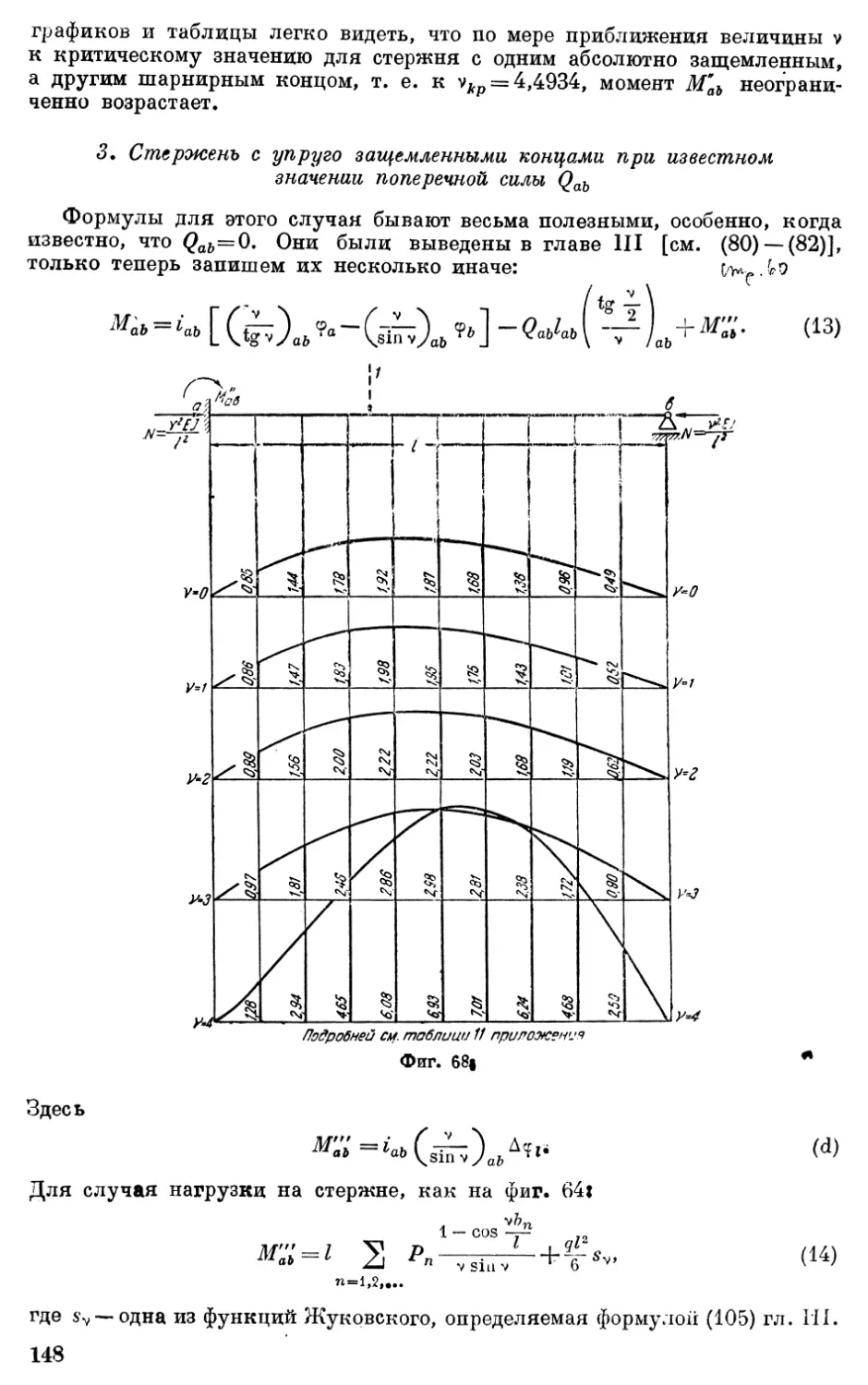
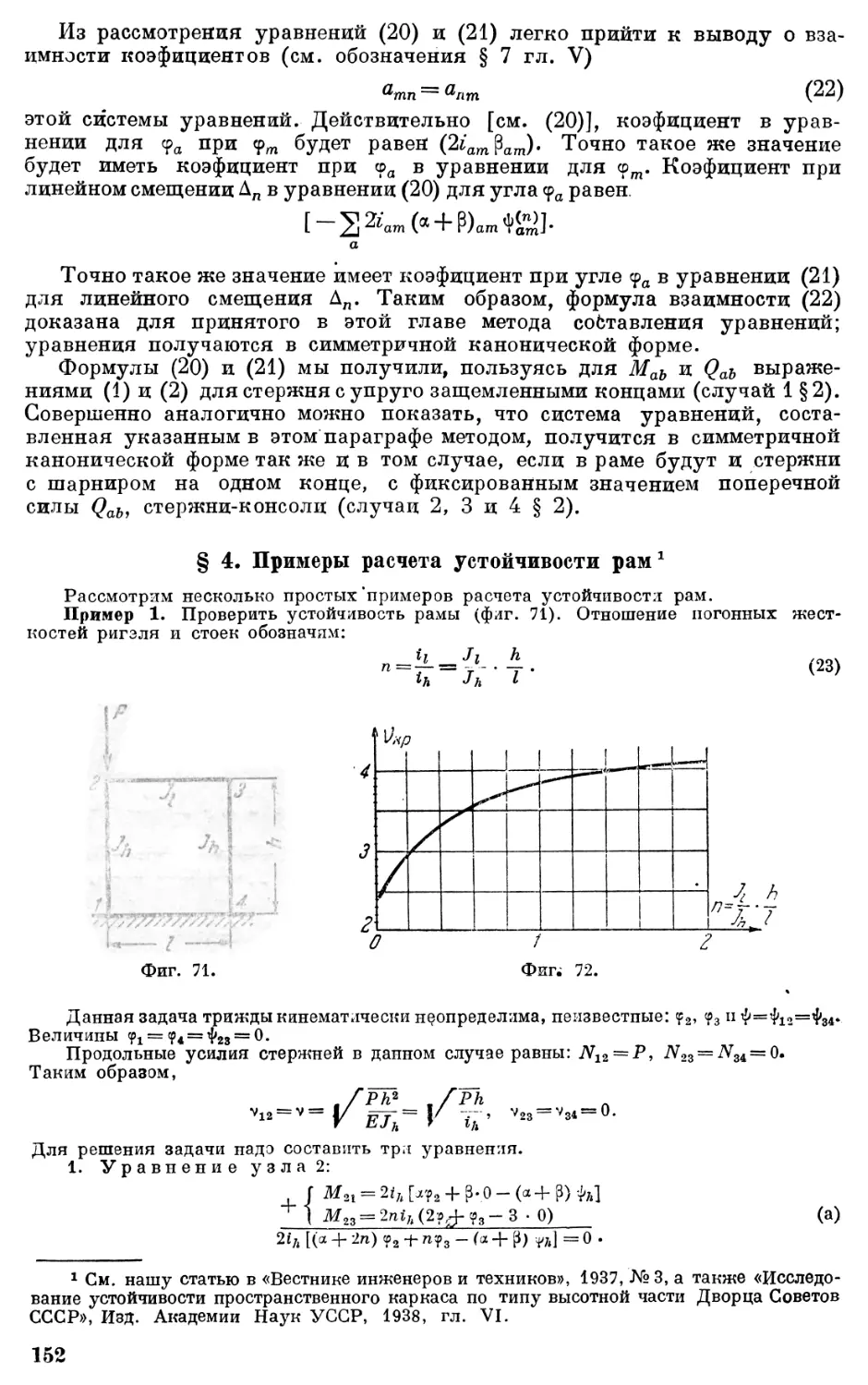
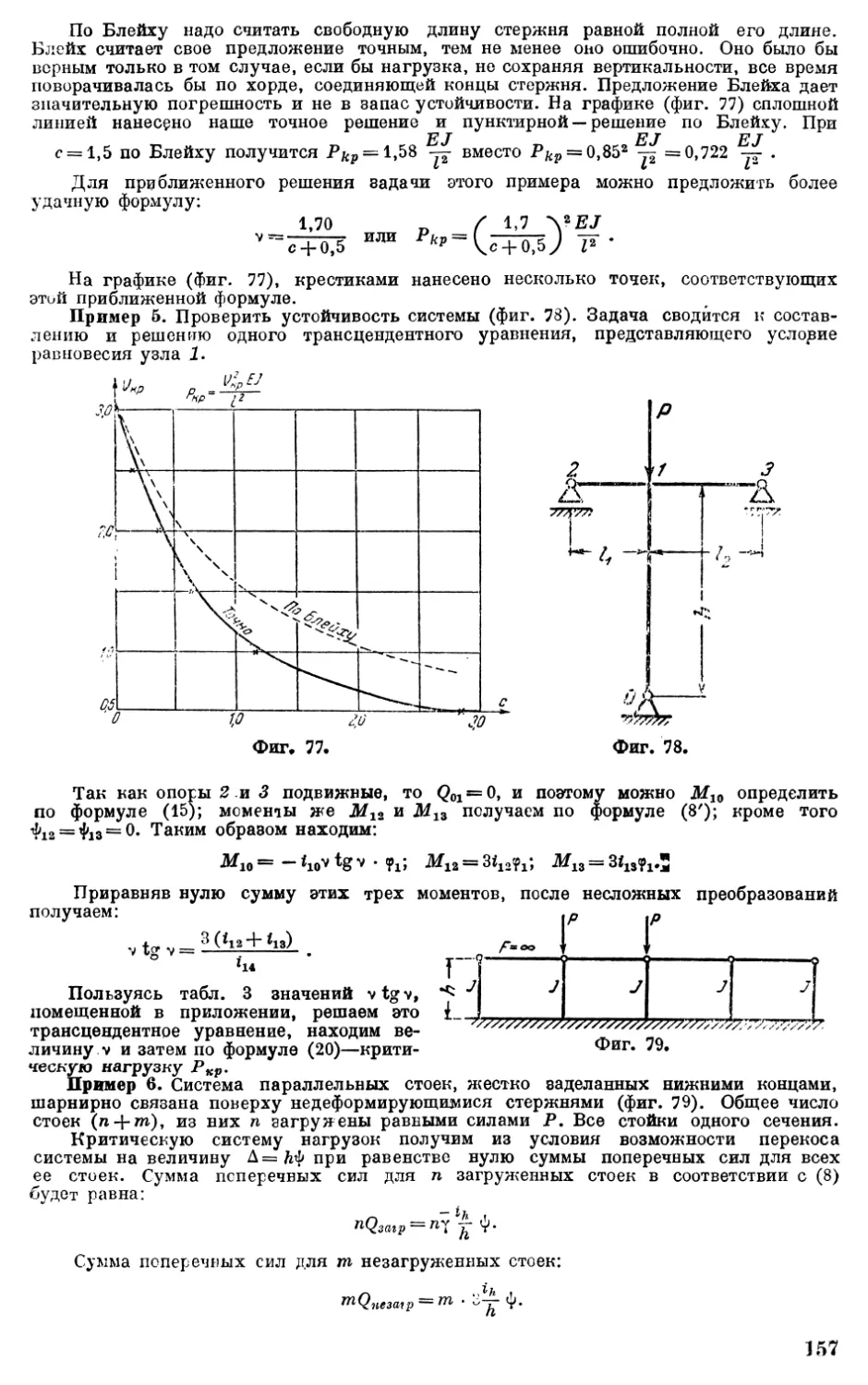
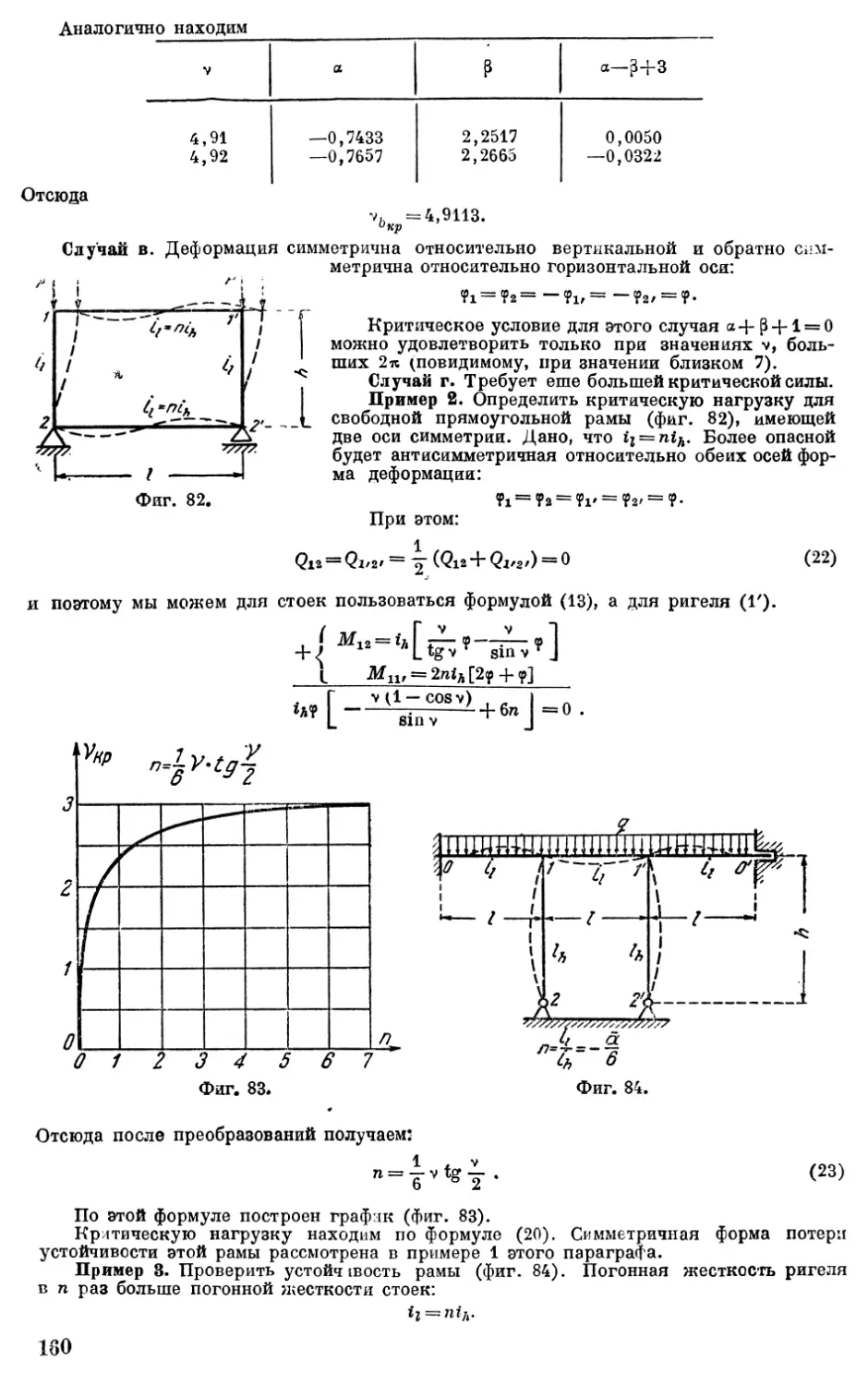
Автор: Корноухов Н.В.
Теги: строительство инженерия инженерное дело стройиздат стержневые системы
Год: 1949
Текст
Н. В.КОРН оухов
ПРОЧНОСТЬ
устойчивость
СТЕРЖНЕВЫХ
СИСТЕМ
С ТР О Й И 3 Д А Т 1949
Н. В. КОРНОУХОВ
ЧЛЕН-КОРРЕСПОНДЕНТ АН УССР, ПРОФ., Д-Р ТЕХН. НАУК
ПРОЧНОСТЬ и УСТОЙЧИВОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
УПРУГИЕ РАМЫ, ФЕРМЫ И КОМБИНИРОВАННЫЕ СИСТЕМЫ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО СТРОИТЕЛЬНОЙ ЛИТЕРАТУРЫ
Москва — 1 9 4 9
ОПЕЧАТКИ
Стра
ница
Строка
Напечатано
ж
Должно быть
По чьей вине
15
4 сверху
б- 0
S—1
Автора
30.
Формула 59
О-3 0
СО
1
Типографии
58
13 сверху
4-
о
147
Формула 8
ЧьЧi fa Фа
аЪаЪ а Фл
195
Формула 18
Gab ЕаЪ Fab СаЪ ЕаЪ аЪ О
Автора
198
1 снизу
f 2
- 2 vfc
Типографии
224
5 снизу
V 1 л, п1
ГМ
V Ул 1, п
Автора
245
Табл. 26, 3 строка и 14 снизу
2vii cos в
2хк cos 20
261
2 снизу
0,32240,0079-0,37151
—0,3224 — 0,00790,3715j
Издательства
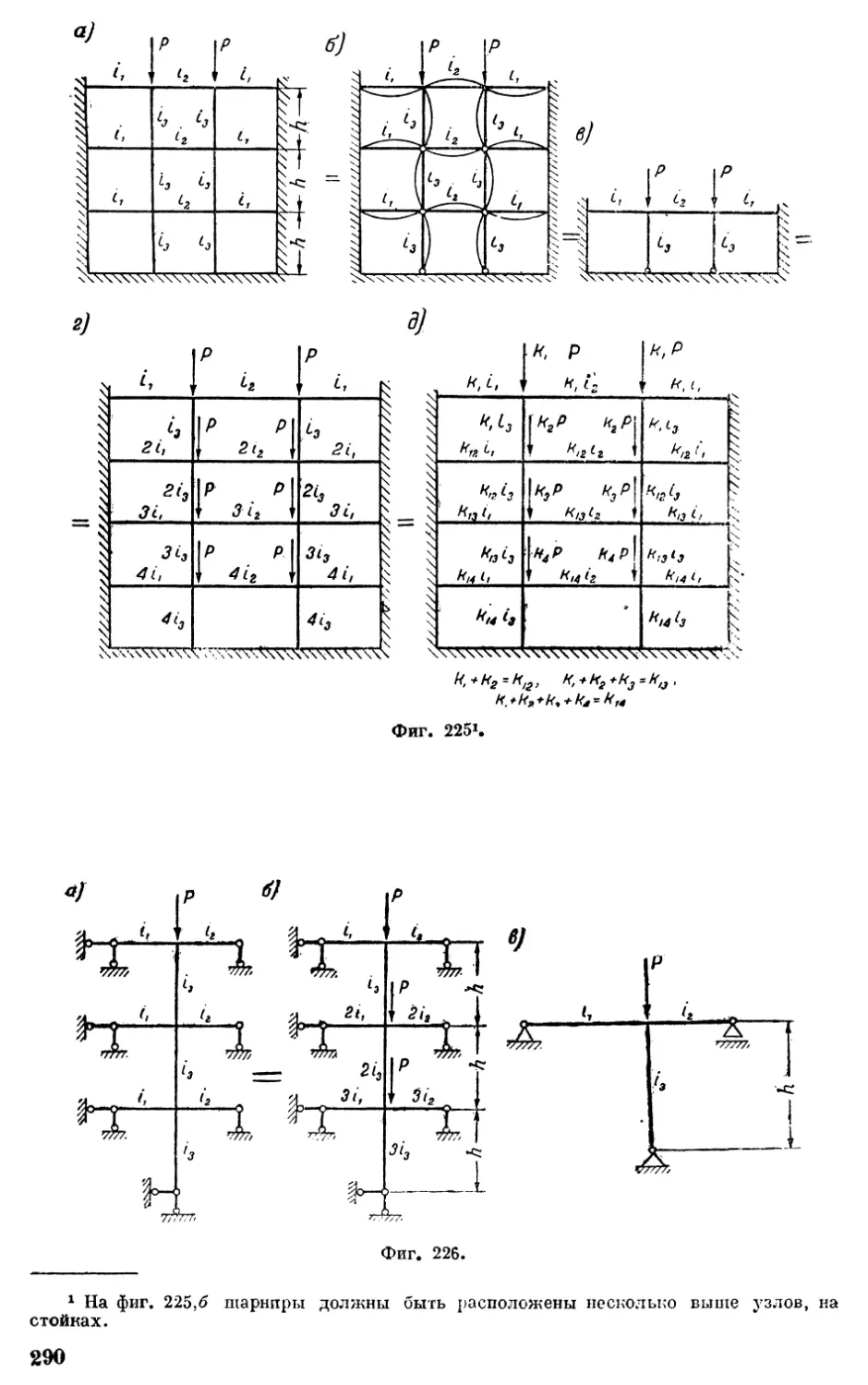
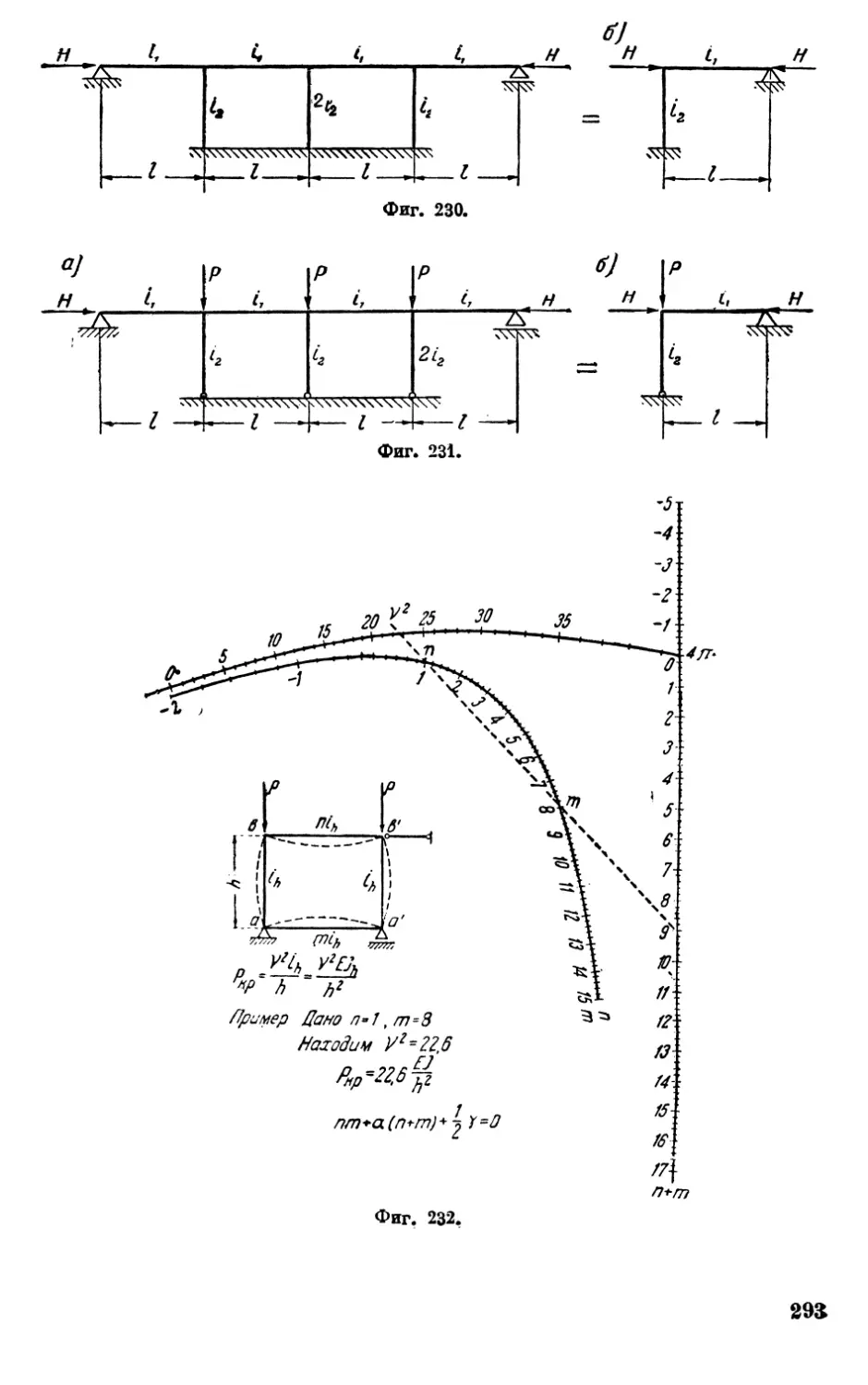
293
Фиг, 231, а
Средний груз
равняется 2Р
Автора
329
2 снизу
0
0
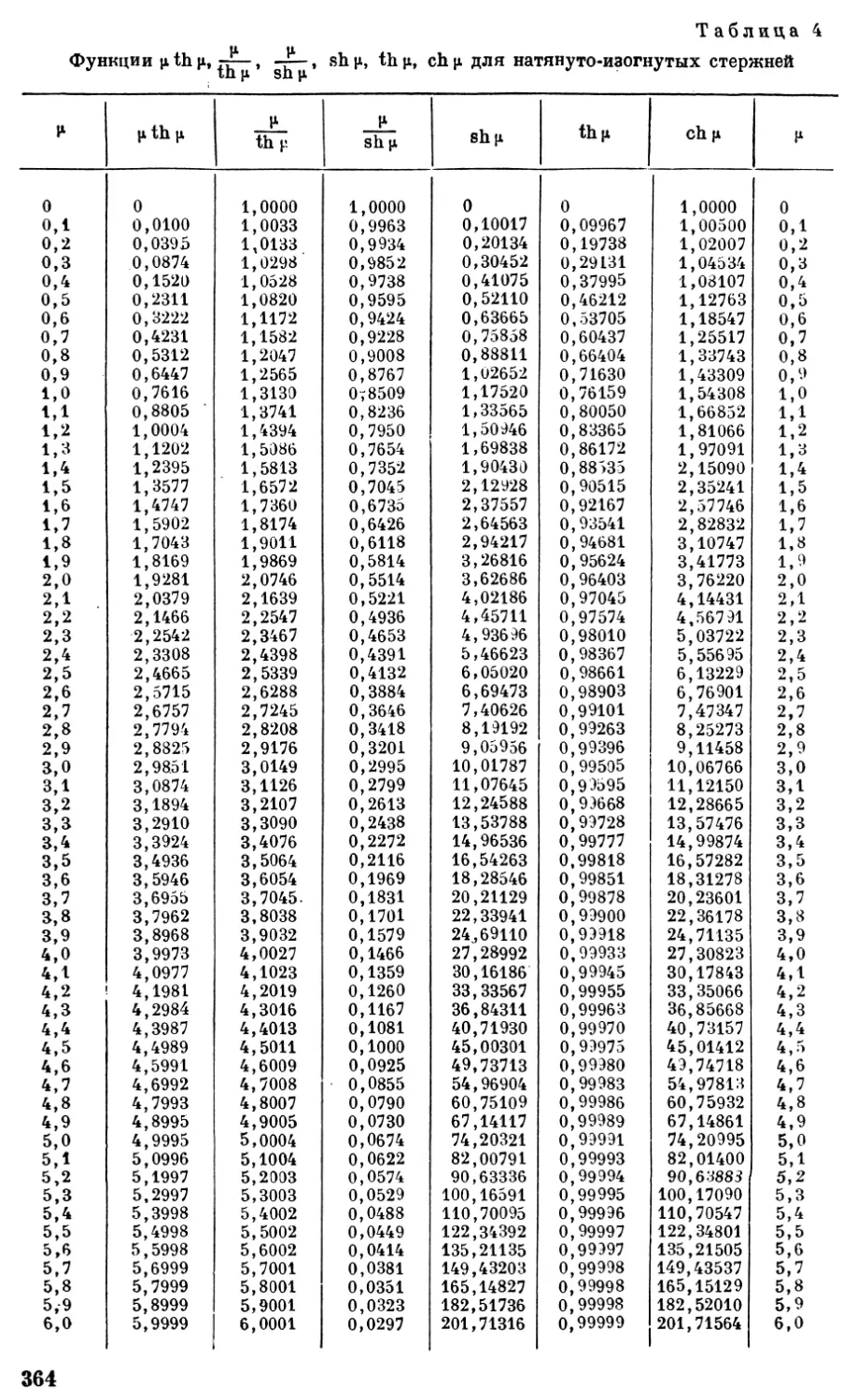
364
2 сверху
натянуто-
растянуто-
Издательства
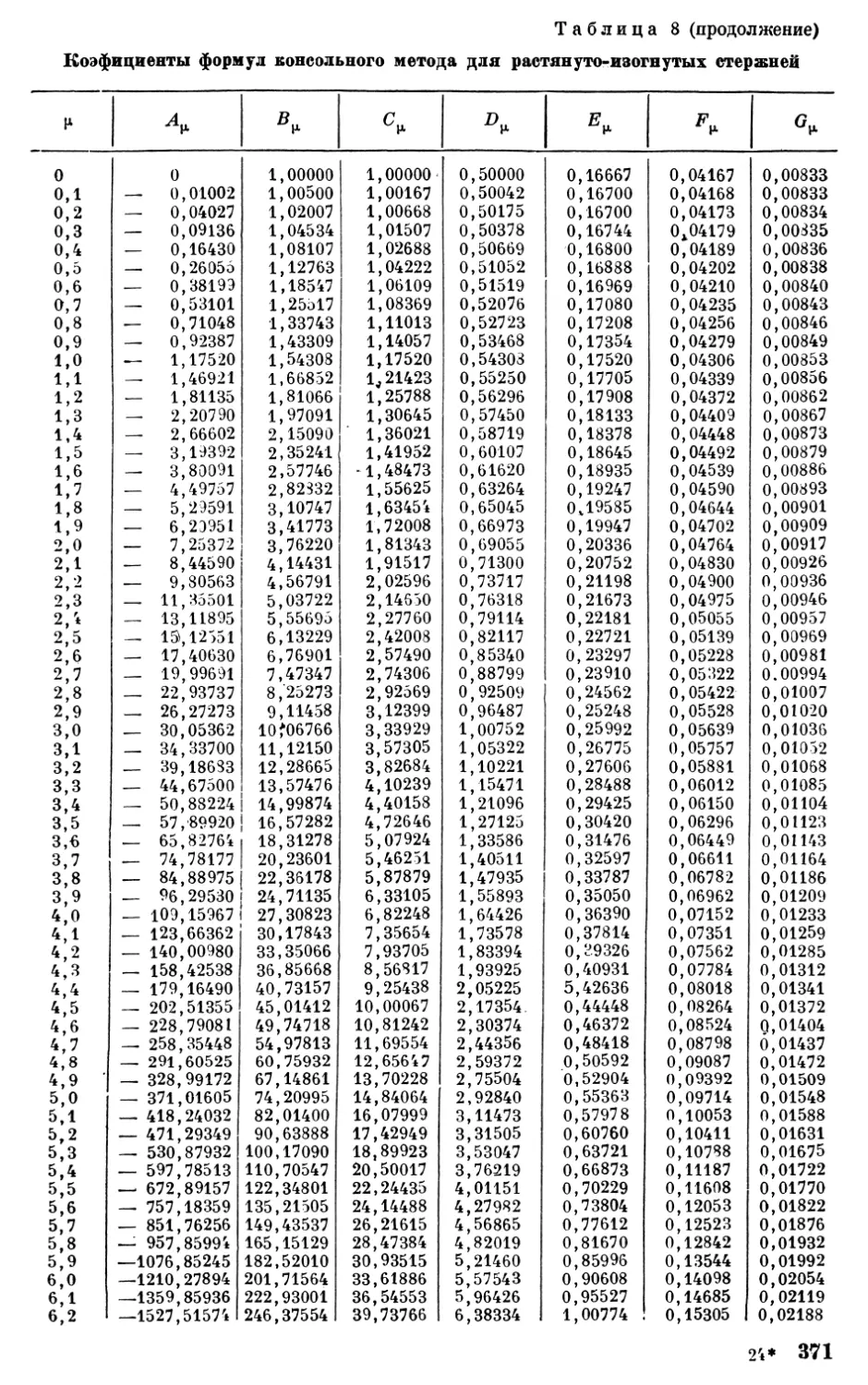
31
1 сверху
Таблица 8 продолжение
Таблица 9
Редактор—доц. А, М. АФАНАСЬЕВ
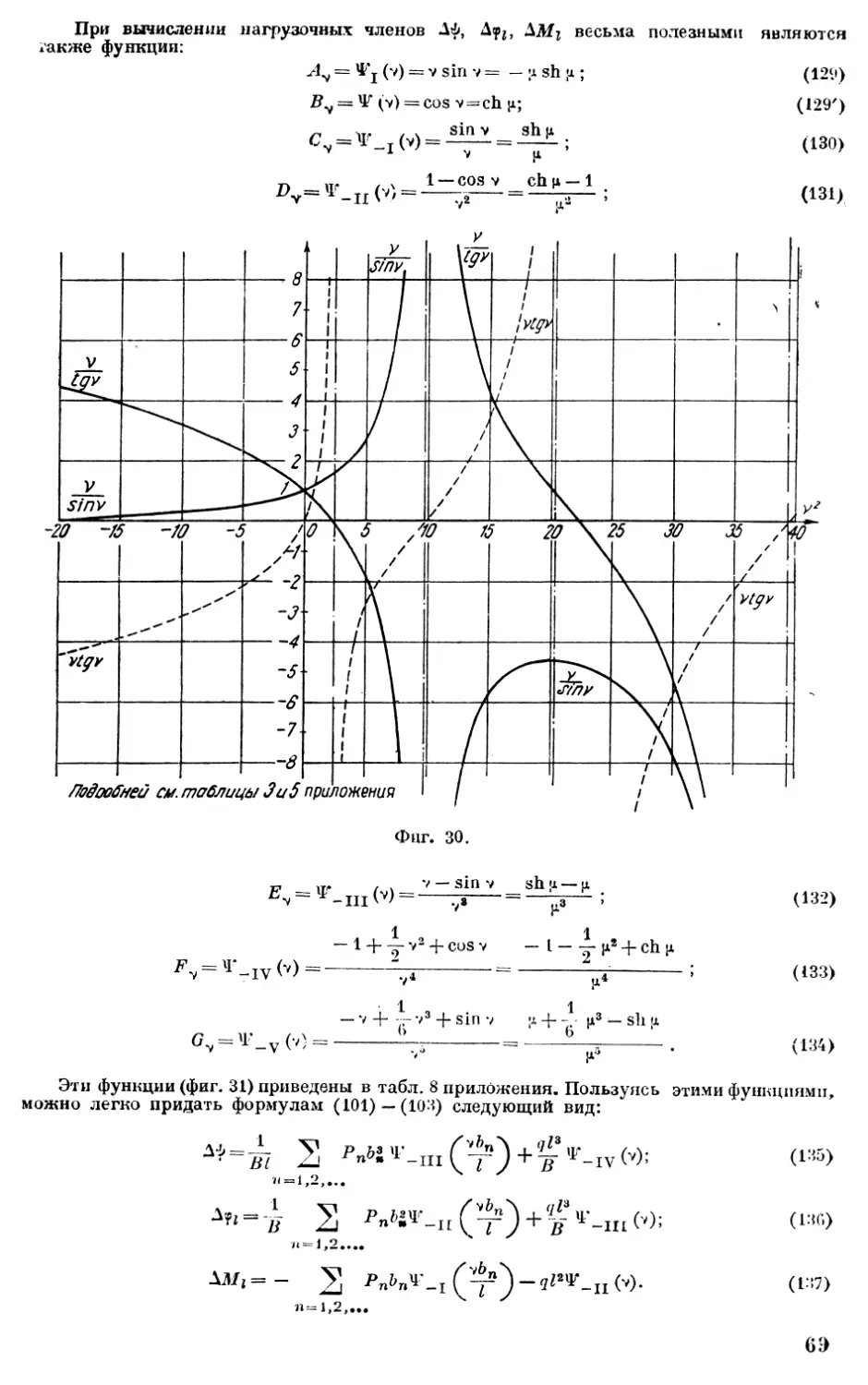
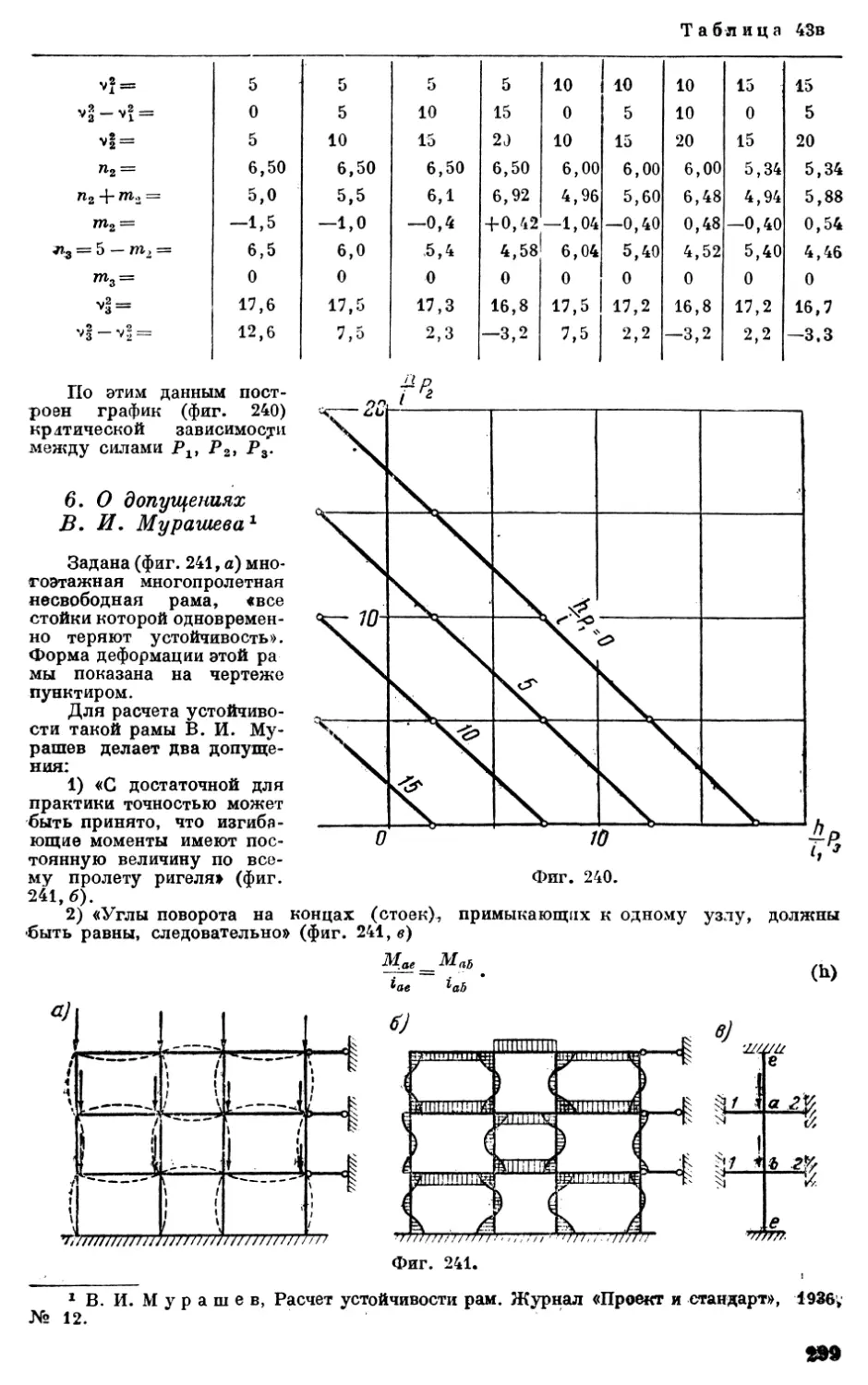
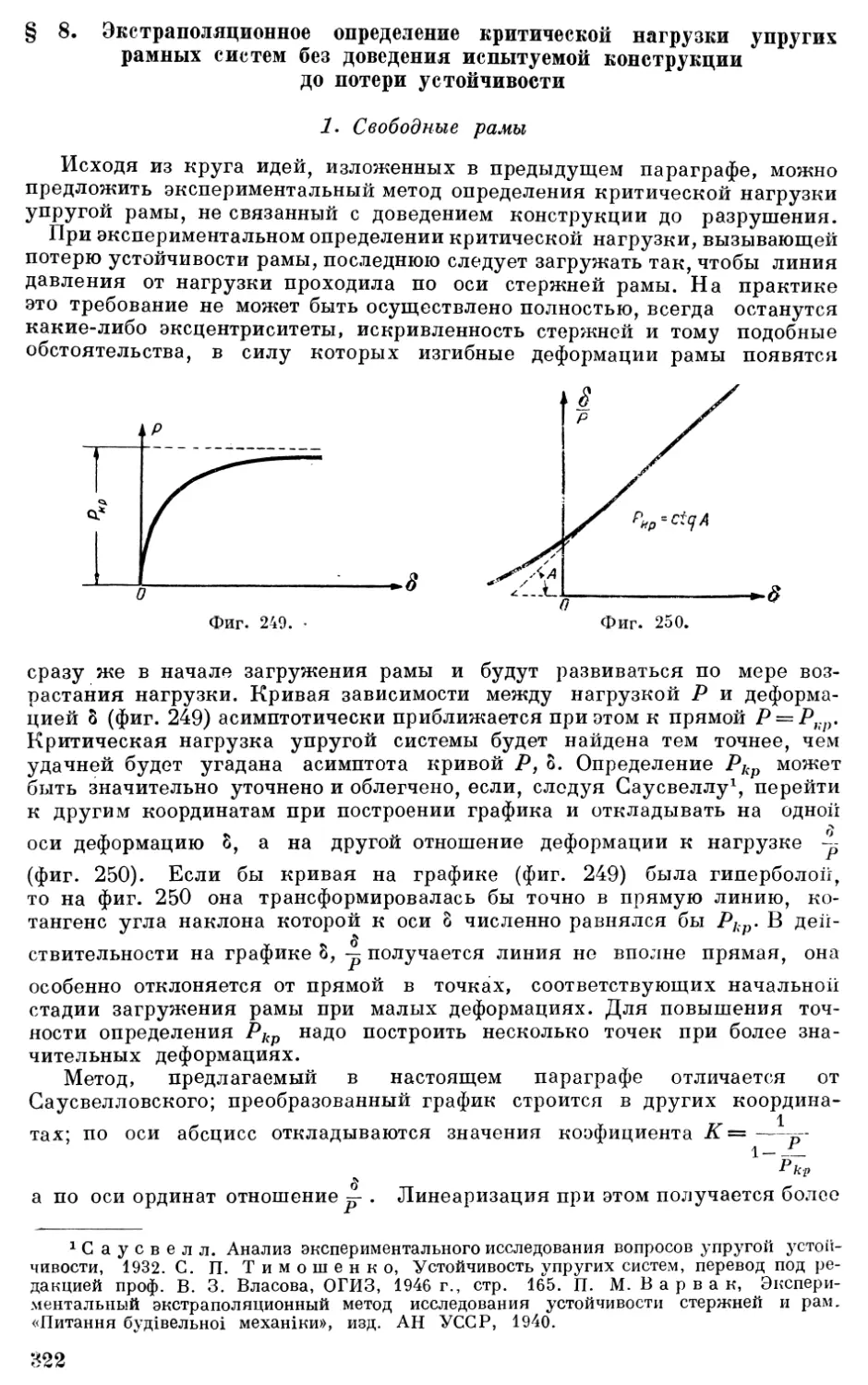
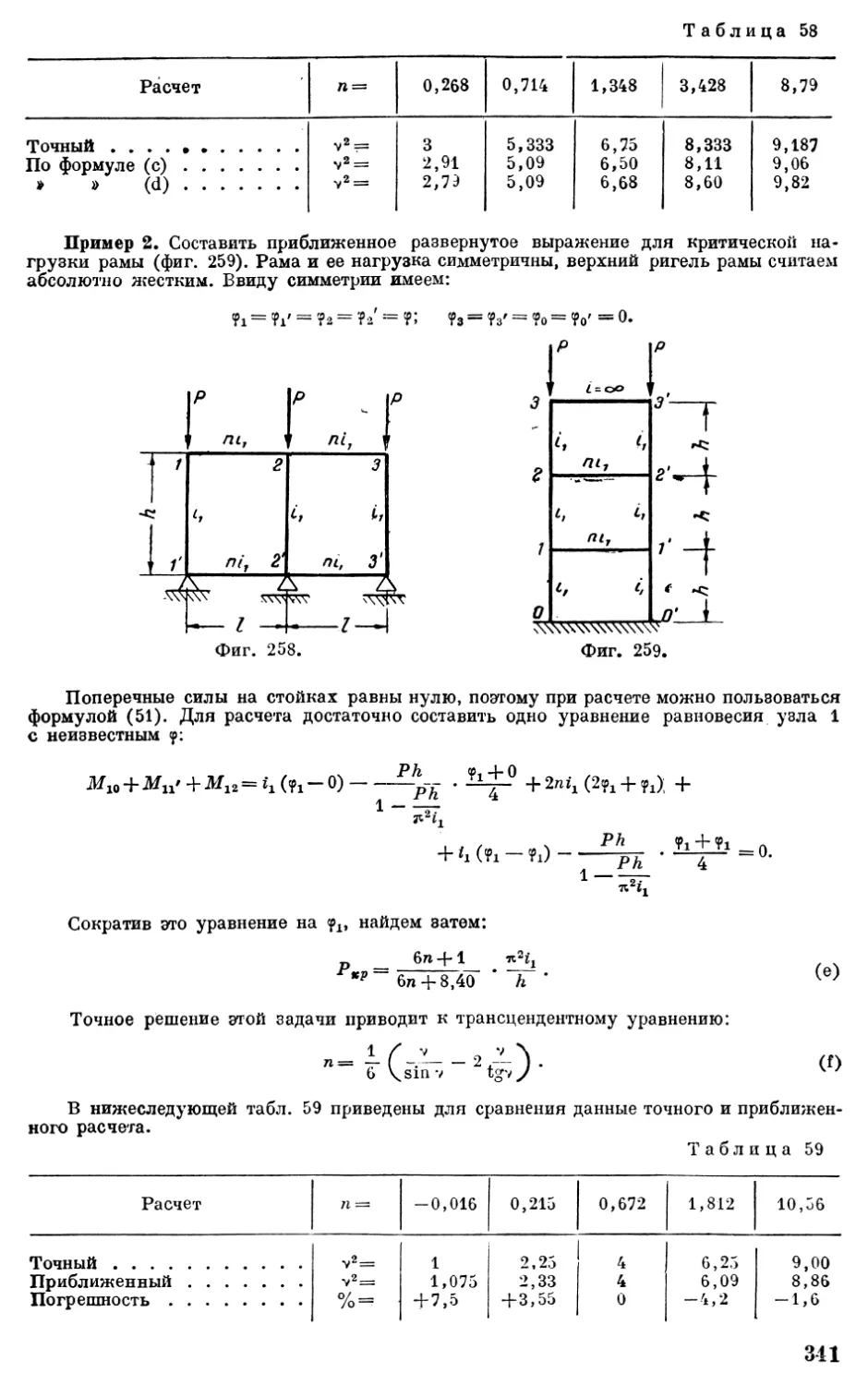
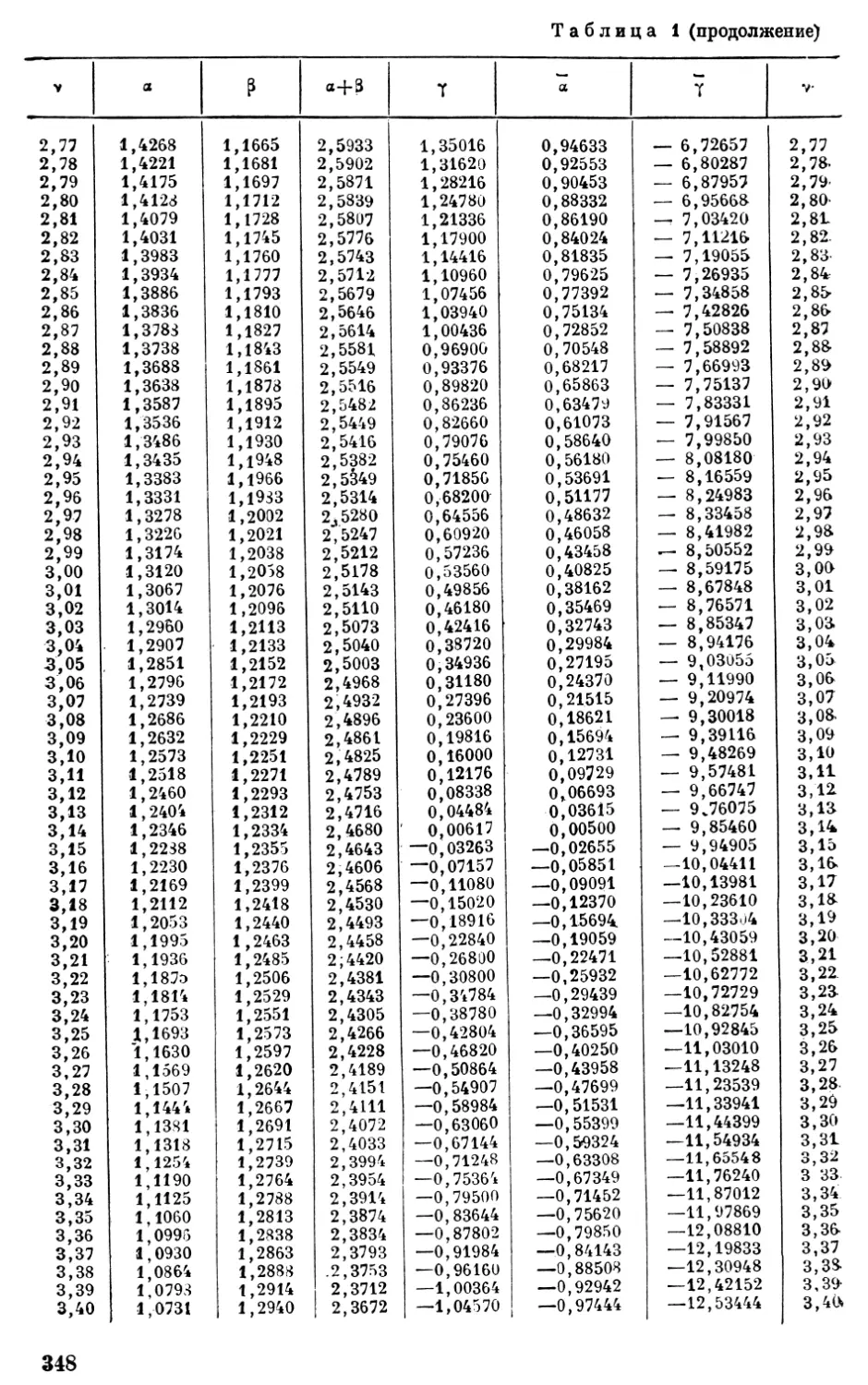
Настоящая книга посвящена таким методам статического расчета стержневых конструкций, которые одновременно учитывают как вопросы их прочности, так и вопросы их общей устойчивости. Труд всесторонне охватывает теорию расчета стержневых сжато-изогнутых упругих систем и в первую очередь рам. Наряду с точными методами в работе освещены и приближенные методы, причем дается возможность оценить степень погрешности.
Работа содержит большое количество числовых примеров. В приложении к книге даны таблицы специальных функций, необходимых для точного решения задач устойчивости.
Книга рассчитана на научных работников аспирантов и инжеиеров-проектировщиков.
ПРЕДИСЛОВИЕ
В исследовании вопросов устойчивости сооружений, в создании и развитии теории устойчивости наши отечественные ученые уже с давних пор играют важнейшую роль. Достаточно указать в этом отношении на имена таких ученых, как Ф. С. Ясинский,И. Г. Бубнов, Б. Г. Галеркин, П. Ф. Папкович, А. Н. Динник, В. 3. Власов, К. С. Завриев, Е. JI. Николаи, И. Я. Штаерман и др. На эту тему в СССР опубликован ряд работ, значительно опережающих зарубежную науку.
Большое внимание вопросам устойчивости сооружений уделяет в своей работе Институт строительной механики Академии наук УССР. Сложные стержневые системы—фермы и рамы—стали объектом многолетних исследований Института. В Институте были разработаны методы расчета устойчивости сложных стержневых конструкций, мощного портового поворотного молотовидного крана грузоподъемностью 350 т и др. На базе работ Института автор дал основанный на методе деформаций точный расчет упругих рамных систем на устойчивость.
Настоящая работа представляет собой теоретическое обобщение частных решений ряда задач, поставленных перед Институтом практикой нашего проектирования и строительства. Работа посвящена таким методам статического расчета стержневых конструкций, которые одновременно учитывают как вопросы их прочности, так и вопросы их общей устойчивости. Мы не говорим здесь о поверке местной устойчивости, так как предполагаем, что последнюю можно обеспечить на основе существующих методов расчета.
Обычные общепринятые методы расчета стержневых систем вырабатывались постепенно, причем с целью упрощения расчетов был сделан ряд допущений, вполне законных и оправдывающихся при известных условиях для обычных в инженерной практике стержневых систем. Однако в связи с этими допущениями вопрос об обеспечении общей устойчивости конструкции как стержневой системы в сущности выпал из рассмотрения. В то же время опыт строительства и анализ аварий различных сооружений ясно свидетельствуют о том, что во многих случаях одной из основных причин таких аварий является недостаточная устойчивость сооружения. Особенно это относится к случаям отступления от обычных норм или в связи с применением новых, не проверенных на практике, конструктивных решений и, в частности, решений с повышенными гибкостями элементов.
Прогресс техники выдвигает на сцену материалы повышенного качества, применение которых вызывает к жизни новые конструкции повышенной гибкости. Для обеспечения надежности этих конструкций обычные методы расчета не всегда достаточны. Нужно переходить либо к экспериментированию над моделями, либо к опытному строительству, либо заняться разработкой новых методов расчета, которые обеспечивали бы сооружению не только прочность, но и общую его устойчивость. В противном случае, действуя вслепую, проектировщик бывает вынужден отказаться от рациональных решений.
Без разработки новых уточненных методов расчета применение новых рациональных типов конструкций становится весьма затруднительным, так как у конструктора нет полной уверенности в достаточной надежности новой конструкции в отношении ее устойчивости. Каждый же раз прибегать к экспериментированию и дорого и требуется много времени. Значительно проще в сомнительных случаях производить расчет на основе более уточнен-
8
ных методов. Как увидит читатель, эти методы не так уже сложны, они вполне практически применимы и в ряде случаев лишь немногим более трудоемки, чем обычные методы статического расчета стержневых систем. Автор поставил себе целью изложить эти методы в максимально доступной форме с тем, чтобы всемерно облегчить внедрение их в практику инженерных расчетов и тем самым способствовать более смелому проектированию рациональных конструкций новых типов.
Изложение построено так, что для ознакомления с тем или другим методом расчета достаточно в основном познакомиться с материалом соответствующей главы и не требуется изучения всей книги.
Настоящая книга в весьма значительной мере представляет собой оригинальное исследование автора. Автор не стремился специально к оригинальности, он старался приспособлять известные методы обычного статического расчета стержневых систем к новой задаче расчета, одновременно учитывающего вопросы прочности и устойчивости. Автор старался возможно объективней оценить достоинства и недостатки каждого из рассмотренных им методов расчета. Параллельно с изложением точных методов расчета автор уделил много внимания также и приближенным методам, дающим в ряде случаев весьма простые и надежные приемы решения.
Первые две главы содержат введение, некоторые общие соображения и теорию объединенного расчета на прочность и общую устойчивость теорию расчета устойчивой прочности плоских и пространственных ферм. Здесь рассмотрены точный метод узловых перемещений и два приближенных метода: вариационный, основанный на начале виртуальных работ, и метод эквивалентной дополнительной нагрузки, с помощью которого расчет фермы по деформированному ее состоянию приводится к расчету фермы по ее первоначальной недеформированной схеме. Кроме того, здесь даны общие указания по расчету комбинированных систем по типу ферм с неразрезными стержнями.
Последующие главы содержат теорию объединенного расчета на прочность и устойчивость плоских рам, составленных из призматических стержней.
Глава III посвящена продольно-поперечному изгибу отдельного стержня, элемента рамной конструкции. В этой главе приводятся зависимости между нагрузками и концевыми усилиями стержня, с одной стороны, и перемещениями его концов, с другой стороны. Этими зависимостями, приводимыми в различных формах, в основном предопределяются различные точные методы расчета рам. В 17 этой главы дается подробное исследование специальных функций, входящих в эти зависимости; 21 посвящен решению задачи продол ьно-поперечного изгиба призматического стержня при учете деформаций сдвига.
В главе IV приводится вывод обобщенной формулы начала виртуальных работ применительно к задачам устойчивой прочности рамных систем, выясняется возможность применения принципа наложения для поперечных, искривляющих факторов при условии сохранения неизменной эпюры продольного усилия стержня. Затем в этой главе вводится новое понятие об единичных равносжатых состояниях системы и даются формулы для перемещений и реакций этих состояний.
Глава V содержит общие положения расчета устойчивости и устойчивой прочности плоских рам безотносительно к конкретному методу расчета. В 6 этой главы идет речь о составлении уравнений, соответствующих неизвестным—кинематически независимым смещениям узлов рамы; в 7—о взаимности коэфициентов канонической системы уравнений, в 8—об особенностях расчета симметричных, симметрично загруженных систем. Для таких систем оказывается достаточным произвести раздельно проверку на потерю устойчивости в симметричной форме и проверку на потерю устойчивости в анти симметричной форме, не рассматривая комбинированной формы деформаций.
4
Глава VI посвящена применению известной обобщенной теоремы трех или четырех моментов к задачам устойчивости и устойчивой прочности рам. В 7 этой главы указаны частные случаи рационального использования этогог вообще говоря, мало удачного метода.
Глава VII содержит изложение, пожалуй, основного метода расчета устойчивости и устойчиво л прочности рамных систем—метода деформаций. Эта глава снабжена большим количеством примеров, иллюстрирующих простоту этого метода. В 7 этой главы даны примеры расчета шпренгельных рам. В примерах же 8 показана возможность спрямления при специальном выборе системы координат графиков зависимостей усилий и деформаций от нагрузки в сжато-изогнутых рамных системах.
В главе VIII изложен метод узловых поворотов и поперечных сил, являющийся естественным дополнением к методу деформаций. 2 этой главы содержит уравнение трех узловых поворотов, весьма удобное при расчетах рам с ломаными стержнями. В 5 приведены формулы для ступенчатых стержней, a Bv 7—для стержней рам с жесткими узловыми фасонками. В 8 показано, как сильно повышается устойчивость рам при наличии жестких узловых фасонок.
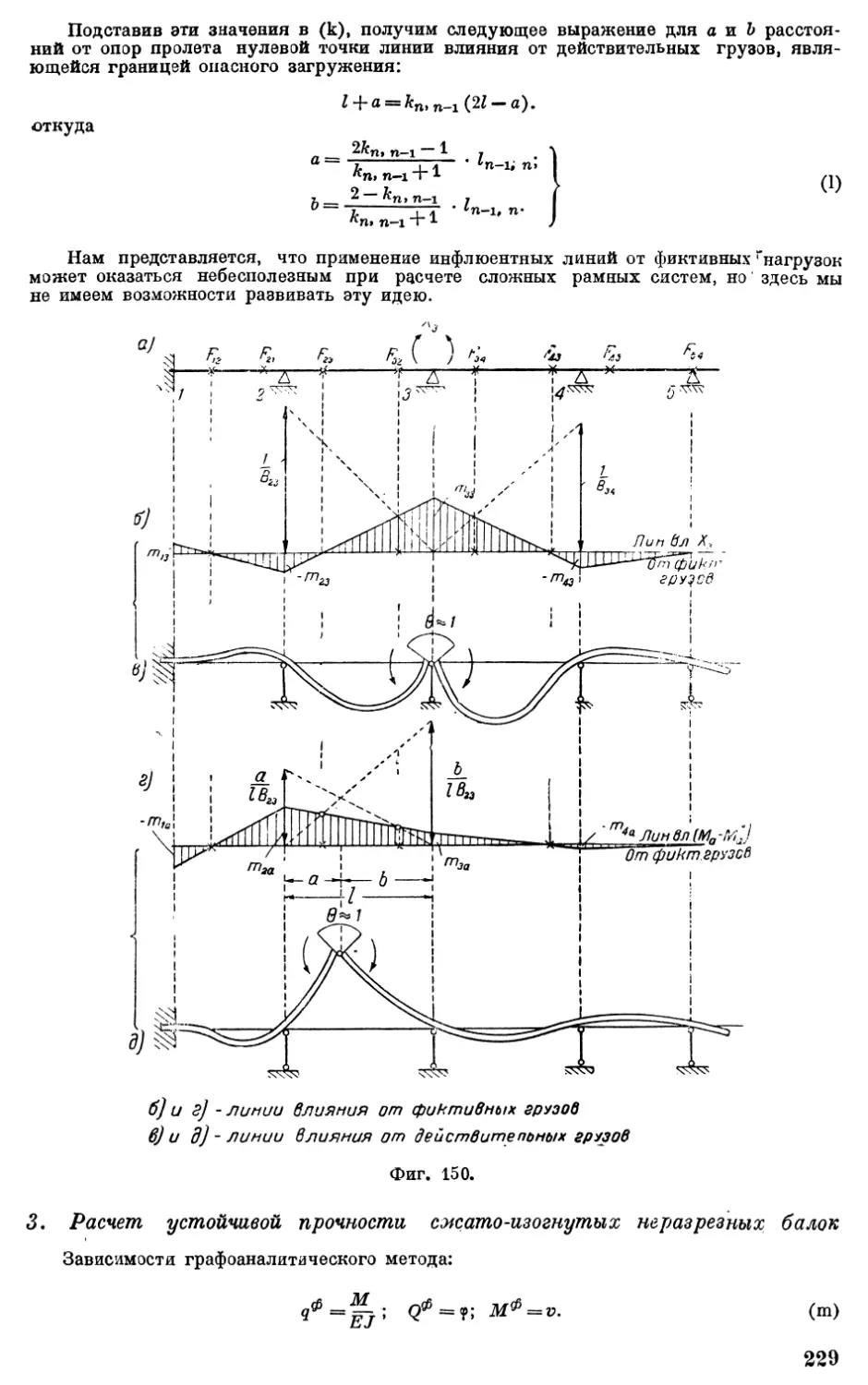
Глава IX посвящена ряду других методов расчета рам. В 1 изложен консольный метод, основанный на последовательном применении формул метода начальных параметров, данных в главе III. Этот метод особенно удобен для расчета малоконтурных рам с многоугольными контурами. В 2 приведен метод узловых моментов и поперечных сил, который с удобством может быть применен к расчетам многоугольных одноконтурных рам с шарнирами или без них. В примере 3 этого параграфа путем предельного перехода от стержня с многоугольным ломаным очертанием даны результаты проверки устойчивости двухшарнирной арки, очерченной по дуге круга, и показано, в какой мере поведение нагрузки при деформации влияет на величину ее критического значения. В 3 показаны случаи рационального применения к задачам устойчивости и устойчивой прочности метода сил в его обычном виде. 4 посвящен расчету рам по методу фокусов. В 5 изложен графоаналитический метод расчета устойчивости и устойчивой прочности неразрезных балок. По этому методу задача расчета неразрезной балки приводится к условиям равновесия шарнирной цепи жестких звеньев, загруженных фиктивной нагрузкой. Этот метод приводит к весьма интересным, составленным из прямолинейных участков для каждого отдельного пролета, линиям влияния от действия фиктивных грузов. 6 трактует об ограничениях, накладываемых на решение выбором метода расчета. Оказывается, что некоторые методы расчета, особенно основанные на применении обобщенной теоремы трех и четырех моментов, должны применяться с осторожностью, чтобы из рассмотрения не выпала наиболее опасная форма потери устойчивости. Безусловно надежным является метод деформаций, при пользовании которым могут выпасть из рассмотрения только высшие формы потери устойчивости, не имеющие никакого практического значения.
ГлаваХ посвящена в основном уточнению расчетов устойчивости и устойчивой прочности рам при учете деформаций сдвига и обжатия оси стержней. В 3 приведены примеры расчета устойчивости рамы со стойками на планках или с решеткой. В 4ив 5выяснено, при каких обстоятельствах необходимо учитывать и при каких обстоятельствах можно пренебречь продольными деформациями стержней рамы. В 5 дан расчет устойчивости рамного стержня, и данные точного расчета сопоставлены с приближенными решениями. 8 посвящен исследованию случая нагружения силой, направленной к полюсу.
В весьма обширной главе XI излагаются некоторые общие положения и приближенные методы расчета устойчивости и устойчивой прочности плоских рам. В 1 этой главы показано, как путем введения дополнительных
нулевых связей можно из нескольких равноустойчивых систем образовать новую сложную равноустойчивую с ними систему. Показано также, что постановка дополнительных не нулевых связей повышает общую устойчивость системы. Выяснены принципы замены сложной многопролетной и многоэтажной рамы эквивалентной ей по устойчивости однопролетной и даже однопролетной одноэтажной рамой. В 2 приведены расчетные графики и номограммы для определения устойчивости свободной одноконтурной прямоугольной рамы с разной в том числе и отрицательной жесткостью ригелей. В 3 показано, как пользуясь графиками 2 и принципами расчленения 1 для многоэтажной рамы, загруженной рядом нагрузок, получить всю область критических соотношений между этими нагрузками. В 4 те же вопросы рассмотрены для задач устойчивости несвободных рам для рам с линейно несмещающимися узлами. Кроме того, в 1 показано, что принятое рядом авторов для приближенного расчета устойчивости многопролетных рам допущение об отсутствии поперечных сил в стойках рамы в деформированном ее состоянии дает весьма большую погрешность в сторону преуменьшения критической нагрузки. В 5 даны простые формулы, связывающие между собой коэфициент запаса устойчивости для комбинированного загружения системы с коэфициентами запаса устойчивости той же системы для случаев раздельного действия отдельных компонентов этой составной нагрузки. В 6 дан ряд приемов получения из точных трансцендентных уравнений критического состояния развернутых приближенных достаточно точных рациональных алгебраических выражений для критического значения нагрузки. Приводимые формулы для ряда простых рам могут быть весьма полезны при практическом расчете их устойчивости. В 7 изложен метод составления простых приближенных формул для усилий и деформаций рам со сжато-изогнутыми стержнями на основе полученных ранее критических значений нагрузок для этих рам. В 8 даны формулы, позволяющие без доведения упругой конструкции до разрушения, определить критическую ее нагрузку на устойчивость по экспериментально определенным ее деформациям при нескольких ступенях загружения. В 9 дан ряд вариантов приближенных выражений разной степени точности для основных формул, связывающих между собой усилия и деформации по концам стержня. Часть этих формул получена по методу замены прямолинейными секущими кривых трансцендентных выражений коэфициентов точных формул. Другие упрощенные варианты получены с помощью статического интерполяционного метода так, чтобы возможно снизить ошибку для ряда частных граничных случаев расчета. В 10 приведены примеры расчета устойчивости рам на основе приближенных формул 9 и выяснена степень погрешности результатов такого расчета. В ряде случаев такой приближенных расчет, разрешающий одновременно задачу прочности и общей устойчивости, оказывается не намного более сложным, чем обычный статический расчет рамы по методу деформаций, совершенно игнорирующий вопросы устойчивости.
В приложевии к книге даны подробные таблицы специальных функций, необходимых для точного решения задач устойчивости и устойчивой прочности.
Книга набрана двумя шрифтами. Основной теоретический материал дан крупным шрифтом, а детализация теории и примеры расчета—мелким.
Автор считает своим приятным долгом выразить глубокую благодарность члену-корреснонденту АН СССР проф. И. М. Рабиновичу, проф. А. А. Уманскому и действительному члену АН УССР проф. Ф. П. Белянкину, ознакомившимся с рукописью и давшим ряд ценных указаний. Автор приносит также глубокую благодарность научному сотруднику Института строительной механики АН УССР—Н. Н. Гуслистой за ценную помощь в вычислительной работе.
ГЛАВА I
ВВЕДЕНИЕ
1. Классификация задач статического расчета конструкций с точка
зрения обеспечения их устойчивости
В основе установления тех или других закономерностей в прикладных науках лежат прежде всего накопление, систематизация и классификация подлежащих изучению фактов, а затем схематизация и обобщение их. Прежде всего нужно установить схему изучаемого явления, выяснить факторы, имеющие к нему отношение, и установить, какие из них являются основными и какие второстепенными. При составлении математических зависимостей прикладного порядка естественно принять во внимание сначала только основные факторы, пренебрегая влиянием второстепенных или учитывая их интегрально путем введения эмпирических коэфициентов. Затем на более высокой стадии науки, по мере накопления фактов, вполне уместно уточнение первоначально установленных зависимостей путем введения в рассмотрение факторов второстепенных. Иногда после изучения одной какой-нибудь области технических задач развитие техники выдвигает также и другие смежные с ней области. Естественно, что для этих смежных областей влияние факторов, вводимых в исследование, может оказаться иным: факторы второстепенные становятся главными и наоборот. При этом происходит резкое изменение значения приближенных закономерностей; уточненные закономерности, учитывающие более широкую область явлений, оказываются более устойчивыми, зато они и более сложны. Интересы практического применения, требующие максимальной возможности простого оперирования установленными закономерностями, склоняют чашку весов в сторону приближенных закономерностей, в то же время ограничивая область их применения.
Вышесказанное с полным основанием может быть отнесено также к задачам статического расчета сооружений и конструкций. При этом расчете мы связаны с рядом условностей: 1 при выборе расчетной схемы сооружения,
2 при определении свойств материала, 3при назначении расчетных нагрузок,
4 при установлении требований, предъявляемых к сооружению при установлении критериев пригодности и надежности сооружения1, 5 при проведении расчета, на основе которого мы определяем, удовлетворяет ли сооружение поставленным требованиям. Последний вопрос мы решаем с помощью аппарата строительной механики.
В современном своем виде строительная механика стержневых систем базируется на ряде допущений и гипотез, имеющих большую или меньшую область применения. Назовем некоторые из них, имеющие отношение к предмету настоящего исследования:
1 См. проф. Н. С. С т р е л е ц к и й, Об исчтлонч t запасов прочности сооружений, Сборник 1 МИСИ им. Куйбышева, Госстройиздат, 193S г.; Строительная промышленность 7, 1940.
7
1 расчет в пределах упругости по допускаемым напряжениям, а не по разрушающим нагрузкам;
2 расчет на основе теории малых деформаций. На основе этой теории мы принимаем приближенное выражение для кривизны — —— и предполагав
р а оо
ем, что перемещение поворота стержня фермы направлено перпендикулярна к первоначальному направлению стержня допущение Виллио;
3 предположение о пропорциональности упругих деформаций внешним нагрузкам обобщенный закон Гу к а и связанный с ним принцип независимости действия принцип аддитивности, или принцип наложения;
4 расчет сооружения по недеформированному состоянию по первоначальной геометрической схеме, не учитывающий возрастающего действия внешних нагрузок вследствие возникновения деформаций. При таком расчете не учитывается изгибающее влияние продольной силы и крутящего момента при наличии деформаций изгиба, и вопросы общей устойчивости конструкции выпадают из рассмотрения;
5 гипотезу плоских сечений и основанные на ней формулы для напряжений и деформаций из теории сопротивления материалов;
6 гипотезы и формулы теории тонкостенных стержней1;
7 пренебрежение деформациями сдвига и обжатия оси стержня по сравнению с его изгибными деформациями;
8 неучет возможности появления крутильных форм деформации в случае открытого тонкостенного сечения стержней;
9 пренебрежение шириной эдемента по сравнению с его длиной;
10 неучет пространственности конструкции.
В нашей работе мы будем исходить из соображения, что при расчете инженерных конструкций вполне допустимо применение теории малых деформаций д о п у щ е н и е 2. Мы покажем, что расчеты, построенные на этой теории, идут в запас надежности см. ниже, 7.
Мы выясним, что для поперечных факторов можно пользоваться принципом наложения допущение 3 при условии сохранения неизменными осевых факторов продольной силы и крутящего момента. Это чрезвычайно облегчит и упростит теорию расчета.
Основным же предметом настоящего исследования является разработка теории расчета стержневых систем, свободной от допущения Это допущение о возможности расчета усилий в элементах стержневой системы без учета влияния величины ее деформаций в свое время сыграло большую положительную роль. На нем основана современная теория статического расчета стержневых систем. Но это оправдывающееся обычно допущение в иных случаях, как показывает инженерный опыт, может привести к неожиданному разрушению, казалось бы, правильно рассчитанного сооружения. Дело в том, что из такого обычного статического расчета совершенно выпал вопрос а проверке общей устойчивости системы. Ясно, что проверка местной устойчивости отдельных элементов сооружения еще не обеспечивает его общей устойчивости. Анализ ряда аварий различных инженерных конструкций показалг что во многих случаях основной причиной аварий является недостаточный учет вопросов устойчивости при проектировании конструкций2. Так стали
1 В развитии теории тонкостенных стержней особенно велика роль советской науки. В 1941 г. был удостоен Сталинской премии 1-й степени проф. В. 3. Власовза капитальный труд Тонкостенные упругие стержни прочность, устойчивость, колебания, Госстройиздат, 1940.
2 См., например: предисловие к книге акад. А. Н. Д и н н и к, Устойчивость упругих систем, ОНТИ, 1935; Ф. С. Я с и и с к и й, Собрание сочинений, т.1, стр. 228, 1902; Н. В. Терпугов, Крушение моста через реку св. Лаврентия у Квебека, 1908; А. Д. Голов, Деформация раскосов ферм Мозырского моста, изд. MB О НК ПС, 1925; П. Ф. П а п к о в и ч, Строительная механика корабля, ч. II, стр. 180 — 182, Оборонгиз, 1940,
8
создаваться учение о продольном изгибе и теория устойчивости упругих: систем вообще.
Стали говорить, что сооружение нужно рассчитать не только на прочность, но и на устойчивость. При этом потерей устойчивости стали называть неожиданное появление деформаций нового типа, по характеру своему в корне отличных от деформаций, обычно соответствующих приложенной нагрузке. Но о возникновении деформаций нового типа можно говорить только в том случае, если деформаций такого типа, в том числе и весьма малых по величине, до этого не было. Последнее обстоятельство накладывает определенные ограничения на характер приложения нагрузок; оказывается, что при комбинированных нагрузках,
вызывающих деформации раз- фиг- 1
ных типов, говорить о возникновении деформаций нового типа зачастую нельзя. Таким образом в большинстве случаев, если от комбинированной нагрузки не отбросить некоторых ее составляющих, то говорить о потере устойчивости в классическом смысле этого термина не представляется возможным1. Очевидно, что в таких случаях следует производить объединенный расчет прочности и устойчивости, представляющий собой расчет прочности с учетом влияния величины деформаций системы на усилия в ее элементах. Для краткости такой объединенный расчет мы предлагаем называть расчетом устойчивой прочности, так как в результате его конструкции будет обеспечена прочность устойчивым образом, так что при некотором превышении расчетной нагрузки не произойдет внезапного разрушения конструкции в силу пренебрежения вопросами общей ее устойчивости.
Введение в обиход понятия о расчете устойчивой прочности будет полезным при решении весьма широкой области практических задач и будет, способствовать развитию общей теории.
Рассматривая различнее задачи строительной механики, нетрудно прийти к выводу, что их можно классифицировать по различным признакам: задачи статические и динамические, задачи упругие и неупругие, задачи статически-определимые и статически-неопределимые. Теперь мы можем добавить еще такую классификацию: 1 задачи прочности, 2 задачи устойчивости, 3 задачи устойчивой прочности. Кроме того, ввиду некоторых качественных особенностей целесообразно выделить еще особую категорию: 4 задачи на потерю устойчивости второго рода задачи предельного сопротивления. Поясним вышесказанное, подробней осветив каждую из четырех перечисленных выше категорий задач предлагаемой нами классификации.
2. Задачи прочности
Задачи прочности обнимают обычный статический расчет сооружений. Основная особенность этих задач—вычисление усилий на базе недеформированной схемы сооружения. Это значительно упрощает расчет и во многих случаях дает вполне надежные для практического использования результаты. Конечной целью расчета является определение напряжений и деформаций при заданных нагрузках, причем в пределах упругости деформации и нагрузки сохраняют пропорциональность.
1 Поэтому, папример, И. Ратцерсдорфер при проверке устойчивости шарнирностержневых ферм, рассматривает столь мало реальные примеры, как изображенный на фиг. 1. В этом случае верхний и нижний пояса фермы имеют одинаковые относительны удлинения в элементах решетки нет усилий и потому в 1-ой стад.ш деформации фермы до потери ею устойчивости пояса фермы остаются прямолинейным;,
9
3. Задачи устойчивости
Потерей устойчивости сооружения мы называем, вообще говоря, нарушение равновесия между внешними и внутренними его силами. Такое нарушение равновесия может быть двух родов.
Потеря устойчивости первого рода при постепенном возрастании нагрузки происходит внезапно, с появлением и сильным развитием совершенно новых форм деформации. Такая потеря устойчивости не может быть свойственна всем конструкциям, она возможна только в особых случаях и только для таких конструкций и нагрузок, для которых деформации имеют строго определенный характер, нарушение которого становится возможным лишь в случае потери устойчивости. К таким особым случаям можно отнести симметричные, симметрично нагруженные системы. Нарушение симметрии их деформации может быть отнесено к потере устойчивости первого рода.
Потеря устойчивости второго рода происходит в результате сильного развития предшествующих деформаций без появления деформаций нового типа, вследствие невозможности поддержания статического равновесия между внешними нагрузками и внутренними усилиями системы без уменьшения внешних нагрузок системы. При такой потере устойчивости отпорность системы сопротивление системы росту деформаций, достигнув максимума, начинает затем уменьшаться при дальнейшем росте деформаций. Известные автору случаи потери устойчивости второго рода связаны либо со столь большими упругими деформациями, которые невозможны для применяемых на практике строительных материалов, либо с работой сооружения частично или полностью за пределами упругости. Потеря устойчивости второго рода за пределами упругости—явление, неизбежное для всех строительных конструкций, имеющих сжатые элементы. Задачи на потерю устойчивости второго рода мы будем называть задачами предельного сопротивления предельного равновесия. Известные методы расчета сооружений по разрушающим нагрузкам, проводящегося с учетом пластических деформаций, относятся как бы к упрощенному частному случаю задачи предельного сопротивления.
Поэтому, когда мы будем говорить о задачах устойчивости, то будем иметь в виду задачи устойчивости первого рода. Конечная цель исследования в этих задачах заключается в определении тех критических значений нагрузок, при которых становится возможным внезапное возникновение деформаций нового типа, качественно отличных от прежних деформаций, имевших место при меньших нагрузках. Основная особенность решения задач устойчивости заключается в расчете сооружения на основе возможной деформированной его схемы, иначе говоря, в учете само влияния деформаций. Например, в сжатом стержне случайная деформация искривления его вызывает изменение величины изгибающих моментов, что в свою очередь благодаря упругим свойствам стержня вызывает дополнительное его искривление. Потеря устойчивости сооружения возможна, когда деформации увеличивают эффект влияния внешних сил, и, наоборот, невозможна, если деформации уменьшают этот эффект.
Характерная особенность потери устойчивости упругих систем: обычно достаточно незначительного превышения величины критической нагрузки, чтобы ставшие возможными при этой нагрузке деформации нового типа необычайно сильно возросли, что может привести и, как правило, приводит к разрушению сооружения.
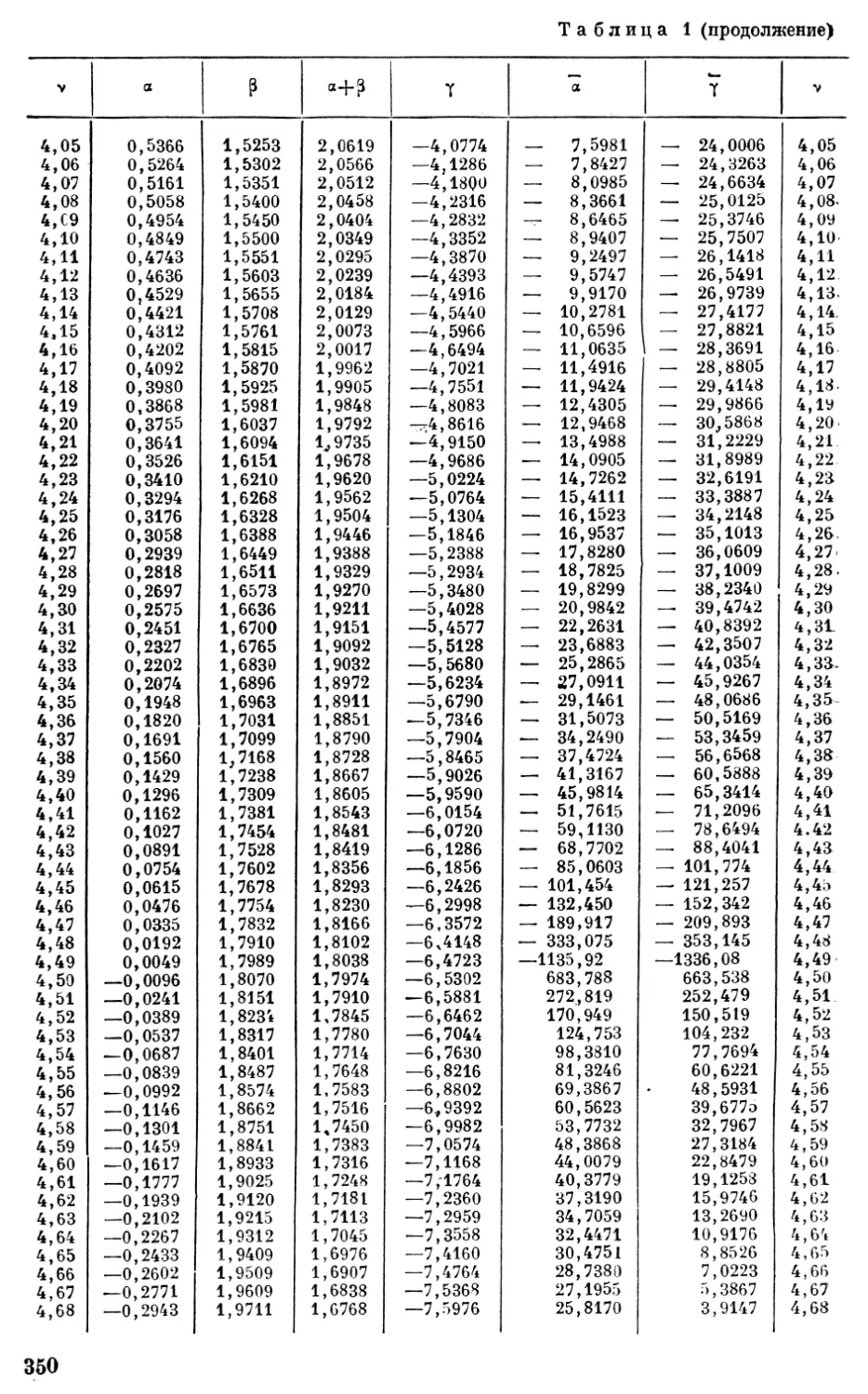
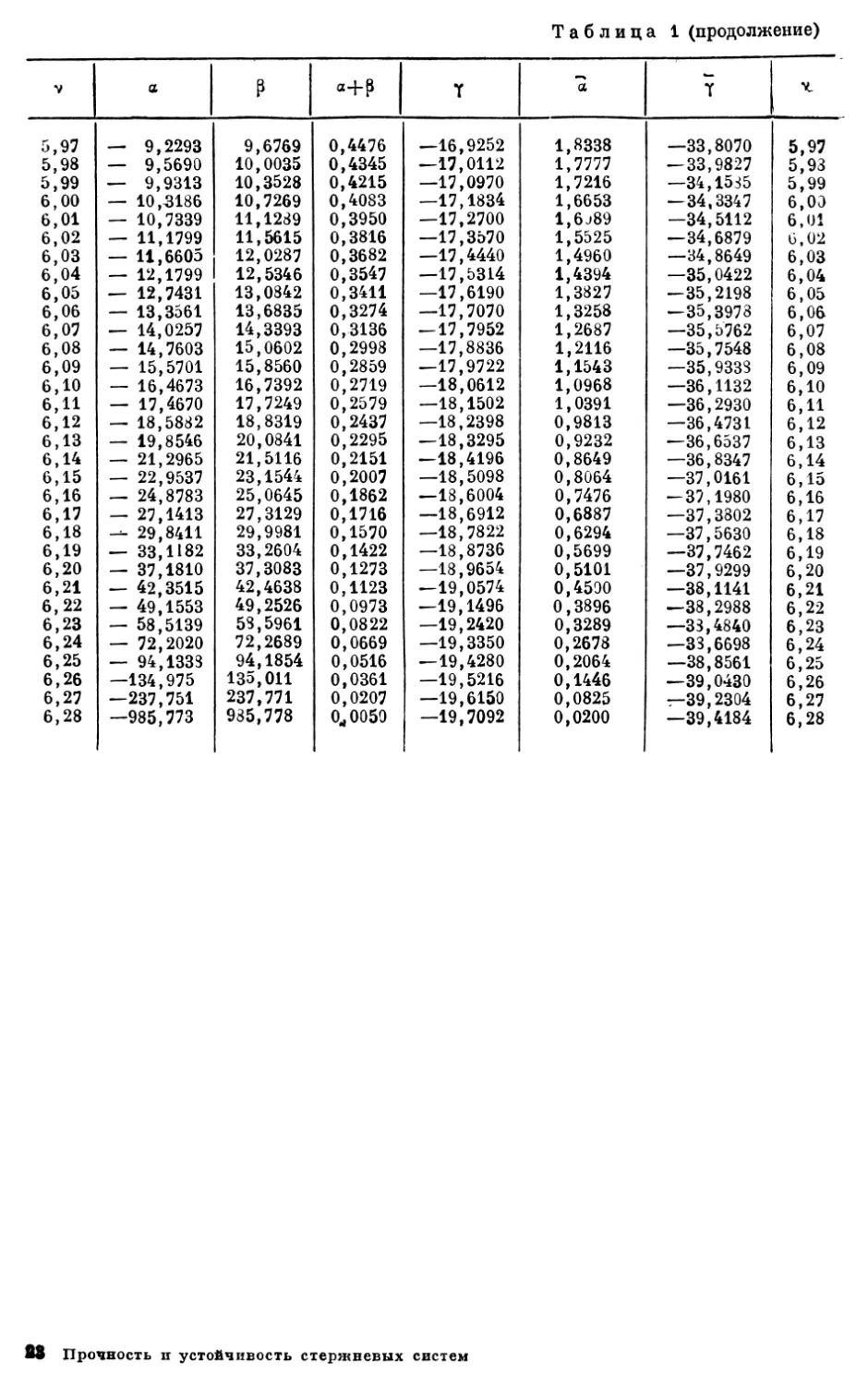
Основные случаи потери устойчивости вкратце представлены в виде табл. 1.
10
Таблица 1
Основные случаи потери устойчивости
Начальная деформация
Новая, внезапно возника
Объекты, теряющие
элементов сасгемы
ющая деформация системы
устойчивость примеры
1. Чистое осевое сжатие
Изгиб искривление
Стержень, арка, ферма
2. Кручение
Башня, тонкостенный стержень
3. Крученне
Изглб
Вал, винтовая рессора
4. Изглб
5. Симметричная деформация
Кручение потеря плоской деформации
Полная или частичная утрата симметрии деформации понижение степени симметрии дзформации
Балка с высокой стенкой, арка
Стержень, арка, рама, ерма
4. Задачи устойчивой прочности
В большинстве случаев практики вопросы устойчивости не могут быть отделены от вопросов прочности. Это связано с тем, что обычно на систему, кроме осевых нагрузок, характерных для постановки задачи устойчивости, действуют еще поперечные или искривляющие факторы, например, поперечные нагрузки, эксцентриситеты, искривление оси и т. д. Эти факторы с самого начала, задолго до возрастания нагрузки до критического значения, вызывают деформации, типичные при отсутствии этих дополнительных факторов для потери устойчивости системы. Лишь при отсутствии этих искривляющих факторов можно говорить о потере устойчивости первого рода, т. е. о внезапном возникновении качественно новых деформаций. Увеличение осевых нагрузок до критической величины с точки зрения устойчивости при наличии таких искривляющих факторов вызывает несоразмерно высокий рост деформаций. При определенных упрощениях расчета, вполне оправдывающих себя, пока деформации малы, в результате расчета мы даже получим, что деформации возрастают до бесконечности.
Отсутствие процорциональности между нагрузками, с одной стороны, и напряжениями и деформациями, с другой стороны, объясняется изменением расчетной схемы сооружения по мере роста нагрузок и деформаций. Для решения этих задач сооружение нужно рассчитывать на основе деформированной его схемы.
Принцип наложения независимости действия в этих задачах для осевых нагрузок, вообще говоря, неприменим, для искривляющих же факторов конечно, если не выходить за пределы теории малых деформаций им вполне можно пользоваться. Это происходит благодаря тому, что влияние искривляющих факторов на усилия можно считать с достаточной для практики точностью независимым от величины деформации.
Обычно еще до достижения сооружением стадии потери устойчивости второго рода его деформации становятся настолько большими, что сооружение можно считать практически переставшим быть пригодным к эксплоатации. Поэтому для практических целей не столько важно знать критические значения нагрузок, при которых нарушается равновесие между внутренними и внешними силами системы, сколько значения нагрузок, при которых напряжения и деформации системы перестают быть допустимыми. Ясно, что такой расчет нужно проводить по деформированной схеме. Поскольку он должен обеспечить сооружение от нарушения проч-
11
ности и от внезапного резкого нарастания деформаций, мы его называем расчетом устойчивой прочности.
Расчеты устойчивости первого и второго рода также являются расчетами по деформированной схеме сооружения, но при них мы разыскиваем некоторые определенные критические состояния системы, при расчете же устойчивой прочности мы ограничиваемся определением напряжений и деформаций, соответствующих некоторым промежуточным состояниям, отличным от критических. Если сооружению надо обеспечить коэфициент безопасности не ниже к. то рассчитываем сооружение по деформированной схеме на нагрузки, увеличенные в к раз против заданных значений1. Если при этом деформации и напряжения в сооружении не превзойдут известных пределов например, можно поставить требование, чтобы напряжения были меньше предела текучести и не вызывали местной потери устойчивости и если при нагрузках, меньших принятых в расчете, не может иметь место общая потеря устойчивости такой добавочный расчет выполняется одновременно с основным расчетом и составляет его часть, то нужный коэфициент безопасности сооружению обеспечен.
5. Задачи на потерю устойчивости второго рода
Эти задачи сводятся к определению предельного сопротивления предельной несущей способности системы. Как было указано выше, для применяемых на практике строительных материалов и конструкций эти задачи связаны с учетом пластических деформаций. Как только в сооружении начинают появляться напряжения выше предела упругости, то дальнейшее увеличение нагрузки приводит к расширению зоны пластических деформаций и одновременно с этим к уменьшению жесткости сооружения; рост Нагрузок вызывает непропорционально ускоренное возрастание деформаций. Конечной целью расчета является определение предельной сопротивляемости, т. е. определение величины нагрузки, при которой сопротивляемость сооружения начинает понижаться, а деформации его продолжают расти без увеличения или даже при некотором дальнейшем уменьшении нагрузки. Таким образом, благодаря учету пластических деформаций, появляется возможность при решении задач устойчивой прочности говорить о своего рода критической нагрузке, соответствующей предельной сопротивляемости сооружения при потере устойчивости равновесия между внешними и внутренними силами в опасных элементах или сечениях сооружения.
Сравнивая эти четыре типа задач прочности, устойчивости, устойчивой прочности, предельного сопротивления, мы видим, что все они в основном относятся к одному вопросу—обеспечению определенного коэфициента безопасности сооружения. Наиболее сложная постановка задачи соответствует определению предельного сопротивления; только решив эту задачу, мы можем говорить об определении действительного коэфициента безопасности сооружения. Однако из-за высокой трудности решения задачи в такой постановке вполне целесообразны более схематизированные постановки задачи.
6. Примеры использования предлагаемой классификации
Приведенная классификация задач по определению коэфициента безопасности, помимо ее формального значения, весьма облегчает постановку задачи.
Рассмотрим, например, сквозную ферму с параллельными поясами. Считая эту ферму шарнирной, можно ставить вопрос о так называемой ферменной потере устойчивости за счет удлинений или укорочений от-
1 Бел4 ставится требование о созданяи для временной нагрузки определенного запаса, выраженного в тоннах см. проф. Н. С. Стрелецкий, Курс металлических конструкций, Стройиздат, 1940, ч. 1, стр. 166 и дальше, то к величине расчетной нагрузки надо прибавить этот запас нагрузки вместо умножения расчетной нагрузка на коэфициент безопасности.
12
дельных стержней при сохранении прямолинейной формы каждого из них. Этот вид потери устойчивости заключается в том, что ось фермы, при малых нагрузках прямолинейная, внезапно искривляется при достижении критического состояния. Конечно, когда нагрузки с самого начала вызывают искриление оси фермы, тогда нельзя уже говорить о такой потере устойчивости; в этом случае приходится говорить о проверке устойчивой прочности. Впрочем, если ферма и нагрузка симметричны, то можно поставить вопрос о ферменной потере устойчивости, но уже в ином смысле, а именно как о потере устойчивости симметричной деформации. Если же отсутствует симметрия фермы или нагрузок, то от проверки устойчивости фермы необходимо перейти к проверке ее устойчивой прочности и, как всегда, к проверке местной устойчивости прямолинейной формы ее отдельных стержней. N Далее можно пренебречь удлинениями
Г
pi
А
1
t
t Фиг. 2.
.
отдельных стержней фермы и в то же вре- д мя рассматривать ее как систему с жесткими узлами. Тогда при произвольной системе узловых нагрузок можно будет говорить о рамной потере устойчивости фермы, заключающейся во внезапном искривлении стержней фермы при
отсутствии линейных перемещений ее узлов. При размещении поперечных нагрузок кроме узлов также на стержнях фермы можно говорить о потере устойчивости лишь как о потере симметрии деформации, в ином случае надо перейти к расчету устойчивой прочности.
Если рассматривать ферму как систему жестко соединенных в узлах стержней, которые могут иметь и продольные и поперечные деформации, то о потере устойчивости можно говорить лишь как об искривлении первоначально прямолинейной оси фермы или как о потере симметричной деформации. Понятно, что в обоих случаях нагрузки не могут быть произвольными, они должны быть такого типа, чтобы до потери устойчивости характерных для них деформаций не возникало. Итак, о потере устойчивости фермы с жесткими узлами при учете удлинений ее стержней можно говорить только в исключительных случаях, только для особых случаев ее загружения, в общем же случае речь может быть только о задаче устойчивой прочности.
Второй пример—аксиально сжатый стержень или какой-нибудь другой случай чистой начальной деформации. В этом случае нельзя ставить задачи
о расчете устойчивой прочности, а задача распадается на две отдельные: проверку устойчивости и проверку прочности.
Задачу об определении предельного сопротивления с принципиальной точки зрения можно ставить во всех случаях.
7. Надежность расчетов, основанных на теории малых деформаций
Покажем, что расчет сжато-изогнутого стержня по теории малых деформаций
7
EJgZ M-O
1
дает, как правило, при тех же нагрузках большие значения прогибов v, чем расчет по теории конечных деформаций:
Е1 м 0. 2
р
Величины прогиба и изгибающего момента, относящиеся к теории малых деформаций, будем обозначать: v и М фиг. 2, а. Те же величины, полученные по теории конечных деформаций, обозначим: v и М фиг. 2,6.
13
В первом случае сечения стержня имеют только вертикальные перемещения и длина отрезка стержня s равна длине его горизонтальной проекции во втором случае xs.
Выражения для изгибающих моментов можно представить:
М М Nv; М М N7.
Здесь М и М — изгибающие моменты от действия поперечных грузов. Так как плечи поперечных нагрузок при определении М больше, чем
js j при определении Л, то
М М.
Пользуясь выражением кривизны г:
dh
1
ds2
Л-
dv2
3
уравнение 2 запишем так:
Фиг. 3.
1-5Л 0.
2
Введем обозначения:
N
Мв
‘-СЮ-:-
3
Тогда расчет по теории конечных деформаций приводится к уравнению:
d-v
EJiNxv M 0,
4
1 Эта формула эквивалентна обычной;
1_
Р
d2v dx1
2 , 3i
. J
Формулу 3 можно получить так. Из рассмотрения фиг. 3 получаем:
, ,. dv
ds oa; smср —
Продиференцировав последнее выражение, находим:
dv d2v
C0S 5F-
Таким образом:
7
i
d2v
dy
—- -. — — ds cos ds1
d2v
14
расчет же по теории малых деформации s — х —к уравнению:
EJd Nv M Q. 5.
Сравним эти два уравнения. Граничные условия обеих задач одинаковы: о 0; i;Sso 0.
Очевидно, что
N, N; М М М.
Определение прогиба v по уравнению 4 совершенно аналогично
определению прогиба v по уравнению 5, но прогибы v соответствуют как бы меньшим значениям продольной силы Nx N и меньшим значениям поперечных нагрузок М1 М. Таким образом, для балки на двух опорах при исследуемом характере ее загружения прогибы v получаются меньше прогибов v.
Отсюда следует, что р а счет по теории малых деформаций дает в этом случае результаты в запас надежности.
Если граничные условия при переходе от расчета по теории малых: деформаций к расчету по теории конечных деформаций существенно менялись бы, то наш вывод мог бы усложниться. Не исследовав этого вопроса подробней, мы допускаем возможность специальных случаев, которые могут явиться исключением из общего правила. Кроме того, нетрудно видеть, что при расчете по теории конечных деформаций прогиб консоли не может быть больше ее длины фиг. 4,а, прогиб балки на двух опорах не может быть больше половины ее длины фиг. 4,6, горизонтальное смещение узла рамы не может быть больше длины стойки, связывающей этот узел с землей. При расчете же конструкций по теории малых деформаций мы не имеем такого ограничения: прогибы могут получаться как угодно большими. Это еще раз подтверждает, что расчет по теории малых деформаций должен, вообще говоря, итти в запас надежности, так как он дает результаты в сторону некоторого увеличения прогибов конструкции. Чем меньше величина деформаций, тем ближе сходятся данные таких двух расчетов.
Реальные инженерные конструкции не приходится рассчитывать на большие деформации. Допускаемые перемещения для них невелики так что вполне рационально рассчитывать их по теории малых деформаций. Такой расчет будет неизмеримо проще, и, кроме того, он идет в запас надежности конструкции. Расчет устойчивости инженерных конструкций по теории конечных деформаций, вообще говоря, не вызывается необходимостью и для практических расчетов не может считаться целесообразным.
1 Мы утверждали вышэ, что эпюра прогибов балки по теории конечных деформаций лежит внутри такой же эпюры по теории малых деформаций. Это еще не значит, что углы поворота сечений по теории конечных деформаций всегда меньше соответствующих углов, вычисленных по теории малых деформаций. Может быть и наоборот.
ГЛАВА II
ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ШАРНИРНО-СТЕРЖНЕВЫХ ФЕРМ И КОМБИНИРОВАННЫХ СИСТЕМ
Длинные фермы, подвергнутые одновременному действию сжатия и изгиба высокие башни, стрелы подъемных кранов, решетчатые арки фиг. 5, решетчатые колонны и пр., нуждаются в расчете, учитывающем вопросы их прочности и общей их устойчивости. Проверка местной устойчивости отдельных элементов этих ферм не всегда обеспечивает надлежащую устойчивость ферм в целом. Метод объединенного расчета ферм на прочность и общую их устойчивость в литературе не известен г. Автором разработано несколько способов такого расчета устойчивой прочности, сводящегося к расчету сооружения по его деформированному состоянию, а не по первоначальной геометрической его схеме без учета деформаций, как это принято обычно.
1 Основные зависимости
Пусть координаты учла а пространственной фермы будут ха, уа, za. Тогда проекции на осикоординат стержня 1атУ соединяющего узел а с узлом т9 можно обозначить фиг. 6:
ат У am Ут Уп ат а
Эти проекции связаны между собой зависимостью
am Хат 4 Уат ат
Пользуясь этими обозначениями, можно условия равновесия узла а шарнирно-стержневой фермы при расчете ее по первоначальной геометрической схеме записать в таком виде:
2
2 sm г”р:о,
1 ат
У 1
а
Уат
т I
ат
а
0. am 1 _ 1 а
ат
а
со
О
Здесь Sam — усилие стержня 1ат, рассчитанное по первоначальной схеме фермы, не учитывающей деформаций ее not нагрузки.
Значок а под знаком 2 обозначает, что суммирование распространяется на все стержни, сходящиеся в узле а.
При деформировании фермы координаты узлов ее ха9 уа, za получают соответствующие приращения uaJ va, wa, а проекции длин стержней приращения:
иат ат
Wa.
4
1 О потере устойчивости ферм см. проф. И. М. Рабинович, Об устойчивости стержней в статически-неопределимых системах, Гострансиздат, 1932.
16
Продиференцировав 2 и заменив диферепциалы приращениями, получим формулу для удлинения к стержня через разность перемещений его концов:
t хпт У am i zam ш сс
ат am i am i j Wam J
am lam Lam
или в более короткой записи:
f fyf , 5, Продиференцируем теперь аналогично условия равновесия 3 и заменим диференциалы приращениями будем помнить при этом, что нагрузки узлов фермы остаются неизменными. Тогда получим:
2 Гл5атриат-0о, 1
L lam lam am У J
а
2 Гд5атрат-рОо,
L 1ат 1ат Ч 1am У J
а
ЕГ Л С zam I ат f zam , Л 1 n
I am j 1 ™am i am
L am lam lam У J
a
6
Полное усилие Sam стержня lam при расчете фермы по деформированной ее схеме иначе говоря, при учете деформаций фермы, вызываемых
нагрузками, равно:
ат ат ат С
В соответствии с законом Гука:
о EFam, EFam Г х.у , z оч
S— - , Г.ат -т— у В f V т W. 8
am lam L 1 1 1 J am
am 7 При выводе уравнений 5—8 мы допустили, что перемещения узлов фермы, вызываемые ее нагрузками, малы по сравнению с генеральными размерами сооружения. Формула 5 вполне соответствует допущению Виллио о том, что перемещение конца стержня, вызываемое его поворотом на малый угол, может быть принято нормальным к первоначальному направлению стержня.
2. Метод узловых перемещений1
Расчет фермы по ее деформированной схеме, объединяющий вопросы прочности и устойчивости этой фермы, может быть произведен точно при использовании, например, метода деформаций.
Для этого надо исключить из 6 приращение усилий AS. Это можно сделать, сложив соответствующие строки уравнений 3 и 6 и заменив величину ее значением по формуле 8, а Хат — его значением по формуле 5. Введем для сокращения записи обозначение:
г EFam —
am 1ат
9
1 Этот метод был разработан автором в 1939 г. в связи с расчетом устойчивости башни мощного портового молотовидного крана.
2 Прочность и устойчивость стержневых систем
17
Тогда получим для узла в:
2 Ит-вЛт гтвт ит-а gf f а
2 .—J ef- 10
K-osf t0Jp
2 гтвт п — gj тот
а
Wm—Wa 7 ё ji em -Рв 0.
Уравнения 10 представляют собой условия равновесия узла а пространственной фермы, выраженные через перемещения ее узлов и учитывающие влияние деформаций фермы на усилия ее стержней.
Расчет прочности и устойчивости фермы может быть выполнен в следующем порядке. Для каждого из смещающихся узлов фермы составляем по три уравнения типа 10. Уравнения эти записаны в канонической форме в табл. 2.
Таблица 2
иг
u2
Л 1
а11
Д12
аъ
1
а14
1
аЮ
а21
агг
a2Z
Д24
а20
Л81
azz Л84 аъо 1 I
И
Решив эту систему уравнений и найдя неизвестные иш, vm9 wm для всех узлов фермы, затем по формуле 8 определяем усилия всех ее стержней Sam.
При расчете фермы по ее деформированной схеме, вообще говоря, нарушается пропорциональность между нагрузками фермы и усилиями ее стержней. Поэтому для обеспечения определенного коэфициента к запаса надежности фермы нужно предварительно умножить на этот коэфициент всю расчетную нагрузку фермы и уже после этого по формулам 3, 9 и 10 произвести расчет. Если при такой увеличенной нагрузке не произойдет ни общей потери устойчивости фермы, ни местной потери устойчивости отдельных ее стержней, и если при этом напряжения в элементах фермы не выйдут за пределы упругости, то можно будет утверждать, что коэфициент Л запаса надежности фермы действительно обеспечен.
Таким образом, при расчете фермы по деформированной ее схеме коэфициенты all9 а12,.,япп системы уравнений И, а также и свободные члены а1о, а20,.,япд являются линейными функциями коэфициента запаса к.
Величина какой-либо неизвестной, например ип может быть найдена как отношение двух детерминантов:
12
98
где D — детерминант, составленный из коэфициентов а119 а12, при
неизвестных в системе уравнений 11. Величина D является функцией коэфициента к запаса надежности:
. 13
Устойчивость фермы теряется при таком значении к, при котором
Z А 0. 14
Для определения минимального коэфициента устойчивости ктш нужно решить уравнение 14. Проще всего это можно сделать, построив график зависимости D от к и по этому графику1 определить минимальное значение к, при котором D 0.
При объединенном расчете фермы на прочность и устойчивость нужно убедиться, что при значениях к, меньших желаемого, ферма устойчива. Это будет, если при этих значениях к знак детерминанта D остается без изменения таким же, как и при к, принятом равным нулю2. На практике обычно вполне достаточно, кроме значения D к при заданном
значении к, найти еще значение 0 и fkx, где 0 кг к.
Если все эти три значения 0, fki и одного знака и плавно укладываются ка графике, то можно не опасаться потери устойчивости при значениях к, меньших заданного.
Как мы видим из вышесказанного, точный расчет прочности и устойчивости пространственной фермы по методу деформаций связан с составлением и решением весьма большого числа уравнений.
Практически этот метод, и то в измененном несколько виде, может быть рекомендован только для расчета конструкций, обладающих весьма высокой степенью симметрии. К таким конструкциям могут быть, например, отнесены пространственные купольные покрытия по типу системы Шведлера. Но в этом случае систему основных уравнений надо перестроить, приспособив ее либо к цилиндрическим координатам, либо к пространственным косоугольным координатам. При решении системы уравнений надо максимальным образом использовать симметрию системы или применить аппарат разностного исчисления.
3. Вариационный метод3
Расчет может быть значительно упрощен и облегчен, если отказаться от точного решения и перейти к приближенному решению, основанному на применении начала возможных перемещений,
а Расчет пространственных ферм
Будем представлять себе, что окончательные соответствующие расчету фермы по деформированному состоянию значения усилий S, удлинений X и перемещений и, v, w с достаточным приближением можно выразить так:
SS AS; Х л АХ;
M tt Aw; y i; Au; ww Aw
л л
1 Иследование устойчивости пространственного каркаса по типу Дворца Советов СССР. Изд. Ак. наук Ъ ССР, Киев 1938 г., стр. 39—41, 219—224.
2 В этом случае коэфициенты системы уравнений 11 будут совпадать со значениями, соответствующими обычному расчету фермы по ее первоночальной недзформироваиной схемз.
8 См. статью автора в Доповда АН УРСР 3, 1947 г. Этот метод с разрешения автора был использован при проверке надежности плоских и пространствзыных ферм в кандидатских диссертациях Н. Н. Беляшевского и И. С. Бондаренко.
15
2 19
где S, л иу0
w соответствуют расчету фермы по первоначальному недеформирова иному состоянию, а
ф
AS са5 с,5П1
Да. Cl.i с2,и сп1.; А и 4 4 До Ci1 сгип C3uni 4- ; Ди tv1 c2cvn c3cvin 16
Здесь S1, SH,
Xi.
a1, и
ii
v vu,
w
rll виртуальные усилия, удлинения ствующие единичным состояниям
у f стержней и перемещения, соответнекоторых нагрузок сх 1; с3 1; с3 1;., рассчитанные обычным способом по недеформйрованной схеме фермы. Характер нагрузок с19 с2, с3,. надо выбрать так, чтобы возможные формы деформаций при потере устойчивости фермы можно было с достаточной для практики степенью точности получить как линейные комбинации деформаций фермы от воздействия этих нагрузок с19 с2, с3,.
В качестве неизвестных в этом способе фигурируют эти неопределенные параметры с19 с2, сз,. Чем меньшим количеством этих параметров мы сможем ограничиться, тем проще получится решение задачи.
Рассмотрим, например, мостовую ферму фиг. 7, симметричную по своей схеме и симметрично загруженную вертикальными грузами Р. Пусть нам надо определить критическое значение этой величины Ркру при котором нарушается симметрия деформации и начинается боковое выпучивание сжатого верхнего пояса х.
В этом случае деформацию в начальный момент боковой потери устойчивости можно с достаточной точностью представить как сумму деформаций состояния Р и помноженных на сг й с2 деформаций соответственно состояний I и И, изображенных на фиг. 7:
и а сци1 -f- с2 н11; v v9 CjV1 c2in;
Фиг. 7.
Более того, принимая во внимание, что стремление к боковому выпучиванию свойственно собственно верхним сжатым поясам фермы и не свойственно нижним растянутым, можно даже ограничиться одним неопре-
1 Такой вопрос может представлять практический интерес при большой вертикальной нагрузке и малой жесткости горизонтальных и поперечных связей.
20
деленным параметром cxi
и и cxul х v9 4 сгх
Итак, пользуясь вариационным методом, число неизвестных можно, как мы видим, снизить для данного случая даже до единицы.
Если мы желаем учесть непропорциональный нагрузке рост вертикальных симметричных деформаций, то мы можем взять еще одно виртуальное состояние деформации, состояние III, отличающееся от состояния Р лишь постоянным множителем:
ш-р.
Тогда:
и и схи1 сиш; v v CjV1 с3рш.
Нетрудно видеть, что неизвестные параметры —антисимметричный с и симметричный сь — в дальнейшем дадут два раздельных уравнения.
Покажем теперь, как в общем случае составляются уравнения вариационного метода. Пусть S, л соответственно усилия и удлинения
стержней, а и, и, v — перемещения узлов фермы в некотором виртуальном состоянии ее деформации. Очевидно, что для какого-нибудь стержня 1пт эти величины должны быть связаны между собой зависимостями 5 и 8:
7 W f U 7 ат 17
и
-5вт Гат. 18
1ат
Нам нужно приравнять нулю суАмму работ всех внешних и внутренних сил, действующих на пространственную ферму в ее деформированном состоянии, соответствующем некоторой виртуальной деформации этой фермы. Для этого надо составить выражение виртуальной работы для отдельного узла дефорМрованной фермы и затем приравнять нулю сумму таких выражений для всех ее узлов. Сделаем это так.
Уравнения равновесия 6 были составлены для отдельного узла а
фермы. Умножим первое из них на иа, второе на va и третье на wa
и сложим все три произведения вместе. Затем выполним аналогичные операции для всех других узлов фермы и результаты их сложим все вместе:
хпт и Ь УатР. znmwa а аШ ат
I Sam I 7_ I. хатиа Ь УатРп Ь znmwa л
Г иатиа Г vamva Г WamWa Лат f U.
Lam L lam J Каждый стержень lam фермы имеет два конца: конец а и конец т, причем:
A S
ат
s
fim
со.
u mat
I — I
vam
ат :г
mai
У am
Уma-
7 — ГГ
am mai
Иат
am
ma
Warn —Wma-
1
Ц
В состав суммы а для каждого стержня 1ат входят два выражения: одно для конца а, другое для конца т.
Сделав приведение подобных членов в этих цвух выражениях и учитывая при этом соотношения Ь, получим для отдельного стержня lamt
д с хат Цд ит У пт д Ущ zg т wg wrrd
I Gm — bnI 0 Г _ _ _ am a m vam wa — m am a wm
ьаШ L.
xam ua um f У am Pa m h am i.wa win 1 hm amJJ
или на основе равенств 4 и 17:
S2
1 i j amdm Ь amPam awS
L am
am
i
Таким образом, уравнение а приобретает вид:
У Гд5Х 4ш то ww — а1 0.
L J am
19
am
Суммирование в этом уравнении распространяется на все стержни пространственной фермы. Уравнение 19 представляет собой начало виртуальных работ для деформированного состояния пространственной фермы. Оно является основным уравнением объединенного расчета прочности и устойчивости пространственных ферм вариационным методом.
Каноническую систему уравнений такого расчета табл. 3 получим,
Таблица 3
Cl
С2
3
♦ 1
11
Aiz
-13
10
21
А2
23
А 20
-31
32
33
зо
t 0
20
подставив в 19 вместо AS его выражение 16 и вместо и, v, w, X. их выражения 15. При этом принимаем последовательно в формуле 19 в качестве виртуального состояния S, к, и, v, w одно
за другим единичные состояния S1, л1, и1, v1, w1; Su, X11, и11, v11, w11 и т, д., рассчитываемые каждое по недеформированной схеме фермы на нагрузки соответственно сх 1; с2 — 1 и т. д.
Как легко видеть из 19 и 16, коэфициенты системы уравнений 20 имеют следующие выражения:
Атп Апт 2 Г MmMn ”;” _ 1 ; 21
J ab
Атл 2 Т wyW WWm — X0Xm j
ab
ab
1 Для получения коэфициента Л12 мы вместо значка -записываем I, вместо значка д записываем II и т. д. 22
Для обеспечения пространственной ферме коэфициента к запаса надежности заменяем коэфициенты Атп и Ато в системе уравнений 20 соответственно коэфициентами Атп и Ат0:
Атл 2 iSmXn kj a”Vn j ; 21
22
Amo VA
mo
так как при увеличении нагрузки в с раз усилия S также возрастают в к раз, а произведения Su, Sc, Sw в к2 раз.
Если пространственная ферма может быть рассчитана методом разложения ее на плоские системы, то расчет может быть в значительной
мере выполнен графически. Усилия стержней S в нагрузочном и 51, S11,. в единичных состояниях можно будет определить с помощью построения
диаграмм усилий, удлинения стержней Х, к1, Хп,. — вычислить по формуле Гука, перемещения узлов — найти из кинематических соображений, определив их проекции на плоскости граней фермы при помощи диаграммы Виллио.
Решив систему уравнений табл. 4:
Таблица 4
С1
1
А
11
А
Ар
Aiq
23
А 21
Аз
Л
-1 -2р
А
J
найдем величины с19 с2, с3,., ср.
После этого по формулам 15 и 16 определяем полные усилия стержней, соответствующие расчету фермы по деформированной ее схеме:
5 5 c.S1 с25п. cpiS‘p 24
Эти усилия не должны вызывать ни местной потери устойчивости стержней фермы, ни появления в них пластических деформаций:
S С FepQ крФ уст или I 25
SFHmGj,
Коэфициент запаса кг на появление деформаций нового типа или на неограниченное возрастание старых найдем как минимальный корень уравнения:
Агг
А
12
А
Л1 р
А21
А Jrx22
А
Jr2p
II
о
26
4
Jrxp2 ф
а;р
Этот коэфициент кг должен быть не меньше желаемого коэфициента запаса к:
К к. 27
Если условия 25 и 27 будут выполнены, то пространственной ферме действительно будет обеспечен желательный коэфициент к запаса надежности.
23
Примечание. При расчете циклически симметричных систем па
типу купола Шведлера вместо уравнения 19 рациональней пользоваться формулой:
в которой 6 и О —углы поворота стержня в вертикальной плоскости,
проходящей через стержень, а в и 6 — соответственно углы поворота стержня в плоскости, перпендикулярной к предыдущей и также проходящей через стержень. Эти углы поворота проще всего определить аналитически по формуле Максвелла —Мора.
При расчете плоских ферм могут быть сделаны значительные упрощения. Начало виртуальных работ для деформированного состояния
повернутого по сравнению с первоначальной геометрической схемой фермы на угол фа5, равна
Мы записали сейчас работу сил St и Sba, приложенных к отдельному стержню 1аЪ работа внутренних сил взаимодействия ваъ и приложенных к узлам а и , будет такая же, но со знаком минус. Все узлы фермы находятся в равновесии, поэтому сумма работ сил внешних и внутренних, приложенных к этим узлам, на соответствующих виртуальных перемещениях может быть приравнена нулю:
Здесь Р — внешние нагрузки фермы;
др — соответствующие им виртуальные перемещения:
S и ф — действительные усилие и угол поворота стержня в деформированном состоянии;
Я и ф —виртуальные удлинение стержня и угол его поворота.
Запишем работу сил, соответствующих недеформированному состоянию фермы на тех же виртуальных перемещениях:
Вычтя 30 из 31 и пренебрегая малыми высших порядков, получаем уравнение начала возможных перемещений для деформированного состояния фермы:
а это и есть уравнение 29, им мы и будем пользоваться при расчете плоских ферм
24ssvwe6ebo,
28
ab
б Расчет плоских ферм
плоской фермы удобней записать не по формуле 19, а через углы поворота h стержней фермы:
am
При этом значительная часть расчета может быть выполнена графически.
Фиг. 8.
Приведем здесь совершенно элементарный вывод формулы 29. Чтобы записать ее, нам надо приравнять нулю работу сил внешних Р и внутренних S S S деформированного состояния фермы на соответствующих им виртуальных перемещениях. Пусть в виртуальном состоянии фиг. 8 удлинение стержня
1аъ равно Aaj, а взаимный сдвиг его концов от поворота стержня равен 1аьаЪ Тогда работа усилия Sai в действительном деформированном состоянии стержня.
30
31
29
24
S0
Г77
тГТ77.
Примем, что окончательные, соответствующие расчету фермы по деформированному состоянию, значения усилий S, удлинений X и углов поворота ф стержней с достаточным приближением можно выразить так:
5 Л; ХХДХ; ф ф Дф, 32
где
AS сг Sl c2Sn c3S™.;
АХ а XI с2 Х с3 X111.; 33
Дф с1ф1 С2фП сзфШ Здесь Sl , S11,., X1 , X11,., ф1 , ф11,. — усилия, удлинения и углы поворота стержней фермы, соответствующие единичным состояниям некоторых нагрузок сх 1, с2
1,., рассчитанные обычным способом например, при помощи диаграмм усилий и Виллио по недеформированной схеме фермы фиг. 9. Характер нагрузок с19 с2, с3,. надо выбрать так, чтобы возможные формы деформации при потере устойчивости фермы можно было с достаточной для практики степенью точности получить как линейные комбинации деформаций фермы от воздействия этих нагрузок сг, с2, с3,.
Подставив эти выражения в 29, получим:
2 -Ь с2 Sn c8Sin. X
S Sl ф Ci ф1 с2фп
с8фш. ф 0. 34
Давая последовательно вирту альным удлинениям X и виртуальным углам поворота ф значения а X1, Хп, ХШ,., ф ф1, ф11,
фш,., получим систему уравнений относительно величин clf с2, с9,. табл. 5:
Таблица 5
Фиг. 9.
С1
С.у
С3
1
-11
, 1
;
1 -
; 1з
1
10 20 -30 У
-22
1
23
1
31
32
33
35
где
Атп 2 54 р s VS s I ф” ф А
т. 36 37
S 5 1 Фт-
Решив систему уравнений 35, находим сг, с2, с3,., затем определяем
5 с25п с,5ш 38
Далее мы постуцаем аналогично сказанному зыше о расчете пространственных ферм.
На фиг. 9 в единичных состояниях приложено по одной силе с 1, сг 1. Совершенно очевидно, что зачастую рациональнее прикладывать в единичных состояниях обобщенные еилы, представляющие собой целые
Фиг. 10.
группы сосредоточенных сил. Например, при расчете устойчивой прочности решетчатой трехшарнирной арки фиг. 5 единичные состояния следует выбирать так, как это показано на фиг. 10.
4. Метод эквивалентной дополнительной нагрузки1
Довольно простым является и другой графический приближенный способ расчета, но он относится в основном к расчету устойчивой прочности и менее удобен для обнаружения внезапных новых форм деформаций. Способ этот основан на аналогии между условиями равновесия узла при расчете фермы по первоначальной схеме:
9
ат
хат
lam
ат
У am
lam
РХа 0,
Ко,
а
39
и между условиями б, связывающими приращения усилий стержней A Sam Sam — Sam Sam — усилие стержня при расчете фермы по деформированному состоянию:
С1 О,
am
a
40
Здесь Са, Са, Са определяются формулами:
V С 0 f итиа хат am
а — qm I 7 I
Ч Lam am Lam
ч
41
J
1 Н. В. Корноухо в, СтШкють стиржневих систем, статья в Юбилейном сборнике Академии наук УССР, т. 1, 1944 и СтШтсть та стка мщшсть шаршрно-стиржйевих систем в Доповщ1 АН УРСР, JNft 2, 1947.
См. также сноску к 2.
8
Для плоских ферм формулы 41 могут быть заменены:
42
Если не интересоваться пока критическими состояниями, а ограничиться расчетом устойчивой прочности, то его можно выполнить в следующем порядке. Сначала определяются усилия Sam всех стержней фермы от заданной нагрузки обычными методами например, при помощи диаграммы усилий или по способу моментных точек. Затем определяются удлинения всех стержней фермы по формуле
Потом при помощи диаграммы Виллио или другими способами определяются перемещения узлов ит, vm или углы поворота стержней фаш
После этого вычисляются величины Са и Са Для всех узлов фермы. Прикладывая их в виде нагрузок к узлам недеформированной схемы фермы, строим диаграмму усилий и находим усилия в стержнях, которые будут равны ASam. Если
и не вызывает местной потери устойчивости стержня, то ускоренный рост деформаций при заданных нагрузках для фермы не опасен.
Для обеспечения коэфициента запаса к на появление пластических деформаций или на местную потерю устойчивости стержня нужно, чтобы
для всех стержней фермы было меньше соответственно предела текучести аТ или критического напряжения скр. уст.
Этот способ расчета удобен для систем, у которых первоначальные деформации совпадают по характеру с наинизшей формой потери устойчивости. Его можно с некоторыми изменениями в виде метода последовательных приближений применить также к проверке устойчивости 1-го рода.
При выполнении определенного цикла расчета устойчивости фермы по методу последовательных приближений, мы обычно принимаем перемещения и, v, w, ф и удлинения стержней к из предыдущего приближения. В первом же приближении систему этих перемещений и удлинений стержней можно принять на-глаз, ставя лишь требование, чтобы эти величины были кинематически связаны друг с другом для данной фермы и чтобы соответствующая им деформация фермы была сходна с деформацией, на появление которой мы проверяем устойчивость фермы.
Коэфициент запаса устойчивости фермы в n-ом приближении может быть найден как отношение соответствующих перемещений либо усилий стержней фермы, взятых: числитель из предыдущего, а знаменатель из
Замена в 43 полного усилия Sam его приближенным значением т приводит
к тому, что из рассмотрен ля исключается изучение форм деформаций, отличных па характеру от вызываемых заданной нагрузкой.
Samlam
am Пч F am
43
hSam -f с2 AiSam
44
27
последующего приближения:
кп,Мп: 45
Обычно можно считать, что результат не вызывает сомнений, если значения всех этих отношений одинаковы, либо мало отличаются друг от друга. Чтобы этого добиться, нужно сделать несколько циклов последовательных приближений.
Процесс определения коэфициента запаса устойчивости может быть ускорен, т. е. число циклов последовательных приближений может быть уменьшено, если перейти к интегральным характеристикам и принять равным отношению величин потенциальной энергии деформации фермы предыдущего к последующему приближению
2
Sn4 46
2.J 2 EF
5. Прочность и устойчивость комбинированных стержневых систем1
К числу комбинированных систем мы относим следующие системы: шпренгельные балки и рамы, фермы с неразрезными поясами, фермы с жесткими узлами и вообще все системы, часть элементов которых ферменные стержни работает, как стержни шарнирно-стержневых ферм тодько на продольные усилия, а другая часть рамные стержни — как стержни рамных конструкций в основном на изгиб. Такие комбинированные системы занимают промежуточное положение между рамами и фермами. На практике, поскольку шарниры в узлах отсутствуют, к ферменным стержням относят обычно стержни большой гибкости с малыми поперечными сечениями, не воспринимающие на себя значительных изгибающих моментов. К рамным же стержням относят обычно стержни малой гибкости и с большими поперечными сечениями. При этом зачастую для рамных стержней учитывают только изгибные деформации а для ферменных—только продольные.
Метод узловых перемещений. При учете в общем случае как продольных, так и изгибных деформаций расчет комбинированных систем сильно усложняется. Действительно, при расчете плоских комбинированных стержневых систем, например по методу деформаций, число неизвестных в общем случае равно утроенному числу узлов. На каждый узел а приходится по три неизвестных перемещения узла: 1 горизонтальное иа,.
2 вертикальное va и 3 угловое сра. Для каждого узла надо составить
по три уравнения: 1 уравнение равновесия горизонтальных проекций
внешних и внутренних сил, действующих на узел, 2 такое же уравнение для вертикальных проекций и 3 уравнение равновесия моментов сил, действующих иа узел
2 Qam COS Qam, Ж 2 ат COS Nam, x P Q; 47
a a
2am cos Qam, y 2 Nam cos Nam, y P 0; 48
2 Mam M 0. 49
1 См. статью автэра: Ст1йтсть та стШка мщтсть комбшованпих отрижневих систем — Допов1д1 АН УРСР, 3, 1947.
28
В этих уравнениях нужно вместо концевых моментов Мат, поперечных сил Qam и продольных сил Ndm подставить их выражения через деформации1:
Мат 2‘ат аат а Рат а Рат Фат Мат 50
Qam f m Рвт а ь Чат Qam, М
ifim
N Wim 52
am у чат lam
-Здесь: р— углы поворота узлов, 6 — углы поворота стержней, X — удлинения стержней; последние две величины через перемещения узлов и и v выражаются так:
ат - m - Ua р vrn в; 53
1ат ат
аmtyam Рт уа Ь ат
W у, 54
УатУат Цт а ат J
1ат
Этот способ расчета при значительном числе неизвестных перемещений весьма сложен. Он несколько упрощается при расчете симметричных, симметрично загруженных комбинированных систем на антисимметричную форму потери устойчивости.
Вариационный метод. В наиболее общем и в то же время практически вполне применимом виде расчет устойчивости и устойчивой прочности комбинированных систем может быть осуществлен с достаточной степенью точности при помощи вариационного метода. Этот метод базируется на обобщенной автором формуле Мора для расчета комбинированных систем по их деформированному состоянию2:
2-2 ш 2 5 Nwds 2 5 - о- 55
В этой формуле: Р —внешние нагрузки системы, Ър — соответствующие им виртуальные перемещения, S и — действительные усилия и угол
поворота ферменного стержня в деформированном состоянии, Хиф — виртуальные удлинения стержня и угол его поворота; N, М и р — продольное усилие3, изгибающий момент и угол поворота поперечного сечения рамного
стержня в деформированном состоянии; М и р — те же величины, относящиеся к виртуальному состоянию.
Запишем формулу Мора для недеформированного состояния:
Вычитая 55 из 55, получаем пренебрегая малыми высших порядков следующую расчетную формулу:
2 5 - 2 I 2 Д. 2 SVM - 0. 56
Совершенно аналогично расчету ферм по этому способу будем принимать, что окончательные усилия и деформации, соответствующие расчету комбинированной системы по деформированному состоянию, могут быть с до-
1 См. главу VII.
а См. 3, формула 30, а также главу IV, 2 настоящей работы и статью автора: Основные теоремы строительной механики в задачах объединенного расчета
стержневых конструкций на прочность и устойчивость, Сборник, посвященный 75-летию действительного члена АН УССР—Е. О. Патона, изд. АН УССР, 1946.
3 Продольное услляе ферменного стержня S мы считаем положительным в Слу
чае растяжения, а для рамного стержня N—в случае сжатия.
29
57
1
I
I
J
58
сдаточным приближением выражены так:
М М AM; S S AS; l l Дл;
р р Др; ф ф4.Дф,
ifae:
AM cxMl с2Мп csMm.;
Д5 с151 c2S11 CgiSm ;
Ah CjJ j- -j Д Ctf1 C2cp1t с8срш.;
Дф с11 С3ФШ Здесь Ml , М11,., Sl, S11,., X1, X11, ср , срп, ф1, фп,.—изгибающие моменты, продольные усилия, удлинения стержней, углы поворота поперечных сечений и углы поворота стержней, соответствующие единичным состояниям некоторых нагрузок сх— 1, с2 1,. и рассчитанные по недеформированной схеме системы. Характер нагрузок с19 с29 с3,.,
надо выбирать так, чтобы возможные формы деформации при потере устойчивости комбинированной системы можно было с достаточной для практики степенью точности получить как линейные комбинации деформаций от воздействия этих нагрузок с19 с2, с8,. фИГв Давая последовательно виртуальным
величинам М, р и ф, входящим в формулу 56, значения М1 , ср1 и ф1 , потом Ми9 fn и ф11, потом Мш, ср111, фШ и Тв дв получаем каноническую систему уравнений для определения известных с19 с2, с3,.
Решение этих уравнений и составление критерия потери устойчивости для комбинированных систем производится совершенно аналогично тому, как было описано нами ранее при расчете шарнирно-стержневых ферм
производится, как при обычных расчетах проч-
AMMds
EJ
ности рамных систем. Для вычисления интегралов fNyvds в случае, когда N const по длине стержня 1аь, можно пользоваться следующей формулой;
i
j рр ds фф
о
з
8МаМа 7 МаМь МьМа тмь
360ЕУ2
2 1 yn7-3 M6l 7-3
п—1, 2, 3,.
J ql Ма Мь. 59
Эта формула фиг. 11 соответствует загрузке стержня 1оЪ моментами Ма и МЪ9 равномерно распределенной нагрузкой q и сосредоточенными грузами Р19 Р29.
Число неизвестных параметров с19 с2,. определяется теми формами возможной деформации системы, которые мы желаем учесть при расчете ее устойчивости. Иногда в единичных состояниях сг 1, с2 1,. рационально прикладывать обобщенные силы, представляющие группы нагрузок.
Вообще говоря, обычно бывает достаточным для инженерной практики ограничиться двумя, тремя надлежаще выбранными параметрами с19 с2У с3.
Аналогичный изложенному здесь энергетический метод был нами практически применен при расчете устойчивости конструкции одного из вариантов стального каркаса Дворца Советов СССР1.
1 Исследование устойчивости пространственного каркаса Дворца Советов СССР,
Изд. АН УССР, Киев, 1938 г.
30
ГЛАВА 111
СЖАТО-ИЗОГНУТЫЙ СТЕРЖЕНЬ
1, О внешних воздействиях, определяющих деформацию балки
С развитием теории балок вводится ъ рассмотрение все большее числовоздействий или факторов, определяющих их деформации. Общепринята рассматривать воздействие на балку внешних сосредоточенных сил Р и распределенной нагрузки q фиг.
12.
Часто также рассматривают влияние внешних сосредоточенных моментов; во избежание путаницы с обозначением изгибающего момента М будем их обозначать М, отмечая индексом а, что момент приложен в сечении х а, а звездочкой , что момент этот является внешним сосредоточенным1.
При составлении формул для балок обозначениями Рид мы будем пользоваться, главным образом, для поперечных нагрузок. Продольные сосредоточенные нагрузки мы будем обозначать символом N в отличие от продольной силы N, а распределенные продольные нагрузки, вернее их интенсивность, буквою п.
Иногда рассматривают также Енешнюю распределенную моментную нагрузку интенсивностьюJm. С такой нагрузкой нам приходится, например,
встречаться в случае приложения внешней распределенной продольной нагрузки п с эксцентриситетом с. Такая нагрузка приводится к сумме двух распределенных нагрузок: продольной осевой ть и моментной т пс.
Кроме того, можно рассматривать как внешние воздействия на стержень также и первоначальные малые деформации, если они по величине своей такого же порядка, как и упругие деформации. К таким первоначальным деформациям можно отнести неточности, вызываемые несовершенством изготовления, искривление от неравномерного нагрева, наконец, специальное искривление прямолинейного стержня для создания строительного подъема.
Эти первоначальные деформации могут быть: 1 в виде сосредоточенных сдвигов 8 смежных сечений фиг. 13 без изменения угла между сечениями; 2 в виде сосредоточенных углов б перелома оси стержня;
3 в виде распределенной деформации сдвига интенсивностью у, при которой
1 Обобщением понятия нагрузка, особенно в связи с теорией инфлюен, ванимался Я. М. Риппенбейн. См., например, его статью в Трудах МИИТ, вып. 3, 1927 г.
Проф.А- А. Гвоздев также в связи с теорией i нфлюент рассматривает нагрузку в виде перелома оси, движущегося вдоль оси балки. См. книгу А А. Гвоздева Общий метод расчета статическл неопределимых систем, 1927 г., стр. 19.
Проф. А. А. Уманский в своем Специальном курсе строительной механики, ч. 1. 1935 г. и ч. 2, 1940 г. излагает теорию балок на основе подробного систематического изучения влияния сосредоточенных и распределенных, силовых и деформационных факторов.
Различные достижения, связанные с обобщением понятия нагрузок, освещены в Курсе строительной механики стержневых систем ч. 1, 1938 г. и ч. 2, 1940 г. проф. И. М. Рабиновича.
Фиг. 12.
31
искривление оси стержня достигается без взаимного поворота смежных сечений; 4 в виде распределенной угловой деформации первоначальной кривизны интенсивностью х. Для криволинейных балок особенно при построении инфлюент могут иметь также значение: 5 сосредоточенное поступательное взаимное продольное расхождение Д двух смежных сечений стержня и 6 распределенная продольная деформация относительное удлинение г.
Правило знаков для всех этих нагрузочных и деформационных факторов примем согласно фиг. 12 и 13, на которых они показаны положительными. Размерность этих факторов в технической системе единиц будет: Р — кг q — кгм; il-— кгм; т — кг ммкг; 8 — м; у и 0 — величины отвлеченные;
у. — погонный угол —; А — м; г — величина отвлеченная.
ЛЬ
В обычных расчетах прочности стержней при определении внутренних усилий в поперечном сечении стержня пренебрегают влиянием деформации стержня. При этом про-
устойчивой прочности следует учитывать деформации стержня. Нам представляется целесообразным в связи с этим внести некоторую диференциацию в терминологию и обозначения. Истинную продольную силу фиг. 14 поперечного сечения деформированного стержня, направленную по касательной к изогнутой оси стержня, будем обозначать N и называть ее либо сжимающей, либо растягивающей силой в зависимости от ее направления. Истинную поперечную силу, направленную по нормали к изогнутой оси,
будем обозначать Q и называть перерезывающей силой. Истинный изгибающий момент, взятый относительно центра смещенного сечения, будем обозначать, как обычно Мх и называть его, как обычно, изгибающим
моментом. Момент Мх взятый относительно точки на первоначальной прямолинейной оси стержня, удобнее будет не называть изгибающим моментом. Его можно было бы назвать либо моментом полеречных н а г р уз о к, либо основным моментом внешних сил последнее название будет более общим, одинаково пригодным и для прямолинейных и для криволинейных стержней. Термины же продольная и поперечная сила и обозначения Nx и Qx будем применять по отношению к составляющим равнодействующей Rx сил сечения, направленным соответственно вышесказанному вдоль и поперек первоначальной оси стержня.
Между силами Nx и N образуется фиг. 14 такой же угол, как и между силами Qx и Qx, равный углу поворота сечения фх. Вообще говоря:
2. Внутренние усилия деформированного стержня
неинои оси стержня, поперечная сила Qx — перпендикулярна к этой оси, а изгибающий момент
будем его обозначать Mix берут относительно точки встречи поперечного сечения с этой первоначальной прямолинейной осью. Для определения действительных напряжений и деформаций в задачах
дольная сила Nx направлена вдоль первоначальной прямоли-
— tc
Фиг. 14.
a
b
32
При решении задач теории сооружений приходится рассматривать лишь малые деформации, поэтому полагаем:
dx л dv dv , ч
dT1 и ds di v- с
Таким образом, истинные поперечная и продольная силы равны:
Qsx х Nj; 1
Nsx Nx-Qxvx. 2
В задачах устойчивости линия давления направлена по оси стержня и Qx 0, поэтому в этом случае:
— Nxvx и NSXNX. 3
При переходе от значения Мх к истинному значению изгибающего момента Мх учтем как поперечные перемещения v сечений стержня, так и продольные, вызванные поворотами и обжатием элементов стержня.
Рассмотрим зависимость между приращениями этих моментов dM и dMx на элементе стержня длиною ds. Приращение поперечного перемещения для этого элемента ds будет dv, приращение продольного перемещения, зависящее от поворота элемента, будет ds — dx, а зависящее от обжатия
Nxds
элемента будет.
Таким образом
Ns dx
dMx—dHTx Nxdv — Qxds — dx — Qx F. d
Учитывая, что в задачах теории сооружений т. е. при малых деформациях ds — dx, можно представить:
ds-dx А т2 в
на длине от начального сечения стержня до данного его сечения получаем:
XX X
rs
Мх М N0V0Nxdx- QxXdx- 5 Qxgp dx. f
0 0 0
Последними двумя членами этого выражения вследствие малости
соответствующих деформаций, рассматриваемых в задачах теории сооружения, можно пренебречь.
Тогда:
X
Мх — Мх N0v0 Nxvxdx. 4
о
Если продольная сила по длине стержня постоянна, то:
Mx Mx Nvx. 4
3. Диференциальные условия равновесия
Рассмотрим фиг. 15 условия равновесия элемента dx деформированного стержня при действии на него распределенных нагрузок: поперечных—qx, продольных — пх, моментных — тх. Из условия равновесия проекций сил на оси координат получаем:
Nx nxdx NX dNx; Qx — qxdx QX dQx,
3 Прочность и устойчивость стержневых систем зз
откуда
nx Nx; 5
Qx Qx 6
Из условия равновесия моментов вокруг центра правого сечения:
Mx QxdxNxdv тх dx — qxdxd nx dx Mx dMx;
отбросив бесконечно малые высших порядков, получаем:
Mx — Qx-x-Nxvx 7
Аналогично, пренебрегая деформациями стержня, находим:
MQx mx. 8
Уравнению 7, использовав зависимость 1, можно придать вид;
Mx Qx mx. 9
При отсутствии распределенной
моментной нагрузки уравнения 8 и 9 приобретают вид формулы Журавского:
NzdNx
Фиг. 15.
MVQx
II
8
9
MxQi.
4. Зависимость между усилиями и деформациями. Учет деформаций сдвига
В соответствии с элементарной теорией сопротивления материалов
будем считать, что деформация элемента ds стержня состоит из трех
V
частей: 1 продольной: zdx — jdx, 2 поперечной деформации сдвига:
— dx и 3 угловой:
dpF — v.dx — dx
Y dx
Согласно элементарной теории деформации поперечного сдвига не нарушают параллельности поперечных сечений стержня, поэтому взаимный угол поворота двух поперечных сечений стержня определяется только деформациями изгиба Деформации поперечного сдвига создают разницу между углом поворота оси и углом поворота поперечного сечения срг
равную углу поперечного сдвига:
Ю
V г-
Здесь Fx —приведенная площадь, равная Fx —F1, где к—коэфициент, учитывающий неравномерность распределения по сечению касательных напряжений при изгибе. Его обычно принимают равным:
см., например, проф. И. М. Рабинович, Курс строительной механики стержневых систем, ч. 2, 13, Стройиздат, 1940.
34
Угол поворота сечения р:
X X
4Z 4d4fs4-mdx И
О О
В связи с этим будем различать: полные прогибы оси стержня:
X
v v5dx о
прогибы, зависящие от жесткости изгиба:
х
Ч iVbо 5 йх а
и
и прогибы, зависящие от жесткости сдвига:
х
Kt05 чах
о
Ясно, что
v — vbvt 13
В случае наличия первоначальных деформаций: сосредоточенных
деформаций сдвига 8, сосредоточенных угловых деформаций б, распределенных деформаций сдвига у и распределенных угловых деформаций первоначальной кривизны х надо прежде всего внести поправку в формулу И для угла поворота поперечного сечения:
X X
Fo 5 шАх 2 е— 5 xdx О ах 0
C2J X
и в выражение угла сдвига у-
_
S
Yx Ф
Теперь на основании выражения 12 при зависимостях 10 и 11 получим для полного прогиба v следующее выражение:
X X
v vt x- dz jjfrdx
0 0 о
х х
2 а 2 р 5х 0
ах ах 0 0 0
Для точного решения задач устойчивой прочности уравнение 14 не пригодно, так как подинтегральные выражения его правой части М и зависят от неизвестной величины прогибов и.
Поэтому продиференцируем его два раза:
йж—м- 15
Ясно, что это диференциальное уравнение кривой прогибов может быть получено непосредственно, на основе суммирования деформаций от разных причин, без рассмотрения уравнения 14. Если продольная сила по длине стержня постоянна, то, подставив 4 и 1 в 15, получим:
16 г‘ 35
Если стержень призматический, то и Fx — величины по длине стержня постоянные, и тогда, принимая во внимание 6, получаем:
16
Если пренебречь деформациями поперечного сдвига, то уравнение 16 принимает вид:
vejv 16
Сличая уравнения 16 и 16, приходим к выводу, что с математической стороны нет принципиального различия между решением этих двух уравнений. Действительно, введем обозначения:
i l— GFl
Ml М q, d
ж
1 1-
е
1 —
GFt
О
N
GFX
Тогда, разделив уравнение 16 на множитель в скобке при v, получим:
vf,tv,-mt-М 16а
— уравнение, совершенно аналогичное 16.
Итак, элементарный учет деформаций поперечного сдвига приводит при определении прогибов v к замене диференциального уравнения 16, не учитывающего этих деформаций, уравнением 16а, отличающимся от него в основном: 1 величиной жесткости изгиба EJX — вместо EJ и 2 некоторой дополнительной распределенной нагрузкой, интенсивEJ
ностыо —ртдг fx Откладывая до 21 более подробное исследование вопроса,
Г j
мы сейчас уже можем сказать, что учет влияния деформаций поперечного сдвига может быть произведен элементарно при наличии развернутого решения диференциального уравнения 16, не учитывающего деформаций сдвиг а.
Поэтому мы пока будем пренебрегать деформациями сдвига; более того, составим сначала развернутое решение для случая действия только сосредоточенных нагрузок и сосредоточенных первоначальных деформаций. Наличие распределенных воздействий легко будет учесть, как мы это увидим дальше, путем интегрирования решений для соответствующих сосредоточенных воздействий. Диференциальные уравнения 15 и 16 изогнутой оси в этом случае можно записать:
Для стержней постоянного сечения в иных случаях вместо уравнения 17 удобно бывает также пользоваться уравнениями:
I о ЖГ -ЩТ ит-д-
или уравнениями:
I М Р -gj-T- -
M -jlTM-q,
Q
EJ
N
Q‘ EjQ‘ —я и т. д.
17
17
18
18
18
Последние два уравнения получаются путем последовательного диференцирования уравнения 18 и замены
М
-.жИ м.
5. Решение диференциального уравнения прогибов
Проинтегрируем диференциальное уравнение 17 сжато-изогнутого призматического стержня. Продольная сила N постоянна по длине стержня. В сечении на расстоянии х а от левого конца стержня действуют фиг. 16 сосредоточенные сила Ра и внешний момент Мау а также сосредоточенная деформация сдвига 8а и сосредоточенная угловая деформация 0а. Обозначим прогибы для левого участка балки при а буквой vl9 а для правого при а буквой v2. Тогда пограничные условия между этими двумя участками при х а будут:
tf ia 8z Уа
Wa— 6a a-
a
а
b
Момент поперечных нагрузок на левом участке выразится уравнением:
М Ml Qax,
а на правом:
м Ml Ма — Ра х — а.
Диференциальное уравнение кривой прогибов 17 для левого участка примет вид:
vi gj vi ”” ej
а для правого:
h-lK Q Ml-PAx-a. d
, N
— У,
EJ
EJ
Введем обозначение
N_
EJ
L 7
19
37
или:
L
EJ N
Эта вспомогательная величина L имеет размерность длины.
Нетрудно убедиться непосредственной подстановкой, что уравнение с имеет следующее решение:
Постоянные интегрирования Сг и С2 находятся из условий закрепления на концах стержня. Об их определении будем говорить в следующем параграфе.
Интегрируя уравнение d для правого участка стржня, применим прием, аналогичный приему Клебша для случая поперечного изгиба балки. Решение уравнения d составим, дописав к решению е уравнения с такие члены, которые, удовлетворяя уравнению d, в то же время удовлетворяют также и условиям а и Ь сопряжения левого и правого участков стержня.
Итак, будем искать для правого участка решение в форме:
Заметив, что, таким образом, v2 — vt Av, вычтем из диференциального уравнения d уравнение с и получим:
т. е. уравнение, вполне аналогичное уравнению с. Влияние величины Av распространяется от сечения х а, а не от начального, как это было для величины ь в уравнении с Проинтегрировав j, получаем для Av решение, аналогичное решению для vx:
Сравнивая выражения т с пограничными условиями а и Ь, находим:
Перегруппировав члены, получим общее решение для левого и правого участков в такой форме:
е
— -j- Аи
i
Av”
Jbv-JMa-Pax-a,
j
00
а для разности производных:
1
Подставляя в к и х а, получаем:
т
п
Итак:
v Cj cos С2 sin — Л Ml Qox
20
38
или, при замене по формуле М М0 — NvQf в таком виде:
X 1
I Uq 4- 01 cos у 4 С о sm
Здесь:
kv
v и0 4- Ccos — С2 sin М0 Qo 20 ГЛ ж —а Гл ж— а Ша ГА ж —аЛ
80 cos-g L6asin— jl-cos— J
¥т-8т , 2i
В дальнейшем для сокращения записи жесткость изгиба будем обозначать буквой В:
В EJ 22
Используя фЬрмулу 19 и заменяя в формулах 20 и 21
JL — 4i
N В
получаем:
V и0 Сх cos Сг sin М0 Qx Ди 20
и
Г я — а Гл. х — а MIL2 Л х — а
Ди joa cos -g L6a sin 1— 1 — cos —J
. Pa3 fx—a. ж — a I смv
т.ти_г. 21
Очевидно, что если на стержне будет не одно, а несколько нагруженных сечений x alf а2, аъ, то каждый раз при переходе от участка левее такого сечения ап к участку правее, надо будет дописывать к выражению прогиба v левее сечения новую добавку по типу 21, удовле
творяющую уравнению вида j, в котором вместо а будет стоять соответствующее ап, и новым пограничным условиям по типу а и Ь.
Итак, в случае действия ряда сосредоточенных воздействий в различных сечениях стержня формула 20 будет справедлива для всей длины стержня, если Av дать форму:
2 eacos — L 2 SaSinr —
L
CL Я1 j Cloy t Ci Cl , Cloy L2 В
Ci — CJL j CLo 9 1 9 Clo 2 Ml-cos g 2 aVsinir 23
которой суммирование распространяется на все воздействия, приложенные левее сечения х, т. е. для всех а19 а2, , меньших х.
Воспользуемся обозначением отрицательной производной:
X X
Фх-П 5 5 фх dxn. 24
Если принять, что
Фх cos ,
ЗУ
то
Фх
фх-2
Фх3
Фх4
ф-5
Фг зт 2 , ф;и2 i-cos ,
Ъш Л-Ат
g co.,
vs-fl rsinr
25
Причем при х О
Ф 1
ф0-гф0-ф0-1п
о.
26
Приняв эти обозначения, формулу 23 можно переписать в следующем виде:
2 К Ф-а — 2 Ф-а
CL в flj do t
1
О— Cl, 02
-j- 2 2
23
CL—Я 2 9
в которой
2 3 Х-
Формулы 20 и 23 или 23 выражают собой принцип независимости действия поперечных нагрузок и первоначальных деформаций для случая продольно-поперечного изгиба стержня.
6. Распределенные воздействия
Пусть стержень кроме сосредоточенных воздействий загружен также и распределенными: распределенным поперечным сдвигом у, распределенной угловой деформацией первоначальной кривизной у., распределенной моментной нагрузкой тх и распределенной силовой нагрузкрй qx. В этом случае к выражению 23 надо добавить еще следующее:
X X
л X
— W S Ми ф- du F 5 q Ф da
О ft
27
Подробно покажем, как развернуть какой-нибудь из интегралов формулы 27, например, последний. Пусть нагрузка qx до сечения х с равна нулю, а начиная от этого сечения, может быть представлена рядом Тейлора:
c f ж— С — С2 х —С3.
28
Тогда, пользуясь интегрированием по частям и имея в виду 26, получаем:
XX X
Яи Ф- du дц Фх1ц du Яи ЙФ-Ц — Яи ф-и
Ос с
и аг
и—с
40
X ФСЬ ui-uU. сФ-Т яс Фх-с Jcx-c Яс Фх-с Аналогично, пользуясь разложениями:
fx fcx-c х-су. ; 1
J р
т,
I
l Ti х-с х-су
тс х-с х-сГ.; j
получаем развернутую формулу для Дих вместо формулы 27:
г
А. 2 уФ-с fc Ф”с fcФх-с1 С Cj С2
— 2 KI-C XC ФЛ1 с Фх-
— g- 2 гс Фх-с1 тсФх-У тпсФх-с -
СС1, С2
g- 2 С Фх-С Яс Ф-С 9с Ф— с 4. 29
C—Cij C21 Знаки 2 в этй формуле даны для различных распределенных воздействий, начинающихся с разных сечений сг с2 с3. х и простирающихся за сечение х, для которого определяем vx.
Если какое-нибудь распределенное воздействие, начинаясь в сечении elf заканчивается в сечении с2, причем сх
с2 х, то такое воздействие надо считать за два: одно положительное, начинающееся в сечении сг и простирающееся
за интересующее нас сечение х, и другое отрицательное, начинающееся в сечении с2 и также простирающееся за сечение х.
Пусть, например, надо найти влияние равномерно-распределенной нагрузки q фиг. 17.
Для этого случая пишем:
О
1 —с, X Фиг. 17.
Aqvx — jf Ф-са Фж—сг
30
7. Развернутое уравнение эпюр перемещений и усилий
для сжато изогнутого стержня
Полученное нами решение для прогиба v, представленное совокупностью формул 20 и 23, соответствует диференциальному уравнению
17, а с присоединением к решению влияния распределенных факторов
по формуле 29 — диференциальному уравнению:
-j- Y0; 31
Уравнение рх углов поворота легко получить, диференцируя уравнение изогнутой оси:
Р Vi. 31
41
32
33
34
35
Уравнение эпюры моментов получим согласно формуле 31:
мх — В vx X — Y. 31
Уравнение эпюры перерезывающих сил Qx получим по формуле 9:
Ql Mx-mx. 31
Приведем эти уравнения:
vx v0 C1cos- Сг sin — Мл 0я До;
х - —Cisin- -f С2 cos j- J
Mx n Сг cos J- C2 sin ДДx;
Ql X- — С г sin — -f C. cos - д.
Добавки ДУд., px, АМхи AQsx, учитывающие влияние пролетных факторов нагрузок и первоначальных деформаций в пролете стержня, определяются следующими формулами:
Д А; 2х 36
где Доопределяется по формуле 23 или 23 a Д—-по формуле 29.
Затем, аналогично формулам 31 — 31:
Дсрх Дух; 36
Шх-В Асху - fj; 36
Щ8х ХШх-тх. _ 36
Понятно, что при x 0:Av0 0; Др0 0; АМ0 0; Д 00.
Для примера запишем выражения этих добавок от влияния пролетных поперечных нагрузок Р и q:
1 лц-Ш ,
Р,рх —
2 РаФха
CL dj у CL 2 у В
ССС2 j I
лр,ях
i 2 сФ™ сФх- дЖ-с.;
С Clj С2 j р,Мх — —
X Q, - 2 I сф ”ф-Ж - ;
С С1,2 P,oQx 2 -РаФх-а
С1 — d j 12 9 — 2 сфх -с cx ”с ОсФхЦ1.
37
С— Cl,Со
J
Поперечная сила Qx, нормальная к первоначальной прямол шейной оси стержня, определяется формулой:
Qx Qo AQx. 35
Тот же результат можно получить из формулы 1:
Qx Q N Фх
после подстановки в нее значений 35 и 33, учитывая, что
ДО - Мп Д Q - лгх Дх.
42
Рассмотрим еще один пример. Пусть стержень по всей своей длине подвергается действию неравномерного нагрева: температура сверху
стержня равна t0, снизу tu. Такое воздействие температуры эквивалентно наличию первоначальной распределенной угловой деформации
О о
А h
где а,— линейный коэфициент температурного расширения, к — высота сечения стержня.
В этом случае, согласно формуле 29:
— 0фхП
или на основании второй из формул 25:
- vL l - cos -J. - V l - cos - J.
После этого по формулам 36 и 36 легко получим:
AtMx B Af В4cos 1.
S. Граничные параметры. Определение постоянных интегрирования Сх и С2
Постоянные интегрирования Сг и С2 могут быть различным образом определены через граничные параметры: М0, Мг, ср0, pz, Q0 и угол поворота стержня или просто , определяемый формулой:
VJP 38
Разность прогибов vl — v0, так называемый взаимный сдвиг концов стержня еще обозначается:
01 vi — ио 39
Для определения Сг л С2, вообще говоря, достаточно двух независимых уравнений. Рассмотрим разные способы их определения. Для этого достаточно в формулах 32, 33 и 34 приравнять абсциссу х сначала 0, а потом Z, где I — длина стержня. При этом будем помнить, что Avx, Дсрх, АМх, отражающие собой влияние пролетных факторов, при х 0 обращаются в нули. Кроме того, примем обозначение:
V -i L
VТГ 4
равносильное формуле:
N —
г- I2
напоминающей формулу Эйлера.
N — 41
В число граничных параметров нецелесообразно вводить кроме Q0 также и Qi, так как поперечные силы на концах стержня связаны столь простой зависимостью:
Qz QoAQi, 35
где AQi — сумма всех пролетных поперечных нагрузок стержня, что не имеет смысла считать Q0 и. Qi за два различных параметра.
Структура формулы 32, в которую входят не две величины vx и v0, а по существу только их разность vx — v0, также делает целесообразным представление прогибов концов стержня vt и v0 в виде одного граничного параметра, именно их разностью по формуле 39.
43
В результате подстановки ж 0 и х 1 в уравнения 32 —34 получим следующие шесть равенств:
Уравнение 43 является своеобразной формой условия равновесия моментов всех сил, приложенных к стержню. Его можно записать еще в таком виде:
Таким образом, равенства 4 и 6 взаимно преобразуются одно в другое при использовании условия равновесия внешних сил. Они могут быть записаны;
В зависимости от условий задачи мы можем при определении Сг и С,
Отметим, что шесть граничных параметров М0, Мг, ср0, pz, Q0 и ф связаны между собой при условии учета упругих свойств и нагрузок стержня тремя зависимостями: 1 условием 44 равновесия моментов всех сил приложенных к стержню; 2 и 3 — условияхми, определяющими углы поворота концов стержня ср0 и р через его упругие свойства в зависимости от его нагрузок. Такие условия можно, например, получить, под-
п Мо
w- N
Четвертое и шестое при их сравнении дают:
М - АМг М QJt N У, - Ди, - v0.
42
43
г Mt - А Мг - Ма -NQ-Щ,
44
где
45
Сх cos v Сг sin v -i- Mt — ДДj
46
или
С, cos v С2 sin v.¥ Q0l -f — Дф.
46
Равенство второе дает:
47,
Равенство пятое может быть записано:
48
использовать любые два из вышеприведенных уравнений 42, 46 или.
46, 47 и 48.
44
ставив выражения Ct и Сг по 42 и 47 в формулы 46 и 48:
cos -ir L. J- Bin 4 i Mi - Л 49
Упругие свойства стержня в этих формулах отображены величиною L:
Понятно, что уравнениям 49 и 50 можно придать и другой вид, исключая из них при помощи условия равновесия 44 одну из величин М0, Mi и вводя новый фактор — угол поворота стержня ф.
Итак, условия упругости стержня 49 и 50 и условие 44 равновесия моментов сил, к нему приложенных, дают три зависимости между шестью его граничными параметрами.
Эти параметры могут быть подразделены на три взаимно-сопряженные пары параметров: М0 и р0, Мг и pz, Q0 и ф. Произведения
Л0р0, Mfti и 0ф дают работу обобщенных сил М0, Mit Q0 на соответствующих им обобщенных перемещениях ср0, cpz, ф.
Из шести параметров стержня три могут быть названы активными и три пассивными. Это значит, что для постановки задачи о расчете сжато-изогнутого стержня нужно кроме его поперечных нагрузок и продольной силы N знать также любые три из шести его граничных параметров. Число различных распределений шести параметров натри активных и три пассивных весьма велико, оно равно числу сочетаний из
6 элементов по 3, а именно: Г 20. Но наиболее естественно
s у 1-23
принять такие симметричные относительно концов 0 и I стержня распределения, при которых один из параметров взаимно сопряженных пар считался бы активным, а другой пассивным. Таких распределений всего четыре:
Как мы увидим позже см. 16, этим четырем распределениям соответствуют четыре основных метода расчета устойчивости и устойчивой прочности плоских рам.
Отметим также, что параметры левого конца стержня Д0, Q0 и срв носят название начальных параметров. Параметры Мх, ср и ф можно было бы назвать конечным и.
В качестве простейшей иллюстрации к вышесказанному приведем окончательные формулы для эпюр vx, срж, Мх и Qx для случая, когда постоянные интегрирования Сг и С2 определяются см. 42 и 47 из условий в начальном сечении стержня:
19
активные I М0, Мь Q М0, Мг, Ь 0. 4 о ь Qa
пассивные р0, г, ф 0, Q0 М, Mi, Q0 I М, Мг, Ф
9. Формулы метода начальных параметров
45
При таких значениях С1 и С2 формулы 32 —35 приобретают вид формул метода начальных параметров1:
о ,яп J — l — cos j — — sin Arx, 32,.
X ocosZ-r sin-jr - 1 - cos J Afx; 33
тcsin z Mcos т sin г 34
Ql N0 cos - — sin cos Д. 35
V
Этим формулам можно Придать еще другой вид, если исключить из них всюду L, N и х, пользуясь следующими обозначениями:
x R, 51
L 7 40
iV f. 41
Величина S называется относительной абсциссой; значению
я соответствует значение 1
При таких обозначениях формулы 32 — 35 приобретают вид:
1 М J2 П 73
X v0 - 0 sin V — 1 — cos V — v — sin v5 Д; 32
x 0 cos v — sin v — 1 — cos v Дсрж; 33
Mx p0 sin v M0 cos v sin v -f- ДМЯ; 34
7 Pо cos v — v-y- sin v 0 cos v AQx. 35
Используя для определения С и С2 другие комбинации двух уравнений из 42, 46, 46, 47 и 48, можно получить ряд иных выражений для vx, ох Мх и Qx.
10. Растянуто-изогнутый стержень
Решение задачи о растянуто-изогнутом стержне совершенно аналогично решению для сжато-изогнутого стержня. Все различие ограничивается переменой направления знака продольной силы iV. Для сжато-изогнутого стержня мы исходим из диференциального уравнения 17:
f N М
v А V В В
1 Методу начальных параметров, применительно к задачам продольно-поперечного изгиба, посвящены статьи:
Проф. Н. К. С н и тко Расчет сжато-изогнутых стержней при применении общего уравнения упругой линии. Журнал Проект и стандарт, 1938 г., 1.
Доц. В. М. Макушин Теория упругой линии при продольно-поперечном изгибе, выпуск 563 Трудов Московского Механ. Машиностроительного Института им- Баумана, 193 Э г.
Инж. В. А. Киселев Уравнение упругой линии продольно-поперечного изгиба Научные записки московского Гидромелиоративного института, т. VII, вып. 14, 1939 г
Если в формуле 32 поставить согласно 4
M0 Mi Nv0,
то получим:
х х Mo f А QoL f х. a:V ,
vx v0 cos — L sin —-_f :l-cos — J — — —sin - J Avx.
46
Для растянуто-изогнутого стержня фиг. 18 вместо этого уравнения надо взять:
V
т м
в v В 9
52
где Т — продольное растягивающее усилие.
Все предыдущие выводы и формулы, полученные нами для сжатоизогнутого стержня, сохраняются и для растянуто-изогнутого, надо будет их только освободить от выражений, связанных с мнимой единицей. Аналогично обозначению 40:
введем обозначение:
Iх
N1
В
- Т Ясно, что эти величины связаны зависимостью:
v —р.
или
54
54
Тригонометрические функции величины v превращаются в гиперболические функции величины р.:
cosv chp.; sin v i sh -; tgv ithji.
55
Очевидно, что и входящие в формулы 32 — 35 величины соответственно преобразуются:
СС X
cos cos vS ch sin — sin v i sh
JLi JLs
55
Точно так же преобразуются. величццы,. входящие в формулы для Avx, Ах, Шх и Д:
рх — а.
х — a v х — а 1
COS — COS СП
sin
I jx ж — а
I
Для примера приведем ддя растянуто-изогнутого стержня формулы метода начальных параметров:
1 Напомним разложение в ряды этих величин:
.3
2 1 4
,2 4
4
6
Р1
chfl-т бГ
Кроме того:
sinv v_____. ehtti-j-f -.
sh х
tg v
sin V -
COS V
th x —
ch i e
47
J 0 sb tS 1 — ch ; prgf fS — sh i Д vx
ch sh iS -grl — sh j4 Дх;
A — pe sh Д0 ch - sh AMX;
l Г
QI тг o k h 7 sb o QX
56
57
58
59
Правильность произведенной замены величины v через jx в этих формулах нетрудно проверить непосредственным диференцированием, помня:
или
ch хх sh х sh хх ch х
ch р1х ch j sh i; sh jt -y ch fi;.
Определ ение пролетных членов AvXP А рх, АМХ и AQ может быть произведено по формулам 23, 29, 37, но надо иметь в виду, что формулы 25 для растянуто-изогнутого стержня примут вид:
Ф.
Ф
-I
Фас
-И
Ф
-III
Фх1У
icv
Chf;
Sh ;
к‘т
chT T
0
г у
J_. —.
2 i 1 i ржЛ
Tl Г у
60
J
11. Случай поперечного изгиба iV 0
Вышеприведенные формулы пригодны также и для случая поперечного изгиба, т. е. для значения v i 0. Раскрытие получающихся при этом неопределенностей удобнее всего произвести, используя разложения тригонометрических или гиперболических функций в ряды см. сноску к 10.
В результате раскрытия неопределенностей получаем выражения:
оvo9ох— я2—х
9х о — Ъ Х—-Шх2 АР;
МХ М0 Qtx АМХ;
Qx QoAQ
известные из курсов сопротивления материалов.
1 См., например, проф. М. М. Ф я л о н е н к о-Б о р о д и ч и др. Сопротивление материалов, изд. 2-е, стр. 312, Стройиздат, 1940 г.
48
12 Принцип независимости действия поперечных факторов на сзкато-изогнутый стержень
Формулы метода начальных параметров 32 —35, а также формулй. 23 и 29 полностью подтверждают справедливость для сжато-изогнутого призматического стержня принципа наложения независимости действия поперечных нагрузочных il0, Q0, Ра, Ма, т9 q и деформационных у0, р0, а, 6а, у0, х воздействий при условии сохранения без изменения величины продольного усилия.
Этот принцип останется справедливым независимо от того, будет ли сжатый стержень, изгибающийся в плоскости, иметь постоянное или переменное по длине поперечное сечение, будет ли продольное усилие по длине стержня постоянным или переменным, нужно только, чтобы при наложении нагрузочных и деформационных воздействий факторов отдельные слагаемые определялись каждый раз при одной и той же, остающейся неизменной эпюре продольных усилий Nx. Иначе говоря, принцип независимости действия для различных факторов справедлив, если М, определяемый при совместном действии этих факторов, равен сумме М, соответствующих действию отдельных факторов.
Это можно показать совершенно независимо от вышеприведенного вывода формул метода начальных параметров. Диференциалыюе уравнение изгиба для стержня переменного сечения при переменном по длине значении продольной силы можно получить, подставив в уравнение
EJx Mx-0 61
вместо Мх его значение по формуле 4 отсчитывая прогибы так, чтоб . 0:
X
Mx MlNsdx.
О
Таким образом:
X
EJjf -f Njodx Мх 0. 62
О
Пусть для стержня при разных силовых и деформационных воздействиях, но при одних и тех же граничных условиях и одной и той же эпюре продольного усилия Nx известны значения прогибов v и моментов М: прогибы vx и моменты М, соответствующие первому воздействию,
прогибы v2 и моменты М, соответствующие второму воздействию, и т. д.
Для первого воздействия будет справедливо уравнение:
X
EJjo NTvdx f М 0; а
О
для второго:
х
EJxV2 Ь - М — 0; Ь
о
для третьего:
X
FJА Nxvadx Мг — 0. с
U
4 Прочность и устойчивость стержневых систем
49
При одновременном действии всех трех воздействий:
W МиЩЩЧ-Щ d
и
X
ВД. Ndx Ml -f Ш м 0. е
О
vG5io5k4Ib fa, b и с, Получим:
X
EJX vx -f- v2 vz rf iVx vL -f- v2 4- v.9dx -f- M -f- Л - jtif 0. f
0
Из сравнения e с f находим:
12 3 1 2 Ь 3
а это и требовалось доказать.
‘В заключение отметим, что принцип наложения действия поперечных факторов справедлив только для малых деформаций, при которых можно считать неизменными плечи поперечных факторов. Для больших поперечных деформаций, при которых заметно меняются плечи поперечных факторов, принцип наложения теряет свою силу.
13. Другие варианты вывода формул метода начальных параметров
Приведем в общих чертах еще три других варианта вывода формул метода начальных параметров, интересных с методической точки зрения. В предыдущем параграфе мы выяснили возможность применения принципа наложения для поперечных факторов при условии сохранения неизменными продольных факторов величины ародольной СиЛы. Поэтому мы можем рассмотреть сначала случай действия распределенных непрерывно по длине стержня внешних факторов, формулы же для действия сосредоточенных или прерывных распределенных факторов.получим потом на основе принципа наложения.
1-й вариант. Надо получить развернутое решение для стержня, загруженного непрерывно распределенными факторами, причем:
М Mq-tQqX— q0 - 63
Дйференциальное уравнение Изгиба Для этого стержйй:
BJv Nv -М. а
Если бы продольная сила JV 0, то при тех же значениях Ж0 дрошбы v нмелы й другие значения, которые обозначим через v. Слёдователыю:
BJv - Jf ; Ъ
ЕЖШ-ЯЛ. с
отсюда:
Используя обозначение 49
N _1 EJL1
ч1й6жем уравнение с записать в таком виде:
я 5 d
Величину v0 можно представить при помощи ряда Маклорена:
- М — - х -ту ж2 -у а;3 -ут х т
v gjr ГГ 0 ч 0 ЗГ 0 4 Коэфициенты при одинаковых степенях х в рядах 63 и 63 имеют постоянное отношение, равное —EJ—B.
Решение для неполного уравнения
.г: 0 е
60
элементарно:
v
X
v0 cos f- Lvt sin —
JLj Lj
o
Чтобы получить решение полного уравнения d к f, надо добавить частное решение V:
v — г0 cos -f- Lv0 sin — -f- F,
j
причем, очевидно, F надо подобрать так, чтобы при ж 0
Fo 0 и F0 0.
Решение для V в соответствии с h и 63 будем искать в следующем виде:
V trt vV9 Jvr4 F,.
Величины F2, F3, F4. должны удовлетворять следующим уравнениям:
1 Л
4. у 1
2Т Г2 - U
1
а;
Г д.1. F — _ L2 3 11 1
F 4- —- F — — F 4- — F — .L 5 31 J
g
h
i
b
Очевидно см. формулу 24:
V
Г3 K2 dxV ;
0
3C
0
Я
FC rAdx Vtni x;
ii
1
Из уравнений k следует, что F2 найдем, решив уравнение:
Vl Vt l.
Решение для него получим в следующей форме:
У г Сх cos С 2 sin- 4- L2.
JLj JLj
Произвольные постоянные Ct и С2 найдем из условий h при я 0:
У 20 cos 0 С2 sin О -Ь L2 О,
Fос —- у— С7 sin 0 -f у— О2 cos 0 — 0.
L L
Отсюда Сх — L2 и С2 0 и
F2X2 1 —cos. ш
Сравнивая ш с формулами 25, находим: 4
f2ф;и. 64
Затем, в соответствии с 1:
Га Ф-Ш; Г4 Ф-1У;.; Гп-Ф-П. 64
Итак, решение уравнения d при использовании формул g и i, получит вид:
t; г Фх г ФГ1 la Ф1т г; Фх-Ш v™ IV-f. ф. 65
4 51
или, после замены производных от v их выражениями согласно 63:
р0ФроФ1-ФГ11-гФшФ;1Уф jvjvi- 66
Пользуясь этим методом ипринципом наложения, легко можно написать все ранее приведенные в 5, 6, 7,. 11 формулы метода начальных параметров.
2-й вариант. Получим решение путем разложения в бесконечный степенной ряд1; загрузка стержня такая же, как и в первом варианте, для которой:
х
хг
хч
M M8 Q0a:-5 — - q0 — - gj f- -.
2
Нам нужно проинтегрировать уравнение1
4
63
В М М 0.
а
Обозначим
dry
dx2
Ь
где у—прогиб у, соответствующий эпюре М по формуле 63 при тех же граничных условиях и. отсутствии продольной силы iV 0. Кроме того, используем обозначения:
— А
В L2
х dy 1 dy у d2i 1 dtyy
L dx L dS L dx2 L2 ‘ dp L
В этих обозначениях уравнение а перепишется так:
У У У
Здесь у мы считаем величиной известной, действительно:
5 dy Ш
у dx N dx2 N
Уравнение е проинтегрируем при помощи строки Маклорена:
c
d
е
О
У
С2 С3 TV С
io уо т Уо 2J 2оГ
1
3, . 4Т-
67
Начальные параметры у0 и считаем известными, остальные же коэфициенты 2о У о 2oV этого ряда определим из уравнения е как функции от у0 и у0 и производных от у. Эти выражения получим, диференцируя уравнение е много раз, заменяя все время получающиеся производные у -уЛ-у
Таким образом найдем:
У о — Уо У о
иг
У о
Уо Уо
III
IV г , JV
Vt —Уо-Уо Vi
V , _v
У о —УоУо У о
2У1 - Уо У о У1У Уо
VI
Ю
— С2 2 S зГ
4 4 5
6
С
1 Здесь принято для краткости записи и во избежание путаницы для прогиба
обозначение у вместо г, так как выше было принято а здесь у
52
Умножив обе части выражений g на множители, стоящие справа от вертикальной черты, подставив результаты в 67 и отобрав подобные члены, получим:
Г С2 С4 С С8 1 ГС С3 С6 С7 1
У У 1_ 2 4 -6 81 J J4lT _ ‘ЗТ Ы 7Т - J
ИЙ-пГт-
jC
Заметив, что см. сноску в 10 скобка при у0 равна cos С — cos — , скобка при
х
равна sinCsin — , скобка npntJ равна 1— cos С 1 —cos — и т. д., мы в соответ-
L X-
ствии с формулами 25 можем записать:
У УоФх Уо Г 2о У Y ФГ1П 2оУ ФГ1УЧ-.-
Но:
у.-г.; Й. . Щ; УоиЪ
таким образом:
г г0 Фж Ф J1 v0 Ф J11 vq ФГш Ф-1У. 65
Дальше, как в первом варианте.
8-й вариант. В 12 мы доказали возможность применения принципа наложения для величины последнего свободного члена v диференциального уравнения:
2v v. а
1 Пусть сначала о 0, тогда
X
v v0 cos — -f Lvf0 sin r-. b
JLi Li
2 Теперь пусть v0 -0, v0 0, a v равно нулю для всех значений х, кроме бесконечно малого интервала между значениями xt — dt и Для всех значений х с хг
прогиб г 0; интервал dt считаем настолько малым, что v для этого интервала можно считать величиной постоянной. Поэтому к концу этого интервала при ж г:
v vdt, vtdt с
В соответствии с принципом независимости действия для всех значений х t
v vt cos Lv‘t sin d
J
Но согласно с vt — бесконечно малая высшего порядка по сравнению с v, пиэтому первым членом правой части 1 мы можем пренебречь
х — t
ttLsin——vtdti е
JLd
3 Если мы теперь будем считать, что го 0, го 0, ас отлично от нуля на всем протяжении от значения х 0 до значения х х, то
X
_ С —. х — t. v — L vt sin —dt. f
u
4 Общее же и полное решение уравнения а получим, просуммировав влияние
начальных параметров v0 и v0 по формуле Ь с влиянием члена Vе на всем протяжении
значений х от нуля до х по формуле f:
или в соответствии с формулами 25:
х
__ j р __п j
с ОоФд4 Ь
о
Интегрируя по частям последний член и помня, что ФГп Фо111 получаем:
v г0 Ф 4 г;Ф J1 11 -Ьоф х1ПаУфГ1У -
ФГ1У
60. о
65
Дальше, как в первом варианте.
14. Правила для запоминания формул метода
начальных параметров
Формулы метода начальных параметров мэжно легко и безошибочно писать на память, если обратить внимание на следующее обстоятельства.
Прежде всего нужно запомнить формулы:
1
70
e4,coefoein5-.l_cosi-i-8in.;
Г -Sinr Ь Ы-meiar1 N l-cosjA;
м — Nv0 — cos J — NLо — sin J M0 cos J Q0L sin J -f-AM.
В этих формулах коэфициенты при скобках содержат множителями в первом члене я0, во втором р0 в третьем—Ml, в четвертом—Q0. Выражения, стоящие в скобках, величины отвлеченные, поэтому коэфициенты, стоящие перед скобками, в строке для v должны иметь размерность длины, в строке для f должны быть отвлеченными, в строке для М должны иметь размерность произведения силы на длину. Нужная размерность достигается путем умножения и деления на величины N, L и В. Таким образом, эти коэфициенты должны иметь вид:
1 в строке для v:
2 в строке для :
3 в строке дляЛ1:
v
9
щ
L
—
Bv о
L2
¥о
-NL0 —:
Bio
м;
MIL
QoL_
QoL
N
В
N
В
Ml
MIL
_
QoL-
NL
В
iV
B
Ml
QoL
Эти коэфициенты представляют собой как бы ряд последовательных производных по производная от v будет L, производная от L будет слс
дующая производная Точпо так же выражения, стоящие в скобках,
связаны между собой. Производная по г от каждой последующей правой скобки представляет собой предыдущую левую. При.т0 все скобки, кроме cos J , обращаются в нуль, a C0ST J обращается в единицу. Таким образ зм при ж 0 получаем
из первой строки 70: v — vQJ из второй: р р0 и из третьей: М М0 iv0 М0.
Достаточно запомнить первую строку, чтобы последующие получить обыкновенным
диференцированкем: М — В
dx
1 В формулах 70 можно опустить первые члены, так как всегда можно выбрать ось отсчета прогдбов v так, чтобы го 0. При этом М можно будет заменить просто М0, так как M0 M Nv0. Первые члены мы в формулах 70 сохраняем только для
удобства записи развернутых выражений Дг, Д и ДМ при наличии вынужденных деформаций сдвига да или к0 в пролете стержня.
54
Добавки Ду, Др, ДЛ, учитывающие влияние пролетных воздействий, записываются легко по аналогии с влиянием начальных параметров. Влияние сосредоточенного сдвига да в сечении xL а аналогично влиянию г; влияние сэсредоточенного угла перелома оси 6Л при принятом нами выше правиле знаков аналогично влиянию минус угла поворота — влияние сосредоточенного внешнего момента Ма аналогично влиянию М0 и влияние поперечной сосредоточенной силы Ра аналэгично влиянию — Q0. Надо помнить,; что влияние начальных параметров начинается от значения х 0 и простирается на всю область значений я0; влияние пролетных воздействий, приложенных в сечении ж1 а, начинается в этом сечении и распространяется на всю область ха. Расстояние от текущего сечения до места приложения начальных факторов равно х, до места приложения какого-либо пролетного фактора равно ж —а, где а — расстояние от места приложения этого пролетного фактора до начала координат. В соответствии с этим мы, например, пишем для ДМ:
m-N 2 e-cosA-L 2 .-8Пг
j CL li2 2 m;cos-l 2 psinL
Cl —
y 2 —cs daNL 2- -sinda
-f 2 m C0S IT da L S 5 q sin 77 Jda-
15. Примеры применения метода начальных параметров
1. Сждтогизогнутая балка, со свободно оперыми концами фиг. 39. В этом случае го 0, ifcf0 Д О,
Фиг. 19.
Неизвестен один начальный параметр р0. Его ведтдну легко найдем либо из условия, что гг 0, либо из условия, что Мг 0. Используем, например, последнее:
Mi NLf0 sin j LQo sin l- L 2sin 0,
откуда
- _ Qj. V Pn L Vi p f К N 2j N. I. l
Cl n x nil- Sin z Sill y-
J-j L
2. Сжато-изогнутая консоль флг. 20. Известно: v0 0, 0 0, Qa Яiat — aiНеизвестный: начальный параметр MJilf0 можно найтд из условия, чта JVf 1 — 0:
12
Mi — М cos — QdL sin — L q sin - du 0,
ai
отсюда
Mo - LQ0 tg Qos- — cos ,
C0SL
5
ак как
2
С. I — и , Г _ 1 — и1 2 _ f Ъ Ь N
8Ш __ dtt i cos— J oi L Qcos -cos-LJ.
ax
3. Сжато-изогнутая балка с одним защемленным и д ру г и м свободно-опертым концом фиг. 21. Известно: v0 0; 0 0. Надо составить два уравнения для определения неизвестных начальных параметров Q0 и М9
Фдг 22
Одно из них можно составить из условий статики, приравняв нулю сумму моментов всех сил относительно правой опоры:
Mo Qol Ml 0,
а другое, использовав формулы метода начальных параметров записав М — 0 или г1 0:
Mi Ml cos -fQ0L sin — Ma sin — 0.
Решив эти два уравнения, найдем Ml и Q01 4. Сжато-ивогнутая балка с защемленными концами фиг. 22 Известно юо 0; Роив0, надо найти Q0 и М0 М1
Фиг, 23.
Составляем два уравнения vi 0 и — 0:
Mof l QoLfl. I PL Ъ. Ь Л
4-Nl-C0SL-N-VL-SinLlf Cr-SlnrJ0;
Mo. I l-NZSmL
-1-со8г1-со8е 0-
Решив эти два уравнения, найдем М0 и Q0.
5. Однопролетная балка с шарниром в пролете фиг. 23. Дано го0, 90 ; неизвестны М0, Q0 и угол 0Я перелома оси в шарнире. Нужно составить, три уравнения, одно из них может быть условием статики:
а
Два других получим, приравняв нулю Ма и Mi или v:
la — М0 cos г- Ч- Q0L sin — qL 1 — cos J 0; b.
i M0 cos —j- Q0L sin j- — qL2 1 — cos J — 0a sin 0. c
M,
Ml
Если не интересоваться величиной угла 0Л перелома оси стержня в шарнире, то можно ограничиться решен ем двух первых уравнений.
6. Проверка устойчивости сжатой балки постоянного сечения с шарниром в пролете фиг. 24. Задача отличается от предыдущей отсутствием поперечной нагрузки. Получающаяся система уравнений а, Ь и с приведена в табл. 6.
Таблица 6
м0
QoL
В
-L
1
1
1
L
0
0
а
С 06Z
а
sili L
0
0
1
С081
1
gin L
b
sinL
0
Тривиальное решение этой системы уравнений дает:
Мо 0; Qq 0; 0а 0.
Потеря устойчивости становится возможной при таких значениях вспомогательной длины L, при которых детерминат матрицы из козфициентов этой системы уравнений обращается в нуль:
2 -sin-
L
cos -4- lsinr- 0.
. b
L
Таким образом, потеря устойчивости возможна в двух случаях: 1 когда
2 когда
В первом случае
Здесь
а I Л 81П Т-Г 008 0
. а I
tg LT V-
L- I,
V N V
дт EJ v7
Nkp l
a
0
Давая отношению последовательно значения от 0 до 1,5, получаем для v и зна
чения, приведенные в табл. 7.
Таблица 7
a
7
0
0,25
0,50
0,75
1,00
1,20
1,30
1,35
1,40
1,50
V tg — _
L L
0
0,2554
0,546
0,932
1,557
2,572
3,602
4,455
5,793
14,10
a
1
0,979
0,915
0,805
0,642
0,466
0,361
0,303
0,2415
0,1064
Ь Ъ
Вр втором случае: sin- 0, -nw, где л —целое ча ело. Наименьшему значению критической силы соответствует п 1 и
кр L2 Ъг
67
Т0 Я 1 f N
Кривые зависимости между отношением —и величиной v I —
t f Ei
Л72
EJ
показаны на
фиг. 25. Из рассмотрения ихмы вид im, что, примерно, д значений — 0,303 устой-
чивость теряется прп критической силе по формуле Ь, то есть в результате выпучивания подвесной балочкл СВ, а для значений
0.303 1 устойчивость теряется вследствие искривления консоли АС.
16. Основные решения в граничных параметрах для сжато-изогнутых и растянуто-изогнутых призматических стержней
1. Классификация различных форм зависимостей между граничными параметрами
Как мы уже указали выше, можно представить себе 20 раз
личных комбинаций выбора трех активных параметров стержня из общего числа его параметров, равного шести. Но парахметры М0 и Mlt а также параметры р0 ц pz симметричны, поэтому число принципиально различных комбинаций будет меньше 20. После пересмотра всех 20 комбинаций и устранения аналогичных1 мы убеждаемся, что число принципиально различных комбинаций равно 12. Эти комбинации записаны в следующей табличке:
1 М, М Q. 3 М, Mi, J, 5 М, Mv f0
7 Qt, b 9 M, e, 90
11 Mt, Q9, qi
2
4 0- 6 . Ф 8 . Ml
10 P, Mt 12 90, ф, Mt
Табличка составлена из двух столбцов и шести строк, причем в каждой строке перечислены все шесть параметров. Если считать параметры одного столбца активными, то параметры другого будут соответствующими пассивными, и наоборот.
Если для простоты и ясности расчетной схемы поставить условие, чтобы при расчете рамы все жесткие узлы ее находились в отношении расчетных формул в равных условиях, то наиболее естественными будут формулы, симметричные относительно параметров на левом и правом концах стержня. Симметричные формулы получим, если в качестве активных параметров выберем:
1 М0, Мь Q0— метод сил;
2 — метод концевых моментов и углов перекоса;
3 о0, cpz, Q0 —метод узловых поворотов и поперечных сил;
4 ф0, рь cl —метод деформаций.
1 Аналогичными комбинацэяма мы считаем такие, которые могут быть получены одна из другой путем взаимной замены значков 0 и I у М и Например, М0, Q0t Vo и Мг, Q0t M0, Q0 Vi и Mh Qo ; MQy Q0, Ф и Mt, Q0, ф и т. д. Замена Q0 на Qi при этом не требуется, так как сэгласнэ условно обэ этд велдчины мы по существу считаем одним параметром.
58
Этим симметричным комбинациям грашичных параметров стержня соответствуют четыре основных метода расчета устойчивой прочности плоских рам. Каждому методу соответствуют по три основных формулы для пассивных параметров. Основные формулы метода сил представляют собой выражения для перемещений р0, и ф в зависимости от М0, М и Основные формулы метода концевых моментов и углов перекоса представляют выражения для р0, ср и Q0 в зависимости от MQ, Mi и ф. Основные формулы метода узловых поворотов и поперечных сил дают выражения для М0, Мt и ф в зависимости от р0, рг и Q0.
Основные формулы метода деформаций дают выражения для М0 Мг и ф в зависимости от р0, cpt и ф.
В число расчетных формул кроме основных формул полезно включить еще ряд специальных формул для стержня с шарниром на одном конце, для стержня с одним жестко заделанным концом, для стержня со свободным концом стержень-консоль и пр.
Для составления таких специальных формул полезно выбрать в качестве активных параметров:
11 М, Р
12 М, рг, ф.
Особо отметим еще так нааываемый консольный метод или метод начальных параметров, все три активных параметра которого сосредоточены на одном конце:
9 Qt, р0.
Для комбинаций активных параметров 5, 6, 7, 8 и 10 мы пока не видим случаев целесообразного их практического применения.
Прежде чем перейти к составлению конкретных формул, перепишем полученные нами выше зависимости 44, 49 и 50 между граничными параметрами стержня, придав им несколько более удобный для дальнейших преобразований вид; при этом используем обозначения 19, 40 и 41. Получаем:
М - ЛГ, - ДМ, QJ ф- Дф 0, 71
М cos V — 4- QJ, 0v sin v 0, 72
Мл sin v Q0l 1os v — -y- p0 v cos v pt — Apt v 0. 73
2. Основные формулы метода сил
Активные параметры этого метода: Мо9 Mlt Q01. Из 72 получаем:
о — __ Mj—JbMl Qoi ja
vtgv v sili v v2
Подставив 74 в 73, найдем:
ер,—Дф — -М-. 75
l TL В vsmv v tg v va J v
Из 71 имеем:
ф—Дф 5 — АГ. _ДДГО —.г. 76
3. Основные формулы балочного метода метода моментов
и углов перекоса
Активные параметры этого метода: Мщ, Mi9 ф.
Подставив в формулы 74 и 75 вместо QJL его выражение из 71,
59
после преобразований получим
р,—д, — j
Кроме того, имеем:
I Г V—sin v
V4 sm v
м Ml- AM, ф-Дф.
77
78
— M Мг — ДЛj —ф — Дф- 79
4. Основные формулы метода узловых поворотов и поперечных сил
Активные параметры этого метода: ср0, р Qa. Из формулы 73,
V
2
V 1 — cos V
учитывая, что tg — sinv получаем:
М-Т iFvf.--, - 4 -ft Подставив 80 в 72, найдем:
80
Mi - AMt у Г-;— 1 1 I L sin
0
sin V 4 w tg V
Подставив 80 и 81 в 76, получим:
t—
2
г—д QJ
tg
81
ф—Дф-V- К —Ар 1
2 tg 2 v Qo v8 В
82
5. Основные формулы метода деформаций
Активные параметры этого метода: ср0, р, ф. Заменив в 80 и 81 его выражением из 82, получим:
tgv-v , v
- Р. Т
v2tg-
v - sm v у. v 2
- i—i —
sm v _ , v
2tgY-v
2tgT-v
ф - Дф
83
М - АМ —
в
smv
v
tsr
tar v - v
2tg j-у
v — sm v
2tg¥-v
2tgJ-v
ф_Дф
84
Из 82 имеем:
О —
V i-i
2tg7-v
P Ti — Pi —
atsr-g-v
Ф _ Дф
85
б. О симметрии между граничными параметрами для левого и правого
концов стержня
Три зависимости, связывающие между собой граничные параметры стержня М0, Дj, 90, 9 , Q0, ф, могут быть записаны в различных формах эквивалентных по существу друг другу, как это сделано выше в пунктах 2, 3, 4 и 5 этого параграфа. Из рассмотрения формул 74
60
75 и 76 мы приходим к выводу, что, если в них заменить величину М0 величиной — ЛГ.—ДЛ и величину р0 величиной р — ДРг то совокупность формул не изменится, только формулы 74 и 75 поменяются местами. Такой же результат мы получим при рассмотрении любого другого варианта трех формул зависимости между граничными параметрами. Таким образом, мы приходим к выводу, что при принятом нами выше правиле знаков для моментов М0 и Мх мы их считаем положительными, если они изгибают балку выпуклостью книзу и правиле знаков для углов поворота р0 и pj мы их считаем положительными, если они направлены по часовой стрелке, величины М0 и Mi — Ailj стоят в формулах обратно симметрично, а величины сра и 90 — Арг прямо симметрично.
Если изменить правило знаков для концевых моментов М0 и Мг м считать их положительными, когда они, например, будут направлены по часовой стрелке, то формулы граничных параметров станут прямо симметричными относительно обоих концов стержня. Это обстоятельство будет нами использовано в дальнейших параграфах, там, где это окажется выгодным.
Заметим еще, что величины Мг — АМг, рг—А и ф— Дф представляют собой величины Мг cpz и ф для случая отсутствия пролетных нагрузок на стержне.
7. Формулы для специальных случаев для опорных стержней
Рассмотрим систему активных параметров: М0, рг, 0. Из формул 74 и 75 получаем:
9ш 2. м, Q1 86
,0 В v 01 v2cosv 0 у cos v N 7
Из формулы 75 получаем:
МI — AMt — Af pV vtgv-9j — 87
Использовав этот результат, найдем из формулы 71:
-Ati. 88
Рассмотрим другую систему активных параметров; М0, р, ф. Из 88
— , находим;
V tg V tg
—5ТГГ- Т W. - 89
Из 78 получаем:
90
Из 83 имеем:
о Ц1- tgvlv МВ lv-v2 sliTV—vbs v 1 91
Формулы 86 — 91 могут быть полезны для стержней, примыкающих к опорным узлам, и, вообще, во всех тех случаях, когда имеет место разрыв непрерывности в упругом контуре рамы. Применение этих формул сокращает число неизвестных при расчете рамы по одному из основных методов. С помощью этих формул как бы заранее исключаются неизвестные, связанные с опорными узлами рамы Формулы эти могут быть применены , для опорных стержней с_ неподвижным шарниром
6Х
ш оворе, с катком в опоре, с жестким защемлением в алоре. В последующих иуяктйх этого параграфа покажем это детальней. При составлении соответствующих формул надо помнить следующие уравнения для опорнот узла, приведенные в табл. 8,
Таблица 8
.ТЧв пп
На конце 0 стержня 1ог
Уравнения
1
1
Шарнир о
II
О
2
Жесткое защемление.
о
И
е
3
1
t
I
Каток, не позволяющий поворота и не препятствующий прогибу конца стержня
I
4
Каток с шарниром свободный конец стержня 200; Л0О
Для случая упругой податливости опорного узла мы формул составлять не будем, так как ввиду их громоздкости такие формулы не дают экономии в расчете по сравнению с применением общих методов.
8. Дополнительные формулы метода сил М0 Мх Q
Основные формулы 74 — 76 метода сил непосредственно охватывают случай шарнирной и катковой опор.
Формулы для стержня о1 с жестко-з аще м л ен н ы м кон до л I получим из формул 86 и 88. В этом случае нам дано: фг 0.
Тогда:
л4тл. таг-; 92
♦ - - Т ггшг- У - Ч- а. 93
Если жесткое защемление имеет место на конце 0, а не на конце t
стержня i0, то в соответствии с замечанием п. 6 этого параграфа мы
предварительно заменяем в формулах 86 и 88 М0 через—Mt —AM t, а фа через pj— А и обратно. Помня, что в этом случае нам даног
—О,
получаем:
Т — д S v cosy4 J 93
Если при расчете рамы по методу сил будет известно, что угол, поворота какого-либо из ее стержней Ф 0, то для такого стержня уместно вместо формул 74 и 75 применить формулы 77 и 78, чтобы исключить из рассмотрения лишнюю величину Qt.
9. Дополнительные формулы метода моментов и углов
перекоса М9, Mi, j
Основные формулы 77—79 этого метода охватывают случаи шарнирной опоры ЛО и случай, когда известно, что опоры стертая не имеют взаимного сдвига х 0. В случае катковой
62
опоры для стойки Q0 0 здмеет смысл вместо формул 77 и 78 пользоваться формулами 74 и 75, тем самым исключаем из рассмотревши лишнюю величину ф.
В случае наличия жесткого защемления на конце 0, стержня о1 что равносильно р0 0, можно пользоваться формулами 89 и 91, поело замены в них соответственно р0 через pz — Apz и М0 через — Мг — АЛ,, н наоборот. Это приводит к следующим результатам:
0
0;
v v tg _ __ ддг з
. - -Tjrr — т F 577 - о о
4 t-v 2 -v. vtgvtgY
l _ Д1 —. -t— l-v V- Av- 9i
10. Дополнительные формулы летода узловых поворотов и поперечных
1 о
Основные формулы 80 — 82 этого метода непосредственно охватывают случай жесткого защемления опорного узла ф0 0 и катковой опоры, не препятствующей прогибу и не позволяющей поворота конца стержня
р.-о.
Если известно, что концы какого-либо стержня рамы не имеют взаимного сдвига Ф 0,то для такого стержня целесообразно вместо формул 80 и 81 пользоваться формулами 83 и 84, тем самым исключается из рассмотрения лишняя неизвестная 0.
Если на конце 0 стержня lot имеется шарнир, то соответствующие формулы получим, приравняв Л00 в формулах 87 и 88:
М 00;
Л, — AMt Ql у tg v ifj — Др,; 96
- М - - - Т, - ад. 97.
Если конец 0 стержня свободный, то: Л0 0, 0 0, и из фор
мулы 87 получаем:
Mt — ДMt v tg v . y fi — Afi- 98
Если свободным является конец I стержня l9l, т. е. если Мг — О
и 0, то:
в,-2 л
и из форхмулы 74 получаем:
и, - -, ,g А , 2 р. ,98-
11. Дополнительные формулы метода деформаций р0 Основные формулы 83 — 85 этого метода охватывают случаи жесткого защемления конца р0 0 и отсутствия взаимного сдвига концов стержня ф0.
63
Для случая наличия шарнира на конце 0 стержня 1о1 формулы 90 и 89 дают следующие результату:
л0о,
-Д1--ДФ ,
99
100
При этом исключается необходимость рассматривать в числе неизвестных величину р0.
Если шарнир стоит на правом конце стержня ilt 0, то:
Я Jt t V- А 1 i Sill V I Л
Мл — - - v- 0 - f- Дy silv__ i tg V
В Г V2tgV V3 , A 1
T LtV37.-tvJ
V COS V
vtvtT Шг
99
100
tgv-v T0 tg V — V VT TJ tg V — V Z
Если конец 0 стержня свободный, тоЛГ0 0; QoO, и из 87, получаем:
В
М — v tg v. — рг — Дер,.
98
Если известно, что поперечная сила Q0 0, то рациональней вместо формул 83—84 пользоваться формулами 80 и 81, исключается тем самым необходимость рассматривать угол перекоса этого стержня как величину неизвестную.
12. Формулы консольного метода метода начальных
параметров р0, М0, Q
о
sin V
Формула 72 дает:
Mt — ДЛ, у pv sin v -f. МЛ сое v Qel
Подставив этот результат в формулу 71, получаем:
. А, sinv МЛ 1—cos v Q0l2 v —sinv
О — ДО 5 сс — л-. т То v в v2 В V8
Из 73 находим:
t—Ai
101
ЮГ
Ср0 cos V
M0l sinv Q0l2 1 — cos v
В
В
101
Формулы этого метода полезны в качестве вспомогательного средства ири составлении специальных формул для ломаных и ступенчатых,
ступенчато загруженных стержней см. 9, гл. IV.
Pi
ъ
Рг
А о,
-—
9
Ъ N
1 1-
-
Фиг. 26.
Составим выражения нагрузочных членов для случая загружения стержня 1аЪ равномерно-распределенной нагрузкой интенсивностью q по всему пролету и рядом сосредоточенных грузов Р19 Р2,. на расстояниях ах, а2,. от конца а и расстояниях Ьх 1 — ах; Ьъ 1 — а2,. от конца Ь стержня фиг. 26. Для этого заменим в формулах 37 х через I, а величины Ф их триго-
64
нометрическими выражениями 25, принимая во внимание, что L — :
, , V0
Ф1-.а Фь cos J ;
, т. v
-II V1
ф
-III
13
1—а —
V3
-IV
1—а
7
72Ь2
COS
т: ‘
ФГЛ ;1-сов;
В результате получим формулы:
ЛЛРvi 2 л. т-‘ -sin -г йй С1 - ¥ -cos v;
h
vsF
ч
Л Л, —2 рп sin т” Тг- — cos v
103
17. Специальные функции в формулах продольно-поперечного изгиба
призматического стержня
2. jСокращенные обозначения
Для облегчения пользования формулами 16-го параграфа, здесь приводятся графики, а в конце книги в приложении даются таблицы для определения численных значений коэффициентов этих формул. При этом для сокращения записи нами применены следующие обозначения для коэфициентов, представляющих собой сложные функции.
Коэфициенты формул 77 и 78, так называемые функции Жуковского 1, мы в нашей работе обозначаем фиг. 27:
v6
Для
tgv-v
v2 tg v
v — sin v v2 sin v
104
105
растянутоизогнутых сте рж ней формулы этих коэффициентов легко получим, заменяя по формулам 54 и 55:
vi; cosv chn; sinv shA; tgv ithtx.
Таким образом, для растянуто-изогнутых стержней
Цу-
tm3 у2ду
S-6
Фиг. 27.
3
St6
ji — th ц
Ii2 th jjl
sh ц — i ji2 sh x
104 105
104
1 Таблицы этих коэфициентов были составлены Н. Е. Жуковским см. примечание проф. В. П. Ветчинкина на стр. 188 VIII тома Полного собрания сотенений проф. Н. Е. Жуковского ЦАГИ, 1937.
Если продольное усилие стержня N 0, то оба эти коэфициента
tsSl.
Прочность и устойчивость стержневых систем
65
При использовании этих обозначений формулы 77 и 78 балочного метода при-, обретают вид:
6 в
Ма1 Мг-Шг1 , , д
Коэфициенты формул метода деформаций 83— 85 обозначаем фиг. 28:
v
106
107
а
v 2 tg v
tgv — V 2tg-J-v
V — sin V
108
109
К
X 1 ч
ч
я
1
-го -ts
-ю
-s
a.-¥- 1уу
2t9y Ztg-У
д _ у У-Sin У
r zsiny гtgi-y _ y‘2
V —1_ V3
2 г97У-У
Фиг. 28
1 vHgY
а v y ;
2tg— v
1
Tv y
Джя растянуто-изогнутых стержней эти коэфициенты имеют вид:
ч
ц ц — th ji
а.
11 21Ъ ц — 2 th
Ji sh Ц — ji
iv
2 8Ь 4. 1
И - 2 th -
110
111
108
109
м
ufi th —
1 p 2
aVj 11-2 tt-t
.-2 th Л
110
1117
Если продольно усилие iV 0, то:
a 2; jjl; a P 3; -y 6.
При использовании этих обозначений формулы 83 —85 метода деформаций получают вид:
Мо лр0 4- р — Лр — а Э Ф Ф1
-f а — Дсрх — а Р ф — А;
OR
Q - -Г о П Дг ТГ Ф Д401
112
ИЗ
114
Коэфициенты формул 99 и 100 метода деформаций для стержня с шарниром на одном конце обозначаем фиг. 29:
— V2 tg V
av tsr v — v
Tv tg v - v
Для растянуто-изогнутого стержня они имеют вид:
— ji2 th ц
Шц
3
TV Ц —tg ц
115
116
115
116
5 67
Используя эти обозначения, а также нижеследующие формулы 128 и 124, формулы 99 и 100 метода деформаций для стержня с шарниром на конце I, можно записать следующим образом:
Мг 0;
М,. 4ав-.-Дф А.дм,; 117
I а
Q. - - J- й. - т - д1 - dv в
Коэфициент формулы 82, пользуясь обозначением 111 записываем так:
V 1 2tg2 V i — 2 th i
12 2y vs jx8
Коэфициенты формул 92 и 93 обозначаем:
119
1 — cos v ch ц, — 1 v2 cos v jx2 ch a 1 ts v — v p — th ii
v2 cos v ns ch i 120
Y v
V
121
Таким образом, формулы 92 и 93 метода сил для стержня с жестко защемленным концом I получают виц:
¥г 0;
1 ЛЯ7 Л Л д1 -
cos V
122
То М сv Q0l
♦ -A-g-cv.aft iQ.i-A,. 123
Коэфициенты формул 94 и 95:
I th ц th
dw z ; 12i
tg V — V JX th JX
2tgTv thy i-2thf
2v v ‘ tgv — v a ix—thjx
125
В результате формулы 94 — 95 балочного метода для стержня с левым защемленным концом приобретают вид:
о 0:
Q. —г-— -f2 f - А; 126
уг- Ду, - JL М; г rfv ф - Дф. 127
Отметим, что коэфициент формул 90 и 91 может быть представлен в виде:
v — sin v sh jx— ix s p
sin v — v cos v jx ch jx — shtx 21
128
В приложении, приведенном в конце книги, даны таблицы коэфициентов:
V V
а , 4 Y а Y а также величин sin v, cos v, tg v, 7— , -7— , v tg v фиг. 30, s, t, и
‘ tgv sin v
n величин sh a, ch jx, th jx, - , txthu.
th jx sh jx
При вычислении нагрузочных членов Д, Дг, ДМг весьма полезным являются ханже функции:
ylv у v sin v — u sh x ;
B4f v cos vch ji;
sin v sh fi
Cv F4v Pv-V_nv
v n
1 — cos v ch ц — 1
v2
u.
5
12‘.i
129
130
131
E v_ v-sinv _shi-n.
-inW —— jTa ,
1 1
1 v2 -cos v — i — —- jx2-ch jx
V4
v -vC
1 1
v -f v3 -f- sin v ;л 4 H3 — sli u, b
132
133
134
Эти функции фиг. 31 приведены в табл. 8 приложения. Пользуясь этими функциями, можно легко придать формулам 101 —103 следующий вид:
Р г
ВС —1 п —
ii—i
ЛЛ, - V-i т9 ff,v-n v-
135
Ш
6г
Если v 0, то
ЧГДО-ЧГ-аО-; -п0 2 ;
41
51
Приведем здесь некоторые формулы, связывающие между собой специальные функции этого раздела Формулы эти мы даем здесь без вывода, правильность их может
У у У у4
Подробней см. таблицы и9б приложении
Фиг. 31.
быть проверена непосредственной подстановкой
ТГ 8
Р JL.
т 6
а 21 : -т 3
a t
2 -
г
Т 2 - Л ;
♦ -v
138
133
140
141
142 14-1
а —
z Р2 V
144
145
146
147
-
М:
2 sin v
-Ргт;
а tg v
Т v
d g —
dv 2.
а
Т-п.
V COS V
-ш W
6 v
, 6t 18
48 — 5- — ;
а T
3
2f s
148
149
150
151
152
153
154
155 155a
155b
70
2. Разложение специальных функций в ряды
Приведем здесь, не останавливаясь на математических преобразованиях они весьма элементарны, результаты разложений специальных функций сжато-изэгнутого стержня в степенные ряды с указанием границ их применения границ сходимости рядов. Тригонометрические функции:
чуЗ у5 9
1 sin v v — si— 79Т -oovoo;
2 4 8
2 cosv 1 2Г4ГбГ 8Г —оо v оо;
3 tv v v34-2 v6-f -7- v7 -I—— v9 4- v - :
5 Г 3 15 315 2835 2 2
v 17 41 127
4 ihTT1Vv2 v4 i5i20 v бШоГ8 -v-;
5 -v.
is
сл 2 _ 1 -1- 1 2. 1 i , 17 e , 31
v 2 24 V 240 V 40 320 V 725 760V v ;
-Функции Жуковского:
v 3- vatgv 115v2315 v4 1575 V31135 v —
o с v - sin v 7. 31 127 , 73 , ,
8 sv — v2sirtv— 60 V 2520 V 100 800 V 570 240 —1tvw-
Функции формул метода деформаций:
v t V — v 1 11 1
9 а _—. _12_ 2 v2 — v4 Vе -
2tgv v 15 12 600 54 000
О о r 2tg-
509 14617 1в
V 1 QUO ППЛ v 2 V 2;
1 164 240 000 1 362 160 800 000
,м v V - sin V 1 13. , 11. ,
2 sin v . v — 60 V 25 200 V 756 000 V
2tg -2 -v
907 л 27641
2 328 430 000 V 2 724 321 600 000 v - 2 v 2;
v tf
ч - 1 a 1 2 O v v
11 aS —. 3-——
2 . v 20 2 800 252 000
2tg-v
37 59
8 ——— -v1——8,986 v 8,986;
776 160 000 100 900 800 000
1 v3 4 1 1
12 V . 1 _ v2 v4 1 _
1 2 _. V 0 5 1400 126 000
2tct v
2
w Я 59
388 030 000 7 50450400 000V —8,986 v 8,936.
Функции формул метода деформаций для стержня с шарниром на одном конце
Коэфициенты специальных формул:
1 у 1 17 31
15 2-f v l2l2QV 20160 V 3,62880 v 7 K‘
104 c __ 1 COS V ___ 1_ , 2 I V4J v6 i _ v . V v2 cos v 2 24 720 8064 ‘ 2 2 -Ч 1 tV — V 1 2 , 62 Л TC
V V 3 15V 315V 2835V 7 v 2 ;
4
v tar v tor
2 S 1 11 67
18 dv tgv-v 240v2 8403vt 1003 000 v- - MS v 4.4M-
v
2 - - — v
1 tgV 2 11 13 19
1- 2a v tgv-v 7l20V r 3:iOOv4 10080007 v я;
20 1 vsinv. 1 va LV4 7., —4,493 v 4,493.
7 a sm V — V cos V 2 40 8400 1008000
Фулкции v, 4T_j v, ЧГ_ц v,. входящие в формулы для нагрузочных членов Av, Др, ДМ:
м 4 6 ,8
2Г 4ГбГ 8
sin v V3 v4 v v
22 47Iv SV1-3foT-7T 9T-
21 ¥v cos v l-t7T-fГГ-А-. - ос y со
— ОО V оо
IT- ч 1 — COS V 1 V2 V4 V6 V8
-3 _ц 5 — 2J- — 4Т -6Г _8Г 10 —oovoo
_ , ч w. ч V — sin V 1 V2 , V4 V6 V8
24 V_UIv - со у со
1
— 1-Ь V2 -I- COSV 2 4 в
25 V_lvv- 5, __7_7_-_. — оо v оо;
1
— V — V8 sin V 2 4 26 Ф у у 6 5 т yj fjj оо v оо
и так далее.
3. Разложение специальных функций в бесконечные произведения
При решении задач устойчивости требуется знать, при каких значениях аргумента v специальные функции обращаются в 0 и в оо. В этом отношении весьма полезно иметь разложения специальных функций в бесконечные произведения.
Считаем не лишним сказать предварительно несколько слов о разложении трансцендентных функций в бесконечные произведения. Регулярные функции F ж, которые ни при каких конечных значениях аргумента не обращаются в оо к таким функциям могут быть отнесены целые полиномы, отдельные члены которых представляют произведения степеней аргумента на sin я, cos, shx, ch, могут быть представлены в виде бесконечного произведения
Здесь с19 сг, с3, корни функции, обращающие ее в нуль:
F Cj F с2 F с3. 0.
Условие сходимости бесконечного произведения состоит в том, чтобы ряд:
ГГГ-
1 2 3
был сходящимся, причем сумма его должна быть отлична от нуля.
Корни Cj, с2, сг. могут быть действительными или комплексными:
сп п
72
Подставив в F х вместо х комплексную величину a-j-Ьг, получи
F с — F a-f hi f a; b-Ma; 5,
где a; Ь и f a; 6 вещественны.
Определение комплексных корней F х приводится к определению вещественных корней а19 а2, а3,.,. и blt Ъ2, 68,. системы уравнений:
fa Ъ 0 и у а; 0.
Примеры. 1 Дана функция:
Для нее:
Решая совместно
F х х — sin х.
а; Ь а—sin а ch Ъ и f a; Ъ—cos a sh Ь.
a h
ch 0 и -r—v cos a,
sin a
sh b
получаем корни:
п
1
2
3
1
1
4
ап
7,498
13,90
20,24
26,55
Ъп
2,769
I
1
3,350
1
3,715
3,983
Каждому комплексному корню a-hi соответствует сопряженный корень а — Ыг поэтому:
С1 х х — 1— ах х2
V a6i V a-bi а Ь as Ьг
2 Дана функция: Fj sin х — ж cos х. Если бы эта функция имела комплексные корни, то уравнения:
f a, Ъ sin а ch Ь -f- Ъ sh Ъ -j- a cos а ch Ь О,
р а, 6 cos а sh — Ь ch Ь - a sin а sh О,
приводящиеся к уравнениям;
a2 b2 -1
sh 2
siu а
должны были бы иметь вещественные корня для а и Ъ. Нетрудно видеть, что гри. любых вещественных значениях а и Ь
0 1 —
2 Ъ
1, а — 1 —
2 а
2,
sh 2b i sin 2а
следовательно, а, Ь и а, 6 не имеют вещественных корней а и Ъ, a Fj я не
СО
имеет комплексных корней. Поэтому бесконечное произведение Пж — ап, где ап — только вещественные корни F2aO полностью представит функцию Fxx.
Трансцендентные функции F ж, обращающиеся в бесконечность имеющие разрывы непрерывности при конечных значениях аргумента например, при x dltd2, следует представить в виде дроби, числитель и знаменатель которой являются конечными функциями, тогда:
F х — Ах
П
‘-а Ю о-;-
С 1- ld0 О
Наши специальные функции всегда могут быть приведены к этому виду, если заменять в них всюду tgx и tha отношениями sin ж к cos х или sh к ch.
Приведем теперь без вывода интересующие нас разложения функций в бесконечные произведения. Сначала дадим несколько формул разложений, которые будут
7
нужны при составлении бесконечных произведений для наших специальных функций:
i, - О -S 0 -О - , - 1йг. 492 У
Очевидно, что разложения shv и chv получаются из разложений sin v и cosv путем замены знака минус на плюс перед v2.
Приведем еще четыре разложения, полученных нами:
I. х
х С1- 14,066
V V V у yi Ч у уЛ И. V- sin V — Q1 262 63 89J 1-7736 2043j С1_1М5 42374У Х
Х С1_13758 72м-”
Г. shv-vchv-l1li___ х
Х С114,06бО
V8 V V f V V у Ч
II. v-shv J i-308 204J 1-57n 5237V Х
Отстжд-
Пользуясь разложениями 1, 2, I и II, получаем:
з.г— yg С1-1
-‘-S‘-S - ;
V 1
4
sinv Z v2 Л v2 v2
‘О О-ЕГ. 1
ГЧ V
v -. -й‘-й
т ‘-е‘-да‘- -
7 , Функции Жуковского:
С‘-лр ‘тэт о-яэт С‘-ял-
О-йЗО-О-О-п-
V — sin у С1-4.262 63,89 О-,36 204,б С_ 10,45 423,4 J 74
Функции формул метода деформаций: v sin v — v cos v
9 х
, V. V V V
8sInT SinTTC0S2
f i———— i _ — i v.Л
V 4,493V v 7,725 7 V iof90,ee
0-Й O-i-sO 0- - С1- О-ст 0-S0-
Ю p —v vsinv
8sin sinl-Icos
1_ 1— I V _L yt Л V , I Л
у 4,262 63,89 7,36 204,5 у 10,45423,4 С-й От - - ‘т0 Отда C‘-son -
V2
V
Sin -Г
11 a-f-8 —-
4. v v v
sin cos —
2 2 2
-0-pC‘-ro0-ip0-ip-
O-CTj. O-i ‘-5Щ. -sot-
t-T
V
s cos T
v3 2
V V V
sm — COS —
2 2 2
.ЛЧ — v2 sin v 13 a —
sm v — v cos v
-5С-й0чр0-го-
_ C‘-ra. ‘тот ОтгаО О-япр - ‘
Коэфиционты метода деформаций для стержня с шарниром на одном конце:
-
‘тот ‘тэт 0-ш- -ял
sin V—v cos v v2i v31 v2 Л
V 47493V V1 7,7252V1 10,902У V 14,07V
Коэфициенты специальных формул:
1 2 81п2-2 C03 2_ C18,987a О-ЦГО СпЖ
cosi 12 0-S 0-Й ‘-5Й-. in Г‘-0-А0-зй.-
1 __sin v—v cos v
75
18 d
_ С‘-ет -да - 2
smv-v cos v
‘-4тЙз0-0-тЙг.-
4 sin
19Ъ — 2а
V
V V V
S 2 2 C0S 2
sin V—v cos v
- Ст С-ю - ‘-да ОчиЛ О
21,81
I _Vi r_Vi
V 4,4932. 7,725V
725V V. 10
v Л ,90V
20 1 v-sinv
a Sin V—v COS V
Л Л Л_ Л Л
V 4,262 63,89 J 7,36 204,5 J 10,45 423,4
‘-от‘-г‘-иэт
4. Разложение специальных функций в дробные ряды
Большинство наших специальных функций являются функциями мероморфными. обращающимися в бесконечность при определенных значениях аргумёнта. Такие функции можно представить в виде разложения в ряды, составленные из простейших дробей. Приведем здесь без вывода эти разложения, весьма полезные в ряде случаев при решении практических задач.
При составлении таких рядов во многих случаях удобно бывает использовать разложения функций в бесконечные произведения. Пусть известно, что
п а
Ч di.S
А 1,2,3,. Л
где п и rrik могут быть как положительны, гак и отрицательны.
Тогда
In х In А п In х -f mk hi —.
Al,2,3,. k
Продиференцпровав, получим выражение логарифмической производной
f х _ _ 9г V Шк
f х х а-х2 А 1,2,3,. К
Пользуясь этой формулой, непосредственно получаем разложения для дробных
функций, числитель которых равен производной от знаменателя, как, например:
, sin х cos xf , sin xY x sin x sin x—x cos xY
— tgx — ; ctg x — ;. —: cos a; cos x sm a; sin x — x cos r sin x — x cos x
и так далее.
Если числитель и знаменатель дроби не имеют общих корней, причем чис
литель рациональная, а знаменатель трансцендентная функция, разлагающаяся в бесконечное произведение и не имеющая кратных корней:
х — ах х — а.л х — а2. то такая дробь может быть разложена в ряд:
F х XI Лк
2 -ь— с jLJ х — a l.
х x-ak
к — If 2 76
Коэфицйенты этого ряда легко найдем, умнбжая обе части с йа я последо-
о
вательно приравнивая х а1У а2, я3,.♦ При этом, раскрывая неопределенность —
получаем:
а Р ак
лс-77
Г ак
1
Разложим дня примера по этому способу дробь. Известно, что корни знамс
cos ос
иателя будут равняться:
тс те 3 3 5 5
а — - - : ; —тс; тс; -тс; -тс;.
К 2 2 9 9 2
Таким образом
sm
отсюда:
1 — 1 1 1 — 1 — 1 1
—— —4- —4- г—4- с—
cos х тс тс 3 3 о э
х—2 V ЖТ х— ж2
или:
secx in тез_4а;2_9гГ4г 25ж2-4а:2_49-4ж Начнем с известных разложений
14 _;Г 1 1 1 1 - 1-
v L тс2 —4v2 9тс2 — 4v2 1 25тс2 — 4v2 49тс2 — 4v2 J v _ 2v2 2v2 2v2 2v2
2 7—rt
tor v тс2 — v2 4tc2—v2.tc2 — v2 16tc2 — v2
O
v 2v2 2v2 2v2 2v2
sin v тс2 — v2 4tc2 — v2 9tc2 — v2 16тс2—v2 4 tg2 — if 1 - I 1 I 1 1 1 1
V L2-v2 92 —v2 25tc2 — v2 49tc2 — v2 J
Из этих разложений нетрудно получить формулы для функций Жуковского:
tg v — v Г 1 1 1 1 1
0 — 3 7TZ 6 I —2 2 ”7—2 4 Т—2 2 2 2 ”Ь I
v v- tg v L—v тс2—v —V 16 —V2 J
П с V - Sin V _ i9 Г 1 1. 1 _ , 1
5v-D‘ v2 sin v L2- 4tc2 — v2 9tc2 — v2 lbTC2-v2t J ‘
Коэфициенты метода деформаций:
n — v sin v — v cos v g Г 1 1 1
2 2 1 — cos v — v siii v L 4tc2 — v2 162— v2 Збтс2—v2
L_ ‘ 1 1.
8,9872-v2 15,45 — v2 21,81 —v J 8 — я i ct 2 i v 42: 16—v2‘зб1 —v2 ‘ —
1 1 1 I
8,9873 — v2 15,45s-v2 21,81s —v2 :
9 a P3—2v2 8,987—va 15,452v2 21,812-v2 28,132 — vs J
10 y 2 i-f-3 1 1 1 1 f 1 -
8 8,9872-v2 15,45s — v5 21,81s-vs 28,13s —vs J ‘
Коэфициенты метода деформаций для стержня с шарниром на одном конце
у sin v ;
11 а v —
sm V—v cos
3 — 2v2 Г I - -.
L 4,4932 — v2 7,7252 — v2 10,902-v2 l4,072-v2 J
12 ,-
I 1 I
т 10,902—v2 т 14,07-vs J
Коэфициенты специальных формул:
I ъ. V 1
О, -8 о о м2
2f v1
8 Г 1 1 1 1 11 1 I
L2_V2 9 9it2 — v2 25 25те2— va 49 49те2 — v2 e J
14 с
v v2 cos V V2
16 Г 1 1 1 1 1 1 1 1
те L те2 — 4v2 3 9те2 —4v2 5 25теа —4va 7 49те2 —4v2 J
1 t0 v 1
15 т
v3 v1
32 Г 1 1 1 1 1 1 1 1
nL -n2 —4va 9 ‘ 9те2 —4те2 25 25те2 — 4va 49 ‘ 492-4v2 eJ
,1 V2 Y
16 d _ , v sm v — v cos v v2
, , 2r7i 211-1 2тГТ;1 2Гм-1
T2 — v2 T2 — 2 2— v2 2 — v2
где Сл — корни уравнения: tgTn-cn, причем: 4,4934; с2 7,7252; 10,904:
4 14,066. Таким образом:
11,21 13,58 23,89 26,21
v —1 20,19- v 59,68 - v2118,8 - v2 197,96 - v2 2 t2 — 2 tgf2 -2- 2 tsr2 Jl 2 1 — COS v — v sin v 2 2 ё 2
2л v sin v — v COS v : — v2 C2 — v2 — v2
шли
1 _ 3,111 1,539 2,407 1,749
2л 20,19 - v2 59,68 - v2 118,8 - v2 197,96 - v2 ft v — sin v , 11,21 13,58 23,89 26,21
a sinv-vcosv v 20,19 — v2 59,68 —v2 118,8 — v2 197,96 — v2-
Для примера покажем, как нами подучено разложение су. Выше было дано разложение —-—. Пользуясь им, получаем: cos v
_J 4 Г 1- 1— 5 v2cosv v2n2-4v2 29те2 —4v2 7225те2 —4v2
Замечая, что:
k k_ _4_ 1
V2 Au2TC2 — 4v2 с2Л2 V2 ЙГГС2 27t2 — 4v2
находим:
1 1 , Г , 5 I 4 4ic Г 1 1 1 1
v2COS v v2 L теа 9теа 25теа J L 1 те2—4v2 3 3теа — 4v2
, 1 1 л
_г 5 5 - 4v J
78
Здесь:
4Г- 5 -
L2 9а 25™ ‘J cos О
Принимая во внимание, что
с. —
v V2 cos V V2 окончательно получаем для cv приведенное выше разложение.
5 О повышении сходимости дробных рядов. Комбинированные
дробно-степенные ряды
Пусть известно, что функция р я разлагается в ряд простейших дробей:
Для того чтобы повысить сходимость разложения ж в ряд возле значенм xbt разделим и умножим каждый член ряда на х — Ъ
,_,-2; х_ьап_ху
о
о
Таким образом:
1 Г 1 1 1_
— Ь аЛ — х х — Ъ ап — х J ап — Ь
Разлагая вторую сумму по этой же формуле, получаем:
у 00 - у X - 6 у. 7-n— X - Ь У - 1—
rw - - - впг
Продолжая разложение, получаем:
Сравнивая это уравнение с разложением в строку Тейлора:
т
ь6 i Ь находим:
тЬ _ у7. VI Лп _ У Ь ,
eT5efW ап-Ъ И ZjLan-fc 21
и вообще:
у-1 Ь
вп-Г т-11 Таким образом:
Если р2 Функция четная: р 2я Ф и, гДе и х2, то
- 2 sfb - 2 - ь 2 яй. j.‘ - ь, 2 .- т-‘ 2 s-tir - ‘ш 2 cfeji Ь
Здесь
v Сп - Ь
Zj а-Ъгт т-1
7
В частном случае, если 6 0:
- 2 2 31 2 ij- 2 4.sme Cn -L згт V _cn 1
а 2л alm esm а -ж
с
В этом случае:
v ___ J2m 0
Zi a™ 2m —21
и
2 53 f 4 2- J0 4 jj V 4-
4
2m — 21
fa
0 -f x
2m
лт а—хг
d
Примеры
fg y_y 11 1 1 1 lV tv 3 vitgv 6 _vi l_v d4-V3 16- V
1 Г5 vS A v4 15 v v‘ С
Давая в формуле d последовательно значения для то 1; 2; 3;., получаем:
1.1 1.1 1
. 6v S 1
ti —-
7С2 1C2 — V2 4 4л2 — V2
--
т 9 9 —v 16 16 —v
,А
1., бу 1
v 15 V 4 s —716 4 — VsИ81 9г — v
1 1 1
‘ о-2_,.2 256 16
t 1 1 v2 - v — v 15 315 П
2 ,.2
64 4i2— v2 729 9теа — v2
V
I
-va 0 : 1.
л Т. Д.
. v —sinv 7 31 127
2 sv — 6 oo V 2520 V
loo doa
v‘.
12v 1
svH I
i2f_J 1 I 1 V
— v2 4n2 —v2 9n2— v2 16tc2 — v2 J 9
V
I
,ч4
л2 ie2 —v 4 4icv2 1 9 __ 7 g t 12v4 1 1 1 1
60 V л4 к,л2 — v2 16 4w2— v2 81
1
9ic2 — v2 16 16tt2 — v2
9ic2 — v2 256 16л2 — v1
4
1, 1
7 2 31 12ve Г 1
5v1 60V ” 2520 V e ,г-v2 64 42 —v2 1 729 92
я т.д.
1 5 61
3 secv l ¥v 24 7-v.
b-
, 1 3,5. 7 тс2 — 4v2 У8 —4v8 25it2—‘4v 49w2 — 4v2 yk
Для удобства применения формулы d последнее разложение запишем так:
3.5 7
sec v
-сь
92
т
— v
г
252
— V3
49г
4
.2
Затем получаем:
, , 16v2 1 1
sec v — 14 Л те2 — 4v2 3
1
sec v 1 ——- v2 4
Ал
64v
4
1 1 9 - 4v 5 25
1 _ i ч.
— 4v2 7 49-4vл‘
;4v4 Г l l l l
тс it2 — 4v2 27 9-ж2 — 4v2
4 , 1 г , 5 4 , 256v f 1
8eCV l21 24 v —
27 9 - 4va 125 25 - 4va 343 49 - 4v
256v Г 1 1 1
4v2 243 92-4v2 ‘ 3125
1 i N
125 25 Л2—4v2 80
— v2tgv v2 v4 2v6
О a -7—2— 3—— — —
tg v —v 5 175 7875
0 0 а 1 1 1 1
3—2v2 44932_v2 77252-v2 10,902-v314,072-v21 В этом случае получим: v2 1 1 1 1 1 1 Л
a q__I 2v4 I. 1 1 L. 5 4,4932 4,4932—v2 7,7252 7,7252-v2 10,9o2 10,90e-v2 у о v2 V4 0 1 1
a 3_‘5 _175 _ v4,4934 4.4У32-2
__. 1 1 Л.
T7,724 7,7252—v2 10,904 10,902-v2 т у
Приведенные примеры относятся к случаю повышения сходимости рядов в окрестности v 0; они рассчитаны на применение, главным образом, в пределах значений
от 0 до значения первого корня те в формулах для v и sv ; — в формулах для secv,
4,493 в формуле для а.
Если нужно повысить сходимость ряда в окрестности значения аргумента х Ь, далекого от нуля и не совпадающего со значениями корней уравнения, то удобней будет вместо формулы Ь применять последовательно формулу:
Если значение Ъ совпадает со значением одного из корней 6 ас, то в формулу е надо внести корректив. В этом случае:
2 лГж2 аГж2 2 а2 -а. 2 а-а
:2 а — х2 О
пфк п л пфс
где
Л1 л I , I U I. М, V , йм ОС4
ь п к . в п к
XCLh пф л л - причем в этом случае придется раскрыть неопределенность оо — оо по обычным правилам.
Для примера применим эти формулы для повышения сходимости ряда функции tv вблизи значения аргумента v.
Cv2 vtgv Сте2 —v247c2 —V2 9те2 —v2 ”16те2—v2 Раскрываем неопределенность:
Г l_ 1 3 Г_1 1 1 JT
L ы те2 —v2Jv—те Ь2 vtgv те2 — v2Jv-re 2те2
После этого получаем:
tv rZ 2v212 т 4л2 —v2 Т А ‘ 162-i-‘
Еще раз повысим сходимость по формуле f, применив ее для выражения во второй круглой скобке. Раскрыв неопределенноеть, получаем:
6 9
Таким образом:
Г I ь п
I ft2 —V2 2те2 1 33
L v2 — те2 2те2 8те4 v Z5 5KZi v2 те2 — v теа _ v2 2те2 2те2 8те4 J
v-22.—.
Аналогично получаем также:
-. 44i-lls 4-rv2-. А Г 1 1 1 1 1 , 1
я L 27 42_ V2 512 9те2 — v2 3375 162— v2 J
Прочность и устойчивость стержневых систем 81
те2 —v2 ‘ 2те2
6. Решение трансцендентного уравнения
f х sin ж — х cos х 0.
а
Выше, в пунктах 3, 4, 5 этого параграфа, нам приходилось пользоваться корнями уравнения a: sinar — a: cos ж 0. Покажем, как можно их определить с любой степенью точности. Прежде всего построим графики фиг. 32 периодической функции,
sin ж
2 и прямой Уг х.
Абсциссы точек их пересечения отвечают корням уравнения а. Из рассмотрения этого графика мы заключаем, что положительные корни а 0, а именно а,:а., аг, а. будут: Л
л 3 5 2п 1
ао 0; fli —u-l; а2 — я-s2;. , ап—
где elf е2 е3 ,.. — сравнительно малые положительные величины — поправки к значениям — , - Отрицательные же корни уравнения а будут соответственно
У I равны:
а_2 — а2;.
Для сокращения записи обозначим
271 1
те с
п
Ь
-277
12л
или просто
и
з2л SztT тогда
Фиг. 32.
а б — е.
Подставим это выражение в а 0:
а sin с — е — с — е cos с — е 0.
_ 2п 1
Заметив, что cos с cos —-— 0, получим:
sin с — е sin с cos е; cos с — е sin с sin е а sin с cos е — с — е. sin е 0,
— сп в
п
с
откуда
ctg е г - с — е.
d
Здесь е —малая поправка, и поэтому можно пользоваться разложением ctge в ряд, не занимаясь вопросом о его сходимости:
ctge
It 1 , 2 , 1 , ,
— — р.3 — -— е — Гр7 —
3 е 45 е 945
4725
Подставив это выражение в d и умножив на —, получим:
С
1 Л , 2 2 1 4 2 в 1 8 е- — 1 — е2 — — е4 — е тг е8 —.
с 3 45 94э 4725 у
е
Учитывая, что е малая величина, значительно меньшая единицы, можно уравнение е удобно использовать для разложения е в степенной ряд по степеням
при помощи метода последовательных приближений.
Первое приближение получим, игнорируя члены со степенями е выше первой;
1 1
найдем ет —. Второе приближение получим, отбрасывая члены со степенями — выше
Ас С
третьей:
1 Л , 2 1 Л , 2 1 1,2
еИ- с С 3 SI J с. 3 с J с 3с3
82
Третье приближение найдем, пренебрегая членами со степенями — выше пятой:
еш
в2.Л-.
с 3с3 15с5
f
Четвертое приближение получим, пренебрегая в е членами со степенями — быше
с
седьмой:
1 f л , 2 9 1 Л 2 в Л
8IV- — ч1 3- еШ 46 еШ 945 eIllJ-
-I- 1 .S4-
1 41 _ 1 , 5
945 Чс У с 1
2_ 1, 13 _1 , 146 J_
3 с3 15 с 105 с7
Дальнейшие члены разложения в случае надобности мы можем получить ана
логичным образом. Корни уравнения я 0 в соответствии с формулой с мы
получаем в следующем виде:
1 2 1 13 1 146 1 m
а с 3 с 15 ‘ с5 105 с7
Подставив вместо с сп его значение по формуле Ь, получим:
2п 1 2 JL_Af —. JLY- 12 2
вп 2 2га 1 я 3 2д 1 ж 15.2га 1.
146
га 4-
105
Давая п в этой формуле последовательно значения: 1; 2; 3; 4;., находим:
3 2 16 416 18688 а
2 П 3 81 3645 ж5 229 635 я7
5 _ 2 16 416 18 688
г 2 5я 375л3 46 875 те5 8 203125 л7 a 1,-А - У -. 10,9041
2 7 1029 л1
9 2 16
а 2 9я 2187 л8 —
К этим корням надо добавить: а0 0; аг — а2; а_2 — а2;. и т. д. Комплексных корней это уравнение не имеет, как это показано в п. 3 настоящего параграфа.
7. Представление специальных функций в виде непрерывных дробей
Приведем без вывода ряд формул могущих оказаться полезными при приближенном решении задач, в частности, при составлении подходящих дробей для специаль-
1 Составление их основано на следующих формулах преобразования степенного ряда в непрерывную дробь:
2С2 X4 X X8 X2 1
1 -Г -оГ -FT.-1
А В С D г , , х2
Н гг 1 X2 X2
ъ ч I
с ТТ 61Н 2
а. , х
С1
А и В
Здесь: а А; Ъ — ;
4-
с Л А2С d В2 — АС и
Кроме того:
а1_а; сх -Ь 1с; 1 - 51 l и т. д.
83
еых функций.
1 cosv 1 —
V2
2
va
6 3v
io 1342
126 .V. V2 1
2 -TTT71 sinv. 7v2 v2
6 Г7-. 1 —
10 6
98 -55178 10 - 11V
198 . 42 25v2
66 J;.
V. V2
tg V V2 , V2
3 -j- 1 5- 3- 6V2
7 - — 5-
9 —. 42 —.
Функции Жуковского:
v2 3
4 4v i 1_ t 1
10v2 v2
lo r 3 7 — xT—r- 5- V
9—.
5 sv -2 Is 1
v2 SlftV J
310 v2 7v2
60 ——г 6 —
49 10 lb-
3720 . Q 551v
У о —
198 . Функции метода деформаций:
fis v tgv-v v2 2
212Г v л , v llv2. v2
2 tg -— v 15 1 -f
2 56-5- 30- 39v
И-‘- 28- 5V
78 4- v v —siiv ,. v2
2
2 tor у go s 6 —
о 9 v2 v2
74-гт 10
24 Ч v21 —
, о 1 2 _ О V2 _ 30
8 Р-2-——- 3 - —- -2
2tg —v 20 10
36 . v2
7 —
120 .1 Vs З2 30
9 Г у 6 2tgr-v 5 r-j 5 2 5v2 1 17v2
16В — — 2-
3- 84- 72
102 4i Функции метода деформаций для стержня с шарниром на одном конце
— v2 tfir v v2 3
10 т- 3-
rv-v 5_ 1_
v2 10v4
7 15 -
v2 _ V2
9- -г-— 7-
11- 30 —. 84
V
11 Т Г 3 2 — 0 2
tgv—v - V2 2v2
5v2 85v2
42 — ——- о —
3. 42 V2
51.
Разложение функции fx ж в непрерьлвную дробь может быть осуществлено также при помощи формулы:
х2Го
fx — о Ь
2_oIV
-r 2I-10IV2l 00 —
лу х2; 5б У12 - 3Qv0vm 0 21tVI-10JV2
18. Эпюры прогибов, углов поворота и изгибающих моментов стержня, подверженного продольно-поперечному изгибу
Для построения таких эпюр можно воспользоваться формулами метода начальных параметров:
sinv_Af0Z2 1 — cosv Q0l vC-sinAi4 e м vx—v в V3 В v3 lOOJ
ь qI sin V Qj 1 cos v. i г и
T 0 cos v f- —1-1 _дя; 157
MX — J f0v sin Д, cos v AMX. 158
При расчете рам по другим методам зачастую более удобными будут другие формулы с иными активными параметрами. Приведем уравнения эпюр vx, срж, Мх для упомянутых выше четырех основных методов расчета устойчивой прочности плоских рам см. 16.
Заменяя в формулах 156 —158 р0 выражением 74
If Мр Мг-Шг Q0l
В vtgv I vsinv v2 после преобразований получаем формулы метода сил активные параметры М0, Mit Q0:
.-к 159
Q.I АТ,; 160
И,-И, - ln‘-v Л,-ДИ,. ДЛ 161
Подставив в эти формулы вместо Qq его выражение 79
-1 - М0 Mt - AM г - - Д ф,
получим формулы балочного метода активные параметры
М0 Мх, ф:
—ш м- - 1р - 0- тег - 0
j — ДфЛ Avx; 162
Здесь мы отсчитываем прогибы от прямой, проходящей через левый конец стержня параллельно его первоначальному положению, иначе говоря, мы считаем,
ЧТО 10а 0.
85
т.—4- и, c”v‘b,sv-v-w- ф—Цд; 163
мм -insLv-W - АЛГ ТГШ 164
Заменив Л0 в формулах 156 —158 его выражением 80
Т tiT—iE7 ¥--Ql
юсле преобразований получим формулы метода узловых поворотов и поперечных сил активные параметры р0, pz, Q0:
7 cos 1 — С v — cos v , 7, А. 1 — cos Еу t
Vx 535 ьфа h Ф,-Аф, : ф
х то vsinv ти V S1QV
-. — - fi ,ьр -а
166
g V
мх — -7 Ро008 1 —5 V — , — Ар, с os Sv
SiL сое 1—6 v—cos Ь Шх. 167
Используя формулы 112 —114 и подставляя в формулы 159 —161
вместо
о о
м г Р ь — Аь — а Р Ф — Д 4,
о
М1—Ш1 — у ftpe а 9, — др, — а -ff J — Дф,
— QJ Щ- а Р о t — А Т Ф — АФJ
после преобразований получаем формулы метода деформаций:
- iО-тШ ь
- сЙ sl‘,r,Sv - ог -МО 168 Р1-хй1- -4й
- 1— S v coafiv — y t—AiI 169
Мх — Щ- a sin 1 — 0 v — Р sin EvJ
р sin 1 — v — а sin Sv р, — Дрх —
- а р sin 1 - v - sin Ь ф - Д1 Шх. 170
83
Приведем также выражения для Аиж, и АМх для самого
общего случая действия на стержень внешних сосредоточенных сил Р и моментов Му внешних распределенных поперечных q и моментных т нагрузок, а также при наличии первоначальных сосредоточенных деформаций сдвига Ь и перелома оси 0, первоначальной распределенной деформации сдвига оси и первоначальной распределенной кривизны х. В соответствии с формулами 23, 25 и 29:
азс
2 8аФ-а - 6аФ а - Щ- ФЛ Фх-а 2t
сх
2 уГФ” тГФ”сх.-
CeCj С2
- КФГ-ф ГФ5Т.-
б ИсФ-с тсФх1с.
4- -0 чЖ-с . 171
Взяв от 171 производную по х, получим:
ах
Дх Ц 5вФ- - - Ф- W 2
СХ
2 ШсФ-с Т2Ф-е ТГФ-с —
C2t
— хсФх-с хс Фх-с хс Ф. —
—7Г лЪсФхс 4 в2Ф-в 172
Пользуясь формулой 36:
Шх - - В Аху - ЯТ,
получаем:
ах
АДд. 2 — ВЬаФха - 56аФЛ-а Ь аФж-а -РдФ— ”f
сх
2 — - ТФх-с Yc Фзс-с — 1 Yc Фх-с П”0 CCj С2
в х2 Фя_с- 1 с Ф-с-V Г тсФя1с Фх-Пс Ь 10 —
— всФ.-1; Н” ЗсФх-с1 сФх-с J 173
87
I
г — doc
19, Интеграл Мора МХМ для двух эпюр моментов:
о
эпюры продольно-поперечного изгиба Мх и эпюры поперечного изгиба Мх М0 Q0
Такими интегралами нам придется в дальнейшем пользоваться при решении задач устойчивой прочности плоских рам. Мы приведем здесь вывод соответствующей формулы, основанный на применении начала возможных перемещений. Значительно более сложный вывод, основанный на непосредственном интегрировании подинтегральной функции после
подстановки в нее выражений для Мх и Мх, мы здесь опускаем, так как по существу единственным его результатом является подтверждение применимости начала возможных перемещений в обычной его форме к обычной задаче поперечного изгиба, что соверженно излишне. В случае равновесия работа внешних сил М0, Mt, Q0 и Q0 и внутренних Мх состояния поперечного изгиба на любой возможно малой деформации стержня должна равняться нулю. Возьмем фиг. 33 в качестве возможной
деформации — деформацию стержня от действия продольного усилия N и поперечных нагрузок. Тогда внешним силам будут соответствовать следующие перемещения:
обобщенная сила М0 Мх Q0l
перемещение р0 — ф ф
I, и таким образом:
i
5 J мхмх ¥0 - Мт Q0l.
JZl
9
I—1_
Фиг. 33.
Имея в виду, что
Qtl Мг- М
а
запишем
полученный результат еще в таком виде:
Мхмх dx
О
ч
В
М0 0 — 9i — Ф. 174
Более общий вид для формулы 174 получим, если в состоянии продольно-поперечного изгиба, кроме продольного усилия и поперечных нагрузок, будут иметь место также первоначальные деформации: сосредоточенные сдвиги оси 8а, сосредоточенные переломы оси 0а, распределенные сдвиги оси у и первоначальная кривизна х. В этом случае, еще до приложения внешних нагрузок, концевые сечения стержня будем его рассматривать как балку на двух опорах повернутся на углы1:
1 1 1 Л А Д I 7 V 4 t J XI f 0 Tf. I
0
9
о о
1 1
-2 6.8.-1 Я-2-у - 5 fxК.
о и
175
1 Величины р и помимо непосредственного их вывода легко также получить
как поперечные силы от нагрувки балки фиктивными грузами 0а, сосредоточенными моментами да и т. д.
88
Работа внешних сил останется без изменения:
м0 9о — Ф — Ж, — Ф,
к работе же внутренних сил нужно будет добавить работу изгибающих
моментов Ма и Мх на соответствующих перемещениях 0а и х dx и работу
поперечных усилий Q на перемещениях Ьа и 4dx.
Таким образом получим:
i i _ м0 — — ч1 — МХМХ 2 а9а Mxdz
о U
I
о
Учитывая, что:
Ма М01аМа шМх М0 1-5 , а также формулы а и 175, окончательно получаем:
мхмх J¥0 0-j- сре - м, -1 - 176
О
Заменим в формуле 174 р01 и i— Ю выражениями см. 106 и 107:
. М01. Мг1 Л. б
. _ au м,г. , б I
pz_d_ _ —sv_ v pj. J
Здесь ср и pf—углы поворота концов сжатого стержня как балки
на двух опорах, возникающие от воздействия пролетных факторов:
2М1_Дф, 1
fo 6 ВТ I 178у.
р гдм1_д1 д11 j
Таким образохм, вместо 174 получим:
a Is
МХМХ р Sf. Л0 МгМг МйМ1 MtM, т. 179
0
Этой формулой удобно пользоваться при решении задач устойчивой прочности по методу сил. Формулу эту можно записать еще в таком виде:
1
МХМХ f 2fv F0 svi 2vM, svF M0 Ж, cpf. 179
0
Преобразуем формулу 174 еще иначе, приведя к виду, удобному при решении задач по методу узловых поворотов и поперечных сил. Для этого используем формулу 114 метода деформаций
для поперечной силы:
е.-Т Р. -ТФ 180
где
; Р АТ, — уАф. 181.
Решая уравнение 180 относительно угла поворота стержня 1, получаем:
182
Подставив это выражение в формулу 174, найдем: i
мхмхр9ошо
tg 2
tg Ql 2- 183
2Т
20. О форме эпюры моментов и кривой прогибов сжато-изогнутого стержня
При рассмотрении этого вопроса ограничимся случаем, когда по длине стержня нет нагрузок. В этом случае см. 161
Мх М0 М
х 0 sm v 1 sm v
йли
ikfj — ikf0cos v
Мх Мс cos Sv -f-
sm v
sin v.
184
Приведем это выражение к виду:
Мх Ам sin v Ф Ам sin Ф cos Sv Ам cos Ф sin сv. Сравнивая почленно 184 с 185, получаем:
и
. М0 sin v
фагсмгщ
Ocos V
185
186
187
Форма кривой эпюры моментов представляет синусоиду с амплитудой Ам и сдвигом фазы на величину Ф. Длину волны Л синусоиды найдем из условия:
откуда
0туф-ьф12те
188
Длина волны А всецело определяется величиной отношения жесткости изгиба стержня к величине продольного усилия. По мере роста продольного усилия N длина волны меняется обратно пропорционально f N.
На фиг. 34, а толстая линия должна быть от точки 0 до точки I
90
Для определения характера кривой нужно еще знать две отвлеченные характеристики 0 и которые мы будем называть фиг. 34, а относительными абсциссами концов стержня.
Величины их найдем, положив в выражении 185 для Мх S 0 и 1:
Мл A sin Ф; Л, Двту Ф.
С другой стороны:
ЛГ, AMain 20; Мг АМ sin 2,.
Таким образом:
‘-г-.к 189
или
г 1. Мо sin v arctg Ml _ м0 cos v r 1. Мг sin v 2 arctg jjf cqs v — M0 j
190
Введем еще понятие относительной ординаты vx кривой прогибов, которую мы будем отсчитывать от линии давления, иначе говоря, от прямой, соединяющей точки перегиба синусоиды.
Тогда, очевидно:
Y МХ. MQ Ml , Д Q V
х— N 0 А и 41 1УД
Относительная эпюра прогибов будет выражаться уравнением:
ух sin Ь Ф, 192
в котором — амплитуда кривой прогибов
А 193
Очевидно, что относительные абсциссы С0 и С кривой прогибов те же, что у эпюры моментов.
Для стержня с постоянным продольным усилием по длине мы см. 4 получили выше:
MX MX Nvx,
отсюда:
Vx Мх хМ г1х—ПХ- 194
Если стержень не загружен пролетными нагрузками, то
п MqQqX
UX lx Решим такую задачу. Продольное усилие N сжато-изогнутого, не загруженного в пролете стержня растет, моменты же по концам сохраняют
постоянное отношение Как меняются относительные абсциссы С0
JVLq
и концов стержня
Возьмем производные по v от выражений 189 и 190:
dKfi п cos у — 1 в
dv 2 тс 1 — 2 л cos v л2
di 1 п2 — n cos v 57 2 Г— 2п cos v л2
С-Со_ 1
dv 2гс
Если М0 Mt, то п 1 и
__1.
dv 4те
91
Это значит, что в случае одновременного действия чистого изгиба и сжатия при росте продольной силы N абсцисса 0 уменьшается фиг. 34,6, а С увеличивается, причем кривая прогибов стремится развиться в более значительную дугу синусоиды. Относительные абсциссы 0 и в этом случае равны:
- 1 sinv те —v те-j-v
W- 2-arctgST
Если v тг, то С0 0, Сг 0,5 и кривая прогибов обращается в полуволну синусоиды. При дальнейшем росте силы N продолжается развитие кривой прогибов и при v абсциссы С0 —0,25; С 0,75 и кривая прогибов охватывает целую волну синусоиды между двумя горбами фиг. 34, в.
Если М0 — Ми то
—
4те
В этом случае кривая прогибов обратно-симметрична относительно своей середины, являющейся точкой перегиба фиг. 34, г. Вообще говоря, формула 189,. пригодная для любых соотношений между М0 и Мг и дающая
r- —г - v 189
легко позволяет судить о том, какую часть волны синусоиды охватывает кривая изгиба. Эта формула показывает, что при v 7r кривая изгиба соот
ветствует — , т. е. одной полуволне синусоиды, при v 2tc — целой волне, при v 3tc — трем вторым волны и т. д.
21. Развернутое решение задачи продольно-поперечного изгиба призматического стержня при учете деформаций сдвига
В 4 мы для этой задачи получили следующее диференциальное
уравнение 16:
у Л JLV J V0 4- v0 а
Ч GF1 EJ EJ GFX a
Для упрощения записи введем следующие обозначения:
1 — с J 195
N 1
c2EJ L 1
fjGk -Wy 197
В последнем уравнении 197 v представляет собой прогиб, который
мы получили бы из уравнения а, если бы пренебрегли в нем вторым
членом левой части, иначе говоря, если бы пренебрегли влиянием
продольного усилия N на деформации изгиба.
При этих обозначениях уравнение а можно записать:
0 . 198
Здесь Lj const и по длине стержня не меняется.
92
Решению уравнения см. 13 можно придать вид:
v v0 cos sin Y V. b
Первые два члена правой части являются общим решением однородного неполного уравнения v 4- а последний член F —частным
решением, удовлетворяющим последнему члену v.
Совершенно очевидно, что при составлении выражения для V можно пользоваться принципом наложения1.
Итак, решение уравнения 198 с принципиальной стороны должно совпадать с решением уравнения d 13 в форме 65:
. Ъ-0Ф ф1 11 ;ИФП1 tV.0D. С
Здесь мы дописали член который на основе принципа наложения аналогично указаниям 14 должен представлять собой влияние факторов, приложенных в пролетных сечениях стержня. Заменив функцию Ф и ее последовательные интегралы значениями по формулам 25, уравнению с придадим вид:
v v0 cos jr 1ч sin IX 1 — COS -f- - sin ф 12cs. .8. d
Применяя обозначения, аналогичные принятым ранее см. 14, мы можем всю совокупность членов, помещенных во второй строке уравнения d, обозначить через Av:
Av — 1 cos. е
Все члены правой части е, кроме последнего 8у, отражают влияние см. ниже уравнения i распределенных нагрузок и деформаций w, q, у0 начинающихся с левого конца стержня и имеющих интенсивность:
В уравнении d при учете деформаций сдвига мы должны вместо v взять в соответствии с формулами 4:
1 Действительно, если
v A2v; 4- A3v;,
причем
KYjrViv; r;nl пцГ
и, кроме того, при 0:
Fi F2 F3 0 и f; F FJ0,
то
Если факторы г, v2, приложены в разных сечениях х а19 х а2, ж я3, то и частные решения Vlt V2t F надо распространять в одном направлении — вправо от этих сечений, в которых приложены внешние факторы, их вызывающие.
93
откуда:
-VF-H0Kpsy;O- Затем:
1 G1
f в I— Т -if Г Ю
В этих уравнениях cpF — угол поворота поперечного сечения, у0 — первоначальная распределенная деформация сдвига оси стержня, х — первоначальная кривизна стержня, ш — распределенная моментная нагрузка. Таким образом:
Vo -Г Го ‘ Ь
Пользуясь формулой 197, находим:
- - ел; ; —k LsPйж;-I-1
Подставив выражения h и i в формулу d, мы получим развернутое уравнение кривой прогибов сжато-изогнутого стержня с учетом деформаций сдвига. В случае отсутствия у0, х и т и при уо 0 оно будет
WXfQTt. тэт тт
иметь вид:
Л-i, f r Sin X-Ц Д 1 -CC-i -
я-_1 2ЦСШ; - оу- 9
Взяв последовательные производные от этого уравнения, получим:
fp4-cVrfc,8-iwAsi4-
- 1-C08i i:j-J;5-i”-8fr: 200
ТП -cV- х Ж i SAMft-l7J;,ir1-
1—co8f1-s даг, 201
В уравнениях 199 — 201 qQ, qr0, — величины известные. Внешний вид этих уравнений весьма мало отличается от уравнений 32 34
см. 9, полученных нами при пренебрежении деформациями сдвига.
Более общие уравнения можно легко получить, подставив h и i в d
Мы всегда можем условиться отсчитывать прогибы v от прямой, параллельной первоначальному направлению стержня и проходящей черев его левый конец. В этом случае мы принимаем го 0; М0 М.
94
и продиференцировав дважды; в них будут известными также величины х, у0, т и их производные.
Сравнив 19 см. 5 с 196, мы получим:
Lx cL. 202
Подставив в формулы 199 — 201 х1 и согласно данному
1 в 8 обозначению 40, мы получим формулы зависимости между граничными параметрами обоих концов стержня:
g0l 1 — cos vt
2.tj Лил frF I Qo Л sinvi q0l N
— -tzjgfJ
-
Qof , qii EJ r GF
я V,
-sin Vj.
vi
— -Г Gii у
F.Ql д I _
V‘iTcfJ
COSV _ Ml I qol Л sin V1 Qo12 I C0SV1 vt cr-t-
q0l2 1 — COS Vj
EJ 1 GF
У 203
if S19‘_AM‘ 30 TVlSinVl
.jr g. cos Vl Щ.
Здесь А —знак приращения стоящей за ним величины, возникающего от влияния внешних воздействий на стержень, расположенных в его пролете. Правила составления выражения для этого приращения по формулам 199 — 201 совершенно аналогичны правилам, изложенным в 14., Сравнивая формулы 2ЭЗ с формулами 101, 101 и 101 см. 16 замечаем в них следующее соответствие:
Формулы 101
V
Ро
п
м0
Mi
Qo
Формулы 203
V
v11
сЧ
mF , Qo 0 GFX
1 GFt
QP 0
hj , Е M Qj
gjFx ;
На основе формул 101 —101 могут быть получены все формулы 16 и 17, относящиеся к различным методам расчета устойчивой прочности рам. Легко видеть, что для получения уточненных формул, учитывающих деформации сдвига оси стержня, достаточно в формулах 16 и 17 заменить величины v, ф, ср0, р М0, Мх и Q0 им соответствующими по вышеприведенной табличке. Для примера уточдим формулы 112 —114 метода деформаций 17:
..-¥ као
-.,О - - т р ОЮ
Гст;-дГда. --♦; а Р -4 Г т --4 204
205
206
9
Этим формулам можно придать более простой вид:
м acpfPf-aPc2— ;
м1-™ы Г- Р с- МЧ;
Qi -:™ Р f f 2 JQ - я.
204
205
206
где:
К - - Щ1 рДРГ - Р.вДф;
-;пп аАГ - аР ; I
QHo -Sffi Ke P А-ТС-
2Е
207
GFX
Z2
В случае отсутствия пролетных воздействий величины il, Mnlt Qt равны нулю. В формулах 204—207 величины а, р, у определяются в зависимости от численного значения величины vx.
Совершенно аналогично могут быть уточнены все остальные формулы 116 и 17.
ГЛАВА IV
НАЧАЛО ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ В ПРИМЕНЕНИИ К ЗАДАЧАМ УСТОЙЧИВОЙ ПРОЧНОСТИ ПЛОСКИХ СИСТЕМ
1. Общие соображения
Особенность применения начала возможных перемещений к задачам устойчивой прочности заключается в том, что в этом случае оно должно
отображать условия равновесия системы в деформированном ее состоянии при учете деформаций изгиба от действия продольных усилий стержней.
При этом, как это было показано выше, в задачах, относящихся к расчету инженерных сооружений, можно ограничиться рассмотрением малых деформаций.
Непосредственное применение формулы начала возможных перемещений или вытекающей из нее формулы Мора в обычном их виде, принятом в статике стержневых систем, при решении задач устойчивой прочности зачастую приводит н неправильным результатам.
Например, для задачи, показанной на фиг. 35, при непосредственном применении начала возможных перемещений в его обычной форме, каза-
N
1
1
1
1
—1
Рг
-—
1
1
1
1
N
мда
Uf Vz
4,
rt
r7777
M,Nta
Kir
Фиг. 35.
лось быестественным записать:
а
Pii Pv Nif — 2 -M We Y ds 0,
а при применении формулы Mopat
Рл 22 Nn 2 RJ ef Q Gf J 0.
ВГслучае пренебрежения деформациями сдвига и обжатия оси стержня казалось бы естественным:
Ь
1 Впервые доложено автором в Институте строительной механики АН УССР всентябре 1942 г.
96
Как мы убедимся дальше, все эти результаты а, Ь и Ь совершенно не верны.
Для применения к решению задач устойчивой прочности формулы эти нуждаются в некоторых коррективах.
Нужно рассматривать равновесие деформированного состояния системы, т. е. виртуальные деформации надо отсчитывать от деформированного состояния системы.
Пусть дан прямолинейный стержень переменного сечения с переменным по длине продольным сжимающим усилием Nx, изогнутый в одной из главных плоскостей жесткости. Изгибающий момент Мх и поперечная сила Qx в сечении х такого стержня в задачах устойчивой прочности определяется формулами:
X
Mx MlNxfxdx-, 1
U
2
где г;— прогиб стержня, а ; М и Qx — значения изгибающего момента и поперечной силы без учета деформаций. Если на стержень действуют сосредоточенные нагрузки Рп, распределенная поперечная нагрузка q,
кг м
распределенная моментная нагрузка т, имеющая размерность — кг,
М
а также в начальном сечении момент М0 и сила Q0, то:
XX X
Af —2 — qdxmdx. 3
0 0 о
Таким образом, можно считать, что при переходе от Мх к Мх как бы
добавляется влияние новой распределенной моментной нагрузки интен
сивностью:
4
Иначе говоря, расчет прогибов с учетом изгибающего действия продольных нагрузок расчет устойчивой прочности можно вести, как обычный расчет по недеформированной схеме при условии замены продольных нагрузок эквивалентной им воображаемой распределенной
моментной нагрузкой Nx , величина которой возрастает с возрастанием
прогибов.
Диференциальное уравнение изгиба сжато-изогнутого стержня:
5
о
дает линейную зависимость между прогибом v и поперечными нагрузками
М0, Q0, Р19 Р2 q, т, так как Мх является их линейной функцией см. 3, чего нельзя сказать относительно продольных нагрузок ввиду
Л у
наличия в 5 произведения продольной силы Nx па.
Поэтому в задачах устойчивой прочности можно пользоваться принципом наложения независихмости действия для поперечных нагрузок, при условии, что изменение последних не влечет за собой изменения продольных сил Nx.
При обычных расчетах мы пользуемся формулой Мора:
2p-2 ffTW s 6
7 Прочность и устойчивость стержневых систем 97
для работы внешних и внутренних сил Р, М, N, Q одного состояния
f — Mds Nds Qds
системы на соответствующих им перемещениях оР, , qT
другого состояния той же системы. Левая часть этой формулы охватывает собой работу всех внешних сил. Для отдельного стержня можно написать подробнее:
i i
2 РЬр му0 — Q0v — Mtvt Qfii 2 PnVn qv dx mvdx. 7
0 0
Непосредственное применение формулы 6 к задачам устойчивой прочности встречает затруднение. В этих задачах нужно рассматривать равновесие системы в деформированном состоянии, а добавление к наличным
перемещениям прогибам v дополнительных перемещений прогибов v должно вызвать существенное изменение внутренних сил. Эту трудность можно обойти, заменяя расчет по деформированной схеме обычным расчетом по недеформированной схеме и вводя при этом некоторую дополнительную внешнюю нагрузку, которая сделает оба расчета эквивалентными. Как мы показали выше см. формулу 4 такой дополнительной нагрузкой должна являться распределенная моментная нагрузка интенсивностью
mNxd Nxv
Работа такой нагрузки на соответствующих перемещениях углах поворота v другого состояния будет:
Xvdx 2 Noodx, или, после замены для общности записи dx на ds:
2 Nvvda.
В результате формула 6 для задач устойчивой прочности примет следующий вид:
Вышеприведенный вывод формулы 8 несколько схематичен. Ввиду
того, что эта формула является основной, докажем ее еще другим, более
строгим способом.
2. Вывод основной вариационной формулы 1
В основу вывода положим начало возможных перемещений для системы точек: если система точек находится в состоянии равновесия, то сумма работ сил, приложенных к этим точкам, на любых возможных элементарных перемещениях этих точек равняется нулю 2.
При выводе нам будут нужны диференциальные условия равновесия элемента стержня длиной dx:
dN п dx; 9
dQzz —qdx; 10
dM -Np m dx 11
1 Вывод, аналогичный приводимому здесь, был применен ранее автором для более простой задачи в его статье: Принцип возможных перемещений для упругой системы в Сборнике трудов Киевского строительного института, вып. 1, 1933.
2 Элементарными перемещениями называем перемещения столь малые, что они не вызывают изменения в величинах и направлениях действующих сил.
98
и зависимости между перемещениями и деформациями:
dtf — г dx 12
dvydx; 13
dcp dy— dx 14
В этих уравнениях и и и перемещения вдоль и поперек оси стержня
см, фиг. 36, ср — угол поворота элемента оси, з — относительное укороче-
ние, у —угол сдвига оси, х—кривизна изогнутой оси стержня, иначе
говоря, погонный угол изгибной деформации см. фиг. 13, х — координата по длине стержня.
Пусть нам задана какая-то стержневая система в деформированном сжато-изогнутом состоянии. Подразделим ее бесконечно большим числом дискретных поперечных сечений стержней на бесконечно-малые по длине элементы dx, причем обязательно будем брать поперечные сечения в местах приложения внешних сосредоточенных сил. На каждое поперечное сечение в центре его тяжести в местах отсутствия сосредоточенных нагрузок будут действовать фиг. 36 с одной стороны силы N, Q и М и с другой стороны силы такой же величины, но направленные в противоположном направлении. Можно сказать, что силы, приложенные к незагруженному сечению, уравновешены и что работа их на всяком элементарном перемещении равна нулю. Если к сечению хг приложены сосредоточенные продольные и поперечные наг- Qt-fрузки Тх и Рх и сосредоточенный внешний момент М, то по одну сторону от сечения действуют силы фиг. 36
Ml, Qi, м1г а по другую Nt N1 Tl, Qi Qi—Plt Фйг. Зб.
М Мг все же девять сил, приложенных к сечению, находятся в равновесии и работа их на любом элементарном перемещении сечения равна нулю. Вообразим какую-нибудь виртуальную возможную систему элементарных перемещений и деформаций для нашей стержневой системы, которую в отличие от истинных перемещений и деформаций системы и, v, ср, г, у, х будем обозначать с черточками и9 v, ср, а, у, х, причем:
du —adx; t2
dv — pdx; 13
dy — dy — xdx. 14
Запишем сумму работ сил, приложенных ко всем выбранным нами поперечным сечениям стержней нашей деформированной системы, на этих
виртуальных перемещениях и, v и р, являющихся функциями координаты х.
Для каждого отдельного поперечного сечения, согласно вышесказанному, сумма работ будет равна нулю; следовательно, и для совокупности всех рассматриваемых поперечных сечений сумма работ будет также равна нулю. Так как от перестановки слагаемых сумма не меняется то вместо того, чтобы сначала суммировать работы отдельных сил по сечениям, а затем работы для всех сечений, нагруженных внешними сосредоточенными силами Т, Р, М и не нагруженных, можно сначала
отдельно взять сумму работ внешних сосредоточенных сил и реакций
опор г.
1 К работе реакций опор относится и работа сил N, Q, М, действующих с внешней стороны торцевых крайних сечений стержней.
; 99
2 Тит2 Рр2
а
Ф
и к ней прибавить сумму работ сил N, Q и М, приложенных ко всем
рассматриваемым сечениям. Подразделим только работы этих сил на
группы, но не по сечениям, а иначе. Будем брать работы для групп
сил, приложенных между двумя смежными сечениями изогнутого стержня, из числа выбранных нами выше.
Общая сумма работ от этого не изменится. Такие два сечения фиг. 37 будут отстоять друг от
друга на расстоянии dx, а груп
па сил, между ними заключенная, будет состоять из сил N, Q и М, действующих на одно сечение и сил N -dN, Q dQ и М- dM, действующих на другое. Этим силам будут соответствовать следующие виртуальные перемещения:
-й
А
Л
У- If
Фиг. 37.
сила
Q Q dQ i N N dN I
M
M dM
перемещение
v
— v — do
— и
u-du
-T
-r df- ay
Для пояснения последних столбцов этой таблички отметим, что ф — угол поворота элемента оси, угол же поворота поперечного сечения меньше
его на угол сдвига, т. е. равняется ср — у: момент М приложен к поперечному сечению и соответствующее ему перемещение будет углом поворота
сечения, т. е. — 9 — у. Если взять сумму работ сил N, Q и М для всех интервалов между сечениями, то получим:
2 у - о do — Nu N dN 1a da —
— M 9 — у M dM 9 — у dcp — dy.
После приведения подобных членов и отбрасывания бесконечно малых высших порядков
dQ-dv; dN-du; rfifcf rfp — tfy
эта сумма примет вид:
— Qdc —- vdQ Ndu udN M dy — dy p — y dM.
2
Заменяя в этом выражении диференциалы виртуальных перемещений их выражениями 12 —14 через виртуальные деформации и диференг циалы усилий dN, dQ, и dM их выражениями 9 —11, получаем:
2 — ип — О У Q 9 rridx
или после приведения подобных членов:
2 пи СР m Np 9 — y dx — 2 Y N г dx. b
Сложив выражение а с выражением Ь, получим полную сумму работ сил всех сечений, которая должна быть равна нулю:
21 РоР Mf м 2 tre 4 m — Y1dx
2мр -тг-2Ф Лгв0‘ 15
100
Это и есть формула начала возможных перемещений применительно к задачам устойчивой прочности. Первая сумма в этой формуле представляет собой работу внешних сосредоточенных сил Т, Р и М, вторая — работу внешних распределенных нагрузок п, q и тп, четвертая — работу внутренних сил М, Q и N, Новой, по сравнению с обычным видом формулы начала возможных перемещений для стержневых систем в задачах прочности, является в задачах устойчивой прочности третья сумма. Наличие ее объясняется тем, что к категории внешних нагрузок добавляется еще нагрузка Ny, действующая по типу распределенной моментной нагрузки т.
Условно, для сокращения записи, будем обозначать виртуальную работу внешних сосредоточенных и распределенных сил через
2р2.Ттрр м.2 5 пи qv m р — у dx. 16
Принимая во внимание, что истинное перерезывающее усилие Qs при учете деформаций изгиба см. 2 равняется:
Q Q N9f 17
формулу 15 начала возможных перемещений для задач устойчивой прочности приводим к окончательному виду:
2 Мх ЛГг 2у dx 2р 2 N9 dx 18
Если, как это делается обычно при расчете рамных конструкций, мы пренебрежем работой сдвигов и обжатия, то формула 18 упростится:
2 М dx 1 2 9 dx. 19
Если для у. воспользоваться упрощенным выражением, соответствующим малым деформациям стержневой системы инженерного сооружения:
х —и
и, кроме того, иметь в виду, что
ср у и ср г, то формула 19 приобретет вид:
2 Modx 2 Nvvdx 2-PSp 0. 20
Наконец, если в этой формуле заменить:
М - EJv”,
то получим:
2 JEJvvdx 23р 2 Nvvdx- 21
3 Другой вывод основной вариационной формулы
Приведем еще другой вывод формулы 18, интересный с методической стороны.
Вывод этот построен на применении интегрирования по частям:1
udv — uv J — vdu.
Для простоты вывода будем считать, что наша система загружена только распределенными нагрузками пу q и ш. Учитывая, что сосредоточенные нагрузки можно рассматривать как предел распределенных нагрузок при концентрации их неравномерности, мы сможем обобщить вывод и на случай сосредоточенных нагрузок
1 В этой формуле и дальше в этом параграфе интегрирование мы проводим по всей длиье стержня для значений х от 0 до I.
101
Работа распределенной поперечной нагрузки одного стержня на виртуальных перемещениях равна:
qvdx — vdQ — vQ 20 -f Qydx. с
Здесь мы использэвали зависимости 10 и 13:
q dx —dQ и dv у dx
Подставим в с в соответствии с 11
Q dx dM — mdx — Ny dx
и затем заменим:
р dM М р о — М dy.
Получим:
gu dx — Qu М р о — р пг iVp dx — М df. d
Вычислим последний интеграл, заменив в нем согласно с 14 — х dx dy:
— М df Mxdx— М df Мх dx — MyJ-f- ydM —
Mv.dx — Му о у Q dx.
В результате подстановки этого выражения в d получим:
qv dx — Qy -r Mp — у J — у — y m iVp d -f-
J
0
Mdx Qdx. e
Составим выражение для работы распределенной продольной нагрузки:
udiV I Nu J- J Ndu.
Имея в виду, что da — sdx, получаем:
nudx Nu i Nedx.
Сложив выражения e и f, находим:
qv nu my — y dx-Qi-Qo-МгСп — Ъ-
oPo To — NiUi N0u0 MxQy-f Nedx- 22
— N p — уdx.
Левая часть этого уравнения представляет работу распределенных пролетных
нагрузок 7, п и т и опорных реакций, — она может быть сокращенно обозначена
через тогда 22 приобретает вид:
2 Рр Мх Qy 4 Ne dx — Ny — у dx. 22
Подставив согласно 17
Q QS_7V,
где Q —истинная поперечная сила перерезывающее усилие, получим:
2 Мр Мх Ni QtI dx С22
Обобщая это выражение на систему из ряда стержней перед знаками интегралов ставим 2, приходим к ранее нами полученному виду основной вариационной формулы 18 для задач устойчивой прочности стержневых систем.
102
4. Обобщение формулы Мора
Возьмем в качестве виртуальных перемещений перемещения той же стержневой системы, но в ином ее состоянии, соответствующие другой нагрузке, отличной от заданной. В этом случае:
ё — N т
EJ 4GF1 EF I
и формула 18 приобретает вид:
2 СШШ- 2v 2 24
В этой формуле, чтобы придать ей более обычный вид, мы заменили dx — ds.
5. Действие неравномерного нагрева
Возьмем в качестве виртуальных перемещения от действия на нашу систему неравномерного нагрева:
_af tu-t0 e
х
d
Y 0; 6 — ats- 25
Здесь at—линейный коэфициент температурного расширения; tu, tof ts — температуры снизу, сверху и по оси стержня, с —толщина стержня. Подставляя 25 в 18, получаем:
s 5 м :s 5 Nds 2б
где ор и р— перемещение и угол поворота из температурного состояния
системы.
6. Принцип взаимности работ
Если в формуле 24 поменять местами оба состояния системы: заданное без черточек и виртуальное нагрузочное с черточками, то левые части уравнения 24 не изменяются, значит, и правые части должны быть равны друг другу:
S 5 Nds25р 2 5 Nds- 27
Обычный свой вид принцип взаимности работ при обретает лишь в случае N N. Тогда:
2 2 27
7. Переход от обобщенной формулы в обычной формуле Мора
Если продольное усилие стержня N — 0, то в формуле 24 отпадает последний член. Такой же результат получится, если внутренние усилия стержня будут определены без учета влияния абсолютной величины деформаций, т. е. будут представлять собой М, Q0 и. Они должны уравновешиваться нагрузками Ру следовательно, формула 24 приобретает в этом случае обычный вид:
2С ММ. QQ , N , ооч
-eTgf1 ef ds2jpp- 28
Этот результат вполне понятен, так как тут силы М, Q, N, Р
взяты не из задачи устойчивой прочности, а просто из задачи прочности,
соответствующими же им перемещениями могут быть какие угодно возможные перемещения, в том числе и из задачи устойчивой прочности.
ЮЗ
8. Определение перемещений в задачах устойчивой прочности
При определении деформаций систем со сжато-и растянуто-изогнутыми стержнями, естественно усилия соответствующих единичных виртуальных состояний определить попроще, по недеформированной схеме сооружения, без учета изгибающего влияния продольной силы. Это позволит нам пользоваться обычной формулой 28. Пусть нам нужно определить перемещение ок сжато-изогнутой системы с усилиями М, Q, N, соответствующее обобщенной силе 1 k-то единичного виртуального состояния с усилиями Ми QL Nfc. Записав работу сил внешних lft и внутренних Mk, QI, Nk k-то единичного состояния на соответствующих им перемещениях действительного:
Mds Qds Nds
k ЁТ GF И W
получим:
ОТ
Если при расчете устойчивой прочности рамной конструкции пренебречь, как это принято при обычных расчетах, деформациями сдвига и обжатия оси, то:
Заметим, что в этих формулах Ьк—действительное перемещение сжато-изогнутой системы. Представление об единичном перемещении для сжато-изогнутой системы является условным ввиду того, что в общэм случае в задачах устойчивой прочности нельзя пользоваться принципом независимости действия сил. Символы okti и bkfP единичного и нагрузочного перемещений в задачах устойчивой прочности имеют особое, несколько условное, отличное от обычного значение, но об этом речь будет дальше.
9. Об условиях применения принципа аддитивности в задачах устойчивой прочности. Понятие о равносжатых состояниях системы
В 9 главы III мы получили формулы 32 — 35 метода начальных параметров для призматического сжато-изогнутого стержня. Эти формулы показывают, что действие на стержень, сжатый определенным и неизменным продольным усилием, поперечных сосредоточеных и распределенных нагрузок и деформаций подчиняется закону аддитивности, иначе говоря закону независимости действия. В 12 гл. III нами доказано, что это свойство остается справедливым для любого прямолинейного стержня также и в том случае, если жесткость изгиба этого стержня EJх и продольное усилие NX9 будучи величинами переменными по длине стержня, остаются неизменными в процессе загружения стержня. Для такого стержня можно, например, символически записать формулы метода начальных параметров для прогиба vx, угла поворота срж и изгибающего момента Мх в сечении на расстоянии х от левого конца стержня 0:
vx ВХМ0С XQ0
4xvx Axq- ВхМъ CxQo x 30
— vx АхУо ВхМ9 CXQ0 А В этих формулах коэфициенты Ах, Вх, Сх, А9Х,. совершенно не зависят поскольку мы для инженерных сооружений ограничиваемся рассмотрением деформаций малой величины от величин ср0, MQt Q0
101
и других поперечных нагрузок, расположенных в пролете стержня. Для данного стержня, определяемого его геометрическими размерами и упругими свойствами, при сохранении неизменной эпюры продольного усилия Nx эти коэфициенты Ах, Вх СХУ. всецело определяются положением сечения я, и не меняются при изменении действующих на стержень поперечных факторов: нагрузок Р, q, ilf, т и активных деформаций
о, б, у, х. Пролетные члены Аух, Дсрж, Д—также являются линейными функциями типа:
Ра Ь Ех-а,2 Рх-а а3 4 Gx-a4 0а4 Ь от пролетных поперечных факторов. Коэфициенты Dx-aif Ех-а2 ПРИ них вполне определяются эпюрой изгибной жесткости EJX стержня и эпюрой продольного усилия Nx.
Подставив в формулах 30 х1, где I—длина стержня, мы для
прямолинейного стержня 1аъ переменного поперечного сечения с перемен
ной по длине эпюрой Nx получим в общем случае следующие зависимости между граничными параметрами концов а и стержня:
U f В1М 1Q А; 31
Ма CiQa Acpa; 31
-ж.-4;,в:с:1-дё7.- 31
Пусть дан фиг. 38 стержень ломаного очертания аЬсЛ нагрузки стержня заданы. Предположим сначала, что нам известны продольное усилие Nab и граничные параметры МаЬ, Qab, cpa на конце а первого звена 1аЪ этого ломаного стержня. Тогда, проектируя силы, лежащие слева от сечения, на касательную и нормаль к оси стержня в этом сечении, мы легко строим эпюры продольного усилия Nx и поперечного усилия Qx для всего ломаного стержня. В дальнейшем мы считаем величины Nx и Qx известными. Это получается так просто благодаря принятому нами ранее условию
см. 2, гл. III о том, что величины Q и N мы считаем направленными в соответствии с первоначальной недеформированной схемой сооружения. Имея эпюру Nx, можно считать, что коэфициенты формул 30 и 31 величины А, В, С, ,. тоже известны.
Зная величины сра и Ма, мы по формулам 31, 31 и 31 легш найдем величины фа6, срь и Мъ. Затем, заменив в этих формулах индексы а и Ь через бис, легко найдем фьс Те и Ме Совершенно аналогично мы сможем найти параметры для всех остальных вершин и для правого конца ломаного стержня. Зная длины и углы поворота аЪ, Ьс, ФСсь. всех звеньев ломаного стержня, из кинематических соображений легко находим также линейные перемещения всех узлов ломаного стержня1. После этого, пользуясь формулами 30, мы можем найти величины
vx —10, рхи gy- для любого промежуточного сечения любого из прямолинейных звеньев ломаного стержня. Такой метод определения перемещений мы будем называть ко н с о л ь н ы м.
Решение получается просто, если известны величины усилий и перемещений на одном из концов стержня. Если не все эти величины известны,
1 Мы здесь ограничиваемся рассмотрением деформаций изгиба и пренебрегаем деформациями сдвига и обжатия оси стержня.
105
то задача несколько усложняется. Для определения некоторых из неизвестных на исходном конце ломаного стержня приходится привлечь граничные условия на другом его конце. Подробно об этом мы будем говорить дальше, в следующих главах. Сейчас же для нас важно отметить, что перемещения и усилия во всех точках ломаного стержня определяются при помощи линейных операций с выражениями типа 30 и 31. Эти же выражения в свою очередь линейны относительно поперечных нагрузок, если коэфициенты А, В, С, D,.формул 30 и 31 при этом определить по продольным усилиям Nx, соответствующим полной нагрузке стержня. Можно сказать фиг. 39, что линейные и угло-
выа перемещения, а также изгибающие моменты состояния 2 одноконтурной рамы равны суммам соответствующих величии состояний Р19 Р2, PZy если только для всех этих состояний 2, Pi Р2 Рз эпюры Nx одинаковы. Равенство эпюр продольного усилия Nx при разных нагрузках рамы может быть достигнуто путем добавочных взаимно-погашающихся на стержнях рамы местных продольных нагрузок см. фиг. 39 Р19 Р2, Рг, вызывающих дополнительное сжатие или растяжение элементов оси рамы1.
На фиг. 39 в состояниях Р19 Р2 и Р3 показаны тонкими стрелками такие дополнительные взаимно-уравновешенные нагрузки, уравнивающие желательным образом эпюры продольных сил состояний Р19 Р2 и Ps с эпюрой продольных сил для полного загружения рамы состояние 2
Пополним несколько нашу терминологию. Нагрузки типа Р19 Р2, РВ9. на фиг. 39, 2 мы будем называть изгибающими, или еще точнее искривляющими2, нагрузки продольные — осевыми. Два разно загруженных состояния одной и той же рамы мы будем называть р а в н о с ж а т ы м и, если в результате одновременного действия различных осевых и различных искривляющих нагрузок в этих состояниях получатся во всех соответственных сечениях одинаковые продольные усилия Nx безразлично усилия сжатия или усилия растяжения. Пользуясь этой терминологией, мы можем относительно рамы фиг. 39 сказать следующее: если искривляющие нагрузки состояния 2 представляют собой сумму искривляющих нагрузок отдельных, равносжатых с состоянием 2 состояний Р19 Р29 jPs,.,to: 1 изгибающие моменты в состоянии У равны сумме соответствующих изгибающих моментов состояний Р19 Р29 PSy.; 2 углы поворота р сечений состояния 2 равны суммам соответствующих углов поворота состояний Р19 Р2У jP3.; 3 вертикальные и горизонтальные перемещения в состоянии 2 равны суммам соответствующих перемещений в состояниях Ply Р2у PZ9.
Очевидно также, что если в двух равносжатых состояниях одной и той же рамы искривляющие нагрузки пропорциональны, то изгибающие
1 Например, если продольное усилие по длине стержня должно быть постоянно, т дополнительная нагрузка для этого стержня представляет собой систему из двух равнопротивоположных, взаимно-уравновешивающихся сил, приложенных по его концам.
2 Понятно, что в категорию искривляющих нагрузок искривляющих факторов входят также распределенные нагрузки д, внешние сосредоточенные и распределенные моменты М и га, а также активные внешние сосредоточенные или распределенные деформации сдвига и искривления оси стержня деформации d, 0,.
106
моменты, углы поворота сечений, вертикальные и горизонтальные прогибы в этих состояниях прямо пропорциональны искривляющим нагрузкам.
Ра вносжатыми единичными состояниями системы в дальнейшем будем называть состояния, равносжатые с заданным расчетным состоянием системы, но загруженные единичными искривляющими нагрузочными или деформационными факторами. Например, для системы фиг. 40, ив качестве равносжатых единичных состояний можно принять состояния, показанные на фиг. 40, б. В соответствии с вышесказанным очевидно, что изгибающий момент расчетного состояния:
М2 XMi qMi PMv-,
32
тде Мх, Mqs1, Mpi — изгибающие моменты в соответствующих сечениях
равносжатых единичных состояний. То же можно сказать и о прогибах и углах поворота р сечений рамы:
срЕ Xxi qyqi Ppvi.
32
32
о
I
N,
N,
t
N I
H,
n Nz 1 p-1
Фиг. 40.
Формулы 32 и 32” в математической форме отображают сформулированный выше принцип аддитивности искривляющих факторов. В более общем виде их можно записать так:
опЕ хг 1 X2 2 Х3 Вп,3. Рт1 РтЪпут. 32
Здесь oik — перемещение в к-м равносжатом единичном состоянии по направлению lf силы единица i-го единичного состояния.
Хотя вышеприведенные рассуждения были проведены нами для одноконтурной рамы, тем не менее не трудно видеть, что они справедливы и в более общем случае, т. е. для многоконтурных рам. Нужно оговориться, что сделанные в этом параграфе выводы относятся, собственно говоря, к случаю, когда рассматриваются одни изгибные деформации. При учете деформаций сдвига и обжатия оси эти выводы нуждаются еще в некоторой дополнительной трактовке; этот вопрос ввиду второстепенного его значения оставляем пока в стороне.
Ограничимся указанием, что формула 29:
‘ 2trw 29
остается верной в самом общем случае. Принцип же аддитивности искривляющих факторов мы будем относить пока только к первому ее члену:
V С ds, которым обычно ограничиваются при решении практиче-
EJ
ских задач.
107
10. Определение перемещении единичных равносжатых состояний
Такие перемещения можно определить по формуле 29 или, если пренебречь деформациями сдвига и обжатия оси стержня, по формуле 29:
kt
Ml
О Mids
EJ
33
Для удобства пользования формулой 33 введем еще одно новое понятие. Момент М19 входящий в эту формулу, относится к i-му единичному равносжатому состоянию. Величину такого момента мы определяем по деформированной схеме этого состояния. Что же касается момента il, то о нем мы будем говорить, что он относится к А-му
первоначальному единичному состоянию, так как момент М к,
в соответствии с 7 и 8
7X7.
Л
I
0
1
t
Л
и
V7,
к
7t77
Фиг. 41.
мы определяем по первоначальной недеформированной схеме этого состояния. Таким образом, для каждого типа единичного загружения например, для загружения lfc у нас будет по два единичных состояния: равно
сжатое с нагрузкой 1к — ед иница A-я и первоначальное
с нагрузкой 1 — единица A-я нулевая. Моменты и перемещения А-го равносжатого состояния мы будем обозначать Мк и Bl7c, моменты и перемещения первоначального А-го состояния мы будем обозначать теми же буквами,
но с добавлением нуликов в виде показателей степени: Мк и Ък.
На фиг. 41 показаны два таких состояния, каждое в двух вариантах. Пользуясь формулой:
РЕр 2n9ds мм, 34
запишем работу сил внешних и внутренних А-го состояния на соответствующих им перемещениях сначала г-го, а потом г-го состояния. Получим:
Аналогично для работы сил А-го г-го и г-го состояний получим:
i2 s к,2
EJ СОСТОЯНИЯ
на
a
b
перемещениях
c
d
Состояния А-е и -е равносжатые, поэтому:
Nk Nt N. е
Поменяв местами состояния А-е и -е в формуле а, приходим к выводу:
kiik 3
Сделав то же в формуле d, получим:
108
Использовав формулу с, найдем:
36
Сравнив а и с, найдем:
37
38
Аналогично можно получить формулы для главных перемещений:
36
а также для перемещений нагрузочных равносжатых состояний
36
Итак, перемещения равносжатых состояний могут быть определены по формулам 36, 36 и 36. Интегралы этих формул могут быть вычислены в соответствии с данными 18 главы III. Для вычисления этих интегралов нужно знать по концам каждого стержня рамы либо изгибающие моменты М, либо углы поворота р — ф, либо углы поворота р и поперечные силы Q. Именно в этом состоит основная трудность определения перемещений равносжатых состояний. Задача эта может быть решена различными путями: можно использовать консольный способ, намеченный в предыдущем параграфе, можно, наконец, последовательно и многократно использовать формулы 36 — 36, введя добавочные первоначальные единичные состояния для определения недостающих перемещений в узлах рамы1. Обо всем этом подробно будем говорить в следующих главах.
11. Определение реакций единичных равносжатых состояний
При обычном расчете прочности рам по методу деформаций принято на действительную систему накладывать дополнительные связи, соответствующие неизвестным перемещениям. Искомые неизвестные определяются из уравнений, представляющих собой условия равенства нулю реакций этих дополнительных связзй
Представим себе к-е единичное равносжатое состояние основной системы с наложенными дополнительными связями, загруженное активным перемещением одной гз Дополнительных связей А:-й связи , равным единице. Составам формулу для реакции i-й связи к-ю равносжатого состояния. Для этого нам придется
заплсать по формуле 84 работу сил внешних ть r2fc, г,. и внутренних Ми к-го равносжатого едингчного состояния основной системы на соответствующих им перемещениях i-ro первоначального единичного состояния основной системы. В i-м состоянии перемещение, соответствующее реакции равно lj l, перещения
же, соответствующие всем остальным реакциям г2к отличным от г,
равны нулю. Таким образом, получим:
1 С помощью узловых перемещений зачастую легко из условий статики найти также узловые моменты.
2 См., например, И. М. Рабинович, Курс строительной механики стержневых систем, часть 2-я, Стройиздат, 1940, 138, 151; А. А. Гвоздев, Общий метод расчета статически неопределимых систем, Москва, 1927; И. П. Прокофьев, Теория сооружений, Стройиздат, ч. 2-я, 1940, 61, 73, 74.
3 Вычисления по формуле 39 достаточно сложны, поэтому при решении задач устойчивой прочности на практике приходится искать другую трактовку для метода деформаций.
Mids EJ
откуда
39
100
12 Переход к формулам энергетического метода
Применяя в формуле 24 силы и перемещения одного и того же деформирован ного состояния системы, т. е. принимая в качестве виртуальных перемещений действительные, мы формулу 24 можем переписать в следующем виде:
2U
М2 Q2 N2
2 EJ 2 GFt 2 EF
42рр2
v2 ,
ds.
2
40
Сформулировать ее можно так. При переходе от задач прочности к задачам устойчивой прочности в формулу равенства потенциальной энергии дзформации — работе внешних сил, должна быть внесена поправка: работу внешних сил нужно увеличить на работу продольных усилий на перемещениях, связанных с отклонением осей стержней системы при ее деформации от их первэначальных направлений. Действительно,
работу силы N на перемещении, вызванном по-
0 воротом элемента ds на угол р г, можно пред-
N ставить:
Фиг. 42.
N ds 1 — cos р Nds 2 sin2 Nds 2 v2
— N ds.
2
Если пренебречь деформациями сдвига и обжатия оси и, кроме того, подставить вместо М —EJv, то формула 40 приобретает вид:
2 ej ds 2 рР2 N ds-
41
Формулы 40 и 41 относятся к задачам устойчивой прочности. Пзрэходя к таким задачам устойчивости, в которых до потери устойчивости, деформации не имеют мэста точнее не учитываются, мы можзм в уравнениях 49 и 41 отброзить также и тогда придем к формулам:
или
2 -2
2 EJ vf ds 2 N ds.
42
43
13. Пример неправильного применения начала возможных перемещении
В развитие сказанного в начале 1 этой главы покажем на элементарном примере, к каким ошибкам может привести непосредственное примзнзниз начала возможных перемещзний, взятого в его обычной форме бзз коррективов, предложенных в этой главе. Примзням начало возможных перемещзннй к внзшним и внутренним силам балки на двух опорах, сжатой сллами N и изогнутой моментом М0 фиг. 42,1, и
к перемещзниям той же балки, изогнутой моментом М0 при отсутствии продольных сил
- Ml
фиг- 42, II. Моменту М0 состояния I соответствует угол поворота Рооё7 состояния
Ож2 J
И, продольной силе N соответствует казалось бы так сближение опор а и b состояния II:
-—о
1 г - 1 г Г , ‘Л2-х Зх2 л2 , м;3
jL 0 6IEJ J У0 EJ2
о о
1 Эти две формулы обычно без знаков S широко использовались многими исследователями при решении задач устойчивости стержней. Формула 43 соответствует методике, широко применявшейся С. Г1. Тимошенко в его брошюре Об устойчивости упругих систем, Киев 1910, и в последующих его работах. Энергетический метод применялся нами также в ряде работ, в частности, в Исследовании устойчивости пространственного каркаса по типу высотной части Дворца Советов СССР, изд. Акад. наук УССР, 1938.
110
Изгибающему моменту Мх, равному см. 161 гл. III, 18:
ъг М0. i — я V
3fx -т—- sin —j-t— sinv I 9
соответствует взаимный угол поворота двух сечений:
1i ydx ilg t Л j
-—- dx.
EJ IEJ
Итак, применяя нескорректированную формулу начала возможных перемещений, мы получшм бы:
1 _
- - Г Mxdx
0 - а
о
или после подстановки приведенных выше значений:
М01 му _ М0 ; -v М0 -. МОЗЁ7ЛГ90Б7- з sTTv —I Tej—
D
N12
Выполнив интегрирование и заменив v2, найдем:
M0M0l 2 M1 _M0M0l siv —vcosv
wv 90Ё7 Ё7 v2 sin v
Если бы формула а была взрна, то уравнзние Ь должно было бы превратиться
в тождество. Но уравнение Ь преврашаэтся в тождество только при v 0, т. е.
при N 0.
Итак, формула а для задач продольно-поперечного изгиба не верна. Применив к этой же задаче скорректированное уравнение начала возможных перемещзиий, получим:
i I __
Mofo No4,dx мх. с
6 О
Здесь v в соответствии с 160 гл. III, 18:
1-х v
_М01 I ll
v EJ L v sin v v2J
Подставив это выражение в с и выполнив все операции, получим тождество:
M0M0l sin v — v cos v _ M0M0l sin v — v cos v EJ v2sinv — EJ v2siav
что и требовалось покаэать.
ГЛАВА V
ОБЩИЕ ПОЛОЖЕНИЯ ПО РАСЧЕТУ УСТОЙЧИВОЙ ПРОЧНОСТИ И РАСЧЕТУ УСТОЙЧИВОСТИ ПЛОСКИХ РАМ
1. О предварительном определении продольных усилий в стержнях рам,
Моноциклические н полицикличесвие задачи
Как нами было выяснено в 9 гл. IV, при расчете устойчивой прочности плоских рам, точнее при определении их изгибных деформаций, а также изгибающих моментов и поперечных сил, можно пользоваться принципом аддитивности, если каким-либо образом до этого определены продольные усилия в стержнях рамы. Таким образом, расчет подразделяется на две части. Сначала, хотя бы приближенно это зачастую оказывается вполне достаточным, нужно найти продольные усилия стержней рамы. Тогда вторая часть расчета приведется к составлению и решению системы линейных уравнений. Если же считать продольные усилия стержней неизвестными, точнее, если определять продольные усилия
111
стержней и изгибающие моменты или деформации одновременно, то уже нельзя будет пользоваться принципом аддитивности так как он недействителен для продольных нагрузок в задачах устойчивой прочности и задача сведется к решению совместной системы сложных трансцендентных уравнений. Поясним это подробнее.
При расчете устойчивой прочности плоских рам приходится в основном опираться на зависимости между граничными параметрами для отдельных стержней рамы, подробно рассмотренные в главе III. Эти зависимости линейно связывают между собой величины М0, 0, Мг, срь Q, О и нагрузки стержня. В то же время коэфициенты при этих величинах представляют сложные трансцендентные функции от величины
решения сложных трансцендентных уравнений, желательно величины N, т. е. продольные усилия стержней, рассматривать как величины известные. Если нельзя сразу указать их окончательные значения, то в большинстве случаев не представляет особого труда определить их с достаточным приближением и затем по этим приближенным значениям продольных усилий N вычислить для всех стержней рамы величины
v V -ру. После этого, пользуясь таблицами или графиками, нетрудно
найти значения трансцендентных коэфициентов формул t, s, а, 3,., или каких-либо других, связывающих граничные параметры. Дальнейший расчет устойчивой прочности рамной системы сводится к решению системы линейных уравнений для нахождения граничных параметров отдельных стержней рамы. Затем из условий равновесия узлов рамы следует определить уточненные продольные усилия стержней и сравнить их с ранее принятыми. В случае малой разницы расчет можно считать окончательным. Если же разница в значениях N получится заметной, то нужно по новым уточненным значениям N найти опять значение трансцендентных функций величины v и принять их за основу для повторного цикла расчета. Зачастую даже при заметных разницах в значениях N величины трансцендентных коэфициентов наших формул, старые и уточненные, настолько мало отличаются друг от друга, что надобность в повторном цикле расчета отпадает. Это легко понять, так как обычно трансцендентные коэфициенты формул меняются значительно медленнее, чем величины соответствующих им продольных усилий стержней1.
Задачи, при решении которых с самого начала можно указать точные значения продольных усилий N, будем называть моноциклическими, а задачи, до решения которых нельзя получить точных значений продольных усилий стержней, будем называть полициклическими. Очевидно, что при решении задач моноциклических сразу получается окончательный расчет, при решении же задач полициклических могут быть случаи, когда нельзя будет ограничиться первым циклом расчета. Другое различие заключается в том, что моноциклические задачи приводят к решению системы линейных уравнений, а полициклические задачи, решаемые в несколько циклов, соответствуют по существу приближенному определению корней трансцендентных уравнений.
При выполнении отдельного цикла расчета в задачах устойчивой прочности разыскиваются усилия и деформации, соответствующие вполне определенным значениям внешней нагрузки. При решении задач устойчивости разыскивается величина критической нагрузки, вызывающей потерю устой
1 9то особенно относится к коэфициентам а, р, а-J-B, Формул метода деформаций см. фиг. 28 пливно и медленно меняющимся в широких пределах значелмй v. Зн ачительно сложнее обстоит вопрос с балочным методом, коэфициенты которого t и s претерпевают разрывы непрерывности см. фиг. 27 при сравнительно малых значениях величины v.
Поэтому, чтобы в задачах устойчивой прочности избежать
112
чивости системы. Так как значение нагрузки в задачах устойчивости неизвестно, то ясно, что все задачи устойчивости рамных систем должны быть отнесены к категории задач полициклических. Добавим к этому, что решение задач устойчивости рамных систем приводит к нахождению корней трансцендентных уравнений, что также является отличительным признаком полициклических задач.
Отметим еще, что к задачам устойчивости и устойчивой прочности, вообще говоря, не подходит классификация в смысле статической определимости. Статически определимыми мы называем задачи, которые можно решить на основе одних условий равновесия без привлечения к решению данных об упругих свойствах системы. Поскольку при решении задач устойчивости и устойчивой прочности рамных систем мы не можем
Фиг, 43.
отвлечься от их упругих свойств, постольку не приходится говорить
о статически определимых задачах в этой области.
Тем не менее, в так называемых статически определимых системах не всегда —но зачастую можно точно определить продольные усилия N стержней в зависимости от внешних нагрузок. Например, систему по типу ломаной консоли фиг. 43, а мы можем назвать моноциклической. Задачи же, показанные на фиг. 43 б, в, г, вообще говоря, задачи полициклические, так как деформации системы вызывают некоторые изменения реакций, а, следовательно, и усилий N стержней. Мы такие задачи предлагаем называть квази-моноциклическими, потому что в этих задачах, хотя и не вполне точно, но с вполне достаточной степенью приближения можно указать продольные усилия стержней.
В задачах моноциклических не составляет трудности параллельно с деформациями изгиба учесть сразу же и продольные деформации оси стержня. В задачах полициклических, приближенно намечая продольные усилия стержней для определения трансцендентных коэфициентов формул, можно одновременно с этим подсчитать также по формуле Гука приближенные удлинения стержней и ввести их в дальнейший расчет. Но, как это принято обычно и подтверждается приводимыми дальше примерами расчета, при расчете рам не только можно, но даже и следует во избежание излишних усложнений пренебрегать продольными деформациями стержней по сравнению с деформациями их изгиба. В особо же ответственных случаях влияние продольных деформаций можно учесть в порядке уточнения при специальном повторном цикле расчета аналогично тому, как это делается при обычном расчете прочности рам по методу деформаций2.
Предварительное приближенное определение продольных усилий N стержней рамы может быть выполнено различными способами. Можно, например, распределение продольных усилий принимать в соответствии с обычным статическим расчетом прочности рамы; можно распределение усилий получить более точно на оспове описываемых далее приближен -
1 Напоминаем, что продольное усилие N мы считаем направленным параллельно первоначальному направлению стержня до деформации системы см. 2, гл. III.
2 См., например, проф. И. М. Р а б и н о в и ч, Курс строит, механики стержневых систем, ч. 2, 148 и 144, Стройиздат, 1940.
8 Прочность и устойчивость стержневых систем
113
ных методов расчета устойчивой прочности рамы; в простейших случаях можно даже распределить нагрузку ригелей рамы между стойками, как для системы разрезных балок с шарнирами над стойками.
В задачах устойчивости, если нагрузка приложена в узлах рамы так, что до момента потери устойчивости изгибные деформации вообще отсутствуют, распределение продольных усилий можно производить по шарнирной схеме рамы. Такое распределение не требует последующих коррективов, так как приращения усилий, возникающие в момент потери устойчивости, могут рассматриваться как величины бесконечно малые по сравнению с величинами продольных усилий N, имевших место до момента потери устойчивости.
2. Об отдельном цикле расчета устойчивой прочности плоской рамы
При расчете устойчивой прочности мы будем рассматривать раму как систему, составленную из отдельных стержней и узлов, связанных между собой. Рама будет правильно рассчитана, если будут удовлетворены:
1 условия статики, 2 условия кинематики и 3 условия упругости.
Условия статики заключаются в том, что каждый стержень и каждый узел рамы должен находиться в состоянии равновесия под влиянием внешних нагрузок и концевых усилий, передающихся на него со стороны смежных с ним элементов. Условия равновесия узла а можно записать в таком виде:
Здесь Qamy Nam, Мат — поперечная сила, продольная сила и изгибающий момент на конце а стержня 1ат рамы; Ра и Ма — внешние нагрузки узла а. Индексы х, у, и z обозначают оси, на которые проектируются величины, заключенные в скобки ось z — перпендикулярна плоскости рамы. За знаком сумм в уравнениях 1 — 3 стоят все величины, примыкающие к узлу а.
Условия равновесия стержня 1о1 если на стержне нет продольных нагрузок могут быть записаны так:
Условия кинематики заключаются в том, что во всех узлах рамы, включая и опорные, должны быть удовлетворены условия сопряженности, соответствующие кинематической схеме рамы, в отношении линейных и угловых перемещений между узлами и примыкающими к ним элементами. Так, например, если узел жесткий, то концы всех стержней, в нем сходящихся, имеют одинаковые углы поворота:
Замкнутость контуров рамы, обусловливаемая ее связями, не нарушается при деформации рамы:
1
а
а
а
2
а
а
а
О
а
а
Qi QoJr Qii ,
Mt - ДМ, M0 Q0l N11,-
5
4
9аЪ — ас — ad — 6
2j Wabk 2j bu W-h U J
7
114
В этих уравнениях А 1аЪ — удлинение стержня 1аЬ, направленное вдоль оси его на первоначальной недеформированной схеме рамы; oab labab — перемещение от поворота стержня рамы, направленное под прямым углом к этому удлинению; AL — изменения длин хорд, соединяющих свободные или опорные концы цепи стержней рамы. Уравнения 7 означают, что суммы проекций этих величин для отдельной цепи стержней рамы на оси х и у равны нулю.
Присоединяя к цепи стержней хорду как некоторый воображаемый стержень, замыкающий цепь и приравнивая величину AL — удлинению этого стержня, мы можем отбросить в уравнениях 7 последние слагаемые и записать их так:
2 маъ cos и 2 sin x
— 2 008 Vab У 2 Sb sin U У 0. I
Во избежание путаницы со знаками синусов и косинусов, будем придавать всем стержням контура направления, обходя контур по часовой стрелке, и брать углы по часовой стрелке от положительного направления оси х или у до положительного направления стержня. Отметим, что оси хну могут не пересекаться под прямым углом, нужно только, чтобы они не были параллельны друг другу. В замкнутом многоугольном контуре фиг. 44 мы можем, пользуясь двумя уравнениями
7, выразить перемещения поворота Sob
— аъУаь любых двух непараллельных стержней контура, как функцию от удлинений стержней если мы их учитываем и от перемещений поворота остальных стержней контура. Можно при этом избежать совместного решения системы двух уравнений; для этого достаточно выбрать оси х и у вдоль стержней, перемещения поворота ЪаЬ —
— labtyab которых мы примем за величины кинематически зависимые
Например, если для рамы фиг. 44 мы примем как кинематически независимые перемещения 8о1, 23, 845 стоек и горизонтального стержня, то для определения 812 наклонного стержня надо спроектировать удлинения и перемещения поворота всех стержней контура на ось другого наклонного стержня 34 и, наоборот, для определения 834— на ось 112. Так, проектируя на ось 1 — 2, имеем:
Фиг. 44.
— 2д cos Л оо1 sin Л01 012 0-f 023 sin A3 5S1 sin Аы 845 sin Л45 0,
откуда
j
734 34
lz4 sin А
34
Г 041 sin Ао1 023 sin А3 sin45 2 созЛ
Условия упругости заключаются в соблюдении для каждого стержня рамы двух зависимостей между нагрузками и деформациями. Такие зависимости могут быть записаны, например, в виде уравнений 101 и 101 16 главы III, связывающих между собой граничные параметры стержня1:
1 Уравнение 101 гл. III непосредственно вытекает из уравнений 8 и 9 и условия равновесия стержня 5 этой главы,
8 115
Mt — Mt t sm v -f. M cos v -f QJ
8
0
Условия кинематики рамы и условия равновесия ее узлов дают зависимости между граничными параметрами различных ее стержней.
Условия упругости стержня 8 и 9 и условие 5 равновесия моментов сил, к нему приложенных, дают три зависимости между шестью граничными параметрами данного стержня.
Шесть граничных параметров стержня разбиваются на три пары: Ма и р0, Мг и Q0 и ф взаимосопряженных параметров. Произведения Л0р0, Mfli и Ql дают работу обобщенных сил M0,MU Q0 на соответствующих им обобщенных перемещениях р0, рг, 0. Из шести параметров стержня три могут быть названы активными и три пассивными. Это значит, что для постановки задачи о расчете сжатоизогнутого стержня нужно кроме его поперечных нагрузок и продольной силы N знать также любые три из шести его граничных параметров. Число различных распределений шести параметров на три активных и три пассивных весьма велико, оно равно числу сочетаний из 6 эле-
являются такие симметричные относительно концов О ж I стержня распределения, при которых один из параметров взаимносопряженных пар считается активным, а другой пассивным. Таких распределений всего четыре:
Этим четырем распределениям соответствуют четыре основных метода расчета устойчивой прочности плоских рам.
Расчет рамы в основном заключается в определении из условий равновесия, кинематики и упругости активных параметров для всех стержней з тем, чтобы заменить расчет системы расчетом отдельных ее стержней В принципе он может быть подразделен на следующие этапы:
1 выбор активных параметров рамы выбор основной системы и назначение неизвестных;
2 составление системы уравнений, соответствующей выбранным неизвестным;
3 решение системы уравнений с определением активных граничных параметров для всех стержней;
4 расчет по граничным параметрам отдельных стержней, заключающийся в построении эпюр М, Q и v и в определении напряжений для опасных сечений рамы.
В связи с тем, что для каждого стержня рамы надо найти по три активных параметра, мы приходим к выводу, что максимальное число неизвестных, подлежащих определению для перехода к расчету отдельных стержней, равно утроенному числу стержней рамы. Для определения этих неизвестных используются условия статики для узлов рамы и условия кинематики для узлов шарнирной схемы рамы,1
Многие из этих условий дают настолько простые зависимости между граничными параметрами стержней рамы, что по несколько граничных параметров для различных стержней могут быть объединены вместе и в дальнейшем расчете представлены в виде одного неизвестного.
1 Шарнирной схемой рамы называется шарнирно-стержневая изменяемая или неизменяемая система, получающаяся из рамы при замене в ней всех жестких узлов шарнирами.
ментов по 3, а именно
Но наиболее естественными
активные M0,MhQ0 М0,Мг, ф 0, Ф То. i Qo
пассивные р0, р;, ф 0 рг, Q0 М0, Mh Q0 ilf0, Мь ф
116
Так, например, условия кинематики узла дают равенство друг другу и углу поворота р узла углов поворота всех жестко прикрепленных к узлу концов стержней. Условия кинематики шарнирной схемы рамы позволяют выразить углы ф поворота всех ее стержней в виде линейных функций нескольких независимых смещений Аи Д2, Д8,., число которых равно числу степеней кинематической свободы шарнирной схемы рамы, величине значительно меньшей числа стержней рамы. Поэтому при расчете нецелесобразно вводить в качестве неизвестных углы поворота всех ее стержней, а достаточно принять за неизвестные независимые смещения ltA2 Д3,.
Если рама представляет собой многоугольный контур, то величины N и Q для всех стержней могут быть представлены в виде суммы проекций на первоначальные направления стержней и нормалей к ним продоль ной и поперечной силы в опорном закреплении рамы, возникающих при ее искривлении, и известных внешних нагрузок, лежащих между этим опорным закреплением и рассматриваемым сечением рамы. Таким образом, граничные параметры — силы Q для всех стержней рамы могут быть представлены в виде линейных функций двух независимых параметров рамы: сил N и Q в опорном сечении.
Из условия равновесия узлов рамы легко получить простые выражения для момента М на одном из прилегающих к узлу концов стержней через такие же выражения моментов на других прилегающих к узлу концах стержней. Таким образом, число неизвестных может быть значительно снижено против Зп, т. е. максимального числа неизвестных, равного утроенному числу узлов п.
После выбора неизвестных, являющихся активными параметрами рамы, мы как бы заменяем заданную нам раму другой системой, в которой все неизвестные из пассивных величин, вызываемых нагрузками рамы, превращаются в активные воздействия. Для этого в местах приложения неизвестных, относящихся к категории внутренних усилий системы, удаляются соответствующие им упругие связи, в местах приложения неизвестных, относящихся к категории перемещений, вводятся новые кинематические связи.
Полученная таким образом упругая система, являющаяся основой последующего расчета, ногит название основной системы. Работа основной системы совпадает с работой заданной нам рамы в том случае, если величины всех назначенных неизвестных—активных параметров рамы, приложенных к основной системе, будут равны соответствующим пассивным величинам из заданной рамы. В противном случае работа основной системы будет отличаться от работы заданной рамы: в местах приложения неизвестных — сил в основной системе возникнут разрывы непрерывности в деформациях, а в местах приложения неизвест ных — перемещений в основной системе возникнут дополнительные реакции во вновь введенных кинематических связях. Систему уравнений для определения этих неизвестных получим, приравняв нулю выражения для величин разрывов непрерывности в деформациях и для реакций дополнительно введенных связей.
Составление системы уравнений для определения неизвестных всегда может быть выполнено в каноническом виде при ус ловии использования начала возможных перемещений.д
Уравнение, соответствующее основному неизвестному — внутреннему усилию, — надо составлять приравнивая нулю виртуальную работу сил соответствующего этому неизвестному первоначального единичного состояния гл. IV, 10 на перемещениях действительного, сжатоизогнутого состояния основной системы. При этом перемещение, соответствующее неизвестному внутреннему усилию, мы принимаем равным нулю.
117
Уравнение, соответствующее основному неизвестному — перемещению, надо составлять, приравнивая нулю виртуальную работу сил действительного сжато-изогнутого состояния основной системы на перемещениях соответственного данному неизвестному первоначального единичного состояния. При этом реакцию дополнительной связи в действительном состоянии мы считаем равной нулю, так что и работа ее на перемещении первоначального состояния отпадает. Для избежания
осложнений с вычислением NytfdSy в отличие от обычной трактовки
см. 11 гл. IV, можно в качестве единичных состояний выбирать состояния шарнирной схемы рамы с единичным перемещением, соответствующим данной неизвестной. Подробней об этом будет сказано в 6 этой главы.
3 О расчете устойчивости рам
Пусть для заданной рамы нами составлена система уравнений устойчивой прочности в виде табл, 9.
Таблица 9
1
1
Яц
1
1г
10
21
22
1
ат
20
i
т
П1
а а 2
i
1 апп
1
ПО
Здесь для общности мы обозначили буквами Xlt Х2 Хп неизвестные нам основные параметры рамы. Коэфициенты aki и свободные члены aki этих уравнений являются как об этом говорилось выше в этой главе функциями продольных усилий N стержней рамы, точнее — функциями
Г 2
для стержней рамы. Если система уравнений 10
составлена в канонической форме, то коэфициенты с одинаковыми индексами равны друг другу:
aki aik. 11
Решение этой системы уравнений удобно записать при помощи детерминантов:
D,
и вообще
т 1 12
где
а
а
11
la
D
21
22 13
И
Детерминант Dm получим, заменив в детерминанте D wi-ый столбец: т соответственно свободными членами а10,а20,.,апо.
Если все свободные чдены этой системы уравнений равны нулю: 1о а2о лпо 0, то мы.тогда имеем дело с так называемой чис
той задачей устойчивости.
Тривиальное решение системы уравнений 10 даст нам в этом случае нулевые значения.
Для того чтобы рама потеряла устойчивость, нужно наоборот, чтобы эти параметры или хотя бы некоторая их часть могла отличаться от нуля. А это при а1о а2д. 0, т. е. при D1D2. 0, может получиться только в том случае, когда детерминант D знаменателя дробей 12 обращается в нуль. Итак, можно сказать, что необходимым условием для критического состояния такой рамы будет равенство нулю детерминанта 13. Раскрывая этот детерминант, мы, вообще говоря, получаем трансцендентное уравнение, связывающее между собой величины v для различных стержней рамы. В простейших случаях определение критических значений vKp может быть выполнено непосредственно из этого уравнения. В более -сложных случаях приходится прибегать к графическому определению критического значения нагрузки. Для этого нужно выразить все величины v для разных стержней рамы в функции от некоторого коэфициента пропорциональности к, на который мы будем множить продольные усилия N, соответствующие заданным расчетным нагрузкам.
Мы будем отыскивать kiq— Л критическое коэффициент запаса устойчивости, которому соответствует наинизшее критическое состояние рамы. Для этого нужно построить график зависимости значений детерминанта D от величин А
Давая к различные числовые значения, начиная от нуля и больше1, мы вычисляем соответствующие значения детерминанта и по точкам строим график фиг. 45. Ближайшая к началу координат точка пересечения кривой графика с осью к даст нам наименьшее значениие к критического: Amin- Для уменьшения количества вычислений мы, вычислив значение D при к 0, увеличиваем к до тех пор, пока D не изменит знака. Тогда мы начинаем уточнять значение ктп. Практика вычислений3 показала нам, что численные значения детерминанта D удобней всего выполнять с помощью алгоритма Гаусса3.
Решая по Гауссу систему уравнений 10, мы последовательно исключаем неизвестные Х19 затем Х2 и т. д.
При этом мы имеем возможность выполнить все текущие проверки и таким образом гарантировать себя от арифметических ошибок. В результате последовательного исключения неизвестных мы придем вместо системы 10 табл. 9 к системе уравнений, приведенной в табл. 10.
Известно, что величина детерминанта не меняется, если из любой его троки вычесть помноженную на произвольный конечный коэфициент любую другую из его строк. Так как переход от системы уравнений 10
1 Значению к 0 соответствует расчет рамы по ее первоначальной недеформированной схеме. Коэфициенты апт, определенные при к 0, получатся такими же, как при обычном статическом расчете рамы.
2 См. нашу работу: Исследование устойчивости пространственного каркаса Дворца Советов СССР, стр. 40, 148—150 и 222, изд. АН У ССР, Киев 1938.
3 См., например, А. А. У м а н с к и й, Специальный курс строительной механики,
ч. 1, гл. IV, ОНТИ, 1935.
11
Таблица 10
1
Хг
Хп
1
kn
Л12
Д18
а1
22
23
а2
а33
а
m
а
ю
а
21
а:
1
а
2
Зп
а
20
2
30
у 14
птг
апП_1
По
к системе уравнений видеть, что:
14 совершался именно этим путем, то легка
D
a н
О
О
О
О
О
12 а13
ati
О
О
О
О
41
42
о
о
о
in
а2п
Ж
ПП
что D равно произведению
Раскрывая этот детерминант, находим, коэфициентов главной его диагонали, т. е.
D йц с . йпп 15
Если все или часть свободных членов системы уравнений 10 не равны нулю, то мы, вообще говоря, имеем дело с задачей устойчивой прочности. Но при этом могут быть случаи, когда при постепенном деформировании рамы, связанном с ростом нагрузки, внезапно появляются отсутствовавшие до того, принципиально новые, формы деформации. Момент возникновения этих деформаций соответствует некоторому критическому состоянию, за которым следует потеря устойчивости предшествовавшей деформации. Легко представить себе пример такой деформации. Пусть нам дана симметричная и симметрично загруженная система; деформация такой системы вначале будет также симметричной нарушение ее симметрии будет соответствовать потере устойчивости.
Обнаружить такое состояние можно различными способами. В случае симметричной симметрично загруженной системы можно прибегнуть к групповым неизвестным, составить несимметричные неизвестные Хп —
Хп Хп из двух составляющих: прямо симметричной Хп и обратно симметричной X. Тогда система уравнений разделится на две независимые системы. Одна из них будет включать в себя только симметричные неизвестные; эта система будет иметь свободные члены, и она будет соответствовать задаче устойчивой прочности. Другая система уравнений будет содержать только антисимметричные неизвестные; эта система не будет иметь свободных членов, она соответствует задаче устойчивости подробнее см. 8 настоящей главы.
4. Введение обозначении, удобных при расчете рам
На чертеже рамы каждому ее узлу присвоим особое численное или буквенное наименование фиг. 46. Величины, относящиеся к узлам например, величины их углов поворота или величины их линейны
12Р
перемещений, будем обозначать буквой, соответствующей данной величине, с индексом, соответствующим названию узла например, рх, р2,. 9 Ра А2, , У обозначений величин, относящихся
к стержням, будем ставить в индексе два знака, соответствующих наименованиям узлов, к которым относится стержень. При обозначениях граничных параметров мы в индексе на первом месте будем ставить значок, относящийся к тому же концу стержня, к которому относится данный параметр. Так, например, момент или поперечную силу на конце h
3
Фиг. 46, Фиг. 47.
стержня 1аЬ мы будем соответственно обозначать МаЪ и Qab, а такие же величины на конце Ъ—буквами МЪа и Qba.
Для придания большего единообразия формулам для символа момента с двумя значками в индексе МаЪ или МЪа примем другое правило знаков, чем это было раньше. Мы уже не будем их называть изгибающими моментами на концах стержня, а концевыми моментами и будем их считать положительными в том случае, если они будут действовать на стержень по часовой, а на узел — против часовой стрелки фиг. 47.
В неразрезных прямолинейных или ломаных балках мы будем ставить в символе для момента в узле п один значок Мп и будем считать такой момент изгибающим с сохранением для него обычного правила знаков.
Изгибающие моменты по концам стержня 1аЪ будем обозначать: Мьа на конце а и Ml на конце 6; понятно, что Ма — Маъ и Мъ —МЬа. На схеме рамы будем проводить пунктирную тень по одну сторону от ее стержней фиг. 48 и будем считать изгибающий момент положительным, если он изгибает стержень выпуклостью в сторону пунктирной тени.
Ниже мы будем пользоваться формулами для стержня 1аЬ, для составления которых надо будет всюду в формулах главы III произвести, замену:
р———
F.
1
1
1
1
1
1 1
1
1 1
1
1 1
7777У77777777Г
Фиг. 48.
обозначений:
м0
Ml
Q
о ;
г
♦
В
i
V
на обозначения:
МаЪ
ИЛИ
Мь
а
-МЬа
ИЛИ
маь
Qab
Р
1
1
ь
bib
tab
Величины АМи Ау1 Д1 будем обозначать соответственно: — АМЪаг
Путем введения этих и некоторых других дополнительных обозначений вместо AMbay AfbafAfpba мы в дальнейшем объединим основные формулы для МаЪ и МЪа, для fa и ,f br тдк что формулы для разных КОНЦОВстержня станут симметричными в смысле знаков.
121
5. Кинематические зависимости между углами поворота стержней свободных рам
Этот вопрос достаточно и с разных точек зрения освещен в литературе, посвященной обычному расчету рам. Поэтому мы остановимся нэ нем только вкратце. В 2 мы говорили о нахождении этих зависимостей аналитически при помощи уравнений 7 замкнутости контуров рамы. Очень часто эти зависимости выясняются также графическим путем с последующим аналитическим оформлением. Мы здесь ограничимся как более общим приемом, позволяющим учитывать удлинения стержней построениями полярного плана диаграммы Виллио. О применении неполярного плана диаграммы скоростей можно найти в литературе Ч
Пусть дана какая-нибудь рама фиг. 49, а. Прежде всего выясняем число кинематически независимых углов 6 поворота ее стержней
036
4Ш47
8
Фяг. 49.
О но равно числу степеней кинематической свободы шарнирной схемы рамы. Иначе говоря, оно равно числу стержней, которое нужно добавить к раме после постановки в ней шарниров во всех узлах с тем, чтобы превратить ее в статически определимую геометрически неизменяемую систему. Легко видеть, что рама фиг. 49 имеет две степени кинематической свободы. Линейные перемещения ее узлов при известных удлинениях стержней вполне определяются двумя величинами, например, горизонтальными сдвигами узлов 1 и 2, или углами поворота стержней 101 и 112. Обозначим кинематически независимые углы поворота r 60l и 0И 112. Тогда для угла поворота любого стержня 1аЬ можно записать:
В этой формуле —угол поворота стержня 1аЬу вызванный поворотом Iil при фп0 и при равенстве нулю удлинений всех стержней;
OS—угол поворота стержня 1аЪ, вызванный поворотом ц 1 приф1 0 и при равенстве нулю удлинений всех стержней; — угол поворота стержня 1аЬ, вызванный удлинениями стержней рамы при
1 ц 0.
Если в качестве кинематически независимых величин мы примем не углы поворота и п стержней, а линейные смещения узлов Дх и Ди, то формула 16 запишется так:
tyab 1 ФаЬ Ац 1 См., например, И. М. Р а б и и о в и ч, Методы расчета рам, ОНТИ, ч. II, 1934, гл. 1; И. П. Прокофьев, Теория сооружений, Стройиздат, ч. II, 1940, 67;
Б. И. Жемочкин, Расчет статически неопределимых рамных систем. Способ угловых деформаций, Гостроййздат, 1931, в; А А. У м а н с к и й, Статика и кинематика рамных конструкций 3, статья в сборнике Исследования по теории сооружений, ОНТИ, 1936.
122
Обозначая через oab взаимный сдвиг концов стержня 1аЪу вызываемый
SS
-его поворотом на угол 1аЬ , мы формуле 16 можем придать такой ид:
1 , и ab , аЪ 1лп
ь — 1Т Фи 1 Ьу- 17
ab аЬ 1аЪ
В этих формулах bj и фи или Aj и Ап величины неизвестные;
д1 а11
— и 1 -—вполне определяются геометрической схемой рамы;
— определяются значениями удлинений стержней и геометрической схемой рамы.
Углы поворота стержней 1а6 и соответствующие им величины ьаЬ Цаъаъ мы считаем положительными в случае поворота стержней по часовой стрелке.
Определение величин оможет быть выполнено при помощи: по
строения диаграммы Виллио фиг. 49, б. Точки 0, 3, 6, как неподвижные, будут находиться в полюсе этой диаграммы, точка 1 при повороте стержня 0 — 1 на угол 11 переместится от полюса вправо на величину tyi 01 l‘Ai hi Для получения точки 4 проводим на диаграмме через точку 1 нормаль к направлению 1 — 4 и через точку 3 нормаль к направлению 3— 4 и затем ищем точку пересечения этих нормалей. Аналогично находим точку 7. Точка 2 совпадает с точкой 1, так как при построении этой диаграммы мы считаем фп ф12 0. Аналогично найдем точки: 5 и 8.
Таким образом, мы приходим к выводу, что
7. 1 51 51 1 rm
U 1 — Ч1 14 25 — 12 45 78 V,
l7 68-,itg; Sj7.
На фиг. 49, в ц г показаны аналогично построенные диаграммы Виллио
для определения величин при п 1; AZ 0; i 0 и для определения величин lab при ф1 фи 0; Мф 0. При построении последней предположено, что удлинения всех стержней рамы положительны. Обычно при решении задач устойчивости и устойчивой прочности рамных кон
струкций мы пренебрегаем деформациями обжатия их стержней. Учет этих деформаций производится только в особых случаях, когда влияние их сравнимо с влиянием изгибных деформаций.
6. Составление уравнений, соответствующих неизвестным — кинематически независимым смещениям
Покажем общий прием составления таких уравнений в канонической форме, удобный для задач устойчивой прочности. Пусть для рамы фиг. 50,. а надо составить уравнение, соответствующее неизвестному— кинематически независимому углу поворота Представим основную
систему этой рамы в виде шарнирной цепи фиг. 50, б, загруженной кроме заданных внешних нагрузок моментами Ма Мь,. в местах постановки дополнительных шарниров и удерживаемую в состоянии геометрически неизменяемой системы дополнительными стержнями на фиг. 50, б показанными пунктиром, соответствующими кинематически независимым смещениям. Усилия этих стержней должны равняться нулю, так как в действительном состоянии рамы фиг. 50, а они отсутствуют. В качестве виртуального единичного состояния этой системы рассмотрим фиг. 50, в перемещение шарнирной цепи схемы нашей рамы при на
133
рушении целостности одного из дополнительных стержней, а имёйно при
деформации tyil. Запишем в соответствии с формулой 18 главы IV работу сил состояния б на перемещениях состояния в:
2 2-2
Замечая, что для отдельного стержня 1аЪ величина г tyab, после приведения подобных членов получаем:
I
2 РЬ 2 Ма-Мь Nv ds фаа 0.
о
18
7Л 1
7777777777777.
7777777777
777777777777.
0.4.3
Фиг. 50.
Из условий равновесия для стержня 1аЪ можно записать следующее равенство:
г
Ма Nv ds — Mh Qab — 2 Pnbn 0, а
о
где Ъп — плечо для силы Рп относительно конца Ъ стержня 1аЪ.
Введем обозначение:
-ъ 2рк
19
для поперечной реакции от заданных внешних нагрузок Р стержня аЬу рассматриваемого как свободно опертая балка. Тогда уравнение а можно переписать так:
i
Ма-Мь 5 Nv ds Qab - Qab lab 0, b
0
а уравнению 18 можно придать следующий вид:
2 Р 2 - Qab Кь,
20
где
Подставив в формулу 20 вместо Qab его выражение через принятые нами основные неизвестные — параметры рамы, получим требуемое уравнение, соответствующее заданной неизвестной — кинематически независимому смещению. Формуле 20 можно дать еще другой вид, преобразовав
выражение для работы внешних сил 2-РЗр- Из диаграммы Виллио, соответствующей единичному состоянию i l, мы можем легко получить горизонтальные ul и вертикальные vl перемещения любого узла а шар-
iu
мирной цепи в виртуальном состоянии фиг. 50, г. Пусть фиг. 51 Hat Нъ, Vat Vb гРизонтальные и вертикальные опорные реакции; по концам стержня 1аЪ рассматриваемого как абсолютно жесткое тело, уравновешивающие нагрузку стержня внешними силами Pl9 Piy. Располагая тремя условиями равновесия стержня и произвольно задавая по своему выбору одну из этих четырех реакций например, полагая, что
Нъ 0, мы остальные три выражаем вполне определенно через нагрузки Р стержня. Произвол в выборе одной из этих четырех реакций не оказывает никакого влияния на дальнейшие результаты. Запишем теперь работу внешних нагрузок рамы на соответствующих им перемещениях виртуального состояния:
2р2 н- 2 v- 21
- 1
Использовав это уравнение, из 20 получим:
Vi
а
Фиг. 51;
2 2 Но 2 Qab Kb-
22
Этой формулой мы и рекомендуем пользоваться при составлении уравнений, соответствующих неизвестным — кинематически независимым смещениям.
Пусть, например, требуется составить уравнение, соответствующее неизвестной Д1—горизонтальному смещению узлов ригеля рамной эстакады с параллельными стойками фиг. 52, а,.В этом случае, как легко зидеть из диаграммы Виллио фиг. 52, б и как это, вообще, известно,
горизонтальные смещения всех узлов ригеля: u1 uz. и9 Дв 1.
Вертикальные же смещения этих узлов vx vs. v9 можно считать равными нулю. В результате, применив формулу 22, получим:
W- 12 Qab-Qab- 1,
стосп
или ввиду отсутствия поперечных нагрузок на стойках Qab 0:
Ф
б
2 Qab W. 23
стоек
0,246.8 1.Щ9
Фиг. 52.
Это легко может быть получено непосредственно из условий равновесия отсеченного ригеля рамы при проектировании на горизонталь действующих на него сил. Этот простой пример выбран нами с целью показать, что составление уравнений изложенным выше способом приводит к знакомым нам результатам.
Этот способ составления уравнений особенно эффективен в сложных случаях, когда составление уравнений другими способами представляет затруднения.
В качестве более сложного примера рекомендуем снова раму, изобра-
jn г
женную на фиг. 50, а. Для этой рамы можно принять: Ff У2 считая
Г р
все остальные V и Н равными нулю. Из диаграммы Виллио фиг. 50, г,
125
соответствующей виртуэльному состоянию фиг. 50, в, мы легко находим что:
1 0; v2 — TtgA 01 h h ll 2vSin И 23 2 sin Л
В результате получаем искомое уравнение:
v оу , 2 О -
или
л-да.-. вЬлп
При составлении этого уравнения мы учли, что нагрузки на стержнях 0—1 и 2 — 3 нет, и поэтому положили
Qu1 Q23 — 0.
7. О взаимности коэфициентов канонической системы уравнений
отдельного цикла расчета устойчивой прочности
Выше см. 9 гл. IV и 1 и 2 гл. V мы выяснили, что при со
ставлении уравнений для отдельного цикла задачи устойчивой прочности для всех искривляющих факторов можно пользоваться принципом
аддитивности при условии сохранения неизменными осевых факторов Это значит, что мы можем выразить в виде линейной функции от основных искривляющих параметров рамы назовем их для общности Xlf Х2, Х3,. любое перемещение и любое усилие:
— Ъкр Хгок1 -f Х2ок2 Х3ол.3 4-. ;
Р х2 ХгФ3. ;
М Мр ХгМг Х2М2 Х3М3.;
Q—Qp X1Q1 X2Q2 XZQZ.;
N NPNX N NZ.
Подставим эти выражения в обобщенную формулу Мора см. формулу 24;
2 5 т87ггЯ -2 5 w0.
При составлении канонического уравнения для Хп нужно будет в него
подставить вместо М, Q, N, р, ор соответственно выражения Мп, Qn, Nn 9nt рп Легко видеть, что коэфициент апт в этом уравнении при Хт будет иметь вид:
2 И Т2 - 2 S 24
Аналогичное выражение можно составить для коэфициента апт при Хл в каноническом уравнении для Хт. Это выражение отличается от 24 только порядком букв тип. Таким образом получаем, что
тп пт
Этот результат совершенно не зависит от природы неизвестных Хп и Хт. Они могут быть оба — усилиями, оба — перемещениями, одно — усилием, а другое — перемещением, во всех случаях формула 25 остается справедливой.
126
В предыдущем параграфе нами предложен метод составления уравнений, соответствующих неизвестным — кинематически независимым перемещениям. Хотя этот метод по существу своему отличается от метода составления канонической системы уравнений, на основе которого нами получена формула 24, тем не менее системы уравнений, составленные этими двумя различными способами, тождественно совпадают. Мы не будем приводить здесь доказательства этого положения и ограничимся указанием, что уравнения, составленные для какого-либо кинематически независимого перемещения по обоим способам выражают собою равенство нулю реакции определенной дополнительной связи, препятствующей этому перемещению, и совершенно не содержат в себе условий, соответствующих другим дополнительным связям и неизвестным. В 3 главы VII покажем, что способ составления уравнений, данный в 6 настоящей главы, обеспечивает взаимность коэфициентов системы уравнений метода деформаций по формуле 25.
8. О расчете симметричных, симметрично загруженных систем
Симметричные, симметрично загруженные системы до потери их устойчивости деформируются симметрично, причем эпюры продольного усилия iV, изгибающего момента М прямо-симметричны, а эпюры поперечной силы Q и уголов поворота 9 или — обратно-симметричны.
При расчете таких систем неизвестные следует выбирать симметрично, то есть в симметричных сечениях и симметрично направленными. Если число неизвестных получается нечетным, то одно из неизвестных или несколько можно выбрать в сечении по оси симметрии системы. Условимся симметрично приложенные в симметричных сечениях неизвестные обозначать соответственно: Хг и XXt и Х2,. и, вообще, Хп и Хп. Каждую из них можно разложить на симметричную Yn и антисимметричную Ъп составляющие, причем:
Хя Yn Zn и Хл, Yn -Zn. 26
Ясно, что до потери устойчивости при симметричном загружении в симметричных системах могут иметь место только симметричные составляющие, т. е. до потери устойчивости
Х Х- У И z 0.
В 7 мы доказали, что в плоской задаче устойчивости или устойчивой прочности систему уравнений для неизвестных можно всегда составить в канонической симметричной форме так, что коэфициенты при неизвестных:
nm :sz тп
В симметричных, симметрично загруженных системах к этому можно будет добавить
пт тп nni тгп I 27
1тгп пт J J
no no- 28
Вследствие этих соотношений систему уравнений для неизвестных
можно представить в виде табл. 11.
Матрица коэфициентов при неизвестных получается симметричной относительно обеих своих главных диагоналей. Рассмотрим два симметричных уравнения, п-ое и п-ое:
Хгапг X2an2 Xzanz. Хапгг Хапг2-гХгапг1 яло 0, Хха.г 4 Xtcinf2 -f- Xzanz-j-. - X9dnz rj- X2n2 -j- Хат апо — 0. J
127
Таблица 11
Хг
3
з
l
1
11
18
_
13
а12
11
ю
12
22
23
п а 23
_ а22
2l
20
. 29
ап
Я 22
а23
23
22
12
20
л аг1
12
13
13
12
11
.Заменим в них Хп и Хпг по формуле 26:
Y1 ат ani апг ап2 ani ani 2 апг апг П0
1 ani Ь ат h 2 апТ2 Ь ат Zi аЛ artl - -Za д2 лЛ.
апо- О5
Заменим теперь эти два последних уравнения их полусуммой и их
полуразн остью:
Y1 ат ап,1 Y яП2 апг2 Уз апз anz Ь апо 0; с
1 Л1 Vl Ь 2 12 2 Z3 лз ц f Ь 0 В результате таких преобразований можно систему уравнений а с неизвестными X заменить двумя независимыми системами уравнений с одинаковым общим количеством неизвестных, равным та к см. дальше 30 и 31. В одной системе уравнений останутся только Yn симметричные составляющие неизвестных и свободные члены, во второй системе уравнений только Zn антисимметричные составляющие неизвестных, причем эта последняя система получится однородной без свободных членов. Вид этих систем уравнений будет:
1 для симметричных составляющих табл. 12
Таблица 12
У
Уг
Ут
1
а1111
aib2i
12Ь12
азЬ2
imim
2tnbam
10 1 20
;
Y 30
mifmi
т2Ьт-
тт1тт
то j
128
2 для антисимметричных составляющих табл. 13
Таблица 13
Zk
all а11
aU aki
ак-2 к 2
ахк
a2fc ” 2к
акк акк
О
О
о
31
Легко видеть, что эти системы уравнений получаются опять в симметричном каноническом виде.
Если система и ее нагрузка имеют несколько осей симметрии, то совершенно аналогично можно продолжать разложение систем уравнений 30 и 31 на новые составляющие, симметричные относительно второй оси симметрии, потом третьей оси симметрии и т. д.1
Полученный нами результат можно было бы представить несколько иначе. Известно, что детерминант не меняет своей величины, если к любой из его колонок прибавить или от нее отнять любую другую кроме данной колонку. То же самое можно сказать и о строках детерминанта: величина детерминанта не меняется, если к любой его строке прибавить или от нее отнять любую другую его строку. Выполняя выше операцию Ь замены Хп и Хп через Yn и Z, мы как бы заменяем одну из симметричных колонок детерминанта, составленного из коэфициентов при нейзвестных в системе уравнений 29, их суммой, а другую — их разностью, от этого величина детерминанта не изменяется. Заменяя уравнения Ь их полусуммой с и полуразностью d, величину детерминанта уменьшаем в 4 раза. В результате этих замен, выполненных со всеми колонками и строками детерминанта 29, мы его приводим, примерно, к виду:
ООО ООО ООО
4Р WWW 0 0 0
о
о
о
о
о
о
о
о
о
о
о
о
Иначе говоря, детерминант, составленный из коэфициентов при неизвестных системы уравнений 29, можно представить с точностью до нешторого постоянного множителя 4Р как произведение детерминантов, составленных из коэфициентов при неизвестных систем уравнений 30 и 31. Любой корень детерминанта системы 29 является корнем или дегр минанта системы 30 или детерминанта системы 31.
1 Этот прием был использован по нашему совету инж. М. Я. Бородянским в его кандидатской диссертации, посвященной исследованию устойчивости пространственных рамных куполов.
9 Прочность и устойчивость стержневых систем
189
Применим вышесказанное к задачам устойчивости, для которых в системе уравнений 29 отсутствуют свободные члены. Исследование системы уравнений устойчивости для определения наименьшей критической нагрузки требует большой вычислительной работы. Для симметричных, симметрично загруженных систем такое исследование можно значительно облегчитьДело в том, что детерминант устойчивости всегда1 может быть составлен в канонической форме с симметрией коэфициентов относительно главной диагонали. В случае симметрии системы и нагрузок, симметрично располагая соответствующие уравнения устойчивости, можно достигнуть симметрии в этом детерминанте относительно обеих его главных диагоналей. Такой детерминант, как показано выше, может быть разложен на два множителя — детерминанта низших порядков: один из них отвечает симметричным формам потери устойчивости, а другой обратно-симметричным. Таким образом, при исследовании упругой устойчивости симметричных, симметрично загруженных систем достаточно отдельно рассмотреть симметричные и отдельно обратно-симметричные формы потери устойчивости. Комбинированные формы не могут дать меньшей критической нагрузки, чем наиболее опасная чистая форма. Использование этого принципа значительно облегчает исследования устойчивости сложных систем2.
В конце 3 настоящей главы мы уже говорили о расчете устойчивой прочности симметричных, симметрично загруженных систем. Здесь мы можем более углубленно проиллюстрировать сказанное там.
Во всех случаях, при решении таких задач следует систему уравнений типа 29 расчленять на две независимые системы по типу 30 и 31. Таким образом задача устойчивой прочности симметричной и симметрично загруженной системы распадается на две задачи :1 собственно задачу устойчивой прочности, для изучения которой служит система уравнений 30, и 2 задачу устойчивости, для которой используется система уравнений 31. Первая задача состоит в изучении ускоренного роста наличных симметричных деформаций и усилий по мере увеличения внешних симметричных нагрузок. Вторая задача состоит в определении наименьшей критической нагрузки, при которой становится возможным появление цовых несимметричных составляющих усилий и деформаций.
Выше мы показали, как можно подразделить общую систему уравнений на две отдельные системы уравнений: 30 для симметричных составляющих и 31 для антисимметричных составляющих наших неизвестных. Эти системы уравнений можно получить также сразу, не составляя общей системы уравнений.
Систему уравнений для симметричных составляющих можно получить легко: для этого достаточно положить, что не только нагрузки симметричны, но также симметричны опорные реакции, деформации и все вообще неизвестные заданной системы. Этот результат легко достигается приравниванием нулю всех антисимметричных составляющих. Понятно, что при этом уменьшается число неизвестных, и поэтому соответственно придется составлять меньшее количество уравнений.
Система уравнений для антисимметричных составляющих получается следующим образом. Мы сразу исключаем из рассмотрения как бы приравниваем нулю симметричную внешнюю нагрузку и все симметричные составляющие реакций и принятых неизвестных,
1 Точнее—для эадач, в которых исключена необходимость рассмотрения секториальной жесткости стержней EJ, столь важной в конструкциях из тонкостенных стержней.
2 Это использовано, между прочим, в нашей работе, посвященной расчету устойчивости пространственных рам. См. Вестник инженеров и техников, 1939, Ns 2.
сохраняя при этом значения величин
неизменными
130
такими же точно, какими мы их принимали при расчете симметричных составляющих. Система как бы лишается искривляющих нагрузок, но остается равносжатой с заданной см. 9, гл. IV путем соответствующего регулирования осевых нагрузок. При этом надо учитывать антисимметричные приращения опорных реакций, появляющихся при потере устойчивости системы. Иногда симметричные составляющие реакций например, вертикальные реакции стоек одноконтурной рамы при симметричной нагрузке являются величинами вполне определенными, в то время как антисимметричные составляющие реакций будут неизвестными. Бывает и наоборот: так, например, распор дэухшарнирной рамы при потере ее устойчивости от действия симметричных вертикальных нагрузок не имеет антисимметричной составляющей1.
В заключение отметим, что разделение симметричной и антисимметричной задач при расчете устойчивой прочности симметричных и симметрично загруженных систем вполне естественно и с другой точки зрения. В то время, как величины симметричных составляющих вполне определяются из уравнений 30, антисимметричные составляющие при нашем решении, основанном на теории малых деформаций, находятся лишь во вполне определенных между собой соотношениях, выражаемых системой уравнений 31, но не имеют в то же время определенных по абсолютной величине значений. Они представляют собой как бы величины
неопределенного масштаба формулы 12, 3, внезапно появляющиеся в момент потери устойчивости и затем быстро и как бы неограниченно возрастающие при дальнейшем увеличении нагрузки.
ГЛАВА VI
БАЛОЧНЫЙ МЕТОД МЕТОД МОМЕНТОВ И УГЛОВ ПЕРЕКОСА 1. Формулы для отдельного стержня
Начнем рассмотрение основных методов расчета устойчивости и устойчивой прочности плоских рам с этого метода, известного под названием обобщенной теоремы трех или четырех моментов. Это первый по времени появления метод расчета устойчивой прочности неразрезных балок и рам, получивший особое развитие применительно к задачам строительной механики самолета2.
Основные формулы этого метода для стержня 1аЪ, подверженного продольно-поперечному изгибу, могут быть записаны так см. формулы 77 —
1 См. пример 4, 2, гл. IX, в котором приведено раздельное составление уравнений для симметричных и антисимметричных составляющлх.
2 О применении обобщенной теоремы трех моментов см. например: Мюллер-Бреслау Графич. статика сооружений, т. II, ч. 2, стр. 277—282, Петербург, изд. 1913 г. С. П. Тимошенко Курс теории упругости, Петроград, ч. 2, 1916, стр. 37—38.
Весьма интересное и оригинальное решение дано в статье Н. Е. Жуковского Исследование устойчивости конструкций аэропланов в Трудах авиац. расчетно-испытательного бюро, вып. 5, 1918 г. см. также том VIII полн. собран, сочин. Н. Е. Жуковского, ЦАГИ, 1937. Ряд применений уравнения четырех моментов показан в работах Ф. Блейх и Е. Мелан Уравнения в конечных разностях статики сооружений, Харьков, 1936, гл. 9; Ф. Блейх Теория и расчет жел. мостов, Гострансиздат, 1931, гл. XI; Ф. Блейх Стальные сооружения, Госстройиздат, т.1, 1938, стр. 183—196.
С. П. Тимошенко Устойчивость упругих систем, Гостехиздат, 1946.
Г. Д. Абрамов Упругая устойчивость ступенчато-сжатых рам,журнал Строит, промыщленость 4—5, 1939.
П. ф. Попкович Строительная механика корабля, Судпромгиз, 19И, ч. 2. стр. 51 г 237—158.
9 131
—79 — 16, гл. Ill:
Та
Qob -
f i_ Mbl _ ; t _i ms
S ”Г фай Ь Tab
_ W c , A , Б
3 6Z ”та”ГРЬа
Ма-Мь v2B 0Б
: j Та- Ta6 i Vafc
Z:
1
2
3
В этих формулах t и s — коэфициенты Жуковского:
70 Р CtKT-1
-Ki-v-O-pC1-
4
5
Если продольное усилие стержня N 0, то оба эти коэфициента обращаются в единицу: гб 1. Об этих коэфициентах см. 17 гл. III.
Величины pfb, pfa, — углы поворота и поперечная сила по концам сжатого стержня, возникающие от его пролетных и поперечных нагрузок, если этот стержень рассматривать как балку на двух
5
Pf
1
5
I г
а -ь Oi -
опорах1:
в
а6
— Д
til
I
sM I
Фиг. 53.
Ьа— — — tLMx
_1дЛГ1 дф
6
г В случае, если стержень загружен сосредоточенными грузами Р19 Р2,. и равномерно распределенной нагрузкой q по всему пролету фиг, 53:
в __ 1Ъ
УаЬВ 2л
п 1,2,.
sinV J р
n L sin V г J Т 4Вт,
sin I п I jt
sin v I J 4Лу
7
8
9
При v 0:
Б VI p Ьу f A Л i.
Pab — 6B V1 W J 24B
г 1,2,
24 S
7
8
nl,2,.
Здесь в 7 и 8 коэфициент yv определяется формулой:
Yv
i_
Т
.8
10
— V
и табл. 1 приложения к настоящей работе.
1 Индекс Б в формулах 6—первая буква слова балка.
132
В частном случае, если коцец а стержня 1аЪ жестко защемлен, ра О, и тогда формулы 126. и 127 главы III дают:
Ш.1 dy ь ЪаБ, И
QabT-dy QabB, 12
где коэфициенты а, у и d определяются формулами 108, 116 и 124
главы III, а нагрузочные члены: к st: e
l
i.
о
БЬ Ьа, 13 Г
Qaf Qab Ub. 14
2. Обобщенное уравнение трех моментов
Пусть в жестком узле Ь сходятся два стержня фиг. 54,я. Углы поворота концов Ь этих стержней в соответствии с формулами 2 и 1 J
будут: Фиг. 54.
п. - - гг., - Св.4
л м‘., Ввиду жесткости узла углы pbd и вЪс равны друг другу: рЬа flc fb. Таким образом:
ш‘ GOGO J 00
— 6фгс 1а bc Ьа-
Умножив это уравнение на некоторую произвольную погонную жест-
Б
К
15
кость общую для всей рамы, и применив обозначения:
о
приведем уравнение трех моментов к ооычному виду:
ма Sab 2Мь lab tic 4- Мс Sbc б-Ь - с fa - . 16
10
3. Обобщенное уравнение четырех моментов
Если в жестком узле сходятся три или более стержней фиг. 54, б, то, вообще говоря:
Уьс ¥bd — Ъе
Таким образом число взаимно независимых условий неразрывности угловых перемещений в узле на единицу меньше числа жестко примыкающих к узлу стержней. Эти условия могут быть записаны в виде уравнения четырех моментов;
МЬа sab ml tab 2Ml tbc Mbc Sbc tab c fc- i 7
133
4. Составление урэвнвния неразрезности для узлэ, снежного с неповорачивающимся узлом
Пусть нам известно, что узел а не поворачивается фа 0. Пользуясь тогда для стержия 1аЪ уравнениями 11 — 14, можно уменьшить на единицу число совместных уравнений, исключая временно из рассмотрения изгибающий момент Ма. В этом случае согласно 11:
Ьа — МЬ jTiab аЬ 9baB
согласно 1: Mi — -МьГЛ _1_л
J ,е ЯЧ 35 ЬсМс ьвЛИ 9ьс
Приравняв друг другу эти два угла, получим уравнение неразрезности контура abc в узле Ь:
Mbtab 2Ml tbc м Sbc — фйс dab tlafr cpfc — cpfaB. 18
Здесь для сокращения записи принято обозначение:
3В0 S 1 1
17ваЬь- 19
б. Расчет несвободных рам
Несвободными рамами мы называем такие системы, которые остаются геометрически неизменяемыми при постановке шарниров во всех их узлах. Как обычно, пренебрегая при расчете рамы деформациями обжатия оси ее стержней по сравнению с деформациями их изгиба, мы тем самым дону-
I
vV
4
скаем, что углы несвободной рамы не имеют линейных смещений, а углы поворота всех ее стержней-равны нулю: фа 0.
Для примера рассмотрим расчэт устойчивой прочности рэмной эстакады с линейнонесмещающимися узлами флг. 55. Правлло знаков изгибающ лх момэнтов дано на чертзже прл помощи пунктирной тени: положительными мы считаем те моменты, которые выгибают сгержн х в сторону этой тени. В качестве неизвестных расчета мы примем момепты М, М, М и М. Моменты вверху стоек мы из условия равновесия узлов 1 и 3 будэм записывать в видз разности моментов по концам ригелей.
м Ml - М; Mi М1-М1
Ввиду шарн хрности узлов 0, 2, 4 и 5 моменты М0 М2 М4 М5 0. Для определения четырех неизвзстных нам надо состав,ть четыре уравнения неразрезности. При этом, составляя уравнения четырех моментов 17, мы будем следить за тем, чтобы пунктирная тень лежала по одну сторону от сочетаемых каждым такам уравнением двух стержней1.
1 iMbi никогда не напишем лишнего уравнения, если будем следить, сочетая два стержля, за тем, чтобы пунктирная тень лежала с одной стороны для обоих этих стержней.
134
Итак, мы получили следующие четыре уравнения:
0 — 1 — 3 0 — 1 — 2 1-3-5 1-3-4
шю.2МММ,- - _ fBy
2Mt01 2 MJ - М t;2 f;
l0
Msltl 2MJ, 2Mta5 - Л-зБ1;
0
лК,гм f;32 M - m tM tg.
a
Прежде чем решать эту систему четырех уравнений, нужно определить по формулам 4 — 5 или из таблиц.1 данных в приложении, величины коэфициентов t и s и по формулам 7 и 8 величины свободных членов, но для этого надэ иметь значения
Г jji2
величины v у -jjjj для всех стержней рамы. Их можно в соответствии со сказанным в 1, гл. V взять сначала приближенно, а потом уточнить, если это потребуется. Конечно, если имеется обыкновенный расчет прочности рамы для этой нагрузки, то лучше всего принять распределение продольных сил N между стержнями рамы, полученное по этому расчету.
Если такого расчета нет, то при определении i продольных сил стоек можно воспользоваться линиями влияния для неразрезных балок и принять, например
N21 0,511 0,889Р2 0,770Р3 0,363Р4 2,533Р; iV43 - О,118Р1-0,148Р2 0,363Р8 0,770Р4 0,867Р.
Продольное усилие ригеля 0; можно принять равными нулю также: iVol iV130. Так как поперечная нагрузка дана только на ригеле, а для ригеля мёс приняли v 0, то по формулам 7 и 8 получаем:
Б_аВ__ъВ_аБ П ,1
Тх — 36 Тз1 Tie 6Вг L з 9 3 9 J 9j
В в
Примем отношение 7——г, тогда при v 0 для ригеля мы получим в соответствие
It
с 15:
I
slt tni tU tU 1.
01
13
85
Таким образом, система уравнений а для первого цикла расчета получится в аде табл. 14.
Таблица 4
М1
м
м
Ml
1-
2
2
—
2
2 1,,
— 21 12
—
—
j ‘
1
I 2
t
2
2
1
1 21-Мм
34
1
В этой записи свободные члены перенесены также на левую сторону уравнений. Система уравнений получилась в неканоническом виде. Для достижения каноничности нужен был другой порядок составления уравнений. При нашем выборе в качестве неизвестных концевых моментов рлгелей нужно было взять уравнения: 0 — 1 — 2;
2 — 1 — 3; 1 — 3 — 4 и 4 — 3 — 5. Но в таком случае все четыре уравнения имели бы
1 Распределяя продольные силы в стойках, как в разрезной балке, мы получили бы
1 2 2 1 1 2
si -Ь — — 4-— Р 2Р и iY43 у — Р Р. Величина v21 при этом умень-
2 533 Г 1
—— 1,12 раза, а величина v43 увеличилась бы в у 5357 в рава
Величины же трансцендентных коэфициентов t и s для стоек рамы изменились бы значительно меньше.
135
трансцендентные коэфициенты. Кроме того, при таком составлении уравнений нам пришлось бы перерезать пунктирную тень и в связи с этим менять знаки в уравнении четырех момептов.
В задачах устойчивой прочности нет пропорциональности между нагрузками, с одной стороны, и усилиями и деформациями, с другой стороны. Поэтому, еслл мы хотим обеспечить конструкции коэфициент безопасности, равный Аг, то мы должны определлть усллия и деформации конструкции от действия нагрузок, в к раз превышающих заданные расчетные. По этим увеличенным нагрузкам мы отыскиваем продольпые усилия N стержней и затем уже определяем числовые значения величин v и коэфлцлентов t этой системы уравнений.
Решив систему уравнений табл. 14, мы затем легко строим эпюры М, Q и N соответствующие заданным значениям нагрузки.
На стойках эпюра М получится слегка криволинейной в результате учета деформаций изгиба при наличии продольной силы.
Для контроля точности расчета следует по новым уточненным значениям продольных усилий N в стойках и в ригеле найти коэфициенты системы уравнений а. Если они будут мало отличаться от принятых в системе уравнений табл. 14, то выполненный расчет считаем приемлемым, если же полученная точность решения нас не удовлетворит, то переход im ко второму циклу расчета при новых численных значениях системы коэфициентов.
Предположив при подсчете коэфициентов t системы уравнений табл. 14, что v 0, мы получим систему уравнений для обычного расчета прочности. При малой разнице между коэфициентами этой системы уравнений и коэфициентами системы табл. 14 уравнений расчет устойчивой прочности для заданных значений нагрузок Р не является актуальным. Если характеры эпюры моментов при расчетах обыкновенном и по деформирован ной схеме существенно отличаются друг от друга, то нужно исследовать поведение рамы при нагрузках меньших, чем принятые в расчете. Надо выяснить, не обращается ля в пуль при меньших нагрузках детерминант, составленный из ксэфиц лентов при неизвестных. В частности, при таком исследовании может помочь сравненле знаков D — детерминанта при заданном значении к и при значении А: 0см. 3, гл. V.
В заключение надо указать, что расчет разбираемой рамы фиг. 55 по методу деформаций был бы значительно проще.
6. Расчет свободных рам
При расчете свободных рам, кроме моментов по концам стержней в качестве неизвестных фигурируют также кинематические независимые
линейные смещения узлов рам: Дх , Дхх,., или кинематические независимые углы поворота стержней tyi Фи - см гл. V. Не все моменты по концам стержней мы будем считать неизвестными, часть из них мы сразу же выразим через другие неизвестные. Действительно, рассматривая условия равновесия какого-либо узла а рамы фиг. 5, мы один из моментов на концах стержней, жестко примыкающих к узлу,
можем выразить через остальные:
Ml - Ml Ml Mi. 20
неизвестных моментов легко определить, подсчитав число жестко примыкающих к узлам концов стержней и вычтя число прикрепленных узлов. Общее количество неизвестных для рам типа,
показанного на фиг. 57 для рам без шарниров в пролетах стержней, равно:
m 2s — п — h k, а
Где — число стержней, ть — число прикрепленных узлов, h — число шарниров, к—число степеней кинематической свободы шарнирной схемы рамы. Как известно из курса статики сооружений, А 2п — s, поэтому формуле а можно придать вид:
ms n — ft. 21
Для рамы фиг. 57 14, л — 8, А 4 и, таким образом:
тп 14 8 — 4 18.
Фиг. 56.
Поэтому число
133
,л
II
3
3 с
Фиг. 57.
Для контроля на фиг. 57 возле каждого узла рамы написано число неизвестных моментов, оно в сумме равно 16; число неизвестных кинематически независимых смещений равно 2, числу этажей рамы. Таким образом, опять получаем для рамы фиг. 57 т 16 2 18. Мы можем сказать, что для расчета рамы фиг. 57 надо составить 16 уравнений неразрезности по типу трех или четырех моментов 16 или 17 j 7 i
и 2 дополнительных уравнения, соответствующих углам перекоса и фи первого и второго этажей рамы уравнения типа 22 6 гл. V.
Для получения системы уравнений в каноническом виде ее надо составлять так, чтобы каждому из выбранных неизвестных соответствовало определенное уравнение. Пусть, например, в качестве основных неизвестных моментов возле узла 1 рамы фиг. 58, а мы выбрали моменты М, и М и М.
Это значит, что на основной системе этой рамы возле узла 1 должны быть поставлены шарниры так, как это показано на фиг. 58, б.
В соответствии с этим надо составить уравнения неразрезности в точке 1 между ригелем 2 — 1 и стойкой j — 5 уравнения 2—1 — 5, между стойкой 3 — 1 и стойкой 1 — 5 уравнения 3—1 — 5 и между ригелем 4 — 1 и стойкой 1 — 5 уравнения 4— 1 — 5. Можно сформулировать это так. Для того чтобы уравнения трех и четырех моментов получились в каноническом виде, нужно, чтобы в основной системе между стержнями, сочетаемыми в этих уравнениях, был только один шарнир. Эти уравнения должны выразить следующее:
— 9i 0; is — pu 0; р14 — ф16 0.
Иначе говоря, деформации раскрытия швов, ставшие возможными в месте постановки дополнительных шарниров в месте выбора неизвестных
изгибающих моментов, должны равняться нулю.
Если при записи такого уравнения будет перерезаться пунктирная тень, определяющая правило знаков для изгибающих моментов, как например, при составлении уравнения 2 —1 — 5 фиг. 58, то в формуле 17 уравнения четырех моментов нужно у стержня, для которого пунктирная тень получается сверху при обходе стержней слева направо, знаки у моментов переменить на обратные. Таким образом уравнение 2 — 1 — 5 запишется так:
О
f 1
i j 1
4
Si
б
J
T -
г
WM
—г
Фиг. 58.
М 12 2М t2 — 2М ti
fl 6Z0
5 15 т
12 — 16 12 — .
Б
Углы поворота стержней и углы поворота узлов саь мы считаем при этом положительными, если они направлены по часовой стрелке. При составлении уравнений трех и четырех моментов нужно во избежании ошибки внимательно следить за направлением по часовой стрелке
Г1
или против углов сраъ, вызываемых собственной нагрузкой стержня, рассматриваемого как балка на двух опорах.
Дополнительные уравнения, соответствующие углам перекоса tyi и йц мы составляем в соответствии с указаниями 6 гл. V по формуле 22:
Пользуясь формулой 3, мы исключаем из эдго уравнения величину и придаем ему вид:
2 МаъЛ-МЪа аЪ 2 Va HgUg — Q.
22
Суммирование в этой формуле мы распространяем на все стержни рамы. Моменты МаЪ и МЪа мы считаем положительными, если они действуют на конец стержня по часовой стрелке. В соответствии с положением пунктирной тени мы заменяем моменты МаЬ и
МЪа обозначениями Мъа и Мь
Если пунктирная тень расположена так, как на фиг. 58, то:
У
lh Фиг. 59.
В заключение этого параграфа дадим пример
составления уравнений для простейшей свободной
рамы, изображенной на фиг. 59.
Неизвестных расчета в этом случае три: Mlt Шг и фа.
Ясно, что М0 — М — 0 и oi Фгз 12 0.
Составим два уравнения неразрезности для узлов 1 и 9
0-1-2
1-2-3
2М, м,6-Ь. 64- -о;
М4 2Мs t2 tjj -—— 0.
о
a
b
При составлении дополнительного уравнения для угла перекоса по формуле 22 примем:
Фв1 Фа1; 12 0; v1v1 0:
u1 m2 A; Ff rH 0;
пБ 1 У
Тогда дополнительное уравнение можно записать так:
-. х - т - -¥ -
Этот же результат легко можно получить нзпэсрздственнэ бзз применения уравнения 22 из условия равновесия ригеля Q104 Q23 — 0 с послздующзй заменой выражений Q по формуле 3.
Из условий равновесия рамы сумма ее вертикальных рзакций равна нулю:
с
vB В _
рп Поэтому дополнительное уравнение получает вид:
-М1М, 0.
с
Для придания системе уравнений а, Ь и с полной каноничности нужно было
бы уравнение с умножить на как это сделано с уравнением 16, по которому
составлены уравнзнля а и Ь.
Уравнения а, Ь и с решаем так. Сложив а и Ь, исключаем ф затем вместо Мг подставляем его выражение из с:
В результате находим:
М., ML— f.
1 У,
с
ВI
h
toi t 4 4 1
Вд Toi
А
138
Пользуясь уравнениями с и Ь, обратным ходом нетрудно получить значения
.для М2 и
Фа 12 Ь 2j si2 212 -f 223. e
Поперечные силы находим, пользуясь формулами 3 и 9 при tis 0:
_МХ qh. М2
Qoi—д аГТ Qi2 j д
Сравнив выражение для Q12 с формулой с, получим:
12 21
Из условия равновесия узлов I и 2 фиг. 60 получаем:
Л Фа
AToi Qi2 — N2s - ; f
42
iv п Мг К1 Мъ qh2 , Lw ,
bit-Qn д-2уа h 57Фл- g Г
ю
Итак, продольные усилия в стойках мы сразу поручаем по формуле f в окончательном вдде. Продольное усилие в рягеле сначала примем приближенно в соответствии с обычным расчетом прочности по не- Фнг. 60.
сформированной схеме рамы.
Для получения численных значений зададим следующие соотношения: h l l0; Bh Bl B0.
Тогда в соответствии с формулой 15 выражение для Мг упростится:
ah2 5i22ii22j231”
МЦ 191-. dO
01 4 2 tl2 123 - s12
При обычном расчете прочности s l, у 6 и таким образом по формуле d
п
а по формуле с: М2 — 0,525 .Продольные усилия стоек iV2g — N0l — Продольное усилие ригеля находим
Л.jf nh
пока приближенно, пренебрегая в формуле g вторым членом N1 j-a 0,525 —
2 Обозначим для сжатой стойки v23 v, тогда для растянутой стойки jl01 v, для ригеля vi2 10,526,70,725 v при этом —. Полученные соотношения между
величинами v для разных стержней используем при расчете устойчивой прочности.
Выясним зависимость между величиной внешней нагрузки рамы, ее усилиями и деформациями. Для этого последовательно даем v разныз значения: 0; 1; 2; 3 и т. д., выплсываем из таблиц, данных в приложении, соответствующие им значения t и s для всех стержней рамы, а затем по формулам d с и е вычисляем значения М19 Мг и ф. Результаты таких подсчетов сведены в табл. 15.
При vvKp 3,2693 знаменатель выражения d обращается в нуль, вследствие
этого значения Mlt М2 и Жд неограниченно возрастают, точнее при v vKp эти значения
как бы испытывают разрыв непрерывности от со до — оо. Этот противоречащий данным опыта результат вполне объясняется особенностями нашего расчета, основанного на теории малых деформаций. В последней строке таблицы выписаны значения в радианах угла перекоса фд стоек рамы. При значении v l этот угол фЛ 0,2764 - 1547 уже достаточно велик, а при v 2 он, вообще говоря, превышает всякое вероятие фА 1,915 10946 90. Поэтому табличные данные для значений v2 не имеют никакого реального значения.
Перейдем теперь ко второму циклу расчета устойчивой прочности. Как это нами выяснено выше, продольные усллия стоек вполне определяются формулой f и не требуют уточнений. Продольное же усилие ригеля может быть легко уточнено
139
Таблица 15
0
1
2
3
3.26
3.27
4
28
1
1,074
1,436
7,349
-7,453
-6,825
-0,460
01
1
0,935
0,806
0,672
0,644
0,643
о,5ба
Toi
6
5,400
3,588
0,536
-0,468
-0,509
—3.82J
V12
0
0,725
1,450
2,175
2,362
2,370
2,90
Sl2
1
1,075
1,315
2,084
2,538
2,562
7,934
12 —
1
1,043
1,176
1,586
1,823
1,835
4,555
мх
qh2
0,2375
0,2428
0,2593
0,323
19,09
-207,3
0,2408
м2
qh2
0,2625
0,2572
0,2407
0,177
-18,59
207,8
0,2592
С I
1
И
0,1354
0,1377
0,1529
0,4145
26,82
-257
0,0353
Л
0
0,2754
1,915
7,4
569
- 5500
1,13
по формуле g;
Лточ _ К4 В _ _ М А_ ii. Л. 1
12 - Р V 2 дЛ V Вд
gAV А А2 ЧгАУ
Отсюда
Пользуясь формулой h, уточняем данные табл. 15. Уточненные данные приведены в табл. 16.
Таблица 16
v
0
1
2
3
v12
S12 12 —
0
1
1
0,489
1,029
1,017
0,864 0,916 0,9 1
2,67 V-i
0,529
0,714
И
а
0,2375
0,2432
0,2605
0,347
Mi
qh2
0,2625
0,2568
0,2395
0,153
I
И
0,1354
0,1372
0,1506
0,380
т
Сравнивая данные уточненного расчета с данными первого цикла расчета, мы кон статируем весьма хорошее совпадение в пределах реальных значенай деформаций.
Итак, для данной рамы можно вполне ограничиться расчетом первого цикла. Боль ше того, можно сказать, что коэфяциенты при обычном расчете прочности коэфдц ленты столбца со значениями v 0 достаточно близки к коэфлциентам, полученным при расчете устойчивой прочностл если не выходить за пределы реально возможных в инженерных сооружениях деформаций. Поэтому, при заданной нагрузке для данной рамы нет надобности в расчете ее устойчивой прочности, для нее вполне достаточен обычный расчет прочности.
7 Случаи рационального применения балочного метода
Балочный метод был разработан ранее см. 1 настоящей главы других методов расчета устойчивости и устойчивой прочности плоских рам. Этот метод был предложен вначале для расчета неразрезных балок на жестких и на упруго-податливых опорах. Для этих задач этот метод достаточно удобен и не требует большей затраты труда для решения, чем метод деформаций. Для расчета сложных многопролетных многоэтажных рам этот метод неудобен. В примере расчета рамной эстакады см. 5 по балочному методу нам пришлось составить 4 уравнения, в то время как при применении метода деформаций можно было бы ограничиться всего двумя уравнениями с неизвестными cpt и р2-
Однако, отказавшись от канонической формы системы уравнений, можно зачастую дополнительные уравнения по этому
методу составить так, что исключение ряда неизвестных сильно облегчается и практически придется иметь дело с меньшим числом неизвестных. Так, в примере, разобранном в 6, относящемся к двухшарнирной прямоугольной раме, из двух уравнений а и Ъ легко исключается угол перекоса рамы фл, а третье уравнение с позволяет так же легко исключить еще одно неизвестное и, таким образом, сложность определения отдельных неизвестных см., например, формулу d 6 не превышает сложности решения одного уравнения с одним неизвестным.
При расчете устойчивой прочности одноконтурных многоугольных рам фиг. 61, пользуясь общей методикой см. 6, вообще говоря, надо составить п — 1 уравнений неразрезности и л —2 дополнительных уравнений для кинематически независимых углов поворота Jj, фц. фп_2, а всего 2п — 3 уравнений. Но удобней такие рамы рассчитывать иначе. Сначала составляем два уравнения непрерывности контура см. 2, гл. V:
Фиг. 61
2 Ьаъ sin 4г. х 0 и 2 Sabsin4b- 2 0.
а
из которых получаем выражения для углов поворота фп_2, п_х и ф.п через кинематически независимые углы поворота фь фп,. фп2
Эти уравнения можно составить так см. 2, гл. V, что сразу получаются развернутые выражения для фл_2, п_х и фп_ьп без какой-либо необходимости решать систему двух уравнений.
Затем составляем выражения для горизонтальных ит и вертикальных vm перемещений всех узлов рамы:
Jfcm- 1
т 2 tyk, к1 Ук1 — укУ,
к—О
ш
bTR- 1
35 ОЛl : Ь
A0
Составляем выражения узловых моментов М, М,. Мп_г для недеформированной схемы по формуле:
к т—1
Мт — Нут Vxm — 2. Рк Хт — хп- су
к1
Полное выражение узлового момента Мт при расчете рамы по недеформированной схеме получим как сумму:
Мт Мт АМт, d
в которой добавку АМт можно получить как вариацию выражения с для Мт. Имея в виду, что вариации ук, хк, Н0 п V соответственно будут: — vk, ик, АН и AV, получаем:
к—т 1
АМт—AH-ym AV xm Hcm V0um— 2 ркит — е
к1
В формулах с и е Н и У0 —опорные реакции при расчете рамы по недеформированной схеме, а АН и AV их добавки при переходе к расчету рамы для деформированного состояния так, что:
Я Я ДЯ,
F F4 AV. j O
Величины V и AV легко находим из условий равновесия:
An — 1
т 2 рк1-кУ g
к 1
Jc—1
2 ркак ь
к1
Подставив h в е, получим:
к —п — 1 к—т- 1
Шт — AH-ym HOm VUm — 2 Ркик— 2 Рк.ит — ик- U
fc- 1 к 1
Итак, мы видим, что пользуясь формулами, d, i и b, легко можно представить выражения узловых моментов М19 М2,. , Мп_г, как линейные функции внешних нагрузок Р, приращения распора АН и кинематически независимых углов поворота. , йЛ-2:
Мт М 2 АткЪк Аю, Л АН. к
Здесь Атк и Ат, а — некоторые коэфициенты, зависящие от нагрузок; они определяются в результате обычного расчета рамы по недеформированной схеме.
Теперь составим п — 1 уравнений неразрезности по формуле трех моментов. Подставив в них вместо моментов Мг, М2,. , Мп_х их выражения по формуле к, получим систему п—1 уравнений с п — 1 неизвестными, из которых п — 2 — кинематически независимые углы поворота. , п_2 и одно — приращение распора АН. Таким обра
зом, пользуясь указанным выше приемом, мы можем значительно упростить.для одноконтурных многоугольных рам расчет их по балочному методу, сведя задачу к системе п — 1 уравнений вместо 2п — 3 уравнений, составленных в канонической форме, как это описано выше в 6
142
Дальнейшие упрощения цодучедэдся при расчете рам со ступенчатосжатыми стойками фиг. 62. Изложенная выше методика, относящаяся к расчету устойчивой прочности многоугольных одноконтурных рам, в основном, сохраняется. Подразделяем раму на шесть стержней 0 — 2, 2 — 2у.,.,5—6 из кинематических соображений получаем
Bl и2 1з 14 и5 0; a3 — ut; 034 0;
кроме того:
О,
и,
У12 —
и2 — щ
‘23 I,
23
qh
а
k
1
1
Р4
1
4 -
к
2
3
1
4
9
qhH
в
zp-v
Фиг. 62.
01 уха 01 bia
Из условий равновесия:
У0 -Pi Рг 3 2Ь AV - J Л1 Л. Л иа Узловые моменты на левой стойке равны:
Мг М - АН ух Vва;
Mt M — АН у Уи — — tti:
Л3 Л, — ДЯ yt Vu3 — Рх и3 — гг3 — иг.
На правой стойке узловые моменты равны:
М М1-АН-у-2Р- V
л;-дя. -2 -v , -.
В результате подстановки этих выражений для М19 М2,. , i¥6 в уравнения неразрезности задача сводится к пяти уравнениям с пятью неизвестными их9 и2, и3иА, и5 и АН.
Еще проще получится задача расчета устойчивости той же рамы фиг. 62 при отсутствии распределенной нагрузки q. В этом случае1 отпадает необходимость в предварительном расчете прочности рамы по ее недеформированной схеме, так как и без такого расчета легко видеть, что:
М М2- М9 М 0;
У рг р рг
ГЛАВА VII
МЕТОД ДЕФОРМАЦИЙ
1. Общие соображения о значении метода деформаций в задачах
уотойчивой прочности2
При расчете сложных систем принято расчленять их на более простыесистемы, легче поддающиеся расчету. Такое расчленение может быть выполнено двумя различными способами: либо путем отбрасывания части наличных связей например, постановки дополнительных шарниров,
1 См. статьи проф. Г. Д. Абрамова в журнале Строительная промышленность 1938 г., 5—Новый метод исследования устойчивости двух-и многоопорных стержней при сложной продольной нагрузке и 1939 г., 4—5 — Упругая устойчивость ступенчато-сжатых рам.
2 О расчете устойчивости рам по методу деформаций впервые было доложено автором 25 июня 1936 г. на заседании общего собрания Ак. наук УССР. См. также: Н. В. Корноухов Точный метод проверки устойчивости плоских рам в Вестнике инженеров и тех-
143
либо путем введения новых дополнительных кинематических связей гнапример, фиксирования линейных или угловых перемещений узлов рамы. При первом способе нарушенные связи системы заменяют силами — неизвестными расчета; величину их затем находят из условия равенства нулю дополнительных перемещений системы, ставших возможными вследствие отбрасывания связей. Такой способ расчета носит название метода сил.
При втором способе неизвестными расчета являются фиксированные перемещения, соответствующие дополнительным кинематическим связям. Величину этих фиксированных перемещений находят з условия равенства нулю реакций дополнительных связей. Этот способ расчета носит название метода деформаций. Кроме того, возможны различные варианты смешанного метода, при котором часть неизвестных являются усилиями системы, соответствующими нарушаемым связям, а часть неизвестных—фиксированными перемещениями, соответствующими новым накладываемым связям. Рассмотренный в предыдущей главе балочный метод является одним из вариантов такого смешанного метода.
Вообще говоря, при переходе от обычного расчета прочности рам к их расчету по деформированному состоянию приходится произвести переоценку сравнительной выгодности и удобства различных методов расчета рам. Прежде всего надо отметить, что в задачах устойчивой прочности теряется основное различие между статически-определимыми и статически-неопределимыми системами; трудность их расчета по методу сил сильно возрастает и примерно уравнивается. Исходя лишь из условий статики, без рассмотрения упругих свойств рамы, оказывается невозможным построение эпюр моментов для статически-определимых систем. Поэтому преимущества метода сил при переходе к расчету рам по деформированному состоянию в общем случае почти совершенно парализуются, а недостатки возрастают. В то же время выполнение цикла расчета устойчивой прочности рамы методом деформаций не на много сложней обычного расчета прочности рамы. В результате, из различных.методов расчета устойчивости и устойчивой прочности рамных систем в соответствии со спецификой этого расчета, связанной с определением усилий по деформированному состоянию, главным и основным является метод деформаций. В большинстве случаев этот метод приводит к меньшему числу уравнений и требует более простых и менее трудоемких вычислений, чем другие методы.
Трансцендентные коэфициенты формул метода деформаций при изменении продольной силы меняются медленнее й более плавно, чем коэфициенты при применении других методов. Некоторая неточность при предварительном определении продольных усилий стержней рамы сказывается на результатах расчета по этому методу в значительно меньшей степени, ем при применении других методов.
Только в особых случаях, о которых будем говорить ниже, следует отдать предпочтение другим методам расчета.
ников, 1937, 3, главу VI Исследования устойчивости пространственного каркаса Дворца Советов СССР, изд. АН УССР, 1938.
Метод этот с соответствующими ссылками на автора этой работы приведен в курсах проф. Раэяновяча И. М., Строительная мэханчка стержневых сястем, 227. Стройяздат, 1945 и проф. П. Ф. Папковича Строительная механика корабля, часть II Судпромгиз, 1941, стр. 258—270. См. также: С. Н. Никифоров Устойчивость сжатых стерж 1ей сварных ферм, Стройиздат, 1938.
Метод деформаций с успехом применен к задачам динамики рамных конструкций в работах: А. А. Белоус Собственные и вынужденные колебания рам иэд. АН УССР, 1939 см. также сборник Исследования по теории сооружений, Госстройнэдат, 1939, В. Г. Чудновский Частота собственных колебаний стержней и рам и динамический критерий их устойчивости, изд. Академии наук УССР, 1939.
144
Прежде чем перейти к вопросу о составлении уравнений по методу деформаций, сделаем обзор ранее полученных нами формул, которыми придется пользоваться.
2. Основные формулы для отдельного стержня
1. Общий случай стержня с упруго защемленными концами Для практического применения при расчете рам формулам 112 — 114 гл. Ill удобно придать следую- я
щий вид фиг. 63:
а у-
чЗ
Фиг. 63.
Маъ — 2iаЪ.ab9a а Ь
РаЬаб Ь МаЪ 1
Qab а Раа —
Y abab-Qab Правило знаков, указанное в 4 гл. V делает эти формулы в одинаковой мере пригодными как для левого, так и для правого конца стержня. На фиг. 63 величины МаЬ, Mba, Qab, Qba, Nab, Nba, pa,p, аь Кь изображены положительными. Если в формулах 1 и 2 везде поменять индексы а на 6 и наоборот, то получим формулы для МЪа и Qba. Символами МаЬ и Qab в этих формулах обозначены момент защемления и поперечная сила защемления конца а стержня 1аЪ. Значения этих величин вполне определяются собственными нагрузками и продольным усилием Nab данного стержня 1аЬ.
Действительно, если сохранить продольное усилие Ndb и нагрузки стержня, а концы его сделать неподвижными так, чтобы ра рь О,
ТО МаЬ МаЪ И Qab —Qab Величины эти могут быть в соответствии с формулами 112 — 114 гл. III выражены следующим образом:
МаЬ 2iab - рДр a J Дф; а
Ь
О ч
и
i
1 —
:U1IL
1Г0Т111ЩЦ
гг Л.
Vi к, Л-
”2 - Ш г ш
Фиг. 64.
Для частного случая фиг. 64, когда стержень 1аЪ загружен сосредоточенными силами Рг, Р2,. и1 равномерно распределенной нагрузкой q по всему пролету, величины эти могут быть определены по следующим формулам:
М.
_ fj 0 sin v _sin т - 4ЙТ :
2 ysinv —sin—
V.
i
3
v sm v
Ti—19 2 gV
Ktsin v -sin x P
ЧаЪ —
lab
Ql
4
Здесь Qb —поперечная сила на конце а стержня, рассматриваемого как балка со свободно опертыми концами, возникающая от собственных
10 Прочность II устойчивость стеряшепых сгстем
145
нагрузок стержня;
Формуле 4 можно придать вид:
- sm —— sin———
2 2
I
I
Т
v v
2 sin - — со
2 2
Лг
W-
va
Линии влияния - j-аЪ сжато-изогнутого стержня.
1г
У-0
5
6
Подробней см. таблице 1 О приложения Фиг. 65.
На фиг. 65 изображены линии влияния для МаЪ при значениях v 0; 1,0; 2,0;.; 6,0; в табл. 10 приложения ординаты у этих линий даны для сечений через одну десятую пролета. Определив необходимые значения ординат линий влияния по графику фиг. 65 дли: по табл. 10, легко найти моменты защемления от действия сосредоточенных грузов по формуле:
МаЬРпУп- 7
Из рассмотрения графика фиг. 65 и таблЛЮ приходим к выводу, что по мере приближения величины v к значению 2к моменты МаЬ и МЬа неограниченно возрастают яри наличии самой малой поперечной нагрузки на данном стержне. Это вполне понятно, так как при v 2tu
146
аксиально сжатый стержень с абсолютно защемленными концами теряет
ЯГ 4
устойчивость iYKps—р—
Стержень с ШйрнироМ на одном конце
Формулы 117 —118 гл. III удобно записать в следующем шде фиг. 66:
МqJj а 4 а,Ъ
Qab аа9а Yab1ab ”Ь
8
9
I I
7К
ШИШ
iramt
h
г77т:
t-аЪ
Qbo
Фиг. 67
Символами МаЪ и Qab обозначены момент и поперечная сила фиг. 67, возникающие от действия поперечных нагрузок сжатого стержня на абсолютно защемленном его конце при наличии шарнира на другом его койце.
В соответствии с формулами 117 и 118 эти величины могут быть выражены так:
AM,
V_T
c
d
Момент защемления МаЪ может быть выражен через моменты защемления МаЬ и МЬа следующим образом:
к,-;.,
10
а поперечнаясила защемления Qabi
-те5.
Н
Для частного случая действия на сжатый стержень поперечных сосредоточенных нагрузок Р19 Р2,. и равномерно распределенной нагрузки q по всему пролету фиг. 67:
sin
ъпУ
2 р п
I
sm V
ii2
4
12
Если шарнир Ь будет на левом конце, а заделка а на правом конце стержня, то в формуле 12 надо знаки поменять на обратные.
На фиг. 68 изображены инфлюентные линии для МаЪ а в табл. 11 приложения даны ординаты этой инфлюентной линии. Из рассмотрения
ю 147
графиков и таблицы легко видеть, что по мере приближения величины v к критическому значению для стержня с одним абсолютно защемленным, а другим шарнирным концом, т. е. к vp 4,4934, момент М”аЬ неограниченно возрастает.
3. Стержень с упруго защемленными концами при известном
значении поперечной силы Qab
Формулы для этого случая бывают весьма полезными, особенно, когда известно, что Qab0. Они были выведены в главе III см. 80 — 82, только теперь запишем их несколько иначе:
0;н , 5 О
Мab lab tg vafi 8in vob Qabl
fey,
-1аЬ М
13
Здесь
M
ab
Для случая нагрузки на стержне, как на фиг. 64
1 — cos
Л-I 2 P.-TiETT-Tv.
d
14 til ,2
где sv —одна из функций Жуковского, определяемая формулой 105 гл. Ш. 148
Для полноты картины приведем здесь формулу 82 гл. III, выражающую угол поворота стержня:
4‘тЛ.п4;- 13
где уа5 определяется формулой 111 гл. III, а
7 14а
4. Консольный сжато-изогнутый стержень фиг. 69
Используем для этого случая формулу 72 гл. III. Приравняв в ней Мх 0, получим:
o-7oVtgv-e-i. е
Для случая загружения стержня распределенной нагрузкой по всему пролету и; сосредоточенными грузами Р Р
л 1 л 2 .
Q, 2Pn qi
И
I ХЧ Л V
ДЛГ, -i. 2 Psin-
1,2,.
О,
72l-COSV
— ql —2— Фиг. 69.
Подставив эти выражения в е и перейдя к новым обозначениям, получим:
МаЬ — lab v tg Veft p0 Mlb, 15
где момент защемления
M-b 2 PnsinV-8in-Z2tv-tg. 16
n—1,2,.
5. Переход к обычным формулам расчета по недеформированной схеме
Для перехода к обычным формулам достаточно в вышеприведенных формулах 1 — 16 принять v 0. Тогда соответственно получим: а Для стержня с упругозащемленными концами:
Маъ 2аЪ 2а Уь ЗДа МаЪ 1
Qab - Ра 9Ъ 2U Qab 2
1аЪ
2
2 V- 12
п1,2,.
Маь — РчапЬп _ gl.
Мьа- 2 3
12 1 12
п1,2,.
2
I
п—1,2,.
в Для стержня с шарниром на конце Ь:
Mab 3iabfa — ab iiab; 8
аЪ
lab
Qab-97Ta-U Qab; 9
149
Маъг S Pe6n i Ь - Т ; 12,
П1,2,.
i SpAM,-; 1Г
Пв12 с Для стержня с упруго-защемленными концами при известном значении поперечной силы Qab:
маь iab - Ъ - Qab-i М”; 13
м”ь Yi 2 Pnbn -ql- 140.
n 1,2,.
д Для консольного стержня:
Mab Mkab-lQba- 2 Pnan-ql 16
1,2,.
3. Составление системы уравнений
Рассмотрим методику составления уравнений при расчете рам по методу деформаций с расчленением их на отдельные простейшие элементы: стержни и узлы фиг. 701.
В качестве неизвестных принимаем пять неизвестных углов поворота узлов: рх, р2, р3, р4 и р5 и три кинематически независимых смещения
шарнирной схемы А1У Д2 и Д3. Через эти смещения мы должны используя методику 2 или 5 гл. V выразить углы поворота фа6 для всех стержней рамы:
Val РаЬ Д Д2 Д.,. 2 Дп ФЙ- 17 ‘
Этими выражениями мы заменяем величины Ьа в формулах 2 настоящей главы для отдельных стержней нашей рамы.
После этого можно перейти к составлению системы уравнений для выбранных неизвестных.
Уравнение, соответствующее углу рг поворота узла п рамы, составим так. Дадим этому узлу на схеме расчленения рамы фиг. 70, б угол поворота, равный 1 единице, и затем запишем работу сил действительного состояния рамы при этом угле поворота. Так как этот узел, схематически изображенный в виде маленького кружочка, имеет только угловое единичное перемещение и не имеет линейных перемещений, то указанная работа окажется численно равной сумме моментов на концах стержней, примыкающих к этому узлу. Напомним, что концевые моменты стержней мы считаем положительными, если они действуют на стержень по часо
1 Возможно расчленение на более крупные элементы, состоящие из нескольких стержней, но тогда необходимо предварительно всесторонне изучить такие составные элементы.
160
вой стрелке, а на узел против часовой стрелки. Таким образом для узла п мы, вообще говоря, получим:
na nft nc 18
Для узла 4 рамы фиг. 70, а это уравнение имело бы вид:
43 45 4 46 0
Такое уравнение можно составить непосредственно без начала возможных перемещений, записывая условие равновесия моментов, действующих на данный узел.
Моменты в этом уравнении должны быть заменены через принятые неизвестные при помощи формул 2, в которых, в свою очередь, величины tyai должны быть заменены пр формуле 17.
Уравнение, соответствующее кинематически независимому смещению Ат составим так. Осуществим на схеме расчленения рамы она же является
шарнирной схемой рамы смещение Дт, равное 1 единице, но так, чтобы при этом не появилось никаких перемещений, соответствующих прочим принятым неизвестным. Затем запишем работу сил действительного состояния на этом перемещении шарнирной схемы рамы, полностью в соответствии с указаниями гл. V. В результате мы получим уравнение типа 22 гл. V:
ЛУа 2a 2а- Qab Kb-. 19
TTJ
В этом уравнении мы заменяем величину QabQab по формулам 2 и по формуле 17 через принятые неизвестные перемещения. Вот краткое изложение стандартного приема составления уравнений метода деформаций в задачах устойчивости и устойчивой прочности. Для таких задач этот прием, невидимому, более удобен, чем какие-либо другие.
В дальнейшем уравнения типа 18 мы будем называть уравнениями узлов, а уравнения типа 19 дополнительными уравнениями или уравнениями линейных смещений.
Запишем эти уравнения в развернутом виде.
Уравнения узла а можно записать так:
2 Мат 22iam Km Та Pam Tm а Pam Ф2т SАп Феб 2Mam 0-
а а па
Здесь суммирование распространяется на все стержни ат19 ат2, ат3,., сходящиеся в узле а. Расположив члены этого уравнения в порядке неизвестных, получим:
Та 22 iam аат т 2am Pam
а а па
Warn Фат 2 Мат h Pam 0. 20
а а
Уравнение для линейного смещения Дп можно записать так:
2 Qab Qabhb ¥ab - 2a 2a вП 0
или, используя формулы 2 и 17:
2 ab ta Pa а b — Tab ab 2с ab
Qab Qab lab 2 Vfv™ 2И a П 0.
Перегруппировав члены и объединив символом ра оба угла ра и получим:
— 2а 2am а ат tyam ат Yam Фат фат а к
2m-Sn4m1-2a 1П 2 in 22iamTamm1. 21
161
Из рассмотрения уравнений 20 и 21 легко прийти к выводу о взаимности коэфициентов см. обозначения 7 гл. V
тп 22
этой системы уравнений. Действительно см. 20, коэфициент в уравнении для сра при 9т будет равен 2iamarr Точно такое же значение будет иметь коэфициент при сра в уравнении для срш. Коэфициент при линейном смещении Дп в уравнении 20 для угла сра равен.
-Кт PemI-
а
Точно такое же значение имеет коэфициент при угле ра в уравнении 21 для линейного смещения Дп. Таким образом, формула взаимности 22 доказана для принятого в этой главе метода собтавления уравнений; уравнения получаются в симметричной канонической форме.
Формулы 20 и 21 мы получили, пользуясь для МаЪ и Qab выражениями 1 и 2 для стержня с упруго защемленными концами случай 1 2. Совершенно аналогично можно показать, что система уравнений, составленная указанным в этом параграфе методом, получится в симметричной канонической форме так же ив том случае, если в раме будут и стержни с шарниром на одном конце, с фиксированным значением поперечной силы Qab, стержни-консоли случаи 2, 3 и 4 2.
4. Примеры расчета устойчивости рам1
Рассмотрим несколько простыхпримеров расчета устойчивости рам.
Пример 1. Проверить устойчивость рамы фиг. 71. Отношение погонных жесткостей ригзля и стоек обозначим:
Ji h
м — Jl n h Jh I
23
Фиг. 71.
Данная задача трижды кинематически неопределима, пеизвестпые: р2, р3 и ФФ12 Величины р 1 р4 Ф2з0
Продольные усилия стержней в данном случае равны: jV12 P, 2з 34 0. Таким образом,
34-
,Ph2 ,Ph.
vi2vf ЁТГУ и vv-
ч
Для решения задачи надо составить три уравнения. 1. Уравнение узла 2:
Г М21 2ih Vf2 -f- 30 — а Р ЗД 1 Jf28 2yift28- 3 - 0
2ih а-2п р2 f- — а 4 Р щ 0.
а
1 См. нашу статью в Вестнике инженеров и техников, 1937, 3, а также Исследо
вание устойчивости пространственного каркаса по типу высотной части Дворца Советов СССР, Изд. Академии Наук УССР, 1938, гл. VI.
2. Уравнение узла 3
JW32 2д р2 3 0
MM2ij2b 0-3A
Ь
2й 12 2 2 з-Зй 0.
Дополнительное уравнение см. формулу 23 гл. V
21-2а3 Ь-тМ
Ь
34- h
33—6a
VC
Да 2 3fg— Y 6 Фл
Полученная система уравнений приведена в табл. 17.
Таблица 17
з
а 2.ч п а-f-ji
а3 3
Т6
о
о
о
Для критического состояния детерминант этой системы уравнений должен равняться нулю.
а 2 п п а Р
п 2л-2 3
Р 3 т 6
D
0
il Раскрыв этот детерминант, иолучим уравнение, трансцендентное относительно
ii
v v12 и квадратное относительно величины тг.
lh
В отличие от общей методики 3 гл. V, связанной с построением графика этого детерминанта, задачу в этом сравнительно простом случае следует поставить так. Давая v v12 ряд последовательных числовых значений в пределах, примерно, от v 1,4те когда п оо до v0,7re когда д 0, разыскиваем по табл. 1 приложения соответственные числовые значения коэфлциентов а, ар и у и затем решаем наше квадратное уравнение 0 относительно п. Из двух корней для п мы выбираем паабольший положительный, как соответствующий более опасному критическому состоянию.
По найденным таким образом значениям п и v построен график фиг. 72. Критическое значение груза находим по формуле:
р kpEJh ,
h Для примера найдем положение одной точки на этом графике
Пусть v3,0, тогда по табл. 1 приложения находим:
а 1,3120; a J 2,5178; 6 6,5356.
Подставйв эти значения в d, получим квадратное уравнение:
19,61 и2 27,70 71-7,34 0.
Корни этого уравнения дх 0,2280 и п2 —1,6414.
Отрицательный корень мы отбрасываем, как не имэющяй реального смысла отношение погонных жесткостей стержней не мэжзг быть отрицательным. Таким образом, мы находдм точку на графике с координатами
7 3,0; п 0,2280.
153
Пример 2. Проверить устойчивость системы фиг. 73; отношение погонных жесткостей ригелей и стоек равно п. Продольные усилия можно считать для ригелей равными нулю, а для стоек равными
iV01 AT12 -ql,
т. е. реакции средней опоры двухпролетной неразрезной балки 4—2—4. Рассматриваемая рама не свободна, все углы поворота стержней ф 0. В качестве неизвестных расчета мы примем углы поворота узлов и р2Уравнение узла 1:
f М10 по формуле 8
8
I М12 2
api frp2 h а 2a fx 2fty2 О
1
a
Уравнение узла 2:
М21 — 2 аКр2 4 Pi
J 3ix Ь 9-
М
- —
i 23у1 2а4-61 2J0.
Детерминант для критического состояния:
D
a 2a-f6i 2р 2Р 2а 6гс
0.
Раскрывая его, находим:
2а бтг4,2 а 2а 6га -42 0,
-откуда
2а 6п —4г.
по формуле 1 8 и 12
8 и 12
Ь
Выбираем для п больший положительный корень, соответствующий более опасному критическому состоянию:
С
Давая v последовательно значения vis; 3,3; 3,5 и т. д., по таблицам приложения находим соответствующие значения а, а и р и затем вычисляем п.
164
Результаты этих вычислений приведены в табличке:
v
T.
3,3
3,5
3,7
3,9
4,0
n—
0
0,0907
0,2363
0,465
0,8133
1,086
По данным этой таблички построен график фиг. 74. По этому графику легко находим для заданного значения п соответствующее значение укр после чего величину критической нагрузки определяем по формуле:
7 _ 5 al-.wHl_y2EJh
-откуда
Пусть, например, По графику находим v 3,98, откуда
- 3,98 12,6
Пример 8. Определить критическую силу Ркр для ступенчатой стойки фиг. 75. Задано: ТТ И VT вди
l23 01
В этом случае величины v01 v32 v23 v. Очевидно, что поперечная
сила
Qjo Q21 Q32 О
Поэтому при решении этсй задачи уместно для стержней 1—2 и 2—3 использовать формулу 13, которая для данного частного случая запишется так:
GiV
а для стержня 2—0 формулу 15:
Mat tab v tg v e.
В качестве неизвестных в этой задаче мы можем принять , и . Уравнение узла 1:
j м10 — г01 v tg v
M™ 2i t7 1 slHV 0
0lV
-tgvt-l-v1:bo.
Уравнение узла 2:
Mii2oi t; _ sTSTfi
8V. b - b1j o
SF 2
sm v
Детерминант для критического состояния:
w
tg V
2
sin V
sin V
5
tg v
0,
Фиг. 75.
0
b
155
Раскрываем его:
и преобразуем так:
Dil-5 rV tgaV Slir V
p I D— 10 cos2 v — 5 sin2 v — 41 -Дг 15 cos2 v — 91 0,
f A sin2 v sin3 v J
i откуда
I
cos2v — 0,6 и cosv o,6 0,7746.
ft
15
1
По таблицам Петерса1 легкэ находим v 39o4610 или v 0,6836, откуда
_ v2EJx л ,спл EJX кр If 04673 дГ
Пример 4. Проверить устойчивость сжатой стойки с односторонней консолью фаг. 76. Длина пролета стойки—I, длину консоли обозначим через cl, где с — некоторый отвлеченный коэфициент. В этом случае:
01
,рг2
К Юv; vi2cv;
EJ
t
Фиг. 76.
i _ ti_ —
01 у 112 — c
Составим одно уравнение с одним неизвестным рх, ислользуя формулы: 8 для стержня 0 — 1 и 15 для консоли 1 — 2;
Ml0 i10 М12 — cv tgcvyx
С
hob а —v tg cv 0.
Для того чтобы pj могло отличаться от нуля, нужно, чтобы выражение в скобке равнялось нулю. Таким образом:
4. а
tg cv —.
В табл. 18 приводим подсчеты, выполненные по этой формуле.
Таблица 18
V
0
0,5
1,0
1,5
2,0
2,5
3,0
те
tg cv — ь v
со
5,8993
1
2,7940
1
1,6785
1,0442
0,5752
0,1361
0
cv
7С
2
1,4029
1,2271
1,0335
0,80702
0,52195
0,13526
0
с
оо
2,8058
1,2271
0,6890
0,40351
0,2088
0,04509
0
По этим данным построен график фиг. 77. Критическую нагрузку определим по формуле:
v2
Р
кр JT
20
Если воспользоваться указаниями, помещенными в курсе Ф. Блейх Стальные конструкции т. 1, 1938, стр. 191—192, то
Ркр —
EJ
14-с2 г2
не верно
1 И. Петерс, Шестизначные таблицы тригонометрических функций, ГТТИ, 1932,
156
По Блейху надо считать свободную длину стержня равной полной его длине. Блейх считает свое предложение точным, тем не менее оно ошибочно. Оно было бы верным только в том случае, если бы нагрузка, не сохраняя вертикальности, все время поворачивалась бы по хорде, соединяющей концы стержня. Предложение Блейха дает значительную погрешность и не в запас устойчивости. На графике фиг. 77 сплошной линией нанесено наше точное решение и пунктирной — решение по Блейху. При
EJ EJ EJ
с 1,5 по Блейху получится РЛр 1,58 вместо РС2, 0,852 0,722.
Для приближенного решения задачи этого примера можно предложить более удачную формулу:
1,70 D 1,7 EJ
или kpc 0fi
с 0,5
I
На графике фиг. 77, крестиками нанесено несколько точек, соответствующих этой приближенной формуле.
Пример 5. Проверить устойчивость системы фиг. 78. Задача сводится к составлению и решению одного трансцендентного уравнения, представляющего условие равновесия узла 1.
f J
мр
к; ej
Рнр ; 2
4 к4 ч
V
1
С.
V
ч
1 v
Чс
_
г,
с
Фиг 77.
жг
Фиг. 78.
Так как опоры 2 и 3 подвижные, то Q01 0, и поэтому можно М10 определить по формуле 15; моменцл же Д12 и M1Z получаем по формуле 8; кроме того 1р12 ф13 0. Таким образом находим:
Л10 — Jiotgv 4it Miz 13 i3
Приравняв нулю сумму этих трех моментов, после несложных преобразований получаем:
v tg V
14
Фиг. 79.
Пользуясь табл. 3 значений vtgv, помещенной в приложении, решаем это трансцендентное уравнение, находим величину v и затем по формуле 20—критическую нагрузку Ркр.
Пример 6. Система параллельных стоек, жестко заделанных нижними концами, шарнирно связана поверху не деформирующимися стержнями фиг. 79. Общее число стоек n m, из них п загружены равными силами Р. Все стойки одного сечения.
Критическую систему нагрузок получим из условия возможности перекоса системы на величину Дф при равенстве нулю суммы поперечных сил для всех ее стоек. Сумма поперечных сил для п загруженных стоек в соответствии с 8 будет равна:
- h ftQsatp — д V
Сумма поперечных сил для т незагруженных стоек:
ftQne3aip
т ф, h
157
Таким образом, уравнение критического состояния будет:
пг 3 т О
или
3 т
Пользуясь табл. 1 значений у, помещенной в приложении, определяем v, а затем по формуле 20
Пусть, например, n 2; т 3. Нам надо найги v, для которого —4,5. Из табл. 1
при v 2,45 находим: т —4,43623 и при v 2,46 находим f — 4,55077, Путем интерполяции получаем искомое значение:
4 5 л 4362Я
7 245 4,550774,44628 01 245 0021 24521
EJ EJ
откуда Ркр 2,4522 -2 6,01 —.
5. Примеры расчета устойчивости симметричных,
симметрично загруженных рам
Выше в 8 гл. V мы выяснили, что в случае симметричной, симметрично загруженной системы достаточно рассмотреть отдельно симметричные и отдельно обратно симметричные формы потери устойчивости.
В 20 гл. III мы выясндли, что при отсутствии нагрузок по длине стержня сжато изогнутый стержень искривляется по дуге синусоиды, причем длина волны Л этой синусоиды определяется формулой 188:
Л
EJ
N
V77777777777777. Фиг. 80.
а продольное усилие
42 EJ
N
Л2
21
Эта формула позволяет во многих случаях без предварительного расчета выяснить, какая из форм потери устойчивости, симметричная или антисимметричная, является наиболее опасной, т. е. соответствует меньшей критической нагрузке. Формула 21 показывает, что критическое усилие N будет тем менее, чем больше будет квадрат длины волны А2 кривой изгиба стержня. Легко видеть, что для свободной многоэтажной рамы фиг. 80 длина волны Аа при антисимметричной форме потери устойчивости фиг. 80, б больше длины Дс при симметричной форме фиг. 80, а
поэтому
Na Ncy
и, следовательно, для таких рам антисимметричная форма потери устойчивости является более опасной.
Относительно сравнительной опасности различных форм потери устойчивости можно высказать еще одно общее положение, основанное на энергетических соображениях см. 12 гл. IV, формула 43:
158
Вслучае равенства работы, внешнихсил 2 при двух формах потери устойчивости — более опасной является форма, которой соответствует меньшая работа
деформации 2 EJ v2 ds.
На основе этих принципов легко, например, без всякого расчета установить, что из четырех различных форм потери устойчивости для
OJ
1
г
I
I
I
2
V
Г
2
Л
б
ГГ- г
I I
несвободной прямоугольной замкнутой рамы фиг. 81, наиболее опасной является форма а. Действительно, формы б и г менее опасны, так как им соответствует меньшее значение Л; форма б менее опасна, так как в ней нужно затратить больше энергии на S-образное искривление ригеля.
Перейдем к примерам.
Пример 1. Сравнить критические нагрузки, соответствующие различным формам потери устойчивости несвэбодной одноконтурной прямоугольной рамы фиг. 81. Погонные жесткости стоек и ригелей равны 1г 1к10.
Углы ф 0 для всех стержней
В соответствии со сказанным в 8
гл. V мы можем считать, что в данной раме, имеющей две оси симметрии — вертикальную и горизэнтальную, углы поворота узлов должны быть либо прямо, либо обратно симметричны относительно этих осей. Иначе говоря, по абсолютной величине углы
¥i ¥1 и 2 должны быть равны друг другу, они могут только различаться знака
ми. В качестве неизвестной мы поэтому примем р — абсолютную величину такого угла поворота.
Случай а. Деформация прямо симметрична относительно обеих осей:
Уравнение узла 1:
Г Mllf 2e2y-rt
I Ml2 2i0ap-
2i0p a— р 1 0. По табл. 1 приложения легко находим:
V
a
P
a-p1
4,03
0,5366
1,5233
0,0113
4,06
0,5264
1,5302
—0,0038
Таким образом:
О 0114
V -.05 0,01 0,0113 0,0038 ‘05,5‘
Случай б. Деформация симметрична относительно горизонтальной оси и обратнгсямметрична относительно вертикальной:
1 -2 ¥i- — Уравнение узла 1:
Mn, 2f0 2 f
M12 2i0 ay-Py
2i0f a - J 3 - 0.
15
Аналогично находим
4.91
4.92
Отсюда
0,7433
-0,7657
2,2517 2,2665
0,0050 —0,0322
V,
кр
4,9113.
Случай в. Деформация симметрична относительно вертикальной и обратно симметрична относительно горизонтальной оси:
Pl2 , — 2 Р.
Критическое условие для этого случая а- fi-f- 1 0 можно удовлетворить только при значениях v, больших 2 те повидимому, при значении близком 7.
Случай г. Требует еше большей критической силы. Пример 2. Определить критическую нагрузку для свободной прямоугольной рамы фиг. 82, имеющей две оси симметрии. Дано, что ii nih. Более опасной будет антисимметричная относительно обеих осей форма деформации:
1 Р2 Рг Р2 -
При этом:
Ql2 — Ql2— 2 Qi2— 0
j
и поэтому мы можем для стоек пользоваться формулой 13, а для ригеля 1.
L V т sin V r J
22
tg v sm v Mllr 2nih 2р р
v 1 cos у sin v
- Ъп
j-
0.
¥
J
Фаг. 83
Отсюда после преобразований получаем:
,. гкnJi _ а
Th—6
Фиг. 84.
1. V
ng vtgj.
23
По этой формуле построен график фиг. 83.
Критическую нагрузку находим по формуле 20. Симметричная форма потери устойчивости этой рамы рассмотрена в примере 1 этого параграфа.
Пример В. Проверить устойчивость рамы фиг. 84. Погонная жесткость ригеля в п раз больше погонной жесткости стоек:
hnh-
180
В соответствии с энергетическим принципом, изложенным в начале этого параграфа, более опасной в данном случае является симметричная форма потери устойчивости :
i —Pi До потери устойчивости в этой раме углы рг 0, так как моменты защемле-
ql2
ния М0 — Mlf взадмно погашают друг друга в свободных членах. Поэтому
распор в раме до потери ее устойчивости отсутствует и продольные усилия JV в стержнях ригеля можно считать равными нулю. Продольные усилия стоек Nh ql.
-А-Н
Фаг; 85;
Задача приводится к составлению одного уравнения с одним неизвестным:
gl2
I
M10 2nth2l 0 —
S —0
alz
Mllf 2nih 2 — — —
iji 6ra -f- j, s 0.
Зная га, легко находим a—6га, а затем по табл. 1 приложения определяем
после чего получаем
ql 1ЛР.
h1
Если га 2, то а —12 и vwp 6,0365.
Пример 4. Определить крлтические нагрузки антисимметричной и симметричной форм потери устойчивости для рам фиг. 85.
Все эти случаи трзбуют составления одного уравнения равновесия узла с одним неизвестным рх. В случае антисимметричной деформации случаи а и в поперечные силы на стойках равны друг другу и сумма их равна нулю, следовательно, эта поперечные с ялы равны нулю. Поэтому момент М10 мы для случая а определяем по формуле 15:
м10 — tAV tgvft,
а для случая в по формуле 13:
Для случая б этот момент находим по формуле 8:
М10 t haVlf
а для случая г по формуле 1:
М j_o 214в.
Критические условия при этом получаются1:
для случая а
1 1 т1 га —v tgv;
h 6
б
в
6 tg V
п — —а.
23
24
25
26
1 См. статью автора в сборнике 3 Исследования по теории сооружений, Госстройиздат, 1939.
11 Прочность и устойчивость стержневых систем
161
Все эти функции приведены в табл. 1 и 3 приложения и определение по ним значения укр не представляет никаких затруднений см. также графики фиг. 86.
Прлмер 5. Проверить устойчивость трехэтажной рамы фиг. 87. Отношение погонных жесткостей ригеля и стоек обозначам:
а
Более опасной деформацией рамы при потере устойчивости будет антисимметрия ная, т. е.:
itePio 2 ь ;
Точно так же:
QoieQolM Ql2 Ql2i Q28Q23 а так как из условия равновесия:
Qoi 4 Qol в Ф Ql2 Qi2 ; Q23 bQ28 — О
то поперечные силы на стойках рамы и при потере устойчивости равны нулю. Поэтому прл определении моментов на концах стоек рамы можно пользоваться формулой 13.
Моменты на концах стержней, сходящихся в узле 1, будут:
Мц, 22f —3 0.
Приравняв нулю сумму этих трех моментов, получим условие равновесия узла 1:
Из фиг. 87 видно, что
N23 Р Nlt2P и N01Z Р9
отсюда
Ь
v23 v; v12 v2; v0l — v з.
с
162
На основании а и с перепишем условие Ь в таком виде:
V уз , V2 , 1 _ ч V2
f
mh
— -I r 4-бл f i
Ч V 3 tg v 2 J
P
J
sin
v2
dr
И
c
H
I
p p nth ,
I p p
nlh
1
4
4 r
4
A,
- Фиг 87.
Аналогичным образом получим уравнения равновесия для узлов 2 и 3:
О
т
V2
i
v У 2
г
sin v 2 1 Ltgvl2 tgv
p2 Г— Ьп Рз 0.
smvт Lg v J
6n 1 p2 p3 0; d
J sin v T
e
77-1
Приравняв нулю детерминант этих трех уравнений, получим условае критического состояния нащзй рамы. Раскрыв этот детерминант, получдм уравненде третьей степени относдтельно коэфлциента п. Давая аргументу v ряд последовательных значений,
меньших pi этому случаю соответствует оо, решаем полученное кубдческое уравнение относительно п и из трех корней его берем нааболыпай положительный действительный корень. По данным вычислендй построен графак фаг. 88, Критическое значение груза Рир находим по формуле 20.
Пример 6. Рассмотрим ряд прлмеров, когда проверка устойчивости многоэтажных рам может быть сведена к проверке устойчдвости одноклеточной рамы, изученной нами в примере 2. Проверам на устойчдвость самметричную m-этажную раму фиг. 89,а. Погонные жесткости стоек рамы равны погонные жесткости крайядх верхнего и нижнего ригелей в два раза меньше погонных жесткостей промежуточных ригелей, которые равны г‘ 2дд. Так же, как и в прлмере 5, при антисимметричной форме потера устойчлвоста попзречныэ сдлы стоек равны нулю, что дает возможность пользоваться для концевых моментов стоек формулой 13. Составив уравнение для какого-нибудь промежуточного узла к по тапу:
Мк к-1 Л Мк сЧ Mkt к i525 0,
p
4
2nit,
4
2nih
4
2rih
4
2nih
4
nth
1 -i
Н
С
-4
-t
5
P
nlh
4
;
nih
т
получим:
Фиг 89.
fkl г‘0 4п 2
tgvfc sin v
ила после преобразований:
-3 0
. f , sin v
- fk-t 2 f cos v 6n —Jfk — fk-,1
27
ll 163
Аналогично для крайних верхнего и нижнего узлов получим-:
¥m-i cos v 6г- pm 0; а
. sin v
Cos v бп —— J po1 0. b
Для краткости обозначим:
. sin v , v
cos v 6w : a. c
v
Тогда уравнение 27 получит вид:
- Pc-i 2арк - pfc j 0. 23
Таким образом, эадача сводится к решению линейного однородного уравнения
второго порядка в конечных разностях. Решение этого уравнения может быть дано
в виде:
Чк С1 cos6fc C2sin0fc, d
где Сг и С2 — независимые параметры, определяемые из граничных условий а и Ь, а 0 — вспомогательная величина, определяемая по формуле:
cos б а е
В правильности решения d легко убедиться непосредственной подстановкой
в уравнение 27.
Определим параметры Сг и С2, для чего подставим в уравнения а и Ъ:
- Ртп-1 Ы cos в 0 а
и
р0 cos 0 — рх 0 b
вместо рт-1 ¥т Ро и их значения по формуле d.
После некоторых преобразований, получлм:
— С sin б sin 6m C2sin 0 cos 0m 0: а
— С2 sin 6 0. b
Так как рама может потерять устойчивость только при условии, что Сг и Са оба или одно из них отличны от нуля, то критическое условие получим, приравняв нулю детерминант, составленный иэ коэфициентов при Сг и Сг в этих двух
уравнениях:
sin2 б sin бт 0. f
Это уравнение f может быть удовлетворено в следующих случаях:
1-й -случай: sin 0 0, cos 64-1, тогда согласно е и с
. sinv. , cos V -f- 6 tl - 1,
откуда
n A- v tg. 23
Уравнения a, b и 28 при этом дадут:
¥о Pi з т-
5-й случай: sin б 0; cos б — 1: тогда
Ро 1.v
n-vctgY.
s-случай: sin 6m 0, 6m prc, где коэфициент p может быть равен любому целому числу.
рт6
cos cos v
m
n — v.
6 sm v
Для величины p нужно выбрать такэе целое число, чтобы отношение погонных жесткостей п получило наиболыпзе положительное значение.
Так как нас интересуют только значения v, меньшие, чем п, то нужно выбрать.
Рп л
такие значения р, при которых cos- l; тогда
1 — cos v 1 х V
П -бЖ-76- 2
т.е. получается та же формула, что и для первого случая.
164
Очевидно, что форма искривления рамы, соответствующая второму случа-ю а -— 1 требует бблыплх значений крлтлческой сллы, а поэтому более опасным является первый случай, для которогомы получили:
1 , v
rtgI
23
Эта формула вполне совпадает с формулой 23 примера 2. Таким образом, одноэтажная рама фиг. 89, б равноустойчива с многоэтажной рамой по фиг. 89, а.
Пример 7. В раме флг. 90 крайние ригеля 0 — 0 и т — т имеют такие же сеченяя, как и промежуточные, т. е. в отллчие от рамы фиг. 89, а погонные жесткости крайних ригелей также равны 2ni. Граничные условия а и Ь несколько меняются:
т
А
W
р
f
tb
ii
4
it
4
it
4
ii
— m-14 cos v - 12д
11 v л
— т 0;
COS V 12п .
Ь
О
Vp
3.14
V.
Iftnis Фиг. 90
m100
773
2 3
Фиг. 91.
Подставив решение d в Ь и i, после некоторых преобразований получим:
Сг 6 cos 0m — cos 9 m — 1 С2 sin Отта — sin 0 m — 1 0: h
Cx 6 — cos — C2sin 9 0. i
Здесь для краткости обозначено:
. sin v
cosv-f-12Ti. k
Критическое условие получим, приравняв ;нулю детерминант, составленный из коэфлциентов при Сг и С2.
Раскрыв этот детерминант, получим квадратное уравнение относительно , ив которого найдем:
sin б яг — 1 sin 0 1Ч
0
о sin Qm
Подробный анализ формулы 1 показывает, что более опасным является верхний знак в числителе этой формулы.
Согласно формулам с, е и к:
6 2 cos 0 — cos v. m
Подставив значение m в 1, после преобразований получим:
0 иг-f 2
cos
cos v
cos
0 т
Y
29
Кроме того, решая формулы с и е относдтельно п и учтя , что -Л 2п, полу-
Ч
чаем:
Н
Из формул 29 и Зо следовало бы исключить вспомогательную величину 0 для
того, чтобы получить критическую зависимость между v, отношением а и ч хлом
этажей т. Удобнее поступить иначе, сохранив величину б, как вспомогательный параметр. Давая величине 0 последовательно различные значения в промежутке1
, по формулам 29 и 30 вычисляем соответствующие значения для
между 0 и —i v в пределах от 0 до те и отношения
h
а
п
л-1
pi
2Р
А
ZST
;
12Р 12Р I
i 21,
2U
75Г
А
Р
D
Ч
В
В результате таких вычислений построен
график фаг. 91 для рам с числом этажей га 1, 3 и 10Э.
Пример 8. Дэкажем, что многопролетная и многоэтажная рама фиг. 92,а для случая загружения, показанного на фигурз, имеет такую же степень устойчдвости, как и одноклеточная рама фиг. 92, б. Дано, что погонные жесткости всех средних рлгелзй и стоек лежащих внутри пунктира нафлг.92,а вдвое больше соответственно погонных жесткостей ригелей и стоек, расположенных по внешнему контуру рамы. Продольные силы крайних стоек вдвое меньше продольных слл промежуточных стоек, —таким образом, для всех стоек велдчина одна и та же, а для ригелей v0.
Предположим, что при потере устойчивости рамы в ее плоскости все узлы повернутся на один и тот же угол ср и все этажи перекосятся на одинаковые углы ф. Еслл окажется, что, при таком допущении, можно будет удовлетворить всем уравнениям, составляемым по методу деформаций для проверки устойчивости этой рамы при значениях риф, отличных от нуля, то будем считать это допущение доказанным. Уравнение равновесия для какого-нибудь внутреннего узла А фиг. 92, а будет:
т-1
Фиг. 92.
т
2мдо
или
2 2 2ii 2зр -f- — 3 0 -Ь2 2 2ар-j- р — л4- ф 0. После приведения подобных членов и сокращений получим:
Р3 -рф 0.
А
Совершенно такой же вид имеют уравнения и для наружных узлов типа В, С и D фиг. 92, а, в чем нетрудно убедиться.
Уравнение горизонтальных проекций усилий стоек одного этажа имеет вид:
или
2 h
Т a W 14- 2 m — 1 -f 1 0,
где т — число пролетов.
Такой же вид имеет уравнение и для любого другого этажа нашей рамы. После преобразований его можно записать:
2 а - Р р — тФ 0- Q
Таким обраэом, наше допущение о равенстве для всех узлов рамы углов р и для всех этажей — углов ф можно считать доказанным, так как мы показали, что такая форма потери устойчивости возможна; также очевидно, что такой форме потери устойчивости соответствует наименьшее значение критической нагрузки. Критическое условие получим, приравняв нулю детерминант из коэфициентов при р и ф в уравнениях А и Q. Раскрыв его, найдем:
3aP,yiiii,
ч т
1 Более подробный анализ показывает, что этот промежуток охватывает весь интер вал значений, соответствующих наиболее опасному случаю потери устойчивости.
166
Использовав выражения дляфункций a, J и у через v, приведем это выражение к виду:
а
Эта формула совпадает с формулой 23 для одноклеточной рамы фаг. 92, б. Выходит, что многоэтажная рама фиг. 92, а как бы составлена из поставленных друг на друга одноклеточных рам фиг. 92, б, прячем все они теряют устойчвосаь одновременно, одинаково при этом деформируясь.
6. Об устойчивости однопанельных рам с прямоугольными клетками при отсутствии симметрии в нагрузках
и жесткостях их стоек
Исследуем сначала одноклеточную раму фиг. 93 со стойками разной жесткости. Пусть рама имеет горизонтальную ось симметрии. Рассмотрим более опасную, антисимметричную относительно этой оси деформацию:
i р4; 2 а-
Углы поворота ригелей: ф12 43 — 0. Углы поворота стоек равны друг другу: ф14 ф,3.
Итак, задача сводится к составлению трех уравнений с неизвестными рх, р2, 1.
Для загруженной стойки v23v, причем:
р у _lJt. а
п Фиг. 93.
Здесь А — отвлеченый коэфициент, изменяющийся в пределах от 0 до 1. Для остальных элементов рамы va 0.
Уравнение узла 2:
Г ifcfia 27102 1 Мла —
14 — 2 1 — к 2у1 -Ь — Зф
2i0 2л - S 1 — к пр2 — 3 1 — к ф 0
Уравнение узла 2:
I Г М21 2nt0 23 i I М23
2f0 пух 2п 1 к а 4- Ь р2 - 1 к а- ф 0
Дополнительное уравнение:
fa,
h
3 4 3ft— 6ф
23 -31-Л1-1Ла рЬ 3l-A l-TlftJ ф10 Раскрыв детерминант этих трех уравнений, использовав зависимость
V у2ат-р получим условие критического состояния рамы
ns4l Y 9l-il A 31 — Лv2 Зу —
— -Ш- v8 а р — 1 — к 1 Av3 а р 0.
Ь
167
При помощи этого уравнения построен график фиг. 94, на котором представлены для сравнения следующие четыре случая:
А — симметричная рама к 0 загружена симметрично пример 2 5; В — несимметрично;
С — несимметричная рама к 0,5 загружена над сильной стойкой; D— к —0,5 слабой стойкой.
Для построения графика фиг. 94 мы последовательно задавались численными значениями v и по табл. 1 приложения, разыскивали соответствующие им значения коэфициентов ар и у. Затем решалось квадратное уравнение Ь и определялся его боль-
- Р
р
2
р
2
Л10
to
пс0
,
it
к
Д
7777.
Фиг 94.
Фиг. 95.
ший положительный корень п, представляющий абсциссу точки на графике; соответственные ординаты вычислялись и по формуле а.
На графике фиг. 94 кривые для случаев А и В практически сливаются, кривые же для случаев С и D идут ниже, причем случай положения груза над слабой стойкой оказывается наиболее опасным.
Аналогично примеру 6. рассмотренному в 5, нетрудно показать, что многоэтажная рама по типу фиг. 95 равноустойчива с одноклеточной рамой по типу фиг. 93, если погонная жесткость средних ригелей равна 2i3.
График фиг. 94 показывает, что для упругой устойчивости однопанельных многоэтажных и одноэтажных рампри наличии симметрии в жесткостях стоек практически безразлично, как распределяется нагрузка Р между стойками рамы: будет ли нагрузка действовать вдоль одной из стоек или будет частично действовать на одну, а частично на другую стойку. Важно только, чтобы сумма продольных усилий стоек сохранялась без изменения.
В случае отсутствия симметрии в жесткостях стоек распределение нагрузки между стойками уже сказывается в той или другой мере на устойчивости рамы. Для случаев С и D фиг. 94 жесткость сильной стойки превышает жесткость слабой в три раза, при этом перенос нагрузки с сильной стойки на слабую снижает в пределах графика фиг. 94 устойчивость рамы всего, примерно, на 15 0. Если жесткости стоек не будут так сильно отличаться друг от друга, то перенос нагрузки с одной стойки на другую и вообще перераспределение нагрузки между стойками будет в значительно меньшей мере отражаться на величине
168
критической нагрузки рамы. График фиг. 94 показывает, что при расчете устойчивости однопанельных многоэтажных рам фиг. 96 для упрощения расчетов можно:
1 неравные в пределах одного этажа моменты инерции колонн заменить равными—их средними арифметическими значениями, превратив, таким образом, несимметричную конструкцию в симметричную;
2 неравные нагрузки узлов левой и правой колонн заменить рав
ными—их средними арифметическими значениями, превратив, таким образом, нагрузку конструкции в симметричную. I
Степень погрешности, соответствующую такому у проще- нию расчета, можно оценить примерно, пользуясь кривыми графика фиг. 94.
дне балки, балки Лангера,
9
7. Примеры расчета устойчивости шпренгельных коне тру БЦИЙ
Шпренгельными конструкциями, несколько во изменение и обобщение этого понятия, мы будем называть также такие стержневые системы, в которых для усиления и увеличения жесткости изгибаемых элементов ставятся дополни- утельные стержни, работающие на продольные усилия и вое- Фиг. 96.
принимающие на себя часть общего изгибающего усилия. Конструкции эти занимают промежуточное положение между рамами и шарнирно-стержневыми системами. К ним можно отнести шпренгель-
мачты на оттяжках, рамы с решетчатыми ригелями и рамы с угловыми подкосами2.
Основные, изгибаемые элементы в таких конструкциях имеют сравнительно мощные сечения, и продольными деформациями их обычно можно пренебрегать по сравнению с продольными деформациями дополнительных стержней, работающих на осевые усилия.
Рассмотрим несколько примеров расчета устойчивости таких конструкций.
Пример 1. Проверить устойчивость портальной рамы с перекрещивающимися подкосами фиг. 97, а. Наиболее опасной формой потери устойчивости рамы будет антисимметричная форма.
Таким образом:
pi i; Ф01 ; 12 ф12-
При перекосе верхней части рамы фиг. 97, б в подкосах возникнут усилия S, равные по величине, но противоположные по знаку.
При смещении узла 2 вправо на величину Ь12 подкос 1—2 фиг.97, б удлинится на величину:
А
Фиг. 97
8lt cos А
1 Мы здесь не имеем в виду шарнирно-стержневых ферм со шпренгельной решеткой.
2 Такие рамы названы шпренгельными в книге Д. Я. Акимова-Перетц Расчет рамных систем, стр. 21, Стройивдат, 1932.
16
откуда
EF
S -y-i httylt cos A EFi sin A cos A 1W- a.
Проектируя. на горизонтальную ось силы, приложенные к верхней отрезанной часты рамы, получим:
2 1з 5 cos А 0. Ь
Подставив сюда вместо Q12 его выражение по формуле 9
_ 12 Ц- 12 — YlA
и вместо S его выражение а, получим после преобразований:
с
Tl2T
Здесь для краткости обозначено:
С -у- h sin A cos2 A. d
Момент М1г на конце стержня 1 — 2 можно получить по формуле 8
EJ —
Pi —
или после подстановки вместо Ф12 его значения из с:
М1г5i. 1 -ттг в
2 Ч Yia С У
Момент М10 на конце стержня 1 — 0 найдем по формуле 15:
ю vi tg f
Условие равновесия узла 1:
м10 МХ2 0
после подстановки в него вместо М10 и М1 их значений из е и f
покажет, что угол может отличаться от нуля только в случае, если:
В этом уравнении критического состояния С — величина постоянная
для данной рамы, величины же alt и у12 определяются по табл. 1 при
ложения, как функции величины
Via
Давая последовательно величине v01 различные численные значения, ищем значение v01, при котором удовлетворится уравнение g; тогда
р __ V
КРh
Пример 2 Проверить устойчивость монотонной двенадцатиярусной рамы фиг. 98, представляющей собой ,деталь сложной системы. Задано, что вследствие особенностей конструкции продольные деформации колонн не следует учитывать. В силу этого деформация нашей рамы при потере устойчивости носит характер деформаций сдвига. Наиболее опасной формой потери устойчивости будет антисимметричная форма, как относительно вертикальной, так и относительно горизонтальной осей симмет
170
рии конструкции. В силу этого изгибающие моменты в колоннах на высоте горизонтальной оси симметрии равны нулю. Двенадцатиярусная рама оказывается равноустойчивой со своей половиной —рамой шестиярусной, а та в свою очередь на тех же основаниях рав- р pi ноустойчива с рамой трехъярусной фиг. 99.
Опасной формой потери устойчивости конструкции будет антисимметричная, при которой:
3 8 Л 2 2М 0 ¥
Кроме того, ввиду симметрии конструкции относительно горизонтальной оси 1 — 1 фиг. 99
i T и 9 р3. а
Таким образом, задачу можно свести к одному уравнению равновесия узла 1:
Ь -ю 0. Ь
Момент М12 можно выразить по формуле 13:
М
12 — in t
Sill V
.
а момент Ml0— по формуле е примера 1:
М1о lea10 l - 1,
d
Tl0
где вспомогательная величина С, как и в примере 1, имеет значение:
V7Z
Фиг. 98.
F
- A2 sin A cos3 Л.
Фиг. 99.
31
Подставив выражения с и d в формулу Ь и учитывая при этом, что р2 9и а получим:
Угол рх сможет отличаться от нуля, а рама сможет потерять устойчивость, когда коэфициент в квадратных скобках будет равен нулю, или когда:
Подставив в это уравнение критического состояния вместо функций а и у их выражения через аргумент v, после ряда тригонометрических преобразований получим:
V3
с sm v sm
. 3v sm
2
32
Подставляя в формулу 32 ряд последовательных значений аргумента v и пользуясь табл. 5 приложения для тригонометрических функций углов, выраженных в радианах, получаем следующие зависимости С и v:
1 Этот пример, как и следующий, заимствован из нашей книги Исследование
устойчивости пространственного каркаса, изд. Ак. наук УССР, 1938.
171
v
1,1
1,3
1,5
1,6.
1,7
7
2,10
3,26
5,30
7,58
13,22
По данным этой таблицы построен график фиг. 100.
Определим по формуле 31 значение величины С для нашей рамы. Дано: h 3,783 м, 6 2,35 м, cos А 0,534 и sin А 0,846. После подстановки числовых значений в 31 получаем:
С 10,73.
Этому значению С соответствует значение v 1,656, следовательно:
Ркр 1,6562гл 2,742Ел
Л2
6 to
Фиг. 100.
Если бы раскосы 0 — 1, 0 —1,2 — Зг и 2 —3 фиг. 99 были сконструированы так, что они могли бы работать только на растяжение, то из двух раскосов креста в панелях 0 — 1 и 1—2 работал бы только один, и тогда в формулу 31 вместо Fd
следовало бы внести только половинную площадь. В этом случае
С 10,73 5,36, чему соответствует см. фиг. 100 значение v l,50, и
кР 1,50
Л2
2,25
EJ
Л
Пример 3. Проверить устойчивость сложной шпренгельной рамы фиг. 101, симметрично загруженной во всех узлах. Пример этот заимствован из расчета конкретной конструкцди. Задано, что вследствие особенностей конструкции продольные деформации колонн не следует учитывать. Числовые значендя, вытекающие из величин нагрузок рамы, а также геометрических размеров рамы и ее элементов, мы будем приводить по мере возникновения в них необходимости при проведении расчета.
Вследствие симметрии рамы и антисимметрии ее деформации при потере устойчивости имеем возможность значительно понизить число неизвестных. В качестве основных неизвестных выберем углы поворота узлов:
1. а, Ъ. 4 5 11 Рб
всего семь основных неизвестных.
Углы ф0 ф7 о, так как внизу имеется абсолютное защемление концэв рамы, а вверху ригель 7 — 7 считаем абсолютно жестким.
Кроме семи основных неизвестных в расчет прлдется временно ввести 4 вспомогательных неизвестных — взаимные сдвиги узлов:
6
J
3
2
г
е4 у45 и5в
67е
Наша задача—найти — коэфициент запаса устойчивости рамы при заданных нагрузках.
Вспомним формулу:
Фиг. 101.
УаЬ
Nfiblgb EJ,
аЪ
Заменим неизвестное нам пока усилие в стержне в гмомент потери устойчивости рамы iVa6 —через коэфициент запаса к и известное нам расчетное усилие NabvaC4:
Nabk iabpac4
172
Тогда получим:
vei F Nab2 lh
Второй множитель правой части этой формулы является функцией известных нам величин и может быть вычислен заранее. Обозначим его через
-1 j, а
тогда
Jah vаЪ Ь
В”результате подстановки числовых значений в формулу а получаем для отдель
ных элементов следующие значения vj:
— ei 0,141695;
Т45 0,136910;
v5e 0,45-7022;
v670,435755.
v 0,327613 712 0,324787 7230,3412o3 v3 0,325248
При составлении уравнений вследствие симметрии рамы и аптисимметряи деформаций изгибающ ie моменты по концам стоек в интервале между узлами 0 и в могут быть вычислены по формуле:
МаЬ Къ tg0 П с
В интервале между узлами е и 7 эта формула не будет верна, и придется пользоваться общими формулами:
МоЪ 2iol aabfa pabfb - a 35 j ; d
- fa П — tab e
Составим систему уравнений.
Уравнение узла 1;
1
t
21 21 i 30
I М1г tlt tj-vi2 fi- iiJv и
tivie Ь6г tgv12 J - ж71в f,r
Аналогично получим для у з л а 2:
- iibl2w ia‘ 6‘и w‘s -
и для узл а 3:
- 5Шт23h 2 t2, 6W тт Ь-
_ Csinv 8 Т 0‘
Для узла е:
2leA aetfe -f- — a -f- Ре4 j J
- sITve3 Gl7.n,-21-. PbAd4-
-ЮЛ у 0.
Ьлл
173
Для узла 4:
МА 2iu ae4f 4 — Рв4 J
М45 2f45 a46p4-f Р46Т5 аР45 J
2б4в4 е 4 2е44 2a4545 f4 24545 ¥5 —
-12 - 2 а o.
64 46
Аналогично получим для уз л а б;
24545 4 24б45 Ь 2a6eiw 6 -f 2бв66 —
45 ГО - I Q 4 1 66
45 56
и для узла 6:
J,56 56
67 67
— 2х -j- Р4645 — 2 a fOse — 0
AK t
2рбббб 5 4 25656b 2ae7ie7 — 2 a-f Pse seL — 2 a4-
Lt
Ь Рб7 67 7 e
w
В уравнения узлов e, 4 б и 6 входят 4 вспомогательных неизвестных—взаимные сдвиги узлов: дв4, д4б, 5вА7- Аналогично тому, как это сделано в примере 1 этого параграфа, составлм для исключения этих вспомогательных неизвестных 4 дополнительных уравнения, приравняв нулю суммы горизонтальных проекцлй усилий стержней, попадающих в поперечные разрезы рамы флг. 101, произведенные на уровне между узлами е и 4, 4 и 5, б и 6, 6 и 7.
Ввиду самметрли рамы и нагрузки и антислмметрии деформации прл потере устойчивости, эти уравненияможно записать следующлм образом.
Разрез между узлами ей 4:
Qe Sb cosЛ50-
Фиг. 102.
Разрез между узлами 4 и б:
Q45 — 1 cos У2 cos А2 0.
Разрез между узлами б и 6:
56 — C0S А3 0.
Разрез между узлами в и 7:
Qe7 4C0S з е-4
4-5
5-6
6-7
В этих уравнениях поперечные сллы Qe4 Q45, Qse и Q67 следует заменить по формуле е через углы р и смещзнля д. Величлны S — усилий стержней решетки, возникающих при потере устойчивости рамы, выраз.ш через смещэния dtf4, tf45, дбв и дв7. Для этого решим следующую 4 раза статическл-неопределлмую задачу.
Определить усилия в стержнях 1, 2, 3, 4 и 5 стержневой системы фиг. 102, возникающ хе от изменения длин опорных стержней: стержня 8 — на величину — 4 стержня 9 — на величину 46, стержня 10 — на веллчину д45- 5в и стержня 11 — на величину 454-бб4- Фет Стержнл, показанные жлрными линиями на ф хг. 102, считаем недеформирующимися. Решаем эту задачу по методу сил. Выбрав неизвестные, как показано на фиг. 102, получим следующую систему уравнений:
Хгап Х2а12 а1Д0;
21 4 Xyfl 22 4 323 4_а2Д0 I 232 4 Х3а8з 4 ЛзД 4Л44 4 Я4Д 0. J
Остальные коэфициенты, как это будет вддно дальше, равнынулю, т.- е
13 ai4 a24 a34 0
Коэфициенты при неизвестных определяем по формуле:
Wf
О
g
174
а свободные члены по формуле:
ЛтД 2 т дгЛ
h
Последнюю формулу в развернутом виде, применительно к задаче фиг. 102, можно записать так:
тЛ S™ - 5т , 51т 9. i
Усилия 1, Siiyf S9, Su стержней четырех единичных состояний нашей системы и величины Дд выписаны для всех стержней в табл. 19
Таблица 19
Стержень
Si1
.SW
S
Д К
2
3
4
6
7
В
9
10
11
1
О
о
о
2 cos Аг 0
cos
cos Аг 0 0
0
1
о
о
sin а2
sin Аг
cos А2 — sin А2 ctgAx
— cos А2 sin А2 ctg Ax
— cos A2
0
0
0
0
1
0
0
0
— cos A3
0
— cos A3 cos A3
0
0
0
0
1
0
0
0
0
0
cos A3 - cos A
0
0
0
0
0
0 0 -ft ft
4
45
45 56
45 467
Площадя сечений F опорных стержней 8, 9, 10 и 11 считаем бесконечно большими:
Fв 9 — 11 СО,
чаем
В результате использования данных табл. 19, применяя формулы g и h, полу-
ш
Еа1
sin А2 13 — 14 53 24 — 34— О
11 4 Fj cos2l1:
Еа1г 8 - 2 cos At cos Л2 - sin Az ctg At ;
sin A V ь
Ea23 cos A2cos A3 ;
7.
Еазг -f- cos2 Л8 ;
з
I
а44 J 1Д 48 COS
Efl2A Я — de4 sin A2 ctg Ax — 45 cos A2
Я 5 cos A3
Л4Д E 67 COS A3.
После подстановки численных значений приводим систему уравнений f к следующему виду:
Хг 3,4875 Ха. 1,7523 — 16935 0;
Xi 1,7523-Ь-ЗГа 1,9209 Хг 0,20649 - 26420в4 - 8102,4 0;
Х2 0,20649 Х9 0,75821 10б946в 0;
ХА 0,48566- 10694 в7 0
175
Решив эти уравнения, получим:
2 г
— 4287,79 а4-13336,18 8is- 1486,80 S6; Ч 18198,17 е4 16877,77 645 2959,09 м; I -4956,07 et- 4596,47 4 -14910,15и; J Х4 22019,52 Ь.
00
Полученные выражения Х, Xs, ХА надо подставять в уравнения е-4, 4-5,
5-6 и 6-7, которые можно записать через X в следующем влдс:
Qe4 - Xt cos At X2 sin Аг ctg Ax 0;
Qib — Xx cos Ax X2 cos Л2 0;
Q5g JSTj cos j4j 0j Qe7 Xt cos 0.
Вместо X в эти уравнения подставляем их значения к, а вместо поперечных сил Q— их выражения по формуле е.
В результате получаем следующую систему уравнений:
4,53693 y4 1,94378 Sei 1,04793 SiB 0,25239 д 19,96247 а Р, , ; 1,04793 6е4 4,53693 г 1,72668 845 0,23407 19,96247 р45 ;
0,25239 ое1 0,23407 45 0,12552 Ги 0,75928 1,66313 а Р5 5 ,
Решив эти уравнения относительно 8ci, й45 и й56, найдем:
4аЕ04 - e 4 fs s 1
Ьа в4
4
45 а Р5 Г й Ь 94 4 4 б Ь Ps ei
4 45 V
a
56 Рбв J— в 4 4 ¥ С 5 в
If
67 а 4 Рб7 — 6
tW
66
56
67
67
J
1
Здесь для краткости обозначено:
D 2,58367 уе4 45 Тбв 4 15,6288 ув4 45 4 0,98330 Убв 4 10690 45 Кбв 4 5,6995 4 4
6,4069 Т45 0.28344 т 1,62191;
А -а Р4 5,4032f4SТм 32,685 2,0564 Ти 11,919; В - Р 5,4127 Ти 32,685 Г1 2,3150 13,399;
С — i- Р1 1,3551 y,4 f4t 0,51573 f4 0,58057 т45 0,14866; в i а Р4 f04s 1,2480 f, 6,9889; у
д — jj Р4 а Ри 0,90499 0,15056;
6 i Р 0,83931 Тв4 0,15056;
т.w ц j
Подставив выражения де4. д45 и fl5e по формулам 1 в уравнения равновесия узлов, получим в результате систему сема уравнений, представленную в виде табл. 20.
Уравнение критического состоянля нашей рамы легко получить, прираввдга пулю детерминант системы уравнений табл. 20.
176
ш
Таблица 20
2
Ь
и
5
Рв
Свободный
член
11
Г12
—
0
Г21
Г 23
0
32
Г33
0
—
гег
гее
теь
геа
0
—
Ге
Г44
Г45
Г4в
0
—
rse
Гб4
Г55
Г56
0
ге
Гв4
Гв5
Г6в
0
Коэфициенты гik гм имеют значения:
4 Пе 2 Рм е4 - Л а;
Геь гье — 2 а д;
вгв - 2d;
г44 2 ав4 е4 - а45 i45 Л. - 2а -J- -S
г45 г64 2 Р45 Я4б а -f д - 4 -Д
4в в4 -2 6 9;
гб5в 2 45 45 Ь абв бв Р Ь 2 С;
бв 5 2 J6e i6e - Ь С;
Г66 2 5в 56 Ь ав7 67 fi. Дальнейшие вычисления были произведены следующим образом1. Был принят ряд значений к 0; 9; 16, и 14,44 и для каждого иэ этих значений были выполнены следующие операции:
1 По формуле Ь были определены численные значения величин для всех восьми элементов колонн:
1-1, 1 — 2, 2 — 3, 3-е, -4, 4-5, 5-6 и 6-7.
2 Для полученных значений уаЬ по формулам 17 гл. III были подсчитаны чис
ленные значения: a Sa и чаъ-
3 По формулам т были подсчитаны численные значения вспомогательных величин D, Л, В, С, а, Ъ, ду.
4 По формулам п были определены численные значения коэфициентов г.
5 По методике 3 гл. V было определено численное значение детерминанта А,
составленного из коэфициентов системы уравнений табл. 20.
В результате получились следующие значения:
с
0
9
14,44
16
Д
4648,378
955,875
86,587
—33,557
1 Вычисления произвели в 1937 г. студенты Киевского инженерно-строительного института т. т. Бородянский, Штильман и Шумейко.
12 Прочность и устойчивость стержневых систем 17 Т
По этим данным был построен график фиг 103 зависимости между к и , из которого оказалось, что Д0 при значении к, равном, примерно 15,40.
Таким образом, коэфициент запаса устойчивости рамы определен по методу деформаций и получился равным 15,4.
Пример 4. Проверить устойчивость сжатого стержня, усиленного шпренгелем фиг. 104,а. Удлинениями стержней 0—1, O—1 и 1—2 можно пренебречь. Будем считать, что первоначальное натяжение тяг невелико, и поэтому в случае смещения
узла 1 будет работать только одна пара растянутых тяг. Допустим, что в этом случае более опасна симметричная деформациях:
i Ф12 Ф12 0; К Задача свэдится к составлению одного уравнения с неизвестным ф. Вырежем стержень 1 — 2 и приравняем нулю сумму проекций на вертикаль всех сил, действующих на этот стержень фиг. 104, б:
2 Q10 S sin А 0. а
Величину Ql0 найдем по формуле 9:
ia — EJ -j
7™ 5
Величину S определим по формуле Гука: S — EF
Д02; из диаграммы Виллио фиг. 104, в
it
‘оа
находим:
Следовательно: EF
S
a sec А
M02 atysin А.
аф sin А EF sin A cos А ф.
Подставив значения Q10 и в уравнение а, получим критическое условие:
EF sin2 А cos Л О,
а2
откуда
F
Y —у a2 sin2 A cos А.
J а
Зная площадь сечения F тяги, момент инерции Ja поперечного сечения балки, а также длину а полупролета балки и угол А наклона тяги к балке, нахэдим численное
г9
Ь
6
а
О
б о ы02
Фш 104.
значение коэфициента у затем по табл. 1 приложения отыскиваем соответствующее
D vBJa
значение v, после чего определяем Fp —
а‘
Пример б. Проверить устойчивость стойки, усиленной вертикальными тягами 2 фиг. 105.Поперечину 2 — 2 будем считать абсолютно жесткой. При потере устойчи
1 При антисимметричной деформации узел 1 не имеет линейного поперечного смещения, кривая деформации стержня будет состоять из двух полуволн и
Ри -
гкц- аг
2 Модель такой стойки демонстрировалась в 1939 г. Я. JI. Нудельманом на совещании
по строительной механике при ОТН АН СССР.
178
вости стойки одна из тяг натянется, а другая выйдет из работы. Удлинение тяги вызывается двумя причинами: поворотом узла 1 на угол рх и поворотом стойки на угол ф. Первая часть удлинения равна а1э вторая же будет функцией квадрата угла ф и поэтому ею можно пренебречь, как бесконечно малой высшего порядка.
Итак, добавочное усилие в тяге при потере устойчивости стержня равно:
с EF
—ai-
Задача свэдится к системе уравнений
Ml0- Sa 0;
Qio 0.
Подставив в с вместо S его выражение а, получим:
EF
Qio -j аф 0.
h
V
2—
Г
С
о-
IT
Т7
4
к
to
1
штптипп
Л
3
К
у Г-Г9
Фиг. 105.
jV
Фиг. 106.
t
Отбрасывая второе слагаемое как величину высшего порядка малости, мы приходим к выводу, что в нашей задаче можно считать: Q10 О, а поэтому М10 можно определять по формуле 13:
. EJ v
ML0 -у— рх
J. I tgv
с EF
-Ofl
I
а21
EJ
v EF
Г
I tg V EJ Критическое условие получает влд:
Л,0.
у _ EF 2 tsr v EJ а
Пользуясь табл. 3 приложения легко находим vp, а затем и Pjp
n2EJ
33
v2EJ
12
__ 2 t
Есля считать тягу неудлиняющейся F co, то v и Ркр—; в случае слабой тяги F 0 fgv oo, откуда v у и Р, 8. Примеры расчета устойчивой прочности рамных систем Начнем с простейшей моноциклической задачи.
Пример 1. Рассчитать раму, изображенную на фиг. 106 и исследовать закон изменения в ней усилий и деформаций в связи с ростом нагрузкиДано:
I — h i0l i12 ilz
Опорные реакции в точках 0 ж 2 вертикальны, нагрузка ql также вертикальна. Значит, реакция в точке 3 не имеет горизонтальной составляющей: Q13 0.
12 17
Таким образом, для стойки можно пользоваться формулой 15:
М1г — i0vtg v-px.
Продольные усилия ригелей равны нулю, поэтому в соответствии с 8:
и 301 и 3i,Tl-.
Сложив эти три момента и приравняв сумму нулю, получим:
72
а
u‘0 v т vb т
после чего легко найдем:
8 о 6-
V tg V j
V tgv
N I 1
6—vtgv 8
3
6 —V tgv
8
v tg v — 3
ql2
М™ б-vtgv ‘ 8 b
12 6-vtgv 8
Горизонтальное перемещение ригеля hty13 найдем из условия равновесия стойки:
N MO,
откуда
д М33_ Mlzl tgv ql
1 N v2i0 v 6—v tg v Si0 Для вычисления всех этих величин нужно выразить величину v
в функции от нагрузки ql. Величина продольного усилия стойки
см. 9 и И:
NQlt-хо —т4ql- т1 qi d
Таким образом:
- Г и наоборот:
еч
Т5
В этом простейшем примере продольные усилия стержней могут быть определены сразу достаточно точно, поэтому рассматриваемая задача может быть отнесена к моноциклическим см. 1 гл. V.
Из рассмотрения выражений а, Ь и с мы заключаем, что при значениях v, которым отвечает равенство 6 — vtgv 0, величины деформаций срх, Дх и моментов М13, М10, М12 неограниченно возрастают1.
Назовем эти значения v критическими vKp.
Пользуясь табл. 3 приложения, легко находим:
Укр 1,3495; qKpl 2,914.
Легко видеть, что при обычном расчете рамы по ее первоначальной недеформированной схеме, т. е. считая в формулах а, Ь и с v 0, мы получим:
о Ql2 ао Ql
Ш0 1 48ф
Щз — 0; 1 Этот преувеличенный результат мы получаем вследствие применения теории малых деформаций изгиба см. 7 гл. 1.
180
Для разных значений v нами вычислены отношения результатов подсчета перемещений рх и Дх и моментов М1о и М12 по деформированной и по недеформированной схеме см. таблицу 21. При этом приведены
также отношения т —и значения коэфициента K Кроме того,
Якр 1 в таблице даны величины - М13 и углы рх и 6.
10
Во втором для v 0 столбце приведены данные, соответствующие расчету рамы по недеформированной схеме.
Таблица 21
V
0
0,5
1,0
1,2
1,25
1,3
1,34
1,3495
6 — vtgV
6
5,727
4,443
2,912
2.238
1,320
0,300
0
0 -и л-0
1 Мю
1
1,046
1,346
2,060
2,680
4,540
20,00
оо
д1_
К
1
1,142
2,095
4,41
6,45
12,59
63,5
ОО
м12
2
1
0,954
0,656
—0,060
—0,681
—2,54
—18,0
—оо
q v2 __
аи у2
Vkp ykp
0
0,1374
0,550
0,791
0,858
0,928
0,938
1
II
1 Н
11
и
1
1,16
2,22
4,79
7,04
13,9
83,4
оо
1
н.
fe:
М
со
II
0
0,00233
0,0701
0,305
0,525
1,198
6,23
оо
1
qi2
48 i0
ч
О
СО
234
1540
00
о
о
ч
1439
6335
оо
II
II
gl2
48 i0
со
со
ч
41
210
1915
4038
218
оо
Выясним пределы практической применимости данных табл. 21, так как для значений нагрузки, близких к дкр, получаются практически несуразные, чрезмерно завышенные результаты. Ясно, что эти пределы являются пределами применимости теории малых деформаций изгиба.
Допуская, например, ошибку до 25 в значении кривизны для наиболее повернутого сечения ошибка в прогибах и углах поворота будет значительно меньшая, мы допускаем тем самым для знаменателя выражения кривизны максимальное значение:
1 ввР1.25,
которому соответствует значение v tg р у 1,25 3 — 1 0,4 и значение угла поворота ф 22. Такому значению в 22 для угла ф в табл. 21 соответствуют значения для 1,27 и для д 0,89 qKp. Таким образом, данные таблицы для значений v, больших 1, 27, должны быть отброшены.
181
На фиг. 107 приведена картина деформации рамы и эпюра изгибающих моментов, соответствующие значению vl,25.
Изучим графически зависимость между коэфициентом К ; и взаимными
1 — Y
отношениями деформаций и усилий, рассчитанных по деформированной и недеформированной схеме. Для этого фиг. 108 построим график, по оси абцисс которого
будем откладывать коэфициент К а по оси ординат отношения 10 1
Л12 щ-. Мы видим, что для каждого из этих отношений на графике получается прак-
V426
г
птииппттгп
12
10
8
2
Ч, -8О Г395
Г -
ь,
А
Г
пГ-
Л_ _
1 У,
к
4
6
Hi
1 к
7 К
14
Фиг. 107.
Фиг 108.
тически прямая линия. Все три этих прямых проходят через точку с координатами 1; 1. Измерив угловые коэфициенты этих кривых, мы получаем следующие уравнения:
Й 1 0,895 К - 1; h 1 0,274 К - 1;
1 Vi
м
12
1 -0,274 К- 1.
12
После преобразований получаем следующие приближенные формулы для деформаций:
___ 1 — 0,726rj gZ2 1 —0,105 ql2
i
1 — у 48i0 т 1 — к 48i0
О
и для концевых моментов:
_ 1-0,726V ql
м1 1_Г 16 12
— 1-И,274ч
1-V 16 — 0,548iq ql2
10
12
1-Y,
16
g
выраженные через отношение нагрузок —.
Якр
В ряде случаев при расчете устойчивой прочности рам могут быть получены аналогичные простые приближенные формулы. Формулы такого типа, как f и g, получаются тем точнее, чем больше разница между первым наинизшим и последующим за ним значениями критической нагрузки, обращающими в нуль детерминант знаменателя системы уравнений подробнее см. 7 гл. XI.
182
р
1-Щ
Lh
2
7Р77777.
1 г
Пример 2. Рассчитать на устойчивость и устойчивую прочность симметричную, симметрично загруженную раму фиг. 109.
Общие указания по расчету симметричных, симметрично загруженных рам даны в 8 гл. V; в силу этих указаний можно было бы независимо друг от друга изучить симметричные и антисимметричные составляющие деформации рамы. Но мы, ввиду простоты поставленной задачи, а также с целью придания большей поучительности разбираемому примеру, повторим отчасти эти рассуждения вновь, предполагая вначале, что деформация в общем случае может оказаться несимметричной, хотя бы в момент потери устойчивости. Ясно, что до боко-, вой потери устойчивости рама деформируется симметрично и усилия в стойках Nh N12
iVi23P. Поэтому при расчете рамы коэфициенты ah, рЛ, уЛ для обеих стоек могут быть приняты соответственно одинаковыми, поскольку мы ограничиваем наше исследование только начальным моментом потери устойчивости.
Перейдем к решению. Из условий закрепления ср2 — 0. Из условий кинематики ц 0;
ф12 12 ф. Итак, в общем случае несимметричной деформации задача трижды кинематически неопределима: неизвестны углы поворота узлов pi и ffu ч угол перекоса стоек ф.
Уравнение равновесия узла 1:
M 2ihahf1 — РЛ1
J i
У777.-Л
Фиг. 109.
М1г 2nih агсрг -f 1, 4. МХ1,
2Л аЛ 1 PlcPi — а Pft ф Mi Уравнение равновесия узла 1:
Мхг 2ih аЛср1 — а рй ф
2nih a9i ptpx7 — М
0.
а
Мхъ —
I мг.х
2л lah пг р nfx - a Рл 4 - Ми,
Дополнительное уравнение:
0.
Ь
Г 12 — -J а РЛ — Тлф
2i
Разложим наши составляющие:
а Рь 1 TiO — — 0.
неизвестные на симметричные и
c
антисимметричные
d
i р; i — i
Величина ф не имеет симметричной составляющей, она антисимметрична по природе ф ф.
Подставив в уравнения а, Ь и с вместо 91 и cpi их выражения d и заменив затем уравнения а и Ь их полусуммой и полуразностью,
получим раздельные уравнения: для симметричной составля
ющей деформации ср:
Ч nxi — ni i Ь МГ1Х, 0 е
и для антисимметричных составляющих р и ф:
ah — а Рлф 0, f
2ih — а Ph р Y1 0. g
183
Эти уравнения е, f и g легко получить непосредственно без предварительного составления уравнений а, Ь и с. Действительно, предположив деформацию рамы симметричной и сохранив в ней симметричную нагрузку, мы сразу имеем: ф 0; Pi —Подставив эти выражения в уравнение а равновесия узла 1, получим уравнение е. Предположив деформацию рамы антисимметричной и отбросив изгибающую нагрузку при сохранении старых значений величин v для элементов рамы, мы получим: уг срх ср; 1 Подставив эти выражения в уравнения а и с, мы получим уравнения f и g. Таким образом, можно раздельно рассматривать две разные задачи и раздельно составлять для них уравнения, в одной задаче заняться изучением симметричных, а в другой— антисимметричных составляющих деформации.
Уравнение е сразу дает конкретную величину симметричной деформации:
С _ Мц, ,1V
2гЛаА дсх-рг
Уравнения же f и g, не имеющие свободных членов, дают для антисимметричных деформаций тривиальное решение: cpj ф 0. Антисимметричные составляющие деформации рамы могут появиться только в результате потери устойчивости, которой соответствует равенство нулю детерминанта, составленного из коэфициентов уравнений f и g:
D xft п а рг1 — а 0. i
Завершим теперь этот пример численным расчетом.
Пусть нам заданы следующие соотношения:
I 2Л, ih ti, тогда п 1.
Прежде всего для назначения соотношений между продольными усилиями ригеля и стоек и для дальнейших сравнений выполним обыкновенный расчет прочности нашей рамы. Для этого надо в формулу h подставить аА а1 2; рЛ1 и Mix по формуле 3:
РкаМ
2 Tj—— — Р1 0,2.0,82 0,4.0,62 0,6.0,42 0,8.0,22 - 0,4 Р1.
Таким образом получим:
Теперь найдем концевые моменты стойки и продольные усилия ригеля и стоек: Mia 2iAxAy А р г 0.2667PZ; М2 2Лрд Ч Р1 0,1333 Р1;
Щ QZzх WitMilо.вР; ч3р.
Изгибающий момент посредине длины ригеля:
ms, - -взр4 -р т - 4 -р 4 -1- -1Pi-Мш Pl
а посредине длины стойки:
MB0bh МЪ-МЪ -0,06667Р1.
Перейдем теперь к расчету рамы по деформированной схеме. Соотношение
Приближенно для первого цикла расчета примем соотношение между продольными силами на основе вышеприведенного обычного расчета прочности:
vv Щр”1871,
Для большей наглядности запишем все выкладки для случая значений v 1,37 и vj 1. Из табл. 1 приложения выписываем аЛ 1,872; рЛ 1,033: а Рд 2,905;
184
YA 4,871; 1,932; p 1,017. Значение МХ1, определим no табл. 10 приложения
для значения vj l и 0,2; 0,4; 0,6 и 0,8 соответственно расположению грузов Р на ригеле:
Мц, - 0,129500,14674 0,098200,03270 Р1 -0,40714 PL По формуле h получаем;
0,40714
PI Р1
21,872 1,932-1,017 - 0,07305 —
После этого находим:
MU ЩчГг 0,2734PJ; Мсп 2 0,1508PZ.
Уточняя теперь значение продольного усилия ригеля, ранее ориентировочно принятое равным Лг 0,8Р, получаем:
Л, - Q, М МЬ 0,8484Р.
Изгибающие моменты посредине ригеля и стоек найдем по формулам метода начальных параметров 158 гл. III:
п 0
Щ,ы htPi sin 0,5vj М cos 0,5v2 Sin- ov1 —
PI
sin 0,3vj sin 0,lvj;
MJ,5A M cos 0,5vA - Kth
vl
sin 0.5vA
v
1
Для значений V-l и vA l,37 эти формулы дают:
M,5l 0,359PZ и Mc05h -0.0791PZ. Уточненному значению Ni соответствует величина согласно к;
-v.1 -v.2-М484_ v _ 1,37
-VAK ж VA К 3чж 1Ж
Уточняем теперь по табл. 1 приложения значения аг и Pi: г 1,928, рг 1,018, а было принято соответственно 1,932 и 1,017. Очевидно, что для значения vA l,37 вполне достаточно ограничиться первым циклом расчета.
Совершенно аналогично, исходя из того же отношения1 v2 ——
1,37
выполняем рас
чет для значения vA 2,74 и, следовательно, vj 2 и получаем:
Р1
tpf 0,1032— ;
ili;a 0,2975PZ;
К1 0,2400Р;
Ni 1,075Р;
Moc,5i 0,503PZ;
Ml бА -0,1445PZ.
При vA 2,742 рама теряет устойчивость с нарушением симметрии деформации, действительно, детерминант D смотри i при этом значении vA обращается в нуль. Приводим табличку изменения этого детерминанта:
0
1,37
2,74
2,75
2,4717
D
21
15,01
0,156
—0,76
0
Исследуя
получаем:
закон изменения знаменателя выражения h для угла поворота
0
1,37
2,74
1
4,11
4,38
4,436
ал л — Рг
о
2,787
2,083
0,5805
0,10Э
0
1 Точнее было бы взять отношение ——, полученное нами выше
X у о о
185
Итак, критическая нагрузка Ркр1 при которой рама теряет устойчивость с нарушением симметрии деформации, равна:
Pfcp4-. 2,472-2,04-
m
На фиг. 110 приведены эпюры моментов для трех последовательных стадий загружения рамы v 0; v l,37 и v 2,74. Из рассмотрения этих эпюр можно сделать выводы о характере перераспределения нагрузки между элементами рамы при расчете рамы по деформированной схеме.
До потери устойчивости деформации рамы симметричны; чтобы исследовать их
1
изменение в зависимости от коэфициента К- см. пример 1 этого параграфа,
1 — Y,
следует в отношении г —
Рк
В
Р
VA
кр
знаменателе подставить значение v 4,436, при котором знаменатель выражения 5 обращается в нуль. В табл. 22 приведены значения коэфициента К и отношения угла поворота р и изгибающих моментов, подсчитанных по деформированной схеме рамы, к соответствующим величинам, вычисленным по недеформированной схеме.
Если по данным табл. 22 построим график, откладывая по одной оси коэфи-
циенты К, а по другой отношения
и
Мс
—, то получим так же, как и на графике
фиг. 108, нечто вроде пучка прямых лучей, исходящего из точки с координатами 1;1. При этом можно составить приближенные выражения:
1 0,9ЛГ—1;
Vi-2;
0,145 PI vh-Z,7b
—7 VT 0,240 PI
flpuV- 2,742 теряется бопоЬая устойчидость Фиг. 110.
Mo,sh -Jg1 1,9 -11 PI.
Таблица 22
к- 1
М
mi
-05Л
1 4,436
1 —
М
м
о 51
-ВДбЛ
0
0
1
1
1
1
1
1
1,37
0,095
1,106
1,095
1,023
1,133
1,08
1,19
2,74
0,380
1,612
1,55
1,115
1,801
1,51
2,17
ГЛАВА VIII
МЕТОД УЗЛОВЫХ ПОВОРОТОВ И ПОПЕРЕЧНЫХ сил
1. Общие соображения о методе. Формулы для отдельного стержня
В ряде случаев можно достигнуть уменьшения числа неизвестных расчета, если принимать в качестве активных параметров для отдельного
186
стержня lab углы поворота его концов ра и и поперечную силу1 на одном из концов Qab. Особенно значительные упрощения получаются в том случае, когда по условиям конструкции и загружения рамы поперечные силы в ряде сжато-изогнутых стержней заранее вполне известны, например равны нулю 2. При расчете многоугольных одноконтурных рам поперечные силы всех стержней могут быть легко представлены как функции внешних нагрузок и вертикальной и горизонтальной реакций одной из опор.
Вообще говоря, этот метод тесно примыкает к методу деформаций и его зачастую бывает удобно сочетать с ним. Основные формулы этого метода приведены нами в главе VII формулы 13 — 16. Их нужно только дополнить формулой для угла поворота стержня 1аЬ в случае наличия шарнира МЬа 0 на конце 6 см. фиг. 66:
и, v I v v Qabab лА 3
где буквой tyab обозначена следующая величина:
2 РпОт-— fl V4-secv 2
V lab V. Z COSV У v4a 2 J 4 J
ni, 2,.
В формуле 2 силы P и нагрузку q считаем положительными, если они действуют по часовой стрелке вокруг защемленного конца стержня.
2. Уравнение трех узловых поворотов
В случае, если в узле Ъ рамы сходятся всего два стержня 1Ъа и he фиг. 111, то условие равновесия моментов, приложенных к этому узлу, соответствующее неизвестной — углу поворота фъ этого узла, можно составить так: Фиг. 111.
МЬа Kb tg jfb sin v aia QbJab v tg 2 ai M
Mbc hc QgObc9 jUbcfc Ьс1ъс jtg t,c M
ft
ba
be
ab С sin ia6 tg0oj4c tgOjcl isc С sin v
7 tg abQablab 7 tg itQbJbo Ка KJ- 3
Уравнение 3 мы будем называть уравнением трех узловых поворотов.
Совершенно аналогично можно составить соответственное уравнение в том случае, если в узле а будет находиться шарнир МаЬ0, но тогда
вместо уравнения 13 гл. VII уместнее будет с целью исключения неиз
вестной сра использовать уравнение 15 той же главы. Таким образом, получим:
— Къ v tg va ibc bc CsliTbc
v tg yc Qbclbe - Ml MZ. 4
1 Напоминаем, что поперечную силу стержня мы в отличие от перерезывающей силы считаем направленной нормально к первоначальной прямолинейной оси стержня см. 1 гл. IV.
2 См. примеры расчета в главе VII, 4 примеры 3 и 5; 5 примеры 2, 5, 6, 7 и 7
примеры 1, 2 и 3.
8 Формулы 1 и 2 получены в результате преобразования формулы 88 главы III
в соответствии с пунктом 6 16 и с последующим использованием формул 103 гл. III.
187
Применяя формулу 16 гл. VII для вычисления величины Ма, нужно помнить правило знаков для силы Р и распределенной нагрузки qf указанное в конце предыдущего параграфа; защемленным концом стержня считается конец Ь.
3. Составление системы уравнении
Рассмотрим этот вопрос на конкретном примере фиг. 112, а. Неизвестными расчета по этому методу для данной рамы являются углы пово
рота узлов: срх, ср2, срз, Если вертикальную и
о
о
Мл
4
о
t Те
горизонтальную
6
поперечные силы Qab стержней рамы, составляющие усилия стержня в каком-либо его сечении фиг. 112, б обозначить через Vs и Hsr то поперечная и продольная силы в этом сечении могут быть выражены следующим образом:
Qs VscosAs — HssinAs-,
Г
N. Vs sin As Hо cos А,
5
Составляющие Vs и Hs для любого сечения s рамы фиг. 112, б, а также поперечные силы Qab для всех стержней рамы легко могут быть выражены через Н0 и V0 И нагрузку рамы силы Р. Величины Н0 и V0 следует представить так:
77777777777777777777777777777.
Фиг. 112.
я0 я: дя0 и V0 Vl AVt. 6
В этих формулах Щ и Fo — реакции рамы, определенные на основе обыкновенного расчета прочности рамы, а АН0 и AV0— поправки к этим величинам, получаемые при расчете рамы по деформированной схеме. Величины vab, входящие в коэфициенты расчетных формул, для первого цикла расчета мы тоже можем определять по продольным усилиям Nab стержней, полученным из обыкновенного расчета рамы по ее недеформированной схеме:
vь-у ё7;-
Общее число неизвестных для нашей рамы таким образом составляет восемь: шесть углов поворота узлов: срх, р2,., срв и две величины А и AV0. Для неизвестных—-углов поворота узлов рамы срп мы составляем уравнения трех узловых поворотов. Для неизвестных АН0 и AV0 надо составить два уравнения кинематики замкнутого контура рамы, выражающих собой равенство нулю взаимных вертикального и горизонтального передвижений опор рамы, точек 0 и 7 см. уравнения 7 2 гл. V, а также уравнения а 7 гл. VI:
2 hbabSin 1аЬ, ж 0;
I I fabtyab fabj 2 e
В формулы 7 вместо углов tyab надо вставить их выражения по формуле 13а гл. VII. В случае наличия в раме шарнирных узлов фиг. 113 углы поворота шарнирных узлов ср0, р4, р8 легко исключаются из расчета. Для этого следует пользоваться при составлении уравнений узловых поворотов для узлов 1, 3, 5 и 7 формулой 4 вместо формулы 3
188
д подставлять в формулы 7 для стержней 0 — 1, 3 — 4, 4 — 5 и 7 — 8 выражения для углов по формулам 1 и 2 этой главы, а для стержней 1 — 2, 2 — 3, 5 — 6 и 6 — 7 по формулам 13а и 14а гл. VII.
Этот метод может быть применен также и при расчете двухконтурных рам фиг. 114, но в этом случае поперечные силы Qab стержней рамы
придется выразить для левого контура как функции НА и VА, для пра вого контура как функции Нс иУс и для средней стойки как функцию НА и Нс. Кроме уравнений узловых поворотов нужно будет составить 4 дополнительных уравнения по типу 7: два для одного и два для другого контура.
Уравнение узловых поворотов для узла D нужно будет составить, суммируя моменты в этом узле:
Mde Ч Mqb Mbf 0 8
изаменяя в уравнении 8 моменты их выражениями через pD, Че и f, а также через Qde, Qdf, Qdb по формулам 13 и 15 гл. VII.
4. Примеры расчета устойчивости
Пример 1. Найти критическую нагрузку для рамы фиг. 115, ау соответствующую антисимметрич- gn ной форме потери устойчивости.
На основе соображений, изложенных в 5 гл. VII, лс легко видеть, что для данной рамы более опасной является антисимметричная форма потери ее устойчивости.
Поперечные силы левой и правой стоек из условий антисимметрии деформации должны быть равны друг другу, а так как сумма их должна равняться нулю, то каждая из них тоже равна Qa 0; поэтому для определения концевых моментов стоек можно пользоваться формулой 13 гл. VI:
Фиг. 115.
Распор Н ломаного двухскатного ригеля 2 — 3 — 2 рамы:
Н Q21 —Qa 0i
а
Ь
а поэтому для этого ригеля в случае антисимметричной деформации можно пользоваться формулой фиг. 115, б:
и EJ
Mac -7- о 3tac.
С
Вследствие антисимметрии деформации:
Ь2.
С
А
Таким образзм, задача сводится к составлению двух уравнений с двумя неизвестными i и fa-
189
Для узла 1 используем уравнение трех узловых поворотов и, так как р0 0,. получим:
тк.if lib - - Для узла 2 составляем уравнение по общей схеме:
М 2з — 3l232
О
Условие критического состояния получим, приравняв нулю детерминант этой системы уравнений:
D
ioi t.l12txJ ; _in uft12
-12 CiKTvl3 ; i23 tiVl2 323
0.
g
Пусть дано: P1 P2; i01 i12 i23; l01 2ll2 последнее соответствует 01 212. Кроме того, получаем:
Л12 Ру iV10 2P; iV23 0,
откуда
Р112 1 2Z12
vi2l -r-v; voil —l2v;v23 0.
Г ll2 V i12
При этих условиях детерминант D приобретает вид:
Давая v значения 0; 1; 0,7;. и пользуясь табл. 1 приложения, получаем:
0Г
V
0
1
0,7
0,8
0,9
0,887
0,8875
N.
о
II
7,0Э0
—2,400
2,93
1,513
—0,228
0,010
0
Таким образом:
Р кр —
-у2_ 0,887 52 0,7876 12 12
Е112
12 12
Пример 2. Для рамы, рассмотренной в примере 1, найти критическую нагрузку соответствующую симметричной форме потери ее устойчивости. В этом случае задача сводится к составлению трех уравнений с тремя неизвестными:
1-1; ьн0 нв.
Вследствие симметрия деформации р3 0; кроме того Н 0.
Уравнение узла 1 получаем по формуле 3:
Gfktir -sifv2-Stgv2vtgi-A-
При составлении уравнения для узла 2 надо иметь в виду, что для стержня2 —3: величина v23 0, а поэтому из табл. 3 приложения находим:
Кроме того:
Qa3 - о sin A — tf0
f
I
23
Итак, уравнение для узла 2
v f v i H0h 1. v
sin v tgv J i10 v 2
H0f
2 i
i
k
10
19Э
Дополнительное уравнение, соответствующее 0, должно отражать равенства нулю горизонтального перемещения конькового узла рамы 3 см. уравнение 7:
Критическое условие для симметричной формы потери устойчивости получим, приравняв нулю детермлнант из коэфициентов уровнений h, к и п:
В этом детерминанте у01 является функцией v01 2v, а у12 — функцией v12 v. Задавая соотношение между и h например, Л, затем давая v последовательно значения 0; 1; 2: 3 и пользуясь таблицами 1 и 3 приложения, подсчитываем значения детерминанта D. Определив между какими значениями v детерминант D обращается в нуль, последовательно уточняем значение v. Арифметических операций мы тут не производим, так как заранее знаем, что получим большую критическую силу, чем в примере 1. Этот пример приведен нами с целью показать, как составляются уравнения,
5. Формулы для ступенчатых стержней, загруженных поперечной нагрузкой и продольными сосредоточенными силами
Формулы, которые мы здесь получим, могут быть применены для расчета ступенчатых стоек фиг. 116, а также для расчета наклонных ригелей, загруженных вертикальными силами фиг. 117. Мы дадим вывод этих формул в качестве примера применения рассматриваемого метода к задачам устойчивой прочности.
призматических участков. Формулы для стержней из двух или трех участков можно будет получить как частный случай из формул для стержня с четырьмя участками, полагая равными нулю длины некоторых из его участков.
Пусть дан стержень фиг. 118, состоящий из четырех призматических участков: 1аЪ lx l2 l3 4. Участки имеют разную жесткость изгиба: B1 l1i1 B2 l2i2, B3 — l3i3, ВА 1ь и разные продольные усилия
0101 4 1212 4 2323 si11 — 0
или
2фО1 Лф12 ф23 0.
Для углов фаб мы воспользуемся формулой 13 а гл. VI:
0
т
Таким образэм, мы получим:
0. о
1. Стержень из четырех участков Здесь мы ограничимся рассмотрением стержней, состоящих из четырех
191
Для сокращения записи введем обозначения:
г
vn
io
rn
sin v
a —
Uni i l0
tgvn
rvtg C; bn b 0 vn A
m
ьп,
rimi Cn f
1
-c I
ьпту J
9
в которых i0 и l0 — некоторые вспомогательные величины.
Равнодействующие поперечной нагрузки каждого из участков причисляя к ним для определенности правую пограничную силу будем
обозначать соответственно через: Rly R2, R3, Д4. Тогда:
Qdb Q 21 : Q
Qba
Qai
2з :
Qsb
Qbz
Qa Qla Q12 :
Qa Q21
Qa 2 Дз:
.Qa-RXR2-Rz
3;
4 Qb
9a
Пользуясь обозначениями 9 — 9a и формулой 13 гл. УП можем записать уравнения для концевых и промежуточных моментов:
МаЬ Мъъ
М1а
м12
Ма1 0 ”
0 btfb — 4з
11 - в1Ра
0 621 — Й22
Я ii — cQaK ai a
c4 а— — R2 — Rs—RJ l0 Мм ; a
Cl Qa-R1l0 M1a 1
с2юв-л1влгг; J
b
192
Чтобы получить выражения для концевых моментов МаЬ и МЬа
стержня 1аЬ, рассматриваемого как единое целое, нужно из выражений а и а исключить величины промежуточных углов поворота рх и р8. Для этого нужно составить систему уравнений трех узловых поворотов см. формулу 3:
I 1 2 i0 i12 i t 2г Ч” 12 а i Ь 1
1 — 2 — 3 i0aif1 — bi3f2 aif3 c2aQa — R1 — Rtl0 mt 0; с
2 — 3 — 6 i0 а32 — 6318 а4г. с34 а — — Л2 — R h тя 0. J
В этих уравнениях для сокращения записи принято:
ш1-ДГ ЛГд;,АГЭ;
тл-М М М1У, d
т3-М3г М М1. J
Неизвестными в уравнениях с мы будем считать ог, р2, р8, рассматривая независимые от них члены уравнений, как свободные:
Сi 65 ioTa f nQao 4 ji i2il 1
С 2 CzzQaJo Ь 23 l Ьг 1 e
С г QJcffb Ь zQafo 4е Щъ 34 Ci Ь Ь Л J
Запишем уравнения с в табличной форме табл. 23
Таблица 23.
01
Ь
08
1
12
CL о
0
Ci
а2
23
аз
с
0
аз
-t34
Решая эти уравнения, получаем:
Dt Dz. D.
01 ; VP2 n 5 г03 —2
jD
где
D —b12b23b3i a22634 ab12;
D1 2334 j 1 ”1” 2342 5
2 2341 12342 f 8183
3 231 f 3122 f 1223 2 3 j
Q
g
h
Подставив выражения h в f, выразим неизвестные 9 cp2, ра с помощью чисел влияния через свободные члены:
oTl И1 Ь 122 Ь АхзСз;
02 211 4 Л22С2 Ь 288
оТз зА 4 322 1 ЗЗЗ
Числа влияния равны:
2 л —2334.2, 2. a234. z. 2. Л2а3
Л11 J 12 — 4l 2Г 13 81 jj”
. г. лт. _ л- л8 —bib
D
i
2. 1234.2. 2. a812
Л22 П 5 л23 32 . 2. 2
J ЗЗ
гггз
k
33 D
Подставляя в i вместо C19 Сг, Сг их значения по е, после приведения подобных членов находим:
офп lnioTa 4 4пзМ nQao Н nii 1 л22 Ъ л8з
адв Л22 3 1 1384 20 Л83430 1
13 Прочность и устойчивость стержневых систеи
193
В этой формуле для сокращения записи принято обозначение:
Кп л112 71223 П334 Из формулы 1 легко получим 91, р2, 3, заменяя в ней соответственно индекс п на 1, 2, 3.
Заменив срг в формуле а, по формуле 1 получим следующее выражение для концевого момента МаЪ:
а
Маъ о АаъЧа abQabh аЪ- Ю
Здесь отвлеченные коэфициенты АаЬ, ВаЬ, СаЬ и нагрузочный член Dab имеют следующие значения:
Dab il;v — аг 4 к12т2 fclzm3 аг10 К к12с23 I 11
Ч” 1334 2 Ь 1834з J
Формулу для МЪа получим из формул 10 и 11, поменяв в них всюду индексы а на b, 1 на 3 и наоборот, а также изменив знаки перед R на обратные. Чтобы решение поставленной задачи было полным, нужно составить еще формулу для ЪаЬ Jaab ai 12-f 823 88г. Величины 8а1, о12, 828 и оз8 найдем, использовав формулу 13а гл. VII:
у 8ai ci ai 2n Т а71
i 8,2 С2 рх - р 2Ti -Г 1 Г Уп
Со 01Ч 12 с0
i 8 с, р2 ср3 А ‘ v1 Q -R- R Г
оз Тз о
8зь с4 з б 7 7 а — 2 — Я3 у ФзГ
1л 04 14 0
¥ ъ 77 е ClP Cl2 С2 Сзсрз Cipb
4. Ss Г А 4- А 4- -L Д ГД Д —-
2Zq b_Yi гТг ЬТз 4Т4 J ЧгТг зТз
_ f Д П _ А i до- ,;; , ж 1 2i0 1зТз 14Т4У VUW ‘о
Подставивв п вместо, р2, р3 их выражения по;формуле 1, получим:
К -EdftTa db 12
Здесь отвлеченные коэфициенты ЕаЬ, Fab, Gab, НаЬ имеют следующие выражения:
ЕаЬг Кг СаЬ, Fab С4 вД,; 13
с5щ.; 14
И-ЫЛ-ЛЛ‘-1Й‘Л-ЙЬ
— Г c12K1R1 c2zK2 Rx R2 cZiK3 R2 Rz
Чыъ L
— j- 77l2K2 зз J Ь
Ulai 323 434
Формулы 10 и 12 относятся к методу узловых поворотов и поперечных сил. Их нетрудно преобразовать в формулы метода деформации,
194
для этого надо из формулы 12 получить:
Qab 15 l0Qab Ь аЪЬ ФаЬ 1 аъ
16
и затем подставить 16 в 10:
мл - i. А. в. -
-згФ‘-с-г- 17
Формула 17 соответствует формуле 1 гл. VII, а 16—формуле 2 гл. VII.
В частных случаях формулы 10 —17 упрощаются. Например, в случае загрузки стержня по фиг. 118, когда поперечная нагрузка состоит только из сосредоточенных грузов, приложенных в сечениях, пограничных между смежными участками, и продольные силы приложены без эксцентриситетов М М М 0, величины Ма. т1 т2 т3 0, точно так же ф ф ф ф; 0.
При полном отсутствии поперечных нагрузок в пролете стержня
R2 Rz Л4 0 и тогда Dab 0 и НаЪ 0.
Как мы видим, для получения коэфициентов формул 16 и 17 нужно выполнить довольно много арифметических операций. Для проверки правильности полученных результатов частично может служить следующее правило: сумма коэфициентов при ра, р6, 1аЬ в формуле 17 должна равняться нулю:
Ааъ Bab Gab Gab Eab Fab — 1 0; 18
Действительно, как мы видели выше, коэфициенты, входящие в формулу 18, не зависят от внешней поперечной нагрузки. Предположим, что она равна нулю. Тогда свободный член момент защемления в формуле 17 пропадает. Предположим далее, что стержень вообще не загружен и не изгибается, а только слегка поворачивается на малый угол tlGd ра ср6. Тогда МаЬ МЬа 0, а это по формуле 17 может получиться только в том случае, если справедлива формула 18.
2. Стержень из трех участков
Общий вид формул 10, 12, 16, 17 и 18 сохраняется при любом числе участков стержня, но выражения для входящих в эти формулы коэфициентов А, В, С, Z, Е, F, G, Н могут несколько измениться. Формулы 11, 13, 14 и 15 для стержня из трех участков можно
легко получить как частный случай из соответственных формул, приве
денных в п. 1 этого параграфа. Для этого нужно положить, что четвертый участок стержня отсутствует, т. е. 4 0, и р3 срь. Равенство: 4 0
влечет за собой: i. оо; v4 0; я4 64 оо; с4 0 и т. д.
Вычисляем по формулам 9 коэфициенты ant Ьп и сп для всех трех участков стержня, затем определяем числа влияния:
1 к21 -1- _ к
12 2 3 2 1223 а2 1223
Эти формулы легко получаются из к после сокращения числителя и знаменателя на бесконечно большое 634. При этом получается также
13 23 33 Коэфициенты Кп равны:
1Cj 1112 Ь 12235 2 1212 4 2223
13 195
Формула 10 сохранится, а вместо 11 получим:
х ок1Х ВаЬ j812 Саъ сг
Dab Mai — ai mkn m212 aJo ii iC232 Коэфициенты формулы 12 приобретут вид:
.
110
ЕаЬГ, С1aiU СЬ ForJc а;
,aft Lab
Gab24й; м;Ci2‘сДг :
13
140
я- - it - д‘ - сад
С2ВК2 Дх Д2 т11 22 4 7— lai 326
‘О 1аЪ
15
3. Стержень из двух участков
Дальнейшие упрощения получим, если стержень будет состоять всего
из двух участков. В этом случае: ц-г—
12
А А а В ав2 С С I aiCli 1
АаЬ1 S оЬ- Ьиг Ьаь — Сi 12 12
ai
17 I aiC12 lo fi.
babClhJ-hbtab
P n I 2С12 Л.
Fab-uV-br
С — 0
ab Vo lab
Hab —
2ie ЧТ2 1
f_l З.Л. ii. is.
V4Ti ЧТ2 12 Лб fe ft-
130
14
г
ad
Z2. 0 labo
W W-
15
С. О расчете устойчивой прочности рамы со ступенчато загруженными
стержнями
Пусть дана симметричная и симметрично загруженная рама фиг. 119, а. Стойки рамы ступенчаты и ось стоек имеет сдвиги в пограничных сечениях а и 6, однако для упрощения расчета в виду большой
УZ V77Y77777777777777T7
777У77У7Т77777Т777777777Г777777777777777777777
Фиг. 119.
жесткости горизонтальных ступенек оси в пограничных сечениях а и 6 будем считать ось стойки прямолинейной фиг. 119, б. Силы Ра и Рь будем считать действующими по этой прямолинейной оси и вместо налич-
196
ных эксцентриситетов приложим в этих сечениях эквивалентные сосредоточенные моменты М и Ма. Эти моменты выбираем так, чтобы в отдельно взятых стойках по фиг. 119, а и по фиг. 119, б, рассматриваемых как статически определимые консоли, закрепленные нижними концами, возникали одинаковые эпюры изгибающих моментов при расчете их по иедсформированной схеме.
При использовании формул 16 и 17 5,. относящихся к методу деформаций, число неизвестных при расчете симметричной деформации рамы равно двум: рх и ф01
Кроме того, pi —pi; фо1 —di; 12 — —tyiv —j- фа При решении
той же задачи по формулам 10 и 12, относящимся к методу узловых поворотов и поперечных сил, число неизвестных также равно двум
и Qoi-
При расчете устойчивости рамы на появление антисимметричных составляющих деформации применяем методику, изложенную в примере 1 4, а также в 8 гл. V.
7 Формулы для стержней рам с жесткими узловыми фасонками
Жесткие узловые фасонки сокращают длину деформирующихся элементов рамы, повышают ее общую жесткость, а, следовательно, и устойчивость. Для упрощения расчета мы в этом параграфе будем считать узловые фасонки абсолютно жесткими и соответственно с этим концы стержней рам от места их
жесткого скрепления с фасонкой и до центра узла рамы — абсолютно йедеформирующимися.
Рассмотрим сначала отдельный сжато-изогнутый стержень фиг. 120 е абсолютно жесткими недеформирующимися участками на обоих его концах. Формулы для этого стержня можно цолучить как частный случай формул 5, но мы изберем другой путь.
Будем считать, что поперечная нагрузка приложена только в пределах между узловыми фасонками, нагрузку же, действующую на фасонках, мы будем непосредственно передавать на узел, приводя ее к равнодействующей и внешнему сосредоточенному моменту. Величину v0 мы будем относить только к среднему упругому участку стержня:
Mab
L C
r
уУпЬ ‘
— a
Qab
1 1
Я i.
1 i 1
j 4t
J —
tab
ь
N,
аЪ
VgZ ЕЗаЬ Фиг, 120.
vhEJab
IEJ
пЪ
Vhl
г
аЪ
н
00
1о
Вследствие недеформируемости концевых участков мы получим следующие зависимости:
и, кроме того,
12
a
i2 — Qab Mab-Qaba-j- асрц; Qi Qbai -21 Mba Qbab - 6cpj. j
b
197
Записав выражения М12 и 12 по формулам 13 и 13, а гл. VII
и использовав зависимости а и Ь, после преобразований получим формулы метода узловых поворотов и поперечных сил:
м- ; - х0 - шт: - 0 i м; 19
_ _ . ‘в а. т.б1, tg - 4 I ж 20
Записав выражения М12 и 12 по формулам 1 и 2 гл. VII и применив те же зависимости а и Ь, получим формулы метода деформаций:
ч
о
Qab —
2EJab
П
аЪ
А В 9аС В 9ь - D Ql2.
21
22
7
а
1 1 1
аА Ua-
_. 1
jAfo-fJBfy- it
f
л.
Г
с
Фиг. 121, А.
В
ОТ СП
1 п
Фиг. 121, В.
f
О. го
0.17.4
0.15 —0.125
0,10
005
1
0
0 12 3 4
5 V
В этих формулах для сокращения записи приняты обозначения:
следующие
л Z а i г Yo
ьввРтМ;
C 7fa i1 ToY;
D JfiyA 2B C lb.
23
198
По формулам 23 построены графики этих коэфициентов в зависимости от величины v va v0 jWJb для ДВУХ частных случаев: 1 случая, когда а 6фиг. 121, и 2 случая, когда 60 фиг. 122.
Эти графики показывают, что наличие жестких участков по концам упругого стержня чрезвычайно сильно влияет на величину коэфициентов.
Совершенно аналогичным способом нами получены формулы для стержня с шарниром на одном конце конце Ъ и жестким участком на другом конце а.
Формулы метода узловых поворотов и поперечных сил:
D
т:
j
мьа 0;
МаЪ — го votg V0-f la-Qab Mk
ЪаЬ Qa lo а
24
v0 vo Qab la
.3
25
Величины Mib и определяются
oo формулам 16 гл. VII я 2 гл. VIII.
Формулы метода деформаций соответствующие формулам 8 и 9 гл. VII для призматического стержня с шарниром на конце:
МаЬЦ-А - М1ь-aQib- 26
Qab тг СIfa 5 ё Qlb
Здесьдля сокращения записи обозначено:
J
ЬьтА ,вч
v
I
F
2
v
Фиг. 121, Dt
27
28
Графики этих коэфициентов А и С в зависимости от величины
y va yv0 приведены на фиг. 123.
0
8. Устойчивость рам с жесткими узловыми фасонками
Прдведем оформленные в виде графиков решения для двух простых рам. Из этих графиков будет наглядно видно, как сильно влияет на устойчивость рам наличие жестких узловых фасонок.
Дана свободная прямоугольная рама фиг. 124 с жесткими узловыми фасонками. Примем, что узловые фасонки в одинаковом отношении сокращают упругую длину ригелей и стоек рамы.
Рама имеет две оси симметрии: вертикальную и горизонтальную. Наиболее опасной будет форма деформации, антисимметричная относительно обеих этих осей: рх р2 р3 р.
Учитывая, что поперечные силы стоек Q12 i Qtt 0
199
МаЪ жЦА ь8ЪУаьМе
гс -в Чг,м
VlT
V EJ
Фиг. 123.
1-0
cs
a
Q-
u
я
e
20 f
и что углы поворота ригелей ф14 ф2з0 можно было бы обойтись одним неизвестным 9 и пользоваться для стоек формулой 19, а для ригелей 21 при значении vo 0. Мы изберем другой путь и будем пользоваться только уравнениями 21 — 22, т. е. будем решать задачу с двумя неизвестными ср и фЛ 12 Ф48. Соответствующие уравнения получим в виде М1гМы 0 и 12 0;
Ah Bh - At Bt ср 0;
2 AhBh ср — Dhb 0n
Решив эти уравнения, найдем:
n_Jih __ Ah Bh
При определении коэфициентов Ah, Bhj Dh по формулам 23 надо меть в виду, что в соответствии с нашим заданием аЛ 6Л 0г, j
l0 1 - 20 A; v, - 1 - 29 v 1 - 201
и х0, ро, у0 являются функциями v0; при определении коэфициентов Ах и Bt длина 0 1 — 26, a vo0, вследствие чего ос0 2, 30 1 и
Из рассмотрения графика фиг. 124, относящегося к этому случаю видим, что при значении 0 0,05, т. е. в том случае, когда жесткие фасонки по концам стержня сокращают его упругую длину на 10, величина критической нагрузки возрастает примерно на 30, при в 0,10 на 80, ПРИ 0 0,15 на 135 и т. д.
Примерно такие же результаты получаются для рамы с защемленными пятами фиг. 125
ГЛАВА IX
О ДРУГИХ МЕТОДАХ РАСЧЕТА РАМ
Кроме изложенных выше в главах VI, VII и VIII основных методов расчета устойчивости И устойчивой прочности плоских рамных систем мы кратко изложим и несколько других методов, имеющих меньшее значение, но все же представляющих известный интерес и могущих оказаться полезными в некоторых специальных случаях.
1. Консольный метод
Консольный метод основан на последовательном применении формул метода начальных параметров см. 9 и формулы 101—101 16 гл. III:
Mb aaysin vab COS vab -f- Qabhb V ab - 5 - C-3
Пользуясь обозначениями 17 гл. Ill см, формулы 129— 134, эти формулы можно записать так:
М Aabiabya BabMa CabQabab Ь bi 1
BabPa - Cab g - Dab Afr0; 2
ab Caba-DabTf -Eabf- Mab. 3
labi lab
202
Функции А, В, С, D приведены в табл. 8 приложения к книге, а на фиг. 31 даны их графики.
1. Задачи с одним неизвестным
Если нам нужно рассчитать какую-либо ломаную консоль, жестко или упруго закрепленную одним концом фиг. 126, а, то прежде всего по недеформированной схеме конструкции находим Qab и Nab для всех стержней консоли1. Таким образом мы сразу получаем величины vab для всех стержней. После этого можно, пользуясь формулами 1 и 2, выразить начальные параметры р6 и Мь каждого следующего стержня ломаной консоли через начальные параметры сра, ма, Qab предыдущего. Из трех начальных параметров свободного конца стержня 0-1 мы сразу знаем два начальных параметра 01 Р2 и М0, неизвестным остается ср0. По формулам 1 и 2 мы находим Мг и Рх, как функцию нагрузок стержня 0-1 и неизвестного р0. Затем так же выражаем М2 и р2 как функции от ранее определенного Ql2 и величин срх и Мх.
Запишем это:
М. г Qoih
¥ — С0г D
Аф
10
A0i0y0 В 0М0 C0Q01l0 А М1о
Вх
С_г
U
Вх.
a
b
За первой вертикальной чертой стоят множители, на которые надо умножить по формуле 2 рх и Мг при составлении выражения для р2, а за второй чертой то же по формуле 1 для М2:
ад- вхс, Аад_
- ад С,Сг Вг Д10 - Д21 ; С
лг, ад -адг0 ад- лг.
вгС. - AXD Qllt AJAVu BAM10 C.QJ, Шг1. d
Понятно, что операции по вычислению ср2 и Л2 следует производить сразу в числах, а не записывать их в виде громоздких формул по типу с и d. Символически результаты с и d можно записать так:
о — 7 о Г — D 01 Л- Acs
V 2 02 V О 02 у 0 2 у 1 V 2 0
М2 А0л0.Р0 В02М 0C02Q0J0 Д-20
С
ю
После этого мы точно так же, пользуясь формулами 1 и 2, находим ср3 и Мг и потом р4 и М4.
1 Qab и мы отличаем см. 2 гл. III от истинных перерезывающих и сжимающих усилий и iVJj.
203
Пусть последние выражения будут иметь вид:
Мо.
0
4 -Во4 — Cot
Dai Л40;
e
f
М4 A04i0q0 B0tM0 C0tQ0ll0 ЛМ40.
В соответствии с вышеуказанным в этих уравнениях неизвестна лишь одна величина — угол поворота р0. Если конец 4 ломаного стержня упруго заделан, причем задан коэфициент упругой заделки к то,
подставив е и f в формулу
g
получим уравнение, из которого найдем неизвестное ср0. Если конец 4 жестко заделан, то найдем р0, приравняв ср4 по формуле е нулю.
После того как определено ср0, подставляем его численное значение в формулы а, Ь, с, d и т. д. и последовательно получаем все углы поворота узлов р0 рх, ср2,. и все узловые моменты М0, ilx, ilf2, Для получения линейных смещений узлов мы по формуле 3 находим последовательно численные значения углов поворота стержней 101 у
н
ф12 , 128 - 23 , а затем по формулам или графически, строя диа-
1Х 12
грамму Виллио фиг. 126, б, находим линейные перемещения узлов ломаной консоли. При построении этой диаграммы мы допустим, что все стержни ломаной консоли вращаются по часовой стрелке. Полные перемещения узлов получаем на диаграмме как радиусы-векторы из ее полюса—неподвижной точки 4.
2. Задачи с двумя и многими неизвестными
Разобранная нами выше задача о ломаной консоли принадлежит
к задачам моноциклическим, так как в этом случае мы можем сразу
получить окончательные значения vab. Несколько сложнее задача для
I I,
01
1о
.-JV Ко М.
гт - U- — —— I И
Фиг. 127.
Фиг. 128.
ломаного стержня фиг. 127, один конец которого шарнирно закреплен, а другой опирается на каток. Такую задачу по классификации 1 гл. V мы считаем квазимоноциклической, так как вертикальные опорные реакции не могут быть определены вполне точно без учета деформации рамы. Но при практических расчетах инженерных конструкций, не имеющих больших деформаций, для определения величин va можно исходить из расчета по недеформированной схеме и считать достаточно точными полученные опорные реакции рамы и продольные усилия Nab ее стержней. Вообще же надо учесть, что при деформации рамы N0l AN01 и,
следовательно:
QI АЯ.г, Q Ш,
01
Ь
204
На конце 0 рамы нам сразу известны два начальных параметра М щ Q0. Неизвестными являются две величины: угол поворота р0 и приращение вертикальной реакции AN01, влияющие см. h на поперечные силы ригелей.
Составляя выражения по типу а, Ь, с,., для углов поворота i Тз и моментов Ми Мг, М3 и Д4, мы должны все время учитывать, что 12 и 23 содержат неизвестное AiV01. Для определения неизвестных ф0 и AiV0l служат уравнения:
Mt 0 и б,, 0. i, k
Уравнение к удовлетворяет условию кинематики, а именно, что взаимный сдвиг по вертикали точек 0 и 4 равняется нулю. В уравнения i д к вместо ilf4, ф1а и 23 должны быть подставлены их выражения
через неизвестные ср0 и АЛГ01, полученные так, как это описано в п. 1
этого параграфа.
Задача расчета устойчивости рамы фиг. 128 моноциклическая см. 1 гл. V, так как осевые усилия Nab могут быть определены сразу:
V0 - pip. и0 _ р. дг 0- N Р Р
01 -11 2 ‘МЗ 2 28 — 84 57 V 45 iV56 -8 iV78 4
и, таким образом, сразу же могут быть найдены величины vab для всех стержней. Тем не менее при потере устойчивости рамы произойдет перераспределение усилий; появятся поперечные силы во всех стержнях, я продольные усилия изменятся на малые величины:
N01 N1 AN01; Ni7 Nl7 ANs,-, Nts - ANol AN. 1
Поперечные усилия элементов, которые надлежит подставлять в формулы начальных параметров 1, 2 и 3, могут быть выражены через четыре величины: Q0i Qoi 5д5 ANi и ANS,
Qib Qsi — 01 Qt 5J Qi1 Q, ls 01 4 7 W AN- m
Рама состоит из двух контуров: 0—1—2—3—4—5 и 6—5—7—8. В первом контуре М0 О, если кроме этого мы знали бы р0, Q01 и A7V01, то мы могли бы, пользуясь последовательно формулами 1, 2 и 3, найти узловые моменты Ml9 М2У Mzy il4, Л54, а также угловые и линейные перемещения узлов первого контура. Во втором контуре ile 0, AN95 — AN0l — AiV87. Если бы мы, кроме того, знали ср6 и в5, то мы
могли бы также определить все величины, относящиеся ко второму
контуру 6—5—7—8. Итак, общее число неизвестных равно шести: р0, 0i AiV0l, AiV87, ср0 и вб. Уравнения, служащие для определения этих неизвестных, должны выражать собой следующие зависимости:
4 Р5.; 2 Mol1012 l23 —Ю—Й4145 Л5в; 3 ♦,. 0; 4 6 0; 5 М9 0; 6 А ф - ф78 0. п
При составлениии уравнения 5 мы рассматриваем контур 6—5—7—8, причем учитываем загрузку этого контура в узле 5 сосредоточенным моментом Af54, величину которого мы определили из рассмотрения первого контура 0—1—2—3—4—5 через неизвестные р0, Q0l и AN0l. Уравнение
2 выражает собой равенство горизонтального смешения узла 5 первого контура и конца 5 стойки 5—6 второго контура. Уравнение 3 выражает собой равенство нулю вертикального перемещения узла 5 первого контура. Во все уравнения 1 — 6 мы, вместо входящих в них величин, подставляем их выражения через неизвестные р0, Q0l, AN0l, ANs7, ф6 и Qes, полученные путем последовательного применения уравнений I, 2 и 3.
205
В качестве следующего примера рассмотрим схему расчета устойчивой прочности бесшарнирного замкнутого контура фиг. 129. Задача расчета— полициклическая. Из предварительного расчета рамы по недеформированной ее схеме находим продольные усилия аЪ всех ее стержней, на основе которых определяем величины va для первого цикла расчета. Очевидно, что приняв в качестве неизвестных 0, N0l, Q01 и М01 мы можем затем из условий статики определить для всех стержней рамы величины Qah, как функции внешних нагрузок и неизвестных N0l и Q0l. После этого по формулам 1, 2, 3 можем последовательно найти для всех узлов 1, 2, 3,., 7 и 0 величины углов поворота рп, узловых моментов Мп и углов поворота всех стержней фп,л1 как функции от внешних нагрузок и неизвестных расчета ср0, N01, Q0l, Мо1. Задача отдельного цикла
расчета устойчивой прочности замкнутого контура по этому способу приводится к определению четырех неизвестных из уравнений, выражающих собой следующие зависимости:
п 7
1 Мо1 М07; 2 п1 Q
п О
п—7
3 2 0; 4 р01 7. v
nsQ
При составлении формул 2 и 3 мы должны помнить, что величины проекций длин стержней направленного контура рамы на оси у я х: h0, h19 h29 b2, b3 и 64 — положительны; hz h7 bx bb 0;гвеличины й4, hb9 йв, b09 b7, b9 — отрицательны.
Если в результате первого цикла расчета продольные усилия изменятся настолько значительно, что это заметно отразится на трансцендентных коэфициентах формул 1 —3, то нужно перейти ко второму циклу расчета для уточнения полученных результатов.
В заключение этого параграфа отметим, что, хотя предложенный в нем способ расчета в ряде случаев значительно сокращает число уравнений, подлежащих совместному рассмотрению, тем не менее составление этих уравнений связано с громоздкими операциями по последовательному применению формул метода начальных параметров. Последнее обстоятельство несколько сокращает область рационального применения этого метода. Кроме того, неизбежные погрешности расчета накопляются в самом процессе составления уравнений и проверка полученных численных решений путем подстановки в систему совместных уравнений в этом способе не гарантирует правильности решения, так как наиболее громоздкая часть расчета по составлению системы уравнений остается вне контроля.
Консольный метод по идее своей, как это легко заметить, несколько похож на обычный расчет статически неопределимых систем по методу сил, так как большая часть неизвестных в этом методе — статически неопределимые величины в обычном смысле этого термина. Неизвестные же деформации в этом методе являются как-бы неизвестными, относящимися к основной в обычном смысле этого понятия статически определимой системе, которую нельзя рассчитать по деформированной схеме, исходя из одних условий равновесия.
2. Метод узловых моментов и поперечных сил
Предлагаемый ниже метод Ма, Qab, Мь находится примерно в таком же отношении к балочному методу Ма9 ЬаЪ, М9 как метод узловых поворо
—х
Фиг. 129.
206
тов и поперечных сил ра, Qab, fb относится к методу деформаций ра, фа, рь Формулы этого метода могут применяться при расчете по балочному методу как вспомогательные для стержней, для которых величина поперечных сил известна до начала расчета например, для стержней с поперечным усилием, равным нулю. Кроме того, этот метод может быть с удобством применен к расчетам многоугольных одноконтурных рам с шарнирами или без них.
7 л
р,
Pz
X
1 ч - а,-
г — —-
N а-
; ниш
rUlLLlJ
: LIJ1U1 К
—
Фиг. 130.
относятся к категории внутренних сил МаЪ, Qab то метод этот может быть назван также методом сил. Но надо оговориться, что этот метод не является обобщением известного метода сил при расчете сооружений по не-
деформированной схеме и поэтому мы будем воздерживаться называть так этот метод.
Основные формулы этого метода см. формулы 74 — 76 гл. III могут быть записаны так:
-г
чъ L
УаЪ—
Маъ
Mba
та ,. I у tg уЛ 1 v sin чаЬ
1
Qab I
ab
v2 ab
J a;
Mab Mba Qabhb tyabt
4
5
lab v ab
где fab и выражают собой влияние поперечных пролетных факторов стержня:
1 ШЬа
СаЪ tab у Sin va
1 д мЪа
6
ab АЬаЬ V2”b Для случая загрузки стержня силами Р и нагрузкой q по всему пролету фиг. 130 формулы 6 и 7 получают вид:
vbn
I
2
sin -j- tg -1
qi
sin v
a6 4iab L n 1,2,.
2 Tl
Tl 1 I 2;
6
T
Если конец Ь стержня lab жестко защемлен, т, е. рь0, то в соответствии с формулами 86 и 88 гл. III будем иметь:
Ьь гаь МаЬ С. аЬ аЬ
аЬ 1Ь С V2C0SV ьМаЬ аЬ аЬ 1аЬ где аь и выражают собой влияние пролетных факторов на стержне:
10
8
9
ъ —.
‘а cos veft
ДЬа-абДер6а.
И
Если известно, что концы стержня 1аЪ не имеют взаимного сдвига ab 0, то вместо формул 4 и 5 целесообразно применять формулы балочного метода 1 главы VI:
12
207
Уравнения для расчета рам по этому методу представляют собой условия неразрывности их деформаций в узлах и на опорах. Одни из них выражают собой равенства углов поворота концов стержней, жестко вязанных в узлах:
ab:aci ¥ab Pa.d И Т. Д., -3
другие — условия неразрывности шарнирной схемы отдельных контуров рамы уравнения 7 гл. V:
21 Yab 08 Iat О, 2 1Ъ ФаЬ COS у, 1аЬ 0.
14
В формулах 14 суммирование распространяется на все стержни, входящие в замкнутый контур, причем направление стержня 1аЬ должно
соответствовать обходу контура по часовой стрелке. Формулы 14 можно записать проще:
14
где
;1аъ Хь — а t IаЬ — Уь У а I
tab Iab fat ab htb ab у.
15
Фиг. 131.
Применение этого метода покажем на нескольких пря0 мерах.
Пример 1. Проверить устойчивость симметричной рамы фиг. 131.
Более опасной здесь является антисимметричная форма потери устойчивости:
01 412 412 ФЬ2
Мх — М2— Мг,;
Qoi Qoa 2 Qoi Qoi 0.
Задача сводится к составлению двух уравнений с неизвестными Mt и ilf2.
Для стоек мы будем пользоваться формулой 4, а для ригеля формулой 21. Для узла 1 получаем1:
In V
э tg v0
1 Г _М_ Мг I
Ч L Vi tg Vi vx sin vA J
a
Аналогично для узла 2 находлм:
2 -i Г 1 2M2 iM2.
1 LviljVi vjsmvj 6i2 Полученную систему уравнений можно представить в виде:
Ь
1
М2
1
1 111
1 1
о VotgvoЧ tgv,
vjsinvj
0
1 1
11 1
0
it ViSinvjL
4 vivi -i-i
1 Напоминаем наши обозначения 4 гл. V:
М10—М1; Af12Mj; Mn—Mi; М2 — Мг, Мг1——Мг.
208
Критическое условие устойчивости получим, приравняв нулю детерминант этой системы уравнений:
Г JL 1 , 1 11Г1 1 11 Г 1 1 1 0
L о VitgVjJ L vx tg v, 2i2J L h Vj si.i vx J —
C
Пусть: P Plf h0 h1; 10 2; тогда v0 v1 v и критическое условие с,
получает вид:
_3
2
_LJL_L L_ 0
tg v Jg v 2тг у sin2 v 9
откуда
i9 3v tg v 0,75 v tg v
n — 0 —
iL 2 — 4 tg2 v 0,5 — tg2 v Результаты подсчетов по этой формуле даны в следующей табличке:
d
1
v
1
I 0
1
1
0,2
0,3
0,4
j
0,5
1
0,6
0,6155
n
0
0,0662
0,1721
0,3947
1,016
9,620
00
НАН
Пример 2. Проверить устойчивость двухшарнирной рамы, составленной из 2т равных хорд, вписанных в дугу окружности, и подверженной действию равных радиальных сил во всех ее узлах фиг. 132, а.
Задано, что: 1 при переме- Р Р iP
тениях узлов, связанных с потерей устойчивости рамы, линии действия грузов перемещаются параллельно своим прежним нап- ндн равлениям, проходя через новые положения узлов, и 2 изгибная деформативность стержней рамы неизмеримо превышает их осевую деформативность, так что стержни рамы можно считать несжимаемыми.
Ось рамы очерчена по линии давления от нагрузок. Продольные усилия всех стержней рамы до потери устойчивости равны Р
N0. Длины всех стерж-
vA
Фиг. 132.
2 cos —
пей равны I, а погонная жесткость
тр Т
и равна i0 —. Величины аЪ для всех стержней равны v
L
Поперечные усилия, появляющиеся в момент потери устойчивости, равны:
Qn AV cos
2n-lA 2n-lA
Sill
По формуле 4 получаем:
2 2 фиг. 132,6, помня, что Мпг; п Мпг и Мп ni
Мп
а
тг
10П, ГИ 1
ioin, n-i
Мпг Qnil
v siii v v2
М п—1 QrJ
V tg У
Мп
v tg v v sin v 1 v
Дпi i о Mni , Qn Qni j Г I ,.2
v gt v v si П V
0
V sin V
Прочность и устойчивость стержневых систем
b
209
Подставив в b вместо Qn и Qn1 их выражения по а, после умножения на vsinv и преобразований получим1 симметричное линейное разностное уравнение второго порядка с постоянными коэфициентами:
С1Т1 ч
— 2 cos v МпМЛ- 2 sin — I AF sin nA ДЯ cos дЛ. с
JL V
В соответствии с правилами разностного исчисления будем искать решение уравнения с в следующем ваде:
Мп Сг cos nv 4- С2 sin nv -f- Dx cos nA D2 sin nA, d
Первые два члена d являются общим решением уравнения с при правой части, равной нулю, последние два—частным решением, удовлетворяющим правой части. Для определения величин Dx и D2 подставим в с вместо Мп1, Мп и их выра
жения по d:
С1 cos п - 1 V — 2 cos v cos nv cos п — 1 v -f4 С2 sin n 1 v — 2 cos v sin nv sin n — 1 v 4
Dx cos n 1 A — 2 cos v cos nA -f cos n — 1 A
Hr D2 sin n 1 A — 2 cos v sin nA sin n — 1 A —
2 sin -ф l ДГ sin пАШ cos nA, d
Выражения в скобках при Сг и С2 тождественно равны нулю, как и следовало ожидать. Для того чтобы все уравнение d обратилось в тождество, нужно приравнять друг другу в левой и правой части d отдельно коэфициенты при sin пА и сопА. В результате получим:
D1 D - ДЯ; D2 D ДГ, е
где для краткости записи обозначено:
. А.
sm sin v
D —. I. f
v cos A — cos v v Итак, решение d приобретает вид:
Mn Сг cos nv С2 sinnv -f D ДГ sin nA -f ДЯ cos nA.
Постоянные Сг и С2 находим из граничных условий, используя шарнирность опорных узлов рамы: Мт М_т 0 Решив эти два уравнения, находим:
_ cos тА ЛГ_ п sin тА АТГ
С. — D ДЯ; С2 — — D —. ДГ.
cos mv sm mv
Таким образом:
Mn D Г ДГ С sin пА — -s.n sin д. cos —cos тЛ I
n L ч sin mv у V cos mv J J Из условия равновесия отдельного стержня рамы:
2 Mn —1 -f- Qnl И J
найдем угол поворота стержня фп:
л г. 2л-1Л,. 2п— 1 v Атг Г 2п-1л , ДЯ a sin - —- - с sin - — - — ДК а cos - Ь о cos j. n
Здесь для краткости записи приняты обозначения:
Csinv 1 — cos Л I2
1 г -т-;
cos V — cos A J- V2l0
о А. V
2 sin - sm —-. 72
2 2 sin v cos тА 12.
g. ; j
cos v — cos A v cos mv v2i0 1 4 7
Л. Л. v
2sm — sin—. y2
2 2 sm v sin тА 12
cos v — cos A v siimv v2i0 e
Чтобы получить уравнение критического состояния рамы, нужно выяснить условия, при которых возможно появление приращений реакций ДЯ и AV. Для этого нужно записать два уравнения замкнутости шарнирной цепи рамы:
nm пт
I ♦всов.А 0; г 2 sia 2al1d0- k
n-m1 n—m1
1 Умножая на sin v, мы вводим паразитные корни в уравнение а v п; 2п; 3-тс,.
Будем об этом помнить.
210
Подставив в уравнения к вместо фл его выражение по h и выполнив суммирование г, получим следующие два уравнения:
sin 2тА
к
т-f
2 siii А
sin т Л-f-v sinm — v
Н 2 sin
А — v
2 2 sin 2mА , л sir га А — v sin m A -fv
171 : — I j С
2 sm A J
2 sin
А — v 1
in т Л уУ
. Л v 1 2 sin —— j
ДГ 0;
ДЯ о,
р
q
Приравняв нулю выражение в квадратной скобке уравнения р, получим критическое условие для антисимметричной формы потери устойчивости, при которой нарушается симметрия вертикальных реакций рамы. Аналогично приравняв нулю выражение в квадратной скобке уравнения q, получим критическое условие для симметричной формы потери устойчивости.
7С
Пусть нам задано: А 30— и га 3, тогда критическое условие для более
опасной антисимметричной формы потери устойчивости после некоторых преобразований запишется так:
0,1340 sinv I sin
7 I О ЯААП — г.п и J 3tg
Д 1
8660 - cos v -1П 1 0.
g 3v J
v. 0,8660 — cos v2 Подставляя сюда вместо v численные значения, получаем:
р
V
0
0,5
0,7
0,9
1,0
0,96
0,9615
д
0,830
0,7820
0,7064
0,3975
—0,746
0,029
0
Итак:
Ркр 2Л кр cos 4 1 -732 0 96152 Т 1 600 Т
Заменив длину стороны многоугольника I через радиус описанной окружности
R —-j- и через радиус вписанной окружности г ——г соответственно получим:
2sin 2tg-
ЛКР 344632157
г
1 При суммировании пользуемся следующими формулами:
т т
2 cos 2п-1 В ; 2 sin 2n—1 В 0. 1
ri —тп1 п — тп1
На основе формул 1 путем простых тригонометрических преобразований получаем:
т т
2 cos2L ro M: 2 8in- m-; ш
jLI 2 2 sm Л 2 2 sm Л 4 71 —7711
m
2 cos 2ra 1 v sin
2
71 — 7711
m
2
71 —7711
771
s
71 - 7711
2п-1Л. 2w-lv л
cos - — sm 7 0; n
2rc — 1 A 2n — 1 v __ sin га Л v sin га Л — v
cos cos 2
о Л -h 2 sm —
о — v
2 sin —2-
V dn2”-1 cin 2n-1v - sinm4—v sin тА ч
2 2. A — v. Лv
2 sm —-— 2 sm
71 - 7711
2
o
14 211
Пример 3. Использовать решение предыдущего примера для определения критической нагрузки двухшарнирной круговой арки постоянного сечения, загруженной равномерно распределенной радиальной нагрузкой фиг. 133. Считать, что при потере устойчивости элементы нагрузки qds следуют за осью арки, сохраняя параллельность своим прежним направлением, благодаря чему происходит перемещение линии давленая при потере устойчивости арки. Сравнить это решение с решением С. П. Тимошенко, относящимся к случаю такого поведения нагрузки, когда элементы нагрузки qds при искривлении оси арки сохраняют линии своего действия и линия давления при потере устойчивости арки не перемещается2.
С. П. Тимошенко для этого случая предложим формулу
EJ те2 ч
Лкрг ЯкР r2 w2 J
15
Заранее, a priori можно сказать, что в разбираемом случае действия нагрузки потребуется большая величина критического усилия, чем в случае, рассмотренном
С. П. Тимошенко. Действительно, в разбираемом случае при антисимметричной деформации оси арки точки приложения нагрузок будут на одной половине арки опускаться вниз, а на другой подыматься вверх, причем все они будут иметь горизонтальные смещения в ту сторону арки, которая будет подыматься вверх. Благодаря этому на опускающейся стороне арки останется меньше половины всей нагрузки, на этой стороне произойдет как бы разряжение нагрузки, а на подымающейся стороне как бы ее сгущение. Выходит таким образом, что подымающаяся сторона арки в разбираемом случае получает как бы дополнйтельное сопротивление своему движению вверх, которого не имеется в случае, разобранном С П. Тимошенко. Представляет практический интерес выяснить, насколько в разбираемом случае действия нагрузки должно увеличиться критическое усилие NKp-
Чтобы из формул примера 2 для многоугольной рамы получить формулы для круговой арки, надо положить, что т — число сторон рамы, стремится к бесконечности, а величины Л и I неограниченно убывают:
r2CJy Фиг. 133.
причем:
I— 0; А— 0; т— оо,
шА о; 1 г А; 1т юг.
S
Величина v I также стремится к нулю, a j0-y- стремится к бес
конечности.
г f Nfl Обозначим отношение у —
тогда:
I г ч Т ТА ПА.
t
В связи с вышесказанным выражения, входящие в формулы р и i, получат следующий вид:
а
1— 1
т2
ГА
гА
d
А — т. Л 1 1
1
Sin О
г А
гг - 1 N
sin со г А
si л со iV 1 — rf sin or i
1 С. П. Т и м о ш е и к о, Курс теории упругости, ч. II, 30, 1916.
2 В то время как статические нагрузки, вызываемые весом сооружения, действуют всегда вертикально, поведение наклонных нагрузок может быть различным в зависимости от условий загружения. В частности, наклонные нагрузки могут: 1 сохранять свой наклон к горизонту и точку приложения к поверхности разбираемый нами случай; 2 сохранять свой наклон к поверхности и точку приложения гидростатическое действие; перемещаясь с поверхностью, несколько поворачиваться, сохраняя направление на какой-то определенный полюс; 4 сохранять свою линию действия, не следуя вбок за смещающейся поверхностью сооружения.
212
т -Ь
sin 2mA __ 2о sin 2о
2 sin А
2 А
sin т А v sin m A — vJ _ sin o 14. sin fo 1 — _
0. A v A — v A 1-f 4 1 — 73
2 sm —2 sm 4 u i
2
2
2
A 1 - r,2
sin 0 cos 07 — 73 cos O sin 17.
Таким образом, критическое условие для антисимметричной формы потери устойчивости круговой двухшарнирной арки будет:
Oi
згу ,3 4sia - i7sin 2u1 t::r - lg
Величина угла o задается условиями задачи, величину же т мы определяем гак минимальный корень трансцендентного уравнения 16, после чего находим:
ЛГ __
N кр— Г1кр— г2
17
В нижеследующей табличке для сравнения приведены результаты вычислений величины -q2JVkp cry по формуле 16 и по формуле 15 С. П. Тимошенко:
JU J
Формула
2ш
3
9
мл
7Ъ
Л
Т
тс
1 Ь 1
7С
т
16
ТГ
3,270
6,750
8,736
15,86
35,94
63,97
15
ГГ
3,000
6,111
8,000
15,00Э
35,000
63,000
Таким образом, допущение С. П. Тимошзнко о сохранении без изменения линии давления арки при потере устойчивости действительно идет в запас надежности расчета.
Пример 4. Рассчитать трехшарнирную раму фиг. 134 на действие симметричной нагрузки. Поставленная задача — квази-моноциклическая, поэтому мы прежде всего на
Фиг. 134.
основе обыкновенного расчета определяем распор II V0 — P,. —— —.f8.
л 2 А а затем находим величины и v2 для стоек и ригеля рамы.
В соответствии с соображениями, высказанными в 8 гл. V, данная задача может быть подразделена на две отдельных задачи; 1 симметричную — для определения симметричных составляющих усилий и деформаций и 2 антисимметричную — для выяснения критической нагрузки, при которой нарушается симметрия деформации. Решим каждую из этих задач отдельно.
1. Симметричная задача. В этол случае: F0 F4 P1 - Р2 и Мх М. Неизвестных в расчете два: М и распор IIе. Этим неизвестным соответствуют уравне-
21а
ния выражающзе собой: 1 равенство углов поворота хэ и.
1 Mf Hh 1 Г М Рг Ь si
h vi vi v J h L tg v2 V. 2 4- у vS J 2 отсутствие горизонтального перемещения узда 2: или и2 йф01 -f ф12 О,
-Ренгав эти уравнения, находим неизвестные Mf и.й.
2. Антисимметричная задача. Задачу эту мы решаем в соответствии с указаниями, данными в конце 8 гл. V. Вместо заданной сжато-изогнутой рамы мы рассчитывазм на устойчивость равнссжатую см. 9 гл. IV систему, подверженную действию осевых нагрузок с теми же значениями Vj и v2, как и в симметричной задаче. При этом учитывается появление антисимметричных составляющих AV вертикальных реакций рамы; распор рамы Н не может иметь антисимметричных составляющих, поэтому Д 0.
Неизвестными расчета будут: AV и М —М. Из условий антисимметрии:
Qoi Q43 О
Поперечные силы ригеля:
Неизвестным соответствуют уравнения, выражающие собой: 1 равенство друг другу
1 МЧ X Г МЧ. Ь
Ч vi Ч vi h V v2 tr vs
—ДГ
rO и 2 равенство нулю антисимметричной составляющей вертикального перемещения узла 2: i ф2 0:
d
Из уравнения d находим:
ДГ - 4- мь
о
Подставив этот результат в с, получаем:
f г -г— 0.
4ivi vl tg va wi J
Приравнивая нулю выражение в скобках, получаем условие критического состояния рамы, при котором становится возможной потеря симметрия деформации:
1а V V о 4 V
i t7VVltgVl 0
11 2 о 2
или, пользуясь обозначениями 115 гл. III:
U to-
- - — 1 о
3. О применении метода сил в его обычном виде к задачам
устойчивости и устойчивой прочности
1. Основные предпосылки
Изложенный в предыдущем параграфе метод является одной из разновидностей метода сил. Здесь мы будем говорить о другой его разновидности, более близкой к классическому методу сил в задачах расчета прочности рам.
Используем при этом представления о равносжатых единичных и нагрузочном состояниях и о первоначальных единичных состояниях основной системы рамы, развитые нами в 9 и 10 гл. IV.
Пусть дана рама, изображенная на фиг. 136. С обычной точки зрения эта рама трижды статически неопределима. Основную систему и неиз-
214
вестяые для нее можно было бы выбрать так, как это показано на фиг. 137. Эту же систему неизвестных Xlf Х2, Х8 можно принять и при расчете рамы по деформированной схеме и воспользоваться той же канонической системой уравнений:
XAiXA.XA,ipo,
-Х21 222 Х382з- о2р О, 18
181 Ь2з2 Хззз зр О J
при условии, что все перемещения 8ц, 812,. , 81р,. , входящие
в эгу систему уравнений, будут определяться для равносжатых состояний с такими же значениями величин va, какие соответствуют полной нагрузке рамы фиг. 136. Пренебрегая при этом деформациями сдвига
и обжатия оси рамы, можем определять эти перемещения по формулам 33, 35 и 36 10 гл. IV:
J _vf MlM,ds _ V f. Й MlMpds Jim
tk — ki — 2d J EJ kk 2л J EJ Kp 2l J EJ В этих формулах Mk — изгибающий момент Л-го первоначального единичного состояния, определяемый по недеформированной схеме рамы; Мь Мк, Мр — изгибающие моменты г-го и А-го единичных и Р-го нагрузочного равносжатых состояний рамы. Таким образом, для каждого неизвестного нужно взять не по одному, а по два единичных состояния: по одному равносжатому и по одному первоначальному. Кроме того надо взять еще одно нагрузочное равносжатое состояние основнэй системы.
На фиг. 138 показаны все эти состояния для рамы фиг. 137.
Эпюры моментов первоначальных единичных состояний 1, 2 и 3 получаются по правилам статики, без рассмотрения деформаций. Эпюры моментов равносжатых состояний 1, 2, 3, Р получить не так легко. Расчет каждого равносжатого состояния представляет отдельную задачу, для решения которой может быть применен любой метод из описанных выше в главах VI — IX. Фактически для вычисления интегралов 19 не нужны эпюры моментов равносжатых состояний, достаточно знать изгибающие моменты или даже какие-либо другие граничные параметры по концам всех стержней в этих состояниях. Вычисление интегралов 19 для отдельных стержней можно затем выполнить по формулам 179, 174, 183 гл. III 19. Если расчет равносжатого состояния нами выполнен по методу узловых моментов и поперечных сил в этом случае можно считать, что весь расчет рамы в целом и в его отдельных частях выполнен по методу сил, либо по балочному методу, то мы можем использовать формулу:
lj ММ ds М0Мй МХМХ MMi лгм0 Мм Mtf.
20
EJ
О
215
Если расчет равносжатого состояния выполнен по методу деформаций, то можно использовать формулу:
1 MMds мл К - мг - ф.
21
Наконец, если при расчете равносжатого состояния был применен метод узловых поворотов и поперечных сил, то воспользуемся формулой:
ilf Л
I
JL С
О
В этих формулах 20 — 22 величины М, , rf, 6 без черточек отно-
Фиг. 138.
сятся к равносжатому состоянию, величины Л, Q относятся к первоначальному состоянию; правило знаков для М0 и Мг берем как для изгибающих моментов, т. е. считаем их положительными в случае изгиба стержня рамы выпуклостью в сторону пунктирной тени.
Отметим одну особенность расчета устойчивой прочности рамы фиг. 136. Ввиду отсутствия симметрии нагрузок рама как бы сама теряет сихмметрию, так как в симметричных элементах значения va получатся различными. Поэтому нельзя уже считать, как при расчете симметричной, симметрично загруженной рамы, что состояния 1 и Я см. фиг. 138 симметричны, а состояние 2 — антисимметрично. Коэфн-
216
циенты 312 и 823 при несимметричной нагрузке рамы фиг. 136 отличаются от нуля.
Вообще говоря, в связи со сложностью расчета отдельных равносжатых состояний, расчет устойчивой прочности рам методом сил в изложенной в этом параграфе трактовке нельзя признать достаточно удобным. Этот метод оправдывает себя лишь в тех случаях, когда известно, что продольные усилия большинства стержней рамы равны нулю: 7Va 0.
Более простым представляется получение системы уравнений 18 путем непосредственной записи по формуле Мора 28 гл. IV работы сил первоначальных единичных состояний 1, 2 и 3 на перемещениях сжато-изогнутого состояния 2 см Фиг 137 основной системы, одновременно загруженного нагрузками и неизвестными Х1у Х2, Х3:
MlMds
EJ
188з
0;
1
-2
М М ds EJ
0;
М М ds
EJ
0.
23
Для вычисления этих интегралов по формулам 20 или 21, или 22 надо предварительно по одному из изложенных выше методов гл. VI—IXг считая известными vab для всех стержней рамы, найти для равносжатого состояния 2 значения входящих в эти формулы величин. Для первого цикла расчета можно значения vab определить в соответствии со значениями продольных усилий Лг2ь, полученными из обьдчного расчета рамы по недеформированной схеме.
Таким образом мы объединим в единой записи все операции, относящиеся к четырем различным равносжатым состояниям 1, 2, 3 и Р.
Этот способ легко позволяет учесть не только деформации изгиба оси, но также и деформации ее сдвига и обжатия, если вместо формул 23 воспользоваться формулами типа:
1
о
Ml М ds EJ
sSisJJ-o- 24
2. Расчет устойчивости рам с большим числом стержней, из которых только немногие имеют продольные усилия, отличные от нуля
В этом случае применение метода сил может оказаться весьма целесообразным. Покажем это на примере рамы фиг. 139 с одним сжатым стержнем — левой
X, 4 X,
стойкой. Для всех остальных стерж-
ней величины va6 0, так как до потери устойчивости рамы продольных усилий в них не возникает. Вообще говоря, нужно различать при расчетах устойчивости величины двух разных порядков малости: величины, имею
щие конечные значения уже до потери устойчивости, и величины, возникающие в момент потери устойчивости.
Последние величины, если
ограничиться изучением момента потери устойчивости, мы можем рассматривать как величины бесконечно малые, произведениями которых вполне можно пренебрегать по сравнению с первыми их степенями.
В рассматриваемой задаче конечной величиной является только нагрузка Р и равное ей продольное усилие N12 левой стойки. Угловые и линейные смещения узлов рамы, изгибающие моменты и поперечные
217
усилия, дополнительные реакции, а также значения неизвестных Хи X2f Xs мы можем рассматривать как величины бесконечно малые. Поэтому при определении изгибающих моментов в части рамы, лежащей справа от загруженной стойки, можно не учитывать перемещений узлов даже при расчете ее устойчивости, так как эти моменты здесь определяются суммами произведений неизвестных Х1у Х2 и Х3 на соответствующие плечи. Таким образом эпюры моментов равносжатых единичных состояний для этой части рамы вполне совпадают с эпюрами моментов соответствующих единичных первоначальных состояний. Иначе дело обстоит с загруженной стойкой и левым ригелем 0 — 2. Чтобы найти в них моменты, нужно отдельно рассмотреть систему из двух стержней 0 — 2 — 1, загруженную, как показано на фиг. 140.
Учитывая, что поперечное усилие стойки Q12 —Х1у моменты в этой системе рассчитаем по методу деформаций, пользуясь формулами 8, 15 и 16 гл. VII:
Р х-
-I,
Фиг. 140.
М23 ХЛ-Х2 ;- Х3;
М20 302 92
М21 — vtg v-cfj-f -2kXt.
Приравняв сумму этих моментов нулю, найдем выражение для р2:
04
а
Имея в виду в дальнейшем пользоваться при вычислении интегралов 19 формулой 21, находим также по формуле 1 гл. VIII величину угла поворота ф12 загруженной стойки:
12
tg V tg V — V
— 2 — h
Хг.
12
Ь
Для ригеля 102 из условий кинематики фог — О Таким образом для загруженной стойки по формуле 21 получим:
i
MMKds Мк21 2 - j
ft
Мк21 А V2 3h j Хг V2 - У Хг Х3 , с
где для сокращения записи обозначено:
tgv-v
V3 302 12VoV
d
Для ригеля Z02 аналогично получим
i
1 ММ dsМки ср2 - 1о2 М:20 в лХг-4Х2 Х3, 1
tgv
где для сокращения записи обозначено:
1
5 -
3оа — tg V
0
218
Для всех остальных стеркнеи рамы, учнтыввя что для них уз,ъ О, яайдем:
i i
2ммм 2 т ХКХМ mi ds
О о
3 мк
EJ
ds
xxx.k x.b
5o
zk
is
В этой формуле при определении величин 5Г, 8 и 8 суммирование распространяется на все стержни рамы, кроме двух 1о2 и 12.
Сложив выражения с, е и g, получим перемещение 8s равносжатого состояния 2 Фиг 19, соответствующее неизвестной Хк:
Oki Хг Ok А Mhzi ЗА В M2o j J Ь
Х2 82fe - A Mftn - 5 Mft2o j хз 8
А Мй21 v2 В Л20 0. h
Давая последовательно в формуле h значения к 1, к 2 и 3, получим систему трех уравнений с неизвестными Хг,Х2 и Х3. Приравняв нулю детерминант, составленный из коэфициентов этой системы уравнений, получим критическое условие, из которого мы сможем
2 ЕТ
VKPCJ 12
hz
найти vKp и затем РКр
Можно несколько видоизменить вышеприведенный расчет рамы1, нигде не выходя ни в целом, ни в частях расчета за пределы метода сил. При этом придется увеличить ч юло неизвестных на единицу, добавив к неизвестным Х19 Х2, Хг неизвестный изгибающий момент вверху загруженной стойки М21. Уравнение для неизвестных Хг, Х2, Хг составляем, приравнивая нулю перемещения dls, 3i:
MjMdsQ MSMds
2 С ММ ds J EJ
EJ
0. I, II, III.
0;
Фиг. 141.
Уравнение для неизвестной М21 составим так. Сначала по формуле 29 гл. IV
г М. М ds
аайдем горизонтальное перзмзщзние Д2 узла 2 в состоянии S Состояние Мк получим, прдложив к статически олредзлдмой ге шетрлческа нелзменяемой части рамы 0—2—1 фиг. 141 в узле 2 горизонтальную силу еддндца. Затем из условия равновесия -стойки 1 — 2, прзнебрегая малым д высших порядков, найдем выражение для момента М21:
М21 — РД34 XJi.
Итак, четвертое уравнение получдт в едз
М
21
М, М ds
IV
Заменив в уравнениях I и IV момент М через Xlt Х2, Хь и Мг1. выполняем интегрирование. Интегралы для загруженной стойки берем по формуле 2Э. Критическое условие устойчдвостд получим, приравняв нулю детерминант, составленный из коэфициентов при неизвестных Х19 Х2, Хг и М21 в этих уравнениях
1 См. статью В. Г. Чудновского впервые применившего метод сил к расчету устойчивости рам в Сборнике, посвященном 75-летию и 50-летию научной деятельности акад. Е. О. Патона, Изд. Ак. Наук УССР, 1946, г. Киев.
219
4. О расчете рам по методу фокусов
В 9 гл. IV и в 1 гл. V мы выяснили, что при расчете устойчивой прочности рам можно пользоваться принципом наложения аддитивности для искривляющих факторов при условии, что для всех стержней рамы коэфициенты чаъ остаются постоянными и соответствуют продольным усилиям Nab стержней рамы при ее полном расчетном загружении. Ясно, что при соблюдении этого условия можем к расчету устойчивой прочности рамы применить любой метод расчета прочности рамы с соответствующими изменениями. При этом такой расчет будет отчасти напоминать расчет прочности рамы со стержнями переменного сечения1.
Таким образом, к расчету устойчивой прочности рам при соблюдении: вышеприведенного условия вполне можно применить и методы фокусов:
моментный и угловой2. К сожалению
с
при переносе этих методов на задачи устойчивой прочности теряется основм г ное их преимущество, состоящее в воз-
я Ъможности использования раз навсегда
полученных для данной рамы фокусных отношений и коэфициентов распределения в методе моментных фокусов к самым различным случаям заФиг. 142. гружения рамы. В задачах устойчивой
прочности при всяком изменении продольных усилий стержней наново приходится пересчитывать величины аъу трансцендентные коэфициенты уравнений и затем значения фокусных отношений и коэфициентов распределения.
Принимая коэфипиенты va в соответствии с полным расчетным загружением рамы и рассматривая потом последовательно случаи загружения отдельных ее стержней, мы получаем правильные окончательные суммарные значения концевых моментов стержней углов поворота узлов для полной расчетной нагрузки, в то время как для отдельных частных загружении решения не будут при этом верны.
Тем не менее метод фокусов с удобством может быть применен для точного расчета устойчивости одноэтажных рамных эстакад и для приближенного расчета многоэтажных рам3.
Мы ограничимся приведением некоторых формул, относящихся к методу угловых фокусов, и примером расчета устойчивости несвободной рамной эстакады по этому методу.
Пусть два узла а и Ь несвободной рамы связаны между собой только одним стержнем фиг. 142 Za, узел с— шарнирный, узел d — жестко защемленный, узел е — упруго защемленный. Пусть также значения
vJДля всех стержней известны. Легко представить себе, что
если изгибающие раму нагрузки находятся только справа от узла Ьу, то во всяком случае, пока нагрузка рамы мала, далека от своего критического значения углы поворота правых узлов будут больше углот
1 Коренное различие между такими расчетами состоит в следующем. При расчет опрочности рам со стержнями переменного сечения эпюры моментов на незагруженных поперечной нагрузкой прямолинейных стержнях прямолинейны, при расчете устойчивой прочности эти эпюры криволинейны даже при отсутствии поперечной нагрузки, если только продольное усилие стержня i аъ не равно нулю.
2 СхМ. И. М. Рабинович, Методы расчета рам, ч. III, ОНТИ, 1937; Б. И. Ж ем о ч к и н, Расчет статически неопределимых рамных систем. Способ угловых фокусов,
2-е изд., Госстройиздат, 1932.
3 О применении метода моментных фокусов см. статью проф. Н. К. Снитко Устойчивость рамных конструкций при узловой нагрузке, Вестн. инж. и техн. 0, 1939.
220
поворота левых узлов рь ра ое. Отношения между углами поворота, взятые с обратным знаком, в незагруженной изгибающими нагрузками сосредоточенные узловые нагрузки могут быть левой части рамы мы назовем левыми фокусными отношениями
Ъ Чъ. 7л а
аЬ еа е Д. __ fa _ __ qq
da id О
25
25
Если изгибающие нагрузки будут находиться слева от узла е, то между углами поворота узлов рамы установятся правые фокусные отношения:
k - —
Га
—
ts
Чь
25
а
Первый этап расчета рамы по методу угловых фокусов состоит в определении левых и правых фокусных отношений для ее стержней. Составим формулу зависимости между левыми фокусными отношениями, для этого запишем уравнение для узла а:
Мab 2iab ab Та Раб аЬ 9а
Мао асас fa
Mad 2faJ aad cpu - pad ;
Mae 2tae oca cn — pae.
Приравняв нулю сумму этих моментов, получим формулу для левого фокусного отношения каЬ в зависимости от левых фокусных отношений предыдущих стержней:
ub adad Ь аеае асас ftacf I 1
V kea J J
пли в более общей записи:
:б
тФс
тф Ь тфс
am
та
26
Первая сумма уравнений 26 не распространяется на стержни с шарнирами в узлах т, вторая относится только к стержням с шарнирами в узлах су третья не распространяется на стержень, для которого мы ищем фокусное отношение каЬ и на стержни с шарнирами в узлах га.
Для правых фокусных отношений аналогично получим:
7- — 1 Г XV 1 V; V hmhm
1т 1аЪЪа1ЬтЬт12-1Ьс Ьс ктЬ
тфс тфа
тфс
В частном случае расчета прочности, если считать все v 0, формула 26 получает вид:
i 2 2 -12 - 21 26
27
m-7-c
тфЬ
тфс
В случае нахождения искривляющей нагрузки только на одном стержне рамы lab9 углы поворота сра и ь получим, решив систему двух уравнений равновесия для узлов а и 6. Составим уравнение для узла а:
МаЪ Mac Мad Мае 0. Ь
221
В этом уравнении МаЪ возьмем по формуле 1 гл. VII, сумму же моментов Mac Mad Мае мы заменим в соответствии с первой строкой системы уравнений а:
Мае 1 Ма -f- Мае аЪ faab¥a Pababa
Маъ abPa Ь РаЬб Ч Mgi,
Ziabfiab Kb9a b МаЪ 0.
Аналогично для узла Ь находим:
abfiab а ЬаЬ Мьа 0.
c
d
в
Решив эти два уравнения, получим:
аЪ
о
Mfa Ъа Ма
ab
Ь
4 а abPab ftabkba
Мab ” ab Mfra
I
J
28
abab НаЬЪа 1
Показателем ab у обозначений углов a и cpt мы отмечаем, что
нагрузка находится на стержне 1аЪ.
Не вдаваясь в дальнейшие подробности теории расчета устой
чивой прочности рам по методу угловых фокусов, укажем только, что вопросы, касающиеся 1 расчета рам с изгибающей нагрузкой на ряде стержней, 2 расчета рам свободных, многопролетных и многоэтажных, и другие аналогичные при соблюдении условия, указанного в начале параграфа, решаются совершенно так же, как и при обычном расчете прочности рам по этому методу1.
Затронем только вопрос о составлении критического условия при расчете устойчивости несвободных рам по этому
методу. Если на несвободную раму при отсутствии изгибающих нагрузок действуют только узловые нагрузки, то мы имеем дело с чистой задачей устойчивости. Числители дробей формул 28 обращаются при этом в нуль. Для того чтобы искривление рамы могло произойти, надо чтобы знаменатели этих дробей тоже равнялись нулю:
аЛа-1 0. 29
Иначе говоря, в критическом состоянии для любого из стержней несвободной рамы, связанных между собой ее упругой деформацией,
произведение его левого и правого фокусных отношений должно равняться единице.
Для свободных рам со-
0
Ж
5
I
6
4
К
7
I
Фиг. 143.
ставление точного критерия L неустойчивости во много раз усложняется и применение метода фокусов становится нерациональным.
Пример. Проверить устойчивость несвободной рамной эстакады фиг. 143. Дано: 1 2 2, 2 для загруженных стоек:
v2e v37 v; a2e a37 a; 326 837 S.
Для всех остальных стержней рамы величины va5 0; aa52; и 1.
Определим фокусные отношения. В соответствии с формулой 25:
51 62 73
1 См. вторую сноску в начале параграфа.
222
По формулам 26 и 26 находим:
i2 2 1 2 -Ь 2 — — J 4,5;
—2- 1-ег1 fт-
Пойдем теперь в обратном направлении, используя формулу 27
-f - 2. т 2 3 -М Т
Согласно 29 условие критического состояния будет:
1тт‘-
Решая это квадратное уравнение, находим два корня для а:
4—5,24 и а2 — 9,32.
Им соответствуют значения v2 5,777 и v2 5,973. Критическое значение нагрузки:
Pkr S.7772 33,37
5. Графоаналитический метод расчета неразрезных балов. Применение линий влияния от фиктивных нагрузок
i. Общие соображения
Методы графического и графоаналитического расчета устойчивости и устойчивой прочности стержневых конструкций представляют большой интерес1. Не имея возможности здесь подробно на них остановиться, мы ограничимся кратким изложением применения графоаналитического метода к задачам расчета устойчивой прочности неразрезных балок 2.
В основу этого метода кладется, как известно, равенство прогибов v и углов поворота сечений у изогнутой балки соответственно v МФ — изгибающим моментам и — поперечным силам некоторой фиктивной взаимной балки от действия фиктивной распределенной нагрузки интенсивностью дф.Взаимноесоответствие между
JuiJ
действительной и взаимной фиктивной балкой в смысле устройства их опор представлено в виде таблицы 3 на фиг. 144.
Таким образом многопролетной статически определимой балке фиг. 145, а соответствует фиктивная балка фиг. 145, б. Соответствие здесь взаимное: если бы действительная балка была по схеме а, то фиктивной балке отвечала бы схема б.
ногопролетной п раз статически неопределимой балке фиг. 146, а отвечает фиктивная балка, представляющая собой геометрически изменяемую цепь с п степенями кинематической свободы фиг. 146,6.
Несмотря на геометрическую изменяемость фиктивная балка фиг. 146,6 под
влиянием фиктивней нагрузки должна находиться в состоянии мгновенного
равновесия, поскольку ее езтс бающие моменты и поперечные силы должны иметь определенные значения прогибов и углов поЕсрота сечений действительной балки. Таким образом, задача определения льшньх неизвестных Хл, -ЗГ3,. статически неопределимой Оалки может быть приведена к задаче нахождения некоторых фиктивных
1 Г. Д. Абрамов, Графический расчет сжатых и сжато-изогнутых стержней, Оборонгиэ, 1939.
А. Р. Р ж а н и ц ы н, Графоаналитический метод определения деформаций сжатоивогнутых стержней, Сборник трудов 2 Инж. строит, ин-та им. КуйСь:шеЕа, под редакцией проф. И. М. Рабиновича, 1939 г.
2 Докладывалось автором на семинаре Института строительной механики АН УССР весной 1945 г.
3 Таблица заимствована нами из Курса строительной механики стержневых систем проф. И. М. Рабиновича, часть 1, Стройивдат, 19S8, 53, 54. См. также: прсф. И. М. Раб и н о в и ч, Кинематический метод в строительной механике, Москва, 1928. В 46 этой книги изложены осноеы графоаналитического метода расчета неразрезных балок.
223
лагрузок, соответствующих этим неизвестным Хи Х2, -ЗГ3,. и уравновешивающих на
_ 0
кинематически изменяемой цеп i фиктивной балки фиктдв гую нагрузку дф —- ,
Hi J
соответствующую нагрузочному состояняю основной статлческл: определимой системы действительной балки.
а
Устройство опор
Действительной балки
Фиктивной балНи
1
II
а мФа о
я - Ча о
II
2
а иа0 1
Ча
Ч1о
3
a va 0
а Мд — 0
Г - Л
С Ча
4
a v-a- о
L.
, о
г V Jie6
1
плев_ п пР
Ча г а
5
,.2.
ф лев Фпр
J а Ма —Ма
У ЧаР
1 д7евФ9;пр
Фиг. 144. в
til
б
I
Фиг 145.
Фиг. 146.
2. Расчет прочности не раз резной балки переменного сечения
Применим изложенные общие соображения сначала для расчета прочности неразрезной балки переменного сечения, причем используем обозначения фиг. 147, относящиеся к отдельному ее пролету. Углы поворота концов балки мы обозначаем буквами А и В с соответственными индексами, их суммы, равные равнодействующим фиктивной нагрузки, — буквами D:
4n,ni -ri,ni—Dn,n1 -ni; п Ь гп1 -пъп
гъпi nin Aini
Кроме того: ВПуП1 BnliYl
D П,П 1
I -у 1
Ч п,п1 Ч- n,n1
а
Ь
Если на отдельный пролет кроме внешних пролетных нагрузок действуют еще опорные моменты JSTj и Х2 фиг. 148,а, то фиктивная нагрузка пролета может быть приведена к трем силам фиг. 148, б: XnDn,nu ХП1ХП1П и Хп,п1, не считая опорных реакций от этой нагрузки по концам стержня.
224
В соответствии с вышесказанным расчет неразрезной балки фиг. 149, а приводится к расчету равновесия шарнирной цепи с жесткими эвеньями фиг. 149, б1, загруженной грузами ZJX, XxD10y XxD12, Du XD Условия равновесия проще всего записать с помощью начала возможных перемещений. Если дать, например,
в
ВП,П1 П1П
Bnt,n An frt
Фиг. 147.
узлу 2 фиг. 149, в перемещение вверх на 1 единицу, а все прочие узлы оставить на прежнем уровне, то сумма работ нагрузок цепи на таком перемещении будет равна:
X 2-21221 X2D2zy2z Ъ -33223223 DitPib -ззРгз с
В соответствии с Ь, имеем:
A.Vi.-A.VА. тг в
12
Ь
Сп; Dtlytl Ап и т. д.
Подставив Ь в с, получим:
112 Ь2 С21 Ьи42з Ь X С2 ”Ь 23 30
Легко видеть, что уравнение 30 — обычное уравнение трех моментов. Пользуясь на ча л омА возможных перемещений, нетрудно составить условия равновесия шарнирной
цепи так, что в каждом из них будет только по одному неизвестному. Зададим какое-нибудь возможное перемещение шарнирной цепи, удовлетворяющее ее граничным условиям. Пусть при этом перемещения, соответствующие силам XxD10, XxD12y X2D2x, X2I23,. соответственно будут: у10, y12i y21, y2z,., а перемещения, соответствующие известным нагрузкам цепи Di, U, D2Z,. будут p01, р12, р2з,. Тогда работа сил шарнирной цепи на таких перемещениях будет:
-1 ю2ю 12212 X2 -2121 -2з22з
Xz Dz2yz2 Ь -3434 . Хп Dn
,п-Уп, п—1 Ь nni2nni —
e 4 12р12 -D23P23 Ь Ч Dn,nlPn;nl d
1 Между расчетом неразрезной балки и шарнирной цепи, находящейся на плаву, существует аналогия. См:
Б. Н. Жемочкин, Некоторые гидростатические аналогии. Труды МИИТ, вып. 6, 1927.
А. А. У м а н с к и й, Наплавные мосты, Трансжелдориздат, 1939.
А. А. У м а н с к и й, Лекции по строительной механике, Изд. Наркомхоза РСФСР, 1939, стр. 50.
15 Прочность и устойчивость стержневых систем
225
Для того чтобы получить уравнение с одним неизвестным, надо, чтобы коэфициенты при других неизвестных обратились в нули. Этого легко можно достигнуть путем следующего графического построения фиг. 149,г. На вычерченной с соблюдением масштаба схеме неразрезной балки намечаем сначала t10, tl2l 21. — вертикали действия грузов ХхВ10, X1JD12,. для балки постоянного сечения они носят название третных вертикалей, затем для каждой опоры проводим смещенные опорные вертикали г1э г2, г3,., —вертикали равнодействующих двух фиктивных грузов,
относящихся к этой опоре. Ясно, что смещенная опорная вертикаль тп делит расстояние между вертикалями n,n-i и nni обратно пропорционально величинам
А, п-i и 1- —
Переходим теперь к построению перемещений шарнирной цепи. Построим такое
перемещение для неизвестной Хь четырехпролетной балки фиг. 149, а. Звено 0 — 1
шарнирной цепи повернем вокруг опоры 0 до некоторого положения 0—1. Следующее
звено должно занять такое положение 1 — 2, чтобы коэфициент при Хг в уравнении
d обратился в нуль. Ординаты у10 и у12 должны иметь разные знаки и быть обратно
пропорциональными величинам 10 и Dl2. Поэтому прямая, соединяющая вершины
ординат у10 и у1г, должна проходить через смещенную опору—1С. Прямую 1 —2
проводим через точку V и вершину ординаты г12. Эта прямая отсечет на вертикали
t21 отрезок 221- Чзрез вершину этого отрезка и смещенную опору 2С проводим прямую,
которая отсечет на вертикали г2, отрезок Через взршииу этого отрезка и точку 2
проводим прямую 2 —3. Точку 3 создиняем прямой с опорой 4. Полученная лома-
226
ная О—1 — 2 — 3 — 4 будет линией влияния Хг от действия фиктивных грузов1. Действительно, приняв ее за линию вертикальных перемещений шарнирной цепи и записав работу фиктивных грузов на таких перемещениях, получим, уравнение с одним неизвестным Х:
г Д23з2 34234 Доо1 DizPiz -гзРаз -34Р34- е
Читатель, знакомый с графическим расчетом неразрезных балок2, заметит, что эта линия влияния проходит через левые фокусы неразрезной балки в первых трех пролетах и через правый фокус в четвертом пролете. Итак, метод графического определения фокусов неразрезяой балки предстает перед нами в новой точнее, в своей первичной трактовке. Линия влияния от действия фиктивных грузов состоит из прямолинейных участков, построение ее значительно проще, чем построение криволинейных линий влияния от действия сосредоточенных действительных грузов. Переход от действительных нагрузок пролета Р19 Р2, Р3,. к фиктивному грузу несложен —этот груз представляет собой равнодействующую двух фик
тивных опорных давлений Сп, ni и Сп1, п, равных углам поворота концов балки 1п,л г на двух опорах от действия заданной действительной ее нагрузки см. фиг. 147, 3.
Линию влияния от действия фиктивных нагрузок для неизвестной Х3 балки фиг. 149, а, можно получить просто, отложив над опорой 3 некоторую ординату т33 и приняв для ординат над другими опорами следующие значения:
_ тза. т _ _ т2з __ зз_.
23— Z 13 h k к
л23 л12 л12ге23
т т33. т т43 _ т33 Р
т43— 7. 53 г. к к л 13 ”-54 43 64
Здесь к12, к23, fc34 — левые, а А:21, 32, 43,.—правые фокусные отношения. Зависимость между двумя левыми фокусными отношениями с12 и к23 получим, приравняв нулю коэфицаент при Х2 в уравнении d, в котором предварительно нужно выразить через т2, к12, к2Ь величины у21 и г23:
21у21-В2гу2ъ В21 т1 т21т2 ”23 т2
тг — 7 -4г1 23 2згз J
g
Отсюда:
7. 21 -23
23 R 23
В 21 1
В2з к12
, получаем:
А-П, П—1 Ь ПП 1
Вп, п-1
1
П, П1
Вщ ni
к 9 П—1 п
ПЪ п 1, П2
Bfl4 1; П2
1
ВпV п
Bnin
П2 П 1
с, ni- -ВГТГ ЕГГ:; 31
31
v А. V II 1 I If I JL
Величину т33 в f мы получим подобным же образом, приравняв в d коэфициент прл Х3единице4
Г В г В 1
34234 — тзз 3234— J 1.
Ь
1 Идея о линиях влияния от действия угла перелома оси балки, перемещающегося вдоль этой оси, впервые была высказана в книге: А. А. Г в о з д е в, Расчет статически неопределимых систем, МИИТ, 1927, стр. 19. Понятно, что действие фиктивного груза эквивалентно действию угла перелома.
2 См. 66: Графическое построение фокусов в книге: проф. И. М. Рабинович Курс строительной механики стержневых систем, ч. 2, Стройиздат, 1940.
3 Очевидно, что линии влияния от фиктивных нагрузок могут быть применены не только при расчете неразрезных балок, но и при расчете других статически-неопределимых систем.
4 Величину т33 мы могли бы получить графически следующим образом. Над опо-
1
рой 4 отложим отрезок — и вершину этого отрезка см. пунктирное построение на
фиг. 150, б соединяем прямой с опорой 5, затем через точку пересечения этой прямой с фо
кусной вертикалью F34 и фокус F43 проводим прямую, которая отсечет над опорой 3 отрезок т33, а под опорой 4—отрезок га43. См. статью автора в Сборнике научных тру
дов Укр. научн. иссл. ин-та сооружений, 1932.
15 22
Аналогично g мы могли бы записать:
32
— т — з4з4 —0 0
с
23
Использовав g, придаем h следующий вид:
W3334 34 J — 0
Обобщая результаты h и i, можно записать:
1
тп п— Б Б 2
Dnn-1 , , л _ п П1
Г 3 г -гп п-i I Л‘П п1 Т КП—1; п кп 1,п
или:
m _ П 1 П П-1 П оо
п1 п. п1 kni, п 1 п, п—1 п; n-i 1 п 1
Если разрезать неразрезную балку над опорой п и приложить в месте разреза
два равнопротивоположных момента единица, то шов над этой опорой раскроется на угол, равный выражению, стоящему в знаменателе формулы 32. Таким образом, эта формула показывает, что mn, п является значением ьзгибающего момента на опоре п, возникающего от действия вынужденного угла перелома 0Л 1 оси неразрезной балки на этой опоре.
Для неразрезной балки фиг. 150, а показана на фиг. 150,6 эпюра моментов,
соответствующая перелому оси на опоре 3 по фиг. 150,я.
Изгибающий момент Ма в пролете Zn-i,rt равен: Ма М—j Хп_х — у Хп, поэтому
линию влияния от действия фиктивных грузов для разности моментов Ма — М можно построить при помощи известного перекрестного построения, как это показано на фиг. 150, г.
Определение величины изгибаюшего момента Мп на опоре п может быть выполнено при помощи чисел влияния В виду прямолинейности участков линий
влияния от действия фиктивных грузов, фиктивные грузы для каждого пролета 1п, п1 неразрезной балки могут быть заменены фиктивными опорными давлениями Сп п1 И П1 п
Применяя обозначение для суммы фиктивных давлений п-й опоры
П-1 nij 34
величину изгибающего момента на опоре п при наличии нагрузок во всех пролетах неразрезной балки можно выразить так:
Мп nhPk 71 лп Т, С n-i 7 т С Л_2 —. —
L Kn—i,n КП—2П—1КП—1П
— 7 Сп1 7 7 П2 7 7 7 Сп3 Ь 1 З1
П 1 п П1, П 122 П1 1, П2 П13. П2 J
Если нужно найти эпюру моментов неразрезной балки при вполне определенном ее загружении, то, конечно, проще воспользоваться формулами типа 35, не строя линий влияния от фиктивных грузов. Если же нужно найти невыгоднейшее загружение неразрезной балки подвижной нагрузкой, то такие линии влияния могут оказаться весьма полезными. Определив при помоши прямолинейных линий влияния границы опасного загружения балки фиктивными грузами, нетрудно затем пересчитать их и определить границы опасного загружения балки действительными грузами. Пусть границей фиктивного загружения является фокус Fn, n-1. Положению фиктивного
груза Zn-i,n наД этим фокусом соответствует отношение между фиктивными опорными реакциями:
Сщ n-ie n-i Cn-i9 п к
Если балка постоянного сечения, то грузу Р, находящемуся на расстоянии а от опоры — 1 и на расстоянии Ъ от опоры п соответствуют значения:
п РаЪ 7 Pab, N
Cn-ii п — — -qJ- 2Z —а
п РаЪ
ьm n-i 1 г а.
1 Эта формула впервые дана в работе проф. М. М. Филоненко - Бородич, Общее решение системы основных уравнений трех моментов для неразрезной балки постоянного поперечного сечения, Москва, 1921. См. также проф. М. М. Ф и л о н е н к оБородич, Основы теории работы упругих сил, 1932, глава X.
228
Подставив эти значения в к, получим следующее выражение для а и Ь расстояний от опор пролета нулевой точки линии влияния от действительных грузов, являющейся границей опасного загружения:
откуда
I л — ся, п—1 я
а 2п п-1 1. I
Ъ -J- 1 п-1; п
кп П—1 А
т, 2 п, п—1 у
ПГТ пь п-
Лп П-1 Г А
1
Нам представляется, что применение инфлюентных линий от фиктивных гнагрузок может оказаться небесполезным при расчете сложных рамных систем, но здесь мы не имеем возможности развивать эту идею.
f. О 1
4алинвлм-г;:J Оп7 фикт.грузов
б и 2 - линии влияния от фиктивных грузов
в и д - линии влияния от действитепьных грузов
Фиг, 150.
3. Расчет устойчивой прочности сжато-изогнутых неразрезных балок
Зависимости графоаналитического метода:
m
229
остаются справедливыми также и для задач устойчивой прочности. Формулы ш верны независимо от природы происхождения момента М, ясно только, что в задачах устойчивой прочности:
М M Nv
4 EJ
EJ
m
Поэтому весьма многое из вышесказанного о графоаналитическом способе расчета прочности неразрезных балок вполне применимо также и к расчету их устойчивой прочности.
Для сжато-изогнутой балки постоянного сечения величины углов фиг. 151 Ли В имеют следующие значения:
А
I
3 EJ I
JL v EJ
I
I tgv — V
- J 6EJ Sy EJ
v2tgv v— sinv v2sinv
j
36
Dab-ABat
Фиг. 151.
ab
Dab Фиг. 152.
При загружении пролета балкиравномерно распределенной нагрузкой q по всей его длине и рядом сосредоточенных грузов Рг, Р2величины С фиг. 152 равны:
37
Для нанесения на схеме неразрезной балки единичных вертикалей—вертикалей действия единичных фиктивных грузов а HDja численно равных сумме углов A -f Ваъ для каждого ее пролета нам нужно знать отношение см. фиг. 151
Ъ В В I D А В
Для краткости записи мы будем обозначать это отношение буквой Я. Для обеих единичных вертикалей пролета 1аъ оно равно
Г Д772
На фиг. 153 приводится график зависимости величины Я, от v J Пунктиром
1 1 на этом графике дано отношение для значений Я 1. При v 0 величина Я и
единичные вертикали пролета taj, и tba делят его тогда на три равных отреэка они становятся третными вертикалями.
По мере роста величины v обе единичных вертикали пролета сближаются, при v они сливаются в одну вертикаль, проходящую через середину пролета. При дальнейшем росте v левая единичная вертикаль перемещается на правую половину пролета, а правая на левую. При v 4,4934 т. е. при v tgv Я 1 и единичные вертикали пролета проходят: левая через его правую опору, а правая через левую. При дальнейшем увеличении v единичные вертикали выходят за пределы пролета Я1.
230
Графическое построение фокусов сжато-изогнутой неразрезной балки выполняется совершенно аналогично тому, как показано на фиг. 14Э, г. Аналитическое определение левых и правых фокусных отношений может быть выполнено по формулам 31 и ЗГ. Главные числа влияния тпп могут быть вычислены по формуле 33, а побочные mni по формулам, аналогичным f. При определении неизвестных опорных моментов Мп незачем каждый раз для каждого момента пользоваться формулой 35. Достаточно по этой формуле найти один из крайних неизвестных опорных моментов; например, для балки фиг. 150 достаточно найти М4 или Мг, а потом остальные моменты найти последовательно по цепной зависимости уравнений трех моментов 30. Зная Мь и М4, находим М3; зная ikf4 и М3, находим М2 и т. д., пока не получим в качестве контроля точности расчета вновь уже ранее известное значение момента на крайней опоре. Этим мы избежим при определении моментов Мп излишнего суммирования многих слагаемых, требующегося по формуле 35. При графическом расчете все неизвестные опорные моменты, кроме одного, можно определить при помощи построения веревочного многоугольника для шарнирной цепи, загруженной фиктивными грузами, при этом ординаты веревочного многоугольника на промежуточных опорных вертикалях балки должны равняться нулю.
Найдя, таким образом, на плане сил неизвестные фиктивные силы, легко определяем затем все опорные моменты1.
4. Расчет устойчивости сжатых не раз резных балок
Потеря устойчивости неразрезной балки соответствует таким значениям v, при которых достаточно наличия самой ничтожной поперечной нагрузки, чтобы нарушить равновесие шарнирной цепи. Иначе говоря, устойчивость теряется, когда все коэфициенты при всех неизвестных Хх, Х2, Х8, в уравнении d обращаются в нули. Это получается тогда, когда знаменатели выражений 33 обращаются в нули:
Bab 0аЪ Ъа О —
39
Геометрический смысл уравнения 39 состоит в том, что во всех пролетах неразрезной балки в критическом ее состоянии правые и левые фокусы Faj, и Fj,a совпадают.
Действительно, равенство каЪ — — обозначает, что оба фокуса Fab и Fba делят пролет 1аЪ
kba
на левый и правый участки в одном и том же отношении, иначе говоря, сливаются в одну точку.
Критическое условие можно сформулировать еще так:
Если можно построить такое виртуальное перемещение шарнирной цепи, на котором работа всех неизвестных Х19 Хп
о б р а ща ется в нуль, то неразрезная балка находится в критическом состоянии. Действительно, в этом случае равновесие шарнирной цепи может сохраниться только случайно, при специальном подборе известных фиктивных грузов.
Впрочем надо оговориться, что наше толкование критерия 39 справедливо только в том случае, если Ваь не обращается в бесконечность, как это имеет место см. 36 при v it.
При значении v те единичные давления А, В и величина единичного фиктивного
I 1 V
груза D А-В gj— 2” обращаются в оо, и оба приведенных выше графических
У словия критического состояния для этого случая теряют смысл.
Применим вышеизложенную методику для расчета устойчивости неразрезной балки с пятью равными прилетами и с заделанными концами фиг. 154, а. В этом случае вследствие равенства пролетов и отсутствия промежуточных продольных нагрузок вели
чины v
N12
EJ
и D Л-f В для всех пролетов будутодинаковы. Величины Л, опре-
1 См. аналогичные построения в 46 стр. 386 книги: И. М. Р а б ин о в и ч, Кинематический метод в строительной механике, изд. МВТУ, Москва, 1928.
Возможны также и другие построения, в том числе построение, предложенное автором. См. проф. А. А. У м а н с к и й, Специальный курс строительной механики, ч. 1, стр. 162, ОНТИ, 1935.
231
деляемые по формуле 38 или по графику фиг. 153 в зависимости от значений v, также во всех пролетах будут равны друг другу. Поэтому единичные вертикали tab и tba во всех пролетах должны расположиться одинаково фиг. 154, Ъ.
Учитывая условия закрепления концов балки, мы заключаем, что ур должно быть
больше ъ. Прймем сначала v 3,30, для него значение Я 0,5275 см. также
график фиг. 153. Приступим теперь к построению линии виртуальных прогибов для шарнирной цепи, выбирая последовательно перемещения ее эвеньев так, чтобы обращались в нули коэфициенш при Хх, Х2 Х8,. в уравнении d работы фиктивных грузов. На первое звено шарнирной цепи действуют два фиктивных груза: DXx на вертикали t12 и JDX2 на вертикали t21, на второе 8вено—грузы 10Х2 на вертикали 23и DXZ на вертикали tz2 и т. д. Прямую 1—2 проведем через нулевую точку на вертикали tlZf
а
V2J
А -
Докрити-
ческое
сестояние
Уе0
V 3,30 0,5275
В 3,815
1
2
3
‘1
h
А
А
— 1 —
SjS — —
—
— L
ч
f
Hpurfiu
веское
состояние
ув-
V 3,42 А 0,551 d-P5-k
U J
Фиг. 154.
чтобы обратить в нуль работу груза DXr. Но при этом фиктивный груз DX2 навертикали i21 получает перемещение вверх. Нужно, чтобы равный ему фиктивный грузDX на вертикали t2z получил такое же перемещение у2, но только вниз, тогда неизвестное Х2 не войдет в уравнение работы цепи на виртуальном ее перемещении. Итак, прямую 2—3 проводим через нижний конец отрезка y2i отложенного на вертикали t2z. Эта прямая отсечет снизу на вертикали tz2 отрезок yz; отложив такой же отрезэк сверху на вертикали г34, проводим через его вершину и точку 3 прямую 3—4. Продолжая построение аналогичным образом, дойдем до прямой 5—6, изображающей эпюру вертикальных прогибов последнего звена шарнирной цепи. Полученная ломаная 1—2 — 3—4—5—6 в некотором масштабе будет представлять собой линию влиянияот фиктивных грузов для последней неизвестной XQi причем см. d:
DXtijb 5Я7.
У нас, при v 3,30 отрезок у9 на вертикали te5 получился отличным от нуля, эначит vcp Ф 3,30. При этом мы получаем из чертежа, что отношение ординат
4-1,48.
Уз
OQO
Сделаем вторую попытку. Построим линию влияния от фиктивных грузов для Х3 при значении v 3,50. В этом случае Л 0,568. Выполнив аналогично пре
дыдущему все построения их выполнение занимает меньше времени, чем их описание,
мы в результате получим отношение — — 0,6. Очевидно, что критическое отношена
ние аас 0 должно соответствовать значению v, большему 3,30 и меньшему 3,50.
2а
При третьей попытке v 3,40, получаем —0,3. Наконец, при v 3,42 получаем
У 2
ув о. Таким образом, 3,42. Ясно, при нашем построении нулевые точки эпюр виртуальных прогибов шарнирной цепи являются левыми фокусами неразрезной балки. На фиг. 154 мы привели эпюры виртуальных прогибов шарнирной цепи только для значений v 3,30 и vp 3,42. Последняя получилась совершенно симметричной. Это вполне понятно, так как только при этом условии левые фокусы сольются с правыми.
Графический расчет устойчивости неразрезных балок выполняется довольно быстро, но степень его точности ограничивается степенью точности графических построений.
В заключение, давая оценку графоаналитическому методу, мы можем сказать, что он представляет интерес для расчета устойчивой прочности неразрезных балок, особенно в том случае, когда нужно рассчитать несколько вариантов поперечного загружения при одной и той же продольной нагрузке. В основном же метод интересен больше с теоретической, чем с практической стороны, как геометрическая ; интерпретация аналитического решения.
Особый интерес представляют линии влияния от фиктивных грузов.
6. Ограничения, накладываемые на решение выбором
метода расчета
При выборе метода расчета мы для упрощения последнего стремимся максимально сократить количество неизвестных. При этом может случиться, что из рассмотрения выпадут величины, характеризующие ту или иную форму потери устойчивости
Поясним это на примерах. Пусть дана симметричная двухшарнирная рама фиг. 155, а, составленная из двух стержней; она симметрично загружена силой, приложенной в ее коньке.
В этом случае оба стержня рамы одинаково напряжены, задача расчета устойчивости этой рамы эквивалентна задаче расчета двухпролетной неразрезной балки фиг. 155, б. Опасной форме потери устойчивости этих систем соответствует выпучивание каждого стержня по полуволне синусоиды при значении изгибающего момента в узле 1, равном нулю:
Мг 0.
Если бы мы при расчете устойчивости этих систем выбрали балочный метод с неизвестной М1у то мы тем самым исключили бы из рассмотрения наиболее опасную форму потери устойчивости. Действительно, составив уравнение трех моментов см. гл. VI, уравнение 16 для этого
.0 , 2
4,- -4-
h I I Фиг. 155.
Более точный аналитический расчет дает для этого случая 3,43. Вообще говоря, для неразрезной балки по типу фиг. 154 с п равными пролетами и с защемленными концами при п3 критическое усилие достаточно точно можно определить по приближен-
тсЧ EJ
19,883—10,014 cos - J ,
233
случая, получим:
2 MX1 10 t12 О
или
471 0, а
где t 1 —г —функция Жуковского, обращающаяся в нуль при значениях v 4,4934; 7,7252; 10,9041 и т. д. Итак, из рассмотрения при использовании балочного метода для этой задачи выпало наименьшее критическое значение v tc 3,1416.
Легко видеть, что значению v 4,4934 соответствует форма потери устойчивости, показанная на фиг. 156, когда каждый стержень теряет устойчивость как балка с одним шарнирным, а другим защемленным концом фиг. 156, б при значении угла поворота конька рамы cpi 0.
6J 0 1 2
Чтобы не потерять наименьшего критического значения v, нам нужно при исследовании уравнения а разобрать не только случай, когда множитель 0, но и другой случай, когда множитель Мг0. Иначе говоря, нам нужно обратиться кроме балочного метода еще к другому методу, дающему выражение для Мх. Пользуясь для этой цели формулой 8 гл. VII для стержня с шарниром на одном конце, мы получаем:
Мх 10шр 1 0. Ь
Если мы допустим в Ь, что ср5 0, мы придем к значениям vp 4,4934; 7,7252;., рассмотренным выше.
Полагая в Ь, что pj Ф 0, мы тем самым приравниваем нулю
— V2 tg V а,—5— 0.
t g V — V
Легко видеть, что этот коэфициент обращается в нуль при значениях v тг; 2тг; Зтс; 4тс;. Сочетая эти знечения v с ранее полученными v 4,4934; 7,7252;., мы охватим критические значения v для всех возможных форм потери устойчивости нашей системы в ее плоскости.
Сделаем общее заключение. Выбирая ту или другую систему неизвестных для расчета, мы устраняем тем самым из рассмотрения формы потери устойчивости, возможные при значениях этих неизвестных, равных нулю. Применяя для расчета метод деформаций, мы можем устранить из рассмотрения высшие формы потери устойчивости. Действительно превращение в нуль тех или иных деформаций соответствуют ожествлекию системы и, следовательно, повышению ее устойчивости. Поэтому, пользуясь методом деформаций, мы можем быть спокойными, что не упустим из рассмотрения наиболее опасной формы потери устойчивости. Применяя другие методы особенно при использовании балочного метода, нужно проявлять некоторую осторожность, чтобы не встретиться с исключительным случаем, при котором выпадет из рассмотрения наиболее опасная форма потери устойчивости.
234
ГЛАВА X
УЧЕТ ДЕФОРМАЦИЙ СДВИГА И ОБЖАТИЯ
С
1. Уточнение выражения критического усилия призматического стержня при различных закреплениях его концов
При нашем анализе мы будем пользоваться формулами 21 гл. III. Уточним выражение критической силы для стержня фиг. 157, а с шарнирным закреплением концов. В этом случае из условий опирания следует; il0 ij 0; Q0 Qt 0; 1о иг 0.
У
V s
0
1
N
Фиг. 157.
Пользуясь формулой метода начальных параметров 199 гл. III, получаем уравнение изогнутой оси стержня:
v7Vo
X
sm-. Li
а
Здесь величины с и Lx определяются формулами 195 и 196 гл. III:
Ь
,. n тг cmj
с 1-oF1 и
Приравнивая в а х 1г — обжатой длине стержня:
i
С
а прогиб на правом конце стержня vix 0, находим:
sin 4- О.
d
Для того чтобы cpf могло отличаться от нуля, нужно, чтобы
sin ф 0, или
е
где 1; 2; 3;. —любому целому числу. Подставив в е вместо 1Х и Lx их значения по формулам с и Ь, а вместо 1, получим наименьшее значение критического усилия NKp в результате следующих преобразований:
h V г21-Ю2лг V LXJ cEJ
I2 1 — 2е c2EJ
N
N12
А72
с21 -f- 2s EJ Nl2
EJ 0 - sk 0 - E1 -Kw,-w
или
1
V.CF, EFJ
N12 2
235
откуда
NKp— 12 12
7Б JfEJ GF EF
Подставляя в 1 вместо -т:, получаем критическое усилие для
1
сжатого стержня с шарнирно закрепленными концами:
NKp —Ji I 2 n2EJ GF WF
Используя обозначения приведенной площади сечения на сдвиг
F J I
Fx радиуса инерции г у , гибкости стержня Х —и эйлеровой
дГ те2Е ГЧ
величины силы уу9 — , в результате получаем вместо 2:
Легко видеть, что для стержней сплошного сечения знаменатель 2
может без заметной погрешности быть приравненным единице. Действи-
Е
тельно, пусть, например, 2,5, для двутаврового сечения к2,
ч 40, тогда Лгхр 0,982 ЛГд, при Х 100 величина NKp 0,997 Nd. Иначе получается для составных рамных или решетчатых стержней. Для таких стержней можно пренебрегать равномерным обжатием оси стержня, но необходимо сохранять член, зависящий от деформаций сдвига оси:
Nkp JL Q-1 2
rEJ Т
Здесь обозначено через YQ1‘ — у т е угол сдвига оси
стержня при значении поперечной силы Q 1.
В составных стержнях деформация сдвига не получается плавной, поэтому вместо приходится брать среднее его значение, относящееся к одной панели составного стержня.
Так сделал С. П. Тимошенко в своих работах, относящихся к продольному изгибу составных стержней1.
Для консольного стержня фиг. 157, б: v0 0; ср 0; Мгг 0; Q0 Qtl 0. Пользуясь формулой 201 гл. III, получаем:
тмчюи™ёг0-
I те
Отсюда у1- — , и минимальное значение критической силы в соот-
ветствии с 1 получается:
Nkp 42 I 2 1 См. статью Тимошенко С. П. в Известиях Киевского политехнического института 1908 г. См. также его же Сопротивление материалов, часть II, ОНТИ, 1934 г. 42.
236
Для стержня с двумя защемленными концами фиг. 157, в точно так же находим
NP Т 2 krfEJ GF1EF
Для стержня с одним защемленным и другим шарнирным концом фиг. 157, г задача решается несколько сложней. В этом случае и0 0 Mh 0; 0 г 0.
Пользуясь уравнением 201 гл. III, получаем:
Г 1 h. 1 I 1 л
GF1sint B7Sin t J Г oe--0.
Кроме того, из условий равновесия следует:
м0 — А-
Сочетая эти два уравнения, получаем критическое условие в следующем виде:
. EJ 1 N. h 1г 1г
С1 GFt L L, Lx 00 Lx
или, после использования обозначений b:
T-tg т- с.
1 Х1
Это уравнение1 удобней всего решать, применяя метод последовательных приближений. Для первого приближения можно взять с2 1, для
этого случая 4,4934 20,19 и:
кр,I
J2 , 1 2
Г 77 20,2 EJ GF1 EF
Пользуясь этим значением 7VKp, находим уточненное численное
значение:
кр, I
1 CF1
и подставляем его вместо с2 в уравнение 5. Решив это уравнение, находим уточненное значение Ц-, после чего определяем NKp по формуле 1.
В случае надобности, повторяя этот процесс последовательных приближений, можем получить NKp с любой степенью точности.
2. Формулы метода деформаций с учетом деформаций сдвига
Преобразуем формулы 204 — 206, полученные нами в 21 гл. III; их следует переделать, исключив в них величину Q0 из правой части уравнений и перейдя к обозначениям 4 гл. V. Формула 206 после этого получит вид:
Qab 7 У.аЬ К РЬ К D ГаЬЬъ1 У-abQab- 6
Величины а, р, у в этой формуле и последующих представляют
собой функции аргумента:
L 11 — г 1—е v Р_Ч
Vi -r —- v— 7
Lx Lc w
1 Заменяя с2 его значением и применяя обозначение vx А-, уравнению 5 можно придать вид:
Vl 1
tgv1 1 GFth I1
237
Коэфициент имеет значение:
Хл,
8
аь l 4ia Pab
где т — отвлеченная величина, характеризующая соотношение жесткостей изгиба и сдвига:
. С EJ - iab -Л Я
Vab—GFJJabiGFJU V v2 Jab G А2 Jab К Вводя еще одно обозначение:
а2ТГХ а Р2Ц, можем формулам 204 и 205 придать вид:
” --ой
р-;цг-рц1
2TOab1at МаЪ
Ю
N
а
а,-
ГГ11 и и Г11111111111II11111 гт
И
В формулах 6 и 11 величины О at и
нн
Маъ зависят от пролетных нагрузок стержня и исчезают при их отсутствии. Эти величины для случая загрузки стержня равномерно распределенной нагрузкой q и рядом сосредоточенных грузов Pl9 Р2,. фиг. 158 определяются так.
Сначала вычисляем величины:
Vl Ьп
Фиг. 158.
n1, 2,.
vlbn.
4111 - - -
К I I я1 Г _L 1—-cosv
I VjC2 N_ 1 J n 1,2,.
Затем находим:
12
2 i.
Qab a P Afa — ус2АЦаЬ;
Mab — 2iab a W C2Aiab — ba5
Mab Mab 2Qab lal,
В случае, если продольное усилие стержня Nab — 0, то:
с 1; vt v; a 2; р 1; у 6;
13
l12i
и формулы И и 6 получают вид:
2iab
:
щ
1121
Л
2 6ч 1 - 6ч - Зфаь Л;
6L
1 12
Qab га6 i 12ij
В этих формулах:
М”ьН - 2 6 С1 8ri rlJ 1 6ч - 1 8nff -
1Т21 Г2 471 3072 ;
Qab 2 12Ч 3-2г ql т 64.
14
15
16
17
n 1, 2,.
238
3. Примеры расчета устойчивости рам с учетом деформаций сдвига
Мы будем предполагать, что деформации сдвига и изгиба узловых фасонок рамы ничтожны по сравнению с деформациями соединяемых ими стержней. Иначе говоря, мы будем предполагать, что углы поворота касательных к концам стержней, сходящихся в одном узле а фиг. 159, могут быть разными:
18
но что углы поворота поперечных сечений по концам стержней жесткого узла должны быть одинаковы:
ab ас
Л — pF pF
tad тае а
19
При таком предположении методика расчета рам, разработанная в главах IV — IX, в основном не потребует изменений. В качестве неизвестных при расчете рамы по методу деформаций мы попрежнему будем принимать углы поворота узлов и углы поворота стержней ф.
Фиг. 159.
Пример 1. При расчете рамы фиг. 160 на антисимметричную форму потери устойчивости мы заключаем, что Q0i Qoi 0- В этом случае деформации сдвига в стойках вообще отсутствуют и формулы 204 — 206 гл. III вырождаются в обычные формулы метода деформаций. Иначе говоря, сдвиг в стойках для этой задачи учитывать не нужно. Продольное усилие ригеля равно нулю, поэтому для рлгеля можно использовать формулу 14. Пусть, например, дано, что сечение ригеля двутавровое, причем
F
k jr— 2. а гибкость ригеля А 50. Тогда по формулам 9 и 14 находим:
_Е к г 2 1 G 502 М1Х, 2Ц 1,965 р 0,964 - 2,929 фаЬ.
a
b
t
О
ТО
Lh
O
Фиг. 160.
Если бы мы не учитывали деформаций сдвига оси ригеля, то:
Mu, 22f-3. Ь
Сравнивая формулы Ь и Ь видим, что учет деформаций сдвига не вносит в
результаты расчета нашей рамы сколько-нибудь ощутительной разницы.
Точно так же учет обжатия стоек для этой рамы не имеет смысла, так как обе стойки обжимаются одинаково.
Пример 2. Рассчитать на устойчивость раму фиг. 161. Учесть, что колонны рамы составные на планках.
Прежде всего нужно определить величину rh см. 9 и 2.
fEJ 1 Л __EJ Qi
г2 GFjab V г2 Т Jab
с
Для составного стержня с планками фиг. 162 С. П. Тимошенко принимает 1
аЪ
TQ-
о
г
12EJb ‘ 24 EJC‘
d
1 См. сноску к 1.
39
Таким образом:
J а 25 а 7li I 24 ТЬ Те‘
20
Пусть дано: J 20 ООО см, 600 сл, а 60 см. 5 30 еле, 1 300 еле, Jr 260 еле4; тогда: 0,0385.
Ригель сплоппюго сечения; пусть для него как в примере 1 дано 177 0,002. Переходим к расчету устойчивости рамы фиг. 161. Наиболее опасной формой
потери устойчивости рамы будет симметричная: yf — yf,. Задача сводится к составлению одного уравнения с неизвестной величиной углы поворота всех стержней равны нулю:
Мп, 2, 1,965 f- 0,964 f,
Mlt 2j 1,965 f,
I M10 2a — C1Bf3,
2f -2,966п а-Ы 0.
M
сз
777777777777У
—ь
Фиг. 162
Фиг. 163.
Фиг. 164.
Таким образом, критическое условие устойчивости для нашей рамы:
n L Ом.
ih 2,966
Для определения.величины воспользуемся формулами 8 и 10:
1 1 1 10 1 4чя — Рю 1 4 0,0385 а р10 1 0,154 лр10
t -r9wj-Rvn 0,077gPfB. i Vя -т- Р Л-1 0,154аР1в1,30 2а Р1О
V
Здесь а и 3 функция величины — t где с определяется формулой 9
С
С jl — 1V2.
е
О
21
Удобнее выразить зависимость между v и несколько иначе. Подставив в 21
вместо с —, после преобразований получим:
v2
1VV
21
240
Для колонн рамы фиг. 161:
v2
V2,
l 0,0385vf
g
Давая величине последовательные значения: 2; 4; 5; 6; 2те, по табл. 1 приложения находим соответствующие значения х10 и а-ЬЭю- Затем по формуле f находим 10 и по формуле е величину п. По формуле g вычисляем 2, после чего определяем критическое значение груза Р:
PkPy2EJ
Данные этих вычислений сведены в табл. 24.
Таблица 24
Vl
2
4
5
6
2 те
a
1,718
0,5865
—0,9544
—10,319
—оо
a -f- 3
2,794
2,0884
1,4379
0,4083
0
1,135
0,797
0,495
0,079
0
h
—0,197
0,0708
0,489
3,50
оо
V2
3,47
9,90
12,73
15,10
15,67
Если бы мы не учитывали деформаций сдвига, то критерий е принял бы вид: п —и между v и п установилась бы зависимость, приведенная в табл. 25.
О
Таблица 25
7
4,493
5
5,5
5,75
6
2 те
Т1
0
0,318
0,945
1,635
3,440
оо
v2
20,19
25
30,25
33,06
36
39,5
Достаточно взглянуть на табл. 24 и 25, чтобы увидеть, как сильно падает критическая нагрузка рамы фиг. 161 при замене сплошных колонн составными на планках.
При расчете составных колонн со стержневой решеткой фиг. 163, следуя вышецитированной работе С. П. Тимошенко, величину принимаем но формуле:
EFd cos2 A sin А
h
а величину ун:
Чй-
12 F cos2 А sin А
22
При плохой центрации решетки эта формула может дать завышенные значения критического усилия.
4. Расчет рам с учетом продольных деформаций их стержней
При самой общей постановке этого вопроса получаются большие усложнения. При расчете рамы по методу деформаций число неизвестных в этом случае равно утроенному числу узлов. Каждому узлу а соответствуют три неизвестных перемещения: вертикальное иа, горизонтальное иа и угловое ра. Для узла 1 рамы фиг. 164, а надо составить
16 Прочность и устойчивость стержневых систем
241
в соответствии с этим три уравнения:
Nu 12 Ql Ф
Ql2 QlO 14 а
м10 - М12 4 0.
В эти уравнения мы должны подставить:
МаЬ 2iab Къа PafrTb — аЬ Ы Мл Ь
а —77- а РаЬ а Тб YabW Q. с
NabEff Uab- d
lab
Величины Jd и А 1аЪ мы без труда выражаем через горизонтальные иа и вертикальные va перемещения узлов рамы, например:
ф — И — Ц3Ц4. И, 3-2. е
Т01— 7 Т 34— I Т23— 7 ь Vе
01 34 123
AZoi — V, А34 У4 — Vl А23 Uz — U2. f
Таким образом, для рамы фиг. 164 в общем случае надо составить
3 412 уравнений с 12 неизвестными.
Число неизвестных значительно сократится в случае симметрии конструкции и нагрузок рамы. В соответствии с указаниями 8 гл. V в этом случае мы можем решать отдельно две задачи: симметричную и антисимметричную. При расчете устойчивости рамы фиг. 164, а можно ограничиться рассмотрением одной, более опасной формы деформации, а именно — антисимметричной. При этом1:
b4Bi; и3 и2; и,; и3 — v2;
4 i5 ¥; 45 10 12 4S0-
Равенство нулю поперечных сил на стойках сразу позволяет нам исключить из рассмотрения горизонтальные перемещения узлов рамы и пользоваться для стоек формулой:
Маъ iab tgOab Gin0abb
Таким образом, задача вместо 12 сводится к составлению четырех уравнений с четырьмя неизвестными: Pi р2 ui, Уравнение для рх:
12 tgv1 sinv2
М 1о ih
Мц 2i,29l срх - 3 -З-р.
2г 60 шг; С1- Ui g
Для р2 аналогично составляем:
sib г,бг0 ¥Ь-. h
Уравнение для vx и v2 составим так см. фиг. 164, г.
Поперечные силы ригелей равны разностям приращений продольных усилий стоек, возникающих при потере устойчивости рамы:
Qu ANlt-AN; , ДЛГИ. i
1 Симметричные составляющие вертикальных перемещений узлов, вызываемые обжатием стоек нагрузками Р, здесь нами не рассматриваются; их учет относится к симметричной задаче.
242
Применяя обозначение для погонной продольной жесткости, стержня fab
17. С23
1аЪ
и учитывая, что для нашей рамы 10 12 , мы можем записать для AN10 и ANlt следующие выражения:
AN к, о; ANlt AN21 fva—ej. k
Подставляя в i вместо и AiV их выражения, получаем:
-.1.-2J
Эти уравнения легко решаются относительно рх и
i - т 0 Шг v 1
Р1 ш,0”С5 1, v J
Но мы изберем другой путь, решим их относительно и г3:
2-Ь4 д 1— Л2 64 4 I v
- _ Л1 2 2Л2 т
42 6Л 4 J
Здесь для краткости записи принято обозначение:
1211. л. L. ib 24
12г YlJxh nFlh 12 Fbh где ч - —гибкость ригеля рамы Легко видеть, что коэфициент А, вообще
говоря, представляет большое число1, порядка около 100—1000. В связи
с этим формулы т можно переписать приближенно так:
.;
11 г т — х1 22-
Считая углы поворота узлов рх и ср2 величинами малыми, видим из
у 2
формул т, что величины и у можно считать как бы величинами
второго порядка малости. Отбрасывая их в уравнениях g и h, приходим к уравнениям обычного типа, соответствующим расчету рам без учета величины продольных деформаций обжатия стержней рамы.
Из вышесказанного нетрудно сделать вывод, что при расчете устойчивости и устойчивой прочностирам с небольшим числом этажей и с ригелями обычной гибкости вполне допустимо и целесообразно пренебрегать продольными деформациями стержней по сравнению с деформациями их изгиба. Только в случае большого числа этажей или повышенной жесткости ригелей учет продольных деформаций стержней может оказать заметное влияние на результаты расчета. Этот вопрос мы разберем подробней в следующем параграфе см. конец 5.
1 Сказанное не относится к рамному стержню, у которого ригелями являются планки. Гибкость А планок невелика и поэтому величина А для рамного стержня не может быть
большим числом.
16 24Х
5. Расчет устойчивости рамного стержня
Р
т
77
1, Расчет устойчивости т-этажной рамы фиг. 1651, с учетом как
изгибньгх, так и продольных деформаций стержней
Погонные жесткости изгиба стоек равны ih, промежуточных ригелей
1
il nifl9 верхнего ригеля гг у Погонные продольные жесткости всех
стоек равны.
Более опасной формой потери устойчивости в данном случае будет антисимметричная форма.
В соответствии с примером 4 легко видеть, что в качестве неизвестных здесь можно избрать т углов поворота: р19 ср2, т и т вертикальных перемещений узлов: v19 v2f
Ввиду монотонности конструкции число неизвестных не играет роли — задача может быть решена в разностных уравнениях, причем результативные формулы можно будет применить для любого числа этажей т.
Совершенно аналогично задаче 4 уравнения g и Г для узла к нашей рамы мы можем составить два следующих уравнения 2:
к1
и-1
гг
1
2 I
1
-с
ч
II
г
гЛ
-с
1
0 1
к1
Kt,
— I
—
Slfl V
-Vk — Vk
7T Vk 0
f — ”c-l - i — ”
6VTc -2 b
После некоторых преобразований приводим эти уравнения к виду:
12п sin v
Т
Т
Фиг. 165. где попрежнему:
— Та-1 2 cos V-j-Зл фк1
к у - - 2 vk.
v 0,
a
b
А
12 ц ‘
С
Для верхнего узла m точно так же получим:
,. о sin v ,6п sin v
9m-1 cos v 3г —J m J V w
Pm у 2m-l - 2 Для нижнего узла:
v0 0; cp0 0.
0;
a
fl
d
1 Изображенная на фиг. 165 рама соответствует половине рамного стержня. Ось
0—0 рассматривается как ось симметрии деформации стержня при потере устойчивости.
2 При расчете реального составного стержня на планках нужно учитывать также сокращение планками длины элементов поясов, характер прикрепления планок, их жесткость на сдвиг и т. д.
244
Нетрудно видеть, что уравнения а и Ь совпадут с а и Ь, если условно принять:
И
m-i mi 9т-1 Tmi
хотя узла т 1 и нет в нашей раме.
Итак, нам нужно найти такие выражения для рк и vk, которые удовлетворяли бы уравнениям а и Ь для промежуточных узлов рамы и граничным условиям d д е. Выполним это следующим образом. Исключив с помощью Ь углы поворота узлов р из уравнения а, найдем:
2Dvk — 2В tti уа-2 улг — 0. 0
Здесь для сокращения записи приняты обозначения:
r А 1. , о sin v
В —-А—- cos v 3п ;
А 1 v
D 1 -j- 2 —”— COS V 072, e
Уравнение f — однородное линейное разностное уравнение четвертого порядка с постоянными симметричными коэфициентамц. Частные решения для vk будем искать в форме sin Q и cos0. При этом имеют место следующие зависимости табл. 26.
Таблица 26
Vk
sin 0
cosfc 0
Vk
Vk-i ус1
2 sin Л 0 cos 0
2 cos 0 cos 0
2vk cos 0
2 sin к 0 cos 20
2 cos 0 cos 20
cos 0
Таким образом:
vk-i Wfc1 2vk cos 6; vk-2 vkt 2 u cos 0.
h
Подставляя h в f, получим:
vk D — 2В cos 0 cos 20 0.
Заменяя здесь cos20 2 cos20 — 1, запишем характеристическое уравнение в следующем виде:
2 cos 02 — 2В 2 cos О 2D — 2 О,
i
откуда
cos 01 -1 В —2D 2; cos 02 1Я_В1 —2D 2.
Ь
Таким образом, уравнение f имеет следующее решение: vk С sin С2 sin Лб2 Cz cos kbx -f- CA cos 02.
Подставляя это выражение в b, для рк находим:
рк — 2 —1 Ус - cos 0 Сх sin 0X Сд cos А0Х cos 02 С2 sin А02 С4 cos 04.
1
ш
246
Удовлетворяя граничным условиям d и е, получаем:
С8 Ct — 0; п1
совесовбО; п2
С г cos тбх — Сг sin mOJ sin 0Х С2 cos тВ2 — С4 sin тВ2 sin д2 0; п3
Ci cos mGi — Съ sin тЬ sin 0Х cos 0Х С2 cos тб2 —
— С4 sin тд2 sin 02 cos 02 0. п4
Из рассмотрения условий пх и п2 заключаем, что могут быть два случая:
1-й случай: С3 С4 0;
2-й случай: cos 02 — cos 0Х 0.
Обратимся сначала к 1-му случаю. Критическое условие из п8 и п4 при этом будет:
Д cos тд1 sin 0Х cos m02 sin 02 cos 02 — cos т 0Х sin Oj cos 0 x
x cos m02 sin 02 0
пли, после выноса за скобки общих множителей:
Д cos т 0Х cos т 02 sin 0г sin 02 cos 02 — cos 0Х 0. о
Во втором случае мы заранее задаем критическое условие:
cos 02 — cos 0Х 0. р
Это предположение не противоречит уравнениям п3 и п4, так как р входит в качестве множителя в детерминант о. Таким образом, все возможные для данной задачи формы потери устойчивости охватываются критическим условием о.
Проанализируем его. Первый множитель cosmOx обращается в нуль, если:
тб1 2 1 у,
где любое целое число: 0; 1; 2; 3;.
Второй множитель обращается в нуль, если:
7П02 2р 1 у.
В обоих этих случаях критическое значение cos 6:
cos 0 cos. г 2 т v
Третий множитель sin обращается в нуль при вх тг, четвертый — при 02 ж. В обоих этих случаях критическое значение cos0:
cos 0 1. г2
Пятый множитель критического условия о обращается в нуль при:
CO8 02 COS0x. г
Эти критерии гх, г2 и г8 соответствуют различным формам потери устойчивости. Наша задача — выделить из них критерий, соответствующий наименьшему значению критической нагрузки. Обратимся для этого к характеристическому уравнению i, которое мы перепишем так:
cosa 0 — В cos 6 0.
После подстановки в него вместо В и D их значений оно примет вид:
П— COS 6 cos 0 — cosvl — сояб Л. s
246
Из различных возможных форм потери устойчивости при одном и том же значении v наиболее опасной является форма, которой соответствует наибольшая жесткость связей, в нашем случае — наибольшее отношение
п у. Поэтому при подстановке в s вместо cos 6 значений по формуле гх надо так выбрать величину р, чтобы cos0 возможно более приближался к своему максимальному значению, т. е. к единице. Иначе
говоря, надо принять р- 0, тогда 6 и
nfcos-cosvV 1 Т Цг-V 25
3 sm v v 2m J I 1 А те
1 — COS Л
2 m
После подстановки в s вместо cos б его значений 1 и — 1 по формуле г2 соответственно получим:
OvtTe0
чему соответствует: v 2рк — результат, не представляющий интереса, и
л 2А -J-1 , v
2 П 6А V CtТ ‘
Для того чтобы п получило положительное значение как это должно
быть нужно, чтобы ctg 0 или чтобы v те. Этот результат также
не представляет интереса. Достаточно вспомнить, что даже для рамы с абсолютно жесткими ригелями при пренебрежении продольными деформациями стоек vKp ir в соответствии со случаем критического состояния для стержня со смещающимися, но с неповорачивающимися концами. Наконец, критерий г8 в соответствии с к равносилен равенству:
B-2D 2 0.
После подстановки в него значений g коэфициентов В и D получим квадратное уравнение:
3S-v2-2-1-cos v Зи -соз vy 0, из которого найдем:
v f А — 1 , ircosv — l
5—: —-А COS V -л.
3 sm v А ¥ А У
Подкоренное выражение здесь отрицательно, и п получается ком-
ч
плексным числом, что невозможно.
Итак, наинизшая критическая нагрузка рамного стержня определяется формулой 25.
Для рам, как мы указали выше в 4, коэфициент А—большое число. Если принять А оо, т. е., если пренебречь продольными деформациями стоек, то критерий 25 получит вид:
п z-Z— cos — cos v. 25
3 sin v V 2m J
Если, кроме того, предположить, что число этажей весьма велико т оо, то получим:
nb1-coev Tvti- - 25
Эта формула нам уже знакома по примеру 6 5 гл. VII. Формула 25
относится к раме с защемленными нижними узлами р0 0, формула 25
относится к раме фиг. 89, у которой нижний и верхний ригели имеют половинную по сравнению с промежуточными ригелями погонную жесткость изгиба. Доведение числа панелей пг рамы фиг. 165 до бесконечно
247
п
большого числа эквивалентно, таким образом, ликвидации эффекта защемления нижних концов ее стоек.
Но если в формуле 25 положить т сю, то мы получим п со. Это значит, что при учете продольной деформативности стоек никакая сколь угодно большая жесткость распорок не может обеспечить рамный стержень от потери устойчивости при возрастании числа его панелей до бесконечности.
2. Стержень с бесконечно-жесткими крайними распорками
Выше мы разобрали случай, когда жесткость изгиба крайних распорок в 2 раза меньше жесткости изгиба промежуточных распорок рамного стержня.
Остановимся кратко на случае, когда жесткость крайних распорок неизмеримо превышает жесткость остальных элементов рамного стержня ir oo. Уравнения а и Ь придется в этом случае заменить другими:
2 Ъ
9т vm‘i — ANmm-i .V,
Второе из этих уравнений может быть переписано в следующей форме:
fb sin v
-m-i mCOSV— —— Ут-i
lih v
Критическое условие для этого случая при сохранении тех же обозначений чрезвычайно усложняется:
A sinm01 sin m02cos62— cos бЗтг V H- sin jn — 1 sin m02 cos 02 — 1 cos 0X — — 3n —
— sin m — 1 02 sin mQ1 cos 0X — 1 cos 02 — 26
Практическое использование этого критерия довольно затруднительно. Сначала нужно по одной из приближенных формул 1 найти ориентировочно критическое зна-
Р
——-—, затем по формулам с и g вычислить велиtJh
чины Л,В и D. После этого по формулам к находим cos 0Х и cos02. Подставляя
их в 26, после двух-трех проб мы найдем, наконец, vKp, при котором Д 0.
3. Приближенное решение для рамного стержня
Приведем здесь, в порядке уточнения формулы С. П. Тимошенко, одно приближенное решение. Воспользуемся формулой 2 из 1 настоящей главы:
idhsr.1 2
JV,
относящейся к расчету устойчивости стержня сплошного сечения при учете его деформаций сдвига. Следуя С. П. Тимошенко, видоизменяем эту формулу так:
— 27
W3 ¥d
Здесь Nd — критическое усилие рамного стержня, соответствующее одним только деформациям сдвига без учета удлинений поясов стержня. В самом деле, если принять, что продольная деформативность поясов стержня равна нулю, то Na oo
1
и формула 2 дает, что критическая нагрузка на сдвиг NKp — Nd ”q Величина NB может быть определена по формуле:
n2EJ _ 2h Fh 2 пНЛ С fb 28
12 2mh2 ‘2m2h V
1 Имеется достаточное количество приближенных формул, вполне удовлетворитель
ных для целей практики. Упомянем работы Тимошенко, Виноградова, Ржаницына и др.
248
Величину Nd 2Ркр для рамного стержня мы можем найти как для многоэтажной рамы по данным примеров расчета 6 и 7, рассмотренных в 5 гл. VII. Если погонные жесткости крайних распорок стержня в два раза меньше погонных жест-
1
костей промежуточных распорок: iT-Ц, то пользуемся для определения величины Nd формулой:
v 2ъ.
Nd 2 _2l , t,
h
причем величину мы находим из уравнения:
Прлближенно величину можно найти по формуле:
9ге 2га -f- 3 f ,v
V Г8л 5iii 44 Если жесткость крайних распорок равна жесткости промежуточных гг ь то для
определения величины можно воспользоваться графиком фиг. 91 или приближенной формулой:
где т1 — полное число панелей стержня тг 2т в наших обозначениях.
Наконец, если крайние распорки абсолютно жестки ir oo, то определяем по формуле 1:
п -г- —— cos — cos Л. w
in 3 sm v V 2m J
Чтобы избежать решения трансцендентного уравнения w, можпо воспользоваться приближеиным уравнением, квадратным относительно v:
0,0325 0,021n v2 - 0,481 0,492га v2 Qt,995га 0,989 - cos 0, w
наиболее точным для интервала значений v между 1 и 2.
Формула w выводится из w с помощью приближенных равенств:
sin v
3 2,995-0,49l8v2-b0,0210v4,
cos v 0,989 - 0,4812v2 -f 0,0325v4,
составленных, главным образом, для интервала значений v между 1 и 2.
Для сравнения приведем здесь простую приближенную формулу, вытекающую из теории рамного стержня, разработанной С. П. Тимошенко:
2 121
v Ь 71 2
х
По характеру вывода этой формулы, связанному с предположением, что нулевые точки эпюры моментов на поясах стержня располагаются по середине длины панелей, следует ожидать, что эта формула ближе всего должна подходить к формулам и
и и.
В табл. 27 мы даем значения величин v для формулы t, вычисленные при
п I и т 2: 3 и 4.
Ч
Принимая во внимание, что формула критического усилия NKp для рамного стержня см. 27, 28 и t имеет вид:
Atkd
мы видим, что определение vh но формуле х вполне допустимо. В формуле 29 I — полная длина шарнирно опертого по концам сжатого рамного стержня. В сокра-
1 Вывода этой формулы мы здесь не приводим. Он отличается от вывода примера 7 5 гл. VII только другими граничными условиями: p0 mio.
24
Таблица 27
ir
1. T11
1
h
00
oo
Th
Формула
M
u
M
w
W
mx 2m 4
3,91
3,93
4,24
6,03
6,24
4
m1 2m 6
3,91
3,93
4,21
4,86
4,92
4
m1 2m 8
3,91
3,93
4,15
4,46
4,47
4
щенных обозначениях этого параграфа формулу 29 можно еще записать так:
ъЧь 1 3 Ап
NKp — 1PKp— 2т2д
29
Сравним теперь величину критического усилия для какого-либо частного случая
рамного стержня, подсчитанную по С. П. Тимошенко и по точной формуле 25.
ft-. 2 Пусть дан шестипанельный т 3 стержень, причем А — 2 и л-Л 1.
ihi ч
По С. П. Тимошенко получим:
ко — - 1 3 2 1 4 _д
Р 2 3 h. it2 1 Л 1
4 36
7
Этому решению соответствует значение:
Подсчитаем по точной формуле 25 для ряда значений vA близких к 1,138, величины соответствующих им отношений погонных жесткостей распорок и элементов поясов:
I v тс
п — cos — cos v
ih 3 sin v V. 2m
y I 1 — cos
те
2m
Подставив сюда вместо A2 и вместо cos—— cos - 0,86603, приводим эту
ть о
-формулу для нашего случая к виду:
1 1,577
sin v
0,866 — cos v.
V
Пользуясь табл. 3 приложения для величин —: и cos v, легко получаем:
sm v
VA
1,12
1,14
1,16
1,19
1,20
n
0,640
0,885
0,930
1,000
1,020
Отсюда следует, что точное значение критической нагрузки для нашего шестипанельного стержня л 1; А 2:
Ч
Ч
NKp 2 1,192 - 2,832.
h
250
Итак, формула С. П. Тимошенко, основанная на переносе на рамный стержень зависимости 27, относящейся к сплошному стержню, дает для нашего стержня погрешность в сторону запаса устойчивости на
2,832-2,594 ЛЛЛ л.
2,832 100 8,4.
Принимая во внимание неизбежные дефекты в изготовлении стержня, снижающие его отпорность, приходим к выводу, что пользование приближенной формулой С. П. Тимошенко в большей мере обеспечит его надежность, чем применение точной формулы.
В соответствии с полученным выше результатом, мы приходим к выводу, что в приближенной формуле 27 знак равзнства может быть заменен знаком неравенства:
кр I т 30
Оценим теперь степень погрешности, которую мы получим, если пренебрежем рамностью стержня, т. е. будем считать NKpN9i а также степень погрешности при пренебрежении продольными деформациями его поясов, т. е. если считать NKp iV.
По формуле 28:
Т384 т1‘385-
По табл. 27
2v.- 2- 3,91 7,822,76.
При дав. формуле 30 вид:
111 — Ч ЗСГ
после подстановки в нее численных значений, получаем:
0,353 0,260 4- 0,128 0,388.
На основании изложенного можно сделать такой вывод. При расчете рамного стержня необходимо учитывать как его рамность, так и продольные деформации его поясов, причем можно пользоваться приближенной теорией С. П. Тимошенко4.
4. Заключение
Необходимость учета продольных деформаций поясов для рамного стержня и ненужность такого учета при расчете обычных рам вполне обосновываются формулой 25. Вопрос о том, является ли данная конструкция многоэтажной рамой или рамным стержнем, решается подсчетом по этой формуле.
Для рам коэфициент А
, Ь2 _ Fh ь_ Ъ у Fh I
Л 12i, 12F h rb J 12Fb h
имеет большие значения, поскольку велика гибкость ригелей Хг. Поэтому для рам в формуле 25 можно пренебрегать членом, содержащим множитель -т , тем самым отказываясь от учета продольной деформативности
стоек рамы.
Для рамных стержней
а
ГЬ 12 где а—ширина планки, и коэфициент
4__ Y
l Ft h aj
сравнительно не велики, колеблется примерно в пределах от 0,3 до 3. Поэтому при расчете рамных стержней необходимо учитывать продольную деформативность их поясов.
1 С. П. Тимошенко, Сопротивление материалов, т. 2, 1934, 42, формула 194.
251
6. Изменение категории задачи при учете деформаций обжатия
стержней рамы
Э, F
Особенность учета деформаций обжатия стержней рамы состоит в том, что при таком учете зачастую с уточнением меняется категория задачи. Действительно, учитывая продольные деформации стержней рамы фиг. 166, а, мы видим, что загруженная стойка рамы укорачивается больше, чем незагруженная, в результате чего стержни рамы при самом малом значении нагрузки Р уже будут искривляться, а узлы перемещаться. Итак, при учете продольных деформаций стержней расчет рамы фиг. 166, а представляет задачу устойчивой прочности. При пренебрежении продольными деформациями стержней расчет той же рамы — задача устойчивости. Категория задачи при уточнении расчета рамы, связанном с дополнительным учетом продольных деформаций ее стержней, не меняется только в том случае, если такой учет не влечет за собой появления углов поворота стержней Обе стойки симметричной, симметрично загруженной рамы фиг. 166, б укорачиваются одинаково. В этом случае и при учете и без учета продольных деформаций стержней рамы задача остается задачей устойчивости.
Фиг. 166.
7. Практический прием учета продольных деформаций
стержней рам
В 4 мы показали, что учет продольных деформаций обжатия стержней не вносит существенных изменений в результаты расчета рам со стержнями нормальных гибкостей. Этот учет существенно влияет на результаты расчета лишь для конструкций со стержнями пониженной гибкости, как, например, распорки в рамном стержне см. 5. В нормальных же случаях учет деформации обжатия стержней вносит лишь некоторое уточнение в результаты расчета. В таких случаях общая методика, изложенная в 4, может быть упрощена и обжатие стержней рамы может быть учтено с помощью последовательных приближений, совершенно аналогично тому, как это делается при расчетах прочности рам по методу деформаций
По принятым для первого цикла расчета значениям продольных
NI
усилий стержней рамы вычисляем укорочения этих стержней АI
Затем, пользуясь методикой 5 гл. III, выражаем углы поворота стержней рамы по формуле:
ФиФй 31
Первый член отражает влияние изменений длин стержней АI, а остальные—влияние кинематически независимых смещений рамы: Фь фи Величины фаЬ, определяемые по формуле 31, подставляем в выражения для МаЪ и Qab, необходимые при составлении уравнений для расчета рамы по методу деформаций. В результате первого цикла расчета определяем уточненные значения продольных усилий стержней рамы. Если они мало разнятся от усилий Nab, принятых при первом цикле расчета, то произведенный расчет считаем окончательным. В про-
1 См. проф. И. М. Рабинович, Курс строительной механики стержневых систем, ч. II, Стройиздат, 1940, 141, 145, 148.
262
тивном случае выполняем аналогично повторный расчет, приняв в его основание продольные усилия стержней Nab, полученные в первом цикле расчета
8. Нагружение силой, направленной к полюсу
При испытании моделей сооружений на устойчивость зачастую вместо непосредственного приложения грузов нагружение их приходится осуществлять при помощи тяг со стяжками. При дефор- i
мировании модели верхний конец тяги перемещается вместе с точкой приложения нагрузки, а нижний закрепленный конец остается на месте. Таким образом, при испытании модели нагрузка меняет свое первоначальное вертикальное направление, все время поворачиваясь вокруг полюса — нижнего закрепленного конца тяги. Рассмотрим на примерах, как влияет такое загружение на величину критической силы.
Пример 1. Пусть дана консоль фиг. 167 длиною Л, загруженная силой, проходящей через полюс А, находящийся на расстоянии а ниже корня консоли.
Диференциальное уравнение изогнутой консоли в этом случае можно записать так: Ъ
или
EJ
d2v dx2
d2v
dx2
Pv-Px 0,
1 ah 1
hVaТлЖ--
Фиг. 167.
Интегрируя это уравнение, получаем:
Д. NX
г Л , yoi. УХ
v hx CcosTC sin 7Г-
Из граничных условий: у0 0 и ул Д находим:
аД 1
Сх 0; С2
а h sin v
Итак:
f I а VX
I X —— sin
a -f h sin v h
Критическое условие устойчивости получим, приравняв v
0;
i
а
sin v h
COS v 0,
или
tg V
h
a
32
Пользуясь табл. 3 приложения для функции получаем ряд зна
чений vKp, приведенных в табл. 28.
4v2 ;
В табл. 28 даны также значения — и выражения l-f-0,7 —. Из рас-
Г
смотрения таблицы видно, что величина Ркр -,а h может быть в этом
h2
интервале значений - от 0 до 1 приближенно с точностью до 20 пред-
253
Таблица 28
а
1
0,5
0,4
0,3
0,2
0,1
0
Ж
45
и
2,029
1,838
1,790
1,741
1,689
1,633
1,571
vk2 —
4,117
3,378
3,204
3,031
2,853
2,667
2,468
II
i
1,667
1,368
1,297
1,227
1,155
1,080
1,000
1,70
1,35
1,28
1,21
1,14
1,07
1,00
ставлена формулой:
Л,р1 0,7
EJ_k h2 e
32
Пример 2. Пусть при расчете того же консольного стержня фиг. 167 нужно учесть также деформации сдвига его оси. В этом случае в соответствии с 4 и 21 гл. III диференциальное уравнение изогнутого стержня может быть записано:
Р Г Д
х
d2v а Р , р Г Д Л А
GF1EJtV a hX Пользуясь обозначением:
h2
EJ 1
мы аналогично предыдущему получаем:
Д Г I а via; Л v ——т х4-.— sin.
я h ч sin vi Л у
а
Ь
Для получения критического условия устойчивости надо приравнять нулю рд:
ь — vh Yft— gf,—0 gfX. ahPP 0 —
Иначе:
0.
Л GFX
Подставив сюда вместо его выражение цз Ь, найдем:
О Т Й С11 Щ ‘
Отсюда, используя формулу а, получаем для критического состояния:
14-. Ll _о пъ
1 A tg vx Л2 Ue
Из этого трансцендентного уравнения определяем величину vx, после
чего находим критическое усилие Ркр по той же формуле а:
Р КР Д2
34
EJ ‘ GFX
254
Если мы не будем учитывать деформаций изгиба стержня, а ограничимся только учетом деформаций сдвига, то в 33 нужно положить EJ оо
V v2 jp
и согласно с aJvO, l и EJ-ф — —
1 —
В результате мы получим вместо 33:
GFX
1f
GFX
1—Р-
GFX
0.
Раскрыв это уравнение, мы найдем величину критической нагрузки Р
на сдвиг:
в
а
351
Этот же результат легко получить непосредственно, учитывая только деформации сдвига, из уравнения:
L v Л
GFXGFXU a hj
Интегрируя его, находим:
Л
-г
vwXv-hxc-
7777.
Из условия, что при ж 0, v0 0 находим постоянную интегрирования С 0. Приравнивая x h, а1Л Д, получаем:
77777Т
. Р Г а АД
A — GfA а АУ
Л
7Г
Фиг. 168.
откуда
Pd Gi.
а
Ha основе формулы 35 нетрудно заключить, что критическая нагрузка рамы фиг. 168 с абсолютно жестким верхним ригелем, загружаемой при помощи натяжения стяжки АВ длиной а Л, будет примерно
в раз больше критической нагрузки той же рамы, осуществляемой
CL
непосредственно приложением нагрузок в узлах С и D. В самом деле непосредственное загружение рамы вертикальными грузами в узлах С uD эквивалентно случаю, когда а со.
Но тогда:
Pd1 GFX.
Итак
а Ь п Г1Х
а
36
Нежелательный эффект замены непосредственного приложения грузов действием стяжек может быть несколько снижен путем увеличения
1 На первый взгляд кажется, что Р можно получить из 34, положив в последнем EJ оо, а потом сократив числитель и знаменатель на v. В результате получилось бы вместо 34, что Pd GFX. Ошибка этого вывода заключается в следующем. Приоо величина v0 и поэтому нельзя отбрасывать в знаменателе 34 первый член: он вполне сравним со вторым.
266
их длины. Он может быть совершенно уничтожен путем удвоения конструкции, подлежащей испытанию на устойчивость. В случае необходимости испытать раму ABCD фиг. 169 надо изготовить еще такую же раму A1B1C1D1 и установить обе эти рамы строго симметрично, как
это показано на фиг. 169. В этом случае действие стяжки ЕЕХ при симметричной деформации системы будет эквивалентно действию нагрузки постоянного направления.
1. Упрощение расчетной схемы в задачах устойчивости свободных
многопролетных многоэтажных рам
1. Замена многопролетной рамы эквивалентной однопролетной
В 6 главы VII мы указали на возможность упрощения расчета однопролетных многоэтажных рам. На основе изучения числовых примеров мы пришли к следующим выводам: а устойчивость однопролетных многоэтажных симметричных рам практически не меняется при замене несимметричной нагрузки этих рам симметричной путем перераспределения нагрузок между узлами одного уровня; Ь если моменты инерции стоек одного уровня не слишком сильно отличаются друг от друга, то они могут быть заменены без значительной погрешности в расчете их средними арифметическими значениями.
Конечно, эти заключения относятся к работе элементов конструкций в пределах упругости. Возникновение в одной из стоек напряжений, выходящих за пределы упругости, при наличии заметной площадки текучести на диаграмме растяжения—сжатия материала этой стойки, может сразу привести конструкцию к разрушению, так как перенапряженная стойка как бы исключается цз работы конструкции. Оговорив это обстоятельство, особо требующее проверки напряжений в сжатых элементах, мы в дальнейшем в этой главе будем говорить об упругой устойчивости.
Выводы, полученные нами для однопролетных рам, могут быть в значительной мере использованы также и при расчете многоэтажных, многопролетных рам по типу рамы фиг. 170, а, если известно, что погонные жесткости it ригелей одного уровня этих рам одинаковы.
При приближенном расчете упругой устойчивости таких рам можно последовательно пройти через следующие ступени упрощения их расчетной схемы.
а Перераспределить жесткости стоек отдельно в каждом ярусе рамы. При этом удобно в упрощенной схеме рамы жесткости крайних стоек взять в два раза меньшими, чем жесткости промежуточных стоек, не меняя общей суммы жесткостей стоек одного
Фиг. 169.
ГЛАВА XI
НЕКОТОРЫЕ ОБЩИЕ ПОЛОЖЕНИЯ И ПРИБЛИЖЕННЫЕ
МЕТОДЫ РАСЧЕТА
266
яруса фиг. 170, а и б:
б II е р е р а с п р еде лить нагрузки узлов отдельно в каждом уровне. При этом на крайние узлы одного уровня точно так же передаются нагрузки в два раза меньшие, чем на промежуточные узлы этого уровня см. фиг. 170, б.
После такого перераспределения жесткостей стоек и нагрузок узлов нетрудно показать см. пример 8 5 гл. VII, что рама фиг. 170, б
Pi
Р2
J
1
7,
4
3
777Г7УУ77П7УИ7Т
и
1
ъ 1
t
I
1r
1
1- J
1
— 1
7
1
t
1
I1-—J
1
1 I
. J
1
1
4
з
i
J
Фиг. 170.
равноустойчива с однопролетной рамой фиг. 170, в. Действительно, значения v для крайних и промежуточных стоек одного яруса рамы фиг. 470, б получаются одинаковыми:
iA—
V EJ
1р г г
и
i J
I I
2J 2J
—Р - Р 2н
I I
I I
- Р -Р 2Н 2Н
I I
Углы о поворота узлов одного уровня для наиболее опасной формы потери устойчивости рамы фиг. 170,6 и рамы фиг. 170, в также одинаковы. Это вытекает из того, что уравнение равновесия моментов для промежуточного узла рамы фиг.
170, в отличается от уравнения равновесия крайнего узла только постоянными множителями 2 в уравнение промежуточного узла входят два одинаковых ригеля вместо одного и жесткость промежуточных стоек, вдвое большая жесткости крайних. Отсюда следует, что рама фиг. 170, б в смысле устойчивости v;7тх;Ьт;. эквивалентна системе фиг. 171, состоя- Фиг. 171.
щей из трех одинаковых симметричных,
симметрично загруженных рам, связанных между собой нерастяжимыми связями, обеспечивающими равенство линейных смещений соответствующих узлов. Ввиду одинаковой нагрузки этих рам соединение их такими связями не повышает их устойчивости и поэтому устойчивость многопролетной рамы фиг. 170, б такая же, как и однопролетной рамы фиг. 170, е.
Проиллюстрируем вышесказанное на примерах.
Пример 1. Для рамы фиг. 172 сравнить три случая загружения:
а вся нагрузка сосредоточена над крайним узлом фиг. 172, а;
б вся нагрузка сосредоточена над средним узлом фиг. 172,6;
в нагрузка распределена равномерно менаду всеми тремя узлами фиг. 172, в.
17 Прочность и устойчивость стержневых систем
257
Погонные жесткости ригелей — , стоек — ihj причем
Ttlfr.
В результате точного решения для случая п 1 мы получим следующие значения критических нагрузок:
Случай
а
6
в
н
ft
18,49
17,14
18,38
100,6
93,4
100
В табл. 28 а сопоставлены значения п для всех трех случаев нагрузки
Л2
соответствующие одному и тому же значению ту 2 Р кр
а зр
в
Фиг 172.
СТО:
Таблица 23а
w уР. EJh 2jrP
0
9
16
20,25
25
27,56
З2
а
п
0
0,263
0,702
1,319
3,817
15,38
Случаи: б
п
0
0,272
0,819
1,795
6,37о
28,01
п
0
0,268
0,714
1,348
3,428
8,79
оо
По данным табл. 28 а на графике фиг. 173 для всех трех случаев загружения приведены кривые зависимостей величины 2 Ркр от от-
tLJji
ношения и. Итак, мы видим, что даже весьма значительное перераспределение нагрузок между узлами рамы сравнительно мало влияет на суммарную величину критической нагрузки.
На основе соображений, аналогичных приведенным в примере 8 5 гл. VII, можно отнести полученные выше данные и график фиг. 173 также и к рамам, изображенным на фиг. 174, а и бу у которых жесткости промежуточных ригелей в 2 раза больше жесткости ригелей крайних. Рама фиг. 174, б представляет собой верхнюю половину рамы фиг. 174,а.
1 Сплошная кривая на фиг. 173 соответствует случаю загружения фиг. 172 а; примыкающая к ней нижняя пунктирная кривая—случаю б; верхняя—случаюв. На первый взгляд кажется несколько странным, что при загружении рамы фиг. 172 одной силой симметричное 8агружение случай б оказывается более опасным, чем несимметричное случай а. Это, повидимому, можно объяснить так. В обоих случаях потеря устойчивости происходит по типу перекоса рамы. Перекос рамы в целом не возможен без перекоса каждой ее отдельной стойки, в том числе и наиболее отдаленной от места приложения груза. В случае а влияние груза на наиболее отдаленную стойкг меньше, чем в случае б.
258
Аналогичное заключение из рассмотрения графиков 1 можно сделать также для рам фиг. 175 и фиг. 176.
Только при малых жесткостях ригелей ,n 1 перераспределение нагрузок между стойками рамы может практически заметно сказаться до 15 — 20 на величине критической суммарной нагрузки, но и то
г
Р
Г
77Z.
777.
777,
н
II
7777.
0
2
4
й
а
р
р 1
L Ч
2ч
V
г it
Big
и
и
V77,
1 р 2И
в
1н
21
р
lL
Г
2ц
гч
77
7777.
V
7777.
777
7771
VS.
77777,
7771
7777 Т7тг
Фиг. 174.
7777. ГТ77
Фиг. 175.
7777.
только в том случае, если такое перераспределение нагрузки будет очень резким.
Пример 2. Проверить устойчивость трехпролетной двухэтажной рамы фиг. 177, а. Погонные жесткости верхних стоек и ригелей равны il9 нижних стоек 2ilf ригелей первого этажа тг. Приближенное решение, полученное на основе упрощения расчетной схемы, сравнить с точным.
Для заданной рамы наиболее опасной формой потери устойчивости будет антисимметричная. Величины v для стоек второго и первого этажа равны действительно
Ph , flPh
h У i
Для ригелей величины vt 0.
1 Эти графики построены на основе изложенного выше метода деформаций. Они приведены в статье А. П. Раковицан, Точность расчетов и устойчивость рамных систем по проекту ТУН, Вестник инж. и техн. 10, 1938.
17 259
Точный расчет устойчивости рамы требует составления шести уравнений с неизвестными olf р2, ср8, ср4, 6х фхз и фп ф35 177, а, б. При Iр составлении системы уравнений мы должны
t пользоваться формулами:
1 для стоек:
Маъ 2аЬ аа — а Р
1Р
Vffrr.
7р
V7‘
J
4
777,
Фиг. 176.
Хр
Qab — гг я Р ь — 7Ы;
топ
lab
2 для ригелей:
Ла6 2га6 2fa b.
Результаты этого расчета показаны на графике фиг. 178 сплошной линией. Для частного случая, при гг 1,660, приводим данные, характеризующие форму потери устойчивости рамы. Критическая величина груза Ркр — б,25. Соотношения между углами поворота узлов рамы и углами перекоса этажей будут:
р
щФиг. 177.
i 1,50464; р2 0,8270у4; 3 1,6696р4; Ц1 13 3,0103р4;
ФИ 35 1,606.
Значения поперечных усилий стоек:
13 -3,6004 р4; Qti 3,6004 4;
- 3,5790 р4; 3,5790 4.
Форма деформации рамы при потере устойчивости показана на фиг. 179.
Приближенное решение осуществляется путем перехода от заданной трехпролетной рамы фиг. 177, а к эквивалентной приблизительно ей по устойчивости однопролетной раме фиг. 180. В соответствии с указаниями, данными в начале этого параграфа, жесткости стоек этой рамы равны двум третям жесткостей стоек заданной рамы так как 32 - —
4ihJ, а нагрузки узлов равны двум третям нагрузок узлов полной
трехпролетной рамы. Поэтому величины vh для эквивалентной рамы равны попрежнему:
У ч
1 Расчет произведен II. Н. Гуслистой, мл. научи, сотрудником Инст. строит, механики АН УССР.
260
Ввиду симметрии системы и нагрузок эквивалентной рамы при наиболее опасной антисимметричной форме ее деформации: ср1 ср1; cp2 ip2; 12 Q , 0; 2з 2з:0- Таким образом, моменты на концах стоек могут
быть определены по формулам, не содержащим выражения для угла перекоса а стержня:
Л™
I,
V V
tg v sin v
Поэтому при решении задачи устойчивости эквивалентной рамы достаточно составить всего два уравнения с двумя неизвестными срА и ср2:
б — т—1 — — 0;
V 3 tg v J 3 sm v
-J- Гбл 2 r—— o 0.
3 sin V T1 1 V tg V Приравняв нулю детерминант, составленный из коэфициентов при 1 о и ср2 в этих уравнениях, после неко- торых преобразований получим уравнение критического состояния в следующем виде:
У
робяН
homJPF ному рос1
-р. 1 1
1 1
Г
i
А
Рл
5 1
Я
1
1
4
Фиг. 178.
п
п
sm v
С
9 9
v
tgv
-L
Т tgv
Jl JL_
fit o,83 1,67 1,00 301 1,61
Фиг. 179.
Фиг. 180.
Давая v последовательно ряд значений и определяя по табл. 3 приложения функций и , мы по этой формуле получаем соответ
ствующие значения п. Вычисления приведены в табл. 29.
Таблица 29
V
0
1,5
2,0
2,5
2,75
2,801
2,836
V
1
1,5038
2,1995
4,1773
7,205
siii v
У
1
0,1064
-0,9153
-3,3466
-6,660
- - я
- -
tgv
л -0,3224
0,0079
-0,3715
1,4585
4,685
ОО
пточп
-0,310
-0,004
0,390
1,660
7,83
оо
—
261
В последней строке табл. 29 приведены для сравнения результаты точного расчета, по которым нанесена сплошная кривая на графике фиг. 178. Данные приближенного расчета нанесены на этом графике пунктирной кривой. Из рассмотрения этих кривых приходим к заключению, что, пользуясь указанным приближенным способом, мы сделаем ошибку в определении критической нагрузки рамы фиг. 177, а примерно не свыше 2,50. Такая точность для практических расчетов может быть признана вполне удовлетворительной.
2. Неточность допущения об отсутствии поперечных сил в стойках
многопролетных рам
При рассмотрения задач устойчивости многопролетных рам весьма заманчиво сделать допущение об отсутствии поперечных сил в стойках, так как такое допущение снижает количество неизвестных. В одной статье1 это допущение мотивируется так:
Примем, что смещение всех узлов перекрытия в одном направлении вызывает однородную по своему характеру деформацию изгиба стоек фиг. 181, иначе говоря, такую, при которой имеем постоянство знака поперечных сил Q всех стоек рамы.
Такое предположение возможно распространить на случаи большой жестокости ригелей по сравнению со стойками или при одинаковых отношениах сжимающих сил к моментам инерции стоек.
Составляя условие равновесия рамы по разрезу, проходящему через стойки,
in
получаем il
Учитывая постоянство направления всех поперечных сил, имеем:
Qi0; 0; Qn0
Условие неустойчивого состояния представляется как ряд условий равенства нулю поперечных сил Qi в стойках.
К сожалению, это, казалось бы, довольно естественное допущение оказывается довольно грубым. В результате его применения получаются весьма значительные погрешности в сторону преуменьшения критической нагрузки.
Погрешность цитированной выше мотивировки заключается в следующем. Из равенства и одинаковой направленности взаимного смещения Д узлов стоек рамы фиг. 181 в момент потери устойчивости совершенно нельзя сделать заключение о постоянстве направления поперечных усилий этих стоек. Такое допущение, естественное при обычном расчете прочности рамы расчете по недеформированной схеме, оказывается ошибочным прлмэнительно к задачам устойчивости. Изгибающие моменты против часовой стрелки по концам стойки фаг. 182, а в задачах прочности могут быть уравновешены только парой концевых поперечных сил, действующей в обратном направлении: по часовой стрелке. В задачах устойчивости, составляя условия равновесия стержня фиг. 182, б, мы должны учесть также и пару, образованную продольными силами. При этом концевые моменты Маъ, Mba и момент пары поперечных сил Qabh могут действовать в одном направлении, уравновешиваясь моментом пары продольных сил
1 Проф. Н. К. С н и т к о, Устойчивость рамных конструкций при узловой нагрузке, Вестник инженеров и техников 6, 1939.
Аналогичное допущение делают и другие авторы, на них мы не ссылаемся, так как их работы не напечатаны.
282
JVA, действующим в противоположном направлении. Надо принять во внимание, что концевые моменты и поперечные усилия в задачах устойчивости малы, они возникают только при потере устойчивости, в то время как продольные усилия весьма Значительны.
При одном и том же взаимном сдвиге концов стержня Д и при одинаковых значениях продольного усилия Лт фиг. 182, бив знак у поперечной силы Q может оказаться тем или другим в зависимости от величины концевых моментов. Сказанное здесь вполне подтверждается численными величинами деформаций и поперечных усилий стоек рамы фиг. 179 в момент потери устойчивости, определенными в примере 2 этого параграфа:
и - 3,6004- 4 и Qu 3,6004 -1- 4 и т. д.
Поперечные усилия стоек одного этажа получаются разных знаков, а сумма их равняется нулю
Нетрудно видеть, что допущение о равенстве нулю поперечных сил стоек рамы, теряющей устойчивость, должно давать заниженные значения критической нагрузки. Действительно, оно соответствует замене рамы с неразрезными стойками системой более деформативной со стойками, не работающими на сдвиг фиг. 183, а. Это может быть достигнуто путем рассечения этих стоек и постановки в местах разреза механизмов из двух параллельных стерженьков фиг. 183, б.
Для сценки степени возможной погрешности рассматриваемого допущения на основе его нами перерассчитана рама примера 2 этого параграфа. Нам пришлось составить всего 4 уравнения с неизвестными рх, р2, р3, р4.
Концевые моменты стоек определялись при этом по формуле:
МаЬ г а п
Результаты этого расчета показаны штрих-пунктирной линией на графике фиг. 178. Сравнивая эту кривую со сплошной кривой, соответствующей точному расчету, мы заключаем, что рассматриваемое допущение для данной задачи дает погрешность до.35 в сторону преуменьшения критической нагрузки. Столь же неудачным, как мы в этом убедились, оказалось это допущение и для других задач см. фиг. 173.
Итак, допущение это, взятое само по себе, весьма грубо, его никак нельзя признать удачным.
3. Замена многоэтауюной рамы эквивалентной одноэтажной
В главе VII 5, примеры 6, 8; 6 и в этом параграфе см. фиг. 172 и 174 мы уже применяли и обосновывали замену многоэтажных рам эквивалентными им по устойчивости одноэтажными рамами.
Сейчас мы сделаем некоторые обобщения по этому вопросу. Раньше всего вспомним одно очевидное свойство, относящееся к задачам устойчивости упругих рам. При пропорциональном увеличении в несколько раз например, в т раз погонных жесткостей всех элементов рамы с одновременным сохранением их длин критическая нагрузка рамы увеличивается во столько же раз, величины же vab, относящиеся к критическим состояниям рамы, остаются без изменения. Больше того, форма потери устойчивости, характеризующаяся соотношениями между различными деформациями системы например, углами поворота узлов и стержней рамы, также остается при этом без изменения.
Представим себе несколько фиг. 184 одинаковых по схеме рам с одинаковыми длинами элементов, у которых жесткости соответственных стержней пропорциональны. Пусть нагрузки этих рам также пропорциональны. Тогда критические состояния этих рам наступят при одинаковых значениях величин va соответственных элементов этих рам.
стоем
Фиг. 183.
263
w
Г 1
1
- 4
42
4
tj
-
h
и
т
A
7777
7777.
777;
Поставим теперь эти рамы друг на друга и свяжем соответственные узлы их шарнирами фиг. 185, Чтобы сохранить эти рамы в критическом состоянии, нужно, не меняя нагрузки верхних узлов новой системы, уменьшить нагрузки других уровней таким образом, чтобы величины продольных усилий NаЬ, а следовательно, и величины va6 в стеряшях
новой системы оставались такими же, какими они были до ее образования в критических состояниях отдельных рам см. фиг. 184.
Если жесткости верхних и: нижних ригелей отдельных рам одинаковы, иначе говоря, если эти рамы имеют горизонтальные оси симметрии, то деформации их при потере устойчивости будут антисимметричны относительно этих осей и пропорциональны у всех отдельных рам и у новой составной рамной системы.
Вследствие неопределенности масштаба деформаций при потере устойчивости, мы можем положить, не меняя при этом величины критической нагрузки, что деформации всех ригелей составной системы фиг. 185 не только пропорциональны, но и равны. Тогда ее деформации ничем не будут отличаться от деформаций трехэтажной рамы фиг. 186, у которой погонные жесткости промежуточных ригелей равны суммам погонных жесткостей примыкающих друг к другу ригелей составной системы фиг. 185, а все прочие элементы и нагрузки совершенно одинаковы.
Приняв коэфициенты к1у к2у й3,. постоянными, мы можем считать, что нагружение рам фиг. 184, фиг. 185 и фиг. 186 определяется некоторыми силами Ри Р2у Будем называть все эти рамы эквивалентными
Pz j
I U Hi
-21
T
j
L3H1
hi
i4hV
-1
7777
S
5Г
V
ТУ
777777
А
77777
Р,г
r 1
P2X2
UH2
22
l3H2
1
с
22
u
77777. 7777Z
Фиг. 184.
r 1
- 4r
Pi
I J
г Ц
r
1
1
4
U-
P,x,-0
1
1 Lj
I H t2
1
i4t
I
T
1
i Ц,мг
1
f 42
1 U 2
l4Hz
V77fr
Ж
777777 777X7.
Фиг. 185.
V.
7
-с
-I
7S Д Л
ТТТТ ГГГГ777 7777777.
Фиг. 186.
по устойчивости иначе равноустойчивыми, если критическое состояние их достигается при одинаковых для всех их значениях силовых характеристик Рг, Р2,. В соответствии с данными выше пояснениями об образовании этих систем они являются действительно эквивалентными по устойчивости.
Мы видели, что задачу нахождения критической системы нагрузок Pi, 2У сложной рамы фиг. 186 можно заменить задачей расчета устомчи-
264
вости одноэтажной рамы фиг. 184, а. Величины Ри Р2,., являющиеся критическими для этой рамы, будут также критическими и для рамы фиг. 186.
Нетрудно видеть, что все приведенные выше соображения останутся в силе и в том случае, если мы заменим отдельные одноэтажные рамы фиг. 184 более сложными системами фиг.487, а и б, имеющими горизонтальные осц симметрии. На фиг. 187, а пунктиром показан характер деформации шарнирной схемы рамы. Несмотря на наличие наклонных элементов, в силу симметрии относительно горизонтальной оси крайние верхний и нижний ригели остаются параллельными.
4. Общие принципы образования из нескольких равноустойчивых простых систем равноустойчивой с ними сложной
системы
Продолжим наши обобщения. Пусть дано несколько систем, находящихся в критическом состоянии: I, II, III фиг.
188, а. Если мы соединим их дополнительными связями фиг. 188, б, то критическое состояние системы не изменится. Действительно, при этом связываются между собой только масштабы деформаций отдельных систем I, II, III, и не создается препятствий к осуществлению в полной пропорциональности прежних форм деформаций отдельных соединяемых частей. В силу этого обстоятельства, а также ввиду неопределенности масштаба деформаций при потере устойчивости и того, что соединяемые части были самоуравновешенными и без постановки дополнительных связей, усилия этих связей
2 ИР
б
кр PfHP
III
7777777777777777777777777777777777777777 г77777777777777777777777777777777777777
P3Kf.
t
Ш
Фиг. 188.
при потере устойчивости соединенной системы, остаются равными нулю Поэтому такие связи мы в дальнейшем будем называть нулевыми связям и.
Выше мы условились называть равноустойчивыми системы, нагрузки которых нужно увеличить в одинаковое число раз, чтобы каждая из этих систем достигла критического состояния.
Итак, постановка нулевых связей между несколькими равноустойчивыми системами не изменяет коэфициента запаса их устойчивости.
Если мы возьмем несколько одинаковых, одинаково загруженных рам фиг. 189 и соединим соответственные узлы их дополнительными стержнями то эти стержни будут нулевыми связями. Соединяя одинаковые, одинаково загруженные рамы дополнительными связями так, как это показано на фиг. 180, мы накладываем новые кинематические ограничения на форму деформаций этих рам мы лишаем возможности перекоса третий
26Г
этаж левой рамд. Такие связи мы будем называть ненулевыми. Ясно, что постановка ненулевых связей повышает устойчивость системы.
Нулевые связи могут осуществляться не только при помощи допол нительных стержней, но и при помощи выбрасывания шарниров и объединения примыкающих друг к другу стержней. Покажем это на примерах.
Фиг. I90j
Пусть даны две равноустойчивых симметричных, симметрично загруженных однопролетных рамы равной ширины b фиг. 191, а, б, из которых одна по крайней мере шарнирно присоединена к земле. Поставим ее на другую раму фиг. 191, в и уменьшим на величину силы Рг нагрузки Р2 и Pz с тем, чтобы сохранить старые значения продольных сил стержней Nab.
о
рг
777777777777777.
L 6 Уравнения, составленные для системы фиг. 191, в по методу деформаций при обычном пренебрежении изменениями длин стержней, разделятся на две независимых системы: одну для рамы а и другую для рамы б. Это получится в связи с тем, что угол поворота ригеля ААг
AAi 0.
Если мы теперь введем в систему в дополнительные связи, заменив шарниры А я А жестким присоединением, мы получим систему фиг. 191, г, равноустойчивую с системами а и б.
Действительно, такая замена: 1 не вносит новых кинематических зависимостей между деформациями: каждой из соединяемых равноустойчивых частей отдельно взятой; углы поворота узлов А и Аг рамы а при
266
атотере устойчивости равны друг другу cpA pAl; точно так же рарны друг другу углы поворота концов А и Ах стоек рамы б; 2 не нарушает имевших место до соединения условий равновесия сумма нулей равна нулю; 3 связывает между собой только масштабы угловых деформаций верхней и нижней части рамы г, что ввиду неопределенности масштаба деформаций при потере устойчивости не имеет никакого значения.
б
Л
г 6
J2
A Pi
1 I
1 1
ъ
Т777777У77А
777.:
в
в
А
1
г
1
I—Z—1
Pz-P,
А д
1 I
Jz 1
А А
I I
1 1
Ps-Pi
L J
в
Ггв
А.
в
Фиг. 192.
Итак, жесткие крепления вточках Ап Аг рамы в являются нулевыми связями и поэтому система а равноустойчива с системами а и б.
Другой случай: пусть даны две симметричных, симметрично загруженных равноустойчивых рамы одинаковой ширины 6 фиг. 192, а и б, причем по крайней мере у одной из них нижние концы стоек жестко связаны с упругим ригелем, шарнирно опертым по концам. Поставив раму б на раму а и соответственно изменив узловые на- 0 грузки, мы получим в силу кинематических особенностей этих рам aai — O, систему фиг. 192, в, равноустойчивую с рамами а ж б. Заменив два идущих рядом ригеля ААг одним стержнем, жесткость изгиба которого равна Jx J2,
т. е. сумме жесткостей изгиба ; j 3
соединяемых ригелей, мы по- j2 1-1 1 Л
лучим раму фиг. 192, г,
равноустойчивую рамам а и б. Ц jf — 1
Соединение двух стержней в один здесь равносильно вве- Jiwssssssfo 7 дению нулевых связей, так как J
формы изгиба стержней ААг в соединяемых рамах одинаковые, пропорциональные.
На основе вышесказанного легко сделать вывод, что симметричные многоэтажные рамы фиг. 193, а и фиг. 194, а, симметрично загруженные двумя силами Р в верхних узлах, при постоянстве высот этажей и жесткостей Jx стоек и при прочих условиях, отмеченных на чертеже, ‘равноустойчивы с системами фиг. 193, б, фиг. 194, б и одноэтажными рамами фиг. 193, в, фиг. 194, в.
р р
6
Р Р
л
Jl у
If
J2
г т
j,
— Г
Л
j,
J,
л У Л
Г
7
Jf
в — Фиг. 193.
777777777777777.
3
267
Легко видеть1 также, что для рам по типу фиг. 195 не требуется симметрии системы и нагрузки. Отдельные клетки; системы должны лишь иметь горизонтальные оси симметрии для того, чтобы сохранялось
р
постоянное отношение — между углами поворота левых и правых узлов
Фпр
одного уровня. Многоэтажная и одноэтажная рамы, изображенные на
фиг. 195, равноустойчивы.
о
р
р
г
Jz
у,
Vt
у,
2Jz
у,
2JZ
J
4
Я
л
4
J,
Х
Л
л
Этот вопрос подробнее нами разобран выше в пункте 3 этого параграфа. По аналогии со сказанным в том пункте легко также заключить, что симметричная, симметрично загруженная рама фиг. 196, а равноустойчива с двухшарнирной рамой фиг. 196, б. При этом для равенства величин vWj0a укрб не требуется ни равенства высот этажей, ни равенства пролетов этих рам, достаточно, чтобы погонные 777 жесткостные характеристики этих рам it и i2 были у них соответственно пропорциональны.
Если бы в раме фиг. 196, а нагрузка была несимметричной, то это значило бы, что в отдельных составляющих рамах фиг. 196, б нет пропорциональности между углами поворота узлов:
А , Ai
ф g
Поэтому для получения системы фиг. 197, а из системы фиг. 197, б на последнюю нужно было наложить ненулевые связи. Итак, рама р
U— б — Фиг. 194.
U—S
Г
с
I
t-
1—
J,
Я
У,
Ml
h
J,
Уз
2Уг
у,
Уз
Уг
I
р
Уг
у,
Уз
7
г
fa-tJP
I - р
з - г
V7777
в
Уро тУмрЪ
777777777777777
в
77777777777777
Фиг. 195.
Фиг. 196.
1 См. статью автора Точный метод проверки устойчивости плоских рам в Зб1рник присвячений сорокал1ттю науковой д1яльност1 акад. Е. О. Патона АН УССР, 1937 Проф. Н. П. Павлюк, Устойчивость прямоугольных рамных систем, Труды ЛИИКС 1938, вып. 5.
268
фиг. 197, а устойчивей системы фиг. 197,6 и равной ей по устойчивости одноэтажной рамы фиг. 197,. Следует заметить, что вышеприведенные соображения не могут быть распространены на случай соединения равноустойчивых рам с непараллельными стойками. Система фиг. 198, в, образованная из рам фиг. 198, а и фиг. 198, б, не равноустойчива им, а менее устойчива чем они, так как рама б представляет в ней упруго деформирующееся основание для надстройки а.
Соединение двух рам в третью равноустойчивую может быть произведено не только по вертикали, но и по горизонтали. Пусть, например, даны две аналитически ввиду пропорциональности погонных жесткостей стержней и нагрузок к одному аналитическому и численному решению. В силу этой пропорциональности кривая деформации правой трехэтажной стойки рамы фиг. 199, а отличается только масштабом а, может быть, и знаком от кривой деформации левой трехэтажной стойки рамы фиг. 199, б. Поэтому объединение этих стоек в одну в системе фиг. 199, в равносильно добавлению нулевых связей. Значит система в равноустойчива с системами а и б.
Очевидно, что в случае отсутствия или хотя бы частичного нарушения такой пропорциональности подобное соединение двух таких рам в одну будет равносильно накладыванию ненулевых связей и приведет -к образованию системы более устойчивой, чем системы-составляющие.
4
б
hl
4
б
Pf
4
Р, ♦
. ъ
1
b
hLj
м
Hi
н14
U
iz
Pj I 4
hl4
15
в
8
KLq
мз
кРг
1
s
1
1kC8
h
is
hP2
As
71
Ь
У:
7:777777777777777777
HLg
77Г
r7
0kl9
777777777777
77Т77У777777777.
rr:
Фиг. 199.
Если соединяемые равноустойчивые рамы будут не только аналитически подобны, но и симметричны и симметрично загружены, то число слагаемых рам может быть любым, как мы это для частного случая
б к Р,
Фиг. 198.
О
н,-1р
г -ЪУ3
6
н,-гР
Фиг. 197.
подобные задачи фиг. 199, приводящиеся
269
Л 1 на основе примера 8 5 гл. VII установили в начале этого параграфа. Это вполне понятно, так как кривые деформаций стоек всех соединяемых рам будут пропорциональны фиг. 200 и 201.
5. Общие принципы расчленения сложной системы на более простые
Расчленение сложной системы на более простые может быть осуществлено либо путем удаления некоторых наличных связей, либо путем введения новых связей. Конечно, расчленение можно осуществить
7777777777,
7777777777.
177777777777: Г7777,
V
Фиг 200.
У,,
I I
itt
1
id
AzLz
О
H3L1
О
4-1
H4lz
С
7777777у7
только тогда, когда в результате его можно рассматривать устойчивость, отдельных частей рамы независимо друг от друга. Так, например, раму фиг. 198, б с непараллельными стойками в нижнем этаже нельзя расчленить на две независимые системы фиг. 198, а и фиг. 198, б ввидутого, что боковое выпучивание нижнего этажа вызовет поворот ригеляv
г
1-1
i-i i 2с
Т
2Р
2,
2i,
2it
2i
2
4it
21 it
212
2ii
2iz
2lt
2L7
4L
r r
2if Li 2
2ii
212
4t
2 it
2t2
If
2ii
41
777777777777777777777777777777777777777777
Фиг. 201,
г
Р
1
1-г
s
it.
Lz
T
с
r r-
I
7777777777:-J
являющегося основанием для вышележащей части, и силы, приложенные к последней, как бы повернутся относительно ее основания, ускоряя потерю устойчивости системы.
В случае удаления связей, общая устойчивость системы должна либо понизиться, либо остаться без изменения. Она понизится, если систему расчленить на неравноустойчивые части: устойчивость одних частей повысится, а других — снизится. Коэфициент общей устойчивости нерасчлененной системы будет при этом заключаться между наибольшим и наименьшим коэфициентами запаса устойчивости ее отдельных частей.
270
Общая устойчивость системы не изменится, если она будет расчленена на равноустойчивые части так, как это описано в пункте 4 этого параграфа.
В случае введения новых связей например, закреплений от поворота узлов рамы или абсолютного ожествления отдельных ригелей рамы общая устойчивость системы и устойчивость отдельных ее частей повышается.
Проиллюстрируем на примере расчленение сложной фиг. 202 рамы на отдельные части путем удаления связей. Выясним, при каких обстоятельствах устойчивость однопролетной многоэтажной рамы фиг. 202, ак
77777777777777
6
Р
I
h
б 2Р
1
2Р
Т7777777777777.
Lh
77777777777777
Фиг. 202.
Фиг. 203.
будет равна устойчивости системы из поставленных друг на друга одноконтурных рам фиг. 202,6. Это будет в том случае, если уравнения для рамы фиг. 202, а могут быть приведены к уравнениям для рамной системы фиг. 202,6. При этом ввиду неопределенности масштаба деформаций при потере устойчивости рамной системы фиг. 202,6 можно принять, что ср1о р12 ср1, а фгх — Ъз р2- Сравним уравнения для узла 2 в обеих рамных системах. Для цельной системы фиг. 202, а получаем:
2 М28 22 Ь -21 — —1
23 sin v3 тз
Ь 6i2
tgv3
V 2 Л V2 f
21 4 Фо 21 Ф1 ;_А 0.
SlllVg kl
а
Для расчлененной системы фиг. 202,6 получаем два уравнения:
2 М23 М2г, — г23 рз Q2s t- 6iQ 92 0; b
2 м:2,Mtl itl t- 9t -itl 9l0. c
Сложив уравнения b и с и сравнив их сумму с уравнением а,
приходим к выводу, что
d
и вообще
I о —
-р 141 — La9
Составим еще одно уравнение для узла 3 системы фиг. 202,6:
3 MS3i -J- Mit -j- i32 3 г32 siivj 2 —
271
Приравнявдруг другу отношения , полученные из уравнений Ь и se, найдем величину i2:
i
б
23 7з2 зЧз
о V3
32
tg v3
6,
О
После этого из уравнения d найдем i. Аналогично можно найти ix и г. В результате мы получим систему расчлененную фиг. 202,6,
равноустойчивую с системой цельной фиг. 202, а.
При другом распределении жесткостей ригелей в расчлененной системе
га; и i—
мы уже не получим равноустойчивости: для этих систем. Если возьмем величину i большей, чем следует по формуле f, то повысим устойчивость одноконтурной рамы третьего яруса расчлененной системы и уменьшим устойчивость нижележащей части, и наоборот. Отдельные части расчлененной системы получатся при несоблюдении условий типа f более устойчивыми, чем цельная система, а другие менее устойчивыми.
Пример 3. Трехэтажная рама фиг. 203, а расчленена на отдельные части фиг. 203, б, в, г с помощью постановки шарниров в стойках над первым и вторым ригелем. На графике фиг. 204 показаны зависимости
силовой характеристики Ркр от соотношения п. Из рассмотрения
этого графика мы приходим к выводу, что коэфициент запара устойчивости цельной рамы действительно заключается между коэфициентами запаса для отдельных ее частей. График построен в соответствии с данными табл. 30.
Таблица 30
,5 2,0
Фиг. 204.
II
С. 1
0-
0,4
0,7
1
1,5
2,0
2,5
3,0
Случай а б в г
р
ч
Г 0,184
i 0
10
0,82
1,36
1,28
0,64
1,86
1,82
1,63
0,815
2,24
2,15
1,82
0,91
2,46
2,47
2,00
1,00
2,63
2,66
2,10
1,05
2,81
2,79
2,17
1,085
2,89
2,88
2,21
1,11
2,96
Пример 4. Та же трехэтажная рама фиг. 205, а расчленена на три одноконтурных рамы по фцг. 205, б, в, г. И в этом случае коэфициент запаса устойчивости цельной рамы заключается между коэфициентами запаса отдельных частей. График фиг. 206 построен по данным табл. 31.
272
Таблица 31
1
II
0
0,4
0,7
1
1,5
2,0
2,5
3,0
Случай: а
Г 0,184
1,36
1,82
2,15
2,47
2,66
2,79
2,88
б
0
2,56
3,84
4,78
5,72
6,43
6,92
7,30
в
-Р й
0
0,99
1,52
1,95
2,47
2,84
3,12
3,34
г
1
0,82
1,46
1,78
2,01
2,28
2,46
2,59
2,68
Г 4 1
V.77:
Фиг. 205.
Примеры расчленения сложных рам на более простые равноустойчивые системы приведены в пп. 4 и 7 этого параграфа.
1 2. Вспомогательная задача: одноконтурная прямоугольная свободная рама с разной жесткостью ригелей
1. Постановка задача
Для решения задачи расчленения сложной рамы на более простые гравноустойчивые рамы весьма полезны приводимые ниже графики для проверки устойчивости одноклеточной симметричной, симметрично загружен-
-ТР
4 р
г
1
t
f
- i
У
У
у
J7 i
t
1б
i
-mm А
X
Г
1
1
1
1
✓ 1 г 1 А Ч 1
V t 1
к t if
Е
, ,
1 ——♦ t 1
L
i
05
25
ми верхнего и нижнего ригеля фиг. 208, в. Погонные жесткости элементов этой рамы обозначим: о
ih — левой и правой стоек, it
nih — одного из ригелей и kit
knih — mih — другого ригеля. Если к 0, рама вырождается в двухшарнирную, для которой см. гл. VII 5 известно решение
15 2
Фиг. 206.
При к 1
п — v tg v.
о
1. V
TvtgT.
1
2
При к со рама превращается в бесшарнирную с жестко заделанными пятами, для которой:
6 tg
18 Прочность и устойчивость стержневых систем
3
273
В оэщвхМ случае, для любых значений к адача сводится к составлению двух уравнений с неизвестными углами поворота верхнего и нижнего концов стойки рамы. Детерминант критического состояния
3бит 6 п т — v2 О,
или в друглх обозначениях
4
36 for 6 1 к А- гг - V2 о 4
о v
представляет собой трансцендентное уравнение относительно величины
. Его удобней решать
v
как квадратное уравнение относительно величины п:
12к tg v
к v
-
l lk tsr v
V—
J 3b
5
сохраняя знак плюс перед радикалом для более опасного критического состояния рамы. Еще проще уравнение 4 решается относительно к:
к
tgv
6
61 -f-
tsr v
В частном случае при v О уравнение 6 получает вид:
к -
61 1
7
Фиг. 207.
При решении задач расчленения сложных систем на более простые равноустойчивые зачастую приходится расчленять жесткости отдельных элементов на составляющие разных знаков. Дикое и нереальное понятие отрицательной погонной жесткости стержня в отдельной раме, рассматриваемой как одно целое, становится рациональным и реальным для стержня рамыг представляющей собой часть более сложной системы.
2. Расчетный график в декартовых координатах
Зависимость между отношениями погонных жесткостей стержня рамы п -V
lh
7П h
и к — и характеристикой критической нагрузки, величиной v2 — NKp наиболее п
наглядно можно представить при помощи графика, построенного в декартовых координатах по формулам 5 и 6 фиг. 207. Несмотря на известную сложность построения такого графика, преимущество наглядности его бесспорно; на нем приведены не только данные для положительных значений к и п, но й для отрицательных. По оси абсцисс
этого графика отложены величины отношения п , по оси ординат—величины
h
274
h
— H-2 -r кривые построены для различных значений отношения к настолько lh
густо, что интерполяция между ними не представляет больших затруднений.
При наличии в составе рамы ригелей с отрицательными погонными жесткостями возможны случаи, когда критическому состоянию ее соответствует усилие растяжения
в стойках. Для таких случаев величины и v2 в формулах 4 —6 надо соответ-
tg V
ственно заменить величинами— и —ц2. Формула 7 дает значения к для одноконтурных рам, находящихся в критическом состоянии при отсутствии продольных усилий в стойках при vA 0.
Результаты вычислений по формуле 5, на основе которых построен график, частично приведены в табл. 32.
Таблица 32
it
Значения п—
ч
1
2,56
5,76
6,76
7,84
8,41
9,61
9,87
оо
1
0,75
0,5
0,25
0,1
-0,107
0,091
0,104
0,125
0,160
0,201
0,0078
0,275
0,317
0,388
0,553
0,887
0,1526
0,519
0,602
0,753
1,149
2,186
0,437
1,029
1,198
1,521
2,444
5,116
0,720
1,561
1,817
2,323
3,798
8,15
1,313
2,706
3,153
4,05
6,69
14,59
1,962
3,982
4,65
5,96
9,89
21,67
3,507
7,051
8,22
10,56
17,60
38,4
12,42
24,84
30,01
37,22
62,13
90,0
оо
оо
оо
оо
оо
оо
Кривая для к со пересекает ось абсцисс в точке 0 -Ь у2 и ось орди-
Г те2 пп
нат в точке 0; у 2,467. Все остальные кривые кф оо проходят через начало координат. Все эти кривые для значений к 0 имеют общую асимптоту v2 те2;
те2
кривая для к 0 имеет асимптоту v2. Кривые для отрицательных значений к
для к 0, проходя через начало координат, достигают при значении п
V 12к tgvy максимУма ЛРИ значении п — пересекают рсь абсцисс
и затем переходят в область отрицательных значений продольного усилия стоек Nh.
3. О правилах интерполяции по расчетным графикам, представляющим
семейство кривых, связывающее три переменных1
На фиг. 208, а приведен тот же график, что и на фиг. 207, но только с меньшим числом кривых. Покажем, как пользуясь графиком фиг. 208, а, можно путем интерполяции провести кривую для любого не показанного на чертеже значения параметра Л. Семейство кривых с отметками графика фиг. 208, а представляет собой некоторую плавно меняющуюся криволинейную поверхность. Пересечем эту поверхность, например, плоскостью п 5 и по точкам построим плавную кривую зависимости между v2 и к для п 5 фиг. 208, б. Пользуясь этим поперечным разрезом, наносим на вертикали п 5 фиг. 208, а более подробную шкалу значений к.
Введем вспомогательную величину 0, представляюшую собой отношение двух ординат V2 и v25 на одной и той же кривой при одном и том же значении к.
Очевидно, что для всех точек вертикали п 5 величина 0 1. Возьмем какую-нибудь одну кривую, например, для к 0,75. Для этой кривой по графику легко находим значение v58,500. Итак, точкам со значением 0 0,4; 0,5; 0,6; 0,7; на этой
кривой будут соответствовать ординаты: 0,48,5 3,40; 0,58,5 4,25; 0,6-8,5 5,10; 0,7 8,5 5,95 и т. д. По этим ординатам нетрудно нанести на кривой к 0,75 точки
1 Излагаемый здесь способ интерполяции может быть весьма полезным в самых различных случаях, в частности при расчете стенок цилиндрических резервуаров ho графикам проф. И. Я. Штаермана.
18 276
с этими значениями 0. Нанеся аналогично точки с такими же значениями 0 и на других кривых нашего графика, соединяем затем точки с одинаковыми значениями 0 плавными кривыми. Таким образом на графике фиг. 208, а нанесены пунктирные кривые для
0 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 0,95; 1,00; 1,05; 1,10; 1,15 и 1,20.
Пусть нам нужно теперь провести кривую для к 0,2. На шкале при п 5 читаем
для к 0,2 значение vn6— 6,94. Умножая затем это значение v2 6,94 на разные аначения 0, для которых построены пунктирные кривые, мы на этих кривых по орди-
Фиг. 208.
натам наносим точки, лежащие на кривой к 0,2. Если нам нужна только отдельная ордината кривой к — 0,2 для определенного значения абсциссы д, например для п 2, то мы ограничиваемся построением части кривой к 0,2 между значениями 0 0,7 и 0,8 фиг. 208, а. В результате находим v2 4,92. Такое же значение мы получим и на более подробном графике фиг. 207.
4. Сетчатая номограмма без правых линий
У Графики типа фиг. 207, обладая наглядностью, имеют вместе с тем ряд существенных недостатков. Построение их связано с проведением большого числа кривых линий. Для возможности надежного интерполирования по такому графику нужно провести также весьма густую сетку прямых, параллельных осям координат. Степень возможной точности отсчетов для разных точек поля этого графика весьма различна. Отсчеты, соответствующие малым значениям координат, получаются с меньшей относительной точностью, чем для координат с бблыпими значениями. Пересечение кривых под острыми углами также снижает степень точности отсчетов. Поэтому значительно удобней пользоваться вместо сетчатых шкалярными номограммами, обычно номограммами ив выравненных точек1. Для более удобного перзхода к шкалярной номограмме сначала покажем, как можно построить для данной задачи сетчатую номограмму без кривых линий.
Рассматривая уравнение 4: I
Збтп б п -т v2 0, 4
1 Проф. Н. М. Герсеванов, Основы номографии, ГМТИ, 1932.
Г. Швердт, Номография на основе геометрии отображения, ДНТЗУ, 1935.
Н. А. Глаголев, Теоретические основы номографии, ОНТИ,1936.
276
мы видим, что, приняв обозначения:
у пт; я п-т, а
мы можем уравнению 4 придатьвид уравнения прямой в декартовых координатах:
тгО- ь
если считать величину v постоянной. Давая v ряд последовательных значений, мы можем представить уравнение 4 в виде семейства прямых сплошные прямые на фиг. 209 в декартовых координатах с надписанным над каждой прямой значением параметра v.
Исключив из а параметр получим:
у п с
Это уравнение дает нам на графике другоесемейство прямых пунктирныелинии на фиг. 209 с надписанным над каждой прямой значением п. Каждой точке графика фиг. 209 в пределах нанесенных на него семейств прямых отвечают однозначение величины v и два значения величины п. При этом, если одно из этих значений мы примем за п, другое значение будет соответствовать величине т.
График типа фиг. 209 неудобен для расчетов. Семейства прямых пересекаются в нем иод острыми углами, неравномерность степени точности отсчетов для этого графика весьма значительна. Эти дефекты можно было бы несколько снизить с помощью надлежащей перспективной анаморфозы, но значительно удобней перейти к другому типу графика: номограмме из выравненных точек.
5. Шкалярная номограм
ма
ХП7
Фиг. 209.
Зависимости Ъ и с могут быть совершенно иначе геометрически интерпретированы, если вместо координатной системы Декарта перейти к параллельным координатам Шаля.
Сопоставим системы координат Декарта и Шаля см. табл. 32а на стр. 278.
Эта таблдца отражает известный принцип двойственности, аналогию между точкой и прямой иа плоскости. На нем основано коррелятивное преобразование плоскости, с помошью которого сетчатые номограммы из трех семейств прямых получают вид шкалярных номограмм.
Таким образом, в системе параллельных координат каждой прямой L графика фпг. 209 будет соответствовать точка т, каждой точке М прямая I, каждым трем прямым Lu Li Х3, проходяшим через одну точку М — три точки mlt m2, w3, лежащие на одной прямой Z, семействам помеченных прямых прямых с отметками третьей переменной Ь и с — две криволинейные шкалы с надписанными значениями v или v2 на одной и значениями п на другой. Семейству прямых л т, параллельных оси ординат графика фиг. 209, и семейству прямых пт, параллельных оси абсцисс, будут соответствовать прямолинейные шкалы значений п-т и пт вторую из этих шкал мы на номограмме — фиг. 210 за ее ненадобностью не показываем.
Принимая в этой координатной системе разные масштабы для отрезков х и у, различным образом выбирая положение полюсов О и 01 в одну или разные стороны направляя положительные течения осей х и у, мы можем значительно варьировать вид шкалярной номограммы.
Пусть оси х и у заданы на чертеже фиг. 2111 и пусть масштаб отсчетов по оси у в К раз меньше, чем по осп х.
Тогда уравнение
Ах By С 0 cl
С С
1 На фиг. 211 вместо— должно быть — fig
2 77
Таблица 32а
Координаты Шаля
Координаты Декарта
-—
1. Образ х, у представляет точку М
X
N
С
в
г
2. Образ АхВу-
-f С 0 представляет
3. Любая точка, лежащая на прямой L, имеет координаты х, у, удовлетворяющие этому уравнению
4. Если три прямых
Ар Вгу С О,
М 222 0,
Л3ж В3у -f- С з 0 проходят через одну точку, то
Ах Bt Ct
A Bt ct
А Вь С
0
А В 2 С 2
А3 В3 Сг
А3 В3 С3
5. Бели три точки lf 2х, я , 22, 3, у3 лежат на одной прямой, то
хг ух 1 2 У 1
ж,
0
1. Образ х, у представляет прямую
-Г
л
У 2. Образ Лж 4- By С 0
представляет точку m
1
77,
С
В
3. Любая прямая, проходящая через точку п, отсекает на осях координат отрезки х и у, удовлетворяющие этому уравнению
4. Если три точки
Агх Вгу Сг А2х-В2у С2 А3х -f В3у С3 лежат на одной прямой, то
0
0, : 0
0
5. Если три прямых xlf ух, ж2, ts, х3, у3 проходят через одну точку, то
1
2i
1
ж2
У 2
1
0
3
Уз
1
273
в координатах Шаля представит собой точку т с декартовыми координатами
КВ
КВ —А KBh C
ь,
4 -КВ-А
Такимобразэм, уравнение Ь даст точку координатами:
, Ь; У :—.
6К-
tgv
д 8 1 6 5 4 vj
6iT —
tg v
jl.V. ijIirt j- r i i
j: V V 6-j-i
7 JL Jl
8 i nm
О
p -Уг1.-Уга
Чр h —7jl
Пример. Дано: nQ,1; m5 Находим: v4j35;PHpa5
ЗЬппгб1т-тпъдч V2-Q
о
Фиг. 210.
Для того чтобы шкала Гзначений v2 в пределах интересующего нас интервала —2 v22 была непрерывной, нужно, чтобы знаменатели формул f в этих пределах
у
не меняли своего знака. Примем К 0,5, тогда: 1,4 6J5T — т—оо. Положим, кроме
того, что h 0, тогда, подставив; в формулы f
tgv
А
в-1; с—я;
6 tgv
ЛГ 0,5; Л 0,
получим
; —
.2
tgv
f
Фиг. 211.
Пользуясь этими формулами, и да- ;
вая v2 различные значения от — 2 до п
п2 включительно, построим шкалу v2 фиг. 210 в виде трансцендентной кривой линии, довольно близкой к прямой.
Шкалу значений п строим аналогично. В соответствии с уравнением с подставляем в формулы е
А — п; В 1; С п2; К 0,5; h 0
я получаем:
Ь 2 п2
Примем 6 10 см. Исключив из g параметр л, получим уравнение кривой, на которой лежит шкала п:
С2 — 20i - 20С 100 0. h
Это гипербола, асимптоты которой:
0 и — 20т, — 0,1 0,
Уравнение а х — п т при соответственных значениях А — 1; 0; С — —пт дает точку с координатами:
5 0; т п -т.
Шкала п т прямолинейна и равномерна. Эта шкала не является безусловно необходимой, но она полезна для контроля правильности и для повышения точности отсчетов по шкалярной номограмме.
Покажем на примере, как пользоваться номограммой фиг. 210. Пусть даны значения л 0,1 и т 5, находим соответствующие им точки на гиперболической шкале. Прямая, проведенная через эти точки, должна на шкале пт отсечь соответственно показание п-т 0,1 5 5,1, на шкале v2 эта прямая дает отсчет v23,35. Итак,
РкР 3,35.
Если п mf то прямая-секущая превращается в касательную к гиперболической шкале, мы ее проводим через точку п на этой шкале и точку п п 2п на прямолинейной шкале.
Если п — конечная величина, а т оо, то прямая-секущая становится параллельной прямолинейной шкале, так как эта шкала является асимптотой гиперболической шкалы п; ш.
Отрицательные части шкал v2 и п; т служат для решения задач расчленения сложных систем на более простые равноустойчивые системы см. 3.
3. Эквивалентные критические системы нагрузок рамы
1. Критическая совокупность нагрузок для однопролетной
двухэтажной рамы
Пользуясь графиком фиг. 207 или номограммой фиг. 210, легко можно составлять различные критические комбинации нагрузок для
однопролетных многоэтажных рам. Покажем это на примерах. Пусть задана двухэтажная рама с защемленными пятами фиг. 212, а, симметрично загруженная некоторыми нагрузками Рг и Р2 в двух ярусах, и требуется выяснить различные комбинации критических значений этих нагрузок.
Варьируя величины грузов Pt и Рг и удаляя в соответствии с указаниями п. 4 1 нулевые связи, будем расчленять заданную раму на две одноконтурных равноустойчивых с ней рамы фиг. 22, б. Для каждой из этих отдельных рам используем график фиг. 207 или номограмму фиг. 210.
Для верхней рамы величина пг 1-г-. Задав для ее стоек какое-
h 4
нибудь критическое значение v N19 на этом графике по значениям
li
ординат v2 и абсциссы nt находим точку, которая будет лежать между какими-либо двумя кривыми с заданными значениями к. Интерполируя на глаз между этими значениями, находим отношение кх. Для верхней рамы погонная жесткость нижнего ригеля равна kxiZy а погонная жесткость верхнего ригеля нижней рамы равна разности
i — Jq i
4 — Итак, для нижней рамы п2 -——. По этому значению пь
Фиг. 212
380
на кривой Аоо, соответствующей абсолютному защемлению пят рамы,.
находим точку, ордината которой дает критическое значение Nt для нижней рамы. После этого получаем критические значения нагрузок
Px Nt и PN-Nx.
Задав другое критическое значение v, найдем соответственно другие значения kly п2, vf, Д и Р2.
Таким образом нетрудно по ряду точек построить график критических соотношений Рг и Р2 для заданной рамы.
Вместо того, чтобы задавать различные значения vj, а потом находите путем интерполяции соответствующие значения ки можно поступить наоборот: сначала задавать значения к1у для которых проведены кривые на графике фиг. 207, а потом по этому графику, имея определенные значения абсцисс п19 определять соответствующие значения vj как ординаты.
Такой порядок действий для двухэтажных рам более предпочтителен, так как результаты будут получены без интерполирования и, значит с большей точностью.
Пример 1. Для частного случая рамы фиг. 212 с равными погонными жесткостями всех элементов: ix f2 i3 4 в табл. 33 приводится расчет по графику фиг. 207.
Таблица 33
1
1
1
1
1
1
1
1
1
1
1
0,75
0,50
0,25
0,10
0
—0г05
—0,10
—0,15
V2 - Рг 1 i 1
5,5
5,27
4,74
3,67
2,72
1,83
1,27
0,64
—0,10
л2
0
0,25
0,50
0,75
0,90
1,0
1,05
1,10
1,15
грр0
2,47
4,75
6,03
6,85
7,17
7,38
7,48
7,56
7,63
-
—3,18
—0,52
1,29
3,18
4,45
5,55
6,21
6,92
7,73
fhpi Itll 6 ‘U; h, л2
4:
I Tt
О
L N
4
i X I
-2 0
2 4
6
8
p, -ft
1 i t
4 1
__ 1
0
L
L
т
Фиг. 213.
Фиг. 214
По данным табл. 33 построен график фиг. 213, дающий критическую совокуп-
h ry h
ность величин —Pj и —г2.
1 I
Пример 2. Для двухконтурной рамы фиг. 214 с равными погонными жесткостями всех ее элементов аналогичный расчет приведен в табл. 34.
28Г
Таблица 34
1
1
1
1
1
1
1
0,5
0,25
0
—0,10
—0,15
2 h D
4,73
3,66
1,83
0,64
—0,08
П2
0,5
0,75
1,00
1,10
1,15
КРР
4,73
5,27
5,65
5,80
5,82
1
0
1,61
3,82
5,16
5,90
На фиг. 215 приведена кривая критической совокупности нагрузок Рг и Р2 для этой рамы.
Пример В. Для двухшарнирной двухэтажной7рамы фиг. 216 с равными погонными жесткостями i всех ее элементов расчет дан в табл. 35.
г
Фиг. 216.
Таблица 35
ni
1
1
1
1
1
0,1
0
—0,05
—0,10
—0,15
V2 - Л 1 i 1
2,72
1,83
1,27
0,64
—0,08
п2
0,9
1,0
1,05
1,10
1,15
v- РгPt i V у
1,78
1,83
1,86
1,88
1,91
-р i
—0,94
0
0,59
1,24
1,99
Кривая критической совокупности для нагрузок Р и Р2 приведена на фиг. 217.
2. Критическая совокупность нагрузок для трехэтажных рам
Критическую совокупность трех грузов Р1у Р2 и Р3 можно геометрически интерпретировать в виде криволинейной поверхности в трехмерном пространстве с осями координат Р1у Р2 и Р3. Графическое пред
282
ставление о такой поверхности легче всего дать при помощи плана с горизонталями, соответствующими различным постоянным значениям одной из переменных, например, Рг. Построение таких горизонталей выполняется в полном соответствии с первым приемом, описанным в предыдущем пункте этого параграфа.
Пусть дана симметричная, симметрично загруженная трехэтажная рама фиг. 218, а.
Совершенно аналогично предыдущему мы, варьируя нагрузки Р1у Р2 иР3, расчленяем ее на три равноустойчивых одноконтурных рамы фиг. 218,6. Понятно, что при этом величины n2i2 и nziz мы получим как разности:
ТЬъЬ2 — 5 j nzlz I JCqTIqI2
Для построения горизонтали Рг v
мы по принятому значению v и величине из графика фиг. 207
li
Ъ 1с ъ
находим величину ки потом вычисляем п2 1 4 , задаем к2 и нахо
дим v
2
б
Рх Рз. После этого мы находим тг3-—и зная к
с2
р.
и
4
1
KiU
n2iz
рл
—
HZnZZ
j, 1
Г
1
LZ
nsh
7х;;;Я7777УУЯ7
I I
и J
Фиг. 218.
для случая жесткого защемления пят рамы А3 оо, для шарнирного закрепления А, 0, находим по графику фиг.
207 величину vj А5
Рг Р Р9. Так, точка за точкой строим нужную нам горизонталь. После первой горизонтали переходим ко второй, третьей и т. д.
При Рг 0 величина v г 0 и тогда в соответствии с формулой 7
—
Пример 4. В частном случае i1 i2 t3 iA ii i6 i фиг. 218, а выкладки можно провести так:
Горизонталь v-yP1 0; п1 1.
В этом случае кг —
118 6ГТГ-Т: Пг у1-143-
h 7 62 Если v —Р2 0, то Лг2 — — ; п3 — 1,127; v7,61. Далее вычисления
t DO 00
даны в табл. 36а.
Горизонталь vf Р11; 1; к1 — 0,075; л2 1,075. Дальнейшие вы-
ъ
числения даны в табл. Збб.
Аналогично производим выкладки и для других горизонталей. Сводку результатов приводим в табл. 36 в.
283
Таблица 36а
пг
1,143
1,143
1,143
1,143
2
_ 7
55
0
0,25
0,60
Vр -0
1,90
4,00
5,43
пг — 1 — 22
1,127
1
0,715
0,316
p. p,-v5-.
7,61
7,38
6,75
5,20
р 3
7,61
5,4f
2,75
—0,23
Т а б л иц а 36б
п2
1,075
1,075
1,075
1,075
1,075
2 —
—0,074
0
0,25
0,50
0,60
г _.
-Ро v —1
0
0,85
2,87
3,91
4,26
3 1 — 2П2
у
1,08
1,00
0,731
0,463
0,355
7PiPP v-
7,52
7,38
6,75
5,90
5,35
-ЛР 8
6i52
5,53
2,88
0,99
0,09
Т а б л и ц а 36в
4-
0
0
0
0
1
1
II
0
1,90
4,00
5,43
0
0,85
II
7,61
5,48
2,75
—0,23
6,52
5,53
J э-
H
II
1
1
1
2
2
2
2,87
3,91
4,26
0
1,65
2,67
4.-
2,88
0,99
0,09
5,36
3,20
1,35
P 2
3
3
3
3
3
Ap i
3,21
0
0,40
1,36
1,88
2,32
iP_ 8
—0,36
i
4,02
1
3,50
1,86
0,48
—1,32
JLP _ i
4
4
4
4,50
0
0-
Ар 1
0
0,37
0,75
0
5,33
0
iP
2,40
1,55
0,30
0
0
7,61
284
По данным табл. 36в построен график фиг. 219, а. Пользуясь им, можно графически решать различные вопросы о критической совэкупности нагрузок для данной рамы. Например, решим задачу: найти Ркр, если известно, что Р1 Р2 Р3 Р. Нужно найти точку на критической поверхности, для которой все три координаты равны друг другу. Рассекаем нашу поверхность плоскостью Р2Рз иначе говоря, проводим
биссектрису между осями -уРг и -Р3 на графике фиг. 219, а и до точкам ее пе
ресечения с горизонталями строим новый график фиг. 219, б зависимости между
— рг и — Р2-—Рз- Проведя биссектрису на этом графике находим точку ее пере-
i i i
сечения с кривой:
Р1 Р2 Р3 2,15 j.
Этот результат вполне совпадает с данными табл. 30 и 31, приведенных в примерах 3 и 4 1 этой главы.
Пример б. Для трехэтажной двухшарнирной рамы с равными погонными жесткостями всех ее стержней фиг. 220 результаты приведены в табл. 37.
Таблица 37
Ар , 1
0
0
0
0
0,5
0,5
0,5
0,5
А
i 2
0
0,47
1,25
1,89
0
0,44
0,78
1,38
тр‘-
1,90
1,41
0,60
—0,06
1,37
0,92
0,57
—0,05
4-
1
1
1
1,5
1,5
1,83
0
0
Ар i
0
0,23
0,87
0
0,34
0
1,86
0
1 5
0,87
0,61
—0,04
0,35
—0,01
0
0
1,90
График фиг. 221, построенный по табл. 37, показывает, что критическая поверхность весьма близка в этом частном случае к плоскости, отсекающей на осях координат h h
— Pi, -7Р2 и -г-Р3 отрезки 1,83, 1,86 и 1,90.
I ъ
На основе сказанного выше 1,1 и 1,4 в этой главе нетрудно видеть, что результаты, полученные нами для многоэтажных однопролетных рам в равной мере относятся к равноустойчивым рамам, изображенным на фиг. 222, а, 6.
285
В соответствии с 1,1 настоящей главы эти результаты могут быть распространены как приближенные на более общий случай, несколько отличающийся от изображенных на фиг. 222 другим распределением: жесткостей между стойками и другим распределением нагрузок между
узлами. Нужно только см. 1,1, чтобы сумма жесткостей всех стоек для каждого этажа рамы не изменялась и чтобы сумма нагрузок узлов для каждого яруса рамы оставалась прежней.
3. Критическое состояние при любом числе нагрузок
Если нагрузка упругой системы состоит из т обобщенных грузов Р1уР21. , Рт9 то критическая их совокупность может быть интерпретирована геометрически в виде некоей критической по вер х-
а 1КР, КК,Р, к,в б
Фиг; 222;
ности в яг-мерном пространстве с осями координат: Р1у Р2,. , Рт Обобщенным грузом мы называем здесь совокупность ряда внешних сил, одновременно и с сохранением пропорциональности между ними меняющихся в процессе нагружения системы. Все точки тп-мерного пространства, лежащие между критической поверхностью и началом координат, относятся к состояниям устойчивого равновесия системы; точки на поверхности относятся к различным критическим состояниям
286
наконец, точки за этой поверхностью соответствуют потере устойчивости системы.
Совершенно очевидно, что метод получения отдельных точек этой критической поверхности, примененный нами выше в пунктах 3 и 4 отого параграфа для двухэтажных и трехэтажных рам, с таким же успехом может быть применен для рам с любым числом этажей. Пользуясь этим методом, можно составить таблицы критических совокупностей этих нагрузок Р1уР2,.,Рт вполне аналогично табл. сб и 37 примеров 4 и 5. Графическое же представление критической поверхности в многомерном пространстве значительно усложнится.
В случае четырех сил PlfP2,Ps и 4 ЭТУ поверхность можно задать рядом графиков по типу фиг. 219, а, связывающих между собой три силы Р1уР2,Рз при некотором постоянном значении четвертой силы РА. Число таких графиков будет соответстствовать числу желательных интервалов между значениями Р4 0 и Р4 гпахР4. Каждый из этих графиков будет представлять собой как-бы некоторую горизонталь поверхности четырехмерного пространства, соответствующую определенному значению у р о в н я РА,
В 5 настоящей главы мы покажем, что критическая поверхность или обращена выпуклостью в сторону области неустойчивости1, или в частных случаях является плоскостью2.
4. Упрощение расчетной схемы в задачах устойчивости несвободных рам
1. Недопустимость перераспределения нагрузок между стойками
Вопрос об упрощении расчетной схемы для несвободных рам решается несколько иначе, чем для свободных рам. При расчете свободных рам, не делая большой ошибки, можно известным образом перераспределять жесткости стоек и нагрузки см. 1.
При расчете несвободных рам такое перераспределение может явиться источником больших ошибок. Это легко себе представить. Потеря устойчивости свободной многопролетной многоэтажной рамы связана, главным образом, с перекосом ее стоек. При этом деформации всех стоек одного и того же этажа рамы примерно одинаковы, независимо от того, одинаково ли загружены эти стойки или нет. При потере устойчивости несвободной рамы ее узлы в пределах теории малых деформаций не имеют линейных смещений, а только поворачиваются, причем деформации стоек одного и того же этажа могут весьма значительно отличаться друг от друга. Стойки несвободной рамы менее зависят друг от друга, нагрузка соседних стоек не так сильно отражается на предельной нагрузке данной стойки.
Покажем это на примере одноэтажной трехпролетной рамы фиг. 223 с равными догонными жесткостями стоек ih и ригелей
1
в
Рг
Г ,
Р
Г
2
i, 3
, 4
и
4
lh Lh
2‘
3
4
Фиг. 223.
1 Вышеприведенную формулировку мы здесь в известной мере заимствуем у проф. П. Ф. Папковича. См. главу IV Некоторые общие теоремы, относящиеся к устойчивости упругих систем в курсе проф. П. Ф. Папковича Строительная механика корабля, часть II, 1941. Отсылая читателя к этой весьма интересной работе, мы здесь ограничимся изложением результатов, полученных автором непосредственно.
2 В конце книги дано добавление к 3 о способз выяснения критичесЕюй совокупности грузов без использования вспомогательных графиков.
287
Расчет устойчивости этой рамы но методу деформаций приводится iK рассмотрению системы уравнений равновесия ее узлов табл. 38.
Таблица 38
Ь
3
4
1
ах -f 2 п
п
0
п
аЪ Ьп
п
0
—
п
ctj -f- 4ti
п
0
—
—
п
а4 - 21
0
Здесь. 1-1, 2-2,. , 1
а
б
F
в
ччч1
о-ч
г
11
д
vVwx4444v Sx4 444444v
Фиг. 224.
После раскрытия детерминанта критического состояния получаем следующие трансцендентные уравнения для определения минимальных критических нагрузок для разных случаев загружения рамы фиг. 224.
Примечание
Схема затруднений
Уравнение
я
б
9
а
а
t
7л3 12пг 4 п 26 п 60я2 40п 8
11 п3 - 20п2 8п
Г, Ни3 - 20п2 8ге
L 2г 2 7п 12д 4 I
п
2
а
2 3 п
а
пъ 2 -2 л
2л
— 3 п
— 5 V5 _
а — г г
Наиболее опасной является симметричная форма деформаций
Пользуясь этими формулами и табл. 1 приложения, по коэфициентам а легко находим численные значения величины v, а затем и
2кр Ддя загруженных стоек рамы при разных значениях п т-.
Ч
В табл. 39 приведены результаты расчета устойчивости для разных случаев загружения этой рамы при разных отношениях п Л.
ч
Из рассмотрения табл. 39 можно сделать следующие заключения. 1 Общая критическая нагрузка несвободной рамы фиг. 224 примерно равна сумме предельных нагрузок отдельных стоек. 2 По мере увеличения жесткости заделки концов стойки критическая ее нагрузка возра-
888
Таблица 39
Схема по
Случай загружения
Значения SP кр h
фиг. 224
Рг
ЪР
Р 2
SP
Рг
ЪР
Ра
ЪР
п 0
п 1
п 2
п 3
п 4
а
1
0
0
0
20,19
27,94
31,49
33,45
34,66
б
0
1
0
0
20,19
31,48
34,57
35,96
36,74
12
0
0
7а
40,38
55,72
62,73
66,64
69,08
г
0
72
7
0
40,38
60,17
66,91
70,16
72,05
д
lU
11а
74
7
80,76
106,28
120,44
128,94
134,47
стает. 3 Наличие других загруженных сжатых стоек как бы уменьшает жесткость заделки концов данной стойки и снижает ее предельную нагрузку.
Становится естественной постановка вопроса о приближенном определении критической нагрузки несвободных рам как суммы критических нагрузок для отдельных ее стоек, рассматриваемых изолированно как сжатые стержни с упруго защемленными концами.
2i Равноустойчивые несвободные рамы
Общие принципы образования из ряда равноустойчивых систем новой, равноустойчивой с ними системы путем постановки нулевых связей, изложенные выше в 1, в пунктах 3, 4 и 5, пригодны в равной мере как для свободных, так и для несвободных рамных систем. Постановка или удаление нулевых связей не изменяет запаса устойчивости системы, постановка ненулевых связей увеличивает, удаление ненулевых связей снижает общую устойчивость системы. При расчленении сложной системы на более простые путем удаления связей запас устойчивости одних частей может повыситься, других понизиться, общий же коэфициент запаса нерасчлененной первоначальной системы будет заключаться во всяком случае между наибольшими и наименьшими коэфициентамц запаса устойчивости отдельных частей.
Напомнив эти положения, мы ограничимся здесь приведением ряда примеров сложных и простых равноустойчивых несвободных рамных систем.
Очевидно, что симметричные, симметрично загруженные несвободные рамы по типу изображенных на фиг. 225, а, б ив равноустойчивы друг другу. Действительно, опасные формы потери устойчивости этих рам симметричны, углы поворота нижних концов стоек отдельной рамы рис. 225, в равны друг другу по величине и противоположны по направлению, то же самое можно сказать о верхних концах этих стоек, жестко связанных с ригелем. Различие между углами поворота нижних и верхних концов стоек только масштабного порядка см. 1,4, поэтому связи, которые надо поставить в системе б, чтобы обратить ее в систему а, могут быть отнесены к категории нулевых связей. Равноустойчивы с рамами а, б и в будут также системы, изображенные на фиг. 225, гид.
На основе аналогичных соображений легко сделать заключение о равноустойчивости систем фиг. 226, а, б, в. То же самое можно сказать о симметричных системах фиг. 227, а, б, в и г. Последняя система
19 Прочность и устойчивость стержневых систем
289
а
N
N1
р I р ‘г 1 i.
6
L,
L, С 2
3 З
L
L,
С
I,
У
::
S -
ч
N н
I
, DJ
p
h t, 3
1 i
h
, J Jr _
lr
J-i
i,
h
П
h
I в
3
it ,
P
t 12
p
Lj
h
2,
r1
i
Si, I
h
3i,
1 M1
2h 3i,
:
3h
4i,
г4 1
3iз 4i, :
4io
v r; г тлр1
4i3
K, P
к, - T X, ‘j
k,p k, i,
K,-3
к TP. 7
k,P k.P 1 ,. 1
h Z k lj K t,
k3p k3p 1 к 132 t
г т 4
I
13 3
км
k4P k4P T к l4 iz 1
v
ИЭ1Э к,4 i,
4 h
у
.43 1
,
К кгкг, K,ksk3k,3, И, Н к с i4
Фиг, 2251.
Фиг. 226.
1 На фиг. 225,6 шарниры должны быть расположены несколько выше узлов, на стойках.
290
фиг. 227, а дана дяя расшифровки равноустойчивости систем а я в с одноконтурной раной б Очевидно также, что можно получить равноустойчивые системы до типу фиг. 227, взяв за основу их образования
J
it
21г
Ч
2 tg
ч
—I Н1
кР
НР
Нг
1
Hi,
М,
м
I,
2i,
Jit
Г 1
1 1г 1
Р
I
Р
У Г
Г
Р
♦ Si,
. г
Г
Р
7it
1
4t2
2i,
3h
г
р р
i.
2i,
3i,
Р
Р j
.jill
J
t1 у i - ‘2 Р
.у
Р
21г
1
3Lz
Р
V 3ib
4
4il
A
Фиг. 227
вместо одноконтурной рамы фиг. 227, б одноконтурную симметричную раму с неравными жесткостями верхнего и нижнего ригелей фиг. 28,
а, б и в.
у г ♦
12
кг г
р
V ф
К,-1Р к,-TIP,
Т I
I
кг-к,Р н2-н,.
ffih
t II II I IЛ
Ut
3—i k,i,
1
6
kP
H It
7,
Hi, — -
— a
7777
d k,p
H,P
tg 11 Hf t
H3P
Hz it
H3p
3 l2
k3i,
t
I
Hg k3JP
H2hji,
H44
Фиг. 229.
По тем же соображениям равноустойчивы рамы, изображенные на фиг. 229 а, б, в. В основу их образования положена простая Г-образная рама фиг. 229, б. С этими же рамами будут равноустойчивы системы фиг. 229, г9 д.
19 291
В заключение на фиг. 230 й 231 показаны рамы go сжатыми ригелями и стойками, равноустойчивые с соответственными простыми рамами.
3. Вспомогательная задача: одноконтурная несвободная прямоугольная
рама с разной жесткостью ригелей
По аналогии с 2 решим сначала задачу устойчивости для рамы, изображенной на фиг. 232. Рама симметрична и симметрично загружена. Наиболее опасной является симметричная форма потери устойчивости:
Ра
Условия равновесия узла а:
Маа — 2тЛ 2ра — ра;
Mah 2ih ара РРь;
а
2ih п а ¥
Аналогично получим уравнение для узла 6:
2ih Ра а т 0 Ь
Приравняв нулю детерминант из коэфициентов.этих уравнений, найдем условие критического состояния рамы:
ос п а m — Р2 0.
Раскрывая скобки и пользуясь формулой 149 гл. III:
а2 — р2 - у,
приводим условие критического состояния к виду:
пт а я ти у у 0.
Решая это уравнение, мы получаем коэфициенты v‘ NKp т приведенные в табл. 40а.
с
формулы
Коэфициенты
Таблица 40а
п т
0
0,25
1
4
оо
0
9,87
10,80
12,90
16,53
20,19
0,25
10,80
11,77
13,98
17,83
21,66
1
12,90
13,98
16,46
20,85
25,18
4
16,53
17,83
20,85
26,43
32,06
оо
20,19
21,66
25,18
32,06
39,48
Пересчитав табл. 40а для коэфициента с — свободной длины стоек рамы на продольный изгиб, из формулы
получим1 табл. 406:
chy
1 Эта таблица соответствует таблице В. И. Мурашева из статьи Расчет устойчивости рам, помещенной в журнале Проект и стандарт, 1936 г., 12. При сличении таблиц надо помнить, что наши коэфициенты пт т связаны с коэфициентами В. И. Мурашева
1 1
Уд и Vs зависимостями: Vд — — и V-.
1т 2 п
292
б
н
t,
н
L
Фиг. 230.
Фиг 231.
т р
Р h hг
Пример Дано п1, тд Находим У222,6
пта пт 1 40
nJt
V-
ч
9
ю- 1л i-
1Г-
г-
Я
f4i 5. 7 пт
Фиг. 232.
29а
Т а б л и ц а 40б
Коэфициент с
0
0,25
4
1
4
4
00
0
1,000
0,956
0,875
0,773
0,699
0,25
0,956
0,916
0,840
0,744
0,675
1
0,875
0,840
0,774
0,688
0,626
4
0,773
0,744
0,688
0,611
0,555
00
0,699
0,675
0,626
0,555
0,500
т Для облегчения интерполяции по этим таблицам при решении задач по расчленению сложных систем на простые приводим также шкалярную номограмму фиг. 232, связывающую между собой величины v2, п, ту и п т. Эта номограмма построена совершенно аналогично номограмме фиг. 210.
4. Сжатая стойка с уцруго-защемленными концами
Эта задача легко может быть приведена к предыдущей. Угол поворота 9a ai конца а стержня 1а1 фиг. 233 равен:
Уа
Mgilrti Мтahn 1 91 Ilf
6EJal 6EJal Ыа1Ша1 Mla
Но между Ма1 и М1а существует зависимость:
М1а -М
К1 а
ai
гДе 1а —моментное фокусное отношение, равное двум в случае абсолютно жесткой заделки узла 1 и равное бесконечности, если в узле 1 находится шарнир. Отсюда:
d
Ля1
6
К1 а
а-
Составим условие равновесия для узла а рамы фиг. 233
6 iai
Mai Ма2 — V2-_
МаЬ 2ih apa pcpfr;
cp
a
L2a.
2‘ U ЙЙт-р,‘0
ka kyaj
Обозначив
71
3i
a
3t
12
1 1 2 — 2 — j-kXa k
h
e
0
приведем уравнение e к виду а. Приняв также обозначение:
т
3i
Ы
2-
3ig 2-
ci3
г
g
294
приводим расчет устойчивости рамы фиг. 233 к определению минимального корня v трансцендентного уравнения с:
пт а п - т у О,
ы
для решения которого нами выше приведены табл. 40а и 406 и шкалярная номограмма фиг. 232.
5. Критическая система нагрузок для несвободной рамы
Пример 1. Построить график критической зависимости между Рг и Р2 для рамы фиг. 234. Для простоты будем считать, что погонные жесткости i для всех стержней рамы одинаковы.
Кб
п—:
Ь К
А
1—
г —
Я
Фиг. 233.
Фиг. 234.
В нашем расчете будут фигурировать коэфициенты защемления пг и пг1 для стойки 12 и коэфициенты и2 и т для стойки Л23. В соответствии с формулами f и g
3 _135;
1 ,
1711 П 2 I —
1 л 1
2 — —- 2 2 оо
2-1 2- i
,2 оо
т2 оо;
2-
2 ——
1
оо
- 3,5
Весь расчет запишем в табл. 41.
Таблица 41
5 м
II
II
0
5
10
15
20
25
24
1
3,50
3,50
3,50
3,50
3,50
3,50
3,50
1 1
1,68
2,07
2,60
3,30
4,34
6,78
6,05
171
- 1,82
—1,43
—0,90
—0,20
0,84
3,28
2,55
3,50
3,50
3,50
3,50
3,50
3,50
3,50
п2
5,32
4,93
4,40
3,70
2,66
0,22
0,95
т2
оо
оо
оо
оо
оо
оо
оо
V2 —
v2 —
33,3
33,1
32,5
31,6
29,8
21,5
25,9
-JLpv-vf-
33,3
28,1
22,5
16,6
9,8
—3,5
1.0
295
Строки п1э m17i2 т2 3аполняем до начала расчета. Строку пх т4 заполняем с пси мощью номограммы, строку т1 и п2 получаем с помощью вычитания, строку v опять получаем при помощи номограммы. По данным табл. 41 построен график фиг. 2351 критической зависимости между нагрузками Рг и Р2.
На фиг. 236 изображен график зависимости между продольными усилиями Nx и Лг2 верхней и нижней стоек, соответствующий критическому состоянию рамы. Кривая этого графика имеет две асимптоты:
h
TL
— Лл 31,36 и ЛТ, 42 39,48 Ч Ч hp t
Г” f
о
QCVJ
cU
A
Фиг. 235
Фиг. 236.
V7V-
Из рассмотрения этого графика мы заключаем, что наличие продольного усилия
в верхней стойке может оказать сильное влияние на величину критического усилия для нижней стойки и наоборот. i
Пример 2. Представить графически критическую поверхность Р2, Р2, Р3 для неразревной стойки фиг. 237, а.
ti
V
4
У
у
V -о
Zi
it
-2it
3i
o
у у у V,
7777777777777,У
Фиг. 237.
го
Фиг. 238.
Рассматриваем систему, состоящую из трех равноустойчивых частей, шарнирно между собой связанных фиг. 237, б. Тогда по формулам и g:
U
o;
3
mi2
T2
3
. 2
21
1
YFlc
2
nz
3 2
со 1
II
2
in ;
3
s
CO
II
о
1.
ч
1 На фиг. 235 и 236 двойными кружками отмечены точки, соответствующие допущениям В. И. Мурашева см. ниже п. 6.
Попутно обращаем внимание читателя на следующее: идеально прочный прямолинейный стержень, растягиваемый бесконечно большим усилием, становится как бьг абсолютно жестким для деформаций изгиба.
296
Кроме того:
Р JL р —. 1 2 — v 3
или
Т-Л-vl; -у-Ра 2vt-v;; Ap3 3v_2v.
Расчет, произведенный по номограмме фиг. 232, затем был уточнен. При этом былоиспользовано критическое условие
D 4а2 i 42 -f Зз - О,
v — —4х,а1 —8y. _
из которого была получена формула а3 ——. По заданным значениям
3 4аа ах _
и v2 определялись по табл. 1 приложения коэфициенты ах, а2, и затем по значению а3 — значения v3. Результаты представлены на графике фиг. 238 и в табл. 42.
Таблица 42
Ар i
0
0
0
0
5
5
5
5
Ар t
0
10
20
26
0
о
15
21
Ар3
39,4
26,94
12,88
2,20
33,01
26,60
11,65
0,16-
4-
10
10
10
10
12,5
12,5
12,5
15,0-
АР -
Т2
0
О
10
14
0
2,5
7,5
0
АР i 3
25,70
18,42
9,19
—0,51
20,2
15,6
3,31
О
Пример 3. Выяснить критическую зависимость между грузами Plt Р2, Р3 для симметричной рамы фиг. 239, а. Дано fa 2fr
tfj
Л,
Л
J
р,
в
1
г 1
1 п
Й Ml
jYj
г. 4
Л
к
К
‘
О
У 9 JT
г
✓
с
г
I
л
♦
УР
i
it
с,
и
I ,
1г УУ
IJ
г
1-С
г I
ц
I 1
У
;; V.
Фиг. 239.
Подразделим раму на части фиг. 239, б. При потере устойчивости рамы средние ригели h находятся в состоянии чистого изгиба. Поэтому, вычисляя по формулам f и g коэфициенты пит для средних ригелей, примем моментные фокусные отношения -1.
297
Таким образом получим:.для верхней стойки
n1
3i2
-т 1 1
2- — 2 Ц-
оо —1
5
1 1. v
-для средней стойки:
для нижней стойки:
М2 —
i — i
ff
5 г m, — — ; 2 2 i
m3 0.
Исключая из этих зависимостей неизвестные i и f, найдем:
1 5; т1-п2 — 5; 7п2 л8 5; т3 0.
Кроме того
Р _чч.
ГгТ
PlP
ч 21.
k
РхЛ-РЛ-Ръ —
vli
3 Ч
Л
откуда
-Р1 ч1; 1 2 vl-v; 4 ps5:VI — vi-
С помощью номограммы фиг. 232 расчет выполняется очень просто1. Мы приводим его здесь полностью в табличной форме. Заменим сначала верхний ярус рамы с его нагрузками эквивалентным коэфициентом защемления л2 для верхних концов
стоек среднего яруса табл. 43а.
Таблица 43а
ni —
Ар — v2 __ i
гх -f- 5 -f- 7lo 0
га,
5
5
5
5
0
5
10
15
3,12
3,50
4,00
4,66
6,88
6,50
6,00
5,34
5
20
5,60
4,40
Получим теперь данные для проведения на критической поверхности грузов лРх, Р2, -Рз горизонтали РО, т. е. для v 0 табл. 43б.
Таблица 43б
i
1
0
5
10
15
20
v2 2 —
0
5
10
15
20
п2 —
6,88
6,88
6,88
6,88
6,88
n2 m2
4,92
5,36
5,80
6,40
7,20
,п3 5 - m211,88 - п2 m2—
6,96
6,52
6,08
5,48
4,68
m3
0
0
0
0
0
ve —
v3
17,7
17,6
17,5
17,3
16,9
.A P — 2 __ v2 — у 3 3 2 ‘ 1
17,7
12,6
7,5
2,3
3,1
Аналогично получаем данные для проведения горизонталей vf 5; vf 10irvf 15 табл. 43в.
- — 1 Приводимый ниже расчет отнял у автора всего 50 минут времени.
398
Таблица 43в
vf-
V2 — V vl
n2 — n2 4 m2
Tft2
5 - m2
m3
va
О о
v — vl
5
0
5
6,50
5,0
-1,5
6,5
0
17.6
12.6
5
5
10
6,50
5.5 -1,0
6,0
0
17,5
7.5
5
10
15
6,50
6,1
-0,4
5,4
0
17,3
2,3
5
15
20
6,50
6,92
10
0 10 6,00 4,96
0,42—1,04 4,58 6,04
0
16,8
-3,2
0
17,5
7,5
10
10
15
5
10
0
15
20
15
6,00
6,00
5,34
5,60
6,48
4,94
—0,40
0,48
—0,40
5,40
4,52
5,40
0
0
0
17,2
16,8
17,2
2,2
-3,2
2,2
15
5
20
5,34
5,88
0,54
4,46
0
16,7
—3.3
По этим данным построен график фиг. 240 критической зависимосуи между силами Р1Э Р2, Р3.
6. О допущениях В. И. Мурагиева1
Задана фиг. 241, а многоэтажная многопролетная несвободная рама, все стойки которой одновременно теряют устойчивость.
Форма деформации этой ра мы показана на чертеже пунктиром.
Для расчета устойчивости такой рамы В. И. Мурашов делает два допущения:
1 С достаточной для практики точностью может быть принято, что изгибающие моменты имеют постоянную величину по всему пролету ригеля фиг.
241,6.
2 Углы поворота на концах стоек, примыкающих к одному узлу, должны быть равны, следовательно фиг. 241, в
Фиг. 240.
Ж
ае
а
4
f
I
4
4
I
J
LJ
ае
М ab
tab
Ь
t I
l
штпмпи.ЙПЕПЕЖ
iiciiuiwini;
б
ЛШИ
е
шшш
1
VTJT7777TPT77
Фиг. 241.
к
,1
N
I
1
,
И;
7. 77Т.
1 В. И. М у р а ш е в, Расчет устойчивости рам. Журнал Проект и стандарт, 1936; 12.
ю
Как мы увидим ниже, допущение h накладывает значительные ограничения на характер приложения критической нагрузки рамы1.
Оставив пока в стороне 1-ое из этих допущений, используем второе. Составим уравнения равновесия для узлов а и Ь многоэтажной стойки фиг. 241, в. На основа а и h получим:
Ма1 Маг ———— a-Vv.
I 2-Л- 2 —
Л1 а Л2а
eb2feiafe P4;
мае421 м
аеч— Шаб lab
—1 ”—Ь 2 iab iae J а 2 tab tae 0.
2 — 2 — -
kia k2a
Сравним это уравнение с уравнением fa. Чтобы можно было при дальнейшем расчете использовать нашу номограмму фиг. 232, надо принять:
3
ta5 r
la Л2 a
Из условия равновесия для узла Ь аналогично получим:
3
т
rVrl- k
ha he t 2 2 —
к
1 б К2 Ъ
Если принять также первое допущение В. И. Мурашева о чистом изгибе ригелей, то kla к2а klb fc25 1 и
Я tК О
1аЬ 1ав
mifVr k
lba Т he
Применим второе допущение В. И. Мурашева к расчету устойчивости рамы фиг. 234 см. пример 1 этого параграфа. Погонные жесткости i всех стержней рамы одинаковы. Формулы i и к дадут:
3 Г 1 , 1 1 А е
-————J 35-
п,
1 ‘ 0.,. 2——
2 оо
тгттггЬ5
2 оо
и аналогично: п2 1,75; т2 оо.
По этим данным, пользуясь номограммой фиг. 232, мы находим:
Api v 22,5 и AP1 l2 vl 27,7.
I I
Итак, мы получаем всего одну и при этом довольно случайную нехарактерную точку2 кривой графика фиг. 235 критической зависимости между нагрузками Рх и Р рамы примера 1-го. Этого и следовало ожидать, так как условия, полученные нами на основе второго допушения В. И. Мурашева
пг 3,5; т1 1,75; п2 1,75; т2 оо,
соответствуют только одному частному случаю более общих условий задачи примера
1-го:
пх 3,5; тп1 и2 3,5; тп2 — оо;
при добавочном случайном ограничении m1 n2.
1 Такое же допущение принимается В. И. Мурашовым также и для расчета устой чивости свободных рам. ,
Эта точка на графиках фиг. 235 й фиг. 236 отмечена двойным кружком.
Пользуясь методом В. И. Мурашева, нельзя найти коэфициент запаса устойчивости для заданной системы внешних нагрузок многоэтажной рамы. В результате расчета устойчивости многоэтажной рамы по этому методу получается, вообщз говоря, приближенное выражение для одного частного случая критической системы нагрузок рамы, довольно далекого но характеру распределения нагрузок от разных возмож- ных загружений рамы.
777777777777777777
Груо Рр
5. Сопоставление запасов устойчивости при комбинированном загружении упругой системы и при загружении отдельными составляющими1
Мы будем представлять себе, что комбинированное загружение состоит из ряда обобщенных грузов. Два обобщенных груза Рх и Рг мы будем называть подобными, если оба они состоят из одинакового числа компонентов, между которыми существует соответствие в смысле их направлений и точек приложения, и если соответствующие компоненты будут пропорциональны друг другу. Короче говоря, подобный обобщенный труз может быть получен из другого подобного путем пропорционального увеличения всех его компонентов: Р2 тР1. На _ фиг. 242 показаны для примера два уз
подобных груза Рг и Р2У состоящие из че- фиг
тырех компонентов: аРу ЬР, сР, dP.
Два обобщенных груза Рг и Р2, не удовлетворяющих вышеуказанным условиям, мы будем называть неподобными друг другу.
В главе IV, 9 мы ввели представление о нагрузках осевых и искривляющих. Осевые нагрузки до потери устойчивости системы вызывают в ней только продольные усилия без изгиба. Искривляющие нагрузки в силу наличия в них некоторых компенсирующих составляющих не влияют на величины продольных усилий стержней, вызывая исключительно их изгиб. В общем случае нагрузка состоит из осевых и изгибающих составляющих. Там же 9 гл. IV мы установили, -что для искривляющих нагрузок в пределах малых деформаций упругой системы вполне применим принцип наложения, на осевые же нагрузки этот принцип, вообще говоря, не распространяется. Рост искривляющих нагрузок вызывает соответственный пропорциональный рост деформаций упругой системы. Рост осевых, сжимающих нагрузок при наличии деформаций изгиба вызывает ускоренный рост последних.
Пусть дан искривленный стержень, сжатый силами Р. Изгибающий момент в каком-либо сечении этого стержня равен произведению продольного усилия Р на соответствующую ординату искривления: M Pv. Увеличим продольное усилие в т раз, очевидно, при этом должны возрасти также и ординаты искривления стержня. Итак, множитель Р возрастает в т раз, множитель v тоже возрастает, значит произведение — изгибающий момент М возрастает более, чем в т раз, значит деформации изгиба искривленного стержня, пропорциональные изгибающему моменту, растут скорее его продольного усилия.
Совместное действие двух или нескольких осевых сжимающих нагрузок при наличии первоначального искривления стержня вызывает дополнительные прогибы, которые превышают сумму дополнительных
1 См. статьи автора в 1 Зб1рник памят1 акад. К. К. Симшського, Киев, 1933 г., стр. 225—232; 2 Сборник трудов Киевского Строительного Института, выпуск 3, Киев, 1936 г., 22, стр. 101; 3 Юв1лейний Зб1рник Акад. Наук УРСР, том 1, Куйбышев, 1944 г., стр. 559.
301
прогибов, соответствующих действию каждой из них отдельно взятой. Пусть для одной и той же упругой системы нам известны два различных неподобных критических загружения: в одном случае системой сил
Р1у в другом — системой сил Р2. Очевидно, что этим системам нагрузок при потере устойчивости системы соответствуют несколько отличные
друг от друга неподобные формы деформаций.
1 —
Если мы к упругой системе приложим нагрузку Рх у Рг или на1 —
грузку Р2 -—Р2у то ни в одном из этих случаев мы не получим кри-
тического состояния. Мы получим его, если одновременно приложим
1 — 1 —
к системе две одинаковых нагрузки: либо две Pi, либо две тР2.
2,
1 — 1 —
Но если мы приложим одновременно нагрузки - Рх и — Р2У то мы
тоже не получим критического состояния. Это вполне понятно, так как действие этих разных неподобных нагрузок не будет столь согласован-
1 n 1 — 1 — 1 — ным, как действие двух одинаковых Pi и — Pj или — Р2 и — Рг. В
1 —
то время как нагрузка — Рг будет стремиться вызывать большие про-
1 —
гибы в одном месте и меньшие в другом, нагрузка Р2 будет стре-
миться вызвать деформации несколько другого характера. Поэтому совместное действие двух половин различных неподобных критических нагрузок должно оказать меньшее действие, чем совместное действие двух половин одного и того же критического загружения.
г 4 Итак, совместное действие двух одинаковых половин — Рх и — Рг
I 2
приводит упругую систему к критическому состоянию, а совместное дей-
1 — 1 етвие двух половин разных неподобных нагрузок — Рг и — j2 не дает
еще критической совокупности нагрузок.
Обобщим вышеприведенные соображения. Пусть обобщенные нагрузки Рг и Р2 составляют некоторые части
рг тпхРх и Р2 т2Р2 8
от соответствующих их критических значений Рх и Р2.
Правильные дроби шг и тг мы будем называть относительными коэфициентами нагрузок Рг и Р2. Очевидно, что относительные коэфициенты нагрузок тх и т2 представляют собой обратные дроби от соответствующих коэфициентов запаса устойчивости кг и2:
mi AA; тг 1- Ь-. 9
Ki Р г Л2 Р2
Прикладывая одновременно нагрузки Рх ж Р2у мы получим нагрузку Рi2 Пусть относительный коэфициент этой нагрузки будет т12, а соответствующий ей коэфициент запаса устойчивости 12.
Тогда:
l-J-2 jPl4 2
где Р12—критическое значение нагрузки Рх2-
Если нагрузка Р равна критической Р, то соответствующее значение т — относительного коэфициента нагрузки равно единице т 1. Если нагрузка больше критической, то т1.
Приложив к упругой системе одновременно две подобные сжимающие осевые нагрузки с коэфициентами т1 и т2у получим для совместного их
302
действия коэфициеит тг29 в точности равный сумме коэфициентов тх и т2:
т2 подобные нагрузки. 10
Если мы загружаем одновременно систему двумя различными неподобными сжимающими осевыми нагрузками с коэфициентами mt и т2, та ввиду некоторой противоречивости, несогласованности их действия относительный коэфициент т12 будет меньше суммы тх и тг:
неподобные нагрузки. 11
Если неизвестно, подобны или не подобны одновременно прилагаемые к упругой системе нагрузки Рх и Р2, то, объединяя 10 и 11, можем вообще записать, что
nh2mi M2-
Очевидно, что, если одновременно к упругой системе прилагается несколько нагрузок Р1у Р2у Рпг то
wlf 2.-hn т1 Ь Н ЬWjf 12
Для сокращения записи вводим обозначения:
l 2.n 72 , 13
Р Г Л1
и формулу 12 можем переписать так:
тхт1 т2. тп, 12
или
или
или
Л srfcrs Pi Р 2 Р П
ИЛИ
1П
1Л
16
Истолкуем уравнение 15 геометрически. В пункте 5 предшествующего параграфа мы говорили о представлении критической совокупности грузов Р19 Р2,. , Рп при помощи критической поверхности в n-морном пространстве с осями координат Рг, Р2, Рп, подразделяющей это пространство на две части: область устойчивости и область неустойчивости.
Если совокупность сил Р1У Р2,. , Рг образует критическую систему нагрузок, то jP2 и зависимость 15 можно переписать так:
17
1 1 1 2 П
Эта зависимость в известной мере характеризует критическую поверхность. Знаменатели дробей 17 представляют собой отрезки, отсекае
303
мые на осях координат Pif Рг. , Рп этой критической поверхностью.
Эти отрезки численно равны критическим значениям Plf Р2,. , Рп, изолированно действующих компонентов общей комбинированной нагрузки
Рх 4- Рг Внесли нагрузки Ри Р2,. , Рп подобны1, то зависимость 17 превращается в равенство:
-1, 18
---.РгР, Рп
а критическая поверхность становится плоскостью в -мерном пространстве.
Если нагрузки Р1г Р2,. , Р неподобны или если не все из них подобны друг другу, то зависимость 17 превращается в неравенство:
19
I
I.J
Р1 Рг
Займемся теперь анализом этого неравенства. Каждой комбинированной нагрузке Рх Р2 рп соответствует некоторая точка с координатами Рх, Р2, Рп в тг-мерном пространстве. Если эта точка
лежит между началом координат и критической поверхностью, то упругая система устойI чива; если она лежит на этой поверхности,
то система находится в критическом состоянии;
если она лежит за критической поверхностью,
то система уже потеряла устойчивость. Пусть координаты Р1У Р2,. , Рп подобраны так, что точка лежит на критической поверхности. Для того чтобы от точки на критической поверх ности 19 перейти к точке на плоскости 18, надо по крайней мере уменьшить хоть одну из положительных координат либо увеличить по абсолютной величине хоть одну из отрицательных координат, если таковые мы допускаем по условиям задачи. Итак, в пределах положительных значений координат Р19 Р2,. , Рfi плоскость 18 лежит между началом координат и критической поверхностью, имея общие с ней отрезки на осях координат.
Используя различные обобщенные комбинированные нагрузки Р1У Р2У. , Рп, мы можем производить по-своему преобразование координат в я-мерном пространстве. Пусть Рг Р2,. , Рп будет система новых координатных осей этого пространства, причем новые координаты являются линейными однородными функциями старых координат:
Рх Q,lPl I- 12-2 Ь f пРП1
JD.К V7777777777,
Фиг. 243.
Р — 21-1 22Р2 1” I- 2TlPП1
Рп i Ь л22 i Н аппРП
а
При таком преобразовании координат тг-мерного пространства все приведенные выше в этом параграфе соображения и формулы остаются справедливыми, критическая поверхность остается прежней, начало координат остается на старом месте, оси же новых координат будут представлять собой новые лучи из этого начала
1 Если в упругой системе ввиду наличия шарниров или абсолютно жестких элементов фиг. 243 при потере устойчивости деформации локализируются имеют местный характер на небольшой ее части, то все действующие на эту часть груэы Plf Р2 Рз Рп можно считать подобными, так как все они оказывают одинаковое влияние на решающую опасную теряющую устойчивость часть упругой системы. Для рам типа фиг. 243 критическая поверхность превращается в плоскость.
304
Выбирая различные значения для параметров аи, а12,., апп, можно осуществить различные преобразования координат.
Теперь нетрудно показать, что критическая поверхность, подчиняющаяся неравенству 19, во всех своих точках направлена выпуклостью в сторону области неустойчивости и обращена своей вогнутой стороной к началу координат1. Другими словами, критическая поверхность имеет ко всех точках положительную гауссову кривизну.
Действительно, возьмем любую точку А на критической поверхности и проведем бесконечно близко от нее п прямых, проходящих через начало координат. Прямые эти надо выбрать линейно независимыми, такими, чтобы никакие три из них нельзя было пересечь прямой, не проходящей через начало координат. Эти п прямых мы примем за новые оси координат Р1У Р2, Рп. Путем надлежащего выбора параметров
преобразования а11у а12,., апп новые координаты могут быть связаны со старыми зависимостями а. Новые координатные оси пересекут критическую поверхность в п точках, бесконечно близких к А. Эти точки
отсекают на новых осях координат отрезки, численно равные Р1у Р2У. уРп. Через эти точки можно провести только одну плоскость я-мерного пространства:
В соответствии с вышесказанным эта плоскость, имея на новых осях координат общие точки с критической поверхностью, будет проходить между началом координат и точкой А. Итак, мы доказали, что в любой точке А критической поверхности эта поверхность обращена вогнутой своей стороной к началу координат, а выпуклой к области неустойчивости. Примеры 1 — 5 и графики 3 и 4 вполне подтверждают и хорошо иллюстрируют это положение.
В заключение обратим внимание на формулу 16:
Имея решения для отдельных составляющих комбинированной нагрузки и пользуясь этой формулой, можно легко определить выполняя операции правой части формулы 16 несколько преуменьшенное значение критической комбинированной нагрузки. Известно, что энергетический метод при решении задач устойчивости дает для задач критической нагрузки несколько преувеличенные значения. Используя одновременно оба приема, можно определить для критической нагрузки два значения, из которых одно будет несколько преуменьшенным, а другое несколько преувеличенным, и, таким образом, можно выяснить величину возможной ошибки такого приближенного решения.
В тех случаях, когда критическая поверхность линия близка к плоскости прямой примеры 2, 3 и 5 3, пример 3 4, формула 16 может дать сама по себе вполне достаточное по точности решение. Если
1 Это положение по праву может быть названо теоремой Н. Ф. Папковича. Хотя автор еще в 1932 г. в своих работах см. сноску в начале этого параграфа использовал для построения линий влияния продольных нагрузок на продольный изгиб стержней основную идею этого параграфа, но он не дал ей геометрического толкования, как это было сделано проф. П. Ф. Папковичем. Можно привести еще одно простое доказательство, основанное на свойствах энергетического метода.
Р.
i6
20 Прочность и устойчивость стержневых систем
305
критическая поверхность сильно искривлена, то формулы 12 —16 могут быть надежно использованы для линейной интерполяции между близкими комбинированными нагрузками.
6. Составление приближенных развернутых выражений для критической нагрузки на основе точного расчета устойчивости
В главе V, 3 и в многочисленных примерах расчета гл. VI — IX мы показали методы определения критической нагрузки рам, основанные на построении графиков по точкам, полученным на основе точного расчета. При наличии таблиц специальных функций, данных в приложении, построение таких графиков не представляет большой трудности
на приближенном решении точных трансцендентных уравнений устойчивости. В дальнейших параграфах этой главы мы покажем, как выражение для критической нагрузки может быть получено с помощью применения приближенных методов расчета.
В самом общем случае решение трансцендентных уравнений приходится основывать на угадывании приближенных значений корней с последующим их уточнением при помощи метода Ньютона и regula falsi. Здесь мы на примерах продемонстрируем другие приемы.
В 17,6 гл. III мы показали метод разложения в ряд по приближенному значению корней уравнения
f я sin х — х cos х 0.
Аналогичный прием может быть применен и в ряде других случаев. Пусть, например, нужно найти выражение для критической нагрузки рамы фиг. 244 с погонными жесткостями стоек ih и ригелей il nih. Точное решение для этого случая:
Здесь v наименьший положительный корень трансцендентного уравнения
заключается в пределах между 0 и те.
В главе III 17, 2 и 17, 4 приведены следующие разложения:
Мы можем использовать их для решения нашей задачи, представив уравнения а так:
лы для величин критических нагрузок, не связанные I с с применением специальных функций. Такие формулы. 1 для простых рам могли бы быть помещены в справоч-
Iр Однако в отдельных случаях полезно иметь простые,
I хотя бы несколько приближенные развернутые форму-
i
7777
77777 мулам должно быть совершенно элементарным. Ниже
Фиг. 244. мы покажем различные приемы построения таких фор
мул. В этом параграфе приводится способ, основаняый
77777
никах, вычисление критической нагрузки по этим фор-
1. Разложение в бесконечный ряд
1 V
П 6 2
а
Ь
с
а
306
1 V
Величина п, так же как и функция — tg — при v 7r обраща-
V JL
1
ются в бесконечность. Функцию — tg — можно представить так:
тН7вг179 d
где символом cv обозначена вся совокупность остальных членов ряда с, кроме его первого члена. Величина ov в пределах интересующего нас интервала 0vtc сохраняет конечные значения, меняется плавно и является величиной, значительно меньшей единицы. Действительно, при v 0:
So
lim Г — tg 4 г- — т— 0,09472.
v_o L V 6 2 i v-0
По мере увеличения v значения
4. 4. 4.
9те2 — Vй 25те2— v2 49л2— v2
растут, достигая при v u величины:
т riCOSv 4 1 1 v Г те2 — v2 1 — cos v — 4v sin vl 1 Л iAi0o
07Tlim —: —I — lim v 9-2—or- —. 0,10132.
L vsinv те- —v2J те v_ L те2 — v2 Sin v J те-
Представим ov в виде степенного ряда, используя при этом формулу Ь и разложение
4 4 f л. v2. v4.Vе. Ч
те2 — v2 да V 1 да да у получаем:
3T-rA A_v2 rio-ev4 4Ш0 - A v‘ е
Вернемся теперь к формулам а вс d:
n-rwriTe0 f
Умножив на 6ir2 —v2, найдем:
6 к2п 6 п 4 тс2 — Vs av v2. Г
Подставив сюда вместо cv его выражение е, после преобразования подобных членов получим:
г 2 гГа , да2 12-те2 а 10-те2 4 163 -17те2 в бтг Л V 2 24 V 240 v 40 320 V J
Введем сокращенные обозначения для этих сложных коэфициентов:
с 6я a4 0,0887667; g
ae 102 0,000543333; a8 0,00000537698.
Тогда:
6п2п cv2 — a4v4 -f a6ve a8v8 откуда
V4 V a8v8 - b
В пределах значений 0 v п каждый следующий член в скобках значительно менее предыдущего. Выражение h мсжет быть удобно использовано для разложения в ряд путем итерационного процесса величины v2 по степеням приближенного значения. В качестве начально 307
ного нулевого приолижения примем:
2 6л2д 6К2п ТС2Л V
v — с , те2 п 0,8225
6п —
Первое приближение v получим, подставив v0 вместо v. в правую часть h и сохраняя при этом члены до vj включительно:
2 2 г 1 4
v;vo К-
Второе приближение v найдем, подставив вместо v в правую часть h и удерживая при этом члены до v включительно:
-т-Ч-1г у5 Т‘у т 0т
Третье приближение v2 найдем, подставив v2 вместо v в правую часть h и сохраняя при этом члены до v включительно:
VV-vJ V4VP-Vo 2SvV- tvo3tv- v-
Аналогичным образом можно получить любое число членов разложения v2 в степенной ряд по степеням приближенного значения v2:
v2
:т-у7т v6-fv:. а
Подставляя вместо коэфициентов а их численные значения, мы этому ряду придадим вид:
ч 3497,20 241,150 , 5,37693 8 , 1 Гл,
— Н 3 1 I v oj- UJ
Пользуясь разложением v2 в ряд по степеням v20, можно получить величину v2 с любой степенью точности.
2. Метод последовательных приближений
Несколько скорее, причем с любой степенью точности можно получить решение с помощью метода итерации. Продемонстрируем этот метод на той же задаче решения относительно v2 уравнения:
1 V
п 6v
Для этого уравнения выше мы получили см. Ь:
CV f 6в 1 67Ti
ИЛИ
6 Л1
V
С — V2 а4 V2 я6 V2 а8. к
Эта формула может быть положена в основу процесса итерации. Нулевое приближение мы получим, ограничившись двумя членами в знаменателе к и приняв вместо va его среднее возможное значение
308
1 о
— mm в интересующем нас интервале v- — 7с:
2 6тс2г п v
— к,
С —7 Л4
Первое приближение получим в следующем виде:
Второе приближение:
ki
v2 Ьт.-П.
2_c-va4 v6K Третье:
2 _ Ъ2П v
c-vla4 — vf ae — v2a 3
и т. д. до достижения необходимой степени точности. Впрочем, для
практических расчетов можно ограничиться значительно более простыми приближенными решениями.
3. Составление приближенных формул
На том же примере для рамы фиг. 244 покажем прием составления приближенного выражения для критической нагрузки. Точное решение
а
аналогично предыдущему приводим к виду
Т ”7 30
Как мы видели выше, в интересующем нас интервале значений v2 между 0 для п 0 и va —тс2 для п со величина av плавно меняется, имея значения при v 0 и при v тг:
а0 0,09472; а 0,10132.
о 1 о 7Ъ2
Вычислим еще значение av для среднего значения v2 - 0 тг2 —.
Jmt В этом случае v 2,2215 и a q — 5 -г 0,09788. Это доволь-
47 7 СР 2,221о те 7
Г 2
но близко к Y q0 a 0,09802.
Итак, величина о7 может быть приближенно представлена как линейная функция от v2:
п
со
7 q0 -4—тг V2 0,09472 0,0006728 v2.
— и 7
Подставляем это выражение в формулу f:
п Т 7 -9472 0,0006728 v2.
Умножив обе части уравнения на тс2— v2, после преобразований получим:
тz2n п 0,8225 v2 — 0,01468 v4 1 0,00855 v2.
Заменяя в последней скобке v2 средним возможным значением v2 y0 tc2, запишем:
я2и п - 0,8225 — 0,0153 v2 v2.
30
Последний член в скобке — относительно малая величина, его множитель Vй заменяем приближенным:
V п
0 те2 п 4- 0 746 п 0,8225.— 0,0153 —
JL
Тогда приближенное значение для Vs получим в следующем виде:
кп
п -f- 0,746 ИЛИ
2_ 0,1125 П0.6715- _ п 0,746
Еще проще получим результат, дав cv в формуле f постоянное среднее значение по Симпсону:
с а0 4J , з I 0,09472 4 0,09788 - 0,10132 0,0980.
Г2
Тогда
т..0980-
Замена av средним постоянным значением вполне обоснована, так как при v 0 отношение п также равно нулю независимо от величины av, а при v тс первый член в скобках безгранично возрастает, так что конечное значение av не влияет на общий результат Величину cv надо выбирать так, чтобы возможно точнее получить результат для средних возможных значений v2 между 0 и тс2, как мы это выше и сделали. Итак,
2 2 ч Г 4 , 0,0980 , 2 9ч 1
71 я2 — V2 V- _ к —V J ,
или
ш2 п 0,828 - 0,01633 V2 V2.
Заменяя v2 в последнем члене скобки аналогично предыдущему:
2 ПП2 ПТ.2
п 0,828-0,01633- 0,747
JL
получаем приближенную формулу для v3:
v2. , n
0,828
0,747
или
тс тъ
V-
Lftfn, 0,120
n -f- 0,667 Т7Г7
n 4 0,47
n
Для оценки степени точности приближенных формул может служить табл. 44.
310
Таблица 44
0,5
1
2
3
4
3,961
5,653
7,188
7,904
8,318
3,911
5,685
7,277
7,999
8,408
3,906
5,686
7,282
8,004
8,413
3,906
5,688
7,285
8,007
8,416
h
ч
1L
8
v
п2П
п 0,746
v2
п 0,8235 -
0,151п п 0,746
v2
п 0,828 —
0,1611 п0,747
v2 точное
1 V
по формуле И — vt —
О ил я по формуле j
8,778
8,854
8,859
8,860
9,028
9,092
9,096
9,097
Из рассмотрения табл. 44 мы заключаем, что формула 1 дает ошибку в величине критической силы до 1,33, формула т до —0,11 и формула п до —0,04.
г
i Р
а
ч
I Lh
I
1
I
I
I
I
.
у м
Г,Г7Т.7Г,ГГГЛт:
h Гг
”7
i
t
i
7 r.
Фиг. 245.
Примеры приближенных формул для других случаев Для рам фиг. 245, а, б, и г в табл. 45 приводятся точные1 и приближенные решения; погрешность последних выражается в малых долях процента.
Таблица 45
Рама
Точное решение
Приближенное решение
Фиг. 243, а
ь 245, б
П — — vtgv о
1 V
п —
6 tgv
v2
к2п
4м 1,333
0,483 4 п 1,49а
v2
2 6л 1
6гс 3
3,57
Ьп 3,53
1 Точные решения были приведены выше в гл. VI, 5, пример 4
311
Продолжение табл. 45
Рама
Точное решение
Приближенное решение
Фиг. 245, в
245, г
v2
20,19 л 1,5
п 2,5
1,528
п 2,8
4гс2 п 2
п 3
3,05
При составлении этих приближенных формул мы ориентировались на следующие интервалы значений v:
Рама
Фиг. 245, а
Фиг. 245, б
Фиг. 245, в
Фиг. 245, г
Интервал
0v4
2
V
V
к
v4,493
4,493v 2
5. Симметричная одноконтурная рама с ригелями разной жесткости
ния для рамы фи
I
р I
f
1
nth
f
1
lh
mih
1
, i
36пт 6 п т т— v2 0.
v tor v
а
Величина v может здесь изменяться примерно в пределах д с от 0 до п. Пользуясь формулами 17, 4 гл. III представим приближенно:
777
Фиг. 246.
tg v А л2 — v2 Малый коэфициент cv имеет значения:
V 0
1 ,
7b
2
2
cv
0,13069
0,14005
0,15198
Среднее значение этого коэфициента примем по Симпсону;
уо 4оте сж 0,1405. Г2
Уравнение а перепишем теперь тан:
ч2_-:ъ2 Л -V2 бит. п т I — с,- — — 0.
Умножив на те2—v2, приведем оо уравнение к виду:
v2 бит Я сто2 п т — v2 с д т J п2 бит п т,
Ь
с
312
Приравняв v2 при последнем члене фигурной скобки его среднему возможному зиа
чению — и2, получим нулевое приближение для v2:
2
v2 п2
1 -
2 12
J7C2S 7С2
6пт -f 3 4 —- j п 4 т 4 _
Уточним это решение, заменив через vjj величину v2 при последнем члене фигурной скобки в с:
л2 6пт п. -j- т
v2
6пт 3 п 4- т -f а2 2 4
Подставив сюда с 0,1405, получим:
птк птуггшд
6тп 3 п т‘п
d
v2
п2 6пт 4- г т
бпт-ЬЗ п 4т 3,733
или, отбрасывая лишние знаки:
1,187 гг -m-f- 0,3053
6тп 4 3,693 п 4 т 4 0,8225
Г
v2
те2 бтгтп 44 га
6717714 3 тг 4 ти 4 3,73
n4m 1Д9 д 4т-4 0,305 6пт 4 3,69 п -4 т 0,82
е-
В приводимой ниже табличке результаты вычислений по этой приближенной формуле е сравнены с точными;
Случай
1 3; 7П со
п 3; т 3
п 3; т 0
v2
8,86
7,99
2,22
V2 ss точно —
8,870
8,006
2,215
Очевидно, что более универсальная формула е дает несколько менее точные результаты, чем специализированные формулы предыдущего раздела, при выводе которых апроксимация трансцендентных функций производилась для более узк1х пределов.
7. Составление приближенных развернутых решений для сжатоизогнутых рам на основе их точного расчета
2 Общие соображения
Пусть для всех нагрузок Рх, Р2у РЪ1. упругой рамы принимается один и тот же коэфициент запаса. Это равносильно допущению, что все эти нагрузки пропорциональны некоторому переменному коэфициенту нагрузки ку меняющемуся в процессе загружения рамы:
Р, Р к;Ъ Рг -Р; к; Р3 Pzk; а
Здесь jP , jP,.—некоторые постоянные величины.
При расчете устойчивой прочности рамы по деформированной схеме надо решить систему уравнений:
ап 4 Xodi2. Xn0in-f- aio 0; i 1; 2;.; п. b
Тут X19 X2, ., Xn — неизвестные основные параметры рамы. Приближенно рассчитывая ту же раму по первоначальной ее недеформирован-
3ia
ной схеме, как это делается в обычных расчетах, мы пользуемся упрощенной системой уравнений:
аа 2 Xlain ао 0; 1; 2;.т. г
Коэфициенты при неизвестных anj последней системы уравнений не зависят от нагрузок, не зависят также и от коэфициента нагрузки к. Коэфициенты же aj системы уравнений Ь являются функциями величин
v стержней рамы и, следовательно, в конечном счете являются
-функциями коэфициента нагрузки к:
aif aifk. d
Полагая к 0, мы тем самым как бы отказываемся от расчета рамы по деформированной схеме и переходим к обычному ее расчету по первоначальной недеформированной схеме. Поэтому
aif 0 аг е
Свободные члены ai0 будем представлять в виде произведений
я t
считая ct функциями коэфициента нагрузки к:
с с. g
Естественно принять, что
ci 0 1 Ь
Решение системы уравнений Ь устойчивой прочности можно символически записать с помощью детерминантов:
V 1. V — 2
1 77 77
и вообще:
где
i 21 22 2П
0
ЙЩ Л2 Пi
Детерминант Dt получим, заменив в j столбец я1г, я2г,., ал соответственно свободными членами а1о, апо. Понятно, что детер
минанты Dy D и значения неизвестных Х являются функциями коэфициента нагрузки к:
D Dk; Dt Dt к; Xt к. к
Для сокращения записи и удобства последующего изложения формально условимся не считать свободные члены а0 упрощенной системы уравнений с функциями коэфициента нагрузки к; мы будем считать, что они непосредственно зависят от нагрузок Ри Р2, Р3 Таким образом
б‘о 0 яо У
и для упрощенной системы уравнений с
Z Z0; Dl Dt 0; Х Х,0. ш
Приравняв детерминант знаменателя Dk нулю:
к 0, п
314
аты получим в общем случае трансцендентное относительно к уравнение, корни которого в порядке их возрастания мы обозначим:
к к2 С kz С Если бы все свободные члены я10 0, то коэфициенты ки къ, Л,. соответствовали бы первому, второму, третьему,. критическим в смысле устойчивости состояниям упругой системы. Коэфициент кг в этом случае является коэфициентом запаса упругой устойчивости рамы.
Легко видеть, что детерминант D может быть представлен в виде произведения:
D - D 0 1 — - А 1 - 0 , о
а неизвестная X так:
у Ю п
Если Dt к регулярная функция, непрерывная и конечная при конечных значениях А, к тому же не имеющая общих корней с знаменателем D А, то выражение р может быть разложено в дробный ряд:
- . К -I
где rt rf к или равно нулю, или является также регулярной функций от к. Если Dtk не удовлетворяет вышеуказанным условиям, то путем умножения числителя и знаменателя на один и тот же множитель приводим выражение Х к такому виду:
Т ___
D к
в котором будут удовлетворены поставленные выше условия, после чего выполняем разложение q.
, Величина г к по сравнению с остальными членами ряда q меняется весьма медленно. Член ряда с Ах соответствует первому разрыву непрерывности при k klf член с А2 — второму разрыву непрерывности при к к2 и т. д.
Коэфициенты At могут быть определены так. Сравнив р и q, имеем:
-л,хг,Л 2 г
При kkj детерминант й; 0 и правая часть г обращается яз неопределенность. Раскрыв ее, получим:
откуда
Используем обозначения 8 гл. VII:
I к
ч г; 8
1 1
Ki 1 ;
315
Коэфициент К мы рассматривали в гл. VII, 8 см. табл. 21. Перепишем теперь формулу q:
X,- Хг.i г -41 А2К2 -АгК2. q
.Для практических расчетов представляет интерес интервал значений к между нулем и к1:0Ск к1. Для этого интервала мы можем с достаточной точностью считать величину rt постоянной. Замечая, что щи А 0 неизвестные X, Xi и все Гу 1, получаем:
О
U
I i Li,
О
Со
-I
7л
ТГ7
ft
1 4l 2 Л3 -
Исключив теперь rt из q, найдем:
Х, Х 1 Аг Кг-1 А2 ЛГ, —1 -М. АГа —1. 21
Если Aj значительно меньше к2 кг с2, то в пределах интересующего нас интервала 0 А члены с Л2, Л3 и т. д. разложения q регулярны и имеют почти неизменную величину, так что они могут быть причислены к величине rtТогда формула 21 получит вид:
-X‘ Xli4iAT1 —1. 22
Зависимость между неизвестной X,и коэфициентом Кг линейна. Исполь-
L
3
тгптг
t
i
л
Фиг. 247,
зуя обозначения s и t, получаем:
к-—— к 1 —
л 1ki-k 1 -
к
I
Таким образом выражение 22 можно представить так:
V 1 Ь -1 1 с 1 1 — 1 Vi
q-Тс Ai-
U
23
Формулы 22 и 23 с успехом могут применяться при расчете свободных рам, потеря устойчивости которых в основном связана с линейной подвижностью их узлов; для таких рам обычно кг к2.
Если к2 мало отличается от klf a i3 к2, то можно ограничиться двумя членами дробного ряда q, присоединив остальные его члены к г:
или
2
v
25
Покажем применение этих формул на примере.
Пример 1. Вернемся к задаче, рассмотренной нами в примере 1 8 гл. VII фиг. 247. Там мы получили выражения для углов поворота и ф13, а также для изгибающих моментов по концам стержней, сходящихся у узла 1. Приведем здесь эти выражения в несколько преобразованном виде с тем, чтобы числители дробей были регулярными функциями, не имеющими общих корней со знаменателями:
6 cos V
А
qV
Величина v здесь связана с нагрузкой q следующей зависимостью:
2 5_ qJl
Ч 8 Детерминант знаменателя
D — 6 cos v — v sin v имеет следующие корни, при которых он обращается в нуль:
v1 l,351; v2 4,114; v3 6,994;.
Примем в качестве коэфициента нагрузки к величину v2, тогда:
Лх vj 1,825; 2 16,925; А, 48,916;.
Так как кгк2, то применение формул 22 и 23 вполне обосновано. Для вычисления по формуле 20 величин Аг составим сначала выражение:
kjy к v2 — 6 sin vx — sin — Vj cos vt Учитывая, что 2 7 и П0ЛУая из D 1 6 cos — VjSin v1 0,
что Vj sin vx 6 cos Vj, находим:
k1Dkl 7vx sin tv, cos vt - 42 vf cos vx.
Теперь по формуле 20 легко находим значения коэфициентов Ах:
А л1
— 6f J COS Vj 12
42 vj
0,273S
—6фа 72
vi42vf
sin v
0,900
6M0 cos Vj_ 0,2738
— MJ2 — 6 cos vx —0,2738
Затем по формуле 23 получаем следующие простые приближенные выражения:
_ 1 -0,726у gl2 в 1-0,100 12
1 —
481
М
ю
_1 -0,726У ql_ а
М 12-
16
16 1-7
Сравнивая эти результаты с формулами f и g примера 1 8 гл. VII, констатируем почти их полное совпадение. В главе VII мы эти формулы получили в результате утомительного составления таблицы численных значений величин р17 ф13, М10, М12 для разных значений нагрузки и последующей интерполяции но этим таблицам. Здесь же эти формулы получены без сколько-нибудь заметных вычислительных операций на основе общих теоретических соображений этого параграфа.
2. Симметричные, симметрично загруженные системы
В 8 гл. V мы говорили уже о том, что симметричные, симметрично загруженные системы деформируются симметрично, пока не произойдет потеря устойчивости с потерей симметрии характера деформации если, конечно, коэфициент соответствует такой потере устойчивости. Совершенно очевидно, что было бы неправильно составлять выражения для симметричных составляющих деформаций и усилий, подставляя в формулу 23 значения kl9 соответствующие потере устойчивости в виде появления антисимметричных составляющих деформаций. Но этого у нас и не получится при точном соблюдении условий, указанных нами выше при переходе от формулы р к формуле q, связанных с предварительным исключением общих множителей из числителя и знаменателя выра
жений Xi —
4l
I
3. Симметричные системы, почти симметрично загруженные
К такой категории мы будем относить системы, в симметричных элементах которых продольные усилия почти одинаковы, точнее на столько
317
близки друг к другу, что специальные функции продольно-поперечногоизгиба: а, р, у и тому подобные для этих элементов практически приходится принимать одинаковыми. Такие системы подвергаются с самого начала одновременно действию симметричных и антисимметричных загружений1. Расчет на симметричные и на антисимметричные изгибающие воздействия может быть произведен раздельно см. 8 гл. V при условии, что эти раздельные задачи будут относиться к системам, равносжатым
с заданной см. 9 гл. IV. Как показано в 8 гл. V, детерминант D
критического состояния, соответствующий общему загружению системы, может быть представлен как произведение детерминантов D и Da, из которых первый соответствует симметричному, а второй антисимметричному загружению равносжатых с заданной упругих систем:
D — DcDa 26
Значение неизвестной Xt может быть представлено как сумма двух составляющих: симметричной Х и антисимметричной Х:
XiXl Xl 27
причем каждая из этих составляющих может быть найдена независима от другой:
Xic-i и Х 28
Dc Da 4 Пусть наинизшей симметричной форме потери устойчивости соответствует коэфициент нагрузки с а наинизшей антисимметричной форма потери устойчивости той же системы коэфициент 0. Тогда общее значение неизвестной Xt может быть представлено как сумма:
х iy-,1 Х‘ iAyi Хоа _ 29
Здесь приняты обозначения:
к к Ъ kj ка
и, кроме того, через Хс и Ха обозначены соответственно симметричная и антисимметричная составляющие неизвестной X, получаемой
обычным расчетом сооружения по его первоначальной недеформированной схеме.
4. Случай, когда первая и вторая критические нагрузки близки
друг к другу
Для этого случая, возможного, главным образом, при расчете несвободных рам, могут быть использованы формулы 24 и 25, приведенные
выше. Применение их покажем на примере.
Пример 2. Симметричная рама фиг. 248 загружена в узлах четырьмя равными силами Р, причем силы действуют с небольшими эксцентриситетами с1У с2, сз с4 Требуется составить по формуле 25 приближенные развернутые выражения для углов поворота узлов р2, р3 и р4 а также выяснить степень точности этих выражений. Вследствие малой величины экцентриситетов можно считать продольные усилия стоек равными нагрузкам Р. Для простоты погонныз жесткости всех элементов рамы принимаем равными i0.
1 К системам такого типа могут быть отнесены симметричные арки с большой постоян
ной и малой временной нагрузкой.
С,
2
г-
1
1
1
to
2
to
3 и 4
1
с
1
to
to
to
и
1
Y
.5
; Г7.
iti7V, т.
6
rrr
ТГТГГГПТГГ.-
777
7 t
Г7Г777Т7ТГГ,ТГГ77Г7
Фиг. 248.
318
Каждый из эксцентриситетов с разложим на две со став ляющ ix: антисимметрична.с. ную са и симметричную с.
с1сcf;
-
4 — 1 с1
с2 с с ;
Со с — с.
Это дает нам возможность решать независимо две задачи: ную и другую симметричную.
Антисимметричная задача Система уравнений для этой задачи:
одну антисимметряч
о
ТР
л 2
1 ч
С С,
Значения неизвестных:
о Ь 4 5 Рсi ci , Рс2 с.
2 —1Г —D—v0—
_о 2 з 1 Р С1 Cl 4-2 Рс4 са
4—2Д 4 5 41 .а
Л У1 1 v 1 I
D 4 D 4i0 J
Детерминант знаменателя
Z a 2a 5-l a2 7a 9 b
7 I 113 7 _ ‘iJjj
равняется нулю при значениях: ах — —1,6965 и а2 - —5,303.
Этим значениям аг и о2 соответствуют значения 5,2497 и va 5,7817 см. табл. 1 приложения. Принимая коэфициент нагрузки равным v2, иолучим 27,562 и к2 33,427. Эти значения Агх и 2 достаточно близки друг к другу, поэтому мы при составлении развернутых упрощенных выажень-й для углов р вынуждены вместо простой формулы 23 пользоваться более сложной формулой 25. Определим па
л 4- 5 1 а 1 2
формуле 20 коэфициенты Аг и Л2 отдельно для множителей ; — ; — ,
а 4- 5
входящих в выражения а. Для первого из них :
л - Д 1 5. А Р0. 5
1_” 5e ktD к a о w
Здесь1 D0 227-2 9 27; а 50 2 5 7;
D. Ц - i 7. Ц _v_ - .
Величину Для значения vx 5,2497 найдем с помощью интерполяции
по табл. 1 приложения для функции а. При v 5,23 величина а —1,6272, при v 5,25 величина а —1,6976. Значит для v 5,24 можно иринять
da - 1,6976 1,6272
Vl
dv 5,25 — 5,23
- 3,52.
d
Точно также для v 5,25 находим —3,58. Для значения vx 5,2497 получаем:
Итак:
7
j- - 3,52 0,97 - 3,58 - - 3,52 яв - 3,58.
D l 24 - 358 - 1229-
1 При к 0 величина v 0 и а— 2.
319
Аналогично:
у А:, -2 ,Э;3П 7 -13,303 4,14.
2-5,7817
Подставив полученные численные значения в формулы с, получим:
0,377;
27 :.,:035
1— 7 27,э62 1,229
88.Ш М4 --008И-
Таким же образом находим коэфициенты Аг и Л2 для множителя —
D 0
00
и для множителя —
Al k,D к, 79: 2 с21У к2
CL -J- 2
—0,1945
J90 а.2
Al - а20 ,060о;
Л — 2 2 _ л lft0r:
2 20 к31Ук, 1605-
Теперь входящие в формулы а трансцендентные множители апроксимируем по формуле 25 рациональными функциями:
5 Г , 0,377vji , 0,00844i2 7. 1 Г, , 0.9Ч 0,1945ч, П. t
z L1tv—
а 2 Г , О.ОбОбг , 0,1605i21 f 4 ТГ L 1:Г ТчГ J 27 J 1
где
Р 2 кр 33,427
а 5
В табл. 46 сопоставлены результаты подсчета коэфициснтов формул а по их приближенным выражениям d с точными значениями.
е
а-2 D
Таблица 46
v
1
2
3
4
4,5
5
5,2
0,0384
0,170
0,485
1,385
2,765
9,76
51,8
0,0308
0,136
0,369
0,918
1,535
2,97
4,23
0,263
0,276
0,308
0,397
0,533
1,22
5,33
0,264
0,280
0,317
0,415
0,558
1,25
5,37
0,038
0,041
0,049
0,071
0,108
0,301
1,535
0,038
0,042
0,050
0,074
0,112
0,310
1,545
0,149
0Д53
0,161
0,182
0,209
0,309
0,712
0,149
1
0,155
0,166
0,191
0,223
0,223
0,732
1 2
а 5 I приближенно
D
точно
Г
_1 J приближенно
D
точно а 2 приближенно
D I
точно
320
Симметричная задача Система уравнений в этом случае имеет вид:
01
01
ct 4 2
1
Ci—c4
1
a -j- 3
c2 c3
Значения неизвестных:
_3 Pcx-c4 1 Рсг-с3
2 D 4i0 D 4i, 1 Peici 2 Рс.-с3
2 D Ы D 4 i0
Детерминант знаменателя Z
D a 2 a -f 3 — 1 a2 5 5
-5 4-lTT — 5 — lT
оораща ется в нуль при значениях аг -— — 1,382 и а2 —
О
2 — -3 — 3,618.
Этим значениям ах и а2 соответствуют величины vx 5,155 и v 5,616. Считая v2, получаем 26,57 и fc2 31,54.
Действуя совершенно аналогично предыдущему, получаем упрощенные приближенные выражения для трансцендентных коэфициентов формул f:
3_ Г 0,347 0,04852I f 5
L l-li 1-4. J Ч IV
D
-1- Г1 I 1070lJi 3921ь 1 f
d 1- l-Ч, J V1V
a 2
ZJ
1
0,1653v t 0,1587yj2
g
где:
4i
26,57
31,54
В табл. 47 для сравнения приведены результаты вычислений по формулам g и точные значения.
Таблица 47
v
1
1
2
3
4
4,5
4,8
5
0,0391
0,1772
0,5125
1,535
3,210
6,54
15,9
0,0327
0,1452
0,399
1,030
1,793
2,61
3,82
0,267
0,281
0,315
0,416
0,579
0,893
1,763
0,268
0,285
0,324
0,433
0,604
0,923
1,795
0,054
0,060
0,073
0,118
0,197
0,368
0,860
0,054
0,060
0,075
0,120
0,202
0,371
0,877
0,213
0,222
0,242
0,299
0,382
0,525
0,891
0,214
0,225
0,249
0,312
0,402
0,552
0,918
1 — П1
ъ
точно
— У 2
a 4 3 _ Г приближ
—D D
а 4- 2
ZT
женно
I
f приближенно I точно
Г приближенно
точно
Из рассмотрения таблиц 46 и 47 мы приходим к заключению, что формула 25 дает для случая близости значений кг и к2 для первой и второй критических нагрузок погрешность, примерно, до 5.
21 Прочность и устойчивость стержневых систем
321
8. Экстраполяционное определение критической нагрузки упругих рамных систем без доведения испытуемой конструкции до потери устойчивости
1. Свободные рамы
Исходя из круга идей, изложенных в предыдущем параграфе, можно предложить экспериментальный метод определения критической нагрузки упругой рамы, не связанный с доведением конструкции до разрушения.
При экспериментальном определении критической нагрузки, вызывающей потерю устойчивости рамы, последнюю следует загружать так, чтобы линия давления от нагрузки проходила по оси стержней рамы. На практике это требование не может быть осуществлено полностью, всегда останутся какие-либо эксцентриситеты, искривленность стержней и тому подобные обстоятельства, в силу которых изгибные деформации рамы появятся
сразу же в начале загружения рамы и будут развиваться по мере возрастания нагрузки. Кривая зависимости между нагрузкой Р и деформацией 8 фиг. 249 асимптотически приближается при этом к прямой Р Р Критическая нагрузка упругой системы будет найдена тем точнее, чем удачней будет угадана асимптота кривой Р, 8. Определение Ркр может быть значительно уточнено и облегчено, если, следуя Саусвеллу1, перейти к другим координатам при построении графика и откладывать на одной
оси деформацию 8, а на другой отношение деформации к нагрузке
фиг. 250. Если бы кривая на графике фиг. 249 была гиперболой, то на фиг. 250 она трансформировалась бы точно в прямую линию, котангенс угла наклона которой к оси 8 численно равнялся бы Ркр. В действительности на графике 8, получается линия не вполне прямая, она
особенно отклоняется от прямой в точках, соответствующих начальной стадии загружения рамы при малых деформациях. Для повышения точности определения Ркр надо построить несколько точек при более значительных деформациях.
Метод, предлагаемый в настоящем параграфе отличается от Саусвелловского; преобразованный график строится в других координа-
l
тах; по оси абсцисс откладываются значения коэфициента К —-р-
1-__
Р кр
а по оси ординат отношение. Линеаризация при этом получается более
1 С ау свел л. Анализ экспериментального исследования вопросов упругой устойчивости, 1932. С. П. Тимошенко, Устойчивость упругих систем, перевод под редакцией проф. В. 3. Власова, ОГИЗ, 1946 г., стр. 165. П. М. В а р в а к, Экспериментальный экстраполяционный метод исследования устойчивости стержней и рам, Питания буд1вельжп мехатки, изд. АН УССР, 1940.
822
совершенной, чем при методе Саусвелла, причем практически могут быть использованы также и отсчеты при малых нагрузках.
Для рамы, разобранной в 8 гл. VII и; в примере 1 предыдущего параграфа приведены для сравнения графики в координатах Саусвелла
фиг. 251, а и наших фиг. 251, б. Эти графики построены по данным, приведенным в табл. 48.
Таблица 48
V
0
0,5
1
1,2
1,25
1,3
1,32
1,34
1,3495
1
Pi
1
1
0
0,0087
0,0449
0,0989
0,1394
0,256
0,411
1,196
оо
II
1411 И
0,0333
0,0349
0,С449
0,0687
0,0893
0,1516
0,236
0,667
оо
1 , Щ к rnd
1
1,16
2,22
4,79
7,04
13,9
23,1
83,4
оо
1 - —
V
укр
В предыдущей параграфе мы показали, что для свободных рам спрямление графиков по типу фиг. 251,6 объясняется формулой 22 или 23. Введем обозначение:
Xiki. а
Тогда формулу 23 можно переписать так:
Ь
Величина Х соответствует расчету рамы по ее первоначальной неде-
х-
формированной схеме, поэтому отношение не зависит от величины
нагрузки. Таким образом, формулу Ь в несколько более общем виде можно записать так:
хв к 30
21 323
Здесь В и С постоянные коэфициенты. При постановке экспериментов величина к задается для каждого этапа загружения, величина X может быть замерена, три величины В, С is. кг не известны. Надо найти коэфициенты запаса устойчивости кг Для этого надо составить три уравнения для трех этапов загружения с коэфициентами нагрузки ка, къ, кс :
1-V ьВ ку-кь -CB Jkc
и затем исключить из этих уравнений коэфициенты В и С. Исключая В, получаем:
У.а-У.ь с -кпга—ккь откуда
С 1 -. 1 - К gEff Ах - К - К,
ИЛИ
У.а Хб а с 1 Ха Хс а 1 с
Решая это уравнение относительно к1У находим коэфициент запаса устойчивости свободной рамы:
h Ха Xb ка с Ь Уд Хс а СМ
Ха-ХъЬа-кс-Ха-Ус.-, или после приведения подобных членов:
Ь, Хч kb с kg Ь У.Ь с ка къ f Ус а 31
УакЪ-ксЪЬс-ка Хска-кь ‘ V
Для уточнения результатов надо этапы нагрузки выбирать так, чтобы в формулах 31 и 31 не получались малые разности больших чисел.
Пример 1. По данным для трех этапов загружения рамы Фиг. 252. примера 1 7, приведенным в табл. 48
0,25; ft v 1,44; ftc v l,69;
у, 7г -0349; f-ъ 0687: У-о -1516
определить коэфициент запаса устойчивости рамы, соответствующий такому осевому загружению рамы, при котором сохраняются продольные усилия ее стержней фиг. 252. Воспользуемся формулой 31:
0,0338-1,442 — 0,1167-1,19.1,69 ооо
0,0338-1,44-0,1167-М9д1823 ош ка
Этот ответ отличается от точного кг v2 1,34952 1,8212 меее, чем на 0,1. Метод Саусвелла требует всего двух показаний на прямолинейной части графика фиг. 251, а. Если исходить из отсчетов для ка и ку:
;r:S:5s267 ошибка 4б5-
Если исходить из отсчетов для ка и кс:
т. с 0,0087 0,256. 0 nrrTTTprTfr л оо
х-с 6,0349 -о; 1516—2Д2 ШИбКа 163ов
Наконец, если исходить из данных для kj, и кс,
-о.обвУ-Го0:гв 1 -8 35 шибка
Отсюда следует, что по Саусвеллу — нужно по ряду точек построить всю кривую графика фиг. 251, а, между тем по нашему способу для определения кг достаточно ограничиться тремя точками графика, причем среди них могут быть использованы также и точки при небольших нагрузках.
324
2. Несвободные рамы
Как мы указывали выше в 7, для несвободных рам значения кг и к2 могут быть весьма близки друг к другу. Поэтому для них экстраполяционное определение кг из опыта не может быть осуществлено на основе формулы 31. Для несвободных рам следует базироваться на формулах 24 и 25. Пользуясь обозначением:
Xi кЪ, а
эти формулы можно переписать так:
v _Л с
7-г.к1-кк2—к к
Ограничивая задачу разысканием значения кг и пренебрегая определением значения к2, первый и третий член выражения в скобке с
Ак
можно объединить приближенно в виде г—г при каком-то новом А и к2.
К К
х
Учитывая затем постоянство отношения f формулу с можно приближенно преобразовать к следующему виду:
k1 — kk2 — к
В этой формуле величины X и к считаем заданными, постоянные же коэфициенты к1у к2, В и С — неизвестными величинами. Для того чтобы найти кх из формулы 32, надо рассмотреть четыре разных этапа загружения с коэфициентами нагрузки ка, къ, кСу kd:
В С _ В С
Хак1-ктк2-ка bki_kb k2_h;.
в. с в. с Хс 1-сс Л2-сс: к1-как1-
ка
и из формул d исключить коэфициенты Ву Су к2. Это довольно необычная задача, поэтому изложим решение ее несколько подробнее. Исключим сначала1 коэфвдиент С:
С у.ак2-ка-кВ у.ькг-кь-кьВ.
Найдем теперь выражение для В:
р __ Хт 2 kg Хъ к2 kjf f a к2 kg Хс з с рЧ
h-ka к2 kfr к,-ка с2 —Лгс ‘
кх ка кх kfr ка к с
Для краткости записи обозначим:
к2 ка а2; К — ка
к 2 — кь Ь2; кх — кь Ь1;
к2 — к б2 5 1 С 1
С 2 2 1 1
Тогда уравнению е можно придать вид:
.. - -Л О; - 5 - ха - ZA - -
О
1 Здесь и в дальнейшем мы будем применять круговую подстановку букв: а, Ъ, с, а, Ъ,.
325
или после приведения подобных членов:
аА S Sbc S - Юса S Заменяя здесь:
ClA К — а 2 — К 2 — 2 а ь
Ь2с2 к — к2 къ кс кькСу
с2а2 к — к2 кс 4 ка кскПУ
получаем квадратное уравнение относительно к2;
jr Г Хс-У.Ь Ум-7с Ъ-Ха 1 — ft Г Xzhh-Xbkgh
L ai ci J L ai
-j. Xfl к fy Ус кс j 7ft fy с — А:с ка П I Г оХс кьУ.ь к кау-ксулСУ кс къХъ аХо ” L —— J-0-
Умножим его на произведение а1Ь1с1 и затем произведем замену: blCl к — къ кг — кс к — кг къ кс кьксCiUi кс 4 а кскаУ
а1Ь1 к — кх ка4- А аА.
После приведения подобных членов и сокращения на к2— кхФ О, получим уравнение:
ркгк2 —qk1 k2r 0, g
в котором для краткости записи обозначено:
Р Ха кь—кс Хъ кс — ка Хс а— й;
Ха — с а X с — а АЬ Хс а ь Лс5 33
г — Ха Ас У,Ъ кс — Йа 6 Хс а къ к2с.
Из g находим й2:
.
До сих пор мы использовали данные трех этапов загружения: Ха йа;
Хь, къ; хс йс Чтобы исключить г2 нужно использовать также данные
четвертого этапа: Xd kd. Заменим в формулах 33 данные одного из
этапов данными четвертого этапа и результаты такой замены обозначим _ _ _
Р Q 1 Тогда:
gCj — Г gf — г
рк 1 - q ркх - д
или
i — 9 рг — г гд - гд 0. 34
Это квадратное уравнение по физическому смыслу задачи должно иметь два положительных корня, меньший 1 из них должен соответствовать искомому значению кг.
Формула 31 для свободных рам в обозначениях 33 может быть записана кратко:
h-p 31
1 Что касается большего корня, то казалось бы, что он должен соответствовать к2. Но это не совсем так из-за упрощающего допущения, сделанного нами при переходе от формулы с к формуле 32 и позволившего нам в структуре формулы 32 опустить третье слагаемое.
326
Пример 2. По формуле 34 определить коэфициент запаса кг при симметричной форме потери устойчивости рамы примера 2 7 фиг. 248.
Предположим, что для четырех этапов загружения
a v 12; къ 22; кс З2; ка 42 нами получены из эксперимента значения углов поворота рх и р4. Пользуясь формулой
т-1-У4
ri 2 мы сразу же определим симметричные составляющие этих деформаций. Пусть они, нанример, соответствуют случаю с2 с3 с4 0, тогда эти данные в соответствии
ОС 1 3
с точными значениями —гг— из табл. 47 7, могут быть записаны в табл. 49.
Таблица 49
Этап загружений
а
Ъ
с
d
V
1
2
3
4
к V2 :
1
4
9
16
1 С
х т 1
0,268
0,285
0,324
0,433
Пользуясь этими данными, по формулам 33 вычисляем для этапов загружения
а, Ь, с:
р 0,268 - — 5 0,285 80,324 -3 —0,032;
7 0,268 -50,285 8 4 0,324 - 3 9 -0,968; г 0,268 — 5 0,285 8 420,324 -3 92 -43,592
и для этапов загружения a,b, d:
р 0,268 - 12 0,285. 15 0,433 - 3 - 0,240;
0,268 —12 0,285 15 4 0,433-3 16 —6,900; г 0,268 -12 0,285 15 42 0,433 -3 162 -267,36.
После подстановки этих значений в 34 получаем квадратное уравнение
0,0108 к - 1,901 42,0 0.
Корни этого уравнения
1
1,90 1,34 0,0216
Меньший из них дает искомое значение 25,9, которое отличается от точного значения кх 26,57 на — 2,5.
Посмотрим, какую погрешность даст упрощенная формула 31 рекомендованная нами для расчета устойчивости свободных рам. Применяя ее для этапов загружения а, 6, с, получаем:
_ q 0,968 b-J-o7m
Несколько более точный результат получим, использовав данные этапов загружештя a, byd:
к — б,900 28 75 1 р 0,240
В этом случае погрешность составляет 8,2. Ясно, что чем ближе будут используемые этапы загружения к критическому состоянию, тем точнее упрощенная формула 31 даст коэфициент запаса устойчивости. Очевидно, что значительно надежнее пользоваться формулой 34, причем для контроля значение кг следует определить дважды: раз по данным этапов загружения: а, Ъ, с, d и другой Ь, с, d, е.
327
9. Приближенные выражения основных формул, связывающих граничные параметры стержня
1. Формулы для расчета свободных рам
Точные формулы для расчета устойчивости рам содержат ряд трансцендентных коэфициентов а, р, а 3, у, а, у,., таблицы значений которых приводятся нами в приложении:. Пользование этими таблицами не составляет особого труда; тем не менее, в ряде случаев желательно иметь формулы, хотя бы приближенные, свободные от этих коэфициентов.
В 6 и 7 настоящей главы показаны примеры составления таких приближенных формул с помощью апроксимации предварительно полученных точных решений; там же мы указали на другой метод получения приближенных формул с помощью замены приближенными точных формул связывающих граничные параметры стержня.
Точные формулы метода деформаций имеют вид:
сят трансцендентные коэфициенты этих формул а, р, у., обычно не превышает величины тс:
Величина vkp tc имеет место для стержня свободной рамы, концы которого не могут поворачиваться, но могут сдвигаться без препятствий со стороны других стержней рамы.
Пользуясь разложением этих коэфициентов в степенные ряды гл. III, 17, 2 и сохраняя члены со степенями v не выше второй, получаем следующие приближенные выражения:
Выражения d, е и f линейны относительно величины v2, значит они линейны также и относительно продольного усилия стержня N В этом заключается преимущество этих формул. Чем меньше величина v, чем она ближе к нулю, тем точнее эти формулы.
Метод, примененный нами выше при составлении приближенных формул d, е и f, эквивалентен замене функции y fx:
Маь — 2iab р0 — р Фаь Маь;
Qab — — rf а Р а b — Ylab Qa
lab
a
Ь
Для стержней свободных рам величина
которой зави-
VTC.
С
2
2
d
Кроме того при загружении стержня по фиг. 253:
fln гг
; е
f
q
первыми двумя членами ее разложения в ряд Макл.орена:
h я 0 1 Ь
328
С геометрической точки зрения фиг. 254 это равносильно заменеотрезка АВ кривой y fx между значениями 0 и х х1У касательной АВг к ней в начальной точке А.
Такая замена вполне годится для участка кривой вблизи точки касания А, но для всего интересующего нас интервала она дает
апроксимацию менее совершенную, чем ее можно получить с помощью прямолинейной секущей А2В2- Секущую эту мы предлагаем проводить так, чтобы предельная абсолютная ошибка в величинах ординат или что
N
ab
в
ft
V II1II
11111
А
Г я,
п _
. А —.
2
0,—
Фиг. 253.
то же самое, в величинах абсцисс, была минимальной1. Если добавить еще одно вообще говоря совершенно не обязательное пожелание, чтобы приближенные выражения для ос, р,. при значении v 0 были точными, то вместо формул d, е и f мы получим:
а 2 — 0,076v2; P l0,022v2; а -f р 3 — 0,054v2; 4 6-0,Q08v j 35
Mab iS-i- 2яi-s2 x
x 1 5-2 64 - 5 1 - 0,2 - 0,43S2 ; 36
j21-21 2 S2 2,89 - 5,35 5 — 1,29 V 0,86 V.
37
Для сокращения записи выше принято обозначение
Eef pn. i‘
В табл. 50 сопоставлены точные значения а, 3, а р и у с приближенными, вычисленными по формулам d и 35.
Примерно такова же степень точности формул е, f, 36 и 37.
Для стержня с шарниром на одном конце конце 6 точные формулы момента и поперечной силы на другом конце имеют вид:
Маъ iab а а — ab Маь
Qab — 77 Те — Ттаь Qab- 1 Если в этом требовании абсолютную ошибку мы заменим относительной, то мы получим две разных апроксимирующих секущих: одну для разыскания ординат по заданным абсциссам и другую для определения абсцисс по заданным ординатам.
Формула 36 дана для левого конца стержня. Чтобы получить формулу для правого концевого момента Мьа надо в формулах 36 и j поменять местами буквы а и Ъ, а также изменить знак на обратный.
329
Т а б л и ц а 50
v2
1
5,29
9,61
по табл.
по фор
по фор
по табл.
по фор
по фор
по табл.
по фор
по фор
Функции
1 приложения
муле
муле
1 прило
муле
муле
1 прило
муле
муле
точное
d
35
жения
d
35
жения
d
35
а
1,93
1,93
1,92
1,62
1
1,65
1,69
1,26
1,36
1,27
1,02
1,02
1,02
1,11
1,09
1,12
1,23
1,16
1,21
а 3
2,95
2,95
2,95
2,72
2,74
2,71
2,48
2,52
2,48
Т
5,40
5,40
5,39
2,80
2,83
2,7Э
0,16
0,24
1
0,16
1
Совершенно аналогично формулам 35 и 36 можно для стержней свободных рам. приближенно принять:
38
а 3 — 0,22 v2; у 3 —1,22 v2;
М1ъ - -j-2l 0,0394 v2 - А- 2 Р 2,25 70,5 —75,0 S2
v2 - 0,3 4,32 - 4,09 5;
nl. ъ MU
hb
Qb Pi-k-
39
39
40
2. Формулы для расчета несвободных рам при значениях rCv4,5 Для этого случая точно так же получаем:
а 2,446-0,119 v2; р 0,664 0,0546 v2;1
а р 3,11—0,0644 V2; у 622 — 0,629 - v2;
AT,.- ql2 1 v2
ab 15,45 V 18,15
— I 2 P 0,0593 0,2018 -0,2906¥—0,002440,03821—0,0387 v. 41
3. Формулы для расчета несвободных рам при значениях 4,5v2:r
Для этого интервала составление формул по типу 40 и 41 не представляется возможным. Величины а, 3, Маъ растут с увеличением v2 настолько ускоренно, что они никак не могут быть апроксимированы линейными функциями от v2. Выделяя иррегулярный член, претерпевающий разрыв непрерывности через оо при значении v 2к, можно составить для интервала 4,5 v 2tz следующие приближенные выражения для аир:
а 3,30 — 0,062 V2— 42 1
4тс2 — у 4 п2
р 0,37 - 0,028 v2. j
42
По своей структуре эти формулы достаточно громоздки и поэтому надо считать, что возможности практического применения их довольно ограничены.
4. Выделение иррегулярного члена, как средство составления приближенных рациональных выражений
для трансцендентных функций
Пользуясь этим приемом и приведенными в 17 гл. III разложениями трансцендентных функций в степенные и дробные ряды, нетрудно получить приближенные рациональные выражения для этих функций. Степень их точности зависит от степени сложности числа членов структуры этих выражений.
330
Пусть например, надо получить приближенное выражение коэфициента а в пределах интервала 0 v 2п.
В 17 гл, III приведены следующие формулы:
а 2 —
15
2 _
11
12 ЬОО
—
54 ООО
к
я 2 — V2 Г 1 j l 4.
L 2я2 - V2 Т 42 - v2 on - V2 1 1 1 Л
8,9372 — v2 15,452 —v2 21,812-v2 J
О
Для заданного интервала значений v между нулем и 2тс сумма всех членов кроме первого члена ряда в квадратных скобках формулы 1 представляет собой конечную непрерывную, плавно и медленно меняющуюся функцию от v. Первый же член мы его называем иррегулярным претерпевает разрыв непрерывности, проходя при этом значения оо при v 2u. Выделим этот член и разложим его в степенный ряд:
а
2п2 — v2 4тъ2 Вычитая ш из к, получаем:
4п2 — v2 15 4тс2 J
i
4 и2 16я4
ш
И
12 600 161
Л v4r_i — Л
J V54 ООО б4 J
V6.,
или
a 3 —
4
4rt2—v2
- 4,133637 у - 2,313920 - 2,265996 -. n
Сохраняя то же количество членов и ту же степень точности, перепишем формулу п так:
3-Т2-жУм336-2 2,3142,27 -2. пх
Степень точности этой формулы характеризуется табл. 51.
Таблица 51
V
1
1
1
2
3
4
5
6
По формуле дх a — По табл. 1 приложения a
1.9324
1.9324
1.7180
1.7180
1,3123 1,3120
0,5886
0,5865
1
—0,9402
—0,9544
1
—10,234
—10,318
Дадим здесь без вывода ряд аналогичных формул:
р-.ЧЧМбб4ЧйУ1258, У ;
-и Ю 1
О МП JL‘ 1,927 8,33 . ;
-tor V
— 4v
8 v
-0,1894 0i
0.
03
0.
0.
Ч
V
_l-13j.-l8,069 -l6,90 36,1-ir.; .
- тг м8 Gnr . -йг- j 2v2
— 1 2 ГУ
Эти формулы могут служить основой для составления структурно болеэ простых, jvieHee точных приближениях формул.
331
Для примера составим несколько более простых приближенных формул из формулы , пригодных для интервала значения v от нуля до 2да. Среднее значение v2
2 2те220. Сокращая формулу пх на один
20
при коэфициенте 2,27 величину qq — 02:
член, подставим вместо
1 3 —
для этого интервала можно принять v;
У
4да2
,
Применяя тот же прием, сократим эту формулу еще на один член:
4 те2
а 3 —
4 те2 — vJ
— 0,0468v2.
П3
Результаты вычислений, выполненных по этой формуле, записаны в третьей строке табл. 52; во второй ее строке даны значения по табл. 1 приложения, а в четвертой, приведены значения v, соответствующие по табл. 1 приложения значениям а третьей строки.
Таблица 52
v
1 1
1
2
3 4
5
6
а
1,932
1,718
1
1,312
0,586
-0,954
-10,32
апр
1,927
1,700
1,284
0,571
-0,895
-10,04
1,04
2,06
3,052
1
4,015
1
4,976
5,993
Точность формул по типу п2 может быть повышена при условии сужения интервала значений v, для которых она предназначена. Вообще говоря, чем ближе значение v к положенному в основу приближенной формулы vcp, тем точнее получится значение
искомой функции. При этом можно пойти даже по пути дальнейшего упрощения
структуры приближенной формулы. Пусть на основе ориентировочного расчета, например, известно, что v заключается для данного стержня рамы в пределах от 5 до 6,
среднее значение v2 для этого случая будет около 30,5 в связи с чем формула п3
несколько видоизменяется:
g3- — 0,0505v2. n4
Заменяя в последнем члене v2 его средним для данного интервала значением. v2p 30,5, получаем:
а 1,46 —
4тс5
4u2-v2
Степень точности этой формулы иллюстрируется табл. 53:
Таблица 53
n4V
V
о
5,5
6
а
-0,954
-2,836
— 10,32
пр
— 0,71
-2,82
- 9,89
упр
4,895
5,497
5,989
Если разница в значениях а и апр заметна, то разница в соответствующих им. значениях v и vnp достаточно мала.
5. Другая запись полученных формул1
Пользуясь полученными выше приближенными выражениями коэфициентов а, 3, у, а и помня, что
NabU р
можно формулы a, Ъ, j записать иначе.
1 Предлагаемые здесь формулы входили в состав доклада автора, сделанного на всесоюзном совещании по строит, механике при ОТН АН СССР в конце 1939 г. См. Известия АН СССР, 1940, 2, стр. 77.
332
Для расчета свободных рам им можно придать вид:
маь 2iab 2сра оь — 3U
Nablab - 0,152 сра 0,044 9ь 0,108 Ы МаЬ-,
43
Если на конце b стержня 1аЬ шарнир, то:
Mab 3iab-0,22 Nablat fa—bab MlbV
Г
Qab - c0 - Фа6 Nab 0,22 fa - 1,22 Ы.
44
Для расчета несвободных рам фаЬ 0 при тс v 4,5 формулу а можно переписать так:
6. Получение статическим интерполяционным методом более упрощенных
формул для расчета свободных рам
Выше, при составлении приближенных формул, мы шли по пути упрощения полученных ранее точных формул. Здесь мы применим другой прием. Мы постараемся применить формулы для деформаций поперечного изгиба, известные из курса сопротивления материалов, к более сложной задаче продольно-поперечного изгиба. Деформации, зависящие от продольной силы, будем определять как функции от окончательной взаимной деформации сдвига 1аъ концов стержня и некоторых пока неопределенных множителей сх и с2. Значения этих множителей в последующем мы подберем так, чтобы для некоторых частных случаев приближенные решения совпадали с точными1.
Перейдем к выводу формул. Стержень 1аЪ фиг. 255 будем рассматривать как консоль, заделанную левым концом а, причем сечение консоли в плоскости заделки будем считать повернувшимся на угол ра. Консоль загружена в пролете поперечным грузом Р и на правом конце 6 моментом МЪа и поперечной и продольной нагрузками Qba и Nba. Угол поворота правого конца консоли относительно левого, равный разности г — может быть получен как сумма углов поворота концов консоли от воздействия Р Mba, Qba и Nba:
Последний член правой части выражения q получен по аналогии с предпоследним: момент в корне консоли от действия Qba, равный Qbal, заменен моментом от действия Nba, равным Nbaltyab и, кроме того, введен пока неопределенный поправочный коэфициент сг.
1 См. нашу статью в сборнике 3 Исследования по теории сооружений, Госстройяздат, 1939.
а-6 МоЬ.
46
В последней формуле:
q
ш
Прогиб правого конца консоли относительно Левого, равный величине Фпь—- Ча может быть получен как сумма прогибов консоли: от воздействия Р, МЪа, Qba и 1Ъа:
л, л. Ра I 2 7 -L —6а- - I у г
vVab Va — у, 2EJ Г Г 2 ‘а6
2Е
ЗЯ
3EJ
07
Последний член правой части выражения г получен по аналогии с предпоследним: момент в корне консоли от действия Qba заменен моментом от действия -Nba, равным Nbaltyab и, кроме того, введен пока неопределенный поправочный коэфициент с2. Если бы деформации искривления стержня были исчезающе малы по сравнению с перемещениями от поворота его на угол ФаЬ, то эпюра моментов от действия продольной силы Nba превратилась бы из криволинейной в прямолинейную, пропорциональную эпюре моментов от действия силы Qba. В этом случае-
Ci — С2 1
Из условий равновесия стержня имеем:
Nab Nbai Qab Qba Р
Ра
— V. 11 лЪ I 7Т . л. м 1 V
1УаЪЧа Ъа I аЪЧаЪ J ь
V
н
4
—
Фиг. 255.
Фиг. 256.
Подставим последнее выражение для Qba в уравнения q и г; решив их относительно МаЬ и МЪа, получим:
МаЬ — Т 2а 96 3afe аЪ ЩиЪ С1 2с2—
м
I
2EJ
Ьа
Ь а — ЗДай Nba ЩаЪ С1 2с2 V
Ра2Ь
t
Г0 та ап I - oa-iaoK —х i —-z yi
Поставив требование о взаимообратимости уравнений t при замене левого конца стержня правым и наоборот, приходим к выводу, что:
— 1 2с2 — 2сг -j- 2с2,
откуда
сх — 1. и
Пользуясь формулами s и t, получаем также:
РЪ2 Q7 __ -7Л
v
л 6Я.Г ,. О. , лг - о ч , РЬ3-2Ь
Г- а й — 2Vai Vafr 3 — 4с2 Величину коэфициента с2 можно найти, поставив треоование, чтооы для какой-либо частной задачи формулы t и v давали решение, совпадающее с точным. Если взять в качестве такой частной задачи определение критического усилия для стержня со взаимно смещающимися, но не поворачивающимися концами фиг. 256, то надо принять:
Nab jr-, a i. 0; Qab 5 Подставив эти данные в формулу v, получим:
EJ
V
12 тс2 3 — 4с2 tyob — О,
откуда
з
1,054.
w
334
Итак, уравнения t и v приводятся к следующему виду:
Маь 2tab 2 ъ — 31аь 0,108 Nab 1аЬ аЬ МаЬ Qab-47 ь-21а6-1,2167Уа6фаЬ ь.
Lab
47
48
Величины Маъ и Qab мы берем здесь как в обычном расчете рам по недеформированной схеме.
Если в качестве частной задачи выбрать не предельный случай, как мы взяли выше фиг. 256, а какую-нибудь другую задачу, то мы получим несколько другое значение коэфициента с2. Пусть такой задачей будет определение критической нагрузки для рамы фиг. 257. В этом случае:
12 4 4
Л12 -14 2г 2ср ср — 31 Nlty 2с2 —2 - 2nix 2р р 0; У
Qii Q - 9-Щ Щ3-Ьег 0.
Обозначая, как обычно:
х
N1 , — v2,
приводим два последние уравнения к виду:
1
V2
п -J- 1
1 - — 1 — С2
о
0
V2
1
1 3 — 4 с2
0
Фиг. 257.
,ЧЧЧЧЧЧ
Приравнивая детерминант критического состояния нулю, после некоторых преобразований получаем
12v2
0-1
4v
, 2
У
Если принять, что ригели нашей рамы абсолютно жестки, иначе говоря, что п оо, то тогда v tt и формула у даст для с2 то же самое значение с2 1,054, которое уже нами получено выше w.
Если принять, что п 2, то v2 7,285 х и
с0 1.036.
Вид формул 47 и 48 несколько меняется:
МаЪ 2гаЪ 2 ра рь — Зфаь 0,072 NаЬ 1аЪ фа Маъ
Qab Т а 9ь 2аЬ — 1,144 Nab фоЬ Qab
Lab
Xi
47
48
При расчете рам с обычными жесткостями ригелей формулы 47 и 48 дают результаты несколько более точные, чем 47 и 48. Вообще же говоря для практических целей и те и другие формулы при разных значениях п дают достаточно точные результаты.
1 См. табл. 44 в 6,3 этой главы; При п 1 из этой же таблицы v2 5,688 и с2 1,027.
335
Для стержня с шарниром на одном конце конце 6 вывод формул значительно упрощается. Для этого случая вместо выражений s и г будем иметь:
M6a0; Mab - Qab —Qlbl Nabfyab м:ь. tO
I Л. P-a— - _L _L с bglZ ф ,
1 lYab TaJ ZEj T 2EJ -t SEJ -f C- 3EJ fab- 1.Г
Из последнего уравнения легко находим:
‘Qba —ТГ 9а - Ы CNabbb Qla- z
Величина Qla принимается здесь как для случая поперечного изгиба. Значение коэфициента с определим из условия, чтобы формула z
ТУТ n2EJ
давала точное значение УУкр-для консольного стержня длиною I,
абсолютно защемленного на одном конце и загруженного продольной нагрузкой N на свободном конце. В этом случае ра 0 и Qba a 0;
откуда
3 EJ , -ntEJ , Л
Qba 2 ЧаЬ С Фаб —
с - 1,216.
It 7
Таким образом, формулы для стержня свободной рамы с шарниром в конце Ъ получают вид:
МЬа Ъ 1
МаЬ 3iab fa -1ab 0,2164 M”ab. J 49
Qab-ZJf-a-b -1,216 50
vab
Приведем еще формулы для двух специальных случаев, которые будут полезны для приближенного решения задач устойчивости плоских рам. Будем считать, что поперечная нагрузка на стержне отсутствует.
Если оба конца стержня упруго заделаны и он расположен в конструкции так, что его поперечная силаа 0, то, исключив
из формул 47 и 48 угол поворота стержня tyab, получим:
Qab Qba 0; 1
Mab iab 9a 9b 1
Если один конец стержня упруго заделан, а другой конец Ь свободен, то, исключив из 49 и 50 угол поворота стержня фа, получим:
МЪа О Qba Qab М h -Stlsl. ф I 52
Ша 4 АаЪ1аЬ V V ;
7. Дальнейшие упрощения формул для расчета устойчивости
свободных рам
Обратимся к формулам 43. Пусть известно, что потеря устойчивости многоэтажной рамы происходит за счет перекоса ее в целом при сравнительно небольших искривлениях ее стержней. Допустим, что в этом
336
случае для стоек рамы величины углов поворота их концов ра и ср6 будут мало отличаться от углов поворота этих стоек Полагая,
что рa — Фаь мы придем к формулам:
53
Формулы эти подкупают своей простотой. Не усложняя их структуры, но учитывая, что углы сра и ь не вполне равняются углу поворота стержня введем некоторый поправочный коэфициент с перед Nabtyab в формуле для поперечной силы, который мы подберем затем так, чтобы повысить точность расчета. Тогда мы получим:
Маъ 2ia 2cpa d — 3a6;
Qab — jfb b — 2фвй — cNabb. j
1
53
В первых параграфах этой главы мы видели, что расчет устойчивости многоэтажных многопролетных рам во многих случаях может быть приведен к расчету отдельной прямоугольной ячейки фиг. 257. Применим поэтому в первую очередь формулы 53 к расчету такой ячейки и подберем оптимальное значение коэфициента с. Для этой рамы справедливы зависимости х. Уравнения Л1а Л14 0 и Qlt 0 после использования формул 53 приводятся к виду:
Исключая ip и , получаем:
с — -
12 п
12 п
1 п N1 1 п v2
В табл. 44 6,3 этой главы приведены данные точного расчета этой рамы. Используем их здесь и для ряда значений п вычислим по формуле zx соответствующие значения с см. табл. 54.
Таблица 54
п
0,5
1
2
3
4
6
8
2
у точи —
3,906
1
5,688
7,285
8,007
8,416
8,860
9,097
С
1,023
1,054
1
1,097
1,124
1,141
1,160
1,172
;з ю
о
II
3,64
5,46
7,27
8,18
8,73
9,36
9,70
погрешность в -6,8
-4,0
-0,2
2,2
3,7
5,65
6,65
Как на среднем остановимся на значении с 1,1 и определим по формуле zx значения vp, соответствующие расчету рамы по формулам 53 при с 1,1:
12тг
v2
1,1 1-М
Эти значения приведены в четвертой строке табл. 54, а в пятой записаны в процентах ошибки этого расчета, полученные путем сравнения с данными точного расчета, записанными во второй строке таблицы. В довольно широких пределах отношения п погонных жесткостей ригеля и стоек, данных в этой таблице, ошибка в величине
22 Прочность и устойчивость стержневых систем
337
критической силы нигде не достигает 70. Мы видим, что даже довольна грубые формулы 53 при значении с 1,1 дают достаточную для практических задач точность.
8. Получение статическим интерполяционным методом более упрощенных формул для расчета устойчивости несвободных рам
При деформировании несвободных рам их стержни искривляются, а узловые точки поворачиваются на месте без линейных смещений, иначе говоря, углы аЪ поворота стержней равны нулю. Составим приближенную формулу для определения концевого момента МаЪ стержня с упруго защемленными, но линейно несмещающимися концами. Применим для этого нижеследующий интерполяционный прием, поставив следующие три требования:
1 при Nab 0 формула для определения МаЪ должна иметь обычный вид:
Маъ 2iab 2сра ср6;
2 формула должна удовлетворять частному случаю стержня с двумя абсолютно защемленными концами. В этом случае:
а РЬ 0 И Nab t ,
а моменты МаЪ и МЪа должны отличаться от нуля;
3 формула должна удовлетворять частному случаю стержня с двумя шарнирными концами. В этом случае:
а -ь МаЬ МЬа 0 и Nab.
Легко видеть, что первым двум требованиям удовлетворяет следующая формула:
МаЬ - 2iab 2fa Ъ с - - Ть.
1_4Г
Коэфициент сг найдем, удовлетворяя третьему требованию:
О 2iab2va — ра с3 0 9а,
откуда
з
Итак:
МаЬ iab 7. b 54
4-UL
где
1ab
Составим теперь приближенную формулу МаЪ для стержня несвободной рамы с шарниром на конце 6. Опять применим интерполяционный прием, причем поставим следующие три требования:
1 при Nab 0 формула для определения МаЬ должна иметь обычный вид:
Мab аЬау
338
2 формула должна удовлетворять частному случаю стержня с абсолютно защемленным концом а и шарнирным концом Ь. В этом случае:
3 формула должна удовлетворять частному случаю стержня с двумя шарнирными концами. В этом случае:
Легко видеть, что первым двум требованиям удовлетворяет следующая формула:
Как показывают примеры расчета1, упрощенные формулы — 4955 дают при решении задач устойчивости достаточно точные для целей практики результаты: ошибка в величине критической нагрузки колеблется, примерно, от 2 до 60. Точность формул 43 — 46 несколько выше. Надо еще отметить, что при расчете свободных рам по формулам этого параграфа получается большая точность, чем при расчете несвободных рам.
10. Примеры приближенного расчета рам по методу деформаций
Пример 1. Составить развернутое выражение для критической нагрузки рамы фиг. 258. Из условий симметрии заключаем, что:
Углы поворота ригелей фг 0, углы поворота стоек фд. Итак, лля решения задачи надо составить три уравнения с неизвестными рх, р2 фд. Схема составления этих уравнений следующая:
Первый вариант приближенного решения. Используем формулы 43. Обозначив для краткости буквой х величину
получим систему уравнений, приведенную в табл. 55.
1 См. нашу статью Приближенный расчет устойчивости плоских упругих рам по
методу деформаций в сборнике 3 Исследования по теории сооружений, Госстройиздат, 1939.
а— К ЧъФ 0,
Коэфициент с4 найдем, удовлетворив третьему условию:
20,19
откуда
с4 —0,1553.
Итак:
55
1 М12 Мг1 0; 2 2М21 Мы 0; 3 2Qn Q22- 0.
х 0,108
Nk
0,103v2,
a
1
22 339
Таблица 55
Ъ
Фа
1
4 п 6 — х
2 п
- 6 X
0
2 п
. х 4п3-т
- 7
0
— 6 X
1
СО
9 - 8,45 ж
0
Для определения критической нагрузки надо составить детерминант из коэфициентов трех этих уравнений, приравнять его нулю и решить относительно х полученное кубическое уравнение. Величину NKp найдем затем по формуле:
N —
хл
V 0.108А
Ь
Мьгвидимчтоэтот вариант не дает возможности составить простое развернутое выражение для критической нагрузки.
Второй вариант приближенного решения. Используем формулы 47 и 48. Система уравнений примет при этом вид, данный в табл. 56.
Таблица 56
1
и
Фа
1
4 п 6
2 п
- 6 ж
0
2 п
kn 3
-3
л
0
- 6
- 3
9 — 8,45 х
0
Система уравнений при использовании формул 47 и 48 не получается канонической, но детерминант критического состояния приводит нас к линейному относительно х уравнению. Решив это уравнение, получим:
дг п п 2 кр п2 2,824л1,233 h
С
Третий вариант приближенного решения. Используем формулу 53 при значении с 1,1. Система уравнений, получающихся при этом, дана в табл. 57.
Таблица 57
1
2
1
kn -f 6
2 п
1
-6
0
2 ть
Ьп 3
-3
0
—6
-3
9—0,825 v2
0
Решив эту систему уравнений, получим:
_ п п _2_
кр п Зп 1,5
10,91,
ЬГ
d
В примере 1 1 этой главы приведены данные точного расчета этой рамы. В нижеследующей табл. 58 мы сопоставляем данные точного расчета, приближенного расчета по формуле с и приближенного по формуле d.
340
Таблица 58
Расчет
п
0,268
0,714
1,348
3,428
8,79
Точный. . По формуле с d v2 v2 v2
3
2,91
2,79
5,333
5.09
5.09
6,75
6,50
6,68
8,333
8,11
8,60
9,187
9,06
9,82
Пример 2. Составить приближенное развернутое выражение для критической нагрузки рамы фиг. 259. Рама и ее нагрузка симметричны, верхний ригель рамы считаем абсолютно жестким. Ввиду симметрии имеем:
1 1 Ъ ь Г з з о 0 0.
Р
Р
т, у
ni, v
1
2
3
it
if if
Г
ni, 2
т, 3
ж
Фиг. 258.
ЧЧЧЧЧЧЧЧЧЧЧ Фиг. 259.
Поперечные силы на стойках равны нулю, поэтому при расчете можно пользоваться формулой 51. Для расчета достаточно составить одно уравнение равновесия узла 1 с неизвестным
М10 Мг1 М12 tx pj — 0 —
Ph
1 -
Ph
2n2cpx jpi;
h fi — h -
Ph
1 —
ti ft _ о Ph 4 Сократив это уравнение на найдем эатем:
_ 6п 1 п Чг р бп 8,40 h
Точное решение этой задачи приводит к трансцендентному уравнению:
Ь Vsinv tgvy
е
О
В нижеследующей табл. 59 приведены для сравнения данные точного и приближенного расчета.
Таблица 59
Расчет
п
-0,016
0,215
0,672
1,812
10,56
Точный v2
1
2,25
4
6,25
9,00
Приближенный v2
1,075
2,33
4
6,09
8,86
Погрешность 7,5
3,55
0
-4,2
-1,6
341
Пример 3. Рассчитать на устойчивость симметричную двухэтажную трехпролетную раму фиг. 260 примера 2 1 этой главы; результаты приближенных расчетов по формулам 47—48 и по формулам 53 сравнить между собой и с точным решением. Погонные жесткости ригелей и стоек второго этажа равны it, ригелей и стоек первого этажа равны соответственно nix и 2it. Величины v для стоек обоих этажей одинаковы, для ригелей они равны нулю.
Наиболее опасной является антисимметричная форма потери устойчивости. Задача приводит к составлению и решению шести уравнений с неизвестными ф13, ф3б, ¥и ¥з
Г г г
A 2i i, 2 i, iir
i
3
2i.
i
I,
ni, 4
2i,
Pl
ni, i
21,
i 1 4 П1, T
2i,
S
T
it
3
8
6
4
г
s
ТТТТТТТТТТТТТТТТТТТТтаТТТТТТТТТТТТИ
Фиг. 260.
f —1 — 1
р
ъ
J
i
i 1
о
4 6 8
Фиг. 261.
to 12
И
ft
Первый вариант приближенного решения. В этом случае мы пользуемся формулами:
Маь 2iafi 2в — Зфад 0,108ЛгвйФа5 47
48
Система уравнений дана в табл. 60.
Таблица 60
♦и
35
ft
ft
з
4
1
—а
0
1
1
1
1
0
0
—а
0
0
1
1
0
-Ь
0
4
1
1
0
0
-Ь
0
1
7
0
1
0
-Ъ
-2 Ь
1
0
б2л
п
0
-Ь
-2 Ъ
0
1
п
65д
0
Здесь для сокращения записи обозначено:
а 4 - 0,4053 v2; Ъ 3 - 0,054 v2. g
Исключив неизвестные ф13 и ф35, систему уравнений приводим к виду табл. 61.
Таблица 61
1
2
Ь
п
1
4-с
1 —С
1 —с
— с
0
1-с
1-с
— с
1 —с
0
1-с
—с
64-2га—Зс
г
1
00
Л
0
—с
1 —с
п—Зс
6Ъть — Зс
0
Здесь принято еще одно обозначение:
Ь __ 3 - 0,054v2 а 4 - 0,4053v
h
342
Приравняв нулю детерминант этой системы уравнений, получим условие критического состояния:
D 3 - с 9п 121 - 80с Юс2 9л 907 - 1141с 203с2 0.
Pk
О
Теперь мы задаем ряд значений v2 — , по формуле h вычисляем соответствующие
им значения с и затем из квадратного уравнения i находим больший положительный корень п. Результаты вычислений записаны в табл. 62 х.
Таблица 62
v2
0
2,25
4,0
6,25
7,5625
8,0
7,74
71
-0,310
-0,050
0,341
1,861
14,17
-2,34
оо
Второй вариант приближенного решения. Используем формулы;
Маь 2tafi 2ра4- уь Зфд;
Qab — 7— 9a f6 2Фab —
1аЪ
53
Совершенно аналогично предыдущзму задача приводится к четырем уравнениям табл. 61 с неизвестными у1э р2 з 4 но только коэфициент с имеет теперь другое значение:
9
с
12—l,lv
к
В результате решения квадратного уравнения i получаем данные, приведенные в табл. 63.
Таблица 63
v2
2,05
3,64
5,69
6,88
7,50
7,88
8,19
п —
0,061
0,262
1,163
2,576
5,061
10,70
оо
Приведем здесь также данные точного расчета табл. 64.
Таблица 64
V2
0
2,25
4,0
6,25
6,76
7,29
7,56
7,67
7,848
71
-0,310
-0,004
0,390
1,660
2,441
4,385
7,83
12,3
оо
Данные этих трех таблиц нанесены на график фиг. 261, точному расчету соответствует сплошная линия, первому варианту приближенного расчета точки в квадратиках, а второму крестики.
1 Значение v2, соответствующее абсолютно жесткому ригелю первого этажа поо, определяем, приравняв нулю коэфициент при 9пъ в уравнении i. Находим с3, после
чего по формуле h получаем v2.
343
Итак, приближенные решения вполне удовлетворительны для практических расчетов. Дальнейшее упрощение расчета получим, заменив трехпролетную раму фиг. 260 однопролетной в соответствии с указанием 1,1 гл. XI.
Выяснение критической совокупности грузов без использования вспомогательных графиков
Пусть нужно определить критическую совокупность величин vlf v2, v,. Из условия критического состояния определяем какую-либо табулированную функцию р уп одного из этих коэфициентов ylt v2, v8,. через табулированные функции остальных коэфициентов. Задавая числовые значения последних, находим числовое значение этой функции р vn и затем по таблицам получаем величину vn. Таким образом найдена одна точка на критической поверхности. Получив аналогично еще ряд точек, строим горизонтали критической поверхности.
Пример. Степенчатая стойка фиг. 75 загружена силой Р в узле О и силами Р1 и Р2 в узлах 2 и 2.
Решая задачу аналогично примеру 3 4 гл. VII, получаем условие критического состояния в следующем виде:
2т2 1г3г2ж72 0- а
Чтобы построить горизонталь v1 0 критической поверхности, задаем v1 0, a v2 даем ряд последовательных значений например: v2 l; 2;., и для каждого из них
по формуле а находим числовое значение и потом по табл. 3 приложения —
соответствующее значение v3. Так же строятся затем горизонтали v1 l; 2; 3 и т. д.
ПРИЛОЖЕНИЕ
ТАБЛИЦЫ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
Таблица 1
Коэфициеиты формул метода деформаций а, р, а-ffJ, у, а, у
для сжато-изогнутых стержней
V
а
Р
V
1
а
V
0
2,00000
1,00000
3,00000
6,00000
3,00000
3,00000
0
0,10
1,99933
1,00017
2,99950
5,99400
2,99800
2,98800
0,10
0,20
0,30
1,99733
1,00067
2,99800
5 , 97600
2,99199
2,95199
0,20
1,99399
1,00150
2,99550
5,94599
2,98195
2,89195
0,30
0,40
1,98931
1,00268
2,99199
5,90398
2,96785
2,80785
0,4
0,50
1,9832J
1,00420
2,98748
5,84996
2,94964
2,69964
0,50
0,60
1,97589
1,00607
2,98195
5,78391
2,92725
2,56725
0,60
0,70
1,96712
1,00829
2,97541
5,70583
2,90060
2,41060
0,70
0,80
1,95697
1,01088
2,96785
5,61571
2,86959
2,22959
0,80-
0,90
1,94542
1,01385
2,95926
5,51353
2,83411
2,02411
0,90
1,00
1,93244
1,01720
2,94964
5,39928
2,79402
1,79402
1,00
1,01
1,93107
1,01755
2,94862
5,38719
2,78975
1,76965
1,01
1,02
1,92967
1,01792
2,94759
5,37498
2,78543
1,74503
1,02
1,03
1,92827
1,01828
2,94655
5,36265
2,78107
1,72017
1,03-
1,04
1,92685
1,01865
2,94550
5,35019
2,77666
1,69506
1,04
1,05
1,92541
1,01902
2,94444
5,33762
2,77220
1,66970
1,05
1,06
1,92396
1,01940
2,94336
5,32493
2,7676
1,64409
1,06
1,07
1,92250
1,01978
2,94228
5,31211
2,76313
1,61823
1,07
1,08
1,92102
1,02017
2,94119
5,29918
2,75852
1,59212
1,08
1,09
1,91953
1,02056
2,94008
5,28612
2,75386
1,56576
1,09
1,10
1,91802
1,02095
2,93897
5,27294
2,74916
1,53916
1,10
1,11
1,91650
1,02135
2,93785
5,25964
2,74440
1,51230
1,11
1,12
1,91496
1,02175
2,93671
5,24622
2,73960
1,48520
1,12
1,13
1,91341
1,02215
2,93556
5,23268
2,73474
1,45784
1,13
1,14
1,91184
1,02256
2,93441
5,21902
2,72983
1,43023
1,14
1,15
1,91026
1,02298
2,93324
5,20523
2,72488
1,40238
1,15
1,16
1,9086
1,0234
2,9320
5,19124
2,71987
1,37427
1,16
1,17
1,9072
1,0238
2,9309
5,17736
2,71481
1,34591
1.17
1,18
1,9053
1,0242
2,9295
5,16276
2,70969
1,31730
1,18
1,19
1,9038
1,0247
2,9285
5,14900
2,70455
1,28845
1,19
1,20
1,9021
1,0251
2,9272
5,13448
2,69934
1,25934
1,20
1,21
1,9005
1,0255
2,9261
5,12012
2,69410
1,23000
1,21
1,22
1,8989
1,0260
2,9248
5,10540
2,68876
1,20036
1,22
1,23
1,8970
1,0264
2,9234
5,09038
2,68340
1,17049
1,23
1,24
1,8953
1,0269
2,9222
5,07570
2,67796
1,14037
1,24.
1,25
1,8938
1,0274
2,9212
5,06126
2,67241
1,11000
1,2.
1,26
1,8920
1,0279
2,9198
5,04590
2,66699
1,07938
1,26
1,27
1,8901
1,0283
2,9184
5,03036
2,66140
1,04850
1,27
1,28
1,8884
1,0288
2,9172
5,01520
2,65578
1,01737
1,28
1,29
1,8866
1,0293
2,9159
4,99976
2,65008
0,98598
1,29
1,30
1,8848
1,0298
2,9146
4,98420
2,64434
0,95435
1,30
1,31
1,8830
1,0303
2,9132
4,96836
2,63854
0,92245
1,31
1,32
1,8810
1,0307
2,9117
4,9520
2,63271
0,89030
1,32
1,33
1,8792
1,0312
2,9103
4,93616
2,62681
0,85790
1,33-
1,34
1,8774
1,0317
2,9091
4,92040
2,62085
0,82525
1,34
1,35
1,8755
1,0322
2,9077
4,90426
2,61482
0,79233
1,35
1,36
1,8736
1,0327
2,9063
4,88780
2,60878
0,75917
1,36
1,37
1,8717
1,0332
2,9049
4,87136
2,60265
0,72574
1,37
1,38
1,8697
1,0333
2,9034
4,85460
2,59646
0,69206
1,38
1,39
1,8677
1,0342
2,9019
4,83786
2,59022
0,65813
1,39
1,40
1,8658
1,0347
2,9006
4,82114
2,58394
0,62394
1,40
1,41
1,8639
1,0353
2,8992
4,80436
2,57760
0,58949
1,41
1,42
1,8619
1,0358
2,8977
4,78718
2,57118
0,55478
1,42
1,43
1,8599
1,0364
2,8962
4,77006
2,56472
0,51982
1,43
1,44
1,8578
1,0369
2,8947
4,75260
2,55820
0,48459
1,44
1,45
1,8558
1,0375
2,8933
4,73536
2,55161
0,44911
1,45
1,46
1,8537
1,0380
2,8917
4,71760
2,54498
0,41337
1,46
1,47
1,8516
1,0386
2,8902
4,69976
2,53828
0,37738
1,47
1,48
1,8497
1,0391
2,8883
4,68225
2,53152
0,34112
1,48
34
Таблица 1 продолжение
V
в
Y
а
Y
V
1,40
1,8475
1
0397
2,8872
4
66436
2,52471
0,30460
1,49
1,50
1,8453
1
0400
2,8853
4
64560
2,51782
0,26783
1,50
1,51
1,8433
1
0408
2,8841
4
62816
2,51090
0,23079
1,51
1,52
1,8412
1
0415
2,8826
4
61000
2,50390
0,19349
1,52
1,53
1,838
1
0421
2,8809
4
59136
2,49683
0,15593
1,53
1,54
1,8366
1
0426
2,8793
4
57280
2,48971
0,11811
1,54
1,55
1,8345
1
0432
2,8777
4
55416
2,48254
0,03003
1,55
1,56
1,8323
1
0438
2,8762
4
53560
2,47529
0,04169
1,56
1,57
1,8301
1
0445
2,8746
4
51676
2,46798
0,00308
1,57
1,58
1,8279
1
0450
2,8729
4
49760
2,46062
—0,03578
1,58
1,59
1,8257
1
0456
2,8713
4
47856
2,45318
—0,07491
1,59
1,60
1,8233
1
0463
2,8696
4
45920
2,44569
—0,11431
1,60
1,61
1,8210
1
0469
2,8679
4
43976
2,43814
—0,15397
1,61
1,62
1,8185
1
0475
2,8661
4
42000
2,43052
—0,19339
1,62
1,63
1,8162
1
0482
2,8644
4
40036
2,42233
—0,23403
1,63
1,64
1,8141
1
0489
2,8629
4
38100
2,41506
—0,27453
1,64
1,65
1,8116
1
0495
2,8612
4
36116
2,40725
—0,31525
1,65
1,66
1,8092
1
0502
2,8594
4
34100
2,39937
—0,35624
1,66
1,67
1,8069
1
0508
2,8577
4
32096
2,39140
—0,39749
1,67
1,68
1,8044
1
0515
2,8559
4
30060
2,38340
—0,43901
1,68
1,69
1,8020
1
0522
2,8541
4
28016
2,37531
—0,48079
1,69
1,70
1,7996
1
0528
2,8524
4
25980
2,36714
—0,52285
1,70
1,71
1,7369
1
0535
2,8505
4
23896
2,35893
—0,56517
1,71
1,72
1,7946
1
0542
2,8488
4
21840
2,35064
—0,60776
1,72
1,73
1,7921
1
0549
2,8470
4
19756
2,34228
—0,65062
1,73
1,74
1,7896
1
0536
2,8453
4
17680
2,33384
—0,69376
1,74
1,75
1,7871
1
0563
2,8434
4
15556
2,32534
—0,73715
1,75
1,76
1,7845
1
0571
2,8416
4
13440
2,31678
—0,78082
1,76
1,77
1,7819
1
0577
2,8397
4
112
2,30813
—0,82476
1,77
1,78
1,7794
1
0585
2,8378
4
09140
2,29942
—0,86898
1,78
1,79
1,7768
1
0592
2,8360
4
06996
2,29064
—0,91347
1,79
1,80
1,7742
1
0599
2,8341
4
04822
2,28177
—0,95822
1,80
1,81
1,7715
1
0607
2,8322
4
02636
2,27285
—1,00325
1,81
1,82
1,7689
1
0614
2,8303
4
00440
2,26384
—1,04856
1,82
1,83
1,7662
1
0622
2,8284
3
93236
2,25476
—1,09414
1,83
1,84
1,7635
1
0630
2,8265
3
96020
2,24560
—1,14000
1,84
1,85
1,7608
1
0637
2,8245
3
93776
2,23637
—1,18613
1,85
1,86
1,7581
1
0645
2,8226
3
91540
2,22707
—1,23253
1,86
1,87
1,7553
1
0653
2,8206
3
89276
2,21768
—1,27922
1,87
1,88
1,7526
1
0660
2,8187
3
87020
2,20821
—1,32618
1,88
1,89
1,7493
1
0668
2,8166
3
84716
2,19363
—1,37342
1,89
1,90
1,7470
1
0677
2,8147
3
82440
2,18906
—1,42094
1,90
1,91
1,7442
1
0684
2,8126
3
80116
2,17937
—1,46873
1,91
1,92
1,7413
1
0692
2,8106
3
77800 ,
2,16959
—1,51681
1,92
1,93
1,7385
1
0701
2,8086
3
75476
2,15974
—1,56517
1,93
1,94
1,7356
1
0709
2,8065
3
73120
2,14979
—1,61330
1,94
1,95
1,7328
1
0717
2,8045
3
70776
2,13978
—1,66272
1,95
1,96
1,7299
1
0726
2,8024
3
68400
2,12967
—1,71193
1,96
1,97
1,7269
1
0734
2,8003
3
66016
2,11943
—1,76141
1,97
1,98
1,7240
1
0742
2,7982
3
63620
2,10922
—1,81118
1,98
1,99
1,7210
1
0751
2,7961
3
61216
2,09887
—1,86123
1,99
2,00
1,7180
1
0760
2,7940
3
58800
2,08843
—1,91157
2,00
2,01
1,7150
1
0768
2,7919
3
56376
2,07791
—1,96219
2,01
2,02
1,7120
1
0777
2,7897
3
53920
2,06729
—2,01311
2,02
2,03
1,7090
1
0786
2,7876
3
51476
2,05659
—2,06430
2,03
2,04
1,7060
1
0795
2,7354
3
49000
2,04581
—2,11573
2,04
2,03
1,7029
1
0804
2,7833
3
46536
2,03493
—2,16757
2,05
2,06
1,6998
1
0813
2,7811
3
44040
2,02396
—2,21963
2,06
2,07
2,07
1,6967
1
0822
2,7738
3
41516
2,01291
—2,27198
2,03
1,6936
1
0831
2,7767
3
39020
2,00176
—2,32463
2,08
2,09
1,6904
1
0840
2,7744
3
35476
1,99052
—2,37757
2,09
2,10
1,6872
1
0849
2,7722
3
33940
1,97919
—2,43080
2,10
2,11
1,6840
1
0859
2,7699
3
31376
1,96777
—2,48433
2,11
2,12
1,6309
1
0868
2,7677
3
28820
1,95625
—2,53815
2,12
346
Таблица 1 продолжение
V
а
Р
аР
Т
а
V
2,13
1,6777
1,0878
2
7654
3
26236
1,94462
—2,59227
2
2,14
1,6744
1,0887
2
7631
3
23640
1,93292
—2,64668
2
2,15
1,6711
1,0897
2
7608
3
21036
1,92110
—2,70139
2
2,16
1,6678
1,0907
2
7585
3
18420
1,90920
—2,75641
2
2,17
1,6645
1,0916
2
7562
3
15796
1,89719
—2,81131
2
2,18
1,6612
1,0927
2
7539
3
13160
1,88508
—2,86732
2
2,19
1,6579
1,0937
2
7515
3
10496
1,87287
—2,92323
2
2,20
1,6545
1,0946
2
7491
3
07820
1,86056
—2,97944
2
2,21
1,6511
1,0956
2
7468
3
05156
1,84814
—3,03596
2
2,22
1,6477
1,0967
2
7444
3
02460
1,83562
—3,09278
2
2,23
1,6443
1,0977
2
7420
2
99756
1,82300
—3,14990
2
2,24
1,6408
1,0987
2
7396
2
97040
1,81026
—3,20733
2
2,25
1,6374
1,0998
2
7372
2
94316
1,79742
—3,26507
2
2,26
1,6339
1,1008
2
7347
2
91568
1,78448
—3,32312
2
2,27
1,6305
1,1019
2
7323
2
88816
1,77142
—3,38148
2
2,28
2,29
1,6269
1,1030
2
7298
2
86040
1,75825
—3,44015
2
1,6233
1,1040
2
7273
2
83266
1,74498
—3,49912
2
2,30
1,6198
1,1051
2
7249
2
80480
1,73158
—3,55842
2
2,31
1,6162
1,1062
2
7224
2
77676
1,71807
—3,61802
2
2,32
1,6126
1,1073
2
7199
2
74860
1,70445
—3,67795
2
2,33
1,6089
1,1084
2
7173
2
72016
1,69071
—3,73819
2
2,34
1,6053
1,1095
2
7148
2
69180
1,67685
—3,79874
2
2,35
1,6016
1,1106
2
7122
2
66316
1,66287
—3,85962
2
2,36
1,5979
1,1118
2
7097
2
63460
1,64877
—3,92083
2
2,37
1,5942
1,1129
2
7071
2
60576
1,63454
—3,98235
2
2,38
1,5914
1,1143
2
7062
2
58020
1,62021
—4,04419
2
2,39
1,5867
1,1152
2
7019
2
54776
1,60574
—4,10636
2
2,40
1,5829
1,1164
2
6993
2
51860
1,59113
—4,16887
2
2,41
1,5791
1,1176
2
6967
2
43936
1,57642
—4,23168
2
2,42
1,5753
1,1187
2
6940
2
45980
1,56156
—4,29484
2
2,43
1,5715
1,1200
2
6914
2
43036
1,54657
—4,35832
2
2,44
1,5676
1,1211
2
6888
2
40080
1,53146
—4,42214
2
2,45
1,5637
1,1224
2
6861
2
37096
1,51622
—4,48628
2
2,46
1,5598
1,1236
2
6834
2
34100
1,50083
—4,55077
2
2,47
1,5559
1,1248
2
6807
2
31096
1,48531
—4,61559
2
2,43
1,5519
1,1261
2
6780
2
28080
1,46964
—4,68076
2
2,49
1,5479
1,1273
2
6752
2
25036
1,45384
—.4,74626
2
2,50
1,5439
1,1286
2
6725
2
22000
1,43790
—4,81210
2
2,51
1,5399
1,1298
2
6697
2
18936
1,42182
—4,87828
2
2,52
1,5358
1,1311
2
6669
2
15860
1,40558
—4,94482
2
2,53
1,5318
1,1324
2
6642
2
12796
1,38919
—5,01171
2
2,54
1,5277
1,1337
2
6614
2
09700
1,37267
—5,07893
2
2,55
1,5236
1,1350
2
6586
2
06596
1,35598
—5,14652
2
2,56
1,5194
1,1363
2
6557
2
03474
1,33915
—5,21445
2
2,57
1,5153
1,1377
2
6529
2
00336
1,32216
—5,28274
2
2,58
1,5110
1,1390
2
6500
1
97180
1,30501
—5,35139
2
2,59
1,5069
1,1413
2
6472
1
94036
1,28771
—5,42039
2
2,60
1,5026
1,1417
2
6443
1
90860
1,27024
—5,48976
2
2,61
1,4983
1,1431
2
6414
1
87676
1,25261
—5,55943
2
2,62
1,4940
1,1449
2
6386
1
84500
1,23481
—5,62959
2
2,63
1,4807
1,1459
2
6356
1
81276
1,21684
—5,70006
2
2,64
1,4854
1,1472
2
6327
1
78060
1,19871
—5,77089
2
2,65
1,4810
1,1487
2
6297
1
74816
1,18041
—5,84209
2
2,66
1,4767
1,1501
2
6264
1
71580
1,16192
—5,91368
2
2,67
1,4723
1,1515
2
6238
1
68316
1,14326
—5,98564
2
2,68
1,4678
1,1530
2
6208
1
65040
1,12441
—6,05799
2
2,69
1,4629
1,1540
2
6169
1
61576
1,10540
—6,13070
2
2,70
1,4589
1,1559
2
6148
1
58460
1,08619
—6,20381
2
2,71
1,4544
1,1573
2
6118
1
55156
1,06679
—6,27731
2
2,72
1,4499
1,1589
2
6088
1
51840
1,04720
—6,35120
2
2,73
1,4453
1,1604
2
6057
1
48496
1,02744
—6,42546
2
2,74
1,4407
1,1619
2
6026
1
45140
1,00745
—6,50015
2
2,75
1,4361
1,1634
2
5996
1
41796
0,98729
—6,57521
2
2,76
1,4315
1,1649
2
5964
1
38400
0,96690
—6,65070 I
2
347
Таблица 1 продолжение
Р
а3
а
2.77
2.78
2.79
2.80 2,81 2,82
2.83
2.84
2.85
2.86
2.87
2.88
2.89
2.90
2.91
2.92
2.93
2.94
2.95
2.96
2.97
2.98
2.99
3.00
3.01
3.02
3.03
3.04
3.05
3.06
3.07
3.08
3.09
3.10
3.11
3.12
3.13
3.14
3.15
3.16
3.17
3.18
3.19
3.20
3.21
3.22
3.23
3.24
3.25
3.26
3.27
3.28
3.29
3.30
3.31
3.32
3.33
3.34
3.35
3.36
3.37
3.38
3.39
3.40
1,4268 1,4221 1,4175 1,4128 1,4079 1,4031 1,3983 1,3934 1,3886 1,3836 1,3783 1,3738 1,3688 1,3638 1,3587 1,3536 1,3486 1,3435 1,3383 1,3331 1,3278 1,3226 1,3174 1,3120 1,3067 1,3014 1,2960 1,2907 1,2851 1,2796 1,2739 1,2686 1,2632 1,2573 1,2518 1,2460 1,2404 1,2346 1,2238 1,2230 1,2169 1,2112 1,2053 1,1995 1,1936 1,187э 1,1814 1,1753 1,1693 1,1630 1,1569 1,1507 1,1444 1,1381 1,1318 1,1254 1,1190 1,1125 1,1060 1,0993 1,0930 1,0864 1,0793 1.0731
1,1665 1,1681 1,1697 1,1712 1,1728 1,1745 1,1760 1,1777 1,1793 1,1810 1,1827 1,1843 1,1861 1,1878 1,1895 1,1912 1,1930 1,1948 1,1966 1,1933 1,2002 1,2021 1,2038 1,2058 1,2076 1,2096 1,2113 1,2133 1,2152 1,2172 1,2193 1,2210 1,2229 1,2251 1,2271 1,2293 1,2312 1,2334 1,2355 1,2376 1,2399 1,2418 1,2440 1,2463 1,2485 1,2506 1,2529 1,2551 1,2573 1,2597 1,2620 1,2644 1,2667 1,2691 1,2715 1,2739 1,2764 1,2788 1,2813 1,2838 1,2863 1,2888 1,2914 1,2940
2,5933 2,5902 2,5871 2,5839 2,5807 2,5776 2,5743 2,5712 2,5679 2,5646 2,5614 2,5581 2,5549 2,5516 2,5482 2,5449 2,5416 2,5382 2,549 2,5314 2,5280 2, 5247 2,5212 2,5178 2,5143 2,5110 2,5073 2,5040 2,5003 2,4968 2,4932 2,4896 2,4861 2,4825 2,4789 2,4753 2,4716 2,4680 2,4643 2,4606 2,4568 2,4530 2,4493 2,4458 2;4420 2,4381 2,4343 2,4305 2,4266 2,4228 2,4189 2,4151 2,4111 2,4072 2,4033 2,3994 2,3954 2,3914 2,3874 2,3834 2,3793.2,3753 2,3712 2,3672
1,35016 1,31620 1,28216 1,24780 1,21336 1,17900 1,14416 1,10960 1,07456 1,03940 1,00436 0,96900 0,93376 0,89820 0,86236 0,82660 0,79076 0,75460 0,71856 0,68200 0,64556 0,60920 0,57236 0,53560 0,49856 0,46180 0,42416 0,38720 0,34936 0,31180 0,27396 0,23600 0,19816 0,16000 0,12176 0,08338 0,04484 0,00617 —0,03263 —0,07157 —0,11080 —0,15020 —0,18916 —0,22840 —0,26800 —0,30800 —0,34784 —0,38780 —0,42804 —0,46820 —0,50864 —0,54907 —0,58984 —0,63060 —0,67144 —0,71248 —0,75364 —О,79500 —О,83644 —0,87802 —0,91984 —0,96160 —1,00364 —1,04570
0,94633 0,92553 0,90453 0,88332 0,86190 0,84024 0,81835 0,79625 0,77392 0,75134 0,72852 О,70548 0,68217 0,65863 0,63479 0,61073 0,58640 0,56180 О,53691 0,51177 0,48632 0,46058 0,43458 0,40825 0,38162 0,35469 0,32743 0,29984 0,27195 0,24370 0,21515 0,18621 0,15694 0,12731 0,09729 0,06693 0,03615 0,00500 —0,02655 —0,05851 —0,09091 —0,12370 —0,15694. —0,19059 —0,22471 —0,25932 —0,29439 —0,32994 —0,36595 —0,40250 —0,43958 —0,47699 —0,51531 —0,55399 —0,59324 —0,63308 —0,67349 —0,71452 —0,75620 —0,79850 —0,84143 —0,88508 —0,92942 —0,97444
- 6,72657
- 6,80287
- 6,87957
- 6,95668
- 7,03420
- 7,11216
- 7,19055
- 7,26935
- 7,34858
- 7,42826
- 7,50838
- 7,58892
- 7,66993
- 7,75137
- 7,83331
- 7,91567
- 7,99850
- 8,08180
— 8,16559
— 8,24983
— 8,33458
— 8,41982
— 8,50552
— 8,59175
— 8,67848
— 8,76571
— 8,85347
— 8,94176
— 9,03055
— 9,11990
— 9,20974
— 9,30018
— 9,39116
— 9,48269
— 9,57481
— 9,66747
— 9.76075
— 9,85460
— 9,94905 —10,04411 —10,13981 —10,23610 —10,33304 —10,43059 —10,52881 —10,62772 —10,72729 —10,82754 —10,92845 —11,03010 —11,13248 —11,23539 —11,33941 —11,44399 —11,54934 —11,65548 —11,76240 —11,87012 —11,97869 —12,08810 —12,19833 —12,30948 —12,42152 —12,53444
2,77
2.78.
2.79. 2,80 2,81 2,82. 2,83 2,84
2.85-
2.86-
2.87
2.88
2.89
2.90
2.91
2.92
2.93
2.94
2.95
2.96
2.97
2.98
2.99
3.00
3.01
3.02 3,03.
3.04
3.05
3.06 3,07 3,08. 3,09 3,Ю
3.11
3.12
3.13
3.14
3.15 3,16. 3,17 3,1
3.19
3.20 3,21 3,22 3,23
3.24
3.25
3.26 3,27 3,28.
3.29
3.30
3.31
3.32 3 33
3.34
3.35 3,363,37 3,383,39 3,40.
348
Таблица 1 продолжение
3.41
3.42
3.43.3,44 3,45.3,46
3.47
3.48.3,49.3,50
3.51
3.52
3.53
3.54.3,55.3,56
3.57
3.58
3.59 -3,60 3,61.3,62
3.63
3.64
3.65.3,66 3,67 -3,68
3.69
3.70 Я, 71
3.72
3.73.3,74
3.75
3.76
3.77 -3,78.3,79
3.80
3.81.3,82
3,83
.3,84
3.85
3.86
3.87
3.88.3,89
3.90
3.91
3.92
3.93
3.94
3.95
3.96
3.97
3.98
3.99
4.00
4.01
4.02
4.03 Л, 04
а
1,0664 1,0597 1,0529 1,0460 1,03У2 1,0323 1,0253 1,0183 1,0113 1,0041 0,9970 0,9898 0,9827 0,9754 0,9681 0,9608 0,9534 0,9459 0,9384 0,9309 0,9233 0,9157 0,9080 0,9003 0,8925 0,8347 0,8769 0,868а 0,8610 0,8530 0,8450 0,8368 0,8286 0,8204 0,8121 0,8038 0,7954 0,7870 0,7785 0,7700 0,7613 0,7530 0,7440 0,7352 0,7264 О,717о 0,7086 0,6995 0,6905 0,6814 0,6721 0,6629 0,6536 0,6442 0,6348 0,6253 0,6157 0,6061 0,5963 0,5865 0,5767 0,5668 0,5568 0,5i68
р
аР
Г
UL
Т
1,2966
2,3630
—1,08804
—1,02017
—12,64827
1,2992
2,3589
—1,13040
—1,06669
—12,76309
1,3018
2,3547
—1,17304
—1,11397
—12,87887
1,3046
2,3506
—1,21560
—1,16201
—12,99561
1,3073
2,3465
—1,25824
— 1,21088
—13,11338
1,3101
2,3423
—1,30124
—1,26057
—13,23218
1,3127
2,3380
—1,34444
—1,31116
—13,35206
1,3155
2,3338
—1,38760
—1,36259
—13,47299
1,3183
2,3296
—1,43084
—1,41489
—13,59499
1;3211
2,3253
—1,47440
—1,46820
—13,71820
1,3241
2,3211
—1,51784
—1,52241
—13,84251
1,3269
2,3167
—1,56180
—1,57763
—13,96803
1,3298
2,3125
—1,60544
—1,63385
—14,09475
1,3327
2,3081
—1,64960
—1,69114
—14,22274
1,3357
2,3038
—1,69364
—1,74949
—14,35199
1,3387
2,2994
—1,73796
—1,80893
—14,48284
1,3416
2,2950
—1,78244
—1,86954
—14,61444
1,3447
2,2906
—1,82693
—1,93138
—14,74778
1,3478
2,2862
—1,87164
—1,99438
—14,88248
1,3508
2,2817
—1,91660
—2,05869
—15,01869
1,3540
2,2773
—1,96144
—2,12424
—15,15634
1,3571
2,2728
—2,00660
—2,19120
—15,29560
1,3603
2,2683
—2,05184
—2,25950
—15,43640
1,3635
2,2638
—2,09720
—2,32930
—15,57890
1,3667
2,2593
—2,14264
—2,40054
—15,72304
1,3700
2,2548
—2,18828
—2,47334
—15,86894
1,3733
2,2501
—2,23424 1
—2,54774
—16,01664
1,3766
2,2456
—2,28000
—2,62330
—16,16620
1,3800
2,2410
—2,32604
—2,70157
—16,31767
1,3834
2,2363
—2,37240
—2,78107
—16,47107
1,386S
2,2317
—2,41864
—2,86246
—16,62656
1,3902
2,2271
—2,46500
—2,94581
—16,78421
1,3937
2,2223
—2,51184
—3,03134
—16,94424
1,3973
2,2177
—2,55844
—3,11842
—17,10602
1,4008
2,2129
—2,60544
—3,20792
—17,27042
1,4044
2,2082
—2,65236
—3,29968
—17,43728
1,4080
2,2034
—2,69964
—3,39374
—17,60664
1.4117
2,1987
—2,74680
—3,48991
—17,77831
1,4153
2,1939
—2,79424
—3,58919
—17,95329
1,4190
2,1890
—2,84200
—3,69088
—18,13087
1,4227
2,1841
—2,88984
—3,79526
—18,31136
1,4266
2,1793
—2,93760
—3,90246
—18,49487
1,4304
2,1745
—2,98544
—4,01269
—18,68159
1,4344
2,1696
—3,03362
—4,12606
— 18,87166
1,4383
2,1647
— 3,08184
—4,24273
—19,06523
1,4422
2,1597
—3,13040
—4,36272
—19,26232
1,4462
2,1548
—3,17884
—4,48636
—19,46326
1,4502
2,1498
—3,22760
—4,61382
—19,66822
1,4543
2,1448
—3,27644
—4,74508
—19,87718
1,4584
2,1398
—3,32540
—4,88057
—20,09056
1,4626
2,1347
—3,37464
—5,02041
—20,30851
1,4667
2,1296
—3,42400
—5,16486
—20,53127
1,4710
2,1246
—3,47324
—5,31403
—20,75892
1,4753
2,1195
—3,52280
—5,46835
—20,99195
1,4796
2,1143
—3,57264
—5,62802
—21,23052
1,4839
2,1092
—3,62240
—5,79337
—21,47496
1,4884
2,1040
—3,67244
—5,96462
—21,72551
1,4928
2,0989
—3,72240
—6,14221
—21,98260
1,4973
2,0937
—3,7726
—6,3265
—22,2466
1,5018
2,0884
—3,8232
—6,5179
—22,5179
1,5064
2,0831
—3,8733
—6,7168
—22,7970
1,5111
2,0779
—3,9244
—6,9238
—23,0842
1,5158
2,0726
—3,9752
—7,1393
—23,3802
1,5205
2,0673
—4,0262
—7,3639
—23,6855
3.41
3.42
3.43
3.44 3,4о
3.46
3.47
3.48
3.49
3.50
3.51
3.52
3.53
3.54
3.55
3.56
3.57
3.58
3.59
3.60
3.61
3.62
3.63
3.64
3.65
3.66
3.67
3.68
3.69
3.70
3.71
3.72
3.73
3.74
3.75
3.76
3.77
3.78
3.79
3.80
3.81
3.82
3.83
3.84
3.85
3.86
3.87
3.88
3.89
3.90
3.91
3.92
3.93
3.94
3.95
3.96
3.97
3.98
3.99
4.00
4.01
4.02
4.03
4.04
349
Таблица 1 продолжение
V
а
Р
хр
г
а
т
V
4
05
0
5366
1,5253
2,0619
—4,0774
7,5981
24,0006
4,05
4
06
0
5264
1,5302
2,0566
—4,1286
7,8427
—
24,3263
4,06
4
07
0
5161
1,5351
2,0512
—4,1800
8,0985
—
24,6634
4,07
4
08
0
5058
1,5400
2,0458
—4,2316
8,3661
—
25,0125
4,08
4
С9
0
4954
1,5450
2,0404
—4,2832
—
8,6465
—
25,3746
4,09
4
10
0
4849
1,5500
2,0349
—4,3352
8,9407
—
25,7507
4,10
4
11
0
4743
1,5551
2,0295
—4,3870
9,2497
—
26,1418
4,11
4
12
0
4636
1,5603
2,0239
—4,4393
9,5747
—
26,5491
4,12
4
13
0
4529
1,5655
2,0184
—4,4916
9,9170
—
26,9739
4,13.
4
14
0
4421
1,5708
2,0129
—4,5440
10,2781
—
27,4177
4,14.
4
15
0
4312
1,5761
2,0073
—4,5966
г
10,6596
—
27,8821
4,15
4
16
0
4202
1,5815
2,0017
—4,6494
11,0635
—
28,3691
4,16
4
17
0
4092
1,5870
1,9962
—4,7021
11,4916
—
28,8805
4,17
4
18
0
3980
1,5925
1,9905
—4,7551
11,9424
—
29,4148
4,18
4
19
0
3868
1,5981
1,9848
—4,8083
12,4305
—
29,9866
4,19
4
20
0
3755
1,6037
1,9792
4,8616
12,9468
—
30,5868
4,20.
4
21
0
3641
1,6094
1 9735
—4,9150
13,4988
—
31,2229
4,21
4
22
0
3526
1,6151
1,9678
—4,9686
14,0905
—
31,8989
4,22
4
23
0
3410
1,6210
1,9620
—5,0224
14,7262
—
32,6191
4,23
4
24
0
3294
1,6268
1,9562
—5,0764
15,4111
—
33,3887
4,24
4
25
0
3176
1,6328
1,9504
—5,1304
16,1523
—
34,2148
4,25
4
26
0
3058
1,6388
1,9446
—5,1846
16,9537
—
35,1013
4,26.
4
27
0
2939
1,6449
1,9388
—5,2388
17,8280
—
36,0609
4,27-
4
28
0
2818
1,6511
1,9329
—5,2934
18,7825
—
37,1009
4,28.
4
29
0
2697
1,6573
1,9270
—5,3480
19,8299
—
38,2340
4,29
4
30
0
2575
1,6636
1,9211
—5,4028
20,9842
—-
39,4742
4,30
4
31
0
2451
1,6700
1,9151
—5,4577
22,2631
—
40,8392
4,31
4
32
0
2327
1,6765
1,9092
—5,5128
23,6883
—
42,3507
4,32
4
33
0
2202
1,6830
1,9032
—5,5680
25,2865
—
44,0354
4,33.
4
34
0
2074
1,6896
1,8972
—5,6234
27,0911
—
45,9267
4,34
4
35
0
1948
1,6963
1,8911
—5,6790
29,1461
—
48,0686
4,35
4
36
0
1820
1,7031
1,8851
—5,7346
31,5073
—
50,5169
4,36
4
37
0
1691
1,7099
1,8790
—5,7904
34,2490
—
53,3459
4,37
4
38
0
1560
1,7168
1,8728
—5,8465
37,4724
—
56,6568
4,38
4
39
0
1429
1,7238
1,8667
—5,9026
—
41,3167
—
60,5888
4,39
4
40
0
1296
1,7309
1,8605
—5,9590
45,9814
—
65,3414
4,40
4
41
0
1162
1,7381
1,8543
—6,0154
—
51,7615
—
71,2096
4,41
4
42
0
1027
1,7454
1,8481
—6,0720
59,1130
—
78,6494
4.42
4
43
0
0891
1,7528
1,8419
—6,1286
68,7702
—-
88,4041
4,43
4
44
0
0754
1,7602
1,8356
—6,1856
85,0603
—
101,774
4,44
4
45
0
0615
1,7678
1,8293
—6,2426
101,454
—
121,257
4,45
4
46
0
0476
1,7754
1,8230
—6,2998
132,450
—
152,342
4,46
4
47
0
0335
1,7832
1,8166
—6,3572
189,917
—
209,893
4,47
4
48
0
0192
1,7910
1,8102
—6,4148
333,075
—
353,145
4,48
4
49
0
0049
1,7989
1,8038
—6,4723
—1135,92
—1336,08
4,49
4
50
—0
0096
1,8070
1,7974
—6,5302
683,788
663,538
4,50
4
51
—0
0241
1,8151
1,7910
—6,5881
272,819
252,479
4,51
4
52
—0
0389
1,8234
1,7845
—6,6462
170,949
150,519
4,52
4
53
—0
0537
1,8317
1,7780
—6,7044
124,753
104,232
4,53
4
54
—0
0687
1,8401
1,7714
—6,7630
98,3810
77,7694
4,54
4
55
—0
0839
1,8487
1,7648
—6,8216
81,3246
60,6221
4,55
4
56
—0
0992
1,8574
1,7583
—6,8802
69,3867
48,5931
4,56
4
57
—0
1146
1,8662
1,7516
—6,9392
60,5623
39,677э
4,57
4
58
—0
1301
1,8751
17450
—6,9982
53,7732
32,7967
4,58
4
59
—0
1459
1,8841
1,7383
—7,0574
48,3868
27,3184
4,59
4
60
—0
1617
1,8933
1,7316
—7,1168
44,0079
22,8479
4,60
4
61
—0
1777
1,9025
1,7248
—7,-1764
40,3779
19,1253
4,61
4
62
—0
1939
1,9120
1,7181
—7,2360
37,3190
15,9746
4,62
4
63
—0
2102
1,9215
1,7113
—7,2959
34,7059
13,2690
4,63
4
64
—0
2267
1,9312
1,7045
—7,3558
32,4471
10,9176
4,64
4
65
—0
2433
1,9409
1,6976
—7,4160
30,4751
8,8526
4,65
4
66
—0
2602
1,9509
1,6907
—7,4764
28,7380
7,0223
4,66
4
67
—0
2771
1,9609
1,6838
—7,5368
27,1955
5,3867
4,67
4
68
—0
2943
1,9711
1,6768
—7,5976
25,8170
3,9147
4,68
350
Таблица 1 продолжение
V
а
Р
aji
Y
а
Т
V
4,69
—0,3116
1,9815
1,6699
— 7,6582
24,5772
2,5811
4,69
4,70
—0,3291
1,9920
1,6629
— 7,7192
23,4558
1,3659
4,70
4,71
—0,3467
2,0026
1,6559
— 7,7802
22,4365
0,2525
4,71
4,72
—0,3646
2,0134
1,6488
— 7,8416
21,5059
— 0,7726
4,7 г
4,73
—0,3827
2,0243
1,6416
— 7,9031
20,6524
— 1,7205
Ь,Г4
4,74
—0,4009
2,0354
1,6345
— 7,9648
19,8663
— 2,6008
it,Ilk
4,75
—0,4193
2,0467
1,6274
— 8,0264
19,1412
— 3,4213
4,75
4,76
—0,4379
2,0581
1,6202
— 8,0884
18,4689
— 4,1887
4,76
4,77
—0,4568
2,0698
1,6130
— 8,1504
17,8439
— 4,9090
4,77
4,78
—0,4758
2,0815
1,6057
— 8,2123
17,2614
— 5,5870
4,78
4,79
—0,4950
2,0934
1,5984
— 8,2752
16,7170
— 6,2271
4,79
4,80
—0,5144
2,1056
1,5912
— 8,3377
16,2070
— 6,8330
4,80
4,81
—0,5341
2,1179
1,5838
— 8,4005
15,7280
— 7,4080
4,81
4,82
—0,5540
2,1304
1,5764
— 8,4634
15,2774
— 7,9549
4,82
4,83
—0,5740
2,1430
1,5690
— 8,5264
14,8526
— 8,4763
4,83
4,84
—0,5944
2,1559
1,5615
— 8,5397
14,4512
— 8,9744
4,84
4,85
—0,6149
2,1690
1,5541
— 8,6530
14,0713
— 9,4511
4,85
4,86
—0,6357
2,1823
1,5466
— 8,7166
13,7113
— 9,9084
4,86
4,87
—0,6568
2,1958
1,5390
— 8,7804
13,3693
—10,3476
4,87
4,88
—0,6780
2,2095
1,5315
— 8,8443
13,0440
—10,7703
4,88
4,89
—0,6996
2,2234
1,5238
— 8,9084
12,7343
—11,1779
4,89
4,90
—0,7213
2,2375
1,5162
— 8,9726
12,4389
—11,5711
4,90
4,91
—0,7433
2,2517
1,5084
— 9,0372
12,1568
—11,9513
4,91
4,92
—0,7657
2,2665
1,5008
— 9,1016
11,8870
—12,3194
4,92
4,93
—0,7882
2,2813
1,4931
— 9,1662
11,6286
—12,6763
4,93
4,94
—0,8111
2,2964
1,4853
— 9,2312
11,3811
—13,0225
4,94
4,95
—0,8342
2,3117
1,4775
— 9,2962
11,1435
—13,3590
4,95
4,96
—0,8577
2,3273
1,4696
— 9,3615
10,9152
—13,6864
4,96
4,97
—0,8814
2,3431
1,4617
— 9,4270
10,6957
—14,0052
4,97
4,98
—0,9054
2,3592
1,4533
— 9,4926
10,4844
—14,3160
4,98
4,99
—0,9297
2,3756
1,4459
— 9,5582
10,2808
—14,6193
4,99
5,00
—0,9544
2 3923
1,4379
— 9,6242
10,0845
—14,9155
5,00
5,01
—0,9793
2,4092
1,4299
— 9,6902
9,8949
—15,2052
5,01
5,02
—1,0046
2,4264
1,4218
— 9,7566
9,7118
—15,4886
5,02
5,03
—1,0302
2,4439
1,4137
— 9,8230
9,5347
—15,7662
5,03
5,04
—1,0562
2,4618
1,4056
— 9,8896
9,3633
—16,0383
5,04
5,05
—1,0825
2,4799
1,3974
— 9,9564
9,1973
—16,3053
5,05
5,06
—1,1099
2,4988
1,3889
—10,0240
9,0312
—16,5724
5,06
5,07
—1,1363
2,5172
1,3809
—10,0906
8,8804
—16,8245
5,07
5,08
—1,1637
2,5363
1,3726
— 10,1580
8,7290
—17,0774
5,0.3
5,09
—1,1915
2,5558
1,3643
—10,2254
8,5819
—17,3262
5,09
5,10
—1,2197
2,5757
1,3560
—10,2930
8,4389
—17,5711
5,10
5,11
—1,2483
2,5959
1,3476
—10,3608
8,2998
—17,8123
5,11
5,12
—1,2773
2.6165
1,3392
—10,4289
8,1645
—18,0499
5,12
5,13
—1,ЗС68
2,6375
1,3306
—10,4972
8,0326
—18,2842
5,13
5,14
—1,3367
2,6589
1,3222
—10,5654
7,9042
—18,5154
5,14
5,15
—1,3670
2,6806
1,3136
—10,6340
7,7790
—18,743,5
5,15
5,16
—1,3978
2,7028
1,3050
—10,7028
7,6568
—18,9688
5,16
5,17
— 1,4291
2.7255
1,2964
—10,7716
7,5375
—19,1914
5,17
5,18
—1,4608
2,7485
1,2877
—10,8408
7,4211
—19,4113
5,18
5,19
—1,4930
2,7720
1,2790
—10,9100
7,3072
—19,6289
5,19
5,20
—1,5258
2,7960
1,2702
—10.97С6
7,1959
—19,8441
5,20
5,21
—1,5591
2,8205
1,2614
—11,0492
7,0871
—20,0570
5,21
5,22
—1,5928
2,8454
1,2526
—11,1190
6,9805
—20,2679
5,22
5,23
—1,6272
2,8709
1,2437
—11,1890
6,8762
—20,4767
5,23
5,24
—1,6621
2,8969
1,2348
— 11,2592
6,7739
—20,6837
5,24
5,25
—1,6976
2,9235
1,2259
—11,3294
6,6733
—20,8887
5,25
5,26
—1,7337
2,9506
1,2169
—11,4000
6,5755
—21,0921
5,26
5,27
—1,7705
2,9782
1,2077
—11,4710
6,4791
—21,2938
5,27
5,28
—1,8078
3,0065
1,1987
—11,5418
6,3845
—21,4939
5,28
5,29
—1,8457
3,0353
1,1896
—11,6128
6,2917
—21,6924
5,29
5,30
—1,8844
3,С648
1,1804
— 11,6842
6.2004
—21,8896
5,30
5,31
— 1,9237
3,0949
1,1712
—11,7556
6,1107
—22, 0854
5,31
5,32
—1,9638
3,1257
1,1619
—11,8274
6.0226
—22,2793
5,32
351
Таблица 1 продолжение
V
а
Г
а
Т
V
5.33
5.34
5.35 t, 36 5,37
5.35 о,39
5.40
5.41
5.42
5.43
5.44 о,45
5.46
5.47
5.48
5.49
5.50
5.51
5.52
5.53
5.54
5.55
5.56
5.57
5.58
5.59 0,60
5.61
5.62
5.63
5.64
5.65
5.66
5.67
5.68
5.69
5.70
5.71
5.72
5.73
5.74
5.75
5.76
5.77
5.78
5.79
5.80
5.81
5.82
5.83
5.84
5.85
5.86
5.87
5.88
5.89
5.90
5.91
5.92
5.93
5.94
5.95
5.96
—2,0046 —2,0461 —2,0885 —2,1316 —2,1756 —2,2203 —2,2662 —2,3127 —2,3602 —2,4087 —2,4583 —2,5088 —2,5605 —2,6132 —2,6672 —2,7223 —2,7787 —2,8364 —2,8953 —2,9557 —3,0176 —3,0809 —3,1458 —3,2123 —3,2805 —3,3505 —3,4224 —3,4961 —3,5719 —3,6497 —3,7298 —3,8120 —3,8969 —3,9841 —4,0739 —4,1666 —4,2621 —4,3607 —4,4625 - 4,5676 —4,6763 —4,7888 —4,9053 —5,0258 —5,1509 —5,2806 —5,4152 —5,5552 —5,7008 —5,8525 —6,0104 —6,1750 —6,3471 —6,5268 —6,7150 —6,9120 —7,1188 —7,3358 —7,5641 —7,8043 —8,0580 —8,3260 —8,6094 —8,9100
3,1572
3,1894
3,2224
3,2560
3,2905
3,3257
3,3621
3,3989
3,4367
3,4755
3,5153
3,5560
3,5978
3,6407
3,6846
3,7298
3,7760
3,8236
3,8724
3,9226
3,9742
4,0272
4,0817
4,1379
4,1956
4,2551
4,3163
4,3794
4,4445
4,5116
4,5808
4,6523
4,7261
4,8024
4,8812
4.9628 5,0472 5,1345 5,2252 5,3190 5,4163 5,5173 5,6223 5,7313 5,8448
5.9628 6,0857 6,2140 6,3476 6,4872 6,6332 6,7858 6,9455 7,1132 7,2891 7,4738 7,6681 7,8725 8,0884 8,3159 8,5570 8,8122 9,0830 9,3706
1,1526 1,1433 1,1339 1,1244 1,1149 1,1054 1,0959 1,0862 1,0765 1,0668 1,0570 1,0472 1,0373 1,0275 1,0174 1,0075 0,9973 0,9872 0,9771 0,9669 0,9566 0,9463 0,9359 0,9256 0,9151 0,9046 0,8939 0,8833 0,8726 0,8618 0,8510 0,8403 0,8292 О,8184 0,8073 0,7962 0,7851 0,7738 0,7627 0,7514 0,7400 0,7285 0,7170 0,7055 0,6939 0,6822 0,6705 0,6587 0,6468 0,6347 0,6228 0,6108 0,5984 0,5864 0,5741 0,5618 0.5493 0,5368 0,5243 0,5116 О,4990 0,4862 О,4736 0,4606
—11,8992 —11,9712 — 12,0434 —12,1160 —12,1886 —12,2614 —12,3342 —12,4076 —12,4810 —12,5546 —12,6284 —12,7024 —12,7766 —12,8509 —12,9256 —13,0001 —13,0753 —13,1506 —13,2253 —13,3014 —13,3772 —13,4532 —13,5294 —13,6056 —13,6822 —13,7590 —13,8362 —13,9134 —13,9908 —14,0686 —14,1464 —14,2243 —14,3028 —14,3811 -14,4598 —14,5388 —14,6178 —14,6974 —14,7766 —14,8564 —14,9364 —15,0168 —15,0972 —15,1778 -15,2586 —15,3398 —15,4210 -15,5026 —15,5844 —15,6668 —15,7488 -15,8312 —15,9144 -15,9970 —16,0802 —16,1636 —16,2474 —16,3314 —16,4154 —16,5900 —16,5844 —16,6694 —16,7540 —16,8396
5,9359 5,8506 5,7666 5,6839 5,6025 5,5222 5,4431 5,3651 5,2881 5,2121 5,1371 5,0631 4,9899 4,9176 4,8461 4,7755 4,7056 4,6364 4,5680 4,5002 4,4331 4,3667 4,3008 4,2355 4,1707 4,1065 4,0429 3,9796 3,9169 3,8546 3,7928 3,7314 3,6703 3,6096 3,5493 3,4893 3,4297 3,3704 3,3113 3,2526 3,1941 3,1358 3,0777 3,0199 2,9623 2,9049 2,8477 2,7906 2,7337 2,6769 2,6203 2,5637 2,5073 2,4510 2,3947 2,3385 2,2823 2,2262 2,1702 2,1142 2,0581 2,0020 1,9460 1,8900
—22,4730 —22,6650 —22,8559 —23,0457 —23,2344 —23,4222 —23,6090 —23,7949 —23,9800 —24,1643 —24,3478 —24,5305 —24,7126 —24,8940 —25,0748 —25,2549 —25,4345 —25,6136 —25,7921 —25,9702 —26,1478 —26,3249 —26,5017 —26,6781 —26,8542 —27,0299 —27,2052 —27,3804 —27,5552 —27.7298 —27,9041 —28,0782 —28,2522 —28,4260 —28,5996 —28,7731 —28,9463 —29,1196 —29,2928 —29,4658 —29,6388 —29,8118 —29,9848 —30,1576 —30,3306 —30,5035 —30,6764 —30,8494 —31,0224 —31,1955 —31,3686 —31,5418 —31,7152 —31,8886 —32,0622 —32,2359 —32,4098 —32,583 8 —32,7579 —32,9322 —33,1068 —33,2815 —33,4565 —33,6316
5.33
5.34
5.35
5.36
5.37
5.38
5.39
5.40
5.41
5.42
5.43
5.44
5.45
5.46
5.47
5.48
5.49
5.50
5.51
5.52
5.53
5.54
5.55
5.56
5.57
5.58
5.59
5.60
5.61
5.62
5.63
5.64
5.65
5.66
5.67
5.68
5.69
5.70
5.71
5.72
5.73
5.74
5.75
5.76
5.77
5.78
5.79
5.80
5.81
5.82
5.83
5.84
5.85
5.86
5.87
5.88
5.89
5.90
5.91
5.92
5.93
5.94
5.95
5.96
352
Таблица 1 продолжение
V
а
Р
аР
Т
а
Т
У.
5,97
— 9,2293
9,6769
0,4476
—16,9252
1,8338
—33,8070
5,97
5,98
— 9,5690
10,0035
0,4345
—17,0112
1,7777
—33,9827
5,93
5,99
— 9,9313
10,3528
0,4215
—17,0970
1,7216
—34,1535
5,99
6,00
— 10,3186
10,7269
0,4083
—17,1834
1,6653
—34,3347
6,0Э
6,01
— 10,7339
11,1289
0,3950
—17,2700
1,6j89
—34,5112
6, U1
6,02
— 11,1799
11,5615
0,3816
—17,3570
1,5525
—34,6879
0,02
6,03
— 11,6605
12,0287
0,3682
—17,4440
1,4960
—34,8649
6,03
6,04
— 12,1799
12,5346
0,3547
—17,5314
1,4394
—35,0422
6,04
6,05
— 12,7431
13,0842
0,3411
—17,6190
1,3827
—35,2198
6,05
6,06
— 13,3561
13,6835
0,3274
—17,7070
1,3258
—35,3978
6,06
6,07
— 14,0257
14,3393
0,3136
—17,7952
1,2687
—35,5762
6,07
6,08
— 14,7603
15,0602
0,2998
—17,8836
1,2116
—35,7548
6,08
6,09
— 15,5701
15,8560
0,2859
—17,9722
1,1543
—35,9333
6,09
6,10
— 16,4673
16,7392
0,2719
—18,0612
1,0968
—36,1132
6,10
6,11
— 17,4670
17,7249
0,2579
—18,1502
1,0391
—36,2930
6,11
6,12
— 18,5882
18,8319
0,2437
—18,2398
0,9813
—36,4731
6,12
6,13
— 19,8546
20,0841
0,2295
—18,3295
0,9232
—36,6537
6,13
6,14
— 21,2965
21,5116
0,2151
—18,4196
0,8649
—36,8347
6,14
6,15
— 22,9537
23,1544
0,2007
—18,5098
0,8064
—37,0161
6,15
6,16
— 24,8783
25,0645
0,1862
—18,6004
0,7476
— 37,1980
6,16
6,17
— 27,1413
27,3129
0,1716
—18,6912
0,6887
—37,3802
6,17
6,18
29,8411
29,9981
0,1570
—18,7822
0,6294
—37,5630
6,18
6,19
— 33,1182
33,2604
0,1422
—18,8736
0,5699
—37,7462
6,19
6,20
— 37,1810
37,3083
0,1273
—18,9654
0,5101
—37,9299
6,20
6,21
— 42,3515
42,4638
0,1123
—19,0574
0,4500
—38,1141
6,21
6,22
— 49,1553
49,2526
0,0973
—19,1496
0,3896
—38,2988
6,22
6,23
— 58,5139
53,5961
0,0822
—19,2420
0,3289
—33,4840
6,23
6,24
— 72,2020
72,2689
0,0669
—19,3350
0,2678
—33,6698
6,24
6,25
— 94,1333
94,1854
0,0516
—19,4280
0,2064
—38,8561
6,25
6,26
—134,975
135,011
0,0361
—19,5216
0,1446
—39,0430
6,26
6,27
—237,751
237,771
0,0207
—19,6150
0,0825
—39,2304
6,27
6,28
—985,773
935,778
0, 0050
—19,7092
0,0200
—39,4184
6,28
Прочность и устойчивость стержневых систем
Т а блица 2
Коэфициенты формул метода деформаций а, р, зсЭ, у, а, у для растянуто- изогнутых стержней
а
Р
Р
—
а
Y
И
О
o,i
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1.3
1.4
1.5
1.6
1.7
1.8
1.9 2,0 2,1 2,2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
4.0
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9 5,п
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9 6,0
2,0000 2,0007 2,0027 2,0060 2,0106 2,0166 2,0239 2,0325 2,0423 2,0534 2,0658 2,0794 2,0943 2,1103 2,1275 2,1458 2,1653 2,1858 2,2074 2,2301 2,2537 2,2786 2,3041 2,3306 2,3581 2,3865 2,4157 2,4457 2,4765 2,5081 2,5405 2,5735
2.6072 2,6415 2,6765 2,7121 2,7483 2,7851 2,8223 2,8601 2,8984 2,9372 2,9764 3,0160 3,0561 3,0966 3,1373 3,1786 3,2201 3,2620 3,342 3,3466 3,3895 3,4326 3,4759 3,5194 3,5633
3.6073 3,6516 3,6961 3,7408
1,0000 0,9998 0,9993 0,9985 0,9973 0,9959 0,9941 0,9920 0,9895 0,9868 0,9838 0,9806 0,9770 0,9732 0,9692 0,9650 0,9605 0,9558 0,9510 0,9459 0,9407 0,9354 0,9299 0,9244 0,9187 0,9129 0,9071 0,9012 0,8952 0,8892 0,8832 0,8772 0,8711 0,8632 0,8591 0,8531 0,8472 0,8412 0,8354 0,82У6 0,8237 0,8180 0,8124 0,8069 0,8014 0,7960 0,7907 0,7854 0,7802 0,7753 0,7703 0,7655 0,7607 0,7560 0,7514 0,7468 0,7426 0,7381 0,7340 0,7300 0,7258
3,0000
3,0005
3,0020
3,0045
3,0080
3,0125
3,0Ш
3,0244
3,0319
3,0403
3,0496
3,0600
3,0713
3,0835
3,0967
3,1108
3,1258
3,1416
3,1584
3,1760
3,1944
3,2140
3,2340
3,2550
3,2768
3,2994
3,3228
3,3469
3,3718
3,3973
3,4237
3,4507
3,4783
3,5067
3,5356
3,5652
3,5955
3,6263
3,6577
3,6897
3,7221
3,7553
3,7883
3,8229
3,8575
3,8926
3,9280
3,9640
4,0003
4,0373
4,0745
4,1121
4,1502
4,1886
4,2273
4.2662
4,3059
4,3455
4,3856
4,4261
4,4666
6,0000 6,0060 6,0241 6,0540 6,0У60 6,1500 6,2159 6,2938 6,3837 6,4855 6,5993 6,7250 6,8626 7,0120 7,1734 7.3466 7,5316 7,7282 7,9368 8,1570 8,3388 8,6330 8,8882 9,1550 9,4336 9,7238 10,0256 10,3388 10,6636 10,9998 11,3474 11,7064 12,0766 12,4584 12,8512 13,3556 13,6710 14,0976 14,5354 14,9844 15,4444 15,9156 16,3976 16,8908 17,3950 17,9102 18.4360 18,9733 19,5208 20,0796 20,6490 21,2292 21,8204 22,4220 23,0378 23,6576 24,2918 24,9360 25,5912 26,2572 26,9332
3,0000 3,0020 3,0080 3,0180 3,0319 3,0496 3,0713 3,0967 3,1257 3,1.84 3,1945 3,2341 3,2768 3,3228 3,3718.3,4237 3,4784 3,5357 3,.955 3,6577 3,7222 3,7888 3,8575 3,9281 4,0004 4,0745 4,1502 4,2273 4,3058 4,3856 4,4667 4,5489 4,6321 4,7163 4.8И5 4,8875 4,9743 5,0619 5,1501 5,2390 5.3286 5,4186 5,5092 5,6003 5.6919 5,7838 5,8763 5,9690 6.0621 6,1556 6,2403 6,3433 6.4376 6,5321 6,6269 6,7220 6,8171 6,9126 7,0082 7,1040 7,1999
4
4
4
5
6
6
6
7.
7:
3,0000 3,0120 3,0480 3,1080 3,1919 3,2996 3,4313 3,5867 3,7657 3,9684 ,1945 ,4441 ,7168 ,0128 5,3318 5,6737 ,0384 ,4257 8355 2677 ,7222 81988 8 6975 9,2181 9,7604 10,3245 10 9102 11,5173 12,1458 12,7956 13,4667 14,1589 14,8721 15,6063 16,3615 17,1375 17,9343 18,7519 19,5901 20,4490 21,3286 22,2286 23,1492 24,0903 25,0519 26,0338 27,0363 28,0590 29,1021 30,1656 31,2493 32,3533 33,4776 34,6221 35,7869 36,9720 38,1771 39,4026 40,6482 41,9140 43,1999
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 О,У 1,0 1,1 1,2
1.3
1.4
1.5
ч
ч
1,8
1.9 2,0 2,1 2,2
2.3
Ч
2.5
Ч
2.7
2.8
2.9
3.0
3.1
3I
3.3
Ч
3.5
ч
3.7
3.8
Ч
Ч
ч
4.2
Ч
ч
4.5
Ч
4.7
4.8
4.9 5,
Ч
5.2
4
5.4
5 5
Ч
5.8
5.9 6,0
354
Таблица 3
Функции slnv vtev cosv, sinv, igv для сжато-изогнутых стержней
V
V
tgv
V
sin v
vtg V
COS V
sin v
tgv
V
0
1,0000
1,0000
0,0000
1,00000
0,00000
0,00000
0
0,10
0,9967
1,0017
0,0100
0,99500
0,09983
0,10033
0,10
0,20
0,9866
1,0067
0,0405
0,98007
0,19867
0,20271
0,20
0,30
0.9698
1,0152
0,0928
0,95534
0,29552
0.30J34
0,30
0,40
0,9461
1,0272
0,1691
0,92106
0,3842
0,42279
0,40
0,50
0,9152
1,0429
0,2731
0,87758
0,47343
0,54630
0,a0
0,60
0,8770
1,0626
0,4105
0,82u34
0,56464
0,68414
0,60
0,70
0,8311
1,0866
0,5896
0,76484
0,64422
0,84229
0,70
0,80
0,7770
1,1152
0,8237
0,69671
0,71736
1,02964
0,80
0,90
0,7142
1,1489
1,1341
0,62161
0,78333
1,26016
1,55741
0,90
1,00
0,6421
1,1885
1,5574
0,54u30
0,84147
1,00
1,01
0,6343
1,1927
1,6081
0,53186
0,84683
1,59221
1,01
1,02
1,03
0,6265
1,1970
1,6607
0,52337
0,85211
1,62813
1,02
0,6185
1,2014
1,7152
0,51482
0,85730
1,66524
1,03
1,04
0,6105
1,2059
1,7717
0,50622
0,86240
1,70361
1,04
1.05
0,6023
1,2105
1,8305
0,49757
0,86742
1,74332
1,05
1,06
0,5940
1,2151
1,8915
0,48887
0,87236
1,78442
1,06
1,07
0,5856
1,2198
1,9549
0,48012
0,87720
1,82703
1,07
1,08
0,5772
1,2245
2,0209
0,47133
0,88196
1,87122
1,08
1,09
0,5686
1,2214
2,0896
0,46249
0,88663
1,91709
1,09
1,10
0,5599
1,2343
2,1612
0,45360
0,89121
1,96476
1,10
1,11
0,5510
1,2392
2,2359
0,44466
0,89670
2,01434
1,11
1,12
0,5421
1,2443
2,3139
0,43568
0,90010
2,065.6
1,12
1,13
0,5331
1,2414
2,3953
0,42666
0,90441
2,ll97o
1,13
1,14
0,5239
1,2546
2,4805
0,41759
0,90863
2,17-88
1,14
1,15
0,5147
1,2599
2,5697
0,40849
0,91276
2,23450
1,15
1,16
0,5053
1,2653
2,6631
0,39934
0,91680
2,29580
1,16
1,17
0,4958
1,2707
2,7612
0,39015
0,92075
2,35998
1,17
1,18
0,4861
1,2762
2,8642
0,38092
0,92461
2,42727
1,18
1,19
0,4764
1,2818
2,9725
0,37166
0,92837
2,49790
1,19
1,20
0,4665
1,2875
3,0866
0,36236
0,93204
2,57215
1,20
1,21
0,4565
1,2933
3,2069
0,3j302
0,93562
2,65032
1,21
1,22
0,4465
1,2991
3,3339
0,34365
0,53910
2,73275
1,22
1,23
0,4362
1,3050
3,4684
0,33424
0,94249
2,81982
1,23
1,24
0,4258
1,3111
3,6108
0,32480
0,4j78
2,91193
1,24
1,25
0,4153
1,3172
3,7620
0,31532
0,94-98
3,00957
1,25
1,26
0,4047
1,3234
3,9227
0,30582
0,95209
3,11327
1,26
1,27
0,3940
1,3297
4,0940
0,29628
0,95510
3,22363
1,27
1,28
0,3831
1,3351
4,2769
0,28672
0,95802
3,34135
1,28
1,2Э
0,3721
1,3426
4,4727
0,27712
0,96084
3,46721
1,29
1,30
0,3609
1,3493
4,6827
0,26750
0,96356
3,60210
1,30
1,31
0,34
1,3558
4,9087
0,25785
0,96618
3,74708
1,31
1,32
0,3382
1,3626
5,1524
0,24818
0,96872
3,90335
1,32
1,33
0,32o6
1,3695
5,4162
0,23848
0,97115
4,07231
1,33
1,34
0,3149
1,3765
5,7025
0,22875
0,97348
4,2j562
1,34
1,35
0,3030
1,3836
6,0145
0,21901
0,97572
4,45522
1,35
1,36
0,2910
1,3908
6,3559
0,20924
0,97786
4,67344
1,36
1,37
0,2788
1,3981
6,7309
0,19945
0,97991
4,91306
1,37
1,38
0,2665
1,4055
7,1449
0,18964
0,98185
5,17744
1,33
1,39
0,2541
1,4130
7,6043
0,17981
0,98370
5,47069
1,39
1,40
0,2415
1,4207
8,1170
0,16997
0,98545
5,79788
1,40
1,41
0,2287
1,4284
8,6932
0,16010
0,98710
6,16536
1,41
1,42
0,2158
1,4363
9,3452
0,15023
0,98865
6,58112
1,42
1,43
0,2027
1,4443
10,0893
0,14033
0,99010
7,05546
1,43
1,44
0,1894
1,4524
Ю, 9466
0,13442
0,99146
7,60183
1,44
1,45
0,1760
1,4606
11,9452
0,12050
0,99271
8,23809
1,45
1,46
0,1624
1,4690
13,1234
0,11057
0,99387
8,98861
1,46
1,47
0,1487
1,4775
14,5344
0,10063
0,99492
9,88737
1,47
1,48
0,1347
1,4861
16,2554
0,09067
0,99588
10,98338
1,48
1,49
0,1206
1,4949
18,4013
0,08071
0,99674
12,34986
1,49
1,50
0,1064
1,5038
21,1521
0,07074
0,99749
14,10142
1,50
23 355
Таблица 3 продолжение
V
V
tgv
V
sin v
v tgv
cosv
Sin v
tgv
V
1,51
0,0919
1,5128
24
8064
0,06076
0
99815
16
42809
1,51
1,52
0,0773
1,5220
29
8977
0,05077
0
99871
19
66953
1,52
1,эЗ
0,0624
1,5313
37
4S26
0,04079
0
99917
24
49841
l,o3
1,54
0,0474
1,5407
49
9902
0,03079
0
99953
32
46114
1,54
11 о а
0,0322
1,5503
74
5216
0,02079
0
99978
48
07848
1,55
1,56
0,0168
1,5601
144
4880
0,01080
0
99Э94
92
62050
1,56
1,57
0,0013
1,5700
1971
5520
0,00080
1
00000
1205
7656
1,57
1,58
-0,0145
1,5801
171
6657
-0,00920
0
99996
108
64920
1,58
1,59
—0,0305
1,903
82
7865
-0,01920
0
99982
52
06697
1,59
1,60
-0,0467
1,6007
54
7721
-0,02920
0
99957
34
23253
1,60
1,61
-0,0632
1,6112
41
0465
-0,03919
0
99923
25
49475
1,61
1,62
—0,0738
1,6220
32
8978
-0,04918
0
99879
20
30728
1,62
1,63
-0,0966
1,6329
—
27
4999
-0,05917
0
99825
—
16
87110
1,63
1,64
—0,1137
1,6439
23
6603
-0,06915
0
93761
14
42703
1,64
1,65
—0,1310
1,6552
20
7888
-0,07912
0
99687
—
12
59926
1,65
1,66
-0,1485
1,6666
—
18
5597
-0,08909
0
99602
ll
18055
1,66
1,67
-0,1662
1,6783
16
7788
-0,09904
0
99508
10
04718
1,67
1,68
-0,1842
1,6901
15
3229
-0,10899
0
99404
9
12077
1,68
1,69
-0,2024
1,7021
14
1102
-0,11892
0
93290
8
34923
1,69
1,70
-0,2209
1,7143
13
0842
0,12884
0
99166
7
69660
1,70
1,71
—0,2396
1,7267
12
2047
-0,13875
0
99033
7
13726
1,71
1,72
-0,2586
1,7393
11
4422
-0,14865
0
98889
6
6244
1,72
1,73
-O, 2778
1,7522
10
7746
-0,15853
0
98735
6
22810
1,73
1,74
-0,2973
1,7652
—
10
1851
-0,16840
0
98572
5
85353
1,74
1,75
-0,3170
1,7785
9
6607
0,17825
0
98399
5
52038
1,75
1,76
-0,3370
1,7920
9
1909
-0,18808
0
98219
—
5
22209
1,76
1,77
-0,3573
1,8057
8
7675
0,19789
0
98022
4
95341
1,77
1,78
-0,3779
1,8197
8
3840
-0,20768
, 0
97820
—
4
71009
1,78
1,79
—0,3988
1,8339
8
0347
0,21745
0
97607
4
48866
1,79
1,80
-0,4199
1,8483
7
7153
-0,22720
0
97385
4
28626
1,80
1,81
-0,4414
1,8630
7
4219
—0,2c693
0
97153
4
10050
1,81
1,82
— 0,4632
1,8780
7
1514
0,24663
0
96911
3
92937
1,82
1,83
-0,4853
1,8932
6
9013
-0,25631
0
96659
—
3
77118
1,83
1,84
-0,5077
1,9087
—
6
6691
0,26596
0
96398
3
62449
1,84
1,85
-0,5304
1,9245
6
4529
0,27559
0
96128
3
48806
1,85
1,86
-0,5534
1,9406
6
2511
-0,28519
0
95847
3
36083
1,86
1,87
-0,5768
1,9569
—
6
0623
-0,29476
0
95557
3
24187
1,87
1,88
-0,6006
1,9736
5
8851
0,30430
0
95258
—
3
13038
1,88
1,89
-0,6247
1,9905
5
7185
-0,31381
0
94949
3
02567
1,89
1,90
-0,6491
2,0078
5
5615
0,32329
0
94630
2
92710
1,90
1,91
-0,6739
2,0254
5
4132
0,33274
0
94302
2
83414
1,91
1,92
-0,6991
2,0433
5
2729
0,34215
0
93965
2
74630
1,92
1,93
-0,7247
2,0616
—
5
1399
0,35153
0
93618
2
66316
1,93
1,94
-0,7507
2,0802
—
5
0136
0,36087
0
93262
2
58433
1,94
1,95
-0,7770
2,0991
4
8935
0,37018
0
92896
2
50948
1,95
1,96
-0,8038
2,1184
4
7790
-0,37945
0
92521
2
43828
1,96
1,97
-0,8311
2,1381
4
6698
0,38868
0
92137
2
37048
1,97
1,93
-0,8587
2,1582
—
4
5655
-0,39788
0
91744
2
30582
1,98
1,99
-0,8868
2,1786
—
4
4657
0,40703
0
91341
—
2
24408
1,99
2,00
-0,9153
2,1995
4
3701
0,41615
0
90930
2
18o04
2,00
2,01
-0,9443
2,2208
4
,2783
0,42522
0
90509
2
12853
2,01
2,02
-0,9735
2,2425
4
1902
0,43425
0
90079
2
07437
2,02
2,03
-1,0037
2,2546
—
4
1055
0,44323
0
89641
—
2
02242
2,03
2,04
-1,034
2,2872
4
0239
-0,45218
0
89193
1
97252
2,04
2,05
-1,062
2,3102
3
9453
0,46107
0
88736
—
1
92456
2,05
2,06
-1,0967
2,3337
3
P695
-0,46992
0
88271
—
1
87841
2,06
2,07
— 1,1237
2,3577
3
7Э63
-0,47873
0
87796
1
83396
2,07
2,08
-1,1613
2,3822
3
7255
0,48748
0
87313
—
1
79111
2,08
2,09
-1,1944
2,4072
3
6570
-0,49619
0
86821
1
74977
2,09
2,10
-1,2282
2,4328
i
5907
0,50485
0
86321
1
70985
2,10
2,11
— 1,2625
. 2,4589
3
5264
0,51345
0
85812
—
1
67127
2,11
2,12
-1,2375
2,4855
3
4640
0,52201
0
8594
1
63396
2,12
2,13
-1,3330
2,5127
3
4034
0,53051
0
84768
1
59785
2,13
356
Таблица 3 продолжение
2.14
2.15
2.16
2.17
2.18
2.19
2.20 2,21 2,22
2.23
2.24
2.25
2.26
2.27
2.28
2.29
2.30
2.31
2.32
2.33
2.34
2.35
2.36
2.37
2.38
2.39
2.40
2.41
2.42
2.43
2.44
2.45
2.46
2.47
2.48
2.49
2.50
2.51
2.52
2.53
2.54
2.55
2.56
2.57
2.58
2.59
2.60 2,61 2,62
2.63
2.64
2.65
2.66
2.67
2.68
2.69
2.70
2.71
2.72
2.73
2.74
2.75
2.76
tgv
-1,3693 -1,4062 -1,4437 -1,4820 -1,5211 -1,5608 -1,6014 -1,6427 -1,6849 -1,7279 -1,7717 -1,8165 -1,8622 -1,9090 -1,9566
— 2,0052
— 2,0550 -2,1059 -2,1579 -2,2110 -2,2654 -2,3211 -2,3780 —2,4364 -2,4961 -2,5573 -2,6201 -2,6844 -2,7503 —2,8180 -2,8375 —2,9о89 -3,0322 -3,1075 -3,1850 -3,2646 -3,3466 -3,4310 -3,5180 -3,6076 -3,7000 -3,7954 -3,8938 -3,9955 -4,1006 -4,2093 -4,3218 -4,4383 —4,5j91 —4,6843 -4,8143 —4,949
— 5,0895 -5,2356 -5,3877
— 5,5462 -5,7115 -5,8843 -6,0649 -6,2539 -6,4521
— 6,6599 -6,8783
V
sin v
v tgv
COS V
sin v
tgv
2,5406
-3,3446
-0,53896
0,84233
-1,56288
2,5690
-3,2873
-0,54736
0,83690
-1,52898
2,5981
-3,2316
-0,55570
0,83138
-1,49610
2,6278
-3,1773
-0,56399
0,82578
-1,46420
2,6582
-3,1244
-0,57221
0,82010
-1,43321
2,6893
-3,0728
-0,58039
0,81434
— 1,40310
2,7211
-3,0224
-0,58850
0,80850
-1,37382
2,7537
-2,9732
—0,59656
0,80257
-1,34534
2,7869
-2,9251
-0,60455
0,79657
-1,31761
2,8211
-2,8781
-0,61249
0,79048
-1,29061
2,8560
-2,8323
-0,62036
0,78432
-1,26429
2,8918
-2,7869
-0,62817
0,77807
-1,23863
2,9284
-2,7427
-0,63592
0,77175
-1,21359
2,9660
-2,6994
-0,64361
0,76535
-1,18916
3,0044
-2,6569
-0,65123
0,75888
-1,16530
3,0439
-2,6152
-0,65879
0,75233
-1,14200
3,0843
-2,5742
-0,66628
0,74571
-1,11921
3,1258
-2,5339
-0,67370
0,73901
-1,09694
3,1684
-2,4943
-0,68106
0,73223
-1,07514
3,212
-2,4554
-0,68834
0,72538
-1,05381
3,2570
-2,4171
— 0,69556
0,71846
-1,03293
3,3030
-2,3793
-0,70271
0,71147
-1,01247
3,3503
-2,3421
-0,70979
0,70441
-0,99242
3,3989
-2,3054
-0,71680
0,69728
-0,97276
3,4489
-2,2693
-0,72374
0,69007
-0,95349
3,5003
-2,2336
-0,73060
0,68280
-0,93458
3,5531
-2,1984
-0,73739
0,67546
-0,91601
3,6075
-2,1637
-0,74411
0,66806
-0,89779
3,6634
-2,1293
-0,75075
0,66058
-0 87989
3,7211
-2,0954
-0,75732
0,65304
-0,86230
3,7804
-2,0618
-0,76382
0,64544
-0,84501
3,8416
-2,0286
-0,77023
0,63776
— 0,82802
3,9046
-1,9958
-0,77657
0,63003
—0,81130
3,9696
-1,9633
-0,78283
0,62223
-0,79485
4,0362
-1,9311
-0,78901
0,61437
-0,77866
4,10a
-1,8992
-0,79512
0,60645
-0,76272
4,1773
-1,8675
-0,80114
0,59847
-0,74702
4,2511
-1,8362
-0,80709
0,59043
— 0,73156
4,3274
-1,8051
-0,81295
0,58233
-0,71632
4,4064
-1,7743
-0,81873
0,57417
-0,70129
4,4879
-1,7437
-0,82444
0,56596
-0,68648
4,5725
-1,7387
-0,83005
0,55768
-0,67186
4,6600
-1,6831
— 0,83559
0,54936
-0,65745
4,7507
-1,6531
-0,84104
0,54097
-0,64322
4,8448
-1,6233
-0,84641
0,53253
-0,62917
4,9424
-1,5936
-0,85169
. 0,52404
-0,61530
5,0436
-1,5642
-0,85689
0,51550
-0,60160
5,1488
-1,5348
-0,86200
0,50691
-0,58806
5,2603
-1,5057
-0,86703
0,49826
-0,57468
5,3721
-1,4766
-0,87197
0,48957
— 0,56145
5,4906
-1,4477
-0,87682
0,48082
-0,54837
5,6140
-1,4189
— 0,83158
0,47203
-0,53544
5,7425
-1,3902
— 0,88626
0,46319
-0,52264
5,8770
-1,3616
-0,89085
0,45431
-0,50997
6,0175
-1,3331
-0,89534
0,44537
-0,49743
6,1641
-1,3047
-0,89975
0,43640
-0,48502
6,3176
-1,2764
-0,90407
0,42738
-0,47273
6,4783
-1,2481
-0,90830
0,41832
-0,46055
6,6469
-1,2199
-0,91244
0,40921
-0,44848
6,8238
-1,1917
— 0,91643
0,40007
-0,43653
7,0098
-1,1636
-0,92044
0,39088
-0,42467
7,2054
-1,1355
-0,92430
0,38166
-0,41292
7,4114
—1,1075
—0,92807
0,37240
-0,40126
2.14
2.15
2.16
2.17
2.18
2.19
2.20 2,21. 2,22
2.23
2.24
2.25
2.26
2.27
2.28
2.29
2.30
2.31
2.32
2.33
2.34
2.35
2.36
2.37
2.38
2.39
2.40
2.41
2.42
2.43
2.44
2.45
2.46
2.47
2.48
2.49
2.50
2.51
2.52
2.53
2.54
2.55
2.56
2.57
2.58
2.59
2.60 2,61 2,62
2.63
2.64
2.65
2.66
2.67
2.68
2.69
2.70
2.71
2.72
2.73
2.74
2.75
2.76
357
Таблица 3 продолжение
V
V
tgv
V
sin v
V tg V
COS V
sin v
tgv
V
2,77
7,1080
7
6287
-1,0795
-0,93175
0,36310
-0,38970
2,77
2,78
—
7,3502
7
8584
-1,0514
-0,93533
0,35376
— 0,37822
2,78
2,79
—
7,6057
8
1013
-1,0235
-0,93883
0,34439
-0,36683
2,79
2,80
—
7,8756
8
3535
-0,9955
-0,94222
0,33499
-0,35553
2,80
2,81
—
8,1612
8
6315
-0,9675
-0,94553
0,32555
-0,34431
2,81
2,82
—
8,4644
8
9218
-0,9395
-0,94873
0,31608
-0,33316
2,82
2,83
—
8,7866
9
2309
-0,9115
— 0,95135
0,30657
-0,32208
2,8a
2,84
—
9,1295
9
5610
-0,8834
-0,95486
0,29704
-0,31108
2,84
2,85
—
9,4952
9
9137
-0,8554
-0,95779
0,28748
-0,30015
2,85
2,86
—
9,8866
10
2918
-0,8273
-0,96061
0,27789
-0,28928
2,86
2,87
—
10,3063
10
6982
-0,7992
-0,96334
0,26827
-0,27347
287
2,88
—
10,7571
11
1360
-0,7711
-0,96593
0,25862
-0,26773
2,83
2,89
—
11,2434
11
6083
-0,7428
-0,96852
0,24895
-0,25704
2,89
2,90
—
11,7690
12
1212
-0,7146
-0,97096
0,23925
-0,24641
2,90
2,91
—
12,3399
12
6781
-0,6862
-0,97330
0,22953
-0,23582
2,91
2,92
—
12,9611
13
2860
-0,6578
-0,97555
0,21978
-0,22529
2,92
2,93
—
13,6400
13
9510
-0,6294
-0,97770
0,21002
-0,21481
2,93
2,94
—
143857
14
6831
-0,6008
-0,97975
0,20023
-0,20437
2,94
2,95
—
15,2085
15
4921
-0,5722
-0,93170
0,19042
_0,19397
2,9o
2,96
_
16,1202
16
3898
-0,5435
-0,98356
0,18060
-0,18362
2,96
2,97
—
17,1379
17
3933
-0,5147
-0,98531
0,17075
-0,17330
2,97
2,98
—
18,2810
18
5220
-0,4858
-0,98697
0,16089
-0,16301
2,98
2,99
—-
19,5726
19
8000
-0,4568
-0,98353
0,15101
-0,15276
2,99
3,00
—
21,0452
21
2585
-0,4276
-0,98999
0,14112
-0,14255
3,00
3,01
—
22,7410
22
9403
-0,3984
-0,99135
0,13121
-0,13236
3,01
3,02
—
24,7136
24
8990
-0,3090
-0,99262
0,12129
-0,12220
3,02
3.03
—
27,0391
27
2090
- 0,3395
-0,99378
0,11136
-0,11206
3,03
3,04
—
29,8215
29
9744
-0,3099
-0,99484
0,10142
-0,10194
3,04
3,05
—
33,2063
33
3479
-0,2801
-0,99581
0,09146
-0,09185
3,05
3,06
—
37,4220
37
5460
-0,2502
-0,99667
0,08150
-0,08177
3,06
3,07
—
42,8053
42
9190
— 0,2202
-0,99744
0,07153
—0,07172
3,07
3,08
—
49,9432
50
0402
-0,1899
-0,99810
0,06155
-0,06167
3,03
3,09
—
59,8373
59
9186
-0,1596
-0,99867
0,05157
-0,05164
3,09
3,10
—
74,4383
74
5533
-0,1321
-0,99914
0,04158
-0,04162
3,10
3,11
—
98,4177
98
4489
-0,0983
-0,99950
,03159
-0,03160
3,11
3,12
—
lit, 471
144
505
-0,0674
-0,99977
,02159
-0,02160
3,12
3,13
—
269,937
270
005
-0,0363
-0,99993
0,01159
-0,01159
3,13
3,14
4
1971,55
1971
56
-0,0050
-1,00000
0,00159
-0,00159
3,14
3,15
374,663
-374
677
0,0265
-0,99996
-0,00841
0,00841
3,15
3,16
171,651
-171
630
0,0582
-0,99983
-0,01841
0,01841
3,16
3,17
111,5 И
-111
606
0,0901
-0,99960
-0,02840
0,02841
3,17
3,18
82,7478;
- 82
8125
0,1222
—0,99926
-0,03840
0,03843
3,18
3,19
65,8411
- 65
9227
0,1545
-0,99883
-0,04839
0,04845
3,19
3,20
54,7289
- 54
8227
0,1871
-0,99829
-0,05837
0,05847
3,20
3,21
46,8545
- 46
9641
0,2199
-0,99766
-0,06835
0,06851
3,21
3,22
40,9326
- 41
1081
0,2530
-0,99693
-0,07833
0,07857
3,22
3,23
36,4395
- 36
5840
0,2863
-0,99609
-0,08829
0,08864
3,23
3,24
32,8168
- 32
9771
0,3199
-0,99516
-0,09825
0,09873
3,24
3,25
29,8631
- 30
0370
0,3537
-0,99413
-0,10820
0,lp883
3,25
3,26
27,4042
- 27
5967
0,3878
—0,99300
-0,11813
0,11896
3,26
3,27
25,3253
- 25
5369
0,4222
-0,99177
-0,12805
0,12912
3,27
3,28
23,456
- 23
7740
0,4569
-0,99044
-0,13797
0,13940
3,23
3,29
22,0052
- 22
2508
0,4919
-0,98901
-0,14786
0,14951
3,29
3,30
20,6573
- 20
9192
0,5272
-0,98748
-0,15775
0,15975
3,30
3,31
19,4683
- 19
7482
0,5628
-0,98585
-0,16761
0,17002
3,31
3,32
18,4107
- 18
7084
0,5987
-0,98413
-0,17746
0,18033
3,32
3,33
17,4647
- 17
7799
0,6349
-0,98230
-0,18729
0,19067
3,33
3.34
16,6128
- 16
9448
0,6715
-0,98038
-0,19711
0,20105
3,34
3,35
15,8407
- 16
1914
0,7085
-0,97836
-0,20690
0,21148
3,35
3,36
15,1385
- 15
5067
0,7457
-0,97624
-0,21668
0,22195
3,36
3,37
14,4971
— 14
8832
0,7834
—0,97403
-0,22643
0,23246
3,37
3,38
13,9077
- 14
3123
0,8214
-0,97172
-0,23616
0,24303
3,38
3,39
13,3649
- 13
7883
0,8599
-0,96931
-0,24586
0,25365
3,39
338
Таблица 3 продолжение
V
V
tgv
V
sin v
v tg V
cos v
sin v
r-
tgv
V
3,40
12,8632
-13,3052
0,8987
-0,96680
-0,25554
0,26432
3,40.
3,41
12,3982
-12,8582
0,9379
-0,96419
-0,26520
0,27504
3,41
3,42
11,9651
-12,4445
0,9775
-0,96149
-0,27482
0,28583
3,42
3,43
11,5613
-12,0592
1,0176
-0,95870
-0,28443
0,29668
3,43
3,44
11,1837
-11,7007
1,0581
-0,95581
-0,29400
0,30759
3,44
3,45
10,8296
-11,3659
1,0991
-0,95282
-0,30354
0,31857
3,45
3,46
10,4969
-11,0525
1,1405
-0,94974
-0,31305
0,32962
3,46
3,47
10,1834
-10,7584
1,1824
-0,94656
-0,32254
0,34075
3,47
3,48
9,8878
-10,4822
1,2248
-0,94328
-0,33199
0,35195
3,48
3,49
9,6085
-10,2226
1,2676
-0,93992
-0,34140
0,36322
3,49
3,50
9,3433
- 9,9778
1,3111
-0,93646
-0,35078
0,37459
3,50
3,51
9,0926
- 9,7465
1,3550
-0,93290
-0,36013
0,38603
3,51
3,52
8,8538
- 9,5279
1,3994
-0,92925
-0,36944
0,39757
3,52
3,53
8,6268
- 9,3211
1,4444
-0,92551
-0,37871
0,40919
3,53
3,54
8,4101
- 9,1249
1,4901
-0,92168
-0,38795
0,42092
3,54
3,55
8,2035
- 8,9387
1,5362
— 0,91775
-0,39715
0,43274
3,55
3,56
8,0061
- 8,7618
1,5830
-0,91374
-0,40631
0,44466
3,56
3,57
7,8171
- 8,5937
1,6304
-0,90963
-0,41542
0,45669
3,57
3,58
7,6339
- 8,4334
1,6784
-0,90543
-0,42450
0,46884
3,58
3,59
7,4622
- 8,2809
1,7271
-0,90114
-0,43353
Q, 48109
3,59
3,60
7,2953
- 8,1352
1,7765
-0,89676
-0,44252
0,49347
3,60
3,61
7,1349
- 7,9961
1,8265
-0,89229
-0,45147
0,59596
3,61
3,62
6,9805
- 7,8632
1,8773
-0,88773
-0,46037
0,51859
8,62
3,63
6,8318
- 7,7362
1,9288
-0,88308
-0,46922
0,53134
3,63
3,64
6,6882
- 7,6146
1,9810
-0,87835
-0,47803
0,54424
3,64
3,65
6,5498
- 7,4979
2,0340
-0,87352
-0,48679
0,55727
3,65
3,66
6,4160
- 7,3865
2,0878
-0,86861
-0,49550
0,57045
3,66
3,67
6,2866
- 7,2794
2,1425
-0,86361
-0,50416
0,58378
3,67
3,68
6,1614
- 7,1767
2,1979
-0,85853
-0,51277
0,59727
3,68
3,69
6,0401
- 7,0780
2,2543
-0,85336
-0,52133
0,61092
3,69
3,70
5,9226
- 6,9832
2,3115
-0,84810
-0,52984
0,62473
3,70
3,71
5,8085
- 6,8922
2,3696
-0,84276
-0,53829
0,63872
3,71
3,72
5,6977
- 6,8046
2,4288
-0,83733
-0,54669
0,65289
3,72
3,73
5,5901
- 6,7202
2,4888
-0,83183
-0,55504
0,66725
3,73
3,74
5,4855
— 6,6391
2,5499
-0,82623
- 0,56333
0,68180
3,74
3,75
5,3837
- 6,5610
2,6121
-0,82056
-0,57156
0,69655
3,75
3,76
5,2845
- 6,4557
2,6753
-0,81480
-0,57974
0,71151
3,76
3,77
5,1880
- 6,4131
2,7396
- 0,80896
-0,58786
0,72668
3,77
3,78
5,0939
- 6,3431
2,8050
-0,80305
-0,59592.
0,74207
3,78
3,79
5,0020
- 6,2757
2,8716
-0,79705
-0,60392
0,75769
3,79
3,80
4,9123
- 6,2106
2,9395
-0,79097
-0,61186
0,77356
3,80
3,8.1
4,8248
- 6,1477
3,0086
-0,78481
-0,61974
0,78967
3,81
3,82
4,7393
- 6,0872
3,0790
-0,77857
-0,62755
0,80603
3,82
3,83
4,6556
- 6,0285
3,1508
-0,77226
-0,63531
0,82266
3,ea
3,81
4,5738
- 5,9720
3,2239
-0,76587
-0,64300
0,83957
3,84
3,85
4,4937
- 5,9173
3,2985
-0,75940
-0,65063
0,85676
3,85.
3,86
4,4152
- 5,8646
3,3746
-0,75285
-0,65819
0,87425
3,86.
3,87
4,3383
- 5,8136
3,4522
-0,74624
-0,66568
0,89205
3,87
3,88
4,2629
- 5,7643
3,5315
-0,73954
-0,67311
0,91017
3.8
3,89
4,1890
- 5,7166
3,6124
— 0,73277
-0,68047
0,92863
3,89
3,90
4,1164
- 5,6705
3,6949
-0,72593
-0,68777
0,94742
3,90
3,91
4,0452
- 5,6260
3,7793
-0,71902
-0,69499
0,96658
3,91
3,92
3,9752
- 5,5828
3,8656
—0,71203
-0,70215
0,98612
3,92
3,93
3,9064
- 5,5412
3,9537
-0,70498
-0,70923
1,00604
3,9a
3,94
3,8388
— 5,5009
4,0439
-0,69785
-0,71625
1,02636
3,94
3,95
3,7723
- 5,4619
4,1361
-0,69065
-0,72319
1,04711
3,95.
3,96
3,7068
- 5,4242
4,2305
-0,68338
-0,73006
1,06830
3,96
3,97
3,6424
- 5,3877
4,3271
-0,67605
-0,73686
1,08994
3,97
3,98
3,5789
- 5,3525
4,4260
-0,66865
-0,74358
1,11206
3,98
3,99
3,5164
- 5,3184
4,5274
-0,66118
-0,75023
1,13468
3,99
4,00
3,4548
- 5,2854
4,6313
-0,65364
-0,75680
1,15782
4,00
4,01
3,3940
— 5,2535
4,7378
-0,64604
-0,76330
1,18150
4,01
4,02
3,3340
- 5,2227
4,8471
-0,63838
-0,76972
1,20575
4,02
36
Таблица 3 продолжение
V
V
tgv
V
sin v
v tgv
cos v
sin v
tgv
V
4,03
3,2748
-5,1928
4,9593
-0,63065
-0,77607
1,23059
4,03
4,04
3,2164
-5,1649
5,0744
-0,62286
— 0,78234
1,25604
4,04
4,05
3,1588
-5,1361
5,1927
-0,61500
— 0,78853
1,28215
4,05
4,06
3,1018
-5,1092
5,3143
-0,60709
—0,79464
1,30893
4,0ft
4,07
3,0454
-5,0832
5,4393
-0,59911
—0,80067
1,3363
4,07
4,08
2,9897
-5,0581
5,5678
-0,59107
-0,80662
1,36467
4,08
4,09
2,9347
-5,0339
5,7002
-0,58298
-0,81249
1,39369
4,09
4,10
2,8802
-5,0105
5,8365
-0,57482
-0,81828
1,42353
4,10
4,11
2,8262
-4,9830
5,9769
-0,56661
-0,82398
1,45423
4,11
4,12
2,7728
-4,9662
6,1217
-0,55834
-0,82961
1,48534
4,12
4,13
2,7200
-4,9452
6,2710
-0,55002
-0,83515
1,51840
4,13
4,14
2,6676
-4,9250
6,4251 j
-0,54164
-0,84061
1,55197
4,14
4,15
2,6157
-4,9055
6,5343
-0,53321
-0,84598
1,53659
4,15
4,16
2,5642
—4,8368
6,7489
-0,52472
-0,85127
1,62233
4Д6
4,17
2,5132
-4,8688
6,9191
-0,51618
-0,85648
1,65925
4,17
4,18
2,4626
-4,8514
7,0952
-0,50759
-0,86160
1,69742
4,18
4,19
2,4123
-4,8348
7,2776
-0,49895
-0,86663
1,73690
4,19
4,20
2,3625
-4,8188
7,4667
-0,49026
-0,87158
1,77778
4,20
4,21
2,3130
-4,8036
7,6628
-0,4815.2
-0,87643
1,82014
4,21
4,22
2,2639
-4,7839
7,8663
-0,47273
-0,88121
1,86407
4,22
4,23
2,2150
-4,7749
8,0779
-0,46390
-0,88539
1,90967
4,23
4,24
2,1665
-4,7615
8,2978
-0,45501
— 0,89048
1,95704
4,24
4,25
2,1183
-4,7487
8,5268
-0,44609
-0,89499
2,00631
4.25
4.26
4,26
2,0704
-4,7364
8,7653
-0,43712
-0,89941
2,05759
4,27
2,0227
-4,7249
9,0141
-0,42810
-0,90373
2,11103
4,27
4,28
1,9753
-4,7133
9,2733
-0,41904
-0,90797
2,16677
4,28
4,29
1,9281
-4,7034
9,5452
- 0,40994
-0,91211
2,22499
4,29
4,30
1,8811
-4,6934
9,8291
-0,40080
— 0,91617
2,28535
4,30
4,31
1,8344
-4,6841
10,1266
— 0,39162
-0,92013
2,34956
2,41633
4,31
4,32
1,7878
-4,6753
10,4385
-0,38240
—0,92400
4,32
4,33
1,7415
-4,6670
10,7662
-0,37314
— 0,92778
2,48642
4,33
4,34
1,6953
-4,6593
11,1107
-0,36334
-0,93146
2,56007
4,34
4,35
1,6492
-4,6522
11,4736
-0,35451
-0,93505
2,63760
4,35
4,36
1,6033
—4,6455
11,8563
-0,34514
-0,93855
2,71933
4,36
4,37
1,5576
-4,6393
12,2606
-0,33574
-0,94196
2,80562
4,37
4,38
1,5120
-4,6336
12,6884
-0,32630
—0,94527
2,89690
4,38
4,39
1,4664
-4,6285
13,1420
-0,31683
-0,94848
2,99363
4,39
4,40
1,4210
—4,6238
13,6238
-0,39733
-0,95160
3,09632
4,40
4,41
1,3757
-4,6196
14,1366
-0,29780
-0,95463
3,20558
4,41
4,42
1,3305
-4,6159
14,6836
1 -0,28824
-0,95756
3,32208
4,42
4,43
1,2853
-4,6127
15,2683
-0,27865
-0,96039
3,44658
4,43
4,44
1,2402
-4,6100
15,8951
-0,26903
-0,96313
3,57997
4,44
4,45
1,1952
-4,6077
16,5685
-0,25939
-0,96577
3,72327
4,45
4,46
1,1502
-4,6059
17,2943
-0,24972
-0,96832
3,87765
4,46
4,47
1,1052
— 4,6946
18,0789
-0,24002
-0,97077
4,04449
4,47
4,48
1,0603
-4,6037
18,9297
-0,23030
-0,97312
4,22539
4,48
4,49
1,0153
-4,6034
19,8559
-0,22036
-0,97537
4,42225
4,49
4,50
0,9704
-4,6034
20,8630
-0,21030
-0,97753
4,63733
4,50
4,51
0,9254
-4,6040
21,9787
-0,20101
-0,97959
4,87333
4,51
4,52
0,8805
—4,6050
23,2035
-0,19120
-0,98155
5,13351
4,52
4,53
0,8355
-4,6064
24,5610
-0,18138
-0,98341
5,42186
4,53
4,54
0,7905
-4,6083
26,0744
-0,17154
-0,98518
5,74326
4,54
4,55
0,7454
-4,6107
27,7724
-0,16168
-0,98684
6,10333
4,55
4,56
0,7003
-4,6135
29,6914
-0,15180
-0,98341
6,51128
4,56
4,57
0,6551
-4,6167
31,8780
-0,14191
-0,93988
6,97549
4,57
4,58
0,6099
-4,6204
34,3927
-0,13200
— 0,99125
7,50932
4,58
4,59
0,5646
-4,6246
37,3159
-0,12208
— 0,99252
8,12983
4,59
4,60
0,5192
-4,6292
40,7568
-0,11215
-0,99369
8,86017
4,60
4,61
0,4737
-4,6343
44,8669
-0,10221
-0,99476
9,73252
4,61
4,62
0,4281
-4,6398
49,8635
-0,09226
-0,99574
10,7930
4,62
4,63
0,3823
-4,6457
56,0696
-0,08230
-0,99661
12,1101
4,63
4,64
0,3365
-4,6522
63,9852
-0,07233
-0,99738
13,7901
4,64
4,65
0,2905
-4,6591
74,4357
-0,06235
-0,99805
16,0077
4,65
360
Таблица 3 продолжение
V
V
tgv
V
sin v
vt
COS V
sin v
tgv
V
4,66
0
2444
-4
6664
88
8686
-0
05237
-0
99863
19
0705
4
66
4,67
0
1981
-4
6742
110
104
-0
04238
-0
99910
23
576Э
4
67
4,68
0
1516
-4
6324
144
443
-0
03238
-0
99948
30
8639
4
68
4,69
0
ЮоО
-4
6912
209
443
-0
02239
-0
99975
44
6574
4
69
4,70
0
0582
-4
7004
379
350
-0
01239
-0
99992
80
71276
4
70
4,71
0
0113
-4
7100
1971
55
-0
00239
-1
00000
418
587
4
71
4,72
-0
0359
-4
7201
— 620
141
0
00761
-0
99997
131
336
4
72
4,73
-0
0833
-4
7308
-268
554
0
01761
-0
99984
56
7768
4
73
4,74
-0
1309
-4
7418
-171
627
0
02761
-0
99962
—
36
20S2
4
74
4,75
-0
1787
-4
7534
-126
233
0
03760
-0
99329
26
5754
4
75
4,76
-0
2268
-4
7654
- 99
9013
0
04759
-0
99887
20
9377
4
76
4,77
-0
2751
-4
7779
- 82
7050
0
05758
-0
99834
17
3336
4
77
4,78
-0
3237
— 4
7909
- 70
5907
0
06756
-0
99772
14
7679
4
78
4,79
-0
3725
-4
8045
- 61
5940
0
07753
-0
99699
12
3539
4
79
4,80
-0
4216
— 4
8185
- 54
6474
0
08750
-0
99616
11
3849
4
80
4,81
-0
4710
-4
8330
- 49
1206
0
09746
-0
99524
Ю
2122
4
81
4,82
-0
5207
-4
8480
- 44
6179
0
10740
-0
99422
9
25633
4
82
4,83
-0
5707
-4
8636
- 40
8781
0
11734
-0
9Э309
—
8
46336
4
83
4,84
-0
6210
-4
8797
- 37
7216
0
12726
-0
99187
7
79373
4
84
4,85
-0
6717
-4
8963
- 35
0215
0
13718
-0
99055
7
22093
4
85
4,86
-0
7226
-4
9134
- 32
6849
0
14708
-0
98913
6
72529
4
86
4,87
-0
7740
-4
9311
- 30
6426
0
156 Э6
-0
98761
6
29211
4
87
4,88
-0
8257
-4
9493
- 28
8419
0
16683
-0
98599
5
91022
4
83
4,89
-0
8778
— 4
9681
- 27
2419
0
17668
-0
98427
5
57095
4
89
4,90
-0
9302
-4
9875
- 25
8107
0
18651
-0
93245
5
26749
4
90
4,91
-0
9831
-5
0074
- 24
5225
0
19633
-0
98054
4
99440
4
91
4,92
-1
0364
-5
0279
- 23
3567
0
20612
-0
97853
4
74730
4
92
4,93
-1
0901
-5
0491
- 22
2964
0
21590
-0
97642
—
4
52259
4
93
4,9
-1
1442
-5
0708
- 21
3276
0
22565
-0
97421
4
31733
4
94
4,95
-1
1988
-5
0931
- 20
4388
0
23538
-0
97190
4
12906
4
95
4,96
-1
2539
-5
1160
- 19
1737
0
24509
-0
96950
3
95572
4
96
4,97
-1
3094
-5
1396
- 18
8640
0
25477
-o
96700
3
79557
4
97
4,98
-1
3655
-5
1638
- 18
1627
0
26443
-0
96441
3
64713
4
93
4,99
-1
4220
-5
1887
- 17
5107
0
27406
-0
96171
3
50915
4
99
5,00
-1
4791
-5
2142
- 16
9026
0
23366
-0
95392
3
33052
5
00
5,01
-1
5367
— 5
2404
- 16
3341
0
29324
-0
95604
о
С
26030
5
01
5,02
-1
5948
-5
2672
- 15
8013
0
30278
-0
95306
3
14767
5
02
5,03
-1
6536
-5
2948
- 15
3009
0
31230
-0
94998
3
04192
5
03
5,04
-1
7129
-5
3231
- 14
8297
0
32178
-0
94681
2
94241
5
04
5,05
-1
7728
-5
3521
- 14
3854
0
33123
-0
94355
2
84359
5
05
5,06
-1
8334
-5
3819
- 13
965
0
34065
-0
94019
2
75996
5
06
5,07
-1
8945
-5
4124
- 13
5678
0
35004
-0
93674
2
67610
5
07
5,08
-1
9564
-5
4437
- 13
1908
0
35939
-0
93319
2.
,59661
5
08
5,09
-2
0189
-5
4758
- 12
8326
0
36870
-0
92955
2
52114
5
09
5,10
-2
0821
-5
5087
- 12
4919
0
37798
-0
92581
2
44Э39
5
10
5,11
-2
1461
-5
5424
- 12
1673
0
38722
-0
92199
2
38107
5
11
5,12
-2
2108
— 5
5769
- 11
8575
0
39642
-0
91807
2
31592
5
12
5,13
-2
2762
-5
6123
- 11
5616
0
40558
-0
91406
—
2
25372
5
13
5,14
-2
3425
-5
6486
- 11
2785
0
41470
-0
90996
2
19427
5
14
5,15
— 2
4095
— 5
6858
- 11
0074
0
42378
-0
90577
—
2
13737
5
15
5,16
— 2
4774
-5
7238
- 10
7475
0
43281
-0
90148
2
08285
5
16
5,17
—2
5461
-5
7629
- 10
4979
0
44181
-0
89711
2
03055
5
17
5,18
-2
6157
-5
8029
- 10
2582
0
45076
-0
89265
1
98034
5
18
5,19
-2
6862
-5
8439
- 10
0275
0
45966
-0
88810
—
1
93208
5
19
5,20
-2
7577
-5
8860
- 9
8053
0
46852
-0
83345
1
88564
5
20
5,21
— 2
8301
-5
9290
- 9
5912
0
47733
-0
87873
1
84093
5
21
5,22
-2
9035
-5
9732
- 9
3847
0
48609
-0
87391
1
79733
5
22
5,23
-2
9779
-6
0184
- 9
1852
0
49481
-0
86900
1
75625
5
23
5,24
-3
0534
-6
0647
- 8
9924
0
50347
-0
86401
1
71611
5
24
5,25
-3
1300
-6
1123
- 8
8060
0
51209
-0
85893
1
67733
5
25
5,26
-3
2077
-6
1610
- 8
6254
0
52065
-0
85377
1
63982
5
26
5,27
-3
2865
-6
2108
- 8
4506
0
52Э16
-0
84852
1
60352
5
27
5,28
-3
3665
-6
2619
- 8
2810
0
53762
-0
84319
—
1
56837
5
28
361
Таблица 3 продолжение
V
V
tgv
V
sin v
v t g v.
cos v
sin v
tgv
V
5
29
- 3
4478
е
3144
-8
1165
0
54602
-0
83777
-1,53431
5,29
5
30
- 3
5303
—
6
3681
— 7
9567
0
55437
-0
83227
-1,50127
5,30
5
31
- 3
6142
—
6
4233
-7
8015
0
56267
-0
82668
-1,46922
5,31
5
32
- 3
6993
—
6
4798
-7
6506
0
57091
-0
82101
-1,43809
5,32
5
33
— 3
7859
—
6
5378
-7
5038
0
57909
-0
81526
-1,40784
5,33
5
34
- 3
8740
—
6
5972
-7
3603
0
58721
-0
80943
-1,37843
5,34
5
35
- 3
9635
—
6
6582
-7
2215
0
59528
-0
80352
-1,34982
5,35
5
36
- 4
0545
—
6
7207
-7
0858
0
60328
-0
79753
-1,32198
5,36
5
37
- 4
1472
—
е
7850
-6
9534
0
61123
-0
79145
-1,29486
5,37
5
38
- 4
2414
—
6
850Э
-6
8242
0
61911
-0
78530
-1,26844
5,38
5
39
- 4
3374
—
6
9185
-6
6930
0
62693
-0
77907
-1,24267
5,39
5
40
- 4
4352
—
6
9879
-6
5747
0
63469
-0
77276
-1,21754
5,40
5
41
- 4
5347
—
7
0592
-6
4542
0
64239
-0
76638
-1,19301
5,41
5
42
- 4
6362
—
7
1323
-6
3364
0
65002
-0
75992
-1,16907
5,42
5
43
- 4
7396
—
7
2075
-6
2210
0
65759
-0
75338
-1,14567
5,43
5
44
- 4
8450
—
7
2347
-6
1081
0
66509
-0
74677
-1,12281
5,44
5
45
- 4
Э525
—
7
3641
-5
9974
0
67252
-0
74008
-1,10045
5,45
5
46
- 5
0622
—
7
4456
-5
880
0
67989
-0
73332
-1,07858
5,46
5
47
— 5
1742
—
7
5295
-5
7828
0
68719
-0
72648
-1,05718
5,47
5
48
- 5
2884
—
7
6157
-5
6785
0
69442
-0
71957
-1,03622
5,48
5
49
- 5
4051
—
7
7043
-5
5762
0
70158
-0
71259
-1,01570
5,49
5
50
— 0
5244
—
7
7954
-5
4757
0
70867
-0
70554
-0,99558
5,50
5
51
- 5
6462
—
7
8892
-5
3770
0
71569
-0
69842
-0,97587
5,51
5
52
- 5
7709
—
7
9853
-5
2300
0
72264
-0
69123
-0,95653
5,52
5
53
- 5
8933
—
8
0851
-5
1847
0
72951
-0
68397
-0,93756
5,53
5
54
- 6
0286
—
8
1875
-5
0910
0
73632
-0
67664
-0,91895
5,54
5
55
- 6
1621
—
8
2930
-4
9987
0
74305
-0
66924
-0,90067
5,55
5
56
- 6
2987
—
8
4016
-4
9192
0
74970
-0
66178
-0,88272
5,56
5
57
- 6
4337
—
8
5136
-4
8185
0
75628
-0
65425
-0,86508
5,57
5
58
- 6
5821
—
8
62Э1
-4
7304
0
76279
-0
64665
-0,84775
5,58
5
59
- 6
7292
—
8
7482
-4
6437
0
76921
-0
63899
-0,83071
5,59
5
60
- 6
8801
—
8
8710
-4
5581
0
77557
-0
63127
-0,81394
5,60
5
61
- 7
0349
—
8
9979
-4
4737
0
78184
-0
62348
-0,79745
5,61
5
62
- 7
1939
—
9
1289
-4
3905
0
78804
-0
61563
-0,78122
5,62
5
63
- 7
3572
—
9
2641
-4
3083
0
79415
-0
60772
-0,76524
5,63
5
64
- 7
5249
—
9
4039
-4
2272
0
80019
-0
59975
-0,74951
5,64
5
65
- 7
6975
—
9
5484
-4
1471
0
80615
-0
59172
-0,73400
5,65
5
66
- 7
8750
—
9
6981
-4
0680
0
81202
-0
58362
-0,71873
5,66
5
67
- 8
0577
—
9
8526
-3
9898
0
81782
-0
57548
-0,70367
5,67
5
68
- 8
2460
—
0129
-3
9125
0
82353
-0
56727
-0,68882
5-, 68
5
69
- 8
4399
—
0
1789
-3
8361
0
82916
-0
55900
-0,67418
5,69
5
70
- 8
6399
—
0
3506
-3
7605
0
83471
-0
55069
-0,65973
5,70
5
71
- 8
8463
—
0
5290
-3
6856
0
84018
-0
54231
-0,64547
5,71
5
72
- 9
0592
—
0
7140
-3
6116
0
84556
-0
53388
-0,63140
5,72
5
73
- 9
2793
—
0
9060
-3
5383
0
85086
-0
52540
-0,61750
5,73
5
74
- 9
5069
—
1
1054
-3
4656
0
85607
-0
51687
-0,60377
5,74
5
75
- 9
7425
—
1
3127
-3
3936
0
86119
-0
50828
-0,59020
5,75
5
76
- 9
9861
—
1
5283
-3
3224
0
86623
-0
49964
-0,57680
5,76
5
77
-Ю
2337
1
7527
-3
2517
0
87119
-0
49095
-0,56355
5,77
5
78
-Ю
5005
—
1
9862
-3
1816
0
87605
-0
48222
-0,55045
5,78
5
79
-Ю
7723
—
2
2299
-3
1121
0
88083
-0
47343
-0,53749
5,79
5
80
-11
0546
_
2
4839
-3
0431
0
88552
-0
46460
-0,52467
5,80
5
81
-И
3481
—
2
7491
-2
9746
0
89012
-0
45572
-0,51198
5,81
5
82
-11
6535
—
3
0260
-2
9066
0
89463
-0
44680
-0,49942
5,82
5
83
-11
9715
—
3
3157
-2
83Э1
0
89906
-0
43783
— 0,48699
5,83
5
84
-12
3030
—
3
6183
-2
7721
0
90339
-0
42882
-0,47468
5,84
5
85
-12
6492
—
3
9365
-2
7055
0
90763
-0
41976
-0,46248
5,85
5
86
-13
0107
—
2694
-2
6393
0
91179
-0
41067
-0,45040
5,86
5
87
-13
3890
—
6191
-2
5735
0
91585
-0
40153
-0,43842
5,87
5
88
-13
7850
—
9866
-2
5081
0
91982
-0
39235
-0,42655
5,88
5
89
-14
2003
—
5
3734
-2
4430
0
92369
-0
38313
-0,41478
5,89
5
90
-14
6362
—
5
7805
-2
3783
0
92748
-0
37388
-0,40311
5,90
5
91
-15
0946
—;
2104
-2
3139
1
0
93117
-0
36458
-0,39153
5,91
362
Таблица 3 продолжение
V
V
ч
V
V
sin v
v fcg v
cos V
sin v
tgv
V
5
92
15
5772
16
6642
-2
2499
0,93477
-0
35525
-0,38004
5
92
5
93
16
0862
17
1442
-2
1860
0,93828
-0
34589
-0,36864
5
93
5
94
16
6238
—
17
6528
-2
1225
0,94169
-0
33649
-0,35732
5
94
5
95
17
1921
—
18
1929
— 2
0592
0,94501
-0
32705
-0,34609
5
95
5
96
17
7948
—
18
7663
-1
9962
0,94823
-0
31759
-0,33493
5
96
5
97
18
4350
—
19
3775
-1
9333
0,95136
-0
30809
-0,32384
5
97
5
98
19
1158
—
20
0295
-1
8707
0,95439
-0
29856
-0,31289
5
98
5
99
19
8420
—
20
7264
-1
8083
0,95733
-0
28900
-0,30189
5
99
6
00
20
6178
—
21
4731
-1
7461
0,96017
-0
27942
-0,29101
6
00
6
01
—
21
4497
—
22
2758
-1
6839
0,96292
-0
26980
-0,28019
6
01
6
02
22
3430
—
23
1399
-1
6220
0,96557
-0
26016
-0,26944
6
02
6
03
23
3055
—
24
0729
-1
5602
0,96812
-0
25049
-0,25874
6
03
6
04
—
24
3455
—
25
0S35
-1
4985
0,97058
-0
24080
-0,24810
6
04
6
05
—
25
4730
—
26
1816
-1
4369
0,97294
-0
23108
-0,23751
6
05
6
06
—
26
7000
—
27
3791
-1
3754
0,97520
-0
22134
-0,22697
6
06
6
07
28
0403
—
28
6897
-1
3140
0,97736
-0
21157
-0,21647
6
07
6
08
—
29
5105
—
30
1303
-1
2527
0,97943
-0
20179
-0,20603
6
08
Г
09
31
1310
—
31
7211
-1
1914
0,98140
-0
19199
-0,19562
6
09
6
10
32
9263
—
33
4867
-1
1301
0,98327
-0
18216
-0,18526
6
10
6
11
34
9267
—
35
4571
-1
0639
0,98504
-0
17232
-0,17494
6
11
6
12
37
-1699
—
37
6703
-1
0077
0,98671
-0
16246
-0,16465
6
12
6
13
—
39
7034
—
40
1738
-0
9464
0,98829
-0
15259
-0,15439
6
13
6
14
42
5880
—
43
0284
-0
8852
0,98977
-0
14270
-0,14417
6
14
6
15
45
9031
—
46
3130
-0
8240
0,99114
-0
13279
-0,13398
6
15
6
16
49
7529
—
50
1327
-0
7627
0,99242
-0
12287
-0,12381
6
16
6
17
54
2795
—
54
6288
-0
7013
0,99360
-0
11294
-0,11367
6
17
6
18
59
6796
—
59
9988
-0
6399
0,99468
-0
10300
- 0,10355
6
18
6
19
—
66
2344
—
66
5230
-0
5785
0,99566
-0
09305
-0,09346
6
19
6
20
74
3604
—
74
6184
-0
5170
0,99654
-0
08309
-0,08338-
6
20
6
21
—
84
7016
—
84
9289
-0
4553
0,99732
-0
07312
- 0,07332
6
21
6
22
98
3096
—
98
5062
-0
3935
0,99800
-0
06314
-0,06327
6
22
6
23
117
027
—
117
193
-0
3317
0,99859
-0
05316
-0,05324
6
23
6
24
144
40
—
144
538
-0
2697
0,99907
-0
04317
-0,04321
6
24
6
25
188
267
—
188
371
-0
2075
0,99945
-0
03318
-0,03320
6
25
6
26
269
950
—
270
023
-0
1452
0,99973
-0
02318
-0,02319
6
26
6
27
475
501
—
475
543
-0
0827
0,99991
-0
01318
-0,01319
6
27
6
28
У
1971
55
1971
56
-0
0200
0,99999
-0
003185
-0,003185
6
28
Т аблица 4
Функции jithji, shy, thji, chp для натянуто-изогнутых стержней
1
ц th ц
th д
sh р
shp
thi
ch ц
И
О
0
1,0000
1,0000
0
0
1,0000
0
0,1
0,0100
1,0033
0,9963
0,10017
0,09967
1,00500
0,1
0,2
0,0395
1,0133
0,9934
0,20134
0,19738
1,02007
0,2
0,3
0,0874
1,0298
0,9852
0,30452
0,29131
1,04534
0,3
0,4
0,1520
1,0528
0,9738
0,41075
0,37995
1,08107
0,4
0,5
0,2311
1,0820
0,9595
0,52110
0,46212
1,12763
0,5
0,6
0,3222
1,1172
0,9424
0,63665
0,53705
1,18547
0,6
0,7
0,4231
1,1582
0,9228
0,75858
0,60437
1,25517
0,7
0,8
0,5312
1,2047
0,9008
0,88811
0,66404
1,33743
0,8
0,9
0,6447
1,2565
0,8767
1,02652
0,71630
1,43309
0,9
1,0
0,7616
1,3130
0т8509
1,17520
0,76159
1,54308
1,0
1,1
0,8805
1,3741
0,8236
1,33565
0,80050
1,66852
1,1
1,2
1,0004
1,4394
0,7950
1,50946
0,83365
1,81066
1.2
1,3
1,1202
1,5086
0,7654
1,69838
0,86172
1,97091
1,3
1,4
1,2395
1,5813
0,7352
1,90430
0,8835
2,15090
1,4
1,5
1,3577
1,6572
0,7045
2,12928
0,90515
2,35241
1,5
1,6
1,4747
1,7360
0,673а
2,37557
0,92167
2,57746
1,6
1.7
1,5902
1,8174
0,6426
2,64563
0,93541
2,82832
1,7
1,8
1,7043
1,9011
0,6118
2,94217
0,94681
3,10747
1,8
1,9
1,8169
1,9869
0,5814
3,26816
0,95624
3,41773
1,3
2,0
1,9281
2,0746
0,5514
3,62686
0,96403
3,76220
2,0
2,1.
2,0379
2,1639
0,5221
4,02186
0,97045
4,14431
2,1
2,2
2,1466
2,2547
0,4936
4,45711
0,97574
4,56731
2,2
2,3
2,2542
2,3467
0,4653
4,936 96
0,98010
5,03722
2,3
2,4
2,3308
2,4398
0,4391
5,46623
0,98367
5,55635
2,4
2,5
2,4665
2,5339
0,4132
6,05020
0,98661
6,13223
2,5
2,6
2,5715
2,6288
0,3884
6,69473
0,98903
6,76901
2,6
2,7
2,6757
2,7245
0,3646
7,40626
0,99101
7,47347
2,7
2,8
2,7794
2,8208
0,3418
8,19192
0,99263
8,25273
2,8
2,9
2,8825
2,9176
0,3201
9,05956
0,99396
9,11458
2,9
3,0
2,9851
3,0149
0,2995
10,01787
0,99505
10,06766
3,0
3,1
3,0874
3,1126
0,2799
11,07645
0,90595
11,12150
3,1
3,2
3,1894
3,2107
0,2613
12,24588
0,93668
12,28665
3,2
3,3
3,2910
3,3090
0,2438
13,53788
0,93728
13,57476
3,3
3,4
3,3924
3,4076
0,2272
14,96536
0,99777
14,99874
3,4
3,5
3,4936
3,5064
0,2116
16,54263
0,99818
16,57282
3,5
3,6
3,5946
3,6054
0,1969
18,28546
0,99851
18,31278
3,6
3,7
3,6955
3,7045.
0,1831
20,21129
0,99878
20,23601
3,7
3,8
3,7962
3,8038
0,1701
22,33941
0,93900
22,36178
3,8
3,9
3,8968
3,9032
0,1579
24,69110
0,93918
24,71135
3,9
4,0
3,9973
4,0027
0,1466
27,28992
0,93933
27,30823
4,0
4,1
4,0977
4,1023
0,1359
30,16186
0,99945
30,17843
4,1
4,2
4,1981
4,2019
0,1260
33,33567
0,99955
33,35066
4,2
4,3
4,2984
4,3016
0,1167
36,84311
0,99963
36,85668
4,3
4,4
4,3987
4,4013
0,1081
40,71930
0,99970
40,73157
4,4
4,5
4,4989
4,5011
0,1000
45,00301
0,93975
45,01412
4,5
4,6
4,5991
4,6009
0,0925
49,73713
0,99380
43,74718
4,6
4,7
4,6992
4,7008
0,0855
54,96904
0,99983
54,97813
4,7
4,8
4,7993
4,8007
0,0790
60,75109
0,99986
60,75932
4,8
4,9
4,8995
4,9005
0,0730
67,14117
0,99989
67,14861
4,9
5,0
4,9995
5,0004
0,0674
74,20321
0,93991
74,20995
5,0
5,1
5,0996
5,1004
0,0622
82,00791
0,99993
82,01400
5,1
5,2
5,1997
5,2003
0,0574
90,63336
0,99994
90,63883
5,2
5,3
5,2997
5,3003
0,0529
100,16591
0,99995
100,17090
5,3
5,4
5,3998
5,4002
0,0488
110,70095
0,99996
110,70547
5,4
5,5
5,4998
5,5002
0,0449
122,34392
0,99997
122,34801
5,5
5,6
5,5998
5,6002
0,0414
135,21135
0,99397
135,21505
5,6
5,7
5,6999
5,7001
0,0381
149,43203
0,99998
149,43537
5,7
5,8
5,7999
5,8001
0,0351
165,14827
0,99998
165,15129
5,8
5,9
5,8999
5,9001
0,0323
182,51736
0,99998
182,52010
5,9
6,0
5,9999
6,0001
0,0297
201,71316
0,99999
201,71564
6,0
364
Таблица 5
Круговые и гиперболические функции для аргумента 0 v 1
V
sin v
cos v
tgv
sh v
ch v
th v
0,00
0,00000
1,00000
0,00000
0,00000
1,00000
0,00000
0,01
0,01000
0,99995
0,01000
0,01000
1,00005
0,01000
0,02
0,02000
0,99980
0,02000
0,02000
1,00020
0,02000
0,03
0,03000
0,99955
0,03001
0,03000
1,00045
0,02999
0,04
0,03999
0,99920
0,04002
0,04001
1,00080
0,03993
0,05
0,04998
0,99875
0,05004
0,05002
1,00125
0,04996
0,06
0,05996
0,99820
0,06007
0,06004
1,00180
0,05993
0,07
0,06994
0,99755
0,07011
0,07006
1,00245
0,06989
0,03
0,07991
0,99680
0,08017
0,08009
1,00320
0,07983
0,09
0,08988
0,99о95
0,09024
0,09012
1,00405
0,08976
0,10
0,09983
0,99500
0,10033
0,10017
1,00500
0,09967
0,11
0,10978
0,99396
0,11045
0,11022
1,00606
0,10956
0,12
0,11971
0,93281
0,12058
0,12029
1,00721
0,11943
0,13
0,12963
0,99156
0,13074
0,13037
1,00846
0,12927
0,14
0,13954
0,93022
0,14092
0,14046
1,00982
0,13909
0,15
0,14944
0,98877
0,15114
0,15056
1,01127
0,14889
0,16
0,15932
0,98723
0,16138
0,16068
1,01283
0,15865
0,17
0,16918
0,98553
0,17166
0,17082
1,01448
0,16338
0,18
0,17903
0,98384
0,18197
0,18097
1,01624
0,17808
0,19
0,18886
0,98200
0,19232
0,19115
1,01810
0,18775
0,20
0,19867
0,98007
0,20271
0,20134
1,02007
0,19738
0,21
0,20846
0,97803
0,21314
0,21155
1,02213
0,20697
0,22
0,21823
0,97590
0,22362
0,22178
1,02430
0,21652
0,23
0,22798
0,97367
0,23414
0,23203
1,02657
0,22603
0,24
0,23770
0,97134
0,24472
0,24231
1,02894
0,23550
0,25
0,24740
0,96891
0,25534
0,25261
1,03141
0,24492
0,26
0,25708
0,96639
0,26602
0,26294
1.03399
0,25430
0,27
0,26673
0,96377
0,27676
0,27329
1,03667
0,26362
0,28
0,27636
0,96106
0,28755
0,28367
1,03946
0,27291
0,29
0,28595
0,9824
0,29841
0,29408
1,04235
0,28213
0,30
0,29552
0,95534
0,30934
0,30452
1,04534
0,29131
0,31
0,30506
0,95233
0,32033
0,31499
1,04844
0,30044
0,32
0,31457
0,94924
0,33139
0,32549
1,05164
0,30951
0,33
0,32404
0,94604
0,34252
0,33602
1,05495
0,31852
0,34
0,33349
0,94275
0,35374
0,34659
1,05836
0,32748
0,35
0,34290
0,93337
0,36503
0,35719
1,06188
0,33638
0,36
0,35227
0,93630
0,37640
0,36783
1,06550
0,34521
0,37
0,36162
0,93233
0,38786
0,37350
1,06923
0,35399
0,38
0,37092
0,92866
0,39941
0,38921
1,07307
0,36271
0,39
0,38019
0,92491
0,41105
0,39996
1,07702
0,37136
0,40
0,38942
0,92106
0,42279
0,41075
1,08107
0,37995
0,41
0,39861
0,91712
0,43463
0,42158
1,08523
0,38847
0,42
0,40776
0,91309
0,44657
0,43246
1,08950
0,39693
0,43
0,41687
0,90897
0,45862
0,44337
1,09388
0,40532
0,44
0,42594
0,90475
0,47078
0,45434
1,09837
0,41364
0,45
0,43497
0,90045
0,48306
0,46534
1,10297
0,42190
0,46
0,44395
0,89605
0,49545
0,47640
1,10768
0,43008
0,47
0,45289
0,89157
0,50797
0,48750
1,11250
0,43820
0,48
0,46178
0,88699
0,52061
0,49865
1,11743
0,44624
0,49
0,47063
0,88233
0,53339
0,50984
1,12247
0,45422
0,50
0,47943
0,87758
0,54630
0,52110
1,12763
0,46212
0,51
0,48818
0,87274
0,55936
0,53240
1,13289
0,46995
0,52
0,49688
0,86782
0,57256
0,54375
1,13827
0,47770
0,53
0,50553
0,86281
0,58592
0,55516
1,14377
0,48538
0,54
0,51414
0,85771
0,59943
0,56663
1,14938
0,49299
0,55
0,52269
0,85252
0,61311
0,57815
1,15510
0,50052
0,56
0,53119
0,84726
0,62695
0,58973
1,16094
0,50798
0,57
0,53963
0,84190
0,64097
0,60137
1,16690
0,51536
0,58
0,54802
0,83646
0,65517
0,61307
1,17297
0,52267
0,59
0,55636
0,83094
0,66956
0,62483
1,17916
0,52990
365
Таблица 5 продолжение
V
sin v
COS V
tg v
shv
ch v
thv
0,60
0,56464
0,82534
0,68414
0,63665
1
1,18547
1
0,53705
0,61
0,57287
0,81965
0,69892
0,64854
1,19189
0,54413
0,62
0,58104
0,81388
0,71391
0,66049
1,19844
0,55113
0,63
0,58914
0,80803
0,72911
0,67251
1,20510
0,55805
0,64
0,59720
0,80210
0,74454
0,68459
1,21189
0,56490
0,65
0,60519
0,79608
0,76020
0,69675
1,21879
0,57167
0,66
0,61312
0,78999
0,77610
0,70897
1,22582
0,57836
0,67
0,62099
0,78382
0,79225
0,72126
1,23297
0,58498
0,68
0,62879
0,77757
0,80866
0,73363
1,24025
0,59152
0,69
0,63654
0,77125
0,82534
0,74607
1,24765
0,59798
0,70
0,64422
0,76484
0,84229
0,75858
1,25517
0,60437
0,71
0,65183
0,75836
0,85953
0,77117
1,26282
0,61068
0,72
0,65938”
0,75181
0,87707
0,78334
1,27059
0,61691
0,73
0,66687
0,74517
0,89492
0,79659
1,27849
0,62307
0,74
0,67429
0,73847
0,91309
0,80941
1,28652
0,62915
0,75
0,68164
0,73169
0,93160
0,82232
1,29463
0,63515
0,76
0,68892
0,72484
0,95045
0,83530
1,30297
0,64108
0,77
0,69614
0,71791
0,96967
0,84838
1,31139
0,64693
0,78
0,70328
0,71091
0,98926
0,86153
1,31994
0,65271
0,79
0,71035
0,70385
1,00925
0,87478
1,32862
0,65841
0,80
0,71736
0,69671
1,02964
0,88811
1,33743
0,66404
0,81
0,72429
0,68950
1,05046
0,90152
1,34638
0,66959
0,82
0,73115
0,68222
1,07171
0,91503
1,35547
0,67507
0,83
0,73793
0,67488
1,09343
0,92863
1,36468
0,68048
0,84
0,74464
0,66746
1,11563
0,94233
1,37404
0,68581
0,85
0,75128
0,65998
1,13833
0,95612
1,38353
0,69107
0,86
0,75784
0,65244
1,16156
0,97000
1,39316
0,69626
0,87
0,76433
0.64483
1,18532
0,98398
1,40293
0,70137
0,88
0,77074
0,63715
1,20966
0,99806
1,41284
0,70642
0,89
0,77707
0,62941
1,23460
1,01224
1,42289
0,71139
0,90
0,78333
0,62161
1,26016
1,02652
1,43309
0,71630
0,91
0,78950
0,61375
1,28637
1,04090
1,44342
0,72113
0,92
0,79560
0,60582
1,31326
1,05539
1,45390
0,72590
0,93
0,80162
0,59783
1,34087
1,06998
1,46453
0,73059
0,94
0,80756
0,58979
1,36923
1,08468
1,47530
0,73522
0,95
0,81342
0,58168
1,39838
1,09948
1,48623
0,73978
0,96
0,81919
0,57352
1,42836
1,11440
1,49729
0,74428
0,97
0,82489
0,56530
1,45920
1,12943
1,50851
0,74870
0,98
0,83050
0,55702
1,49096
1,14457
1,51988
0,75307
0,99
0,83603
0,54869
1,52368
1,15983
1,53141
0,75736
1,00
0,84147
0.54030
1,55741
1,17520
1,54308
0,76159
Таблица 6
Коэфициенты формул балочного метода
,_A.V
—sin v.
J-3-tgv
6 2tiv n IO
v2 sin v
v2tg
V
T
V3
V
s
t
и
V
s
t
и
0
1,0000
1,0000
1,0000
2,35
2,5022
1,8041
2,2529
0,50
1,0300
1,0171
1,0256
2,36
2,5320
1,8195
2,2774
1,00
1,1304
1,0737
1,1113
2,37
2,5625
1,8354
2,3025
1,05
1,1455
1,0822
1,1241
2,38
2,5939
1,8516
2,3284
1,10
1,1617
1,0912
1,1379
2,39
2,6262
1,8683
2,3550
1,15
1,1792
1,1009
1,1527
2,40
2,6596
1,8854
2,3822
1,20
1,1979
1,1114
1,1686
2,41
2,6935
1,9031
2,4103
1,25
1,2180
1,1225
1,1856
2,42
2,7287
1,9212
2,4391
1,30
1,2396
1,1345
1,2039
2,43
2,7649
1,9398
2,4687
1,35
1,2628
1,1473
1,2235
2,44
2,8021
1,9589
2,4993
1,40
1,2878
1,1610
1,2445
2,45
2,8403
1,9786
2,5306
1,45
1,3146
1,1757
1,2671
2,46
2,8798
1,9989
2,5630
1,50
1,3434
1,1915
1,2914
2,47
2,9204
2,0198
2,5964
1,55
1,3744
1,2084
1,3174
2,48
2,9624
2,0413
2,6307
1,60
1,4078
1,2266
1,3455
2,49
3,0056
2,0635
2,6662
1,65
1,4439
1,2462
1,3758
2,50
3,0502
2,0864
2,7027
1,70
1,4830
1,2673
1,4085
2,51
3,0963
2,1100
2,7405
1,75
1,5252
1,2901
1,4438
2,52
3,1438
2,1343
2,7794
1,80
1,5710
1,3147
1,4821
2,53
3,1931
2,1595
2,8197
1,85
1,6208
1,3414
1,5237
2,54
3,2437
2,1855
2,8612
1,90
1,6750
1,3704
1,5689
2,55
3,2963
2,2124
2,9043
1,95
1,7343
1,4020
1,6182
2,56
3,3508
, 2,2402
2,9488
2,00
1,7993
1,4365
1,6722
2,57
3,4072
2,2690
2,9949
2,01
1,8130
1,4438
1,6836
2,58
3,4657
2,2988
3,0427
2,02
1,8270
1,4512
1,6953
2,59
3,5262
2,3297
3,0922
2,03
1,8413
1,4587
1,7071
2,60
3,5890
2,3618
3,1435
2,04
1,8558
1,4664
1,7192
2,61
3,6542
2,3950
3,1968
2,05
1,8706
1,4742
1,7315
2,62
3,7220
2,4295
3,2522
2,06
1,8858
1,4822
1,7440
2,63
3,7925
2 ,-4654
3,3097
-2,07
1,9012
1,4904
1,7568
2,64
3,8659
2,5027
3,3696
2,08
1,9168
1,4987
1,7698
2,65
3,9421
2,5415
3,4319
U, 09
1,9329
1,5071
1,7832
2,66
4,0218
2,5819
3,4969
2,10
1,9494
1,5158
1,7967
2,67
4,1047
2,6241
3,5646
2,11
1,9661
1,5246
1,8106
2,68
4,1914
2, 6680
3,6353
2,12
1,9831
1,5336
1,8247
2,69
4,2820
2,7140
3,7092
-2,13
2,0005
1,5427
1,8392
2,70
4,3766
2,7619
3,7863
2,14
2,0184
1,5521
1.8539
2,71
4,4757
2,8121
3,8671
2,15
2,0366
1,5616
1,8689
2,72
4,5795
2,8648
3,9517
2,16
2,0552
1,5713
1,8843
2,73
4,6885
2,9199
4,0405
2,17
2,0741
1,5813
1,9000
2,74
4,8029
2,9778
4,1337
2,18
2,0935
1,5914
1,9160
2,75
4,9233
3,0386
4,2317
2,10
2,1133
1,6018
1,9323
2,76
5,0499
3,1027
4,3349
2,20
2,1336
1,6124
1,9491
2,77
5,1835
3,1702
4,4436
2,21
2,1543
1,6233
1,9663
2,78
5,3245
3,2414
4,5584
2,22
2,1754
1,6343
1,9837
2,79
5,4736
3,3166
4,6797
2,23
2,1972
1,6457
2,0016
2,80
5,6315
3,3963
4.8082
2,24
2,2194
1,6572
2,0199
2,81
5,7990
3,4807
4,9444
2,25
2,2421
1,6690
2,0386
2,82
5,9770
3,5704
5,0892
2,26
2,2654
1,6812
2,0578
2,83
6,1664
3,6659
5,2432
2,27
2,2891
1,6936
2,0775
2,84
6,3685
3,7676
5,4075
2,28
2,3135
1,7062
2,0976
2,85
6,5845
3,8764
5,5832
2,29
2,3384
1,7192
2,1181
2,86
6,8160
3,9928
5,7713
2,30
2,3641
1,7325
2,1.392
2,87
7,0646
4,1179
5,9733
2,31
2,3902
1,7461
2,1608
2,88
7,3322
4,2525
6,1907
2,32
2,4171
1,7601
2,1830
2,89
7,6212
4,3977
6,4255
2,33
2,4448
1,7744
2,2057
2,90
7,9343
4,5550
6,6798
2,34
2,4731
1,7891
2,2290
2,91
8,2745
4,7259
6,9561
367
Таблица О продолжение
V
S
t
и
V
S
t
и
2,92 1
8,6455
4,9121
7,2573
3,22
—24,3683
—11,5688
—19,4845
2,93
9,0516
5,1160
7,0871
3,23
—21,6142
—10,1909
—17,2515
2,94
9,4982
5,3101
7,9496
3,24
—19,4202
— 9,0929
—15,4725
2,95
9,9915
5,5875
8,3о00
3,25
—17,6312
— 8,1975
—14,0218
2,96
10,5393
5,8622
8,7946
3,26
—16,1447
— 7,4532
—12,8161
2,97
11,1510
6,1688
9,2910
3,27
—14,8899
— 6,3248
—11,7983
2,98
11,8386
6,5134
У,8489
3,28
—13,8166
— 6,2872
—10,9276
2,99
12,6171
6,9035
10,4804
3,29
—12,8881
— 5,8220
—10,1743
3,00
13,5057
7,3486
11,2013
3,30
—12,0770
— 5,4154
— 9,5162
3,01
14,5295
7,8613
12,0317
3,40-
— 7,4248
— 3,0787
— 5,7378
3,02
15,7219
8,4583
12,9988
3,50
— 5,3769
— 2,0433
— 4,0697
3,03
17,1282
9,1623
14,1393
3,60
— 4,2292
— 1,4572
— 3,1308
3,04
18,8116
10,0049
15,5044
3,70
— 3,4990
— 1,0787
— 2,5292
3,05
20,8629
11,0314
17,1677
3,80
— 2,9961
— 0,8128
— 2,1113
3,06
23,4176
12,3096
19,2388
3,90
— 2,6314
— 0,6147
— 1,8043
3,07
26,6860
13,9446
21,8886
4,00
— 2,3570
— 0,4603
— 1,5694
3,08
31,0160
16,1105
25,3989
4,10
— 2,1454
— 0,3355
— 1,3840
3,09
37,0244
19,1156
30,2701
4,20
— 1,9792
— 0,2317
— 1,2342
3,10
45,9234
23,5659
37,4839
4,30
— 1,875
— 0,1430
— 1,1105
3,11
60,4566
30,8334
49,2647
4,40
— 1,7429
— 0,0652
— 1,0069
3,12
88,4522
44,8321
71,9577
4,50
— 1,6603
0,0044
— 0,9188
3,13
16,7487
82,9812
133,8017
4,60
— 1,5962
0,0682
— 0,8431
3,14
1199,1629
600,1900
972,2562
4,80
— 1,5152
0,1851
— 0,7126
3,15
—227,1668
—112,9747
—183,8716
5,00
— 1,4914
0,2975
— 0,6234
3,16
—103,7576
— 51,2692
— 83,8391
5,25
— 1,5482
0,4495
— 0,5296
3,17
— 67,2348
— 33,0068
— 54,2342
5,50
— 1,7446
0,6470
— 0,4563
3,18
— 49,7313
— 24,2541
— 40,0458
5,75
— 2,2314
0,9747
— 0,3974
3,19
— 39,4600
— 19,1176
— 31,7195
6,00
— 3,7455
1,8015
— 0,3492
3,20
— 32,7063
— 15,7398
— 26,2445
6,25
—29,0867
14,5346
— 0,3088
3,21
— 27,9276
— 13,3495
— 22,3703
2те
F
со
— 0,3940
6,50
4,1490
— 2,0242
— 0,2745
Таблица 7
Коэфициенты формул балочного метода для растянуто-изогнутых стержней
Ц
t
и
1
S
t
и
0,00
1,0000
1,0000
1,0000
2,10
0,6501
0,7918
0,6950
0,50
0,9716
0,9837
0,9756
2,15
0,6389
0,7847
0,6850
1,00
0,8945
0,9391
0,9092
2,20
0,6278
0,7777
0,6750
1,05
0,8848
0,9334
0,9009
2,25
0,6167
0,7707
0,6652
1,10
0,8748
0,9277
0,8922
2,30
0,6058
0,7637
0,6554
1,15
0,8647
0,9216
0,8833
2,35
0,5950
0,7568
0,6457
1,20
0,8542
0,9155
0,8743
2,40
0,5843
0,7499
0,6360
1,25
0,8436
0,9093
0,8651
2,45
0,5737
0,7430
0,6265
1,30
0,8328
0,9028
0,8557
2,50
0,5683
0,7362
0,6170
1,35
0,8218
0,8963
0,8461
2,55
0,5530
0,7295
0,6077
1,40
0,8107
0,8897
0,8364
2,60
0,5429
0,7228
0,5985
1,45
0,7994
0,8830
0,8266
2,65
0,5329
0,7162
0,5893
1,50
0,7881
0,8762
0,8167
2,70
0,5230
0,7097
0,5803
1,55
0,7767
0,8694
0,8067
2,75
0,5133
0,7032
0,5715
1,60
0,7652
0,8625
0,7967
2,80
0,5037
0,6967
0,5627
1,65
0,7537
0,8555
0,7867
2,85
0,4943
0,6903
0,5542
1,70
0,7421
0,8485
0,7766
2,90
0,4851
0,6840
0,5457
1,75
0,7305
0,8415
0,7664
2,95
0,4760
0,6778
0,5372
1,80
0,7189
0,8344
0,7560
3,00
0,4670
0,6716
0,5288
1,85
0,7073
0,8273
0,7457
3,05
0,4583
0,6655
0,5205
1,90
0,6958
0,8202
0,7355
3,10
0,4496
0,6595
0,5125
1,95
0,6843
0,8131
0,7253
3,15
0,4411
0,6536
0,5045
2,00
0,6728
0,8060
0,7152
3,20
0,4328
0,6476
0,4968
2,05
0,6614
0,7989
0,7051
388
Таблица 8
Коэфициенты формул консольного метода
А
sin v
vsinv; В cosv; С ; Dv
1 —cosv _ : Е.
V — sin V
VI3
1i
F —.
-V2rJ- COS V
G
, V 6
- v3 sin v
V
A 1
V4
V
Vs
V
ЛУ
Cv
F
V
0
0
1,00000
1,00000
0,50000
0,16667
0,04167
0,00833
0,1
0,00998
0,99500
0,99833
0,49953
0,16652
0,04166
0,00833
0,2
0,03973
0,98007
0,99335
0,49825
0,16625
0,04161
0,00832
0,3
0,08866
0,95534
0,98507
0,49622
0,16539
0,04155
0,00831
0,4
0,15577
0,92106
0,97355
0,49337
0,16531
0,04145
0,00830
0,5
0,23971
0,87758
0,95886
0,43963
0,16456
0,04133
0,00828
0,6
0,33879
0,82534
0,94107
0,48617
0,16369
0,04117
0,00826
0,7
0,45095
0,76484
0,92031
0,47992
0,16263
0,04099
0,00823
0,8
0,57388
0,69671
0,89670
0,47389
0,16141
0,04078
0,00820
0,9
0,70499
0,62161
0,87037
0,46715
0,16004
0,04055
0,00817
1,0
0,84147
0,54030
0,84147
0,45970
0,15353
0,04023
0,00813
1,1
0,98033
0,45360
0,81019
0,45157
0,15686
0,04002
0,00811
1,2
1,11845
0,36236
0,77670
0,44281
0,15507
0,03972
0,00806
1,3
1,25263
0,26750
0,74120
0,43343
0,15314
0,03940
0,00801
М
1,37963
0,16997
0,70389
0,42348
0,15108
0,03904
0,00795
1,5
1,49624
0,07074
0,66499
0,41300
0,14839
0,03367
0,00790
1,6
1,59932
-0,02920
0,62473
0,40203
0,14659
0,03327
0,00784
1,7
1,68583
-0,12884
0,58333
0,39060
0,14418
0,03785
0,00778
1,8
1,75293
-0,22720
0,54103
0,37877
0,14166
0,03742
0,00772
1,9
1,79797
-0,32329
0,49805
0,36656
0,13904
0,03696
0,00765
2,0
1,81859
-0,41615
0,45465
0,35404
0,13634
0,03649
0,00758
2,1
1,81274
-0,50485
0,41105
0,34124
0,13355
0,03600
0,00751
2,2
j.1,77869
— 0,58850
0,36750
0,32820
0,13063
0,03j50
0,00744
2,3
1,71512
-0,66628
0,32422
0,31499
0,12775
0,03497
0,00736
2,4
1,62111
-0,73739
0,23145
0,30163
0,12475
0,03444
0,00728
2,5
1,49618
-0,80114
0,23939
0,23818
0,12170
0,03389
0,00720
2,6
1,34030
-0,85689
0,19827
0,27469
0,11860
0,03333
0,00711
2,7
1,15393
-0,90407
0,15829
0,26119
0,11541
0,03276
0,00703
2,8
0,93797
-0,94222
0,11964
0,24773
0,11229
0,03218
0,00694
9 1
2,9
0,69382
I -0,97096
0,08250
0,23436
0,10910
0,03159
0,00685
3,0
0,42336
-0,98999
0,04704
0,22111
0,10583
0,03099
0,00675
3,1
0,12890
-0,99914
0,01341
0,20803
0,10266
0,03038
0,00666
3,2
-0,18680
-0,99829
-0,01824
0,19515
0,09887
0,02977
0,00662
3,3
-0,52056
—0,98748
-0,04730
0,18251
0,09622
0,02915
0,00647
3,4
-0,86884
-0,96630
—0,07516
0,17014
0,09301
0,02853
0,00637
3,5
1-1,22774
-0,93646
-0,10022
0,15803
0,08931
0,02791
0,00627
3,6
—1,593Э7
-0,89676
-0,12292
0,14635
0,03713
0,02729
0,00614
3,7
-1,96039
-0,84810
-0,14320
0,13500
0,03351
0,02666
0,00607
3,8
-2,32506
-0,79097
-0,16102
0,12403
0,03040
0,02604
0,00597
3,9
— 2,63229
-0,72593
-0,17635
0,11347
0,07734
0,02641
0,00581
4,0
1 — 3,02721
-0,65364
-0,18920
0,10335
0,07432
0,02479
0,00577
4,1
j-3,35494
-0,57482
-0,19958
0,09368
0,07114
0,02417
0,00568
4,2
1-3,66062
-0,49026
-0,20752
0,08443
0,06345
0,02356
0,00557
4,3
-3,93951
-0,40080
— 0,21306
0,07576
0,06561
0,02294
0,00547
4,4
-4,18705
-0,30733
-0,21627
0,06753
0,06282
0,02234
0,00536
4,5
-4,39889
-0,21080
— 0,21723
0,05979
0,06011
0,02174
0,00526
4,6
-4,57098
-0,11215
-0,21602
0,05256
0,05747
0,02115
0,00516
4,7
-4,69964
-0,01239
-0,21275
0,04583
0,05490
0,02056
0,00506
4,8
-4,78159
0,08750
-0,20753
0,03960
0,05241
0,01998
0,00496
4,9
-4,81402
0,18651
-0,20050
0,03388
0,05000
0,01941
0,0086
5,0
-4,79462
0,28366
-0,19178
0,02865
0,04767
0,01885
0,00476
5,1
-4,72165
0,37798
-0,18153
0,02391
0,04543
0,01830
0,00466
5,2
-4,59396
0,46852
-0,16989
0,01966
0,04327
0,01776
0,00456
5,3
-4,41102
0,55437
-0,15703
0,01536
0,04119
0,01724
0,00447
5,4
-4,17293
0,63469
-0,14310
0,01253
0,03920
0,01672
0,00437
Табл. 8, 9, 10 и 11 составила Н. Н. Гуслистая, 24 Прочность и устойчивость стержневых систем
369
Таблица 8 продолжение
V
Ay
Bv
Cv
Dv
E v
Fw
Gv
5,5
-3,88047
0,70867
-0,12828
0,00963
0,03730
1
0,01621
0,00428
5,6
-3,53509
0,7757
-0,11273
0,00716
0,03548
0,01572
0,00418
5,7
-3,13891
0,83471
-0,09661
0,00509
0,03375
0,01523
0,00409
5,8
-2,69469
0,88552
— 0,08010
0,00340
0,03211
0,01476
0,00400
5,9
-2,20587
0,92748
-0,06337
0,00208
0,03055
0,01430
0,00391
6,0
-1,67649
0,96017
-0,04657
0,00111
0,02907
0,01386
0,00382
6,1
-1,11119
0,98327
-0,02986
0,00045
0,02768
0,01342
0,00374
6,2
-0,51515
0,99654
- 0,01340
0,00009
0,02636
0,01300
0,00365
о
о
о
о
о
о
о
о
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4,
4,
4,
4,
4,
4,
5,
t
5,
5,
5,
5
5,
5,
5,
5,
6,
6,
6,
Таблица 8 п консольного метода для растянуто-изогнутых
В.
clL
Ftt
и-
и-
1,00000 1,00500 1,02007 1,04534 1,08107 1,12763 1,18547 1,25517 1,33743 1,43309 1,54308 1,66852 1,81066
1,97091 2,15090 2,35241 2,57746 2,82332 3,10747 3,41773 3,76220 4,14431 4,56791 5,03722 5,55695 6,13229 6,76901 7,47347 8,25273 9,11458 1006766
11,12150 12,28665 13,57476 14,99874 16,57282 18,31278 20,23601 22,36178 24,71135 27,30823 30,17843 33,35066 36,85668 40,73157 45,01412 49,74718 54,97813 60,75932 67,14861 74,20995 82,01400 90,63888 100,17090 110,70547 122,34801 135,21505 149,43537 165,15129 182,52010 201,71564 222,93001 246,37554
1,00000 1,00167 1,00668 1,01507 1,02688 1,04222 1,06109 1,08369 1,11013 1,14057 1,17520 1.21423 1,25788 1,30645 1,36021 1,41952 -1,48473 1,55625 1,63454 1,72008 1,81343 1,91517 2,02596 2,14650 2,27760 2,42008 2,57490 2,74306 2,92569 3,12399 3,33929 3,57305 3,82684 4,10239 4,40158 4,72646 5,07924 5,46251 5,87879 6,33105 6,82248 7,35654 7,93705 8,56817 9,25438 10,00067 10,81242
11,69554 12,65647 13,70228 14,84064 16,07999 17,42949 18,89923 20,50017 22,24435 24,14488 26,21615 28,47384 30,93515 33,61886 36,54553 39,73766
0,50000
0,50042
0,50175
0,50378
0,50669
0,51052
0,51519
0,52076
0,52723
0,53468
0,54303
0,55250
0,56296
0,57450
0,58719
0,60107
0,61620
0,63264
0,65045
0,66973
0,69055
0,71300
0,73717
0,76318
0,79114
0,82117
0,85340
0,88799
0,92509
0,96487
1,00752
1,05322
1,10221
1,15471
1,21096
1,27125
1,33586
1,40511
1,47935
1,55893
1,64426
1,73578
1,83394
1,93925
2,05225
2,17354
2,30374
2,44356
2,59372
2,75504
2,92840
3,11473
3,31505
3,53047
3,76219
4,01151
4,27982
4,56865
4,82019
5,21460
5,57543
5,96426
6,38334
0,16667 0,16700 0,16700 0,16744 0,16800 0,16888 0,16969 0,17080 0,17208 0,17354 0,17520 0,17705 0,17908 0,18133 0,18378 0,18645 0,18935 0,19247 0Д9585 0,19947 О,20336 0,20752 0,21198 0,21673 0,22181 0,22721 0,23297 0,23910 0,24562 0,25248 0,25992 0,26775 0,27606 0,28488 0,29425 0,30420 0,31476 0,32597 0,33787 0,35050 О,36390 0,37814 0,29326 О,40931 5,42636 0,44448 0,46372 0,48418 0,50592 0,52904 О,55363 0,57978 0,60760 0,63721 0,66873 0,70229 0,73804 0,77612 0,81670 0,85996 0,90608 0,95527 1,00774
0,04167
0,04168
0,04173
004179
0,04189
0,04202
0,04210
0,04235
0,04256
0,04279
0,04306
0,04339
0,04372
0,04409
0,04448
0,04492
0,04539
0,04590
0,04644
0,04702
0,04764
0,04830
0,04900
0,04975
0,05055
0,05139
0,05228
0,05322
0,05422
0,05528
0,05639
0,05757
0,05881
0,06012
0,06150
0,06296
0,06449
0,06611
0,06782
0,06962
0,07152
0,07351
0,07562
0,07784
0,08018
0,08264
0,08524
0,08798
0,09087
0,09392
0,09714
0,10053
0,10411
0,10788
0,11187
0,11608
0,12053
0,12523
0,12842
0,13544
0,14098
0,14685
0,15305
9
А
Таблица 10 Ординаты линии влияния МаЬ сжато-изогнутой балки
V
0
0,5
1,0
1,5
2,0
2,5
3,0
0
0
0
0
0
0
0
0
0,1
0,081
0,08105
0,08154
0,08220
0,03314
0,08450
0,08626
0,2
0,123
0,12340
0,12950
0,13146
0,13426
0,13832
0,14372
0,3
0,147
0,14743
0,14936
0,15242
0,15696
0,16348
0,17232
0,4
0,144
0,14460
0,14674
0,15042
0,15584
0,16368
0,17450
0,5
0,125
0,12556
0,12763
0,13124
0,13656
0,14423
0,15502
0,6
0,096
0,09656
0,09820
0,10103
0,10542
0,11178
0,12062
0,7
0,063
0,06336
0,06440
0,06633
0,06924
0,07350
0,07944
0,8
0,032
0,03208
0,03270
0,03364
0,03508
0,03716
0,04006
0,9
0,009
0,00911
0,00916
0,00943
0,00978
0,01032
0,01104
1,0
0
0
0
0
0
0
0
ч V
3,5
4,0
4,5
5,0
5,5
6,0
6,25
0
0
о-
0
0
0
0
0
0,1
0,08880
0,09226
0,09734
0,10570
0,12302
0,19442
1,0046
0,2
0,15154
0,16248
0,17904
0,20704
0,26700
0,52184
3,4508
0,3
0,18526
0,20372
0,23236
0,28202
0,39142
0,86904
6,4167
0,4
0,19046
0,21362
0,25016
0,31510
0,46142
9 ч
1,11496
8,7763
0,5
0,17106
0,19466
0,23252
0,30094
0,45834
1,17520
9,6419
0,6
0,13406
0,15402
0,18644
0,24596
0,38508
1,02872
8,6847
0,7
0,08858
0., 10224
0,12462
0,16639
0,26512
0,72830
6,2684
0,8
0,04468
0,05156
0,06294
0,08432
0,13568
0,37892
3,3023
0,9
0,01230
0,01412
0,01718
0,02294
0,03696
0,10400
0,9125
1,0
0
0
0
0
0
0
0
♦ МаЪ — момент защемления конца балки. См. графики фиг. 65.
372
Таблица 11
Ординаты линии влияния — у МаЬ
V
с
0
0,5
1,0
1,5
2,0
2,5
0
0
0
0
0
0
0
0,1
0,0855
0,08566
0,08636
0,08749
0,08928
0,09205
0,2
0,1440
0,14465
0,14671
0,15039
0,15625
0,16550
0,3
0,1785
0,17957
0,18326
0,18979
0,20036
0,21722
0,4
0,1920
0,19350
0,19843
0,20734
0,22189
0,24542
0,5
0,1875
0,18913
0,19488
0,20518
0,22210
0,24978
0,6
0,1680
0,16978
0,17544
0,18581
0,20306
0,23146
0,7
0,1365
0,13304
0,14303
0,15225
0,16757
0,19302
0,8
0,0960
0,09710
0,10086
0,10771
0,11918
0,13828
0,9
0,0495
0,05014
0,05208
0,05574
0,06186
0,07210
1,0
0
0
0
0
0
0
N. v
с
2,5
3,0
3,5
4,0
4,49
0
0
0
0
0
0
0,1
0,09205
0,09655
0,10499
0,12840
6,4465
0,2
0,16550
0,18083
0,21035
0,29448
23,435
0,3
0,21722
0,24571
0,30180
0,46552
46,295
0,4
0,24542
0,28581
0,36634
0,60300
69,168
0,5
0,24978
0,29794
0,39614
0,69312
86,217
0,6
0,23146
0,28144
0,38465
0,70101
92,737
0,7
0,19302
0,23818
0,33233
0,62390
86,136
0,8
0,13828
0,17242
0,24409
0,46760
66,389
0,9
0,07210
0,09045
0,12914
0,25036
36,127
10
0
0
0
0
0
МаЬ— момент защемления конца сжато-изогнутой балки с шарниром на другом ее конце. См. графики фиг. 63.
ОГЛАВЛЕНИЕ
Стр.
Предисловие ;; Глава I. Введение
1. Классификация задач статического расчета конструкцгй с точка зрения
обеспечения их устойчивости 7
2. Задачи прочности 9
3. Задачи устойчивости 10
4. Задачи устойчивой прочности 11
5. Задача на потерю устойчивости второго рода 12
6. Примеры использэвандя предлагаемой классификации —
7. Надежность расчетов, основанных на теории малых деформаций 13
Глава II. Прочность и устойчивость шарнирно-стержневых
ферм и комбинированных систем
1. Основные зависимости 16
2. Метод узловых перемещен :хй 17
3. Вариационный метод 19
4. Метод эквивалентной дополнительной нагрузки 26
5. Прочность и устойчивость комбинированных стержневых систем. 28
Глава III. Сжато-изогнутый стержень
1. О внешних воздействшх, определяющих деформацию балки 31
2. Внутренние усдлия деформированного стержня 32
3. Диференциальные условия равновесия 33
4. Зависимость между усилиями и деформациями. Учет деформаций сдвига 34
5. Решение диференциального уравнения прогибов 37
6. Распределенные воздействия. 40
7. Развернутое уравнение эпюр перемещений и усилий сжато-изогнутого
стержня 41
8. Граничные параметры. Определение постоянных интегрирования Ct и С2 43
9. Формулы метода начальных параметров. 45
10. Растянуто-изогнутый стержзнь 46
11. Случай поперечного изгиба iV 0 48
12. Принц ш независимости действия поперечных факторов на сжато-изогнутый
стержень 49
13. Другие варианты вывода формул метода начальных параметров 50
14. Правила для запоминания формул метода начальных лараметров 54
1-5. Примеры применения метода начальных параметров 55
16. Основные решения в граничных параметрах для сжато-изогнутых и рас-
тянуто-изэгнутых призматических стержней 58
17. Специальные функции в формулах продольно-поперечного изгиба призматического стержня 65
18. Эпюры прогибов, углов поворота и изгибающих моментов стержня, подверженного продольно-поперечному изгибу 85.
— d v
19. Интеграл Мора Для двух эпюр моментов: эпюры продоль-
о __ _
но-поперечного изгиба Мх и эпюры поперечного изгиба M;cM0Q0:r. 88
20. О форме эпюры моментов и кривой прогибов сжато-изогнутого стержня. 90
21. Развернутое решение задачи продольно-поперечного изгиба призматического стержня при учете деформаций сдвига 92
374
Глава IV. Начало возможных перемещений в применении в задачам
устойчивой прочности плосбих систем Стр.
1. Общие соображения 96
2. Вывод основной вариационной формулы 98
3. Другой вывод основной вариационной формулы 101
4. Обобщение формулы Мора ЮЗ
5. Действ е неравномерного нагрева _
6. Пр щип взаимности работ —
7. Переход от обобщенной формулы к обычной формуле Мора —
8. Определение перемещений в задачах устойчивой прочности 104
9. Об условиях применения принц па аддитивности в задачах устойчивой
прочности. Понятие о равносжатых состояниях системы —
10. Определение перемещений единичных равносжатых состояний 108
11. Определение реакций единичных равносжатых состояний 109
12. Переход к формулам энергетического метода 110
13. Пример неправильного применения начала возможных перемещений. —
ч
ч
Глава V. Общие положения по расчету устойчивой прочности и расчету
устойчивости плоских рам
1. О предварительном определении продольных усилий в стержнях рам.
Моноцикл ические и полициклические задачи. 111
2. Об отдельном цикле расчета устойчивой прочности плоской рамы 114
3. О расчете устойчивости рам 118
4. Введение обозначений, удобных при расчете рам 120
5. Кинематические зависимости между углами поворота стержней свободных рам 122
6. Составление уравнений, соответствующих неизвестным кинематически
независимым смещениям 123
7. О взаимности коэфициентов канонической системы уравнений отдельного
цикла расчета устойчивой прочности 126
8. О расчете симметричных, симметрично загруженных систем 127
Глава VI. Балочный метод метод моментов и углов перекоса
1. Формулы для отдельного стержня. ; ;. 131
2. Обобщенное уравнение трех моментов 133
3. Обобщенное уравнение четырех моментов —
4. Составление уравнения неразрезности для узла, смежного с неповэрачи-
вающимся узлом 134
5. Расчет несвободных рам —
6. Расчет свободных рам. 136
7. Случаи рационального, применения балочного метода 141
Глава VII. Метод деформаций
1. Общие соображения о значении метода деформаций в задачах устойчивой
прочности 143
2. Основные формулы для‘отдельного стержня 145
3. Составление системы уравнений. 150
4. Примеры расчета устойчивости рам 152
5. Примеры расчета устойчивости симметричных, симметрично загруженных
рам 158
6. Об устойчивости однопанельных рам с прямоугольными клетками при от-
сутствии симметрии в нагрузках и жесткостях их стоек 167
7. Примеры расчета устойчивости шпренгельных конструкций 169
8. Примеры расчета устойчивой прочности рамных систем 179
Глава VIII. Метод узловых поворотов и поперечных сил
1. Общие соображения о методе. Формулы для отдельного стержня 186
2. Уравнение трех узловых поворотов 187
3. Составление системы уравнений 188
4. Примеры расчета устойчивости 189
5. Формулы для ступенчатых стержней, загруженных поперечной нагрузкой и продольными сосредоточенными силами 191
6. О расчете устойчивой прочности рамы со ступенчато-загруженными
стержнями 196
7. Формулы для стержней рам с жесткими узловымд фасонками. 197
8. Устойчивость рам с жесткими узловыми фасонками 199
375
Глава IX. О других методах расчета рам Стр.
1. Консольный метод 202
2. Метод узловых моментов и поперечных сил 206
3. О применении метода сил в его обычном виде к задачам устойчивости
и устойчивой прочности 214
4. О расчёте рам по методу фокусов 220
5. Графоаналитический метод расчета неразрезяых балок. Применение
линий влияния от фиктивных нагрузэк. 223
6. Ограничения, накладываемые на решзние выбором метода расчета. 233
Глава X. Учет деформаций сдвига и обжатия
1. Уточненные выражения критического усилия призматического стержня
при различных закреплениях его концов 235
2. Формулы метода деформаций с учетом деформаций сдвига 237
3. Примеры расчета устойчивости рам с учетом деформаций сдвига 230
4. Расчет рам с учетом продольных деформаций их стержней 241
5. Расчет устойчивости рамного стержня 244
6. Изменение категории задачи при учете деформаций обжатия стержней рамы 252
7. Практический прием учета продольных деформаций стержней рам —
8. Нагружение силой, направленной к полюсу 253
Глава XI. Некоторые оЗщие положения и приближенные методы расчета
1. Упрощение расчетной схзмы в задачах устойчив эста свэбодных много-
пролетных многоэтажных рам. 256
2. Вспомогательная задача: одноконтурная прямоугольная свободная рама
с разной жесткостью ригелей 273
3. Эквивалентные критические системы нагрузэк рамы 280
4. Упрощение расчетной схемы в задачах устойчивости несвободных рам. 287
5. Сопоставление запасов устойчивости при комбинированном загружении
упругой системы и при загружении ее отдельными составляющими. 301
6. Составление приближенных развернутых выражений для критической
нагрузки на основе точного расчета устойчивости 306
7. Составление приближенных развернутых решений для сжато-изогнутых
рам на основе их точного расчета 313
8. Экстраполяционное определение критической нагрузка упругих рамных
систем без доведения испытуемой конструкции до потери устойчивости 322
9. Приближенные выражения основных формул, связывающих граничные
параметры стержня 328
10. Примеры приближенного расчета рам по методу деформаций 339
Добавление в В гл. XI
Приложение. Таблицы специальных функций,. 345
Техн. редакторы В. С. Дахнов и Е. С. Герасимова.
Сдано в производство 17Х1 1948 г. Подп. к печати 27IV 1949 г. Форм, бум. 70xl08Vu Печ. л. 23,5. Уч.-изд. л. 34,59. Уч. 8000. JI-139975. Тираж 2000 экз. Заказ 866
Цена 31 р. 15 к. -Ь переплет 2 р.
16-я типография Главполиграфиздата при Совете Министров СССР.
Москва, Трехпрудный пер., д. 9.