Текст
НАГЛЯДНЫЙ
С П РАВ 04 Н И К
Алгебре
И НАЧАЛАМ АНАЛИЗА
с приллерсцыи
для 7-11 классов
• ФУНКЦИИ
• ГРАФИКИ
• УРАВНЕНИЯ
• НЕРАВЕНСТВА
• СИСТЕМЫ УРАВНЕНИЙ
• ПРОИЗВОДНАЯ
• ИНТЕГРАЛ
• СПРАВОЧНЫЕ ТАБЛИЦЫ
Л. Э. Генденштейн, А. П. Ершова, А. С. Ершова
НАГЛЯДНЫЙ
СПРАВОЧНИК
Алгебре
И НАЧАЛАМ АНАЛИЗА
с примерами
дла 7-11 классов
Издание 2-е, переработанное
ИЛЕКСА
ГИМНАЗИЯ
Москва-Харьков
1997
Справочник отличается максимальной наглядностью:
каждая тема элементарного курса алгебры и начал математи-
ческого анализа иллюстрируется «говорящими» графиками.
Книга поможет учащимся школ, лицеев и гимназий,
независимо от того, по какому учебнику и по какой программе,
изучается курс алгебры и начал анализа, наглядно представить
изучаемый материал и быстро найти необходимые сведения.
Такой справочник на столах учеников позволит учителю осво-
бодить время урока для решения задач.
Выпускникам и абитуриентам справочник даст возмож-
ность увидеть предмет в целом и систематизировать свои знания.
Перепечатка отдельных разделов и всего издания запрещена.
Любое коммерческое использование данного издания возможно только
с разрешения издателя.
Рецензенты:
Ю.В. Гандель, доктор физико-математических наук,
профессор Харькоэдсого государственного университета;
В.В. Голобородъко, учитель Академической гимназии № 45 г. Харькова
Лев Элевич Генденштейн,
Алла Петровна Ершова,
Анна Сергеевна Ершова
Наглядный справочник по алгебре и началам анализа
для 7-11 классов
Ответственный за выпуск JI.A. Кирик
Художник-оформитель МЛ. Курдюмов
Корректор О.Ф. Крижановский
ЛР № 064344 от 9.12.1995. Подписано в печать 17.3.97.
Печать офсетная. Формат 60x90 1/16.
Бумага книжно-журнальная.
Тираж 100 000 экз. (1-й завод 50 000 экз.) 3.457
ООО "Илекса", 121354, г. Москва, Измайловское шоссе, 48а
Творческое объединение «Гимназия», г. Харьков, ул. Тобольская, 46а
Заказы по телефонам: в Москве (095) 365-30-55
в Харькове (0572) 11-80-62, 32-98-50
Ордена Трудового Красного Знамени Чеховский полиграфический
комбинат Комитета Российской Федерации по печати
142300, г. Чехов Московской области
ISBN 5-89237-011-9 © Генденштейн Л.Э.,
Ершова А.П.,
Ершова А.С., 1997
3
СОДЕРЖАНИЕ
ФУНКЦИИ..................................................б
Основные свойства функций.............................7
Четность и нечетность...............................7
Периодичность.......................................8
Нули функции....................................... 8
Монотонность (возрастание, убывание)................9
Экстремумы (максимумы и минимумы)...................9
Асимптоты..........................................10
Обратные функции...................................11
Нахождение формулы для функции, обратной данной....11
Преобразования графиков функций......................12
Преобразование симметрии относительно оси х........12
Преобразование симметрии относительно оси у........13
Параллельный перенос вдоль оси х...................14
Параллельный перенос вдоль оси у...................15
Сжатие и растяжение вдоль оси х....................16
Сжатие и растяжение вдоль оси у....................17
Построение графика функции у = |/(х)|..............18
Построение графика функции у = f(\x\)..............18
Построение графика обратной функции................19
Построение графиков сложных функций с помощью
последовательных преобразований графиков
элементарных функций..............................20
Линейная функция.....................................22
Частные случаи линейной функции (прямая
пропорциональность и постоянная функция)...........22
Взаимное расположение графиков линейных функций....22
Свойства линейной функции..........................23
Построение графика линейной функции по двум точкам.24
Построение графика линейной функции у = kx + b
с помощью элементарных преобразований графика
функции у = х.................................25
Квадратичная функция.................................26
Различные представления квадратичной функции.......26
Выделение полного квадрата...................26
Разложение на линейные множители.............26
Свойства квадратичной функции и ее графика.........27
Направление ветвей, характерные точки и ось симметрии
параболы......................................28
4
Построение графика квадратичной функции
по направлению ветвей, характерным точкам
и оси симметрии параболы (примеры)...............29
Построение графика квадратичной функции
с помощью элементарных преобразований
графика функции у — х2.......................30
Степенные функции с натуральными показателями степени.32
Степенные функции с целыми отрицательными
показателями степени.............................33
Функции у = tfx ...................................34
Степенные функции с действительными
показателями степени.............................35
Показательная функция..............................36
Логарифмическая функция............................37
Тригонометрические функции.........................38
Обратные тригонометрические функции................42
УРАВНЕНИЯ.............................................44
Линейные уравнения.................................45
Квадратные уравнения...............................46
Неполные квадратные уравнения....................47
Теоремы Виета....................................48
Формулы Виета для корней приведенного квадратного
уравнения...................................48
Уравнения, сводящиеся к квадратным...............49
Иррациональные уравнения...........................50
Простейшие показательные уравнения.................51
Простейшие логарифмические уравнения...............51
Простейшие тригонометрические уравнения............52
Уравнение с двумя переменными и его график.........55
НЕРАВЕНСТВА...........................................57
Линейные неравенства.............................. 58
Квадратные неравенства.............................59
Метод интервалов для неравенств вида
(х-а1)‘*(х-о2)*‘...(х-ая)*->0 60
Применение метода интервалов для решения дробно*
рациональных неравенств......................61
Иррациональные неравенства.........................62
Показательные неравенства..........................63
Логарифмические неравенства........................63
Простейшие тригонометрические неравенства..........64
5
СИСТЕМЫ ДВУХ УРАВНЕНИЙ С ДВУМЯ
НЕИЗВЕСТНЫМИ........................................67
Основные методы решения систем уравнении..........68
Метод подстановки..............................68
Метод сложения.................................69
Графический метод решения системы двух уравнений
с двумя неизвестными......................70
Системы двух линейных уравнений с двумя неизвестными.71
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ.........................72
Производная.......................................72
Геометрический смысл производной..................72
Уравнение касательной.............................72
Вторая производная................................73
Физический смысл производной......................73
Правила дифференцирования.........................73
Производная сложной функции....................73
Применение производной к исследованию функций.....74
Монотонность...................................74
Экстремумы.....................................75
Схема применения производной для нахождения
интервалов монотонности и экстремумов.....76
Наибольшее и наименьшее значения функции,
непрерывной на отрезке.........................77
Схема нахождения наибольшего и наименьшего значений
функции, непрерывной на отрезке...........77
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ............................78
Первообразная.....................................78
Основное свойство первообразных................78
Неопределенный интеграл...........................78
Правила интегрирования............................78
Определенный интеграл.............................79
Связь между определенным интегралом и первообразной
(формула Ньютона-Лейбница)................79
Основные свойства определенного интеграла.........79
Геометрический смысл определенного интеграла......80
Физический смысл определенного интеграла..........80
Вычисление площадей и объемов с помощью определенного
интеграла........................................81
СПРАВОЧНЫЕ ТАБЛИЦЫ..................................82
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ................................94
6
Функции
ФУНКЦИИ*)
Числовой функцией называется соответствие, которое
каждому числу х из некоторого заданного множества
сопоставляет единственное число у.
Обозначение: у = /(х), где
X — независимая переменная (аргумент функции),
у — зависимая переменная (функция).
Множество значений х называется областью определе-
ния функции (обычно обозначается D}.
Множество значений у называется областью значений
функции (обычно обозначается Е).
Графиком функции назы-
вается множество точек
плоскости с координатами
(х, /(х)).
СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ
• Аналитический способ: функция задается с помощью
математической формулы.
Примеры: у = х2, у = In х
Табличный способ: функция задается с помощью таблицы.
Пример.
X 1 2 3 4 5
У 2 4 6 8 10
• Описательный способ: функция задается словесным
описанием.
(1 для рациональных х,
О для иррациональных х.
• Графический способ: функция задается с помощью
графика.
^Все параметры функций, в том числе коэффициенты многочленов, счи-
таются действительными.
Функции
7
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ
Функция называется
четной, если:
• область определения
функции симметрична
относительно нуля,
• для любого х из об-
ласти определения
Л-Х) = Г(х).
Функция называется
нечетной, если:
• область определения
функции симметрична
относительно нуля,
• для любого х из облас-
ти определения
Г(-Х) = -Г(х).
График четной функции
симметричен относительно
оси у.
График нечетной функции
симметричен относительно
начала координат.
Многие функции не являются ни четными, ни нечетными.
Пример арефика функции, не являющейся ни четной, ни нечетной:
Примеры четных функций: у = х2п, п е Z\ у - cos х
Примеры нечетных функций: у = x2n+1, п е Z\ у = sin х
Примеры функций, не являющихся ни четными, ни нечетными:
У = 2х, у = In х, у = х - 2, у = (х 4- I)2
8
Функции
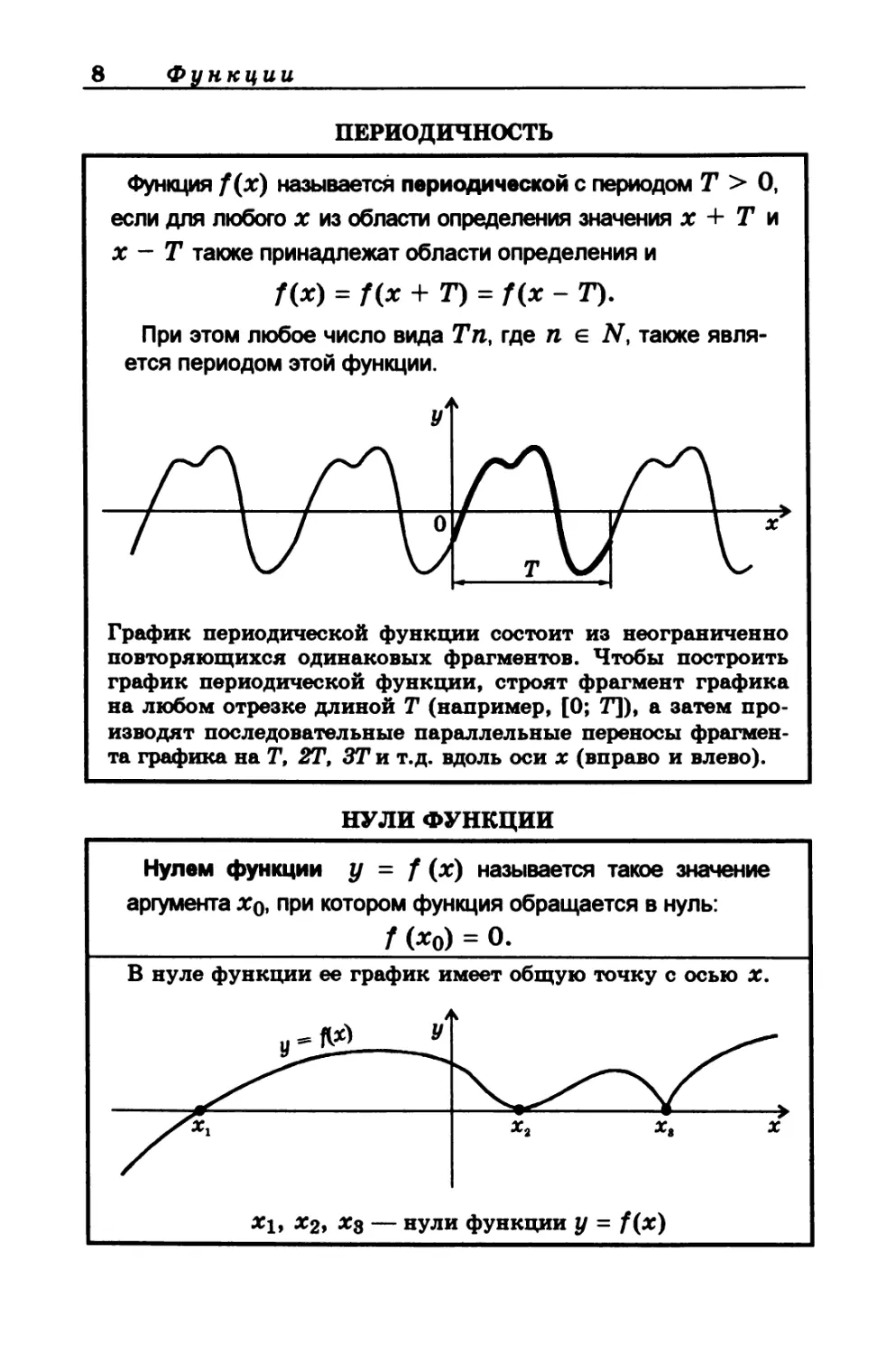
ПЕРИОДИЧНОСТЬ
Функция f{x) называется периодической с периодом Т > О,
если для любого х из области определения значения х + Т и
х - Т также принадлежат области определения и
Г(х) = f(x + Т) = f(x - 73.
При этом любое число вида Тп, где п е N, также явля-
ется периодом этой функции.
График периодической функции состоит из неограниченно
повторяющихся одинаковых фрагментов. Чтобы построить
график периодической функции, строят фрагмент графика
на любом отрезке длиной Т (например, [0; Т]), а затем про-
изводят последовательные параллельные переносы фрагмен-
та графика на Т, 2Т, ЗТ и т.д. вдоль оси х (вправо и влево).
НУЛИ ФУНКЦИИ
Нулем функции у = f (х) называется такое значение
аргумента Xq, при котором функция обращается в нуль:
_____________________f М = о.______________________
В нуле функции ее график имеет общую точку с осью х.
Функции
9
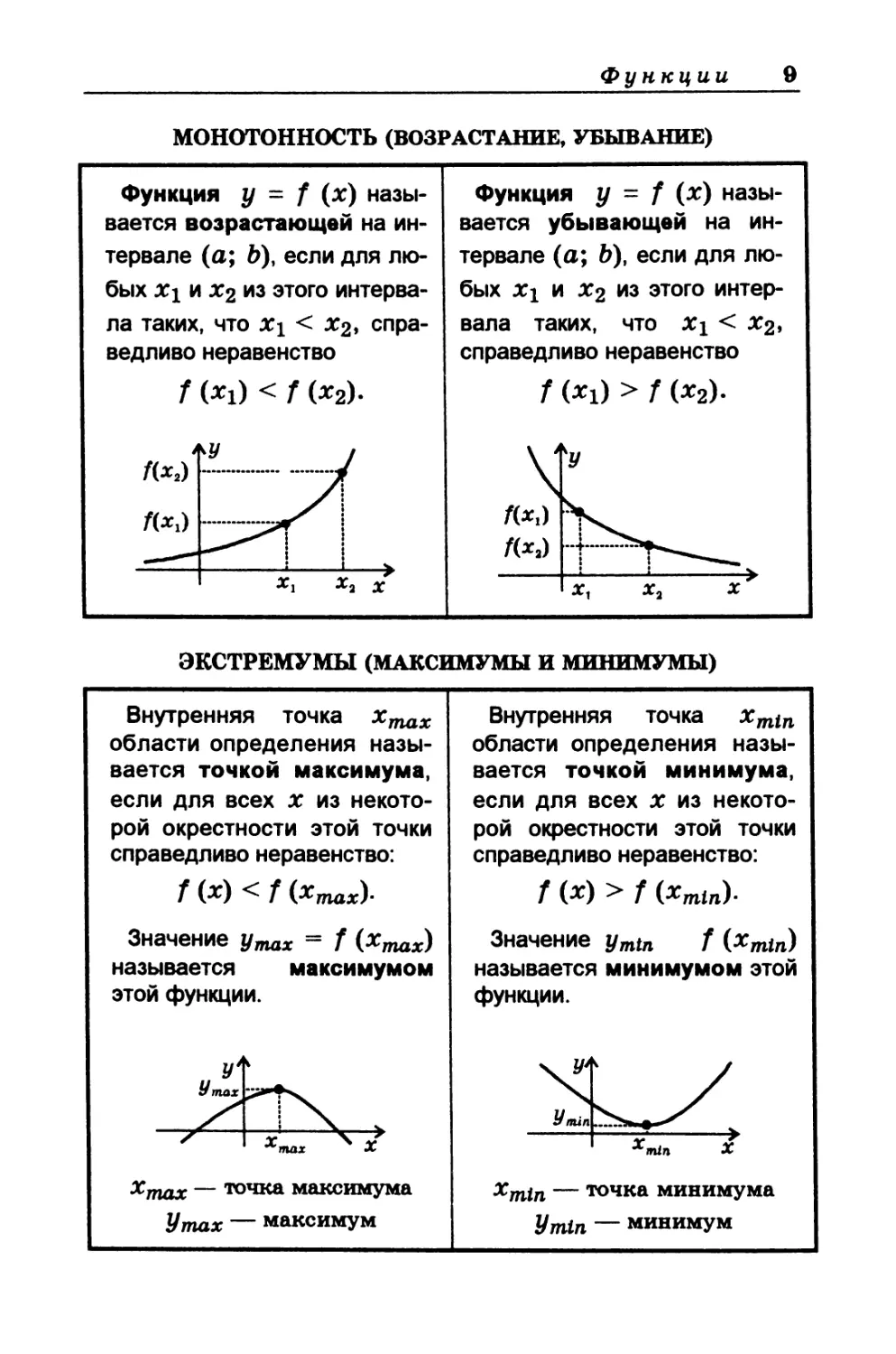
МОНОТОННОСТЬ (ВОЗРАСТАНИЕ, УБЫВАНИЕ)
Функция у = f (х) назы-
вается возрастающей на ин-
тервале (а; Ь), если для лю-
бых Xi и Х2 из этого интерва-
ла таких, что Xi < Х2, спра-
ведливо неравенство
f (*1) < f (х2).
Функция у = f (х) назы-
вается убывающей на ин-
тервале (а; Ь), если для лю-
бых Xi и х2 из этого интер-
вала таких, что Xi < Х2,
справедливо неравенство
t (*1) > f (*2).
ЭКСТРЕМУМЫ (МАКСИМУМЫ И МИНИМУМЫ)
Внутренняя точка х^х
области определения назы-
вается точкой максимума,
если для всех х из некото-
рой окрестности этой точки
справедливо неравенство:
f 00 < f (Хтах)-
Значение у щах = f (х^)
называется максимумом
этой функции.
Внутренняя точка xmin
области определения назы-
вается точкой минимума,
если для всех х из некото-
рой окрестности этой точки
справедливо неравенство:
f (Л') > f (xmtn)'
Значение ymtn f (xmin)
называется минимумом этой
функции.
XmftT — точка максимума
У та г — максимум
xmin — точка минимума
У min — минимум
10
Функции
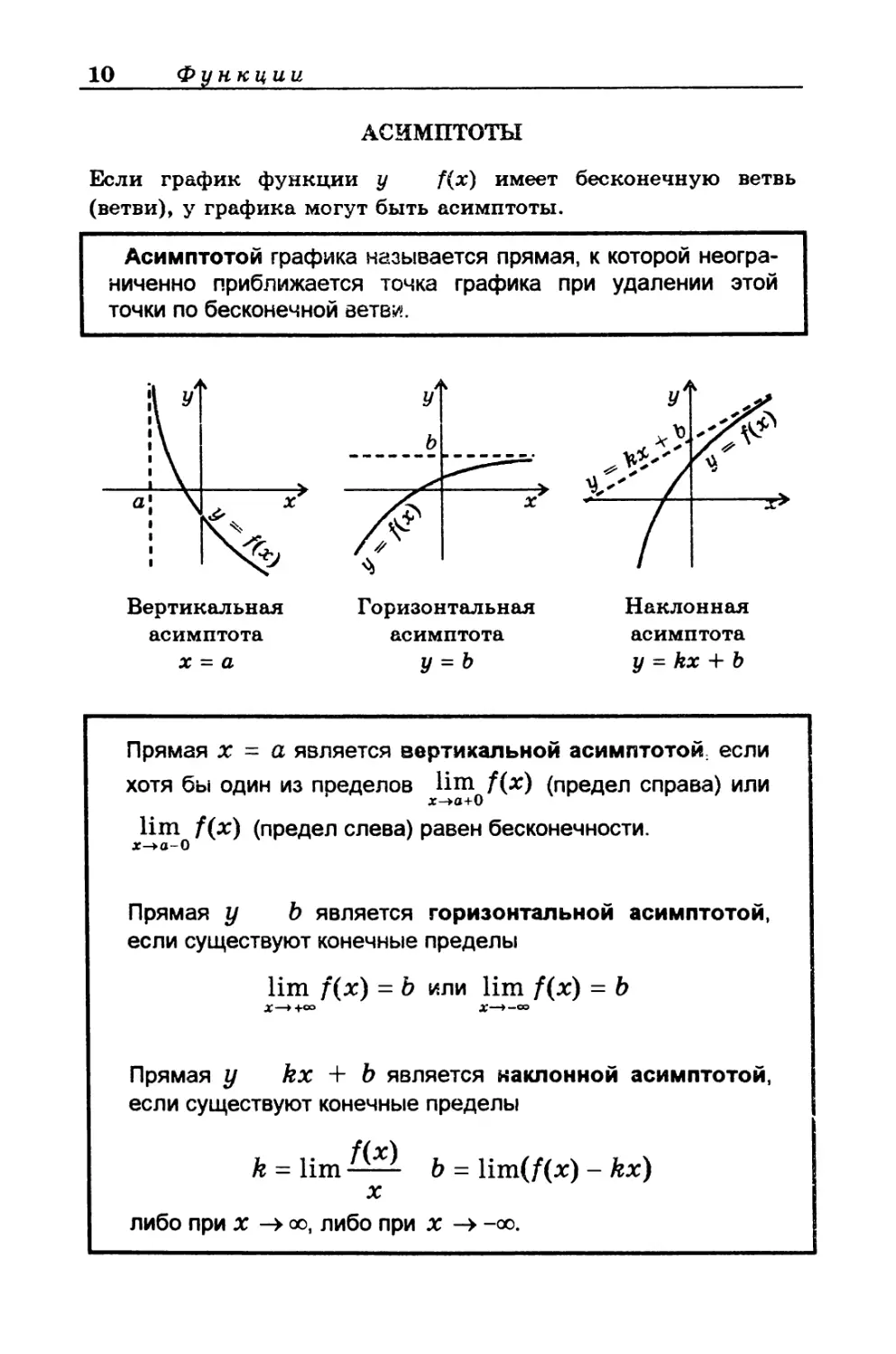
АСИМПТОТЫ
Если график функции у f(x) имеет бесконечную ветвь
(ветви), у графика могут быть асимптоты.
Асимптотой графика называется прямая, к которой неогра-
ниченно приближается точка графика при удалении этой
точки по бесконечной ветв^*.
Вертикальная
асимптота
х = а
Горизонтальная
асимптота
у = ъ
Наклонная
асимптота
у = kx + b
Прямая х - а является вертикальной асимптотой если
хотя бы один из пределов Нт /(х) (предел справа) или
х->а+0
Нт /(х) (предел слева) равен бесконечности.
х-»а-0
Прямая у Ъ является горизонтальной асимптотой,
если существуют конечные пределы
lim /(х) = Ъ или lim /(х) = b
х—»+оо х—
Прямая у kx + b является наклонной асимптотой,
если существуют конечные пределы
k - lim b = lim(/(x) - kx)
х
либо при X —> 00, либо при X —> -00.
Функции
11
ОБРАТНЫЕ ФУНКЦИИ
Понятие обратной функции применимо к функциям,
обладающим следующим свойством: каждому значению у из об-
ласти значений функции соответствует единственное значение х
из области определения этой функции.
Замечание, &ля многих функций это свойство выполняется лишь на
части области определения, в частности, на любом промежутке
монотонности (для функции у = х2 таким промежутком является,
например, луч [0; оо), для функции у = sin х — отрезок [~я/2; я/2]).
Функция g называется обратной для функции /, если каждо-
му у из области значений функции / функция g ставит в соот-
ветствие такое х из области определения функции /, что
у = /(х). Таким образом, если у = f(x), то х = g(y).
Функции f v\ g являются взаимно обратными.
• Область определения функции f является областью зна-
чений функции £, а область значений функции f явля-
ется областью определения функции g.
• Графики взаимно обратных функций симметричны друг
ДРУГУ относительно прямой у = х (построение графика
обратной функции см. на стр. 19).
Примеры взаимно обратных функций:
у = х3 и у = у[х , у = 2х и у = log2x
НАХОЖДЕНИЕ ФОРМУЛЫ ДЛЯ ФУНКЦИИ, ОБРАТНОЙ ДАННОЙ
• Пользуясь формулой у = /(х), следует выразить х через у,
а в полученной формуле х = g(y) заменить х на у, а у на х.
Пример. Найти формулу для функции,
обратной функции
1
у = — х +1 .
* 2
Выражение х через у: х = 2у - 2.
Замена х на у, у на х дает: у = 2х - 2.
Результат: функция у = 2х - 2 является
1
обратной для функции у = — X 4-1.
12
Функции
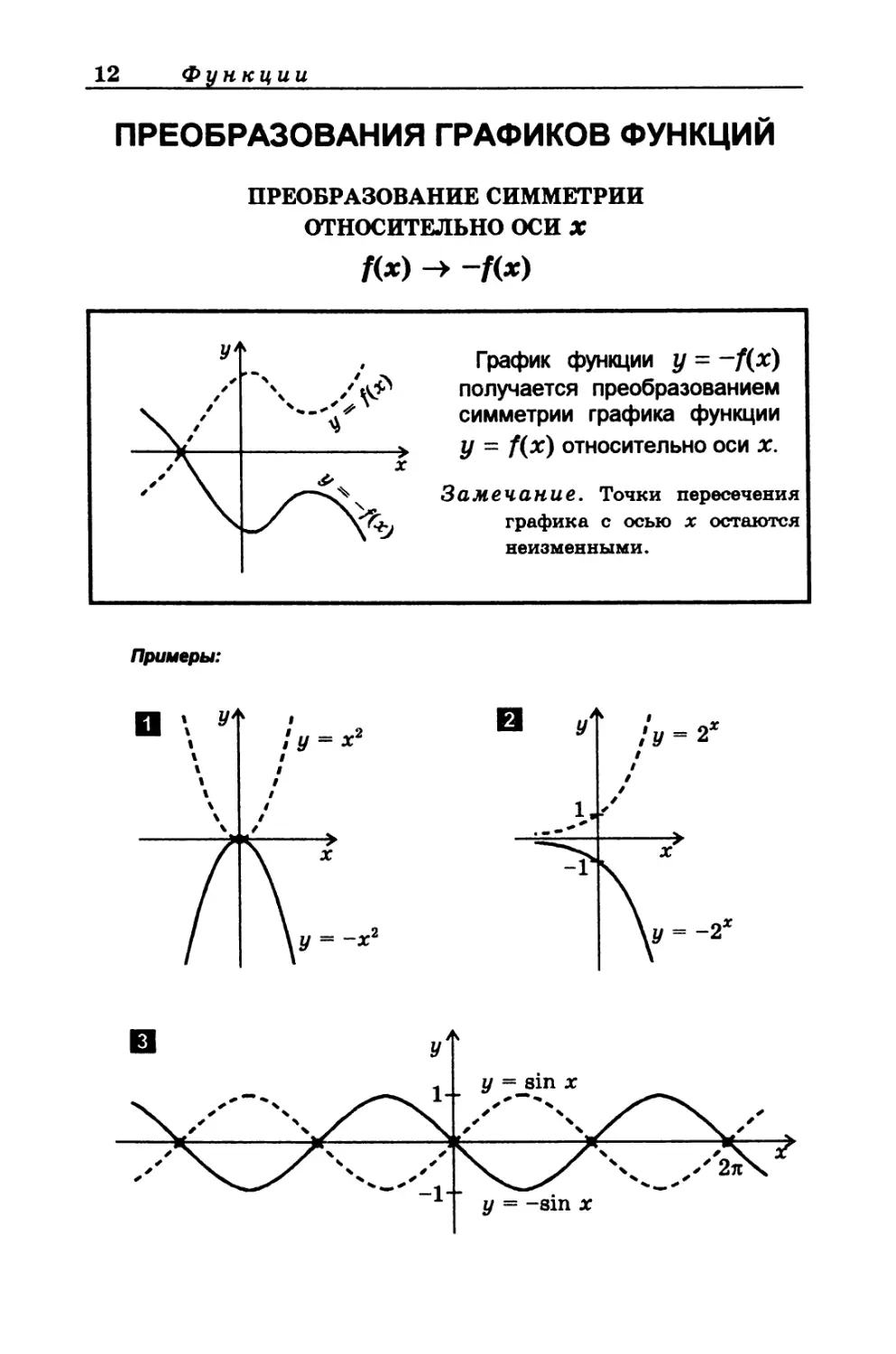
ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
ПРЕОБРАЗОВАНИЕ СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ X
fix) -> -f(x)
График функции у = ~f(x)
получается преобразованием
симметрии графика функции
У - f(x) относительно оси х.
Замечание. Точки пересечения
графика с осью х остаются
неизменными.
Примеры:
Функции
13
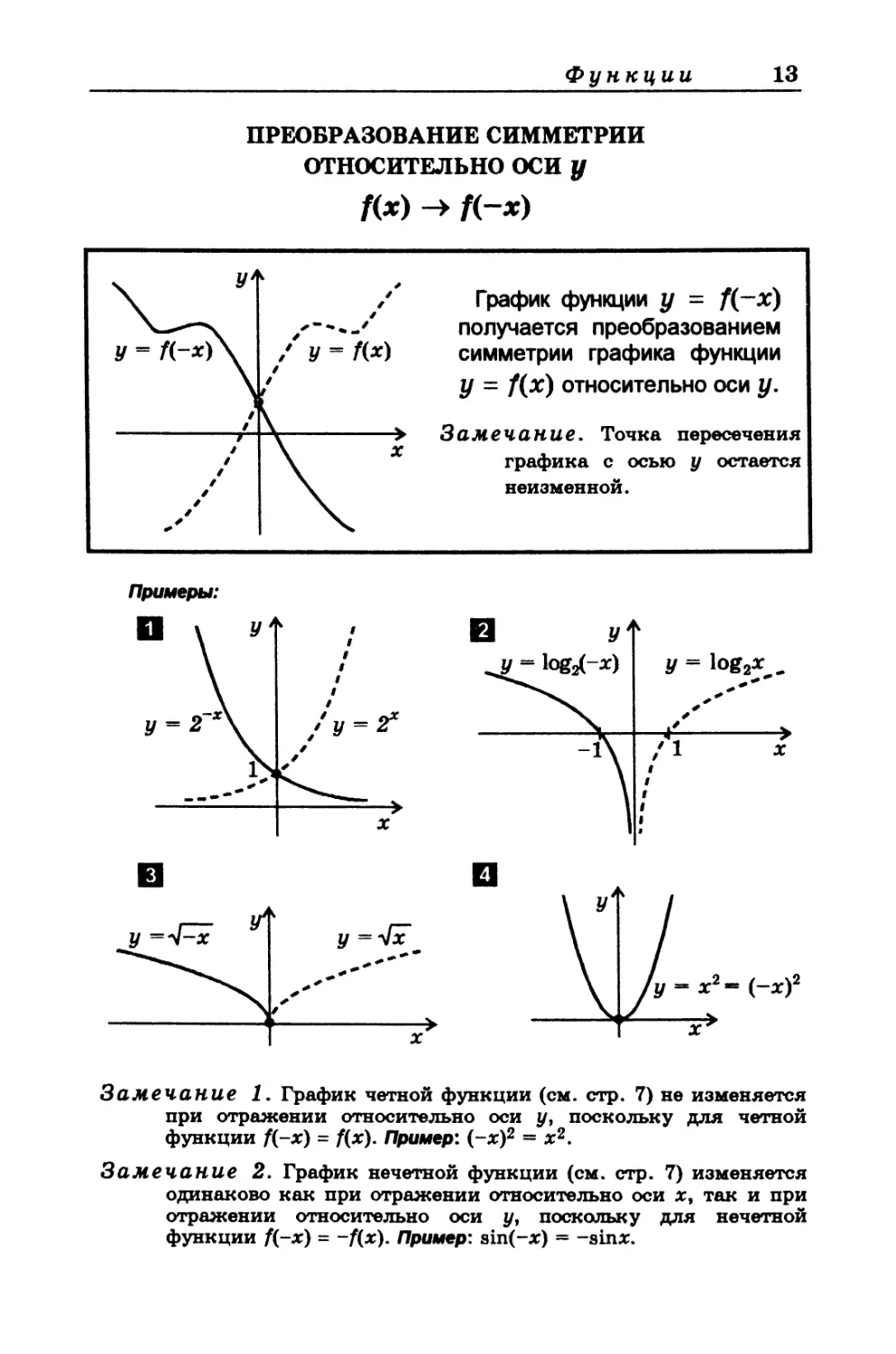
ПРЕОБРАЗОВАНИЕ СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ у
-> f(-x)
График функции у = f(~x)
получается преобразованием
симметрии графика функции
у = /(г) относительно оси у.
Замечание. Точка пересечения
графика с осью у остается
неизменной.
Замечание 1. График четной функции (см. стр. 7) не изменяется
при отражении относительно оси у, поскольку для четной
функции f(-x) = f(x). Пример: (-х)2 = х2.
Замечание 2. График нечетной функции (см. стр. 7) изменяется
одинаково как при отражении относительно оси х, так и при
отражении относительно оси у, поскольку для нечетной
функции Д-х) = -Дх). Пример: sin(-x) = -sinx.
14 Функции
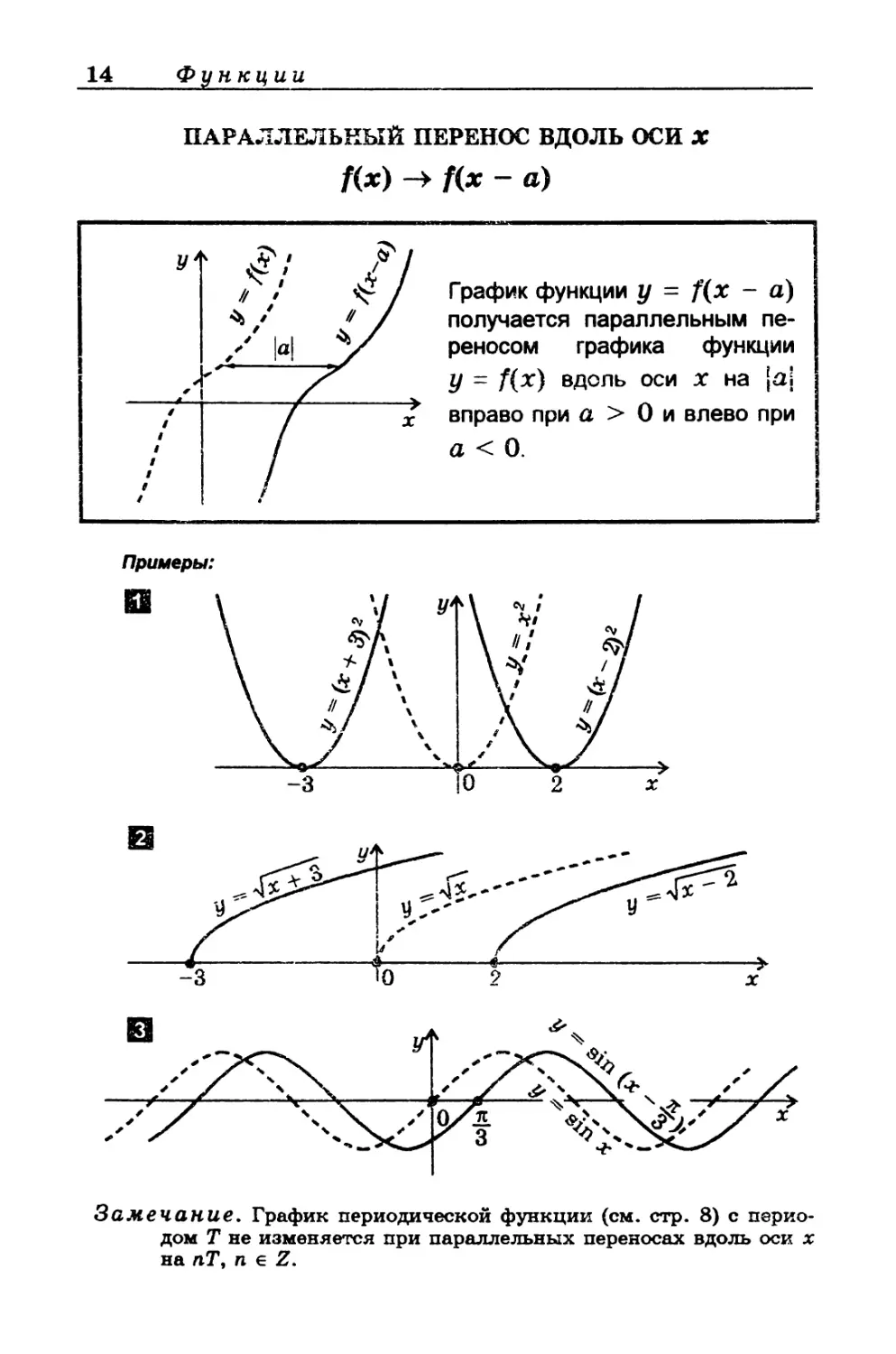
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ X
f(x) -» f(x - а)
Г рафик функции у = f(x - а)
получается параллельным пе-
реносом графика функции
у = f(x) вдоль оси х на jai
вправо при а > 0 и влево при
а < 0.
Замечание. График периодической функции (см. стр. 8) с перио-
дом Т не изменяется при параллельных переносах вдоль оси х
на пТ, п е Z.
Функции
15
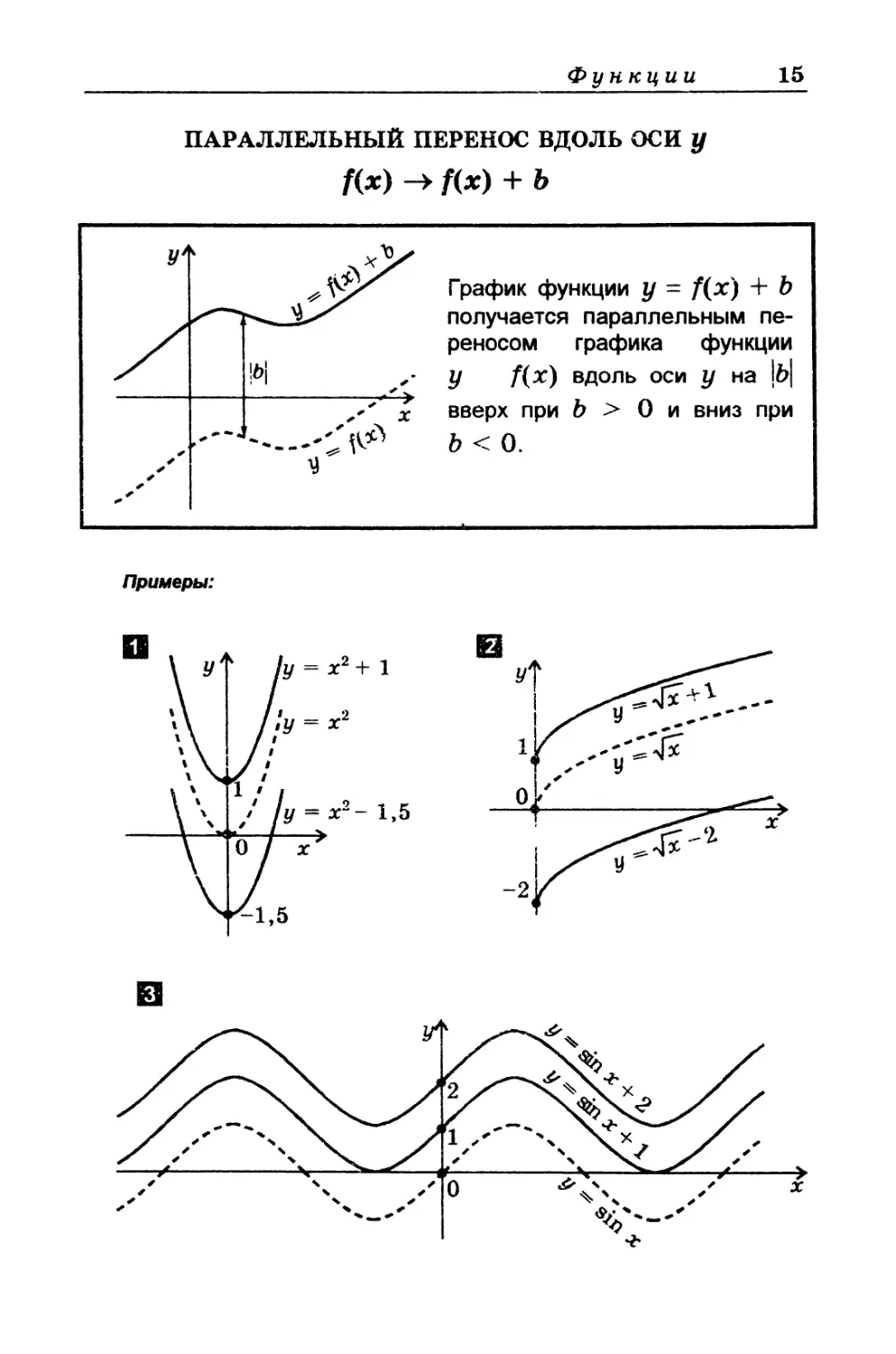
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ ОСИ у
f(x) -> f(x) + Ь
График функции у = f(x') + Ъ
получается параллельным пе-
реносом графика функции
у f(x) вдоль оси у на 1&|
вверх при b > О и вниз при
Ь < 0.
16 Функции
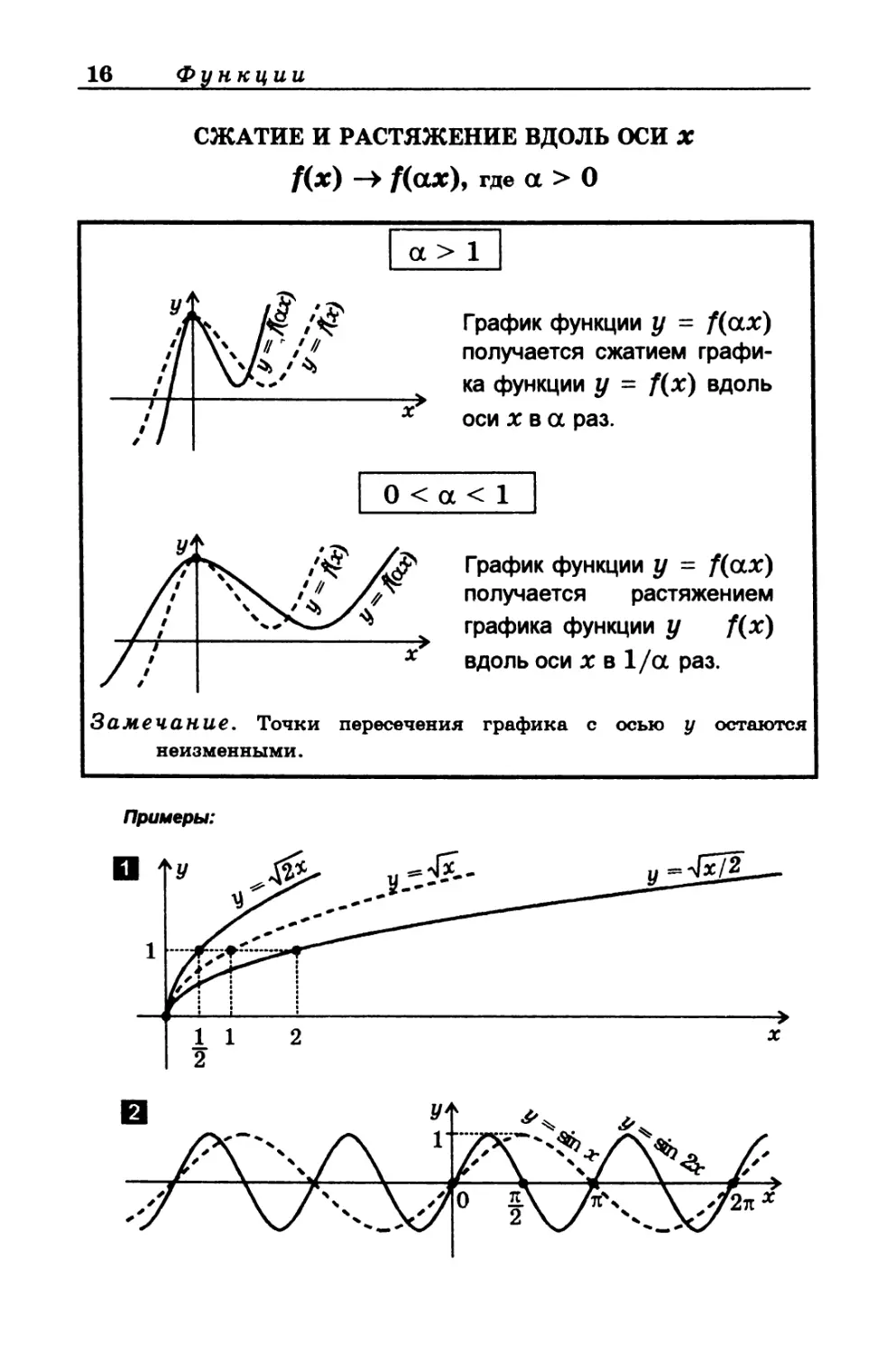
СЖАТИЕ И РАСТЯЖЕНИЕ ВДОЛЬ ОСИ X
f(x) -> /(ах), где а > О
График функции у = /(ах)
получается сжатием графи-
ка функции у = f(x) вдоль
оси х в а раз.
График функции у = /(ах)
получается растяжением
графика функции у f(x)
вдоль оси х в 1/а раз.
Замечание. Точки пересечения графика с осью у остаются
неизменными.
Примеры:
Функции
17
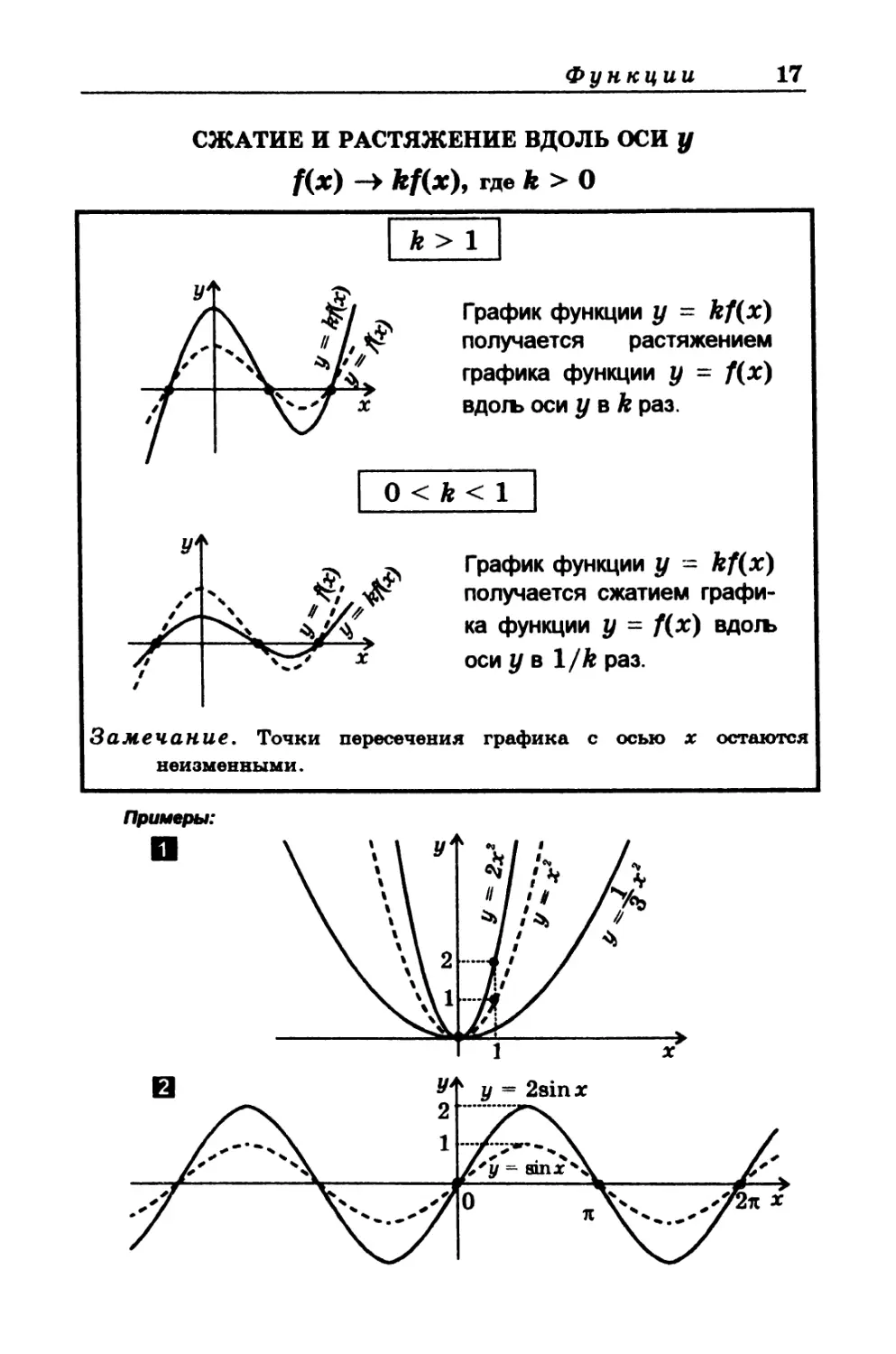
СЖАТИЕ И РАСТЯЖЕНИЕ ВДОЛЬ ОСИ у
f(x) -> kf(x), где k > О
Л > 1
График функции у = kf(x)
получается растяжением
графика функции у = f(x)
вдогъ оси у в k раз.
График функции у - kf(x)
получается сжатием графи-
ка функции у = f(x) вдогъ
оси у в 1/k раз.
Замечание. Точки пересечения графика с осью х остаются
неизменными.
18 Функции
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = |f(x)|
Части графика функции у = f(x), лежащие выше оси х и на
оси х, остаются без изменения, а лежащие ниже оси х —
симметрично отражаются относительно этой оси (вверх).
Замечание. Функция у = |/(х)| неотрицаФельна (ее график рас-
положен в верхней полуплоскости).
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ у = f (|х|)
Часть графика функции у = /(х), лежащая левее оси у, удаля-
ется, а часть, лежащая правее оси у — остается без изменения и,
кроме того, симметрично отражается относительно оси у (влево).
Точка графика, лежащая на оси у, остается неизменной.
Замечание. Функция у = Д|х|) четная (ее график симметричен
относительно оси у).
Функции
19
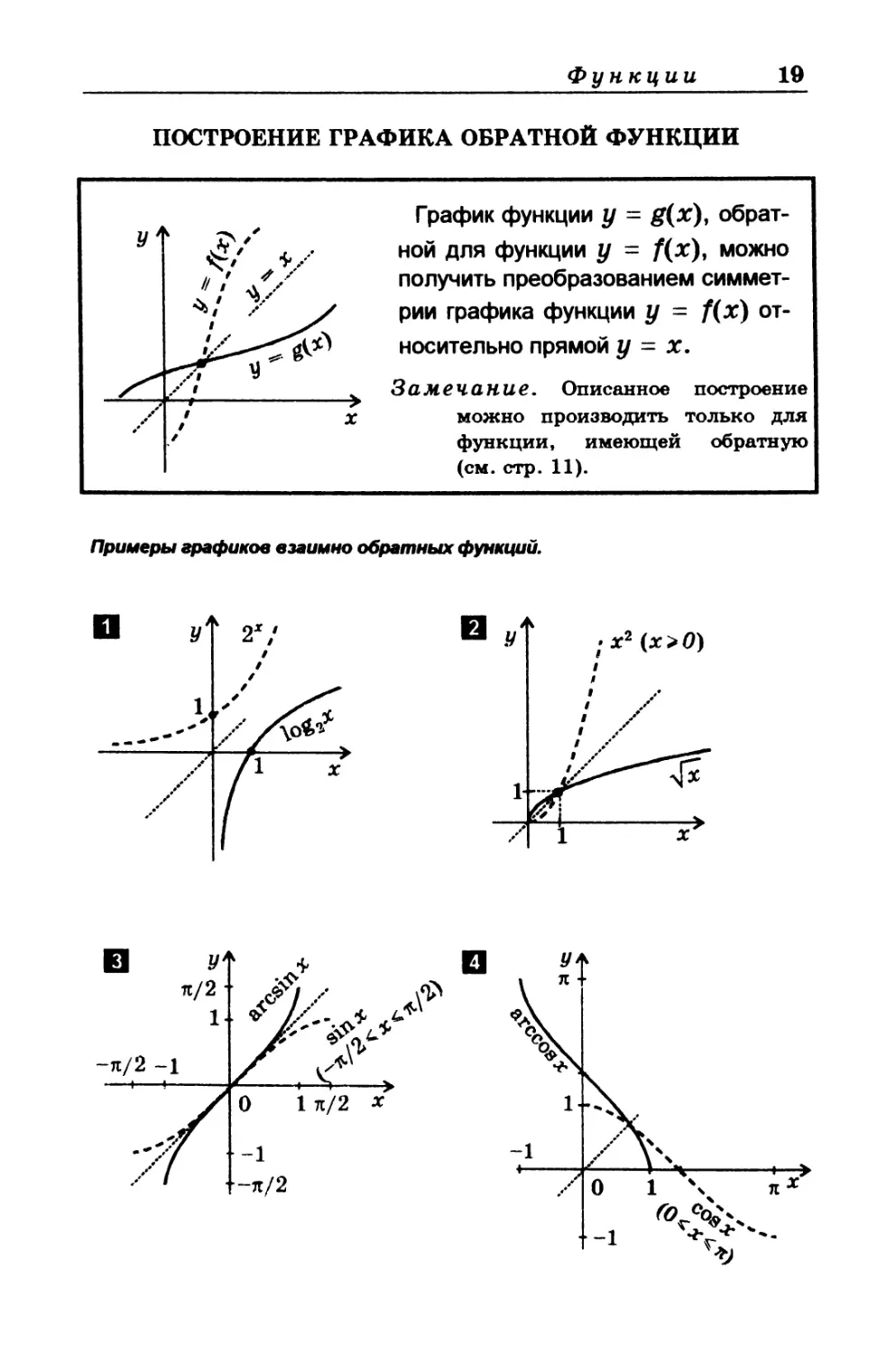
ПОСТРОЕНИЕ ГРАФИКА ОБРАТНОЙ ФУНКЦИИ
График функции у = g(x), обрат-
ной для функции у = f(x), можно
получить преобразованием симмет-
рии графика функции у = f(x) от-
носительно прямой у = х.
Замечание. Описанное построение
можно производить только для
функции, имеющей обратную
(см. стр. 11).
Примеры графиков взаимно обратных функции.
20
Функции
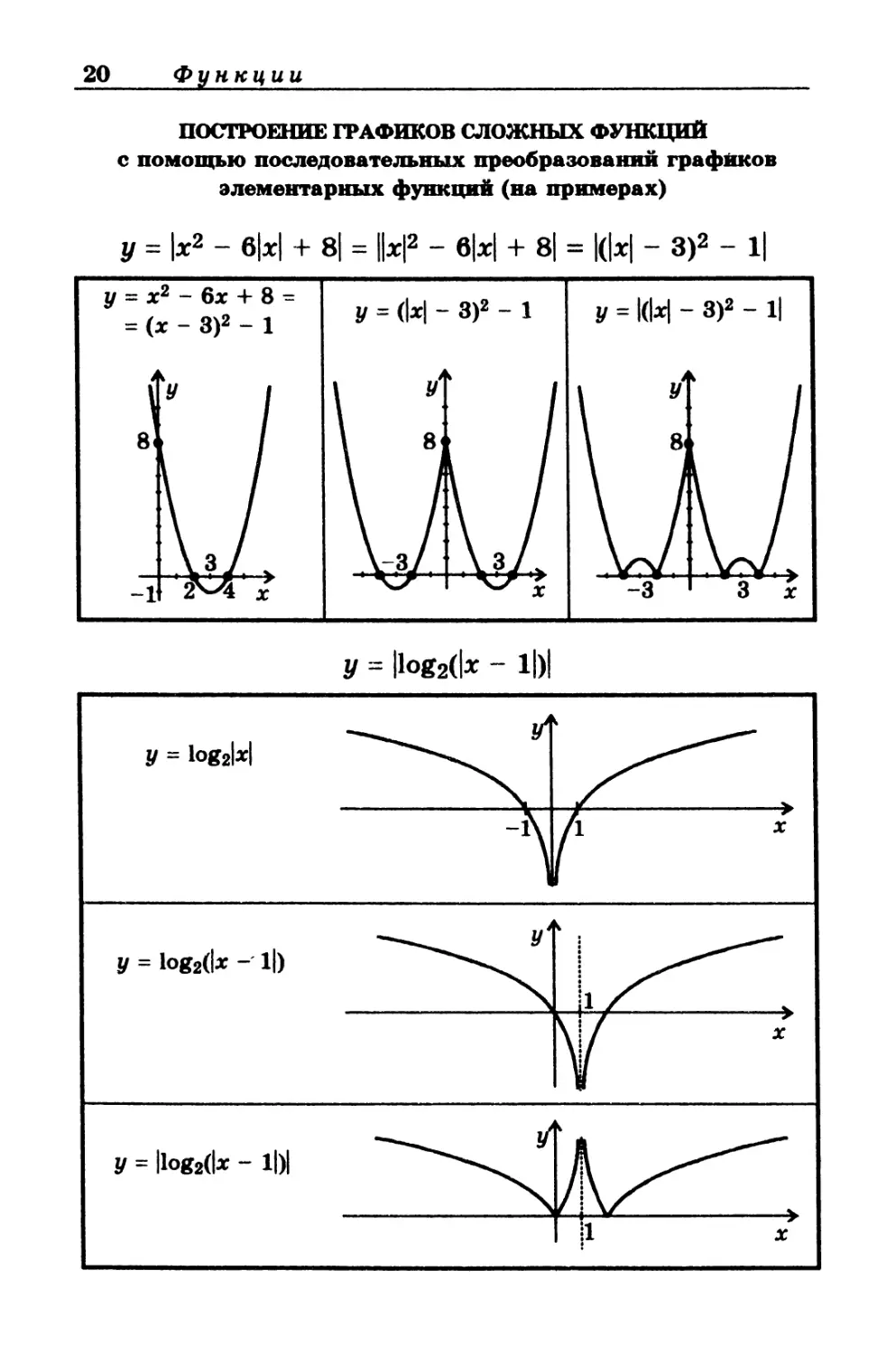
ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНЫХ ФУНКЦИЙ
с помощью последовательных преобразований графиков
элементарных функций (на примерах)
У = |х2 - б|х| + 8| = ||х|2 “ 6|х| + 8| = |(|х| - З)2 - 1|
Функции
21
у = |3sin2x| - 1
у = sin2x
у = |3sin2x|
Уф
у = |3sin2x| -1
22
Функции
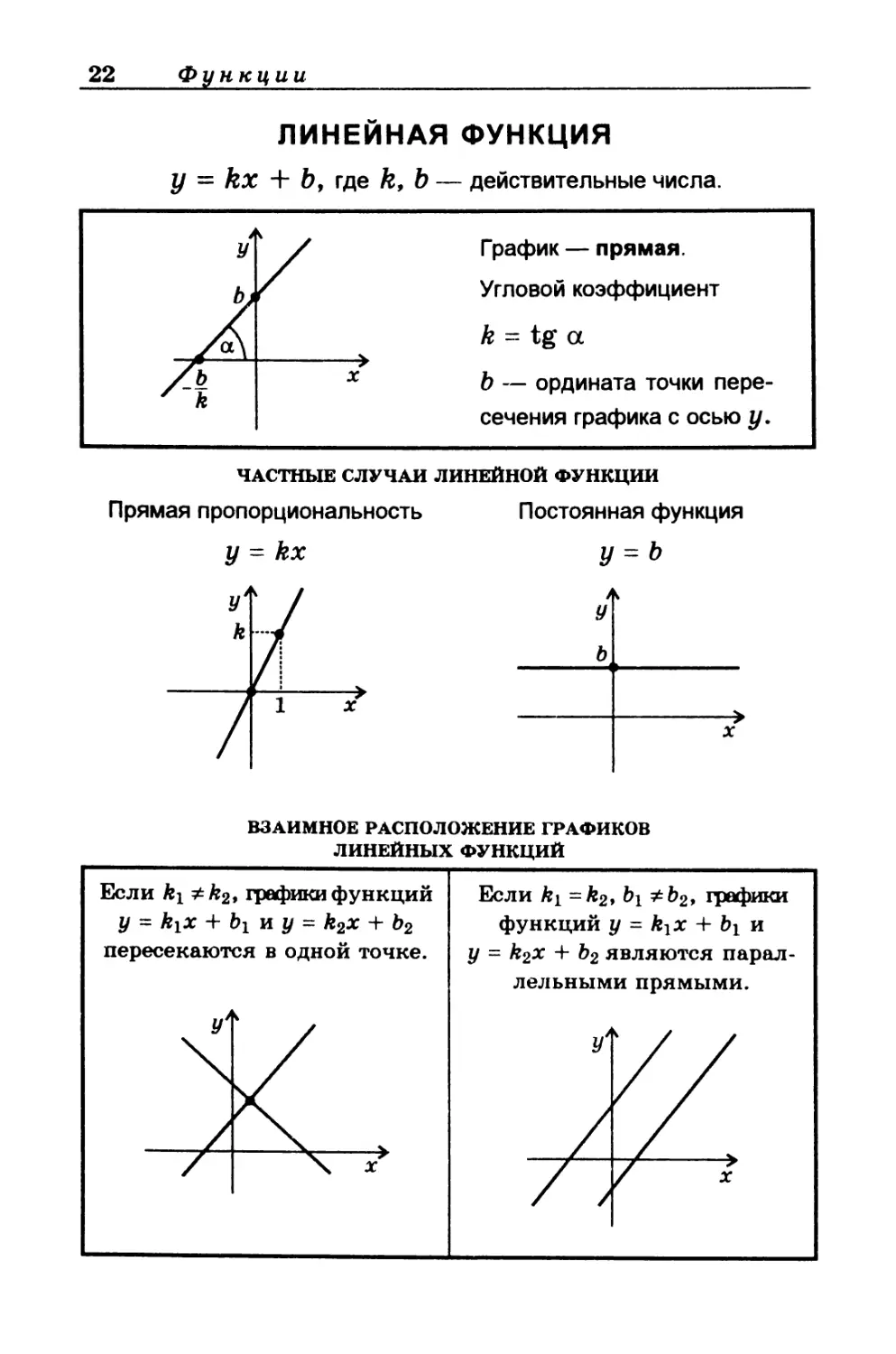
ЛИНЕЙНАЯ ФУНКЦИЯ
у = kx + Ь, где k, b — действительные числа.
График — прямая.
Угловой коэффициент
k = tg а
b — ордината точки пере-
сечения графика с осью у.
ЧАСТНЫЕ СЛУЧАИ ЛИНЕЙНОЙ ФУНКЦИИ
Прямая пропорциональность
У = kx
Постоянная функция
У = Ъ
у'
д
----------------->
х
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ
ЛИНЕЙНЫХ ФУНКЦИЙ
Если ki графики функций
у = kix + bi м у = k2x + b2
пересекаются в одной точке.
Если ki = k2, bi *b2, графики
функций у - kiX + Ьх и
у = k2x + b2 являются парал-
лельными прямыми.
Функции
23
свойства линейной функции у - kx + Ъ
• Область определения: R
• Область значений:
при k * О R
при k = О {Ъ}
• Четность, нечетность:
если k * О, Ь Ф 0, то функция не является ни четной,
ни нечетной
если k ф О, Ь = 0, то функция нечетная
если k = О, Ь * 0, то функция четная
если k = О, Ъ = 0, то функция тождественно равна нулю,
то есть является одновременно четной и нечетной
• Нули: если k * 0, то если k = 0, Ь ф 0, то если k = 0, b = 0, то у = 0 при х = —b/k нулей нет у - 0 при х е R
• Промежутки знакопостоянства:
если k > 0, то (у > 0 при х е (-b/k; оо) (z/ < 0 при х g (-оо; —b/k)
если k < 0, то (у > 0 при х е (-оо; -b/k) |z/ < 0 при х g (~b/k; оо)
если k = 0, Ь > 0, то если k = 0, Ь < 0, то если k = 0, Ь = 0, то у > 0 при х е R у < 0 при X G R у = 0 при X G R
• Промежутки монотонности:
если k > 0, то функция возрастает при х е R
если k < 0, то функция убывает при х е R
если k = 0, то функция постоянна при х е R
• Экстремумов нет
24
Функции
ПОСТРОЕНИЕ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ
ПО ДВУМ ТОЧКАМ
Часто удобно выбирать = О, Х2 1. Соответствую-
щие точки прямой (0; Ъ) и (1; b + k).
Пример.
у = Зх + 2
Если Xi = 0, то yi = 2;
если х2 = 1, то 1/2 ~ 5.
Через точки (0; 2) и (1; 5)
провести прямую.
Если k Ф 0, Ь Ф 0, можно выбирать точки (0; Ь) и
(~b/k; 0) на осях координат.
у = 2х + 2
Если = 0, то yi = 2;
если 1/2 - то х2 = ~1-
Через точки (0; 2) и (-1; 0)
провести прямую.
Если коэффициент перед х дробный, удобно выбирать
Х1 и Х2 так, чтобы у± и У2 были целыми.
Пример.
У = - — х + 2
3
Если Xt = 3, то ух = 1;
если х2 = -3, то 1/2 = 3.
Через точки (3; 1) и (-3; 3)
провести прямую.
Функции
25
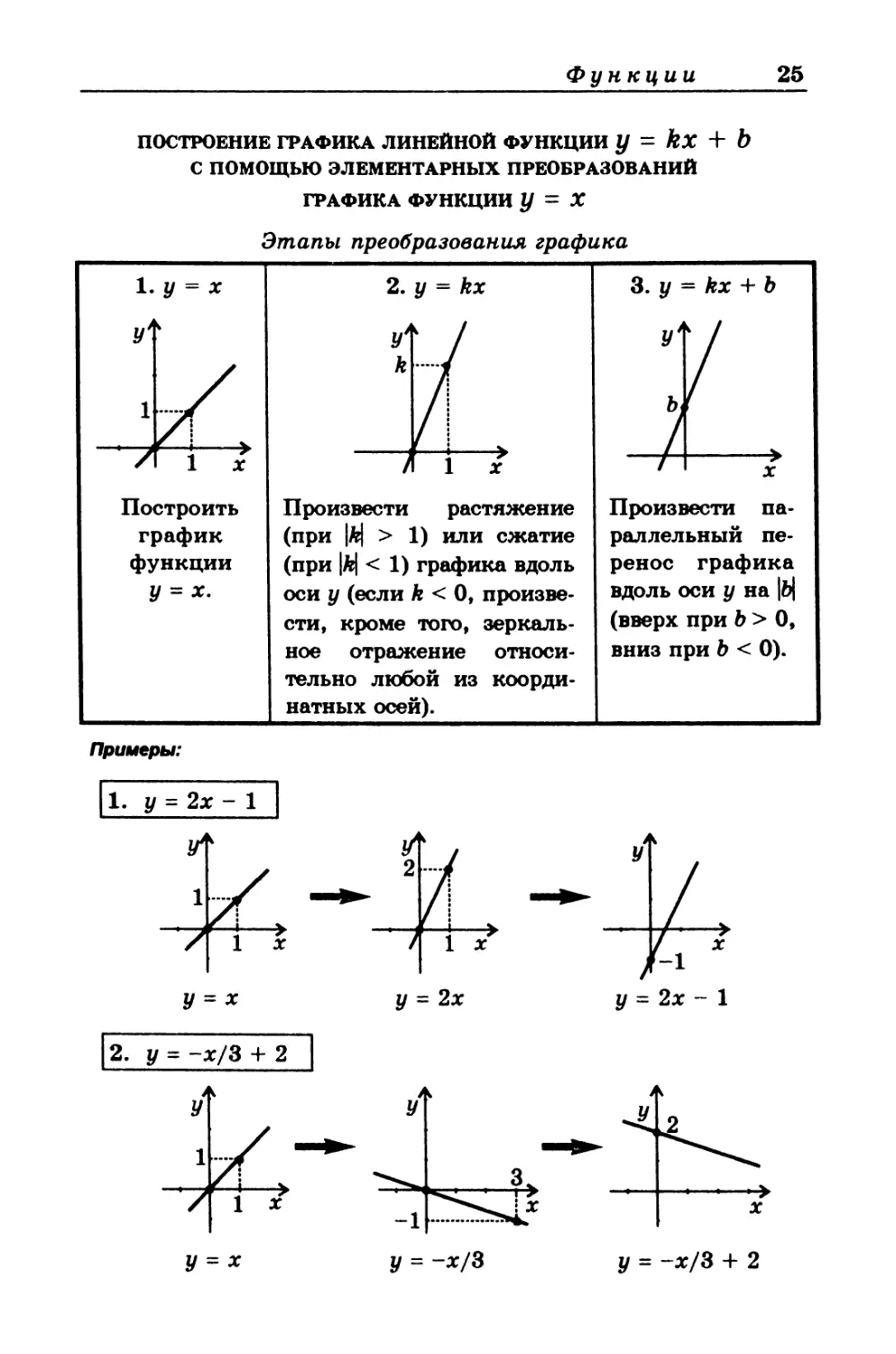
ПОСТРОЕНИЕ ГРАФИКА ЛИНЕЙНОЙ ФУНКЦИИ у - kx + Ъ
С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ
ГРАФИКА ФУНКЦИИ У ~ X
Этапы преобразования графика
3. у = kx 4- Ь
Построить
график
функции
У = х.
Произвести растяжение
(при |&| > 1) или сжатие
(при |fe| < 1) графика вдоль
оси у (если k < 0, произве-
сти, кроме того, зеркаль-
ное отражение относи-
тельно любой из коорди-
натных осей).
Произвести па-
раллельный пе-
ренос графика
вдоль оси у на |b|
(вверх при Ь > О,
вниз при Ь < 0).
Примеры:
1. у = 2х - 1
У = х
У = -х/3
у = -х/3 + 2
26
Функции
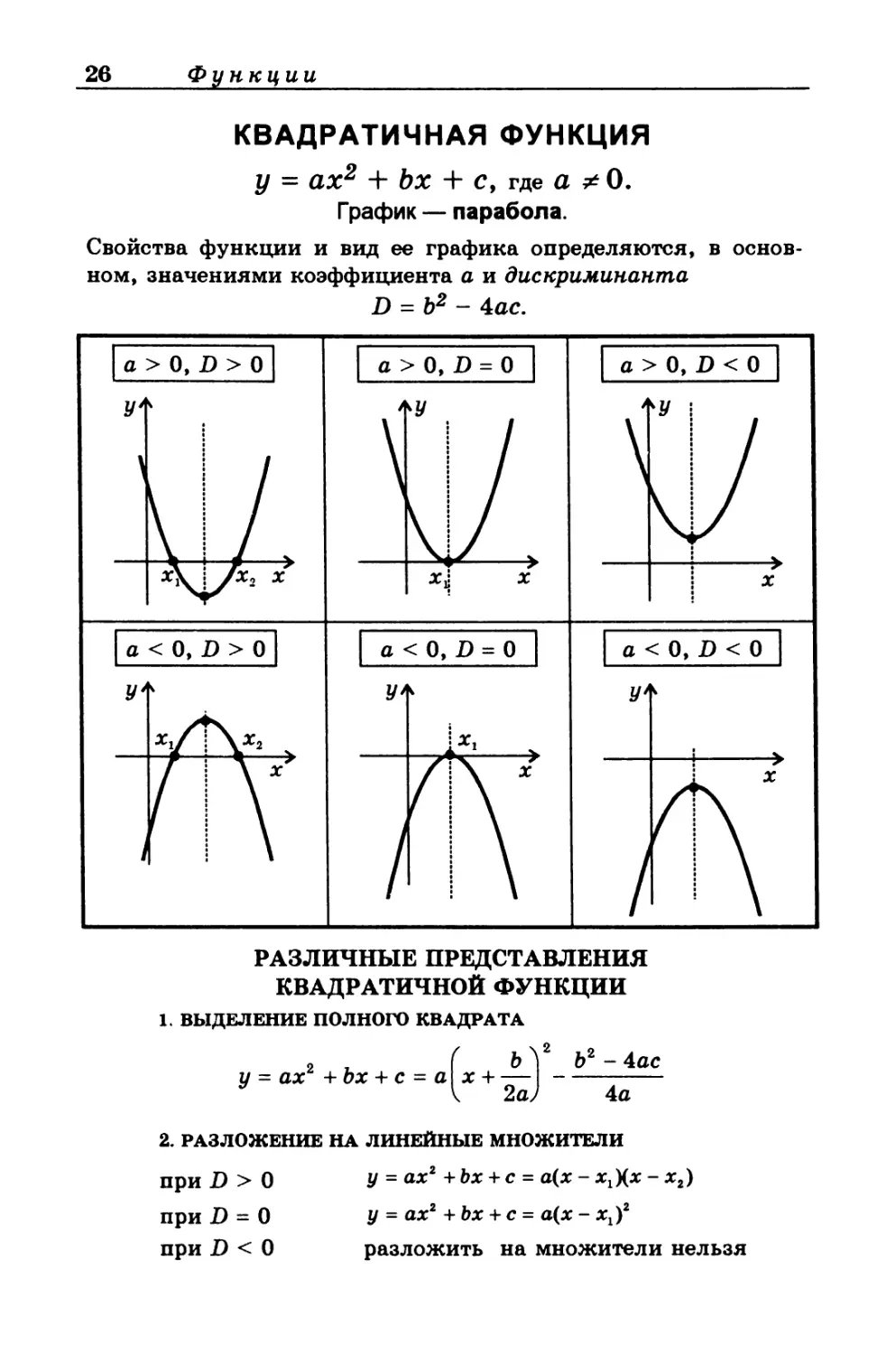
КВАДРАТИЧНАЯ ФУНКЦИЯ
у = ах2 + Ьх + с, где а # 0.
Г рафик — парабола.
Свойства функции и вид ее графика определяются, в основ-
ном, значениями коэффициента а и дискриминанта
D = Ь2 - 4ас.
РАЗЛИЧНЫЕ ПРЕДСТАВЛЕНИЯ
КВАДРАТИЧНОЙ ФУНКЦИИ
1. ВЫДЕЛЕНИЕ ПОЛНОГО КВАДРАТА
2 ( Ь V Ь2 - 4ас
у = ах + Ьх + с = а х + —----
у V 2а) 4а
2. РАЗЛОЖЕНИЕ НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ
при D > 0 у = ах2+Ьх + с = а(х-х^х-хг)
при D = 0 у = ах2 + Ьх + с = а(х - хх)2
при D < 0 разложить на множители нельзя
Функции
27
свойства квадратичной функции у = ах2 + Ьх + с
• Область определения: R
• Область значений:
при а > 0 [-D/(4a); оо)
при а < 0 (-оо; -В/(4а)]
• Четность, нечетность:
при Ь = 0 функция четная
при Ъ Ф 0 функция не является ни четной, ни нечетной
• Нули:
при D > 0 -ь-Jd два нуля: xt = , х2 = 2а -b + JD 2а
при D = 0 один нуль: Xi = -Ь/(2а)
при D < 0 нулей нет
• Промежутки знакопостоянства:
(у; > 0 при х G (“00; xjLK^; оо)
если а - > 0, D > 0, то (У < 0 при х е (Хр х2)
если а - > 0, D = 0, то У > > 0 при х е (-оо; Xi)U(xi; оо)
если а - > 0, D < 0, то У > ► 0 при х е R
(у : > 0 при х е (х,; х2)
если а < - 0, D > 0, то \у < 0 при х G (-оо; X1)U(X2; оо)
если а < - 0, D = 0, то У < : 0 при х е (-оо; XxXXxi; оо)
если а * - 0, D < 0, то У < : 0 при х g R
• Промежутки монотонности:
при а > О
при а < О
функция возрастает при х е [~Ь/(2а); оо)
функция убывает при х е (-оо; -Ь/(2а)]
функция возрастает при х е (-оо; -Ь/(2а)]
функция убывает при х е [~Ь/(2а); оо)
• Экстремумы:
при а > О xmtn = - Ь/(2а); ymln = - D/(4a)
при а < 0 Хм: = - Ь/(2а); утах = - D/(4a)
28
Функции
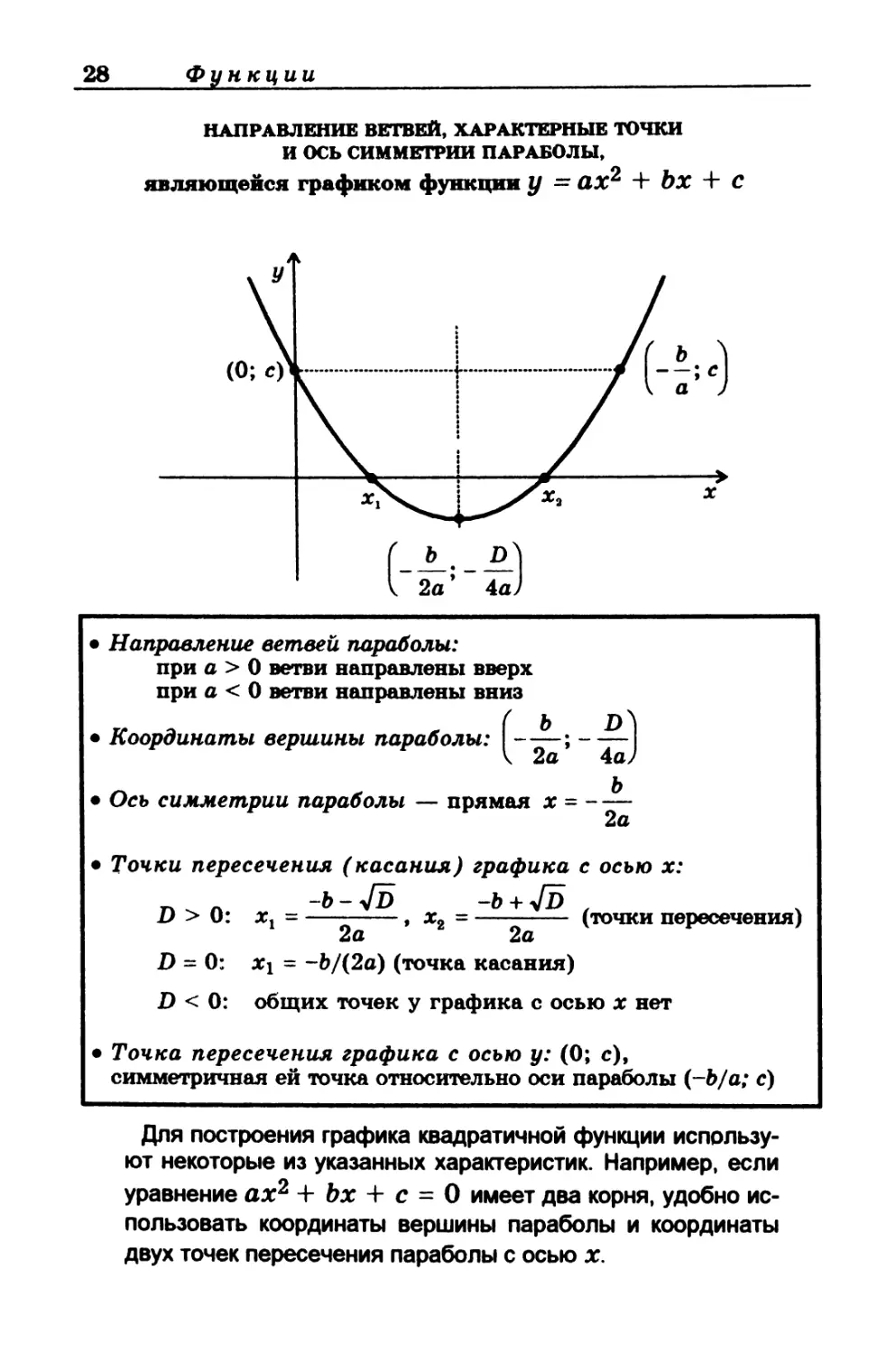
НАПРАВЛЕНИЕ ВЕТВЕЙ, ХАРАКТЕРНЫЕ ТОЧКИ
И ОСЬ СИММЕТРИИ ПАРАБОЛЫ,
являющейся графиком функции у = ах2 + Ьх + С
• Направление ветвей параболы:
при а > 0 ветви направлены вверх
при а < 0 ветви направлены вниз
• Координаты вершины параболы:
• Ось симметрии параболы — прямая х =-
• Точки пересечения (касания) графика с осью х:
n n -ь-Jd -ь + Jd t
D > О: хг =--------, х2 =------- (точки пересечения)
2а 2а
D = 0: Xi = -Ь/(2а) (точка касания)
D < 0: общих точек у графика с осью х нет
• Точка пересечения графика с осью у: (0; с),
симметричная ей точка относительно оси параболы (~Ь/а; с)
Для построения графика квадратичной функции использу-
ют некоторые из указанных характеристик. Например, если
уравнение ах2 + Ьх + с = 0 имеет два корня, удобно ис-
пользовать координаты вершины параболы и координаты
двух точек пересечения параболы с осью х.
Функции
29
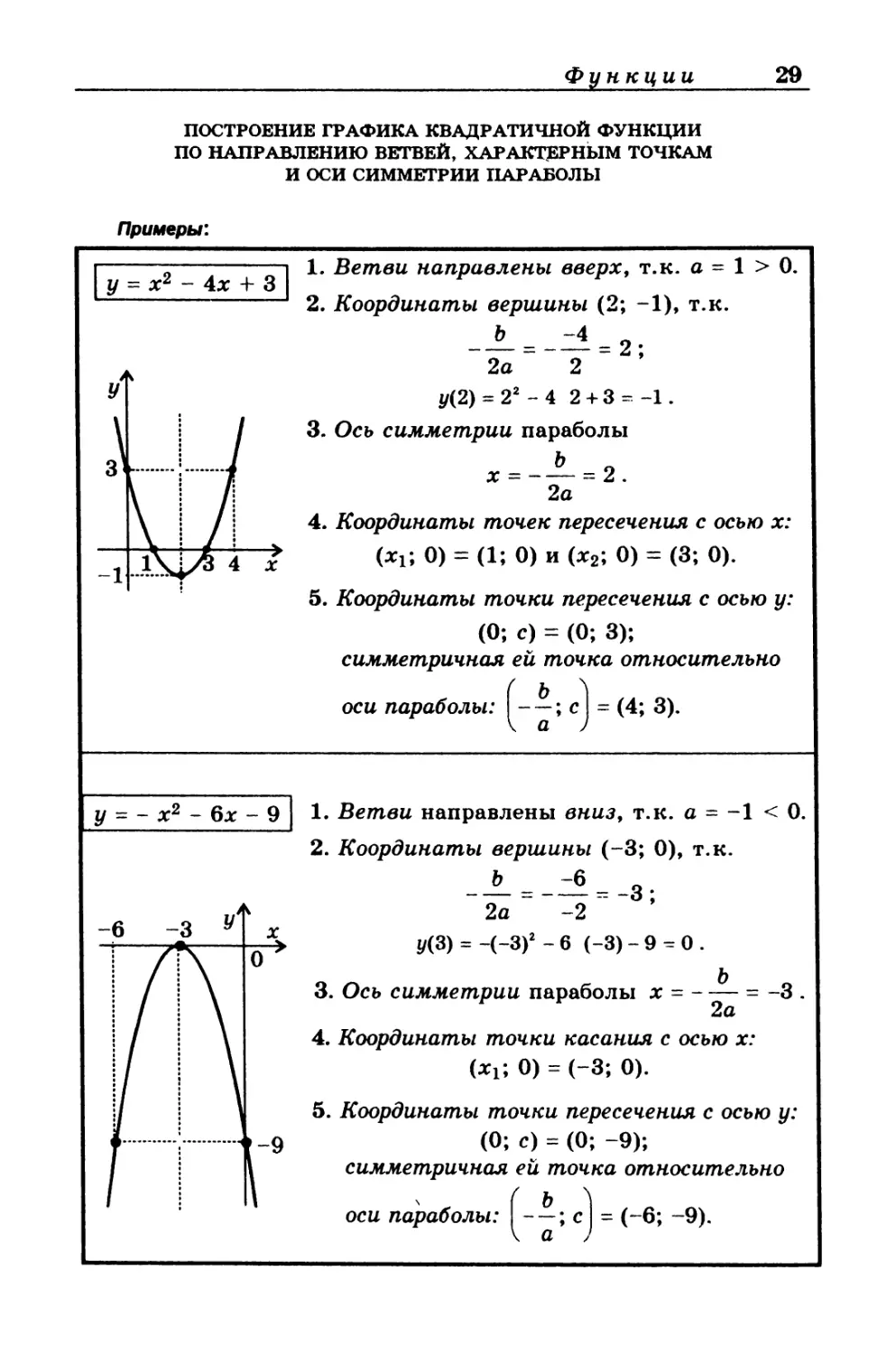
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ПО НАПРАВЛЕНИЮ ВЕТВЕЙ, ХАРАКТЕРНЫМ ТОЧКАМ
И ОСИ СИММЕТРИИ ПАРАБОЛЫ
Примеры:
у = х2 - 4х + 3
у = - х2 - 6х - 9
1. Ветви направлены вверх, т.к. а - 1 > 0.
2. Координаты вершины (2; -1), т.к.
-± = -Zl = 2;
2а 2
i/(2) = 22 - 4 2 + 3 = -1.
3. Ось симметрии параболы
х = -—= 2.
2а
4. Координаты точек пересечения с осью х:
(*Г, 0) = (1; 0) и (х2; 0) = (3; 0).
5. Координаты точки пересечения с осью у:
(0; с) = (0; 3);
симметричная ей точка относительно
оси параболы: | ; с | = (4; 3).
\ a J
1. Ветви направлены вниз, т.к. а = -1 < 0.
2. Координаты вершины (-3; 0), т.к.
2а -2
i/(3) = -(-З)2 - 6 (-3) - 9 - 0 .
3. Ось симметрии параболы х - - — = -3 .
2а
4. Координаты точки касания с осью х:
(х1; 0) = (-3; 0).
5. Координаты точки пересечения с осью у:
(0; с) = (0; -9);
симметричная ей точка относительно
оси параболы: (- —; с | - (-6; -9).
\ а )
30
Функции
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ С ПОМОЩЬЮ
ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ ГРАФИКА ФУНКЦИИ у - X2
С помощью выделения полного квадрата (см. стр. 26) любую
квадратичную функцию можно представить в виде:
2 , ( Ъ V Ь2 - 4ас 2
у = ах 4- Ьх + с = а х + —---------= а(х - ту 4- п,
к 2а) 4а
Ь Ь2 - 4ас
где т = - —, п =---------.
2а 4а
Это позволяет построить график квадратичной функции с по-
мощью элементарных преобразований графика функции у = х2.
Этапы построения графика функции у — а(х - т)2 4- п:
У % В 1. Растяжение графика у = х2 вдоль оси у в |а| раз (при |а| < 1 — это сжатие в 1/|а| раз). Если а < 0, произвести, кроме того, зеркальное отражение графика отно- сительно оси х (ветви параболы бу- дут направлены вниз). Результат: график функции у = ах2.
1 X
У 1 2. Параллельный перенос графика
1 1 \ ! / функции у = ах2 вдоль оси х на |тп|
1 1 \.и/ (вправо при т > 0
% и влево при т < 0).
ч % ДА т х Результат: график функции у = а(х - т)2.
У U 3. Параллельный перенос графика функ- ции у = а(х - т)2 вдоль оси у на |п| (вверх при п > 0
п Up' — > т х и вниз при п < 0). Результат: график функции у = а(х - т)2 4- п.
Функции
31
Примеры:
у = 2хг - 12х + 19 = 2(х - З)2 +1
1. Растяжение
графика
функции
у = х2 вдоль
оси у в 2 раза.
2. Параллельный
перенос графика
функции
у = 2Х2 вдоль оси х
на 3 вправо.
3. Параллельный
перенос графика
функции
у = 2(х - З)2 вдоль
оси у на 1 вверх.
г2 1
jZ = -±--2x-3 = -|(x + 2)2-1
---у = ~(х+2)2/2
---у = -(х+2)2/2 - 1
1. Сжатие графи-
ка функции
у = х2 вдоль оси у
в 2 раза и преоб-
разование симмет-
рии относительно
оси х.
2. Параллельный
перенос графика
функции
у = -х2/2 вдоль
оси х на 2 влево.
3. Параллельный пере-
нос графика функции
у = ~(х 4- 2)2/2 вдоль
оси у на 1 вниз.
32
Функции
СТЕПЕННЫЕ ФУНКЦИИ
с натуральными показателями степени
у = Хп, где П € N
Примеры графиков
п нечетное
п четное
СВОЙСТВА ФУНКЦИЙ
• Область определения: R
• Область значений:
при п нечетном R
при п четном [0; оо)
• Четность, нечетность:
при п нечетном функция нечетная
при п четном функция четная
• Нули: у = 0 при х = 0
• Промежутки знакопостоянства:
(у > 0 при х е (0; оо)
если п нечетное, то < ,
(I/ < 0 при х с (-ос; 0)
если п четное, то у > 0 при х е (-оо; 0) U (0; оо)
• Промежутки монотонности:
если п нечетное, то функция возрастает при х е R
функция возрастает при х е [0; оо)
функция убывает при х е (-ос; 0]
• Экстремумы:
если п нечетное, экстремумов нет
если п четное, У min - 0 ПРИ xmin ~ 0
• Графики функций проходят через точки:
при п нечетном (-1; -1), (0; 0), (1; 1)
при п четном (-1; 1), (0; 0), (1; 1)
Замечание. При п = 0 функция у = хп определяется так:
х° = 1 при х 0; при х = 0 функция не определена.
если п четное, то
Функции
33
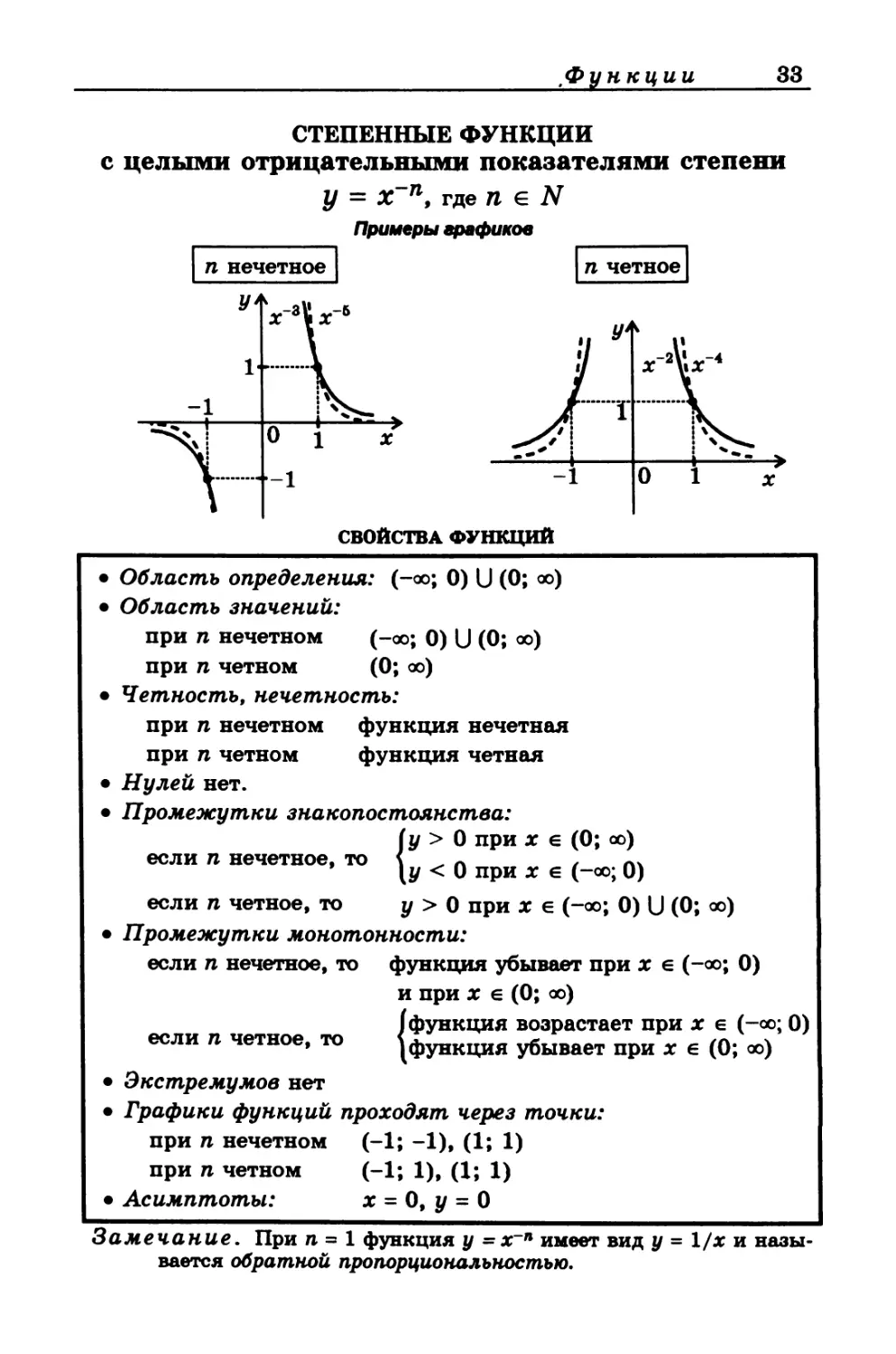
СТЕПЕННЫЕ ФУНКЦИИ
с целыми отрицательными показателями степени
у = Х~п, где п е N
Примеры графиков
п четное
СВОЙСТВА ФУНКЦИЙ
• Область определения: (-оо; 0) U (0; оо)
• Область значений:
при п нечетном (-оо; 0) U (0; оо)
при п четном (0; оо)
• Четность, нечетность:
при п нечетном функция нечетная
при п четном функция четная
• Нулей нет.
• Промежутки знакопостоянства:
(у > 0 при х е (0; оо)
если п нечетное, то \ Л
’ [у < 0 при х е (-оо; 0)
если п четное, то у > 0 при х е (-оо; 0) U (0; оо)
• Промежутки монотонности:
если п нечетное, то
функция убывает при х е (-оо; 0)
и при х е (0; оо)
(функция возрастает при х е (-оо; 0)
[функция убывает при х е (0; оо)
если п четное, то
• Экстремумов нет
• Графики функций проходят через точки:
при п нечетном (-1; -1), (1; 1)
при п четном (-1; 1), (1; 1)
• Асимптоты: х = 0, у = 0
Замечание. При п = 1 функция у = х~п имеет вид у = 1/х и назы-
вается обратной пропорциональностью.
34
Функции
ФУНКЦИИ
У = V* , где П е N
Примеры графиков
п нечетное п четное
СВОЙСТВА ФУНКЦИЙ
• Область определения:
при п нечетном R
при п четном [0; оо)
• Область значений:
при п нечетном R
при п четном [0; со)
• Четность, нечетность:
при п нечетном функция нечетная
при п четном функция не является
ни четной, ни нечетной
• Нули: у = 0 при х = О
• Промежутки знакопостоянства:
(у > 0 при х е (0; оо)
если п нечетное, то < 0 При х в (-оо; 0)
если п четное, то у > 0 при х е (0; оо)
• Промежутки монотонности:
функция возрастает при всех х из области определения
• Экстремумов нет
• Графики функций проходят через точки:
при п нечетном (-1; -1), (0; 0), (1; 1)
при п четном (0; 0), (1; 1)
Функции
35
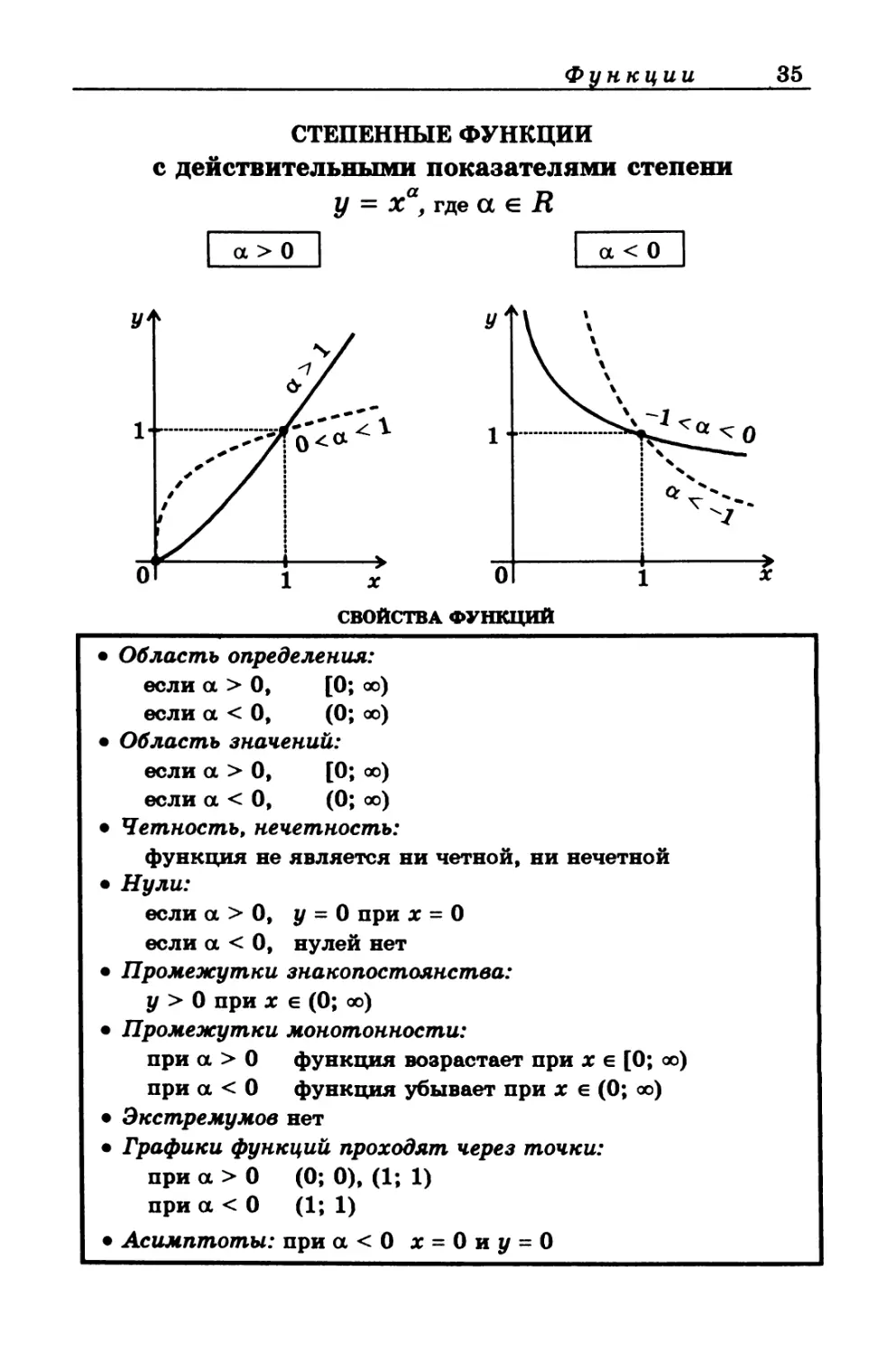
СТЕПЕННЫЕ ФУНКЦИИ
с действительными показателями степени
у = ха, где а е Я
а > О
а < О
СВОЙСТВА функций
• Область определения:
если а > 0, [0; оо)
если а < 0, (0; оо)
• Область значений:
если а > 0, [0; оо)
если а < 0, (0; оо)
• Четность, нечетность:
функция не является ни четной, ни нечетной
• Нули:
если а > 0, у = 0 при х = 0
если а < 0, нулей нет
• Промежутки знакопостоянства:
у > 0 при х е (0; оо)
• Промежутки монотонности:
при а > 0 функция возрастает при х е [0; оо)
при а < 0 функция убывает при х е (0; оо)
• Экстремумов нет
• Графики функций проходят через точки:
при а > 0 (0; 0), (1; 1)
при а < 0 (1; 1)
• Асимптоты: при а<0 х = 0 и у = О
36 Функции
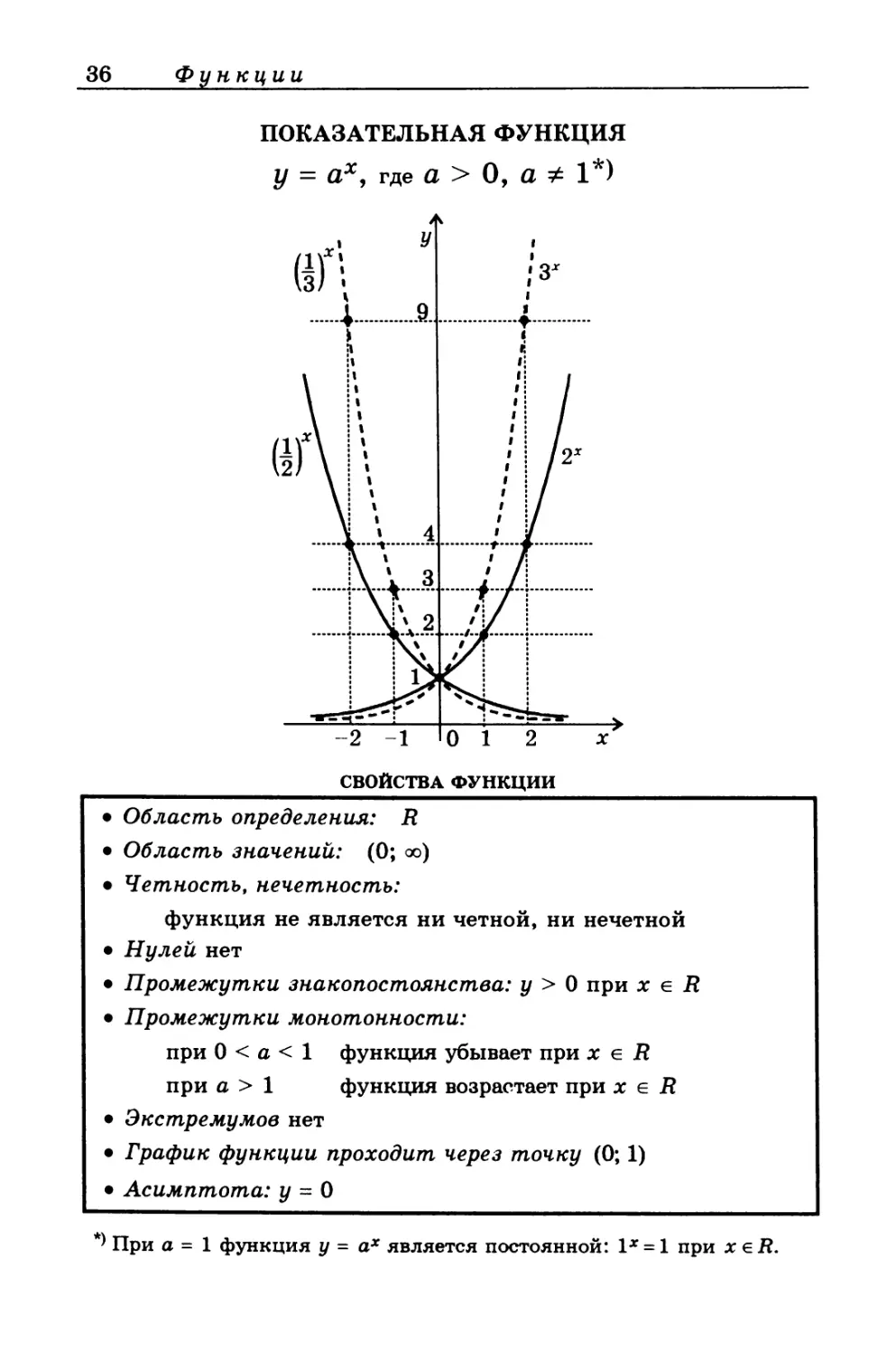
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
__________________СВОЙСТВА ФУНКЦИИ____________
• Область определения: R
• Область значений: (0; оо)
• Четность, нечетность:
функция не является ни четной, ни нечетной
• Нулей нет
• Промежутки знакопостоянства: у > 0 при х е R
• Промежутки монотонности:
при 0 < а < 1 функция убывает при х е R
при а > 1 функция возрастает при х е R
• Экстремумов нет
• График функции проходит через точку (0; 1)
• Асимптота: у - 0
При а = 1 функция у = ах является постоянной: Iх = 1 при х е R.
Функции
37
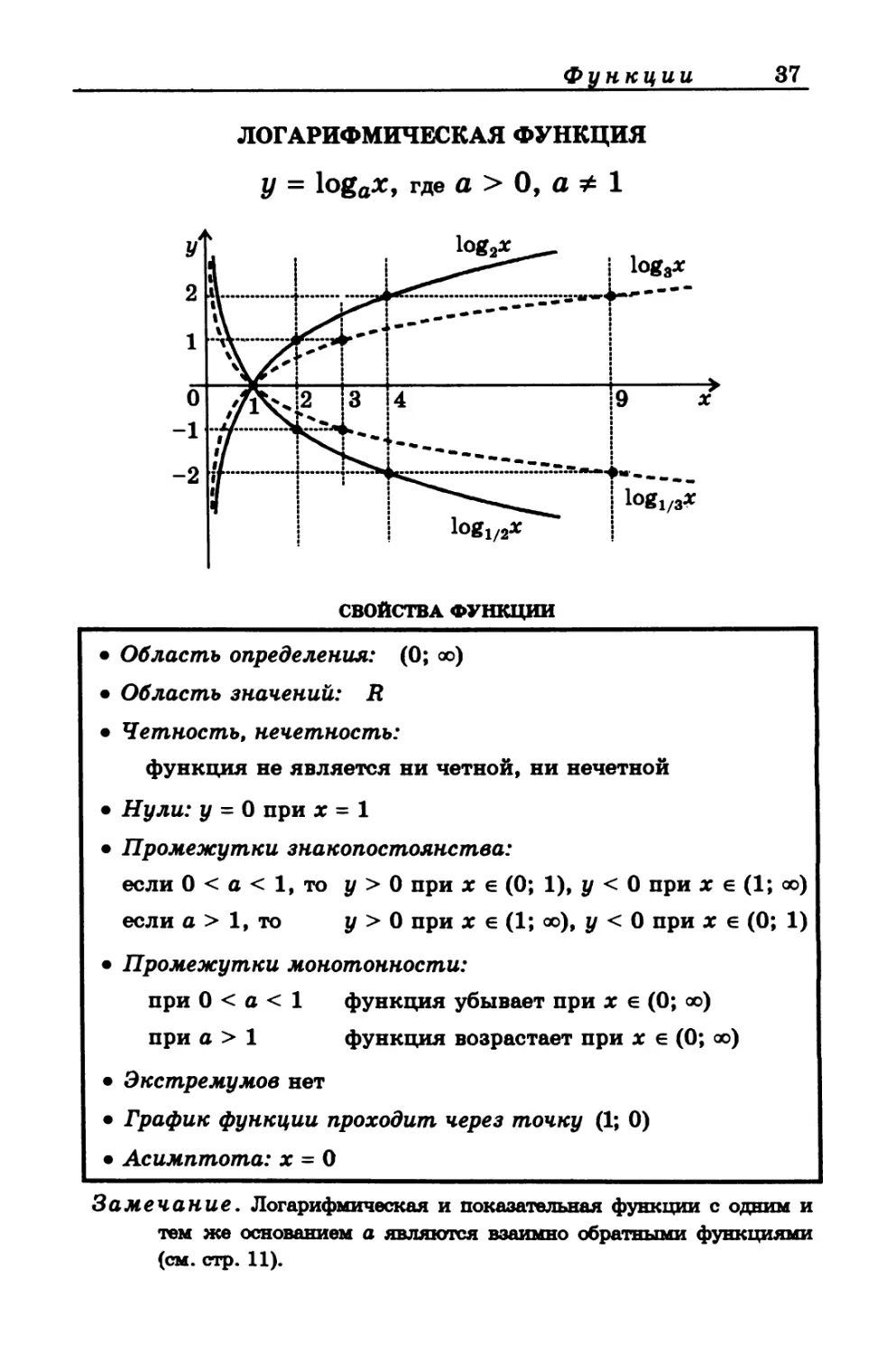
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
у = logex, где а > 0, а * 1
• Область определения: (0; оо)
• Область значений: R
• Четность, нечетность:
функция не является ни четной, ни нечетной
• Нули: у = 0 при х = 1
• Промежутки знакопостоянства:
если 0 < а < 1, то у > G при х е (0; 1), у < 0 при х е (1; оо)
если а > 1, то у > 0 при х е (1; оо), у < 0 при х е (0; 1)
• Промежутки монотонности:
при 0 < а < 1 функция убывает при х е (0; оо)
при а > 1 функция возрастает при х е (0; оо)
• Экстремумов нет
• График функции проходит через точку (Г, 0)
• Асимптота: х = 0
Замечание. Логарифмическая и показательная функции с одним и
тем же основанием а являются взаимно обратными функциями
(см. стр. 11).
38
Функции
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ*’
у = sinx
график — синусоида
СВОЙСТВА ФУНКЦИИ
• Область определения: R
• Область значений: [-1; Л
• Четность, нечетность: функция нечетная
• Период: 2п
• Нули: sin х = 0 при х = пп, neZ
• Промежутки знакопостоянства:
sin х > 0 при х е (2пп; л + 2лп), п е. Z
sin х < 0 при х е (-л + 2лп; 2лп), п е Z
• Экстремумы:
xmin = ~ + 2™. n^Z-, ymin = -1
л л _
хт(1Т = — + 2лп, п е Z; и r = 1
max 1 7 v max
Промежутки монотонности:
Г* Г» ГУ
функция возрастает при хе-----------+ 2лп; — + 2лп , п е Z
2 2
функция убывает
л л Зл _
при х е — + 2лп; — + 2лп , п е Z
2 2
Основные формулы тригонометрии см. на стр. 88-90.
Далее в качестве периода функции рассматривается ее наи-
меньший положительный период.
Функции
39
СВОЙСТВА ФУНКЦИИ
• Область определения: R
• Область значений: [-1; 1]
• Четность, нечетность: функция четная
• Период: 2л
• Нули: у = 0 при х = — + лп, п g Z
2
• Промежутки знакопостоянства:
cos х > О при х е - - + 2лп; — + 2 л п , п е Z
I 2 2 )
cos х < 0 при х е [ — + 2лп; — + 2лп п е Z
\ 2 2 )
• Экстремумы:
хтш = л + 2лп, п е Z; ymln = -1
Хтах = 2лп, е ута1 = 1
• Промежутки монотонности:
функция возрастает при х е [-л + 2лп; 2лп], п е Z
функция убывает при х е [2лп; л + 2лп], п с Z
Замечание. Графики функций у sin х и у = cos х получаются
друг из друга с помощью параллельных переносов вдоль оси х
на л/2 : cos х = sml х + — , sin х = cos х-
I 2) I 2)
40
Функции
СВОЙСТВА ФУНКЦИИ
• Область определения: объединение интервалов
( П П „
---4- ли; — + 7tn , п е Z
I 2 2 )
• Область значений: R
• Четность, нечетность: функция нечетная
• Период: it
• Нули: у = 0 при х = лп, п е Z
• Промежутки знакопостоянства:
f 71 „
tg х > 0 при х g пп; — + ля , п е Z
к 2 )
( 71 „
tg х < 0 при х е I-—+ ли; ли I, neZ
• Экстремумов нет
• Промежутки монотонности:
функция возрастает на каждом интервале
области определения
А 71
• Асимптоты: х = — + пп, п е Z
?
Функции
41
СВОЙСТВА ФУНКЦИИ
• Область определения: объединение интервалов
(лп; л 4- лп), п е Z
• Область значений: R
• Четность, нечетность: функция нечетная
• Период: п
• Нули: у - 0 при х - — + лп, п е Z
2
• Промежутки знакопостоянства:
( л „
ctg х > 0 при х е I лп; — + лп I, п е Z
( л „
ctg х < 0 при х е------+ лп; лп , п е Z
\ 2 )
• Экстремумов нет
• Промежутки монотонности:
функция убывает на каждом интервале
области определения
• Асимптоты: х = лп, п eZ
Замечание. График функции у = ctgx получается из графика функции
у = tgx отражением относительно любой из координатных осей и
последующим параллельным переносом вдоль оси х на л/2.
42
Функции
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
у = arcsin х
функция, обратная функции
у - sin х, -л/2 < х < л/2
у = arccosх
функция, обратная функции
у = cos х, 0 < х < л
СВОЙСТВА ФУНКЦИЙ*)
У = ; arcsin х у = arccos х
• Область определения: [-1; 1] [-1; 1]
• Область значений: 71.71 ~ 2'2 [0; л]
• Четность, нечетность: нечетная ни четная, ни нечетная
• • Нули: Промежутки знакопосто- янства: у = 0 при х = 0 у > 0 при х е (0; 1] у < 0 при х е [-1; 0) у = 0 при х = 1 у > 0 при х е [-1; 1)
• • Экстремумы: Промежутки монотон- ности: нет возрастает на всей области определения нет убывает на всей области определения
arcsin х + arccos х = я/2
См. также стр. 91.
Функции
43
у = arctg х
функция, обратная функции
у = tg х, -п/2 < х < п/2
у - arcctgх
функция, обратная функции
у = ctg х, 0 < х < л
СВОЙСТВА ФУНКЦИЙ
у = arctg х у = arcctg х
• Область определения: R R
• Область значений: 1 tO | а tO I (0; л)
• Четность, нечетность: нечетная ни четная, ни нечетная
• Нули: у = 0 при х = 0 нулей нет
• Промежутки знакопосто- янства: у > 0 при х е (0; оо) у < 0 при х е (-оо; 0) у > 0 при х е R
• Экстремумы: нет нет
• Промежутки монотонности: возрастает при х е R убывает при х е R
• Асимптоты: П П У = и у = — 2 * 2 у = 0 и у = Т1
arctg х + arcctg х = я/2
44 Уравнения
УРАВНЕНИЯ*»
Уравнением называется равенство, содержащее одно
или несколько неизвестных.
Общий вид уравнения
с одним неизвестным:
Л (*) = Л>(*).
с и неизвестными:
f1(xl9...9xTl) = f2(x19...9xn).
Часто все функции переносят в одну часть уравнения, и тогда
уравнения принимают вид:
/(х) = 0;
f(xi,.= 0.
Областью допустимых значений уравнения называется
область определения функций f(x) или f(xi,...,xn).
Пример. Областью допустимых значений уравнения
у1х - 2 = V3 - х является х е [2; 3].
Решением уравнения с одним неизвестным (корнем уравне-
ния) называется такое значение неизвестного, при подстановке
которого уравнение обращается в верное числовое равенство.
Решить уравнение — значит найти все его корни или до-
казать, что корней нет.
Примеры. Решить уравнение х2 - 4 = 0 — значит найти его
корни = -2; х2 2; решить уравнение х2 + 4 0 —
значит доказать, что корней нет.
Равносильными называются уравнения, множества кор-
ней которых совпадают.
В частности, равносильны все уравнения, не имеющие корней.
Примеры равносильных уравнений:
1. х - 2 = 0 и 2х = 4,
2. sinx = 2 и Jx = -1.
Решения всех уравнений, неравенств и систем рассматриваются толь-
ко на множестве действительных чисел.
Уравнения
45
ЛИНЕЙНЫЕ УРАВНЕНИЯ
ах + b = О,
где а и Ъ —действительные числа
Наличие корней и их число зависит от значений а и Ъ.
а О, Ъ — любое число
Уравнение ах + Ъ - О име-
ет один корень:
Ь
х =--------------
а
Прямая у = ах 4- b пересекает
ось х в одной точке.
Пример: 2х 4- 3 - 0 <=> х = -1,5
а = О, Ь Ф О
Уравнение 0 • х + Ь = 0 не
имеет корней.
Прямая у = Ох 4- b не пересекает
ось х.
-С II
л
Пример: О х 4- 2 = О — уравнение не имеет корней.
а = О, Ъ = О
Уравнение 0 х + О О
имеет бесконечно много кор-
ней: корнем является любое
число.
Прямая у 0x4-0 совпадает
с осью х.
Пример: 0х4-2 = 2<=>0х = 0 — корнем является любое
число.
46
Уравнения
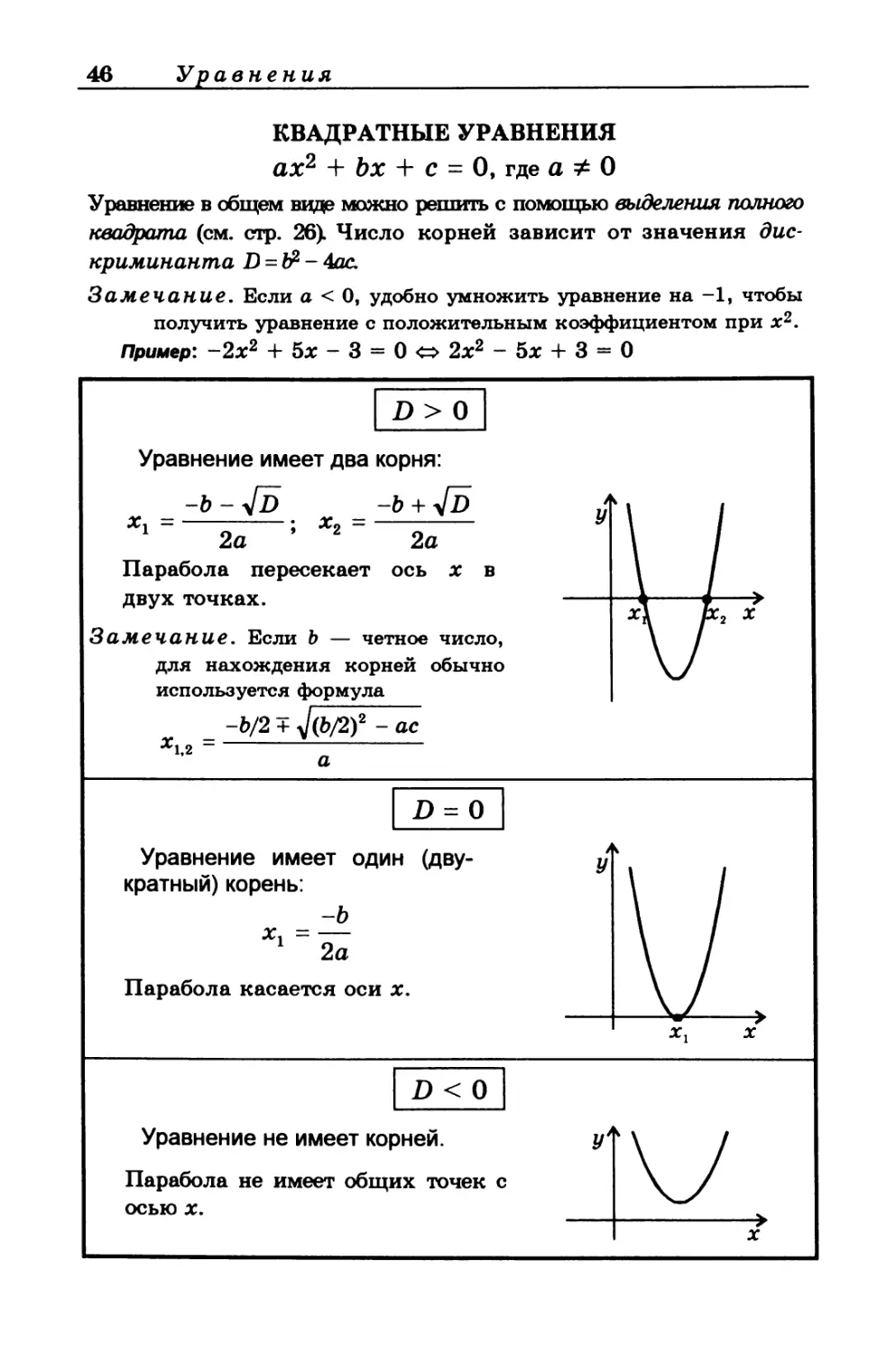
КВАДРАТНЫЕ УРАВНЕНИЯ
ах2 + Ьх + с - 0, где а * О
Уравнение в общем виде можно решить с помощью выделения полного
квадрата (см. стр. 26). Число корней зависит от значения дис-
криминанта D = t?~ 4ас.
Замечание. Если а < 0, удобно умножить уравнение на -1, чтобы
получить уравнение с положительным коэффициентом при х2.
Пример: -2х2 + 5х - 3 = 0 <=> 2х2 - 5х + 3 = О
D > О
Уравнение имеет два корня:
-ь + 4р
2а
Парабола пересекает ось х в
двух точках.
Замечание. Если b — четное число,
для нахождения корней обычно
используется формула
_ -Ъ/2 + ^(Ь/2)2 - ас
Х1,2
а
D = О
Уравнение имеет один (дву-
кратный) корень:
Парабола касается оси х.
D<0
Уравнение не имеет корней.
Парабола не имеет общих точек с
осью х.
Уравнения
47
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
ах2 + Ьх = 0, ах2 + с = О, ах2 = О
Такие уравнения решают обычно без применения общей фор-
мулы для корней квадратного уравнения.
ах2 + Ьх = О, Ь О
Уравнение всегда имеет два корня.
Решается с помощью разложения ле-
вой части уравнения на множители:
х (ах + Ь) = О
л Ь
Xj = 0; х2 =-----
а
Парабола пересекает ось х в двух точках, одна из кото-
рых является началом координат.
Пример: х2 - 2х = 0 <=> х (х - 2) = 0 <=> Xi = 0; х2 = 2
ах2 + с = 0, с О
Уравнение не имеет корней, если зна-
ки а и с совпадают; уравнение имеет
два корня, если знаки а и с различны:
Парабола или не пересекает ось х, или пересекает ее в двух
точках, симметричных относительно начала координат.
Примеры: х2 + 1 = 0 — нет решений
х2 - 1 = 0 <=> Xj = -1; х2 = 1
ах2 = 0
Уравнение имеет один (двукратный) » у корень: Xj = 0. \ Парабола касается оси х в начале ко- \
ординат. о' г > X
48
Уравнения
ТЕОРЕМЫ ВИЕТА
1. Если Xi и х2 — корни квадратного уравнения
ах2 + Ьх + с - 0, то Xi + х2 = -Ь/а\ Xi х2 = с/а.
2. Если Xi и х2 таковы, что х^ + х2 = ~Ь/а, Xi х2 = с/а,
то Xi и х2 являются корнями квадратного уравнения
ах2 + Ьх + с - 0.
ПРИВЕДЕННЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
Приведенным квадратным уравнением называется урав-
нение вида х2 + рх + q - 0
Замечание. Любое квадратное уравнение ах2 + Ьх + с = 0 можно
привести к такому виду с помощью деления уравнения на а.
ФОРМУЛЫ ВИЕТА ДЛЯ КОРНЕЙ
ПРИВЕДЕННОГО КВАДРАТНОГО УРАВНЕНИЯ
*1 + х2 = -р; Xi х2 = q
Теоремы Виета часто используются для:
• Подбора корней без решения уравнения
• Определения знаков корней без решения уравнения (при
условии D > 0) по следующим правилам:
р>0 Р < 0
q>0 Оба корня отрицательны Оба корня положительны
g<0 Корни имеют противоположные знаки
Примеры подбора корней с использованием теорем Виета:
1. х2 - 7х + 6 = 0. Нетрудно подобрать пару чисел, сумма
которых равна 7, а произведение равно 6 — это 1 и 6.
Согласно теоремам Виета корнями квадратного уравне-
ния х2 - 7х + 6 = 0 являются 1 и 6.
2. х2 - 4х - 5 = 0. Нетрудно подобрать пару чисел, сумма
которых равна 4, а произведение равно -5 — это -1 и 5.
Согласно теоремам Виета корнями квадратного уравне-
ния х2 - 4х - 5 = 0 являются -1 и 5.
Уравнения
49
УРАВНЕНИЯ, СВОДЯЩИЕСЯ К КВАДРАТНЫМ
af2(x) + bf(x) + с = О
СХЕМА РЕШЕНИЯ
1. С помощью введения новой переменной t f(x) уравне-
ние приводят к виду
at2 + bt + с - О
2. Если это уравнение имеет корни t\ и t2 (или один корнень t^),
решения исходного уравнения ищут как решения совокуп-
= t,
(или одного уравнения Дх)=^).
Т(х) — t2
ности уравнений
Частный случай уравнений, сводящихся к квадратным — биквад-
ратные уравнения (уравнения вида ах4 4- Ьх2 + с 0). В этом
случае вводят переменную t = х2.
Примеры:
Биквадратное уравнение
х4 - х2 - 2 = 0; замена t = х2
t2 - t - 2 = 0 о
t = -1 х2 = -1
t = 2 х2 = 2
корней нет
Иррациональное уравнение
х2 + V*2 - 2 = 4 о (х2 - 2) + у/х2 - 2 -2 = 0;
замена t = ^х2 - 2
t2 + t - 2 = 0 «> f ~~
t = 1
ух2 - 2 = -2 корней нет
л/х2- 2 = 1 х, = ±<3~
Тригонометрическое уравнение
sin2x - cosx + 1 - 0 <=> cos2x + cosx -2 = 0; замена t = cosx
cosx = -2 корней нет
cosx = 1 х = 2пп, п е Z
t = -2
t = 1
Показательное уравнение
32х - 12 3х-1 + 3 = 0 <=> 32х - 4 3х + 3 = 0;
замена t = 3х
4t + 3 = 0 <=>
t = 1
t = 3
3х = 1
3х =3
х = 0
х = 1
50
Уравнения
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Как правило, иррациональное уравнение сводится к равно-
сильной системе, содержащей уравнения и неравенства.
1. = -Jg(x) <=> < Замечание. Из двух си< ще. 7(Х) = g(x) f(x) > 0 или < зтем выбирают ту, в f(x) = g(x) g(x) > 0 юторая решается про-
Пример: у/З - х = у/х2 - 5х - 2
3-х = х2-5х-2^
3-х >0
х2 - 4х - 5 = О
х <3
х = 5
х = -1 <=> х = -1
х <3
2. 7/(х) = а
Если а < 0, уравнение не имеет корней.
Если а > 0, уравнение равносильно уравнению f(x) = а2.
Замечание. Иногда иррациональное уравнение можно свести к
приведенному виду с помощью введения новой переменной.
Пример: х - -Jx +1 = 5 <=> (х + 1) - Jx +1 -6 = 0
2 = Vx + 1 ,
22 -2-6 = 0 <=>
2 = -2 -Jx + 1 = -2
2 = 8 [Vx + 1 = 3
Первое уравнение совокупности не имеет корней, ко-
рень второго уравнения х = 8.
з. ' g(x) > 0 f(x) = g2(x)
Пример: V7-x = x- l<=>* х-1 >0 7 - х = (х - I)2
х>1
х2 - х - 6 = 0
х>1
х = -2 х = 3
х = 3
Уравнения
61
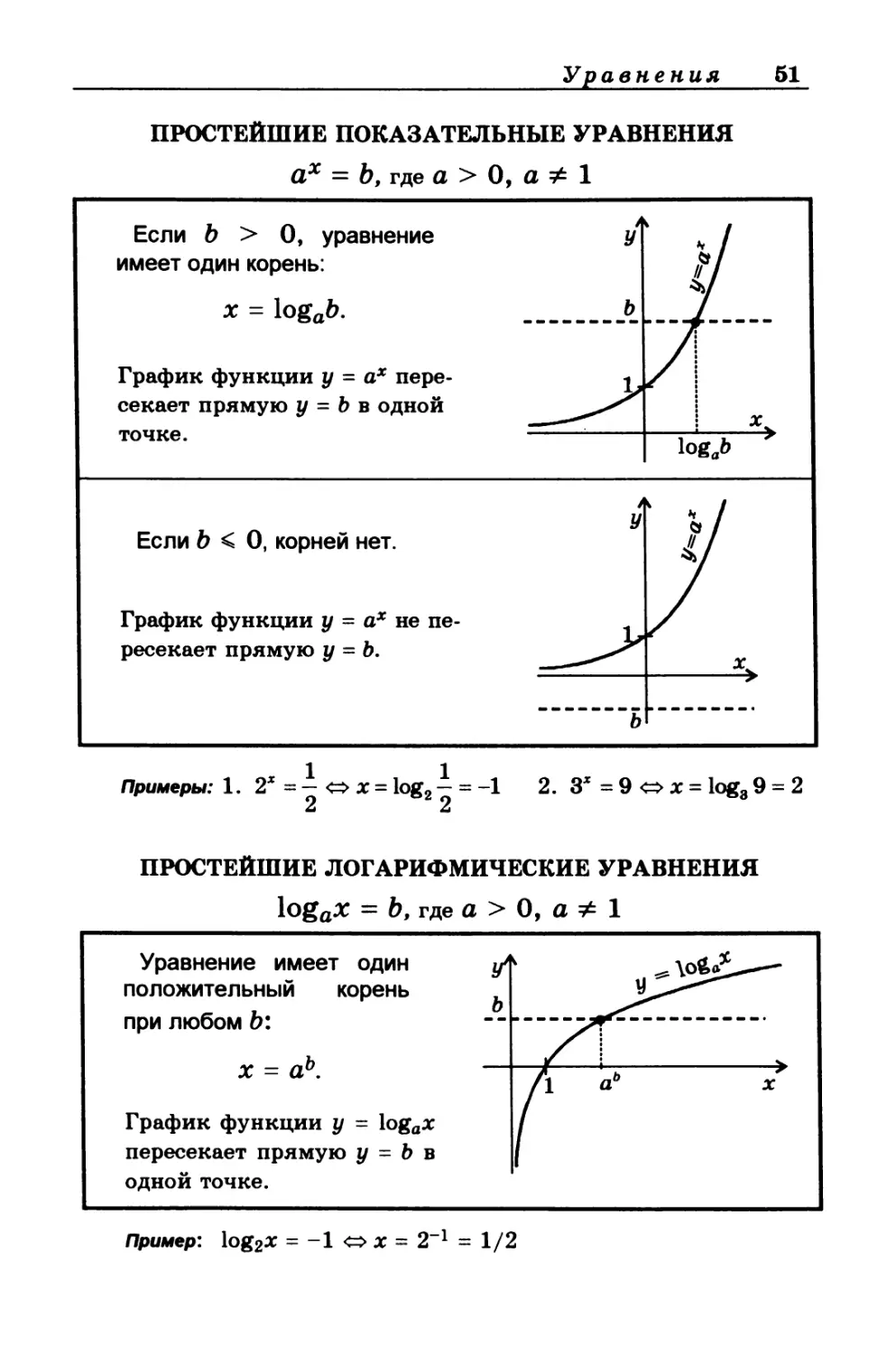
ПРОСТЕЙШИЕ ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
ах = Ъ, где а > 0, а & 1
2. 3х = 9 <=> х = log8 9 = 2
Примеры: 1. 2х = — <=> х = log2 — = -1
2 2
ПРОСТЕЙШИЕ ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
logox = Ь, где а > О, а * 1
Уравнение имеет один
положительный корень
при любом Ь:
х = аь.
График функции у - logax
пересекает прямую у = b в
одной точке.
Пример: \og2x = -1 <=> х = 2 1 = 1/2
52
Уравнения
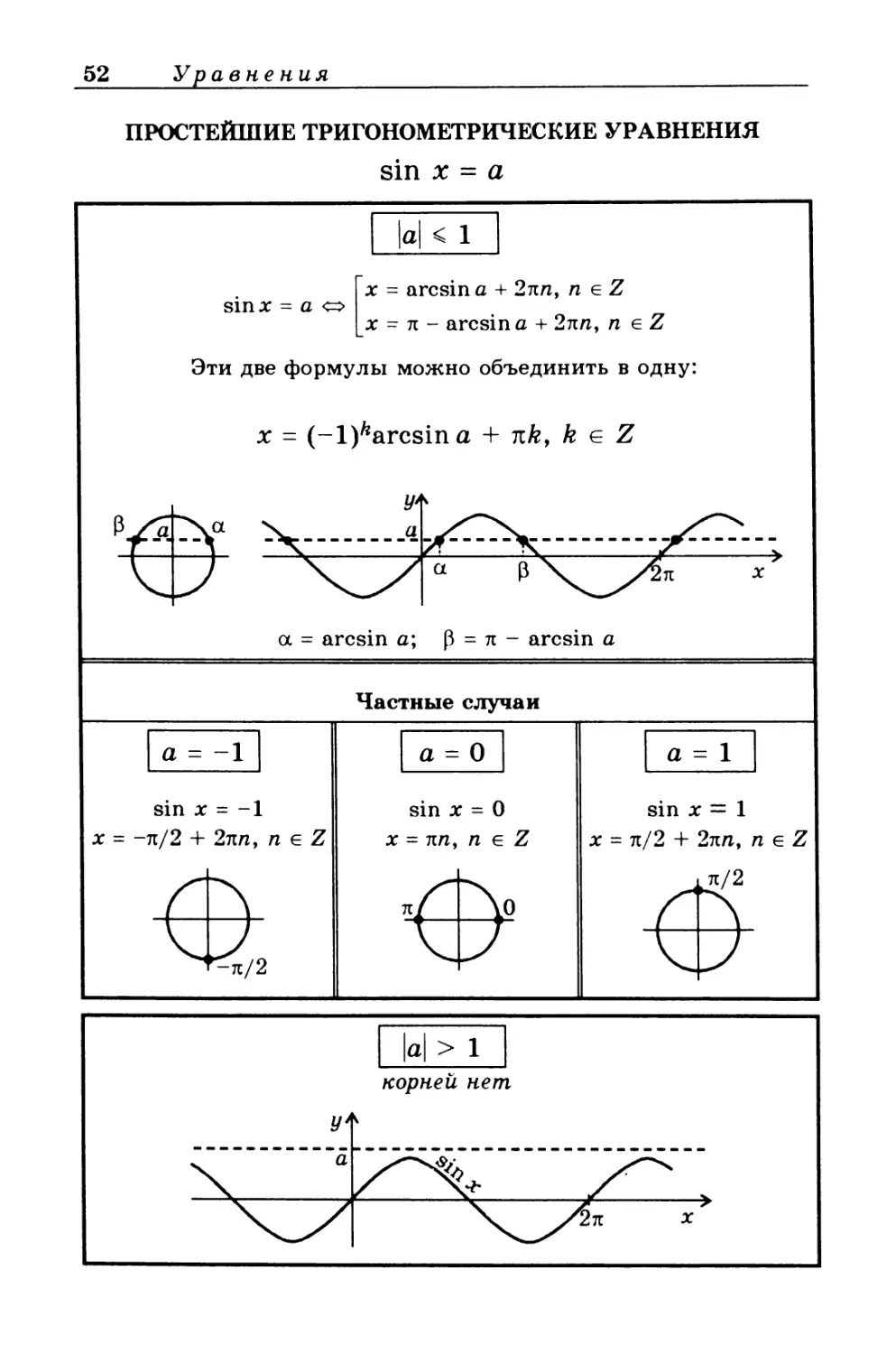
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
sin х = а
Уравнения
53
cos х = а
х = arccos а + 2лп, п е Z
х = - arccos а + 2лп, п е Z
Эти две формулы можно объединить в одну:
х = ±arccos а + 2лп, п g Z
2л х
а = -arccos а; р = arccos а
Частные случаи
а - -1
а = О
а = 1
cos х = -1
X = л + 2лп, П G Z
cos х = О
х = л/2 + лп, п е Z
COS X = 1
х = 2tui, п е Z
л/2
-л/2
54
Уравнения
tg х = a ctg х = а
a sin х + b cos x = c (a,b*O)
Уравнение не имеет корней, если а2 + Ь2 < с2.
Если а2 + Ь2 > с2, уравнение можно привести к виду:
а Ь с
Tfe2
Поскольку .—_
Wa2 4
sin X 4- cosX =
+ b2 7a2+b2
\2
—1 =1.
+ b2)
\2
можно ввести новую
a
переменную <p такую, что cos q> =
4a2 4-fe2
c
Уравнение примет вид: sin(x 4- ср) = f .
yla2 4- b2
Корни этого уравнения:
x = -q> 4- (-1)* arcsinl .—-
, sincp =
ч- л/г, k e Z
Пример: sin x 4- <3 cos x =
b___
'Th2
1 v3 \2
— sin х ч- COS X =----<=>
2 2 2
<=> sinf х 4- — | = —— <=> х = - — 4- (-1)* — 4- л/г, k eZ
I 3J 2 3 ' 4
Уравнения
55
УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ
И ЕГО ГРАФИК
Общий вид:
= f2(X,y)
Решением уравнения с двумя переменными называется
пара чисел (хо, уо), при подстановке которых вместо со-
ответствующих переменных х, у уравнение обращается в
верное числовое равенство.
Решить уравнение с двумя неизвестными — значит найти
все его решения или доказать, что решений нет.
Примеры:
1. х2 + у2 = 1 — бесконечно много решений: решением яв-
ляется любая пара чисел, совпадающих с координатами
точки, лежащей на единичной окружности, т.е. окруж-
ности радиуса 1 с центром в начале координат
2. х2 + у2 = 0 — одно решение: х = 0, у = О
3. х2 + у2 = -1 — решений нет
Решения уравнения с двумя переменными представляют
часто в виде графика.
Графиком уравнения с двумя переменными называется
множество всех точек плоскости, координаты которых х, у
являются решениями этого уравнения.
Примеры графиков уравнения с двумя переменными:
1. (x-2)? + (i/ + 1)2=9 2. ху = 1
з. = 1
56
Уравнения
Неравенства
57
НЕРАВЕНСТВА
Неравенствами называются выражения вида а < Ь,
а < Ь, а > Ь, а > Ъ, где а и Ъ могут быть числами (число-
выми выражениями) или функциями. Неравенства, содер-
жащие знаки < или >, называются строгими, а содержащие
знаки < или > — нестрогими.
Различают два вида неравенств: числовые и неравенства с пе-
ременными.
Примеры:
1. 5 < 10 — числовое неравенство
2. 2х > 3 — неравенство с одной переменной
3. 2х < 5у — неравенство с двумя переменными
Решением неравенства с одной переменной называется
такое значение переменной, при подстановке которого нера-
венство обращается в верное числовое неравенство.
Решить неравенство — значит найти все его решения
или доказать, что решений нет.
Примеры:
1. х2 + 5>0»хей
2. х-4с0охе (-оо; 4]
3. х2 < 0 — решений нет
Равносильными называются неравенства, множества
решений которых совпадают.
В частности, равносильны все неравенства, не имеющие решений.
Примеры равносильных неравенств:
1. х > 2 и х3 > 8 Л
2. sinx > 2 и 7х < -1
Из неравенств так же, как из уравнений, составляют системы
и совокупности (примеры см. на стр. 62). Кроме того, часто
рассматриваются системы и совокупности, содержащие одно-
временно уравнения и неравенства (примеры см. на стр. 50).
58 Неравенства
ЛИНЕЙНЫЕ НЕРАВЕНСТВА
ах + b > 0, ах + b > О, ах + b < О, ах + b < О
Замечание. Если неравенство нестрогое (ах + Ъ > 0, ах + Ь < О),
его решением является объединение решений соответствующе-
го строгого неравенства и уравнения ах + b = О. Например,
х + 2 > О <=> хе [-^2; оо); О-х<О«хеЯ.
Неравенства
69
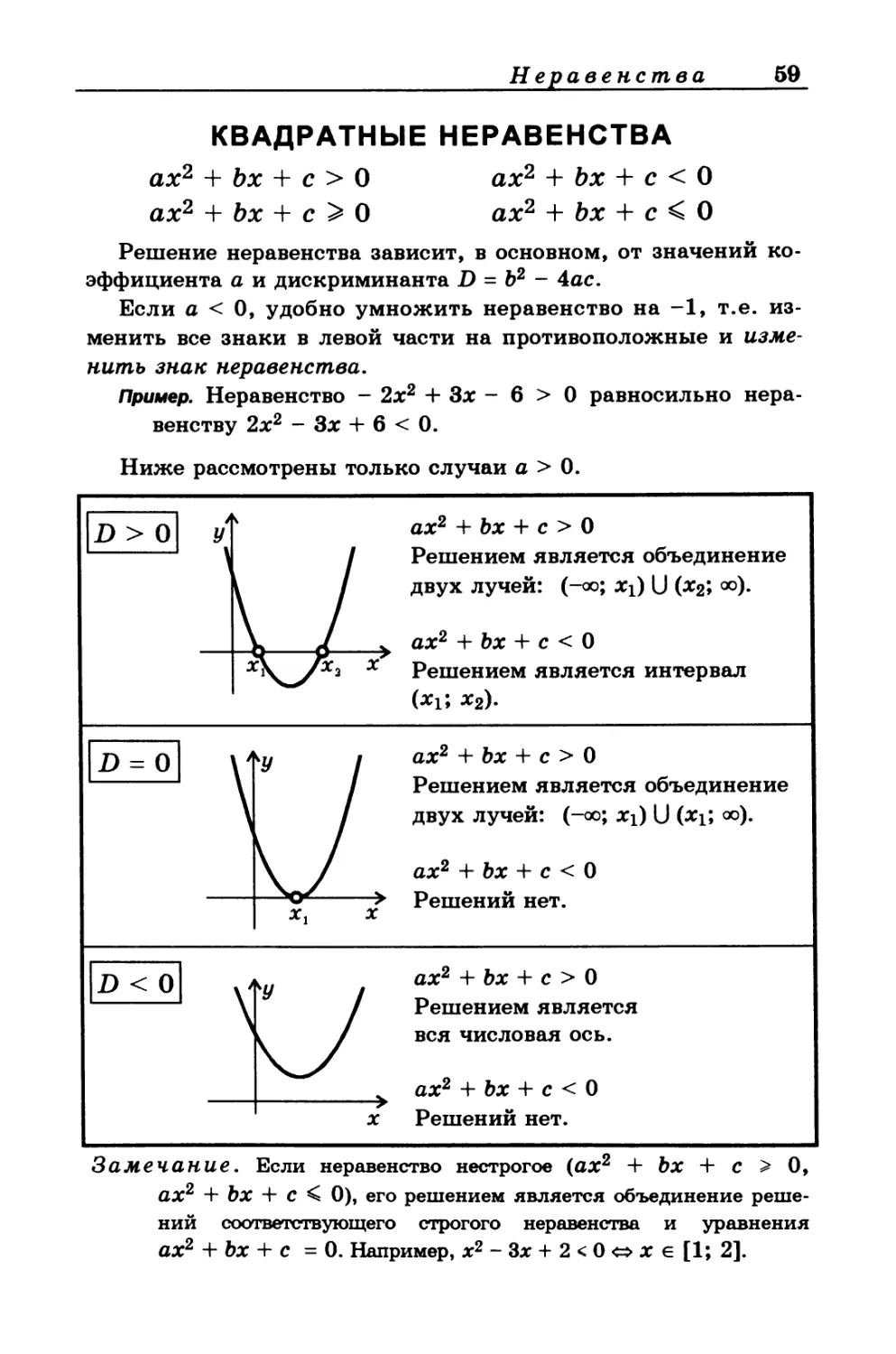
КВАДРАТНЫЕ НЕРАВЕНСТВА
ах2 + Ьх + с > 0 ах2 + Ьх + с < О
ах2 + Ьх + с О ах2 + Ьх + с < О
Решение неравенства зависит, в основном, от значений ко-
эффициента а и дискриминанта D = Ь2 - 4ас.
Если а < 0, удобно умножить неравенство на -1, т.е. из-
менить все знаки в левой части на противоположные и изме-
нить знак неравенства.
Пример. Неравенство - 2х2 4- Зх - 6 > 0 равносильно нера-
венству 2х2 - Зх 4- 6 < 0.
Ниже рассмотрены только случаи а > 0.
ах2 4- Ьх 4- с > 0
Решением является объединение
двух лучей: (-оо; х^ U (х2; <»).
ах2 4- Ьх 4- с < 0
Решением является интервал
(*i; *2)-
D-0
ах2 4- Ьх 4- с < 0
Решений нет.
ах2 4- Ьх 4- с > 0
Решением является объединение
двух лучей: (-оо; xj U (Xi; оо).
ах2 4- Ьх 4- с > 0
Решением является
вся числовая ось.
ах2 4- Ьх 4- с < 0
Решений нет.
Замечание. Если неравенство нестрогое (ах2 4- Ьх 4- с > 0,
ах2 4- Ьх 4- с С 0), его решением является объединение реше-
ний соответствующего строгого неравенства и уравнения
ах2 4- Ьх 4- с =0. Например, х2 - Зх 4- 2 < 0 <=> х е [1; 2].
60 Неравенства
МЕТОД ИНТЕРВАЛОВ
для неравенств вида
(х - ах)к1(х - а2)*2...(х - ап)*л >0 (> 0; < 0; < 0), где е N
СХЕМА РЕШЕНИЯ
1. Найти нули функции, стоящей в левой части неравенства.
2. Отметить положение нулей на числовой оси и определить
их кратность (если А/ четное, то нуль четной кратности,
если kt нечетное — то нечетной).
3. Найти знаки функции в промежутках между ее нулями,
начиная с крайнего правого промежутка: в этом промежут-
ке функция в левой части неравенства всегда положитель-
на для приведенного вида неравенств. При переходе справа
налево через нуль функции от одного промежутка к сосед-
нему следует учитывать:
• если нуль нечетной кратности, знак функции изменяется;
• если нуль четной кратности, знак функции сохраняется.
4. Записать ответ.
Пример: (х - 2)(х - 3)2(х - 4)3 > 0
1. нули: х = 2, х = 3, х = 4
4. х е ( -оо; 2] U {3} U [4; оо)
Замечание. Если функция, стоящая в левой части неравенства,
содержит множители вида (at - х)*1 , следует заменить их со-
ответствующими множителями (х - а,)*1 с учетом четности /?/.
Примеры:
1. (2 - х)2 = (х - 2)2; 2. (2 - х)3 = -(х - 2)3
Неравенства
61
ПРИМЕНЕНИЕ МЕТОДА ИНТЕРВАЛОВ
ДЛЯ РЕШЕНИЯ ДРОБНО-РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ
СТРОГИЕ НЕРАВЕНСТВА
(х - а.)*1 ...(х-а„)*" л , хг
-----< 0 (или > 0), где kt, р; 6 N
равносильно неравенству
(x - aj*1 • (x - аУ" (x - by • (x - bm)Pm < 0 (или > 0)
Схему решения таких неравенств см. на стр. 60.
(х — 2)(х — З)2 „ , _
Пример:-----------< 0 <=> (х - 2)(х - 3)2(х - 1) < О
х - 1
+ > х е (1;2)
1V^X2 3
НЕСТРОГИЕ НЕРАВЕНСТВА
———-----————< о (или > 0), где kit Pj е N
(х-by (х-Ъ„У
равносильно системе
(х-аУ (х - anY" (х - by • (х - Ьт)Рт < 0 (или > 0)
х *bltb2,...,bm
Схему решения первого неравенства системы см. на стр. 60.
„ , (х-2)(х-3)2 п (х - 1)(х - 2)(х - З)2 < О
Примеры: 1. ---------— < 0 <=> v
х - 1 х # 1
х е (1;2]U{3}
2 (х - 3)(х - 2) > 0 1(х - 3)2(х - 2)> О
X - 3 |Х Ф 3
Замечание. Сокращение числителя и знаменателя на (х 3) во
втором примере привело бы к неравенству х - 2 > 0, решение
которого [2; оо) содержит значение х = 3, которое не является
решением исходного неравенства.
62
Неравенства
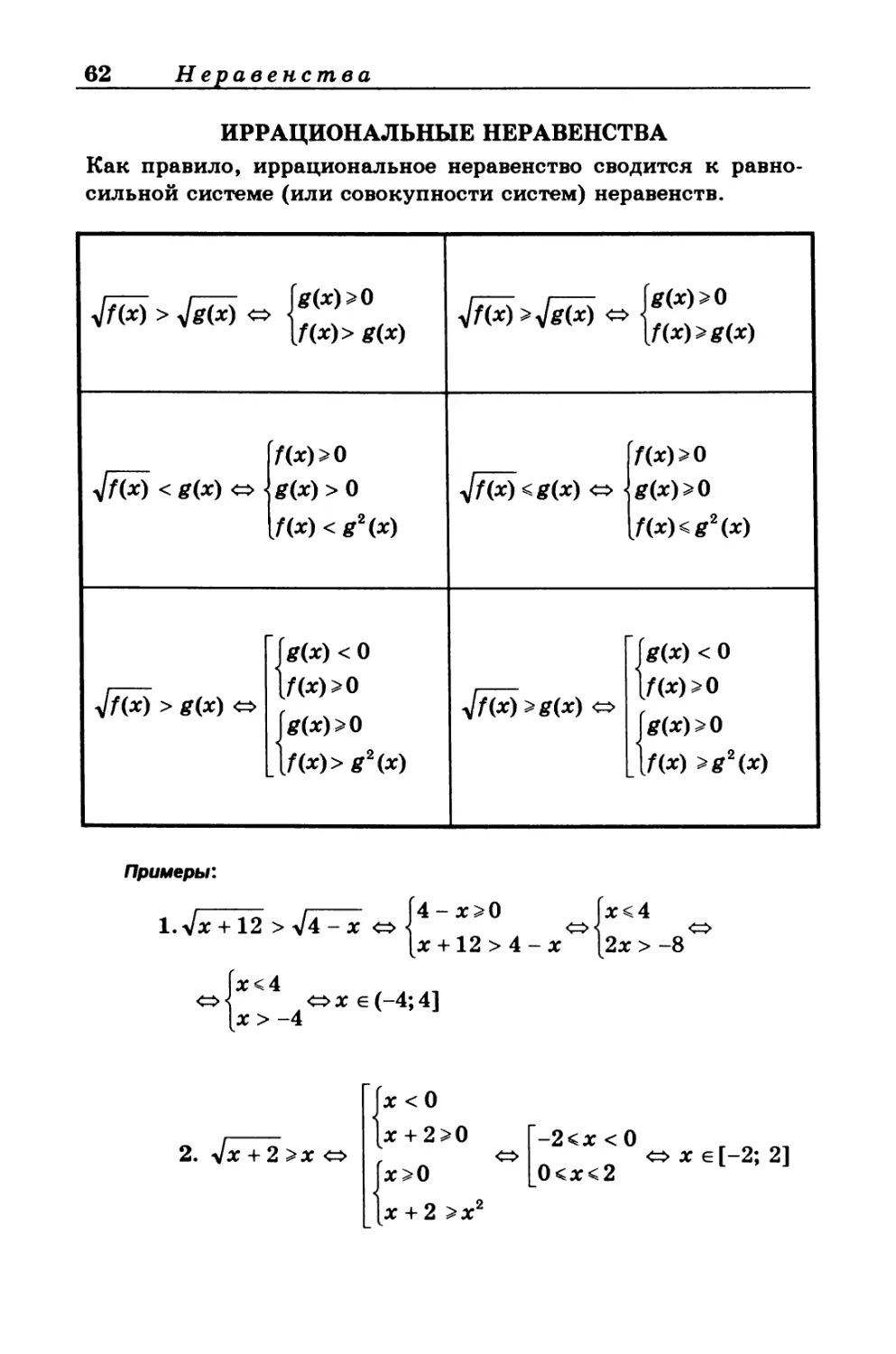
ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Как правило, иррациональное неравенство сводится к равно-
сильной системе (или совокупности систем) неравенств.
/ 1—— [я(х)>0 4f&)>4g&) <=> ] ч . ч [f(x)> g(x) <=> |g(x)>0 V(x)>g(x)
< g(x) о • 7(х)>о g(x) > 0 [f(x) < g2(x) 4fw<g(x) <=> 7(x)>0 g(x)>0 [f(x)<g2(x)
Tftx) > g(x) о fg(x) < 0 V(x)>0 g(x)>Q . /(x)> g2(x) 77(x)>g(x) ftf(x) < 0 V(x)>0 g(x)>0 . /(x) >g2(x)
Примеры:
l.Vx + 12 > V4-x <=>
4-х>0 (х<4
х + 12>4-х |2х>-8
2. Vx + 2 >х <=>
[х < О
|х + 2>0
х>0
х + 2 >х2
-2<х < О
0<х<2
<=> х е [-2; 2]
Неравенства
63
ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
где а > О, а Ф 1
а > 1 0 < a < 1
а«х> > о f(x) > ’ g(x) afM > о«(х) дх) < g(x)
Примеры:
1. 2х2 > 2х+2<=> х2 > х+2 <=> х е (-оо; -1) U (2; оо)
fiVx Г ГТ1
2. — < — <=>2х>х-1<=>хе [-1; оо
Замечание. В случае нестрогих неравенств знаки > и < в решениях
заменяются соответственно на > и < .
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
10gaZ(*) > ^Sag(x), где а > О, а Ф 1
a > 1 0 < a < 1
logaf(x)>log^(r) > ° [/(x) > g(x) 10ga/(x) >10gag(x) > ° lf(x) < g(x)
10ga/(X)>10gag(x) <=4f (X) > l/(x)>g(x) 10ga/(x)>10gag(x) <=4^*5 > ° [f(x)<g(x)
Примеры:
log2(x + 8) > log2(2x + 4)<=>]2* + 4 > 0 <=>5 > ^ <=> х е (-2; 4)
[х + 8 > 2х + 4 |х < 4
2. log! (х - 2) >logj (х2 - Зх + 1) <=>
х - 2 > О
<
х - 2 < х2 - Зх + 1
Замечание. Следует обратить внимание на область определения
функции у = loga х: решения нестрогих неравенств не всегда
получаются из решений соответствующих строгих неравенств
просто заменой знаков > и < на знаки > и < .
64 Неравенства
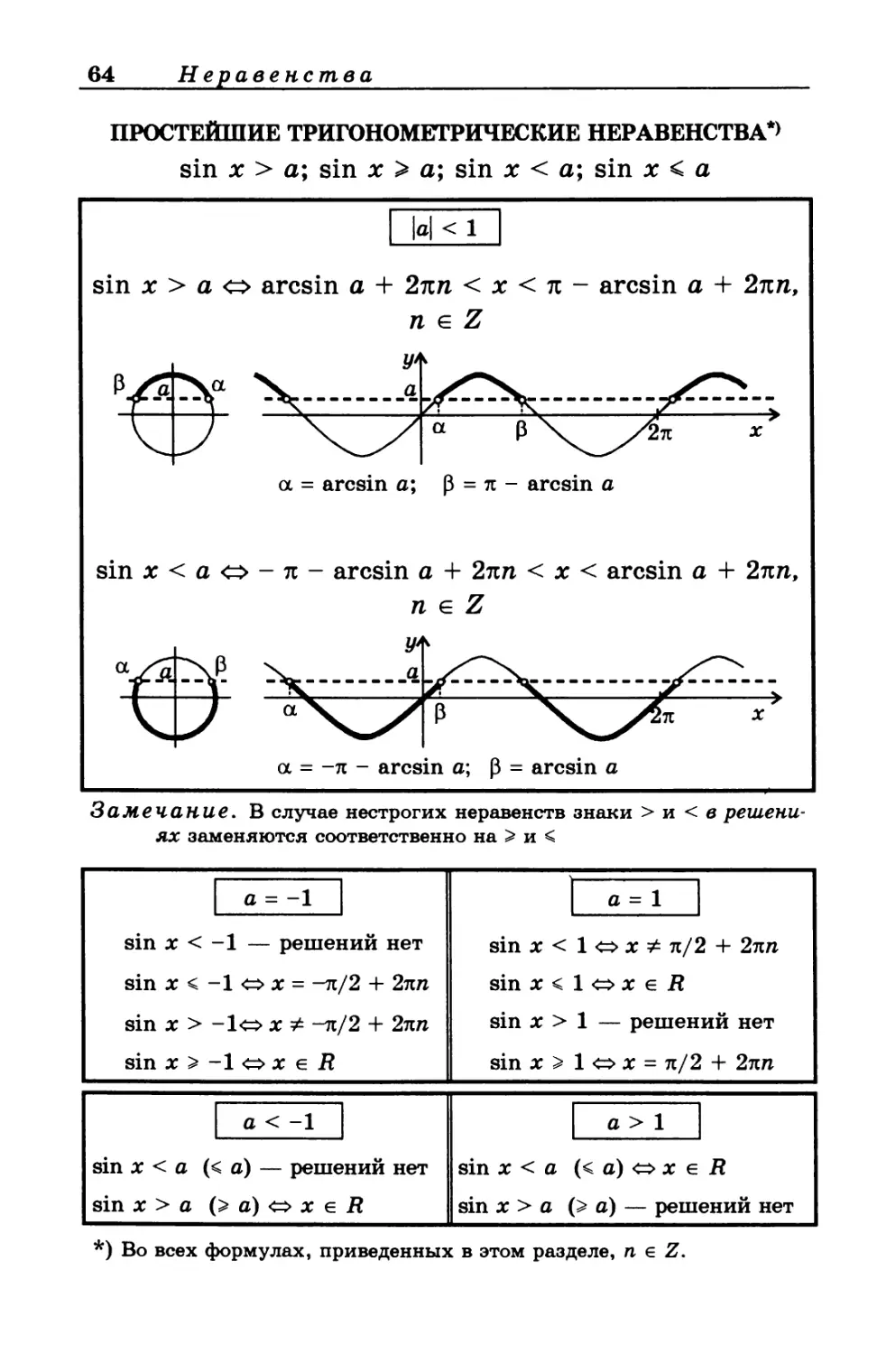
ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА*)
sin х > a; sin х > a; sin х < a; sin х < а
|о| < 1
sin х > а о arcsin а + 2яи < х < л - arcsin а + 2пп,
п е Z
у*
ос = arcsin а; р = л - arcsin а
sin х < а <=> - п - arcsin а + 2пп < х < arcsin а + 2лп,
и е Z
У*
а = -л - arcsin а; р = arcsin а
Замечание. В случае нестрогих неравенств знаки > и < в решени-
ях заменяются соответственно на > и <
а = -1
sin х < -1 — решений нет
sin х < -1 <=> х = -л/2 -I- 2лп
sin х > -1<=> х Ф -л/2 4- 2лп
sin х > -1 <=> х е R
а < -1
sin х < а (< а) — решений нет
sin х > а (> а) <=> х е R
а = 1
sin х < 1 <=> х Ф л/2 4- 2лп
sin х < 1 <=> х е R
sin х > 1 — решений нет
sin х > 1 <=> х = л/2 4- 2лп
а > 1
sin х < а (< а) <=> х е Я
sin х > а (> а) — решений нет
*) Во всех формулах, приведенных в этом разделе, п е Z.
Неравенства
65
а = -1
COS X < -1 — решений нет
COS X < -1 - с=> х = п 4- 2пп
COS X > -1 <=> х Ф л 4- 2лп
COS x > -1 <=> х е R
а = 1
COS X < 1 <=> x Ф 2лп
COS X < 1 < :=> х е R
COS X > 1 — решений нет
COS X > 1 с=> х = 2пп
а < -1
cos х < а (с а) — решений нет
cos х>а(> a) <^xeR
а > 1
cos х < а (< а) <^> х е R
cos х > а (> а) — решений нет
66
Неравенства
tg х > a; tg х > а\ tg х < а; tg х < а
tg х > а
arctg а + тт < х < л/2 + лп,
п е Z
tg х > а
arctg а + лп < х < л/2 + лп,
п е Z
tg х < а
-л/2 + Tin < х < arctg а + лп,
п е Z
tg х < а
-л/2 + тт < х с arctg а + лп,
п е Z
ctg х > а; ctg х > a; ctg х < а; ctg х < а
ctg х > а
тт < х < arcctg а + лп, neZ
тт < х < arcctg а + лп, neZ
ctg х < а
arcctg a + Tin<x<Ti + тт, neZ
ctg x < a
arcctg а + лп<х<л + лп, neZ
ctg х > а
Замечание. Следует обратить внимание на область определения
функций у = tg х и у = ctg х: решения нестрогих неравенств
не всегда получаются из решений соответствующих строгих
неравенств просто заменой знаков > и < на знаки > и < .
Системы уравнений
67
СИСТЕМЫ ДВУХ УРАВНЕНИЙ
С ДВУМЯ НЕИЗВЕСТНЫМИ
Общий вид:
= gi(x,y)
f2(x,y) = g2(x,y)
Решением системы двух уравнений с двумя неизвестны-
ми называется пара чисел (xq, у$), при подстановке кото-
рых вместо соответствующих переменных х, у оба уравне-
ния системы обращаются в верные числовые равенства.
Примеры:
J | X - 2у = 1
|2х + Зу - 9
Решение системы: (3; 1)
У = х2
У = х 4- 2
Решения системы: (-1; 1) и (2; 4)
Решить систему уравнений — значит найти все ее ре-
шения или доказать, что решений нет.
Равносильными называются системы, множества реше-
ний которых совпадают.
В частности, равносильны все системы, не имеющие решений.
Система, не имеющая решений, называется несовместной.
Пример несовместной системы:
х 4- 2у = 2
Зх 4- бу = 5
Замечание. Наряду с системами уравнений часто рассматривают-
ся совокупности уравнений. Решением совокупности является
объединение решений всех уравнений совокупности.
Для обозначения совокупности уравнений используют квад-
ратную скобку.
68
Системы уравнений
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
МЕТОД ПОДСТАНОВКИ
Этапы решения Примеры
1. С помощью какого- либо из уравнений выразить одно неиз- вестное через другое. (2х-у = 4 |х + Зу = 9 из первого уравнения У = 2х - 4 X2 + ху - у2 = 1 X + у = 2 из второго уравнения У = 2 - х
2. Подставить найденное выражение в другое уравнение системы: в результате получится одно уравнение с од- ним неизвестным. х + 3(2х-4) = 9; 7х = 21 х2 + х(2 - х) - - (2 - х)2 = 1; х2 - 6х + 5 = 0
3. Найти корень (кор- ни) этого уравнения, то есть найти значе- ние (значения) одно- го из неизвестных системы. х = 3 Xi = 1; х2 = 5
4. Использовать найден- ное выражение одно- го неизвестного через другое (подстановку), то есть найти значе- ние (соответствую- щие значения) вто- рого неизвестного. у = 2х - 4 = = 2 3-4=2 У1 = 2 - хг = 2-1 = 1; у2 = 2 - х2 = = 2 - 5 = -3
б. Записать ответ. (3; 2) (1; 1), (5; -3)
Системы уравнений
69
МЕТОД СЛОЖЕНИЯ
Этапы решения Примеры
1. Сложить почленно уравнения системы, умножив предвари- тельно каждое из уравнений на подхо- дящее число так, что- бы в результате сло- жения получилось одно уравнение с од- ним неизвестным. |4х + бу = 191x4 |7х - 4у = -5|х5 (16х + 20у = 76 (35х - 20г/ = -25 (2ху + х2 = 2 1x3 (Зху - 4х = 51 х(-2) ( бху + Зх2 = 6 (-бху + 8х = -10
51х = 51 Зх2+ 8х = -4
2. Найти корень (кор- ни) этого уравнения, то есть найти значе- ние (значения) одно- го из неизвестных системы. х = 1 Xi = -2; х2= -2/3
3. Подставить найденное значение (значения) одного из неизвест- ных в любое из урав- нений системы: в ре- зультате снова по- лучится уравнение (уравнения) с одним неизвестным. Подстановка в первое уравнение дает: 4 1 + 5у = 19; 5у = 15 Подстановка во второе уравнение дает: при х = Xi = -2 бу = 3; при х = х2 = “2/3 2у = -7/3
4. Найти решение (реше- ния) этого уравнения (этих уравнений), то есть найти значе- ние (соответствую- щие значения) вто- рого неизвестного. со и У1 = 1/2; У2 = -7/G
5. Записать ответ. (1; 3) (-2; 1/2), (-2/3; -7/6)
70
Системы уравнений
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ
СИСТЕМЫ ДВУХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ
Надо построить графики обоих уравнений и найти координа-
ты общих точек этих графиков — эти координаты являются
решениями системы.
Примеры:
(х2 + у2 =2
|х3 - у = О
График первого уравнения —
окружность радиуса ^2 с цен-
тром в начале координат, гра-
фик второго уравнения — ку-
бическая парабола у = х3. Эти
два графика пересекаются в
двух точках с координатами
(-1; -1) и (1; 1).
2 jx2 +/ =25
[ху = 12
График первого уравнения —
окружность радиуса 5 с цен-
тром в начале координат, гра-
фик второго уравнения — ги-
12 ГА
пербола у = — . Эти два графи-
х
ка пересекаются в четырех точ-
ках с координатами (-4; -3),
(-3; -4), (4; 3) и (3; 4).
Замечание. Хотя графический метод не всегда позволяет найти
точные решения системы уравнений, он помогает обнаружить
решения, которые часто упускаются из виду при аналитиче-
ском решении (например, отрицательные значения неизвест-
ных в приведенных примерах).
Системы уравнений
71
СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ДВУМЯ НЕИЗВЕСТНЫМИ*)
f^x + bxy = с}
[а2х + Ь2у = с2
Возможные случаи Граф интер] ическая третация
1. Коэффициенты при неизвестных в уравнениях не пропорциональны, т.е. * &2^1- Система имеет единственное решение: х _ С\^2 ~ с2^1 ^1^2 ^2^1 у _ а\С2 ~ а2С\ ^1^2 ^2^1 Прямые уравнен: пересекаь точке, в которой 5 шениеа — графики ий системы отся в одной юординаты шляются ре- « системы: / _
/
2. Коэффициенты при неизвестных в уравнениях пропорциональны, т.е. ~ &2^1» но они не пропорциональны свобод- ным членам, т.е. ахс2 * fl2ci или b)C2 * &2С1- Система не имеет решений. Прямые уравнен napaj у' — графики ий системы тлельны: s
X
3. Коэффициенты при неизвестных и свободные члены в уравнениях про- порциональны, т.е. ^1^2 = а\с2 — а2с1» ^1с2 - ^2С1- Система имеет бесконечно много ре- шений: решениями является любая пара (х; 1/), удовлетворяющая одному (любому) уравнению системы. Прямые уравнен СОВ! У/ — графики :ий системы 1адают: s
X
*) Предполагается, что в каждом уравнении системы хотя бы один
из коэффициентов при неизвестных отличен от нуля, т.е. графиком
каждого уравнения системы является прямая.
72 Производная
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ*)
_________________ПРОИЗВОДНАЯ___________________
Производной функции /(х) в точке Xq называется предел
отношения приращения функции Д/ = /(хо + Дх) - /(xq) к
приращению аргумента Дх при Дх -> 0, если этот предел
существует:
Г(х0) = Кт +-4х_).т:.ЛЛо)
° д~о ДХ
„ , 2ч, 1. (Х + Дх)* 1 2 3 4-Х2 ,п А _
Пример: (х )' = hm -----= hm(2x + Дх) = 2х .
Дх->0 Дх Дх->0
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Производная в точке Хд равна угловому коэффициенту
касательной к графику функции у = f(x) в этой точке:
Z'(*o)=tga>0 /'(xo)=tga = O f'(x0) = tg a < 0
УРАВНЕНИЕ КАСАТЕЛЬНОЙ
к графику функции у = f(x) в точке Xq:
У = /(х0) + Г(х0)(х - х0)
Пример. Нахождение уравнения касательной к графику
функции f(x) = у[х в точке х0 = 1:
1. Г(х0) = Г(1) = 1
2.
3. Нх0) = Н1) = |
, 1, 1 1
4. у = 1 + — (х - 1) = — х + —
2 2 2
*>Таблицу производных см. на стр. 92.
Производная
73
ВТОРАЯ ПРОИЗВОДНАЯ
Второй производной функции у = f(x) называется произ-
водная от производной f'(x) (обозначается
ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Если точка движется вдоль оси х и ее координата изме-
няется по закону x(i), то мгновенная скорость точки:
г + Д<) “ х(0 ,,.ч
v(t) = lim —-----------= х (t),
At—>0
а ускорение:
a(t) = lim + = v'(t) = x"(t)
At-»O At
gt2
Пример. При свободном падении x(t) = , v(t) = х'(0 = gt ,
a(t) = v’(t) = g
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Если у функций u(x) и v(x) существуют производные, то
(и ± и)’ = и' ± и'
(си\ = си’, где с — const
(ииу = и'и 4- uv'
u'v — uv'
= ---- (V # 0)
и
V
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Если у = f(g(x)) и существуют производные fg и g'x, то
Ух = fg g'x ,
где индексы g и х указывают, по какому аргументу вычис-
ляются производные.
Примеры: 1. k/sinx) = —. .. (sinx) = —°sx (sinx > 0)
' ' 2<sinx 2vsinx
о /1 • x' 1 z • ч' cosx
2. (in sm x) =-----(sin x) =----= ctg x (sin x > 0)
sin x sin x
3. (Xх)' =(exlnx) = exlnx(xlnx) =xz(lnx + l) (x > 0)
74
Производная
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
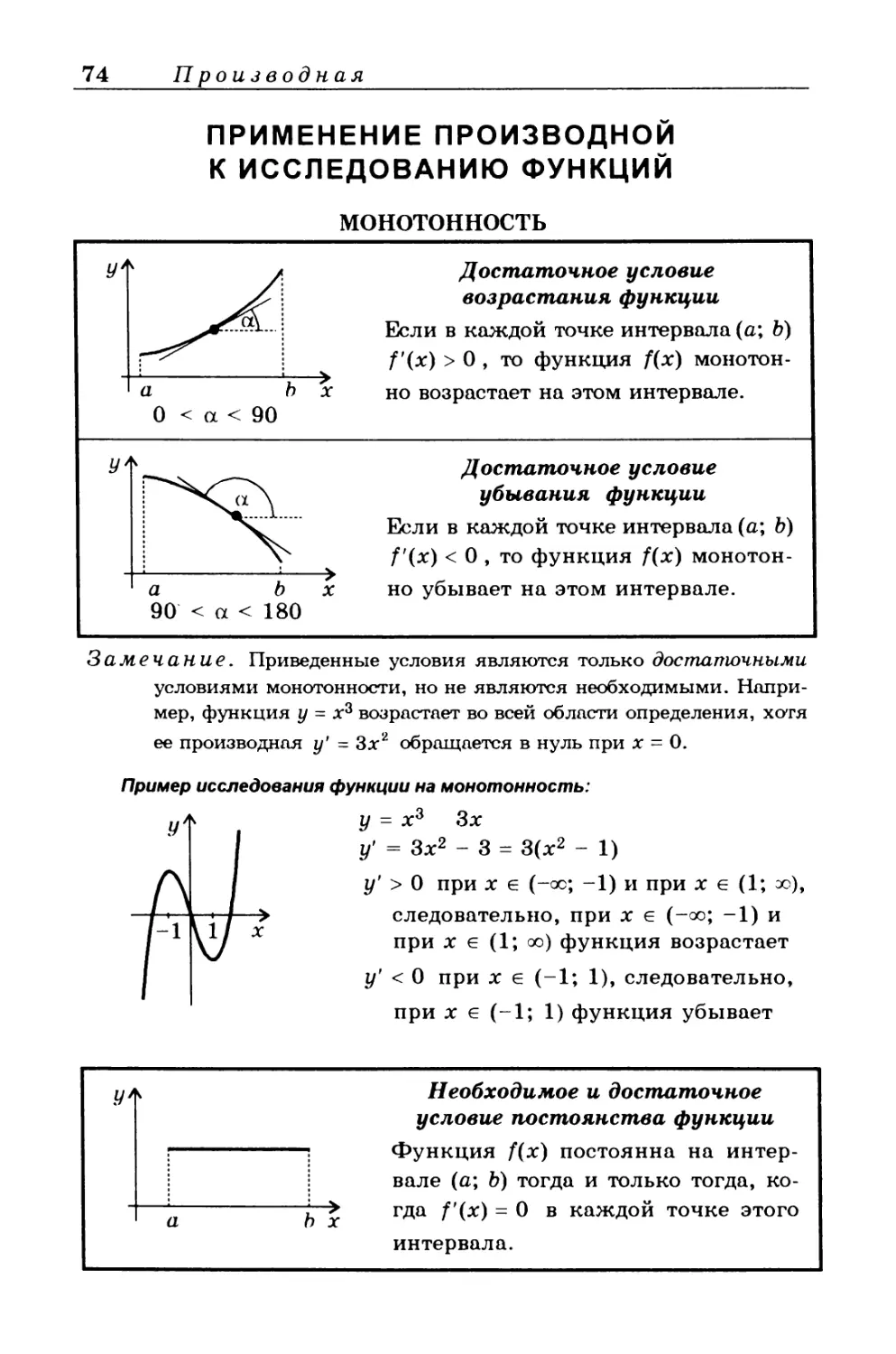
МОНОТОННОСТЬ
Достаточное условие
возрастания функции
Если в каждой точке интервала (а; Ь)
f'(x) > 0 , то функция f(x) монотон-
но возрастает на этом интервале.
Достаточное условие
убывания функции
Если в каждой точке интервала (а; Ь)
f'(x) < 0 , то функция f(x) монотон-
но убывает на этом интервале.
Замечание. Приведенные условия являются только достаточными
условиями монотонности, но не являются необходимыми. Напри-
мер, функция у = х3 возрастает во всей области определения, хотя
ее производная у’ = Зх2 обращается в нуль при х = О.
Пример исследования функции на монотонность:
у = х3 Зх
у' = Зх2 - 3 = 3(х2 - 1)
у' > 0 при х е (-ос; -1) и при х е (1; х>),
следовательно, при х е (-оо; -1) и
при х 6 (Г, оо) функция возрастает
у' < 0 при х е (-1; 1), следовательно,
при х е (-1; 1) функция убывает
У' < Необходимое и достаточное условие постоянства функции
: Функция f(x) постоянна на интер- вале (а; Ь) тогда и только тогда, ко-
| а > гда f’(x) - 0 в каждой точке этого интервала.
Производная
75
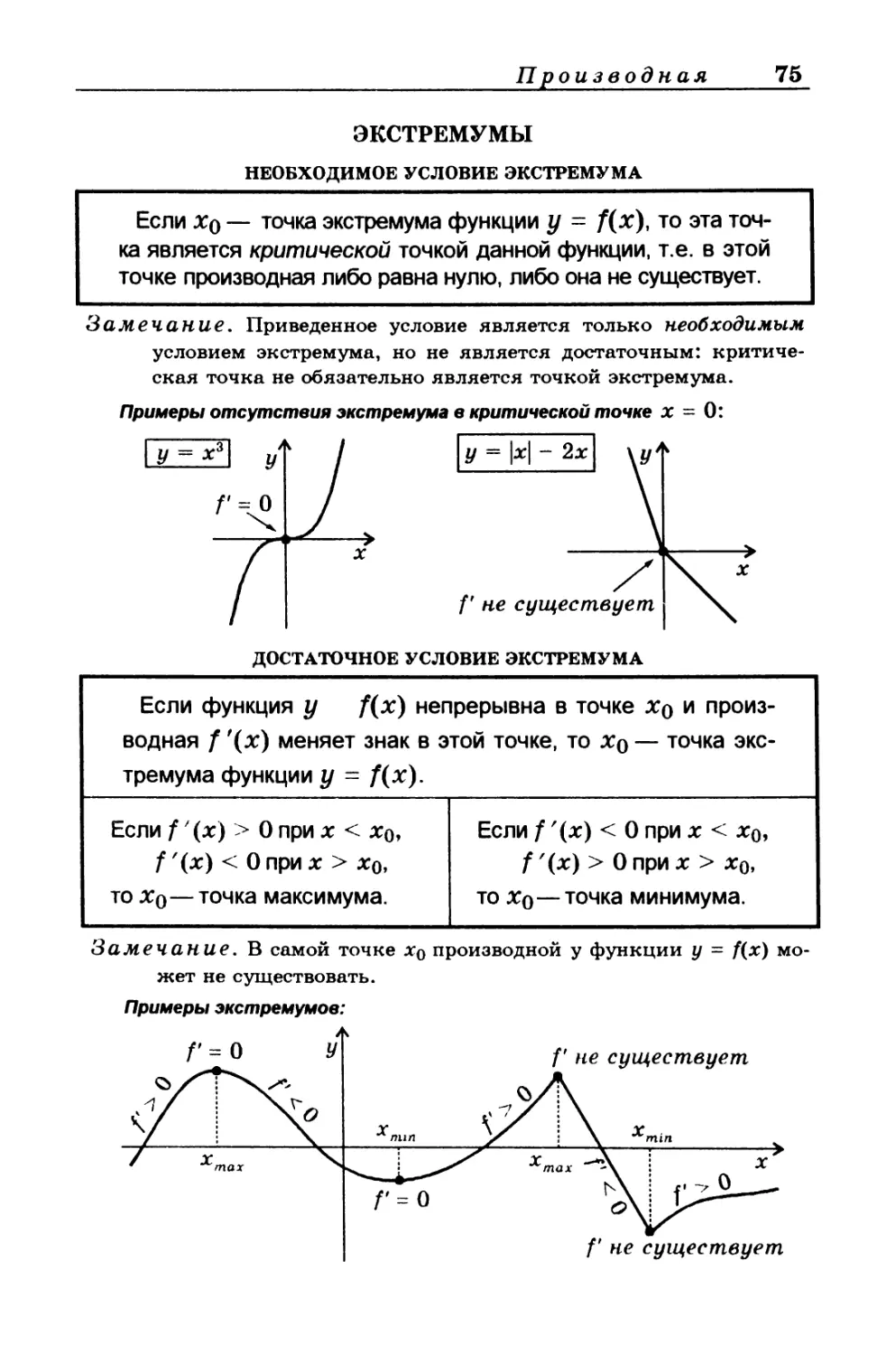
ЭКСТРЕМУМЫ
НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА
Если Хо — точка экстремума функции у = /(х), то эта точ-
ка является критической точкой данной функции, т.е. в этой
точке производная либо равна нулю, либо она не существует.
Замечание. Приведенное условие является только необходимым
условием экстремума, но не является достаточным: критиче-
ская точка не обязательно является точкой экстремума.
Примеры отсутствия экстремума в критической точке х - 0:
ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА
Если функция у /(х) непрерывна в точке Xq и произ- водная f '(х) меняет знак в этой точке, то Xq — точка экс- тремума функции у = /(х).
Если f '(х) > 0 при х < хо, f'(x) < Оприх > Хо, то Хо—точка максимума. Если f '(х) < 0 при х < хо, f'(x) > Оприх > Хо, то Xq—точка минимума.
Замечание. В самой точке х0 производной у функции у = f(x) мо-
жет не существовать.
Примеры экстремумов:
/' не существует
76
Производная
СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ
ИНТЕРВАЛОВ МОНОТОННОСТИ И ЭКСТРЕМУМОВ
Этапы Пример для функции у = 2х3 - Зх2 - 36х + 5
1. Найти область определения функции и интервалы, на ко- торых функция непрерывна. Об л. определения: R Функция непрерывна во всей обл. определения
2. Найти производную f'(x). f'(x) = 6х2 - 6х - 36
3. Найти критические точки, т.е. точки, в которых произ- водная функции равна нулю или не существует. /'(«) = о при х - -2, х = 3
4. В каждом из интервалов, на которые область определения знак Г + ” +
разбивается критическими точками, определить знак производной и характер из- менения функции (с помо- щью достаточных условий монотонности). характер изменения функции 1 • Л' -2 3
б. Относительно каждой крити- ческой точки определить, яв- ляется ли она точкой макси- мума, минимума или не яв- ляется точкой экстремума. х = -2 точка максимума; х = 3 точка минимума
6. Записать результат исследо- вания функции: промежутки монотонности и экстремумы. f(x) возрастает при х 6 (-оо; -2) и при х е (3; оо); f(x) убывает при х 6 (-2; 3); Хтах = “2, Утах = /(~2) = 49;
xmin = 3, У min = Г(3) = -76
Производная
77
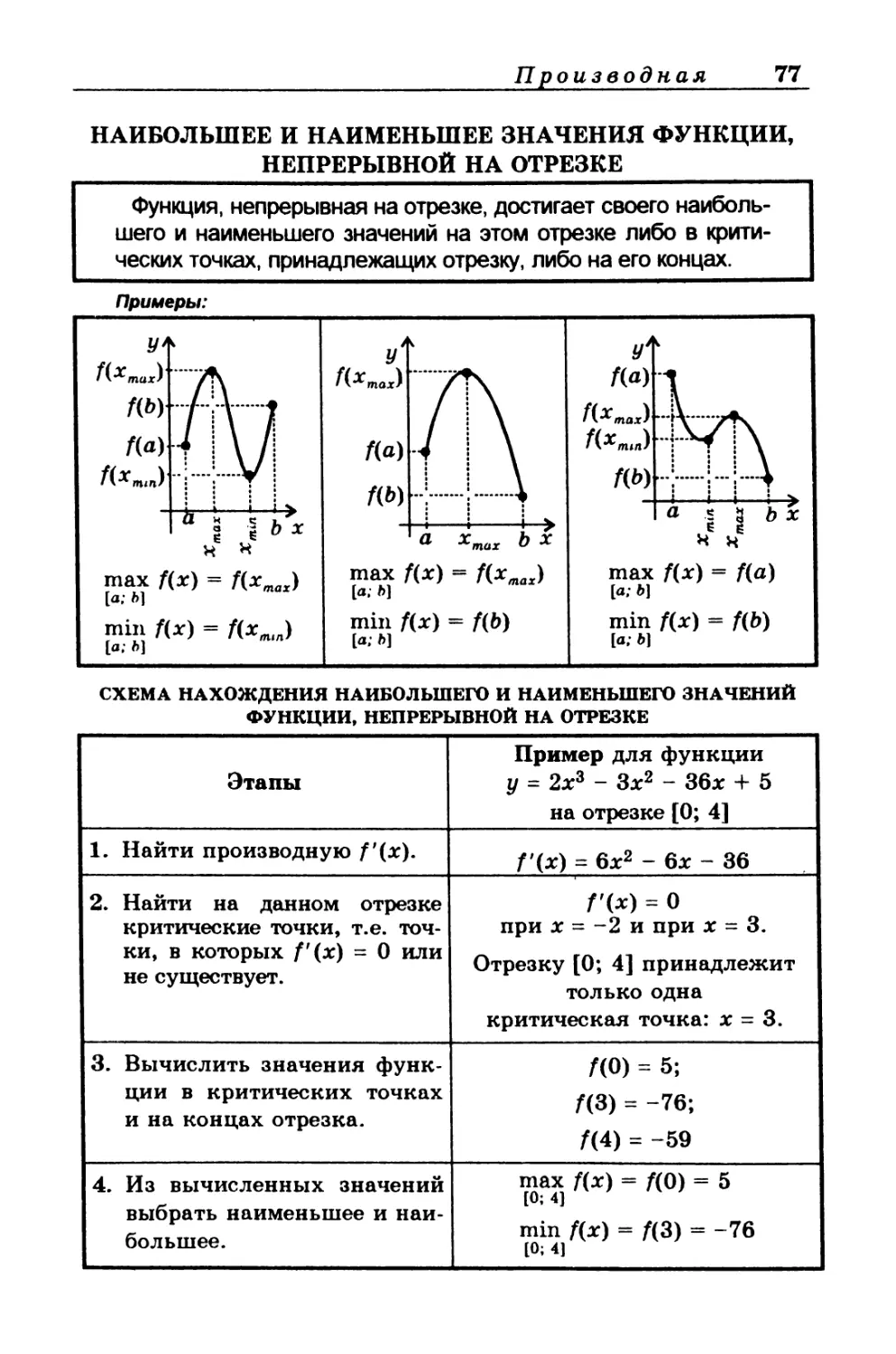
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ,
______________НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ___________________
Функция, непрерывная на отрезке, достигает своего наиболь-
шего и наименьшего значений на этом отрезке либо в крити-
ческих точках, принадлежащих отрезку, либо на его концах.
Примеры:
max f(x) = f(xmai)
[а; Ь]
min f(x) = f(xmm)
[a; *]
max f(x) = f(xmax)
[a, b)
min f(x) = f(b)
[a; M
max f(x) = f(a)
[a; ft]
min f(x) = f(b)
[a; ft]
СХЕМА НАХОЖДЕНИЯ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ
ФУНКЦИИ, НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ
Этапы Пример для функции у = 2х3 - Зх2 - 36х + 5 на отрезке [0; 4]
1. Найти производную f’(x). Г(х) = 6х2 - 6х - 36
2. Найти на данном отрезке критические точки, т.е. точ- ки, в которых Г(х) = 0 или не существует. Г(Х) = 0 при х = -2 и при х = 3. Отрезку [0; 4] принадлежит только одна критическая точка: х = 3.
3. Вычислить значения функ- ции в критических точках и на концах отрезка. Г(0) - 5; ЦЗ) = -76; /(4) = -59
4. Из вычисленных значений выбрать наименьшее и наи- большее. max f(x) = f(0) = 5 min f(x) = /(3) = -76 [0; 4]
78 Интеграл
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ*)
ПЕРВООБРАЗНАЯ
Функция F (х) называется первообразной для функции
/(х) на данном промежутке, если для любого х из этого
промежутка F'(x) - f(x).
Пример. Первообразной для функции f(x) х на всей число-
вой оси является F(x) = х2/2, поскольку (х2/2)' = х
ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНЫХ
Если F (х) — первообразная функции f (х), то и функция
F(x) + С, где С — произвольная постоянная, также явля-
ется первообразной функции /(х).
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Графики всех первообразных данной
функции /(х) получаются из графи-
ка какой-либо одной первообразной
параллельными переносами вдоль
оси у.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Совокупность всех первообразных данной функции f (х)
называется ее неопределенным интегралом и обознача-
ется | f(x)dx
f(x)dx = F(x) + С, где С — произвольная постоянная.
ПРАВИЛА ИНТЕГРИРОВАНИЯ
J cf(x)dx = с J f(x)dx, где с — const
f (/(х) 1 g(x))dx = J f(x)dx ± f g(x)dx
f f(ax + b)dx = — F(ax + b) + С , а Ф 0
3 a
^Таблицу интегралов см. на стр. 93.
Интеграл
79
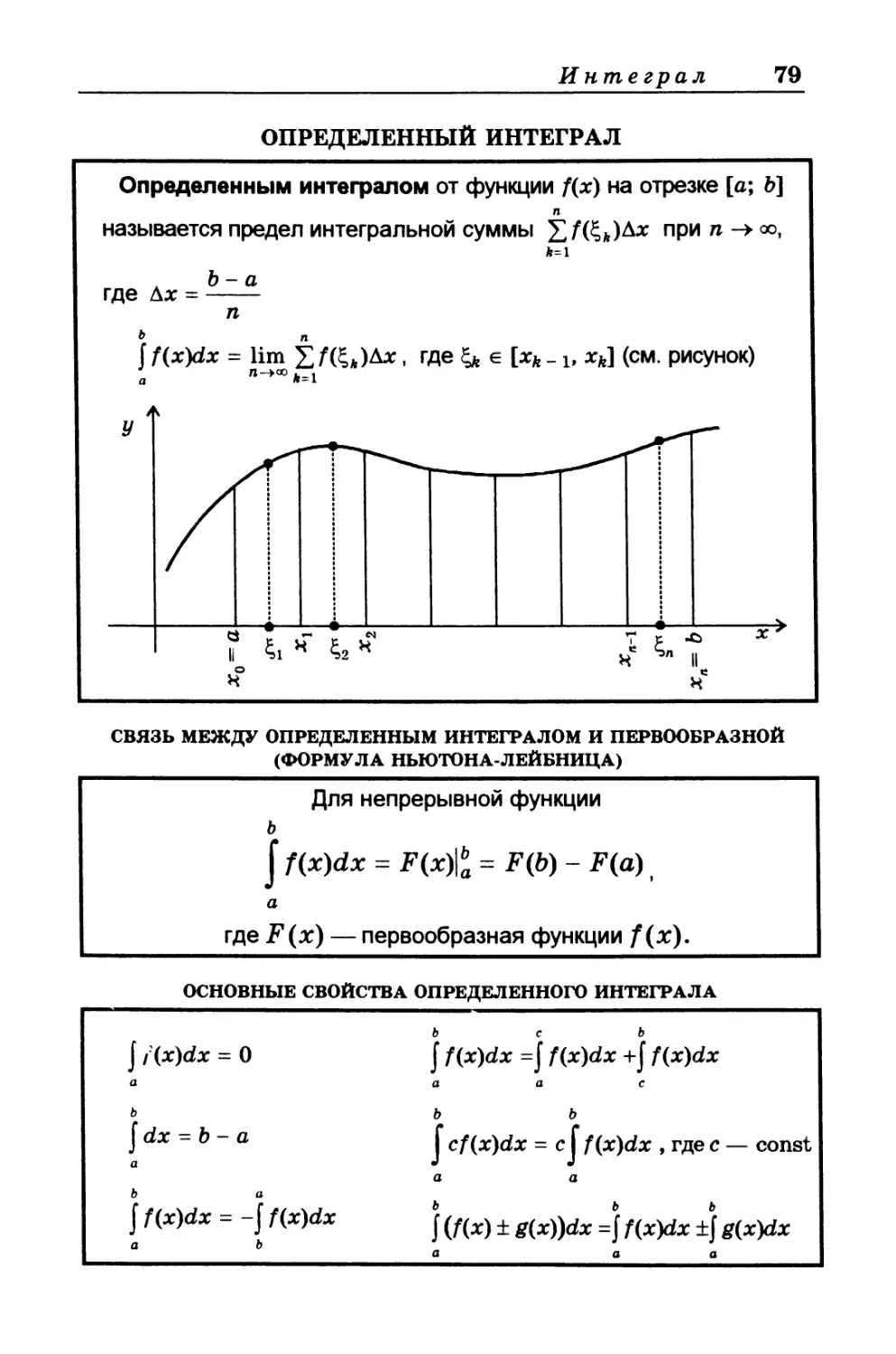
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенным интегралом от функции f(x) на отрезке [а; &]
называется предел интегральной суммы прип-»оо,
Ь - а
где Ах =-------
п
ь п
СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ И ПЕРВООБРАЗНОЙ
(ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА)
Для непрерывной функции
ь
JZ(x)dx = F(x)|$=F((>)-F(a),
а
где F (х) — первообразная функции /(х).
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
j / (x)dx = 0 а Ь j dx - b - а а b c b j f(x)dx =j f(x)dx -i-j f(x)dx a a c b b J cf(x)dx = cJ f(x)dx , где c — const
b а j f(x)dx = - j f(x)dx o b J (/(x) ± g(x))dx = j f(x)dx ±f g(x)dx
a a a
80 И нте грал
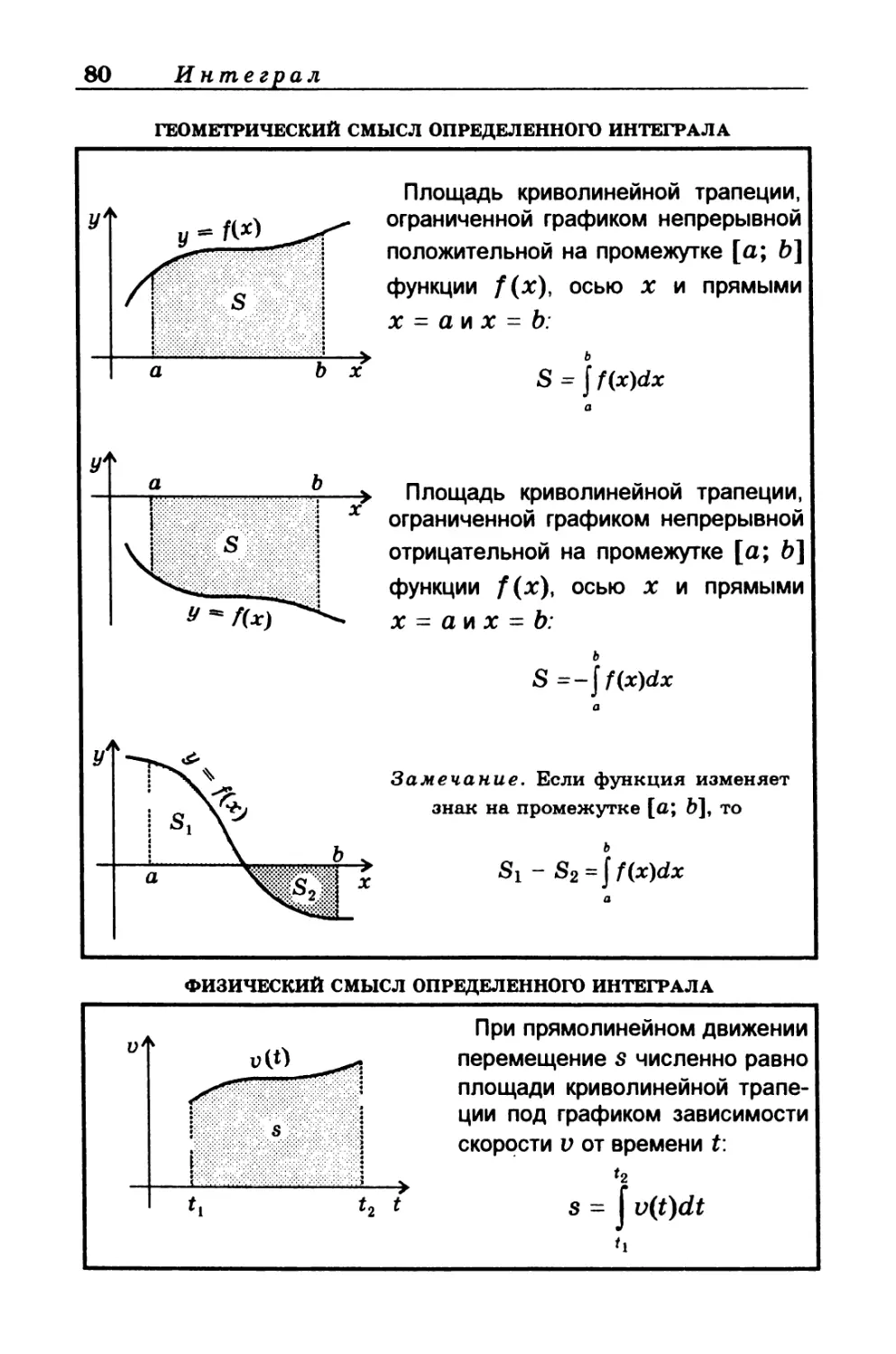
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
положительной на промежутке [а; Ь]
функции f(x), осью х и прямыми
х = а и х = Ь:
S = J f(x)dx
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
отрицательной на промежутке [а; Ь]
функции f (х), осью х и прямыми
х = а и х = Ь:
ь
s = -p(x)dx
Замечание. Если функция изменяет
знак на промежутке [а; Ь], то
ь
Si - S2 =| f(x)dx
ФИЗИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
При прямолинейном движении
перемещение $ численно равно
площади криволинейной трапе-
ции под графиком зависимости
скорости v от времени t:
*2
s = J v(t)dt
Интеграл
81
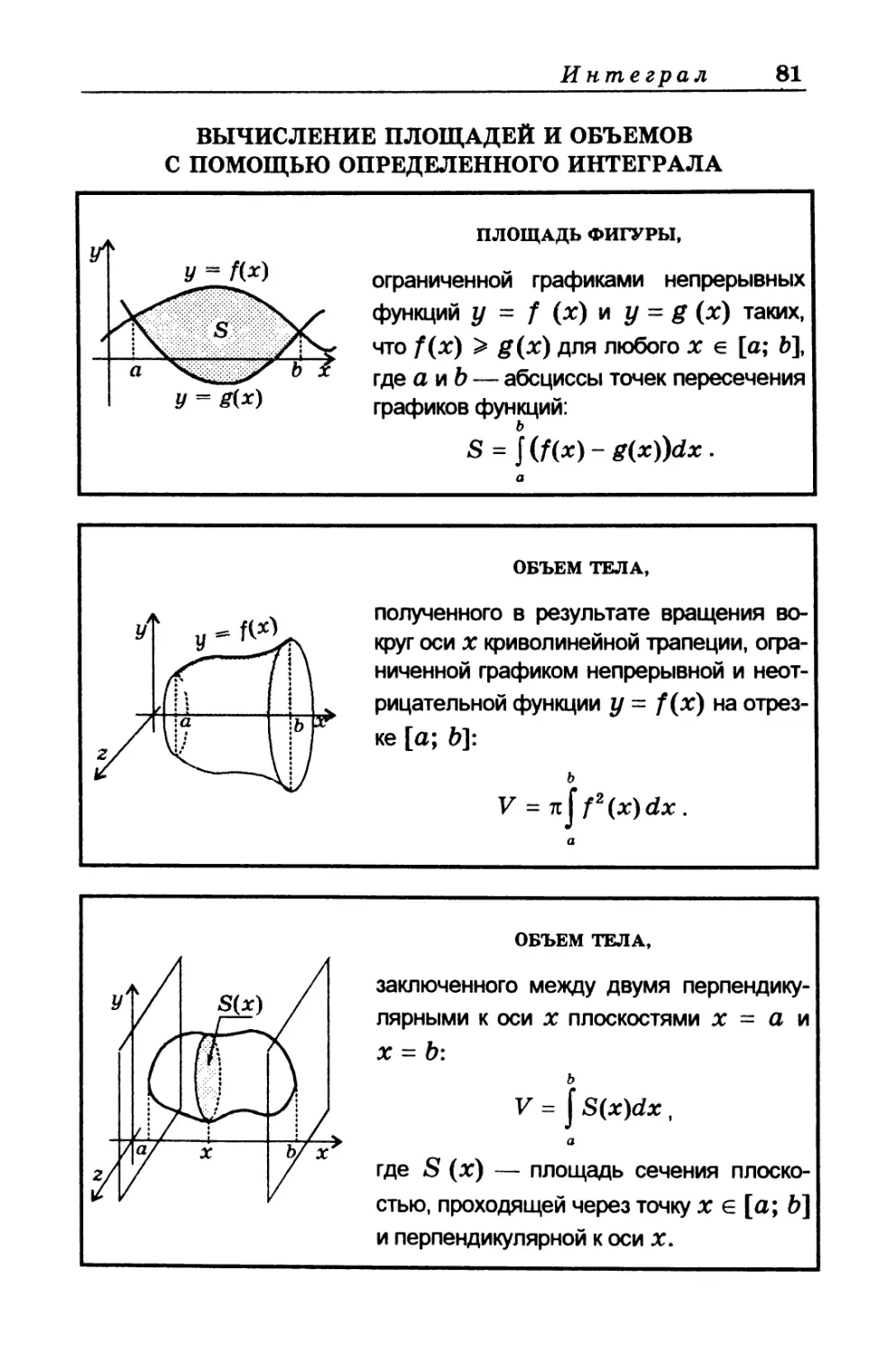
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ПЛОЩАДЬ ФИГУРЫ,
ограниченной графиками непрерывных
функций у = f (х) и у = g (х) таких,
что f(x) > g(x) для любого х е [а; Ь],
где а и b — абсциссы точек пересечения
графиков функций:
S = f (f(x) - g(x))dx.
ОБЪЕМ ТЕЛА,
полученного в результате вращения во-
круг оси х криволинейной трапеции, огра-
ниченной графиком непрерывной и неот-
рицательной функции у = f(x) на отрез-
ке [а; д]:
ь
V = 7tJ f2(x)dx .
а
ОБЪЕМ ТЕЛА,
заключенного между двумя перпендику-
лярными к оси х плоскостями х = а и
х = Ь:
ь
V = J S(x)dx ,
а
где S (х) — площадь сечения плоско-
стью, проходящей через точку х е [а; д]
и перпендикулярной к оси х.
82
Справочные таблицы
СПРАВОЧНЫЕ ТАБЛИЦЫ
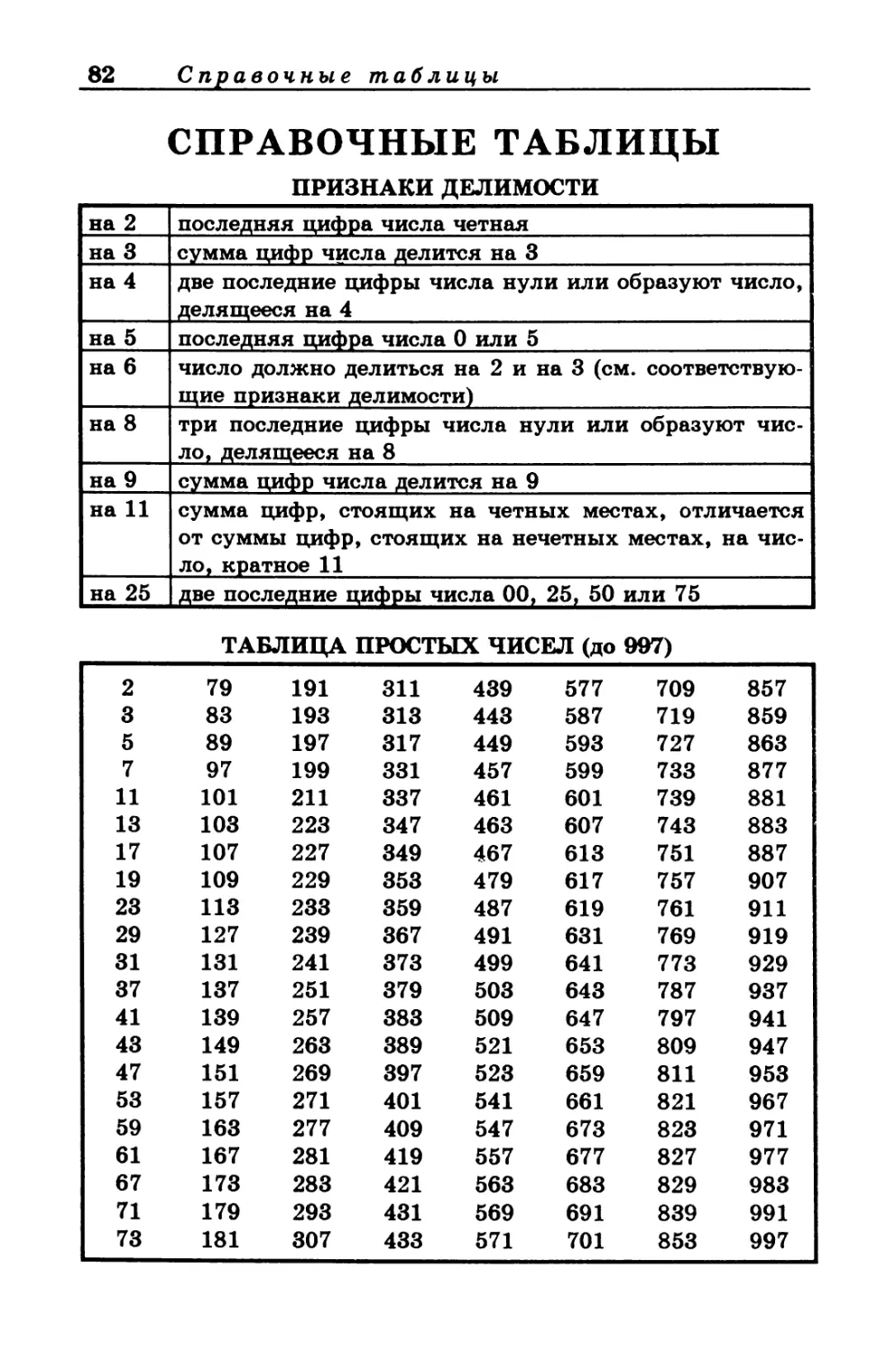
ПРИЗНАКИ ДЕЛИМОСТИ
на 2 последняя цифра числа четная
на 3 сумма цифр числа делится на 3
на 4 две последние цифры числа нули или образуют число, делящееся на 4
на 5 последняя цифра числа 0 или 5
на 6 число должно делиться на 2 и на 3 (см. соответствую- щие признаки делимости)
на 8 три последние цифры числа нули или образуют чис- ло, делящееся на 8
на 9 сумма цифр числа делится на 9
на 11 сумма цифр, стоящих на четных местах, отличается от суммы цифр, стоящих на нечетных местах, на чис- ло, кратное 11
на 25 две последние цифры числа 00, 25, 50 или 75
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ (до 997)
2 79 191 311 439 577 709 857
3 83 193 313 443 587 719 859
5 89 197 317 449 593 727 863
7 97 199 331 457 599 733 877
11 101 211 837 461 601 739 881
13 103 223 347 463 607 743 883
17 107 227 349 467 613 751 887
19 109 229 353 479 617 757 907
23 113 233 359 487 619 761 911
29 127 239 367 491 631 769 919
31 131 241 373 499 641 773 929
87 187 251 379 503 643 787 937
41 189 257 383 509 647 797 941
43 149 263 389 521 653 809 947
47 151 269 397 523 659 811 953
53 157 271 401 541 661 821 967
59 163 277 409 547 673 823 971
61 167 281 419 557 677 827 977
67 178 283 421 563 683 829 983
71 179 293 431 569 691 839 991
78 181 807 433 571 701 853 997
Справочные таблицы 83
ТАБЛИЦА КВАДРАТОВ ДВУЗНАЧНЫХ ЧИСЕЛ
ДЕСЯТКИ ЕДИНИЦЫ
0 1 2 3 4 5 6 7 8 9
1 100 121 144 169 196 225 256 289 324 361
2 400 441 484 529 576 625 676 729 784 841
3 900 961 1024 1089 1156 1225 1296 1369 1444 1521
4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401
5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481
в 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761]
7 4900 5041 5184 5329 5476 5625 5776 5929 6084 62411
8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921
9 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801|
ПРОПОРЦИИ*»
СВОЙСТВА ПРОПОРЦИЙ
1. Произведение крайних членов равно произведению средних,
а с I
т.е. если — = — , то ad = Ъс
Ъ d j
2. В пропорции, все члены которой отличны от нуля, можно |
менять местами средние и крайние члены пропорции, т.е. ес-
ас abdcdb i
ли — - — , то — <
bdcdbaca
ПРОИЗВОДНЫЕ ПРОПОРЦИИ, 5
а с
полученные из пропорции — = — : i
Ъ d 1
а ± Ъ _ с ± d a + b _ с 4- d
а с a-b c-d
а±Ъ _ с ±d a ± с _ a _ c
ъ d b ± d b d
ааъ^ 4~ Ьа^ cmr + dnx 4- cnx _ bmx 4- dnx
ат2 + Ьп2 cm2 + dn2 am2 4- cn2 bm2 4- dn2
где mi , ТП2, П1, 7^2 произвольные числа.
Во всех приведенных формулах знаменатели не должны
равняться нулю.
84
Справочные таблицы
МНОГОЧЛЕНЫ
а2 - Ь2 = (а - Ь)(а + Ь) (а + Ь)2 = а2 + 2аЬ + Ь2 (а - Ь)2 = а2 - 2аЬ + Ъ2 (а + Ъ + с)2 - а2 + Ь2 + с2 + 2аЬ + 2Ьс + 2ас а3 + Ь3 = (а + Ь)(а2 - ab + Ъ2) а3 - Ъ3 = (а - Ь)(а2 + аЪ 4- Ь2) (а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3 = а3 + Ь3 + ЗаЬ(а + Ь) (а - Ь)3 = а3- За2Ь + ЗаЬ2 - Ь3 = а3 - Ь3 - ЗаЪ(а - Ь) Для п е N ап-Ьп = (а- Ъ)(ап~х + ап~2Ь + ап~3Ь2 + Ч-аЬ71'2 + Ь71’1) Если п — четное, ап - Ь" = (а Ч- Ь)(ап-1 - an~2b + an~3b2 - + ab71-2 - Ь71"1) Если п — нечетное, а" Ч- Ь7* = (а Ч- Ь)(ап~1 - ап~2Ь Ч- ап~3Ь2 - - аЫ2 + Ь71”1) БИНОМ НЬЮТОНА (а + b)" = £сХ’*Ь‘ = *=0 = С°пап +С1пап-1Ь1 +С2ап-2Ъ‘ +... + С:’,а,Ь"’1 +С?ЬП где С_ = — — число сочетании из п по k. k\(n - fe)!
МОДУЛЬ ЧИСЛА
|а| = |а| > 0; |а |а| = 0 <=> а = 0 а» п 0 II / о , а = Vflz -fl, fl < 0 11 •b| = |а|-|Ь| |а + b| < |а| + |Ь| |а - Ь| > ||а| - |Ы| h ь
Справочные таблицы
85
ПРОГРЕССИИ
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Лд + 1 = ип 4~ d, Ь/1 + 1 = 9»
где d - разность прогрессии где q 0 - знаменатель прогрессии
Формулы 71-го члена
ап = -h (n - l)d
an = ak + (n- k)d
- _ ^n-k + ’ 2 ~~ ^n~k ’ bfl+k
Формулы суммы первых п членов
2аг +(п- l)d О = • п = п 2 _а1+ап п Sn - bl n, q = 1
2
Формула для разности Формула для знаменателя b„ ,
d = аЛ + 1 — аЛ ?=r
Если п 4- т = k + p, TO
ап + ат “ ak + ар 4? II В Л st
Сумма последовательных Сумма бесконечно убывающей
натуральных чисел от 1 до п: геометрической прогресии:
g = п(и -ь 1) 1-9
2
ПРОСТЕЙШИЕ НЕРАВЕНСТВА*»
а2 + Ь2 > 2аЪ; — + — > 2 , аЬ > О
Ь а
а + Ь I—
-----> уаЪ , а > О, Ь > О
2
(Среднее арифметическое не меньше среднего геометрического)
*) Равенства в приведенных неравенствах достигаются тогда и
только тогда, когда а = Ь.
86
Справочные таблицы
АРИФМЕТИЧЕСКИЙ КОРЕНЬ
Арифметичзс.::;?.; корнем n-ой степени из неотрицательного чис-
ла а называется такое неотрицательное число о, п-ая степень кото-
рого равна а, т.е. tfa = b , если Ъп = а (а > О, Ъ > О).
СВОЙСТВА КОРНЕЙ
Основное свойство корня = f а> Q
Умножение корней -tfab ,а>0, Ь>0
Деление корней д/Т уа — п %[ъ Ч о-1&] & V о о- V о
Возведение корня в степень (V^)m = №, а > 0
Извлечение корня из корня tftfa = ntfa , а > 0
Вынесение множителя из-под знака корня 2Va2"b = |а| • 2$>, Ь > 0 в частности, -Ja2b = | а| 4b 2п+^а2п+1Ъ = а 2п^Ь
Внесение множителя под знак корня а-2^Ь = ! 2Va2nb,(a>0, b>0) |-2^а2"Ь,(а <0, Ь>0) а • = 2п+\<а2п+1Ь
СТЕПЕНИ
С натуральным показателем ап = а • а • ...• а» аУ = а п раз
С положительным дробным показателем an = tfa?' ,1два>0,7n,ne^
С нулевым показателем а0 = 1, где а * 0
С отрицательным рациональным показателем а~г = — , где а > 0 аг
Умножение степеней ар -а4 = ap+q ; а” Ъ" = (аЪ)р
Деление степеней ?L = ap-4-, £f. = |£.y а4 Ър УЪ)
Возведение степени в степень (ар)4 = ам
87
С правочные таблицы
_________________ЛОГАРИФМЫ___________________
Логарифмом положительного числа b по основанию а
(а > О, а * 1) называется такой показатель степени с, в
которую надо возвести число а, чтобы получить число Ь:
logab = с <=> ас = Ь.
СВОЙСТВА ЛОГАРИФМОВ*)
• Основное логарифмическое тождество: alofife ь = Ь9 Ь > 0
• logaa = l • logo 1 = 0 • Логарифм произведения: loga ху = log J x|+loge|i/|, ху > 0
• Логарифм частного: loge - = loge|x|- loga|y|, - > 0 У У
• Логарифм степени: loge хР =Plogal*l. ХР >0
• Логарифм корня: loge, хр = —loge|x|, ХР >0 Я loga Vx = -loge X, X > 0 n
• Формула перехода к другому основанию: logo Ь = , где b > 0, с>0, с 1 logca
1 1- 1 Is'tCf — — , где Ь > 0, Ь Ф 1
log» a
Во всех приведенных формулах а > 0, а Ф 1
_______ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
Число перестановок из п элементов:
Р„=п! = 1-2-3- п
Число размещений из п элементов по k элементов:
= ( П= п • (п - 1) • (п - 2) •• (n - fe + 1)
(п - к)!
Число сочетаний из п элементов по k элементов:
_ п • (п - 1) • (п - 2) •• (n - fe +1)
n~k\(n-k)\~ 1-2-3- k
88 Справочные таблицы
ОСНОВНЫЕ ФОРМУЛЫ ТРИГОНОМЕТРИИ*)
СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
ОДНОГО И ТОГО ЖЕ АРГУМЕНТА
sin2 х + cos2 х = 1 tgxctgx = 1
. sinx tgx = 1 4- X —
CO8X x COSX ctgx = sinx 1+Lg X- COS X 1 4- rfo*2 T - 1
1 -1- Cbg X — 81П X
ФОРМУЛЫ СЛОЖЕНИЯ
sin(x + у) - sin х сов у + cos х sin у
sin(x - у) - sin х сов у - сов х sin у
cos(x + у) - cos х cos у - sin х sin у
cos(x - у) = сов х сов у + sin х sin у
, . . tgx + tgy , . . ctgxctgy-1
tg(* + y) = -r5——ctg(x + y) = ---
1-tgxtgy ctgx + ctgy
, . . tgx-tgy ± , . ctgxctgy + 1
tg(x - y) = -— -Ctg(x - y) =---------s--
1 + tgxtgy ctgx-ctgy
ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО УГЛА
5* 1 to £ to| H tgx = to ьэ|Н
0АД1 —
1 x 2 x 1-tg2^
COS X = — ctgx = 2
ч X 2 x i + tg - x 2t«o 2
*>Во всех формулах, приведенных в этом разделе, следует
учитывать область допустимых значений левой и правой час-
тей формул.
Справочные таблицы
89
ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА
sin2x = 2 sinx cosx
cos 2x = cos2 x - sin2 x = 1 - 2 sin2 x = 2 cos2 x - 1
2
tg2x = 2t«f
l-tgzx ctgx-tgx
ctg2 x — 1 ctgx-tgx
ctg2x = —5------- — ---5—
2ctgx 2
ФОРМУЛЫ ПОЛОВИННОГО АРГУМЕНТА
• 2 х sm — 2 1 - COS X , 9 х 1 - COS X = tg — = 2 2 1 + cos x
2 * cos — 2 1 + COS X 9 X 1 + COS X = ctg2 — - 2 2 1 - cos x t x sin x 1 - cos x tg _ =, 2 1 + cos x sin x t x sin x 1 + cos x ctg— = = 2 1 - cos x sin x
ФОРМУЛЫ ТРОЙНОГО АРГУМЕНТА
sin3x = 3sinx - 4sin3 x cos3x = 4cos3 x - 3cosx 1 - 3tg2 x Sctg2 x - 1
90
Справочные таблицы
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ СУММЫ В ПРОИЗВЕДЕНИЕ
x + 1/ x — у sinx + siny = 2sin —cos — я 2 2 x — у X + у sinx - siny = 2sin —cos — я 2 2 „ X +у X-y cosx + cosy = 2 cos —cos — v 2 2 X + у X — у cosx - cosy = -2sin — sin — 2 2
, , sin(x + y) , , sin(x + y) tgx + tgy = - — ctgx + ctgy = -7-1— cosx cos у sinx sin у , , sin(x - y) , , sin(x - y) tgx —tgy = — ctgx-ctgy =— cosx cos у sinx sin у
. , cos(x - y) tgx + ctgy = — cosx sin у . . cos(x + y) tgx - ctgy = . cosx sin у X X 1 2 tg x + ctgx = — = ——- sinx cosx sin2x tgx - ctgx = -2 0082* _ -2ctg2x sin 2x
cosx + sinx = V2 cos(45o-x) = V2 sin(45°+x) cosx - sinx = V2 sin(45°-x) = 72 cos(45°+x) asinx + bcosx = 7a2 + b2 sin(x + <p)» b a где sincp = , созф = - Va2 +b* 4a*+b*
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ПРОИЗВЕДЕНИЯ В СУММУ
sinx sin у = —[сов(х - у) - cos(x + у)]
2
cosx cos у = —[cos(x - у) + cos(x + у)]
2
sinxсову = —[sin(x - у} + sin(x + у)]
2
Справочные таблицы
91
ФОРМУЛЫ ПРИВЕДЕНИЯ
угол функция^^ Р = — ± а 2 Р = п ± а 2 Р = 2л ± а
sin Р сова Т sin а -сова ±sina
СО8 Р Т sin а -сова ±sina сова
tgp Т ctg а ±tga Т ctg а ±tga
Т tga ±ctga Т tga ±ctga
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ НЕКОТОРЫХ УГЛОВ
Угол в градусах 0° 30° 45° 60° 90° 180° 270° 360°
Угол в радианах 0 л 6 л 4 я 3 я 2 п Зл ~2 2л
sin a 0 1. 2 1 Уг Уз 2 1 0 -Г 0
cos a 1 Уз 2 1 Уг j. 2 0 -1 0 1
tga 0 1 Уз 1 Уз не сущ. 0 не сущ. 0
ctg a не сущ. Уз 1 1 Уз 0 не сущ. 0 не сущ.
СВОЙСТВА ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
arcsin (-a) = - arcsin а9 |а| <. 1
arccos (-а) = я - arccos а, |а|^1
arctg (-а) = - arctg а, а е R
arcctg (-а) = я - arcctg а, а € R
я arcsin а + arccos а = —, 2 |а|£1
. А П arctg а + arcctg а = —, 2 а е R
92
Справочные таблицы
НЕКОТОРЫЕ ПРЕДЕЛЫ
.. sinx lim = 1 X ->0 X 1- 1 hm = 1 X >0 X
ех -1 lim = 1 .. ах -1 lim = In а, а > 0
х->0 X х *° X
lim(l + х)1/х = е х-*0 lin,l"(ltI) = l х
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Функция Производная
/(х) = с c' = 0 , где c — const
Г(*) = Ха (xa)' = axa-‘
fix) = ех (ex)'=ex
fix) = а* (az)' = a1 Ina
f(x) = 1пх (Inx)' = - X
f(x) = loga х
xlna
f(x) = sinx (sinx)' = cosx
/(x) = cosx (cosx)' = -sinx
f(x) = tgx (iff yY - 1
COS X
f(x) = ctgx (t>i cr yV —
(CLgX) - sin X
f(x) = arcsin x / • У 1 (arcsin x) = = Vi - x2
f(x) = arccosx / v 1 (arccosx) = —7--- Vi -x2
f(x) = arctgx (cr yY —
tarcig X) - 1 + X
f(x) = arcctgx / * v 1 f П 1*ЛПт ff Y 1 —
(arccigxj - 1 + xz
Справочные таблицы 93
ТАБЛИЦА ИНТЕГРАЛОВ
10 • dx = С
J1 • dx = х + С
г ха+^
Г xadx =----+ С, (а * -1)
J а +1
J—dx = 1п|*| + С
г 1 , ’агент* + С
, dx= \
J - х2 l~ arccos x + С
[-i-dx.J + C
Jl + *2 [-arcctg* + C
f axdx = —— + C
J Ina
J sinxdx = -cos* + C
J cosxdx = sin* + C
jtgxdx = - ln|cos*| + C
J ctgxdx = ln|sin*| + C
J—— dx = tgx + C
J cos *
f ——dx = -ctgx + C
J sin *
—-—dx = In sinx *4 + C
—-—dx = In tgf- + -^ +c
CO8X 12 4 J
• x arcsin—+ C
. . * dx — . a
l„2 ~2 ya — x arccos— + C
a
1 -arctg— + C
— -dx = a a
a2 +* 1 A X П -arcctg— + C
, a i a
a2
1 , 1 . = -X-ln a + x
-Xs 2a a-x
ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение радиоактивного распада: у' = -ау
у = Се'ах, где С — произвольная постоянная.
Уравнение гармонических колебаний: у" = -а2у
у = A cos(cd* + ср), где А и ф — произвольные постоянные.
94 Предметный указатель
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аргумент 6
асимптота 10
— вертикальная 10
— горизонтальная 10
— наклонная 10
Возрастание функции 9
— — , достаточное условие 74
выделение полного квадрата 26, 30
График функции, определение 6
графики сложных функций, построение 20-21
— функций, преобразования 12-21
Дискриминант 26
дифференцирования правила 73
Интеграл неопределенный 78
— определенный 79
— определенный, вычисление площадей и объемов 81
— определенный, геометрический смысл 80
— определенный, физический смысл 80
интегрирования правила 78
Касательная к графику функции, уравнение 72
квадратов таблица 83
комбинаторика, основные формулы 87
корень арифметический 86
корень уравнения 44
Логарифмы 87
Максимум 9
минимум 9
многочлены 84
модуль числа 84
монотонность функции 9
Наибольшее и наименьшее значения функции,
непрерывной на отрезке 77
неравенства 57-66
— дробно-рациональные, метод интервалов 61
— иррациональные 62
— квадратные 59
— линейные 58
— логарифмические 63
— показательные 63
— тригонометрические, простейшие 64-66
— числовые 85
неравенства, метод интервалов 60
Предметный указатель 96
нуль функции 8
Область допустимых значений уравнения 44
объемы тел, вычисление с помощью определенного
интеграла 81
Первообразная 78
период функции 8
площади поверхностей, вычисление с помощью
определенного интеграла 81
постоянства функции необходимое и достаточное условие
74
признаки делимости 82
прогрессия арифметическая 86
— геометрическая 85
производная 72-77
— сложной функции 73
— вторая 73
— , геометрический смысл 72
— , применение к исследованию функций 74-77
— , физический смысл 73
производные элементарных функций, таблица 92
пропорции 83
пропорциональность обратная 33
— прямая 22
простых чисел таблица 82
Разложение квадратного трехчлена на линейные
множители 26
Системы двух линейных уравнений с двумя неизвестными
71
— — уравнений с двумя неизвестными 67-71
— — уравнений с двумя неизвестными,
графический метод решения 70
— — уравнений с двумя неизвестными, метод подстановки
68
— — уравнений с двумя неизвестными, метод сложения
69
сокращенного умножения формулы 84
способы задания функции 6
степени 86
Тригонометрические формулы 88-91
Убывание функции 9
----, достаточное условие 74
угловой коэффициент прямой 22
уравнение asinx + bcosx = с 54
уравнения 44-56
96 Предметный указатель
уравнения иррациональные 50
— квадратные 46-48
— — неполные 47
— — приведенные 48
— линейные 45
— логарифмические, простейшие 51
— показательные, простейшие 51
— равносильные 44
— с двумя переменными и их графики 55-56
— тригонометрические, простейшие 52-54
уравнения, сводящиеся к квадратным 49
Формула Ньютона-Лейбница 79
формулы Виета для корней квадратного уравнения 48
функции 6-48
— y = Vx 34
— , область значений 6
— обратные тригонометрические 42-48
— степенные с действительными показателями степени 35
— степенные с натуральными показателями степени 32
— степенные с целыми отрицательными показателями
степени 33
— тригонометрические 38-42
функция, область значений 6
— , область определения 6
функция возрастающая 9
— Дирихле 6
— квадратичная 26-31
— квадратичная, график 28-31
— линейная 22-25
— логарифмическая 37
— нечетная 7, 13
— обратная 11
— обратная, график 19
— обратная, формула 11
— периодическая 8, 14
— показательная 36
— убывающая 9
— четная 7
Экстремум 9
* экстремума достаточное условие 75
экстремума необходимое условие 75