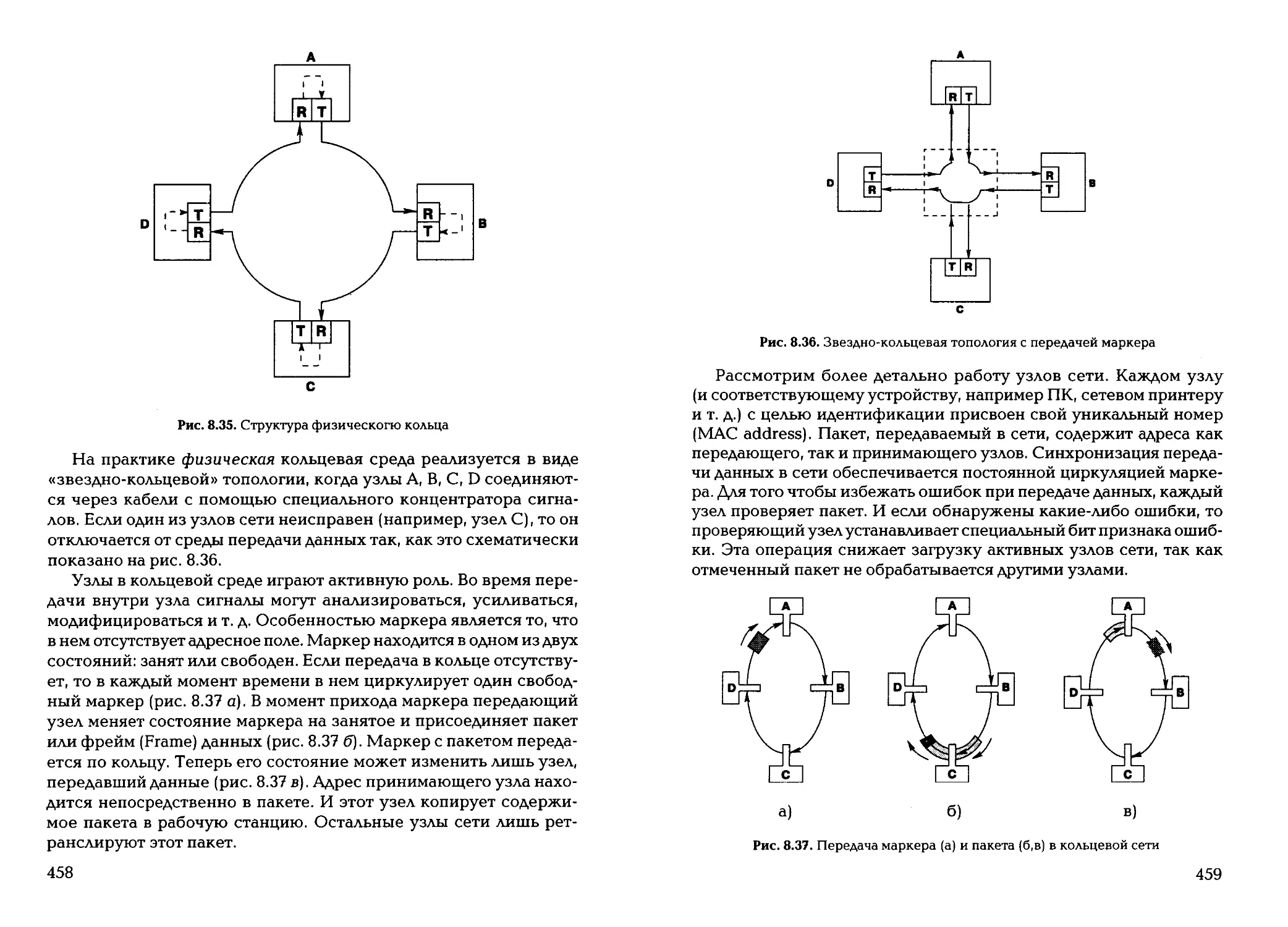
/
Текст
УЧЕБНИК ДЛЯ ТЕХНИЧЕСКИХ ВУЗОВ
О.А. АКУЛОВ,
Н.В. МЕДВЕДЕВ
Информатика
БАЗОВЫЙ КУРС
Структура и свойства
информации
Принципы построения
вычислительных устройств
Системы обработки, хранения
и передачи информации
Контроль и защита информации
«Ж ОМЕГА-А
О.А. Акулов
Н.В. Медведев
базовый курс
2 издание,
исправленное и дополненное
Допущено УМО по университетскому
политехническому образованию
в качестве учебника
для студентов высших учебных заведений,
бакалавров, магистров,
обучающихся по направлениям
Информатика и вычислительная техника»
Жомега-л
Москва 2005
УДК 004(075.8)
ББК32.81я73-1
А44
Рецензенты:
доктор технических наук, заведующий кафедрой АСУ МГТУ
им. Н.Э. Баумана, профессор В.М. Черненький;
доктор физико-математических наук, заведующий сектором ВЦ РАН,
профессор В. К. Леонтьев
Акулов, Олег Анатольевич, Медведев, Николай Викторович.
А44 Информатика: базовый курс: учеб, пособие для студентов
вузов, обучающихся по направлениям 552800,654600 «Инфор-
матика и вычислительная техника»/О.А. Акулов, Н.В. Мед-
ведев. 2-е изд., испр. и доп. — М.: Омега-Л, 2005. — 552 с. —
ISBN 5-98119-630-Х.
I. Медведев, Николай Викторович.
Агентство CIP РГБ
В книге изложены основы современной информатики как комп-
лексной научно-технической дисциплины, включающей изучение
структуры и общих свойств информации и информационных про-
цессов, общих принципов построения вычислительных устройств,
а также систем обработки, хранения и передачи информации. Рас-
смотрены актуальные вопросы контроля и защиты информации
в автоматизированных системах. Представлены определения клю-
чевых понятий и конкретные вопросы по темам курса.
Для студентов высших учебных заведений, бакалавров, магист-
ров, обучающихся по специальности «Информатика и вычислитель-
ная техника», а также студентов, изучающих естественные науки.
УДК 004(075.8)
ББК32.81я73-1
ISBN 5-98119-630-Х
© О.А. Акулов, 2005
© Н.В. Медведев, 2005
© Омега-Л, 2005
Предисловие
Учебник охватывает основные разделы современной информа-
тики как комплексной научно-технической дисциплины, занима-
ющейся изучением структуры и общих свойств информации, ин-
формационных процессов, разработкой на этой основе информа-
ционной техники и технологии, а также решением научных и ин-
женерных проблем создания, внедрения и эффективного исполь-
зования компьютерной техники и технологии во всех сферах об-
щественной практики.
Учебник создан на основе чтения авторами курса лекций по
информатике в Московском государственном техническом уни-
верситете им. Н.Э.Баумана.
Главы с первой по пятую закладывают теоретическую базу ин-
форматики.
В главах с шестой по восьмую излагаются общие характерис-
тики процессов обработки, хранения и передачи информации,
способы их технической реализации.
Девятая глава посвящена актуальным вопросам контроля и за-
щиты информации в автоматизированных системах.
В заключение представлен список использованной литературы.
Учебник рассчитан на студентов младших курсов высших учеб-
ных заведений, бакалавров, магистров, обучающихся по направ-
лению «Информатика и вычислительная техника». По существу
это базовый курс, который знакомит их с широким спектром зна-
ний в данной области. Кроме того, может быть использован в ка-
честве ознакомительного курса по информатике для студентов,
изучающих естественные науки.
Тлава /
Информация и информатика
1.1. ПОНЯТИЕ ИНФОРМАЦИИ
Вся жизнь человека так или иначе связана с накоплением и об-
работкой информации, которую он получает из окружающего мира,
используя пять органов чувств — зрение, слух, вкус, обоняние и ося-
зание. Как научная категория «информация» составляет предмет
изучения для самых различных дисциплин: информатики, кибер-
нетики, философии, физики, биологии, теории связи и т. д. Несмот-
ря на это, строгого научного определения, что же такое информа-
ция, до настоящего времени не существует, а вместо него обычно
используют понятие об информации. Понятия отличаются от опре-
делений тем, что разные дисциплины в разных областях науки и тех-
ники вкладывают в него разный смысл с тем, чтобы оно в наиболь-
шей степени соответствовало предмету и задачам конкретной дис-
циплины. Имеется множество определений понятия информации,
от наиболее общего философского (информация есть отражение ре-
ального мира) до наиболее частного прикладного (информация есть
сведения, являющиеся объектом переработки). Вот некоторые из них:
сообщение, осведомление о положении дел, сведения о чем-
либо, передаваемые модели;
уменьшаемая, снимаемая неопределенность в результате по-
лучения сообщений;
передача, отражение разнообразия в любых процессах и
объектах, отраженное разнообразие;
товар, являющийся объектом купли-продажи знаний для до-
стижения определенных целей;
данные как результат организации символов в соответствии
с установленными правилами;
продукт взаимодействия данных и адекватных им методов;
сведения о лицах, предметах, фактах, событиях, явлениях и
процессах независимо от формы их представления.
Наряду с названными существуют сотни других, зачастую про-
тиворечащих друг другу или взаимоисключающих определений
4
информации. Многообразие этих определений свидетельствует о
широте подхода к понятию информации и отражает становление
концепции информации в современной науке.
Первоначально смысл слова «информация» (от лат. Informatio —
разъяснение, изложение) трактовался как нечто присущее только
человеческому сознанию и общению: «знания, сведения, сообще-
ния, известия, передаваемые людьми устным, письменным или дру-
гим способом». Затем смысл этого слова начал расширяться и обоб-
щаться. Так, с позиций материалистической теории познания од-
ним из всеобщих свойств материи (наряду с движением, развити-
ем, пространством, временем и др.) было признано отражение, зак-
лючающееся в способности адекватно отображать одним реальным
объектом другие реальные объекты, а сам факт отражения состоя-
ний одного объекта в состояниях другого (или просто одного объек-
та в другом) и означает присутствие в нем информации об отражае-
мом объекте. Таким образом, как только состояния одного объекта
находятся в соответствии с состояниями другого объекта (напри-
мер, соответствие между положением стрелки вольтметра и напря-
жением на его клеммах или соответствие между нашим ощущени-
ем и реальностью), это значит, что один объект отражает другой,
т. е. содержит информацию о другом.
Высшей, специфической формой отражения является сознание
человека. Кроме этого, существуют и другие формы — психичес-
кая (присущая не только человеку, но и животным, несущая в себе
информацию, способную влиять на их эмоциональные состояния
и поведение), раздражимость (охватывающая, помимо прочего, ра-
стения и простейшие организмы, реагирующие на слабые меха-
нические, химические, тепловые контакты с окружающей средой)
и самая элементарная форма — запечатление взаимодействия
(присущая и неорганической природе, и элементарным частицам,
т. е. всей материи вообще) (рис. 1.1).
Формы отражения Сознание
Психика
Раздражимость
Запечатление взаимодействия
Неорганическая природа Растительный мир Животный мир Человек
Рис. 1.1. Формы отражения в живой и неживой природе
5
Так, кусок каменного угля несет в себе «отражение» событий, про-
изошедших в далекие времена, т. е. обладает свойством информатив-
ности. Деловое письмо с предложениями сотрудничества информа-
тивно, постольку-поскольку отражает серьезные намерения опреде-
ленного учреждения или ведомства. Команда приступить к конкрет-
ным действиям (запуску ракеты, отправке груза, производству вы-
числений и т. п.) содержит информацию о подготовленности соот-
ветствующих служб и своевременности предпринимаемых шагов.
Информация не является ни материей, ни энергией. В отличие
от них она может возникать и исчезать. В указанных примерах ин-
формация в куске каменного угля или делового письма может ис-
чезнуть, если исчезнет ее носитель, например сгорит.
Особенность информации заключается в том, что проявляется
она только при взаимодействии объектов, причем обмен инфор-
мацией может совершаться не вообще между любыми объектами,
а только между теми из них, которые представляют собой органи-
зованную структуру (систему). Элементами этой системы могут
быть не только люди: обмен информацией может происходить в
животном и растительном мире, между живой и неживой приро-
дой, людьми и устройствами. Так, информация, заключенная в кус-
ке каменного угля проявится лишь при взаимодействии с челове-
ком, а растение, получая информацию о свете, днем раскрывает
свои лепестки, а ночью закрывает их.
Понятие «информация» обычно предполагает наличие двух
объектов — «источника» информации и «приемника» (потреби-
теля, адресата) информации (рис. 1.2).
Среда
распространения
Рис. 1.2. Структурные компоненты обмена информацией
6
Информация передается от источника к приемнику в матери-
ально-энергетической форме в виде сигналов (например, электри-
ческих, световых, звуковых и т. д.), распространяющихся в опре-
деленной среде.
Сигнал (от лат. signum — знак) — физический процесс (явление),
несущий сообщение (информацию) о событии или состоянии объек-
та наблюдения.
Информация может поступать непрерывно или дискретно, т. е.
в виде последовательности отдельных сигналов. Соответственно
различают непрерывную и дискретную информацию.
Информация — специфический атрибут реального мира, представ-
ляющий собой его объективное отражение в виде совокупности сиг-
налов и проявляющийся при взаимодействии с «приемником» инфор-
мации, позволяющим выделять, регистрировать эти сигналы из окру-
жающего мира и по тому или иному критерию их идентифицировать.
Из этого определения следует, что:
• информация объективна, так как это свойство материи —
отражение;
информация проявляется в виде сигналов и лишь при взаи-
модействии объектов;
одна и та же информация различными получателями может
быть интерпретирована по-разному, в зависимости от «на-
стройки» «приемника».
Человек воспринимает сигналы посредством органов чувств, ко-
торые «идентифицируются» мозгом. Поэтому, например, при на-
блюдении одного и того же объекта человек с лучшим зрением мо-
жет получить больше информации об объекте, чем тот, у которого
зрение хуже. В то же время, при одинаковой остроте зрения, в слу-
чае, например, прочтения текста на иностранном языке, человек,
не владеющий этим языком, вообще не получит никакой инфор-
мации, так как его мозг не сможет ее «идентифицировать». При-
емники информации в технике воспринимают сигналы с помощью
различной измерительной и регистрирующей аппаратуры. При
этом приемник, обладающий большей чувствительностью при ре-
гистрации сигналов и более совершенными алгоритмами их обра-
ботки, позволяет получить большие объемы информации.
7
Информация имеет определенные функции и этапы обращения
в обществе. Основными из них являются:
познавательная, цель которой — получение новой инфор-
мации. Функция реализуется в основном через такие этапы
обращения информации, как:
— ее синтез (производство),
— представление,
— хранение (передача во времени),
— восприятие (потребление);
* коммуникативная — функция общения людей, реализуемая
через такие этапы обращения информации, как:
— передача (в пространстве),
— распределение;
* управленческая, цель которой — формирование целесооб-
разного поведения управляемой системы, получающей ин-
формацию. Эта функция информации неразрывно связана
с познавательной и коммуникативной и реализуется через
все основные этапы обращения, включая обработку.
Без информации не может существовать жизнь в любой фор-
ме и не могут функционировать созданные человеком любые ин-
формационные системы. Без нее биологические и технические
системы представляют груду химических элементов. Общение,
коммуникации, обмен информацией присущи всем живым суще-
ствам, но в особой степени — человеку. Будучи аккумулирован-
ной и обработанной с определенных позиций, информация дает
новые сведения, приводит к новому знанию. Получение инфор-
мации из окружающего мира, ее анализ и генерирование состав-
ляют одну из основных функций человека, отличающую его от
остального живого мира.
1.2. ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ И СИСТЕМЫ
В общем случае роль информации может ограничиваться эмо-
циональным воздействием на человека, однако наиболее часто она
используется для выработки управляющих воздействий в автома-
тических (чисто технических) и автоматизированных (человеко-
машинных) системах [8]. В подобных системах можно выделить
отдельные этапы (фазы) обращения информации, каждый из ко-
торых характеризуется определенными действиями.
8
Последовательность действий, выполняемых с информацией, на-
зывают информационным процессом.
Системы, реализующие информационные процессы, называют ин-
формационными системами.
Основными этапами (фазами) обращения информации в сис-
темах являются:
сбор (восприятие) информации;
подготовка (преобразование) информации;
передача информации;
обработка (преобразование) информации;
хранение информации;
отображение (воспроизведение) информации.
Так как материальным носителем информации является сигнал,
то реально это будут этапы обращения и преобразования сигна-
лов (рис. 1.3).
Рис. 1.3. Этапы обращения информации в автоматизированных системах
На этапе восприятия информации осуществляется целенаправ-
ленное извлечение и анализ информации о каком-либо объекте
(процессе), в результате чего формируется образ объекта, прово-
дятся его опознание и оценка. Главная задача на этом этапе — отде-
лить полезную информацию от мешающей (шумов), что в ряде слу-
чаев связано со значительными трудностями. Простейшим видом
восприятия является различение двух противоположных состояний:
наличия («да») и отсутствия («нет»), более сложным — измерение.
9
На этапе подготовки информации осуществляется ее первич-
ное преобразование. На этом этапе проводятся такие операции, как
нормализация, аналого-цифровое преобразование, шифрование.
Иногда этап подготовки рассматривается как вспомогательный на
этапе восприятия. В результате восприятия и подготовки получает-
ся сигнал в форме, удобной для передачи, хранения или обработки.
На этапе передачи информация пересылается из одного места в
другое (от отправителя получателю — адресату). Передача осуществ-
ляется по каналам различной физической природы, самыми распро-
страненными из которых являются электрические, электромагнит-
ные и оптические. Извлечение сигнала на выходе канала, подвержен-
ного действию шумов, носит характер вторичного восприятия.
На этапах обработки информации выявляются ее общие и су-
щественные взаимозависимости, представляющие интерес для си-
стемы. Преобразование информации на этапе обработки (как и на
других этапах) осуществляется либо средствами информационной
техники, либо человеком.
В общем случае под обработкой информации понимается любое
ее преобразование, проводимое по законам логики, математики, а
также неформальным правилам, основанным на «здравом смысле»,
интуиции, обобщенном опыте, сложившихся взглядах и нормах по-
ведения. Результатом обработки является тоже информация, но либо
представленная в иных формах (например, упорядоченная по каким-
то признакам), либо содержащая ответы на поставленные вопросы
(например, решение некоторой задачи). Если процесс обработки
формализуем, он может выполняться техническими средствами. Кар-
динальные сдвиги в этой области произошли благодаря созданию
ЭВМ как универсального преобразователя информации, в связи с чем
появились понятия данных и обработки данных.
Данными называют факты, сведения, представленные в формали-
зованном виде (закодированные), занесенные на те или иные носите-
ли и допускающие обработку с помощью специальных технических
средств (в первую очередь ЭВМ).
Обработка данных предполагает производство различных опе-
раций над ними, в первую очередь арифметических и логических,
для получения новых данных, которые объективно необходимы
(например, при подготовке ответственных решений).
10
На этапе хранения информацию записывают в запоминающее
устройство для последующего использования. Для хранения инфор-
мации используются в основном полупроводниковые, магнитные и
оптические носители. Решение задач извлечения хранимой инфор-
мации (поиска информации) связано с разработкой классификаци-
онных признаков и схем размещения хранимой информации, сис-
тематизацией, правилами доступа к ней, порядком ее пополнения и
обновления, т. е. всем тем, что определяет возможность целенаправ-
ленного поиска и оперативного извлечения хранимой информации.
Этап отображения информации должен предшествовать эта-
пам, связанным с участием человека. Цель этого этапа — предос-
тавить человеку нужную ему информацию с помощью устройств,
способных воздействовать на его органы чувств.
Информационные системы можно классифицировать по различ-
ным признакам. Так, по сфере применения информационные систе-
мы подразделяются на: административные, производственные, учеб-
ные, медицинские, военные и др. По территориальному признаку: ин-
формационные системы района, города, области и т. п. С точки зрения
возможности организации конкретных информационных процессов
различают информационно-справочные, информационно-поиско-
вые системы, системы обработки и передачи данных, системы связи.
Большинство автоматизированных информационных систем
являются локальными системами и функционируют на уровне
предприятий и учреждений. В настоящее время происходит ин-
тенсивный процесс интеграции таких систем в корпоративные
системы и далее — в региональные и глобальные системы.
Системы более высокого уровня становятся территориально рас-
средоточенными, иерархичными как по функциональному принципу,
так и по их технической реализации. Обеспечение взаимодействия
территориально рассредоточенных систем требует протяженных вы-
сокоскоростных и надежных каналов связи, а увеличение объема об-
рабатываемой информации—ЭВМ высокой производительности. Это
приводит к необходимости коллективного использования дорогосто-
ящих средств автоматизации (ЭВМ и линий связи) и обрабатываемой
информации (баз данных). Техническое развитие как самих электрон-
ных вычислительных машин, так и средств связи, позволило решить
эту проблему путем перехода к созданию распределенных информа-
ционно-вычислительных сетей коллективного пользования.
Централизация различных видов информации в одной сети дает
возможность использовать ее для решения широкого спектра за-
11
дач, связанных с административным управлением, планировани-
ем, научными исследованиями, конструкторскими разработками,
технологией производства, снабжением, учетом и отчетностью.
Если поставляемая информация извлекается из какого-либо
объекта (процесса), а выходная применяется для целенаправлен-
ного изменения состояния того же объекта (процесса), причем або-
нентом, использующим информацию для выбора основных управ-
ляющих воздействий (принятия решения), является человек, то
такую автоматизированную информационную систему называют
автоматизированной системой управления (АСУ).
Управление и информация служат основными понятиями ки-
бернетики — науки об общих принципах управления в различных
системах: технических, биологических, социальных и др.
Управление — функция организованных систем различной при-
роды (технических, биологических или социальных), направленная на
реализацию их целевых установок и поддержание внутренне присущей
им структуры.
Понятие «кибернетика» как научный термин введено в первой
половине XIX века французским физиком Андре Мари Ампером,
который назвал кибернетикой (от греч. слова кибернетикос —
искусный в управлении) науку, занимающуюся изучением искус-
ства управления людьми, обществом. В Древней Греции этого ти-
тула удостаивались лучшие мастера управления боевыми колес-
ницами. Впоследствии слово «кибернетикос» было заимствовано
римлянами — так в латинском языке появилось слово «губерна-
тор» (управляющий провинцией).
Кибернетика — наука, изучающая с единых позиций связь и уп-
равление (самоуправление) в организованных системах любой физи-
ческой природы.
Основоположником кибернетики считается выдающийся аме-
риканский математик Норберт Винер (1894—1964), а датой ее рож-
дения —1948 г., когда он опубликовал книгу «Кибернетика или уп-
равление и связь в животном и машине». Сущность кибернетики
в самом общем виде может быть выражена основными ее закона-
ми, структура и содержание которых приведены на рис. 1.4 [7].
12
Формулировка общих законов управления
1. Всякое управление есть 2. Всякое управление есть 3. Всякое управление обычно
целенаправленный процесс информационный процесс осуществляется
в замкнутом контуре
1. Процессы сбора
информации
2. Процессы обработки
и представления
информации
для принятия решений
3. Процессы хранения
и передачи информации
Управляющий
объект
Рис. 1.4. Состав и содержание общих законов управления
Таким образом, кибернетическая система (система управления)
может рассматриваться как совокупность двух систем — управля-
ющего объекта и объекта управления. При этом управляющая си-
стема воздействует на объект управления, подавая на него управ-
ляющие сигналы (управляющие воздействия). Для выработки уп-
равляющих решений, обеспечивающих достижение цели управ-
ления, управляющая система получает информацию о состоянии
объекта управления по линии обратной связи.
Автоматизированные системы управления нашли широкое при-
менение во всех сферах современного общества, в первую очередь
как системы управления технологическими процессами и коллек-
тивами людей. АСУ технологическими процессами служат для ав-
томатизации различных функций на производстве. Они широко
используются при организации поточных линий, изготовлении
микросхем, для поддержания технологического цикла в машино-
строении и т. п. Информационные системы организационного уп-
равления предназначены для автоматизации функций управлен-
13
ческого персонала, например информационные системы управле-
ния банками, гостиницами, торговыми фирмами и т. п.
1.3. ИНФОРМАЦИОННЫЕ РЕСУРСЫ И ТЕХНОЛОГИИ
Особенностью современного этапа развития общества является
переход от индустриального общества к информационному. Про-
цесс, обеспечивающий этот переход, называют информатизацией.
Информатизация общества — организованный социально-эконо-
мический и научно-технический процесс создания оптимальных усло-
вий для удовлетворения информационных потребностей и реализации
прав граждан, органов государственной власти, органов местного са-
моуправления, организаций, общественных объединений на основе
формирования и использования информационных ресурсов [25].
Неизбежность информатизации обусловлена резким возраста-
нием роли и значения информации. Для нормального функциони-
рования организации любого масштаба уже не достаточно только
традиционных для индустриального общества ресурсов (материаль-
ных, природных, трудовых, финансовых, энергетических), необхо-
димо знать, как наиболее эффективно эти ресурсы использовать,
иметь информацию о технологиях. Поэтому существенным ресур-
сом стала информация. Информационные ресурсы в настоящее
время рассматриваются как отдельная экономическая категория,
важнейший стратегический ресурс общества.
Информационные ресурсы — отдельные документы и отдельные
массивы документов, документы и массивы документов в информа-
ционных системах (библиотеках, архивах, фондах, банках данных, дру-
гих информационных системах).
Информационная система — организационно упорядоченная со-
вокупность документов, информационных технологий, в том числе с
использованием средств вычислительной техники и связи, реализую-
щих информационные процессы [25].
В общем случае под информационными ресурсами понимают
весь имеющийся в информационной системе объем информации,
14
отчужденной от ее создателей и предназначенной для обществен-
ного использования.
Основной особенностью информационных ресурсов является то,
что в отличие от других видов ресурсов (материальных, природных и
др.) они практически неисчерпаемы; по мере развития общества и
роста потребления информации их запасы не убывают, а растут. Эта
специфика информационных ресурсов хорошо иллюстрируется сле-
дующим высказыванием: «Если у вас есть по яблоку и вы обменяе-
тесь ими, у вас опять будет по яблоку, но если у вас есть по идее и вы
обменяетесь ими, то у каждого их будет по две». Более того, в процес-
се применения информационные ресурсы постоянно развиваются и
совершенствуются, избавляясь от ошибок и уточняя свои параметры.
Выделяют пассивную и активную формы информационных ре-
сурсов. К пассивной форме относятся книги, журнальные статьи,
патенты, банки данных и т. п. Примерами активных форм служат:
модель, алгоритм, проект, программа и т. п.
Государственная политика в сфере формирования информацион-
ных ресурсов и информатизации направлена на создание условий
для эффективного и качественного информационного обеспечения
решения задач социально-экономического развития. Основными на-
правлениями государственной политики в этой области являются:
• обеспечение условий для развития и защиты всех форм соб-
ственности на информационные ресурсы;
• формирование и защита информационных ресурсов;
создание и развитие федеральных и региональных информа-
ционных систем и сетей, обеспечение их совместимости и вза-
имодействия в едином информационном пространстве РФ;
создание условий для качественного и эффективного инфор-
мационного обеспечения граждан, органов государственной
власти, органов местного самоуправления, организаций и об-
щественных объединений на основе государственных инфор-
мационных ресурсов;
содействие формированию рынка информационных ресур-
сов, услуг, информационных систем, технологий и средств
их обеспечения;
формирование и осуществление единой научно-технической
и промышленной политики в сфере информатизации с уче-
том современного мирового уровня развития информацион-
ных технологий;
" создание и совершенствование системы привлечения инве-
стиций и механизма стимулирования разработки и реализа-
ции проектов информатизации;
15
• развитие законодательства в сфере информационных про-
цессов, информатизации и защиты информации.
Базовой технической составляющей процесса информатизации
общества является компьютеризация.
Под компьютеризацией понимается развитие и внедрение тех-
нической базы — компьютеров, обеспечивающих оперативное по-
лучение результатов переработки информации и ее накопление.
Научным фундаментом процесса информатизации общества яв-
ляется информатика, призванная создавать новые информацион-
ные технологии и системы для решения задач информатизации.
Технология (от греч. techne — искусство, мастерство, умение и греч.
logos — слово, учение) — совокупность методов обработки, изготов-
ления, изменения состояния, свойств, формы сырья, материала или
полуфабриката, осуществляемых в процессе производства продукции.
Основными компонентами материальных технологий являют-
ся: подготовка сырья и материалов, производство материального
продукта, сбыт произведенных продуктов потребителям.
В информационной технологии в качестве исходного материа-
ла выступает информация. В качестве конечного продукта — так-
же информация, но это качественно новая информация о состоя-
нии объекта, процесса или явления. При этом основными компо-
нентами информационных технологий служат: сбор данных (пер-
вичной информации), обработка данных, получение результатной
информации и передача ее потребителю.
Выделяют несколько поколений информационных технологий:
• самую древнюю — «наскально-берестяную»;
«бумажную», связанную с изобретением печатного станка
(середина XVвека);
«безбумажную», или «электронную», относящуюся к появ-
лениюм ЭВМ (середина XX века);
«новую информационную технологию», связанную с внедре-
нием персональных ЭВМ и телекоммуникационных средств
(с середины 80-х годов прошлого века).
Новая информационная технология (компьютерная информаци-
онная технология) — технология, основанная на использовании пер-
сональных компьютеров и телекоммуникационных средств.
16
В процессе информатизации общества происходит проникно-
вение информационных технологий во все сферы жизнедеятель-
ности общества, в том числе и связанные с принятием ответствен-
ных решений. При этом уже сейчас информационные технологии
оказывают решающее воздействие на многие сферы деятельнос-
ти людей, человеческих коллективов и общество в целом. Однако
указанное воздействие в некоторых случаях может иметь и нега-
тивный характер [7].
Во-первых, вычислительная техника все более широко внедряет-
ся в системы управления такими технологическими процессами, вы-
ход которых за регламентированные пределы грозит не только круп-
ными авариями, но и крупномасштабными катастрофами (системы
управления вооружением, атомными реакторами и т. п.). Отличитель-
ной особенностью таких систем управления является необходимость
осуществления сложных видов обработки больших объемов инфор-
мации в крайне ограниченные сроки. В силу этого сложность систем
неуклонно растет, а гарантировать отсутствие ошибок в программ-
ном обеспечении, исчисляемом многими десятками миллионов ма-
шинных команд, практически невозможно. Помимо этого, возмож-
ны сбои или отказы аппаратуры, провокационные и диверсионные
действия персонала, заражение компьютеров электронными виру-
сами и т. п. Нетрудно представить себе возможные последствия та-
ких событий в системе военного назначения. Иными словами, в со-
временных условиях надо защищать как системы обработки инфор-
мации от воздействия внешней среды, так и среду от воздействия ин-
формации, находящейся в системах обработки. Должна быть обес-
печена не только безопасность информации, накапливаемой, храни-
мой и обрабатываемой в системах, но также и информационная бе-
зопасность окружающей среды, т. е. предупреждение негативного
воздействия на окружающую среду, которое может иметь место в
результате непредусмотренных (ошибочных или злоумышленных)
видов обработки.
Во-вторых, массовое использование вычислительной техники
в различных сферах деятельности резко увеличивает потенциаль-
ные возможности нарушения гражданских прав и свобод челове-
ка, поскольку в условиях повсеместного внедрения новых инфор-
мационных технологий расширяются возможности ведения досье
на людей, подслушивания телефонных разговоров, несанкциони-
рованного чтения электронной почты, контролирования вкладов,
осуществления компьютерной слежки и т. п.
2 А-210
17
В-третьих, увеличивается опасность нарушения авторского пра-
ва и права собственности, в первую очередь на программные про-
дукты. Во многих случаях программное обеспечение как отдель-
ными пользователями, так и целыми организациями приобретает-
ся в результате незаконного копирования, т. е. хищения.
В-четвертых, информатизация может являться и источником со-
циальной напряженности. Так, автоматизация производства ведет
к полному изменению технологии, что влечет за собой смену но-
менклатуры профессий и сокращение численности персонала. При
этом не все люди могут легко освоить новую специальность или
найти новое место работы.
Заслуживает быть отмеченным и такой несколько необычный
аспект, как опасность профанации искусства, поскольку широкие
возможности современных ЭВМ позволяют существенно интен-
сифицировать процесс творчества, а интенсификация его сверх
некоторой меры неизбежно скажется на качестве произведения.
Кроме того, по мнению некоторых ученых, у руководителей и спе-
циалистов, длительное время и регулярно использующих вычис-
лительную технику в процессе своей деятельности, атрофируют-
ся опыт и интуиция относительно важных своих функций.
Негативные аспекты информационных технологий необходимо
учитывать при решении задач информатизации. Эти проблемы дол-
жны также стать предметом изучения современной информатики.
1.4. ИНФОРМАТИКА И ЕЕ ПРЕДЫСТОРИЯ
Задачи накопления (хранения), обработки и передачи информа-
ции стояли перед человечеством на всех этапах его развития. Каж-
дому этапу соответствовал определенный уровень развития средств
информационного труда, прогресс развития которых всякий раз
придавал человеческому обществу новое качество. Долгое время
средства хранения, обработки и передачи информации развивались
отдельно по этим трем направлениям табл. 1.1. Этот период в исто-
рии развития информатики можно назвать ее предысторией.
В течение долгого времени основными инструментами для ре-
шения задач обработки и передачи информации были мозг, язык
и слух человека. Первое кардинальное изменение пришло с при-
ходом письменности (по мнению ученых, речь возникла более ты-
сячи веков назад, изобретение письменности относится к третьему
18
Q
ST
3
*5
rQ
X
f
X
s
8
tQ
<
о
©
я
x
о
x
tr
«
s
a.
о
•e
X
X
и
a>
R
X
H
X
n
м
я
ua
E
fl
h
Г)
X
§
я
£
I
я
e
X
I
f
£
X
8
о
5
S
I
s
J X
H
s
3 &
X
8
5
5
111
ill?
3 3
al
= s
K
hil
§
a
m
g
X
i I*
§.x *
S л x
о S g
e; Я g
s
X
s
X
S
Ух
г
g “ I
Г
sS
<3 S
s'
s
=:
s
5
8 =
ij
“ X
о
e
3
ffi
si
11
3
s
s 3
x
я
g
s
X
5
s!
4 !S
a ®
s
X
s
3
5
a
г :s
i S
5
o -
5
X
- Й
1 I
z
s
f?
о
3
g
s
-e-
X
2
2
8
X
2
Л
g
2
о
X
X
I
B®x
C s s 2
-I *
>f2fS
X o. x
S
В J §
s s< Z,
X
2
x
x
2
X
3
и
X
X
s
8
s
X
I
I
X
g
8
X
S'
E(
X
X
g
£
X
X
I
X
cq a
X
a
i
3
&
X
X
г>
3
я
s
3
s
з
x
s
53“
X
Й
1 I
5 |
X
5
X
2
s
ЭХ
thii
8 S
4 A
Q>
г
о
Ч
X
I
3
о
z
I
X
X
X
о
z
£
s
I
X
Q.
x
s
s
X
X
H
8
X
I
X
S
«j
S
3
X
li
i
z
5!
X
X
3
fiB
5
?s
§8
2
о
x
s
X
3
X
3
X
a
s
s
_ о
gs
x
s
X
3
x.
i
5
1
§
X
ЗГ
s
§
V -
= g
8.C
8 *
зХ
X
X
X
i
s
U!
x •©• 2
§ 5 x
E < E
3^2
ffi s
§
8
A
§
9 9 5
I 8 .
h! h
3
S'S
X
8
X
s
I
2
3 £ §
g
X
3
X
X
X
s
8
Z
z
i!
b
& 5
3
X
3
i
<4
s
*
§
*
3
H
X
Cu
E
a
X
KJ
s
В
s
4
I
V
5
9X
-sz-л!
gifts iliafF
7 X X U U ©
X X
11
§ §
5
3
о
8.U |
ШН
8
p
5
3
8
s
з
i
!
z
a
§ _
“'g
z
5
u
= :X
a ©
O. x
2 e-
Б =
* X
I
p
a
g.
S
о
X
3
г
s
z
S !<>
X X E
S X
я x 3
Ц-
s 3
i*
X
i I
« 3
5^
z m
о
5
s
ц
I
rt X
= s
il
x
S
a
4
з
s
8
ч
s
X
x
X
B-F §=i
i = i Й
Я
s
X
X
E
Zl&bg'l
S £ g >x
§ p § i
2 " «
f Hit
1
«g
О Л
S
X
8
3
3
5 e s
x S o.
§ u
м x x
§3 я
I §
г a
ьс
8 5
E
£m В
i
-s
0^7?
x
X
©
5
X
X
s° Ovi
ht
НИН:
£
t X
X
3 ?
Hi
Id J
5
co
X
*
S
g
g
CM
g
2
3
5
3
8
X
M
X
*
s
и a. M
f S I
S
*
з
X
:X
3
ffi
8
%
X
г
8
g
fll p
* g
S
8
C £! §
X д£_
« aS"
ex
X и
X s
* X
i.
з «ecg
Ц*
Ш
Hi"
P
k
3
03
s
s a
Й
I®
X
x
5,8
8 3
II
о a
» i,
s
a
s -
g g
§ 8.
§
§
X
8
z'
s,
s
§ 3
« ¥
3 g
8 8
° 2
о
z
8
'g
if 8 Oi
x 3
§ о s
3
о
о =:
lii
W
Hi
— e E
w
x
x
I
!a
rO \©
. з
M
2.
19
Окончание табл. 1.1
20
тысячелетию до н. э.). Это привело к гигантскому качественному
и количественному скачку в развитии общества, появилась воз-
можность передачи знаний от поколения к поколению. Изобрете-
ние книгопечатания (середина XV века) радикально изменило ин-
дустриальное общество, культуру, организацию деятельности.
Эти два этапа (письменность и книгопечатание) создали прин-
ципиально новую технологию накопления и распространения (пе-
редачи) информации, избавившую человечество от необходимос-
ти всецело полагаться на такой зыбкий и ненадежный инструмент,
каким является человеческая память.
Конец XIX века ознаменован изобретением электричества,
благодаря которому появились телеграф, телефон, радио, позво-
ляющие оперативно передавать и накапливать информацию в лю-
бом объеме.
Бурное развитие науки и промышленности в XX веке, неудер-
жимый рост объемов поступающей информации привели к тому,
что человек оказался не в состоянии воспринимать и перерабаты-
вать все ему предназначенное. Возникла необходимость класси-
фицировать поступления по темам, организовать их хранение, до-
ступ к ним, понять закономерности движения информации в раз-
личных изданиях и т. д. Исследования, позволяющие разрешить воз-
никшие проблемы, стали называть информатикой. В этом смысле
информатика — научная дисциплина, изучающая структуру и об-
щие свойства научной информации, а также закономерности всех
процессов научной коммуникации.
Информатика, являясь базой библиотечного дела, многие годы
так и занималась узкоконкретной областью изучения структуры
и общих свойств научной информации, передаваемой посредством
научной литературы. Постановка вопроса о завладении информа-
тикой всем кругом вопросов, который связан с разработкой эф-
фективных методов сбора, хранения, обработки и преобразования
имеющейся информации в знания, прежде была неправомерной,
так как не существовало почти ничего общего в методах сбора и
обработки информации у медиков, географов, психологов, физи-
ков, филологов и т. д. С этой точки зрения много общего между
собой имели математика и физика, химия и медицина. Примеров
отдельных связей было много, но общего стержня, вокруг которо-
го объединились бы все науки, не было.
Положение существенно изменилось с появлением электрон-
но-вычислительных машин (ЭВМ).
21
Первые ЭВМ создавались для проведения расчетов в атомной
физике, в летательной и ракетной технике. Последовавшее да-
лее внедрение ЭВМ в области административного управления и
экономики дало не только большой экономический эффект, но и
привело к созданию и бурному росту новой промышленной от-
расли — средств и методов электронной обработки информации.
Электронно-вычислительные машины стали обрабатывать чис-
ловую, текстовую, графическую и другую информацию. Появи-
лись новые ЭВМ, новые методы и средства общения с ними. Ин-
формация стала товаром.
Вычислительная техника сразу же показала свою эффектив-
ность в тех областях человеческой деятельности, где широко ис-
пользовались методы математического моделирования — точные
количественные методы. Сюда относятся физика, механика, хи-
мия, геофизика и т. д.
Развитие электронно-вычислительной техники, средств и мето-
дов общения с ней, создание автоматизированных информацион-
но-поисковых систем, методов распознавания образов привели к
тому, что ЭВМ стали эффективным инструментом и для «описатель-
ных» наук, которые раньше считались недоступными для методов
математического моделирования (биология, юридические науки, ис-
тория и т. п.). В них шло накопление отдельных фактов, давалось
качественное описание объектов и событий. Использование ново-
го рабочего инструмента значительно повысило эффективность
проведения описательного анализа изучаемых объектов в таких
науках. Появилось новое направление исследований, связанное с
машинным моделированием человеческих интеллектуальных фун-
кций, — разработка «искусственного интеллекта».
Миниатюризация средств вычислительной техники, снижение ее
стоимости позволили создавать станки с программным управлени-
ем, гибкие автоматизированные производства, станки-роботы, в ко-
торых ЭВМ решает задачи сбора, хранения, обработки, преобразо-
вания информации и на основании ее анализа вырабатывает соот-
ветствующие решения. В более сложных задачах человек, используя
электронную технику, берет ответственность за принятие решения
на себя. В этом случае ЭВМ анализирует огромные объемы инфор-
мации и предлагает возможные варианты. Человек, познакомившись
с этими вариантами, либо выбирает лучший, с его точки зрения, либо
ставит перед машиной новые условия и ждет следующего совета. Так,
в режиме диалога происходит процесс принятия решения.
22
Проведение любого эксперимента связано с получением инфор-
мации, регистрируемой различными датчиками или непосред-
ственно органами чувств человека. В ходе эксперимента инфор-
мацию надо принять и записать, обработать по специальным алго-
ритмам, преобразовать к удобному для анализа виду. Далее, иссле-
дуя полученные результаты, необходимо сделать выводы.
При этом не имеет значения, какой это эксперимент — физи-
ческий, биологический, химический и т. д., передают ли датчики
данные прямо в ЭВМ или показания приборов сначала записыва-
ют в тетрадь, а потом вводят их в машину. Главное в том, что нуж-
ны алгоритмы сбора данных и записи их в запоминающие устрой-
ства в таком виде, который позволяет находить эти данные повтор-
но, считывать и анализировать.
Другой важнейшей составной частью эксперимента является
обработка данных по разработанным алгоритмам и составленным
на их основе программам для вычислительной машины.
На следующем этапе активно используются программы преоб-
разования данных к удобному для исследования виду (построение
графиков, таблиц, рабочих чертежей и т. д.) и их выдача (отобра-
жение информации) или передача другим участникам эксперимен-
та, находящимся на значительном расстоянии. Как правило, такие
программы не ориентированы на конкретную предметную область,
они достаточно универсальны.
Таким образом, мы выделили задачи, которые являются общи-
ми для всех наук при обработке информации с помощью ЭВМ. На-
учным фундаментом для их решения и стала новая наука — ин-
форматика.
В этом смысле слово «информатика» второй раз появляется в
научной среде. Теперь — как перевод с французского informatique.
Французский термин informatique (информатика) образован пу-
тем слияния слов information (информация) и automatique (автома-
тика) и означает «информационная автоматика или автоматизи-
рованная переработка информации». В англоязычных странах это-
му термину соответствует синоним computer science (наука о вы-
числительной технике).
Появление ЭВМ сыграло решающую роль в оформлении ин-
форматики как науки, но и сама ЭВМ, ее создание, функциониро-
вание и применение — тоже предмет изучения информатики.
Практика показала, что использование ЭВМ резко повысило про-
изводительность труда на производстве и в науке, оказало силь-
23
ное влияние на научно-технический прогресс. В то же время су-
ществует и обратное влияние — задачи науки и практики предъяв-
ляют конструкторам и разработчикам программ требования для
создания новых, более высокопроизводительных ЭВМ, ориенти-
рованных на решение конкретных проблем.
Раннее употребляемый в русском языке термин «информатика»,
связанный с узкоконкретной областью изучения структуры и об-
щих свойств научной информации, передаваемой с помощью науч-
ной литературы, в современных условиях приобретает более ши-
рокое значение — название комплексной научно-технической дис-
циплины, призванной создавать новые информационные техноло-
гии и средства для решения проблем информатизации в различных
областях человеческой деятельности: производстве, управлении,
науке, образовании, торговле, финансовой сфере, медицине и др.
Информатика — комплексная научно-техническая дисциплина,
занимающаяся изучением структуры и общих свойств информации,
информационных процессов, разработкой на этой основе информа-
ционной техники и технологии, а также решением научных и инже-
нерных проблем создания, внедрения и эффективного использования
компьютерной техники и технологии во всех сферах общественной
практики.
1.5. СТРУКТУРА ИНФОРМАТИКИ
И ЕЕ СВЯЗЬ С ДРУГИМИ НАУКАМИ
Ядро современной информатики образуют три составные час-
ти, каждая из которых может рассматриваться как относительно
самостоятельная научная дисциплина (рис. 1.5).
Теоретическая информатика — часть информатики, занимаю-
щаяся изучением структуры и общих свойств информации и ин-
формационных процессов, разработкой общих принципов пост-
роения информационной техники и технологии. Она основана на
использовании математических методов и включает в себя такие
основные математические разделы, как теория алгоритмов и ав-
томатов, теория информации и теория кодирования, теория фор-
мальных языков и грамматик, исследование операций и др.
24
Теоретическая
информатика
Основные
разделы:
теория алгорит-
мов и автоматов;
теория
информации;
теория
кодирования;
математическая
логика;
теория
формальных
языков
и грамматик;
исследование
операций и др.
Средства информатизации
технические программные
средства обработки информации; средства передачи информации; средства хранения информации; средства представления информации системное программное обеспечение; инструментарий технологии программирования; пакеты прикладных программ
Информационные системы и технологии
• ввода/вывода, сбора, хранения, передачи и обработки данных;
• подготовки текстовых и графических документов;
• защиты информации;
• программирования, проектирования, моделирования, обучения,
диагностики, управления объектами, процессами, системами
(информационно-справочные, информационно-поисковые системы,
современные глобальные системы хранения и поиска информации,
включая Интернет и др.)
Рис. 1.5. Структура информатики
Средства информатизации (технические и программные)—раздел,
занимающийся изучением общих принципов построения вычисли-
тельных устройств и систем обработки и передачи данных, а также
вопросов, связанных с разработкой систем программного обеспечения.
Информационные системы и технологии — раздел информа-
тики, связанный с решением вопросов по анализу потоков инфор-
мации, их оптимизации, структурировании в различных сложных
системах, разработкой принципов реализации в данных системах
информационных процессов.
25
Иногда информационные технологии называют компьютерны-
ми технологиями или прикладной информатикой. Само слово
«компьютер» произошло от английского computer, переводимого
на русский язык как «вычислитель», или электронная вычислитель-
ная машина — ЭВМ.
Технические (аппаратные) средства, или аппаратура компьюте-
ров, в английском языке обозначаются словом hardware, которое пе-
реводится как «твердые изделия». Для обозначения программных
средств, под которыми понимается совокупность всех программ, ис-
пользуемых компьютерами, и область деятельности по их созданию
и применению, используется слово software (в переводе — «мягкие
изделия»), которое подчеркивает способность программного обес-
печения модифицироваться, приспосабливаться и развиваться.
Изучением закономерностей и форм движения информации
в обществе, возникающих в современном обществе информаци-
онных, психологических, социально-экономических проблем и
методов их решения занимается новое направление исследований
в области информатики — социальная информатика.
Информатика — очень широкая сфера научных знаний, возник-
шая на стыке нескольких фундаментальных и прикладных дисциплин.
Фундаментальная наука — наука, изучающая объективные зако-
ны природы и общества, осуществляющая теоретическую системати-
зацию знаний о действительности.
К фундаментальным принято относить те науки, основные по-
нятия которых носят общенаучный характер, используются во мно-
гих других науках и видах деятельности.
Как комплексная научная дисциплина информатика связана
с (рис. 1.6):
философией и психологией — через учение об информации
и теорию познания;
математикой — через теорию математического моделирова-
ния, дискретную математику, математическую логику и те-
орию алгоритмов;
лингвистикой — через учение о формальных языках и о зна-
ковых системах;
кибернетикой — через теорию информации и теорию уп-
равления;
физикой и химией, электроникой и радиотехникой — через
«материальную» часть компьютера и информационных систем.
26
Рис. 1.6. Связь информатики с другими науками
Роль информатики в развитии общества чрезвычайно велика.
Она является научным фундаментом процесса информатизации
общества. С ней связано прогрессивное увеличение возможнос-
тей компьютерной техники, развитие информационных сетей,
создание новых информационных технологий, которые приводят
к значительным изменениям во всех сферах общества: в произ-
водстве, науке, образовании, медицине и т. д.
Контрольные вопросы =
1. Какие определения понятия «информация» Вы знаете?
2. Назовите формы отражения в живой и неживой природе.
27
3. Назовите основные структурные компоненты процесса обмена ин-
формацией.
4. Какие функции и формы движения в обществе имеет информация?
5. Что такое информационный процесс?
6. Назовите основные этапы обращения информации в автоматизи-
рованных системах.
7. Что такое данные?
8. Назовите состав и содержание общих законов управления.
9. Что такое информационный ресурс и в чем его особенности?
10. В чем состоит процесс информатизации?
11. В чем отличие процессов компьютеризации и информатизации?
12. Определите суть информационных технологий.
13. Какие негативные последствия несет с собой появление новых
информационных технологий?
14. Расскажите об истории развития средств информационного труда.
15. Как и для чего появилась информатика?
16. Дайте определение информатики.
17. Какова общая структура современной информатики?
18. Как информатика связана с другими науками?
Тлава 2
Количество и качество информации
2.1. УРОВНИ ПРОБЛЕМ ПЕРЕДАЧИ ИНФОРМАЦИИ
При реализации информационных процессов всегда происхо-
дит перенос информации в пространстве и времени от источника
информации к приемнику (получателю) (см. рис. 1.2). При этом для
передачи информации используют различные знаки или симво-
лы, например естественного или искусственного (формального)
языка, позволяющие выразить ее в некоторой форме, называемой
сообщением.
Сообщение — форма представления информации в виде совокуп-
ности знаков (символов), используемая для передачи.
Сообщение как совокупность знаков с точки зрения семиоти-
ки (от греч. semeion — знак, признак) — науки, занимающейся ис-
следованием свойств знаков и знаковых систем, может изучаться
на трех уровнях [8]:
синтаксическом, где рассматриваются внутренние свойства
сообщений, т. е. отношения между знаками, отражающие
структуру данной знаковой системы. Внешние свойства изу-
чают на семантическом и прагматическом уровнях;
семантическом, где анализируются отношения между зна-
ками и обозначаемыми ими предметами, действиями, каче-
ствами, т. е. смысловое содержание сообщения, его отноше-
ние к источнику информации;
прагматическом, где рассматриваются отношения между со-
общением и получателем, т. е. потребительское содержание
сообщения, его отношение к получателю.
Таким образом, учитывая определенную взаимосвязь проблем
передачи информации с уровнями изучения знаковых систем, их
разделяют на три уровня: синтаксический, семантический и праг-
матический.
29
Проблемы синтаксического уровня касаются создания теоре-
тических основ построения информационных систем, основные
показатели функционирования которых были бы близки к предель-
но возможным, а также совершенствования существующих сис-
тем с целью повышения эффективности их использования. Это
чисто технические проблемы совершенствования методов пере-
дачи сообщений и их материальных носителей — сигналов. На этом
уровне рассматривают проблемы доставки получателю сообщений
как совокупности знаков, учитывая при этом тип носителя и спо-
соб представления информации, скорость передачи и обработки,
размеры кодов представления информации, надежность и точность
преобразования этих кодов и т. п., полностью абстрагируясь от
смыслового содержания сообщений и их целевого предназначе-
ния. На этом уровне информацию, рассматриваемую только с син-
таксических позиций, обычно называют данными, так как смыс-
ловая сторона при этом не имеет значения.
Современная теория информации исследует в основном про-
блемы именно этого уровня. Она опирается на понятие «количе-
ство информации», являющееся мерой частоты употребления зна-
ков, которая никак не отражает ни смысла, ни важности переда-
ваемых сообщений. В связи с этим иногда говорят, что теория ин-
формации находится на синтаксическом уровне.
Проблемы семантического уровня связаны с формализацией
и учетом смысла передаваемой информации, определения степе-
ни соответствия образа объекта и самого объекта. На данном уров-
не анализируются те сведения, которые отражает информация,
рассматриваются смысловые связи, формируются понятия и пред-
ставления, выявляется смысл, содержание информации, осуществ-
ляется ее обобщение.
Проблемы этого уровня чрезвычайно сложны, так как смысло-
вое содержание информации больше зависит от получателя, чем
от семантики сообщения, представленного на каком-либо языке.
На прагматическом уровне интересуют последствия от полу-
чения и использования данной информации потребителем. Про-
блемы этого уровня связаны с определением ценности и полезно-
сти использования информации при выработке потребителем ре-
шения для достижения своей цели. Основная сложность здесь со-
стоит в том, что ценность, полезность информации может быть
совершенно различной для различных получателей и, кроме того,
она зависит от ряда факторов, таких, например, как своевремен-
30
ность ее доставки и использования. Высокие требования в от-
ношении скорости доставки информации часто диктуются тем,
что управляющие воздействия должны осуществляться в реаль-
ном масштабе времени, т. е. со скоростью изменения состояния
управляемых объектов или процессов. Задержки в доставке или
использовании информации могут иметь катастрофические по-
следствия.
2.2. МЕРЫ ИНФОРМАЦИИ
Для каждого из рассмотренных выше уровней проблем переда-
чи информации существуют свои подходы к измерению количе-
ства информации и свои меры информации. Различают соответ-
ственно меры информации синтаксического уровня, семантичес-
кого уровня и прагматического уровня.
2.2.1. Меры информации синтаксического уровня
Количественная оценка информации этого уровня не связана
с содержательной стороной информации, а оперирует с обезли-
ченной информацией, не выражающей смыслового отношения
к объекту. В связи с этим данная мера дает возможность оценки
информационных потоков в таких разных по своей природе объек-
тах, как системы связи, вычислительные машины, системы управ-
ления, нервная система живого организма и т. п.
Для измерения информации на синтаксическом уровне вводят-
ся два параметра: объем информации (данных) — Vg (объемный
подход) и количество информации — I (энтропийный подход).
Объем информации Vg (объемный подход). При реализации ин-
формационных процессов информация передается в виде сообще-
ния, представляющего собой совокупность символов какого-либо
алфавита. При этом каждый новый символ в сообщении увеличи-
вает количество информации, представленной последовательнос-
тью символов данного алфавита. Если теперь количество инфор-
мации, содержащейся в сообщении из одного символа, принять за
единицу, то объем информации (данных) V в любом другом сооб-
щении будет равен количеству символов (разрядов) в этом сооб-
щении. Так как одна и та же информация может быть представле-
на многими разными способами (с использованием разных алфа-
31
битов), то и единица измерения информации (данных) соответ-
ственно будет меняться.
Так, в десятичной системе счисления один разряд имеет вес,
равный 10, и соответственно единицей измерения информации
будет дит (десятичный разряд). В этом случае сообщение в виде п-
разрядного числа имеет объем данных Vg — п дит. Например, четы-
рехразрядное число 2003 имеет объем данных V = 4 дит.
В двоичной системе счисления один разряд имеет вес, равный
2, и соответственно единицей измерения информации будет — бит
(bit — binary digit — двоичный разряд). В этом случае сообщение в
виде n-разрядного числа имеет объем данных V = п бит. Напри-
мер, восьмиразрядный двоичный код 11001011 имеет объем дан-
ных V = 8 бит.
д
В современной вычислительной технике наряду с минимальной
единицей измерения данных «бит» широко используется укруп-
ненная единица измерения «байт», равная 8 бит. При работе с боль-
шими объемами информации для подсчета ее количества приме-
няют более крупные единицы измерения, такие как килобайт
(Кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт):
1 Кбайт = 1024 байт = 210 байт;
1 Мбайт = 1024 Кбайт = 220 байт = 1 048 576 байт;
1 Гбайт = 1024 Мбайт = 230 байт = 1 073 741 824 байт;
1 Тбайт = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт.
Следует обратить внимание, что в системе измерения двоичной
(компьютерной) информации, в отличие от метрической системы,
единицы с приставками «кило», «мега» и т. д. получаются путем
умножения основной единицы не на 103= 1000, 106= 1000 000 ит. д.,
а на 2,0= 1024, 220= 1048576 и т. д.
Количество информации I (энтропийный подход). В теории ин-
формации и кодирования принят энтропийный подход к измере-
нию информации. Этот подход основан на том, что факт получе-
ния информации всегда связан с уменьшением разнообразия или
неопределенности (энтропии) системы. Исходя из этого количе-
ство информации в сообщении определяется как мера уменьше-
ния неопределенности состояния данной системы после получе-
ния сообщения. Неопределенность может быть интерпретирова-
на в смысле того, насколько мало известно наблюдателю о данной
системе. Как только наблюдатель выявил что-нибудь в физичес-
кой системе, энтропия системы снизилась, так как для наблюдате-
ля система стала более упорядоченной.
32
Таким образом, при энтропийном подходе под информацией
понимается количественная величина исчезнувшей в ходе како-
го-либо процесса (испытания, измерения и т. д.) неопределеннос-
ти. При этом в качестве меры неопределенности вводится энтро-
пия Н, а количество информации равно:
I = H —Н , (1)
где Нарг — априорная энтропия о состоянии исследуемой системы
или процесса.
HQps— апостериорная энтропия.
Апостериори (от лат. a posteriori — из последующего) — проис-
ходящее из опыта (испытания, измерения).
Априори — (от лат. a priori — из предшествующего) — понятие,
характеризующее знание, предшествующее опыту (испытанию),
и независимое от него.
В случае когда в ходе испытания имевшаяся неопределенность
снята (получен конкретный результат, т. е. Haps = 0), количество
полученной информации совпадает с первоначальной энтропией
I = Нарг’
Рассмотрим в качестве исследуемой системы дискретный ис-
точник информации (источник дискретных сообщений), под ко-
торым будем понимать физическую систему, имеющую конечное
множество возможных состояний {а;}, / = 1, т .
Все множество А = { at, а2, ..., аш} состояний системы в теории
информации называют абстрактным алфавитом, или алфавитом
источника сообщений.
Отдельные состояния at, а? ат называют буквами или симво-
лами алфавита.
Такая система может в каждый момент времени случайным обра-
зом принять одно из конечных множеств возможных состояний —
а. При этом говорят, что различные состояния реализуются вслед-
ствие выбора их источником.
Поскольку одни состояния выбираются источником чаще, а
другие реже, то в общем случае он характеризуется ансамблем А,
т. е. полной совокупностью состояний с вероятностями их появле-
ния, составляющими в сумме единицу:
3 А-210
33
. ( a, a2 ... aN ] "
P2-^]'причем2л" • (21)
Введем меру неопределенности выбора состояния источника.
Ее можно рассматривать и как меру количества информации, по-
лучаемой при полном устранении неопределенности относитель-
но состояния источника. Мера должна удовлетворять ряду есте-
ственных условий. Одним из них является необходимость моно-
тонного возрастания с увеличением возможностей выбора, т. е. чис-
ла возможных состояний источника N, причем недопустимые со-
стояния (состояния с вероятностями, равными нолю) не долж-
ны учитываться, так как они не меняют неопределенности.
Ограничиваясь только этим условием, за меру неопределенно-
сти можно было бы взять число состояний, предположив, что они
равновероятны. Однако в этом случае при N= 1, когда неопреде-
ленность отсутствует, такая мера давала бы значение, равное еди-
нице. Кроме того, она не отвечает требованию аддитивности,
состоящему в следующем.
Если два независимых источника с числом равновероятных со-
стояний N и М рассматривать как один источник, одновременно
реализующий пары состояний nf,m., то естественно предположить,
что неопределенность объединенного источника должна равнять-
ся сумме неопределенностей исходных источников. Поскольку
общее число состояний объединенного источника равно NM, то
искомая функция должна удовлетворять условию:
f(MN) = f(M) + f(N). (2.2)
Соотношение (2.2) выполняется, если в качестве меры неопре-
деленности источника с равновероятными состояниями и харак-
теризующего его ансамбля А принять логарифм числа состояний:
Н(А) = logN. (2.3)
Тогда при N= 1 Н(А) = 0 и требование аддитивности выполняется.
Указанная мера была предложена американским ученым
Р. Хартли в 1928 г. Основание логарифма в формуле (2.3) не имеет
принципиального значения и определяет только масштаб или еди-
ницу измерения. В зависимости от основания логарифма приме-
няют следующие единицы измерения:
1. Биты — при этом основание логарифма равно 2:
Н(А) = log2N.
(2.4)
34
2. Наты — при этом основание логарифма равно е:
H = InN;
3. Диты — при этом основание логарифма равно 10:
H = IgN.
Так как современная информационная техника базируется на
элементах, имеющих два устойчивых состояния, то в информати-
ке в качестве меры неопределенности обычно используют форму-
лу (2.4). При этом единица неопределенности называется двоич-
ной единицей, или битом, и представляет собой неопределенность
выбора из двух равновероятных событий.
Формулу (2.4) можно получить эмпирически: для снятия не-
определенности в ситуации из двух равновероятных событий не-
обходим один опыт и соответственно один бит информации, при
неопределенности, состоящей из четырех равновероятных собы-
тий, достаточно двух бит информации, чтобы угадать искомый
факт. Эти рассуждения можно продолжить: 3 бита информации
соответствуют неопределенности из 8 равновероятных событий,
4 бита — 16 равновероятных событий и т. д. Например, для опре-
деления карты из колоды, состоящей из 32 карт, достаточно 5 бит
информации, т. е. достаточно задать 5 вопросов с ответами «да»
или «нет», чтобы определить искомую карту.
Таким образом, если сообщение указывает на один из п равно-
вероятных вариантов, то оно несет количество информации, рав-
ное log2n. Действительно, из наших примеров 1од232 = 5,1од216 = 4,
1од28 = 3 и т. д. Ту же формулу можно словесно выразить иначе:
количество информации равно степени, в которую необходимо
возвести число 2, чтобы получить число равновероятных вариан-
тов выбора, т. е. 2‘= 16, где /=4 (бита).
Предложенная мера позволяет решать определенные практи-
ческие задачи, когда все возможные состояния источника инфор-
мации имеют одинаковую вероятность.
В общем случае степень неопределенности реализации состоя-
ния источника информации зависит не только от числа состояний,
но и от вероятностей этих состояний. Если источник информации
имеет, например, два возможных состояния с вероятностями 0,99
и 0,01, то неопределенность выбора у него значительно меньше,
чем у источника, имеющего два равновероятных состояния, так
как в этом случае результат практически предрешен (реализация
состояния, вероятность которого равна 0,99).
35
Американский ученый К. Шеннон обобщил понятие меры нео-
пределенности выбора Н на случай, когда Н зависит не только от
числа состояний, но и от вероятностей этих состояний (вероятно-
стей р выбора символов а. алфавита А). Эту меру, представляю-
щую собой неопределенность, приходящуюся в среднем на одно
состояние, называют энтропией дискретного источника инфор-
мации.
Н = -Zp,log р,..
/=1
(2-5)
Если снова ориентироваться на измерение неопределенности
в двоичных единицах, то основание логарифма следует принять
равным двум.
N
н = -Xp,log2p,..
/=1
(2.6)
При равновероятных выборах всеp=l/Nn формула (2.6) пре-
образуется в формулу Р. Хартли (2.3):
w 111
Н = -Zp. log p,=-N—log — = -N—(log 1 - log N) = log2 N.
/=1 2 N 2 N N 2 2
Предложенная мера была названа энтропией не случайно. Дело
в том, что формальная структура выражения (2.5) совпадает с энт-
ропией физической системы, определенной ранее Больцманом.
Согласно второму закону термодинамики энтропия Н замкнутого
пространства определяется выражением:
1 лг т.
Н =--------Дли, In------ глр
Мп — число молекул в данном пространстве; т. — число молекул,
обладающих скоростью v. + Av. Так как т./Мп есть вероятность
того, что молекула имеет скорость v.+Av, то Н можно записать
N
как И = -£ Pjlnp^ Данная формула полностью совпадает с (2.5) —
/=1
в обоих случаях величина Н характеризует степень разнообразия
системы.
Используя формулы (2.4) и (2.6), можно определить избыточ-
ность D алфавита источника сообщений — А, которая показыва-
36
ет, насколько рационально применяются символы данного алфа-
вита:
D= [HmJA)~H(A)]/[HmJA)], (2.7)
где Нтах(А} — максимально возможная энтропия, определяемая по
формуле (2.4);
Н(А) — энтропия источника, определяемая по формуле (2.6).
Суть данной меры заключается в том, что при равновероятном
выборе ту же информационную нагрузку на знак можно обеспе-
чить, используя алфавит меньшего объема, чем в случае с нерав-
новероятным выбором.
Пример. Согласно экспериментальным данным безусловные
вероятности букв русского и английского алфавитов характери-
зуются табл. 2.1 и 2.2 соответственно.
Требуется найти энтропии источников А1 и А2, выдающих текст
из букв русского и английского алфавитов соответственно, при от-
сутствии статистических связей между буквами, а также вычис-
лить избыточность источников, выдающих тексты, обусловленную
неравновероятностью выбора букв.
Талица 2.1 Таблица 2.2
Бук- ва Вероят- ность Бук- ва Вероят- ность Бук- ва Вероят- ность
Про- бел 0,175 к 0,028 ч 0,012
0 0,090 м 0,026 и 0,010
Е 0,072 д 0,025 X 0,009
А 0,062 п 0,023 ж 0,007
И 0,062 У 0,021 ю 0,006
т 0,053 я 0,018 ш 0,006
Н 0,053 ы 0,016 ц 0,004
С 0,045 3 0,016 щ 0,003
Р 0,040 ь, ъ 0,014 э 0,002
В 0,038 Б 0,014 ф 0,002
Л 0,035 Г 0,013
Бук- ва Вероят- ность Бук- ва Вероят- ность Бук- ва Вероят- ность
Про- бел 0,2 н 0,047 W 0,012
Е 0,105 D 0,035 G 0,011
Т 0,072 L 0,028 В 0,010
О 0,065 С 0,023 V 0,008
F 0,063 F 0,023 К 0,003
N 0,058 и 0,023 X 0,001
I 0,055 м 0,021 J 0,001
R 0,052 р 0,018 Q 0,001
S 0,052 Y 0,012 Z 0,001
Решение. Найдем энтропии источников А1 и А2, используя фор-
мулу (2.6).
37
Н(А1) = — 0,1751og20,175-0,091og20,09-...-0,0021og20,002 = 4,35
(бит/символ).
Н(А2) = — 0,21од20,2 — 0,1051од20,105-...-0,0011од20,001 » 4,03
(бит/символ).
По формуле (2.4) находим:
Нтах(А1) = 1од232 = 5 (бит/символ).
Нтах(А2) = 1од227 = 4,75 (бит/символ).
Избыточность источников находим по формуле (2.7):
£>(А1) = (5 —4,35)/5 = 0,13.
О(А2) = (4,75 —• 4,03)/4,75 = 0,15.
Полученные результаты позволяют сделать вывод о том, что
избыточность, а следовательно, и неравномерность распределения
вероятностей букв источника А2 — латинского алфавита больше,
чем у источника А1 — русского алфавита.
2.2.2. Меры информации семантического уровня
Для измерения смыслового содержания информации, т. е. ее
количества на семантическом уровне, наибольшее распростране-
ние получила тезаурусная мера, которая связывает семантические
свойства информации со способностью пользователя принимать
поступившее сообщение [14]. Действительно, для понимания и ис-
пользования полученной информации получатель должен обладать
определенным запасом знаний. Полное незнание предмета не по-
зволяет извлечь полезную информацию из принятого сообще-
ния об этом предмете. По мере роста знаний о предмете растет и
количество полезной информации, извлекаемой из сообщения.
Если назвать имеющиеся у получателя знания о данном пред-
мете «тезаурусом» (т. е. неким сводом слов, понятий, названий
объектов, связанных смысловыми связями), то количество инфор-
мации, содержащееся в некотором сообщении, можно оценить
степенью изменения индивидуального тезауруса под воздействи-
ем данного сообщения.
Тезаурус — совокупность сведений, которыми располагает пользо-
ватель или система.
Иными словами, количество семантической информации, из-
влекаемой получателем из поступающих сообщений, зависит от
38
степени подготовленности его тезауруса для восприятия такой
информации.
В зависимости от соотношений между смысловым содержани-
ем информации S и тезаурусом пользователя Sp изменяется коли-
чество семантической информации 1с, воспринимаемой пользова-
телем и включаемой им в дальнейшем в свой тезаурус. Характер
такой зависимости показан на рис. 2.1. Рассмотрим два предель-
ных случая, когда количество семантической информации 1с рав-
но 0:
при Sp = 0 пользователь не воспринимает (не понимает) по-
ступающую информацию;
при Sp —> оо пользователь «все знает», и поступающая ин-
формация ему не нужна.
Рис. 2.1. Зависимость количества семантической информации,
воспринимаемой потребителем, от его тезауруса Ic = f(Sp)
Максимальное количество семантической информации потре-
битель приобретает при согласовании ее смыслового содержания
S со своим тезаурусом Sp (Sp = Sp opt), когда поступающая ин-
формация понятна пользователю и несет ему ранее неизвестные
(отсутствующие в его тезаурусе) сведения.
Следовательно, количество семантической информации в со-
общении, количество новых знаний, получаемых пользователем,
является величиной относительной. Одно и то же сообщение мо-
жет иметь смысловое содержание для компетентного пользовате-
ля и быть бессмысленным для пользователя некомпетентного.
При оценке семантического (содержательного) аспекта инфор-
мации необходимо стремиться к согласованию величин S и Sp.
39
Относительной мерой количества семантической информации
может служить коэффициент содержательности С, который оп-
ределяется как отношение количества семантической информа-
ции к ее объему:
С=//Уд
С Д.
Еще один подход к семантическим оценкам информации, раз-
виваемый в рамках науковедения, заключается в том, что в каче-
стве основного показателя семантической ценности информации,
содержащейся в анализируемом документе (сообщении, публика-
ции), принимается количество ссылок на него в других докумен-
тах. Конкретные показатели формируются на основе статистичес-
кой обработки количества ссылок в различных выборках.
2.2.3. Меры информации прагматического уровня
Эта мера определяет полезность информации (ценность) для
достижения пользователем поставленной цели. Она также вели-
чина относительная, обусловленная особенностями использования
этой информации в той или иной системе.
Одним из первых отечественных ученых к этой проблеме об-
ратился А.А. Харкевич, который предложил принять за меру цен-
ности информации количество информации, необходимое для до-
стижения поставленной цели, т. е. рассчитывать приращение ве-
роятности достижения цели. Так, если до получения информации
вероятность достижения цели равнялась а после ее получения —
pt, то ценность информации определяется как логарифм отноше-
ния р/р0-.
р,
I = log2рх - log2p0 = log2 — (2.8)
Pq
Таким образом, ценность информации при этом измеряется
в единицах информации, в данном случае в битах.
Выражение (2.8) можно рассматривать как результат норми-
ровки числа исходов. В пояснение на рис. 2.2 приведены три схе-
мы, на которых приняты одинаковые значения числа исходов 2
и 6 для точек 0 и 1 соответственно. Исходное положение — точка 0.
На основании полученной информации совершается переход
в точку 1. Цель обозначена крестиком. Благоприятные исходы
40
изображены линиями, ведущими к цели. Определим ценность по-
лученной информации во всех трех случаях:
а) число благоприятных исходов равно трем: р=1/2, р, = 3/6 = 1/2
и, следовательно,
/=log2(p/p0) = log2l = 0;
б) имеется один благоприятный исход: р=1/2, pt = 1/6,
I = log2 — = —log2 3 = -1,58;
в) число благоприятных исходов равно четырем: рд = 1/2, р( =
= 4/6 = 2/3,
Рис. 2.2. К вопросу о ценности информации:
а) I = 0; б) I = — 1,58 (дезинформация); в) / = 0,42
В примере б) получена отрицательная ценность информации
(отрицательная информация). Такую информацию, увеличива-
ющую исходную неопределенность и уменьшающую вероят-
ность достижения цели, называют дезинформацией. Таким об-
разом, в примере б) мы получили дезинформацию в 1,58 двоич-
ной единицы.
Дальнейшее развитие данного подхода базируется на статис-
тической теории информации и теории решений. Сущность мето-
да состоит в том, что, кроме вероятностных характеристик не-
определенности объекта, после получения информации вводятся
функции штрафов или потерь и оценка информации производит-
ся в результате минимизации потерь. Максимальной ценностью
41
обладает то количество информации, которое уменьшает потери
до ноля при достижении поставленной цели.
2.3. КАЧЕСТВО ИНФОРМАЦИИ
Эффективность применения и качество функционирования
любых систем во многом определяется качеством информации, на
основе которой принимаются управляющие решения. Составля-
ющие качества информация отражены на рис. 2.3.
Качество информации — совокупность свойств информации, ха-
рактеризующих степень ее соответствия потребностям (целям, цен-
ностям) пользователей (средств автоматизации, персонала и др.).
Выделяют внутреннее качество — содержательность (присущее
собственно информации и сохраняющееся при ее переносе в дру-
гую систему) и внешнее — защищенность (присущее информации,
находящейся или используемой только в определенной системе) [16].
Рис. 2.3. Составляющие качества информации
42
Содержательность информации — совокупность сведений о
конкретном объекте (системе) или процессе, содержащаяся в сооб-
щениях и воспринимаемая получателем. Содержательность отра-
жает семантическую емкость информации, содержащейся в инфор-
мационных массивах (массивах данных, массивах программ, сооб-
щениях, фактах). Содержательная информация используется, как
правило, для выработки и принятия управляющего воздействия.
Содержательность информации определяется такими свойства-
ми, как значимость и кумулятивность.
Значимость информации — свойство информации сохранять
ценность для потребителя с течением времени, т. е. не подвергать-
ся «моральному» старению.
Составляющими значимости являются полнота и идентичность.
Полнота информации — свойство содержательной информа-
ции, характеризуемое мерой ее достаточности для решения опре-
деленных задач. Полнота (достаточность) информации означает,
что она обеспечивает принятие правильного (оптимального) реше-
ния. Из этого следует, что данное свойство является относитель-
ным: полнота информации оценивается относительно вполне оп-
ределенной задачи или группы задач. Поэтому, чтобы иметь воз-
можность определить показатель полноты информации, необхо-
димо для каждой существенно значимой задачи или группы задач
иметь перечень тех сведений, которые требуются для их решения.
Как неполная, т. е. недостаточная для принятия правильного ре-
шения, так и избыточная информации снижают эффективность
принимаемых пользователем решений.
Идентичность — свойство, заключающееся в соответствии
содержательной информации состоянию объекта. Нарушение
идентичности связано с техническим (по рассогласованию призна-
ков) старением информации, при котором происходит расхожде-
ние реальных признаков объектов и тех же признаков, отображен-
ных в информации. Обычно закон старения информации представ-
ляют в виде рис. 2.4.
На данном рисунке tg обозначает момент времени генерирова-
ния (получения) оцениваемой информации, при этом коэффици-
ент К, характеризующий идентичность информации, равен 1. За-
кон старения информации определяется четырьмя характерными
интервалами:
Atj— продолжительностью времени, в течение которого оце-
ниваемая информация полностью сохраняет свою идентичность;
43
At, — продолжительностью времени, в течение которого иден-
тичность информации падает, но не более чем на одну четверть;
At3 — продолжительностью времени, в течение которого иден-
тичность информации падает наполовину;
At4 — продолжительностью времени, в течение которого иден-
тичность информации падает на три четверти.
Рис. 2.4. Общий вид закона старения информации
Кумулятивность информации — свойство содержательной
информации, заключенной в массиве небольшого объема, доста-
точно полно отображать действительность.
Задачу обеспечения кумулятивности информации можно ре-
шать без учета и с учетом опыта и квалификации конкретного по-
требителя информации, применяя соответственно формально-тех-
нические и социально-психологические приемы. К числу формаль-
но-технических приемов относится, например, агрегирование —
получение сводных показателей различного уровня обобщения или
выбор отдельных показателей из массивов исходных данных. Эти
и другие формальные приемы направлены на построение моделей
типа «многое в одном», когда действительность отображается
с помощью малого числа символов. Такие модели называются
44
гомоморфными, а соответствующее свойство — гомоморфизмом
информации. Это формально-техническая составляющая кумуля-
тивности информации.
Гомоморфизм информации — свойство содержательной инфор-
мации, связанное с достаточно полным отображением действи-
тельности, представленной информационными массивами большо-
го объема, с помощью малого числа информационных единиц (сим-
волов) на основе соответствующих моделей агрегирования.
Информационное обеспечение конкретного потребителя мо-
жет осуществляться с учетом его опыта, квалификации и других
свойств, а также с учетом решаемых им задач. Информация, спе-
циально отобранная для конкретного потребителя, обладает опре-
деленным свойством — избирательностью. Это социально-психо-
логическая составляющая свойства кумулятивности.
Избирательность информации — свойство содержательной
информации, заключающееся в достаточно полном отображении
действительности, представленной информационными массивами
большого объема, с помощью малого числа информационных еди-
ниц (символов) на основе учета квалификации, опыта и других
качеств конкретного потребителя.
Защищенность отражает внешнее качество информации, оп-
ределяемое совокупностью свойств информации, обеспечиваемых
системой контроля и защиты информации (КЗИ) в конкретной
информационной системе. Основными из них являются свойства,
заключающиеся в способности не допускать случайного или целе-
направленного искажения или разрушения, раскрытия или моди-
фикации информационных массивов, соответственно достовер-
ность, конфиденциальность и сохранность информации. При пе-
реносе информации в другую систему (среду) эти свойства исче-
зают.
Достоверность информации — свойство информации, харак-
теризуемое степенью соответствия (в пределах заданной точнос-
ти) реальных информационных единиц (символов, знаков, запи-
сей, сообщений, информационных массивов и т. д.) их истинному
значению и определяемое способностью КЗИ обеспечить отсут-
ствие ошибок переработки информации, т. е. не допустить сниже-
ния ценности информации при принятии управленческих реше-
ний, искажений информационных массивов (ИМ), их смыслового
значения, замены единичных символов ИМ и других из-за несо-
вершенства организации (структуры) процесса переработки,
45
несовершенства алгоритмов, ненадежной работы аппаратно-про-
граммных средств, ошибок пользователей и т. д.
Требуемый уровень достоверности информации достигается
путем внедрения методов контроля и защиты информации на всех
стадиях ее переработки, повышением надежности комплекса тех-
нических и программных средств информационной системы, а
также административно-организационными мерами (моральным
и материальным стимулированием, направленным на снижение
числа ошибок, улучшением условий труда персонала и др.).
Критериями оптимальности при этом, как правило, являются:
минимизация вероятности искажения единичного массива
информации;
" максимизация достоверности переработки информации как
некоторой функции вероятности ошибки;
• минимизация времени переработки ИМ и материальных зат-
рат при ограничении на достоверность;
* минимизация суммарного среднего времени на обработку,
контроль и исправление ИМ;
* минимизация суммарных потерь с учетом затрат на разра-
ботку и функционирование структур контроля, исправление
ошибок и на потери в информационной системе (ИС) при
использовании недостоверной информации и т. п.
Конфиденциальность информации — свойство информации,
позволяющее сохранять предоставленный ей статус. Конфиден-
циальность информации характеризуется такими показателями,
как доступность, скрытность и имитостойкость информации.
Доступность информации характеризуется степенью разгра-
ничения действий объектов информационной системы (операто-
ров, задач, устройств, программ, подсистем и др.) и заключается в
возможности использования ИМ по требованию объектов систе-
мы, имеющих соответствующие полномочия (мандаты).
Скрытность информации характеризуется степенью маски-
ровки информации и отражает ее способность противостоять рас-
крытию смысла ИМ (семантическая скрытность на основе обра-
тимых преобразований информации), определению структуры
хранимого ИМ или носителя (сигнала-переносчика) передавае-
мого ИМ (структурная скрытность на основе необратимых пре-
образований, использования спецаппаратуры, различных форм
сигналов-переносчиков, видов модуляции и др.) и установлению
факта передачи ИМ по каналам связи (энергетическая скрыт-
46
ность на основе применения широкополосных сигналов-перенос-
чиков ИМ, организации периодического маскирующего обмена
ИМ и др.).
Имитостойкость информации определяется степенью ее защи-
щенности от внедрения ИМ, имитирующих авторизованные (за-
регистрированные) массивы, и заключается в способности не до-
пустить навязывания дезинформации и нарушения нормально-
го функционирования информационной системы.
Требуемый уровень конфиденциальности ИМ достигается пу-
тем дополнительных преобразований (семантических, криптогра-
фических и др.) информации, контроля полномочий программно-
технических средств, ресурсов ИС и лиц (операторов, персонала,
пользователей и др.), взаимодействующих со средствами автома-
тизации и разграничения доступа к ИМ. Критериями оптимально-
сти при этом, как правило, являются:
минимизация вероятности преодоления («взлома») защиты;
максимизация ожидаемого безопасного времени до «взло-
ма» подсистемы защиты;
минимизация суммарных затрат (интеллектуальных, финан-
совых, материальных, временных и др.) на разработку и эк-
сплуатацию подсистемы КЗИ при ограничениях на вероят-
ность несанкционированного доступа к ресурсам ИС;
минимизация суммарных потерь от «взлома» защиты и зат-
рат на разработку и эксплуатацию соответствующих элемен-
тов подсистемы КЗИ и т. п.
Сохранность информации — свойство информации, харак-
теризуемое степенью готовности определенных ИМ к целево-
му применению и определяемое способностью КЗИ обеспечить
постоянное наличие и своевременное предоставление ИМ, не-
обходимых для автоматизированного решения целевых и функ-
циональных задач системы, т. е. не допускать разрушения ИМ
из-за несовершенства носителей, механических повреждений,
неправильной эксплуатации, износа и старения аппаратных
средств, ошибок персонала и несанкционированных корректи-
ровок, недостатков в программных средствах и т. д. Основными
показателями сохранности являются целостность и готовность
информации.
Целостность информации характеризуется степенью аутентич-
ности (подлинности) ИМ в информационной базе и исходных до-
кументах (сообщениях) и определяется способностью КЗИ обес-
47
печить, насколько это возможно, физическое наличие информа-
ционных единиц в информационной базе в любой момент време-
ни, т. е. не допустить случайных искажений и разрушения ИМ из-
за дефектов и сбоев аппаратных средств, действия «компьютер-
ных вирусов», ошибок оператора (при вводе информации в инфор-
мационную базу или обращении к ней), ошибок в программных
средствах (операционных системах, СУБД, комплексах приклад-
ных программ и др.).
Готовность информации характеризуется степенью работо-
способности ИМ при выполнении целевых и функциональных за-
дач системы и определяется возможностью КЗИ обеспечить сво-
евременное предоставление необходимых неразрушенных ИМ.
Необходимый уровень сохранности ИМ достигается путем вве-
дения специальной организации хранения и подготовки, регене-
рации и восстановления ИМ, использования дополнительных ре-
сурсов для их резервирования, что позволяет значительно умень-
шить влияние разрушающих факторов на эффективность функ-
ционирования ИС в целом. Основными критериями оптимальнос-
ти при этом являются:
* максимизация вероятности успешного решения определен-
ной частной задачи системы при наличии соответствующих
ИМ, их дубликатов, копий;
* максимизация вероятности восстановления ИМ;
минимизация среднего времени решения задачи системы;
* минимизация среднего времени восстановления ИМ;
максимизация вероятности сохранности ИМ за фиксирован-
ный интервал времени их эксплуатации;
минимизация стоимостных затрат на дополнительные носи-
тели информации для размещения резервных ИМ, потерь от
разрушения ИМ и т. п.
2.4. ВИДЫ И ФОРМЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ
В ИНФОРМАЦИОННЫХ СИСТЕМАХ
Все многообразие окружающей нас информации можно клас-
сифицировать по различным признакам. Так, по признаку «об-
ласть возникновения» информацию, отражающую процессы, яв-
ления неодушевленной природы, называют элементарной, или
механической, процессы животного и растительного мира —
48
биологической, человеческого общества — социальной. Инфор-
мацию, создаваемую и используемую человеком, по обществен-
ному назначению можно разбить на три вида: личная, массовая
и специальная. Личная информация предназначается для конк-
ретного человека, массовая для любого желающего ею пользо-
ваться (общественно-политическая, научно-популярная и т. д.),
а специальная — для применения узким кругом лиц, занимаю-
щихся решением сложных специальных задач в области науки,
техники, экономики и т. п. Информация может быть объектив-
ной и субъективной. Объективная информация отражает явле-
ния природы и человеческого общества. Субъективная инфор-
мация создается людьми и отражает их взгляд на объективные
явления.
В автоматизированных информационных системах выделяют:
структурную (преобразующую) информацию объектов си-
стемы, заключенную в структурах системы, ее элементов
управления, алгоритмов и программ переработки инфор-
мации;
содержательную (специальную, главным образом осведом-
ляющую, измерительную и управляющую, а также научно-
техническую, технологическую и др.) информацию, извле-
каемую из информационных массивов (сообщений, команд
и т. п.) относительно индивидуальной модели предметной об-
ласти получателя (человека, подсистемы).
Первая связана с качеством информационных процессов в си-
стеме, с внутренними технологическими эффектами, затратами на
переработку информации. Вторая — как правило, с внешним це-
левым (материальным) эффектом.
Один из возможных вариантов классификации информации в
автоматизированных системах представлен на рис. 2.5.
При реализации информационных процессов передача инфор-
мации (сообщения) от источника к приемнику может осуществ-
ляться с помощью какого-либо материального носителя (бумаги,
магнитной ленты и т. п.) или физического процесса (звуковых или
электромагнитных волн).
В зависимости от типа носителя различают следующие виды
информации (рис. 2.6):
документальную;
акустическую (речевую);
• телекоммуникационную.
4 А-210
49
:. 2.5. Классификация информации в автоматизированных системах
50
Информация
Рис. 2.6. Классификация информации в зависимости от типа носителя
Документальная информация представляется в графическом
или буквенно-цифровом виде на бумаге, а также в электронном
виде на магнитных и других носителях.
Речевая информация возникает в ходе ведения разговоров, а так-
же при работе систем звукоусиления и звуковоспроизведения. Но-
сителем речевой информации являются акустические колебания
(механические колебания частиц упругой среды, распространяю-
щиеся от источника колебаний в окружающее пространство в виде
волн различной длины) в диапазоне частот от 200...300 Гц до 4...6 кГц.
Телекоммуникационная информация циркулирует в техничес-
ких средствах обработки и хранения информации, а также в кана-
лах связи при ее передаче. Носителем информации при ее обра-
ботке техническими средствами и передаче по проводным кана-
лам связи является электрический ток, а при передаче по радио- и
оптическому каналам — электромагнитные волны.
Источник информации может вырабатывать непрерывное со-
общение (сигнал), в этом случае информация называется непре-
рывной, или дискретное — информация называется дискретной.
Например, сигналы, передаваемые по радио и телевидению, а так-
же используемые в магнитной записи, имеют форму непрерывных,
быстро изменяющихся во времени зависимостей. Такие сигналы на-
зываются непрерывными, или аналоговыми сигналами. В противо-
51
положность этому в телеграфии и вычислительной технике сигналы
имеют импульсную форму и называются дискретными сигналами.
Непрерывная и дискретная формы представления информации
имеют особое значение при рассмотрении вопросов создания, хра-
нения, передачи и обработки информации с помощью средств
вычислительной техники.
В настоящее время во всех вычислительных машинах инфор-
мация представляется с помощью электрических сигналов. При
этом возможны две формы представления численного значения
какой-либо переменной, например X:
• в виде одного сигнала — например, электрического напря-
жения, которое сравнимо с величиной X (аналогично ей). На-
пример, при X=2003 единицам на вход вычислительного уст-
ройства можно подать напряжение 2,003 В (масштаб представ-
ления 0,001 В/ед.) или 10,015 В (масштаб представления 0,005
В/ед.);
в виде нескольких сигналов — нескольких импульсов напря-
жений, которые сравнимы с числом единиц в X, числом де-
сятков в X, числом сотен в X и т. д.
Первая форма представления информации (с помощью сходной
величины — аналога) называется аналоговой, или непрерывной. Ве-
личины, представленные в такой форме, могут принимать принци-
пиально любые значения в определенном диапазоне. Количество зна-
чений, которые может принимать такая величина, бесконечно вели-
ко. Отсюда названия — непрерывная величина и непрерывная ин-
формация. Слово непрерывность отчетливо выделяет основное свой-
ство таких величин — отсутствие разрывов, промежутков между зна-
чениями, которые может принимать данная аналоговая величина.
Вторая форма представления информации называется дискрет-
ной (с помощью набора напряжений, каждое из которых соответ-
ствует одной из цифр представляемой величины). Такие величи-
ны, принимающие не все возможные, а лишь вполне определен-
ные значения, называются дискретными (прерывистыми). В отли-
чие от непрерывной величины количество значений дискретной
величины всегда будет конечным.
Сравнивая непрерывную и дискретную формы представления
информации, нетрудно заметить, что при использовании непрерыв-
ной формы для создания вычислительной машины потребуется
меньшее число устройств (каждая величина представляется одним,
а не несколькими сигналами), но эти устройства будут сложнее (они
должны различать значительно большее число состояний сигнала).
52
Непрерывная форма представления используется в аналоговых
вычислительных машинах (АВМ). Эти машины предназначены в
основном для решения задач, описываемых системами дифферен-
циальных уравнений: исследования поведения подвижных объек-
тов, моделирования процессов и систем, решения задач парамет-
рической оптимизации и оптимального управления. Устройства для
обработки непрерывных сигналов обладают более высоким быст-
родействием, они могут интегрировать сигнал, выполнять любое его
функциональное преобразование и т. п. Однако из-за сложности
технической реализации устройств выполнения логических опера-
ций с непрерывными сигналами, длительного хранения таких сиг-
налов, их точного измерения АВМ не могут эффективно решать за-
дачи, связанные с хранением и обработкой больших объемов ин-
формации, которые легко решаются при использовании цифровой
(дискретной) формы представления информации, реализуемой
цифровыми электронными вычислительными машинами (ЭВМ).
Контрольные вопросы ~
1. Какие уровни проблем передачи информации Вы знаете?
2. Назовите меры информации синтаксического уровня.
3. Охарактеризуйте сущность понятия энтропии.
4. Как связаны между собой понятия количества информации и эн-
тропии ?
5. Что определяет термин «бит»? Приведите примеры сообщений,
содержащих один (два, восемь) бит информации.
б. Запишите формулы Хартли и Шеннона. При каком условии фор-
мула Шеннона переходит в формулу Хартли ?
7. Что такое абстрактный алфавит?
8. Дайте определение избыточности алфавита источника сообщений.
9. Какие меры информации семантического уровня Вы знаете?
10. Что такое тезаурус?
11. Какие меры информации прагматического уровня Вы знаете?
12. Дайте определение дезинформации.
13. Что такое качество информации?
14. Назовите основные составляющие качества информации.
15. Как Вы понимаете защищенность и содержательность информации ?
16. Чем достигается требуемый уровень защищенности информации?
17. Назовите основные классификационные признаки информации?
18. Какие виды и формы представления информации в информаци-
онных системах Вы знаете?
Тлава 3
Представление информации
в цифровых автоматах
3.1. СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления — совокупность приемов и правил наимено-
вания и обозначения чисел, позволяющих установить взаимно одно-
значное соответствие между любым числом и его представлением
в виде конечного числа символов.
В любой системе счисления выбирается алфавит, представля-
ющий собой совокупность некоторых символов (слов или знаков),
с помощью которого в результате каких-либо операций можно
представить любое количество. Изображение любого количества
называется числом, а символы алфавита — цифрами (от лат. cifra).
Символы алфавита должны быть разными и значение каждого из
них должно быть известно.
В современном мире наиболее распространенной является де-
сятичная система счисления, происхождение которой связано с
пальцевым счетом. Она возникла в Индии и в XIII веке была пере-
несена в Европу арабами. Поэтому десятичную систему счисле-
ния стали называть арабской, а используемые для записи чисел циф-
ры, которыми мы теперь пользуемся, — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 —
арабскими.
С давних времен для подсчетов и вычислений применялись раз-
личные системы счисления. Например, на Древнем Востоке доволь-
но широко была распространена двенадцатеричная система. Мно-
гие предметы (ножи, вилки, тарелки и т. д.) и сейчас считают дю-
жинами. Число месяцев в году — двенадцать. Эта система счисле-
ния сохранилась в английской системе мер (например, 1 фут = 12
дюймов) и в денежной системе (1 шиллинг = 12 пенсов). В Древ-
нем Вавилоне существовала весьма сложная шестидесятеричная
54
система. Она, как и двенадцатеричная система, в какой-то степе-
ни сохранилась и до наших дней (например, в системе измерения
времени: 1 ч = 60 мин, 1 мин = 60 с, аналогично в системе измере-
ния углов: 1° = 60 мин, 1 мин = 60 с).
Первые цифры (знаки для обозначения чисел) появились у егип-
тян и вавилонян. У ряда народов (древние греки, сирийцы, фини-
кияне) цифрами служили буквы алфавита. Аналогичная система
до XVI века применялась и в России. В Средние века в Европе
пользовались системой римских цифр, которые и сейчас часто при-
меняют для обозначения глав, частей, разделов в различного рода
документах, книгах, для обозначения месяцев и т. д.
Все системы счисления можно разделить на позиционные и
непозиционные.
Непозиционная система счисления — система, в которой симво-
лы, обозначающие то или иное количество, не меняют своего значения
в зависимости от местоположения (позиции) в изображении числа.
Запись числа А в непозиционной системе счисления D может
быть представлена выражением:
Ad = Z)j + + ••• + Dn = % D; f
где Ad — запись числа А в системе счисления D; Di — символы сис-
темы.
Непозиционной системой счисления является самая простая
система с одним символом (палочкой). Для изображения какого-
либо числа в этой системе надо записать количество палочек, рав-
ное данному числу. Например, запись числа 12 в такой системе
счисления будет иметь вид: 111111111111, где каждая «палочка»
обозначена символом 1. Эта система неэффективна, так как фор-
ма записи очень громоздка.
К непозиционной системе счисления относится и римская, сим-
волы алфавита которой и обозначаемое ими количество представ-
лены в табл. 3.1.
Таблица 3.1
Римские цифры I V X L С D М
Значение (обозначаемое количество) 1 5 10 50 100 500 1000
55
Запись чисел в этой системе счисления осуществляется по сле-
дующим правилам:
1) если цифра слева меньше, чем цифра справа, то левая цифра
вычитается из правой (IV: 1 < 5, следовательно, 5 — 1=4, XL: 10 < 50,
следовательно, 50 — 10 =40);
2) если цифра справа меньше или равна цифре слева, то эти
цифры складываются (VI: 5+1 =6, VIII: 5+14-1 + 1=8, XX:
10+10 = 20).
Так, число 1964 в римской системе счисления имеет вид
MCMLXIV (М — 1000, СМ — 900, LX — 60, IV — 4), здесь «девять-
сот» получается посредством вычитания из «тысячи» числа «сто»,
«шестьдесят» — посредством сложения «пятидесяти» и «десяти»,
«четыре» — посредством вычитания из «пяти» «единицы».
В общем случае непозиционные системы счисления характери-
зуются сложными способами записи чисел и правилами выполнения
арифметических операций. В настоящее время все наиболее распро-
страненные системы счисления относятся к разряду позиционных.
3.1.1. Позиционные системы счисления
Систему счисления, в которой значение цифры определяется ее
местоположением (позицией) в изображении числа, называют пози-
ционной.
Упорядоченный набор символов (цифр) fa0,a;,...,an7, используе-
мый для представления любых чисел в заданной позиционной си-
стеме счисления, называют ее алфавитом, число символов (цифр)
алфавита р = п + 1 — ее основанием, а саму систему счисления
называют р-ичной.
Основание позиционной системы счисления — количество различ-
ных цифр, используемых для изображения чисел в данной системе
счисления.
Самой привычной для нас является десятичная система счис-
ления. Ее алфавит — {0,1,2,3,4,5,6,7,8,9}, а основание р = 10, т. е. в
этой системе для записи любых чисел используется только десять
разных символов (цифр). Эти цифры введены для обозначения пер-
56
вых десяти последовательных чисел, а все последующие числа, на-
чиная с 10 и т. д., обозначаются уже без использования новых цифр.
Десятичная система счисления основана на том, что десять единиц
каждого разряда объединяются в одну единицу соседнего старшего
разряда, поэтому каждый разряд имеет вес, равный степени 10. Сле-
довательно, значение одной и той же цифры определяется ее мес-
тоположением в изображении числа, характеризуемым степенью
числа 10. Например, в изображении числа 222.22 цифра 2 повторя-
ется пять раз, при этом первая слева цифра 2 означает количество
сотен (ее вес равен 102); вторая — количество десятков (ее вес ра-
вен 10), третья — количество единиц (ее вес равен 10°), четвертая —
количество десятых долей единицы (ее вес равен 10 ’) и пятая циф-
ра — количество сотых долей единицы (ее вес равен 102). То есть
число 222.22 может быть разложено по степеням числа 10:
222.22 = 2х 102 + 2х 10* + 2х 10° +2 х 10 1 + 2 х 10’2.
Аналогично:
725 =7х 102 + 2х 10Ч-5х 10°;
1304.5 = 1 х 103 + Зх 102 + 0х 10Ч-4Х 10° + 5х 10';
50328.15 = 5х 104+0х 103 + Зх 102+2х 1О‘ + 8х 10°+1 х 1О‘ + 5х 102.
Таким образом, любое число А можно представить в виде поли-
нома путем разложения его по степеням числа 10:
А10 = аах 10" +ап1 х 10п1 + ... + а1 х 104-аох 10°-Та , х 10 * + ...+
+ а.тх 10т-Т..., (3.1)
последовательность из коэффициентов которого представляет со-
бой десятичную запись числа А10:
А,0 = апапл -а1а,-а.1-а.т- <3-2)
Точка, отделяющая целую часть числа от дробной, служит для
фиксации конкретных значений каждой позиции в этой последо-
вательности цифр и является началом отсчета.
В общем случае для задания р-ичной системы счисления необ-
ходимо определить основание р и алфавит, состоящий из р раз-
личных символов (цифр) a., i= 1,...,р.
За основание системы можно принять любое натуральное чис-
ло — два, три, четыре и т. д. Обычно в качестве алфавита берутся
57
последовательные целые числа от 0 до (р— 1) включительно. Для
записи произвольного числа в двоичной системе счисления ис-
пользуются цифры 0, 1, троичной — 0, 1,2, пятеричной — 0, 1, 2, 3, 4
и т. д. В тех случаях, когда общепринятых (арабских) цифр не хва-
тает для обозначения всех символов алфавита системы счисле-
ния с основанием р> 10, используют буквенное обозначение цифр
a,b,c,d,e,f.
Для примера в табл. 3.2 приведены алфавиты некоторых сис-
тем счисления.
Таблица 3.2
Основание Система счисления Алфавит системы счисления
2 Двоичная 0,1
3 Троичная 0,1,2
4 Четверичная 0,1,2,3
5 Пятеричная 0,1,2,3,4
8 Восьмеричная 0,1,2,3,4,5,6,7
10 Десятичная 0,1,2,3,4,5,6,7,8,9
12 Двенадцатеричная 0,1,2,3,4,5,6,7,8,9,А,В
16 Шестнадцатеричная 0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F
Таким образом, возможно бесчисленное множество позицион-
ных систем: двоичная, троичная, четверичная и т. д. Запись чисел
в каждой из систем счисления с основанием р означает сокра-
щенную запись выражения:
Ар = авхрп+ап_1хрЛ,+...+а1хр'+аохро+а_1хр-,+...+а тхрш =
п
= X акРк,
к=-т
(3.3)
где а( — цифры системы счисления; пит — число целых и дроб-
ных разрядов, соответственно, Ар— запись числа А в р-ичной сис-
теме счисления.
Изображением числа А в р-ичной системе счисления является
последовательность цифр ак.
Например, десятичное число 35 в системах счисления с основа-
нием Р будет иметь вид:
Р разряды 1 о
12 число 2 В12 = 2x12' +Вх12°
58
10
8
4
3
2
1 о
3 510= 3x10’+ 5x10°
1 о
4 38 = 4х8‘ + 3x8°
2 10
2 0 34 = 2х42 + 0x4* + 3x4°
3 2 10
1 0 2 23 = 1x3’ + ОхЗ2 + 2x3' + 2x3°
5 4 3 2 1 0
1 0 0 0 1 12 = 1х25 + 0х24 + 0х23 + 0х22 + 1х2‘+1x2°
Из приведенных примеров видно, что с уменьшением основа-
ния системы счисления уменьшается число используемых цифр,
но возрастает количество разрядов. Так, в двенадцатеричной, де-
сятичной и восьмеричной системах для записи числа 35 требова-
лось два разряда, в четверичной — три разряда, а в двоичной —
шесть разрядов.
Все известные позиционные системы счисления являются ад-
дитивно-мультипликативными. Особенно отчетливо аддитивно-
мультипликативный способ образования чисел из базисных вы-
ражен в числительных русского языка, например пятьсот ше-
стьдесят восемь (т. е. пять сотен плюс шесть десятков плюс во-
семь).
Арифметические действия над числами в любой позиционной
системе счисления производятся по тем же правилам, что и в де-
сятичной системе, так как все они основываются на правилах вы-
полнения действий над соответствующими полиномами. При этом
нужно только пользоваться теми таблицами сложения и умноже-
ния, которые имеют место при данном основании р системы счис-
ления.
Отметим, что во всех позиционных системах счисления с лю-
бым основанием Р умножения на числа вида Рт , где т — целое
число, сводится просто к перенесению запятой у множимого на т
разрядов вправо или влево (в зависимости от знака т), так же как
и в десятичной системе.
Рассмотрим в качестве примера выполнение арифметических
операций в троичной и пятеричной системах счисления, таблицы
сложения и умножения для которых представлены соответствен-
но на рис. 3.1 и 3.2.
59
+ 0 1 2
0 0 1 2
1 1 2 10
2 2 10 11
X 0 1 2
0 0 0 0
1 0 1 2
2 0 2 11
a)
б)
Рис. 3.1. Таблицы сложения (а) и умножения (б) в троичной системе счисления
+ 0 1 2 3 4
0 0 1 2 3 4
1 1 2 3 4 10
2 2 3 4 10 И
3 3 4 10 И 12
4 4 10 И 12 13
а)
X 0 1 2 3 4
0 0 0 0 0 0
1 0 1 2 3 4
2 0 2 4 11 13
3 0 3 11 14 22
4 0 4 13 22 31
б)
Рис. 3.2. Таблицы сложения (а)
и умножения (б) в пятеричной системе счисления
Пример 1. Выполните действия в троичной системе счисления:
а) 2113 + 1013; б) 2013 — 1223; в) 121зх 103.
Решение:
а> 2 1 1 б) __ 2 0 1 в) 12 1
1 0 1 1 2 2 Х 1 о
1 0 1 2 002 000
1 2 1
12 10
Пример 2. Выполните действия в пятеричной системе счисле-
ния: 3245 + 1025; 4315 - 1225; 142зх 135.
Решение:
а) 324 б) _ 4 з i в) 142
1 0 2 1 2 2 х 1 з
4 3 1 3 0 4 1 0 3 1
1 4 2
3 0 0 1
60
Системы счисления используются для построения на их осно-
ве различных кодов в системах передачи, хранения и преобразо-
вания информации.
Код (от лат. codex) — система условных знаков (символов) для пред-
ставления различной информации.
Любому дискретному сообщению или знаку сообщения можно
приписать какой-либо порядковый номер. Измерение аналоговой
величины, выражающееся в сравнении ее с образцовыми мерами,
также приводит к числовому представлению информации. Пере-
дача или хранение сообщений при этом сводится к передаче или
хранению чисел. Числа можно выразить в какой-либо системе
счисления. Таким образом будет получен один из кодов, основан-
ный на данной системе счисления.
Каждому разряду числа можно поставить в соответствие какой-
либо параметр электрического сигнала, например амплитуду. На
рис. 3.3 в качестве примера приведено изображение числа 35 в виде
импульсов длительностью т0 с разными амплитудами (при разных
системах счисления) [9].
Основание
системы
счисления
Запись
числа
{код числа)
Электри-
ческие
сигналы
(кодовая
комби-
нация)
Р= 12
2В
Р= 10
35
Р = 8
43
Рис. 3.3. Изображение числа 35 в виде сигналов при разных системах счисления
Анализ систем счисления и построенных на их основе кодов с по-
зиций применения в системах передачи, хранения и преобразования
информации показывает, что чем больше основание системы счис-
ления, тем меньшее число разрядов требуется для представления дан-
ного числа, а следовательно, и меньшее время для его передачи.
61
Однако с ростом основания существенно повышаются требо-
вания к аппаратуре формирования и распознавания элементарных
сигналов, соответствующих различным символам. Логические эле-
менты вычислительных устройств в этом случае должны иметь
большее число устойчивых состояний.
С учетом этих обстоятельств в качестве показателя эффектив-
ности системы может быть выбрано число, равное произведению
количества различных символов q на количество разрядов N для
выражения любого числа. Тогда наиболее эффективной будет си-
стема, обеспечивающая минимум значения данного показателя.
Обозначим произведение основания системы q на длину раз-
рядной сетки N, выбранную для записи чисел в этой системе, — С:
С= qxN. (3.4)
Если принять, что каждый разряд числа представлен не одним
элементом с q устойчивыми состояниями, a q элементами, каждый
из которых имеет одно устойчивое состояние, то показатель (3.4)
определит условное количество оборудования, которое необходи-
мо затратить на представление чисел в этой системе. В связи с этим
показатель (3.4) называют показателем экономичности системы.
Максимальное число, которое можно изобразить в системе с
основанием q:
A =qN — 1. (3.5)
Из (3.5) можно найти требуемую длину разрядной сетки:
N = ^gq(Amax+l). (3.6)
Тогда для любой системы счисления С = q logq(Aqmax + 1).
Допустим, что величина q является непрерывной величиной.
При этом будем рассматривать величину С как функцию от вели-
чины q. Теперь если за единицу измерения оборудования принять
условный элемент с одним устойчивым состоянием, то для срав-
нения двух систем счисления можно ввести относительный пока-
затель экономичности:
F = qlogq(Aqmax + 1)/[21од2(А2ш<а + 1)], (3.7)
позволяющий сравнить любую систему счисления с двоичной.
Из приведенного ниже соотношения видно, что функция F име-
ет минимум.
q 2 3 4 6 8 10
F 1,000 0,946 1,000 1,148 1,333 1,505
62
На рис. 3.4 представлена зависимость величины For основания
системы счисления q, если функция Fнепрерывна. Нижняя точка
графика соответствует минимуму функции F, определяемому из
условия dF/dq = 0, что соответствует значению q = е = 2,72.
Следовательно, с точки зре-
ния минимальных затрат услов-
ного оборудования наиболее
экономичной является система
счисления с основанием 3.
Незначительно уступают ей
двоичная и четверичная. Систе-
мы с основанием 10 и более су-
щественно менее эффективны.
Сравнивая эти системы с точки
зрения удобства физической ре-
ализации соответствующих им
логических элементов и просто-
ты выполнения в них арифмети-
ческих и логических действий,
Рис. 3.4. Зависимость относительного
показателя экономичности
от основания системы счисления
предпочтение в настоящее время отдается двоичной системе счис-
ления. Действительно, логические элементы, соответствующие
этой системе, должны иметь всего два устойчивых состояния. За-
дача различения сигналов сводится в этом случае к задаче обнару-
жения (есть импульс или его нет), что значительно проще. Ариф-
метические и логические действия также легче осуществляются в
двоичной системе.
3.1.2. Перевод чисел из одной системы счисления в другую
Рассмотрим задачу перевода числа из одной системы счисле-
ния в другую в общем случае [20]. Пусть известна запись числа А
в системе счисления с основанием р:
Ар = ап х р” + ап1 х р"1 +...+ а, хр1 + аох р° + а( х р1 +...+
п
+ axp'm = S а р ,
•Ш L— ...
«——т
(3.8)
где а. — цифры р-ичной системы (0 < а. £р-1)-
63
Требуется найти запись этого же числа А в системе счисления с
основанием d:
A=b xdn + b .х dnl +...+ b.xd1 + bnxd° + b .xd‘ + ... +
а П П-J J U -I
+ b xd^= X bKdK ,
k=-m
(3.9)
где b — искомые цифры d-ичной системы (0 < Ь <d-l}. При этом
можно ограничиться случаем положительных чисел, так как пере-
вод любого числа сводится к переводу его модуля и приписыва-
нию числу нужного знака.
При переводе чисел из р-ичной системы счисления в d-ичную
(Ар -> AJ нужно учитывать, средствами какой арифметики должен
быть осуществлен перевод, т. е. в какой системе счисления (р-ич-
ной или d-ичной) должны быть выполнены все необходимые для
перевода действия.
Пусть перевод Ар —>Ad должен осуществляться средствами d-ич-
ной арифметики. В этом случае перевод произвольного числа А, за-
данного в системе счисления с основанием р, в систему счисления
с основанием d выполняется по правилу замещения, предусматрива-
ющему вычисление полинома (3.8) в новой системе счисления. То есть
для получения d-ичного изображения выражения (3.8) необходимо
все цифры а и число р заменить d-ичными изображениями и выпол-
нить арифметические операции в d-ичной системе счисления.
Правило замещения чаще всего используется для преобразова-
ния чисел из любой системы счисления в десятичную. Правило
перевода для этого случая можно конкретизировать.
Перевод в десятичную систему числа А, записанного в р-ичной
системе счисления в виде А;) = (апап1 ... а0 , а_, а2 ... а т)р сводится
к вычислению значения многочлена А|о = ап р" + ап, р" ' + .. + аор° +
+ а,р'' + а2р-2 + ... + аш р” средствами десятичной арифметики.
Пример 3.
Разряды 3 2 1о -1
Число 10 11, 12 = 1х23 + 1x2'+ 1x2° + 1х2‘= 11,5](|.
6, 58 = 2х82 +7Х81 + 6x8° + 5х8> = 190,6251О.
31й = 1х162 +15Х161 + 3x16° = 499...
10 IV
64
При переводе следует придерживаться правила сохранения точ-
ности изображения числа в разных системах, причем под точностью
понимается значение единицы самого младшего (правого) разряда,
используемого в записи числа в той или иной системе счисления.
Пусть теперь перевод Ар —> Ad должен осуществляться сред-
ствами р-ичной арифметики. В этом случае для перевода любого
числа используют правило деления — для перевода целой части
числа, и правило умножения — для перевода его дробной части.
Перевод целых чисел. Выражения (3.8) и (3.9) для целых чисел
будут иметь следующий вид соответственно:
Ар = ап х р" + ап1 х р"1 +... + at х р' + а0, (3.10)
Ad = bnxd" 4-Ьп1хсГ‘+...+ b, х d1 4- Ьо, (3.11)
где а. — цифры р-ичной системы (0 < а< р-1) и Ь. — искомые циф-
ры d-ичной системы (0 < b. < d-1).
Так как А — А„, то можно записать:
р d'
Ар= bnxd"+ b^xd"' + ...+ b(xd’ + b0, (3.12)
где b. — искомые цифры в d-ичной системе счисления.
Для определения Ьо разделим обе части равенства (3.12) на число
d, причем в левой части произведем деление, пользуясь правилами р-
ичной арифметики (так как запись числа Ар в р-ичной системе счис-
ления известна). Выделим в частном [Ар/ d] целую и дробную части:
[Ap/d]= [Ap/d]4-HAp/d]A, (3.13)
где [Ар/ d]4 — целая часть частного — неполное частное;
остаток
<V
— дробная часть частного, остаток — оста-
ток от деления Ар на d.
Правую часть перепишем в виде:
[Ар/ d] =bnх d"1 + bnix dn2 +... + bi + b0/d. (3.14)
Учитывая, что b < d, приравняем между собой полученные це-
лые и дробные части равенства (3.14):
[Ар/ d]v = bnxdn l +bn.lxdn'2 +...+ br (3.15)
остаток
5 A-210
65
Таким образом, младший коэффициент Ьо в разложении (3.11)
определяется соотношением:
остаток
d
= остаток,
b0= dx
т. е. Ьд является остатком от деления Ар на d. Положим:
A1 = [A/d] =b xdnl+b ,xdn2 + ... + b,.
р 1 Р JI< П П-1 /
(3.16)
(3.17)
Тогда А1 будет целым числом и к нему можно применить ту же са-
мую процедуру для определения следующего коэффициента bt и т. д.
Этот процесс продолжается до тех пор, пока неполное частное
не станет равным нолю:
[А‘р/dj4 = 0. (3.18)
Поскольку все операции выполняются в системе счисления с
основанием р, то в этой же системе будут получены искомые ко-
эффициенты bt, поэтому их необходимо записать d-ичной цифрой.
Правило деления чаще всего используется для преобразования
целых чисел из десятичной в любую другую систему счисления.
Таким образом, правило перевода целых чисел из р-ичной сис-
темы счисления в d-ичную средствами р-ичной арифметики мо-
жет быть сформулировано в следующем виде.
Для перевода целого числа А из р-ичной системы счисления
в систему счисления с основанием d необходимо Ар разделить
с остатком («нацело») на число d, записанное в той же р-ичной сис-
теме. Затем неполное частное, полученное от такого деления, нужно
снова разделить с остатком на d и т. д., пока последнее полученное
неполное частное не станет равным нолю. Представлением числа Ар в
новой системе счисления будет последовательность остатков деления,
изображенных d-ичной цифрой и записанных в порядке, обратном
порядку их получения.
Пример 4. Переведем число А10 = 47 в двоичную систему с ис-
пользованием десятичной арифметики. Применяя формулы
(3.12)—(3.18) при d = 2, имеем:
47:2 = 23(1); м
23:2 = 11(1);
11:2 = 5(1);
5:2 = 2(1);
2:2 = 1(0);
1:2 = 0(1).
66
Поскольку числа ноль и единица в обеих системах счисления
обозначаются одинаковыми цифрами 0 и 1, то в процессе деления
сразу получим двоичные изображения искомых цифр: А~ 101111.
Пример 5. Переведем число А]0 = 75 в шестнадцатеричную си-
стему счисления с использованием десятичной арифметики. При-
меняя формулы (3.12)—(3.18) при d= 16, имеем:
75:16 = 4(11);
4:16 = 0(4).
Первый остаток 1110 в 16-ричной системе счисления обознача-
ется шестнадцатеричной цифрой В16, поэтому окончательно полу-
чим: А|6=4В.
Перевод правильных дробей. Выражения (3.8) и (3.9) для пра-
вильной дроби будут иметь следующий вид соответственно:
Ар = ал хр-‘ + а 2 хр2 +...+ а т хрт+..., (3.19)
Ad = b, х d1 + Ь 2 х d2 +...+ b ш х d* +..., (3.20)
где at — цифры р-ичной системы (0 < а( < Р-1) и bt — искомые циф-
ры d-ичной системы (0 < Ц < d-1).
При этом:
А = b.xd1 + b,xd'2 + ...+ b xdm. (3.21)
p -1 -2 -m ' •
определения b t умножим обе части равенства (3.21) на чис-
ло d, причем в левой части произведем умножение, пользуясь пра-
вилами р-ичной арифметики (так как запись числа Ар в р-ичной
системе счисления известна). Выделим в произведении [Арх d] це-
лую и дробную части:
[Ар х d] = [Ар х d]q+ [Ар х d]A, (3.22)
где [Ар х d]q — целая часть произведения;
[Ар х d]A — дробная часть произведения.
Правую часть перепишем в виде:
[Apxd]=b1 + b2xd1 + ... + bmxdm+1 + .... (3.23)
Учитывая, что 0<b.<d, приравняем между собой полученные
целые и дробные части равенства (3.23):
[ApXd]q=b1, (3.24)
[Axd] = b, х d1 +...+ b х d‘m+1 +....
i p лд -L -ХП
67
Таким образом, младший коэффициент b_t в разложении (3.21)
определяется соотношением:
b, = [A xd] .
-1 1 р
Положим:
А'р = [Apxd]4 = b2xd' + ... + bmxd“+1 +... . (3.25)
Тогда А' будет правильной дробью и к нему можно применить
ту же самую процедуру для определения следующего коэффици-
ента b 2 и т. д.
Этот процесс продолжается до тех пор, пока дробная часть про-
изведения не станет равной нолю:
[А‘рха]д=0, (3.26)
или не будет достигнута требуемая точность представления числа.
При переводе приближенных дробей из одной системы счисле-
ния в другую необходимо придерживаться следующего правила.
Если единица младшего разряда числа А, заданного в р-ичной
системе счисления, есть р*, то в его d-ичной записи следует сохра-
нить j разрядов после запятой, где j удовлетворяет условию:
d> > р к/2 > ,
округляя последнюю оставляемую цифру обычным способом.
Поскольку все операции выполняются в системе счисления с ос-
нованием р, то в этой же системе будут получены искомые коэффи-
циенты Ье поэтому их необходимо записать d-ичной цифрой. Прави-
ло умножения чаще всего используется для преобразования правиль-
ных дробей из десятичной в любую другую систему счисления.
Таким образом, правило перевода правильных дробей из р-ич-
ной системы счисления в d-ичную средствами р-ичной арифмети-
ки может быть сформулировано в следующем виде.
Для перевода правильной дроби Ар из р-ичной системы счисления в
систему счисления с основанием d необходимо Ар умножить на d,
записанное в той же р-ичной системе, затем дробную часть получен-
ного произведения снова умножить на d ит.д. до тех пор, пока дробная
часть очередного произведения не станет равной нолю, либо не бу-
дет достигнута требуемая точность изображения числа Ар в d-ичной
системе. Представлением дробной части числа Ар в новой системе
счисления будет последовательность целых частей полученных про-
68
изведений, записанных в порядке их получения и изображенных d-ичной
цифрой. Если требуемая точность перевода числа Ар составляет
j знаков после запятой, то предельная абсолютная погрешность при
этом равняется d ('+0 / 2.
Примерб. Переведем число А10 = 0.2 в двоичную систему счис-
ления с использованием средств десятичной арифметики. Приме-
нение формул (3.23)—(3.25) приводит к такой последовательности
действий:
0.2 х 2 = 0.4 = 0 + 0.4 => b , = 0;
0.4 х 2 = 0.8 = 0 + 0.8 => b 2 = 0;
0.8x2 = 1.6= 1 + 0.6 =>Ь3 = 1;
0.6 х 2 = 1.2= 1 + 0.2 => b . = 1 и т. д. ' ’
-4
Если десятичная дробь А)0=0.2 является точным числом, то в
результате перевода в двоичную систему счисления получена пе-
риодическая дробь А2 = 0.(0011) (в скобках указан период дроби).
Пример 7. Переведем число А10 = 0.36 в восьмеричную и шест-
надцатеричную системы счисления с использованием средств де-
сятичной арифметики. Применив формулы (3.23)—(3.25), получим:
0.36 х 8 = 2.88 = 2 + 0.88 => b , = 2;
0.88 х 8 = 7.08 = 7 + 0.08 => b 2 = 7;
0.08 х 8 = 0.64 = 0 + 0.64 => b 3 = 0 и т. д. ,,
Таким образом, А* = 0.270, при этом предельная абсолютная по-
грешность равна 8'4/2 = 213.
0.36 х 16 = 5.76 = 5 + 0.76 =>Ь4 = 5; I
0.76x8 = 12.16 = 12 + 0.16 => Ь2 = 12ит.д. |
Число 1210 в 16-ичной системе счисления обозначается цифрой
С16, поэтому окончательно получим А16 = 0.5С, при этом предель-
ная абсолютная погрешность равна 16V2 = 213.
Особого внимания заслуживает случай перевода чисел из од-
ной системы счисления в другую, когда основания данных систем
счисления pud связаны равенством р = dK, где К — целое положи-
тельное число. В этом случае перевод из d-ичной в р-ичную систе-
му счисления может быть осуществлен по следующему правилу.
69
В исходной, d-ичной, записи числа разряды объединяются впра-
во и влево отточки в группы длины К (добавляя в случае необходи-
мости левее старшей или правее младшей значащих цифр соот-
ветствующее количество нолей), и каждая такая группа записыва-
ется одной цифрой р-ичной системы счисления. Для обратного
перевода из р-ичной в d-ичную систему счисления — каждая циф-
ра числа, заданного в р-ичной системе счисления заменяется ее d-
ичным изображением. Например,
01 21 21 12 = 1996,,;
4 1о
1996, = 0001 1001 1001 ОНО,;
0 1 22.11 023 = 18.429;
5259 = 12 01 123.
3.1.3. Двоичная, восьмеричная и шестнадцатеричная
системы счисления
Примеры изображения чисел в данных системах счисления
представлены в табл. 3.3.
Таблица 3.3
Системы счисления
10-ичная 2-ичная 8-ичная 16-ичная
0 00000 0 0
1 00001 1 1
2 00010 2 2
3 00011 3 3
4 00100 4 4
5 00101 5 5
6 00110 6 6
7 00111 7 7
8 01000 10 8
9 01001 И 9
10 01010 12 А
10-ичная 2-ичная 8-ичная 16-ичная
И 01011 13 В
12 01100 14 С
13 01101 15 D
14 01110 16 Е
15 ОНИ 17 F
16 10000 20 10
17 10001 21 И
18 10010 22 12
19 10011 23 13
20 10100 24 14
70
Как было отмечено выше, в современной вычислительной тех-
нике, в устройствах автоматики и связи используется в основном
двоичная система счисления, что обусловлено рядом преимуществ
данной системы счисления перед другими системами. Так, для ее
реализации нужны технические устройства лишь с двумя устой-
чивыми состояниями, например материал намагничен или размаг-
ничен (магнитные ленты, диски), отверстие есть или отсутствует
(перфолента и перфокарта). Этот обеспечивает более надежное и
помехоустойчивое представление информации, дает возможность
применения аппарата булевой алгебры для выполнения логичес-
ких преобразований информации. Кроме того, арифметические
операции в двоичной системе счисления выполняются наиболее
просто.
Недостаток двоичной системы — быстрый рост числа разря-
дов, необходимых для записи больших чисел. Этот недостаток не
имеет существенного значения для ЭВМ. Если же возникает не-
обходимость кодировать информацию «вручную», например при
составлении программы на машинном языке, то используют
восьмеричную или шестнадцатеричную системы счисления. Чис-
ла в этих системах читаются почти так же легко, как десятичные,
требуют соответственно в три (восьмеричная) и в четыре (шест-
надцатеричная) раза меньше разрядов, чем в двоичной системе
(числа 8 и 16 — соответственно третья и четвертая степени числа
2), а перевод их в двоичную систему счисления и обратно осуще-
ствляется гораздо проще в сравнении с десятичной системой
счисления.
Перевод восьмеричных и шестнадцатеричных чисел в двоичную
систему осуществляется путем замены каждой цифры эквивален-
тной ей двоичной триадой (тройкой цифр) или тетрадой (чет-
веркой цифр) соответственно.
Например:
537,1 = 101 011 111,001,; 1 АЗ, F.= 1 10100011,1111,
ММ JM i i
5 3 7 1 1 А 3 F
Чтобы перевести число из двоичной системы в восьмеричную
или шестнадцатеричную, его нужно разбить влево и вправо от
запятой на триады (для восьмеричной) или тетрады (для шест-
надцатеричной) и каждую такую группу заменить соответству-
ющей восьмеричной или шестнадцатеричной цифрой.
71
Например:
10101001,10111, = 10 101 001, 101 110, = 251,56я
J, i 4- X
2 5 15 6
10101001,10111, = 1010 1001, 1011 1000, = А9,В81Й.
г г г г
А 9 В 8
Правила выполнения арифметических операций сложения, вы-
читания, умножения и деления в 2-, 8- и 16-ичной системах счисле-
ния, как было отмечено выше, будут такими же, как и в десятич-
ной системе, только надо пользоваться особыми для каждой сис-
темы таблицами сложения и умножения.
Рассмотрим примеры выполнения арифметических операций
в данных системах счисления.
Сложение
Таблицы сложения для 2-ичной, 8-ичнойи 16-ичной систем счис-
ления представлены на рис. 3.5.
Сложение
в восьмеричной системе
+ 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7 10
2 2 3 4 5 6 7 10 11
3 3 4 5 6 7 10 11 12
4 4 5 6 7 10 11 12 13
5 5 6 7 10 11 12 13 14
6 6 7 10 11 12 13 14 15
7 7 10 11 12 13 14 15 16
Рис. 3.5. Таблицы сложения для двоичной, восьмеричной
и шестнадцатеричной систем счисления
72
Сложение
в шестнадцатеричной системе
+ 0 1 2 3 4 5 6 7 8 9 А В С D Е F
0 0 1 2 3 4 5 6 7 8 9 А В С D Е F
1 1 2 3 4 5 6 7 8 9 А В С D Е F 10
2 2 3 4 5 6 7 8 9 А В С D Е F 10 И
3 3 4 5 6 7 8 9 А В С D Е F 10 11 12
4 4 5 6 7 8 9 А В С D Е F 10 11 12 13
5 5 6 7 8 9 А В С D Е F 10 11 12 13 14
6 6 7 8 9 А В С D Е F 10 11 12 13 14 15
7 7 8 9 А В С D Е F 10 И 12 13 14 15 16
8 8 9 А В С D Е F 10 11 12 13 14 15 16 17
9 9 А В С D Е F 10 И 12 13 14 15 16 17 18
А А В С D Е F 10 11 12 13 14 15 16 17 18 19
В В С D Е F 10 И 12 13 14 15 16 17 18 19 1А
С С D Е F 10 11 12 13 14 15 16 17 18 19 1А 1В
D D Е F 10 И 12 13 14 15 16 17 18 19 1А 1В 1С
Е Е F 10 И 12 13 14 15 16 17 18 19 1А 1В 1С 1D
F F 10 11 12 13 14 15 16 17 18 19 1А 1В 1С 1D 1Е
Рис. 3.5. Таблицы сложения для двоичной, восьмеричной
и шестнадцатеричной систем счисления (окончание)
При сложении цифры суммируются по разрядам, и если при
этом возникает избыток, то он переносится влево.
Пример 8. Сложить десятичные числа 15 и 6 в 2-, 8- и 16-ичной
системах счисления.
Двоичная: 11112 + 1102 Восьмеричная: 17g + 68
ill 1
+ ИИ 17
ОНО _£
10101 25
73
Шестнадцатеричная: Fie + 6,6
1
+ F
15
Ответ: 15 + 6 = 2110 = 10 1 012 = 258 = 1516.
Проверка. Преобразуем полученные суммы к десятичному
виду:
101012 = 24 + 22 + 2° = 16 + 4 + 1 = 21,
258 = 2 81 + 5x8° = 16 + 5 = 21,
15,. = 1 х 16, + 5х 16 = 16 + 5 = 21.
1о 1 и
Пример 9. Сложить десятичные числа 141,5 и 59,75 в 2-, 8- и 16-
ичной системах счисления.
Двоичная: 10001101,12 + 111011,112
1111111
10001101,1
+ 111011,11
11001001,01
Восьмеричная: 215,48 + 73,68 Шестнадцатеричная: 8D,816 + ЗВ, С16
ill 1 1
, 215,4 , 8D,8
+ 73.6 ЗВ,С
311,2 С9,4
Ответ: 141,5 + 59,75 = 201,25, п = 11001001,01, = 311,2. = С9,4,,.
Проверка. Преобразуем полученные суммы к десятичному
виду:
1100 1001,012 = 27 + 26 + 23 + 2° + 2‘2 = 201,25;
311,28= Зх82+ 1 х 81 + 1 х 8° + 2х 81 = 201,25;
С9,4,„ = 12х 161 + 9х 16° + 4х 161 = 201,25.
1О
74
Вычитание
Пример 10. Вычесть единицу из чисел 102, 108 и 1016.
Двоичная: 102 — 12 Восьмеричная: 108 — 18
1 1 Заемы
_ 10 _ 10
____1 ___________________1
1 7
Шестнадцатеричная: 1016 — 116
1
_ 10
____1
F
Пример 10. Вычесть число 59,75 из числа 201,25.
Двоичная: 11001001,012 - 111011,112
1 1 1
11001001,01
00111011.11
10001101,10
Восьмеричная: 31 l,2g — 73,68 Шестнадцатеричная: С9,416 + ЗВ, С16
111
311,2
215,4
1 1
С9,4
ЗВ.С
8D,8
Ответ: 201,2510 - 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному
виду:
10001101,12 = 27 + 23 + 22 + 2° + 21 = 141,5;;
215,48 = 2-82+1-8’ + 5-8° + 4-81 = 141,5,•
8D,8,K = 8' 161 + D-16° + 8-161 = 141,5.
10
75
Умножение
Выполняя умножение многозначных чисел в различных позици-
онных системах счисления, можно использовать обычный алгоритм
перемножения чисел в столбик, но при этом результаты перемноже-
ния и сложения однозначных чисел необходимо брать из соответству-
ющих рассматриваемой системе таблиц умножения и сложения.
Таблицы умножения для 2-ичной, 8-ичной и 16-ичной систем
счисления представлены на рис. 3.6.
Умножение Умножение
в двоичной системе в восьмеричной системе
X 0 1
0 1 0 0 0 1
X 0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7
2 0 2 4 6 10 12 14 16
3 0 3 6 И 14 17 22 25
4 0 4 10 14 20 24 30 34
5 0 5 12 17 24 31 36 43
6 0 6 14 22 30 36 44 52
7 0 7 16 25 34 43 52 61
Умножение в шестнадцатеричной системе
X 0 1 2 3 4 5 6 7 8 9 А В С D Е F
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 А в с D Е F
2 0 2 4 6 8 А С Е 10 12 14 16 18 1А 1С 1Е
3 0 3 6 9 С F 12 15 18 1В 1Е 21 24 27 2А 2D
4 0 4 8 С 10 14 18 1С 20 24 28 2С 30 34 38 ЗС
5 0 5 А F 14 19 1Е 23 28 2D 32 37 ЗС 41 46 4В
6 0 6 С 12 18 1Е 24 2А 30 36 ЗС 42 48 4Е 54 5А
7 0 7 Е 15 1С 23 2А 31 38 3F 46 4D 54 5В 62 69
8 0 8 10 18 20 28 30 38 40 48 50 58 60 68 70 78
9 0 9 12 1В 24 2D 36 3F 48 51 5А 63 6С 75 7Е 87
А 0 А 14 1Е 28 32 ЗС 46 50 5А 64 6Е 78 82 8С 96
В 0 В 16 21 2С 37 42 4D 58 63 6Е 79 84 8F 9А А5
С 0 С 18 24 30 ЗС 48 54 60 6С 78 84 90 9С А8 В4
D 0 D 1А 27 34 41 4Е 5В 68 75 82 8F 9С А9 В6 СЗ
Е 0 Е 1С 2А 38 46 54 62 70 7Е 8С 9А А8 В6 С4 D2
F 0 F 1Е 2D ЗС 4В 5А 69 78 87 96 А5 В4 сз D2 Е1
Рис. 3.6. Таблицы умножения для 2-ичной, 8-ичной и 16-ичной систем счисления
76
Ввиду чрезвычайной простоты таблицы умножения в двоичной сис-
теме умножение сводится лишь к сдвигам множимого и сложениям.
Пример 11. Перемножим числа 5 и 6.
Двоичная: 1012 х 1102 Восьмеричная: 58 х 68
101 36
101
11110
Шестнадцатеричная: 516 х 616.
5
Х_6
1Е
Ответ: 5 х 6 = 30 = 11110 =36 = 1Е .
10 2 о 16
Проверка. Преобразуем полученные произведения к десятич-
ному виду:
111102 = 24 + 23 + 24- 21 = 30;
368 = 3 х 81 + 6 х 8° = 30;
IE, = 1 х 16’4-Ех 16°= 30.
1Ь
Пример 12. Перемножим числа 115 и 51.
Двоичная: 11100112 х 1100112 Восьмеричная: 1638 х 638
1110011 163
Х 110011 _£3
1110011 531
1110011 1262
1110011 13351
1110011
1011011101001
Шестнадцатеричная: 7316 х 3316
159
159
16Е9
77
Ответ: 115x51 = 5865 = 1011011101001 = 13351 = 16Е9,К.
Проверка. Преобразуем полученные произведения к десятич-
ному виду:
101101110 1 0012 = 212 4- 210 + 29 + 2’4- 26 4- 25 + 23 4- 2° = 5865;
133518 = 1х 84 4-3х 83 4-3х 82 4- 5 х8‘4-1х8° = 5865;
16Е9,, = 1 х 163 4- 6х 162 4- Ex 161 4- 9х 16° = 5865.
10
Деление
Деление в данных системах счисления, как и в любой другой
позиционной системе счисления, производится по тем же прави-
лам, как и деление углом в десятичной системе. В двоичной систе-
ме деление выполняется особенно просто, так как очередная циф-
ра частного может быть только нолем или единицей.
Пример 13. Разделим число 5865 на число 115.
Двоичная: 10110111010012: 11100112 Восьмеричная: 133518:1638
_10110111010011 1110011 1110011 110011 1000100 1110011 _10101100 3351 | 163 1262 63 531 531 0
1110011
_1110011
1114)011
0
Шестнадцатеричная: 16Е9: 73
_16Е91 73
159 33
_ 159
159
0
Ответ: 5865: 115 = 51, = 110011= 63 = 33,к.
1U 2 о 1о
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 4- 21 4- 2° = 51;
638 = 6х8‘ 4- 3x8° = 51;
33,й = Зх 161 4- Зх 16° = 51.
ID
78
Пример 14. Разделим число 35 на число 14.
Двоичная: 1000112:11102 Восьмеричная: 438: 168
100011 |1110
' 1110 10,1
_ 1110
1110
0
43 |_lfi
34 2,4
70
‘ 2Q
0
Шестнадцатеричная: 23 : Е
_23 |Е
1С 2,8
70
23
0
Ответ: 35 : 14 = 2,51П = 10,1, = 2,4Я = 2,81К.
10 2 о 10
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 21 = 2,5;
2,48 = 2x8° + 4x8* = 2,5;
2,8|К = 2х 16° + 8х 16'1 = 2,5.
10
3.1.4. Двоично-десятичная система счисления
Двоично-десятичная система счисления (ДДСС) широко ис-
пользуется в цифровых устройствах, когда основная часть опера-
ций связана не с обработкой и хранением вводимой информации,
а с ее вводом и выводом на какие-либо индикаторы с десятичным
представлением полученных результатов (микрокалькуляторы,
кассовые аппараты и т. п.) [6].
В двоично-десятичной системе десятичные цифры от 0 до 9 пред-
ставляют 4-разрядными двоичными комбинациями от 0000 до 1001,
т. е. двоичными эквивалентами десяти первых шестнадцатеричных
цифр (см. табл. 3.3). Преобразования из двоично-десятичной систе-
мы в десятичную систему счисления (ДСС) (и обратные преобра-
зования) не вызывают затруднений и выполняются путем прямой
замены четырех двоичных цифр одной десятичной цифрой (или об-
ратной замены). Например,
(ООП 0111)2_10
4, 4,
(3 -7)10
79
Две двоично-десятичные цифры составляют 1 байт. Таким об-
разом, с помощью 1 байта можно представлять значения от 0 до
99, а не от 0 до 255, как при использовании 8-разрядного двоичного
числа. Используя 1 байт для представления каждых двух десятич-
ных цифр, можно формировать двоично-десятичные числа с лю-
бым требуемым числом десятичных разрядов.
Так, если число
1001 0101 ООН 1000
рассматривать как двоичное, то его десятичный эквивалент
(1001 0101 0011 1000)2 — (38200) 10
в несколько раз больше десятичного эквивалента двоично-десятич-
ного числа
(1001 0101 ООП Ю00)2,10= (9538)10.
Сложение двоично-десятичных чисел, имеющих один десятич-
ный разряд, выполняется так же, как и сложение 4-разрядных дво-
ичных чисел без знака, за исключением того, что при получении
результата, превышающего 1001, необходимо производить коррек-
цию. Результат корректируется путем прибавления двоичного кода
числа 6, т. е. кода 0110. Например:
ДСС ДДСС ДСС ДДСС
, 4 0100 , 5 0101
+ 0101 + 9 1001
9 1001 14 1110
~г 0110 —коррекция
10 + 4 1 0100
ДСС ДДСС
, 9 , 1001
+ 9 + 1001
18 1 0010
0110 —коррекция
10 + 8 1 1000
Если первоначальное двоичное сложение или прибавление кор-
ректирующего числа приводит к возникновению переноса, то при
80
сложении многоразрядных двоично-десятичных чисел перенос
осуществляется в следующий десятичный разряд:
Дес ДДСС
1889 + £37£ 0001 + 1110 + 1000 ИШ + 1000 0111 + 1001 жш
8265 0111 1011 1111 1111
+__L Z 1000 + 4- оно 1 ' + < + 0110^ 1 1- оно 0101
г 0010 оно г
г г
8 2 6 5
3.2. ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ
В ЦИФРОВЫХ АВТОМАТАХ
Информация в памяти ЭВМ записывается в форме цифрового
двоичного кода. С этой целью ЭВМ содержит большое количество
ячеек памяти и регистров (от лат. regestum — внесенное, записан-
ное) для хранения двоичной информации. Большинство этих яче-
ек имеет одинаковую длину п, т. е. они используются для хране-
ния п бит двоичной информации (бит — один двоичный разряд).
Информация, хранимая в такой ячейке, называется словом. Дво-
ичное слово, состоящее из 2 байт, представлено на рис. 3.7 [6].
Рис. 3.7. Бит, байт и слово
Ячейки памяти и регистры состоят из элементов памяти. Каж-
дый из таких электрических элементов может находиться в одном
из двух устойчивых состояний: конденсатор заряжен или разря-
жен, транзистор находится в проводящем или непроводящем со-
стоянии, специальный полупроводниковый материал имеет высо-
кое или низкое удельное сопротивление и т. п. Одно из таких фи-
зических состояний создает высокий уровень выходного напря-
бА-210 81
жения элемента памяти, а другое — низкий. Обычно это электри-
ческие напряжения порядка 4—5В и ОВ соответственно, причем
первое обычно принимается за двоичную единицу, а второе — за
двоичный ноль (возможно и обратное кодирование).
На рис. 3.8 показан выходной сигнал такого элемента памяти
(например, одного разряда регистра) при изменении его состоя-
ний (при переключениях) под воздействием некоторого входного
сигнала. Переход от0к1иот1к0 происходит не мгновенно, одна-
ко в определенные моменты времени этот сигнал достигает значе-
ний, которые воспринимаются элементами ЭВМ как 0 или 1 [6].
Область
напряжений,
соответствующих
сигналу "1"
Идеальный
сигнал
Реальный
сигнал
Область
напряжений,
соответствующих
сигналу"О"
---►
t
Рис. 3.8. Графическое изображение двоичного сигнала
Память ЭВМ состоит из конечной последовательности слов, а
слова — из конечной последовательности битов, поэтому объем
представляемой в ЭВМ информации ограничен емкостью памяти,
а числовая информация может быть представлена только с опре-
деленной точностью, зависящей от архитектуры памяти данной
ЭВМ.
В вычислительных машинах применяются две формы представ-
ления двоичных чисел:
естественная форма, или форма с фиксированной запятой
(точкой);
82
• нормальная форма, или форма с плавающей запятой (точкой).
С фиксированной запятой все числа изображаются в виде пос-
ледовательности цифр с постоянным для всех чисел положением
запятой (точкой), отделяющей целую часть от дробной. В общем
случае разрядная сетка ЭВМ с фиксированной запятой имеет вид,
показанный на рис. 3.9.
Диапазон представления чисел по модулю для такой формы:
2r< |N| < 2п - 2 Г. (3.27)
Если в результате операции получится число, выходящее за до-
пустимый диапазон, происходит переполнение разрядной сетки,
что нарушает нормальное функционирование вычислительной
машины. В современных ЭВМ естественная форма представления
используется как вспомогательная и только для целых чисел.
С плавающей запятой каждое число изображается в виде
двух групп цифр. Первая группа цифр называется мантиссой,
вторая — порядком, причем абсолютная величина мантиссы
должна быть меньше 1, а порядок — целым числом. В общем
случае число в форме с плавающей запятой может быть пред-
ставлено в виде:
N=±Mp*s, (3.28)
где М — мантисса числа (|М|< 1);
s — порядок числа (s — целое число);
р — основание системы счисления.
При р = 2 и наличии п разрядов у мантиссы и г разрядов у по-
рядка (без учета знаковых разрядов) диапазон представления чи-
сел с плавающей запятой:
2 Лх2 (У ° <JV<(l-2 ")х2(2Г ° (3-29)
Нормальная форма представления является основной в совре-
менных ЭВМ.
83
3.2.1. Выполнение арифметических операций
над целыми числами. Прямой, обратный
и дополнительный коды
Целые числа могут представляться в компьютере без знака или
со знаком.
Целые числа без знака. Обычно занимают в памяти компьюте-
ра один или два байта (рис. 3.10). В однобайтовом формате принима-
ют значения от 000000002 до 111111112. В двубайтовом формате —
от 00000000 000000002 до 11111111 111111112.
Формат числа в байтах Диапазон
Запись с порядком Обычная запись
1 0 ... 28 - 1 0 ... 255
2 0 ... 216 - 1 0 ... 65535
Рис. 3.10. Диапазоны значений целых чисел без знака
Примеры:
а) число 72|0 — 10010002 в однобайтовом формате:
Номера разрядов 76543210
Биты числа |0 1 0 0 1 0 0 0
б) это же число в двубайтовом формате: Номера разрядов 15 14 13 12 И 10 9 8 7 6 5 4 3 2 1 0
Биты числа 0 0 0 0 0 0 0 0 0 1 0 0 10 0 0
в) число 65535 в двубайтовом формате: Номера разрядов 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
Биты числа 1111111 1 1 1 1 1111 _1
Целые числа со знаком: прямой, обратный и дополнительный
коды. Целые числа со знаком обычно занимают в памяти компью-
тера один, два или четыре байта (рис. 3.11).
84
Формат числа в байтах Диапазон
Запись с порядком Обычная запись
1 -27... 27 - 1 -128 ... 127
2 -215... 215 - 1 -32768 ... 32767
4 -231 ... 23' - 1 -2147483648 ... 2147483647
Рис. 3.11. Диапазоны значений целых чисел со знаком
В цифровых автоматах применяются три формы записи (коди-
рования) целых чисел со знаком: прямой код, дополнительный
код, обратный код.
Прямой код. Прямой n-разрядный двоичный код отличается от
двоичного тем, что в нем отводится один, как правило, самый стар-
ший разряд для знака, а оставшиеся п-1 разрядов —для значащих
цифр. Значение знакового разряда равно 0 для чисел Д2>0, и 1 —
для чисел А,<0 (рис. 3.12).
а)
Число 110 = 12
|0|0|0|0|0|0|0|1|
I Знак числа « + »
Число 12710= 111 11112
[о]Т|1|1|1|1|1|1|
Т Знак числа « + »
б)
Прямой код числа — 1
fl|O|O|O|O|Q|O|l|
f Знак числа « — »
Прямой код числа —127
ишшшшз
f Знак числа « — »
Рис. 3.12. Представление чисел в прямом коде:
а) положительных, б) отрицательных
Для прямого кода справедливо следующее соотношение:
<=о
(3.30)
где п — разрядность кода; азн — значение знакового разряда.
Например, десятичная запись числа, представленного в прямом
коде как 1101, будет иметь вид:
А10= (- 1)41 х 2° + 0 х 2>+ 1 х 22] = -5.
85
Дополнительный код. Использование чисел со знаком (прямо-
го кода представления чисел) усложняет структуру ЭВМ. В этом
случае операция сложения двух чисел, имеющих разные знаки,
должна быть заменена на операцию вычитания меньшей величи-
ны из большей и присвоения результату знака большей величины.
Поэтому в современных ЭВМ, как правило, отрицательные числа
представляют в виде дополнительного или обратного кодов, что при
суммировании двух чисел с разными знаками позволяет заменить
вычитание на обычное сложение и упростить тем самым конст-
рукцию арифметико-логического устройства компьютера.
Смысл перевода отрицательных чисел из прямого в дополни-
тельный и обратный коды поясним на примере с десятичными чис-
лами. Допустим, вычислительная машина, которая оперирует с
двухразрядными десятичными числами, должна сложить два чис-
ла: Х{ = 84 и Х2 = — 32. Заменим код отрицательного слагаемого Х2
егб дополнением до 100, так чтобы [Х2]доп = 100+ Х2 = 68. Сложив
числа X] + [Х2]доп, получим:
У= X, + [X,] = 84 + 68= 1 52.
1 1 2JAOn
Учитывая, что вычисления проводятся на устройстве с двумя
десятичными разрядами, конечный результат будет равен 52. Ра-
венство полученного результата истинному значению объясняет-
ся тем, что при формировании дополнительного кода к Х2 мы при-
бавляли 100, а затем из результата вычитали 100 отбрасыванием
старшего разряда:
Y = X, + [Х2]доп - 100 = X, + [Х2 + 100] - 100 =
= 84 + 1 — 32 +100] -- 100 = 52.
Операция вычитания 100 заключается в том, что не учитывает-
ся код третьего десятичного разряда.
Таким образом, дополнением М л-разрядного целого числа К
называют разность
М = рп — К, (3.31)
где р — основание системы счисления.
Так как количество различных целых n-разрядных чисел равно
рп (от 0 до рп — 1), то половину этих чисел рассматривают как по-
ложительные (от 0 до рп/2 — 1), а другую половину — как отрица-
тельные (т. е. как дополнения к первой половине чисел). Полный
же набор таких чисел называют числами, представленными в до-
полнительном коде (табл. 3.4) [6].
86
Дополнительные коды чисел
Таблица 3.4
Прямой код ряда 5-разрядных десятичных чисел Дополнительный код чисел
5-разрядных десятичных 4-разрядных шестнадцатеричных 16-разрядных двоичных
-50 000 50 000 —
-49 999 50 001 — —
-49 998 50 002 — —
-32 769 67 231
-32 768 67 232 8000 1 000 0000 0000 0000
-32 767 67 233 8001 1 000 0000 0000 0001
-3 99 997 FFFD 1 111 1111 1111 1101
-2 99 998 FFFF 1111 1111 1111 1110
-1 99 999 FFFF 1111111111111111
0 00 000 0000 0 000 0000 0000 0000
+ 1 00 001 0001 0 000 0000 0000 0001
+2 00 002 0002 0 000 0000 0000 0010
+3 00 003 0003 0 000 0000 0000 ООН
+32 766 32 766 7FFF 0 111 1111 1111 1110
+32 767 32 767 7FFF 0 111 1111 1111 1111
+32 768 32 768 — —
+49 998 49 998 — —
+49 999 49 999 — —
Легко проверить правильность получения дополнений (кодов
отрицательных чисел) в столбцах табл. 3.4. Для этого надо сложить
число из нижней половины таблицы с его дополнением, располо-
женным над кодом 0. Например:
а) для пятиразрядных десятичных чисел:
99999 + 00001 = 1 00000;
99998 + 00002 = 1 00000;
б) для четырехразрядных шестнадцатеричных чисел:
FFFF + 0001 = l 0000;
FFFE +0002=1 0000;
в) для шестнадцатиразрядных двоичных чисел:
1 111 1111 1111 1111 +0 000 0000 0000 0001 =
= 1 0 000 0000 0000 0000;
1 111 1111 1111 1110 + 0 000 0000 0000 0010 =
= 1 0 000 0000 0000 0000;
87
Как видно из примера, результатом такого суммирования бу-
дут числа 10s = ( 1 00 000) 10, 164 = (1 00 00) 16 и 216 = (1 0 000 0000 0000
0000)2. В связи с тем что разрядность чисел (см. табл. 3.4) ограниче-
на 5, 4 и 16 разрядами соответственно, единица в старшем разряде
полученных сумм не учитывается, так как она «выходит» за раз-
рядную сетку. Следовательно, все суммы равны нолю, т. е. правиль-
ному результату сложения двух одинаковых по величине чисел,
имеющих разные знаки.
Дополнения числа можно получить и без вычитания. Перепи-
шем формулу (3.31) в виде:
М = рп — К = ((рп-1) -К) +1.
(3.32)
Здесь число рп — 1 состоит из п цифр (р— 1), т. е. старших цифр
используемой системы счисления (для чисел в табл. 3.4 это 99 999,
FFFF или 1111111111111111).
Поэтому (рп — 1)—К можно получить путем образования допол-
нений до р—1 для каждой из цифр числа К в отдельности, а иско-
мое дополнение — суммированием этого числа с 1. Так как в дво-
ичной системе дополнения цифр до 1 соответствуют их инверс-
ным значениям (дополнение 0 равно 1, а дополнение 1— 0), то
можно дать простое правило для получения дополнения двоич-
ных чисел [6]:
1. Получить инверсию заданного числа (все его 0 заменить на 1,
а все 1 — на 0):
0 000 0010 1100 0101 число
1 111 11010011 1010 инверсия числа
2. Образовать дополнительный код заданного числа путем до-
бавления 1 к инверсии этого числа:
1 111 1101 ООП 1010 инверсия числа
________________1 слагаемое 1
1111 110100111011 дополнительный код числа
Проверим правильность перевода:
1 in ini ini nil
0 000 0010 1100 0101
1 111 1101 ООП 1011
10 000 0000 0000 0000
переносы
число
дополнительный код числа
0
88
(3.33)
где аы
Так как перенос из старшего разряда не учитывается, то резуль-
тат суммирования равен 0, что подтверждает правильность преоб-
разования.
Старший бит дополнительного кода двоичных чисел выполняет
функцию знака числа, т. е. равен 0 для положительных чисел и 1 —
для их дополнений (отрицательных чисел). При этом положитель-
ные числа в дополнительном коде изображаются так же, как и в
прямом, — двоичными кодами с цифрой 0 в знаковом разряде.
Для дополнительного кода справедливо следующее соотношение:
и-2
Ли=а,(-2-') + ^О?2'
1=0
0, для положительных чисел
1 д ; п — разрядность
1, для отрицательных чисел н
машинного слова.
Например, десятичная запись отрицательного числа, представ-
ленного в дополнительном коде как 1011, будет иметь вид:
А10 = lx (— 23) + [1 х2° + 1 х2’ + 0х22] = -8 + 3 = -5.
Обратный код. Для представления отрицательных чисел исполь-
зуется также обратный код, который получается инвертировани-
ем всех цифр двоичного кода абсолютной величины числа: ноли
заменяются единицами, а единицы — нолями. При этом, необхо-
димо помнить, что все операции с отрицательными числами вы-
полняются в формате машинного слова. Это значит, что к двоич-
ному числу слева дописываются ноли до нужного количества раз-
рядов. Например, для 8-разрядного машинного слова:
Число: — 1 Число: — 127
Код модуля числа: 00000001 Код модуля числа: 01111111
Обратный код числа: 11111110 Обратный код числа: 10000000
ПИЕИИИ
(3.34)
Для обратного кода справедливо следующее соотношение:
п-2
4о=«зи(-2'”* 1+1) + Х<2'.
i=0
0, для положительных чисел
, ч ; п — разрядность
1, для отрицательных чисел
машинного слова.
где азн
89
Например, десятичная запись отрицательного числа, представ-
ленного в обратном коде как 1010, будет иметь вид:
А)0 = 1 х (-23 + 1) + [0x2° +1x2' + 0х22] = -7 + 2 =-5.
Для положительных чисел ази = 0 и представление числа полнос-
тью совпадает с представлением в прямом и дополнительном кодах.
Таким образом, положительные числа в прямом, обратном и
дополнительном кодах изображаются одинаково — двоичными
кодами с цифрой 0 в знаковом разряде.
Обычно отрицательные десятичные числа при вводе в машину
автоматически преобразуются в обратный или дополнительный
двоичный код и в таком виде хранятся, перемещаются и участву-
ют в операциях. При выводе таких чисел из машины происходит
обратное преобразование в отрицательные десятичные числа.
Выполнение арифметических операций
Сложение и вычитание
В большинстве вычислительных устройств с целью упрощения
их конструкции операция вычитания не используется. Вместо нее
производится сложение обратных или дополнительных кодов
уменьшаемого и вычитаемого.
Сложение обратных кодов. В этом случае при сложении чисел
X и Y имеют место четыре основных и два особых случая:
1. Хи У положительные. При суммировании складываются все
разряды, включая разряд знака. Так как знаковые разряды поло-
жительных слагаемых равны нолю, разряд знака суммы тоже ра-
вен нолю. Например:
Десятичная запись Двоичные коды
3 0 0000011
+ _7 + 0 0000111
10 0 0001010
Получен корректный результат.
2. X положительное, У отрицательное и по абсолютной вели-
чине больше, чем X.
Например:
Десятичная запись Двоичные коды
3
nlQ
— 7
0 0000011
1 1110101
1 1111000
Обратный код числа — 10
Обратный код числа — 7
90
Получен корректный результат в обратном коде. При переводе
в прямой код биты цифровой части результата инвертируются:
1 0000111 = -710.
3. X положительное, Y отрицательное и по абсолютной вели-
чине меньше, чем X. Например:
Десятичная запись Двоичные коды
7
0 0001010
1 1Ш100
0 0000110
+1
0 0000111
Обратный код числа — 3
Компьютер исправляет полученный первоначально некоррек-
тный результат (6 вместо 7) переносом единицы из знакового раз-
ряда в младший разряд суммы.
4. X и У отрицательные. Например:
Десятичная запись Двоичные коды
-10
1 1111100
1 1111000
1 1110100
—
1 1110101
Обратный код числа — 3
Обратный код числа — 7
Обратный код числа — 10
Полученный первоначально некорректный результат (обрат-
ный код числа — 1110 вместо обратного кода числа — Ю10) компью-
тер исправляет переносом единицы из знакового разряда в млад-
ший разряд суммы. При переводе результата в прямой код биты
цифровой части числа инвертируются: 1 0001010 = — 101О.
При сложении может возникнуть ситуация, когда старшие разря-
ды результата операции не помещаются в отведенной для него обла-
сти памяти. Такая ситуация называется переполнением разрядной
сетки формата числа. Для обнаружения переполнения и оповеще-
ния о возникшей ошибке в компьютере используются специальные
средства. Ниже приведены два возможных случая переполнения.
5. X и У положительные, сумма Х+У больше либо равна 2"-1, где
п — количество разрядов формата чисел (для однобайтового фор-
мата п = 8, 2П-1 = 27 = 128). Например:
Десятичная запись Двоичные коды
65 01000001
+ 97 + 01100001
162 0 0100010 Переполнение
91
Семи разрядов цифровой части числового формата недостаточ-
но для размещения восьмиразрядной суммы (162]0 = 101000102),
поэтому старший разряд суммы оказывается в знаковом разряде.
Это вызывает несовпадение знака суммы и знаков слагаемых, что
является свидетельством переполнения разрядной сетки.
6. X и У отрицательные, сумма абсолютных величин X и У боль-
ше либо равна 2""1. Например:
Десятичная запись Двоичные коды
-63
' ^95
- 158
1 1000000 Обратный код числа —63
1 0100000 Обратный код числа — 95
0 1100000 Переполнение
Здесь знак суммы тоже не совпадает со знаками слагаемых, что
свидетельствует о переполнении разрядной сетки.
Сложение дополнительных кодов. Здесь также имеют место
рассмотренные выше шесть случаев. Примеры сложения целых чи-
сел X и У при 16-разрядном машинном слове сведены в табл. 3.5 [6].
В двух случаях (пятом и шестом) ограниченная разрядность чи-
сел приводит к искажению не только величины, но и знака ре-
зультата. Исправить положение можно, добавляя к результату (слу-
чай 5) или вычитая из него (случай 6) число 216= 65536.
Для обеспечения корректности вычислений перед суммирова-
нием необходимо анализировать знаки слагаемых и результата.
Разные знаки слагаемых или совпадение знаков слагаемых со зна-
ком суммы свидетельствуют о том, что результат будет коррект-
ным.
Таблица 3.5
Различные случаи сложения двоичных чисел со знаком
Случай Слагаемые и результат Комментарий
1 Х>0, Y>0, X+Y<2'5 0 000 0110 0011 1010 Х-+1594 + 0 100 0100 1001 1011 Y-+1756.3 0 100 1010 1101 0101 Z=+19157 Результат корректный
2 Х>0, Y<0, IX|<|Y| 0 000 0110 0011 1010 X=+1521 + 1 011 1011 01100101 Y--17563 1 100 0001 1001 1111 Z--15969 Результат корректный.
92
Окончание табл. 3.5
Случай Слагаемые и результат Комментарий
3 Х>0, У<(), |Х|>|У| 0 100 0100 1001 1011 Х-+17563 + 1 111 1001 1100 0110 Y=-159-1 1 0 011 1110 0110 0001 Z-+15969 Результат корректный. Перенос из старшего разряда не учитывается
4 Х<0, Y<0, |X|+|Y|<215 1 111 1001 1100 0110 X—1594 + 1011 10110110 0101 Y—1756.3 1 1 011 0101 0010 1011 Z—19157 Результат корректный. Перенос из старшего разряда не учитывается
5 X>0, Y>0, X+Y>2'5 0 100 0100 1001 1011 X-+17563 + 0 100 1010 1101 0101 Y-+19157 1 000 1111 0111 0000 Z--28816 При сложении положительных чисел получен отрицательный результат - ПЕРЕПОЛНЕНИЕ!
6 X<0, Y<0, |X|+|Y|>2‘5 1 011 1011 0110 0101 X--17563 + 1 011 0101 0010 1011 Y—19157 1 0 111 0000 1001 0000 Z-+28816 При сложении отрицательных чисел получен положительный результат — ПЕРЕПОЛНЕНИЕ!
Для контроля за выполнением арифметических операций в про-
цессоре ЭВМ (устройстве, в котором выполняются арифметичес-
кие операции) содержатся два индикатора — индикатор переноса
и индикатор переполнения. Каждый индикатор содержит 1 бит
информации и может иметь значение, равное 1 (индикатор уста-
новлен) или равное 0 (индикатор сброшен). Индикатор переноса
указывает на перенос из знакового бита, а индикатор переполне-
ния — на перенос в знаковый бит. Таким образом, после заверше-
ния операции, в которой происходит перенос в старший бит, про-
цессор устанавливает индикатор переполнения. Если такого пере-
носа нет, то индикатор переполнения сбрасывается. Индикатор
переноса обрабатывается аналогичным образом.
После выполнения операции процессором, ЭВМ сигнализирует о
состоянии индикаторов, и их можно проверить. Если состояние ин-
дикаторов указывает на неправильный арифметический результат,
то необходимо предпринять меры, исправляющие эту ситуацию,
т. е. пользователю ЭВМ предоставляется возможность контролиро-
вать правильность выполнения арифметических операций.
Операции сложения и вычитания являются основными опера-
циями в ЭВМ. Это объясняется тем, что они легко выполняются и
любые более сложные операции (умножение, деление, вычисле-
ние тригонометрических функций и т. д.) могут быть сведены к
многократным сложениям и вычитаниям. Так, во многих компью-
93
те pax умножение производится как последовательность сложений
и сдвигов, а деление реализуется путем многократного прибавле-
ния к делимому дополнительного кода делителя.
3.2.2. Смещенный код и код Грея
Смещенный код, или, как его еще называют, двоичный код с из-
бытком, используется в ЭВМ для упрощения операций над порядками
чисел с плавающей запятой. Он формируется следующим образом [4].
Сначала выбирается длина разрядной сетки — пи записываются пос-
ледовательно все возможные кодовые комбинации в обычной двоич-
ной системе счисления. Затем кодовая комбинация с единицей в стар-
шем разряде, имеющая значение 2n l, выбирается для представления
числа 0. Все последующие комбинации с единицей в старшем разряде
будут представлять числа 1,2,3,... соответственно, а предыдущие ком-
бинации в обратном порядке — числа —1, — 2, —3,.... Двоичный код
с избытком для 3- и 4-разрядных сеток представлен в табл. 3.6.
Таблица 3.6.
Номер кодовой комбинации Код с избытком 4 Десятичное значение Номер кодовой комбинации Код с избытком 4 Десятичное значение
7 111 3 15 1111 7
6 110 2 14 1110 6
5 101 1 13 1101 5
4 100 0 12 1100 4
3 011 -1 И 1011 3
2 010 -2 10 1010 2
1 001 -3 9 1001 1
0 000 -4 8 1000 0
7 0111 -1
6 ОНО -2
5 0101 -3
4 0100 -4
3 ООН -5
2 0010 -6
1 0001 -7
0 0000 -8
94
Так, числа 3 и — 3 в формате со смещением для 3-разрядной сет-
ки будут иметь представление 111 и 001 соответственно, в форма-
те со смещением для 4-разрядной сетки 1011и0101 соответствен-
но. Нетрудно заметить, что различие между двоичным кодом с из-
бытком и двоичным дополнительным кодом состоит в противопо-
ложности значений знаковых битов, а разность значений кодовых
комбинаций в обычном двоичном коде и двоичном коде с избыт-
ком для 3- и 4-разрядных сеток равна соответственно 4 и 8.
Например, кодовые комбинации 111 и 001 в обычном двоичном
коде имеют значения 7 и 1, а в двоичном коде с избытком: 3 и — 3
соответственно. Таким образом, разность значений кодовых ком-
бинаций в обычном двоичном коде и двоичном коде с избытком:
7—3 = 4 и 1—(—3) = 4.
Для 4-разрядной сетки кодовые комбинации 1011 и0101 в обыч-
ном двоичном коде имеют значения 11 и 5 соответственно а в двоич-
ном коде с избытком: 3 и — 3. Таким образом, 11 — 3 = 8и5—( — 3) = 8.
В связи с этим смещенный код для 3-разрядной сетки называют
двоичным кодом с избытком 4, для 4-разрядной — с избытком 8.
Смещенный код можно создать для любого значения п-разряд-
ности сетки. При этом он будет называться двоичным кодом с из-
бытком 2Л/.
Как было отмечено выше, смещенный код используется для уп-
рощения операций над порядками чисел с плавающей запятой. Так,
при размещении порядка числа в 8 разрядах используется двоич-
ный код с избытком 128. В этом случае порядок, принимающий
значения в диапазоне от — 128 до + 127, представляется смещен-
ным порядком, значения которого меняются от 0 до 255, что по-
зволяет работать с порядками как с целыми без знака.
Код Г рея широко используется в различных преобразовательных
устройствах (для кодирования положений валов, дисков и т. д.),
с тем, чтобы разрешить проблемы, связанные с возможностью од-
новременного изменения нескольких разрядов кодового слова.
Характерной особенностью кода Грея является то, что в нем
соседние кодовые слова различаются только в одном разряде.
Комбинации кода Грея, соответствующие десятичным числам от 0
до 15, приведены в табл. 3.7 [8].
Правила перевода числа из кода Грея в обычный двоичный код
сводятся к следующему:
1. Первая единица со стороны старших разрядов остается без
изменения.
95
2. Последующие цифры (0 и 1) остаются без изменения, если
число единиц, им предшествующих, четно, инвертируются — если
нечетно.
Число в десятичном коде Двоичный код Код Грея
0 0000 0000
1 0001 0001
2 0010 ООН
3 ООН 0010
4 0100 оно
5 0101 0111
6 оно 0101
7 0111 0100
Таблица 3.7.
Число в десятичном коде Двоичный код Код Грея
8 1000 1100
9 1001 1101
10 1010 1111
И 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000
Пример 15. Выразим число 1011, записанное в коде Г рея, в обыч-
ном двоичном коде:
1. Первую слева цифру (1) переписываем — 1;
2. Вторую слева цифру (0) инвертируем, так как перед ней толь-
ко одна единица — 1;
3. Третью цифру (1) опять инвертируем, так как перед ней толь-
ко одна единица — 0;
4. Четвертую цифру (1) оставляем без изменений, так как пе-
ред ней две единицы — 1.
Таким образом, числу 1011 в коде Грея соответствует двоичное
число — 1101.
Код Грея широко используется для кодирования положений
валов, дисков и т. д., позволяя свести к единице младшего разряда
погрешность при считывании.
96
На рис. 3.12 представлен один из вариантов кодирующей мас-
ки, выполненной в виде диска с обычным двоичным кодом [8].
Внешняя дорожка диска соответствует младшему разряду. Каж-
дому дискретному значению угла
ставится в соответствие определенное
двоичное число. Для считывания с каж-
дого из разрядов могут использоваться
различные чувствительные элементы:
щетки, фотоэлементы и т. д. При ис-
пользовании такой маски с обычным
двоичным кодом в местах, где одно-
временно изменяется состояние не-
скольких чувствительных элементов,
при считывании могут возникать
значительные погрешности. Так,
если чувствительные элементы рас-
полагаются на границе между числом 7
(0111) и 8 (1000), то преобразователь
может выдать на выходе любое чис-
Рис. 3.12. Кодирующая
маска в виде диска
с двоичным кодом
ло от 0 до 15.
Указанный недостаток устраняется при использовании масок
с кодом Грея. Кодирующая маска в виде прямоугольной пластины
с кодом Грея изображена на рис. 3.13 [8].
Рис. 3.13. Кодирующая маска в виде прямоугольной пластины с кодом Грея
В коде Грея при последовательном переходе от числа к числу
изменяется только один разряд, поэтому погрешность при счи-
тывании не может превосходить единицы младшего разряда не-
зависимо от того, в каком разряде имела место неопределен-
ность.
7 А-210
97
Ъ.ЪЪ. Представление вещественных чисел
и выполнение арифметических операций над ними в ЭВМ
Любое вещественное число N, представленное в системе счис-
ления с основанием р, можно записать в виде:
N — ±М х р**,
где М — мантисса; к — порядок числа (целое число).
Например, десятичное число 234,47 или двоичное число 1011,01
можно представить следующим образом:
234,47 = 234470 х 103 = 23447 х 102 = 2344,7 х 101 = 234,47 х 10° =
= 2,3447 х 102 = 0,23447 х 103 = 0,023447 х 10\
1011,01 = 101101 х 10 10 = 1011,01 х 10° =10,1101 х 1010 =
= 0,101101 х 10100 = 0,0101101 х Ю101.
Такое представление чисел называется представлением с пла-
вающей запятой, где порядок определяет, на сколько разрядов не-
обходимо осуществить сдвиг относительно запятой.
Если «плавающая» запятая расположена в мантиссе перед пер-
вой значащей цифрой, то при фиксированном количестве разря-
дов, отведенных под мантиссу, обеспечивается запись максималь-
ного количества значащих цифр числа, т. е. максимальная точность
представления числа. Из этого следует то, что мантисса должна
быть правильной дробью (|М| < 1), у которой первая цифра а пос-
ле запятой отлична от ноля (|М|= 0,а... ). Для двоичной системы
счисления а = 1, поэтому |М| = 0,1... . Если это требование выпол-
нено, то число называется нормализованным. Нормализованная
мантисса в двоичной системе счисления всегда представляется
десятичным числом п, лежащим в диапазоне 0,5 < n < 1.
При написании вещественных чисел в программах вместо при-
вычной запятой принято ставить точку.
Примеры нормализованного представления:
Десятичная система Двоичная система
753.15 = 0.75315x10’; -101.01= -0.10101 х 1011 (порядок 112 = 310);
-0.000034= -0.34Х10Л 0.000011 = 0.11х101Ю(порядок -1002 = -41О).
Вещественные числа в компьютерах представляются, пак пра-
вило, в трех форматах — одинарном, двойном и расширенном,
имеющих одинаковую структуру вида рис. 3.14.
98
Рис. 3.14. Формат представления вещественных чисел
Здесь порядок n-разрядного нормализованного числа задается
смещенным кодом (см. п. 3.2.2), позволяющим производить опера-
ции над порядками как над беззнаковыми числами, что упрощает
операции сравнения, сложения и вычитания порядков, а также
операцию сравнения самих нормализованных чисел.
Чем больше разрядов отводится под запись мантиссы, тем выше
точность представления числа. Чем больше разрядов занимает по-
рядок, тем шире диапазон от наименьшего отличного от ноля чис-
ла до наибольшего числа, представимого в машине при заданном
формате.
Нормализованное число одинарной точности, представленное
в формате с плавающей запятой, записывается в память следую-
щим образом: знак числа (знак мантиссы) — в бите 15 первого слова
(О — для положительных и 1 — для отрицательных чисел); порядок
размещается в битах 7 — 14 первого слова, а мантисса занимает
остальные 23 бита в двух словах. При этом, хотя для мантиссы от-
ведены 23 разряда, в операциях участвуют 24 разряда, так как стар-
ший разряд мантиссы нормализованного числа не хранится (он
всегда равен 1), т. е. имеет место так называемый скрытый разряд,
который при аппаратном выполнении операций автоматически
восстанавливается и учитывается при выполнении операций. По-
рядок числа также учитывает скрытый старший разряд мантиссы.
Нормализованное число двойной точности представляет собой
64-разрядное нормализованное число со знаком, 11-разрядным
смещенным порядком и 53-разрядной мантиссой (размер поля,
выделенного для хранения мантиссы, составляет 52 разряда, а стар-
ший бит мантиссы не хранится).
Расширенный формат позволяет хранить ненормализованные
числа в виде 80-разрядного числа со знаком: 15-разрядным смещен-
ным порядком и 64-разрядной мантиссой.
99
Следует отметить, что вещественный формат с ш-разрядной
мантиссой дает возможность абсолютно точно представлять
m-разрядные целые числа, т. е. любое двоичное целое число, со-
держащее не более т разрядов, может быть без искажений пре-
образовано в вещественный формат.
Примеры представления чисел с плавающей запятой:
1) 0,110 = 0,000(1100)2 = 0,(1100)2 х 102(-3)10, при этом порядок
числа представляется двоичным кодом с избытком 128:
-310= (-3 4- 128)10 = 011111012.
fo o|l|l|l|l|l|o|l|l|o|o|l|l|ojo]
1 i|o|o|i|i|o|o i|i|o|o|i|i|o|i
Заметим, что в этом примере мантисса представлена бесконеч-
ной периодической дробью, поэтому последний учитываемый раз-
ряд мантиссы округляется.
2) -49,510 = - 110001,1002 = - 0,11000112 х 102|6Ч при этом по-
рядок числа:
610 =(6 4- 128)10 = 100001102.
11|1|о|о|о|о|1[Т о|1|о|о|о|1|1|о]
Выполнение арифметических действий
над нормализованными числами
При алгебраическом сложении и вычитании чисел, представ-
ленных в формате с плавающей запятой, сначала уравниваются
порядки слагаемых. В процессе выравнивания порядков мантисса
числа с меньшим порядком сдвигается в своем регистре вправо на
количество разрядов, равное разности порядков операндов. Пос-
ле каждого сдвига порядок увеличивается на единицу. В результа-
те выравнивания порядков одноименные разряды чисел оказыва-
ются расположенными в соответствующих разрядах обоих регис-
тров, после чего мантиссы складываются или вычитаются. В слу-
100
чае необходимости полученный результат нормализуется путем сдви-
га мантиссы результата влево. После каждого сдвига влево порядок
результата уменьшается на единицу. Ниже в примерах для упроще-
ния расчетов порядок представлен в обычной двоичной форме.
Пример 16. Сложите двоичные нормализованные числа
0.10111 х 10 1 и 0.11011 х 1010. Разность порядков слагаемых здесь
равна трем, поэтому перед сложением мантисса первого числа
сдвигается на три разряда вправо:
0.00010111 х 1010
+ 0.11011 хЮ10
0.11101111 х 1010
Пример 17. Выполним вычитание двоичных нормализованных
чисел 0.10101 х 1010и 0.11101 х 10’. Разность порядков уменьшаемо-
го и вычитаемого здесь равна единице, поэтому перед вычитани-
ем мантисса второго числа сдвигается на один разряд вправо:
_ 0.10101 хЮ10
0.011101 х 1Q10
0.001101 х Ю10
Результат получился не нормализованным, поэтому его мантис-
са сдвигается влево на два разряда с соответствующим уменьше-
нием порядка на две единицы: 0.1101 х 10°.
При умножении порядки складываются, а мантиссы перемно-
жаются.
Пример 18. Выполним умножение двоичных нормализованных
чисел:
(0.11101 х 10101) х (0.1001 х 10") = (0.11101 х 0.1001) х 10>101 + 11> =
= 0.100000101 х Ю1000.
При делении из порядка делимого вычитается порядок делите-
ля, а над мантиссами совершается обычная операция деления.
В случае необходимости полученный результат нормализуется, что
приводит к изменению порядков, так как каждый сдвиг на один
разряд влево соответствует уменьшению порядка на единицу, а
сдвиг вправо — увеличению его на единицу. Введение термина
«плавающая запятая» как раз и объясняется тем, что двоичный
порядок, определяющий фактическое положение запятой в изоб-
101
ражении числа, корректируется после выполнения каждой ариф-
метической операции, т. е. запятая в изображении числа плавает
(изменятся ее положение) по мере изменения данной величины.
Пример 19. Выполним деление двоичных нормализованных
чисел.
0.11 llxlO100: 0.101 хЮ11 = (0.1111 : 0.101) хЮ1100"111 =
= 1.1x10' = 0.11x10”.
32.4. Погрешности представления числовой информации в ЭВМ
Представление числовой информации в ЭВМ, как правило, вле-
чет за собой появление погрешностей (ошибок), величина кото-
рых зависит от формы представления чисел и от длины разрядной
сетки цифрового автомата [21].
Абсолютная погрешность Д [А] представления кода числа в раз-
рядной сетке ЭВМ определяется по формуле:
Д[А] = |А| - |А„|,
где |А| — модуль числа А, код которого требуется представить
в ЭВМ;
|Ам| — модуль числа Ам, код которого представлен в разрядной
сетке.
Относительная погрешность представления — величина
5[А]= Д[А]/|Аи|.
Для чисел с фиксированной запятой, представленных в форма-
те рис. 3.9, наибольшее значение абсолютной погрешности равно
весу младшего разряда разрядной сетки:
МА]тм = 2-1. (3.35)
Другими словами, максимальная погрешность перевода деся-
тичной информации в двоичную не будет превышать единицы
младшего разряда разрядной сетки автомата. Минимальная по-
грешность перевода равна нолю.
Отбрасывание младших разрядов кода числа, не вошедших в раз-
рядную сетку, может быть выполнено с округлением. В этом слу-
чае, если число ДА, код которого отбрасывается, меньше половины
веса младшего разряда разрядной сетки ЭВМ (ДА < 0,5x2'), то код
числа в разрядной сетке остается без изменений. В противном слу-
чае в младший разряд кода разрядной сетки добавляется единица.
102
Наибольшая абсолютная погрешность представления числа в
разрядной сетке с округлением равна:
= 0,5x2'.
Пределы изменения относительной погрешности при представ-
лении чисел с фиксированной запятой в ЭВМ с округлением оп-
ределяются по формулам:
= [А’]ти/|А|тах = 0,5х2'/(2п - 2-'); (3.36)
«ЯА1тах = A [A’U/HL = 0,5 х 2' / 2-' = 0,5. (3.37)
Из (3.37) видно, что погрешности представления чисел в форме
с фиксированной запятой могут быть значительными.
Для представления чисел в форме с плавающей запятой
(см. рис. 3.14) абсолютное значение мантиссы МЛ:
2'1 < |МД| < 1 - 2~т, (3.38)
где Л1 — количество разрядов, отведенных под мантиссу.
В этом случае, как и для формата с фиксированной запятой,
наибольшее значение абсолютной погрешности представления
мантиссы равно весу младшего разряда разрядной сетки, а наи-
большая абсолютная погрешность представления мантиссы в раз-
рядной сетке с округлением равна:
Д1М.1 = 0,5 х 2т.
Для нахождения погрешности представления числа Ат в форме
с плавающей запятой величину этой погрешности надо умножить
на величину порядка числа РА:
- 0.5 X 2- Р, / (2-РЛI - 2-;
4A.U-A|A.U'KI„“°.5x2-Pa/|(l -2-|Ра)-0,5х2-/(1 -2™).
где т — количество разрядов для представления мантиссы числа.
Для ЭВМ т > 16, тогда 1 — 2 “=/ и 5[Am]min = 0,5 х 2“ш.
Таким образом, относительная точность представления чисел
в форме с плавающей запятой почти не зависит от величины чис-
ла и определяется количеством разрядов, отведенных под ман-
тиссу.
103
3.3. ПРЕДСТАВЛЕНИЕ СИМВОЛЬНОЙ ИНФОРМАЦИИ В ЭВМ
Символьная (алфавитно-цифровая) информация хранится и
обрабатывается в ЭВМ в форме цифрового кода, т. е. каждому сим-
волу ставится в соответствие отдельное бинарное слово-код. При
выборе метода кодирования руководствуются объемом и спосо-
бами обработки символьной информации. Так как многие типы
информации содержат в значительном объеме цифровую инфор-
мацию, то применяются две системы кодирования: символьной
информации и десятичных чисел.
Необходимый набор символов, предусмотренный в конкретной
ЭВМ, обычно включает в себя:
буквенно-цифровые знаки алфавита (алфавитов);
• специальные знаки (пробел, скобки, знаки препинания и др.);
знаки операций.
Кроме того, в состав набора входят управляющие символы, со-
ответствующие определенным функциям.
Среди наборов символов наибольшее распространение полу-
чили знаки кода ASCII (ASCII — American Standard Code for
Information Interchange) — американский стандартный код обмена
информацией и кода EBCDIC (Extended Binary Coded Decimal
Interchange Code) — расширенный двоично-десятичный код обме-
на информацией. Набор EBCDIC используется главным образом
на «больших» машинах, тогда как набор ASCII, созданный в 1963 г. и
введенный в действие институтом стандартизации США (ANSI —
American National Standard Institute), находит наиболее широкое
применение в мини- и микроЭВМ, в том числе в персональных
компьютерах.
ASCII — это семиразрядный код, обеспечивающий 128 различ-
ных битовых комбинаций. Стандартный знакогенератор современ-
ного персонального компьютера IBM PC имеет 8-битную кодиров-
ку символов, состоящую из двух таблиц кодирования: базовой и
расширенной. Базовая таблица построена по стандарту ASCII и оди-
накова для всех IBM-совместимых компьютеров. Расширенная
относится к символам с номерами от 128 до 255 и может отличать-
ся на компьютерах разного типа (рис. 3.15).
Первые 32 кода базовой таблицы, начиная с нолевого, отданы
производителям аппаратных средств (в первую очередь произво-
дителям компьютеров и печатающих устройств). В этой области
104
размещаются так называемые управляющие коды, которым не со-
ответствуют никакие символы языков, и соответственно эти коды
не выводятся ни на экран, ни на устройства печати, но они могут
управлять тем, как производится вывод прочих данных.
Начиная с кода 32 по код 127 размещены коды символов анг-
лийского алфавита, знаков препинания, цифр, арифметических
действий и некоторых вспомогательных символов.
СО сч 5 8 176 О} см <35 208 224 1240
00 Е а til Г" и а = 00
01 U 2В i 1 1 т Р ± 01
02 ё А б 1 т тг г > 02
03 а О й 1 1 Ц я < 03
04 а О й 1 - ь X т 04
05 А 6 N I г о J 05
06 Ь U ас dl I- ГТ Ц “Г 06
07 С U О Tl II- 'Т 07
08 ё У 4 =1 S о 08
09 ё б 1— =11 If J 0 09
10 ё и —• II JT г S • 10
11 1 С Т1 Тг 1 б И
12 1 £ 'А JJ !г оо п 12
13 1 т JJ = 1 я6 X 13
14 А « =1 яг тг 1 е 14
15 А f » 1 "Г” п 15
Рис. 3.15. Стандартная кодировка фирмы IBM:
а) для кодов 1...127; б) для кодов 128...255
В расширенной таблице стандартной кодировки фирмы IBM три
смежные колонки (коды 176...223) занимают символы псевдогра-
фики, колонки с кодами от 128 до 175 и от 224 до 239 используются
для размещения некоторых символов национальных алфавитов
различных европейских языков, а последняя колонка (коды
105
240...255) — для размещения специальных знаков. С учетом этого
расположения символов разрабатывается подавляющее большин-
ство программ зарубежного производства.
Для представления букв русского алфавита в рамках ASCII
первоначально был разработан ГОСТовский вариант кодиров-
ки — КОИ-7 (код обмена информацией 7-битный). Расположе-
ние символов во второй половине таблицы этой кодировки рез-
ко отличается от принятого фирмой IBM, что затрудняет исполь-
зование зарубежного программного обеспечения на отечествен-
ных ЭВМ. В связи с этим он практически не применяется, а на
отечественных ПК введена так называемая ГОСТ-алыпернатив-
ная кодировка, главное достоинство которой — расположение
символов псевдографики на тех же местах, что и в кодировке
IBM (рис. 3.16).
00
01
02
03
04
05
06
07
08
09
10
И
12
13
14
15
СО-Ч'ФЮГЯСО’Ч'О
счч'ФГ'ФОСЧ'Ч'
— — CNCSC4
А -р а и “Г и р =
Б с б 1 1 т с
'В т в 1 т тт т >
Г У г 1 1 и У <
Д ф д i - 1= ф f
Е X е 1 + г X J
Ж ц ж 11 F ГТ Ц ч-
3 ч 3 т IF ч
И ш и т U. + ш о
Й щ й 41 (г Т Щ
К ъ к II X Г ъ •
Л ы л Т1 Тг ы
м ь м JJ lh ь п
н э н JJ г э к
о ю О =1 ГТГ" пг 7 ю
п я п 7 "Г W я
00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
Рис. 3.16. ГОСТ-альтернативная кодировка
106
В настоящее время находят широкое применение и другие виды
кодировки [13].
Так, в связи с массовым распространением операционных сис-
тем и других продуктов компании Microsoft в нашей стране нашла
применение кодировка символов русского языка, известная как
кодировка Windows-1251 (рис. 3.17).
128 Ъ 144 $ 160 176 0 192 А 208 Р 224 а 240 р
129 Г 145 ‘ 161 V 177 ± 193 Б 209 С 225 б 241 с
130 , 146 ’ 162 у 178 I 194 В 210 Т 226 в 242 т
131 f 147 “ 163 J 179 i 195 Г 211 У 227 г 243 у
132 „ 148 ” 164 о 180 г 196 Д 212 Ф 228 д 244 ф
133 ... 149 • 165 Г 181 ц 197 Е 213 X 229 е 245 х
134 f 150 - 166 | 182 198 Ж 214 Ц 230 ж 246 ц
135 $ 151 — 167 § 183 • 199 3 215 Ч 231 з 247 ч
136 € 152 ~ 168 Ё 184 ё 200 И 216 Ш 232 и 248 ш
137 %о 153 ™ 169 © 185 № 201 Й 217 Щ 233 й 249 щ
138 Л> 154 л> 170 186 с 202 К 218 Ъ 234 к 250 ъ
139 < 155 > 171 « 187 » 203 Л 219 Ы 235 л 251 ы
140 Н» 156 н> 172 - 188 j 204 М 220 Ь 236 м 252 ь
141 К 157 к 173 - 189 S 205 Н 221 Э 237 н 253 э
142 Ъ 158 h 174 ® 190 s 206 О 222 Ю 238 о 254 ю
143 Ц 159 ц 175 I 191 Т 207 П 223 Я 239 п 255 я
Рис. 3.17. Кодировка Windows 1251
Эта кодировка используется на большинстве персональных
компьютеров, работающих на платформе Windows.
Другая распространенная кодировка носит название КОИ-8
(код обмена информацией восьмизначный) (рис. 3.18) — ее проис-
хождение относится ко временам действия Совета Экономичес-
кой Взаимопомощи государств Восточной Европы. Сегодня коди-
ровка КОИ-8 имеет широкое распространение в компьютерных се-
тях на территории России и в некоторых службах российского сек-
тора Интернета. В частности, в России она де-факто является стан-
дартной в сообщениях электронной почты и телеконференций.
107
128 144Ш 160 — 176 1 192 ю 208 п 224 Ю 240 П
129 I 145 И 161 Ё 177 1 193 а 209 я 225 А 241 Я
130 Г" 146 162 Г 178 -1 194 6 210р 226 Б 242 Р
131 1 147 f 163 ё 179 Ё 195 ц 211 с 227 Ц 243 С
132 L 148 164 г 180 ’I 196 д 212т 228 Д 244 Т
133 -1 149. 165 Г 181 -1 197 е 213у 229 Е 245 У
134 F 150 "V 166 1 182 т 198 ф 214ж 230 Ф 246 Ж
135-1 151 = 167 I 183 т 199 г 215в 231 Г 247 В
136 т 152 < 168 -| 184 т 200 х 216ь 232 X 248 Ь
137-L 153 > 169 L 185 -J- 201 и 217ы 233 И 249 Ы
138 + 154 170 1_ 186 -L 202 й 218з 234 Й 250 3
139- 155 J 171 L 187 J- 203 к 219 ш 235 К 251 Ш
140- 156- 172 -1 188 + 204 л 220 э 236 Л 252 Э
141 | 1572 173 -> 189 + 205 м 221 щ 237 М 253 Щ
142 1 158. 174 -> 190 + 206 н 222 ч 238 Н 254 Ч
143 1 159 + 175 h 191 ё 207 о 223 ъ 239 О 255 Ъ
Рис. 3.18. Кодировка KOH-8R
В последнее время все большее распространение получает уни-
версальная система кодирования текстовых данных — UNICODE.
В данной системе символы кодируются не восьмиразрядными дво-
ичными числами, а 16-разрядными числами. Шестнадцать разря-
дов позволяют обеспечить уникальные коды для 65536 различных
символов — этого достаточно для размещения в одной таблице всех
широкоупотребляемых языков.
В отличие от символьной для десятичной цифровой информа-
ции при байтовой организации в целях экономии памяти и удоб-
ства обработки используют специальные форматы кодирования
десятичных чисел — зонный и упакованный. При этом десятич-
ные числа рассматриваются как десятичные со знаком, имеющие
переменную длину.
108
В упакованном формате /ул каждой десятичной цифры отво-
дится по 4 двоичных разряда (полбайта), при этом знак числа ко-
дируется в крайнем правом полубайте числа (1100 — знак « + » и
1101 — знак « —»).
Структура поля упакованного формата1:
цф Цф Цф Цф ... цф знак
байт байт байт
Упакованный формат применяется обычно в ЭВМ при выпол-
нении арифметических операций: сложения, вычитания, умноже-
ния, деления и сравнения.
В зонном формате для каждой десятичной цифры отводится по
целому байту, при этом старшие полубайты (зона) каждого байта
(кроме самого младшего) заполняются кодом 1111, а в младших (ле-
вых) полубайтах обычным образом кодируются десятичные циф-
ры. Старший полубайт (зона) самого младшего (правого) байта ис-
пользуется для кодирования знака числа.
Структура поля зонного формата:
зона Цф зона Цф зона Цф знак Цф
байт байт байт байт
Зонный формат удобен для представления вводимой в ЭВМ де-
сятичной информации, когда каждая десятичная цифра вместе
с кодом зоны занимает целый байт.
Пример 20. Число —283(10) = —0010 1000 0011(210) в ЭВМ будет
представлено:
В упакованном формате 0010 1000 ООН 1101
В зонном формате 1111 0010 1111 1000 1101 ООП
1 Здесь и далее: цф — цифра; знак — знак числа.
109
3.4. ПРЕДСТАВЛЕНИЕ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ
Современные компьютерные системы способны обрабатывать
не только простейшие текстовые и цифровые данные. Они позво-
ляют работать также с изображениями и с аудио- и видеоинфор-
мацией. В отличие от методов представления символьной и число-
вой информации, для представления изображений, аудио- и видео-
информации пока не существует общепризнанных стандартов.
Наиболее распространенные из существующих методов пред-
ставления изображений можно разделить на две большие катего-
рии: растровые методы и векторные методы.
При растровом методе изображение представляется как сово-
купность точек, называемых пикселями (pixel — сокращение от
picture element — элемент изображения). Поскольку линейные
координаты и индивидуальные свойства каждой точки (яркость)
можно выразить с помощью целых чисел, то можно сказать, что
растровое кодирование позволяет использовать двоичный код для
представления графических данных. Общепринятым на сегодняш-
ний день считается представление черно-белых иллюстраций в
виде комбинации точек с 256 градациями серого цвета, и, таким
образом, для кодирования яркости любой точки обычно достаточ-
но восьмиразрядного двоичного числа.
Для кодирования цветных графических изображений приме-
няется принцип декомпозиции произвольного цвета на основные
составляющие. В качестве таких составляющих используют три
основных цвета: красный (Red, R), зеленый (Green, G) и синий (Blue,
В). На практике считается, что любой цвет, видимый человечес-
ким глазом, можно получить путем механического смешения этих
трех основных цветов. Такая система кодирования называется
системой RGB (по первым буквам названий основных цветов).
Если для кодирования яркости каждой из основных составляю-
щих использовать по 256 значений (восемь двоичных разрядов), как
это принято для полутоновых черно-белых изображений, то на ко-
дирование цвета одной точки надо затратить 24 разряда (рис. 3.19).
• ОЛ Лыт _ ь.
Ч с- 1 UH1
Красный Зеленый Синий
8 бит 8 бит 8 бит
Рис. 3.19. Кодирование цветного изображения
ПО
При этом система кодирования обеспечивает однозначное оп-
ределение 16,5 млн различных цветов, что близко к чувствитель-
ности человеческого глаза. Режим представления цветной графи-
ки с использованием 24 двоичных разрядов называют полноцвет-
ным (True Color).
Графические файлы, в которых применяется цветовая система
RGB, представляют каждый пиксель в виде цветового триплета —
трех числовых величин (R, G, В), соответствующих интенсивнос-
тям красного, зеленого и синего цветов (рис. 3.20).
Голубой (0,255,255)
Рис. 3.20. Цветовая система RGB
Для 24-битового цвета триплетом (0, 0, 0) обычно представляет-
ся черный цвет, а триплетом (255, 255, 255) — белый. Если все три
величины RGB имеют одинаковые значения, например (63, 63, 63),
(127, 127, 127) или (191, 191, 191), то результирующим будет один
из оттенков серого цвета.
Кроме RGB, другими популярными системами кодирования
цветных изображений являются CMY и HSB.
CMY (Cyan-Magenta-Yellow — голубой-пурпурный-желтый) —
цветовая система, применяемая для получения цветных изображе-
ний на белой поверхности. Эта система используется в большин-
стве устройств вывода, таких как лазерные и струйные принтеры,
когда для получения твердых копий краски наносятся на белую
бумагу. При освещении каждый из трех основных цветов погло-
111
щает дополняющий его цвет: голубой цвет поглощает красный,
пурпурный — зеленый, а желтый — синий. Например, если увели-
чить количество желтой краски, то интенсивность синего цвета в
изображении уменьшится.
Новые цвета в системе CMY получают вычитанием цветовых
составляющих из белого цвета. Они имеют длину волны отражен-
ного света, не поглощенного основными цветами CMY. Например,
в результате поглощения голубого и пурпурного цветов образует-
ся желтый, т. е. можно сказать, что желтый цвет является резуль-
татом «вычитания» из отраженного света голубой и пурпурной
составляющих. Если все составляющие CMY будут вычтены (или
поглощены), то результирующим цветом станет черный. На прак-
тике же получить идеальный черный цвет без дорогостоящих кра-
сителей в системе CMYвесьма сложно.
Существует более практичный вариант CMY— система CMYK,
в которой символ К означает черный цвет. Введение в эту цвето-
вую систему черного цвета в качестве независимой основной цве-
товой переменной позволяет использовать недорогие красители.
Систему CMYK часто называют четырехцветной, а результат ее
применения — четырехцветной печатью. Во многих моделях точ-
ка, окрашенная в составной цвет, группируется из четырех точек,
каждая из которых окрашена в один из основных цветов CMYK.
Данные в системе CMYK представляются либо цветовым трип-
летом, аналогичным RGB, либо четырьмя величинами. Если дан-
ные представлены цветовым триплетом, то отдельные цветовые
величины противоположны величинам RGB. Так, для 24-битового
пиксельного значения триплет (255,255, 255) соответствует черно-
му цвету, а триплет (0, 0, 0) — белому. Однако в большинстве слу-
чаев для представления цветов в системе CMYK используется пос-
ледовательность четырех величин.
Как правило, четыре цветовые составляющие CMYK задаются
в процентах в диапазоне от 0 до 100.
Модель HSV (Hue, Saturation, Value — оттенок, насыщенность, ве-
личина) — одна из многих цветовых систем, в которых при представ-
лении новых цветов не смешивают основные цвета, а изменяют их
свойства. Оттенок — это «цвет» в общеупотребительном смысле этого
слова, например красный, оранжевый, синий и т. д. Насыщенность
(также называемая цветностью) определяется количеством белого
в оттенке. В полностью насыщенном (100%) оттенке не содержится
белого, такой оттенок считается чистым. Ча-стично насыщенный от-
112
тенок светлее по цвету. Красный оттенок с 50%-ной насыщенностью
соответствует розовому. Величина (также называемая яркостью) оп-
ределяет интенсивность свечения цвета. Оттенок с высокой интен-
сивностью является очень ярким, а с низкой — темным.
Модель HSV напоминает принцип, используемый художника-
ми для получения нужных цветов, — смешивание белой, черной и
серой с чистыми красками для получения различных тонов и от-
тенков [tint, shade и tone}. Оттенок tint является чистым, полнос-
тью насыщенным цветом, смешанным с белым, а оттенок shade —
полностью насыщенным цветом, смешанным с черным. Тон [tone] —
это полностью насыщенный цвет, к которому добавлены черный
и белый цвета (серый). Если рассматривать систему HSVс точки
зрения смеси этих цветов, то насыщенность будет представлять
собой количество белого, величина — количество черного, а отте-
нок — тот цвет, к которому добавляются белый и черный.
Режим, когда для кодирования цвета каждой точки использует-
ся 32 двоичных разряда, так же как и рассмотренный выше с ис-
пользованием 24 разрядов, называют полноцветным (True Color).
Если уменьшить количество двоичных разрядов, используемых для
кодирования цвета каждой точки, то можно сократить объем дан-
ных, но при этом диапазон кодируемых цветов заметно сокраща-
ется. Кодирование цветной графики 16-разрядными двоичными
числами называют режимом High Color.
При кодировании информации о цвете с помощью восьми бит
данных можно передать только 256 цветовых оттенков. Такой ме-
тод кодирования цвета называют индексным. Смысл названия со-
стоит в том, что, поскольку 256 значений недостаточно, чтобы пе-
редать весь диапазон цветов, доступный человеческому глазу, код
каждой точки растра выражает не цвет сам по себе, а только его
номер (индекс) в справочной таблице, называемой палитрой. Эта
палитра прикладывается к графическим данным.
Одним из недостатков растровых методов является трудность
пропорционального изменения размеров изображения до произ-
вольно выбранного значения. В сущности, единственный способ
увеличить изображение — это увеличить сами пиксели. Однако
это приводит к появлению зернистости — пикселизации.
Векторные методы позволяют избежать проблем масштабиро-
вания, характерных для растровых методов. В этом случае изобра-
жение представляется в виде совокупности линий и кривых. Вме-
8 А 210
ИЗ
сто того чтобы заставлять устройство воспроизводить заданную
конфигурацию пикселей, составляющих изображение, ему пере-
дается подробное описание того, как расположены образующие
изображение линии и кривые. На основе этих данных устройство
в конечном счете и создает готовое изображение. С помощью по-
добной технологии описываются различные шрифты, поддержи-
ваемые современными принтерами и мониторами. Они позволя-
ют изменять размер символов в широких пределах и по этой при-
чине получили название масштабируемых шрифтов. Например,
технология True Туре, разработанная компаниями Microsoft и Apple
Computer, описывает способ отображения символов в тексте. Для
подобных целей предназначена и технология PostScript (разрабо-
тана компанией Adobe Systems), позволяющая описывать способ
отображения символов, а также других, более общих графичес-
ких данных. Векторные методы также широко применяются в ав-
томатизированных системах проектирования, которые отобража-
ют на экране мониторов чертежи сложных трехмерных объектов
и предоставляют средства манипулирования ими. Однако вектор-
ная технология не позволяет достичь фотографического качества
изображений объектов как при использовании растровых мето-
дов.
Контрольные вопросы
1. Что такое система счисления?
2. В чем отличие позиционной системы счисления от непозиционной?
3. Что называется основанием системы счисления?
4. Что понимают под алфавитом системы счисления?
5. Сформулируйте правила выполнения арифметических действий
в позиционных системах счисления?
6. Что такое код?
7. Какие системы счисления являются более эффективными для ис-
пользования в цифровых автоматах?
8. Какие способы перевода чисел из одной системы счисления в дру-
гую Вы знаете?
9. В чем заключается преимущество использования восьмеричной и
шестнадцатеричной систем счисления?
10. Дайте определение двоично-десятичной системы счисления.
11. Что такое машинное слово?
12. Что представляет собой выходной сигнал элемента памяти ЭВМ?
114
13. Назовите формы представления двоичных чисел в ЭВМ.
14. Что такое прямой, обратный и дополнительный коды?
15. Сформулируйте правила, определяющие правильность выполне-
ния операций сложения чисел со знаком и без знака в ЭВМ.
16. Что такое смещенный код?
17. Что такое код Грея?
18. Как представляются вещественные числа в ЭВМ?
19. Чем определяется погрешность представления числовой инфор-
мации в ЭВМ?
20. Как представляются символьные данные в ЭВМ?
21. Какие системы кодировки символьной информации Вы знаете?
22. Какие системы кодирования графической информации Вы знаете?
Тлава У
Логические основы построения
цифровых автоматов
Основу любого дискретного вычислительного устройства со-
ставляют элементарные логические схемы. Работа этих схем ос-
нована на законах и правилах алгебры логики, которая оперирует
двумя понятиями: истинности и ложности высказывания.
Алгебра логики — раздел математики, изучающий высказывания,
рассматриваемые со стороны их логических значений (истинности или
ложности) и логических операций над ними.
Высказывание — некоторое предложение, в отношении которого
можно однозначно сказать, истинно оно или ложно.
Аппарат алгебры логики {булевой алгебры) создан в 1854 г. Дж.
Булем как попытка изучения логики мышления математическими
методами. Впервые практическое применение булевой алгебры было
сделано К. Шенноном в 1938 г. для анализа и разработки релейных
переключательных сетей, результатом чего явилась разработка ме-
тода представления любой сети, состоящей из совокупности пере-
ключателей и реле, математическими выражениями и принципов их
преобразования на основе правил булевой алгебры [1]. Ввиду нали-
чия аналогий между релейными и современными электронными схе-
мами аппарат булевой алгебры нашел широкое применение для их
структурно-функционального описания, анализа и проектирования.
Использование булевой алгебры позволяет не только более удобно
оперировать с булевыми выражениями (описывающими те или иные
электронные узлы), чем со схемами или логическими диаграммами,
но и на формальном уровне путем эквивалентных преобразований и
базовых теорем упрощать их, давая возможность создавать эконо-
мически и технически более совершенные электронные устройства
любого назначения. Операции булевой алгебры часто встречаются и
в программном обеспечении вычислительных устройств, где они ис-
пользуются для замены аппаратной логики на программную.
Аппарат булевой алгебры, как и любая другая формальная ма-
тематическая система состоит из трех множеств: элементов, опе-
раций над ними и аксиом.
116
Элементы. Схемы вычислительных устройств можно условно
разделить на три группы: исполнительные, информационные и
управляющие. Первые производят обработку информации, пред-
ставленной в бинарной форме; вторые служат для передачи би-
нарной формы информации; третьи выполняют управляющие
функции, генерируя соответствующие сигналы. Во всех случаях в
тпх или иных точках логических схем сигналы двух различных
уровней могут представляться бинарными символами {0,1} или
логическими значениями {Истина (True), Ложь (False)}. Поэтому
множество элементов булевой алгебры выбирается бинарным
В “ {0,1}, а сама алгебра называется бинарной, или переключатель-
ной. Ее элементы называются константами, или логическими 0 и
1, которым в ряде случаев соответствуют бинарные цифры, в дру-
гих случаях — логические значения, соответственно ложь (False) и
истина (True). В дальнейшем для обозначения булевых перемен-
ных будем использовать буквы латинского алфавита — х, у, z... .
Набор переменных х, у, z...может рассматриваться как п-разряд-
ный двоичный код, разрядами которого являются эти переменные.
Операции. Основными, или базовыми, операциями булевой
алгебры служат (табл. 4.1): И (AND), ИЛИ (OR) и НЕ (NOT). Опера-
ция И называется логическим умножением или конъюнкцией и
обозначается знаком умножения {•, л}. Операция ИЛИ называет-
ся логическим сложением или дизъюнкцией и обозначается знаком
сложения { +, v}. Операция НЕ называется логическим отрицани-
ям или инверсией (дополнением) и обозначается знаком {', —>}.
Таблица 4.1
Базовые логические операции
Операция Название операции Обозначение операции
И (AND) Логическое умножение — конъюнкция л
ИЛИ (OR) Логическое сложение — дизъюнкция + V
НЕ (NOT) Логическое отрицание — инверсия / —1
При выполнении операций применяются отношение эквивален-
тности « = » и скобки «()», которые определяют порядок выполне-
117
ния операций. Если скобок нет, то операции выполняются в сле-
дующей последовательности: логическое отрицание, логическое
умножение и логическое сложение.
4.1. ОСНОВНЫЕ ЗАКОНЫ
И ПОСТУЛАТЫ АЛГЕБРЫ ЛОГИКИ
Аксиомы (постулаты) алгебры логики
1. Дизъюнкция двух переменных равна 1, если хотя бы одна из
них равна 1:
0 + 0 = 0;
0+1 = 1;
1 + 0=1;
1 + 1 = 1.
2. Конъюнкция двух переменных равна 0, если хотя бы одна
переменная равна 0:
0x0 = 0;
0x1=0;
1x0 = 0;
1x1 = 1.
3. Инверсия одного значения переменной совпадает с ее дру-
гим значением:
1 = 0;
0 = 1.
Законы алгебры логики
1. Законы однопарных элементов:
а) универсального множества:
х + 1 = 1;
X • 1 = X.
б) нулевого множества:
х + 0 = х;
х-0 = 0.
2. Законы отрицания:
а) двойного отрицания: х = х
118
х + х = 1;
б) дополнительности: -
х • х = 0;
в) двойственности (де Моргана):---- — —
X, -Х2 =Х] +х2.
3. Комбинационные законы:
х + х = х;
а) тавтологии:
хх = х;
X] +х2 = х2 +Хр
б) коммутативные:
х, -х2 = х2 • х3;
х1+(х2+х3)=(х1+х2)+х3;
в) ассоциативные (сочетательные): / \ / \
X] (х2 x-J-lx, -х2) х3;
г) дистрибутивные (распределительные):
хг(х2+хз)7хГх2 + х1хз:
Xj +х2 -х3 = (х| +х2дх] +х3);
д) закон абсорбции (поглощения):
Xj+XjXj = х(.
х.^ + х^ = х);
е) склеивания:
X] -х2 +XjX2 = х,;
(х1+х2)(х1+х2) = х1.
Законы двойственности де Моргана были обобщены Шенноном
на произвольное количество двоичных переменных: инвертиро-
вание произвольной комбинации двоичных переменных, связан-
ных знаками дизъюнкции и конъюнкции, эквивалентно инверти-
рованию комбинаций переменных с одновременной заменой конъ-
юнкции на дизъюнкцию, и наоборот:
*1 ’ Х2 ’ Х3 ' ’ ’ Хп ~ Х1 + Х2 + Х3 + ’ ’ ’ + Хп •
X, + X, Ч---------F X = X, • X, • • Х„ .
1 Z п 1 1 п
119
Рассмотрим на примерах некоторые приемы и способы, при-
меняемые при упрощении логических формул:
1) х + у • (х • у )= х • у (х • у ) = х • х • у • у = 0 • у • у = 0 • у = О
(законы алгебры логики применяются в следующей последователь-
ности: правило де Моргана, сочетательный закон, законы допол-
нительности и нулевого множества);
2) х-у + х + у + х = х-у + х-у + х = х-(у + у) + х = х-1-х = 1
(применяется правило де Моргана, выносится за скобки общий
множитель, используется закон дополнительности);
3) xy + xyz + xz-p = х • (у • (1 + z) + z • р) = х • (у + z • р)
(выносятся за скобки общие множители; применяется закон уни-
версального множества);
4) Рассмотрим доказательство соотношения (хг + х2)(х! + х3) = х, +
-I- х2х3 (распределительный закон):
(х, +х,)(х, +х,) = х,х, +х,х, + х,х, +х,х = Х. + Х.Х. + Х-Х.+Х-Х =
' J Z* * 1 о* 11 1«5 Z 1 Z «5 1 1 и л. 1 Z О
= х) + х2х1+х2х3 = Х( (1+Х2) + Х2Х3 = xt+x2x3
(применяются законы тавтологии и универсального множества).
4. 2. ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
Булевой (переключательной, двоичной) функцией называется
двоичная переменная у значение которой зависит от значений дру-
гих двоичных переменных (х;, х? ...,хп), именуемых аргументами:
у = у(х,, х2.хп).
Задание булевой функции означает, что каждому из возмож-
ных сочетаний аргументов поставлено в соответствие определен-
ное значение у.
При п аргументах общее число сочетаний N = 2Л . Так как каж-
дому сочетанию аргументов соответствует два значения функции
(О, 1), то общее число функций F = 22”.
Булевая функция может быть задана на словах, таблично, ал-
гебраически или числовым способом.
В табл. 4.2 представлена функция одной переменной у = у(х). При
п = 1 существует 4 функции, каждая из которых имеет свое название.
120
Таблица 4.2
Табличное задание функции одной переменной
' у0 = 0 — const ноля, или генератор 0;
У] = х — повторитель;
у2 = х — инвертор;
у3 = 1 — const 1; или генератор 1.
Для алгебры логики установлено, что если у = у (zt,z^, где zt
и z2— двоичные функции, т. е. z; = z;fx;,x2), z2= z2(x3,x4), то
y = y(xt,x2lx3,x4).
Операцию замены одной функции другими функциями назы-
вают суперпозицией. Эта операция дает возможность с помощью
функций малых аргументов получить функции большего числа
аргументов. Так, при помощи суперпозиции можно получить фун-
кцию с требуемым числом аргументов, используя только функцию
двух аргументов.
Рассмотрим функцию двух аргументов.
По определению существует 16 функций двух аргументов (табл 4.3).
При помощи набора булевых функций двух аргументов можно
описать любую цифровую систему.
На практике используют не все функции, а лишь те из них, ко-
торые методом суперпозиции обеспечивают представление любой
другой функции. Набор таких функций называют функционально
полным набором (ФПН).
Существует несколько ФПН. В качестве ФПН применяются
дизъюнкция, конъюнкция и инверсия. Этот набор называют ос-
новным ФПН (ОФПН).
Кроме ОФПН, широкое применение получили:
функционально-полная система, включающая в себя только
одну функцию — функцию Пирса (ИЛИ-НЕ);
функционально-полная система, включающая в себя только
одну функцию — функцию Шеффера (И-НЕ).
При помощи этих функций можно построить любую цифровую
систему.
Синтез логических устройств в базисе ОФПН состоит из пред-
ставления этих функций в нормальных формах и минимизации.
121
Таблица 4.3
Табличное задание функции двух переменных
хх 0 1 0 1
х2 0 0 1 1
Уз 0 0 0 0 Const 0, - 0
У, 0 0 0 1 Конъюнкция: yt - х,х2
У2 0 0 1 0 Запрет по х,: у2-х,-х2
Уз 0 0 1 1 Повторитель х2: у3 - х2
У, 0 1 0 0 Запрет по х2: У<"*1 Л
Уз 0 1 0 1 Повторитель х,: ys - х,
Уз 0 1 1 0 Исключающее «или»: 1/б “ Xj • Х2 + Х| • х2, или сложение по модулю 2: Уз~хх®хг
У1 0 1 1 1 Дизъюнктор (или) У7 “ Х< + х2
Уз 1 0 0 0 Функция Пирса (или-не) % - х, + х2
Уз 1 0 0 1 Логическая равнозначность ^-x-Xj + x^-x;
1 0 1 0 Инвертор х,: ую -"х,
У» 1 0 1 1 Импликация от х2 к х,: Ун ~Хх + Х2
У\2 1 1 0 0 Инвертор х2: _у12 - х2
У\з 1 1 0 1 Импликация от х, к х2: У»-*! + Х2
У» 1 1 1 0 Функция Шеффера (и-не) У" ~Х,'Х2
У,з 1 1 1 1 Генератор 1: г/15 ~ 1
Нормальной формой считают представление этих функций по-
средством суперпозиций вспомогательных функций — минтермов
и макстермов.
122
Минтерном называют функцию, которая принимает 1 только при
одном значении аргументов и 0 — при других (иногда в литературе
используется термин «конституэнта единицы»).
Например, для функции двух аргументов имеем:
х2 С» С, сг С’з
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1
Таким образом, для функции двух аргументов имеем четыре
минтерма:
Со = Х| • х2;
= Х1-х2;
с,1
С*
d
Макстермом называют функцию, которая принимает 0 только при
одном значении аргументов и 1 — при другом (иногда в литературе
используется термин «конституэнта ноля»).
Например, для функции двух аргументов имеем:
*1 х2
0 0 0 1 1 1
0 1 1 0 1 1
1 0 1 1 0 1
1 1 1 1 1 0
123
Таким образом, для функции двух аргументов имеем также че-
тыре макстерма:
Со =Х[ + х2;
С] = х, +х2;
С, = Х| +Х2>
С3 = X! + Х2.
^При этом, минтерм есть инверсия макстерма: С- =Cf, С? = С-.
Форму представления функций посредством суперпозиции их мин-
термов называют формой представления посредством совершенных
дизъюнктивных нормальных форм (СДНФ), а посредством суперпо-
зиции макстермов — посредством совершенных конъюнктивных нор-
мальных форм (СКНФ).
В общем случае форма представления функций посредством
суперпозиции их минтермов имеет вид:
у(х3х2...хя) = f у -с', N = 22".
1=1
Для функций одной переменной:
Я^) = У(1) -х, +у(0)-х, .
Для функций двух переменных:
у(х|,х2) = у(1,х2)х1 + у(0, х2) • х, =
= у(1,1) • х, • х2 + у(1,0) • х, х2 + у(0,1) • X] • х2 + у(0,0) Х| • х2
ИТ. д.
Аналогично алгебраическая запись СКНФ имеет вид:
Л-1 0
y(xjX2...xn)= П(у,+С,. ).
i=i
Любую функцию можно представить путем суперпозиции их
минтермов (СДНФ) или макстермов (СКНФ).
124
Пример. Представим функцию Шеффера путем суперпозиции
минтермов (СДНФ) и макстермов (СКНФ).
Табличное представление функции Шеффера имеет вид (см. табл. 4.3):
х, 0 1 0 1
х2 0 0 1 1
Ум 1 1 1 0
Тогда совершенная дизъюнктивная нормальная форма функ-
ции Шеффера будет иметь вид:
у14 = %! • Х2 + х1*2 + *1 ‘ *2'
Соответственно СКНФ функции Шеффера:
у14 =*1+Х2 •
Применив закон де Моргана, получим:
У14 =xt-x2.
Из примеров видно, что данная функция посредством СКНФ
представляется значительно проще, чем посредством СДНФ и, сле-
довательно, имеет меньшее число схем для реализации.
4.3. ЛОГИЧЕСКИЙ СИНТЕЗ ПЕРЕКЛЮЧАТЕЛЬНЫХ
И ВЫЧИСЛИТЕЛЬНЫХ СХЕМ
4.3.1. Синтез переключательных схем
В вычислительных и других автоматических устройствах ши-
роко применяются электрические схемы, содержащие множество
переключательных элементов: реле, выключателей и т. п. При раз-
работке таких схем с успехом может быть использован аппарат
алгебры логики.
125
Переключательная схема — схематическое изображение некото-
рого устройства, состоящего из переключателей и соединяющих их
проводников, а также входов и выходов, на которые подается и с кото-
рых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое
и разомкнутое. Переключателю X поставим в соответствие логи-
ческую переменную х, которая принимает значение 1 только в том
случае, когда переключатель X замкнут и схема проводит ток; если
же переключатель разомкнут; то переменная х равна нолю. При
этом два переключателя X и X связаны таким образом, что когда
X замкнут, то X разомкнут, и наоборот. Следовательно, если пе-
реключателю X поставлена в соответствие логическая переменная
х, то переключателю X должна соответствовать переменная х.
Всей переключательной схеме также можно поставить в соот-
ветствие логическую переменную, равную единице, если схема
проводит ток, и равную нолю — если не проводит. Эта перемен-
ная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.
Рассмотрим функции проводимости F некоторых переключа-
тельных схем:
а| о
о
Схема не содержит переключателей и проводит ток всегда, сле-
довательно, F= 1;
б)
О-------------------о
Схема содержит один постоянно разомкнутый контакт, следо-
вательно, F=0;
О--------х--------О
Схема проводит ток, когда переключатель х замкнут, и не про-
водит, когда х разомкнут, следовательно, F(x)=x;
г) О--------*--------О
Схема проводит ток, когда переключатель х разомкнут, и не
проводит, когда х замкнут, следовательно, F(x)= х;
126
Д) _ _
О--------х-------у О
Схема проводит ток, когда оба переключателя замкнуты, сле-
довательно, F(x)=х • у,
е)
Схема проводит ток, когда хотя бы один из переключателей зам-
кнут, следовательно, F(x) = х v у.
При рассмотрении переключательных схем решают, как пра-
вило, одну из основных задач: синтез или анализ схемы.
Синтез переключательной схемы по заданным условиям ее ра-
боты сводится к следующим трем этапам:
1. Составление функции проводимости по заданным условиям.
2. Упрощение этой функции.
3. Построение соответствующей схемы.
Анализ схемы характеризуется следующими этапами:
1. Определение значений функции проводимости при всех воз-
можных наборах входящих в эту функцию переменных.
2. Получение упрощенной формулы.
Рассмотрим примеры решения задач синтеза и анализа неслож-
ных переключательных схем.
Задачи синтеза.
1. Построим схему, содержащую 4 переключателя х, у, z и t, та-
кую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трех кон-
тактов.
Решение. Функция проводимости для данного случая имеет вид
F(x, у, z, t) = t (xv у vz), а схема имеет вид:
2. Построим схему с пятью переключателями, которая прово-
дит ток в том и только в том случае, когда замкнуты ровно четыре
из этих переключателей.
127
Решение:
F(a,b,c,d,e) =
= abcdevaB-cdeva-bcdeva-bcdevab-c-de
Схема имеет вид:
I
Задачи анализа.
3. Найдем функцию проводимости схемы:
Решение. Имеется четыре возможных пути прохождения тока
при замкнутых переключателях a, b, с, d, е: через переключатели
а, Ь; через переключатели а, е, d; через переключатели с, d и через
переключатели с, е, Ъ. Функция проводимости F(a, b, с, d, е) =
= a-b v a-e-d v c-d v c-e-b.
4. Упростим переключательные схемы:
а)
Решение:
F(x, у) = х • у v у • х = х • (у v у) = х -1 = х.
128
Упрощенная схема: О------х-------О
Решение:
F(x,y,z) = z (х v у) v (z v х • у) = 1.
Здесь первое логическое слагаемое z • (х v у) является отрицани-
ем второго логического слагаемого (z v х • у), а дизъюнкция пере-
менной с ее инверсией равна 1.
Упрощенная схема: О-------О
Анализ и синтез более сложных переключательных схем мо-
жет проводиться по тем же правилам, что и для вычислительных
схем.
4.3.2. Синтез вычислительных схем
Синтез вычислительных схем по заданным условиям работы
сводится к следующим трем этапам:
1. Образование СДНФ (СКНФ) функции по заданной таблице
истинности.
Таблица истинности — табличное представление вычислительной
(логической) схемы (операции), в котором перечислены все возмож-
ные сочетания значений истинности входных сигналов (операндов)
вместе со значением истинности выходного сигнала (результата опе-
рации) для каждого из этих сочетаний.
2. Упрощение этой функции (преобразованию СДНФ (СКНФ)
в формулу с наименьшим числом вхождений переменных);
3. Построение соответствующей схемы.
9а-210
129
Образование СДНФ функции по заданной таблице истиннос-
ти. Этот этап включает в себя следующие шаги:
1) в заданной таблице истинности выделяются наборы значе-
ний аргументов, при которых функция принимает единичное зна-
чение; '
2) для каждого выделенного набора образуется конституэнта
единицы (минтерм), принимающая единичное значение придан-
ном наборе значений аргументов;
3) составляется логическая сумма образованных конституэнт
единицы.
Для образования конституэнты единицы С'(, принимающей еди-
ничное значение при z-м наборе значений аргументов, необходи-
мо составить логическое произведение аргументов, в которое ар-
гументы, принимающие в z-м наборе единичное значение, входят
без знака отрицания, а аргументы, принимающие в z-м наборе но-
левое значение, входят со знаком отрицания.
При образовании совершенной конъюнктивной нормальной
формы (СКНФ) функции:
1) в таблице выделяются наборы значений аргументов, при ко-
торых функция принимает нолевое значение;
2) для каждого выделенного набора образуется конституэнта
ноля, принимавшая нолевое значение при данном наборе значе-
ний аргументов;
3) составляется логическое произведение образованных консти-
туэнт ноля.
Упрощение функции. При преобразовании СДНФ (СКНФ)
в формулу с наименьшим числом вхождений переменных (мини-
мизация формулы) используют следующие основные приемы:
вынос за скобки XYv XZ =_Х(YvZ);
• полное склеивание XY v XY = X;
• поглощение X v XY = X;
минимизация по методу Квайна;
* минимизация с использованием карт Карно или диаграмм
Вейча.
При минимизации по методу Квайна предполагается, что исход-
ная функция задана в СДНФ. Введем несколько определений.
Конъюнкция, получаемая в результате склеивания двух консти-
туэнт единицы, называется импликантой.
Импликанта поглощает конституэнты единицы, при склеивании
которых она образовалась.
130
Простая импликанта — импликанта, склеивание которой с дру-
гой импликантой невозможно.
Задача минимизации по методу Квайна состоит из следующих
шагов:
1) в СДНФ функции выполняются все возможные склеивания
конституэнт единицы и получаемых импликант, и выделяются все
простые импликанты;
2) из набора простых импликант выделяется наименьший по
числу импликант поднабор простых импликант, поглощающих
в совокупности наибольшее число конституэнт единицы;
3) образовывается логическая сумма простых импликант, во-
шедших в выделенный поднабор, и конституэнт единицы, не уча-
ствующих в склеивании.
Полученная таким образом формула называется минимальной
ДНФ функции.
Диаграмма Вейча или карта Карно — таблица, облегчающая на-
хождение склеивающихся конституэнт единицы и получение набора
простых импликант.
Таблица для функций п аргументов содержит 2“ клеток. Каждая
клетка соответствует одной определенной конституэнте единицы.
Соответствие клетки таблицы определенной конституэнте еди-
ницы устанавливается:
* для диаграммы Вейча с помощью обрамления таблицы, где
каждой клетке таблицы соответствует набор всех аргумен-
тов, в который каждый из аргументов входит или без знака
отрицания, или со знаком отрицания;
для карты Карно с помощью двух входов в таблицу, где ука-
заны две части набора значений аргументов, при котором со-
ответствующая конституэнта единицы принимает единичное
значение.
Карты Карно обычно используют для ручной минимизации бу-
левых функций при небольшом числе переменных (не более пяти).
На рис. 4.1 представлены карты Карно для трех переменных.
Каждая клетка соответствует логическому произведению прямо-
го или инверсного значения переменных, присвоенных столбцу
или строке, на пересечении которых она находится. Например,
клетка с номером 4 находится на пересечении строки со значени-
ем переменной xt и столбца со значениями переменных х2 и х3
131
и соответствует логическому произведению х15уг3. В картах Карно
значения переменных присваиваются таким образом, чтобы со-
седние клетки по строкам и столбцам отличались между собой зна-
чением только одной переменной, при этом обозначение значе-
ния логического произведения переменных соответствует .номе-
ру клетки, записанному в коде Грея (см. рис. 4.1).
Х2 Х2 Х2
4 (ПО) 5 (П1) 6 (101) 7 (100)
3 2 1 0
(010) (0П) (001) (000)
х3 хз хз х3
Х2 Х2 х2 х2
XjX2X3 Xj^2X3 XjX2X3
Л'|Х2Х3 XjX2X3
х3 Х3 хз
а)
б)
Рис. 4.1. Карты Карно для трех переменных:
а) с номером клетки (десятичным и в коде Грея);
б) с логическим обозначением клетки
На рис. 4.2 представлены аналогичные карты для четырех пе-
ременных.
Хз X) Х) Хз
12 (1010) 13 (ЮН) 14 (1001) 15 (1000)
И 10 9 8
(ИЮ) (1111) (1Ю1) (1100)
4 5 6 7
(ОНО) (ОШ) (0101) (0100)
3 2 1 0
(0010) (ООП) (0001) (0000)
Х4 Xf Xt
а) б)
Рис. 4.2. Карты Карно для четырех переменных:
а) с номером клетки (десятичным и в коде Грея);
б) с логическим обозначением клетки
132
При упрощении логических функций с использованием карт
Карно в ячейки карты записывают значения логических произве-
дений из таблицы истинности. Пусть, например, логическая фун-
кция трех переменных задана таблицей истинности (табл. 4.4).
х, х2 хз Y
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
Таблица 4.4
х. х2 хз Y
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
На рис. 4.3 представлена карта Карно, соответствующая дан-
ной логической функции.
х2 х2 х2 х2
illll Illll 0 0
0 яшш 0 0
Рис. 4.3. Карта Карно логической функции, заданной табл. 4.4.
Карта Карно позволяет легко выделить произведения, которые
можно упростить. Так, если произведения стоят в соседних клет-
ках, то из общего выражения можно исключить одну переменную.
В нашем случае элементы 2 и 5 клеток (см. рис. 4.1 а) можно преоб-
разовать к виду:
Х[Х2Х3 + Х]Х2Х3
= х2х3
Элементы 4 и 5 клеток — соответственно к виду:
Х]Х2Х3 +Х]Х2Х3 = х{х2
'2-
133
Таким образом, функция, представленная табл. 4.4, определя-
ется уравнением:
У = Х]Х2 + х2х3.
Построение схемы. В качестве примера логического синтеза
вычислительных схем рассмотрим построение одноразрядного
двоичного сумматора, имеющего два входа (х( и х2) и два выхода
(S и Р) рис. 4.4.
s — сумма
Р — перенос
в старший разряд
Рис. 4.4. Двоичный сумматор
Зададим таблицу истинности сумматора.
X, 0 0 1 1
х2 0 1 0 1
5-/,(х1,х2) 0 1 1 0
р “ /2(^'1» ^2) 0 0 0 1
Представим выходные функции S и Р в виде СДНФ:
5 = /1(х1,х2) = Х]Х2 + х1х2<
Р = f2(xitx2) = х}х2.
Логическая схема сумматора, реализующего данные функции,
представлена на рис. 4.5.
Для логических схем И, ИЛИ, НЕ существуют типовые тех-
нические схемы (логические элементы), реализующие их на по-
лупроводниковых структурах (см. п. 4.4.1).
134
X, хг
Рис. 4.5. Логическая схема сумматора
Логический элемент — часть электронной логической схемы, ко-
торая реализует элементарную логическую функцию.
Тогда структурная схема сумматора будет иметь вид, показан-
ный на рис. 4.6.
Рис. 4.6. Структурная схема сумматора
135
4.4. ОСНОВЫ ЭЛЕМЕНТНОЙ БАЗЫ
ЦИФРОВЫХ АВТОМАТОВ
4.4.1. Логические элементы
К основным логическим элементам современных вычислитель-
ных устройств относятся электронные схемы, реализующие опе-
рации И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие, а также триггер.
С помощью этих схем можно реализовать любую логическую
функцию, описывающую работу устройств компьютера. Обычно
у них бывают от двух до восьми входов и один или два выхода.
Входные и выходные сигналы, соответствующие двум логичес-
ким состояниям в логических элементах — 1 и 0 — имеют один из
двух установленных уровней напряжения. Например, +5 В и О В.
Высокий уровень обычно соответствует значению «истина»
(«1»), а низкий — значению «ложь» («О»),
Каждый логический элемент имеет свое условное обозначение,
которое выражает его логическую функцию.
Работу логических элементов описывают с помощью таблиц
истинности.
Схема И. Эта схема реализует конъюнкцию двух или более ло-
гических значений. Условное обозначение на структурных схемах
схемы И с двумя входами представлено на рис. 4.7.
X У хху
0 0 0
0 1 0
1 0 0
1 1 1
Рис. 4.7. Условное обозначение и таблица истинности схемы И
136
Единица на выходе схемы И будет тогда и только тогда, когда на
всех входах будут единицы. Когда хотя бы на одном входе будет
ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами х и у описыва-
ется соотношением: z = х ху (читается как х и у). Операция конъ-
юнкции на структурных схемах обозначается знаком & (читается
как амперсэнд), являющимся сокращенной записью английского
слова and.
Схема ИЛИ. Эта схема реализует дизъюнкцию двух или более
логических значений. Когда хотя бы на одном входе схемы ИЛИ
будет единица, на ее выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с
двумя входами представлено на рис. 4.8. Знак 1 на схеме соответ-
ствует обозначению, т. е. значение дизъюнкции равно единице,
если сумма значений операндов больше или равна 1. Связь между
выходом z этой схемы и входами х и у описывается соотношени-
ем: z = х v у (читается как х или у).
Рис. 4.8. Условное обозначение и таблица истинности схемы ИЛИ
Схема НЕ. Схема НЕ (инвертор) реализует операцию отрица-
ния. Связь между входом х этой схемы и выходом z можно запи-
сать соотношением z = х, где х читается как «не х» или «инвер-
сия х».
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на вы-
ходе 0. Условное обозначение инвертора представлено на рис. 4.9.
137
X X
0 1
1 0
Рис. 4.9. Условное обозначение и таблица истинности схемы НЕ
Схема И—НЕ. Схема состоит из элемента И и инвертора и осу-
ществляет отрицание результата схемы И. Связь между выходом
z и входами х и у схемы записывают следующим образом: z = х X у,
где хху, читается как «инверсия х и у». Условное обозначение
на структурных схемах схемы И—НЕ с двумя входами представ-
лено на рисунке 4.10.
X У хху
0 0 1
0 1 1
1 0 1
1 1 0
Рис. 4.10. Условное обозначение и таблица истинности схемы И—НЕ
Схема ИЛИ—НЕ. Схема состоит из элемента ИЛИ и инвертора
и осуществляет отрицание результата схемы ИЛИ. Связь между
выходом z и входами х и у схемы записывают следующим обра-
зом: z = xv у, где xv у, читается как «инверсиях и у». Условное
обозначение на структурных схемах схемы ИЛИ—НЕ с двумя
входами представлено на рисунке 4.11.
138
X
У
X У xvy
0 0 1
0 1 0
1 0 0
1 1 0
Рис. 4.11. Условное обозначение и таблица истинности схемы ИЛИ НЕ
Триггер — (от англ, trigger — защелка, спусковой крючок) элект-
ронное устройство с двумя устойчивыми состояниями равновесия,
чередующимися под воздействием внешних сигналов, предназначен-
ных для записи и хранения 1 бита данных.
Для обозначения этой схемы в английском языке чаще употреб-
ляется термин flip-flop, что в переводе означает «хлопанье».
В отличие от рассмотренных выше логических схем, триггеры —
это логические устройства с памятью. Выходные сигналы тригге-
ров в общем случае зависят не только от их входных сигналов, дей-
ствующих в настоящий момент, но и от сигналов, действовавших
на входы до этого (рис. 4.12).
Рис. 4.12. Функциональная схема триггера
139
Триггер функционирует следующим образом. Устройство уп-
равления (УУ) преобразует входные сигналы так, что ячейка памя-
ти (ЯП) принимает одно из двух устойчивых состояний, в зависи-
мости от входных сигналов. Входные сигналы поступают на входы
S1 и R , преобразуются устройством управления (УУ) и поступают
на внутренние входы ячейки памяти (ЯП). В общем случае устрой-
ство управления может отсутствовать. Тогда сигналы подаются
непосредственно на входы RnS ячейки памяти.
В триггерах также может осуществляться синхронизация
приема информации с помощью входа С. При наличии входа С
триггер называют синхронным, в противном случае — асинх-
ронным. В асинхронных триггерах информация может записы-
ваться непрерывно. В этом случае она определяется информа-
ционными сигналами, действующими на входах в данный мо-
мент времени, т. е. изменение состояния ячейки памяти проис-
ходит мгновенно после изменения состояния информационных
входов.
В синхронном (или тактируемом) триггере информация зано-
сится только в момент действия так называемого синхронизирую-
щего сигнала. Синхронизация триггера может осуществляться как
импульсом (потенциалом), так и фронтом (перепадом потенциа-
ла) . В схемотехнике приняты следующие обозначения входов триг-
геров:
Q — прямой выход триггера;
Q — инверсный выход триггера;
S— раздельный вход установки в единичное состояние (напря-
жение высокого уровня на прямом выходе Q);
R — раздельный вход установки в нолевое состояние (напря-
жение низкого уровня на прямом выходе О);
D — информационный вход (на него подается информация,
предназначенная для занесения в триггер);
С — вход синхронизации;
Т — счетный вход.
В основе любого триггера находится кольцо из двух инверто-
ров (рис. 4.13). Это кольцо принято изображать в виде так называ-
емой защелки (рис. 4.14).
Однозначную запись 1 бита информации в защелку можно осу-
ществить, если снабдить ее цепями управления и запуска.
140
DD1 DD2
Рис. 4.13. Кольцо инверторов
DD1
DD2
Рис. 4.14. Элемент-защелка
DD2
Рис. 4.15.
Принципиальная
схема RS-триггера
Самый распространенный тип триггера — RS-триггер. Принци-
пиальная схема RS-триггера (рис. 4.15) содержит защелку (два эле-
мента И—НЕ или ИЛИ—НЕ), а также два раздель-
ных статических входа управления. В зависимости
от используемых элементов можно получить
триггеры с прямыми входами (за активный логичес-
кий уровень принимают уровень логической едини-
цы) — элемент ИЛИ—НЕ — или с инверсными вхо-
дами (за активный уровень принимается уровень
логического ноля). Эти входы управления называ-
ют R (reset — сброс) и S (set — установка).
По сути дела, RS-триггер, изображенный на
рис. 4.15, это триггер без устройства управления.
Для триггера с прямыми входами подача на вход
S -триггера логической единицы, а на вход R — ло-
гического ноля приведет к тому, что на выходе триг-
гера Q установится сигнал единицы и, наоборот,
при подаче на R единицы, а на S — ноля на выходе Q установится
сигнал ноля. Таким образом, таблица истинности для данного триг-
гера будет иметь вид, показанный в табл. 4.5.
Как видно из табл. 4.5, комбинация R = 1 и S = 1 является зап-
рещенной. После нее состояние выходов триггера становится нео-
пределенным. На выходе Q может установиться как состояние ло-
гического ноля, так и состояние логической единицы.
Иногда режим работы триггера, при котором R = 1, a S = О,
называют режимом очистки, при R = О, S = 1 — режимом записи,
а при R = О, S = 0 — режимом хранения, так как информация на
выходе триггера в этом случае не изменяется. Для триггера с ин-
версными входами таблица истинности имеет вид, представлен-
ный в табл. 4.6.
141
Таблица 4.5
Входы Выходы
R S Q Q
0 0 Без изменений
0 1 1 0
1 0 0 1
1 1 Не определено
Таблица 4.6
Входы Выходы
R 5 Q Q
0 0 Не определено
0 1 0 1
1 0 1 0
1 1 Без изменений
Поскольку один триггер может запомнить только один раз-
ряд двоичного кода, то для запоминания байта нужно 8 тригге-
ров, для запоминания килобайта соответственно 8x2'° = 8192
триггеров. Современные микросхемы памяти содержат милли-
оны триггеров.
4.4.2. Схемотехника логических элементов
По принципу построения базовые логические элементы делят-
ся на следующие основные типы: элементы диодно-транзисторной
логики (ДТЛ), резистивно-транзисторной логики (РТА), транзис-
торно-транзисторной логики (ТТЛ), эмиттерно-связанной логики
(ЭСЛ), элементы на так называемых комплементарных МДП-
структурах (КМДП). Элементы КМДП используют пары МДП-
транзисторов (со структурой металл—диэлектрик — полупровод-
ник) с каналами р- и п-типов. Базовые элементы остальных типов
выполнены на биполярных транзисторах. В основе построения
транзисторов и других полупроводниковых приборов лежат свой-
ства и характеристики электронно-дырочного перехода.
Образование и свойства электронно-дырочного перехода. Ос-
новой построения логических элементов являются полупроводни-
ковые структуры. Электрические свойства такой структуры опре-
деляются в первую очередь степенью связи носителей заряда с
атомами в кристаллической решетке. В полупроводниковой тех-
нике чаще всего используют четырехвалентные германий и крем-
ний — вещества кристаллической структуры с ковалентными меж-
атомными связями, при которых каждый атом связан с соседними
посредством восьми обобщенных электронов. Это обстоятельство
схематически отображено на рис. 4.16 а, где двойными линиями
142
показаны связи между соседними атомами в кристаллической
решетке, большими кружками обозначены четырехвалентные
атомы, а малыми кружками с горизонтальной чертой — элект-
роны.
Рис. 4.16. Схематичное изображение кристаллической структуры
с ковалентными межатомными связями (а)
и нарушения ее электрической нейтральности (б)
Такая связь весьма устойчива, и для ее разрыва требуется зат-
ратить определенную энергию. При разрывах ковалентных свя-
зей в полупроводнике появляются свободные носители заряда —
электроны и дырки, которые совершают хаотическое (тепловое)
движение в кристалле.
Появление дырок в полупроводнике и их перемещение в нем
связаны с возбуждением валентных электронов, когда в результа-
те поглощения энергии один из валентных электронов освобож-
дается от связи с атомом, становясь подвижным носителем заря-
да. Нарушение электрической нейтральности в месте разрыва ва-
лентной связи эквивалентно появлению там элементарного поло-
жительного заряда. Образовавшаяся вакантная связь может быть
заполнена электроном из соседней связи (рис. 4.16 б), так как та-
кой переход не связан с большими энергетическими затратами (все
валентные электроны в решетке взаимодействуют со своими ато-
мами примерно в одинаковой степени). Перемещение электрона
из одной связи в другую эквивалентно непрерывному перемеще-
нию подвижного положительного заряда — дырки.
143
Процесс возникновения свободных носителей заряда носит
название генерации. В процессе хаотического движения носите-
ли могут заполнять освободившиеся ранее связи, тогда происхо-
дит исчезновение двух носителей заряда — электрона и дырки, их
рекомбинация. Среднее число актов генерации и актов рекомби-
нации в единицу времени при постоянной температуре одинако-
во, поэтому среднее число дырок и электронов в кристалле при
данной температуре является вполне определенным. При этом
кристалл в целом электрически нейтрален.
Если к кристаллу приложить напряжение, то в образовавшем-
ся электрическом поле у электронов и дырок появляется состав-
ляющая дрейфовой скорости по силовым линиям. Электроны пе-
ремещаются к положительному полюсу, а дырки — к отрицатель-
ному. При этом полный ток равен сумме электронной и дырочной
составляющих.
Если в рассматриваемый кристалл с ковалентными связями вне-
сти примеси элементов III или V группы периодической системы
Менделеева, то относительное количество электронов и дырок изме-
нится. Процесс внесения примесей часто называют легированием.
Атомы примеси элемента V группы называют донорами. В неко-
торых узлах кристаллической решетки доноры замещают атомы ос-
новного вещества (рис. 4.17 а). Четыре валентных электрона донора
связываются в кристаллической решетке с соседними атомами, а
пятый электрон, оставшийся неиспользованным, оказывается слабо
связанным с атомом донора (лишь силами кулоновского притяжения).
При этом обеспечивается электрическая нейтральность атома.
а)
Рис. 4.17. Схематичное изображение замещения атомов
основного вещества: а) донорами; 6) акцепторами
б)
144
Для отрыва указанного электрона от атома достаточно затра-
тить небольшую энергию. Поэтому уже при комнатной темпера-
туре пятые электроны доноров оказываются свободными и могут
участвовать в создании тока через кристалл. Атомы примеси, ли-
шенные одного электрона, превращаются в положительные ионы,
расположенные в узлах кристаллической решетки. Следует особо
отметить, что появление свободного электрона в данном случае не
связано с появлением дырки, т. е. в кристалле с пятивалентной при-
месью ток будет иметь в основном электронную составляющую.
По этой причине полупроводник с донорной примесью называют
электронным, или полупроводником п-типа. В полупроводнике
n-типа также имеется и дырочная составляющая, но она значитель-
но меньше электронной. Наличие дырочной составляющей объяс-
няется разрывом отдельных связей атомов основного вещества с
образованием электронов и дырок.
Добавление в чистый полупроводник трехвалентных атомов
примеси, называемых акцепторами, приводит к замещению ими в
отдельных узлах решетки атомов основного вещества (рис. 4.17 б).
Трехвалентный атом примеси имеет на один электрон меньше того
числа электронов, которое требуется для образования устойчивых
ковалентных связей. Иными словами, при введении такого атома
примеси появляется вакантная связь, на которую может перейти
электрон из соседней связи. Необходимая для такого перехода
энергия весьма мала, и уже при комнатной температуре все сво-
бодные места у атомов примеси оказываются занятыми, а сами
атомы вследствие этого превращаются в отрицательные ионы. На
местах ушедших к этим атомам электронов образуются дырки,
которые хаотически перемещаются в кристалле и могут участво-
вать в создании тока через кристалл. Появление дырок не связано
с появлением свободных электронов, поэтому дырочная составля-
ющая общего количества подвижных носителей заряда в таком
полупроводнике преобладает над электронной составляющей. Рас-
смотренный полупроводник называют дырочным, или полупро-
водником р-типа.
Полупроводники п- и p-типа называют примесными, или легиро-
ванными. Носители заряда, однотипные с примесным полупровод-
ником, называют основными, а неоднотипные — неосновными.
В полупроводнике n-типа основными носителями являются электро-
ны, а неосновными—дырки, а в р-полупроводнике, наоборот, дырки
являются основными носителями, а электроны — неосновными.
10 А-210
145
Принцип действия большинства полупроводниковых приборов
и элементов интегральных схем основан на использовании свойств
электронно-дырочного перехода (р—п-перехода) — переходного
слоя между двумя областями полупроводника, одна из которых име-
ет электропроводность p-типа, а другая — n-типа. На рис. 4.18 а
показаны два образца полупроводника с различным типом элект-
ропроводности. В каждом полупроводнике подвижные носители
заряда (электроны и дырки) совершают хаотическое движение,
обусловленное их тепловой энергией. Неподвижные положитель-
ные и отрицательные примесные ионы обозначены знаками плюс
и минус соответственно, а дырки и электроны — теми же знаками
в кружках. Оба образца нейтральны, т. е. подвижные и неподвиж-
ные заряды в них взаимно скомпенсированы.
Р П
б)
Рис. 4.18. Проводники с различным типом электропроводности:
а) до соприкосновения, б) при соприкосновении
После приведения полупроводников в соприкосновение из-за
значительного различия в концентрациях подвижных носителей
заряда будет происходить диффузия электронов из n-области в
p-область и дырок из p-области в n-область, т. е. наблюдаться диф-
146
фузионный ток. Переход электронов из приконтактной области
Л-полупроводника в р-полупроводник нарушает электрическую
нейтральность указанной области. Заряды положительных ионов
примеси оказываются нескомпенсированными, т. е. со стороны
n-полупроводника у границы контакта появляется положительный
заряд (рис. 4.18 б). Появлению этого заряда способствует также
диффузия дырок из p-области и их рекомбинация с электронами
n-области, вследствие чего избыточный положительный заряд со
стороны n-области увеличивается.
Аналогично в слоях p-области, примыкающих к контакту, об-
разуется нескомпенсированный отрицательный заряд доноров,
вызванный уходом дырок в n-область и рекомбинацией дырок с
электронами, пришедшими из n-области. Появление противопо-
ложных по знаку зарядов по обе стороны контакта вызывает по-
явление электрического поля с напряженностью Е, направленно-
го из n-области в p-область (рис. 4.19).
Рис. 4.19.'Образование
р—п-перехода
Возникшее электрическое поле препятствует диффузии основ-
ных носителей заряда, но способствует перемещению неосновных
носителей заряда, т. е. электронов из p-области в n-область и ды-
рок из n-области в p-область, так как для них направление поля
является ускоряющим. Движение неосновных носителей заряда
под воздействием поля образует ток проводимости (дрейфа), на-
правленный противоположно току диффузии.
Состояние равновесия в структуре, очевидно, наступит тогда,
когда ток диффузии и ток проводимости сравняются. При этом в
области перехода установится некоторое значение напряженнос-
ти электрического поля, а между областями полупроводника —
разность потенциалов Vk (см. рис. 4.19).
147
Таким образом, вблизи границы двух полупроводников обра-
зуется слой, лишенный подвижных носителей заряда и поэтому
обладающий высоким электрическим сопротивлением, так назы-
ваемый запирающий слой. Толщина запирающего слоя обычно не
превышает нескольких микрометров.
Использование свойств р—n-перехода в полупроводниковых
приборах в большинстве случаев связано с приложением к пере-
ходу разности потенциалов. При этом в переходе возникает допол-
нительное электрическое поле, изменяется высота потенциально-
го барьера, а вместе с этим изменяются и потоки основных и нео-
сновных носителей.
Если к р—п-переходу приложить разность потенциалов таким
образом, чтобы плюс источника подключился к п-области, а ми-
нус — к p-области, то это приведет к увеличению потенциального
барьера в переходе на U, так как поле, обусловленное внешним
источником, добавляется к внутреннему полю, существующему в
переходе (рис. 4.20 а).
Увеличение напряженности электрического поля означает уве-
личение объемного заряда неподвижных ионов на участках, при-
легающих к контакту, а последнее может быть достигнуто только
за счет увеличения расстояния, на котором располагаются ионы с
нескомпенсированным зарядом, т. е. за счет толщины перехода. При
этом сопротивление р—л-перехода велико, ток через него мал — он
обусловлен движением неосновных носителей заряда. В этом слу-
чае ток называют обратным, а р—л-переход — закрытым.
Рис. 4.20. Электронно-дырочный переход во внешнем электрическом поле:
а) к р—n-переходу приложено обратное напряжение;
б) к р—n-переходу приложено прямое напряжение
148
При противоположной полярности источника напряжения
(рис. 4.20 б) внешнее электрическое поле направлено навстречу внут-
реннему полю в р—л-переходе, толщина запирающего слоя уменьша-
ется, и при напряжении 0,3...0,5 В запирающий слой исчезает. Сопро-
тивление р—n-перехода резко снижается, и возникает сравнительно
большой ток. Ток при этом называют прямым, а переход—открытым.
На рис. 4.21 показана полная вольт-амперная характеристика
открытого и закрытого р—п-переходов. Как видно, эта характери-
стика является существенно нелинейной. На участке 1 прямой ток
мал. На участке 2 внешнее электрическое поле больше внутренне-
го, запирающий слой отсутствует, ток определяется только сопро-
тивлением полупроводника. На участке 3 запирающий слой пре-
пятствует движению основных носителей, небольшой ток опреде-
ляется движением неосновных носителей заряда. Излом вольт-ам-
перной характеристики в начале координат обусловлен различны-
ми масштабами координатных осей при прямом и обратном на-
пряжении, приложенном к р—п-переходу. И наконец, на участке 4
происходит пробой р—л-перехода, и обратный ток быстро возрас-
тает. Это связано с тем, что при движении через р—л-переход под
действием электрического поля неосновные носители заряда при-
обретают энергию, достаточную для ударной ионизации атомов
полупроводника. В переходе начинается лавинообразное размно-
жение носителей заряда (электронов и дырок), что приводит к рез-
кому увеличению обратного тока через р—л-переход при почти
неизменном обратном напряжении. Этот вид электрического про-
боя называют лавинным. Обычно он развивается в относительно
широких р—л-переходах, которые образуются в слаболегирован-
ных полупроводниках.
Рис. 4.21. Вольт-амперная характеристика р—п-перехода
149
Закрытый р—л-переход обладает электрической емкостью С,
которая зависит от его площади и ширины, а также от диэлектри-
ческой проницаемости запирающего слоя. При увеличении обрат-
ного напряжения ширина р—n-перехода возрастает, и емкость
р—л-перехода уменьшается.
Свойства чистых и легированных полупроводников и р—л-пе-
рехода лежат в основе построения двухэлектродных полупровод-
никовых приборов — полупроводниковых резисторов и диодов.
В основе построения более сложных приборов — транзисторов —
лежат свойства и характеристики, определяемые взаимодействи-
ем нескольких р—п -переходов.
Биполярные и полевые транзисторы. Транзистором называ-
ют полупроводниковый прибор с тремя и более выводами, пред-
назначенный для усиления, генерирования и преобразования элек-
трических колебаний.
В зависимости от того, носители одного или обоих знаков уча-
ствуют в образовании тока, различают униполярные и биполяр-
ные транзисторы соответственно.
Основу биполярного транзистора составляет транзисторная
структура с двумя взаимодействующими р—п-переходами, обла-
дающая усилительными свойствами, обусловленными явлениями
инжекции и экстракции неосновных носителей заряда. На рис. 4.22
показана структура такого транзистора с выводами от каждой об-
ласти.
В зависимости от порядка чередования областей различают
транзисторные структуры р—п—р и л—р—л. На рис. 4.23 показаны
схемы и условные обозначения этих структур. Среднюю часть кри-
сталла с электрическим выводом называют базой, одну из край-
них — эмиттером, вторую — коллектором.
Рис. 4.22. Структура
биполярного транзистора
Рис. 4.23. Типы транзисторов (а)
и их условное обозначение (б)
a)
б)
150
Переход между эмиттером и базой обычно называют эмиттер-
ным, а между коллектором и базой — коллекторным. В зависимо-
сти от напряжения смещения переходов различают три режима
включения: активный, отсечки и насыщения.
В активном режиме один из переходов смещен в прямом на-
правлении, другой — в обратном. Если в прямом направлении
включен эмитгерный переход, то такой режим называют нормаль-
ным. Токи во внешних цепях в активном режиме определяются
высотой управляемого потенциального барьера открытого пере-
хода, т. е. способностью перехода инжектировать неосновные но-
сители в базу.
Режим отсечки имеет место в том случае, когда оба перехода
смещены в обратном направлении. В этом случае токи во внешних
цепях малы и соизмеримы с обратным током одного из переходов.
О транзисторе при этом говорят, что он заперт.
В режиме насыщения оба перехода открыты, в базу инжекти-
руются неосновные носители из области эмиттера и из области
коллектора. Так как оба перехода открыты, то на структуру падает
небольшое напряжение. По этой причине режим насыщения час-
то используют в тех случаях, когда транзистор выполняет роль клю-
ча, предназначенного для замыкания цепи. Размыкание цепи осу-
ществляется переводом транзистора в режим отсечки, при этом
транзисторная структура обладает большим сопротивлением.
Физические процессы в транзисторной структуре определяют-
ся состоянием эмиттерного и коллекторного переходов. При этом
все положения, рассмотренные ранее для единичного р—л-пере-
хода, справедливы для каждого из р—п-переходов транзистора.
В равновесном состоянии наблюдается динамическое равновесие
между потоками дырок и электронов, протекающими через каж-
дый р—n-переход, и результирующие токи равны нулю.
В активном нормальном режиме при подключении к электро-
дам транзистора напряжений U'^ и J7'6, как показано на рис. 4.24,
эмиттерный переход смещается в прямом направлении, а коллек-
торный — в обратном.
В результате снижения потенциального барьера дырки из об-
ласти эмиттера диффундируют через р—л-переход в область базы
(инжекция дырок), а электроны — из базы в область эмиттера.
Однако поскольку удельное сопротивление базы высоко, дыроч-
ный поток носителей заряда преобладает над электронным. Поэто-
151
му электронным потоком в первом приближении можно пренеб-
речь. Для количественной оценки составляющих полного тока р—
п-перехода используют коэффициент инжекции:
Л) ~ ^зр^зр "* ^зп) ~ Мз’
где I и /эп — дырочная и электронная составляющие тока эмиттерного
перехода; 1з — полный ток перехода.
Рис. 4.24. Токи в транзисторе
Вследствие разности концентраций инжектированные в базу
носители заряда диффундируют (в диффузионных транзисторах)
или движутся под действием поля (в дрейфовых транзисторах) в
глубь ее по направлению к коллектору. Так как ширина базы во
много раз меньше диффузионной длины, то большинство дырок,
инжектированных в базу, не успевает рекомбинировать в ней с
электронами и, попав вблизи коллекторного перехода в ускоряю-
щее поле, втягивается в коллектор (экстракция дырок). На воспол-
нение числа электронов, рекомбинированных с дырками, переме-
щающимися в базе, из внешней цепи по выводу в область базы
поступает такая же часть электронов, которая и создает ток базы
16. Таким образом, ток эмиттерного перехода несколько больше
тока коллекторного перехода. Относительное число неосновных
носителей заряда, достигших коллекторного перехода транзисто-
ра, характеризуется коэффициентом переноса:
= ^эр-
152
Если бы рекомбинация в базе отсутствовала, то все носители
заряда, инжектированные эмиттером, достигали бы коллекторно-
го перехода. В действительности только часть (у0) тока эмиттера
составляют дырки и только эта часть доходит до коллекторного
перехода. Поэтому ток коллектора равен:
где ад — коэффициент передачи эмиттерного тока, а0 = у080.
Кроме тока, вызванного инжектированными в базу неосновны-
ми носителями заряда, через р—л-переход, смещенный в обратном
направлении, протекает обратный ток 1кбо. Результирующий ток
в коллекторной цепи равен:
/ = aJ + К.
к 0 э кбо
Изменение напряжения, приложенного к эмиттерному переходу,
вызывает изменение числа инжектируемых в базу неосновных но-
сителей заряда и соответствующее изменение тока эмиттера и кол-
лектора. Следовательно, для изменения по определенному закону
коллекторного тока необходимо приложить к эмиттерному перехо-
ду напряжение, изменяющее по этому же закону ток эмиттера.
Поскольку сопротивление прямосмещенного эмиттерного пе-
рехода мало по сравнению с сопротивлением обратносмещенного
коллекторного перехода, то и мощность управления по входной
эмиттерной цепи оказывается намного меньше мощности, цирку-
лирующей в выходной цепи, содержащей коллекторный переход.
Именно с этим обстоятельством связаны в конечном итоге усили-
тельные свойства транзистора.
Полевой транзистор — полупроводниковый прибор, работа ко-
торого основана на модуляции сопротивления полупроводниково-
го материала поперечным электрическим полем, а усилительные свой-
ства обусловлены потоком основных носителей заряда одного знака,
протекающим через проводящий канал.
Управляющий электрод, изолированный от канала, называют
затвором. По способу изоляции затвора различают два типа поле-
вых транзисторов: с управляющим р—п-переходом, или с р—л-зат-
нором, и с изолированным затвором.
153
Транзистор с управляющим переходом представляет собой по-
левой транзистор, в котором проводящий канал изолирован от
подложки и затвора р—п-переходами, смещенными в обратном
направлении и расположенными вдоль базы (подложки) транзис-
тора. По каналу между электродами стока и истока протекает ток
основных носителей.
Истоком называется электрод, от которого начинают движение
основные носители заряда в канале. Электрод, к которому движут-
ся носители заряда, называется стоком. Управляющее напряже-
ние прикладывают к третьему электроду, называемому затвором.
Структура такого транзистора со схемой подачи напряжений и
направлений тока стока изображена на рис. 4.25.
Рис. 4.25. Полевой транзистор с управляющим переходом
Принцип работы полевого транзистора с управляющим пере-
ходом основан на изменении сопротивления канала за счет изме-
нения под действием обратного напряжения ширины области
р—п-перехода, обедненной носителями заряда. Так как во входной
цепи ток практически отсутствует, в такой структуре существует
возможность усиления по мощности.
Основными преимуществами полевых транзисторов с управ-
ляющим переходом являются высокое входное сопротивление, ма-
лые шумы, простота изготовления, отсутствие в открытом состоя-
нии остаточного напряжения между стоком и истоком открытого
транзистора.
Полевые транзисторы с изолированным затвором отличаются
от полевых транзисторов с управляющим р—n-переходом тем, что
электрод затвора изолирован от полупроводниковой области ка-
нала слоем диэлектрика. Эти транзисторы имеют структуру ме-
талл — диэлектрик — полупроводник и называются кратко МДП-
154
транзисторами. Если в качестве диэлектрика используется оксид
кремния, то их называют также МОП-транзисторами.
МДП-транзисторы могут быть двух видов: с индуцированным
каналом (канал наводится под действием напряжения, приложен-
ного к затвору) и со встроенным каналом (канал создается при из-
готовлении). МДП-транзисторы с индуцированным каналом изоб-
ражены на рис. 4.26 а. Они выполнены на основе кристалличес-
кой пластинки 1 слабо легированного п-кремния, называемого
подложкой П. В толще подложки созданы две сильно легирован-
ные области 2 с противоположным типом электропроводности р
(или р+). Металлические пластинки 5 над ними с проволочными
выводами являются электродами истока И и стока С. Поверхность
кристалла между указанными областями покрыта диэлектричес-
ким слоем диоксида кремния SiO2 3, который изолирует электрод
затвора 3 от области канала. На границе областей р у истока И —
стока С образуются р—n-переходы, один из которых при любой
полярности напряжения стока оказывается включенным в обрат-
ном направлении и препятствует протеканию тока 1с.
Рис. 4.26. Структуры МДП-транзисторов:
а) с индуцированным каналом; б) со встроенным каналом
В рабочем режиме транзистора канал 4 возникает (индуциру-
ется) под воздействием соответствующего напряжения на затво-
ре. При отрицательном напряжении затвора электрическое поле
через диэлектрик проникает в глубь подложки, выталкивает из нее
электроны и притягивает дырки (обогащает приповерхностный
слой). При некотором напряжении, называемом пороговым U ,
между стоком и истоком образуется проводящий канал, имеющий
такой же тип электропроводности, как и у стока и истока.
155
Толщина канала (инверсного слоя) незначительная, дырки ин-
дуцированного канала «сжаты» в приповерхностном слое. Дырки,
образующие канал, поступают в него не только из подложки, но
также из слоев p-типа стока и истока.
В транзисторах со встроенным каналом (рис. 4.26 б) ток в цепи
стока будет протекать и при нулевом напряжении на затворе.
В зависимости от полярности напряжения на затворе канал может
обогащаться дырками (сопротивление канала падает) либо обед-
няться, вплоть до прекращения тока ([7зи отс).
Полевые транзисторы успешно применяют в различных уси-
лительных и переключающихся устройствах, их часто использу-
ют в сочетании с биполярными транзисторами.
Схемотехника РТА и ДТЛ. На рис. 4.27 представлена принци-
пиальная схема трехвходового элемента, построенного по техно-
логии резисторно-транзисторной логики. Данная технология до-
вольно широко применялась в 60-х годах XX века при производ-
стве логических элементов.
Если на вход логического элемента (например, на вход А) по-
дать напряжение высокого уровня, то от положительного полюса
источника питания через резистор R1 и через базу транзистора
потечет насыщающий ток. Транзистор будет открыт, соответствен-
но на выходе логического элемента будет действовать сигнал ло-
гического нуля. Если на все входы подать напряжение низкого
уровня (заземлить), то транзистор VI'1 не будет получать открыва-
ющего тока и поэтому закроется. Таким образом, рассмотренный
элемент реализует логическую функцию ИЛИ—НЕ. Таблица ис-
тинности для данной функции имеет вид, показанный на рис. 4.11.
Рис. 4.27. Элемент РТА
156
Следующим этапом в развитии цифровой схемотехники стало
использование диодно-транзисторной логики, когда на входе вме-
сто резисторов использовались диоды.
Рассмотрим схемотехнику трехвходового логического элемен-
та И—НЕ (рис. 4.28), построенного по технологии ДТЛ. Таблица
истинности для функции И—НЕ имеет вид, представленный на
рис. 4.10.
Транзистор VT1 закрывается дополнительным внешним напря-
жением смещения. Элемент ДТЛ DD1 можно включить, если за-
землить один из его входов. Пусть это будет, например, вход А.
Тогда диод VD1 откроется, напряжение в точке схемы S понизится
до 0,7 В (это прямое падение напряжения на кремниевом диоде).
Отрицательное напряжение переведет транзистор VT1 в режим
отсечки. На выходе Q появится напряжение высокого уровня. От-
метим, что от входа логического элемента ДТЛ в это время стекает
на землю входной ток низкого уровня.
Рис. 4.28. Элемент ДТЛ
Когда на вход А будет подано напряжение высокого уровня,
диод закроется, и поэтому входной ток высокого уровня окажется
пренебрежимо малым. На выходе Q появится выходное напряже-
ние низкого уровня, так как транзистор VT1 получит от источника
питания через диод VD4 большой открывающий ток (учтем, что UK п
существенно превышает — Ц.м). Таким образом, в схеме ДТЛ база
ключевого транзистора VT1 непосредственно не связана с источ-
157
ником сигнала. Следовательно, транзистор не принимает многие
помехи от источника питания.
В элементе ДТЛ входным запускающим током служит ток низ-
кого уровня, для такой схемы активным является входное напря-
жение низкого логического уровня. Переход к низкому запускаю-
щему уровню оказался необходимым для обслуживания источни-
ков кодовых, цифровых, командных сигналов — кнопок, переклю-
чателей и контактов реле. Замыканию их контактов на провод с
нулевым потенциалом сопутствует гораздо меньше ложных им-
пульсов запуска (так называемый дребезг контактов), чем при их
замыкании на высокий потенциал.
Заметим, что если оставить все входы неподключенными
(«в воздухе»), это будет равнозначно подаче на них сигнала, соответ-
ствующего логической единице. Если при этом заземлен хотя бы один
из входов элемента, смена логических уровней на остальных входах
не влияет на выходное напряжение.
Схемотехника ТТЛ. После перехода к широкому выпуску интег-
ральных полупроводниковых микросхем ДТЛ довольно быстро вы-
яснилось, что для улучшения электрических параметров цифровых
микросхем выгоднее заменить матрицу диодов VD1—VD3 много-
эмиттерным транзистором (рис. 4.29). Поэтому название ДТЛтранс-
формировалось в ТТЛ, т. е. транзисторно-транзисторная логика.
Элементов ТТЛ на дискретных компонентах не было, так как мно-
гоэмиттерный транзистор разработали лишь на этапе интегральной
схемотехники. Три р—п-перехода транзистора VT1 образуют мат-
рицу диодов, соответствующую диодам VD1—VD3 элемента ДТЛ.
Рис. 4.29. Эквивалентная схема элемента ТТЛ
158
Логическую функцию И в элементе ТТЛ выполняет многоэмит-
терный транзистор (рис. 4.30).
Рис. 4.30. Элемент ТТЛ
Транзистор VT2 служит в качестве простого инвертора. Если
хотя бы один вход транзистора VT1 заземлить (сигнал логического
ноля), то соответствующий переход база—эмиттер транзистора от-
кроется. Появится входной стекающий ток /вх0 от источника пи-
тания через резистор R6 и переход база—эмиттер транзистора.
Силу базового тока нормирует резистор 7?в:
В этом случае переход база—коллектор транзистора УТ/ не
может открыться, на нем не создается избыточного напряжения
0,7 В как на переходе база—эмиттер. Транзистор VT2 в результате
будет закрыт. Соответственно на выходе появится высокий потен-
циал (логическая единица).
Будем теперь считать, что на все входы логического элемента
подан высокий потенциал (единица). В этом случае все переходы
база—эмиттер транзистора VT1 будут закрыты, так как нет разно-
сти потенциалов между базой и эмиттером, поскольку эти элект-
роды подсоединены к общему источнику питания +5 В. От поло-
жительного полюса источника питания на входы поступает лишь
входной ток утечки /вх, не превышающий при нормальной темпе-
ратуре нескольких наноампер. Направление этого тока будет про-
тивоположно проводимости транзистора. Потенциал базы тран-
159
зистора VT2 близок к нолю, а переход база — коллектор транзис-
тора VT1 открыт приложенным в прямом направлении напряже-
нием источника питания. Большой по силе ток базы теперь поте-
чет через открытый переход база—коллектор транзистора VT1 и
далее через переход база—эмиттер транзистора VT2, переводя его
в режим насыщения. На выходе в этом случае появляется низкий
потенциал (сигналлогического ноля).
Рис. 4.31. Схема работы элемента ТТЛ
Таким образом, видно, что сигнал ноля на выходе может быть
только при сигналах единицы на всех входах логического элемен-
та, что соответствует операции И—НЕ (рис. 4.31).
Схемотехника ЭСЛ. Цифровые микросхемы эмиттерно-связан-
ной логики (ЭСЛ) имеют наибольшее быстродействие, достигшее
в настоящее время субнаносекундного диапазона. Особенность
ЭСЛ заключается в том, что схема логического элемента строится
на основе интегрального дифференциального усилителя (ДУ),
транзисторы которого могут переключать ток и при этом никогда
не попадают в режим насыщения.
Дифференциальным усилителем называют усилитель, предназ-
наченный для усиления разности двух входных сигналов. При этом
полученное выходное напряжение не должно зависеть от абсолют-
ного значения входных сигналов, температуры окружающей сре-
ды и других факторов:
U = (U —U ,)К,
вых ' вх1 вх2' у’
где Ку — коэффициент усиления.
160
DD1
Рис 4.32. Схема простейшего дифференциального усилительного каскада
Базовая схема дифференциального усилителя приведена на рис.
4.32. Усилитель состоит из дифференциального каскада, выполнен-
ного на транзисторах VT1 и VT2. Базы транзисторов являются вхо-
дами усилителя, а выходное напряжение снимают с одного из кол-
лекторов транзисторов VT1 и VT2 (несимметричное подключение
нагрузки) или включают нагрузку между коллекторами двух тран-
зисторов.
Сумма токов, протекающих через эмиттеры транзисторов VT1
и VT2, не зависит от входных напряжений, а определяется режи-
мом генератора стабильного тока (ГСТ):
Ъ = 7о-
где /0 — ток генератора стабильного тока.
Если входным сигналом Д17вх открыть транзистор VT1, то через
него потечет весь ток /0. На коллекторе этого транзистора окажется
напряжение низкого уровня. В этот момент через транзистор VT2
ток не течет, транзистор вынужденно находится в состоянии отсеч-
ки. На его коллекторе присутствует напряжение высокого уровня.
Будем считать, что теперь на базу транзистора VT2 подано опор-
ное напряжение [7оп. Это напряжение будет фиксировать порог
срабатывания переключателя тока. Таким образом, дифференци-
альный усилитель выполняет функции логического элемента, у
которого два состояния выходов, переключающиеся только при
условиях Ubx < Uoa и UB* > Uon. Наличие генератора стабильного тока
принципиально: с его помощью строго фиксируются логические
уровни.
Отметим существенный недостаток данной схемы — выходное
сопротивление выходов велико, что не позволяет обеспечить вы-
1 1 А-210
161
сокое быстродействие схемы. Для снижения выходного сопротив-
ления к коллекторным выходам подключают эмиттерные повтори-
тели на транзисторах VT4 и VT5. Для получения нескольких логи-
ческих входов используют один пороговый транзистор и несколь-
ко параллельно включенных входных транзисторов (рис. 4.33).
Рис. 4.33. Базовая схема двухвходового элемента ЭСЛ
Нетрудно заметить, что данная схема реализует логические опе-
рации И, ИЛИ в зависимости от используемого выхода. Действи-
тельно, при подаче на один из входов элемента напряжения высо-
кого уровня соответствующий транзистор VT2 или VT3 откроется.
Через открытый транзистор будет протекать ток, который создаст
на резисторе R3 падение напряжения отрицательной относитель-
но корпуса полярности. Это напряжение низкого уровня (— 1,6 В)
через эмиттерный повторитель передается на выход Yr Порого-
вый транзистор вынужденно перейдет в режим отсечки, поэтому
на выходе У2 будет напряжение высокого уровня (логическая еди-
ница), равное —0,98 В. При наличии на входах X, иХ2 напряжения
низкого уровня транзисторы VT2 и VT3 закроются, а состояние
выходов изменится на противоположное. Таким образом, на вы-
ходе У, реализуется операция ИЛИ—НЕ, а на выходе У2 — опера-
ция ИЛИ (табл. 4.7).
Следует отметить очень важную черту элементов ЭСЛ. Все ло-
гические уровни ЭСЛ имеют место в отрицательной области по-
тенциалов. Такие уровни непосредственно не совместимы со схе-
мами ТТЛ и КМДП, что считается большим недостатком ЭСЛ.
162
Таблица 4.7
у. Y1
00 1 0
01 0 1
10 0 1
11 0 1
Рис. 4.34.
Ключевой
каскад
Элементы ЭСЛ отличаются повышенным быстродействием в
результате использования в них принципа переключения тока и
из-за отсутствия насыщения транзисторов. Но вместе с тем они
характеризуются повышенным энергопотреблением, низкой по-
мехоустойчивостью и повышенной чувствительностью к кратков-
ременным помехам.
Схемотехника КМДП. В основе всех цифровых микросхем
КМДП находятся три логических элемента: И, ИЛИ и коммутаци-
онный ключ (КК). С помощью КК реализуются выходы с третьим
состоянием очень большого выходного импеданса
Z (практически разомкнуто). Полевые транзисторы
можно соединять последовательно («столбиком»),
поэтому элементы И, ИЛИ строят по различным схе-
мам. В отличие от ТТЛ здесь не нужно переименовы-
вать логические уровни. Для КМДП принято, чтобы
единица отображалась высоким уровнем, а ноль —
низким.
Основу таких микросхем составляет ключевой
каскад на двух соединенных стоками МДП транзи-
сторах VT1 и VT2 (рис. 4.34). Данные транзисторы
имеют каналы с различными типами проводимости:
VT1 — канал с проводимостью п-типа; VT2 — канал с проводимос-
тью p-типа. На соединенные вместе затворы подается входной сиг-
нал. Напряжение питания положительной полярности может со-
ставлять от 3 до 15 В. Напряжение низкого уровня для микросхем
КМДП равно 0,001 В, а напряжение высокого уровня практически
равно напряжению питания.
При подаче на вход напряжения низкого уровня транзистор VT1
открывается, а транзистор VT2 закрывается. Напряжение источ-
ника питания через открытый транзистор VT1 подается на выход
163
каскада — это напряжение высокого уровня. При подаче на вход
напряжения высокого уровня транзистор VT1 закрыт, а транзис-
тор VT2 открыт. На выходе устанавливается напряжение низкого
уровня. Таким образом, данный ключевой каскад реализует логи-
ческую функцию НЕ.
Следует отметить одну важную особенность КМДП-ключа и
интегральных микросхем на его основе: в статическом режиме
потребляемая от источника питания мощность меньше на несколь-
ко порядков по сравнению с мощностью самых маломощных ло-
гических элементов ТТЛ и ТТЛШ. Это объясняется тем, что в ста-
тическом режиме один из транзисторов закрыт и, следовательно,
ток через ключ не проходит.
Схема логического элемента на основе КМДП-ключа приведе-
на на рис. 4.35. Если на оба входа подать сигналы низкого уровня,
то транзисторы VT3 и VT4 будут открыты, так как имеют канал с
проводимостью p-типа, а транзисторы VT1 и VT2 — закрыты, так
как имеют канал с проводимостью н-типа. Таким образом, на вы-
ходе установится напряжение высокого уровня (логическая еди-
ница). При подаче напряжения высокого уровня хотя бы на один
из входов соответствующий транзистор VT3 или VT4 закроется, а
транзистор VT1 или VT2 соответственно откроется. На выходе ус-
тановится напряжение низкого уровня (логический ноль). Видно,
что данная схема реализует логическую функцию ИЛИ—НЕ.
Устройство базового элемента И—НЕ как бы обратно устрой-
ству элемента ИЛИ—НЕ: параллельно соединены транзисторы с
каналами p-типа, а последовательно — с каналами n-типа (рис. 4.36).
Рис 4.35. Логический элемент ИЛИ—НЕ на основе КМДП-ключа
164
Работа данной схемы абсолютно идентична работе элемента
ИЛИ—НЕ с тем исключением, что напряжение низкого уровня на
выходе устанавливается только при одновременной подаче на оба
входа элемента напряжения высокого уровня, а во всех остальных
случаях на выходе будет присутствовать напряжение высокого уров-
ня. Действительно, при одновременной подаче на входы и Х2 на-
пряжения высокого уровня транзисторы VT1 и VT2 открываются, а
транзисторы VT3 и VT4 закрываются. На выходе устанавливается
напряжение низкого уровня (логический ноль). При подаче хотя бы
на один из входов напряжения низкого уровня один из параллельно
включенных транзисторов VT3 или VT4 открывается, а соответству-
ющий ему комплементарный транзистор (VT1 или VT2) закрывает-
ся. На вход в этом случае через соответствующий открытый тран-
зистор передается напряжение источника питания. На выходе ус-
танавливается напряжение высокого уровня (логическая единица).
Рис. 4.36. Логический элемент И—НЕ на основе КМДП-ключа
Чтобы построить логический элемент с тремя состояниями, с
выходом логического элемента нужно включить последовательный
двухполярный полевой ключ коммутации (рис. 4.37).
Затворы транзисторов VT1 и VT2 управляются сигналами с про-
тивоположными фазами <!>! и Ф2. При высоком уровне сигнала и
низком уровне S2 транзисторы VT1 и VT2 закроются, и ключ ра-
зомкнется. При обратной фазе сигналов Sj и S2 ключ будет открыт.
Когда ключ закроется, выходная цепь схемы станет высокоомной,
с очень большим сопротивлением Z. Сигналы от выхода логичес-
кого элемента не смогут пройти в выходной провод. Таким обра-
зом, выходы после ключа коммутации можно непосредственно
165
подключать к общей шине данных. При этом следует соблюдать
одно правило: при соединении нескольких элементов с третьим со-
стоянием сигналы разрешения должны быть сформированы так,
чтобы для соседних каналов они не перекрывались. Для формиро-
вания сигналов S, и S2 различного уровня (с различной фазой) мож-
но использовать один источник сигнала, при этом включив в схе-
му дополнительный инвертор.
Рис. 4.37. Двухполярный ключ коммутации
4.4.3. Элементы интегральных схем
Основными элементами полупроводниковых интегральных
схем (ИС) являются биполярные и полевые транзисторные струк-
туры. В схемах, как правило, применяют планарные транзистор-
ные элементы, у которых эмиттерные, базовые и коллекторные
области выходят на одну сторону подложки. На этой же стороне
подложки, на ее поверхности, располагаются и контактные выво-
ды от этих областей.
На рис. 4.38 показан разрез кристалла фрагмента интегральной
схемы. Транзисторы размещены в одной изолированной области
1, а резисторы — в области 2. Затемненными участками на повер-
хности кристалла обозначены металлизация, контактные площад-
ки и межсоединения. Транзисторы имеют общий коллектор.
Основой для изготовления ИС служит полупроводниковая пла-
стина кремния с проводимостью p-типа, на которую наносят тон-
кий эпитаксиальный слой n-типа. В этом случае протравливают
166
канавки для разделения отдельных элементов схемы. Путем диф-
фузии в эпитаксиальный слой под канавками вводятся примеси
p-типа, вследствие чего между созданной областью p-типа и при-
мыкающими к ней участками эпитаксиального слоя п-типа обра-
зуются р — n-переходы, служащие для изоляции отдельных элемен-
тов схемы. С этой целью при работе схемы на подложку подают
наибольший отрицательный потенциал, и р—п-переходы оказыва-
ются включенными в обратном направлении, т. е. между элемен-
тами отсутствует электрическая связь.
Рис. 4.38. Поперечное сечение фрагмента микросхемы
На оставшихся участках эпитаксиального слоя л-типа создают
необходимые структуры для получения активных и пассивных эле-
ментов. Так, путем двойной диффузии может быть создана пла-
нарная п—р—л-структура с выводами от всех электродов в одной
плоскости. При образовании полупроводниковой структуры боль-
шую роль играет пленка диоксида кремния, которая предохраня-
ет поверхности от внешних воздействий. В промежуточных опе-
рациях по изготовлению полупроводниковой структуры эта плен-
ка служит экраном, предохраняющим от диффузии примесей те
участки, в которых необходимо сохранить прежний тип проводи-
мости.
В процессе изготовления полупроводниковых ИС широко ис-
пользуют метод фотолитографии, сущность которого кратко сво-
дится к следующему. Поверхность пластины покрывают слоем
167
фоторезиста — материала, чувствительного к ультрафиолетовому
облучению. Затем пластину облучают через фотомаску, имеющую
рисунок, соответствующий последующей технологической опера-
ции. Облученные участки фоторезиста после операции закрепле-
ния полимеризуются, поэтому на них не действуют травители, с
помощью которых на необлученных участках удаляют слой диок-
сида кремния с фоторезистом. В дальнейшем производится диф-
фузия примесей в протравленные «окна», покрытие слоем диок-
сида кремния и, если необходимо, снова слоем фоторезиста с пос-
ледующим облучением через новую фотомаску и т. д.
В ходе изготовления интегральной схемы обычно приходится
использовать несколько фотомасок и выполнять соответственно
несколько по существу одинаковых технологических операций.
Однако число операций здесь примерно такое же, как и при изго-
товлении дискретного планарно-эпитаксиального транзистора, а
число одновременно изготовляемых из одной пластины схем мо-
жет быть достаточно велико, поэтому стоимость производства уни-
фицированных ИС сравнима со стоимостью производства диск-
ретных транзисторов.
Соединения между элементами в полупроводниковой ИС осуще-
ствляются путем вакуумного напыления металлических (обычно алю-
миниевых) пленок с использованием методов фотолитографии.
Транзисторный элемент отличается от обычного транзистора
тем, что содержит три р—n-перехода и четыре области. Переход,
образованный коллектором и подложкой, как уже отмечалось, ис-
пользуется для изоляции элементов схемы друг от друга. Однако
из-за наличия емкостей изолирующих переходов между отдель-
ными элементами схемы существует связь по переменному току.
Повышение эффективности изоляции элементов достигается
применением в качестве изолирующих материалов диэлектриков
(например, диоксида кремния) и воздушной изоляцией, частным
случаем которой является выращивание по технологии КНС (крем-
ний на сапфире) эпитаксиальных слоев кремния на изолирующей
подложке из сапфира, имеющего примерно такую же, как и крем-
ний, структуру кристаллической решетки, а также использовани-
ем комбинированных методов изоляции (например, сочетанием
смещенных в обратном направлении р—n-переходов с диэлектри-
ческой изоляцией, реализуемым по технологии, получившей на-
звание изопланарной, и др.). При этом удается уменьшить значе-
ние разделительной емкости между элементами схемы, повысить
168
напряжение пробоя изоляции и значительно уменьшить ток утеч-
ки изоляции.
В интегральных схемах используют вертикальные и горизонталь-
ные транзисторные элементы п—р—п- и р—п—p-типа, многоэмиттер-
ные и многоколлекторные элементы, транзисторные элементы с ба-
рьером Шотки и др. Наибольшее применение в ИС находят кремни-
евые транзисторные элементы п—р-н-типа, которые обладают луч-
шими по сравнению с р—п—p-элементами усилительными и частот-
ными свойствами. Показанные на рис. 4.39 н—р—n-элементы получи-
ли название вертикальных. В них основной поток электронов, инжек-
тируемых в базу, направлен вертикально по отношению к поверхно-
сти подложки. Эти элементы могут иметь очень тонкую базу.
Однако из-за планарного расположения контактного вывода
коллектора у таких элементов увеличивается последовательное
сопротивление коллекторного слоя в горизонтальном направле-
нии, и возрастает падение напряжения на нем, что ведет к увели-
чению энергетических затрат и ухудшению характеристик и
параметров элементов. Уменьшение этого сопротивления дости-
гается введением в нижнюю часть коллекторной области скры-
того низкоомного п+-слоя, через который и протекает основная
часть коллекторного тока.
Транзисторные элементы р—п—p-типа в ИС обычно не имеют
самостоятельного значения и применяются в сочетании с п-р—п-
элементами в одной и той же схеме, обеспечивая в ряде случаев
упрощение схемы и оптимизацию ее параметров. Транзисторные
элементы в таких схемах и сами схемы называют комплементар-
ными (дополняющими).
Многоэмиттерные транзисторные элементы (см. рис. 4.39 а) от-
личаются от обычных транзисторных элементов главным образом
наличием в базе нескольких эмиттеров. Для устранения взаимно-
го влияния эмиттеров последние располагают друг от друга на рас-
стоянии, превышающем диффузную длину носителя заряда.
В качестве эмиттерного слоя многоколлекторного транзистор-
ного элемента (рис. 4.39 б) используют эпитаксиальный n-слой, а
коллекторами служат низкоомные слои n-типа. Для увеличения
коэффициента передачи тока от эмиттера к каждому коллектору
скрытый п+-слой располагают в непосредственной близости от
базового слоя (или даже в контакте с ним), а сами коллекторы,
имеющие малые размеры, размещают на минимальном расстоя-
нии друг от друга.
169
Рис. 4.39. Транзисторный элемент:
а) многоэмиттерный; б) многоколлекторный
Важное место в производстве ИС занимает вопрос повышения
их быстродействия. Одним из путей улучшения частотных и вре-
менных свойств ИС является применение транзисторных элемен-
тов в сочетании с диодами Шотки. На рис. 4.40 а схематично пока-
зано устройство транзисторного элемента с диодом Шотки, а на
рис. 4.40 б—его эквивалентное представление. Диод Шотки обра-
зован алюминиевой полоской и n-слоем коллектора, при этом кон-
такт полоски с p-слоем базы выполняется невыпрямляющим.
Э |Б AI |К
б)
Рис. 4.40. Транзисторный элемент с диодом Шотки:
а) схематичное изображение; б) эквивалентное представление
При напряжении на коллекторном переходе, соответствующем
активному режиму или режиму отсечки транзисторного элемен-
та, диод Шотки находится под напряжением обратного смещения
и не влияет на работу элемента. При смене полярности напряже-
170
ния на коллекторном переходе диод Шотки открывается раньше
коллекторного перехода и, шунтируя его, предотвращает накоп-
ление неосновных носителей заряда в базе, что повышает быстро-
действие транзисторного элемента.
Одной из особенностей ИС является использование транзис-
торных элементов в диодном включении, обусловленное тем, что
при изготовлении ИС технологически проще получить одинако-
вые транзисторные структуры, чем специально диодные.
Существует пять основных вариантов схем диодного включе-
ния транзисторных элементов, используемых в ИС и отличающих-
ся друг от друга способом соединения электродов (рис. 4.41).
Рис. 4.41. Варианты схем диодного включения транзисторных элементов
Свойства полученных таким образом диодных элементов суще-
ственно различаются. Например, наибольшее напряжение пробоя
получается в схемах, использующих переход коллектор—база, а
наименьшее — в схемах, использующих переход эмиттер—база.
Схема с разомкнутой цепью коллектора обладает наименьшей ве-
личиной нежелательной емкости между коллектором и подлож-
кой.
Из полевых транзисторных элементов (ТЭ) наиболее широко в
интегральных схемах используют полевые ТЭ с изолированным
затвором. Их применение в интегральных схемах обусловлено осо-
бенностями МОП-элементов: высоким входным сопротивлением
(-1016 Ом); отсутствием необходимости в изоляции; возможностью
использования поверхности кристалла, созданной в результате
однократной диффузии, для стоков и истоков большой группы
транзисторных элементов; возможностью применения ТЭ в каче-
стве резисторов с высоким сопротивлением вследствие особенно-
сти входной характеристики; малой потребляемой и, следователь-
но, рассеиваемой мощностью; возможностью получения высокой
плотности элементов. Привлекательной стороной МОП-элементов
является также технология их изготовления, которая проще тех-
171
нологии изготовления биполярных ТЭ и во многом сходна с тех-
нологией получения пассивных элементов.
Основной недостаток полевых ТЭ в интегральных схемах зак-
лючается в относительно малом их быстродействии, обусловлен-
ном довольно высокими значениями емкостей затвор—исток и
затвор—сток.
МОП ТЭ имеют более низкое напряжение отсечки (или поро-
говое напряжение) по сравнению с аналогичными дискретными
компонентами. Это позволяет, в частности, снизить напряжение
питания ИС на полевых ТЭ до уровня напряжения питания ИС на
биполярных ТЭ и тем самым обеспечить условия для их совмест-
ного эффективного применения.
Внешне схема устройства МОП ТЭ практически не отличается
от схемы устройства дискретного полевого компонента. На рис.
4.42 показаны варианты МОП ТЭ со встроенным n-каналом и ин-
дуцированным p-каналом соответственно. Изоляция ТЭ от других
элементов ИС осуществляется путем смещения в обратном направ-
лении р—n-перехода, образуемого подложкой с областями истока
и стока.
В настоящее время в схемах с высокой степенью интеграции
интенсивно используются комплементарные МОП-элементы
(КМОП), обладающие рядом ценных свойств: малой потребляемой
мощностью в статическом режиме, относительно высоким быст-
родействием, хорошей помехоустойчивостью, большой нагрузоч-
ной способностью и высоким уровнем интеграции.
Рис. 4.42. МОП ТЭ:
а) со встроенным n-каналом; б) с индуцированным р-каналом
172
В КМОП ИС изоляция полевых элементов достигается как пу-
тем смещения в обратном направлении р—n-переходов, образуе-
мых подложкой с областями ТЭ (рис. 4.43 а), так и с помощью диэ-
лектрика, в частности воздуха (рис. 4.43 б), когда ИС изготовляет-
ся по упоминавшейся ранее технологии КНС.
|И|3|С
а)
Сапфир
PHUMI
б)
Рис. 4.43. Изоляция в КМОП ТЭ:
а) путем смещения р—n-переходов; б) с помощью диэлектрика
Схематическое устройство полевых ТЭ с управляющим р—п-пе-
реходом показано на рис. 4.44. Транзисторный элемент с п-кана-
лом (рис. 4.44 а) имеет скрытый р+-слой, предназначенный для
снижения напряжения отсечки элемента за счет уменьшения на-
чальной толщины канала. Транзисторный элемент с р-каналом
(рис. 4.44 б) содержит два затвора — верхний 3 и нижний 3', меж-
ду которыми и расположен p-канал. Затворы могут быть соедине-
ны друг с другом, что условно показано штриховой линией.
Рис. 4.44. Устройство полевых ТЭ с управляющим р—п-переходом:
а) ТЭ с n-каналом; б) ТЭ с р-каналом
173
Технология изготовлении ТЭ с управляющим р—п-переходом
хорошо согласуется с технологией биполярных ТЭ, поэтому они
часто изготовляются совместно на одной подложке.
Среди полевых ТЭ особое место занимают МНОП ТЭ (МНОП —
металл—нитрид—окись—полупроводник), у которых диэлектрик
затвора состоит из слоев нитрида и оксида кремния (рис. 4.45 а).
Характерной особенностью МНОП ТЭ является гистерезисная
зависимость порогового напряжения от напряжения затво-
ра. На рис. 4.45 б в качестве примера показана зависимость
[7зи пор(Ц,и) •Мя одного из МНОП элементов. Из рисунка видно, что
при подведении к затвору ТЭ напряжений, больших 30 В и мень-
ших —30 В, у ТЭ устанавливаются различные пороговые напря-
жения. В качестве управляющих сигналов обычно используют
импульсы напряжения длительностью около 0,1 мс. Так, при пода-
че импульса напряжения 17зи = 30 В устанавливается пороговое
напряжение Узи = — 5 В, которое сохраняется при работе ТЭ в
режиме малых сигналов. В таком режиме МНОП-элемент ведет
себя как обычный МОП ТЭ с индуцированным p-каналом. Если
теперь подать напряжение (7зи = — 30 В, то установится другое по-
роговое напряжение Ц, = —20 В и ТЭ окажется закрытым.
б)
Рис. 4.45. МНОП ТЭ:
а) схематичное изображение; б) гистерезисная характеристика
В основе работы МНОП ТЭ лежат процессы накопления носи-
телей заряда вблизи границы между нитридным и оксидным слоя-
ми. При напряжении затвора, превышающем 25 В, через слой диэ-
лектрика протекают токи проводимости, различные по значению
и зависящие от напряжения затвора (при малых напряжениях зат-
174
вора эти токи пренебрежимо малы). Локализация и соответствен-
но накопление носителей заряда происходят в слое нитрида крем-
ния. Накопленный заряд индуцирует на поверхности подложки
заряд противоположного знака, в результате чего изменяется по-
роговое напряжение. После снятия напряжения затвора заряд в
нитриде кремния может сохраняться в течение нескольких лет. Это
обстоятельство позволяет использовать МНОП ТЭ в запоминаю-
щих устройствах с неразрушаемой энергонезависимой памятью.
При относительно большом отрицательном напряжении затво-
ра ток проводимости, протекающий через слой окиси кремния,
превышает ток, протекающий через нитрид, что приводит к на-
коплению положительного заряда в слое нитрида и увеличению
отрицательного порогового напряжения. При относительно боль-
шом положительном напряжении затвора в слое нитрида накап-
ливается отрицательный заряд, что влечет за собой уменьшение
отрицательного порогового напряжения.
Для снятия накопленного заряда достаточно приложить к зат-
вору относительно высокое напряжение обратной полярности.
Контрольные вопросы
1. Что такое алгебра логики ?
2. Назовите области применения булевой алгебры.
3. Что такое элементы булевой алгебры?
4. Назовите базовые операции булевой алгебры.
5. Какие основные законы и постулаты алгебры логики Вы знаете?
6. Дайте определение булевой функции.
7. Перечислите булевые функции двух переменных.
8. Что такое функционально полный набор?
9. Какие функционально полные системы Вы знаете?
10. Дайте определение минтерма и макстерма.
11. Как называются формы представления функций посредством су-
перпозиции их минтермов и макстермов?
12. Что такое переключательная схема?
13. В чем состоит синтез переключательной схемы по заданным ус-
ловиям ее работы?
14. Что такое таблица истинности ?
15. Для чего применяют карты Карно?
16. Назовите основные этапы синтеза вычислительных схем.
17. Что такое логический элемент компьютера ?
175
18. Какие базовые логические элементы современных вычислитель-
ный устройств Вы знаете?
19. Что такое триггер?
20. Назовите основные свойства и характеристики электронно-ды-
рочного перехода.
21. Что такое транзистор ?
22. Какие типы транзисторов Вы знаете?
23. Назовите основные типы базовых логических элементов, их пре-
имущества и недостатки.
24. Что такое транзисторный элемент?
25. Назовите основные этапы процесса изготовления полупроводни-
ковых интегральных схем.
26. Какие типы транзисторных элементов, используемых в интеграль-
ных схемах, Вы знаете?
Тлава 5
Понятие алгоритма
и алгоритмические системы
Понятие алгоритма является одним из основных понятий совре-
менной информатики. Термин алгоритм (алгорифм) происходит
от имени среднеазиатского ученого IX века аль-Хорезми, который
разработал правила выполнения четырех арифметических дей-
ствий в десятичной системе счисления.
Вплоть до 30-х годов прошлого столетия понятие алгоритма но-
сило сугубо интуитивный характер и имело скорее методологичес-
кое, чем математическое значение. Общей теории алгоритмов
фактически не существовало, а под алгоритмом понимали конеч-
ную совокупность точно сформулированных правил, которые по-
зволяли решать те или иные классы задач. Основными свойства-
ми такого «интуитивного» понятия алгоритма являются [2]:
1. Массовость алгоритма. Подразумевается, что алгоритм позво-
ляет решать не одну конкретную задачу, а некоторый класс задач
данного типа. В простейшем случае массовость обеспечивает воз-
можность изменения исходных данных в определенных пределах.
2. Детерминированность алгоритма. Процесс применения пра-
вил к исходным данным (путь решения задачи) однозначно опре-
делен.
3. Результативность алгоритма. На каждом шаге процесса при-
менения правил известно, что считать результатом этого процес-
са, а сам процесс должен прекратиться за конечное число шагов.
В течение длительного времени пока дело касалось задач, име-
ющих положительное решение, математики довольствовались
этим определением. В этом случае достаточно и интуитивного по-
нятия алгоритма, чтобы удостовериться в том, что описанный про-
цесс решения задачи есть алгоритм. Совсем другое дело, когда за-
дача или класс задач могут и не иметь решения. В этом случае тре-
буется строго формализованное понятие алгоритма, чтобы иметь
возможность доказать его отсутствие.
В 20-х годах прошлого века задача такого определения понятия
алгоритма стала одной из центральных математических проблем.
Решение ее было получено в середине 30-х годов в работах извес-
12 А-210
177
тных математиков Д. Гильберта, К. Геделя, А. Черча, С. Клини,
Э. Поста и А. Тьюринга в двух эквивалентных формулировках: на
основе особого класса арифметических функций, получивших
название рекурсивных функций (Д. Гильберт, К. Гедель, А. Черч,
С. Клини) и на основе абстрактных автоматов (Э. Пост, А. Тью-
ринг) . Впоследствии в работах А. Маркова, Л. Калужнина появи-
лось толкование теории алгоритмов, поставившее в основу опре-
деление алгоритма как особого соответствия между словами в том
или ином абстрактном алфавите.
Таким образом, первоначально теория алгоритмов возникла
в связи с внутренними потребностями теоретической математи-
ки. Математическая логика, основания математики, алгебра, гео-
метрия и анализ остаются и сегодня одной из основных областей
приложения теории алгоритмов. Кроме того, теория алгоритмов
оказалась тесно связанной и с рядом областей лингвистики, эко-
номики, физиологии мозга и психологии, философии, естествоз-
нания. Примером одной из задач этой области может служить опи-
сание алгоритмов, реализуемых человеком в процессе умственной
деятельности.
Вместе с тем в 40-х годах прошлого века в связи с созданием
электронных вычислительных и управляющих машин возникла
область теории алгоритмов, тесно взаимодействующая с инфор-
матикой. Появление ЭВМ способствовало развитию разделов этой
теории, имеющих ярко выраженную прикладную направленность.
В настоящее время положения теории алгоритмов являются тео-
ретической основой таких составных частей современной инфор-
матики, как теории программирования, построения алгоритмичес-
ких языков и ЭВМ, анализа алгоритмов с целью выбора наиболее
рационального для решения на ЭВМ, анализа алгоритмических
языков и их синтаксического контроля при разработке трансля-
торов.
В общем случае при составлении алгоритма конкретной зада-
чи актуальное значение имеет такое представление алгоритма,
которое позволяет наиболее быстро реализовать его механизи-
рованным путем, и в частности с помощью ЭВМ. При этом для
решения задачи с помощью ЭВМ ее необходимо запрограмми-
ровать, т. е. представить алгоритм решения задачи в виде после-
довательности команд, которые может выполнять машина. Одна-
ко процесс записи алгоритма в виде последовательности машин-
ных команд очень длительный и трудоемкий. Его также можно
178
автоматизировать, если использовать для записи алгоритмов ал-
горитмические языки, представляющие собой набор символов и
терминов, связанных синтаксической структурой. С их помощью
можно по определенным правилам описывать алгоритмы реше-
ния задач. Алгоритмы, записанные в алгоритмическом языке, ав-
томатически самой ЭВМ с помощью специальной программы-
транслятора могут быть переведены в машинные программы для
конкретной ЭВМ.
Наиболее важными понятиями теории алгоритмов с точки зре-
ния информатики являются: алгоритм, алгоритмические системы,
а также системы и методы алгоритмизации.
5.1. ПОНЯТИЕ АЛГОРИТМА И ЕГО СВОЙСТВА
Алгоритм — конечный набор правил или команд (указаний), по-
зволяющий исполнителю решать любую конкретную задачу из неко-
торого класса однотипных задач.
Исполнителем может быть человек, группа людей, станок, ком-
пьютер и др. С учетом особенностей исполнителя составленный
алгоритм может быть представлен различными способами: с по-
мощью графического или словесного описания, в виде таблицы,
последовательностью формул, записанных на алгоритмическом
языке (языке программирования) и др. [2].
Язык — знаковая система (множество символов и правил) любой
физической природы, выполняющая познавательную и коммуникатив-
ную (общение) функции в процессе человеческой деятельности.
Язык может быть естественным и искусственным. Естествен-
ный язык — форма выражения мыслей и средство общения меж-
ду людьми. Искусственный язык — вспомогательный, созданный
на базе естественного языка людьми для каких-либо частных це-
лей.
Первоначально для записи алгоритмов пользовались средства-
ми естественного языка.
179
Словесный алгоритм — описание последовательных этапов обра-
ботки данных на естественном языке.
Уточним понятие словесного алгоритма на примерах сложения
п
п чисел а;, а2, ап, т. е. вычисления по формуле 5 = и нахож-
/=1
дения минимального числа х в массиве из п чисел а{, а? ап,.
В первом случае процесс может быть записан в виде следую-
щей системы последовательных указаний:
1. Полагаем S равным нолю и переходим к следующему указа-
нию.
2. Полагаем i равным единице и переходим к следующему ука-
занию.
3. Полагаем S равным S+a. и переходим к следующему указа-
нию.
4. Проверяем, равно ли i числу п. Если i = п, то вычисления пре-
кращаем. Если 1 < п, то увеличиваем i на единицу и переходим
к 3-му указанию.
Процесс нахождения минимального числа х в массиве из п чи-
сел а(, а? ад, осуществляется следующим образом. Первоначаль-
но в качестве числа х принимается а;, т. е. полагаем х = а/( после
чего х сравниваем с последующими числами массива, начиная с
а2. Если х < а2, то х сравнивается с а3, если х < а3, то х сравнивается
с а4, и т. д., пока не получим число а. < х. Тогда полагаем х = а. и
продолжаем сравнение с х последующих чисел из массива, начи-
ная с ai+), и так до тех пор, пока не будут просмотрены п чисел.
В результате просмотра всех п чисел х будет иметь значение, рав-
ное наименьшему числу из массива (г — текущий номер числа из
массива). Этот процесс может быть записан в виде следующей си-
стемы последовательных указаний:
1. Полагаем i = 1 и переходим к следующему указанию.
2. Полагаем х = а. и переходим к следующему указанию.
3. Сравниваем i с п, если i < п, то переходим к следующему ука-
занию, если i = п, процесс поиска останавливаем.
4. Увеличиваем i на единицу и переходим к следующему указа-
нию.
5. Сравниваем а. с х. Если at > х, то переходим к указанию 3,
если а, < х, переходим к указанию 2.
180
Алгоритмами в современной математике принято называть кон-
структивно задаваемые соответствия между словами в абстракт-
ных алфавитах [2].
Как было отмечено выше, под абстрактным алфавитом пони-
мают любую конечную совокупность объектов, называемых бук-
вами или символами данного алфавита. При этом природа этих
объектов не имеет значения. Символом абстрактных алфавитов
можно считать, например, буквы алфавита какого-либо языка,
цифры, любые знаки, рисунки и т. п.
Алфавит, как любое множество, задается перечислением его эле-
ментов, т. е. символов. Например, А = В = {п,6,с,Т, ?},
С = /х,у/.
Слово (строка алфавита) — любая конечная упорядоченная после-
довательность символов. Число символов в слове называют длиной слова.
Так, в алфавите А словами будут любые последовательности at,
ар* afl3a4, а4а4 и т. п., в алфавите С — х, у, ху, ух, хх, уу и т. п.
При расширении алфавита, т. е. при включении в его состав но-
вых символов, понятие слова может претерпеть существенное изме-
нение. Так, в алфавите А = {0,1,2,3,4,5,6,7,8,9} выражение «15+ 68»
представляет собой два слова, соединенные знаком суммы, а в алфа-
вите А' = {+, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} это будет одно слово.
Алфавитным оператором, или алфавитным отображением на-
зывают всякое соответствие, сопоставляющее словам некоторого ал-
фавита слова в том же или в другом фиксированном алфавите.
При этом первый алфавит называется входным, второй — вы-
ходным алфавитом данного оператора.
В случае совпадения входного и выходного алфавитов говорят,
что алфавитный оператор задан в соответствующем алфавите.
Если а — слово в алфавите А, а /3 — слово в алфавите В, то алфа-
витный оператор Га = /3 «перерабатывает» входное слово а в вы-
ходное слово ft.
Буква Г в алфавитном операторе означает отображение. Если каж-
дому входному слову алфавитный оператор ставит в соответствие не
более одного выходного слова, то такой алфавитный оператор назы-
вают однозначным, в противном случае — многозначным.
181
Алфавитный оператор, не сопоставляющий данному входному
слову а. никакого выходного слова b, не определен на этом слове.
Совокупность всех слов, на которых алфавитный оператор оп-
ределен, называется его областью определения.
Наиболее простыми являются алфавитные операторы, осуще-
ствляющие посимвольные отображения. Посимвольное отображе-
ние состоит в том, что каждый символ s входного слова а заменя-
ется некоторым символом выходного алфавита В.
Большое значение имеют так называемые кодирующие отобра-
жения [2].
Кодирующее отображение — соответствие, сопоставляющее каж-
дому символу входного алфавита некоторую конечную последователь-
ность символов в выходном алфавите, называемую кодом.
Например, если заданы входной А = {а,Ь,с,(1} и выходной
В = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} алфавиты, а также отображение симво-
лов А символами В (рис. 5.1), то для построения искомого кодиру-
ющего отображения достаточно заменить все символы любого сло-
ва а. в алфавите А соответствующими кодами алфавита В.
/7 ь. о? 7
(4 h 7Я
и ь. 454
с /)/??
и
Рис. 5.1. Пример кодирующего отображения
Так, для слова а = bccd имеем Га = 784564560123. Полученное
таким образом слово в алфавите В называется кодом исходного
слова а.
Процесс, обратный кодированию, т. е. замена в слове jB кодов
алфавита В символами из алфавита А, называется декодировани-
ем и обозначается Г1 ft. = а..
182
Например, для слова Д = 9314567878 в алфавите В декодирова-
ние Г'р дает слово а = acbb.
Кодирование называется обратимым, если при кодировании
слова а. получаем некоторое слово Д’, а декодирование дает исход-
ное слово а, (Га, = , Г1 Д;. = а).
В приведенном выше примере обратимость имеет место.
Пусть теперь имеем А = {а, Ь, с}, В = {0,1}, Га = О, ГЪ = 1, Гс —
01 и слово aabca в алфавите А. Тогда
ГааЬса = 001010 и
Г'001010 = aababa (либо одно из слов acaba, aabca, асса), т. е. об-
ратимость отсутствует.
Для обратимости кодирования должны выполняться следующие
условия:
1. Коды разных символов исходного алфавита А должны быть
различны.
2. Код любого символа алфавита А не может совпадать ни с ка-
ким из начальных подслов кодов других символов этого алфавита.
Слово р называется подсловом слова q, если слово q можно пред-
ставить в виде q = рг, где г — любое слово, в том числе и пустое,
т. е. не содержащее ни одного символа.
Второе условие выполняется в том случае, если коды всех сим-
волов исходного алфавита А имеют одинаковую длину.
Кодирование, при котором все коды имеют одинаковую длину, на-
зывают нормальным.
Кодирование позволяет сводить изучение произвольных алфа-
витных отображений к алфавитным отображениям в некотором
стандартном алфавите. Наиболее часто в качестве стандартного
алфавита выбирается двоичный алфавит, состоящий из двух сим-
волов, которые обычно отождествляют с цифрами 0 и 1: В = {0, 1}.
При этом, если п — число символов в алфавите А, то всегда
можно выбрать длину слова 1 так, чтобы удовлетворялось усло-
вие 2’ > п.
Поскольку число различных слов длины 1 в двоичном алфавите
равно 2’, то все символы в алфавите А можно закодировать слова-
ми длины 1 в алфавите В так, чтобы коды различных букв были раз-
ными. Любое такое кодирование будет нормальным и порождает
обратимое кодирующее отображение слов в алфавите А в слова в
алфавите В.
183
В общем случае к алгоритму сводятся любые процессы преоб-
разования информации, поэтому теория любых преобразователей
информации фактически сводится к изучению алфавитных опе-
раторов.
Наиболее явно это выражено при преобразовании лексической
или числовой информации. В этом случае как входная, так и вы-
ходная информация может быть представлена в виде слов, а пре-
образование информации сводится к установлению некоторого
соответствия между словами. Например, при переводе текстов
с одного языка на другой можно считать словами предложения или
отдельные абзацы книги, а задача перевода полностью сводится к
задаче установления соответствия между такими обобщенными
словами, т. е. процесс перевода с одного языка на другой может
трактоваться как процесс реализации некоторого алфавитного
оператора. При этом качественный и грамотный перевод допус-
кает, как известно, возможность известных модификаций пере-
водного текста, поэтому процесс перевода описывается не обыч-
ным однозначным алфавитным оператором, а многозначным.
Основой теории алфавитных операторов являются способы их
задания [2].
В случае если область определения алфавитного оператора ко-
нечна, оператор может быть задан простой таблицей соответствия,
связывающей все слова, входящие в область определения рассмат-
риваемого оператора (входные слова), и выходные слова, получа-
ющиеся в результате применения оператора к каждому входному
слову.
В случае бесконечной области определения алфавитного опе-
ратора задание его с помощью таблицы принципиально невозмож-
но. В этом случае оператор задается системой правил, позволяю-
щей за конечное число шагов найти выходное слово, соответству-
ющее любому наперед заданному входному слову из области оп-
ределения рассматриваемого алфавитного оператора.
Алфавитные операторы, задаваемые с помощью конечной системы
правил, называют алгоритмами.
Таким образом, всякий алфавитный оператор, который можно
фактически задать, обязательно является алгоритмом.
Однако между понятиями алфавитного оператора и алгорит-
ма существует различие. Так, в понятии алфавитного оператора
184
существенно лишь само соответствие, устанавливаемое между
входными и выходными словами, а не способ, которым это соот-
ветствие устанавливается. В понятии алгоритма, наоборот, основ-
ным является способ задания соответствия, устанавливаемого ал-
горитмом.
Алгоритм — алфавитный оператор вместе с правилами, определя-
ющими его действие.
Два алфавитных оператора считаются равными, если они име-
ют одну и ту же область определения и сопоставляют любому на-
перед заданному входному слову из этой области одинаковые вы-
ходные слова.
Два алгоритма считаются равными, если равны соответствую-
щие им алфавитные операторы и совпадает система правил, зада-
ющих действие этих алгоритмов на выходные слова.
Два алгоритма считаются эквивалентными, если у них совпада-
ют алфавитные операторы, но не совпадают способы их задания
(система правил).
Из свойства алгоритма результативности вытекает понятие об-
ласти применимости алгоритма под которой понимается множе-
ство строк, для которых алгоритм результативен.
Таким образом, эквивалентность алгоритмов может быть опре-
делена следующим образом: два алгоритма эквивалентны, если
совпадают их области применимости и результаты переработки
любого слова из этой области.
В общем случае различают случайные и самоизменяющиеся
алгоритмы [2]. Алгоритм называется случайным, если в системе
правил, описывающих алгоритм, предусматривается возможность
случайного выбора тех или иных слов или тех или иных правил.
Им соответствуют многозначные алфавитные операторы.
Алгоритм называется самоизменяющимся, если он не только
перерабатывает входные слова, но и сам изменяется в процессе
такой переработки. Результат действия самоизменяющегося алго-
ритма на то или иное входное слово зависит не только от этого сло-
ва, но и от истории предыдущей работы алгоритма.
В теории алгоритмов большое внимание уделяется общим спо-
собам задания алгоритмов, характеризующимся свойством универ-
сальности, т. е. таким способам, которые позволяют задать алго-
185
В общем случае к алгоритму сводятся любые процессы преоб-
разования информации, поэтому теория любых преобразователей
информации фактически сводится к изучению алфавитных опе-
раторов.
Наиболее явно это выражено при преобразовании лексической
или числовой информации. В этом случае как входная, так и вы-
ходная информация может быть представлена в виде слов, а пре-
образование информации сводится к установлению некоторого
соответствия между словами. Например, при переводе текстов
с одного языка на другой можно считать словами предложения или
отдельные абзацы книги, а задача перевода полностью сводится к
задаче установления соответствия между такими обобщенными
словами, т. е. процесс перевода с одного языка на другой может
трактоваться как процесс реализации некоторого алфавитного
оператора. При этом качественный и грамотный перевод допус-
кает, как известно, возможность известных модификаций пере-
водного текста, поэтому процесс перевода описывается не обыч-
ным однозначным алфавитным оператором, а многозначным.
Основой теории алфавитных операторов являются способы их
задания [2].
В случае если область определения алфавитного оператора ко-
нечна, оператор может быть задан простой таблицей соответствия,
связывающей все слова, входящие в область определения рассмат-
риваемого оператора (входные слова), и выходные слова, получа-
ющиеся в результате применения оператора к каждому входному
слову.
В случае бесконечной области определения алфавитного опе-
ратора задание его с помощью таблицы принципиально невозмож-
но. В этом случае оператор задается системой правил, позволяю-
щей за конечное число шагов найти выходное слово, соответству-
ющее любому наперед заданному входному слову из области оп-
ределения рассматриваемого алфавитного оператора.
Алфавитные операторы, задаваемые с помощью конечной системы
правил, называют алгоритмами.
Таким образом, всякий алфавитный оператор, который можно
фактически задать, обязательно является алгоритмом.
Однако между понятиями алфавитного оператора и алгорит-
ма существует различие. Так, в понятии алфавитного оператора
184
существенно лишь само соответствие, устанавливаемое между
входными и выходными словами, а не способ, которым это соот-
ветствие устанавливается. В понятии алгоритма, наоборот, основ-
ным является способ задания соответствия, устанавливаемого ал-
горитмом.
Алгоритм — алфавитный оператор вместе с правилами, определя-
ющими его действие.
Два алфавитных оператора считаются равными, если они име-
ют одну и ту же область определения и сопоставляют любому на-
перед заданному входному слову из этой области одинаковые вы-
ходные слова.
Два алгоритма считаются равными, если равны соответствую-
щие им алфавитные операторы и совпадает система правил, зада-
ющих действие этих алгоритмов на выходные слова.
Два алгоритма считаются эквивалентными, если у них совпада-
ют алфавитные операторы, но не совпадают способы их задания
(система правил).
Из свойства алгоритма результативности вытекает понятие об-
ласти применимости алгоритма под которой понимается множе-
ство строк, для которых алгоритм результативен.
Таким образом, эквивалентность алгоритмов может быть опре-
делена следующим образом: два алгоритма эквивалентны, если
совпадают их области применимости и результаты переработки
любого слова из этой области.
В общем случае различают случайные и самоизменяющиеся
алгоритмы [2]. Алгоритм называется случайным, если в системе
правил, описывающих алгоритм, предусматривается возможность
случайного выбора тех или иных слов или тех или иных правил.
Им соответствуют многозначные алфавитные операторы.
Алгоритм называется самоизменяющимся, если он не только
перерабатывает входные слова, но и сам изменяется в процессе
такой переработки. Результат действия самоизменяющегося алго-
ритма на то или иное входное слово зависит не только от этого сло-
ва, но и от истории предыдущей работы алгоритма.
В теории алгоритмов большое внимание уделяется общим спо-
собам задания алгоритмов, характеризующимся свойством универ-
сальности, т. е. таким способам, которые позволяют задать алго-
185
Используя данные функции в качестве исходных, путем при-
менения простых операций суперпозиции, примитивной рекурсии
и минимизации можно получить любую сколь угодно сложную
числовую функцию.
Операция суперпозиции функций заключается в подстановке
одних арифметических функций вместо аргументов других ариф-
метических функций.
Операция примитивной рекурсии позволяет строить функцию
от п + 1 аргумента по двум заданным функциям — функции п-го
аргумента и (п + 2)-го аргумента.
Функции, которые могут быть построены из элементарных
арифметических функций с помощью операций суперпозиции и
примитивной рекурсии, примененных любое конечное число раз
в произвольной последовательности, называются примитивно ре-
курсивными функциями.
Операции суперпозиции и примитивной рекурсии, будучи при-
менены ко всюду определенным функциям, дают в результате сно-
ва всюду определенные функции.
Большинство арифметических функций относятся к примитив-
но рекурсивным. Тем не менее примитивно рекурсивные функ-
ции не охватывают всех арифметических функций, которые мо-
гут быть определены конструктивно. При построении всех этих
функций используются другие операции, в частности операция
минимизации.
Операция минимизации позволяет определить новую арифме-
тическую функцию f(x, ..., xj от п переменных с помощью ранее
построенной арифметической функции g(xt,..., хп, у) от n + 1 пере-
менных. При этом оператор минимизации р определяется следу-
ющим образом.
Пусть (n+ 1) переменных функции g имеют неотрицательные
целые значения, тогда py(g(xI,x2,...,xn,y) = 0) образует наимень-
шее неотрицательное целое значение у, для которого
g(xl,x2,...,xn,y) = 0, при всех фиксированных значенияхх^х^...^.
Если у существует, то частичная функция f от п переменных мо-
жет быть определена из выражения g с помощью оператора ц:
/(xj, х2.хп) = ру (g(x,, х2.хп, у) = 0), в противном случаеf/x/,x2,...,xj
неопределима.
Например, для/(х) - ду(|2у-х| = 0) имеем Дх) = х/2 при всех
четных значениях х.
188
Арифметические функции, которые могут быть построены из
элементарных арифметических функций с помощью операций
суперпозиции, примитивной рекурсии и минимизации, называют-
ся частично рекурсивными функциями.
Частично рекурсивные функции представляют собой наиболее
общий класс конструктивно определяемых арифметических фун-
кций, а понятие частично рекурсивной функции является одним
из главных понятий теории алгоритмов.
Таким образом, каждая заданная частично рекурсивная функ-
ция вычислима путем определенной процедуры механического
характера, и наоборот, числовые функции, вычислимые посред-
ством алгоритмов, являются частично рекурсивными. В соответ-
ствии с тезисом Черча: класс алгоритмически (или машинно) вы-
числимых частичных числовых функций совпадает с классом всех
частично рекурсивных функций.
Этот тезис дает алгоритмическое толкование понятию частич-
но рекурсивных функций. Практически понятие частично рекур-
сивных функций используют для доказательства алгоритмической
разрешимости или неразрешимости проблем. Использование же
частично рекурсивных функций для представления того или ино-
го конкретного алгоритма практически нецелесообразно ввиду
сложности такого процесса алгоритмизации.
5.3. МАШИНЫ ТЬЮРИНГА
В 1936—1937 гг. независимо друг от друга и почти одновременно
с работами А.Черча и С. Клини было дано определение понятия ал-
горитма американским и английским математиками Э. Постом
и А.Тьюрингом. Их подход базируется на определении специальных
абстрактных (т. е. существующих не реально, а лишь в воображе-
нии) автоматов (машин). Основная мысль при этом заключалась
в том, что алгоритмические процессы — это процессы, которые мо-
жет совершать подходяще устроенная «машина». В соответствии
с этим ими с помощью точных математических терминов были описа-
ны классы машин, способные осуществить или имитировать все алго-
ритмические процессы, когда-либо описываемые математиками [2].
Машины, введенные Постом и Тьюрингом, отличались не очень
существенно и в дальнейшем стали называться машинами Тьюринга.
189
В общем случае такая машина состоит из следующих частей
(рис. 5.2):
1) информационной ленты, представляющей собой бесконеч-
ную (неограниченную) память машины. В качестве информацион-
ной ленты может служить магнитная или бумажная бесконечная
лента, разделенная на отдельные ячейки. В каждой ячейке можно
поместить лишь один символ, в том числе и ноль;
2) «считывающей головки» — специального чувствительного
элемента, способного обозревать содержимое ячеек. Вдоль голов-
ки информационная лента перемещается в обе стороны так, что-
бы в каждый рассматриваемый момент времени головка находи-
лась в одной определенной ячейке ленты;
3) управляющего устройства, которое в каждый рассматривае-
мый момент находится в некотором «состоянии». Предполагает-
ся, что устройство управления машины может находиться в неко-
тором конечном числе состояний. Состояние устройства управле-
ния часто называют внутренним состоянием машины. Одно из этих
состояний называется заключительным и управляет окончанием
работы машины.
Рис. 5.2. Состав машины Тьюринга
Рассмотрим алгоритмическую систему, предложенную Постом [2].
В алгоритмической системе Поста информация представляет-
ся в двоичном алфавите А = {1,0}. То есть в каждой ячейке инфор-
мационной ленты можно поместить либо 0, либо 1. Алгоритм пред-
ставляется в виде конечного упорядоченного набора правил, на-
зываемых приказами. Работа алгоритма начинается с некоторой
начальной ячейки, соответствующей первому приказу алгоритма.
Составляющие алгоритм приказы могут принадлежать к одному
190
из 6 приказов, выполняемых устройством управления машины
Поста:
1. Записать в рассматриваемую ячейку 1 и перейти к i-му при-
казу.
2. Записать в рассматриваемую ячейку 0 и перейти к i -му при-
казу.
3. Сдвинуть ленту вправо на одну ячейку и приступить к выпол-
нению i -го приказа.
4. Сдвинуть ленту влево на одну ячейку и перейти к выполне-
нию I -го приказа.
5. Если в рассматриваемой ячейке записана 1, то перейти к вы-
полнению j-ro приказа, а если записан 0, то перейти к выполне-
нию i -го приказа.
6. Окончание работы алгоритма, остановка.
Алгоритмы, составленные из любого конечного числа правил,
представленных приказами машины Поста, называются алгорит-
мами Поста.
Алгоритмы Поста сводятся к алгоритмам, реализуемым с помо-
щью частично рекурсивных функций, и наоборот, любая частич-
но рекурсивная функция может быть представлена алгоритмом
системы Поста.
В отличие от машины Поста машина Тьюринга может работать
в произвольном конечном алфавите и выполнять некоторое конеч-
ное число приказов. При этом машины Тьюринга, как и машины
Поста, могут сдвигать ленту на одну ячейку вправо или влево, ос-
тавляя содержимое ячеек неизменным, или могут изменять состо-
яние воспринимаемой ячейки, оставляя ленту неподвижной [2].
Машина Тьюринга называется стандартной, если она при сдвиге
ленты может предварительно изменять состояние воспринимае-
мой ячейки.
Пусть алфавит машины Тьюринга задан в виде множества А =
{So S;,..., Sгде So соответствует пустой ячейке, а число состояний
устройства управления задано в виде множества Q — {qtf qt, ..., qj,
где q0 соответствует заключительному состоянию.
Конечную совокупность символов алфавита, с которой работа-
ет машина, называют внешним алфавитом, конечную совокуп-
ность состояний устройства управления —внутренним алфави-
том.
Совокупность, образованную последовательностью состояний
всех ячеек ленты и состоянием устройства управления, называют
191
конфигурацией машины. Конфигурация задается в виде слова,
описывающего конкретное состояние машины.
Пусть в некоторый момент времени машина Тьюринга находит-
ся в состоянии, представленном на рис. 5.3.
Внешний
алфавит
Внутренний
алфавит
S
1 2
Рис. 5.3. Состояние машины Тьюринга
Конфигурация машины для данного случая будет представлена
в виде слова:
...S„S,S,...qS.k...S.Sn...,
О jl j2 ]к jr 0 '
где So — символ, обозначающий пустую ячейку;
г — число заполненных ячеек на ленте;
Sjt — состояние первой слева непустой ячейки;
Sk — состояние ячейки, просматриваемой в данный момент вре-
мени;
qt — состояние устройства управления.
Каждая конфигурация содержит лишь одно вхождение симво-
ла ф из внутреннего алфавита. Этот символ может быть в слове
самым левым, но не может быть самым правым, так как справа от
него должен помещаться символ состояния обозреваемой ячейки.
Если стандартная машина Тьюринга, находясь в состоянии q. и
воспринимая записанный на ленте символ Sk, переходит в новое
состояние q^ осуществляя при этом замену символа в рассматри-
ваемой ячейке на символ Sm и сдвиг ленты влево на одну ячейку, то
говорят, что машина выполняет команду qSk —>qSmA.
При манипуляциях с лентами используют следующие обозна-
чения:
Л — движение ленты влево;
П— движение ленты вправо;
С — нет движения ленты.
192
Команды стандартной машины Тьюринга могут задаваться на-
бором пятерок символов вида qsk qsmA, т. е. стрелка опускается.
Рассмотрим пример машины Тьюринга с алфавитами А = {0, 1},
Q = {qg qt} и командами qtl qt 1Л, qfi qg 1С.
Пусть на ленте имеется слово 11100. Головка стоит над первой
слева единицей (рис. 5.4). В результате работы машины Тьюринга
за 4 шага это слово превращается в 11110. По окончании работы
машины головка стоит над крайней правой единицей. Можно ска-
зать, что данная машина выполнила сложение в двоичной системе
десятичных чисел 28 + 2.
№ Конфигурация Исполняемые
шага команды (программа)
1 1 4- 1 0 0 <у,11100 <Т,Ч1Л
1 1 1 1 г 0 0 1g, 1100 <7,Ч1Л
2 1 1 1 0 4 0 11g, 100 д,1д,1Л
3 1 1 1 0 4 0 Illg,00 <?;Одо1С
4 1 1 1 1 0 Illg,10
а) б) в)
Рис. 5.4. Алгоритм работы машины Тьюринга
по переработке слова «11100» в слово «11110»
Совокупность всех команд, которые может выполнять маши-
на, называется ее программой [2].
Машина Тьюринга считается заданной, если заданы:
ее внешний и внутренний алфавиты;
программа;
• начальная конфигурация;
символы обозначающие пустую ячейку и заключительное
состояние.
13 А 210
193
Пусть машина Тьюринга задана внешним алфавитом А = {0, а,
Ь, с, d}, внутренним алфавитом Q = {g# q, q? q3, q4, qj и совокуп-
ностью команд:
<?oaqr;aA qobqobA, q2aqsdll, qocqocA, q,dq2cn, q3aq4dn, q4dq2cll.
Пустую ячейку обозначает символ S°, а заключительное состо-
яние — q5.
На рис. 5.5 представлен процесс переработки машиной Тьюрин-
га исходного слова bcadc в слово bcdcc. Начальная конфигурация
имеет вид qgbcadc.
№ шага Конфигурация Исполняемые команды (программа)
bqQcadc (<70b<70M)
1 bcqoadc (qocqocA)
2 bcaqtdc (qoaqtaA)
3 bcq2acc (4i<iq2cn)
4 bq5cdcc (q2aq5dn)
Рис. 5.5. Алгоритм работы машины Тьюринга
по переработке слова «bcadc» в слово «bcdcc»
Программа рассмотренной машины Тьюринга может быть пред-
ставлена в виде таблицы соответствия:
Q A S° a b c d
9» 9,аЛ qobJl qocA
- - - - 92M
92 - 954П - - -
- — - —
<?4 - - - <726П
9s Останов
Машины Тьюринга представляют собой универсальных испол-
нителей, с использованием которых можно имитировать все алго-
ритмические процессы, описываемые математиками. Было дока-
зано, что класс функций, вычислимых на этих машинах, точно со-
впадает с классом всех частично рекурсивных функций.
194
Таким образом, вопрос о существовании или несуществовании
алгоритма для задачи того или иного типа следует понимать как
вопрос о существовании или несуществовании машины Тьюрин-
га, обладающей нужным свойством.
В зависимости от числа используемых лент, их назначения и
числа состояний устройства управления определяются различные
модификации машин Тьюринга, например машина Тьюринга с дву-
мя выходами, многоленточная машина Тьюринга. При этом различ-
ные алгоритмы осуществляются на различных машинах Тьюринга,
отличающихся набором команд, внутренним и внешним алфавита-
ми. Но можно построить и универсальную машину Тьюринга, спо-
собную в известном смысле выполнять любой алгоритм [2].
В универсальной машине Тьюринга, как и во всякой тьюринго-
вой машине, информация изображается символами, расположен-
ными одновременно на магнитной ленте. При этом универсальная
машина Тьюринга может располагать лишь фиксированным ко-
нечным внешним алфавитом. Между тем она должна быть приспо-
соблена к приему в качестве исходной информации всевозмож-
ных состояний устройства управления и конфигураций, в которых
могут встречаться символы из разнообразных алфавитов со сколь
угодно большим числом различных символов.
Это достигается путем кодирования конфигурации и програм-
мы любой данной машины Тьюринга в символах входного (внеш-
него) алфавита универсальной машины. Само кодирование долж-
но выполняться следующим образом:
1) различные символы должны заменяться различными кодо-
выми группами, но один и тот же символ должен заменяться всю-
ду, где бы он ни встречался, одной и той же кодовой группой;
2) строки кодовых записей должны однозначным образом раз-
биваться на отдельные кодовые группы;
3) должна иметь место возможность распознать, какие кодовые
группы соответствуют различным сдвигам, т. е. каждой из букв Л,
П, Св отдельности, и различать кодовые группы, соответствующие
символам внутреннего алфавита и символам внешнего алфавита.
Рассмотрим пример такого кодирования для машины Тьюрин-
га Т, имеющей внешний алфавит А = fs(, s?..., sk} и внутренний ал-
фавит Q = {qt, q?..., qj.
Если внешний алфавит универсальной машины Тьюринга со-
стоит из символов А = {0, 1}, то эти условия будут выполнены при
следующем способе кодирования.
195
1. В качестве кодовых групп используются 3 + к + т различных
слов вида 100 ... 01 (между единицами — ноли), где к — число сим-
волов внешнего алфавита; т — число состояний устройства уп-
равления.
При этом разбивка строк на кодовые группы производится од-
нозначным образом путем выделения последовательностей нолей,
заключенных между двумя единицами.
2. Сопоставление кодовых групп с исходными символами внеш-
него и внутреннего алфавитов осуществляется согласно следую-
щей таблице кодирования:
Буква Кодовая группа
Л 101
п 1001
с 10001
(5, 100001 - 4 ноля
Внешний 10000001-6 нолей Четное
алфавит 2 число нолей,
больше
к 10...01 - 2(к +1) нолей) чем 2
1000001-5 нолей 1 Нечетное
Внутренний д 100000001 - 7 нолей числ0 нолей-
алфавит больше
(состояния) чем 3
flm 10...01 - 2(т +1) + 1нолей
Так, для машины Тьюринга, перерабатывающей слово bcadc в
слово bcdcc (см. рис. 5.5), входное слово в универсальной машине
Тьюринга с данным кодом будет представлено следующей строкой:
1000000110000000011000011000000000011000000001,
где 100001 — а, 10000001 — Ь, 1000000001 — с, 100000000001 — d.
Вся программа будет иметь вид:
(qobqobJl) 1000001 10000001 1000001 10000001 101
{qocqocJT) 1000001 1000000001 1000001 1000000001 101
(qoaqiaJI) 1000001 100001 100000001 100001 101
(qid2q2cll) 100000001 100000000001 10000000001 1000000001 10001
(q2aq5dFI) 10000000001 100001 100000000000001 100000000001 10001
196
Таким образом, если какая-либо машина Тьюринга Тп решает
некоторую задачу, то и универсальная машина Тьюринга Та спо-
собна решить эту задачу при условии, что кроме кодов исходных
данных этой задачи на ее ленту будет подан код программы маши-
ны Тп. Задавая универсальной машине Тьюринга Тц изображение
программы любой данной машины Тьюринга Тп и изображение
любого ее входного слова Хп, получим изображение выходного
слова Уп, в которое машина Тц переводит слово Хп.
Если же алгоритм, реализуемый машиной Тп, неприменим к сло-
ву Хп, то алгоритм, реализуемый универсальной машиной Ти так-
же неприменим к слову, образованному из изображения Хп и про-
граммы машины Тп.
Таким образом, машина Тьюринга Тп может рассматриваться
как одна из программ для универсальной машины Т.
При изучении моделей вычислений обычно проводят различие
между детерминированными и недетерминированными машинами
Тьюринга. В детерминированной машине Тьюринга общий ход вы-
числений полностью определяется машиной Тьюринга (программой),
начальным символом и начальными вводами с ленты. В недетерми-
нированной машине Тьюринга на каждой стадии вычислений суще-
ствуют альтернативы, т. е. она может работать в одном из несколь-
ких основных режимов. При этом класс задач, решаемых на детер-
минированных машинах Тьюринга за полиноминальное время, назы-
вают классом Р, а класс задач, решаемых на недертеминированных
машинах Тьюринга за полиноминальное время, — классом NP [2].
Современные электронные вычислительные машины строятся
как универсальные: в запоминающее устройство наряду с исход-
ными данными поставленной задачи вводится также и программа
ее решения. Однако в отличие от машины Тьюринга, в которой
внешняя память (лента) бесконечна, в любой реальной вычисли-
тельной машине она конечна.
Для сравнения структур различных машин и оценки их слож-
ности используют произведение числа символов внешнего алфа-
вита на число внутренних состояний, отличных от заключитель-
ного. В этом смысле представляет интерес задача построения уни-
версальных машин Тьюринга минимальной сложности. Здесь не-
обходимо отметить теоремы Ватанабе о существовании универ-
сальной машины с 5 символами и 6 состояниями, Минского о су-
ществовании машины с 4 символами и 7 состояниями и теорему
Триггера о существовании универсальной машины с 4 символами
и 6 состояниями.
197
5.4. НОРМАЛЬНЫЕ АЛГОРИТМЫ МАРКОВА
Как было отмечено выше, всякий общий способ задания алго-
ритмов называется алгоритмической системой. Алгоритмическая
система, основанная на соответствии между словами в абстракт-
ном алфавите, включает в себя объекты двух типов: элементарные
операторы и элементарные распознаватели [2].
Элементарные операторы представляют собой алфавитные
операторы, предназначенные для реализации алгоритмов в рас-
сматриваемой алгоритмической системе.
Элементарные распознаватели служат для распознавания на-
личия тех или иных свойств перерабатываемой алгоритмом инфор-
мации и для изменения, в зависимости от результатов распознава-
ния, порядка следования элементарных операторов.
Для указания набора элементарных операторов и порядка их
следования при задании конкретного алгоритма используют ори-
ентированные графы, называемые граф-схемами соответствую-
щих алгоритмов.
Граф-схема алгоритма представляет собой конечное множество
соединенных между собой вершин (или геометрических фигур),
называемых узлами граф-схемы. Каждому узлу, кроме особых уз-
лов, называемых входом и выходом, сопоставляется какой-либо
элементарный оператор (ЭО) или элементарный распознаватель
(ЭР). При этом из каждого узла, которому сопоставлен оператор, а
также из входного узла исходит по одной дуге, а из каждого узла,
которому сопоставлен распознаватель, исходит по две дуги. Из
выходного узла не исходит ни одной дуги. Число дуг, входящих
в узел граф-схемы, может быть любым.
Вариант такой граф-схемы представлен на рис. 5.6. Алгоритм,
определенный граф-схемой, работает следующим образом. Вход-
ное слово поступает на вход и двигается по направлениям, указан-
ным стрелками. При попадании слова в распознавательный узел
осуществляется проверка условия, сопоставленного этому узлу.
При выполнении условия слово направляется в операторный узел,
при невыполнении — к следующему распознавателю.
Если входное слово р, поданное на вход граф-схемы, проходя
через узлы схемы и преобразуясь, попадает через конечное число
шагов на выход, то считается, что алгоритм применим к слову р
(слово р входит в область определения этого алгоритма). Результа-
те
том воздействия на слово р будет то слово, которое оказывается на
выходе схемы. Если после подачи слова р на вход графа его преоб-
разование и движение по граф-схеме продолжается бесконечно
долго, не приводя на выход, считается, что алгоритм неприменим
к слову р, т. е. слово р не входит в область определения алгоритма.
Рис. 5.6. Вариант граф-схемы алгоритма
В нормальных алгоритмах в качестве элементарного оператора
используют оператор подстановки (ОП), а в качестве элементар-
ного распознавателя — распознаватель вхождения (РВ).
Распознаватель вхождения проверяет условие — имеет ли мес-
то вхождение рассматриваемого слова р{ в качестве подслова не-
которого заданного слова q.
Оператор подстановки заменяет первое слева вхождение слова
Р] в слово q на некоторое заданное слово р2. Оператор подстановки
задается обычно в виде двух слов, соединенных стрелкой р1—> р2.
Например, для слова 01230123применение подстановок 01—>32
и 23—>10 через четыре шага приводит к слову 32103210 (рис. 5.7):
01230123—>32230123—>32233223—>32103223—>32103210.
Последовательность слов pt, р?.рп, получаемых в процессе
реализации алгоритма, называется дедуктивной цепочкой, веду-
щей от слова pt к слову рп
Алгоритмы, которые задаются графами, составленными только
из распознавателей вхождения слов и операторов подстановки,
199
называют обобщенными нормальными алгоритмами. При этом
предполагается, что к каждому оператору подстановки ведет толь-
ко одна дуга, исходящая из соответствующего распознавателя.
ОП,
«01—>32»
оп2
«23—>10»
Рис. 5.7. Граф-схема алгоритма преобразования
входного слова «01230123» в слово «32103210»
Нормальными алгоритмами называют обобщенные нормаль-
ные алгоритмы, граф-схемы которых удовлетворяют следующим
условиям [2]:
1. Все узлы, соответствующие распознавателям, упорядочива-
ются путем их нумерации от 1 до п.
2. Дуги, исходящие из узлов, соответствующих операторам под-
становки, подсоединяются либо к узлу, соответствующему перво-
му распознавателю, либо к выходному узлу. В первом случае под-
становка называется обычной, во втором — заключительной.
3. Входной узел подсоединяется дугой к первому распознавателю.
Нормальные алгоритмы принято задавать упорядоченным мно-
жеством подстановок всех операторов данного алгоритма, назы-
ваемым схемой алгоритма. При этом обычные подстановки запи-
сываются, как и в обобщенных алгоритмах, в виде двух слов, со-
единенных стрелкой (pt—>р2), а заключительные подстановки обо-
значаются стрелкой с точкой (р:—> р2). Процесс выполнения под-
становок заканчивается лишь тогда, когда ни одна из подстановок
схемы не применима к полученному слову или когда выполнена
(первый раз) какая-либо заключительная подстановка.
Вариант граф-схемы нормального алгоритма в общем виде пред-
ставлен на рис. 5.8.
200
Рис. 5.8. Вариант граф-схемы нормального алгоритма
В качестве примера рассмотрим работу нормального алгорит-
ма А.А. Маркова, алфавит которого представлен алфавитом рус-
ского языка и задано множество подстановок:
1. Б—>В 4. 0->Х
2. Л->У 5. В->Я
3. С^М 6. Н—>А
Тогда, если на вход подать слово «СЛОН», то оно переработает-
ся алгоритмом в выходное слово «МУХА» (рис. 5.9):
«СЛОН» -»«СУОН» ->«МУОН» -^«МУХН» —>«МУХА».
На рис. 5.10 представлена граф-схема нормального алгоритма
А.А. Маркова, реализующего сложение единиц в непозиционной
системе счисления при заданном алфавите А = {+, 1} и системе
подстановок «1 + 1»—>' 1 Г, «1»—>•’ Г. При подаче на вход строки
’ 11 + 11 + Г она перерабатывается алгоритмом в строку «11 + 11
+ 1»—>'1111 +Г—>' 1111 Г—>'11И Г.
Наличие в нормальных алгоритмах подстановок двух видов —
заключительной и обычной — необходимое условие универсаль-
ности нормальных алгоритмов, т. е. возможности построения нор-
мального алгоритма, эквивалентного любому наперед заданному
алгоритму.
201
Новые алгоритмы могут быть построены из уже известных ал-
горитмов путем суперпозиции, объединения, разветвления алго-
ритмов и повторения (итерации).
В теории алгоритмов строго доказано, что по своим возможно-
стям преобразования нормальные алгоритмы эквивалентны маши-
не Тьюринга и другим моделям, уточняющим понятие алгоритма.
Рис. 5.9. Граф-схема алгоритма
преобразования входного
слова «СЛОН» в слово «МУХА»
Рис. 5.10. Граф-схема алгоритма
преобразования входного
слова «11 + 11 + 1» в слово «11111»
5.5. ОПЕРАТОРНЫЕ СИСТЕМЫ АЛГОРИТМИЗАЦИИ
Одной из особенностей рассмотренных выше алгоритмических
систем является неизменность набора допустимых средств, исполь-
зуемых для построения записи алгоритма. Например, все частич-
202
но рекурсивные функции получаются из некоторого фиксирован-
ного набора базисных функций с помощью трех операторов —
подстановки, примитивной рекурсии, минимизации. Элементар-
ные акты при вычислениях на машине Тьюринга ограничиваются
фиксированным набором операций, которые выполняет описыва-
емый класс машин и т. п.
В то же время при изучении конкретных алгоритмов желатель-
но, чтобы каждый алгоритм мог изучаться в терминах тех элемен-
тарных средств, которые наиболее удобны для его описания. На-
пример, алгоритмы линейной алгебры удобнее всего описывать
с помощью четырех арифметических действий, а алгоритмы вы-
числения функций алгебры логики — с помощью тех базисных ло-
гических операций, в терминах которых функции и записаны. По-
этому одним из требований, которое предъявляется к определе-
нию алгоритма при его практическом использовании, является то,
чтобы форма представления перерабатываемой информации и
средства ее переработки выбирались в зависимости от класса рас-
сматриваемых алгоритмов [2].
Кроме того, для классических алгоритмических систем харак-
терно, что в каждом алгоритме список предписаний о выполнении
элементарных актов — «команд» алгоритма фиксируется заранее
и явно указывается в записи алгоритма. Например, в нормальных
алгоритмах все применяемые формулы подстановки заранее ука-
заны в записи алгоритма. Список допустимых действий машины
Тьюринга при ее работе остается неизменным. Частично рекур-
сивная функция задается фиксированной последовательностью
уравнений. В то же время допущение формирования команд алго-
ритма в процессе его реализации приводит к существенному со-
кращению и упрощению записи алгоритма. В связи с этим следу-
ющим требованием, предъявляемым к понятию алгоритма, при его
практическом использовании является возможность формирова-
ния команд алгоритма в процессе его выполнения.
В общем случае все элементарные операции, производимые
в процессе выполнения алгоритмов, распадаются на две группы
операций, которые обычно называют арифметическими и логи-
ческими. Арифметические операции осуществляют непосред-
ственное преобразование информации. Логические операции оп-
ределяют дальнейшее направление счета, т. е. последовательность
выполнения арифметических операций. При этом во многих слож-
ных алгоритмах преобладают логические операции, в то время как
преобразование информации носит иногда очень простой характер.
203
Элементарные акты, аналогичные логическим операциям, в яв-
ном или неявном виде вводятся и при определении понятия вы-
полнения алгоритма в абстрактной теории алгоритмов. Например,
при выполнении нормального алгоритма после рассмотрения оче-
редной формулы подстановки осуществляется либо переход к сле-
дующей формуле подстановки, либо остановка, либо переход к
первой формуле подстановки схемы алгоритма. В машине Тьюрин-
га логической операцией можно считать движение ленты вправо
или влево в зависимости от состояния машины и прочитанного
символа.
Однако, как правило, логические операции в классических ал-
горитмических системах носят тривиальный характер. Во многих
случаях такая тривиальность логических операций сильно услож-
няет построение конкретных алгоритмов. В связи с этим следую-
щим требованием, которое предъявляется к определению алгорит-
ма при его практическом использовании, является допущение бо-
лее универсальных логических элементарных операций, нежели те,
которые имеются в абстрактной теории алгоритмов.
В той или иной мере этим требованиям отвечают так называе-
мые операторные алгоритмические системы [2].
5.5.1. Операторные алгоритмы Ван Хао
Операторный алгоритм Ван Хао задается последовательностью
приказов специального вида. Каждый приказ имеет определенный
номер и содержит указания: какую операцию следует выполнить
над заданным объектом и приказ с каким номером следует далее
выполнить над результатом данной операции. Общий вид такого
приказа:
CD а Р
где i — номер приказа;
со — элементарная операция над объектом;
а, Р — номера некоторых приказов.
В терминах машин Тьюринга номера приказов соответствуют
номерам конфигураций машины, а элементарная операция над
объектом — элементарному действию над конфигурацией при
некотором состоянии.
Выполнить приказ (5.1) над числом х в операторном алгоритме —
значит найти число со(х) и далее перейти к выполнению над й)(х)
204
приказа с номером а. Если же со(х) не определено, то перейти к
выполнению над числом х приказа с номером Д.
Заключительному состоянию машины Тьюринга в операторных
алгоритмах соответствует приказ вида:
i :|сшоп|,
который означает, что вычисления следует остановить. Число, над
которым следует выполнить этот приказ, есть результат вычисле-
ний.
Программой операторного алгоритма называется последова-
тельность приказов вида:
со, а.
ОДч-5 (Xi+s fli+s
стоп
i+n
где co/xj,coi+s(x) — заданные функции, определяющие элемен-
тарные операции над объектом х;
а , Д. — натуральные числа из последовательности i, i+l,
i -I- n.
Переработать x согласно данному операторному алгоритму —
значит выполнить над х последовательность следующих действий.
i-шаг. Находим со.(х). Если о\(х) определено, то результатом бу-
дет пара чисел [со(х),а]. Если со.(х) не определено, то результатом i-
го шага будет пара (х, Д.).
i+ 1-шаг, если результат предыдущего шага х, Д , где Д. = i + 1.
Находим coj+t (х). Если она определена, то результатом будет пара
[й)/+Дх/,а/+/], если не определена, то результатом будет пара (х, Д+1)
ИТ. д.
i+п-1 -шаг. Если в качестве результата на данном шаге получит-
ся пара, указывающая на заключительный оператор (z, i+п), то
процесс завершается и число z является результатом переработки
числа х согласно заданному алгоритму z = <о.+п ;(х).
Тип функций, вычисляемых посредством операторных алгорит-
мов Ван Хао, зависит от того, какие функции to. входят в записи
приказов.
205
5.5.2. Операторные алгоритмы Ляпунова
Алгоритмическая система отечественного ученого А.А. Ляпуно-
ва, предложенная им в 1953 г., является одной из первых, учитываю-
щих все требования, предъявляемые к конкретным алгоритмам. Она
возникла в связи с реализацией алгоритмов различных задач на ЭВМ.
Важнейшим понятием, введенным А.А. Ляпуновым, было поня-
тие оператора, являющегося одновременно и единицей действия,
и единицей конструирования программы. Как единица действия
оператор выполняет некоторое преобразование над информаци-
ей, а как единица конструирования программы — имеет некото-
рое обозначение, показывающее тип оператора, его место в про-
грамме и конкретное содержание оператора (спецификацию).
Важным свойством оператора было то, что трактовка операто-
ра как единицы действия носит относительный характер. Два опе-
ратора Ап В, выполненные друг за другом, осуществляют какое-то
совокупное преобразование информации, т. е. также образуют
некоторый оператор С. Для того чтобы операторы Ап В выполня-
лись подряд, их записывают один за другим: АВ, а связь с операто-
ром С выглядит как: С = АВ. Информация, например, о том, что
Ап В можно выполнять в любом порядке, получая один и тот же
результат, может быть выражена равенством А В = В А.
Выражаясь языком алгебры, можно сказать, что операторы про-
грамм образуют полугруппу, в которой могут существовать опре-
деляющие отношения. Изучение полугруппы операторов приоб-
рело фундаментальную роль в теоретическом программировании.
Аналогия двух рядом стоящих операторов АВ с произведени-
ем двух чисел делала понятными такие обозначения, введенные
А.А. Ляпуновым, как:
П^0)ВС(/)_
1=1
Эта запись обозначает n-кратное повторение операторов АВС,
причем символы A(i) и C(i) показывают, что спецификация этих
операторов зависит от значения индекса повторения I.
Для записи передач управления в зависимости от условий А.А. Ля-
пунов ввел понятие логических операторов:
i i
...г...р?...,
где Р — символ логического оператора;
ф — передающая и приемная стрелки соответственно.
206
Обозначение i используется, чтобы выделять пары соответству-
ющих друг другу приемных и передающих стрелок. При одном
значении Р управление передается на оператор, стоящий вслед за
передающей стрелкой I, а при другом — на оператор, стоящий
вслед за принимающей стрелкой i.
Запись алгоритма по А.А. Ляпунову состоит из двух частей. Пер-
вая часть — схема алгоритма — образована символами операто-
ров и показывает порядок расположения операторов в програм-
ме, а также направления передач управления. Вторая часть — это
спецификация всех операторов, образующих программу.
Рассмотрим пример записи операторного алгоритма Ляпунова для
решения 10 квадратных уравнений вида cz,x2 +bix + cj =0 (i = 1,...,10).
Для каждого уравнения, представив общую формулу решения
- b ± л/й2 — 4 ас J Ь2 - 4ас
Х\2=--------------- в виде р = -Ь/2а и q = --------------,
2а 2а
в зависимости от знака дискриминанта Ь2 — 4ас найдем для дей-
ствительного случая (призн = 1), корl=p+qn кор2 = p-q, для ком-
плексного — (призн = — 1), кор\ = у[р2 +q2 и кор2 = arcsin-у=г-
у1р2 + я2
Схема алгоритма:
2 1 2
4П Л2(0Л3Л4Р5?А6ТIА7 I AgA^i) 410 СТОП.
Спецификация:
At — ввод всех коэффициентов a., b., с. (I = 1,..., 10);
А2 — присвоение переменным а, b и с значений коэффициен-
тов а(, б,, с.;
А3—вычисление дискриминанта: tt = 2а, t2 — 2c, дискр = b2— ttt2\
А4—вычисление вспомогательных значений: р = —b/tt, q = ^дмск-р]//!;
Р5 — проверка условия: дискр < 0?;
Ag — вычисление модуля и аргумента комплексной пары кор-
ней:
t = р2 + q2, кор! = Vt, кор2 = arcsin (q/кор!);
207
А7 — вычисление пары действительных корней:
кор1= р + q, кор2 = р— q;
Ag — сохранение знака дискриминанта: призн = sign (дискр);
Ад — запоминание в массиве решений пары корней z-го урав-
нения;
А10 — печать всех решений.
На основе данного операторного метода в период 1955—1960 гг.
были созданы первые алгоритмические языки и трансляторы,
а также разработаны первые формализмы теоретического програм-
мирования.
5.5.3. Блок-схемный метод алгоритмизации
При блок-схемном методе алгоритмизации весь процесс реше-
ния задачи расчленяется на отдельные этапы-блоки. В блок-схеме
каждому типу действий (вводу исходных данных, вычислению зна-
чений выражений, проверке условий, управлению повторением
действий, окончанию обработки и т. п.) соответствует геометри-
ческая фигура, представленная в виде блочного символа, блоку при-
сваивается номер (метка), и он снабжается пояснительным текстом.
Направление процесса обработки в блок-схеме указывается путем
соединения отдельных элементов блок-схемы линиями переходов
(стрелками). В табл. 5.1 приведены наиболее часто употребляемые
символы.
Блок «Процесс» применяется для обозначения действия или
последовательности действий, изменяющих значение, форму пред-
ставления или размещения данных. Для улучшения наглядности
схемы несколько отдельных блоков обработки можно объединять
в один блок.
Блок «Решение» используется для обозначения переходов уп-
равления по условию. В каждом таком блоке должны быть указа-
ны вопрос, условие или сравнение, которые он определяет.
Блок «Модификация» используется для организации цикли-
ческих конструкций. (Слово модификация означает видоизме-
нение, преобразование.) Внутри блока записывается параметр
цикла, для которого указываются его начальное значение, гра-
ничное условие и шаг изменения значения параметра для каж-
дого повторения.
208
Таблица 5.1
Название символа Обозначение и пример заполнения Пояснение
Процесс I х = (а — b)/sin(l Вычислительное действие или последовательность действий
Решение Проверка условий
Модификация у I i-К i = 1,50,2 > 1 1 ' * Начало цикла
Предопределенный процесс - 1 II Расчет || параметров 1 Вычисления по подпрограмме, стандартной подпрограмме
Ввод-вывод / Ввод / / а,Ь, с / Ввод-вывод в общем виде
Пуск-останов С27началсГ^> Начало, конец алгоритма, вход и выход в подпрограмму
Документ 1 [Печать | уа, Вывод результатов на печать
Блок «Предопределенный процесс» используется для указания
обращений к вспомогательным алгоритмам, существующим авто-
номно в виде некоторых самостоятельных модулей, и для обраще-
ний к библиотечным подпрограммам.
При построении блок-схемы сложных вычислительных процес-
сов не всегда целесообразно дробить весь процесс решения зада-
чи на мелкие блоки. Иногда для большей обозримости соединяют
в один блок целую группу этапов, т. е. в зависимости от сложности
задачи необходимо составлять блок-схемы с различной степенью
детализации.
В качестве примера рассмотрим применение блок-схемного
метода алгоритмизации при решении двух задач: вычисления дей-
ствительных корней квадратного уравнения ах2+Ьх+с = 0 и на-
хождения максимального числа из массива целых чисел.
Блок-схема алгоритма вычисления действительных корней
квадратного уравнения показана на рис. 5.11.
14 А-210
209
Начало
Рис.5.11. Вычисление корней квадратного уравнения
В блоке 1 задаются исходные данные, в блоке 2 вычисляется зна-
чение дискриминанта d по заданным значениям а, b и с. В блоке 3
это значение проверяется: если оно меньше ноля, выдается сооб-
щение «Решения нет» (блок 5); если d больше или равен нолю, вы-
числяются квадратный корень из дискриминант, а затем — значе-
ния двух корней (х 1 и х2). В частном случае, если d = 0, получают-
ся два равных корня (х1 = х2 = -Ь/2а), и выводится значение ре-
зультата (блок 8).
На рис. 5.12 представлена блок-схема поиска максимального
числа из чисел a. (i = 1, 2, .... п).
Здесь сначала вводятся две дополнительные переменные: т —
значение максимального числа и i — порядковый номер (индекс)
числа в последовательности (i — 1, 2, ..., п). Присваивается т зна-
чение «ноль», a i — значение 1 (блок 3).
В блоке 4 сравнивается текущее значение т с очередным чис-
лом из заданной последовательности. Например, пусть в начале
210
последовательности указаны at = 3,
а3 = 6, а3 = 2, ... При первом выполнении
блока 4 проверяется условие а. > т (т. е.
3 > 0). В результате проверки переменной
т будет присвоено значение а. (т. е. т = 3).
Далее значение i увеличивается на едини-
цу (блок 6). Если i не больше п (блок 7), сно-
ва выполняется блок 4. На втором шаге а =
6, т. е. at > т, и т примет значение 6. На тре-
тьем шаге а = 2 (а.< ш), и т сохранит значе-
ние 6. Как только i превысит число элемен-
тов последовательности (все числа просмот-
рены), выполнение алгоритма заканчивает-
ся, а переменная т сохраняет значение мак-
симального числа последовательности.
Блок-схемным методом удобно пользо-
ваться при составлении сложных алгорит-
мов, в качестве предварительной проверки
и наглядного представления логики реше-
ния задачи.
В связи с возникновением ЭВМ и их ис-
пользованием для решения различных за-
дач возникла необходимость перевода алго-
ритмов, представленных аппаратом той или
иной алгоритмической системы, в команды
конкретной машины. Первоначально этот
перевод выполнялся вручную и требовал
много труда и времени. Для ускорения про-
Рис.5.12. Поиск
цесса перевода алгоритмов задач с языка ал- максимального числа
горитмической системы в язык машины
были разработаны специальные алгоритмические системы, полу-
чившие название алгоритмические языки программирования. В на-
стоящее время разработано и используется несколько сотен алго-
ритмических языков программирования. Строгая формализация и
однозначность описания алгоритмов в таких языках позволила пе-
реложить на машину и сам перевод с алгоритмического языка на
язык машины. Для этого ЭВМ снабжается так называемой програм-
мирующей программой — транслятором, которая, анализируя опи-
сание, сделанное на алгоритмическом языке, перерабатывает его в
программу, состоящую только из машинных команд.
211
5.6. МЕТОДЫ ОЦЕНКИ АЛГОРИТМОВ
И АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
В теории алгоритмов понятие «алгоритм» обычно уточняется
посредством описания «математической модели» вычислительной
машины. При этом возможны два подхода в зависимости от того,
оценивается ли сложность алгоритма (машины, программы) или
сложность вычислительного процесса, протекающего в соответ-
ствии с алгоритмом [2].
В качестве меры сложности алгоритмов используется функци-
онал, соотносящий каждому алгоритму А некоторое число ц(А),
характеризующее (в подходящем смысле) его громоздкость, напри-
мер: число команд в А, длина записи А или какой-нибудь другой
числовой параметр, характеризующий объем информации, содер-
жащийся в А. Подобные функционалы применяются в теоретико-
кибернетических исследованиях схем, реализующих функции ал-
гебры логики, а также в вычислительной математике, где мощность
схемы, по которой вычисляется многочлен, измеряется числом
арифметических операций, фигурирующих в схеме.
В качестве меры сложности вычислений рассматривается фун-
кционал, соотносящий каждой паре (А, а), где А — алгоритм, а —
индивидуальная задача из того класса задач, которые алгоритм А
решает, некоторое число о(А, а). Это число характеризует слож-
ность работы алгоритма А применительно к исходным данным а до
выдачи соответствующего результата. Например, в качестве а(А, а)
можно брать число элементарных шагов, из которых складывает-
ся эта работа (иначе говоря, длительность процесса вычисления)
или объем памяти, который может понадобиться для реализации
всех выкладок по ходу данного процесса, и т. д. Поскольку для каж-
дого алгоритма А однозначно определен тот класс задач W, кото-
рый он решает (например, та функция f, значение которой он вы-
числяет), то можно считать, что в рассматриваемой ситуации каж-
дый алгоритм А характеризуется функцией переменного а
оА(а) = о(А, а). Иными словами, мерой сложности работы алгорит-
ма (вычисления) является оператор, сопоставляющий с каждым
алгоритмом А соответствующую функцию оА(а).
Введение некоторой меры сложности для алгоритмов (или вы-
числений) позволяет получить удобный инструмент для сравнения
алгоритмов, а также для оценки объективной трудности, прису-
212
щей различным вычислимым функциям. Обычно считают, что мера
сложности алгоритма принимает лишь натуральное значение, по-
этому для каждой вычислимой функции существует вычисляющий
ее алгоритм с минимальной сложностью.
Классификации по сложности обычно подвергаются задачи,
решаемые с помощью машины Тьюринга (МТ). В процессе вычис-
ления с помощью такой машины могут использоваться различные
ресурсы, например «пространство» и «время». Эти ресурсы фор-
мально могут быть определены следующим образом. Пусть зада-
ны программа М машины Тьюринга и входная цепочках, тогда вре-
менной ресурс Т(М,х) определяется как число шагов в вычислении
М на х до останова М. Время будет неопределенным (т. е. равным
бесконечности), если М не останавливается на х. Временная слож-
ность М определяется как целочисленная функция Тм, где TJn)=
e max (Т (М, х); | х | = п) для неотрицательного целого числа п.
Аналогичным образом, пространственный ресурс S(M,x) опре-
деляется как число ячеек ленты, используемых М на х, а простран-
ственная сложность Sm — как SM(n)= max (SfM, х); | х | = п). Чтобы
не путать пространство, необходимое для работы, с пространством,
выделяемым для входной цепочки х, предполагается, что машина
имеет ленту ввода, работающую только на считывание, a S(M,x)
определяется как число ячеек (куда можно записывать данные),
используемых М на х.
Алгоритм, для которого критерий сложности Тм(п) или Бм(п)
возрастает при увеличении п не быстрее, чем полином в п, назы-
вается полиномиально ограниченным; алгоритм, сложность кото-
рого возрастает по экспоненте, называется экспоненциально огра-
ниченным. При этом в обоих случаях подразумевается, что алго-
ритм завершается.
Одна из главных нерешенных в настоящее время задач теории
вычислительных систем — задача тождества Р = NP. Суть ее со-
стоит в следующем [2].
Р — класс задач полиномиального типа, или в терминологии
алгоритмической системы Тьюринга, — класс формальных язы-
ков, которые считаются распознаваемыми за полиномиальное вре-
мя. Язык L входит в Р, если существует программа М машины Тью-
ринга и некоторый полином р(п), при котором эта программа рас-
познает язык L, и для всех неотрицательных значений целых п со-
блюдается условие Тм (п) < р(п), где Тм является временной оцен-
кой сложности программы М. Если какой-либо язык не входит в Р,
213
то не существует алгоритма, который распознает его за полино-
миальное время.
NP — класс задач, имеющих недетерминированное решение с
полиномиально затрачиваемым временем на решение, или в тер-
минологии алгоритмической системы Тьюринга, — класс язы-
ков, распознаваемых за полиномиальное время недетерминиро-
ванной машиной Тьюринга. При этом PQNP, но вопрос тождествен-
ности до настоящего времени не решен, несмотря на интенсивные
исследования.
Успешное решение данной проблемы может иметь значитель-
ные последствия. Например, в криптографии, где надежность шиф-
ровальных систем основывается на нереальном времени, необхо-
димом для решения задачи расшифровки, решение данной про-
блемы может привести к компрометации шифровальных систем.
Таким образом, в зависимости от сложности практической ре-
ализации все алгоритмически разрешимые задачи подразделяют-
ся на задачи полиномиального типа и задачи неполиномиального
типа.
Одним из свойств алгоритма является его массовость. Это оз-
начает, что алгоритм представляет собой способ решения некото-
рой массовой проблемы, формулируемой в виде проблемы отобра-
жения не одного, а целого множества входных слов в соответству-
ющие им выходные слова. Таким образом, всякий алгоритм мож-
но рассматривать как некоторое универсальное средство для ре-
шения целого класса задач.
Однако существуют такие классы задач, для решения которых
нет и не может быть единого универсального приема — алгорит-
ма. Другими Словами, все задачи (проблемы) можно разделить на
алгоритмически разрешимые и алгоритмически неразрешимые.
В качестве примера доказательства алгоритмической нераз-
решимости рассмотрим проблему распознавания самопримени-
мости [2].
Существуют как самоприменимые, так и несамоприменимые
алгоритмы. Примером самоприменимого алгоритма является так
называемый тождественный алгоритм в любом алфавите А, содер-
жащем две или более двух букв. Этот алгоритм применим к любо-
му слову р в алфавите А и перерабатывает любое входное слово в
себя. Примером несамоприменимого алгоритма является так на-
зываемый нолевой алгоритм в любом конечном алфавите В. Этот
алгоритм задается схемой, содержащей единственную подстанов-
214
ку —>у (где у — любая буква алфавита В), и по своему определе-
нию он не применим ни к какому входному слову.
Проблема распознавания самоприменимости алгоритмов состо-
ит в том, чтобы найти единый конструктивный прием, позволяю-
щий за конечное число шагов по схеме любого данного алгоритма
узнать, является алгоритм самоприменимым или несамопримени-
мым.
Для доказательства алгоритмической неразрешимости данной
проблемы можно использовать алгоритмическую систему Тью-
ринга.
В терминологии машины Тьюринга проблема самоприменимо-
сти может быть сформулирована следующим образом. Пусть в
машине Тьюринга зафиксирована какая-нибудь конфигурация.
Возможны два случая:
1) машина применима к этой конфигурации, т. е. после конеч-
ного числа тактов (шагов) она останавливается в заключительной
конфигурации (самоостанавливающаяся программа);
2) машина неприменима к этой конфигурации, т. е. машина
никогда не переходит в заключительную конфигурацию, она впа-
дает в бесконечный процесс (несамоостанавливающаяся про-
грамма) .
Пусть на ленте машины Тьюринга изображен ее собственный
шифр (шифр таблицы соответствия и исходной конфигурации),
записанный в алфавите машины. Если машина применима к дан-
ной конфигурации, то будем называть ее самоприменимой, в про-
тивном случае — несамоприменимой.
Тогда проблема распознавания самоприменимости состоит в
следующем: по любому заданному шифру установить, к какому
классу относится машина — к классу самоприменимых или неса-
моприменимых?
Данная проблема распознавания самоприменимости алгорит-
мически неразрешима.
Доказательство проведем методом от противного, т. е. покажем,
что исходное предположение о распознавании самоприменимос-
ти приводит к противоречию, вследствие чего мы будем вынужде-
ны сделать вывод о неразрешимости проблемы распознавания са-
моприменимости. Предположим, что такая машина МТ существу-
ет. Тогда в МТ всякий самоприменимый шифр перерабатывается
в какой-то символ, например 1 (имеющий смысл утвердительного
ответа на поставленный вопрос о самоприменимости), а всякий
215
несамоприменимый шифр — в символ 0 (имеющий смысл отрица-
тельного ответа на поставленный вопрос).
В таком случае можно было бы построить и такую машину МГ;,
которая по-прежнему перерабатывает несамоприменимые шиф-
ры в 0, в то время как к самоприменимым шифрам МГ; уже непри-
менима. Этого можно добиться путем такого изменения схемы
машины (таблицы соответствия) МТ, чтобы после появления сим-
вола 1 вместо остановки машина стала бы неограниченно повто-
рять этот же символ.
Таким образом, получаем, что MTt применима ко всякому неса-
моприменимому шифру (вырабатывая при этом символ 0) и непри-
менима к самоприменимым шифрам. Однако это приводит к про-
тиворечию.
Действительно:
1) пусть машина MTt самоприменима, тогда она применима к
своему шифру М/ и перерабатывает его в символ 0, но появление
этого символа как раз и должно означать, что машина несамопри-
менима;
2) пусть MTt несамоприменима, тогда она применима к М/, что
должно означать, что Mt самоприменима.
Полученное противоречие доказывает теорему, т. е. наше пред-
положение о машине МТ неверно. Таким образом, мы показали,
что существуют алгоритмически неразрешимые задачи, т. е. зада-
чи, решение которых не может быть получено с помощью ЭВМ.
К типу алгоритмических проблем относится и теорема Геделя о
неполноте арифметической логики, утверждающая, что любая
адекватная непротиворечивая арифметическая логика неполна,
т. е. существует истинное утверждение о целых числах, которое
нельзя доказать в такой логике [2].
Под арифметической логикой понимается совокупность акси-
ом и правил вывода теорем в элементарной теории чисел (теории
положительных целых чисел). Логика называется полной, если в
ней можно доказать истинность или ложность каждого утвержде-
ния. Логика называется непротиворечивой, если она свободна от
противоречий. Гедель показал, что невозможно доказать непро-
тиворечивость арифметической логики (даже неполной) теми ме-
тодами, которые выразимы в самой этой логике.
Чтобы было понятно значение результатов, полученных Геде-
лем, вспомним, что первой аксиоматической системой была гео-
метрия Евклида (III век до н. э.). В основе евклидовой геометрии
216
лежит совокупность определений и аксиом, отражающих простей-
шие геометрические свойства, подтвержденные многовековым
человеческим опытом.
В число аксиом, которые в геометрии Евклида принимаются без
доказательств, входит и аксиома о параллельных линиях. Аксиому
о параллельных линиях нередко называли темным пятном в гени-
альном труде Евклида. Не была также доказана полнота и непро-
тиворечивость евклидовой геометрии. И очень рано начались упор-
ные попытки математиков очистить евклидову геометрию от вся-
ких пятен. С этой целью стремились доказать аксиому о параллель-
ных линиях. Пытались логически вывести ее утверждение из ос-
тальных аксиом Евклида. Такие попытки продолжались на протя-
жении двух с лишним тысячелетий. Почти все выдающиеся мате-
матики испытывали свои силы на решении этой проблемы (Декарт,
Лейбниц, Гаусс и др.).
Полную бесплодность попыток доказать аксиому о параллель-
ных линиях впервые строго научно установил великий русский
математик Я.И. Лобачевский в XVIII веке. Он доказал, что утверж-
дение этой аксиомы нельзя вывести из остальных аксиом Евкли-
да. Лобачевский постулировал особую неевклидову геометрию,
названную его именем. Она отвергала истинность следующей ак-
сиомы Евклида: «Если даны прямая и точка, не лежащая на ней, то
существует только одна прямая, которая проходит через данную
точку параллельно данной прямой». В геометрии Лобачевского па-
раллельных линий не существует. По отношению к этой новой гео-
метрии евклидова геометрия является только частным случаем.
Контрольные вопросы
1. Какие определения понятия алгоритма Вы знаете?
2. Назовите роль и место теории алгоритмов в современной инфор-
матике.
3. Чем вызвана необходимость формализации понятия алгоритма?
4. Какие способы представления алгоритма Вы знаете?
5. Что такое алфавитный оператор?
6. Дайте определение кодирующего отображения.
7. Назовите основные свойства алгоритма.
8. Что такое алгоритмическая система?
9. Что такое рекурсия?
10. Дайте определения вычислимой и частичной функций.
217
11. В чем состоит тезис Черча?
12. Назовите элементарные арифметические функции и операции.
13. Дайте определение частично рекурсивной функции.
14. Что такое абстрактные машины Поста и Тьюринга, для чего они
предназначены ?
15. Как «устроена» машина Тьюринга?
16. Перечислите приказы, выполняемые машиной Поста.
17. Что понимают под конфигурацией машины Тьюринга?
18. Каков принцип работы машины Тьюринга?
19. Что такое универсальная машина Тьюринга?
20. В чем различие между детерминированной и недетерминирован-
ной машинами Тьюринга?
21. Что такое граф-схема алгоритма?
22. Дайте определение нормального алгоритма Маркова.
23. Назовите основные требования, предъявляемые к определению
алгоритма при его практическом использовании.
24. Что представляет собой операторный алгоритм Ван Хао?
25. Назовите основные особенности операторных алгоритмов Ляпу-
нова.
26. В чем состоит особенность блок-схемного метода алгоритмиза-
ции?
27. Какие меры сложности алгоритмов Вы знаете?
28. Что такое полиномиально ограниченный алгоритм?
29. В чем состоит суть проблемы тождества PQNP1
30. Что означает алгоритмическая разрешимость или неразрешимость
задачи?
31. Приведите примеры алгоритмически неразрешимых задач.
Тлава 6
Обработка информации
6.1. КОМПЬЮТЕРНАЯ ОБРАБОТКА ИНФОРМАЦИИ
Обработка является одной из основных операций, выполняе-
мых над информацией и главным средством увеличения ее объе-
ма и разнообразия. Для осуществления обработки информации
с помощью технических средств ее представляют в формализован-
ном виде — в виде структур данных («информационных объек-
тов»), представляющих собой некоторую абстракцию фрагмента
реального мира. Абстракция (от лат. Abstraction — отвлечение)
подразумевает выделение наиболее существенных с точки зрения
задачи обработки свойств и связей. Так, например, информация
о студенте, необходимая для учета его успеваемости, может быть
представлена набором таких идентифицирующих данных, как фа-
милия, имя, отчество, номер учебной группы. При этом несуще-
ственные для данной задачи характеристики, например рост, вес,
цвет волос и т. п., не будут учтены.
Обработка информации — получение одних «информационных
объектов» (структур данных) из других путем выполнения некоторых
алгоритмов.
Исполнитель алгоритма — абстрактная или реальная (техни-
ческая, биологическая или биотехническая) система, способная
выполнить действия, предписываемые алгоритмом. Для механиза-
ции и автоматизации процесса обработки информации и вычис-
лений, выполняемых в соответствии с заданным алгоритмом, ис-
пользуют различные типы вычислительных машин: механические,
электрические, электронные (ЭВМ), гидравлические, пневмати-
ческие, оптические и комбинированные.
В современной информатике основным исполнителем алгорит-
мов является ЭВМ, называемая также компьютером (от англ.
computer — вычислитель).
219
ЭВМ — электронное устройство, предназначенное для автомати-
зации процесса алгоритмической обработки информации и вычислений.
В зависимости от формы представления обрабатываемой инфор-
мации вычислительные машины делятся на три больших класса:
цифровые вычислительные машины (ЦВМ), обрабатываю-
щие информацию, представленную в цифровой форме;
аналоговые вычислительные машины (АВМ), обрабатыва-
ющие информацию, представленную в виде непрерывно ме-
няющихся значений какой-либо физической величины
(электрического напряжения, тока и т. д.);
гибридные вычислительные машины (Г'ВМ), содержащие как
аналоговые, так и цифровые вычислительные устройства.
В основе функционирования АВМ заложен принцип модели-
рования. Так, при использовании в качестве модели некоторой
задачи электронных цепей каждой переменной величине задачи
ставится в соответствие определенная переменная величина элект-
ронной цепи. При этом основой построения такой модели является
изоморфизм (подобие) исследуемой задачи и соответствующей ей
электронной модели. Согласно своим вычислительным возможно-
стям АВМ наиболее приспособлены для решения математических
задач, содержащих дифференциальные уравнения, не требующие
сложной логики. В отличие от ЦВМ, точность которых определяет-
ся их разрядностью, точность вычислений на АВМ ограничена и
характеризуется качеством изготовления элементной базы и основ-
ных узлов. В то же время для целого класса задач скорость решения
задач на АВМ может быть значительно больше, чем на ЦВМ. Это
объясняется параллельным принципом решения задач на АВМ, ког-
да результат решения получается мгновенно и одновременно во всех
точках модели. Данная особенность обусловливает использование
АВМ в замкнутых системах автоматического регулирования и для
решения задач в режиме реального времени. Гибридные вычисли-
тельные машины, содержащие как аналоговые, так и цифровые
вычислительные устройства, совмещают в себе достоинства АВМ и
ЦВМ. В таких машинах цифровые устройства обычно служат для
управления и выполнения логических операций, а аналоговые уст-
ройства — для решения дифференциальных уравнений.
Поскольку в настоящее время подавляющее большинство ком-
пьютеров являются цифровыми, далее слово «компьютер», или
220
«ЭВМ», будем употреблять в значении «цифровой компьютер». Для
обработки аналоговой информации на таком компьютере ее сна-
чала преобразуют в цифровую форму (см. п. 6.2).
Современный компьютер (ЭВМ) как реальная система обработ-
ки данных имеет ряд общих черт с рассмотренной в предыдущей
главе абстрактной алгоритмической системой — машиной Тью-
ринга (МТ):
подобно МТ-модели ЭВМ располагает конечным множе-
ством команд, лежащих в основе реализации и выполнения
каждого алгоритма;
• подобно МТ-модели ЭВМ функционирует дискретно (потак-
тно) под управлением программы, хранящейся в оператив-
ной памяти;
устройство управления ЭВМ по назначению в общих чертах
аналогично устройству управления МТ-модели.
Однако ЭВМ имеют относительно МТ-моделей существенно
более сложную организацию и широкий набор более крупных ко-
манд, что позволяет эффективно представлять разнообразные ал-
горитмы решаемых задач. Более того, в предположении о возмож-
ности наращивания памяти в необходимых объемах каждая ЭВМ
может моделировать любую МТ, являясь потенциально универ-
сальной. Потенциальность объясняется тем, что ни одна ЭВМ не
может считаться универсальной в смысле вычислимости произ-
вольной, частично рекурсивной функции, т. е. для нее существует
класс нерешаемых задач при условии неизменности ее ресурсов
(в первую очередь памяти).
Основу современных компьютеров образует аппаратура
(Hardware) — совокупность электронных и электромеханических
элементов и устройств, а принцип компьютерной обработки ин-
формации состоит в выполнении программы (Software) — форма-
лизованном описании алгоритма обработки в виде последователь-
ности команд, управляющих процессом обработки.
Команда представляет собой двоичный код, который определя -
ет действие вычислительной системы по выполнению какой-либо
операции.
Операция — комплекс совершаемых технологических действий
над информацией по одной из команд программы.
221
Основными операциями при обработке информации на ЭВМ
являются арифметические и логические. Арифметические опера-
ции включают в себя все виды математических действий, обуслов-
ленных программой, над целыми числами, дробями и числами с пла-
вающей запятой. Логические операции обеспечивают действия над
логическими величинами с получением логического результата.
В вычислительных системах последовательность действий, состав-
ляющих задачу обработки информации, называют процессом.
Так, обработка некоторого текста программой-редактором явля-
ется процессом, а редактирование другого текста с помощью этой
же программы представляет собой другой процесс, даже если при
этом используется одна и та же копия программы. Процесс опреде-
ляется соответствующей программой, набором данных, которые в
ходе реализации процесса могут считываться, записываться и ис-
пользоваться, а также дескриптором процесса, который описывает
текущее состояние любого выделенного процессу ресурса ЭВМ.
Дескриптор процесса — совокупность сведений, определяющих
состояние ресурсов ЭВМ, предоставленных процессу.
Каждый сеанс пользователя с вычислительной системой, напри-
мер ввод-вывод данных в ЭВМ, также является процессом. В об- J
щем случае в вычислительной системе может одновременно су- |
ществовать произвольное число процессов, поэтому между ними j
возможна конкуренция за обладание тем или иным ресурсом, *
в первую очередь временем процессора — основного вычислитель- •
ного устройства ЭВМ. Это обусловливает необходимость органи-
зации управления процессами и их планирования. В современных
ЭВМ для решения данных задач служат операционные системы ।
(ОС), включающие совокупность программ для управления про- I
цессами, распределения ресурсов, организации ввода-вывода и
интерфейса с пользователем.
С точки зрения организации вычислительных процессов в ЭВМ
выделяют несколько режимов:
однопрограммный однопользовательский режим, в котором
вычисления носят последовательный характер, а ресурсы
ЭВМ не разделяются;
222
мультизадачный, когда несколько программ последователь-
но используют время процессора, при этом возможно раз-
деление как аппаратных, так и программных ресурсов ЭВМ;
многопользовательский, когда каждому пользователю выде-
ляется квант (интервал) времени процессора, при этом зада-
ча распределения ресурсов, в первую очередь времени про-
цессора и памяти, значительно усложняется;
мультипроцессорный, когда вычислительная система, вклю-
чающая несколько процессоров, позволяет выполнять реаль-
ные параллельные процессы, при этом распределение ресур-
сов носит наиболее сложный характер.
При выполнении задач обработки информации на компьютере
выделяют пакетный и интерактивный (запросный, диалоговый)
режимы взаимодействия пользователя с ЭВМ.
Пакетный режим первоначально использовался для снижения
непроизводительных затрат машинного времени путем объедине-
ния однотипных заданий. Его суть заключается в следующем. Зада-
ния группируются в пакеты, каждый со своим отдельным компиля-
тором. Компилятор загружается один раз, а затем осуществляется
последовательная трансляция всех заданий пакета. По окончании
компиляции пакета все успешно транслированные в двоичный код
задания последовательно загружаются и обрабатываются. Такой ре-
жим был основным в эпоху централизованного использования ЭВМ
(централизованной обработки), когда различные классы задач ре-
шались с использованием одних и тех же вычислительных ресур-
сов, сосредоточенных в одном месте (информационно-вычислитель-
ном центре). При этом организация вычислительного процесса стро-
илась главным образом без доступа пользователя к ЭВМ. Его функ-
ции ограничивались лишь подготовкой исходных данных по комп-
лексу информационно-взаимосвязанных задач и передачей их в
центр обработки, где формировался пакет заданий для ЭВМ.
В настоящее время под пакетным режимом также понимается
процесс компьютерной обработки заданий без возможности вза-
имодействия с пользователем. При этом, как правило, задания вво-
дятся пользователями с терминалов и обрабатываются не сразу,
а помещаются сначала в очередь задач, а затем поступают на обра-
ботку по мере высвобождения ресурсов. Такой режим реализует-
ся во многих системах коллективного доступа.
Интерактивный режим предусматривает непосредственное
взаимодействие пользователя с информационно-вычислительной
системой и может носить характер запроса (как правило, регла-
223
ментированного) или диалога с ЭВМ [12]. Запросный режим позво-
ляет дифференцированно, в строго установленном порядке предос-
тавлять пользователям время для общения с ЭВМ. Диалоговый режим
открывает пользователю возможность непосредственно взаимодей-
ствовать с вычислительной системой в допустимом для него темпе
работы, реализуя повторяющийся цикл выдачи задания, получения
и анализа ответа. При этом ЭВМ сама может инициировать диалог,
сообщая пользователю последовательность шагов (предоставление
меню) для получения искомого результата. Организация взаимодей-
ствия пользователя и ЭВМ представлена на рис. 6.1. Взаимодействие
осуществляется путем передачи сообщений и управляющих сигна-
лов между пользователем и ЭВМ. Входные сообщения генерируют-
ся оператором с помощью средств ввода: клавиатуры, манипулято-
ров типа мышь и т. п., выходные — компьютером в виде текстов, зву-
ковых сигналов, изображений и представляются пользователю на эк-
ране монитора или других устройствах вывода информации. Основ-
ными типами сообщений, генерируемыми пользователем, являются:
запрос информации, запрос помощи, запрос операции или функции,
ввод или изменение информации и т. д. В ответ со стороны компью-
тера он получает: подсказки или справки, информационные сообще-
ния, не требующие ответа, приказы, требующие действий, сообще-
ния об ошибках, нуждающиеся в ответных действиях и т. д.
I---------------------------------------------------------------------------------------------------------------------------------------!
I---------------------------------------------------------------------------------------------------------------------------------------1
Рис. 6.1. Организация взаимодействия пользователя и ЭВМ
224
Данный режим является основным на современном этапе разви-
тия компьютерных систем обработки информации, характерной чер-
той которого является широкое внедрение практически во все сфе-
ры деятельности человека персональных компьютеров (ПК) — одно-
пользовательских микроЭВМ, удовлетворяющих требованиям обще-
доступности и универсальности применения. В настоящее время
пользователь, обладая знаниями основ информатики и вычислитель-
ной техники, сам разрабатывает алгоритм решения задачи, вводит
данные, получает результаты, оценивает их качество. У него имеют-
ся реальные возможности решать задачи с альтернативными вари-
антами, анализировать и выбирать с помощью системы в конкрет-
ных условиях наиболее приемлемый вариант. Основные этапы ре-
шения задач с помощью компьютера представлены на рис. 6.2.
Практика применения персональных компьютеров в различных
отраслях науки, техники и производства показала, что наибольшую
эффективность от внедрения вычислительной техники обеспечи-
вают не отдельные ПК, а вычислительные сети — совокупность
компьютеров и терминалов, соединенных с помощью каналов свя-
зи в единую систему распределенной обработки данных.
6.1.1. Поколения электронных вычислительных машин
Развитие электронных вычислительных машин можно условно
разбить на несколько этапов (поколений ЭВМ), которые имеют
свои характерные особенности.
Первый этап (ЭВМ первого поколения) — до конца 50-х годов
XX века.
Точкой отсчета эры ЭВМ считают 1946 г„ когда был создан первый
электронный цифровой компьютер «Эниак» (Electronic Numerical
Integrator and Computer). Вычислительные машины этого поколения
строились на электронных лампах, потребляющих огромное количе-
ство электроэнергии и выделяющих много тепла.
Числа в ЭВМ вводились с помощью перфокарт и набора пере-
ключателей, а программа задавалась соединением гнезд на специ-
альных наборных платах. Производительность такой гигантской
ЭВМ была ниже, чем современного калькулятора. Широкому ис-
пользованию этих ЭВМ, кроме дороговизны, препятствовали так-
же низкая надежность, ограниченность их ресурсов и чрезвычайно
трудоемкий процесс подготовки, ввод и отладка программ, написан-
ных на языке машинных команд. Основными их пользователями
15 А-2Ю
225
1. Постановка задачи:
* сбор информации о задаче;
формулировка условия задачи;
определение конечных целей решения задачи;
определение формы выдачи результатов;
описание данных (их типов, диапазонов величин, структуры и т. п.).
I -
2. Анализ и исследование задачи, модели:
анализ существующих аналогов;
анализ технических и программных средств;
разработка математической модели;
разработка структур данных.
3. Разработка алгоритма:
• выбор метода проектирования алгоритма;
выбор формы записи алгоритма (блок-схема, псевдокод и др.);
выбор тестов и метода тестирования;
* проектирование алгоритма.
4. Программирование:
выбор языка программирования;
уточнение способов организации данных;
запись алгоритма на выбранном языке программирования
5. Тестирование и отладка:
синтаксическая отладка;
отладка семантики и логической структуры;
тестовые расчеты и анализ результатов тестирования;
совершенствование программы
--- I
6. Анализ результатов решения задачи и уточнение
в случае необходимости математической модели
с повторным выполнением этапов 2—5
I
7. Сопровождение программы:
доработка программы для решения конкретных задач;
составление документации к решенной задаче,
математической модели, алгоритму, программе, по их использованию
Рис. 6.2. Этапы решения задач с помощью компьютера
226
были ученые, решавшие наиболее актуальные научно-техничес-
кие задачи, связанные с развитием реактивной авиации, ракетос-
троения и т. д.
Среди известных отечественных машин первого поколения не-
обходимо отметить БЭСМ-1 (большая электронная счетная ма-
шина), Стрела, Урал, М-20. Типичные характеристики ЭВМ пер-
вого поколения (на примере БЭСМ-1, 1953 г.): емкость памяти —
2048 слов; быстродействие — 7000—8000 оп./с; разрядность —
39 разрядов; арифметика — двоичная с плавающей запятой; сис-
тема команд — трехадресная; устройство ввода — перфолента;
количество электронных ламп в аппаратуре — около 4000; вне-
шние запоминающие устройства — барабаны на 5120 слов; маг-
нитная лента — до 120 000 слов; вывод на быструю цифровую
печать — 300 строк в минуту. Отечественная ЭВМ М-20 (20 тыс.
оп./с) была одной из самых быстродействующих машин первого
поколения в мире.
Основной режим использования машин первого поколения со-
стоял в том, что математик, составивший программу, садился за
пульт управления машиной и производил необходимые вычисле-
ния. Чаще всего работа за пультом была связана с отладкой своей
собственной программы — наиболее длительным по времени про-
цессом. При этом класс математика-программиста определялся его
умением быстро находить и исправлять ошибки в своих програм-
мах, хорошо ориентироваться за пультом ЭВМ.
В этот период началась интенсивная разработка средств авто-
матизации программирования, создание входных языков разных
уровней, создание систем обслуживания программ, упрощающих
работу на машине и увеличивающих эффективность ее использо-
вания.
Второй этап (ЭВМ второго поколения) — до середины 60-х го-
дов XX века.
Развитие электроники привело к изобретению в 1948 г. нового
полупроводникового устройства — транзистора, который заменил
лампы (создатели транзистора — сотрудники американской фир-
мы Bell Laboratories физики У. Шокли, У. Браттейн и Дж. Бардин
за это достижение были удостоены Нобелевской премии). Появ-
ление ЭВМ, построенных на транзисторах, привело к уменьшению
их габаритов, массы, энергопотребления и стоимости, а также
к увеличению их надежности и производительности. Одной из
227
первых транзисторных ЭВМ была созданная в 1955 г. бортовая
ЭВМ для межконтинентальной баллистической ракеты ATLAS.
Если с технической точки зрения переход к машинам второго
поколения четко очерчен переходом на полупроводники, то со
структурной точки зрения ЭВМ второго поколения характеризу-
ются расширенными возможностями по вводу-выводу, увеличен-
ным объемом запоминающих устройств, развитыми системами
программирования.
В рамках второго поколения все более четко проявляется диф-
ференциация ЭВМ на малые, средние и большие, позволившая
существенно расширить сферу применения ЭВМ, приступить
к созданию автоматизированных систем управления (АСУ) пред-
приятиями, целыми отраслями и технологическими процессами.
Стиль использования ЭВМ второго поколения характерен тем,
что теперь математик-программист не допускается в машинный
зал, а свою программу, обычно записанную на языке высокого
уровня, отдает в группу обслуживания, которая занимается даль-
нейшей обработкой его задачи — перфорированием и пропуском
на машине.
Среди известных отечественных машин второго поколения не-
обходимо отметить БЭСМ-4, М-220 (200 тыс. оп./с), Наири, Мир,
МИНСК, РАЗДАН, Днепр. Наилучшей отечественной ЭВМ второ-
го поколения считается БЭСМ-6, созданная в 1966 г. Она имела
основную и промежуточную память (на магнитных барабанах)
объемами соответственно 128 и 512 Кбайт, быстродействие поряд-
ка 1 млн оп./с и довольно обширную периферию (магнитные лен-
ты и диски, графопостроители, разнообразные устройства ввода-
вывода).
В этот период появились так называемые алгоритмические язы -
ки высокого уровня, средства которых допускают описание всей
необходимой последовательности вычислительных действий в на-
глядном, легко воспринимаемом виде. Программа, написанная на
алгоритмическом языке, непонятна компьютеру, воспринимающе-
му только язык своих собственных команд. Поэтому специальные
программы, которые называются трансляторами, переводят про-
грамму с языка высокого уровня на машинный язык.
Появился широкий набор библиотечных программ для реше-
ния разнообразных математических задач. Были созданы монитор-
ные системы, управляющие режимом трансляции и исполнения
программ. Из мониторных систем в дальнейшем выросли совре-
228
менные операционные системы (комплексы служебных программ,
обеспечивающих лучшее распределение ресурсов ЭВМ при испол-
нении пользовательских задач).
Первые ОС просто автоматизировали работу оператора ЭВМ,
связанную с выполнением задания пользователя: ввод в ЭВМ тек-
ста программы, вызов нужного транслятора, вызов необходимых
библиотечных программ и т. д. Теперь же вместе с программой и
данными в ЭВМ вводится еще и инструкция, где перечисляются
этапы обработки и приводится ряд сведений о программе и ее ав-
торе. Затем в ЭВМ стали вводить сразу по нескольку заданий
пользователей (пакет заданий), ОС стали распределять ресурсы
ЭВМ между этими заданиями — появился мультипрограммный
режим обработки.
Третий этап (ЭВМ третьего поколения) — до начала 70-х годов
XX века.
Элементной базой в ЭВМ третьего поколения являются интег-
ральные схемы. Создание технологии производства интегральных
схем, состоящих из десятков электронных элементов, образован-
ных в прямоугольной пластине кремния с длиной стороны не бо-
лее 1см, позволило увеличить быстродействие и надежность ЭВМ
на их основе, а также уменьшить габариты, потребляемую мощ-
ность и стоимость ЭВМ.
Машины третьего поколения — это семейство машин с единой
архитектурой, т. е. программно-совместимых. Они имеют разви-
тые операционные системы, обладают возможностями мульти-
программирования, т. е. одновременного выполнения нескольких
программ. Многие задачи управления памятью, устройствами и
ресурсами стала брать на себя операционная система или же не-
посредственно сама машина.
Примеры машин третьего поколения — семейство IBM-360,
IBM-370, PDP-8, PDP-11, отечественные ЕС ЭВМ (единая система
ЭВМ), СМ ЭВМ (семейство малых ЭВМ) и др.
Быстродействие машин внутри семейства изменяется от не-
скольких десятков тысяч до миллионов операций в секунду. Ем-
кость оперативной памяти достигает нескольких сотен тысяч слов.
В этот период широкое распространение получило семейство
мини-ЭВМ. Простота обслуживания мини-ЭВМ, их сравнительно
низкая стоимость и малые габариты позволяли снабдить этими
машинами небольшие коллективы исследователей, разработчиков-
экспериментаторов и т. д., т. е. дать ЭВМ прямо в руки пользовате-
229
лей. В начале 70-х годов с термином мини-ЭВМ связывали уже два
существенно различных типа средств вычислительной техники:
универсальный блок обработки данных и выдачи управляющих
сигналов, серийно выпускаемых для применения в различных
специализированных системах контроля и управления;
универсальную ЭВМ небольших габаритов, проблемно-ори-
ентированную пользователем на решение ограниченного
круга задач в рамках одной лаборатории, тех. участка и т. д.,
т. е. задач, в решении которых оказывались заинтересованы
10—20 человек, работавших над одной проблемой.
В период машин третьего поколения произошел крупный сдвиг
в области применения ЭВМ. Если раньше ЭВМ использовались в
основном для научно-технических расчетов, то в 60—70-е годы все
больше места стала занимать обработка символьной информации.
Четвертый этап (ЭВМ четвертого поколения) — по настоящее
время.
Этот этап условно делят на два периода: первый — до конца 70-х
годов и второй — с начала 80-х по настоящее время.
В первый период успехи в развитии электроники привели к со-
зданию больших интегральных схем (БИС), где в одном кристалле
размещалось несколько десятков тысяч электронных элементов. Это
позволило разработать более дешевые ЭВМ, имеющие большую
память и меньший цикл выполнения команд: стоимость байта памя-
ти и одной машинной операции резко снизилась. Но так как затра-
ты на программирование почти не сокращались, то на первый план
вышла задача экономии человеческих, а не машинных ресурсов.
Разрабатывались новые ОС, позволяющие программистам от-
лаживать свои программы прямо за дисплеем ЭВМ, что ускоряло
разработку программ. Это полностью противоречило концепци-
ям первых этапов информационной технологии: «процессор вы-
полняет лишь ту часть работы по обработке данных, которую прин-
ципиально люди выполнить не могут, т. е. массовый счет». Стала
прослеживаться другая тенденция: «все, что могут делать маши-
ны, должны делать машины; люди выполняют лишь ту часть рабо-
ты, которую нельзя автоматизировать».
В 1971 г. был изготовлен первый микропроцессор — большая
интегральная схема (БИС), в которой полностью размещался про-
цессор ЭВМ простой архитектуры. Стала реальной возможность
размещения в одной БИС почти всех электронных устройств не-
сложной по архитектуре ЭВМ, т. е. возможность серийного вы-
230
пуска простых ЭВМ малой стоимости. Появились дешевые мик-
рокалькуляторы и микроконтроллеры—управляющие устройства,
построенные на одной или нескольких БИС, содержащих процес-
сор, память и системы связи с датчиками и исполнительными орга-
нами в объекте управления. Программа управления объектами вво-
дилась в память ЭВМ либо при изготовлении, либо непосредствен-
но на предприятии.
В 70-х годах стали изготовлять и микро-ЭВМ — универсальные
вычислительные системы, состоящие из процессора, памяти, схем
сопряжения с устройствами ввода-вывода и тактового генерато-
ра, размещенных в одной БИС (однокристальная ЭВМ) или в не-
скольких БИС, установленных на одной плате (одноплатная ЭВМ).
Примерами отечественных ЭВМ этого периода являются СМ-1800,
«Электроника 60М» и др.
Во втором периоде улучшение технологии БИС позволяло из-
готовлять дешевые электронные схемы, содержащие сотни тысяч
элементов в кристалле — схемы сверхбольшой степени интегра-
ции — СБИС.
Появилась возможность создать настольный прибор с габари-
тами телевизора, в котором размещались микро-ЭВМ, клавиату-
ра, а также схемы сопряжения с малогабаритным печатающим ус-
тройством, измерительной аппаратурой, другими ЭВМ и т. п. Бла-
годаря ОС, обеспечивающей простоту общения с этой ЭВМ, боль-
шой библиотеки прикладных программ по различным отраслям
человеческой деятельности, а также малой стоимости такой пер-
сональный компьютер становится необходимой принадлежностью
любого специалиста и даже ребенка. Кроме функций помощника
в решении традиционных задач расчетного характера, персональ-
ный компьютер (ПК) может выполнять функции личного секрета-
ря; помогать в составлении личной картотеки; создавать, хранить,
редактировать и размножать тексты и т. п.
С точки зрения структуры машины этого поколения представ-
ляют собой многопроцессорные и многомашинные комплексы,
работающие на общую память и общее поле внешних устройств.
Для этого периода характерно широкое применение систем управ-
ления базами данных, компьютерных сетей, систем распределен-
ной обработки данных.
Последующие поколения ЭВМ будут представлять, по-видимо-
му, оптоэлектронные ЭВМ с массовым параллелизмом и нейрон-
ной структурой — с распределенной сетью большого числа (десят-
231
ки тысяч) несложных процессоров, моделирующих структуру ней-
ронных биологических систем, произойдет качественный переход
от обработки данных к обработке знаний.
6.1.2. Классификация средств обработки информации
Существуют различные системы классификации электронных
средств обработки информации: по архитектуре, по производи-
тельности, по условиям эксплуатации, по количеству процессоров,
по потребительским свойствам и т. д. Один из наиболее ранних
методов классификации — классификация по производительнос-
ти и характеру использования компьютеров. В соответствии с этой
классификацией компьютерные средства обработки можно услов-
но подразделить на:
микрокомпьютеры;
• мэйнфреймы;
* суперкомпьютеры.
Данная классификация достаточно условна, поскольку интен-
сивное развитие технологий производства электронных компонен-
тов и значительный прогресс в совершенствовании архитектуры
компьютеров и наиболее важных составляющих их элементов при-
водят к размыванию границ между указанными классами средств
вычислительной техники. Кроме того, рассмотренная классифи-
кация учитывает только автономное использование вычислитель-
ных систем. В настоящее время преобладает тенденция объедине-
ния разных вычислительных систем в вычислительные сети раз-
личного масштаба, что позволяет интегрировать информационно-
вычислительные ресурсы для наиболее эффективной реализации
информационных процессов (рис. 6.3).
Вычислительная (компьютерная) сеть — комплекс территори-
ально рассредоточенных ЭВМ и терминальных устройств, соединен-
ных между собой каналами передачи данных.
Оценка производительности ЭВМ всегда приблизительна так
как при этом ориентируются на некоторые усредненные или, на-
оборот, на конкретные виды операций. Реально при решении раз-
личных задач используются и различные наборы операций. Поэто-
му для характеристики ЭВМ вместо производительности обычно
указывают тактовую частоту, более объективно определяющую
232
быстродействие машины, так как каждая операция требует для
своего выполнения вполне определенного количества тактов.
Такт — время однократного срабатывания логического элемента.
Во всех ЭВМ есть специальное устройство — генератор так-
товой частоты, которое выдает так называемые тактирующие
импульсы, инициирующие срабатывание схем. Т. е. прежде чем
логический элемент снова выполнит какую-либо минимальную
функцию — микрооперацию, должно пройти некоторое время, на-
зываемое тактом. Зная тактовую частоту, можно достаточно точ-
но определить время выполнения любой машинной операции.
Часто для оценки производительности ЭВМ используют некото-
рое число MIPS (Mega Instruction Per Second — миллион команд в се-
кунду) или число FLOPS (FLoating Operations Per Second — операций
над числами с плавающей запятой (точкой) в секунду). Например:
— запись 50 MIPS (МИПС) означает 50 миллионов команд в секунду;
— 100 MFLOPS (МФЛОПС) — сто миллионов (Меда) операций
над числами с плавающей запятой (точкой) в секунду;
— 100 GFLOPS (ГФЛОПС) — сто миллиардов (Giga) операций
над числами с плавающей запятой (точкой) в секунду.
Рис. 6.3. Классификация компьютерных средств обработки информации
Микрокомпьютеры. Первоначально определяющим признаком
микрокомпьютера служило наличие в нем микропроцессора,
т. е. центрального процессора, выполненного в виде одной микро-
схемы. Сейчас микропроцессоры используются во всех без исклю-
233
чения классах ЭВМ, а к микрокомпьютерам относят более компак-
тные в сравнении с мэйнфреймами ЭВМ, имеющие производитель-
ность до сотен МИПС.
Современные модели микрокомпьютеров обладают нескольки-
ми микропроцессорами. Производительность компьютера опре-
деляется не только характеристиками применяемого микропроцес-
сора, но и емкостью оперативной памяти, типами периферийных
устройств, качеством конструктивных решений и др.
Микрокомпьютеры представляют собой инструменты для ре-
шения разнообразных сложных задач. Их микропроцессоры с каж-
дым годом увеличивают мощность, а периферийные устройства —
эффективность.
Разновидность микрокомпьютера — микроконтроллер. Это ос-
нованное на микропроцессоре специализированное устройство,
встраиваемое в систему управления или технологическую линию.
Персональные компьютеры (ПК) — это микрокомпьютеры уни-
версального назначения, рассчитанные на одного пользователя и
управляемые одним человеком. В класс персональных компьюте-
ров входят различные вычислительные машины — от дешевых до-
машних и игровых с небольшой оперативной памятью, с памятью
программы на кассетной ленте и обычным телевизором в качестве
дисплея (80-е годы), до сверхсложных машин с мощным процессо-
ром, винчестерским накопителем емкостью в десятки гигабайт,
с цветными графическими устройствами высокого разрешения, сред-
ствами мультимедиа и другими дополнительными устройствами.
Персональные компьютеры можно классифицировать и по кон-
структивным особенностям (рис. 6.4).
Рис. 6.4. Классификация ПК по конструктивным особенностям
234
Переносные компьютеры обычно нужны руководителям пред-
приятий, менеджерам, ученым, журналистам, которым приходит-
ся работать вне офиса — дома, на презентациях или во время ко-
мандировок.
Laptop (наколенник, от lap — колено и top — поверх) по раз-
мерам близок к обычному портфелю. По основным характерис-
тикам (быстродействие, память) примерно соответствует настоль-
ным ПК. Сейчас компьютеры этого типа уступают место еще
меньшим.
Notebook (блокнот, записная книжка) по размерам ближе к кни-
ге крупного формата. Имеет вес около 3 кг. Помещается в порт-
фель-дипломат. Для связи с офисом его обычно комплектуют мо-
демом. Ноутбуки зачастую снабжают приводами CD-ROM.
Многие современные ноутбуки включают в себя взаимозаме-
няемые блоки со стандартными разъемами. Такие модули предназ-
начены для очень разных функций. В одно и то же гнездо можно
по мере надобности вставлять привод компакт-дисков, накопитель
на магнитных дисках, запасную батарею или съемный винчестер.
Ноутбук устойчив к сбоям в энергопитании. Даже если он получа-
ет энергию от обычной электросети, в случае какого-либо сбоя он
мгновенно переходит на питание от аккумуляторов.
Palmtop (наладонник) — самые маленькие современные пер-
сональные компьютеры. Умещаются на ладони. Магнитные дис-
ки в них заменяет энергонезависимая электронная память. Нет и
накопителей на дисках — обмен информацией с обычными ком-
пьютерами идет по линиям связи. Если Palmtop дополнить набо-
ром деловых программ, записанных в его постоянную память, по-
лучится персональный цифровой помощник (Personal Digital
Assistant).
Возможности портативных компьютеров постоянно расширя-
ются. Например, современный карманный компьютер iPAQ 3150
располагает всем необходимым для ведения списка задач, хране-
ния записок, включая аудиофайлы, работы с календарем, чтения
электронной почты, синхронизации с ПК, мобильным телефоном.
Помимо этого iPAQ позволяет проигрывать видео- и звуковые ро-
лики, работать с Интернетом, просматривать и редактировать до-
кументы и электронные таблицы, хранить файлы, искать в них сло-
ва, просматривать картинки, вести домашнюю бухгалтерию,
235
играть в игры, читать электронные книги с помощью Microsoft
Reader, полноценно работать с программным обеспечением.
Мэйнфреймы. Предназначены для решения широкого класса
научно-технических задач и являются сложными и дорогими ма-
шинами. Их целесообразно применять в больших системах при
наличии не менее 200—300 рабочих мест.
Централизованная обработка данных на мэйнфрейме обходит-
ся примерно в 5—6 раз дешевле, чем распределенная обработка
при клиент-серверном подходе с использованием микроЭВМ.
Известный мэйнфрейм S/390 фирмы IBM обычно оснащается
не менее чем тремя процессорами. Максимальный объем опера-
тивного хранения достигает 342 терабайт.
Производительность его процессоров, пропускная способность
каналов, объем оперативного хранения позволяют наращивать
число рабочих мест в широком диапазоне с помощью простого
добавления процессорных плат, модулей оперативной памяти и
дисковых накопителей.
Несколько мэйнфреймов могут работать совместно под управле-
нием одной операционной системы над выполнением единой задачи.
Суперкомпьютеры. Это очень мощные компьютеры с произво-
дительностью свыше 100 МФЛОПС. Они называются сверхбыстро-
действующими. Создать такие высокопроизводительные ЭВМ по
современной технологии на одном микропроцессоре не представля-
ется возможным ввиду ограничения, обусловленного конечным зна-
чением скорости распространения электромагнитных волн (300 000
км/с), так как время распространения сигнала на расстояние несколь-
ко миллиметров (линейный размер стороны МП) при быстродействии
100 млрд оп./с становится соизмеримым со временем выполнения
одной операции. Поэтому суперЭВМ создаются в виде высокопарал-
лельных многопроцессорных вычислительных систем (МПВС).
6.1.3. Классификация программного обеспечения
Под программным обеспечением (Software) понимается сово-
купность программных средств для ЭВМ (систем ЭВМ), обеспечи-
вающих функционирование, диагностику и тестирование их ап-
паратных средств, а также разработку, отладку и выполнение лю-
бых задач пользователя с соответствующим документированием,
где в качестве пользователя может выступать как человек, так и
любое внешнее устройство, подключенное к ЭВМ и нуждающее-
ся в ее вычислительных ресурсах [1].
236
Программное обеспечение (Software) — совокупность программ,
выполняемых вычислительной системой, и необходимых для их экс-
плуатации документов.
К программному обеспечению (ПО) относится также вся об-
ласть деятельности по проектированию и разработке ПО:
технология проектирования программ (например, нисходя-
щее проектирование, структурное и объектно-ориентиро-
ванное проектирование и др.);
• методы тестирования программ;
анализ качества работы программ;
документирование программ;
разработка и использование программных средств, облегча-
ющих процесс проектирования программного обеспечения,
и многое другое.
Все программы по характеру использования и категориям
пользователей подразделяют на два класса — утилитарные про-
граммы и программные продукты (изделия) [14J.
Утилитарные программы («программы для себя») предназначе-
ны для удовлетворения нужд их разработчиков. Чаще всего ути-
литарные программы выполняют роль сервиса в технологии обра-
ботки данных либо являются программами решения функциональ-
ных задач, не предназначенных для широкого распространения.
Программные продукты (изделия) предназначены для удовлет-
ворения потребностей пользователей, широкого распространения
и продажи.
Программный продукт — программа или комплекс взаимосвязан-
ных программ для решения определенной проблемы {задачи) массо-
вого спроса, подготовленные к реализации как любой вид промыш-
ленной продукции.
Программные продукты можно классифицировать по разным
признакам. Наиболее общей является классификация, в которой
основополагающим признаком служит сфера (область) использо-
вания программных продуктов:
аппаратная часть компьютеров и сетей ЭВМ;
технология разработки программ;
функциональные задачи различных предметных областей.
237
Исходя из этого выделяют три класса программных продуктов:
системное программное обеспечение;
инструментарий технологии программирования;
пакеты прикладных программ.
Системное программное обеспечение ЭВМ
Системное программное обеспечение управляет всеми ресур-
сами ЭВМ (центральным процессором, памятью, вводом-выводом)
и осуществляет общую организацию процесса обработки инфор-
мации и интерфейсы между ЭВМ, пользователем, аппаратными и
программными средствами. Оно разрабатывается так, чтобы ком-
пьютер мог эффективно выполнять прикладные программы.
ч _____________________________________________________
Системное программное обеспечение (System Software) — сово-
купность программ и программных комплексов для обеспечения ра-
боты компьютеров и сетей ЭВМ.
Системное ПО тесно связано с типом компьютера, является его
неотъемлемой частью и имеет общий характер применения, неза-
висимо от специфики предметной области решаемых с помощью
ЭВМ задач.
Структура системного программного обеспечения представле-
на на рис. 6.5.
Рис. 6.5. Классификация системного программного обеспечения компьютера
238
Системное ПО состоит из базового программного обеспечения,
которое, как правило, поставляется вместе с компьютером, и сер-
висного программного обеспечения, которое может быть приоб-
ретено дополнительно.
В базовое программное обеспечение входят:
» базовая система ввода-вывода (BIOS-Basic Input/Output System);
операционная система (сетевая операционная система);
операционные оболочки.
Базовая система ввода-ввода (BIOS) представляет собой набор
программ, обеспечивающих взаимодействие операционной сис-
темы и других программ с различными устройствами компьютера
(клавиатурой, видеоадаптером, дисководом, таймером и др.).
В функции BIOS входят также автоматическое тестирование ос-
новных аппаратных компонентов (оперативной памяти и др.) при
включении машины, поиск на диске программы-загрузчика опе-
рационной системы и ее загрузка с диска в оперативную память.
Програмные модули BIOS находятся в постоянном запоминаю-
щем устройстве — ПЗУ (см. п. 7.2.3), они имеют определенные ад-
реса, благодаря чему все приложения могут использовать их для
реализации основных функций ввода-вывода.
BIOS (Basic Input/Output System — базовая система ввода-вывода) —
совокупность программ, предназначенных для автоматического тес-
тирования устройств после включения питания компьютера, загрузки
операционной системы в оперативную память и обеспечения взаимо-
действия операционной системы и приложений с различными устрой-
ствами компьютера.
Операционная система предназначена для управления выпол-
нением пользовательских программ, планирования и управления
вычислительными ресурсами ЭВМ. Она выполняет роль связую-
щего звена между аппаратурой компьютера, с одной стороны, и
выполняемыми программами, а также пользователем — с другой.
Операционная система обычно хранится во внешней памяти
компьютера — на диске. При включении компьютера, как было
отмечено выше, она считывается с дисковой памяти и размещает-
ся в оперативном запоминающем устройстве.
Этот процесс называется загрузкой операционной системы.
В функции операционной системы входит:
осуществление диалога с пользователем;
239
ввод-вывод и управление данными;
планирование и организация процесса обработки программ;
распределение ресурсов (оперативной памяти, процессора,
внешних устройств);
запуск программ на выполнение;
всевозможные вспомогательные операции обслуживания;
* передача информации между различными внутренними ус-
тройствами;
программная поддержка работы периферийных устройств
(дисплея, клавиатуры, дисковых накопителей, принтера и др.).
Операционную систему можно назвать программным продол-
жением устройства управления компьютера. Она скрывает от
пользователя сложные ненужные подробности взаимодействия с
аппаратурой, образуя прослойку между ними. В результате этого
люди освобождаются от очень трудоемкой работы по организации
взаимодействия с аппаратурой компьютера. >
Операционные системы для компьютеров делятся на:
одно- и многозадачные (в зависимости от возможного числа
запускаемых и выполняемых прикладных процессов);
одно- и многопользовательские (в зависимости от числа
пользователей, одновременно работающих с операционной
системой);
• несетевые и сетевые, обеспечивающие работу в локальной
вычислительной сети ЭВМ.
Операционная система для компьютера, ориентированного на
профессиональное применение, должна содержать следующие
основные программные компоненты:
управление вводом-выводом;
управление файловой системой;
• планирование процессов;
* анализ и выполнение команд, адресованных операционной си-
стеме.
Каждая операционная система имеет свой командный язык,
который позволяет пользователю выполнять те или иные действия:
обращаться к каталогу;
" выполнять разметку внешних носителей;
* запускать программы и др.
Анализ и исполнение команд пользователя, включая загрузку
готовых программ из файлов в оперативную память и их запуск,
осуществляет командный процессор операционной системы.
240
В секторе программного обеспечения и операционных систем
ведущее положение занимают фирмы IBM, Microsoft, UNISYS,
Novell. Рассмотрим наиболее распространенные типы операцион-
ных систем.
Операционная система MS DOS (Microsoft Disk Operating
System) — самая распространенная ОС на 16-разрядных персо-
нальных компьютерах. Она состоит из следующих основных мо-
дулей (рис. 6.6):
• блок начальной загрузки (Boot Record);
модуль расширения базовой системы ввода-вывода (IO.SYS);
модуль обработки прерываний (MSDOS.SYS);
командный процессор (COMMAND.COM);
утилиты MS DOS.
Каждый из указанных модулей выполняет определенную часть
функций, возложенных на ОС.
MS-DOS
Блок начальной
загрузки
(Boot Record)
Модуль расширения
базовой системы
ввода/вывода
(Io. SYS)
Модуль обработки
прерываний MS-DOS
ввода/вывода
(MsDos. SYS)
Командный
процессор
(Command.COM)
Утилиты
Format.COM, Chkdsk.COM,
Mode. COM, Graphics. COM,
FDisk. COM,...
Рис. 6.6. Состав операционной системы MS-DOS
Блок начальной загрузки (или просто загрузчик) — это очень
короткая программа, единственная функция которой заключает-
ся в считывании с диска в оперативную память двух других частей
DOS — модуля расширения базовой системы ввода-вывода и мо-
дуля обработки прерываний.
Модуль расширения базовой системы ввода-вывода дает воз-
можность использования дополнительных драйверов, обслужива-
ющих новые внешние устройства, а также драйверов для нестан-
дартного обслуживания внешних устройств.
Модуль обработки прерываний реализует основные высоко-
уровневые услуги DOS, поэтому его и называют основным.
Командный процессор DOS обрабатывает команды, вводимые
пользователем.
<6а-2ю 241
Утилиты DOS — это программы, поставляемые вместе с опера-
ционной системой в виде отдельных файлов. Они выполняют дей-
ствия обслуживающего характера, например разметку дискет,
проверку дисков и т. д.
Долгое время эта операционная система была установлена на
подавляющем большинстве персональных компьютеров. Начиная
с 1996 г. MS DOS была заменена ОС Windows — 32-разрядной мно-
гозадачной и многопоточной операционной системы с графичес-
ким интерфейсом и расширенными сетевыми возможностями.
Операционные системы Windows. Windows 95 представляет со-
бой универсальную высокопроизводительную многозадачную 32-
разрядную ОС с графическим интерфейсом и расширенными се-
тевыми возможностями. Windows 95 — интегрированная среда,
обеспечивающая эффективный обмен информацией между от-
дельными программами и предоставляющая пользователю широ-
кие возможности работы с мультимедиа, обработки текстовой,
графической, звуковой и видеоинформации. Интегрированность
подразумевает также совместное использование ресурсов компь-
ютера всеми программами.
Эта операционная система обеспечивает работу пользователя
в сети, предоставляя встроенные средства поддержки для обмена
файлами и меры по их защите, возможность совместного исполь-
зования принтеров, факсов и других общих ресурсов. Windows 95
позволяет отправлять сообщения электронной почтой, факсимиль-
ной связью, поддерживает удаленный доступ.
Windows 98 отличается от Windows 95 тем, что в ней операцион-
ная система объединена с браузером Internet Explorer. Кроме это-
го, в ней улучшена совместимость с новыми аппаратными сред-
ствами компьютера, она одинаково удобна как для использования
на настольных, так и на портативных компьютерах.
Windows NT (NT— от англ. New Technology) — 32-разрядная ОС
со встроенной сетевой поддержкой и развитыми многопользова-
тельскими средствами. Она предоставляет пользователям много-
задачность, надежность, многопроцессорную поддержку, секрет-
ность, защиту данных и многое другое. Эта операционная система
очень удобна для пользователей, работающих в рамках локальной
сети, для коллективных пользователей, особенно для групп, рабо-
тающих над большими проектами и обменивающихся данными.
Семейство Windows 2000 — операционная система нового поко-
ления для делового использования на самых разнообразных компь-
ютерах — от портативных до серверов. Эта ОС является одной из
лучших для ведения коммерческой деятельности в Интернете. Она
242
объединяет присущую Windows 98 простоту использования с прису-
щими Windows NT надежностью, экономичностью и безопасностью.
Семейство Windows ХР обладает улучшенной защитой систем-
ных файлов, программное обеспечение, поддерживающее запись
СД и СД-RW, включено в состав самой ОС, имеет ряд новых драй-
веров устройств, полностью настраиваемый интерфейс, а также
множество новых программ и мультимедийных добавлений. По-
мимо 32-разрядного варианта ОС имеется и 64-разрядная модифи-
кация, предназначенная для установки на компьютеры, оснащен-
ные 64-разрядным процессором.
Packet (Windows СЕ) — операционная система для мобильных
вычислительных устройств, таких как карманные компьютеры, циф-
ровые информационные пейджеры, сотовые телефоны, мультиме-
дийные и развлекательные приставки, включая DVD-проигрывате-
ли и устройства целевого доступа в Интернет. Это 32-разрядная,
многозадачная, многопоточная операционная система, имеющая от-
крытую архитектуру, разрешающую использование множества уст-
ройств. Packet (Windows СЕ) позволяет устройствам различных кате-
горий «говорить» и обмениваться информацией друг с другом, свя-
зываться с корпоративными сетями и с Интернетом, пользоваться
электронной почтой. Она компактна, но высокопроизводительна. Это
мобильная система, функционирующая с микропроцессорами раз-
личных марок и изготовителей.
Операционная система Unix была создана в Bell Telephone
Laboratories. Unix — многозадачная операционная система, способ-
ная обеспечить одновременную работу очень большого количество
пользователей. Ядро ОС Unix написано на языке высокого уровня
С и имеет только около 10% кода на ассемблере. Это позволяет за
считанные месяцы переносить ОС Unix на другие аппаратные плат-
формы и достаточно легко вносить в нее серьезные изменения и
дополнения. UNIX является первой действительно переносимой
операционной системой. В многочисленные существующие вер-
сии UNIX постоянно вносятся изменения. С одной стороны, это
расширяет возможности системы, делает ее мощнее и надежнее,
с другой — ведет к появлению различий между существующими
версиями. В связи с этим возникает необходимость стандартиза-
ции различных свойств системы. Наличие стандартов облегчает
переносимость приложений между различными версиями UNIX
и защищает как пользователей, так и производителей програм-
много обеспечения. Поэтому в 80-х годах разработан ряд стандар-
тов, оказывающих влияние на развитие UNIX. Сейчас существу-
ют десятки операционных систем, которые можно объединить под
общим названием UNIX. В основном это коммерческие версии,
243
выпущенные производителями аппаратных платформ для компь-
ютеров своего производства. Основными факторами, обеспечива-
ющим популярность UNIX, являются следующие:
1. Код системы написан на языке высокого уровня С, что сдела-
ло ее простой для понимания, изменения и переноса на другие плат-
формы. При этом UNIX является одной из наиболее открытых си-
стем.
2. UNIX — многозадачная многопользовательская система.
Один мощный сервер может обслуживать запросы большого ко-
личества пользователей. При этом необходимо администрирова-
ние только одной системы. Кроме того, система способна выпол-
нять большое количество различных функций, в частности рабо-
тать, как вычислительный сервер, как сервер базы данных, как
сетевой сервер, поддерживающий важнейшие сервисы сети, и т. д.
3. Наличие стандартов. Несмотря на разнообразие версий UNIX,
основой всего семейства являются принципиально одинаковая
архитектура и ряд стандартных интерфейсов. Для администрато-
ра переход на другую версию системы не составит большого тру-
да, а для пользователей он может и вовсе оказаться незаметным.
4. Простой, но мощный модульный пользовательский интер-
фейс. Имея в своем распоряжении набор утилит, каждая из кото-
рых решает узкую специализированную задачу, можно конструи-
ровать из них сложные комплексы.
5. Использование единой, легко обслуживаемой иерархической
файловой системы. Файловая система UNIX — это не только дос-
туп к данным, хранящимся на диске. Через унифицированный
интерфейс файловой системы осуществляется доступ к термина-
лам, принтерам, сети и т. п.
6. Большое количество приложений, в том числе свободно рас-
пространяемых, начиная от простейших текстовых редакторов и
заканчивая мощными системами управления базами данных.
Операционная система Linux. Начало созданию системы Linux
положено в 1991 г. финским студентом Линусом Торвальдсом (Linus
Torvalds). В сентябре 1991 г. он распространил по Интернету пер-
вый прототип своей операционной системы и призвал откликнуть-
ся на его работу всех, кому она нравится или нет. С этого момента
многие программисты стали поддерживать Linux, добавляя драй-
веры устройств, разрабатывая различные приложения и др. Атмос-
фера работы энтузиастов над полезным проектом, а также свобод-
ное распространение и использование исходных текстов стали ос-
новой феномена Linux. В настоящее время Linux — очень мощная
система, и при этом она бесплатная (free).
244
Л. Торвальдс разработал не саму операционную систему, а толь-
ко ее ядро, подключив уже имеющиеся компоненты. Довольно ско-
ро другие программисты стали насыщать ОС утилитами и приклад-
ным ПО. Недостаток такого подхода — отсутствие унифицирован-
ной и продуманной процедуры установки системы, и это до сих
пор является одним из главных сдерживающих факторов для бо-
лее широкого распространения Linux.
Традиционные стадии жизненного цикла программного продук-
та таковы: анализ требований, разработка спецификаций, проек-
тирование, макетирование, написание исходного текста, отладка,
документирование, тестирование и сопровождение. Главное, что
отличает этот подход, — централизация управления разными ста-
диями и преимущественно «нисходящая» разработка (т. е. посто-
янная детализация). Однако Linux создавалась по-иному. Готовый
работающий макет постоянно совершенствовался и развивался
децентрализованной группой энтузиастов, действия которых лишь
слегка координировались. Налицо «восходящая» разработка: сбор-
ка все более крупных блоков из ранее созданных мелких. Здесь
можно отметить и другое. При традиционной разработке в основу
кладется проектирование и написание текстов, при разработке по
методу Linux — макетирование, отладка и тестирование. Первые два
этапа распараллелить сложно, а с отладкой и тестированием дело
обстоит полегче. Иными словами, разработка по методу Linux — это
метод проб и ошибок, построенный на интенсивном тестировании.
Сетевое программное обеспечение предназначено для органи-
зации совместной работы группы пользователей на разных ком-
пьютерах. Оно позволяет организовать общую файловую струк-
туру, общие базы данных, доступные каждому члену группы, обес-
печивает возможность передачи сообщений и работы над общи-
ми проектами, возможность разделения ресурсов.
Основными функциями сетевых ОС являются:
управление каталогами и файлами;
управление ресурсами;
коммуникационные функции;
• защита от несанкционированного доступа;
" обеспечение отказоустойчивости;
управление сетью.
Управление каталогами и файлами в сетях заключается в обеспе-
чении доступа к данным, физически расположенным в других узлах
сети. Управление осуществляется с помощью специальной сетевой
файловой системы. Файловая система1 позволяет обращаться к фай-
245
лам путем применения привычных для локальной работы языковых
средств. При обмене файлами должен быть обеспечен необходи-
мый уровень конфиденциальности обмена (секретности данных).
Управление ресурсами включает в себя обслуживание запросов
на предоставление ресурсов, доступных по сети.
Коммуникационные функции обеспечивают адресацию, буфе-
ризацию, выбор направления для движения данных в разветвлен-
ной сети (маршрутизацию), управление потоками данных и др.
Разграничение доступа — важная функция, способствующая
поддержанию целостности данных и их конфиденциальности. Сред-
ства защиты могут разрешать доступ к определенным данным толь-
ко с некоторых терминалов, в оговоренное время, определенное чис-
ло раз и т. п. У каждого пользователя в корпоративной сети могут
быть свои права доступа с ограничением совокупности доступных
директорий или списка возможных действий, например, может быть
запрещено изменение содержимого некоторых файлов.
Отказоустойчивость характеризуется сохранением работос-
пособности системы при воздействии дестабилизирующих фак-
торов и обеспечивается применением для серверов автономных
источников питания, отображением или дублированием инфор-
мации в дисковых накопителях. Под отображением обычно пони-
мают наличие в системе двух копий данных с их расположением
на разных дисках, но подключенных к одному контроллеру. Дуб-
лирование отличается тем, что для каждого из дисков с копиями
используются разные контроллеры. Очевидно, что дублирование
более надежно. Дальнейшее повышение отказоустойчивости обус-
ловлено дублированием серверов, что однако требует дополнитель-
ных затрат на приобретение оборудования.
Управление сетью связано с применением соответствующих
протоколов управления. Программное обеспечение управления
сетью обычно состоит из менеджеров и агентов. Менеджером на-
зывается программа, вырабатывающая сетевые команды. Агенты
представляют собой программы, расположенные в различных уз-
лах сети. Они выполняют команды менеджеров, следят за состоя-
нием узлов, собирают информацию о параметрах их функциони-
рования, сигнализируют о происходящих событиях, фиксируют
аномалии, следят за трафиком, осуществляют защиту от вирусов.
Агенты с достаточной степенью интеллектуальности могут участво-
вать в восстановлении информации после сбоев, в корректировке
параметров управления и т. п.
246
Программное обеспечение сетевых ОС распределено по узлам
сети. Имеется ядро ОС, выполняющее большинство из охаракте-
ризованных выше функций, и дополнительные программы (служ-
бы), ориентированные на реализацию протоколов верхних уров-
ней, выполнение специфических функций для коммутационных
серверов, организацию распределенных вычислений и т. п. К се-
тевому программному обеспечению относят также драйверы се-
тевых плат. Для каждого типа ЛВС разработаны разные типы плат
и драйверов. Внутри каждого типа ЛВС может быть много разно-
видностей плат с разными характеристиками «интеллектуальнос-
ти», скорости, объема буферной памяти.
Среди распространенных сетевых ОС необходимо отметить
UNIX, Windows NT/2000/XP и Novell Netware.
ОС UNIX применяют преимущественно в крупных корпоратив-
ных сетях, поскольку эта система характеризуется высокой надеж-
ностью, возможностью легкого масштабирования сети. В UNIX име-
ется ряд команд и поддерживающих их программ для работы в сети.
Во-первых, это команды, реализующие файловый обмен и эмуляцию
удаленного узла на базе протоколов TCP/IP. Во-вторых, команды и
программы, разработанные с ориентацией на асинхронную модем-
ную связь по телефонным линиям между удаленными Unix-узла-
ми в корпоративных и территориальных сетях.
ОС Windows NT включает в себя серверную (Windows NT Server)
и клиентскую (Windows NT Workstation) версии и тем самым обес-
печивает работу в системах «клиент-сервер». Windows NT обычно
применяют в средних по масштабам сетях.
ОС Novell Netware состоит из серверной части и оболочек, раз-
мещаемых в клиентских узлах. Предоставляет пользователям воз-
можность совместно использовать файлы, принтеры и другое обо-
рудование. Содержит службу каталогов, общую распределенную
базу данных пользователей и ресурсов сети. Эта ОС наиболее при-
менима в небольших сетях.
Операционные оболочки — специальные программы, предназ-
наченные для облегчения общения пользователя с командами опе-
рационной системы. Операционные оболочки имеют текстовый и
графический варианты интерфейса конечного пользователя.
Наиболее популярны следующие виды текстовых и графичес-
ких оболочек операционной системы Windows (MS DOS):
Norton Commander;
Far;
" Windows Commander;
247
XTree Gold 4.0;
Norton Navigator и др.
Эти программы существенно упрощают задание управляющей
информации для выполнения команд операционной системы, умень-
шают напряженность и сложность работы конечного пользователя.
Например, пакет программ Norton Commander обеспечивает:
• создание, копирование, пересылку, переименование, удале-
ние, поиск файлов, а также изменение их атрибутов;
отображение дерева каталогов и характеристик входящих
в них файлов в форме, удобной для восприятия человека;
создание, обновление и распаковку архивов (групп сжатых
файлов);
просмотр текстовых файлов;
• редактирование текстовых файлов;
выполнение из ее среды практически всех команд DOS;
запуск программ;
выдачу информации о ресурсах компьютера;
создание и удаление каталогов;
поддержку межкомпьютерной связи;
поддержку электронной почты через модем и др.
Сервисное программное обеспечение. Расширением базового
программного обеспечения компьютера является набор сервис-
ных, дополнительно устанавливаемых программ, которые можно
классифицировать по функциональному признаку следующим об-
разом [14]:
* программы контроля, тестирования и диагностики, которые
используются для проверки правильности функционирова-
ния устройств компьютера и для обнаружения неисправно-
стей в процессе эксплуатации; указывают причину и место
неисправности;
программы-драйверы, которые расширяют возможности
операционной системы по управлению устройствами ввода-
вывода, оперативной памятью и т. д.; с помощью драйверов
возможно подключение к компьютеру новых устройств или
нестандартное использование имеющихся;
программы-упаковщики (архиваторы), которые позволяют
записывать информацию на дисках более плотно, а также
объединять копии нескольких файлов в один архивный файл;
антивирусные программы, предназначенные для предотвра-
щения заражения компьютерными вирусами и ликвидации
последствий заражения вирусами;
248
программы оптимизации и контроля качества дискового про-
странства;
программы восстановления информации, форматирования,
защиты данных;
коммуникационные программы, организующие обмен ин-
формацией между компьютерами;
программы для управления памятью, обеспечивающие бо-
лее гибкое использование оперативной памяти;
программы обслуживания сети;
• программы для записи CD-ROM, CD-R и многие другие.
Эти программы часто называются утилитами. Они либо расши-
ряют и дополняют соответствующие возможности операционной
системы, либо решают самостоятельные важные задачи.
Утилиты (от лат. utilitas — польза) — программы, служащие для
выполнения вспомогательных операций обработки данных или обслу-
живания компьютеров (диагностики, тестирования аппаратных и про-
граммных средств, оптимизации использования дискового простран-
ства, восстановления разрушенной на магнитном диске информации
и т. п.).
Часть утилит входит в состав операционной системы, другая
часть функционирует независимо от нее — автономно.
Инструментарий технологии программирования
Инструментарий технологии программирования обеспечива-
ет процесс разработки программ и включает специализирован-
ные программные продукты, которые являются инструменталь-
ными средствами разработчика. Программные продукты данно-
го класса поддерживают все технологические этапы процесса
проектирования, программирования (кодирования), отладки и те-
стирования создаваемых программ. Пользователями технологии
программирования выступают системные и прикладные програм-
мисты.
Инструментарий технологии программирования — совокуп-
ность программ и программных комплексов, обеспечивающих техно-
логию разработки, отладки и внедрения создаваемых программ.
249
Выделяют следующие группы инструментальных средств тех-
нологии программирования (рис. 6.7) [14]:
• средства для создания приложений, включающие:
— локальные средства, обеспечивающие выполнение от-
дельных работ по созданию программ;
— интегрированные среды разработчиков программ, обес-
печивающие выполнение комплекса взаимосвязанных
работ по созданию программ;
CASE-технология (Computer-Aided System Engineering), пред-
ставляющая методы анализа, проектирования и создания про-
граммных систем и предназначенная для автоматизации про-
цессов разработки и реализации информационных систем.
Рис. 6.7. Классификация инструментария технологии программирования
Рассмотрим средства для создания приложений более подробно.
Локальные средства разработки программ наиболее представи-
тельны на рынке программных продуктов и состоят из языков и
систем программирования, а также инструментальной среды
пользователя.
Язык программирования — формализованный язык для описания
алгоритма решения задачи на компьютере.
250
Языки программирования, если в качестве признака классифи-
кации взять синтаксис образования его конструкций, можно ус-
ловно разделить на классы:
машинные языки (computer language) — языки программи-
рования, воспринимаемые аппаратной частью компьютера
(машинные коды);
• машинно-ориентированные языки (computer-oriented
language) — языки программирования, которые отражают
структуру конкретного типа компьютера (ассемблеры);
• алгоритмические языки (algorithmic language) — не завися-
щие от архитектуры компьютера языки программирования
для отражения структуры алгоритма (Паскаль, Фортран, Бей-
сик и др.);
• процедурно-ориентированные языки (procedure-oriented
language) — языки программирования, где имеется возмож-
ность описания программы как совокупности процедур (под-
программ);
проблемно-ориентированные языки (universal programming
language) — языки программирования, предназначенные
для решения задач определенного класса (Лисп, Симула
и др.);
интегрированные системы программирования.
Программа, подготовленная на языке программирования высо-
кого уровня, проходит этап трансляции.
Трансляторы реализуются в виде компиляторов или интерпре-
таторов. С точки зрения выполнения работы компилятор и интер-
претатор существенно различаются.
Компилятор (от англ, compiler — составитель, собиратель) читает
всю программу целиком, делает ее перевод и создает законченный ва-
риант программы на машинном языке, который затем и выполняется.
Интерпретатор (от англ, interpreter—истолкователь, устный пере-
водчик) переводит и выполняет программу построчно.
После того как программа откомпилирована, ни сама исход-
ная программа, ни компилятор более не нужны. В то же время
251
программа, обрабатываемая интерпретатором, должна заново пе-
реводиться на машинный язык при каждом очередном запуске
программы.
Откомпилированные программы работают быстрее, но интер-
претируемые проще исправлять и изменять.
Современные системы программирования обычно предостав-
ляют пользователям мощные и удобные средства разработки про-
грамм. В них входят:
компилятор или интерпретатор;
« интегрированная среда разработки;
средства создания и редактирования текстов программ;
« обширные библиотеки стандартных программ и функций;
отладочные программы, т. е. программы, помогающие нахо-
дить и устранять ошибки в программе;
«дружественная» к пользователю диалоговая среда;
многооконный режим работы;
мощные графические библиотеки;
« утилиты для работы с библиотеками;
встроенный ассемблер;
встроенная справочная служба и др.
При создании сложных прикладных систем часто возникает
необходимость использования машинно-ориентированных ассем-
блерных программ. При этом с целью повышения быстродействия
или сокращения требуемых объемов памяти на ассемблере иног-
да составляется значительное количество прикладных процедур
Помимо языка ассемблера, который дает возможность использо-
вать все особенности машины и потому может быть применен для
решения задач любого типа, существуют языки программирова-
ния высокого уровня, ориентированные на различные классы за-
дач. К ним относятся: Фортран, Паскаль и Си.
Язык Фортран — один из самых старых языков высокого уров-
ня, активно используется на персональных компьютерах. Приме-
няется он главным образом при разработке прикладных систем,
ориентированных на научные исследования, автоматизацию про-
ектирования и другие области, где уже накоплены обширные стан-
дартные библиотеки программ. Имеется несколько версий этого
языка, из которых наиболее популярна версия Фортран-90, отдель-
ные элементы которой реализованы в Microsoft Fortran, а в пол-
ном объеме — в Fortran PowerStation.
252
Язык Паскаль, выпущенный в 1969 г., — сегодня один из широ-
ко распространенных алгоритмических языков, компиляторы с
которого разработаны для компьютеров практически всех архи-
тектур. Существует несколько развитых диалектов языка, снаб-
женных разнообразными дополнительными инструментариями
и средствами поддержки разработки программного обеспечения.
В качестве примера можно назвать средства Borland для персо-
нальных компьютеров. Паскаль является классическим языком
программирования, который первоначально был создан как учеб-
ный язык и лишь позже стал применяться для решения научных
задач.
Язык Си, в отличие от Паскаля, с момента своего появления
(1972 г.) был ориентирован на разработку системных программ.
Он, в частности, послужил главным инструментом для создания
многих операционных систем и программных продуктов. В этом
языке имеются более гибкие средства для эффективного исполь-
зования особенностей аппаратуры, чем в Паскале. Благодаря это-
му порождаемые машинные программы, как правило, более ком-
пактны и работают быстрее, чем программы, полученные Пас-
каль-трансляторами. С другой стороны, синтаксис языка Си ме-
нее прозрачен, чем у Паскаля; возможностей для внесения оши-
бок больше; чтение текстов программ требует определенного
навыка. В связи с этим язык Си применяется главным образом
для создания системных и прикладных программ, в которых ско-
рость работы и объем памяти являются критическими парамет-
рами.
Несмотря на то что Паскаль представляется как ортодоксаль-
ный язык, а Си позволяет программисту точнее учитывать ап-
паратные особенности, в целом эти языки сравнимы. Основны-
ми достоинствами, необходимыми при построении больших про-
граммных систем, у этих языков являются возможность работы
с данными сложной структуры; наличие развитых средств для
выделения отдельных частей программ в процедуры, модуль-
ность, т. е. возможность независимой разработки отдельных
частей программ и последующего их связывания в единую сис-
тему.
Недостатками подхода, реализованного в процедурных языках,
выступают сложность организации процесса внесения в систему
изменений, обязательное последовательное выполнение всех эта-
253
пов разработки, несовместимость с эволюционным подходом и, как
следствие, слабая пригодность их для разработки сложных про-
граммных систем. Развитием процедурных языков является объек-
тно-ориентированный подход, впервые возникший в комплекте с
компилятором Turbo Pascal 5.5. Начиная с Turbo Pascal 6.0 в пакет
входит библиотека Turbo Vision, позднее перенесенная в среду
Turbo С + +. Данные библиотеки основаны на объектно-ориенти-
рованном программировании и принципах построения программ,
управляемых событиями. Объектно-ориентированный подход
представляет собой последовательный итеративный процесс, ко-
торый позволяет безболезненно вносить изменения в уже отла-
женный программный продукт и в котором результаты одного из
этапов могут влиять на решения, принятые на предыдущих.
Наиболее полное отражение концепция объектно-ориентиро-
ванного программирования и визуального подхода к построению
приложений нашла в языках для разработки Windows приложе-
ний: Visual Basic, Delphi, Си + +. Общим для них является про-
стота и наглядность процесса создания программ, основанных на
использовании технологий визуального программирования. Ком-
понентный подход позволяет легко и быстро создавать не только
интерфейс программ, но и достаточно сложные механизмы дос-
тупа к данным, а также проверять и тиражировать удачные про-
граммные решения. Несмотря на идентичность идеологии, зало-
женной в данных языках, в их применении имеются отличия. Со-
временные тенденции показывают, что Delphi ориентируется
фирмой Inprise (прежнее название — Borland) на создание пол-
ноценных распределенных корпоративных систем доступа к дан-
ным. Visual Basic (фирмы Microsoft) применяется в основном для
создания приложений и расширений для готовых программных
продуктов под Windows и Веб-приложения, a Visual Си+ +
(Microsoft) и Borland C++ Builder используется для разработки
интернет-обозревателей, корпоративных приложений и опера-
ционных систем.
Инструментальная среда пользователя представлена специаль-
ными средствами, встроенными в пакеты прикладных программ,
такими как:
• библиотека функций, процедур, объектов и методов обра-
ботки;
254
макрокоманды;
клавишные макросы;
языковые макросы;
программные модули-вставки;
конструкторы экранных форм и отчетов;
генераторы приложений;
языки запросов высокого уровня;
• языки манипулирования данными;
конструкторы меню и многое другое.
Дальнейшим развитием локальных средств разработки про-
грамм, которые объединяют набор средств для комплексного их
применения на всех технологических этапах создания программ,
являются интегрированные программные среды разработчиков.
Основное назначение инструментария данного вида — повыше-
ние производительности труда программистов, автоматизация со-
здания кодов программ, обеспечивающих интерфейс пользовате-
ля графического типа, разработка приложений для архитектуры
клиент-сервер, запросов и отчетов.
Пакеты прикладных программ
Пакеты прикладных программ (ППП) служат программным
инструментарием решения функциональных задач и являются са-
мым многочисленным классом программных продуктов. В данный
класс входят программные продукты, выполняющие обработку
информации различных предметных областей.
Пакет прикладных программ (application program package) — ком-
плекс взаимосвязанных программ для решения задач определенного
класса конкретной предметной области.
Единую классификацию ППП провести затруднительно ввиду
большого разнообразия решаемых на ЭВМ задач и соответствую-
щих им ППП. В общем случае ППП могут быть разделены на два
больших класса: общего назначения и специального назначения.
К ППП общего назначения можно отнести наиболее распрост-
раненные программные продукты, такие как текстовые и таблич-
ные процессоры, графические редакторы, системы управления
базами данных, различные интегрированные пакеты и др.
255
Текстовый редактор — программа, используемая специально для
ввода и редактирования текстовых данных.
Текстовые редакторы могут обеспечивать выполнение разно-
образных функций, а именно:
и редактирование строк текста;
возможность использования различных шрифтов символов;
• копирование и перенос части текста с одного места на дру-
гое или из одного документа в другой;
контекстный поиск и замена частей текста;
задание произвольных межстрочных промежутков;
автоматический перенос слов на новую строку;
автоматическая нумерация страниц;
обработка и нумерация сносок;
выравнивание краев абзаца;
создание таблиц и построение диаграмм;
проверка правописания слов и подбор синонимов;
• построение оглавлений и предметных указателей;
распечатка подготовленного текста на принтере в нужном
количестве экземпляров и т. п.
Возможности текстовых редакторов различны — от программ,
предназначенных для подготовки небольших документов простой
структуры, до программ для набора, оформления и полной подго-
товки к типографскому изданию книг и журналов (издательские
системы).
Наиболее известный текстовый редактор — Microsoft Word.
Графический редактор — программа, предназначенная для авто -
матизации процессов построения на экране дисплея графических
изображений.
Графический редактор предоставляет возможности рисования
линий, кривых, раскраски областей экрана, создания надписей
различными шрифтами и т. д. Большинство редакторов позволя-
ют обрабатывать изображения, полученные с помощью сканеров,
а также выводить картинки в таком виде, чтобы они могли быть
включены в документ, подготовленный с помощью текстового ре-
дактора.
256
Некоторые редакторы позволяют получать изображения трех-
мерных объектов, их сечений, разворотов, каркасных моделей
и т. п.
Пользуется известностью Corel DRAW— мощный графический
редактор с функциями создания публикаций, снабженный инст-
рументами для редактирования графики и трехмерного модели-
рования.
Табличный процессор — комплекс взаимосвязанных программ,
предназначенный для обработки электронных таблиц.
Электронная таблица — компьютерный эквивалент обычной
таблицы, состоящей из строк и столбцов, на пересечении которых
располагаются ячейки, содержащие числовую информацию, форму-
лы или текст.
Значение в числовой ячейке таблицы может быть либо введе-
но, либо рассчитано по соответствующей формуле; в формуле мо-
гут присутствовать обращения к другим ячейкам.
Каждый раз при изменении значения в ячейке таблицы в ре-
зультате ввода в нее нового значения с клавиатуры пересчитыва-
ются также значения во всех тех ячейках, в которых стоят величи-
ны, зависящие от данной ячейки.
Столбцам и строкам можно присваивать наименования. Экран
монитора трактуется как окно, через которое можно рассматри-
вать таблицу целиком или по частям.
Табличные процессоры представляют собой удобное средство
для проведения бухгалтерских и статистических расчетов. В каж-
дом пакете имеются сотни встроенных математических функций
и алгоритмов статистической обработки данных. Кроме того, име-
ются мощные средства для связи таблиц между собой, создания и
редактирования электронных баз данных.
Специальные средства позволяют автоматически получать и
распечатывать настраиваемые отчеты с использованием десятков
различных типов таблиц, графиков, диаграмм, снабжать их ком-
ментариями и графическими иллюстрациями.
Табличные процессоры имеют встроенную справочную систе-
му, предоставляющую пользователю информацию по конкретным
командам меню и другие справочные данные. Многомерные таб-
лицы позволяют быстро делать выборки в базе данных по любому
критерию.
17 А-210
257
Самые популярные табличные процессоры — Microsoft Excel и
Lotus 1—2—3.
В Microsoft Excel автоматизированы многие рутинные операции,
специальные шаблоны помогают создавать отчеты, импортировать
данные и многое другое.
Lotus 1—2—3 — профессиональный процессор электронных таб-
лиц. Широкие графические возможности и удобный интерфейс паке-
та позволяют быстро ориентироваться в нем. С его помощью можно
создать любой финансовый документ, отчет для бухгалтерии, соста-
вить бюджет, а затем разместить все эти документы в базах данных.
База данных — это один или несколько файлов данных, предназ-
наченных для хранения, изменения и обработки больших объемов вза-
имосвязанной информации.
В базе данных предприятия, например, может храниться:
вся информация о штатном расписании, о рабочих и служа-
щих предприятия;
сведения о материальных ценностях;
данные о поступлении сырья и комплектующих;
" сведения о запасах на складах;
данные о выпуске готовой продукции;
приказы и распоряжения дирекции и т. п.
Даже небольшие изменения какой-либо информации могут
приводить к значительным изменениям в разных других местах.
Базы данных используются под управлением систем управле-
ния базами данных (СУБД).
Система управления базами данных (СУБД) — система про-
граммного обеспечения, позволяющая обрабатывать обращения
к базе данных, поступающие от прикладных программ конечных
пользователей.
Системы управления базами данных дают возможность объ-
единять большие объемы информации и обрабатывать их, сорти-
ровать, делать выборки по определенным критериям и т. п. Совре-
менные СУБД дают возможность включать в них не только тек-
стовую и графическую информацию, но и звуковые фрагменты и
даже видеоклипы. Простота использования СУБД позволяет созда-
258
вать новые базы данных, не прибегая к программированию,
а пользуясь только встроенными функциями.
СУБД обеспечивают правильность, полноту и непротиворечи-
вость данных, а также удобный доступ к ним.
Популярные СУБД — FoxPro, Access for Windows, Paradox.
Для менее сложных задач вместо СУБД используются инфор-
мационно-поисковые системы (ИПС), которые выполняют следу-
ющие функции:
хранение большого объема информации;
быстрый поиск требуемой информации;
• добавление, удаление и изменение хранимой информации;
вывод ее в удобном для человека виде.
Интегрированные пакеты представляют собой набор нескольких
программных продуктов, объединенных в единый удобный инстру-
мент.
Наиболее развитые из них состоят из текстового редактора, орга-
найзера, электронной таблицы, СУБД, средств поддержки электрон-
ной почты, программы создания презентационной графики.
Результаты, полученные отдельными подпрограммами, могут
быть объединены в окончательный документ, содержащий таблич-
ный, графический и текстовый материал.
Интегрированные пакеты, как правило, включают в себя неко-
торое ядро, обеспечивающее возможность тесного взаимодей-
ствия между составляющими.
Наиболее распространенным интегрированным пакетом явля-
ется Microsoft Office. В этот мощный профессиональный пакет вош-
ли такие необходимые программы, как текстовый редактор
Win Word, электронная таблица Excel, программа создания презен-
таций PowerPoint, СУБД Access, средство поддержки электронной
почты Mail. При этом, все части этого пакета составляют единое
целое, и даже внешне все программы выглядят единообразно, что
облегчает как их освоение, так и ежедневное использование.
ППП специального назначения предназначены для решения за-
дач в некоторой предметной области.
Например, одним из наиболее эффективных и распространен-
ных программных средств моделирования сложных дискретных
систем на персональных ЭВМ является ППП GPSS (General Purpose
259
Simulating System). Он успешно используется для моделирования
систем, формализованных в виде систем массового обслуживания.
Язык GPSS построен на предположении, что моделью сложной дис-
кретной системы является описание ее элементов и логических
правил их взаимовлияния в процессе функционирования модели-
руемой системы. Далее предполагается, что для определенного
класса моделируемых систем можно выделить небольшой набор
абстрактных элементов, называемых объектами. Причем набор ло-
гических правил также ограничен и может быть описан неболь-
шим числом стандартных операций. Комплекс программ, описы-
вающих функционирование объектов и выполняющих логические
операции, является основой для создания программной модели
системы данного класса. Эта идея и была реализована при разра-
ботке языка GPSS.
На сегодняшний день среди широко известных программных
сред для проведения научно-технических расчетов можно выде-
лить: MathCad, MatLab и Mathematica. Важным достоинством сре-
ды MathCad является возможность записи алгоритмов в есте-
ственном научно-техническом виде. Данная среда на сегодняш-
ний день является одной из наиболее удобных сред для проведе-
ния математических расчетов. В последних реализациях MathCad
значительно облегчен ввод математических выражений, увели-
чено число встроенных процедур и приложений, расширены воз-
можности языка программирования, усовершенствованы сред-
ства обмена с Windows приложениями. Наглядность среды, а так-
же большое количество разнообразной литературы делают эту
среду весьма привлекательной для проведения имитационного
моделирования.
Среда MatLab (Matrix Laboratory — матричная лаборатория)
предложенная фирмой The MathWorks Inc. представляет собой
апробированную и надежную систему, рассчитанную на реше-
ние широкого круга инженерных задач с представлением дан-
ных в универсальной матричной форме. Благодаря интеграции
в ней среды Maple, разработанной фирмой Waterloo Maple
Software, так же как и в MathCad, среда MatLab позволяет при-
менять символьную запись математических выражений. Широ-
кому применению MatLab при имитационном моделировании
способствует не только разнообразный набор матричных и иных
операций и функций, но и наличие большого количества спе-
260
циализированных расширений. Так, версия MatLab 5.0/5.3 рас-
пространяется с 35 расширениями, самое мощное из которых
Simulink for Windows непосредственно предназначено для про-
ведения имитационного моделирования. Важным достоинством
системы является ее открытость и расширяемость, а также при-
способляемость к решению широкого класса задач. Расширяе-
мость достигается за счет встроенного языка программирова-
ния. При этом язык системы MatLab в части программирования
математических вычислений намного богаче большинства уни-
версальных языков программирования высокого уровня. Он
реализует почти все известные средства программирования, в
том числе объектно-ориентированное и визуальное программи-
рование. Расширения системы хранятся на жестком диске ком-
пьютера и вызываются в нужный момент без какого-либо пред-
варительного объявления или описания, необходимого в боль-
шинстве универсальных языков программирования. При этом
по скорости выполнения задач эта система превосходит другие
подобные системы.
Универсальная среда Mathematica разработана фирмой Wolfram
Relearch, является мощным средством для математических и дру-
гих вычислений и выполняет численные, аналитические и графи-
ческие операции. Ввод и представление информации, графичес-
кая оболочка среды, набор дополнительных библиотек — все со-
ответствует самым современным требованиям и тенденциям.
Встроенный, высокого уровня, язык программирования позволя-
ет быстро и качественно решать разнообразные инженерные за-
дачи, имеет богатые возможности для визуализации данных и ре-
зультатов расчетов. По богатству и разнообразию средств высо-
кого уровня данная среда уникальна. Пакет позволяет создавать
интерактивные документы, объединяющие в себе текст, анимацию
и активные формулы.
6.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВОЙ ИНФОРМАЦИИ
В ЦИФРОВУЮ ФОРМУ
При использовании ЭВМ для обработки информации от различ-
ных устройств (объектов, процессов), в которых информация пред-
ставлена непрерывными (аналоговыми) сигналами, требуется пре-
261
образовать аналоговый сигнал в цифровой — в число, пропорцио-
нальное амплитуде этого сигнала, и наоборот.
В общем случае процедура аналого-цифрового преобразования
состоит из трех этапов [8]:
дискретизации;
квантования по уровню;
* кодирования.
Под дискретизацией понимают преобразование функции непре-
рывного времени в функцию дискретного времени, а сам процесс дис-
кретизации состоит в замене непрерывной функции ее отдельными
значениями в фиксированные моменты времени.
г)
Рис. 6.8. Процесс аналого-
цифрового преобразования
Дискретизация может быть
равномерной и неравномерной.
При неравномерной дискрети-
зации длительность интервалов
между отсчетами различна. Наи-
более часто применяется равно-
мерная дискретизации, при кото-
рой длительность интервала меж-
ду отсчетами Тд постоянна. Пери-
од дискретизации Т непрерывно-
го сигнала u(t) (рис. 6.8 а) выбира-
ется в соответствии с теоремой
Котельникова:
Т=—, (6.1)
д 2Fe
где Fb — высшая частота в спектре
частот сигнала u(t) (рис. 6.8 б).
Под квантованием понимают
преобразование некоторой вели-
чины с непрерывной шкалой зна-
чений в величину, имеющую дис-
кретную шкалу значений.
Для этого весь диапазон значе-
ний сигнала u(t), называемый шка-
262
лой, делится на равные части — кванты, h — шаг квантования. Про-
цесс квантования сводится к замене любого мгновенного значе-
ния одним из конечного множества разрешенных значений, на-
зываемых уровнями квантования.
Вид сигнала u(t) в результате совместного проведения опера-
ций дискретизации и квантования представлен на рис. 6.8 в.
Дискретизированное значение сигнала u(t), находящееся меж-
ду двумя уровнями квантования, отождествляется либо с ближай-
шим уровнем квантования, либо с ближайшим меньшим (или боль-
шим) уровнем квантования. Это приводит к ошибкам квантования,
которые всегда меньше шага квантования (кванта), т. е. чем мень-
ше шаг квантования, тем меньше погрешность квантования, но
больше уровней квантования. Для ускорения процесса преобра-
зования, упрощения и удешевления преобразователя надо выби-
рать максимально допустимый шаг квантования, при котором по-
грешности еще не выходят за допустимые пределы.
Число уровней квантования на рис. 6.8 в равно 8. Обычно их
значительно больше. Можно провести нумерацию уровней и вы-
разить их в двоичной системе счисления. Д ля восьми уровней дос-
таточно трех двоичных разрядов. Каждое дискретное значение
сигнала представляется в этом случае двоичным кодом (табл. 6.1)
в виде последовательности сигналов двух уровней.
Таблица 6.1
Значение уровня Двоичное представление значения уровня
6 011
5 101
4 001
5 101
6 011
7 111
Наличие или отсутствие импульса на определенном месте ин-
терпретируется единицей или нолем в соответствующем разряде
двоичного числа. Цифровая форма представления сигнала u(t) по-
казана на рис. 6.8 г. Импульсы старших разрядов расположены
крайними справа.
Таким образом, в результате дискретизации, квантования
и кодирования аналогового сигнала получаем последовательность
263
n-разрядных кодовых комбинаций, которые следуют с периодом
дискретизации Т. При этом рациональное выполнение операций
дискретизации и квантования приводит к значительному эконо-
мическому эффекту как за счет снижения затрат на хранение и
обработку получаемой информации, так и вследствие сокращения
времени обработки информации.
Рассмотрим в качестве примера аналого-цифровое преобразо-
вание речевого сигнала при использовании его в цифровых систе-
мах передачи. Согласно рекомендациям Международного консуль-
тативного комитета по телефонии и телеграфии для передачи те-
лефонных сообщений достаточна полоса частот от 300 до 3400 Гц,
динамический диапазон — до 35 дБ. При этом слоговая разборчи-
вость, определенная экспериментально, составляет 90%. Так как
в реальном телефонном канале данная полоса частот выделяется
фильтром, имеющим конечный спад частотной характеристики,
в качестве расчетной ширины спектра стандартного телефонного
канала используют ширину полосы частот в 4 кГц.
Для дискретизации такого сигнала в соответствии с формулой
(6.1) частота дискретизации fg=2FB при FB=4 кГц равна 1=8 кГц, что
соответствует максимальному периоду дискретизации сигнала
Tg=l/f = 125 мкс. Данные период и частота дискретизации приня-
ты в качестве основы при разработке стандартов цифровых сис-
тем передачи.
Для кодирования квантованных значений амплитуды аналого-
вого сигнала используют, как правило, 7- или 8-битный двоичный
код, обеспечивающий соответственно N=2’= 128 или N=28 = 256
уровней квантования. Это гарантирует передачу качественного
речевого сигнала с динамическим диапазоном по амплитуде
D= 201g 128 = 42 дБ или D = 201g256 = 48 дБ соответственно. При
этом скорость передачи такого цифрового потока при 7-битном
кодировании равна 8 кГц х 7 бит = 56 кбит/с, при 8-битном коди-
ровании — 8 кГц х 8 бит = 64 кбит/с.
На практике преобразование аналогового сигнала в цифровую
форму осуществляется с помощью аналого-цифрового преобразо-
вателя (АЦП). Для решения обратной задачи преобразования чис-
ла в пропорциональную аналоговую величину, представленную
в виде электрического напряжения, тока и т. п. служит цифроана-
логовый преобразователь (ЦАП). В ЦАП каждая двоичная кодовая
комбинация преобразуется в аналоговый сигнал и на выходе со-
здается последовательность модулированных по амплитуде им-
264
пульсов с периодом Т . Восстановление аналоговой структуры про-
изводится при помощи специальных схем, обеспечивающих филь-
трацию либо экстраполяцию этих сигналов.
В основе построения ЦАП лежит принцип суперпозиции токов
(напряжений), каждый из которых пропорционален шагу кванто-
вания. При этом член суммы не равен 0, если соответствующий
разряд входного слова равен 1. На рис. 6.9 представлена одна из
наиболее простых схем ЦАП, включающая:
« источник опорного напряжения (ИОН), Е;
аналоговые ключи (АК);
цепи формирования выходных сигналов (резистивные цепи).
Рис. 6.9. Цифроаналоговый преобразователь с весовыми резисторами
На вход ЦАП поступает п-разрядный код преобразуемого чис-
ла X. Состояние электронного ключа определяется значением со-
ответствующего разряда преобразуемого числа, при этом, если
двоичный разряд числа равен единице, то соответствующий рези-
стор соединяется с источником опорного напряжения Е, в против-
265
ном случае ключ разомкнут. Сопротивления резисторов подбира-
ют следующим образом:
R0=2°R;
R1=2‘R;
Кп., = 2"^..
При этом на выходе ЦАП для каждого кода имеем:
Л-1 г Л-1
1=0 К i=0
где х. — значение /-го разряда входного двоичного кода.
Точность такого преобразования определяется разрядностью
ЦАП, а также точностью изготовления резисторов и стабильнос-
тью опорного напряжения Е. Для уменьшения количества номи-
налов резисторов используют цепную схему, составленную из
вдвое большего числа резисторов всего лишь двух номиналов —
Rn2R.
Цифроаналоговые преобразователи могут преобразовывать
в аналоговый сигнал лишь параллельные коды. При преобразова-
нии в аналоговый сигнал последовательных кодов их сначала пре-
образуют в параллельные.
Схема простейшего АЦП представлена на рис. 6.10. Она вклю-
чает в себя суммирующий счетчик, ЦАП, сравнивающее устрой-
ство (К-компаратор) и генератор тактовых импульсов (ГТИ).
По принципу действия такой АЦП называется последователь-
ным. Временные диаграммы на рис. 6.11 поясняют принцип его
работы. На один вход компаратора поступает входной сигнал Ubx.
На другой — формируемое ЦАП напряжение порога срабатыва-
ния компаратора. При достижении равенства данного напряже-
ния и напряжения входного сигнала на выходе компаратора появ-
ляется сигнал, останавливающий счет и суммирование тактовых
импульсов в суммирующем счетчике. Одновременно считывается
выходной цифровой код хдхг.лп.
Основной недостаток такой схемы — низкое быстродействие,
так как время преобразования Тпр пропорционально амплитуде
сигнала.
266
Рис. 6.10. Схема простейшего каскада АЦП
Значительно большим быстродействием отличаются АЦП па-
раллельного кодирования. В них для преобразования аналогового
сигнала в л-разрядный двоичный код используется 2П1 компарато-
ра. На один из двух дифференциальных входов каждого компара-
тора подается свое опорное напряжение, формируемое резистор-
ным делителем. Разность между опорными напряжениями двух
ближайших компараторов равна Е/2, где Е — опорное напряже-
ние, соответствующее максимальному значению преобразуемого
аналогового сигнала. Другие входы компараторов объединены, и
на них подается входной сигнал. Приоритетный шифратор фор-
мирует выходной цифровой сигнал, соответствующий самому
старшему сработавшему компаратору.
Способ параллельного кодирования (иногда он называется спо-
собом мгновенного кодирования) отличается наибольшим быст-
родействием. Время задержки при передаче сигнала от входа
к выходу равно сумме запаздываний компараторов и шифратора.
267
Ш1ШМ
Рис. 6.11. Временные диаграммы работы АЦП
В некритичных к быстродействию применениях используют
также преобразователи, построенные по методу двойного интег-
рирования. Такие преобразователи состоят из конденсатора (ин-
тегрирующий элемент), который в течение фиксированного про-
межутка времени заряжается током, пропорциональным входно-
му сигналу, после чего он разряжается до тех пор, пока напряже-
ние на нем не станет равным нолю. Время разряда конденсатора
пропорционально значению входного сигнала и используется для
подсчета тактовых импульсов фиксированной частоты при помо-
щи счетчика. Полученное число, пропорциональное входному
уровню, является выходным цифровым сигналом.
6.3. ФУНКЦИОНАЛЬНАЯ И СТРУКТУРНАЯ
ОРГАНИЗАЦИЯ ПРОЦЕССОРНЫХ УСТРОЙСТВ
ОБРАБОТКИ ИНФОРМАЦИИ
6.3.1. Общая структура процессорных устройств
обработки информации и принципы фон Неймана
Со времени появления в 40-х годах XX века первых электрон-
ных цифровых вычислительных машин технология их производ-
ства была значительно усовершенствована. В последние годы бла-
годаря развитию интегральной технологии существенно улучши-
268
лись их характеристики, значительно снизилась стоимость. Одна-
ко, несмотря на успехи, достигнутые в области технологии, суще-
ственных изменений в базовой структуре и принципах работы
вычислительных машин не произошло. Так, в основу построения
подавляющего большинства современных компьютеров положе-
ны общие принципы функционирования универсальных вычис-
лительных устройств, сформулированные еще в 1945 г. американ-
ским ученым Джоном фон Нейманом.
Согласно фон Нейману, для того чтобы ЭВМ была универсаль-
ным и эффективным устройством обработки информации, она
должна строиться в соответствии со следующими принципами:
1. Информация кодируется в двоичной форме и разделяется на
единицы (элементы) информации, называемые словами.
Использование в ЭВМ двоичных кодов продиктовано в первую
очередь спецификой электронных схем, применяемых для пере-
дачи, хранения и преобразования информации. Как уже отмеча-
лось, в этом случае конструкция ЭВМ предельно упрощается, и
ЭВМ работает наиболее надежно (устойчиво). Совокупности но-
лей и единиц (битов информации), используемые для представле-
ния отдельных чисел, команд и т. п., рассматриваются как само-
стоятельные информационные объекты и называются словами.
Слово обрабатывается в ЭВМ как одно целое — как машинный эле-
мент информации.
2. Разнотипные слова информации хранятся в одной и той же
памяти и различаются по способу использования, но не по спосо-
бу кодирования.
Все слова, представляющие числа, команды и прочие объекты,
выглядят в ЭВМ совершенно одинаково, и сами по себе неразли-
чимы. Только порядок использования слов в программе вносит
различия в слова. Благодаря такому «однообразию» слов оказыва-
ется возможным использовать одни и те же операции для обра-
ботки слов различной природы, например для обработки и чисел,
и команд, т. е. команды программы становятся в такой же степени
доступными для отработки, как и числа.
3. Слова информации размещаются в ячейках памяти машины
и идентифицируются номерами ячеек, называемыми адресами
слов.
Структурно основная память состоит из перенумерованных
ячеек. Ячейка памяти выделяется для хранения значения величи-
ны, в частности константы или команды. Чтобы записать слово
269
в память, необходимо указать адрес ячейки, отведенной для хра-
нения соответствующей величины. Чтобы выбрать слово из памя-
ти (прочитать его), следует опять же указать адрес ячейки памяти.
То есть адрес ячейки, в которой хранится величина или команда,
становится машинным идентификатором (именем) величины и ко-
манды. Таким образом, единственным средством для обозначения
величин и команд в ЭВМ являются адреса, присваиваемые вели-
чинам и командам в процессе составления программы вычисле-
ний. При этом выборка (чтение) слова из памяти не разрушает
информацию, хранимую в ячейке. Это позволяет любое слово, за-
писанное однажды, читать какое угодно число раз, т. е. из памяти
выбираются не слова, а копии слов.
4. Алгоритм представляется в форме последовательности управ-
ляющих слов, называемых командами, которые определяют наи-
менование операции и слова информации, участвующие в опера-
ции. Алгоритм, представленный в терминах машинных команд,
называется программой.
В общем случае алгоритм в ЭВМ представляется в виде упоря-
доченной последовательности команд следующего вида:
bb...b bb...b bb...b... bb...b.
t 1___ I 1 1 I
коп A, A2 Ak
Здесь b — двоичная переменная, принимающая значение 0 или
1. Определенное число первых разрядов команды характеризует
код операции (КОП). Например, операция сложения может пред-
ставляться в команде кодом 001010. Последующие наборы двоич-
ных переменных bb ... b определяют адреса А(,..., Ак операндов (ар-
гументов и результатов), участвующих в операции, заданной ко-
дом КОП.
На рис. 6.12 в общем виде представлен формат (структура) ко-
манды.
1 ...т 1...п 1...п_______________1 ...п
КОП Ai а2 Ак
Рис. 6.12. Общая структура команды
Составные части команды называют полями. Так, КОП, А/(..., Ак —
поля команды, представляющие соответственно код операции и
270
адреса операндов, участвующих в операции. Сверху указаны но-
мера разрядов полей: поле КОП состоит из т двоичных разрядов,
каждое поле А,,..., Ак содержит п двоичных разрядов. С учетом это-
го представленная на рис. 6.12 команда позволяет инициировать
одну из 2т операций, и каждый адрес может принимать до 2П раз-
личных значений, обеспечивая ссылку на любую из 2Л величин или
команд. Требуемый порядок вычислений предопределяется алго-
ритмом и описывается последовательностью команд, образующих
программу вычислений.
5. Выполнение вычислений, предписанных алгоритмом, сводит-
ся к последовательному выполнению команд в порядке, однознач-
но определяемом программой.
Первой выполняется команда, заданная пусковым адресом
программы. Обычно это адрес первой команды программы. Ад-
рес следующей команды однозначно определяется в процессе
выполнения текущей команды и может быть либо адресом сле-
дующей по порядку команды, либо адресом любой другой ко-
манды. Процесс вычислений продолжается до тех пор, пока не
будет выполнена команда, предписывающая прекращение вы-
числений.
Необходимо подчеркнуть, что вычисления, производимые ма-
шиной, определяются программой. Именно программа «настраи-
вает» ЭВМ на получение требуемых результатов. Замена програм-
мы приводит к изменению функций, реализуемых ЭВМ. Следова-
тельно, многообразие программ, которые могут быть выполнены
ЭВМ, определяет класс функций, который способна реализовать
данная ЭВМ.
Перечисленные принципы функционирования ЭВМ предпола-
гают, что компьютер должен иметь следующие устройства:
арифметико-логическое устройство (ААУ), выполняющее
арифметические и логические операции;
устройство управления (УУ), которое организует процесс
выполнения программы;
запоминающее устройство (ЗУ), или память для хранения
программ и данных;
* внешние устройства для ввода (устройства ввода) и вывода
(устройства вывода) информации.
При рассмотрении компьютерных устройств принято различать
их архитектуру и структуру.
271
Под архитектурой ЭВМ понимают ее логическую организацию,
состав и назначение ее функциональных средств, принципы кодиро-
вания и т. п., т. е. все то, что однозначно определяет процесс обработ-
ки информации на данной ЭВМ.
ЭВМ, построенные в соответствии с принципами фон Нейма-
на, называют фон-неймановскими, или компьютерами фон-ней-
мановской (классической) архитектуры.
Структура ЭВМ — совокупность элементов компьютера и связей
между ними.
Ввиду большой сложности современных ЭВМ принято пред-
ставлять их структуру иерархически, т. е. понятие «элемент» жес-
тко не фиксируется. Так, на самом высоком уровне сама ЭВМ мо-
жет считаться элементом. На следующем (программном) уровне
иерархии элементами структуры ЭВМ являются память, процес-
сор, устройства ввода-вывода и т. д. На более низком уровне (мик-
ропрограммном) элементами служат узлы и блоки, из которых
строятся память, процессор и т. д. Наконец, на самых низких уров-
нях элементами выступают интегральные логические микросхе-
мы и электронные приборы.
Несмотря на разнообразие современных компьютеров, обоб-
щенная структурная схема подавляющего большинства из них
может быть представлена схемой, изображенной на рис. 6.13.
Рис. 6.13. Обобщенная структурная схема ЭВМ
272
Все устройства ЭВМ соединены линиями связи, по которым
передаются информационные и управляющие сигналы, а синхро-
низация процессов передачи осуществляется при помощи такто-
вых импульсов, вырабатываемых генератором тактовых импуль-
сов (ГТИ).
Устройство управления и арифметико-логическое устройство
в современных компьютерах объединены в один блок — процес-
сор, предназначенный для обработки данных по заданной програм-
ме путем выполнения арифметических и логических операций и
программного управления работой устройств компьютера.
Процессор (центральный процессор, ЦП) — программно-управля-
емое устройство, осуществляющее процесс обработки цифровой ин-
формации, управление им и координацию работы всех устройств ком-
пьютера.
Процессор, построенный на одной или нескольких больших интег-
ральных микросхемах, называют микропроцессором.
Как было отмечено выше, микропроцессор включает в себя:
арифметико-логическое устройство (АЛУ), предназначенное
для выполнения всех арифметических и логических опера-
ций над числовой и символьной информацией. Для ускоре-
ния выполнения арифметических операций с плавающей
точкой к АЛУ подключается дополнительный математичес-
кий сопроцессор;
устройство управления (УУ) — формирует и подает во все
блоки машины в нужные моменты времени определенные
сигналы управления (управляющие импульсы), обусловлен-
ные спецификой выполняемой операции и результатами
предыдущих операций; формирует адреса ячеек памяти, ис-
пользуемых выполняемой операцией, и передает эти адреса
в соответствующие блоки ЭВМ; опорную последователь-
ность импульсов устройство управления получает от гене-
ратора тактовых импульсов (ГТИ).
Для кратковременного хранения, записи и выдачи информации,
непосредственно используемой в вычислениях в ЦП имеется про-
цессорная память (ПП), состоящая из специализированных ячеек
памяти, называемых регистрами.
18а-210 273
В общем случае регистры состоят из элементов памяти, каж-
дый из которых может находиться в одном из двух устойчивых со-
стояний: конденсатор заряжен или разряжен, транзистор находит-
ся в проводящем или непроводящем состоянии, специальный по-
лупроводниковый материал имеет высокое или низкое удельное
сопротивление и т. п. Одно из таких физических состояний созда-
ет высокий уровень выходного напряжения элемента памяти, а
другое — низкий. Например, электрическое напряжение порядка
5В может приниматься за двоичную единицу, а ОВ — за двоичный
ноль [6].
Регистры часто изображают так, как показано на рис. 6.14 а.
Регистр характеризуется единственным числом: количеством би-
тов, которые могут в нем храниться. Помещенная в регистр ин-
формация остается там до тех пор, пока она не будет заменена дру-
гой. Процесс чтения информации из регистра не влияет на содер-
жимое последнего, другими словами, операция чтения информа-
ции, хранимой в регистре, сводится к созданию копии его содер-
жимого, оригинал же сохраняется в регистре без изменений.
а) Номер бита 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
00001011 01000111
б)
Регистр
(источник информации)
в)
Регистр
(источник информации)
(приемник информации)
Рис. 6.14. Регистры, шины и вентильные схемы
274
Шина состоит из параллельных проводов, каждый из которых
предназначен для передачи соответствующего бита регистра (рис.
6.146). Если два 8-битовых регистра соединяются между собой ши-
ной из восьми проводов, то говорят, что ее ширина равна 8, или
восьмиразрядная шина. В действительности шина обычно содер-
жит несколько дополнительных проводов, используемых для пе-
редачи сигналов синхронизации и управления.
Шина служит для передачи информации лишь в направлении,
обозначенном стрелкой на шине (рис. 6.14 б, в). Такая однонап-
равленность передачи обусловлена не свойствами шины (прово-
да, из которых состоит шина, позволяют передавать сигналы в лю-
бом направлении), а характеристиками схем, соединяющих шину
с регистром или другими устройствами ЭВМ. Специальные схемы
дают возможность, например, в одни моменты времени передавать
информацию по шине в одну сторону, а в другие — в обратном
направлении, т. е. организовать двунаправленную шину. Такие
электронные ключевые схемы, предназначенные для управления
потоком информации из регистров в шины и обратно, называют
вентильными схемами. На рис. 6.14 в показано применение вен-
тильной схемы В. Такая схема имеет два входа и один выход. На
один вход подается информационный сигнал (данные с регистра),
а на другой — управляющий. Если управляющий сигнал равен еди-
нице, то данные проходят через схему, а если нолю — информация
через схему не пройдет. Таким образом, при подаче единичного
управляющего сигнала на вентильную схему В состояние регист-
ра приемника информации изменится с (00100110)2 на (10011101)2,
т. е. в него поступит копия содержимого регистра источника ин-
формации.
Простейшим вариантом организации взаимодействия между
процессором и любым другим устройством ЭВМ было бы исполь-
зование отдельного набора проводов для подключения данного
устройства к процессору. При этом количество проводов и разъе-
мов процессора было бы неимоверно большим. В большинстве
современных ЭВМ для организации процессов обмена информа-
цией между различными устройствами ЭВМ используется общая
шина (системная магистраль). Физически магистраль представля-
ет собой многопроводную линию с гнездами для подключения элек-
тронных схем. Совокупность средств сопряжения и связи уст-
ройств компьютера, обеспечивающая их эффективное взаимодей-
ствие, называют интерфейсом.
275
Системный интерфейс — набор цепей, связывающих процес-
сор с памятью и контроллерами внешних устройств, алгоритм пере-
дачи сигналов по этим цепям, их электрические параметры и тип
соединительных элементов.
Для согласования интерфейсов периферийные устройства подклю-
чаются к шине не напрямую, а через свои контроллеры (адаптеры).
Устройства ввода обеспечивают считывание информации (ис-
ходных данных и программы решения задачи) с определенных
носителей информации (клавиатур, магнитных лент или дисков,
датчиков состояний управляемых объектов и т. п.) и ее представ-
ление в форме электрических сигналов, воспринимаемых други-
ми устройствами ЭВМ.
Устройства вывода представляют результаты обработки инфор-
мации в форме, удобной для визуального восприятия (индикато-
ры, печатающие устройства, графопостроители, экран дисплея
ит. п.). При необходимости они обеспечивают запоминание ре-
зультатов на носителях, с которых эти результаты могут быть сно-
ва введены в ЭВМ для дальнейшей обработки, или передачу ре-
зультатов на исполнительные органы управляемого объекта (на-
пример, робота, станка с программным управлением и т. п.).
Память ЭВМ, или ЗУ, обеспечивает хранение команд и данных.
Это устройство состоит из блоков одинакового размера — ячеек
памяти, предназначенных для хранения одного слова информации
(рис. 6.15). В свою очередь, ячейка памяти включает в себя элемен-
ты памяти, состояние каждого из которых соответствует одной
двоичной цифре (0 или 1). Совокупность нолей и единиц, храня-
щихся в элементах одной ячейки, представляет собой содержимое
этой ячейки памяти [6].
Ячейки нумеруются числами 0, 1, 2, ... , называемыми адресом
ячеек. Запись в память слова осуществляется подачей на шину ад-
реса памяти сигналов, соответствующих адресу ячейки, в которую
надо поместить записываемое слово, и подачей самого слова на
шину записи (см. рис. 6.15). Память устроена так, что заданное сло-
во будет передано в ячейку с указанным адресом для хранения,
причем в любой момент, обратившись к памяти, можно получить
содержимое хранимого там слова. Для этого в память посылается
адрес, определяющий местоположение требуемого слова, и она
выдает по шине чтения копию слова.
276
Рис. 6.15. Организация памяти ЭВМ
При считывании содержимое ячейки остается без изменения,
так что, один раз записав слово, можно сколько угодно раз полу-
чать его копии. Это аналогично записи информации на магнито-
фонную ленту. Запись можно прослушивать с ленты (читать с лен-
ты) сколько угодно раз, но если на ее место записать другую ин-
формацию, то первая будет стерта. Однако время доступа к ин-
формации на магнитной ленте зависит от того, где записана эта
информация (иногда надо перемотать почти всю ленту, чтобы най-
ти нужную запись), тогда как время доступа к любой ячейке памя-
ти всегда одинаково (не зависит от ее номера).
На рис. 6.15 показана память, имеющая 4096 = 212 8-разрядных
слов, т. е. содержащая 4096 байт информации. При том же самом
числе запоминающих элементов можно было бы организовать па-
мять из 32 768 1-битовых слов; 2048 16-битовых слов, 1024 32-бито-
вых слов и т. д.
Тактовые импульсы вырабатываются генератором тактовых
импульсов ЭВМ и используются для синхронизации процессов пе-
редачи информации между устройствами ЭВМ. Необходимость
распределения во времени отдельных операций по передаче инфор-
мации в цифровых устройствах рассмотрим на примере работы
упрощенной модели школьного микрокалькулятора (рис. 6.16 а) [6].
277
Рис. 6.16. Структурно-функциональная схема микрокалькулятора и управляющие
сигналы: а) при вводе первой цифры слагаемого; б) при вводе второй цифры;
в) при нажатии клавиши « + »
В состав микрокалькулятора входят:
цифровая (0, 1,.... 9, «.») и функциональная (С, %, х,-*-, — , +,
=) клавиатуры;
основной регистр X, в который вводится операнд (набирае-
мое на клавиатуре число) и по окончании какой-либо опера-
ции засылается ее результат (сумма, разность и т. п.);
табло для индикации содержимого регистра X, т. е. вводимого
числа (в момент набора его на цифровой клавиатуре) или резуль-
тата вычислений (после нажатия функциональной клавиши);
вспомогательный регистр У, в который переписывается со-
держимое регистра X при вводе в последний нового операн-
да (это позволяет, например, сохранить в У значение преды-
дущего слагаемого или ранее накопленной суммы в момент
ввода в X нового слагаемого);
278
* арифметико-логическое устройство (АЛУ), предназначенное
для выполнения операций над содержимым регистров Хи У
(сложение, умножение, вычитание и деление) или только
регистра X (извлечение квадратного корня и нахождение
процентов), а также ряда служебных операций (например,
сдвига старших цифр числа при вводе его новой цифры);
• устройство управления вводом числа и выполнением опера-
ций, которое после любого нажатия цифровой или функци-
ональной клавиши вырабатывает определенную последова-
тельность управляющих сигналов (У.) для осуществления не-
обходимых пересылок информации между устройствами
микрокалькулятора и (или) перестройки АЛУ на ту или иную
операцию.
Рассмотрим работу микрокалькулятора при сложении чисел
27 + 48+129 + 36... [6]. При этом для удобства будем использовать
десятичное представление цифр в регистрах микрокалькулятора.
Начнем с момента нажатия клавиши « + », завершающей ввод пер-
вого слагаемого, т. е. с момента, когда в регистрах содержатся сле-
дующие числа:
Регистр У О
Регистр X 27
1 -й шаг. Ввод цифры 4 — старшей цифры второго слагаемого:
Регистр У 27
Регистр X 4
Содержимое регистра X переписалось для сохранения в регистр
У, регистр X был очищен и в его младший разряд записан код на-
жатой клавиши, т. е. цифра 4.
Рассмотрим последовательность управляющих сигналов У, вы-
рабатываемых при этом устройством управления.
Ввод первой цифры любого операнда (первое нажатие цифро-
вой клавиши после выполнения какой-либо операции) должен
инициировать перепись содержимого регистра X в регистр У,
т. е. выработку управляющего сигнала УЗ (рис. 6.16 а). Одновре-
менно с этим сигналом может быть выработан сигнал Уб, устанавли-
вающий 0 на выходе АЛУ. Теперь производятся очистка регистра X,
суммирование его содержимого с вводимой цифрой и перезапись
полученной суммы в регистр X. Для этого сначала подается сигнал
У2 (0 с выхода АЛУ переписывается в регистр X), затем одновре-
279
27
48
менно сигналы У7, У1 и У5 (У7 для настройки АЛУ на суммирова-
ние) и, наконец, сигнал У2.
2-й шаг. Ввод цифры 8 — младшей цифры второго слагаемого:
Регистр У
Регистр X
Число, содержащееся в регистре X, было сдвинуто влево на один
разряд, а в освободившийся младший разряд записан код нажатой
клавиши, т. е. цифра 8.
Рассмотрим последовательность управляющих сигналов У, вы-
рабатываемых устройством управления на втором шаге.
Ввод второй цифры (или любой из следующих) осуществляет-
ся путем умножения на 10 (сдвига влево на один десятичный раз-
ряд) содержимого регистра X и суммирования сдвинутого значе-
ния с вводимой цифрой. Для этого вырабатывается последователь-
ность управляющих сигналов, показанная на рис. 6.16 6 (сигнал У8
служит для организации сдвига).
3-й шаг. Нажатие клавиши « + »:
Регистр У 27
Регистр X 75
Зафиксировался ввод последней цифры второго слагаемого (48),
выполнились операция сложения содержимого регистров X и У
(48 + 27 = 75) и операция пересылки полученного результата в ре-
гистр X.
Суммирование содержимого регистров X и У (сигналы У7, У1 и
У4) и перезапись полученной суммы в регистр X (сигнал У2) иллю-
стрируются временной диаграммой на рис. 6.16 в.
4-й шаг. Ввод цифры 1 — старшей цифры третьего слагаемого:
Регистр У
Регистр X
Содержимое регистра X переписалось для сохранения в регистр
У, регистр X был очищен и в его младший разряд записан код на-
жатой клавиши, т. е. цифра 1. Дальнейшие шаги не представляют
интереса, так как в них будут повторяться ранее описанные опе-
рации.
Анализ временных диаграмм на рис. 6.16 а, б, в показывает, что
некоторые из управляющих сигналов вырабатываются одновре-
менно, а другие — через те или иные интервалы времени. Напри-
75
1
280
мер, нельзя при суммировании содержимого регистров X и У од-
новременно вырабатывать сигналы У1, У2, У4, У7, так как при од-
новременной выработке сигналов У1 и У2, а также при настройке
АЛУ на выполнение какой-либо операции с содержимым регист-
ра X возникает полная неопределенность: содержимое регистра X
попадает в АЛУ, через него обратно в регистр X и т. д. В то же вре-
мя, если при суммировании X и У не будет обеспечена одновре-
менная выработка сигналов У1, У4 и У7, то суммы не получится.
Минимальный промежуток времени Т между управляющими
сигналами, которые должны быть сдвинуты относительно друг
друга (например, промежуток времени между сигналами У1 и У2
на рис. 6.16 в), выбирается исходя из максимального времени пе-
реключения элементов цифрового устройства (пока, например, не
окончилось формирование суммы X+Y, бессмысленно подавать
управляющий сигнал У2 на перезапись этой суммы в регистр X).
Для задания нужных временных интервалов в управляющих уст-
ройствах ЭВМ устанавливаются генераторы тактовых импульсов
(ГТИ), синхронизирующие управляющие сигналы У .
Генератор тактовых импульсов генерирует последовательность
электрических импульсов, частота которых определяет тактовую
частоту ЭВМ. Промежуток времени между соседними импульса-
ми определяет время одного такта работы ЭВМ, или просто такт
работы ЭВМ. Частота генератора тактовых импульсов является
одной из основных характеристик компьютера и во многом опре-
деляет скорость его работы, так как каждая операция в ЭВМ вы-
полняется за определенное количество тактов.
6.3.2. Исполнение команд программы процессором
Первоначально команда ЭВМ содержала следующую информа-
цию (рис. 6.17 а) [6]:
1. Код операции, указывающий операцию, которую должна
выполнить ЭВМ (сложение, вычитание, умножение, сравнение,
изменение знака и т. п.).
2. Адреса двух операндов — аргументов операции, например
слагаемых, уменьшаемого и вычитаемого, сомножителей и т. п.
Если какой-либо из операндов является константой, то вместо его
адреса в команде может быть задано само значение операнда. Од-
нако это обстоятельство должно быть отражено в коде операции,
чтобы ЭВМ использовала соответствующую часть команды в ка-
281
честве операнда, а не адреса ячейки памяти, в которой хранится
этот операнд.
3. Адрес ячейки памяти, в которую должен быть помещен ре-
зультат операции.
4. Адрес следующей команды.
Такая команда, состоящая из пяти полей (код операции и четы-
ре адреса), может быть реализована процессорами самых разно-
образных структур.
а)
Рис. 6.17. Форматы команд:
а) четырехадресная; б) одноадресная; в) безадресная
Простейшая из этих структур (рис. 6.18) напоминает структуру
процессора микрокалькулятора, приведенную на рис. 6.16 [6]. Про-
цессор содержит устройство управления, АЛУ, регистр для разме-
щения исполняемой команды (регистр команд) и регистр для раз-
мещения одного из операндов или результата операции в процес-
се выполнения этой команды — аккумулятор (на рис. 6.16 а роль
аккумулятора выполнял регистр X). Рассмотрим, что происходит
в процессоре после того, как в его регистр команд была переписа-
на из памяти какая-либо команда, например команда вычитания.
Так как поле регистра команд, в котором хранится код опера-
ции, связано шиной с устройством управления, то последнее по-
282
лучит приказ на выполнение операции «вычитание» и перейдет
в режим генерации управляющих сигналов:
одновременной выработкой сигналов У1, У5, У10 и У8 обес-
печиваются пересылка из памяти численного значения
уменьшаемого, прохождение его через АЛУ (сигнал У10,/ и
запись в аккумулятор;
следующий тактовый импульс инициирует выработку сигна-
лов У2, У5, Уб и У11, что приводит к пересылке из памяти чис-
ленного значения вычитаемого, к выполнению операции вы-
читания этого значения (сигнал У11/ из содержимого аккуму-
лятора (из уменьшаемого); по сигналу У8 производится запись
полученной разности в аккумулятор вместо уменьшаемого;
затем сигналы УЗ и У9 обеспечат пересылку разности из ак-
кумулятора в ячейку памяти, на которую указывает предпос-
леднее поле команды;
* наконец, с помощью сигналов У4 и У7 будет произведена пе-
резапись в регистр команд следующей команды программы.
При такой структуре процессора и реализуемой им структуре
четырехадресной команды первый операнд приходится сохранять
в процессоре до момента получения следующего операнда, так как
нельзя одновременно получать из памяти оба операнда. Поэтому в
состав процессора включен аккумулятор (он назван так потому,
что может быть использован для накопления — аккумуляции —
слагаемых в процессе получения суммы многих слагаемых или
накопления результатов других вычислений).
Нужен и регистр для хранения в процессоре исполняемой ко-
манды (регистр команд), так как во время выполнения этой коман-
ды из нее должна выбираться различная информация, используе-
мая устройством управления и памятью.
Четырехадресная команда (см. рис. 6.17 а) длиной в 16 бит мо-
жет адресовать лишь 23 = 8 ячеек памяти. Современные же микро-
ЭВМ адресуются к памяти, содержащей не менее 216=65536 яче-
ек. Если создавать четырехадресную команду, работающую даже
с этим минимальным размером памяти, то на каждое адресное поле
команды придется отвести 16 бит, а на всю команду (при 16-бито-
вом коде операции) — 80 бит.
В связи с этим в современных ЭВМ практически не встречают-
ся четырехадресные команды. Мало и трехадресных команд, так
как результат операции почти всегда можно записать на место од-
ного из уже использованных операндов.
283
Рис. 6.18. Простой процессор, работающий с четырехадресной командой,
целиком выбираемой из одной ячейки памяти
Если команды программы размещать в памяти ЭВМ друг за дру-
гом (а не в произвольной последовательности), то адрес следую-
щей команды чаще всего будет отличаться от адреса исполняемой
команды (или ее последнего поля) лишь на единицу, а добавление
единицы к текущему адресу можно возложить на ЭВМ. Это по-
зволяет сократить длину команды (изъять из ее содержимого ад-
рес следующей команды), но приводит к необходимости исполь-
зования специальных команд перехода, размещаемых в тех мес-
тах программы, где может потребоваться изменение естественной
последовательности выполнения команд в зависимости от резуль-
тата вычислений. Обычно команды перехода — одноадресные ко-
манды (см. рис. 6.17 б), где код операции оговаривает проверяемое
условие (знак результата предыдущей операции, наличие перено-
284
са из старшего разряда и т. п.), а адрес — адрес команды, к кото-
рой нужно перейти, если условие выполняется (при невыполне-
нии условия выбирается команда, расположенная вслед за коман-
дой перехода).
Во многих случаях результат выполнения предыдущей коман-
ды используется как операнд в следующей. Если результат выпол-
нения команды не пересылать в память, а сохранять, например,
в аккумуляторе, то можно обойтись одноадресными командами:
арифметической (логической) обработки, которые дают
приказ на выполнение какой-либо арифметической или ло-
гической операции, используя в качестве операндов содер-
жимое аккумулятора и содержимое адресуемой ячейки па-
мяти (регистра данных, куда переписывается содержимое ад-
ресуемой ячейки);
пересылки, которые дают приказ на обмен информацией
между аккумулятором и памятью (через регистр данных),
т. е. на загрузку аккумулятора содержимым адресуемой ячей-
ки памяти или запись в эту ячейку содержимого аккумуля-
тора (результата вычислений);
передачи управления, обеспечивающими условный или бе-
зусловный переход к адресуемой ячейке памяти (т. е. к ко-
манде, которая должна быть помещена в процессор при вы-
полнении какого-либо условия или вне зависимости от ре-
зультата предыдущих вычислений), обращение к подпрог-
рамме и выход из нее;
ввода-вывода.
На рис. 6.19 представлена одна из возможных структур процес-
сора, реализующего программы из одноадресных и безадресных
команд. Он состоит из следующих устройств [6];
• арифметико-логического устройства, производящего опе-
рации над двумя величинами в целях получения результата
и выработки ряда признаков (результат меньше ноля, равен
нолю или больше ноля, был перенос из старшего разряда
результата);
регистра состояния, в котором хранятся признаки результа-
та последней операции, используемые командами перехода;
• аккумулятора — регистра, в котором размещаются подле-
жащие обработке данные или результат обработки;
• регистра команд —регистра, служащего для размещения ис-
полняемой команды;
285
регистра адреса — регистра, содержащего адрес ячейки па-
мяти, из которой будет считана команда (операнд) или запи-
сан результат обработки;
регистра данных — регистра, используемого в качестве бу-
фера между памятью и остальными регистрами процессора;
через него пересылаются в процессор команды (операнды)
и передаются в память результаты обработки;
счетчика команд — регистра, содержимое которого увели-
чивается на единицу в момент выборки из памяти исполняе-
мой команды и, если выбрана команда перехода, может быть
заменено на содержимое адресной части команды перехо-
да; в конце цикла исполнения команды в счетчике команд
всегда хранится адрес той команды, которая должна испол-
няться вслед за текущей, это может быть как следующая по
порядку команда, так и команда, к которой требуется перейти
при выполнении условий, заданных кодом операции коман-
ды перехода.
ПАМЯТЬ
26
41
77
102
134
135
136
137
Рис. 6.19. Простой процессор, работающий
с одноадресными и безадресными командами
286
Для решения задачи на такой ЭВМ необходимо:
1) через устройства ввода информации загрузить в память ЭВМ
программу решения задачи (алгоритм, написанный на языке
ЭВМ) и исходные данные; и программа, и данные могут быть раз-
мещены в любой области памяти, начиная с ячейки 0 или другой
ячейки с любым адресом (сначала программа, а затем данные, или
наоборот).
2) «сообщить» процессору адрес ячейки памяти, в которой раз-
мещена первая команда программы, для чего занести адрес этой
ячейки в счетчик команд;
3) нажать кнопку «ПУСК», что приведет к передаче в память
адреса первой команды программы и к пересылке ее содержимо-
го из памяти в регистр команд; с этого момента процессор начнет
выполнять последовательность достаточно простых операций, по-
казанных на схеме алгоритма выполнения команды (рис. 6.20).
Как видно из схемы алгоритма, два первых действия (блоки 1
и 2) выполняются для каждой команды. Эти действия (а также дей-
ствия по определению типа команды — блоки 3, 6 и 9) обычно на-
зывают «выборкой команды». Последующие действия алгоритма
(«Исполнение команды») полностью зависят от того, какая это ко-
манда.
Рассмотрим исполнение команды, расположенной в ячейке 135
на рис. 6.19 [6]. Оно начинается в момент, когда в аккумуляторе
хранится значение уменьшаемого, записанное туда при выполне-
нии предыдущей команды, а в счетчике команд — адрес 135.
1. Адрес, содержащийся в счетчике команд, переписывается
в регистр адреса и далее в память ЭВМ (сигнал У1), а оттуда счи-
тывается команда «Выч. 26», помещаемая в регистр команд (сиг-
нал У4).
2. Счетчик команд наращивается на единицу (сигнал +1), что-
бы он указывал на команду (адрес 136), расположенную в памяти
вслед за выбранной командой.
3. Устройство управления считывает из регистра команд код
исполняемой команды, выясняет, что это команда вычитания, и
переходит к ее выполнению.
4. Из регистра команд считывается (сигнал УЗ) и пересылается
в память (через регистр адреса) адрес вычитаемого (26), а из памя-
ти переписывается в регистр данных численное значение вычита-
емого.
287
Рис. 6.20. Схема алгоритма выполнения команд простого процессора
288
5. Выполняется операция вычитания содержимого регистра дан-
ных из содержимого аккумулятора (сигналы У5, Уб и У11), а затем
полученная разность переписывается с выхода АЛУ в аккумуля-
тор (сигнал У8_), заменяя значение уменьшаемого.
Таким образом, процесс выполнения команды сводится к опре-
делению последовательности открывания и закрывания вентиль-
ных схем. Описание того, какую вентильную схему и когда откры-
вать, составляет программу для машины, система команд которой
включает в себя команду «Открыть вентильную схему». Такой ма-
шиной и является устройство управления ЭВМ, в котором хранят-
ся программы реализации всех команд ЭВМ. Эти программы обыч-
но называются микропрограммами, а их команды — микроко-
мандами. Простейшая микрокоманда состоит из набора битов, каж-
дый из которых управляет одной из вентильных схем процессора:
единица означает, что вентильная схема открыта, ноль — закрыта.
В заключение отметим, что процессор, изображенный на рис.
6.19, не является единственно возможным процессором, исполь-
зуемым для реализации одноадресных команд. Так, сумму произ-
ведений ахв + схе + fxh + qxk +... лучше вычислять с помощью про-
цессора, имеющего два аккумулятора (один — для вычисления
произведений, а другой — для накопления суммы). Это позво-
лит исключить пересылку в память промежуточных результатов,
т. е. ускорить вычисления и уменьшить число используемых ячеек
памяти. Существуют и другие виды процессоров.
6.4. ОБЩАЯ СТРУКТУРА ЭВМ
6.4.1. Структурная схема ПЭВМ
Персональный компьютер (ПК), или персональная ЭВМ
(ПЭВМ) — электронная вычислительная машина, с которой мо-
жет работать пользователь, не являющийся профессиональным
программистом.
Она характеризуется развитым («дружественным») человеко-
машинным интерфейсом, малыми габаритами, массой, относитель-
но невысокой стоимостью и многофункциональностью (универ-
сальностью) применения.
Одним из основных достоинств ПЭВМ, обеспечивших им по-
трясающий успех, явился принцип открытой архитектуры, заклю-
19 А-210
289
чающийся в том, что при проектировании ПЭВМ регламентиру-
ются и стандартизируются только принцип действия компьютера
и его конфигурация (определенная совокупность аппаратных
средств и соединений между ними). Построение ПЭВМ не единым
неразъемным устройством, а на основе принципа открытой архи-
тектуры (модульности построения), обеспечивает возможность их
сборки из отдельных узлов и деталей, разработанных и изготов-
ленных независимыми фирмами-изготовителями. Кроме того, та-
кой компьютер легко расширяется и модернизируется за счет на-
личия внутренних расширительных разъемов, позволяющих
пользователю добавлять разнообразные устройства, удовлетворя-
ющие заданному стандарту, и тем самым устанавливать конфигу-
рацию своей ЭВМ в соответствии со своими личными предпочте-
ниями. Специалисты часто называют такие операции upgrade (рас-
ширить, обновить).
Упрощенная блок-схема, отражающая основные функциональ-
ные компоненты ПЭВМ в их взаимосвязи, изображена на рис. 6.21.
Конструктивно современный персональный компьютер состо-
ит из трех основных компонентов (рис. 6.22):
системного блока, в котором размещаются устройства обра-
ботки и хранения информации;
* дисплея — устройства отображения информации;
* клавиатуры — основного устройства ввода информации
вПК.
Для упрощения взаимодействия пользователя с ПК в тех или
иных случаях используют различные манипуляторы (мышь, трек-
бол, джойстик и др.).
Корпус системного блока может иметь горизонтальную (Desk-
Top) или вертикальную (Tower — башня) компоновку. В систем-
ном блоке размещаются основные элементы компьютера, необхо-
димые для выполнения программ:
* микропроцессор (МП), или центральный процессор (CPU, от
англ. Central Processing Unit) — основной рабочий компонент
компьютера, который выполняет арифметические и логичес-
кие операции, заданные программой, управляет вычисли-
тельным процессом и координирует работу всех устройств
компьютера;
" память (внутренняя — системная, включающая ОЗУ и ПЗУ и
внешняя дисковая). ПЗУ (от англ. ROM, Read Only Memory —
память только для чтения) служит для хранения неизменяе-
290
Рис. 6.21. Блок-схема ПЭВМ
291
Рис. 6.22. Состав
персонального компьютера
мой (постоянной) программной и справочной информации.
ОЗУ (от англ. RAM, Random Access Memory — память с про-
извольным доступом) предназначено для оперативной за-
писи, хранения и считывания информации (программ и дан-
ных), непосредственно участвующей в информационно-вы-
числительном процессе, выполняемом ПК в текущий пери-
од времени. Дисковая память относится к внешним устрой-
ствам ПК и используется для долговременного хранения
любой информации, которая может когда-либо потребо-
ваться для решения задач, в ней, в частности, хранится все
программное обеспечение компьютера. В качестве уст-
ройств внешней памяти, размещаемых в системном блоке,
используются накопители на жестких (НЖМД) и гибких
(НГМД) магнитных дисках, накопители на оптических дис-
ках (НОД) и др;
контроллеры (адаптеры) служат для подключения перифе-
рийных (внешних по отношению к процессору) устройств к
шинам микропроцессора, обеспечивая совместимость их
интерфейсов. Они осуществляют непосредственное управ-
ление периферийными устройствами по запросам микро-
процессора. Контроллеры реализуются, как правило, на от-
дельных печатных платах, часто называемых адаптерами
устройств (отлат. adapto — преобразовываю);
системная шина — основная интерфейсная система компь-
ютера, обеспечивающая сопряжение и связь всех его уст-
ройств между собой. Системная шина включает в себя: шину
данных (ТТТД), содержащую провода и схемы сопряжения для
параллельной передачи всех разрядов числового кода (ма-
шинного слова) операнда,
шину адреса (ША), состоя-
щую из проводов и схем со-
пряжения для параллельной
передачи всех разрядов кода
адреса ячейки основной па-
мяти или порта ввода-вывода
внешнего устройства, шину
управления (ШУ), содержа-
щую провода и схемы сопря-
жения для передачи инструк-
292
ций (управляющих сигналов, импульсов) во все блоки ком-
пьютера, и шину питания, имеющую провода и схемы со-
пряжения для подключения блоков ПК к системе энергопи-
тания. Системная шина обеспечивает три направления пе-
редачи информации: между микропроцессором и внутрен-
ней (основной) памятью, между микропроцессором и пор-
тами ввода-вывода внешних устройств, между внутренней
(основной) памятью и портами ввода-вывода внешних уст-
ройств (в режиме прямого доступа к памяти).
Устройства, непосредственно осуществляющие процесс обработ-
ки информации (вычисления), в том числе микропроцессор, опера-
тивная память и шина, размещаются на системной (материнской)
плате компьютера, на ней же располагается и контроллер клавиа-
туры. Схемы, управляющие другими внешними устройствами ком-
пьютера, как правило, находятся на отдельных платах, вставляемых
в унифицированные разъемы (слоты) на материнской плате. Через
эти разъемы контроллеры устройств подключаются непосредствен-
но к системной магистрали передачи данных в компьютере — шине.
Иногда эти контроллеры могут располагаться на системной плате.
Наборы микросхем, на основе которых исполняются системные
платы, называют чипсетами (ChipSets).
В системном блоке располагается также блок питания, преоб-
разующий переменное напряжение электросети в постоянное на-
пряжение различной полярности и величины, необходимое для
питания системной платы и других устройств компьютера, разме-
щенных в системном блоке. Блок питания содержит вентилятор,
создающий циркулирующие потоки воздуха для охлаждения сис-
темного блока, сетевого энергопитания ПК. Кроме сетевого, в ком-
пьютере имеется также автономный источник питания — аккуму-
лятор. К аккумулятору подключается таймер — внутримашинные
электронные часы, обеспечивающие при необходимости автома-
тический съем текущего момента времени (год, месяц, часы, ми-
нуты, секунды и доли секунд). Таймер продолжает работать и при
отключении компьютера от сети.
Важнейшую роль в работе ЭВМ играет контроллер прерываний.
Прерывание — временный останов выполнения одной программы
в целях оперативного выполнения другой, в данный момент более важ-
ной (приоритетной) программы.
293
Контроллер прерываний обслуживает процедуры прерывания,
принимает запрос на прерывание от внешних устройств, определя-
ет уровень приоритета этого запроса и выдает сигнал прерывания
процессору. Процессор, получив этот сигнал, приостанавливает
выполнение текущей программы и переходит к выполнению спе-
циальной программы обслуживания того прерывания, которое зап-
росило внешнее устройство. После завершения программы обслу-
живания восстанавливается выполнение прерванной программы.
6.4.2. Устройства ввода-вывода информации
Устройства вывода информации. Основным устройством вы-
вода информации в ПЭВМ является дисплей. Дисплей (монитор) —
устройство визуального отображения текстовой и графической
информации без ее долговременной фиксации.
Для обозначения этого типа устройств с учетом функций, вы-
полняемых ими в ПК, в английском языке используются как сино-
нимы термины monitor display, monitor, video monitor, video display.
Соответственно в русском переводе также в качестве синонимов
используется ряд терминов, таких как монитор, видеомонитор,
видеодисплей. Мониторы бывают алфавитно-цифровые и графи-
ческие, монохромные и цветного изображения.
В современных ПЭВМ в качестве устройств отображения ин-
формации наиболее широкое распространение получили цветные
графические дисплеи на базе электронно-лучевых трубок, газораз-
рядные и жидкокристаллические дисплеи.
Дисплей на базе электронно-лучевой трубки. Основной элемент
такого дисплея — электронно-лучевая трубка (рис. 6.23), а прин-
цип его работы аналогичен принципу работы телевизора. Форми-
рование изображения производится на внутренней поверхности
экрана, покрытого слоем люминофора — вещества, светящегося
под воздействием электронного луча, генерируемого специальной
«электронной пушкой» и управляемого системами горизонтальной
и вертикальной развертки.
Люминофор наносится в виде наборов точек трех основных цве-
тов — красного, зеленого и синего. Эти цвета называют основными,
потому что их сочетаниями (в различных пропорциях) можно пред-
ставить любой цвет спектра.
Наборы точек люминофора располагаются по треугольным три-
адам (рис. 6.24). Триада образует пиксель — (от англ, pixel — picture
element—элемент картинки) точку, из которых формируется изоб-
ражение.
294
Рис. 6.23. Схема электронно-лучевой трубки
Расстояние между центрами пикселей называется точечным
шагом монитора. Это расстояние существенно влияет на четкость
изображения. Чем меньше шаг, тем выше четкость. В современ-
ных цветных мониторах шаг составляет 0,24 мм и менее. При та-
ком шаге глаз человека воспринимает точки триады как одну точ-
ку «сложного» цвета.
На противоположной стороне трубки расположены три (по коли-
честву основных цветов) электронные пушки. Все три пушки «наце-
лены» на один и тот же пиксель, но каждая из них излучает поток
электронов в сторону «своей» точки люминофора. Чтобы электроны
беспрепятственно достигали экрана, из трубки откачивается воздух,
а между пушками и экраном создается высокое электрическое на-
пряжение, ускоряющее электроны. Перед экра-
ном на пути электронов ставится маска — тонкая
металлическая пластина с большим количеством
отверстий, расположенных напротив точек люми-
нофора. Маска обеспечивает попадание электрон-
ных лучей только в точки люминофора соответ-
ствующего цвета.
Величиной электронного тока пушек и, сле-
довательно, яркостью свечения пикселей, управляет сигнал, посту-
пающий с видеоконтроллера.
Отклоняющая система монитора обеспечивает прохождение
электронным лучом поочередно всех пикселей — строчка за строч-
кой от верхней до нижней, затем возвращается в начало верхней
строки и т. д. (рис. 6.25).
Рис. 6.24.
Пиксельные триады
295
Рис. 6.25. Ход электронного пучка по экрану
Количество отображенных строк в секунду называется строч-
ной частотой развертки. А частота, с которой меняются кадры изоб-
ражения, называется кадровой частотой развертки. Кадровая ча-
стота развертки должна быть такой, чтобы глаз человека не заме-
чал последовательной смены кадров. (Ассоциация видеоэлектрон-
ных стандартов (VESA — Video Electronics Standards Association}
рекомендует частоту не ниже 75 кадров в секунду).
Синхросигналы строчной и кадровой разверток, а также сиг-
налы управления яркостью лучей формируются видеоконтролле-
ром, часто называемым видеокартой, или видеоадаптером. Основ-
ным компонентом видеокарты (рис. 6.26) является память, где хра-
нятся передаваемые процессором числа, характеризующие каж-
дый пиксель монитора. Цифроаналоговые преобразователи пре-
образуют эти числа в аналоговые сигналы, необходимые для рабо-
ты монитора. Для ускорения процесса обработки видеоданных и
разгрузки при этом центрального процессора ЭВМ современные
видеокарты имеют свой собственный видеопроцессор.
Минимальный размер видеопамяти определяется количеством
цветов и разрешающей способностью монитора. Так, для представ-
ления на мониторе 16,7 млн цветов (цвет каждого пикселя задает-
ся 24-разрядным числом) с разрешающей способностью 640x480
пикселей необходимый объем видеопамяти равен 0,9 Мбайт, при
разрешающей способности 800x600 — 1,4 Мбайт.
Газоразрядные и жидкокристаллические дисплеи. Такие дисп-
леи часто называют панелями. Газоразрядную панель образуют два
плоскопараллельных стекла, между которыми размещены мини-
атюрные газоразрядные элементы. В инертном газе газоразрядного
элемента под действием управляющих сигналов, формируемых
296
микропроцессором устройства синхронизации и подаваемых на
прозрачные электроды одного или обоих стекол, возникает раз-
ряд с ультрафиолетовым излучением. Это излучение вызывает све-
чение нанесенного на переднее или заднее стекло люминофора
одного цвета черно-белой панели или люминофоров красного, зе-
леного или синего цветов цветной панели.
Рис. 6.26. Структура видеоконтроллера
Основой жидкокристаллической панели служат также две плос-
копараллельные стеклянные пластины. На одну из них нанесены
прозрачные горизонтальные и вертикальные токопроводящие
электроды. В местах их пересечения укреплены пленочные тран-
зисторы, два вывода которых соединены с электродами на стекле,
а третий образует обкладку конденсатора. Вторую пластину кон-
денсатора представляет прозрачный металлизированный слой на
второй стеклянной пластине, расположенной параллельно первой
на расстоянии, измеряемом микронами. Между пластинами поме-
щено органическое вещество (жидкий кристалл), поворачивающее
под действием электрического поля плоскость поляризации про-
ходящего через него света. С двух сторон панели укреплены поля-
роидные пленки, плоскости поляризации которых повернуты на
90° относительно друг друга (рис. 6.27).
297
Растр телевизионного изображения формируется сигналами,
генерируемыми устройством синхронизации и подаваемыми на
электроды стеклянных пластин. При подаче на эти электроды на-
пряжения в точке их пересечения конденсатор заряжается, и воз-
никает электрическое поле между соответствующими обкладка-
ми конденсатора. В зависимости от величины напряжения изме-
няется угол поляризации жидкого кристалла между обкладками
конденсатора. При отсутствии напряжения и соответственно элек-
трического поля жидкий кристалл поворачивает угол поляризации
света от лампы подсветки на 90°, в результате чего свет свободно
проходит через поляроидные пленки. В зависимости от напряже-
ния на обкладках конденсатора угол поляризации может изменять-
ся от 90° до 0°, а прозрачность ячейки панели — от максимальной
до непропускания света. Панель цветного дисплея содержит крас-
ный, зеленый и синий светофильтры, образующие триаду элемен-
та разложения изображения.
Плоские панели имеют преимущества перед вакуумными кинес-
копами по техническим параметрам, экологической безопасности
и сроку службы. Экран современных ЖК-мониторов (панелей)
с разрешением 1280x1024 имеет до 5 млн точек, каждая из которых
управляется собственным транзистором. Такие мониторы занима-
ют в 2—3 раза меньше места, чем мониторы с ЭЛТ и во столько же
раз легче; потребляют гораздо меньше электроэнергии и не излуча-
ют электромагнитных волн, воздействующих на здоровье людей.
Свет
Лампа
подсветки
Поляризующий
фильтр
Светофильтр
Поляри-
зующий
фильтр
Стеклянная
пластина
Жидкие
кристаллы
Стеклянная --------
пластина
Рис. 6.27. Жидкокристаллический дисплей
298
Сигналы, которые получает монитор (сигналы управления яр-
костью лучей и синхросигналы строчной и кадровой разверток),
формируются соответствующим контроллером, который называ-
ют видеокартой, или видеоадаптером. Монитор преобразует эти
сигналы в зрительные образы.
Другим широко распространенным устройством вывода тексто-
вой и графической информации, обрабатываемой ПЭВМ являет-
ся принтер.
Принтер — печатающее устройство для регистрации информации
на твердый, как правило, бумажный носитель.
Существует огромное количество наименований принтеров. Но
основных видов принтеров три: матричные (игольчатые), лазерные
и струйные.
Матричные принтеры. Их печатающая головка содержит не-
которое количество «иголок», которые под воздействием управ-
ляющих сигналов наносят удар по красящей ленте, благодаря чему
на бумаге остается отпечаток символа. Каждый символ, печатае-
мый на таком принтере, образуется из набора 9 или 24 игл, сфор-
мированных в виде вертикальной колонки. При использовании
многоцветной печатной ленты можно получить цветную печать.
Недостатками этих недорогих принтеров являются их шумная ра-
бота и невысокое качество печати.
Струйные принтеры. Печатное устройство этого принтера пред-
ставляет собой емкость со специальными чернилами, которые через
крошечные сопла под большим давлением выбрызгиваются на бума-
гу. Диаметр полученной таким образом точки на бумаге в десятки
раз меньше, чем диаметр точки от матричного принтера, что обеспе-
чивает значительно лучшее качество печати. Цветные струйные прин-
теры, кроме черного картриджа, дополнительно имеют картридж
с чернилами ярко-голубого, пурпурного и желтого цветов.
Лазерные принтеры. Основным печатающим устройством ла-
зерного принтера (рис. 6.28), так же как ксерокса, является валик-
«барабан», имеющий светочувствительное покрытие, изменяющее
свои электрические свойства в зависимости от освещенности.
Принцип работы лазерного принтера заключается в следующем.
Компьютер формирует в своей памяти «образ» страницы текста
и передает его принтеру. Информация о странице проецируется
с помощью лазерного луча на вращающийся барабан. После чего на
299
Рис. 6.28. Лазерный принтер
барабан, находящийся под электричес-
ким напряжением, наносится красящий
порошок — тонер, частицы которого на-
липают на засвеченные участки повер-
хности барабана. Принтер с помощью
специального горячего валика протяги-
вает бумагу под барабаном; тонер пере-
носится на бумагу и «вплавляется» в нее,
оставляя стойкое высококачественное
изображение. В отличие от лазерных
принтеров в светодиодных принтерах (которые часто также назы-
вают лазерными) информация на барабан проецируется не лазер-
ным лучом, а светодиодной матрицей. Из-за сложности техноло-
гии цветной лазерной печати цветные лазерные принтеры стоят
значительно дороже черно-белых.
Устройства ввода информации. Важнейшими устройствами
ввода информации, которыми укомплектован практически каж-
дый ПК, являются клавиатура и манипулятор типа «мышь».
Клавиатура — клавишное устройство для ручного ввода числовой,
текстовой и управляющей информации в ПК, оно обеспечивает диа-
логовое общение пользователя с ПЭВМ.
Клавиатура содержит стандартный набор клавиш печатной ма-
шинки и некоторые дополнительные клавиши — управляющие и
функциональные клавиши, клавиши управления курсором и ма-
лую цифровую клавиатуру. Все символы, набираемые на клавиа-
туре, немедленно отображаются на мониторе в позиции курсора
(светящийся символ на экране монитора, указывающий позицию,
на которой будет отображаться следующий вводимый с клавиату-
ры знак). В настоящее время наиболее распространена клавиату-
ра с раскладкой клавиш QWERTY (читается «кверти»), названная
так по клавишам, расположенным в верхнем левом ряду алфавит-
но-цифровой части клавиатуры.
Такая клавиатура имеет 12 функциональных клавиш, размещен-
ных вдоль верхнего края. Нажатие функциональной клавиши при-
водит к посылке в компьютер не одного символа, а целой совокуп-
ности символов. Функциональные клавиши могут программиро-
ваться пользователем. Например, во многих программах для полу-
300
чения помощи (подсказки) задействована клавиша F1, а для выхо-
да из программы — клавиша F10.
Название управляющих клавиш и их назначение представле-
ны в табл. 6.2.
Таблица 6.2
Название клавиши Назначение
Enter Клавиша ввода информации, служащая для завершения ввода очередной строки информации
Esc (Escape — выход) Отмена каких-либо действий, выход из программы, из меню и т. п.
Ctrl и Alt Самостоятельного значения не имеют, но при нажатии совместно с другими управляющими клавишами изменяют их действие
Shift Обеспечивает смену регистра клавиш (верхнего на нижний, и наоборот)
Insert Переключает режимы вставки (новые символы вводятся посреди уже набранных, раздвигая их) и замены (старые символы замещаются новыми
Delete Удаляет символ с позиции курсора
Back Space или <— Удаляет символ перед курсором
Home и End Обеспечивают перемещение курсора в первую и последнюю позицию строки соответственно
Page Up и Page Down Обеспечивают перемещение по тексту на одну страницу (один экран) назад и вперед соответственно
Tab Клавиша табуляции, обеспечивает перемещение курсора вправо сразу на несколько позиций до очередной позиции табуляции
Caps Lock Фиксирует верхний регистр, обеспечивает ввод прописных букв вместо строчных
Print Screen Обеспечивает печать информации, видимой в текущий момент на экране
Длинная нижняя клавиша без названия Предназначена для ввода пробелов
Клавиши Т, i, <— и Служат для перемещения курсора вверх, вниз, влево и вправо на одну позицию или строку
Малая цифровая клавиатура используется в двух режимах —
ввода чисел и управления курсором. Переключение этих режимов
осуществляется клавишей Num Lock.
301
Клавиатура содержит встроенный микроконтроллер (местное
устройство управления), который выполняет следующие функции:
последовательно опрашивает клавиши, считывая введенный
сигнал и вырабатывая двоичный скан-код клавиши;
осуществляет буферизацию (временное запоминание до 20
отдельных кодов клавиш на время между двумя соседними
опросами клавиатуры процессором);
управляет световыми индикаторами клавиатуры;
проводит внутреннюю диагностику неисправностей;
осуществляет взаимодействие с центральным процессором.
При поступлении любой информации в буферную память кла-
виатуры посылается запрос на аппаратное прерывание, иниции-
руемое клавиатурой. При выполнении прерывания скан-код пре-
образуется в ASCII и оба кода пересылаются в соответствующее
поле ОЗУ ЭВМ.
ч________________________________________________________
Манипуляторы (мышь, трекбол и др.) — специальные устройства
ввода и управления, облегчающие взаимодействие пользователя и
ПЭВМ.
Несмотря на большое разнообразие форм и размеров манипу-
ляторов типа мышь, они имеют единые принципы работы. При
перемещении мыши по поверхности это перемещение преобра-
зуется в последовательности импульсов, передаваемых в ПК. При
нажатии кнопок мыши их код также передается в ПК, где специ-
альная программа управления мышью (драйвер мыши) преобра-
зует последовательности импульсов и коды нажатия кнопок в оп-
ределенные действия. В зависимости от способа определения пе-
ремещения — механического, связанного с перемещением частей
устройства, или оптического, основанного на фиксации переме-
щения с помощью оптических приборов, различают соответствен-
но механические и оптические мыши.
На рис. 6.29 представлено устройство механической мыши.
Принцип ее работы заключается в следующем.
При перемещении мыши по поверхности расположенный в ее
основании шарик начинает вращаться, приводя в движение рас-
положенные внутри корпуса ролики. Эти ролики смонтированы
относительно друг друга под углом 90° и, соприкасаясь с шариком,
могут вращаться только по часовой или против часовой стрелки,
преобразуя произвольное движение шарика в движение в двух
302
взаимно-перпендикулярных направлениях (X и Y). При перемеще-
нии мыши строго горизонтально или строго вертикально приво-
дится в движение только один из роликов, показывающий движе-
ние либо в направлении X, либо Y соответственно. Электронные
схемы мыши преобразуют движения роликов в последовательно-
сти импульсов, передаваемые в ПЭВМ.
Переключатели
кнопок
К компьютеру
Кнопки
Корпус
Детектор
вращения
ролика
Два ролика,
смонтированных под углом 90°
друг к другу, вращающиеся
при перемещении шарика
Шарик, который
вращается
при перемещении
мыши
Схема,
которая передает
компьютеру информацию
о вращении роликов
и нажатии
переключателей
Рис. 6.29. Устройство механической мыши
Оптическая мышь, в отличие от механической, не имеет ника-
ких движущихся элементов, а для фиксации перемещения исполь-
зуются оптические приборы.
Трекбол по своему функциональному устройству аналогичен
механической мыши, с той лишь разницей, что вместо перемеще-
ния мыши для вращения шарика, пользователь вращает рукой сам
шарик, встроенный в верхнюю часть корпуса. В отличие от мыши,
трекбол не требует свободного пространства около компьютера,
его можно встроить в корпус машины.
303
Одним из широко распространенных манипуляторов, приме-
няемых в компьютерных играх, является джойстик. Обычно это
стержень-ручка, отклонение которой от вертикального положе-
ния приводит к передвижению курсора в соответствующем на-
правлении по экрану монитора. В некоторых моделях в джойстик
монтируется датчик давления. В этом случае, чем сильнее пользо-
ватель нажимает на ручку, тем быстрее движется курсор по эк-
рану дисплея.
Для ввода в ПЭВМ графической информации наиболее часто
используется сканер. Он создает оцифрованное изображение до-
кумента и помещает его в память компьютера. Существуют руч-
ные сканеры, которые прокатывают по поверхности документа
рукой, и планшетные сканеры (рис. 6.30), по внешнему виду напо-
минающие копировальные машины. Принцип работы сканера от-
носительно прост. Луч света (специальная лампа, расположенная
в корпусе сканера) «пробегает» по сканируемой поверхности, при
этом светочувствительными датчиками воспринимается яркость
Рис. 6.30. Планшетный сканер
и цветность отраженного света и
преобразуется в двоичный код.
Введенную с помощью сканера и
графическую, и текстовую ин-
формацию компьютер восприни-
маеткак «картинку», поэтомудля
преобразования графического
текста в обычный символьный
формат используют программы
оптического распознавания об-
разов.
6.4.3. Системная магистраль и шины ЭВМ
Отличительным признаком современных ПЭВМ, построенных
по модульному принципу, является единая системная магистраль
(шина), связывающая все входящие в систему модули [3]. Правила
подключения модулей к магистрали определяются системным
(внутренним) интерфейсом. Различают также внешние интер-
фейсы или интерфейсы периферийного оборудования, задаю-
щие правила сопряжения с устройствами ввода-вывода.
304
Под интерфейсом (interface) понимают совокупность информаци-
онно-логических, электрических и конструктивных требований, вы-
полнение которых обеспечивает работоспособное, с определенными
характеристиками сопряжение различных модулей (элементов, узлов,
устройств) системы.
Информационно-логические требования определяют структуру
и состав линий и сигналов, способы кодирования и форматы дан-
ных, адресов, команд, протоколы обмена для различных режимов и
фаз работы. Информационно-логические условия непосредствен-
но влияют на основные характеристики интерфейса — пропускную
способность, надежность обмена, аппаратурные затраты.
Электрические требования задают необходимые статические
и динамические параметры сигналов на линиях интерфейса: уров-
ни, длительности фронтов и самих сигналов, нагрузочные способ-
ности, уровни помех и т. п.
Конструктивные требования указывают на тип соединительно-
го элемента, распределение линий по контактам соединительного
элемента, допустимую длину линий, геометрические размеры пла-
ты, каркаса и других конструктивных элементов.
Системный интерфейс в целом существенно влияет на все ха-
рактеристики ЭВМ, особенно на производительность, так как
она может ограничиваться не быстродействием микропроцес-
сора, а возможностями магистрали по скорости передачи инфор-
мации.
Когда некоторый модуль выполняет обмен информацией с дру-
гим модулем или несколькими модулями, то первый называют ве-
дущим (master), а второй — ведомым (исполнителем, slave). Веду-
щий модуль управляет магистралью, т. е. генерирует определен-
ную последовательность сигналов, обеспечивающую выполнение
требуемой операции. Ведомый модуль посылает сигналы в магис-
траль только в ответ на соответствующие сигналы ведущего. Сиг-
налы между модулями передаются по линиям — электрическим
цепям, связывающим одноименные контакты на всех соедините-
лях (разъемах) магистрали. Как правило, линия и сигнал, который
по ней передается, называются и обозначаются одинаково. Сово-
купность линий, передающих сигналы одного функционального
назначения, называют шиной (bus). Отметим, что в англоязычной
литературе термин bus используется для обозначения и шины,
20 А-210
305
и магистрали. Различают следующие основные шины системной
магистрали:
• шину данных, предназначенную для передачи кодов данных
между модулями, характеризуется своей разрядностью, фак-
тически это количество линий в шине. Некоторые магистра-
ли допускают изменение разрядности передаваемых кодов
данных (но не шины) в процессе функционирования;
ш ину адреса, обеспечивающую выбор ведущим модулем тре-
буемого ведомого (передает адрес модуля), а внутри ведомо-
го модуля — выбор требуемого элемента, например ячейки
памяти (передает адрес ячейки) или регистра контроллера
ввода-вывода (передает адрес порта устройства ввода-выво-
да) . Адресная шина также характеризуется разрядностью —
количеством линий. В некоторых магистралях коды адреса
и данных передаются по одним и тем же линиям. Такую шину
называют мультиплексируемой шиной адреса/данных;
* шину управления, включающую в себя линии, по которым пе-
редаются сигналы управления обменом, запросы прерыва-
ния, сигналы синхронизации и т. п.;
* шину питания, подводящую питающие напряжения ко всем
потребителям, подключенным к магистрали.
Различают три фазы (режима) работы магистрали: обмена, ар-
битража, обработки прерываний [3].
В фазе обмена происходит передача информационного кода
между ведущим и ведомым модулями. В этой фазе выполняется
одна из двух операций: чтение, когда код данных передается из
ведомого модуля в ведущий, или запись, когда код данных переда-
ется из ведущего модуля в ведомый. Существуют два основных спо-
соба организации обмена — асинхронный и синхронный. Отли-
чительная особенность асинхронной организации заключается во
взаимной зависимости смены состояний ведущим и ведомым мо-
дулями (рис. 6.31 а). Ведущий модуль устанавливает на шине адре-
са код адреса модуля и элемента в модуле, из которого он хочет
получить информацию. Сигналом «Чтение» ведущий сообщает
всем модулям, что он начинает операцию чтения и что адрес уже
установлен на шине. Все модули, подключенные к магистрали, ана-
лизируют адрес. Однако активизируется только тот модуль, кото-
рому принадлежит установленный на шине адрес, он и становит-
ся ведомым. Этот модуль считывает код данных из требуемого эле-
мента (ячейки ЗУ или порта ввода-вывода) и выставляет его на
306
шину данных. Истинность кода ведомый подтверждает сигналом
готовности данных. Только получив сигнал готовности, ведущий
может принимать данные. Завершив прием, ведущий снимает ад-
рес и сигнал «Чтение». Теперь и ведомый может снять код данных
с шины и сбросить сигнал готовности. На этом фаза обмена завер-
шается. При такой организации не требуется никаких особых сиг-
налов синхронизации.
Шина
адреса
Истинный адрес
из ведущего
Чтение
Сигнал генерируется ведущим
Шина
данных
Данные
из ведомого
Сигнал генерируется
Готовность
данных
Рис. 6.31. Организация обмена в магистрали:
а) асинхронное чтение; б) синхронное чтение
307
При синхронном способе смена состояний модулей, участвую-
щих в обмене, происходит в строго оговоренные моменты времени,
определяемые специальным сигналом синхронизации. На рис. 6.31 б
показан пример синхронной организации обмена. Операция обя-
зана завершиться за три такта. Причем в первом такте ведущий
модуль должен выставить адрес и управляющий сигнал, определя-
ющий операцию, в рассматриваемом примере — низкий уровень
сигнала «Чтение». Ведомый модуль, распознав в первом такте, что
ведущий обращается к нему и желает прочитать содержимое неко-
торого элемента (ячейки ЗУ или порта ввода-вывода), должен во вто-
ром такте выбрать эту информацию и выставить ее на шину дан-
ных. Ведущий модуль всегда принимает код данных в начале тре-
тьего такта и затем снимает адрес и сигнал «Чтение». На этом опе-
рация завершается. Важно, что модули работают совершенно неза-
висимо и при выполнении всех временных требований нет необхо-
димости в сигнале подтверждения готовности данных от ведомого.
Считается, что асинхронная организация обмена упрощает сопря-
жение устройств с различной скоростью передачи данных, но сни-
жает пропускную способность магистрали. Синхронная организа-
ция позволяет достичь максимальных скоростей, но затрудняет
связь между устройствами, существенно различающимися по вре-
менным характеристикам. Для устранения последнего недостатка
в реальных синхронных магистралях так или иначе вводится под-
тверждение готовности ведомого к выполнению операции.
Возможны случаи, когда нескольким модулям одновременно не-
обходимо выполнить обмен. Но магистраль одна, и пользоваться ею
в каждый отдельный момент времени может только один ведущий.
Поэтому возникает необходимость в фазе арбитража, в которой
выбирается один модуль из всех, желающих стать ведущим. Выб-
ранному модулю и предоставляется право управления магистралью.
Существуют два принципиально различных способа арбитра-
жа [3]. Первый — централизованный, параллельный (рис. 6.32 а).
В этом случае к магистрали подключается специальный модуль —
арбитр (контроллер) магистрали, имеющий входы запроса и вы-
ходы разрешения. Каждый модуль, который пытается стать веду-
щим, формирует сигналы запроса магистрали (ЗМ) и передает их
арбитру. Последний по некоторому алгоритму выбирает модуль,
который должен стать ведущим в очередной фазе обмена, и сооб-
щает ему об этом, формируя сигнал разрешения (Р) на занятие
магистрали. Фаза арбитража на этом завершается и начинается
фаза обмена под управлением выбранного модуля.
308
Второй способ арбитража — последовательный (цепочечный,
daisy-chain). Все потенциально ведущие модули пронизывает линия
(цепочка) разрешения занятия магистрали (рис. 6.32 б). Так, пусть
модуль 2 пытается захватить управление. При этом в фазе арбитра-
жа он разрывает цепочку и анализирует состояние входа разреше-
ния. Если на входе установлена логическая единица, т. е. ни один
модуль, расположенный правее, не разорвал линию и, следователь-
но, не требует магистрали, то модуль 2 может ее занимать. Если на
входе разрешения отсутствует единичный сигнал, то какой-то мо-
дуль справа тоже стремится выполнить обмен, и управление шиной
получает он, а не модуль 2. Таким образом, между модулями уста-
навливается «географический» приоритет — чем правее, тем при-
оритетнее (для нашего примера), и никакого специального арбитра
не требуется. Фактически при последовательном способе арбитр
магистрали как бы распределяется между всеми модулями, в каж-
дом из которых есть схемы, выполняющие его функции.
б)
Рис. 6.32. Арбитраж магистрали:
а) централизованный параллельный арбитраж; б) последовательный арбитраж
309
И последовательный, и параллельный способы допускают час-
тичное или полное совмещение фазы обмена и фазы арбитража.
Это требует дополнительной регламентации и дополнительных
линий. Например, вводится линия «Занято», и модулям разреша-
ется запрашивать магистраль, только если она свободна (на линии
«Занято» низкий уровень). Получив управление шиной, ведущий
модуль переводит линию в единичное состояние. Следовательно,
пока ведущий модуль не завершит обмен, никакой другой, даже
старший по приоритету, не получит управление магистралью, но
и никаких специально выделенных тактов для арбитража не тре-
буется. К преимуществам параллельного арбитража относятся
малое время выбора ведущего, возможность программной на-
стройки системы приоритетов между модулями. Но количество
ведущих модулей, подключаемых к магистрали, ограничивается
количеством входов и выходов арбитра. И схемно, и организаци-
онно более прост последовательный способ, однако его эффектив-
ность снижается большими задержками в распространении сиг-
нала разрешения по длинной цепочке и невозможностью про-
граммного управления приоритетами модулей. Реальные магист-
рали допускают то или иное совмещение двух основных способов
арбитража, позволяющее сочетать достоинства каждого.
Фаза прерывания наступает, когда некоторый модуль стремит-
ся обратить внимание ведущего на свое состояние. Например,
принтер завершил печать сообщения и может печатать следующее,
контроллер должен сообщить об этом процессору. Или в процессе
передачи группы данных в память из дискового накопителя про-
изошла ошибка, канал прямого доступа должен немедленно поста-
вить в известность об этом процессор. Организация прерываний
в системных магистралях достаточно проста, пока допускается
только один обработчик прерываний, как правило, процессорный
модуль, а само количество запросов невелико. В шине управления
выделяется несколько линий, по которым запросы от всех уст-
ройств передаются обработчику. Получив запрос или запросы,
обработчик инициализирует на магистрали фазу прерывания, во
время которой происходит выделение наиболее приоритетного
запроса и идентификация модуля, который его выставил. Фаза
прерывания завершается передачей в процессор вектора преры-
вания — кода адреса программы, обслуживающей данное устрой-
ство. При росте числа источников запросов и ограниченном коли-
честве линий их передачи усложняется организация прерываний.
310
Вводятся, например, линии последовательной передачи запросов
типа daisy-chain и программный поиск в цепочке устройства, выс-
тавившего запрос. Если разрешается подключение к магистрали
нескольких обработчиков (мультипроцессорные системы), то орга-
низация прерываний еще более усложняется. Принципиальным
преодолением этих затруднений является введение виртуальных
прерываний — передачи сообщений специального вида между
модулями в стандартных фазах обмена. Виртуальные прерывания
полностью снимают проблемы количества запросов, их идентифи-
кации и множественности обработчиков. Однако реакция на зап-
росы при этом замедляется, что существенно при использовании
ЭВМ в системах реального времени.
В качестве системной магистрали в современных ПЭВМ исполь-
зуются:
шины расширений — шины общего назначения, позволяю-
щие подключать большое число самых разнообразных уст-
ройств;
локальные шины, специализирующиеся на обслуживании
устройств определенного типа.
Рассмотрим кратко основные из них [13].
ISA (Industry Standard Architecture — архитектура промышлен-
ного стандарта). Это 16-разрядная шина с 24 адресными линиями
(адресное пространство шины — 16 Мбайт), с 16 линиями аппа-
ратных прерываний и с 8 каналами DMA (Direct Memory Access,
прямого доступа к памяти). Несмотря на низкую пропускную спо-
собность (шина ISA работает асинхронно на частоте 8 МГц, ско-
рость обмена данными — до 5,5 Мбайт/с), эта шина продолжает
использоваться в компьютерах для подключения сравнительно
«медленных» внешних устройств, например звуковых карт и мо-
демов.
EISA. Расширением стандарта ISA стал стандарт EISA (Extended
ISA), имеющий 32-разрядную шину данных и 32-разрядную шину
адреса (адресное пространство шины — 4 Гбайт) и увеличенную
производительность (до 32 Мбайт/с). Как и ISA, в настоящее вре-
мя данный стандарт считается устаревшим.
VLB (VESA LocalBus — локальная шина стандарта VESA). Раз-
работана в 1992 г. Ассоциацией стандартов видеооборудования
(VESA— Video Electronics Standards Association), поэтому ее часто
называют шиной VESA. Понятие «локальной шины» впервые по-
явилось в конце 80-х годов XX века. Оно связано с тем, что при
311
внедрении процессоров третьего и четвертого поколений (Intel
80386 и Intel 80486) частоты основной шины (в качестве основной
использовалась шина ISA/EISA) стало недостаточно для обмена
между процессором и оперативной памятью. Локальная шина,
имеющая повышенную частоту, связала между собой процессор
и память в обход основной шины. Впоследствии в эту шину «вре-
зали» интерфейс для подключения видеоадаптера, который тоже
требует повышенной пропускной способности, — так появился
стандарт VLB, который позволил поднять тактовую частоту ло-
кальной шины и обеспечил пиковую пропускную способность до
130 Мбайт/с. В настоящее время данный стандарт не использует-
ся.
PCI (Peripheral Component Interconnect — стандарт подключения
внешних устройств). Шина PCI разработана в 1993 г. фирмой Intel.
По своей сути это тоже интерфейс локальной шины, связываю-
щей процессор с оперативной памятью, в которую врезаны разъ-
емы для подключения внешних устройств. Для связи с основной
шиной компьютера (ISA/EISA) используются специальные интер-
фейсные преобразователи — мосты PCI (PCI Bridge). В современ-
ных компьютерах функции моста PCI выполняют микросхемы
микропроцессорного комплекта (чипсета). Шина может работать
параллельно с шиной процессора, т. е. обмен данными процессор —
память и, например, видеоадаптер — память может осуществлять-
ся параллельно. Шина PCI является синхронной 32-разрядной или
64-разрядной шиной, работающей на частоте 33 или 66 МГц. Шина
PCI при частоте 33 МГц обеспечивает пропускную способность
132 Мбайт/с, при частоте до 66 МГц обеспечивают производитель-
ность 264 Мбайт/с для 32-разрядных данных и 528 Мбайт/с для
64-разрядных данных.
FSB. Шина PCI, появившаяся в компьютерах на базе процессо-
ров Intel Pentium как локальная шина, предназначенная для связи
процессора с оперативной памятью, недолго оставалась в этом ка-
честве. Сегодня она используется только как шина для подключе-
ния внешних устройств, а для связи процессора и памяти, начиная
с процессора Intel Pentium Pro применяется специальная шина,
получившая название Front Side Bus (FSB). Эта шина работает на
частоте от 100 МГц и выше. Пропускная способность шины FSB
при частоте 100 МГц составляет порядка 800 Мбайт/с.
AGPfAdvanced Graphic Port — усовершенствованный графичес-
кий порт). Видеоадаптер — устройство, требующее особенно вы-
312
сокой скорости передачи данных. Как при внедрении локальной
шины VLB, так и при внедрении локальной шины PCI, видеоадап-
тер всегда был первым устройством, «врезаемым» в новую шину.
Сегодня параметры шины PCI уже не соответствуют требованиям
видеоадаптеров, поэтому для них разработана отдельная шина,
получившая название AGP.
Другие локальные шины: IDE (Integrated Device Electronics), EIDE
(Enhanced IDE), SCSI (Smati Computer System Interface) используют-
ся чаще всего в качестве интерфейса только для внешних запоми-
нающих устройств.
6.4.4. Организация ввода-вывода информации в ЭВМ
В системах ввода-вывода большинства современных ЭВМ мож-
но выделить два уровня сопряжения внешних устройств (ВУ) с про-
цессором и памятью [6]. На первом уровне контроллеры ВУ сопря-
гаются с процессором и памятью через системный интерфейс
ЭВМ, который обеспечивает комплексирование отдельных уст-
ройств ЭВМ в единую систему. На втором уровне сопряжения кон-
троллеры посредством шин связи соединяются с соответствующи-
ми внешними устройствами ЭВМ.
На первом уровне сопряжения набор шин интерфейса ввода-
вывода и алгоритм его функционирования полностью определя-
ются системным интерфейсом ЭВМ. Несмотря на широкое раз-
нообразие системных интерфейсов ЭВМ, в общем случае можно
выделить два основных способа использования системного интер-
фейса для организации обмена информацией с ВУ: 1) с примене-
нием специальных команд ввода-вывода; 2) по аналогии с обраще-
ниями к памяти.
Рассмотрим, как используются для обмена информацией с ВУ
шины адреса и данных системных интерфейсов ЭВМ и какие не-
обходимы для этого управляющие сигналы [6].
При использовании для обмена с ВУ команд ввода-вывода ад-
рес (номер) ВУ передается по шине адреса. Однако по этой же шине
передаются и адреса ячеек памяти. Информация на шине адреса
имеет смысл адреса (номера) ВУ только при наличии специальных
управляющих сигналов. Такими сигналами могут быть, например,
«Ввод из ВУ» и «Вывод в ВУ» (рис. 6.33, а), инициируемые соответ-
ствующими командами ввода-вывода ЭВМ [6].
313
а) б)
Рис. 6.33. Простейшее сопряжение контроллера ВУ с системным интерфейсом:
а) с применением специальных команд ввода-вывода;
б) по аналогии с обращением к памяти
Для синхронизации работы процессора ЭВМ и контроллеров
ВУ, а точнее, для указания моментов времени, определяющих го-
товность данных в ВУ для передачи либо подтверждающих их при-
ем, может служить управляющий осведомительный сигнал «Готов-
ность ВУ».
Такого простого набора управляющих сигналов в общем слу-
чае достаточно для организации программно-управляемого обме-
на данными с ВУ на первом уровне (процессор — контроллер ВУ).
Порядок использования описанных выше управляющих сигналов
при выполнении операций ВВОД и ВЫВОД проиллюстрирован
рис. 6.34.
Операция ВЫВОД, инициируемая соответствующей коман-
дой микропроцессора, выполняется следующим образом. Мик-
ропроцессор выставляет на линиях адресной шины адрес (но-
мер) ВУ, на линиях шины данных — значения разрядов выводи-
мого слова данных и единичным сигналом по линии «Вывод
в ВУ» указывает тип операции. Адресуемый контроллер ВУ при-
нимает данные, пересылает их в ВУ и единичным сигналом по
линии «Готовность ВУ» сообщает процессору, что данные при-
няты ВУ и можно снять информацию с шин адреса и данных,
а также сигнал «Вывод в ВУ».
314
обмена *
Адрес
Ввод
из ВУ
Данные
Готовность
ВУ
а) б)
Рис. 6.34. Временные диаграммы операций для простейшего набора
управляющих сигналов: а) ВЫВОД; б) ВВОД
Выполнение операции ВВОД начинается с того, что микропро-
цессор выставляет на линиях адресной шины адрес (номер) ВУ
и единичным сигналом на линии «Ввод из ВУ» указывает тип вы-
полняемой операции. По сигналу «Ввод из ВУ» контроллер адре-
суемого ВУ считывает слово данных из ВУ, выставляет на линиях
шины данных значения разрядов считанного слова и единичным
сигналом по линии «Готовность ВУ» сообщает об этом процессо-
ру. Приняв данные из контроллера ВУ, процессор снимает сигна-
лы с шины адреса и линии «Ввод из ВУ».
При реализации в ЭВМ обмена с ВУ по аналогии с обращения-
ми к памяти отпадает необходимость в специальных сигналах, ука-
зывающих, что на шине адреса находится адрес ВУ. Для адресов
ВУ отведена часть адресного пространства ЭВМ, и в контроллерах
ВУ удается легко организовать селекцию адресов ВУ — выделение
собственного адреса ВУ из всего множества адресов, передавае-
мых по линиям адресной шины. Однако остается необходимость
передавать в ВУ приказ на ввод или вывод информации. Для этих
целей используются линии управляющей шины «Чтение» и «За-
пись», обеспечивающие обмен информацией микропроцессора
с модулями памяти (см. рис. 6.33 б).
315
Временные диаграммы операций ВВОД и ВЫВОД при органи-
зации обмена с ВУ по аналогии с памятью полностью соответству-
ют рассмотренным ранее (см. рис. 6.34).
Приведенный минимальный набор управляющих (осведомитель-
ных) сигналов позволяет организовать обмен с ВУ не только в асин-
хронном режиме, но и в режиме прерывания программы. Однако при
этом существенно усложняются алгоритмы использования управля-
ющих сигналов и, как следствие, аппаратура для их обработки. Более
рациональным оказывается увеличение числа управляющих сигна-
лов с тем, чтобы каждый режим обмена идентифицировался отдель-
ным сигналом или набором сигналов. Для этого в системных интер-
фейсах вводятся линии для передачи сигналов запроса на прерыва-
ние и предоставления прерывания, запроса на предоставление пря-
мого доступа к памяти и его предоставления и т. п.
Но в ЭВМ необходимо управлять еще и режимами работы кон-
троллеров разнообразных ВУ, многие из которых являются доста-
точно сложными устройствами. При этом каждый контроллер вос-
принимает определенный, присущий только данному ВУ набор
команд управления (приказов ВУ). Организовать в этом случае
передачу каждого приказа ВУ по отдельной линии системного ин-
терфейса не представляется возможным по двум причинам. Во-
первых, при разработке микропроцессора и системного интерфей-
са достаточно трудно предусмотреть все возможные применения
ЭВМ на его основе, а следовательно, и используемые в ЭВМ ВУ.
И во-вторых, для каждого дополнительного управляющего сигна-
ла потребуется отдельный вывод в БИС микропроцессора. Таким
образом, возникают чисто конструктивные ограничения на коли-
чество используемых в системном интерфейсе управляющих сиг-
налов, связанных с числом выводов в БИС микропроцессора [6].
Решение указанной проблемы осуществляется путем мульти-
плексирования шины данных, т. е. использования ее для обмена
с контроллерами ВУ как данными (в одни моменты времени), так и
частью управляющей информации (в другие моменты времени).
Однако пересылаемая информация должна размещаться в различ-
ных регистрах контроллера ВУ: данные — в регистре данных,
а управляющая информация — в одном или нескольких регистрах
состояния и управления (количество этих регистров возрастает
с увеличением сложности ВУ и уменьшением разрядности переда-
ваемых слов, т. е. разрядности шины данных). Это ставит новую за-
дачу — выбор одного или нескольких регистров контроллера ВУ.
316
Наиболее просто эта задача решается выделением каждому ре-
гистру контроллера собственного адреса в системе адресов ЭВМ.
В этом случае организация обмена информацией микропроцессо-
ра с регистрами контроллеров не потребует дополнительных ли-
ний системного интерфейса, так как для адресации регистров ис-
пользуется шина адреса. Таким образом, в ЭВМ каждому ВУ выде-
ляется столько адресов, сколько регистров в его контроллере.
Итак, подключение любого внешнего устройства к ЭВМ осуще-
ствляется через контроллер ВУ, при этом способы структурной и
функциональной организации контроллеров ВУ определяются дву-
мя основными факторами:
форматами данных и режимами работы конкретных ВУ;
типом системного интерфейса ЭВМ.
Влияние первого из этих факторов на организацию контролле-
ров ВУ достаточно очевидно. В самом деле, нерационально было
бы создавать единый универсальный контроллер, обеспечиваю-
щий, например, подключение к компьютеру простых устройств
типа цифровых индикаторов и сложных устройств типа накопи-
телей на магнитных дисках. Именно поэтому на практике приме-
няют самые разнообразные контроллеры ВУ: от простейших для
подключения к ЭВМ датчиков одиночных сигналов до очень слож-
ных, сравнимых по сложности с процессорами ЭВМ, например,
для сопряжения ЭВМ с аппаратурой видеозаписи.
Второй фактор — тип интерфейса — определяет способ орга-
низации электронных схем контроллеров ВУ, обеспечивающих
связь с шинами интерфейса, в первую очередь — схем распозна-
вания адресов ВУ.
Однако такое положение дел, когда для каждого типа ВУ требу-
ется уникальный контроллер, не устраивало ни разработчиков
средств вычислительной техники (ЭВМ и ВУ), ни ее пользовате-
лей. Наиболее перспективным оказался путь стандартизации на-
бора информационных и управляющих сигналов, которыми обме-
ниваются контроллер и ВУ. Так, для разных типов ЭВМ были раз-
работаны контроллеры, обеспечивающие связь с ВУ по стан-
дартному параллельному и по стандартному последовательному
каналам передачи данных.
Рассмотрим типичные структуры контроллеров ВУ, применяемых
в ЭВМ с различными системными интерфейсами [6]. На рис. 6.35 а
приведена блок-схема типичного контроллера ВУ, обеспечиваю-
щего программно-управляемый обмен информацией с ВУ (опера-
ции ВВОД и ВЫВОД).
317
Системный интерфейс Системный интерфейс
б)
Рис. 6.35. Блок-схема типичного контроллера ВУ для системного интерфейса:
а) с раздельными шинами адреса и данных;
б) с мультиплексированной шиной «адрес/данные»
318
Основу контроллера ВУ составляют несколько регистров, ко-
торые служат для временного хранения передаваемой информа-
ции. Каждый регистр имеет свой адрес, и часто такие регистры
называют портами ввода-вывода. Регистры входных и выходных
данных работают соответственно только в режиме чтения и толь-
ко в режиме записи. Регистр состояния работает только в режиме
чтения и содержит информацию о текущем состоянии ВУ (вклю-
чено/выключено, готово/не готово к обмену данными и т. п.). Ре-
гистр управления работает только в режиме записи и служит для
приема из ЭВМ приказов для ВУ. В контроллерах, используемых
для подключения достаточно простых ВУ (клавиатура, мышьит.п.),
удается совместить в один регистры состояния и управления, что
позволяет сократить количество используемых в контроллере пор-
тов ввода-вывода, а следовательно, и адресов, выделенных для дан-
ного ВУ.
Логика управления контроллера ВУ выполняет селекцию адре-
сов регистров контроллера, прием, обработку и формирование
управляющих сигналов системного интерфейса, обеспечивая тем
самым обмен информацией между регистрами контроллера и ши-
ной данных системного интерфейса ЭВМ.
Приемопередатчики шин адреса и данных служат для физичес-
кого подключения электронных схем контроллера к соответству-
ющим шинам системного интерфейса.
На рис. 6.35 б приведена блок-схема типичного контроллера ВУ
для системного интерфейса с мультиплексируемой шиной «адрес/
данные». Сравнение двух контроллеров показывает, что между
ними нет принципиальных различий в порядке использования ре-
гистров. Различия в структурах контроллеров, вызванные различ-
ной организацией системных интерфейсов, проявляются только в
построении логики управления (по-разному организованы прием
и селекция адресов) и способе подключения к шинам системного
интерфейса [6].
В настоящее время используются в основном программируемые
контроллеры, режимы работы которых устанавливаются специаль-
ными командами ЭВМ или определяются программами обмена с
ВУ. Программируемые контроллеры настраивают на конкретный
режим обмена данными, присущий ВУ: синхронный или асинхрон-
ный, с использованием сигналов прерывания или без их использо-
вания, на заданную скорость обмена и т. д.
319
Настройка таких контроллеров на требуемый режим обмена
производится программным путем с помощью специальных ко-
манд (управляющих слов), передаваемых из процессора в контрол-
лер ВУ перед началом обмена. Управляющее слово записывается в
специальный регистр и инициирует заданный режим обмена с ВУ.
Стандартизация интерфейсов ввода-вывода и использование
БИС для реализации логических схем интерфейсов и контроллеров
ВУ позволяет конструктивно реализовать контроллер (интерфейс
ввода-вывода) на материнской плате либо непосредственно в ВУ.
Такая реализация интерфейсов и контроллеров создает у пользова-
теля иллюзию их отсутствия и некоторую несогласованность
в структурных и функциональных схемах ЭВМ. Тем не менее в лю-
бой ЭВМ всегда можно достаточно четко выделить компоненты си-
стемы ввода-вывода, что крайне необходимо при изучение как ЭВМ,
так и способов их использования в различных системах.
Примерами контроллеров, как правило, располагаемых на ма-
теринских платах современных ПЭВМ, могут служить устройства
последовательного и параллельного интерфейсов, называемые так-
же последовательным и параллельным портами соответственно.
Контроллеры дисковых накопителей размещаются непосредствен-
но на диске, а контроллеры видеомонитора, называемые также
видеоадаптерами, — на отдельной плате (видеоплате).
6.5. СИСТЕМЫ ПАРАЛЛЕЛЬНОЙ ОБРАБОТКИ ДАННЫХ
Любая вычислительная система (будь то суперЭВМ или персо-
нальный компьютер) достигает своей наивысшей производитель-
ности благодаря использованию высокоскоростных элементов и
параллельному выполнению большого числа операций. Именно
возможность параллельной работы различных устройств системы
является основой ускорения основных операций.
Параллелизм — параллельное выполнение двух или более процес-
сов (программ).
Параллельное выполнение нескольких процессов может быть
реализовано путем следующих аппаратных решений:
многомашинности;
320
мультипроцессорности;
* однопроцессорности с несколькими исполнительными уст-
ройствами;
конвейеризации обработки данных.
Типичными примерами двух последних подходов являются спе-
циализированные векторные процессоры, использующие паралле-
лизм обработки, допускаемый векторно-матричными вычислениями.
Векторная обработка — единообразная обработка последователь-
ностей данных, встречающаяся, как правило, при манипулировании
матрицами (элементами которых являются векторы) или другими ин-
формационными массивами.
Векторные процессоры включают в свой состав векторные и
скалярные исполнительные устройства с быстрыми регистрами
и индексной арифметикой и имеют производительность почти на
порядок выше по сравнению с традиционными процессорами ска-
лярного типа. Конвейеризация обработки данных расширяет па-
раллелизм во времени вычислительного процесса за счет увеличе-
ния числа исполнительных устройств. Основу конвейерной обра-
ботки составляет раздельное выполнение некоторой операции
в несколько этапов. При этом, когда первый этап завершается, ре-
зультаты передаются на второй этап, на котором используются
другие аппаратные средства. Устройство, используемое на первом
этапе, используется для начала обработки новых данных.
Конвейерная обработка — вид обработки, при котором обработ-
ка в функциональном узле вычислительной системы разбивается на
несколько этапов.
Такая технология обеспечивает быструю обработку последова-
тельных процессов, но требует использования сложного управля-
ющего устройства, которое должно вести учет операций, выпол-
няемых одновременно. Производительность при этом возрастает
благодаря тому, что одновременно на различных ступенях конвей-
ера выполняются несколько операций. Конвейеризация эффек-
тивна только тогда, когда загрузка конвейера близка к полной,
а скорость подачи новых операндов соответствует максимальной
производительности конвейера. Если происходит задержка, то па-
21 А-210
321
раллельно будет выполняться меньше операций и суммарная про-
изводительность снизится. Идеальную возможность полной загруз-
ки вычислительного конвейера обеспечивают векторные операции.
В многомашинной вычислительной системе каждый компьютер,
входящий в систему, имеет классическую архитектуру. Такая сис-
тема применяется достаточно широко, однако эффект от ее при-
менения может быть получен только при решении задач, имею-
щих специальную структуру: она должна разбиваться на столько
слабо связанных подзадач, сколько компьютеров в системе.
В настоящее время существует ряд классификаций параллель-
ных архитектур вычислительных систем (Flynn, Share, структурная
и др.), однако они не охватывают всего спектра параллелизма и раз-
нообразия существующих и разрабатываемых параллельных струк-
тур. Все параллельные вычислительные системы являются мульти-
процессорными с различной архитектурой. При их описании часто
используют классификацию Флинна, в которой, определен парал-
лелизм потока команд и параллелизм потока данных в системе. Со-
гласно этой классификации системы делятся на четыре категории:
• SISD (Single Instruction Single Data) — система с одним пото-
ком команд и одним потоком данных;
SIMD (Single Instruction Multiple Data) — система с одним по-
током команд и несколькими потоками данных;
• MISD (Multiple Instruction Single Data) — система с несколь-
кими потоками команд и одним потоком данных;
MIMD (Multiple Instruction Multiple Data) — система с несколь-
кими по токами команд и несколькими потоками данных.
Первая из этих систем — SISD — представляет собой обычный
процессор последовательной обработки. Третья система—M1SD —
в существующих устройствах обработки данных практически не
встречается. Наибольший интерес для мультипроцессорных сис-
тем представляют две оставшиеся архитектуры. Система SIMD
пригодна для обработки данных, представленных в виде векторов
и матриц; здесь используется преимущество внутреннего парал-
лелизма данных такого типа. В качестве примера такой системы
можно привести матричный процессор.
Матричный процессор — ЭВМ или процессор со специальной ар-
хитектурой, рассчитанной на обработку числовых массивов, напри-
мер матриц.
322
Эта архитектура включает в себя матрицу процессорных элемен-
тов (например, 64x64), работающих одновременно. Каждый из них
обрабатывает один элемент матрицы, так что за одну операцию мо-
гут быть параллельно обработаны все элементы матрицы. Чтобы
получить тот же самый результат при использовании обычного про-
цессора, надо обрабатывать каждый элемент матрицы последова-
тельно, поэтому время вычислений значительно больше. Матрич-
ный процессор может быть выполнен в виде отдельного блока, под-
ключаемого к основному компьютеру через порт ввода-вывода или
внутреннюю шину. Это может быть также распределенный матрич-
ный процессор, обрабатывающие элементы которого распределе-
ны по всей вычислительной системе и тесно связаны с определен-
ной частью памяти ЭВМ. В отличие от ограниченного конвейерно-
го функционирования векторного процессора, матричный процес-
сор (синоним для большинства SIMD-машин) может быть значитель-
но более гибким. Обрабатывающие элементы таких процессоров -
это универсальные программируемые ЭВМ, так что задача, реша-
емая параллельно, может быть достаточно сложной и содержать вет-
вления. Матричные процессоры — очень мощное средство реше-
ния задач, характеризующихся высокой степенью параллелизма.
Однако они требуют другого подхода к программированию. Преоб-
разование обычных (последовательных) программ с целью их реа-
лизации на матричных процессорах представляет собой непростую
задачу, и часто приходится выбирать иной (параллельный) алгоритм,
который был бы пригоден для параллельной обработки.
Система MIMD представляет широкий диапазон архитектур —
от больших симметричных мультипроцессорных систем до неболь-
ших асимметричных миниЭВМ в комбинации с каналами прямо-
го доступа к памяти. В такой системе, как правило, каждый про-
цессорный элемент (ПЭ) выполняет свою программу достаточно
независимо от других процессорных элементов. В мультипроцес-
сорах с общей памятью (сильносвязанных мультипроцессорах)
имеется память данных и команд, доступная всем ПЭ. С общей
памятью ПЭ связываются с помощью общей шины или сети обме-
на. В противоположность этому варианту в слабосвязанных мно-
гопроцессорных системах (машинах с локальной памятью) вся па-
мять делится между процессорными элементами и каждый блок
памяти доступен только связанному с ним процессору. Сеть обме-
на связывает процессорные элементы друг с другом.
Базовой моделью вычислений на MIMD-мультипроцессоре яв-
ляется совокупность независимых процессов, эпизодически обра-
щающихся к разделяемым данным. Существует большое количество
323
вариантов этой модели. На одном конце спектра — модель распре-
деленных вычислений, в которой программа делится на довольно
большое число параллельных задач, состоящих из множества под-
программ. На другом конце спектра — модель потоковых вычисле-
ний, в которых каждая операция в программе может рассматривать-
ся как отдельный процесс. Такая операция ждет своих входных дан-
ных (операндов), которые должны быть переданы ей другими про-
цессами. По их получении операция выполняется и полученное зна-
чение передается тем процессам, которые в нем нуждаются.
Многопроцессорные системы за годы развития вычислитель-
ной техники претерпели ряд этапов своего развития. Историчес-
ки первой стала осваиваться технология SIMD. Однако в настоя-
щее время наметился устойчивый интерес к архитектурам MIMD.
Большинство самых быстрых вычислительных систем в мире мож-
но отнести к MIMD архитектуре, при этом их относительное коли-
чество увеличивается. Интерес к MIMD системам главным обра-
зом определяется двумя факторами:
Архитектура MIMD дает большую гибкость: при наличии адек-
ватной поддержки со стороны аппаратных средств и программно-
го обеспечения MIMD система может работать как однопользова-
тельская система, обеспечивая высокопроизводительную обработ-
ку данных для одной прикладной задачи, как многопрограммная
машина, выполняющая множество задач параллельно, и как неко-
торая комбинация этих возможностей.
Архитектура MIMD может использовать все преимущества со-
временной микропроцессорной технологии на основе строгого
учета соотношения стоимость/производительность. В действитель-
ности практически все современные многопроцессорные систе-
мы строятся на тех же микропроцессорах, которые можно найти
в персональных компьютерах, рабочих станциях и небольших од-
нопроцессорных серверах.
6.6. ПРОЦЕССОРЫ И ПРОЦЕССОРНЫЕ ЭЛЕМЕНТЫ
ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ
6.6.1. Микропроцессоры с расширенной
и сокращенной системой команд
В ходе выполнения заданной программы процессор обслужи-
вает данные, находящиеся в его регистрах, в поле оперативной
324
памяти, а также данные, находящиеся во внешних портах процес-
сора. Часть данных он интерпретирует непосредственно как дан-
ные, часть данных — как адресные данные, а часть — как коман-
ды. Совокупность всех возможных команд, которые может выпол-
нить процессор над данными, образует так называемую систему
команд процессора. Процессоры, относящиеся к одному семейству,
имеют одинаковые или близкие системы команд. Процессоры,
относящиеся к разным семействам, различаются по системе ко-
манд и являются невзаимозаменяемыми.
Если два процессора имеют одинаковую систему команд, то они
полностью совместимы на программном уровне. Это означает, что
программа, написанная для одного процессора, может исполнять-
ся и другим процессором. Процессоры, имеющие разные систе-
мы команд, как правило, несовместимы или ограниченно совмес-
тимы на программном уровне.
Группы процессоров, имеющих ограниченную совместимость,
рассматривают как семейства процессоров. Например, все процес-
соры Intel Pentium относятся к так называемому семейству х86.
Родоначальником этого семейства был 16-разрядный процессор
Intel 8086, на базе которого собиралась первая модель компьютера
IBM PC. Впоследствии сменилось восемь поколений процессоров
фирмы Intel: 8088, 80286, 80386, 80486, Pentium, Pentium II, Pentium III,
Pentium IV. В каждом поколении имеются еще и модификации,
отличающиеся друг от друга назначением и ценой. Все эти моде-
ли, и не только они, а также многие модели процессоров компа-
ний AMD и Cyrix относятся к семейству х86 и обладают совмести-
мостью по принципу «сверху вниз».
Принцип совместимости «сверху вниз» — это пример непол-
ной совместимости, когда каждый новый процессор «понимает»
все команды своих предшественников, но не наоборот. Благода-
ря такой совместимости на современном компьютере можно вы-
полнять любые программы, созданные для любого из предшеству-
ющих компьютеров, принадлежащего той же аппаратной плат-
форме.
Чем шире набор системных команд процессора, тем сложнее
его архитектура, тем длиннее формальная запись команды (в бай-
тах), тем выше средняя продолжительность исполнения одной ко-
манды, измеренная в тактах работы процессора. Так, система ко-
манд процессоров Intel Pentium в настоящее время насчитывает
порядка тысячи различных команд. При этом команды имеют длину
325
от 8 до 120 бит. Такие процессоры называют процессорами с рас-
ширенной системой команд — CISC-процессорами (CISC —
Complete Instruction Set Computer).
Лидером в разработке микропроцессоров с полным набором
команд (CISC) считается компания Intel со своей серией х86 и
Pentium. Эта архитектура является практическим стандартом для
рынка микрокомпьютеров. Для CTSC-процессоров характерно:
сравнительно небольшое число регистров общего назначения;
большое количество машинных команд, некоторые из которых
нагружены семантически аналогично операторам высокоуровне-
вых языков программирования и выполняются за много тактов и
методов адресации; большое количество форматов команд различ-
ной разрядности; преобладание двухадресного формата команд;
наличие команд обработки типа регистр-память.
Основой архитектуры современных рабочих станций и серве-
ров является архитектура компьютера с сокращенным набором
команд — (RISC — Reduce Instruction Set Computer), созданная
в середине 80-х годов XX века. Зачатки этой архитектуры уходят
своими корнями к компьютерам CDC6600, разработчики которых
(Торнтон, Крэй и др.) осознали важность упрощения набора ко-
манд для построения быстрых вычислительных машин. Эту тра-
дицию упрощения архитектуры С. Крэй с успехом применил при
создании широко известной серии суперкомпьютеров компании
Cray Research.
При такой архитектуре количество команд в системе намного
меньше, они имеют одинаковую длину и каждая из них выполня-
ется намного быстрее. В этих микропроцессорах на выполнение
каждой простой команды за счет их наложения и параллельного
выполнения тратится 1 машинный такт (на выполнение даже са-
мой короткой команды из системы CISC обычно расходуется
4 такта).
Таким образом, программы, состоящие из простейших команд,
выполняются этими процессорами намного быстрее. Оборотная
сторона сокращенного набора команд состоит в том, что сложные
операции приходится эмулировать далеко не эффективной после-
довательностью простейших команд сокращенного набора.
В 1980 г. в университете Беркли были изготовлены две маши-
ны, которые получили названия RISC-In RISC-П. Главными идеями
этих машин было отделение медленной памяти от высокоскорост-
ных регистров и