К. Ф. ЧЕРНЫХ
ВВЕДЕНИЕ
В ФИЗИЧЕСКИ
И ГЕОМЕТРИЧЕСКИ
НЕЛИНЕЙНУЮ
ТЕОРИЮ ТРЕЩИН
МОСКВА
НАУКА • ФИЗМАТЛИТ
1996

ББК 22.251	Федеральная целевая программа
4-45	книгоиздания России
УДК 539.3
Черных К. Ф. Введение в физически и геометрически не-
нелинейную теорию трещин,—М.: Наука. Физматлит, 1996.—288 с—
ISBN 5-02-014523-8.
Приводятся основные зависимости предложенной автором нелиней-
нелинейной плоской теории упругости. Компактность и сравнительная простота
аппарата теории позволили получить ряд точных решений краевых задач
для разрезов, вырезов и включений. Сопоставление последних с соответст-
соответствующими решениями линейной плоской теории упругости позволило
прояснить вопрос о применимости линейной теории трещин в механике
разрушений. Излагаются результаты автора по построению общей, фи-
физически и геометрически нелинейной теории трещин.
Для механиков, занимающихся проблемами хрупкого и квазихрупко-
квазихрупкого разрушения.
Табл. 6. Ил. 87. Библиогр. 125 назв.
Рецензент доктор технических наук Е.М. Морозов,
Научное издание
ЧЕРНЫХ Климентий Феодосьевич
ВВЕДЕНИЕ В ФИЗИЧЕСКИ И ГЕОМЕТРИЧЕСКИ
НЕЛИНЕЙНУЮ ТЕОРИЮ ТРЕЩИН
Редактор H.IJ. Рябенькая.
Художественный редактор Г.М. Коровина.
Технический редактор С.Я. Шкляр.
Корректоры О. А Бутусова, О.М. Ki
Карпова.
ИБ№41149
ЛР№ 020297 от 27.11.91.
Сдано в набор 20.08.91. Подписано к печати 28.02.96. Формат 84x108/32.
Бумага книжно-журнальная. Гарнитура обыкновенная. Печать офсетная.
Усл. печ. л. 15,12. Уч.-изд. л. 16,54. Тираж 1000 экз. Заказ N5 4042
С-011.
Издательская фирма «Физико-математическая литература» РАН
117071 Москва В-71, Ленинский проспект, 15
Отпечатано в Московской типографии № 2 РАН
121099 Москва Г-99, Шубинский пер., 6
* I?1190-96, Наука. I полугодие	О К.Ф. Черных, 1996
- "~*в	©Оформление.
ISBN 5-02-014523-8	Физматлит, 1996

Светлой памяти
дорогого учителя и друга
ВАЛЕНТИНА
ВАЛЕНТИНОВИЧА
НОВОЖИЛОВА
посвящается эта книга
ПРЕДИСЛОВИЕ
У истоков этой книги, как, впрочем, и других книг
автора, стоял Валентин Валентинович Новожилов. Мно-
Многочисленные беседы с ним и споры выкристаллизовали
общее направление книги и ключевые вопросы, подлежа-
подлежащие рассмотрению. По установившейся традиции к каж-
каждой моей книге Валентин Валентинович писал краткое
предисловие, глубину и содержательность которого труд-
трудно переоценить. К великому сожалению, предисловия
к этой книге написано не было — Валентина Валентино-
Валентиновича не стало... Основные тезисы этого несостоявшегося
предисловия на стадии написания проспекта книги ча-
часто обсуждались, и я попытаюсь «на память» изло-
изложить их:
—	Основные результаты теории трещин получены на
базе линейной теории упругости либо геометрически ли-
линейной теории пластичности, имеющих в своей основе
предположения о малости деформаций и поворотов. В то
же время наиболее интересны именно окрестности особых
точек (концы трещин, угловые точки), где эти предпо-
предположения заведомо нарушаются.
—	Казалось бы, классическая теория трещин не мо-
может иметь право на существование. Но это не так: по-
полученные на ее базе результаты часто, но не всегда,
неплохо коррелируют с экспериментальными данными.
Одной из главных задач создаваемой нелинейной теории
является выяснение пределов применимости линейной
теории.
—	Геометрически и физически нелинейные задачи от-
относятся к наиболее сложным. К тому же в механике раз-
разрушения приходится иметь дело с областями сложного
вида, содержащими особые точки. Для рассмотрения та-
таких задач необходимы предельно простые, хорошо разра-
разработанные теории. Таковой и является полученная авто-

4	ПРЕДИСЛОВИЕ
ром унифицированная плоская задача нелинейной теорий
упругости.
—	Основное в механике разрушения — це численные
результаты, хотя и они безусловно нужны, а понимание
характерных особенностей самого механизма разрушения.
Важны прежде всего новые качественные результаты.
Поэтому особенно ценны полученные автором книги точ-
точные, эталонные решения нелинейных краевых задач, по-
позволившие в известной мере выявить влияние нелиней-
нелинейности и, в частности, преимущества условных напряже-
напряжений перед истинными.
—	Насколько можно судить по проспекту книги и
опубликованным статьям автора, книга пробудит интерес
к нелинейной теории и найдет своего читателя.
Многие замечания Валентина Валентиновича, но, ко-
конечно, далеко не все, были учтены при написании книги.
В частности, его идеи, изложенные в статьях [41, 42],
послужили канвой при написании главы 4.
Автор благодарен рецензенту Евгению Михайловичу
Морозову, основательно вникшему в содержание книги
и сделавшему ряд ценных замечаний. Большую помощь
в оформлении книги оказали И. М. Лосева и Э. Н. Чер-
Черных.
Автор заранее благодарен за все замечания и подме-
подмеченные недостатки книги, неизбежные в новой для него
области.
К. Ф. Черных

ВВЕДЕНИЕ
Поистине необъятным разделом механики твердого
деформируемого тела стала дисциплина, именуемая тео-
теорией трещин. Значительная ее часть базируется на соот-
соотношениях, полученных в рамках линейной теории упру-
упругости. Ситуация воистину парадоксальная! В самом деле,
в основе линейной теории упругости лежат предположе-
предположения о малости деформаций и поворотов, нарушаемые в
окрестностях наиболее интересных для теории сингуляр-
сингулярных точек (концы трещин и острых включений, угловые
точки). Казалось бы, так полученная теория не может
претендовать на достоверность. Тем не менее линейная
теория трещин (создание которой связывается с именами
Вейхардта, Гриффитса, Орована, Ирвина и более позд-
поздних исследователей) зачастую дает вполне приемлемые
результаты, неплохо согласующиеся с экспериментами.
Из сказанного следует необходимость разобраться в
ситуации; очертить круг проблем, для рассмотрения ко-
которых пригодна линейная теория; построить нелинейную
теорию для остальных проблем. Естественным здесь пред-
представляется путь решения задач по линейной и нелиней-
нелинейной теориям с последующим сопоставлением полученных
результатов. Реализовать этот путь, однако, непросто,
поскольку решение нелинейных краевых задач для слож-
сложных областей с сингулярными точками — проблема не из
легких. К тому же требуется получить не приближенные,
численные решения, а точные, аналитические, пригодные
для теоретического анализа.
В механике разрушения используется термин «нели-
«нелинейная». Но под этим обычно понимается рассмотрение
физически нелинейных проблем (главным образом учет
пластичности в геометрически линейной постановке).
Геометрическая нелинейность либо совсем не учитывает-
учитывается, либо учитывается частично. Например, учитываются
большие деформации, ио не рассматривается поворот

в	ВВЕДЕНИЕ
главных осей деформации. Необходимо, конечно, учиты-
учитывать общую (физически и геометрически) нелинейность.
При этом построенная теория должна быть предельно
проста (но, как принято говорить, без потери общности).
Такого рода общая нелинейная теория упругости и из-
изложена в главе 1. Достойно здесь специального упоми-
упоминания дальнейшее развитие (применительно к нелиней-
нелинейной теории) комплексного метода Колосова [24]. По
сравнению с изложенным в [81, 84] приведены некото-
некоторые новые результаты. В частности, по-новому рассмат-
рассматривается малосжимаемый упругий материал, приводится
комплексная форма интегральных тождеств.
В линейной теории трещин наиболее часто использу-
используют антиплоскую деформацию (которой по классификации
отвечает тип разрушения III) и плоскую (типы разру-
разрушения I и II). Первая (гармоническая) проблема про-
проще второй (бигармонической). Поэтому новые подходы
обычно «обкатывают» на антиплоской деформации.
При нелинейном же подходе преимущества антипло-
антиплоской деформации уже не так ощутимы, поскольку ей в
общем случае отвечают переопределенные задачи [81]
и, вообще говоря, не вполне разделяются типы разруше-
разрушения I—II—III. К тому же плоские задачи и более инте-
интересны по своим приложениям. Этим и объясняется то,
что в книге рассматривается в основном плоская задача.
Антиплоской посвящена глава 9.
Особенностью изложенного в главе 2 варианта нели-
нелинейной плоской задачи является его предельная простота
(насколько этот термин может быть применим к нели-
нелинейной теории) и почти полная унификация восьми са-
самостоятельных проблем, отвечающих сочетанию: обоб-
обобщенной плоской деформации и плоского напряженного
состояния; сжимаемого и несжимаемого материалов; ста-
статических (динамических) и геометрических (дисторсион-
ных) граничных условий.
Рассмотрение линейно-упругого материала специаль-
специального вида позволило получить точные решения ряда ос-
основных (эталонных) задач. Подробно рассмотрен вопрос
об асимптотике решений в окрестностях сингулярных
точек для нелинейного материала. Сформулированы ва-
вариационные уравнения.
В главе 3 рассмотрена линейная плоская задача,
включающая в себя обобщенную плоскую деформацию,
учитывающую предварительную всестороннюю деформа-

ВВЕДЕНИЕ	7
цию и несжимаемость материала. Изложенное дано в
терминах функций Ф(?), ^it), в унифицированной фор-
форме, с использованием дисторсионных граничных условий.
В главе 4 дается краткое изложение основных идей
и результатов линейной теории трещин. В основу изло-
изложения положена концепция Новожилова, в двух статьях
которого [41, 42] дан единый критический взгляд на
многочисленные предложения и подходы в теории тре-
трещин. Сказанное там во многом прояснило пути построе-
построения нелинейной теории.
Центральная в книге глава 5 посвящена выявлению
влияния учета геометрической нелинейности на хрупкое
разрушение. Производится это сопоставлением точных
решений эталонных задач по линейной и нелинейной
теориям. Проведенное сопоставление привело к обосно-
обоснованию возможности использования линейной теории в
задачах, где «ведущим» параметром является коэффици-
коэффициент интенсивности напряжений. Вместе с тем по линей-
линейной теории неправильно могут определяться величины
максимальных нормальных и тангенциальных напряже-
напряжений, а также направления площадок, на которых они
действуют. Таким образом, представляются сомнительны-
сомнительными полученные с помощью линейной теории более «тон-
«тонкие» результаты (структура устья трещины, критерии
хрупкости разрушения и т. п.). Наконец, анализ полу-
полученных решений показывает неоспоримые преимущества
условных напряжений перед истинными.
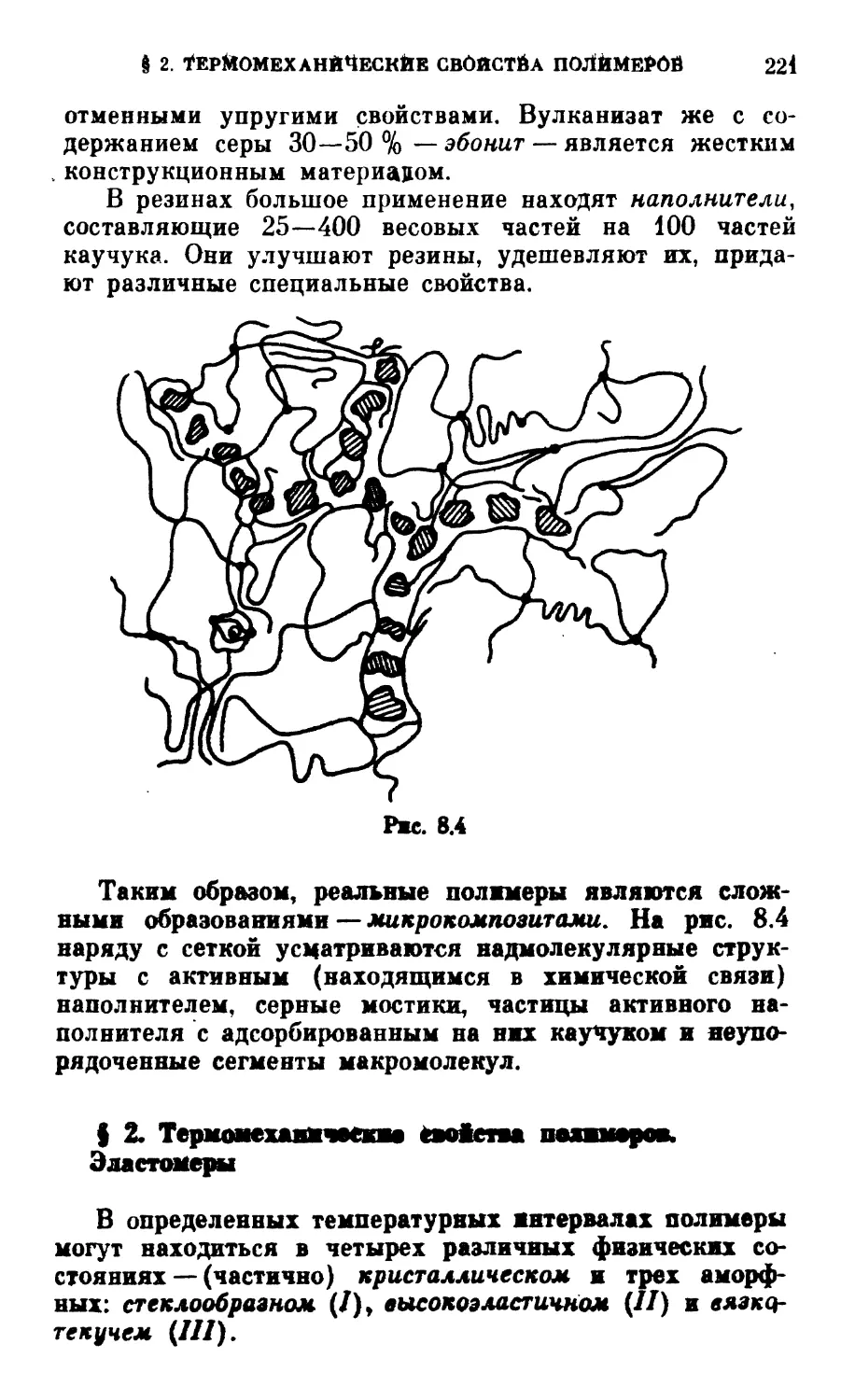
В главе 6 дается весьма краткое изложение круга
вопросов, связанных со структурой идеальных (безде-
(бездефектных) решеток и идеальной прочностью твердых тел.
В следующей, 7 главе рассматриваются дислокации
Вольтерра в сплошной упругой среде. Особое внимание
уделяется клиновой дисклинации. Для нее развита не-
нелинейная теория, применительно к малосжимаемым ма-
материалам.
В главе 8 излагается круг вопросов, связанных с раз-
разрушением полимеров и эластомеров. Особое внимание
уделяется применимости теории трещин.
В последней главе 10 подводится итог. Прежде всего
сводятся воедино аргументы в пользу использования в
нелинейной механике твердого деформируемого тела со-
сопряженной по Хиллу (энергетической) пары тензоров:
условных напряжений — кратностей удлинений (относи-
(относительных удлинений). Обсуждается вопрос об особенно-

стях напряжений в сингулярных точках. Идет речь
о ближних и дальних перспективах построения общей
нелинейной теории трещин.
Опыт преподавания в Ленинградском университете
утвердил автора во мнении, что печальным побочным
результатом внедрения ЭВМ явилось снижение внимания
к теории функций комплексной переменной (ТФКП).
В теории же трещин ТФКП занимает видное место, хотя
объем требуемых здесь познаний сравнительно невелик.
Поэтому в Приложении даны необходимые сведения по
ТФКП. При этом использованы некоторые оригинальные
результаты автора.
Более подробно с содержанием книги можно ознако-
ознакомиться по оглавлению и § 3 гл. 10.
Читатель, по-видимому, обратит внимание на отсут-
отсутствие ссылок на работы предшественников по учету (фи-
(физической и геометрической) нелинейности. Но, во-первых,
у автора нет сколь-нибудь полных сведений о таких ра-
работах. Во-вторых, с некоторыми из них он категорически
не согласен. Очень не хотелось начинать свою первую
монографию по разрушению с критики альтернативных
подходов. Во всяком случае автор осознает этот пробел
в книге и надеется ъ дальнейшем «искупить свою вину».

Глава 1
ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ
ТЕОРИИ УПРУГОСТИ
В книгах [81, 84] изложен предложенный автором
сравнительно простой «рабочий» вариант нелинейной
теории упругости. В этой главе дается его краткое изло-
изложение. Приводятся и некоторые новые результаты. Для
простоты изложение ведется в прямоугольных декарто-
декартовых координатах. Широко используются комплексные
координаты и компоненты, весьма удобные как при из-
изложении общих вопросов, так и для решения конкретных
задач.
§ 1. О тензорах второго ранга
В прямоугольных декартовых координатах тензор вто-
второго ранга можно записать в диадном представлении
T-i«g.g,.	A.1)
Здесь gi, g2, gs — координатные орты, удовлетворяющие
условиям ортонормированности
при j~J	A.2)
Величины gigi называют координатными диодами, наде-
наделяя их следующими свойствами:
e«gb	A.3)
g/ (g* • gi) ft - 6Mg,g,.
При написании представления A.1) было использовано
следующее (употребляемое и ниже) правило суммирова-
суммирования: по каждому повторяющемуся греческому индексу
производится суммирование от 1 до 3. Таким образом,
правая часть представления A.1) — двойная сумма, со-
содержащая девять слагаемых ^, —компонент тензора Т.
Если наряду с Т рассмотреть еще один такой же тен-
тензор S=-*^gHgYt то с учетом свойств диад A.3) можно оп-

Ю ГЛ. 1. ОСНОЙНЬГЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ
ределить операцию скалярного умножения тензоров ра-
равенством
Т • S == UifiSmgafy ' giigv = faft*»A»gagv = Uzptyvgagv,
т. е.
T S = U^vgagv, (T - S){i - *„*«.	A.4)
Повторное свертывание полученного тензора по индексам
а = v приводит к двойному скалярному произведению
(свертке) пары тензоров:
Т: S
Аналогично, с учетом первых двух из соотношений
A.3), вводятся скалярные произведения вектора на тен-
тензор (соответственно справа и слева):
Т • а = Ь -> tiada = bi,
A6)
Из этих соотношений видно, что тензор можно рас-
рассматривать как оператор, переводящий вектор в некото-
некоторый другой. Наибольший интерес представляют векторы,
претерпевающие при этом минимальные изменения. Эти
так называемые главные векторы тензора а удовлетво-
удовлетворяют соотношению
Т-а = *а.	A.7)
Число t называют главным значением тензора.
Согласно выражениям A.6) векторные соотношения
A.7) записываются в виде следующей однородной систе-
системы уравнений:
0,
0,	A.8)
0.
Как известно, необходимым и достаточным условием су-
существования нетривиального (ненулевого) решения яв-
является равенство нулю определителя системы A.8):
<-<и -'it
-<3i -'«'-
или в развернутом виде
-0, A.10)

1. б ТЕНЗОР А* ВТОРОГО РАНГА
где
til +
*33'
«11
'n
'u
«и
«и
«2,
hi
«13
*S3
22
32
'я
«33
hi «13
«3! «33
(l.H)
— так называемые главные инварианты тензора. Соотно-
Соотношение же A.10) называют характеристическим урав-
уравнением.
Поскольку коэффициенты характеристического урав-
уравнения инвариантны (не зависят от выбора системы коор-
координат), таковыми же являются и его корни — главные
значения тензора t\, t%, tz и, следовательно, определяемые
из системы A.8) (для каждого t) главные векторы аь
а2, аз. Перечисленные инвариантные величины определя-
определяют внутреннюю структуру тензора.
Сопряженным Т называют тензор (см. A.1))
T* = *aPgpga, ty = ^.	A.12)
Таким образом, сопряженному тензору отвечает переста-
перестановка векторов в координатных диадах или, что то же,
перестановка индексов в компонентах тензора. Из A.10)
и A.11) усматривается
tf = **, A13)
т. е. сопряжение тензора не меняет его главных значе-
значений и главных инвариантов.
Переходя к компонентам, нетрудно проверить спра-
справедливость следующих свойств сопряженного тензора:
(T-S)*-S*-T*;	A.14)
Т-а-а-Т*, Т»-а-а-Т.	, A.15)
Напомним, что при переходе от одной прямоугольной
декартовой системы координат к другой такой же (штри-
(штрихованной) компоненты тензора преобразуются но фор-
формулам
A-16)
где qiy — косинус угла между i-м старым и ;-м новым
ортами.

12 tX i. ОСНОВНОЕ ЗАВИСИМОСТИ НЕЛИНЕЙЙОЙ ТЕОРИЙ
§ 2. Каноническое представление тензора
С учетом вещественности главных инвариантов ве-
вещественного тензора (т. е. тензора с вещественными ком-
компонентами) операция комплексного сопряжения характе-
характеристического уравнения A.10) приводит к равенству
Отсюда следует, что наряду с t характеристическому
уравнению удовлетворяет и комплексно сопряженная ве-
величина L Поэтому для корней кубического уравнения
возможны две ситуации:
а)	все главные значения (tu t2, h) вещественны;
б)	два главных значения комплексно сопряжены
(h — h), а третье (fo) вещественно,
В начале рассмотрения будем считать корни некрат-
некратными (*i Ф *2 + *з * h). При этом
Т-*1-»*|«ь Т-аг^аг, Т аэ«*заз. B.1)
Покажем, что в этом случае главные векторы линейно-
независимы, т. е. соотношение
0	B.2) х
может выполняться лишь при с\ >¦ с*в с%« 0. Скалярно
умножая это векторное равенство слева на Т, а затем
полученное еще раз на Т, получаем с учетом B.1)
0.	' м
Определитель однородной системы уравнений B.2) 1,2,3
111
t* ta t*
Ч *% *з
отличен от нуля в силу предположенной некратности
главных значений тензора. Отсюда и следует, что систе-
система B,2) 1,2,з имеет лишь тривиальное решение С\*=С2 =
= сз = 0, т. е. главные векторы линейно-независимы.
Как известно, линейная независимость означает, что
главные векторы не лежат в одной плоскости. Поэтому
их можно принять в качестве векторного базиса. Пусть
i + j. Тогда согласно B.1) и A.15)

§ 2. КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ТЕНЗОРА	13
Скалярно умножая первое уравнение на а^, а второе — на
а, и вычитая из полученного первого второе, находим
аНТ-Т*)-а, = (*,-*,)а,-а*	B.4)
Определяющими для симметричного тензора являются
следующие свойства:
Т* = Т, tn^ta.	B.5)
Для него при ti"?=tj из B.4) следует а, а; = 0, т. е. орто-
ортогональность главных векторов. Но согласно A.7) послед-
последние определяются с точностью до скалярного множителя.
Поэтому можно считать главные векторы не только вза-
взаимно ортогональными, но и единичными (единичной дли-
длины), т. е. ортами.
Далее, из B.3) i следует
a,-T-a*-*tA-a,-*,lail2.	B.6)
Заменяя индексы суммирования и используя симметрич-
симметричность рассматриваемого тензора, имеем
а< Т -a«-
Отсюда видно, что левая часть равенства B.6) вещест-
вещественна и, стало быть, U вещественно. Из A.8) при этом
следует вещественность главных векторов а».
Заменим обозначения а, на е, и будем называть еь е2,
вз главным (ортонормированным) векторным базисом
тензора. Отметим, что при тензоре, зависящем от коор-
координат, главный векторный базис поворачивается при пе-
переходе от точки к точке.
Согласно соотношениям A.1) и B.1) имеем (а<-*е<)
Ub = Т е, *= ta&* (е* • е{) = *аЛ«еа — ta<ea.
Отсюда следует г# = ?Д,. Таким образом, в своем главном
векторном базисе или, как говорят, в своих главных осях
тензор имеет следующий канонический вид:
Т — heiei + *2е2е2 + *3езе3.	B.7)
Выше была предположена некратность главных значе-
значений тензора. Теперь можно отказаться от этого ограни*
чения. Так,
Т — U (eiei + ejej) + ^Зезе3 (при t\
Т—

14 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
Таким образом, симметричному тензору отвечает случай
а) — вещественных главных значений.
Несимметричным же тензорам отвечает случай б) —
комплексно сопряженных главных значений
*1=Я + 1'ц, *2 = А-*ц, h	B.9)
(А, |Л, h — вещественные величины).
Поскольку t\ n t2 = t\ комплексно сопряжены, таковыми
же будут и определяемые из системы A.8) главные век-
векторы ai = ai + ia2, аг = ai — ia2. Внося их, а также выра-
выражения B.9) в B.1), получаем после разделения веще-
вещественных и мнимых частей
Т • at = k&i - ца2, Т • а2 = \хец + Хаг, Т • а3 — *3а3. B.10)
Как и выше для симметричного тензора, можно считать
[65, 81] главные векторы а< ортами е<. Отсюда с учетом
выражений A.1) получаем паноническое представление
несимметричного тензора:
T«X(eiei + в2е2)+ |i(eie2 —егеО + ^езвз B.11) i
и согласно определению сопряженного тензора A.12)
T*-X(e,ei + e2e2)-n(eie2-e2ei)+^e8e3. B.11)*
Кососимметричным (антисимметричным) называют
тензор К, для которого
К» = -К, *;; = -*«.	B.12)
Согласно же выражениям B.10) и B.11) ему отвечает
следующее каноническое представление:
K«G)(eie2-e2ei).	B.13)
Ортогональным называют тензор Q, для	которого
Q.Q*-Q*.Q-1,	B,14)
где
1 ¦* eiei + егег + езвз	B.15)
— единичный тензор, обладающий (как нетрудно прове-
проверить с помощью соотношений A.1) и A.3)) свойством:
т-1-1-т-т:	B.16)
Согласно соотношениям B.10), B.11) и A.3)

§ 3. КЛАССИЧЕСКИЕ ТЕНЗОРНЫЕ ФУНКЦИИ	15
Сопоставляя полученное с B.14), B.15), имеем
X — coso), jj, = sin со, fee=tl.
Различают ортогональный тензор первого рода
Q = cos со (е^! + егвг) + sin а) (е^г — e^i) + езвз B.17) i
и ортогональный тензор второго рода
Q — cos со (eiei + егвг) + sin со (eie2 — егеО — езвз. B.17J
Для невырожденного тензора (т. е. тензора с ///г =¦
= 1 ^о I S96s 0) можно ввести обратный тензор Т, опреде-
определяемый равенствами
Т.Т-*-Т-1-Т-1.	B.18)
При этом имеет место равенство
(T-S)-1-S-lT-1,	B.19)
справедливость которого проверяется скалярным умноже-
умножением на Т • S.
Отметим, что свертка симметричного S(s<;) и кососим-
метричного К(Аг/тп) тензоров равна нулю. Действительно,
согласно A,5), B.5) и B.12)
S: К-!.,*».-
- 72 (i«k* + tpJe*) = 7и^ (*«> + М- 0. B.20)
§ 3. Классические тензорные функции
Тензорные функции, значения которых являются тен-
тензорами второго ранга [65, 81], являются естественными
обобщениями скалярных функций. Будем вначале счи-
считать, что главные значения тензора-аргумента вещест-
вещественны и некратны. Принимая для тензора каноническое
представление B.7), находим с учетом A.3)
Т* = &Л + t$e2e2 + *5еае, (Т* = 1). C.1)
Теперь произвольному скалярному полиному
2y*'*	C.2)
можно сопоставить тензорный полином
2 Y*T* - g (*i) ел + g (tt) efr + g (*,) e,er C.3)

16 ГЛ. 1. ОСНОВНОЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
Большую роль играет характеристический полином
Д (t) ^t3- ITt2 + IITt - IIIt,	C.4)
обращающийся согласно A.10) в нуль на главных зна-
значениях тензора U:
Д(*<)-0 (i = l,2,3).	C.5)
С учетом этого, полагая в тензорном полиноме C.3)
g(t)*& &(t), приходим к тождеству Гамильтона -^ Кэли
(А (Т) -) Т3 - /ТТ2 + //ГТ - Шт\ = 0, C.6)
дающему возможность снижать (редуцировать) порядок
любого тензорного полинома до второго. Тем самым мож-
можно ограничиться рассмотрением тензорных полиномов
лишь второго порядка.
Будем называть классической тензорной функцией
/(Т) тензорный полином второго порядка g(T), удовлет-
удовлетворяющий соотношениям
g(ti) = f(ti) 0 = 1, 2, 3).	C.7)
Таким образом, отвечающий тензорному полиному ска-
скалярный полином второго порядка должен совпадать с
порождающей скалярной функцией f(t) на главных зна-
значениях тензора-аргумента.
Как нетрудно проверить, условию C.7) удовлетворя-
удовлетворяет интерполяционный полином Лагранжа — Сильвестра
Отсюда и следует, что согласно данному определению
классической тензорной функции (Т° == 1)
Это разложение, полученное из канонического представ-
представления, справедливо для любого тензора с некратными
главными значениями.

§ 3. КЛАССИЧЕСКИЕ ТЕЙЗОРНЫЕ ФУНКЦИИ
17
Для иллюстрации полученных зависимостей подсчи-
подсчитаем тензорную функцию / (К) = е , где К — кососим-
метричный тензор B.13). Составляя для него характери-
характеристическое уравнение A.9)
t
0)
0
— со
t
0
0
0
t
находим отсюда
*1 = Ш,	/(tt)-в*-,
и по C.9) —
ек =
sin со
0)
(ЗЛО)
Подстановка в это равенство представления B.13) и сле-
следующего из него К2^—co2(eiei+ егег) дает
ек = cos со
+ е2е2) + sin со (е^ — е^
Отсюда и из B.17) 1 усматривается, что
е8е3.
C.11)
где Q — ортогональный тензор первого рода.
С вектором (большого) поворота абсолютно твердого
тела
C.12)
C.13)
О) « 0)igi + (d2g2
обычно связывают кососимметричную матрицу
О — сов
— 3
О —CD,
Подстановка выписанных матриц в отвечающее C.11)

ig ГЛ. f. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ
матричное равенство (/ — единичная матрица, со —
= Г %ЧШ2 + Юз)
Q = 1 + ^K+1^LK»	C.14)
дает связь косинусов углов поворота с компонентами век-
вектора поворота:
Kl ?12 «181	II 1 0 011	. I] - -«а
Q-\*n*n*u =cosco 010+ i?? «, 0 -со,
|0 0 1| Ш „-и
2 
+
1 — 009@
. C.15)
Отсюда следуют обратные зависимости
+ g22 + g33- 1),
со	2 sin со ' со	2 sin со ' со	2зщсо f
определяющие компоненты вектора поворота по извест-
известным косинусам углов поворота.
§ 4. Полярное разложение тензора
Получим весьма полезное в дальнейшем так называе-
называемое полярное разложение тензора. Прежде всего соглас-
согласно соотношению A.14)
т. е. тензор Т* • Т симметричен и по сказанному в § 2,
D.1)
где х< — вещественные главные значения, а а< — главные
векторы тензора Т* Т. Отсюда и из A.15) имеем
Т).а,]-а,
Но согласно D.1)
Сопоставление двух полученных выражений показывает,
что все главные значения тензора Т* • Т неотрицательны.

§ 4. ПОЛЯРНОЕ РАЗЛОЖЕНИЕ ТЕНЗОРА	19
Будем рассматривать только невырожденные тензоры,
для которых (см. § 2) ШТФО. Согласно A.4), A.13)
и хорошо известным свойствам определителей
ШТ*Т = | Ctaj | = |& | | *« | = (Шт? > 0.
Но тогда из записываемого для тензора Т* • Т характери-
характеристического уравнения A.10)
% 17/
%i тТ7/л + ттХг	тт = 0
следует, что Xi^O. Выше была установлена неотрица-
неотрицательность %и так что
Х*>0.	D.2)
Рассмотрим симметричный тензор А, для которого
А • а<
А2 • а, = Л • (Л • аО =
Сопоставление полученного с D.1) дает
Л = УТ* Т.	D.3)
Таким образом, УТ* • Т — симметричный тензор с поло-
положительными главными значениями.
Покажем справедливость следующего утверждения:
произвольный невырожденный тензор с вещественными
компонентами может быть представлен в виде полярного
разложения
		T-Q.A,	D.4)
где А «* УТ* • Т ~ симметричный тензор с положительны-
положительными главными значениями, a Q — ортогональный тензор
первого рода.
Действительно, при тензоре Л, определяемом выраже-
выражением D.3), равенству D.4) очевидно удовлетворяет тен-
тензор Q = TA~1. Остается показать, что последний орто-
ортогонален. Из соотношений D.3) и B.19) следует
т*-т = л2, л-2=(т*-т)-1 = т-1-т*-1.
Но с учетом A.14)
и утверждение доказано.

20 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
§ 5. Движение и деформация материальной частицы
Рассмотрим кинематику и деформацию материальной
частицы тела. Ее движение будем описывать в единой
пространственной прямоугольной декартовой системе ко-
координат (системе отсчета). Используем при этом мате-
материальный (лагранжев) способ описания движения, при
котором как бы следят за движущейся материальной точ-
точкой. Рассматриваемые величины будем относить как к
исходной (недеформированной), так и к текущей (дефор-
(деформированной) конфигурациям тела. В первом случае ве-
величины будем снабжать значком °.
Пусть
х{ r==Xi(xl,xl,xl;t) (i = 1,2,3)	E.1).
— уравнения движения материальных точек тела в про-
пространстве, отнесенном к выбранной системе отсчета с
прямоугольной декартовой системой координат. Здесь
хи Х2, #з — пространственные координаты движущейся
материальной точки, a xl,x2,xa— ее материальные ко-
ординаты, выделяющие из тела материальную точку.
Примем в качестве материальных пространственные
координаты материальной точки в некоторый фиксиро-
фиксированный момент времени fo, так что
*? = *i|«-V	E.2)
Дифференцирование уравнений движения E.1) дает
dx^^dxl	E.3)
дха
Введем в рассмотрение радиусы-векторы материальных
точек и их дифференциалы соответственно в исходной и
текущей конфигурациях тела:
E.4)
и тензоры (см. A.12) и B.18))
.'	ES)

§ 5. ДВИЖЕНИЕ И ДЕФОРМАЦИЯ МАТЕРИАЛЬНОЙ ЧАСТИЦЫ 21
(То, что в соответствии с обозначением тензор F явля-
является обратным тензору F, легко проверяется с учетом
соотношений A.3) и B.15). Так,
FF
dx,t дх„
дх
Jx° дХа
дх°а дх^
Используя соотношения E.4), E.5) и A.3), записы-
записываем равенства E.3) в виде
dR = F dR°.	E.6)
Геометрический смысл введенных величин усматривается
из рис. 1.1; dR°, сЖ — векто-
векторы, определяющие положе-
положение произвольной точки ма-
малой частицы относительно ее
центра, в начальной и теку-
текущей конфигурациях тела. Из
соотношения E.6) видно,
что тензор F определяет ло-
локальное (относительно свое-
своего центра) движение точек
материальной частицы. Бу-
Будем называть его градиентом
движения.
Применяя к градиенту движения полярное разложе-
разложение D.4), получаем с учетом A.14) и B.19)
Рис. 1.1
F«Q Л", F*
Q«\
E.7)
F-i
Напомним, что здесь Л° ~ VF* • F — симметричный тензор
с положительными главными значениями (Л°* = Л°),
а Q — ортогональный тензор (Q — Q*).
В механике деформируемого тела под деформацией
понимают движение тела, при котором изменяются рас-
расстояния между его материальными точками. Если таких
изменений не происходит, тело движется как абсолютно
твердое — деформация отсутствует.
Обозначим через
ds°-\dR°\, ds-IJR!
E.8)

22 Гл. i. осноёныё зависимости нелинейной теории
— длины элемента материального волокна до и после
деформации. Согласно формулам E.6), E.7) и A.15)
(dsJ = dR-dR = dR° (F* F)-dR° =
= dR°-Ao-(Q*Q)-Ao-dR = dRo.A°2-<m0,
(^J = dR0-A°2-dR°.	E.9)
Отсюда усматривается, что тензор Л° определяет изме-
изменение расстояний между точками материальной частицы,
т. е. деформацию. Ортогональный же тензор Q опреде-
определяет поворот материальной частицы.
Пусть е1,е2,е3— главный (ортонормированный) век-
векторный базис тензора Л°. С учетом соотношений B.7)
и A.3) имеем
Л° = Xae°e°, Л°2 - А?е?<?.	E.10)
В i-м главном направлении тензора A0 dRi = ds^e* и по
формулам E.9), E.10)
W = Я" (dslY(ele°a) (elel) = Л? {ds\y
и
h = dsi/dsl	E.11)!
Тем самым показано, что главные значения тензора Л°
являются кратностями удлинений материальных воло-
волокон, следующих главным направлениям тензора. Поэто-
Поэтому тензор Л° будем называть тензором кратностей удли-
удлинений, а величины h —главными кратностями удлине-
удлинений. Помимо h используются еще две меры деформации
[65, 81, 86]: главные относительные удлинения
ds,
Наряду с А° используется и тензор
A-Q-Ae-Q*.	E.12) i
При этом согласно E.10) и A.15)
или
E.13)

§ 5. Движение и деформация материальной Частицы ?3
где
ei-Q-e,0 (et°-Q*.e0.	EЛ4)
Таким образом, А — тензор с теми же, что и у Л°, глав-
главными значениями, но с главными осями (направления-
(направлениями), повернутыми тензором поворота материальной ча-
частицы Q, введенным полярным разложением градиента
движения F E.7).
Далее,
Л2 - Q Л° (Q* Q) Ae Q* - Q Л°2 Q* E.12J
и, очевидно,
I-Q-1-Q*.	E.12).
Поскольку произвольная классическая функция является,
по существу, тензорным полиномом второго порядка (см.
§ 3), из E.12I,2,3 и C.9) следует
/(A) = Q./(A°).Q«.	E.15)!
Из сказанного следует, что в качестве тензоров де-
деформации могут быть, в принципе, выбраны любые из
следующих пар классических тензорных функций*)
имеющих общие главные значения — меру деформации
/(Л<) —и главные оси, направления которых связаны за-
зависимостями E.14). При этом рассмотренные два семей-
семейства тензоров деформации имеют следующие канониче-
канонические представления:
/(А°)==/(Яа)еХ /(Л) = /(Яа)еаеа. E.15)а,3
Упоминания заслуживают прежде всего следующие,
наиболее часто используемые тензоры деформации:
Л°, А — кратностей удлинений,
Ee~V2(Ae2-l), E~V2(A2-i)-Грина, E.16)
вв = 72A-Ав-2), в = V2 A-А-2)-Ллъжаиси,
lnAe, In A — логарифмических (Генки) деформаций.
*) В § 9, а также в § 1 гл. 9 будут приведены доводы в поль-
пользу разумного сокращения числа конкурирующих мер деформации.

24 РЛ. 1- ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ
Отметим, что внутри каждого из двух рассматривае-
рассматриваемых семейств тензоры соосны между собой. Иногда для
того, чтобы четче различать одноименные тензоры обоих
семейств, добавляют к первым название — Лагранжа,
а ко вторым — Эйлера. Так, С° — тензор Коши — Лагран-
жа, а С — Коши — Эйлера. Отметим также, что в на-
настоящее время нет установившихся наименований тен-
тензоров деформации: разными именами называют один и
тот же тензор, и наоборот, одним и тем же величают
разные тензоры. Помочь здесь может лишь «визитная
карточка» тензора E.16), т. е. его выражение через Л°
или Л.
Приведем полезные, устанавливаемые с помощью со-
соотношений E.16), E.15) и E.7) зависимости
C° = F* F, C = F F*, C'-'-F-'-F-1*,
C-i-T-^-F-1. E.17)
С учетом соотношений E.4) векторы скорости и уско-
ускорения подсчитываются по формулам ( = d/dt)
у = R" = vygyj	vi - dxi/dt;
E.18)
w = v = R = Wygy, Wi = d2Xi/(dtJ.
§ 6. Основные деформационные зависимости
Получим необходимые в дальнейшем деформационные
зависимости. Прежде всего вдоль i-й главной оси dR^ =*
= ъ\йх\ и согласно E.6) и E.7)
<ffi«) - F-dRj, - Q-CA0^0) dx\ =
= Q•[Яae;(e^e0]dxio = Лi^io(Q.eio)==Яi(гx4oe^ F.1)
Обозначая
объем материальной частицы до и после деформации,
находим с учетом выражений F.1)
«то	-О-О-ОО/О	О\	,0,0.0
dv° = dxxdxtdx&i • (е2 X e3j = dxxdx%dx9i
dV = k1dx°1k2dx2^3dxle1-{e2xeB) = h^^dx^dx^dxl.
Отсюда и следует выражение для деформационной крат-

§ 6. ОСНОВНЫЕ ДЕФОРМАЦИОННЫЕ ЗАВИСИМОСТИ	25
ности изменения объема
Рассмотрим деформацию элементарного тетраэдра, вы-
вырезанного из недеформированного тела (рис. 1.2) в гра-
гранями, проходящими через глав-
главные оси деформации. Обозначая
через dS° площади его граней, А
а через dSn— площадь основания
и через п° — единичный вектор
нормали к основанию, находим
2dS°nn° = PjP, - PjPs =
О О	_ О О
= dxldxle°1 + d.°'00 '°'oe
dxxdx3es = 2dSaea, F.3)
т. е.
Пусть n, dSn, dSi — соответствующие величины в де-
деформированном тетраэдре. Очевидно, что для него можно
использовать зависимость F.3), производя в ней замены
(см. F.1))
о	о	о
Gi —> e<, dx\ —> dx{ в hidxi.
В результате проделанного получаем с учетом F.2)
». F.5)
Согласно же равенствам E.7), E.15) и E.14)
Отсюда и из выражений F.5), F.4J следует соотноше-
соотношение
ndSn = n°-JF-ldSl	F.6)
называемое в зарубежной литературе теоремой Наясова.

26 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
Пусть F°, Sn — часть тела и окружающая ее поверх-
поверхность до деформации, a F, 5„ — после деформации. Со-
Соотношения F.2) и F.6) позволяют переходить от инте-
интегрирования по деформированным объему и поверхности
к интегрированию по недеформированным. Так, для про-
произвольной функции W
r= JWdV0.	F.7)
У	у»
Введем в рассмотрение набла-векторы
Г = вц-?_., V = ga^-.	F.8)
Известные формулы Гаусса — Остроградского
?„ F.9)
после умножения на постоянные векторы g, и суммиро-
суммирования по / принимают согласно F.8) вид
f \°WdV° - f n°WdS°n, f \WdV = f nWdSn. F.10)
Если здесь W ¦= T — тензор, то производя под знаком ин-
интегрирования операцию скалярного умножения, находим
с учетом C.6)
n-TdSn
= f ^.(F./T)dSj = J V.^-.nOdF0. F.11)
Согласно известному правилу подсчета определителя
произведения и соотношениям F.2), E.16), E.17) и
A.Н)
Р = ///\= 7//л,=|А01| = |С°| = |F*-F| = |F*||F| =
Отсюда и из первого выражения в E.5) находим
| F | = | F{j | = | дхг/дхо$ |. F.12)

§ 7. НАПРЯЖЕНИЯ. УРАВНЕНИЯ ДВИЖЕНИЯ	27
§ 7. Напряжения. Уравнения движения
Из деформированного тела мысленно вырежем его
часть F, ограниченную поверхностью 5„. Обозначая через
р плотность деформированного тела, запишем интеграль-
интегральное равенство
Г tpdV + J ondSn = J wpdV,	G.1)
механический смысл которого будет установлен ниже.
Здесь f — интенсивность массовых сил;
a.-«MR, n)	G.2)
— вектор интенсивности поверхностной силы, действую-
действующей через поверхность Sn и являющейся в силу произ-
произвольности V и Sn функцией двух векторов: радиуса-век-
радиуса-вектора точки R и единичного вектора нормали к поверхно-
поверхности п = rcTgT.
Величину оп называют вектором напряжений. Вектор
напряжений, представляющий обусловленные деформа-
деформацией тела внутренние силы, обладает свойством
о-п^-Оп,	G.3)
являющимся для деформируемого тела, по существу, за-
записью закона Ньютона (действие равно противодей-
противодействию) .
Так как
dm	G.4)
— элемент массы, aw — вектор ускорения, интеграл в
правой части равенства G.1) представляет собой силу
инерции выделенного объема. Левая же часть представ-
представляет действующие на него (массовые и поверхностные)
силы. Таким образом, равенство G.1) означает, что дей-
действующие на выделенный объем силы уравновешиваются
силой инерции. В отсутствие последней G.1) —условие
равновесия выделенного объема.
Равенство G.1) должно выполняться для любого ма-
материального объема. Применим его к элементарному тет-
тетраэдру, показанному на рис. 1.2. Так как
имеющим третий порядок малости объемным вкладом
можно пренебречь по сравнению с поверхностным —

28 гл. i. основные зависимости йЕЛйнёййой теории
второго порядка малости. В результате получаем
ondSn + a~adSa = 0.
Отсюда с учетом равенств G.3) и F.4) 2 (записанных
для деформированной конфигурации тела) следует
On = ПаОа.	G.5)
Если представить векторы напряжений о< разложе-
ниями
G.6)
то равенство G.6) можно записать в виде
где
G.7)
G.8)
— тензор истинных напряжений Ноши. Знание его позво-
позволяет подсчитать векторы напряжений на площадках лю-
любого направления. Действительно, согласно G.5), G.6)
ж G.8)
On — n • 2,
G.9)
С учетом соотношений G.6) и G.3) покажем на эле-
элементарном параллелепипеде (рис. 1.3) Положительные
Рис. 1.3
направления компонент тензора напряжений. Из рисун-
рисунка усматривается, почему компоненты с одинаковыми ин-
индексами называют нормальными напряжениями, а с раз-
разными — тангенциальными.

§ 1. напряжения. Уравнений Движения	29
Подсчитаем главный момент приложенных к рассмат-
рассматриваемому параллелепипеду поверхностных сил относи-
относительно проходящей через центр параллелепипеда оси,
параллельной прямой х$:
dx\ —
Поскольку главный момент должен равняться нулю, от-
отсюда следует 012 = 021. Аналогично выводятся остальные
условия симметричности тензора истинных напряжений
Коши:
2* = 2: O12 — O21, О2з = 0з2, O3i=Oi3. G.10)
Вернемся к интегральному равенству G.1). С учетом >
равенств G.9) и F.11) можно получить
Sn. G.11)
f undSn= f n-2dSn= J nMir^
Sn	sn	sQn
Введем вектор напряжений 0П» в расчете не единицу пло-
площади исходной недеформированной поверхности
°n*Sn dSn
Qn° —	5— = —о" °п*	GЛ2)
При этом очевидно
" 'n-dS°n,	G.13)
а сопоставление последнего равенства с G.11) дает
Несимметричный тензор
(F-1-/!}	G.15)
будем называть номинальным тензором напряжений.
Получим уравнения движения материальной частицы.
Прежде всего согласно соотношениям G.11) и F.11)
f GndSn= j ^.{F^.JZUV0.	G.16)
К	v°
Далее, согласно G.4) закон сохранения массы записы-
записывается в виде
(dm~) pdV*=p°dV\	G.17)

30 гл. 1. Основные зависимей нелинейной теорий
Подставляя выражения G.16) и G.17) в интегральнбе
равенство G.1), получаем с учетом произвольности объ-
объема уравнения движения в недеформированной конфигу-
конфигурации тела:
Vе. {F./!} + р°A - w) = 0,
дх!
§ 8. Работа напряжений
Подсчитаем работу внешних сил на вариациях коор-
координат материальных точек 6х{. Обозначая через 6W плот-
плотность этой работы (в расчете на единицу массы), полу-
получаем интегральное выражение — начало возможных пере-
перемещений (принцип Лагранжа):
\bWpdV = f an*
v	sn
(8.1)
Здесь anp6xp, /рбхр, —шрбхэ— плотности работ поверх-
постных, массовых и инерционных сил. С учетом соотно-
соотношений G.12) и G.17) перейдем здесь к интегрированию
по недеформированным объему и поверхности
f bWp'dV- Jano.te,dS°n + J (ft-wtNxtP°dV. (8.2)
*	°
С учетом уравнений движения G.18)а, F.9) и E.5) пре-
преобразуем последний интеграл
J fo-iprtteip-dr- - J

§ 9. СОПРЯЖЕННЫЕ ПО ХИЛЛУ ПАРЫ ТЕНЗОРОВ	31
Подстановка этого выражения в (8.2) дает с учетом
G.14)
j p°6WdV°= f [F-^Jl}a^F^dV°.
v°	v°
С учетом же произвольности объема и A.4) отсюда сле-
следует
Но согласно соотношениям E.7) и A.12)
(8.4)
С учетом того, что A^a(A°~1)av = (А°« А9")^ =
(l)ixv = Sjav» преобразуем подчеркнутую сумму
(8.5)
Варьирование следующих из B.14) условий ортогональ-
ортогональности дтд^еи ^ бТР дает ^тмбдрц^— дрцбдТц. С учетом этого
находим, меняя индексы суммирования (f ** ^) и ис-
используя симметричность тензора напряжений,
Отсюда и из (8.5) следует, что подчеркнутая в (8.4)
сумма равна нулю, и окончательно
pW = [/ (Л0-1^:^^] 6Л°ца.	(8.6)
§ 9. «Сопряженные по Хиллу (энергетические)
пары тензоров
Рассмотрим подробнее равенство (8.6), записав его с
учетом соотношений E.7) и A.4) в виде
pW = (/^-/Е-фацбЛ'а = (F^./S.Q): 8А°.
Разбивая первые сомножители правой части на суммы
симметричных и кососимметричных частей, получаем
с учетом того, что (см. B.20)) свертка кососимметричной
Части с симметричными компонентами 6Лца равна нулю,

32 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
выражение для плотности (в расчете на единицу неде-
формированного объема) работы напряжений
р W = V, (F~l J2Q + Q+J2F-1* )а|4 6Л;а =
= V2 (F^./S.Q + Q^/S-F*): 6Л°. (9.1)
Р. Хилл предложил [76] называть свернутые в правой
части тензоры сопряженной парой тензоров. Тем самым
выше была получена четвертая пара из следующих пяти
сопряженных пар:
2Э	Е9
ИЛИ ?О =
(9.2)
II
III
IV
V
F*
Q«
i/ 1
Л-
'¦Л.
;p-i.
F
Q
Я QH
удовлетворяющих
P°
—72C ~
или в°
+ Q* /2F-1*)Ae или
h Q* • /2 ¦ F) -Л" или
соотношению
2л . Ou :=: A I ?4 Of ^ Gc
= — /2.
-7«A-
Г
Ae-i
1 — \'~
(9.3)
и представляющих собой для деформируемого тела ла-
гранжевы пары: обобщенная сила — обобщенное переме-
перемещение. Остальные пары выводятся аналогичными пре-
преобразованиями [76, 81].
Тензор F^/ZF* называют симметричным тензо-
тензором Пиала— Кирхгофа. Тензор Т° вводится «не го л оном-
ным» соотношением:
Г* - Vs (A°* • А0-1 + А0 • А°).	(9.4)
Для изотропного материала*), а также для деформации
без поворота главных осей деформации тензор Т° можно
заменить на 1пА° [76, 81]. Именно этими двумя случая-
случаями и ограничивается область применимости тензора ло-
логарифмических деформаций, если оставаться в рамках
использования сопряженных по Хиллу пар тензоров.
¦) Изотропным будем называть материал, для которого соосны
тензоры Q* • /2 • Q ж Л°.

§ 9. СОПРЯЖЕННЫЕ ПО ХИЛЛУ ПАРЫ ТЕНЗОРОВ	33
Рассмотрим подробнее тензор напряжений из четвер-
четвертой пары в (9.2), записывая с учетом E.7)
Г = у* [{F-1 - /2) • Q + Q* {F 72}*] =
-2Q)A°-1]. (9.5)
В зарубежной литературе его называют симметричным
тензором напряжений Био. Считая материал изотропным,
имеем по формулам E.15J, E.14) и выражению тензора
истинных напряжений в главных осях 2 = оаеаеа следу-
следующие соотношения в главных осях деформации и напря-
напряжений:
Отсюда и из (9.5) находим с учетом F.2) (i?"j ?*кФ1)
*	(9.6)
Величина ddSi является силой, передаваемой через эле-
элемент деформированной поверхности. Отсюда и из (9.6)
усматривается, что для изотропного материала главные
значения симметричного тензора Био 0* являются ус-
условными напряжениями (подсчитанными без учета де-
деформационного изменения площади элементарной пло-
площадки, через которую они передаются). Поэтому в даль-
дальнейшем симметричный тензор Био будем называть тен-
тензорам условных напряжений (с компонентами 0$ и глав-
главными значениями о<).
Из второго столбца таблицы (9.2) и E.И)з,з следует,
что четвертому и пятому тензорам деформации отвечают
основные определения относительных удлинений.
Из соотношения (8.3) следует шестая (номинальная)
пара тензоров
2*	Е*
VI {F-1 Л!) F	<9.7)
Таким образом, шестую пару сопряженных тензоров со-
составляют тензор номинальных напряжений и градиент
движения. В отличие от первых пяти шестая пара зави-
зависит не только от деформации, но и от поворота матери-
материальной частицы. В случае деформации без поворота
главных осей Q = 1 н согласно (9.5)
Г - Ч* [<F-! • 7» + <F-f • J»*b	(9.8)
2 к Ф. Чержых

54 Гл. i. Основные злййсймбстй нелинейной теорий
Таким образом, при деформации без поворота главных
осей тензор условных напряжений совпадает с симметри-
зованным тензором номинальных напряжений.
Фундаментальность полученных сопряженных по Хил-
лу пар тензоров определяется тем, что они являются
следствием лишь начала возможных перемещений (8.1),
определяющего работу действующих на произвольную
часть тела внешних сил, и ничего более. Приведенные
сопряженные по Хиллу пары тензоров не зависят от
свойств материала и вида деформации.
В случае упругого материала вариация работы напря-
напряжений совпадает с вариацией энергии деформации, и со-
сопряженные по Хиллу пары тензоров уместно называть
энергетическими. В дальнейшем из энергетических (со-
(сопряженных) пар выделим четвертую: условные напря-
напряжения — кратности удлинений. О ее преимуществах будет
сказано в § 1 гл. 9. В качестве вспомогательной будет
широко использоваться шестая пара: номинальные на-
напряжения «-*» компоненты градиента движения.
Отметим, что систематический вывод сопряженных
пар был дан Р. Хиллом [76]. Пятая и, по-видимому, по-
последняя пара такого рода была получена автором [80].
Ранее вопрос о сопряженных парах рассматривался Но-
Новожиловым [39].
§10. Закон упругости
Для получения закова упругости рассмотрим две кон-
конфигурации A) и B). Переходу из первой во вторую от-
отвечает плотность работы напряжений
[p°6W.	A0.1)
ш
Вообще говоря, эта работа зависит от пути деформирова-
деформирования, т. е. от того, в какой последовательности деформи-
деформировалась материальная частица при переходе от первой
конфигурации ко второй.
Для упругого материала, по определению, работа на-
напряжений не зависит от пути деформирования и опреде-
определяется только начальной и конечной конфигурациями*).
*) Следует отметить, что рассматривается изотермическая ли-
либо адиабатическая деформация.

6 10. ЗАКОН УПРУГОСТИ	35
Согласно соотношениям (9.3) независимость интеграла
A0.1) от пути интегрирования влечет равенства
где Ф (е^) — некоторая функция компонент деформации
из пар сопряженных тензоров (9.2), (9.7). Из (9.3)
и A0.2) следует
- 0,	A0.3)
Отсюда в силу произвольности вариаций следует закон
упругости сжимаемого материала
°ъ = 7Т- (М = 1-2,3).	A0.4)
В дальнейшем наиболее удобной окажется шестая пара
энергетических тензоров, для которой (см. E.5))
Для несжимаемого материала имеем согласно F.12)
условие несжимаемости \FI — 1 — 0, из которого следует
O.	A0.6)
Таким образом, в рассматриваемом случае несжимаемого
материала вариации уже не являются произвольными,
будучи связанными соотношением A0.6). Для того что-
чтобы обойти возникшую трудность, умножим условие не-
несжимаемости A0.6) на произвольную вещественную
функцию (—/?). Прибавляя полученное к записанному
для шестой пары равенству A0.3), получаем
Как было сказано выше, здесь одна из вариаций линей-
линейно зависит от остальных. Выберем функцию р так, чтобы
обращалась в нуль величина, входящая в скобки перед
этой вариацией. Остальные вариации независимы, и по-
поэтому равны нулю и остальные скобка. Таким образом

36 f Л 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ
приходим к закону упругости несжимаемого материала
-1
д{дх}1дх°.) У
Как будет видно из дальнейшего, функция р(х\,х\,х\)
определяется из статических соображений.
§ 11. Приведение к комплексным координатам
к компонентам
В нелинейной теории упругости широко используют-
используются комплексные координаты, а также комплексные ком-
компоненты векторов и тензоров. Введение комплексных
величин существенно упрощает промежуточные выклад-
выкладки и придает окончательным зависимостям более ком-
компактный и обозримый вид. Оправдано также использова-
использование функций комплексной переменной и конформного
отображения, облегчающих, в частности, переход к кри-
криволинейным координатам и решение конкретных крае-
краевых задач.
Комплексную запись можно рассматривать как аль-
альтернативу векторной. Изложенное же в § 11-—15 следует
считать дальнейшим развитием комплексного подхода,
широко использованного в свое время в линейной теории
упругости Г. В. Колосовым [24].
Введем комплексные координаты
о
Со	о -	о . о
= Хг + 1Хг, t = Хг — |gS9
-	A1.1)
z = хх + izt, z = xx — ixt
к дифференцирование по первым из них
д 1 / д
"
Для тензора второго ранга T = k»g<ig» удобно ввести
следующее комплексные компоненты:
A1.3)

§ II. ПРИВЕДЕНИЕ К КОМПЛЕКСНЫМ КООРДИНАТАМ	37
Разовьем необходимый в дальнейшем аппарат. Пусть
S = S(tvgMgv — еще один тензор второго ранга. Расписывая
скалярное произведение Т • S = lap^vgagv и используя
комбинации A1.3), находим
(Г • su - 'ЫГА + г*)+ ГА, (И.4)
Из выражений для компонент сопряженного тензора
A.12) следует
7? = Тг, Tt = Тгч Т1 = Г4Т Г; - Г„ Г5* = Г5. A1.5)
Для единичного тензора legaga B.15) подсчитываем
по формулам A1.3)
li«2, 12«1з~14~0, 1в-1.	A1.6)
Полагая теперь в соотношениях A1.4) S^T
(Т-8в1) и решая полученную систему уравнений от-
относительно комплексных компонент (Г~')<, находим ком-
комплексные компоненты обратного тензора
(г-1)»
A17)
4D - (J,f, - J2f,)
Используя формулы A.11) и A1.3), подсчитываем
выражения для главных ввварнантов тензора

38 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
Сопоставление последнего выражения с последним в
A1.7) дает
D = IIIT.	A1.9)
Для симметричного тензора А = aa»gogp, в« =¦ в# и
А\ =ац + 022,	Аг — Си — a22 + i2ai2,
A1.10)
= V4 {А\ - AtAt) А, - »/ИИА + V* (^йз2 + А2А\).
Используем формулы A1.4) для подсчета комплекс-
комплексных компонент тензоров истинных и условных напряже-
напряжений. Так, из очевидного соотношения /S = F • (F /2}
находим
/2, - 'MW-1 • /2}, + FtiF-1 ¦ /2J] + №' • /2}4,
'/2 [W-' • /2>, + FiiF-1 ¦ /2}2] + F3{F~l ¦ /2L,
'/г [№"' • /2)з + F2lF-l-W»] + F3{f-' • /2)s,
/24 = 4*[FtiF-1 ¦ /2), + ^{F-1 • /2J] + FbiF-1 ¦ /2L,
/25 - '/г[W-'-y2>3 + Л^ • /2)з] + F5{^-1 • /2>5.
A1.12)
Аналогично для тензора условных напряжений (9.5)
находим с учетом A1.4) и A1.5)
2; = v4
A1.13)

§ 12. ДЕФОРМАЦИОННЫЕ СООТНОШЕНИЯ	39
В заключение параграфа получим две полезные в
дальнейшем изложении формулы. Из F.9) имеем
f 4%dV° = \umld&- f v^dV\
jo dxi	Jo	jjo dxl
f и Ц, dV° = f uvn°a dS°n-\v -^0 dV°.
Jo dx%	Jo	jo дхг
sn
Умножая второе выражение на ±i и прибавляя к перво-
первому, получаем с учетом A1.2) первые два из следующих
соотношений:
o
(ll)o- \vd?dV°, A1.14)
уо b	о
8П
^dVo= \wm\dSl- \v%dV
д*а	Jo	jo дхз
§ 12. Деформационные соотношения в комплексной
записи
По формулам (И.З) и C.15) подсчитаем комплекс-
вые компоненты тензора поворота Q:
A2Л)
1 + (О*
Здесь
V sin со/ , . ч v sin©	/jr» ov
со/ = -jj- К + *оJ), oJv = —?- (о8	A2.2)
комплексные компоненты вектора большого поворота
A23)

40 ГЛ. I. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИЙ
В общем случае для вектора а = aaga имеем
«iV = «1 + «аг- a»V = «з-
Из соотношений E.5), A1.3), A1.5) и A1.7) находим
„ 9d~z р* 9 дг	т(р-1\ 9(#гдхз ^ дх
4,
дгТг
где величина
является согласно A1.8K? A1.9) и F.12) кратностью
изменения объема.
Рассмотрим основной в дальнейшем случаи поворота
вокруг третьей координатной оси, при котором
©3 = ©1 <01 = Сд2 *==*0	A2.7) 1
и согласно соотношениям C.15) отличны от нуля лишь
компоненты
qu = дм == cos о), ?21 ¦* —gi2e sin о). A2.7J
Отсюда и из соотношений A.16), A1.3) следует
A2.8)
= e-*« (a, + ia2), ^ - а,.	A2.9)
Из равенств же A2.7J и A1.3) получаем
0,-2е-*\ ft-ft-04-Qt ^5-1. A2.10)

S IS. ДИВАкЙЧЕСКИЁ СбОТНОШЕЙИЯ	41
При этом соотношения A1.13) принимают вид
11
2S° = 2? =
В случае отсутствия поворота в рассматриваемой точ-
точке тела (например, в бесконечно удаленной) @ = 0 и
A2.12)
В этом случае тензор условных напряжений совпадает
с симметризованным тензором номинальных напряжений.
§ 13. Динамические соотношения. Комплексная
вались закона упругости
Распишем уравнения движения G.18)
Ч-р°/,-
Умножая второе уравнение на г и складывая с первый,
подучаем с учетом соотношений A1.2) и A13) комп-
комплексные уравнения движения
К ¦ Т	*	Т дж\	'
'' +^-^1==0' A3.1)
+p \/f~^?

42 ?Л. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ ЙЁЛИНЁЙНбЙ ТЕОРИЙ
Совершенно аналогично, считая, что левые части й
выражениях G.14) являются заданными функциями
точки поверхности тела, получаем комплексные силовые
(статические) граничные условия
П1
П2/
A3.2)
ns
Рассмотрим цилиндр с образующими, параллельными
оси х3. Пусть g° — граничный контур области S°, полу-
полученной при пересечении деформированного цилиндра
плоскостью, перпендикулярной оси. Из рис. 1.4 следует
(при замене на боковой по-
поверхности nQ на v°)
о
— 11 = sin y = —
AJ
vj - 0),
A3.3)
Рис. 1.4
а о а , о a
_ = Vl -o + V2 -T5
d*	дх	дх
Здесь d/ds° — производная вдоль контура	области,
a d/dsy— но нормали к нему. Из выражений	A3.3) и
A1.1), A1.2) следует
§	A3.4)
Теперь из соотношений A3.2), A3.4) получаем на
части поверхности ?0, где заданы напряжения, комп-

g 13. ДИНАМИЧЕСКИЕ СООТНОШЕНИЯ	48
лексные силовые граничные условия
= 2 [о.л(»\хо,) + и,и{?,хЦ, A3.6)
8°, X°3<=S°a.
На части боковой поверхности 5U, где задана конфи-
конфигурация деформированной поверхности, имеем следую-
следующие комплексные геометрические граничные условия:
l
z = z{s°,xl), xB = x3{s°,xll s°,xl<=S°u. A3.7)
Дифференцирование последних условий вдоль контура
приводит согласно A3.5) i к комплексным дисторсион-
ным *) граничным условиям
#?	as	7 *
Частным случаем A3.7) является условие заделки
* = ?, xB = xl s°,xl<=S°u.	A3.9)
Ему отвечают согласно A3.8) и A3.5) i условия жестко-
жесткого края
Последние отличаются от условий заделки тем, что в
многосвязной области частичные контуры могут сме-
смещаться как жесткие целые.
Подсчитаем компоненты главного вектора и главного
Момента действующих на цилиндрическую поверхность
напряжений (в расчете на единицу ее высоты), проходя-
проходящую через кривую &° (в частности, ею может быть
граничный контур g°) сечения 5е недеформированного
*) Термин предложен JI. М. Зубоэьш.

44 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
цилиндра:
Используя эти выражения, а также A3.2) и A3.3),
получаем
, = - Jm f [F-l.J2)t d?,	A3.11)
i
», = -»/.Re f
В поперечных сечениях цилиндра S", со стороны по-
положительного направления оси х3:
о	о .	о .
Пг = П, = О, П3 = 1,
и согласно A3.2) аналогично выводим
F^.JSUdS0, 5, = f
»! + ш4 = t f с{F-^/sibi^0, A3.12)
s°
Получим комплексную запись закона упругости. Со-
Согласно соотношениям A1.1) — A1.3) имеем для сжимае-
сжимаемого материала из A0.5)
е,

8 14. ИСПОЛЬЗОВАНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ	45
= 2^2-, A3.13)
Будем считать, что
Ф = Ф(/С, //с, ///с),	A3.14)
где согласно A1.11), A1.4), A1.5) и E.7) C = F F* и
/с = С; + С;, /7С - V,(C1 - С°?°г) - С°?3 + C\d
A3.15)
///с = V,(C1-	1 №
С; = V, {FiFi + *г) + Л. Й ЛЛ + !,
Для несжимаемого же материала имеем согласно
A0.7), F.12), A2.5) и A2.6)
A3.17)
jf jsj - ^ л-nZU-l
\F .J2U-. — +P-L--
где
— +P-L--
о	О
Ф(/С, //с);	A3.18)
!/4(JVl - F^i)^. A3.19)
§ 14. Использование конформного отображения
В дальнейшем окажется полезным использование
конформного отображения рассматриваемой области ком-
комплексной плоскости ? на внутренность либо внешность
единичной окружности комплексной области, осущест-

46 гл. i. основные зависимости нелинейной теорий
вляемого функцией
С-х(х).	A4.1)
Функции переменных ?, ? преобразуются при этом
к новым переменным х» X по формуле
х). A4.2)
Поскольку
д _ д	д
К ~ *' (х) V д\
из A4.2) получаем
х)
т. е.
х'(Х)«Х	к'(Х)*Х'
(X, X) ««,.&	1 дХ^хЛ)
Рис. 1.5
Из рис. 1.5 видно, что вдоль линий первого семейства
_ dt	хЧ
Ix'(X)I
Г. €.
A4.5)

§ 75. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛЬНЫХ ТОЖДЕСТВ 47
На единичной окружности, точки которой будем обо-
обозначать через о,
г° = 1, a = <?-ie° = a~i, a = a	A4.6)
и вдоль контура области, отвечающего единичной ок-
окружности,
d	I d
ds° I к'(a) I
A4.7)
Как известно, концентрация напряжений обычно
имеет место на контуре отверстия и существенно зависит
от кривизны последнего К° = dy'/ds*. Дифференцируя
по s° выражение A4.5)з на контуре ei2?°= -=Д, полу-
Xх (О)
чаем с учетом A4.7)
§ 15. Комплексная форма интегральных тождеств
В теории трещин часто используются интегральные
тождества, связываемые с именами Раиса, Черепанова и
других механиков. Получим их в удобной для практиче-
практического использования комплексной форме.
В отсутствие массовых и инерционных сил имеем со-
согласно соотношениям G.18), E.5) и A0.5) для сжимае-
сжимаемого материала
'<*-'/*> = 0,	A5.1)
дФ
Умножая уравнение равновесия A5.1) на F{j и сумми-
суммируя полученное по iea, получаем интегральное тож-
тождество
= 0.	A5.3)
Интегрируя его по частям, находим с учетом равенств

48 гл. t. осйовнЫе зависимости нелинейной Теорий
A5.2), F.9), и G.14J
J {/}«»; = 0 G = 1,2,3),	A5.4)
О
а»
где
М^Фп'-пЦр-^ЛЯ^Ръ^Фп'-о Fa}. A5.5)
п°а
Из полученных соотношений, а из также A1.1) и A1.3)
следуют удобные для практического использования ком-
комплексные интегральные тождества.
О	О
A5.6)
где
,-V/,, A5.7)
f 16. Основные варианты закона упругости
В конце § 13 были получены комплексные аналоги
закона упругости для сжимаемых и несжимаемых изо-
изотропных материалов. Для описания упругих свойств ре-
реального материала необходимо конкретизировать в них
вид упругого потенциала. Единственные требования
к нему:
1. Удовлетворительное онисанвзе упругих свойств*
рассматриваемого материала в требуемом интервале де-
деформации.

§ 16. ОСНОВНЫЕ ВАРИАНТЫ ЗАКОНА УПРУГОСТИ	49
2. Возможно большая аналитическая простота потен-
потенциала, облегчающая решение краевых задач.
Для «живых носителей» больших деформаций—эла-
деформаций—эластомеров — проблема рационального выбора упругого по-
потенциала рассматривалась, например, в работах автора
(81,84,88,89].
Так, для несжимаемого материала IIIАп = /п = 1 и
Ф = Ф(/А«, //Лп),	A6.1)
где
К 1	ВД ВД + Я3%п, A6.2)
IIIАП = ВД? = (Я^)* = Г.
При этом переход отвечающего упругому потенциалу
A6.1) закона упругости при малых деформациях в за-
закон Гука обеспечивается условием
Простейшее семейство этого типа составляют упругие
потенциалы «типа неогуковского»
удовлетворякшще условию A6.3) и содержащие неогу-
ковскян потенциал при /п == 1.
Часто упругие потенциалы задают в виде
Ф«Ф(Х,,А* U)	A6.5)
с заменой условия A6.3) на следующее:
Так, хорошо себя зарекомендовала трехяонстантный
A6.7)
¦ двухконстантный
З»(	3)	A6.8)

5 0 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
упругие потенциалы. Здесь ц, = ?УЗ, п, $ — постоянные
материала. Значение я = 2 в A6.8) отвечает неогуков-
скому материалу, а п = 1 — материалу Бертенева — Ха-
зановича. Значение /г = 2 в A6.7) отвечает материалу
Муни, а п = 1 — материалу, предложенному автором.
Для того чтобы можно было воспользоваться приве-
приведенными в конце § 13 соотношениями при задании по-
потенциала в виде A6.5), требуется обратить выражения
1С = /Ai = Хх -f Я2 -f ^з*
IIс = П А% = XX + \\Х\ + Х\ХЪ	A6.9)
III с =	JJJ
(При рассмотрении в гл. 2 плоской задачи такое обра-
обращение легко проводится.)
Из A6.9) находим
dic
c_ «"с
Обращение этих соотношений дает
- х;)+я,4(^ - А)

§ 17. СЖИМАЕМЫЙ И СТАНДАРТНЫЙ МАТЕРИАЛЫ	51
дФ _ dtf дФ	д*1 дФ	д^\
дф
Итак, приведенные соотношения при условии обраще-
обращения выражений A6.9) позволяют использовать упругие
потенциалы вида A6.5) в произвольных (не обязатель-
обязательно главных) осях.
§ 17. Сжимаемый, малосжимаемый и стандартный
материалы
Для изотропных сжимаемых материалов примем
(см. A6.2))
)>	A7.1)
Переход отвечающих этому упругому потенциалу зако-
законов при малых деформациях в закон Гука обеспечивает-
обеспечивается равенствами [81]
Етг*
Большинство конструкционных материалов (если ис-
исключить из рассмотрения пористые) малосжимаемы. Это
следует учитывать при конструировании упругих потен-
потенциалов. Применительно к эластомерам предложено боль-
большое число вариантов закона упругости для малосжимае-
мых материалов [81, 88, 89].
В этом параграфе будет предложен еще один подход
к проблеме, особенно удобный (как выяснится в следую-
следующей главе) в плоской задаче. Малость сжимаемости дает
возможность учесть «ответственный» за изменение объ-

52 ГЛ. 1. ОСНОВНЫЕ ЗАВИСИМОСТИ НЕЛИНЕЙНОЙ ТЕОРИИ
ема третий главный инвариант Ш Ап = /п простейшим,
линейным образом:
Ф = С (IIIАП - 1) + V (/л„, //дП).	A7.3)
Здесь С — постоянная материала, a W — некоторая
функция своих аргументов, ответственная главным обра-
образом за формоизменение. Подстановка выражения A7.3)
в A7.2) приводит к условиям, обеспечивающим при ма-
малых деформациях переход принимаемого закона в закон
Гука:
Err*
Л-\	,Г	Еп~*	,47 /\
Еще удобнее для практического использования сле-
следующее более простое выражение:
для которого условия A7.4) принимают вид
дУ\	г Еп~*
A7.6)
Стандартными п-го порядка называют материалы, от-
отвечающие упругому потенциалу
A7.7)
Потенциал A7.7) получен из упругого потенциала ли-
линейно-упругого материала заменой инвариантов линейно-
линейного тензора деформации Е на инварианты тензоров
(Л°п—1)/л. Преимуществом их является то обстоя-
обстоятельство, что при малых деформациях отвечающий им

§ 17. СЖИМАЕМЫЙ Й СТАНДАРТНЫЙ МАТЕРИАЛУ	53
упругий закон автоматически переходит в закон Гука.
Стандартный материал 1-го порядка (он же гармониче-
гармонический, полулинейный, материал Джона) широко исполь-
используется, несмотря на то, что обладает рядом недостатков
физического характера [81].
Вполне оправданно использование стандартных мате-
материалов при расчете гибких изделий, когда напряжения
малы, а повороты велики. В этом случае тензоры дефор-
деформации (Л°п—1)/н, в отличие от линейного тензора де-
деформации Е, «правомочны».

Глава 2
НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Хорошо известно (см., например, [36]), что в линей-
линейной теории упругости рассмотрение плоской деформации
и плоского напряженного состояния приводит к почти
идентичной математической постановке. Соответствую-
Соответствующие зависимости различаются лишь упругими постоян-
постоянными. В нелинейной же теории различие между ними
значительно больше. Поэтому их и рассматривают по-
порознь, независимо друг от друга. В этой главе показы-
показывается, что и в нелинейной теории обе проблемы сводят-
сводятся в одну унифицированную нелинейную плоскую зада-
задачу: для обобщенной плоской деформации и плоского на-
напряженного состояния, для сжимаемого и несжимаемого
материалов, силового и дисторсионного граничных усло-
условий. Таким образом, по существу, в унифицированной
форме представлена восемь самостоятельных краевых
задач. При этом полученные зависимости существенно
проще предлагавшихся ранее. Это позволило значитель-
значительно дальше продвинуться в решении актуальных «плос-
«плоских» проблем.
Нелинейной (физически и геометрически) плоской за-
задаче посвящено сравнительно небольшое число публика-
публикаций. Изложенное ниже подводит итог работам автора
[79,81].
§ 1. Обобщенная плоская деформация
Получим зависимости обобщенной плоской деформа-
деформации, понимая под ней деформацию, при которой прямо-
прямоугольные координаты материальной точки, до и после
деформации, связаны соотношениями
хг = хх{х1, х°2; t), х% = х2(х°г, xl; t\ х3 = Xxl,
или
z = *(?,?; *), х3 = Кх1	A.1)
Таким образом, при обобщенной плоской деформации
нормальное к плоскости х\ = О материальное волокно

§ i. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
55
смещается поступательно вдоль плоскости, удлиняясь с
постоянной кратностью удлинения Яз = Я =• const. Собст-
Собственно же плоской деформации отвечает Я= 1.
Конкретизируем применительно к закону движения
A.1) соотношения § 11 —13 гл. 1, опуская при этом со-
соотношения, удовлетворяемые тождественно. При очевид-
очевидном предположении об углах поворота
0I=0J = 0, 0)з==0)	A-2)
из выражений A.12.1), A.12.2) имеем для тензора
поворота
01=2<Г'\ 02 = 0, 05=1 @3 = 04 = 0). A.3)
Далее, по формулам A.12.5), A.12.6) подсчитываем
р 	9 _?. р 	2—- Р 	5l (Р 	Р 	0V (\ А\
1	««. *	2	?Z '5	V 3	4	/* \ • */
/-ЯА,
где
A.5)
— кратность изменения площади плоскости х3 = const.
Из соотношений A.3), A.4), A.11.4), A.5.7) находим
с учетом симметричности тензора кратностей удлинений
А°
По равенствам A.5) —A.7) и A.11.11) подсчитываем
главные инварианты тензора кратностей удлинений
А ° . Л	п I ^2 I . «
+2Х
A.8)
Упрощаются и уравнения движения A.13.1):

56	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Поскольку рассматриваемые величины не зависят от
?3< можно вместо цилиндрического тела рассматривать
его произвольное поперечное сечение — область 5е с гра-
граничным контуром g° (рис. 1.4). При этом согласно соот-
соотношениям A.13.6), A.13.8), A.13.10), A.12.9) на кон-
тУре g° могут быть заданы: силовое граничное условие
= 2
o (О + toy». (*•)], A.10)
дисторсионное граничное условие
в частности, условие жесткого края
На цилиндрическую поверхность единичной высоты,
проходящую через кривую 2" области 5° (могущую
быть и граничным контуром g°), действуют напряжения
с главными вектором и моментом, определяемыми со
гласно A.13.11) выражениями
Si + *», = -(г/2) J [{F^
A.13)
]
На поперечном же сечении цилиндра действуют (со сто-
стороны положительного направления оси xs) напряжения
с главными вектором и моментом A.13), A.12)
аи,
Далее, из соотношений A.11.12), A.11.13), A.3)
A.5) следуют выражения для: истинных напряжений

§ 1. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
57
A.15)
а условных напряжении
у° - дг Г1
A.16)
Получим удобные для практического использования
формы закона упругости. Прежде всего в силу того, что
^3 = ^4 = 0, получаем из соотношений A.13.15), A.13.16)
"с = 7„ (ЗД - ?гРг? + V, (ЛЛ + FtF2) F\,
IIIc = Ух. (F& - FtFt)*F\, F = lU PA - FtFt) ръ-
Отсюда усматривается, что
0 = 0(^1^1, FJP2, Fb),
и соотношения A.13.13), A.13.17) записываются в виде
aKFiFi>
дф
A.17)
С учетом выражений A.4) имеем
ш из первой группы равенств в A.17) получаем для
сжимаемого материала

58
frl. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
дф
д | dz/dl I '
A.19)
Для несжимаемого материала находим из второй
группы выражений
г -1 dФ
di
д |
+
A.20)
Введем новую произвольную функцию
A.21)
В силу несжимаемости материала и выражений A.5)
имеем
= А;
Если ввести обозначение
то согласно A.22) имеем
2 \дг
д |
дФ
d\dz/dl\
дф	2 \dz
A.22)
A.23)
A.24)
d\dz/dl\ d\dz/dl\
Теперь с помощью выражений A.21) —A.24) закону
упругости для несжимаемого материала A.20) придаем
искомую форму
дг
"Ж
дг
Ж
дг
-1 ЭФЛ
д\дг/дЦ
A.25)
Иногда удобно вести рассмотрение в главных осях
деформаций и напряжений, Получим соответствующие

i 1 Плоское йапряЖенйОё состояние тбнкой пластины 59
зависимости. Прежде всего согласно A.8) при Xi > Хг
_к±к
к
A.26)
Далее, из соотношений A.16), A.19) и A.11.3) находим
дФ
2 d\dzidi\ + 4
1 (~di dz dz Tz\ \dz\-l
+ 4 \a?^ + *C*c jk'
dz 1-1
О ад, =
4 \^ ag ^ dl)\^\ \dl
—1
4
Вводя главные условные напряжения о1ч а2 и используя
только что полученные выражения, запишем инварианты
двояко
о о о о аФ
Oi + О* = Оц + О„ - щ
Отсюда следуют выражения для сжимаемого материала
дф	дф \ о JL/ дФ	^Ф \
о _
01 ~
_ 1 /
~ 2 [
d\dz/dt\
A.27)
Аналогично выводятся выражения для несжимаемого
материала
к
A.28)
15" \Ч
§ 2. Плоское напряженное состояние тонкой
пластины
Рассмотрим тонкую пластину, считая, что прямо-
прямоугольные декартовы координаты ее материальной точки,
До и после деформации, связаны соотношениями
(ОО\	/ О ' О \	л/°О\°
xi,xt;t), хг = *,(*!, x,,t), х, = Цх!, xt;t)xs,
B.1)
\

бО	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
При этом материальное волокно, нормальное к средин-
срединной поверхности х3 = О, перемещается параллельно себе,
испытывая удлинение с кратностью удлинения
л^х1т хг\ t), постоянной для каждого волокна и меняю-
меняющейся при переходе от волокна к волокну.
Принятому закону движения B.1) отвечают согласно
формулам A.12.5), A.12.6) комплексные компоненты
градиента движения:
^& = л,	/^5=Л,	\1 Л = л •	Vz-^)
Здесь
/ = ЯД, L ~ -ку
дг дг дг дг
дз
'¦ B.3)
По формулам A.11.4), A.5.11), A.11.11) получаем
выражения для главных инвариантов тензора деформа-
деформации Коши —- Лагранжа
3
о2 Г^Х ^Я / дг Tz dz Tt \ (dXJdi dz /?M2 dz di
Пусть А° — толщина недеформированной пластины,
а Г — характерный размер ее срединной плоскости, либо
«длина волны» динамического воздействия. По определе-
определению, для тонкой пластины
*7Г<1.	B5)

§ 2. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ ТОНКОЙ ПЛАСТИНЫ 61
Введем безразмерные величины
Бели внедрить их в зависимости B.4) и считать, что ве-
величины дХ/д^ дХ/д% не слишком велики по сравнению
с дт\1д%, дх\1д\, то нетрудно проследить, что подчеркну-
подчеркнутые величины малы по сравнению с остальными. С точ-
точностью до пренебрежения величинами порядка (А°/ГJ
по сравнению с 1 ими можно пренебречь в выражениях
B.4), а значит, и в плотности энергии деформации
ф = ФAСуПСуШс).
Изложенные «энергетические» соображения и_оправ-
и_оправдывают пренебрежение величинами dX/dt, и dX/dt, в от-
отвечающих рассматриваемому случаю зависимостях*).
Так, соотношения B.2) принимают вид
|Д-1, B.6)
(F3 = Fl = (F-lK = Ft = F\ = (F-% = 0),
совпадающий с A.4), с той лишь разницей, что послед-
последние являются не приближенными, а точными.
С ПРИНЯТОЙ ТОЧНОСТЬЮ МОЖНО ПОЛОЖИТЬ @1 == 0J * 0,
юз — со, т. е. считать, что окрестность материальной
точки поворачивается вокруг нормали к срединной
плоскости. При этом согласно A.12.1), A.12.2)
Отсюда в иэ соотношений A.5.7), A.11.4), B.6) находим
B.7)
д*
Получим закон упругости. На лицевых поверхностях
йластины {х\ = ± k°/2) п{ = п\ = 0, п, = ± 1 и сотласно
¦) Это, конечно, не означает отказа от зависимости X от ? ж ?

62
ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
соотношению A.7.14)г отсутствию там напряжений отве-
отвечают равенства {F~l • /Shi =* {F~l • /2}32 = {F~l • /2}33 = 0
или согласно A.11.3)
Первое из полученных равенств согласно B.6) и A.10.5)
выполняется тождественно. Из второго и A.13.13),
A.13.6), B.6) следует для сжимаемого материала закон
упругости
IF JV) -dz\d* I
B.9)
—1
дф
и соотношения для определения функции Х(д?, х^; 0
55^ = 0.	B.10)
Для несжимаемого материала находим из соотноше-
соотношений B.8J, A.13.17), A.17) и B.1)
1 ?Ф
-1 dФ
д |
dФ
d\dz/dl\ ^ & дКу
С учетом соотношений A.21) —A.24) отсюда следует
-1
-1
B.11)
Остальные, не выписанные здесь зависимости совпадают
с полученными в § 1 для обобщенной плоской дефор-
деформации.
§ 3. Основная краевая задача
Используя полученные в двух предыдущих парагра-
параграфах соотношения, сформулируем основную краевую за-
задачу (включающую в себя, по существу, восемь само-
самостоятельных задач: обобщенная плоская деформация *

§ 3. ОСНОВНАЯ КРАЕВАЯ ЗАДАЧА
63
плоское напряженное состояние, для сжимаемого и не-
несжимаемого материала, при силовом и дисторсионном
граничных условиях 2X2X2 = 8). При этом будем счи-
считать, что граничный контур недеформированной области
5° может быть представлен суммой
g =
C.1)
где на части ga заданы напряжения, а на ^и — положе-
положение материальных точек граничного контура после де-
деформации. Итак, имеет место
основная краевая задача
При этом
функ-
функция
w
р
Обобщенная плоская
деформация
сжимае-
сжимаемый мате-
материал
Ф
0
несжи-
несжимаемый
материал
Я
Плоское напряженное
состояние
сжимае-
сжимаемый мате-
материал
Ф
0
несжимаемый
материал
Фд
0
C.3)
Поясним сведенные в C.3) восемь самостоятельных
«адач:

64	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
1.	При обобщенной плоской деформации сжимаемого
материала постоянная Я определяется из соотношения
(см. A.14),, A.19)8)
?$?««•	C.4)
при задаяной осевой силе 5з.
2.	При обобщенной плоской деформации несжимае-
несжимаемого материала постоянная X определяется по-прежнему
из C.4), а соотношение (см. A.22)ь A.5))
\дъ\г
к
= Г	C.5)
следует рассматривать как дополнительное дифферен-
дифференциальное уравнение, «компенсирующее» появление до-
дополнительной вещественной искомой функции #(?, ?).
3. При плоском напряженном состоянии^ сжимаемого
материам для определения функции Я{?, ?) следует ис-
пользовагь уравнение (см. B.10))
4. При плоском напряженном состоянии несжимаемо-
несжимаемого материала функция Х{?, ?) определяется из вы-
выражения
,	1(^J	0**1-1
Приведем остальные зависимости, пригодные для всех
случаев: угод поворота окрестности (см. A.6), B.7))
кратность изменения площади
»1 at
компоненты тензора истинных напряжений (см. A-15),
C.2), (IS))
(МО)

1 ОСЙОбНАЯ КРАЕВАЯ ЗАДАЧА
65
Компоненты тенгора условных напряжений (см. A.16),
C.2), C.3))
2,=
dW
дг дъ
\dz\
+pk\
-l dz
el
a | dzldl |
C.11)
Кроме того, согласно A.15), A.16), A.19), A.25) и
B.8)г имеем:
Напряже-
Напряжение
Обобщенная плоская
деформация
Сжимае-
Сжимаемый мате-
материал
1 дФ
дФ
дХ
Несжи-
Несжимаемый
материал
2
2
Плоское напряжен-
напряженное состояние
Сжимае-
Сжимаемый мате-
материал
0
0
Несжи-
Несжимаемый
материал
0
0
C.12)
При переходе к главным осям деформаций — напря-
напряжений получаем из A.27), A.28) и их аналогов (соглас-
(согласно C.3)) для плоского напряженного состояния выра-
0 °
жения для главных условных напряжении ах, а2 и глав-
главных кратностей удлинений К\, Яг:
о i т aw
i
о 1 Г dW
°* 2[d\dz/di\
2 ~~
dW 1 p /
Ях — X2 dz
2
•
C.13)
Исключение из выписанных соотношений величин ldz/d?|
и |dz/d?| приводит к закону упругости в главных
осях.
Приведем с учетом A.13), A.Ц) выражения для
главных вектора и момента напряжений, действующих
на цилиндрическую поверхность единичной высоты, про-
проходящую через кривую &° области S° (которая может
быть и граничным контуром g°). Напомним, что при
обобщенной плоской деформации 5° — произвольное
(в силу независимости напряженно-деформированного
3 К. ф. Черных

66	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛбСКАЯ ЗАДАЧА
состояния от х9) поперечное сечение, а при плоском на-
напряженном состоянии — часть срединной плоскости.
Итак,
= - (*/2) f
C.14)
= - V. Re J
?,0
На поперечном сечении SQ со стороны положительно-
положительного направления оси xs имеем
go
C.15)
Напомним, что величина г подсчитывается по формуле
i-Tf?dc+5<ft	(зле)
Вернемся к задаче C.2). Если на контур действует
нормальное давление ап =• —аоп, то с учетом соотноше-
соотношений A.7.12), A.6.6), A.13.4), A.4) и B.6) имеем
Итак,
где во — величина нормального давления.

§ 4. НЕОГРАНИЧЕННО-ЛИНЕЙНЫЙ МАТЕРИАЛ	67
§ 4. Неограниченно-линейный материал
Рассмотрим материал, отвечающий упругому потен-
потенциалу
W =
D.1)
Отсюда и из соотношений C.13) следует закон упруго-
упругости (связь между энергетической парой величин: глав-
главными условными напряжениями о°г и главными относи-
относительными удлинениями (Л<— 1))
D.2)
переходящий при малых деформациях в своеобразный
закон Гука в главных осях
D.3)
о
При At = Яг =1, т. е. в отсутствие деформации, о^ =
= о2 = о*. Таким образом, о* — величина предваритель-
предварительного всестороннего (в плоскости) условного напряжения.
Линейность соотношения D.2) показывает, что упругий
потенциал D.1) отвечает неограниченно-линейному пред-
предварительно напряженному материалу.
Строго говоря, следовало бы сделать оговорку, что
линейность имеет место по отношению к энергетической
паре величин сг* «-> (К — 1)- Ниже, однако (см. § 1 гл. 9),
будут сведены воедино аргументы в пользу преимущест-
преимущественного использования именно этой пары. Так что (если
согласиться с ними) надобность в такой оговорке отпа-
отпадает. Использование упругого потенциала D.1) позволя-
позволяет получить точные решения ряда краевых задач и с их
Помощью выявить влияние учета геометрической нели-
нелинейности на особенности напряженно-деформированного
состояния.
Так, из соотношений C.2J,з при р = 0 следует
:2а g. D.4)

68	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Подстановка полученных выражений в однородное урав-
уравнение равновесия (C.2)i при /i = /2 = d2z/(dtJ = 0) при-
приводит к гармоническому уравнению
из коего следует
Отсюда и из соотношений C.8) — C.11) находим
X = 2 [а*Ф (О Ф(С) +
Ф1ё}	D.6)
С учетом полученных выражений, а также C.2),
C.3), C.17) приходим к граничным условиям:
(I)	при заданном на контуре области нормальном
давлении оо
(а* + Ха0) Ф @ eiy° + (а - Ч) Щ5) e"iy° = 0; D.7)
(II)	при условии жесткого края
Задачи однотипные. Решив одну, нетрудно получить ре-
решение другой. Существенно, что обе они линейны отно-
относительно искомых функций Ф(?) и ^(S), так что при-
применимы все известные методы решения плоских задач
линейной теории упругости.
Так, можно принять представления

§ 5. ОДНОРОДНАЯ ДЕФОРМАЦИЯ	69
обеспечивающие конечность напряжений, однозначность
смещений и самоуравновешенность краевой нагрузки в
плоскости с отверстиями, одно из которых содержит на-
начало координат ? = 0.
Свяжем постоянные ао, Ьо со значениями условных
напряжений и угла поворота на бесконечности (ai/0,©00)-
Согласно соотношениям D.6) и D.9) имеем
а а I/2 2°~ - 2а *°*°	J»°° - ( М
а°ао) ' 1% ~ (VoI/2t	"U/
D.10)
Отсюда следует
2a4 = 2?V#eDf 2abo = ^^w.	D.11),
Если поворот на бесконечности отсутствует, то ©"«О и
Подстановка выражений D.9) в D.7) и D.8) приво-
приводит к граничным условиям для регулярных частей иско-
искомых функций Фо(?), Yo(?):
(I)	(о* + Ла0)Ф0Ш«1уО + (а-Л(т0) ^j<T<V° =
« _ (а* + hj0) ао^° - (а - Ла0) V"*"; D.12)
(II)	Ф,©е^ - ад)^7°= A ~ ee)e^+V-^. D.13)
| 5. Однородная деформация
Изучение структуры получаемых с помощью гранич-
граничных условий D.12), D.13) решений начнем с рассмот-
рассмотрения однородной деформации, которой отвечают
ФF)-«о,
Отсюда е из соотношений D.5), D.6) следует
е'- —ao/laol; A - laol2- lbol2;	E.1)
а°п + а^ = 2а* | а01, аГх - а^ + i2a°1% = 2ааЛ/| а01.
Рассмотрим наиболее характерные частные случаи.

70
ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
а) Двустороннее растяжение. Для него, очевидно,
«о =0,Gx2= 0и из соотношений E.1) следуетСсг^^О,а^^
)
^22
2а*
2а
2а*
2а
При аи = а22 = ст*? т.е. при начальном (предварительном)
растяжении имеем, как и следовало ожидать, хх = хх,
х2 = хъ т. е. деформация отсутствует.
/
/
/
1
1
h
,х2"
/
/
1
1
V
Рис. 2.1
Рис. 2.2
б) Простой сдвиг. Для него (рис. 2.1) прямоугольная
декартова координатная сетка скашивается и
или
Сопоставление полученного выражения с E.1) дает
ао - 1 - (i/2)ctg р, tool - VTTvTFK
Отсюда и из соотношений E.1) находим
Д-1;

? 6. ПЛОСКОСТЬ С ЭЛЛИПТИЧЕСКИМ ОТВЕРСТИЕМ	?1
4 К i + V4ctg2p
„° _ a	ctgp
2 /l + 1/4ctg2p"
Из полученных соотношений усматривается, что при со-
сохраняющей объем деформации простого сдвига в геомет-
геометрически нелинейной теории имеют место не только тан-
тангенциальные напряжения (как в линейной теории), но и
нормальные.
в) Дополнительный сдвиг. Так назовем напряженно-
деформированное состояние, при котором
о	о	. о -	л
стц = а22 = ст *, а12=7^и, (о = U,
т. е. на исходное	(предварцтельное) всестороннее растя-
растяжение наложены	тангенциальные напряжения в отсут-
отсутствие поворота.
Согласно E.1)	при этом
Координатная сетка скашивается, как показано
на рис. 2.2.
§ 6. Плоскость с эллиптическим отверстием
Рассмотрим задачу о деформации плоскости с эллипти-
эллиптическим отверстием, к (контуру которого приложено равно-
равномерное нормальное давление Со, а на бесконечности дей-
действуют напряжения сГ|/°. Отображение внешности эллип-
эллипса на внешность единичного круга и обратно реализуют
функции (см. с. 259 и рис. 2.3)
? + W — Ас2т
= ——Тс	'
F.1)

72	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Вводя обозначения
Фо (х) = фо [х (x)L ^oV (X) = ^о fx (ХI	F-2)
и используя соотношения A.14.5), A.14.6) на единичной
окружности ( где % = о = ег )
приводим граничное условие D.12) к виду
И + (а -
„v (а) «
i (<** + Ч) % - (« - ко0) Ъо -~(а* + ;
+ m (а -
а	а
В соответствии со сказанными в § 4 Приложения при-
приравняем первое слагаемое левой части первому слагаемому
12
правой, а второе — второму. Уходя при этом с контура
внутрь области (что отвечает замене о на %), находим
F.4)
Возвращаясь теперь с помощью второго из соотношений
F.1) на комплексную плоскость ?, получаем, используя

§ 7. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ	73
легко проверяемое равенство
-l\ F.5)
и D.9):
1.1/
I
1т (а* + Ка0)
2т(а-Яа0)
§ 7. Плоскость с прямолинейным разрезом
F.6)
Рассмотрим плоскость с прямолинейным разрезом
(— a^xl^a, #2 — О) (рис. 2.4), нагруженную на берегах
разреза нормальным давлением Оо, а на бесконечности
условными напряжениями 0Г|/°.
* i
Рис. 2.4
Эта задача является частным случаем рассмотренной в
§ 6 при
с «а/2, т-|.	G.1)
С учетам этого из F.6) и D.11J следует
Ф@« А z , в
(а
4 (о*
G-2)

74	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
где
?)
Г
- (l-?) КГ-
1A) . G.3)
J
Отсюда и из D.5) находим
А Г У г2 —. а2 V^E2 — а* 1 В Г t	С 1
Z = '4 ["о^ТЦ; а-Ха0 J ^ Т [о* + Яа0 + а - KoQ J *
G.4)
Иопользуя теперь соотношения D.6), можно подсчи-
подсчитать все величины, определяющие напряженно-деформи-
напряженно-деформированное состояние. Так, в окрестности правого конца раз-
разреза (рис. 2.4) имеем асимптотические равенства
G.5)
и до формулам D.6) находим для сжимаемого материала
при обобщенной плоской деформации, а также для сжи-
сжимаемого и несжимаемого материала в плоском напряжен-
напряженном состоянии
А
Ы
16
TSyiJ Ы '

§ 7. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ
О* | Л | / а \1/2	о _ «|Л| f 0/ а \1/1
!(o4-Xoe)Br«J ' А*~ 2(а-Хо0)« \W) '
Из последних двух выражений, а также формул пере-
перехода к полярным Координатам (рис. 2.5)
= ап cos2 фс
° 2 ф°
°\г 2sin ф° cos ф° + ^l2 sin2
фО'= а°п sin2 ф° — ol2 2sin ф° cos ф°
cos2
°, G.7)
(Угофо = (а22 — сги^зтф^озф0 + С12(с082фо— sin2 ф°)
получаем выражения для компонент тензора условных
напряжений:
о	о	| Л
4
о
СГгого
Часто рассматривают случай одноосного растяжения
на бесконечности под углом а к координатным осям
/7Щ
ч f/fft
Рис. 2.5
Рис. 2.6
(рис, 2.6). При этом по формулам, аналогичным G.7),
имеем
<»ii =a sm2 а, aaa =a cos2 а, а1а =а sin а cos а.
G.9)
Полагая также, что угол поворота на бесконечности ра~

?6	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
вен нулю (оK0 =0), а берега разреза свободны от нагруз-
нагрузки (оо = 0), получаем из G.3)
A =oOo°(l-be-i2a), B = aO00(l~e-i2a), \A\ =oOo°2cosa.
G.10)
Рассмотрим далее наиболее интересный случай отсут-
отсутствия сдвига и поворота на бесконечности. При этом
o-i,00 = 0, со00 = 0 и по G.3)'
А = [2 + Ч (* " k)\ & + И (± + ?) <#.
5 = [2+ч (^ -1)] air+ч (ол+!)#.GЛ1)
Во введенной локальной полярной системе координат
имеем согласно G.5) и рис. 2.4 на верхнем (+) и ниж-
нижнем (—) берегах разреза
= ±i\/a-x\,	G.12)
— a2 = ± * у #2 — x^i v s — fl2 ~ "*f" f fl2'— ^i*
(|хП<«).
Отсюда и из G.4), имеем на берегах разреза
Из полученных выражений следует, что в рассматривае-
рассматриваемом случае разрез переходит в эллипс с полуосями
а\ Ъ\ где
GЛ4)

§ 7. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ	77
f-i
В частном случае всестороннего растяжения с исходной
интенсивностью (ojf = а2" = а*) разрез переходит в
окружность радиусом R:
Я 1
Обметим, что последнему случаю отвечает задача о «на-
«нанесении пореза» всесторонне растянутой плоскости.
Для несжимаемого материала в плоском напряженном
состоянии имеем согласно C.7), C.10), D.1) и G.6)
1 16
1 1-1 / a \-i,
-(a-Xog)«J I2r°j '
UV G-16)
(«-Xao) J127J-
Остальные соотношения совпадают с приведенными выше
для сжимаемого материала.
Вернемся к соотношениям G.6). Прпо0=Ои=Ом~0
имеем согласно GЛ1)А = 2о2? и с учетам A.11.3)
°и ^ ai2 ^ 0, ог22 ^ -J-
Отсюда усматривается, что в рассматриваемом случае
асимптотика истинных напряжений не зависит от внеш-
внешней нагрузки (cr2sT). Это обстоятельство нельзя не рас-
рассматривать как один из (многочисленных, см. § 1 гл. 9)
недостатков истинных напряжений.
Подробный анализ полученных зависимостей и их со-
сопоставление с решением той же задачи по линейной тео-
теории будут проведены в § 1 гл. 5.

78	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЛА
§ 8. Плоскость с жестким включением
Рассмотрим задачу о деформации плоскости с- жест-
жестким эллиптическим включением. С помощью соотношений
F.1) — F.3) краевое условие жесткого края D.13) при-
принимает вид
Как и в § 6, приравнивая первые слагаемые левой и пра-
правой частей, затем вторые и переходя с граничного конту-
контура вовнутрь области (т. е. проводя замену с-*%), по-
лучаам
Испблшуя затем соотношения F.5) и D.9), находим
Отсюда и из соотношений D.5), D.6) можно определить
все величины, описывающие напряженно-деформирован-
напряженно-деформированное состояние плоскости с жестким эллиптическом вклю-
включением.
Рассмотрим далее жесткое линейное включение
(— а^^х^а, х% = 0), для которого согласно G.1) полу-
получаем из (8.1) и D.11J
(8.2)
где
455
(8.3)
л	2	Г"*" 4a5	"a	4a5	'
Из соотношений D.5), D.6) и G.5) получаем в окрест-

§ 8. ПЛОСКОСТЬ С ЖЕСТКИМ ВКЛЮЧЕНИЕМ	79
яости правого конца включения асимптотические выраже-
выражения для сжимаемого материала
(8-4)
Что касается кратности изменения площади Д, то непо-
непосредственная подстановка первых двух из выражений
(8.4) в C.9) приводит к физически несуразному резуль-
результату: Д ~ 0. Полученное свидетельствует, однако, лишь о
выпадении старших членов асимптотического представле-
представления этой величины. Подстановка же выражений (8.2) в
D.6J дает
Д ~ [(АВ +АВ)-А] уЛ== + [(АЁ	?
~ {[АВ + АВ-А] Г™ + [АВ + АВ - A] ^(jpf'*.
(8.5)
Отсюда и из D.6) следуют асимптотические выражения
для истинных напряжений
Из соотношений (8.5) — (8.6) видно, что в рассматривае-
рассматриваемом случае истинные напряжения имеют особенность
(a/2r°I/2, a не конечны, как в плоскости с разрезом
(см. G.6)).
Для несжимаемого (материала в плоском напряженном
состоянии К = А и в (8.6) выражения для истинных на-
напряжений заменяются следующими:
+^(?)\ (8.7,
При ф° = 0 (на продолжении разреза) и 0^=0 из
Последних двух выражений в (8.4) и A.11.3) следует, что

80
ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
при жестком линейном включении определяющим являет-
ся условное напряжение <Уц, в то время <как для линей-
линейного разреза (ом, G.6)) таковым является а22- То же
относится и « истинным напряжениям.
Далее, согласно D.5) и (8.2) для комплексного сме-
смещения имеем выражение
щ + iu2 = z - ? = Л( УТ^Т2 + /?2-а2) +ЯС+A
(8.8)
Для контроля правильности полученных результатов не-
нелишне убедиться, с учетом G.12), что на жестком вклю-
включении смещения равны нулю.
§ 9. Плоскость с отверстием в виде симметричной
лунки
Рассмотрим плоскость, ослабленную отверстием в ви-
виде симметричной лунки с углом раствора 2[J (рис. 2.7).
Функция, отображающая внешность лунки на внешность
Рис. 2.7
единичной окружности, и ей обратная имеют вид (П.2.21)
к =
. я
При этом разрезу отвечает р-0 (к — 1/2), а окружности

§ 9. ПЛОСКОСТЬ С ОТВЕРСТИЕМ В ВИДЕ ЛУНКИ	81
E = я/2 (&=1). Таким образом, параметр к меняется в
пределах 1/2 ^ к < 1.
Будем считать, что берега лунки свободны от внешних
воздействий (оо = 0) и окрестность бесконечно удаленной
точки не поворачивается (о)°°==0). Тогда согласно соот-
соотношениям D.12), F.2) и F.3) имеем на единичной
окружности (х = а = eiQ°) граничное условие
о*ок' (a) 0>0v (а) + аах' (а) ?ov (а) =
= — о*а0ох' (а) — аЬ0ох' (а). (9.2)
Согласно (9.1) 1
Решим эту задачу двумя способами: методом интегра-
интегралов типа Коши (§ 3 П.) и элементарным методом расчле-
расчленения граничного условия (§ 4 П.).
В первом случае, умножая условие (9.2), а затем
1 da
комплексно сопряженное ему на х—. ¦_ ¦ и интегрируя по
единичной окружности, получаем
, 1 Г о(^-1)"»-*ФеУ(а) da
0 Ш } [
_ (а _
а -
f
< J [@ +1}1/* _ (а _ 1I/*!* о -
Г
v [(a + l)lA - (a - Л*'*!38 о -
Г a(a»-
i J [(a _|. i)i/* _ (a _ i)*/*j2 cr —
V
2Ж
[(o + !, _ (o _ 1}i/k|* о -

82	frt 2. ЙЕЛИНЕЙЙАЙ ПЛбС^АЙ ЗАДАЛА
= _ а а* — f g(g2-lI/fe~1	da
0 2niJ [(<j+ lI/ft — (a— lI/fe]2 a— 5
v
[(a + l)i/"_(a-l)^h]2 o-x*
С учетом соотношений (П.3.13, 3.16, 3.18) и (9.3) i по-
получаем
1 f q(g2-i)i/fe-i da -x(x2-lI/*-1 ,Л2
2л/J [(o + lI''1	(a	lI^]2 a ~* X [(X+lI^	(X	lI^]2 ^
v
— f
2Я1J
a(a2-lI/''-1	da	fc2 1
4 x'
(Z Р1/к1 Фоу (Х)
|(a+i)i/"_(a-lI'"i]2 a-X
f(a + I)»/* - (a - l)i/"l2 о - x	[(x+lI/ft -(X-lI/hJ2'
2niJ
	 0 da
[@ + l)iA^(a-i)i/ft]2 o-x:
J) da
2n<J
	da
Y
При выводе этих выражений мы учли, что согласно
(9.3) 1 Goo(x)= — х и по (П.3.16) получили первое в
(9.4)_ выражение. Второй интеграл преобразовался к ви-
виду Со ==s o~ )
1 ff a(g2-i)i/*-~	ifc ] ^ . А2/4 f da
V L	J	T
Здесь первый интеграл согласно (П.3.18) равен нулю, по-
поскольку функция под знакам сопряжения регулярна вне
7 (см. (9.3)). Второй же интеграл является интегралом
Каши и согласно (П. 1.15) равен — 1/х. Знак минус обу-
обусловливается те«м, что здесь обход контура противополо-
противоположен принятому в § 1 Приложения. Далее, с учетам D.9)

§ 9. ПЛ(!>СКОСТЬ С ОТВЕРСТИЕМ В ВИДЕ ЛУНКИ	83
плотности третьего и четвертого интегралов являются
предельными значениями функций, регулярных вне v.
А тогда по формулам (П.3.13), (П.3.18) и следуют по-
последние четыре выражения в (9,4). Подстановка выраже-
выражений (9.4) в уравнения (9.3J приводит к формулам
•WW+.J-? ^Г (
(9.5)
Перейдем ко второму способу — методу расчленения
граничных условий. Для этого, используя равенства о =
«о*1 и (9.3) 1, проведем расчленение условия (9.2), при-
приведя его к виду
t>V (a)
г
[(о + II/" - (о - l)^f т [(о +1I/" - (о - lI/h]2
-г к2
b
t(g+ f^ _ (L
Смысл проведенного преобразования заключается в том,
что в квадратных скобках правой части стоят предель-
предельные значения функций, регулярных в бесконечной обла-
области. Приравняем первое слагаемое левой части первому
слагаемому правой, а второе — второму. Уходя далее с
контура вовнутрь области (т. е. заменяя о на х), прихо-
Ди\м к полученным ранее методом интегралов типа Кош и
выражениям (9.5). Нетрудно видеть, что метод расчле-
расчленения граничного условия элементарен и технически бо-
более прост.
Вернемся к выражениям (9.5). Возвращаясь с по-
помощью второго из выражений (9.1) на комплексную плос-
плоскость ?, получаем с учетом D.9)

84	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
г	'	*	i
I	ocb	о а	I
-(?2_a2)i-*| l(? + a)ft—°(С —a)fe]2 ~ [(? + a)fe + (?-a)fe]2J'
С помощью выражений D.6) теперь можно подсчитать
все величины, характеризующие напряженно-деформиро-
напряженно-деформированное состояние.
Так, в окрестности правого конца лунки (ом. рис. 2.7)
имеют место асимптотические выражения
? = а + rV<*>°, (Е + a)h ~ Ba)fc, (? — af ~ r°keik(*0,
и согласно (9.6) и D.11J
°оо . °оо	/ \1—h
а*	V р 1
(9-7)
+fg
Теперь из соотношений D.6), G.7) и A.11.3) находим
16А:2		"		1~"
X sin(l - /c)<p°cos(l - А)фв^У;
(9.8)
(9.9)
В частности, при ах* =0 имеем с учетом A.11.3) вы-
выражения для истинных напряжений
*ii~ai2~0, a22~-f 5^5,	(9.10)
совпадающие с таковыми для плоскости с прямолинейным
разрезом G.17). Таким образом, асимптотика истинных
напряжений не зависит не только от внешней нагрузки
() но в от угла раствора лунки 2§. Это, конечно, яв-

§ 10. О НЕЛИНЕЙНОЙ АСИМПТОТИКЕ НА КОНЦАХ РАЗРЕЗА 85
ляется одним из (многочисленных, ом. § 1 гл. 9) недо-
недостатков истинных напряжений.
Возвращаясь к соотношениям (9.8), видим, что для
условных напряжений показатель особенности (сингуляр-
(сингулярности) п($) равен (рис. 2.8)
|||f	(9.11)
принимая для разреза (§ = 0) уже известное (см. G.8))
значение п = 1/2. Как видно из рис. 2.8, при развертыва-
развертывании входящего угла показатель сингулярности уменьша-
уменьшается, обращаясь для развернутого угла B[i = л) в нуль
Рис. 2.8
и становясь отрицательным при 2(i > я. Последнее согла-
согласуется с известным фактом ненагруженности выходящего
угла области.
§ 10. О нелинейной асимптотике на концах
прямолинейного разреза
Вернемся к плоскости с пря)молинейным разрезом, рас-
рассматривая теперь, однако, упругий потенциал общего ви-
вида. В § 15 гл. 1 были получены комплексные интеграль-
интегральные тождества A.15.6). Применим их ос находящемуся в
обобщенном плоском деформированнсш состоянии цилин-
цилиндрическому телу, для которого5п = S+ + 5L + Sv- На
верхнем основании цилиндра (S+)nx = п2 =0, nz = 1; на
нижнем (S_) л2= п°2 = 0, п3 = — 1; на боковой поверх-
поверхности (iSv) имеем согласно A.13.4) п[ -\- in2 ss v^ + ivl —
= e*\ n3 = 0.
Поскольку рассматриваемое напряженно-деформиро-
напряженно-деформированное состояние не зависит от х3, интеграл в A.15.6) i
до S+ + S- выпадает, а интеграл по Sv можно заме-
нить на интеграл по контуру какого-нибудь поперечного

86	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
сечения g°'. Тем са/мым рассматривается цилиндрическая
поверхность единичной высоты.
Сказанное справедливо с учетом B.8) и для плоско-
плоского напряженного состояния. При этом боковая нагрузка
на пластину пересчитывается на единицу ее толщины,
а упомянутым сечением является срединная плоскость
пластины. Согласно C.3) в плоском напряженном со-
состоянии для несжимаемого материала р = О, и в получае-
получаемых ниже зависимостях следует заменять Ф на Фд.
В рассматриваемой плоской задаче отличны от нуля
лишь Fh F2 и Fs. Поэтому из A.15.7), A.15.8) следует
{3} =0, а с учетом A.4) и B.6) получаем
{1} + 1 {2} =	g	)^
A0.1)
(V, + ftvt = ± [[^.ЛЪе* + [F^.JZUe-**]. A0.2)
Подстановка второго выражения в первое дает с учетом
C.2) и C.3) для сжимаемого материала
д\дг/д1\1
(Ю.З)
Рассмотрим интеграл
ReJ[{l} + i{2}]d^=0,	A0.4)
8°
характерным свойством (которого является то, что на сво-
свободных от нагрузки берегах разреза (— а^хг ^а, х2 =
= 0)y°= ±я/2 и подынтегральное выражение в нем об-
обращается согласно A0.1) в нуль.
С учетом этого рассмотрим криволинейный контур,
положительное направление обхода которого показано на
рис. 2.9. На участке Го («который будем считать окруж-
окружностью достаточно малого радиуса г° для того, чтобы в
ее точках можно было использовать асимптотику напря-
напряженно-деформированного состояния) имеем
A0.5)

§ 10. О НЕЛИНЕЙНОЙ АСИМПТОТИКЕ НА КОНЦАХ РАЗРЕЗА 87
Отсюда и из A0.3), A0.4) следует равенство
Y - -/,
где
Re f
A0.6)
A0.7)
д I dzldl\
дг
—1
h -1 дФ
К d\dzidl\
Отметим, что интеграл /, в силу сказанного о нем, может
быть взят по произвольному контуру, не охватывающему
второго конца разреза.
Примем в окрестности правого конца разреза асимпто-
асимптотические представления
дг
Ж'
?i_ ii ew9\ (ю.9)
dl dl	v '
Отсюда и из C.2) (при р —
«= 0 и W — Ф) следует
A0.10)	Рис- 29
На берегах свободного от нагруаки разреза (av°v° =¦
= av°to = 0 при ч° = ±п/2) вьшолияется согласно C.2L
асимптотическое равенство
Подставляя сюда выражения A0.10), получаем на верх-
верхнем (<р°=*л) и нижнем (<р° = —я) берегах разреза
дФ I
A0.11)

88	frl. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Далее, подстановка выражений A0.9) в A0.8) дает
Re
ф
дг
дф
дг
д\
дФ W в*фэ -
2 У К \
дФ
d\dtldl\
d\dz/dl\)
[X
Xdq>°~Y/r°. A0.13)
Соотношениям A0.11) — A0.13) необходимо должны
удовлетворять искомые функции
дг
К
Безусловно, этих соотношений в общем случае недостаточ-
недостаточно для полного определения искомых функций.
Отметим, что согласно C.11), A0.9) (при р = 0 и
W = Ф)
дф	2о _ _^ф_^ ^(го.фо^^.фо,^	A0Л4)
Обратим внимание читателя на то, что именно экспонен-
экспоненциальный множитель второго выражения и входит в со-
соотношения A0.12) и A0.13). Это характерное преимуще-
преимущество условных напряжений перед истинными и будет ис-
использовано в следующем параграфе.
§ И. Асимптотика простейшего вида
Рассмотрим полученные необходимые условия
A0.11) — A0.13) применительно к асимптотике простей-
простейшего вида, подсказываемой видом асимптотики получен-
полученного в § 7 точного решения. Примем
+*-я A1.1)
(к, I, m, s — постоянные) и будем считать, что в окрест-
окрестности правого конца разреза (см. рис. 2.4) величины
\dz/d%\ ъ \dz/dt,\ зависит только от г°. Тогда из соотно-
соотношений A0.11) —A0.13) следует
— К Т 1, 5 — *,	^11.^
ао ^ф
дх
дФ
дг
дФ
2/
A1.3)

ll. АСИМПТОТИКА ЙРОСТЕЙШЕГО ВИДА
Отсюда и из соотношений A0.9), A1.1), A1.2), C.2),
C.8) — C.11) находим для сжимаемого материала при
обобщенной плоской деформации и плоском напряженном
состоянии, а также для несжимаемого материала при
плоском напряженном состоянии (при замене Ф на Фд)
со
A1.4)
Отметим, что входящий в выражения A1.4) угол по-
поворота окрестности <о не определяется из использованных
асимптотических соотношений. Существенно, что в отли-
отличие от истинных напряжений условные напряжения
B1? 22) не зависят от этого утла. Последние определя-
определяются с точностью до постоянной /. В тех случаях, когда
вдали от концов разреза напряженно-деформированное
состояние определяется из линейной теории, постоянную J
можно считать известной, и асимптотические значения
условных напряжений определяются полностью (коль ско-
скоро найдены \dz/d%\ и \dz/d?\).
Рассмотрим, например, класс упругих потенциалов с
асимптотикой
ф
дФ
d\dzldl\
дг
пА
—1
пВ
' d\dz/di\
Подстановка выписанных выражений в систему асимпто-
асимптотических уравнений A1^3) и последующее ее решение
дает с учетом A1.4), D0.9) и A0.2)
дг	А-1/пЯ1/п(п-1)	I от \1/п ( „ \1/п
(	pi® I jl—
\ппа) * \2г°) '
дг
д~
\ппа ]
/ a
Г(?)"*

ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЛА
В1/(п-1))B-п)/пА2/пвг/п

(л-2)/2
Х
2/ \(п-
nAllnBlln
-Dj(n-i)/n \lHxa"/	\2г
2/ Yn-
2г
A1.6)
Показатели особенностей (сингулярности) условных
(п) = (л — 1)/п) и истинных ($(п)*--(п — 2)/п) налря-
1/2
а(п)
3 5
Рис. 2.10
7 п
жений показаны на рис. 2.10. Постоянную п можно рас-
рассматривать как показатель физической нелинейности ма-
материала.
§ 12. Вариационные уравнения
После того как более или менее выяснен вопрос об
асимптотическом представлении напряженно-деформиро-
напряженно-деформированного состояния в окрестностях сингулярных точек,
имеет смысл подробнее рассмотреть вариационные урав-
уравнения плоской задачи.
Прежде всего согласно соотношениям C.2), C.3),
A.12) имеем для статических задач сжимаемого упругого

§ 12. ВАРИАЦИОННЫЕ УРАВНЕНИЯ	91
тела: уравнения равновесия
6 F 1С ' + a{F^n)t + Р°(Л + ih) - 0; A2.1)
закон упругости
о dz	дФ
статическое граничное условие
A2.3)
дистореионное граничное условие
dz_ iv° _ dz_ iy° _	d,{,°)	,2
и его частный случай — условие жесткого края
дг iy° dz_ -4Y° _ iY#
В соотйошениях A2.2)
— упругий потенциал — плотность энергии деформации.
При этом величину X бущем рассматривать как параметр,
не включая ее в число аргументов Ф.
Вариационное уравнение Лагранжа примем в виде
J 60>dS°-=:¦ J ovo.6rds° + j f.6rd5°. A2.6)
о
во
З^десь, как и выше, 5° •— произвольное (в силу независи-
независимости напряженно-деформированного состояния от х3)
поперечное сечение недеформированнаго цилиндрического
тела в случае обобщенной плоской деформации и область
срединной плоскости при плоском напряженном состоянии

92	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
пластины. Далее, g° = gl+ gl, где g°o — часть граничного
контура, на которой заданы напряжения, а на gu — поло-
положение 'материальных точек после деформации (г) и, зна-
значит, бг = 0.
Вариационное уравнение A2.6) имеет очевидный ме-
механический смысл: отвечающая 6г вариация энергии де-
деформации равна работе поверхностных и массовых сил
на 6г.
Прежде всего согласно A.11.1)
avo. 6г = о^бх! + cy26z2 = Re [(a^ + *ауо2) 6~z ],
|.бг = р° {fx6xx + /28*2) - Re [р° (Д + ift) 6z
вариацио
в следую
Re Г J 6Od5° - J
°	4
Теперь вариационное уравнение Лагранжа A2.6) записы-
записывается в следующей комплексной форме:
=0. A2.7)
Для дальнейших преобразований используем следующие
из A.11.14), A.13.4) (при заменах щ -> v{) комплексные
аналоги формул Гаусса — Остроградокого:
j и % dS° -1 j и»*"*0 - f v% dS°'
f и ^r dS° = 1 Г шЛ° - f ^ d^°.
. ^	Л	Л
8	g	S
Далее, согласно соотношениям A2.2), A2.5) имеем,
меняя порядок дифференцирования и варьирования,
-фдФ
= Re2 4?
^]. A2.9)

§ 12. ВАРИАЦИОННЫЕ УРАВНЕНИЯ
93
Подстановка этого выражения в A2.7) и последующее
использование формул A2.8) приводит ко второй^ форме
комплексной записи уравнения Лагранжа (на gu 6z = 0):
Re -
«С
8zdS°
AS
О
8а
= 0. A2.10)
В силу произвольности 6z отсюда следуют: уравнение рав-
равновесия A2.1) и статическое граничное условие A2.3),
являющееся, таким образам, естественным граничным ус-
условием.
Для получения вариационного уравнения Кастильяно
(широко используемого в линейной теории упругости) не-
необходимо, прежде всего, обратить уравнения A2.2). За-
Записывая их снова в виде
IF-.
дг I дг
дг
дф
дФ
находим отсюда
t -
дф
д |
дф
d\dz/dl
A2.11)
тт- A2-12)
Пусть эта нелинейная алгебраическая система одно-
однозначно разрешима:
\dzldt\=X2(HF-l-J2)i\,
-1 • /2Ы),
-* -72Ы).
A2.13)
Используя известное преобразование Лежандра, введем
функцию
4^l|tl~~(I)-A2Л4)
При этом, заменяя величины |dz/d?i, \.dzjd?\ их выраже-

&4	ГЛ. 2. НЕЛИНКЙНЛЯ ПЛОСКАЯ ЗАДАЧА
ниями из A2.13), будем считать
ЛJ\)
(V
A2.15)
Теперь из соотношений A2.14), A2.15) и A2.5) на-
находим
дФ
"*Ш~ЛЩ\
дг
= 0.
Отсюда и из A2.12), в силу произвольности 6IW •
и 6\{F~l -/Shi, следует
дг
дг
-. A2.16)
Согласно же равенствам A2.11), A2.12)
дг
-, A2.17)
либо
— 9
l} A2.18)
Величину A2.15) называют плотностью дополнительной
$нергии.

§ 12. ВАРИАЦИОННЫЕ УРАВНЕНИЯ	9$
Примем вариационное уравнение Кастильяно в следую-
следующей комплексной форме:
Re Г f 6VdS° +
г (О [е*°

1./^] ds'l = 0.
J
el	J
A2.19)
Здесь согласно A2.15) и A2.18)
./Д}«1
. A2.20)
Комплексную функцию напряжения <р(?, ?) введем
соотношениями
^	./S).--!, A2.21)
тождественно удовлетворяющими однородному уравнению
равновесия. При этом будем считать
Тогда согласно A2.19), A2.20) имеем
4- f z (s°) ( e*v° Ц& - e-4'%1 )ds°] =
2 J >{. *\	a; ) J
Ни

96	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
С учетом соотношений A2.8) имеем
-г» С (dz dSw dz дбф \ joo о Г Г / ®*z о
) ~д? —=	=	~dF~ )	= I — I "^
gu	J
Далее, считая контур и искомые функции гладкими (так
что внеинтегральные члены отсутствуют), находим с уче-
учетом A.13.5) 1
*6	dl J
8ч
8ч
Подстановка полученных выражений в A2.23) приводит
ко второй форме комплексного вариационного уравнения
Кастильяно
" °- <12-24>
В силу произвольности бф из полученного вариацион-
вариационного уравнения следует (естественное) дисторсионное
граничное условие A2.4) и условие неразрывности (сов-
(совместности) деформации
обеспечивающее возможность определения функции
z(?, l) по найденным величинам dz/dt» dz/dt,.
Подстановка выражений A2.21) в A2.18) приводит к
зависимостям
dz ду/д? dW dz	dyldj

§ 13. ДЕФОРМАЦИЯ БКСКОНЕЧНОГО КЛИНА
97
Подстановка их в уравнение неразрывности A2.25) при-
приводит к уравнению
dW I , д [ ду/dl dW
д I
I d |
= 0, A2.27)
определяющему комилексную функцию напряжений. Гра-
Граничное условие для нее получаем из условий A2.3)
и A.13.4):
-t~o" === ^ [Ov°i (^ ) ~г ^^v°2 (^ ) •	(l^.Zo)
Вернемся к системе нелинейных алгебраических урав-
уравнений A2.12). Как известно, для ее разрешимости необ-
необходимо и достаточно выполнение неравенства
D =
d\dzid\\
d\dz/dl\
дгФ
д2Ф
д\дг/дЦд\дг/д1\
д2ф
Ф0,
т. е.
a |
§ 13. Деформация бесконечного клина
). A2.29)
В геометрически нелинейной постановке рассмотрим
деформацию бесконечного клина (рис. 2.11). Примем для
этого
2 = Й(*+1)/2/(х).	A3.1)
Здесь (? = r°ei4>°) / (х) — искомая функция,
О = Й = гч, х = С/1 = «i24>° (^Х)- A3.2)
При этом	ч
A3 Ч
К. Ф. Черных

98
ГЛ. 1 НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
С помощью соотношений A3.1) —A3.3) уже нетрудно
подсчитать:
A3.4)
Принимая теперь закон упругости D.1), получаем с
учетом D.4)
- 2а*| в
ф / (Х) + х/' (х)],
Подстановка последних выражений_в однородное уравне-
уравнение равновесия C.2)i дает d2z/d% д% «О. Отсюда и из по-
к* ь\<
Рис. 2.11
следнего выражения в A3.4) получаем определяющее
уравнение
с общим решением
A3.6)

§ 13. ДЕФОРМАЦИЯ БЕСКОНЕЧНОГО КЛИНА	99
Подстановка найденного решения в A3.1) дает с уче-
учетом A3.2) (А, В — вещественные постоянные)
Теперь по формулам C.11), C.3), D.1) и A.11.3) на-
находим
о°п = (ft + 1) r°h [о* А + аВ cos 2Ачр°],
о°22 =(k + l)roh[o*A-aBcos2kq>°l A3.8)
а°12 = (ft + 1) г°к [- аВ sin 2Лф°].
Отсюда и из G.7) лолучаем
афОфо= (ft + l)r°h [a*A - аВ cos 2 (ft + 1) <pe],
0^ОфО = (ft + 1) г0" [- afi sin 2 (ft + 1) ф°].
Отсутствие напряжений на сторонах клина
о |	о |	п
о^р = агофо |фО«±р = U
привадит к уравнениям
0, o*A -
Минимальному допустимому корню первого	уравнения
fc = ^-l	A3.10)!
отвечает
Д=_?Л;	A3.10),
и согласно A3.7) — A3.9)
">??«*);	A3.11)
= ar°oro = Ао* ^ (re)«/*P-i sin» (J - l) Ф°,
; = 4<т* -J. (г°)«/*Р-1 cos* (J - l) Ф°,	A3.12)
= Ao*f(rY'*t-isin(^ - l) <peco8(j - l)q>°.

100
РЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Как и следовало ожидать, особенность в условных на-
напряжениях та же, что и в задаче о симметричной лунке
(§ 9). (При сопоставлении (9.8) и A3.12) следует иметь
в виду, что в § 9 2р — угол раствора лунки, а здесь ана-
аналогичная величина обозначена через 2д — 2[J, так что сле-
следует провести замену ji -* л — ji.)
§ 14. Малосжимаемый материал
Заканчивая главу, рассмотрим перспективные для
практического использования в плоской задаче малосжи-
маемые материалы. С учетом выражений A.8) упругий
потенциал для малосжимаемого материала A.17.5) при-
принимает При П = 1 ВИ|Д
Ф
Согласно последним двум из равенств C.13), условиям
кк = 1 (к = 1, 2, 3) отвечают следующие:
U
= 0, -A, =
A4.2)
и условия перехода при малых деформациях закона упру-
упругости в закон Гука A.17.6) принимают (при /1 = 1) вид
В плоской задаче близок по своей структуре ок потен-
потенциалу A4.1) получаемый из A.17.7) и A.8) упругий по-
тейциал (при п = 1)
отвечающий стандартному материалу 1-го порядка (он же
гармонический, полулинейный, материал Джона). Следу-
Следует отметить, что при X Ф 1 он не является частным слу-
случаем «потенциала A4.1).

I 14. МАЛОСЖЯМЛЕМЫЙ МАТЕРИАЛ
101
Вернемся к потенциалу A4.1). Ему с учетом A4.3)
отвечают
?ф
Е
Подстановка полученных выражений в однородное урав-
уравнение равновесия C.2) приводит к уравнению
д \дг дг
из которого следует
-1
дг
где / — произвольная функция своего аргумента. Отсюда
находим, определяя модуль левой части,
B
С, Я) |«
Т). A4.7)
Пусть решение этого нелинейного алгебраического
уравнения (при заданном х?) имеет вид
A4.8)
Тогда из выражений A4.6) — A4.8) последовательно на-
находим

102	ГЛ. 2. НЕЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Рассмотрим, например, семейство упругих потенциа
лов, удовлетворяющих A4.3):
1	1-уГ| Л3 1-v
A4.10)
Подстановка этого выражения в A4.7) и разрешение по-
полученного алгебраического уравнения дают
)-^, я],
Q = 4 [(/(ЬЦ/р)-^, я],	A4.11)
Разумно распоряжаясь парой функций /(?, Я,),
можно строить различные точные решения плоских задач.

Глава 3
ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
В этой главе рассматривается линейная плоская зада-
задача теории упругости. От традиционного изложения пред-
предлагаемое ниже отличается рассмотрением обобщенной
плоской деформации, учетом несжимаемости и предвари-
предварительной деформации. Все восемь рассматриваемых задач
приводятся к унифицированной форме. При этом изложе-
изложение ведется в терминах функций Ф(?), W (?) с исполь-
использованием дисторсйонных граничных условий.
Сопоставление решений одних и тех же задач по ли-
линейной (гл. 3) и нелинейной (гл. 2) теориям позволяет
выяснить роль нелинейных факторов в теории трещин
(гл.5).
§ 1. Линеаризация плоской задачи
Линеаризуем полученные в гл. 2 основные зависимо-
зависимости. Для этого прежде всего введем смещения:
и1 = х1 — х°1, и2 = х2 — х°2, и3 = х3 — х°3. A.1)
Отсюда и из соотношений A.11.1) следует
z = t> + (u1 + iu2), х3 = х°в + и3.	A.2)
В линейной плоской теории упругости рассматривают-
рассматриваются: компоненты линейного тензора деформации Е
ди	#ц
fduo диЛ	ди.
ш единственный угол поворота
1

104	ГЛ. 3. ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
С учетом A.11.2), A.11.3) из выражений A.3) и A.4)
следует
Е, , '<•¦+"¦> + <<--+'Ч Е, = 2 '-Ь+^: A.5)
Отсюда и из соотношений A.2), A,5) находим
|+^2^.O.	A.9)
(«СI («С)8 ее ^
Соотношение A.9) является (единственным в плоской
задаче) уравнением совместности (неразрывности дефор-
деформации), гарантирующим разрешимость при заданных Е\
и Еч системы уравнений A.7) —A.8) относительно комп-
комплексного смещения щ + ш2-
В дальнейшем будем использовать неравенства
ди• ди•
-?, -^<1, (Я-1=е3Д«1),	A.10)
обеспечивающие согласно A.5) и A.6) малость деформа-
деформации и поворота. С учетом равенств A.10) и A.7) нахо-
находим согласно B.1.4), B.1.5)
= A + V^j + to) A + V,?i - iw) - х/4^2^*»1 + ^i + e3.
Отсюда и из A.6.2), A.2) усматривается, что величина
E1 + e3KJ-l = d-?j^.	A.11)
представляет собой в линейной теории относительное из-
изменение объема, а Е\ — относительное изменение площа-
площади в плоскости х% в const.

§ i. ЛИНЕАРИЗАЦИЯ ПЛОСКОЙ ЗАДАЧИ	105
Далее, линеаризация соотношений § 3 гл. 2 дает с
учетом A.10) упрощенные выражения для: уравнений
движения *)
силового (статического) граничного условия
(*) + to* («)];	A.13)
дисторсионного граничного условия
A.14)
в частности, условия жесткого края
d^ + itl>)e«-d^ + tu>>e-» = 0;	A.15)
для (комплексных компонент главных вектора и момента
напряжений, действующих на цилиндрическую поверх-
поверхность единичной высоты, проходящую через кривую &
области S (.могущую быть и граничным контуром g, см.
рис. 1.4):
	(l/2)Re
для комплексных компонент главных вектора и момента
напряжений, действующих на (произвольное) поперечное
сечение цилиндра со стороны положительного направле-
направления оси х$:
J4	ftf,<W. A.17)
*) Поскольку в линейной теортц в силу малости смещений и
*х градиентов, не различают положения материальной точки до
* после деформации, значок ° в дальнейшем опускаем.

10б	ГЛ. 3. ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Рассмотрим вопрос о виде закона Гука. В главных осях
деформации имеем для изотропного материала
Ev	f	ч Е
01 = (l + v)(l-2v) ^ + *г + е*) + Т+Ъе»
t?*.	jp
СТ	(? + в + е> +	' <118)
v)(l-2v)
Рассмотрим четыре наиболее интересных для дальнейше-
дальнейшего случая.
1. Обобщенная плоская деформация сжимаемого мате-
материала, В отличие от обычно полагаемого при плоской де-
деформации равенства е% = 0 считаем ег = езз = const. При
этом из A.18) 12 следует
»i = (l + V)(l-2v) К1 ~ v)*x + v^l + (i+v)(l-2v) е»'
A.19)
Сумму первых двух выражений A.18) запишем в виде
Подставляя полученное выражение в A.18)з, получаем
C3—v(Oi + O2)+?es.	A.20)
С учетом зависимостей A.11.3), A.12.8)
2i в 0п "Ь ^22 === (Jl "t" О2» S2 s==s <Jl 1 — 022 "I" ?2<Ji2 e
= (oi - 02)e-<2e, ?1 = en + e22 eei + e2,
?2 - en - e22 + i2ei2 -(ei - e2)e-i2e\ A.21)
где со — угол поворота от осей рассматриваемой декарто-
декартовой системы координат к главным осям тензоров Е, 2,
совпадающим для изотропного материала.
Соотношения A.19), A.20) можно записать в виде
1-2») <**
«' ^8 = v21 + ^3. A-22)
Что касается постоянной ез, то согласно A.17) i н A.22)з

I i. Линеаризация плоской Задачи	Ю?
Она связана с осевой силой $з соотношением
A.23)
2. Обобщенная плоская деформация несжимаемого ма-
материала. Для нее [84] v = 1/2 и
2Е .	2Е .	2Е .
ai= — *i + P> <*i = т «i + Р* а3 = -г^3 + р.
Если ввести новую статически определимую функцию
Я = Ц-е3 + р,	A.24)
то
A.25)
При этом согласно A.11) из условия несжимае«мости
/ ~ 1 mm 0 следует
Е\ — е3 — const	A.26)
и согласно A.21), A.25)
22 = Щ- (Е1 — 2е3) + 2д, 22=^?2, а3 = д. A.27)
Наконец, из формул A.17)i и A.27)з получаем соот-
соотношение
A.28)
связывающее осевую силу &з со статически определимой
вещественной функцией q.
3.	Плоское напряженное состояние сжимаемого мате-
материала. Для него оз = 0 и из A.18)з следует
'з = -г^Л; ^ = j^-yEv 2t=JLEv A.29)
4.	Плоское напряженное состояние несжимаемого ма-
материала. Для него v =• 1/2 и
е>--?|,	A.30),
и по A.25) —A.27) с учетом того, что о$ —0, имеем
A.30J

ЮЙ	frl. 3. ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Нетрудно видеть, что полученные в главных осях дефор-
деформации, но записанные в инвариантной форме соотноше-
соотношения A.22), A.27), A.29) и A.30) справедливы и в про-
произвольных декартовых координатах.
§ 2. Использование функций комплексной
переменной
С давних пор в линейной плоской задаче для сжимае^
мого материала широко использовались [24, 36] функции
комплексной переменной. Введем их. Прежде всего не-
нетрудно убедиться, что однородному уравнению равнове-
равновесия (см. A.12))
If+ "^г==
тождественно удовлетворяют выражения
B.1)
Отсюда и из соотношений A.22) и A.29) находим: для
обобщенной плоакой деформации
(Ф©
B.2)
для плоского напряженного состояния
5
Нетрудно (проверить, что полученные выражения удов-
удовлетворяют уравнениям неразрывности A.9), так что из
системы уравнений A.7), A.8) и B.2) определяется
комплексное смещение.
Используя выражения B.2), B.3) и A.8), находим с
учетом вещественности величины со и постоянства ез: для
обобщенной плоской деформации
B.4)

§ 2. ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ Ю9
для плоского напряженного состояния
. 2
§	B.5)
Из полученных соотношений B.1), B.4) и B.5) сле-
следуют широко используемые соотношения Колосова
B, = ) оц + ой + iEpo
(-22 -) о22 - он + i2o12
B.6)
(__ |A — v2)" при обобщенной плоской деформацииЛ
1 1 при плоском напряженном состоянии./
Далее, из соотношений A.7), B.2) —B.5) и A.16) на-
находим
B.7)
гЗ-4а
l=: {3-v • X
|1 при обобщенной плоской деформацииЛ
(О при плоском напряженном состоянии;/
	^
J	Ф @)« + «Ф' (С) + V (С))) <*Ь
зял = - Re J ; {(Ф (о + ф1)) d; + (iff® + Щ» ф.
B.9)
Перецдем к (краевым задачам, определяющим функции
Ф(?), W(t). Согласно соотношениям A.13), A.15) и
B.1), B.7) имеем
При этом для плоского напряженного состояния и обоб-
обобщенной плоской деформации при силовом (статическом)

НО	ГЛ. 3. ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
грани/чном условии
при обобщенной цлоокой деформации и условии жесткого
края
W + tftW«-;~ea; B.11),
X-3-4V,
при плоском напряженном состоянии и условии жесткого
края
Рассмотрим плоскость комплексной переменной с вы-
вырезом, содержащим начало координат. Принятие функций
ФE), ?(?) в виде
B.12)
обеспечивает конечность напряжений. Подстановка
Рмс. 3.1
приведенных выражений в B.6) и предельный переход
при % -* оо дают
-, 2Ь§« aS - аП + ЙоГ.. B.13)
4а0 = аП + а
Подстановка же выражений B.12) в B.9) \ и интегри-
интегрирование по контуру &, охватывающему вырез (рис. 3.1),
дают
- f
Вводя полярные координаты (рис; 3.1) t^pe", щмееы

§ 3. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ
при обходе контура по часовой стрелке
и, стало быть,
Аналогично, обходя контур выреза и требуя однозначно-
однозначности смещений, полугааем из соотношения B.8)
ца»! + Ь-1 = 0.
Отсюда и из предыдущего равенства находим
Будем в дальнейшем считать нагрузку самоуравнове-
самоуравновешенной. Тоща 8i e 82 e 0 и
a-i-ft-i-0.	B.15)
Кроме того, положим, что отсутствует поворот на беско-
бесконечности. Тогда о" — 0 и по B.13)
*о = *о = ги (°?г + <*п), \ = V» (аи - aS + i2°T*). B.16)
При этом граничные условия B.10) с учетом B.12) и
B.15) записываются так:
[- хФо @+«та ^ - [сф; (о+
= № W + <A W + (X - 1) «•! ^i? + V-<T- B.17)
§ 3. Плоскость с прямолинейным разрезом
Рассмотрим плоскость с разрезом по вещественной оси
(—а<*Х\ <а, Х21а=0) (см. рис. 2.4). На верхнем (+) берегу
разреза f+ -¦ —я/2, на нижнем ("*) if" ¦- я/2 и на обоих
? = ? = xj. С учетом этого силовое граничное условие
B.17), B.11) 1 записывается на берегах разреза в виде
) + ^t (хг) =
- a+ (xx) - fo$ (x,) - (аГ. + ta" ),
= a^ (xx) — iavl (xx) — (a^ + to5)«
Здесь и ниже значками +(") снабжаются предельные «на-

Ш	ГЛ. 3. ЛИНЕЙНАЯ ПЛОСКАИ
чения искомых функций при приближении из области
к точке верхнего (нижнего) берега разреза.
Введем в рассмотрение функцию (П.3.4)
Q(t)-YE)+tO'(C)+O(t).	C.2)
Здесь Ф(?), Ф'(?), ?(?) — функции, принимающие комп-
комплексно сопряженные с функциями Ф(?), Ф'(?), ? (?)
значения в точках комплексной плоскости, симметричных
относительно вещественной оси:
p C.3)
Согласно равенствам B.12), B.13) и B.15) при ю~ = 0
С (С) = «. (С) + V4 (оП + аи) + V, (аи - о^ - Йа5),
C.4)
Устремляя теперь точку области ? соответственно из
нижней (верхней) полуплоскости к точке разреза xi, по-
получаем с учетом равенств C.3):
Qo~ (»i) = Уо+ (»,) + а:,Ф;+ (х,) + фТЙ.	„
Й+ & ^(	Ф;( Ф(
(—а <Х| < а).
С учетом полученных соотношений условия C.1)
после операции комплексного сопряжения записываются
в виде
Фо+ <*i) + «Г (*0 = <&(*i) + to^i (*i) - (<й - tof,),
Фо~ (г,) + Qj (*!> = о; (jfj) + iff7i (*i) ~ (ой - ia5)i
или
)] = /(«I), C 6)
[Ф, (X,) + Йо (*!)]+ + [Ф. (*,) + «о («I)]" = g (*l),
где
/ (*l) = [ow (^i) — <*w (^i)] + » [Ov< (*i) — Ow (*i)J,
f (*i) = [a^, (a:,) + a? (a;,)] + ' [ow (xx) + o^ (xx)] —

I 3. ЙЛбСКОСТЬ С ЙРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ	{{3
Решение задачи C.6), C.7) дается формулами
(П.3.10), (П.3.11):
am- i
Заменяя далее в выражениях C.4) ? на ? и проводя опе-
операцию комплексного сопряжения, получаем с учетом C.3)
^о @ = «о (С) - №i @ - Фо (О-	C.9)
Остается воспользоваться формулами B.12), B.16),
B.15), B.8) и B.6).
Пусть, например, на берега разреза действует равно-
равномерное нормальное давление Оо, т. е. (Tw = avv = — ^о,
o&=a^ = 0. Тогда согласно C.7) /(xi)==0, g{x^) =
- ~2(аГ2 + а0- toS) и с учетом C.8), (П.3.16), C.9),
B.15) и B.16) имеем
При помощи полученных выражений находим из
B.6) и B.8)
= 2 {о?, + о9-

Гл. з. Лийейная плоская
C.11)
(« + *И)
= V,И(aS + а0 - toS) /F^1 + 1аГ, Kg1-a» +
6 локальной полярной системе координат с полюсом
в правом конце разреза (рис. 2.4)
5 = а + re* ~ а, % - f = ilr sin <р, УС2 - а2 ~ У2аге*>*
C.13)
и из равенств C.12), B.7.7) следуют асимптотические
выражения
ап ~ 1(аГг + <*о) cos -f- (l ~ sin -i sin -|-J —
- аГя sin f B + cos -f cos Ц-)] YjL,
+ <^o) cos-f- (l + sin -f- sin 2f-j +
^(X?f)]/Z. C.14)
(c
sin -f" (cos "f- cos
cos2 -J. [(a- + a0) cos -J- - оГ»3 sin -J.J j/^,
~y +
o»r ~ cos~?- \[aM + aft) sm -J- cos -

§ 3. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ
115
На продолжении разреза ? = Х\ > 0, хг = О и согласно
C.11) приог? = 0
. C.15)
На верхнем (+) и нижнем (~) берегах разреза имеем с уче-
учетом C.13) {\хх\ <а)
и по выражению C.12) имеем
и±(т т-
щ \хх, V) —
a2-*? C.16)
)
Рассмотрим, наконец, задачу о расклинивании разреза
парой сосредоточенных сил (рис. 3.2). В формулах C.7),
C.8) этой задаче отвечают f{xx) = о^ — о\^ = 0, g(xx) =
= <Jvv + счГу = — %Q (хо) 6 (^i — хо)у где Q(xo) — величина
«*,)
*»t
-п
Рис. 3.2
силы, а б (х\ - с) — обобщенная Ь-фунщия Дирака, рав-
равная нулю при х\ Ф с и бесконечности при х\ = с, но так,
что
ь
\g(xi)8(x1-c)dxl = g(c) при а<с<Ъ. C.18)
а
Поэтому из выражений C.8) следует
2я

116	ГЛ. 3, ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
Отсюда ж из B.12), B.13), B.15) и C.9) следует
при о% = 0
V ° '	C.19)
и по формулам B.6)
		C.20)
<)(х0) /««_*2(;_йу 1 ¦
„
В частности, полагая здесь хо — % » хо — а и используя
C.13), приходим к следующим асимптотическим фор-
формулам в окрестности правого конца разреза:
Для определения величины расхождения берегов раз-
разреза удобно воспользоваться формулой A.14), которая с
учетом B.7) принимает вид
C.22)

§ 4. ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫЙ МАТЕРИАЛ	Ц7
Используя теперь выражения C.19), C.16) и то, что
на берегах разреза
ds± = =р dxv y± - =р -у,
получаем
Напомним, что верхние знаки отвечают верхнему берегу,
а нижние — нижнему.
Следуя [52] ,* введем функцию
«i) (з24)
), C.24)
обладающую следующими легко проверяемыми свойст-
свойствами:
Lfl
С учетом второго из них находим из C.23)
ut (*!, 0; х0) = ± (>t+^1 + v) ^ (х0) Г (а; ^, xj. C.26)
Отсюда находим для произвольной симметричной от-
относительно оси абсцисс нормальной нагрузки на берегах
разреза:
а
и? (*„ 0) = ± (|Х+4яД+У) J Q (*о) Г (а; х,, ха) dx0 C.27)
—а
§ 4. Предварительно напряженный материал
Получим решения линейных задач — аналогов рас-*,
смотренных в § 6—9 гл. 2. Прежде всего с учетом соот-
соотношений A.21) запишем закон Гука B.4.3) для ма-
материала с начальным всесторонним (в плоскости хз ¦* 0)

i!8	til. 3. ЛИЙЕЙНЛЯ ПЛОСКАЯ ЗАДАЧА
растяжением о* в виде
11 = а*[Е1 + 2), 2,=а?2;
F 2' 2	F * S	DЛ)
Функции комплексной переменной введем соотношениями
	 		D Z)
2, --2[?Ф#(?)"+?(?)]
удовлетворяющими однородным уравнениям равновесия
(A.12) при fi=f2 = d2(ui + iu2)/(dtJ = 0). Отсюда и из
D.1), A.5), A.6) находим
со =
]; D.3)
4)i
Нетрудно проверить, что выражения D.3) удовлетворяют
уравнениям неразрывности A.9), что обеспечивает сущест-
существование комплексного смещения. Для него согласно соот-
соотношениям A.5), D.3) и D.4)
В дальнейшем ограничимся рассмотрением краевой за-
задачи с заданными на контуре области напряжениями. Для
этого используем силовое граничное условие B.1.10),
опуская в нем (в соответствии со сказанным в § 1) круж-
кружки и производя замены: {F~! •/2)»—*2<. В результате
проделанного приходим к силовому граничному условию:
записываемому согласно D.2) в виде
*- ЦФ») + V(t)]е
!,|A)-0^Л D.6)

§ 5. ЧАСТНЫЕ СЛУЧАЙ
Как и в § 4 гл. 2, примем представления
обеспечивающие конечность напряжений, однозначность
смещений и самоуравновешенность краевой нагрузки в
плоскости с отверстиями, одно из которых содержит нача-
начало координат. В отсутствие поворота на бесконечности
(со00 =0) имеем согласно D.2)
J22 " "u
D.8)
2°°	G°° — C°° -
b° = "" T ^	2	~*
Подстановка выражений D.7), D.8) в D.6) приводит
к требуемой форме силового (статического) гранич-
граничного условия
[ф0 (о + ф0 (см ^ - [де>; (о + % @1 ^-iv =
= e*v [0VV E) + iQv< (s) - 2a0 - a*] + e-«*5e. D.9)
§ 5. Частные случаи
Используя соотношения предыдущего параграфа, рас-
рассмотрим несколько необходимых в дальнейшем частных
случаев.
а) Рассмотрение начнем с плоскости с эллиптическим
отверстием (рис. 2.3), нагруженной напряжениями на
бесконечности о% и нормальным давлением на берегах
отверстия (Ow(s) e —Оо, avt($)=O). Согласно B.6.1)
имеем отображающую функцию и ей обратную
С учетом этих соотношении, а также зависимостей B.6.3)

120	ttl. 3. ЛИЙЕЙНАЙ ПЛОСКАЯ ЗАДАЧА
получаем, вводя замены Фо (С) -*• Фо I* (%)]
следующую запись граничного условия D.9) на единич-
единичной окружности
а — т
(а) =
Приравнивая первые слагаемы^ левой и правой частей
этого равенства, а затем — вторые, получаем, переходя с
контура внутрь области (т. е. заменяя о на %)'
0 ш
+ IY9/T	| /-.$ I -- \ [ will 1
*\ О '	I U/ I	IN 2
Используя затем формулы B.6.5), D.7), вернемся на
комплексную плоскость ?:
Зная же Ф(^), ^(С)» можно по формулам D.2) и D.5)
подсчитать напряжения и смещения.
б) Для плоскости с разрезом (си. рис. 2.4) в получен-
полученных выражениях следует положить Ь*0, с = а/2, m = 1.

§ 5. ЧАСТНЫЕ СЛУЧАИ	121
Из соотношений E.2), D.2), D.5) и D.8) находим
2—'
E.3)
= aj°i — <т — 2<т0 +
+ а. - <2) . j	 + (о? + а, +
<2) . j
а
ап — а22
С учетом соотношений C.13) получаем асимптоти-
асимптотические выражения для напряжений в окрестности пра-
правого конца разреза
2» - [(ой + ae + fcu
2, ~ [гой!*^ + (ой + а„ + Юй) i sin ф^л] (^IЛ,
ли
и ~ [(ой + o0)cos-J. (t - sin -|- sin -^ J -
или
sin -^J —
- ой sin -f- (- coa Л- cos Щ У-~

122	ГЛ. 3. ЛИНЕЙНАЯ ПЛОСКАЯ ЗАДАЧА
22 + оJ sin-|-cos-|- cos—J. +	п
ф ~ cos2 -|- [(о + а0) cos -J - ЗаГ»sin -f j V "^'
cos -|-1 (о + а0) sin -|- cos -|- +
Из соотношений C.11), C.14), C.20), C.21), E.4)
и E.6) следует, что в линейной плоской задаче напря-
напряжения в плоскости с разрезом и их асимптотика не зави-
зависят от упругих постоянных и всестороннего предваритель-
предварительного растяжения в плоскости о*.
Вернемся к соотношению E.6). На верхнем (+) и ниж-
нижнем ("} берегах разреза имеют место соотношения B.7.12).
Добавляя к ним выражение (ф = ±л)
а2 — Й — — 2arcos<p — г2 = 2а(а — хг) — (а— ххJ == а2 — х{
и полагая а^ = 0, получаем из E.5)
Таким образом, в отсутствие сдвига на бесконечности раз-
разрез переходит в эллипс с полуосями а , Ъ'\
При Ои=Оп — о*
Последний случай отвечает всестороннему растяжению
плоскости с разрезом, берега которого нагружены нормаль-
нормальным давлением о0. Анализ полученного решения и его
сопоставление с решением этой задачи по нелинейной
теории (| 7 гл. 2) будут приведены в § 1 гл. 5.

Глава 4
ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
Слово «разрушение» для большинства людей ассо-
ассоциируется прежде всего с некими бедствиями, несчас-
несчастиями. Это и катастрофические землетрясения и разру-
разрушения цунами прибрежных сооружений, построек, и раз-
разрушительные тайфуны с красивыми женскими именами,
п усталостные разрушения самолетов, кораблей, разру-
разрушения атомных реакторов, трубопроводов и многое, мно-
многое другое.
Вместе с тем, если подумать, обычное принятие пи-
пищи — прежде всего процесс разрушения (измельчение
пищи). Почти три миллиона лет тому назад доистори-
доисторический человек, отламывая сук дерева и раскалывая кам-
камни, изготовлял орудия для добывания пищи и огня.
В наше время процессы разрушения приобрели гло-
глобальный, индустриальный характер. Здесь и взрывные
вскрышные работы, дробление горных пород, бурение на
нефть, газ, воду; измельчение цементного клинкера, на-
наконец.
Широко используется разрушение в быту (помол ко-
кофейных зерен, использование терки), в искусстве («удале-
(«удаление всего лишнего» при ваянии скульптуры), в строитель-
строительстве (сооружение фундаментов, траншей), в сельском хо-
хозяйстве (пахота) и, конечно, в военном деле.
Итак, с одной стороны, разрушения стараются всячески
избежать, с трех других — стремятся добиться максималь-
максимального разрушения при минимальной затрате энергии.
Различают два типа разрушения: вязкое и хрупкое.
Вязкое сопровождается большими остаточными деформа-
деформациями, оно реализуется, например, при медленном растя-
растяжении сургуча. При хрупком же разрушении остаточная
деформация пренебрежимо мала (например, быстрый удар
по палочке сургуча), так что процесс разрушения может
быть рассмотрен в рамках теории упругости. Обычно при
этом используют зависимости линейной теории упругости.
Возникшее в двадцатых годах направление в механике
разрушения — теория трещин — бурно развивается до

124	ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
сих пор. К настоящему времени написано большое число
содержательных (и не очень содержательных) книг и
необозримое число статей, малая толика которых указана
в приведенном списке литературы. За прошедшие деся-
десятилетия почти устоялись представления, гипотезы и кон-
концепции теории.
Целью этой главы является краткое изложение основ-
основных идей и результатов линейной теории. В качестве
организующей канвы принята концепция Новожилова,
изложенная им в статьях [41, 42]. Связано это, прежде
всего, с тем, что в этих статьях был дан единый крити-
критический взгляд на многочисленные предложения в теории
трещин. Кроме того, изложенная там оригинальная кон-
концепция подсказывает путь построения нелинейной теории
трещин — основной цели настоящей книги.
§ 1. Основные понятия линейной теории трещин
Линейная теория трещин базируется на зависимостях
линейной теории упругости. При этом разрушение счи-
считается хрупким, причем материал остается линейно-упру-
линейно-упругим, вплоть до своего разрушения. Рассматривается также
и квазихрупкое разрушение, при котором в окрестности
конца трещины образуется небольшая пластическая зона.
Вследствие малости последней, при анализе напряженно-
деформированного состояния пластическая деформация не
учитывается.
Рис. 4.1
Характерные особенности линейной теории трещин
продемонстрируем на примере рассмотренных в § 3 гл. 3
задач о прямолинейной трещине при плоской деформации.
Имеет место следующая установившаяся классификация
(рир.4.1):

i i. Осйовн&е понятия линейной те6рий т^ещий 125
1.	Задача о нормальном отрыве, для которой на бере-
берегах разреза действует нормальное напряжение <5п, а па
бесконечности а^, а^.
2.	Задача о поперечном сдвиге, для которой на берегах
разреза действует касательное напряжение On, а на бес-
бесконечности о™2.
В соответствии с этой классификацией имеем согласно
соотношениям C.3.14) следующие асимптотические вы-
выражения для напряжений в окрестности конца трещин
(при берегах трещины, свободных от нагрузки): в задаче
о нормальном отрыве (тип разрушения I)
*i	Ф
0п~у!ГгС03 2
-f
= a?2 Vita);
в задаче о поперечном сдвиге (тип разрушения II)
*И	ф (л	Ф • Зф \
а" " viHF cos  I sm 2 8Ш "Г/;
В общем случае величины ки кп — называемые коэф-
коэффициентами интенсивности напряжений — зависят от ве-
величины нагрузки, расположения и длин трещин. В полном
соответствии со своим названием они характеризуют ин-
интенсивность напряжений в окрестностях концов трещин
и играют в линейной теории разрушения выдающуюся
роль.

126 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕбРЙД)
Понятие коэффициентов интенсивности деформации и
классификация типов разрушения, показанная на рис. 4.1,
была введена Ирвином [106]. Выражения для коэффи-
коэффициентов интенсивности в различных задачах собраны в
работе [64].
Третий тип разрушения — продольный сдвиг — отно-
относится к антиплоской деформации и в нашей книге не рас-
рассматривается. В общем случае рост трещины в однородном
теле может быть описан при помощи комбинации трех
указанных типов разрушения.
Основными задачами механики разрушения тел с тре-
щинами являются: определение разрушающей (критиче*
ской) нагрузки при заданной системе трещин и установле-
установление критических размеров трещин, отвечающих началу
разрушения при данном уровне нагрузки.
Эти задачи решаются на базе той или иной модели
разрушения, включающей в себя модель трещины и кри-
критерий разрушения. Чаще всего трещину моделируют
бесконечно тонким разрезом, берега которого «экраниро-
«экранированы» (по всей длине или везде, кроме концевых зон)
от взаимного влияния*). Критерий же разрушения — не-
некоторое условие, при выполнении которого становится воз-
возможным рост (страеивание) трещины.
§ 2. Энергетический критерий Грнффнтса
В своих основополагающих для теории трещин работах
[102, 103] Гриффите предложил энергетический подход
к проблеме хрупкого разрушения. Предположив изначаль-
изначальное существование трещин в хрупких телах, он рассмот-
рассмотрел вопрос об энергетическом балансе тела с трещиной**).
*) Механическое содержание этой модели обсуждается в § б
этой главы.
**) Основой для работ Гриффитса послужила статья Инглиса
[104], посвященная исследованию напряженно-реформированного
состояния в упругой пластине с разрезами. Работы Гриффитса
[102, 103] A921, 1925) намного опередили свое время. Этим и объ-
объясняется отсутствие работ в этой области вплоть до 1940 г. (статья
Ирвина [106]). Существенное развитие подхода Гриффитса было
дано в работах [97, 105, 1071. Следует отметить еще более раннюю
работу Вейхардта [123] A907), содержащую асимптотику напря-
напряженного состояния в конце разреза и формулировку критерия раз-
разрушения. Об этой работе, «воскрешенной» Б. М. Морозовым, см.
в [94].	.

S 2. ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ ГРИФФИТСА	|27
Суть его подхода состояла в следующем. Любое дефор-
деформированное тело обладает некоторым запасом энергии* де-
деформации. С образованием в нем трещины появляются
две новые свободные поверхности, обладающие поверх-
поверхностной энергией, аналогичной создаваемой поверхностным
натяжением жидкости. Появ-	^оо
ление в теле трещины} вызы-	к к ilk
вает также уменьшение энер-	*х | [ 111
гии деформации, компенси-	* *
руемое (в отсутствие других
видов энергии) энергией
вновь образующихся поверх-
поверхностей. Если баланс нару-
нарушается и при продвижении
трещины освобождается боль-	Рис. 4.2
ше энергии, чем требуется на
образование вновь появляющейся поверхности, происходит
рост трещины, приводящий к разрушению тела.
Рассмотрим линейно-упругое весьма протяженное
тело со сквозной прямолинейной трещиной длиной & = 2а,
подверженное однородному поперечному растяжению на
бесконечности а = af%. Считая, что тело подвергнуто плос-
плоской деформации, имеем задачу о нормальном отрыве, по-
показанную на рис. 4.2.
Энергия деформации вырезанной из тела пластины
(единичной толщины вдоль оси х3) представляется в виде
W~W0+T(a)-U(a).	B.1)
Здесь Wo — энергия деформации пластины без трещины,
Г (а) — поверхностная энергия (двух) берегов трещины,
U (а) — высвобождающаяся при раскрытии трещины энер-
энергия деформации.
Рассмотрим три мыслимые ситуации:
dW > 0, dW - 0, dW < 0.	B.2)
Поскольку
dW = dT (a) - dU (а) - (i? - g) da,	B.3)
первое неравенство означает, что при продвижении конца
трещины на величину da освобождающейся энергии де-
деформации не хватает на образование новой поверхности,
и трещина не будет развиваться. Наоборот, третье условие
означает, что высвобождающаяся энергия превышает по-
поверхностную энергию вновь образующейся поверхности,

128 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
и трещина будет продвигаться. Второе (промежуточное)
условие отвечает критическому значению нагрузки, при
котором трещина получает возможность двигаться. Со-
Согласно B.2)г и B.3) этому и отвечает критерий разру-
разрушения Гриффитса
d±*L
da da#
Далее, Гриффите принял простейшее предположение
B.5)
Поскольку поверхность двух берегов равна 2 • 2а • 1 = 4а,
постоянная if имеет физический смысл плотности поверх-
поверхностной энергии (работы, необходимой для образования
единицы площади свободной поверхности).
В рассматриваемом случае высвобождающаяся энергия
деформации равна, очевидно, работе по закрытию тре-
трещины с конечным напряжением a = a^. Для подсчета
этой работы используем теорему Клапейрона, согласно
которой работа равна интегралу вдоль разреза от поло-
половицы произведения расстояния между берегами разреза
на отвечающее ему конечное значение напряжения.
Используя формулу C.3.17), подсчитываем
U(a) -4
(i-уУЛ
(l*2"aV	B-6)
Подстановка выражений B.5) и B.6) в B.4) приводит
к значению критической нагрузки
а* =
отвечающей трещине длиной 91 л = 2а.
Если же фиксирована внешняя нагрузка о (в рассмат-
рассматриваемой задаче 0п)> то е* отвечает критическая

§ 2. ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ ГРИФФИТСА	129
(гриффитская) длина трещины
По сказанному выше, трещина будет развиваться, коль
скоро ее длина превосходит критическое значение:
2 > 2й.	B.9)
Отметим, что для трещины критической длины обычно
используют термин — предельно равновесная трещина.
Существенно, .что в рассматриваемой задаче значение
критического напряжения падает по мере удлинения тре-
трещины. В этом смысле пре-
предельно равновесную трещи-
трещину в рассматриваемой задаче
следует рассматривать как
неустойчивую. При достиже-
достижении нагрузкой критического
для неустойчивой трещины
значения происходит про-
прогрессирующее удлинение тре-	,
щины. Объясняется это боль-
шим запасом энергии дефор-
деформации в разрушаемом теле. Интенсивность высвобожде-
высвобождения растет по мере удлинения трещины.
Бывают, конечно, и устойчивые предельно равновесные
трещины. Так, для расклинивающей пары сосредоточен-
сосредоточенных сил (рис. 4.3) находим при хо = О с помощью соот-
соотношений C.3.20), C.3.26)
1
i
-я
xz
a
Q
н критическое значение величины расклинивающей пары
п* в
Отсюда видно, что в рассматриваемом случае предельно
равновесная трещина может продвигаться лишь при уве-
увеличении расклинивающей пары сил, т. е. предельно рав-
равновесная трещина устойчива. Объясняется это тем, что
в рассматриваемом случае запас энергии деформации в те-
теле сравнительно невелик.
Теория Гриффитса показывает, что появление трещины
в теле еще не означает его разрушения, пока действующие
5 К. Ф. Черных

130 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
на тело нагрузки не достигли критической для рассмат-
рассматриваемой трещины величины. Отсюда и следует практи-
практическая значимость теории — возможность определить, яв-
является ли при заданных нагрузках опасной имеющаяся
в теле (конструкции) система трещин?
Гриффите подтвердил справедливость своего подхода
экспериментами на стеклянных колбах и цилиндрических
трубах, ослабленных трещинами различной длины. Экспе-
Эксперименты подтвердили следующее из формулы B.7) соот-
соотношение
а* У а = const.
Для металлов критерий Гриффитса оказался неприем-
неприемлемым, давая слишком заниженные значения критической
нагрузки. Область применения критерия Гриффитса была
существеннр расширена Ирвином [106] и Орованом
[111—112], принявшими во внимание, что для ряда ма-
материалов разрушение происходит при небольших пласти-
пластических деформациях, сосредоточенных в весьма тонком
слое, примыкающем к берегу трещины, так что рас-
рассеянная (диссипированная) энергия остается пропорцио-
пропорциональной вновь образованной поверхности. Такое разруше-
разрушение называют квазихрупким. Была введена поправка на
пластичность, так. что вместо формулы B.7) была пред-
предложена следующая:
B.10)
/•2?0
V A-
I па
Здесь fn — удельная (в расчете на единицу поверхности
берега трещины) работа пластической деформации. Экспе-
Экспериментальные данные свидетельствуют, однако, что вели-
величина fn на несколько порядков превосходит у. Так [52],
для стали 7 » 103 эрг/см2, чп ™ Ю6 эрг/см2. Поэтому в фор-
формуле B.10) можно пренебречь величиной т, приняв
Выписанную формулу использует и в общем случае,
понимая под fn плотность поверхностной (приповерхност-
(приповерхностной) энергии, обусловленной различными физическими
факторами. При этом собственно плотность энергии обра-
образования новой поверхности включают в v В § 3 гл. 8 мы
вернемся к этому вопросу, уще применительно к поли-

§ 3. ЛОКЛЛЬЙЫЁ СИЛОВУЁ KPHtEPHH РАЗРУШЕНИЯ 131
мерам. Полученные выше зависимости относятся к плос-
плоской деформации. Как известно, соответствующие зависи-
зависимости для плоского напряженного состояния можно полу-
получить из выписанных заменой A — v2) —> 1. Так, формула
B.11) 1 заменяется следующей:
§ 3. Локальные силовые критерии разрушения
В этом параграфе рассмотрим два критерия разру-
разрушения:
а) Критерий Ирвина.
Введем прежде всего обозначения
Q яA-у2)да* с» лA-у')дд"	(ЗД)
При раскрытии трещины, связанном с появлением сво-
свободной поверхности d2 = 2 • da • 1 (в расчете на единицу
длины в направлении оси х$ и с учетом того, что берегов
два), имеем согласно равенствам B.6) ад C.1)
Отсюда видно, что Q можно рассматривать как обобщен-
обобщенную (ее называют итрещиноподвижной*) силу. При этом
Q* — ее критическое значение.
Критерием Ирвина является утверждение: трещина
в теле начинает расти после того, как трещиноподвижная
сила достигает своего критического значения, т. е. при
Q>Q*.	C.3)
Согласно равенствам C.1) и B.7) критерии Ирвина и
Гриффитса равносильны при
2f - <?*.	C.4)
Сопоставление выражений C.1) и A.1) при a = aft
дает*)
Q^^~Lk\.	C.5)
Поэтому критерий Ирвина можно записать в терминах
*) Связь трещиноподвижной силы с коэффжцмептамж жнтен-
сжвности нацряженмй была установлена Ирвином в [105].
5*

132 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
коэффициента интенсивности напряжений:
C.6)
где к* — критическое значение коэффициента интенсив-
интенсивности напряжений.
Соотношение C.6) получено нами из рассмотрения
частной задачи, но оно имеет место при произвольном
напряженно-деформированном состоянии, и критерий
Ирвина можно сформулировать так: продвижение трещины
начинается после того, как коэффициент интенсивности
напряжений достигает своего критического значения (обоз-
(обозначаемого обычно через kiC), т. е. при
к > к1С.	C.7)
При такой записи выясняется, что критерий Ирвина
связан с наиболее напряженной окрестностью конца тре-
трещины. В этом смысле он является локальным критерием.
Критерий Ирвина и более удобен, поскольку его можно
использовать, зная лишь асимптотику, напряженного со-
состояния в окрестностях концов трещин, например, со-
соотношения A.1), A2). Не сле|дуетг однако, при этом
забывать, что коэффициент интенсивности напряжений
определяется из напряженно-деформированного состояния
всего тела.
б) Модель Баренблата.
Предложенная Г. И. Баренблатом [1, 2] модель
трещины (рис. 4.4) представляет собой полость, концы
1*2
2а
Рмс. 4.4
которой смыкаются под действием больших (порядка
идеальной прочности*)) сил сцепления. При этом пред-
предполагается:
1. Длина d концевой (тупиковой) зоны трещины, где
действуют значительные силы сцепления, мала по срав-
•) См. f 4—5 гд. 6.

$ 3. ЛОКАЛЬНЫЕ СИЛОВЫЕ КРИТЕРИИ РАЗРУШЕНИЯ 133
нению с длиной трещины. Такие трещины назовем, сле-
следуя [52j, макротрещинами. В противном случае имеем
дело с микротрещиной.
2.	Конфигурация тупиковой части трещины (а значит,
и распределение сил сцепления в ней) не зависит от дей-
действующих на тело нагрузок. При продвижении трещины
ее тупиковая часть сохраняет свою форму (гипотеза авто-
автономности концевой части трещины). Конфигурация кон-
концевой части трещины зависит, однако, от материала и
окружающих физических условий (температура, состав и
давление газа и т. п.).
3.	Противоположные берега трещины в ее концах
плавно смыкаются, что обеспечивает конечность напря-
напряжений в тупиковой части трещины (гипотеза Христиано-
вича — Баренблата).
Для анализа ситуации в тупиковой части трещины,
следующей из сделанных предположений, воспользуемся
соотношениями § 3 гл. 3. Так, при переходе от пары
сосредоточенных сил (рис. 3.2) к нагрузке, показанной
на рис. 4.4, необходимо проинтегрировать решение C.3.21)
по хо и добавить решение A.1). В результате проделан-
проделанного имеем
^11 —
где
a	.—___
J /??> <3'9>
Заменяя здесь переменную интегрирования на % = а - х0
и считая (в силу малости d) а + х0 « 2а, получаем ве-
величину, называемую модулем сцепления:
Подсчитаем вертикальные смещения берегов в окрест-
окрестности конца трещины. Так, в формуле C.3.23) можно

134 гл. 4. хрупкое разрушение (линейная теория)
приближенно считать
А тогда интегрирование по х\ и хо дает
Объединяя полученное с C.3.17), имеем с учетом того,
что по A.1)
ki = of% ]fna при ао=0;
C.11)
яа
Из выражений C.8) следует, что условие конечности
напряжений в конце трещины имеет вид
C.12)
Полученное равенство определяет модуль сцеплбикл.
Критерий же разрушения
C.13)
согласно которому трещмна распространяется после дости-
достижения модулем сцепления своего критического значения,
согласно C.12) совпадает, по существу, с силовым кри-
критерием Ирвина C.6).
В силу равенства C.12) обращаются в нуль входящие
в C.11) асимптотические представления, обусловливаю-
обусловливающие скругление тупиковой зоны. Оставшиеся слагаемые,
не вошедшие в асимптотику, обеспечивают плавное смы-
смыкание берегов тупиковой зоны (см. § 4).
§ 4. Деформационный критерий
Леонова — Панасюка — Дагдейла
В рассмотренных силовых критериях оценка крити-
критического состояния трещины производятся по одному па-
параметру — коэффициенту интенсивности напряжения
(модулю сцепления). Более общим является деформа-
деформационный критерий Леонова — Панасюка — Дагдейла. Кри-

S 4. КРИТЕРИЙ ЛЕОНОВА — ПАНАСЮКА — ДАРДЕЙЛА 135
тическое состояние здесь определяется двумя параметра-
параметрами (постоянными материала): 6*, ос-
При построении своей 6*-модели М. Я. Леонов и
В. В. Панасюк исходили из следующих предпосылок:
1)	максимальное растягивающее напряжение в теле
не превосходит предела хрупкой прочности ос;
2)	напряжения и деформации связаны законом Гука;
3)	в теле образуются микротрещины (области ослаб-
ослабленных связей между частицами тела), если подсчитанные
по линейной теории упругости максимальные значения
растягивающих напряжений достигают значения ос;
4)	противоположные берега таких микротрещин при-
притягиваются напряжениями ос, если расстояние между
ними не превышает величины 6к — так называемого кри-
критического раскрытия трещины, и не взаимодействуют меж-
между собой, коль скоро это расстояние больше 6*.
о (О
<5
У
\
Рже. 4.6
Последнее сводится к закону взаимодействия берегов,
показанному на рис. 4.6 (ср. рже. 4.9). Из рас. 4.5 следует
D.1)
Действительно, интеграл в левой части равен работе по
разъединению берегов трещины (в расчете на единицу
ее длины). В правой части — энергия образующихся при
этом двух свободных поверхностей (опять же в расчете
на единицу длины трещины). Таким образом, равенство
D.1) означает, что работа по разъединению берегов раз-
разреза уходит на образование новых свободных поверх-
поверхностей. При принятой на рис. 4.6 схематизации находим
из D.1)
2f.	D.2)

136 1*л. * Хрупкое разрушение (линейная теорий)
Развитая Леоновым и Панасюком теория предназна-
предназначалась для рассмотрения не только макро-, но и микро-
микротрещин, а также для выявления тонкой структуры ту-
тупиковой части трещины. Поэтому здесь уже недостаточно
использованных выше асимптотических выражений для
(ь 0) и m?(#i), требуются более точные выражения.
Так, из формул C.3.15), |3.3.20), A.1) получаем
на продолжении разреза, где ? = ? =	(	V
Переходя от пары сосредоточенных сил к нагрузке, по-
показанной на рис. 4.5, получаем после интегрирования
по zo (d — длина зоны взаимодействия берегов)
Г h °с ( ef V«2-^
Использование здесь легко проверяемого тождества
+ zx arccos
_
:+ V a* —
дает
D.3)
Отсюда видно, что условие конечности напряжений в кон-
конце трещины (при х\ = а) имеет вид

14. критерий Леонова — ИанаС<ока — даГдейла 137
Из полученного выражения и определяется длина туци-
ковой зоны:
— = 1 — cos *	или У d = у 2а sin
2\/аос	с
D.5I§1
Для определения величины раскрытия трещины ис-
используем теперь соотношения C.3.23), C.3.25), C.3.26),
J Г (а; х0, ^) dc0 + J Г (а; *„ *,) Лг„ . D.
—а	а-*4	J'
С помощью соотношений C.3.24), C.3.25) нетрудно про-
проверять равенство
J Г dx0 = (х0 — хО Г — 2 W — xj arcsin
Используя его, приводим D.6) i к виду
"
-a + d,¦ *,)+
+ (a ~ d - х,) Г (a; a - d, x,)]}. D:6),
Согласно равенству D.4) последнее выражение еще упро-
упрощается:
4 (х,) = =F i-=^-^-{(a-d^x1)T(a; -a + dtXl) +
+ (a-d-xi)T(a;a-d,x1)}. D.7)
С учетом второго нз равенств C.3.25) псееы отсюда

138 гл- 4- ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЙ)
Наконец, из полученного выражения и D.7) находим
и?(а) = ^(а).= 0.	D.8)
Итак, в отличие от подхода Гриффитса, подходу Леоно-
Леонова — Панасюка отвечает, как уже было сказано выше,
плавное смыкание берегов в конце трещины.
Риб. 4.7
Возвращаясь к выражению D.7), получаем с учетом
рис. 4.7 величину 6* — критическое раскрытие трещины;
6k ж б as и% (а — d) — mJ" (а ^- d) в
Используя равенство D.5) ь введем «чистую» (за вычетом
зоны ослабленных связей) полудлину трещины
oo-a-d.	D.10)
В результате получаем
или
«I =
-т=
У я
с
=—arccos
D.И),
Полученная формула в теории Леонова — Панасюка при
заданной начальной чистой длине трещины по и постоян-
постоянных материала Е, v, ас, бк определяет критическое зна-
значение коэффициента интенсивности напряжений ^i:

§ 5. ЛОКАЛЬНЫЙ ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ	139
Для макроскопической трещины б* < по « а и
arccos
- v2) aca'
С учетом этого из равенств D.11) и D.2) находим
D.12)
В рассматриваемом нами случае нормального отрыва (см.
A.1)) aS = а*, к* = а* Упа и из D.12) следует выраже-
выражение B.7). Тем самым показано, что для макротрещины под-
подхода Леонова — Панасюка, по существу, равносилен рас-
рассмотренным выше.
При а—>О формула Гриффитса B.7) дает для а*
бесконечное значение. Из формулы же D.11)? следует,
что ао —> 0 влечет а* —> ос. По мнению авторов метода,
это обстоятельство и возможность обследовать «тонкую
структуру» тупиковой зоны оправдывают применение изло-
изложенного метода к микротрещинам. Некоторые критические
соображения по этому поводу приведены в статье [42].
Эксперименты на металлах с хорошо выраженным
пределом текучести показывают, что в окрестности бере-
берегов трещины образуются тонкие пластические зоны. Это
дало возможность Дагдейлу предложить [98] модель тре-
трещины, аналогичную модели Леонова — Панасюка. Ее за-
зависимости следуют из полученных выше заменой ос на
От — предел текучести материала, отвечающий образованию
пластических зон в конце трещины. Формальной эквива-
эквивалентностью обоих подходов объясняется их объединение
в единую модель Леонова — Панасюка — Дагдейла.
} 5. Локальный энергетический критерий
В линейной теории хрупкого разрушения широко ис-
используется критерий, связанный с интегральным тождест-
тождеством A.15.4), A.15.5). Считая Sn цилиндрической по-
поверхностью единичной высоты, проходящей через кривую
со скругленным корцом, охватывающую конец разреза

140 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
(рис. 4.8,а), находим, заменяя n*—> v* и опуская индек-
индексы (рассмотрение ведь идет в рамках линейной теории
упругости):
V+AB-Tt+CD
E.1)
При_разрезе, свободном от напряжений, oVj в 0 на 1\, АВ
и CD. Кроме того, на А В и> CD vi = 0. С учетом этого
a+da
Рис. 4.8
к A.13.3) тождество E.1) записывается в виде
Ov, dt =
ft
U^-
При этом Г — произвольный контур показанного на
рис. 4.8,а вида, а Г, проходится в показанном стрелкой
направления.
Выясним механический смысл интеграла в правой
части
E.3)
Из рис. 4.8, б видно, что при продвижении конца трещины
на da из тела как бы выбывает объем (в расчете на еди-
единицу длины в направлении хъ) dV — da • dxi -1. С этим
связано уменьшение энергии деформации на величину
— dU — da J Ф dx%. Отсюда и из E.3) следует
. ___ аи
J	"й'
E.4)
т. е. / — спорость уменьшения энергии деформации тела
(слоя единичной толщины) при продвижении трещины.

§ 5. ЛОКАЛЬНЫЙ ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ	141
Пусть при возрастании растягивающего напряжения
на бесконечности <х^ половина трещины удлиняется на
величину da. Работа, потребная для закрытия вновь появ-
появляющейся при этом части трещины (точнее, ее половины),
равна по теореме Клапейрона
a+da
dA = ±- J [ut(xi;a+da)-
a
— w7 (хг; а + da)] on (xv 0; a) dxv E.5)
Здесь (u? — щ)— взаимное перемещение берегов, а
022 — статически отвечающее этому смещению напряже-
напряжение на продолжении исходной трещины. Согласно равен-
равенствам C.3.15), C.3.17)
*i>a,.
Х\<а+ da.
Подстановка этих выражений в E.5) дает
*А = 2-^(аГ,)'«Х,	E.6)
где
а
Полагая здесь х\ « а, Х\ + а « х\ + da + х\ « 2а и ис-
используя таблицы интегралов, находим
a+da r-
Отсюда и из E.6), A.1)) следует
ЙЛ = Ц^( J/Wr,)fda = i^!fcf da.
Приравнивание полученной работы по закрытжю трещи-

142 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЁЙЙАЯ ТЕОРИЙ)
ны уменьшению энергии деформации приводит по E.4)
к зависимости
E.7)
В общем случае суммарной плоской задачи A.1), A.2)
имеем
/-4^(*S + *ii).	E-8)
В качестве критерия разрушения здесь принимается до-
достижение /-интегралом своего критического значения:
E.9)
По-видимому, первой среди основополагающих работ
по созданию концепции /-интеграла была статья Эшелби
[100]. Отметим кроме нее еще работы [77, 97, 115, 117].
I 6. Концепция Новожилова
В предыдущих параграфах было показано, что приме*
нительно к макротрещинам различные so своему содер-
содержанию подходы привели в базовой задаче к тому же
критерию Гриффитса B.8), B.9)
F.1)
В статьях Новожилова [41, 42] была предложена трак-
трактовка основных концепций линейной теории хрупкого
разрушения. Ниже дается ее краткое изложение.
Рассмотрим прежде всего кристаллический материал
с идеальной (бездефектной) простой кубической решеткой
(рис. 4.9). Пусть Г— сила взаимодействия между парой
близлежащих атомов, расстояние между которыми в нена-
ненапряженном состоянии обозначим через D и назовем атом-
атомным диаметром. Величина
является условным нормальным напряжением в дефор-
деформированной решетке. В плоском деформированном со-
состоянии, рассмотрением которого мы и ограничимся, имеем
(в расчете на единицу длины уходящей за плоскость

S в. КОНЦЕПЦИЯ НОВОЖИЛОВА
143
чертежа 4.9 оси зд)
т
Зависимость условного напряжения о° от расстояния
между центрами атомов описывается экспериментальной
кривой типа показанной на рис. 4.5 сплошной линией.
При увеличении расстояния между атомами отталкивание
и

—
с
с
г
4 ¦
Э
Рис. 49
Рже. 4.10
при 㫦D/2 сменяется притяжением, достигающим при
г = гс максимального значения — т. н. идеальной проч-
прочности Ос*). При г>гс происходит дальнейшее расхож-
расхождение атомов при прогрессирующем снижении напряже-
напряжений, т. е. появление микротрещины.
Введем кратности удлинений
JL = -JU, ^- го	F.2)
так, что значение Я -* 1 отвечает 2г — D — расстоянию
между атомами в ненапряженном состоянии. Модуль Юн-
ра естественно определить равенством
шр da01	/А л,
Е = Ж1-г	F'3)
Экспериментальную кривую на рис. 4.5 можно аппрокси-
аппроксимировать функцией
<у° =* <Jc г——-? е	,	F.4)
так что по F.3)
Л Более подробно об идеальной прочности речь будет идти и
гл. б.

144 ft* 4 «УПКОЁ РАЗРУШВЙИЕ (ЛИНЁЙЙАЙ ТЕОРИЙ)
т. е.
F.5)
На рис. 4.10 показаны три атома из трех смежных
атомных слоев (ср. с рис. 4.9). Рассмотрим ситуацию,
когда хо > 2гс, т. е. когда при х = 0 средний атом взаимо-
взаимодействует с каждым из крайних по закону нисходящей
ветви на рис. 4.5. Предполагая, что притяжение проис-
происходит по закону F.4), найдем возможные равновесные
положения среднего атома, считая положения крайних
фиксированными. В соответствии с рис. 4.10 средний
атом притягивается к внешним следующими силами:
Dal = Doc Vя е1-^-1^1),
Приравнивание сил притяжения F.6) дает три положе-
положения равновесия:
ХA) = 0, ЛA) = Хф, № « - Лф,	F.8)
где Яф — положительный корень трансцендентного урав-
уравнения
Неравенства
или (что то же, в силу F.7))
К— К — 2*с < 0, к0 — Хф — 2ХС > 0 F.10)
определяют, будет ли средний атом взаимодействовать
с верхним по восходящей ветви (первое неравенство) или
по нисходящей (второе неравенство). Неравенства F.10)
можно записать с помощью F.9) и так:

I в. КОНЦЕПЦИЯ НОВОЖИЛОВА	145
Рассмотрим корни F.8). Первый из них отвечает три-
тривиальному положению равновесия, равноудаленному от
верхнего и нижнего атомов. Это положение равновесия
неустойчиво. Действительно, небольшое смещение внут-
внутреннего атома из положения равновесия увеличивает его
притяжение в направлении движения и уменьшает в про-
противоположном. Нетрудно убедиться, что для второго по-
положения равновесия выполняются первые соотношения
в F.10) и F.11). Отсюда следует, что второе положение
равновесия относится к восходящему участку кривой
о <*> г и, стало быть, устойчиво. Таким образом, атом,
взаимодействующий с двумя смежными по закону нисхо-
нисходящей ветви, неминуемо будет притянут к одному из
них, взаимодействуя при этом с этим атомом по закону
восходящей ветви.
Отправляясь от этого, полученного на предельно про-
простой модели, результата, Новожилов показал [41, 42]:
механизмом хрупкого разрушения является потеря ус-
устойчивости тривиальных форм равновесия атомной ре-
решетки. При этом трещина рассматривается не как изна-
изначально данный разрез, а как нетривиальная форма равно-
весия упругого тела, возможная при интенсивной растя-
растягивающей нагрузке.
Принятый Леоновым и Панасюком закон взаимодей-
взаимодействия берегов трещины (рис. 4.6) в свете сказанного
можно рассматривать как простейшую кусочно-линейную
аппроксимацию кривой взаимодействия берегов трещины.
Длина горизонтальной площадки 6* определяется форму-
формулой D.2) у Полученный при подсчете по формуле D.1)
работы, идущей на образование новой поверхности.
Принимая же закон F.4) и вводя обозначения
находим с учетом соотношений F.5), F.2) и D.1)
(б.12)ж
Записывая теперь соотношение F.5) в виде

146 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
получаем отсюда и из F.12) i выражение Новожилова
С л ос С	/а лОч
Y =-j ~!Г ' "/Г*	F-12)i
Подсчет же по формулам D.1) и выражениям
о facsin2n(X —1), 1<Я<3/2 (^ = 5/4),
° 10,	Я,>3/2,	F.13)
отвечающим аппроксимации кривой полусинусоидой
(штриховая кривая на рис. 4.5), приводит к выражению
Орована
Тж0,5^р.	F.14)
Поскольку последняя аппроксимация грубее, истинное
значение f, по-видимому, ближе к F.12) 2.
Вернемся к равенствам D.3) и предшествовавшему
D.7). С учетом того, что d/a<l, и равенства C.3.24)
находим после некоторых преобразований следующие
приближенные выражения:
OcVTi + ±ac{d-:IпЩ^} F.15)
Из последнего выражения видно, что при этом
F.17)
,
у конца трещины имеют место бескондешо большие растя-
растягивающие напряжения, а при
/J	F.17),

S 7. КОНЦЕПЦИЯ НОВОЖИЛОВА (ПРОДОЛЖЕНИЕ)	147
— бесконечно большие сжимающие напряжения. И толь-
только при
напряжения конечны. Выполнение последнего равенства
и есть для рассматриваемой задачи упомянутый выше по-
постулат Христиановича — Баренблата, согласно которому
наличие бесконечно больших напряжений у концов тре-
трещины считается физически некорректным.
Далее, из выражения F.15) следует при выполнении
условия F.17) з
Отсюда и из равенства D.2) следует
Исключая из F.17)з и полученного равенства d, имеем
(ср. B.7))
Итак, принятие гипотезы конечности напряжений (рас-
(растягивающих и сжимающих) приводит для каждого зна-
значения нагрузки о к определенной (и именно гриффитской)
длине равновесной трещины. Равновесная трещина не
может быть ни длиннее, ни короче гриффитской. Она
является всегда неустойчивой — столь угодно малое
изменение о приводит к появлению бесконечных напря-
напряжений, воспрещаемых гипотезой Христиановича — Ба-
ренблата.
§ 7. Концепция Новожилова (продолжение)
Стремление «избавиться» от бесконечно больших зна-
значений напряжений связано с понятным желанием согла-
согласовать классический критерий наибольших нормальных
напряжений
о»<0с	G.1)
(On — максимальное значение напряжений в рассматри-
рассматриваемой задаче) с несомненным фактом существования

148 frl. 4.'ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТГ.ОРЙЯ)
равновесных трещин, в концах которых имеют место
бесконечно большие напряжения.
В упомянутых работах [41, 42] Новожилов показал,
что не следует наотрез отказываться от решений линейной
теории упругости только из-за того, что они приводят
к появлению бесконечно больших напряжений. Проследим
ход его рассуждений.
Прежде всего разрушение твердых тел — процесс дис-
дискретный: нельзя, например, отделить половину атома от
половины другого. «Квантом» (элементарным актом раз-
разрушения) является разрыв связи у одной пары атомов —
при достижении в этой паре растягивающей силой своего
предельно возможного значения
или
Интегрирование здесь производится по содержащему одну
связь «атомному квадрату» со стороной D.
Если во всех точках тела выполняется обратное нера-
неравенство
G.3)
то прочность обеспечена, так как действующие на него
внешние силы недостаточны для разрыва хотя бы одной
пары атомов.
Из этого, однако, не следует, что условие G.2) можно
считать критерием разрушения. Оно является всего лишь
условием разрушения одного элемента многократно стати-
статически неопределимой системы, каковой является атомная
решетка. Поэтому будучи необходимым критерием разру-
разрушения, неравенство G.2) не является достаточным. Стро-
Строго говоря, формулировка достаточного критерия раз-
разрушения должна быть связана с оценкой несущей
способности атомной решетки тела при действии на него
данной внешней нагрузки.
Практически дискретный критерий G.3) отличается
от континуального критерия G.1) лишь в окрестностях
сингулярных точек поля напряжений. Существенно, что
там, наряду с бесконечностью напряжений, бесконечно ве-
велики и градиенты напряжений, так что усреднение по «атрм-
ному квадрату» (а это, по существу, ж делается при пер*-

I 1. КОНЦЕПЦИЯ НОВОЖИЛОВА (ПРбДОЛ&ЙЙИЁ)	149
*оде от континуального критерия к дискретному) устра-
устраняет отмеченные сингулярности. Поэтому бесконечность
напряжений, категорически воспрещаемая континуальным
критерием, не противоречит дискретному.
Для плоской задачи критерий G.3) заменяется еле-
дующим:
D
у J о» «•
ас, 6 - * - а.	G.4)
При этом знаку равенства в нем отвечает критическое
состояние трещины, при котором сила взаимодействия
между ближайшими к вершине трещины парой атомов
достигает своего предельно возможного значения.
Определим критическую длину трещины 3?n e 2а, от-
отвечающую этому состоянию. Подставим для этого выра-
выражение F.16) в критерий G.4), при знаке равенства
в нем. Используя легко проверяемые равенства
получаем
Далее, с помощью формулы F.15) шкодим
6h^uUd)-uT (d) -4Aд^ (а
Отсюда и из равенства D.2) следует
Введем обозначения
5Ь ""-т* GЛ)

150 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
С их помощью уравнения G.6) записываются в следую-
следующих двух формах:
или
Из второго равенства следует, кстати, & %
Вычитание равенства G.8) i из G.5) дает
р = A + a) /a[l- 4 arcsin^i].
<7-8>'
G.9)
Согласно первому из выражений G.7) величина A явля-
является функцией физических постоянных материала — за-
заданной величиной. Таким образом, G.9) можно рассмат-
рассматривать как трансцендентное уравнение для величины
а
2 4
Рис. 4.11
u**d/D. На рис. 4.11 показана зависимость Уа от р
Из этого графика и формул G.7), G.8)i и G.8J под-
вчитываются коэффициенты Лих, вводимые соотноше-
соотношениями
о
G.10)
2	1	а ' q2	АТ7%	I	¦ О \
а \ * - \ *• Р	„	*U ш. ITT я Р	11 Ai\
Значения коэффициентов приведены на рис. 4.12, 4.13.
Предельному значению р»0 (т. е. ife 0) отвечает
пренебрежение межатомными связями на нисходящей вет-
ветви графика о со т). При этом согласно третьему выра-
выражению в G.7) -2% = 0. Из рис. 4.13 (либо непосредствен-

I 7. КОНЦЕПЦИЯ НОВОЖИЛОВА (ПРОДОЛЖЕНИЕ)
151
но из соотношений G.10), G.11)) следует, что при этом
2 м *?• 0. В другом предельном случае (при р —> <*>) имеем
согласно первому из выражений в G.7) D—>О. При ко-
конечном if этому случаю отвечает переход к сплошной сре-
среде. Естественно, что при этом согласно рис. 4.12, 4.13 а
G.10) 2N = 2t. Из сказанного следует, что 2'* > 2в
и 2N — верхняя граница для длины равновесной тре-
трещины 2.
А
a
2 4
Рис. 4.12
fi
0 1 2
Рже. 4.13
Для определения нижней границы рассмотрим рав-
равновесную трещину с длиной 2 < 2?к, которой отвечает
в соотношении G.4) знак неравенства. Однако при этом
сохраняется равенство G.8J
G.12)
являющееся следствием лишь соотношения G.6), не свя-
связанного, как нетрудно проследить, с G.4). Из последнего
равенства следует SB > 9?t.
Итак, все возможные длины равновесных трещин удов-
дятворяют двустороннему неравенству
St9<St<SM.	G.13)
Как было отмечено выше, при (J = 0(ч = 0) этот интервал
переходит в 0 < 2 < 2N, т. е. для материала с пренебре-
пренебрежимо малой плотностью поверхностной энергии могут
существовать равновесные трещины любой длины, мень-
меньшей чем критическая по Новожилову 2V При р—> «
(D —> 0) допустимый интервал стягивается в точку 2 =*
=*21 = 2n. Таким образом, для сплошной среды возможна
равновесная трещина лишь строго определенной (гриф-
фитской) длины. Из рис. 4.13 усматривается, что в наибо-
наиболее вероятном интервале изменения параметра § @,5 <
<р< 1,3) имеем 0,6 <2J2*< 0,9,

152 ГЛ. 4. ХРУПКОЕ РАЗРУШЕНИЕ (ЛИНЕЙНАЯ ТЕОРИЯ)
В статье [42] приводятся также интересные сообра-
соображения о возможности расширения интервала G.13) в ле-
левую сторону и о том, что в рассматриваемой задаче дискрет-
дискретный критерий является не только необходимым, но и
достаточным. Отметим, что (по мнению Новожилова) по-
полученные количественные оценки следует рассматривать
как первое приближение. Желательно их уточнение пу-
путем более аккуратного рассмотрения ситуации в конце
трещины.
В цитированных статьях Новожилова имеется еще
ряд интересных соображений, усиливающих познаватель-
познавательную ценность этих глубоких, но оставшихся малоизвест-
малоизвестными работ. Отсылая читателя к первоисточникам, отме-
отметим следующее:
1.	Дискретный критерий Новожилова рриложим не
только к трещинам (как критерий Гриффитса), но и к уг-
угловым точкам.
2.	Заманчиво распространить изложенную концепцию
Новожилова на нелинейную теорию хрупкого разрушения.
Кое-что в этом направлении уже делается (см. сле-
следующую главу).

Глава 5
ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
В публикациях по теории трещин под нелинейной тео-
теорией обычно понимают учет физической нелинейности
материала (главным образом учет пластичности). Совсем
мало уделяется внимания учету геометрической нелиней-
нелинейности. При этом последняя зачастую учитывается лишь
частично (например, рассматриваются большие дефор-
деформации, но без учета поворота главных осей деформации).
Целью этой главы и является выяснение (на приме-
примерах полученных выше аналитических решений) влияния
геометрической нелинейности.
| 1. Задача о прямолинейном paspete
Сопоставим решения задачи о плоскости с прямоли-
прямолинейным разрезом в геометрически нелинейной (§ 7 гл. 2)
и линейной (§ 5 гл. 3) постановках. Прежде всего, по-
полагая для простоты и наглядности aJJ° = aj^ = а[™ =
= a?= a0 = 0, со00 = 0; aj~, a? > 0, имеем согласно выра-
выражениям B.7.8), B.7.3) и C.5.6J асимптотические вы-
выражения для: истинных напряжений
линейных
Прежде всего из соотношений A.1) следует, что
асимптотики истинных напряжении в рассматриваемой

154 ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
задаче не имеют реального физического смысла, будучи
независимыми от внешней нагрузки (о?™).
Что касается условных напряжений, то они при уме-
умеренных напряжениях на бесконечности (при oj* « a^)
имеют тот же коэффициент интенсивности напряжений,
что и линейные. Тем не менее различие зависимостей
от полярного угла может существенно повлиять на ре-
результаты рассмотрения ряда тонких вопросов теории тре-
трещин (см., например, § 2).
Далее, из соотношений D.1.2), B.7.3), B.7.8) полу-
получаем при
а17 = аГ1-а;Г = аГ,-0, ао«О, аГ=0; о1
для условных напряжений
для линейных напряжений
Здесь также (в еще большей степени) различаются за-
зависимости от полярного угла.
В литературе по теории трещин бытует мнение, что
геометрическая нелинейность слабо влияет на конфигу-
конфигурацию трещины (разреза). На примере рассмотренной
задачи покажем, что и это не так. Согласно соотноше-
соотношениям B.7.15) и C.5.7) при исходном всестороннем ра-
растяжении плоскости с разрезом на бесконечности (aJJ° =
s= aj?° = an = о%2 = a*, aj* = o™2 = 0) и нормальном дав-
давлении на берегах разреза Оо имеем: с учетом геометри-
геометрической нелинейности разрез переходит в круг
«' Ь' i ( о* , а»
( +

§ i. ЗАДАЧА 6 ПРЙМОЛЙНВИИОМ РАЗРЕЗ*	155
и без учета — в эллипс с полуосями
В частности, при оо в О
?-0. ^-(* + ?>	СТ..
Отметим, что в последнем случае мы имеем дело с «на-
«нанесением разреза» предварительно всесторонне растяну-
растянутой пластине. При этом геометрически нелинейному ре-
решению A.6J отвечает переход разреза в круглое отвер-
отверстие. Этот результат качественно подтверждается в эк-
экспериментах на резиновых пластинах.
Полученное круговое отверстие имитирует (в рамках
плоской задачи) возникновение пор (микропор) в мат-
матрице с жесткими включениями, где, как известно [13],
возникает напряженное состояние, близкое к всесторон-
всестороннему растяжению.
Возвращаясь к линейному решению A.7) 2, отметим,
что оно приводит к физически несуразному результату:
разрез, располагавшийся по горизонтальной оси, пере-
переходит в разрез по вертикальной. Этого и следовало ожи-
ожидать, поскольку линейная теория неадекватно учитывает
большие повороты.
Рассмотрим подробнее характер учета действия на
контур отверстия нормального давления. Согласно равен-
равенствам B.4.7) и C.4.6) при 0у*вво, оУ(=0 имеем два
вида статических граничных условий: в нелинейной по-
постановке
и в линейной
(Ф(С) + ФОе»° - (CW) + ТЩ)Г* - (а,- а»)
Отсюда и усматривается качественное различие в спосо-
способе учета нормального давления. При нелинейном подходе
Со, входя в коэффициенты граничного условия, являются
своеобразной «параметрической нагрузкой*, цри линей-
линейном же подходе 0о — обычный «нагрузочный член».

156 ГЛ. 5. ВЛИЯЙИК ГЕОМК»ГРИ^ЕСКОЙ НЕЛИНЕЙНОСТИ
§ 2. Условия хрупкого разрушения
В статье [108] было приведено необходимое условие
хрупкого разрушения Кейли — Тайсона — Котрелла
Здесь тс, Ос — максимально допустимые (идеальные)
значения тангенциальных и нормальных напряжений в
рассматриваемом материале (см. § 4—5 гл. 4),
а (см. A.3))
овтиа„~--—-,	<р = 0,
*	-	<2-2>
т 35 шах (V ~ * -0,385? <р « 70,5%
Ф	у 2л г
— максимальные значения нормальных и касательных
напряжений в рассмотренной нами задаче. Механический
смысл условия B.1) состоит в том, что реализующееся
в рассматриваемой задаче максимальное значение нор-
нормального напряжения ближе к своему цредельно воз-
возможному значению, чем максимальное значение танген-
тангенциального — к своему предельно возможному. Так что
хрупкое разрушение путем отрыва более вероятно, чем
вязкое разрушение путем сдвига.
Переходя к геометрически нелинейному решению, ус-
условие B.1) необходимо заменить на следующее:
где согласно A.2) (в рассмотренной нами задаче)
а° э= max о?офо ~ 1	,	<р° = 0,
Т° _ <2-4>
—7==г«0,5, ф°==90°.
ф°	у2пг°
Из соотношений B.2) и B.4) при к\^кг следует
ас хс
р	[8] автор рр () (фр
мулированного ими, строго говоря, для Г-=0°К) отме-
В своей работе [108] авторы критерия B.1) (сфор-
(сфорГ0°К)

I 3. УТОЧНЕНИЕ ДИСКРЕТНОГО КРИТЕРИЯ ОТРЫВА	157
чали его грубость. Критерий, безусловно, справедлив в
двух крайних случаях. Так, при ас/тс достаточно боль-
больших (скажем, больших 10), характерных для металлов
с гранецентрированной кубической решеткой, разруше-
разрушение всегда вязкое, с интенсивным пластическим тече-
течением. Если же вс/тс порядка 1 (например, для алмаза,
поваренной соли), то разрушение (с учетом того, что
обычно Ощдх > Тлю) при низких температурах всегда
хрупкое.
Между этими двумя типами твердых тел нельзя про-
провести резкой границы. Если отношение ос/тс лишь в не-
несколько раз (скажем, меньше чем в 5) больше единицы,
то на вид разрушения влияют многие вторичные факто-
факторы (температура; напряжения по нормали к плоскости
максимального значения тс; неоднородности на берегах
трещины и в атомной решетке, приводящие к случайно-
случайному излучению дислокаций, затупляющих трещину; трех-
трехмерность эффектов, не учитываемая двумерными моде-
моделями и т. п.).
Итак, в этом случае необходим более детальный ана-
анализ, в том числе и напряженно-деформированного состоя-
состояния в конце трещины. Такой анализ стал проводиться
в более поздних работах по атомистике разрушения.
Ссылки на них можно найти в [9, 23, 32, 48].
Одним из упомянутых факторов является учет гео-
геометрической нелинейности проблемы, приведший к более
жесткому (согласно равенствам B.5)) условию хрупкого
разрушения B.3).
f 3. Уточнение дискретного критерия
нормального отрыва
В § 7 гл. 4 был приведен, применительно к задаче
нормального отрыва прямолинейной трещины, дискрет-
дискретный критерий D.7.4)
D
5- J
F, 0) d\ < а* 6 = *! - а.	C.1)
о
Внимательное рассмотрение проделанного в статьях Но-
Новожилова [41, 42] показывает, что там речь, по суще-
существу, идет о больших (хотя и не .очень) деформациях.
Кроме того, при рассмотрении разрыва атомной решетки
не учитывалась ее поперечная деформация. Кстати об

158	ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
этом, по существу, сказано в [48, с. 145]. Поэтому в
C.1) 022 следует заменить на соответствующее условное
напряжение о22, a D — на начальное расстояние между
рядами недеформированной решетки Д>. Таким образом,
критерий C.1) следует записывать в виде
Я- J o\t ($, 0)« < ac (\ = x\- а). C.2)
0 о
Последний естественным образом обобщается на слу-
случай произвольной трещины (выреза):
7Г f
max
О	<ро
При этом в общем случае DQ — характерный размер не-
недеформированной структуры рассматриваемого материа-
материала (композита).
§ 4. Нелинейный подход
к задаче Леонова — Панаеюка — Новожилова
Рассмотрим задачу Леонова — Панаеюка (§ 4 гл. 3).
Новожилов высказал мнение ([42], с. 812), что здесь й
первом приближении можно пренебречь геометрической
нелинейностью. Покажем, что так оно и есть.
По аналогии с изложенным в § 3 гл. 3 рассмотрим
задачу о деформации плоскости с прямолинейным разре-
разрезом (— а^.хг^а, #2=0) (см. рис. 2.4). На верхнем (+)
берегу разреза •уо+ = — я/2, на нижнем -у0" = я/2 и на
обоих С = t = х\- С учетом этого силовые граничные ус-
условия B.3.2), B.4.6), B.4.9), B.4.11) записываются в
виде
ОС. D1)
Аналогично проделанному в § 3 гл. 3 введем функцию
йо(?)-^о(?) (ЧЧ?)=йо(Ш,	D.2)
где	_ _ 	 _
Vo(t)-Vo«), Qo(t)-Oo(t),	D.3)
т. е. функции 4*0E), йо(?) принимают в симметр^ичных

§ 4. ЗАДАЧА ЛЕОНОВА — ПАНАСЮКА — НОВОЖИЛОВА 159
относительно оси абцисс точках комплексно сопряжен-
сопряженные с Ч^оС^), йо(?) значения. Согласно D.2) и D.3)
при выходе из области на верхний берег разреза
(?-***) и нижний (t-+x7) имеем
и граничные значения D.1) записываются в виде
D.4)
где
g {xl) = [atovo (xl) + a7ovo (xl)] +
+ i [atoto (xl) + a-oto(xl)] - 2 (aja°° - to;,"). D.5)
Решение выписанных задач (см. (П.3.10), (П.3.11)) да-
дается формулами
Рассмотрим первый частный случай
«;)= 0; Лх1)=0, g(xl) = - 2 (а^- toff).
При этом с учетом соотношений (П.3.16), B.4.11J и
D.2) находим

160	ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
Второй частный случай отвечает расклинивающей па-
паре вертикальных сил (рис. 3.2), для которой (см.
C.3.18))
a12 = O22 = u>
Отсюда и из D.6) следует
i2— хг
1 X0
-. D.8)
При заданном распределении вертикальной нагрузки, оп-
определяемой функцией Q(xo), находим, интегрируя по х0,
TTT^i ° *<>-? ° °'
2n
D.9)
Перейдем к задаче Леонова — Панасюка (§ 4 гл. 4),
для которой
о, -.
D.10)
a —
Отсюда и из D.9) находим
D.11)
С учетом этого, а также легко проверяемого соотношения
1 — о2 arcsin —т=—^-г +
	? = _Ё_ I
arccos (zo/fl) + |/ о2 — x\
2 — x\

§ 4. ЗАДАЧА ЛЕОНОВА —ПАНАСЮКА —НОВОЖИЛОВА
получаем
=р +
D.12)
Далее, интегрируя выражения D.11) по ? и меняя
порядок интегрирования, находим
о*
Используя же второе из легко проверяемых тождеств
ж - (;_,о)ув._^' -. - (,, -о V* - 4(¦ }
где
находим отсюда
[— a+d	а	т
j f(a;*0,C)d»e+ J f(a;*Q,?)d*e
J
С помощью легко проверяемого тождества
e @С)+ 2 /?^?
б К. Ф. Ч»рных

162 ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
предыдущие выражения можно записать и так:
= ос [- 4Н I(a ~ d + О Г (а; - а + d, С) + (а - d - ?) X
хТ(а; a-d, ?)] - ± arccos (l - 4) /F17^2}- D.15)
arccos (l 4
Для получения функций Гурса — Колосова (?),
W (I) рассматриваемой задачи Леонова — Панасюка к
выражениям D.12) и D.15) следует добавить (при
аг7 = ОгГ == 0) соотношения D.7)
а*Ф (С) - - аТ @ - ^1 yJ==r D.16),
и следующие аз них
— aJ^K'^/F^. D.16),
В результате проделанного имеем (при OjS° = a0)
D.17)
1 [а' - § arccos (l ^ ±)\ V?=* - «g [(« - d +
P	(a-d-OP(a;o-d,0]. D.18)
С помощью полученных для функций Гурса — Коло-
Колосова выражений имеем из формул B.4.6), B.4.5):
; D.19)
. D.20)
Так, на продолжении разреза, вправо от его конца, имеем

§ 4. ЗАДАЧА ЛЕОНОВА — ПАНАСЮКА — НОВОЖИЛОВА 163
согласно D.17), D.19) и A.11.3)
a; («10) = [а° - § arccos (l - |)
+ oc 1 + - arcsin 0 ——r -arcsm -^	—, I
I *\	a(x1-a + d)	a^-ra-d))]
D.21)
Далее (см. рве. 2.4) на верхнем (+) в нижнем (-) бере-
берегах разреза
; = о + г°е * , ф + = я, ф = — я,
		D.22)t
_ ж-«, /^ГГ^-± = ± уаш _ ^*;
Согласно же формулам D.14) и C.3.24)
Г± = ±Г.	D.22J
Теперь формулы D.20) н D.18) дают
D.23)
Сопоставление асимптотического выражения для уп-
упругого потенциала линейной плоской задачи
с соответствующим упругим потенциалом для геометри-
геометрически нелинейной теории B.4.1) обнаруживает в них
следующие соответствия:
6*

164 ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
Если к тому же считать, что вдали от трещины имеем
линейно-упругое состояние, то
а0 = о!? = а? = а.	D.26)
С учетом последних двух зависимостей выражение D.23)
совпадает с рассмотренным Новожиловым D.4.6) 2,
а D.21)-с D.4.3).
Возвращаясь теперь к первому абзацу параграфа,
можно опустить в высказывании Новожилова оговорку —
«в первом приближении» и констатировать полное сов-
совпадение решений задачи Леонова — Панасюка по линей-
линейной и геометрически нелинейной теориям. Причиной то-
тому является отсутствие в окрестности конца трещины
больших поворотов и деформаций.
§ 5. Страгивание трещины смешанного типа
(линейный подход)
Рассмотри»! случай комбинированного нагружения,
когда в эталонной задаче деформации плоскости с пря-
прямолинейной трещиной (рис. 2.4) «в игре участвуют» оба
коэффициента интенсивности напряжений: кг ж ки. Зна-
Значительное внимание этому вопросу уделено в книге
К. Хеллана [75, с. 202—207]. Изложим кратко часть его
Рис. 5.1
концепции, касающейся хрупкого разрушения, с тем что-
чтобы в следующем параграфе сопоставить ее с результа-
результатами, полученными из геометрически нелинейной теории.
Прежде всего предполагается, что направлением про-
продвижения трещины является такое направление <р = — cfс
(рис. 5.1), для которого трещнноподвижная сила имеет,
црж заданных внешних воздействиях, максимальное зна-

§ 5. СТРАГИВЛНИЕ ТРЕЩИНЫ СМЕШАННОГО ТИПА
165
чение. Критическое значение внешних воздействий долж-
должно быть таким, чтобы отвечающая им трещиноподвиж-
ная сила была равна сопротивлению растрескиванию.
Рассмотрим соотношение
где к1С — критическое значение коэффициента интенсив-
интенсивности напряжений для трещин нормального отрыва (см.
D.1.1)). Со ссылкой на работу [113] отмечается, что
нтм*
* л' <• \\W\\\"
Рис. 5.2
Рже. 5.3
согласие теории с экспериментом имеет место при ах
«с4*0, агж Заг/2, т. е.
На рис. 5.2 кружками показаны экспериментальные зна-
значения коэффициентов интенсивности в момент страги-
вания трещины [114, 118], сплошной линией доказана
кривая E.2). Материалом здесь является застеклованный
полимер полиметилметакрилат (ПММК).
В частном случае растяжения плоскости (широкой
пластины) со сквозной трещиной, наклоненной под углом

1в6 гл. 5. влияние Геометрической нелинейности
а* к оси Х[ (рис. 5.3), имеем (см. B.7.9))
*?=*<*• ein« а*,
а~ = а* sin а* cos а*, a?t = a°° cos2 a*;
h = а~2 /я? = а°° cos2 а* /да,
А;ц = Ом Vяа = or00 sin а* cos а* Упа.
E.3)
Подстановка последних выражений в условие E.2) при-
приводит к критическому значению растягивающего напря-
напряжения на бесконечности:
__ he Vi + 6 tg2 a* - 1
3sin2a*
E.4)
Результаты подсчета по полученной формуле показаны
на рис. 5.4 сплошной линией. Точками показаны экспе-
экспериментальные значения из [ИЗ]. Видно, что для уме-
умеренных значений угла а* разрушающаяся нагрузка поч-
почти не меняется.
л/2 а*
Рис. 5.4
Рис. 5.5
На рис. 5.5 приведены теоретические и эксперимен-
экспериментальные значения угла поворота трещины фс в функции
угла а*. Экспериментальные результаты (точки) заим-
заимствованы из работы [ИЗ], теоретические — из [99,
110]. В отличие от критической нагрузки угол излома
фс сильно зависит от угла наклона а*, и для малых зна-

I 5. СТРАГИВЛНИЁ ТРЕЩИНЫ СМЕШАННОГО ТИПА	167
чений этого угла — даже сильнее, чем это дает «правило
большого пальца рукт, согласно которому трещина
должна продвигаться перпендикулярно направлению ра-
растягивающих усилий, приложенных на удаленных от
трещины границах образца (на бесконечности). Послед-
Последнее показано на рисунке штрихпунктирной линией.
В ранних исследованиях Эрдогана и Си [99] был
предложен критерий о„:
1)	Трещина растет в направлении, по которому ве-
величина Vraw, определяемая асимптотикой (формулы
D.1.1), D.1.2)), максимальна.
2)	Трещина будет страгиваться тогда, когда указан-
указанная величина совпадает с критическим значением ко-
коэффициента интенсивности напряжений для типа I. При
этом установлено (согласно D.1.1)), что
VmJf-o * *,с/У^.	E.5)
Используем сформулированный критерий. Согласно
D.1.1), D.1.2)
Приравнивая второе выражение нулю, а первое (соглас-
(согласно E.5)) постоянной А1С/У2я, получаем систему двух
уравнений
кг sin Ц cos ^ Ч- *и (l - 3 sin* ^) - О,
кг cos3 ^ - АП3 sin ^ cos2 ^ - к1С,
связывающую три величины: kh kn и <рс. Решение этой
системы имеет вид
cos2(Vc/2) |pq	sin(9/2)
кЮ	соз3(Фс/2) ' he
Исключение отсюда угла фс приводит к связи между
&i и кц9 показанной на рис. 5.2 штрихами. Используя

168 IVL 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИЙЕЙНОСТЙ
же выражения E.3) и E.4), можно получить зависим
мости, показанные на рисунках 5.4 и 5.5 штрихами.
Изложенное в этом параграфе (как отметил Хеллан)
основано прежде всего на экспериментах. Результаты,
помещенные на рис. 5.5, получены только для поли-
полиуретана.
§ 6. Страгивание трещины смешанного типа
(геометрически нелинейный подход)*)
Рассмотрев в предыдущем параграфе этот вопрос в
линейной постановке, сравним приведенные там резуль-
результаты с таковыми же, но полученными в геометрически
нелинейной постановке. Для этого несколько преобразу-
преобразуем соотношения § 7 гл. 2. Полагая в них Оо = 0 и со* ==
•»0г получаем прежде всего из B.7.3)
Из соотношений B.7.8) следуют асимптотические выра-
выражения для условных напряжений
)	F.2)
Далее, из выражения B.7.4) получаем
Рассмотрим, во что при деформации переходит прямоли-
прямолинейный разрез (— а^хг ^а, х2 = 0) и его продолжение
*) Параграф натшсан совместно с И. М. Лосевой.

§ 6. ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫЙ ПОДХОД	169
(х2 = 0, |xi|>a). Прежде всего согласно B.7.12)
± i \/~аг - xi*>
F.4)
Л Г °2 	 2	° <*-
(верхний знак отвечает верхнему берегу, нижний
нижнему).
Из F.3) и F.4) получаем
f
F.5)
Отсюда следует параметрическое задание берегов трещины

170	ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
с помощью выражений
2 \ a/jo* a ^ о*
F.6)
При OiJ°= 0 полученные выражения совпадают с B.7.13)
(при Оо = 0).
Вернемся к результатам предыдущего параграфа и
посмотрим, как они трансформируются при геометриче-
геометрически нелинейном подходе? Прежде всего критерий Эрдо-
гана — Си E.5) принимает согласно F.2) следующий
вид:
l	Ф° = 0.	F.7)
Таким образом, независимо от соотношения между коэф-
коэффициентами интенсивности напряжений A*i и кц трещина
согласно критерию Эрдогана — Си распространяется
«вдоль себя» (ф° = 0, х°2— 0). Этот, странный на пер-
первый взгляд результат мы объясним ниже. Далее, подста-
подстановка в F.7) выражений E.3) приводит к более про-
простому, чем E.4), выражению для критического значения
растягивающего напряжения на бесконечности:
Отвечающие этой формуле значения показаны на рис. 5.2
кривой с крестиками.
Вернемся к соотношению F.7). Достоинством этой
зависимости является не то, что в нее коэффициенты
интенсивности напряжений входят нелинейным образом
(это естественно при нелинейном подходе), а в том, что
они входят именно в той комбинации, в какой они при-
присутствуют в выражении для трещиноподвижной силы
[Q = ^—- (к{ + к*п) (см., например, [75], формула
C.29)). На рис 5.2 соотношению (критерию) F.7) от-
отвечает единичная окружность с крестиками.

§ 6. ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫЙ ПОДХОД	171
Остается открытым вопрос о повороте трещины, объ-
объясняющем отмеченный выше парадокс. Для того чтобы
выяснить ситуацию в окрестности правого конца тре-
трещины, введем локальную координату ? = х\ — а. Из со-
соотношений F.5) получаем при |?| <а
( ©00
Г12
О*
— х.
где
F.9)
?)* «>¦'»)
— безразмерные координаты конца трещины.
Полагая для простоты и наглядности ог~ = atj°, полу-
получаем отсюда

172	ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
Д±/2 1^=1, ?<(),
•' №/«•)
F.11)
тЬ 1>0,
где
а = -7Г
= a%- = tg«, P-|f?g. F-12)
Если ввести еще обозначения
то
У- 2|/а
F.13)
На рис. 5.6 показаны локальные (материальные) тра-
траектории наибольшего нормального напряжения в зави-
Рже. 5.6
симости от параметра § (при к = 1/2), подсчитанные по
формулам F.11). Из F.13) следует формула для под-
подсчета угла поворота траектории
<Рс = arctg
5>о.
F.14)

§ 6. ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫЙ ПОДХОД	|?3
В вершине трещины (при 1 = 0) находим отсюда (см.
F.12))
Фс = arctg(-?) = -a,	F.15)
т. е. независимо от значений упругих постоянных точно
w
п/г-
п/2
п/2 а4
Рас 5.7
JS'1/Z
t-<S*/a
f+e*/a
0,001
Я/2 в*
Рис. 5.8
выполняется правило большого пальца руки. Отметим,
что в ряде публикаций по линейной теории трещин это
правило рассматривается как грубо приближенное.

174 ГЛ. 5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКОЙ НЕЛИНЕЙНОСТИ
Часто рекомендуют для лучшего совпадения теоре-
теоретических изысканий с экспериментальными данными рас-
рассматривать характеристики напряженно-деформированно-
напряженно-деформированного состояния в некотором отдалении от конца трещины.
Имеется в виду как-то отстроиться от пластической де-
деформации и избежать трудности фактического наблюде-
наблюдения только что формирующегося ответвления трещины.
В связи с этим на рис. 5.7, 5.8 рассматриваются зна-
значения фс на некотором расстоянии (?' = \la = x°Ja — l)
от конца трещины.
Накопленные экспериментальные данные свидетель-
свидетельствуют об отсутствии универсального критерия. Каждый
из существующих критериев сносно описывает лишь
поведение группы материалов, близких по своим физи-
физическим свойствам. Поэтому на практике часто исполь-
используют эмпирические формулы типа E.1). Кстати, форму-
формулы F.7) являются частным случаем E.1), полученным,
однако, из четких теоретических предпосылок.
Проведенное выше на ограниченном материале сопо-
сопоставление с экспериментами не свидетельствует убеди-
убедительно в пользу нелинейного подхода. Необходима даль-
дальнейшая работа в этом направлении, проводимая в на-
настоящее время. Тем не менее уже сейчас можно сказать
в пользу нелинейного ^подхода следующее: а. Видна
разумность и приемлемость уже полученных по нелиней-
нелинейной теории первых результатов, б. Как уже было сказа-
сказано выше, «нелинейное» соотношение F.8) проще «ли-
«линейного» E.4). в. Критерий F.7) естественным образом
связан с трещиноподвижной силой. Более того, из него
следует «равноправность» величин к\ и к°ц (встречаю-
(встречающееся в литературе утверждение об определяющей роли
kj свидетельствует, в силу полученного выше, лишь
о неприменимости к соответствующим материалам это-
этого критерия), г. Установлено, что критерий «большого
пальца руки» является не грубо приближенным, а точным.
д. Установлено, что отклонение трещины реализуется по-
поворотом материальной окрестности конца трещины.
Отметим в заключение, что с учетом предварительного
всестороннего напряжения а* сопоставление полученных
выше формул с результатами экспериментов следует про-
проводить по дополнительным напряжениям
<* = O а* О О о* ^1 0*

Глава 6
КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ
ПРОЧНОСТЬ
Вольно или невольно автор вынужден вторгнуться в
область микромеханики разрушения. Поэтому и возникла
необходимость в этой скромной по объему вспомогатель-
вспомогательно-информационной главе. В ней приводится минималь-
минимальный набор сведений, необходимых в дальнейшем для раз-
развития нелинейной механики трещин.
§ 1. Соображения симметрии. Кристаллографические
классы
Трудно найти область человеческих знаний, где в той
или иной степени не использовались бы соображения
симметрии. Не обходится без них и при рассмотрении
кристаллов.
Рассмотрим какую-нибудь трехмерную фигуру. Речь
о ее симметрии может идти лишь в случае, если фигура
может быть разбита на несколько одинаковых частей,
расположенных в некотором правильном порядке. При
этом правильность определяется преобразованиями сим-
симметрии, переводящими одинаковые части фигуры друг
в друга. Если же не делать различия между одинаковы-
одинаковыми частями, то можно сказать, что преобразования сим-
симметрии самосовмещают фигуру. Подробно о преобразо-
преобразованиях симметрии сказано в фундаментальной моногра-
монографии А. В. Шубникова [90] (см. также [81]). Ниже бу-
будет дано очень краткое наложение вопроса, насущно
необходимое для понимания содержания книги.
Несложные геометрические преобразования показы-
показывают [90], что основными преобразованиями симметрии
являются: отражение в плоскости, поворот вокруг оси и
зеркальный поворот.
Так, на рис. 6.1 показана фигура, составленная из
двух тетраэдров с основаниями, лежащими в плоскости
рисунка. Отражение в плоскости симметрии (проходящей
через общее ребро тетраэдров перпендикулярно плоско-

|76 ГЛ 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
сти рисунка) самосовмещает фигуру. Плоскость симмет-
симметрии обозначают символом т.
Ось поворота называют осью симметрии п-то порядка
(обозначая символом я), если при каждом повороте на
угол 2п/п фигура самосовмещается. На рис. 6.2 показана
фигура с осью симметрии 3-го порядка.
Рис. 6.1
Рис. 6.2
Ось называют зеркальной осью п-то порядка (обозна-
(обозначая символом п), если фигура самосовмещается при по-
повороте на угол 2л/п и последующем отражении в пло-
плоскости, перпендикулярной оси. На рис. 6.3 показана фи-
фигура с зеркальной осью 4-го порядка.
Рже. 6.3
Кроме перечисленных основных преобразований сим-
симметрии, употребляются и некоторые другие, например
инверсия — отражение в точке. Но они не являются са-
самостоятельными преобразованиями, а могут быть полу-
получены через рассмотренные выше. Так, из рис. 6.4 видно,
что инверсия эквивалентна зеркальному повороту 2-го
порядка.
Периодичность кристаллической решетки существенно
уменьшает число допустимых элементов симметрии. По-
Покажем, например, что не каждая ось симметрии допу-

§ 1. СООБРАЖЕНИЯ СИММЕТРИИ	177
стина. Пусть через узел А (рис. 6.5) проходит перпен-
перпендикулярно плоскости чертежа ось симметрии n-го по-
порядка. Через любой другой узел решетки В проходит
ось того же порядка. Совершая поворот вокруг узла А
на угол <рп = 2л/п, мы должны, очевидно, совместить ре-
решетку саму с собой. При этом узел В переходит в не-
некоторый узел В'. Аналогично при повороте вокруг В
на тот же угол, но в противоположном направлении,
узел А переходит в узел А'. Таким образом, отрезок
В'А' должен быть кратен периоду решетки а, т. е.
а + 2а sin (<pn — я/2)
	^U	L = 1 -
2COS фп =
где р — целое число. Отсюда следует, что cos <pn = ?/2,
где д —также целое число. Поскольку lcos<pj<l, из
этого неравенства следует; что имеются лишь пять зна-
значений <ря (отвечающих д = 0, ±1, ±2): 0, 180, 120, 90,
60°. Таким образом, в кристаллах возможны оси сим*
метрии лишь 1, 2, 3, 4 и 6-го порядков.
Показано [90], что существуют 32 существенно раз-
различных кристаллических класса, отнесенных к семи кри-
кристаллическим системам — сингониям. Все они сведены в
табл. 6.1. В третьем столбце ее помещены порождающие
элементы симметрии^ комбинации которых позволяют по-
получить все преобразования симметрии кристаллического
класса. В четвертом столбце помещены порождающие
элементы симметрии, которые с дополнительным преоб-
преобразованием инверсии позвляют получить все преобразо-
преобразования симметрии рассматриваемого кристаллического
•класса. В третьем и четвертом, столбцах точка сопровож-
сопровождает плоскость, параллельную оси, а двоеточие — перпен-
перпендикулярную. Косая черта сопровождает следующую за
ней ось симметрии, равнонаклоненную к координатным
осям.

178 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
Таблица 6.1
Порождающие элементы симметрии
Сингония
Триклинная
Моноклинная
Ромбическая
Тетрагональная
Тригональная
(ромбоэдрическая)
Гексагональная
Кубическая
Номер класса
по Гроту
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Порождающие элементы
симметрии
1
2
2
т
2 :т
2:2
2-т
т>2 : т
4
4-771
4:2
4:т
4-т
/7i«4 : m
3
6
3:2
3-т
3: т
т-Ъ : т
6
6:2
6 : т
6-т
т-6 : т
3/2
3/4
6/2
3/4
6/4
1
1
to to to
CM CM CM
CM CM CM
4
4
4:2
4:2
4
4:2
4:2
3
3
3:2
3:2
3:2
6
6:2
6
6:2
6
6:2
6:2
3/2
3/4
3/2
3/4
3/4'
f 2. Идеальные кристаллические решетки
Симметрия кристаллов и анизотропия их физических
свойств тесно связаны с наличием кристаллической ре-
решетки, в узлах которой расположены атомы, ионы либо
молекулы. Тройная периодичность (бесконечной, идеаль-

§ 2. ИДЕАЛЬНЫЕ КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ
179
ной) решетки дает возможность бесконечным числом
трансляций (поступательных смещений) совмещать ре-
решетку саму с собой. При этом всегда можно выбрать
такие не лежащие в одной плоскости векторы аь а2, а3
(рис. 6.6), что любая трансляция может быть представ-
представлена в виде
Si&x + s2a2 + s3a3,
где $\у S2, Sz — целые числа (положительные, отрицатель-
отрицательные или нули). Векторы аь а2, а3 называют основными
векторами (периодами), а построенный на них парал-
параллелепипед — элементарной ячейкой кристаллической ре-
решетки.
Рис. 6.6
Если одинаковые атомы располагаются только в углах
элементарной ячейки, кристаллическую решетку (и эле-
элементарную ячейку) называют простой. Поскольку у ячей-
ячейки восемь вершин и в каждой вершине сходятся восемь
ячеек, в простой решетке на элементарную ячейку при-
приходится по одному атому (иону, молекуле). Если же в
элементарную ячейку попадает \i (ц>1) атомов, одина-
одинаковых либо различных, решетку (и элементарную ячей-
ячейку) называют сложной, а совокупность атомов, прихо-
приходящихся на элементарную ячейку,— базисом кристаллы-
ческой решетки. Элементарная ячейка, повторяясь, за-
заполняет всю решетку. При этом каждый атом базиса
повторяется с периодами ai, as, аз.
Совокупность всех узлов, которые могут быть сов-
совмещены друг с другом посредством трансляций на целое
число основных периодов кристаллической решетки, на-
называют решеткой Праве кристалла. Таким образом, каж-
каждый атом базиса определяет свою решетку Браве, а вся
сложная кристаллическая решетка как бы состоит из
вдвинутых друг в друга простых решеток Браве.

180 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
Отметим, что выбор основных периодов, а стало быть
и элементарной ячейки, неоднозначен. Покажем это на
двумерной решетке (сетке), изображенной на рис. 6.7.
Нетрудно видеть, что сетку можно заполнить элементар-
ньши^ячейками а1? а2; ai, 82; aj, aj. Ячейки же a'i', а^;
at , a2 не являются таковыми, поскольку узлы, помечен-
помеченные крестиками, не могут быть достигнуты из точки О
трансляциями, кратными отвечающим этим ячейкам пе-
периодам.
Та же ситуация имеет место и для трехмерной ре-
решетки: элементарные решетки не могут содержать узлов
внутри себя и на гранях. Каждая элементарная ячейка
объединяет восемь расположенных в ее вершинах узлов.
Таблица 6.2
Кристаллографические системы (сннгонии)
1
2
3
4
5
6
7
Кристаллографическая
система
Триклинная
Моноклинная
Ромбическая
Тетрагональная
Тригональная (ромбо-
(ромбоэдрическая)
Гексагональная.
Кубическая
Осевые единицы
а ф b Ф с Ф а
а Ф b Ф с Ф а
аф b фс Ф а
а= Ьфс
а = b = с
а= Ьфс
а = b = с
а
а
а
а
а
Y
Осевые
= у =
= р =
= R =
= Р =
= 120°
= р =
углы
УФ
90S
? =
Y=^
90°,
Tf =
а
90°
90°
90°
90°
Поэтому при любом выборе элементарной ячейки макро-
макрообъем V разбивается на # равных частей, и объем эле-
элементарной ячейки равен Vq = VjN. В приложениях ис-
используют
ягаешот.
как элементарные, так и неэлементарные

§ 2. ИДЕАЛЬНЫЕ КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ	181
Решетка Браве полностью определяется заданием три-
триэдра основных векторов (периодов) аь аг, аз. С послед-
последними связана так называемая кристаллическая система
координат (рис. 6.8), оси которой направлены вдоль ос-
основных векторов. При этом в качестве масштабных (осе-
(осевых) единиц принимают величины a = Iail, Ь = Ia^19
c = |a3l. Углы а, р, -у называют осевыми. Браве показал,
что все названные его именем решетки могут быть раз-
разбиты на 14 типов, отнесенных к семи кристаллографи-
кристаллографическим системам — сингониям (табл. 6.2 и рис. 6.9).
Для триклинной сингонии A\г) узлы решетки Браве
располагаются в вершинах параллелепипеда с произволь-
произвольными сторонами и углами.
Моноклинной сингонии отвечают два типа решеток.
Для первого узлы располагаются в вершинах прямого
(в направлении Ь) параллелепипеда с произвольным ос-
основанием. Для второго (решетка с центрированным ос-
основанием (—Гго)) имеются дополнительные * узлы в
центрах противоположных граней параллелепипедов.
К ромбической сингонии относятся четыре типа ре-
решеток. В простой ромбической решетке (Го) узлы рас-
располагаются в вершинах прямоугольных параллелепипе-
параллелепипедов. В решетках с центрированными основаниями (Го)
имеются также узлы в центрах двух противоположных
граней. В объемно-центрированной решетке (Г^), поми-
помимо вершин, узлы находятся в центрах параллелепипедов.
В гранецентрированной решетке (Г^) узлы находятся
в вершинах параллелепипеда и центрах его граней.
Для тетрагональной сингонии имеет место либо про-
простая решетка (Г,) с узлами в вершинах призмы с квад-
квадратным основанием, либо объемно-центрированная с до-
дополнительным узлом в центре призмы (Г?).
В (ромбоэдрической) тригональной сингонии (Ггл) узлы
расположены в вершинах ромбоэдра (фигуры, получен-
полученной путем растяжения — сжатия куба вдоль его про-
пространственной диагонали).
В кристаллах гексагональной сингойии A\) узлы рас-
располагаются в вершинах правильных шестигранных призм
и центрах их оснований.
Кубической сингонии отвечают три типа решеток:
простая кубическая (Ге), объемно-центрированная (П)
и гранецентрированная (Г{).

182 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
Рис. 6.8
и
7
Триклинная
Моноклинные
/<
с
1
/
V-
—
/
У
/
У
у
/
•
У
/
Ромбоэдрическая
(Триаональная)
Тетрагональные
Гексагональная	Кубические
Рже. 6.9

§ 3. УЗЛОВЫЕ ПРЯМЫЕ И ПЛОСКОСТИ РЕШЕТКИ	183
В соответствии со сказанным выше объемно-центри-
объемно-центрированные, гранецентрированные и решетки с центриро-
центрированными основаниями заданы на рис. 6.9 своими слож-
сложными (неэлементарными) решетками.
§ 3. Узловые прямые и плоскости кристаллической
решетки
Рассмотрим сложную кристаллическую решетку с ба-
базисом из ц атомов. Введем косоугольную систему коор-
координат с осями OX, OY, OZ, параллельными основным
векторам кристаллической решетки ai, аг, аз. При этом
начало координат О совместим с первым узлом основ-
основной (нулевой) элементарной ячейки. Положение любого
узла решетки в принятой системе отсчета определяется
вектором
R.x = Ro*+R,.	C.1)
Здесь
C.2)
— радиус-вектор х-го (х = 1, ..., ц) узла основной (ну-
(нулевой) элементарной ячейки, а
R, = siai + S2&2 + $заз,	C.3)
где, напомним, s< — произвольные целые числа.
Векторному равенству C.1) — C.3) отвечают скаляр-
скалярные (а(= lat|)
C.4)
Введем относительные координаты
I - Фи Ц в У1<*>ь I -
измеряя тем самым координаты узлов в единицах, рав-
равных соответствующим основным периодам кристалличе-
кристаллической решетки. Тогда из C.4) следует
6* —6ои'+*ь Л.* — Лон + $2, UeU + ^ C.5)
В частном случае простой решетки, содержащей узлы
только в вершинах элементарных ячеек, индекс х сле-
следует опустить, и относительные координаты всех узлов
определяются формулами
5.в*Ь *Ьв*2, ke*3.	C.6)
При этом соответствующий узел обозначается тройкой
i, ?2> ?3*

184 IV'J. G. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
В сложных решетках, с учетом периодичности решет-
решетки, структуру нулевой ячейки задают величинами ?ок,
Лох, ?ох — т. н. индексами точки. Так, например, узел,
лежащий в центре определяемой векторами ai, аг грани
имеет своими индексами величины 1/2, 1/2, 0, а узел в
центре ячейки — 1/2, 1/2, 1/2. Описанный способ приме-
применим и в случаях, когда построенная на векторах ai, аг,
аз ячейка не является элементарной.
Рассмотрим линию, проходящую через начало коор-
координат и узел в вершине решетки с координатами S\au
$2^2, $зяз-. Координаты этой прямой удовлетворяют урав-
уравнениям
Vi V« Vs
или, после введения относительных координат,
jL = 2L==i..	C.7)
fl *2 *3
Узел S\, 5j, $з на рассматриваемой прямой будет бли-
ближайшим к началу координат, если целые числа s\, s?, s$
не имеют общего целого множителя. Пусть такой бли-
ближайший узел имеет относительные координаты и, v, w.
Эти целые числа называют индексами данной узловой
прямой и обозначают символом [а, и, w]. Так, для ко-
координатных осей: 0Х-*[1ОО], OF+ [010], 0Z->[OO1].
Прямые, являющиеся диагоналями граней, имеют индек-
индексы [110], [101], [011]. Прямая [111] является про-
пространственной диагональю ячейки и т. д. Если прямая
проходит через узел с отрицательными коэффициентами,
знак минус ставится над координатой узла. Так, [101] —
индекс прямой, проходящей через начало координат и
узел 1, 0, —1.
Каждой узловой прямой [иуш], проходящей через
начало координат, отвечает семейство прямых, проходя-
проходящих через идентичные узлы решетки. Указанное семей-
семейство обозначают тем же символом [и, у, w].
В кристаллических решетках преобразованиями сим-
симметрии связаны узловые прямые, имеющие разные на*
правления, но физически эквивалентные между собой.
Совокупность семейств таких узловых прямых образует
форму узловых прямых и обозначается символом <u, v,
w). Так, в кубических кристаллах форма <1, 0т 0> со-
содержит семейства узловых прямых [100]* [100], [010],

§ 3. УЗЛОВЫЕ ПРЯМЫЕ Й ПЛОСКОСТИ РЕШЕТКИ
185
[010], [001], [001]. Форму диагоналей граней кубиче-
кубической решетки обозначают символом <110>, а простран-
пространственных диагоналей — <111>. На рис. 6.10 показаны
важнейшие направления в кубической кристаллической
решетке.
[001]
[101]
Рис. 6.10
Рис. 6.11
Важной характеристикой узловых прямых является
расстояние между идентичными узлами этих прямых, на-
называемое периодом идентичности. Оно равно расстоянию
точки с координатами иа\, VQ2, wa% от начала координат,
т. е. (см. рис. 6.8)
= \и2а\ + lAig + w%a\ + 2uva1a2 cos у +
-f 2uwa1a3 cos 0 + 2vwa2a3 cos a]*/*. C.8)
В частности, для простой кубической кристаллической
решетки п\ «- а% =* аз =* а, а «= ^ =-* "к « 90* и
/ = аУ и2 + v2 + w2.	C.9)
Из формул C.8) —C.9) видно, что чем меньше индексы
и, v, и;, тем меньше /, т. е. тем плотнее заполнено соот-
соответствующее направление атомами (ионами, молекула-
молекулами). Ребра природных кристаллов обычно параллельны
направлениям с малыми индексами. Отметим, что для
сложных решеток с базисом периоды идентичности мо-
могут быть меньшими, чем определенные по C.8).
Рассмотрим узловые плоскости (плоскости, проходя-
проходящие через лежащие в вершинах ячеек узлы). Каждой
такой плоскости отвечает целое семейство параллельных
равцоотстоящих плоскостей. Из эквивалентности всех
рассматриваемых узлов решетки следует, что плоскости
рассматриваемого семейства делят ребра нулевой эле-

186 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
ментарной ячейки на целые числа равных частей
(рис. 6.11), скажем, А, к, I. На координатных осях бли-
ближайшая к началу координат плоскость отсекает отрезки
ai/A, <hJk, аз//. Уравнение этой плоскости имеет вид
или в относительных координатах
hl+kr\ + lt-l.	C.10)
Можно показать, что числа А, ?, I являются взаимно
простыми, т. е. не содержат общего целого множителя.
Действительно, если бы для них был общий целочислен-
целочисленный множитель t, то было бы: А = h't, к = k't, I = I't,
где А', к', V — взаимно простые целые числа. Уравне-
Уравнение C.10) при этом принимает вид
Этому уравнению не удовлетворяют координаты % = s\,
Ц = $2, С3*^ ни одного лежащего в вершине ячейки
узла, так как в левой части равенства располагается
целое число, а в правой — правильная дробь. Получен-
Полученное противоречие и доказывает взаимную простоту ко-
коэффициентов в C.10).
Уравнения следующих, более удаленных от начала
координат плоскостей, отсекающих на координатных осях
отрезки
"т- пт> "т<	C-")i
записываются в виде
hl + kr\ + lt-nf	C.11J
где л — целое (положительное либо отрицательное) чис-
число (значение /1 = 0 отвечает плоскости семейства, про-
проходящей через начало координат).
Итак, тройка взаимно простых целых чисел А, /с, I
(геометрический смысл которых был выяснен) опреде-
определяет семейство узловых плоскостей. Эти числа называют
индексами Миллера (индексами системы плоскостей) и
обозначают символом (hkl). Если известны отрезки, от-
отсекаемые узловой плоскостью на осях OX, OY, OZ, то
согласно C.11) для определения индексов Миллера не-
необходимо найти три взаимно простых числа, пропорцио-

§ 3. УЗЛОВЫЕ ПРЯМЫЕ И ПЛОСКОСТИ РЕШЕТКИ
187
нальных обратным значениям относительных длин этих
отрезков. Отрицательные индексы отвечают пересечению
плоскости с отрицательной координатной полуосью и обо-
обозначаются, например, 7г.
kZ
U
@000
A11)
'011)
A01) A11)
Рис. 6.12
Рис. 6.13
На рис. 6.12 показаны индексы Миллера основных
плоскостей в кубическом кристалле. Из рисунка видно,
что в кристалле имеются физически равноценные пло-
плоскости разной ориентации. Например, таковыми явля-
являются плоскости, параллельные граням кубической ячей-
ячейки A00), @10), @01). Совокупность этих плоскостей
обозначают символом И 00). В общем случае совокуп-
совокупность плоскостей, получаемых из плоскости (h к I) пре-
преобразованиями симметрии кристалла, обозначают симво-
символом {h к 1} и называют формой плоскостей. Так (см.
рис. 6.12), форма {110} содержит так называемые пло-
плоскости ромбического додекаэдра, получаемые срезанием
ребер куба этими плоскостями на одинаковом расстоянии
от центра. Форма {111} состоит из т. н. плоскостей ок-
октаэдра, полученных срезанием вершин куба этими пло-
плоскостями на одинакоЁом расстоянии от центра.
В гексагональных кристаллических решетках наряду
с достаточными для описания кристаллической решетки
тремя осями (OX, OY, OZ) вводят в четвертую ось (ОС/).
Эта ось (рис. 6.13) лежит в плоскости XY, равнонакло-
ненно к первым двум осям. При этом используются осе-
осевые единицы аи <*2, <*з, с. С их помощью можно опреде-
определить относительные длины отрезков, отсекаемых рассмат-
рассматриваемой узловой плоскостью на осях, и, взяв их обрат-

188 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
ные значения, привести последние к отношению взаимно
простых целых чисел. Полученная таким образом четвер-
четверка чисел А, к, i, l называется индексами Миллера —
Браве и обозначается символом (A k i I). При этом
можно показать, что всегда i = — (А + к).
Введение добавочного, четвертого, индекса оправды-
оправдывается тем преимуществом, что эквивалентным плоско-
плоскостям при этом отвечают одноименные символы. Так, бо-
боковые грани изображенной на рис» 6.13 гексагональной
призмы имеют индексы Миллера — Браве A 1 0 0),
A0 10), @110), тогда как соответствующие ин-
индексы Миллера A10), A0 0), @ 1 0) для гекса-
гексагональных решеток не являются однотипными. Иногда
в гексагональных кристаллах используют четыре оси и
для определения узловых прямых.
§ 4. Идеальная прочность твердых тел
(экспериментальный подход)
Прочность каждого материала в данных условиях эк-
эксплуатации или испытаний имеет верхнюю грань, назы-
называемую идеальной прочностью.
Первым подходом к определению идеальной прочности
является постановка специальных (прецизионных) эк-
экспериментов, в которых удается получить очень высокие
значения прочности, значительно превышающие обычно
наблюдаемые.
При проведении экспериментов к образцам предъяв-
предъявляются довольно жесткие требования. Так, они не долж-
должны содержать границ зерен, быть свободными от боль-
больших внутренних дефектов (пустот, трещин и включе-
включений), ступенек и трещин на свободных поверхностях.
Дисклинации и дислокации должны либо отсутствовать,
либо быть заторможенными. Кроме того, достаточно со-
совершенный образец не должен разрушаться вследствие
контакта с испытательной машиной. Из-за значительных
трудностей в изготовлении и испытании образцов обна-
обнаруживаются большие расхождения в определяемых экс-
экспериментальным путем величинах прочности.
Так, для нитевидных кристаллов имеем A ГПа«
«104 кгс/см2) табл. 6.3. В табл. 6.4 приведены данные
по прочности стержней и волокон
Приведенные таблицы представляют выборки из при-
приведенных в [32]. Там же дан развернутый обзор работ

k. ИДЕАЛЬНАЯ ПРОЧНОСТЬ (ЭКСПЕРИМЕНТАЛЬНЫЙ ПОДХОД) 189
по экспериментальному определению идеальной прочно-
прочности. Характерно следующее высказывание (с. [32], 47):
«...Таким образом, ясно, что идеальная прочность по-
подобно прочности, измеренной в любом эксперименте, яв-
является функцией не только частного вида испытываемого
Таблица 6.3
Прочность нитевидных кристаллов
Материал
Макси-
Максимальное
растягива-
растягивающее
напряже-
напряжение (ГПа)
Деформа-
Деформация
Примечания (ГПа)
NaCl
NaCl
А1аО8
Си
1и
Си
Си
Си
Fe
С(гра-
С(графит)
1,6
1,08
22,3
2,94
«1,50
1,74
1,59
1,71
13,40
20,7
0,039
0,026
—
0,015
0,028
0,030
0,016
0,012
0,049
0,02
Растяжение в направлении A00)
воде; т {110} (НО) = 0,8 = 0,044 G
Растяжение в направлении A00);
т. {110} A10)- 0,54 = 0,030 G
Растяжение в направлении A120)
В направлениях @001) и A010) со
ответственно 10,9 и 15,3
Растяжение в направлении A11)
х-{111} (НО) = 0,80 =0,022 G
Растяжение в направлении A00)
T.{lll}<lT0> = 0,61 = 0,017 G
Растяжение в направлении A00);
т {411} A10) = 0,71 = 0,020 G
Растяжение в направлении A10);
т {111} (НО) = 0,65 = 0,018 G
Растяжение в направлении A11);
т {111} (НО) = 0,46 = 0,013 G
Растяжение в направлении A11);
т {110} A11) = 3,58 = 0,060 G
Растяжение
т {hkl} (uvw)— наибольшая касательная компонента напряжений
плоскости {hkl} и направлении (uvw), G, —соответствующий мо-
модуль сдвига.
материала, но и процедуры, испытания. Следовательно,
идеальная прочность зависит от геометрии образца, ти-
типа деформации, температуры, скорости деформации, типа
нагружения (например, статическое нагружение, сжатие
и т. п.), создаваемого испытательной машиной, и т. д......

190 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
Почти всегда остается неясным, является ли наиден-
наиденное значение максимальной прочности действительно
максимально возможным и не будет ли обнаружена при
последующих испытаниях еще более высокая прочность?
Таблица 6.4
Материал
Е (стекло)
SiO2 (крем-
(кремнезем)
« «
Fe — С (чу-
(чугун)
А1
Полиэтилен
Прочность стержней и волокон
Максималь-
Максимальное растяги-
растягивающее
напряжение
(ГПа)
3,59
13,1
13,8
5,68
10,45
2,27
3,04
Деформа-
Деформация
«0,18
«0,19
«0,08
«0,06
0,060
Примечания
Прочность не зависит от диа-
диаметра волокна при диаметрах
5—20 мкм
Изгиб стержней при 78 К диа-
диаметром 0,5—3,0 мм
Растяжение при 78 К волокон
диаметром 30 мкм
Изгиб огнеполир'ованных
стержней диаметром 1 мм
Вытянутые тонкие проволоки
Изгиб волокна с поперечным
сечением 0,7X13 мкм, получен-
полученного травлением из большого
кристалла
Растяжение. Крученые (тяну-
(тянутые из раствора нити)
Поэтому всегда желательны теоретические подходы к
определению идеальной прочности. Они и будут рассмот-
рассмотрены в следующем параграфе.
§ 5. Идеальная прочность (теоретические подходы)
По-видимому, первыми попытками теоретического оп-
определения идеальной прочности были работы Полани и
Орована [111, 112]. При этом руководящей идеей здесь
было получение связи идеальной прочности с другими
макроскопическими физическими (механическими) вели-
величинами. Рассматривая одноосное равномерное растяжение
атомной решетки (рис. 6.14), авторы [111, 112] приняли
зависимость напряжения от относительного удлинения
в виде полусинусоиды (рис. 6.15)
а° = ас sin
E.1)

5. ИДЕАЛЬНАЯ ПРОЧНОСТЬ (ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ)
Отсюда находится начальный модуль упругости (модуль
Юнга)
Е —¦*•
do0
Работа напряжения на деформации раскрытая трещины
X—1—L--J
а-аа
Рис. 6.14
Рис. 6.15
отождествляется с плотностью энергии образования сво-
свободных поверхностей у. С учетом того, что поверхностей
две, находим из E.1)
«(Хе
= J
•(Хе-1)
J
)
J 8in^^jd(X-l) = i.
Таким образом,
E.3)
Исключение из формул E.2) и E.3) величины (Яс — 1)
приводит к соотношению
^7^	E.4)
позволяющему расчетным путем определить идеальную
прочность по известным величинам: модулю Юнга Е, по-
поверхностной энергии Y и расстоянию между атомными
плоскостями (нормальными к направлению растяжения)
в недеформированной конфигурации о<ь В табл. 6.5 при-
приведены результаты расчетов по полученной формуле,
проведенных Келли [32]. Приведенные дАнные отвечают

192 ГЛ. 6. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
комнатной температуре B93 К), кроме заключенных в
скобки, отвечающих О К. Из приведенной таблицы усмат-
усматривается, в частности, что формула E.4) предполагает
слабую зависимость ос от температуры.
Т а б л и ц а 6.5
Расчеты идеальной прочности при одноосном растяжении
методом Орована — Полани
Материал
Си
Си
W
a-Fe
or-Fe
Si
С (алмаз)
SiO2 (крем-
NaCl
А12О3
Направ-
Направление ра-
растяжения
A11)
A00)
<100)
<100>
A11)
A11)
A11)
A00)
@001)
Е, ГПа
192
67G5)
390D05)
132A43)
260
188
1210
73
44
460
у, мДж/м*
1650
1650C630)
3000F415)
2000D520)
2000
1200
5400
560
115
1000
О(у, ГПа
39
25C8,7)
61(90,8)
30D7,9)
46
32
205
16
4,3
46
ос/Е
0,20
0,37@,51)
0,16@,22)
0,23@,34)
0,18
0,17
0,17
0,22
0,10
0,10
Аналогичный изложенному подход предложил Френ-
Френкель [32] для расчета идеальной сдвиговой прочности хс
в условиях простого сдвига. Изложим его на примере
решетки, сечение двух соседних плоскостей которой пло-
плоскостью рисунка показано на рис. 6.16. Пусть под влия-
влиянием сдвигового напряжения т° верхняя атомная плос-
плоскость сместилась, как целое, на расстояние х (рис. 6.16).
J
JL

j
/
1
F
—^
X
Рис. 6.16
Напряжение т° является периодической функцией х с
периодом bo. В исходном положении устойчивого равно-
равновесия (при х = 0) т°=0. С ростом т° растет и х. При
этом при х = Ьо/2 система (из двух атомных плоскостей)
достигает положения неустойчивого равновесия, при ко-
котором т° = 0. При еще больших значениях х система са-
сама стремится к новому положению устойчивого равно-

? 5. ИДЕАЛЬНАЯ ПРОЧНОСТЬ (ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ) 193
весия, причем г° становится отрицательным. Наконец,
при х=Ьо система переходит в конфигурацию, эквива-
эквивалентную исходной.
Простейшей зависимостью, описывающей сказанное
выше, является выражение
т° = TcsmBnz/bo).	E.5)
При малом х т° « тсBяд:/Ьо). Из рис. 6.16 видно, что
сдвиг равен х/ао. Отсюда следует выражение для модуля
Таблица 6.6
Расчеты идеальной сдвиговой прочности чс методом Френкеля
Материал
Си A0 К)
Си
А1
А1
Fe
W
A\fi9
С (графит)
Плоскость и направ-
направление сдвига
{111} <Н2)
{111} A12)
{111} A12)
{111} A10)
{110} A11)
{110} A11)
{0001} A120)
{0001} A010)
G, ГПа
33,2
30,8
23,0
23,0
60,0
150,0
147,0
23,0
tc/G
0,028-0,039
0,028-0,039
0,028-0,039
0,114
0,11-0,13
0,11-0,13
0,Н5
0,05
0,93-1,29
0,86-1,20
0,65—0,90
2,62
6,6-7,8
16,5-19,5
16,9
0,0115
сдвига G = T°/(x/ao)sssic{2jiuo/bo) и для идеальной сдви-
сдвиговой прочности имеем
тс = y ^.	E.6)
В табл. 6.6 показаны некоторые результаты, полученные
Келли для идеальной сдвиговой прочности тс методом
Френкеля. Кроме первой строки, остальные результаты
относятся к комнатной температуре.
Существует много путей уточнения полученных с по-
помощью описанного метода результатов. Так, можно рас-
рассмотреть более реальный закон межатомного взаимодей-
взаимодействия (рис. 6.17), приняв, например, закон Леннарда —
Джонса
ов=Л(Х-7~Х-13).	E.7)
Отсюда, прежде всего, находится модуль Юнга
ТУ 	 «U I		 Л л	#(Р Qv
EL = -гг" I ==^ ОЛ.	IЭ.О}
* К Ф, Ч»рянх

|94 ГЛ. в. КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ. ИДЕАЛЬНАЯ ПРОЧНОСТЬ
Далее обычным путем находим
ос -<w = ов(Хс)- А -0,224 (Хс~A3/7I/в«1,11). E.9)
Наконец, подсчитываем плотность энергии образования
Рис. 6.17
новой поверхности при раскрытии трещины
что образуются две поверхности)
(напомним,
9О
J (Я -
E.10)
Йз соотношений E.8) — E.10) теперь получаем (ср. с
E.4)) Ос = 0,448У7?/ао.
Отметим, что отсутствие детального знания межатом-
межатомных сил и чрезмерная сложность (квантовомеханиче-
ских) расчетов препятствуют существенному уточнению
приведенных сильно упрощенных расчетов.
Что касается сопоставления экспериментальных и рас-
расчетных значений идеальной прочности для различных ма-
материалов, то здесь наблюдаются как значительные рас-
расхождения (по различным причинам, обсуждаемым в
[32]), так и вполне приличные совпадения.
С современным состоянием проблемы идеальной проч-
прочности твердых тел читатель может ознакомиться по об-
обстоятельной публикации Н. Макмиллана [32]. Там же
приведена обширная библиография по данному вопросу.
Отметим в заключение, что идеальная и реальная
(обычная) прочности твердых тел могут различаться на
несколько порядков. Объясняется это наличием дефектов
(в том числе дислокаций и диск ли наций) структуры ре-
реальных тел.

Глава 7
ДИСЛОКАЦИИ ВОЛЬТЕРРА
В главе рассматриваются дислокации Вольтерра в изо-
изотропно-упругой сплошной среде. По причинам, изложен-
изложенным в § 5, основное внимание уделяется, в рамках не-
нелинейной теории упругости, клиновой дисклинации.
§ 1. Дислокации Вольтерра в линейной теория
упругости
Применительно к линейно-упругому изотропному телу
понятие дислокаций было введено еще в работах италь-
итальянской школы теории упругости [122]*). Наиболее на-
наглядно дислокации Вольтерра можно ввести следующим
Рис. 7.2
образом. Рассмотрим цилиндр (рис. 7.1), разрезанный по
полуплоскости ОО'АА\ берегам которого отвечают зна-
значения <𠦦 ф~ = 0 и ф = ф+ = 2я. Пусть плоскость ф~
остается неподвижной, а ф+ получает малое смещение,
*) Термин был предложен Лявом [30]. Сам Вольтерра исполь-
использовал другой термин — дисторсад.
7*

196	гл. 7. дислокации вольтеррА
как жесткое тело*),
XR.	A.1)
При этом полагаем, что образовавшиеся щели заполнены
тем же материалом, а при взаимном внедрении берегов
лишний материал изымается.
Рассмотрим вектор смещений
иа = иж<р/Bл).	A.2)
Отсюда и следующих из рис. 7.2 выражений
R — гег + х3ез,
ei «= cos<p er — sin ф e^, e^ = sin <p er + cos ф ещ
Ь « b\e\ + 6262 + Йзвз, © = coiei + соавз +
находим .
где
и^ = Ь3 cos ф + Ь2 sin ф + (— ых sin ф + со2 cos ф) х3,
и™ = — 6Х sin ф -f fc2 cos ф — ((Oi cos Ф + co2 sin ф) ars + co3rf
a^ = b3 + (^i s^n ф — co2 cos ф) г.
A.4)
Подстановка выражений A.3)—A.4) в формулы для
компонент деформации
_ 1 (dU9 , 1 5"г «ф\
et*~~ Т\~дГ~т~Т дф г/'
ди9	j /дит \ диа
дает
¦) В теоржн упругости рассматриваются и дисдокаднн Со-
медьяяа, щш которых упомянутые влоскостж деформируются.

g 1. ДИСЛОКАЦИЙ В ЛИНЕЙНОЙ ТЕОРИЙ УПРУГОСТИ 197
Отсюда и из закона Гука
находим
_ 2v) 2пг1 афф A + v) A — 2v) 2яг'
Согласно соотношениям A.6) и A.8) на оси цилиндра
имеют место особенности (сингулярности) напряженно-
деформированного состояния порядка (г/г*)*1. Такие ли-
линии обычно называют дислокационными.
Контуры, охватывающие дислокационную линию, на-
называют контурами Бюреерса. В рассматриваемом случае
в качестве такового удобно выбрать окружность с центром
на оси цилиндра. При ее обходе (от <р = 0 до <р = 2я)
вектор A.2) получает приращение иж A.1), представ-
представляющее собой, как уже было сказано, взаимное жесткое
смещение берегов разреза. Кроме того, как это видно из
A.4), A.6) и A.8), отвечающие смещению A.1) дефор-
деформации и напряжения однозначны. Таким образом, дисло-
дислокационному вектору A.2) отвечают неоднозначные сме-
смещения и однозначные деформации, напряжения. Попут-
Попутно выяснилось, что в формулах A.6) и A.8) никак не
фиксировано положение разреза. Последний может быть
произвольным поперечным разрезом цилиндра рассмот-
рассмотренного вида.
Величину Ь называют вектором Бюргерса, а ю — век-
вектором Франка. В наше время поворотные дислокации
Вольтерра (отвечающие вектору Франка) называют
диск ли нациями, сохраняя термин дислокации за линей-
линейными дислокациями (определяемыми вектором Бюр-
герса).
На рис. 7.3 показаны 6 типов дислокаций Вольтерра.
Первые две относятся к т. н. краевым дислокациям,

198
ГЛ. 7. ДИСЛОКАЦИИ ВОЛЬТЕРРА
третья — к винтовой дислокации, четвертая — к клиновой
дисклинации, пятая и шестая — к дисклинациям кру-
кручения.
Полученным для напряжений выражениям A.8) от-
отвечают, вообще говоря, ненулевые массовые силы и по-
поверхностная нагрузка. Действительно, подстановка выра-
выражений в левые части уравнений равновесия
darr . 1 допр . даг* . °rr'
дг ' Г дф "^" ^х8 "•
*ФФ .
и
A.9)
да
гз
да.
4- 12 —
' г
дает
Е
1 + v
?
1
г8 J'
1 д (и?\ 1 —v I d"i
2г27ф" 1 — 2v р ах3 J"
2г
A.10)

6 1. ДИСЛОКАЦИИ В ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ	199
Далее, согласно выражениям A.8) имеем: на боковой
поверхности (при г = гф)
а0 — п° ! —
A + v) A - Zv)
If г»
A.11),
на верхнем (хз = /) и нижнем (#з = 0) торцах цилиндра
2яг •
= — (Тфз |*,-0 = — ;
2яг '
I — 2v) 2nr »
•v	цф [^-0
A— 2v) 2яг #
Рассмотрим подробнее относящиеся к рассматривае-
рассматриваемой в книге обобщенной плоской деформации случаи от-
отличных от нуля &i, Ь2, о)з. Имеем согласно A.4), A.8),
A.10) а A.11)
и? = Ьх cos ф + Ь% sin ф,
и™ = — bj sin ф + Ь2 cos ф + (ozr, u\ = 0; A-12)
в в I Ev Г — b^in ф + Ь2 совф
<*гг= ааз eST(l + v)(l-2v)l	?	+
*(l-v) Г-
2^-rf
+ v
1 + v
— fcj sin ф + 6g cos ф
2(l-2v)	P*
j	6j COS I
2 A — 2v)
A.14)
0;

200	ГЛ. 7. ДИСЛОКАЦИИ ВОЛЬТЕРРА
на боковой поверхности
д	Е\	Г — 6j sin ф + b2 cos ф
A,15),
fct cos ф + b ain ф ] .
	f;	J ?
на верхнем основании
на нижнем основании
- 6 sin <р + 6 cos ф	]
	s	r-J	+ o>3J- A.15),
Для того чтобы получить требуемые нулевые массо-
массовые силы и граничные условия, добавим к дислокацион-
дислокационным смещениям A.3) следующие, уже однозначные:
иг = и(г0) (г) + и(гг) (г) cos ф + и(т2) sin ф,
им согласно A.5) и A.7) отвечают ('«
Отт =
- v) i4-lr+ v r r У j cos ф +
(-,B) u(
Г	иA) 4- иа) 1
+ Ыг1У + A - V) Г ^ Ф j COS ф +

§ 1. ДИСЛОКАЦИИ В ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ 201
= v
= 0.
Подстановка полученных выражений в уравнения
равновесия A.9) при /г = — ft, /»=—/», /» = — /s да-
дает три системы уравнений:
@)"
„@)' „@)
Ur _ "г
.(•)' „о
Шз 1-2V 1
2л Г^Т г '
AЛ8I
4.
4 Zdl
г ' 2(t-v)
2я 2A-v) r2'	A
,1Г и«У 3 + 4v«<«lJ 1 «<»' .-.8+4vg
"ф "Г-Г^ l-2v г2 J ' I l-2v"T"r l-2v r2
1	1
A)" , ujr__ I —
3 + 4у^1 Г 1 и«У 3 + 4у"У1 _
-v) Г2 ] [2A —v) г +2A —v) г2 J ~"
2n2(l-v)r«' A.18),
l-2v
1 u<«'
1
STl — 2v ^*
Начнем с рассмотрения первой, общее решение кото-
которой имеет вид
AЛ9>

202	#л. 7, Дислокации
Отсюда и из A.17) находим
"rr -(l+V)(l-2«
Используя теперь выражения A.15) i и удовлетворяя
граничному условию агг |г«г# = — gr, находим
Таким образом, из соотношений A.19), A.3), A.12),
A.13), A.5) и A.17) следует
-т]' ^-ё^ "-0; A.20)
»з Г 1 —2v , г	v
2A—v)J*
^з, = 0; A.21)
Для плотности энергии деформации
Ф = % • « ? (^гг + еффJ + ^?г + ^фф | A.23)
имеем
A.24)
Полученным значениям напряжений отвечает на торцах

S l, НЕЛИНЕЙНАЯ КЛИНОЁАЙ ДИСКЛИЙАЦЙЯ 203
цилиндра осевая сила
Таким образом, реализующееся на торцах цилиндра на-
напряжение Озз статически эквивалентно нулю — осевая си-
сила отсутствует.
Аналогично рассматриваются системы уравнений
A-18J,з. Им отвечают
= fe {- * sin f + [ln 77 ~ T Ш1cos ф
h. {ф cos ф + [in ^ - -f (j^-)] Siu ф},
0.
§ 2. Нелинейная клиновая дисклинация
В рамках нелинейной теории упругости (обобщенной
плоской деформации) рассмотрим клиновую дисклина-
цию. Для этого положим
(х>0).	B.1)
Здесь /(•) —искомая деформационная функция. Для вы-
выяснения геометрического смысла постоянной х использу-
используем полярные представления
==rV*°.	B.2)

204
гл. 7. Дислокации вольтеАра
С их помощью получаем из B.1)
г-/<f« Я) (г*)-,
При х>1 соотношения B.3)
B.3)
соотношения B.3) описывают деформацию,
возникающую после удаления из кругового цилиндра сек-
сектора 2я/х < <р° < 2я и последующего стягивания берегов.
Такую клиновую дисклинация называют положительной.
При х < 1 в разрез qp = 0 как бы вставляют клин с углом
раствора х===2яA — х). Такую клиновую дисклинацию
называют отрицательной.
Вернемся к выражению B.1). Принимая (см.
B.1Л8))
дг
К
и вводя обозначения
B.4)
B5)
получаем из формул B.1) и B.3.2), B.3.3)
; B.7)
Подстановка последних выражений в однородное урав-
уравнение равновесия B.3.2) приводит к разрешающему
уравнению
определяющему при заданном упругом потенциале Ф ис-
искомую деформационную функцию /(Q, Я).
Коль скоро последняя найдена, из соотношений
B.6) —B.8), B.3.8) —B.3.12) последовательно находим:
угол поворота материальной частицы
B.10)
B.11)
кратность изменения площади

ft 3. СЛУЧАЯ МАЛОСЖИМАЕМОГО МАТЕРИАЛА	205
комплексные компоненты тензора условных напряжений
2*1 = Фг, S^O.U/t). <4 = Фх	B.12)
и тензора истинных напряжений
- l(/eQ)Oi +(/eQ - х
B.13)
Перейдем к полярной системе координат. Для этого
будем считать, что последней в соотношениях A.12.8)
отвечают штрихованные величины. Заменяя там о на <р°
и используя выражения A.11.3), B.12) и B.2), по-
получаем
о	о	_о	_
Ororo + a^o^o = 1ч = Фх,
агого — ОфОфО + йагофо
(ф + фЬ
B.14)
о
= 0.
Полученные выражения позволяют удовлетворить ус-
условию свободы боковой поверхности от нагрузки
^=0	B.15)
и равенству нулю осевой силы на торцах цилиндра
О»	г*
j	J l
0
al/4r° = 0.	B.16)
§ 3. Случай малосжимаемого материала
Как уже говорилось выше, сплошные (не пористые)
материалы малосжимаемы. Поэтому имеет смысл исполь-
использовать полученные в § 14 гл. 2 зависимости. Так, со-
согласно B.145), B.14.3)

206	ГЛ. 7. ДИСЛОКАЦИИ ВОЛЬТЕРРА
Подстановка полученных выражений в разрешающее
уравнение B.9) приводит к уравнению
с общим решением
-l)/2,	C.2)
определяющим при заданном законе упругости (функции
^(^а)) деформационную функцию, по которой уже на-
находится напряженно-деформированное состояние.
Подстановка выражений C.2) и B.7) в C.1) дает
1А
Ф2 - 2Я (/Л - x/)fl-(1)/2,	.	C.3)
*+1) + А (к) Q("-l)/a.
С помощью этих выражений, а также соотношений
B.14) — B.16) получаем условия свободы боковой по-
поверхности цилиндра от нагрузки и равенства нулю осе-
осевой силы на торцах:
-	Як/* + А (К) 02 - 0 (/¦ =
-	к f / B/ofl - х
или
ч—х
о*
f / B/nQ - x/) Q-(K+1)dQ - -2*? Qr(H"lVt = 0.
C.4)
Из последнего уравнения определяется постоянная X.
Рассмотрим, например, семейство упругих потенциа-
потенциалов B.14.10), для которого согласно B.7) и C.4)
(У—) Дп[2/0?Г(*-1)/2+ Я]" + D -
C.5)
1-у п_.	3 1-У

§ 3. СЛУЧАЙ МАЛОСЖИМАЕМОГО МАТЕРИАЛА	207
Отсюда находим
X Q(*~1)/adQ - К = 0. C.6)
Входящая в подынтегральное выражение постоянная
/* определяется из уравнения
X Q(x")/sldQ - ^ = 0, C.7)
следующего из C.6) при Q == Q*.
Найдем асимптотику разыскиваемого решения в окре-
окрестности оси цилиндра. Для этого опустим в C.6) и C.7)
подчеркнутые постоянные. В результате содеянного из
соотношений C.7), C.6), C.4), B.7) и B.11) после вве-
введения обозначения
Ж n(x-
последовательно находим
1 ill
. C-9)
/о (П, к) ~ Т -|- B,
Х-1

2о8	рл. 7. дислокаций вольте?рА
Отсюда и из соотношений C.3), B.14), B.13) и
B.14.4) находим
1 + у °
—g- Ororo ~
X—1	X—1
^^ """"" Ах	/	л\ \ с% /	л
X—1
1+v о	1/г (х —!) + (" —1)
ii	Л IX	 1/ ~+~ U \71 	 1
X—1
О
Е "»	*" ln(x_i) + 2(n-l)f
(«Г+
х— i
щ) г ; C.12)
l+Vy	9 ,
(п-гкх-1)
+ 2(п-1)]г 1а\ «"-«
	^ (и -^ 2) [п (х - 1) -f 2 (п — 1» х - 1 / Q \ 1<я"> /^.\х^
Я (л~1)[(х — 1} + (л — 1)] х W*/	\С/
1+v ^ _ 4 ! ^У" f и (х - 1) + 2 (» - I)}2 /^Q \ «*-!>
^ °» ^ * "Г х ^ _ |j цх _ и + (Л _ 1)] ^Q^)
C.13)
i)""). C.14)

i l слУЧлй малосжимаемого Материала	20§
Подсчитывая теперь энергию деформации цилиндра
(в расчете на единицу его длины)
П = J d(f° j ФгЧг* *-- я J 0Ш,	C.15)
а а	о
7!
При переходе от выражения C.14) к (ЗЛ6) было опу-
опущено значение первообразной на нижнем пределе. Тем
самым, как нетрудно видеть, были использованы нера-
неравенства
Более «жестким» из них является первое. Прежде чем
анализировать его, напомним, что (см. начало § 2) при
положительной клиновой дисклинации х > 1 и согласно
соотношениям C.10) —C.14) все характеризующие на-
напряженно-деформированное состояние величины конечны
на оси (напомним еще раз, что по предположению л > 2).
При отрицательной же дисклинации х < 1 и в разрез
как бы вставляется клин с углом раствора % « 2л A — х).
При этом более «жесткое» первое из неравенств C.17)
накладывает на угол раствора ограничение
Х<(п-1Jл,	C.18)
выполняющееся при п>2. Отметим, что полученное не-
неравенство обеспечивает и законность использования соот-
соотношений C.6), C.7) в окрестности оси цилиндра.
В § 7 гл. 2 было показано, что при деформации раз-
разрез переходит в эллипс. При этом в конце трещины ну-
нулевой угол между берегами разреза становится равным
л. Согласно сказанному в начале § 2 этому как бы от-
отвечает внедрение клина с углом раствора л, т. е.
2лA-х)«л или х = 1/2.	C.19)
Отсюда ¦ из выражений C.12)—C.14) следует, что на

210	ГЛ. 7. ДИСЛОКАЦИИ ВОЛЬТЕР?А
оси цилиндра имеют место следующие сингулярности
(	2)
crr°oro
фф
C.20)
Отметим, что показатели сингулярности близки к полу-
полученным в § 11 гл. 2, хотя и не совпадают с ними при
п Ф2.
В этом параграфе был предложен путь решения зада-
задачи, состоящий в определении из уравнения C.2) при за-
заданном упругом потенциале (функции XF(-)) деформа-
деформационной функции /(Я, Я). Это, так сказать, прямой ход.
Можно предложить и обратный ход, состоящий в задании
деформационной функции (с теми или иными произволь-
произвольными элементами) с последующим определением отве-
отвечающего ей упругого потенциала.
Подучим исходные зависимости для обратного хода.
Так, согласно соотношению B.7) i
]	0.21)
?
. 24" [/flaQ + tfi/a] О
Отсюда и из C.2) получаем упомянутое исходное соот-
соотношение
Q
2А (X) J [/M (Q, X) + 1^-к/0 (Й, Я)] dft + В (К). C.22)
о
| 4. Случай стандартного материала
Известно [81], что стандартный материал (он же гар-
гармонический, полулинейный, материал Джона) имеет су-
существенные недостатки физического характера. Однако
его простота позволяет прояснить структуру полученных

§ 4. СЛУЧАЙ СТАНДАРТНОГО МАТЕРИАЛА	211
в § 2 зависимостей. Согласно B.14.4), B.5) и B.7)
Л (i + v)(l-2v)
дг
2Е
-<K-iV»
OP
« 1 -f v
(l + v) (l -;
Подстановка полученных выражений в разрешающее
уравнение B.9) приводит к уравнению
-tt)/ofl = X4H ^v
D.2)
с общим решением
^ 	X	q(x+1)/2
A v) (х ¦! 1)
Отсюда и из B.3) следует
D.3)
Поскольку х > 0, из конечности смещения на оси ци-
цилиндра (при г° = 0) следует В = 0. При этом
2Е
(l-2v)x
D.4)
D.5)
¦ согласно B.14)
1—V
1
чИ-l

212	ГЛ. 7. ДИСЛОКАЦИИ ВОЛЬТЕРРА
Подстановка полученного выражения в граничное усло-
условие B.15) дает
СГ	D6)
С учетом этого получаем из соотношений D.3) —
D.5), B.11) —BЛЗ)
Д = г
A-V)* (Х+1)
\ D.7)
Огого =
x-i
-v)* (х
, f(l - 2v)x ff
0 f "*/С\x.
Ф =
?v(l-v)x+l Г /r°\*-i
1 + v X	jj
r°\*-i 1 + x]
rj Г x J
l(r.)	2)
Подсчитывая по этому выражению энергию деформа-
деформации цилиндра (в расчете на единицу его длины)
«Я	Гу	Гф
Д = J Жр° j Фг°йг° = 2я j Фг°<*г°,

§ 4. СЛУЧАЙ СТАНДАРТНОГО МАТЕРИАЛА	213
находим
Как нетрудно убедиться, переход от выражения D.10) к
D.11), связанный с опусканием значения первообразной
функции на нижнем пределе, обеспечивается неравен-
неравенствами
2(х-1)+1^0, х>0.	D.12)
Они, безусловно, выполняются при положительной кли-
клиновой дисклинации, при которой (см. начало § 2) х > 1.
Для отрицательной же дисклинации (х<1) второе не-
неравенство выполняется, а первое с учетом того, что (см.
там же) % = 2лA — х) — угол раствора клина, наклады-
накладывает условие
%<п.	D.13)
Из третьего выражения в D.8) и условия отсутствия
осевой силы на торцах цилиндра B.16) находим
Это значение Я и необходимо подставить в предыдущие
выражения.
Рассмотрим использованный _в § 4 гл. 2 упругий по-
потенциал <t> = o*\dz/d?\2 + a\dz/d%>\2. Повторяя для него
проделанное выше, получаем
г = ();	();
ol^ol^Do^rOf-i), <& = ?«<»;	D.15)
Отсюда прежде всего обнаруживается нечувствительность
(при рассматриваемом законе упругости) к величине
дисклинации истинных напряжений — еще один недоста-
недостаток истинных напряжений. Согласно C.19) при раскры-
раскрытии трещины показатель сингулярности условных напря-
напряжений равен 1/2, а истинные напряжения конечны. Ре-
Результат — хорошо знакомый по § 7 гл. 2, но полученный
теперь из точного решения совершенно иной задачи.
• Из выражений D.8) — DЛ0), как и в предыдущем
параграфе, усматривается конечность при положительной

214	ГЛ. 1. Д0СЛОКАЦЙИ
дисклинации деформаций, напряжений и плотности энер-
энергии деформации (упругого потенциала). Правдоподобно
утверждение у что отмеченное обстоятельство является
общим свойством напряженно-деформированного состоя-
состояния при положительных дисклинациях.
§ 5. Заключение
В § 1 была изложена «линейно-упругая» версия тео-
теории дислокаций Вольтерра в форме, предложенной авто-
автором в теории оболочек [78]. Поскольку в книге рассмат-
рассматривается в основном плоская задача, предметом рассмот-
рассмотрения в § 1 были краевые дислокации и клиновая
дисклинация. Более того, дислокации, по-видимому,.впол-
по-видимому,.вполне сносно описываются в рамках линейной теории упру-
упругости. Не так обстоит дело с клиновой дисклинацией.
Полная (идеальная, совместимая с симметрией кристал-
кристаллических решеток) дисклинация сопровождается поворо-
поворотами, не меньшими 60°. Так что для ее адекватного опи-
описания требуется привлечение нелинейной теории упру-
упругости.
В свете сказанного основное внимание в главе было
уделено клиновой дисклинации. При этом рассмотрение
ограничилось изотропной сплошной средой. Попытка из-
изложения предмета с привлечением кристаллической
структуры неизбежно вывела бы автора далеко за преде-
пределы поставленной задачи (см. введение).
На необходимость создания теории дисклинации в не-
нелинейно-упругой постановке неоднократно указывалось
специалистами по физике твердого тела. Так, в диссер-
диссертации А. Е. Романова «Экранированные дисклинации в
твердых телах» (Ленинград, 1989) был использован под-
подход, основанный на использовании квадратичной теории
упругости с законом упругости Мурнагана.
Известна критика В. В. Новожиловым квадратичной
теории упругости [40], основанной на формальном отбра-
отбрасывании в геометрических и физических соотношениях
нелинейной теории упругости членов выше второго по-
порядка малости. Отмечались и недостатки закона Мурна-
Мурнагана. К тому же в упомянутой работе использовались
заимствованные из [29] «упругие постоянные» для арм-
ко-железа, которые таковыми не являются (данные от-
относятся к упругопластическому состоянию).

§ 5. ЗАКЛЮЧЕНИЕ	215
Прорыв в нелинейную теорию дислокаций Вольтерра
обозначился в работах Л. М. Зубова [16—18]. В этих
первых, основополагающих работах, естественно, не обо-
обошлось без недостатков. Применительно к клиновой ди-
склинации следует упомянуть:
1)	использование плоской (а не обобщенной плоской)
деформации и
2)	использование случайных, не всегда физически
корректных, законов упругости.
Результатом первого упущения явилось то, что полу-
полученным решениям отвечали приложенные к торцам ци-
цилиндра осевые сжимающие силы. Так, для стандартного
материала (см. § 4) упомянутая сила равна
Введение в рассмотрение в этой главе обобщенной пло-
плоской деформации позволило «снять» осевую силу.
Что касается второго упущения, то оно в значитель-
значительной мере было устранено введением в рассмотрение ши-
широкого класса малосжимаемых материалов B.14.1) и его
конкретизацией B.14.10).
Отметим, что в конце § 4 было подмечено преимуще-
преимущество при описании дисклинации условных напряжений
перед истинными.
По мнению автора, построение общей нелинейной тео-
теории дислокаций Вольтерра и ее использование в физике
твердого тела — проблема вполне созревшая.
Более подробно с нелинейным подходом к теории
дислокаций можно ознакомиться по статье: Чер-
Черных К. Ф., Мил яков а Л. В. Дислокации Вольтерра
в теории упругости / Вопросы физики материалов.—
Новгород: ADVELA, 1992.—С. 69—98. В ней, в частно-
частности, рассмотрены и краевые дислокации.

Глава 8
ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
ПОЛИМЕРОВ И ЭЛАСТОМЕРОВ
Полимеры обладают столь специфичными строением
и физико-механическими свойствами, что их иногда от-
относят к особому — высокополимерному — состоянию ве-
вещества. В главе дается краткая «справка» о строении и
механических свойствах полимеров. Механизм разруше-
разрушения полимеров существенно отличается от таковых для
низкомолекулярных твердых тел. Тем не менее (и это
основной предмет разговора) теория трещин находит при-
применение и здесь.
Особое место среди полимеров занимают эластомеры
(резиноподобные материалы) — материалы, обладающие
уникальным механическим свойством — большими обра-
обратимыми (высокоэластическими) деформациями, могущи-
могущими достигать десятков и даже сотен процентов. Это —
натуральный и синтетические каучуки, полиуретаны, ма-
материалы биологического происхождения. После соответ-
соответствующей технологической обработки эластомеры широко
используются как конструкционные материалы.
Строго говоря, в общем случае расчет изделий из эла-
эластомеров сводится к решению задач геометрически и фи-
физически нелинейной связной задачи термовязкоуиругости.
Вместе с тем в достаточно долго работающем изделии из
эластомера неупругие эффекты успевают отредактиро-
отредактировать, и оно практически находится в упругом состоянии.
К тому же вклад упругой (точнее — высокоэластической)
деформации, по-видимому, всегда составляет не менее
80 % общей величины. Тем самым неупругость для эла-
эластомеров является эффектом второго порядка, и нелиней-
нелинейная теория упругости представляет надежную основу для
прочностных расчетов изделий из эластомеров.
Теория трещин находит применение и при рассмотре-
рассмотрении разрушения эластомеров, хотя систематические ис-
исследования в этом направлении только разворачиваются.
Одной из фундаментальных трудностей здесь является
необходимость адекватного описания процесса разруше-
разрушения при больших деформациях ж поворотах. Затрудняет

§ L СТРОЕНИЕ ПОЛИМЕРОВ	217
интерпретацию результатов эксперимента и значительный
разброс в значениях механических характеристик мате-
материала.
Косвенным подтверждением применимости теории
трещин является и следующее любопытное обстоятель-
обстоятельство: зачастую теоретики при рассмотрении вопросов раз-
разрушения металлических материалов используют (за не-
неимением других) эксперименты на эластомерах.
§ 1. Строение полимеров
Полимеры — высокомолекулярные вещества, молекулы
которых построены из большого числа мономерных звень-
звеньев, связанных в длинные цепи химическими связями.
Примером, наиболее простым по своей структуре, мо-
может служить полиэтилен. Образуется он при раскрытии
двойной связи в молекуле этилена СНг=СН2 и после-
последующем объединении мономерных звеньев СНг—СНг в
цепочку
—СНг—СНг—СНг—СНг—-
Схематически полученную цепочку обозначают так:
(СН2~СН2)Я.
Более сложен натуральный каучук (НК)
/-СН2-СН8=С-СНЛ
\	CHL )п
СН,
мономерным звеном которого является изопрен. В отли-
отличие от полиэтилена, он обладает боковой (обрамляющей)
группой СНз (метиловой группой) и двойной связью в
цепи. Последняя сильно влияет на химическую актив-
активность каучука, в частности, на процесс вулканизации.
Некоторые полимеры (например, найлон) образуют
цепочку из регулярно чередующихся звеньев (А), (В):
- (А) - (В) - (А) - (В) -.
Для многих синтетических каучуков (СК) характерен
случайный порядок чередования мономерных звеньев,
например,
- (А) - (А) - (В) - (А) - (А) - (А) - (В) -.
Полимеры такого тиц* называют сополимерами.

218	ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
Приведенные полимеры относят к линейным, имею-
имеющим четко прослеживаемую главную цепь, окамленную
боковыми группами. Существуют и так называемые раз-
разветвленные полимеры типа
(A)-W-(A) - (в/
-(А)-(В/	(А)-(В).
В физике полимеров наряду с линейными различают
еще плоские и пространственные сетчатые полимеры,
подразделяемые в зависимости от частоты сшивок на
а	6
Рже. 8.1
макро- и микросетчатые. К макроскотгческим полиме*
рам (рис. 8.1, а) относятся, например, резины- (умерен-
(умеренно сшитые каучуки), к микроскопическим (рис. 8.1, б) —
эпоксидные смолы, кварцевое стекло, полностью сшитые
каучуки (эбониты).
По своему химическому составу полимеры делятся на
органические, элементоорганические и неорганические.
Органическими называют полимеры, в главную цепь ко*
торых входят углерод и его соединения с кислородом
азотом, серой и фосфором (т. е. вещества, образующие
органические соединения). По своему происхождению
они могут быть как природными, так и синтетическими.
Элементоорганическими называют полимеры с неоргани-
неорганической главной цепью, но органическими боковыми груп-
группами. Наконец, неорганические полимеры обладают не-
неорганическими главными цепями и боковыми группами.
Число молекулярных звеньев цепи полимеров имеет
порядок 103— 105т что отвечает огромным молекулярный

8 1. СТРОЕНИЕ ПОЛИМЕРОВ	219
массам 5 • 103—105*). Поэтому полимеры часто называ-
называют высокополимерами, а их молекулы — макромолекула-
макромолекулами. Так, для молекулы полиэтилена с молекулярным
весом 3,5 • 105, диаметр которой равен 5 А0**), длина
вытянутой цепи превышает диаметр в 6000 раз. Макро-
Макромолекула состоит из громадного числа звеньев, отож-
отождествляемых с простыми связями макромолекулы.
Рис. 8.2	Рис. 8.3
Простейшей при рассмотрении макромолекулы явля-
является модель свободно сочлененной цепи, состоящей из
п звеньев одинаковой длины /, направления которых
произвольны, не зависят друг от друга (рис. 8.2). Про-
Простейшие статистические предположения приводят к сле-
следующему наиболее вероятному (квадратичному) значе-
значению расстояния между концами цепи:
г» - 11~п.
При этом длина растянутой цепи (контурная длина)
равна
/max e In.
Конечно, модель свободно сочлененной цепи довольно
груба. Прежде всего соседние звенья (простые связи)
сочленяются цод определенным (т. н. валентным углом
Р ж 109,5°) (рис. 8.3). Кроме того, вращение звена по
конусу соседнего звена затормаживается вследствие дей-
действия боковых групп цепи. Учет этого приводит к не-
несколько уточненным формулам
= 0,82/п,
*) Соединения с меньшей молекулярной массой, состоящие
из повторяющихся звеньев, называют олигомерами.
••) 1А° — 10-« см — 10~10 м.

220 гл. 8. Хрупкое и квазихрупкое разрушёййё
где т] — параметр заторможенности вращения звена Пб
конусу. Можно ввести уточнение и на случай звеньев
неодинаковой длины.
Из приведенных формул усматривается, что при боль-
большом числе звеньев (п) расстояние между концами мак-
макромолекулы много меньше ее контурной длины. В своей
обычной (наиболее вероятной) форме (т. н. конформа-
ции) гибкая цепь напоминает спутанный клубок шерсти.
Мысленно потянем за концы цепи. Расстояние между
концами увеличится во много раз. После того как мы
(опять же мысленно) отпустим концы, макромолекула
под действием теплового движения начнет сокращаться,
снова превращаясь в клубок.
Сказанное объясняет природу неотъемлемого фунда-
фундаментального свойства гибкой макромолекулы — ее высо-
коэластичностъ, т. е. возможность испытывать большие
обратимые деформации. При этом деформация в основ-
основном определяется изменением внешней формы макромо-
макромолекулы — ее конформацией.
• До сих пор мы говорили о единичной макромолекуле.
Совокупность макромолекул образует материал — поли-
полимер. Макромолекулы в материале ведут себя иначе, что
связано с межмолекулярным взаимодействием соприка-
соприкасающихся частей различных макромолекул. С межмоле-
межмолекулярным взаимодействием связано появление различ-
различных над сегмент ар них и надмолекулярных структур, спон-
спонтанно возникающих и разрушающихся в различных ме-
местах полимерного тела.
При понижении температуры или приложении сил,
усиливающих упорядочение структуры материала, над-
надмолекулярные структуры способствуют кристаллизации
полимера. При этом кристаллизуются полимеры с макро-
макромолекулами, имеющими правильное, регулярное строе-
строение. Кристаллизация никогда не бывает полной, так что
кристаллические области чередуются с аморфными.
Перепутанность макромолекул с достаточно большим
молекулярным весом способствует превращению их сово-
совокупности в некую пространственную сетку. Более прочны
и устойчивы сетки с поперечными химическими связями
между макромолекулами. Применительно к каучукам их
можно получить вулканизацией — термохимическим про-
процессом, при котором образуются поперечные связи (мо-
(мостики) между макромолекулами. Так, умеренно вулкани-
вулканизированные A—5 % S) каучуки — резины — обладают

2. ТЕР&ОМЕХАНЙ**ЕСКЙЕ СВОЙСТЙА
221
отменными упругими свойствами. Вулканизат же с со*
держанием серы 30—50%—эбонит — является жестким
v конструкционным материалом.
В резинах большое применение находят наполнители,
составляющие 25—400 весовых частей на 100 частей
каучука. Они улучшают резины, удешевляют их, прида-
придают различные специальные свойства.
Рже. 8.4
Таким образом, реальные полимеры являются слож-
сложными образованиями — микрокомпозитами. На рис. 8.4
наряду с сеткой усматриваются надмолекулярные струк-
структуры с активным (находящимся в химической связи)
наполнителем, серные мостики, частицы активного на-
наполнителя с адсорбированным на них каучуком и неупо-
неупорядоченные сегменты макромолекул.
Эластомеры
В определенных температурных интервалах полимеры
могут находиться в четырех различных физических со-
состояниях — (частично) кристаллическом и трех аморф-
аморфных: стеклообразном (/), высокоэластичном (II) и вязко-
текучем (III).

222
ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
Рассмотрим полимерный образец при фиксированной
постоянной нагрузке. Схематически кривая 1 зависимо-
зависимости деформации от температуры выглядит так, как по-
показано на рис. 8.5. При низких температурах до темпе-
температуры стеклования (Гст) полимер находится в стекло-
стеклообразном состоянии, деформируется как обычное твердое
Температура
Рже. 8.5
упругое тело. Выше температуры стеклования появля-
появляется высокоэластическая деформация (на рисунке пока-
показано высокоэластическое плато — протяженный горизон-
горизонтальный участок). Выше же температуры течения (Тт)
начинается вязкое течение с накоплением необратимой
остаточной деформации. Рассмотрим подробнее каждый
из этих температурных интервалов.
При низких температурах, меньших температуры
хрупкости (Гхр), тепловое движение недостаточно для
преодоления молекулярных сил и проведения переориен-
переориентации сегментов макромолекулы в направлении прило-
приложенной силы. Тепловое движение лишь обусловливает
крутильные колебания звеньев. Поэтому слабая нагрузка
вызывает лишь малые упругие деформации при больших
значениях модулей упругости. Большая же нагрузка
нриводит к хрупкому разрушению. Деформация связана
с изменением средних межатомных расстояний в поли-
полимере и деформацией валентных углов в макромолекулах.
Полимер ведет себя как обычное низкомолекулярное не-
неорганическое стекло.
При температурах, больших Тхрг но меньших Гст, по-
полимер еще застеклован. Но более интенсивное тепловое
движение приводит к совместным крутильным колеба-

§ 2. ТЕРМОМЕХАНИЧЕСКИЕ СВОЙСТВА ПОЛИМЕРОВ	223
ниям соседних звеньев, активизированным приложенной
нагрузкой. Из-за слабой подвижности звеньев тепловое
движение еще не может преодолеть действие межмоле-
межмолекулярных сил. При этом образец все же получает боль-
большую деформацию, связанную с конформацией молекул.
Назвать такую деформацию высокоэластической нельзя
из-за ее необратимости. При снятии нагрузки деформа-
деформация (опять же по причине малой подвижности звеньев)
не исчезает. Для снятия деформации следует нагреть
образец. Описанную деформацию называют вынужденно-
эластической. Вынужденноэластическая деформация при-
приводит к ориентированному состоянию полимера с суще-
существенной анизотропией механических (физических)
свойств. Все химические волокна и пленки находятся в
вынужденноэластическом состоянии. Таким образом, за-
стеклованный полимер при Т > Гхр отличается от низко-
низкомолекулярных неорганических стекол возможностью вы-
нужденноэластической деформации и, тем самым, отсут-
отсутствием хрупкости. Именно поэтому можно использовать
застеклованные пластмассы в качестве конструкционных
материалов в температурном интервале Гхр < Т < Тсг.
При температуре выше Тст полимер получает высоко-
высокоэластическую деформацию, могущую достигать сотен
процентов и отвечающую малому модулю высокоэластич-
ности (?«0,1—1 МПа«1—10 кгс/см2).
Наконец, при температуре, превышающей температу-
температуру течения (Тгсч), появляется вязкая необратимая дефор-
деформация, обусловливаемая взаимным проскальзыванием
макромолекул, приводящим к накоплению необратимой,
остаточной деформации. Предотвратить вязкотекучесть
можно, сшив полимер. При этом узлы сетки препятству-
препятствуют проскальзыванию полимерных цепей. Поэтому сши-
сшитый полимер «игнорирует» температуру течения. Интер-
Интервал высокоэластичности расширяется, и его верхней
границей становится температура химического разложе-
разложения полимера (Тхиы) (кривая 2 на рис. 8.5). Последнее
свойство наиболее характерно для слабосшитых макро-
сетчатых вулканизатов каучуков — резин.
Наличие в линейном полимере кристаллической фазы
приводит к тому, что ниже температуры плавления —
кристаллизации (Гкр) он находится в твердом состоянии
(кривая 3 на рис. 8.5), но обладает меньшей жесткостью
при Т > Тсг. Последнее объясняется взаимодействием
кристаллической фазы с аморфной частью полимера.

224	ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
При Т > Тир кристаллическая фаза плавится, и кривая
почти скачкообразно достигает высокоэластического пла-
плато кривой 7, характерной для аморфных полимеров.
Многочисленные полимерные материалы можно услов-
условно разделить на шесть групп по соотношению их Тхр и
Тст с комнатной температурой.
1.	Исходные линейные полимеры — каучуки — высо-
высокоэластичны при комнатной температуре. Температура
стеклования (а тем более хрупкости) значительно мень-
меньше комнатной. Так, например, для натурального каучу-
каучука Гст = — 70 °С, для се л ико нового каучука Т„ =
= -125°С.
2.	Резины (умеренно сшитые каучуки) также имеют
низкие температуры стеклования. Так, морозостойкие
марки резины могут быть использованы в температурном
интервале (-40, +50 °С).
3.	Эбонит (сильно сшитый каучук) застекло-
ван, а иногда даже хрупок уже при комнатной темпе-
температуре.
4.	Линейные полимеры, образующие пластмассы, от-
отличаются от каучуков большим межмолекулярным вза-
взаимодействием. Поэтому изготовленные из них термопла-
термопласты, как правило, застеклованы уже при комнатной тем-
температуре.
5.	Добавление специальных веществ -— пластификато-
пластификаторов — ослабляет межмолекулярное взаимодействие и при-
приводит к пластикатом — материалам, высокоэластичным
при комнатной температуре.
6.	Густосшитые микросетчатые полимеры — реакто-
пласты — имеют еще большие температуры стеклования.
В отличие от термопластов, они при комнатной темпе-
температуре хрупки. С высокой температурой стеклования
связано их основное свойство — термостойкость.
Данная классификация относится к обычной продол-
продолжительности воздействия (минуты, часы). При быстрых,
ударных нагрузках высокоэластичный материал ведет
себя как застеклованный и даже хрупкий. Наоборот, про-
продолжительное воздействие приводит к тому, что застекло-
застеклованный материал ведет себя как высокоэластичный и
даже вязкотекучий, если он не сшит.
После всего сказанного можно определить эластомеры
как полимерные материалы, проявляющие высокоэла-
высокоэластичные свойства в широком температурном интервале,
содержащем шэднатную температуру.

§ 2. ТЕРМОМЕХАНИЧЕСКИЕ СВОЙСТВА ПОЛИМЕРОВ	225
Остановимся на основных механических свойствах
эластомеров (в высокоэластичном состоянии).
1.	Достигающая сотен процентов высокоэластичная
деформация носит сдвиговой характер. Модуль сдви-
сдвига (в зависимости от степени наполнения эласто-
эластомера) меняется примерно в пределах 0,1—15 МПа
A—150 кгс/см2). Поэтому эластомеры относят к низко-
низкомодульным материалам.
2.	При деформации эластомеров проявляются вязкие
свойства (ползучесть, релаксация напряжений), связан-
связанные с разрушением связей и надмолекулярных образо-
образований, возможно, с деформацией наполнителя. Обрати-
Обратимость высокоэластичной деформации носит геометриче-
геометрический характер: тело восстанавливает форму. Однако
вследствие существенного отставания деформации от на-
напряжений (широкая петля гистерезиса) часть энергии
теряется, выделяясь в виде тепла.
3.	При всестороннем сжатии эластомер ведет себя
как низкомолекулярное тело (твердое либо жидкое),
поскольку при этом меняются межмолекулярные расстоя-
расстояния, а конформация макроцепей не реализуется. Модуль
объемного сжатия имеет порядок 102—103 МПа A03—
104 кгс/см2), близкий к таковому для жидкости. Сопо-
Сопоставление значений модулей объемного сжатия и сдвига
показывает, что последний на два-три порядка меньше.
Эластомер значительно «охотнее» меняет форму, чем
объем. Отсюда и следует обычно используемое предпо-
предположение о несжимаемости эластомеров. По величине же
сжимаемости эластомер имеет тот же порядок, что и у
жидкостей [81, с, 76], [89, 951.
Эластомеры и по некоторым .другим свойствам близки
к жидкостям. Так, коэффициенты термического объем-
объемного расширения близки между собой C—6 • Ю^),
но намного больше, чем у твердых тел C—6 • Ю*^").
Природа высокоэластичной деформации, связанная с
изменением под действием напряжений конформации гиб-
гибких макромолекул, имеет энтропийный характер. В этом
она аналогична кинетической (энтропийной) природе
упругости газов.
Отметим характерное для линейных полимеров свой-
свойство: взаимодействие между звеньями вдоль цепи (хи-
(химическое) значительно сильнее, чем между цепями (меж-
(межмолекулярное). Несколько иная ситуация в полимерных
волокнах и цленках, представляющих собой полимерные
8 к. ф. ч*ржнх

22<* Wt в. Хрупкое и квазиХрупк6ё разрУШйий
материалы, находящиеся в одноосно- и двухосно-ориенти-
рованном состоянии. При обычных температурах боль-
большинство волоконобразующих полимеров находится в
кристаллическом состоянии и характеризуется сильными
межмолекулярными воздействиями.
| 3. Хрупкое и квазихрупкое разрушение
метекдованных полимеров
В отличие от низкомолекулярных твердых материа-
материалов, разрушение полимеров имеет ряд характерных осо-
особенностей, обусловленных их строением и механически-
механическими свойствами (§ 1—2). Характер разрушения полиме-
полимера существенно зависит от температуры, скорости нагру-
жения, условий эксперимента. Очевидно (на многое
влияющее) различие между химическими и межмолеку-
межмолекулярными связями, если вспомнить, что последние на
1^—2 порядка слабее, Никуда не уйти от необходимости
учитывать наличие кристаллической фазы, надмолеку-
надмолекулярных и надсегментальных структур, наполнителей и
армирования (в композитах с полимерной матрицей).
Следует также отметить, что (в отличие от низкомо-
низкомолекулярных материалов) зачастую отсутствует возмож-
возможность непосредственного наблюдения деталей структуры
деформируемых аморфных полимеров. Поэтому при изу-
изучении процесса разрушения последних значительно чаще
используются косвенные методы и общефизические сооб-
соображения.
Начнем рассмотрение с одноосно-ориентированного
линейного полимера. Для него характерны следующие
четыре типа разрушения (рис. 8.6): растяжение вдоль
(/) и поперек (//) волокна, сдвиг вдоль (///) и попе-
поперек (IV). При разрушении по типам I n IV преодоле-
преодолеваются химические связи, а по типам // и /// — межмо-
межмолекулярные, намного менее прочные. Величины проч-
прочности неориентированных полимеров занимают промежу-
промежуточное положение.
По характеру книги в этом параграфе нас должна
интересовать роль трещин при разрушении застеклован-
ных полимеров. Прежде всего следует отметить, что су-
существует (кинетический) подход к проблеме разруше-
разрушения, вовсе не принимающий во внимание влияние тре-
трещин — ато термофлуктуационная теория Журкова.

I 3. §АС*ЁкЛ0ВАЙНкЕ Й0ЛЙМЙР*>1	227
Коротко об этой феноменологической теории. Под
руководством С. Н. Журкова была проведена большая
серия экспериментов на различных твердых материалах
в широких диапазонах температур и времен A0~ls—
I	Ж	Ж	Ш
i
}
\
11
t
t
Рже. 8.6
уЛолимштилнета-
\ крилат
у V
Рис. 8.7
107 с). Часть из полученных результатов приведена на
рис. 8.7. Усматриваемые из него линейные зависимости
логарифма времени разрушения т от напряжения растя-
растяжения а и обратной абсолютной температуры привели

228	1*Л. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
к уравнению Журкова [15]
U —уо
т = тоехр °к1Г.	C,1)
Здесь Т — абсолютная температура; к — постоянная
Больцмана; ю — коэффициент порядка 10~14—10~12 с,
находящийся в хорошем соответствии с периодом коле-
колебаний молекулы; U^ — энергия активации; f—структур-
f—структурно чувствительный эмпирический коэффициент, служа-
служащий мерой неоднородности распределения напряжений
по молекулярным связям и определяющий интенсивность
снижения потенциального барьера вследствие действия
растягивающего напряжения о.
Проведенные наблюдения привели Журкова к выво-
выводу, что разрушение есть термически активируемый ки-
кинетический процесс, энергия активации которого снижа-
снижается приложением (растягивающего) напряжения.
Критика концепции Журкова (особенно интенсивная
на Западе) сводилась к тому, что будучи по своей при-
природе феноменологической, она не содержит механизма
и критерия разрушения, а также не принимает во вни-
внимание влияния трещин.
Описание (качественное) процесса разрушения по
Журкову делится на три стадии: 1) возбуждение моле-
молекулярных связей при приложении нагрузки; 2) разру-
разрушение молекулярных связей вследствие тепловых коле-
колебаний; 3) критическая концентрация разрушенных свя-
связей (от 50 до 100%), приводящая к разрушению тела
(образца).
Таким образом, в изложенной концепции не учиты-
учитывается существенное влияние на процесс разрушения
возникновения и развития трещин. Что касается обла-
области применимости теории Журкова (для полимеров), то
Бартенев ограничивает ее [3] сверхпрочными и высоко-
высокопрочными полимерами. Поясним последние термины.
К сверхпрочным относят полимеры, имеющие хоро-
хорошо организованную бездефектную структуру, обладаю-
обладающие прочностью, сравнимой с идеальной (см. § 4, 5
гл. 6). Такие материалы существуют пока в виде отдель-
отдельных лабораторных образцов.
Высокопрочными являются материалы, не имеющие
начальных микротрещин. Их прочность 1—3 ГПа
A—3 • 104 кгс/см2). Это на порядок ниже идеальной
прочности, но ж на порядок выше прочности обычных

§ 3. ЗАСТЕКЛОВЛННЫЕ ПОЛИМЕРЫ	229
технических материалов с начальными микротрещинами.
Поскольку образования микротрещин легче избежать в
малых образцах, высокопрочное состояние обычно реали-
реализуется в полимерных волокнах, тонких пластинах и т. п.
Причин тому, что полимеры в отсутствие микротре-
микротрещин не обладают идеальной прочностью, несколько.
Во-первых, полимерные цепи из-за неидеальности их
структуры (включение других атомов, нарушение ло-
локальной структуры при полимеризации, образование
звеньев различной регулярности, окисления С—С связей
и т. д.) содержат наряду с основными прочными и сла-
слабые связи. Во-вторых, прочность снижается из-за нерав-
неравномерного распределения нагрузки по цепям вследствие
существования коротких и длинных цепей, а также их
различной ориентации. В-третьих, снижение прочности
связано с тепловым движением и термофлуктуационным
механизмом разрыва главных цепей (возрастающими с
увеличением температуры). И, наконец, в-четвертых,
прочность снижается из-за неоднородной структуры ре-
реальных материалов. Прочность материала определяется
слабыми местами последней.
Для объяснения характерных для полимеров времен-
временных эффектов использовались различные теоретические,
в том числе и молекулярные модели [3, с. 49—52].
Другой подход к рассмотрению разрушения полиме-
полимеров — механический — состоит в использовании теории
трещин Гриффитса, хорошо зарекомендовавшей себя
применительно к низкомолекулярным твердым материа-
материалам (см. гл. 4—5).
Для его применимости следовало прежде всего про-
проверить для аморфных полимеров выполнение следующей
из формулы D.2.11)г зависимости разрушающего напря-
напряжения (а*) от полудлины трещины (а):
а*Уа - const - V2#f,.	C.2)
Была проведена [41 серия экспериментов на образцах
из полиметилметакрилата (ПММА) и полиэтилена (ПС),
ослабленных трещиной заданной длины. Результаты экс-
экспериментов сведены на рис. 8.8 для ПММА и на рис. 8.9
для ПС. Сплошные линии отвечают формуле Гриффитса
C.2). Данные на рис. 8.8 и 8.9 отвечают значениям:
?Ти«5,0±1,4 1015 дин2/см3 (т.-2,1±6,5-104 эрг/см2)
для ПММА и ?т,-3,4±1,1-101в дин2/см3 (TlI«l,7=fc
± 6,0 • 105 эрг/см2) для 1ГС (с — дджнц разреза).

230
ГЛ. 8. ХРУПКОЕ И КВЛЗИХРУПКОЕ РАЗРУШЕНИЕ
6
5
N
^о
2
1
1
¦ \Й
- V
-
-
	1	1
•
ш
\о ©о
кЛлп
Ж??
:
-
-
-
т
1 1 1.
0JS
1,0 1,5
с,ми
Рже. 8.3
2,0	2,5
Рже. 8.9

§ 3. ЗАСТЕКЛОВАННЫЕ ПОЛИМЕРЫ	231
Из рис. 8.9 усматривается выпадение эксперимен-
экспериментальных точек из зависимости Гриффитса при малых
разрезах для ПС. Берри объяснил это тем, что наряду
с разрезами образец содержит малые трещины, на кото-
которых при сравнимом с ними по величине малом разрезе
может развиваться разрушение. Испытания образцом без
разреза и постулирования зависимости C.2) позволяет
найти из последней характерный дефект (длиной 2а0).
Таким образом, считается, что образец содержит опасную
гриффитскую трещину длиной 2ао. При этом обнаружи-
обнаружилось, что при комнатной температуре а0»0,05 мм для
ПММА и а0 ш 1 мм для ПС. Этим и объясняется, что
выпадение экспериментальных точек реализуется именно
для ПС, обладающего сравнительно длинными началь-
начальными трещинами.
Анализ данных различных авторов показал [4, с. 20—
24], что для ПММА чи ^ 1,2—10 • 105 эрг/см2, а для ПС
Чп ж 3—17 • 105 эрг/см. Эти величины на несколько по-
порядков превышают прикидочные значения плотности
энергии образования новой поверхности *уп да 555 эрг/см2.
Выявленную колоссальную разницу можно, по-видимо-
по-видимому, объяснить (Т>Тхр) переходом материала в окрест-
окрестности концов трещины в вынужденноэластичное состоя-
состояние (играющее здесь ту же роль, что пластическая де-
деформация при квазихрупком разрушении металла),
В упомянутой статье Берри [4] рассматриваются раз-
различные факторы, влияющие на характер разрушения
полимера: температура, молекулярный вес, поперечные
связи, ориентация макромолекул, скорость роста тре-
трещин.
Так, показывается, что процесс разрушения (в отсут-
связи, ориентация макромолекул, скорость роста тре-
треления в теле (образце) плотной сетки волосяных тре-
трещин. Последние не являются трещинами в точном смыс-
смысле этого термина, а представляют собой четко ограни-
ограниченные области, содержащие интенсивно ориентирован-
ориентированный полимерный материал, способный передавать напря-
напряжения. Растягиваемый до 60 % ориентированный поли-
полимер перемежается сообщающимися порами D0—60 %
объема волосяной трещины). Считается, что образование
волосяной трещины связано с реализующимся в поли-
полимере всесторонним растяжением. Процесс разрушения
всегда начинается в области волосяных трещин. Пола-
Полагается, что в некоторый момент поры центральной пло-

232 гл. 8. Хрупкое и квлзихрупкоё разрушение
скости волосяной трещины сливаются, образуя макро-
макроскопическую гриффитскую трещину.
Итак, исследования разрушения застеклованных по-
полимеров развивалось в двух, почти не пересекающихся
направлениях. Первое (механическое), учитывающее де-
дефекты структуры, использовало линейную теорию тре-
трещин. Второе (кинетическое) исследовало временные эф-
эффекты прочности. Интересную попытку объединить оба
направления предпринял выдающийся специалист в об-
области физики стекол и полимеров Г. М. Бартенев.
Не имея возможности подробно рассказать о его подходе,
остановимся на некоторых принципиальных, узловых во-
вопросах [3].
Так, предложенная им формула
C.3,
отличается от уравнения Журкова C.1) «структурно-
«структурностью» входящих в нее величин. Здесь ^ = vAx — уже не
эмпирический коэффициент, х = Х($ — коэффициент пе-
перенапряжения вблизи конца трещины. При этом Хо —
коэффициент перенапряжения отдельных полимерных
цепей, обусловливаемого неоднородностью структуры по-
полимера, a {J — коэффициент концентрации напряжений в
вершине трещины. Величина vA = AoAm — так называе-
называемый флуктуационный объем, определяемый межмолеку-
межмолекулярным расстоянием Ао и разрывной величиной химиче-
химической связи Am. Величина А зависит от длины трещины,
температуры, растягивающего напряжения и молекуляр-
молекулярных параметров. Применительно к конкретным материа-
материалам эта величина определяется. Таким образом, в под-
подходе Бартенева учитываются как структура полимера,
так и влияние микротрещин.
Далее, при рассмотрении хрупкого и квазихрупкого
разрушений Бартенев принимает молекулярную модель
трещины, показанную на рис. 8.10. На границе перехода
от сплошного тела к свободной поверхности (штриховая
линия) происходят последовательные разрывы и восста-
восстановления (рекомбинации) химических связей. В момент,
фиксированный на рис. 8.10, атомы 1—5 находятся еще
в объеме тела, а 6, 7, ...— на свободных поверхностях.
Следующий акт разрыва сводится к переходу 5 -+ 6.
Вследствие тепловых флуктуации атомы в вершине
трещины приобретают кинетическую энергию, достаток-

3. 3АРЕНДОВАННЫЕ ГГОЛИМЕРЬ*
233
ную для разрыва связи или ее восстановления, если раз-
разрыв уже произошел. Как процесс разрыва, так и процесс
восстановления связей при о = О сопровождаются затра-
затратой кинетической энергии на преодоление потенциаль-
потенциальных барьеров Uo и Uo соответственно (рис. 8.11).
ю
еее
еее
еее
Рис. 8.10
На рис. 8,11 показана двухуровневая модель Стюарта —
Андерсона — Бартенева. Кинетические энергии частиц,
равные указанным барьерам, являются соответственно
энергиями активации и восстановления одной связи. Раз-
Разность потенциальных барьеров равна свободной поверх*
ностной энергии, возникающей при разрыве связи. По-
Потенциальная энергия в объеме является функцией рас-
расстояния между атомами в направлении растяжения х,

234
ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
а для частиц на свободной поверхности — функцией рас-
расстояния х' (рис. 8.10).
В ненагруженном состоянии (при о = 0) х = Ло и
;г' = Л0, что отвечает равновесному межатомному рас-
расстоянию в объеме и в поверхностном слое. Так что ле-
левый минимум на рис. 8.И отвечает равновесному поло-
положению в объеме, правый — равновесному положению
атомов на поверхности трещины. Максимум на кривой
потенциальных энергий возникает вследствие того, что
Рис. 8.12
на процесс разрыва связей влияют соседние атомы сле-
следующих атомных слоев. Как видно из рис. 8.11, в нена-
ненагруженном состоянии вероятность нахождения атомов в
левом минимуме кривой (т. е. в объеме) больше, чем в
правом (на поверхности). Таким образом, трещина после
разгрузки будет смыкаться.
В нагруженном состоянии (при о > 0) растягивающее
напряжение способствует разрыву связей и препятствует
их восстановлению (рис. 8.12). При этом (ср. C.3))
и = 170-ила, U' = U'0 + vAo.	C.4)
При некотором значении растягивающего напряжения
о0 в вершине трещины V"= ?/', т. е. вероятности разрыва
и восстановления связей равны. Имеет место динамиче-
динамическое равновесие и трещина не растет. Отвечающее этой
ситуации напряжение
C.5)

§ 4. ОСОБЕННОСТИ РАЗРУШЕНИЯ ЭЛАСТОМЕРОВ	235
является постоянной материала. Бартенев назвал его
безопасным локальным напряжением.
Им же использовано понятие критического напря-
напряжения
ok = U0/vA,	C.6)
при котором энергия активации обращается в нуль
(?/= С/о — vAo = 0) и происходит переход от активацион-
ного термофлуктуационного разрыва к безактивационно-
му атермическому, при котором разрыв связей происхо-
происходит под действием механической силы, и тепловые флук-
флуктуации не нужны.
Интересным является указание [3, с. 191] на то, что
для ПММА и направленного волокна критическое на-
напряжение Гриффитса 0G отвечает не aft, а Оо. Отсюда
делается вывод: «...aG и теория Гриффитса не имеют
отношения к критерию разрушения и критическому на-
напряжению Ой. Критерий Гриффитса скорее является
критерием безопасности (как и безопасное напряжение
Оо в термофлуктуационной теории прочности)*.
Отметим, что имеется несомненная связь сказанного
в конце этого параграфа с изложенным в § 7 гл. 4 под-
подходом Новожилова.
§ 4* Особенности разрушения эластомеров
Проблема разрушения эластомеров (более общо — по-
полимеров в высокоэластичном состоянии) чрезвычайно
сложна. И тому много причин. Прежде всего (см. § 2)
реальные эластомеры (главным образом резины) явля-
являются сложными микрокомпозитами. Напомним, что их
основой являются хаотически переплетенные цепи (мак-
(макромолекулы), сшитые (коль скоро подвергались термо-
термомеханическому процессу — вулканизации) в трехмерные
сетки. Обычно эластомеры содержат наполнители, неак-
неактивные и активные. Последние адсорбируют на своих
частицах каучук. Эластомеры содержат различные до-
добавки (жидкости, пластификаторы и т. п.). Зачастую
наполнители вводятся по соображениям, весьма далеким
от прочностных, например, по коммерческим.
Необходимо далее отметить слабую регулярность
структуры эластомеров. Так, макромолекулы имеют раз-
различные длины и жесткости. Сшивками (мостиками) они
разделяются на сегменты различной длины. При этом

236	?Л. 8. ХРУПКОЕ И КВЛЗИХРУПКОЕ РАЗРУШЕНИЕ
часть сегментов неупорядоченна (рис. 8.4). Макромоле-
Макромолекулы образуют спонтанно возникающие и разрушающие-
разрушающиеся надмолекулярные и надсегментальные образования
(структуры). Нерегулярно распределен и наполнитель,
частицы которого имеют различные формы и размеры и
способны объединяться в различные конгломераты. Вслед-
Вследствие локальных изменений температуры и деформаций
образуются области кристаллизации. Последние в упроч-
упрочнении эластомеров играют ту же роль, что и наполнитель.
Реальные эластомерные материалы часто являются и
макрокомпозитами с эластомерной матрицей, будучи уси-
усиленными нерастяжимыми и малорастяжимыми волокна-
волокнами, тканями, металлом либо пластмассами.
Многочисленность факторов и неоднозначность их
влияния на процесс разрушения еще более запутывает
ситуацию. Так, например, наполнитель и частота сши-
сшивок макромолекул могут служить как упрочнению мате-
материала, так и его ослаблению.
Как уже говорилось в § 2, обратимость высокоэла-
высокоэластичной деформации носит геометрический характер и
зачастую сопровождается солидной петлей гистерезиса
и соответственно большой диссипацией энергии. Кроме
того, в реальных эластомерах проявляются и вязкие
свойства (ползучесть и релаксация напряжений). Ска-
Сказанное относится к части интервала высокоэластичности
Тег + 10 °С — Тсг + 50 °С, называемой иногда кожеподоб-
кожеподобным состоянием. В последнем, таким образом, процесс
разрушения сильно зависит от температуры и скорости
деформации.
Значительные трудности при выявлении предельных
свойств эластомеров (разрушающее условное напряже-
напряжение оь, предельная кратность удлинения Хь) создает не-
необходимость учета геометрической и физической нели-
нейностей. При этом обычно используемые законы нели-
нелинейной упругости «исчерпывают себя» задолго до разру-
разрушения эластомера. Сказанное существенно затрудняет
интерпретацию экспериментальных данных.
Что касается последних, то приходится считаться с
их плохой воспроизводимостью. Так, раэброс в механи-
механических свойствах образцов, изготовленных из материала
одного замеса, в 10—20 % экспериментаторов совсем не
удивляет. Следует иметь в виду и чисто технические
трудности, например использование методов фотоупруго-
фотоупругости при больших деформациях и поворотах.

§ 4. ОСОБЕННОСТИ РАЗРУШЕНИЯ ЭЛАСТОМЕРОВ	237
Указанными (конечно, это не все) трудностями объ-
объясняется то, что до построения законченной теории раз-
разрушения эластомеров еще очень и очень далеко. Не го-
говоря уже о количественной стороне дела, многие каче-
качественные эффекты до конца не поняты и не получили
однозначного объяснения. Поэтому, с учетом целей на-
нашей книги, ограничимся ниже обсуждением основных
факторов, влияющих на прочность эластомеров.
Начнем с диссипации энергии, интенсивной в обла-
области кожеподобного состояния. Появление ее объясняют
несколькими причинами. Так, при изменении конфигу-
конфигурации макромолекул их сегменты скользят друг по дру-
другу. При этом трение, сопровождаемое выделением тепла,
возрастает по мере приближения к Тст.
При понижении температуры и ориентирующем
влиянии деформации макромолекулы регулярного строе-
строения образуют микрокристаллические ансамбли. Дальней-
Дальнейшая деформация сопровождается разрушением образо-
образовавшихся кристаллитов, сопровождаемым диссипацией
энергии.
Жесткие частицы наполнителя (обычно это техниче-
технический углерод) усиливают эластомер путем образования
длинных цепей частиц, прочно слипающихся с макромо-
макромолекулами. Разрушение этих связей при деформации со-
сопровождается диссипацией энергии.
Диссипация энергии существенно зависит от темпе-
температуры (Г) и скорости деформации \е = Я ). На рис. 8.13
показана доля энергии Я, поглощаемая за цикл дефор-
деформации вулканизата натурального каучука при малых де-
деформациях [13]. На рис. 8.13, а показана зависимость Я
от температуры при частоте 1000 циклов в минуту.
Из рисунка видно, что при понижении температуры Я
проходит через максимум, снова падая по мере прибли-
приближения к стеклообразному состоянию. На рис. 8.13, б по-
показана зависимость Я от скорости деформации i/t (t вы-
выражается в секундах) при постоянной температуре 20 °С.
Усматривается переход (слева направо) от сравнительно
упругого состояния через область интенсивной диссипа-
диссипации энергии к стеклообразному состоянию. Сопоставле-
Сопоставление обоих рисунков показывает, что рост скорости де-
деформации и понижение температуры оказывают сходное
влияние на диссипацию энергии. Область интенсивной
диссипации энергии особо интересна при проектировании
эдастомерных ударозащитных конструкций.

238
ГЛ. 8. ХРУПКОЕ И КВАЗИХРУПКОЕ РАЗРУШЕНИЕ
Отмеченный выше характер зависимости диссипации
энергии от скорости деформации и температуры имеет
место и для разрушающего условного напряжения оь.
-80 -40
О 40
Температура, °С
а
Рис. 8.13
Так, в [13, с. 70] со ссылкой на Т. Л. Смита для нена-
полненного бутадьенстирола приведена обобщенная зави-
зависимость разрывной прочности оь, приведенная к темпе*
Г + 50°С10°С ( 814)
ратуре
р
(рис. 8.14).
Рис. 8.14
Рис. 8.15
Поясним этот рисунок. Прежде всего включение мно-
множителя TJT исключает влияние (возрастающего пропор-
пропорционально температуре) модуля упругости. Далее, ис-
используется вязкость несшитых эластомеров qT, подсчи-
подсчитываемая по эмпирической формуле
*О(Т-Т„)
D.1)
Таким образом, подмечено, что зависимость от тем-
температуры (Т) и скорости деформации (е = А\ измеряв-

§ i. ОСОБЕННОСТИ РАЗРУШЕНИЯ ЭЛАСТОМЕРОВ	230
кой в с) определяется единственной совмещенной пере-
переменной е'т|г, характеризующей вязкую часть сопротивле-
сопротивления деформации. С увеличением этой переменной оь рез-
резко возрастает до максимального значения (когда сегменты
уже не движутся, а материал разрушается как хрупкое
стекло). На рис. 8.15 в функции все той же пере-
переменной приведена обобщенная зависимость для относи-
относительного удлинения при разрыве (eb~Xb — 1). Предель-
Предельное относительное удлинение вначале возрастает, отра-
отражая растущую прочность, а затем падает, поскольку
сегменты макромолекул становятся неспособными реаги-
реагировать достаточно быстро на возрастающую нагрузку.
Часто в качестве меры разрушения принимают плот-
плотность работы (в расчете на единицу объема) Wb, требуе*
мую для разрыва резины. Эмпирическим путем Грош,
Харвуд и Рэйн установили связь между Wb и энергией
Wd, рассеиваемой при растяжении до разрыва:
Wb = 8,9И1/8	D.2)
(Wb и Wd измерялись в кгс/см2). При этом было рас-
рассмотрено большое число наполненных, ненаполненных,
аморфных и кристаллизующихся при деформации эла-
эластомеров.
Разрушение происходит в результате затраты упругой
энергии {Wb — Wd). Естественно, что эластомеры, у ко-
которых большая часть энергии перед разрушением рас-
рассеивается, и являются наипрочнейшими.
Часто определяющим прочность фактором является
наполнитель. Так, прочность аморфного эластомера мо-
может существенно повысить тонкодисперсный наполни-
наполнитель (например, технический углерод — сажа). Предло-
Предложено несколько более или менее прабдоподобных тому
объяснений [13, 91].
Так, после разрыва сильнонапряженной макромоле-
макромолекулы несомая им нагрузка передается не только смеж-
смежным цепям. С помощью частиц наполнителя (конгломе-
(конгломерата последних) усилия перераспределяются между зна-
значительным числом макромолекул. Тем самым предотвра-
предотвращается прогрессирующее разрушение материала.
Другим возможным механизмом может служить
скольжение по поверхностям наполнителя, приводящее
к разгрузке высоконапряженных участков цепей.
Вблизи конца продвигающейся трещины в наиболее
напряженных местах наблюдается отделение эластомера

24o fri. 8. хрупкое и квазихрупкое разрушение
от наполнителя. Характерным при этом является про-
продвижение трещины не в определенной плоскости, а от
одной частицы наполнителя к другой. При этом возни-
возникают многочисленные повреждения, способствующие по-
повышенному сопротивлению раздиру наполненных резин.
Отклонению пути раздира может способствовать и воз-
возникающая деформационная анизотропия — переход к во-
волокнистой структуре. Своеобразным самонаполнителем
являются возникающие в процессе деформации кристал-
кристаллиты эластомера.
Повышенную прочность наполненных эластомеров
приписывают также сложному вязкому сопротивлению
наполнителя. Имеются и другие объяснения [13,91, 116].
Наконец, наполнитель способствует образованию в
материале трехосного напряженного состояния, сопро-
сопровождаемого возникновением в эластомерной матрице не-
небольших полостей (вакуолей).
Основным механизмом разрушения сшитых, напол-
наполненных эластомеров является образование и развитие
микротрещин, с последующим их объединением в макро-
макротрещины и в магистральную трещину. При этом не обя-
обязательно развиваются микротрещины максимального раз-
размера. Большинство трещин затупляются вследствие
большой поперечной деформации либо блокируются. Раз-
Развиваются трещины, «оказавшиеся в благоприятных усло-
условиях»,—в местах концентрации напряжений или де-
дефектов.
Одной из первых попыток применить энергетический
подход Гриффитса к проблеме разрушения эластомеров
явилась работа Ривлина и Томаса [116]. Так (в наших
обозначениях), из D.2.2), D.2.3) следует, что условие
возможности продвижения трещины имеет вид
da ^ da'
где а — длина (здесь односторонней) трещины
(рис. 8.16), dU/da—скорость высвобождения энергии
деформации при продвижении трещины, а
— энергия образования новой поверхности. Подстановка
последнего выражения в предшествующее приводит к
условию
%	D.3)

§ 4. ОСОБЕННОСТИ РАЗРУШЕНИЯ ЭЛАСТОМЕРОВ
241
Справедливо полагая, что, в силу неполной упругости
эластомера, требуемая для продвижения трещины энер-
энергия превышает энергию образования новой поверхности,
Ривлин ц Томас предложили считать величину
f = 2*f	D.4)
плотностью характеристической энергии раздира мате-
материала, не зависящей от формы
образца и способа приложения
к нему сил. Конечно, величина Т
существенно зависит от темпера-
температуры и скорости раздира. Введен-
Введенная величина является аналогом
суммы ч + ^п, введенной при рас-
рассмотрении квазихрупкого разру-
разрушения (§ 2 гл. 4).
Pic. 8.16
Рмс. 8.17
Наиболее удобным при испытаниях на раздир явля-
является образец, показанный на рис. 8.17. В нем области А
находятся в условиях растяжения, а область В факти-
фактически не нагружена. Если образец достаточно широк,
то деформацией в областях А можно пренебречь и эле-
элементарную работу раздира осуществляет сила F на пу-
пути Ida. При этом dU = F • Ida и согласно D.4) критерий
раздира D.3) принимает вид
Таким образом, для рассматриваемого образца вели-
величина растягивающей силы может служить мерой плот-
плотности энергии разрыва, независимо от упругих свойств
материала и длины разреза а. Измерение этой силы ши-
широко используется для определения величины Т и иссле-
исследования влияния структуры материала и условий испы-
испытания на сопротивление раздиру [13].

Глава 9
НЕЛИНЕЙНАЯ АНТИПЛОСКАЯ ЗАДАЧА
Во введении к книге было сказано об ограниченной
применимости антиплоской деформации в нелинейной
теории трещин. Тем не менее ее рассмотрение приводит
к любопытным результатам (§ 8), подтверждающим це-
целесообразность создания нелинейной теории разрушения.
Излагаемая в главе версия антиплоской деформации яв-
является существенным продвижением по сравнению с из-
изложенным в монографии [81].
§ 1. Основные геометрические
и деформационные зависимости
Обобщенной антиплоской деформацией (продольным
сдвигом) назовем деформацию, при которой
* = *?, х3 = Х-*х°3 + и;(ъЦ	A.1)
Таким образом, при обобщенной антиплоской деформации
на сохраняющее объем равномерное двухосное растяже-
растяжение (с кратностью X) накладывается произвольное сме-
смещение вдоль оси Xz(w). Просто антиплоской деформации
отвечает Xе 1.
Прежде всего из соотношений A.1), A.12.5),
A.12.16) находим
A.2)
где
G(U) = 2|	A.3)
— разрешающая функция.
По характеру деформации естественно принять шз = О,
полагая отличными от нуля углы поворота coi, 0J. При

§ 2. ТЕНЗОР ДЕФОРМАЦИИ КОШИ — ЛАГРАНЖА	243
этом согласно выражениям A.11.5), A.12.1) и A.12.2)
имеем
A.4)
где
©y^^K + tat), со =/со? + со*. A.5)
Применяя теперь формулы A.2), A.4) и A.11.4) к
полярному разложению Л° = Q* • F, находим
Л* = - *а>Уй + X A + cos со),	A.6)
Л3 = ш^Я", Л4 = — iXtoi + cos со Q.
В силу симметричности тензора Л° должны выполняться
равенства
1тЛ; = 0, Л; = ,С	A.7)
Из второго, а также выражений A.6), A.12.2) находим
A.8)
Нетрудно проверить, что полученные выражения удов-
удовлетворяют и первому из условий A.7). _
Согласно A.3) dQ/dt, = 2d2w/d% dt, — вещественная
функция. Поэтому равенство
является условием вещественности определяемого по Q
смещения
^=BTljQ«,t)« + jQU,C)«J. A.9)
§ 2. Использование тензора деформации
Коши — Лагранжа
К наиболее простым соотношениям приводит исполь-
использование тензора деформации Коши — Лагранжа С° = Л°2.
Прежде всего по формулам A.2), A.13.13) —A.13.19)
находим для сжимаемого материала
- 2АГ4 + QQ)|^-+ 4X"^-,

24-4	ГЛ. 9. НЕЛИНЕЙНАЯ АНТИПЛОСКАЯ ЗАДАЧА
и для несжимаемого материала
С учетом того, что входящие сюда величины не за-
зависят от х3, получаем из соотношений A.13.1), A.13.6),
A.13.8) однородные уравнения равновесия
B.3)
статические (силовые) граничные условия
^^ 2avos(O	B.4)
и дисторсионное граничное условие
Qe*v° _ Qe-<v° = _ i2 ^L.	B.5)
dt
Наконец, из соотношений A.11.12), A.11.13), A.2)
и A.4) получаем выражения для истинных напряжений
B.6)

jj 3. НЕСЖИМАЕМЫЙ МАТЕРИАЛ «ТИПА НЁОГУКОВСКОГО»	245
и для условных напряжений
^^}8, B.7)
1	COS2O) ft2
I _|_ \Y 1 + COS Ф
COS 0) fi
,~ 2fi
I COS 0)
Наличие двух уравнений движения B.3) при двух
граничных условиях B.4), но при одной искомой функ-
функции Q(?, ?) (задача явно переопределена) накладывает
в случае сжимаемого материала довольно жесткие усло-
условия на внешнюю нагрузку. Положение существенно
улучшается с появлением у несжимаемого материала ста-
статически определимой вещественной функции р(?, ?).
§ 3. Несжимаемый материал «типа неогуковекого»
«Типа неогуковского» будем называть несжимаемый
материал, для которого
Ф-Ф(Л)	C.1)
и согласно B.2) (f=d/dlc)
4ЛФ7 + 2X-Jp, {F-1 • /2h - 0,
>\ C.2)

246	гл. 9. Нелинейная айтиплоская задача
С учетом полученных выражений из второго уравне-
уравнения равновесия B.3J следует разрешающее уравнение
0.	C.3)
Из первого же находим р = — 2А2Ф' +%{1), где %Ц)
произвольная функция. Поскольку р и Ф'- веществен-
вещественные величины, таковой должна быть и х(?)- Но извест-
известно, что функция комплексной переменной может быть
вещественной, лишь будучи постоянной, т. е. x(S)===Xo==s
— const. Таким образом,
{F-1 • Л!>1 - гх-^о, iF-1 • /2J - 0, {F~l • /2K - 2QO',
{F-1 -Л!}4~ЯОBЯ2Ф'-хо), IF'1 /2}5=	C.4)
В случае статических граничных условий подстанов-
подстановка первых двух из этих выражений в граничное условие
B.4) 1 дает Хо =^avcv0 E°)' °voio(s°) — 0- Полученные равен-
равенства накладывают следующее ограничение: в процессе
деформации постоянная нагрузка ffo(=av°v=(s°)) направ-
направлена по нормали к недеформированному контуру. Заме-
Заметим, что это не нормальное давление, отслеживающее
положение нормали по отношению к деформирующемуся
контуру. Такую нагрузку можно назвать начальным нор-
нормальным давлением. Итак,
Хо — ta*o = const.	C.5)
Подстановка третьего из выражений C.4) во второе
граничное условие B.4J дает:
Согласно же соотношениям A.13.12) и C.4) на попереч-
поперечное сечение действует осевая сила (Р = 8?з)
Р = 2 (?Г2 - Я4) J O'dS0 + Я8Хо5°.	C.7)
8°
§ 4. Неогуковский материал
Простейшим «представителем» рассмотренного в пре-
предыдущем параграфе семейства упругих потенциалов яв-
является собственно неогуковский материал, для которого
[см. § 16 гл. 1]
-3), Фх = 1/а|А.	D.1)

§ 4. НЕОГУКОВСКИЙ МАТЕРИАЛ	247
Здесь прежде всего разрешающее уравнение C.3) при-
принимает вид
и может быть согласно выражению A.3) записано в ви-
виде d2wjd% д% = 0. Отсюда следует
W = -гг-
а = УЩ).	D.3)
С учетом выражений D.1) и D.3) получаем из C.4)
-* ¦ /2), - 2k-lxo, iF-i JlJ - 0, (F~l ¦ /Е}3 = »W, D.4)
Отсюда и из соотношений B.6), B.7) находим
		D.5)
v*	cos со W 1 +cos со
у0 	 Г COS СО	1	COS2C0	]
Согласно же формулам C.6), B.5) и C.7) имеем:
статическое (силовое) граничное условие
yeiv° +.? e-iy = j- av», (О,	D.7)
дисторсионное граничное условие
_ T|fe-V e _ B -^?i	D.8)

248	ГЛ. 9. НЕЛИНЕЙНАЯ АНТИПЛОСКАЯ ЗАДАЧА
и осевую силу на поперечном сечении
о]5°.	D.9)
В случае задания силы Р отсюда определяется X.
§ 5. Плоскость с отверстием
Итак, согласно D.7) и D.8)
'~&! = ?оу.я(*в),	E.1)
dx (j°)
= - i2 -ЦА	E.2)
ds
Рассмотрим плоскость с отверстием, содержащим начало
координат. Принятие выражения [ср. § 4 гл. 2]
обеспечивает конечность смещений и напряжений в бес-
бесконечной области, самоуравновешенность нагрузки на
контуре отверстия и однозначность смещений. При этом
с учетом соотношений D.5)
а„ = W (оо) = 2, (оо)/(цХ) = (aS - й&)/(цЯ), E.4)
где а^, а^ — значения напряжений на бесконечности.
Подстановка выражения E.3) в граничные условия
E.1), E.2) приводит к граничным условиям для регу-
регулярной части ?(?)
E.5)
Пусть, в соответствии со сказанным в § 14 гл. 1,
С-*(Х), Х-х-ЧС)	E.7)
— соответственно функция, отображающая рассматривае-
рассматриваемую бесконечную область на внешность единичного кру-
круга, и ей обратная. Вводя функцию
^(х) = %1х(х)]	E.8)
и используя соотношения [см. A.14.5) и A.14.6)] на
единичной окружности

g в. ПЛОСКОСТЬ С ПРЯМОЛИНЕЙНЫМ РАЗРЕЗОМ	249
приведем граничные условия E.5) и E.6) к виду
?0V (а) ах' (а) + уЧ(о)ох'(о) =
= - а0ох' (а) - а0ох' (а) + Bcv$ (в°)/ц) | х' (а) |, E.10)
= - аоах' (а) + Я^Р>) - 12 -^-1 х' (а) |. E.11)
as
§ 6. Плоскость с прямолинейным разрезом
Рассмотрим плоскость с прямолинейным разрезом
(— а^х3^.а, х2 = 0) (рис. 2.4), берега которого свобод-
свободны от нагрузки, а на бесконечности заданы напряжения
<*Гз> а2з- Отображение плоскости с разрезом на внешность
единичного круга и обратно осуществляют функции (см.
§ 6-7 гл. 2)
( !)	?+//2. F.D
Граничное условие E.10) с учетом F.1) и E*9) прини-
принимает вид
В соответствии со сказанным в § 4 Приложения удов-
удовлетворим этому граничному условию, положив ^0 (х) =
а -а,
—-. Используя соотношения E.3) и E.4), находим
Отсюда и из соотношений D.2), D.3), D.9) и A.8)
находим
w = ^f.{Ylz-a* - VtF1*) + °7**i + constj, F.4)
ХГ% + Х	ai	Im Y щ _ Re У
F.6)

250 М. 9. ЙЕЛЙНЕЙЙАЯ АЙТИЙЛОСКАЙ ЗАДАЧА
Наиболее интересна асимптотика смещений, углов по-
поворота и напряжений в окрестности (правого) конца
разреза. Вводя локальные полярные координаты
(рис. 2.4), находим
*~ а,
Отсюда и из F.3) —F.5) находим (а?>0)
w ~ "г ^2ar°sin (ф0/2^+ const> ^6#7^
Далее, из выражений D.5), D.6) следует при во-
l^il^o;	F.8)
L - а°22 + t2o°12	- ^ i a vi/a
а23	^Г /
F.9)
Изложенная задача, по-видимому, впервые была рас-
рассмотрена Ноулсом при К = 1. Ее можно рассматривать
как схематизацию напряженно-деформированного состоя-
состояния, реализующегося в цилиндре с малым плоским раз-
разрезом, параллельным оси стержня и свободным (при
Оо = 0) от нагрузки. При этом вдали от разреза имеется
равномерный так называемый продольный сдвиг. На опи-
описанное состояние может накладываться осевое растяже-
растяжение силой Р и начальное нормальное давление (—Оо).

§ 7. ТРЕЩИНА ПРОДОЛЬНОГО СДВИГА	251
§ 7. Трещина продольного сдвига
Полученные в § 6 зависимости дают возможность рас-
рассмотреть тип разрушения III — продольный сдвиг. При
этом обнаруживается любопытное обстоятельство. Преж-
Прежде всего, из соотношений F.8), F.9) и известных зави-
зависимостей линейной теории [21, 67, 69] имеем:
для ^линейных* напряжений
km/yscr sincp' *in/y2^~coscp;
для истинных напряжений
3	г*^
для условных напряжений
V»
Что можно сказать о приведенных соотношениях?
Прежде всего они относятся к несжимаемому материалу.
Выражения для истинных напряжений Oi3, 023 совпадают
с таковыми из линейной теории. Но выражение для Озз
обладает (как и в плоской задаче) куда более серьезной
особенностью. Следует отметить, что последняя «экрани-
«экранируется» малым (для высокомодульного материала) мно-
множителем <*2з/ц« Условные же напряжения <J13, с2з конеч-
конечны, хотя имеют величины порядка ft (что опять же суще-
существенно для высокомодульного материала).
В плоской задаче одним из неоднократно подчерки-
подчеркивавшиеся преимуществ условных напряжений являлась

252	Г*Л. 9. НЕЛИНЕЙНАЯ АЙТИПЛОСКАЙ ЗАДАЛА
их стандартная особенность. Это преимущество (перед
истинными напряжениями) сохраняется и здесь.
Неожиданным является лишь то, что обладают стан-
дартнои особенностью не а13, а23 (как в линейной тео-
теории), а напряжения о1Ь а12, о22, стзз' которых в линейной
теории просто нет. Таким образом в нелинейной теории
конечный продольный сдвиг, как бы формирует сингу-
сингулярные нормальные растяжения и поперечный сдвиг,
обладающие стандартной особенностью. Если принять
это во внимание, то к антиплоской деформации приме-
применимы аппарат и критерии разрушения плоской задачи.
Окончательно ситуация здесь прояснится после поста-
постановки специальных целенаправленных экспериментов.
Известные автору экспериментальные результаты допу-
допускают, к сожалению, неоднозначную трактовку.

Глава 10
ОСНОВНЫЕ ПРОБЛЕМЫ
И ПЕРСПЕКТИВЫ ПОСТРОЕНИЯ
ОБЩЕЙ НЕЛИНЕЙНОЙ ТЕОРИИ ТРЕЩИН
В этой главе мы не будем касаться многочисленных
не решенных должным образом проблем линейной тео-
теории трещин, о которых говорится в различных обзорах
[9, 19, 45, 53, 58, 91]. Остановимся лишь на вопросах,
связанных с созданием общей физически и геометриче-
геометрически нелинейной теории трещин.
§ 1. Об «истинных» мерах напряжений и деформаций
В § 9 гл. 1 было приведено пять пар сопряженных
по Хиллу тензоров, применительно к упругому материа-
материалу названных энергетическими. В механике сплошных
сред они, по существу, являются введенными еще Лаг-
ранжем парами «обобщенная сила — обобщенное пере-
перемещение». Фундаментальное значение приведенных пяти
пар объясняется тем, что они являются простыми след-
следствиями вариационного начала Лагранжа (§8 гл. 1)
и непосредственно не связаны со свойствами материала
Ц видом деформации.
Напомним, что определяющим для сопряженной по
Хиллу (энергетической) пары тензоров 2Э «-* Еэ являет-
является равенство
2Э: 6ЕЭ = 2Э: 2э'б*,
где р° — плотность недеформированного материала,
a 6W — вариация плотности работы обобщенных сил Лэ
на вариациях обобщенных перемещений 6ЕЭ = Еэ*6*.
В случае упругого материала b\V — вариация плотности
энергии деформации.
Величины Еэ* являются объективными скоростями
изменения напряжений, не зависящими от поворота ма-
материальной частицы как жесткого целого [65, 76, 81].
В статьях [76, 80] был подробно рассмотрен критерий
устойчивости материала
V: Е** >>0.	A.1)

254 ГЛ. 10. ОСНОВНЫЕ ПРОБЛЕМЫ НЕЛИНЕЙНОЙ ТЕОРИИ ТРЕЩИН
Систематическое изложение связанного с ним круга во-
вопросов дано в монографии [84]. Очевидно, что механи-
механическое содержание выписанного критерия устойчивости
материала существенно зависит от выбора сопряженной
по Хиллу (энергетической) пары тензоров.
Как выбрать из пяти представленных пар одну-един-
ственную, пригодную для теоретических исследований и
удобную для практического использования? Наиболее
часто в качестве таковой нарекается пара: истинные
напряжения — логарифмические (истинные) деформации.
При этом одним из самых весомых доводов здесь слу-
служит то обстоятельство, что при больших деформациях
первый главный инвариант логарифмической деформации
равен логарифму кратности изменения объема. Это по-
позволяет естественным путем отделить деформацию фор-
формоизменения от объемной.
Рассмотрим эту (третью ц A.9.2)) пару более вни-
внимательно. В общем случае в ней роль обобщенного пере-
перемещения играет не тензор логарифмических деформаций,
а «неголономный» тензор Т°, задаваемый в A.9.4) своей
производной по времени. Замена Т° на 1пА° возможна
лишь в двух случаях: для изотропного материала*) и
при деформации, не сопровождаемой поворотом главных
осей. Таким образом, тензор 1пА° пригоден к употребле-
употреблению лишь при частных (хотя и весьма важных) пред-
предположениях о свойствах материала или виде деформации.
Строго говоря, тензор истинных напряжений относит-
относится к паре 2 -«-* Т, где Т — также «него л оном ный» тен-
тензор, определяемый своей производной:
Но сказанное выше целиком относится и к этой паре,
являющейся аналогом третьей пары в A.9.2) в дефор-
деформированном главном базисе A.5.14).
Отметим, что использование логарифмических дефор-
деформаций в общем случае связано с большими математиче-
математическими трудностями. Сказанное относится и к объектив-
объективной скорости изменения напряжений по Яуману [84].
Основной целью этого параграфа является изложение
аргументов в пользу того, что наиболее приемлемой явлй-
*) Под изотропным пондмаем материал, для которого соосжы
тенворд Л° к (Q*-X-Q).

§ i. ОБ «ИСТИННЫХ) МЕРАХ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 255
ется четвертая пара: тензор условных напряжений*) —
тензор кратностей удлинений Лагранжа (тензор относи-
относительных удлинений Лагранжа).
Инженерная. практика давно уже выявила преиму-
преимущества использования условных напряжений перед истин-
истинными при определении механических свойств материала.
Так, известная величина — временное сопротивление — на
условной диаграмме растяжения (отвечающая знаку ра-
равенства в критерии устойчивости материала A.1) при
рассматриваемой паре) является одной из основных ха-
характеристик материала, входящей в его технический
паспорт. При этом условное напряжение и кратность
удлинений (относительное удлинение) являются изме-
измеряемыми величинами, в то время как истинное напря-
напряжение — величина экспериментально-расчетная.
При экспериментальном изучении больших деформа-
деформаций, как правило, используют условные напряжения.
Эпизодические пересчеты на истинные напряжения не
вносят дополнительной ясности в рассматриваемую фи-
физико-механическую ситуацию.
Дальнейшие преимущества условных напряжений
выясняются при выявлении особенностей (сингулярно-
стей) решений в концах трещин и угловых точках. Пе-
Перечислим основные из них.
Прежде всего для линейного материала истинные на-
напряжения имеют различные особенности (сингулярно-
(сингулярности). Так, в задаче о плоскости с разрезом (§ 7 гл. 2)
для сжимаемого материала они конечны, а для несжи-
несжимаемого имеют сильную особенность (а/Bг°)I. Нако-
Наконец, для линейного жесткого включения (§ 8 гл. 2)
особенность стандартная — (а/ Bг°)I/2. В то же время
во всех трех случаях условные напряжения имеют стан-
стандартную особенность, ту же, что и линейное решение
рассматриваемой задачи. Это дает возможность исполь-
использовать при нелинейном подходе весь арсенал приемов,
разработанных в линейной теорий трещин, при учете,
однако, должным образом реализующихся в окрестностях
концов трещин и угловых точек больших поворотов и
деформаций.
Да и сама, часто возводимая в ранг достоинств, ко-
конечность цстинных напряжений физически представля-
*) Его в зарубежной литературе называют симметричным ген-
дороМ напряжений Био.

256 1*Л. 10. ОСЙОВНЫЕ ПРОБЛЕМЫ НЕЛИНЕЙНОЙ ТЕОРИИ ТРЕЩИН
ется мало убедительной. В самом деле, как видно из со-
соотношений B.7.6), конечность являемся результатом
раскрытия неопределенности типа оо/оо? с существенным
использованием обращения в бесконечность площади при-
примыкающих к сингулярным точкам площадок.
Истинным напряжениям отвечают довольно грубые
асимптотики. Так B.7.17), при растяжении плоскости с
разрезом поперечной нагрузкой на бесконечности o2t
асимптотика напряжений не зависит от этой внешней
нагрузки. Согласно выражениям B.9.10) то же обстоя-
обстоятельство имеет место и для плоскости с симметричной
лункой. При этом асимптотика не зависит и от угла
раствора лунки. От указанных недостатков полностью
свободны условные напряжения.
При использовании асимптотики простейшего вида
B.11.4) истинные напряжения находятся с точностью
до оставшегося неопределенным угла поворота окрест-
окрестности оз. В то же время условные напряжения, не зави-
зависят от со, определяются полностью.
В дискретный критерий нормального отрыва входят
именно условные напряжения (§ 3 гл. 5). Более того,
при упрощенных вычислениях идеальной прочности так-
также используются условные напряжения [48, с. 145, 146].
Собранное на истинные напряжения «досье» может
быть еще пополнено. Перечисленные многочисленные
конкретные преимущества условных напряжений явля-
являются, по-видимому, различными проявлениями их более
глубокого свойства. В самом деле, переход от дискрет-
дискретной структуры тела к сплошной среде связан с «разма-
«размазыванием» действующих внутренних сил. Условные на-
напряжения, являющиеся (с точностью до не зависящего
от деформации масштабного множителя) силами, могут,
по-видимому, рассматриваться «полномочными предста-
представителями» этих исходных сил.
Статья [46], специально посвященная рассматривае-
рассматриваемому здесь вопросу, заканчивается так: «...Только боязнь
внести еще больший беспорядок в и без того чрезвычай-
чрезвычайно запутанную терминологию не позволяет назвать вы-
выделенную пару (условные напряжения — кратность удли-
удлинений) единственно истинными напряжениями — дефор-
деформациями».
Сказанное объясняет большое внимание, уделяемое
нами в книге условным напряжением. Более того, по
глубокому убеждению автора, нелинейную механику де-

§ 2. ОСОБЕНЙОСТИ СОСТОЯНИЙ В СЙНГУЛЯРЙЫХ ТОЧКА* 257
формируемого твердого тела необходимо излагать в тер-
терминах: условные напряжения — кратности удлинений
(относительные удлинения).
Отметим в заключение, что сказанное в этом парагра-
параграфе имеет и сугубо практическое значение в стратегии
проведения экспериментальных работ. Так, например,
проектируются сложные устройства, обеспечивающие в
процессе эксперимента постоянность истинных напряже-
напряжений. В силу сказанного, в этом вряд ли есть какой-то
смысл.
§ 2. Особенности напряженно-деформированного
состояния в сингулярных точках
Автор книги был невольным свидетелем спора двух
известных специалистов по теории разрушения. Один из
них утверждал, что учет в теории трещин геометриче-
геометрической нелинейности не оказывает влияния на особенности
напряжений. Возражая ему, другой говорил, что переход
от линейной теории к геометрически нелинейной, как бы
«размягчает» жесткие связи, обусловленные принятием
линейной теории. Результатом этого должно быть сни-
снижение особенностей в напряжениях.
Полученные в главах 2 и 3 точные решения краевых
задач показали, что истинная ситуация отлична от обоих
предположений. Прежде всего в задаче для плоскости
с прямолинейным разрезом (§ 7 гл. 2) истинные напря-
напряжения конечны для сжимаемого материала и имеют ано-
аномально сильную особенность (а/Bг°)I—для несжимае-
несжимаемого. В задаче же о линейном жестком включении
(§8 гл. 2) истинные напряжения имеют стандартную
(как для линейного решения) особенность (а/Bг°)I/2.
Что касается условных напряжений, то для них осо-
особенности во всех перечисленных случаях остаются стан-
стандартными*). Таким образом, возвращаясь к упомянутому
спору, отметим, что особенности в решениях могут уве-
увеличиваться, уменьшаться и не меняться.
Полученная в § 11 гл. 2 асимптотика простейшего
вида при сжимаемом материале дала следующие показа-
показатели сингулярности: для истинных напряжений
а(п) = п-^,	B.1)
¦) Что послужило дополнительным аргументом в пользу пред
почтительного использования условных напряжений, см. § 1.
9 к. Ф. Черных

258 гл. ю. основные проблемы нелинейной теории трещин
а для условных напряжений
«W-^JT1.	B.2)
Здесь п — показатель физической нелинейности в асимп-
асимптотике упругого потенциала B.11.5). Как и следовало
ожидать, для линейного материала (»= 2) эти показа-
показатели стыкуются с полученными в § 7 гл. 2 из точного
решения краевой задачи.
Что касается острого выреза с углом раствора 2{J, то
для него B.9.11)
— выражение, принимающее для разреза (при C = 0)
значение а@)=1/2. Сказанное полностью относится и
к рассмотренной в § 13 гл. 2 задаче о деформации бес-
бесконечного клина.
Следует отметить еще раз (см. конец § 4 гл. 7), что
точное решение совершенно другой задачи о нелинейной
клиновой дисклинации дает ту же стандартную особен-
особенность для условных напряжений.
Нетрудно убедиться, что все упомянутые решения
задачи о плоскости с разрезом приводят к стандартной
(той же, что и в линейном решении) особенности в упру-
упругом потенциале (плотности энергии деформации):
Ф~(а/Bг9)I.	B.4)
Этим подтверждается, что концепция «стекания энергии
в конец трещины» выполняется и в проделанном нели-
нелинейном подходе. Для. автора соотношение B.4) служило
одним из контролей правильности полученных нелиней-
нелинейных решений.
Знание показателей сингулярности облегчает исполь-
использование вариационного подхода (§ 12 гл. 2) к областям
с разрезами, острыми включениями и угловыми точками.
§ 3. Перспективы построения общей нелинейной
теории трещин
Как уже говорилось в предисловии, целью книги яв-
является стремление пробудить интерес к общей (геометри-
(геометрически и физически) нелинейной теории трещин и оказать
посильную помощь читателю, рискнувшему связать свою

ft 3. ПЕРСПЕКТИВЫ ПОСТРОЕНИЯ ОБЩЕЙ ТЕОРИИ ТРЕЩИН 259
деятельность с этой сложной, но так много обещающей
областью механики.
Исходя из этого, автор стремился максимально сузить
круг рассматриваемых вопросов. Так, рассмотрена в ос-
основном плоская задача. При этом изучались лишь основ-
основные (эталонные) задачи, для которых были найдены
простые аналитические решения. Совсем не использова-
использовались численные методы. Да и вообще использованный
математический аппарат почти не выходит за пределы
традиционных курсов анализа и теории функций комп-
комплексной переменной.
Не рассматривались задачи динамики и распростра-
распространения волн. Почти не рассматривались неупругие дефор-
деформации. За пределами книги осталась малоцикловая уста-
усталость и усталостное разрушение, анизотропные и ком-
композитные материалы. Одним словом, автор всячески
старался избежать «работы вширь». Многие вопросы не-
нелинейной механики трещин в книге не только не решены,
но и едва обозначены. Включение в книгу в таком виде
оправдывается их значимостью для теории и приложений.
Нельзя требовать от только что создаваемой нелиней-
нелинейной теории каких-либо законченных результатов и прак-
практических рекомендаций. Достаточно вспомнить, что раз-
развиваемая на протяжении десятков лет линейная теория
во многих своих важных разделах далека от завершения.
Тем не менее в изложенном в книге содержится немало
полезного:
1.	Более или менее обосновано утверждение, что в
качестве пары «обобщенная сила — обобщенное переме-
перемещение» следует рассматривать условные напряжения —
кратности удлинений (относительные удлинения). При-
Принятие сказанного, например, освобождает эксперимента-
экспериментатора от необходимости определять (и пересчитывать)
истинные напряжения.
2.	Выявленные особенности решений в «сингулярных
точках позволяют выделять сингулярные части решений,
улучшая тем самым структуру искомого решения. Это
особенно полезно при использовании численных методов.
3.	Найденные нелинейные зависимости позволяют
провести «ревизию» полученных по линейной теории ре-
результатов, в том числе критериальных соотношений.
Изложенное в книге позволяет прояснить ближайшие
и более далекце перспективы создания нелинейной тео*
ржж трещин. Прежде всего для придания большей общ-

260 ГЛ. 10. ОСНОВНЫЕ ПРОБЛЕМЫ НЕЛИНЕЙНОЙ ТЕОРИИ ТРЕЩИН
ности полученным результатам следует, помимо плоской
задачи, рассмотреть осесимметричную деформацию тел
вращения, теорию оболочек. Требуется существенно рас-
расширить круг рассмотренных задач, продублировав с уче-
учетом нелинейности известные линейные решения. Нет
принципиальных препятствий к рассмотрению динамиче-
динамических и волновых задач, малоцикловой усталости и уста-
усталостной прочности, учету структуры материала. Просмат-
Просматриваются пути построения адекватной геометрически
нелинейной деформационной теории пластичности. Вид-
Видны подходы к рассмотрению нелинейных контактных за-
задач (штампов). В физике твердого тела возник все ра-
растущий интерес к нелинейной теории дисклинаций, при
построении которой можно использовать результаты гла-
главы 8. Поистине непочатыц край представляет нелинейная
теория разрушения полимеров и эластомеров.
По глубокому убеждению автора, построение общей
нелинейной теории трещин реально и своевременно.

Приложение
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ФУНКЦИЙ
КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Опыт преподавания в Ленинградском университете утвердил
автора в мысли, что негативным побочным результатом широкого
внедрения ЭВМ в учебный процесс явилось неизбежное снижение
внимания к преподаванию теории функций комплексной перемен-
переменной (ТФКП). Еще меньше с ней знакомы выпускники техниче-
технических вузов. Между тем в теории трещин ТФКП занимает видное
место, хотя объем требуемых здесь знаний сравнительно невелик.
Сказанное привело автора к мысли дать краткое изложение сведе-
сведений из ТФКП, необходимых для чтения литературы по теории
трещин, в том числе для понимания изложенного в главах 2—4
книги. Для более глубокого и полного ознакомления с излагаемы-
излагаемыми разделами теории рекомендуем руководство [36].
§ 1. Понятия и основные свойства функций
комплексной переменной
Отнесем плоскость к прямоугольным декартовым координатам
хи х2 (рис. П.1). Каждой точке плоскости можно сопоставить ком-
комплексное число
Z = ХХ + 1X2.	A.1)
Поэтому указанную плоскость называют плоскостью комплексной
переменной z. Далее,
2=*re*V	A.2) 1
Здесь
— соответственно модуль и аргумент комплексного числа г.
Пусть z меняется в некоторой области комплексной плоскости.
Если каждому значению г из 5 отвечает число из = щ + Шг, то го-
говорят, что в области S задана функция комплексной переменной
w ш f(z) = их(хи х2) + iu2{xu x2).	A.3)
Выявим структуру правой части этого равенств*. Прежде все-
всего, вводя наряду с комплексной переменно! z A.1) ей комплексно

262	ПРИЛОЖЕНИЕ
сопряженную z ¦¦ хх — ix2, имеем
н при произвольных u\(xh а?2), щ(х\, х2)
Для того чтобы правая часть была функцией только переменной *,
необходимо и достаточно выполнения условия
Из равенств A.4) следуют правила дифферен-
дифференцирования по комплексным переменным
д i ( д	д
Xf	dz ~~ 2
РйС. П.1	4-= 4
dz *
Используя их, а также A.3), получаем искомые ограничения на
вещественную й мнимую части функции комплексной переменной
ди. дио дил	ди9
—*_.—I —?=*_—?	A.7)
дх дх* ох	ох '	'
называемые условиями Коши — Римана. При этом A.5) можно
рассматривать как комплексную форму записи условий Коши —
Римана.
Функция f(z) регулярна (голоморфна) в области 5, если она
однозначна там и имеет непрерывную производную.
Как было только что выяснено, для регулярности f(z) необ-
необходимо, помимо наличия у u\(xi, x2), и2(хи х2) непрерывных част-
частных производных, и их удовлетворение условиям Коши — Рима-
на A.7).
Рассмотрим, например, функции
их =z е * cos arg, u% = t l sin x?.
Для них выполняются условия Коши — Римана, поскольку
Отсюда н яз сформулированных выше условий регулярности

§ i. ПОНЯТИЙ И ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
следует, что
является регулярной функцией в любой конечной области.
На положительной вещественной полуоси z = ц и f <х ) = е*1.
Поэтому введенную функцию можно рассматривать как определе-
определение показательной функции комплексной переменной
/ (*) шт ez = *(*i+i*i) = e*i (cos x% + **in а^.	A.8)
Далее, из A.8) и A.6) t находим
df (а) 1 / д	д
= е*1 (cos х% + i sin *2) = / (д),
т. е.
(е'У - е*.	A.9)
Таким образом, на примере конкретной функции показаны два
общих правила построения теории функций комплексной пере-
переменной:
а)	функции комплексной переменной получаются из соответ-
соответствующих функций вещественной переменной путем замены их
переменных хна z;
б)	сохраняются правила дифференцирования.
Из соотношения A.8) усматривается известная формула
Эйлера
е*ф = cos ф + i sin ф,
с помощью которой комплексной переменной z A.2) можно при-
придать следующее полярное разложение:
z = г*'» — r(cos ф + i sin ф).	A.10)
Пусть в односвязной области S задан криволинейный интег-
интеграл по некоторой кривой i?. Используя соотношения A.1) и A.3),
его можно представить в виде суммы двух обычных вещественных
криволинейных интегралов
I
" lu»(xv *t)dxi + ui(*i> **)***]
2
Как известно, условия независимости от пути интегрирования

264	ПРИЛОЖЕНИЕ
интегралов правой части имеют в одяосвяаиой области виД
ди ди	дип дил
а совпадают с условиями Коши —Римана A.7). Поэтому криволи-
криволинейный интеграл от регулярной функции не зависит в односвяз-
ной области от пути интегрирования. Отсюда следует и то, что
интеграл по замкнутому контуру равен нулю.
В дальнейшем будем рассматривать и функции, регулярные в
замкнутой области S (включающей границу области g). Под ними
понимают функции, регулярные в области, целиком содержащей S.
В этом случае в качестве замкнутого контура можно принять гра-
границу области g, и полученный Еыше результат сформулировать
следующим образом:
Теорема Коши. Интеграл от регулярной в замкнутой об-
ласти S функции, взятый по границе области, равен нулю.
Выявленная независимость интеграла от пути интегрирования
дает возможность ввести неопределенный интеграл от регулярной
функции
являющийся в односв язвой области S однозначной функцией.
Не так будет в случае многосвязной области. Здесь величина
F(z) может зависеть от пути интегрирования, а интеграл по замк-
замкнутому контуру быть не равным нулю. Пусть, например,
Подынтегральная функция является регулярной в двухсвязной об*
ласти (рис. П.2). Вычислим интеграл по контуру, показанному на
рис. П.2 стрелками. Поскольку на вещественной оси t = xi, dt «*
«= dxu а на дуге окружности t » re% dt = irt^dy, имеем
A.11)
Бели i принадлежит положительной вещественной полуоси (ер =•
» 0, 2 = r«=i1), то F(i) я= lnxi. Естественно принять выраже-
выражение A.11) в качестве определения логарифмической функции в

265
§ 1. ПОНЯТИЯ И ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
комплексной плоскости, т. е. положить
In z = In г + up.
A.12)
Коль скоро контур 2? охватывает начало координат, при его обхо-
обходе функция In z получает приращение
и тем самым является в многосвязной области многозначной функ-
функцией. С помощью соотношений A.10) и A.12) показывается, что
Рис. П.2
Рис. П.З
логарифмическая функция является обратной к показательной.
Действительно,
elnz в е\пгегц> в ге{щ в г
Теорема Коши справедлива и для многосвязных областей, ес-
если брать интеграл по суммарному контуру 5й =• &о + &\ + .«.
... + 2*пу проходимому в положительном направлении (гшк, что-
чтобы область оставалась слева по ходу, рис, П.З). Применим теоре-
теорему к функции
/(*)/(*-iQ)f	A.13)
регулярной в 5 всюду, кроме точки z » zq. Вырежем аз S малый
кружок радиусом г с центром в точке z = z0. Для точек этого
кружка 1**1о+ге**. В оставшейся части S функция регулярна
и к вей применима теорема Коши
Г
A.14)
Пусть г~*0. Тогда в селу непрерывности /(*)
J

266	ПРИЛОЖЕНИЕ
Подставим полученное выражение в A.14). В нем zq может быть
любой точкой 5. Опуская поэтому индекс 0, приходим к фундамен-
фундаментальной для теории функций комплексной переменной формуле
Коши
показывающей, что регулярная в замкнутой области S функция
полностью определяется заданием ее граничных значений.
Из формулы Коши извлекается ряд замечательных следствий.
Так:
1. Регулярная в S функция имеет в S производные любого по-
порядка, причем
2. Функция разлагается в окрестности любой точки области
г « а в степенной ряд
f(z) - ce + ci (i - а) + с*(* - аK + ...	A.47)
При этом согласно A.16)
" /О* .	A.18)
3. Пусть функция регулярна в кольце А < |а| < В. Тогда она
разлагается в ряд Лорана
/ w - S а-*г*+«о + 2е*1*-	(*•19)
При этом первый ряд сходится вне внутреннего кольца, а второй —
внутри внешнего.
Если первая сумма содержит лишь конечное число членов:
a-iz~l +... + a-\z~x, то функция f(z) регулярна внутри круга
|z| < В, за исключением точки z = 0, где она имеет полюс 1-го
порядки. Аналогично, если вторая сумма имеет конечное число чле-
членов: a\z + ... + anzn, то f(z) регулярна при R > \z\ > А, где Я —
любое (положительное) число. В бесконечной точке z = оо функ-
функция имеет полюс п-го порядка. Если же здесь я « 0, то функция
/(*) регулярна в бесконечной области |*| > А.

§ 1. ПОНЯТИЯ И ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ	267
§ 2. Конформное отображение
Пусть в некоторой области В плоскости комплексной перемен-
переменной % задана регулярная функция к(%). Значения этой функция
можно рассматривать как точки некоторой другой области В' плос-
плоскости комплексной переменной
С = *1 + "? = *(Х)-	B.1)
Считая, что х'(х) отлична от нуля в В, выясним геометриче-
геометрический смысл ее модуля и аргумента. Для этого рассмотрим в В не-
некоторую кривую I и на ней две близкие (смежные) точки М(%) и
MIX)	M'
Рис. П.4
(Рис- П.4) с соединяющим их вектором Л%. Преобразо-
Преобразование B.1) сопоставляет I некоторую кривую V из В' с выделен-
выделенными на ней точками ЛГ(?), W(C + AC) и соединяющим их векто-
вектором Л?. Из рис. П.4 следует
l4^l НИЧИ	B-2)
Таким образом, модуль производной определяет измевевяе линей-
линейных размеров в точке %, обусловленное преобразованием B.1).
Далее, arg A% — угол, составленный вектором MN с осью абс-
абсцисс, a arg AS — аналогичный угол для M'N'. А тогда (arg At —
— argAx) —угол, отсчитываемый (против часовой стрелка) от на-
направления вектора MN до M'N\ Но из полярных представлений
ЛХ — | Ах | е* аг« А*, АС * | АС | е« аг« * следует
lim {arg AC - arg Ax} ~ lim argi4L\ = arg x' (x). B.3)
лх-*о	Дх-*о IAXJ
Отсюда усматривается, что аргумент производной определяет угол
поворота касательной к кривой в точке х* обусловленный преобра-
преобразованием B.1).
Если провести через точку % в области В две кривые, то каса-
касательные к ним повернутся на один ш тот же угод, так что угол

268	Приложение
между ними сохранит свою величину. Преобразование, сохраняю-
сохраняющее величины углов, называют конформным. Таким образом, пре-
преобразование, осуществляемое регулярной функцией, в точках, где
*'(х) Ф- О* является конформным. В частности, прямолинейная
декартова сетка переходит в криволинейную, но обязательно ор-
ортогональную. Из соотношения B.2) видно, что при рассматривае-
рассматриваемом конформном преобразовании происходит изотропное (равно-
(равномерное во всех направлениях) растяжение (или сжатие) коорди-
координатной сетки.
Итак, преобразование B.1) конформно отображает область В'
на В, Естественно возникает вопрос. Пусть имеются две односвяз-
ные области В и В'. Можно ли найти такую регулярную в В функ-
функцию х(х), чтобы преобразование ? = х(х) конформно отображало
область В' на В? При этом ограничимся взаимно однозначным ото-
отображением и будем считать, что В — внешность или внутренность
единичного круга, а В' ограничена кусочно-гладким контуром.
Ответ на поставленный вопрос положителен [36]: во внутрен-
внутренности (внешности) единичного круга существует непрерывная
вплоть до контура (|х| = 1) регулярная функция х(х) такая, что
? = у,(у) — конформное отображение В' на В.
При этом х(х) не единственна. Для фиксации произвола в
отображающей функции х(х) можно поставить дополнительные
условия:
а.	В случае конечной области (не содержащей бесконечной
точки ? 5к= оо)
>с@) = 0, и7@) ~ И (R — положительное число),
т. е. при отображении точка х = 0 переходит в точку f = 0 и (см.
B.3)) ее окрестность не поворачивается.
б.	В случае бесконечной области окрестности точки % = 0 от-
отвечает окрестность бесконечно удаленной точки ? = оо, не испы-
испытывающая поворота. При этом с учетом взаимной однозначности
отображения
о
х (х) = — + регулярная функция.
Л
При отыскании отображающей функции полезен принцип со-
соответствия границ, состоящий в следующем. Пусть в единичном
круге задана регулярная функция х(х), непрерывная вплоть
до контура. Пусть, далее, точка ? = х(х) описывает на плоскости
? некоторый замкнутый контур g, когда точка х движется по еди-
единичной окружности о (|о| = 1), причем различным точкам g от-
отвечают различные точки о. Тогда ? = х(х) отображает на внут-
внутренность единичной окружности: область, лежащую внутри ?, дри

i 2. КОНФОРМНОЕ ОТОЁРАЖЕЙИК
2б9
совпадении направлений обхода обеих кривых (либо внешность —
на внешность), и область, лежащую вне g, при несовпадении на-
направлений обхода.
Рассмотрим несколько конформных отображений, используе-
используемых в главах 2—4.
1. Начнем с отображающей функции
Полагая
—	(О 0, 0<т<1).
получаем из B.4)
' + j^-l ссюв% х°% = с |г° — -р-1 sin 9°.
Окружности г" = const отвечает эллипс
B.4)
B-5)
B.6)
Отсюда видно, что единичной окружности а(г° = 1) отвечает эл-
эллипс с полуосями а = сA + лг), 6 = сA — т), где
BЛ)
В частности, окружности (а » & =в= Д) отвечают с =¦ Л, m = 0, а
разрезу длиной 2а(Ь « 0) —значения с = а/2, m *= 1.
Рже. П.5
Из выражений B.6) и рис П.5 усматривается, что обходу еди-
единичной окружности против часовой стрелки отвечает такой же об-
обход эллипса. Поэтому, согласно принципу соответствия границ,
функция B.4) отображает внешность эллипса на внешность еди-
единичной окружности.

270	ПРИЛОЖЕНИЕ
Нетрудно проверить, что
2. Рассмотрим дробно-линейное преобразование
Z = RJT7>	B-9)!
где R — вещественная, а Ъ Ф d — комплексные постоянные. Из
B.9) 1 следует обратное, также дробно-линейное преобразование
R
?	-	B.0),
Таким образом, формулы B.9) 12 определяют взаимно однозначные
отображения комплексных плоскостей х и ?.
Покажем, что дробно-линейное преобразование переводит ок-
окружности в окружности. При этом прямые рассматриваются как
частные случаи окружностей (с бесконечно большим радиусом).
Окружность на комплексной плоскости ? определяется урав-
уравнением
где х*. х* — координаты ее центра, Л; — ее радиус, Используя ра-
равенства
придадим уравнению B.10) комплексную форму
(С-С*)(Е-?Ф)-Д?«о.	B.11)
Подстановка сюда выражеция B.9) i приводит в случае невыпол-
невыполнения условия
(?•?• +Л8-Л?)-Я (?• + ;•) = 0	B.12)
к окружности в плоскости х
(Х-Х*)(Х-Х#)-ДЦ = О,	B.1Э)
где
_ ягь + (?*;« - д|) d - л (ь?" + <*?»)
х	ч-л"-^)-л(р + 1«) '
+ (?*?*- л|) d5 - л Cbdj* + ь5;»)
(;•;• + л8 -я\)- л

2. КОНФОРМНОЕ ОТОБРАЖЕНИЕ
271
В случаях, когда условие B.12) выполняется, окружность B.11)
переходит в прямую на плоскости х
[яЧ + (р? - я») 1 - я Сь? + к*)] х +
+ [R2b + (?*?¦ - Л\) d - Я (bl* + *?)] х +
+ [Я2ЪЪ + (?¦?¦ - R\) dl-R (Id? + bdl*)] = 0. B.15)
3. Используя полученные формулы, рассмотрим конформное
отображение внешности симнегричной лунки (рис. П.6) на внеш-
7
Рис. П.7
ность единичного круга. Прежде всего дробно-линейное преобра-
преобразование
отображает внешность лунки на внешность угла (рис. П.7). При
этом условие B.12) переходит в очевидное (см. рис. П.З) равенство
a* + c2=*R^. Кроме того, согласно B.16), B.9) i
и . 1—СОВР.
a +
J* s. — ic = — fa ctg p
и уравнение прямой B.13) принимает вид (d
aa — cf «я 0.
При отображении точки верхнего берега лунки ?: —a; ih\ а пере-
переходят в точки li: 0, —cos р — i sin p; oo. Отсюда по принципу соот-
соответствия границ следует, что внешность лунки отображается на
внешность угла с тем же углом раствора 2ji (легко проверяется,
что условие конформности в вершине угла не нарушается).

272
ПРИЛОЖЕНИЕ
Преобразование
B.18)
как следует из полярных представлений ?х = рге	1t J2 = р9е 2И
B.17Х, разворачивает внешность угла в правую	полуплоскость
(рис. П.8).
Далее, преобразозание
ч- *~ sbin/2 ;v	/О 4О\
ЦЗ := Ь2^ == *<э2	1^-*"/
осуществляет поворот против часовой стрелки на угол я/2, так что
Рис. П.9
правая полуплоскость переходит в верхнюю полуплоскость Im
>0 (рис. П.9).
Наконец, как и в B.16), преобразование
B.20)
отображает вещественную ось в единичную окружность, а верх-
верхнюю полуплоскость — во внешность единичного круга.
Функции, составленные из рассмотренных B.16) —B.20),
Xl + 1
" х? - ¦
B.21)
(*-2(я-Р))'
дают искомую, отображающую внешность симметричной дуикя на
внешность единичного круга и «•¦ обратную.

§ 3. ИНТЕГРАЛЫ ТИПА К0П1И	273
§ 3. Интегралы типа Коши
Рассмотрим интеграл
где f(t) — некоторая интегрируемая функция. В отличие от функ-
функций, входящих в интегралы Коши A.15), не предполагается, что
она является значением регулярной функции f(z) на контуре SB.
Поэтому, в отличие от интеграла Коши, выражение C.1) называют
интегралом типа Коша. Теория интегралов типа Коши развита в
работах Мусхелишвиля, его учеников и многочисленных после-
последователей. В главах 2—4 нам понадобится несколько результатов
из этой далеко не элементарной теории. Их-то мы и приведем в
этом параграфе.
Прежде всего видно, что интеграл типа Коши является функ-
функцией, регулярной на всей комплексной плоскости, кроме точек са-
самого контура. Пусть, далее, на контуре установлено направление
обхода (рис. П. 10). Точки области, расположенные справа по ходу,
обозначим через ?~, слева — через S+. Пусть t — некоторая точка
на SB. При довольно общих предположениях о гладкости SB и f(t)
(которые обычно выполняются) существуют пределы
C.2)
связанные со значениями f(t) соотношением
F+(t)-F-(t)*=f(t).	C.3)
Пусть, далее, F(z) —некоторая функция комплексной перемен-
переменной, определенная в некой области S+ (рис. П.11). Введем в рас-
рассмотрение функцию
]*(*)= Уф,	C.4)
принимающую комплексно сопряженные с F(z) значения в точ-
точках z, симметричных относительно вещественной оси. Например,
для
имеем

tn
ПРИЛОЖЕНИЕ
Если F(z) регулярна в S+, то F(z) регулярна в 5~. Йусть t «* xx —
точка вещественной оси и (см. C.2))
F+ (z1) = lim F(z),
f- (хх) = lim F B),
S~.
C.5)
Из определения C.4) следует, что существование одного из
Рис. П. 10
Рис. П. 11
выписанных пределов обязательно влечет существование анало-
аналогичного предела для F{z), причем
W&	^Г).	C.6)
В главах 2—4 рассматриваются следующие задачи линейного
сопряжения: найти функцию F(z), исчезающую на бесконечности
и удовлетворяющую на линии скачка 3? условию;
I.	F+(t)-F~(t) **f(t) на 2	C.7),
для первой задачи или
II. F+(t)+F~(t) ..;(*) на Я
C.8)!
для второй задачи.
Для первой задачи решением является согласно C.3) интеграл
типа Коши
(V) dt	/л я>
для второй — несколько более сложное выражение
* Г h(t)g(t)dt
=HiJ 	jZTl
C-8),

$ 1 ИНТЕГРАЛЫ ТИПА КОШЙ	275
где
h(z) -У(*-а)(*-&)	C.9)
ив, b (см. рис. П. 10) — концы линии скачка.
Если линия скачка является отрезком вещественной оси
~ л ^ хх ^ а, то решение второй задачи дается выражением
C.10)
2я У zm — a" J	~i "
—а
а первой —
а
CL11)
Приведем несколько полезных формул, облегчающих подсчет
интегралов типа Кошя. Пусть S+ — конечная, ограниченная зам-
замкнутым гладким контуром g область, a S~ — внешняя но отноше-
отношению к g область, содержащая бесконечную точку. На контуре ус-
установлено положительное направление обхода, оставляющее об-
область 5+ слева. При этом справедливы следующие утверждения.
I.	Если f(z) — функция, регулярная в 5+ и непрерывная в
S+ = S+ + g, то
1 Cf(*)dt	ZeiS+,
g
g
Первая из этих формул представляет собой полученную при не-
несколько более общих предположениях о функции f(z) формулу
Коши A.15). Вторая — следствие теоремы Коши (поскольку функ-
функция f(t)l(t — z), рассматриваемая как функция t, регулярна в ?+
и непрерывна в S+ = S+ + g).
II.	Пусть f(z) — функция, регулярная в ?~, включая бесконеч-
бесконечную точку ¦), и непрерывная в S1 = S~ + g. Тогда при принятом
*) Т. е. при достаточно больших \z\ справедливо разложение

2?6	ПРИЛОЖЕНИЕ
положительном направлении обхода
Равенство C.13) 2 называют формулой Коши для бесконечной об-
области.
Пусть f(z) — функция, имеющая в конечной точке г *¦= а по
люс /-го порядка, т. е.
/(*)«(?(*)+/„<*),
где
— главная часть функции, а
В случае же полюса в бесконечной точке
G(z) =A* + Axz + ... + AizK	C.14),
Применительно к рассмотренным функциям формулы C.12)—
C.13) обобщаются следующим образом:
III. Пусть функция f(z) регулярна в 5+ и непрерывна в5+»
= S+ + g, кроме, быть может, точек аи ..., ап области S+, где она
может иметь полюсы с главными частями G\(z)y ..., Gn(z). Тогда
C.15)
IV. Пусть функция f(z) регулярна в S" и непрерывна в5- =
— ^~ + ^» за исключением, быть может, точек cj, ..., an и г = оо,
где она может иметь полюсы с главными частями ?i(z), ..., Gn{z)*
G«(z). Тогда
C.16)

I 4. МЕТОД РАСЧЛЕНЕНИЯ ГРАНИЧНЫХ УСЛОВИЙ	277
Для практического использования полезны также соотношения:
V.	Для того чтобы непрерывная на окружности f функция
/(о) была предельным значением некоторой функции, регулярной
внутри окружности ^» необходимо и достаточно, чтобы
1 р f (a) do -
2^1 \ q__g =a для всех g внутри у.	C.17)
v
Здесь а — постоянная, равная значению упомянутой функции в
точке z = 0.
VI.	Для того' чтобы непрерывная на окружности f функции
/(а) была граничным значением функции, регулярной вне f» необ-
необходимо и достаточно, чтобы
1 0-2 ° для всех * вне У'
У
Далее, пусть
ф(з) = ao-f axz + a2z2 + ...
— функция, регулярная внутри ч, вплоть до контура. Тогда
У
для всех z внутри ч> В частности,
§ 4* Метод расчленения граничных условий
При всей своей общности метод интегралов типа Коши требует
все же специальной подготовки читателя. В монографии [40] был
изложен полученный автором в дипломной работе A952 г.) алге-
алгебраический метод расчленения граничных условий. Для полино-
полиномиальных отображающих функций он давал те же результаты, что
и метод интегралов типа Коши. В главах 2—4 отмеченный подход
применяется (в том числе и для отображающей функции более
общего вида, см. § 9 гл. 2) в следующей форме.
Пусть удастся привести граничное условие к виду
где Fi(o), F2(a), /i(o), /2@) —граничные значения функций Fi(%),

278	ПРИЛОЖЕНИЕ
)» /i(x)» h(x)i регулярных в области S (конечной либо беско-
бесконечной), ограниченной контуром g. Из D.1) следует
*(Х)-МХ). ^(х)=Ых) (Хб5).	D.2)
Йе имея возможности (и желания) как-то теоретически обосно-
обосновать этот метод, отметим, что для всех рассмотренных задач полу-
полученные с его помощью решения совпадают с найденными (более
сложным и требующим специальной подготовки) методом инте-
интегралов типа Коши. Отметим также, что метод расчленения гранич-
граничных условий, конечно, не универсален. Иногда он неудобен, а то
в просто неприменим (см., например, § 3 гл. 3 — случай сосредо-
сосредоточенной силы).

СПИСОК ЛИТЕРАТУРЫ
1.	Баренблат Г. И. Математическая теория равновесных тре-
трещин, образующихся при хрупком разрушении II ПМТФ.—
1961.- № 4.- С. 3-56.
2.	Баренблат Г. И. О некоторых общих представлениях
математической теории хрупкого разрушения / ПММ.—
1964.— Т. 28, № 4.- С. 630-643.
Д Бартенев Г. М. Прочность и механика разрушения поли*
меров.— М.: Химия, 1931— 280 с.
4.	Берри Дж. И. Разрушение стеклообразных полимеров /
Разрушение.— М.: Мир, 1976.-- Т. 7, ч. 2.— С. 8—65.
5.	Болотин В. В. Прогнозирование машин и. конструкций.—
М.: Машиностроение, 1984,—312 с.
6.	Бугаков И. И., Демидова И. И. Квазихрупкое разру-
разрушение образцов с вырезами, имеющими угловые точки II
МТТ.- 1980.- № 3.- С. 70-75.
7.	В а к у л е н к о А. А. О связях между напряжениями и дефор-
деформациями в неупругих средах / Исслед. по упругости и плас-
пластичности.—Л.: Изд-во Ленингр. ун-та, 1961.—№ 1.—С. 3—35.
8.	В а с и л ь е в В. В., С о л д а т о в С. А. Соотношения нелиней-
нелинейной механики композитных материалов // Механика компо-
композитных материалов.— Рига.— С. 38—43.
9.	Гольдштейн Р. В. Некоторые вопросы механики в ато-
атомистике разрушения / Атомистика разрушения.— М.: Мир,
1987.- С. 236-245.
10.	Греков М. А. Поле напряжений в области пластических де-
деформаций около трещины / Деформация сплошных сред н
управление движением.— Л.: Изд-во Ленингр. ун-та, 1984.—
С. 59-74.
11.	Гузь А. Н. Механика хрупкого разрушения материалов с
начальными напряжениями.— Киев: Наукова думка, 1983.—
296 с.
12.	Д а л ь Ю. М. Влияние малой геометрической нелинейности
на характер напряженно-деформированного состояния у вер-
вершины трещины / МТТ.— 1980.— № 2.— С. 17—25.
13.	Д ж е н т А. Н. Разрушение эластомеров // Разрушение.— М.:
Мир, 1976.— Т. 7, ч. 2.- С. 66-103.
14.	Е к о б о р и Т. Научные основы прочности и разрушения ма-
материалов.— Киев: Наукова думка, 1978.— 385 с.
15.	Ж у р к о в С. Н. Кинетические концепции прочности твердых
тел II Изв. АН СССР. Сер. неорганич. материалы.—1967.—
Т. 3, № 10.- С. 1767—1771.
16.	Зубов Л. М. Изолированная дисклинация в нелинейно-уп-
нелинейно-упругом сжимаемом теле / МТТ.—1986.—№ 1.—С. 69—73.

2Й0	список литературы
17.	Зубов Л. М. Теория дислокаций Вольтерра в нелинейно-уп-
нелинейно-упругих телах / МТТ.—1987.—№ 5.—С. 140—147.
18.	3 у и о в Л. М., К а р я к и н М. П. .Многозначные смещения и
дислокации Вольтерра в плоской нелинейной теории упруго-
упругости // ЖПМТФ.— 1987.— № 6.—С. 146—152.
19.	11 в л ев Д. Д. О теории трещин квазихрупкого разрушения /
ЖПМТФ.— 1967.— № 6.—С. 88—128.
20.	Ильюшин А. А. Об одной теории длительной прочности /
МТТ.— 1967.— Да 3.- С. 3—12.
21.	Качанов Л. М. Основы механики разрушения.— М.: Нау-
Наука. 1974.— 267 с.
22.	Кер штейн И. М., Клюшников В. Д., Ломакин Е. В.,
Шестериков С. А. Основы экспериментальной механики
разрушения.— М.: Изд-во Моск. ун-та, 1989.— 140 с.
23.	К н о т т Дж. Микромеханизмы разрушения и трещиностойкость
конструкционных сплавов / Механика разрушения. Разруше-
Разрушение материалов. Механика, вып. 17.—М.: Мир, 1979.—С. 40—
82,
24.	К о л о с о в Г. В. Применение комплексной переменной к тео-
теории упругости.— М.; Л.: ОНТИ, 1935 — 224 с,
25.	Костров Б. В., Н и к и т и н Л. В., Ф л и т м а н Л. М. Ме-
Механика хрупкого разрушения // МТТ.— 1969.— № 3.—С. 112—
125.
26.	К о у т Г. Разрушение полимеров— М.: Мир, 1981.—440 с.
27.	Леонов М. Я. Механика деформаций и разрушения. —
Фрунзе: Илим, 1981.— 237 с.
28.	Л и х а ч е в В. А.. X а й р о в В. Ю. Введение в теорию дис-
клинаций. — Л.: Изд-во Лепингр. ун-та, 1975.— 183 с.
29.	Л у р ь е А. И. Нелинейная теория упругости.—М.: Наука,
1980.-512 с.
30.	Л я в А. Математическая теория упругости.— М.: ОНТИ,
1935.— 674 с.
31.	М а к к л и н т о к Ф. А.. Аргон А. С. Деформация и раз-
разрушение материалов.— М.: Мир, 1970.— 444 с.
32.	М а к м и л л а н И. Идеальная прочность твердых тел // Ато-
Атомистика разрушения.—М.: Мир, 1987.—С. 35—103.
33.	Махутов Н. А. Деформационные критерии разрушения и
расчет элементов конструкций на прочность.— М.: Машино-
Машиностроение, 1981.— 272 с,
34.	М о р о з о в Е. М. Расчет на прочность конструкционных
элементов с трещинами.— М.: Машиностроение, 1982.—
48 с.
35.	Морозов Н. Ф. Математические вопросы механики тре-
трещин.-^ М.: Наука, 1984.— 256 с.
36.	М у с х е л и ш в и л и Н. И. Некоторые основные вопросы ма-
математической теории упругости.— М.: Наука, 1966.— 708 с.
37.	Н а д а и А. Пластичность и разрушение твердых тел.— М.:
Мир. 1969.— Т. 2.— 864 с.
38.	Ней бер Г. Концентрация напряжений.—М.: Гостехиздат,
1947.— 204 с.
39. Новожилов В. В. О принципах обработки статических ис-
испытаний изотропных материалов / ПММ.—1951.— Т. 15,
вып. 6.— С. 709—722.
40. Новожилов В. В. Теория упругости.—Л.: Судпромгжз,
1958.- 370 с.

СПИСОК ЛИТЕРАТУРУ	281
41.	Новожилов В. В. О необходимом и достаточном критерии
хрупкой прочности / ПММ.—1969.—Т. 33, вып. 2.—С. 212—
222.
42.	Новожилов В. В. К основам теории равновесных трещин
в упругих телах / ПММ.—1969.—Т. 33, вып. 5.—С. 797—812.
43.	Н о в о ж и л о в В. В. Достижения и перспективы развития
механики разрушения Ц Проблемы механики разрушения.—
Калинин: Калининский ун-т, 1987.—С. 6—9.
44.	Н о в о ж и л о в В. В., Даль Ю. М. Об эффективном радиусе
кривизны квазихрупкой трещины / Избранные проблемы при-
прикладной механики.— ВИНИТИ, 1974.— С. 299—303.
45.	Новожилов В. В., С л е п я н Л. И. Некоторые проблемы
и достижения механики разрушения / Вестн. АН СССР.—
1987.-№ 9,-С. 96-111.
46.	Н о в о ж и л о в В. В., Черных К. Ф. Об «истинных» мерах
напряжений и деформаций в нелинейной механике деформи-
деформируемого тела И МТТ.— 1987.— № 4.-- С. 191—197.
47.	Н о т т Дж. Ф. Основы механики разрушения.— М.: Метал-
Металлургия, 1978.— 256 с.
48.	Н о т т Дж. Ф. Механика разрушения / Атомистика разру-
разрушения.— М.: Мир, 1987.— С. 145—176.
49.	Образцов И. Ф.. Васильев В. В. Нелинейные феноме-
феноменологические модели волокнистых композитных материалов Ц
Механика композитных материалов,—1982.—№ 3.—С. 390—
393.
50.	О с а д ч у к В. А., Подстригая Я. С. К определению на-
напряженного состояния в замкнутой цилиндрической оболочке
и бесконечной пластине с трещинами / МТТ.— 1973.— № 3.—
С. 69—78.
51.	Павлов А. А., Жунисбеков С. Исследование началь-
начальной стадии развития трещины при растяжении и сжатии об-
образцов из полиметилметакрилата / Проблемы прочности.—
1973.- № 8.- С. 14—18.
52.	П а н а с ю к В. В. Предельное равновесие хрупких тел с тре-
трещинами,— Киев: Наукова думка, 1968.— 246 с.
53.	II а н а с ю к В. В. Деформационные критерии в механике
разрушения JJ Физ.-хим. механика материалов.— 1986.— Ms 7.—
С. 7-17.
54.	Панасюк В. В., Б е р е ж н и ц к и й Л. Т., К о в ч и к С. Е.
О распространении произвольно ориентированной прямолиней-
прямолинейной трещины при растяжении пластины / Прикл. механи-
механика.- 1965.-№ 2.—С. 48—55.
55.	Парис П., Си Дж. Анализ напряженного состояния око-
около трещины II Прикладные вопросы вязкости разрушения.—
М.: Мир, 1968.- С. 64-142.
56.	П а р т о н В. 3. Механика разрушения. От теории к практи-
практике.— М.: Наука, 1990.— 240 с.
57.	П а р т о н В. 3., Морозов Е. М. Механика упругопластиче-
ского разрушения.— М.: Наука, 1985.— 504 с.
58.	Пар тон В. 3., Черепанов Г. П. Механика разруше-
разрушения / Механика в СССР за 50 лет.— М.: Наука, 1972.— С. 365—
467.
59.	П и с а р е н к о Г. С, Науменко В. П. Экспериментальные
методы механики разрушения материалов / Физ.-хим. меха-
механика материалов.— 1982.— № 2.— С. 28—40.

282	СПИСОК ЛИТЕРАТУРЫ
60.	П о б е д р я Б. Е. Механика композиционных материалов.—
М.: Изд-во МГУ, 1984.
61.	Райе Дж. Не зависящий от пути интеграл и приближед-
ный анализ концентрации деформаций у вырезов и трещин /
Прикладная механика, сер. Е.— 1968.— Т. 35, № 4.— С. 340—
350.
62.	Райе Дж. Математические методы в механике разрушения /
Разрушение.— М.: Мир, 1974.— Т. 2.— С. 202—235.
63.	С а в р у к М. П. Двумерные задачи упругости для тел с тре-
трещинами.— Киев: Наукова думка. 1981.— 324 с.
64.	С а в р у к М. П. Коэффициенты интенсивности напряжений в
телах с трещинами / Механика разрушения и прочности ма-
материалов. Киев: Наукова думка, 1988.— Т. 2.— 620 с.
65.	Седов Л. И. Введение в механику сплошной среды,— М.:
Наука, 1962.- 284 с.
66.	Седов Л. И. Механика сплошной среды.— М.: Наука»
1974.- Т. 2.- 640 с.
67.	С и Дж., Л и б о в и ц Г. Математическая теория хрупкого
разрушения / Разрушение.— М.: Мир, 1975.— Т. 2,— С. 83—
203.
68. Сиратори М., Миеси Т., МацуситаХ. Вычислитель-
Вычислительная механика разрушения.— М.: Мир, 1986.— 336 с.
69.	Слепян Л. И. Механика трещин.—Л.: Судостроение. 1981.—
295 с.
70.	Солнцев С. С, Морозов Е. М. Разрушение стекла.—
М.: Машиностроение, 1978.— 152 с.
71.	С т е п а н о в А. В„ Основы практической прочности кристал-
кристаллов.— М.: Наука, 1974.— 132 с.
72.	Т о м п с о н Р. Физика разрушения / Атомистика разруше-
разрушения.-М.: Мир, 1987.-С. 104-144.
73.	Ф и н к е л ь В. М. Портрет трещины,— М.: Металлургия,
1989.- 192 с.
74.	Фролов К. В. Методы совершенствования машин и совре-
современные проблемы машиностроения.— М.: Машиностроение,
1984.- 224 с.
75.	Хеллан К. Введение в механику разрушения.—"М.: Мир,
1988.— 364 с.
76.	X и л л Р. Об определяющих неравенствах для простых мате-
материалов // Механика.— 1969.—№ 4 A16)—С. 94—118.
77.	Ч е р е п а и о в Г. П. Механика хрупкого разрушения,— М.:
Наука, 1974.— 640 с.
78.	Черных К. Ф. Линейная теория оболочек.—Л.: Изд-во Ле-
нингр. ун-та, 1964.— Ч. 2.— 395 с.
79.	Черных К. Ф. Определяющие неравенства >пругих тел /
Механика сплошпой среды и родственные проблемы анализа
(к 80-летию акад. Н. И. Мусхелишвили).—М.: Наука, 1972.—
С. 623-633.
80.	Черных К. Ф. Большие деформации упругого тела / Ме-
Механика деформируемых тел и конструкций.— М.: Машино-
Машиностроение, 1975.— С. 508—516.
81.	Черных К. Ф. Нелинейная теория упругости в машино-
машиностроительных расчетах.—Л.: Машиностроение, 1986.—336 с,
82.	Черных К. Ф. Нелинейно-упругое (плоское') напряженное
состояние / Вестник Ленингр. ун-та. Сер. 1,— 1986.— Вып. 3.—
С. 72-77.

СПИСОК ЛИТЕРАТУРЫ	283
83.	Ч с р н ы х К. Ф. О построении нелинейной теории хрупкого
разрушения / Вестн. Ленингр. ун-та. Сер. 1,— 1987.— Вып. 1.—
С. 83-88.
84.	Черных К. Ф. Введение в анизотропную упругость.—- М.:
Наука, 1988.- 190 с.
85.	Черны х К. Ф. О необходимости учета геометрической не-
нелинейности в проблеме хрупкого разрушения / ДАН АН
СССР.— 1989.— Т. 306, № 6.— С. 1336—1338.
86.	Ч е р н ы х К. Ф., Алешков Ю. 3., П о н я т о в с к и й В. В.,
Ш а м и на В. А. Введение в механику сплошных сред.— Л.:
Изд-во Ленингр. ун-та, 1984.— 280 с.
87.	Ч е р н ы х К. Ф., М и л я к о в а Л. В. Общая линейная тео-
теория тонкослойных резино-металлических элементов II МТТ.—
1986.-№ З.-С. 110-120.
88.	Ч е р н ы х К. Ф., Шубина И. М. Законы упругости для
изотропных материалов (феноменологический подход) / Меха-
Механика эластомеров.— Краснодар: Изд-во Краснодар, политехи,
ин-та, 1977.- Т. 1.— С. 54-65.
89.	Черных К. Ф., Ш у б и и а И. М. Об учете сжимаемости ре-
резин / Механика эластомеров.— Краснодар:* Изд-во Краснодар,
политехи, ин-та, 1978.— Т. 2.— С. 56—62.
90.	Шубников А. В. Симметрия и антисимметрия конечных
фигур.— М.: Изд-во АН СССР, 1951.— 253 с.
91.	Эйрих Ф. Р., Смит Т. Л. Молекулярно-механические ас-
аспекты изотермического разрушения эластомеров / Разруше-
Разрушение.- М.: Мир, 1975.- Т. 7, ч. 2.- С. 104-301.
92.	Э р д о г а н Ф. Теория распространения трещин / Разруше-
Разрушение.- М.: Мир, 1975.- Т. 2.- С. 521-615.
93.	Я р е м а С. Я., И в а н и ц к а я Г. С. Предельное равновесие
и развитие косых трещин. Обзор критериев // Физ.-хим. меха-
механика материалов.— 1986. -№ 1.—С. 45—57.
94.	Ярема С. Я., Иваницкая Г. С, Майстренко А. Л..
Зборомирский А. И. Развитие трещины в твердом спла-
сплаве при комбинированной деформации I и II видов Ц Пробл.
прочности.—1984.—№ 8.— С. 51—56.
95.	Adams L. G., Gibson R. E. The Compressibility of Rub-
Rubber II T. Washington: Acad. Sci.— 1930.- V. 20, N 12.- P. 213—
223.
96.	A w a j i H., Sato S. Combined Mode Fructure Toughness Mea-
Measurement by the Disk Test / Trans. ASME. Ser. J.— 1978.—
V. 100, N 9.- P. 175-182.
97.	Bueckner H. F. // Trans. ASME.- 1958.- V. 80.—P. 1225-
1229.
98.	Dug dale D. S. Yielding of Steel Sheets, Containing Slits //
J. Mech. and Phys. Solids.- I960.- V. 8, N 2.-P. 100-108.
99.	Erdogan F., Sih G. С // J. Basic Eng.—1963L—V. 85.-
P. 519-527.
100.	E shelby J. D. / Solid State Phys.-1956.—V. 3.-P. 79-
144.
101.	Gent A. N., Lindley P. B. / Proc. Roy. Soc. (London).
Ser. A.- 1959.- V. 249. — P. 195.
102.	Griffith A. A. The Phenomena of Rupture and Flow in So-
Solids / Phil. Trans. R. Soc. (London).-1921,-A 221.-P. 163-
198.

284	список литературы
103.	Griffith A. A. The Theory of Rupture ff Proc. 1st Int. Cong.
Appl. Mech. (Delft).—1925.—P. 55—63.
104.	Inglis С. Е. Stresses in a Plate Due to Cracks and Sharp
Corners / Trans. Inst. Nav. Archit.—1913.—55.—P. 219—241.
105.	lrwin G. H. / J. Appl. Mech.— 1957.— V. 24.—P. 361—364.
106.	lrwin G. R. Fructure // S. Fltigge (ed) Encyclopedia of Phy-
Physics.—Berlin: Springer.- 1958.— V. 6.—P. 551—590.
107.	I r w in G. R. / Fructure Mechanics, Proc. 1st Symp. Nev.
Struct. Mech. A358), I960.—New York: Pergamon Press.—
p 557	5Q2
108.	Kelly A., Tyson W., Cot re 11 A. Dictile and Brittle
Crystals /I Philos. Mag.- 1967.— V. 15.—P. 567.
109.	Liu A. F. Crack Growth and Failure of Aluminium Plate un-
under In-Plane Shear / AIAA 73-253, 11th Aerospace Sciences
Meeting, D. С Jan., 1973.
110.	Marandet В., Sanz С // Flaw Growth and Fructure,
1979.—ASTM STP 631.— ?. 72-95.
111.	О г о w a n E. / Z. Krist.— 1934.- A 89.- P. 327.
112.	Or о wan E. // Rep. Prog. Phys.- 1949.- V. 12.-P. 185.
113.	P a I a n i s w a m у К., К n a u s s W. G. On the Problem of
Crack Extention in Brittle Solids Under General Louding. Mecha-
Mechanics Today/Ed. S. Nemat-Nasser.— New York: Pergamon Press,
1978.—V. 4.—P. 87—148.
114.	Pook L. P. / J. of Engineering Fructure Mechanics.— 1971.—
V. 3.-P. 205-218.
115.	Rice J. R. / J. Appl. Mech.-1968.-V. 35.-P. 379-386.
116.	R i v 1 i n R. S., Thomas A. G. // J. Polymer Sci.— 1953.—
V. 10.— P. 291.
117.	Saunders J. L. / J. Appl. Mech.-I960.-V. 27.-P. 352-
353
118.	Shah R. С Fruclure Under Combined Modes in 4340 Steel.
Fructure Analysis. / ASTM STP 560, American Society for Tes-
Testing and Materials, 1974.— P. 29—52.
119.	Sih G. C, Cha В. С A Fructure Criterion for Three Dementio-
nal Crack Problem. / Eng. Fract. Mech.— 1974.— V. 6, N 4.—
P. 699-723.
120.	Theocaris P. S., Andrianopouloz N. P. A Modified
Strain-Energy Density Criterion Applied to Crack Propagation. /
Trans ASME, Ser. E., J. Appl. Mech.- 1982.— V. 49, N 1.—
P. 81-86.
121.	Unpublished Data.— Boeing Aeraspaoe Co.— Seattle, Washing-
Washington.
122.	Volterra V. I/ Ann. Ecole Normale Sup., Paris C).— 1907.—
V. 24.— P. 400.
123.	W e i h а г d t K. t)ber da's Spalten- und Zerressen Elastischer
Korner. / Zeitschr. fur Math, und Phys— 1907.— Bd. 55, N 1/2.—
S. 60—103.
124.	Williams J. G., Ewing P. D. Fructure Under Complex
Stress. The Angled Crack Problem. / Jnt. J. Fruct. Mech —
1972.- V. 8, N 4.— P. 445-446.
1?5. Wilson W. K. On Combined Mode Fructure Mechanics / Re-
Research Report 69-1E7 FMECH-R1, Westinghouse Research Labo-
Laboratories, June, 1969.

ОГЛАВЛЕНИЕ
Предисловие		3
Введение		5
Глава 1. Основные зависимости нелинейной теории упру-
упругости 		9
§ 1. О тензорах второго ранга		9
§ 2. Каноническое представление тензора ....	12
§ 3. Классические тензорные функции .	15
§ 4. Полярное разложение тензора		18
§ 5. Движение и деформация материальной частицы	20
§ 6. Основные деформационные зависимости	24
§ 7. Напряжения. Уравнения движения ....	21
§ 8. Работа напряжений		30
§ 9. Сопряженные по Хиллу (энергетические) пары тен-
тензоров 		31
§ 10. Закон упругости		34
§ 11. Приведение к комплексным координатам и компо-
компонентам 		36
§ 12. Деформационные соотношения в комплексной
записи		39
§ 13. Динамические соотношения. Комплексная запись
закона упругости		41
§ 14. Использование конформного отображения . .	45
§ 15. Комплексная фсГрма интегральных тождеств . .	47
§ 16. Основные варианты закона упругости изотропного
несжимаемого материала	 .	48
§ 17. Сжимаемый, малосжимаемый и стандартный ма-
материалы 		51
Глава 2. Нелинейная плоская задача		54
§ 1. Обобщенная плоская деформация		54
§ 2. Плоское напряженное состояние тонкой пластины	59
§ 3. Основная краевая задача		62
§ 4. Неограниченно-линейный материал .....	67
§ 5. Однородная деформация		69
§ 6. Плоскость с эллиптическим отверстием ...	71
§ 7. Плоскость с прямолинейным разрезом ....	73
§ 8. Плоскость с жестким включением		78
§ 9. Плоскость с отверстием в виде симметричной лунки	80
§ 10. О нелинейной асимптотике на концах прямолиней-
прямолинейного разреза		85

286	оглавление
§ 11. Асимптотика простейшего вида		88
§ 12. Вариационные уравнения		90
§ 13. Деформация бесконечного клина		97
§ 14. Малосжимаемый материал		100
Г л а в а 3. Линейная плоская задача		103
§ 1. Линеаризация плоской задачи		103
§ 2. Использование функций комплексной переменной	108
§ 3. Плоскость с прямолинейным разрезом . . . .	111
§ 4. Предварительно напряженный материал . . .	117
§ 5. Частные случаи		119
Глава 4. Хрупкое разрушение (линейная теория) . .	123
§ 1. Основные понятия линейной теории трещин . .	124
§ 2. Энергетический критерий Гриффитса . . . .	126
§ 3. Локальные силовые критерии разрушения ...	131
§ 4. Деформационный критерий Леонова — Панасюка —
Дагдейла		134
§ 5. Локальный энергетический критерий . . . .	139
§ 6. Концепция Новожилова		142
§ 7. Концепция Новожилова (продолжение) . . .	147
Глава 5. Влияние геометрической нелинейности . . .	153
§ 1. Задача о прямолинейном разрезе		153
§ 2. Условия хрупкого разрушения		156
§ 3. Уточнение дискретного критерия нормального от-
отрыва 		157
§ 4. Нелинейный подход к задаче Леонова — Панасю-
Панасюка — Новожилова		158
§ 5. Страгивание трещины смешанного типа (линейный
подход)		164
§ 6. Страгивание трещины смешанного типа (геометри-
(геометрически нелинейный подход)		168
Глава 6. Кристаллические решетки. Идеальная прочность	1?5
§ 1. Соображения симметрии. Кристаллографические
классы . 		175
§ 2. Идеальные кристаллические решетки . . . .178
§ 3. Узловые прямые и плоскости кристаллической ре-
решетки 		183
§ 4. Идеальная прочность твердых тел (эксперименталь-
(экспериментальный подход) .		188
§ 5. Идеальная прочность (теоретические подходы) .	190
Глава 7. Дислокации Вольтерра		195
§ 1. Дислокации Вольтерра в линейной теории упругости	195
§ 2. Нелинейная клиновая дисклинация		203
§ 3. Случай малосжимаемого материала ....	205
S 4. Случай стандартного материала		210
5 5. Заключение		214

ОГЛЛВЛЕЙИЁ	28?
Глава 8. Хрупкое и квазихрупкое разрушение полимеро!
и эластомеров .			216
§ 1. Строение полимеров		217
§ 2. Термомеханические свойства полимеров. Эласто-
Эластомеры 		221
§ 3. Хрупкое и квазихрупкое разрушение застеклован-
ных полимеров		226
§ 4. Особенности разрушения эластомеров ....	235
Глава 9. Нелинейная антиплоская задача ....	242
§ 1. Основные геометрические и деформационные зави-
зависимости 		242
§ 2. Использование тензора деформации Коши — Лаг-
ранжа		243
§ 3. Несжимаемый материал «типа неогуковского» . .	245
§ 4. Неогуковский материал		246
§ 5. Плоскость с отверстием		248
§ 6. Плоскость с прямолинейным разрезом ....	249
§ 7. Трещина продольного сдвига		251
Глава 10. Основные проблемы и перспективы построения
общей нелинейной теории трещин		253
§ 1. Об «истинных» мерах напряжений и деформаций	253
§ 2. Особенности напряженно-деформированного состоя-
состояния в сингулярных точках	 .	257
§ 3. Перспективы построения общей нелинейной теории
трещин		258
Приложение. Основные сведения из теории функций
комплексной переменной		261
§ 1. Понятия и основные свойства функций комплексной
переменной		261
§ 2. Конформное отображение		267
§ 3. Интегралы типа Коши ........	273
§ 4. Метод расчленения граничных условий ....	277
Список литературы .			279