Текст
Д.Е МЕРКИН
ВВЕДЕНИЕ В МЕХАНИКУ ГИБКОЙ НИТИ
<0
ш,
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1980
22.23 М 52
УДК 531
Меркип Д. Р. Введение в механику гибкой нити.—М.: Наука. Главная редакция физико-математической литературы, 1980.— 240 с.
Теория абсолютно гибкой нити широко используется в различных научных исследованиях, при расчете и конструировании инженерных устройств, машин, технологических процессов и т. п.
Книга, рассматриваемая как раздел теоретической механики, посвящена изложению тех вопросов теории абсолютно гибкой нити, которые наиболее близки к инженерным задачам. В связи с этим особое внимание обращено на выбор рациональных форм дифференциальных уравнений равновесия или движения нити, построение граничных условий, сравнение и оценку различных методов. Почти все примеры доведены до численного ответа, расчетных таблиц или математической модели, легко реализуемой на ЭВМ.
Книга не требует специальной математической подготовки — небольшие сведения, не излагаемые обычно во втузах, приведены в двух очень кратких приложениях. Рассчитана книга на студентов, преподавателей, научных работников и инженеров, для которых теория гибкой пити и ее приложения представляют научный или производственный интерес.
Табл. 6, илл. 65, библ. 30
Давид Рахмильевич Меркип ВВЕДЕНИЕ В МЕХАНИКУ ГИБКОЙ М., 1980 г., 240 стр. с илл.
Редактор А. Б. Елагин
Техн. редактор Я. В. Кошелева
Корректоры О. А. Сигал, Н* Д. Дорохова
ИБ № 11358
Сдано в набор 19 02 80 Подписано к печати 07.08 80. Т-14665. Бумага 84x108732, тип. JsTb 1. Обыкновенная гранитура. Высокая печать. Условн. печ. л. 12,6. Уч -изд. л. 12,06. Тираж 2500 экз. Заказ Кв 72. Цена книги 2 р 10 к.
Издательство «Наука»
Главная редакция физико-математической литературы 117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука», 630077, Новосибирск, 77, Станиславского, 25.
Издательство «Наука,>. Главная редакция физико-математической литературы, 1980
хк 20^02 — 108
053(02)-80 ' 1^2~80- 1703020000
ОГЛАВЛЕНИЕ
ЧАСТЬ 1
основы статики' нити 7
Глава I. Дифференциальные уравнения равновесия нити 7
§ 1.1. Основные определения 7
§ 1.2. Дифференциальные уравнения равновесия нити . 14
§ 1.3. Естественные уравнения равновесия нити ... 22
§ 1.4. Потенциальные силы . 26
§ 1.5. Уравнения равновесия нити в криволинейпых
(обобщенных) координатах 29
§ 1.6. Канонические уравнения равповесия нити . . 35
§ 1.7. Связь задачи о форме равновесия нити с задачей о
движении материальной точки 39
§ 1.8. Интегральные методы . . 41
Глава II. Цепная линия . . 45
§ 2.1. Цепная линия 45
§ 2.2. Неоднородная цепная линия 56
§ 2.3. Влияние упругой деформации ...... 58
Глава III. Равновесие тяжелых нитей с малой стрелой провисания . 67
§ 3.1. Уравнение равновесия 67
§ 3.2. Влияние дополнительной равномерно распределенной нагрузки 74
§ 3.3. Влияние сосредоточенной силы 81
§ 3.4. Влияние линейных деформаций нити .... 86
Глава IV. Нити равного сопротивления ..... 93
§ 4.1. Постановка задачи 93
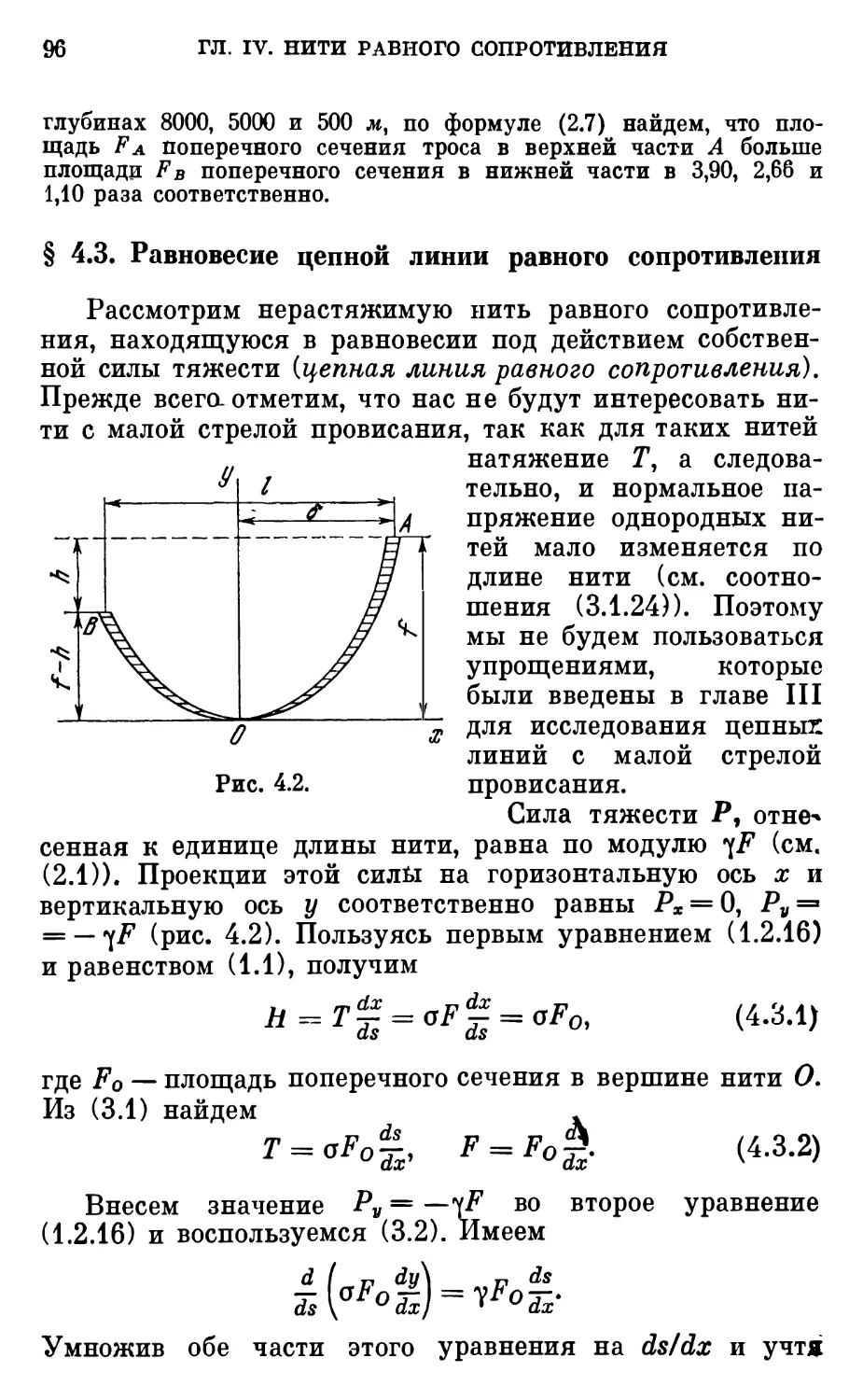
§ 4.2. Равновесие тяжелой вертикально подвешенной нити равного сопротивления 94
§ 4.3. Равновесие цепной линии равного сопротивления 96
Глава V. Равновесие тяжелых нитей, находящихся в установившемся потоке 101
§ 5.1. Силыг действующие на нить 101
§ 5.2. Дифференциальные уравнения равновесия нити . 1^7
§ 5.3, Граничные условия . . 112
4
ОГЛАВЛЕНИЕ
§ 5.4. Задача о равновесии троса, удерживающего неукрепленное тело в однородном потоке . . . . 116
§ 5.5. Влияние силы давления ветра на цепную линию . 124
Г л а а в VI. Равновесие нити (цилиндрической гибкой оболочки), находящейся под действием гидростатической нагрузки 126
§ 6.1. Постановка задачи 126
§ 6.2. Форма поперечного сечения плавающего пучка и
натяжение в обвязке 128
§ 6.3. Методы решения граничных уравпепий и примеры
расчета пучка 135
§ 6.4. Расчет пучка, лежащего на суше 137
§ 6.5. Влияние сил внутреннего трения 140
Глава VII. Равновесие нити на поверхности' .... 146
§ 7.1. Равновесие нити на гладкой поверхности . . . 146
§ 7.2. Равновесие нити на поверхности при наличии трения 151
ЧАСТЬ 2
ОСНОВЫ ДИНАМИКИ НИТИ 159
Глава VIII. Дифференциальные уравнения движения нити 159 § 8.1. Дифференциальные уравнения движения нити в
декартовых координатах 159
§ 8.2. Естественные уравнения движения нити . . . 161
Глава IX. Контурное движение нити 170
§ 9.1. Основные определения и уравнения движения . 170
§ 9.2. Кажущийся покой 176
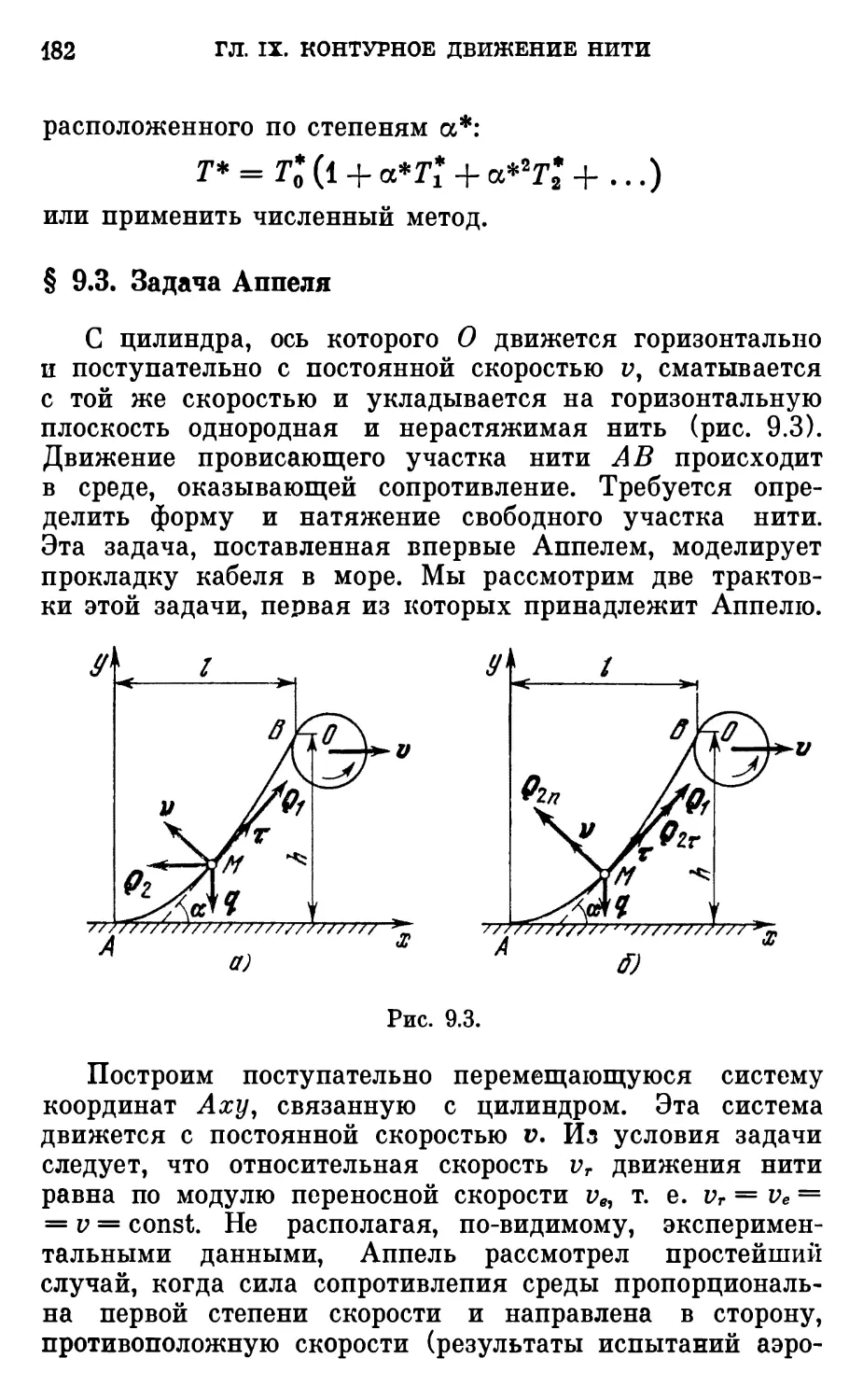
§ 9.3. Задача Аппеля 182
§ 9.4. Относительное равновесие вращающейся пити . 186
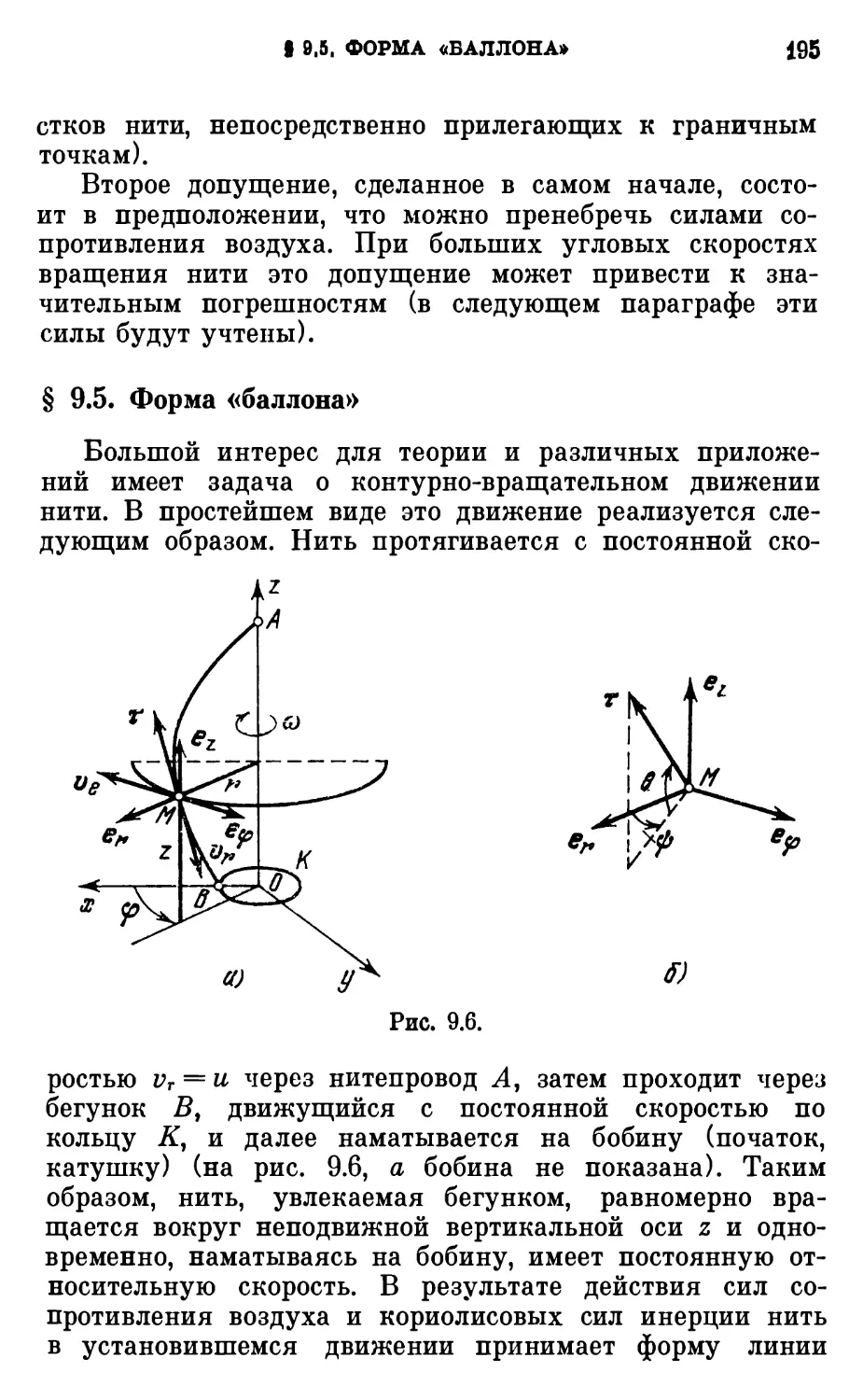
§ 9.5. Форма «баллона» 195
Глава X. Свободные колебания нитей ...... 204
§ 10.1. Введение 204
§ 10.2. Поперечные колебания сильно натянутой нити
(струны) 204
§ 10.3. Колебания однородной нерастяжимой нити с грузом на конце 214
§ 10.4. Колебания нерастяжимой цепной линии . . . 225
Приложение 1. Гиперболические функции . . . 237
Прил о ж е н и е 2. Фупкции Бесселя 238
Литература 239
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга принадлежит к серии пособий, выходящих в издательстве «Наука» в качестве дополнения к «Курсу теоретической механики» Н. В. Бутенина, Я. Л. Лунца и Д. Р. Меркина. Издание этих пособий связано с тем, что учащиеся некоторых вузов, преподаватели, инженеры, научные сотрудники НИИ часто нуждаются в более подробном ознакомлении с рядом проблем механики, чем это можно сделать в основном курсе. Книги, входящие в эту серию, посвящены аналитической механике, теории устойчивости движения, теории гироскопов, теории колебаний, теории гибкой нити, теории удара; в будущем этот перечень предполагается продолжить.
Современная теория гибкой нити представляет широко разветвленную дисциплину, охватывающую самые различные аспекты этой науки. В Советском Союзе и в других странах опубликовано много работ, в которых теория гибкой нити излагается с различных точек зрения, различной полнотой и строгостью. Некоторые из них представляют монографии, посвященные узкой проблеме, часть работ охватывает очень широкий круг вопросов, главнь1м образом, теоретического характера; теории нити посвящены и отдельные главы в курсах теоретической механики.
Естественно, что включить в небольшую по объему книгу все вопросы современной теории гибкой нити не представляется возможным. Поэтому предлагаемая книга, рассматриваемая как раздел теоретической механики, содержит лишь некоторые вопросы теории абсолютно гибкой нити, которые наиболее близки к инженерным задачам. В связи с этим в книге значительное место отведено не только теории, но и ее приложениям. Особое внимание обращено на выбор рациональной формы
6
ПРЕДИСЛОВИЕ
дифференциальных уравнений равновесия или движения нити, определение граничных условий, сравнение и оценку различных методов. Почти все примеры доведены до численного ответа, расчетных таблиц или математической модели, легко реализуемой на ЭВМ. В конце книги даны два очень кратких приложения, содержащих определения и сводку основных формул гиперболических функций и функций Бесселя нулевого порядка.
Учитывая, что в [1, 13, 16, 19, 22] содержится свыше пятисот различных библиографических ссылок и в той или иной форме дано изложение истории развития механики гибкой нити, мы ограничились очень кратким списком литературы, который носит, как правило, справочный характер и включает некоторые работы (далеко не все), опубликованные в последние годы и имеющие непосредственное отношение к содержанию данной книги.
Книга рассчитана на студентов, преподавателей, научных работников и инженеров, для которых теория абсолютно гибкой нити и ее приложения представляют научный или производственный интерес.
Проф. В. А. Светлицкий взял на себя труд прочитать рукопись и сделал ряд очень полезных замечаний, позволивших улучшить текст книги. Все вычисления на ЭВМ выполнены И. Н. Лопыревым (глава V) и В. М. Меркиным (главы II и VI). Всем этим лицам автор приносит свою искреннюю благодарность.
Часть 1 Основы статики нити
ГЛАВА I
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
§ 1.1. Основные определения
В механике под нитью понимается материальная система одного измерения, которая под действием приложенных сил может принять форму любой геометрической линии. Нить, не оказывающая сопротивления изгибу и кручению, называется идеальной или абсолютно гибкой нитью. Идеальная нить может быть растяжимой или нерастяжимой (крайняя абстракция). В дальнейшем, при отсутствии специального указания, под термином «гибкая нить» или просто шить» будем понимать идеальную нерастяжимую или растяжимую нить.
При расчете нити на прочность, вычислении поверхностных сил, действующих на нить, а также в ряде других случаев необходимо учитывать поперечные размеры нити. Поэтому, говоря об одномерности нити, мы, конечно, имеем в виду, что поперечные размеры малы по сравнению с длиной и что они не нарушают перечисленных выше свойств идеальной нити.
Модель идеальной нити представляет некоторую абстракцию, однако во многих случаях пряжа и нитки (в процессе их изготовления), тросы, цепи и канаты вполне удовлетворительно отвечают этой модели. К этой же модели сводятся иногда плоские задачи механики некоторых лент и оболочек. Поэтому теория идеальной нити имеет большое прикладное значение *).
Пусть нить А В под действием приложенных к ней сил приняла некоторую равновесную конфигурацию.
*) Нити, в которых учитывается сопротивление на изгиб и кручение, рассматриваются в монографии В. А. Светлицкого [22].
8 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТЙ
Положение каждой точки М растянутой или нерастяжимой нити будем определять дуговой координатой s, отсчитываемой от фиксированной точки нити, например точки А (рис. 1.1). Выделим на нити какой-нибудь ее отрезок ММ' длиной A s и массой А т. Плотностью растянутой нити ц в точке М (иногда говорят линейной плотностью) называется предел отношения Атп к As
Рис. 1.1.
Рис. 1.2.
при условии, что точка М' стремится по нити к точке М:
т A m u = lim -г—.
^ As->-0 AS
В общем случае линейная плотность нити зависит от выбранной точки, т. е.
\i =
Если до растяжения плотность нити \iq была одинакова во всех точках, то нить называется однородной, в противном случае — неоднородной. При данном определении линейной плотности нити ее неоднородность может быть вызвана неоднородностью материала или различной площадью поперечного сечения нити.
Пусть нить А В находится в равновесии под действием распределенных сил. Сделаем в точке М нити мысленный разрез и рассмотрим силу Т, с которой часть нити, расположенная в направлении положительного отсчета дуговой координаты s (на рис. 1.2 правая часть нити) действует на другую (левую) часть нити. Очевидно, что эта сила, называемая натяжением нити, направлена по общей касательной к нити в точке М (в § 1.2 это утверждение будет доказано). Естественно, что левая часть нити действует на правую часть с та¬
§ 1 1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
9
кой же по модулю, но направленной в противоположную сторону силой, т. е. силой —Т.
В каждой точке нити имеется свое натяжение Т. Поэтому при равновесии натяжение нити Т будет функцией дуговой координаты
T = T(s).
Если ввести единичный касательный вектор т, то будем иметь *)
Т = Тт, (1.1.1)
где Т — модуль натяжения нити.
Нормальное напряжение пити а определяется, как обычно, равенством
ог = -£. (1.1.2)
Здесь F — площадь поперечного сечения нити.
Пусть до растяжения длина элемента нити была dso, а после растяжения она сделалась равной ds. Так как растяжение нити зависит от нормального напряжения, то отношение ds/ds0 представляет некоторую функцию а
^=/(0)-
Для однородной нити можно считать, что это отношение зависит только от натяжения Т
■^ = /(Л- (1-1-3)
Задавая функцию /, мы получим соответствующий закон растяжения, например упругое, пластическое растяжение и т. п. Остановимся более подробно на упругом растяжении однородной нити по закону Гука, когда
выполняется равенство
*) Формулы пумеруются тремя числами: первое число означает номер главы, второе — номер параграфа в данной главе, третье — номер формулы в данном параграфе. При ссылках на формулы данной главы приводятся только два последних числа; при ссылках на формулы из другой главы приводятся все три числа. Рисунки нумеруются двумя числами: первое число означает номер главы, второе — номер рисунка в этой главе.
10 гл. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
где Е* — модуль упругости нити *). Пользуясь равенством (1.3), получим
Т = EHf — 1); (1.1.5)
отсюда
f(T) = 1 + а*Т, (1.1.6)
где а* = 1/Е* — удельное относительное удлинение нити. Если нить нерастяжима, то / = 1, а* = 0, Е* = Заметим, что модуль упругости нити Е* имеет размерность обычной силы: в Международной системе фи¬
зических единиц [Е*] =;*, в технической системе [£*Г = = кГ; соответственно [a*]=w”1 и кГ~1. Очевидно, что
E* = EF, (1.1.7)
где Е — модуль упругости материала нити ([Е] = н/м2 или кГ/см2).
Пусть d0 и d — диаметры нити до и после растяжения. Тогда относительное изменение диаметра нити определится равенством
— d а
р — _0 _ А
О о
Считая, что нить изотропна и что растяжение подчинено закону Гука, будем иметь
* 8 ^s ^so
LI* = , 8=< -j
* е1 *0
где jti* — коэффициент Пуассона. Пользуясь равенствами (1.4) и (1.6), найдем значение диаметра нити после растяжения
d=(l-a*|Li*r)do. (1.1.8)
Как правило, величина а*|и*Г ничтожно мала по сравнению с единицей. Поэтому изменением диаметра нити при ее растяжении обычно пренебрегают (по крайней мере для стальных тросов) и полагают, что для растянутого троса d « do.
Рассмотрим нить, на которую действует распределенные по ее длине силы, например силы тяжести, силы
*) В прикладной теории упругости величину Е* называют «жесткостью на растяжение».
§ i 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
11
давления ветра и т. п. Главный вектор сил, действующих на элемент нити М'М", обозначим через AG и будем считать, что он приложен к точке Л/, находящейся
между М' и М" (рис. 1.3). Силой, отнесенной к едини¬
це длины нити, или интенсивностью распределенных сил называется выражение
Р = lim (1.1.9)
Дв-»о л* '
Отсюда с точностью до членов высшего порядка относительно Л s получим
AG = PAs. (1.1.10)
Размерность силы, отнесенной к единице длины нити, отличается от размерности обычной силы: в системе СИ она равна н/м, в технической системе — кГ/м.
Распределенные силы, действующие на нить, можно разбить на массовые и поверхностные. К первым относятся силы, зависящие от массы нити, например силы тяжести и силы инерции.
Поверхностные силы, например силы давления 'набега- Рлс
ющего потока, от массы нити не зависят (они могут зависеть от площади продольного диаметрального сечения нити, т. е. от ее диаметра, скорости набегающего потока и других факторов).
Остановимся более подробно на массовых силах. Если через Р обозначить силу, отнесенную к единице длины, то сила Р*, отнесенная к единице массы нити, определится равенством
Р = (аР*. (1.1.11)
В частности, для силы тяжести будем иметь
Р = Я = №, (1.1.12)
гДв ё— ускорение силы тяжести, a q-— сила тяжести, отнесенпая к единице длины нити. Для однородной нерастянутой нити сила q численно равна весу едипицы длины нити.
12 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Так как масса нити при растяжении не изменяется, то будем иметь
[ids = iio ^So-
Отсюда, пользуясь равенством (1.3), получим
^=-^=/(Г), (1.1.13)
ИЛИ
, = ^ (1.1.14)
Таким образом, массовые силы, отнесенные к единице длины растяжимой нити, можно представить равенством
Р = ~ПтТР*' (1ЛЛ5)
Поверхностные силы, отнесенные к единице длины, обычно пропорциональны диаметру d нити
P=Xd,
где коэффициент пропорциональности X зависит от разных факторов (например, от скорости потока, плотности среды и т. п.). Как уже отмечалось, в подавляющем большинстве случаев изменением диаметра растяжимой нити можно пренебречь, и тогда число d в последней формуле следует считать постоянным. Для растяжимых нитей, модуль упругости которых очень мал, возможен случай, когда изменение диаметра нити нужно учесть. Тогда следует воспользоваться формулой (1.8).
В общем случае сила Р, отнесенная к единице длины нити, зависит от дуговой координаты s точки М, положения последней в пространстве, направления касательной или нормали к нити и натяжения Т. Действительно, плотность и, следовательно, сила тяжести неоднородной нити зависят от положения точки М на нити, т. е. от ее дуговой координаты s. Сила гидростатического давления направлена по нормали к нити и модуль ее пропорционален высоте уровня, т. е. эта сила зависит от координат точки. Из формулы (1.15) следует, что в аналитическое выражение силы Р, отнесенной к единице длины растянутой нити, явно входит модуль натяже-
6 1.1. ОСЙОВЙЫЁ ОПРЕДЕЛЕНИЯ
13
ыия Т. Поэтому, если рассматривать нить в прямоугольной системе координат Oxyz, то в общем случае будем иметь
P = P(s,z. г) (1.1.16)
или в векторных обозначениях
р = р(з,г,^,т}, (1.1.17)
где г — радиус-вектор точки М и dr Ids = т— единичный касательный вектор.
Помимо распределенных сил на нить могут действовать конечные силы, приложенные к одной или нескольким точкам нити. Такие силы называются сосредоточенными. Например, сила тяжести вагонетки, находящейся на канатной дороге, представляет сосредоточенную силу. На участках действия распределенных сил нить является гладкой, т. е. в каждой ее точке имеется вполне определенная непрерывно изменяющаяся касательная, а точки приложения сосредоточенных сил являются угловыми. На рис. 1.4 участки нити AM и MB находятся
Рис. 1.4.
Рис. 1.5.
под действием распределенных сил, а в угловой точке М приложена сосредоточенная сила G. В дальнейшем для простоты изложения распределенные силы, отнесенные к единице длины нити, будем называть просто силами, а конечные силы — сосредоточенными. Отметим также, что нить может быть нагружена и распределенными моментами (в настоящей книге они не рассматриваются).
Для полного решения задачи на равновесие нити, кроме активных сил (распределенных и сосредоточенных) и закона растяжения нити нужно определить еще граничные условия. Если концы нити А и В не закреп¬
14 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
лены, то к ним необходимо приложить конечные силы На и Нв, причем они должны удовлетворять условиям (см. рис. 1.2 и 1.5)
Ra = -TAi Rb = Tb. (1.1.18)
Если же концы нити закреплены, то эти равенства могут служить для определения реакций точек закрепления. Чаще всего встречаются нити с двумя закрепленными концами, реже — нити с одним закрепленным и одним свободным концами, причем задается или можно определить из дополнительной информации значение силы, приложенной к свободному концу (положение его, как правило, неизвестно). Встречаются и более сложные граничные условия. Многие из них будут рассмотрены при изучении конкретных задач. Кроме непосредственных условий на границах, должны быть заданы геометрические (один или несколько) лараметры, например длина нити, стрела провисания и т. п. Эти элементы мы будем условно относить также к граничным условиям.
Теперь можно сформулировать основную задачу о равновесии идеальной нити: даны действующие на нить силы (распределенные и сосредоточенные), закон растяжения нити и найдены в необходимом числе граничные условия. Требуется определить форму равновесия нити, натяжение ее в любой точке и изменение длины (для растяжимых нитей).
В заключение отметим, что при решении конкретных задач основные трудности возникают, как правило, при интегрировании дифференциальных уравнений равновесия нити. Однако следует иметь в виду, что во многих случаях уравнения равновесия нити интегрируются сравнительно легко, а наибольшие затруднения появляются при построении решения, удовлетворяющего граничным условиям.
§ 1.2. Дифференциальные уравнения равновесия нити
Рассмотрим гибкую нить, находящуюся в равновесии под действием распределенных сил. Возьмем на нити произвольную точку М и достаточно близкую к ней точку Л/'; пусть точке М соответствует дуговая координа¬
§ 1 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 15
та s, а точке М' дуговая координата s + A s. Мысленно выделим отрезок нити ММ' действующие на него (рис.
1.6). Прежде всего, на отрезок нити ММ' действуют распределенные силы, главный вектор которых AG равен, согласно (1.10), PAs.
Кроме того, в точке М действует сила —Т (s), а в точке М' — сила Т (s + As). Так как участок нити ММ' по условию находится в равновесии, то геометрическая сумма всех приложенных к нему сил должна равняться нулю
T{s + As)-T(s) + PAs = 0 или, деля на As и учитывая, что Т (s -f As) — Т (.ч) = ДТ,
-тг + р = 0-
As
Переходя к пределу в предположении, что точка М' стремится по кривой равновесия к точке М, получим
-f + P-0. (1.2.1)
Здесь и в дальнейшем под Р понимается, копечно,
равнодействующая всех распределенных сил, отнесенных к единице длины нити и приложенных к точке М.
Векторное дифференциальное уравнение (2.1) равновесия идеальной нити, справедливое как для нерастяжимой, так и для растяжимой нити, является основным, и из него могут быть получены дифференциальные уравнения равновесия нити в других формах.
Для вывода уравнения (2.1) мы не делали никаких предположений о направлении вектора натяжения Т. Докажем, что натяжение нити Т направлено по касательной. Для этого составим уравнения моментов. Обозначим через г(5), г(s + Д5) и г(s + в*Д$),где 0^6^ 1, радиусы-векторы точек Л/, М' и N соответственно (рис. 1.6). Тогда уравнение моментов примет вид
г {$ As)xT(s -J- As) —г {s)xT(s)-|-r (5 + Q-As)xPA$=Q,
и рассмотрим все силы,
-T(S)
Рис. 1 6.
16 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Разность первых двух членов равна А(гхТ). Поэтому, разделив последнее равенство на As, получим
Д(д*Г) +r(s + e-As)xP = 0.
Переходя к пределу при As -*■ 0, найдем
±{гхТ) + гхР = 0. (1.2.2)
Дифференцируя произведение, будем иметь
£хГ + гх£ + гхР-о,
или, группируя члены,
txT + rx(f- + P) = 0,
где т = dr Ids — орт касательной.
Принимая во внимание уравнение (2.1), получим
т х Т = 0.
Из этого равенства следует, что векторы т и Т параллельны, а так как они имеют общую точку М, то вектор натяжения нити Т направлен по касательной (в § 1.1 это было принято a priori).
Если считать это обстоятельство известным, то дифференциальные уравнения (2.1) и (2.2) эквивалентны. Мы будем, как правило, пользоваться уравнением (2.1), как более простым.
Пусть нить ориентирована относительно прямоугольной декартовой системы координат Oxyz. Возьмем на нити произвольную точку М с координатами х, у, z и проведем в этой точке касательную к нити. Как известно, направляющие косинусы касательной (проекции вектора х) определяются равенствами
dx о dy dz ,л 0v
cosa=dT> cosP=dT’ cosY = -2T’ t1'2'3)
где a, p, Y — углы между касательной и осями координат соответственно.
§ 1.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 17
Так как вектор Т направлен по касательной, то проекции его на координатные оси будут равны
где Т — модуль натяжения в точке М.
Проектируя обе части векторного уравнения (2.1) на координатные оси, получим
Здесь Рх, Ру, Pz — проекции силы Р на соответствующие координатные оси.
При решении конкретных задач используются чаще всего уравнения (2.5) или уравнения, получающиеся из них путем несложных преобразований. Поэтому остановимся на этих уравнениях несколько подробнее.
Будем, как и прежде, считать, что положение точки на нити определяется ее дуговой координатой s. Тогда координаты точек нити х, г/, z, а также модуль натяжения Т будут функциями параметра s:
x = x(s), у = y(s), z = z{s), Т = Tis), (1.2.6)
причем первые три равенства определяют уравнения кривой равновесия нити в параметрической форме. Дуговая координата s точки М и декартовы координаты х, у, z той же точки связаны известным соотношением
Это уравнение определяет неинтегрируемую (неголономную) дифференциальную связь, которой должны удовлетворять координаты точки нити *).
*) Дифференциальная связь называется неголономной, если уравнение связи нельзя проинтегрировать без уравнений равновесия нити (в динамике — без уравнений движения). Конечно, совокупность уравнения неголономпой связи и уравнений равновесия (движения) нити представляет систему интегрируемых дифференциальных уравнений.
(1.2.5)
(1.2.7)
18 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Уравнения (2.5) содержат производные второго порядка по s относительно трех координат х, у, z и первого порядка относительно Т (эти производные возникают при дифференцировании членов, стоящих в скоб¬
ках). Общий интеграл такой системы должен содержать, вообще говоря, семь произвольных постоянных, но поскольку существует одна связь (2.7), независимых постоянных будет только шесть. Поэтому общее решение можно представить в следующей форме:
X = x(s, Си ■ ■Сб), у = y(s, С1, ..С6),
z = z(s, Cl, ..Съ), Т = T(s, Си ..С6).
Произвольные постоянные интегрирования Сi, ..., Cq определяются из граничных условий на концах нити.
Если кроме непрерывно распределенной нагрузки имеются сосредоточенные силы, приложенные к одной или нескольким внутренним точкам, то нить нужно разбить на части, на которые она делится этими точками. Пусть число сосредоточенных сил и, следовательно, число угловых точек равно п. Тогда число участков будет п + 1, и для каждого из них имеется свое решение, содержащее в общем случае шесть произвольных постоянных. Все бгс + 6 произвольных постоянных найдутся из граничных условий, из которых шесть, как и прежде, отвечают концам нити и 6п — точкам приложения сосредоточенных сил (для каждой точки три условия определяют ее равновесие и три условия — общую точку двух участков нити).
Если нить и все силы, приложенные к ней, находятся в одной плоскости (будем считать, что это плоскость ху), то вместо трех уравнений (2.5) будем иметь только два уравнения:
т(г'-я)+г>»=0. а-2-8»
причем координаты хну подчинены неголопомной связи
(£)’ + (-зг)’ - *• (1-2.9)
ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ У*>АВНЕЙИЯ РАЁНОВЕСЙЯ НЙ*Й 19
Общее решение уравнений (2.8) зависит от четырех независимых произвольных постоянных и имеет вид
x = x(s, Сь С4), y = y(s, Си с4),
T = T(s,Cu С4). (1.2.10)
Во многих задачах, имеющих прикладное значение, распределенные силы не зависят явно от криволинейной координаты 5. В этом случае целесообразно исключить координату s из уравнений равновесия. Это можно «делать, например, следующим образом. Найдем из равенства (2.9) дифференциал дуги ds (для сокращения выкладок мы приводим все преобразования и вид общего решения для плоской системы):
ds=]/ 1 + y^dx, У'=%■ (1.2.11)
После подстановки в (2.8) получим
4- , ■т■ ■ + V1 + у'2рх = о,
dx У А + „'2 *
. (1.2.12)
-ЕТ7а=. + ^1+^,р»-°-
]/1 + У2
Общее решение уравнений (2.12) имеет вид
у = у{х, Си С2, С3), Г = TU, Сь С2, С3). (1.2.13)
Это решение полностью определяет кривую равновесия нити и ее натяжение Т, причем роль независимой переменной играет не вспомогательная величина 5, а координата х. Это решение имеет еще и то преимущество, что содержит не четыре, а три произвольных постоянных Ci, С2, Сз, которые определяются из граничных условий.
Рассмотрим частный случай параллельных сил. Построим систему координат так, чтобы ось у была параллельна силам. Тогда Рх = Рг = 0 и два уравнения (2.5) примут вид
Отсюда
20 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Деля почленно полученные равенства, найдем dx
=~с~2
или, разделяя переменные и интегрируя,
C/qoCs С/ \Z — С3.
Полученное уравнение определяет в пространстве плоскость, параллельную оси у. Так как координаты любой точки нити должны удовлетворять этому уравнению, то, следовательно, под действием параллельных сил нить располагается в плоскости, параллельной силам. Не нарушая общности, можно считать, что плоскость нити совпадает с плоскостью ху (z = 0). Тогда третье уравнение (2.5) обращается в тождество и задача сводится к интегрированию уравнений
т£-н’ -s(tJst) + p*-0’ <‘-2-1в>
где Н = С\.
Постоянная Н имеет простой физический смысл — она равна проекции натяжения нити па ось х, т. е. на
Рис. 1.7.
прямую, перпендикулярную силам (см. первое равенство (2.4)). Таким образом, во всех точках нити, находящейся в равновесии под действием параллельных сил, проекция натяжения на направление, перпендикулярное силам, есть величина постоянная. На рис. 1.7 показана нить, находящаяся под действием сил, параллельных оси у. НатяженияТц Г2 и Г3в точках Л/i, М2 и М$ име-
§ 1 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 21 *
ют различные направления и модули, но их составляющие по оси х равны между собой.
В некоторых случаях полезно воспользоваться уравнением моментов (2.2), которое в проекциях на координатные оси эквивалентно трем уравнениям
Если сила Р находится в одной плоскости с какойнибудь осью, то ее момент относительно этой оси равен нулю. Это дает интеграл моментов. Так, если Мх = О, то из первого уравнения (2.17) получим
Наличие этого интеграла может существенно упростить решение задачи.
В заключение остановимся на некоторых особенностях применения уравнений равновесия к растяжимым нитям. Во всех уравнениях этой книги ds означает дифференциал дуги, находящейся в рассматриваемом состоянии нити, в частности, если нить растяжима, то ds — дифференциал дуги растянутой нити. В тех случаях, когда на растянутую нить одновременно действуют массовые и поверхностные силы, их следует строго различать (для нерастяжимой нити это различие не имеет значения). Массовые силы Р, отнесенные к единице длины растянутой нити, нужно выражать по формуле (1.15)
где Р* — сила, отнесенная к единице массы нити,— величина, в отличие от Р, известная.
Поверхностные силы обычно зависят от диаметра нити, который в большинстве случаев при растяжении нити практически не изменяется (см. прцмечание
(1.2.18)
Р = ^0 Р*,
ПТ)
22 ГЛ. I. ДЙФФЕРЕНЦЙАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
к формуле (1.1.8)). Поэтому можно считать, что поверхностные силы при растяжении нити остаются без изменения (в крайнем случае нужно учесть формулу (1.1.8)).
Таким образом, если на растяжимую нить одновременно действуют массовые и поверхностные Р2 силы, то уравнение равновесия (2.1) будет иметь вид
— -I р* 4-Р0 = 0. (1.2.19)
ds ^ / (Т) 2 Ut 4 1
Заметим, что в некоторых статьях и книгах все си¬
лы, действующие на нить, считаются массовыми. Поэтому в этих работах основное уравнение равновесия
(2.1) для растяжимой нити преобразуется к следующей форме (с точностью до обозначений):
+ Р* = 0. (1.2.20)
ц0 ds т ' '
Это приводит к ошибочным результатам, когда в силу Р* включают не только массовые, но и поверхностные силы (например, силы давления потока, силы сопротивления среды и т. п.).
§ 1.3. Естественные уравнения равновесия нити
Во многих случаях удобнее пользоваться так называемыми естественными уравнениями равновесия нити.
Для вывода их возьмем на нити произвольную точку М и построим оси естественного трехгранника. Обозначим через т, v, р орты касательной, главной нормали и бинормали соответственно
(рис. 1.8). Напомним, что векторы т и v определяют соприкасающуюся плоскость (если нить плоская, то соприкасающаяся плоскость совпадает с плоскостью нити) и что единичный вектор главной нормали v всегда направлен в сторону вогнутости кривой. Кроме того, напомним формулы Френе *)
*) Подробности можно найти в любом курсе дифференциальной геометрии.
§ 1.3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 23
— J- *1
ds р ’ ds
где 1/р — кривизна, a 1/pi — кручение дуги в данной точке (р и pi — радиусы кривизны и кручения соответственно) *).
Внесем значение Т из равенства (1.1) в векторное уравнение равновесия нити (2.1)
Продифференцируем выражение, стоящее в скобках,
Проектируя на касательную, главную нормаль и бинормаль, получим
где Рт, Pv, Рр — проекции силы Р на соответствующие оси естественного трехгранника.
Уравнения (3.3) называются естественными или натуральными уравнениями равновесия гибкой нити. Не останавливаясь на доказательстве, заметим, что их можно получить из уравнений (2.5).
Из последнего уравнения (3.3) следует, что проекция силы Р на бинормаль равна нулю. Это означает, что под действием приложенных сил нить принимает форму линии, в каждой точке которой соприкасающаяся плоскость содержит силу Р.
Кривизна линии определяется в общем случае равенством
-&W + P- 0.
(1.3.2)
или, учитывая первую формулу (3.1),
М- + Рт = 0, j- + Pv = 0, Рр = 0, (1.3.3)
(1.3.4)
*) Иногда кручение 1/рх называют второй кривизной, а лицщо, для которой 1/рд ф 0,— линией двоякой кривизны.
24 ГЛ. 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
где е — угол смежности (угол между двумя близкими касательными). Из этого видно, что кривизну линии можно рассматривать как скорость поворота касательной по дуге s. Для плоской кривой угол смежности е равен приращению угла а между касательной и какимлибо неизменным направлением, например осью х, т. е. 8 = Да. Поэтому для плоской линии кривизна равна производной от. угла а по дуге s
Если плоская линия задана уравнением у = у(х), то последняя формула приводится к виду
В отличие от плоской линии, направление касательной пространственной кривой определяется не одним, а двумя углами. Поэтому для пространственной кривой не существует одного угла, приращение которого равно углу смежности. Из этого следует, что кривизну (скорость поворота касательной) пространственной линии нельзя рассматривать как производную от некоторого угла а по s, что имеет место для плоской кривой *).
Для пространственной линии, заданной уравнениями
Здесь R — радиус цилиндра, а — угол между касательной к випто-
*) Аналогично при вращении твердого тела вокруг неподвижной оси угловая скорость равна производной по времени от реального угла поворота, а при движении твердого тела, имеющего одну неподвижную точку, угловая скорость (точнее квазискорость) существует, а угла поворота нет (см., например, [4] т. 1).
(1.3.6)
x = x(s), y = y(s), z = z(s), (1.3.7)
кривизна вычисляется по формуле
Пример. Уравнения винтовой линии имеют вид x=Rcosks, у=R sin ks, z = s sin a.
§ 1.3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 25
вой линии и плоскостью поперечного сечения цилиндра, и = = cos а/Л. Имеем:
d2x о о d2z
—2 = — Rk cos XS, ■—2 = — 1Ы sinxs, —2 = 0, ds db ds
Пользуясь формулой (3.8) и учитывая значение х, получим
J_ = cos2a (1.3.9)
р Я
Естественными уравнениями (3.3) пользуются чаще всего в тех случаях, когда форма линии равновесия нити известна. Однако в некоторых случаях плоской нити эти уравнения можно эффективно использовать для определения основных параметров, в том числе и формы нити. Действительно, если проекции силы Р на касательную и главную нормаль зависят только от угла а между касательной и осью абсцисс х, то решение задачи можно провести в следующем порядке (см. [16]). Пусть РХ = РХ(а) и P„ = PV{а). Тогда первые два уравнения (3.3) примут вид
§ = -Рх(а), L = -P,(a). (1.3.10)
Деля первое уравнение па второе и учитывая, что для плоской кривой имеет место равенство (3.5), получим
dT рч (<*) Т ~ Pv (а)
или, интегрируя,
da,
т = Схе«*\ Ф (а) = J da. (1.3.11)
Пользуясь этим выражением для натяжения Т и вторым уравнением (3.10), найдем радиус кривизны
еФ(а)
е=-с*т^у (1.3.12)
Для решения конкретных задач нужно от уравнения (3.12) перейти к уравнениям, с помощью которых легко учитываются граничные условия. Для этого воспользу¬
26 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
емся двумя выражениями для радиуса кривизны
ds 1 dx ds 1 tdy о л о\
Р — da ~ cos a da * Р — da ~ sin а л da * ' '
Сопоставляя с (3.12), найдем уравнения равновесия нити в параметрической форме
Описанный здесь метод не является, как правило, самым простым, но в некоторых случаях оп весьма эффективен (см. § 9.3).
§ 1.4. Потенциальные силы
Пусть на нерастяжимую пить действует потенциальная не обязательно массовая сила Р, т. е.*)
где П — потенциальная энергия, отнесенная к единице длины нити (растяжимая нить будет рассмотрела ниже). В проекциях па координатные оси будем иметь
По определению потенциальная энергия зависит только от координат точки
причем предполагается, что эта функция однозначна и дважды дифференцируема по всем координатам.
Следует различать потенциальную энергию, отнесенную к единице длины нити, от обычной потенциальпой энергии. Потенциальная энергия, рассматриваемая в фи-
*) Напомним, что градиентом скалярной функции <р = *= ф(*> У, z) называется вектор, определенный равенством
(1.3.14
Р = — grad П,
(1.4.1)
П = Щя;, г/, z),
(1.4.3)
§ 1.4. ПОТЕНЦИАЛЬНЫЕ СИЛЫ
27
зике, в частности в механике, имеет размерность работы (например, н*м = дж или кГ-ле), а потенциальная энергия, отнесенная к единице длины нити, имеет размерность силы (соответственно н или кГ).
Вычислим проекцию Рх потенциальной силы Р на касательную к нити. Имеем
Рх = Рх cos а + Ру cos (3 + Р2 cos у,
где а, (3, 7 — углы между касательной и осями координат х, г/, z.
Пользуясь равенствами (2.3) и (4.2), получим
р I<Ш dx . дП dy . дП dz \
т \ дх ds ' ду ds ' dz ds J
Величина, стоящая в скобках, равна полной производной от П по s. Поэтому для потенциальных сил будем иметь
Внесем это значение для Рх в первое уравнение (3.3) Отсюда
Т = П + С, (1.4.5)
где С —постоянная интегрирования. Этот интеграл называется интегралом натяжения.
Рассмотрим теперь растяжимую нить, на которую действует массовая сила, определяемая равенством (1.15)
р — р* f(T) Г ’
где Р* — сила, отнесенная к единице массы. Если эта сила потенциальная и П* ее потенциальная энергия, то равенство (4.4) примет вид
рг = (1 4 б\
т f(T) ds ' '
Подставляя в первое уравнение (3.3), получим
dr ^П* л
ds / (Т) ds — и
dT dU _ 0
ds ds
28 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
илц, сокращая на ds, разделяя переменные и интегрируя,
^f(T)dT = non* + C.
Это равенство определяет интеграл натяжения для растяжимой нити, находящейся под действием массовой потенциальной силы. В частности, для растяжимой по закону Гука нити интеграл натяжения примет вид (см. равенство (1.6))
Т + Щ-Т2 = ц0П* + С. (1.4.8)
Заметим, что интеграл натяжения (4.5) или (4.7) существует и в том случае, когда, помимо потенциальных сил на нить действует распределенная сила, перпендикулярная касательной (так как она не изменяет равенства (4.4) или (4.6)). Конечно, это не означает, что добавление такой распределенной силы не изменяет натяжения нити.
Пример. Если однородная нерастяжимая нить находится в равновесии под действием силы тяжести, то П = gz, где g — сила тяжести единицы длины нити, a z — вертикальная координата рассматриваемой точки. Интеграл натяжения (4.5) принимает вид
T=qz+C. (1.4.9)
Если же тяжелая однородная нить растяжима, то q = jug = = H0g/f(T) = nn/f(T), где g0 —вес единицы длины нити до ее растяжения Теперь P* = g, n* = gz и интеграл (4.8) растяжимой по закону Гука нити будет
T + ^jT* = q0z + C. (1.4.10)
Эти интегралы не изменяются, если на нить будут дополнительно действовать силы, перпендикулярные касательной.
Интеграл натяжения может в некоторых случаях существенно упростить процесс интегрирования дифференциальных уравнений равновесия нити, в частности с его помощью можно уменьшить число уравнений равновесия.
§ 1.5. УРАВНЕНИЯ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ 29
В заключение отметим, что вместо потенциальной энергии П иногда вводят силовую функцию U, которая отличается от П только знаком
U=- П.
§ 1.5. Уравнения равновесия нити в криволинейных (обобщенных) координатах
Напомним основные определения (см., например, [4J, т. I). Любые три параметра qi, q,2, <73, однозначно определяющие положение точки в пространстве, называются криволинейными или обобщенными координатами. Так как положение точки определяется также радиусом-вектором г, то будем иметь
г = г (qu ?2, q3) или в скалярной форме х = x(qh q2, q3), у = y(qu q2, q3), z = z(qu q2t ?3).
(1.5.1)
Координатная линия представляет годограф радиусавектора г при изменении только одной координаты qi и неизменном значении двух других координат. Если изменять сразу две координаты, а третью оставить без изменения, то получим координатную поверхность. Через каждую точку М пространства можно провести три координатных линии и три координатных поверхности.
Касательные [gj к координатным линиям в точке М, направленные в сторону возрастания соответствующих координат, называются координатными осями (рис. 1.9). Направления этих осей задаются ортами ег, е2, е3, которые вычисляются по формулам
Ht dqt ~ 2’ 3)’
(1.5.2)
30 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
где коэффициенты Ляме Нг определены равенствами
Я'=111=/(1Й1Г+Ж (,-5-3>
С помощью формулы (5.2) легко находятся косинусы углов между ортами криволинейной координатной системы и осями декартовых координат. Наприм;ер,
. дг_ . _ 1 ду
^J-TT.dq.J-H-.dq-
cos {erj)
Таким образом, получим таблицу косинусов
1 дх
ИЛ,
1
1 dz H.Tq,
(1.5.4)
Если в каждой точке пространства координатные оси взаимно перпендикулярны, то такая система криволинейных координат называется ортогональной. Условие ортогональности et*ej = 0 (i=7^/), согласно таблице (5.4),
имеет вид
дх дх ду ду . dz dz ~
(1.5.5)
причем эти условия должны выполняться для всех i и /, для которых i Ф /. Построим в данной точке нити единичный касательный вектор т = dr Ids. По правилам дифференцирования сложных функций будем иметь з
2 dr ' / ' dQ\\
Введем функцию
3 3
т 1 о 1 W ^
-тт - 2 22^^:?т-
(1.5.6)
(1.5.7)
Функция I представляет квадратичную форму производных q', и поэтому, согласно соответствующей теореме
§ 1.5. УРАВНЕНИЯ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
31
Эйлера, будем иметь
2fWi = 2/. (1.5.8)
г=1 дЯ\
Дифференциал дуги в криволинейной системе координат непосредственно получается из равенства (5.7), если только учесть, что {ds)2 = т2 (ds)2
з з
(dsr=2^i^-wdqidq3. (1.5.9)
i=lj=l 4i
Для ортогональной системы координат:
^ з
(1.5.10)
i= 1
{dsf = 21 (1.5.11)
i=l
Установим два тождества, первое из которых получается, если продифференцировать обе части равенства
(5.6) по q\
дт дг /. r
Ц = эГ, (<-1.2,3). (1-5.12)
Продифференцируем теперь обе части равенства (5.6) частным образом по qt, изменив предварительно индекс суммирования с i на /:
з
д2г
дт __ V - д9г ~ Р дЯ3дЧг9*'
Пользуясь правилом дифференцирования сложных функций, будем иметь
— — — V дУ
ds dq • Zddqflq.
Яг
3-1
Сравнивая последние два равенства, получим второе тождество
= (* = 1,2,3). (1.5.13)
32 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Перейдем теперь к выводу дифференциальных уравнений равновесия нити в криволинейных (обобщенных) координатах. Для этого умножим обе части уравнения
(2.1) скалярно на dr/dqii
^W + PW = ° (г = 1’2’3)- d-5-14)
Имеем очевидное равенство
dT dr d у d дг
ds dq i ds у dqiJ ds dq^
Пользуясь тождествами (5.12), (5.13) и равенством
(1.1), получим
Ц- iL = -L( тх - Тх р-.
ds dq{ ds \ dqJ dq{
Скалярные произведения, стоящие в правой части, можно представить следующим образом (см. (5.7)):
_ JL/JEi'l — 2L дт д I т2 \ _ д!
Х dq'i ~ dq\ l~I ~ dq'.' * “ «*Д 2 > ~
Тогда получим
%-£- = (1.5.15)
ds dq{ ds у dq'J dq{ v >
Второе слагаемое в уравнении (5.14) можно записать так (см. (5.2)):
Р^- = Н?.ек = НкРх = (}ь (1.5.16)
где Р\ = Р*е\ —проекция силы Р на координатную ось LgJ. В дальнейшем величину Qt будем называть обобщенной силой, соответствующей обобщенной координате qt и отнесенной к единице длины нити.
Подставив равенства (5.15) и (5.16) в уравнения (5.14), получим
Это и есть уравнения равновесия нити в криволинейных (обобщенных) координатах. Их можно назвать уравнениями равновесия нити в форме Лагранжа (по аналогии с соответствующими уравнениями Лагранжа в динамике).
§ 1.5, УРАВНЕНИЯ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ 33
Обобщенные силы вычисляются по одной из следующих формул:
Qi = HiPu (1.5.18)
дх , „ ду ^ р dz
dqC
О — Р —4-Р 4- Р —
xdq.% dq{ + ^z
dQi
(1.5.19)
(1.5.20)
Формула (5.19) непосредственно вытекает из равенства
(5.18) и таблицы косинусов (5.4), а формула (5.20) следует из (5.19) и равенств (4.2).
Заметим, что размерность обобщенной силы, отнесенной к единице длины нити, зависит от размерности соответствующей обобщенной координаты.
Рассмотрим примеры.
Пример 1. Уравнения равновесия нити в цилиндрической системе координат. В цилиндрических координатах положение точки М определяется радиусом г, углом ср и аппликатой z. На рис. 1.10 показаны эти координаты, координатные линии и поверхности. Пользуясь рисунком, получим х = г cos ф, у = г sin ф, z = z.
По формулам (5.3) найдем коэффициенты Ляме
' Нг = 1, ЯФ = г, Нг = 1. (1.5.21)
Цилиндрическая система координат ортогональна и, следовательно, согласно формулам (5.10) и (5.11), будем иметь
/ = -2 (r'2+rV2 + *'2), (1-5.22)
m2 =
= (dr)2 + г2 (dq>)2 + (dzf. (1.5.23) Рис. 1.10.
Пользуясь схемой (5.17) и равенством (5.18), получим дифференциальные уравнения равновесия нити в цилиндрической системе координат
d
34 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
где Рг, Рф, Рг — проекции силы Р на координатные оси [г], [<р] и [z] соответственно. К этим уравнениям нужно присоединить уравнение связи (5.23).
Рис. 1.11.
Пример 2. Уравнения равновесия нити в полярной системе координат (рис. 1.11). Если нить плоская, то дифференциальные уравнения равновесия ее в полярных координатах г и <р получаются из уравнений (5.24) при z = 0. Таким образом, в полярных координатах мы имеем первые два уравнения (5.24) и уравнение связи
(ds)2 =, (dr)2 + r2(dq>)2. (1.5.25)
Пример 3. Уравнения равновесия нити в сферической системе координат. В сферических координатах положение точки определяется полярным радиусом г, углом <р и углом 0 (полюсный угол). На рис. 1.12 показаны значения этих величин, координатные линии и поверхности. Имеем
х = г sin 0 cos ф,
у = г sin 0 sin ф, (1.5.26)
z = Г COS 0.
По формулам (5.3) найдем коэффициенты Ляме Вт = 1,
Яе = г, (1.5.27)
ЯФ = г sin 0.
Сферические координаты ортогональны, и, следовательно, согласно формулам (5.10) и (5.11), будем иметь
/ = l(r'* + rV2+r2sinV2).
(<fo)2 в (dr)9 + г2 (d0)2 + г2 sin20 (<2ф)2
(1.5.28)
(1.5.29)
§ 1.6. КАНОНИЧЕСКИЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 35
Пользуясь схемой (5.17) и равенством (5.18), получим дифференциальные уравнения нити в сферических координатах
я(г1)-г''[(г)‘+а|Л(вГ
Л (Тг8 ^) — Гг2 с os 0 sin е f
ds \ ds) \ds)
■(*>*,• ef)
+ ^r=0,
+r/>e = 0.
(1.5.30)
£
ds
+r sin 0 Рф = 0.
Здесь РТу P&, Pq> — проекция силы P на координатные оси [г], [0], [<р] соответственно.
К уравнениям (5.30) нужно присоединить уравнение связи (5.29).
§ 1.6. Канонические уравнения равновесия нити
Во многих случаях решение дифференциальных уравнений равновесия нити нельзя довести до квадратур и приходится прибегать к численным методам интегрирования на ЭВМ. Для этих целей ранее полученные уравнения недостаточно удобны, так как они содержат производные второго порядка. Если же ввести новые переменные, обозначив q\ через (£ = 1, 2, 3), то полученная в результате этого система уравнений первого порядка не будет симметрична и вычисления существенно усложнятся. Большими удобствами для численного (иногда и не только численного) интегрирования дифференциальных уравнений равновесия нити представляют канонические уравнения в форме Гамильтона. Для их вывода введем в рассмотрение новую функцию
G = TI. (1.6.1)
Эта функция зависит явно от Г, q% и q\, причем ыатяжение Т рассматривается как функция дуговой координаты s:
G = G {т, (?2, q3, q%, ?з)*
Обозначим через рг частные производные от G по q\ (в динамике соответствующие величины называются обобщенными импульсами)
Pi = rr=Trr (« = 1,2,3). (1.6.2)
36 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Выразим из равенств (6.2) производные q' (они входят в правые части линейно) через Г, q и р:
Яг = Qi {Т, ^17 Яз"> Pli Ръч Рз)* (1.6.3)
Составим теперь функцию Ж по следующему правилу:
з
Ж = 2 q'iPi-G. (1.6.4)
i=l
Внесем в эту функцию вместо производных q% их значения из (6.3), считая в дальнейшем, что Ж зависит от
T{s), q и р: Ж = Ж(Т, р). Вычислим от функции Ж
вариацию, считая s неизменным. Имеем
<w-5)
i=l °Pi i=1
Варьируя теперь (6.4), получим
ЬЖ = 2 Pibq'i + 2 g&Pi — 2 w. ^9i ~ 2 т7 8g'h i=1 i=l i=l i=l ^ i
или, учитывая (6.2) и сокращая первый и последние слагаемые,
з з
ЬЖ = 2 9ibPi-2S- S?*- (1.6.6)
i=i i=l
Пользуясь равенством (6.1), запишем уравнения (5.17) в следующей форме:
d dG dG Q _ Q
* eg'. dq{ + и.
Преобразуя первое слагаемое с помощью равенства
(6.2), найдем
Теперь соотношение (6.6) примет вид
§ 1.0. КАНОНИЧЕСКИЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
37
Сравнивая коэффициенты при вариациях 6р* и 6д< в (6.5) и (6.8), получим шесть уравнений равновесия нити в форме Гамильтона (аналогичные уравнения получены Гамильтоном в динамике)
дХ dPi_ дЖ п. fi_< , /4 ft q\
-dF=Wi' V-1’*’6)' (a-b-y)
Для растяжимых нитей эта форма уравнений сохраняется, нужно только массовые силы Рэ входящие в ()г, заменить на их значение по формулам (1.15). Уравнения равновесия нити в форме Гамильтона имеют симметричную форму и они решены относительно производных.
Если действующие силы потенциальны, .то введем новую функцию
Н = Х-П. (1.6.10)
Учитывая теперь равенство (5.20), приведем уравнения.
(6.9) к канонической форме
% = ъ--щ 0 = ‘.*3). (1.6.11)
Для полного интегрирования уравнений (6.9) или
(6.11) к ним нужно присоединить уравнение связи (5.9) и граничные условия.
Упростим выражение для функции Ж. Для этого внесем в (6.4) значение р\ из (6.2). Имеем
г=1 д<1х
Пользуясь равенством (5.8), последовательно получим Ж = Т • 21-G = 2G-G = G.
Таким образом, функция Ж совпадает с функцией G, если в последней выразить производные q\ через импульсы р{
» Qn #2» Qzi Qh 9з) = Ж (T, qv q2, q& Рц р2ч Рз)ш
(1.6.12)
Перед тем как перейти к примерам, отметим, что все выводы получены здесь для любых криволинейных координат.
38 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Пример. Уравнения равновесия нити в форме Гамильтона в декартовой системе координат. Для прямоугольной декартовой системы координат имеем
/ = у (*'* + »'*+ *'*)•
Пользуясь (6.1) и (6.2), найдем
G = f + у'2 + z'2); рх = Тх', ру = Ту’, pz = Tz'.
(1.6.13)
Сравнивая эти выражения с равенствами (2.4), видим, что величины рх, Ру, pz равны проекциям натяжения нити Т на соответствующие оси координат я, г/, z.
Из равенств (6.13) найдем х\ уz' и внесем их в функцию G. Тогда получим
M = yT{pI + pI + p\)- (1.6.14)
Уравнения равновесия (6.9) примут вид
ds Т — —
л (1*6.15)
Рх — р ^ = г г = ±
ds *’ ds У' ds 2
(ds)2= (dx)2+(dy)2+ (dz)2.
Из равенств (6.13) и последнего уравнения (6.15) найдем натяжение нити
т = -/р1 + р2у + р1. (1.6.16)
Если внести это значение для Т в первые три уравнения (6.15),
то получим следующие дифференциальные уравнения равновесия
нити в форме Гамильтона:
dx Рх dy Ру
dy _Ру
dz
ds Т’
ds
d!l = -p ,
dpz _
ds «'
ds
ds
У р%+р\+р\ ds + + р\
dz _ Pz
ds
^ р1 + р1 + р?
(1.6.17)
dpx _ _ D dpy р dpz _ _ D
1Г~ х' У'
Впервые уравнения (6.17) были получены акад. Б. Г. Ишменецким [6].
§ 1.7. ФОРМА РАВНОВЕСИЯ НИТИ И ДВИЖЕНИЕ ФОЧКИ
39
§ 1.7. Связь задачи о форме равновесия нити с задачей о движении материальной точки
Сравним основное дифференциальное уравнение равновесия нити (2.1)
§ + Р = 0 (1.7.1)
с дифференциальным уравнением движения материальной точки
m§=F. (1.Г2)
Легко видеть, что оба уравнения имеют одинаковую аналитическую структуру, причем натяжению Г, направленному по касательной к кривой равновесия, в первом уравнении отвечает скорость*?, направленная по касательной к траектории точки, во втором уравнении, силе Р, отнесенной к единице длины нити, уравнения (7.1) отвечает сила — F/иг, отнесенная к единице массы точки, уравнения (7.2). Этой аналогией объясняется сходство между другими формами уравнений равновесия нити и уравнений движения материальной точки. Так, например, уравнениям равновесия нити в естественных осях, в обобщенных (криволинейных) координатах, в канонической форме Гамильтона отвечают соответствующие уравнения движения материальной точки. Можно привести w другие формы уравнений равновесия нити, имеющие соответствующие аналоги в динамике, например уравнение в частных производных в форме Гамильтона — Остроградского (впервые оно было получено акад. В. Г. Ишменецким [6]); используются также вариационные принципы (см. § 10.4) и т. п. Наконец, есть много общего и между интегралом натяжения нити и интегралом энергии материальной точки.
Основное различие уравнений (7.1) и (7.2) состоит в независимой переменной: в дифференциальном уравнении равновесия нити (7.1) это дуговая координата 5, а в дифференциальном уравнении движения материальной точки
(7.2) это время t. Однако это различие можно сгладить и провести более глубокую аналогию. В самом деле, рассмотрим для простоты случай потенциальных сил, когда —grad П. Тогда уравнение равновесия нити (7.1)
40 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
примет вид
■§-8шШ = 0.
Умножим обе части этого уравнения на модуль натяжения Т
J'f-J’gradn-O
и преобразуем с помощью интеграла натяжения Т = П + + С второе слагаемое. Имеем (С = const)
Т grad П = (П + С) grad (П + С) = grad .
Теперь уравнение равновесия нити примет вид
Т^ = grad^2i£L2. (1.7.3)
Это векторное уравнение или эквивалентные ему три уравнения в проекциях на оси координат вместе с уравнением связи (2.7) определяют координаты х, у, z кривой равновесия нити и натяжение Т как функцию параметра s.
Перейдем к рассмотрению дифференциального уравнения движения материальной точки, на которую действует консервативная сила F с потенциальной энергией П1Т
F = — grad Пх.
Уравнение движения имеет вид
m = — grad Пь
где m — масса точки, a v — ее скорость.
Ускорение dv/dt можно преобразовать следующим образом:
dv dv ds dv
dt ds dt ds'
Внося это значение для ускорения в уравнение (7.2), получим
dv j
8 1.8. ИНТЕГРАЛЬНЫЕ МЕТОДЫ
41
Это векторное уравнение или эквивалентные ему три уравнения в проекциях на оси неподвижной системы координат вместе с уравнением связи, которое в данном случае имеет тот же вид (2.7), определяют координаты х, г/, z траектории движения точки и скорость v как функцию параметра s.
Сравнение уравнений (7.3) и (7.4) показывает, что если нить находится в равновесии под действием отнесенной к единице длины нити силы Р с потенциальной энергией П, то линия равновесия нити будет совпадать с траекторией движения материальной точки, к которой приложена консервативная сила с потенциальной энергией — ти(П + + С)2/2 (конечно, при равных соответствующих граничных и начальных условиях).
§ 1.8. Интегральные методы
Основное уравнение равновесия нити (2.1) характеризует условие равновесия не конечного участка нити, а одного ее элемента. Поэтому это уравнение, так же как и все другие уравнения §§ 2—6, полученные из него, носят дифференциальный характер. Представляет интерес составить такие уравнения, которые отражали бы условия равновесия не одного элемента нити, а конечной ее части. В этом случае уравнения равновесия будут носить не дифференциальную, а интегральную форму.
Рассмотрим вначале равновесие всей нити, находящейся под действием распределенных Р и сосредоточенных сил Gi (i = 1,..., п). Для простоты изложения будем считать, что нить плоская и концы нити закреплены. Введем систему координат, совместив начало осей с точкой закрепления нити А (рис. 1.13). Разложим реакции Да и Rb точек закрепления на составляющие Ха, Yа, Хв, У в и, рассматривая равновесие всей нити, составим уравнения проекций:
п г
— Ха + Хв + 2 Gix + ] Pxds О, i==1 о
L (1-8.1)
-YA-YB + ^Giy+ \pyds= О, i=1 о
где оба криволинейных интеграла первого рода вычисля-
42 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
ются по длине L всей нити, уравнение которой нам неизвестно. Наличие интегралов создает определенные трудности в применении уравнений (8.1), но в некоторых случаях эти уравнения могут быть эффективно использованы для определения величин — Ха + Хв и
Рис. 1.13.
Рассмотрим теперь равновесие участка нити AM, где М(х, у) — произвольная точка нити с координатами х и у. Участок нити AM находится в равновесии под действием активных распределенных Р и сосредоточенных Gi сил, реакции Ra(Xa, У а) точки закрепления А и силы натяжения Т, которую нужно приложить к точке Л/, чтобы заменить действие отброшенной части нити
§ 1.8. ИНТЕГРАЛЬНЫЕ МЕТОДЫ
43
(рис. 1.14). Уравнения проекций имеют вид
s
Т'М - Ха+2G*+i p*ds=°>
1 i О
i О
В этих уравнениях s — длина нити на участке AM, а суммы проекций сосредоточенных сил относятся только к тем силам, которые действуют на этом участке нити.
Составим теперь уравнение моментов относительно точки М. Моменты сил Да» G\ ж Р ds будут, очевидно, равны
-уХА + xYa, (у - yJGb -(х- Xi)G{y,
Ку—у\)Рх— (х—l)Py]ds,
где х%, уг, |, ц — координаты точек приложения сосредоточенной силы G\ и распределенной силы Р ds соответственно (см. рис. 1.14).
При вычислении суммы (интеграла) моментов распределенных сил нужно иметь в виду, что меняются только координаты | и г\ текущей точки N, а координаты х и у остаются без изменения. На этом основании сумму моментов распределенных сил относительно точки М можно представить так:
s s S S
у J Pxds — j г]Pxds — х j Pyds -f- \ \>Pvds.
0 0 oo
Заменим в этом выражении | и ц на х и у, не вынося их, конечно, за знак интегралов. Тогда уравнение моментов конечного участка нити можно записать в следующей форме:
-yXA + xYA + M = 0, (1.8.3)
где М — момент всех активных (распределенных и сосредоточенных) сил относительно точки мысленного разреза нити — определен равенством
М ^ 2 [(у — J/i) GiX — (х — Xi) Gij] -f-
s я s s
+ У j Pxds — j yPxds — x j* Pyds + j xPyds. (1.8.4)
Oo 0 0
(1.8.2)
44 ГЛ. I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ
Три уравнения (8.2), (8.3) решают поставленную задачу: они определяют условия равновесия не одного элемента нити, а конечного участка ее.
Рассмотрим частный случай, когда все активные силы параллельны и направлены в одну сторону. Выбрав координатную систему так, чтобы ось у была параллельна силам, будем иметь Рх = 0, Gix = 0, Ру = Р, Giy = Из первого уравнения (8.2) найдем
Т^ = ХА = Я = const, (1.8.5)
т. е. проекция натяжения на направление, перпендикулярное силам, одинакова во всех точках нити (так как левая часть равенства (8.5) вычисляется в любой точке нити, а величина ХА не зависит от выбора точки нити (см. примечания к уравнениям (2.16)). Уравнение (8.3) принимает теперь вид_
У А
— A- I ^ (х ~ xi) Gi + х f Р ds — | xP ds .
Li 0 0 J
(1.8.6)
Если сила Py отнесенная к единице длины нити, зависит только от положения точки нити, т. е. Р = Р(х, у), то, учитывая равенство ds = Vi + у'2 dx, последнему уравнению можно придать вид
У = -fTx—-Jf 1^2 (х — Xi)Gi +
X X "I
+ x\pV\ +y'2dx-\xP-/l +y'tdx\. (1.8.7)
Уравнение (8.7) можно рассматривать как нелинейное интегро-дифференциальное уравнение относительно неизвестной функции у = у(х). В некоторых случаях уравнение (8.7), а также уравнения (8.3) и (8.6) существенно упрощаются и тогда они сразу определяют линию равновесия нити (см. главу III). В общем случае эти уравнения можно использовать для приближенных вычислений.
В заключение отметим, что в терминах сопротивления материалов уравнения (8.3), (8.6) получаются из условия равенства нулю изгибающего момента в любой точке нити.
ГЛАВА II
ЦЕПНАЯ ЛИНИЯ
§ 2.1. Цепная линия
Линия равновесия абсолютно гибкой и нерастяжимой однородной нити, находящейся в поле силы тяжести, называется цепной линией. В более широком смысле под цепной линией понимается линия равновесия тяжелой неоднородной и растяжимой нити. В этом параграфе мы рассмотрим однородную нерастяжимую цепную линию.
Силы тяжести, действующие на каждый элемент нити, направлены вертикально вниз и, следовательно, параллельны между собой. Поэтому цепная линия является плоской кривой (см. § 1.2).
Для вывода уравнения цепной линии совместим начало координат с ее вершиной О, ось у направим вертикально д вверх, а ось х горизонтально так, чтобы координатная плоскость ху являлась плоскостью нити (рис. 2.1). Как было показано ранее (см. при- Рис. 2.1.
мечание к формуле (1.1.12)),
модуль силы Р для однородной тяжелой нити равен весу единицы длины нити q, причем q = const. При данном выборе координатных осей будем иметь: Р*=0, Pv=—q. Подставляя значение Ру во второе уравнение (1.2.16), получим Т% = И‘ = <211> где II = const — проекция натяжения нити на горизон¬
46
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
тальную ось х. Из первого уравнения (1.1) найдем
Г-я£. (2.1.2)/
Подставим это выражение для Т во второе уравнение
(1.1) и учтем равенство
ds = 1 + у'2 dx. (2.1.3)
Тогда после разделения переменных уравнение (1.1) примет вид
dy' dx
7Т+Р~~
где
a=*L. (2.1.4)
Интегрируя полученное уравнение, найдем*)
х — Сл
Arcsh у' = ——L.
Здесь С1 — постоянная интегрирования. Из последнего равенства будем иметь
^ = (2.1.5)
Интегрируя еще раз, получим уравнение цепной линии
у = ach—-—- С2, (2.1.6)
где С2 — новая постоянная интегрирования.
Уравнения цепной линии (2.6) можно получить,
конечно, и с помощью других методов, в частности,
если воспользоваться результатами § 1.3 (см. формулы
(1.3.10)—(1.3.14)).
*) Символ Arcshz обозначает функцию, обратную shz, т. е. из равенства у = Arcsh z следует z = sh у. Легко показать, что
Arcsh z = ln(z + У1 + z2).
Определение гиперболических функций и краткая сводка основных формул даны в Приложении 1.
§ 2.1. ЦЕПНАЯ ЛИНИЯ
47
Так как при выбранной системе координат ось у проходит через вершину цепной линии, касательная к которой параллельна оси х (рис. 2.1), то у'= 0 при я = 0. Внося эти значения для х и у' в равенство (1.5), получим С\ = 0. Следовательно, уравнение (1.6) примет вид
Учтем теперь, что цепная линия проходит через начало координат х = 0, у = 0. Поэтому С2 = — я и последнее уравнение принимает каноническую форму
Это уравнение получено практически одновременно Лейбницем, Гюйгенсом и Иоганном Бернулли.
В технических приложениях обычно задается взаимное расположение точек закрепления А и В (пролет I и превышение h — рис. 2.2), а также длина L цепной линии (или другой какой-нибудь ее элемент). При этих условиях приходится определять не только параметр а, входящий в уравнение (1.7), но и положение начала координат относительно точек закрепления (заметим, что начало координат может и не принадлежать цепной линии —
у = ach-2- + C2.
(2.1.7)
Н /
У
Рис. 2.2.
рис. 2.2, б).
48
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
Обозначим расстояние по горизонтали и вертикали от > вершины О до верхней точки закрепления А через б и,
/ соответственно, т. е. положим хА = в и у a — / (прй Л «= 0 величина / называется стрелой провисания; длй краткости Мы будем употреблять этот термин и в общем случае при h Ф 0). Тогда координаты точки В будут: а;в = — (Z—б), yB = f—h. Внесем координаты точки А в уравнение (1.7)
/ = a(chA-l). (2.1.8)
Подставим теперь в уравнение (1.7) координаты точки В и используем при этом полученное значение для /. После очевидных упрощений получим
h = a ^ch -jj ch —р )• (2.1.9)
Вычислим дифференциал дуги цепной линии,^ для чего
внесем в равенство (1.3) значение производной у' из (1.5),
учтя при этом, что при выбранной системе координат постоянная С\ = 0. Имеем
ds = ]/ 1 + sh2-^- dx.
На основании хорошо известной формулы для гиперболических функций
ch2 2—sh2 2 = 1 (2.1.10)
получим
ds = ch — dx. (2.1.11)
a ' '
Интегрируя это равенство от хв = — (I—б) до хА = б,
найдем длину цепной линии
L = a(shJL +8ьЦ^). (2.1.12)
Пользуясь равенствами (1.2), (1.4) и (1.11), найдем натяжение
Т = aq ch
(2.1.13)
8 2.1. ЦЕПНАЯ ЛИНИЯ
49
или, учитывая уравнение (1.7),
T = q(a + y). (2.1.14)
Заметим, что это равенство очень просто получается также и из интеграла натяжения (1.4.5У. Действительно, для силы тяжести потенциальная энергия
U = qy (2.1.15)
и, следовательно, интеграл натяжения принимает вид
T = qy + C. (2.1.16)
Постоянную С найдем из условия, что в вершине нити при у = 0 натяжение Т = Н = qa (см. рис. 1.7). Таким
образом, С = qa и интеграл натяжения (1.16) принимает
форму (1.14).
Равенство (1.14) позволяет дать простую интерпретацию параметра а. Проведем горизонтальную прямую N — N на расстоянии а от вершины цепной линии О (рис. 2.3, а). Пользуясь рисунком и равенством (1.14), найдем, что натяжение нити в любой ее точке
Рис. 2.3.
равно весу нити, длина которой равна расстоянию от данной точки До прямой N — N. Из этого следует, что тяжелая однородная нить, лежащая на двух бесконечно малых блоках, будет в равновесии, если свободные концы ее опущены ниже вершины на расстояние а (рис. 2 3, б).
Все элементы цепной линии легко определяются, если известны параметры а и б. Их вычисление зависит от
50
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
условий задачи. Мы рассмотрим три наиболее распространенные схемы расчета цепной линии.
1-я схема. Заданы вес единицы длины нити q, ее длина L, пролет I и превышение h.
Воспользуемся следующими формулами для гиперболических функций:
sh и + sh v = 2 sh ch ,
: _ (2.1.17)
ch и — ch v = 2 sh и ^ v sh и 2 v.
С помощью этих формул преобразуем равенства (1.12) и (1.9) к виду
2sh^-ch^p^ = —, 2sh^-sh^^ = —. (2.1.18)
2а 2а а ’ 2а 2а а ' 7
Деля второе равенство на первое, получим
,ь^=т- <2U9>
Если h = 0 (точки закрепления находятся на одном
уровне), то из этого равенства найдем: 6 = 1/2 — резуль¬
тат, очевидный из условия симметрии. Если же h Ф 0, но мало отношение h/Ly то гиперболический тангенс можно заменить на его аргумент
26 — I _ h 2 a L
Отсюда
б=4"+4а- (2Л-2°)
Эта приближенная формула дает ошибку меньше 1,5% при h/L < 0,2.
Возведем теперь оба равенства (1.18) в квадрат и вычтем из первого равенства второе. Тогда, учитывая формулу (1.10), получим после очевидных преобразований
Положив
<2Л-2,>
±._{, h = ^L'-4, (2.1.22)
6 2.1. ЦЁПЙАЙ ЛИНИЯ
51
приведем уравнение (1.21) к виду
sh£ = A£.
(2.1.23)
Заметим, что параметр к > 1. Действительно, длина нити L больше расстояния между точками закрепления А и 5, т. е. L2 > I2 + h2. Сравнивая с (1.22), получим к > 1. Каждому значению /с отвечает один положительный корень уравнения (1.23), которое легко решается на
Таблица 2.1
Корни уравнения sh£=k£
к
1
k
С
k
h
Т
С
k
t
1,00
0,000
1,10
0,763
1,20
1,065
1,70
1,877
2,20
2,342
1,01
0,244
1,11
0,800
1,25
1,183
1,75
1,933
2,25
2,380
1,02
0,345
1,12
0,834
1,30
1,287
1,80
1,986
2,30
2,416
1,03
0,422
1,13
0,867
1,35
1,382
1,85
2,037
2,35
2,452
1,04
0,487
1,14
0,898
1,40
1,468
1,90
2,086
2,40
2,486
1,05
0,544
1,15
0,928
1,45
1,548
1,95
2,132
2,45
2,520
1,06
0,595
1,16
0,958
1,50
1,622
2,00
2,177
2,50
2,553
1,07
0,641
1,17
0,986
1,55
1,692
2,05
2,221
2,55
2,584
1,08
0,685
1,18
1,013
1,60
1,757
2,10
2,262
2,60
2,615
1,09
0,725
1,19
1,039
1,65
1,819
2,15
2,303
2,65
2,646
ЭВМ, графическим, табличным или аналитическим методами. В таблице 2.1, составленной с помощью ЭВМ, приведены корни уравнения (1.23) для различных значений к.
Порядок вычисления основных параметров цепной линии очевиден.
Пример. Длина нити L=100 м, пролет 1 = 65 м, превышение одной опоры над другой h=20 м, вес погонного метра нити 9=0,8 кГ/м. Определить основные параметры цепной линии.
Прежде всего вычисляем число к:
: 1,507.
* i—
С помощью интерполяции по таблице 2.1 найдем % = 1,631. Пользуясь формулой (1.22), определим параметр а:
I
а = 2£ = 19,90 м.
52
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
Применим теперь формулу (1.19)
По таблицам гиперболических функций [21] находим
26 — I
—2^— =0,203; 6 = 36,54 м
(приближенная формула (1.20) дает 6=36,48 м).
Стрелу провисания найдем по формуле (1.8) и таблицам гиперболических функций
Горизонтальная составляющая натяжения Н = aq = 15,92 кГ. Натяжения в точках закрепления найдем по формуле (1.14), учтя при этом, что у а = / и ув = f — h:
ТА = q(a+f) = 51,0 «Г, Тв = q(a + f — h) =35,0 кГ.
Реакции опор RA и RB равны по модулю натяжениям ТА иТв соответственно.
2-я схема. Даны стрела провисания / точки закрепления (числа I и h) и вес единицы длины нити q.
Если точки подвеса находятся^а одном уровне (Л=0), то б = 1/2 и уравнение (1.8) принимает вид
Найдя из этого уравнения число £, вычислим затем параметр а, после чего длина нити L, натяжение в точках А и В и горизонтальная составляющая натяжения Я найдутся по формулам (1.12), (1.14) и (1.4) соответственно.
Если же опоры находятся на разных уровнях (h Ф 0), то положим
Внесем эти значения для б и а в равенства (1.8) и
(1.9), после чего представим их в следующем виде:
6 =■ у («ь с -1) - с, i = (oh I — 1) — t (2.1.27)
ch£ = 2-j £ + 1,
(2.1.24)
(2.1.25)
Отсюда
(2.1.26)
8 2.1. ЦЕПНАЯ ЛИНИЯ
53
Эта система двух трансцендентных уравнений легко решается на ЭВМ. Найдя при данных Z, h и / числа £ и £, по формулам (1.26) определяем 6 и а, после чего обычным путем вычисляются остальные величины.
3-я схема. Цепная линия с одним свободным концом (задача о натяжении якорной цепи).
Имеются интересные задачи, в которых один конец цепной линии свободен и может перемещаться. Мы рассмотрим одну из таких задач на примере якорной цепи.
Пусть якорная цепь удерживает судно, находящееся под воздействием установившегося ветра, причем будем считать, что влиянием течения можно пренебречь (гидро- и аэродинамическое давление на нить рассматриваются в главе V). При этих условиях якорная цепь будет находиться в равновесии под действием сил тяжести (конечно, с учетом архимедовой силы), т. е. примет форму цепной линии.
Судно под действием ветра будет перемещаться до тех пор, пока сила давления ветра не уравновесится горизонтальной составляющей Н натяжения якорной цепи. Считая, что сила давления ветра на судно (в положении равновесия она равна Н) определена из аэродинамических характеристик судна и скорости ветра (внешняя информация для нити), придем к следующей задаче: при известной горизонтальной составляющей натяжения Н и одной закрепленной точке В (рис. 2.4) требуется определить основные параметры якорной цепи. Для полного решения задачи нужно задать еще длину цепи L, глубину моря h в месте якорной стоянки и вес единицы длины цепи в воде д.
Так как судно (верхняя точка А) может перемещаться, то при достаточно большой длине цепи последняя частично ляжет на дно и собственно цепная линия будет начинаться не от якоря В, а от точки О, в которой цепь отделяется от дна (рис. 2.4, а).
Решение задачи можно осуществить в следующей последовательности. По известной величине горизонтальной составляющей натяжения Я и по заданному значению q находим параметр a = H/q. Предположим, что якорная цепь не лежит на дне и имеет одну общую точку В (рис. 2.4, б). Тогда, пользуясь формулой (1.21) и таблицами гиперболических функций, найдем отношение Z/2a,
54
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
а затем число Z. Из равенства (1.19), зная й, L, Z, а, по таблицам найдем сначала (26—Z)/2a, после чего вычислим 6*
Затем следует рассмотреть два возможных случая,
а. Случай б ^ Z. Это означает, что точка В (якорь) принадлежит цепной линии (рис. 2.4, б), и найденные
Рис. 2.4.
значения для I и б можно использовать для дальнейших расчетов: по формуле (1.8) определяется стрела /, после чего по (1.14) находятся натяжения в точках А и В (г/л=/, yB = f—h).
б. Случай 6<Z. Это неравенство означает, что часть якорной цепи лежит на дне и цепная линия начинается в точке О (рис. 2.4, а). Расчет нужно производить
в другой последовательности. Точка О является вершиной цепной линии и, следовательно, б = Zj, а стрела f = h. Пользуясь формулой (1.8), получим
chA = i + A. (2.1.28)
Зная h и а, по таблицам найдем Zi/a, а затем и 1\. Длину L\ участка АО якорной цепи найдем по формуле
(1.12) при б = l\ = Z
Lx = a sh-^. (2.1.29)
§ 2.1. ЦЕПНАЯ ЛИНИЯ
55
Общее расстояние Z* по горизонтали от судна до якоря определяется равенством
z* = h + h, (2.1.30)
где h = L—L\. Остальные параметры вычисляются обычным способом.
Пример. Сила давления ветра на судно Н=2 г, вес погонного метра цепи в воде д —25 кГ/м, глубина h = 40 м, вытравлено Ь = 150 м цепи.
Находим а = H/q = 80 м\ вносим a, h, L в формулу (1.21):
sh 2а = 0,904.
По таблицам [21] находим 1/(2а) = 0,812. Отсюда I = 129,9 м. По формуле (1.19) имеем
26 — I
L “
По таблицам находим
tb 2a L ~ °*267,
Отсюда 6 = 86,8 м. Так как 6 < Z, то часть троса лежит на дне и, следовательно, вычисления нужно вести по формулам (1.28) и (1.29). Имеем:
chil=l,5, !± = 0,963, 1 =77,0 л»,
а а 1
I
L = a -1 = 89,5 м.
1 а
На дне лежит l2 = L — Ь{ = 60,5 м цепи. Расстояние по горизонтали от судна до якоря I* = l\ + h = 137,5 м.
Мы закончим этот параграф разбором одного очень важного для приложений случая малой стрелы провисания. Для простоты изложения рассмотрим цепную линию, граничные точки закрепления которой находятся на одном уровне (й = 0). Стрела провисания / называется малой, если она мала по сравнению с пролетом I:
(2.1.31)
Вернемся к равенству (1.24). При f/l < 1 правая и, следовательно, левая части этого равенства будут близки к единице. На этом основании ch £ можно разложить в ряд до степеням £ и ограничиться первыми двумя
56
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
ch^ = l + ^- +
(2.1.32)
Теперь равенство (1.24) принимает вид
или, учитывая, что £ = I/(2а),
12
(2.1.33)
й~ 8/’
Далее, если число £ = 1/(2а) = 6/а мало по сравнению с единицей, то будет мало и число х/а (так как |х| < 6). Поэтому, разлагая правую часть уравнения
(1.7) в ряд по степеням х/а и ограничиваясь принятой точностью, получим
Таким образом, цепная линия с малой стрелой провисания достаточно точно совпадает с отрезком параболы. Мы не останавливаемся здесь на этом вопросе более подробно, так как цепной линии с малой стрелой провисания будет посвящена вся третья глава.
§ 2.2. Неоднородная цепная линия
В приложениях иногда встречаются неоднородные цепные линии, когда сила тяжести, отнесенная к единице длины нити, зависит от положения точки М на нити. В этом случае будем иметь
где q(s) — заданная функция дуговой координаты s, которую будем отсчитывать от нижней точки нити О (рис. 2.2). Относительно функции q(s) будем предполагать, что она интегрируема, в частности она может быть кусочно-непрерывна (нить составлена из нескольких различных частей, каждая из которых однородна).
(2.1.34)
q = q(s),
(2.2.1)
§ 2.2. НЕОДНОРОДНАЯ ЦЕПНАЯ ЛИНИЯ
57
Для решения задачи воспользуемся дифференциальными уравнениями равновесия нити в канонической форме (1.6.17) и учтем при этом, что z = 0:
dx Рх dy
~ l/n2 _U n2
•2)
* VA + 4 d! VA + rl (2.2.;
dPx P dpv _ p
Ts -~^x' ~ds
В нашем случае Px = 0, Py = — q(s). Из последних двух уравнений (2.2) найдем
8
Рх = н = const, Ру = Q {s) = J q(s) ds + С. (2.2.3)
Постоянная Н имеет прежний смысл — она равна горизонтальной составляющей натяжения нити, а постоянная С = ру(0) = T(0)(dy/ds)o = 0, так как в точке О касательная к нити параллельна горизонтальной оси х.
Внесем значения рх и ру в первые два уравнения
(2.2) и проинтегрируем их от 0 до s, учтя, что при s = 0 х = у = 0:
ds
о ^
VНг- + Q2 (•)'
(2.2.4)
—Ш *.
J /я2 + £2 (s)
Мы получили уравнения равновесия неоднородной цепной линии в параметрической форме, в которых роль параметра играет дуговая координата s (читатель без труда может доказать, что при q = const после исключения параметра s получится обычное уравнение цепной линии (1.7)).
Натяжение нити Т найдем из формулы (1.6.16)
Т = УН2 + <?2Ы.
(2.2.5)
58
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
Положение вершины О (начала координат) относительно граничных точек А ж В ж остальные параметры нити определяются обычным путем из граничных условий.
§ 2.3. Влияние упругой деформации
До сих пор мы считали, что нить нерастяжима. Рассмотрим, какое влияние оказывает на однородную цепную линию упругая деформация, подчиняющаяся закону Гука. Задачу будем решать строгими методами (в рамках принятой модели абсолютно гибкой нити) и только в конце дадим оценку целесообразности применения их.
Как уже отмечалось в главе I, основное уравнение статики нити (1.2.1), а следовательно, и дифференциальные уравнения цепной линии (1.1) справедливы как для нерастяжимой, так и для растяжимой нити. Нужно только иметь в виду, что для растянутой нити сила тяжести д, отнесенная к единице длины нити, является величиной переменной, зависящей от натяжения Т. Поэтому для нити, подверженной линейной деформации, во втором уравнении (1.1) величину q нужно выразить через закон растяжения нити.
Пользуясь равенствами (1.1.12) и (1.1.14), получим
где до — сила тяжести, отнесенная к единице длины еще нерастянутой нити. При растяжении по закону Гука
где а* — удельное относительное удлинение нити (см.
(1.1.6)). Следовательно,
(2.3.1)
f(T) = 1 + а*Т,
(2.3.2)
(2.3.3)
Воспользуемся уравнениями равновесия (1.1)
Я_г£_сош,1, 4-(т£)=д. (2.3.4)
§ 2.3. ВЛИЯНИЕ УПРУГОЙ ДЕФОРМАЦИИ
59
Второе уравнение с помощью (3.3) принимает вид
(1 + a*T)d(T%f) = q0ds. (2.3.5)
Решение этого уравнения целесообразно провести в параметрической форме, выбрав в качестве параметра угол а между осью х и касательной к нити. Имеем
-J = cosa, ^ = sin a, -|jf=tga. (2.3.6)
Следовательно,
Т = — • (2.3.7)
cos ot 4 7
ме:
Теперь уравнение (3.5) приводится к следующей фор-
(* + а* 5мо) d tg ^ = q°ds• (2,3-S)
Из (3.6) найдем два выражения для ds:
ds = —, ds = S-. (2.3.9)
cos a’ sm a 47
Внесем в (3.8) сначала первое, а затем второе значения для ds и решим полученные уравнения относительно dx ж dy:
dx = a( l +
cos a) cos a dy = a(l+cc*^)^-da,
или, интегрируя,
x = a [in tg (x + -f-) + a*aQo tg a] + £i>
» = ‘[5h+-b,,,*sk]+c" (2'311>
где a = Н/q0.
Эти уравнения в параметрической форме определяют растянутую по закону Гука цепную линию. Дальнейшие
60
ГЛ. II. ЦЕПНДЯ ЛИНИЯ
вычисления можно несколько упростить, если перейти к новой переменной
« = In tg (-£+-!-). (2.3.12)
Пользуясь этим равенством легко установить следующие формулы *):
tg-T = thl-> (2-3-13)
seca = chu, (2.3.14)
sin a = th и, (2.3.15)
tga = shu. (2.3.16)
В новой переменной уравнения (3.11) принимают вид х = а (и + a*aq0 sh и) + Cv
I a* . \ (2.3.17)
у = a I ch и + aq0 ch2 и J + Cv
Покажем, что при a* = О из этих уравнений вытекает обычное уравнение цепной линии. Действительно, при а* = 0 получим
х = аи + С\, y = achu + C2.
Отсюда
х - Су = a ch — h С2»
т. е. уравнение (1.6).
Обозначим через щ и и2 значения параметра и в точках А и В соответственно. Так как растянутая цепная линия проходит через точку В, для которой хв — — (Z —б) и yB = f—h, то постоянные С\жС2 определятся равенствами
Сх = — (I — 6) — я (иг + a*ag0 sh их), сй = / — h — a ^ch щ + Ц- aq0 ch2 и^.
*) Угол ос, связанный с переменной и соотношениями (3.13) — (3.16), называется «гудерманианом ш> и обозначается символом a = gd и (по именй Гудермана, который, пользуясь этими формулами, составил таблицы гиперболических функций).
§ 2.3. ВЛИЯНИЕ УПРУГОЙ ДЕФОРМАЦИИ
61
Цепная линия проходит и через точку А. Поэтому х = 8, у = / при и = и2. Подставляя эти граничные условия в уравнения (3.17) и учитывая значения С\ и С2, получим после очевидных преобразований
и2 — ui + (sh и2 — sh их) = —,
h <2-3-18)
ch и2 — ch иг + — aq0 (ch2 u2 — ch2 ux) = —.
Эти два уравнения содержат.три неизвестные величины а, щ, и2. Для составления третьего уравнения проще всего воспользоваться условием равновесия всей нити. Если обозначить длину нити до растяжения через Lo, а через YA и YB — вертикальные проекции реакций точек закрепления, то будем иметь
Ya + Yb = Logo, (2.3.19)
где Logo — вес нити. Из условия равновесия точек А и В следует
YB = ТВу = —Я tg oci = —Я sh Hi,
Ya = TAy = Я tg 0С2 = Hshu2.
Здесь TBy и ТАу — вертикальные проекции натяжения в точках S и i, а «1 и а2 — значения угла а в тёх же точках. Подставив эти значения для YA и YB в (3.19), получим
Ьл
sh щ — sh их = -А (2.3.20)
С помощью этого равенства можно упростить уравнения (3.18). Упрощение первого уравнения очевидно, а для второго уравнения учтем следующее преобразование (см. формулу (1.10)):
ch2 и2 — ch2 щ = (1 + sh2 и2) — (1 + sh2 щ) =
= (shu2 — shu\)(shu2 + sh щ).
Пользуясь равенством (3.20) и присоединяя его к преобразованным уравнениям (3.18), получим
и2 ui = а*£оА)>
ch u2 — ch + ^j-q0L0 (sh ux + sh u2) = (2.3.21)
L
sh щ — sh ил = —.
- z 1 a
62
ГЛ. И. ЦЕПНАЯ ЛИНИЯ
Из этих уравнений по заданным go, U К ос* можно найти щ, и,2 и а. Предположим, что уравнения (3.21) решены и числа щ, щ п а найдены. Тогда натяжение растянутой цепной линии в любой ее точке найдем по формулам (3.7) и (3.14):
Т = Н ch и. (2.3.22)
В вершине О цепной линии а = 0, следовательно, и = 0. Стрелу провисания / растянутой линии найдем из второго уравнения (3.17)-, подставив в него и = 0, у = 0 и учтя значение С2:
/ = h + a [ch ut — 1 + Ц- aq0 (ch2 щ — 1) j, или, принимая во внимание равенство (1.10),
/ = h + a ^ch иг — 1 + aq0 sh2 (2.3.23)
Нам осталось определить длину L растянутой цепной линии. Для этого, пользуясь равенствами (3.10), найдем сначала дифференциал дуги:
(ds)2 = (dx)2 + (dy)2 =
= a2 (l + а* ——) (—~2 \~ —4—1 (da)2.
\ cos а/ \cos2 а cos а /
Отсюда
ds=a(l + a*^-)-^-. (2.3.24)
v cos a/ cog2 а 4
Интегрируя в пределах от а\ до аг, получим L = a (tg а2 — tg 04) +
или, учитывая равенства (3.12), (3.14), (3.16) и (3.21), L = L0 + i£a*?0Jch и2 sh иг — ch их sh их + — a*?0L0) |.
(2.3.25)
§ 2.3. ВЛИЯНИЕ УПРУГОЙ ДЕФОРМАЦИИ
63
Таким образом, задача свелась к решению уравнений
(3.21). Вычисления значительно упрощаются, если граничные точки А и В находятся на одном уровне. Действительно, в этом случае h = 0 и из второго уравнения
(3.21) вытекает единственное решение
U\ = —U2 (oci = —#2), (2.3.26)
что очевидно в силу симметрии.
Оставшиеся два уравнения принимают вид
и’ = "г(4 a*9oLo\ sh (2.3.27)
или, исключая и2,
Р-3-28*
Это уравнение содержит одну неизвестную величину а. При h = О упрощаются и выражения для длины растянутой цепной линии и стрелы провисания. Действительно, учитывая равенства (3.27) и (3.26), получим
L = L0 + aq0 [I + Lq (ch u2 — оь*Д(7о)Ь (2.3.29)
/ = a (ch - 1 + £ q0 ii). (2.3.30)
В сделанных предположениях все полученные формулы являются точными. Основные трудности решения задачи при h Ф 0 состоят в определении корней щ, и2, a уравнений (3.21), а при h = 0 — корня а уравнения (3.28). Для конкретных числовых условий решение легко реализуется на ЭВМ.
Для случая, когда модуль упругости нити £* (см.
(1.1.4)) значительно превосходит ее вес q^Lo, можно дать приближенное аналитическое решение. Мы покажем это на примере растяжимой цепной линии, концы которой закреплены на одном уровне (А = 0).
Если вес нити qoLo значительно меньше модуля упругости Е*, то число a*qoLQ/2 = qQLQ/(2E*) будет значительно меньше единицы. Положим
•удА = е< 1. (2.3.31)
64
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
Теперь уравнение (3.28) принимает вид
<2-332>
Будем искать решение этого уравнения в форме ряда, расположенного по степеням е:
а = ао(1 + d\z + а2г2 +...), (2.3.33)
где ао — значение параметра а при отсутствии растяже¬
ния нити. Внесем это выражение для а в уравнение (3.32) и разложим обе части в ряды по степеням е. Тогда, ограничиваясь членами первого порядка малости, получим
sh^ е + l\ ch^- =
2ао \ о / 2ао о о
Отсюда, сравнивая коэффициенты при одинаковых степенях е, получим
sh ^ + 0 ch ^ ах. (2.3.34)
2а0 2а0’ \2а0 т J 2aQ 2«0 1 v '
Первое равенство определяет параметр ао для нерастяжимой нити (см. равенство (1.21) при h = 0), а из второго находим
2aochi
аг = 2j-. (2.3.35)
Lo-lch2T0
Подставим это значение для а\ в (3.33). Тогда, учитывая равенство (3.31) и ограничиваясь принятой точностью, найдем
I
а—а. Н — Н. aoqoLo ch 2оТ
rix = —0 = = Г° а*. (2.3.36)
• ‘.-'Ы
Для длины растянутой нити будем иметь L—Ln Vo I
§ 2.3. ВЛИЯНИЕ УПРУГОЙ ДЕФОРМАЦИИ G5
Пример. Длина однородного стального троса в нерастянутом состоянии равна L0 = 110 м, площадь поперечного сечения F = 2 см2. Концы троса подвешены на одном уровне на расстоянии I = 100 м друг от друга. Полагая, что удельный вес стали у = 7,80 Г/сле3, а модуль упругости Е = 2 • 106 кГ/см2у определить растяжение троса и изменение горизонтальной составляющей натяжения.
Пользуясь формулой (1.1.7), найдем
Е* = EF = 4-10® кГ, а* = £; = -£. 1(ПвкГ-1.
Вес одного погонного метра троса до растяжения Яо = чР = = 1,56 кГ/м, вес всего троса q0L0 = 171,6 кГ. Это число мало по сравнению с Е*, поэтому можно воспользоваться приближенными формулами.
С помощью уравнения (1.23) и таблицы 2.1 находим значение параметра а0 троса, если бы он не подвергался растяжению. Имеем (h = 0)
к = Ь = 1,1, £ = 0,763, а0 = ± = 65,5 м,
I
ch 2^" = 1,305, /0 = 20 м,
^де /о — стрела провисания нерастянутого троса.
Подставляя найденные величины в (3.36) и (3.37), получим*)
jj jj
= н 0 = — 0,00018 = — 0,018%,
L-L0
Т|2 = L = 0,000028 = 0,0028%.
О
Эти числа наглядно показывают, почему во многих случаях не следует учитывать растяжение нити. Заметим здесь же, что если натяжение нити сравнимо с модулем упругости £*, то растяжение дает ощутимые результаты, в частности растяжение цепной линии необходимо учитывать при малой стреле провисания, когда натяжение троса достаточно велико. Однако при этом следует пользоваться не точными формулами этого параграфа, а приближенными формулами, которые будут даны в § 3.4.
Этот пример поучителен еще в одном плане. Строгое решение задачи о равновесии растяжимой цепной линии
*) Легко проследить, что и г\2 не зависят от площади поперечного сечения троса F.
66
ГЛ. II. ЦЕПНАЯ ЛИНИЯ
приводит к сравнительно сложному анализу и требует даже применения ЭВМ для определения корней системы уравнений (3.21). Между тем простой прикидочный расчет дает оценку метода. Действительно, натяжение нерастянутого троса в нижней точке равно Го = Но = qoao = = 102,2 кГ, а в верхней точке ТА = Tq+ qofo = 133,4 кГ. Среднее значение натяжения будет
Тср = Т°+2Та = 117,8 кГ.
Отклонения крайних значений натяжения от среднего значения не очень велико и для инженерного расчета можно считать, что Т = Гср = const. Но тогда относительное растяжение будет определяться равенством
= а*Гср = 0,000029 = 0,0029%.
о
Эта величина практически совпадает со значением т]2, вычисленной точными методами.
Приведенный элементарный расчет полезен не столько для приближенного вычисления относительного удлинения троса, сколько для оценки целесообразности применения строгих методов. Так, в данном примере, получив прикидочное значение для т]2 = 0,0029 %, можно сразу пренебречь растяжением троса — ведь исходные данные известны нам с меныпей точностью, да и модель идеальной нити, на которой построена вся теория, не может дать такое приближение к реальным объектам.
ГЛАВА III
РАВНОВЕСИЕ ТЯЖЕЛЫХ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
§ 3.1. Уравнение равновесия
Как уже отмечалось в § 2.1, стрела провисания тяжелой нити (цепной линии) называется малой, если она мала по сравнению с горизонтальным пролетом между граничными точками (рис. 3.1), т. е.
f<l. (3.1.1)
Случай малой стрелы провисания очень часто встречается в различных устройствах (радиоантенны, провода контактных сетей электрофицированных железных до-
Рис. 3.1.
рог и трамваев и т. п.). Кроме того, теория нити с малой стрелой провисания имеет непосредственное отношение к расчету висящих конструкций, например мостов. Это объясняется тем, что при малой стреле провисания нить мало отклоняется от горизонтальной проекции ее и можно считать, что распределение силы тяжести висящей нити происходит не по ее длине, а по горизонтальной прямой, т. е. так же как и распределение нагрузки ви5*
68 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
сящей конструкции (рис. 3.2). Поэтому мы считаем целесообразным посвятить теории тяжелой нити с малой стрелой провисания отдельную главу *).
Перейдем к составлению дифференциальных уравнений равновесия в предположении, что нить нерастяжима (влияние линейных деформаций на нить с малой стрелой
Рис. 3.2.
провисания будет рассмотрено в § 3.4). Так как па нить действуют вертикально направленные параллельные силы тяжести, то уравнения равновесия имеют вид (см.
(1.2.16))
Г £ = if.-const, +
В этих уравнениях постоянная интегрирования Н равна проекции натяжения нити Т в любой ее точке на горизонтальную ось х. Обозначим через q силу тяжести, отнесенную к единице длины горизонтальной оси х, и будем считать ее заданной функцией абсциссы х: q = q(x). Сила, действующая на элемент dx, равна q dx. Поэтому сила, приходящаяся на единицу длины нити, равна qdx/ds, и она равна проекции на направленную вертикально вниз ось I/**):
Py=q(x)^. (3.1.3)
*) Приложение теории гибкой нити с малой стрелой провисания к различным прикладным задачам подробно изложено в монографиях В. К. Качурина 1[7] и Р. Н. Мацелинского [13].
**) В отличие от главы II, здесь мы направляем ось у вертикально вниз, а начало координат выбираем в верхней точке закрепления. Такой выбор координатных осей более удобен для тех задач, которые будут рассмотрены в этой главе.
в 3.1. УРАВНЕНИЕ РАВНОВЕСИЯ
69
Из первого уравнения (1.2) найдем натяжение нити: Г = я£. (3.1.4)
Подставив во второе уравнение (1.2) значения Т и Ру и сократив его на ds, получим дифференциальное уравнение равновесия нерастяжимой нити, находящейся под действием вертикальной нагрузки, распределенной по горизонтали по произвольному закону:
d(tf-g-) + <z(*)d* = 0. (3.1.5)
Это уравнение решается простым повторным интег¬
рированием
X х
у = х — J<? (х) dx -f Съ, Q(x) = ^q(x)dx,
(3.1.6)
где С\ и С2 — новые произвольные постоянные.
Решение (1.6), справедливое при любом законе распределения нагрузки q(x), значительно упрощается при однородной нагрузке. Действительно, в этом случае qix) = q = const, и решение (1.6) принимает вид
У = -£-х — Jijx* + Cb. (3.1.7)
Таким образом, нить, находящаяся в равновесии под действием вертикальной нагрузки, равномерно распределенной по горизонтали, принимает форму параболы. Такдй же вывод мы получили, рассматривая цепную линию с малой стрелой провисания (см. окончание § 2.1). Это служит обоснованием сделанного предположения, что для тяжелых нитей с малой стрелой провисания можно считать, что нагрузка распределена не по нити, а по ее горизонтальной проекции.
Прежде чем перейти к определению основных параметров параболической нити, покажем, что те же результаты можно получить с помощью интегро-дифференциального уравнения равновесия нити (1.8.6). Действительно, дри отсутствии .сосредоточенных сил (Сг* = 0) ц
70 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
при Р = q dx/ds уравнение (1.8.6) приводится к виду
(\Х X к
x^qdx— ^'xqdx\, (3.1.8)
О 0 /
или, учитывая, что q = const,
у = х2
у Н 2Н
Это уравнение отличается от уравнения (2.7) только формой обозначения постоянной интегрирования (Су = = Ya) и отсутствием постоянной С2 (последняя обращается в нуль, если начало координат совпадает с любой точкой нити).
в Перейдем к определению основных параметров параболической нити. Найдем прежде всего значение х, при котором правая часть уравнения (1.7) имеет минимум. Для этого вычислим производную dyldx и приравняем ее к нулю. Имеем
7/ _ L х — о
у ~ Н II ~
Отсюда
х = 6 = —,
Я
причем постоянная интегрирования имеет простой геометрический смысл (см. рис. 3.1). Теперь уравнение
(1.7) принимает вид
У =!?[**- 4-) + С*’ <зл-9)
или
у=±(ьх--^) + С2, (3.1.10)
где параметр а определен прежним равенством (2.1.4)
a = f. (3.1.11)
При сделанном выборе начала координат (рис. 3.1) у 0 при х = 0. Внося эти значения для х и у в урав¬
§ 3.1. УРАВНЕНИЕ РАВНОВЕСИЯ
71
нение (1.10), найдем ^2 = 0. Следовательно,
у = -^г(Ьх- 4
Имеем
(3.1.12)
(3.1.13)
Внося в уравнение (1.12) значение х = б, найдем стрелу провисания
(3.1.14)
J 2а
Заметим, что вершина параболы С может не принадлежать нити, так как последняя совпадает только с частью параболы (рис. 3.1, б).
Горизонтальную составляющую Н можно вычислить теперь по формуле
я = |г?.
(3.1.15)
Обозначим через h превышение по вертикали одной граничной точки над другой. Очевидно, что у = h при х = Z. Внося эти значения в уравнение (1.12) и решая полученное равенство относительно б, найдем
я 1 . h л
б = Т + -Г ’
(3.1.16)
jEШ
Если граничные точки находятся на одном уровне, то h = 0 и 8 = 1/2 — результат, очевидный из условия симметрии (рис. 3.3).
Для нитей с малой стрелой провисания угол а между касательной к нити и горизонтальной осью х мал. Но тогда величина Itgal = \у'\ будет мала по сравнению с единицей.
На этом основании выражение для дифференциала дуги
Рис. 3.3.
ds = Vi -f у'2 dx
72 ГЛ. III РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
можно разложить в ряд по степеням у' и ограничиться первыми двумя членами. Имеем
ds = (l+-|-!/,!!)dx. (3.1.17)
Внесем в это равенство зпачение производной у' из формулы (1.13):
ds =. |l + (в — х)2^ doc- (3.1.18)
Интегрируя в пределах от 0 до Z, найдем длину L параболической нити при малой стреле провисания
L = l+±[(l-8)* + 6s\, (3.1.19)
Ьа-
или, учитывая значение б из равенства (1.16),
ь=1+£>+£- (зл-20>
Если точки закрепления находятся на одном уровне, то h = 0; согласно формулам (1.14) и (1.20) получим
£-!+i-r-
Найдем натяжение нити. Пользуясь равенствами
(1.4), (1.18) и (1.11), получим
Т = q [а + ~t (6 ~ ХУ] = 9 [а + 4" ~ "Г (6х - х)]-
Если учесть теперь формулу (1.14) и уравнение (1.12), то получим следующее выражение для натяжения параболической нити в любой ее точке:
'T = q(a + f-y). (3.1.22)
В точках закрепления уА = 0, ув = h. Поэтому
ТА = qU + /), Тв = q(a + /- h). (3.1.23)
§ 3.1. УРАВНЕНИЕ РАВНОВЕСИЯ
73
Дадим две оценки для параболических нитей с малыми стрелками *), граничные точки которых находятся на одном уровне. Из формул (1.21), (1.22) и (1.11) найдем
L-1 8 /2 Т — Н ^ с, /2 m О/Л
I _ 3 ;S’ Н ^ I2' (0.1.2а)
Если / = 0,11 (такую стрелку принято считать относительно большой), то длина нити L будет превосходить пролет I на 2,7%, а максимальное натяжение Т превышает его горизонтальную составляющую на 8%. Для стрелы / = 0,021 эти числа соответственно составляют 0,11% и 0,32%.
Пример 1. Определить основные параметры нити при следующих условиях I = 120 ле, h = Ь м, / = 10 ле, q = 0,8 кГ/м.
В данном примере f/l = 0,083, и поэтому стрелу провисания можпо считать малой. Найдем сначала параметр 6. Исключив из равенств (1.14) и (1.16) параметр а, получим
б2 - 2/ -L б + = 0. (3.1.25)
h h
Отсюда
f> = j(f-Vf2-fh) (3.2.26)
(при задании стрелы провисания / вершина нити С лежит между граничными точками А и В и перед радикалом нужно брать знак
минус).
Подставляя заданные числа, получим б = 70,3 м. Теперь, по формулам (1.14), (1-20), (1.11) и (1.23) последовательно найдем:
а = 247 м, L = 122,2 м, Н = 198 «Г, Т А = 205 кГ, Тв= 202 кГ.
Если при тех же I и q опоры находятся на одном уровне (h = 0), а стрела провисания / = 3 м, то будем иметь:
б = 60 м, а = 600 м, L = 120,2 м, Н = 480 кГ, ТА '= Тв = 482 кГ.
Из этих примеров видно, что длина нити L ненамного превышает величину пролета I (во втором примере всего на 0,2 ле), а максимальное натяжение нити ТА несущественно превышает горизонтальную составляющую Я (во втором примере на 0,5%).
Пример 2 Сравним результаты вычислений по точным формулам главы II и приближенным формулам этого параграфа.
а —^П/ Qb . Т ^алпп L Ъ 101 М1 h = Формулы § 2.1 дают ^U4,y м] j — Ь,127 м. По приближенным формулам § 3.1 полу-
стрелкойТР0ЛУ провисания часто называют просто стрелой или
74 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
чим а* = 204,1 м; /* = 6,124 м. Как видно, точность приближенных формул вполне удовлетворительна (исходные данные нам известны обычно с меньшей точностью). Заметим, что в данном примере / = 0,0612 I. Если стрела провисания будет составлять меньшую долю от то погрешность вычисления будет еще меньше.
§ 3.2. Влияние дополнительной равномерно распределенной нагрузки
Одной из задач теории подвесных конструкций является определение влияния на основные характеристики удерживающих нитей (тросов, канатов, цепей) дополнительной нагрузки. В этом параграфе мы исследуем случай, когда на нить с малой стрелой действует дополнительная равномерно распределенная нагрузка.
Рассмотрим сначала более общую задачу. Пусть пить с малой стрелой провисания находится в равновесии под действием вертикальной кусочно-равномерной распределенной по горизонтали нагрузки. Для определенности будем считать, что весь пролет разбит на три участка, как показано на рис. 3.4. Случай дополнительной нагрузки получится при q\ = #з = q и q2 = q + q*, где q* — дополнительная нагрузка. Мы рассмотрим два способа решения этой задачи, начав с метода припасовывания решений, применимого к любой кусоч^ но-непрерывно распределенной нагрузке.
Прежде всего заметим, что в силу независимости первого интеграла Н = Рис. 3.4. = const из (1.2) от зако¬
на распределения нагрузки q(x) все участки нити имеют одинаковую горизонтальную составляющую Н натяжения нити Т. Так как отдельные участки нити находятся под действием равномерно распределенной по горизонтали нагрузки, то к каждому из них можно применить готовые результаты, полученные ранее, в частности, каждый участок нити будет совпадать с отрезком соответствующей параболы, уравнение которой возьмем в форме (1.9). Таким образом, мы получим три уравнения, каждое из которых
S 9.2 н ВЛИЯНИЕ ДОПОЛНИТЕЛЬНОЙ НАГРУЗКИ 75
отвечает своему участку нити:
у = Zl(82x-^) + C2, (3.2.2)
у = тг{6*х-4) + с*‘ <3-2-3)
Эти уравнения содержат семь неизвестных величин: бь 62, бз, Сг, C2l С3 и Я. Для их определения воспользуемся сначала двумя гранйчными условиями:
у = 0 при х = 0, у = h при х = Z,
причем первое условие относится к уравнению (2.1), а второе к уравнению (2.3). Имеем
сг = о, + = (3.2.4)
Еще два уравнения получим из условия, что точка С с абсциссой х\ является общей для парабол (2.1) и (2.2), а точка D с абсциссой х2 — общая для парабол (2.2) и
(2.3):
~ Х% ^б2 j-j + С2 = -jf %% 2~) ^3*
В точках Си/) соответствующие параболы имеют общие касательные, и, следовательно, производные, вычисленные в этих точках, должны быть равны между собой. Это дает еще два условия
?i(6i - хО = q2(б2 - XI), q2(62 - х2) = д3(б3 - х2). (3.2.0
Решая совместно уравнения (2.4)—(2.6), получим (уравнения (2.5) и (2.6) составляют сущность метода припасовывания):
сх = 0, сг = 2^- (?1 — ?2) хи
1 (3-2.7)
Сз = 2Я 1(?1 й) “Ь ((?2 — (7з) ^2]?
76 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
§i — (21 — ^1)(?х — 92) ~Ь
-f- ^2 (2i — а:г)(5г2 — Яв) “Ь ]}*
(3.2.8)
f>2 = “|д" ~Ь 2“ [^1 (?2 —9l) + Х2 (2i—Хъ){Яъ 9з) “Ь ?3^2]J*
63 = ^ {ял + Ы (91 - ffi) + xt (я, - ff.) + Яз12]}‘
Перейдем теперь к вычислению длины нити. Пользуясь формулой (1.18) и интегрируя для первого участка нити в пределах от 0 до х\л для второго от х\ до Х2 и для третьего участка от х% до Z, получим:
Ьг = Х1 4- [(яг — 6i)3 + 6l],
L2 = хг — хх + ^5 [(a:2 — 62)3 — (х± — б2)8], (3.2.9) Ь, = 1-*ш + ц l(i - 6з)8 - (*, - Ш
где L\y L2, Lz — длины соответствующих участков нити.
Теперь, учитывая, что ak = H/qkj найдем длину всей нити
£ = Z + [(^1 ““ ®i)s + 81] +
~Ь я\ [(^2 — ®г)3 — (хх — ^г)3] ~Ь Яъ [(^ — ®з)3 (^2 83)3]).
(3.2.10)
Легко проверить, что из полученных формул вытекает случай однородной нагрузки. Действительно, если Я\ = ?2 = ?з = 9, то из равенств (2.8) будем иметь
=в, - 6, _ £(я*+«£.)=4+«f,
что совпадает с (1.16). Кроме того, при этом условии С{ = С<2 = Сг = 0. Таким образом, все три уравнения
(2.1)—(2.3) определяют одну параболу. Наконец, формула (2.10) упрощается и переходит в (1.19).
9 3.^ ВЛИЯНИЕ ДОПОЛНИТЕЛЬНОЙ НАГРУЗКИ
77
Предположим, что горизонтальная составляющая Я натяжения: Т определена* Найдем для каждого участка нити свое значений параметра ак
«1 = ^-, = a3 =f (З-2-11)
п затем, пользуясь уравнениями (2.6) и (2.8), вычислим соответствующие стрелки (Д = у(6*))
^ = 2^’ f*=db + C" /а = 4 + ^3- (3-2.12)
Так как каждый участок нити совпадает только с частью параболы, то вычисленные Д являются по существу не стрелками нити (одна из них может действительно принадлежать нити), а просто значениями соответствующих ординат парабол при xh = 8h (см. рис. 3.1, б).
Вычислим значения ординат точек, в которых определяется натяжение нити Т. Для точек А, С, Z), В имеем
и-0, +
(3.2.13)
Ув = к, Уо=-^-{ьг — -£?j + ct=*-±(b, — -fj + C,.
Натяжения нити в рассматриваемых точках определяются по формуле (1.22)
ТА = qM\ + fi),
Тв = дгЫг + /з-й),
(3.2.14)
Тс = qMI + fi- Ус) = Q2(CL2 + /2 - Ус),
TD = g2(^2 + /2 — Ud) = дз(«з + U — Ув).
Таким образом, для полного решения задачи осталось определить один параметр Я, который легко вычисляется, если известна длина нити L. Действительно, внесем значения 61, 62, 63 из (2.8) в равенство (2.10). Тогда последнее будет содержать только одну неизвестную величину Я. Решая полученное уравнение, найдем значение Я, после чего все остальные параметры нити определятся по полученным формулам.
78 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛО^ПРОВИСАНИЯ
/
/
/
Второй метод основан на комбинировании уравнений
(2.1) —(2.3) с уравнением равновесия н^ти в интегральной форме, которое при горизонтально распределенной нагрузке имеет вид (см. (1.8)) /
х х
У = ^ х — j q (х) dx + -iyj xq (ж) dx. (3.2.15) li о о
Функция qix) на участке (0, X\) равна q 1, на участке (x\, X2) — <72, а на последнем участке (x2, I) — дз. Напишем теперь уравнение (2.15) сразу для третьего участка, считая, что абсцисса х принадлежит промежутку (#2, D- Для вычисления интегралов разобьем весь промежуток (0, х) на три части: (0, х\), Ui, х2) и (х2, х). Имеем
(*1 *2 х \
J qidx + j q2dx + J q3dx J +
о *i *2 /
*2 * \
J xq^dx + J xq2dx + Jxqzdx I, о x2 J
или, интегрируя,
Y A x
У= ~нх— ~н foA + 9t (хг — X1) + Яз (x — ^2)] +
+ Yjj hixl + {x\ — xt) + q3 (x2 — ^2)]• (3.2.16)
Для того чтобы получить уравнение кривой равновесия для второго участка СД достаточно в уравнении
(2.16) положить £з = 0 и заменить Х2 на х:
Y л х
У — х —jf \q\xi + ?2 (х — ^i)] +
+ 2^[?i*? + g2(*2-*?)]• (3.2.17)
Уравнение кривой равновесия для первого участка АС получается из (2.17) при q2 = 0 и х\ = х
У=Чх-Шх2- (3-2-18)
§ 3.^ ВЛИЯНИЕ ДОПОЛНИТЕЛЬНОЙ НАГРУЗКИ 79
Для определения постоянной YA учтем, что у = h при х = 1. Внося 9тй\ значения для у и х в уравнение (2.16) и решая полученное равенство относительно YА, найдем
уА =-р{яь+V* w -х^ - q*)+
+ х2 (21 — х2) (д2 — д3) + q3l2] j. (3.2.19)
Если теперь сравнить коэффициенты при одинаковых степенях х уравнений (2.18), (2.17) и (2.16) с соответствующими коэффициентами уравнений (2.1), (2.2) и
(2.3), то получим сразу формулы (2.7) и (2.8). Второй метод практически применим только при нагрузке, распределенной по горизонтали, в то время как первый метод может быть использован при любой кусочно-непрерывной нагрузке. В частности, для цепной линии с кусочно-непрерывной нагрузкой весь первый метод остается без изменения — нужно только вместо уравнений парабол (2.1)—(2.3) написать соответствующие три уравнения цепной линии.
Пример. Нить находится в равновесии под действием вертикальной равномерно распределенной нагрузки q. Длина пролета нити равна J, граничные точки А и В находятся на одном уровне (h'=0) и стрела провисания равна /0. На участок (яь х2) положена дополнительная нагрузка q* '= д. Определить, как изменится натяжение и форма нити, если хх '= г/4 их2 = г/2 (рис. 3.5).
Прежде всего найдем все основные параметры нити без дополнительной нагрузки, причем все значения их будем обозначать нижним индексом нуль, а значения тех же параметров при дополнительной нагрузке будем обозначать теми же символами, но без индекса.
Так как по условию задачи граничные точки А и В находятся на одном уровне (h = 0), то, согласно формулам § 2.1, будем иметь
60=f H° = 9ijr0’ L0 = l + TV TOA = ToB^ff0 + qf0.
(3.2.20)
80 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
Ординаты точек С и D при отсутствии дополнительной нагрузки определим из уравнения
X / X \
, = Г0(б°—2 )-
где а0 = H0/q = I2/ (8/0). В точке С абсцисса х = Z/4, а в точке D она равна 1/2. Поэтому ординаты этих -точек равны (б0 = I/2)
^ОС = |-/о- ^oD f o' (З-2-21)
Перейдем к вычислению основных параметров нити с дополнительной нагрузкой q* = q. Очевидно, что в данном примере будем иметь: gi = g, g2 = 2g, g3= g. По формулам (2.13) найдем
с 21 у с 291 с 13»
1 = 32 2 = 64 8 = 32
Пользуясь формулой (2.10), найдем горизонтальную составляющую Н натяжения Г, при этом учтем, что длина нити остается без изменения, так что L = LQ = I + Sf2/(3l). Подставляя соответствующие величины в эту формулу, найдем
ql
// = 0,1697-.
•о
Сравнивая с Но, получим
Н — Нл
• н ° = 0,352,
о
т. е. горизонтальная составляющая натяжения увеличилась на 35,2%.
Вычислим по формулам (2.11) парахметры аи:
I2 I2 I2
^=0,1697, а =0,0845 т, а_ = 0,1697.
h 2 То 3 То
По формулам (2.12) найдем стрелки всех трех парабол:
и = 1,27 /о, и = 1,03 /о, /з = 1,04 /о.
Из этих трех величин только стрела /2 принадлежит нити, так как координата 61 находится вне первого промежутка (0, I/4), координата 63 — вне третьего промежутка (I/2, I) и только 62 принадлежит своему промежутку (I/4, 1/2).
Вычислим по формулам (2.13) ординаты точек С и D:
Ус — 0,784 /о, yD = 1,016 /0.
Сравнивая с уос и i/od, найдем
"-^-0,034, ».»«.
У ОС У0D
§\3.3. ВЛИЯНИЕ СОСРЕДОТОЧЕННОЙ СИЛЫ 81
Таким обрашш, ординаты точек С и D остались практически без изменения. \
По формулам \2.14) найдем натяжения в отдельных точках
(учтено равенство akQk)'
ТА = яу 1,274 g/о, Тс = Н + 0,490 д/0,
Тв = Я X 1,042 д/о, Т d = Н + 0,026 д/0.
Если /о = 0,1 £, то б^дем иметь
mm fp Ф Т Т
Ат °* = 0,346, °С = 0,350, ” oD = 0,352,
У 0 А 1 ОС i ОД
т. е. натяжение в отдельных точках увеличилось примерно па 35%. На такую же величину возросла и горизонтальная составляющая Я натяжения Т. Это следовало ожидать, так как при малой стреле провисания основной частью натяжения в любой точке нити является горизонтальная составляющая Я (см. примечание к соотношениям (1.24) и пример § 2.1).
§ 3.3. Влияние сосредоточенной силы
Пусть однородная нить с малой стрелой провисания находится в равновесии. Требуется определить, как изменится форма нити и ее натяжение, если в точке С с абсциссой хо к нити будет приложена сосредоточенная сила G, направленная вертикально вниз (рис. 3.6).
Мы будем решать задачу методом, применимым к лю- А бым силам. В данном случае на оба участка нити АС и СВ действуют равномерно распределенные по горизонтальной прямой вертикально рис 3 g.
направленные силы. Поэтому
каждый участок нити совпадает с отрезком соответствующей параболы, уравнения которых запишем в форме (2.1)
y = -H-1{^x-4) + Cl' (3-3>1)
У=ТГ (бгХ — 1~) + С2’ (3.3.2)
причем первое уравнение относится к участку нити АС, а второе — к участку СВ\ считается также, что каждому
82 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
участку нити соответствует своя горизонтальная составляющая Нк натяжения нити Т. /
Для определения неизвестных 61, /2, С\, С2, Н1, Н2 воспользуемся прежде всего граничными условиями: у = О при х = О и у = h при х = 1, причем первое условие относится к уравнению (3.1), к второе — к уравнению (3.2). /
Имеем
сх = °, £ (бг - J ) + Сг = h. (3.3.3)
Еще одно равенство получим из условия, что обе параболы имеют общую точку С:
+ (3.3.4)
Два уравнения получим из условия равновесия точки С. На эту точку действуют три силы: сосредоточенная сила G, направленная по условию задачи вертикально вниз, сила реакции правой части нити Т2> равная ее натяжению в этой точке, и сила реакции левой части нити, равная по модулю ее натяжению в точке С и направленная в противоположную сторону, т. е. — Тг (см. рис. 1.2 и 3.6). Так как точка С находится в равновесии, то должно выполняться следующее векторное равенство:
-Tx + T2 + G = 0.
В проекциях на оси координат будем иметь
—Т1 cos а\ + Т2 cos <Х2 = 0, (3.3.5)
—Т1 sin а\ + Т2 sin аг + G = 0, (3.3.6)
где ai и о&2 — углы между касательными к соответствующим параболам и осью х в точке С. Слагаемые в уравнении (3.5) равны горизонтальным составляющим натяжения Н\ и #2:
•
Т1 cos а\ = Н1, Т2 cos а2 = Я2. (3.3.7)
Поэтому из уравнения (3.5) получим
Я! = Н2 = Н. (3.3.8)
9 ^.3. ВЛИЯНИЕ СОСРЕДОТОЧЕННОЙ СИЛЫ 83
\
Из формул (3.8) и (3.7) найдем
У = _й_ т =
\ cosc^’ 2 cosa2'
Внесем эти значения для Т\ и Т2 в уравнение (3.6)
—Я tg ai + Н tg «2 + G = О,
9 9
или, учитывая, что tg = уг, tg a2 = у2,
У1 — Уг = тр (3.3.9)
где у[ и У2 — производные по а;, вычисленные от функций (3.1) и (3.2) в точке С (х = #0). Имеем
у'1 = IT(6l _ у'2= ~5~^2 — ^
Равенство (3.9) примет теперь вид
Si — б 2 = (з.з.ю)
где безразмерный параметр и определен равенством
* = |. (3.3.11)
Решая совместно уравнения (3.3), (3.4) и (3.10),
найдем
~ 0, 6i = -г —т & и (I *0),
I г h (3.3.12)
С2 = k — Xq, б2 = j 4- -у л — к*о-
Здесь, как обычно, а = Я/д.
Прежде чем перейти к дальнейшему, заметим, что в данном примере для определения постоянных С\, и 62 можно было использовать уравнение равновесия в интегральной форме (1.8.6), которое в нашем случае принимает вид
У
у Г * * 1
= х — Jjr (а; — а;0) G 4- х J q dx— j* xq dx .
L 0 0 J
Мы не пользуемся этим уравнением, так как оно применимо практически только к горизонтально распределен-
84 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛО*уПРОВИСАНИЯ
ной нагрузке и не обладает общностью изложенного выше метода. /
Для полного решения задачи остаюсь найти один неизвестный параметр а. Для его определения выразим длину нити L через a, 6j и 62. Для этсто достаточно проинтегрировать выражение (1.18), разбив промежуток интегрирования (О, I) на два промежутка (0, xq) и (я0, I). Имеем
Li = #0 + — ^i)3 +
а < (3.3.13)
ь2 = I - Х0 + JL [{I - 62)* - (x0 - б2)3],
где Li и L2 — длины соответствующих участков нити. Складывая, получим длину всей нити
L = I [(:г0 — б2)3 + S? + (Z — б2)3 — (хо — 62)3]»
о а
(3.3.14)
или, раскрывая скобки и учитывая равенство (3.10),
L = I + [l2 — Зкяо + Зха:0 (fix + 62) — 362 (I — 62)].
6а
(3.3.15)
Если внести сюда значения Si и 62 из равенств (3.12), то получится квадратное уравнение относительно параметра а; взяв положительный корень, найдем затем Я, 61, 62 и С2. При h¥= 0 это решение в общем виде будет выглядеть несколько громоздко, но в каждом конкретном случае довести его до конечного результата не представляет никакого труда.
Дальнейшее исследование мы проведем в предположении, что обе граничные точки находятся на одном уровне, т. е. при h = 0. Будем считать, что нить без сосредоточенной силы определялась пролетом I и стрелой /0. Тогда все ее параметры будут определены равенствами (2.20)
о _ I а = 12 г _ ; , 8 /о
0 — 2 ’ 0 8/# ’ 3 I ’
Но = ^ Т0А = Т0В = //„ + qf0. (3.3.16)
Й\8.3. ВЛИЯНИЕ СОСРЕДОТОЧЕННОЙ силы 85
\
Найдем изкенение горизонтальной составляющей натяженйя нити $Г при действии сосредоточенной силы G. Пользуясь равей^твом (3.15) и значением L из (3.16) и учитывая, кроме foro, что нить нерастяжима, получим
а2 = ~~ло*2 I1* — (fix + 62) — Зб2 (I — 6а)].
16/о
Внеся сюда значения Si и 62 из (3.12) при h = 0 и произведя элементарные преобразования, найдем
а = - J- 1Лг + 12(1 + х)(^0- х$). (3.3.17)
Отсюда
я = £- Vp+ 12х (1 + и) О0 - х\). (3.3.18)
5/0
Из этого выражения видно, что горизонтальная составляющая Н натяжения нити Т зависит от точки приложения сосредоточенной силы G. Найдем экстремальные значения Н. Имеем
dH _ gl 6х (1 + у) (I — 2х0)
dxo 8*о ]f + 12и (1 + ус) (lxQ — xjj
В точках максимума и минимума dH/dxQ = 0, что дает
I
%о — 2 *
Из полученных выражений видно, что горизонтальная составляющая натяжения имеет только одно экстремальное значение, когда сосредоточенная сила приложена в середине пролета. Легко проверить, что в этой точке имеется максимум, равный
Я та* = |г- ]Л + Зи(1 + *). (3.3.19)
На рис. 3.7 показана зависимость горизонтальной составляющей Н натяжения Т от относительной координаты #о/I точки приложения сосредоточенной силы G. Зависимость дана в долях Я0, где Hq = Н при G = 0. График
86 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ^РОВИСАНИЯ
построен по формуле '
которая легко получается сравнением равенств (3.18) и
(3.16). Из графика видно, что значение горизонтальной
И/Но
составляющей натяжения нити быстро растет с увеличением мф*уля сосредоточенной силы G (напомним, что х = G/ql).
§ 3.4. Влияние линейных деформаций нити
Все выводы, полученные до сих пор, сделаны в предположении, что нить нерастяжима. Однако на практике приходится считаться с тем, что под влиянием температуры и упругих свойств материала нить деформируется, изменяя свою длину.
1. Влияние температуры. Пусть при температуре t°
о
длина нити равна Ь$. Тогда при температуре длина нити будет
L = L0 [1+<*(£-О],
где а — коэффициент линейного расширения.
Отсюда найдем относительное приращение длины нити
Ц = L т L° = a(tl — t°). (3.4.1)
О
Оценим величину т]. Считая, что а = 12° • 10"6 (для стального троса) и что разность между летней и зимней
§ З.А ВЛИЯНИЕ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ НИТИ
87
температурами равна 70°С, получим
г\ = 0,00084.
Таким образом, при изменении температуры на 70°С длина стального троса изменится на 0,084%- Рассмотрим как эта деформация скажется на натяжении троса, предполагая для простоты выкладок, что граничные точки закрепления находятся на одном уровне (h = 0).
Считая, что деформация нити происходит равномерно
по всей длине и учитывая, что вес нити при этом остается
без изменения, будем иметь
Loqo = Lq,
где qo и q — вес единицы длины нити до и после ее деформации. Пользуясь равенством (4.1), получим
Logo = Zro(l + ri)g.
Отсюда
g = (3.4.2)
или, с точностью до членов высшего порядка относительно малой величины rj,
q = (1—T|)ff0- (3.4.3)
Из сделанного предположения о равномерном растяжении нити следует, что деформированная нить принимает форму параболы.
Обозначим значение параметра а при температуре t° через Оо, а при температуре h через а. Пользуясь формулой (1.20), получим при h = 0
а=\/' 24 (L — 1) ’
где L — длина нити при измененной температуре. Согласно равенству (4.1) Ь = Ь^(\ + у\). Следовательно,
а= V24(£0-г+^) •
При h = 0 длина нити L0 определяется формулой (1.21)
8 ft |
88 ГЛ. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ /ЙРОВИСАНИЯ
После подстановки и очевидных преобразований получим
12 / \-i/a
Первый множитель равен значению ао до температурной деформации. Разлагая второй множитель в ряд по степеням т] и ограничиваясь членами первого порядка малости, найдем
3
а = а0 (l —
16
Имеем
H = aq = a0^ 1 - П U (1 - Л),
16
или с принятой точностью
/2
'О
о
'0
л
где Но — значение горизонтальной составляющей натяжения нити до температурной деформации.
Внесем в последнее равенство значение Lq и вычислим относительное изменение Н:
<3-«>
При малой стреле провисания горизонтальная составляющая натяжения может существенно измениться даже при очень малом значении т]. Так, например, если летом стальной трос имел стрелу провисания, равную 0,02/, то зимой при перепаде температуры на 70°С будем иметь: т] = —0,00084, l/fo = 50, и, следовательно,
Я“Я° = 0,395,
#о
т. е. горизонтальная составляющая натяжения увеличится почтд на 40%. Если же стрела провисания составляет
0,01 Z, то горизонтальная составляющая натяжения увеличится на 160%. Зимой это может вызвать обрыв туго натянутых тросов.
§ 3.4. ВЛИЯНИЕ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ НИТИ
89
2. Влияние упругих деформаций. Будем считать, что растяжение нити подчиняется закону Гука. Тогда равенство (1.1.3) на основании (1.1.6) примет вид
-|L = l+a*7\ (3.4.5)
где ds0 и ds — длины одного и того же элемента нити до и после растяжения, а а* = 1/£* — удельное относительное удлинение нити.
Для нитей с малой стрелой провисания горизонтальная составляющая натяжения Н мало отличается от натяжения Т (см. примечание к соотношениям (1.24) и пример § 3.1). На этом основании в равенстве (4.4) натяжение Т заменяют на его горизонтальную составляющую Н. Тогда это равенство принимает вид
ds = (1 + a*H)dso, или после интегрирования
L= (l + a*H)L0, (3.4.6)
где Lo и L — длины нити до и после растяжения, а Ягоризонтальная составляющая после растяжения.
Из условия сохранения веса нити получим аналогично (4.2)
^— (3.4.7)
1 + а*Н
Из сделанного предположения о возможности замены Т на Н следует, что растяпутая по закону Гука нить с малой стрелой провисания с принятой точностью принимает форму параболы.
Параметр нити а будет равен
„=«-= "» + “•*». (3.4.8)
q Ч
Дальнейшие вычисления зависят от заданных элементов нити.
а. Предположим, что заданы пролет Z, превышение Л, вес единицы длины нити до деформации и стрела провисания / после деформации нити. Из уравнения (1.26) найдем параметр б, затем по формуле (1.14) найдем па-
90 гл. III. РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
раметр а после деформации нити
а=£. (3.4.9)
Подставляя это значение параметра а в (4.8), получим квадратное относительно Я уравнение
а*Я2 + Я-?0|1 = 0. (3.4.10)
Отсюда находим натяжение растянутой нити.
б. Заданы пролет Z, превышение h, вес единицы длины нити qo и ее длина Ьо до деформации. Пользуясь формулами (1.20), (4.7) и (4.8), получим после очевидных преобразований
24LqH* (1 + <х*Я)3 -24 (* + Я2 (1 + <х*Я)а - l3ql = 0.
(3.4.11)
Рассмотрим случай, когда модуль упругости нити £* значительно больше горизонтального натяжения нерастянутой нити #о, т. е. £* > Я0; отсюда HJE* = а*Я0 < 1. Положим
а*Я0 = е < 1 (3.4.12)
и будем искать решение уравнения (4.11) в форме ряда, расположенного по степеням е:
Н = Я0(1 + еЯ1 + ...). (3.4.13)
Подставим это выражение для Я в уравнение (4.11) и сгруппируем члены по степеням е. Тогда, ограничиваясь членами первого порядка малости, получим
24 (b0-l-?p)H2-Pq2 + + 24Н20[зЬ0 - 21 - -f + 2[l0 - I -1?) Ях] 8 = 0.
Так как это равенство должно выполняться при всех е, то свободный член и коэффициент при е должны равняться нулю. Следовательно,
JS, 3L0-2l-*L
Я02=— —ГгГ’ Н1 7 Ат* (3-4.14)
24
§ 3.4. ВЛИЯНИЕ ЛИНЕЙНЫХ ДЕФОРМАЦИЙ НИТИ
91
Рассмотрим частный случай, когда граничные точки нити находятся на одном уровне (h = 0). При этом условии L0 = I + 8/2/(3Z) и равенства (4.14) принимают
простой вид
я,--4тг(1+*4)-(3-4-15)
Пользуясь равенствами (4.13), (4.15) и (4.12), найдем
ч. = ^--Т§г-£(1+87)®>‘“*- <3-4-16>
Для нитей с малой стрелой провисания отношение fill2 очень мало. Поэтому, если пренебречь этим членом по сравнению с единицей, то окончательно получим
41= л*»*- (3-4-17)
0 / о
Пример. Пусть пролет стального троса I — 100 м, площадь поперечного сечения F = 1 еле2, стрела провисания нерастянутого троса /о = 0,021. Для стали примем модуль упругости Е = 2 • 106 кГ/см2, а удельный вес f = 7,6 Г/сле3. Согласно равенству (1.1.7) найдем модуль упругости для троса Е* = EF = 2* 106 кГ; отсюда а* = i/E* = 0,5• 10—6 кГ~К Вычислим теперь до. Имеем: q0 = Fy = 0,76 кГ/м. Пользуясь формулами (4.14), (4.15) и (4.6), получим
Н — Нл L — Ln
Н =475 кГ, — = — 0,112, —J—- = 0,00024. (3.4.18)
о о
Таким образом, при упругой деформации стального троса с малой стрелой провисания его длина изменяется очень мало, но это вызывает существенное изменение горизонтальной составляющей Н натяжения Т (в нашем примере на 11,2%).
Все выводы о упругой деформации нити с малой стрелой провисания получены в предположении, что во всех точках нити ее натяжение Т можно заменить на горизонтальную составляющую Я, в результате чего нить после деформации примет снова форму параболы, мало отличающуюся от параболы, форму которой она имела бы при отсутствии растяжения. Это рассуждение, конечно, не является строгим, поэтому представляет интерес оценить полученные результаты. Для этого воспользуемся формулой (2.3.36), свободной от сделанных предположений о
92 ГЛ. IIL РАВНОВЕСИЕ НИТЕЙ С МАЛОЙ СТРЕЛОЙ ПРОВИСАНИЯ
форме растянутой нити,
* Н — #„ °о?о£о cJl 2а~
ЧГ у-* f- а» (3.4.19)
*
(звездочка в коэффициенте % поставлена для того, чтобы отличить его от соответствующего коэффициента (4.16), вычисленного в упрощающих предположениях).
Для нерастянутой нити с малой стрелой провисания и h = 0 были установлены следующие формулы:
а - *2 L -Z + 8 /S
0 - 8/0’ 0 ~ + тт "Г-
Следовательно, l/(2a0) = 4/0/Z 1. Поэтому гиперболи¬
ческие косинусы, входящие в (4.19), можно разложить в ряд по степеням Z/(2a0)<l и ограничиться первыми двумя членами:
ch * « 1 4- — — 14-8 —
2Я0 + 2 Аа2 - 1 + 8 ,2 •
Внося значения для ао, А) и chZ/(2ao) в (4.19) и сравнивая с (4.16), получим после очевидных упрощений
4М±Л
з I» 1в ji
«I ттп~ _о •
4i /5 3 I
1 + 8^
Это означает, что при стреле провисания /о = 0,02 Z ошибка в вычислении коэффициента к)\ по формуле (4.16) составит примерно 0,2%—точность в таких расчетах^ более чем достаточная (в формуле (4.17) мы вообще пренебрегли членом 8fl/l2). Таким образом, приближенная теория упругой деформации тросов с малой стрелой провисания имеет достаточно строгое обоснование.
ГЛАВА IV
НИТИ РАВНОГО СОПРОТИВЛЕНИЯ
§ 4.1. Постановка задачи
В общем случае в каждом сечении нити имеется свое нормальное напряжение. Естественно поставить вопрос о конструировании нитей равного сопротивления, т. е. таких нитей, в которых нормальное напряжение одинаково во всех поперечных сечениях. В этом случае все части нити испытывали бы равные усилия на разрыв, что благоприятно отразилось бы на эксплуатации и отвечало наиболее экономному расходу материала.
Задача о нити равного сопротивления ставится обычно следующим образом: по заданным силам и граничным условиям требуется определить форму равновесия нити и закон распределения площади поперечного сечения, предполагая, что материал нити однороден и что во всех ее точках имеются одинаковые нормальные напряжения. Недостатками нитей равного сопротивления являются, во-первых, отсутствие универсальности (при изменении, например, граничных условий свойство равного сопротивления теряется —см. § 4.3, стр. 100) и, во-вторых, технологические трудности — нужно изготовить нить с переменной площадью поперечного сечения. В связи с этим нити равного сопротивления не нашли широкого распространения. Однако в тех случаях, когда натяжения в разных точках нити существенно отличаются друг от друга, применение нитей равного сопротивления может быть оправдано.
Рассмотрим теперь некоторые общие свойства дитей равного сопротивления.
Натяжение нити Г, нормальное напряжение о и площадь поперечного сечения F связаны очевидным соотношением
I - eF, (4,1.1)
94
ГЛ. IV. НИТИ РАВНОГО СОПРОТИВЛЕНИЯ
причем для нитей равного сопротивления о = const. Поэтому, если будет найден закон распределения площади поперечного сечения F(s), то тем самым будет определен закон изменения натяжения нити T(s).
Пусть нить равного сопротивления испытывает упругое растяжение по зарону Гука. Тогда с помощью равенств (1.1.3) и (1.1.6) получим
Учтем теперь, что удельное относительное удлинение нити а* = 1 /Е* = 1 /{EF) (см. формулу (1.1.7)), а натяжение нити Т = oF. Внося эти значения для а* и Г в последнее равенство, будем иметь
или, интегрируя и учитывая, что для нитей, равного сопротивления а = const,
В следующем параграфе мы начнем изучение поставленного вопроса с рассмотрения хорошо известной, но важной для приложений и нужной нам для сравнения задачи.
§ 4.2. Равновесие тяжелой вертикально подвешенной нити равного сопротивления
Рассмотрим тяжелую нить, подвешенную за один конец и удерживающую на втором конце груз В весом G (рис. 4.1). Требуется определить закон распределения площади поперечного сечения нити F(s), считая, что материал нити однороден, а нормальное напряжение одинаково во всех поперечных сечениях.
ds = (1 + a*T)dso.
(4.1.2)
ds = (1 + c/E)dso,
Отсюда
s~~so _ о m
(4.1.3)
8 4.2. РАВНОВЕСИЕ ТЯЖЕЛОЙ ВЕРТИКАЛЬНОЙ НИТИ
95
Сила тяжести, отнесенная к единице длины нити, определяется равенством
Р = 4F, (4.2.1)
где у — удельный вес материала нити. Для прямолинейной нити первое уравнение равновесия (1.3.3) имеет вид
dT
ds
+ Р = 0.
(4.2.2)
Пользуясь равенствами (1.1) и (2.1), получим
или, разделяя переменные,
где
/с
(4.2.3)
(4.2.4)
А
////////1
Интегрируя уравнение (2.3), найдем закон изменения площади поперечного сечения для рассматриваемой нити равного сопротивления
F (s) = FAe~s/k. (4.2.5)
Здесь Fa — площадь поперечного сечения нити в верхней точке А закрепления нити. В нижней точке В натяжение нити Тв равно силе тяжести G подвешенного груза. Следовательно, если длину нити обозначить через L, то будем иметь
Отсюда
Fb= ?r = FAe
A L/k
тг- = е
-L/k
в
(4.2.6)
(4.2.7)
G
s
Рис. 4.1.
Пример. В воде удельный вес стального троса
Y = 6,8* 10—3 кГ/смг. Если принять о = 4000 кГ/см2, то получим: А *= о/Y = 5,88 • 103 м. Для тросов, удерживающих батисферу на
96
ГЛ. IV. НИТИ РАВНОГО СОПРОТИВЛЕНИЯ
глубинах 8000, 5000 и 500 м, по формуле (2.7) найдем, что площадь Fa поперечного сечения троса в верхней части А больше площади F в поперечного сечения в нижней части в 3,90, 2,66 и 1,10 раза соответственно.
§ 4.3. Равновесие цепной линии равного сопротивления
Рассмотрим нерастяжимую нить равного сопротивления, находящуюся в равновесии под действием собственной силы тяжести (цепная линия равного сопротивления). Прежде всега отметим, что нас не будут интересовать нити с малой стрелой провисания, так как для таких нитей
натяжение Г, а следовательно, и нормальное напряжение однородных ни' тей мало изменяется по длине нити (см. соотношения (3.1.24)). Поэтому мы не будем пользоваться упрощениями, которые f были введены в главе III для исследования ценных линий с малой стрелой провисания.
Сила тяжести Р* отне-* сенная к единице длины нити, равна по модулю yF (см.
(2.1)). Проекции этой силы на горизонтальную ось х и вертикальную ось у соответственно равны Рх = 0, Ру = = — yF (рис. 4.2). Пользуясь первым уравнением (1.2.16) и равенством (1.1), получим
* = *% = ** %-*** (4.3.1)
где F0 — площадь поперечного сечения в вершине нити О. Из (3.1) найдем .
r = ofof, *-Гog. (4.3.2)
Внесем значение Pv= —*(F во второе уравнение
(1.2.16) и воспользуемся (3.2). Имеем
Умножив обе части этого уравнения на ds/dx и учтя
О
Рис. 4.2.
§ 4.3. ЦЕПНАЯ ЛИНИЯ РАВНОГО СОПРОТИВЛЕНИЯ 97
значение параметра к из (2.4), получим
d^_±(^Y („' — da)
dx - к \dx) \У ~ dx]'
или (см. (2.1.3))
Разделяя переменные и интегрируя, найдем
Так как у' = 0 при х = 0 (в начале координат касательная параллельна оси х), то Сi = 0 и, следовательно,
Интегрируя еще один раз и учитывая, что у = 0 при х = 0, получим
Это уравнение цепной линии равного сопротивления впервые было получено Кориолисом. Формально уравнение определяет бесчисленное множество тождественных (конгруэнтных) кривых, имеющих вертикальные асимпто¬
ты и лежащих в интервалах" •
где т = О, ±1, ±2, ± ... Но реальная нить совпадает с отрезком АВ одной ветви и рассматривать нужно только этот участок (рис. 4.3).
Для определения длины дуги воспользуемся последовательно равенствами (2.1.3) и (3.3)
(4.3.3)
у = — к lncos-p
или
7 (-?<*<!)• (4-3-4)
E~yri+y’,~Vi + 4
;2T = secT’ (4-3-5)
или, интегрируя,
98
ГЛ. IV. НИТИ РАВНОГО СОПРОТИВЛЕНИЯ
Будем отсчитывать длину дуги s от вершины нити О. Тогда 5 = 0 при х = 0 и, следовательно, С2 = 0. Таким образом,
* = *lntg(£ + i). (4.3.6)
Отсюда (см. равенства (2.3.12) и (2.3.14))
sec i = ch£. (4.3.7)
Теперь, пользуясь формулами (3.2), (3.5) и (3.7), найдем закон изменения площади поперечного сечения
цеплой линии равного сопротивления
F(s) = F0 ch-i. (4.3.8)
Горизонтальную составляющую Я натяжения и само иатяжение Т найдем из соотношений (3.1), (1.1) и (3.8)
Н = oF0, т = oF0 sec = <xF0ch £ =oF(s). (4.3.9)
Если задана длина нити L и точки подвеса А и В, т. е. пролет I и превышение h (рис. 4.2), то из граничных условий
х А = б, Хв = —(Z—6),
(4.3.10)
У Л = /, у» = i-h
§ 4.3. ЦЕПНАЯ ЛИНИЯ РАВНОГО СОПРОТИВЛЕНИЯ
99
И равенств (3.6) и (3.4) получим
= к In tg (j + L2 = к In tg (д ),
fi — Z-6
L = Lx + L3, ет = sec j, e = sec -j-.
где Li и Z/2 — длины правой и левой частей нити соответственно. Зная L, h и Z, из этих пяти уравнений можно найти /, б, к, L\ и Ь2. Затем по найденному значению к и удельному весу материала нити у по формуле (2.4) определится нормальное напряжение о, а по формуле (3.8) и выбранному значению F0 можно построить цепную линию равного сопротивления, удовлетворяющую заданным граничным условиям. Можно, конечно, использовать и другие схемы расчета. Поясним изложенную здесь теорию расчетом стальной нити (цепи) глубоководного якоря.
Пример. Пусть судно, стоящее на якоре В (рис. 4.4), испытывает горизонтальное давление ветра, равное Qo = 8 т (скоростью течения пренебрегаем). Как уже отмечалось (см. стр. 53), эта внешняя информация определяется из аэродинамических характеристик судна и скорости ветра. В положении равновесия сила Qo
будет уравновешена горизонтальной составляющей Н натяжения нити (цепи) Т. Таким образом, в нашей задаче известна величина " = <?о. Задавшись нормальным напряжением о = 4 т/см2 и считая, что часть цепи лежит на дне, найдем из формулы (3.1) площадь в сечении О: F0 = Н/о = 2 см2. Удельный вес стали в воде К = 6,8• 10—3 кГ/смъ; следовательно, к = о/ч = 5,88 103 м. В условиях задачи б = I (величина нам не известная), а / = h — глубина моря в месте стоянки. Пусть h = 5000 м. Тогда из предпоследнего
100
ГЛ. IV. НИТИ РАВНОГО СОПРОТИВЛЕНИЯ
уравнения (3.11) найдем
По таблицам косинусов находим Ilk -= 1,130; отсюда 1 = б = '= 6640 м. Из первой формулы (3.11) найдем Lx = L (Ь2 = 0)
Площадь поперечного сечения в верхней точке крепления нити (цепи) найдем по формуле (3.8)
Вычислим теперь натяжение нити (цепи) в верхней и нижней точках. Пользуясь формулами (3.9), получим
Несмотря на такой большой перепад в натяжении, построенная по эакону (3.8) нить (цепь) будет иметь во всех поперечных сечениях одинаковое нормальное напряжение а.
Поставим следующую задачу: что произойдет, если скорость ветра изменится и на судно будет давить сила Q, меньшая расчетной (Q < <?о). Сохранит ли нить, изготовленная по условиям задачи, свойство равного сопротивления? Для того чтобы ответить на этот вопрос, обратимся к уравнению Кориолиса (3.4). При выбранном значении нормального напряжения о и данном удельном весе материала f параметр к = о/ч не зависит от других условий задачи и уравнение (3.4) определяет в промежутке (—як/2, тск/2) единственную кривую с двумя вертикальными асимптотами (рис. 4.3). Из этого следует, что граничные точки нити равного сопротивления при заданных о и f нельзя выбирать произвольно— они должны принадлежать графику функции (3.4). Поэтому при уменьшении скорости ветра расстояние I при неизменном h сократится и нить (цепь) глубоководного якоря потеряет свойство равного сопротивления. В частности, при безветрии цепь равного сопротивления должна рассчитываться не по закону (3.8), а по закону (2.5) (при сравнении формул нужно учесть, что в этих задачах отсчет длины дуги производится в противоположных направлениях) .
Учитывая, что нити равного сопротивления не нашли широкого распространения, мы ограничимся изложенным здесь материалом.
L 2
Fa = FqcYl j = 2ch 1,497 = 4,69 см2.
Тл = OF а = 18,76 г, Т0 = Н = 8 г.
ГЛАВА V
РАВНОВЕСИЕ ТЯЖЕЛЫХ НИТЕЙ, НАХОДЯЩИХСЯ В УСТАНОВИВШЕМСЯ ПОТОКЕ
§5.1. Силы, действующие на нить
В практических задачах часто необходимо учесть влияние на тяжелую нить (трос) силы давления ветра или течения жидкости. Анализом таких задач занимались академики А. Н. Крылов, Н. Е. Кочин и др. (см. библиографию в [1, 8]).
Будем считать нить однородной и растяжимой. Обозначим через q силу тяжести, отнесенную к единице длины растянутой нити. Возьмем на нити произвольную точку М, обозначим через т единичный касательный вектор к кривой равновесия и через v вектор скорости набегающего потока в этой точке. Пусть Q означает отнесенную к единице длины силу давления потока на нить в точке М. Испытания, проведенные в аэродинамических лабораториях, дали следующие результаты.
1. Модуль силы давления потока пропорционален плотности обтекающей среды р, квадрату скорости v и диаметру нити d; кроме того, модуль силы давления Q зависит от угла атаки % — угла между направлениями касательной т и скоростью v потока в точке М. Если обозначить коэффициент пропорциональности, не зависящий от угла атаки, через Я, то будем иметь
X = CpJ2d, (5.1 Л)
где С — численный коэффициент, характеризующий данный трос и среду потока. Этой формулой можно пользоваться в известных пределах скорости у, при которых нет срыва и не возникают вихри Кармана.
102 ГЛ V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
2. Силу давления Q потока на нить можно разложить по трем взаимно перпендикулярным направлениям я, т и т:
Q — Qn + Qi + Qm,
или
Q — Ср s- d (Фпл -j- Фхт -f- Фтт).
(5.1.2)
Вектор п направлен по нормали к нити и лежит в плоскости векторов т и v (в общем случае он не совпадает с главной нормалью нити v), вектор т перпендикулярен векторам типи определяется равенством т = т х п. Функции Фп, Фг и Фт зависят от угла атаки их графики, построенные по результатам испытаний, проведенных в аэродинамической лаборатории НИИМ ЛГУ (данные других лабораторий менее подробны и мы их не
0п *
1,0 0,8 0,6 0,4 О,г
о
т
“ 1
X
Ян
-ф-
-4
у
/
!
I
1
■ 1
Фг/Фп,%
ФГШ*0,О2
ГОО 80 60 40
го
20 UO 50 80 Zc
20 40 OO 80 Z°
Рис. 5.1.
Рис. 5.2.
приводим), изображены на рис. 5.1, 5.2 и 5.3 (все графики с точностью до обозначений заимствованы нами из книги
Н. И. Алексеева UJ).
Прежде чем перейти к определению функций Фп, Фт и Фт, сделаем два замечания.
1. Силу давления Q разлагают часто по трем координатным осям, причем одну из осей, например ось я, совмещают с направлением скорости v потока (в [11 приведены графики функций Ф* и Фу). Такое разложение
$ 5.1. СЙЛЫ, ДЕЙСТВУЮЩИЕ НА НИТЬ
103
*т
/
\
к
20 40 00 80 ЛГС Рис. 5.3.
можно применять для потоков, направления скоростей которых во всех точках одинаково. В тех случаях, когда поле скоростей неоднородно по направлению, разложение силы давления потока по неподвижным координатным осям лучше заменить на разложение по ортам л, т и т.
2. Если поменять местами движения нити и среды и считать, что последняя неподвижна, а нить движется со скоростью, равной скорости потока, в противоположную сторону, то сила сопротивления среды движению нити будет равна силе давления движущегося потока на неподвижную нить.
Дадим теперь аналитическое определение функции Фп = Фп(х)» По Н. Е. Кочину [8] Фп = sin/, а А. Н. Крылов [10] считал, что Фп = = sin2x (Кочив ссылается на испытания, но результаты их не приводит, Крылов приводит формулу для Фп без всяких пояснений). В связи с этим установленный экспериментально график функции Фп = Фп(%) был аппроксимирован нами следующей функцией:
Фп = a sin2 .х + Ь sin х-
Методом наименьших квадратов по девяти точкам было получено: а =1,1; Ъ = 0,0 (большую точность из графика, помещенного в [1J, получить нельзя). В соответствии с этим последняя формула принимает вид
Фп = asin2^. (5.1.3)
На рис. 5.1 точками показаны значения функции Фп, вычисленные по формуле (1.3). Принимая во внимание эти результаты и учитывая, что сведения о скорости потока известны обычно с небольшой точностью, следует признать, что формула (1.3), которой пользовался еще А. Н. Крылов, достаточно хорошо отображает значение функции Фп*).
). Если аппроксимировать график рис. 5.1 функцией Фп =
* о sm % и определить коэффициент b тем же методом наимень^вадРатов’ то П0ЛУчим значительно худшее приближение,
104 гл. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
Составляющую Qn можно разложить по направлениям т и v. Имеем (рис. 5.4)
C»e*°»Urx-TCtex), (5Л-4)
где v° — единичный вектор скорости v.
Две другие составляющие определены равенствами
Qx = ^ФтТ, Qm =± ЬФтХ х v°. j (5.1.5)
Направление составляющей Qm (знак во втором равенстве (1.5)) зависит от направления крутки прядей троса. При большом числе прядей или для сплетенных, а не скрученных тросов, а также для цепей составляющая Qm практически равна нулю.
Сопоставляя графики функций Фп и Фт (боковую составляющую Qm как правило, игнорируют), видим, что основная составляющая Qn силы давления пабегающего
потока на нить находится в плоскости векторов т и v и направлена по нормали к нити. Касательная составляющая Qx при больших углах атаки % мала по сравнению с нормальной составляющей Qn и ее следует учитывать только при малых углах % (А. Н, Крылов и
Н. Е. Кочин даже не упоминают о существовании касательной составляющей давления). При % = 0 нормальная составляющая давления Qn обращается в нуль, а касательная составляющая Qx представляет обычную силу трения. В общей постановке задачи мы будем учитывать все три составляющие силы давления потока на нить.
Задачу о равновесии будем решать в предположении, что нить находится в установившемся потоке, скорость которого v и плотность среды р зависят только от вертикальной координаты z рассматриваемой точки М. Обе функции v = v (z) и р = p(z) считаются заданными (их можно определить из гидрологических или метеорологиче-i ских наблюдений). Таким образом, предполагается, 4Tq коэффициент X является известной функцией аппликаты
S 5.1. СИЛЫ. ДЕЙСТВУЮЩИЕ НА НИТЬ
105
z: X = Xiz). Для тросов с небольшой разностью высот отдельных точек (антенн, линий электропередач, не глубоководных тралов и т. п.) можно считать, что X = const. Отметим здесь же, что, считая поток установившимся, т. е. не зависящим от времени £, мы не предполагаем, что он горизонтален и однороден — в потоке могут быть восходящие и нисходящие течения с переменными по высоте z модулем и направлением скорости v.
Совместим начало координат с точкой крепления троса А и направим ось z вертикально вверх, а оси х и у горизонтально. Следуя Н. Е. Кочину 18], введем два угла 0 и яр, определяющих направление касательной. Пользуясь рис. 5.5, найдем проекции единичного касательного вектора т (оси х , у', z' параллельны осям х, у, z соответственно):
тх = ^ = cos 0 cos г|), ту = ^ = cos 0 sin г|),
Преимущество введения углов 0 и ф состоит, в частности, в том, что для трех параметров, z, 0 и ф (в отличие от трех декартовых координат х, у, z), уравнение связи
(1.2.7), согласно (1.6), выполняется автоматически.
Так как модуль и направление силы давления потока Q явно зависят от координаты z (через параметр X и скорость г), то целесообразно в качестве независимой переменной выбрать не дуговую координату s, а аппликату z. Если углы 0 и ф будут найдены как функции z, то координаты х и у и длина дуги s определяется простыми квадратурами. Действительно, пользуясь равенствами (1.6), найдем
dx =-. ctg 0 cos г|) dz, dy — ctg 0 sin г|) dz, ds =
uz . л
T‘ = ^ = sln0-
(5.1.6)
(5.1.7)
отсюда
(5.1.8)
106 гл. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
Пусть в точке М нити направление скорости потока v определяется углами со и £2 (рис. 5.6), причем по условию они являются известными функциями z: со = соЫ, Q —
= Q(z). Тогда проекции единичного вектора скорости v° будут
о о о
vx = cos Q cos со, Vy = cos Q sin со, yz = sinQ. (5.1.9)
Угол x между вектором скорости v и касательной к нити т найдем из равенства: cos% = tf°*T. Выражая скалярное произведение векторов v° и т через их проекции, получим после очевидных преобразований
cos х = cos ® °os Q cos (г|)—со) + sin 0 sin Q. (5.1.10)
Это равенство определяет угол % как функцию координаты z (через со и Q) и углов 0 и -ф:
X = х('0> Ф» *)• (5.1.11)
Пользуясь равенствами (1.4), (1.6) и (1.9), найдем проекции составляющей Qn-
Ф (^)
Qnx = % (z) —?— (cos Й cos (о — cos х cos 0 cos г|>), sm x ф (^)
Qny = X (z) —?—(cos Й sin to — cos x cos 0 simf>), (5.1.12) sin x
Ф (y)
Qnz = X (z) (sin £2 cos x Sin 0).
§5 2. ДЙФФкрЕПЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ Ю7
Проекции касательной составляющей Qx силы давления потока наймутся из формул (1.5) и (1.6):
Qxx = X(z)Фх(%) cos 0 cos
(?TV = Mz)Фх(%) cos 0 sin (5.1.13)
Qtz ЯЫФТ(%) sin 0.
Наконец, из второго равенства (1.5) найдем проекции составляющей Qm:
Qmx = ± Я (Z) Фот (X) (тVVZ — XzV°y),
Qmy — ± х (z) Фш ix) (*zV°x — rxv°2), (5.1.14)
Qmz = i ^ (2) Фш (X.) (тxVy — Tyl?*)*
Если в эти равенства подставить значения проекций
векторов т и v° из (1.6) и (1.9), то проекции составляющей Qm (так же как и Qn и ()т) будут известными функциями углов 0, о|) и координаты z.
Равнодействующая Р всех сил, действующих на нить, складывается из силы тяжести q и силы Q = Qn + Qx + +Q т давления потока на нить. Первая сила является массовой, вторая поверхностной. Проекции массовой силы тяжести q определяются равенствами
Qx = 0, Qy = 0, qz = q* (5.1.15)
Если нить нерастяжима, то q = const; для растяжимой нити
Я = Ш> (5.1.16)
где qo — вес единицы длины нити до растяжения. Проекции силы Р складываются из соответствующих проекций составляющих сил согласно формулам (1.12)—(1.14).
§ 5.2. Дифференциальные уравнения равновесия нити
Для перехода от независимой переменной s к аргументу z воспользуемся третьей формулой (1.6) и очевидным равенством
d d dz л d
108 гл. v. равновесие нитей в установившемся потоке
Внесем в дифференциальные уравнения равновесия нити (1.2.5) значения производных из (1.6) .и оператор
(2.1). Тогда, учитывая равенство (1.15), получим
sin 0 (Т cos 0 cos ф) -j- Qfc = 0, sin 0 (Т cos 0 sin г|)) = 0, (5.2.2)
sin 0 (Т sin 0) -j- Qz — q = 0.
Эти три дифференциальных уравнения равновесия нити относительно трех неизвестных функций 0, ф и Т можно преобразовать к более удобной форме. Для этого запишем их сначала в следующем виде:
sin 0 cos 0 cos г|э —• -f Т sin 0 (cos 0 cos ф) -j- Qx = 0,
sin 0 cos 0 sin г|) ^ -f- T sin 0 (cos 0 sin ф) -f Qy = 0,
sin2 0 -f- T sin 0 (sin 0) + Qz — q — 0.
Умножим первое уравнение на cos 0 cos ф, второе на cos 0 sin г|), третье на sin 0 и сложим все уравнения. Тогда после очевидных преобразований получим
sin 0 ^ + Т sin 0 j^cos 0 cos г|) (cos 0 cos ф) +
-j- cos 0 sin г|) ^ (cos 0 sin г|)) -f sin 0 (sin 0) j -f
+ Qx cos 0 cos г|) + Qy cos 0 sin г|) + Qz sin 0 — q sin 0 = 0.
(5.2.3)
Выражение в квадратных скобках равно нулю. Действительно,
[ ] = JL (cos2 0 cos2 г|) -j- cos2 0 sin2 г|) -f sin2 ®) =*
2a dz
=-f^w = °-
Рассмотрим теперь члены, содержащие проекции силы Q. Если учесть равенства (1.2), (1.12)—(1.14) и (1.6), то
§ 5.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ Ю9
\
после несложных преобразований получим
Qx cos 0 cos ф + Оц cos 0 sin ф + Qz sin 0 = А,ЫФТ(%). (5.2.4)
Внесем все порученные соотношения в уравнение (2.3)
и решим его относительно производной:
^ /~\ ^ /с; о с;\
-%\= я— Mz)lE-§- (5.2.5)
(Это уравнение можно ролучить более простым способом, если использовать первое уравнение (1.3.3) и оператор
(2.1)).
Преобразуем теперь третье уравнение (2.2). Имеем sin20^- + r sin0 cosO^g- + Qz — q = 0.
Внесем сюда значение производной dT/dz из (2.5) и
решим полученное равенство относительно dQ/dz:
ii -9 cos2q + к(z) sin 9 Фх ~ Qz 2 П
dz ~ Т sin 0 cos 0 * ' * ' '
Наконец, запишем первые два уравнения (2.2) в следующем виде:
sin 0 cos г|) -Jj (Т cos 0) — Т sin 0 cos 0 sin г|> ^ + Qx = 0, sin 0 sin г|)-|^(Г cos 0) + T sin 0 cos 0 cos г|) — + Qy = 0.
Умножая первое равенство на —sinвторое на cos и складывая, получим
Qx sin ф Qy cos ф /соГ7ч
dz - T sin 0 cos 0 ‘ (0.4. i)
Уравнения (2.5), (2.6) и (2.7) эквивалентны уравнениям (2.2). Их преимущество состоит в том, что они, в отличие от уравнений (1.2.5), содержащих четыре неизвестных функции х, у, z и Г, подчиненных одной нелинейной неголономной связи (1.2.7), решены относительно производных от неизвестных функций Г, 0 и г|э.
Уравнения (2.5)—(2.7) позволяют решать задачу в предположениях, когда сила давления потока Q имеет все три составляющие, плотность среды р, модуль и направление скорости потока v зависят от высоты рассмат¬
110 гл. V. РАВИОЁЁСЙЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
риваемой точки z, нить растяжима по любому закону j(T), линия равновесия двоякой кривизны. Конечно, для полного решения задачи пужно задать ещ^ граничные условия (о них будет рассказано ниже), Законы изменения плотности среды р = p(z) и скорости пютока v = я (z), для растяжимых нитей силу тяжести q, о/несенную к единице длины нити, нужно определить формулой (1.16) и, наконец, угол атаки %, входящий в функции Фп, Фт и Фт, нужно выразить через углы сo(z){ Q(z), в, по формуле
(1.10). Естественно, что при этом функции Фп, Фт и Фт, заданные графически, целесообразно аппроксимировать соответствующими аналитическими выражениями. Довести решение этих уравнений до квадратур в общем случае нельзя, но реализовать численное решение на ЭВМ не представляет большого труда.
Рассмотрим несколько частных случаев, которые чаще всего встречаются в практических расчетах.
1. Большой угол атаки %. К этому случаю относятся тросы, удерживающие аэростат или плавающие на течении тела (причальный поплавок, буй, измерительный прибор) и т. п. При большом угле % атаки касательная составляющая Qx силы давления потока Q мала по сравнению с нормальной составляющей Qn (см. рис. 5.2), поэтому без большой погрешности можно считать, что Фт = 0. В этом случае уравнение (2.5) принимает вид
Для нерастяжимой нити это дает интеграл натяжения T = qz + C{; (5.2.9)
если же нить растяжима, то интеграл натяжения имеет
вид
j f(T) dT ^ q0z + Сг (5.2.10)
В частности, для растяжимой по закону Гука нити будем иметь (см. (1.4.10))
т +^-T* = q0z + C1. (5.2.11)
Отсутствие в интегралах (2.9)—(2.11) силы давления
потока Q не означает, конечпо, что натяжение нити не
§52 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ НИТИ 1Ц
зависит от Действительно, закрепим нерастяжимую тяжелую нитьV двух точках. При отсутствци ветра (течения) получится обычная цепная линия, для 'которой справедлив интеграл (2.9). Очевидно, что при появлении ветра (течения), с^ла давления которого перпендикулярна нити, линия равновесия, а вместе в ней и натяжение нити Т изменятся, во по-прежнему будет иметь место интеграл (2.9) (только постоянная интегрирования С\ примет новое значений).
2. Скорость потока горизонтальна и неизменна по направлению: v = const. В этом случае целесообразно направить ось х параллельно скорости v, в результате чего получим (рис. 5.6): £2 = 0, со = 0 (этот случай рассматривается чаще всего). Равенство (1.10) примет простой вид
cos х = cos 0 cos ч|), (5.2.12)
и, следовательно, угол % не будет зависеть от аппликаты z. В частном случае плоской нити можно считать, что ф = 0, и тогда угол атаки % будет равен углу между касательной к нити и горизонтальной плоскостью, т. е.
Х = 0. (5.2.13)
3. Сила давления потока и его скорость v не зависят
явно от высоты. В практических задачах этому случаю
отвечают нити (тросы) с небольшой разностью высот отдельных точек. По условию
% = const, £2 = о) — 0, = 0. (5.2.14)
При этих соотношениях правые части уравнений (2.6) и
(2.7) не будут явно зависеть от z. Деля первое из этих уравнений на второе, получим
dQ 0 COs20 + X sin 0 Фт (%) — Qz /ro-ic\
di|> — <?ssint|> — <?j,cosi|> • (O.Z.lO)
Таким образом, задача сводится к решению двух уравнений (2.5) и (2.15).
В заключение отметим, что поверхностная сила давления набегающего потока Q не зависит от массы троса. Если пренебречь изменением диаметра троса при его растяжении, то величина этой силы не будет зависеть от линейной деформаций троса. Поэтому уравнения равновесия
112 ГЛ. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
тяжелого растянутого троса, находящегося тюд действием силы давления набегающего потока, отличаются от уравнений равновесия нерастйжимого троса угольно тем, что в уравнениях (2.5) — (2.7) массовая сшш тяжести q заменяется на qo/f(T). В тех случаях, когда изменение диаметра троса достаточно велико и его цужно учесть, следует воспользоваться равенством (1.1.87. Некоторые авторы допускают ошибку, применяя к сил</ давления потока равенство Q = \iQ*/f (Т), где Q* — си/la, отнесенная к единице массы (см. замечание к формулам (1.2.19) и (1.2.20)).
§ 5.3. Граничные условия
Для тяжелой нити, находящейся под давлением набегающего потока, наиболее характерны граничные условия с одним закрепленным и одним свободным концом, удерживающим ничем другим неукрепленное тело (аэростат [8], мину [10], трал, причальный поплавок, измерительный прибор и т. п.). Здесь возможны два метода задания граничных условий.
1. Определяются углы 0, ф и натяжение Т нити [троса) в точке закрепления А. В этом случае граничные условия имеют вид*)
при zA = 0
0 = 0А, ф = Фа, Т = Та; Zb = h, (5.3.1)
причем предполагается, что начало координат совпадает с точкой закрепления нити А. Для того чтобы учесть реальные условия зависящие от удерживаемого вторым концом нити тела, этот метод требует непосредственного измерения всех трех величин: 0А, Фа и ТЛ. Поэтому задание условий на закрепленном конце нельзя признать достаточно удобным, особенно для составления расчетных таблиц, например таблиц, по которым, зная скорость потока и параметры тела (его вес, объем и т. п.), можно сразу определить величину горизонтального сноса удерживаемого тела. Из этого не следует, конечно, что этот метод нужно исключить из рассмотрения — в тех случаях, когда информация об удерживаемом теле недостаточна (см. сле¬
*) Вместо высоты подъема zb = h можно задать длину троса £, по которой определяется высота h.
§ 5 3. ГРАНИЧНЫЕ УСЛОВИЯ
ИЗ
дующий метод) или для экспериментальной проверки, определение граничных условий на закрепленном конце является наиболее^добным способом решения задачи.
2. Второй метЬд, предложенный для простейшего случая А. Н. Крыловым [10], не требует постановки эксперимента и состоит в задании граничных условий не на закрепленном, а на свободном конце нити. Эти условия определяются из уравнений равновесия удерживаемого тела. Так как этот метод практически одинаков для различных тел, то мы проиллюстрируем его для двух тел; при этом будем считать для простоты, что скорость потока горизонтальна (Q = 0), но может менять свое направление по азимуту (со = (оЫ).
а. Граничные условия для привязного аэростата. На находящийся в равновесии аэростат действуют в первом приближении следующие силы (все приводимые ниже сведения об аэростатах взяты из книги Б. И. Халепского [27]): вес Р, подъемная сила (?£(для невыполненного аэростата подъемная сила на всех высотах одинакова), сила лобового сопротивления Rл, аэродинамическая подъемная сила Rz и сила реакции троса Тв, равная по модулю натяжению его в точке В и направленная в противоположную сторону (рис. 5.7). Кроме того, на аэростат действуют опрокидывающий и стабилизирующий моменты, которые мы не будем учитывать, так как в нужные нам уравнения они не входят. Будем также считать, что скорость ветра по всей высоте аэростата одинакова и равна скорости его в точке 5*).
В сделанных предположениях все силы, действующие на аэростат, находятся в одной вертикальной плоскости, проходящей через вектор скорости vB и составляющей с плоскостью xz угол = со(А), где
Рис. 5.7.
*) Угол атаки а для аэростата определяется из уравнения моментов с учетом способа крепления. Для простоты мы считаем этот угол заданным.
114 гл. Т. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ/ГОТОКК
h — высота подъема аэростата (h = zB). Обозначим через 0* угол между направлением касательной7к тросу в точке Я и горизонтальной плоскостью и составим два уравнения равновесия аэростата /
Rn — Тв cos 0в = О, G + Rz — Р-к sin 0в = 0. Отсюда /
ув = угд*+(б + Л2-РД tgQB=-G^R/iz~P.
11 (5.3.2)
Таким образом, граничные условия будут при zB = h
Т = ТВ, 0=0В, у = ув = с0(h); zA = 0. (5.3.3)
Поясним входящие в формулы (3.2) величины. Если
V — объем аэростата, •у и ^ * — удельные веса воздуха и наполняющего аэростат газа соответственно, то подъемная сила G будет
G-yOf-f*). (5.3.4)
Силы R^ и Rz вычисляются по формулам
Дл = Слр S, Rz = С2р-£ (5.3.5)
где Ст, и Cz — аэродинамические постоянные, зависящие от угла атаки а (см. рис. 5.7), р — плотность воздуха на высоте подъема аэростата h, v = vB — скорость ветра, S — площадь главного поперечного сечения, которая для аэростата вычисляется по следующей приближенной формуле:
S = F2/3 (5.3.6)
Значения аэродинамических коэффициентов в зависимости от угла атаки а приведены в следующей таблице:
а
0
2
4
6
8
10
ci\
ОДО
ОД 1
0,12
0,15
0,20
0,28
Сг
0,00
0,04
0,09
0,14
0,18
0,23
§5 3. ГР АНЙЧНЫЕ УСЛОВЙЯ 115
Удельныи\вес воздуха равен ^ = gp, где плотность воздуха р в зависимости от высоты z определяется равенством \
\ Р = (5.3.7)
В этом равенстве ро = ОД25 кГ*сек2/мА— плотность воздуха на уровне 4 моря при температуре 15°С, v = = 9,8 • 10~5 ле”1, a g* «= 9,81 м/сек2 — ускорение силы тяжести (предполагается, что g = const при всех z, удовлетворяющих условию 0 ^ z ^ h).
Пример 1. Аэростат весом Р = 300 к Г и объемом V = 500 мг поднялся на высоту h — 2000 м; скорость ветра на этой высоте равна 10 м/сек, угол атаки а = 10°. Определить натяжение троса Тв и угол 0в в верхней точке, если считать, что аэростат был заполнен на земле водородом на 90% и его полное выполнение произошло на высоте h = 2000 м.
Объем аэростата на старте равен V\ = 0,9 V = 450 м3, удельный вес воздуха на земле у = 1,225 кГ/м\ удельный вес водорода у* = 0,125 кГ/м3. По формуле (3.4) найдем подъемную силу
G = 450- (1,225—0,125) ■= 495 кТ.
Так как полное выполнение аэростата произошло при h = = 2000 м, то подъемная сила на этой высоте будет равна найденной величине 495 к/1, а объем аэростата сделается равным V — = 500 мъ. Площадь главного сечения на этой высоте найдем по формуле (3.6): S = F2/3 = 63 м2. Плотность р вычислим по формуле (3.7) при z‘= h = 2000 ле; р = 0,103 кГ • сек2/мА. Аэродинамические коэффициенты при угле атаки 10° равны С= 0,28 и Сг *= = 0,23. По формулам (3.5) найдем лобовое сопротивление и аэродинамическую подъемную силу Rz:
Дч.= 90,8 кГ, Rz = 74,6 кГ.
Пользуясь равенствами (3.2), получим
Тв = 285 кГ, tg 0В = 2,97, 0В = 1,246 (71°23'). (5.3.8)
Угол ,фв = а)(/1) определяется из метеорологических наблюдений по направлению скорости ветра v.
б. Граничные условия для шарового тела, находящегося в воде. На находящееся в воде шаровое тело (например, батисферу) действуют в основном те же силы: вес тела Р, архимедова сила G и лобовое сопротивление (подъемная сила Rz для шарового тела равна нулю). Формулы
(3.2) принимают вид
Тв = VRl + (<? - Р)\ tg 0в = . (5.3.9)
116 гл. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
Силу лобового сопротивления для шарового тела* находящегося в воде, А. Н. Крылов [10], рекомендует вычислять по формуле 7
ДЧ=19,8Л5. / (5.3.10)
Здесь S — площадь поперечного сечения шарового тела в квадратных метрах, v — скорость течения в м/сек, —
в кГ (скорость в узлах переведена нами в м/сек).
П р и м е р 2. Пусть радиус шарового тела г = 0,105 ле, скорость течения v = 2 м/сек, чистая плавучесть тела G — Р = 5,5 кГ. Имеем: S = яг2 = 0,0346 м2, = 19,8 v2S = 2,74 кГ,
Тв = 6,14 кГ\ tg 0в = 2,00; 0В = 1,108 (63°,5). (5.3.11)
Условия (3.3) с внешней стороны совпадают с условиями (3.1), но между ними имеется большое принципиальное различие. Условия (3.1) непосредственно не учитывают влияния удерживаемого нитью тела, поэтому они должны устанавливаться экспериментально путем измерепия. Условия (3.3) определяются на основе анализа равновесия удерживаемого тела и они могут быть, вычислены по исходным дапным путем решения элементарных уравнений.
Кроме рассмотренных условий (один конец нити закреплен, а второй свободен, но удерживает ничем другим не укрепленное тело), иногда приходится определять влияние установившегося потока на нить с двумя закрепленными концами. В общем виде уравнения (2.5) — (2.7) при таких граничных условиях решаются даже на ЭВМ более сложными методами. Но, как правило, влияние набегающего потока на нить с двумя закрепленными точками приходится рассматривать для цепной линии с малой стрелой провисания (антенны, линии электропередач и т. п.). В этом случае можно применять приближенные методы, один из которых будет рассмотрен в § 5.5.
§ 5.4. Задача о равновесии троса, удерживающего неукрепленное тело в однородном потоке
Формулы §§ 5.1 и 5.2 позволяет решать различные задачи в достаточно общих предположениях, сделанных ранее. Здесь мы ограничимся рассмотрением равновесия троса, удерживающего тело в однородном потоке. Задачу ре¬
§ 5Л^РАВЙ0ВЕСЙЕ ТРОСА Б ОДНОРОДНОМ ПОТОКЕ Ц7
шим в упрощающих предположениях (более общие условия должны рассматриваться специалистами, работающими в соответствующей области), что дает нам возможность наглядно проследить за порядком построения решения. Упрощение будем вводить постепенно, показывая влияние каждого из них.
Для тросов, удерживающих аэростат или тело на течении, угол атаки %, как правило, достаточно велик. Поэтому касательная составляющая Qx силы давления потока для таких тросов мала (см. рис. 5.2), и без большой погрешности ее можно считать равной нулю. Считая, что трос сплетен из большого числа прядей, мы пренебрежем также и боковой составляющей Qm• Таким образом, будем считать, что на трос действует только нормальная составляющая сила давления потока
Q = Qn.
Зависимость функции Фп от угла % будем определять формулой (1.3). Положив в равенстве (1.1) С = а, где а = 1,1, получим (любой другой числовой множитель С не повлияет на построение решения)
Qn = h(z) sin2 х- (5.4.1)
Здесь
l(z) = ар ^-d. (5.4.2)
Далее, будем считать, что азимут направления скорости потока, т. е. угол со, одинаков по всей высоте подъема тела. Тогда, совместив ось х с плоскостью скорости потока г, получим со = 0.
При Q = Qn и со = 0 будем иметь:
Qx = Qnx = k(z) sin x (cos Q — cos % cos в cos if),
Qv — Qny = k(z)sin /(—cos % cos 0 sin \|>).
Пользуясь этими равенствами, приведем уравнение
(2.7) к виду
л / ч . cosQsimb /г / ov
^ = Mz)smxrsinecosV (5.4.3)
Это уравнение имеет частное решение ^ = 0, означающее, что линия равновесия троса располагается в верти-
118 ГЛ. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМС^ПОТОКЕ
/
кальной плоскости, содержащей скорость обтока v и нижнюю точку закрепления А — результат для троса с одним свободным концом физически очевидны*. Таким образом, задача упрощается и сводится к интегрированию уравнений (2.5) и (2.6), которые при со = ф> О, (?т = О и дополнительном условии, что скорость пбтока горизонтальна (£2=0), приводятся к виду
dT _ dQ_ _ q cos 9 + Я (z) sin29
dz dz T sin 0 ’ v • * /
Рассмотрим частные случаи.
а. Скорость потока v и плотность среды р на всех высотах одинакова, весом троса можно пренебречь (q = 0). Этот случай почти в чистом виде может реализоваться для троса, удерживающих тело на течении в воде. Действительно, плотность воды па всех глубинах практически одинакова, а современные тросы, сплетенные из искусственного волокна, имеют удельный вес почти равный (иногда даже меньший) удельного веса воды. Таким образом, сила тяжести троса в воде может равняться нулю (д = 0) и остается взять только среднее значение скорости течения.
В сделанных предположениях iq = 0 и k = const) уравнения (4.4) принимают вид
Т = ТВ = const, = k sin 0, (5.4.5)
где
к = гг-. (5.4.6)
1 В
Интегрируя второе уравнение (4.5), получим J)
2
In tg = kz + Cv (5.4.7)
Отсюда после очевидных преобразований найдем
_0_
2
tg-f- = eft2+C\ ctg0 = — sh(A;z + C1),
Жё = с hikz + CJ (5.4.8)
Воспользуемся теперь первым и третьим равенствами
§ 5^. РАВНОВЕСИЕ ТРОСА В ОДНОРОДНОМ ПОТОКЕ
119
(1.8) при =0. Имеем
х = — J sh (kz + Сх) dz, s = J ch (kz + Cx) dz, или, учитывая, что при z = 0, а; = 0 и s = 0,
x = -±r[chC1-ch(kz + C1)), (5.4.9)
s = — [sh (/cz + Ci) — sh Сг].
(5.4.10)
Первое уравнение определяет уравнение линии равновесия троса, а второе — его длину от нижней точки крепления z троса А (рис. 5.8).
Пример. Трос, удельный вес материала которого равен удельному весу воды, удерживает на течении шаровое тело с чистой плавучестью G — Р — 5,5 пГ. Скорость течения v = 2 м/сек, диаметр троса d-= 4 лл, расстояние по вертикали от точки крепления тела В до дна hr= 5 м. Определить основные па- Д раметры троса.
Имеем: плотность воды р =
= 102 кГ • сек2/мА; следовательно,
Рис. 5.8.
К = l,lp L d = 0,898 кГ/м.
Для условий задачи были найдены следующие граничные условия (см. (3.11)):
Тв = 6,14 кГ, 0в = 1,108.
Пользуясь равенствами (4.6) и (4.7), вычислим значения параметра к и постоянной интегрирования С\
Во
Сх = In tg“2 — kh = — 1,210.
А
Тв
к= 7рГ = 0,146 м
Расстояние I по горизонтали от якоря А до точки В тела (рис. 5.8) и длину растянутого троса L найдем из формул (4.9) и (4 10) при z = h:
г = 1 [ell С - ch (kh + Сх)] = 4,85 м,
К
I = J [Sh (АЛ + Сг) - sh Сг] = 7,06 м.
120 ГЛ. У. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ЦбТОКЕ
Согласно первому равенству (4.5) натяжение троса в сделанных предположениях одинаково во всех точках. Поэтому растяжение троса найдем из равенства (1.1.3). Для растяжимого по закону Гука троса будем иметь (см. (1.1.6))
ds = (1 + а*Т) dso.
Отсюда при Т = const
L — Ln
— =а*Т,
где а* = 1 /Е* — удельное относительное удлинение нити, L0 — длина нити до растяжения, L — длина растянутой нити.
б. Скорость потока v и плотность среды р на всех высотах одинакова, весом троса пренебречь нельзя. В сделанных предположениях % = const, q Ф 0. Уравнения (4.4) принимают вид
dT= = qcosQ+XsinH^ (5.4.Ц)
dz dz Г sin 0 ' '
Дальнейший ход решения зависит ‘от свойств нити. Рассмотрим сначала нерастяжимую нить, когда q = const (см. [10J). Из первого уравнения находим
T = q(z + Cl), (5.4.12)
где
СХ = Ц--Ь. (5.4.13)
Внося значение Т из (4.12) во второе уравнение
(4.11) и разделяя переменные, получим
dz q sin 0
Z -f- С^ A; (J
^-cos'0 +sin2 0
(5.4.14)
Положив
cos 0 = u, = 2n, k2 = 1 + ra2, -j- = m, (5.4.15)
последовательно найдем dz n du
§ 6.4. РАВНОВЕСИЕ ТРОСА В ОДНОРОДНОМ ПОТОКЕ 121
Интегрируя это равенство, получим
In (z + сх) = т In + In с2;
отсюда
Z -I-
(5'4Л6>
Из этого равенства найдем дифференциал dz:
7 о л (кп — cos 0)771—1 . п ,А
dz = 2пСо —- '—гл sin 0 dQ.
2 (к - п + cos в)т+1
Теперь абсциссу х и длину дуги s найдем из первого и третьего равенств (1.8) при ф = 0:
* = 2 пС% [ {к + п~ cos cos 0 dQ, (5.4.17) * J (к _ п + cos 0)m+1 '
S = 2пСг f (fc + ”-cos6)^~1 de. (5.4.18)
2J (A;-n + cos0)m+1
Постоянная интегрирования C2 определяется из
условия
z = h, 0 = 0В. (5.4.19)
Следовательно,
к — п + cos 0d ^ т с - , f *
Порядок вычисления очевиден. По известным значениям й, Тв и 0В из равенств (4.13) и (4.20) находим С\ и Сг. Зная С\ и Гв, из равенства (4.12) находим при z = 0 натяжение в точке закрепления А. Угол 0А определится из (4.16) при z = 0. Горизонтальное смещение I и длина нити L найдутся из (4.17) и (4.18) при вычислении интегралов от 0а до 0в. Меняя в этих же пределах угол 0, можно по формулам (4.16) и (4.17) вычислить соответствующие значения z и х и по точкам построить кривую равновесия.
Для растяжимой нити нужно в уравнениях (4.11) заменить q на qo/f(T). Первое уравнение дает интеграл натяжения (2.10), а второе уравнение после исключения из
122 ГЛ. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПрТОКЕ
него Т можно проинтегрировать на ЭВМ (мы не останавливаемся на этом более подробно).
Пример. Скорость ветра на высоте h = 2000 м равна 10 м/сек, а на земле — 6 м/сек. Вес погонного метра троса q = = 0,054 кГ/м, его диаметр d = 3,75 мм. Определить снос аэростата по горизонтали I, необходимую для этого длину троса L и его натяжение 7\ если аэростат объемом 500 ле3 требуется поднять на высоту h = 2000 м. Вес аэростата 300 кГ, угол атаки равен 10°, аэростат заполнен на земле водородом на 90% и его полное выполнение произошло на высоте h = 2000 м. Предполагается, что скорость ветра изменяется по высоте равномерно, атмосфера считается стандартной, растяжением троса, касательной и боковой составляющими силы давления ветра пренебречь.
В условиях задачи натяжение Тв и угол 0в в верхней точке крепления троса к аэростату равны (см. пример на стр. 115 и равенства (3.8))
Пользуясь интегралом натяжения (4.12), найдем постоянную Си а затем натяжение троса в нижней точке А. Имеем
Дальнейшее решение проведем двумя методами.
1. Пренебрежем изменениями плотности воздуха и скорости ветра и возьмем их значения на средней высоте 1000 м (см. формулу (3.7) и условия задачи):
Считая эти величины постоянными, воспользуемся формулами
(1.1) и (4.15) — (4.20). При С = а = 1,1 будем иметь
Подставляя сюда значения Сi, С2, п и m и решая получен¬
ное равенство относительно cos0a, получим
Тв = 285 «Г, 0в = 1,246 (71°23').
(5.4.21)
Сл=Т-Л-Нх 3280 м, ТА = 177кГ. (5.4.22)
1 Я
p = pQe vz = 0,113 кГ-секР/м4, v= =8 м/сек.
Из равенства (4.20) найдем С2:
= 1074 ж.
Угол 0а определим пз равенства (4.16) при z = 0. Имеем
тп
cos 0 а = 0,645, 0А = 0,870 (49°51').
§ 5.4. РАВНОВЕСИЕ ТРОСА В ОДНОРОДНОМ ПОТОКЕ
123
Горизонтальный снос I аэростата и длину троса L найдем из равенств (4.17) и (4.18):
0в
I = 2 пП
— cose)”1 1 cos 0d0j
: + COS 0)m+1
L = 2nC f ~ cos 0)m11
2J (k-n
0A
0B
i + cos 0)m+1
dQ.
Вычисления на ЭВМ дали следующие результаты: I = 1067 м, L = 2295 м.
(5.4.23)
Таким образом, при усредненных значениях плотности воздуха и скорости ветра для подъема аэростата па высоту h = 2000 м требуется трос длиной L = 2295 м, при этом аэростат отклонится по горизонтали от нижней точки подвеса на расстояние I = 1067 м.
прибегая к осреднению. Для этого изменим систему координат, поместив ее начало в точку В и направив ось z вертикально вниз, а ось х влево. При этом дифференциальные уравнения (4.4) и (1.7) примут вид W = 0)
dd
dz
д cos 6+A, (z) sin2Q
(TB-qz) sine ’ (5 4 24)
dx ds 1
dz ~ * dz ~ sin 0*
Здесь
X(*) = l,ip£d, р = ров-*'-г)>
v = 10 — 0,002 z,
Рис. 5.9.
где все постоянные имеют прежние значения.
Уравнения (4.24) были проинтегрированы по стандартной программе на ЭВМ от z = 0 до z = h-= 2000 м при начальных условиях
z = 0, 0в = 1,246, х = 0, s = 0.
При небольшом шаге интегрирования, что обеспечило большую точность решения, получены следующие результаты:
0 а '= 0,865, I = 1084 м, L = 2288 м.
124 ГЛ. V. РАВНОВЕСИЕ НИТЕЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ
На рис. 5.9 в старых осях по точкам построена кривая равновесия троса (промежуточные значения координаты х определялись при интегрировании уравнений (4.24)).
Сравнивая полученный ответ с (4.23), следует признать, что оба метода дают практически одинаковые результаты (исходные данные известны с меньшей точностью), и, следовательно, можно пользоваться более простым методом осредненных коэффициентов.
§ 5.5. Влияние силы давления ветра на цепную линию
Существует много приближенных методов учета аэродинамических сил, действующих на тяжелую нить. Мы рассмотрим один из них для случая, когда цепная линия с малой стрелой провисания подвергается действию горизонтально направленного ветра, скорость которого перпендикулярна прямой, соединяющей точки подвеса. Основное допущение, которое при этом делается, состоит в том, что при малой стреле провисания угол атаки в равенстве
(1.3) приближенно равен я/2, и, следовательно, можно считать, что сила давления ветра направлена не по нормали
к нити, а совпадает с направлением скорости и и равномерно распределена по горизонтальной проекции нити. В этих предположениях на нить будет действовать обычная горизонтально распределенная вертикальная нагрузка q и горизонтальная равномерно распределенная сила давления ветра Q (рис. 5.10). Равнодействующая этих сил Р определяется равенством
v
Рис. 5.10.
P = Vq* + Q\
(5.5.1)
9 5.5. ВЛИЯНИЕ ДАВЛЕНИЯ ВЕТРА НА ЦЕПНУЮ ЛИНИЮ 125
где
Q = Cp^-d.
(5.5.2)
Так как сила Р по предположению равномерно распределена по горизонтальной оси х, то проекция этой силы, отнесенной к единице длины нити, будет равна Pdx/ds. Таким образом, мы имеем обычную нить с малой стрелой провисания, расположенную в плоскости, проходящей через горизонтальную ось х и равнодействующую Р сил q и Q (рис. 5.9). Угол а между плоскостью нити и линией отвеса определяется равенством
Все выводы главы III остаются без изменения при замене силы q на Р. В частности, горизонтальная составляющая натяжения Н будет одинакова во всех точках нити: Н = Тх = const.
Пример. Трос диаметра d = 1,13 еле, погонный метр которого весит q = 0,8 кГ/м, подвешен так, что его стрела провисания / мала по сравнению с пролетом. На трос действует аэродинамическая сила давления ветра, модуль скорости которого и = 20 м/сек, а направление перпендикулярно вертикальной плоскости, проходящей через точки закрепления. Определить какое изменение горизонтальной составляющей натяжения троса вызовет ветер.
При С = 1,1, р = 0,125 кГ сек2/м4, d-= 0,0113 м и и = 20 м/сек из формулы (5.2) получим: Q = 0,31 кГ/м. Пользуясь равенством
(5.1), найдем Р = 0,86 кГ/м. Имеем
На такую же величину увеличится горизонтальная составляющая натяжения нити. Плоскость троса отклонится от вертикальной плоскости на угол а = arctg Q/q = 0,369 (21°08').
В заключение отметим, что в работе [25] дано решение пространственной задачи в декартовых координатах.
(5.5.3)
Т) = 0,075 = 7,5%
ГЛАВА VI
РАВНОВЕСИЕ НИТИ
(ЦИЛИНДРИЧЕСКОЙ ГИБКОЙ ОБОЛОЧКИ), НАХОДЯЩЕЙСЯ ПОД ДЕЙСТВИЕМ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
§ 6.1. Постановка задачи
Имеется много устройств, в которых гибкие цилиндрические оболочки находятся под действием гидростатической нагрузки. К таким устройствам относятся, в частности, нейлоновые затворы водосливных плотин. Наиболее интересный в прикладном и теоретическом отношении представляется вопрос о форме поперечного сечения и натяжения плавающей длинной цилиндрической гибкой оболочки, наполненной транспортируемой жидкостью (предполагается, что она идеальная). Эта задача используется как крайняя абстракция и в теории плавающего пучка леса (жидкостная теория), согласно которой пучок состоит из бесконечно большого числа бесконечно тонких и идеально гладких бревен*). Методы, используемые при решении этой задачи, являются общими и могут быть применены для решения других задач, в которых оболочка (нить) находится под действием гидростатической нагрузки.
Для длинной цилиндрической оболочки достаточно рассмотреть плоскую задачу. Поперечное сечение такой оболочки, заполненной жидкостью, удельный вес которой
меньше удельного веса воды 42, принимает форму овала (рис. 6.1). Учитывая, что вес оболочки обычно
*) Жидкостная теория пучка, в пренебрежении поперечными размерами бревен и трением между ними (последнее обстоятельство частично будет учтено в § 6.5), имеет ограниченное применение, но вместе с тем она представляет определенный практический интерес, так как дает верное аначение верхней границы реально существующих натяжений в обвязке '[5, 14, 15, 18].
§ 6.1. ПОСТАНОВКА ЗАДАЧИ
127
ачень мал по сравнению с весом наполняющей ее жидкости, можно считать, что на оболочку действует только сила гидростатического давления Р, направленная по нормали в сторону выпуклости (трением между пучком и оболочкой пренебрегаем). Следовательно, проекции силы Р на касательную и главную нормаль поперечного сечения оболочки будут
рт = 0, Pv = -P. (6.1.1)
Воспользуемся естественными уравнениями равновесия (1.3.3)
Ц- + рт = о, — + Pv = 0.
ds 1 т ’ р 1 v
Подставляя сюда значения и Pv, получим
Т = const, = Р, (6.1.2)
т. е. при действии нормально направленной силы гидростатического давления Р модуль натяжения Т одинаков
во всех точках и пропорционален радиусу кривизны сечения р. Заметим, что для гибкой цилиндрической оболочки, заполненпой жидкостью, под натяжением следует понимать равнодействующую сил, действующих на сечение оболочки по образующей длиной Z, а для обвязок пучков леса величина Т представляет обычное натяжежение нити (троса). Учитывая это обстоятельство, мы из
128 ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
чисто терминологических соображений (книга посвящена механике нити) будем в дальнейшем гибкую оболочку называть обвязкой {нитью, тросом), а наполняющую ее жидкость — пучком.
§ 6.2. Форма поперечного сечения плавающего пучка и натяжение в обвязке
Согласно равенству (1.2) в верхней точке плавающего пучка на обвязку действует сила РА = Т/рА, где рА— радиус кривизны обвязки в точке А. Сила давления на расстоянии у по вертикали от верхней точки А будет складываться из начального давления РА, вызванного давлением обвязки на пучок, и гидростатического давления, равного v\y, где vi = 71Z (для пучков леса Vi = = гДе Л — коэффициент полнодревесности, а I —
длина пучка, приходящаяся па одну обвязку). Таким об¬
разом, в надводной части пучка сила давления на обвязку будет равна
Р = ~- + \1У. (6.2.1)
Ра
Обозначим через а угол между касательной к обвязке пучка и положительным направлением оси х (рис. 6.1). Тогда будем иметь
рх = р sin а = -f vxj/j sin а. (6.2.2)
Воспользуемся первым уравнением равновесия (1.2.8)
Мт£)+р*-°-
Внесем в это уравнение значение Рх, учтя при этом, что sin a = dy/ds и cos а = dx/ds. Тогда, сокращая полученное равенство на ds, будем иметь
d (Т cos а) + + Vij/j dy = 0. (6.2.3)
Введем новую переменную, положив
_—1_ Vjу = VjZ. (6.2.4)
§ 6.2. ФОРМА ПОПЕРЕЧНОГО СЕЧЕНЙЯ ПЛАВАЮЩЕГО ПУЧКА 129
Отсюда dy = dz, и, следовательно, уравнение (2.3) примет вид
d(T cos ос) + Viz dz = 0.
Интегрируя это равенство и учитывая, что в точке А угол а = 0, у = 0, z = PA/vi = 77(pAVi), получим
rcosa + „-r = T+i^r
z = ±]/^Vi-ktcosa, (6.2.5)
kl = -^r-• (6.2.6)
Отсюда
где
viPa
Пользуясь равенствами (1.2), (2.1) и (2.4), получим -у = vxz. (6.2.7)
Кривизна 1/р плоской кривой определяется равенством
1 da dx da da /c* n ov
T = = dF = cosad7- (6-2*8)
Исключая из (2.7) и (2.8) радиус кривизны р, найдем
, Т cos a ,
dx = da
vi z
или, учитывая (2.5),
/~т~ cos a
о— т/ »' da. (6.2.9)
2vx У 1 — cos a v 7
Интегрируя это равенство от 0 до а, получим значение абсциссы надводной части обвязки как функцию параметра а:
130
ГЛ. VI, ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
Функция Ф(а, к) легко преобразуется к эллиптическим интегралам первого и второго рода. Это преобразование используется во всех работах, опубликованных до широкого распространения ЭВМ. Для анализа и вычислений на ЭВМ форма (2.11) функции Ф(а, к) более удобна, так как она более компактна и требует меньшего машинного времени.
Из (2.7) и (2.5) имеем
Пользуясь теперь равенствами (2.4), (2.1), (2.5) и (2.13), легко найдем
Уравнения (2.10) и (2.14) определяют в параметрической форме надводную часть обвязки пучка.
Обозначим через а\ значение угла а на линии водораздела. Тогда высоту надводной части Н\ и длину хорды 2х\ пучка (см. рис. 6.1) получим из (2.14) и (2.10) при а = а\ (во втором равенстве и в дальнейшем учитывается симметрия относительно оси у)
Комбинируя (2.12) и (2.8), найдем дифференциал дуги
Следовательно, длина L\ обвязки надводной части пучка определится равенством
«1
(6.2.12)
Отсюда
(6.2.13)
у (а) = у- (V1 — kl cos а — V1 — к\). (6.2.14)
(6.2.17)
§ 6.2 ФОРМА ПОПЕРЕЧНОГО СЕЧЕНИЯ ПЛАВАЮЩЕГО ПУЧКА 131
Площадь S\ надводной части пучка найдем по формуле
(первое слагаемое в скобке равно площади прямоугольника со сторонами и Я1, а интеграл равен площади криволинейного сектора, ограниченного осью х и обвязкой пучка).
Если внести в последнее равенство значения х\, Ни у и dx, то после очевидных преобразований получим
Аналогично получаются соответствующие величины для нижней подводной части пучка, нужно только во всех формулах индекс 1 заменить на 2 и при этом считать, что для подводной части начало координат находится в нижней точке, ось у направлена вертикально вверх, а угол а отсчитывается против хода часовой стрелки. Кроме того,
где Tf2 — удельный вес воды. Поэтому для подводной час ти пучка будем иметь:
Sx = 2— [V1 — к\ coso^ Ф (ах, — sinaj. (6.2.19)
V|2 = (К2 - IflM,
(6.2.20)
(6.2.21)
Я2 = — к\cosа2 — Vi — кф’
132 ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
Параметры &i, к2, <Х\ и 0С2 нельзя задавать произвольно, так как верхняя и нижняя части пучка связаны
следующими граничными условиями.
1. В точке водораздела должна быть общая касательная к верхней и нижней частям обвязки, т. е.
<Х2 = я — а\. (6.2.26)
2. В точке водораздела обе кривые должны иметь общую абсциссу: х\(а\) = Х2(&2). Подставляя значения #i и Х2, получим
к2Ф(а2 к2) = iii/ciO(ai, A?i), (6.2.27)
где
1* - ]/"^ = j/V** (6.2.28)
т.
и Tfo = Y1/72 — относительный удельный вес пучка.
3. Для пучка должен выполняться закон Архимеда: SiVi = *S2V2. Внесем в это равенство значения S\ и S2 и учтем, что в силу (2.26) sinoc2 = sinai. Тогда получим
Vi — к\ cos аг Ф (<*!, кг) = 1 — к\ cos a2 Ф (a2, к2).
(6.2.29)
Легко проверить (мы не будем останавливаться на этом), что последнее условие эквивалентно равенству давлений на границе водораздела: Р(Н\) = РкН2) или, учитывая (2.1),
— + = — + Voffo.
Ра Ря
При заданном относительном удельном весе То (или параметре ц) для определения значений ai, «2, к\ и к2 к граничным условиям (2.26), (2.27) и (2.29) нужно присоединить еще одно уравнение, определяющее форму пучка (при одной и той же длине обвязки плавающий пучок можно сделать за счет накачанной в оболочку транспортируемой жидкости более вытянутым по ширине или приблизить его к кругу). Так как транспортировка пучка требует знания высоты Н2 подводной части и щирищя 2а его, то в качестве основного коэффициента
§ 6.2. ФОРМА ПОПЕРЕЧНОГО СЕЧЕНИЯ ПЛАВАЮЩЕГО ПУЧКА 133
формы пучка введем следующий параметр
к (6.2.30)
Значение а можно получить из равенства (2.10), если заменить в нем индекс 1 на 2 и положить а = я/2. Тогда, принимая во внимание значение #2, найдем
V1 — к\ cos «2 — V1 — к\
Й Ф
= х. (6.2.31)
Комбинируя равенства (2.27) и (2.29) и заменяя угол аг на его значение из (2.26), получим три уравнения для определения чисел ai, fti и Аг, по заданным параметрам |и и х:
кгФ (я — av кг) = ц&хФ (<%!, кг), (6.2.32)
*, /г — к\ cos аг = \ikx Y1 + A* cos at, (6.2.33)
Kl + fcjcoeo! - Vl-ftS = х^Ф A,)- (6.2.34)
Предположим, что эти трансцендентные уравнения решены и числа ai, fti, к2 найдены (мы еще вернемся к решению этих уравнений). Тогда легко найти следующие отношения, не содержащие неизвестную величину Т:
Ра Рв L xi 2а S /п о ос\
Я,' Я,’ Я,’ Я,’ я,’ с-я1 + я1’ H2'^-z-60>
Здесь L = Li + Ь2 — длина всей обвязки, с — второй коэффициент формы пучка, S = S\ + S2 — площадь поперечпого сечения пучка.
Покажем для примера, как, зная ai, к\ и можно вычислить первое отношение. Пользуясь равенствами
(2.13), (2.22), (2.26) и (2.28), получим
— - J_ м * А
Н2 2 V1 + к\ cos а± — Y1 — к\
Аналогично вычисляются и другие отношения (2.35). Таким образом, все геометрические элементы пучка легко определяются цз этих отношений, еслц зада? одощ
134 ГЛ. VI. ДЕЙСТВДЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
линейный параметр Я2*). Наконец, уравнения (2.10) и
(2.14) позволяют определить относительные координаты надводной части обвязки в долях Яг, т. е. величины х/Нч и у/Яг, как функции угла ос (0<a<o&i); аналогичные уравнения с заменой индекса 1 на 2 дают возможность определить относительные координаты нижней части обвязки (0<а<ос2 = я — ос i). Задавая а в указанных пределах, можно по точкам построить кривую равновесия.
Перейдем к вычислению натяжения в обвязке. Для этого проинтегрируем равенство (2.3). Тогда, учитывая, что при изменении угла а от 0 до а\ ордината у будет меняться от 0 до Яь получим
Складывая оба равенства и принимая во внимание, что cos «2 = — coso&i (так как осг = :гг — oci), будем иметь
Из этой формулы сразу следует, что в сделанных предположениях (жидкостная теория) поперечное сечение пучка не может иметь форму правильного круга. Действительно, при правильном круге радиуса R имеем рл = Рв = К и Ну + Яг = 2 R. Но тогда Т = что невозможно.
VA ~ I
Аналогично для нижней части обвязки
Т cos ос2 — Т -{- —- Я2 + v2 -j- — 0.
-2 Т + (^2+*^)т + + v2#i) = °’
отсюда
(6.2.36)
*) Конечно, вместо глубины осадки Я2 можно задать любой другой линейный размер, например длину обвязки L, ширину пучка 2а и т. п. (см. пример 2 § 6.3).
§ б.З. МЕТОДЫ ЕЕШЕЙИЯ гФаничньй: УРАВНЕНИЙ
135
Натяжение в обвязке лучше всего вычислять в долях веса пучка Q = viS. Таких отношений можно получить несколько. Так, например, из равенства (2.13) найдем
ния. Аналогичные расчетные формулы можно получить, пользуясь равенствами (2.21) и (2.36).
В заключение этого параграфа отметим, что если изогнуть упругий стержень, то его ось (эластика) будет определяться уравнениями вида (2.10) и (2.14) (см., например, [2]). Поэтому некоторые авторы называют теорию пучка эластиковой теорией.
§ 6.3. Методы решения граничных уравнений и примеры расчета пучка
В сделанных предположениях изложенный в § 6.2 материал содержит достаточно полную теорию плавающего пучка, но непосредственно пользоваться им в инженерных расчетах практически нельзя, так как применение полученных результатов связано с большими вычислительными трудностями. В связи с этим мы изложим кратко численные методы решения поставленной задачи и приведем в конце главы таблицы, с помощью которых весь расчет пучка сводится к элементарным действиям.
Из ранее изложенного следует, что для определения основных геометрических элементов пучка и натяжения в обвязке нужно прежде всего решить систему уравнений (2.32)—(2.34). Не останавливаясь на подробностях, поясним, каким методом можно решить эти уравнения.
При заданных fi и и из уравнения (2.34) угол а\ легко выразить через Аъ, а затем из уравнения (2.33) определить к\ через &2. Обозначим эти зависимости следующим образом:
Следовательно,
(6.2.37)
где Sa = Pa/#2 и g = S/H\ —найденные ранее отноше-
а\ =f(k2), fci = (Hfc2)
(6.3.1)
136
ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
(читатель без труда может найти явные выражения для функций / и 00.
С помощью этих зависимостей и уравнения (2.32) составим функционал
F(k2) = к2ФЫ - f(k2), к2.1 - [10(&2)Ф[/(Ы 0Cfe)l. (6.3.2)
Значение к2, при котором F(k2) обращается в нуль, является искомым*).
Изложенный метод решения уравнений (2.32)—(2.34) лучше всего реализовать с помощью ЭВМ. Ручной счет даже с помощью достаточно подробных пятизначных таблиц эллиптических интегралов требует непомерно большого труда и не может дать удовлетворительного результата**). В конце главы даны расчетные таблицы 6.1—6.2 для пяти относительных удельных весов и различных коэффициентов форм плавающего пучка. Эт»и таблицы составлялись следующим образом: по заданным Tfo и х на ЭВМ определялся сначала параметр ц, затем решалось уравнение (3.2), после чего вычислялись значения к\ и Аг, отношения (2.35) и Т/Q (для проверки последнее отношение вычислялось по трем различным формулам). Таблицы содержат соответствующие значения корней уравнений (2.32)—(2.34), т. е. ai, к\ и к2.
При необходимости, пользуясь ими, легко определить элементы пучка, не приведенные в таблицах.
При составлении таблиц коэффициент формы пучка х задавался для каждого Чо с шагом 0,025. Максимальное
*) Вопрос о существовании корня уравнения F(k2) = 0 решается положительно: можно дать строгое аналитическое доказательство (мы не останавливаемся на этом), что при всех Чо и х, удовлетворяющих условиям 0 < 7о < 1 и 0 < х < и0, где х0 — значение коэффициента и, при котором поперечное сечение пучка принимает форму круга, существует единственное решение этого уравнения (каждому гу0 отвечает свое значение Ио).
**) Так, например, при 7о = 0,6 и и = 0,4 перемена знака функции F(k2) обнаруживается при
к2_ = 0,9427623 < к2 < 0,9427631 = к2+,
причем F(k2~) = +0,0000098, a F(k2+) = —0,0000000006. Конечно, такая точность в практических расчетах не нужна, но для получения верных даже первых трех-четырех знаков параметра к2 вычисления на ЭВМ велись в некоторых случаях с точностью до 10“19.
§ €.4. РАСЧЕТ ПУЧКА, ЛЕЖАЩЕГО НА СУШЕ 137
значение к соответствует ближайшему к щ (см. примечание на Стр. 136). Так, например, для То = 0,5 круговая форма пучка получается при Ко = 0,5, а при То = = 0,6 — хо = 0,578. Поэтому в первом случае таблицу оканчивается на х = 0,475, а во втором — на к = 0,575.
Приведем два примера расчета пучка.
Пример 1. Удельный вес бревен ft = 0,7 т/м\ ширина пучка 2а = 4 м, глубина подводной части Я2 = 2 м, коэффициент полнодревесности г\ = 2/3, длина бреван, приходящаяся на одну обвязку Z — 3 м. Пользуясь жидкостной теорией, определить основпые элементы пучка и натяжение в обвязке.
Находим сначала коэффициент формы
По таблице 6.2 для ft = 0,7 (ft = Yi/ft, где ft=1 т/м3 —
удельный вес воды) в первом столбце находим х = 0,500. Для не¬
го имеем:
1. Второй коэффициент формы с = 1,34.
2. Площадь поперечного сечения S = 2,36-Н\ = 9,44 м2.
3. Вес пучка, приходящийся на одну обвязку Q = r\^ilS •= = 13,22 т.
4. Натяжение в обвязке Т = 0,16 •(? = 2,11 т.
5. Длина обвязки L = 5,53-Я2 = 11,06 м
6. Высота надводной части Н\ = 0,49, Я2 = 0,98 м.
Пример 2. Длина периметра гибкой оболочки L •= 15 ле,
второй коэффициент формы с = 1,2, удельный вес транспортируемой нефти ft = 0,9 т/мь. Определить основные параметры поперечного сечения и силу натяжения Гг приходящуюся на 1 м длины образующей оболочки.
По таблице 6.2 для ft = 0,9 и с = 1,2 с помощью интерполяции находим:
1. Глубина подводной части Я2 = £/4,08 = 3,68 м.
2. Площадь поперечного сечения S = 1,31 •Н\ = 17,74 м2.
3. Вес нефти на один метр длины образующей оболочки Q = = blS = 15,96 г.
4. Сила натяжения Т = 0,09 •(? = 1,44 т.
5. Высота надводной части Н\ = 0,17 •#?= 0,62 м.
6. Ширина пучка 2а = Я2/х •= Я2/0,637 = 5,78 м.
Конечно, в практических расчетах большей точности обычно пе требуется.
§ 6.4. Расчет пучка, лежащего на суше [14]
Во многих случаях приходится определять основные параметры пучка, лежащего на суше (рис. 6.2). Все расчетные формулы легко получить из соотношений (2.1)— (2.19). В частности, уравнения контура пучка в парамет-
138 ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
рической форме будут (2.10) и (2.14), длина линии контакта 2d и полная высота Н пучка находятся из этих
уравнений при а = я (нижний индекс 1 опускаем):
2d**2k/'£<b(n, к), (6.4.1)
11 = Т Vк (/ПЛс* - /Г^Р). (6.4.2)
Полную длину обвязкй L получим из равенства (2.18) при а = я и (4.1)
я
L = 2kvr Т f , da | (6.4.3)
V 2v{ ^l_**cosa
Подставив в (2.19) a = я, найдем площадь поперечного сечения
S = 21/Г+fe3ф(я, /с). (6.4.4)
Ширина пучка 2а получается из (2.10) при а = я/2 2а = 2^|ф(|, *). (6.4.5)
Под первым коэффициентом формы пучка будем понимать отношение
§ 6.4. РАСЧЕТ ПУЧКА, ЛЕЖАЩЕГО НА СУШЕ
189
(второй коэффициент формы с в данном случае равен 1/х).
Далее составляем отношения, не содержащие Т и v:
Ра L 2d S /д # «ч
Я * Я ’ Я* я2'
Здесь рА определяется, как и в § 6.2, равенством (2.13).
Все эти отношения при заданном коэффициенте формы пучка х зависят только от параметра к.
Натяжение в обвязке получим из равенства (2.36) при Нч = 0 и Н\ = Н
<6-4-8>
Натяжение в обвязке в долях веса пучка Q можно вычислить по формулам
Т 0 1 — А2 Т 1 «А /й , QV
Q = 2—T' 9-52STT-1- (6-4<9)
Первая формула получена из (2.37), а вторая из (4.8) (6А = ра/Н и 8 = S/H2 — найденные ранее отношения).
При заданном к весь расчет сводится к решению уравнения (4.6). После этого по найденному к вычисляются отношения (4.7) и (4.9). В конце главы приводится расчетная таблица 6.3 для пучка, лежащего на горизонтальной плоскости. При практических вычислениях следует иметь в виду, что от удельного веса пучка, лежащего на суше, зависит только натяжение в обвязке, но не его форма.
Пример. Периметр цилиндрической оболочки L = 12 м. Определить основные параметры оболочки, лежащей на суше и наполненной жидкостью, удельный вес которой у = 0,8 т/мъ, если высота пучка Я = 3 м.
Составим отношение £/Я= 4. По таблице 6.3 находим соответствующий коэффициент формы: х « 0,675. Для этого коэффициента, пользуясь таблицей, получим:
1. Ширина пучка 2а •= Я/х = 4,45 м.
2. Площадь поперечного сечения S = 1,22 Я2 = И м2.
3. Вес жидкости на один метр образующей оболочки Q = ylS = = 8,8 г.
4. Сила натяжения Т = 0,46 • Q = 4,05 т.
6. Длина линии контакта 2d = 0,75-Я=2,25 м.
140 ГЛ, VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
§ 6.5. Влияние сил внутреннего трения
Жидкостная теория пучка не учитывает силы внутреннего трения, а также силы трения между средой пучка и его обвязкой (оболочкой). В этих предположениях было показано, что поперечное сечение пучка не может принять форму правильного круга (см. замечание к формуле (2.36)). Между тем практика показывает, что сформированные пучки могут иметь правильное или почтя правильное круговое поперечное сечение. Покажем, что это может быть объяснено аилами внутреннего трения [14].
Пренебрегая по-прежнему трением между средой пучка и обвязкой и весом последней, мы снова получим, что сила давления пучка на обвязку Р направлена по нормали, а натяженпе в обвязке Т одинаково во всех ее точках (см. § 6.1). Если при отсутствии внутреннего трения сила давления среды пучка на надводную часть обвязки Р определялась формулой (2.1), то при наличии внутреннего трения эта сила (обозначим ее через Р*) уменьшится, т. е.
р* < 1Г + ViyРа
Естественно предположить, что силу Р* можно представить следующей математической моделью:
р* = К (у) (^2 + vtf)« (6-5,1)
где Х\(у) — некоторый положительный коэффициент, удовлетворяющий условию
Ыу) < 1 (6.5.2)
(аналогичный коэффициент М*/) вводится для нижней подводной части обвязки).
Условие равновесия всей обвязки как единого целого требует, чтобы коэффициенты Xk были переменными; легко показать (мы не останавливаемся на этом), что при = Х2 = const это условие нарушается. Конечно, коэффициенты А* зависят от законов внутреннего трения, материала пучка, его формы и т. п. Не уточняя эту вависимость* отметим только, что в каждой точке обвязки бу¬
§ 6.5. ВЛИЯНИЕ СИЛ ВНУТРЕННЕГО ТРЕНИЙ
141
дет свое значение коэффициента К (это выражено нами функциональной зависимостью
kk = Xfc(z/),
где у — ордината рассматриваемой точки).
В сделанных предположениях формула (2.3) принимает вид
d (Т cos а) + (у) ^ -Ь dy = О. (6.5.3)
Интегрируя это равенство и учитывая, что при изменении угла а от 0 до ai ордината у будет меняться от О до Н\, получим
Т cos ax — Т + j* (у) + viy^j ^У = О*
о
Так как множитель при Мг/) в подынтегральном выражении положителен, то, применяя вторую теорему о среднем*), будем иметь (из условия Х\(у) Ф const не следует, конечно, что этот коэффициент нельзя осреднять в интегральном смысле)
Т cos (Xi — Т + Я* J + Vji/j dy = О,
О
или, интегрируя,
Гсоза1 —r + + =0. (6.5.4)
В этом равенстве А*равно значению функции К\(у) в некоторой средней точке интервала [0, Н\].
*) Напомним эту теорему. Если в интервале [а, Ь] функция ■ф(.г) >, то справедливо равенство
ъ ь
J Ф (я) Ф (*) dx = Ф (с) J Ф (я) dx,
а а
гДе а ^ с ^ Ь. (Предполагается, что функция ф(^) непрерывна)
142 ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
Аналогичное выражение получим для подводной части пучка
Прежде всего отметим, что при отсутствии внутренне-
(2.36). Далее, если внутреннее трение бесконечно велико (пучок — твердое тело), то = Яа = 0 и натяжение в обвязке будет равно нулю — вывод, соответствующий физической сущности явления. Если удельный вес пучка 7i равен удельному весу воды 42, то V2 = 0 и из закона Архимеда следует, что 51 = 0 (см. п. 3, стр. 132); отсюда #1 = 0 и Т = 0 — вывод также физически очевидный. Наконец, из равенства (5.6) следует, что при круговой форме поперечного сечения пучка натяжение в обвязке не обращается в бесконечность и, следовательно, такая форма может быть реализована за счет сил внутреннего трения. Действительно, при круговой форме пучка рл = = рв = Д и формула (5.6) принимает вид
Знаменатель этого выражения не может обратиться в
Сложим равенства (5.4) и (5.5) и учтем, что cos 0С2 = —cos ai (0С2 = я — ai).
Имеем
*
'2
отсюда
(6.5.6)
го трения
(к* = к; = 1)
эта формула переходит в
R
§ 6.5. ВЛИЯНИЕ СИЛ ВНУТРЕННЕГО ТРЕНИЯ
143
• Таблица 6.1
Основные параметры плавающего пучка (Vo=0,5; #!=#2; «1=я/2)
и
8!Н\
T/Q
L/H,
кх=к,
0,150
3,333
11,450
0,045
15,010
0,9999
0,175
2,857
9,623
0,055
13,124
0,9997
0,200
2,500
8,279
0,066
11,722
0,9990
0,225
2,222
7,257
0,079
10,644
0,9976
0,250
2,000
6,456
0,095
9,793
0,9947
0,275
1,818
5,816
0,115
9,108
0,9898
0,300
1,667
5,293
0,139
8,547
0,9818
0,325
1,539
4,859
0,170
8,082
0,9691
0,350
1,429
4,494
0,213
7,692
0,9499
0,375
1,333
4,183
0,272
7,362
0,9212
0,400
1,250
3,916
0,362
7,080
0,8784
0,425
1,177
3,684
0,512
6,837
0,8141
0,450
1,111
3,479
0,811
6,626
0,7150
0,475
1,053
3,300
1,715
6,443
0,5461
Таблица 6.2
Основные параметры плавающего пучка
и
SfH\
T/Q
Ь/Нг
/я,
«1.
рад
hi
Ьа
Уо=0,6
0,275
2,154
5,002
0,067
8,773
0,688
1
3717
0,9984
0,9949
0,300
1,969
4,554
0,079
8,199
0,693
1
3730
0,9967
0,9908
0,325
1,813
4,181
0,092
7,721
0,697
1
3748
0,9938
0,9844
0,350
1,680
3,867
0,109
7,318
0,701
1
3770
0,9891
0,9751
0,375
1,564
3,599
0,131
6,976
0,705
1
3797
0,9818
0,9616
0,400
1,463
3,368
0,158
6,682
0,708
1
3827
0,9705
0,9428
0,425
1,375
3,167
0,194
6,429
0,712
1
3861
0,9537
0,9166
0,450
1,296
2,991
0,245
6,208
0,715
1
3898
0,9287
0,8807
0,475
1,226
2,835
0,321
6,015
0,718
1
3938
0,8916
0,8314
0,500
1,163
2,696
0,445
5,845
0,720
1
3980
0,8356
0,7628
0,525
1,106
2,572
0,685
5,696
0,723
1
4024
0,7477
0,6646
0,550
1,054
2,460
1,342
5,563
0,725
1
4070
0,5976
0,5135
0,575
1,007
2,359
10,507
5,444
0,727
1
4117
0,2413
0,1986
144 ГЛ. VI. ДЕЙСТВИЕ ГИДРОСТАТИЧЕСКОЙ НАГРУЗКИ
Таблица 6.2 (продолжение)
н
8/Н1
T/Q
Л-
Ь/я.
HJH,
«1,
рад
hi
k,
0,350
1,952
3,389
0,060
Го=<
7,066
3,7
0,464
1,16631
0,9984
0,9858
0,375
1,815
3,154
0,070
6,712
0,469
1,1694
0,9970
0,9783
0,400
1,696
2,950
0,081
6,408
0,475
1,1731
0,9947
0,9679
0,425
1,590
2,773
0,095
6,143
0,480
1,1775
0,9910
0,9540
0,450
1,497
2,617
0,112
5,912
0,485
1,1826
0,9852
0,9357
0,475
1,414
2,479
0,133
5,710
0,489
1,1884
0,9765
0,9118
0,500
1,339
2,356
0,162
5,530
0,493
1,1947
0,9635
0,3808
0,525
1,272
2,246
0,201
5,372
0,498
1,2016
0,9441
0,8407
0,550
1,211
2,146
0,259
5,230
0,501
1,2090
0,9149
0,7887
0,575
1,156
2,056
0,351
5,104
0,505
1,2167
0,8702
0,7207
0,600
1,105
1,974
0,519
4,990
0,508
1,2249
0,7989
0,6292
0,625
1,059
1,899
0,930
4,888
0,511
1,2333
0,6751
0,4990
0,650
1,016
1,830
3,432
4,795
0,514
1,2419
0,4047
0,2756
0,400
1,949
2,619
0,041
Уо~
6,219
=0,8
0,283
0,9366
0,9995
0,9800
0,425
1,827
2,461
0,047
5,945
0,288
0,9402
0,9991
0,9716
0,450
1,719
2,321
0,054
5,705
0,293
0,9446
0,9983
0,9606
0,475
1,622
2,197
0,061
5,493
0,298
0,9499
0,9970
0,9467
0,500
1,535
2,086
0,071
5,304
0,303
0,9561
0,9948
0,9292
0,525
1,457
1,987
0,083
5,137
0,307
0,9632
0,9915
0,9074
0,550
1,386
1,897
0,097
4,986
0,312
0,9711
0,9863
0,8804
0,575
1,321
1,816
0,116
4,851
0,316
0,9798
0,9783
0,8472
0,600
1,262
1,742
0,142
4,730
0,320
0,9893
0,9662
0,8063
0,625
1,208
1,674
0,178
4,620
0,324
0,9995
0,9477
0,7559
0,650
1,158
1,611
0,234
4,520
0,328
1,0103
0,9186
0,6930
0,675
1,113
1,554
0,328
4,429
0,332
1,0217
0,8712
0,6130
0,700
1,070
1,500
0,526
4,346
0,335
1,0336
0,7877
0,5072
0,725
1,031
1,451
1,196
4,270
0,338
1,0460
0,6146
0,3517
0,500
1,757
1,866
0,027
V
5,147
=0,9
0,137
0,6595
0,9998
0,9535
0,525
1,668
1,775
0,030
4,971
0,142
0,6642
0,9997
0,9399
0,550
1,587
1,693
0,034
4,813
0,146
0,6699
0,9994
0,9235
0,575
1,513
1,619
0,039
4,669
0,150
0,6765
0,9988
0,9039
0,600
1,445
1,551
0,044
4,539
0,153
0,6843
0,9979
0,8806
0,625
1,383
1,489
0,051
4,421
0,157
0,6931
0.9963
0,8532
0,650
1,325
1,432
0,060
4,313
0,161
0,7030
0,9938
0,8209
0,675
1,272
1,223
1,379
0,072
4,214
0,164
0,7140
0,9897
0,7829
0,700
1,330
0,087
4,123
0Д68
0,7261
0,9830
0,7380
0,725
1,178
1,284
0,109
4,040
0,171
0,7392
0,9722
0,6847
0,750
1,135
1,241
0,143
3,963
0,175
0,7533
0,9539
0,6205
§ 6.5. ВЛИЯНИЕ СИЛ ВНУТРЕННЕГО ТРЕНИЯ 145
Таблица 6.2 (окончание)
и
S/H*
T/Q
Ь/Я,
я,/Я,
«1.
рад
kt
ft*
0,775
1,096
1,201
0,201
3,892
0,178
0,7683
0,9214
0,5416
0,800
1,059
1,164
0,327
3,827
0,181
0,7842
0,8571
0,4397
0,825
1,024
1,129
0,791
3,766
0,184
0,8007
0,6939
0,2920
Таблица 6.3 Основные параметры пучка, находящегося на суше
К
S/Я2
T/Q
L/H
2 d/H
k
0,650
1,539
1,276
0,411
4,171
0,824
0,613
0,8814
0,675
1,482
1,226
0,463
4,064
0,750
0,605
0,8592
0,700
1,429
1,180
0,523
3,964
0,680
0,597
0,8343
0,725
1,379
1,136
0,595
3,871
0,613
0,590
0,8065
0,750
1,333
1,095
0,682
3,785
0,549
0,581
0,7756
0,775
1,290
1,057
0,790
3,703
0,487
0,573
0,7415
0,800
1,250
1,021
0,924
3,627
0,428
0,565
0,7037
0,825
1,212
0,987
1,099
3,555
0,370
0,557
0,6618
0,850
1,176
0,954
1,332
3,486
0,314
0,549
0,6155
0,875
1,143
0,923
1,661
3,422
0,259
0,541
0,5637
0,900
1,111
0,893
2,156
3,360
0,205
0,532
0,5053
0,925
1,081
0,865
2,984
3,302
0,153
0,524
0,4382
0,950
1,053
0,837
4,646
3,24G
0,101
0,516
0,3578
0,975
1,026
0,811
9,640
3,193
0,050
0,508
0,2528
ГЛАВА VII
РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
§ 7.1. Равновесие нити на гладкой поверхности
Пусть нить находится на гладкой поверхности, уравнение которой в прямоугольной декартовой системе координат приведено к виду Fix, у, z) =0. При отсутствии трения (поверхность гладкая) на нить в рассматриваемой точке Л/, помимо обычной распределенной силы Р, будет действовать реакция N поверхности, направленная по нормали к последней (рис. 7.1). Конечно, обе силы Р и N отнесены, как обычно, к единице длины нити. Так как градиент функции F есть вектор, направленный по нормали к поверхности Fix, у, z) = 0, то реакция N поверхности отличается от gradF только скалярным множителем %
N = XgvbdF. (7.1.1)
Теперь уравнение (1.2.1) принимает вид
1L + P + N = 0, (7.1.2)
или
-J+P + bgradF = 0. (7.1.3)
В проекциях на оси декартовых координат имеем (см. сноску на стр. 26) уравнения
ЦТ£) + Р’ + >-Ж=0’ т(г £)+*»+*£=0'
ЦтЩ + Ъ + Ьж-0-
§ 7.1. РАВНОВЕСИЕ НИТИ НА ГЛАДКОЙ ПОВЕРХНОСТИ 147
которые совместно с уравнениями
определяют х, у, z, Т и Я в функции s. Когда X будет найдено, то нормальная реакция N определится из (1.1). Уравнение (1.2) можно записать в следующей форме:
T + ^-v + P + tf = 0. (7.1.6)
Проектируя это уравнение на оси естественного трехгранника т, v, р, построенного в рассматриваемой точке М кривой равновесия нити, получим
% + Рх = о, j- + Pv+iVv=0, ^ + iVp = 0. (7.1.7)
Кроме этих, введем другие уравнения, которые получаются из векторного уравнения (1.6) при проектировании его на оси, связанные с поверхностью (рис. 7.2).
Рис. 7.1.
Для этого построим сначала орты касательной т и главной нормали v к кривой равновесия нити АВ (плоскость //, содержащая эти орты, является соприкасающейся плоскостью). Затем построим касательную плоскость I и нормаль К—К к поверхности, а также плоскость III, проходящую через нормаль К—К и касательную т ккри-
148
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
вой равновесия нити. Направим орт п нормали к поверхности в сторону вогнутости нормального сечения (кривой CD, полученной пересечением поверхности плоскостью ///); радиус кривизны этого сечения обозначим через R. Наконец, в касательной плоскости I построим орт g так, чтобы тройка векторов т, п, g образовала правый ортогональный триэдр (очевидно, что векторы п, v и g лежат в одной плоскости).
Спроектируем теперь уравнение (1.6) на оси т, п и g, учтя при этом, что реакция N гладкой поверхности направлена по нормали К—К. Имеем
+ РХ = 0, -^-cosfl+fn +j\Tn=0, ysinft+/><f = 0,
(7.1.8)
Где О — угол между ортами v и п.
Примем во внимание, что Nn = ±N (знак «плюс», если реакция N поверхности совпадает с направлением и, и знак «минус» —в противоположном случае). Теперь урайнения (1.8) примут цид
^Г+Рх = 0, £-совФ + Р„±ЛГ=0, £sm0 + p,=0.
(7.1.9)
Согласно теореме Менье (см. любой курс дифферент циальной геометрии)
p = flcosd, (7.1.10)
где, как отмечено выше, р и R — радиусы кривизны в точке М кривой равновесия нити и нормального сечения соответственно. Поэтому уравнения (1.9) можно записать й так: j
^-+Рг = 0, Х+Р„±АГ = 0, -£-sin<> + />* = 0.
(7.1.11)
Уравнения (1.9) или (1.11) называются естественными уравнениями равновесия нити на поверхности, величина p/sin ft — ради усом геодезической кривизны нити*), а угол Ф углом геодезического отклонения.
*) Если по главной нормали линии, лежащей на поверхности (в нашем случае нити АВ)У отложить в сторону вогнутости радиус кривизны р, то его проекция па касательную плоскость называется радиусом геодезической кривизны данной линии.
§ 7.1. РАВНОВЕСИЕ НИТИ НА ГЛАДКОЙ ПОВЕРХНОСТИ 149
Заметим, что радиус кривизны R = р cos О нормального сечения поверхности и радиус геодезической кривизны p/sin О нити зависят не только от самой поверхности и положения точки М, но и от положения нити на поверхности (точнее, от направления касательной т к нити). Поэтому пользоваться этими уравнениями наиболее целесообразно в тех случаях, когда равновесное положение нити на поверхности известно (см. § 7.2) или для общих выводов (см. пример 1). В тех же случаях, когда требуется определить форму (уравнения) кривой равновесия нити на гладкой поверхности, лучше пользоваться дифференциальными уравнениями равновесия нити (1.4). Во многих случаях более полезными оказываются уравнения равновесия нити в обобщенных координатах
(1.5.17) (при вычислении обобщенных сил нужно учесть, конечно, реакцию поверхности iV).
Пример 1. Геодезические линии. Рассмотрим растянутую на гладкой поверхности нить и будем считать, что активными силами можно пренебречь (Р = 0). Тогда уравнения (1.11) примут вид
dT Т Т
57 = °- r~n = 0< psinfl=0.
Из первого уравнения найдем, что во всех точках такой нити натяжение Т будет одинаково; из третьего уравнения следует, что угол геодезического отклонения нити Ф равен нулю. Это означает, что в каждой точке нити ее главная нормаль v совпадает с нормалью к поверхности п (рис. 7.2). Линии, лежащие на поверхности и обладающие таким свойством, называются геодезическими линиями. Поэтому, если нить, массой которой можно пренебречь, пропустить через два отверстия на гладкой поверхности и натянуть, то в равновесном положении она расположится по геодезической линии. Напомним, что для сферы геодезическими линиями служат дуги большого круга, а для кругового цилиндра — винтовые линии.
Пример 2. Цепная линия на гладкой сфере. Закрепим две точки А и В тяжелой однородной нити на верхней внешней стороне гладкой сферы. Обозначим, как обычно, вес единицы длины нити через д. Тогда на каждый элемент нити будут действовать две силы: q и N. Направим ось z вертикально вверх и воспользуемся сферическими координатами г, 0 и ф (см. рис. 1.12 и 7.3). Так как сила тяжести потенциальна, то будет справедлив интеграл натяжения (1.4.5) (см. замечание к равенству (1.4.8)). В нашем случае будем иметь
Т = qz + С = qR cos 0 + С, (7.1.12)
где qz — потенциальная энергия силы тяжести, R — радиус сферы.
150
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
Если воспользоваться этим интегралом, то из трех уравнений равновесия нити в сферических координатах (1.5.30) независимых будут только два. Для сферы г = R = const и dr = 0. Поэтому первое и третье уравнения (1.5.30) и уравнение связи (1.5.29) примут вид
где Рт и РФ — проекции равнодействующей сил q и N на координатные линии [г] и [ф]. Из рис. 7.3 видно, что Рт = N — q cos 0, РФ = 0. Внесем эти значения для Рг и Рф в первые два уравнения
где М — новая постоянная интегрирования (множитель R введен для удобства). Заметим, что новый интеграл равновесия имеет простой физический смысл — это интеграл момента натяжения относительно оси z, выраженный не через декартовы координаты, как это сделано в (1.2.18), а через сферические координаты. Наличие этого интеграла следует из того, что моменты сил q и iV относительно оси z равны нулю. Использование уравнений равновесия в сферических координатах дало этот интеграл автоматически без каких-либо физических рассуждений и дополнительных преобразований (его можно получить из интеграла (1.2.18) переходом от декартовых к сферическим координатам) — в этом состоит одно из преимуществ метода обобщенных координат.
Возведем второе равенство (1.14) в квадрат, заменим (ds)2 через его значение из третьего уравнения (1.13), а натяжение за¬
(1.13) и заменим квадратную fг скобку в первом уравнении Лг на ее значение из третьего
T^2sin2 6 ^ = MR,
Рис. 7.3.
(7.1.14)
§ 7.2. РАВНОВЕСИЕ НИТИ ПРИ НАЛИЧИИ ТРЕНИЯ
151
меним из (1.12). Тогда после очевидных преобразований получим
(Rq cos 0 + С)2 sin4 0 (йф)2'= Д/2[(<Й>)2 + sin20 (<fcp)2],
или
—sin© Y(Rq COS 0 + С)2 sin2 0 — M2. (7.1.15)
Ось x построим так, чтобы нижней точке цепной линии на сфере отвечало значение угла ф '= 0; пусть при этом 0 = 0О. В этой точке (предполагается, что нить целиком лежит на сфере и нигде не свисает с нее) производная d0/cftp = 0. Учитывая это, выразим с помощью равенства (1.15) постоянную интегрирования М через 0О и С:
М = sin 0о(Дд cos 0О + С). (7.1.16)
Разделяя в (1.15) переменные и интегрируя, получим
е
С dQ
ф = М 7 —■ :: =■:■■■== : ■=. (7.1.17)
J sin 0 у (Rq cos 0 + С) sin 0 — М ео
Заметим, что подстановкой cos 0 = z этот интеграл сводится к эллиптическому интегралу.
Полученное равенство определяет уравнение ф = ф(0, 0О, С) цепной линии на гладкой сфере радиуса R. Если кроме значения 0О известны координаты точек закрепления -4(01, ф0 и #(02, ф2), то постоянная С найдется из (1.17): фг= ф(01, 0о, С) или ф2 = = ф(02, 0о, С). При численных значениях заданных величин определение с помощью ЭВМ постоянной С не представляет труда. Длину дуги от вершины цепной линии до любой ее точки можно вычислить по формуле
Г sin 0 (Rq cos 0 + С) dQ
s = R \ г ■ , (7.1.18)
J у (Rq cos 0 + С) sin 0 — М ео
которая получается (1.14) и (1.15). Таким образом, если известно положение вершины цепной линии на сфере и координаты точек закрепления ее, то все элементы нити легко вычисляются по формулам (1.16) — (1.18). При необходимости читатель без труда составит схему расчета при задании других граничных условий (этой задаче посвящено много работ — см. библиографию в [2]).
§ 7.2. Равновесие нити на поверхности при налячии трения
Задача о равновесии нити на шероховатой поверхности ставится обычно следующим образом: при заданных активных силах, коэффициенте трения к и конфигурации нити на поверхности требуется определить натяжение
152
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
нити и условия, при выполнении которых нить будет находиться в равновесии (предполагается, что силы трения подчинены закону Амонтона).
Сила трения F между поверхностью и нитью расположена в касательной плоскости. Поэтому уравнения
равновесия нити получаются из (1.9), если к первому и третьему уравне-
7ниям присоединить проекции силы трения F на оси т и g. Обозначив угол между касательной т и силой трения F через получим (на рис. 7.4 изображена касательная плоРис. 7.4. скость, сила трения Fn
нормальная реакция N предполагается, что отсчет дуговой координаты s идет в сторону убывания натяжения, поэтому 0 < у < п/2)
+ Р% + F cos v = 0, у cos ft + Pn±N=О,
(7.2.1)
у- sin ft + Pg — F sin у — 0.
К этим уравнениям нужно присоединить условие, которому должна удовлетворять сила трения
F ^ kN, (7.2.2)
где знак равенства отвечает предельному равновесию.
Так как по условию конфигурация нити на поверхности задана, то в уравнениях (2.1) радиус кривизны нити р и угол геодезического отклонения ft будут известными функциями положения точки М на нити, т. е. криволинейной координаты s. Кроме того, известны проекции активной силы P(Px,PnyPg). Неизвестными величинами являются нормальное давление N, натяжение нити Г, модуль и направление силы трения (F и угол у).
В общем случае нужно пользоваться уравнениями
(2.1) п условием (2.2). Мы ограничимся рассмотрением наиболее важного для приложений и вместе с тем наибо¬
§ 7.2. РАВНОВЕСИЕ НИТИ ПРИ НАЛИЧИИ ТРЕНИЯ 153
лее простого случая, когда активными силами, действующими на нить, можно пренебречь СР = 0). В этих условиях уравнения (2.1) принимают вид
~ = — F cos V» N = — cos ft, — sin ft — F sin v.
ds 1 p p 1
(7.2.3)
Пользуясь условием равновесия (2.2) и значением нормального давления N, получим из первого и третьего уравнений
■57^ — -cos О cos7, sin(7-2.4)
Из второго неравенства следует
f А 482Ф A:2 cos2 О — sin2 Ф /79rv
cosy<|/ 1 Ь_ = ^5 . (7-2.5)
Первое неравенство (2.4) только усилится, если cos^f заменить правой частью соотношения (2.5). Следовательно,
-g->-x(*)7\ (7.2.6)
где
, ч 1/л2 cos2 О — sin2 ft /7 О 7\
х (5) = , (7.2.7)
причем параметр х при заданной форме равновесия нити на поверхности является известной функцией дуговой координаты s и коэффициента трения к.
Так как коэффициент хЫ должен быть вещественным, то
к2 cos2 ft > sin2 ft
или, вводя угол трения ф = arctg ку
к = tgcp^tgft, ф ^ ft. (7.2.8)
Это неравенство составляет первое условие равновесия: при отсутствии активных сил для равновесия нитщ лежащей на поверхности, необходимо, чтобы в каждой точке нити угол трения ф был не меньше угла геодезического отклонения ft.
154
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
Проинтегрировав неравенство (2.6), получим второе необходимое условие равновесия нити на шероховатой поверхности
8
—Jx(e)ds
Т^ТАе 0 (7.2.9)
где ТА — сила, приложенная к концу нити А, Т — натяжение нити в любой ее точке М, s — длина нити от А до точки М. В частности, если второй конец нити В свободен, то к нему необходимо приложить силу Тв, удовлетворяющую условию (L — длина всей нити АВ)
ь
—J x(s)ds
Тв>ТАе о (7.2.10)
Таким образом, если при отсутствии активных сил нить, лежащая на поверхности, находится в равновесии, то в каждой точке нити должны выполняться условия
(2.8) и (2.9). Легко видеть, что обратное утверждение тоже справедливо. Следовательно, условия (2.8) и (2.9) являются необходимыми и достаточными для равновесия нити на шероховатой поверхности.
Из неравенства (2.9) нельзя определить значение натяжения в любой точке нити — мы можем только указать его нижнюю границу. Это соответствует природе принятого закона трения. Конечно, в предельном случае, когда имеет место знак равенства, задача становится вполне определенной.
Пример 1. Плоская задача. Пусть нить, находящаяся на цилиндрической не обязательно замкнутой шероховатой поверхности, имеет форму плоской кривой, перпендикулярной образующим поверхности (рис. 7.5, а и б). К концам нити приложены силы Та и Тв. При таком расположении нити ее главная нормаль v в любой точке совпадает с нормалью п к поверхности и, следовательно, угол геодезического отклонения Ф равен нулю. Из формулы (2.7) найдем
*(«)-■£. (7.2.11)
Как уже отмечалось (см. формулу (1.3.5)), для плоской кривой кривизна 1/р определяется равенством
1 da
§72 РАВНОВЕСИЕ НИТИ ПРИ НАЛИЧИИ ТРЕНИЯ
155
где а — угол между касательной и какой-нибудь неподвижной прямой. Если обозначить через ал и а в значения угла а в точках А и В соответственно, то с помощью (2.11) и (2.12) условие равно-
Рис. 7.5.
весия нити (2.10) принимает вид (неравенство (2.8) выполняется автоматически)
а в ~ J kda ТА>Тв>ТАе *А
или, интегрируя,
ТА > Тв > ГАе_А(“в_(ХА). (7.2.13)
Здесь ав —аА —угол поворота касательной (рис. 7.5, б). Для кругового цилиндра (рис. 7.5, в) этот угол равен углу охвата, причем в предельном случае получаем хорошо известную формулу Эйлера *)
rB = 7’Ae“ft(aB-“A)# (7.2.14)
Пример 2. Равновесие нити на круговом конусе. Рассмотрим невесомую нить, охватывающую шероховатый круговой конус по окружности, плоскость которой перпендикулярна оси конуса (рис. 7.6). К переднему свободному концу нити подвешен груз весом G. Требуется определить, какой груз нужно подвесить ко второму концу нити, чтобы последняя оставалась в равновесии. Ось конуса горизонтальна, угол между его образующей и осью равен а0, коэффициент трения к.
В рассматриваемом случае угол геодезического отклонения Ф = a0 = const (так как v и п перпендикулярны оси конуса и его образующей соответственно), радиус кривизны нити р = г, где г —радиус окружности, длина нити, лежащей на конусе, Ь=лг.
*) Если цилиндр не круговой (рис. 7.5, б), то говорить об 'угле охвата можно только условно, так как в общем случае центра криризны для точек А и В не совпадают.
156
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
При G > Q натяжение Т будет убывать от А к В, поэтому в соответствии с принятым ранее условием вектор т имеет указанное на рисунке направление. Сила трения F лежит в касательной плоскости (т, g). Для равновесия нити нужно потребовать прежде
всего, чтобы коэффициент трения к удовлетворял условию (2.8): k^tgao. Из формулы (2.7) найдем
к2 cos2 aQ — sin2a0
X = ^ = const.
г
Натяжения нити в точках А и В соответственно равны Та = G, Тв = Q. Второе условие равновесия (2.10) принимает вид
G>Q>
или
где
х* = V к2 cos2 a0 — Sin2a0. (7.2.15)
В предельном равновесии угол 7 между силой трения F и касательной к нити т определяется из равенства (2.4) и для данного примера = arcsin tg Оо/к.
Пример 3. Равновесие нити, расположенной по геодезической линии шероховатой поверхности. По определению, для любой пространственной геодезической линии угол 'б = 0 (в примере 1 мы тоже рассматривали геодезические линии, но они были плоскими). Поэтому коэффициент x(s)= к/р и условие (2.9) принимает вид
§ 7.2 РАВНОВЕСИЕ НИТИ ПРИ НАЛИЧИИ ТРЕНИЯ
157
Как уже отмечалось (см § 1.3), радиус кривизны любой пространственной, в том числе п геодезической, линии можно рассматривать как функцию дуговой координаты: р = p(s). Поэтому формула (2.16) определяет условие равновесия нити, расположенной по геодезической линии шероховатой поверхности для случая, когда активными силами можно пренебречь.
Рассмотрим пример. Пусть нить, весом которой можно пренебречь, расположена по винтовой линии круглого цилиндра. Радиус кривизны винтовой линии определяется равенством
Пользуясь теперь формулой (2.16), получим в предельном случае натяжение нити, расположенной на круглом шероховатом цилиндре по винтовой линии:
Остановимся несколько подробнее на формуле (2.16). Некоторые авторы называют множитель при коэффициенте трения к в показателе степени «углом охвата» нити, расположенной по геодезической линии. Если обозначить этот угол через Q, то будем иметь
Пользуясь определением кривизны пространственной линии (1.3.4), можно показать, что эта величина равна длине индикатрисы касательной *). В общем случае индикатриса касательной представляет линию двоякой кривизны, но в некоторых случаях она вырождается в окружность (например, для винтовой линии), и тогда величину Q можно найти из геометрических соображений. Заметим только, что стремление свести эффект трения нити о поверхность к формуле Эйлера и рассматривать показатель степени
*) При движении точки по кривой естественный трехгранник будет поворачиваться в пространстве. Индикатрисой касательной (главной нормали или бинормали) называется годограф орта т (соответственно v или (3), т. е. линия, которую описывает конец вектора т, если его начало совмещать все время с одной и той же точкой. Из этого определения следует, что индикаторы представляют линии, лежащие на сфере единичного радиуса (так как |т| = |v| — |р| =1). Почти во всех курсах дифференциальной геометрии показывается, что дифференциал дуги do индикатрисы касательной определяется равенствем da = ds/р. Отсюда непосредственно следует сделанное выше утверждение. В применении к нитям на это обстоятельство впервые обратил вниманце Д. П. Мд-
(1.3.9)
(7.2.17)
(7.2.18)
S
(7.2.19)
о
раков [16].
158
ГЛ. VII. РАВНОВЕСИЕ НИТИ НА ПОВЕРХНОСТИ
в равенстве (2.9) как произведение коэффициента трения к на «угол охвата» может привести к ошибочным заключениям. Действительно, в примере 2 реальный угол охвата равен я, но показатель степени равен не &я, а и*я, где и* определен равенством
(2.15).
В заключение обратим внимание на следующее обстоятельство. Угол у между силой треиия F и касательной к нити т (см. рис. 7.4 и уравнения (2.1)) зависит от действующих на нить активных сил, конфигурации нити на поверхности и коэффициента трения к. Даже при отсутствии активных сил этот угол может быть различным. Так, в примерах 1 и 3 угол у равен нулю» а в примере 2 в предельном равновесии у = arcsin tg а/к.
Часть 2
Основы динамики нити
ГЛАВА VIII
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
§ 8.1. Дифференциальные уравнения движения нити в декартовых координатах
При движении нити, которую мы будем в дальнейшем считать идеальной, однородной и нерастяжимой (исключения оговариваются), положение и скорость каждой ее точки М, а также натяжение Т зависят не только от дуговой координаты 5, но и от времени t. Поэтому, если г — радиус-вектор точки М движущейся нити, a v и w — скорость и ускорение этой точки, то будем иметь
Дуговая координата s отсчитывается от некоторой фиксированной на нити точки. Если нить имеет хотя бы одну неподвижную точку, то за начало отсчета дуговой координаты рационально вы- .
брать эту точку. Если же AffSr(s+As,t)
все точки нити движутся, то начало отсчета будет перемещаться вместе с ^ \
нитью.
Выделим в нити элемент ММ' длиной Дs и ис*
массой цДз. Обозначим, как обычно, через Р силу, отнесенную к единице длины нити. Тогда на этот элемент нити будут действовать сила PAs и в точках М' и М натяжения Т (s -f- As, t) и — T (s, t) соответственно (рис. 8.1). Применим к элементу нити ММ' второй закон
Т = Т (*,*), r = r(s,t),
/ дг dv v = v(s, t) =-gp
dv d2r
(8.1.1)
160 гл. VIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
Ньютона:
jxAsw = Т (s -f- As, t) — Т (s, t) -f- PAs, или, деля на As и переходя к пределу,
(8.1.2)
Это основное дифференциальное уравнение динамики нити в векторной форме. Проектируя его на оси неподвижных декартовых координат, получим
К этим уравнениям нужно присоединить уравнение связи
Дифференцируя это равенство по времени t, получим
te_J>_(dx\ ,£lJ_/dy) , dz д (дг \ л
ds dt yds J ds dt [ds J ds dt yds J ~ ’
или, меняя порядок дифференцирования,
^JL( л_ llLjLt ЁМ.\ л. dz d ( dz\ _
ds ds \ dt J'’ ds ds [ dt J ds ds у dt J ~
Величины, стоящие в скобках, равны соответству щим проекциям скорости V, т. е.
(8.1.3)
(8.1.4)
(8.1.5)
Поэтому последнее равенство принимает вид
dx dvx ду dvu ds dvz
ds ds ds ds ds ds ’
или в векторной форме
do
(8.1.6)
§ «.2. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ 161
(так как первые множители в равенстве (1.6) равны про* екциям единичного касательного вектора т).
Дифференциальные уравнения движения нити (1.3) должны быть проинтегрированы с учетом связей (1.4) и
(1.6), а также граничных и начальных условий. Если концы нити АВ закреплены, то, отсчитывая дуговую координату от конца А, граничные условия можно записать в следующем виде:
£а(0, t) = ai, уА(0, t) = Ьи яА(0г t) = си
(8.1.8)
хв(1, t) = a2, Ув(1, t) = b2, zB(l, t) = c2l
где I — длина нити, а постоянные числа ak, ch (к в
= 1, 2) — координаты точек закрепления А и В.
Если конец нити А закреплен, а конец В свободен и не связан с каким-либо телом, то граничное условие на свободном конце состоит в конечности функций х{1, t)i у {I, t) и zil, t) (см. § 10.3). Если конец В не закреплен, но к нему прикреплено тело (например, груз), граничные условия усложняются (см. § 10.3).
Начальные условия должны предусматривать конфигурацию нити и значения скоростей ее точек в момент времени t = 0. Эти условия имеют вид (конечно, в частных случаях им можно придать другую форму)
x(s, 0) =/1(5), y(s, 0) =/2Ы, z(s, 0) =/3.(5),
(8.1.9)
vx(s, 0) =F\(s), vy(s, 0) =F2(s), v2(s, 0) =F$(s).
Функции fh{s) и Fhis) нельзя задавать произвольно — оыи должны быть подчинены условиям (1.4) и (1.6).
§ 8.2. Естественные уравнения движения нити
В некоторых случаях основное уравнение динамики нити (1.2) целесообразно выразить в проекциях не на оси неподвижной декартовой системы координат, а на оси естественного трехгранника. Для составления этих проекций необходимо йредварительно остановиться на некоторых вопросах кинематики нити.
162 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
Прежде всего нам понадобятся формулы Френе, которые для движущейся нити имеют вид (сравните с (1.3.1))
Здесь р — радиус кривизны (см. § 1.3), a pi — радиус кручения, вычисляемый по формуле
где скобки означают смешанное скалярно-векторное произведение. Аналогично кривизне 1/р (см. формулу (1.3.4)) кручение можно рассматривать как скорость поворота бинормали по дуге, и в общем случае ее нельзя представить как производную от некоторого угла по дуговой координате s. Для плоской кривой 1/pi = 0, pi =
Введем в рассмотрение вектор Дарбу. Для этого зафиксируем время t и дадим дуговой координате приращение As. Тогда естественный трехгранник Mxv$ перейдет в M't'v'p', изменив при этом свою ориентацию (рис. 8.2, а). По теореме Эйлера — Даламбера существует вектор малого поворота е', с помощью которого ориентация трехгранника Mxv$ может быть совмещена с ориентацией трехгранника M'x'v'p *). Векторам Дарбу назы¬
*) Все общие сведения из кинематики, на которые мы будем в дальнейшем ссылаться, можно найти, например, в [14], т. I.
**яс. 8.2.
§ 8.2. ЕСТЕСТВЕННЫЕ СРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
163
вается предел отношения вектора малого поворота с' к приращению дуги As, когда последнее стремится к нулю:
Q = lim-fl. (8.2.2)
As-*o
Из этого определения видно, что вектор Дарбу можно рассматривать как угловую скорость вращения естественного трехгранника, вызванную изменением не времени t, а дуговой координаты s. Для линии двоякой кривизны вектор Дарбу нельзя представить производной от некоторого угла по дуговой координате.
Для вычисления вектора Дарбу напомним, что если с подвижной системой координат жестко связан какоипибудь вектор a[t), то имеет место равенство
^=wxe. (8.2.3)
Здесь со — угловая скорость подвижной системы. Из этого равенства и определения вектора Дарбу следует:
(8.2.4)
где a (s, t) — вектор, жестко связанный с естественным трехгранником. Для вычисления Q положим в этой формуле сначала а = v, а затем а = р. Имеем
4r-°xv, #-Охр,
или, пользуясь формулами Френе (2.1),
— -J-т +-j-p = Qxv, _J_v = ftxp.
Р Pi
Умножим слева первое равенство векторно на V, а второе на Р и учтем, что v X т = — р, v X Р = т и РХ v = —т. Тогда получим
-j!p0 + -^-T = vx(fixv), -^-т = Рх(ЙХР).
Раскрывая двойные векторные произведения *) и учитывая, что v • v = 1, и Р* Р= 1, будем иметь
-Lр + J-т = Q - (v.Q) v, J-т = Q - (р.П) р. (8.2.5) V ^1
*) Напомним формулу: ах (ЬХс) = (а»с)Ь — (а*Ъ)с.
164 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
Вычитая из первого равенства второе, найдем -1P = (P.Q)P_(V.Q) v.
Сравнивая множители при одинаковых ортах, получим
v-Q = О, 6Й=—.
r Р
Подставляя эти значения скалярных произведений в равенства (2.5), найдем вектор Дарбу
Q = — т + — p. (8.2.G)
Рх р v v '
Отсюда получим соответствующие проекции
Qx = -L Qv = 0, Qp=—. (8.2.7)
Pi P
Из определения вектора Дарбу и известной формулы кинематики, связывающей полную и локальную производные *), следует, что для вектора a (s, t), заданного в трехграннике Мт\$ и зависящего от дуговой координаты s и времени t, справедлива формула
_Ё£ = _£« + йха. (8.2.8)
ds ds
При изменении времени t на At нить в общем случае изменит свою форму, а точка Ж, принадлежащая нити, не меняя своей дуговой координаты s, переместится на вектор ММ". Трехгранник Мтх$ займет новое положение М" t"v"P", изменив при этом свою ориентацию (рис. 8.2, б). Угловую скорость естественного трехгранни¬
*) Напомним, что локальной производной вектора называется новый вектор, проекции которого на подвижные оси координат равны производным от соответствующих проекций дифференцируемого вектора. Таким образом, если ах, av и ар — проекции вектора а на оси т, v и р соответственно, то
/да\ = да^ 1$а\ = ^ /|£\ _ да^
\dsfx ds1 \ds )v ds 9 \ds /р ds
Отсюда следует, что локальная производная вектора равна скорости изменения его относительно подвижной системы координат.
§ 8.2. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
165
ка Л/tvfJ, вызванную изменением времени t при неизменной дуговой координате s, обозначим через со. Аналогично формуле (2.2) будем иметь
w=lim дг»
Д4-»0
(8.2.9)
где 8 —вектор малого поворота, с помощью которого ориентация трехгранника Мтх$ может быть совмещена с ориентацией трехгранника М"
Для вектора a (s91) имеет место формула
да да .
~дГ==~дГ + <йХа'
(8.2.10)
Равенства (2.8) и (2.10) справедливы для любого вектора а = a (s, t). Используем их для определения связей, которым должны удовлетворять проекции скорости v точки нити М. Для этого составим два выражения для производной от v по s. Последовательно получим (в конце используется формула (2.10))
dv
ds
д дг ds dt
д дг dt ds
dj
dt
Локальная производная от орта т равна нулю (как относительная скорость вектора, жестко связанного с трехгранником). Поэтому имеем
т v р
dv
Us
= сохт =
®v 1 0
(Dp
о
или, раскрывая определитель, dv
= (Opv - CDvp.
Применим теперь к левой части этого равенства формулу (2.8):
г v р
dv dv , л dv .
Т“=“7Г + ЙХ1;=-Н- +
ds ds 1 ds 1
± 0 -L
Pi p
Пользуясь определением локальной производной и рас-
166 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
крывая определитель, получим
V* ) г 4- (dVy 4- ^ ^ v -4- I 4- ^ ) ft
д. -u “"p-/T+vir+“p"- рГ/ +\*Г + ptJp*
Сравнивая оба выражения для dv/ds, найдем искомую связь для скоростей (формулы Резаля — Флоке):
дих vv _ n dvv , vx % dvt .
ds р ’ ds р р1 ds рх tt>v*
(8.2.11)
Для плоской нити 1/pi =0, (Dv = 0, (i)p = (i) и эти уравнения принимают вид
dv,r ъ' dv„ и.
— = 0, -г-- -J——- = (о. (8.2.12)
ds р ds р 4 7
Уравнения (2.11) и (2.12) справедливы для любого движения нити, в частности они справедливы и для случая, когда нить, не меняя своей формы, перемещается как твердое тело.
Нам осталось установить связь между угловыми скоростями со и Q. Для этого снова возьмем неизменный относительно трехгранника Мтх$ вектор а. Для него локальные производные равны нулю и формулы (2.8) и
(2.10) принимают вид
IT = t)X°' ir = Qxa-
Дифференцируя первое из них по s, а второе по t, получим
д(й , da д(й . ч
= ^rXfl + + (DX (S2 Х«),
dt ds ds ' ds ds
i^=fxa+flx|f = fxa + Qx(a>xa).
Раскроем двойные векторные произведения и вычтем из первого равенства второе:
Йг-§)ха ~ (в,0> ~ Q= °*
Величина, стоящая в квадратных скобках, равна двойному векторному произведению (йхсо)ха, и, следова¬
§ 8.2. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
тельно, последнее равенство принимает вид
j Так как вектор а произволен, то первый множитель этого произведения должен равняться нулю, т. е.
Уравнение (2.13) или эквивалентное ему (2.14) называется уравнением Дарбу, и оно устанавливает связь, которой должны удовлетворять кинематические элементы движущейся нити. В проекциях на оси естественного трехгранника уравнение (2.14) эквивалентно трем скалярным уравнениям (см. равенства (2.7))
Для плоской нити эти равенства обращаются в тождества. Действительно, для плоской нити имеем: =
= cov = 0, 1/pi =0, сор = со = da/dt, 1/р = da/ds, где а — угол между касательной к нити и осью х. Первые два равенства (2.15) принимают вид 0 = 0, а третье переходит в тождество
Перейдем теперь к проектированию основного уравнения динамики нити (1.2) на оси естественного трехгранника. Составим производную вектора Т = Тх по s. Имеем
(8.2.13)
или, пользуясь равенствами. (2.8) и (2.10)
(8.2.14)
д®т д_
ds dt
(8.2.15)
d2a d2a
dt ds ds dt'
168 ГЛ. VIII. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
С учетом этого равенства получим для проекций уравнения (1.2) на оси т, v и р
= §7 + Р%, = -у + Pv, = ■Рр- (8.2.ip
Воспользуемся формулой (2.10) для вектора w = dv/dt: w = ^ + сох г. (8.2.^7)
В проекциях на оси естественного трехгранника будём иметь
д и
wx = -0j-+ (Ovl»p — (Opyv,
Wy = ^ + topi;T — <DT1>0, (8.2.18)
duo
W§ = -qJ -|- (dxVy — (£)VUX.
Теперь дифференциальным уравнениям движения нити (2.16) можно придать следующий вид:
их \ дТ тъ
_ + щщ _ WftVvJ = Ж + РХ,
р (^Г — ®tl7p) = "р"*" Ру' (8.2.19)
^ (l? + — ©v^t) = Ра-
Эти дифференциальные уравнения движения нерастяжимой идеальной нити должны интегрироваться в общем случае с учетом уравнений (2.11) и (2.15). Вся эта система девяти уравнений содержит девять неизвестных функций (ут, i7v, Vi, сох, (Dv, (оp, р, pi, Т) двух независимых переменных s и t. Конечно, для полного решения задачи нужно задать еще в соответствующем виде граничные и начальные условия.
Предположим, что вся система девяти дифференциальных уравнений решена, в частности найдены радиусы кривизны р и кручения pi:
р = p(s, t), pi = pi is, t). (8.2.20)
§ 8.2. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НИТИ
169
Для решения конкретной задачи с учетом граничных и начальных условий натуральные уравнения (2.20) нужно преобразовать к уравнениям в явной форме*). Для линии двоякой кривизны (время t в уравнениях (2.20) играет роль параметра) это требует, как правило, решения сравнительно сложных уравнений, но в случае плоской задачи и для общих теоретических выводов эти уравнения можно использовать с большой эффективностью.
*) Натуральные уравнения p=p(s), pi= pi(s) определяют кривую с точностью до положения ее в пространстве. Так, например, уравнения р = const 'Ф 0, pi = 0 определяют окружность радиуса р, но где находится центр этой окружности и в как&й плоскости она лежит, остается неопределенным.
ГЛАВА IX
КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
§ 9.1. Основные определения и уравнения движения
Рассмотрим движущуюся нить, которая сохраняет все время форму некоторой неизменяемой линии Г. Будем предполагать, что нить движется вдоль линии Г с заданной относительной скоростью vr =vr (t), а сама линия Г неподвижна или перемещается относительно инерциальной системы координат Oi£ri£, вообще говоря, произвольным образом. Такое движение называют контурным или установившимся движением нити.
Свяжем с линией Г координатную систему Oxyz. На рис. 9.1 изображена неподвижная относительно осей Oxyz кривая Г и движущаяся вдоль нее нить АВ (для большей наглядности эти две фактически сливающиеся линии изображены раздельно). Возьмем на нити АВ произвольную
§ 9.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ 171
точку М; в данный момент времени t с ней совпадает точка N линии Г. Соответствующие дуговые координаты обозначим через s и а; первая из них отсчитывается от подвижного начала Л/о, принадлежащего нити АВ (см. замечание к равенствам (8.1.1)), а вторая от неподвижной* в системе Oxyz точки No.
Угловая скорость ю естественного трехгранника Mrvfr (рис. 8.2), связанного с нитью, складывается из угловых скоростей переносного и относительного движений нити:
со = сое + юг.
В этом равенстве юе —угловая скорость координатных осей Oxyz, а юг —угловая скорость трехгранника Мт\$ (на рис. 9.1 он не показан) относительно координатной системы Oxyz.
Для вычисления относительной угловой скорости юг при контурном движении нити поступим следующим образом. Рассмотрим сначала действительное относительное перемещение нити, при котором координатная системаOxyz остается в покое. Пусть за время At точка М нити, совпадающая ранее с точкой N линии Г, переместилась вдоль Г на величину A s\ при этом трехгранник Mtv(V займет положение Л/''t''v''P" и изменит ориентацию на вектор малого поворота е" Теперь при фиксированном времени t мысленно переместим точку N линии Г в положение N' па величину Да = As. Трехгранник Nxxfy займет при этом новое положение N'изменив ориентацию на вектор малого поворота г'. Так как нить АВ фактически совпадает с линией Г и Да = As, то будут совпадать точки М" и Nтрехгранники М"т"х"$" и N't'v'p', а также соответствующие векторы малых поворотов е" и е' Пользуясь равенством (8.2.9) и учитывая, что е" = е', последовательно получим
т г" т As е' т As е'
cor = lim -г- = lim -т— -г- = lim -г- • lim -j—,
At-o А* At^o А* А* At-o А* а«-о А*
или, принимая во внимание (8.2.2),
(or = yrQ, (9.1.1)
где vr = lim As/At = ds/dt — относительная скорость движения точки М нити вдоль линии Г (формулу (1.1) можно* получить другими методами — см., например, [4, 12]).
172
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
Вектор относительной скорости vr точки М нити направлен по касательной к нити. Следовательно, его проекции и проекции вектора сог соответственно равны (см.
Абсолютная скорость v точки М нити складывается из относительной vr и переносной ve скоростей:
Внесем это значение для скорости в первое равенство
При контурном движении нити, когда ее форма не изменяется, переносное движение представляет движение нити как твердого тела. Для такого движения формулы
(8.2.11) сохраняют свою силу (см. замечание к (8.2.12)) и, следовательно, совокупность последних двух членов в
(1.3) равна нулю. Кроме того, rrv = 0. Поэтому равенство
(1.3) принимает вид
нри этом учтено первое равенство (1.2).
Из (1.4) следует, что при контурном движении нерастяжимой нити все ее точки имеют в каждый данный момент одинаковую по модулю относительную скорость vr — факт физически очевидный.
Перейдем к составлению дифференциального уравнения контурного движения нити. Полное ускорение w точки М нити складывается из относительного wf, переносного w и кориолисова ivc ускорений:
(1.1) и (8.2.7))
Vtx = Vr, Vrv = 0, 1>гз = 0;
v г Vr
(Drt = ——, (0rv = 0, (Ofp = .
1*1 К
(9.1.2)
(8.2.11)
dv,
rx
(9.1.3)
ds
(9.1.4)
W = Wr + We + We-
(9.1.5)
Относительное ускорение wr представляет ускорение точки М при ее движении вдоль остановленной линии Г. Лз элементарного курса кинематики известно, что в этом
§ 9 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ 17$
случае проекции ускорения на оси естественного трех* гранника определяются равенствами (их можно получить также из формул (8.2.18), если в правые части внести значения проекций векторов vr и сог из (1.2))
vr
wTX = vr, wr\ = —, MVp = 0. (9.1.6)
Отсюда
V*
wr = vrx -\—- v. (9.1.7)
P
Внесем равенства (1.5) и (1.7) в дифференциальное уравнение движения нити (8.1.2):
vr , дТ , D
liVrX + \1 — V + \iwe + \iwc = + P.
Учтем теперь, что T = Tx, и, следовательно, с помощью первой формулы Френе (8.2.1) последнее уравнение можно привести к виду
1;^ дТ Т
JUVC + (iy V + цм?е + цн>с = + — V + Р,
или, принимая во внимание, что относительная скорость vr(t) не зависит от s (см. равенство (1.4)),
д (т — / о\ V
ds t + (г — — + Р — ЦУгТ — — цм>е = 0.
Объединяя первые два члена и снова учитывая первую формулу Френе, получим
(Т*х) + Р — (uvt — цм?е — цм?с = 0, (9.1.8)
где кажущееся натяжение Т* определено равенством
Т* = Т — \iVr- (9.1.9)
Уравнение (1.8) является основным для контурного движения нити. Оно имеет форму уравнения равновесия
(1.2.1), и его можно прочитать следующим образом: движущуюся вдоль перемещающейся неизменяемой линии Г нить можно рассматривать как находящуюся в покоеf если действительное натяжение Т заменить на кажущееся
174
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
матяжение Т* и к действующим на нить силам Р при-
*соединить относительную касательную (— (и;гт), перегносную (— Ixwe) и кориолисову (— fiwc) силы инерции.
Прежде чем перейти к анализу уравнений (1.8), остановимся на некоторых общих вопросах. До сих пор мы рассматривали движение одной и той же точки нити М. Такой метод принадлежит, по-существу, Лагранжу, который в механике сплошной среды выделял частицу и в дальнейшем следил за ее движением. Эйлеру принадлежит другой метод, сущность которого состоит в следующем. В координатной системе Oxyz (она может быть подвижной или неподвижной) выделяется точка N, определяемая в данной системе отсчета радиусом-вектором г или координатами х, у, z. В каждый данный момент времени t мимо этой точки проходит какая-то частица М сплошной среды, имеющая скорость v. Эйлер предложил выражать скорость v как функцию радиуса-вектора точки N (или ее координат) и времени t:
v = v(r, t) = v(x,y,z, t).
Это равенство определяет поле скоростей, которое называется стационарным, если оно не зависит от времени t явно, и нестационарным в противном случае. Линии, в каждой точке которых скорость v в данный момент направлена по касательным к ним, называются линиями тока. Конечно, уравнения состояния и движения сплошной среды в трактовках Лагранжа и Эйлера отражают одни и те же физические законы, но они выражены через различные переменные.
Для нити метод Эйлера удобно применять при изучении движения гибких шлангов, в которых течет жидкость, контурном движении нити и др. В частности, для контурного движения нити на линии Г через каждую точку N(o) в данный момент времени t проходит какая-то точка нити Ж, имеющая относительную скорость vT. Таким образом, в обозначениях Эйлера имеем: vr = vr (a, t). Это равенство условно можно назвать одномерным полем скоростей, а линию Г — линией тока.
Из вышеизложенного следует, что если в уравнении
(1.8) дуговую координату нити s заменить на а, то оно -будет определять лидию Г, вдоль которой может двигать¬
§9.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ
175
ся нить. Условимся не делать непосредственной замены s па о и на основании сказанного будем в дальнейшем считать, что это уравнение определяет линию Г (г = r(s)) и кажущееся натяжение Т*, причем криволинейную координату s и радиус-вектор г будем относить не к точкам нити, а к точкам линии, вдоль которой нить движется.
Рассмотрим уравнение (1.8) более подробно. В этом уравнении векторы переносного we и кориолисова гой ускорений, а также касательное относительное ускорение »
vr — заданные функции времени t; вектор т определен равенством т = dr/ds. Совместно с уравнением связи IтI = 1 (в координатной форме оно имеет вид (8.1.4)) уравнение (1.8) определяет радиус-вектор г точек линии Г и кажущееся натяжение Г*. Так как уравнение (1.8) получено в предположении, что линия Г неподвижна в системе Oxyz, то его решение относительно радиуса-вектора г не должно содержать время t. Легко видеть, что при не зависящей от времени t силе Р для этого достаточно, чтобы vn we и ivс были постоянными, в частности
они могут равняться нулю. Действительно, если vri we и wc постоянны, то уравнение (1.8) не будет содержать время t в качестве параметра и, следовательно, решение его г = г (s), Т* = Т* (s) не будет также зависеть от t.
Контурное движение нити возможно и при других более широких предположениях. Мы не будем останавливаться на анализе всех возможных случаев и в дальнейшем будем считать, что сила Р и ускорения vr, we и wc от времени t не зависят*). Считая в дальнейшем, что это условие выполнено, заменим в уравнении (1.8) знак частной производной по s на знак полной производной (все члены уравнения не зависят от £):
(Т*х) + Р — ЦУГТ — Ц10* — цн>с = 0. (9.1.10)
Для решения конкретных задач это уравнение целесообразно записать в проекциях на оси естественного трех¬
*) Вопросом существования контурных (установившихся) плоских движений свободной нити при активных силах, зависящих явно от времени t, занимались П. Аппель, А. П. Минаков и др. (см. библиографию в [16, 28]).
176
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
гранника, связанного с линией Г, или на координатные оси х, у, z. В первом случае получим:
dT* •
-fa + Рх — \Я>г — \Ш>ех — = О,
т*
— + Ру — |xwev — \iwcv = 0, (9.1.11)
Р$ — \iWe$ — \iwc$ = 0.
Во втором случае:
Ж (Г* if) + Р* - - \Wex - liWcx = 0,
4г[Т*1б')+Р'1~УЮг%~ М-^г/— М-^cj/= о, (9.1.12) i (Т* 1г) + р*~ WIT ~ - № = °-
В следующих параграфах мы рассмотрим некоторые контурные движения нити.
§ 9.2. Кажущийся покой
Движение нити вдоль неподвижной линии называется кажущимся покоем (переносное движение отсутствует). Рассмотрим несколько частных случаев.
1. Равномерное движение нити вдоль линии кажущегося покоя при отсутствии силового поля. В этом случае ve = 0, uT = v = const, Р = 0, we = wc = 0. Уравнение
(1.10) принимает вид
-jj~ (Т*х) = 0. (9.2.1)
При относительной скорости
» - ]/Ц- (9.2.2)
кажущееся натяжение Т* = Т0 — \iv2 обращается в нуль и уравнение (2.1) будет выполняться при любом направлении в пространстве единичного касательного вектора т. Это означает, что при отсутствии силового поля нить, равномерно бегущая вдоль себя со скоростью (2.2), будет сохранять любую наперед заданную форму (эффект
§ 9.2. КАЖУЩИЙСЯ ПОКОЙ
177
Эткина — Радингера). Заметим, что скорость у, определенная равенством (2.2), равна скорости распространения в нити упругой поперечной волны (см. § 10.2). Конечно, на концах разомкнутой нити должно быть обеспечено натяжение Та = Тв = То = \iv2. Для замкнутой нити это условие отпадает.
Рассмотрим теперь общий случай, когда скорость v не определяется равенством (2.2), т. е. при Г* Ф 0. Заменим уравнение (2.1) на два первых уравнения (1.11):
тг= о* Т = °- (9-2-3)
Из первого уравнения найдем Т* = const Ф 0, а из второго получим р = °°. Это означает, что при отсутствии силового поля и при скорости у, отличной от скорости распространения в нити упругой поперечной волны, в установившемся движении нить может принимать только прямолинейную форму. Только прямолинейную форму принимает нить и в установившемся равнопере-
•
менном движении при и = const. В этом случае Г* =
= ILVS + С И р = оо.
Описанные здесь явления можно моделировать с помощью находящейся на гладкой горизонтальной плоскости гибкой нерастяжимой трубки, внутри которой течет под давлением с постоянной скоростью жидкость.
2. Равномерное движение нити вдоль линии кажущегося покоя при наличии внешних сил (v = const Ф 0). В этом случае линия кажущегося покоя совпадает с линией равновесия нити при тех же силах и тех же граничных условиях и линейных размерах. Натяжение нити увеличивается при этом на величину \iv2. Действительно, при v = 0, ve = 0, we = 0 и wc = 0 уравнение линии кажущегося покоя получим из (1.10):
±(Т*т)+Р = 0. (9.2.4)
Это уравнение в точности совпадает с уравнением равновесия нити (1.2.1). Следовательно, при тех же граничных условиях и линейных размерах будут совпадать лйнии статического и кажущегося равновесий, & Также статическое и кажущееся натяжения, т. е. Т* = Тс
178
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
Из равенства (1.9) найдем динамическое натяжение нити (в нашем случае vr = v)
Т = Тст+ [IV2. (9.2.5)
Пример. Если отвлечься от специфических особенностей движения ремня, то моделью кажущегося покоя нити может служить ременная передача. Пусть такая передача связывает два одинаковых шкива, центры которых находятся на одной высоте. Статическое натяжение ремня в нижней его точке О будет равпо (см. § 3.1)
Гст
где q — вес единицы длины ремня, I — расстояние между точками схода ремня, / — стрела провисания его (предполагается, что она мала).
Пользуясь последними равенствами, найдем относительное увеличение натяжения при равномерном вращении шкивов (ji = q/g)
Т-Тп
Т) =
8/
(9.2.6)
СТ gi
Отсюда видно, что при достаточно большой линейной скорости движения ремня динамическое натяжение может существенно увеличиться по сравнению со статическим натяжением.
3. Движение тяжелой нити вдоль линии кажущегося покоя в сопротивляющейся среде. Рассмотрим встречающийся в приложениях случай, когда однородная тяжелая нить, находящаяся в жидкости, перематывается с постоянной скоростью с одного барабана на другой (рис. 9.2). К точке М нити будут приложены следующие силы, отнесенные к единице длины: сила
тяжести нити в жидкости q и сила сопротивления Q (сила трения), направленная по касательной в сторону, противоположную движению нити. Обе силы для нерастяжимой нити постоянны по модулю, причем первая из них массовая, а вторая поверхност¬
§ 9.2. КАЖУЩИЙСЯ ПОКОЙ
179
ная. Силу сопротивления можно определить по методике, изложенной в работе [11], можно воспользоваться формулой (5.1.2) при нулевом угле атаки, но в конечном счете требуются экспериментальные данные, так как эта сила зависит и от вязкости среды, и от состояния поверхности нити. Заметим здесь же, что если нить движется равноускоренно (равнозамедленно), то все дальнейшие выводы останутся без изменения, если к силе сопротивления Q присоединить силу инерции касательного ускорения, равную = const.
Воспользуемся естественными уравнениями кажущегося равновесия нити *). Для этого составим прежде всего проекции равнодействующей Р сил q и Q на касательную т и главную нормаль V. Пользуясь рис. 9.2, получим
PX = Q — gsina, Pv = — geos a. (9.2.7)
Подставляя эти значения для Р% и Pv в уравнения
(1.11) и учитывая, что в этой задаче vT = 0, we = wc = = 0, будем иметь
^! = gsina — Q, ^- = ? cos a. (9.2.8)
Деля первое уравнение па второе и учитывая, что для плоской нити p = ds/da (см. (1.3.5)), получим
т?-(»*“- sis)**. к=т- <9-2-9)
Интегрируя уравнение (2.9), найдем
In Т* = —In cos a — Zclntg(jt/4 + a/2) + ln(Cig).
Отсюда
T* = Ciqe~hu ch и. (9.2.10)
Здесь С\ — постоянная интегрирования (множитель q введен для удобства), а переменная и определена
*) В работе [22] эта задача решается в декартовых координатах для контурного движения нити, принимающей форму замк¬
нутой петли, расположенной в вертикальной плоскости. В [24] та же задача решается для движения нити в двух различных средах.
180
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
равенством (см. формулы (2.3.12) и (2.3.14))
u = lntg(-^ + -J-). (9.2.11)
Пользуясь полученным выражением для Т* и вто¬
рым уравнением (2.8), найдем радиус кривизны (снова используется формула (2.3.14))
р = cxe-hu ch2 и. (9.2.12)
Имеем
_ ds 1 dx 1 dy /0 9 \
р~ da “cos a da1 Р~ sin а da
Сопоставляя с (2.12), получим
dx = С\e~hu ch2 и cos a da, dy = C\e~hu ch2 и sin a da.
Согласно формулам (2.3.14) —(2.3.16) будем иметь
• < 1 1 j du
sincx = thw, cos ос =-г—, da = —г—.
ch w ch и
Следовательно,
dx = Схе-Ь'^и, dy = Схе-Ш sh и du.
Интегрируя, найдем уравнения линии кажущегося равновесия в параметрической форме *)
с (9.2.14)
у = e~hu (clau + k sh и) + С3.
1 — к
Для определения длины L свободной части нити воспользуемся равенством
Р-£-£<*»• (9.2.15)
Сравнивая с (2.12), получим
ds — С^е-ь*1 ch и du.
*) В тех случаях, когда a > я/2, полезно перейти к декартовым координатам (см. [22, 23]).
§ 0.2. КАЖУЩИЙСЯ ПОКОЙ
181
Интегрируя от щ до и2у найдем L = —^-а [е~Ыг (sh и2 + к ch и2) — e^hUl (sh иг + к ch их)];
1 к (9.2.16)
здесь щ и и2 — значения параметра и в точках А и £ соответственно.
Граничные условия в этой задаче зависят от соотношения между диаметрами барабанов и расстояниями
I и h по горизонтали и вертикали, характера синхронизации вращений барабанов; если верхний барабан не синхронизован и вращается за счет силы натяжения нити, то необходимо учесть момент сил трения на его оси и т. п. Поэтому мы не останавливаемся на этом вопросе, оставляя задачу определения граничных условий для тех, кто имеет дело с конкретными системами.
Рассмотрим теперь эту задачу для растяжимой нити. Сила сопротивления Q— поверхностная и от массы нити не зависит. Поэтому, если пренебречь изменением диаметра растянутой нити (см. замечание к формуле
(1.1.8)), то при растяжении нити значение силы Q не изменится. Сила тяжести д, отнесенная к единице длины,— массовая, и для растянутой нити она определяется равенством: g = qo/f(T), где go — вес единицы длины нити до ее растяжения, a f(T) — закон растяжения. Из этого следует, что для растянутой нити уравнения (2.8) примут вид (мы пренебрегаем временем растяжения нити)
тг-7&в1пв-*’ T = 7Tbcosa’ (9-2Л7)
где Т — истинное, а не кажущееся натяжение нити (Т = Т* + \kv2).
Деля первое уравнение на второе и считая, что нить растяжима по закону Гука, получим вместо (2.9) следующее уравнение:
£ = Г*{«а - [1 + а* (Г* + (**>1 £-}, (9-2.18)
где ko = Q/qo и а* — удельное относительное удлинение нити.
В замкнутой форме это уравнение проинтегрировать нельзя, Решение целесообразно искать в форме ряда,
182
ГЛ. II. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
расположенного по степеням а*:
Т* = Го (1 + а*Т* + а*2Г2* + ...) или применить численный метод.
§ 9.3. Задача Аппеля
С цилиндра, ось которого О движется горизонтально и поступательно с постоянной скоростью v, сматывается с той же скоростью и укладывается на горизонтальную плоскость однородная и нерастяжимая нить (рис. 9.3). Движение провисающего участка нити А В происходит в среде, оказывающей сопротивление. Требуется определить форму и натяжение свободного участка нити. Эта задача, поставленная впервые Аппелем, моделирует прокладку кабеля в море. Мы рассмотрим две трактовки этой задачи, первая из которых принадлежит Аппелю.
Построим поступательно перемещающуюся систему координат Аху, связанную с цилиндром. Эта система движется с постоянной скоростью V. Из условия задачи следует, что относительная скорость vr движения нити равна по модулю переносной скорости ve, т. е. vr = ve = = и = const. Не располагая, по-видимому, экспериментальными данными, Аппель рассмотрел простейший случай, когда сила сопротивления среды пропорциональна первой степени скорости и направлена в сторону, противоположную скорости (результаты испытаний аэро¬
§ 9.3. ЗАДАЧА АППЕЛЯ
183
динамических лабораторий, приведенные в § 5.1, получены спустя несколько десятилетий после работы Аппеля). Таким образом, Аппелю, к точке М нити приложены следующие ^илы, отнесенные к единице длины (рис. 9.3, а): сила тяжести д, сила сопротивления относительному движению (>i = k\v, сила сопротивления переносному движению Q2 = k2v. Проекции равнодействующей этих сил на касательную и главную нормаль будут (см. рис. 9.3, а)
Px = Q\ — (?2 COS а — q sin а, Ру = Q2 sin а — q cos а.
(9.3.1)
Подставим эти выражения в уравнения (1.11) и учтем,
ЧТО Vr = 0, We = We = 0:
Jrp з|с ф e
— = Q2 cos а + q sin а — — = q cos а — Q2 sin a.
P (9.3.2)
Введя вспомогательный угол e по формулам
q = Q0 cose, <?2 = <?0sine, Q0 = V q1 + Q\, (9.3.3)
мы преобразуем уравнения (3.2) к виду
^ = <?оsin t — Qi> y = <?0cos^. (9.3.4)
где
\|) = a + e. (9.3.5)
Уравнения (3.4) совпадают по форме с уравнениями
(2.8). Отличие содержится в равенствах (2.13) — в данном случае они примут вид
1 dx 1 dx ~ 1 dy
Р cos a da ~ cos (ty — е) <2я|)’ ^ sin — ь) dty'
Это отличие приводит к несколько иному, чем (2.14), решению, которое мы приводим без промежуточных выкладок (читатель без труда может провести их самостоятельно):
Т* == CiQ0e~hlU сЪи, х = ^ ^ (ch и + кг sh «)] +Сг, (9.3.0)
у = (ch и + /<1 sh и) + + С3,
184
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
где
и = In tg = (9.3.7)
Рассмотрим теперь эту задачу с учетом результатов аэродинамических испытаний, приведенных в § 5.1. Нить участвует в сложном движении. Сила сопротивления среды относительному движению нити представляет обычную силу трения и она может быть вычислена по формуле (5.1.2) при нулевом угле атаки %. В переносном движении трос набегает на среду со скоростью v, направленной горизонтально (рис. 9.3, б). Сила сопротивления Q2 переносному движению равна силе давления на неподвижную нить потока, движущегося со скоростью — v (см. замечание на стр. 103). Поэтому угол атаки % = л — а. Согласно § 5.1 эту силу можно разложить на три составляющих:
(?2 = (?2П + (?2Т + (?2Ш* (9.3.8)
Пренебрежем, как обычно, боковой составляющей (?2т (для кабеля, заключенного в специальную оболочку, она просто равна нулю (см. § 5.1)) и включим касательную составляющую Q2x в Q1 (обе эти силы направлены по одной прямой). В этих предположениях на точку М нити будут действовать следующие силы, отнесенные к единице длины: сила тяжести нити в среде q, касательная сила сопротивления Qx = Qi + (?2т и сила Qn = (?2п, направленная по нормали к нити, как показано на рис. 9.3, б. Согласно (5.1.1) — (5.1.3) модуль этой силы определяется равенством
2
Qn — k sin2 % — X sin? а, Я = Ср — d, = const. (9.3.9)
В проекциях на касательную и главную нормаль уравнения (1.11) примут вид
dT* л т*
= q sin а — Qx, — = q cos а — X sin5? а. (9,3.10)
Деля первое уравнение на второе и учитывая, что для плоской линии р = ds/da, получим
dT* Я sin а — Qx
§ 9.3. ЗАДАЧА АППЕЛЯ
185
Отсюда
Г* = Сге*Ю,
(9.3.12)
где
а
FW-J
rdl
q cos g — X sin g
(9.3.13)
0
В общем случае Qx = (?i + (?2т является функцией угла атаки х = п *“ а» ПРИ этом (?i = const, Q2x = Q2т(%) (для вычисления (?2* следует воспользоваться графиком па рис. 5.2). Если же Qx = const, то интеграл (3.13) можно выразить через элементарные функции. Однако при этом получается сравнительно сложное выражение, которое для численных расчетов менее удобно, чем непосредственное вычисление интеграла (3.13) на ЭВМ.
Пользуясь вторым уравнением (3.10) и равенствами (2.13), найдем уравнения провисающей части нити
при этом учтено, что в точке А угол а = 0 и х = у = 0.
Длина L провисающей части нити определяется обычпым приемом. Из равенств (3.10) и (3.12) имеем
а
(9.3.14)
а
ds Т*
Р rfr/
П СОЯ CL —
еПа)
q cos а — X sin2oc
1 q cos a — X sin2a’
отсюда
(9.3.15)
о
Форму линии можно построить по точкам, пользуясь уравнениями (3.14).
186
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
Для растяжимой нити нужно в уравнениях (3.10) массовую силу q заменить на qo/f(T), а поверхностные силы Qx и Qv оставить без изменения (см. окончание примера § 9.2).
§ 9.4. Относительное равновесие вращающейся нити
Рассмотрим однородную перастяжимую нить, вращающуюся вместе с координатной системой Axyz с угловой скоростью со вокруг неподвижной оси х; предполагается, что оба конца нити А и В укреплены на оси вращения (рис. 9.4, а). В установившемся движении нить будет находиться в равновесии относительно системы координатных осей Axyz. Если пренебречь силой тяжести и сопротивлением воздуха (корректность этих предположений обсуждается в конце параграфа), то на нить будет действовать только одна центробежная сила инерции. Численное значение ее, отнесенное к единице
длины нити, равно |иго)2, да г — расстояние от рассматриваемой точки М до оси вращення, а |и, как обычно, линейная плотность нити.
Так как центробежные силы инерции, действующие на точки нити, пересекают ось вращения х, то момент этих сил относительйо оси х будет равен нулю: Мх = 0. Из этого следует (см. (1.2.18)), что момент сил натижо-
в 9,4, ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ВРАЩАЮЩЕЙСЯ НИТИ 187
ния относительно этой оси постоянен вдоль всей нити. Но нить прикреплена к двум точкам оси, поэтому моменты сил натяжения на концах равны нулю. Следовательно, этот момент будет равен нулю всюду. Согласно (1.2.18) будем иметь
где С — постоянная. Из этого уравнения видно, что фигура равновесия находится в плоскости, проходящей через ось вращения х. Не нарушая общности, можно считать, что нить находится в плоскости ху. Тогда, пользуясь рис. 9.4, б, получим: г = г/, Р = О, vr = 0, wex = О, wеу = —г/со2, we = 0. Подставляя в (1.12), получим два уравпения относительно равповесия вращающейся нити
(Конечно, применяя принцип Даламбера, эти уравпения можно получить из обычных уравнений равновесия ни¬
где Н — проекция патяжепия Т па ось х. Найдем из этого равенства Т и внесем его во второе уравнение
отсюда
или, интегрируя,
у dz — zdy =* 0, y = Cz,
— It—'1 —n
ds \ dsj ’ ds\ ds)
= — [Ш2*/. (9.4.1)
ти (1.2.8).)
Из первого уравнения имеем
Т Н = const,
ds 1
(9.4.2)
(4.1)
(9.4.3)
Введем обозначение
(9.4.4)
и учтем очевидное равенство
ds = V1 уп dx — ^ У - dy-
188
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
Теперь уравнение (4.3) примет вид
(9.4.5)
или, интегрируя,
(9.4.6)
где новая постоянная интегрирования Ь2 (множитель 1/а2 введен для удобства) должна быть положительной (ибо левая часть положительна). Решая последнее уравнение относительно у' = dy/dx, получим
Легко видеть, что должно выполняться неравенство
Действительно, нить прикреплена к оси х и, следовательно, при у = 0 последнее уравнение должно иметь вещественное значение для у'.
Разделяя переменные и интегрируя, получим
Из этого выражения видно, что ордината у может изменяться в интервале {—1/Ь2 — а2, 1/Ь2 — а2), так как вне его подкоренное выражение в (4.8) будет отрицательно.
Интеграл, стоящий в правой части равенства (4.8), нельзя выразить через элементарные функции (его легко свести к эллиптическим функциям), но, анализируя его, легко построить примерный график функции х = = х(у), определяемой этим равенством, т. е. построить линию относительного равновесия вращающейся нити. Допустим, что график функции (4.8) начинается в точке А (рис. 9.5, а) и хотя бы часть его расположена в углу уАх. Тогда х сначала возрастает вместе с у, производная у' положительна и в правой части равенства (4.8) нужно брать знак «плюс». С возрастанием у бу-
Ь2 > а2.
у
dy
(9.4.8)
а2 - у2) (b2 + а2 - у2)
I 9.4. ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ВРАЩАЮЩЕЙСЯ НИТИ 189
дет увеличиваться и х. Когда у достигнет своего предельного значения 1/Ь2 — а2, абсцисса х сделается равной
где ф(г/, а, Ъ) — многочлен, стоящий под знаком радикала в (4.8). В результате получается ветвь АММ\. Касательная в М\ параллельна оси х, поэтому с этого значения ордината у начнет убывать и, следовательно, dy < 0. Для того чтобы абсцисса х продолжала возрастать, в правой части равенства (4.8) нужно взять знак «минус». Так получается вторая ветвь М\А2, симмет¬
ричная с первой ветвью АМ\ относительно ординаты А\М\. При у = 0 получается точка А2 с абсциссой 2х\. В дальнейшем ветвь линии пойдет влево, и мы получим вторую половину A2M2Ai и т. д. Таким образом, равенство (4.8) определит периодическую функцию с периодом 4^1. При заданных а и Ъ построить по точкам график этой функции не представляет труда. Для этого интеграл, стоящий в правой части (4.8), можно свести к эллиптическим функциям, а затем воспользоваться таблицами этих функций; конечно, еще проще все вычисления провести на ЭВМ.
У Ъ*-а2
dy
(9.4.9)
о
Мг
х
б)
Рис. 9.5.
190
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ ЦИТИ
Применим полученные результаты к анализу формы относительного равновесия вращающейся нити. Если дана однородная нерастяжимая нить длины L и даны точки закрепления на оси А и В (пролет 1 = АВ), то из вышеизложенного следует, что равномерно вращающаяся нить может иметь бесчисленное количество форм отиосительпого равновесия, состоящих из одной, двух, трех и т. д. полуволн (рис. 9.5, б). Естественно, что практически будет реализована только одна, устойчивая, форма равновесия, которой соответствует лииия с одной полуволной. (Это интуитивно очевидное утверждение строго доказано Г. К. Пожарицким [20].)
Рассмотрим, как определяются неизвестные параметры а и Ъ для нити, состоящей из одной полуволны. Будем считать, что заданы расстояние I между точками А л В л длина нити L. Из изложенного ранее следует, что вершине нити точке С соответствует абсцисса х\ = = 1/2. Пользуясь равенством (4.8), получим первое уравнение
Уь2_а2
4 = а2 Г , dy (9.4.10)
2 J V <9 {у, а, ъ)
о
Применяя равенства (4.6) и (4.7), найдем дифференциал дуги
ds = V \ -f- у'2 dx = --- ~ у- — dy. (9.4.11)
/Ф (у* а. Ъ) }
Теперь найдем второе уравнепие
Vb*-a*
4= Г --А dy. (9.4.12)
2 J /ф (У.а.Ъ)
о
При заданных I и L уравнения (4.10) и (4.12) можно решить на ЭВМ и найти неизвестные параметры а
и Ь. Затем из равенства (4.4) определится Н (ц и со —
заданы), после чего натяжение вращающейся нити найдается из (4.2) и (4.6):
Т = ?ЛЪ*-у*). (9.4.13)
а
§ 9.4. ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ВРАЩАЮЩЕЙСЯ НИТИ 191
Это же выражение для натяжения нити можно получить из интеграла натяжения (1.4.5). Действительно, в сделанных предположениях сила, действующая на пить, консервативна и ее потенциальпая энергия, отнесенная к единице длины нити, определяется равенством
П = — цог у, (9.4.14)
или, учитывая (4.4),
U = -%y\ (9.4.15)
а
Интеграл натяжения (1.4.5) примет теперь вид
Т = --2у2 + С1. (9.4.16)
а
Постоянную С\ найдем из условия: Т = Н при у —
= УЬ2 — а2. Внося эти значения для Т и у в (4.16), получим равенство (4.13).
Из (4.13) найдем натяжения на копцах пити
Та = Тв = Ъ-2Н. (9.4.17)
а
Если через / обозначить максимальное отклонение нити от оси вращения х, то будем иметь
/ = Vb^J2. (9.4.18)
Как видно из изложенного, наибольшие трудности встретятся при численном решении уравнений (4.10) и
(4.12).
Приведеппое здесь решение, принадлежащее П. Аппелю [2], значительно упрощается (см. [19]) для достаточно пологих нитей, когда длина вращающейся нити L мало отличается от расстояния I между точками закрепления А и В. В этих предположениях угол а между касательной к нити и осью вращения х будет тоже мал и, следовательно, производная y' = tga будет мала по модулю по сравнению с единицей: \у'\ < 1. На этом основании, разлагая в уравнении (4.5) радикал в ряд по степеням у' и ограничиваясь низшими членами,
192 ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
получцм
у
или
/dy'+Ще^ О,
f2 ,2 2 У & — У
где, как и прежде, 62 — новая постоянная интегрирования. Отсюда находим
Т* = ^УЬ*-У*. (9.4.19)
Разделяя переменные и интегрируя, будем иметь
У 1^2
arcsinf = L^x + cv
Так как нить проходит через точку А с координатами х = 0, у = 0, то постоянная С\=0 и, следовательно,
y = (9.4.20)
Это общее решение задачи для пологой вращающейся нити. Постоянную интегрирования а найдем из условия, что нить проходит через вторую точку закрепления: х = 1, у = 0. Подставляя эти значения для х и у в (4.20), получим
Ъ sin = р. а
Отсюда
a=J£r (« = 1,2,3,...). (9.4.21)
Теперь решение (4.20) принимает вид
у = Ь sin^~ (п = 2, 3, ...). (9.4.22)
Из этого решения видно, что в сделанных предположениях нить имеет бесчисленное множество форм относительно равновесия, каждая из которых состоит из одной, двух, трех и т. д. полуволн синусоиды Ы в (4.22)
§ 9.4. ОТНОСИТЕЛЬНОЕ РАВНО^СИЕ ВРАЩАЮЩЕЙСЯ НИТИ 193
равно числу полуволн). Таким образом, приближенное и полное решения качественно не отличаются друг от друга (см. рис. 9.5, б).
Для определения постоянной Ъ вычислим длину дуги. Имеем
или, учитывая сделанное предположение о малости \у'I,
Пользуясь равенством (4.22), найдем производную у' и внесем ее в это равенство
Интегрируя в пределах от 0 до I, найдем после очевидных преобразований длину нити
Внося это выражение для Ъ в (4.22), получим окончательную форму уравнения относительного равновесия вращающейся нити (конечно, в сделанных предположениях)
Проекцию Н натяжения Т на ось вращения х найдем из равенств (4.21) и (4.4)
Натяжение Т можно определить из равенства (4.2). Имеем
ds = (l + У'2)1/2 dx,
Отсюда
(9.4.23)
y = lVl(L-l) sin^. (9.4.24)
(9.4.25)
194
ГЛ. IX. КОНТУРНО^ДВИЖЕНИЕ НИТИ
Пользуясь равенствами (4.24) и (4.25), получим
В заключение остановимся на правомочности сделанных с самого начала допущепий. Прежде всего, мы предположили, что можно пренебречь силой тяжести q по сравнению с центробежной силой инерции jLico2r. Это равносильно усиленному неравенству
где г — расстояние от точки нити до оси вращения.
Совершенно очевидно, что даже при большой угловой скорости со это неравенство не может быть выполнено для точек нити, расположенных достаточно близко к оси вращения, когда г очень мало. Таким образом, полученное решение не дает верных значений параметров нити для точек, находящихся вблизи граничных точек и точек пересечения нити с осью вращения (для форм равновесия с несколькими полуволнами). Наименьшую погрешность в расчетных формулах будем иметь для нити с одной полуволной (рис. 9.5, б) и с большим отклонением от оси вращения, т. е. для случая, когда должна применяться теория, изложенная в начале параграфа (формулы (4.1)—(4.18)).
Пренебрегая теперь погрешностью в вычислениях для точек, расположенных в непосредственной близости от оси вращения, оценим значение угловой скорости о). Пользуясь соотношением (4.27), найдем
Для точек, отстоящих от оси вращения на расстоянии 1 см, будем иметь: о) > 31,4 сек~*, что соответствует 300 об!мин. Из этого следует, что для быстро вращающихся нитей (угловые скорости, превосходящие 3000 об/мин, типичны для многих технологических процессов, в которых нить участвует во вращательном движении), пренебрежение силой тяжести q = \ig по сравнению с центробежной силой инерции jlig)2# не дает большой погрешности (если не считать небольших уча¬
(9.4.26)
со2г > g,
(9.4.27)
I 9.5. ФОРМА «БАЛЛОНА»
195
стков нити, непосредственно прилегающих к граничным точкам).
Второе допущение, сделанное в самом начале, состоит в предположении, что можно пренебречь силами сопротивления воздуха. При больших угловых скоростях вращения нити это допущение может привести к значительным погрешностям (в следующем параграфе эти силы будут учтены).
§ 9.5. Форма «баллона»
Большой интерес для теории и различных приложений имеет задача о контурно-вращательном движении нити. В простейшем виде это движение реализуется следующим образом. Нить протягивается с постоянной ско¬
ростью vr = и через нитепровод А, затем проходит через бегунок 5, движущийся с постоянной скоростью по кольцу К, и далее наматывается на бобину (початок, катушку) (на рис. 9.6, а бобина не показана). Таким образом, нить, увлекаемая бегунком, равномерно вращается вокруг неподвижной вертикальной оси z и одновременно, наматываясь на бобину, имеет постоянную относительную скорость. В результате действия сил сопротивления воздуха и кориолисовых сил инерции нить в установившемся движении принимает форму линии
П у
Рис. 9.6.
196
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
двоякой кривизны. При большой угловой скорости вращения нити а) (в некоторых современных прядильных машинах она достигает 11—12 тысяч об/мин) глаз наблюдателя воспринимает непрерывно сменяющиеся положения нити как поверхность, которую называют баллоном.
Теорией баллона занимались многие ученые (впервые достаточно строго ее поставил А. П. Минаков [17]) и ей посвящена большая литература (относительно полную библиографию можно пайти в [19]). В рамках настоящей книги мы можем изложить только основные вопросы этой теории.
Введем вращающуюся систему координат Oxyz, направив ось z по неподвижной оси вращения нити вертикально вверх, ось х проведем через бегунок В, а ось у — перпендикулярно осям х и z; система осей Oxyz — правая. Во вращающихся осях Oxyz (рис. 9.6, а) нитепровод А и бегунок В имеют постоянные координаты:
Га = о, у а = о, z = h; хв =R, ув = 0, zQ = 0. (9.5.1)
Здесь R — радиус кольца К, a h — расстояние по вертикали от кольца до нитепровода А.
При выбранных направлениях вращения пити и се относительного движения будем иметь
<а = — со/с, и = — их, (9.5.2)
где (о и и — модули соответствующих скоростей, к— орт оси z, а т — орт касательной (см. рис. 9.6, а).
Простота решения задачи во многом зависит от выбора системы координат. Так как переносная сила инерции — [ли?е (центробежная сила) и, как будет показано в дальнейшем, сила сопротивления воздуха наиболее просто выражаются не через декартовы координаты х, у, z точки М нити, а через ее расстояние г до оси вращения z, то задачу целесообразно решать во вращающейся цилиндрической системе координат г, ф, z. На рис. 9.6, а (см. также рис. 1.10) показаны эти координаты и ортыег, еф и ^направлений координатных линий. Дифференциальные уравнения линии Г, вдоль которой осуществляется контурное движение нити, в ци¬
9 9.5. ФОРМА «БАЛЛОНА»
197
линдрических координатах имеют вид (см. уравнения
(1.10) и (1.5.24))
£ (&)' + *-“•
|.(г.г.^.) + гР; = 0, (9.5.3)
+ 0.
В этих уравнениях Т* = Т — \щ2 — кажущееся натяжение нити, Rr,Ry, Rz— соответствующие проекции равнодействующей Р* всех сил, входящих в уравнение
(1.10), включая силы инерции.
Цилиндрические координаты г, <р, z точек линии должны удовлетворять нелинейной неголономной связи
(1.5.23)
это выражение нужно присоединить к уравнениям (5.3).
Не останавливаясь временно на анализе сил, действующих на нить, займемся преобразованием уравнений
(5.3). Для этого прежде всего введем два угла, 0 и г|), определяющих направление единичного касательного вектора т в цилиндрической системе координат (рис. 9.6, б). Проекции вектора т на направления координатных линий (на ортыег, еф и ez) определяются равенствами
тг = —j- = cos 0 cos яр,
тф = г^ =cos0 simp, (9.5.5)
Преимущество введения углов 0 и \|) состоит, в частности, в том, что три параметра г, 0 и ф, в отличие от цилиндрических координат г, ф и z, удовлетворяют уравнению связй (5.4), согласно (5.5), автоматически.
198
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
В качестве новой независимой переменной возьмем координату г и введем дифференциальный оператор *)
J-cose cos(9.5.6)
Пользуясь теперь вторым и третьим равенствами
(5.5), найдем
_ tg гр dz __ tge т г
dr г 9 dr cos гр 1 ' 9°9 '
£ - • (9'5'8> Если углы 0 и г|? будут найдены как функции г, то из этих равенств простой квадратурой определятся ф=<р(г), z = z{r) и s = sir).
С помощью (5.5) и (5.6) преобразуем уравнения (5.3). Имеем
cos 0 cos (Т* cos 0 cos ty) ^-cos2 0 sin2 -ф + P*r — 0,
cos 0 cos (Г*г cos 0 sin *ф) -f- rP*p -- 0, (9.5.9)
cos 0 cos (Г* sin 0) + Pz = 0.
Эти уравнения можно записать в следующей форме:
[dji* ^
cos 0 cos i|) -jp- + Т* -jp (cos 0 cos г|>) —
— cos2 0 sin2i|) P* =0,
cos 0 cos г)? cos 6 sin г|) ^-^(rcos Osin^j-l-rP^O,
cosO cos\|’ |^sm 0 -J- T* -jp (sin 0)j -|- P* -0.
*) В декартовых координатах расстояние от точки М до оси вращения определяется равенством
Г=ух* + У\
а дифференциальный оператор (5.6) имеет вид d 1
§ 9.5. ФОРМА «БАЛЛОНА»
199
Умножим первое уравнение на cosBcob^ ttt^poe на cos 0 sin ф/r и третье на sin 0. Сложив после этого все уравнения и выполняя очевидные преобразования, получим
cos 0 cos +P*r cos 0 cos ф+Рф cos 0 sin ф+Р* sin 0=0. Отсюда
dT*
dr
= ~ [p;+p; tg *+p: jji). (9.5.10)
Заметим, что это уравнение можно получить более простым методом из первого уравнения (1.11) и оператора
(5.6).
Представим теперь первые два уравнения (5.9) так: cos 0 cos г|) |^— Т* cos 0 sin г|) + cos г|) (Т* cos 0) j —
у- cos2 0 sin2 г|) + Р* = 0,
cos 0 cos г|) T*r cos 0 cos ф + г sin г|) (T* cos 0) +
+ T* cos 0 sin \|>] + = 0.
Умножив первое уравнение на —г sin второе на cos г|) и сложив оба равенства, найдем
*+ = P*r sin cost _ ^ (9 5 И)
T* cos2 0 COS 1|) r
Наконец, преобразуем третье уравнение (5.9):
cos 0 cos г|) ^sin 0 + T* cos 0 j + P*z =0.
Пользуясь (5.10), получим
ii,^.(p; + p;tgt-_|L_). (9.5.12)
Таким образом, вместо трех нелинейных относительно производных уравнений второго порядка (5.3), подчиненных одной нелинейной неголономной связи (5.4), мы получили пять независимых уравнений первого порядка,
200
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
решенных относительно производных (два уравнения
(5.7) и уравнения (5.10) — (5.12)).
Рассмотрим теперь силы, входящие в Р*.. К ним относится прежде всего сила тяжести
q = — qez. (9.5.13)
Затем в равнодействующую Р* входят переносная
— \xwe и кориолисова — \iwc силы инерции (касательная
сила инерции относительного движения — ]ivr равна нулю, так как vr = и = const). Первая из этих сил численно равна ^со2г и направлена по радиусу г от оси вращения.
Следовательно,
— цюе = ца)2гег. (9.5.14)
Для вычисления кориолисовой силы инерции учтем равенства (5.2). Имеем
— \iwc = — 2[Мд х и = — 2jui)wezXT = — 2цож
«г *Ф
0 О 1 т т т
г lz
Отсюда, пользуясь (5.5), получим
(— цн?с)г = 2цсои cos 0 sin tJj,
(— цюс)ф = — 2ц.(ои cos 0 cos (9.5.15)
(- ЦИ>С)г = 0.
Для вычисления сил сопротивления воздуха мысленно будем считать, что движутся не точки нити со скоростью
V = ve + Гг,
а на неподвижную нить движется поток воздуха, скорость которого равна — v (см. замечание на стр. 103). Тогда относительной скорости нити vr = и = —их будет отвечать сила сопротивления Qu определяемая равенством
^1 = Cp-y-d-0T(0)T = ^T (Ь1 = const), (9.5.16)
где все коэффициенты имеют значения, введенные в § 5.1 (угол атаки для относительного контурного движения нити равен нулю).
§ 9.5. ФОРМА «БАЛЛОНА»
201
Скорость переносного движения точки М нити равна по модулю гсо и направлена в сторону, противоположную е<р (рис. 9.6, а). Следовательно,
ve = — согвф.
Скорость — ve = согвф совпадает по направлению с ортом вф, поэтому угол атаки х, отвечающий переносному движению, можно определить из равенства
cos % = 0ф*т = тф = cos 0 втф. (9.5.17)
Согласно § 5.1 силу давления Q2 воздуха, движущегося па нить со скоростью — ve (силу сопротивления воздуха переносному движению нити), можно разложить на три составляющих
= (?2П “Ь (9.5.18)
Боковой составляющей @2т, зависящей от крутки нити, как обычно, пренебрежем, положив (?2т = 0. Модуль касательной составляющей
Q 2т = Ср 4 d- Фх (X) = Cp^d-ox (X)
представим следующим образом:
(?2х = Кг2Фт (X). ** = Ср ^ d, (9.5.19)
где функция Фх(х) определяется графиком на рис. 5.2.
Силы и Q2х направлены по касательной т. Следовательно, модуль их равнодействующей Qx будет
Сх = Я1 + Я2^Ф*(х). (9.5.20)
Главную часть силы сопротивления Q составляет нормальная составляющая Q2n, модуль которой определяется равенством
Qtn = Ср4 d-Фп (х) = Кг2Фп (х), (9-5.21)
где, согласно (5.1.3),
Фп(х) = ^sin2x-
Сила Q2n расположена в плоскости векторов т и — ve9 т. е. в плоскости (т, еф). Пользуясь формулой (5.1.4),
202
ГЛ. IX. КОНТУРНОЕ ДВИЖЕНИЕ НИТИ
будем иметь
Q2n = V2ф„ (Х) |_L_ _ ctg % т). (9.5.22)
Объединяя полученные результаты, получим R* = — qez + цаггет — + Qz т +
+ V2Фп (%) - ctg х т). (9.5.23)
Отсюда найдем проекции этой силы (см. (5.5) и (5.15))
Р* — ц.со2г — 2цош cos 0 sin + Qz cos 0 cos г|э —
— А,2г2Ф„ (х) ctg % cos 0 cos г]),
.Рф = 2uoш cos 0 cos -f- Qx cos 0 sin ^ + ^гГ2Фп (%) —r— —
sin X
— Я2Г?ФД (x) ctg X COS 0 sin
P*z = — q + Qx sin 0 — Я2г2Фд (x) ctg x sin 0. (9.5.24)
Внесем значения этих проекций в уравнения (5.10) —
(5.12) и присоединим к шгм два уравнения (5.7). После очевидных преобразований получим полную систему пяти независимых дифференциальных уравнений первого порядка, решенных относительно производных (Фп^)^ = a sin2/):
dT* dz_ _ 2 Qx
dr ~~ У dr ^ Г cos 0 cos гр ’
£=4* [tg 0 + %*r4 sin *tg ^ • (9'5'25)
sin г|> — Я2г2а sin % — 2\Jl<hu cos 0 tg г|э
dr j1* cos2 0 cos г|? r ’
d(p tg t|? dz tg 0
dr ~ r * dr “ cos г|> *
Для полного решения задачи нужно установить пять граничных условий. Три условия очевидны:
в точке А при г = 0 z = h\ (9.5.26)
в точке В при r = i? z = 0, ф = 0. (9.5.27)
Еще два условия должны содержать легко измеряемые параметры. Так, например, относительно несложно
6 9.5. ФОРМА «БАЛЛОНА»
203
измерить угол в в точках А и В. Тогда дополнительные два условия будут иметь вид
Этих условий достаточно для интегрирования уравнений (5.25) на ЭВМ.
Построенная математическая модель баллона учитывает хотя и не все, но достаточно общие условия. Обычно задачу существенно упрощают, пренебрегая, во-первых, силой тяжести нити д, а во-вторых, касательной силой сопротивления. В этих предположениях q = 0 и Qx = 0, в результате чего первые два уравнения (5.25) упрощаются, причем из первого уравнения сразу получается интеграл натяжения
Как уже отмечалось рапее (см. замечание к равенству (5.2.11)), отсутствие в этом интеграле силы сопротивления воздуха Q не означает, что натяжение нити не зависит от Q (влияние этой силы на натяжение нити скажется через постоянную С\).
В некоторых работах делаются дальнейшие упрощений, а именно, пренебрегают кориолисовой силой инерции (она мала по сравнению с переносной силой инерции (обычно и<гсо)). Наконец, ряд авторов считают, что сила сопротивления направлена в сторону, противоположную скорости (это равносильно предположению, что сила давления потока на нить совпадает по направлению со скоростью потока —см. § 5.1). Это предположение не вносит большой погрешности в вычисления, так как угол г|э мал и тогда, согласно формуле (5.17), угол атаки ~ я/2. Это означает, что основная часть силы сопротивления Qm направлена в сторону, противоположную перепосной скорости ге. '
Мы не останавливаемся более подробно на теории баллона, отсылая интересующихся к специальной литературе.
при г = 0 '0 = 0а, при r = R 6 = 0В.
(9.5.28)
(9.5.29)
ГЛАВА X
СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
§ 10.1. Введение
Изучение колебаний нитей сводится, как правило, к анализу дифференциальных уравнений математической физики и очень часто простой, казалось бы, вопрос приводит к сложным преобразованиям, причем сложность анализа возрастает иногда в несколько раз при несущественном на первый взгляд изменении граничных условий. Учитывая, что в настоящей книге механика нити рассматривается как раздел теоретической механики, мы сочли возможным остановиться здесь только на классических задачах колебаний нити (сравнительно подробное изложение современных методов исследования теории колебаний нити можно найти в книге [22]). Некоторые из рассматриваемых здесь вопросов могут оказаться полезными при решении других инженерных задач. Кроме того, эти задачи изучаются обычно в курсах по теории дифференциальных уравнений математической физики или аналитической механике в отрыве от общей теории гибкой нити. Поэтому вполне естественно остановиться хотя бы кратко на методах составления и решения дифференциальных уравнений колебаний нити. Мы ограничимся рассмотрением только свободных колебаний.
§ 10.2. Поперечные колебания сильно натянутой нити (струны))
Рассмотрим растяжимую нить, натяжение которой Т значительно превосходит по модулю действующие на нее силы, так что последними можно пренебречь. Очевидно, что такая нить, закрепленная в двух точках, принимает
9 10.2, ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТРУНЫ
205
в положении равновесия форму прямой линия. Действительно, при Р«0 и Г^О из второго уравнения (1.3.3) следует р = °°, что соответствует прямой линии. Такую нить называют обычно струной.
Будем изучать поперечные колебания струны, считая, что каждая ее точка М может перемещаться только в направлении, перпендикулярном равновесному положению, т. е. оси х (рис. 10.1).
Кроме того, будем предполагать, что поперечные перемещения uix, t) всех точек струны лежат в одной плоскости и малы.
В соответствии с общей теорией малых колебаний Рис. 10.1.
перемещения и и производные ди/дх и du/dt считаются величинами первого порядка малости. Покажем, что в сделанных предположениях с точностью до членов высшего порядка малости при колебаниях струны ее натяжение будет все время одинаково во всех точках. Действительно, пусть ds и d$o= = dx — длина элемента М\М2 нити в момент времени t и в положении равновесия соответственно. Тогда
+ dx,
или, пренебрегая квадратом производной ди/дх по сравнению с единицей,
ds —" dx dsQ.
Это означает, что при колебании струны растяжение с принятой точностью не изменяется и, следовательно, оно не вызывает с течением времени t изменения ее натяжения в рассматриваемой точке.
Составим теперь дифференциальные уравнения движения нити (8.1.3), помня, что в сделанных предположениях внешние силы равны нулю, колебания нити происходят в одной плоскости и что перемещения точек нити перпендикулярны оси х (рис. 10.1). Из последнего следует, что d2x/dt2 = 0, и, следовательно, первые два уравнения (8.1.3) принимают вид (переменная у
206
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
заменена на и)
Имеем
дх
V1 +tg2a yf ! + /5к\2
\ds J
Теперь первое уравнение (2.1) можно записать следующим образом:
Так как, согласно установленному ранее, натяжение в точке М нити не зависит от времени t, то из последнего равенства находим, что натяжение нити одинаково во всех ее точках, т. е. Т = Го = const. Это полностью доказывает сделанное ранее утверждение.
Подставив во второе уравнение (2.1) значение То = = const, получим дифференциальное уравнение свободных поперечных колебаний струны
где постоянная величина а, имеющая размерность скорости, определена равенством
Уравнение (2.2), называемое волновым уравнением, должно удовлетворять двум начальным и двум граничным условиям. Начальные условия имеют вид при t = 0
Первое из этих уравнений определяет форму, а второе характеризует распределение скоростей точек струны в начальный момент времени t = 0; обе функции fix) и Fix) должны быть заданы.
Граничные условия
(10.2.3)
u=f(x), £ = F(x) (0 (10.2.4)
ы(0, t) — 0, nil, t) =* 0
(10.2.5)
§ 10.2. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТРУНЫ
207
показывают, что перемещения точек закрепления струны равны нулю в любой момент времени.
Волновое уравнение хорошо изучено и ему посвящена большая литература (см., например, [9,26]). Поэтому мы приведем две формы его решения в очень кратком изложении.
1. Решение в форме Даламбера. Подстановкой
\ = х — at, K\ — x + at (10.2.6)
уравнение (2.2) приводится к виду (читатель без труда сможет самостоятельно провести все преобразования)
Шч = 0- (10'2-7>
Запишем это уравнение следующим образом:
lM = 0-
отсюда
ИгеИ>*
где 0(г])—произвольная функция г]. Интегрируя полученное уравнение по т] и рассматривая £ как параметр, найдем
“ = J* © Сп) *) + Ф (I),
где ф(£)— произвольная функция Обозначив теперь
J © Сп) *1 = 'Ф (л)
и возвращаясь к старым переменным х и £, найдем общее решение волнового уравнения (2.2) в форме Даламбера
и = ф(я — at) + а|)(а; + at), (10.2.8)
где ф и ф — произвольные, дважды дифференцируемые функции.
Структуру функций ф и if) найдем, подчинив полученное решение начальным условиям (2.4). Подставляя в
(2.8) t = 0, получим
Ф(х) + ty(x) =f(x), —aq>'(x) + aty'(x) = F(x). (10.2.9)
208
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
Проинтегрируем второе равенство
х
— аф (я) -f аг|э (х) = J F (z) dz + С. (10.2.10)
о
Пользуясь (2.10) и первым равенством (2.9), найдем
я
fP(*) =у/(а:)-^ \F(z)dz~^,
о
X
4(*)=jf(x)+i-a§F(z)dz + £
о
Такова структура функций ф и t|). Внеся полученные выражения в (2.8), получим
x+at
и(х, t) = f.(x.--l9.±.fJx + at'> + I F(z) dz. (10.2.11)
x—at
Непосредственным дифференцированием легко проверить, что полученное выражение для и(х, t) представляет решение волнового уравнения (2.2), удовлетворяющее начальным условиям (2.4).
Решение (2.11) можно записать и в следующей форме:
и(х, t) = и\(х, t) + м2 (a?, t), (10.2.12)
где
x—at
ux (x, t) = / (x — at) — ^ J F (z) dz = <p(x — at),
(10.2.13)
u2 (я, t) = jf (x + at) + ± J F (z) dz = (ж + ai).
0
Рассмотрим случай достаточно длинной струны (в теории говорят иногда о бесконечно длинной струне). Пусть в начальный момент времени t = 0 где-то в середине струны небольшому ее участку дали начальное отклонение и(х, 0) = fix) и каждой точке этого участка сообщили скорость du/dt = Fix). Предположим далее, что в част-
§ 10.2. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТРУНЫ
209
дом решении
uix, t) = ф(я — at), = 0
независимые вообще говоря переменные х и t связаны соотношением х — at = с\= const и, следовательно, dxldt= = а. Физически это означает, что движению точки М(х) с постоянной скоростью а в положительном направлении (слева направо) отвечает постоянное смещение, равное и = щ(с\) (рис. 10.2, а). Такое смещение точек струны называется прямой волной.
и а
aj $)
Рис. 10.2.
Рис. 10.3.
Аналогично, частному решению
и(х, t) = ifi(x + at), ф = 0
отвечает обратная волна и — ^(с2) (рис. 10.2, б), при которой х + at = с2 = const и dx/dt = —а.
Постоянное число а, определяемое равенством (2.3), называется скоростью распространения поперечных волн по струне.
На рис. 10.3 показан процесс распространения волн. На рис. 10.3, а изображено начальное отклонение струны
210
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
на участке (—xq, хо) (для простоты предполагаем, что F = 0). На рис. 10.3, б ив показаны прямая и обратная волны в начальный момент времени, при этом учтено, что, согласно (2.13), при F = 0 и £ = 0 обе волны имеют одинаковую конфигурацию, определяемую равенствами щ,U, 0) = U2^x, 0)=/Ы/2. На рис. 10.3, г показано положение прямой и обратной волн в момент времени t = = Хо/а, а на рис. 10.3, д их положение при х>Хо/а.
Не останавливаясь на процессе отражения волн от точек закрепления, перейдем к рассмотрению второго метода решения волнового уравнения.
2. Метод Фурье. Будем искать решение уравнения
(2.2) в форме произведения двух функций
u{x, t)=X{x)T{t\ (10.2.14)
из которых первая зависит только от х, а вторая — от t. Имеем
д\_<Рхт д2и у d2T
dz2 ~ dx2 ’ dt2 ~ dt2 '
Внесем эти выражения для производных в уравнение
(2.2)
хЦ = а2р^Т,
или
1 d2T 1 d2X
а2Т (t) dt2 X (х) dx2 •
Левая часть этого равенства зависит только от времени t, а правая — только от х. Это возможно только в том случае, если оба отношения представляют постоянное число. Обозначим его через —К2 *). Теперь последнее равенство примет вид
1 d2T _ 1 d2X .2
. а2Т dt2 ~ * dx2 ~
*) Легко показывается (мы не останавливаемся на этом), что это число не может быть положительным или равняться нулю.
§ 10.2. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТРУНЫ
211
Отсюда
% + aWT = 0, (10.2.15)
dt
= 0. (10.2.16)
dx*
Запишем общее решение уравнения (2.16) в следующей форме:
Х(х) — С\ cos Хх + С2 sin Хх. (10.2.17)
Воспользуемся первым граничным условием (2.5) и равенством (2.14). Имеем
и(0, *) = х(от*) = о.
При любом t это равенство возможно только при Х(0) = 0. Теперь из (2.17) найдем, что Сi = 0 и, следовательно.
Х(х) = sin Хх (10.2.18)
(не нарушая общности, можно положить С2 = 1).
Пользуясь вторым граничным условием и (2.14), получим
sin XI = 0.
Это уравнение имеет бесчисленное множество корней h=T (к = 1, 2, 3, ...). (10.2.19)
Внесем значение Хк в уравнение (2.15). Тогда общее решение его будет иметь вид
fry Tldjc т I 7 • TXClIC j
Th = ak cos -J-1 + bk sin-J-1,
где ah и bk — произвольные постоянные.
Учитывая значение Xk из (2.19), получим одно из частных решений волнового уравнения (2.2)
/ .ч • тск ( лак j I т • тсак . j
uk{x, t) = sin у x lak cos— t + bksin— tj.
Так как уравнение (2.2) линейное, то общее решение будет складываться из частных решений
00
и {х, t) = 2 sin X («ft cos ^ + bh sin (10.2.20)
212
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
Введя новые постоянные по формулам
Ак = У а* + Ь\, ви = arctg^, (10.2.21)
°h
общему решению (2.20) можно придать следующую форму:
00 / \ и (х, t) = ^Ah sin sin _|_ Eft j. (Ю.2.22) ft=i
Это решение показывает, что движение каждой точки струны можно рассматривать как наложение бесконечного числа гармонических колебаний (в практических задачах ограничиваются обычно первыми несколькими колебаниями).
Продифференцируем (2.20) по t:
оо
ди V» тк . пкх I .nakt , nakt\
qi l sin j ^ sin ^ -j- Ъь cos j J. (10.2.23)
ft=1
Воспользуемся теперь начальными условиями (2.4). Для этого подставим в (2.20) и (2.23) t = 0 и одновременно правые части заменим на fix) и Fix) соответственно. Имеем
/ (*) = 2 «а Sin = bh sin . (10.2.24)
h=1 ft=l
. nnx
Умножим первое равенство на sin -у— и проинтегрируем его от 0 до I
\ оо i
j / (х) sin dx = 2 ah j sin ^ sin ^ dx. (10.2.25)
0 h=1 0
Учтем теперь формулы ортогональности тригонометрических функций (их можно проверить непосредственным интегрированием)
Г • лкх • Лих j | ^ ^ ^ /ил о о/?\
jsm__sln_r к = п (ю.2.26)
9
§ 10.2. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ СТРУНЫ
213
Пользуясь равенствами (2.25) и (2.26), найдем i
ak =-yJ/(x) sin ^dx,
° , (10\2.27)
ь* = JjF<x)sin2rd*
о
(формула для Ък получается из второго равенства (2.24) аналогичным методом).
Полученные формулы полностью решают задачу о колебании струны: зная натяжение струны Го, ее линейную плотность ц, и длину I, а также начальные условия
(2.4), по формуле (2.3) находим параметр а (скорость волны), затем по равенствам (2.27) вычисляем коэффициенты ак и bh, после чего закон поперечных колебаний любой точки М струны определится по (2.20) или (2.22). Каждый член ряда (2.22) называется к-й гармоникой или стоячей волной; точки струны к-й гармоники совершают гармонические колебания с одинаковой начальной фазой ел, одинаковой частотой сok = nak/l и амплитудой Ahsin(nkx/l). Основная частота coi получается при к = 1:
тса л ■* / Тп
®1 = т = т^ jp
Остальные частоты получаются умножением ее на 2, 3 и т. д. Точки, в которых стоячая волна пересекает ось х при всех £, называются узловыми — они определяются из равенства sin inkx/l).
В практических расчетах на колебания нитей обычно определяют величины, не зависящие от начальных условий. Для струны это скорость распространения волны
(параметр а), основная частота со i, формы колебаний sin(jrкх/l) и узловые точки. На рис. 10.4 показаны формы трех первых колебаций, Основная (первая) гармоника
214
ГЛ X СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
не имеет узловых точек, вторая имеет одну узловую точку х\ = И2, третья — две узловые точки: х\ = Zi/З и х2 = = 2Z/3.
§ 10.3. Колебания однородной нерастяжимой нити с грузом на конце
Рассмотрим однородную перастяжимую нить, подвешенную за один конец и несущую на втором конце груз массы /72-1. В положении равновесия нить располагается
по вертикальной прямой, которую примем за ось х. Пренебрегая размерами груза, исследуем малые колебания нити около положения равновесия, предполагая, что они происходят в одной плоскости.
Йусть в положении равновесия точка М нити определяется абсциссой х\ дифференциал дуги нити в этом положении будет dx. Обозначим координаты той же точки в отклоненном положении через \ и tj, а дифференциал дуги через ds. Тогда
i, = x + v{x, t), Т) = uix,, /),
(10.3.1)
где v{x, t) и иКх, t)—вертикальное и горизонтальное перемещения точки М в момент времени t (рис. 10.5, а). Из условия нерастяжимости ds = dx, и, следовательно, имеем
или, пользуясь (3.1),
Рис. 10.5.
§ 10 3. КОЛЕБАНИЯ НИТИ С ГРУЗОМ НА КОНЦЕ
215
Отсюда
dv
дх
Считая горизонтальные перемещения и и их производные ди/дх и du/dt малыми первого порядка, из последнего равенства найдем, что dv/dx и, следовательно, vix,t) будут величинами второго порядка малости. Согласно (3.1) заключаем теперь, что с точностью до членов первого порядка малости включительно вертикальным перемещением точки М можно пренебречь и считать, что ее положение в момент времени t определяется координатами х и и(х, t), т. е.
Пренебрегая квадратом производной ди/дх по сравнению с единицей, получим
где а — угол между касательной к нити и положительным направлением оси х.
* Натяжение Т нити в точке М с абсциссой х равно сумме силы тяжести груза Ш\ и силы тяжести нити, расположенной ниже точки Л/, т. е.
где |ll — линейная плотность нити, I — ее длина.
Пользуясь вторым уравнением движения нити (8.1.3) и учитывая, что ds = dx и Ру =* Ри = 0, получим
£ =Х, Г)= и(х, t).
ди
дх
sin а =
(10.3.2)
cos а =
1
1
Т = mig + \ig(l — х),
Решение этого дифференциального уравнения мальп поперечных колебаний нити с грузом должно удовлетво¬
216
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
рять двум начальным и двум граничным условиям. Начальные условия имеют тот же вид, что и (2.4):
при t = О
U = f(x), % = F(X).
Граничные условия зависят от наличия или отсутствия груза. Рассмотрим сначала случай, когда груз отсутствует (mi = 0). Верхний конец нити закреплен, и его перемещение при всех t равно нулю; нижний конец нити может перемещаться только на конечную величину. Поэтому граничные условия при отсутствии груза будут
и(0, Й=0, u(Z, (10.3.4)
При наличии груза граничные условия на нижнем конце усложняются (условие на верхнем, закрепленном конце остается без изменения). Для получения этого условия рассмотрим мысленно движение одного груза
без нити, заменив ее реакцией (натяжением). Тогда на груз будут действовать две силы: сила тяжести и сила — T(l,t) (см. рис. 1.2). Первая сила направлена вертикально вниз, параллельно оси х, а вторая — по касательной к нити в нижней ее точке (рис. 10.5, б). Применяя второй закон Ньютона, получим
mxw = rriig — Т (Z, t). (10.3.5)
С принятой точностью ускорение груза направлено перпендикулярно оси х и равно d2u/dt2, причем эта производная должна быть вычислена в нижней точке нити, т. е. при х = Z. Спроектируем равенство (3.5) на ось v, перпендикулярную касательной к нити в нижней точке. Тогда, учитывая направления ускорения w и сил mи
— Т, получим
Г Л* 1 . ,
\mi — cos °Ч = “ miS sin а Iх=и
L dt J x=i
или, принимая во внимание (3.2),
Г д2и ди 1
Уд? \х=1
Присоединяя к этому условию первое равенство из (3.4),
= 0. (10.3.6)
§ 10 3. КОЛЕБАНИЯ НИТИ С ГРУЗОМ НА КОНЦЕ
217
получим граничные условия для колебаний нити с грузом на конце*).
Прежде чем перейти к решению поставленной задачи, преобразуем уравнение (3.3) и граничные условия, введя вместо х новую переменную z по формуле
Уравнение (3.3) в переменных и, t и z примет теперь вид
В тех же переменных граничные условия (3.4) для нити без груза преобразуются к виду
Применяя метод Фурье, изложенный в § 10.2, будем искать решение уравнения (3.8) в форме произведения двух функций Uiz) и Tit), из которых первая зависит только от 2, а вторая от t:
Подставляя в (3.8) и разделяя переменные, получим
1 d ldU\ 4 1 d2T
zU(z) dz V dzj~ a* T(t)
*) Уравнение (3.3) и граничное условие (3.6), полученные здесь из элементарных физических соображений, выводятся в [121 с помощью принципа Гамильтона — Остроградского. Решение этого уравнения и следующий пример заимствованы нами из [12], но излагаются здесь с несколько большими подробностями.
г, + I - X = z2 (г, = mJv). (10.3.7)
(10.3.8)
где
а = 1/g.
(10.3.9)
и(У1, t) = 0, u(0, t) Ф (10.3.10)
а для нити с грузом
(10.3.11)
где для краткости положено
uiz, t) — U(z)Tit).
(10.3.12)
218
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
Так как левая часть зависит только от z, а правая — только от t, то это равенство может существовать, если каждая его часть будет равна постоянному числу. Обозначив, как и в § 10.2, общее значение их через — А,2, получим два обыкновенных дифференциальных уравнения
Mid£)+V*u=0' (10-ЗЛЗ)
—т + -г- Т = 0. (10.3.14)
dt2 4
Первое из этих уравнений представляет уравнение
Бесселя (см. формулу (П2.6) приложения 2}, общее решение которого будет
U(z) = CiMKz) + C2Y0(Xz), (10.3.15)
где Jo и Yo — функции Бесселя 1-го и 2-го родов нулево¬
го порядка.
До сих пор ход решения был практически одинаков для нити с грузом и без него. Дальнейшее решение существенно зависит от наличия или отсутствия груза. Рассмотрим сначала второй случай.
1. Колебания подвешенной нити без груза. Второе граничное условие (3.10) требует, чтобы функция u(z, t), а следовательно, и фуйкция U(z, t) при z = 0 была конечной. Так как Уо(0) = —°°, то постоянная С2 должна равняться нулю: C2 = Q. Полагая С\ = \ (численная величина постоянной С\ не имеет для дальнейшего никакого значения — существенно только, что С\ Ф 0), получим
U(z) = JQ(Xz). (10.3.16)
Подчиним теперь функцию u(z, t) = U(z)T(t) первому граничному условию (3.10). Имеем
и(УX t) = mWT(t)= 0.
Отсюда __ _
и(11)=ЫШ= 0. (10.3.17)
Так как функция Бесселя Joiz) имеет бесчисленное множество положительных корней \х\1 \х2, ..., то имеется
бесчисленное множество чисел Хк, удовлетворяющих по-
S 10 3. КОЛЕБАНИЯ НИТИ С ГРУЗОМ ИЛ КОНЦЕ
\
219
ставленной задаче:
На
(Л = 1,2,3,...). (10.3.18)
Каждому Л), отвечает свое решение уравнения (3.14)
aubf au,,<
Th (t) = ah cos + bh sin
2 УГ
2 Vf
Частное решение уравнения (3.8) равно произведению J0(Xkz)Tk(t), а общее решение равно их сумме. Переходя по (3.7) к переменной х при т.\ = 0, получим
au.t аи. t \
,cos-^= + bhsin—^ ,
2 Vl 1 2 Vl )
(10.3.19)
и (x, t) = 2 Jo V —J1) ( ak
h=1 X 1 \
или, пользуясь формулами (2.21),
rl — x\ . (
h=l
oo
u(x, t) = Vlj=r)
sin
\2 V'l
eft . (10.3.20)
Это решение показывает, что движение каждой точки подвешенной нити можно рассматривать как наложение гармонических колебаний. Частота к-й гармоники равна
ацА/(2У/), а форма (амплитуда) AhJ0(\ihl/(Z — х)/1). Узловые точки определяются из уравнения
I
Отсюда ясно, что эти точки для к-й гармоники находятся из равенств
-(&)1
г,
*к~1 =
1 —
Н-i
н
I,
основная (к = 1) гармоника узловых точек не имеет.
Первые три корня функции Бесселя нулевого порядка имеют следующие значения (см. равенства (П2.3) приложения 2): ц.1 =2,4048; Цг = 5,520; |л.а = 8,654.
Поэтому узловая точка второй гармоники (к = 2) определится из равенства хх = ^1 — | I = 0,810/.
220
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ /
Третья гармоника имеет две узловые точк^ хх = 0*923/, я2 = 0,608Z.
Формы первых трех гармоник в долях |^1А| будут
Ф1(«)=/0 (2,4048 У 1-х)’
Ф,(*) =/o(5,52o/l--^),
Ф3 (*)=/0(8,054 У 1-х)-
С помощью таблиц функций Бесселя [23] были определены значения этих форм колебаний и по точкам
построены их графики (рис. 10.6). Частоты первых трех главных колебаний равны
о)1 = l,2024Vg/Z, (о2 =
= 2,760^ саз = 4,327УвТГ
Для полного решения зада^06081 чи осталось определить посто' янные интегрирования ah и Ък из равенства (3.19). Воспользуемся первым начальным усiOJ/231 ловием. Подставив в (3.19) t = В =0 и и(х, 0)=/(#), получим
оо
f(x) = ^ahJ„к/ Lzf). Рис. 10.6. ftTi V Г 1 I
Умножим обе части этого равенства на /ofunl/L-iJ и проинтегрируем его от 0 до I: i
j* / (х) (fin yi-j^dx =
о
s=2ekJ/o(lA*/' Ц^)/.(|*«|/Ц-2)лс.
h—1 л
^ 10 3. КОЛЕБАНИЯ НИТИ С ГРУЗОМ НА КОНЦЕ 221
\
ОбозначгЦ правую часть этого равенства через I и перейдем к 1^овой переменной интегрирования, положив
м х и>2 j п dw
= -рг, dx = -2w -J-.
После подстановки последовательно получим
k=1 о
= 2 [~¥)d“’ = k=i i
= -J- 2^1 wJo(ph-J-)J° dw•
h=1 о
Все интегралы при к Ф п равны нулю, а при к = п соответствующий интеграл равен l2J\{\i>k)l2 (см. формулы ортогональности (П2.8) приложения 2). Поэтому
I = U1 ([Аа)
и, следовательно,
i
4 = 1TF7L-, I / (*) J0 [н yri-^)dx. (Ю.3.21)
1 v к) о
Продифференцируем теперь равенство (3.19) по времени t и воспользуемся вторым начальным условием. Повторяя затем проведенные выше преобразования, получим
i
bh = afift IF (x) j° (Ца У ~TL) dx' (10-3-22)
Полученными формулами задача о колебании подвешенной однородной нерастяжимой нити без груза полностью решена.
2. Колебания подвешенной нити с грузом. Первое граничное условие (3.11) на основании (3.12) принимает
222
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ /
/
вид
u(yi2, t) = и(У12)тш = о.
Отсюда С/(У/2) =0, что на основании (3.1^) приводит к равенству
СМ%112) + С2Г0(Ш2) = 0. (10.3.23)
Перейдем ко второму граничному условию (3.11). Име-
Подставив эти значения для производных во второе граничное условие (3.11), получим после сокращения на
После подстановки в (3.24) значений U'(z) и U(z) из (3.15) и группировки членов приведем граничное условие
(3.24) к следующей форме:
Сг [X Vh J0 {I А) + 2/0 (X VО] +
+ С, [а, /IIУ0 (х /О + 2Уо (я, /5)] = 0. (10.3.25)
Система линейных однородных алгебраических уравнений (3.23) и (3.25) относительно С\ и С2 должна иметь решение, отличное от нуля. Для этого необходимо и достаточно, чтобы определитель этой системы равнялся нулю:
ем (см. (3.12) и (3.14))
—а2Т
= 0. (10.3.24)
*-y*i
Из равенства (3.15) найдем
U' (*) = XCrJо (te) + XC2Y’2 (Ал)-
'о (*/*.) 1А;о(1А) +
+ 2/0(Х/Т1)
^Ду,(1А)+ =0
10 3. КОЛЕБАНИЯ НИТИ С ГРУЗОМ НА КОНЦЕ 2?3
ИЛИ
\
(10.3.27)
Тогда ЯУ/г = ^VZ2/^i = ^Vl + Z/Zi = ^Vl + m/mi, где m — масса нити без груза. Уравнение (3.26) принимает теперь вид
j0 (с/у О [сп (о+ 2^(0]-
- Го (t/VD [Wo (0 + 2/о (£)] = 0. (10.3.28)
Это трансцендентное относительно £ уравнение зависит только от одного параметра к — т\/т = 1\/1. Оно имеет при заданном значении к бесчисленное множество положительных корней которые можно определить различными методами, но, конечно, лучше всего использовать для этой цели ЭВМ. Не останавливаясь на этом вопросе более подробно, отметим, что в работе [30] вычислены первые пять частот колебаний
для 0 ^ к ^ 50. Для предельных случаев, когда х<1 и к > 1, там же получены упрощенные уравнения для определения частот.
По значениям корней уравнения (3.28) найдем из (3.27) соответствующие %h:
Подставим эти значения для %k в уравнения (3.23) и
(3.25) и обозначим соответствующие значения С\ и С2 через C\h и C2h• Из полученных двух уравнений относительно C\h и C2k независимых будет только одно уравнение (так как при X = %k определитель системы равен нулю).
(10.3.29)
Xft = -^= (*=1,2,3,...). (10.3.30)
V11
224
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
Возьмем уравнение (3.23) как более простое: /
Cik^o О CtkToibhVh) ~
Отсюда
Clk = ^hP^kt
где
*л = -£пгт- (ю.3.31)
Jo\4V h)
Соответствующее частное решение (3.15) для функции U будет (переходим снова к переменной х)
Uk W l2 — x) = vA/0 (xh Yh — х) + У0 (h Yh — х),
(10.3.32)
при этом мы полагаем С2ъ. = 1 (этот множитель можно внести в постоянные ак и bh — см. дальнейшее равенство (3.33)).
Подставим Хк в (3.14) и найдем частное решение этого уравнения
Tk (t) = ак cos соkt + bk sin соkt (cok = aXJ2).
Теперь можно написать и общее решение поставленной задачи
оо
и (х, 0=2 Uh (/— х) (ah cos сoht -j- 6hsin a>ht), h—1
(10.3.33)
или, пользуясь равенствами (2.21),
оо
и (X, 0=2 AhUh {у h — я) sin (®а< + eft). (Ю.3.34) h=l
Функция Uh(l/l2 — x) определяет форму к-й гармоники, узловые точки определяются из уравнения
иЛУк^~х) = о,
или
Vo (К Vh^x) + у0 (К Vh^) = 0. (10.3.35)
§ ЦЛ. КОЛЕБАНИЯ НЕРАСТЯЖИМОЙ ЦЕПНОЙ ЛИНИИ 225
Мы не \станавливаемся на определении постоянных интегрирования ак и Ьк по начальным условиям (3.4), так как для практических целей наибольший интерес представляет ^нание частот, узловых точек и форм колебаний. Заметим только, что теоретически способ определения постоянных ак и Ък несущественно отличается от метода вычисления их при отсутствии груза.
Сравнивая оба случая колебаний подвешенной нити, видим, что добавление груза мало изменяет чисто теоретический анализ, но существенно увеличивает вычислительную часть работы. Если при отсутствии груза для определения частот, узловых точек и форм колебаний нити можно воспользоваться готовыми таблицами бесселевых функций, то для нити с грузом таких таблиц нет.
Можно конечно, использовать результаты упомянутой выше работы [30] и, зная частоты, существенно упростить собственные вычисления. Но остается еще определение узловых точек и форм колебаний. Мы уже не говорим, что существенно усложняется вычисление постоянных ак и Ък по начальным условиям (3.4).
§ 10.4. Колебания нерастяжимой цепной линии
Для составления дифференциальных уравнений колебаний систем с распределенной массой, в частности колебаний нити, с большей эффективностью используются вариационные методы. Эти методы не всегда являются самыми простыми*), но они обладают свойством универсальности. Поэтому мы считаем полезным продемонстрировать их на примере вывода дифференциальных уравнений колебаний цепной линии.
Напомним основные определения и принцип Гамильтона— Остроградского (см. [3, 12]). Рассмотрим систему с идеальными и голономными связями, имеющую s степеней свободы. Пусть при заданных начальных условиях
*) Вывод уравнения (3.3) и граничных условий (3.4) и (3.6) для подвешенной нити с грузом и без него занял у нас немногим более двух страниц текста без сложных преобразований, в то время, как применение вариационного принципа Гамильтона — Остроградского к этой задаче занимает значительно больше места п требует применения более сложного аппарата.
226 гл. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ ^
обобщенные координаты qu ..q9 изменяются по закону qi=*q\(t), qa = qe(t). j (10.4.1)
Говорят, что совокупность функций (4/1) определяет истинный путь системы. Дадим каждой координате qk(t) приращение бqk, где вариации бqk являются произвольными малыми дифференцируемыми функциями времени, допускаемыми связями. Функции
<h (0 = (0 + q* (t) = qs (t) + 6qs
определяют окольный путь.
Составим функцию Лагранжа (кинетический потенциал)— разность кинетической Т и потенциальной П энергий *):
W qs, t) = T — П. (10.4.2)
Вариация функции L определяется следующим образом:
и = 2(^‘+!^)- <10-4-3>
Из всей совокупности мыслимых окольных путей выделим такие, которые в два фиксированных, но произвольно выбираемых момента времени to и t\ совпадают с истинным путем, так что
(Q = бд* (М =0 (к = 1, 2, ..., s). (10.4.4)
Действием по Гамильтону называется величина, опре¬
деляемая равенством
s = J L (д, q, t) dt. (10.4.5)
<о '
Говорят, что действие по Гамильтону S имеет стационарное значение, если его первая вариация бS равна нулю:
65 = 0. (10.4.6)
Принцип Гамильтона — Остроградского формулируется следующим образом: действие по Гамильтону S имеет
*) Мы рассматриваем потенциальную систему, но принцип Г амильтона — Остроградского применим и к непотенциальным и неголономным системам.
§104. КОЛЕБАНИЯ НЕРАСТЯЖИМОЙ ЦЕПНОЙ ЛИНИИ 227
стационарноеч значение на истинном пути системы, если к сравнению р ним привлекается многообразие окольных путей, удовлетворяющих условию (4.4). Доказывается, что из этого принципа вытекают уравнения движения системы (например, уравнения Лагранжа второго рода) и, наоборот, из уравнений движения вытекает равенство (4.6).
Напомним также, что при выводе дифференциальных уравнений движения применяется правило
6d = d6, (10.4.7)
означающее, что операции варьирования и дифференцирования переставимы (это правило доказывается в курсах аналитической механики и вариационного исчисления).
Применим принцип Гамильтона — Остроградского для вывода дифференциальных уравнений малых колебаний нерастяжимой цепной линии. Покажем прежде всего, как с помощью этого принципа получается уравнение равновесия цепной линии. Потенциальная энергия силы тяжести, отнесенная к единице длины нити, равна qy (см. формулу (2.1.15)), поэтому потенциальная энергия П всей нити будет
*2 Н
П = q [ у ds = q j у V1 + у'2 dx.
*1 *1
Здесь х\ и х2 — абсциссы точек закрепления (не внося, надеясь, путаницы, мы сохранили для потенциальной энергии всей нити символ П, которым в § 1.4 обозначали потенциальную энергию, отнесенную к единице длины нити).
Так как при равновесии кинетическая энергия равна нулю, то функция Лагранжа (4.3) принимает вид
*2
L = — Я j yVi + y'2dx,
xi
а интеграл действия S вырождается в L. Следовательно, в положение равновесия вариация бL должна равняться
228 I’Jl- СБОБиДНЫЕ КОЛЕБАНИИ ПИТЕИ I’
нулю. Имеем /
/
*2 I
8L = — q j [ VI + у'2 by + У лГ У , бу,14х=0. (10.4.8)
4 L У 1 + у’2 J
Выделим второе слагаемое, обозначим его через I и применим к нему правило (4.7):
I = q[ -у---— by'dx = q Г (6i/) eta,
J Vi + y'2 ч} Vi + y'*d*y у>
Х1 Х1
или, интегрируя по частям,
1=д-Ж=Ьу '-gb^VSLJbydx.
У1 + у J L У1 + г/ J
Х1 Х1
В точках закрепления
8у(х i) = б у(х2) = 0, (10.4.9)
и первое слагаемое обращается в нуль. Теперь равенство
(4.8) принимает вид
“ " "1 $7г+Р-- УТ+>*)*1"Ь-
Так как вариация 6у(х) произвольна, то функция, стоящая под знаком интеграла, должна равняться нулю
у'
Это уравнение можно переписать следующим образом (справедливость преобразования можно проверить непосредственным дифференцированием):
§ 10.4. КОЛЕБАНИЯ НЕРАСТЯЖИМОЙ ЦЕПНОЙ ЛИНИИ
229
Отсюда
Vi + y’
- а,
где а — постоянная интегрирования*).
Решая относительно у' и разделяя переменные, получим
dy dx
77^Т2=
или, интегрируя и полагая, что у = а при д? = 0 (см. формулу (П1.11) приложения 1),
y = ach^. (10.4.10)
Уравнение (4.10) определяет цепную линию, вершина которой отстоит от начала координат на величину а (рис. 10.7).
Если ввести в рассмотрение угол а между касательной к нити в положении равновесия и осью х, то будут справедливы формулы (см. § 1.2)
X
a
dx 1
COS a = — = ds
x
eh —
a
sin a = th —
a *
(10.4.11)
ad ~a ’ da
где p — радиус кривизны цепной линии
*) Последнее равенство представляет интеграл Эйлера для вариационной задачи
*2
= J F (у, у')
dx.
Если функция F не зависит явно от х, то из равенства 6L = 0 следует интеграл
, dF
У "faj' — F = const,
на который впервые указал Эйлер.
230
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
Переходим к составлению дифференциальных уравнений колебаний цепной линии. Обозначим через г0 и г радиусы-векторы точки М нити в равновесном и в смещенном положениях соответственно. Тогда будем иметь
г = г0 + их + w + (10.4.12)
где и, v, w — проекции вектора перемещения г — г0 на оси естественного трехгранника т, v, Р (бинормаль Р, направленная на читателя, на рис. 10.7 не показана). Эти проекции считаются величинами первого порядка малости; они зависят от времени t и выбранной точки М, т. е. от дуговой координаты s. Орты т, v, Р строятся на нити, находящейся в покое, и поэтому от времени t они не зависят.
Продифференцируем равенство (4.12) по дуге s, учитывая, что нить нерастяжима:
dr dr qu dx . dv . dv . dw 0 , rfB
Для плоской нити dx Ids =— v/p, dv/ds =—т/p, d$/ds =0 (формулы Френе); кроме того, dr0/ds =- т. Следовательно,
dr (. . ди v \ . / и dv\ , dw 0
Модуль левой части равен единице, поэтому
*-(‘+£-тГ+(•?+£)■+(г)'
Раскрывая скобки и группируя члены, найдем
ди р \(ди v \2 . / и dv\2 . (dw\2
y = P^+TLfe-7J +1? + ^) + Ы/
Сохраняя величины первого порядка малости, получим
Разность (du/ds — v/p) имеет второй, а ее квадрат — четвертый порядок малости. На этом основании с точностью до членов второго порядка малости будем иметь
ди р Г/ и dv\2 (dw\2
V = PT*+T Ит+я) +Ы/
§10 4. КОЛЕБАНИЯ НЕРАСТЯЖИМОЙ ЦЕПНОЙ ЛИНИИ 231
Перейдем к новой независимой переменной ос. Пользуясь оператором
д _ д da J_
ds ~dads р да’
получим для первого порядка малости
1 д2и
ди dv ,
V ~ да' ds ~ р 0а2’
для второго порядка малости
ди 1
V = d~a + Tp
(10.4.13)
(10.4.14)
(10.4.15)
Обозначим ординату точки М нити в отклоненном состоянии через т|. Тогда
г) = у + и sin а + v cos а,
где у — ордината той же точки цепной линии при ее равновесии. Поэтому потенциальная энергия нити при ее колебании будет равна
П = q j Л ds = q j у ds + q j (u sin a + v cos a) ds =
a2
= П0 + q J (u sin a + v cos a)p da, ai
где По — значение потенциальной энергии в положении равновесия, а\ и а2 — значения угла а в точках закрепления. Внеся вместо v ее значение из (4.15), получим
0&2
П — I70 = gJ (usina + !£-fosa)p<fot +
“i a2
+
Ы[(
ai L \
I I/ M
U H o’
da
+
dwY
Ja)
cos a da. (10.4.16)
Согласно общей теории малых колебаний первое слагаемое, содержащее отклонения в первой степени, должно равняться нулю (см. например, [4], том 2, § 20.7). Это можно проверить и непосредственно. Дейст-
232
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
вительно, пользуясь равенствами (4.11), будем иметь
ди ди дх ds
ди
х ди
ии, и и и и- иг> и и и л о- и и л а, 7 _
—= - — Е— — = a ch — —, pda = ch—dx
Q(% Я'г Я о ПП т п Я'г ' * п
дх ds da
_ х дх ch — а
а дх '
Следовательно,
J (MSina+-g-cosa)p<fa = j + a-^)ch^cfo-
“1 *1
•^2 x2
= S(ushi + aSchv)dx = af £(uchi)dz =
== au(x, £)ch — 2 = 0,
так как в точках закрепления и(хi t) = и(х2, t) = 0 при любом t. Таким образом,
п-п*-*/[(«+£),+
а! '
дт \2 да )
cos a da. (10.4.17)
ds,
Это равенство показывает, что в положении равновесия потенциальная энергия имеет минимум. Кинетическая энергия колеблющейся нити равна
откуда, учитывая первое равенство (4.14) и что ds = pda, получим с точностью до величин высшего порядка малости
а1 L
Для дальнейшего упрощения целесообразно перейти к новым безразмерным независимым переменным т и | по формулам
- l/ g * t х ,Af, ,
pda. (10.4.18)
§ 10.4. КОЛЕБАНИЯ НЕРАСТЯШИМОЙ ЦЕПНОЙ ЛИНИЙ 233
при этом частные производные по т бУД®“ ?боз??Тт точкой, а по 1-штрихом. Имеем (см. (4.19) и (4.11))
• dx d1~
£u_=todT=1/i.u, da T=d71’
dt дт dt "a ach__
, x i f л- du dl _ , i t
pda = ach2-Jda = ach|dE, = -gf _ ё’ i!|L = -^(u' chg)-^ =uwch26 + «*' ch £ sh I,
cos a aa= -77-• ch |
Пользуясь этими равенствами, преобразуем выражения для кинетической и потенциальной энергий
It
Т = -£. j" (ц2 + и'2 ch21 + u?2) ch £
П-П0 =
^2
= ± j [(и + и" ch21 + «' ch 5 sh I)2 + u^ch2i]
^1
Составим теперь кинетический потенциал L = Т — П, а затем интеграл действия по Гамильтону (4.5), отбросив при этом несущественную постоянную П0:
Т1 ^2
5 = 1 f j'U2ch| + u,2chsi-^+“"ch^+u' shi)N*0 6i
-(- (u;2ch| — u/2)] (10.4.20)
Согласно принципу Гамильтона — Остроградского вариация этого интеграла должна равняться нулю. Так как проведение полных преобразований, связанных с вычислением 65, занимает много места, то мы ограничимся вариацией только одного второго слагаемого, которое обозначим через 7 (остальные вариации вычисляются
234
ГЛ. X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
аналогично). Имеем Ti h
б/ = |б|йт|и'2 ch31 d£ = q j* di j* u' ch3£6 u'd%
4 &i
или, применяя к 6 и' дважды правило (4.7) и меняя порядок интегрирования,
12 ч
67 - g J d\ | и'ch3^
Ei *о
Интегрируя по переменной т по частям, получим
Ы
и' ch3|-^|-6u
* — j u' ch3!-^ (6u)dtJ.
В соответствии с общей теорией бю(|, то)=6и(£, ti) = 0 при всех | (см. (4.4)). Поэтому, отбрасывая первое слагаемое и снова меняя порядок интегрирования, найдем
Ч $2
б/ = — q J dx J и' ch3 g (би)
To ^1
Интегрируя no частям теперь по g, будем иметь б/ =
=—q j* dx
и' ch3 ^ б и
^2 ^2
- J [и" ch3g+3u'ch2 £ sh |) 6u d£
В точках закрепления 6n(£i, т) = би(|2, т) = 0 при всех т. Итак,
т2 *2
6/ = g J f (it* ch31 + Zit’ ch2£ sh £) 8u d£ dr.
T1 ^1
Если проделать аналогичные операции с остальными слагаемыми интеграла действия (4.20), то получим в ре¬
§ 10 4. КОЛЕБАНИЯ НЕРАСТЯЖИМОЙ ЦЕПНОЙ ЛИНИИ
235
зультате следующее уравнение:
Т1 ^2
q j [ и + и" ch21 + 3u' ch £ sli \—*Ы sh \ — Ъи" ch £ —
— 4m'" sh £ — uIY ch £) ch l 6(— w ch £ + и;") 6m;] d% dx.
Так как отклонения и и w независимы, а их вариации б и и 6м;, рассматриваемые как функции £ и т, независимы и произвольны, то последнее равенство возможно только в том случае, если множители при 6и и 6w будут равны нулю. Это дает нам два дифференциальных уравнения в частных производных:
и - и" ch21 - 3и' ch I sh I + 2ur sh I + bu" ch £ +
+ 4«'"sh£ + MIVch£ = 0, (10.4.21)
w ch £ — w” = 0. (10.4.22)
В точках закрепления перемещения и, v = и' и w равны нулю, поэтому искомые функции и и w удовлетворяют следующим граничным условиям:
»(li, т) = 0, в(|2, т) = 0, »'(1ь т) = 0,
(10.4.23)
и'(%2, т)=0, w{%\, т) = 0, w(%2, т)=0.
Кроме того, должны быть заданы начальные условия, но они имеют меньшее значение, и мы не останавливаемся на этом (в практических задачах, как уже отмечалось, наибольшее значение имеют частоты и формы колебаний— величины, не зависящие от начальных условий).
Решение уравнений (4.21) и (4.22) ищется в следующей форме:
и = М(g)sin(coT + е), w = £(£)sin(A;T + 6). (10.4.24)
Отсюда находим
и = — Afco2sin(coT + е), и” = —Af"co2sin(cDT + е),
и{п) — М{п) sin(coT + е),
где = 1, 2, 3, 4. Ацадогдздые выращешя цолучаеад для
236
ГЛ X. СВОБОДНЫЕ КОЛЕБАНИЯ НИТЕЙ
производных w. После подстановки в (4.21) и (4.22), сокращения на общий множитель и группировки членов получим два обыкновенных линейных однородных дифференциальных уравнения с переменными коэффициентами
ch p/IV + 4 sh IM'" + (5 + со2 ch l)ch | • M” +
+ (2 + 3co2 ch l)sh 1 • M' - cd2M = 0, (10.4.25)
B" + k2ch£>B = 0. (10.4.26)
Первое из этих уравнений удовлетворяет четырем граничным условиям
Л/(Ы = 0, м{%2) = 0, M'ih)=0, М'(%2) = 0, (10.4.27)
а второе — двум условиям
Ж|,) = 0, Я(|2) = 0. (10.4.28)
Эти уравнения решаются на ЭВМ — см. [29].
ПРИЛОЖЕНИЕ 1 ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболический синус, косинус и тангенс определяются равенствами
ЛХ —зс х I — X
shz = ? chx= , th ж = (П1.1)
2 2 ch х
подробные таблицы содержатся в [21]. Справедливы следующие формулы:
sh (— я) = — sh г, ch (— х) = ch .г,
(П1.2)
ch2x — sh2x = 1,
(П1.3)
sh (x + у) = sh x ch у ± ch x sh y,
(П1.4)
ch (x ± y) = ch x ch у + sh x sh y,
(П1.5)
2ch2 = ch x + 1, 2sh2 —- = ch x — 1,
(П1.6)
у = Arcsh x, л: = sh
(П1.7)
d r
ch i = sh x, \ sh x dx = ch x + C,
(П1.8)
d r
^ sh x = ch x, \ ch x dx = sh x + С,
(П1.9)
d 1 Г
-т- th x = -72"» \ th x dz = In ch x + C,
ax ch x J
(П1.10)
С dx x -7 — Arcch — + C,
J y**_a2
(П1.11)
P cfa ж
J ArCSh^ + C’
(П1.12)
сЬж=1 + 2Т + 1г + -
(П1.13)
Ph*=x + |j. + |J + ...
(П1.14)
238
ПРИЛОЖЕНИЕ 2. ФУНКЦИИ БЕССЕЛЯ
ПРИЛОЖЕНИЕ 2 ФУНКЦИИ БЕССЕЛЯ
Нас будут интересовать функции Бесселя нулевого порядка. Приведем аналитические выражения для этих функций:
в
/oW=l-i- + 4-2--TT2—2+-- (П2.1)
о 0 2 4 2 *4 *6
у. М-1М Ь5-А 2 (- (ш-2)
При х > 0 функция Бесселя /о(х) имеет бесчисленное множество вещественных корней. В частности, первые три корня имеют следующие значения:
(л, >= 2,4048; ц2 = 5,520; *х3 = 8,654. (П2.3)
Уравнение Бесселя нулевого порядка
sM)+'*-0: ,ш'4)
имеет следующее общее решение:
у (х) = С Jo (х) + C2Y0 (х) . (П2.5)
Уравнение
Цхъ)+х'яу-° <ш-б>
подстановкой \х — и приводится к уравнению (П2.4), поэтому его решение будет
у(х) = СМКх) + C2Y0(lx). (П2.7)
Функции Бесселя обладают свойством ортогональности на любом интервале (0, I), которое состоит в следующем:
0, к =£ п,
-ПК),
где |л& и |лп — любые положительные корни функции /0(я).
Краткие таблицы функций Бесселя нулевого и первого порядков приведены в [21].
ЛИТЕРАТУРА
1. Алексеев Н. И. Статика и установившееся движение гибкой нити — М.: Легкая индустрия, 1970.
2. Аппель П. Теоретическая механика: Перев. с франц. Т. I. — М.: Физматгиз, 1960.
3. Бутенин Н. В. Введение в аналитическую механику.— М.: Наука, 1971.
4. Бутенин Н. В.} Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. Т. I и II.— М.: Наука, 1970.
5. Воробьев А. Г. О расчете по эластиковой теории сигар и пучков пучковых плотов для случая нахождения их на плаву.— Известия вузов. Лесной журнал, 1958, № 6.
6. Ишменецкий В. Г. Канонические дифференциальные уравнения гибкой нерастяжимой нити и брахистохроны.— Протоколы Матем. общества Харьковского университета, 1886, вып. 1.
7. Качурин В. К. Гибкие нити с малыми стрелками.— М:. Гостехиздат, 1956.
8. Кочин Н. Е. Об изгибе троса змейкового аэростата под действием ветра — ПММ, 1946, т. X, вып. 1.
9. Кошляков Н. С., Глинер Э. Б., Смирнов М. М. Основные дифференциальные уравнения математической физики.— М.: Физматгиз, 1962.
10. Крылов А. Н. О равновесии шаровой мины на течении. Собр. трудов, т. IX, ч. 2.— М.: Изд-во АН СССР, 1949.
11. Куркин В. И. О стационарном движении гибкой нити.— Известия вузов. Технология текстильной промышленности, 1964, № 6.
12. Лурье А. И. Аналитическая механика.— М.: Физматгиз, 1961.
13. Мацелинский Р. Н. Статический расчет гибких висящих конструкций.— М.: Стройиздат, 1950.
14. Меркин Д. Р. К вопросу об определении натяжения в обвязке и формы пучка.— Научн. труды Ленингр. лесотехнической академии, 1961, № 96.
15. Меркин Д. Р., Комарницкая О. И. К вопросу об определении натяжения в обвязке и формы плавающего пучка.— Научн. труды Ленингр. лесотехнической академии, 1963, № 102.
16. Минаков А. П. Основы механики нити.— Научно-исследовательские труды Московского текстильного института, 1941, т. 9, вып. 1.
17. Минаков А. П. О форме баллона и натяжении нити в крутильных машинах.—Известия Московского текстильного института, 1929, т. 2.
240
ЛИТЕРАТУРА
18. Можевитинов А. Л. Форма сечения и натяжение обвязок морских плотов.— Известия вузов. Лесной журнал, 1961, № 1.
19. Основы механики нити/Якубовский Ю. В., Шивов В. С., Кори^ тысский Я. И., Мигушов И. И.— М.: Легкая индустрия, 1973.
20. Пожарицкий Г. К. Устойчивость равновесий механических систем, включающих гибкую нерастяжимую нить.— ПММ, 1973, т. 37, вып. 4.
21. Сегал Б. ИСемендяев К. А. Пятизначные математические таблицы — М.: Изд. АН СССР, 1948.
22. Светлицкий В. А. Механика гибких стержней и нитей.— М.: Машиностроение, 1978.
23. Светлицкий В. А., Мирошник Р. А., Куркин В. И. Определение форм стационарного движения нити при произвольном угле запуска.— Известия вузов. Машиностроение, 1972, № 3.
24. Светлицкий В. А., Мирошник Р. А., Куркин В. И. Определение форм стационарного движения нити в средах различной вязкости.— Прикладная механика, 1972, т. VIII, вып. 4.
25. Светлицкий В. Л., Мирошник Р. А. О пространственном расположении идеальной гибкой нити в однородном потоке.— В сб.: Сопротивление материалов и теория сооружений.— Киев: Буд1вельник, 1973, вып. 19.
26. Тихонов А. Самарский А. А. Уравнения математической физики.— М.: Гостехиздат, 1953.
27. Халепский Б. И. Механика привязного воздухоплавания.— М.: Военное изд-во НКО СССР, 1945.
28. Щедрое В. С. Основы механики гибкой нити.— М.: Машгиз, 1961.
29. Saxon D. and Cahn A. S. Modes of vibration of a suspended chain— The Quarterly Journal of Mechanics and Applied Mathematics, 1953, vol. VI, part 3.
30. Woodward J. H. Frequencies of a hanging chain supporting an end mass.— The Journal of the Acoustical Society of America, 1971, vol. 49, N 5, part 2.