Математическая экономия - Аллен Р.

Альб. Л. Вайнштейн. Вступительная статья

Глава 1. Паутинообразная модель и другие простые динамические модели

1.9. Запаздывания в динамических моделях

Глава 2. Кейнс и классические модели: мультипликатор

2.2. Формулировка кейнсианского предпочтения ликвидности

2.5. Макроэкономические модели в «реальном» выражении

2.7. Модель с динамическим мультипликатором

2.8. Зависимость между сбережениями и капиталовложениями

2.9. Рынки товаров и факторов производства

3.5. Модель Филлипса с мультипликатором-акселератором

3.6. Теория роста Харрода — Домара в дискретной форме

3.7. Модель Самуэльсона — Хикса, включающая мультипликатор и акселератор

3.8. Возможность равновесия при росте в геометрической прогрессии

3.9. Распределенные капиталовложения. Дискретный и непрерывный анализ

Глава 4. Математическая часть. Линейные дифференциальные уравнения

4.2. Основные выводы; начальные условия и произвольные постоянные

4.3. Линейные дифференциальные уравнения первого порядка

4.4. Линейные дифференциальные уравнения с постоянными коэффициентами второго порядка

4.5. Линейные дифференциальные уравнения с постоянными коэффициентами произвольного порядка

4.7. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами методом преобразования Лапласа

$4.9. Применение $р = \alpha +i\omega$$

Глава 5. Математическая часть. Линейные разностные уравнения

5.2. Дискретное решение разностного уравнения Основные результаты и свойства

5.3. Линейные разностные уравнения первого порядка

5.4. Линейные разностные уравнения второго порядка

5.5. Линейные разностные уравнения общего вида

5.7. Отставания, распределенные запаздывания и мультипликатор-акселератор

5.8. Непрерывные решения разностных уравнений

Глава 6. Теория экономического цикла Самуэльсона — Хикеа

6.4. Приложение к теории экономического цикла

6.6. Колебания независимых капиталовложений

6.7. Более общая модель с распределенными капиталовложениями

6.9. Анализ распределенных капиталовложений

Глава 7. Теория экономического цикла Гудвина, Калецкого и Филлипса

7.5. Решение дифференциально-разностного уравнения

7.6. Модели Калецкого. Позднейшие варианты

7.7. Модель экономического регулирования Филлипса

7.8. Политика экономической стабилизации

7.9. Некоторые иллюстрации политики экономической стабилизации

Глава 8. Экономическое регулирование. Управляющие системы с замкнутой цепью

8.2. Представление некоторых экономических моделей в форме блок-схем

8.3. Реакция линейной модели на ввод синусоидальных изменений

8.4. Передаточная функция обратной связи

8.5. Свободные вариации в замкнутой линейной системе

8.6. Инженерный подход. Линейные и нелинейные системы

8.7. Регулирование в системах замкнутых цепей

8.8. Политика экономической стабилизации

9.2. Равновесие при неизменных коэффициентах производства

9.6. Некоторые проблемы сравнительной статики

9.8. Производственная функция как матрица

10.4. Матрица межотраслевых потоков в денежном выражении

10.7. Замкнутая система Вальраса — Леонтьева

10.9. Решение динамической системы для случая двух отраслей

Глава 11. Математическая часть. Векторы и матрицы

11.2. Линейные уравнения и преобразования

11.5. Линейные комбинации векторов. Выпуклые множества

$11.8. Сокращенное обозначение суммирования символом $\Sigma$; скалярные произведения$

Глава 12. Математическая часть. Матричная алгебра

12.2. Иллюстрация действий над матрицами

12.3. Равенства, неравенства матриц, сложение матриц и умножение матрицы на скаляр

12.7. Обратные матрицы. Величина определителя матрицы

Глава 13. Применение векторной и матричной алгебры

13.2. Система линейных уравнений и ее решение

13.4. Характеристическое уравнение квадратной матрицы

13.6. Устойчивость состояния равновесия рынка

14.2. Игра двух участников с нулевой суммой и ее платежная матрица

14.3. Математическое ожидание игры; чистые и смешанные стратегии

14.4. Минимакс, седловые точки и решения игр

$14.5. Решение для платежной матрицы $2\times 2$$

$14.6. Графическое решение для игр с платежной матрицей $2 \times n$$

14.7. Общий случай игры двух участников с нулевой суммой

15.2. Простой пример: двойственная задача

15.3. Приведение задачи линейного программирования к решению игры

15.4. Общая прямая и двойственная задачи линейного программирования

15.5. Эквивалентность общих задач линейного программирования и игры с двумя участниками и нулевой суммой

15.6. Преобразование задач линейного программирования для вычислительных операций

15.7. Некоторые свойства выпуклых множеств

15.9. Решение симплексным методом простой задачи линейного программирования

Глава 16. Программирование производственных отраслей и распределение ограниченных ресурсов

16.2. Анализ производственных отраслей: понятия и определения

$16.3. Представление \$

16.4. Заменяемость в открытой системе Леонтьева

16.5. Представление технологических возможностей

16.6. Эффективное распределение при неограниченных ресурсах первичных факторов

16.8. Эффективное распределение при ограниченных ресурсах первичных факторов

16.9. Динамическое программирование; модель роста Неймана

17.3. Предельный анализ и линейное программирование деятельности фирмы

17.5. Две иллюстративные задачи линейного программирования

17.6. Задача линейного программирования для фиксированных факторов и заданных цен на продукты

17.8. Задача линейного программирования для случая неизменной структуры спроса

18.6. Способы потребления и линейное программирование

19.2. Простой пример: укрупнение по индивидуальным потребителям

19.3. Простой пример: укрупнение по товарам

19.4. Противоречия между микро- и макросоотношениями

19.6. Суммирование по потребителям и по товарам

19.7. Общий случай: одно макросоотношение

19.8. Теория экономического благосостояния

$Приложение А. Алгебра операторов 2. Операторы $D$ и $D^{-1}$$

3. Правила применения операторных выражений к некоторым элементарным функциям

4. Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами

$5. Операторы $E$ и $E^{-1}$$

$6. Разностный оператор $\Delta$$

7. Решение линейных разностных уравнение

Приложение Б. Альб. Л. Вайиштейн. Необходимые сведения о комплексных числах
2. Алгебраические действия

3. Тригонометрическая форма комплексного числа

4. Показательная форма комплексного числа
5. Алгебраические уравнения и свойства их корней

7. Комплексное представление колебательного процесса

8. Дифференцирование, интегрирование и комбинирование колебательных процессов

Приложение В. Решения и указания к задачам и упражнениям

$4.9. Применение $р = \alpha +i\omega$$

$11.8. Сокращенное обозначение суммирования символом $\Sigma$; скалярные произведения$

$14.5. Решение для платежной матрицы $2\times 2$$

$14.6. Графическое решение для игр с платежной матрицей $2 \times n$$

$16.3. Представление \$ 16.4. Заменяемость в открытой системе Леонтьева

$Приложение А. Алгебра операторов 2. Операторы $D$ и $D^{-1}$$

$5. Операторы $E$ и $E^{-1}$$ $6. Разностный оператор $\Delta$$ 7. Решение линейных разностных уравнение

Автор: Аллен Р.

Теги: математика экономика математическая экономия

Год: 1963

Похожие

Процессы регулирования в моделях экономических систем

Нобелевские лауреаты ХХ века. Экономика. Энциклопедический словарь

Основные течения современной экономической мысли

Микроэкономика продвинутый уровень

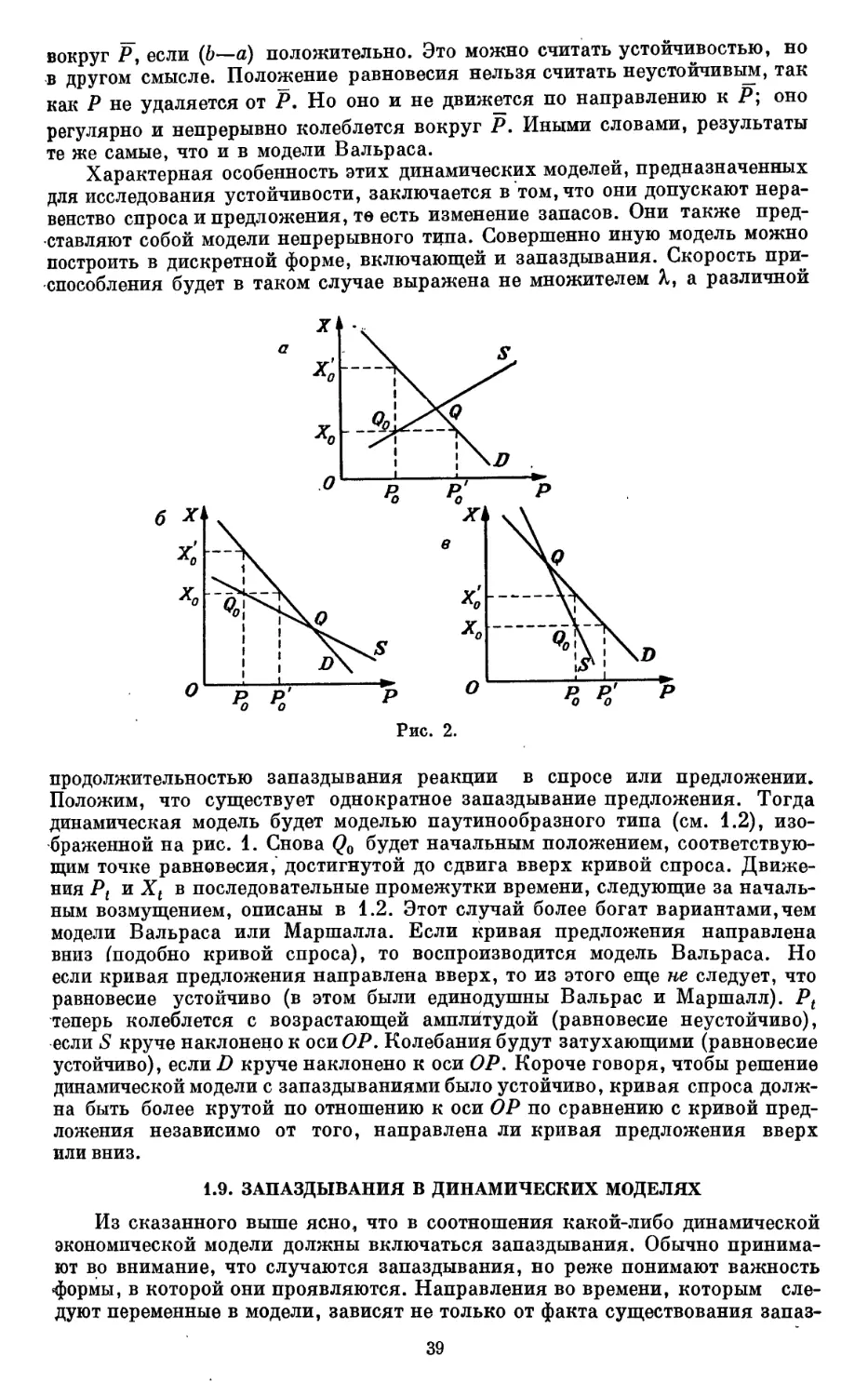
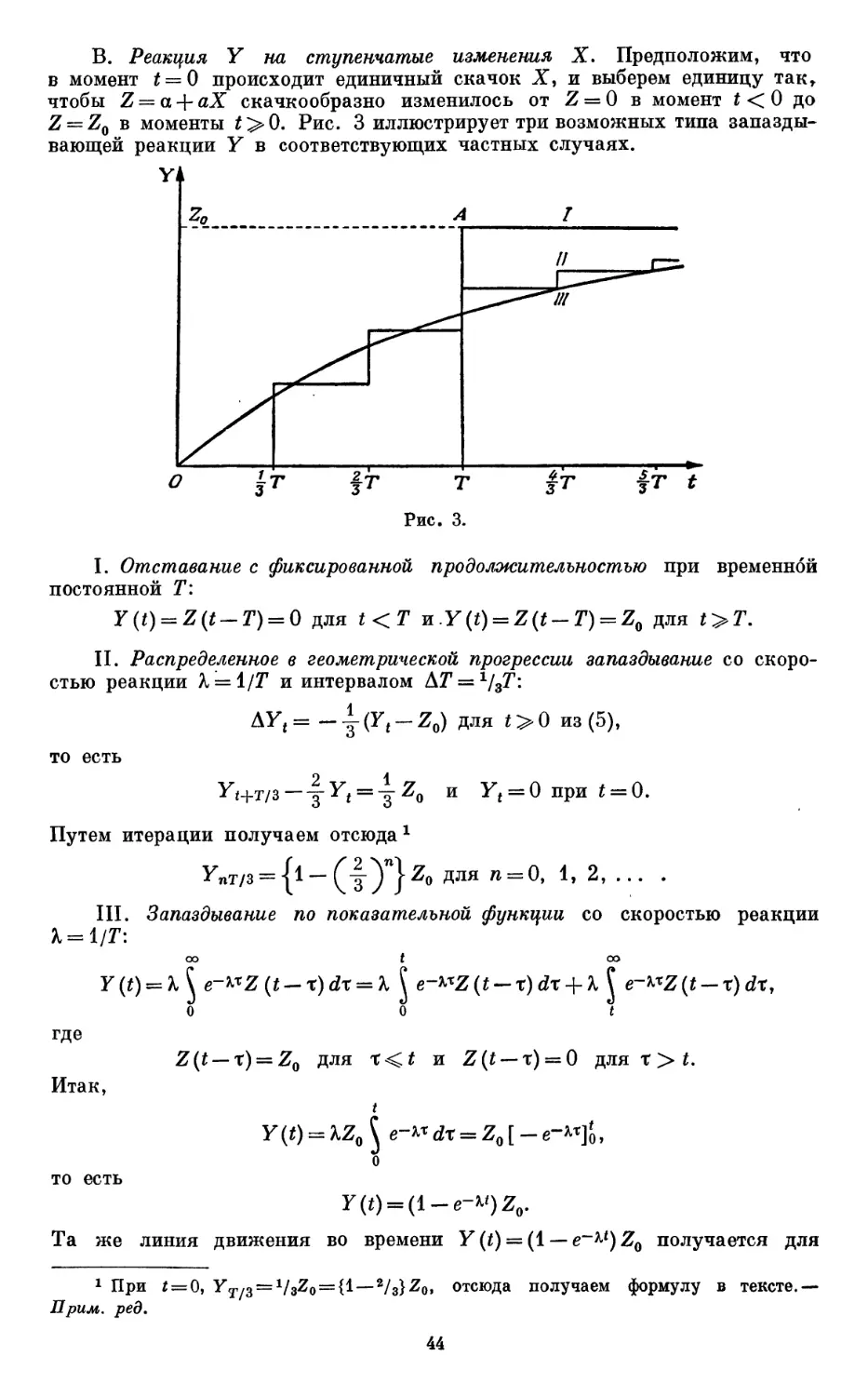
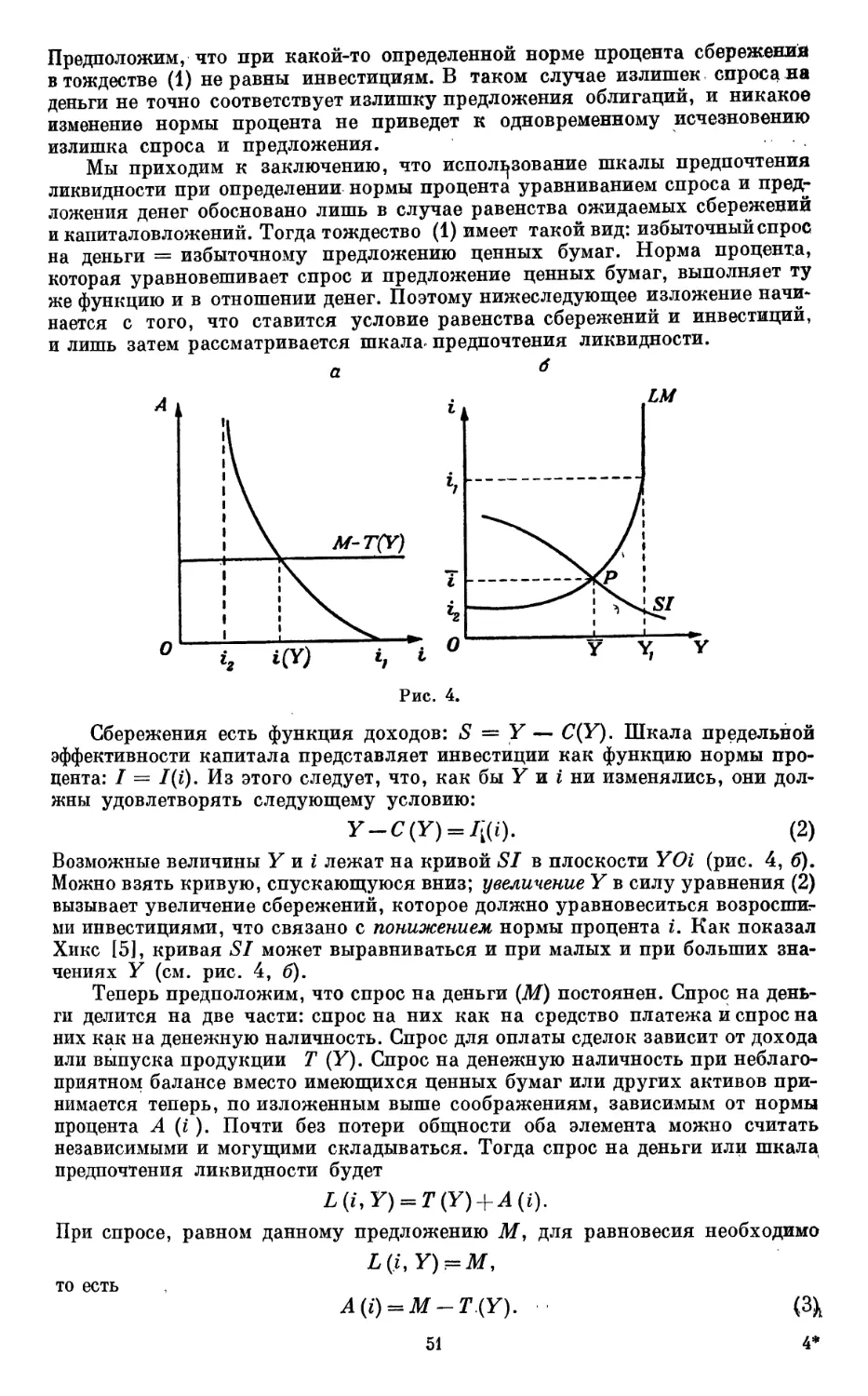
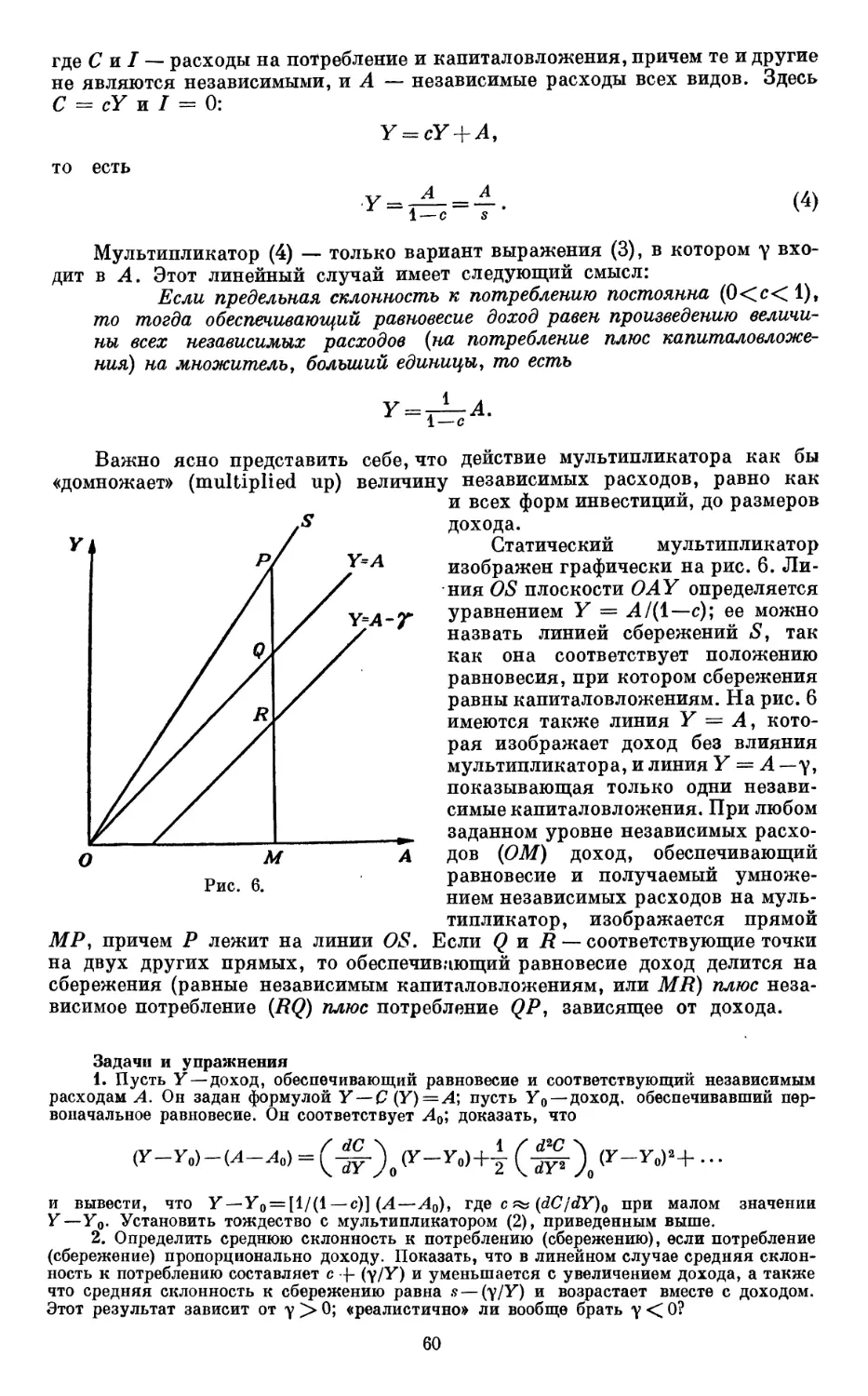
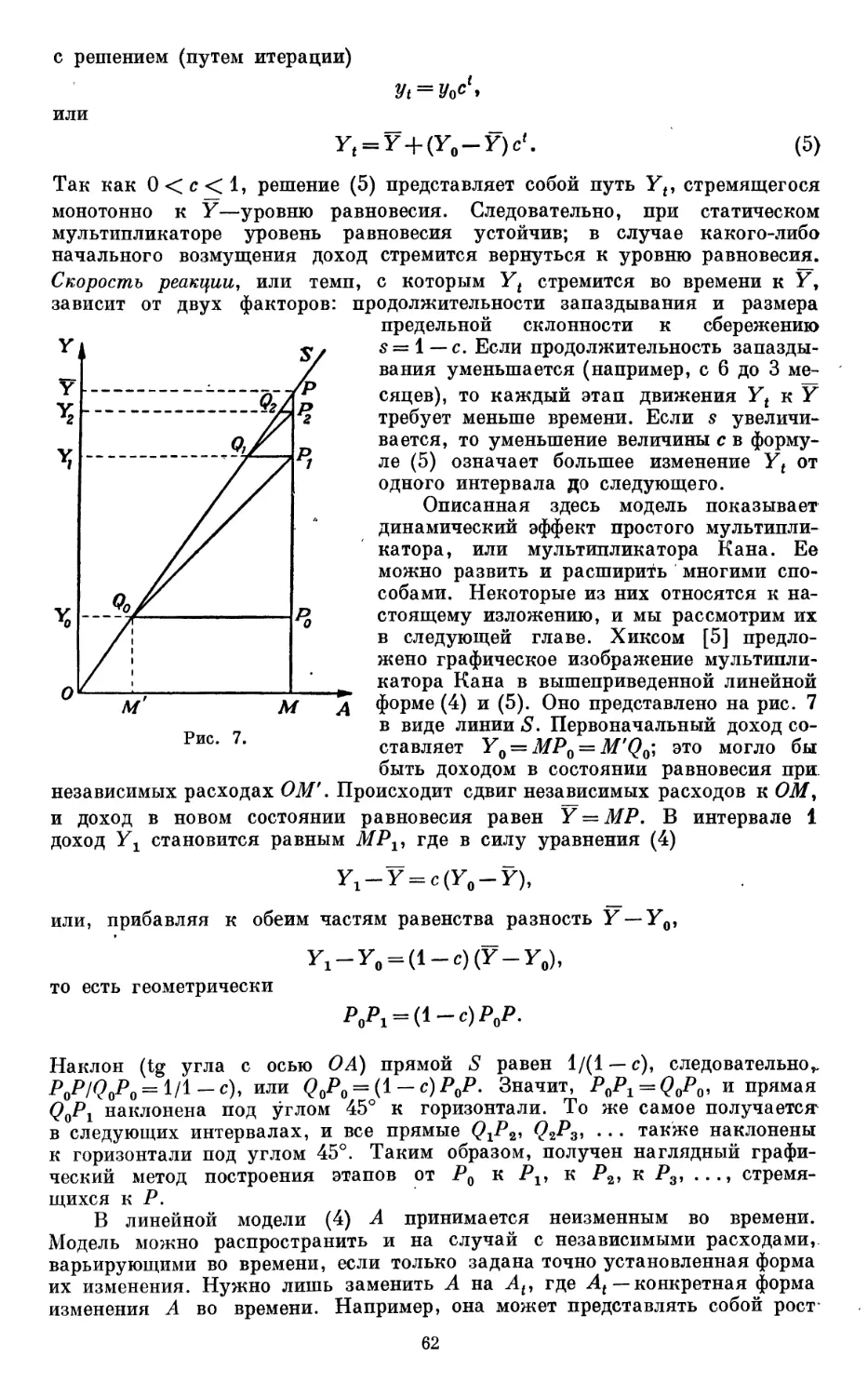
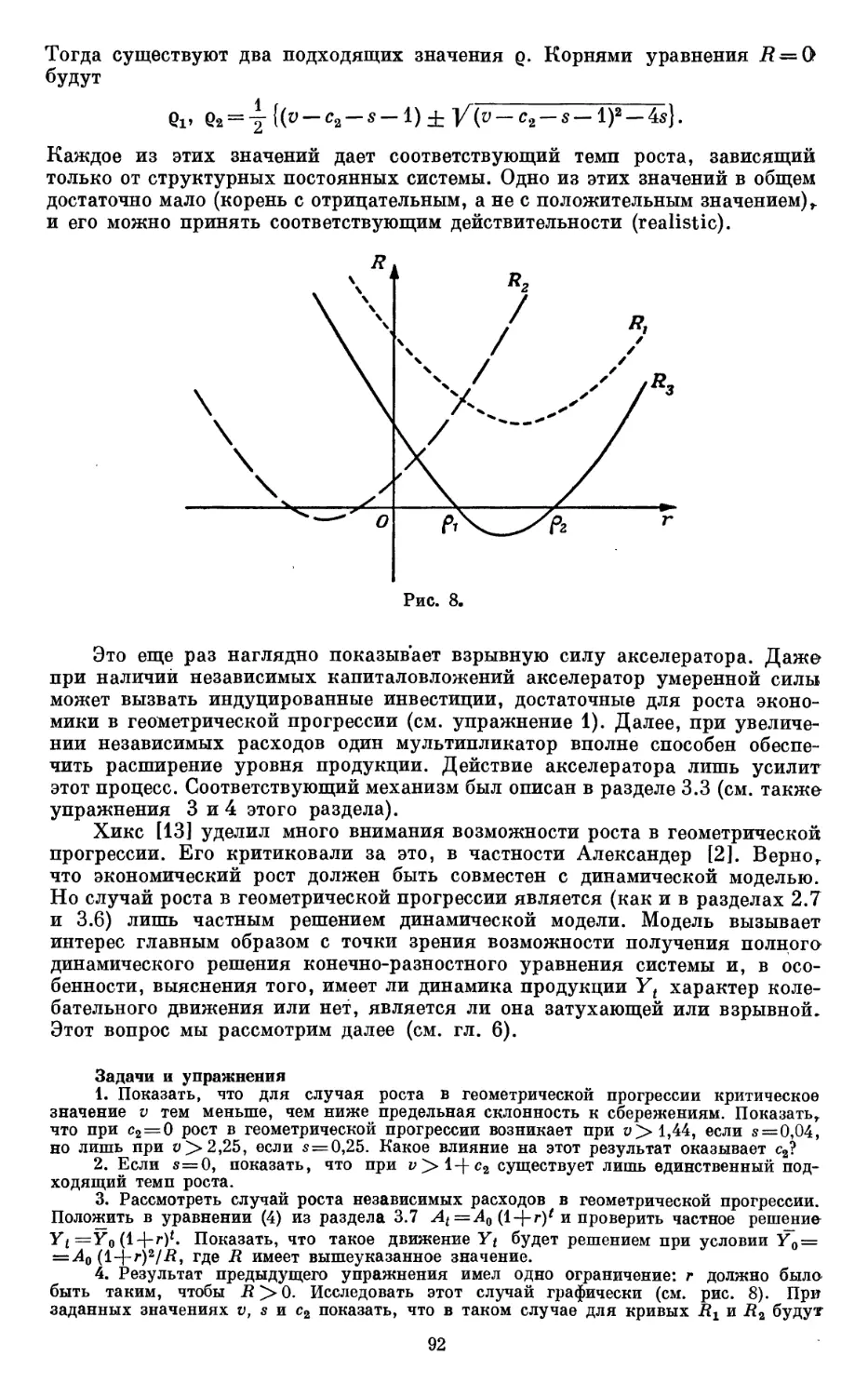
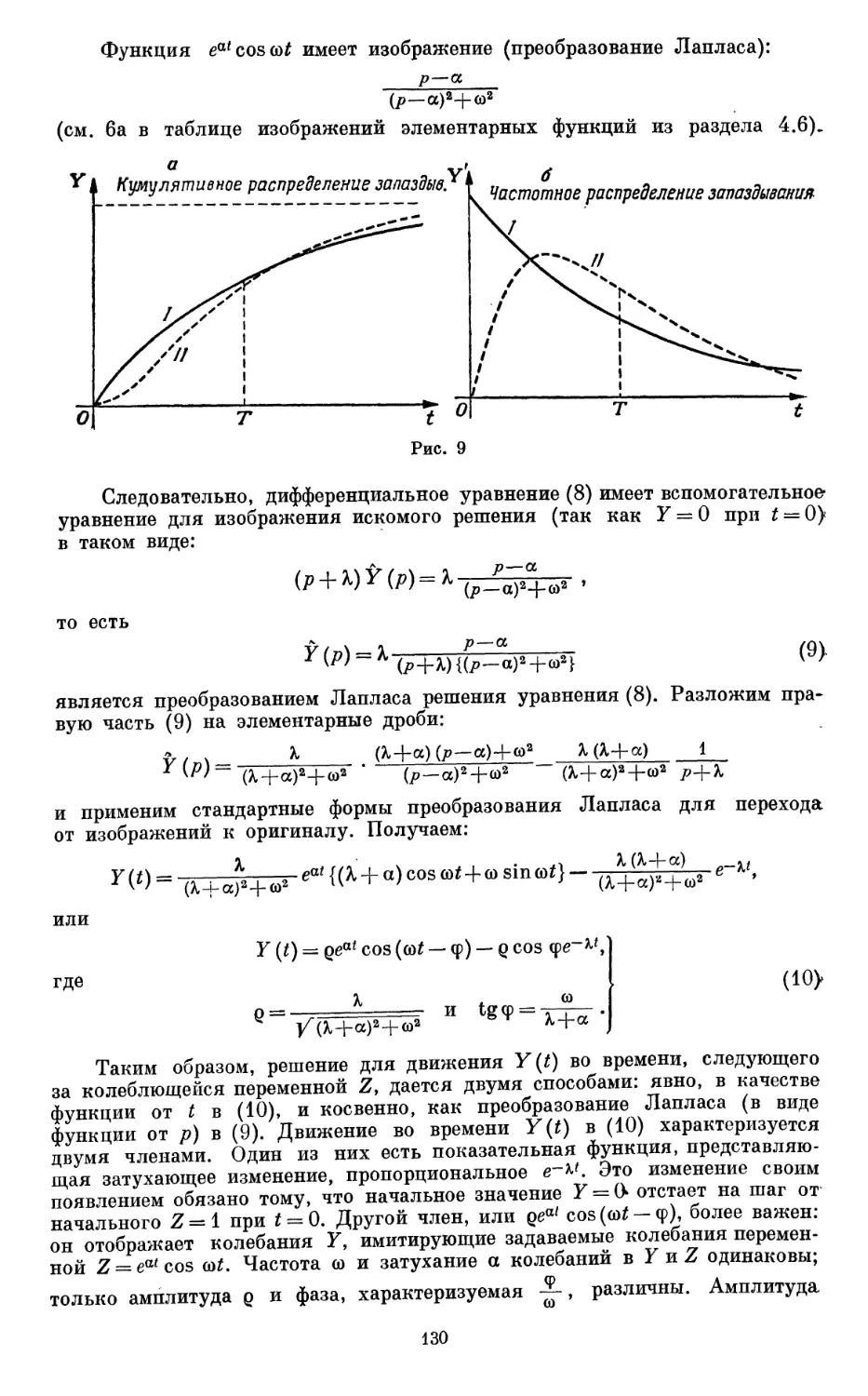
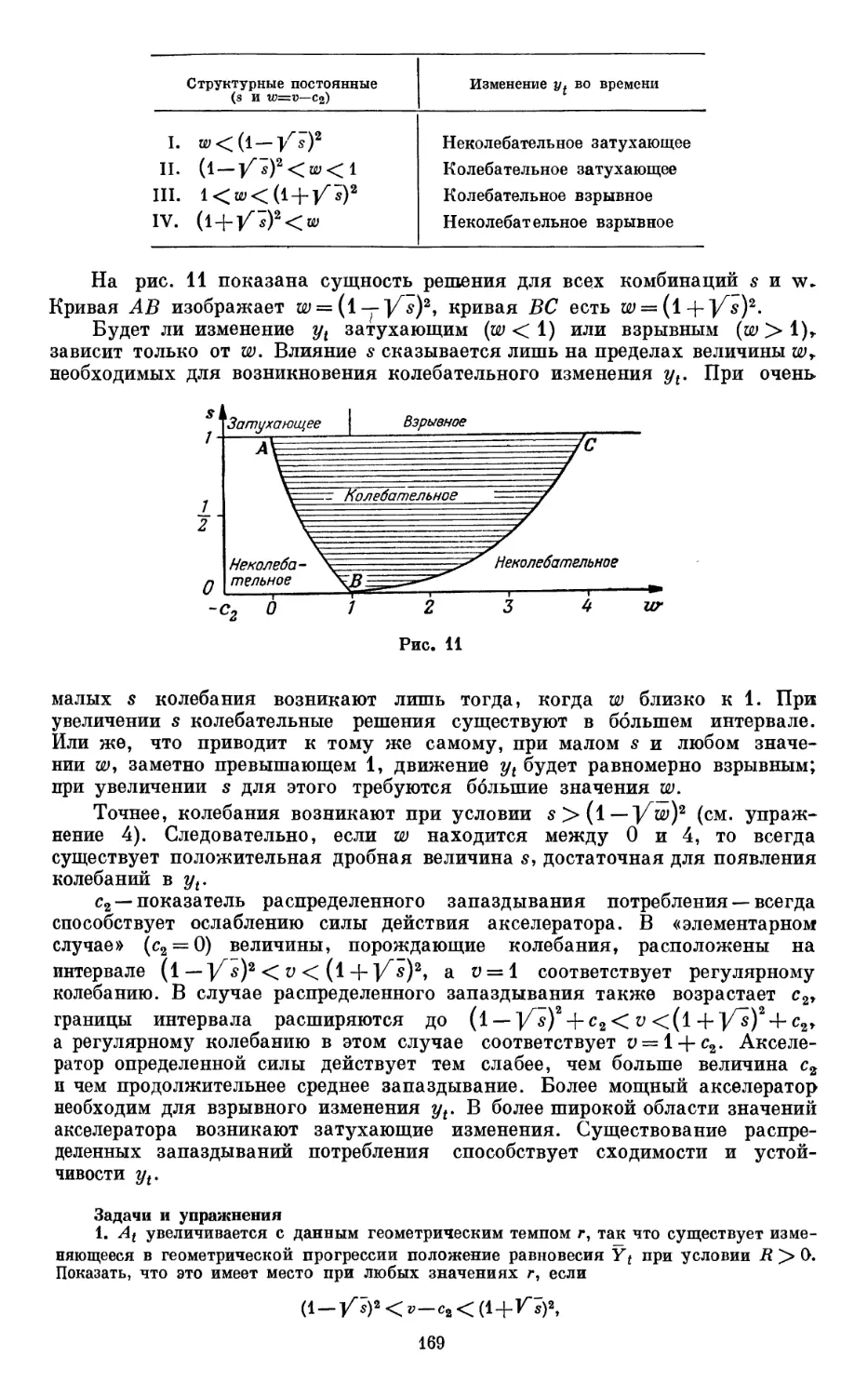
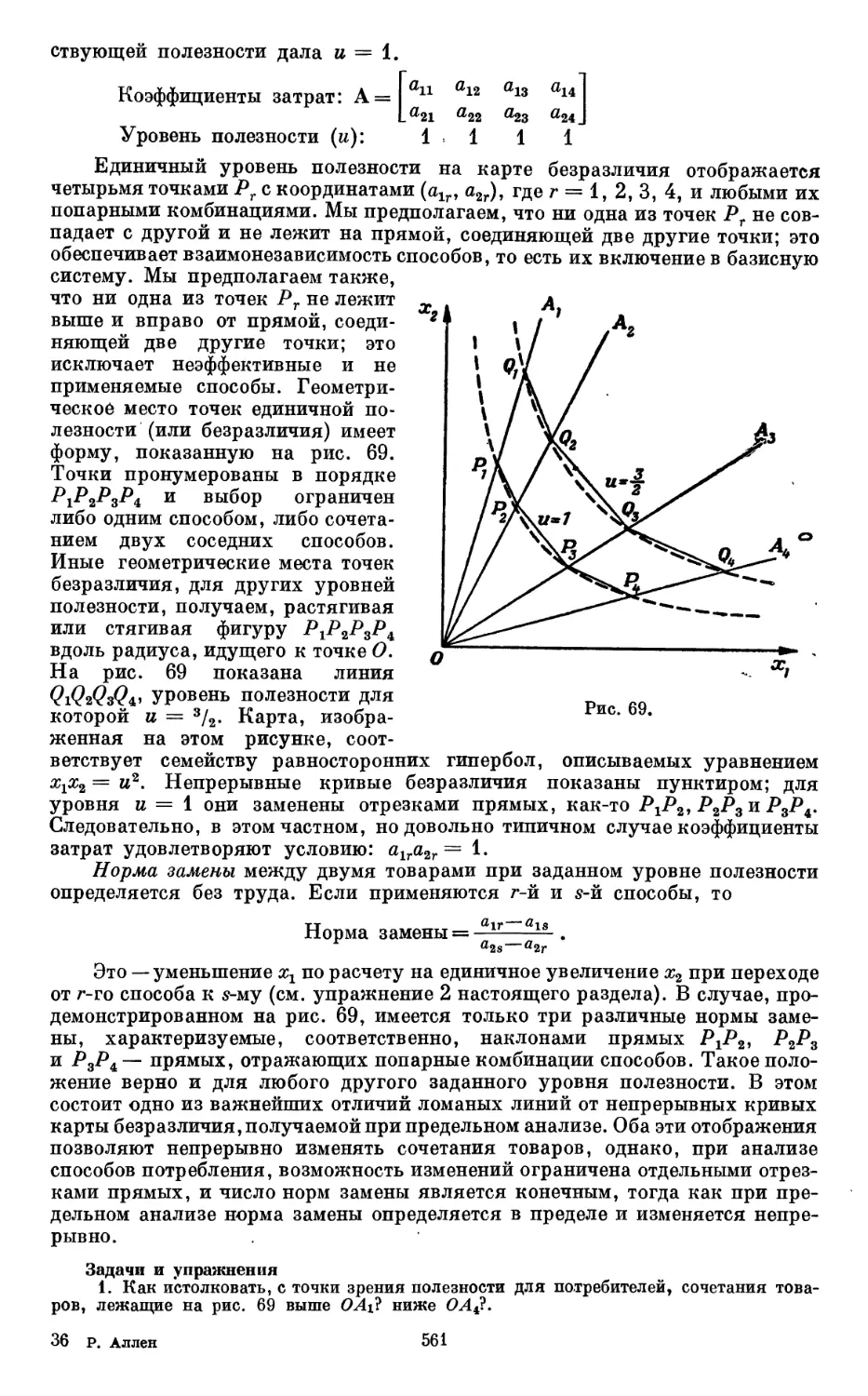
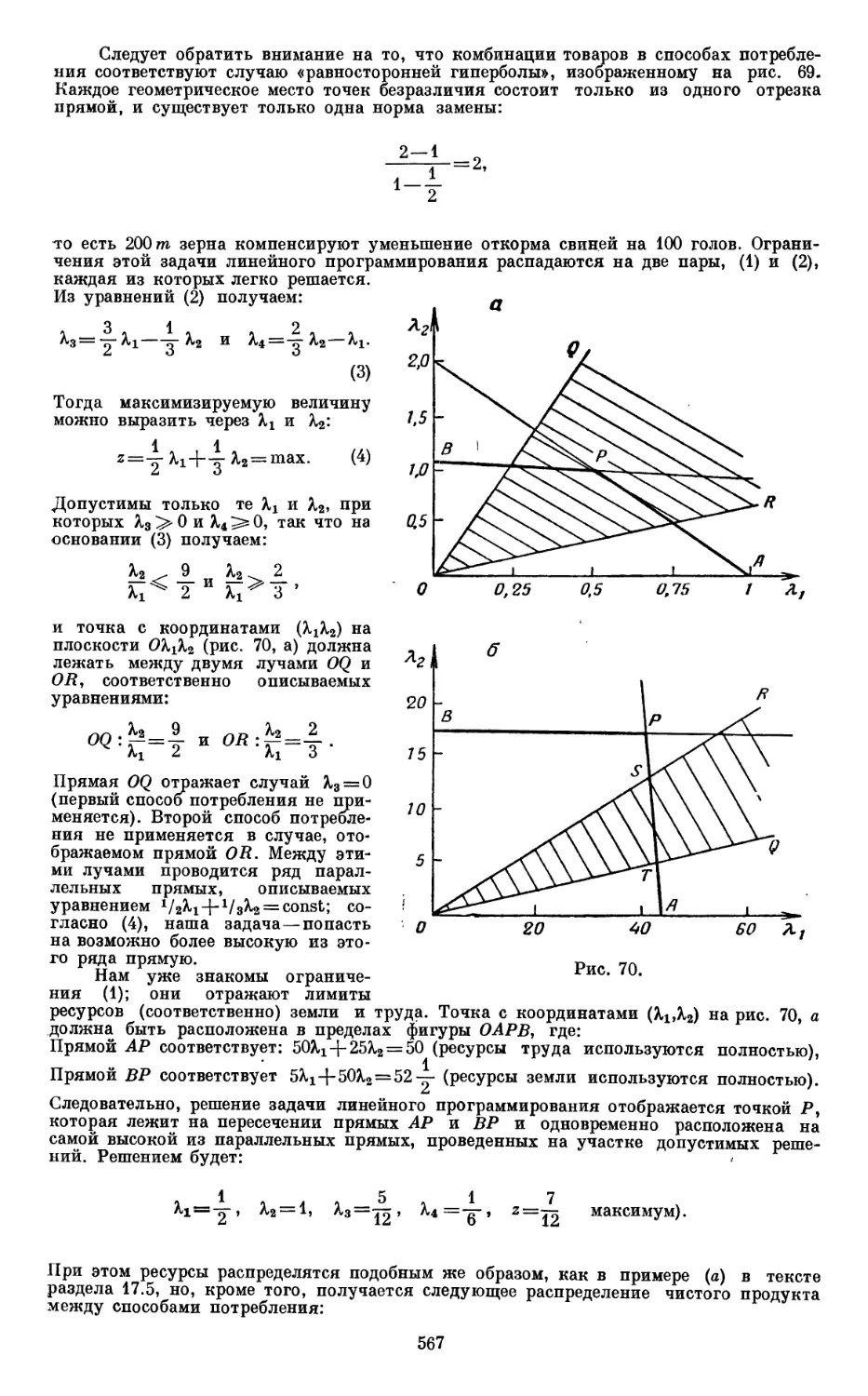
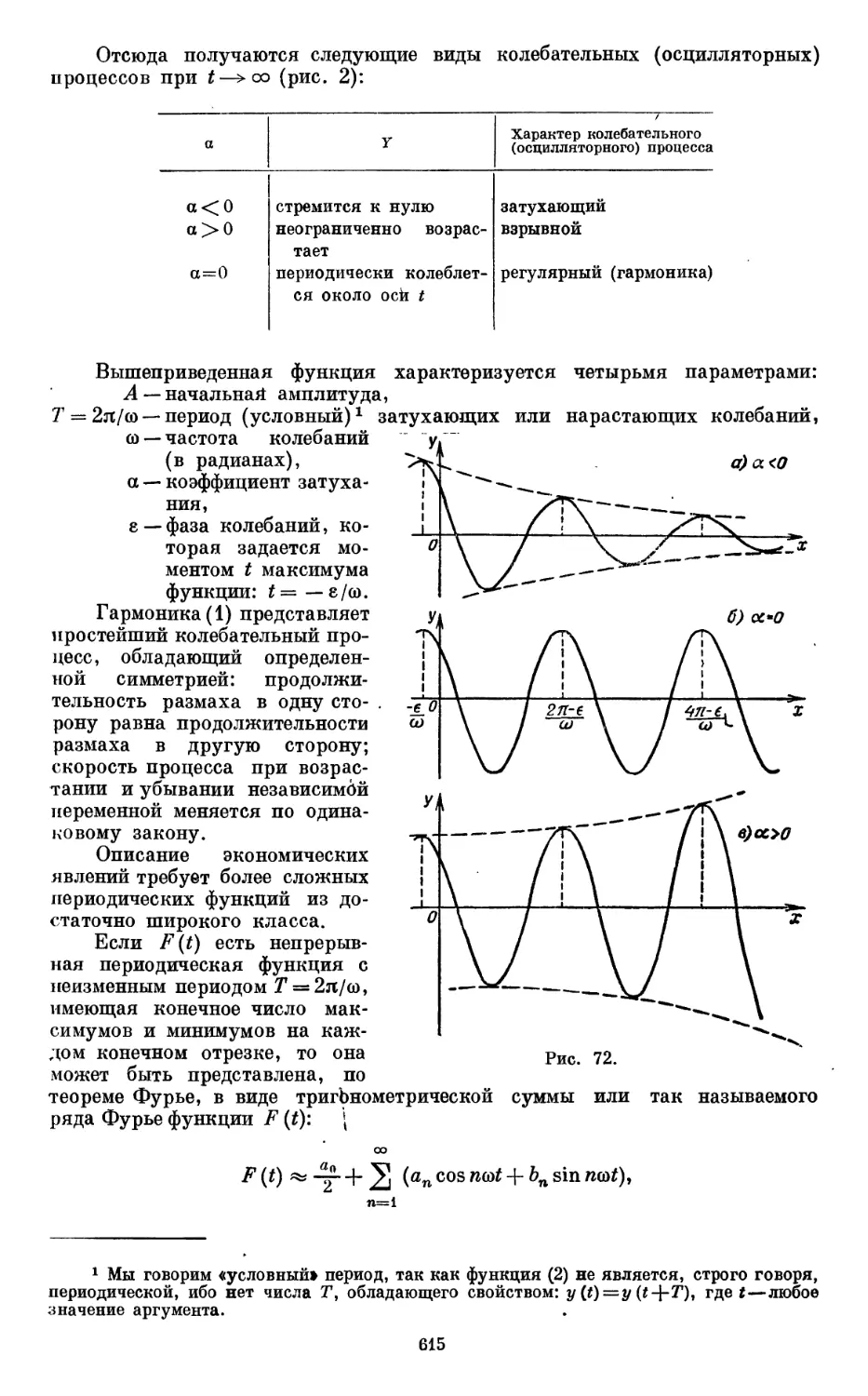
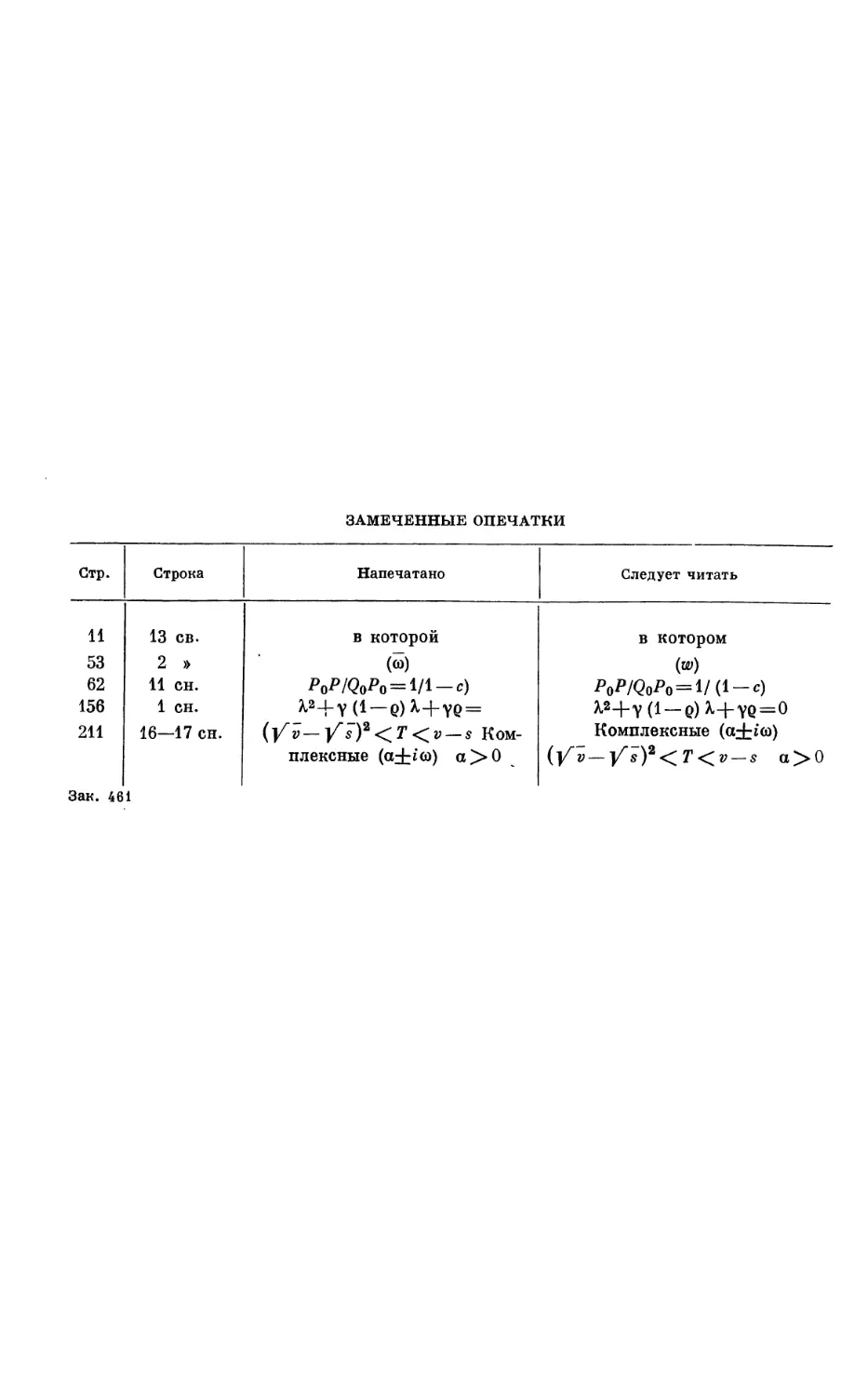
Текст

R. G. D. Allen
MATHEMATICAL ECONOMICS
SECOND EDITION
London
Macmillan and Co LTD
New York
St. Martin's Press
1960

Р. Аллен
МАТЕМАТИЧЕСКАЯ ЭКОНОМИЯ
Перевод с английского
Под редакцией и со вступительной статьей
, АЛЬБ. Л, ВАЙНШТЕЙНА
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва. 1963

АННОТАЦИЯ
Книга известного английского экономиста охватывает все основные
области приложения математики к анализу экономики.
В книге излагаются вопросы анализа системы межотраслевых связей,
применения линейного программирования для решения экономических
и производственных задач, математические методы исследования спроса
и предложения, распределения ресурсов, теории игр, перехода от
микроанализа к макроэкономике и т. д.
Рассматриваемые в книге эконометрические модели основаны на
принципах вульгарной буржуазной политэкономии. Однако методика
использования математического анализа в экономике представляет определенный
интерес для советского читателя.
Книга рассчитана на практиков—экономистов, плановиков,
статистиков — и работников научно-исследовательских институтов.
Перевод книги Р. Аллена выполнили следующие лица:
Э. Б. Ершов — глава 14
B. А. Маги — главы 10,13, 15,16, 17,18, 19
Б. Н. Михалевский — главы 1, 2, 3, 6, 7, 8, 9, введение
и предисловие автора
C. С. Шаталин —'части глав 4 и 5, полностью 11, 12
Редакция литературы по вопросам экономических наук

ВСТУПИТЕЛЬНАЯ СТАТЬЯ
Развитие экономической науки за последние четверть века проходит
под флагом мощного вторжения в нее высшей математики. Исключительную
роль математики и в других отраслях знания уже давно осознали гениальные
исследователи в области экономической науки. По свидетельству Поля Ла-
фарга, «К. Маркс считал, что наука только тогда достигает совершенства,
когда ей удается пользоваться математикой». Больше того, П. Лафарг
сообщает, что «К. Маркс написал работу по исчислению бесконечно малых,
которая, по отзыву читавших ее специалистов, имела большое научное значение».
Высокую роль математики во всех научных исследованиях подчеркивал
и В. И. Ленин. Нужно заметить, что многие из теоретических положений и
законов, выведенных в политэкономии, логически или на арифметических
примерах, можно представить в общем виде в форме математических моделей;
математически могут быть сформулированы как исходные предпосылки
и условия,* лежащие в их основе,1 так и вытекающие из них общие
математические решения. И в советской литературе уже опубликованы такие
интерпретации. Интересно также то, что и теории домарксовой классической
политической экономии (учение Кенэ, Рикардо) можно также перевести на
математический язык1.
В настоящее время наше социалистическое хозяйство нуждается в более
действенной помощи экономической науки в строительстве коммунизма.
«Создание материально-технической базы коммунизма требует постоянного
совершенствования хозяйственного руководства и планирования»
(Программа КПСС, стр. 85). К более решительному применению математического
инструментария в экономике и планировании призывают нас и руководители
/партии и правительства: «...в экономической науке и в планировании,
основанном на экономических научных исследованиях, нужно смелее и шире
переходить к использованию современной электронной вычислительной
техники и математических методов»2.
Применение математических методов в экономике и планировании
распадается на две части. Первая охватывает многие разнообразные частные
задачи, относящиеся к отдельным предприятиям и отраслям народного хозяйства,
в разработке которых математика уже привела к определенным и часто весьма
значительном успехам: рациональное распределение производственной
программы между предприятиями; рациональный|раскрой материалов; расчет
производственных циклов и заделов; оптимальный подбор оборудования
1 Математическое оформление в общем виде схем воспроизводства развертывает
В. С. Немчинов в своей книге «Экономико-математические методы и модели», М., Соц-
экгиз, 1962. Математизирование схем Ф. Кенэ проведено в]ряде работ, в том числе в
двухтомном издании, вышедшем во Франции к двухсотлетию* появления «Экономической
таблицы» Кенэ («Fr. Quesnay et la Physiocratie», Paris, 1958), а также в статье Филлипса
в «Quarterly Journal of Economics», vol. 69, February 1955. В последнем случае автор
интерпретирует схему Кенэ как простейшую систему межотраслевых связей (затраты-
выпуск).
Немецкий исследователь Г. Гейер математизирует теорию Рикардо, которую он
описывает в форме как конечно-разностных, так и дифференциальных уравнений.
2 А. Н. Косыгин, Речь на Всесоюзном совещании научных работников,
«Известия», 14 июня 1961 г. В таком же направлении высказался на этом совещании и
президент АН СССР М. В. Келдыш, «Известия», 12 июня 1961 г.

(тракторного парка и т. д.), подбор поставов для распиловки,
транспортные задачи (математический анализ грузопотоков, оптимальное
планирование перевозок), математические методы планирования массового
обслуживания, анализ межотраслевых связей и т. д. Другое направление применения
математики охватывает основные народнохозяйственные проблемы:
разработку схемы расширенного социалистического воспроизводства, темпы
развития отдельных отраслей, теоретический анализ вопросов ценообразования
и ценоустановления, пути и методы построения оптимального плана и т. п.
В отношении этих вопросов продвижение математики в экономику проходит
у нас гораздо медленнее, с большими трениями, ибо недостаточно разработана
еще теория политической экономии социализма. Немало повинны в этом
промедлении и недавние острые споры о роли и границах полезного применения
математики в экономических исследованиях и высказывавшиеся опасения
относительно того, что расширение применения математического аппарата
для анализа экономических проблем означало бы создание своеобразной
математической экономии, которая якобы сможет претендовать на замену
собой всей теоретической экономии»
Однако нужно заметить, что появление математической физики,
математической логики, статистической физики и т. п. не заменило
экспериментальной физики, классической логики, и вообще возникновение новой области
знания никогда не отметало тех основных, от которых она отпочковалась. Что
касается возможности и полезности применения в экономике математических
методов, то сам Аллен в начале своей книги (см. введение, стр. 17) ставит
вопрос об этом и остроумно отвечает, что качество пудинга познается только
при еде*
Для научного понимания значения современной математики в
экономических исследованиях следует иметь в виду ряд обстоятельств, делающих
ее применение в экономике весьма эффективным.
1. Математика вынуждает экономистов неясное содержание вводимых
ими терминов, расплывчатые выражения и многословные словоизлияния
заменять четкими понятиями, точным перечислением заданных величин,
строгой формулировкой предпосылок, условий и выводов.
2. Она позволяет путем ряда математических выкладок прийти к
математическому (количественному) выражению таких соотношений, которые
нелегко и иногда даже невозможно было бы вывести путем логических словесных
рассуждений или простых арифметических примеров.
3. Математика дает возможность установить связи между явлениями,
факторами, интуитивно не ощущаемыми и не могущими быть обнаруженными
без нее даже в самой общей форме. Например, математическое исследование
уравнений электромагнитного поля показало, что они имеют решение
колебательного характера, что, как известно, послужило основой для создания
электромагнитной теории света.
Несмотря на то что важнейшие из применяемых в настоящее время
математических методов решения экономических проблем начаты были
разработкой в СССР1 и лишь через добрый десяток лет были вновь «открыты» в США,
в дальнейшем использование современных математических методов в
экономических исследованиях продвинулось за рубежом значительно дальше,
нежели у нас. Между тем именно в социалистическом планируемом хозяйстве
применение современных математических методов должно быть весьма
эффективным и сыграть большую роль, что, впрочем, признают и наиболее
проницательные буржуазные экономисты. «...Таким образом, п шет в своей
1 Мы имеем в виду метод анализа «затраты-выпуск», отраженный в первом
«Балансе народного хозяйства СССР за 1923/24 г.», опубликованном ЦСУ в 1926 г., и метод
линейного программирования, открытый советским математиком Л. В. Канторовичем
и изложенный в опубликованной им в 1939 г. работе «Математические методы
организации и планирования производства», ЛГУ. Последняя работа через 20 лет после ее
появления издана в США как признание приоритета советской науки в разработке новой ветви
экономической науки — математической экономии.

книге Р. Аллен, линейное программирование имеет очевидное и
непосредственное отношение к экономике социализма и к планированию коллективистского
хозяйства» (стр. 469). Это он повторяет и по отношению к другим
математическим разделам: «...система межотраслевых связей, предложенная
Леонтьевым, наилучшим образом применима к народному хозяйству в целом и к
проблемам широкого масштаба, например к мероприятиям, проводимым
правительством» (стр. 512), и т. д.
Предлагаемая советскому читателю книга «Математическая экономия»
представляет собой сводку и педагогическое обобщение большого
зарубежного опыта разнообразных применений современной математики в экономике.
Автор ее, Рой Аллен (Roy George Douglas Allen), является одним из
виднейших современных английских статистиков-математиков и экономистов-
математиков.
Научная и научно-педагогическая деятельность Р. Аллена связана
с Лондонским университетом и с Лондонской школой экономических и
политических знаний, находящейся в составе последнего. С 1944 г. Аллеи является
профессором экономической статистики этого университета. Вместе с тем он
читает курс математической экономии в некоторых провинциальных
университетах, консультировал и занимал руководящие постны в центральных
статистических учреждениях Англии, а во время второй мировой войны был
представителем Англии в руководстве статистическими исследованиями
в объединенном министерстве производства и ресурсов в Вашингтоне. Аллен
является членом Совета Королевского статистического, Королевского
экономического и эконометрического обществ, Международного статистического
института и многих других научных обществ и учреждений.
В 1938 г. Аллен выпустил учебник математики для экономистов
(«Mathematical Analysis for Economists»). Эта книга, написанная очень
доходчивым языком, на хорошем математическом уровне, вся пронизанная
экономическими иллюстрациями, была очень положительно встречена научными
буржуазными кругами. Она неоднократно переиздавалась и была переведена
на ряд языков. В 1956 г. Аллен выпустил новую работу — курс
«Математической экономии». В 1957 г. издано стереотипное повторение этого курса,
а в 1959 г. вышло второе, переработанное издание — успех для Англии
немалый. В 1960 г. оно было повторено.
Книга «Математическая экономия» не есть учебник математики. Автор
излагает в ней проблемы, интересующие экономистов, он рассматривает ее
как экономический текст в математических выражениях. Однако книга
Аллена также не есть курс или систематическое изложение какой-либо
экономической теории, а представляет учебник по новой гибридной дисциплине,
четко выявившейся за рубежом в течение последних двух десятилетий на
стыке математики и экономической науки. Она в систематизированной форме
описывает и исследует методы, применяемые для математического оформления
разнообразных экономических проблем как общетеоретического, так и
частнохозяйственного порядка, с целью последующего решения построенных
математических соотношений и нахождения количественного ответа.
Аллен — буржуазный экономист. Его теоретические концепции ярко
отражены в упомянутом выше учебнике «математики для экономистов»,
в котором автор дает экономическую интерпретацию, основных
математических понятий, приемов и задач в духе англо-американской экономической
школы. •
Но математика сама по себе не может обосновать какую-либо
теоретическую концепцию, и Аллен это понимает, когда говорит (стр. 19), что математика
просто ведет от предпосылок к выводам и что последние будут верны, если
предпосылки правильны, правильность же выводов проверяется согласием их
с действительно наблюдаемыми явлениями. Но сами предпосылки или система
исходных положений, аксиом должны быть сформулированы извне. Они
должны вытекать из содержания исследуемого предмета, т. е. в данном случае
из области экономики. Поэтому острие критики математико-экономических

построений должно быть направлено на анализ правомерности предпосылок
кладущихся в их основание, на экономическую интерпретацию получаемых
каждый раз математических решений и соответствие их фактам
экономической действительности и марксистскому учению/
В отдельных случаях сам автор критически относится к исходным
положениям рассматриваемых им построений. Так, разбирая весьма спорную
концепцию известного эконометрика Робертсона о возможности измерения
полезности, если даны две аксиомы, Аллен иронически замечает, что «позиция
Робертсона может быть защитима только при слепом доверии к нему»
(стр. 556). Аллен не считает обязательным принимать основную гипотезу
теории предельной полезности о том, что «решения потребителей совместны
с принципом максимизации ожидаемой полезности». Он полагает, что можно
придумать более фундаментальную систему аксиом, дающую в результате то
же математическое решение (стр. 558). Но все же концепции и модели,
рассматриваемые в «Математической экономии», принадлежат буржуазным
экономистам, прежде всего Кейнсу и кейнсианцам, и, следовательно, Аллен
выступает в этой книге как проводник теоретических взглядов Кейнса.
Теория Кейнса неоднократно критически разбиралась и доказана ее
теоретическая несостоятельность1. Поэтому здесь нам достаточно ограничиться
немногим.
Краеугольным камнем теории Кейнса является движение народного
дохода (определяемого по конечному использованию) и тесно связанного с
доходом объема занятости. Обе эти категории рассматриваются как зависимые
регулируемые величины. Математические модели кейнсианцев строятся на
основе вводимых в экономический анализ предельных категорий:
«предельная склонность к потреблению», «побуждение к инвестированию»,
«предпочтение ликвидности», «предельная эффективность капитала» и связанные с
ними понятия мультипликатора и акселератора. Некоторые из них
представляют модифицированные варианты прежних «классических» категорий
психологического характера.
Аллен рассматривает ряд математических моделей теорий
экономического цикла, принадлежащих различным буржуазным исследователям кейнси-
анского толка. Но вместо анализа кругооборота капитала и соотношений
отдельных его частей, блестяще проведенного К.Марксом, авторы этих
моделей исследуют уравнения обмена и рыночного равновесия и оперируют
отдельными компонентами народного дохода — совокупностью доходов,
совокупностью расходов на потребление, совокупностью сбережений,
совокупными инвестициями,— устанавливая зависимость между этими категориями
в форме уравнений. Но эти уравнения не дают возможности глубоко
проникнуть в экономические процессы и неправильны по существу, ибо отдельные
переменные в этих уравнениях представляют соединение разнородных
элементов. Сумма доходов, например, объединяет и зарплату рабочих, и прибыль
предпринимателей, и доходы прочего населения. Между тем заработная
плата и прибыль антагонистичны по своей природе и ведут себя по-разному
ив процессе производства и в процессе потребления, прочие же формы дохода
(от услуг), как известно, вообще не создаются в процессе производства,
а выплачиваются из создаваемой в последнем прибавочной стоимости. Из
анализа Маркса вытекает, что исходной точкой экономического процесса
является не получение дохода и вытекающие из него сбережения, а
кругооборот капитала, который в капиталистическом обществе есть начало всех
форм дохода. Чем больше капитала вовлечено в оборот, тем большая сумма
переходит в форму товаров, необходимых для производства, тем большая
сумма зарплаты будет выплачена.
1 Из последних работ укажем две: 1) Д ж о н Итон, «Маркс против Кейнса»,-
М., 1958, и 2) содержательнаяТвступительная статья Л. Б. Альтера к книге Э. Хансена
«Экономические циклы и национальный доход», М., 1959. Обе книги выпущены
Издательством иностранной литературы.

В модели Кейнса народный доход распадается на две части: потребление-
и сбережения (У = С + ?), а сбережения S он приравнивает (в условиях
равновесия) к капиталовложениям. Последние являются независимой
переменной, воздействующей через мультипликатор снова на народный доход и
регулирующей весь народнохозяйственный процесс. Однако равенство
фактических сбережений и капиталовложений, а равно и другие принимаемые в
рассматриваемых моделях гипотезы — равенство продукции и дохода,
равенство спроса на предметы потребления и объема их производства — вообще
говоря, не реализуются в капиталистическом хозяйстве, а эти предпосылки
являются краеугольным камнем многих моделей, начиная с простейшей.
Для Кейнса суммы доходов и расходов неизбежно уравниваются, и это
отражено в моделях. Но уравнивание может происходить и происходит на разном
уровне деловой активности, например низкая склонность к потреблению
может не покрываться более высоким побуждением к инвестированию и
обратно. И тогда уравнивание наступит после и в результате значительных
экономических потрясений и кризиса.
Сам отбор переменных, включаемых в модель, зависит от исходных
предпосылок. Например, математическое выражение модели, определяющей
объем капиталовложений, основывается на том теоретическом положении,,
что этот объем является функцией предельной эффективности капитала.
Другой пример. Уровень процента, по Кейнсу, зависит от двух
факторов: от «предпочтения ликвидности» и от количества денег в обращении.
Процент изменяется в прямом отношении к степени «предпочтения
ликвидности» и в обратном — к количеству денег. В соответствии с этим и строится
математическая модель (см. 2.2 и след. разделы этой главы): вся денежная
масса М делится на две части: Т (У) — деньги, обслуживающие сделки
капиталистических предприятий, где У есть объем дохода или выпуска продукциит
и вторую часть — деньги, обслуживающие спрос в сфере биржевой
спекуляции. Последняя величина равна A{i) и зависит, следовательно, от ссудного
процента i. Увеличение А создает возможность роста кредитования
биржевых сделок, увеличивает спрос на ценные бумаги и тем самым повышает их
курс. Курс же ценных бумаг изменяется в обратном отношении к ссудному
проценту. Поэтому рост A(i) влечет за собой снижение процента, и величина
i определена, когда даны УиМ. Это выражается уравнением C) раздела 2.2.
Однако это уравнение и, следовательно, выведенная зависимость не могут
иметь места, ибо неверна исходная предпосылка Кейнса, положенная в основу
модели.
Для того чтобы критически разобрать все модели, представленные Алле-
ном в его книге, и выявить экономически несостоятельные и
несоответствующие марксистскому учению, вероятно, понадобился бы целый том. Однако
этого вовсе не требуется. Предлагаемый труд очень полезен для ознакомления
не с буржуазными экономическими теориями, а с методикой
математического оформления различных экономических гипотез, моделирования
экономических процессов и с вытекающими из них математическими решениями.
В Программе КПСС записано: «Достижение в интересах общества
наибольших результатов при наименьших затратах — таков непреложный закон
хозяйственного строительства». Выполнение же этого требует построения
математических моделей оптимального развития народного хозяйства и его
отдельных отраслей, разработки методов получения их математических решений.
Из книги Аллена советский исследователь сможет увидеть, как
модифицируется математическое построение, какие изменения надо внести в форму
и тип зависимости, когда изменяются исходные предпосылки, направленность
задачи, характер протекания процесса, и он может использовать все это при
построении моделей социалистического хозяйства уже при предпосылках,
свойственных последнему. Нас не должно смущать возможное в ряде случаев
внешнее сходство математических построений экономики социалистического
хозяйства и буржуазной политической экономии, которое вызывается только
общностью математического решения^ многих экстремальных задач. Ведь

одни и те же уравнения математической физики также описывают физические
явления разной природы или допускают различную физическую
интерпретацию.
Надо еще остановиться на характере изложения Алленом
математических частей книги. Математик par exellence (чистый математик) мог бы во
многом упрекнуть автора с точки зрения математической строгости и
последовательности изложения и нашел бы ряд погрешностей в этом отношении.
Аллеи иногда оперирует понятиями до того, как дается их строгое
определение (например, понятиями линейной зависимости и независимости).
Некоторые положения он приводит без доказательства или сначала применяет эти
положения, а доказательства приводит в другом месте. Сами доказательства
им не всегда строго формулируются. С точки зрения математика автор
иногда излишне многословен, несколько раз повторяя одну и ту же мысль,
возвращается к ней в разных местах.
Однако критика в этом направлении била бы мимо цели. Особенности
построения и изложения предлагаемой книги, могущие на первый взгляд
вызвать упреки придирчивого математика, во многих случаях свидетель-
ствуют на самом деле о большом педагогическом опыте и такте автора. Ведь
книга Аллена есть учебник «математической экономии», предназначенный
для студентов-экономистов английских вузов1. Математическая подготовка
этих студентов, конечно, не столь глубока, чтобы воспринимать абстрактное
и лаконическое, хотя бы весьма стройное и логически безупречное
математическое изложение. Нужно к тому же отметить, что математический аппарат,
который предлагает Аллен для экономических исследований, чрезвычайно
широк и разносторонен. Поэтому изложение математических построений
нужно по возможности приспосабливать к уровню математической подготовки
читателя, постепенно вводя его в круг абстрактных идей и понятий,
предварительно или параллельно конкретизируя и иллюстрируя формулируемые
определения и положения геометрическими интерпретациями, графическими
представлениями, примерами из области экономики.
Совершенная строгость и точность математических формулировок на
начальной стадии развития математического мышления у экономиста не только
не обязательна, но иногда даже вредна, ибо может заслонить от него
экономическую сущность и пути применения предлагаемых методов. Книга Аллена
должна прежде всего в максимально доходчивой форме научить экономиста
представлять себе математическое оформление интересующих его
экономических проблем и показать, как в результате решения построенных
уравнений могут быть получены количественные экономические закономерности.
И он достигает своей цели иногда за счет нестрогости доказательства или
замены последнего геометрической интерпретацией или графической
иллюстрацией. Некоторые вопросы (например, доказательство существования решений
для рассматриваемых им видов уравнений) автор оставляет совершенно в
стороне (стр. 141.и др.). Мы, как правило, не указывали и не подчеркивали
в соответствующих местах текста эту нестрогость формулировок и
упрощенность доказательств. В тех случаях, когда изложение в оригинале против
обыкновения было недостаточно подробно, мы в сносках давали пояснения,
элементарные для математика, но необходимые, по нашему мнению, для
читателя-экономиста.
Само изложение математических разделов книги развертывается Алленом
часто не в математико-логической последовательности, а в непосредственной
связи с постановкой экономических проблем. Автор сам говорит об этом во
1 По сообщению проф. Бирмингамского университета А. М. Байкова, курс
математической экономии читается на втором курсе экономического факультета этого
университета, и студенты-экономисты сдают зачет по этой дисциплине в объеме настоящей
книги Аллена.
10

введении (стр. 17). В отдельных случаях мы обращаем (в сносках) внимание
читателя на тесную связь формулировок и операций автора с определениями
и доказательствами, приводимыми только в дальнейшем тексте.
Перевод книги сделан со 2-го, переработанного издания, однако с двумя
купюрами. Во-первых, мы выпустили из математической части главу о
комплексных числах. Поэтому русский перевод Аллена содержит 19 глав вместо
20 глав английского текста. Изложение этой главы в оригинале многословно,
автор приводит в ней много материала, ненужного для понимания
дальнейших математических построений. В СССР комплексные числа и действия
над ними входят в программу полной средней школы. Для тех же читателей,
которые нуждаются в восстановлении в памяти и некотором расширении этого
раздела школьной математики, мы даем приложение Б к книге, написанное
автором настоящей статьи, в которой приводятся краткие элементарные
сведения о комплексных числах и операциях над ними в объеме, достаточном
для понимания остальных глав.
Во-вторых, мы выпустили из приложений к книге два последних раздела
приложения А и полностью приложение Б («Алгебра множеств, групп и
векторных пространств»). Выпущенный текст отсутствовал в первом, но
добавлен Алленом во втором издании. Он представляет изложение абстрактных
разделов современной высшей алгебры и по своему содержанию мало
связан с основной частью книги.
Перевод математико-экономических терминов представлял известные
трудности, ибо нет прочно установленной русской математико-экономиче-
ской терминологии. Бурное развитие применения математических методов
в экономике и планировании за последние десятилетия вызвало к жизни
большое количество новых понятий, введение которых далеко не всегда
считалось с обычным словоупотреблением, с ассоциациями, связанными с
вводимыми терминами, с необходимостью как можно точнее передать смысловой
оттенок и даже с грамматикой русского языка. Поэтому в научный обиход
проникли и неудачные термины, например равновесные цены,
располагаемые ресурсы и т. п., вместо более удовлетворительных, принятых в данном
переводе: цены равновесия, имеющиеся в распоряжении ресурсы или
наличные ресурсы. Иногда, вместо того чтобы подыскать для нового математико-
экономического понятия надлежащий русский термин, пишут просто
соответствующее иностранное (английское) слово русскими буквами. В
результате получаются такие термины, как «бихевиористические отношения» или
«бихевиористическая функция» (behavior function — функция поведения),
статистическое тестирование (statistical testing—статистическая проверка),
инверсионная матрица, которые режут слух русского читателя и менее понятны
ему, чем соответствующие английские словосочетания. Мы решительно
отказались во всех подобных случаях от русифицирования английских слов
и выбирали при переводе по возможности подходящее русское
словосочетание.
Английский термин «aggregation» понимается очень широко, именно как
всякое соединение отдельных элементов и детальных групп в более обширные
подразделения. Перевод этого понятия на русский язык англизированным
термином «агрегирование», как это часто встречается, имеет, быть может,
основание, когда речь идет об объединении разнородных элементов или
частей (агрегатов). Для тех же случаев (а их большинство), когда «aggregation»
относится к процессу объединения отдельных элементов и детальных групп,
однородных по какому-либо признаку или признакам, в более крупные
сводные деления, в русском языке существует слово «укрупнение», адекватно
характеризующее этот процесс. Поэтому в указанных случаях мы оставили
именно его в качестве точного перевода английского «aggregation». К этому
нас побудило еще и то обстоятельство, что обратный процесс — переход
от обширных групп к более детальным — будет при нашей терминологии
характеризоваться словом «разукрупнение», уже издавна вошедшим в
научный и литературный лексикон, в то время как «дезагрегирование» (desaggre-
11

gation), звучало бы совсем непривычно и неблагозвучно для русского
читателя.
Английское сочетание двух существительных, из которых первое
является определением второго (budget line, function, equation; equilibrium price,
position; problem solution и т. д.), не всегда можно и не всегда правильно
передавать прилагательным с существительным; в ряде случаев это звучит
непривычно и часто двусмысленно. Поэтому мы подобные английские
словосочетания передавали на русский язык большей частью также двумя
существительными, из которых второе играет роль прилагательного, например
«положение равновесия», «решение игры» (а не «равновесное положение»,
«игровое решение»).
Некоторые математико-экономические понятия обозначаются в русском
языке несколькими терминами или словосочетаниями, и возникал вопрос,
какое из них выбрать для перевода соответствующего английского
выражения. Так, новая переменная, вводимая в симплексном методе (slack, dummy
variable), в русском языке называется вспомогательной, свободной,
фиктивной, ослабляющей, искусственной, дополнительной, избыточной, скользя-'
щей переменной, псевдопеременной. Autonomous investment, autonomous
expenditure, induced investment могут быть переданы на русском языке чуть
ли не десятком различных терминов, и принятый нами перевод —
независимые капиталовложения и индуцированные капиталовложения — не
является единственно возможным выходом. Множественность односмысловых
терминов-синонимов, конечно, затрудняет чтение математико-экономической
литературы, а в дальнейшем грозит стать серьезным тормозом для
исследовательской работы. Поэтому мы стремились при переводе настоящей книги,
подытоживающей главнейшие направления применения математических
методов в экономике за рубежом, тщательно взвешивать различные
возможности русского перевода, учитывая не только распространенность того или
другого варианта, но и точность, однозначность смыслового содержания,
правильность лингвистического образования, соответствие русским
грамматическим формам, привычным ассоциациям и т. д.
Настоящий перевод является, конечно, лишь начальным вкладом в
установление единой общепринятой математико-экономической терминологии,
создание которой может быть лишь результатом совместной длительной
научной кооперации математиков, экономистов, статистиков и лингвистов. Чтобы
облегчить улучшение этой терминологии в дальнейшем, мы в предметном
указателе наряду с русскими даем и английские выражения.
Все примечания редакции принадлежат нижеподписавшемуся. Ряд
замеченных опечаток и прямых погрешностей в математических формулах,
выкладках, в ответах и указаниях к задачам и упражнениям были исправлены
нами без оговорок в каждом отдельном случае. Число ответов и указаний
к решению задач нами несколько увеличено в переводе, а сами указания
расширены по сравнению с оригиналом. Работы, цитируемые Алленом и
поставленные в переводе в квадратные скобки [ ], приведены в библиографии к
соответствующей главе в конце книги.
Алъб. Л. Вайнгитейн

ПРЕДИСЛОВИЕ
К ПЕРВОМУ ИЗДАНИЮ
Эта книга появилась на основе трех направлений развития
экономической мысли. Когда в начале 30-х годов я впервые заинтересовался
математической экономией, мне представлялось, что главное —это
ознакомить читателя с основами математического анализа. Для этой цели я
в 1938 г. написал учебник «Математический анализ для экономистов»
(«Mathematical Analysis for Economists»), Я не решился ввести в него
высшую алгебру и не использовал аппарат комплексных переменных. Я считал,
что такого рода разделы должны быть написаны теми, кто специально
применяет их в экономических исследованиях. Но впоследствии во многих
разделах математической экономии стали широко применяться матричная
алгебра, векторный анализ, комплексные переменные, операторы и тому
подобные математические методы. Между тем пригодного | для экономистов
учебника по высшей алгебре и операторным методам, с моей точки зрения,
не было.
Второе направление развития экономической науки за последние
20 лет —рост эконометрии. Он происходил столь быстро, что, по моему
мнению, возникла некоторая опасность серьезного отставания в развитии
необходимой экономической теории; последняя должна формулироваться
так, чтобы она имела эконометрический смысл и для статистика. Такого рода
формулировки экономической теории должны были иметь максимально
простую математическую форму.
Наконец, изменение направления экономической мысли за последние
20 лет породило и серьезные сдвиги в соотношении различных частей
экономической теории. Частично, но отнюдь не полностью, это — результат работ
Кейнса. Я полагаю, что теперь возникла действительная необходимость в
некоем синтезе «новых» направлений в экономике — беспристрастном
рассмотрении объема и форм экономической теории.
Эти соображения и привели меня к выводу, что самое лучшее —
написать совершенно новый учебник по экономической теории в ее
математической форме, а не расширять мою книгу 1938 г. Настоящая книга не
является ни учебником математики для экономиста, ни учебником эконометрии.
Ее цель заключается в достаточно систематическом изложении некоторых
наиболее важных и простых разделов математической экономии. Главная
трудность состояла в выборе наиболее важного из широкого круга
экономических проблем — в том, чтобы сделать книгу достаточно современной и в то
же время сохранить умеренный объем ее. Я думаю, что книга была бы
слишком большой, даже если бы я включил в нее лишь то, что представляет
особый интерес лично для меня. И я могу лишь принести извинения антолога
всем, кто интересуется иными темами или другими методами подхода к
проблемам математической экономии.
Я уверен, что книга получилась бы совершенно иной, если бы я писал
ее пять лет назад. И я не могу предсказать, сколь долго она будет, хотя бы
приблизительно, отвечать современным требованиям. Мне кажется, однако,
что многие методы, которые я пытаюсь описать, не потеряют своего значения
и в ближайшем будущем. Эти методы сейчас еще относительно новы, и
нужно время для того, чтобы они сформировались окончательно и были органи-
13

чески впаяны в общее содержание экономической теории. Более того, мой
основной принцип заключался в том, чтобы от начала и до конца оставаться
как можно ближе к реальным экономическим проблемам. Я стремился
только упростить их в такой мере, в какой экономист может это сделать, и облечь
их в математическую форму не более чем средней трудности. Я надеюсь, что
такой подход будет отвечать запросам многих экономистов в настоящее
время и в будущем.
Я не мог бы написать такого рода книгу без помощи столь большого
числа моих коллег, что лишь части из них я в состоянии выразить здесь
признательность. Я благодарен за постоянную помощь и советы в особенности
проф. Лионелю Роббинсу, проф. Джеймсу Миду, м-ру Дэвису Ноксу, м-ру
Ральфу Тёрви. М-р В. М. Горман и д-р Ф. X. Ган из Бирмингамского
университета любезно согласились прочесть всю рукопись. Они сознавали
необходимость такого рода книги и вполне могли бы сами ее написать. И тем не
менее они остались в стороне и позволили мне быть единственным автором.
Кроме того, я признателен д-ру Е. Мейкоуэр, д-ру Дж. Мортону и д-ру
А. В. Филлипсу. Читатель это поймет, когда прочтет середину и конец книги.
Р. Дж. Д. Аллеи
Лондонская экономическая школа

ПРЕДИСЛОВИЕ
КО ВТОРОМУ ИЗДАНИЮ
Я рад представившемуся случаю внести некоторые изменения в книгу.
Во-первых, я исправил ошибки и опечатки, которых, быть может, слишком
много было пропущено мной при правке корректуры первого издания. Во-
вторых, я сделал многочисленные изменения в терминологии и в изложении
текста. Я надеюсь, что это сделает аргументацию более четкой и ясной.
В-третьих, я включил дополнительные ссылки на литературу, главным
образом на книги и статьи, появившиеся после 1956 г. В течение 1957 и 1958 гг.
появилось около полдюжины выдающихся работ: Гольдберг, «Введение
в конечно-разностные уравнения» A958); Мер док, «Линейная алгебра для
студентов последнего курса» A957); Кемени, Снелл и Томпсон, «Введение
в конечную математику» A957); Тролл и Торнхейм, «Векторные
пространства и матрицы» A957); Льюс и Райфа, «Игры и решения» A957I; Дорфман,
Самуэльсон и Солоу, «Линейное программирование и экономический
анализ» A958).
Ни одну из этих работ с математической точки зрения нельзя назвать
очень простой, они являются книгами либо средней трудности, либо же
рассчитаны на высококвалифицированного читателя. И тем не менее
знакомство со всеми ними необходимо для квалифицированного специалиста по
математической экономии.
Наконец, я полностью переработал некоторые важнейшие разделы:
1.9 и 4.8 — о запаздываниях в динамических моделях; 2.3, 9.3, 16.1
и 16.9 — об общем экономическом равновесии и 15.2 — о двойственной
задаче линейного программирования. Значительная часть глав о векторах и
матрицах была коренным образом переделана.
Я расширил приложение А о «практической» математике операторов
и линейных систем.
Я выражаю благодарность ряду читателей, приславших письменные
пожелания. Я особенно признателен за предложения, сделанные Свеном
Дано из Копенгагенского университета; Люсьеном Фолдсом из Лондонской
экономической школы; Морисом Мак-Манусом из Бирмингамского
университета и Школы руководителей предприятий в Миннесоте; Петером Ныомэном
из Вест-Индского университетского колледжа и Чиро Тогнетти из Центра
экономических и эконометрических исследований в Генуе.
Р. Аллен
Калифорнийский университет,
Беркли, январь 1959 г.
1 См. Льюс и Райфа, Игры и решения, Издательство иностранной
литературы, М„ 1961.

ВВЕДЕНИЕ
Вопрос о возможности и необходимости применения математики в
экономике обсуждался уже много раз. Но качество пудинга познается
только при еде. Прочитав нижеследующие главы, всякий экономист должен сам
решить, помогает ли ему математическое изложение некоторых важнейших
экономических теорий в оценке этих теорий и в разработке методов их
практического приложения.
Цель книги сводится к тому, чтобы дать краткое и в известной мере
синтезированное изложение того, что написано специалистами в области
математической экономии относительно некоторых экономических теорий.
Книга носит вводный, но не вполне элементарный характер. Она обращена
к экономистам, а не к математикам, но ее чтение требует известной
математической подготовки.
Принятый в книге порядок изложения материала по экономике может
показаться необычным; он представляет собой отступление от
традиционного подхода. Цель заключается в математической трактовке тех
экономических проблем, которые необходимо знать изучающим экономику. Эти
экономические проблемы в известной мере отражают реальные факты
экономической деятельности. Мы отправляемся от совсем простого к более
трудному. Простота того, что можно расплывчато назвать динамической
макроэкономикой, с которой мы начинаем здесь изложение, объясняется тем, что
она рассматривает лишь несколько основных синтетических категорий.
Приближение к реальным экономическим проблемам осуществляется лишь
благодаря динамическому подходу. Проблемы принятия решений
потребителями, предприятиями или инстанциями, составляющими прогнозы для
народного хозяйства, предполагают включение целого ряда переменных.
Поэтому такого рода проблемы целесообразнее рассмотреть позднее.
Материал в книге излагается не по возрастающей сложности
применяемого математического аппарата. Это учебник по экономике, а не по
математике. Лишь в редких случаях порядок изложения материала зависит от
применяемого математического инструментария. Предполагается известной
математическая техника, изложенная в работах Аллена [2] и Тинтнера [13].
Она охватывает основы математического анализа и некоторые элементы
алгебры и геометрии. В данной книге основная уступка математическим
требованиям заключается в том, что в соответствующих местах —'¦ за счет
нарушения логической последовательности экономического изложения —
вводится более сложный математический инструментарий.
Далее, эта книга посвящена экономической теории, а не прикладной
экономике или эконометрии. Иногда, конечно, изложение неизбежно касает-
17

ся эконометрии, поскольку основное внимание все время уделяется
экономическим теориям с некоторым приложением их к реальным задачам. Автор
пытается так изложить экономические теории, чтобы их можно было
проверить на фактических данных. Однако он никоим образом не делал этого
всегда настолько подробно, чтобы статистик мог прямо приступить к
расчетам. В самом деле, авторы некоторых рассмотренных в книге методов
экономического анализа с самого начала предназначали их для немедленного
приложения к экономическим расчетам. Таковы работы Леонтьева [6, 7],
Купманса [5] и, быть может, также теории экономического цикла Хикса [4],
В этой книге рассматриваются лишь полностью детерминированные модели;
эконометрическое же исследование обычно требует введения в модель каких-
то стохастических элементов.
В очерченных таким образом общих рамках изложение материала
достаточно последовательно. Изложение элементов теории динамической
макроэкономики (гл. 1—3) обусловливает необходимость использования
дифференциальных и конечно-разностных уравнений, а для описания
колебательных движений — комплексных переменных и векторов (гл. 4, 5). На этой
основе становится возможным изложение некоторых наиболее
разработанных теорий экономических циклов, которое подводит к коренным проблемам
экономического регулирования (гл. 6—8). Затем излагается анализ общего
экономического равновесия в моделях Вальраса и Леонтьева (типа баланса
затрат — выпуска продукции). Ему посвящены главы 9 и 10. Здесь
обнаруживается потребность в изложении некоторых элементов векторного анализа
и матричной алгебры (гл. 11—13). Оказывается также, что теория игр имеет
значение для анализа экономических проблем (гл. 14). После этого
становится возможным изложение линейного программирования и теории решений
(гл. 15, 16) с приложением их, в частности, к теории поведения предприятия
и потребителя (гл. 17, 18). Заключительная глава посвящена некоторым
проблемам укрупнения и экономики благосостояния (гл. 19).
Из содержания глав будет видна тесная связь предлагаемой книги
с работами некоторых экономистов англо-американской школы: Хикса
и Самуэльсона, Хансена и Харрода, Леонтьева и Купманса и более молодых
авторов — Варна, Бомоля, Домара, Дорфмана, Дьюзенберри, Гудвина,
Клейна, Мейкоуэр, Нортона, Филлипса, Солоу и Тёрви. Мы отмечаем это не
в порядке оправдания, а считаем своим долгом, ибо с работами именно этих
экономистов хорошо знаком автор настоящей книги и именно о них помнит
большинство читателей. Возможно, что название настоящей книги может
вызвать недоумение, поскольку перечисленные главы освещают не столько
математическую экономию в целом, сколько лишь некоторые наиболее
интересные в настоящее время экономические теории, изложенные в математической
форме экономистами англо-американской школы.
Из перечня глав виден также крайне ограниченный круг
рассматриваемых экономических теорий. В общем ничего или почти ничего не говорится
о теории ожиданий, о международной торговле или проблеме отраслевого
анализа. Но более глубокое размышление покажет, что, хотя
рассматриваемые в книге проблемы ограничены, взятые в целом они занимают
центральное место в общей системе экономической науки. Другие проблемы, например
анализ ожиданий или международной экономики, являются их производ-
18

ными. Более того, анализ экономических циклов и экономического
регулирования (гл. 6—8), линейное программирование и теория решений (гл. 15—
18) являются результатом работ, проведенных главным образом после
второй мировой войны. Они должны занять центральное положение в области
экономической теории, и с их целями должны быть по крайней мере знакомы
все экономисты.
В заключение следует подчеркнуть, что математическая экономия
представляет собой прикладную математику: она воплощает союз между
математикой и экономикой. Сколько-нибудь интересные результаты в
области математической экономии может дать лишь экономист, использующие
математический инструментарий. Это относится и к прочим областям
приложения математики, например к инженерному делу. В самом деле,
экономист может многому научиться у инженера: как способам использования
математических методов, так и умению формулировать технические проблемы,
Довольно широко распространены неправильные представления о
сущности математики и методах ее приложения. Иногда рассматривают чистую
математику как своего рода «язык», подразумевая при этом, что его легко
перевести на обычный. Такое представление абсолютно неверно.
Математика представляет собой скорее специальную форму логики, рассуждения.
Математические доказательства могут совершенно не поддаваться «переводу»,
хотя их исходные предпосылки и получаемые выводы могут и должны
излагаться в «литературной» форме.
Далее, перенесение центра тяжести при изучении математики на
«доказательства» и «что и требовалось доказать» в конце изложения создает
представление, что чисто математически можно доказать какие-то теории. В
действительности это совершенно невозможно. Математика просто ведет от
предпосылок к выводам, но сами эти предпосылки могут быть любой совместной
системой кем-то сформулированных аксиом. Теории возникают лишь иа
особого содержания предмета независимо от того, идет ли речь об экономике
или электротехнике. Так обстоит дело и в прикладной математике.
Следовательно, теоретические концепции облекают в плоть и кровь
первоначальные предпосылки, и таким же образом обстоит дело при логической или
математической интерпретации выводов. Не допуская логической ошибки,
можно сказать, что выводы будут верны, если предпосылки правильны. Но
это не является доказательством какой-либо теории ни в экономии, ни в
какой-либо другой области знаний. Теории проверяются фактами: либо
проверяются предпосылки, либо же, что бывает чаще, — выводы. Проверка
теории может окончиться тем, что последняя будет отвергнута как не
соответствующая фактам. Но такая проверка никогда не может служить
«доказательством» теории, а может привести лишь к предварительному принятию
этой теории как не противоречащей фактам. Поэтому математическую
экономию лучше всего рассматривать как процесс выведения следствий из
специфической системы совместных аксиом экономического содержания.
Испытание системы состоит в получении следствий из аксиом, а не в установлении
обоснованности теории.
Но если математика есть лишь форма логического рассуждения, то
может возникнуть вопрос: зачем применять математику, которую понимают
немногие, вместо общедоступной логики? Это лишь вопрос эффективности,
19 2*

подобно тому как предприниматель решает применять землеройные машины
вместо кирки и лопаты. Часто проще пользоваться киркой и лопатой, и всегда
мыслимо с их помощью выполнение той или иной работы. Но столь же часто
механическая лопата экономичнее. Математика является «механической
лопатой» логического мышления; в одних случаях ее выгодно использовать,
в других — нет. Дело в том, что экономические факты чрезвычайно
сложны, и можно ожидать, что «механическая лопата» математики будет
наиболее эффективным способом их изучения. Математическая форма обычно
надежнее для максимального приближения теории к фактам, для
наименьшего упрощения действительности. Любому экономисту, пытающемуся
построить теоретическую модель, обобщающую конкретные факты,
рекомендуется сделать это в строго математической форме. В противном случае он
рискует потерпеть неудачу либо по меньшей мере упустить важные частные
случаи или возможности и затруднить эмпирическую проверку своей модели.

ГЛАВА 1
ПАУТИНООБРАЗНАЯ МОДЕЛЬ И ДРУГИЕ ПРОСТЫЕ
ДИНАМИЧЕСКИЕ МОДЕЛИ
1.1. ОБОЗНАЧЕНИЯ
Экономическая наука имеет дело с количествами товаров или факторов
производства и их ценами. Товары и факторы производства покупаются
и продаются на рынках. На каждом рынке одна группа лиц или организаций
покупает, а другая продает. В этой главе рассматривается рынок какого-
либо отдельного фактора производства или товара и только одно
агрегирование — объединение покупателей в одну группу и продавцов в другую.
Дальнейшее объединение разных факторов производства или товаров и на
различных рынках будет проведено в последующих главах. Такое
агрегирование выдвигает проблемы оценки, а также суммирования произведений
количеств на цены. Поэтому в первоначальном анализе лучше отказаться от
такого типа объединения.
В модели одного рынка переменными будут цены и количества
покупаемых и продаваемых товаров (спроса и предложения). Обозначим их
прописными буквами, например цену товара через Р. Обычно, в задаче ищутся
значения, при которых достигается равновесие. Такие величины будем
обозначать черточкой над прописной буквой, например Р — цена в условиях
равновесия. Строчными буквами обозначаем отклонения от значений равновесия,
например отклонение цены от ее значения в условиях равновесия р=Р—Р.
Переменные должны отражать изменение во времени. В дискретном
анализе последовательные интервалы времени обозначаются /=0, 1, 2, ..., ty
а соответствующие значения переменных — нижними индексами (например,
значения цены — через Ро, Р19 ..., Pt, ...). Так мы поступаем в случае
отсчета ряда интервалов от начального момента. Но легко пойти и в
обратном направлении. Если t — данный момент времени, то (t—1) —
предыдущий, а (?—2) — предшествующий по отношению к первому и т. д. — до
начального момента 0. Цена в данный момент времени будет Pt, в
предыдущий период Pi_1 и т. д. — до начальной цены Ро.
Другой возможный подход основан на непрерывном анализе, в котором
время4изменяется непрерывно. Переменная t обозначает время; 2=0
соответствует начальному моменту и t > 0 для последующего. В этом случае
переменная выступает как функция времени. Например, цена в момент
t (?>0) будет Р (t) с Р @) как исходным значением в момент 2=0. Функции
типа Р (t) часто принимаются непрерывными, но в действительности они
могут и не быть таковыми. Так, они могут представлять собой ступенчатые
функции. Различие между дискретным и непрерывным анализом сводится
к тому, что в первом случае время разбивается на отдельные отрезки, а во
втором допускаются его непрерывные изменения. Ни в каком случае нельзя
принимать, что такая переменная, как цена, обязательно изменяется плавно
или непрерывно.
Переменные связаны функциональными зависимостями, которые обычно
включают некоторые постоянные и параметры. Их следует точно обозначить.
Например, параметрами могут служить темпы роста, обозначаемые через г
или q. В зависимости от характера исследования они могут быть
неизменными или переменными. Постоянные всегда принимаются неизменными на всем
протяжении. В этой и последующих главах взаимозависимости обычно
принимаются линейными, по крайней мере в порядке аппроксимации, в некоторых
21

областях (например, около значений равновесия). В дальнейшем мы
пользуемся по возможности единообразными обозначениями постоянных в
линейной модели: латинские буквы (с нижними индексами) употребляются для
обозначения^коэффициентов переменных, греческие — для неизменных
выражений. Так, линейная функция спроса в дискретном анализе, где спрос
зависит от цены Данного момента времени и, возможно, от цен предшествующих
периодов, будет иметь вид
или
или
Dt = а + a0Pt
и т. д. Заметим, что в общем предпочтительнее писать Z)t = a + aPf, если
даже а отрицательно, а не Dt = a — aPt при положительном а.
Аналогичные обозначения можно использовать и в непрерывном анализе. Так,
и т. д.
1.2. ПАУТИНООБРАЗНАЯ МОДЕЛЬ
Пусть рынок какого-либо отдельного товара характеризуется следующими
функциями спроса и предложения:
S = S{P).
Для существования равновесия цена должна быть такой, чтобы товар
на рынке был распродан, или
Цена равновесия Р задается этим уравнением (которое может иметь
множество fрешений), а соответствующий объем покупок-продаж, обозначаемый
через X, — следующим уравнением:
Динамическая модель получается при наличии запаздывания спроса или
предложения. Простейшая модель в дискретном анализе включает
неизменное запаздывание или отставание предложения на один интервал:
Это может случиться, если для производства рассматриваемого товара
требуется определенный период времени, выбранный за интервал. Действие
модели таково: при заданном Pt_1 предшествующего периода объем
предложения на рынке в текущем периоде будет S(Pt_1)t и величина Pt должна
установиться так, чтобы был куплен весь объем предложенного товара.
Иными словами, Рь и объем покупок-продаж Xt характеризуются уравнением
Итак, зная исходную цену Ро, с помощью этих уравнений мы можем
получить значения Рх и Хг. Затем, используя имеющуюся цену Р1У из
соответствующих уравнений получим значения Р2 и Х2, и т. д. В общем
изменение Pt характеризуется разностным уравнением первого порядка (одно-
янтервальное отставание):
22

Решение можно проиллюстрировать диаграммой, представленной
на рис. 1, где D и S — соответственно кривые спроса и предложения,
а положение равновесия (со значениями Р и X) соответствует точке их
пересечения Q. В динамической модели D имеет тот же смысл, что
и в статической, но ордината кривой S показывает объем предложения
в данный период времени в зависимости от цен, управлявших рынком
в предшествующий момент времени. Цена в начальный момент времени
равна Ро. Соответствующая точка Qo на кривой S дает объем предложения
в период 1. Весь этот предложенный объем товара раскупается при цене Рх%
заданной точкой Qx на кривой D с той же ординатой (Хг) , что и Qo.
Во второй период времени движение происходит сначала по вертикали
X
(Pis),
i i
1 4
f ^r i
/
I 1
| 1
| 1
0 Pn P2 P P3 P1 P
Рис. 1.
от точки Qt к точке на кривой S, дающей Х2, а затем по горизонтали —
к точке Q2 на кривой D. Последняя точка характеризует Р2.
Продолжение этого процесса и дает график паутины, показанный на рис. 1. Цены
и объемы (покупок-продаж) в последовательные периоды времени являются
соответственно координатами точек Ql9 Q29 QB, ... на кривой спроса D.
В рассматриваемом случае последовательность точек стремится к Q. При
этом точки поочередно располагаются на левой и правой стороне от Q.
Следовательно, и значения цены Pt стремятся к Р, располагаясь поочередно
по обе стороны от Р. Точно так же обстоит дело и с объемами покупок-
продаж (Xt). Предположим, что D идет вниз, a S — вверх. Тогда
интуитивно ясно, что движение с затухающими колебаниями возникнет, если
кривая D в точке равновесия Q опускается к оси абсцисс ОР круче
(под большим углом), чем кривая S. Взрывное колебательное движение
возникает в случае, когда кривая D менее крута по отношению к ОР,
чем S (угол наклона кривой D к оси ОР меньше угла наклона S). При
равных углах наклона D и S возникают регулярные колебания, то есть
незатухающие и невзрывные1.
Решение можно получить алгебраически для случая линейных функ-
ций_спроса и предложения: D = а + аР9 S = р + ЪР. Значения равновесия Р
и X будут заданы уравнениями
1 Под «взрывным» движением здесь и далее понимается движение по кривой,
ордината которой (а в случае «взрывного» колебательного движения —амплитуда)
непрерывно возрастает и уходит в бесконечность. Поэтому правильнее было бы это
движение называть непрерывно возрастающим.—Прим. ред.
23

то есть
? = ?=?,? = *«=?. A)
Ь — а Ь — а х/
Дискретная динамическая модель задается уравнением
Xt^a + aPt = p+bPt_v B)
Ищем сначала решение, дающее равновесие. Для этого положим Pt — P
и Xt = X для всех значений t:
Х = а + аР^$+ЬР. C)
Получаем те же значения Р и X, что и в A). Следовательно, если в каком-
либо периоде существовали цены и объемы, обеспечивавшие равновесие, то
в динамической модели B) они сохранятся и в последующих периодах.
Статическое равновесие согласуется с этой моделью. Вычтем уравнение C)
из B) и положим pl = Pt — P, xt — Xt — X. Тогда
Xt = apt = bpt_1. D)
Уравнения D) аналогичны B), за исключением того, что они описывают
отклонения от уровней равновесия (теперь уже известно, что таковые
существуют). Оба эти уравнения являются разностными уравнениями
первого порядка. Положим с=Ь/а и подставим его в уравнение D), так
что разностное уравнение относительно pt будет
Pt = cPt-i-
При данном значении р0 в момент t — О решение легко получается путем
итерации:
или
Объемы покупок-продаж в каждый период определяются из уравнения D).
Обычно кривая спроса идет вниз (а < 0), а кривая предложения —
вверх (Ь > 0), то есть с = b/а < 0. В этом случае положим г = | с | = Ь/( — а)у
так что г будет положительно. Тогда
и последовательные значения pt при ? = 0, 1, 2, 3, ... будут соответственно
так что pt принимает поочередно положительные и отрицательные
значения. Следовательно, чередуются и знаки Ро которые поочередно будут
располагаться выше и ниже Р. Имею/гся следующие три возможности:
1) Ь > (— а), угол наклона S (к ОР) больше, чем угол наклона Z).
В этом случае г > 1, и ряд последовательных значений pt является
бесконечно возрастающим по абсолютной величине. Следовательно,
Pt~^i00» и имеет место взрывное колебание (при чередовании
знаков).
2) Ь = ( — а), углы наклона D и S равны. В этом случае г=1,
и ряд значений pt будет просто состоять из чередования р0 и (— р0).
Поэтому Pt будет последовательно больше и меньше Р на одну
и ту же величину, равную первоначальному расхождению (Ро — Р),
то есть будет иметь место регулярное колебание (с чередованием
знаков).
3) 6<(—а), угол наклона D (к ОР) больше, чем 5. В этом
случае г<1, и последовательные pt уменьшаются по абсолютной
величине. Значит, Pt—>P последовательно слева и справа, то есть
стремится с затухающими колебаниями к уровню равновесия.
24

В случае C), чем больше будет —а по отношению к 6, то есть чем
круче D сравнительно с S, тем скорее будут затухать колебания и тем
быстрее Pt будет стремиться к Р. Начальные возмущения также
оказывают влияние на амплитуду колебания. Чем дальше Ро от Р, тем больше
будет размах колебаний и тем длительнее промежуток времени,
необходимый для того, чтобы они прекратились.
Следует отметить, что случай B) с продолжающимися и правильными
колебаниями настолько редок, что его можно считать почти тривиальным —
на базе его нельзя построить никакой теории цикла. Интересен случай C),
несмотря на возможное возражение, состоящее в том, что затухающие
колебания «нереальны». Однако существует очень простое развитие модели C)
с затухающими колебаниями, которое позволяет представить движение Pt
с продолжающимися колебаниями во времени. Для этого вместо кривых
спроса и предложения, неизменных во времени, возьмем кривые, которые
под воздействием внешних сил изменяются во времени либо регулярно,
либо циклично, либо случайно, либо как-нибудь иначе. Тогда еще до
прекращения колебаний, показанных на рис. 1, какой-нибудь сдвиг в
кривой D или S приведет к возмущению, и колебания появятся снова.
Например, Qo могла находиться в точке равновесия или вблизи нее до сдвига
вверх кривой D к положению, показанному на рис. 1. Тогда колебания
будут происходить вышеописанным образом, продолжаясь, скажем,
до точки Q3, где колебательное движение будет нарушено сдвигом вверх
кривой S. Возникнет, следовательно, колебательное движение с еще
большей амплитудой, которое постепенно прекратится до появления какого-
либо нового возмущения. Для линейной модели возможно алгебраическое
истолкование в случае параллельного перемещения кривых спроса и
предложения. Уравнение B) тогда будет иметь вид
Xt = at + aPt^^t + bPt,lf
где ctf, Р/ характеризуют сдвиги в момент ? = 0, 1, 2, 3, ... . Разностным
уравнением относительно цены будет
Р — b Р 1 $t — at /гч
Для решения уравнения E) необходимо лишь определить разность Cf — at
сдвигов во времени спроса и предложения. Различные случаи,
возникающие здесь, были рассмотрены Гудвином [4].
Задачи и упражнения
1. Получить D) из B), используя A) для выражения а, р через Р, X. Что
значат а, Р в этой модели? Если дано, что а>0, а<0, 6>0, каковы будут пределы
величины р?
2. Исследовать движение Pj в более редком случае, когда одновременно идут
вниз обе кривые: и спроса, и предложения. Сделать это сначала графически (подобно
рис. 1), а затем для линейного случая и алгебраически (а<0, 6<0).
3. Построить и проанализировать динамическую модель паутинообразного типа с
одноинтервальиым временным запаздыванием спроса, но без запаздывания предложения.
С математической точки зрения между этой моделью и моделью с запаздывающим
предложением нет никаких различий. Существуют ли экономические соображения для
какого-либо предпочтения?
4. Регулярные линейные сдвиги во времени кривых спроса и предложения
характеризуются уравнениямм a^ = ao + ai^ Pf = Po + Pi^ (* = 0, 1, 2, ...)в уравнении E).
Существует ли для цены решение типа Р* = А,о + А,1*, т0 есть регулярный
прямолинейный рост во времени?
1.3. ПРОСТАЯ НЕПРЕРЫВНАЯ МОДЕЛЬ
В непрерывной модели цена есть функция времени P(t). Спрос и
предложение (потоки в единицу времени) суть также функции времени.
Паутинообразная модель (см. 1.2) учитывала запаздывание предложения.
25

Этому будет грубо соответствовать предпосылка об изменении цены
на стороне спроса, а не предложения. Тогда получим модель,
равносильную модели с непрерывным запаздыванием предложения. В дальнейшем
мы покажем, что это запаздывание имеет простую показательную форму
(см. 1.9, упражнение 2). D(t) зависит от Р и dP/dt, a S (t) — только от Р.
Модель действует, как и в предшествующем случае, именно в каждый
момент цена Р устанавливается так, чтобы спрос полностью поглощал
предложение, то есть X(t) и P(t) удовлетворяли уравнению
Если функции линейны, то
X = a + aP + ai~ = $ + bP. A)
Положим P(t)~P и X(t) = X для всех t, то есть для совместного
положения равновесия обеих переменных:
Р. B)
Таким образом, значения равновесия, определяемые уравнением A) из
раздела 1.2, снова совместны с моделью. Вычтем B) из A) и положим р = Р — Р
и х = Х — X. Так как dp/dt = dP/dt9 то
х^ар + а^^Ър. C)
Уравнения A) и C) представляют собой дифференциальные уравнения
первого порядка. Положим с = (b — a)/av Тогда дифференциальное
уравнение относительно p(t) будет иметь вид
Для решения заметим, что
1 dp __ d
Тогда
dt
то есть
In p = const
то есть
или
В обычном случае а < О, аг < О, Ъ > 0, то есть с( = (&— а)/^) < 0.
Следовательно, цена P(t) движется во времени монотонно к Р—цене
равновесия, так как разность р-^0 подобно показательной функции е~*. Менее
обычен случай, когда также Ь < 0. Но если только — Ъ < —а, то есть угол
наклона D к оси ОР в плоскости ОРХ (см. упражнение 1) больше, чем
угол наклона 5, то приходим к тому же результату, что и в первом
случае. Дифференциальное уравнение этой модели имеет меньше решений,
чем соответствующее конечно-разностное уравнение, приведенное выше
<см. 1.2).
Задачи и упражнения
1. Показать, что если а < 0, аг < 0, Ь < 0, то в этой модели существует две
возможности для Р (t)f то есть если —Ь>—а, то монотонно Р —> оо, и если —Ь<—а,
то Р —> Т. Дать графическую интерпретацию полученному результату.
26

2. Построить и исследовать динамическую модель, в которой цена варьирует на
стороне предложения, а не спроса.
3. Дать следующее обобщение модели: D и S зависят каждое от Р и dP/dt.
Решить для линейного случая, где D=<x-\-a0P-\-a1 (dP/dt), S = pJt-b0P-\-bl(dP/dt).
Какое экономическое истолкование может быть дано этой модели? (См. [2, гл.4].)
1.4. ОБЩИЕ СВОЙСТВА МОДЕЛЕЙ
Рассмотренные в разделах 1.2 и 1.3 паутинообразная и непрерывная
модели очень просты и хорошо известны. Они являются частично динамическими,
так как устанавливают соотношение на рынке только одного товара и
учитывают лишь цену его одного, а не цены других товаров и доходы. Тем не
менее они содержат основные формулировки динамики и позволяют вскрыть
некоторые важнейшие свойства, общие для всех динамических моделей.
Позднее, при показе методов построения более сложных динамических моделей,
мы исследуем эти свойства подробнее. Нижеследующие соображения
относятся специально лишь к паутинообразной (дискретной) модели в разделе 1.2.
Отдельное замечание посвящено и непрерывной модели, рассмотренной
в разделе 1.3.
1. Модель предполагает некоторые функциональные соотношения.
В данном случае это — рыночный спрос покупателей и предложение
продавцов. Каждое из них представляет собой функцию цены. Эти функции
являются по существу построениями на основе прошлого или ожиданий (ех
ante). Цена либо дана извне покупателям и продавцам, либо она
предугадывается ими. Спрос предстает как планируемая или предполагаемая величина
покупок, предложение — как планируемая или предполагаемая величина
продаж, причем все эти предположения приурочиваются к началу
промежутка времени t. Продавцы ожидают, что цена будет такой же, как и в
предшествующий период Pt_i и соответственно предполагают продать St=S (Pt_i).
Покупатели считаются лишь с фактической ценой и в соответствии с этим
планируют свои покупки в размере Dt~D(Pt).
2. Форма функции также задана. Задачу можем упростить,
рассматривая частный случай при определенной форме функции (например, линейной
D=a+aP), либо же взяв приближение к данной форме функции (например,
линейную аппроксимацию в ограниченной области около точки равновесия).
Это можно осуществить с помощью разложения в ряд Тейлора функции
спроса с малой разностью Р—Р:
Принятая в задаче линейная (или любая другая) форма должна быть
подходящей и представлять собой или хорошую аппроксимацию, или удобное
упрощение. Так, коэффициент, обозначенный выше через а, может быть либо
коэффициентом при Р в линейной функции спроса, либо наклоном кривой
спроса в точке равновесия. В последнем случае он может приближенно
отражать малые вариации Р вокруг Р.
3. Необходимо точно определить условия, при которых действует модель.
Это предполагает переход от ожидаемых и планируемых величин на основе
прошлого (ex ante) к реализованным фактически (expost). Необходимо точно
определить специфическую нрироду связей между фактическими значениями
переменных и механизм перехода предполагаемых величин в фактические.
В рассматриваемой модели с движением данного товара на одном рынке
фактически сложившиеся отношения характеризуются равенством покупок и
продаж (Xt, по определению). Далее, в рассматриваемом случае переход от
ожидаемых величин к фактическим осуществляется «методом равновесия»,
где цена и является «уравновешивающей» переменной. В начале
периода t продавцы ожидают, что цена будет Pt,l9 и предлагают для продажи
продукцию St. Изменение запасов не предусматривается (хотя возможно, что
27

товар является скоропортящимся), так что предложение должно быть равна
Xt (продажи = покупкам). В процессе установления рыночного равновесия
спрос, следовательно, становится равным предложению (= продажам =
покупкам), так как цена достигает такого уровня, при котором предложение-
полностью поглощается. Все экономические ожидания реализуются.
Исключение составляет лишь цена Pt_i, которую ожидали продавцы. Она не
совпадает с реализуемой ценой Pt, управляющей рынком в данном периоде.
С помощью очень небольшой модификации этой дискретной модели можно
совершенно изменить условия ее действия, введя ступенчатую функцию
(метод последовательного нарушения равновесия). В момент t—1
производители выпускают количество товаров, соответствующее доминирующей
в этот момент цене Pt_i. В конце периода эту массу товаров приобретают
торговцы, так что ее можно продать в течение следующего периода t (как St).
В начале периода t на основе всех известных в тот момент данных торговцы
устанавливают продажные цены Рг. Покупатели тогда решают, сколько
они купят по этим ценам (Dt). В модели (см. 1.2) предполагается, что
торговцы угадывают всегда правильно и устанавливают цены на таком уровне.,
при котором они могут сбыть весь запас товаров:
St =Dt = объему покупок-продаж.
В модели необходимо предусмотреть и варьирование в качестве меры
предосторожности против неправильных предугадываний цен торговцами. Пусть
установленная ими цена Pt такова, что Dt превосходит количество
продаваемых товаров St. При наличии торговых запасов спрос (равный покупкам-
продажам) можно покрыть за счет их уменьшения. Тогда предполагавшееся
предложение St будет меньше фактических продаж и разницу придется
покрыть за счет запасов. В результате покупатели реализуют свои планы
(предположенный спрос=фактическим покупкам), но продавцам придется
произвести неожиданные изъятия запасов. С другой стороны, если
отсутствуют или малы запасы (например, скоропортящихся товаров), то спрос не
удастся удовлетворить, и его вынужденное сокращение потребует
ограничения потребления или других подобных мер. Тогда предполагаемый спрос
будет урезан до величины фактических покупок, и у покупателей возникнут
незапланированные сбережения, продавцы же реализуют свои планы. В
большинстве моделей обычно принимается, что планы покупок реализуются
(ожидаемый спрос равен фактическим закупкам), а возможный «разрыв»
компенсируется вложениями. Такое предположение может быть разумным
или удобным, но, как показывает приведенный пример, оно, конечно, не
необходимо (см. также [5]).
4. Условие действия модели, удовлетворяемое в фактических рыночных
отношениях, записывается в виде уравнения с соответствующей переменной.
В данном случае цена является такой уравновешивающей переменной.
Задача заключается в том, чтобы избавиться от остальных переменных (Dt, St
и обычно фактического значения Xt) и сосредоточить наибольшее внимание
на одной (Pt). Остальные переменные (например, Xt) можно найти, коль
скоро определена важнейшая переменная (Pt). Уравнение паутинообразной
модели является простейшей формой разностного уравнения с одноинтервалъ-
ным запаздыванием (Pt и Ptl явно входят в уравнение). Ищется решение
этого уравнения. В случае равновесия без запаздывания вопрос сводится
к нахождению одного или нескольких значений Р, совместных с условиями
равновесия. При наличии запаздывания в конечно-разностном уравнении
решение предполагает, что заданы и определены какие-то начальные
значения или условия, в данном случае начальная цена Ро. Уравнение
характеризует действие модели в каждый промежуток времени, но результат на
протяжении времени, взятого в целом, зависит от существовавшей начальной
конфигурации, подобно тому как опущенная в автомат монета приводит его в
действие. Модель может «стартовать» лишь из какого-то исходного положения.
Экономически это означает, что изменение цены во времени можно опреде-
28

лить, лишь зная начальное нарушение равновесия или отклонение ее от
положения равновесия. Тот факт, что в данном примере требуется знать
лишь одно начальное значение, является случайным. Он представляет
собой результат существования только одноинтервального запаздывания,
того, что соответствующее конечно-разностное уравнение будет первого
порядка. При многократном или распределенном запаздывании конечно-
разностное уравнение будет иметь более высокий порядок и потребуется
знать не одно, а несколько начальных значений.
5. Решение разностных уравнений является делом математики. Решение
упрощается тем, что в данном случае, как и во многих других, модель этого
типа, описанная Валдом [14], является рекурсивной. Это значит, что если
даны все переменные до (?—1), то модель обеспечивает и получение одного
за другим значений переменных для интервала t. В рассматриваемом случае
при заданных Pi_1 получается сначала Xt=St, а затем и Pt,
Однако относительно решения можно сделать некоторые общие
замечания. Они не только полезны с математической точки зрения, но имеют и
экономический смысл. Первым всегда возникает следующий вопрос: существует
ли положение равновесия, совместное с уравнением? Ответ дается
подстановкой в уравнение Pt—P для всех t. В данном случае такое Р существует,
и это есть статический уровень. В других случаях такое Р может не
существовать. Применяется и другой искусственный прием: определив Р, проследить
не изменение первоначальной величины Pt, а ее отклонения от положения
равновесия, pt=Pt—Р- Это имеет экономический смысл, так как интерес
представляет именно отклонение от положения равновесия. Математически
наилучший способ такого переключения сводится к вычитанию уравнения,
характеризующего точку Р, из уравнения, выражающего Pt\ например»
в разделе 1.2 уравнение C) вычитается из уравнения B).
Модель со всей очевидностью показывает, что статика и динамика не
отгорожены друг от друга водонепроницаемой стеной. Динамическая модель
типа паутинной рассматривает движения вокруг положения равновесия
или отклонения от него. Заметим, однако, что устойчивое существование
положения равновесия (то есть раз достигнутое, оно сохраняется постоянно),
совместного с моделью, вовсе не предполагает, что за всяким отклонением
будет следовать возвращение в исходное статическое положение. Движение
может удаляться от исходного статического положения или быть
направленным к какому-то иному, отличному от исходного. И, наоборот, вопрос об
«устойчивости» положения равновесия в статическом случае должен и
может рассматриваться лишь с точки зрения динамической модели. Положение
равновесия устойчиво, если начальное возмущение порождает возвратное
динамическое движение к положению равновесия, а не в сторону от него
и не к какому-либо другому положению. К этому вопросу мы вновь вернемся
(см. 1.8).
Рассмотренная в разделе 1.3 непрерывная модель имеет в общем те же
свойства, отличаясь главным образом в акцентировании или в деталях.
Функции модели представляют спрос и предложение в зависимости от цены
и скорости изменения последней. Предположения и планы покупателей
и продавцов представляются непрерывно приспосабливающимися во времени
к движению цен. Как и в предыдущем случае, эти ожидания должны
представлять собой звенья одной цепи, чтобы быть совместными. Выражающая
соотношение ожидаемых величин спроса и предложения модель действует
опять-таки по методу приближения к положению равновесия. Рыночные
силы непрерывно изменяют цены так, чтобы предложение было полностью
реализовано. Цена является переменной, обеспечивающей равновесие,
изменяющейся от одного момента к другому для поддержания равенства
спроса и предложения, являясь общей для покупок и продаж (потоков в
соответствующий момент времени). Основное различие заключается в
интерпретации модели с точки зрения решений покупателей и продавцов. В дискретном
29

анализе единицей времени был выбран интервал принятия решений или
пересмотра планов, характерной чертой было различие между ожиданиями
(намерениями) и их осуществлением (реализациями). Все это в общем
исчезает в непрерывной модели, так как предполагается, что принятие-
решений, пересмотр их и приспособление к изменившейся обстановке
происходят непрерывно. Однако многие свойства дискретной модели можно
ввести и в непрерывную, например запаздывания или изменения запасов.
С математической точки зрения непрерывная модель ведет к
дифференциальному уравнению относительно какой-либо переменной [в данном
случае Р (t)]> а не к конечно-разностному. В общем техника решения примерна
одинакова, а существенные различия имеются лишь в деталях. Например,
решение уравнений из раздела 1.3 включает показательную функцию ect
вместо функции с1 уравнений, приведенных в разделе 1.2. Поэтому решение,
полученное из непрерывной модели, охватывает меньшее количество
различных случаев. В последующих главах будет рассмотрена техника решения
конечно-разностных и дифференциальных уравнений, так как и дискретный
и непрерывный анализ применим к решению экономических проблем
различного типа.
1.5. ЭКОНОМЕТРИЧЕСКАЯ ЗАДАЧА
Настоящий раздел не ставит целью рассмотрение проблем эконометрии.
Однако простая паутинообразная модель позволяет выявить основные
проблемы, описанные Леонтьевым [9], и поэтому имеет смысл сделать
краткое отступление. Рассмотрим сначала равновесие на рынке, без
запаздываний. Пользуясь рис. 1, можно сказать, что цена равновесия и объемы
(покупок-продаж) будут заданы точкой пересечения кривых спроса и
предложения на плоскости ОРХ. По мере изменения этих кривых во времени
точка равновесия описывает некоторую траекторию, обусловленную
предшествующим развитием. Соответствующие изменения претерпевают цена и объем.
Вопрос заключается в следующем: можно ли определить углы наклона (или
параметры) кривых спроса и предложения по наблюденным временным рядам
цен и объемов? Ответ в общем отрицательный. Прошлая траектория
движения зависит главным образом от изменений кривых — безразлично,
являются ли эти изменения случайными или регулярными. При линейных функциях
и при изменениях, когда кривые все время перемещаются параллельна
самим себе:
где ut и а, —сдвиги, заданные (но неизвестные) во времени, которые могут
быть регулярными (например, ut = aot, vt = (V) или изменяться
стохастически с присущим данному феномену распределением вероятностей. Без
потери общности можно принять, что ut и vt имеют средние, равные
нулю, и положить, что pt и xt представляют собой отклонения от средних
при любом размахе наблюдений. Тогда
так что
Pt-Т^Г1 Х*-~ b-a '
Таковы наблюдаемые линии движения pt и xv зависящие от заданныхY
но неизвестных utwvt. Чтобы найти а и 6, нужно знать щ и vt. Попытка
элиминировать ut и vt, например с помощью регрессии xt no pt, в общем
окажется неудачной. Решение, имеющее какой-либо экономический смыслг
появится лишь в столь специальных случаях, что его можно
рассматривать почти как тривиальное. Таков, скажем, случай, когда щ = 0 (кривая
спроса фиксирована), так что
_ Vt — aVt
Pt'~ "~^a' Xt "~ b-a '
30

то есть
и можно определить а (наклон фиксированной кривой спроса).
Задача изменится, если в отличие от паутинообразной модели ввести
запаздывание предложения, а не спроса. Соотношение A) тогда будет
иметь вид:
xt = apt + ut = bpt_x + vt. B>
Эти уравнения можно перегруппировать следующим образом:
Наблюденные значения xt и pt имеют «систематическую» часть,
зависящую от pt_v и «ошибку», или «сдвиг», зависящую от ип vt. Если
последняя часть случайна, регрессия xt по pt_± даст 6, а регрессия pt по рг_г
даст b/а. Следовательно, из наблюдений можно вычислить как а, так и Ь.
Резюмируем. Модель A) не идентифицируема, то есть а и Ь нельзя
определить из наблюдений1. Модель B) представляет собой вариант, в котором pt
появляется в одной связи, а переменная pt_x — во второй связи. Это и
составляет всю разницу. Уравнение B) преобразуется в C), так называемую
«приведенную форму», и коэффициенты C) можно оценить и установить с помощью
искомых параметров а и Ъ. Далее, если требуется предсказать значения xt
я pt1 то уравнения регрессии, полученные из «приведенной формы» C), дают
все необходимое для этого.
1.6. УГЛУБЛЕНИЕ ПАУТИНООБРАЗНОЙ МОДЕЛИ
Рассмотренная в разделе 1.2 паутинообразная модель в обычном случае*
(кривая спроса направлена вниз, кривая предложения — вверх) дает
решение, при котором цена в последовательные периоды времени попеременно
принимает значения, лежащие выше и ниже точки равновесия. Это колебание
завершается в течение двух интервалов, то есть при наличии двойного
запаздывания на стороне предложения. Скорость приспособления к
изменившейся обстановке убывает пропорционально увеличению продолжительности;
запаздывания.
Продавцы ожидают, что сохранится цена предшествующего периода,
но то и дело разочаровываются в такого рода ожиданиях. Поставщики
ожидают, что если цена в течение одного периода находилась выше точки
равновесия, то и в следующий период она будет в аналогичном положении. В дей1
ствительности же в следующий период она может оказаться ниже точки
равновесия. И модель исходит из предпосылки, что продавцы ничему не
научились. Однако ее можно распространить и на случай, когда под
влиянием опыта ожидания продавцов меняются. Гудвин [4] исследовал такого*
рода модель.
Цена в период t—1 равна Pt_x. Пусть в период t цена, на которую
рассчитывают поставщики, будет
где APj_2 — увеличение цены по сравнению с периодом t—2, то есть t2
=Pt_1—Pt_2, a q—заданная постоянная. Обычно в такого рода ситуациях
можно принять, что q является положительной дробью @<q<1), to есть
в этом случае ожидается, что цена движется в направлении,
противоположном тому, в котором она изменялась в предыдущий период. Поставщики
ожидают изменения направления движения цены. Реже Q может быть отри-
1 Идентификация есть отождествление анализируемой — здесь экономической —
зависимости с какой-либо математической формой, наиболее свободной от
возможных ошибок, при имеющейся неполной информации о самой зависимости.-—
Прим. ред.
31

дательным, и поставщики будут тогда рассчитывать, что движение цены будет
продолжаться в прежнем направлении. Величина q означает вес
(взвешивающий коэффициент), который продавцы придают возможности поворота или
сохранения направления движения цены. Если q=0, to какого-либо
изменения цены не ожидается; если q—1, ожидается полный поворот в движении
цены.
Уравнение паутинообразной модели (см. 1.2) с линейными функциями
имеет вид
Xt = а + aPt = Р + Ь (/>,_! - QAPt_2),
шли, подставляя выражение APt_2, имеем
Xt = a + aPt = V + b(l-Q)Pt_1 + bQPt_i. A)
Произведем подстановку Pt — P, Xt = X для всех t:
X = a + aP = $ + b(l-Q)P+bQP. B)
Это даст:
^=7' А~ Ъ — а *
Статическое равновесие вновь оказывается совместным с моделью. Вычтем B)
из A) и положим pt=Pt — P, xt = Xt — X и c — bja:
xt = apt=:b(l- q) Л-1 + bQPt_2. C)
Уравнение (З) является разностным относительно отклонений от
положения равновесия. Для цены имеем
pt = с A — q) ри1 + cqpt^ D)
и соответствующее xt определяется из уравнения C). При q=0 уравнение D),
подлежащее решению для определения поведения цены во времени,
сводится к простому конечно-разностному уравнению первого порядка,
рассмотренному в разделе 1.2. При Q=fc Q уравнение D) представляет собой
конечно-разностное уравнение второго порядка, включающее двойное
распределенное запаздывание. Чтобы система, описываемая уравнением D), начала
действовать, должны быть заданы два начальных значения, предположим Ро и Pi
в моменты ?=0, 1. Итерация дает все последующие значения Р2, Р3, Р4, ... .
Чтобы в явной форме написать общее решение относительно pt или Pt,
нужно знать теорию конечно-разностных уравнений. Поэтому мы пока отложим
анализ уравнения D) (см. гл. 5).
Задачи и упражнения
1. В конечно-разностном уравнении D) положить с = —3/4, Q = 1/2- При двух
заданных начальных значениях /?0 = 0, Pi = l с помощью повторяющегося применения
уравнения D) написать последовательные значения отклонения цены от положения
равновесия р2» Рз> Р*> •• • и продолжить ряд настолько, чтобы стала ясна природа
вариации. Объяснить результат.
2. В предыдущем упражнении вместо Q = 1/2 положить q==—*/2- Получить затем
/?2, /?3» Р4> Дать объяснение результата и сопоставить с предыдущим решением.
1.7. МОДЕЛЬ СО ВКЛЮЧЕНИЕМ ЗАПАСОВ
В рассмотренных выше моделях (см. 1.2 и 1.3) цена устанавливалась так,
чтобы полностью поглотить предложение. Наличие запасов товаров (например,
не поддающихся хранению) либо не предполагалось вообще, либо же
предполагалось неизменным. Эти модели могут быть расширены за счет
учета изменения запасов.
А. Для дискретного случая, пользуясь обозначениями раздела 1.2,
обозначим запасы в конце интервала t через Qt. Тогда
32

представляет собой увеличение запасов на протяжении интервала t. В
нижеследующем анализе мы должны рассматривать запасы лишь в смысле
фактически существующих величин (подобно реализованным покупкам-продажам).
Ожидаемые St и Du или планируемые предложение и спрос, равно как
и фактические значения St и Dt, могут быть различными. Фактически
реализуемые поставки вливаются в общую массу запасов, а фактический спрос
удовлетворяется за счет запасов. По определению, на рынке все еще
соблюдается равенство покупок и продаж, а реализованный спрос является их
общей- стоимостью, то есть Xt равняется фактическому Dt. Намерения
покупателей реализуются в покупках (объем последних равен продажам),
намерения поставщиков —в продажах торговцам, которые, как предполагается,
имеют запасы товаров и продают последние покупателям. Поэтому в анализ
придется ввести третью группу — торговцев, имеющих запасы и
производящих продажи. Их функции следует отличать от функций покупателей и
поставщиков. (При совпадении торговцев и поставщиков в одном лице эта группа
приобретает двойные функции.) Действие модели начинается с продаж
торговцев и с установления цен в соответствии с запасами. Рассмотрим два
случая. В первом случае цены устанавливаются в зависимости от изменения
запасов; во втором — в соответствии с уровнем запасов. В обоих случаях
берутся линейные функции спроса и предложения без запаздываний и для
простоты предполагается, что торговцы всегда покупают и продают по одной
и той же цене.
Модель /. В период t торговцы устанавливают цену Pt согласно
следующему условию: цена будет выше, если в предшествующий период запасы
уменьшились, и ее повышение пропорционально сокращению запасов. Имеем
Pt = Pt^-XAQt^ A)
где К — заданная положительная величина. Далее,
Dt = a-\-aPt, St = $+bPt
и
Л<?<-1 = <?f-i ~ Qt-* = St-i ~ Dt-i = (P - «) + (b - а) Л-1-
Уравнение A) сводится к следующему:
то есть
Pt = K(a-P) + [l-k(b-a)]Pt_v B)
Сделаем подстановку Pt = P для всех t:
Р = Ма-Р) + [1^Ц&--а)]Р, C)
то есть
^~~ Ь — а
представляет собой обычный уровень равновесия. Вычтем уравнение C)
пз B) и положим pt = Pt — Р, с = 1-Я (б —а), или Я = A — с)/(Ь — а).
Получаем
Pt = CPi-V
Решение будет иметь вид
Р1=РоСг1
или
-P)c'. D)
Объем покупок (и продаж торговцами) тогда составит Xt = a-\-aPt.
Обычно а < О, Ъ > 0, так что 6 — а > 0. В отношении величины X
возможны три случая. Им будет соответствовать и различное изменение Рп
определяемое уравнением D):
3 Р. Аллен 33

I X < 1/F — а), так что 0 < с < 1, и Pt—>P, то есть Pt монотонно
стремится к Р.
II 1/F — a)< Х< 2/F — а), так что — 1 < с < 0, и PtJ попеременно
меняя знаки, стремится к Р, то есть имеем случай затухающего колебания.
III Х>2/F — а), так что с< -—1, иР(, меняя знаки, стремится
к бесконечности (?\—>±°°)» то есть имеем взрывное колебание.
Величина X определяет движение Pt. Чем больше Я, тем менее
устойчивым становится движение, переходя сначала в затухающее, а затем
во взрывное колебание. Неустойчивость появляется, если, устанавливая
цены, торговцы быстро и энергично реагируют на изменение запасов.
Модель II. Торговцы устанавливают цену Pt в период t следующим
образом: цена повышается, если в предшествующий период уровень
запасов упал ниже данного объема Q, и это повышение цен пропорционально
нехватке запасов до объема Q. Таким образом,
где X — заданная положительная величина.
Как и раньше,
Для определения величины запасов Qt произведем суммирование назад,
вплоть до начального момента (г = 0):
Уравнение E) тогда позволит определить цены на все периоды вплоть
до начального. Но эту зависимость от движения цен в предшествующие
периоды можно выразить и иначе:
Pt = PU1 -1 (QU1 -Q)
И
Произведем вычитание:
Pt -/»,_! = (Р,.х - Pt_J - X (Qt-г - Qt_*). F)
Преобразовывая и развивая уравнение F), можно затем переписать
уравнение E) следующим образом:
то есть
Pt = X(a-P) + [2-W-*)]Pt-i-Pt-* G)
Таково конечно-разностное уравнение, характеризующее модель. Оно
второго порядка, так как включает цены двух предшествующих периодов.
Исходя из уравнения F), можно объяснить механизм действия модели.
Изменение цены, устанавливаемой торговцами, зависит от уровня запасов.
Но норма изменения цен варьирует в зависимости от изменений запасов,
то есть от разности предложения и спроса. Изменения запасов придают
«ускорение» движению цен. Цены повышаются, если уровень запаса низок,,
уменьшение запасов сопровождается ускоренным ростом цен.
Для решения конечно-разностного уравнения G) сделаем подстановку
Pt=P для всех значений t:
Pf (8)
34

то есть Р = (а — р)/(Ь — а), что является опять-таки характеристикой
обычного уровня равновесия. Вычтем уравнение (8) из G) и положим pt=Pt —
— Р. Тогда конечно-разностное уравнение запишется следующим образом:
a)]Pt-i-Pt-*- (9)
Общее решение уравнения (9) с двумя начальными значениями (допустим,
Ро и Рх) мы откладываем до дальнейшего исследования (см. гл. 5).
Б. В случае непрерывного анализа запасы, подобно другим переменным
D, S и Р, непрерывно изменяются во времени. По определению, если
запасы в момент t составляют Q(t), то
Модель III. В каждый момент времени торговцы устанавливают цену
Р так, что скорость возрастания цены пропорциональна скорости
уменьшения запасов:
dPXd®
где А, —заданная положительная величина. При линейности функций
и отсутствии запаздываний, D = а + яР, S = р + ЪР.\ Поэтому
Делаем подстановку P(t) = P для всех t:
то есть Р = (а —Р)/(й —а), и мы снова пришли к обычной характеристике
уровня равновесия. Произведем вычитание и положим
Это дифференциальное уравнение модели. Решение получается точно так
же, как и ранее (см. 1.3):
р = рое-ь(ъ-*)*,
или
p = p+(po-p)e-*'ib-a)t.
В обычном случае а < О, Ъ > 0, так что Ь — а > 0. Следовательно,
движение цены JP(?) во времени монотонно стремится к положению
равновесия Р, так как р—>0, подобно в"'. Это справедливо для всех
положительных значений К. Величина К просто определяет скорость реакции или
приспособления. Чем больше величина X, тем быстрее Р приближается
к Р.
Модель IV. В каждый момент времени торговцы устанавливают цену
Р так, что скорость возрастания цены пропорциональна разности запасов
по сравнению с заданным уровнем Q:
t
§ = -l{Q-Q) = -K [Qo-Q+ ^ (S-D)dt] ,
0
где А, —заданная положительная величина. Имеем
35

и ускорение возрастания цен пропорционально скорости уменьшения
запасов. При линейности ^функций и отсутствии запаздываний;
Делаем подстановку P(t)~P для всех t:
то есть Р = (а — $)/(Ь — а). Снова имеем обычную характеристику
положения равновесия.
Вычтем и положим p(t) = P(t) — P:
Это есть дифференциальное уравнение модели. Оно второго порядка и для
решения требует два начальных условия, например, Р и скорость dPIdt
в момент ?=0. Далее будут рассмотрены уравнения такого типа (см. гл. 4).
Задачи и упражнения
1. Исследовать движение Pi в модели I в случае, когда обе кривые — спроса
и предложения—направлены вниз, причем кривая спроса будет круче, чем кривая
предложения, то есть случай с линейными функциями, когда а<0, &<0 и —6< — а.
Показать, что выводы будут тождественны с теми, которые были сделаны раньше для
обычного случая (а < 0, Ь > 0). Изменятся ли они, если кривая предложения будет
круче, то есть если —6>—а?
2. Построить динамическую модель, соответствующую моделям I и II с
однократным запаздыванием предложения (St = p+&^«-i) и без запаздывания спроса
(Dt = a-\-aPt). Показать, что оба конечно-разностных уравнения относительно
отклонений цены будут второго порядка, то есть соответственно:
3. Какую предельную форму будут иметь модели I и II из предыдущего
упражнения при А, = 0 и X -> оо?
^ 4. Исследовать движение Р (t) в вышеприведенной модели III при я<0 и &<0.
Показать, что Р непрерывно и в прогрессии стремится к Р, если —&< — а, и что
движение Р будет взрывным только в случае —Ь^>—а. Дать объяснение с помощью
кривых спроса и предложения.
5. Построить динамическую модель, соответствующую моделям III и IV, при
функции спроса D = a-\-a [P-\-(dP/dt)] и предложения Sj=$-{-bP. Показать, что
дифференциальные уравнения отклонений цен р (t) будут соответственно:
III (l — ka)-i?
6. Какова будет предельная форма моделей из предыдущего упражнения при
А,=0? Показать, что при X —> оо обе модели будут описываться уравнениями dp/dt =
= [F—а)/а] р. Решить эти уравнения относительно р и объяснить результат.
1.8. УСТОЙЧИВОСТЬ РЫНОЧНОГО РАВНОВЕСИЯ
Цена и объем товара (проданного и купленного) на рынке, находящемся
в состоянии равновесия, заданы уравнениями спроса и предложения,
пересечением кривых спроса и предложения. В противоположность
исследованию вопроса о существовании равновесия задача на его устойчивость
непременно предполагает введение динамических процессов. Проблему можно
сформулировать примерно следующим образом: существует цена,
обеспечивающая равновесие. Раз она установилась, то при ней будет постоянно
поглощаться все предложение товара. Но если в силу каких-либо причин на
рынке установится другая цена, то будет ли последующее движение цены
во времени направлено к положению равновесия и сколь быстро будет про-
36

исходить соответствующий процесс приспособления? Однако может
существовать несколько цен равновесия, а большое начальное возмущение может
качнуть всю систему из одного положения равновесия к другому. Во
избежание такой возможности будем рассматривать проблему устойчивости лишь
при наличии небольших начальных возмущений.
Итак, будем исходить из небольшого отклонения от положения
равновесия. Изучение поведения во времени требует чего-то большего, чем простая
констатация существования равновесия. Оно предполагает построение
подходящей динамической модели, действующей при некоторых принимаемых
условиях и учитывающей несоответствие между ожидаемыми и
фактическими величинами спроса и предложения. Модель может включать
предпосылку о том, что продавцы или торговцы имеют запасы товаров и что изменение
запасов влияет на ценообразование (как, например, в моделях,
рассмотренных в разделе 1.7). В другом случае модель может исходить из гипотезы о том,
что существуют запаздывания спроса или предложения (модели,
рассмотренные в разделах 1.2 и 1.3). И это — лишь два варианта щг большого числа
возможных. Словом, проблема устойчивости является динамической и
разрешается не единственным образом. Следует иметь в виду возможность, что
данное рыночное равновесие может считаться устойчивым при одних
динамических условиях и неустойчивым при других.
Мы рассматриваем лишь небольшие отклонения от положения
равновесия. Поэтому без существенной потери общности можно считать спрос
и предложение линейными функциями, то есть рассматривать последние
как достаточно близкие аппроксимации в малом интервале вокруг
положения равновесия. Итак, возьмем функции D=a-\-aP, S=$-{-bP со
значениями в точке равновесия Р = (а—|3)/(Ь—а), Х — (Ьа—а$)/(Ь—а). Постоянные
а и b характеризуют угол наклона кривых спроса и предложения к оси ОР
в точке их пересечения, которая совпадает с положением равновесия.
Предположим, что а отрицательно. Тогда & может быть либо положительным, либо
отрицательным. Следовательно, принимаем, что кривая спроса направлена
вниз, кривая предложения — либо вверх, либо вниз.
Анализ устойчивости часто проводится слишком грубо. Если цена
установилась слишком низкой, спрос превосходит предложение и цена
повышается до тех пор, пока не будет достигнуто состояние равновесия. Или,
если предложение слишком мало, покупатели предложат более высокие
цены, чем продавцы готовы были бы принять, и предложение возрастает до
установления равновесия. Такого рода аргументацию надо уточнить и
сделать более убедительной, ибо она не только слишком груба: построения
в обоих случаях различны и по существу. В первом случае аргументация
идет в духе концепции Вальраса, во втором случае — согласно концепции
Маршалла. Поэтому они могут привести к различным выводам относительно
устойчивости.
Концепцию типа Вальраса можно выразить с помощью непрерывной
динамической модели. Если в какой-либо момент времени цена отличается
от цены равновесия, или р—Р—РфО, то ожидаемые величины спроса и
предложения не будут равны. Допустим в динамической модели, что цены
повышаются, если предложение отстает от спроса, причем скорость возрастания
цены пропорциональна размерам этого дефицита. Движущей силой в этом
случае может быть уменьшение запасов (см. модель III в разделе 1.7).
Следовательно,
где под А, следует понимать скорость реакции. Чем больше Я, тем быстрее
будет реакция цены на данный дефицит предложения. Как было найдено
(модель III в разделе 1.7), Р равномерно и монотонно стремится к Р, если
37

br-a положительно, и в таком случае равновесие устойчиво. Р монотонно
удаляется от Р, если Ъ — а отрицательно, и равновесие тогда неустойчиво.
Аргументация Маршалла иная. Если в какой-либо момент времени
объем предложения отличается от уровня его, обеспечивающего равновесие,
или х = Х — ХфО, то ожидаемые цены, которые покупатель готов
заплатить, будут отличны от цен, приемлемых для продавца. Построим
динамическую модель, в которой объем предложения увеличивается, если цены
продавцов ниже тех, которые предлагают покупатели. Пусть скорость
этого увеличения пропорциональна размерам дефицита. Получаем:
цена покупателя =
—jj-5- , цена продавца = ——^
й dX/dt = — К (цена продавца минус цена покупателя); dX/dt = Л, [Р/6 — а/а] —
— Я[1/Ь—1/а]Х, где Л по-прежнему означает скорость реакции.
Решение получается точно так же, как и в предыдущем случае. X
монотонно стремится к X, если [lib—На] положительно (устойчивое
равновесие), и X неуклонно удаляется от X, если [lib—lla] отрицательно
(неустойчивое равновесие).
Получаются различные, результаты. Устойчивость в понимании
Вальраса достигается при (Ь—а) >0, в понимании Маршалла—при [A /6)—A1а)] >0.
Таким образом, в зависимости от углов наклона к оси ОР возникают
следующие возможности.
Наименование модели
Модель Вальраса .....
Модель Маршалла ....
—Кривая
предложения
направлена вверх
Ь>0
Устойчиво
Устойчиво
Кривая предложения направлена
вниз Ъ < 0
кривая спроса
D круче
— Ъ<—а
Устойчиво
Неустойчиво
кривая
предложения S круче
— Ь> — а
Неустойчиво
Устойчиво
Во всех случаях принимается, что кривая спроса направлена вниз (а<0).
Результаты показаны на рис. 2. Здесь начальное положение QQ
соответствует прежней точке равновесия — до того как кривая спроса сдвинулась
вверх к положению, указанному линией D, — с точкой Q в качестве нового
положения равновесия. В случае устойчивости новой точки равновесия
значения цены и объема должны переместиться из точки QQ по направлению
к точке Q. При цене Ро (заданной точкой Qo) спрос превосходит ожидаемое
предложение, то есть Х'0>Х0, ив модели Вальраса цена растет. При объеме
предложения Хо (заданном точкой Qo) цена покупателя выше цены
продавца, то есть Р'0>Р0, и в модели Маршалла объем предложения растет. На
рис. 2, а видно, что в каждом случае движение направлено к точке Q, которая
характеризует устойчивое равновесие как в понимании Вальраса, так и в
понимании Маршалла. На рис. 2, б цена повышается в направлении положе-
ния^равновесия Q, но объем движется в противоположном направлении.
Точка Q характеризует устойчивость по Вальрасу и неустойчивость по Маршал-
ду. Обратное положение изображено на рис. 2, в.
Третья динамическая модель для исследования устойчивости учитывает
наличие запасов (неявно это имеет место и в моделях Вальраса и Маршалла),
но несколько иначе, чем в рассматриваемых моделях. Например, можно
предположить, что темп роста цены пропорционален превышению запасов над
«нормальным» уровнем Q в любой момент времени. Такое положение
описывается вышеприведенной моделью IV из раздела 1,7. Предваряя решение
дифференциального уравнения, характеризующего эту модель, можно
сказать, что Р будет описывать регулярные (неизменяющиеся) колебания
38

вокруг Р, если (Ь—а) положительно. Это можно считать устойчивостью, но
в другом смысле. Положение равновесия нельзя считать неустойчивым, так
как Р не удаляется от Р. Но оно и не движется по направлению к Р; оно
регулярно и непрерывно колеблется вокруг Р. Иными словами, результаты
те же самые, что и в модели Вальраса.
Характерная особенность этих динамических моделей, предназначенных
для исследования устойчивости, заключается в том, что они допускают
неравенство спроса и предложения, те есть изменение запасов. Они также
представляют собой модели непрерывного типа. Совершенно иную модель можно
построить в дискретной форме, включающей и запаздывания. Скорость
приспособления будет в таком случае выражена не множителем Я, а различной
Рис. 2.
продолжительностью запаздывания реакции в спросе или предложении.
Положим, что существует однократное запаздывание предложения. Тогда
динамическая модель будет моделью паутинообразного типа (см. 1.2),
изображенной на рис. 1. Снова Qo будет начальным положением,
соответствующим точке равновесия, достигнутой до сдвига вверх кривой спроса.
Движения Pt и Xt в последовательные промежутки времени, следующие за
начальным возмущением, описаны в 1.2. Этот случай более богат вариантами, чем
модели Вальраса или Маршалла. Если кривая предложения направлена
вниз (подобно кривой спроса), то воспроизводится модель Вальраса. Но
если кривая предложения направлена вверх, то из этого еще не следует, что
равновесие устойчиво (в этом были единодушны Вальрас и Маршалл). Pt
теперь колеблется с возрастающей амплитудой (равновесие неустойчиво),
если S круче наклонено к осиОР. Колебания будут затухающими (равновесие
устойчиво), если D круче наклонено к оси ОР. Короче говоря, чтобы решение
динамической модели с запаздываниями было устойчиво, кривая спроса
должна быть более крутой по отношению к оси ОР по сравнению с кривой
предложения независимо от того, направлена ли кривая предложения вверх
или вниз.
1.9. ЗАПАЗДЫВАНИЯ В ДИНАМИЧЕСКИХ МОДЕЛЯХ
Из сказанного выше ясно, что в соотношения какой-либо динамической
экономической модели должны включаться запаздывания. Обычно
принимают во внимание, что случаются запаздывания, но реже понимают важность
формы, в которой они проявляются. Направления во времени, которым
следуют переменные в модели, зависят не только от факта существования запаз-
39

дываний, но также от принимаемой ими частной формы [7, 11]. Полезна
поэтому уделить некоторое внимание (на этом раннем этапе изложения)
могущим встретиться разнообразным типам и формам запаздываний.
А. Дискретный анализ. Возьмем для удобства единицу времени в
качестве интервала для анализа. Тогда с помощью индексов ?(?=0, 1,2, ...)
можно обозначить последовательность во времени двух переменных ХиУ.
Пусть У линейно зависит от X. Тогда, при отсутствии запаздываний,
Запаздывание является отставанием с фиксированной продолжительностью
в Т единиц времени; эта временная постоянная запаздывания Т является
заданной положительной целочисленной величиной:
T. A)
Уравнение A) характеризует зависимость Y от значения X, отстоящего
на Т интервалов назад. В частном случае запаздывание может представлять
собой отставание продолжительностью в один интервал (Г = 1): Yt = а + aXt_x.
Более общим является случай распределенного запаздывания. Он
описывается следующим образом:
Yt = а
где
B)
Таким образом, Y зависит не только от предыдущего значения X, но и от
всей последовательности его прошлых значений. Тогда отсрочка с
фиксированной продолжительностью представится как частный случай, когда
ят = а, а значения остальных а = 0. Заметим, что в уравнениях A) и B)
X, = const (для всех t) соответствует Yt = а + aXt = const (для всех t)t то
есть исходной зависимости без запаздываний.
Постоянные коэффициенты а19 а2, .. ., которые при линейной
зависимости в сумме равны а, характеризуют временную (частотную) форму
запаздывания B). Их можно истолковать и как взвешивающие
коэффициенты (веса). Число их может быть конечным или бесконечным.
Важным видом распределенного запаздывания является геометрическое
запаздывание, то есть распределенное в геометрической прогрессии
Yt = а + а A - г) (Х,_х + гХиг + r2X^3 +...)• C)
В нем взвешивающие коэффициенты уменьшаются по закону бесконечной
убывающей геометрической прогрессии со знаменателем г@ <т"<1).
Первый коэффициент устанавливается в виде аA — г) для того, чтобы сумма
членов бесконечно убывающей геометрической прогрессии оставалась
равной а:
Представляется полезным ввести промежуточную переменную
Zt = a + aXt,
которая будет потенциальным значением зависимой переменной,
получающимся при отсутствии запаздываний. Фактическая величина Yt получается
из X при действии запаздывания. Действительно, Yt является
переменной, которая запаздывает по отношению к Zf. Если X постоянно во
времени, то Yt = Zt= const. Иначе, если Х^ изменяется, то Yt имеет
запаздывание по отношению к Zt. Простое линейное преобразование заменяет
зависимость Yt от Xt зависимостью Yt от Zt. В частности, легко видеть^
что:
40

1) отставание с фиксированной продолжительностью будет
2) распределенное запаздывание есть
Yt = fK1Zt_1
где ^
3) запаздывание, распределенное в геометрической прогрессии, есть
Последний вид запаздывания допускает дальнейшее развертывание.
Напишем первую разность AYt — YUl — Yt:
?± = (Zt+ rZ%_x + r*Zt_t +...)- (Zt-i + rZt_2 + r*Zt_3 +...) =
= Zf - A - r
Положим A, = l —г, где 0<Я<1. Тогда
AYt=-X(Yt-Zt),
ИЛИ
если А рассматривать как оператор (см. приложение А).
Тогда получаем
= _b;(Y,_Z,), или У« = д^„ ^
где I V >
Все это относилось к неизменному временному интервалу, взятому за
единицу времени. Чтобы включить в модель изменение интервала, возьмем
его в виде Д? вместо единицы. Тогда
где
будет распределенным в геометрической прогрессии запаздыванием с
временным интервалом At и приращением AYt = Г<+ДГ— Yt.
Распределенное в геометрической прогрессии запаздывание в форме D)
или E) допускает простое истолкование. Его можно определить как такой
частный случай распределенного запаздывания, в котором веса
уменьшаются в геометрической прогрессии с неизменным знаменателем г. Далее
очевидно, что прирост AYt в единицу времени или средняя скорость роста
AYt/At в интервале AJ всегда пропорциональна дефициту — (У( —Zt), то есть
разности фактической и потенциальной величин в начале интервала.
Запаздывающая переменная Yt стремится достичь потенциальной (незапаздыва-
ющей) величины Zt, и скорость этого процесса пропорциональна разности
фактической и потенциальной величин. Коэффициент
пропорциональности А, = 1 — г называется скоростью реакции.
Б. Непрерывный анализ. Переменные X(t) и Y(?) являются функциями
времени. При линейной зависимости без запаздывания имеем
1 Так как, по определению, Zt_T = a-\-aXt-T. Найдя отсюда Zf_y и подставляя
в уравнение A), получаем yt=Z^y.—Прим. ред.
41

При наличии запаздывания обозначим потенциальную величину зависимой
переменной Z = a-\-aX. При любом запаздывании У будет запаздывать по
отношению к Z.
Можно сразу записать простейший случай отставания с
фиксированной продолжительностью:
где временная постоянная Г —заданная положительная (не обязательно
целочисленная) величина. Более общий случай непрерывно
распределенного запаздывания получается по аналогии с дискретным вариантом
распределенного запаздывания B). Бесконечный ряд коэффициентов а1У а2, а3,...
при переходе к пределу заменяется непрерывным множеством ординат
некоторой функции /(т) непрерывной переменной т, а вместо суммы
появляется интеграл. Следовательно,
где
G)
будет представлять собой непрерывное запаздывание, в котором /(т) будет
временной формой запаздывания, или взвешивающей функцией.
Следовательно, У зависит jHe только от значений X в предшествующие отдельные
моменты времени, как в дискретном ряду, но и от значений X на
протяжении всего прошлого (непрерывного) времени. Функция /(т)
характеризует зависимость У в момент t от значений X за время ? — т, то есть
за промежуток т до этого момента t. После перехода к Z — a-\-aX
уравнение G) примет вид:
где
(8)
Отставание с фиксированным промежутком времени является частным
случаем G) или (8), когда /(т) = 1 в момент т=Ги равно нулю во все
остальные моменты.
Вычисление интегралов G) или (8) представляет значительные
трудности. Однако можно показать, что при некоторых условиях (8)
равносильно дифференциальному уравнению в операторной записи (см.
приложение А):
а F и G — полиномы, причем степень F ниже степени G (см. 4.8).
Вообще говоря, дифференциальное уравнение (9) решается проще, чем
вычисляются интегралы (8).
Важным частным случаем непрерывного запаздывания является запаз<>
дывание в форме показательной функции, представляющее собой
непрерывный вариант распределенного в геометрической прогрессии дискретного
42

запаздывания. Временная форма последнего будет убывающим
геометрическим рядом. Соответствующее непрерывное запаздывание будет иметь вид
f (т) = Хе~кх (к — положительная постоянная), то есть оно будет
представлено непрерывным множеством ординат убывающей показательной функ-
оо
ции. Можно проверить, что \ / (т) dx = 1 (как это и требуется):
о
Следовательно, при Z = a + aX уравнение (8) дает запаздывание в
показательной форме вида
со
^ T)dT. A0)
В этом частном случае легко получить дифференциальное уравнение типа
{9). Произведем в A0) замену переменной интегрирования x = t — т:
Тогда
t
Y(t)eV = % \
—со
Дифференцируя, получаем
то есть
- Z) или
Следовательно, дифференциальное уравнение запаздывания в
показательной форме имеет вид:
Я
Z = a + aX.
В последнем случае мы пользуемся оператором D. Очевиден параллелизм
с распределенным в геометрической прогрессии запаздыванием D) или E).
Действительно, A1) получается из E) при Д?-^0.
Смысл A1) для запаздывания по показательной функции совершенно
аналогичен интерпретации D) или ч E) запаздывания, распределенного
в геометрической прогрессии. Скорость возрастания У всегда
пропорциональна разности —(Y — Z) фактической и потенциальной величин У.
Коэффициент пропорциональности X называется скоростью реакции.
Вместо скорости реакции X можно взять в качестве другого
возможного параметра как для геометрической прогрессии, так и для
запаздывания по показательной функции, обратную величину Т = 1/К9 то есть
временную постоянную запаздывания. Это соответствует употреблению того
же выражения в случае отставания с фиксированной продолжительностью;
тогда параметр Т равен продолжительности отставания. Интересны два
предельных случая: при Т = 0 (А,—>оо), уравнение (И) дает Y = Z —
= a + aX, и запаздывание отсутствует; при Т—> оо, (К = 0) имеем dY/dt = 0,
У есть величина постоянная, и реакции нет.
43

В. Реакция У на ступенчатые изменения X. Предположим, что
в момент ? = 0 происходит единичный скачок X, и выберем единицу так*
чтобы Z = а + аХ скачкообразно изменилось от Z = 0 в момент t < 0 до
Z = Z0 в моменты ?>0. Рис. 3 иллюстрирует три возможных типа
запаздывающей реакции У в соответствующих частных случаях.
У*
§Т {Т t
I. Отставание с фиксированной продолжительностью при временной
постоянной Т:
= Z(t-T) = O для t<T n.Y(t) = Z(t-T) = Z0 для t>T.
II. Распределенное в геометрической прогрессии запаздывание со
скоростью реакции Х'=1/Т и интервалом АТ = г/3Т:
ДУ,= -{(Yt-Z0) для *>0 из E),
то есть
—1^( =4 20 и Уг =
Путем итерации получаем отсюда х
У„т/з = {1-(|)П}ЯО Для п = 0, 1, 2, ... .
III. Запаздывание по показательной функции со скоростью реакции
где
Итак,
то есть
— x) = Z0 для
и Z{t — т) =
= Zo [ -
Та же линия движения во времени У (t) = A — е~-№) Zo получается для
1 При * = 0, y^3 = 1/3Z0 = {l — */3}ZQ, отсюда получаем формулу в тексте.—
Прим. ред.
44

показательно-функционального запаздывания и в результате решения
дифференциального уравнения A1), которое имеет вид
— + XY = KZ0 при условии, что У = 0 в момент t = 0.
Эти три вида реакции У (для случаев I—III) показаны соответственно
тремя линиями движения во времени на рис. 3. Основным вариантом можно
считать случай II—дискретное распределенное (в геометрической прогрессии)
запаздывание. У здесь представлен ступенчатой функцией, в пределе, при
?—> оо, приближающейся к потенциальной величине Zo. Число шагов этого
процесса зависит от временного интервала запаздывания У, распределенного
в геометрической прогрессии. В данном случае интервал равен 273, где
Т — временная постоянная запаздывания. Случай III можно рассматривать
как непрерывный вариант случая И, получающийся при переходе к пределу,
то есть как непрерывно распределенное (по показательной функции)
запаздывание, под действием которого У асимптотически стремится к Zo. Случай I
представляет собой очень специальный случай ступенчатой функции случая II,
когда У достигает Zo за один шаг, при t=T.
В более общем виде случай 1 можно рассматривать как характеристику
отставания на любой фиксированный промежуток времени; случай II как
характеристику любого распределенного дискретного запаздывания с временной
формой, заданной рядом коэффициентов ai, аг, а3, ...; случай III как
характеристику непрерывно распределенного запаздывания с временной
формой, заданной функцией/(т). Вид кривой /// в общем случае определяется
t \
уравнением У — Z0\f(x) dx или dY/dt — f(t)Z0, а не показательной кри-
Jo
вой, нанесенной на графике для частного случая (см. упражнение 5).
Остается нерешенным вопрос: какое запаздывание принять в качестве
«реального» в экономической модели? Отставание с фиксированной
продолжительностью может оказаться подходящим, например, в том случае, когда
речь идет о реакциях единичной фирмы с периодом решения
продолжительностью Т. Ясно, что оно становится менее пригодным, когда переменные
укрупнены и охватывают весь рынок какого-либо товара или все хозяйство.
Специфические свойства отставаний с неизменной продолжительностью
также способствуют их отрыву от реальности, например может возникнуть
ряд краткосрочных колебаний в пределах промежутка отставания Т (см.
гл. 8).
Может быть выдвинут следующий аргумент: при введении
распределенного запаздывания реакция, описываемая ступенчатой функцией (подобная
случаю II на рис. 3), пригодна для случая дискретного анализа. Однако
совершенно неочевидно, что непрерывная форма, в частности реакция,
описываемая показательной функцией (случай III на рис. 3), окажется неподходящей.
Столь удобное для математики непрерывное запаздывание, по-видимому,
вполне уместно применить в макроэкономических моделях, которые включают
множество отдельных лиц и предприятий с различными интервалами
принятия решений. Тогда реакции укрупненных переменных, вероятно, будут
приблизительно непрерывными.
Задачи и упражнения
1. Показать, что па рис. 3 линия О А является касательной к кривой Ш в точке О,
тем самым дать иную интерпретацию временной постоянной Т запаздывания
показательной формы.
2. В задаче из раздела 1.3 принять спрос без запаздывания равным а-{-аР,
ввести непрерывное запаздывание показательной формы на стороне предложения,
фактическая величина которого равна [X/(D-\-k)] ф+ЬР). Показать, что Р удовлетворяет
уравнению
45

Тем самым показать, что «грубо соответствующая действительности предпосылка»
в разделе 1.3 представляет собой на самом деле предпосылку о существовании
запаздывания показательной формы на стороне предложения.
3. Z— потенциальная величина, Yx зависит от Z с запаздыванием показательной
формы (скорость реакции X), а У2—от Ух со вторым аналогичным запаздыванием
(скорость реакции \i). Положить dYxldt=.—% (Ух—Z)h dY2/^ = —M"(^2—Yi) и>
исключив Yu показать, что зависимость У2 от 2 выражается уравнением
Получить то же дифференциальное уравнение из
У»=Т*ТГ Z и У^=
так что
4. В качестве частного случая двойного запаздывания по показательной функции
предыдущего упражнения взять
Y==\D\1 ) Z ZZ Л '>ОиУ
(TV
Z прИ Z=Z° ДЛЯ '>ОиУ="Ж"=О при t = 0-
Нанести на график значения У и сравнить с графиком одинарного запаздывания
показательной формы, то есть с кривой III на рис. 3. Показать, что каждое из
последовательных запаздываний имеет временную постоянную ~-т-, так что в целом временная
^ Л
постоянная двойного запаздывания равна опять-таки Г = 1Д. Обобщить результат
путем рассмотрения запаздывающей переменной Y=^[nX/(D-\-nX)]nZ.
5. Для запаздывающей переменной У в уравнении (8) положить Z(*)=0(*<0)
и Z(*)=Z0 (*>0).
Показать, что
t

ГЛАВА 2
КЕЙНС И КЛАССИЧЕСКИЕ МОДЕЛИ: МУЛЬТИПЛИКАТОР
2.1. МАКРОЭКОНОМИЧЕСКИЕ ПЕРЕМЕННЫЕ И ЗАВИСИМОСТИ
Описанные в предыдущей главе динамические модели просты, но они
содержат основные элементы для дальнейшего анализа. Простота их
объясняется тем, что они динамичны лишь частично. Рассматривается рынок
только одного товара; исследование поведения и решений ограничено в
моделях лишь ценообразованием — установлением цены данного товара. Цены
других товаров, доходы потребителей, техника производства — все это не
принимается во внимание. Совокупности разных рынков или разных
товаров не существует. Только благодаря упрощению анализа, при котором
игнорируется многообразие взаимосвязанных переменных, или укрупнению
(aggregation), мы сразу же получаем результат, то есть движение во
времени цен и количества продукции, проданной и купленной на рынке.
Обобщение может пойти по одному из двух направлений. Можно
увеличить количество переменных, характеризующих предложение и спрос,
например ввести в функцию спроса цены на другие товары и доход
потребителей; можно взять больше товаров и рынков и рассмотреть все их
взаимосвязи. Это — обобщение до микроэкономической системы, очень подробной
со сложными взаимозависимостями. Можно поступить иначе: уменьшить
количество переменных и зависимостей путем укрупнения и рассматривать
отношения лишь между широкими совокупностями. Такое обобщение
приводит к макроэкономической системе. В этой и следующей главах
рассматривается именно последний метод. Первое приближение к действительности
лучше всего достигается чрезвычайно сильным укрупнением; в противном
случае нужно входить в такие подробности, что рискуешь за деревьями не
увидеть леса.
Однако макроэкономический метод плох тем, что с укрупненными
совокупностями трудно оперировать. Довольно легко взять функции спроса или
предложения из предыдущей главы и просто сказать, что они относятся
к совокупности всех товаров, являются функциями общего уровня цен. Но
тогда исчезает ясная взаимозависимость количеств и цен. Объем спроса
и предложения проданных или купленных товаров нельзя объединить в
количественные группы, имеющие какой-либо общий смысл. Вообще говоря,
объединение можно произвести лишь с помощью стоимостного, денежного
выражения. Если движение во времени ценностных показателей
регистрируется в текущих ценах, то его нельзя разделить на «движение реальных
величин» и «движение цен». В этом случае оно может представлять только их
сочетание. Можно попытаться произвести разделение, использовав индексы.
Но такое разделение не будет однозначным. Например, «реальный» спрос или
потребление можно выразить как стоимость спроса или предложения при
некоторых неизменных ценах. Базисные цены выбираются произвольно,
и применяется взвешенный по базисному году индекс объема спроса или
потребления. Соответствующий индекс цен, на который умножают
переменные величины для получения изменяющихся стоимостных значений,
взвешивается тогда по текущим весам. «Реальное значение» переменной получается,
в сущности, путем дефлятирования наблюденных стоимостных значений
47

с помощью индекса цен, основанного на текущих весах. Всю процедуру
можно осуществить и наоборот — получая «реальное значение» переменной
путем дефлятирования стоимостных значений с помощью индекса цен,
взвешенного по базисному году.
Укрупнение уменьшает число переменных и зависимостей. Но этим
нельзя злоупотреблять. Величину всего спроса, предложения или выпуска
продукции можно выразить в денежной форме и свести к «реальным»
величинам делением на индекс цен. В таком случае макроэкономические
вопросы не представили бы большого интереса. Необходимо, по крайней
мере, проводить различие между потреблением и сбережениями, а также
между продукцией, расходуемой на потребление, и продукцией, идущей
на капиталовложения. При приведении к «реальным» величинам возникает
еще одна проблема. Нужно ли дефлятировать продукцию, идущую на
потребление, с помощью того же индекса цен, что и продукцию, предназначенную
для капиталовложений, или для этого нужно пользоваться другим индексом?
Во многих моделях для простоты берется один и тот же индекс. В этом случае
не учитываются изменения соотношений цен, то есть «условия торговли»
между сектором, производящим предметы потребления, и сектором,
продукция которого идет на капиталовложения.
Даже при самых смелых построениях макроэкономических моделей
обязательно все же разграничение потребления, сбережений и
капиталовложений. Кроме того, всегда, за исключением простейшей модели Кейнса,
существует более чем один рынок, например рынок товаров и рынок факторов
производства. Тем самым усложняется вопрос о равенстве переменных по
определению и их фактических значений. Это не всегда учитывается. Если
анализ концентрируется вокруг рынка товаров или факторов, участвующих
в обмене, тогда фактические покупки и продажи равны. С другой стороны,
на каждом рынке имеются две группы (два лица, две фирмы и т.д.): одна —
продает, другая — покупает. Каждая группа фигурирует дважды: как
покупатель — на одном рынке и как продавец — на другом. Фактическое равенство
покупок и продаж на разных рынках не обязательно означает равенство
выручки кого-либо на одном рынке его расходам на другом.
В данной главе анализ редется в дискретной форме; соответствующее
изложение в форме непрерывного анализа дается ниже. Основной
переменной в макроэкономике является доход как совокупная денежная величина
всего народного хозяйства и как поток или скорость в данном периоде. Эту
совокупность лучше всего рассматривать в том виде, в каком она
используется в статистике национального дохода в замкнутой экономике.В этом случае
в доход включаются такие фактические выплаты факторам производства,
как заработная плата, жалованье, прибыли и т. п., а также сбережения
предпринимателей. Последние, правда, не выплачиваются, а сберегаются.
Однако эти сбережения удобно вменить в качестве дохода факторам
производства. Подробнее этот вопрос рассматривается далее, в разделе 2.9.
Согласно общепринятым определениям, национальный доход равен
национальному продукту или выпуску конечной продукции и является
таким образом денежной совокупностью чистой продукции всех отраслей,
производящих товары и оказывающих услуги. С точки зрения
производителей продукция производится факторами производства и распределяется
между ними (или вменяется им). Если рассматривать народное хозяйство
с более широкой точки зрения, то в макроэкономической теории можно
закономерно считать величины дохода и выпуска продукции —
фактические и по определению — равными. Совокупный доход и выпуск продукции
обозначаются нами одной и той же буквой У.
Хотя никто не планирует доход, но его ожидаемая величина может быть
равна фактическому выпуску продукции. Это становится яснее в буквенном
обозначении; например, ожидаемый доход может быть равным Yt}
(фактический доход предыдущего периода); фактический же доход за период t
составляет Yt. Это один из способов включения запаздывания. Существует
48

и другой вид запаздывания: между временем получения заработанного дохода
(переменная У равна фактическому выпуску продукции) и временем
расходования дохода его получателем. Например, при однократном запаздывании
выпуск продукции и полученный доход составляют Yt, а доход, который
тратится в период t, равен Yt_x. Условные обозначения достаточно гибки,
чтобы отразить такие различия в интерпретации.
Норма процента, обозначаемая г, это еще одна переменная,
находящаяся вне контроля отдельных лиц. Ее следует применять или рассматривать
как цену, как норму, управляющую системой в любой момент времени или
установленную в течение какого-либо периода. Здесь не возникает вопроса об
агрегировании в денежной или иной форме. С другой стороны, принятие
единой нормы i было бы абстрагированием от действительности. Ее нужно
считать лишь представителем целого комплекса или системы различных норм —
норм дохода от всех видов капитала.
Основные зависимости макроэкономики относятся к группам
потребителей и производителей. Если в какой-то период доход потребителей,
подлежащий расходованию, составляет У, то решение потребителей будет таково:
У делится на какую-то потребляемую часть (С) и сберегаемый остаток (У—С).
Намечаемое или планируемое потребление есть функция дохода; эта
ожидаемая функция потребления обозначается С = С (У). Тогда, по определению,
сбережения составляют
Это также ожидаемая функция дохода. Хотя вводятся две функции
(потребления и сбережений), но одна из них (S) непосредственно следует из определения,
тогда как другая специфицирована. В дальнейшем анализе мы будем
предполагать, что планы потребителей реализуются, то есть что С означает как
ожидаемое, так и фактическое потребление, а сбережение определяется как
разность всего дохода и его потребленной части. Поэтому обычно функция
потребления записывается единственным образом (как это приведено выше).
Однако можно пойти и обратным путем, предположив реализацию планируемых
сбережений. Тогда функцию сбережений можно записать в виде S = ?(У),
а потребление будет определяться разностью С = У — S(Y).
Производителей интересует главным образом распределение выпускаемой
продукции (У) между капиталовложениями (/) и продукцией, произведенной
для потребителей или проданной им (Y — I). Предназначаемые или
планируемые капиталовложения являются функцией ожидаемой нормы процента.
Эта функция записывается в виде / = I(i). Планируемые капиталовложения
зависят также от уровня и изменения выпуска продукции. Однако в первом
приближении это не принимается во внимание, чтобы сконцентрировать
внимание на рассмотрении зависимости между i и /. Эта функция представляет
собой шкалу предельной эффективности капитала.
Все переменные, за исключением ?, — совокупности, имеющие денежное
выражение: У, С, S и /. Их смысл лучше всего истолковать в категориях
статистики национального дохода. Они представляют собой потоки дохода или
издержек за период или в единицу времени. Так, С — расходы на
потребление, а не величина, характеризующая решения потребителей, и не поставки
потребительских товаров. То же самое можно сказать и относительно /.
Вначале анализ ведется в текущих стоимостных величинах, то есть изменения
«количеств» и «цен» выступают в комбинированном виде. Далее в тех же
обозначениях мы анализируем «реальные» стоимостные величины выпуска
продукции, потребления, сбережений и инвестиций. Предполагается,
следовательно, что денежные совокупности выражены в неизменных ценах или
дефлятированы с помощью какого-либо индекса цен.
Другие переменные и соотношения между ними будут введены далее
в соответствии с рассматриваемой проблемой. Однако в макроэкономике
У, С, S, / и i являются основными переменными, и главные зависимости
устанавливаются между ними.
4 р. Аллен 49

2.2. ФОРМУЛИРОВКА КЕЙНСИАНСКОГО ПРЕДПОЧТЕНИЯ ЛИКВИДНОСТИ
Среди экономистов нет единодушия по вопросам теории процента,
несмотря на работы Кейнса (или, возможно, именно благодаря им). Хороший
анализ существующего положения дал Ган [3]. Много разногласий возникает из-
за частичного характера принятого анализа; из всей системы соотношений
спроса и предложения выбирается одно частное соотношение, и считается, что
именно оно определяет норму процента. Но о каком соотношении идет речь?
Согласно простому варианту теории, норма процента есть та величина
последнего, которая устанавливается при равенстве спроса и предложения
на денежном рынке. Помимо наличных денег для покрытия сделок — этот
спрос постоянен до тех пор, пока денежные величины дохода и выпуска
продукции неизменны,— предъявляется спрос на денежную наличность
как ликвидную статью актива баланса, то есть для того, чтобы держать ее
в резерве.
Спрос на нее зависит от нормы процента — вознаграждения за отказ от
обладания деньгами — и, следовательно, зависит от платы за обладание ими.
Это и есть шкала предпочтения ликвидности. Если предложение денег
неизменно, то шкала предпочтения определяет норму процента, то есть такую
норму, при которой спрос равен данной величине предложения.
Такой подход слишком прост. Из теории «заемнь!х средств»1 известно,
что спрос и предложение денег нельзя рассматривать оторванно от всего
рынка капитала — денег, ценных бумаг и средств инвестиций. Значит,
основным является финансовый баланс; поток всех операций на рынке
капитала в каждый период должен балансироваться. Это есть закон Валь-
раса; его можно выразить с помощью спроса и предложения, просуммировав
возможные потоки спроса и предложения (предполагается, что при этом
рыночные факторы находятся в равновесии):
(Спрос на наличные деньги) -f (Спрос на ценные бумаги) +
(Инвестиции) = (Предложение денег) + (Предложение ценных бумаг) -\-
(Сбережения). A)
Предложение и спрос на деньги появляются в таком случае в виде части
идентичного соотношения, которое содержит как ожидаемые, так и факты-
ческие величины.
Норма процента — не столько вознаграждение за отказ от обладания
деньгами (это в лучшем случае негативное определение), сколько выручка от
единицы всего капитала. В действительности это не единая норма, а
комплекс норм. В качестве характерной нормы возьмем кейнсианский процент
дохода от ценных бумаг с постоянным процентом (облигаций). Можно
предполагать, что доход по облигации выплачивается регулярно в неизменном
размере (например, 1 ф. ст. в год). Цена такого рода ценной бумаги Р есть
обратная величина нормы процента (г) облигации. Цена облигации Р = 1/г,
и, следовательно, норма процента по ней определяется спросом и
предложением таких ценных бумаг при данном общем состоянии рынка капитала2.
Итак, тождество A) в значительной мере дает ключ к решению проблемы.
Предположим, что норма процента такова, что уравнивает спрос и
предложение ценных бумаг (которыми, например, являются облигации). Отсюда
еще не следует, что эта норма процента уравнивает также спрос и
предложение денег, так как потребные сбережения не обязательно должны быть равны
инвестициям. Например, можно частично финансировать капиталовложения,
сократив размеры денежной наличности. Выразим эту же мысль иначе.
1 Согласно этой теории, норма процента определяется спросом и предложением
на денежные средства, которые могут быть предоставлены в качестве кредита.
Предложение таких средств определяется в основном размерами сбережений и приростом
наличных денег, спрос определяется возможностями нового капиталовложения и желанием
увеличить сумму наличных ценностей. Теория «заемных средств» имеет много общего
с теорией предпочтения ликвидности Кейнса.— Прим. ред.
2 Автор неточен: цена облигации будет P = (a/i) 100, где а — приносимый
облигацией ежегодный доход. — Прим. ред.
50

Предположим, что при какой-то определенной норме процента сбережений
в тождестве A) неравны инвестициям. В таком случае излишек спроса на
деньги не точно соответствует излишку предложения облигаций, и никакое
изменение нормы процента не приведет к одновременному исчезновению
излишка спроса и предложения.
Мы приходим к заключению, что использование шкалы предпочтения
ликвидности при определении нормы процента уравниванием спроса и
предложения денег обосновано лишь в случае равенства ожидаемых сбережений
и капиталовложений. Тогда тождество A) имеет такой вид: избыточный спрос
на деньги = избыточному предложению ценных бумаг. Норма процента,
которая уравновешивает спрос и предложение ценных бумаг, выполняет ту
же функцию и в отношении денег. Поэтому нижеследующее изложение
начинается с того, что ставится условие равенства сбережений и инвестиций,
и лишь затем рассматривается шкала* предпочтения ликвидности.
а б
Ш
M-T(Y)
Рис. 4.
Сбережения есть функция доходов: S = У — C(Y). Шкала предельной
эффективности капитала представляет инвестиции как функцию нормы
процента: / = 1A). Из этого следует, что, как бы У и i ни изменялись, они
должны удовлетворять следующему условию:
{) Щ B)
Возможные величины У и i лежат на кривой SI в плоскости YOi (рис. 4, б).
Можно взять кривую, спускающуюся вниз; увеличение У в силу уравнения B)
вызывает увеличение сбережений, которое должно уравновеситься возросши
ми инвестициями, что связано с понижением нормы процента г. Как показал
Хикс 15J, кривая 57 может выравниваться и при малых и при больших
значениях У (см. рис. 4, б).
Теперь предположим, что спрос на деньги (М) постоянен. Спрос на
деньги делится на две части: спрос на них как на средство платежа и спрос на
них как на денежную наличность. Спрос для оплаты сделок зависит от дохода
или выпуска продукции Т (У). Спрос на денежную наличность при
неблагоприятном балансе вместо имеющихся ценных бумаг или других активов
принимается теперь, по изложенным выше соображениям, зависимым от нормы
процента A (i ). Почти без потери общности оба элемента можно считать
независимыми и могущими складываться. Тогда спрос на деньги или шкала
предпочтения ликвидности будет
При спросе, равном данному предложению М, для равновесия необходимо
то есть
A(i) = M-T.(Y).
51

Уравнение C) записано в таком виде с целью показать, что i определено,
когда заданы Y и М. Это построение представляет простейшую форму
предпочтения ликвидности. Возможны различные модификации и дальнейшее
развитие модели. Например, Смизи [9] показал, что спрос А на ликвидную
денежную наличность зависит как от сбережений 5, так и от нормы процента i.
Кривая на рис. 4, а изображает общую форму функции спроса на
денежную наличность A (i). Мы предполагаем, что A (i)=0 при высокой норме
процента (t>ii) и что существует эффективная минимальная норма i = i^
предписанная правительственными учреждениями. Норма процента при
различных зйачениях У определяется уравнением C); ее можно записать в форме
i ±= i(Y). Графически это изображено на рис. 4, а. При увеличении У уровень
М — T{Y) падает, a i(Y) возрастает в интервале г8<*<*1* При i>ix
данное предложение денег не может обеспечить увеличения У выше той
величины Уь которой У достигает при i = iv Следовательно, кривая LM в
плоскости OYi (см. рис. 4, б) изображает зависимость i от У, данную уравнением C).
Условия B) и C) в совокупности определяют У и г в положении
равновесия; таковым является точка пересечения (Р) кривых SI и LM на рис. 4, б
с координатами У и ?. Имеются два крайних случая, представляющих особый
интерес.
«Классический» случай. Уровень У высок, он равен или приближается
к максимуму Y19 какой возможен при данном предложении кредита. Рост
склонности к инвестированию /(г), в результате которого кривая SI
перемещается вверх и вправо, вызывает повышение нормы процента при
постоянном или немного увеличивающемся доходе (и занятости). «Классики» могли
бы также сказать, что результат был бы тот же и при более низких уровнях
дохода и занятости (при условии, что цены и заработная плата свободно
изменяются).
«Особый» случай Кейнса. У находится на низком уровне и норма процента
равна или приближается к минимуму ?2. Усиление склонности к
инвестированию соответствует движению Р вправо вдоль почти горизонтальной части
кривой LM (см. рис. 4, б). Рост дохода (и занятости) при этом не влияет или
почти не влияет на норму процента.
Задачи и упражнения
1. Возьмем линейные функции C = y-\-cY, I=$-\-bi и L = X1Y-\-X2i* Доказать, что
в положении равновесия
Ш+МР+У) _ (
JLft+Ml —с) "
Объяснить смысл постоянных Ь, с, Хг и А,2 (обычно Ь<0, 0<с<1, Xi >0 и Я2<0).
&*# 2. В предыдущем упражнении доказать, что рост склонности к инвестированию
соответствует увеличению р, повышая Y и i в отношении dY/di=—X2Ai- Объяснить
это с помощью «классического» случая и «особого» случая Кейнса.
; -,* 3. Модифицировать уравнения, предполагая, что функция предложения денег
Л/==Л/A, У), если при возрастании У и i финансовые учреждения расширяют кредит.
Показать, что кривая LM (см. рис. 4,6) «тяготеет» вправо. Что теперь можно сказать
о «классическом» случае? Рассмотреть возможность того, что в условиях инфляции
кривая SI становится горизонтальной (см. работы Хикса [5] и Модильяни [8]).
2.3. ОБЩЕЕ РАВНОВЕСИЕ. МОДЕЛЬ МОДИЛЬЯНИ
Проведенный в предыдущем разделе частичный анализ можно уложить
в более общие рамки. Цель состоит в том, чтобы рассмотреть факторы,
определяющие «реальный» выпуск продукции, занятость, и через цены связать
с «деньгами». Такой подход — в основном классический — был предложен
Модильяни [8]. Но наше изложение принимает во внимание и возражения
Патэнкэна, оцененные по достоинству Ганом [31, а также некоторые
неопубликованные работы Папандру.
Имеется семь переменных: совокупный выпуск продукции в денежном У
я «реальном» (#) выражении; занятость тг, выраженная[вчеловеко-часах; норма
52

процента i; уровень цен Р; часовая заработная плата в денежном W и
«реальном» (w) выражении. Заданы: величина предложения денег и минимальная
часовая ставка заработной платы в денежном Wo или в «реальном» w0
выражении. Практически все эти переменные обычно встречаются в виде
индексов. Так, у может быть индексом продукции, взвешенным по базисному
году, Р и W — таким же образом текущими взвешенными индексами цен и
заработной платы. Индексы должны быть таковы, чтобы соблюдались
следующие простые соотношения: у — Y/P и w — W/P.
Классическая модель. В приводимой ниже таблице показаны семь
зависимостей, входящих в модель. Зависимости A) и B) уравнивают сбережения
и капиталовложения, а также спрос и заданное предложение денег Мо.
Эти хорошо известные зависимости теперь лишь обобщаются так, что
каждая функция включает i и У (нас не интересует в данном случае, будут ли
они эластичны или нет). Зависимость C) представляет собой функцию
производства, связывающую выпуск продукции и занятость. Зависимости D) и E)
являются связующими звеньями между «реальными» и денежными
величинами. Величина спроса на рабочую силу определяется просто: спрос
предъявляется до тех пор, пока предельный продукт у'(п) не станет равным w —
ставке заработной платы в «реальном» выражении.
Классическая модель Модильяни
Денежные зависимости
A)
B)
Технико-производственные зависимости C)
D)
E)
Рынок рабочей силы
F)
G)
S(i, Y) = I(i, Y)
L(i, Y)=M0
У = У(п)
Y=Py
W=Pw
w=y'(n)
w—wo=w(n)
Основная трудность при формулировке моделей рассматриваемого типа
заключается в специфической характеристике предложения рабочей силы.
В данном классическом случае предположим, что существует минимальная
реальная заработная плата w0, ниже которой не может быть предложения
рабочей силы. Реальная заработная плата выше этого уровня w определяет
предложение рабочей силы п. Положим w — w0 = w{n)y где w(n) имеет
следующую форму: w(n) = 0 для всех п ниже некоторого значения и0, затем
w (п) возрастает и стремится к бесконечности, когда п стремится к величине,
большей некоторого значения пх. Кривая предложения, связывающая w и тг,
имеет ту же форму, что и кривая LM на рис. 4, б.
Система определена при полной дихотомии между ее «реальной» и
денежной частью. В «реальной» части зависимости F) и G), описывающие рынок
рабочей силы, фиксируют w и п, а функция производства C) определяет у.
Уравнения A) и B), характеризующие денежный рынок, фиксируют i и У.
Это означает следующее: так как «реальный» доход входит в «реальную» часть,
то денежный доход из денежной сферы служит для установления jP, так что
У == Ру, В этом классическом случае масштаб экономической активности
(занятости) определяется рынком рабочей силы, а предложение денег
фиксирует уровень цен.
Модель Кейнса. Вариант модели Модильяни, помещенный в
нижеприводимой таблице, отличается от классического лишь специфическим
определением предложения рабочей силы. Установленный
правительственными учреждениями минимум Wo характеризует теперь уровень денежноц
заработной платы. Предложение рабочей силы при прежнем w(n) буде?
53

описываться следующим образом:
о> —^ = о>(п), или W-W0 =
В ^[модели, все еще имеется семь зависимостей, но исчезла црежняя простая
дихотомия классического случая. Уравнения A) и B) денежной сферы из
нижеприведенной таблицы фиксируют i и У точно так же, как на рис. 4, б.
Рынок рабочей силы описывается уравнениями, получающимися после
подстановки в уравнения F) и G) значений W из уравнения E). Вместе с
функцией производства C) рынок рабочей силы выражает w, n и у, но на этот раз
только через Р. Следовательно, уравнение D) выражает У через Р, но Р
должно быть таково, чтобы оно было совместно с величиной У, полученной из
уравнений денежной сферы. Эта кейнсианская модель не дает четкого
механизма определения уровня цен, но ясно, что они зависят не только от
денежной сферы.
Модель Кейнса
Денежные зависимости
Технико-производственные зависимости
Рынок рабочей силы
A)
B)
C)
D)
E)
F)
G)
Модель Модильяни
r-V:u(,,,
Модель Папандру
it. v)^V)
w^y'(n)
Предложенная Папандру модель также показана в приведенной выше
таблице. Она более точно отражает точку зрения Кейнса и, во всяком случае,
сильнее отличается от классической модели. Существуют два различия. Во-
первых, в уравнениях A) и B) предельная эффективность капитала и шкала
предпочтений ликвидности применяются к «реальному» выпуску продукции.
Предложение денег по-прежнему можно считать равным Мо, но в правой
части уравнения B) должно находиться т0 = Мо/Р. Или же, пользуясь
несколько иной предпосылкой, можно считать, что правительственные
органы так регулируют предложение денег, чтобы оно установилось на уровне т0
в реальном выражении. Во-вторых, предполагается, что на предложение
рабочей силы влияет лишь ставка денежной заработной платы
(превышающая минимум Wo). Кривая предложения W(n), связывающая W — WQ и /г,
имеет ту же J-образную форму, что и w(n). В этом варианте системы Кейнса
уравнения A) и B) дают i и у, а из уравнения C) получаем п. Таким образом,
уровень выпуска и занятости устанавливается на товарном и
денежном/рынках независимо от рынка рабочей силы. На долю рынка рабочей силы, то
есть уравнений, получающихся после подстановки в F) и G) значений E),
остается лишь определение W и Р. Рынок рабочей силы определяет ставку
денежной заработной платы и уровень цен.
Модель является краткосрочной в специальном смысле этого слова,
и в этом состоит ее ограниченность. Функция производства у = у(п)
предполагает, что основной капитал не изменяется, то есть производятся лишь
инвестиции в оборотный капитал. Форт [2] предложил возможное обобщение
модели, но оно не позволяет полностью преодолеть трудности.
2.4. ДИНАМИЧЕСКАЯ ДЕНЕЖНАЯ МОДЕЛЬ
До сих пор мы излагали только условия макроэкономического
равновесия. Теперь остается на основе общих принципов, изложенных в главе 1,
достроить динамические модели. Решения этих моделей покажут динамику
54

такой переменной, как доход У, отправляясь от специфических начальных
условий или внешних возмущений. Следует ожидать, что для одного и того
же положения равновесия можно построить много разных динамических
моделей; они будут варьировать в зависимости от предпосылок механизма
действия системы, например от ее реакции на возмущение или отклонение.
В качестве частного приложения таких моделей можно рассмотреть вопрос
об устойчивости или неустойчивости основных условий равновесия; при этом
будет столько же трактовок стабильности или нестабильности, сколько
и динамических моделей.
В следующих главах нашей книги основной анализ экономической
динамики ведется в физических величинах — норма процента, а также цены на
товары и факторы производства не принимаются во внимание. Для начала —
хотя и не совсем удовлетворительного — рассмотрим динамическую модель,
основанную на уже изложенных в разделах 2.2 и 2.3 условиях денежного
равновесия. Они зависят от предельной производительности капитала и щкал
предпочтения ликвидности; сбережения предполагаются равными ожидаемым
инвестициям при любой норме процента. При доходе У и норме процента i
точка равновесия находится на пересечении кривых SI и LM (см. рис. 4, б).
Условия равновесия можно выразить и в более общей форме:
У-С(У) = /@ и L(UY) = M(UY). A)
Предложение денег или кредита М не обязательно фиксировать; финансовые
учреждения могут регулировать его в соответствии с изменениями дохода
и нормы процента.
Мы пользуемся в динамическом варианте дискретным анализом;
последовательные промежутки времени обозначаются через нижние индексы t
{t = 0, 1, 2, ...). Первое условие равновесия — равенство сбережений и
капиталовложений — соблюдается на протяжении всех временных интервалов.
Поэтому первое уравнение A) просто переписывается в виде
У,-С (У,) = /(*,). B)
Переменные Yt и it не имеют запаздываний и опережений. Возможно, это
объясняется тем, что запаздывания уравновешиваются, ибо сбережения
отстают от дохода, капиталовложения — от нормы процента. Это и
предположил Хикс [5].
Второе уравнение A), выражающее соотношение спроса и предложения
кредита, берем в динамическом варианте с запаздываниями. Мы
предполагаем, что спрос и предложение кредита, хотя на них и влияет текущая норма
процента, зависят и от дохода с запаздыванием в один промежуток времени.
Например, спрос на деньги для оплаты сделок зависит от объема операций
предыдущего периода, а расширение кредита финансовыми учреждениями
является реакцией на изменения дохода также в предыдущем промежутке
времени. В таком случае уравнение примет вид
L(U*Yiml)~M(ii9Yul). C)
Действие динамической модели определяется уравнениями B) и C). Если YU1
дано, из уравнения C) определяем it и затем получаем Yt из уравнения B).
Исключение it из уравнений B) и C) приводит к конечно-разностному
уравнению первого порядка. В него входят Yt и У,_1# Оно непосредственно
определяет динамику Yt. Это изображено графически на рис. 5 в форме обычной
паутинообразной модели. Исходное состояние здесь Ро, скажем, положение
равновесия перед небольшим увеличением склонности к инвестированию
(см. кривую SI). Новое положение равновесия будет Р.
При заданном Уо в точке Ро, h в первом промежутке времени
определяется кривой LM в точке Ро, а Ух — кривой SI с той же ординатой
(сбережения равны устойчивым капиталовложениям). Во втором промежутке гг
55

корректируется в соответствии с i2 по линии LAf, и цикл повторяется. Дина-
мика Yt (и it) представляет колебательное движение с чередованием знаков.
Колебательное движение является
затухающим и стремится к
положению равновесия, если угол наклонаSI
к OY в точке Р больше угла наклона
LM в этой же точке.
В этой модели денежное
равновесие (см. рис. 4, б) устойчиво в
любой точке Р, где кривая SI
пересекает кривую LM под большим
углом к OY. Этого следует ожидать
при низких уровнях дохода и
занятости (например, в «особом»
случае Кейнса) и при повышенных
уровнях, если только предложение
кредита финансовыми учреждениями будет
Рис. 5.
увеличено. Тогда кривая LM
«вытягивается» вправо (см. 2.2, упражнение
3). Это не совсем «правдоподобный»
результат; он указывает на то, что
динамическая модель не является полной и не вполне отражает
действительность. Это затруднение, вероятно, вызвано тем, что концепция предпочтения
ликвидности не подходит к динамическим условиям..
Задачи и упражнения
1. Рассмотреть У/ — С (Yf_1) = / (it) и L (iAYt_i) = M как возможную динамическую
модель, в которой ожидаемый доход потребителей в интервале t составляет Y^i-
Показать, что сбережения не равны предполагаемым капиталовложениям и, таким
образом, предпочтение ликвидности здесь не применимо.
2. Можно ли применить те же построения к Yt— С(У^) = /(^_1) и L(if_i, Yt) = M
как возможным динамическим моделям?
3. Покажите, что описанная в тексте модель включает непредвиденную
ликвидность, а в моделях двух предыдущих упражнений имеются непредвиденные сбережения
или капиталовложения. Проиллюстрируйте, кроме того, что для применения шкалы
предпочтения ликвидности важно соблюдение равенства сбережений ожидаемым
инвестициям.
4. В рассматриваемой модели положить М постоянным и взять линейные функции
как в упражнении 1 раздела 2.2. Покажите, что SI и LM—прямые линии с наклоном
(к OY), соответственно равным [A — с)/Ь] и (—ki/X2). Покажите далее, что модель
приводит к разностному уравнению yt =Yt — У (где У—значение равновесия):
Пользуясь этим, проверьте, что при устойчивости угол наклона j57 должен быть больше,
чем LM.
2.5. МАКРОЭКОНОМИЧЕСКИЕ МОДЕЛИ В «РЕАЛЬНОМ» ВЫРАЖЕНИИ
Макроэкономическая система уже рассматривалась ранее (см. 2.3)
в двух аспектах — реальном и денежном. Но «реальные» величины,
например функция производства и условие равенства предельного продукта
ставке реальной заработной платы, находились на втором плане. «Реальные»
величины введены были там как бы в дополнение к денежной сфере при
изложении широкой схемы общего равновесия. Это не единственный и не
самый важный вклад в теорию Кейнса. Равновесие, описанное в разделе 2.3,
не учитывает взаимодействия между выпуском продукции и
капиталовложениями, между капитальным оборудованием и произведенной продукцией.
А именно эта взаимосвязь через «мультипликатор» и «акселератор» управляет
всеми макроэкономическими динамическими моделями, выраженными
в «реальных» величинах.
56

Здесь и в последующих главах динамические модели рассматриваются
в «реальном» выражении; денежные факторы, в том числе норма процента,
выпадают из поля зрения. В самом деле, их можно ввести позже, например
добавив к «реальной» модели динамический денежный механизм
приблизительно так, как это было сделано в разделе 2.4; именно это и сделал Хикс[5].
Однако ясно, что главное внимание в макроэкономической динамике
обращается на действие «реальных» (а не денежных) факторов, в особенности на
действие мультипликатора и акселератора.
Переменные величины такого анализа следующие: доход и выпуск
продукции У, личное потребление С и дополняющие его сбережения S и
капиталовложения /. Каждая из них представляет «реальную» совокупность в
масштабе всего народного хозяйства. Как и в статистике национального дохода,
каждую из этих совокупностей можно получить, выражая ее в неизменных
ценах или путем эквивалентной операции ее дефлятирования с помощью
индекса цен (или комплекса таких индексов). Строго говоря, для
дефлятирования каждой такой совокупности и даже разных подгрупп внутри нее самой
нужно применять различные индексы цен; например, для выражения
величины потребления в неизменных ценах нужны различные индексы цен на
потребительские товары и услуги, для дефлятирования капиталовложений —
разные индексы одн на отдельные виды капитальных благ. В этом случае
относительное движение цен, изменения «условий обмена» между различными
секторами будут еще одним объектом анализа. Для упрощения модели
(сохраняя при этом ее сущность) предположим, что цены во всех отраслях
движутся параллельно, так что каждую совокупность можно считать дефля-
тированной с помощью одного и того же индекса цен. Предположим, кроме
того, что экономика замкнутая, без государственного бюджета, и что
имеются достаточные неиспользованные ресурсы (труда и других факторов) для
необходимых изменений в выпуске продукции.
Следовательно, как и в статистике национального дохода, можно через У
обозначить доход и выпуск продукции, которые, по определению, равны. Это
верно как для «реального» выражения, так и для денежного, так как
влияние «условий торговли» не учитывается. Доход У — непланируемая
переменная. Фактические условия, определяющие задачу, таковы:
Y = C + S и Yt*C + I. A)
Первое равенство выражает тот факт, что в силу самого определения
фактических соотношений доход разделяется на потребление и сбережение. Что
не потребляется — то сберегается. Второе равенство представляет собой
подобное же деление выпускаемой продукции на продукцию для личного
потребления и продукцию для фактически осуществляемых
капиталовложений. Обе эти формулы связывает личное потребление С, так как предметы
потребления покупаются за счет дохода и продаются из выпускаемой
продукции. Из определения фактических соотношений следует, что S = /,
то есть сбережения равны капиталовложениям.
В моделях, используемых в дальнейшем анализе, У = С + / является
обычным условием для уравнения модели, а значит, и ее решения. Другое
условие A) применяется, между прочим, для определения состояния
сбережений.
Иначе формулируются ожидаемые соотношения. Нет основания полагать,
что такие условия, как A), будут существовать и в ожидаемых отношениях.
Нет никаких причин для равенства или даже строго фиксированного
соотношения ожидаемых сбережений и инвестиций. То, что необходимо уточнить,—
это ряд основных ожидаемых зависимостей или функций.
Первое соотношение такого рода — это функция потребления
если она взята в линейной форме. Ее дополняет функция сбережений
) = A-с)У-<у
57

Обе формулы выражают ожидаемые соотношения. Они определяют
запланированное или имеющееся в виду личное потребление (или сбережения)
через текущий или ожидаемый доход. Второе ожидаемое соотношение
показывает, какими факторами опредедяются капиталовложения. Ожидаемые
инвестиции уже не выражаются в виде функции нормы процента, через
шкалу предельной эффективности капитала. Теперь в каждой из построенных
моделей остается более точно определить факторы, влияющие на инвестиции.
Для начала, на первой стадии анализа, предположим, что ожидаемое
соотношение заключается в том, что инвестиции даны и неизменны:
I = А (независимые капиталовложения). В качестве усложнения можно
принять независимые капиталовложения (autonomous investment)
заданными, но изменяющимися определенным образом (например, колеблющимися)
во времени. А превратится тогда в функцию времени, но по-прежнему
будет представлять независимые капиталовложения.
Чтобы завершить формулирование модели данного типа, предположим,
что осуществляются как планы потребления, так и планы
капиталовложений, то есть что ожидаемые и фактические величины тождественны.
Значит, С и А можно с равным правом употреблять для обозначения как
фактических, так и ожидаемых величин. Для сбережений это необязательно;
фактические сбережения в модели (как остаток после вычитания) будут равны
ожидаемым и фактическим капиталовложениям. Но они не имеют жесткой
связи с ожидаемыми сбережениями. Эта модель допускает появление
непредвиденных сбережений. Можно построить и такую модель, в которой
осуществляются планы сбережений, а не планы потребления, так что возникает
непредвиденное потребление. Но это будет уже другая модель.
2.6. СТАТИЧЕСКИЙ МУЛЬТИПЛИКАТОР
На основе описанного выше общего типа модели статический
мультипликатор получается сразу из условия равновесия
то есть
Y-~C(Y) = A (А дано). A)
Это уравнение выражает Y через А; оно определяет уровень дохода и выпуска
продукции для положения равновесия, допуская и возможность множества
решений. Рассмотрим случай сравнительной статики. Пусть А
меняется. Определим соответствующее изменение уровня дохода, обеспечивающего
равновесие. Дифференцируем A) по А1:
dY dC dY ,
dA dY dA "~ '
то есть
dY __ 1 _ 1
dA ~ 1 —с "~ s '
где
c=zc(Y) = -Ty- и s = sG) = -—г при s = l — c.
Пользуясь малыми конечными приращениями, выразим соотношение
приблизительно так:
№=-??- = — . B)
1 — с s v '
Это и есть мультипликатор.
По определению, с есть предельная склонность к потреблению (dC/dY);
юна в общем варьирует в зависимости от уровня дохода и потребления.
1 Дифференцирование второго слагаемого — дифференцирование сложной
функции С (функции от функции).— Прим. ред.
58

Равным образом s есть альтернативная величина — предельная склонность
к сбережениям (dS/dY), тоже изменяющаяся в зависимости от дохода.
Обе эти величины дополняют друг друга, так как при любом доходе
^= 1 — с и с = 1 — s. В общем только при предположении, что С и S —
возрастающие функции дохода, с и s будут обе положительны и, значит,
обе меньше 1 (так как если s = l — с > 0, то с < 1). В дальнейшем всегда
будет предполагаться, что дело обстоит именно таким образом:
0<с'<1 и 0<s<l.
Теперь соотношение B) имеет следующий смысл:
если независимые инвестиции изменяются на малую величину ДЛ,
то обеспечивающий равновесие доход изменяется на произведение АА
на множитель, больший единицы (мультипликатор), то есть
где с —предельная склонность к потреблению или dC/dY.
Положение даже упрощается, если функции потребления и
сбережения принять линейными. Предельные склонности с и s в этом случае
превращаются в постоянные, неизменные при всех уровнях дохода, то есть
в коэффициенты У в линейных зависимостях:
? = A-с)У-у= -У + sY.
Остается выяснить смысл постоянной у; ее можно принять положительной
(Y > 0) и рассматривать как ту часть потребления, на которую не влияет
доход. Именно благодаря y пРи низких уровнях доходов могут быть
отрицательные сбережения. Далее, обобщая, можно допустить, что y
определенным образом изменяется во времени, представляя собой
«тенденцию» потребления. В таком случае кривая С = cY + y^ на плоскости OYC
перемещается во времени параллельно самой себе.
Условие равновесия A) в этом случае таково:
то есть
у= А+У _ А+У C)
1 — С S ^ '
Таков мультипликатор в линейном случае.
Линейный мультипликатор C) внешне напоминает выражение его
в общем случае B). Различие состоит в том, что в линейном случае
рассматривается зависимость между величинами дохода и капиталовложениями,
а в общем случае — только между изменениями дохода и изменениями
инвестиций. Это служит дополнением еще и того факта, что с и s —
постоянны в выражении C), но не в B).
В линейном случае возникает еще одна особенность. В выражении
мультипликатора C) А и y появляются вместе; они аддитивны1, что и следовало
ожидать, так как А — независимые расходы на капиталовложения, то есть не
зависящие от дохода, а у- независимые расходы на личное потребление,
также не зависящие от дохода. С точки зрения установления дохода эти два
вида расходов просто дополняют друг друга. Поэтому нередко удобно
включать y в А и называть их сумму независимыми расходами. В таком случае
функция потребления С = cY (и функция сбережений S=sY) представляет
ту часть потребления (или сбережений), которая зависит от дохода. Тогда
мультипликатор формулируется следующим образом. Условием равновесия
будет
1 Аддитивными называются величины, суммируемые в том или ином смысле.—
Прим. ред.
59

где С Til — расходы на потребление и капиталовложения, причем те и другие
не являются независимыми, и А — независимые расходы всех видов. Здесь
С = cY и / = 0:
то есть
у . Л _ А
D)
Мультипликатор D) — только вариант выражения C), в котором у
входит в А. Этот линейный случай имеет следующий смысл:
Если предельная склонность к потреблению постоянна @<с<1),
то тогда обеспечивающий равновесие доход равен произведению
величины всех независимых расходов (на потребление плюс
капиталовложения) на множитель, больший единицы, то есть
У-Л
Важно ясно представить себе, что действие мультипликатора как бы
«домножает» (multiplied up) величину независимых расходов, равно как
и всех форм инвестиций, до размеров
дохода.
Статический мультипликатор
изображен графически на рис. 6.
Линия OS плоскости OAY определяется
уравнением У = А 1A—с); ее можно
назвать линией сбережений S, так
как она соответствует положению
равновесия, при котором сбережения
равны капиталовложениям. На рис. 6
имеются также линия У = А,
которая изображает доход без влияния
мультипликатора, и линия У = А —у>
показывающая только одни
независимые капиталовложения. При любом
заданном уровне независимых
расходов (ОМ) доход, обеспечивающий
равновесие и получаемый
умножением независимых расходов на
мультипликатор, изображается прямой
МР, причем Р лежит на линии OS. Если Q и R — соответствующие точки
на двух других прямых, то обеспечивающий равновесие доход делится на
сбережения (равные независимым капиталовложениям, или MR) плюс
независимое потребление (RQ) плюс потребление QP, зависящее от дохода.
Рис. 6.
Задачи и упражнения
1. Пусть У—доход, обеспечивающий равновесие и соответствующий независимым
расходам А. Он задан формулой Y — С (У)=А; пусть Уо — доход, обеспечивавший
первоначальное равновесие. Он соответствует Ло; доказать, что
и вывести, что У—Уо = [1/A — с)] (А—Ао), где с^? (dC/dYH при малом значении
У—Уо- Установить тождество с мультипликатором B), приведенным выше.
2. Определить среднюю склонность к потреблению (сбережению), если потребление
(сбережение) пропорционально доходу. Показать, что в линейном случае средняя
склонность к потреблению составляет с + (y/Y) и уменьшается с увеличением дохода, а также
что средняя склонность к сбережению равна s — (y/Y) и возрастает вместе с доходом.
Этот результат зависит от у > 0; «реалистично» ли вообще брать у < 0?
60

2.7. МОДЕЛЬ С ДИНАМИЧЕСКИМ МУЛЬТИПЛИКАТОРОМ
Остается ввести в анализ запаздывания и ожидания и использовать таким
образом свойства динамической модели, описанныев разделе 2.5. Помимо всего,
это покажет, устойчиво ли равновесие при статическом мультипликаторе.
В рассматриваемой здесь модели мы предполагаем, что потребители
рассчитывают на неизменные размеры дохода в течение каждого ближайшего
промежутка времени, то есть в интервале t ожидаемый доход составит YU1.
Планы потребителей на интервал t таковы:
Ожидаемое потребление = C(Yt_1), \ A)
Ожидаемые сбережения = Ytl — C(Yt_^). J
Далее мы принимаем, что планы потребления осуществляются, то есть
фактическое потребление Ct = C(yt_^), и что реализуются планы
капиталовложений, причем даны независимые инвестиции, постоянные во времени:
Капиталовложения It = A.
Условие действия модели в каждом интервале t будет
что приводит к конечно-разностному уравнению первого порядка
) = A. B)
Если задана величина первоначального дохода Уо, то путем итерации
находим из уравнения B) значения последующих величин Yt при
* = 1, 2, 3, ... .
Планы потребления и инвестиций осуществились; что же происходит
со сбережениями? Ожидаемые сбережения определяются формулой A),
и она не была использована при выводе формулы B) и для характеристики
движения Yt. Однако, коль скоро Yt известно, фактические сбережения
можно определить из Yt = Ct-\-St:
Фактические сбережения St = Yt — C (Y^). C)
Сравнение формул A) и C) показывает, что фактические сбережения
отличаются от ожидаемых в случае изменения дохода от одного
промежутка времени до другого. В модели с конечно-разностным уравнением B)
доход изменяется во времени. Поэтому в этой модели могут быть
непредвиденные сбережения.
В линейном случае независимое потребление включается в
инвестиции Л, а для потребления, зависящего от дохода, берем C = cY. Тогда
где Ctt=cYt_v /j = 0 и At = A (заданные независимые расходы в .сумме
на потребление и капиталовложения). Разностное уравнение будет
иметь вид
Yt-cYt_x = A. D)
Подставим Yt = Y при всех значениях t:
Y-cY = A,
то есть
что характеризует величину дохода, обеспечивающего равновесие при
статическом мультипликаторе. Положим
Тогда выражение D) можно выразить так:
61

с решением (путем итерации)
Vt =
или
E)
Так как 0<с< 1, решение E) представляет собой путь Ур стремящегося
монотонно к Y—уровню равновесия. Следовательно, при статическом
мультипликаторе уровень равновесия устойчив; в случае какого-либо
начального возмущения доход стремится вернуться к уровню равновесия.
Скорость реакции, или темп, с которым Yt стремится во времени к Yy
зависит от двух факторов: продолжительности запаздывания и размера
предельной склонности к сбережению
s=l — с. Если продолжительность
запаздывания уменьшается (например, с 6 до 3
месяцев), то каждый этап движения Yt к Y
требует меньше времени. Если s
увеличивается, то уменьшение величины с в форму*
ле E) означает большее изменение Yt от
одного интервала до следующего.
Описанная здесь модель показывает
динамический эффект простого
мультипликатора, или мультипликатора Кана. Ее
можно развить и расширить многими
способами. Некоторые из них относятся к
настоящему изложению, и мы рассмотрим их
в следующей главе. Хиксом [5]
предложено графическое изображение
мультипликатора Кана в вышеприведенной линейной
форме D) и E). Оно представлено на рис. 7
в виде линии S. Первоначальный доход
составляет Уо = МР0 = M'Q0; это могло бы
быть доходом в состоянии равновесия при
независимых расходах ОМ'. Происходит сдвиг независимых расходов к ОМ,
и доход в новом состоянии равновесия равен Y = MP. В интервале 1
доход Y1 становится равным МР1У где в силу уравнения D)
м
Рис. 7.
или, прибавляя к обеим частям равенства разность Y —
то есть геометрически
Наклон (tg угла с осью О А) прямой S равен 1/A —с), следовательно^
P0P/Qi,Pu = tIl-c), или QoPo = (l-c)PoP- Значит, ^ = ^0» и прямая
Q0P± наклонена под углом 45° к горизонтали. То же самое получается^
в следующих интервалах, и все прямые QxP2i QJP^ • • • также наклонены
к горизонтали под углом 45°. Таким образом, получен наглядный
графический метод построения этапов от Ро к Рг, к Р2, к Р3, ...,
стремящихся к Р.
В линейной модели D) А принимается неизменным во времени.
Модель можно распространить и на случай с независимыми расходами,
варьирующими во времени, если только задана точно установленная форма
их изменения. Нужно лишь заменить А на At, где At — конкретная форма
изменения А во времени. Например, она может представлять собой рост
62

по прогрессии или какой-либо тип колебаний. Возьмем случай, где
независимые расходы возрастают в геометрической прогрессии с темпом г
@)
Тогда конечно-разностное уравнение D) примет вид
Yt - СУ{.1 = Ао A + г)<. F>
Никакое статическое положение равновесия невозможно ни теперь, ни
в будущем; это можно проверить, подставив Yt = Y для всех t в
выражение F). Либо же можно принять другую альтернативу, что доход и
независимые капиталовложения растут с одинаковым темпом. Подставим
5^ = У0A + г)' в выражение F)
то есть, разделив на A+ /•)',
Yo = -^-. G)
1—
1 + г
Следовательно, если увеличение дохода начинается с уровня,
определяемого равенством G), то принятый характер роста дохода У0A + гI
соответствует модели.
Но это еще не все. Далее нужно найти направление движения Yt при
любом другом исходном уровне (или при наличии возмущений) Yo Ф Уо.
Оно легко получается в следующей форме (вывод см. в 5.6):
?^Т0Ц+гУ + (?0-?0)с1. (8)
Первый член выражения (8) означает непрерывный рост; второй член
монотонно затухает, стремясь к нулю. Действительно, в этом случае решение то
же, что и для уравнения E). Различие лишь в том, что Yt устойчиво
стремится не к фиксированному уровню равновесия У, а к растущему уровню
УоA + /•)'. Последний определяется принятым темпом роста независимых
капиталовложений.
Сходные результаты получаются и при иных формах заданного
изменения Ai во времени. Общий вывод таков: любому заданному движению At
соответствует своя форма динамики Yt, являющаяся результатом «домноже-
ния» независимых расходов. Если Yt уклонится с этого пути, то оно будет
стремиться возвратиться к нему, причем скорость этого процесса зависит
от величины s = 1 — с.
Этот вывод представляет некоторый ограниченный интерес.
Мультипликатор воспроизводит в доходе или продукции любой уровень независимых
расходов, соответственно «домножая» их. Но с экономической точки зрения
здесь что-то упущено. Даже если независимые капиталовложения
действительно возрастают в геометрической прогрессии, экономически было бы
неразумно предполагать, что доход будет увеличиваться точно таким же
темпом. Возможно, это было бы верно в отношении роста населения, который
трактуется иначе и проще. Но, как показал Александер [1],рост независимых
расходов в геометрической прогрессии экономически нереален. Более
вероятно, что независимые капиталовложения развиваются «скачками»
(«spurts»), как это описывалШумпетер. Следовательно,соответствующее
движение Ах> подставляемое в выражение D), является не какой-либо
правильной математической формулой, а скорее эмпирическим временным рядом.
Простой мультипликатор лишь показывает, что при любых независимых
расходах «умножение» их на 1/A—с) дает доход или выпуск продукции и что
в динамике этот результат устойчив.
63

Одно расширение простого мультипликатора может быть получено
сразу. До сих пор мы принимали, что функция потребления Ct = С (Y^^
зависит только от дохода предыдущего периода; запаздывание имело форму
простого однократного отставания. В более общем случае существует
распределенное запаздывание, когда Ct зависит от дохода нескольких прошлых
периодов (см. 1.9). В линейном случае Ct = у + cYt-i заменяется
выражением
Cl = y + c1Yi_1 + c2Yt_t+...A
где (9)
В этом случае существует последовательность предельных склонностей
к потреблению (сх, с2, с3, ...), которые в сумме дают общую предельную
склонность к потреблению с @<с<1). В частности, в случае
геометрического запаздывания эти коэффициенты могут уменьшаться в геометрической
прогрессии.
Теперь открывается гораздо больше возможностей. Следует заметить,
что Ct характеризует расходы на потребление в течение промежутка
времени t, а не потребление и даже не поставки потребительских товаров.
Особый случай, характеризуемый уравнением (9), возникает, когда
доход колеблется во времени и потребители как-то «осередняют» (average up)
свои расходы. Наиболее важен тот факт, что расходы на потребление
производятся для приобретения разнородного набора товаров и услуг; решения
о покупках (на которые влияет текущий или недавно полученный доход)
могут привести к увеличению различных видов расходов в будущем.
Примером может служить покупка в рассрочку. Решение о покупке в рассрочку,
принятое сейчас на основании текущего дохода, влечет за собой платежи на
протяжении нескольких последующих периодов; фактическая поставка
товара не имеет значения, ибо в данном случае важны только расходы.
Даже при введении Запаздывания, распределенного в течение двух
интервалов, гибкость модели с мультипликатором возрастает. При Ct =
= ci5Vi+ c2*Va» гДе ci+ С2 ^ с> конечно-разностное уравнение D)
принимает вид
Снова получаем решение Yt — У== Л/A—с), как и для статического
мультипликатора. Положим i/f= Yt—У, и уравнение примет вид
Это конечно-разностное уравнение второго порядка. Полное и общее
решение приводится ниже (см. 5.7). Однако факт существования большего
количества возможностей, включая колебательные и знакочередующиеся
функции, можно проверить методом последовательных решений путем
подстановки разных пар первоначальных значений yt и выписывания
последовательных значений, полученных из разностного уравнения.
Задачи и упражнения
1. Рассмотреть другую возможную модель, в которой выполняются планы
сбережений, а ие потребления. Обозначить ожидаемые сбережения периода t как S (Yt-i)
и показать, что условие модели состоит в том, что S (Vf-i) являются фактическими
капиталовложениями. Если планы капиталовложений реализуются (например,
существует только фиксированная величина независимых капиталовложений), то
S(Yt_1) = Ат Показать, что в результате не получим никакой динамической модели;
только /4/A— с) —доход в состоянии равновесия — будет соответствовать системе.
Почему является столь жесткой двойная предпосылка об осуществлении планов
сбережений и капиталовложений?
2. В динамической модели, представленной уравнением B), взять фактическое
время запаздывания между моментом получения дохода и его расходованием так,
чтобы У/_х была та сумма, которая тратится в период t. Показать, чго применяется
64

то же самое уравнение B) и что единственная разница в истолковании состоит в том,
что фактические сбережения можно разделить:
Объяснить смысл этих двух членов.
3. Использовать рис. 7 для иллюстрации того факта, что при заданном
дискретном запаздывании скорость реакции при изменении Yt до уровня У, дающего
равновесие, изменяется в соответствии с уравнением s = l — с.
4. Для динамической модели, приведенной в тексте, показать что ожидаемая
разность (капиталовложения минус сбережения) равна (Yt—Yj-i)- Объяснить смысл.
Использовать этот результат для построения соответствующей непрерывной модели:
—г- = Капиталовложения—Сбережения==А—У + С (У).
В линейном случае показать, что решением y^=Y—У является выражение
которое представляет собой результат сходимости ряда У к У со скоростью,
зависящей от s=i — с.
5. В уравнении F) для роста в геометрической прогрессии можно ожидать
решения Yt = [Ло/A — с)] A-f-'*)', где Ао — «домножаемый» коэффициент. Действительный
коэффициент равен YO = AO/[1— с/(\-\-г)]. Показать, что при 0<><1 и г>0
У0<Л0/A — с). (См. рис. 3 в работе Хикса [5].)
2.8. ЗАВИСИМОСТЬ МЕЖДУ СБЕРЕЖЕНИЯМИ И КАПИТАЛОВЛОЖЕНИЯМИ
В дискретный динамический анализ входит зависимость между
капиталовложениями и сбережениями (ожидаемыми и фактическими). Эта зависимость
иногда является источником недоразумений при объяснении динамических
моделей. Наиболее четким подходом при решении вопроса является
следующий.
По определению, фактические сбережения и капиталовложения равны.
Это — следствие тождества дохода и выпуска продукции, основного
тождества для развернутого здесь анализа, как и для статистики национального
дохода. Однако ожидаемые сбережения и капиталовложения вовсе не
должны быть равны фактическим величинам или вообще как-либо связаны с
ними. Динамический анализ должен предусмотреть возможность
непредвиденных сбережений, например в форме внеплановых добавлений к балансам
потребителей или фирм. Равным образом он должен помогать предвидеть
неплановые инвестиции, например накопления в виде сверхплановых
запасов. Отсутствие непредвиденных сбережений (или капиталовложений)
должно объясняться лишь тем, что динамическая модель построена на неявном
предположении, что планы сбережений (или капиталовложений)
осуществляются и, значит, ожидаемые и фактические величины равны. Например,
вышеприведенная модель (см. 2.7) предполагает реализацию планов
капиталовложений, но допускает непредвиденные сбережения.
Можно также взять равными как ожидаемые величины сбережений
и капиталовложений, так и фактические (последние по определению), то
есть с самого начала принять наличие равенства между сбережениями
и капиталовложениями. Это равенство вовсе не обязательно; все зависит от
того, является ли данное предположение «реалистичным» в том смысле, что
оно создает динамическую модель, имеющую экономическую значимость.
Можно разработать модели, для которых предпосылка о равенстве
ожидаемых сбережений и капиталовложений является чрезмерным упрощением.
Так обстоит дело в моделях, включающих денежные факторы, в случае если
они основаны на концепции предпочтения ликвидности (см. 2.2). Равенство
ожидаемых сбережений и капиталовложений может быть, следовательно, как
полезным, так и необходимым допущением; непредвиденные сбережения
и капиталовложения исключаются, но лишь потому, что интерес сосредоточен
на непредвиденной ликвидности. Динамический элемент в паутинообразной
5 Р. Аллен 65

модели на рис. 5 заключается не в кривой SI (которая представляет собой
соотношение между сбережениями и капиталовложениями в состоянии
равновесия), а в кривой LM.
Такого оправдания не существует для моделей, основанных на
мультипликаторе, сравнительно простых и общих по форме (см. 2.7). В этом случае
можно утверждать, что допущение равенства ожидаемых сбережений и
инвестиций уводит от реальной проблемы. В самом деле, либо интересующие
нас переменные всегда точно совпадают — ив этом случае они
необъяснимы — либо же совпадение двух шкал представляется случайностью или
тривиальностью (как спрос равен предложению при всех ценах).
Рассмотрим ожидаемые зависимости, свойственные модели
мультипликатора (и акселератора), как это сделано в разделе 2.5. И потребление и
сбережения являются функцией дохода У, причем одно дополняет другое.
Капиталовложения есть функция любых факторов, выбранных в качестве
определяющих. Эти факторы суть планы или шкалы предпочтения; они очень
напоминают кривые спроса и предложения. Вопрос состоит в том: какие
планы осуществляются? Это зависит от предпосылок и их экономического
смысла. Обычная и, как утверждают, экономически наиболее значимая
предпосылка состоит в том, что планы потребления и капиталовложений
реализуются. Следовательно, ожидаемое и фактическое ¦ потребление (или
капиталовложения) равны. Здесь происходит неявный переход от шкал
предпочтения к стоимостям. Для осуществления планов потребления, например,
требуется, чтобы доход был заранее известен, и покупки, соответствующие
(по шкале предпочтения) этому доходу, были бы действительно произведены
независимо от правильности или ошибочности предположений о доходе.
Относительно сбережений такие предположения не делаются —
непредвиденные сбережения вводят в модель элемент гибкости. Положение можно
резюмировать следующим образом:
5? *St = /, = /?,
где верхний индекс п означает ожидаемые (плановые) предполагаемые
величины, а для остальных переменных даны их фактические значения.
Возможна и модель другого типа, в которой принимается, что планы
сбережений и инвестиций реализуются. Она допускает лишь непредвиденное
потребление. Тогда модель будет такова:
?>t — Ot = Л | — If «
Она подразумевает, что сбережения и капиталовложения равны с самого
начала и что отдельные планы сбережений и капиталовложений согласованы.
В более сложных моделях это в любом случае оставляет слишком мало
гибкости в динамическом анализе, основанном на мультипликаторе (см. 2.7, упр. 1).
В этом состоит затруднение в частной формулировке, принятой Харродом
и Домаром в их теории роста (см. 3.6).
Существует еще одна возможная альтернатива для замены
непредвиденных сбережений, взятых в качестве подвижного и гибкого элемента
модели. Она сводится к допущению непредвиденных инвестиций. Для этого надо
отбросить предпосылку о реализации планов капиталовложений. Тогда
формула модели будет такова:
В такой модели есть также место для непредвиденного потребления. Однако
при построении моделей такого типа неизбежны более сложные случаи
планирования капиталовложений, чем описанные в разделе 2.7, где
рассматривались только независимые капиталовложения.
В последующем анализе будут вновь фигурировать соображения

подобного рода. Мы практически испытаем предпосылки, названные здесь
«обычными» (планы потребления и инвестиций реализуются). В главе 8
приводятся схемы различных динамических моделей и при этом выясняется, что
главным фактором, связывающим ожидаемые величины, являются не
сбережения, а капиталовложения. Не совсем случайно, может быть, что в
статистике национального дохода сбережения определяются как остаток. Это
показывает, что сбережения являются не столь жизненно важным звеном
в структуре народного хозяйства.
2.9. РЫНКИ ТОВАРОВ И ФАКТОРОВ ПРОИЗВОДСТВА
До сих пор потребление, а следовательно, и сбережения рассматривались
в нашем анализе как находящиеся в непосредственной зависимости от дохода.
При этом не учитывался тот факт, что только часть сбережений
осуществляется отдельными лицами, то есть потребителями, а остальные сбережения
складываются из нераспределенных прибылей фирм. Подобным же
образом в динамической модели (см. 2.7) предполагалось наличие лишь
единственного запаздывания — между получением и расходованием дохода
потребителями. Два других типа запаздываний — между затратами предприятий
и выпуском ими продукции и между производством и доходом факторов
производства — не рассматривались. Можно легко расширить анализ,
приняв во внимание эти факты; для этого необходимо только различать два
рынка — рынок готовых товаров и рынок факторов производства. При этом
появляются два сектора: один состоит из отдельных лиц (потребителей),
а другой — из фирм (предприятий).
К использовавшимся до сих пор переменным следует добавить еще одну.
Это — личный доход или доход, который получается и расходуется
факторами производства. Он обозначается через F. Как и другие переменные,
F рассматривается здесь в «реальных» единицах.
Функция потребления теперь выражается формулой С = C(F). Ее
ожидаемая величина зависит от личного дохода. Необходима и вторая
функция, характеризующая ожидаемые величины в секторе предприятий.
Она выражает спрос предприятий на факторы производства, зависящий от
выпуска продукции: F — F(Y). В действительности — это простая форма
обратной*функции производства; вид зависимости У от F определяется
техническими условиями производства, а в обратной функции F определяется
через У. Отсюда С = C(F), где F — F(Y), и зависимость потребления от
выпуска продукции является косвенной.
При заданных независимых капиталовложениях А условие равновесия
остается прежним: У = С + А, где С = C(F) nF = F(Y). Подстановкой это
условие сводится к одному уравнению относительно У, в котором У
определяется через А. Теперь можно разделить сбережения на две части:
сбережения предприятий (У — F) и личные сбережения (F — С). Тогда условие
равновесия можно записать следующим образом:
(Y-F) + (F-C)=A, где C = C(F) и F = F(Y).
Здесь У есть функция А. Дифференцируем1:
то есть
dF dY
1 Дифференцирование производится по А9 причем У есть функция A* slF есть
сложная функция от А.— Прим. ред.
67 5*

Мультипликатор теперь является множителем в правой части; в него
входит предельная склонность потребителей и предприятий к расходованию
их дохода соответственно dC/dF и dF/dY. В линейном случае:
C — y + cF (для расходования дохода потребителями),
F = §-\-bY (для расходования дохода предприятиями).
Следовательно,
ф у)
Это выражение есть функция потребления в кейнсианской форме. Тогда
при условиях равновесия У = С-{-А:
Главное различие состоит в том, что кейнсианская предельная
склонность к потреблению теперь выступает как произведение двух видов
предельной склонности к расходованию — предельной склонности
предприятий (Ь) и предельной склонности потребителей (с). Более того, независимые
расходы теперь состоят из трех элементов: затрат на инвестиции,
расходов предприятий и расходов потребителей. В динамическую модель можно
ввести три запаздывания. При однократных запаздываниях каждого
из них, получаем:
1) Запаздывание'.продукция —доход; Ft = F(Yt^1I где выручка от
продукции Yt_x в период (?—1) распределяется предприятиями в виде
доходов по факторам в промежуток t.
2) Запаздывание: доход—расходы; Ct=^C(Ft^1), где личный доход Ftl
в период (t — 1) является основой потребительских расходов в период t.
3) Запаздывание: расходы — продукция; Yt = Ct-1 -)- А, где продукция
в период t состоит из продукции для независимых капиталовложений А
и продукции для потребления, которое базируется на реальных расходах
потребителей Сг_г в период ? — 1.
Третий случай в сочетании с двумя первыми функциями,
содержащими запаздывания^ представляет собой зависимость между Yt и Yt^ то
есть имеет форму конечно-разностного уравнения первого порядка,
включающего трехкратное запаздывание. Таким образом, запаздывание,
рассмотренное в разделе 2.7, имеет тройную форму: это сумма отмеченных
здесь трех отдельных запаздываний.
В линейном случае имеем:
У, = ?,_! + А,
где
C + F и Ft = p + bYt^.
Подставляем значения Ct и Ft в уравнение
то есть
Yt
что идентично выражению D) в разделе 2.7 с тройным запаздыванием
и константами в развернутой форме.
Запаздывания можно полностью объяснить с помощью ожиданий.
В случае A) предприятия ожидают, что их выручка в период t
составит Yt_l4 но в действительности она оказывается иной (Yt). В случае B)
потребители ожидают, что их доход составит Fi_1 в период ?, но
фактически он равен Ft. В случае C) предприятия предполагают, что продажи
в период t достигнут С?-1, но фактически они равны Cv Обозначим
ожидаемые или предполагаемые величины верхним индексом п; фактические
величины не будут иметь этого индекса. Тогда:
A) У? = Yt_i; B) fif = Ft_i; C) С? = Ct.v
68

Сущность модели можно видеть из связи между сбережениями и
капиталовложениями, заданными величиной А.
Сбережения предприятий ....
Личные сбережения
Все сбережения
Капиталовложения
Сбережения— капиталовложения
(Yf
Ожидаемые
Yf—Ft
Ff-Ct
уП _|_ ,^П _р ч_ С
Yt-Cf
-Yt) + (Ff -Ft)+(Cf -Ct)
Фактические
Yt-Ft
Ft-Ct
Y —C
Yt-Ct
0
Следовательно, разность между ожидаемыми сбережениями и
капиталовложениями составляет (последняя строка таблицы):
\ (Yf-Yt) + (Ff-Ft) + {C?-Ct)= ,
= (Разность в выпуске продукции) + (Разность в факторах производства) +
+ (Разность в товарах).
Каждая разность — это избыток спроса, то есть превышение ожидаемой
величины над фактической. Так, разность предполагаемых и фактических
величин факторов призводства — это избыток дохода, ожидавшегося
потребителями, над фактически полученным (F? —Ft = Ft_1 — Ft).
Теперь имеются три запаздывания в кругообороте дохода в течение
цикла: производство — доход — расходы— производство. Соответственно этому
вводятся три разности предполагаемых и фактических величин вместо
одного возможного разрыва между выпуском продукции следующих друг за
другом интервалов времени (Yf —Yt = Ytl — Yt). Два других добавочных
разрыва проявляются на рынке факторов производства и на рынке
потребительских товаров. Запаздывания относятся к соответствующим секторам
(частным лицам или предприятиям); несоответствие плановых и фактических
величин — к рынкам, на которых проявился излишек спроса. Положение
можно резюмировать следующим образом:
1) Запаздывание: продукция — доход. В этом случае платежи
(Ft) за факторы производства отстают от выпуска продукции (Vf_i),
которая обусловливает выручку предприятий; запаздывание возникает
из-за несоответствия предполагаемого и фактического выпусков
продукции: Yf — Yt = Ytl—Yt. В схеме ожидания Робертсона этот
разрыв равен нулю, так как ожидаемый и фактический выпуски
продукции равны.
2) Запаздывание: доход — расходы. Расходы потребителей Ct
отстают от личного дохода /V-i»' 3a счет которого они производятся;
запаздывание соответствует неравенству ожидаемых и фактических
величин факторов производства: Ff —Ft = Ft^ —Ft. Здесь имеет
место робертсоновское запаздывание, обусловленное ожиданием
отдельных лиц (потребителей).
3) Запаздывание: расходы — продукция. Продукция для
потребления отстает от фактических закупок потребителей; запаздывание
соответствует разрыву в потребляемой товарной массе между
ожидаемой и фактической: С1} — Ct = Cf-1—Ct_. Это запаздывание типа
Лундберга, оно объясняется тем, что фирмы (предприятия)
пересмотрели свои планы.
При принятом здесь запаздывании на один интервал времени
кругооборот дохода требует трех интервалов. Весь выпуск продукции в одном
интервале Yt_3 рассматривается как выручка предприятий и частично как
платежи за факторы производства в следующий интервал времени Ft 2. Затем
69

личные доходы потребителей Ft_2 расходуются (частично) на покупку
потребительски^ товаров в следующем периоде Сг_г. Наконец, продажи
потребителям Сь_х ведут в третьем интервале к производству потребительских
товаров предприятиями и, значит, к итогу выпуска продукции Yt.
5
Задачи и упражнения
1. Модель со всеми тремя запаздываниями, как и приведенная выше, основана
на том, что планы сбережений и капиталовложений совсем не осуществляются.
Показать, что сбережения предприятий реализуются в запланированных размерах,
если нет запаздывания «производство — доход», то есть если фирмы правильно
планируют выпуск своей продукции. Показать далее, что плановые капиталовложения
осуществляются, если исчезает запаздывание «расходы—продукция», то есть если
фирмы не должны пересматривать свои планы дли удовлетворения спроса на
потребительские товары.
2. Предположим, что в вышеприведенной модели нет запаздывания
«производство—доход». Показать, что если фирмы правильно предусматривают продажи
товаров, то плановые капиталовложения осуществляются, появляются непредвиденные
личные сбережения и мультипликатор Робертсона. С другой стороны, показать, что
если потребители правильно предвидят, то фактический личный доход равен
плановому, получаются непредвиденные капиталовложения и мультипликатор Лундберга [11].
3. Модель с трехкратным запаздыванием характеризуется конечно-разностным
уравнением, устанавливающим зависимость между Yt и Yt_3. Показать, что одно
начальное значение Уо определяет с этого момента каждое третье значение Yt, но что
для полного решения требуется три начальных значения.

ГЛАВА 3
ПРИНЦИП АКСЕЛЕРАЦИИ
3.1. НЕЗАВИСИМЫЕ И ИНДУЦИРОВАННЫЕ КАПИТАЛОВЛОЖЕНИЯ
В предыдущей главе капиталовложения рассматривались как заданные,
то есть как независимые инвестиции (autonomous investment); они
обозначались буквой А. При помощи мультипликатора исследовалось действие
данной нормы инвестиций. Такой подход односторонен и игнорирует
взаимосвязь между капиталовложениями и выпуском продукции.
Капиталовложения влияют на величину выпуска продукции, но и, наоборот, инвестиции
зависят от выпуска продукции. Точнее, именно изменение величины выпуска
продукции с течением времени или от одного промежутка времени до другого
влияет на размеры чистых капиталовложений, представляющих собой
дополнительный прирост капитальных фондов за рассматриваемый промежуток
времени. Капиталовложения, возникающие в результате изменения объема
продукции, называются индуцированными инвестициями (induced investment)
и обозначаются нами буквой /. Сделаем несколько предварительных
замечаний, так как связь величины выпуска продукции и индуцированных
инвестиций является одновременно и косвенной и сложной, и никогда нельзя
четко разграничить независимые и индуцированные капиталовложения.
Во-первых, формулировка динамической модели должна включать как
независимые, так и индуцированные капиталовложения. Строго говоря,
можно возразить, что ретроспективно все капиталовложения вызваны
изменением выпуска продукции. Однако практически продолжительность
прошлого временного интервала, рассматриваемого в модели, приходится
ограничивать. Некоторая часть капиталовложений в столь незначительной
степени вызвана недавними изменениями объема продукции, что ее в
действительности можно считать независимой. Одним из типов независимых
инвестиций являются капиталовложения государственных и общественных
организаций (например, в строительство дорог и зданий). Инвестиции,
вызываемые изобретениями и нововведениями, относятся к другому типу
независимых капиталовложений.
Во-вторых, существует различие между основным и оборотным
капиталом. Основной капитал состоит из земли, зданий, заводов и оборудования.
Оборотный капитал охватывает запасы готовой продукции, полуфабрикатов
и незавершенного производства. Влияние роста спроса сказывается на
увеличении выпуска продукции и стимулировании необходимых для этого
капиталовложений. Но первая реакция может повлечь уменьшение оборотного
капитала (запасов готовой продукции), и лишь затем последует более или менее
быстрое восстановление оборотного капитала — сначала запасов
полуфабрикатов, а затем и готовой продукции. Тем]временем размещаются заказы
на капитальные блага, составляющие элементы]основного|капитала,
поставка и монтаж которых требуют затрат времени. Мы рассматриваем главным
образом основной капитал, а изменение оборотного капитала в течение
промежуточного периода не принимается во внимание. В дискретном анализе
сделать это сравнительно просто — мы выбираем временной интервал
достаточно длительным, для того чтобы целиком отразить первичное воздействие
увеличения объема продукции на оборотный капитал.
В-третьих, нужно брать чистые капиталовложения в основной капитал,
то есть валовые инвестиции за вычетом затрат на амортизацию. Вообще
71

говоря, именно чистые капиталовложения — независимо от того,
положительны они или отрицательны,— вызываются изменениями в объеме выпуска
продукции. Но и здесь могут возникнуть осложнения, так как увеличение
объема производства иногда стимулирует более раннюю замену оборудования.
Кроме того, прирост основного капитала идет за счет продукции отраслей,
производящих капитальные блага, а эта продукция объемна. Это требует
учета значительной асимметрии в процессе капиталовложений в основной
капитал. В соответствии с выпуском продукции размещаются заказы
и производятся поставки новых капитальных благ. Процесс продолжается да
полной загрузки производственных мощностей отраслей промышленностит
производящих капитальные блага. Увеличение чистых капиталовложений
ограничено только этими производственными мощностями. Но даже и это
ограничение может проявиться скорее в удлинении сроков поставок, чем
в сокращении объема капиталовложений. С другой стороны, уменьшение
выпуска продукции не может повести к быстрому или большому сжатию
инвестиций, то есть к значительной отрицательной величине чистых
капиталовложений. Заказы на капитальное оборудование можно аннулировать или
задержать, но продукция отраслей, производящих эти блага, не может упасть
ниже нуля. Поэтому чистые инвестиции не могут сократиться ниже
определенной отрицательной величины, представляющей действующую норму
списания оборудования.
Наконец, чистые капиталовложения представляют собой производную-
от величины всего наличного капитала (основного и оборотного).
Наличный капитал оценивается в какой-то момент времени. Чистые
капиталовложения представляют собой скорость увеличения запаса капитала, или
возрастание его в течение единицы времени. Уровень выпуска продукции
влияет на величину наличного капитала, необходимого для ее производства.
Изменения объема выпуска влияют на объем потребного капитала и,
следовательно, влекут чистые капиталовложения. Позднее мы изложим метод
анализа с помощью понятий основного капитала. Этот метод, может быть,
лучше соответствует различию между независимыми и индуцированными
капиталовложениями (см. гл. 7). Теперь же мы сосредоточим внимание на чистых
капиталовложениях, не вдаваясь в подробности их отношения к наличному
основному капиталу. Однако общее положение ясно. Если поток выпуска
продукции есть величина постоянная (подобно скорости), тогда наличный
капитал также будет постоянен, а чистые инвестиции будут равны нулю.
Если же поток выпуска меняется (как ускорение), то меняется также и
необходимый наличный капитал, и имеют место положительные или
отрицательные чистые индуцированные капиталовложения. Именно в этом состоит*
принцип акселерации — возросший поток выпуска продукции требует
большего наличного капитала и тем самым вызывает капиталовложения.
Мультипликатор представляет собой отношение между выпуском
продукции и капиталовложениями. Даже динамический мультипликатор явно
непригоден для описания экономической действительности (см. 2.7). При наличии
соответствующим образом подобранного мультипликатора движение
продукции может воспроизводить динамику независимых инвестиций. В
противном случае оно будет неуклонно стремиться к положению равновесия. Это
происходит потому, что мультипликатор использует только одну ожидаемую
зависимость — функцию потребления; он полностью игнорирует другие
возможные обстоятельства на стороне капиталовложений. Необходимо
установить различные факторы, обусловливающие капиталовложения, и ввести
их дополнительно в модель мультипликатора. Воздействие
капиталовложений можно выразить в различных формах. Но мы подробно рассмотрим сейчас
лишь одну из них — вариант, который включает принцип акселерации,
связывающий индуцированные капиталовложения с изменениями выпуска
продукции.
Принцип акселерации — «зависимость» Харрода — давно применяется
в теории капиталовложений и экономических циклов [14]. Им пользовались
72

еще Кларк [6], Фриш [8], Харрод [И] и Лундберг [15]. Первая
формулировка, подчеркивающая взаимодействие мультипликатора и акселератора,
принадлежит Самуэльсону [18, 19]. За ней следовал Хансен, но развитие она
получила лишь у Хикса [13] и других исследователей. Комбинация
мультипликатора и акселератора создает чрезвычайно изящные математические
модели. Основное внимание мы уделим здесь сущности таких моделей, а не
различным возражениям, которые можно сделать против принципа
акселератора с экономической точки зрения. Модели игнорируют, например, тот факт,
что вначале расширение производства может быть осуществлено за счет
использования незагруженных производственных мощностей, и лишь затем
увеличение выпуска продукции требует новых капиталовложений. Многие из
этих возражений связаны с вопросом о «нелинейности» системы,
вопрос,который мы отложим для рассмотрения в дальнейшем.
3.2. АКСЕЛЕРАТОР
Формулировка принципа акселератора зависит от того, пользуемся ли
мы непрерывным или дискретным анализом. Особенно это относится к
введению запаздывания (см. 1.9). Мы теперь уже признаем законность применения
и того и другого типа анализа, так как оба они представляют собой лишь
различные подходы к экономическому «реализму» (в то время как в предыду-.
щей главе рассматривался лишь дискретный анализ). Как и прежде, общая
функциональная зависимость капиталовложений от изменения выпуска
продукции обычно заменяется ее частной линейной формой, по крайней мере
в качестве известной аппроксимации в ограниченной области значений
переменных.
В непрерывной форме без запаздываний простейшее выражение
акселератора таково:
^} A)
Здесь — У (t) —скорость движения выпуска продукции (дохода), I(t) —
движение индуцированных капиталовложений. Обе величины представляют
собой потоки во времени. В линейной форме акселератор выражается таким
образом:
± B)
где и — положительная постоянная, коэффициент инвестиций, указывающий
мощность акселератора. Нет необходимости вводить аддитивные постоянные,
так как их все равно пришлось бы включить в состав независимых
капиталовложений. Следовательно, из уравнения B) следует, что индуцированные
инвестиции представляют собой неизменную долю текущей скорости
изменения выпуска продукции.
В непрерывном анализе запаздывания проще всего можно ввести в виде
непрерывно распределенного запаздывания показательной формы (см. 1.9).
Пусть скорость реакции будет х. Тогда временная постоянная запаздывания
будет Т = 1/х. Скорость изменения индуцированных капиталовложений
будет следующим образом зависеть от выпуска продукции:
C)
Это выражение имеет следующий смысл. Потенциальная скорость роста
капиталовложений в момент t фиксируется акселератором без запаздывания
J(t) = v(d/dt)Y(t). Фактическая скорость роста инвестиций I(t) запаздывает,
и приращение капиталовложений (d/dt)I(t) пропорционально разности
— {I(t) — J(t)} = — {Д?) т v(d/dt)Y(t)}. Коэффициент пропорциональности
и показывает скорость реакции.
Зависимость C), включающую запаздывания показательной формы,
удобно выразить с помощью дифференциального оператора D = dldt (см.
приложение А). Имеем:
73

DI= -x(I-vDY),
то есть
D)
которое и представляет собой выражение акселератора.
Если простая показательная форма считается слишком специфичной,
можно вместо нее ввести в модель два или более таких запаздывания,
действующих последовательно. Для двух запаздываний, каждое из которых
имеет скорость реакции 2х (или имеет временную постоянную 1/2Т),
акселератор D) примет вид (см. 1.9, упражнение 4)
При дискретном анализе акселератор без запаздывания можно
написать при линейной зависимости в такой форме:
yt.1)} = y(Ft-yf.1). E)
Это идентично выражению B) — индуцированные капиталовложения
зависят от изменения текущего выпуска продукции. Тогда простейшая форма
акселератора с запаздыванием будет иметь вид
/(= / {(?м - У,_2)} = v (У,.,- У,_2). F)
В этом случае имеется единственное запаздывание на один временной
интервал. Оно отражает тот факт, что в ожидаемых соотношениях, под влиянием
которых формируются планы капиталовложений, обычно учитывается лишь
самое последнее изменение выпуска продукции, именно изменение в
предыдущий период Yf_! — Yt2. Применение уравнения F) вместо E),
по-видимому, согласуется с использованием функции потребления при
запаздывании Ct = C(YU1) (см. 2.7). Если планируемое потребление принимается
зависимым от уровня дохода прошлого периода, а не от текущей величины
дохода, то столь же важно планировать капиталовложения в зависимости
скорее от изменений в выпуске продукции за прошлый период, чем от
изменений текущего периода.
Легко обобщить дискретную форму акселератора F) на случай с
запаздыванием, распределенным между любым количеством временных
интервалов. При линейной зависимости будем иметь
It = »i(r,-i - У, _,) + v2 (Yt_2 - Yt_3) +..., ]
где G)
v± + v2+...=v. J
Теперь имеем ряд коэффициентов инвестиций (vx, *;2, ...), сумма которых
равна общей мощности акселератора и. В частности, например, коэффициенты
могут уменьшаться в геометрической прогрессии. Этот случай
геометрического изменения запаздывания в наибольшей степени соответствует
запаздыванию в форме показательной функции D).
При уяснении смысла распределенного запаздывания, представленного
как уравнением G), так и уравнениями C)и D), следует принять во внимание,
что / представляют собой затраты на капиталовложения (а не объем решений
о капиталовложениях) и не< величину поставок оборудования. Сказать,
что инвестиционные затраты в интервале времени t зависят от изменения
выпуска продукции на протяжении целого ряда прошлых периодов,
равносильно утверждению, что изменение выпуска продукции в интервале t
повлечет появление затрат на капиталовложения в будущем в течение ряда
интервалов. Между изменением выпуска продукции и моментом решения
о капиталовложениях может существовать временной разрыв. Но в любом
случае, коль скоро такое решение принято, потребуется время на размещение
заказов и производство платежей либо за поставку оборудования, либо
74

в виде авансовых платежей. Если же учесть, кроме того, что
индуцированные данным выпуском продукции капиталовложения представляют собой
«причудливую смесь» (mixed bag) различного рода заводов, машин и запасов,
то вполне резонно предположить, что затраты на капиталовложения
распределяются между целым рядом интервалов времени.
3.3. ТЕОРИЯ РОСТА ХАРРОДА — ДОМАРА
Статический мультипликатор представляет собой устойчивое
соотношение. Следует ожидать, что принцип акселератора приведет к появлению
взрывных тенденций. Вопрос заключается в следующем: каков же будет общий
результат их совместного действия? В первом приближении ответ дает
модель, исключающая запаздывания мультипликатора и акселератора.
Следовательно, совместное действие мультипликатора и акселератора
порождает непрерывный и прогрессирующий рост выпуска продукции или дохода.
Это положение было установлено Лундбергом [15] и развито Харродом [11,
12] и Домаром [7].
Нетрудно понять идею, лежащую в его основе. Если независимые
капиталовложения А растут, например, вследствие внезапного появления крупных
изобретений, мультипликатор порождает соответствующий рост А/A—с)
выпуска продукции, где с — предельная склонность к потреблению @<с<1).
Расширение выпуска продукции приводит в действие акселератор и
сопровождается появлением других (индуцированных) капиталовложений. В свою
очередь эти дополнительные капиталовложения увеличивают («домножают»)
продукцию вследствие действия мультипликатора, и начинается новый
цикл. В общем результате получается прогрессивный рост продукции.
Для описания взаимодействия мультипликатора и акселератора при
отсутствии запаздываний и простейшей форме акселератора (см. 3.2)
больше подходит непрерывный, а не дискретный анализ. Все переменные берутся
как непрерывные функции времени, а зависимости предполагаются
линейными. Если выделить независимые расходы как на капиталовложения,так и на
потребление, то основное условие можно записать в следующем виде:
где [С = cY и / = v-т-— соответственно функция потребления и
соотношение акселератора @ < с < 1, v\> 0). Следовательно,
Y=cY+vir
то есть
является дифференциальным уравнением, решение которого дает
динамику выпуска продукции. Здесь q = s/v> где s = 1 — с и представляет
предельную склонность к сбережениям.
Решение уравнения A) зависит от предпосылки относильно динамики
независимых расходов А. Особого внимания заслуживают два случая.
Случай 1. А = const. Независимые расходы неизменны. Пусть г/ —
отклонение дохода от неизменного уровня A/s, то есть г/ = У — (A/s)
и dy/dt = dY/dt. Следовательно, A) представится в таком виде:
% = Qy, где Q = ^>0. B)
Так как (d/dt) (In у) = (l/y)(dy/dt), то уравнение B) превращается в
следующее:
75

и, таким образом,
1пг/ = q? + const,
то есть
где В — некоторая константа, которую нужно выразить через начальный
уровень дохода. Положим у = у0 в момент ? = 0. Тогда решение B) будег
иметь
Формула C) выражает непрерывный рост по показательной кривой выпуска
продукции или дохода с постоянной относительной скоростью1 q = s/y>0.
Обычно предельная склонность к сбережениям s представляет собой малую
величину по сравнению с коэффициентом инвестиций v; в данном случае Q-
есть положительная дробь, которая может быть совсем малой. Например,
выбрав год за единицу времени, положим s = 0,05 (предельная
склонность к сбережениям 5%) иу = 2,5. Тогда q = 0,02, и доход непрерывно
растет со среднегодовым сложным процентом, равным 2.
Этот пример ясно показывает роль акселератора. Даже при неизменности
независимых расходов взаимодействие мультипликатора и акселератора
вызывает прогрессирующее расширение выпуска продукции. Относительная
скорость роста определяется структурными константами s и и системы.
Очевидно, что акселератор является взрывным фактором.
Случай 2. A =Aoert, то есть независимые расходы увеличиваются по
показательной функции. Относительная скорость роста А, равная г, будег
заданной константой (г > 0). Уравнение A) примет вид
D)
где, как и прежде, e = s/y>0.
Положим, что Y = Yoert есть решение уравнения D), то есть
относительная скорость роста У равна относительной скорости роста А.
Подставим это выражение в уравнение D):
то есть . E)
Следовательно, прогрессирующий рост У с относительной скоростью г
возможен при условии, что Уо имеет указанное частное значение,
определяемое структурными коэффициентами системы.
Остается проследить движение У при любых начальных условиях
и наличии возмущений Уо Ф Уо. Положим y — Y — Yoert, так что начальное
значение г/0 = У0 — Уо при ? = 0. Вычтем уравнение E) из уравнения D)
и заметим, что dy/dt — dY/dt — rYoert. Тогда
и, как и раньше, решением будет
1 Под темпом, или нормой роста (rate of growth), показательной функции автор
понимает отношение производной к функции, то есть относительную скорость в
непрерывном анализе. В дальнейшем мы пользуемся в этом случае термином «относительная
скорость роста». В случае аналогичной дискретной функции (геометрической прогрессии)
темпом мы будем называть отношение приращения дискретной функции в единицу
времени к самой функции; в данном случае это будет величина eQ — 1. Наконец, в случае
изменения функции в геометрической прогрессии по р сложных процентов у = A -ф- ГУ
темпом, или нормой роста, явится величина г = />/100.— Прим. ред.
76

Полученное решение аналогично выражению C) для случая с
неизменными независимыми расходами. Разница заключается в том, что у
представляет собой отклонение выпуска продукции от уровня, растущего по
показательной кривой, а не от неизменного уровня. Следовательно,
решение уравнения D) характеризует рост по показательной кривой,
отклоняющийся от такового же роста выпуска продукции. В развернутом виде
решение будет иметь вид
где
F)
Необходимо тщательно выяснить смысл решения F). Выражение Y=Yoert
характеризует своего рода «равновесие» относительной скорости роста
продукции, то есть увеличение выпуска продукции с той же относительной
скоростью, что и скорость роста независимых расходов. Если рост выпуска
продукции начинается с надлежащего уровня Уо, тогда ее последующий
рост происходит по линии «равновесия». Это — обычный результат, ибо
имеющаяся налицо линия равновесия в точности подобна той, которая имеет
место при тех же обстоятельствах под влиянием динамического
мультипликатора (см. 2.7). Если начальный уровень продукции ненадлежащий,
или Уо Ф Уо, то в ходе последующего динамического изменения он все
в большей мере отклоняется от линии «равновесия». Скорость этого
расхождения дана структурной константой Q = slv. Интересно сопоставить этот
случай с соответствующим влиянием динамического мультипликатора, которое
обеспечивает постоянное возвращение к линии «равновесия». Акселератор
вновь выступает как взрывной элемент.
Но в обоих случаях прогрессирующий рост выпуска продукции с
относительной скоростью q = slv внутренне присущ системе. Он представляет
результат антизатухающего или взрывного действия акселератора
(постоянная и), видоизмененный затухающим влиянием мультипликатора
(постоянная s = 1—с). Это — «гарантированный» темп роста Харрода;
гарантирован он потому, что является результатом непрерывно длящегося во
времени равенства сбережений и инвестиций. В модели отсутствуют
запаздывания, так что основное уравнение A) получается из условия Y = С + / +
+ А. Но это то же самое условие равенства сбережений и капиталовложений.
Равным образом исключаются непредвиденные сбережения и
капиталовложения, а потому нигде нет какого-либо расхождения между этими двумя
величинами.
В основном уравнении A) v(dY/dt) представляет собой акселератор,
связывающий индуцированные капиталовложения с изменениями выпуска
продукции. В другой части уравнения ему равна величина (У — С — А), то
есть сбережения минус независимые капиталовложения. Эта интерпретация
принадлежит Харроду. Домар получает то же самое соотношение A), но
вкладывает в него иной смысл, вернее, он предлагает альтернативное
толкование. Основной подход Домара заключается в том[7, стр. 141], что он
берет постоянную и как обратную величину средней эффективности
капиталовложений. Следовательно, IIv есть отношение прироста выпуска
продукции за счет капиталовложений к самой величине капиталовложений
rl _ dY/dt
v ~~ / #
Это лучше представить в виде dYldt = A1иI, а не в виде формально
эквивалентного выражения / = v(dYldt). В отличие от принципа акселерации
/ не берется как величина, зависимая от dYldt. Напротив, через посредство
показателя эффективности капиталовложений, dY/dt становится здесь
зависимой переменной от /. Теория Домара подчинена требованию полной
занятости или полной загрузки производственных мощностей. Для обеспечения
77

того или.другого выпуск продукции и капиталовложения должны расти
по показательной функции (или гарантированным темпом). Или, говоря
словами Егера [21], соотношение dY/dt = (l/u)I показывает, что «приращение
дохода, необходимое для полной загрузки прироста производственных
мощностей, пропорционально предусматриваемым капиталовложениям,
которые делают возможным получение этого дополнительного дохода».
Во втором подходе Домара [7, стр. 145] трактовка обратная. Если
выпуск продукции растет в геометрической прогрессии, тогда возникает вопросг
достаточна ли величина индуцированных капиталовложений. Ответ будег
утвердительным в случае, если темп роста является гарантированным. В
сущности при этом подходе Домар вводит в модель акселератор.
Многое можно возразить против теории Харрода — Домара.
Возражения направлены не только против того, что теория представляет собой
чрезмерное упрощение— с этой точки зрения критикуются все модели
динамической макроэкономики,— сколько против того, что, говоря опять словами
Егера [21], она претендует на «незаконную точность». В качестве
упрощающих предпосылок можно принять в настоящее время введение в систему двух
простых констант сии — соответственно потребления, пропорционального
выпуску продукции, и капиталовложений, пропорциональных изменению
выпуска продукции. Однако нельзя принять предпосылку о полном
отсутствии запаздываний и тесно связанное с ней исходное положение о равенстве
величин сбережений и капиталовложений не только фактических, но и
ожидаемых.
По существу эту теорию можно считать динамической только в
ограниченном смысле/Мы уже знаем (см. 2.7), что устойчивые или затухающие
колебания порождаются только мультипликатором. Под его воздействием
выпуск продукции следует за движением независимых расходов,
безразлично растут ли они в прогрессии, колеблются или изменяются скачками (ш
«fits and starts»). Теория Харрода — Домара, как в общем и следовало
ожидать, дополнительно вводит акселератор взрывного действия. Она
устанавливает одно существенное обстоятельство, именно что системе, основанной
на совместном действии мультипликатора и акселератора, внутренне
присуще колебательное движение. Для теории экономического цикла
недостаточно выяснить, что колебания независимых расходов имеют результатом
колебания в движении выпуска продукции и дохода. Именно акселератор
порождает структурное колебательное движение, то есть «взрывает» затухающие*
колебания, вызванные действием мультипликатора, превращает их в
колебательные движения вокруг положения равновесия. Можно, конечно,
попытаться преодолеть это, сделав колебание само по себе взрывным. Но это
предвосхищение дальнейшего. Теория Харрода — Домара не описывает
колебательных движений, так как она не включает запаздываний и поэтому
не является динамической в полном смысле слова.
Задачи и упражнения.
1. Сравнить движения У, заданные уравнением A), когда независимые расходы
равны: 1) A (t) и 2) A(t)-\-a0, где а0—постоянно. Показать, что движение во втором
случае на ао/A — с) выше, чем в первом, как данное мультипликатором.
2. В уравнении A) принять A = at, то есть ввести постоянный прирост, а не по
геометрической прогрессии. Показать, что неуклонный рост выпуска продукции задан
выражением Y=*Y0+at/(l—с), которое удовлетворяет уравнению A) при условии
Y0 = av/(l — сJ. Объяснить результат.
3. Положить A~Aoert-\-ao. Так обстоит дело, например, в случае роста
независимых капиталовложений по показательной кривой и постоянной величины
независимых потребительских расходов. Показать, что решение уравнения A) не
изменится (по сравнению со случаем ао = О) при условии замены Y через У —[ао/A—-с)]..
4. Показать, что для случая А = Аоеп, решением для которого является Y=Уоег/,
справедливо Y0 = A0/(s—rv) > A0/s (s = l—с). В каком смысле это предполагает, что У
больше той величины, которая получилась бы при действии только мультипликатора?"
5. Рассмотреть уравнение D) для случая A = Aoert, положить r\ = (Y—Yoert)/Yoert
и показать, что уравнение принимает вид dr\/dt=(Q — r) rj и имеет решение т| = г]ое^"'г^-
78

Показать тождественность этого решения с решением F) в тексте. Дать объяснение
с помощью пропорциональных отклонений от положения «равновесия». Показать
пригодность решения относительно г\ путем, представления решения для Y в виде
функции времени на полулогарифмической шкале.
3.4. МОДЕЛЬ МУЛЬТИПЛИКАТОРА ФИЛЛИПСА
Следующий шаг заключается во введении запаздываний в модель
мультипликатора-акселератора. Если в дальнейшем анализе мы будем
пользоваться непрерывным представлением, дающим дифференциальные
уравнения, то соответствующее запаздывание примет непрерывно распределенную
форму (показательной функции). Такая модель была построена Филлип-
сом [16].
Можно было бы предположить, что путем введения одного или
нескольких отставаний вместо непрерывно распределенного запаздывания
получатся более простые модели. В действительности это не так, поскольку
приводит к неудобным смешанным дифференциально-разностным
уравнениям. Это очевидно из упражнения 1 этого раздела и будет показано
подробнее на некоторых моделях в главе 7.
Акселератор вначале не принимается во внимание, и анализ
ограничивается лишь действием динамического мультипликатора с непрерывным
запаздыванием (по показательной функции). Фактически это является
непрерывным вариантом предыдущей модели (см. 2.7). Все переменные являются
функциями непрерывно меняющегося времени, так что, например, выпуск
продукции или доход У выражает Y(t). Везде предполагаются линейные
зависимости.
Запаздывания спроса отсутствуют. Планируемое потребление будет
С=сУ, а независимые расходы (на капиталовложения и потребление)
составят А, Тогда общий спрос без запаздываний будет
Примем А заданным и постоянным и вместо предельной склонности к
потреблению воспользуемся предельной склонностью к сбережениям 5=1—с.
В самом деле, следуя Филлипсу, s можно истолковать более широко как
«предельную утечку денежных средств» («marginal leakage», см. упражнение 2
данного раздела). В этом случае совокупный спрос без запаздываний будет
Z = (l-s)Y + A. A)
Рассмотрим теперь предложение. Здесь влияние (реакция) выпуска
продукции У на спрос Z не предполагается мгновенным, как в разделе 3.3,
оно имеет непрерывное запаздывание показательной формы. Пусть скорость
реакции будет Ху или постоянная запаздывания Т = 1 Д. Тогда получим
¦?-_MY-Z). B)
Это уравнение описывает изменение выпуска продукции во времени.
Из соотношений A) и B), характеризующих модель, получаем
дифференциальное уравнение, описывающее изменение выпуска продукции во
времени:
%- + %Y = XZ = X{l-s)Y + KA,
CLt л
то есть
Результатом решения уравнения [C) вновь является уровень равновесия
У — У = A /s, свойственный статическому мультипликатору. Положим
79

— Y — Y и подставим это в уравнение C), которое перепишется так:
Как и раньше, воспользуемся тем, что {l/y)(dy/dt) = (d/dt)(lny). Получим
решение уравнения D) в виде
то есть
In г/ = — Xst-{- const,
или
У = Уое~Х8'-
Напишем решение в полном виде:
Y = Y + (Y0-Y)e-№. E)
Пусть задан начальный выпуск продукции Уо в момент ? = 0. Тогда
уравнение E) опишет его движение во времени как неуклонное и
прогрессирующее приближение к положению равновесия У = A/s. Движение
происходит по показательной функции е~*9 и лишь предполагается, что X и s
положительны. Скорость приспособления выпуска продукции к
изменившимся условиям будет задана выражением Xs, которое представляет
комбинацию предельной склонности к сбережениям (как в 2.7) и скорости
реакции при запаздывании производства.
Один частный случай —при особых начальных условиях —был
рассмотрен Филлипсом. Допустим, что вначале имеет место равновесие.
Измеряем У от этого уровня равновесия (У = 0, г = 0), затем происходит
отдельный сдвиг в спросе, представленном А9 например, вследствие роста
независимых капиталовложений. Тогда новое положение равновесия будет
У = A/s. Движение У к новому положению равновесия описывается
уравнением C) с начальным условием У = 0 в момент ? = 0. Значит,
содержащееся в решении E) значение Уо равно 0. Следовательно, в соответствии
со сдвигом в спросе А, движение продукции от одного положения
равновесия (У = 0) к другому (Y — A/s) будет выражаться следующим образом:
Графически это было доказано кривой /// на рис. 3, где Т = 1/Xs и Z0 = A/s.
Действительно, при такой форме динамического мультипликатора
динамика У представлена движением с запаздыванием вида показательной
фунцции со скоростью реакции Xs (см. упражнение 3). Надо сравнить его
с движением, которое порождается динамическим мультипликатором с
единственным однократным запаздыванием (см. 2.7). Решение уравнения E) из
этого раздела с У0 = 0 и У = .4/A —с) будет иметь вид
то есть (так как 1 — с = s)
Это решение непосредственно сопоставимо с выражением F). Решение
непрерывной модели включает в себя показательную временную функцию
вида e'at (в данном случае а = Xs). Решение же дискретной модели дает
функцию вида а1 (где a = c = l — s). Как увидим в главах 4 и 5, это
различие характерно для двух типов анализа — непрерывного и дискретного.
80

Более важное различие, представляющее собой свойство этих моделей,
заключается в том, что в уравнении F) скорость реакции зависит от
величины %s, а в уравнении G) — только от s.
Задачи и упражнения
1. Дифференциальное уравнение A) из 3.3. представляет собой комбинированную
модель мультипликатора-акселератора без запаздываний. Ввести в функцию потребления
отставание продолжительностью 6Х, а в акселератор продолжительностью 62 и
показать, что уравнение A) примет следующий вид:
Даже в простейшем случае (Э1 = 92 = 1) оно будет смешанным
дифференциально-разностным. Показать, что тем не менее Y=Y, где Y—постоянная величина для всех
моментов времени, будет решением, а У = Л/A — с) дано статическим
мультипликатором.
2. Положим, что совокупный спрос равен Z = C-\-A, где С и А оба линейно
зависят от ^величины дохода У. Показать, что совокупный спрос можно выразить
через Z = (l — /)Y-j-6, где I можно истолковать как «предельную утечку денежных
ресурсов» («marginal leakage»), a 6 — как независимый спрос. Показать затем, что
динамический мультипликатор остается точно таким же, как он приведен в данном
разделе.
3. Динамический мультипликатор характеризуется дифференциальным
уравнением C). Написать его в форме dY/dt =—Xs [Y—(A/s)] и истолковать как действие
непрерывного запаздывания.
4. Приведенная в тексте динамическая модель не упоминает о сбережениях.
Показать, что ожидаемое потребление равно A — s) У, сбережения равны sY и
капиталовложения = А (предполагая отсутствие независимых потребительских расходов).
Показать затем, что сумма потребления и сбережений равна У, а сумма потребления
и капиталовложений—ожидаемой величине Z. Вывести отсюда существование
непредусмотренных капиталовложений, за исключением того случая, когда все планы
потребителей не реализуются и в точности балансируются непредусмотренными
сбережениями.
5. Показать, что при движении уравнения F) от одного положения равновесия
к другому dY/dt = XA в * = 0 и дать графическую интерпретацию с помощью кривой III
на рис. 3.
3.5. МОДЕЛЬ ФИЛЛИПСА С МУЛЬТИПЛИКАТОРОМ-АКСЕЛЕРАТОРОМ
Модель, приведенная в разделе 3.4, включает только независимые
капиталовложения, акселератора в ней нет. Добавим теперь акселератор
с запаздыванием, последний в форме непрерывной показательной
функции C) из раздела 3.2, с коэффициентом инвестиций v и скоростью реакции х.
Следовательно, если/ представляет фактические индуцированные
капиталовложения в момент t, вызванные изменениями в выпуске продукции, то
оно будет описано уравнением
?—('-'¦?)
Совокупный спрос будет теперь Z = С +1 + А, где, как и прежде,
С = cY — A — s) Y без запаздываний, то есть
A. B)
Предложение, как и раньше, берется с непрерывно распределенным
запаздыванием и скоростью реакции:
^=-X{Y-Z). C)
Выражения A) —C) являются уравнениями модели. Модель имеет
два непрерывно распределенных запаздывания: одно на стороне
предложения (реакция выпуска продукции на спрос со скоростью А,), второе на
стороне акселератора (индуцированные капиталовложения реагируют на
изменение выпуска продукции со скоростью реакции х). Дифференциальное
6 Р. Аллен 81

уравнение относительно У получается исключением Z и / из выражений
A) — C). Сделаем сначала подстановку выражения B) в C):
dt
то есть
г- i dY
1 -таг
или
dt ~~ Я d*2 ~^5 Л
Подставляем в выражение A)
то есть
Получаем дифференциальное уравнение второго порядка относительно У:
%г+а%- + ЬГ = *ХА, D)
где
а = Л»5 + х — хАх> и & =
Решение уравнения D), постоянное при всех значениях *, будет Y=^Yy
где Y = A/s. Уровень равновесия, заданный статическим мультипликатором,
вновь согласуется с моделью. Пусть y = Y — У. Тогда D) перепишется так:
%L+a^+by = O ' E)
с теми же самыми значениями а и Ь. Решение E) характеризует динамику у,
а следовательно, и У. Подробно это решение рассматривается в главе 7. Там
будет найдено, что в общем случае решение описывает колебательное
движение (оно может быть и взрывным) вокруг Y=Y=A/s.
При подходящих начальных условиях дифференциальное уравнение D)
может представить движение выпуска продукции от одного положения
равновесия до другого. Предполагается, что первое положение равновесия
достигнуто при У=0 в- ?=0 в момент, непосредственно предшествующий
скачку спроса А. Движение от У=0 к новому положению равновесия Y=--Als
задается у равнением; D). Кроме того, теперь нужны два начальных условия
(см. 4.2). Одно из этих условий состоит в том, что Y=0 в f=0. Другое
условие __ начальное значение dY/dt в момент ?=0, заданное мультипликатором,
так как акселератор еще не пришел в действие. Это значение есть dYIdt=KA
(см. 3.4, упражнение 5). Следовательно, динамика от одного положения
равновесия к другому описывается дифференциальным уравнением D),
подчиненным условиям У=0 и dY/dt=KA в ?=0.
Задачи и упражнения
1 Покачать» что модель мультипликатора-акселератора не будет иметь
непредусмотренных сбережений, если все планы потребителей осуществляются, и что весь
разрыв в реализации планов, вызванный наличием запаздываний, выражается в
непредусмотренных капиталовложениях.
2. Иллюстрировать тот факт, что для дифференциального уравнения D) неооходимы
два начальных условия. Для этого показать, что если У = 0 и dY/dt =ХА в * = (),
то d2Y/dt2 в момент *=0 также известно. Каково будет значение d2Y/dt2 и что оно
будет означать с точки зрения графического изображения динамики У?
82

3. Показать, что уравнения A) — C) модели можно написать с помощью
дифференциальных операторов D=d/dt:
где
Доказать, что
и что это выражение соответствует дифференциальному уравнению D).
4. Приведенная в тексте модель предполагает отсутствие запаздываний
потребительского спроса. Ввести в модель непрерывно распределенное запаздывание
потребления, положив dC/dt=—у (С — сУ), где у—скорость реакции. Доказать, что
изменение модели заключается в замене С = cY в уравнении B) на данное здесь значение С,
и показать, что в этом случае получается дифференциальное "уравнение третьего
порядка. Показать, что в обозначении предыдущего упражнения
у=-х -
где
и получить отсюда дифференциальное уравнение третьего порядка относительно У.
3.6. ТЕОРИЯ РОСТА ХАРРОДА — ДОМАРА В ДИСКРЕТНОЙ ФОРМЕ
В разделе 3.3 мы рассмотрели непрерывный вариант теории Харрода —
Домара, в котором не было запаздываний ни потребления, ни сбережений
ни запаздываний капиталовложений. Модель давала гарантированный рост
выпуска продукции по показательной кривой с относительной скоростью
q=s/v. Против этой теории было выдвинуто возражение, что она не вполне
динамична, ибо не включает запаздываний. Условие реализации модели
заключалось в постоянном равенстве сбережений и капиталовложений,
даже в случае рассмотрения ожидаемых планов.
Теперь мы сделаем попытку перевести эту теорию на язык дискретного
анализа. Этим мы больше подчеркнем различие ожидаемых и фактических
величин, планов и степени их осуществления. Если не вводить запаздываний,
то мы получим ту же простую или только формально динамическую модель,
что и в разделе 3.3 (см. упражнение 1). Введение запаздываний приближает
модель к действительности, делает ее менее жесткой и позволяет построить
подлинный динамический вариант ее. Рассмотрим простейший случай с
запаздыванием на один интервал в соотношении потребления и сбережений.
Предположим, что на стороне капиталовложений в акселераторе нет
запаздываний. Этот вариант, по-видимому, ближе всего подходит к изложению самого
Харрода. Нижеследующий анализ основывается на работах Бомоля
и Александера [1, 3, 4].
Вначале сформулируем два вывода Харрода. Первый заключается
в том, что существует гарантированный темп роста выпуска продукции,
который, будучи достигнутым, сохраняется и в дальнейшем. Второй вывод
сводится к тому, что если система достигла какого-либо другого темпа роста,
то в результате внутреннего приспособления темп роста ее не приблизится
к гарантированному, а удалится от него.
Харрод исходит из следующей основной предпосылки: полнее
реализуются не планы потребления, а планы сбережений. Это является одной
возможной предпосылкой при введении запаздываний. В линейной модели;
без независимых расходов функция сбережений будет иметь вид St=sYt_lb
где s — постоянная предельная склонность к сбережениям. Вообще говоря,,
это ожидаемое соотношение. Но, поскольку планы сбережений осущест-
83 6*

вляются, St является также и фактической величиной сбережений.
Ожидаемая величина потребления будет A—s)Yt_lf фактическое же потребление
С t =Yf—St=Yt—sYtl; возможны и непредвиденные затраты на потребление.
Основное уравнение, связывающее фактические величины модели, будет,
как и прежде, Yt=Ct+It+Ao где It — индуцированные, a At—
независимые капиталовложения. Следовательно,
выражает фактическое равенство сбережений и капиталовложений. Мы
рассмотрим важнейший случай — когда отсутствуют независимые
капиталовложения. При At = Q фактические капиталовложения (все индуцированные)
будут
Ожидаемые индуцированные инвестиции выражают действие акселератора
без запаздывания. Они составят
Дальнейшее углубление модели зависит теперь от соотношения между
ожидаемыми и фактическими капиталовложениями, то есть между /J и 1\,
Гарантированный темп роста выпуска продукции Yt следует из условия
равновесия, которое заключается в том, что планы капиталовложений
всегда осуществляются A[ — It) для всех t. Но, по условию, планы
сбережений реализуются в первую очередь. В результате возникает
нединамическая ситуация, в которой сбережения и капиталовложения всегда те
же самые — ожидаемые и фактические. Это условие выражается следующим
образом:
то есть
Положим q = $/v. Тогда полученное путем итерации решение этого
простого конечно-разностного уравнения будет иметь вид
Следовательно, Yt растет в геометрической прогрессии с гарантированным
темпом Q = 5/y.
Теперь допустим наличие внешних возмущений, то есть существование
в период t — 1 темпа роста, отличного от Q. На протяжении этого
промежутка времени ожидаемые капиталовложения фактически не
реализуются, то есть /J-i Ф It_±. Вопрос заключается в следующем: каков будет
механизм приспособления экономической системы в период t? Он зависит
от последующих предпосылок или дальнейших условий действия модели.
Допустим, что в период t превышение планируемых капиталовложений
над фактическими равно
Ut = /{-/,= v (Yt - Гг_г) - *ГЫ = vYt -(v + s) Yt_v A)
Если Ut > 0, то часть плановых капиталовложений не будет реализована.
Если же U% < 0, то имеют место непредвиденные капиталовложения.
Необходимо дополнительное условие для характеристики влияния данного
п11фО в период ^-1 на выпуск продукции Yt в период t.
Первая возможность заключается в предположении, что выпуск
продукции в период t возрос как раз настолько, чтобы компенсировать
недостающую величину Ut_1 (или что производство сократилось, если UU1
отрицательно):
r««r«-i + fft-i. B)
84 .

Из уравнения A) имеем
Yt = Yt_1 + vYt_1
Получаем конечно-разностное уравнение второго порядка:
Yt = H+v)Yt_1-{v + s)YM. C)
Решение его мы дадим в разделе 5.6. При заданном s, которое, как
правило, является небольшой положительной дробью, динамика Yt зависит от
величины коэффициента капиталовложений v. Близкие к действительности
значения v заключены между 1 — 5 и l + 2]/s. Для них движение Ур
описываемое уравнением C), имеет характер взрывного колебательного
движения. Например, если ^ = 1/4, значения v от 3/4 до 2 дают взрывное
колебательное движение. Этот внешне приемлемый результат,
соответствующий и модели Самуэльсона — Хикса (см. 3.7), в действительности создает
большую трудность. Она заключается в том, что условие B) несовместно
с сохранением гарантированного темпа роста. Если темп роста в интервале
t— 1 равен q = s/v, то (поA)) C/i_1 = 0. В таком случае условие B)
превращается в Yt = Yt_1, то есть выпуск продукции остается неизменным
и не может продолжаться с гарантированным темпом роста.
Вторая возможность позволяет избежать такого несоответствия,
а именно мы принимаем, что в период t продукция растет
гарантированным темпом, приспосабливаясь к недостающей величине Ut_v Имеем
Yt = A + Q)Yi.1 + Ut.1. D)
Из уравнения A) и из того, что q = s/v, следует:
Снова имеем конечно-разностное уравнение второго порядка:
)Yt_a. E)
Оно отличается от уравнения C) дополнительным членом s/v в
коэффициенте при Yt_x. Описываемая уравнением E) динамика Yt теперь
представляет собой неуклонный, но неопределенный рост, по крайней мере
для всех вероятных значений и>1 — s (см. 5.6). Это —случай взрывного
и неколебательного изменения Yt. Он на самом деле непосредственно
ведет к двум выводам Харрода, сформулированным вначале. Коль скоро
достигнут гарантированный темп роста, так что Ut_x = 0, то из уравнения D)
следует, что этот темп сохранится и в дальнейшем. Однако если
изменение происходит с каким-либо иным темпом роста, то описываемая
уравнением E) линия движения Yt будет постепенно отклоняться от
направления движения при гарантированном темпе роста, по крайней мере для
всех значений v > 1 — s.
Можно допустить и еще более общее условие. Пусть темп роста
в период ?—1 равен rul, а недостаток фактических капиталовложений
по сравнению с планами инвестиций составляет Utmml. Таким образом,
Yt_1 = Yt_2(l + rt_1). Пусть соответствующий темп роста для периода t
будет гм то есть Yt = Yt_1(l + rt). Введем теперь следующее условие: темп
роста увеличивается при недостатке инвестиций, то есть если часть
запланированных капиталовложений не осуществляется {UU1 > 0), и
понижается в противном случае. Темп роста продукции увеличивается в
соответствии с отклонением фактических капиталовложений от запланирован-
85

ных. Таким образом, условие будет следующим:
rt>rt_v если J7f-1>0,
rt=zrt-v если ^-i = 0, F)
rt < rt_x, если Ut_1 < 0,
Из F) следует, что, коль скоро достигнут гарантированный темп роста
Ut_! = 0, то он сохранится и в дальнейшем (^ = ^t-i)- Это соответствует
первому выводу Харрода. Предположим далее, что достигнутый темп
роста больше гарантированного: rt _1 = E/у) + е, где е > 0. Тогда Ytl =
= Y,_2( 1 +-^- + 8 J , и из выражения A) получим
Отсюда в силу F)
и расхождение между достигнутым и гарантированным темпами роста
продолжает возрастать. Это соответствует второму выводу Харрода.
Теперь ясно, почему теория роста типа Харрода — Домара не дает
удовлетворительной динамической модели. Причину этого надо искать
прежде всего в предпосылке Харрода о выполнении планов сбережений.
Если к тому же предполагается, что осуществляются и планы
капиталовложений, то вся система в существенной мере оказывается «втиснутой»
в рамки подвижного равновесия. Выпуск продукции растет в геометрической
прогрессии гарантированным темпом q=s/v. Это — единственно возможный
вариант в случае осуществления планов капиталовложений. Система не
является динамической моделью в полном смысле слова; например, она
не определяет динамику переменной от одного положения равновесия до
другого, вытекающую из внешних возмущений. Трудности заключаются в
жесткости двойной предпосылки о полном осуществлении планов сбережений
и капиталовложений; эта предпосылка подразумевает, что сбережения
всегда равны планируемым капиталовложениям, что планы всегда
оказываются согласованными.
Исследованная здесь альтернатива состоит в том, чтобы сохранить
предпосылку об осуществлении планов сбережений, но допустить
возможность невыполнения планов капиталовложений. Далее, модель требует
дополнительного условия: нужно установить форму реакции выпуска
продукции на частичное невыполнение планов капиталовложений. Это условие
можно выразить различными способами, и уравнения B), D), F)
представляют собой лишь примеры. Соответственно и результирующая линия
движения Yt может принять различные формы. Главное заключается в том, что
теперь гарантированный темп роста q = — вообще не имеет никакого
отношения к делу. Он появляется лишь тогда, когда налагают условия
равновесия (планируемые сбережения равны ожидаемым капиталовложениям).
Но он не может характеризовать динамические модели рассмотренного типа.
Движение Yt, вытекающее, например, из условий B) или D), следует
оценивать с помощью его собственных требований. Оно может быть колебательным
или взрывным либо же может иметь оба эти свойства. Но в любом случае
это результат взаимодействия мультипликатора и акселератора в
специфической динамической модели. Модели сходны в том, что в них могут быть
непредусмотренные капиталовложения (которые и приводят в действие
механизм приспособления системы), но не может быть непредусмотренных
сбережений. Ни одна из моделей не представляется удовлетворительной,
так как едва ли можно экономически обосновать допущение условий,
подобных B) или D).
86

Итак, мы приходим к тому выводу, что гарантированный темп роста
совсем или почти совсем не применим к динамическим макроэкономическим
моделям. Далее, динамические модели с простыми запаздываниями,
основывающиеся на предпосылке о реализации планов сбережений, не имеют
сколько-нибудь значительного экономического смысла, даже если их
рассматривать в отрыве от понятий гарантированного темпа роста. Более
выгодный подход заключается в том, чтобы вернуться назад к исходной позиции
и ввести иные основные предпосылки: планы потребителей осуществляются,
и остается открытой возможность непредвиденных сбережений.
Рассматриваемая ниже дискретная модель Самуэльсона — Хикса исходит из
предпосылки о том, что реализуются как планы потребления, так и планы
капиталовложений. Такое допущение уже не является столь жестким, как
двойная предпосылка теории Харрода о реализации планов сбережений и
капиталовложений. Остается достаточный простор для введения гибких
вариантов, допускающих возможность непредвиденных сбережений.
Задачи и упражнения
1. Показать, что для рассмотренной нами модели предпосылка об отсутствии
запаздывания означает
It = sYt и JJ=»(y«-y,_i)-
и что осуществляются как планы потребления, так и планы сбережений. Показать, что
в случае реализации также и планов инвестиций Yt~[v/(v—s)] Yt-i и что Yt растет в
геометрической прогрессии с темпом q' = s/(v—s). Почему этот «гарантированный» темп
роста больше темпа Харрода, равного q = s/v (при условии, что v>s)?
2. Рассмотреть случай с таким слабым акселератором, что v < s как для
приведенной в данном разделе модели с запаздываниями, так и модели предыдущего упражнения без
запаздываний. Объяснить дополнительные трудности, обнаруживающиеся в этом
случае в модели тина Харрода—Д омара.
3.7. МОДЕЛЬ САМУЭЛЬСОНА — ХИКСА, ВКЛЮЧАЮЩАЯ МУЛЬТИПЛИКАТОР
И АКСЕЛЕРАТОР
Наиболее полная формулировка взаимодействия мультипликатора
и акселератора в дискретной модели впервые была дана Самуэльсоном [18,19]
и позднее развита Хиксом [13]. Основная предпосылка модели
—осуществление планов потребления. При наличии запаздываний в функциях
ожидаемого потребления и сбережений это оставляет достаточно простора для
появления непредвиденных сбережений. Затем налагается условие, что в ходе
действия модели осуществляются планы капиталовложений, так что
ожидаемые инвестиции равны общей величине фактических сбережений и
капиталовложений. Акселератор с запаздываниями представляет собой функцию
ожидаемых инвестиций. Эта формулировка отличается от соответствующих
положений Харрода (см. раздел 3.6) в двух пунктах: осуществляются планы
потребления, а не сбережений, и запаздывания являются существенным
элементом ожидаемых соотношений потребления и капиталовложений.
В общем модель включает линейную функцию потребления с
распределенным запаздыванием (см. конец 2.7):
t y 1t1 2t2+ |
где A)
Мы принимаем, что общая предельная склонность к потреблению и каждый
из коэффициентов (сг, с2,...) выражаются положительными дробями @ < с < 1).
Функция акселератора также принимается линейной с распределенным
запаздыванием (как в 3.2):
h = »i (У|-х - Yt-t) + vt (Yt_2 - Yf_,) + ...,
где } B)
01^2+ • • • =0.
87

Общий коэффициент инвестиций v и каждый из коэффициентов (р1э v29 ...)
считаются положительными.
Ожидаемые планы, представленные уравнениями A) и B), исчерпывают
все возможности. В зависимости от текущего уровня дохода потребители
принимают те или иные решения об израсходовании имеющихся у них денег.
Соответствующие затраты равными или неравными суммами производятся
в течение нескольких будущих периодов, как, например, при покупках
в кредит. И, что еще более важно, вследствие текущих изменений в выпуске
продукции принимаются решения об инвестициях, и необходимые для этого
затраты планируются на несколько будущих интервалов времени.
Соотношения A) и B) характеризуют расходы на потребление и затраты на
инвестиции. Они могут зависеть и от прежних решений относительно потребления
и от инвестиций. Фактические поставки потребительских товаров и
капитальных благ могут происходить после осуществления затрат, одновременно
с ними или предшествовать им. В данном случае важно лишь, что затраты
производятся на протяжении нескольких промежутков времени.
Фактическое распределение запаздываний в уравнениях A) и B) может принимать
различные формы, например они могут «скучиваться» вместе «бугром»
(«humped») или растягиваться более равномерно. В дальнейшем мы
рассмотрим эти случаи.
Полученную таким образом модель Самуэльсона — Хикса надо
сравнить с соответствующей непрерывной моделью Филлипса (см. 3.5). Обе модели
в полной мере вводят запаздывания или по крайней мере дают возможность
этого. Филлипс берет непрерывно распределенные запаздывания спроса
на потребительские товары и элементы капиталовложений. И случай с
потреблением без запаздываний рассматривается лишь для упрощения
математической трактовки (см. раздел 3.5, упражвдние 4). Модель Самуэльсона —
Хикса включает распределенные запаздывания запланированных затрат
на потребление и капиталовложения. При уменьшении коэффициентов в
геометрической прогрессии они соответствуют типу запаздываний Филлипса.
Во всех других случаях они имеют более общий характер. Различие между
моделями Филлипса и Самуэльсона — Хикса заключается в условиях их
действия. Филлипс рассматривает спрос и предложение отдельно. Планы
потребления и капиталовложений, включающие запаздывания, в сумме
образуют совокупный спрос, а предложение с дальнейшим запаздыванием
приспосабливается к спросу. Из-за наличия запаздывания предложения
центр тяжести лежит на непредвиденных капиталовложениях. Точно так же
могут быть реализованы планы потребления и сбережений. В модели
Самуэльсона —- Хикса также суммируются плановые величины потребления и
капиталовложений, но предполагается, что и те и другие планы реализуются.
Следовательно, планы потребления и капиталовложений с запаздываниями
превращаются в фактические затраты, дающие в сумме выпуск продукции.
Непредвиденные капиталовложения или непредвиденное потребление
отсутствуют. Акцентирование делается на непредвиденные сбережения. Все это
отчасти вопрос удобства применения непрерывного или дискретного анализа.
Но отчасти это и проблема экономической интерпретации. В модели Филлипса
за запаздыванием действия акселератора, создающего спрос на
капиталовложения, следует другое запаздывание в приспособлении предложения
капитальных благ к этому спросу. В модели Самуэльсона — Хикса весь комплекс
запаздываний на стороне инвестиций объединен в единственной зависимости
акселерации B). Именно поэтому наиболее важна гибкость в формулировке
и интерпретации этой зависимости.
Рассмотрим сначала простейший вариант модели Самуэльсона — Хикса.
В нем все затраты на капиталовложения концентрируются, или
«скучиваются», в интервале времени, непосредственно следующем за первоначальным
изменением выпуска продукции. Можно выбрать интервал достаточно
длительным для нейтрализации первоначального влияния изменения выпуска
продукции на оборотный капитал, но не стол*, большим, чтобы этот интервал
88

включал затраты на новый основной капитал. Рассматриваются лишь чистые
индуцированные капиталовложения за вычетом износа. Вторичный эффект
не принимается во внимание, то есть считается, что первоначально
введенная в объем затрат в одном году величина возмещения основного капитала
остается приблизительно такой же и в последующее время.
Рассмотрим лишь первый член акселератора B). Но он включает два
прошлых интервала времени в виде Yt_t и Yt_2. Поэтому мы достигнем лишь
небольшого упрощения оттого, что возьмем мультипликатор типа Кана
и лишь один член (с Уг_г) в функции потребления A). Поэтому берутся два
члена, включающие Уи1*и Yt_2, и получается распределенное запаздывание
в функции потребления. Положив в дальнейшем с2=0, мы придем к
специальному случаю мультипликатора Кана и «элементарному варианту» Хикса [13].
Условие действия модели таково:
где Ct=y+c1Yt_1+c2Yt^2 есть потребление, It = u(Yt_1—Yt_2) —
индуцированные капиталовложения, а4( — независимые капиталовложения. Все
это фактические величины. Вышеприведенное условие эквивалентно
равенству ожидаемых капиталовложений фактическим сбережениям и
инвестициям. Не делается никаких предпосылок относительно ожидаемых
инвестиций, которые в общем случае отнюдь не обязательно равны фактическим
сбережениям и капиталовложениям. Поэтому могут появиться непредвиденные
сбережения.
Вышеприведенное условие сводится к конечно-разностному уравнению
второго порядка относительно Yt:
Y
то есть
Включим у в At и йазовем At . независимыми расходами. Положим
с = с1 + с2 и воспользуемся с и с2, помня, что с1 = с — с2. Тогда
то есть
Yt-cYt-i + iv-c^Y^-Y^ + At. C>
Для получения изменения во времени Yt требуется решить это уравнение
при заданной динамике Аь. Если At = A (постоянной величине), то, как
показывает подстановка в C), одно решение есть Yt = Y (Г = const), где
У = Л/A —с). Уровень статического мультипликатора совместен с моделью.
Положим yt = Yt — F. Тогда уравнение C) примет вид
Уг = су i.i + (v- с2) (уи1 - уи2). D)
Позднее (см. гл. 6) мы найдем общее решение уравнения D), и, как
увидим, изменение Y{ будет представлять обычное взрывное колебательное
движение вокруг Y = -4/A — с).
Элементарный случай Хикса включает следующие простейшие
зависимости: Ct~cYul и It = v(Yul — Yt_2). При с2 = 0 конечно-разностное
уравнение D) примет вид
yt = *И-1 + v (&_х - &_2), E)
где с —предельная склонность к потреблению, а я —мощность
акселератора. Действие распределенного запаздывания потребления,
характеризуемого с2, сводится к простому уменьшению мощности акселератора от v
в уравнении E) до v—c2 в уравнении D). Эффект распределенного
запаздывания капиталовложений можно объяснить, введя в зависимость B)
ненулевое v2. Особенно интересен случай распределенного в геометрической
89

прогрессии запаздывания капиталовложений. Хикс не рассматривал этого
варианта. Пусть при отсутствии запаздывания капиталовложения будут
Z^viY^Y^^vAY^. Тогда
где X —скорость реакции @<Х<1). Как уже было показано в
разделе 1.9,
Подставим это выражение и Ct^=cYt^ в Yt = Ct + It + A D = const):
то есть AYt + XYt = cAYul + cXYt^ + XvAYt^ + XA (так как AA = 0).
Положим AYt = Yul — Yt и AYt^ = Yt — Yt_v Делая приведение подобных
-членов, будем иметь
Решением_снова [будет статический уровень Yt = У = 4/A — с). Положим
yt — Yt — Y и для удобства перейдем от (?+1) к t:
то есть
где } F)
и v' = {l-X)
Заметим, что с'— взвешенная средняя 1 же с весами A—Я) и X, где 0 < X < 1;
и' является такой же взвешенной средней с и v. Следовательно, если с< у,
то, как правило, с < с' < 1 и с < г;' < г;. Сопоставление F) и E) показывает,
что введение распределенного (в геометрической прогрессии) запаздывания
капиталовложений также уменьшает мощность акселератора.
В простой модели Хикса, описываемой конечно-разностными
уравнениями D) или E), акселератор имеет вид It = v(Yt_1—Yt_2). Приводимая
здесь интерпретация принадлежит в основном Хиксу [13]: изменение выпуска
продукции в интервале t—1 при включении запаздываний ведет к
запланированным и реализованным капиталовложениям в период t. Самуэльсон [18]
дает несколько иную интерпретацию: индуцированные капиталовложения
связаны только с изменением выпуска предметов потребления (см.
упражнение 1). Другим путем пришел к тому же самому конечно-разностному
уравнению Смизи [20], элиминировав в своей теории ценных бумаг переменную
норму процента (см. 2.2).
Задачи и упражнения
1. Приравнять нулю независимые расходы и написать функцию
капиталовложений в виде It = k(Ct — Ct_x). Она представляет собой капиталовложения,
вызванные изменением выпуска предметов потребления, и не имеет запаздываний.
Взять функцию потребления с запаздываниями С==сУ^1 и вывести акселератор
в форме 1х = кс(У{_1—Yt^)- Объяснить смысл коэффициента инвестиций v=кс. Это
в действительности и представляет собой вариант Самуэльсона [18].
2. Рассмотреть «элементарный случай» Хикса при s=0 и показать, что конечно-
разностное уравнение будет иметь тогда вид Zt = vZt_1-\-Atj где Zt=Yt—Yf_i«
Решить его относительно Zt при At = A (A = const) и объяснить результат. Почему
яе достигнуто положение равновесия Yt=YH
3. Распространить рассмотренный в предыдущем упражнении случай на вариант
-с распределенным запаздыванием потребления с2ф0, но при s = 0. Что можно сказать
«о необычном случае очень слабого акселератора при v < с2?
90

3.8. ВОЗМОЖНОСТЬ РАВНОВЕСИЯ ПРИ РОСТЕ В ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Как уже было показано, при некоторых условиях возможен рост дохода
и выпуска продукции в геометрической прогрессии вида Yf=yo(l+Q)',
где q — темп роста. Именно так обстоит дело в модели мультипликатора
(см. 2.7), когда независимые расходы увеличиваются с темпом q. Тогда дело
•сводится просто к «доумножению» независимых расходов. Аналогичен
и случай в модели мультипликатора-акселератора даже при неизменных
независимых расходах. Тогда q представляет собой гарантированный темп
роста Харрода slv (см. 3.6). Оба случая представляют собой примеры
взрывного действия акселератора. И в том и в другом случае движение Yt
представляет собой концепцию равновесия и лишь частично-динамическое
решение динамической модели. Это означает, что коль скоро Yt начало двигаться
по линии равновесия, то оно может под действием модели и в дальнейшем
сохранить такое движение.
Та же возможность роста дохода в геометрической прогрессии
существует и в модели Самуэльсона — Хикса. Она опять представляет собой лишь
частное решение, обеспечивающее скорее равновесие, чем динамическое
изменение, и в этом выявляется мощность акселератора. В
конечно-разностном уравнении модели (см. уравнение 4 в разделе 3.7) положим, что
независимые расходы отсутствуют (At=0). Получим
Vt = cVt-i + (v -
Положим, что уг = у0A + гI есть частное решение. Тогда
^0(l+,f = q;jl+r)f-*4^-e^
должно быть удовлетворено для всех t. Это будет выполнено для любого
г/0, если г удовлетворяет соотношению
получаемому делением обеих частей предыдущего выражения на г/0A + 0*~2*
Следовательно, любое значение r = Q, представляющее собой вещественный
и положительный корень квадратного уравнения
дает рост дохода в геометрической прогрессии yt = yo(l + q)' с темпом q.
Можно графически исследовать корни квадратного уравнения Д = 0
(рис. 8). Так как постоянный член s в уравнении Д = 0 положителен,
то на рис. 8 кривая пересекает OR выше точки О. Поэтому корни
уравнения будут либо комплексными (Лх), либо вещественными и
отрицательными G?2)> либо вещественными и положительными (i?3)- Нас интересует
лишь последний случай. Он допускает два возможных темпа роста: qx и q2.
Решение квадратного уравнения легко получить алгебраически. В данном
случае корни уравнения R = 0 вещественны, если
и они в таком случае будут также и положительны, ибо тогда
то есть
Следовательно, возможен рост выпуска продукции в геометрической
прогрессии с соответствующим темпом роста q, если действие акселератора
достаточно сильно. Для этого небходимо лишь, чтобы v > c2 + (l + |AsJ.
91

Тогда существуют два подходящих значения Q. Корнями уравнения
будут
Qii Q2 = -2-{(f — С2 — 5-!)± V>-c2-s — IJ — 4s}.
Каждое из этих значений дает соответствующий темп роста, зависящий
только от структурных постоянных системы. Одно из этих значений в общем
достаточно мало (корень с отрицательным, а не с положительным значением),,
и его можно принять соответствующим действительности (realistic).
\
\
Рис. 8.
Это еще раз наглядно показывает взрывную силу акселератора. Даже
при наличии независимых капиталовложений акселератор умеренной силы
может вызвать индуцированные инвестиции, достаточные для роста
экономики в геометрической прогрессии (см. упражнение 1). Далее, при
увеличении независимых расходов один мультипликатор вполне способен
обеспечить расширение уровня продукции. Действие акселератора лишь усилит
этот процесс. Соответствующий механизм был описан в разделе 3.3 (см. также
упражнения 3 и 4 этого раздела).
Хикс [13] уделил много внимания возможности роста в геометрической
прогрессии. Его критиковали за это, в частности Александер [2]. Верно,
что экономический рост должен быть совместен с динамической моделью.
Но случай роста в геометрической прогрессии является (как и в разделах 2.7
и 3.6) лишь частным решением динамической модели. Модель вызывает
интерес главным образом с точки зрения возможности получения полного
динамического решения конечно-разностного уравнения системы и, в
особенности, выяснения того, имеет ли динамика продукции Yt характер
колебательного движения или нет, является ли она затухающей или взрывной.
Этот вопрос мы рассмотрим далее (см. гл. 6).
Задачи и упражнения
1. Показать, что для случая роста в геометрической прогрессии критическое
значение v тем меньше, чем ниже предельная склонность к сбережениям. Показать,,
что при с2 = 0 рост в геометрической прогрессии возникает при v > 1,44, если s = 0,04,
но лишь при и > 2,25, если 5 = 0,25. Какое влияние на этот результат оказывает с2?
2. Если s=0, показать, что при p>l-f с2 существует лишь единственный
подходящий темп роста.
3. Рассмотреть случай роста независимых расходов в геометрической прогрессии.
Положить в уравнении D) из раздела 3.7 At=A0 (l-f r)' и проверить частное решение
Yt—Y0(l-\-r)t. Показать, что такое движение Yt будет решением при условии У~о =
= Л0 (l-\-rJjR> где R имеет вышеуказанное значение.
4. Результат предыдущего упражнения имел одно ограничение: г должно была
быть таким, чтобы i?>0. Исследовать этот случай графически (см. рис. 8). При
заданных значениях v, s и с2 показать, что в таком случае для кривых R± и i?2 будут
92

подходить любые значения г, но для кривой R3—лишь малые (r<Qi) или большие
величины (r>Q2). Показать, что, при мощном акселераторе, г должно быть достаточно
мало (г < Од) для того, чтобы при росте независимых расходов в геометрической
прогрессии с темпом г был возможен рост выпуска продукции в такой же прогрессии
"С тем же темпом.
5. Объяснить условие i?>0 из предыдущего упражнения для случая с2=0,
доказав, что s> г [l + t>/(l+r)] эквивалентно ему. Вывести отсюда, что при заданном
положительном у>0 и заданной положительной дроби г сбережения должны быть
достаточно велики для покрытия капиталовложений [13, стр. 184].
3.9. РАСПРЕДЕЛЕННЫЕ КАПИТАЛОВЛОЖЕНИЯ.
ДИСКРЕТНЫЙ И НЕПРЕРЫВНЫЙ АНАЛИЗ
В разделе 3.7 рассматривался простейший случай, когда It =
z=v(Yt_l — Yt_2), и все индуцированные капиталовложения
концентрировались (humped) в первом же временном интервале после изменения выпуска
продукции. Распространим теперь вышесказанное на более общий случай
<с распределенным запаздыванием капиталовложений [см. B) в разделе 3.7].
В то же время можно включить в модель и более продолжительные
запаздывания потребления в соответствии с уравнением A) из раздела 3.7.
Сущность этого обобщения достаточно иллюстрируется следующими
равенствами:
Ct = ^iYt-i + c2Yt_2 + c3Yt_3, где сг + с2 + с3 = с, A)
и
it = MYt-i-YU2) + v2{Yt_2^Yt_3), где Vl + tb=v. B)
Из условия действия модели Yt = Ct-\-It-\-At вытекает конечно-разностное
уравнение третьего порядка:
Его можно преобразовать следующим образом:
Yt = cYt_x + (Vl - с') (?г_г - Y,_2) + (v% - с") (Yt_2 - Yt_3) + At, C)
где с = сг + с2 + с3, с' = с2 + с3 и c" = e3. Выражения для с, с', с" можно
назвать кумулятивными предельными склонностями к потреблению в
распределенном запаздывании потребления A).
Наиболее важными свойствами модели являются особенности
акселератора B). В модели имеется теперь распределенное запаздывание. Затраты
на капиталовложения в период t зависят от изменений выпуска продукции
в интервалы t—1 и ?—2, например, от двух совокупностей предыдущих
решений об инвестициях. И наоборот, следствием каждого решения о
капиталовложениях являются затраты на протяжении двух будущих периодов.
Могут представиться два следующих крайних случая: 1) vx=v и v2=0y
когда затраты на капиталовложения концентрируются в первом интервале
времени, и 2) и1=0, v2 = v, когда инвестиции откладываются и производятся
главным образом во втором периоде. Имеются и промежуточные варианты,
когда vl > 0 и и2 > 0, то есть затраты производятся на протяжении обоих
периодов. Они могут производиться равномерно или в большей или меньшей
степени концентрироваться на протяжении того или другого промежутка.
Запаздывание акселератора можно описать с помощью двух констант,
подобно средней и дисперсии или размаха. Такими константами могут служить
коэффициент и, характеризующий общую мощность акселератора, и величина
v2 (по отношению к vx или v), которая показывает размер запаздывания.
Легче определить влияние распределенных запаздываний потребления.
Они описываются кумулятивными величинами предельных склонностей
к потреблению (с, с', с"). Влияние первой из этих величин выражается также
через предельную склонность к сбережениям s=l—с. Прочие две,
отражающие распределение запаздывания, просто служат для уменьшения мощности
93

акселератора. В конечно-разностном уравнении C) с' уменьшает силу vlr
а с"— силу и2.
Как и раньше, можно получить различные частные решения уравнения C).
Если At — постоянно и равно А, то Yt~Y будет решением, где У = А/A—с)
определяется статическим мультипликатором. Далее, подставив в уравнение^
C) yt=Yt—У, получаем
У г = cVt-i + iPi - с') (У*-1 - У<-«) + (Ръ -
Решение этого уравнения дает динамику yt, то есть движение У,
относительно У.
Опять-таки при постоянных независимых расходах D j=const)
возможен рост дохода в геометрической прогрессии. Подставим yt = УоA + гI
в уравнение D), и надлежащий темп роста г найдется как вещественный
положительный корень уравнения
Это — уравнение третьей степени относительно г:
Графически (см. рис. 8) можно убедиться, что из трех возможностей лишь
одна представляет интерес, именно та, которая дает три вещественных корня
уравнения E), из которых один отрицательный и два положительных. В этом
случае имеются опять два возможных темпа роста Yt в геометрической
прогрессии.
Позже мы получим общее решение конечно-разностного уравнения.
Однако уже и сейчас можно сказать, что это уравнение третьего порядка дает
значительно большее разнообразие типов динамики Yt, чем
вышеприведенное уравнение второго порядка (см. 3.7). Более того, по мере расширения
распределения запаздывания, включаемого в функции потребления и
капиталовложений (то есть в мультипликатор и акселератор), повышается
порядок результатного конечно-разностного уравнения, а вместе с ним возрастает
и число решений, то есть количество возможных вариантов динамики Yt.
Таким образом, мы приходим к заключению, что в «реалистичной»
дискретной модели, учитывающей всевозможные запаздывания и отставания^
возникающие в действительности, динамика Yt должна быть найдена из
конечно-разностного уравнения высокого порядка. В таком случае
открывается очень большой выбор возможностей. При экономическом
истолковании результата обилие и многообразие решений являются и преимуществом
и препятствием. Среди большого разнообразия решений уравнения даже
не очень высокого порядка чрезвычайно трудно отличить характерные и
важные случаи и случайные возможности, которыми можно пренебречь. Таково
математическое отражение экономической реальности при дискретном
анализе. Например, если потребление имеет кратковременное отставание,
а последствия решений о капиталовложениях проявляются через более
продолжительные и меняющиеся периоды, тогда на протяжении короткого
отрезка времени могут произойти необычные явления в отношении выпуска
продукции, величины запасов и оборотного капитала; более того, эти
необычные явления вызывают позже отзвук в виде эффекта «эхо» в
последующие периоды, маскируя тем самым реальное действие акселератора.
Одна возможность упрощения заключается во введении жестких
предпосылок относительно продолжительности и единообразия запаздываний
системы. Именно так мы и поступили в данной главе. Риск тут состоите том,
что взятый за единицу промежуток времени — всегда до некоторой степени
произвольный — может быть столь длительным, что уничтожит в себе многие
интересные явления (например, краткосрочные изменения запасов и
величины оборотного капитала).
94

Характерная черта дискретного анализа заключается в трудности
выбора между произвольным упрощением ради удобства математического
решения и сложностью «реальных» моделей с широко распределенными
запаздываниями и большим разнообразием решений, из которых нужно отыскать
и отобрать более важное и менее существенное. Но остается и еще одна
возможность. Так как приближение к действительности требует введения
множества различных запаздываний, то более целесообразно использовать
непрерывный анализ, как это сделано в модели Филлипса (см. 3.5). Тогда
широко распределенное запаздывание (например, в акселераторе) становится
при переходе к пределу непрерывно распределенным, с которым можно
оперировать с помощью дифференциалов, а не с помощью конечных разностей.
Можно было бы ожидать, что непрерывный вариант даст уравнения даже
более высокого порядка с еще большим размахом возможных решений, так
как он представляет собой предел, к которому стремятся соотношения
в дискретной форме, по мере того как запаздывания растягиваются более
широко. Но в действительности, как было показано в разделе 3.5, это не так,
по крайней мере для случая, когда непрерывно распределенные запаздывания
берутся в форме показательной функции. Преимущество непрерывного
анализа в том, что при этом оперируют дифференциальными уравнениями
относительно низкого порядка, которые менее богаты решениями, чем
соответствующие конечно-разностные уравнения, и легче решаются хорошо
разработанными приемами. В дальнейшем мы исследуем различные типы
моделей (см. гл. 6—8), и тогда окажется, что большая амплитуда решений в
дискретном анализе по сравнению с непрерывным вовсе не соответствует
большему приближению к экономической «реальности». Многие из найденных
решений будут представлять собой колебания в пределах допускаемых
фиксированных запаздываний или отставаний. Они мало интересны или не
представляют собой подлинного решения.
Задачи и упражнения
1. Показать, что в дискретном анализе при распределенном запаздывании
акселератора введение краткосрочного запаздывания или полное отсутствие такового
в личном потреблении не является действительным упрощением. Сопоставить это
с упрощением, получающимся в отсутствие запаздываний потребления в непрерывном
анализе (см. 3.5, особенно упражнение 4).
2. Графически исследовать вышеприведенное кубическое уравнение R=Q E),
представив R как функцию от г. Показать сначала, что кривая пересекает OR выше
точки О. Вывести отсюда, что существует лишь три варианта для корней R — 0:
1)один вещественный отрицательный корень; 2) три вещественных отрицательных корня;
3) три вещественных корня, из которых два положительны и один отрицателен.

ГЛАВА 4
МАТЕМАТИЧЕСКАЯ ЧАСТЬ.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4.1, ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С дифференциальными уравнениями мы встречаемся на практике во
многих областях, но последние всегда связаны с понятием непрерывности. Среди
простейших форм дифференциальных уравнений имеются такие, которые
описывают кумулятивный рост некоторой переменной, когда приращение
ее происходит непрерывно и особым образом. Понятие непрерывности
возникает как предельный случай процесса со скачкообразными приращениями
перемегщой так же, как производная функции возникает как предел
отношения конечных приращений. Рассмотрим в качестве примера процесс
возрастания денежной суммы, положенной в банк при условии начисления
р=№0 г сложных процентов в год. Пусть Уо обозначает начальную
денежную сумму, аУя — денежную сумму по истечении х лет. Если бы
проценты начислялись один раз в год, мы бы имели
где # = 0, 1, 2, 3, ... . Если бы проценты начислялись два раза в год
{по истечении каждого полугодия), то мы имели бы
1 3
где я = 0, у, 1, у, ... , Вообще, если проценты начисляются п раз в год
12 3
и х принимает последовательно значения 0, — ,—,—,..., тогда
то есть
Если обозначить — = /г, то предыдущее равенство запишется так:
Неограниченно увеличивая п (при п—>оо, /г—>0), мы в пределе приходим
к процессу возрастания денежной суммы при непрерывном начислении
процентов. Закон возрастания принимает при этом следующий вид:
dx
Изменение, х предполагается непрерывным и закон возрастания выражен
дифференциальным уравнением. Это уравнение содержит производную
от искомой функции Yx по времени. Решение дифференциального
уравнения представляет собой явное выражение искомой функции Yx через

ее аргумент х. В рассматриваемом случае решение имеет следующий вид
(см. 4.3):
Дадим теперь общее определение. Обыкновенным дифференциальным
уравнением называется уравнение, в которое входит неизвестная функция
одной независимой переменной и производные различных порядков от этой
функции. Неизвестная функция должна быть найдена в процессе решения
(интегрирования) дифференциального уравнения. Существуют также и
другие виды дифференциальных уравнений, в которые входят функции
нескольких независимых переменных. Однако такие дифференциальные уравнения
мы здесь не будем рассматривать. Самое общее обыкновенное
дифференциальное уравдение с неизвестной функцией У независимой переменной х имеет
следующий вид:
Порядком дифференциального уравнения называется порядок
наивысшей входящей в это уравнение производной. Так, уравйение первого порядка
содержит dY/dx, но не содержит производных более высокого порядка.
Такое уравнение мы получили, рассматривая процесс возрастания денежной
суммы при непрерывном начислении сложных процентов. Дифференциальное
уравнение второго порядка содержит d2Y/dx2, но не содержит производных
более высокого порядка. Уравнение A) есть дифференциальное уравнение
?г-го порядка в общем виде. Решением дифференциального уравнения
называется всякая функция, обращающая уравнение в тождество. Изложение
технических приемов решения обыкновенных дифференциальных уравнений
различных порядков и типов не входит в нашу задачу; эти сведения можно
найти в учебниках по теории дифференциальных уравнений, например в книге
Пиаджё [7]; приемы интегрирования уравнений некоторых типов
(преимущественно первого порядка), представляющих интерес для экономистов,
можно найти в книге Аллена [1]. В настоящей главе будут рассмотрены более
или менее полно дифференциальные уравнения одного частного вида — так
называемые линейные дифференциальные уравнения с постоянными
коэффициентами.
Обыкновенное дифференциальное уравнение n-го порядка называется
линейным, если функция У и все ее производные входят в линейной
комбинации и не встречаются в какой-либо степени выше первой или в какой-либо
другой алгебраической или аналитической форме. Но независимая
переменная х может появиться в коэффициентах при У, dYldx, d2Y/dx2,... и в члене,
вовсе не содержащем У и его производных. Следовательно, это уравнение
в общем виде будет
^lWi7=/W. B)
где а^х), а±(х), ..., аа(х) — заданные функции, называемые коэффициентами
линейного уравнения, a f(x)— заданная функция, называемая правой
частью линейного уравнения, которая не включает ни У, ни его
производных. Если f(x) Ф 0, уравнение называется неоднородным или уравнением
с правой частью. Если коэффициенты линейного дифференциального
уравнения постоянны, оно называется линейным уравнением с постоянными
коэффициентами. Линейное дифференциальное уравнение с постоянными
коэффициентами тг-го порядка имеет, следовательно, вид
dnY f#i-iy dY
Здесь а0, al1 ..., а,г1, ап суть постоянные коэффициенты (а0 Ф 0), а правая
часть является произвольной функцией от х. В частном случае, если правая
часть тождественно равна нулю, мы получаем однородное линейное уравнение.
7 р. Аллен 97

Общий вид однородного линейного уравнения тг-го порядка с постоянными
коэффициентами таков:
¦апу=О. C)
Мы будем рассматривать здесь линейные уравнения с постоянными
коэффициентами произвольного порядка вида B) и C); при этом особое внимание
мы уделим линейным уравнениям первого и второго порядка. Мы будем,
как правило, для удобства применения в экономике обозначать неизвестную
функцию через Y в случае неоднородного линейного уравнения B) и через у
в случае однородного C).
Приведем несколько примеров линейных дифференциальных уравнений
с постоянными коэффициентами:
dY___i
dx ax-\-b '
— Ь F = sin x -f cos x,
Задачи и упражнения
1. Пусть Y обозначает путь, пройденный прямолинейно движущейся точкой за
время х\ показать, что уравнение dY/dz=const описывает движение с постоянной
скоростью, а уравнение d2Y/dx2 = const —движение с постоянным ускорением. Как
объяснить задачу, если У—национальный доход или объем выпускаемой продукции
в момент х?
2. Показать, что начальная денежная сумма Yo, положенная в банк с условием
начисления 100 г сложных процентов в год, через х лет превращается в
(
1
если начисление процентов производится п раз в год. Проверить для л = 1, п = 2.
Получить как предельный случай закон возрастания Ух при непрерывном начислении
процентов:
Проворить, что полученная функция удовлетворяет дифференциальному уравнению
dYx-rY
4.2. ОСНОВНЫЕ ВЫВОДЫ; НАЧАЛЬНЫЕ УСЛОВИЯ II ПРОИЗВОЛЬНЫЕ
ПОСТОЯННЫЕ
Решение дифференциальных уравнений по существу является делом
практики. Нужно найти тем или другим способом, случайно или путем проб,
функцию, которая удовлетворяет данному уравнению. Мы допускаем, что
такая функция и такое решение существуют. Этим мы избегаем сложных
вопросов о том, имеется ли какая-либо функция определенного типа
(алгебраическая, тригонометрическая и т. д.), удовлетворяющая уравнению. Если
практическая попытка не удается, то это может быть либо потому, что мы
недостаточно далеко продвинулись по намеченному пути, либо потому, что
нельзя найти решения.
Практические руководящие принципы могут быть сформулированы
совсем просто. Первый из них представляет собой общую теорему об обыкно-

венных дифференциальных уравнениях. Она приводится здесь с некоторыми
пояснениями, но без формального доказательства.
Общее решение обыкновенного дифференциального уравнения
порядка п дает Y в виде функции х, включающей точно п произвольных
постоянных:
1 "= jl уХ] л-р -^2' • * * ' п)'
Следующее соображение приводит к этому правдоподобному результату-
Произвольную постоянную всегда можно исключить путем
дифференцирования. Таким образом, если функция содержит две произвольные постоянные,
то первое дифференцирование исключает одну постоянную, а второе —
другую. Решение дифференциального уравнения есть процесс, обратный процессу
дифференцирования, и потому снова появляются произвольные постоянные.
Приведенная теорема относится к общему решению уравнения. Но
существует большое разнообразие частных решений какого-либо данного
уравнения. Смысл теоремы в том, что все частные решения включены в общее;
каждое из них соответствует некоторым определенным значениям постоянных
Аг, А2, ..., Ап. Не существует решений вне частных случаев общего решения.
Частные решения получаются путем установления точного значения
постоянных, которые определяются в соответствии с начальными условиями.
Другой основной результат составляют правила (свойства),
относящиеся к линейному дифференциальному уравнению с постоянными
коэффициентами. Неоднородная форма такого уравнения тг-го порядка следующая:
dnY dn~W . , dY , v ,, ч /;|ч
ао^Г + а1-^^Г+--+ап-1^+^ = /(^)» A)
и соответствующее ему однородное линейное ^уравнение имеет вид
dny , dn~xy . . dy , Л ,пх
Правило I. Если однородное уравнение B) имеет решения у^ух{х)
и ?/=г/2(:г)' т0 У = У\ (х) + У2 (х) есть также его решение.
Правило II. Если однородное уравнение B) имеет решение у = у(х)г
то у = Ау(х) также представляет собой решение с какой-либо постоянной А.
Правило III. Если Y = Y(x) есть какое-либо частное решение любого
общего уравнения A) и если у = у(х;А1,А2, ..., Ап) есть общее решение
соответствующего однородного уравнения формы B), то общее решение A)
есть
Доказательство этих свойств очень простое. Докажем только
последнее свойство.
Рассмотрим линейное неоднородное уравнение с постоянными
коэффициентами:
dnY , dn~*Y v
Пусть найдено какое-нибудь решение У (х) неоднородного уравнения, не
содержащее произвольных постоянных. Докажем, что любое другое
решение У (х) этого уравнения можно представить в виде суммы У (х) и
некоторого частного решения соответствующего однородного уравнения B).
В самом деле, так как У и У —решения уравнения A), мы можем
написать
dny , rfn-iy
+ « + + aY = f (x).
99

Введем разность y=.Y — Y, Вычитая из второго тождества первое, мы полу-
чаем
dn~1
Это значит, что разность у удовлетворяет соответствующему однородному
уравнению и, следовательно, получается из его общего решения, если
постоянным придать определенные значения.
Обратно, сумма какого-либо решения У неоднородного уравнения
и любого решения у соответствующего однородного уравнения есть снова
решение неоднородного уравнения, в чем легко убедиться, подставив сумму
у + У в левую часть неоднородного уравнения A). Из сказанного следует,
что, беря сумму одного произвольного решения неоднородного уравнения A)
и всевозможных решений соответствующего однородного уравнения B),
мы получим все решения уравнения A). Всевозможные решения однородного
уравнения B) или его общее решение выражается формулой
y = Al?l(x) + A2y2{x) + ...+АпУп(х). C)
Сумму Y(x) и общее решение однородного уравнения C)
Y{x)^Y (х) + AlVl (x) + А2у2(х)+...+ АпУп (х) D)
называют общим решением неоднородного уравнения. При этом Y(x) предста-'
вляет собой частный интеграл или частное решение A), а остальную часть
D) — линейную комбинацию с произвольными коэффициентами (то есть
общее решение соответствующего однородного уравнения) — иногда
называют дополнительной функцией. Мы указали выше, что в общем решении D)
содержатся все решения неоднородного уравнения A). Если произвольным
постоянным в общем решении придать определенные значения, мы получим
так называемое частное решение уравнения A).
Из вышеизложенного вытекает практическая процедура решения любого
данного уравнения формы A). Она состоит в отыскании сначала общего
решения однородного уравнения B) с помощью комбинации правил (I)
и (II), а затем в прибавлении частного решения первоначального уравнения
A) для получения общего решения данного неоднородного. Часто
предпочтительнее обратная процедура, и обычно она более подходит при решении
дифференциальных уравнений, получающихся в экономических задачах. В этом
случае практические этапы решения следующие. Данное уравнение A)
выражается в виде функции У (означающей, например, доход или выпуск
продукции), подлежащей исследованию. Должны быть, во-первых, найдены
некоторые частные решения У = Y(x). Какое-либо частное решение, наиболее
подходящее с точки зрения экономического истолкования результата,
будет представлять тенденцию или изменение положения равновесия У.
Интерес обычно сосредоточивается на движении У по мере неопределенного
возрастания х, например на изменении У во времени, если независимая
переменная х есть время. В таком случае ищется частное решение У ~ Y(x),
которое описывало бы движение, совместное с данным уравнением A),
и которое являлось бы в некотором смысле нормой или значением равновесия.
Следующим шагом будет переход к у = У — У, где у есть отклонение от
тенденции или значения равновесия. Из этого следует, что у должно
удовлетворять однородному уравнению B), когда мы подставляем У и У в A), так
как они оба являются решениями, и вычитаем. Последний этап состоит
в получении общего решения однородного уравнения B) в форме, указанной
в C). После этого получается решение, полное и одновременно легкое для
истолкования. Отклонения У от У, обозначенные у, даются уравнением C);
переход обратно к первоначальным переменным дается решением D). Из двух
частей этого решения D) одна представляет собой тенденцию или линию рав-
100

новесия (частное решение), а другая — отклонение от тенденции или линии
равновесия (дополнительная функция). Пример этой практической процедуры
при решении экономической задачи нами уже был приведен [см. 3.3,
уравнение D)].
Некоторое затруднение возникает относительно произвольных
постоянных, появляющихся в общем решении D) в числе, равном порядку
уравнения. Оно вытекает из того обстоятельства, что постоянные, будучи
произвольными, могут появляться в разной оболочке. Общее решение может быть
написано двумя или более способами, которые на первый взгляд кажутся
различными и противоречивыми; на самом же деле они тождественны и
различаются лишь в результате какого-нибудь преобразования. Та же трудность
встречается, когда одно решение сначала написано с одним рядом
произвольных постоянных, а затем — с другим. Это часто бывает удобно, но внешне
видоизменяет характер решения.
Например, решение уравнения dYldx = 11(ах + Ъ) есть У = A/а)Х
Х\п(ах + Ъ) плюс произвольная постоянная (см. 4.3). Это может быть
записано различными способами, где постоянные, смотря по надобности,
изменяют свой вид таким образом:
°, где А = 1пА\
, где А' = (А")~а
Произвольной достоянной может быть по желанию А, А' или Л".
Наиболее обычный способ истолкования произвольных постоянных
отправляется от начальных условий, налагаемых на У и его производные.
Каждой произвольной постоянной в этом случае может соответствовать одно
начальное условие, которое и «определяет» постоянную. Дифференциальное
уравнение первого порядка имеет общее решение в форме У = У (я, -4) с одной
постоянной произвольной А. Предположим, что уравнение подчинено
единственному начальному условию Y — Y0J когда х = 0. Тогда
что определяет А через Уо. И вместо уравнения У = Y(x, А) мы фактически
получаем У = F(x, Уо). Это есть обычная форма решения с постоянной Уо
вместо А. Если дано Уо при х = 0, то дифференциальное уравнение
определяет в таком случае значение dY/dx при х = 0, то есть начальное изменение
У по сравнению с исходной величиной Уо. Основная идея заключается в том,
что решение должно «оттолкнуться» от точно определенной начальной
величины.
Аналогично дифференциальное уравнение второго порядка имеет общее
решение У = Y(x, Ax, А2). Пусть это уравнение подчинено двум начальным
условиям, например,
Y = Y0 и g- = Y; при х=Ь.
Подставляя затем эти значения в уравнение У = Y(x, А1У А2), мы
получаем два уравнения относительно Ах и А2. Из этих уравнений можно
выразить Аг и А2 через Уо и Y'o и включить произвольные постоянные в решения:
У = F(x, Уо, Y'o). Если даны Уо и Y'o при х = 0, то дифференциальное
уравнение устанавливает d2Y/dx2 при х = 0 и «пускает в ход» изменение У. Два
начальных условия необходимы, чтобы построить решение
дифференциального уравнения второго порядка. Ясно теперь распространение этой
процедуры на уравнения более высокого порядка.
Следовательно, начальные значения, подобные Уо и У^, являются как раз
произвольными постоянными. Однако если налагаются особые начальные
101

условия, то в таком случае произвольные постоянные принимают особые
значения, и общее решение становится частным решением, которое подходит
к этим специальным начальным условиям. Для иллюстрации приводим
следующие два примера:
Пример (а)
—г—— г-т- при условии У = 0 и я = 0.
dx ах-\-Ь r J
Общее решение: У = — In (ax-f- Ь) -\- А (см. 4.3);
при х = 0
0 = ~
то есть
А= — — ЫЪ.
а
Частное решение есть У = — Aп(а# + Ь) — In b}=—In a 7~ .
Пример (б)
-j-^—а2у=0 при условии у — У0 и -т^-=0 пРи ^=^0.
Общее решение: y = A1eaxJrA2e~ax (см. 4.4, упражнение 1).
Тогда
Начальные условия при ж=0в таком случае дают
1
— у0.
Частное решение будет
1
то есть А1 = А^ = —
Здесь у0 может рассматриваться как произвольная величина; но решение все еще
является частным, так как другая произвольная постоянная задана особым значением.
Задачи и упражнения
1. Доказать правила (I), (II) и (III), приведенные в тексте.
2. Рассмотреть решение D) уравнения A) как выражение изменения У около
тенденции или положения равновесия У. Провести различие, при неопределенном
возрастании х> между «взрывными» и «затухающими» изменениями и показать, что
достаточно одного ут «взрывной» формы, чтобы У было «взрывным». Что можно
сказать о случае «затухания»? Выразить это в виде понятия «доминирующего» члена
среди уг (г = 1, 2, 3, ..., п).
3. Дано неоднородное уравнение
3B^.
dx6 dx v '
Доказать, что функции ех, е~х и 1—суть линейно-независимые решения
соответствующего однородного уравнения. Проверить, что У(х)=ж3 есть частное решение данного
неоднородного уравнения. Каким начальным условиям оно удовлетворяет при х=0?
Найти частное решение У, при начальных условиях г/@)=0; 2/' @) = 2;г/" @) = 0.
4.3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Простейшее линейное дифференциальное уравнение с постоянными
коэффициентами имеет вид
dY r, v
102

Это уравнение первого порядка, и в нем отсутствует член с неизвестной
функцией Y. Решением этого уравнения является неопределенный интеграл
от функции f(x):
где А — аддитивная произвольная постоянная. Таким образом,
интегрирование дифференциального уравнения сводится в данном случае к
интегрированию функции, то есть просто к действию, обратному дифференцированию.
В следующей таблице приведены решения некоторых наиболее часто
встречающихся уравнений рассмотренного типа, правыми частями которых
являются простейшие элементарные функции.
Формулы дифференцирования
элементарных функций
dx \n-{-iJ X
—— ех = ех
dx
d 1
— пж ——
d .
-г- sin x = cos ?
Дифференциальные уравнения
уравнение
dY
dx
dY
dx
dY
dx
dY
dx
X
= ex
_ 1
X
= COS X
общее решение
А.П+1
Y 14 (n-h W
fi-\-1 '
Эти результаты легко распространить на случай, когда в правых частях
рассмотренных уравнений вместо аргумента х стоит его линейная функция,
то есть выражение вида ах + Ъ. Так, например, уравнение dYldx = eax+b
имеет общее решение Y — (lla)eax+bJr А, а уравнение dYldx = 1/(ах + Ъ) —
общее решение У = A/а)\п(ах + Ь) + А.
Особенностью общего решения уравнений этого типа является то
обстоятельство, что единственная произвольная постоянная в этом общем решении
является аддитивной. Ясно, что это происходит в силу того, что
соответствующее однородное уравнение имеет лишь одно линейно-независимое решение
у^х) = I1. Мы увидим из дальнейшего (см. 4.5), что общее решение любого
однородного дифференциального уравнения с постоянными коэффициентами,
в котором отсутствует член с неизвестной функцией, как это имеет место
в уравнении dYldx = /(#), содержит аддитивную постоянную.
В общем случае линейное дифференциальное уравнение первого порядка
с постоянными коэффициентами имеет вид
a
Так как а0 # 0, мы можем, слегка изменив обозначения, записать это
уравнение в следующем виде:
A)
Соответствующим однородным уравнением будет
dy
dx
¦ = ау.
B)
Как было изложено в разделе 4.2, интегрирование уравнения A) можно
практически осуществить в два этапа. Во-первых, разыскивается какое-либо
1 О понятии линейно-независимых решений см, примечание на стр. 108.—
Прим. ред.
103

частное решение У = Y(x) этого уравнения. Чаще всего это делают методом
последовательного приближения, видоизменяя уравнение в зависимости
от конкретного вида f(x) — правой части уравнения. Во-вторых, мы ищем
общее решение однородного уравнения B). Обозначим у = У — У и заметим,
что У и У должны оба удовлетворять уравнению A):
и *Г
Вычитая одно уравнение из другого, получаем
то есть y=zY — Y должно удовлетворять однородному уравнению B).
Теперь найдем общее решение у.
Перепишем уравнение B) в такой форме:
d л 1 dy
—- In у = — -~- = а.
ах & у dx
Общее решение этого уравнения есть
где А' —произвольная постоянная. Иначе говоря, у = еах+А\ или у-=Аеах,
где А = еА' — новая произвольная постоянная.
Теперь мы можем написать общее решение уравнения A)
Y = Y(x)+Aeax. C)
Произвольная постоянная А получает определенное значение, если задано
начальное условие вида Y = Yo при х = 0.
Имеется другой метод интегрирования однородного уравнения B);
его преимущество состоит в том, что он легко распространяется на однородные
уравнения высших порядков. При другом методе решение уравнения
разыскивается в виде у = evxy где р — неизвестная постоянная, подлежащая
определению. Подставляя это предполагаемое решение в уравнение B),
мы получаем
JJL ерх = аерх, то есть рерх = аерх,
откуда р = а, так как evx Ф 0, Итак, мы нашли частное решение уравнения
B) в виде показательной функции у = еах. В силу общей теории (см. 4.2)
общее решение уравнения имеет вид
где А — произвольная постоянная. Этот результат был получен ранее
другим способом.
Постоянная а задается; она характеризует «структуру» уравнения A).
Поведение решения C) при возрастании х зависит от величины и в
особенности от знака а. Если а > 0, то член Аеах в уравнении C) монотонно
возрастает при, возрастании х — так называемый «взрывной» случай. Если
а < 0, член Аеах по мере возрастания х монотонно уменьшается, стремясь
к нулю, то есть имеет место «затухающий» случай. Член Y(x), какую бы форму
он ни имел, представляет тенденцию или линию равновесия, на которую
накладывается взрывное или затухающее изменение. Характер изменения
зависит от начального возмущения (которым определяется А) и от величины а.
Чем больше численная величина а, тем сильнее взрывное или затухающее
изменение.
Интегрирование линейных дифференциальных уравнений с постоянными
коэффициентами приводит, как правило, к показательным функциям, свой-
104

ства которых необходимо знать читателю [1, гл. IX], (см. также приложение
Б «Комплексные числа» настоящей книги. — Ред.)
Со следующими свойствами чаще всего придется встречаться:
I ех = 1 при х = О,
III еах+ь изменяется с постоянной относительной скоростью, равной а,
возрастая до бесконечности при увеличении х, если а > 0, и уменьшаясь
до нуля при увеличении х, если а < 0.
Подбор частного решения У (х) неоднородного уравнения A)
видоизменяется в зависимости от вида правой части этого уравнения, f(x).
Рассмотрим важный частный случай, когда правая часть неоднородного
уравнения постоянна, то есть f(x) = a. Неоднородное уравнение получает вид
dY V
dx
Будем разыскивать частное решение уравнения в виде постоянной У = [х,
где \х — некоторая постоянная, подлежащая определению. Подставив ее
в дифференциальное уравнение, получим
— а[г = а, то есть ^= .
Мы получаем общее решение уравнения (dY/dx) — аУ = а в виде
Следовательно, решение этого уравнения представляет отклонение (Аеах)
от постоянного уровня У= —а/а.
Неоднородные уравнения первого порядка с правыми частями других
типов рассматриваются в упражнении 6 этого раздела.
Линейные дифференциальные уравнения первого порядка появляются
при изучении простых экономических моделей непрерывного типа. Как
было выяснено выше, такие уравнения описывают изменение цены Р как
функции времени в экономических моделях паутинообразного типа. Так,
в разделе 1.3 мы получили уравнение
dP __Ъ—ар а—р ш
а в разделе 1.7 (модель III)—уравнение
?L -$), E)
где D = a-\-aP и S = Р + ЬР представляют собой соответственно спрос
и предложение в статике, заданные в виде известных линейных функций
цены Р, а ^ — постоянная, определяющая скорость реакции (то есть
изменения цены при изменении запасов товара). Как было выяснено, цена
неуклонно возвращается к своему значению равновесия
если только коэффициенты при Р в дифференциальных уравнениях D)
и E) отрицательны. Так обычно и обстоит дело в силу того, что а < 0,
аг < 0, b > 0, А, > 0. В модели паутинообразного типа (см. 1.3)
абсолютная величина коэффициента при Р равна [Ь + (—а)]/(—а1); в этом случае
мы имеем быстрое приближение к состоянию равновесия, если а± мало.
В модели с запасом товара A.7) скорость возвращения цены к ее
значению равновесия зависит от постоянной к.
Простейшие макроэкономические модели также приводят к линейным
дифференциальным уравнениям первого порядка, описывающим изменение
105

дохода или выпуска продукции У как функций времени. При изучении
простейшей мультипликаторной модели (см. 3.4) получается
дифференциальное уравнение AД) (dY/dt) = — sY-f А, описывающее монотонное
возвращение У к значению равновесия (Y = A/s)\ скорость этого возвращения
зависит от значения s — предельной склонности к сбережению. Однако
в теории роста Харрода — Домара (см. 3.3) действие акселератора
приводит к прогрессивному росту функции У,, удовлетворяющей уравнению
так как в нем q — коэффициент при У — оказывается в этом случае
положительным: q = s/v > 0.
Рассмотрим еще одну экономическую задачу. Пусть доход У
возрастает со скоростью, пропорциональной его величине:
dY -nV
и пусть, кроме того, дефицит в расходах правительства прямо
пропорционален доходу У (при коэффициенте пропорциональности к). Дефицит
в расходах приводит к возрастанию национального долга D: dD/dt = kY.
Здесь мы считаем переменные У и D непрерывными и дифференцируемыми
функциями времени t. Пусть начальные условия имеют вид Y = Y0 и D = D0
при t — 0. Из первого уравнения мы получаем, учитывая начальные
условия, Y = YQ€^. Решение для Y дает постоянный (пропорциональный) рост.
Подставляя У во второе уравнение, получаем dD/dt = kYoeQt. Общее
решение этого уравнения имеет вид
Y0
Постоянную А определим из начальных условий. Именно, подставляя
начальные значения в полученное решение, мы получаем D0 = (k/Q)Y0-\-A.
Итак, окончательно
то есть национальный долг возрастает с той же относительной скоростью
q, что и национальный доход. Рассмотрим отношение
Мы приходим к заключению, что при ?—>оо национальный долг имеет
тенденцию стать определенной долей дохода. Эта задача впервые
рассматривалась Домаром [4] (см., например, работу Бомоля [2]).
Задачи и упражнения
1. Дано уравнение dY/dx = ax; показать, что его общее решение имеет вид
Y = ax/lna-\-A (при а>0, а ф 1). Особо рассмотреть случай а=1.
2. Дано уравнение dY/dx=sin (ax-\- Ь). Показать, что его общее решение имеет
вид У=—(I/a) cos {ах-\-Ъ)-\-А.
3. Показать, что общее решение предыдущего уравнения можно записать также
в форме Y = (l/a) sin (ax-\-b — я/2)+А
4. Дано однородное линейное уравнение dy/dx = Q. Показать, что у = 1 есть его
частное, а у —А—его общее решение. Исходя из этого, найти общее решение
неоднородного уравнения dY/dx — f(x) методом, изложенным в предыдущем разделе.
5. Показать, что уравнение dy/dx-\-y=.O имеет общее решение вида у — Ае~х.
6. Методом подбора найти частные решения уравнений:
^Г 1+*> (II)-?"+Y=sinz+cos *.
Убедиться в том, что общие решения этих уравнений соответственно р
и Y = sinx-\-Ae~x. Дать графическое изображение частных решений при Л=
и истолковать их характер.
106

7. Показать, что общее решение C) уравнения A) при а=0 принимает вид
у=\ /(x)dx-\-A. Что можно сказать в этом случае о тенденции и изменении У по
отношению к тенденции?
8. Рассмотреть комбинацию экономических моделей, описываемых уравнениями
D) и E) (см. 1.7. упражнение 5). Показать, что коэффициент при Р оказывается в этом
случае равным — Х(Ь—а)/A— %а). Что можно сказать тогда о скорости
приближения Р к Р?
4.4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ВТОРОГО ПОРЯДКА
Можно без потери общности линейное дифференциальное уравнение
второго порядка с постоянными коэффициентами и соответствующее
однородное уравнение записать в таком виде:
.*+№_/». (!)
Постоянные а и b могут быть какими угодно величинами (включая
нуль). Они характеризуют «структуру» уравнения. В соответствии с общей
теорией (см. 4.2) общее решение уравнения A) разыскивается в два этапа.
Сначала мы ищем частное решение Y = Y (х) этого уравнения. Возьмем
y = Y — Y, так что у удовлетворяет B). Затем мы должны найти общее
решение соответствующего однородного уравнения B). Метод
интегрирования однородного уравнения, примененный в разделе 4.3, оказывается при-
ложимым и в этом случае. Будем искать решение однородного
уравнения B) в виде показательной функции у = ерх. Подставим это
предполагаемое решение в уравнение B). Заметим, что dy/dx = рерхи d2yjdx2=- p2epx.
В результате мы получим
Так как ерх Ф О, то наша функция будет действительно решением
уравнения B) в том и только в том случае, если р удовлетворяет так
называемому характеристическому уравнению1
= 0. C)
Это — квадратное уравнение с неизвестным р и корнями]
Корни могут оказаться вещественными различными (когда а2 > 4й),
вещественными равными (когда a2 = 4fc) и комплексными сопряженными (в
случае а2 < 46). В каждом из этих случаев мы можем, как это будет сейчас
показано, написать, пользуясь У (ж), общее решение уравнения A).
Случай а2 > 46. Корни характеристического уравнения C) —
вещественные различные числа, заданные формулой D). Мы получаем два част-
1 Характеристическим уравнением линейного дифференциального уравнения
с постоянными коэффициентами вида
называется алгебраическое уравнение, которое получается путем замены функций у
и ее производных соответствующими степенями величины р. то есть уравнение
К этому уравнению приходят при отыскании частного решения вида у = Се&х для
данного дифференциального уравнения. — Прим. ред.
107

ных решения однородного уравнения: ух (х) = epix и у2(х) = ер*х. Эти
решения линейно-независимы1. Следовательно, общее решение уравнения B)
имеет вид
Y = Y(z) + Ахе^х + А2е^ху E)
где Аг и Л2 —произвольные постоянные. Значения этих постоянных можно
найти, если задать два начальных условия, например У = У0 и dY/dx — Yf0
при х = 0. Решение аналогично решению уравнения первого порядка
из раздела 4.3.
Характер решения зависит от знаков и величин р1 и /?2, которые
в свою очередь зависят от аи ft первоначального уравнения. Обычно
вызывает интерес отклонение Y от тенденции равновесия У и то, что
происходит с этим отклонением при возрастании х. Если отклонение
бесконечно возрастает, проходя через положительные или отрицательные
значения, то изменение У будет «взрывным» по отношению к тенденции У.
С другой стороны, если отклонение уменьшается до нуля {с колебаниями
или без них), то тогда У имеет «затухающее>> изменение вокруг
тенденции У. В последнем случае отклонение состоит из двух членов: Аге^х
и А2е*>*х. Вопрос сводится к следующему: который из них является
преобладающим членом, то есть который в действительности определяет
движение y = Y~Y при возрастании х?
Ответ в этом случае прост: численно больший корень
характеристического уравнения определяет преобладающий член в решении.
Предположим, что этот больший или преобладающий корень есть рг. Если рг
положительно, то Ахе^х бесконечно возрастает, и изменение У будет
«взрывным». Другое слагаемое в решении не имеет большого значения; оно может
возрастать (р2 > 0) или уменьшаться (р2<0) без воздействия на
«взрывную» природу изменения У при возрастании х. Если рх отрицательно,
тогда р2 должно быть также отрицательным, и оба слагаемых {Ахе^х
и А2ер*х) уменьшаются до нуля, то есть отклонение У от У «затухает».
Случай а2 = АЬ. Корни характеристического уравнения C)
вещественные равные; иначе говоря, уравнение имеет один двукратный корень.
Из D) следует, что в этом случае pl = p2= —а/2. Однородное уравнение
принимает вид
Его характеристическим уравнением будет р2 + ар + 1/4а2 = [р + (я/2)]2 = 0.
Одно решение однородного*уравнения F) найдено: у = е 2 . Однако, как
известно из общей теории, для построения общего решения линейного
однородного уравнения второго порядка нужно знать два линейно-независимых
частных решения. Недостающее решение мы попробуем найти, подставин
в уравнение F) функцию y — xevx — xe ^ как решение этого уравнения.
Вычислим первую и вторую производные этой функции:
1 г Функции fi(x), /2 (я), ..., fn(x) называются линейно-зависимыми, если
существует какая-либо их нетривиальная линейная комбинация, тождественно равная нулю
то есть если существуют числа Alt A2i ..., Ап, не все равные нулю, такие, что
Л/i (*) +Л/2 (*)+••• +Anfn (x) ~ 0.
Если все числа Ak (A = l, 2, ..., п) равны нулю, то такая линейная комбинация
называется тривиальной, а функции /i(#), /2 W, ..., /n(#) называются
линейно-независимыми, (см. также 13.1).—Прим. ред.
108

где jD= — у а. Подставляя рассматриваемую функцию и ее производные
в уравнение F), получаем:
Г 2р + р2х + а A + рх) + -г а2х 1 ерх = 0, так как р = — у а.
Таким образом, функция у~хе % есть также решение уравнения FI.
Итак, общее решение уравнения F) получает вид:
где Аг и Л2—произвольные постоянные. Общим решением неоднородного
уравнения A) в рассматриваемом случае будет
Y = Y(x) + (A1 + A%x)e~*ax, G)
где Ах и А2 могут быть определены снова из начальных условий.
Это почти такое же по форме решение, как и уравнения первого порядка
из раздела 4.3. Разница заключается в том, что вместо одной
произвольной постоянной теперь в уравнении G) имеются две произвольные
постоянные, объединенные в одном множителе (Ах-\-А2х), умноженном на пока-
_ — дэс
зательную функцию е 2 . Разница эта ощутима для умеренных
значений х, но становится незначительной при бесконечном возрастании х.
Это происходит по той причине, что показательная функция е 2
перекрывает множитель (А1-\-А2х). Показательная функция увеличивается
быстрее, чем какая-либо степень х; например, хех возрастает подобно ех
и хе~х уменьшается до нуля подобно е~х при стремлении х к бесконеч-
—— — — CLX
ности. Изменение У по отношению к У задается выражением (Ах -f- A2x) e 2 ,
-lax
в котором преобладаюу^ая по значению часть есть е 2 . Если а < 0,
изменение будет «взрывным»; если а>0, изменение «затухающее», стремящееся
к нулю.
Случай а2 < АЬ. Корни характеристического уравнения C) —
комплексные сопряженные числа
Pi. 2 = —j> = a ± ico,
где
a=— — a\ (d = —
Составленные с помощью этих корней частные решения однородного
уравнения линейно-независимы. Поэтому общее решение уравнения A)
можно записать в виде
У = У (х)
1 Полученное второе решение является линейно-независимым с найденным
прежде, но автор не оговаривает и не доказывает этого. Докажем, что функции еРх
н хе*>х линейно-независимы. Предположим, что существует тождественно равная
нулю линейная комбинация этих функций:
то есть
еР* (Сг + С2х) = 0.
Так как еРх ф 0 ни при одном значении аргумента, мы должны иметь в этом случае
Но это может быть только в случае С1 = С2 = 0, чго и означает, что функции
и хё°х линейно-независимы. —Прим, ред.
109

то есть
где Вг и В2 — произвольные постоянные. Используя (см. приложение Б„
стр. 612.—Ред.) формулу Эйлера, мы можем преобразовать сумму двух
последних слагаемых следующим образом:
еах El6ifflx + В2е~™х) = еах [Вх (cos (ox + i sin соя) +
+ В2 (cos сох — i sin сод:)] = ea* (Аг cos шя + Л2 sin (ox),
где ^1 = JB1 + JS2 и A2=i(B1 — B2) суть новые произвольные постоянные.
Чтобы эти новые произвольные постоянные оказались вещественнымиу
нужно, чтобы первоначальные постоянные Вг и В2 были комплексными
сопряженными числами.
Общее решение однородного уравнения можно подвергнуть далее
следующему преобразованию. Введем новые постоянные А и е, связанные
с Аг и А2 равенствами
s ^x = i4cos8 и -42=^sine.
Величины А и г можно истолковать как полярные координаты точки
плоскости, декартовы координаты которой суть Аг и А2. Новые
достоянные можно выразить через Ах и А2 следующим образом:
tge = -^-, или (стр. 610) e =
Введя новые постоянные, мы получаем
Y — Y(x) = еах (Аг cos (ох + ^12 sin (ox) =
= еах (A cos (ox cos е + A sin (ox sin е) = Аеах cos (оке — е).
Следовательно, общее решение уравнения A) может быть записано в
рассматриваемом случае в двух эквивалентных формах:
У = Y
или (8)
Y = Y(x) +Aeax cos ((ох — е); J
а и со суть «структурные» постоянные, заданные коэффициентами а и b
первоначального уравнения. Произвольные постоянные суть Аг и Аг
или А и е. Член Y(x) есть частное решение A), зависящее от формы/(х).
Оно может быть определено так, что явится тенденцией или линией
равновесия Y. На него накладываются изменения (y = Y — У), даваемые
вторым членом (8).
Изменение y = Y — У принимает в таком случае форму
синусоидальной функции1 в общем виде Аеах cos ((ох — е)(см. приложение Б, стр. 616)т
и оно будет колебательным. Амплитуда и затухающий множитель
колебания задаются Аеах; уровень фиксируется произвольной постоянной Ау
например начальными условиями, но изменение амплитуды по мере
возрастания х зависит от «структурной» постоянной а= — у а. Период
колебания равен 2я/со; он зависит от другой «структурной» постоянной со =
— —~\f\h — а2. Фаза, или исходный пункт колебаний, зависит от
произвольной постоянной е и устанавливается начальными условиями.
Следовательно, при возрастании х колебание изменяет амплитуду (зависящую
от а), но всегда имеет тот же период (задаваемый со). Из двух произ-
1 Так как функция синуса переходит в функцию косинуса простым увеличением
аргумента на я/2, то автор не разделяет эти функции в колебательных движениях,
называя их обе везде синусоидальными функциями, а соответствующие колебания—
синусоидальными колебаниями.— Прим. ред.
НО

вольных постоянных, одна (А) определяет начальную амплитуду и другая
(е) —начальную фазу колебания.
Так как амплитуда изменяется, то колебательное движение У вокруг У
может быть взрывным, регулярным или затухающим. Это зависит только
от знака а = — —а. Если а > 0, то при возрастании х изменение будет
взрывным; если а = 0, то имеют место регулярные колебания с неизменной
амплитудой; если а < 0, то колебания будут затухающими. Эти три случая
см. на рис. 72. Доминирующим членом в решении (8) является член с еах,
так что если а > 0, то изменение У будет взрывным и колебание является
побочным, тогда как при а < 0 изменения затухают и колебание является
основной характерной чертой движения У.
Итак, в случае комплексных сопряженных корней характеристического
уравнения всякое решение линейного однородного дифференциального
уравнения второго порядка есть колебательный процесс, начальная
амплитуда и фаза колебания которого определяются начальными условиями,
а частота колебания и коэффициент затухания от них не зависят.
Частное решение Y(x) неоднородного уравнения A) во всех случаях
зависит от формы правой части уравнения. Оно разыскивается методом
подбора, при котором решение ищут в той или иной форме в зависимости
от вида f(x). Наиболее прост сдучай, когда f(x) = р. Пусть требуется найти
частное решение следующего уравнения:
n dY L hV ft
Ищем частное решение в виде постоянной У = \i. Подставляя \х в уравнение,
получаем b\i = р, откуда [i = р/&. Поэтому общее решение неоднородного
уравнения имеет в рассматриваемом случае вид
Таким образом, изменение У происходит вокруг постоянного уровня
F= р/б.
Разыскивание частного решения неоднородного уравнения в случае
правой части других типов рассматривается в задачах настоящего раздела.
Линейные дифференциальные уравнения второго порядка находят
применение при изучении, например, экономической модели паутинообразного
типа с запасами товаров (см. 1.7, модель IV), в которой скорость изменения
цены Р зависит от величины запаса. Если спрос и предложение являются
линейными функциями цены, то есть
а А, есть постоянная, определяющая силу реакции изменения цены на
изменение запасов, то процесс изменения цены описывается
дифференциальным уравнением
В качестве частного решения можно взять постоянную
имеющую смысл цены равновесия. Отклонение р — Р — Р удовлетворяет
тогда однородному уравнению
-а)р = 0. (9)
Л*
Найдем общее решение этого уравнения. Характеристическое уравнение,
в котором неизвестная обозначена через q> будет следующее:
111

В обычном случае (а < О, Ъ > О, X > О) член А, F — а) положителен.
Введем обозначение со= J/ Х(Ь — а). Тогда корни характеристического
уравнения будут qlt 2=±*а)- Следовательно, общее решение уравнения (9)
имеет вид
p=Acos((ot — г),
где А и е представляют собой произвольные постоянные, которые
определяются единственным образом, если заданы начальные условия.
Следовательно, присоединив Р, получим закон изменения цены во времени:
Р = Р + A cos (со* - в), A0)
Отметим, что фактор затухания а, входящий в общий случай
колебательного решения (8), здесь равен нулю. Таким образом, цена Р совершает
гармонические колебания относительно уровня равновесия Р. Период колебаний
2я/о> =2л/}/к(Ь —а) не зависит от начальных условий, а определяется
структурой самой модели. Амплитуда и фаза колебаний (А и е соответственно)
устанавливаются начальными условиями. Таким образом, в этой модели
начальное возмущение заставляет цену регулярно колебаться вокруг
положения равновесия с периодом 2я/ш независимо от типа возмущения. Цена
равновесия не может быть названа неустойчивой, так как нет нарастающего
отклонения цены от ее значения в положении равновесия. С другой стороны,
цена не имеет тенденции возвратиться к своему значению равновесия, а скорее
колеблется вокруг него. Период колебаний мал, если величины X и Ъ — а
велики, то есть если цена быстро реагирует на изменение запаса товара,
и если наклоны кривых спроса и предложения — соответственно (—а) и Ъ—
сильно меняются при изменении цены.
Задачи и упражнения
1. Показать, что общим решением уравнения d2y/dx2 = a2y является функция
у = А1еах-\-А2е~ах. Показать также, что знак а не является существенным и что
доминирующий член в решении всегда взрывной (при а Ф 0).
2. а) Проверить, что общее решение уравнения
имеет вид
Y = x-\-A1eax+A2e-ax.
б) Проверить что общее решение уравнения
d2Y
имеет вид
У = е~*+А1еах+А2е-ах.
3. Найти частное решение уравнения d2y/dx*-\-2(dy/dx)-\-y = 0, удовлетворяющее
начальным условиям г/ = 1 и dy/dx-—0 при # = 0. Построить график решения и
объяснить его.
4. Показать, что функция Y = x(l — e~x)-\-Y0 A+яг) е~х есть частное решение
уравнения d^Y/dx2 -(- 2 (dY/dx) -\~ Y = х-\-2, удовлетворяющее начальным условиям
Y = Y0 и dY/dx = 0 при х = 0.
5. С помощью дифференцирования и исключения постоянных А и 8 найти два
дифференциальных уравнения второго порядка, общими решениями которых служат
соответственно функции y=Aexcos(x—е) и у — Ае~х cos (x — е). Проверить,
проинтегрировав уравнения методом, описанным в данном разделе. Начертить графики
решений и объяснить их основные свойства.
-1*
6. Проверить, что функция Y—x-\-Ae 2 cos (x — е) есть общее решение
уравне4 [(d^Y/d2)^ (dY/d) 1] 5 ( У) Нй Л
рр, фуц ( ) щ р ур
ния 4 [(d^Y/dx2)-^ (dY/dx) — 1] =5 (х — У). Найти Л и 8, если заданы начальные условия:
= ±- при *=0.
112

II. 7 = 1 при а?=0, y = y при а:==у Почему А и е-те же бамые?
7. В случае а2 — АЬ найти решение однородного уравнения F) в виде у^ие
где и — некоторая функция от #, подлежащая определению. Показать, что м=Л
есть решение уравнения G).
8. Пусть в экономической модели, описываемой уравнением (9) и решением A0),
графики спроса и предложения суть прямые с отрицательным наклоном к оси Р
(а<0, 6<0). Показать, что цена совершает гармонические колебания, если |а|>|Ь|»
но что будет взрывное изменение по сравнению со значением равновесия, если
| а К | b |. Истолковать эти условия. Исследовать случай | а | = | b j.
9. Обобщить рассмотренную в тексте экономическую модель, взяв вместо
уравнения (9) уравнение вида
* %
(см. 1.7, упражнение 5). Найти общее решение и истолковать полученный результат*
10. Из системы уравнений, к которой мы пришли в задаче о национальном долге
и доходе (см. 4.3), исключить Г и получить уравнение d2D/dt*—Q(dD/dt) = Q с
начальными условиями D=D0J dD/dt=kY0 при * = 0. Показать, что решение имеет вид
D = DQ-\-[(k/Q) Y0(eQt — 1)], что совпадает с результатом, найденным нами другим путем
4.5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ ПРОИЗВОЛЬНОГО ПОРЯДКА
Метод интегрирования линейных уравнений второго порядка с
постоянными коэффициентами, изложенный в разделе 4.4, допускает возможность
обобщения для случая линейного уравнения произвольного порядка с
постоянными коэффициентами. Линейное неоднородное уравнение я-го порядка
и соответствующее ему однородное уравнение имеют вид
A)
B)
Прежде всего разыскивается какое-нибудь частное решение Y = Y(x)
уравнения A). Это может быть сделано путем установления тенденции
или линии равновесия Y при возрастании х. Тогда отклонение у = Y — Y
будет удовлетворять однородному уравнению B), общее решение
которого у = у(х; Ах, А2, ..., Ап) и требуется разыскать. Для этого достаточно
найти п линейно-независимых частных решений ук{х) (к = 1, 2, ..., п)
уравнения B) и составить из них линейную комбинацию с п произвольными
коэффициентами. Для отыскания этих линейно-независимых решений
воспользуемся прежним приемом. Будем искать решение однородного уравнения
в виде показательной функции У = е^х, где р — постоянная, подлежащая
определению. Найдем производные от этой функции до я-го порядка
включительно:
Подставив в уравнение B) рассматриваемую функцию и ее производные,
мы обнаруживаем, что она будет решением этого уравнения в том и только
в том случае, если р удовлетворяет вспомогательному, или так называемому
характеристическому, уравнению (см. выше, стр. 107.—Ред.):
а0Рп + ахрп'г + ... + ап_гр + ап = 0. C)
Это алгебраическое уравнение п-й степени с вещественными коэффициентами
имеет ровно п корней, среди которых могут быть вещественные и
комплексные, образующие сопряженные пары. Обозначим эти корни через р19 р2, ...
..., р,г. Если характеристическое уравнение не имеет кратных корней,
то есть среди чисел р^ р2, •••, Рп нет одинаковых, мы получаем п линейно-
независимых решений уравнения B), имеющих вид
8 р. Аллен

Поэтому общим решением уравнения B) будет
у = А^еР** + А2е^х + ... + АпеР**9 D)
Решение может быть развернуто в другой форме, включающей
синусоидальные функции, когда уравнение C) имеет пары комплексных корней.
В случае, когда характеристическое уравнение имеет кратные корни,
мы получаем лишь столько линейно-независимых частных решений
уравнения B), сколько имеется различных корней характеристического уравнения.
В этом случае формула D) не приводит к общему решению, так как в ней
нет полного комплекта членов. Недостающие линейно-независимые частные
решения мы тогда найдем, воспользовавшись приемом, изложенным во втором
случае, указанном в разделе 4.4, или замечанием в приложении А.З.
Можем быть доказано следующее положение. Если рк есть корень
характеристического уравнения кратности Qk, то этому корню соответствует gk
линейно-независимых частных решений однородного уравнения, имеющих вид.
Итак, и в случае кратных корней нетрудно написать ровно п
линейно-независимых решений линейного однородного уравнения.
Если все корни C) вещественны, то доминирующий член в решении D)
есть тот, в который входит наибольший по абсолютной величине корень р±.
Если Pi > 0, изменение у взрывное при возрастании х. Если рг <0 (каковы
бы ни были другие р), у затухает и стремится к нулю. Хотя у имеет
поворотные точки, ни в том, ни в другом случае нет регулярных колебаний.
Если существуют комплексные корни уравнения C), то они встречаются
парами р = а ±?<о, и два члена формулы D), соответствующие каждой паре
комплексных корней, приводятся к Aeaxcos((ox — е), причем А я е являются
произвольными постоянными. Доминирующий член D) теперь определяется
относительной величиной рх— наибольшим вещественным корнем и аг—
наибольшей величиной из всех а, входящих в Комплексные пары/? = а + /со.
Следовательно, в изменении у в этом случае всегда присутствуют колебания.
Колебания могут быть взрывными сами по себе (ах > 0) или они могут быть
добавлены к монотонно взрывной части (рг > 0). Однако если ах и рх
отрицательны, то взрывного элемента нет, и главным компонентом решения D)<
является затухающее колебание. Корни характеристического уравнения C),.
конечно, нелегко найти для уравнения порядка выше второго. Напримерг
в случае уравнения третьего порядка характеристическое уравнение будет
кубическое: аорг + ахр% + а^р + а3 — 0. Либо все три корня (рг, р2, р3)
будут вещественны, хотя два или даже все могут быть равны по величине;
либо один корень будет вещественным, а два других сопряженными
комплексными (р1? а ± ?(о). Во всех случаях должен существовать по крайней мере*
один вещественный корень рх\ если он может быть найден, то (р — рг) явится
множителем в кубическом характеристическом уравнении, приводимом
к следующему виду:
Коэффициенты а и Ъ находятся из коэффициентов первоначального
характеристического уравнения. Два других корня, будут ли они вещественными
или комплексно-сопряженными, получаются сразу как корни квадратного*
уравнения р2+ ар + Ъ = 0. Раз один вещественный корень кубического
характеристического уравнения определен, нетрудно получить и два других
корня. Схемы нахождения необходимого первого корня содержат различные
методы графического и численного приближения.
В одном частном случае вещественный корень характеристического
уравнения может быть сразу указан. Пусть дифференциальное уравнение
не содержит члена с искомой функцией У. При этом характеристическое
уравнение не будет иметь свободного члена и поэтому обязательно будет
иметь по крайней мере один нулевой корень. Такое однородное уравнение
141

первого порядка исследовано в разделе 4.3. Однородное линейное уравнение
второго порядка в этом случае имеет вид d2yldx2-\- u(dyJdx) = 0.
Характеристическое уравнение р2+ ар = 0 имеет корни р — 0 ж р = — а, и общим
решением будет
Соответствующее уравнение третьего порядка есть d3yldxs+ a(d2y/dx2)+
+ b(dyldx) — 0, а характеристическое уравнение р3 + ap2Jt Ър = 0 имеет
корни р17 р2 = —(—а+Уа2 — 4Ь) и р3 = 0. Общим решением будет
В каждом случае в решении присутствует аддитивная постоянная,
которая соответствует нулевому решению характеристического уравнения.
Это есть общее свойство, справедливое и для уравнения тг-го порядка, ибо
в числе п линейно-независимых решений однородного уравнения также будет
е°х = 1, а, следовательно, общее решение будет содержать произвольную
аддитивную постоянную (см. упражнение 2).
«Классический» метод решения линейного дифференциального уравнения
с постоянными коэффициентами может быть резюмирован таким образом.
Общее решение уравнения A) есть
E)
где все Л представляют произвольные постоянные, заданные начальными
условиями, а все р являются корнями характеристического уравнения
an_lP + an = 0. F)
п корней уравнения F) могут включать вещественные и комплексные
сопряженные величины, и они могут быть не все различны. Для вещественного
корня соответствующий член в уравнении E) будет просто показательной
функцией. Для комплексной сопряженной пары (р = а ± i со) два члена
в уравнении E), соединяясь вместе, дают Ae?xcos((dx — е), где А и г будут
произвольные постоянные, замещающие две постоянные Л в E). В случае
двух равных вещественных корней, рх = р2— р два члена E) замещаются
(Аг + А2х)ерх. Случаи большего количества кратных корней изложены выше
(стр. 114).
Относительно способов разыскания частного решения Y(x), входящего
в E), для неоднородного уравнения A) не было пока сказано ничего, кроме
самой общей рекомендации — действовать методом проб. В качестве простого
примера можно рассмотреть случай постоянной правой части в A). Пусть
f(x) = р. Ищем решение уравнения A) в виде постоянной У = У = const.
Подставляя в уравнение A), получим anY = р, откуда У = $/ап. Это и есть
искомое частное решение E). В этом случае У изменяется около постоянного
уровня.
Классический метод интегрирования линейных уравнений с постоянными
коэффициентами можно облегчить, применяя оператор дифференцирования
D = dldx (см. приложение А).
Операторный метод не приводит к упрощениям выкладок при отыскании
общего решения однородного уравнения. Однородное уравнение B)
записывается в операторной форме следующим образом:
(а0Б» + aiDn-i + . . . + ап_гП + ап)у = 0.
Ищем решение в виде у = evx. Для этой функции Dy = pevx = ру, или D = ру
то есть действие оператора D эквивалентно умножению на р. Замейив поэтому
D через р и, опуская у, мы получаем характеристическое уравнение F).
Таким образом, задача вновь свелась к разысканию корней
характеристического уравнения, то есть операторный метод не дал ничего нового.
115 8*

Однако операторный метод может принести большую пользу при
разысканий частного решения неоднородного уравнения Y(x). Введем обозначение
F(D) = a0Dn + aiDn-i +...+ an_xD + an.
Теперь уравнение A) можно записать в операторной форме следующим обра-
8ом: F{D)Y = /(#). Можем получить формальное решение
Формальное решение может помочь при отыскании частного решения
неоднородного уравнения. Это действительно оказывается так, если
алгебраические действия над оператором D производятся по определенным
установленным правилам. Изложению этих правил посвящено приложение А. Здесь мы
ограничимся тем, что рассмотрим два простых примера дифференциальных
уравнений второго и третьего порядка, показывающих применение опера-
горного метода.
Пример (а)
Характеристическое уравнение имеет вид р2—1=0; его корни plt2:=p= 1. Поэтому
общее решение соответствующего однородного уравнения есть у=А1ех-\-А2е~х, где
Ах и А2—произвольные постоянные. Частное решение ищем из операторного равенства:
Общее решение уравнения G) есть
(см. 4.4, упражнение 2).
Пример (б)
Характеристическое уравнение имеет вид р3—/?2+2=0, то есть (р+1) (р2—2р-\-2) = 0;
его корни: /?Ь2 = 1 zh h Рз= — !• Следовательно, общее решение однородного
уравнения есть
у=Аех cos (х—е)-{-Ве~х,
где А, В, е—произвольны. Частное решение найдем, написав формально
Yхех
Разложим операторную дробь на элементарные:
1 1 \_ /_1 D — 3
D3—D*+2 ~~(D+l)(D*—2D+2)~~ 5 \D+1 D*—2D+
|.'а{сим образом, пользуясь правилами приложения А, получаем частное решение:
d
D2-2D+2
Следовательно
1
Итак, Y~ — Bx—l)ex. Легко проверить, что мы, действительно, получили частное
решение уравнения (8). Находим производные: dY/dx = -y- Bх +1) ех;
116

= -т-Bх-\-3)ех; ddY/dx3='r;Bx+5)ex. Подставляя в левую часть уравнения (8)
значения У и производных, получаем хех, то есть правую часть уравнения (8). Поэтому
общее решение этого уравнения есть
У= Г A cos (x—e)-j--r-Bff— I) | ех-{-Ве~х.
L 4 J
Оно представляет взрывное колебание, наложенное на монотонно развивающуюся
тенденцию -г Bх — 1) ех.
Задачи и упражнения
1. Показать, что частное решение уравнения d2y/dx2 = a (dy/dx), удовлетворяющее
начальным условиям у=у0 и dy/dx=k при а?=0, имеет вид у:=Уо-^(Н/а) (еах—1)*
2. Показать, что общее решение однородного уравнения и-го порядка
л УЛ-п* У-Л- -X*n~ - —1^ = 0 Т
не содержащего у, имеет вид 2/=2/i(#)+-<4, где ух (х) есть общее решение уравнения
(и — 1)-го порядка
а Л—произвольная аддитивная постоянная.
3. Решить уравнение (8), не пользуясь операторным методом. Для этого показать,
что частное решение можно искать в виде Y=(aa;-f b) е*. Подставив его в
дифференциальное уравнение, найти а и Ъ. Показать, что У = -т- Bа:—1) ех есть частное решение,'
4. Показать, что общее решение уравнения
имеет вид у = [A cos (х—е)-\-В]ех, где Л, В> в—произвольные постоянные. Имеется
ли в нем доминирующий член?
5. Что можно сказать относительно решения (и, в особенности, относительно
доминирующего члена) дифференциального уравнения третьего порядка в свете
предыдущего упражнения и примера в тексте, когда характеристическое уравнение имеет
пару сопряженных комплексных решений?
4.6. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Интегрирование линейных дифференциальных уравнений значительно
упрощается, если применять описываемый в разделе 4.7 метод, особенно
удобный для разыскивания частных решений, удовлетворяющих заданным
начальным условиям. Основная идея метода — идея преобразования —
легко объяснима. Она постоянно встречается в математике и в простой форме
уже была нами использована. Если оказывается затруднительным получить
црямое решение задачи, сформулированной в терминах некоторой
переменной величины, то этот прием позволяет перейти к новой переменной,
попытаться решить «преобразованную» задачу, а затем с помощью обратного
преобразования вернуться к исходной переменной. Переход к новой
переменной был применен, например, в разделе 4.3 в форме логарифмического
преобразования при интегрировании однородного линейного уравнения
первого порядка dyldx ~ су. Мы фактически перешли к новой переменной 2,
связанной со старой переменной у зависимостью z = 1щ/, так что dzldx ='
= ily(dyldx) и наше уравнение преобразовалось в dzldx = с. Получив
решение преобразованного уравнения в форме z = сх + const, мы вернулись
к прежней переменной у = ez и отсюда получили общее решение исходного
уравнения в виде у = Аесх, где А есть произвольная постоянная (см. 4.3).
За более сложной техникой так называемого преобразования Лапласа
скрывается та же простая общая идея. Преобразование Лапласа, кроме его
применения к решению дифференциальных уравнений — где оно
представляет наиболее эффективный метод, имеющийся в нашем распоряжении,-^.
117

служит промежуточным звеном для многих результатов, на первый взгляд
не связанных между собой. В частности, оно связано с гармоническим
колебанием у — 4eafcos((o^ + е) и с произведением векторов Aeieepi (p =
= a4- too) (см. приложение Б), р в преобразовании Лапласа может быть
отождествлено с р = а + ico в синусоидальной функции. Условимся
применять преобразование Лапласа к функциям времени, которое мы будем считать
непрерывной переменной и обозначать буквой t. Пусть у — y(t) есть
некоторая функция времени, определенная при ?>0, имеющая значение у0 при
t = 0. Предположим, что функция y(t) непрерывна вместе со своими
производными любого порядка. Можно распространить теорию и на прерывные
(например, ступенчатые) функции; однако мы этого делать не будем.
Обозначим производные и начальные значения производных от функции y(t) при
t = 0 соответственно через
"о' У о' • • •' У а '
Рассмотрим интеграл
A)
где р есть некоторое заданное вещественное или комплексное число. Прежде
всего следует выяснить, существует ли предел в правой части равенства A),
то есть сходится ли интеграл, написанный в левой части. Исследование
сходимости этого интеграла A), вообще говоря, не просто; этим исследованием
мы здесь заниматься не будем. Отметим лишь, что, если вещественная часть
р > 0, множитель e~pt быстро убывает по абсолютной величине при t ->- + оо.
Поэтому расходимость интеграла A) может объясняться либо малостью
вещественной части числа р, либо быстрым ростом функции y(t) по абсолютной
величине. Встречаются функции, для которых предела интеграла A) не
существует ни при каких значениях р\ примером, такой функции служит е*2.
В дальнейшем мы будем, не останавливаясь на доказательстве сходимости,
рассматривать только такие функции времени и такие значения параметра р,
для которых интеграл A) существует, например когда функция представляет
многочлен относительно t. Для рассматриваемых ниже элементарных
функций интеграл A) существует в целой области значений параметра р.
Величина интеграла A) зависит как от вида функции y(t), так и от
значения параметра/?. Другими словами, интеграл A) является некоторой
функцией вещественной или комплексной переменной р. Обозначим эту функцию
через у (р); это обозначение подчеркивает тот факт, что эта функция
аргумента р порождена исходной функцией y(t) аргумента t при разных значениях р.
Определение. Преобразование Лапласа функции y(t) в функцию у(р)
представляется равенством
Функция у(р) называется изображением функции y(t); функция y(t)
называется оригиналом, соответствующим изображению у(рI.
Из многочисленных свойств преобразования Лапласа рассмотрим три
простейших, необходимых для применения этого преобразования при
интегрировании линейных дифференциальных уравнений с постоянными
коэффициентами.
1 В дальнейшем вместо выражения «преобразование Лапласа» нами чаще
употребляется более обычный в русской математической литературе термин «изображение».—
Прим. ред.
118

Свойство I. Данной функции y(t) соответствует ее единственное
изображение у(р); обратно, если данному изображению у(р)
соответствует непрерывный оригинал, то он определяется единственным
образом.
Первая часть этого утверждения очевидна. Доказательство
второй части утверждения можно найти, например, в книге Карслоу
и Егера [3, приложение 1].
Свойство II. Если у(р) есть изображение функции y(t), то
изображение производной n-го порядка от этой функции есть
оо
\ е~*1 уЫ (t) dt = tf% (p) -
о
Свойство III. Если функция у (t) удовлетворяет линейному
дифференциальному уравнению
ап^У , , Л <*У_ . Л „_*/,\ B)
и начальным условиям
г' == У0' л* 2ч)'
при * =
и если / (/?) есть изображение функции fit), то изображение у (р)
решения y(t) удовлетворяет вспомогательному алгебраическому
уравнению
(аорп + atf71'! + ... + ап^р -f an) y(p) = J (p) ¦
C)
• • • + ап-2 (РУо + Уо) + ап-гУо-
Свойство I есть основной результат, позволяющий обратить
преобразование Лапласа. Инверсия при принятых допущениях о непрерывности
является единственной. Для этого имеется разумное основание:
преобразование Лапласа функции y(t) в функцию у (р) вводит интеграл, так что
инверсия от у (р) к y(t) есть действие, обратное интегрированию, и
поэтому не вводит ни аддитивных, ни других постоянных в результат этого
действия. Положение аналогично следующему: интегрирование как
действие, обратное дифференцированию, влечет за собой аддитивные
постоянные; но дифференцирование, будучи обратным интегрированию, не
оказывает такого действия.
Свойство II есть «правило» преобразования Лапласа для производных
ют у (t). Его нетрудно доказать, исходя из определения изображения и
записывая изображения последовательных производных (см. упражнения 1 и 2).
Для последовательных производных первого, второго и третьего порядка
«формула (II) для изо бражения производной соответственно принимает виД|
@ dt=*
119

Заметим, что второе слагаемое в правых частях этих формул есть
многочлен относительйо /?, коэффициентами которого служат начальные значения
функции и ее производных (j/0, y'Qr г/JJ, ...); степень этого многочлена на
единицу меньше порядка производной от y(t), изображение которой ищется.
Применение преобразования Лапласа к интегрированию линейных
дифференциальных уравнений основано на свойстве III, которое нетрудно
получить, применяя свойство II для изображения производной к левой
части рассматриваемого линейного дифференциального уравнения.
Вспомогательное уравнение C), дающее преобразование Лапласа у (р), получается
при этом следующим образом. Умножим обе части уравнения B) на e'vt
и проинтегрируем:
'dt +
Получившиеся интегралы представляют собой изображения неизвестной
функции, ее последовательных производных, а интеграл в правой части —
изображение правой части исходного уравнения.
Если подставить в написанное уравнение
а остальные интегралы заменить их выражениями из свойства II [для
п = 1,293 они приведены в D)], то мы придем к вспомогательному
уравнению C).
В связи со свойством III следует заметить два важных обстоятельства.
Во-первых, для того чтобы составить вспомогательное уравнение C), нужно
знать начальные значения искомого частного решения и его первых п — 1
производных при ? = 0. С другой стороны, эти начальные значения можно
рассматривать как п произвольных постоянных. Следовательно, общее
решение дифференциального уравнения мы получаем в удобной форме,
в которую как бы «вмонтированы» начальные условия и которая делает
излишним весьма трудоемкие вычисления произвольных постоянных,
отвечающих этим начальным условиям.
Во-вторых, заметим, что из вспомогательного уравнения C) мы находим
непосредственно не само искомое решение y{t)<> а его изображение у (р).
Кроме члена f(p), выражение C) дляу(р) дается в форме отношения
одного многочлена! относительно р (степени п— 1) к другому многочлену
относительно р (степени ri). Отсюда у (р) полностью определяется через
постоянные дифференциального уравнения (а0, а19 . . ., ап), начальные
• значения функции и ее производных (у0, у'о, ..., у™'1) и изображение
правой части уравнения, то есть функции f(t). Формула C) выглядит несколько
усложненной, но это только на первый взгляд. При применении формулы C)
необходимо только помнить о преобразовании Лапласа производных
различных порядков, как указано в D) и вообще в свойстве II. Правая
часть C) содержит (если читать снизу вверх) последовательные
многочлены D) преобразований Лапласа производных, умноженные на ап_г>
ап_2, . Таким образом, формула C) даст нам у(р).
От найденного изображения у(р) решения дифференциального
уравнения нужно теперь перейти к самому решению. Здесь мы используем
свойство I, утверждающее, что если функция у(р) есть изображение неко-
120

торого непрерывного оригинала, то есть у(р)= \ e~pty(t) dt, то этот
оригинал y(t) единственный. Последний шаг, состоящий в разыскании у (t) по его
известному изображению у{р)> можно облегчить, составив таблицу
стандартных формул, связывающих отдельные элементарные функции y(t) с их
изображениями y(t), и пользуясь рядом правил для комбинирования y(t)
или у{р), подобно тем стандартным формулам, которые мы получаем для
производных и интегралов. Эти формулы и правила дают возможность
переходить от у(р) в C) к решению y(t) уравнения B), а также от
данной функции f(t) в уравнении B) к f(p), появляющейся в C).
Краткий перечень изображений элементарных функций
Номер
формулы
A)
B)
C)
D)
E)
F)
G)
(8)
Оригинал y(t)
1
t
tn
sin со* = *. (еш е'ш)
2
2
Изображение
у(р)
1
/>
1
Р2
1
1
со
р
@
JD2 — (О2
JO2 —ОJ
Более подробную таблицу изображений можно найти, например, в
книге Карслоу и Егера [3, приложение III]. Рекомендуем читателю про-
оо
верить нашу таблицу, подставив y(t) в \e^pty(t)dt и вычислив все изо*
бражения у (р) непосредственно (см. упражнения 3 и 4).
Заметим, что можно получдть новые формулы для изображений
элементарных функций с помощью дифференцирования оригинала и его
изображения по параметру, например по со, в формулах D) —(8) нашей
таблицы. Возьмем в качестве примера формулу F) таблицы. Она означает, что
е-* cos wtdt =
Продифференцируем по со левую часть этого равенства:
V e~vi cos co? dt == \ е-*>1
d cos Ш
d(x>
dt= — \ е~Щ sin (at dt.
Теперь продифференцируем правую часть:
— (-*—") = —
121

Следовательно,
и
то есть функция ? sin со* имеет изображение 2сор/(р2
Следовательно, если y(p)^
то у(*)=:
—?—t то у(*)=:
Нетрудно доказать четыре следующих простых правила нахождения
изображений по заданным оригиналам.
Правило I. Если у (р) есть изображение функции y(t), a a —
любая постоянная, то ау(р) есть изображение функции ay(t).
Правило II. Если y1(p)f у2{р)> • • • > Уп(р) СУТЬ изображения
соответственно функций уг{г), y%{t)y ...9yn(t), a al9 a2, ..., ап — любые
постоянные, то
• • + <*пУп (Р)
есть изображение линейной комбинации
@ + «22/2 (*) + • • •
Правило III. Если у (р) есть изображение функции y(t), а со
есть постоянная, то A/со) г/ (р/со) есть изображение функции г/(со?).
Правило IV. Если 2/ (р) есть изображение функции у (t) и а есть
постоянная, то у (р — а) есть изображение функции eaty(t) и ?/(р+а)—
функция e~aty(t).
Доказательства этих правил следуют непосредственно из определения
преобразования Лапласа (см. упражнения 6 — 8). Приведем три простых
примера применения последнего, весьма полезного правила, которые
дают стандартные формулы для некоторых функций y(t), умноженных
на eat. Другие свойства преобразования Лапласа и его применения
читатель может найти, например, в книге Егера [6].
Номер
формулы
111
Оригинал г/(О
teat
eat sin со*
eat cos со?
Изображение у(р)
1
(/>-<*)*
со
(р—аJ+со2
/>— а
(р-аJ+со2
Задачи и упражнения
1. Убедиться в справедливости следующей формулы, являющейся частным случаем
формулы «интегрирования по частям»:
С е-ру (*) dt = y @ е-Р*+р С у (*) e'P'dt.
Для доказательства продифференцировать обе части по t. Вывести, что изображение
у'@ есть ру(р) — у0.
2. Распространить предыдущий результат на случаи производных второго и^
третьего порядков, получив приведенные в тексте формулы D) для изображений этих
производных.
122

3. Вычислив интегралы, доказать равенства
о
оо
hi тем самым формулы A) — D) таблицы изображений, приведенной в тексте.
4. Доказать равенства
\ e~Pf sin Ш dt = е'Р* cos Ш—— \ e~vt cos со* dt.
J со © J
\ е~Р* cos at dt =— e-P/sino)i+-^- \ e'^smmtdt.
Доказать с помощью этих равенств формулы E) и F) таблицы изображений.
5. Взяв формулу E) из таблицы изображений, to есть
~р' sin &tdt = -
продифференцировать обе части по ю. Доказать, что функция sin со*—ш* cos со* имеет
изображение
2оK
6. Доказать правила I и II, пользуясь определением преобразования Лапласа,
7. Показать, что
произведя замену переменной интеграции t = art. Вывести отсюда правило III.
8. Убедиться в справедливости равенства
J -^e^y (t) dt=^
о о
и доказать тем самым правило IV. Пользуясь этим правилом, вывести формулу D)
таблицы из формулы A). Показать также, что функция (tn/n\)eat имеет изображение
4.7. ИНТЕГРИРОВАНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ МЕТОДОМ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Пусть дано дифференциальное уравнение относительно y(t):
A)
Требуется найти его решение, удовлетворяющее заданным начальным
условиям
П1)и t -
ПРИ г ~
Методом преобразования Лапласа решение находится в два этапа.
Первый этап состоит в том, что мы составляем вспомогательное уравнение
относительно неизвестного изображения у(р) решения у (?), как изложено
в разделе 4.6. Это вспомогательное уравнение мы разрешаем относительно
у(р), получая
/(/?) + (Многочлен относительно />-степени < п) ,«\
aoPn+alP"-i+... +an_lP+an ' W
123

Второй этап интегрирования состоит в том, что по наиденному
изображению B) мы, идя от у(р), определяем само искомое решение y(t) путем
обратного преобразования Лапласа.
Завершение решения, требующего обратного перехода от y(p)Ky(t)f
встречает много трудностей — не теоретических, а практических. Оно очень
сходно с практической задачей нахождения интегралов, где пользуются
стандартными формулами, рядом правил и приемов. Для преобразования
Лапласа также существуют стандартные формулы и правила. Некоторые
из них приведены в разделе 4.6, другие могут быть найдены. Имеется также
множество приемов, главный из которых состоит в том, что отношение
многочленов выражается в виде суммы элементарных рациональных дробей, как
это излагается в учебниках элементарной алгебры.
Однако, когда практически задача решена и y(t) получено, оно является
единственным решением дифференциального уравнения A), подчиненного
точно установленным начальным условиям. Решение y(t) автоматически
содержит начальные значения (t/0, y'o, у> ...), и больше уже ничего делать
не надо. В отличие от «классического» метода, метод решения, приведенный
в разделе 4.5, не требует приспосабливания произвольных постоянных
к начальным условиям.
Несколько простых замечаний разъяснят существо вопроса.
Стандартные формулы из раздела 4.6 показывают, что для многих распространенных
форм f(t) изображение/(?) правой части исходного уравнения есть
рациональная функция. Так обстоит, например, дело в случае, когда правая часть
уравнения представляет собой многочлен, показательную функцию, синус или
косинус, а также произведение функций указанного типа и суммы таких
произведений. Если же изображение f(t) есть рациональная функция, то из
B) следует, что и преобразование Лапласа у(р) оказывается также
рациональной функцией, и можно ожидать, что оно представит собой отношение
многочленов невысокой степени относительно р, например отношение вида
ар + Р к ар2+ Ьр + с. Кроме того, стандартные формулы и их различные
комбинации очень хорошо подходят для обратного перехода от у(р) как
отношения многочленов к разнообразным распространенным формам y(t) подобно
Г, е?1 или coscoJ. Процесс этот облегчается разложением у(р) на более
простые элементы, то есть на сумму очень простых отношений многочленов,
к каждому из которых стандартные формулы применяются непосредственно.
Таким процессом является представление у(р) в виде «элементарных
рациональных дробей».
Итак, в указанных случаях изображение у(р) искомого решения может
быть представлено в виде отношения двух многочленов относительно р:
C)
При этом полученная рациональная дробь оказывается правильной, то есть
степень многочлена F(p) будет меньше степени многочлена G{p). Отметим
при этом, что G(p) либо представляет собой знаменатель дроби в B), то есть
многочлен аорп+ aip4 + ... + 0n.iP + яп, либо произведение этого
последнего многочлена на некоторый другой многочлен. Это значит, что в любом
случае
G (р) = (аоРп + alP^ +...+an)g(p), D)
где^(р) — либо единица, либо другой многочлен относительно^
положительной степени. Заметим, что многочлен аорп + а1рп~1+ ... + ап представляет
собой левую часть характеристического уравнения, соответствующего
дифференциальному уравнению A), и его множители, соответствующие корням
характеристического уравнения, известны.
Метод «элементарных рациональных дробей», применяемый к C), состоит
в нахождении всех корней уравнения G(p) == 0, то есть рх, .р2» Рз» •••» которые
124

включают вещественные и сопряженно-комплексные величины. Между ними
содержатся все корни характеристического уравнения. Таким образом, если
многочлен G(p) имеет лишь простые корни, число которых в этом случае
равно степени многочлена, то он может быть разложен на п линейных
множителей:
A)"- E)
Выражение E) мы подставляем в C).
Как доказывается в учебниках алгебры, правильная рациональная
дробь
Ж
G(p)
может быть в этом случае единственным образом разложена на сумму
элементарных рациональных дробей вида
При этом каждый линейный множитель в E) порождает соответствующую
элементарную дробь. Можно доказать, что коэффициент Ат в случае простых
вещественных корней можно определить по формуле1
где G'(p) = dG(p)ldpy a F(pr) и G'(pr) обозначают результаты подстановки
значения р = рт в соответствующие функции. Таким образом, если G(p)
представлена в форме E) иг все корни простые и вещественные, то разложение
правильной рациональной дроби на элементарные в случае простых корней
знаменателя может быть записано в следующем виде:
Здесь сумма 2 берется по всем корнямр11др2,... знаменателя исходной дроби.
Теперь у(р) непосредственно обращается~в y(t). Оригинал,
соответствующий каждому слагаемому в правой части F), можно легко написать,
пользуясь стандартной формулой D) таблицы изображений и правилом II из
раздела 4.6. Именно изображению Аг/(р — рг) соответствует оригинал
АгеР**. Поэтому оригинал y(t), соответствующий изображению у(р), можно
записать в виде следующей суммы:
Итак, формула G) позволяет найти оригинал y(t), если его изображение
может быть написано в форме C), то есть является произвольной правильной
рациональной дробью со знаменателем, не имеющим кратных корней.
Все, что говорилось выше относительно F), имело в виду частную
элементарную дробь 1/(р — рг), когда рт и коэффициент при этой дроби
вещественны. Когда же среди корней знаменателя рациональной дроби C)
встречаются комплексные сопряженные корни, то можно идти двумя путями.
Пусть, например, р^ р2 = а± i®. Эти корни могут быть оставлены в E)
в виде Двух множителей (р — а — i (о)(р — а + i со), то есть можно поступить
с ними, как с вещественными корнями, применив ту же процедуру. Тогда
постоянные Аг, А2;\.. будут также комплексными, и каждой паре комплекс-
1 Автор приводит здесь формулу нахождения коэффициентов А, пригодную лишь
для случая простых вещественных корней, но почему-то не излагает метода
неопределенных коэффициентов, применимого во всех случаях — для корней простых и кратных,
вещественных и комплексных. Между тем далее он приводит примеры как раз для
случая кратных и комплексных корней.— Прим. ред.
125

ных сопряженных корней будет соответствовать пара комплексных
сопряженных коэффициентов. Или же можно объединить две элементарные дроби
в правой части F), соответствующие комплексным сопряженным корнямг
в квадратичной форме {(р —- аJ+ со2}. Тогда соответствующие элементарные
дроби примут вид
нетрудно показать, что числитель и знаменатель этой дроби — вещественные
многочлены.
На практике вообще предпочитают избегать комплексных рг и вводимых
с ними в G) комплексных коэффициентов. Поэтому пользуются вторым
способом представления комплексных корней, именно берут их попарно и
элементарные дроби представляют в последней форме.
Оригиц^л, соответствующий дроби [Аг(р — а) + Вг]1[{р — аJ+ аJ],
легко написать с помощью стандартных формул Eа) и Fа) предыдущего
раздела. Он имеет вид
еш ( Ах cos at + —*- sin at) = Aeat cos (at -f- e),
то есть представляет собой знакомый нам колебательный процесс с
характеристическим показателем а + г о (см. приложение Б. 6). Конечно, этот
вещественный оригинал можно получить, объединяя два слагаемых в правой
части G), соответствующих двум показательным функциям или паре
комплексных сопряженных корней а ± i со.
Если f(t) = 0 и уравнение A) однородно, то ясно, что решение G)
равносильно тому, которое получается «классическим» методом, изложенным
в разделе 4.5 (см. упражнение 1 данного раздела).
Проиллюстрируем практическое применение изложенного метода
интегрирования линейных дифференциальных уравнений на двух примерах
с частными формами f(t). Он дает вместе и дополнительную функцию и частное
решение, а также включает начальные условия.
Пример (а)
Найти частное решение дифференциального уравнения
dt2
удовлетворяющее начальным условиям y = (dy/dt)~O при * = 0. Составляем
вспомогательное уравнение
(р2 — 1) у (р) = — изображение t = ^ ,
откуда, разлагая на элементарные рациональные дроби, полз;чим:
У (/>)= —
С помощью формул B) и D) таблицы изображений легко находим решение
дифференциального уравнения:
Заметим, что «классический» метод дал бы общее решение в виде y() \i{
-\-А2е~* (см. раздел 4.5, пример (а)), затем было бы необходимо определить значения
постоянных Ах и А2 так, чтобы удовлетворить заданным выше начальным условиям.
Можно показать, что эти решения эквивалентны (см. упражнение 2).
Пример (б)
Найти частное решение дифференциального уравнения
удовлетворяющее начальным условиям
126

Изображение правой части f(t) = tel по формуле Bа) из раздела 4.6 есть /(р) = 1/(/?—IJ.
Поэтому вспомогательное уравнение C) из раздела 4.6 имеет вид
откуда
Разлагая на элементарные дроби, получаем
(р—1J+1 4 (/>—IJ
. 4(/>-1) + 3 111 1 11
27 КР) ~ (р-1J+1 4р-Г2(р- 1J"^
Следовательно, по формулам таблицы изображений D), Eа), Fа)
111 S
у (t) = 4e< cos * + 3e< sin t — — е'+у /в' -\- — еч = е( D cos f+3 sin i) + -
¦ 4 •
3 3
где tg е = — и 8 = arctg — .
Это есть решение дифференциального уравнения, удовлетворяющее определенным
начальным условиям. Оно эквивалентно общему решению исходного уравнения,
полученного выше «классическим» методом (см. 4.5, пример (б)), в виде
у (*)= [л cos (*—в }+^B*—1)]
Если постоянные Л, В и 8 определить из заданных начальных условий, то мы
получим, конечно, то же частное решение, найденное здесь методом преобразования Лапласа.
Задачи и упражнения
1. Показать, что решение однородного линейного уравнения [/(/) = ()] с
постоянными коэффициентами имеет вид
где P\i Ръ, * - - ч Рп — корни характеристического уравнения. Показать, что решение
уравнения A) имеет в данном случае вид
/а = F(Pi) ePit) *ЧРя) ev*l +
ao(Pi—P2)---(Pi—Pn) ao(P2—Pi)---(P2 — Pn) ~'"#
Показать, что общее решение однородного уравнения A), полученное
«классическим» методом (см. D) в 4.5), совпадет с написанным, если добавить начальные
условия и из них определить постоянные.
2. В решении у (t) = t-\-А^-{-А2е~г (см. 4.4, упражнение 2), найти Аг и Л2 для
начальных условий y = dy/dt=O при г = 0. Получить решение такое, как в примере (а).
3. Если d2y/dt* + 2dy/dt-\-y = t+2. показать, что:
I) г/ = гA — е~1) при y = dy/dt = O и г=0;
II) у = t — A + 20 е"' при 2/= —1, dy/dt = O и * =
4. Решить уравнение
при t/=l, dy/dt = 1/2 при * = 0 (см. 4.4, упражнение 6).
4.8. НЕПРЕРЫВНО РАСПРЕДЕЛЕННОЕ (ЭКСПОНЕНЦИАЛЬНОЕ) ЗАПАЗДЫВАЙИЕ*
Если Z(t) есть заданная функция времени, a Y(t) приближается к ней
со скоростью, пропорциональной расстоянию Y(t) от заданной функции Z(t),
1 Умножая выражение в скобках на -т-cose =1, так как cose = -p- .—Прим. ред.
2 Этот раздел переведен, в целях большей доходчивости, с небольшими
отступлениями от английского оригинала.— Прим» ред.
ill

то мы говорим, что Y(t) изменяется с дифференциальным (экспоненциальным)
запаздыванием относительно переменной Z. Математически такр^г
запаздывание может быть выражено дифференциальным уравнением, которому
должна удовлетворять запаздывающая переменная У, следующего вида:
• j. =—X(У — .Z), или —г:—\-XY = XZ. A)
п.т. N ' ' п.т. N '
dt
где X есть постоянная, которую естественно назвать относительной скоростью
движения или относительной скоростью реакции запаздывающей переменной.
Она равна скорости движения запаздывающей переменной при расстоянии,
равном единице (У — Z = 1). Величина, обратная скорости реакции, Т = у ,
называется временной постоянной системы с постоянным запаздыванием.
Уравнение A) соответствует дифференциальному запаздыванию в форме
показательной функции.
Будем исследовать изменение запаздывающей переменной Y(t), когда
задаваемая функция постоянна:
Z = Z0.
Дифференциальное уравнение A), характеризующее однократное
запаздывание при постоянстве заданной функции Z = Z0, будет иметь вид
%. + bY=XZ0 B)
при начальном условии У=0 при *=0.
Воспользуемся классическим методом интегрирования этого
дифференциального уравнения (см. 4.3). Частное решение уравнения B) будет,
очевидно, F = Z0. Общее решение однородного уравнения -^—[-ЯУ=0,
соответствующего нашему дифференциальному, будет иметь вид у =
Тогда общее решение неоднородного уравнения B) примет вид
где А — произвольная постоянная — определяется из начального условия.
Получаем А = — Zo.
Окончательно изменение запаздывающей переменной У при
однократном экспоненциальном запаздывании описывается функцией
Г@ = A-вгМ)яв1 C)
а скорость ее изменения — функцией
Yf(t)^Xe~^Z0. i D)
Сплошные линии A) на рис. 9 изображают графики функций У и Y' при
однократном запаздывании.
Дифференциальное уравнение A) можно записать в операторной форме
(см. раздел 1.9 и приложение А):
Теперь пусть по-прежнему Z (t) — задаваемая переменная, a Y1(t) —
промежуточная запаздывающая переменная, следующая за Z(t) с
относительной скоростью 2К. Тогда по предыдущему (в операторной записи):
Пусть, далее, переменная У (t) в свою очередь следует за Yx с той же
относительной скоростью 2Х:
D+2XJ
128

Или, принимая во внимание предыдущее равенство:
В этом случае мы говорим, что У изменяется с двойным
экспоненциальным запаздыванием относительно задаваемой переменной Z.
Уравнение E) можно записать в обычной (неоператорной) форме таким образом:
Ea)
с начальными условиями: У = —- = 0 при ? = 0.
Если применить «классические» методы, то частное решение будет
F = Z0, а дополнительная функция получится из характеристического
уравнения р2 + ikp + 4А,2 = 0, имеющего двукратный корень: ^1 = /?2= — 2Х.
Отсюда полное решение:
где постоянные, определяемые из начальных условий, будут:
Следовательно:
А= -Zo и В= -2XZ0.
0 F)
и скорость изменения переменной У
Y'(t) = 4X*te-2MZ0. G)
Временная форма запаздывания воспроизводится формулами D) и G),
описывающими Y' (t), что является общим свойством (см.
упражнение 5 из 1.9).
Реакцию У графически можно показать или в кумулятивной форме
Y(t) или во временной форме, У @» как на Рис- 9,а и 9,6. Кривая /
на графиках относится к однократному экспоненциальному запаздыванию.
Она соответствует уравнениям C) и D).
Кривая // на рис. 9,а и б относится к двойному экспоненциальному
запаздыванию, она нанесена по уравнениям F) и G). Большая
«реалистичность» кривой реакции в случае II — двукратного запаздывания — очевидна.
Можно добиться еще более «реалистичной» формы, если ввести многократные
запаздывания одной переменной относительно другой (см. упражнения 1 и 2
к этому разделу).
Реакцию У на другие типы задаваемого изменения Z можно найти
аналогично. В качестве иллюстрации примем, что Z изменяется как
синусоидальная функция, то есть
= 6*'созю*.
Как будет в этом случае изменяться У, каково будет его фактическое
запаздывающее значение? Можно ожидать, что Y будет колебаться с той же
частотой со и затуханием а, как и Z, но будет иметь другую амплитуду
п фазу. Исследуем это для однократного экспоненциального запаздывания
путем решения дифференциального уравнения этого запаздывания, то есть
уравнения A), где Z будет теперь синусоидальной функцией. Получаем
*? № = №* cos со* (8)
-
с начальным условием Y = 0 при t = 0.
Хотя уравнение (8) легко решить «классическими» методами (см.
упражнение 4 к этому разделу), но целесообразно проинтегрировать его методом
преобразования Лапласа.
9 Р. Аллен 129

Функция eatcos(ot имеет изображение (преобразование Лапласа):
Р—<*
(см. 6а в таблице изображений элементарных функций из раздела 4.6).
А Кумулятивное распределение запаздывУ
Частотное распределение запаздывания
Рис. 9
Следовательно, дифференциальное уравнение (8) имеет вспомогательное*
уравнение для изображения искомого решения (так как Y — 0 при * = 0)
в таком виде:
то есть
р—а
(9)
является преобразованием Лапласа решения уравнения (8). Разложим
правую часть (9) на элементарные дроби:
Ъ, ч_ X (Х+а)(р-а)+(о2 Х(Х+а) 1
- (Я+аJ+со2 р+Х
и применим стандартные формы преобразования Лапласа для перехода
от изображений к оригиналу. Получаем:
Y (t) — qeat cos (со* — ф) — е cos
или
где
Таким образом, решение для движения Y(t) во времени, следующего
за колеблющейся переменной Z, дается двумя способами: явно, в качестве
функции от t в A0), и косвенно, как преобразование Лапласа (в виде
функции от р) в (9). Движение во времени Y(t) в A0) характеризуется
двумя членами. Один из них есть показательная функция,
представляющая затухающее изменение, пропорциональное е~М. Это изменение своим
появлением обязано тому, что начальное значение Y = * отстает на шаг от
начального Z = l при * = 0. Другой член, или Qe** cos (со*-ф), более важен:
он отображает колебания 7, имитирующие задаваемые колебания
переменной Z = ea'cos со*. Частота со и затухание а колебаний bFhZ одинаковы;
только амплитуда е и фаза, характеризуемая -S-, различны. Амплитуда
130

колебаний У составляет долю q(q < 1) от амплитуды колебаний задаваемой
переменной, а по фазе они отстают на ф, то есть по времени на t = ~ *
Задачи и упражнения
(ЗА, \3
J Z есть тройное экспоненциальное запаздывание
по отношению к Z, эквивалентное трем равным последовательным запаздываниям,
1
и что его итоговая временная постоянная Т = -г- .
dY d2Y
Если Я'дано как постоянная Zo и если У = -—==-^- = 0 при * = 0, показать, что
У-[,-(
и представить графически на рис. 9.
2. Обобщить двойное запаздывание E), предполагая различные скорости реакции
в отдельных запаздываниях, и показать, что это можно представить в виде:
/IV
Решите это уравнение для Z = Z0 (const), если заданы начальные условия: У= -?Г=0
при * = 0.
3. Найти дифференциальное уравнение, определяющее л-кратное
экспоненциальное запаздывание при условии: (а) все запаздывания имеют равные скорости реакции
( итоговая временная постоянная Т — -г- ) и (б) имеют место вообще запаздывания
с разной скоростью реакции.
4. Найти решение A0) уравнения (8) «классическими» методами, применяя
оператор D для получения частного интеграла, как мы делали в конце раздела 4.5.
4.9. ПРИМЕНЕНИЕ р =
Комплексная переменная p — a+ito уже несколько раз фигурировала
в нашем изложении. Казалось бы, что появления этой переменной не связаны
друг с другом. Но это не так. В действительности все употребления
p = a+ico имеют общий смысл и связаны между собой. Теперь пришло
время привести все в ясность. Различные случаи применения этой
переменной могут быть сгруппированы следующим образом.
I. р = а + ш, связанная с синусоидальными переменными. Основная
синусоидальная функция1 есть у = Aeat cos((ut + &). Она является
«вещественной» частью комплексной переменной г = Аегеерг> где р = а+шу a z
может быть представлено как векторное произведение. Из четырех
параметров два А я г (амплитуда и фаза) относятся к начальному положению
в момент ? = 0, и они составляют отдельную часть Aeie в виде первого
вектора произведения. Два других параметра со и а (период и
характеристика затухания) служит для описания синусоидальной вариации во
времени. Цель введения р = a -f ico — связать эти два параметра, так что р или,
более строго, комплексное число или вектор ept описывает движение
во времени.
II. Использование переменной р в характеристическом уравнении
линейного дифференциального уравнения. Характеристическое уравнение общего
линейного дифференциального уравнения ?г-го порядка с постоянными
коэффициентами имеет вид:
n~x + • • • + an_lPiL +a - 0.
1 См. наше примечание на стр. НО.—Прим. ред.
131

i Если pv p2, ..., pn есть корни этого уравнения, то дополнительная
функция, являющаяся частью общего решения дифференциального
уравнения, будет:
Предположим, что рг и р2 — сопряженные комплексные корни (а ± гсо).
Тогда два первых члена решения при объединении дадут -4ea'cos((o?-)-e),
где А и е — произвольные постоянные. И в этом случае р = а-\-ш имеет
тот же смысл —она характеризует синусоидальное изменение во времени,
заданное дифференциальным уравнением. Вещественный корень
характеристического уравнения можно рассматривать просто как частный случай,
когда о) = 0. Таким образом, использование переменной р = а + ш в
характеристическом уравнении оправдано; когда возникают колебания, р = a + ш
можно истолковать в соответствии со случаем I.
III. р вводится для оператора D = —=-, примененного к синусоидальным
переменным. В данном случае переменная p = a-\-i(o та же самая, как
в случае I, то есть со и а —два параметра синусоидальной переменной,
которая характеризует движение во времени и поэтому представляется
как -тт. Следовательно, чтобы иметь дело с переменной у — Aeat cos(a)?-f е),
надо ввести переменную z — Aeieevt с Dz = pz, а Dy получится, если взять
«вещественную часть» от pz.
IV. р является переменной преобразования Лапласа:
Этот случай кажется совершенно отличным от других. Действительно,
р является любым вещественным или комплексным числом, независимой
переменной в у(р), полученной из y(t) только при условии, что интеграл
сходится. Однако и здесь в большинстве случаев применения р она опять
оказывается равной a-f гсо, где а и со нужно истолковывать как затухание
и частоту синусоидального компонента в y(t). Далее мы и исследуем этот
вопрос, являющийся главным звеном в цепи.
y(t) определяется линейным дифференциальным уравнением:
п° ~di^ I" al djw-i ~t~ • ' ' ~Ьап-1~^~ + ап^==П0> A)
где мы считаем f(t) или компонент f(t) синусоидальной переменной:
f(t) = Aeut cos {at +г). B)
Предположим далее, что структура дифференциального уравнения,
определяемая его коэффициентами а, такова, что y(t) имеет внутреннее,
присущее ему синусоидальное колебание. Следовательно, часть y(t), получаемая
из A) после исключения из него f(t), есть синусоидальная переменная.
Внутреннее колебание:
у (t) = A'e*'* cos (©'* + е'). C)
Теперь мы должны рассмотреть две синусоидальные вариации, данные
уравнениями B) и C). В отношении своего движения во времени (период
и затухание) они описываются так:
р = а-\-ш и /)' = а' + гсо'
Проанализируем теперь уравнение A). Если исследуется внутреннее
колебание, мы должны опустить / (t) и написать A) как (aQDn-{-a1Dn-1 +
+ .. '+an_iD + an)y = 0. Так как для вариации C) D = p' =a' + ico\ то
132

что как раз представляет характеристическое уравнение, имеющее, как
известно, корень р' = a' -f- ш' и сопряженный ему корень а' — ш\ Таким
образом, здесь нет ничего нового. Но если мы рассматриваем-колебание B),
то встает вопрос: может ли y(t) колебаться подобно /(?)? Если да, то
уравнение A) с /) = /? = <х + ш принимает вид:
(аорп + а^-1 +...+ ап_гр + ап) Y = Z,
где Z есть Aeizevl, или / (t), написанная в форме комплексной переменной,
a Y есть соответствующая комплексная переменная для y(t). Мы пришли
к новому результату, который необходимо исследовать. Этот результат
также тесно связан с вспомогательным уравнением A) в преобразовании
Лапласа, если Y и Z заменить их изображениями у(р) и /(/?).
Система A) имеет вспомогательное уравнение, которое приводит
к изображению (к преобразованию Лапласа) решения (y)t в виде
л , , __ /(р)+многочлен относительно/?
У W - aoP"+a1p"-i+ ... +an_lP + an '
где многочлен, стоящий в числителе, характеризует начальные, условия.
В этом случае f(p) является преобразованием Лапласа (изображением)
уравнения B). Если не учитывать фазу е, то это преобразование таково:
(р— аJ+со2 '
Производя подстановку, получаем:
п+2
многочлен относительно р _ V J ^ (А\
в элементарных дробях, где Аг — некоторые коэффициенты, a pv /?2, ..., рп>
Рп+1» Рп+2 (предполагая, что все они различны) —корни, получаемые
приравниванием знаменателя у(р) нулю. Из приравнивания нулю
характеристического уравнения и (р — аJ4-<о2 следует, что рх, р2, ...,/?п —суть корни
характеристического уравнения A), a /?n+1, jpn+2==a±^(d- Следовательно,
элементы рг выражения D) включают в себя как p = a-{-ia> (и
сопряженный с ним корень), так и p'^a' + ico' (и сопряженный с ним корень),
поскольку р' получается из характеристического уравнения.
Выражение D) прямо превращается в полное решение уравнения A)з
тИ-2
y(t)=%Aret>rt. E)
Две пары членов в выражении E), соответствующие р=^а±^т
ир' = а'± ш', содержащимся среди /?г, объединяются в два синусоидальных
компонента y(t):
у (t) = Beat cos (at + ц) + JB/ea'« cos (id'* + ц') + ..., F)
где В, В', т) и ^' — некоторые постоянные. Теперь мы можем заключить,
что y(t) содержит в аддитивной форме как вынужденное колебание B),
так и внутреннее колебание C). Это и нужно было ожидать; первое
является частным интегралом из /(?), а второе представляет структурные
колебания дополнительной функции. Что теперь стало ясным —это способ
их получения в результате преобразования Лапласа и тот факт, что
p = a-[-?(o и р' = а' + г®' суть значения р в преобразовании Лапласа.
Преобразования Лапласа от y(t) к у(р) и обратно весьма гибки
в интерпретации и применении. Когда вопрос идет и о вынужденных
и внутренних синусоидальных колебаниях, решение дифференциального
уравнения с равным успехом получается в форме D) или F). В последнем
случае y(t) является функцией времени, или самим решением. В первом же
133

случае у (р) есть соответствующая функция переменной р; эту переменную
следует истолковывать как а+ш; функция времени преобразовалась здесь
в функцию частоты (со) и затухания (а) колебания.
Покажем это на простом случае экспоненциального запаздывания,
рассмотренном в конце предшествующего раздела D.8). Дифференциальное
уравнение имеет вид
где Z =
Преобразование Лапласа, или изображение решения (см. (9) в 4.8), будет:
л р—а
Оно является функцией частоты и затухания. Решение, как функция
времени (см. A0) в 4.8), есть
У (t) = Qeat cos (со? — ф) — q cos q>e~M.
Вынужденное колебание относится к Z, отображается p = a-\-i®; оно
фигурирует в Y (р) в виде множителя квадратичной формы (р — аJ + со2,
который дает при приравнивании его к нулю корни р = а ± ко. В этом
случае не существует внутреннего колебания; только имеет место
монотонное затухание, характеризуемое членом е~~м в Y(t) и величиной р= — X
или множителем (р + X) в Y (р).
Истолкование таких решений, как F), может меняться в зависимости
от характера поставленной задачи. Иногда ударение делается на
внутренних колебаниях, с частотами со', задаваемыми структурой системы A). Эти
колебания возникают независимо от того, каково влияние f(t). Если
через*/@ вводятся добавочные колебания, они несущественны. При других
обстоятельствах ударение делается на вынужденных колебаниях, которые
возникают в y(t) вследствие заданных колебаний в /(?), имеющих частоту со.
В этом случае несущественными будут любые внутренние колебания. Однако
8 действительности они не только несущественны; они могут быть
фактически элиминированы при соответствующих начальных условиях. В этом
и лежит разница между вынужденными колебаниями, которые должны
возникать в y(t), если они введены f(t), и внутренними колебаниями,
которые могут вообще не возникнуть, если отсутствуют соответствующие
начальные условия.
Покажем это на примере запаздывания в виде показательной функции.
Внутреннее колебание Y является монотонным и затухающим компонентом,
характеризуемым е~М; оно может представлять наибольший интерес в
анализе, если, например, Z рассматривать как постоянную величину. Однако
если колебание вводится в форме Z = ea*cosco?, то внимание
концентрируется . на соответствующей вариации У, отображаемой компонентом
Qea'cos(co? — ф). Другой компонент е~"М, характеризующий внутреннее
колебание, можно рассматривать как исчезающий во времени. В
действительности он может вообще не возникнуть. Пусть а= — X, так что ф = у »
q =— (см. A0) из 4.8) и со8ф = 0. Второй член в Y(t) тогда исчезает,
и решение становится простым:
что соответствует Z:
= e~M cos at.
Колебание Z вызывает соответствующее колебание в У с амплитудой,
видоизмененной введением множителя — и фазой, сдвинутой на -^-.
СО ?и
134

Задачи и упражнения
/ЯЛ2
1. В двойном экспоненциальном запаздывании Y = ( уггрг ) Z принять Z — cos w*.
Решить уравнение относительно Y и показать, что запаздывание Y относительно Z
задается cp =
2. Разложение у (р) на элементарные дроби в D) зависит от того, что все рг
различны. Как изменится это разложение, если р± = р2 (кратные корни)? Исследуйте
на основе этого случай резонанса, когда вынужденное колебание согласуется по частоте
и затуханию с одним из внутренних колебаний.
d2y
3. Рассмотрите случай резонанса, решив уравнение -~г^-\-у = cosotf и взяв со,
близким к единице.

ГЛАВА 5
МАТЕМАТИЧЕСКАЯ ЧАСТЬ.
ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
5.1. РАЗНОСТНЫЕ УРАВНЕНИЯ
На практике простейшие разностные уравнения возникают при
исследовании изменения переменной Ух, представляющей сумму, накопляемую
по установленному закону при целочисленных значениях аргумента
ж = 0, 1, 2, ..., например Yx возрастает на каждом шаге в установленном
размере. Рассмотрим в качестве примера процесс возрастания денежной
суммы Уо, положенной в банк, при условии начисления 100 г сложных
процентов в год. Пусть начисление процентов производится один раз
в год и х обозначает число лет с момента помещения вклада (# = 0, 1,
2, ...). Обозначим величину вклада по истечении х лет через Yx,
Мы получаем
Если начальная сумма составляет Уо, мы приходим к задаче отыскания
решения полученного разностного уравнения, подчиненного начальному
условию
Yx = Yo при х = 0.
Полученное разностное уравнение содержит Yx и значение этой
переменной на один год раньше, то есть Yx_x\ в данном случае аргумент х
явно не входит в разностное уравнение. Частное решение разностного
уравнения есть явная функция, определенная при х = 0, 1, 2, ... и
удовлетворяющая как самому уравнению, так и начальным условиям.
В рассматриваемом случае Ух = УоA + г)х (см. 5.3).
Возьмем другой вариант. Пусть теперь в конце каждого года делается
вклад Уо, равный начальному вкладу. Разностное уравнение принимает
вид
пусть по-прежнему его решение подчинено условию Yx = Уо при х = 0.
Частное решение этого разностного уравнения, удовлетворяющее
заданному начальному условию, есть
г* = ^4A +'Г1-!]
(см. 5.3, упражнение 10).
Если разностное уравнение выражает общий член ряда и0, uv u21 ...,
то сумма первых х членов этого ряда, то есть
будет удовлетворять разностному уравнению. Член ряда за номером х,
то есть их, есть та величина, которую нужно прибавить к Sx_1 для
получения Sx: Sx — Sx_1=^ux, Раз ux = f(x)9 то есть их определено через х
(х = 0, 1, 2, ...), то это есть разностное уравнение, подлежащее решению
для нахождения Sx, выраженного через х. Пример приведен в разделе 5.3,
упражнение 5.
136

Вообще говоря, обыкновенное разностное уравнение устанавливает связь
между значениями функции Y = Y(x), рассматриваемой для ряда
равноотстоящих значений аргумента х, но можно без ограничения общности
считать, что искомая функция определена для равноотстоящих значений
аргумента с шагом, равным единице. Таким образом, если начальное
значение аргумента есть xf то ряд его равноотстоящих значений будет
х, х-\-1, х-\-2у ... и в обратном направлении: х, х — 1, х — 2, ... .
Соответствующие значения функции мы будем обозначать Ух, Ух+1, Yx+2, ...
или Ух, Yxl, Ух_2, .... Это обозначение удобно; оно достаточно хорошо
подчеркивает, что рассматриваются только изолированные
равноотстоящие значения х. Определим так называемые разности различных порядков
функции Yx с помощью следующих формул:
Разности первого порядка Разности второго порядка
ду v V A2V AV AV
АЛ-«Х — I x + i I х, LX I х = L\I х + 1 lAJL x,
Разности третьего порядка
Ясно, что разность любого порядка есть снова функция, определенная
при тех же значениях аргумента х, х + 1, х + 2, ... .
Дадим теперь следующее определение обыкновенного разностного
уравнения, аналогичное определению обыкновенного дифференциального
уравнения.
Именно обыкновенным разностным уравнением мы назовем уравнение,
связывающее значения одного независимого аргумента х, его функции Yx
и разностей различных порядков этой функции AYX, А2УХ, Д3^' Такое
уравнение можно записать в общем виде следующим образом:
«рО*. Yx, AYx, AWx Д»УЯ) = О, A)
которое по форме аналогично дифференциальному уравнению.
Порядком разностного уравнения называется порядок наивысшей
разности, входящей в это уравнение. Так, уравнение первого порядка
содержит ЛУя, но не содержит разностей более высокого порядка;
уравнение второго порядка содержит А2^, но не содержит разностей
порядков выше второго. Уравнение A) есть уравнение тг-го порядка.
Разностное уравнение вида A) часто удобнее записать, пользуясь
не разностями неизвестной функции, а ее значениями при
последовательных значениях аргумента, то есть выразить AYX, &2YX> A3YX, .. . через
^х> ^jc+i» ^*+2» • • • • При этом разностное уравнение первого порядка
ф(#, YxJ АУЗС) = О приобретет вид 1|)(ж, Yxy Ус+1) = 0 после подстановки
ДУх = Ух+1 — Yx. Разностное уравнение второго порядка ф(х, Yx9 AYX,
A2YX)== 0 запишется в виде ty{x, Ух, Ух+1, YX+2) = Q, так как А2УХ =
= AYX+1 - AYX = (Yx+2 - Yx+l) - (Уя+1 - Yx) = Yx+2 - 2YX+1 + Yx. Заметим,
что уравнения %(xy Yx9 У^^О и co(x, YXJ Yx_v У^_2) = 0 представляют
собой соответственно разностные уравнения первого и второго порядков,
где равноотстоящие значения х отсчитываются в противоположном
направлении. Эти уравнения могут быть приведены к прежней форме с
помощью подстановок соответственно х' = х — 1 и х = х — 2.
Вообще, разностное уравнение гг-го порядка A) может быть
указанным образом приведено, например, к одной из следующих двух
137

форм:
,ф(*, Yx, Уя+1, .... Уя+п) = 0, B)
^(«.У,, У,.! Уя.„) = 0. C)
Рассмотрим пример, наглядно показывающий возможность написания
одного и того же разностного уравнения в одной из трех форм: A) —C).
Пусть задано разностное уравнение первого порядка в форме
(a)
Заменив AYX через Yx+1 — Yx, мы приходим к уравнению
. (б)
Произведем замену аргумента, обозначив х-\-\~%\ Опуская штрих,
получим
(в)
Ясно, что (а), (б), (в) —три различные формы одного и того же
разностного уравнения. Форма записи разностного уравнения несущественна;
это вопрос удобства. Однако мы в дальнейшем будем предпочитать
форму (в), часто используемую при исследовании экономических задач.
Разностное уравнение га-го порядка, записанное в общей форме C),
содержит значение искомой функции Yx при значении х аргумента и при
его значениях, отстающих на 1, 2, ..., п временных единиц, то есть- при
аргументе х — 1, х — 2, ..., причем максимальное запаздывание равно п.
Оно определяет порядок разностного уравнения.
Как в предшествующей главе о дифференциальных уравнениях,
мы будем рассматривать здесь исключительно линейные разностные
уравнения с постоянными коэффициентами. Такое уравнение п-то порядка
имеет следующий вид:
<Л + «1^-1 + • - ¦ + *« А-п+1 + anYx-n = / (*)> D)
где коэффициенты а0, а19 ...,ап суть некоторые постоянные, причем
ап Ф 0 (если ап = 0, то уравнение будет не n-го порядка, а более низкого);
f(x) есть некоторая функция от х, в которую аргумент входит явно,
а независимая переменная отсутствует. Если правая часть f(x) не равна
нулю тождественно, уравнение называется неоднородным. Соответствующее
однородное уравнение мы получим, заменив правую часть D) нулем:
*оУх + ЧУх-i + ¦ • • + *л-1Ух^п*1 + апУх-п = 0- E)
В однородное уравнение E) х явно совсем не входит..Приведем несколько
примеров линейных разностных уравнений вида D) и E), каждое из
которых записано в двух формах: с помощью значений искомой функции
при равноотстоящих значениях аргумента и с помбщью разностей:
I ух__Узс_1==ах-1 или
II У*-аГя-1 = *ж"х или
IV 8^-6^ + ^ = 0 или
V Уа-а2Ух_2==ая + Р или Д*Ух + 2Д Уя - (а
VI ^3^ + 4^-2^-3 = 0 или
138

Задачи и упражнения
1. Пусть */=Л Проверить, что таблица последовательных разностей,
вычисленных при х=0, 1, 2,..., имеет следующий вид:
X
0
1
2
3
4
5
0
1
8
27
64
125
*Ух
1
7
19
37
61
•. •
А2ух
6
12
18
24
• • •
6
6
6
• *
Л4У2С
0
0
• •
Составить аналогичную таблицу для функции у = х*.
2. Обобщить результат предыдущей задачи, установив, что разности п-го порядка
любого многочлена п-й степени постоянны, а разности порядка выше п равны, кроме
того, нулю.
3. Составить таблицу последовательных разностей для функции у=cos х при х=0,
я, 2я, Зя,... и установить, что разность любого порядка постоянна, но что знаки
разностей последовательных порядков чередуются.
4. Выразить ^yx, Д2г/Х и А»ух через yXi ух+1ч ух+2 и т/х+3. Обратно, выразить yx+li
Ух+2 и 2/х+з через уХ1 &yXi &2Ух и Д3^. В примерах (I) — (VI) (стр. 138) каждое разностное
уравнение, стоящее в левом столбце, записать с помощью разностей, проверив тем
самым результат, данный в правом столбце.
5.2. ДИСКРЕТНОЕ РЕШЕНИЕ РАЗНОСТНОГО УРАВНЕНИЯ*
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И СВОЙСТВА
Решение дифференциального уравнения представляет собой функцию,
определенную для всех значений аргумента х из некоторого промежутка
(которым во встречавшихся нам случаях являлась вся вещественная ось).
Иначе говоря, решение дифференциального уравнения есть функция
непрерывно меняющегося аргумента х. В случае разностного уравнения дело не
обстоит так просто. Переменная х не изменяется непрерывно, а принимает
только последовательные значения в ряду равноотстоящих величин.
Неизвестная функция У = Y(x), входящая в разностное уравнение, определена
только для ряда последовательных равноотстоящих значений аргумента,
то. есть в дискретно расположенных равноотстоящих точках числовой оси.
Однако, как мы видели в предыдущем разделе, в разностное уравнение,
вообще говоря, входит начальное значение аргумента, которое может
меняться непрерывно, то есть принимать любое значение. Поэтому можно
говорить о поиске непрерывного решения разностного уравнения (см. 5.8).
Мы начнем с простейшего частного случая, когда начальное значение
аргумента есть фиксированное число. Решение разностного уравнения,
определенное лишь при значениях аргумента, образующих
последовательность равноотстоящих точек с фиксированной начальной точкой, называется
дискретным решением этого уравнения. Никакие другие значения х не
рассматриваются, и не возникает вопроса о непрерывном изменении.
Ясно, что без ограничения общности можно в качестве начального
значения аргумента выбрать х = 0. Мы видели, что расстояние между двумя
последовательными значениями аргумента можно всегда сделать равным
единице. Таким образом, х принимает только целые положительные
значения, и мы всегда можем считать, что дискретное решение определено при
# = 0, 1,2, ...,/г,.... По аналогии с частным решением дифференциального
уравнения мы назовем частным дискретным решением разностного
уравнения такое его дискретное решение, которое удовлетворяет заданным
начальным условиям. Как и в случае дифференциального уравнения, можно ставить
задачу разыскания общего решения разностного уравнения, то есть решения,
139

из которого можно получить любое частное решение, если должным образом
зафиксировать некоторые содержащиеся в общем решении произвольные
постоянные.
Дискретные решения разностных уравнений будут главным предметом
наших исследований в настоящей главе. Важно сосредоточить внимание
на дискретных решениях не только потому, что их гораздо легче получить
и истолковать, но также потому, что их достаточно для широкого круга
проблем. Дело в том, что именно дискретные решения интересуют
исследователя, прилагающего разностные уравнения, например, к экономическим
задачам. Дискретное решение некоторой экономической задачи применимо,
когда мы имеем дело со значениями той или иной переменной (цены, выпуска
продукции и т. п.) к концу каждого года или среднегодовыми ее значениями.
Таким образом, здесь мы имеем дело с некоторым упрощением реального
процесса. Именно мы интересуемся значениями переменных лишь на
определенный момент года или осредненными за каждый год, не интересуясь
особенностями их изменения в течение года, например сезонным изменением
цены или продукции. К этому нужно добавить сравнительную сложность
теории непрерывных решений разностных уравнений.
Методы получения дискретных решений разностных уравнений очень
сходны с методами, применяемыми в теории дифференциальных уравнений.
Некоторые различия будут указаны далее. Отметим здесь одно — наиболее
важное —- различие между (линейным) дифференциальными разностным
уравнениями. Интегрируя дифференциальное уравнение, обычно стремятся найти
его общее решение и уже из него получить частное решение, определив
значения постоянных по заданным начальным условиям. В случае разностного
уравнения частное (дискретное) решение легко найти, оно получается
автоматически. Задача построения общего решения оказывается значительно
сложнее.
Это можно показать на примере некоторого разностного уравнения
первого порядка. В общем виде оно запишется так:
Мы будем считать, что независимая переменная пробегает значения
# = 0,1,2,.... Пусть задано начальное значение искомой функции: Yx = Уа
при х = 0. Подставим в рассматриваемое разностное уравнение х = 1;
так как Уо известно, из уравнения мы можем определить У1# Далее при уже
определенном Ух мы рассматриваем уравнение, подставляя х = 2, и находим
из него У2 и т. д.
Таким образом, зная начальное значение неизвестной функции Уо
и повторно применяя заданное разностное уравнение, мы находим
последовательность Уо, У1? У2, ..., которая и представляет собой искомое частное
решение.
Пусть, например, задано разностное уравнение первого порядка
с начальным условием Уо = 1/2. Тогда последовательность значений искомой
функции будет:
Y — *
У1 = 24+1 = 2,
Частное дискретное решение будет: Yx = V2> 2, 6,15, ... при х = 0,1, 2, 3,... .
Если выбирать другие начальные условия, мы будем получать новые дискрет-
140

ные частные решения исходного уравнения, например:
Ух = 1, 3,8, 19, ..., если Уо = 1,
Yx == 2, 5, 12, 27, ..., если Уо = 2.
Общее дискретное решение должно содержать всякое частное
дискретное решение как частный случай при любом произвольном начальном
значении функции. Это общее решение нужно выразить явно через х, и в этом
заключается основная трудность. Пусть в рассматриваемом случае начальное
значение искомой функции есть произвольное число Уо. Тогда
последовательные значения искомой функции Yx будут таковы:
У1 = 2У0 + 1,
У2= 4У0 + 4,
У3= 8У0+11,
Таким образом, мы получаем общее дискретное решение в форме
последовательности
Уо, 2У0+1, 4У0 + 4, 8У0 + 11, 16У0 + 26, ... ,
определяющей значения Yx при х = О, 1, 2, ... . Как в данном случае
выразить Yx через х в явной форме? Нетрудно увидеть, что первое слагаемое
общего члена записанной последовательности имеет вид У02х; закон
образования второго слагаемого сложнее (см. ниже).
Аналогичным образом можно рассмотреть разностные уравнения
второго и любого более высокого порядка. А именно, чтобы получить частное
дискретное решение разностного уравнения второго порядка, нужно задать
два начальных условия: Уо и У1# Тогда из разностного уравнения мы получим
шаг за шагом последовательные значения решения У2, У3, ... . Ясно, что
для построения частного дискретного решения разностного уравнения я-го
порядка необходимо знать п начальных условий, а именно обычно п
значений функций: Уо, Ух, ..., Уп_!, то есть для решения уравнения первого
порядка достаточно задать Уо, для решения разностного уравнения второго
порядка необходимы значения Уо и Ух и т. д. Таким образом, всегда
возможно решить разностное уравнение численным способом. Главной
трудностью снова является выражение общего дискретного решения через
соответствующее значение аргумента в явной форме.
Мы оставляем в стороне сложные вопросы, касающиеся существования
решения разностного уравнения в определенном классе функций.
Предполагая, что общее дискретное решение рассматриваемых разностных
уравнений существует, мы сформулируем следующую основную теорему.
Общее дискретное решение Yx обыкновенного разностного
уравнения п-го порядка представляет функцию х (х = О, 1, 2, ...),
содержащую ровно п произвольных постоянных:
У х == У \Х, A±i А-%) • • • 9 **.п)т
Не останавливаясь на строгом доказательстве, заметим, что это предложение
кажется весьма правдоподобным, если вспомнить, что для построения
частного дискретного решения уравнения первого порядка необходима была
одна постоянная (начальное условие Уо); частное решение уравнения
второго порядка включало две постоянные (например, два начальных условия
Уо и Yt) и т. д. Для частного дискретного решения уравнения и-го порядка
нам потребуется ровно п начальных условий. С помощью этих начальных
условий мы можем найти значения всех п постоянных в общем решении
и получить таким образом частное решение. В общем решении постоянные
или начальные значения произвольны; в частном решении они являются
141

определенными числами. Все частные решения получаются, однако, иа
общего решения.
Рассмотрим простейшие свойства дискретных решений линейных
разностных уравнений. Как мы увидим, эти свойства аналогичны свойствам
решений линейных дифференциальных уравнений.
Пусть задано линейное неоднородное разностное уравнение тг-го порядка
a*Yx + «x^x-i + • - • + "пУх-п = / (*). A)
Соответствующее однородное уравнение имеет вид:
«оИх + а1Ух-1 + - • - + апУх-п = 0- B)
Свойство /. Если ух{х) и у2(х) суть дискретные решения
линейного однородного уравнения B), то их сумма также является
дискретным решением этого уравнения.
Свойство II. Если у(х) есть дискретное решение однородного
уравнения B), а А — любая постоянная, то Ау{х) также является
дискретным решением того же уравнения.
Свойство III. Если Y{x) есть частное дискретное решение
неоднородного уравнения A), а у(х; Аг, А2У ..., Ап) — общее дискретное
решение соответствующего однородного уравнения B), то их сумма
A1,A2, . .., Ап)
есть общее дискретное решение неоднородного уравнения A).
Доказательства этих свойств следуют непосредственно из определений.
В дальнейшем мы ограничимся случаем линейных разностных
уравнений с постоянными коэффициентами. Пусть найдены п линейно-независимых
частных дискретных решений однородного уравнения B), именно
УЛХ)* УЛХ)> '--,Уп(х)-
Можно показать, что общее дискретное решение этого уравнения есть
линейная комбинация, составленная из этих линейно-независимых частных
решений:
Ух = АУг (*) + КУг (*)+...+ КУп О*). "C)
где А±, А2, ..., Ап — произвольные постоянные. Таким образом, мы получаем
следующую практическую схему решения разностного уравнения A). Именно
мы должны разыскать какое-нибудь частное дискретное решение этого
уравнения Y(x), а затем найти п линейно-независимых частных дискретных
решений соответствующего однородного уравнения. Общее дискретное решение
неоднородного уравнения A) имеет, по свойству III, вид:
Здесь У(х) называется частным интегралом, а общее дискретное решение C)
соответствующего однородного уравнения, то есть линейную комбинацию
иногда называют дополнительной функцией. Не всегда оказывается легким
делом найти п различных частных решений однородного уравнения для
объединения Их в дополнительную функцию, и для этого необходимо применять
разные приемы и ухищрения.
Как и в случае дифференциальных уравнений, часто бывает
предпочтительнее, особенно при решении разностных уравнений, получающихся в
экономических задачах, принять другую процедуру, в которой порядок
главных этапов решения переставлен. Рассматриваемая первоначальная
переменная Yx (например, доход или продукция) должна удовлетворять
разностному уравнению A). Сначала мы пробуем найти его частное дискретное
решение Y(x); легче всего поддается истолкованию решение, которое пред-
142

ставляет тенденцию или изменение положения равновесия Yx по мере
безграничного возрастания х. Если, например, х есть время, тогда Y(x) есть
линия движения Yx во времени, совместная с A), и в то же время норма или
изменение положения равновесия во времени. Иногда частное дискретное
решение Y(x), отвечающее стандартным типичным условиям, называют
невозмущенным решением. Тогда если отклонение Yx от тенденции или линии
равновесия обозначить через ух, то есть ух = Yx -— Y(x), то любое частное
дискретное решение Y(x) можно рассматривать как сумму этого
невозмущенного решения и отклонения ух. Так как и Yx и У(х) оба удовлетворяют
уравнению A), то, если мы подставим Y(x) в A) и затем вычтем одно уравнение
из другого, полученное выражение для ух будет удовлетворять
однородному уравнению B). В конечном счете найденное ух явится общим решением
B), как указано в C). После этого метод завершен, и результат легко
истолковать. Отклонение от тенденции ух дается C); решение D) дает обратный
переход к первоначальной переменной Yx. Мы уже приводили пример такого
метода при рассмотрении экономических проблем (см. 2.7).
Рассмотрим в качестве примера линейное неоднородное разностное
уравнение первого порядка:
Как мы увидим далее (см. 5.3, упражнение 9), общее дискретное решение
этого уравнения имеет вид
где А — произвольная постоянная. Пусть начальное условие есть
?х = ?о при з = 0.
Из общего дискретного решения при х = 0 получаем
У0 = Л —2, то есть Л = У0 + 2.
Таким образом, общее дискретное решение можно записать в виде
Это решение есть все же общее дискретное решение, так как Уо в нем
произвольно; произвольная постоянная имеет здесь смысл начального
значения функции. Если вместо произвольной постоянной Уо подставить
данное начальное значение, общее дискретное решение превратится
в частное. Например, при Уо = 1/2 мы получаем частное решение
то есть Yx — 1/2, 2, 6, 15, ... при я = 0, 1, 2, .... Эту
последовательность значений Yx мы получили выше в числе частных решений (стр. 140)
непосредственно из уравнения. Теперь нам удалось это же самое частное
дискретное решение получить из общего решения Yx> выраженного явно
через х в виде суммы показательной функции и линейной функции от х.
Задачи и упражнения
1. Доказать свойства I, II, III решений линейных разностных уравнений.
2. Написать частное дискретное решение разностного уравнения Ух = 1/2Ух-1
путем его повторного применения, удовлетворяющее начальному условию ух = 1
при # = 0, в виде последовательности и общее его решение, когда ух = у0 при х — 0
(причем у о произвольно). Написать ух в форме конечной комбинации элементарных
функций от х (в каждом случае).
3. Найти таким же способом решение уравнения ух — Ух-\—Ух-ъ подчиненное
начальным условиям ух = у0 и ух~У1 при а?=0 иж = 1 соответственно. Найти частное
решение при у0 = г/х = 1. Убедиться в том, что решение имеет характер периодических
колебаний с периодом 6 интервалов х, то есть у0 повторяется при значениях 07 = 6,12,...,
и аналогично для уъ у2, у3, у&, уь.
143

4, ух или отклонение решения Yx D) от невозмущенного решения Yx (от
тенденции или положения равновесия) имеет вид:
Ух = Лг/i И + ^2^2 С*) + • • • + А#п И,
где ух (х), уъ(х), ..., уп(рс)—линейно-независимые частные решения соответствующего
однородного уравнения. Будем различать среди решений yk (х) взрывные и
затухающие. Именно решение yk (x) мы назовем взрывным, если существует такая
возрастающая последовательность целых положительных чисел
ХЪ хЪч Х3: ••• ->
что \imyk(x)=co. Решение назовем затухающим, если limy^ (х) = 0.
Показать, что движение ух по мере возрастания х будет/«взрывным», если хоть
одно решение у^ (х) взрывное. Выразить это, пользуясь понятием «доминирующего»
члена среди yk (х) (* = 1, 2, ..., п).
5.3. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Решение дифференциального уравнения dYldx — f(x) представляет
неопределенный интеграл с одной аддитивной постоянной; нахождение этого
решения есть действие, обратное дифференцированию.
Простейшее разностное уравнение первого порядка имеет вид
Задача состоит в том, чтобы разыскать такую функцию Ух, первая разность
которой представляла бы собой заданную функцию от х. Таким образом,
мы имеем здесь задачу, обратную задаче вычисления первой разности. Она
имеет дискретное решение, включающее, как при интегрировании,
аддитивную произвольную постоянную, исчезающую при нахождении первой
разности этого решения. Поэтому полезно составить таблицу первых разностей
некоторых элементарных функций. В дифференциальном исчислении
степенная и показательная функции имеют простейшие производные:
-^-(х^^пх71'1 и! ~(еах) = аеах.
dx ч ' * dx v '
В исчислении конечных разностей функциями с наиболее простыми
первичными разностями будут: так называемый «факториал», состоящий из п
последовательных множителей и обозначаемый в дальнейшем хт\ и показательная
функция ах.
Рассмотрим так называемый факториальный многочлен (или просто
факториал) xia\ определяемый формулой
Вычислим первую разность факториала
Итак, мы получили чрезвычайно простую формулу для первой разности
факториала. По этой причине факториалы играют большую роль в
исчислении конечных разностей. Часто, например, применяется разложение
многочленов по факториалам (см. упражнение 4).
Вычислим теперь первую разность показательной функции ау:
Грубо говоря, функции #(п) и ах играют примерно ту же роль в
исчислении конечных разностей, что и функции хп и еах в дифференцировании.
Правила вычисления разностей суммы и произведения вполне
аналогичны известным правилам дифференцирования. Вот простейшие правила,
144

доказательства которых мы предоставляем читателю:
д (аУх + bzx) =
где а я Ь — постоянные, ух и zx — функиии от х.
Достаточная для наших целей таблица первых разностей
элементарных функций имеет следующий вид (для удобства в таблице выписаны
решения уравнений AYx = f(x) для различных видов функций f(x)):
Формулы для первой
разности
а»(п+1)
А * , • *<">
71 + 1
Alna? = lnf 1+^Л
/ sin aa: \
Решения уравнений
уравнение
АУх-я<п>
AYx-ax
АУх = 1пA + ^)
tSYx-cosa(^x+— J
общее решение
у* n+i +А
(пф-1)
(а^1)
Yx = lnx+A
_ sin да;
2 sin —
Заметим, что каждое общее решение в правом столбце таблицы
содержит аддитивную произвольную постоянную А.
Рассмотрим теперь общий случай линейного разностного уравнения
первого порядка с постоянными коэффициентами; такое уравнение имеет вид:
г„-«r,-i=/(*)• A)
Составим соответствующее однородное уравнение:
Ух = <*Ух-1- B)
Воспользуемся общей схемой решения неоднородного уравнения,
рассмотренной в предыдущем разделе. Прежде всего мы ищем частное дискретное
решение Y(x) неоднородного уравнения A) путем проб и приближений.
Успех этих поисков зависит от вида правой части f(x) уравнения A); как
мы увидим, существенную помощь при отыскании частного решения может
оказать так называемый операторный метод (см. 5.5). Затем мы вводим
новую переменную ух = Yx — Y (х) — отклонение решения от Y (х). Так как
Ух и Y (х) оба должны удовлетворять A), то
Вычитая, получаем, что ух удовлетворяет однородному уравнению B).
В конечном счете мы должны найти общее дискретное решение
уравнения B), чего можно достигнуть^ применяя на каждом этапе уравнение B),
Ю р. Аллен
145

которое можно рассматривать как рекуррентное соотношение; мы получаем
то есть
где А — произвольное начальное значение. Таким образом, общее
дискретное решение уравнения A) есть
Уя = ?(х) + Аа*. C)
Рассмотрим более общий метод решения однородного уравнения B),
который применим и к решению линейных разностных уравнений более
высокого порядка. Ищем решение уравнения B) в виде показательной функции
где А, —некоторая постоянная, подлежащая определению. Подстановка
в уравнение B) дает
tf^ak*'1, то есть А, = а.
Итак, ах есть частное решение уравнения B); поэтому общее дискретное
решение однородного уравнения есть ух = Аах. Этот результат уже был
получен другим способом.
Заметим, что возможно еще значение Х — О для уравнения Xх —аХ*,
но оно приводит только к частному решению YX = Y (х) с ух = 0 для всех
значений х.
Характер поведения решения ах при х —> + оо по целым числам и,
следовательно, «структура» уравнения A) зависит от величины и знака а.
Возможны следующие случаи:
1) а > 1; ах—>+со; ух монотонно и неограниченно возрастает;
2) а = 1; а*= 1; ух постоянно и равно А;
3) 0 < а < 1; ах—>0; ух стремится к нулю, оставаясь
положительным;
4) — 1<а<0; ах—>0; ?/х стремится к нулю и знакочередующееся;
5) а= — 1; |ах|==1; решение постоянное по абсолютной
величине | А | и знакочередующееся;
6) а < — 1; |ах|—>оо; решение знакочередующееся и
неограниченно возрастающее по абсолютной
величине.
Диапазон возможностей для разностных уравнений шире, чем для
соответствующих дифференциальных уравнений (см. 4.3). Новым является
возможность знакочередования. Когда а отрицательно, то ух, проходя
значения я = 0, 1, 2, ..., принимает поочередно то положительные, то
отрицательные значения. Когда а положительно, ух изменяется монотонно
в одном направлении. Применяя классификацию из раздела 5.2
(упражнение 4), мы отнесем ах к взрывному типу, если |а|>1 (случаи 1 и 6),
и к затухающему, если | а \ < 1 (случаи 3 и 4). Частное невозмущенное
решение У (х) неустойчиво относительно начальных возмущений при |а|>1.
В этом случае как угодно малое по абсолютной величине начальное
возмущение приводит к взрывному отклонению возмущенного решения от
невозмущенного. В случае |а|<1 частное решение Y (х) устойчиво. При
этом, если |а|<1, к$к угодно большое начальное воЗхМущение
оказывается затухающим.
Член У (х) в решении C) зависит от формы f(x) в первоначальном
уравнении. У легко найти, если /(я) = а (const). Оно представляет тогда
частное решение уравнения Yx — аУх_х = а» Подставим в последнее Ух = [л,
146

где [х — некоторая постоянная, подлежащая определению:
|х — а\л = а, то есть [А = 1^д .
Общее дискретное решение Yx — аУЛ._1 = а есть УЛ = а/A — а)
Вариация происходит теперь от постоянного уровня У = <х/A — а) или
вокруг него. Другие формы f(x) рассматриваются в упражнениях 7 и 8.
Задачи и упражнения
1. Доказать, что
A (yxzx) = zx+1A
2. Доказать равенство
3. Доказать, что A sin ах = 2 sin (a/2) cos а (х-\-1/2), воспользовавшись тождеством
sin а:—sinr/ = 2sin—^ cos
4. Показать, что общее дискретное решение уравнения
имеет вид
У х =
П—{— х
Показать, что любой многочлен относительно х может быть представлен в виде суммы
факториальных многочленов, например
Пользуясь этими двумя результатами, сформулировать метод решения разностного
уравнения вида AYX = P (х), где Р (х) — многочлен. В качестве примера показать, что
общее дискретное решение уравнения
есть
5. Пусть Yx — l2-f-22-f32 + ... + s2 (а:—целое положительное). Показать, что Yx
есть решение разностного уравнения
удовлетворяющее начальному условию У0 = 0. Пользуясь этим, покагать, что
Yx^~x
6. Показать, что линейное уравнение A) при а = 1 имеет общее дискретное
решение вида Yx — Y (x)-\-A. Уравнение при этом можно записать в виде &Yx = f(x).
Почему значение а = 1 может рассматриваться как пограничный случай между
«взрывными» и «затухающими» решениями?
7. Показать, что общее дискретное решение уравнения
^*—аУх-1 = ах (а = const)
имеет вид:
CfX+l
\-Аах (афа)9
х а — а
8. Показать, что общее дискретное решение уравнения
(аир постоянны) имеет вид
147 10*

9. С помощью результатов предыдущих задач показать, что общее дискретное
решение уравнения
Yx=2Yx^+x
есть
YX = A2X — (x+2) (см. 5.2).
10. Рассмотреть уравнение
Yx —аУх_1 = а (a = coist),
являющееся частным случаем уравнения из упражнения 8. Показать, что общее
дискретное решение этого уравнения имеет вид
Найти решение уравнения
Y^aY
удовлетворяющее начальному условию YX = YO при # = 0 (см. задачу о росте
денежной суммы по правилу сложных процентов из раздела 5.1).
5.4. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Рассмотрим линейное неоднородное разностное уравнение второго
порядка
Yx + aYx_1 + bYx_, = f(x) A)
и соответствующее однородное уравнение
Ух + аух-1+Ъух-2 = 0, B)
где а и 6 —постоянные коэффициенты, так называемые «структурные»
постоянные, причем Ь Ф 0. Используя тот же метод (см. 5.2), мы ищем
частное дискретное решение Y (х) неоднородного уравнения A) и вводим
новую неизвестную функцию ух = Yx —- Y (х), которая удовлетворяет
однородному уравнению B). Как и в случае уравнения первого порядка, ищем
решение в виде показательной функции ух = Xх, где X — некоторая
постоянная, подлежащая определению. Подставим это решение в уравнение B)g
Так как X Ф 0 (иначе получим тривиальное решение ух = 0 и YX==Y (x)),
мы можем сократить последнее равенство( на Xх'2. Оказывается, X должно
удовлетворять так называемому характеристическому уравнению
= О. C)
Корни этого уравнения обозначим Хг и Х2:
К 2 = 2 * v4)
Рассмотрим отдельно случаи вещественных (различных или равных) и
комплексных сопряженных корней.
Случай а2 > 4Ь. Корни характеристического уравнения C) вещественны
и различны. Мы получаем два линейно-независимых решения однородного
уравнения: Xf и Х%. Общее дискретное решение уравнения A) имеет,
следовательно, вид:
Уя = У(ж) + Л1^ + ^$, E)
где Ах и А2 — произвольные постоянные. Значения этих постоянных
определяются единственным образом, если задать начальные условия Yx = Уо
при х = 0 и Yx — Yx при х = 1. Это решение аналогично решению
уравнения первого порядка из раздела 5.3.
148

Решение E) зависит от знаков и абсолютных величин кг и А,2,
которые выражаются через «структурные» постоянные а и Ъ разностного
уравнения. Отклонение yx = Yx — Y(x) от рыночного равновесия представляют
два члена А^ + А^Х* уравнения E); при безграничном возрастании х
каждый из них может быть «взрывным» или «затухающим», смотря по тому,
будет ли соответствующее X по абсолютной величине больше или меньше
единицы, и каждый из них может быть положительным или
знакочередующимся в (зависимости от того, будет ли X положительным или
отрицательным). Область возможностей, таким образом, велика. Однако
существенным является то, будет ли Хг и Х2 доминирующим корнем и
соответствующий член доминирующим членом в уравнении E), когда отклонение
рассматривается при безграничном возрастании х, где х получает
целочисленные значения в ряду х-=0, 1, 2, ... . Больший по абсолютной
величине корень из двух, даваемых равенством D), явится доминирующим
корнем.
Если, допустим, l^^l, то в таком случае изменение ух будет
«взрывным»—положительным либо знакочередующимся в зависимости
от того, будет ли Хг > О или кг < 0. В этом случае решение Y(#), как и
в случае линейного разностного уравнения первого порядка (см. 5.3),
оказывается неустойчивым: какое угодное малое по абсолютной величине
начальное возмущение может привести к неограниченно возрастающему
по абсолютной величине отклонению возмущенного решения от У (х).
Если же Кх < 1 по абсолютной величине (а также Х2), то изменение ух
в этом случае будет «затухающим»; ух стремится к нулю, будучи либо
устойчиво положительным, либо знакочередующимся, то есть Yx будет
стремиться к У(я), и решение Y (х) явится устойчивым.
Случай а2 = 4Ь. Характеристическое уравнение C) примет вид Х2-\-аХ +
a2 (fkJ^) =0. Корни характеристического уравнения будут
вещественны и равны: Х1 = Яа= —«/2. Однородное разностное уравнение в
рассматриваемом случае имеет вид:
Ух + аУх-1 + -4а2ух_2 = 0. F)
Одно из решений этого уравнения мы получаем в виде показательной
функции ух = Хх, где Х = —а/2. Второе линейно-независимое решение ищем
в виде ух = хХх, где Х = —а/2. Подставив эту функцию в уравнение F),
мы убеждаемся, что она является его решением:
Итак, мы получили два линейно-независимых решения уравнения F):
А,* и хХх (Х= —а/2). Общее же решение F) есть ух = (А1 + А2х) С — -к-а V.
Поэтому общее дискретное решение неоднородного уравнения A) имеет
в данном случае вид:
Yx = Y(x) + (A1 + Aix)(^-^aJ, G)
где Аг и А2 — произвольные постоянные, которые могут быть найдены
по начальным значениям Уо и Yx.
Решение G) несколько отлично от решения разностного уравнения
первого порядка из предыдущего раздела. Единственная произвольная посто-
149

янная, фигурировавшая там, здесь замещена {Ах-\-А2х) с двумя
произвольными постоянными. Изменение yx = Yx — Y дается теперь выражением
(А1 + А2х)( — 1/2а)х, а доминирующей частью в нем является ( —1/2а)х-
Надо опять различать четыре возможности.
Найденные частные линейно-независимые решения однородного
уравнения hx и хХ00 либо оба взрывные, если |А,|>1, то есть |а|>2, либо
оба затухающие при |А,|<1, то есть |а|<2. При этом если а > О, то
изменение ух будет знакочередующимся; если а < 0, то изменение ух
устойчиво и положительно. В случае |А,| = 1 решение У(х) оказывается
взрывным. Таким образом, решение Y(х) устойчиво при |А,|<1 и неустойчиво
в противном случае, то есть при |Я|>1.
Случай а2 < 46. Характеристическое уравнение имеет в этом случае
пару комплексных сопряженных корней:
Общее дискретное решение уравнения A) имеет в этом случае вид:
Yx = У (х) + Вх (a + fР)* + В2 (а - ф)*,
где Вг и В2 — произвольные постоянные. Преобразуем два последних
слагаемых в правой части последнего равенства, положив предварительно
а± ф = г (cos 9± i sin 0) = re±ie,
где
rcos0 = a= —1Ua и rsin0 = р = 1/2>^46 — a2 (8)
или
= 6 и
Мы получаем
Уя - У (ж) = гх (Вге
= rx [J9X (cos Qx + i sin 0x) + B2 (cos 0x — i si
= rx (A1 cos 0a: + A2 sin 0л:),
где ^х = 5X + В2 и ^42 = i A?! —1?2) — новые произвольные постоянные. Аг
и Л2 вообще считаются вещественными величинами (выражаемыми через
начальные значения Уо и Ух), так что первоначальные произвольные
постоянные Вг и В2 будут сопряженными комплексными величинами.
Введем теперь постоянные А и е, связанные с Аг и А2 соотношениями
и A^
Полученное ранее общее решение неоднородного уравнения принимает
вид YX = Y (x) + rx(A1cosQx + A2sii\Qx), или, вводя Л и е,
-*)t (Ю)
где произвольные постоянные^ и А2, или .4 и 8, находятся по начальным
значениям Уо и Ух, а «структурные» постоянные г и 0 определяются через
а и Ъ первоначального разностного уравнения формулами (8) и (9).
Заметим, что, в силу неравенства E > 0 и (8), всегда sin0>O и,
150

следовательно, 0 удовлетворяет неравенству О<0<я. Знак cos0 в силу
(8) зависит от а. При этом 0 < 0 < я/2, если а > 0 (то есть а < 0),
и я/2 < 0 < я, если а < 0 (то есть а > 0).
Из A0) следует, что решение yx = Yx — Y(x) однородного
уравнения B) имеет (при А Ф 0) колебательный характер. Оно описывается
синусоидальной функцией ^r*cos@# — г). Амплитуда к затухание колебания
представлены в ней множителем Агх = Aevx (где r = ev и у = 1пг). А в нем
определяет начальную амплитуду (зависящую от начальных условий),
а «структурная» (положительная) постоянная г = |/~Ь, определяющая
характер решения, не зависит от начальных условий. Это .решение является
взрывным при г>1 и затухающим при г<1. При г=1 (пограничный
случай) решение однородного уравнения имеет вид
и соответствует регулярному колебанию постоянной амплитуды при х-—> оо.
Период колебания п равен 2я/0, где 0 —другая «структурная» постоянная,
определяемая (9). Так как 0 лежит между 0 и я, то период равен
по крайней мере двум интервалам от х. Следовательно, в отличие от
амплитуды, период устанавливается раз и навсегда структурой первоначального
уравнения; он не изменяется при возрастании х. Наименьшая возможная
величина периода равна двум интервалам (когда 0 = я), и колебание будет
в таком случае знакочередующимся. Чем меньше величина 0, тем длиннее
период; по мере того как 0 приближается к нулевому значению, период
становится весьма длительным и стремится полностью сгладиться. Фаза
колебания, то есть начальная точка колебания при # = 0, зависит от
произвольной постоянной е, определяемой начальными условиями.
' По двум начальным значениям (Уо и Ух) можно установить
начальную амплитуду и фазу колебания. Характер последовательного
колебательного движения при возрастании х будет определяться структурой
разностного уравнения, и он зависит только от г и 0, получаемых из аи 6
с помощью формул (9). Период, как было указано, зависит от 0, и он
будет тем длиннее, чем меньше величина 0. Доминирующей частью в
решении A0) является г*, который определяет взрывной или затухающий
характер колебаний.
Если рассматривать Y (х) как невозмущенное решение, а ух как
отклонение от него, вызванное возмущениями начальных условий, то можно
сделать следующие выводы.
1. При г> 1 решение У (х) оказывается неустойчивым.
2. При г<1 решение У (х) устойчиво. При этом в случае г < 1 сколь
угодно большие начальные возмущения при х—> оо затухают.
При разыскании частного дискретного решения Y(x),
представляющего тенденцию или положение равновесия, рекомендуется пользоваться
операторным методом, описанным далее. В частном случае, когда правая
часть неоднородного уравнения постоянна, разыскать частное решение
нетрудно. Именно пусть Yx + aYx_t + ЬУЯ_2 = /(х) = а; как и в случае
разностного уравнения первого порядка, ищем решение в виде постоянной
Yx — \x, где \i — постоянная, которую нужно найти. Подстановка в
уравнение дает (l-{-a+b)\i = a, или jjl = а/A + а+ 6). Поэтому в рассматриваемом
случае общее дискретное решение уравнения A) имеет вид:
где у(х; Av A2) есть общее решение уравнения B), уже подробно
исследованное нами. Таким образом, колебания Yx происходят вокруг
постоянной тенденции или постоянного уровня равновесия а/A+а+6). Примеры
151

отыскания частного решения для уравнений с правой частью некоторых
специальных типов рассмотрены в упражнении 7.
Задачи и упражнения
1. Найти частное дискретное решение уравнения ух—-г ух_2 = 0, удовлетворяющее
начальным условиям: г/0 = 1 и Ух = О. Проверить, что решение можно записать в виде:
A чэс+1
") •
Показать, что последовательность значений ух состоит из положительных убывающих
до нуля чисел, перемежающихся с нулями. Построить график решения.
2. Рассмотреть уравнение ух—а2ух_2 = 0, являющееся обобщением предыдущего.
Показать, что оно имеет знакочередующееся общее дискретное решение
Когда изменение ух затухает при х —>• оо (при любых начальных условиях)?
3. Найти и сравнить решения следующих уравнений:
(И) Ух—yx-i + -j
4. Показать, что решение уравнения ух—2/X-i+-o" Ух-2 = ° содержит затухающее
колебание ух с периодом в 8 интервалов х. Показать, что уравнение ух-^Ух-г+
+ -2"Ух-2=0 имеет то же решение, за исключением того, что период колебаний в нем
короче.
5. Показать, что решение уравнения ух = уХ-1—Ух-2 содержит регулярные
колебания с периодом в 6 интервалов х (см. 5.2, упражнение 3).
6. Показать, что разностное уравнение второго порядка с & = 1:
приводит к некоторой пограничной линии или предельным случаям решений. В частт
ности, если а2 = 4 и а= ±2,. показать, что ух возрастает линейно по модулю, причем
либо монотонно (при а = — 2), либо знакочередуясь (при а = 2). Прказать, что при а2 < 4
г/х колеблется регулярно, и проверить, что уравнение из предыдущего упражнения
является частным случаем. Каков характер решения, когда а2 > 4?
7. Если Yx=Y(x)-\-y(x; Аъ А2) есть общее решение неоднородного уравнения
^+^^2 = / (#)» показать, что частное решение
8. Почему характеристическое уравнение разностного уравнения второго порядка
никогда не может иметь корня Х = 0? Что случится с вышеприведенным решением E),
когда ^i или Л2 будет равно нулю? Какой вид будет иметь решение, если один из
корней характеристического уравнения равен единице?
9. Пусть временной ряд щ порожден авто регрессивной схемой^ выраженной
разностным уравнением второго порядка:
где а и |5—постоянные, а е* — заданная последовательность случайных слагаемых
с нулевым математическим ожиданием. Исследовать решение и найти условие,
которое нужно наложить на а и E, чтобы решение щ имело внутренние колебания. Какой
вид получает «тенденция» в щ (частное решение), в каком смысле она случайна?
10. В предыдущем упражнении рассмотреть случай р=0, когда авторегрессия
представляет простой Марковский процесс, и показать, что временной ряд Uf не может
иметь колебательного характера.
11. Закон образования авторегрессивного временного ряда таков:
152

При каких значениях а и b этот ряд колеблется? Показать, что при а — 1 первые
разности У/~ Uf — щ_1 есть простой Марковский процесс. Исследовать частный закон
образования временного ряда
который, как показано в работе [8], представляет автррегрессивную схему,
применимую ко многим временным рядам в экономике.
5.5. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА
Теперь ясен общий метод нахождения дискретных решений. Линейное
разностное уравнение тг-го порядка с постоянными коэффициентами и
соответствующее однородное уравнение имеют вид:
a0Yx+a1Yx_i+ ... + an_1Yx_n,1 + anYx_n = f(x)> A)
йоУх + <*1Ух-1 + • • • + ап-1Ух-п+1 + апУх-п = 0. B)
Сперва мы находим некоторое частное решение уравнения A) YX = Y (х),
которое обычно характеризует тенденцию или линию равновесия Ух,
соответствующую возрастанию х. Затем введем новую переменную — отклонение
yx — Yx — Y, которое удовлетворяет однородному уравнению B), и далее
требуется найти его общее дискретное решение, которое содержит п
произвольных постоянных:
yx = Y(x\ Al9 Аг, ..., Ап).
И, наконец, полное решение уравнения A) представляет собой сумму
какого-либо частного решения A) и общего дискретного решения
однородного B), и оно имеет вид:
Yx = Т(х) + у (х; Ах, А2У ..., Ап).
Для нахождения решения однородного уравнения B) ищем его в виде
yx = 'kxJ где постоянная X есть корень характеристического уравнения:
а0Хп + а^'1 + .. - + <*»-!* + ап = 0. C)
Это уравнение имеет п корней (Яп Л2, ..., А,)г), которые могут быть как
вещественными, так и попарно комплексными сопряженными числами. Можно
показать, что эти решения линейно независимы, а потому общее дискретное
решение уравнения B) получится в виде:
Ух = A№ + А*Ч + • • • + Ап^п. D)
Когда уравнение C) имеет пары сопряженных комплексных корней,
соответствующие члены в D) могут быть выражены в различной форме,
включающей синусоидальные функции. Возможно, что два или больше корней в C)
будут равными; в этом случае решение D) «дефектно», так как оно не имеет
требуемого числа различных членов. В таком случае необходимо употребить
прием нахождения решения, который мы применили во втором случае
раздела 5.4.
Если все корни C) вещественные, то доминирующим членом в решении D)
является тот, который содержит наибольший по абсолютной величине корень,
пусть это будет, например, А^*. Если по абсолютной величине l^^l,
то решение относительно ух при возрастании х имеет взрывной характер;
если | \ | < 1, то тогда вариация затухает до нуля. В обоих случаях знак ух
может чередоваться, но ук не колеблется в обычном смысле (то есть с периодом
колебания большим, чем два интервала х).
Если уравнение C) содержит комплексные корни, то они встречаются
парами в форме r(cos0 ± sin 8). Для каждой такой пары два члена в D) при
объединении дают Ar* cos (Qx — е), где А и е — произвольные постоянные.
В этом случае доминирующий член в решении D) зависит от наибольшей
153

величины г (пусть это будет, например, гг) в отношении комплексных корней
и наибольшего по модулю Я (например, XJ в отношении вещественных корней.
Движение ух включает колебания с периодом 2я/Э или несколько таких
колебаний. Колебание само может быть взрывным (если гх > 1) или добавлено
к отдельному неколебательному члену, являющемуся взрывным (если
| Ях | > 1). Однако если по модулю гх Дх < 1, то решение будет
характеризоваться затухающими колебаниями без взрывного элемента. В случае наличия
в C) равных корней возникает дополнительное осложнение. Найти корни
характеристического уравнения для порядка выше второго — нелегкая
задача. Даже для уравнения третьего порядка нужно прежде локализовать
(например, графически) один корень, чтобы найти два других. Но в
некоторых частных случаях можно угадать один или несколько отдельных корней
характеристического уравнения C). Предположим, что сумма коэффициентов
разностного уравнения равна нулю:
В этом случае Я = 1 является корнем C), и один из членов в решении D)
есть дополнительная постоянная. Это соответствует тому случаю
дифференциального уравнения, когда члены с Y отсутствуют (см. 4.5.). Предположим
теперь, что
ао — а1 + а2 — а3+ ... =0.
Тогда Я = — 1 является корнем C), и решение D) включает как слагаемое,
меняющееся по знаку, постоянную (—l)*^. Пока мы ничего не сказали
относительно частного интеграла Y(z), который входит в полное решение
уравнения A). Он зависит от формы f(x), и его приходится находить методом проб
и последовательных приближений, так как любое частное решение уравнения
A) служит для нахождения Y(x). Рассмотрим, например, простейший случай,
когда/(ж) = a (const). Испытаем решение уравнения A) в виде Yx = У (const),
так что (а0 + аг+ ... + an)Y = а. Следовательно, частный интеграл
у а
а полное решение A) представляет вариацию относительно этого
постоянного уровня.
Рассмотрим теперь метод решения разностных уравнений, который можно
применить на практике. Как и в случае дифференциальных уравнений, этот
метод основан на использовании операторов (см. приложение А). В данном
случае мы применяем оцератор сдвига Е или соответствующий разностный
оператор А. Они определяются формулами EYX = YXJ,X и AYX~ Yx+1 — Yx,
где А = Е — 1. С помощью одного из этих операторов можно найти частный
интеграл Y(x) уравнения A).
Запишем разностное уравнение A) в операторной форме, исходя из
следующих формул:
Тогда A) примет вид:
(а0 + а^1 + а2Е~* +...+ апЕ'п) Yx = / (х)9
а это представляет собой операторную форму разностного уравнения A).
Введем теперь функцию F (Е) = а0Е'1 + а^71'1 + ... + ап_гЕ + ап\
преобразуем левую часть полученного выше операторного уравнения и получим,
тогда наше уравнение в следующем виде:
154

Отсюда можно формально написать частный интеграл:
Истолкование и способ алгебраического преобразования выражений с Е
для получения частного интеграла изложены в приложении А. Рассмотрим
применение этого метода на двух примерах.
Пример (а)
Yx-a*Yx_2 = ax.
Корни характеристического уравнения Я2—яа=0 суть Klt 2 = ±«. Поэтому общее
дискретное решение однородного уравнения (дополнительную функцию) получаем
в виде:
ух = {Ах+(— 1)хА2}ах (Ах и А2— произвольные постоянные).
Данное неоднородное уравнение в операторной форме запишется так:
и частный интеграл его будет:
Y*—~m g- ах = 2 J. 2 аХ (п0 Ф°РмУле D) из приложения А).
В результате получаем полное решение исходного разностного уравнения:
которое содержит знакочередующийся элемент, представленный членом с (—1)х.
Решение имеет затухающий или взрывной характер в зависимости от величин а и а.
Пример (б)
Yx-Yx_1+2Yx_z=x+2x.
Характеристическое уравнение А,3—Я2+2 = 0, или (Я+1) (X2—2А,+ 2) = 0, имеет корни
X=i±i и —1. Комплексные корни суть re±lQ = r (cos9± i sin0), где r=]/ и 6 = Jt/4
{см. 5.4, уравнение (9)]
Следовательно, дополнительная функция будет
—А (У)хсо& ( -тх—е) +(— 1)ХВ (А, В и е—произвольные постоянные).
2* [пРиложение Л' Раздел D)].
ух
Частный интеграл данного неоднородного уравнения:
Е3 Е3 23
У^= е*—Е*+2 (*+2>= Е*—Е*+2 W+ 23—22+2
4
Второй член равен просто -~- 2х. Чтобы определить первый член, перейдем от Е к раз-
о
костному оператору А = ^—1. Подставляем в первое слагаемое частного интеграла
ДД+1
Е* _ (Д + 1K _ (Д + 1K _ (А + 1K / 1 Д-2
2+2 "~ (Д+2) (Д2+1) "~ 5 Ч. Д+2
в элементарных рациональных дробях. Разложим дроби в скобках по степеням Д§
Имеем:
Л 2- = B —Д)A + Д2Г1 = B —Д)A —Д2+ ...) = 2—Д—2Д2+ ...
Д2 + 1
и сумма равна —(i — уД — -г- Д2+ ... V Следовательно/первый член в Уж:
— Д —|- Д2+ ... ) ^ = у A+ЗД + ЗД2+Д3) (*-у) =
так как Дх=1 и Д2а7 = Д%= ... =0. Частный интеграл данного неоднородного
уравнения будет
155

и его полное решение имеет вид
Задачи и упражнения
1. Проверить, что yx=A(]/r2)xcos ( — х—г \-\-B является решением
уравнения
Ух — ЗУх-i+4Ух- 2—22/х-з = 0.
Показать, что в этом случае, так. же как и выше, в примере (б), решение ух имеет
взрывной колеблющийся характер с периодом 8. Какая разница между этими двумя
решениями?
2. Линейное разностное уравнение выражается через последовательные разности
Yx, ЛУХ, &2YX Исследовать случай, когда уравнение не содержит Yx, например
AYx = f(x), A2Yx+aAYx~f (x) и т. д. Выразить это в уравнениях, содержащих Yx,
Yx-n Yx_2, •••» и показать, что корень характеристического уравнения X равен 1
и что решение для Yx в каждом случае содержит аддитивную постоянную. (Сравните
с результатом для дифференциальных уравнений в 4.5).
3. Частным решением уравнения a0Y'х-\-а{?'^-1+ •*• + Яп^х-п = а является
у_
Показать, что, когда «0+ai+ ••• +Лп = 0, частным решением этого уравнения будет
СЕ??
У= —-—: : . Каким будет частное решение, если и а14-2а2+ ••-
al-f-za2-\- -\-пап
lf2\
... -\-пап равно 0?
4. Дано разностное уравнение Ух — Заух_1-{-За2ух_2—а3ух^3 = 0. Показать, что
решениями этого уравнения являются ух — ах, ух = хах и ух = х2ах. Вывести отсюда
общее решение данного уравнения, а также обобщить результат для такого типа
разностных уравнений высшего порядка.
5. Характеристическое уравнение разностного уравнения имеет два сопряженных
комплексных корня г (соэ0± /sin 9). Что будет, если 6 = я, и период решения сводится
к 2? Показать, что решение стремится к (А^А^х) ( — г*), то есть что наименьший
период колебания (два интервала х) эквивалентен знакочередованию.
6. Линейное однородное разностное уравнение четвертого порядка имеет
характеристическое уравнение с двукратной парой сопряженных комплексных корней
r(cos0db JsinG). Показать, что общее решение имеет вид
cos ze + (#i + ?2*) sin
5.6. ЭКОНОМИЧЕСКИЕ ИЛЛЮСТРАЦИИ
В паутинообразной модели, которую мы рассматривали в разделе 1.2,
разностное уравнение цены (отклонения от ее уровня в условиях равнове-
сия) есть Pt — —Pt-i- Решением этого уравнения является ^ = ро( — ) , где
р0 — начальное отклонение. Критическое положение характеризуется
отношением b/at где а и Ь — угловые коэффициенты прямых, выражающих
зависимость предложения и спроса от цены. Аналогичное уравнение получится
и для модели I из раздела 1.7, в которой изменение цены зависело
от изменения запасов (степень реакции цены определялась X). В этом
случае критическое положение характеризуется параметром 1 — ХF — а).
В расширенной паутинообразной модели из раздела 1.6 отклонение
цены от ее уровня в условиях статического равновесия, pt = Pt — Ру
описывается разностным уравнением:
Pt = с A - 6) Pt-i + cqpt^ A)
где с = — есть отношение угловых коэффициентов прямых предложения
и спроса, a q (обычно 0<q<1) есть коэффициент, характеризующий
ожидание поставщиком изменения цены в противоположном направлении.
Предположим обычный случай, когда а < 0, Ъ > 0 и, следовательно, с <0.
Введя обозначение у = (— с) = , , мы получим следующее
характеристическое уравнение:
156

с сопряженными комплексными корнями Xly X2 = r(cos0 ± isinG), если
Это будет иметь место при умеренной величине q (примерно г/2) и если
угловой коэффициент предложения не очень большой по сравнению с
угловым коэффициентом кривой спроса. Например, если д = х/2, то Y < §> то
есть b < 8( — а). Если B) выполняется, то на основе раздела 5.4:
C)
а общее дискретное решение уравнения A) получается в виде
Pf='Arl cos (Qt — e), D)
где А я & определяются начальными условиями.
В обычных случаях восходящей кривой предложения и нисходящей
кривой спроса и при средней по размеру величине q условие B)
практически всегда выполняется, и, следовательно, отклонение цены от ее
значения в положении равновесия носит колебательный характер. При этом
совсем не обязательно, чтобы кривая предложения была менее крутой по
сравнению с кривой спроса (как это было в случае простой
паутинообразной модели затухающего типа); кривая предложения может быть значительно
круче кривой спроса, а условие B) будет выполняться.
В колебательном решении D) период равен 2я/0, и колебания затухают,
если г< 1, где г и 0 определяются выражением C). Полученные
результаты интересно сравнить с простой паутинообразной моделью, где
изменение цены знакочередуется (период колебания равен 2) и затухает,
если Ъ < {—а).
Так как tg0<O, то 0 находится между я/2 и я, подходя ближе
к нижнему пределу, если у мало, и к верхнему пределу я, если у велико.
Следовательно, период колебания находится между 2 и 4, приближаясь
к 4 по мере уменьшения у (при заданном qI. Так, если наклон кривой
предложения круче по сравнению с кривой спроса, то период колебания
немного больше 2, и изменение цены не сильно отличается от простой
паутинообразной модели. Если же наклон кривой спроса круче, то период
колебания удлиняется и подходит к 4, то есть становится в два раза
больше, чем в простой паутинообразной модели. Далее, для затухающего
колебания r2 = YQ<l, то есть у = — = — должно быть меньше l/о, кото-
рое больше 1. Следовательно, затухающее колебание может иметь место
даже в том случае, когда & > — а, то есть если даже кривая предложения
наклонена круче, чем кривая спроса.
В рассматриваемой модели затухание колебаний более обычно, чем
в простой паутинообразной модели. По сравнению с последней расширенная
модель имеет более сильное затухание и более продолжительный период
колебания.
Когда в модели изменения цен учитываются запасы товаров (см. 1.7,
модель II), отклонение цены от ее уровня в условиях равновесия
характеризуется уравнением
ГО Л /Г /i\\ г» Т\ t ?\\
где X > 0. Предположим обычный случай восходящей кривой предложения
и нисходящей кривой спроса, так что а < 0, Ъ > 0 и (Ь — а) > 0.
Обозначим с = 1 — — Х(Ь— а), так что с < 1. Тогда разностное уравнение E) будет:
Pt = 2cpt_1-pt_2. Ea)
1 Таким образом, на всяком отрезке ty равном одному периоду колебательного
множителя, лежит от двух до трех точек дискретного решения. —Прим. ред.
157

Оно приводит к граничным решениям (см. упражнение 6 из раздела 5.4)*
Характеристическое уравнение относительно \i имеет вид:
с корнями \ilf \х2 = с ± ]/с2 — 1.
Характер корней зависит от величины X, и мы получаем следующие
случаи:
III
Если X невелико (не больше, чем 4/F —а)), с является положительной или
отрицательной дробью, и вспомогательное уравнение имеет сопряженные
комплексные корни:
— с2,
так что г = 1 и tg 0 = ± у \ — 1 . F)
Решение уравнения E) на основе раздела 5.4 имеет вид
pt=:A(cosQt-e), G)
где А и 8 определяются начальными условиями. Когда А, < 4/F — а),
движение цен всегда имеет характер регулярного колебания с периодом 2я/0.
В выражении F), определяющем tg0, знак плюс берется в том случае,
когда X < 2/(Ь — а) и с положительно; тогда 8 лежит между 0 и я/2. Если же
2/F — а) < i < 4/F — а) и с отрицательно, то tgG берется со знаком минус;
6 лежит здесь между я/2 и я. Следовательно, при увеличении X от 0 до
2/F —а) и далее до 4/F —а), 0 увеличивается от 0 до я/2 и далее до я,
а период колебания убывает от оо до 4 и далее до 2. Таким образом, хотя
колебание всегда регулярно, его период зависит от величины X. Когда
X увеличивается, период колебания укорачивается и при приближении
X к критической величине 4/F — а) он в итоге стремится к 2 (то есть когда
изменение цены знакочередуется).
Разностные уравнения встречаются также в дискретном анализе
динамических моделей с мультипликатором и акселератором, которые мы
рассматривали в разделах 2.7, 3.6 и 3.7. Динамическая модель
мультипликатора (см. 2.7) характеризуется разностным уравнением относительно дохода:
Yt — cYt_1 = Ah где с —постоянная предельная склонность к потреблению,
a At независимые затраты. Если эти затраты At рассматривать
растущими во времени по закону геометрической прогрессии, то это разностное
уравнение примет вид:
Yt-cY^Atil + rY. (8)
Дополнительной функцией (или общее дискретное решение
соответствующего однородного уравнения) для уравнения (8) является yt = Ac\ а его
частный интеграл:
где *о =
1+г
что легко проверить подстановкой в (8). Полное дискретное решение (8)
в случае роста по геометрической прогрессии:
158

Если дано, что при ? = 0 Yt — YOt то произвольная постоянная А = Y0 — У0.
При изложении теории роста Харрода —Домара C.6) были предложены
ее различные динамические варианты. Один из них, описываемый
уравнением C) в разделе 3.6, приводится к разностному уравнению:
где s = 1 — с — предельная склонность к сбережению, a v — мощность
акселератора. Характеристическое уравнение будет иметь вид:
) = 0. (9)
Если уравнение (9) имеет сопряженные комплексные корни, то
движение дохода Y, во времени имеет колебательный характер. Условием этого
является: A + аJ~ 4(v + s) < 0. Следовательно, A — уJ < 4$, и мы
получаем:
или
Этот случай, когда мощность акселератора v около единицы, а предельная
склонность к сбережению s мала, встречается часто. Если уравнение (9)
имеет корни re±ie, то, на основании (9) из раздела 5.4, r2 = (v + s)t и
величина г определяет, будут ли колебания затухающими или взрывными.
Вполне вероятен случай, когда u + s>l, так что следует ожидать
колебаний взрывного характера. Точным условием этого является: l<a + s<
< (l + Ys Y или 1 -~ 5<у<1 + 2]/" 5 (см. упражнение 5 к этому разделу).
Второй динамический вариант модели Харрода — Домара приводит
к уравнению E) из раздела 3.6:
с характеристическим уравнением:
^^k + (v + s) = 0. A0)
Это уравнение отличается от (9) только слагаемым s/v в коэффициенте
при X. Однако этого различия вполне достаточно, чтобы изменить всю
картину. Уравнение A0) будет иметь вещественные корни, если значение
следующего выражения будет неотрицательным:
Это справедливо для всех v и s. Из этого следует, что в
рассматриваемом варианте движение Yt во времени не имеет колебательного
характера. Остается выяснить только вопрос, является ли это движение
затухающим или взрывным. По формулам Виета, два вещественных корня уравнения
A0) ^х и ^2 удовлетворяют следующим условиям:
Следовательно, оба корня положительны, и~движение Yt — А^ + А2М2 имеет
монотонно возрастающий характер. Вполне вероятно, что y + s>l и,
таким образом, \, А,2>1. Из этого следует, что по крайней мере один
из вещественных корней больше единицы, т. е. в рассматриваемом случае
движение Yt имеет взрывной характер, поэтому любое решение окажется
неустойчивым.
' 159

Задачи и упражнения
1. Исследовать решение расширенной паутинообразной модели (уравнение A)),
когда q < 0 и поставщики ожидают, что движение цен будет продолжаться в том же
направлении. Показать, что в обычном случае (а<0, 6>0) характеристическое
уравнение имеет вещественные корни, причем больший по абсолютной величине будет
отрицателен. Вывести отсюда, что преобладающим движением pt является знакочередо-
вание, как и в простой паутинообразной модели, но оно усилено в данном случае
ожиданием поставщиков.
2. В расширенной паутинообразной модели исследовать случай, когда а<0
и 6<0 и (— «)>( — Ь). Что можно сказать об этой модели, если q = 0 и q = 1?
3. В модели с запасами (уравнение E)), предполагая (Ъ — а) > 0, возьмите % > т •
Покажите, что Pt=zA1^ti-\-A2\it2y где \1Ъ Ц2 = с?/с2—1. Покажите также, что
доминирующий член содержит отрицательное [хх, превышающее по абсолютной величине 1.
Описать движение pt. Исследуйте далее случай, когда (Ь — я)<0. Может ли так быть
в действительности с экономической точки зрения?
4. Расширьте модель с запасами, уравнение E), как это делалось в упражнении 2
раздела 1.7. Решите ее и интерпретируйте для обычного случая а < 0, 6>0.
5. Завершите анализ уравнения (9) и покажите, что
Значение v-\-s
(l-— Y^Y < vJrs< i
1 < У-|-5<A+|/Л5"J
Движение У^
Затухающее, неколебательное
Затухающее колебание
Взрывное колебание
Взрывное, неколебательное
При заданном s (обычно небольшом) истолкуйте это, исходя из мощности
акселератора. Сравните полученные результаты с моделью мультипликатора-акселератора
Самуэльсона —Хикса (см. 6.1 и рис. 11).
6. Положить в предыдущем упражнении s = 0 и показать, что в этом случае
колебательное движение Yt невозможно. Докажите, что v < 1 предполагает
затухающее, а у>1 взрывное изменение Yf
5.7. ОТСТАВАНИЯ, РАСПРЕДЕЛЕННЫЕ ЗАПАЗДЫВАНИЯ
И МУЛЬТИПЛИКАТОР-АКСЕЛЕРАТОР
Непрерывное запаздывание имеет то преимущество, что для частных
случаев его временной формы /(т) (например, единичные и многократные
запаздывания показательной формы) оно может быть описано
дифференциальным уравнением типа C) из раздела 4.8, имеющим небольшой порядок
и легко разрешимым. Его же недостатком является то, что с его помощью
трудно оперировать с «реалистическими» или в действительности имеющими
место запаздываниями временной форумы. Для распределенного
запаздывания в дискретном анализе все обстоит наоборот (см. 3.9). Это запаздывание
легко ввести в любой форме, как это было сделано, например, в разделе 3.7,
в модели мультипликатора-акселератора.
Кроме того, результат изменения формы этого запаздывания легко
увидеть (благодаря соответствующим коэффициентам) в решении модели,
включающей в себя запаздывание. Но, с другой стороны, использование широко
распределенных й, следовательно, «реалистических» запаздываний (таких,
как на рис. 9, но в дискретном виде) очень часто приводит к разностным
уравнениям высокого порядка, которые трудно решить и истолковать.
Простейшим видом запаздывания является отставание, то есть
единственное запаздывание в 0 единиц, или периодов времени, причем 0 путем
соответствующего выбора единицы времени часто можно сделать равным 1.
Отставание можно применить одинаково и в дискретном и в непрерывном
анализе. В дискретном анализе это очень просто; отставание является особым
случаем распределенного запаздывания, когда мы берем только первый член.
160

Так, функция потребления в модели мультипликатора Ct = С(Уг_1) означает
отставание в один период, что является особым случаем распределенного
запаздывания Ct = C (Ytl, Yt_2, Yt_3i ...). В непрерывном анализе формальное
введение отставания в Э единиц времени означает только замену в
соответствующих функциях и отношениях t на (t — 9); однако этот простой шаг
«сжимает» (gum up) весь процесс. В результате обычно получается не
дифференциальное, а смешанное дифференциально-разностное уравнение
(дифференциальное уравнение с запаздывающим аргументом). Например, модель
мультипликатора-акселератора (без независимых затрат) при отсутствии
запаздывания описывается следующим дифференциальным уравнением:
ИЛИ
dY 1-е
то есть уравнением Харрода—Домара. Если же ввести отставание на
единицу времени в соотношения и потребления и инвестиций, то мы получим
смешанное дифференциально-разностное уравнение:
или
~dt
Отставания могут быть введены и в непрерывный анализ, но они
ведут к существенным трудностям (см. гл. 7 и 8). Рассмотрим
синусоидальную переменную с затуханием а и частотой со, определяемую
комплексной переменной z = Aeieept (р = а-\-ш). В этом случае Dnz = pnz
(D — символ оператора) является аналогичным синусоидальным
изменением (см. 4.9). Введем теперь переменную с отставанием u(t) = z(t — б):
и (t) = AeieevV-^ = e~*Bz (t).
Влияние члена е~^ проявляется в смягчении амплитуды и задержке фазы
переменной z:
где амплитуда смягчена множителем е~а0, и фаза е уменьшена слагаемым
(—0H). Однако по-прежнему u(t) остается синусоидальной переменной
с тем же затуханием и частотой, что и z(t); при этом член ept остается
неизменным. Это же справедливо для Dnu —pnu = pne~^z.
В общем случае распределенное запаздывание в дискретном анализе
в развернутом виде можно проиллюстрировать на модели
мультипликатора-акселератора. В данном случае:
It = v1(Yt_1 — Yt_2) + v2(Yt_2 — Yf_3) + ..., где u= v1 + vi+ ... .
Первое соотношение характеризует потребление (мультипликатор), а
второе—капиталовложения (акселератор) при условии Yt = CtJrIt + At
(At — независимые затраты).
В распределенном запаздывании потребления коэффициенты сх, с2, с3, ...
могут принимать любые значения при единственном ограничении, что в сумме
они дают общую предельную склонность к потреблению с1. Форма
запаздывания может как угодно варьировать, но в любом случае оно описывается
этими коэффициентами. Например, совсем не обязательно, чтобы сх, с2, с3, ...
уменьшались в геометрической прогрессии, что соответствовало бы распре-
1 Напомним, что с и, следовательно, все сг меньше единицы.— Прим. ред
И р. Аллеи 161

деленному запаздыванию в форме показательной функции в непрерывном
анализе. Аналогичные замечания можно сделать и в отношении запаздывания
инвестиций. Когда учитывающие запаздывания выражения для Ct и It
подставляются в условие модели (Yt = Ct + It + At), то получающееся
в результате разностное уравнение решается относительно Yt, и можно
увидеть влияние коэффициентов запаздываний (отдельных сг и vk) на!
решение. В модели мультипликатора-акселератора важнее запаздывание
инвестиций; мы уже рассматривали предварительно этот вопрос ранее, в разделах
3.7—3.9, но в более общем виде мы исследуем эту проблему в главе 6.
Между тем, и причина этого очевидна, влияние запаздывания
потребления можно легко проследить на простой модели мультипликатора (см. 2.7),
то есть модели мультипликатора-акселератора, в которой It = 0.
Эту модель можно описать разностным уравнением:
Yt = Ct+At, где Ct = c1Yt_1 + c2Yt_2 + c3Yi_3+... .
Если рассматривать только единственное запаздывание (отставание)
Ct — cYt_1 и At считать постоянной величиной, то вышеприведенное
уравнение превращается в уравнение:
решением которого является
Соответствующее уравнение с запаздыванием, распределенным на два периода
(на два временнйх промежутка), будет линейным разностным уравнением
второго порядка:
д
В данном случае частное решение Y — -. , так что, вводя новую пере-
1 — с
менную yt = Yt — Y, получаем однородное уравнение:
Так как с = с1-|-с2, положим сх = с — сг и напишем уравнение:
Уе - (с - с2) уЫ1 - c#%Jt = 0, A)
решением которого является:
yt = ALK[-{- А2Кг2 (Аг и А2 — произвольные постоянные), B)
где Х± и Х2 —корни характеристического уравнения
А»-(с-с,)Л-са = 0. C)
Если значения коэффициентов сг установлены и начальные значения у0 и ух
заданы, то можно найти численное решение уравнения A).
3 1 11
Приведем пример. Пусть с = -г , с2 = -т-, то есть Ct = — Yt_i-\--^Yt.2-
Характеристическое уравнение C): А,2— у ^~" ==° С КОРНЯМИ ^1=-^ A + 1^5) = 0,809 и Л2 =
= -i(l —/5)=— 0,309. Решение уравнения B): у* = Л1@,809)'+-4а ( — 0,309)'. Если
2/о = О и 2/i=l, то, подставляя * = 0 и t = l, получаем Лх = 0,895 и А2= —0,895, и
решение принимает вид:
yt = 0,895 @,809)' —0,895 (—0,309)'.
Первый член доминирует, а второй—быстро исчезает, и, следовательно, yt—^.0 через
положительные значения.
Вообще проблема состоит в том, чтобы определить Ях и А,2 из C),
каковы бы ни были величины коэффициентов с и с2 в запаздывании потреб-
162

ления. Эти корни Х1 и %2 таковы:
Относительно коэффициентов потребления обычно предполагается, что
0<с2<с<1, так как все коэффициенты (с19 с2 и с = сх + с2) принимаются
за положительные правильные дроби. Следовательно, корни кг и ^ —
вещественные; один из них (А,х) положительный, а другой (Я2) —
отрицательный, причем по абсолютной величине положительный корень больше. Для
более точного определения корней находим изменение знака /(А,) = 12 —
— (с — с2)Х— с2, в зависимости от изменения К.
Подстановкой получаем: ^
О с 1
-с.
1-е
Рис. 10
_сяA_с)
Это иллюстрируется графиком f(X) на рис. 10.
Как видно из графика, положительный корень Хг лежит между с и 1,
а отрицательный Х2 между —1 и -—с2. Больший по абсолютной величине
корещ» Хх является
положительной, а корень к2 — отрицатель- fa) График кривой
ной дробью. Теперь мы можем
сделать вывод, что, каково бы
ни было действительное
значение с и с2 @<с2<с<1),
решение относительно ytJ данное
в B), содержит преобладающий
член Ах%[, который монотонно
(steadily) сходится к нулю.
Второй член А2Х\ вносит в решение
знакочередующийся
исчезающий элемент.
Необходимо отметить
несколько крайних случаев.
Сперва мы рассмотрим величину общей^предельной склонности к потреблению с.
Если с мало (следовательно, также и^и с2),то в этом случае график/(X) на
рис. 10 только чуть-чуть опускается ниже 0; следовательно, и Хх и Х2 малы, и уь
быстро сходится к нулю. Если с велико, то точка В на кривой поднимается
только немного выше 0; следовательно, доминирующий корень Яа близок
к 1, и yt сходится к нулю медленно. Таким образом, сходимость yt к нулю
тем медленнее, чем больше величина с или чем меньше величина s = 1 — с =
предельной склонности к сбережению. При данном с решающую роль
начинает играть с2 (которое устанавливает распределение запаздывания); оно
воздействует на сходимость yt через второй (отрицательный) корень Х2.
Если с2 мало, то в этом случае точка А на кривой значительно выше 0
п (— Х2) мало; знакочередующийся член в решении исчезает быстро. Если с2
велико, то А только чуть выше 0 и (— Х2) близко к 1; знакочередующийся
член, так же как и доминирующий, уменьшается медленно. Может быть
очень широкое распределение запаздывания, и запаздывание в среднем будет
велико, когда велико значение с2. Следовательно, сходимость тем медленнее,
чем больше среднее запаздывание.
В общем случае запаздывания, распределенного на п периодов или единиц
времени, разностное уравнение имеет вид:
где все сг и с —
С2 + • • • + сп ~~ положительные правильные
Частное решение этого уравнения опять-таки^-— , и при yf =
дроби.
163
И*

разностное уравнение сводится к однородному уравнению:
Vl = Cl2/*-l + C2Vt-2 + • • • + CnVt-n<>
общим дискретным решением которого является:
В данном случае Xv Х2, ..., Хп представляют п корней характеристического
уравнения:
а А19 А2, ..., Ап — произвольные постоянные, частное значение которых
определяется начальными условиями.
Характеристическое уравнение должно иметь положительный
вещественный корень (Xj), величина которого лежит между с и 1, Подставляя Х = с
и А, —1 в /(А,), получаем:
f(c) = ^-c^-c^-*- ... - сп = с^1 (с-Cl)- с2сп- ... - сЛ =
с3 + ... + сп и с < 1;
/A) = 1 — сх— с2 — ... — сп = 1 — с > 0, так как с<1.
Следовательно, /(я) изменяет знак в промежутке Я=сиЯ = 1,ив нем лежит
корень характеристического уравнения Я1. Можно также показать, хотя
это и несколько затруднительно [6], что А^ является единственным
положительным корнем и имеет самую большую абсолютную величину. Из остальных
(п — 1) корней некоторые могут быть вещественными отрицательными,
а другие — попарно сопряженными комплексными. Для отрицательного
корня | kk | < А,х. Если решение будет содержать и сопряженные комплексные
корни r(cos0 ± sin6), то абсолютная величина г должна быть меньше Ях.
Следовательно, \ — доминирующий корень, и доминирующим членом
в yt будет Агк{. Так как с < кг < 1, то yt сходится к нулю; скорость этой
сходимости зависит прежде всего от абсолютной величины Я1? и вообще
сходимость тем медленнее, чем больше величина с.
Хотя член Ау%\ и доминирует в yt, интересно рассмотреть и другие члены.
Поскольку А,2, Яд, ..., \г имеют отрицательные или сопряженные
комплексные значения, то эти члены вызывают знакочередования или колебания в yt
или и то и другое. Следовательно, вообще ух сходится к нулю, a Yt к У,
но с чередованиями знака и с колебаниями, налагающимися на основное
движение. Эти дополнительные движения замедляют или ускоряют сходимость.
Как показал Солоу [9], в данном случае важно, в противоположность общей
предельной склонности к потреблению с, именно распределение
запаздываний, задаваемых сг: с2: ...: сп. Вообще при прочих равных условиях скорость
сходимости Yt к Y тем медленнее, чем больше среднее запаздывание и
дисперсия коэффициентов ck (к = 1, 2, ..., п) в распределенном запаздывании.
Задачи и упражнения
1. Исследовать модель мультипликатора с запаздыванием, распределенным на два
периода при сг = 0. Чем будет отличаться решение этой модели от решения модели
с единственным запаздыванием?
2. В модели мультипликатора с запаздыванием, распределенным на два периода,
с ^ 1 и сх и с2 являются положительными дробями. Исследовать, в какой форме
выражается решение относительно г/f. Что в данном случае можно сказать о
сбережениях (предполагаемых и фактических)?
3. Пусть в решении для ytJ данном в B), начальные величины будут: при ? = 0
yt = y0 и У1=Ух при * = 1. Показать, что
А = и А
%i — Л-2 ^1 — А/2
Как влияют на характер движения yt знаки и абсолютные величины у0 и
164

5.8. НЕПРЕРЫВНЫЕ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ
Разностное уравнение относительно Yx относится к любому ряду
равноотстоящих (equally-spaced) значений независимой переменной х.
Рассмотренные до сих пор дискретные решения применимы к одному частному ряду
значений переменной х — О, 1, 2, 3, ... Однако разностное уравнение не
ограничивается таким путем; отправной точкой для х может быть любое
значение. Если отправной точкой является х = 0, то разностное уравнение
порождает дискретное решение Уо, Ух, У2, .... Если в качестве начальной
точки выбрать х — -^ , то получится совершенно отличное дискретное реше-
ние Yi/2, Уз/2, Уб/2. Очевидно, что не существует ограничений для того, чтобы
получить какое угодно число различных дискретных решений. Можно
выбрать любое значение х между 0 и 1 в качестве начальной точки, и х можно
заставить изменяться непрерывно. Спрашивается, можно ли все
дискретные решения объединить в отдельное непрерывное решение, выражающее
Ух в виде функции х, вообще для любого ряда равноотстоящих значений х.
Например, предположим, что разностное уравнение характеризует
уровень цен Yx в различные моменты времени ж, а интервал значений х равен
одному году. В этом случае х = О, 1, 2, ... может означать, например, конец
года, и дискретное решение Yx будет тогда показывать изменение цен на
конец года от года к году. Но если положить # = -^,-^,-77,..., то получится
A Z Z
другое дискретное решение Уа, которое будет показывать годовое
изменение цен, но только на середину года. В обоих этих случаях, так же как и в
других, подобных им, изменение цен в пределах года (например, сезонные
колебания цен) в анализе не учитывается. Проблема сводится к тому,
можно ли получить непрерывное решение для Yx, которое характеризовало бы
полностью изменение цен во времени, то есть не только изменение цен год
от года, но и изменение их в пределах каждого года.
Уравнение первого порядка %(х, Yx, Yx^1) = 0 имеет дискретное
решение Yx = Y(x; А), содержащее одну произвольную постоянную А.
Какой бы частный ряд значений х мы ни рассматривали, А всегда можно
выразить через начальное значение У. Если дано Уо, решение относится
к Yx при # = 0, 1, 2, ...; если начальное значение задано У1/2» то ре-
¦\г 13 5
шение относится к Yx при # = у > -«г ' Т ' ••• и так Дадее для всех
задаваемых Yx при х в "интервале 0<ж<1. Теперь мы расширим понятие
произвольного элемента; вместо одного заданного УЛ, например Уо или
У1/2, мы будем рассматривать целую область задаваемых Yx при 0<я<1.
Говоря более точно, вместо одной произвольной начальной величины, мы
возьмем произвольную начальную функцию в области 0 < х < 1. Эта
функция может начинаться с любого значения Уо и изменяться любым
способом от х = 0 до ж=1, возвращаясь при х = 1 к начальному значению.
Наша произвольная функция имеет период 1. Если продолжить наш
пример с ценами, где У^ характеризует уровень цен, то произвольный
элемент, который мы должны указать, — это вся область цен в пределах года,
выраженных в форме сезонных изменений, начинающихся и кончающихся
на одном и том же уровне. Если это сделано, разностное уравнение дает
Yx для любых значений х, изменяющихся непрерывно.
Обозначим через w(x) любую функцию с периодом 1, так что все
значения до, разделенные единичным интервалом х, равны. Следовательно,
для единичного интервала Лдо = 0. Так же как и производная постоянной,
разность функций периода 1 равна нулю. Постоянная исчезает при
дифференцировании, функция периода 1 исчезает при исчислении
дифференцирования по конечной разности. Таким образом, общее непрерывное
решение уравнения % (#, УЛ, Yx_t) = 0 имеет вид YX~Y (хг; w), где w —
произвольная функция периода 1, которая может быть определена через
начальные условия для Yx в интервале 0<#< 1.
165

Понятие непрерывного решения легко обобщить. Разностное уравнение
второго порядка %(#, Yx, YX_VYX_2) =0 имеет дискретное решение
Yx = Y(x; Av А2) при ж = 0, 1, 2, ..., где Ах и А2 — произвольные
постоянные, которые можно отождествить с Уо и Уг Это же уравнение имеет
непрерывное решение Yx = Y(x; wx, w2) для любого х, где wx и ^ —
произвольные функции периода 1, которые можно выразить через начальные
условия для Yx в двух интервалах 0<#<1 и 1<#<2. Очевидно, это
можно обобщить для разностного уравнения любого порядка. Все, что
раньше было сказано о произвольных постоянных или начальных
значениях в дискретном решении, в равной степени относится и к произвольным
функциям периода 1 в непрерывном решении.
Решения разностных и дифференциальных уравнений имеют ряд
отличающих их друг от друга черт. Например, область возможных решений
линейных разностных уравнений (зависящих от показательной функции
типа ах) вообще значительно шире или богаче, чем для линейных
дифференциальных уравнений, решения которых зависят от показательной
функции типа еах. Это ясно из нашего анализа в разделах 5.3-—5.5.
Однако сравнение, настоящей и предыдущей глав показывает, что методы
решения линейных дифференциальных и разностных уравнений имеют
очень много общего, хотя они в значительно большей степени освоены
и разработаны для дифференциальных уравнений.
Наконец, отметим, что разностные уравнения можно решать методами,
аналогичными преобразованию Лапласа для дифференциальных уравнений
(см. 4.7). Если положить YX~YO во всем интервале 0<#< 1, то частное
дискретное решение Yx(x — 0j 1, 2,...) превращается в частное
непрерывное решение. Это решение становится в таком случае ступенчатой
функцией непрерывной переменной:
и можно' применить метод преобразования Лапласа [4]. Альтернативно
для дискретного ряда Yx преобразование можно определить через суммы —
аналогично интегралу преобразования Лапласа для функции непрерывной
переменной. Простым преобразованием такого типа является функция
женератриса (generating functionI:
x=0
в которой коэффициенты при возрастающих степенях s образуют
последовательность значений Yx. Решение разностных уравнений преобразованием
Yx в Y(s) очень похоже на преобразование Лапласа в случае
дифференциальных уравнений (см. [5], особенно пример там на стр. 194).
1 Метод функций женератрис, находящий применение и в теории вероятностей,
тоже принадлежит Лапласу. — Прим, ред.

ГЛАВА 6
ТЕОРИЯ ЭКОНОМИЧЕСКОГО ЦИКЛА САМУЭЛЬСОНА - ХИКСА
6.1. ПРОСТАЯ МОДЕЛЬ МУЛЬТИПЛИКАТОРА-АКСЕЛЕРАТОРА
С КОНЦЕНТРИРОВАННЫМИ КАПИТАЛОВЛОЖЕНИЯМИ
На протяжении последовательных периодов t = 0, 1, 2, ... установлены
независимое потребление и независимые капиталовложения (At). Нет никаких
ограничений в отношении формы динамики At, но она считается заданной.
Доход или выпуск продукции в промежутке t есть Yt. Изменение выпуска
продукции от промежутка времени (t — 2) до (t — 1) вызывает
капиталовложения в промежутке t и в последующие временные интервалы. Эти
капиталовложения так или иначе распределены между отдельными временными
интервалами. В простой модели (см. 3.7) предполагается, что индуцированные
капиталовложения концентрируются в интервале ?, непосредственно следующем
за изменением выпуска продукции. Изменение инвестиций принимается
пропорциональным изменению выпуска продукции, так что:
Индуцированные капиталовложения It = v(Yt_1—Yi^.
Линейная функция потребления включает распределенное запаздывание:
Потребление Ct = c1Yt_1 + c2Yt_2,
Условием действия модели является осуществление планов
капиталовложений и потребления, так что Yt — Ct + It + At. Это условие
предусматривает равенство фактических сбережений и капиталовложений, то есть
(Yt — Ct) = (It + At). Относительно предполагаемых сбережений ничего
не известно, они зависят от того, на какой доход (Yt) рассчитывают
потребители. Модель принимает во внимание возможность непредвиденных
сбережений, но не допускает непредвиденных капиталовложений.
Условие действия модели можно записать в виде
конечно-разностного уравнения второго порядка (см. 3.7):
Yt = (v + ct) Yt_t -(v- et) У,., + AV]
или } A)
Yt = cY^ + (v- с,) (У,.! - У,.,) + AtJ
Структурные постоянные модели суть и, сг и с2; c — c1Jrc2 — совокупная
предельная склонность к потреблению, s = 1 — с — совокупная предельная
склонность к сбережениям. Единственные налагаемые ограничения таковы:
v >0, 0< cv c2, с, s< 1.
Прежде всего нужно найти частное решение уравнения A), которое
было бы, если возможно, выражением линии тенденции или динамическим
уровнем равновесия Yt. Частное решение зависит от принятой формы
динамики независимых расходов At.
Мы уже рассматривали (см. 3.8) возможность динамического
равновесия при росте в геометрической прогрессии Yf = Y0(l + Q)*> где @ —
заданный неизменный темп роста. Когда независимые расходы неизменны
(At=*A для всех t), то имеет место подвижное равновесие,
прогрессирующее с темпом q при условии, что г = q является корнем уравнения
В общем рост в геометрической прогрессии существует как тенденция,
совместная с моделью, даже в случае постоянных независимых расходов.
167

Если же независимые расходы растут в геометрической прогрессии,
то есть At=A0(l + ry для данного г, то Yf = Y0(l + r)' является частным
решением (состоянием равновесия) уравнения A) при
уо = ^о(Н-гI при условии R > о.
Здесь г задано и Yt должно возрастать с тем же темпом г, что и At
(см. 3.8, упражнения 3 и 4). Возрастание выпуска продукции в
геометрической прогрессии обычно имеет место как постоянная тенденция, и темп
роста определяется темпом роста независимых капиталовложений. В
частном случае (г = 0), At—A, т. е. постоянной величине (для всех t), и
существует уровень равновесия Y — -x , заданный мультипликатором.
1 ~~~ С
При другой динамике независимых капиталовложений возникают
иные типы движения выпуска продукции Yt к состоянию равновесия.
Например, динамика At может представлять заданное колебательное
движение; тогда и линия положений равновесия Yt будет также
колеблющейся (см. 6.6).
Теперь предположим, что при заданном изменении независимых
капиталовложений At определена и некоторая соответствующая тенденция
или линия положений равновесия Yt для продукции. Положим, что
yt = Yt — Yt есть отклонение выпуска продукции от уровня равновесия.
Тогда, поскольку оба — и Yt иУ(- удовлетворяют уравнению A), мыполу*
чаем следующее конечно-разностное уравнение:
Уь = (v + сг) уЫ1 - (v - с2) ylJt,
или
где
w — v — с2.
Конечный и наиболее важный шаг — решить уравнение B), чтобы
получить движение yt во времени при любых заданных начальных
возмущениях. Это решение должно ответить на следующие вопросы:
колеблется ли Yt вокруг Yt, и если да, то будет ли. это колебание взрывным
или затухающим при бесконечном возрастании t?
Структурными постоянными являются инвестиционный коэффициент у,
совокупная предельная склонность к потреблению с и вторая частичная
склонность к потреблению с2. Обычно нет необходимости рассматривать другую
частичную склонность к потреблению сх = с — с2. При заданном с
распределенное запаздывание потребления характеризуется с2.
Уравнение B) показывает, что, действительно, важны только две
структурные постоянные с и w = v — c2' Действие распределенного
запаздывания потребления сводится только к уменьшению величины v, то есть
ослабляет силу акселератора. Постоянную w = v — c2 можно назвать
ослабленным инвестиционным коэффициентом. В «элементарном случае»
Хикса (с2 = 0) w является инвестиционным коэффициентом v; по мере
удлинения запаздывания потребления величина w уменьшается при любом
заданном инвестиционном коэффициенте v. Иными словами, данной
величине w соответствует более сильный акселератор. При интерпретации
решения уравнения B) вторую постоянную с удобно заменить предельной
склонностью к сбережениям, равной 5=1 — с.
В разделе 6.2 будет установлено, что встречаются четыре случая:
168

Структурные постоянные
(s и w=v—с2)
I. ш<A —уТJ
II. A —/7J<ш<1
III. 1<ИУ<A + /*J
IV. (l + /7J<>
Изменение yt во времени
Неколебательное затухающее
Колебательное затухающее
Колебательное взрывное
Неколебат ельное взрывное
На рис. 11 показана сущность решения для всех комбинаций s и w-
Кривая АВ изображает w = (l-jY~sJ, кривая ВС есть w = (l+YsJ-
Будет ли изменение yt затухающим (w < 1) или взрывным (w > 1)г
зависит только от w. Влияние s сказывается лишь на пределах величины wr
необходимых для возникновения колебательного изменения yt. При очень
Взрывное
малых s колебания возникают лишь тогда, когда w близко к 1. При
увеличении 5 колебательные решения существуют в большем интервале.
Или же, что приводит к тому же самому, при малом s и любом
значении w, заметно превышающем 1, движение убудет равномерно взрывным;
при увеличении s для этого требуются большие значения w.
Точнее, колебания возникают при условии s>(l — ]/шJ (см.
упражнение 4). Следовательно, если w находится между 0 и 4, то всегда
существует положительная дробная величина s, достаточная для появления
колебаний в уг
с2 — показатель распределенного запаздывания потребления — всегда
способствует ослаблению силы действия акселератора. В «элементарном
случае» (с2 = 0) величины, порождающие колебания, расположены на
интервале (l —VSY < i>< (l + l^sJ, a v = 1 соответствует регулярному
колебанию. В случае распределенного запаздывания также возрастает с2г
границы интервала расширяются до (l — ]/7J + с2 < v <(l + )/sJ4- с2Г
а регулярному колебанию в этом случае соответствует v = l + c2.
Акселератор определенной силы действует тем слабее, чем больше величина с2
и чем продолжительнее среднее запаздывание. Более мощный акселератор
необходим для взрывного изменения yt. В более широкой области значений
акселератора возникают затухающие изменения. Существование
распределенных запаздываний потребления способствует сходимости и
устойчивости yt.
Задачи и упражнения
1. At увеличивается с данным геометрическим темпом г, так что существует
изменяющееся в геометрической прогрессии положение равновесия Yt при условии R > О.
Показать, что это имеет место при любых значениях г, если
169

то есть в случае колебаний. Доказать далее, что трудность возникает только при
v—с2>A+уЛяJ и чт0 в этом случае, когда действует сильный акселератор,
растущее в геометрической прогрессии положение равновесия еще существует, если г
достаточно мало (см. 3.8, упражнение 4).
2. Найти область значений v для решения с колебательным движением: I) при s =
= с2 = 0,25 и II) при s = 0,04, с2 = 0,06.
3. В частном случае при у=с2 показать, что конечно-разностное уравнение
относительно у\ является уравнением первого порядка со сходящимся к нулю решением.
Входит ли это в приведенные в таблице текста случаи I — IV?
4. Дано, что w=zv—с2. Рассмотреть влияние s на характер решения относительно
Ух .Показать, что интенсивность затухания при любых значениях s зависит от величины
Уш.Показать, что в случае s > A — j/oyJ возникают колебания и что при $ < A — }/~wJ
имеет место неколебательное движение. Объяснить это и рассмотреть на примере
5. Пусть 5 = 0. Это не предполагает, что фактические сбережения равны нулю.
Показать, что в этом случае не может возникнуть колебательное движение yt.
Показать, что конечно-разностное уравнение будет иметь вид:
и решить его для zt=yt—Уиг* Согласуется ли это с результатами предыдущего
упражнения? Дать объяснение и сопоставить с упражнениями 3 и 4 из раздела 3.7.
6.2. ПОДРОБНОЕ РЕШЕНИЕ ПРОСТОЙ МОДЕЛИ
Общее решение ищется для уравнения
Юно зависит от корней Хг и Х2 характеристического уравнения
=0, где s = l — с.
<2>
Тогда решение будет иметь вид:
где Ах и А2 — произвольные постоянные, определяемые начальными
возмущениями. Корни уравнения B) могут быть вещественными, и решение C)
будет характеризовать неколебательное движение; корни могут быть
комплексно-сопряженными, и тогда решение C) будет описывать колебания.
В любом случае решение может быть затухающим или незатухающим в
зависимости от величины доминирующего корня и коэффициентов уравнения C).
Решение находится методом, рассмотренным в разделе 5.4.
Расположение корней уравнения B) можем определить, рассмотрев
знак функции f(X) для отдельных значений X:
D)
Заметим также, что
Следовательно, если w < 0, то один корень (XJ будет положительной, а
другой (Х2) отрицательной дробью, так как f(X) в D) будет всегда отрицательно
при X = 0. Из условия E) следует, что большее численное значение будет
иметь положительный корень Хг. Однако в более обычном случае — при
w > 0 — все знаки f(X) в D) будут положительны, так что если оба корня
вещественны, то они будут находиться в одной из четырех областей: (— оо,
— 1), (—1,0), @,1), A, оо). Но по условию E) они могут быть расположены
лишь в одной из двух положительных областей.
—оо
Положительна
- 1
Ziv+cJ + s
положительна
0
W
1
S
положительна
оо
Положительна
170

Решение можно продолжать графически, начертив график f(X). Рис. 12
иллюстрирует два случая. Если -^-/ (Л,) = 2А, —(а; — *+1) = 0, то Я =
1 1
= -2(w — s-\-1) = y(v + ci)> 0- Следовательно, кривая имеет минимум
в точке А, где Я = -^ (w — s+lI, и
Отсюда следует, что точка минимума находится выше оси 0А,, если
A — Y~ST<^< (I +yrs)a. Здесь уравнение B) не имеет вещественных
корней. В противном случае имеются два вещественных корня, и при
о
Я
Случай: 0<w<0 - VTJ
s < A-yUFf
Случай: (/-Vs"J<«r
Q<%<
Рис. 12
X1
A
они или оба находятся в интервале @, 1), или же оба —в
интервале A, со). Величина Кг+_Х2 в уравнении E) достаточна для суждения
об этом. Если w<(l-YsJ, то ^ + ^2 = ^-5 + 1 <2A-|/)<2, то
есть Хг и %2 находятся в интервале @, 1). Аналогично, если w > (l +Y~sJ,
X 2 = w — s + 1 > 2A +VS) > 2, то есть Хх и К2 находятся в интервале
, со).
Разнообразные случаи можно сгруппировать, как это было сделано
в разделе 6.1:
1(а)ау<0, А,! — положительная дробь, А,2— отрицательная дробь и Хг
больше по абсолютной величине, то есть, в силу C), yt, не
испытывая колебательных движений, стремится к 0, но при этом
возможна перемена знака.
(б) 0< w < A — Ys) . %1 и %2 — положительные дроби, то есть yt
стремится к нулю без колебательного движения.
Ih (l — Ys) <w<(l + Y SY- К и Я2 — комплексно-сопряженные корни, то
IIIJ есть изменение yt описывается колебательным движением.
IV (l +YSY < w- К и Ла — положительны и больше 1, то есть
движение yt будет взрывным, но не колебательным.
Остается далее рассмотреть случаи II и III. Область значений w здесь:
(в)
1 Минимум, так как вторая производная от f (К) = 2, то есть положительна.
Значение X подставляем в B) и получаем уравнение в тексте.—Прим* ред.
171

В рассматриваемых случаях корни уравнений B) комплексно-сопряженные.
Обозначим их через г (cos 0±isin0). Тогда
т cos 0 = 4- (w — s+1) и г sin 0 = ~ V^w — (w — s + 1J, G)
то есть
r = Vw H.cos0=i^±i. (8)
Здесь cos0 и sin0, положительны, так что 0 расположено в интервале
(О, я/2). Структурными коэффициентами будут теперь г и 0, которые
выражены с помощью уравнений G) и (8) через w и s.
Теперь общее решение уравнения A) имеет вид:
yt=Ar* cos @*-е), (9)
где А и е — произвольные постоянные, определяемые начальными
возмущениями.
Колебания, описываемые уравнением (9), будут затухающими при
г < 1 и взрывными при г > 1, то есть если соответственно w < 1 и w > 1»
Регулярные колебания будут соответствовать промежуточному случаю
w = l. Таким образом, различие между случаями II д III в области F)
определяется следующим образом:
(II) (l — ]/sJ < w < 1 (затухающие колебания),
(III) I < w < (l + |/sJ (взрывные колебания).
Период колебания в решении (9) уравнения равен 2я;/0, где cos0
определяется из уравнения (8) и 0 находится между 0 и л/2. Период колебания
содержит по меньшей мере четыре интервала времени и не имеет верхнего
предела. Если s задано, то период зависит от величины w в области F).
Дифференцируем cos 0 в выражении (8) по w:
Отсюда
-^-(cos0)<O приш<1,
= 0 при w = 1 — 5,
> 0 при w > 1 — s,
то есть величина cos 0 минимальна при w = 1 —- s. На нижней границе
области F) ш = A— V^)* и cos0 = (ay —5 + 1)/2угг<у=:1. При w — i — s
в области F) cos 0 = j/^l — s, и эта величина будет минимумом. На верхней
границе области F) ш = A+У^^J»и снова cos 0 = 1. Так как cos0
уменьшается от 1 до 0 по мере увеличения 0 от 0 до ~, то 0 увеличивается
от 0 до максимума 0т (где cos0m = }fl — s), а затем вновь уменьшается
до 0 по мере возрастания w в интервале F). Таким образом, период
колебания бесконечно велик в нижнем конце интервала w\ затем он
уменьшается до минимума 2я/0т при &у=1 — s, а потом вновь возрастает,
становясь бесконечно большим в верхнем конце интервала w.
Первоначальная амплитуда и смена фаз колебаний в решении
(9) зависят от двух произвольных постоянных Ли е. Эти постоянные,
характеризующие колебания, определяются начальными возмущениями.
Таким образом, при данном s решение колебательного типа (9)
возникает, если w = v — c2 лежит между
(l-1/sJ и A+у1)«.
172

Затухающие колебания имеют место при небольших величинах w;
при до=1 колебания становятся регулярными, а при больших величинах w
они превращаются во взрывные. В точке w = l — s данной области
значений w колебания будут затухающими и имеют минимальный период
су _,
-^—(где cos0m = "[/I — s). Продолжительность последнего зависит только
от s. В обычном случае, когда s мало, 0т также мало и даже
минимальный период будет длительным. Небольшая величина s означает, что
область возможных значений w для колебаний ограничена, а колебания
в случае их возникновения имеют длительный период.
Задачи и упражнения
1. Написать и объяснить решение для yt при y = 0,05, 5 = 0,04 и с2=0,06.
2. Так как s—положительная дробь, показать, что (l—Y^Y < 1— S<C 1> и отсюда
установить, что величина w для минимального периода лежит в области значений
для затухающих колебаний. Показать, что при s=c2 = 0,25 самый короткий период
заключает 12 временных интервалов и появляется при v = l.
3. Показать, что при 5 = 0 решением будет yt = A1-\-A2wt, которое равномерно
сходится к постоянной при до<1 или будет неколебательным взрывным при до>1.
4. Показать, что в пограничных случаях при до = A ± У^ J решение будет
иметь вид
где Аг и А2 произвольны.
5. Крайние случаи w = (l± Y SY также соответствуют границам области в
выражении F), то есть колебания имеют бесконечно большой период. Имеется ли
несоответствие между этим и результатом, предыдущего упражнения? Или, подходя иначе,
показать, что решение yt сходится к 0 при w = (l — YsJ и будет взрывным при
6. Пусть линия равновесия выпуска продукции Yt=Y0(l-\-Q)t1 причем q
задано и положительно. Положить r\t = —^=—- , так что 4t=-rir—ty-in—гг—х
х ( T]f_i—л 2 ) • Исследовать решение этого конечно-разностного уравнения
относительно г]/. Показать, что оно описывает колебания в той же области значений w
(при 5=1 —с), что и yt, но что ay=(l-j-QJ при регулярном колебании. Почему для
T]f и г/г разница между затухающими, регулярными и взрывными колебаниями
неодинакова?
6.3. ИНТЕРПРЕТАЦИЯ РЕШЕНИЯ
Можно потребовать, чтобы решение модели
мультипликатора-акселератора удовлетворяло одному из двух совершенно различных условий.
Можно пожелать, чтобы yt сходилось к нулю, то есть чтобы Yt
сходилось к Yt в процессе колебательного движения или .как-либо иначе. Это
условие соблюдается только при достаточно слабом действии
акселератора, то есть когда w—v — с2<1. Оно не зависит от совокупной
предельной склонности к потреблению или к сбережениям.
С другой стороны, может быть желательно, чтобы yt колебалось
вокруг нуля, a Yt — вокруг Yt. Колебания могут быть как затухающими, так
и незатухающими. Возникновение колебаний того или иного типа зависит
от комбинации величин w и s. Это можно сформулировать следующим
образом: при данном 5, w должно лежать в интервале от (l—Y^sJ до
(l+V^) , пределы которого будут уже или [шире в зависимости от того,
будет ли s мало или велико. Можно дать и иную формулировку: если w
задано, то $ должно быть больше некоторой величины (l — VWT- Именно
это довольно сложное условие представляет наибольший интерес в теории
экономического цикла.
Чтобы представить себе порядок величины структурных постоянных
при возникновении колебаний, уместно рассмотреть несколько числовых
173

примеров. Как правило, $ может быть взято совсем малым. Если s = 0,04г
тогда колебательное движение возникает при значениях w, лежащих в
интервале 0,64 < w < 1,44. Таким образом, величина w будет близка к единице.
При s, равном 0,25, область значений расширяется до 0,25 < w < 2,25
и почти любая умеренная величина w также вызовет колебания. Такова
область ослабленного коэффициента инвестиций го. Для того чтобы получить
соответствующую область значений и для v — силы действия акселератора,
мы должны эти границы увеличить на с2. Например, в предшествующем
случае при s = 0,04 и с = 0,96 границы v передвигаются с 0,64 < v < 1,44
(при с2 — 0) до 1,6 < v < 2,4, когда с2 = 0,96, и все затраты на потребление
откладываются. По мере возрастания среднего запаздывания потребления
для возникновения колебаний требуется все более сильное действие
акселератора.
Решающей является величина ослабленной мощности акселерации
w = v — с2. Если w близко к единице, то колебания возникнут почти
независимо от величины s. В зависимости от того, будут ли w < 1 или w > 1,
колебания будут слабо затухающими или взрывными. При величинах w,
значительно отличающихся от единицы, колебания будут возникать толька
при достаточно больших значениях s. При этом они будут сильно
затухающими или сильно взрывными. Опыт показывает, что в действительности w
чаще бывает меньше, а не больше единицы. Такой вывод сделал Фишер для
Соединенных Штатов 17]. Вероятны колебательные решения модели
мультипликатора-акселератора; очень возможно, что они будут затухающими, хотя
случаи взрывных колебаний ни в коей мере не исключены. х
Величина предельной склонности к сбережениям s не влияет на
затухание колебаний, и она важна для возникновения колебаний только в случае,
если w отклоняется от единицы. Решающее воздействие s оказывает на длину
периода колебания. Период зависит от обеих структурных постоянных w и sr
а минимально возможныйв модели период, равный 2я/0т, где cos0m = ]/1 — s,
зависит только от s. Если s мало, то существует только довольно
ограниченная область значений w для возникновения колебаний, и даже самый
короткий период будет достаточно длительным. При увеличении $ становятся
возможными колебания с более коротким периодом. Переменная с
меняющимся знаком (как в паутинообразной модели) имеет период из двух
интервалов времени. В модели мультипликатора-акселератора даже при s = 0,25»
невозможны колебания меньшего периода, чем из 12 интервалов времени1.
Если же s равно только 0,04, то период колебаний должен быть больше»
30 интервалов времени.
Колебательные движения Yt внутренне присущи модели. Они заложены
в самой структуре модели и появляются в результате взаимодействия мульти-
пликатора и акселератора. Основные свойства колебаний определяются
структурными постоянными w = v — с2 и s. В частности, степень затухания или
незатухания колебаний определяется величиной г = Уго, то есть мощностью-
акселератора, уменьшенного на величину распределенного запаздывания
потребления. Период колебаний определяется 0, зависящим как от w, так
и от s. Однако период минимальной продолжительности в модели зависит
только от величины 5, то есть от совокупной предельной склонности к
потреблению или к сбережению. Эти свойства колебаний внутренне присущи модели;
они остаются неизменными и не зависят от действия каких бы то ни была
внешних факторов. В частности, на них не влияют начальные возмущения,
порождающие колебания, и любые поддерживающие их позднейшие
возмущения.
С другой стороны, не следует игнорировать влияние внешних факторов.
Чтобы возникли колебания Yt вокруг его линии тенденции, должны
существовать какие-то «начальные» нарушения, то есть что-то внешнее по отноше-
1 При s = 0,25, cos0m = 0,8660, отсюда 0т = я/6, а минимальный период равен,
2я/9т=12 (см. 6.2, упражнение 2). — Прим. ред.
174

нию к модели. Эти нарушения определяют исходный путь или фазу
колебаний. Но еще более важно, что они определяют амплитуду первого колебания,,
которое затем затухает или усиливается в зависимости от внутренних свойств
модели. В частности, если структура модели порождает почти регулярные
колебания Yt (то есть если приблизительно w = 1), то амплитуда колебаний
не является внутренним свойством модели; она скорее зависит от возмущений,
поддерживающих колебательное движение.
6.4. ПРИЛОЖЕНИЕ К ТЕОРИИ ЭКОНОМИЧЕСКОГО ЦИКЛА
Описанный выше механизм мультипликатора-акселератора сам по себе
не представляет теории экономического цикла. Его нельзя применять
механически. Возникает вопрос, является ли он полезным элементом в теории
экономического цикла. Во-первых, следует заметить, что модель
представляет собой взаимодействие мультипликатора и акселератора. Но это
взаимодействие может происходить различно (см. 3.7). Однако, будучи построенной,
модель мультипликатора-акселератора выявляет внутренние колебания У\
при соответствующей комбинации постоянных w и s. Явления, которые мы
должны объяснить в теории экономического цикла, также характеризуются
колебаниями дохода или выпуска продукции. Это внешнее сходство не
предполагает существования причинной или какой-либо иной тесной связи между
колебаниями. Напротив, наблюдаются существенные различия:
1. Экономические циклы более или менее регулярны, их нельзя
безоговорочно назвать затухающими или взрывными. Колебания же в модели
регулярны только в пограничном случае, когда w = v — с2 = 1. Теория не может
опираться на тот случайный вариант, когда акселератор обладает силой
действия как раз надлежащей величины, порождающей регулярные колебания.
2. Экономические циклы хотя и регулярны, но несимметричны. Подъем
и по форме, и по содержанию отличается от спада. В частности, подъем имеет
тенденцию быть длительнее депрессии. Колебания в модели, если отвлечься
от их затухающей или взрывной природы, будут в основном симметричными,
так как они представлены синусоидальными изменениями.
3. Амплитуда экономических циклов, по-видимому, обусловливается
их внутренними свойствами или, по крайней мере, требует объяснения.
Амплитуда же колебаний в модели не зависит от ее внутренних условий;
она произвольна в том смысле, что определяется внешними факторами или
начальными условиями.
Таким образом, для использования модели
мультипликатора-акселератора в качестве основы теории экономического цикла ее нужно
модифицировать или дополнить. Нам надо рассмотреть несколько возможных
модификаций. Быть может, дискретная модель окажется слишком жесткой, и лучше
взять непрерывную вариацию. Предпосылка линейности может быть
причиной «нереалистических» свойств модели, что в ответ потребует, возможно,
введения нелинейного акселератора.
Здесь следует отметить, что не совсем очевидны условия линейности
динамической зависимости или модели; они не так просты, как, например,
гипотеза о линейности функций спроса или предложения в статическом
анализе. В динамическую зависимость могут различными путями войти
производные, интегралы, запаздывания и отставания, и она все-таки
останется линейной. По определению, линейная модель относительно
переменной У это — такая модель, что любая включенная в нее
переменная У имеет вариацию, в которой только затухание и частота
колебания определяются структурой модели; амплитуда же и фаза любого
колебания У устанавливаются внешними факторами (например, начальными
условиями), а не структурой самой модели. Следовательно, для свойственного
системе колебания период и затухание являются структурными качествами,
амплитуда же и фаза не будут таковыми. Далее, если рассматривать
переменную У как «выход» модели, появляющийся под влиянием некоторого
175

входного воздействия, тогда вынужденные колебания на «входе» дают начало
колебаниям на «выходе» с тем же периодом и тем же типом затухания, но
с иной амплитудой и фазой (в зависимости от начальных условий). Например,
в данном случае «выпуск продукции» Yt зависит от независимых расходов At,
представляющих «вложения». Вынужденное колебание At вызывает
колебания в Yt того же периода и типа затухания, но с амплитудой и фазой,
определяемыми внешними факторами (см. 6.6). Модель Самуэльсона — Хикса
на данном этапе ее разработки, очевидно, линейна. Этого нельзя сказать
о модели акселератора Гудвина (см. 7.3 и рис. 18). Мы рассмотрим все это
в главах 7 и 8.
Тем не менее можно кратко перечислить те дополнения, которые вносит
теория цикла в нынешнюю модель Самуэльсона — Хикса. Действительно ли
постоянная акселератора v достаточно мала, и колебания Yt затухают,
или же v скорее велико и Yt внутренне присущи взрывные колебания?
Это один из критических пунктов. Даже при слабом затухании или
незатухании по истечении некоторого времени колебания становятся
«нереальными». Внутренние колебания должны дополняться внешними влияниями.
Внешние воздействия типа «беспорядочных ударов» могут продолжить
затухающие колебания. С другой стороны, взрывное колебание мы можем
удержать в определенных границах, фиксируя его «верхнее» и «нижнее»
значения при помощи внешних факторов.
Другой решающий вопрос — как ввести в колебания модели
необходимый элемент асимметрии. Это можно сделать только с помощью
соответствующих «беспорядочных ударов» или фиксирования надлежащего верхнего
и нижнего пределов. Либо же необходимо смягчить какую-либо исходную
предпосылку о симметрии, в частности гипотезу о том,.что акселератор
действует одинаково при большом и малом выпуске продукции, при росте
и сокращении производства.
Хикс [10] предпочел дополнить свою модель
мультипликатора-акселератора внешними факторами, определяющими ее верхний и нижний пределы,
и ослабить предпосылку об обратимости акселератора. Он предполагает, что v
достаточно велико для возникновения собственных колебаний взрывного
типа, но симметричных. Другие введенные им влияния несимметричны.
Верхний предел выпуска продукции определяется таким образом, что по
достижении «потолка» выпуск продукции остается постоянным и акселератор
перестает действовать. Акселератор не работает, если не происходит изменений
в выпуске продукции. С другой стороны, когда спад приближается к нижнему
пределу, акселератор совсем выключается из действия вследствие излишка
производственных мощностей и вследствие того, что списание на возмещение
основного капитала ограничено остаточной нормой. Акселератор в форме
It= v(Yt^—Yt_2) является обратимым; но для периода спада приходится
отказаться и от этой предпосылки.
Остается лишь одно затруднение. Хотя степень затухания или
незатухания колебания есть внутреннее свойство модели, амплитуда колебаний в этой,
как и в любой линейной, модели зависит только от внешних или начальных
условий. Но раз допускается выключение действия акселератора при каждом
спаде, эти «начальные» условия не относятся к области отдаленной
экономической истории. Они вновь вступают в свои права после спада в каждом цикле.
Когда акселератор вновь начинает действовать и излишних мощностей уже
нет, то начальные условия уже изменились и начинается новое колебание
со своей собственной амплитудой. В той мере, в какой каждая совокупность
начальных условий (зависящих от фактического списания на возмещение
во время спада) является более или менее одинаковой, и амплитуда имеет
тенденцию быть постоянной.
Если, следуя Дьюзенберри [6], глубже рассмотреть этот вопрос, то
окажется, что взрывные свойства колебаний в основном не имеют значения
и нет надобности в фиксировании «потолка». При первом же собственном
колебании акселератор перестает действовать при спаде, и второе колебание
176

начинается, когда акселератор действует уже при новых начальных
условиях. Краткость времени не допускает проявления действия взрывного
элемента, и колебания не обязательно достигают верхнего предела, так как
каждое из них происходит само по себе и начинается с низшей точки каждого
спада. Амплитуда может быть довольно постоянной, но не из-за
взаимодействия мультипликатора-акселератора, а благодаря сходству в начальных
условиях последовательных колебаний.
При таком истолковании применение Хиксом модели мультипликатора-
акселератора выявляет два важных свойства. Во-первых, сила действия
акселератора сможет изменяться в очень широких пределах; годится любая
величина v, соответствующая колебаниям, могущим квалифицироваться как
не слишком сильно затухающие или незатухающие. Во-вторых, хотя
модель формулируется математически как линейная, перерыв в действии
акселератора во время спада вводит нелинейный элемент. Действительно, если
It = v(Yt_1— Yt_2) для некоторых областей значений, в то время как It
является произвольной (отрицательной) величиной для других областей,
то акселератор будет нелинейным. Короче говоря, теория экономического
цикла Хикса представляет собой пример нелинейного акселератора [4,
стр. 281-284].
Этого краткого обзора достаточно для иллюстрации той роли, которую
модель мультипликатора-акселератора может играть в теории
экономического цикла. Существуют, однако, и некоторые добавочные свойства модели,
которые уместно и необходимо рассмотреть.
6.5. ЦИКЛЫ В ДВИЖЕНИИ ЗАПАСОВ
Модель мультипликатора-акселератора в той форме, которая была
приведена в разделе 6.1, можно построить и для капиталовложений в запасы
(то есть в оборотный капитал). Простой вариант модели, основанный на
работах Лундберга [11] и Метцлера [12], получается следующим образом.
Даны независимые капиталовложения At, которые определены в
последовательные периоды t = 0, 1, 2, ... . Продажи предметов потребления в
период t составляют Сп a Kt — запас их у производителей на конец периода t.
Принимаем, что производители стремятся к соответствию запасов уровню
продаж и что между этими величинами соблюдается пропорциональность.
По предположению, производители ожидают, что в период t продажи будут
в размере Ct-\, то есть такими же, как и в прошедший период. Следовательно,
AC/_t есть уровень запасов, планируемый на период t. Фактический уровень
запасов Kt отличается от запланированного уровня на разницу между
действительными продажами Ct и предполагавшимися Ct~i. Итак,
K^kC^-iCt-C^). A)
Мы принимаем, что функция потребления, определяющая продажи Cv
линейна по отношению к доходу юпгвыпуску продукции Yt и не имеет
запаздываний:
Ct = cYt. B)
Выпуск продукции Yt в период t состоит из трех элементов, планируемых
производителями: продукции, предназначаемой для продажи, или Ct—\, для
увеличения запасов (kCt_{—Kt—i) и для независимых капиталовложений At.
Итак, имеем:
Yi^C^ + ikCt^-Kt.J + At. C)
После подстановки A) и B) в уравнение C) условие действия модели будет
выражено конечно-разностным уравнением второго порядка относительно Yt:
У( = сУ(_1 + сA + А;)(У4.1-Уг:2) + ^. D)
Мультипликатор в этой модели действует через посредство функции
потребления B), не имеющей запаздываний. Фактические величины и потребления
12 р. Аллен 177

и сбережений совпадают с плановыми. Появление акселератора обусловлено
воздействием изменений в продажах на запасы и на плановые
капиталовложения в запасы. Однако, как показывает выражение A), плановые
инвестиции в запасы не осуществляются. Модель допускает непредусмотренные
капиталовложения в запасы или сокращение запасов.
Конечно-разностное уравнение D) имеет точно такую же форму, как и в
«элементарном случае» модели Самуэльсона — Хикса с нераспределенным
запаздыванием потребления (см. 6.1). Эта модель описывается уравнением
Yt = cYt_{ + a(Yt—i — Yt_2) + At*. Такова же и модель запасов D), причем
постоянная акселератора принимает форму с{1 -\- к). В данном случае
с — положительная дробь и к > 0. Отсюда следует, что постоянная
акселератора сA + к) положительна, но она может быть и больше и меньше
единицы.
Уравнение D) решается так же, как и соответствующее уравнение из
раздела 6.2. Yt является частным решением уравнения D), зависящим от
формы At. Например, если At = А — const, то Y = г—, уровень
равновесия, определяемый мультипликатором. Тогда yt = Yt — Yt удовлетворяет
уравнению
Уг = cVt-i + c(l+k) (yt_x - yt_2).
Решение описывает колебания yt, если
то есть
L?2L <1 + t< !??.
Колебания будут затухающими, если сA + к) < 1, то есть
37- (8)
Они будут регулярными, если 1 + к = -г— , и взрывными, если
1 —s •
При обычных значениях s условие E) удовлетворяется реально ожидаемыми
величинами к. Условие же F) предполагает, что к мало. Например, если
s = 0,04, к < — достаточно для появления колебаний в силу условия E),
но колебания будут затухающими лишь при &< ^т , что следует из
неравенства F).
Итак, мы приходим к выводу, что следует ожидать колебаний выпуска
продукции Y t относительно какой-то линии равновесия (определяемой
независимыми капиталовложениями)? Это и будут циклы движения запасов.
Циклы могут быть затухающими или взрывными в зависимости от того, мала
или велика постоянная к, определяющая отношение желаемых запасов к
продажам.
Эту модель можно объединить с вышеприведенной моделью (см. 6.1),
если прибавить акселератор индуцированных капиталовложений в основной
капитал (в смысле Хикса) к акселератору данной модели, индуцирующему
капиталовложения в запасы. Как указывал Бомоль [3], модель в этом случае
становится более сложной, она описывается конечно-разностным уравнением
третьего или более высокого порядка.
1 Эта модель получается из уравнения A) в разделе 6.1 при с% = 0 и а= с.-
Прим. ред.
178

Задачи и упражнения
1. Показать, что в вышеописанной модели запасов при s = 0,25 необходимо: для
возникновения колебаний к < 2 и для затухания к<^—.
о
2. Дано к. Найти величину s, необходимую для сходимости (затухания) yit
и объяснить, почему увеличивающееся s является стабилизирующим фактором в
данной модели.
3. Рассмотреть модель при к = 0. Показать, что yt удовлетворяет уравнению
и что yi всегда имеет затухающие колебания.
4. В период t доход или выпуск продукции равен Yti потребительский спрос
равен cYi и желаемые капиталовложения равны v (Yt—Yt_i)-{-kYt-\-A. Все величины
не имеют запаздываний. Оценки производителями ожидаемого потребительского
спроса С( и спроса на капиталовложения It имеют запаздывания и основаны на опыте
предыдущего периода:
Ct^cYt-г и It = viyul-Yt_t) + kYt_1 + A+Ru
где R[ — неудовлетворенный спрос на/капиталовложения (благодаря изменениям
запасов) в конце периода (t — 1). Условие действия модели: Yt = Ct-\-It.
Показать, что:
Rt — Rt_1 = (желаемые капиталовложения) — (фактические
капиталовложения в период t — l) = i;(yf_1—Yt_2)-\-kYt-i — (l— c)Yt_i-\-A.
Вывести отсюда конечно-разностное уравнение третьего порядка для Yt:
5. В модели предыдущего упражнения показать, что имеют место
непредвиденные капиталовложения, но нет непредвиденных сбережений. Модифицировать
уравнение, взяв потребительский спрос равным cYt_ly и показать, что конечно-разностное
уравнение остается уравнением третьего порядка, но что получатся как
непредвиденные сбережения, так и непредвиденные капиталовложения. (См. [3].)
6.6. КОЛЕБАНИЯ НЕЗАВИСИМЫХ КАПИТАЛОВЛОЖЕНИЙ
Теперь мы можем привести несколько дальнейших соображений о неза •
висимых расходах At, изменение которых во времени мы предполагали
всегда данным. Во всех ранее рассмотренных случаях At было либо
постоянным, либо росло с неизменным темпом. Но столь же важен и тот
возможный случай, когда изменение At во времени описывается заданным
колебательным движением. Таким образом, остается определить тенденцию
изменения Yt в этом случае и выяснить ее соотношение с собственными
колебаниями (или с иными изменениями) Yt.
Для любой модели с простым акселератором характеризующее ее конеч-
ио-разностное уравнение можно написать в виде:
t t—I i^ 1-2 f' \ /
где постоянные а и Ъ обычно берутся положительными. Для простой модели,
рассмотренной в разделе 6.1, a—w-\-c и b=w, для модели запасов (см. 6.5)
а = сB-|-А)и b=c(l+k).
Сосредоточим теперь внимание на том важном случае, когда полученное
из уравнения A) решение для Yt имеет собственные, слабо затухающие
пли слабо взрывные колебания с периодом, превышающим 4 интервала
времени. Отсюда а2<4&, и даваемое решением колебательное движение будет
описываться выражением ^r*cos@f —е), где г и 0 выражены через а и Ь:
г cos 0 = тг а и г sin 0 = ^1/46 — а2
ИЛИ
и
2 /Ъ
179 12*

Обратно, а и Ь можно выразить через г и Э:
a = 2rcos0 и Ъ = г\ B)
Мы принимаем, что г — фактор затухания — близко к 1. Далее, для периода
2я/0 > 4 величина 9 заключена в интервале @, я/2), так что sin0, cos 8
и tg0 все будут положительны. На а и Ь налагаются следующие
ограничения:
a2<46; a>0 и 6^1. C)
Для обычных случаев моделей, рассмотренных выше (см. 6.1 и 6.5), эти
ограничения удовлетворяются.
Это все, что можно сказать о собственных колебаниях модели. Теперь
предположим, что изменения независимых расходов At описываются
регулярным колебанием, заданным синусоидальной функцией
At =s Ao cos (kt — к0). D)
Это,—вынужденные (вызванные внешними факторами) колебания с
постоянным периодом 2л/к. Они регулярны, то есть не являются ни
затухающими, ни взрывными, и имеют постоянную амплитуду Ао. Постоянная к0
характеризует фазу, то есть пик колебания приходится на момент t = ко/к.
Чтобы дать представление об основной идее и сконцентрировать
внимание на практически наиболее важном случае, возьмем к < 0.
Следовательно, период вынужденного колебания длительнее периода собственного
колебания модели Bл/к > 2я/0). Нужно определить тенденцию
изменения Ур соответствующую вынужденному колебанию. Она дается частным
решением уравнения A), форма которого подсказывается сама собой:
У, = У0со8(Л*-х0), E)
то есть мы получили тот же период —, что и для вынужденного колебания.
Амплитуда и фаза колебания Ум определяемые Уо и х0, иные, и их еще
нужно найти. Выражение E) для Yt должно удовлетворять
конечно-разностному уравнению для всех значений t.
При трактовке этого условия, включающего синусоидальные функции,
можно применить методы, содержащие комплексные переменные и векторы
(см. приложение Б). Однако в дискретном анализе данной модели лучше
ограничиться элементарными методами и использовать следующие
тригонометрические соотношения:
cos (фх — ф2) = cos фх cos ф2 -}- sin фх sin ф2.
Тогда
cos (kt — х0) = cos (kt — х0),
cqs {k(t — 1) — x0} = cos {(kt — x0) — k] = cos (kt — x0) cos к +
+ sin(Atf—- x0) sin fc,
cos {k(t — 2) — x0} = cos {(kt — x0) — 2k} = cos (kt — x0) cos 2k +
+ sin (kt — k0) sin 2fc,
cos (kt — k0) = cos {(kt — x0) — (k0 — x0)} = cos (kt — x0) cos (k0 — x0) -f-
+ sin (kt - x0) sin (&0 - x0).
Подставим выражение E) в уравнение A), где At задано условием D),
и используем вышеприведенные формулы. Тогда, поскольку результат
верен для всех t, каждый из коэффициентов cos(fc? — х0) и sin (to — x0)
в полученном уравнении должен быть в отдельности равен 0.
Следовательно,
УоA — a cos/с + 6cos2&) = -40cos(A:0 — х0), |
Уо( —asinft+&sin2A:) = ^40sin(A:0 —x0). j
180

При заданных уравнением B) структурных постоянных а и Ъ,
подчиненных условиям C), и известных постоянных Ао, кик0 внешнего
(вынужденного) колебания Аг, показанного условием D), из уравнений
F) можно определить Го и щ.
Общее решение конечно-разностного уравнения A) будет иметь вид:
rl cos@* —e). G)
Очевидно, что динамика Yt будет представлять собой его собственное
колебание, наложенное на вынужденное колебание, определяемое заданным
колебательным движением независимых расходов. При соответствующих
начальных условиях (дающих ^4=0), «выпуск» Yt будет просто колебаться в тон
с вынужденными колебаниями «затрат» At, то есть будет иметь ту же
частоту, но отличную амплитуду и фазу. Более обобщенно можно сказать, что
собственное колебание имеет период 2я/0 и обычно принимается
слабозатухающим или взрывным (так как г близко к 1). Оно поддерживается
начальными возмущениями, которые через произвольные постоянные А и е
определяют амплитуду и фазу колебания. Вынужденное колебание Yt регулярно
(незатухающее) и имеет тот же период Bя/&), что и заданное колебание At.
Мы принимаем, что этот период больше периода собственного колебания.
Однако при превращении вынужденного колебания At в соответствующее
колебание Yt амплитуда и фаза колебания Yt будут другими и
определятся условиями F). В общем они зависят от природы собственных и
вынужденных (внешних) колебаний. Все определяется, следовательно, значениями
Уо и х0, фиксирующими амплитуду и фазу вынужденного колебания Yt.
Решить уравнения F) легко, когда г равно точно единице (г=1) и
собственное колебание регулярно (незатухающее). Тогда в силу B), a = 2cos0>O
и 6=1. В данном частном случае уравнения F) будут иметь вид,
Уо A — 2 cos к cos 0 + cos 2к) = Ао cos (к0 — хо),|
г (8)
Уо ( — 2 sin к cos 0 + sin 2к) = Ао sin (kQ — х0)J
Подставив в уравнение (8) cos2& = 2 cos2 A— 1 и sin 2k — 2 sin к cos /с,
получим:
yocosfc= _^ cos(ft0-x0)
il
Уо sin к — —. r^ gr sin (A:o — x0).
Следовательно,
I ko — xo =&>0 (не считая кратных 2я),
II УЛ =
— ^ ^ О
°~ 2 (cos к — cos 6) ->и'
так как А: и 0 заключены в интервале @, я/2) и так как при к < 0, то
cos/c>cos0. Результат (I) подразумевает, что колебание Yt имеет
запаздывание по отношению к колебанию At. Пик колебательного движения At
приходится на момент t = ко/к, а колебания Уt — в момент t — хо//с =
= (/с0 — к)/к = ко/к — 1, то есть на один интервал времени ранее пика At.
Результат (II) показывает, что амплитуда колебаний Yt пропорциональна
амплитуде колебания At. Множителем пропорциональности будет Х =
= 1/2 (cos к — cos0)y и X увеличивается по мере того, как к возрастает от
нуля до 0. При к — 0 колебание At бесконечно длительно, и X = 1/2A — cos 0).
Л,= 1/A — сI для рассмотренной в разделе 6.1 модели при а = 2cos 0 =
= 1+с. Амплитуда колебания Yt, заданная мультипликатором,
приблизительно равна Ао/A — с) при малом к и вынужденном колебании с про-
1 Напомним, что для модели 6.1 a = w-\-c и b = w, а так как 6=1, то а = 1-[-с,—
Прим. ред.
181

должительным периодом. С другой стороны, когда к —^ 0, то собственное
и вынужденное колебания стремятся иметь тот же период, величина
которого lL—>oo. Следовательно, при совпадении периодов собственного и
вынужденного колебаний, амплитуда колебания Yt бесконечно возрастает.
Оба колебания усиливают друг друга и вызывают значительные
колебания в движении Yt. Это —хорошо известный из физики эффект «резонанса».
Полученные результаты справедливы для строгого равенства г=1,
например для случая, когда уменьшенный коэффициент акселератора в модели
из раздела 6.1 точно равен 1. Можно показать (см. упражнение 3), что почти
то же получается и при г, мало отличном от 1, и слабо затухающих или
взрывных собственных колебаниях. Тогда амплитуда Yo вынужденных
колебаний У будет до некоторой степени затухающей. Полученные
результаты справедливы также и для вынужденных колебаний специальной, в
частности синусоидальной^ формы D). Беннион [5] исследовал эффект
несинусоидальных типов вынужденных колебаний.
Анализ приводит к выводу, что теория экономических циклов может
принимать в расчет колебания различной продолжительности. Относительно
длительные и регулярные колебания выпуска продукции, имеющие характер
тенденции, могут сочетаться с колебаниями независимых расходов того
же периода. На колебания первого типа могут накладываться одно или
более коротких колебательных движений выпуска продукции структурного
характера, присущих самой системе. Они могут возникать, например,
в результате взаимодействия мультипликатора и акселератора или
вследствие изменения запасов. Эти более короткие колебания порождаются
начальными возмущениями и по внутренней природе своей могут быть затухающими
или взрывными. Однако амплитуда длительных колебаний выпуска
продукции зависит и от собственных колебаний. Когда период колебаний
независимых расходов приближается к периоду собственных колебаний выпуска
продукции, возникает эффект «резонанса», и динамика выпуска
характеризуется все большими и большими колебаниями.
Задачи и упражнения
1. Показать, что в модели мультипликатора-акселератора (см. 6.1) г—1 возникает
как частный случай, когда w = l, так что а = 2—s, 6 = 1, Показать также, что cos0 =
= 1— 1/2s, так что период собственных колебаний определяется величиной s.
2. На рис. 13 дано геометрическое
представление частного случая,
рассмотренного в предыдущем
упражнении. Доказать, что проекция ОР на ОХ
будет 1 — B — s)cos?-f- cos 2/с, а
проекция ОР на OY есть —-B —s) sin k-\-
-\-sin2k. с помощью уравнения'(8)
вывести, что если угол РОХ равен
а, то OP cosa = -=~-cos (к0— х0) и
OP sin а = -=?-sm (A:0~x0), так что
а— о о — у0
Заметим, что в этом построении
а = к. Объяснить полученные в тексте
результаты (для г=1), в частности
влияние собственного периода
колебания (фиксируемого s) на Уо.
3. В модели из раздела 6.1 (w Ф 1)
a = w — s-f-1 и b = w. В случае
колебаний, a = 2r cos Э и b — r%. Обобщить
рис. 13 предыдущего упражнения, положив CB=CP = w, и показать, что прежние
выводы будут справедливы. Показать, что при изменении w от единицы в любом
направлении Р движется вдоль линии ВР (рис. 13). Отсюда определить, что произойдет в этом
случае с величиной Yo [10, стр. 197 — 199].
182
Рис. 13

6.7. БОЛЕЕ ОБЩАЯ МОДЕЛЬ С РАСПРЕДЕЛЕННЫМИ КАПИТАЛОВЛОЖЕНИЯМИ
Обобщение модели мультипликатора-акселератора, рассмотренной в
разделе 6.1, допускает распределение индуцированных капиталовложений
на протяжении нескольких периодов и в то же время более широкую
протяженность запаздываний потребления. В общем, функции в линейной форме
имеют вид:
Индуцированные^ капиталовложения: It — v^Yt—i— Yt_2)-\-v2(Yt—2—
-Г«-з)+...'.
Потребление Ct = c1Yt_i + c2Yt_2 + c3Yt_s+ ... .
Независимые расходы снова определяются для последовательных периодов
t=0,1,2, ... . Условие действия модели остается неизменным: Yt = Ct-\-It-{-At.
Порядок получающегося конечно-разностного уравнения зависит от
распределения запаздываний капиталовложений и потребления.
Структурными постоянными являются vt, v2, v3, ... и с1? с2, с3, ... .
В связи с этим уместно несколько уклониться в сторону. Совокупный
коэффициент инвестиций, или сила действия акселератора, будет равен г?= 1^+ v2-\-
-\-vs-{- Часто удобнее вместо vx взять в качестве структурной
постоянной значение г;и оставить обозначения v2, v3,... для фиксирования
распределения запаздываний капиталовложений. Величины с могут кумули-
роваться: с = с1+с2+?>3+.--; с' ==С2+Сз+С4+ •••»' с" = с3-\-с^+...; ...
Совокупная предельная склонность к потреблению равна с, а предельная
склонность к сбережениям будет 5=1—с. Другие кумулированные
величины склонностей к потреблению фиксируют запаздывание потребления.
Единственные ограничения заключаются в том, что все v должны быть
положительны, а все с — положительными дробями.
Достаточно общая для большинства задач модель включает два
запаздывания капиталовложений и три запаздывания потребления. Она
приводит к конечно-разностному уравнению третьего порядка:
,-У,.8)+^ A)
(см, 3.9). Это уравнение можно превратить в однородное и преобразовать.
Частное решение Yt находится по заданному At, и оно характеризует
тенденцию движения. Если положить yt = Yt—Yt, то уравнение A)
превращается в однородное относительно yt без члена, содержащего At.
Распределенное запаздывание потребления уменьшает силу действия
акселератора. Примем w1=^v1 — с' и w2 = v2 — с" и назовем их соответственно
уменьшенными ослабленными или коэффициентами инвестиций, а до = до1 +
4- w2 — v — с' — с" — ослабленной силой действия акселератора. Тогда
уравнение A) будет иметь вид:
Уь = cVt-i + wi (Vt-i - Уг-г) + w* (Vt-г - Уг-з)* B)
wl и w2, а также w могут принимать и отрицательные значения. В
уравнении B) структурными постоянными будут с, wx и w2. Часто удобнее
положить с = 1 — s и w1 = w— w2, так что структурными постоянными
будут s и ^ — соответственно совокупная предельная склонность к
сбережениям и сила действия акселератора, в то время как w2 будет
характеризовать временное распределение капиталовложений.
Для решения уравнения B) нужно найти А^, %2 и А,3— корни
характеристического уравнения:
дз _ (Wi + с) X2 + (w± — w2)X + w2 = О,
или
X3 - (w - w2 - s + 1) X2 + (w - 2w2) X + w2 = 0. C)
Решение будет иметь вид
Уг^АМ + АъЦ + АьЦ, D)
где Ах, А2, А3 —произвольные постоянные, определяемые начальными
возмущениями.
183

Постоянная w2 представляет собой новую особенность, которой не было
в простой модели. Помимо общего случая целесообразно выделить и два
крайних варианта (случая).
Первый крайний вариант: wx =w, w2 = 0. Так же как и в простой модели,
капиталовложения концентрируются на временных отрезках, ближайших
к исходному. Разница состоит в том, что капиталовложения все же
распределяются достаточно (v2=c3), чтобы учесть действие распределенного
запаздывания потребления.
Второй крайний вариант: wi=0^ w2=w. Капиталовложения
откладываются и скучиваются во втором периоде независимо от влияния
запаздывания потребления (v1=c2~{-cz).
Общий случай: ъихф0, го2ф0. Капиталовложения распределены во
времени — часть производится в первый период, а часть откладывается до
второго периода.
В дальнейшем анализе w берется как данное и принимается, что w<l —
случай затухающих колебаний или сходящегося решения в простой модели.
Такими же методами можно исследовать и случай взрывного движения
(г#>1). Величина s — другого характерного признака простой модели —
обычно совсем мала, но мы уделим некоторое внимание и ее влиянию на
решение D). Остается рассмотреть лишь, как влияет на решение величина w2 —
новая постоянная, показывающая распределение капиталовложений.
6.8. ИССЛЕДОВАНИЕ КОНЦЕНТРИРОВАННЫХ (СКУЧЕННЫХ)
КАПИТАЛОВЛОЖЕНИЙ
Так как в настоящем разделе мы применим несколько отличный подход
к вопросу, уместно резюмировать характер решения для первого случая,
концентрированных капиталовложений, совпадающего с простой моделью
(при w2—Q). Пусть s = 0, то есть предельная склонность к сбережениям равна
нулю (хотя сбережения и не фактические). Тогда решение запишется в виде
yt = Al-\-A2wi и будет сходиться к постоянной (см. 6.2, упражнение 4).
В необычном случае (w<0) возможен знакочередующийся ряд, но сходимость
в общем будет равномерной @<г#<1). По мере увеличения s, решения,
дающие колебательное движение, становятся более возможными. При данном
w колебания возникают, когда остановится достаточно большим. Условие
формулируется в виде 5>A—]/гйJ(см. 6.1, упражнение 5). Независимо от того,
будет ли движение колебательным или нет, последовательность уь сходится,
и фактор затухания колебаний определяется w. Второй случай отложенных
и концентрированных капиталовложений является новым.
Характеристическое уравнение C) из раздела 6.7 принимает вид (при wx=0 и w2=w)
или
(X-l)(X2-w) + s№ = 0. ' A)
Если 5 = 0 и 0 < ш < 1, корнями уравнения A) в порядке убывания будут:
Первый корень является доминирующим, и решение уравнения D) из
раздела 6.7 примет вид:
y^A. + A^VwY + A^-VwY. B)
Как и в первом случае, это решение сходится к постоянной. Разница
заключается в наличии знакочередующегося члена с ( — YwY. Хотя он
не является доминирующим, но представляет собой важное дополнение.
Далее, если 5 = 0 и действует лишь слабый акселератор (w < 0), то корни
Я2, Х3 являются комплексными, и yt содержит элементы колебательного
движения, которое будет очень сильно затухающим (см. упражнение 1).
184

Влияние увеличения s во втором случае на три корня уравнения A)
легче всего видеть из графического представления (рис. 14). Значения
корней даются точками пересечения кривых f(X) и g(X):
f(X) = (X-l)(X2-w) и g(X) = -sX2.
Рис. 14 сделан применительно к случаю 0 < w < 1 (необычный случай
до < 0 рассматривается в упражнении 2). Кривая f(X) пересекает ось ОХ
в точках Я = 1, Yw и —Yw, которые будут корнями при s = 0. Кривая
g(X) является параболой, достигающей максимума (вершины) в точке О.
Она слабо выпукла при малом s и более выпукла при больших
значениях s. Таким образом, рис. 14 показывает, что при возрастающих, но
f>9
/
/VST
i
\.
\ Yur
my
J
Рис. 14
достаточно малых значениях s положительные корни Хг и Х2 прибл1-
жаются друг к другу и заключены в интервале (]/ш, 1), тогда как
третий корень Х3 возрастает по абсолютной величине. Пока ( —Я3)<1, все
три корня будут дробями; два — положительными и один —отрицательным.
Решение будет сходиться к нулю с затухающим и знакочередующимся
членом, представленным величиной Х3.
При возрастании s до некоторой критической точки могут иметь место
два следующих обстоятельства. Во-первых, кривая g(X) может совсем не
пересечь кривую f(X) в области положительных значений X. Тогда корни
Хг и Х2 станут комплексными, и в решении будет содержаться элемент
колебательного движения. Это произойдет при весьма малых значениях 5,
во всяком случае меньших, чем в простой модели с условием $ > (l — ]/шJ
(см. упражнение 3). Произведение сопряженных комплексных корней
Xv Х2 = г (cos 0 ± ism 0) будет вещественным числом, то есть ХгХ2 = г2. Из
характеристического уравнения A) имеем
Х1Х2Хг= — w, то есть ХХХ2 = —^—
для любых корней. По мере увеличения s ( — X3) становится больше
значения Yw* показанного на рис. 14, так что ХХХ2 уменьшается и становится
меньше у w. Когда корни становятся комплексными (Я^ = г2), г2 будет
меньше Yw и будет уменьшаться по мере увеличения s. Колебания
в решении для уь будут затухать, и этот процесс будет идти тем сильнее,
чем больше будет становиться s.
185

Во-вторых, что также интересно, отрицательный корень Х3 становится
больше 1 по абсолютной величине: — Х3> I. Критическое значение s
теперь будет достигнуто, когда f{X) = g(X) в точке А. = — 1, то есть после
подстановки в A) 5 ==2A— w). Значит, ( — Х3) > 1, если s>2(l — w). Это
возможно лишь при достаточно большом s (все же остающемся
положительной дробью) при условии, что V2<uy<l. В общем в очень часто
встречающихся случаях, когда w близко к 1, достаточно и не слишком
большой величины s для того, чтобы было — А3>1. Тогда в решении
будет преобладать знакочередующийся элемент, то есть короткий взрывной
цикл с периодом 2.
При s = 0 решение для yt задается выражением B). Для совсем малых
s решение незначительно изменяется и принимает вид:
yt^AM + AM+AM, C)
если Х1 и Х2— положительные дроби, а Х3— отрицательная дробь. Форма
решения C) соответствует равномерной сходимости к нулю (без
колебаний). Для больших значений s решение примет вид
yt = Aricos(Qt-e) + B(--'k)t, D)
где А, В и г — произвольные постоянные. Решение D) получается тогда,
когда характеристическое уравнение имеет два комплексных r(cos 9 + /sin 6)
и третий отрицательный корень —X. Решение D) включает затухающее
колебательное движение с периодом 2я/9 и фактор затухания, определяемый
величиной г и знакочередующимся элементом, содержащим —X, По мере
увеличения s колебания усиленно затухают, но знакочередующийся элемент может
увеличиться настолько, что станет доминирующим и взрывным. При
отложенных капиталовложениях w близко к 1,и s достаточно велико. В этом
случае в движении выпуска продукции yt может преобладать короткий
взрывной цикл с периодом 2.
Несмотря на наличие коротких циклов, решение будет представлять
собой затухающее колебание. Это объясняется тем, что во всех
рассмотренных случаях 0<г#<1. Таков же анализ и для случаев, когда до> 1. Тогда
колебания будут взрывными. Все еще остается верным, что величина w —
ослабленная сила действия акселератора — определяет сходимость решения
(степень затухания колебаний). В общем и целом при любых значениях w,
близких к 1, могут возникнуть короткие циклы или знакочередование
взрывного типа.
Не следует просто Отбрасывать эти новые возможности, в особенности
перспективы появления коротких взрывных циклов. Отсрочка
капиталовложений может быть в большей степени правилом, чем исключением.
Единичный интервал времени выбирается совпадающим с запаздыванием (самым
коротким) потребления. Период для принятия решений о
капиталовложениях может быть более длительным, а запаздывания фактических
инвестиционных затрат и производства капитального оборудования — еще
большими. Однако следует ожидать, что фактические затраты на индуцированные
капиталовложения не будут производиться до второго периода после
изменения выпуска продукции. В этом случае короткий цикл или взрывная смена
фазы в динамике выпуска продукции могут произойти и при умеренной
величине предельной склонности к сбережению.
Задачи и упражнения
1. Исследовать случай II; wl = 0, w2 = w и s=0 при ау<0. Показать, что
отличные от 1 корни характеристического уравнения будут комплексными, г (cos 0 ^ i sin 6),
где г=\/Г — w и 8 = jt/2. Пользуясь этим, показать, что колебательное движение yt
будет иметь период 4 и, как правило, будет сильно затухающим.
2. Рассмотреть предыдущее упражнение (w < 0) при больших s (Ф 0). Произвести
соответствующие изменения в рис. 14 и показать, что характеристическое уравнение,
как правило, будет иметь один вещественный корень (положительную дробь) и два
комплексных корня.
186

3. Доказать, что минимальным значением / (X) будет —^=-{(\-\-?>wf^-\-l-~^w\ при
'v 3 V1
Показать, что при w = 16/27 минимум будет —-16/272 и что g(X)=— 16s/27 в нижней
части области (X=~\/rw) отрицательных значений / (X) (см. рис. 14). Вывести, что при
таком значении w и s> 1/27 = 0,037 отсроченные капиталовложения непременно
породят колебания в yt. Сравнить с условиями возникновения колебательных движений
в простой модели
5> A |/гсГJ = 0,044.
4. Исследовать вышеприведенный критерий ю>1 и показать, что в случае
отсроченных капиталовложений и при достаточно большом s будет происходить
колебательное движение yt в комбинации со сменой знаков или коротким циклом, причем
оба они могут быть взрывными.
6.9. АНАЛИЗ РАСПРЕДЕЛЕННЫХ КАПИТАЛОВЛОЖЕНИЙ
Общий случай распределенных капиталовложений при наличии двух
запаздываний и при ги1ф0 и ги2ф0 можно исследовать по тем же
направлениям, что и в разделе 6.8, начиная с исходной ситуации, когда 5=0. Это
и было сделано Хиксом [10]. Но существует и другой метод, и его полезно
рассмотреть. Когда т1ф0и ю2ф0, конечно-разностное уравнение имеет вид:
Ut = сУ1-1 + Щ (yt-i - У1-2) + Щ (У 1.2 - Уг.з)- ([)
Мы подробно рассмотрим здесь случай, когда задано w—wx-\-w2 и 0<г#<1.
Вообще говоря, это — случай сходимости решения или затухания
колебаний. Этот метод применим и к анализу других случаев: когда действие
акселератора настолько слабо, что w<0, или настолько сильно, что г#>1.
Даже если w = wx-\-w2 положительно, все же возможно, что wx или w2
будет отрицательным, так как оба коэффициента представляют
«ослабленный» тип. Если капиталовложения скучены главным образом в первом
периоде, то w2 может быть отрицательным и wx > w; если же капиталовложения
откладываются главным образом до второго периода, то wx может стать
отрицательным и w2 > w. Мы пользуемся здесь коэффициентами w и w2. Обычным
случаем будем считать 0<w2<w, но в исключительном случае может быть
w2 <0 или w2 > w.
Решение для случая распределенных капиталовложений будет yt =
= -41А,( + -Л2А4 + -43Х?, где Хх, Я2, Х3 — корни характеристического уравнения
[см. 6.7, уравнение C)]
Сравним это с решением для соответствующей простой модели (см. 6.2)
с теми же значениями w и 5, но при отсутствии распределения
капиталовложений, то есть с yt=A1X[-{-A2Xt2, где Хх и Х2 — корни уравнения
X2 - (w - s -\-1) X + w = 0. C)
Так как X Ф 0 до тех пор, пока w2 Ф 0, то уравнение B) можно
преобразовать следующим образом:
то есть
Если приравнять здесь к нулю левую часть f(X) = X2 — (w — s-\- l)X-{-w,
ю получим характеристическое уравнение простой модели C), a g(k) =
= — w2(X — lJА вводит постоянную w2 распределения капиталовложений.
Корни уравнения D) можно найти графически, определив точки
пересечения кривых f(X) и g(k), нанесенных на тех же осях. Кривая f(X)
187

для случая 0,<г^<1 показана на рис. 12. Ее пересечение с осью ОХ
дает корни уравнения C) для решения простой модели. При заданном w
кривая по мере возрастания s перемещается вверх и влево. При малых s
и 5<A — VwJ кривая изображена на рис. 12, а и простая модель имеет
затухающее, но не колебательное решение. При возрастании s, когда
*>A — Vwf> кривая на рис. 12,6 и простая модель характеризуются
затухающими колебаниями yt.
Кривая g(X) (рис. 15) при w2 > 0 представляет собой
гиперболу (случай w2 < О рассмотрен в упражнении 2). Кривая зависит от
значений w2. На рис. 15 показаны два случая. Точка минимума А
приходится на Х = — 1, и для нее величина g равна 4^2, точка максимума В
ч\
Рис. 15
Рис. 16
имеет координаты А, = 1 и ? = (). При возрастании w2 кривая становится
везде круче. Налево от точки О касательная к кривой также сдвигается
вверх, но направо от точки О она проходит вблизи точки В*
На рис. 16 изображены кривые /(к) и g(K) вместе. Хотя w принимается
неизменным, s и w2 могут принимать различные значения. Увеличение s
сдвигает /(Я) вверх и влево, а изменение положения g(X) при росте w2 показано
на рис. 15. При малых значениях s и почти независимо от w2 кривая f(X)
опускается ниже ОХ между 0 и 1 и на этом промежутке пересекает g(X) в двух
точках, а также в одной точке — в интервале @, —1). Уравнение D) имеет
три корня, по абсолютной величине меньших 1: два положительных (Хх и ta)
и один отрицательный (Л3), и решение yt сходится к нулю без колебаний.
Однако при увеличении s или w2, кривые перемещаются так, что они
не пересекаются друг с другом в области значений X @,1). Тогда
положительные, меньшие единицы корни уравнения D) заменяются комплексными, и в
решении yt появляется элемент колебательного движения. Точно так же при
увеличении яили w2 отрицательный корень возрастает по абсолютной
величине. В решении относительно yt более важное значение получает член с Хг3.
Член с XI представляет собой новое свойство, которого не было в простой
модели: он вводит в решение yt чередование знаков или короткий цикл
с периодом 2. Как видно из рис. 16, (—Х3) может быть дробью, но вполне
возможно, что (—Х3) > 1. Если при Х=—1, f(X) < g(X), то пересечение кривых
(в области отрицательных значений X) произойдет налево от Х=—1.
Следовательно, условие, что (—Х3) > 1, равносильно условию
188

то есть s> 2(l + w—2w2), или w2 > %(l + w—%s). При достаточно больших
значениях 5 или w2или соответствующей их комбинации, получается (— Х3) > 1
и знакочередующееся изменение yt будет взрывным. В^ частности, если
отложенные капиталовложения настолько велики, что w* не только
больше w, но и больше w-\-V2{l — w), то условие (—Х3) > 1 будет справедливо
при всех s. При меньших значениях w2 условие (—Х3) > 1 может соблюдаться
все же при достаточно больших значениях s.
В модели с распределенными капиталовложениями, как и в простой
модели, колебания yt при данном w возникают лишь при достаточно
больших 5. В простой модели условием возникновения колебаний является
s> (I—VwJ, и положение кривой/(X) тогда выше оси ОХ. В модели с
распределенными капиталовложениями колебания могут возникнуть и при
несколько меньшей области значений s, так как кривая f(X) может опуститься
ниже оси ОХ и все же не пересечься с кривой g(X). Из характеристического
уравнения B) следует, что произведение трех корней Хх, Я-2 и Х3 будет равно
(—го2), то есть
независимо от того, будут ли Xi и Хъ вещественными или комплексными.
При увеличении s (—Х3) возрастает, а произведение Х±Хг убывает. Когда
оба этих корня вещественны, то они представляют собой положительные
правильные дроби; когда же они комплексны [r(cos0 ± шп 6)], то произведение
ХХХ2 равно г2. Следовательно, г2 меньше 1 и уменьшается по мере
увеличения s. Колебания затухают сильнее при увеличении значений s.
Таким образом, для модели с распределенными капиталовложениями
при заданном w (О < w < 1) и не слишком малом s решение yt будет иметь
следующую форму:
yt = Arl cos @? — е) + В (— XI,
где 4, Вие — произвольные постоянные, а X означает численную величину
отрицательного корня Х3. Как и в простой модели с концентрированными
капиталовложениями, модель с распределенными капиталовложениями
содержит член, выражающий затухающее колебание; различие в том, что оно
возникает при значительно меньших значениях s, а затухание ускоряется
при увеличении s (а не остается постоянным). В добавление к этому в
решении имеется выражение, характеризующее чередование знаков (или
появление короткого цикла) вследствие отсрочки части капиталовложений. Чем
больше величина откладываемых капиталовложений и чем больше s, тем
большую роль играет выражение, характеризующее чередование знаков,
и тем более вероятным становится появление взрывного короткого цикла,
доминирующего в решении. Короткий цикл становится превалирующим
при малых или отрицательных значениях wx и, значит, при величине W2,
близкой или превышающей w. Большая величина предельной склонности
к сбережению s вызывает затухание колебаний yt и усиливает
возможность появления доминирующего в решении короткого цикла. Все это
представляет собой развитие очень сходных результатов, порученных выше
(см. 6.8) для модели с отсроченными .капиталовложениями.
Задачи и упражнения
1. Показать, что g (%) = — w2 (X— 1JД для t02>O имеет максимум 0 при Х = 1
и минимум 4ау2 при Х=—1 (см. рис. 15). Каковы будут результаты при оу2<О?
2. Показать, что при о>2<0 и 0<ку<1 кривая g (X) будет такой же, как на
рис. 15, но отраженной в ОХ. Изменить соответствующим образом рис. 16 и показать,
что решение yt в общем случае будет содержать, кроме выражения, показывающего
наличие колебаний, также и дополнительный член, характеризующий равномерное
затухание. Сравнить с простой моделью (при w2 = 0).
3. Показать, что характеристическое уравнение B) имеет корень Х=-—1 при
^2= х/г( l + w——s J и что два других корня будут заданы выражением:
— 3w2)X+w2 = 0.
189

Объяснить этот случай с помощью рис. 16 и показать, что «короткий цикл»
представлен теперь постоянным знакочередующимся выражением.
4. Показать, что случай с s —0 соответствует корню Х = 1 характеристического
уравнения B) и наоборот. Каким образом этот корень появляется в решении для yt?
Показать далее, что остальные два корня определяются из уравнения X2 — w1X — w2 = 0.
Исследовать это уравнение при положительных wx и w2.
5. Показать, что в случае. 5 = 0 (Х = 1) конечно-разностное уравнение A)
приводится к уравнению второго порядка относительно zt = yt — yt-i- Решить его
относительно zt и сравнить с результатами решения предыдущего упражнения.
6. Привести характеристическое уравнение B) к форме f(X) = g(X), где f(X) =
= X2 — (wx— s~\-l) Я + Ш! и g (X) = w2 ( 1—г- J , и графически расположить корни.
Сравнить с рис. 16.
7. Привести характеристическое уравнение B) к виду:
(X — 1) (X2-w1X~w2) = — sX2.
Исследовать сначала случай 5 = 0 (см. упражнения 4 и 5). Затем для s ф 0 и X Ф 1
привести уравнение к виду f(X) = g(X), где / (Х) = Х2 — wlX—w2i g (X)= ~s-^ — ,
л — 1
и графическим методом найти корни, как это показано на рис. 16. Вывести отсюда
результаты возрастания s от нуля.
8. Рассмотреть случай равномерного распределения капиталовложений на
протяжении двух периодов ( wt = w2= — w j. Показать, что конечно-разностное
уравнение A) примет вид:
yt = cyt-i+-2 w(Vt-i — У1-з)
и будет иметь характеристическое уравнение
Показать, что: а) либо существуют два вещественных корня Я, больших 1, и один
отрицательный X; б) либо существуют два вещественных положительных значения Я, меньших
1; в) либо же не существует вещественных и положительных значений X. Показать, что
случай (а) характеризует неколебательный взрывной рост, а случай (в) —
колебательное изменение дохода во времени. Какой смысл имеет случай (б)?
.- 2
9. Показать, что в предыдущем упражнении F (X) имеет минимум при Я=— х
о
X ( —w-\-c j . Исследовать знак F(X) при Я=1, ЯиГ—до-)"с)и показать, что
« / ч 2 f * . Л
взрывной случаи (а) из предыдущего упражнения наступает, когда — f —w-\-c J
одновременно больше как 1, так и 'fw . Показать, что, когда w = 2, взрывной рост будет
происходить лишь при с>0,9, но что при до=1 взрывной случай не может
возникнуть.
10. Распространить условия двух предыдущих упражнений на модель с
равномерно распределенными капиталовложениями на протяжении п периодов
= w3... =доп = — w j , описываемую конечно-разностным уравнением
w/ = ci//_i-| w (yt-i—yt-n-i)> см. [1].
п

ГЛАВА 7
ТЕОРИЯ ЭКОНОМИЧЕСКОГО ЦИКЛА ГУДВИНА,
КАЛЕЦКОГО И ФИЛЛИПСА
7.1. ВВЕДЕНИЕ
Изложенная в главе 6 теория Самуэльсона — Хикса представляет
собой пример дискретного анализа колебательных движений в
количественной макроэкономической модели. В этой модели особенно интенсивно
применяется дискретный анализ и полностью используются (или по крайней мере
могут быть использованы) преимущества, связанные с введением различного
рода распределенных запаздываний, порождаемых действием
мультипликатора и акселератора. Однако в этом подходе имеются и некоторые свои
теневые стороны. Фактические затраты на потребление и капиталовложения
ставились в зависимость от уровня и изменений дохода на протяжении прошлых
периодов. Эти расходы распределялись во времени в зависимости от
принятой формы запаздывания. Суммирование этих двух видов затрат и
независимых расходов давало в итоге выпуск продукции и доход. Таково было условие
действия модели. Модель включала одно распределенное запаздывание на
стороне потребления и одно на стороне капиталовложений. Однако в
действительности положение не столь просто. Например, в отношении
капиталовложений име^т место запаздывание между изменением дохода и решением
инвестировать (то есть спросом на инвестиционные блага) и дальнейшее
запаздывание между решением инвестировать и фактическими затратами на
покупку произведенного оборудования (то есть запаздывание предложения
элементов капиталовложений). Могут быть и дополнительные запаздывания
или упреждения между расходами на капиталовложения и фактическими
поставками или монтажом оборудования. Но коль скоро эти затраты
рассматриваются в народнохозяйственном разрезе, временные расхождения
между фактическими оплатами и поставками либо вообще игнорируются,
либо считаются чем-то добавочным или второстепенным. В дискретном
анализе — независимо от формы распределенного запаздывания — акселератор
сводит все эти временные разрывы к одной зависимости. Вообще говоря,
возможно выделить различные типы запаздываний, но это нелегко сделать
при дискретной форме модели.
Хотя при непрерывном анализе запаздывания могут носить более
специальную форму (показательной функции), но в этом случае легко различить
запаздывания на стороне спроса и предложения. Наглядной иллюстрацией
тому является теория Филлипса, изложенная выше (см. 3.4 и 3.5). Спрос
распадается на две части: спрос на потребительские товары и на элементы
капиталовложений (каждый из них включает и независимые расходы). Спрос на
предметы потребления может отставать во времени от определяющего его
уровня дохода, то есть решение о потреблении может зависеть и от прежнего
уровня дохода. И, что еще важнее, спрос на инвестиционные блага, то есть
момент принятия решения об инвестировании, может отставать во времени
от изменения выпуска продукции, вызвавшего их. Напротив, предложение
предметов потребления и инвестиционных благ может реагировать на
изменение спроса с совершенно другими различными между собой запаздываниями.
Даже и при отсутствии запаздываний предметов потребления (именно такую
предпосылку вводит для удобства Филлипс) сохраняются все же два
запаздывания: спрос на капиталовложения реагирует с запаздыванием на
изменение выпуска продукции, а предложение их запаздывает при изменении спроса.
191

В настоящей главе рассматриваются некоторые динамические модели,
в которых время принимается непрерывно меняющимся. Такие
экономические величины, как выпуск продукции и доход У, изменяются тогда как
функции времени. Это вовсе не предполагает обязательно непрерывности
функций. Обычно У изменяется во времени непрерывно. Однако могут иметь
место и нарушающие непрерывность резкие скачки в уровне или
направлении изменения У. Следует принять также во внимание возможность
нелинейного изменения У в верхних и нижних пределах. Возможности введения
запаздываний не столь велики, как в дискретном анализе, но все же остается
еще большой выбор. В особенности важно провести различие между
отставанием и непрерывно распределенным запаздыванием. При наличии
временного отставания 0, одна переменная влияет на другую по истечении точно 0
единиц времени. Например, заказы на суда и сумма платежа за них могут
непрерывно изменяться во времени. Но поставки судов, заказанных в
настоящий момент, должны быть оплачены точно через 15 месяцев. Однако для
большинства случаев запаздывающей реакции предпосылка непрерывно
распределенного запаздывания является более «реалистичной». Ответная
реакция становится с течением времени постепенно более сильной, например при
производстве платежей в промежутке между моментом заказа судна и
моментом его поставки. Если Y определяется величиной Z, но эта зависимость
включает запаздывающую реакцию, то соответствующая корректировка
У во времени произойдет даже и в том случае, если имел место только один
сдвиг в Z. Если же изменяется также и Z, то У варьирует тогда во времени
по двум причинам: в своей реакции оно должно отразить прошлые изменения
в Z и не отставать от текущих. Выбор формы непрерывно распределенного
запаздывания отчасти является лишь вопросом удобства для упрощения
математического анализа: можно взять столь хорошо поддающееся анализу
запаздывание в виде показательной функции или более «реалистическую»
форму — последовательность нескольких запаздываний в виде
показательных функций.
В настоящей главе рассматриваются лишь несколько отобранных
моделей разных типов из числа появившихся в литературе начиная с 30-х годов.
Подробно исследуются лишь три модели: отчасти потому, что они
иллюстрируют различные аспекты проблем экономического цикла.
Прежде всего надо назвать модель Гудвина [2J, во многих отношениях
напоминающую модель Самуэльсона — Хикса. Но Гудвин разработал свою
модель самостоятельно и включил в нее некоторые особенности модели
Филлипса. Характерной особенностью модели Гудвина является введение
нелинейного элемента в систему взаимодействия
мультипликатора-акселератора. Основное построение модели Самуэльсона — Хикса приводит к
колебательному движению вообще слабо взрывного типа. И лишь позднее
вводится нелинейный элемент в форме верхних и нижних пределов или в форме
допущения меняющегося соотношения спроса на капиталовложения в
периоды подъема и падения конъюнктуры. Преимущество модели Гудвина
состоит в том, что нелинейный элемент «встроен» в нее в самом начале.
Получающееся в результате колебательное движение совершенно не зависит от
внешних факторов или частных начальных (или бывших до этого) условий. Модель
Гудвина включает запаздывания двух типов: на стороне спроса на
капиталовложения — отставание с фиксированной продолжительностью действия
акселератора, а на стороне предложения имеет место непрерывно
распределенное запаздывание.
Далее, существует модель Калецкого [3] и ее более поздние варианты
[4, 5]. Первая модель Калецкого появилась еще до работы Кейнса,
оказавшей глубокое влияние на направление развития теории экономических
циклов. Вследствие этого она имеет ряд специфических особенностей, в
частности это касается связи между капиталовложениями и величиной основного
капитала. Калецкий вводит в модель как фиксированное отставание (между
решениями инвестировать и поставлять оборудование), так и непрерывные
192

изменения, представленные производными и интегралами. Модель Калец-
кого, как и модель Гудвина, носит смешанный характер. Окончательное
уравнение модели, хотя и совсем простое по форме, является смешанным
дифференциально-разностного типа. Такое уравнение непросто решить
и нелегко объяснить полученное решение. В частности, оказывается, что
возможные колебательные движения охватывают целый ряд циклов с
возрастающей частотой (уменьшающимся периодом). Причина этого лежит
в предпосылке о наличии фиксированного отставания. Его введение
доставляет немало трудностей в дискретной модели Самуэльсона — Хикса, но еще
больше их возникает при комбинировании фиксированного отставания
с непрерывным изменением во времени.
Эти трудности наводят на мысль о том, что сформулированная Филлип-
сом [7] модель мультипликатора-акселератора, возможно, будет более
продуктивной для дальнейшей разработки. Основное построение модели уже
было описано в разделах 3.4 и 3.5. Все запаздывания в модели непрерывно
распределенного вида, и они приводят к дифференциальным уравнениям
невысокого порядка; существует внутренне присущий модели элемент
взрывного характера. Этот элемент необходимо сдерживать с помощью
других факторов. Только акселератор выполняет это. Для этой цели в модели
Самуэльсона — Хикса и Гудвина вводится нелинейный элемент, а в модель
Калецкого — фактор «затухания» колебаний в форме расширения
капитального оборудования. Модель же Филлипса ведет к рассмотрению в более
широком аспекте проблемы экономического регулирования и
стабилизации.
7.2. ПРОСТОЙ ВАРИАНТ МОДЕЛИ ГУДВИНА
Нелинейную форму акселератора Гудвина легче всего пояснить на
примере его простейшей модели с «грубыми допущениями относительно
технического прогресса» [2, стр. 4—8]. Все переменные являются функциями
непрерывно меняющегося времени, и условие действия модели сводится
к известному соотношению для дохода или выпуска продукции:
где С = cY — функция потребления без запаздываний, / — определенная
тем или иным образом сумма чистых капиталовложений и А — независимые
расходы на потребление. Подставив в формулу для Y выражение С,
получаем соотношение, соответствующее мультипликатору без запаздываний:
А принимается постоянным.
Акселератор в нелинейной форме вводится при истолковании чистых
капиталовложений /. Пусть в какой-то момент времени К — фактическая,
а К — желаемая величина основного капитала. Тогда, по определению,
I = — . Примем
K = vY-\-at,
$-»?+••! B)
Здесь а — положительная постоянная, характеризующая тенденцию
технического прогресса, положительный коэффициент v — предельная величина
желаемого отношения капитал—-доход; v предполагается постоянным.
Остается связать фактическую и желаемую величины основного
капитала. Существуют две границы для величины фактических
капиталовложений. Нижняя граница определяется постоянной нормой
возмещения (или износа) М наличного капитала, верхняя — постоянной
мощностью L + M отраслей, производящих капитальные блага. Валовой выпуск
13 р. Аллен 193

этих отраслей должен находиться в интервале (О, L + M), а чистый выпуск
(I~dK/dt) — B интервале ( —М, L). При нелинейном характере
зависимости предполагается, что капиталовложения держатся на высшем уровне-
до тех пор, пока К < ЛГ, что они равны величине тенденции (а) при К— К
и достигают нижней границы при К> К:
I = —- = .?, а или — М C)
в соответствии с тем, что К меньше, равно или больше К.
Нелинейный акселератор, введенный уравнениями B) и C),
характеризует косвенную зависимость / от изменения выпуска продукции dY/dt.
Последнее меняет желаемую величину основного капитала К в силу
B), что в свою очередь через уравнение C) определяет норму
фактических капиталовложений.
Уравнения A) —C) описывают систему. При I=-j- уравнения A) и
B) преобразуются так:
г? v fdK
В любой фазе, определяемой условиями C), I = dK/dt остается постоянным,,
то есть равным L, а или — ЛТ, и, следовательно, из уравнения D) можно
установить следующие возможные фазы:
Таблица 1
Фаза
К—К<0
к—к—о
К К>0
dK
dt
L
а
—М
Y
A+L
1-е
Л+а
1 — с
А — М
1-е
к
-IL-(A+L)+ut
~(A+a) + at
1JL-{A^M)+at
dK
dt
a
a
a
d (K~K)
dt
L a
0
— (Af+e)
Помимо действия тенденции (а), изменения связаны лишь с переходом
системы от одной фазы к другой. Действие системы лучше всего
показывает «фазовая диаграмма» на рис. 17, в которой значения d(K — K)/dt
нанесены против значений К — К.
Точка О на рис. 17 характеризует положение (подвижного)
равновесия при условии, что dK/dt^dKjdt — a и Y = (Л + а)/A — с), как дается
мультипликатором. Капиталовложения развиваются с желаемой скоростью
тенденции, и, коль скоро достигнуто положение равновесия, оно
сохраняется и в дальнейшем. Однако оно неустойчиво. При наличии
начальных нарушений система не будет стремиться к положению равновесия,
она будет описывать регулярные колебания, определяемые циклом ABCDA
на рис. 17. Мы рассмотрим кратко характерные особенности различных:
фаз, изложенных в табл. 1.
Допустим вначале, что К> К, так что d(K — K)/dt= — (М + а) < 0.
Следовательно, К —К положительно, но уменьшается с течением времени
до нуля. На рис. 17 это движение от С до D показано линией CD. По
достижении точки/), K = K = v(A — Af)/A — с) +at. Но тогда d(K — K)/dt
превращается в нуль, и К увеличивается до v(A + a)/(l~~c)-\-at. Сразу же
К<К, так что d(K — K)/dt становится равным (L — a) > 0 и К
возрастает до v(A-{- L)/(l — с) -\-aU Следовательно, по достижении точки D
немедленно, без остановки в точке О, происходит скачок в точку А. Фаза,
194

К—К отрицательна, но в течение времени, пока она находится в
действии, она возрастает до нуля (движение от А к В). Когда достигнута
точка В, то путем обратного процесса следует непосредственное
возвращение в точку D, и цикл начинается снова.
Регулярное колебание представляет собой цикл чередующегося
подъема (АВ) и спада (CD). Следует подчеркнуть, что подъем и спад
имеют разную продолжительность. Во время подъема
dK
dK
= a и К =
то есть К возрастает, так что увеличение К со скоростью L будет
продолжаться до тех пор, пока К не достигнет растущего значения К.
В период депрессии
dK
IF''
= а и К =
то есть уровень К меньше, но, как и прежде, К возрастает. Уменьшение
К (со скоростью М) будет продолжаться до тех пор, пока не совпадут
падающее К и растущее К. Как показывает движение во времени К ж К
dt »
л\
\
\
N
4
\
\
\
в'
0
J
\
\
\
\
\
4
\
V ш
0 \
к; К
Рис. 17
Рис. 18
(рис. 18), подъемы в общем продолжительнее депрессий. Это
подтверждается и соответствующим движением У (рис. 20, а). Из табл. 1 видно,
что значения У чередуются в интервале [(А + L)/(l — с), (А — М)/A — с)], тогда
как I = dK/dt — B интервале (Z, —М). Такие чередования представляют
собой прерывные изменения Y и / и совершенно не соответствуют эконо-v
мической действительности. Они являются результатом введения слишком
специальной формы акселератора —без запаздываний. Более общий и
«реалистический» вариант модели мы рассмотрим в разделе 7.3.
Хотя эта модель и недоработана, она имеет три положительных
свойства. Во-первых, в системе имеются присущие ей самоподдерживающиеся
колебания. Взрывной характер акселератора сдерживается косвенной
(или нелинейной) зависимостью инвестиций dKjdt от изменения выпуска
продукции dY/dt. Нет необходимости ни в «потолке» модели Самуэльсона-
Хикса, ни в ряде «беспорядочных ударов» для сохранения затухающего-
колебательного движения. Более того, колебательное движение совсем
не зависит от начальных условий (см. упражнение 2). Во-вторых,
продолжительность подъема и депрессии неодинакова, они могут совпасть лишь
случайно. На рис. 18 желаемая величина основного капитала К увеличивается,
хотя и скачками, с постоянной скоростью а, фактическая величина
основного капитала в период подъема увеличивается со скоростью L, а во время
депрессии уменьшается со скоростью М. Продолжительность подъема
по сравнению с депрессией больше для высокого темпа технического
прогресса а и для высокой нормы возмещения основного капитала по
отношению к мощности отраслей, производящих капитальные блага. В-третьих,
195 13*

проводится различие между индуцированными и независимыми изменениями
желаемого уровня основного капитала. Изменение желаемой величины
основного капитала представляет собой сумму индуцированных изменений (vY)
и накопленных изменений, связанных с техническим прогрессом, который
является независимым фактором. Так снимается большая часть возражений
против разделения изменений на независимые и индуцированные. В то же
время становится возможным легко приспособить модель к теории обновления
основного капитала, развитой Шумпетером. Равномерный рост желаемой
величины основного капитала отражает тот факт, что технические
изменения во времени могут происходить довольно регулярно. Но фактическая
величина основного капитала возрастает неупорядоченно и с
запаздываниями.
Задачи и упражнения
1. Показать, что падение К в точке В на рис. 17 равно v (L-\~M)/A — с) и
тождественно росту К в точке D. Доказать, что излишек основного капитала,
освобождающегося во время депрессии, равен дефициту его в период подъема. Объяснить это
с помощью рис. 18 и связать с различиями в продолжительности подъема и депрессии.
2. С помощью рис. 17 показать, что при начальном положении К <i? (вместо
К>К) получится тот же самый цикл и что он не зависит от величины
первоначальной разности между К ж К.
3. Показать, что существо модели не изменится, если допустить неуклонный
равномерный во времени рост независимых расходов на личное потребление.
7.3. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МОДЕЛИ ГУДВИНА
Рассмотренный в предыдущем разделе простой вариант модели Гудвина
отражал взаимодействие между мультипликатором и нелинейным
акселератором, но он не учитывал запаздываний. Модель можно расширить в двух
направлениях. Во-первых, можно ввести более общую форму нелинейного
акселератора и, во-вторых, принять, что модель действует с
запаздыванием, имеющим, по Гудвину, форму фиксированного отставания. Вводится
мультипликатор в динамической форме путем присоединения запаздывания
предложения, то есть имеет место замедленная реакция на изменение спроса,
по форме очень напоминающая мультипликатор Филлипса (см. 3.4).
Спрос характеризуется уравнением
Z = C + I + A, A)
где Z — совокупный спрос, складывающийся из спроса на предметы
потребления С, элементы капиталовложений /, а также независимых расходов.
Все эти составные части представляют собой фактические затраты. Как и
прежде, функция потребления имеет простейшую форму С — cY (без
запаздываний). Предполагаем, что фактические затраты на капиталовложения
производятся через фиксированный промежуток продолжительностью в 6 единиц
времени после принятия решений об инвестициях B(t), т. е. I(t) — B(t — 0).
Акселератор здесь выступает как зависимость между объемом решений
о капиталовложениях B(t) и текущей скоростью изменения выпуска
продукции dY(t)/dt. В общей форме это можно записать так:
где ф —некоторая нелинейная функция. Подходящая форма этой функции
Ф показана на рис. 19. Для малых изменений (увеличений или
уменьшений) выпуска продукции действует акселератор в обычной форме В = vdY/dt.
При большом увеличении выпуска продукции уровень В повышается до
верхнего предела L, поставленного наличными мощностями отраслей,
производящих капитальные блага. При большом сокращении выпуска
продукции В понижается до нижнего предела ( —М), поставленного нормой
износа основного капитала.
196

Сравним все сказанное с «грубой» формой акселератора,
представленной уравнениями B) и C) в предыдущем разделе. Теперь между
капиталовложениями / = dK/dt и решениями об инвестициях имеется
запаздывание, а объем решений плавно изменяется в зависимости от изменений
выпуска продукции dY/dt. Но, как и прежде, этот объем ограничен теми
же двумя пределами L и —-М. В уравнениях B) и C) из предыдущего
раздела предполагалось, что 1 = — = В принимает лишь значения L и — М
(не считая неустойчивых промежуточных положений), и переход от одного
значения к другому совершался скачком.
Положение спроса характеризуется функцией С = cF, a
Подставляем эти функции, а также заданную величину независимых
расходов А в уравнение A). Получаем следующее уравнение:
B)
Фактор технического прогресса учитывается вместе с любыми независимыми
потребительскими расходами в члене А уравнения B), причем А может
быть задано в любой форме, например, в форме равномерного роста во
времени: A —at.
На стороне предложения происходит следующее. Выпуск продукции У
берется с запаздыванием по отношению к спросу Z. Это запаздывание
представлено в непрерывно распределенной форме показательной функции
$L=-X{Y-Z), C)
где А,— скорость реакции и 1Д— временная постоянная запаздывания. Сам
Гудвин приравнивает выпуск продукции У выражению B) для потребления
и капиталовложений, добавляя лишь член ( -~г~Л7 \ который, по его
словам, «аналогичен запаздыванию в обычном дискретном динамическом
анализе» [2, стр. 9]. Итак, он берет
или
и е есть временная постоянная обычного запаздывания показательной
формы C).
Объединение спроса и предложения, то есть уравнений B) и C), дает
ИЛИ
Это есть уравнение общей модели Гудвина. По форме оно представляет собой
смешанное дифференциально-разностное уравнение1. Если независимые
расходы А неизменны во времени, то тогда Y(t) = Y (постоянной) будет
совместно с уравнением D) при условии, что У = -4/A — с). Описываемая
уравнением D) модель имеет уровень равновесия, заданный статическим
мультипликатором. Остается определить динамику Y(t) при наличии любых
начальных возмущений. Эта динамика определяется из решения уравнения D).
1 Дифференциальное уравнение с запаздывающим аргументом.-— Прим. ред. ?
197

Сравнение этой модели с моделью, включающей лишь «грубый»
акселератор (см. 7.2), можно провести для специального случая, когда 0 = 0
и нет запаздывания в действии акселератора. Тогда уравнение D)
превратится в дифференциальное уравнение
-т4-,' 'E)
которое можно решить аналитическим или графическим методом, если
определена форма функции ф, то есть если дано ее аналитическое или
эмпирическое (графическое) выражение. Соответствующее уравнение модели из
раздела 7.2, полученное на основе табл. 1 того же раздела, будет иметь вид
,г 1 dK , A
1-е dt ' 1-е ' ^'
где dK/dt = Lb период подъема и dK/dt = — М в период депрессии. Сравнение
уравнений F) и E) явно показывает специальную форму нелинейного
акселератора, рассматривавшегося в предыдущем разделе. Изменение У,
заданное уравнением F) (при
постоянном А), представляет собой
ступенчатую функцию, изображенную на
рис. 20, а. Как показано Гудвином,
динамика У, характеризуемая
уравнением E), будет иметь вид линии, ~~
показанной на рис. 20, б, если А
У
A+L
1-е
AM
О
а
i
i—'
i
!
I
t
I
-
;
|
|
I
\
t
\
L
О
У
~~/'—
/
-Af
tr— /
/
sX ф(
an
dY
dt
Рис. 19
Рис. 20
постоянно, а функция <р имеет форму, изображенную на рис. 19. Доход У
уже не движется скачками; он описывается непрерывной линией,
направление которой испытывает разрывные изменения в моменты кризисов1.
Продолжительность периодов подъема удлиняется по сравнению с
продолжительностью депрессии. Возрастание выпуска.продукции (дохода) У наиболее
быстро происходит в начале подъема, а затем замедляется. Аналогичный
процесс имеет место и при сокращении производства в период депрессии.
Смешанные дифференциально-разностные уравнения формы D)
появляются в связи с предпосылкой о наличии отставания с фиксированной
продолжительностью в функции акселератора. Это допущение вводится
Гудвином для упрощения, а не в качестве выражения экономической «реальности».
В самом деле, 0 есть среднее запаздывание между моментом принятия решений
об инвестициях и фактическими затратами на капиталовложения, равное
1 Такие точки непрерывной кривой носят в дифференциальной геометрии
название особых точек.— Прим. ред.
198

-«приблизительно половине времени, требующегося для производства»
[2, стр. 12]. Отставание лучше заменить непрерывным запаздыванием в форме
показательной функции. Такая замена, вероятно, предпочтительнее с
экономической точки зрения и безусловно облегчает математический анализ
(см. 3.5).
Гудвин дает графическое интегрирование (решение) уравнения D),
основанное на методах, применявшихся для решения аналогичных проблем
в электротехнике и описанных Ле Корбейлем [6]. В главе 8 мы рассмотрим
эту проблему с иной точки зрения и используем подход к ней, предложенный
Тастином [11]. Графическое решение Гудвина можно сравнить с
аналогичными и аналитическими решениями, полученными Стротцем, Мак-Эналти
и Нейнсом [9], приведенными в работе Тастина [11]. Главный результат
сводится к следующему: колебательное движение Y(t), получающееся из
уравнения D), приводится к циклическому движению определенного типа.
Кроме того, в пределах самого фиксированного отставания возникает серия
высокочастотных колебаний (с коротким периодом). Этот «ограниченный
цикл» зависит от пределов L и М, наложенных на акселератор (см. рис. 19),
но он несинусоидальный по форме. Следовательно, восходящая и нисходящая
ветви не имеют одинаковой формы или продолжительности. В частности,
высокие уровни выпуска продукции (дохода) более продолжительны в период
подъема, а низкие уровни выпуска (дохода) держатся дольше (в период
депрессии) по сравнению с продолжительностью их при движении по
обычной синусоиде.
7.4. РАННИЙ ВАРИАНТ МОДЕЛИ КАЛЕЦКОГО
Динамическая модель Калецкого [3], [4], [5] впервые была предложена
в докейнсианский период, и с тех пор она была значительно
усовершенствована. Модель приводит к смешанному дифференциально-разностному
уравнению. Оно в общем мало изменялось по форме в последовательных
вариантах модели, но менялось его истолкование. В настоящем разделе
анализируется по существу ранняя модель Калецкого [3] лишь с незначительными
изменениями.
Переменные снова являются функциями непрерывно изменяющегося
времени. Принимается, что мультипликатор, то есть функция потребления,
или предложения, не имеет запаздываний. Внимание концентрируется на
факторах, определяющих принятие решений об инвестициях и фактических
затратах.
Условием действия модели является хорошо знакомое разложение
выпуска продукции (дохода) на потребление С, накопление / и независимые
расходы А:
где С = cY и А заданы. Следовательно, доход определяется
капиталовложениями в соответствии с мультипликатором без запаздываний:
A)
1 — с
Центральной переменной на стороне капиталовложений является B(t),
определяющая решения об объеме инвестиций в момент t. Предполагается,
что в соответствии с решениями инвестировать (то есть с заказами на
капитальное оборудование) через фиксированный интервал времени 6
производятся поставки и осуществляются денежные платежи в течение периода
производства и установки оборудования. I(t) представляет собой фактические
чистые затраты на капиталовложения в денежном или натуральном
выражении. Чтобы выделить поставки, опять-таки за вычетом возмещения,
обозначим через K(t) запас наличного основного капитала в момент t, так что
скорость поставок нового оборудования, не предназначенного для возмеще-
199

ния, составит dKjdt. Предпосылка о наличии запаздываний на стороне
капиталовложений приводит к следующему:
B)
Q). C)
Определение B(t) напоминает акселератор в других моделях, но взятый
здесь лишь в несколько отличной форме. Предпосылка сводится к
следующему: на B(t) влияет в прямом направлении норма сбережений S(t) —
= A — c)Y(t) и в противоположном направлении наличный запас основного
капитала K(t). Если принять эти зависимости пропорциональными и не
имеющими запаздываний, то в таком случае
где а и к — положительные постоянные и 8 есть член, выражающий
тенденцию, взятый здесь в виде постоянной, но в общем могущий изменяться
с течением времени. Следовательно,
Очевидно, что объем решения об инвестициях зависит не от изменений
дохода dY/dt (как в акселераторе), а от его уровня У. Если коэффициент
а очень велик, эта зависимость может оказывать неустойчивое влияние.
Но решение инвестировать зависит также (в противоположном смысле)
и от наличного запаса основного капитала, и при большом коэффициенте к
эта зависимость оказывает очень важное умеряющее влияние на систему.
Действительно, следует ожидать, что совместное действие изменений У
и К на решения об объеме инвестиций будет подобно влиянию слабого
акселератора.
Важно отметить, что при отсутствии в системе отставания 0, то есть
при отсутствии его в уравнениях B) —D), зависимость между
капиталовложениями и доходом будет точно такая, как при акселераторе с
запаздыванием. При 0 = 0 уравнения будут иметь вид:
Продифференцируем последнее из них и результат подставим в остальные:
— — М— ) — — к—
то есть
dl 7 r 7 dY a A-е)
ж+к1=кг)и> где v—Чг1-
При операторной записи дифференцирования D — j-, получим
Это выражение представляет собой акселератор с непрерывным
запаздыванием в форме показательной функции. Мощность акселератора
а = аA — с)/к, а временная постоянная его запаздывания Г = 1//с.
Постоянная к зависит от выбранной единицы времени; она проявляется
как норма решений об инвестициях по отношению к наличному основном]/
капиталу. Она определяет временную постоянную запаздывания
акселератора. Постоянная а не зависит от выбора единицы времени.
Обычно а представляет собой положительную дробь, причем если
оно мало, то заключающийся в модели Калецкого акселератор действует
200

слабо. Для подтверждения того, что а будет малой величиной, заметим,
что сбережения, за счет которых финансируются капиталовложения,
состоят главным образом из нераспределенных прибылей и прочих
«внутренних» сбережений предприятий, которые значительно меньше общей
величины сбережений в народном хозяйстве.
Система полностью описывается уравнениями A) —D). Она включает
четыре переменные величины: Y(t), I(t), K(t) и B(t). Зависимости
достаточны для исключения трех переменных и получения одного уравнения
относительно четвертой. Выберем для этой цели переменную К (t) — величину
основного капитала в момент t. Подобное же уравнение можно получить
и для любой другой переменной, например Y(t) или I(t). Из уравнений
B) и C) имеем
t-e
то есть
1
= е
Затем из уравнения A) получаем
Подставим это выражение и В (t) = -j-K(t + Q) из C) в уравнение D):
то есть
Приходим к уравнению относительно K(t). Это смешанное дифференциально-
разностное уравнение. При условии, что А и 8 постоянны во времени,
существует уровень равновесия К = (аЛ + е)/й:. Если К измеряет
отклонение от К и если t преобразуется в ? — 9, то уравнение примет вид:
Динамика K(t) находится из решения уравнения G). Остальные
переменные получаются из уравнений C), E) и F). Если Y(t) также измеряет
отклонение от уровня равновесия У = Л/A —с), то в таком случае
Задачи и упражнения
1. Рассмотреть случай, когда сбережения и наличный основной капитал
оказывают влияние на валовые, а не на чистые капиталовложения, так что уравнение D)
будет характеризовать решения относительно объема валовых капиталовложений.
Показать, что модель не изменится, если норма возмещения 1? (t) принимается
неизменной на протяжении цикла. Оправдано ли это? Если нет, то какие затруднения
возникнут в случае R(t)t пропорционального К (t)?
2. Показать, что У (t) удовлетворяет точно такому же уравнению G), как и К (t)y
и что, следовательно, динамика У (t) будет отличаться от динамики К (t) лишь
начальными условиями.
3. Исследовать влияние на уравнение G) введения члена -\-vdY/dt как фактора,,
определяющего объем утвержденных инвестиций [как в уравнении D)]. Объяснить
с помощью акселератора и егб взрывного действия.
201

7.5. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНОГО УРАВНЕНИЯ
Без потери общности единицу времени можно выбрать так, что 0 = 1,
то есть будет равно фиксированному интервалу времени между моментом
размещения заказов и получением по ним капитального оборудования.
Вариация основного капитала в модели Калецкого определяется из
решения уравнения G) из предыдущего раздела:
^-^aK{t)-bK(t-l), A)
где 0<а<1 и Ь — (а-\-к)>0. Решение относительно Y (t) получается сразу
из соотношения:
K(t+l)-K(t)
- tzt
Полная схема решения смешанных дифференциально-разностных уравнений
типа A) была дана Фришем и Хольмом [1]. Она сводится к следующему.
Будем искать решение в форме К = Кое®г, dK/dt = QKoeQt для некоторых
значений q, которые нужно определить. После подстановки этих
выражений в уравнение A) находим
e = a-for-o. B)
Любое q, удовлетворяющее B), дает решение К = Кое& уравнения A). Если
q вещественно, то будет происходить изменение К в виде показательной
функции, которое может быть взрывным (q > 0) или затухающим к 0 (q < 0).
Легко проверить, что в случае комплексного q сопряженные значения
также удовлетворяют уравнению B). Тогда два решения вида К~Кое&
дают одно решение
), C)
д = а±ш есть решение B), а Ко и е — произвольные постоянные,
определяемые начальными условиями. Тогда изменение К будет
представлять собой колебательное движение с частотой со, которое может быть
взрывным (а > 0) или затухающим (а < 0).
Прежде всего нужно исследовать возможные вещественные корни
уравнения B). Удобно применить графический метод решения (рис. 21).
Построим график двух функций:
представляющих собой показательную кривую и прямую линию в плоскости
Oqz соответственно. Вещественные корни B) соответствуют пересечению
кривой и прямой. Кривая z± пересекает Oz в точке Q, где OQ=1. Прямая
линия пересекает координатные оси в точках В и С, причем ОВ = а/Ь
и ОС = а — оба положительны и меньше единицы. Следовательно, не
существует точек пересечения для положительных Q, а, возможно, также и для
отрицательных q. Последний пункт нуждается в полном уточнении.
Выясним условия, необходимые для того, чтобы прямая ВС касалась.
показательной кривой в какой-либо точке Р, где Q < 0 (возможна лишь
одна такая точка). В точке касания Р ординаты и наклоны линий1 z1 и z2
между собой равны, то есть
1 Наклон прямой определяется коэффициентом при q, то есть (—1/6); наклон
кривой— тангенсом угла касательной к кривой в точке q с осью Oq% то есть (— е~с). Отсюда
и получается уравнение в тексте —e~Q= — -т- . — Прим. ред.
202

Следовательно, из второго уравнения Q — lnb. Подставим это выражение
в первое уравнение1 и напишем А = a — In b. Тогда Л = 1 есть условие
касания. Пусть а будет неизменно, а Ь уменьшается. Тогда прямая ВС
будет двигаться по часовой стрелке вокруг точки С, причем В будет
подниматься, но оставаться ниже точки Q. Если же ВС является
касательной к кривой и ее движение начинается из этого положения
D = а — In 6 = 1), то при движении по часовой стрелке будут существовать
две точки пересечения. И обратно, когда линия движется в
противоположном направлении — при неизменном а и возрастающем Ъ—тогда точек
пересечения вовсе не будет. Далее, A = a--lnb возрастает по мере уменьшения
Ъ (и потому А > 1) и падает по мере увеличения Ъ (А < 1). Очевидно, что
в зависимости от того, будет ли -Л>1, А — 1 или Л<1, уравнение B)
будет иметь либо два вещественных различных корня, либо два
вещественных равных корня, либо вообще не будет иметь вещественных корней.
Вещественные корни отсутствуют при условии
Л = а —1п&<1. D)
Это обычный случай; а является дробью а к обычно достаточно велико,
для того чтобы Ъ~а-\-к > 1 (или по крайней мере было близко к единице),
то есть чтобы In Ъ был положительным (или по крайней мере малой
отрицательной величиной). В этом случае имеет место условие D), то есть
вещественные корни уравнения B) отсутствуют, и решение уравнения A)
представляет только колебательное движение.
Затем нужно рассмотреть возможность существования сопряженных
комплексных корней уравнения B). Пусть д = а±ш, так что уравнение A)
имеет решение вида C), характеризующее колебательное движение. Делаем
подстановку q в уравнение B):
а ± i(o = a — be~ae^i<0 = а — be~a(cosw Т г sin со) = (a — be~acos(d) ± ibe~a sin а>.
Приравниваем между собой отдельно вещественные и мнимые части
уравнения:
= be~asin(d.
} E)
J
Затухающий характер колебательного движения К, описываемого
уравнением C), зависит от а. Но это имеет второстепенный интерес по
сравнению с изучением частоты колебаний, характеризуемой со. Поэтому
исключим а из E) и сконцентрируем внимание на о. Из второго
уравнения E) имеем
e6
со
то есть
Подставим в первое уравнение E):
, I., sinco cos со
In Ь +In <*(*>
со * sin со
Следовательно, со задается уравнением
—— + In sin rc = а — In fc = A < 1 в силу уравнения D).
tgCOCO ././r- \/
Положим
г, ч со , , sinco
1 Первое уравнение превращается тогда в уравнение In (a—1дЬ)=0, или
а — In 6=1. — Прим, ред.
203

Таким образом, со мы должны искать как решение уравнения
Функцию /(со), не включающую «структурных» постоянных а и 6, можно
изобразить графически с помощью тригонометрических функций. Фриш
и Хольм [1] получили ее форму (для со > 0); она изображена на рис. 22.
Очевидно, что наряду с одним малым значением со @ < со < я) существует
ряд больших значений со в областях Bя, Зя), Dя, 5я), ....
Наибольший интерес представляет именно минимальное значение со,
так как оно соответствует колебаниям К с малой частотой и с длительным
периодом. Период колебания
равен 2я/со > 2, то есть более
чем вдвое продолжительнее
фиксированного отставания
F = 1) для капиталовложений.
Все остальные значения со
больше 2я и соответствуют
колебаниям с возрастающей ча-
-2-
Рис. 21
Рис. 22
стотой, то есть с уменьшающимися периодами (все периоды меньше 1).
Все циклы высокочастотных колебаний К завершаются в пределах
фиксированного периода отставания капиталовложений, и потому они
представляют лишь ограниченный интерес.
Коль скоро определён единственный длительный цикл (с периодом
больше двух) для 0 < со < я, фактор затухания колебательного движения
а находится из уравнения F). Может случиться, что, в зависимости от
значений а и Ь = а + к, значение а>0 и, следовательно, колебательное
движение будет взрывным. Однако было найдено, что а < 0 для наиболее
часто встречающихся значений а и к, так что колебания будут
затухающими. Один типичный случай встречается, когда а-\-к=Ь = 1 и к = 1 — а
@ < а < 1). Тогда
и из F)
Ь, . , sin со •« sino) . п
b + In = In < 0.
1 со со ^
В этом случае колебательное движение всегда будет более или менее плавно
затухающим. Если а близко к 1, а к мало, то А близко к 1, а со мало
(см. рис. 22). При малом со значение sin со/со примерно равно 1 и, значит,
а ^ 0. Это —случай длительного цикла с почти регулярной амплитудой.
С другой стороны, если а мало и к близко к 1, то А мало и <о близко
204

к л/2. Для такого со значение sin со/со существенно меньше 1 и а
определенно отрицательно. Это — случай короткого цикла (примерно в 4 раза более
продолжительного, чем фиксированное отставание капиталовложений) в
котором можно обнаруживать ярко выраженные затухающие колебания.
В общем относительно модели Калецкого, сформулированной в
разделе 7.3, можно сказать, что, кроме области высокочастотных коротко-
периодовых колебаний в пределах отставания капиталовложений, имеет
место единственное синусоидальное колебательное движение во времени
величины основного капитала K(t). Обычно период колебания в несколько
раз превосходит продолжительность фиксированного отставания
капиталовложений. В зависимости от величины коэффициентов (а и к) факторов,
определяющих объем капиталовложений, колебания могут быть почти
регулярными либо в большей или меньшей степени затухающими.
Задачи и упражнения
1. Показать, что при малых а ж к возможно А = а—1пЬ>1. Доказать, что
в этом случае К (t) включает выражение, представляющее равномерное (затухающее)
движение, стремящееся к нулю.
2. Показать, что в предыдущем случае невозможны большие колебательные
движения К (t), но все же существует область высокочастотных колебаний.
3. Положив а = 0,5 и /г = 0,6, проверить, что Л<1. Показать, что co = Jt/3
приблизительно удовлетворяет /(со)=Л и что основное колебательное движение К (t) имеет
период примерно в 6 раз больший, чем фиксированное отставание капиталовложений.
Показать, что для этого колебательного движения а=—0,1 и, следовательно,
колебание затухающее.
4. Сравнить результат предыдущего упражнения с результатом, полученным
при а = 0,5, к = 0,2. Показать, что основное колебательное движение будет теперь
иметь более длительный период и будет затухать медленнее.
7.6. МОДЕЛИ КАЛЕЦКОГО. ПОЗДНЕЙШИЕ ВАРИАНТЫ
Калецкий [4], [5] развил во многих направлениях модель,
рассмотренную в разделе 7.4. Самый последний вариант теории Калецкого можно
сформулировать следующим образом (помимо уточнений, часть которых
приведена в упражнении 2).
Как и прежде, берется простая форма мультипликатора:
. (^
Однако Калецкий глубже разработал и изменил факторы, влияющие на
решения об инвестициях и на последующие фактические затраты на
капиталовложения и поставки капитального оборудования. Он предполагал, что
капиталовложения производятся не только в основной капитал, но и в запасы сырья,
готовых продуктов и незавершенное производство. Пусть Ik будет
фактической величиной капиталовложений в основной капитал, 18 —
капиталовложения в запасы, так что / = Ih + /s. Затраты на запасы принимаются
зависящими от изменений в выпуске продукции с фиксированным временным
отставанием
где vx — инвестиционный коэффиццент, т' — отставание. Предполагается
также, что фактические затраты на основной капитал производятся
одновременно с установкой оборудования, то есть с оплатой поставок, но имеют
фиксированное запаздывание т по отношению к соответствующим
решениям об инвестициях:
щеК(г) — величина основного капитала, a B(t) — характеризует
утвержденные решения об инвестициях гё основной капитал в момент t.
205

В качестве факторов, влияющих на решения об объеме инвестиций
B(t) (последние берутся за вычетом износа основного капитала),
принимаются теперь следующие: норма сбережений, изменения в скорости выпуска
продукции (оба фактора влияют на увеличение В в прямом направлении)
и изменения в величине основного капитала (оказывает противоположное
влияние на величину В). Тогда при отсутствии запаздываний и наличии
члена, выражающего тенденцию (он принимается постоянным):
k + ^
то есть
Б = аA-С)У + ^-^ + е. D)
Уравнения A) —D) вместе с соотношением / = Jfe-f /s полностью
описывают систему.
Калецкий затем вводит следующее упрощение. Из уравнений C) и D)
получаем
Пусть 0 будет среднее запаздывание (взвешенное по А), такое, что
(о<е<т),
и примем Э неизменным. Тогда предыдущее уравнение перепишется так:
Далее предположим, что отставание в создании запасов равно среднему
запаздыванию инвестиций в основной капитал (т' = 0). Тогда из
уравнения B) находим
а A-е) y(t\ ¦ Г., 1 v* Л d
х W + V^r JU
y(t\ ¦ Г., 1 v* Л d Y (t) 1
х W + V^i-r i+д JUT1 W г
Наконец, пользуясь уравнением A), мы можем в этом уравнении оставить
члены, содержащие либо только капиталовложения /(?)> либо только
доход Y(t). Калецкий выбирает первый вариант и получает:
1 dI{t) i e -
— 0 dt
тт т aA-\-e
Итак, существует постоянный уровень равновесия 1 = —j-рт— ,
совместный с этим уравнением, и если теперь I (t) измерять от этого уровня,,
то зависимость будет следующей:
Выберем единицу времени так, чтобы 9 = 1, то есть единицей времени
пусть будет среднее отставание инвестиций в основной капитал от их
решений. Тогда смешанное дифференциально-разностное уравнение,
характеризующее систему, будет иметь следующий вид:
206

где
a (i —с)
— и р =
Обе постоянные а и Р положительны. Далее, — = гт~т можно считать
положительной дробью, так как 4 , < а < 1 в силу той же предпосылки,
что и в разделе 7.4. Следовательно, в уравнении E) примем а > |3> 0.
Уравнение E) того же типа, что и уравнение, рассмотренное в
разделе 7.4. Поэтому решение, полученное в предыдущем разделе, приложимо
и к данному уравнению, за исключением лишь того, что теперь
запаздывание имеет противоположное направление; в правую часть E) входит
(t + 1) и t вместо t и (t — 1) в уравнении A) из предыдущего раздела.
Решение имеет ту же природу (см. упражнение 1), то есть оно характеризует
одно основное колебательное движение I(t) и ряд высокочастотных
колебаний, укладывающихся в пределы среднего отставания капиталовложений.
Позднейшие варианты модели Калецкого предназначались для обобщения
более ранних вариантов. Калецкий [5] показал, что первоначальный
вариант является лишь частным случаем самой последней модели, которая
в свою очередь включает (как другие частные случаи) модели
мультипликатора-акселератора обычных линейных типов.
Тем не менее, как увидим в главе 8, первоначальный вариант модели
Калецкого все еще представляет интерес. Он обладает рядом очень
характерных особенностей и весьма удобен вследствие своей простоты; несмотря на это,
общий характер его решения тот же, что и более поздних вариантов. Следует
отметить одно обстоятельство: во всех моделях Калецкого нужно с большой
тщательностью установить временную размерность постоянных. В
первоначальном варианте модели к (в отличие от а) зависит от выбранной единицы
времени, и обратная величина к является временной постоянной
запаздывания акселератора. В решении модели из предыдущего раздела (при 0 = 1}
обратная величина к есть продолжительность запаздывания акселератрра
по отношению к фиксированному интервалу времени между моментом заказа
и моментом поставки оборудования. Поэтому к > 1 означает краткое
запаздывание акселератора в том смысле, что продолжительность запаздывания
меньше этого фиксированного интервала между моментом заказа и моментом
осуществления капиталовложений.
Задачи и упражнения
1. Подставить I = IoeQt в уравнение E) и показать, что q должно быть корнем
Q = aeQ—р. Пользуясь диаграммой, подобной изображенной на рис. 21, показать, что,
как правило, не будет вещественных корней q (при а>р). Показать, что возможности
получения комплексно-сопряженных корней в основном те же, что и в разделе 7.5.
2. Примем, следуя Калецкому, что все сбережения и капиталовложения зависят
только от дохода «капиталистов», то есть Р—прибыли после вычета налогов. Заменим
У на Р в уравнении A) и в первом члене в уравнении D). Сохраним, однако, общую
величину дохода У (включая и доход «рабочих», который тратится целиком) в
членах, содержащих акселератор, в dY jdt, именно в уравнениях B) и D). Показать, что
модель в действительности не изменится при условии, что прибыль до вычета налогов
и заработная плата в сумме составляют У в неизменной пропорции и при условии,
что налоговая система такова, что Р связано линейно с прибылями до вычета налогов.
3. Ввести в мультипликатор фиксированное временное отставание а|? и показать,
что уравнение A) заменится следующим:
Принять затем левую часть равной A—с) У (t—(р), объяснить смысл запаздывания ф
и получить для модели соответствующее уравнение формы E).|Какие различия вызывает
введение мультипликатора с запаздыванием?
207

7.7. МОДЕЛЬ ЭКОНОМИЧЕСКОГО РЕГУЛИРОВАНИЯ ФИЛЛИПСА
Особенности модели Филлипса рассматривались в разделах 3.4 и 3.5.
Сейчас мы кратко резюмируем их с помощью дифференциального оператора
D = d/dt, а затем используем модель для освещения проблемы экономического
регулирования. Характерной чертой модели является то, что спрос Z и выпуск
продукции У рассматриваются отдельно, причем один запаздывает по
отношению к другому. Независимые расходы А на предметы потребления и на
капитальные блага рассматриваются вместе как заданные, безразлично, являются
ли они постоянной величиной или же каким-либо определенным образом
изменяются по времени.
Модель мультипликатора описывается следующими уравнениями:
Спрос: Z = С + А, где С = A — s)Y.
Предложение: У = тггт* %.
Реакция предложения на изменение спроса имеет непрерывное
запаздывание типа показательной функции, причем скорость реакции равна X,
а временная постоянная Г = 1Д. Производя подстановки, получаем
г^1
то есть
При Y = Y0 в t = 0 ш А= const решение будет иметь вид1:
y = dfi_e-»
A)
B)
Оно характеризует движение У от начального значения Уо к уровню,
определяемому статическим мультипликатором Y = A/$.
Пример (а)
5 = 0,25, Я = 4, Y=Q в * = 0, ^=
Уравнение A): DY+Y = 4A при У = 0 в * = 0. Решение B) :У=44A — е"%
Решение графически изображается кривой / на рис. 23 (случай А=—1).
Рис. 23
Модель мультипликатора-акселератора описывается следующими
уравнениями:
Cnpoc:;Z = C + / + ^, где С = A-5)У
и
D + к
vDY.
Предложение: У = -jp i ^
1 Уравнение A) есть линейное дифференциальное уравнение первого порядка.
Его интегрирующим множителем будет ^=e^s/.— Прим* ред.
208

Сила действия акселератора равна v. Он имеет запаздывающую
реакцию (скорость х) непрерывной показательной формы. Производя
подстановки, получаем
У- (D-HoVt-*) {A—
то есть
Группируя члены, приходим к дифференциальному уравнению
где
а = %$ + х A —
C)
Если Л = const, то правая часть уравнения станет равна хЫ, так как
DA = 0. Выпуск продукции, определяемый статическим мультипликатором,
У = Л/5, будет совместен с уравнением. Решение уравнения будет иметь
вид (см. 4.4)
где р1 и р2 —корни квадратного уравнения р2 + ар+Ь = 0, а Вгж В2 —
произвольные постоянные. Постоянные нужно определить из двух
начальных условий, например У = У0 и DY = Y'O в ? = 0.
В численных задачах решение уравнения C) в форме D) можно
получить «классическим» методом. Его можно найти и с помощью
преобразования Лапласа (см. 4.7), объединив процесс нахождения частного
решения и постоянных, соответствующих начальным условиям. Так как
преобразование Лапласа будет особенно полезно в дальнейшем — при численном
решении уравнений выше второго порядка, —то мы покажем его
применение теперь для частного случая нахождения решений уравнения C).
Пример (б)
5 = 0,25, о=0,6, х = 1, А,=4,
У = 0 и ?У = 4Л в *=0, ^4 = const.
Уравнение C): D2Y—0,4/)У+У = 4^4, при У = 0 и ?У=4Л в ? = 0. Вспомогательное
уравнение будет иметь вид:
=-y-+4A
Следовательно,
-4Л I 1 (^°'2>
"" IP (/>-0,2J+0,9
°'98
так как
/?2_о14/?+1=:(/?-О,2J+О,96 = (р—0,2J+0,982,
так что р2 — 0,4/?+1 = 0 имеет корни р=0,2± ?0,98. Пользуясь таблицами
изображений элементарных функций при преобразовании Лапласа1, получаем:
У (*) = 4Л A — е°,2< cos O,98*+I,225eo,2< sin0,980 =4Л {1—re°,2f cos @,9
где
8 = arctg 1,225 = 0,89 радиана E1°).
х) См. таблицы в разделе 4.6.—Прим. ред.
14 р. Аллен 209

Следовательно, решение уравнения характеризует колебательное движение взрывного»
типа:
У @ = 4Л{1 —1,58е<>,2* cos @,98^+0,89)}.
Это один из случаев, рассмотренных Филлипсом [7]. Кривая (а) на рис. 9~в [7]
представляет собой графическое изображение решения. Оно воспроизводится здесь
кривой (/) на рис. 24 (для А==—1).
Вернемся к решению D) для общей модели
мультипликатора-акселератора. Динамика Y(t) зависит от вида корней (рг и р2)
характеристического уравнения. Движение Yt будет монотонным или колебательным
в зависимости от того, будут ли корни рх и р2 вещественными или
комплексными, оно будет взрывным или затухающим в зависимости от того*
12
8-
Рис. 24
будут ли рг и рг (или их вещественная часть) положительными или
отрицательными. Возможны все перечисленные варианты в зависимости от
значений, принимаемых структурными постоянными s, v, и и к. В
последующем анализе мы будем считать s и v заданными, а х равным 1. Обратим
особое внимание на зависимость динамики Y (t) от скорости реакции А,
(или временной постоянной Г, равной 1/А.) запаздывания на стороне
предложения, s и v могут принимать любые значения; они ограничены только
неравенствами 0 < s < 1 и v> 0. Однако удобно ограничить обсуждение*
практически встречающимися величинами, в частности малыми
значениями s (до ^0,25) и значениями у, близкими к 1. Анализ главы 6
подсказывает, что силу действия акселератора v можно взять в области
значений от (l — Y~sJ до (l -j-]A?J- В данном случае мы примем здесь:
Движение Y(t), определяемое решением D), будет колебательным,
если корни рг и р2 характеристического уравнения будут комплексно-
сопряженными. Характеристическое уравнение имеет вид:
р2 + {1 - X (v - s)} р + Ks = 0,
то есть
F)
210

При комплексных сопряженных корнях
то есть
Квадратный трехчлен относительно Т принимает отрицательные значения
для всех Т в области Тх < Т < Г2, где
Следовательно, Y(?) имеет колебательное движение для Т в области
Заметим, что в силу неравенства E) нижний предел меньше 1, а верхний
предел больше 1. Колебательное движение Y (t) выражается сочетанием
двух показательных функций в D). Оно имеет форму reaicos((ut + e), где
р = а ± ?со — корни характеристического уравнения F). Нужно различать
колебательное движение взрывное (при а > 0) и затухающее (при а < 0).
Из решения F) имеем
Следовательно, колебательное движение будет взрывным, если Г<а —s,
и затухающим, если T>v — s. Легко присоединить к этим случаям
условия равномерного изменения Y(t), именно условия, при которых р± и р2
будут вещественными корнями F) (см. упражнение 5). Следующая таблица
показывает все возможные случаи.
Значения Т
г<(/»-/7J
{Y~v+Y~s?<t
Корни Pi и р2
Вещественные и
положительные
Комплексные (a ^b l(D)
а>0
а<0
Вещественные и
отрицательные
Движение Y (/>
Неколебательное, взрывное
Колебательное, взрывное
Колебательное, затухающее
Неколебательное, затухающее
В таблице приведены значения временной постоянной (Г = 1/Я)
запаздывания предложения при различных типах движения Y(t). При ее
истолковании нужно помнить, что за единицу времени взята временная постоянная
запаздывания акселератора (х = 1). Следовательно, Т < 1 означает, что
запаздывание предложения короче (реакция быстрее) запаздывания
акселератора. Обратное справедливо при Т > 1. Т будет иметь три следующих
критических значения:
(V~v-V~sY; v-s; {V~v + V~s)\
В силу неравенства E) первое и последнее значения будут соответственна
меньше и больше 1. Среднее значение может быть меньше 1. Например, при
s = 0,04 и v = 1, Т будет принимать значения
0,64; 0,96; 1,44.
211
14*

Если
s = 0,25 и v = 0,6, они будут
0,08; 0,35; 1,62.
Следовательно, нужно ожидать колебательного движения Y(t) лишь в
случае, если запаздывание предложения много короче или длиннее
запаздывания акселератора. Движение, вероятно, будет взрывным, если запаздывание
предложения короче; и только тогда нужно ожидать затухающего движения,
если оно имеет по крайней мере ту же продолжительность (то есть реакцию
по крайней мере такую же медленную), что и запаздывание акселератора.
В итоге взрывное колебательное движение Y(t) является, вероятно, наиболее
характерной чертой этой модели мультипликатора-акселератора.
Ограниченность описанной здесь модели Филлипса заключается в том,
что в ней определяется лишь единственное запаздывание в форме
показательной функции на стороне предложения и акселератора. Смягчая это условие
в формулировке модели, нетрудно ввести в нее множество запаздываний
вида показательной функции и сделать таким образом модель более
«реалистичной». Тогда уравнения типа A) и C) будут иметь более высокий порядок,
и решение их усложнится. Конечно, при введении запаздываний многих
видов увеличиваются возможности вариантов колебательного движения
Y(t) (см. упражнение 6).
Модель мультипликатора, описываемую уравнением A), и модель
мультипликатора-акселератора, описываемую уравнением C), можно
использовать для приспособления выпуска продукции Y к внезапному сдвигу спроса
на величину Л, происходящему в момент t = 0. Предположим, что система
находилась в равновесии вплоть до t = 0. Примем Л = 0иУ = 0за
уровень равновесия (t < 0). В момент t = 0 спрос внезапно изменяется на
постоянную величину А, то есть увеличиваются или уменьшаются независимые
расходы. В модели мультипликатора последовательное (при t > 0)
изменение У задано уравнением A) при условии У = 0 в f = 0. В силу уравнения
B), динамика Y описывается следующим образом: '
Это выражение характеризует равномерное приближение к новому уровню
равновесия У = A/s.
В модели мультипликатора-акселератора динамика У для t > 0 задана
уравнением C) при условии, что А = const. Для решения уравнения C)
нужно знать два начальных условия. Одно из них будет У = 0 при t = 0.
Второе условие задается тем фактом, что в момент t = 0 — когда происходит
сдвиг в спросе — система корректируется сама в соответствии только с
мультипликатором, акселератор же еще не действует. Поэтому, как и в разделе
3.5, DY = ХА, согласно мультипликатору. Движение У от положения
начального равновесия У = 0 находится из уравнения C) при условиях
Y = OnDY — ХАв момент t = 0. Наиболее вероятное решение будет
характеризовать взрывное колебательное движение вокруг У = A/s. Последняя
величина представляет собой уровень, определяемый статическим
мультипликатором после сдвига в спросе.
Следовательно, сдвиг в спросе вводит новый уровень равновесия У = A/s.
Когда действует только мультипликатор, фактическое изменение У будет
представлять собой равномерное приближение к этому уровню. Но
вероятнее всего оно превратится во взрывное колебательное движение, когда
вступит в действие акселератор. В связи с этим возникают две проблемы
экономического регулирования. Во-первых, в случае сокращения спроса
(А < 0) движение У будет направлено к более низкому уровню (У = A/s), чем
первоначальный (У =0), либо же оно будет представлять собой
колебательное движение вокруг этого низкого уровня. Мы можем стремиться достичь
предыдущего, более высокого уровня. В связи с этим возникает вопрос:
как ликвидировать изменение спроса и вернуться или приблизиться к преж-
212

нему уровню выпуска продукции? Во-вторых, если изменение У представляет
собой колебательное движение, в особенности взрывное колебательное
движение, вопрос сводится к следующему: как противодействовать неустойт
чивому влиянию акселератора и парализовать колебания выпуска
продукции? С такой точки зрения эти проблемы исследовал Филлипс [7]. Мы
рассмотрим их в следующих разделах данной главы.
Задачи и упражнения
1. Проанализировать модель мультипликатора-акселератора, характеризуемую
уравнением C), в случае X ->со (отсутствие запаздывания предложения) и А= const.
Показать, что тогда У=—A-е0'), где q= . Сравнить с моделью Хар-
5 WO ~~~ S
рода — Домара (см. 3.3), когда также и х—>со (без запаздывания акселератора).
2. Показать, что линия движения Y (t), полученная для частного случая в
примере (б), идентична решению У=—4—6,32е°>2/ sinE6°i—39°), данному Филлипсом [7],
где А— —1. ;
3. Показать тождественность динамики У (t) в решении примера (б) с
решением D), полученным «классическим» методом.
4. Применить преобразование Лапласа к решению дифференциального
уравнения C) общей модели при условиях А = const и У=0, DY = XA в t = 0. Показать,
что полученное таким образом решение будет иметь вид:
Р(Р2+аР + ь) b \ P
ь+Р1
М (
b \ P Pi — P* P—Pi P1—P2 Р
где
—Р2 J '
Получить отсюда У (t)t используя таблицы элементарных функций для преобразования
Лапласа.
5. Показать, что корни рг и р2 в решении D) будут вещественными, если !Г = 1Д
будет либо меньше (]/у—]/^J, либо больше (}^?>+К$J. Использовать соотношения
Pi-\-p2=—в и PiPz = b для того, чтобы показать, что рг и /?2 будут оба
положительными в первом случае и оба отрицательными во втором. Объяснить это с помощью У.
6. Ввести в модель мультипликатора двойное запаздывание предложения в виде
показательной функции У=( «¦ ) Z и показать, что уравнение A) заменяется
уравнением
D*Y+4U>y+У X*sY = 4АЛ4,
и что решение последнего уравнения дает колебательное движение, если s > 0,25.
Показать далее, что при введении в модель мультипликатора-акселератора двойного
запаздывания типа показательной функции, либо на стороне предложения, либо
в акселератор, либо в то и другое, уравнение C) превратится в уравнение третьего или
четвертого порядка.
7.8. ПОЛИТИКА ЭКОНОМИЧЕСКОЙ СТАБИЛИЗАЦИИ
Существует много вариантов политики стабилизации, которые может
применить правительство для сбалансирования сдвигов в спросе и постепенной
ликвидации колебаний в выпуске продукции. Варианты, рассматриваемые
Филлипсом [7], включают в дополнение к нормальному спросу^ народного
хозяйства на предметы потребления и капиталовложения также создаваемый
или планируемый правительством спрос на товары и услуги. Филлипс
различает следующие типы политики стабилизации:
I. Политика пропорциональной экономическойЩстабилизации.
В этом случае правительственный спрос равен G = —/рУ. Поэтому
при падении выпуска продукции У ниже желаемого уровня (У = 0)
предъявляемый правительством спрос пропорционален сокращению
производства.
П. Политика интегральной экономической стабилизации. Прави-
t
тельственный спрос равен G= — /Д Ydt. Тогда добавочный спрос,
*о
• создаваемый правительством, пропорционален накапливающемуся
дефициту в выпуске продукции ниже желаемого уровня.
213

III. Политика экономической стабилизации, при регулировании
по производной. Правительственный спрос равен G= —fdDY.
В этом случае он связан не с дефицитом продукции Y, а со
скоростью ее сокращения (—DY).
Во всех этих случаях G представляет собой планируемый
правительственный спрос. Обозначим фактический государственный спрос,
оказывающий непрерывное влияние на экономику, через G. Предположим, что по
отношению к планируемому правительственному спросу он имеет непрерывное
запаздывание в виде показательной функции со скоростью реакции р.
Следовательно, если все три типа экономической стабилизации применяются
одновременно, мы получаем следующие уравнения:
Модель мультипликатора, включающая правительственную политику
экономической стабилизации, описывается следующим образом:
Спрос: Z = (l-s)Y + G A
Предложение: У = D , ^ Z.
В результате подстановки получаем следующее дифференциальное
уравнение:
{
то есть
о
После группировки членов:
t
D2Y + aDY-{ bY + c [y dt = X{D + P) A,
где
A)
J
Если Д = 0, то уравнение A) будет дифференциальным уравнением
второго порядка относительно У. Но если Д Ф О, уравнение A) нужно
продифференцировать, чтобы избавиться от интеграла. Тогда оно
превратится в дифференциальное уравнение третьего порядка и заменит
дифференциальное уравнение первого порядка, которое получалось в модели
мультипликатора (см. уравнение A) в 7.7), при отсутствии политики
экономической стабилизации.
Модель мультипликатора-акселератора со стабилизирующим
правительственным спросом описывается уравнениями:
Спрос: Z = (l —
Предложение: У = D . * Z.
214

Снова получаем дифференциальное уравнение
то есть
Производим группировку:
t
DSY + aD2Y + bDY + cY + d ^
о
где
} B)
При fi = 0 это будет дифференциальное уравнение третьего порядка, а при
1гф0 дифференцирование приводит к уравнению четвертого порядка.
Оно заменяет дифференциальное уравнение второго порядка, которое дает
модель при отсутствии политики экономической стабилизации [см. 7.7,
уравнение C)].
Предположим, что Y = О есть желаемый уровень выпуска продукции
в положении равновесия. Он управляет системой до момента t — О, когда
спрос внезапно падает на заданную величину. Для выявления эффекта
политики экономической стабилизации нужно решить уравнение A) или B) с
отрицательной постоянной А (величина, на которую снижается спрос) и
соответствующими начальными условиями в момент t = 0. При выполнении этого
на практике мы встречаемся с двумя затруднениями. Первое заключается
в том, что, как правило, приходится иметь дело с уравнениями третьего
или четвертого порядка, включающими значительное число параметров:
структурные постоянные s и v, скорости реакций р, к, X с различными
запаздываниями и параметры /р, Д, fd принятой политики экономической
стабилизации. Поэтому нельзя рассчитывать на получение общего решения.
Скорее это вопрос численного решения ряда уравнений для различных частных
случаев. Решение лучше всего получить с помощью преобразования Лапласа.
Второе затруднение возникает вследствие того, что независимые расходы
после сдвига в спросе принимаются постоянными. В самом деле, в момент
t = 0 происходит внезапное изменение величины А; А является постоянной
только для t > 0. Значит, соответствующие задаче начальные условия для У,
DY, D2Y, ... будут значениями, существующими в момент, следующий
непосредственно после t = 0. В разделе 7.7 были точно определены два таких
начальных условия, именно У = Ои DY — ХА. Этого было достаточно для
решения дифференциального уравнения второго порядка. Для решения
дифференциального уравнения третьего порядка необходимы начальные
значения и для 2JУ, а для решения уравнения четвертого порядка
требуются значения для D2Y и D3Y. Эти начальные значения, непосредственно
следующие за моментом t = 0, трудно определить, так как они зависят от
приро ы рассматриваемой системы и ее реакции на внешние возмущения
в момент t = 0. (См. Филлипс [7, стр. 319]).
Тизард [10] предложил иной метод — перенести весь анализ назад,
ко времени, непосредственно предшествующему моменту ? = 0. В этом
215

случае начальные условия будут чрезвычайно простыми:
так как У = 0 будет постоянным уровнем равновесия вплоть до момента
? = 0. Однако это упрощение влечет за собой то усложнение, что
независимые расходы А не являются уже больше постоянными, а представляют
собой скорее ступенчатую функцию A(t), определяемую следующим
образом:
Л (*) = 0 (*<0); A(t) = ±A (t = O);A{t) = A (t > 0). C)
Правые части уравнений A) и B) содержат производные от Л, которые
нельзя будет игнорировать, если А не является постоянной величиной.
Далее, чтобы применить производную от ступенчатой функции C),
последнюю нужно сначала аппроксимировать с помощью непрерывной функции^
стремящейся при переходе к пределу к данной ступенчатой функции.
Обобщим задачу. Нужно решить дифференциальное уравнение:
где
= a0Dn + axD^ +...+ an^D + ап > D)
О 1^ 1 I • • • I 971—1 I 771 •
Уравнения A) и B) приводятся к этой форме после исключения
дифференцированием интеграла из первоначальных уравнений. К уравнению D)
нужно добавить соответствующие начальные условия, то есть начальные
значения У и их последовательные производные Уо, У^, У?, ..., а затем
получить решение с помощью преобразования Лапласа. Возможны
следующие альтернативы.
Во-первых, можно принять A (t) = Л = постоянной для t > 0, так что
правая часть уравнения D) станет ЪША — const. Необходимые начальные
условия будут получены для момента, непосредственно следующего за t = 0:
) = ИтУ(е); У^ = 1
Вспомогательное уравнение (см. 4.6) будет иметь вид:
/ (Р) Y(p) = h-If + (Выражения Уо, Y'o, Y'9,...), E)
что и дает У(р) — преобразование Лапласа для получения решения У (t)
уравнения D). Исключение ? = 0 из уравнения E) требует, чтобы
преобразование Лапласа имело следующий смысл:
= lim \e-ptY(t)dt.
8->0
Если Y(t) непрерывно, то с ?(р) не возникает затруднений. Трудность
этого метода решения заключается в определении соответствующих
значений у0, у;, у;;,...
Вторая возможность заключается в том, чтобы считать A (t) ступенчатой
функцией C), а в качестве начальных условий принять начальные
значения в момент, непосредственно предшествующий ? = 0;
(-е); У; = У @-) = ИтУ ( - е); ...,
так что Y0 = Y'0= ... =0, поскольку У = 0 есть установившееся положение
вплоть до момента ? = 0. Тизард [10] показал, что тогда вспомогательное-
216

уравнение для D) будет иметь вид:
^f. F)
Это уравнение снова дает У (р) — преобразование Лапласа для решения
Y(t). В данном случае преобразование Лапласа будет иметь следующий
смысл:
так что t = О включается и не исключается. Никаких трудностей не
возникает, коль скоро Y(t) непрерывно.
Мы можем сравнить и проверить для очень простого случая
альтернативные варианты применения преобразования Лапласа. Рассмотрим
модель мультипликатора-акселератора без применения политики
экономической стабилизации. Пусть модель имеет те же параметры, что и в
примере (б) раздела 7.7: 5 = 0,25, v = 0,6 и = 1, А, = 4. Тогда, в силу
уравнения C) из раздела 7.7, задача сводится к решению следующего
уравнения относительно У:
Положим, во-первых, что А = const (^ > 0), и возьмем следующие
начальные условия:
У = 0 и DY^AA в * = 0+.
Тогда вспомогательное уравнение E) будет иметь вид:
Во-вторых, примем, что А представляет собой ступенчатую функцию
в t = 0, а начальные значения будут
Y = Z>Y = 0 в * = 0-.
Тогда вспомогательное уравнение F) перепишется так:
то есть оно тождественно с предыдущим. Тот и другой методы дают
то же решение, что и в примере (б) (см. 7.7):
В нижеследующих примерах эффективности политики экономической
стабилизации даются решения различных численных уравнений. Можш>
применить любой вариант преобразования Лапласа, но второй способ,
в общем, предпочтительнее.
7.9. НЕКОТОРЫЕ ИЛЛЮСТРАЦИИ ПОЛИТИКИ ЭКОНОМИЧЕСКОЙ
СТАБИЛИЗАЦИИ
Простейший случай представляют собой модели мультипликатора при
проведении только пропорциональной политики экономической стабилизации.
В уравнении A) из раздела 7.8 положим f~ fd~Q. Получаем
Это дифференциальное уравнение характеризует динамику Y(t), начиная
от исходного положения У = 0, в момент t = 0. Его можно решить первым
способом, изложенным в предыдущем разделе. Положим А = const (t > 0}
и возьмем в качестве начальных условий У = 0 и DY = ХА в момент
217

t = 0 +. Решение будет иметь вид:
где рг и р2 — корни квадратного уравнения
а Вх и В2 находятся из начальных условий. Само уравнение и его решение
аналогичны случаю, рассмотренному в разделе 7.7. Наиболее вероятные
значения параметров наводят на мысль, что У колеблется вокруг уровня
У = Л/E + /р). Далее, если рг и р2 — комплексно-сопряженные корни для
случая колебательного решения а ± ico, то сумма корней равна 2а, и тогда
из квадратного уравнения следует
Колебательное движение должно быть затухающим (а < 0), оно не может
быть взрывным.
В модели мультипликатора без экономического регулирования У
равномерно стремится к уровню Y — A/s. При проведении политики
пропорциональной стабилизации У будет, вероятно, колебаться вокруг уровня
Y — A/(s-\-fp). Цель политики экономической стабилизации состоит в том,
чтобы заставить У вновь достичь предшествующего уровня (Y = 0),
и не совершать при этом колебательного движения. Только что рассмотренная
политика увенчалась лишь частичным успехом. Во-первых, 0<A/(s
< — , то есть новый уровень У представляет собой промежуточную вели-
S "
чину между желаемым уровнем У(У = 0) и уровнем, имевшим место
до государственного вмешательства (Y = A/s). Во-вторых, улучшение
экономики обычно достигается за счет введения в модель колебательного
затухающего движения У. Коэффициент /р, выражающий эффективность
экономической политики, появляется лишь как дополнение к предельной
склонности к сбережению s\ он дополняет s и служит для того, чтобы
«пододвинуть обратно» (pull back) обеспечивающий равновесие уровень
выпуска продукции к желаемому объему производства. Но этот
коэффициент вводит также и элемент неустойчивости, именно колебательное
движение выпуска продукции У, которого до этого не было.
Пример (а)
s==0,25, Р = 2, А, = 4, /р = 2.
Уравнение:
Решение производим с помощью преобразования Лапласа (второй способ, см.
раздел 7.8). Вспомогательное уравнение имеет вид:
так как р2-\-Зр-\-18=0 имеет корни —1,5±гЗ,97, то
Итак,
УЫ L1 р+2 Ы{{ p+ifi ИЗО ' 3'97
У @=^ A-е" iM cos 3,97* +1,89*-iM sin 3,970,
1 Здесь знаменатель />2 —{— 3/? —[—18 разложен на произведение двух множителей
(р—рг) (р—р2), а так как корни р1 и />2 — комплексные сопряженные величины, то
это произведение, как известно, дает сумму квадратов вида (р—аJ-)-со2. Далее
разлагаем скобку на элементарные рациональные дроби и по изображениям находим
оригиналы функций по таблице их изображений (см. 4.6). Величину 1,89 затем
представляем как tge (8 = 62,1°) или tg 1,08 (в радианах).— Прим, ред.
218

то есть
у (i) = M{i__2,14e-1'5/ cos C,97*+1,08)}.
у
Для значения А=—1 это решение графически изображено кривой (II) на рис. 23,
и с ней можно сравнить кривую I, характеризующую нерегулируемую модель
мультипликатора.
В данном случае скорость реакции на корректирование работы экономической
системы (р = 2) составляет лишь половину запаздывания предложения (А, = 4). Единица
времени такова, что запаздывание действия экономической политики на повышение
«проса имеет временную постоянную в х/2 единицы, запаздывание
предложения—временную постоянную в х/4 единицы, В качестве единицы времени можно взять,
например, один год. Скорректированная в результате экономической политики динамика У
характеризуется теперь сильно затухающим колебательным движением, и Y колеблется
вокруг уровня У = 4/9Л, то есть недалеко от желаемого уровня (У = 0).
• Следующий случай, подлежащий нашему рассмотрению, это —
проведение смешанной политики экономической стабилизации в рамках модели
мультипликатора. Возьмем дифференциальное уравнение A) из раздела 7.8.
Продифференцируем его, чтобы избавиться от интеграла:
D*Y + aDW + bDY + cY =
где
Пусть А = const (/>0), и уравнение будет однородным с решением вида:
У = Вхе^ + В2е^ + BtfP**,
где pv р2 и р3 — корни характеристического уравнения р3 + ар2 + Ър +
+ с = 0, a Bv B2 и В3 определяются из начальных условий.
Сделаем два общих замечания. Во-первых, пока проводится политика
интегральной стабилизации (Д Ф 0), дифференциальное уравнение с
постоянным А однородно, так что У = 0 будет устойчивым желаемым уровнем
равновесия. Политика интегральной стабилизации должна привести систему
к полному выправлению устойчивого уровня выпуска продукции. Во-вторых,
и при этих условиях колебательные движения Y все еще возможны, даже
вероятны. Корни рх, р2, р3 кубического уравнения либо все вещественны,
либо один из них вещественен, а два комплексно-сопряженны. Если все
корни вещественны, то
Сумма их отрицательна, и все корни могут иметь отрицательные значения;
они будут соответствовать монотонно затухающему колебательному
движению У. Если рг отрицательно, а р2, р3 = а ± i со, то рх + р2 + р3 =
= рх + 2а = —а = — ф + Ks + pX/d) < 0, и снова рх и а могут быть оба
отрицательны. Это означает, что если есть колебательное движение в У, то оно,
вернее всего, будет затухающим. Эта вероятность увеличивается с
возрастанием коэффициента fd политики стабилизации, ориентирующейся на
производную. Никогда нельзя полностью устранить взрывное изменение У.
Но энергичная политика стабилизации, связанная с производной, вызывает
быстрое затухание колебательного движения выпуска продукции.
В общем и целом политика пропорциональной стабилизации достигает
лишь частичного исправления уровня продукции, и только соединение ее
с политикой интегральной стабилизации полностью восстанавливает
положение. Однако возможно, что это случится лишь за счет допущения
колебательного движения выпуска продукции. В этом случае применение политики
стабилизации с помощью введения производной вызывает тенденцию к
затуханию колебаний.
Пример (б)
8 = 0,25, р = 2, Я, = 4, /p = /i = 2f /d = 0.
Уравнение:
219

Вспомогательное уравнение получается вторым из возможных методов
преобразования Лапласа, указанным в разделе 7.8:
Так как /?3+3/?2 + 18/>+16 = 0 имеет корни — 1, — l±i-3,87, то
р+2 Ы [ 1 p+i 1 3 37 3'87
[ 1 3 37
15 \p+i (/?+1J+Cj87)^^/ (p+i)* C,87J
Поэтому г
АЛ
У @=4^- (e-'—e-t cos 3,87*+3,87<Г< sin 3,870,
Id
то есть
АЛ
Y(O=-jj-e-'{l — 4 cos C,87*+1,32)}.
Для случая А=—1 решение показано кривой (///) на рис. 23. Для сравнения дается
кривая II, характеризующая эффект политики пропорциональной стабилизации.
Скорость реакции системы на корректирующую политику остается прежней г
а потому не изменится и сила пропорциональной стабилизации. Действительно, новым
является лишь добавление в модель политики интегральной стабилизации. В
результате корректирование приводит систему до желаемого уровня выпуска продукции
(У = 0), но в то же время вводит в нее колебания медленнее затухающие, чем это
было ранее. Политика интегральной стабилизации избавляет экономическую систему
от первого дефекта политики пропорциональной стабилизации (лишь частичное
исправление уровня выпуска продукции по сравнению с желаемым). Но наряду с
этим она усиливает, а не устраняет второй дефект этой политики—колебания выпуска
продукции во времени.
Политика интегральной стабилизации необязательно сопровождается
колебательным изменением выпуска продукции. Корни кубического
уравнения относительно р могут быть все вещественными (см. упражнение 2). Даже
в этом случае выпуск продукции, как правило, значительно изменяется
фактически без колебаний, прежде чем он установится вблизи уровня или
на уровне Y = 0. Добавление третьего типа политики — политики
стабилизации (корректирование путем введения производной) — может полностью
ликвидировать колебательные движения, вызванные политикой
пропорциональной и интегральной стабилизации. Этот факт иллюстрируется упражнением 3.
Наконец, рассмотрим модель мультипликатора-акселератора с
применением смешанной политики экономической стабилизации. Такая модель
описывается вообще дифференциальным уравнением B) из раздела 7.8.
При столь общей формулировке уравнения немного можно сделать для
исследования характера его решения. Легко сделать лишь одно замечание.
Если Д Ф 0 и применяется политика интегральной стабилизации, то
уравнение B) нужно продифференцировать, чтобы избавиться от интеграла.
Тогда оно превращается в однородное уравнение четвертого порядка.
Следовательно, Y = 0 представляет собой уровень равновесия, и система
полностью отрегулирована. Пусть рг, р2, ps и р^ — корни характеристического
уравнения четвертой степени, так что решение будет иметь вид:
Y = Вге^1 +
Из первого коэффициента уравнения B) из 7.8 получается следующее
равенство:
Оно справедливо как для вещественных, так и для комплексно-сопряженных
корней. Динамика Y несомненно будет взрывной, если выражение в правой
части положительно. Динамика со взрывным элементом еще вполне
возможна, когда выражение отрицательно. И только тогда, когда это
выражение одновременно велико и отрицательно, можно ожидать затухающего
колебательного движения У. Очевидно, что v — сила действия акселера-
1 Преобразования аналогичны указанным в примечании к примеру (а),
стр. 218. — Прим. ред.
220

тора — стремится сделать сумму положительной, a fd — вызвать появление
отрицательных величин. Коэффициент fd измеряет силу воздействия
политики стабилизации* ориентирующейся на производную. Снова мы находим,
что он оказывает затухающее влияние, необходимое теперь для
нейтрализации взрывного действия акселератора.
Для лучшего понимания модели рассмотрим различные численные
примеры и решим соответствующие уравнения с помощью преобразования
Лапласа. Мы возьмем здесь два случая, графики решения которых
изображаются кривыми (//) и (III) на рис. 24. Их нужно сравнить с кривой /,
характеризующей взрывное колебательное движение, возникающее в
соответствующей модели мультипликатора-акселератора без регулирования
{см. 7.7, пример (б)).
Пример (в)
. 5 = 0,25, о = 0,6, р = 2, х = 1, Я=4, /р=г2, /i = /d = 0.
Имеем уравнение B) из 7.8: D*Y + lfi&Y+iGf2Dr+lW = 4(D+i)(D+2)A.
Решая, как и прежде, с помощью второго способа преобразования Лапласа (см. 7.8),
получаем
Так как p3+ifip2+16,2^+18 = 0 имеет корни —1,15, — 0,225±>3,89, то
f» °>056
9 \^
^+0,225 3,89 1
' (Jp+0,225J + 3,892"t"Z>ZD°(p+0,225J+3,892 I "
Итак,
то есть
У @=^{i + 0f056e-«1'lw-2,5e-°'226'сов C,89*+1,13)}.
Для случая Л=— 1 реешние изображается кривой (//) на рис. 24.
В данном случае для регулирования системы применяется только политика
пропорциональной экономической стабилизации. Временная постоянная запаздывания
спроса в связи с проведением политики стабилизации составляет *7г единицы, для
запаздывания акселератора—единицу, для запаздывания предложения х/4 единицы.
Стабилизирующее влияние экономической политики сказывается быстрее влияния
акселератора, но медленнее реакции предложения.
После экономического регулирования установившийся уровень производства
равен Y = A/9A. Он представляет собой частичное улучшение экономической системы
по сравнению с нерегулируемым уровнем (У = 4Л) в направлении желаемого уровня
производства (У=0). Главной составной частью динамики выпуска продукции является
затухающее колебательное движение с периодом 2я/3,89 или приблизительно 1,5
единицы. Но затухание колебания происходит совсем медленно. Политика экономической
стабилизации имеет лишь частичный успех как в корректировании уровня
производства, так ив отношении ликвидации взрывных колебаний выпуска продукции в
первоначальной (нерегулируемой) модели.
Пример (г)
5 = 0,25, о=0,6, р = 2, х = 1, А, = 4, /p=/i = 2, /d = 0-
Уравнение #4У+1,6?3У + 16,2?2У+34?У+16У = 4#A)+1) (D+2) А получается
из уравнения B) раздела 7.8 с помощью дифференцирования, которое уничтожает
интеграл. Тогда вспомогательное уравнение будет иметь вид:
Следовательно,
_0 21
+162/>a+34/>+16=^ {р+0,<Ю+р+1,43
4,03
221

так как —0,69, —1,43, 0,26 ±?4,03 есть корни уравнения четвертой степени
относительно р:
Следовательно,
У@ = Л@,13в-°'69' + 0,07в-'М3*—0,21e°'26f cos 4,03^+l,06e°'26<sin 4,030,
то есть
У (t)=A {0,13е-1°'69'+0,07<Г 1'43f — 1,08е°'Шcos D,03^ + 1,38)}.
Для случая А= — 1 решение изображено кривой (///) на рис. 24.
Сравним это с результатами решения примера (е). Единственное различие
заключается в том, что к политике пропорциональной экономической стабилизации из
предыдущего случая добавляется еще политика интегральной стабилизации. В результате
этого корректирование уровня выпуска продукции до желаемой величины Y = 0 теперь
полностью закончено. Динамика У вокруг уровня У = 0 определяется теперь не только
двумя затухающими и неколебательными компонентами, а включает и более
существенное, чем в предыдущем случае, колебательное движение. Последнее имеет период
2я/4,03, или около 1,5 единицы, то есть почти прежний. Но колебательное движение
носит умеренно взрывной характер. Политика интегральной стабилизации пригодна
для полного регулирования уровня выпуска продукции, но за счет введения в модель
взрывного колебательного движения.
Влияние экономического регулирования достаточно полно разработано
на базе предложенной Филлипсом модели мультипликатора-акселератора
с единственным запаздыванием в форме показательной функции. Если спрос
сокращается на величину А, то соответствующий положению равновесия
уровень выпуска продукции снижается на A/s. В нерегулируемой модели
с действующим акселератором движение дохода от прежнего уровня
равновесия, как правило, будет колебательным и взрывным. Это показывает
кривая (/) на рис. 24. Экономическое регулирование преследует двойную
цель: возместить падение уровня продукции и свести на нет колебания
выпуска ее во времени. Политика пропорциональной экономической
стабилизации лишь частично успешна в обоих отношениях. Добавление политики
интегральной стабилизации позволяет полностью ликвидировать падение
выпуска продукции, но за счет расширения колебательных движений до
такого размера, при котором они могут превратиться снова во взрывные.
Это показывает важное значение третьего типа экономического
регулирования — политики стабилизации, ориентирующейся на производную. Эта
политика стремится к сглаживанию динамики выпуска продукции, и в этом
отношении ее применение может быть весьма эффективным. Она особенно
необходима в случае, когда действует сильный (и, следовательно, взрывной)
акселератор. Политика стабилизации с помощью введения производной
необходима не только для нейтрализации колебаний, создаваемых политикой
пропорциональной (а частично и интегральной) стабилизации, но она должна
противодействовать также и присущим системе колебаниям, возникающим
в связи с действием акселератора.
Таковы результаты, полученные в модели мультипликатора-акселератора
с запаздыванием единственного типа (в виде показательной функции). Они
должны быть весьма существенно модифицированы при наличии более
сложных и «реалистических» форм запаздывания — двойных, тройных
и многократных запаздываний типа показательной функции. Это можно
видеть даже из очень упрощенных случаев (см. упражнения 4, 5 и 6
данного раздела). Подробнее это рассматривается в следующей главе. В общем
и целом можно сказать, что при наличии многочисленных запаздываний
сильнее проявляются колебания, вводимые в модель политикой
пропорциональной или интегральной экономической стабилизации. Очень
возможно, что они будут и взрывными. В то же время регулирование с помощью
политики стабилизации введением производной становится менее
эффективным. В самом деле, если проводится энергичная политика пропорциональной
или интегральной стабилизации, может оказаться, что никакая политика
222

стабилизации, ориентирующаяся на производную, сколь бы энергично она
ни проводилась, не сможет сгладить колебаний выпуска продукции. Все
это по крайней мере помогает понять то обстоятельство, что не только само
существование запаздываний, но и их форма имеет важнейшее значение
при определении динамики экономической системы с мультипликатором
и акселератором [8].
Задачи и упражнения
1. Найти дифференциальное уравнение модели мультипликатора для случая:
5 = 0,25, р = 8, Я = 4./р=2 (при f1 = fd = O). Показать, что его решением будет
У (*) = ^{l_ 1,17*-I*'6' cos G,19*+0,56)}.
Сравнить с результатом решения примера (а) и показать, что следствием более быстрой
реакции на мероприятия правительства (маныпего запаздывания) явится затухание
колебаний в движении У. Этот случай рассматривал Филлипс [7, рис. 4, кривая с].
2 . В модели мультипликатора рассмотреть случай 5 = 0,25, р = 8, Я = 4, /р = /$ =
= 0,5, /ct = O. Показать, что
Начертить свободную от колебаний линию движения У к скорректированной
величине У=0. Это — случай неэнергичной политики пропорциональной и интегральной
стабилизации, оперирующей с коротким запаздыванием. Его рассматривал Филлипс
[7, рис. 8, кривая Ь].
3. Рассмотреть результаты политики стабилизации с введением производной на
следующем примере: s = 0,25, E = 2, Х = 4, /p=/i = 8, /^ = 1. Показать, что
и что колебания У быстро затухают.
4. В регулируемой модели мультипликатора, описываемой дифференциальным
уравнением A) из раздела 7.8, заменить одинарное запаздывание предложения
показательной формы двойным:
Показать, что тогда дифференциальное уравнение примет вид:
D3Y+aD2Y + bDY+cY+d { Y dt =
о
где
(s+fp), d =
5. Рассмотреть модель предыдущего упражнения для случая 5 = 0,25, Р = 2, Х = 4,
fv = 2, /$=^ = 0. Найти решение относительно У (t) и сравнить с результатами
решения примера (а).
6. Рассмотреть модель предыдущего упражнения, заменив /i = 0 на /г = 2.
Сравнить решение относительно У (t) с решением примера (б).

ГЛАВА 8
ЭКОНОМИЧЕСКОЕ РЕГУЛИРОВАНИЕ.
УПРАВЛЯЮЩИЕ СИСТЕМЫ С ЗАМКНУТОЙ ЦЕПЬЮ
8.1. СХЕМАТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЭКОНОМИЧЕСКИХ МОДЕЛЕЙ
В теории электрических цепей и других приложениях замкнутых
управляющих систем инженеры имеют дело с моделями, подобными рассмотренным
выше экономическим моделям. Они считают целесообразным представлять
свои системы в виде блок-схем, дающих наглядное представление об
уравнениях, характеризующих систему. Модели описываются взаимозависимостями
переменных, сложными и многочисленными уравнениями. Блок-схема,
во всяком случае, помогает выяснить эти зависимости.
Нетрудно понять идею, лежащую в основе управляющей системы
с замкнутой цепью и изображения ее в виде блок-схемы. Рассмотрим систему,
в которой три переменные (QL, (?2, Q3) связаны постоянными множителями.
Положим, что Q2 зависит от Qx: Q2 = k12Qly когда третья переменная не
принимается во внимание. Теперь предположим, что начинает действовать
и переменная Q3, которая находится под воздействием Q2 (множитель к23)
и в свою очередь влияет на нее (множитель к32) . Тогда система описывается
так:
откуда получаем
При отсутствии же Q3 мы имели просто Q2 = k12Qx. Такого рода систему
экономисты называют эффектом «мультипликатора», инженеры — системой
с обратной связью.
В схематической форме такая система изображена на рис. 25.
Переменные обведены кружками, которые соединены стрелками, показывающими
направление зависимости. Постоянный множитель, характеризующий
каждую зависимость, помещен в квадрате на соответствующей стрелке. На рис. 25
показывается, под каким влиянием находится каждая переменная (стрелки
направлены к кружку) и как воздействует она на каждую переменную
(стрелки выходят из кружка). Когда к кружку направлены две стрелки,
соответствующие зависимости складываются: Q2 = k12Qx + k32Q3. Если
две зависимости берутся в указанной стрелками последовательности,
множители перемножаются: Q3 ^ к23 Q2 = к12к23 Qt (в случае отсутствия к32).
Эта схема осложняется наличием обратной связи или замкнутой цепи
((?2 —* (?з —> Q%)- (?2 воздействует само на себя через посредство Qs. Если
система представляет течение тока в электрических цепях, то обратная
связь Q2 создает возможность самовозбуждения в цепи, то есть появления
в системе элемента неустойчивости. Пример обратной связи в экономике
представляет собой эффект мультипликатора. Статический мультипликатор
без запаздываний имеет вид:
+ и C =
откуда
Y- Л
224

Это — простая форма обратной связи, изображенной на рис* 25, Необходимо
лишь придать следующий смысл переменным: А — независимые расходы,
У — доход и С — личное потребление. Значения множителей в данном случае
показаны в нижней части рис. 25. Мультипликатор, или обратная связь,
возникает потому, что У через посредство С воздействует само на себя.
С помощью аналогичных блок-схем можно изобразить и более сложные
технические или экономические системы. Такая схема обеспечивает контроль
совместности модели и наглядно показывает сущность зависимостей в ней.
Рассмотрим модель мультипликатора-акселератора типа Харрода —
Домара без запаздываний:
C=cY и I=v§.
Дополнительной переменной здесь являются индуцированные
капиталовложения /. Они связаны с изменением дохода (dY/dt) коэффициентом
акселератора v. Эта система приводится к дифференциальному уравнению
vdY/dt — A — c)Y — А. Схематически она изображена на рис. 26, а. Теперь
в модели необходима двойная обратная связь, так как на У воздействует
Рис. 25
Рис. 26
не только С и /, но и А. Одна обратная связь характеризует мультипликатор
(Y —> С —> У), другая — акселератор (У —> / —> У). Их соединяет
переменная У. Три стрелки, направленные к кружку У, показывают
зависимость У = С + I + А, две стрелки, отходящие от него, характеризуют
зависимости С = cY и / = v(dY/dt). Новое заключается в том, что одна
из зависимостей представлена не постоянным множителем, а величиной
v(dldt), помещенной в квадрате. Однако применение операторов позволяет
обращаться с этой зависимостью так, как если бы она была представлена
постоянным множителем
7— **L-
&dt
Здесь выделение оператора d/dt или D позволяет производить над ним
алгебраические действия.
Особенность динамических моделей заключается в том, что они
включают не только скорости изменений, но и различного рода запаздывания.
Последние также можно вмонтировать в общую блок-схему в виде
отдельных квадратов с надписями, показывающими тип запаздывания (например,
«отставание 0» для неизменного временного отставания или «запаздывание»,
«L^», для показательной функции со скоростью реакции Л,). На рис. 26, б
показана простая модель мультипликатора-акселератора с отставанием
акселератора. Он соответствует системе уравнений
и I = v^Y(t~
где все переменные относятся, если нет какой-либо оговорки, к моменту
времени t. Конечно, блок-схему 26, б мы можем менять, включая в нее запаз-
15 р. Аллен
225

дывания как мультипликатора, так и акселератора и придавая этим
запаздываниям различную форму.
Схемы помогают наглядному выяснению сущности модели. В
дальнейшем будет показано, что еще более полезны они при перенесении в экономику
методов инженерного анализа соответствующих технических проблем. Эта
параллель между экономическими и техническими моделями вовсе не
означает, что механизм их действия одинаков. Нельзя считать, что решение о
капиталовложениях эквивалентно, например, разности напряжений тока.
Необходимо лишь формальное сходство, которое позволило бы ожидать, что
математический аппарат, применяемый инженерами, будет пригоден и для анализа
экономических моделей. Некоторые экономисты, например Гудвин [7],
проектировали экономические модели по аналогии с инженерно-техническими.
Позже Тастин [14] и Филлипс [9] более подробно выяснили связь между
инженерно-физическими и экономическими моделями. Тастин подошел к
вопросу как инженер, изучающий экономические проблемы, а Филлипс —
как экономист, обладающий опытом инженера.
8.2. ПРЕДСТАВЛЕНИЕ НЕКОТОРЫХ ЭКОНОМИЧЕСКИХ МОДЕЛЕЙ
В ФОРМЕ БЛОК-СХЕМ
В качестве упражнения весьма полезно представить различные
экономические модели мультипликатора-акселератора в канонической и
сопоставимой форме, а затем изобразить их в схематическом виде в форме блок-схем.
Тогда будут наиболее точно выявлены черты сходства и различия моделей.
Покажем это на примере четырех частных макродинамических моделей.
Для всех моделей применяется по возможности единая система условных
обозначений. Уравнения каждой модели также пишутся одинаково: сначала
на схему наносятся переменные, связывающие две или более цепи, а затем —
зависимости, которые образуют эти цепи.
Одной из простейших является предложенная Филлипсом модель
мультипликатора-акселератора, рассмотренная в разделе 3.5. Она включает
запаздывания в форме показательной функции. Вводится новая переменная
Z, представляющая спрос, отличный от продукции (дохода) = У. Уравнения
модели таковы:
где
Y
В этой формулировке мы пользуемся оператором D = d/dt; к и X —
скорости реакции двух запаздываний показательной формы. Эти уравнения
приводят к дифференциальному уравнению второго порядка относительно У
(см. 3.5). Схематическое изображение модели дано на рис. 27, /. Здесь L%
означает запаздывание У по отношению к Z, характеризуемое множителем
XI(D + X). Аналогичный смысл имеет и Lx. Запаздывания могут
варьировать в зависимости от скорости реакции. Особый интерес представляют два
предельных случая. Если к = О (бесконечная временная постоянная
запаздывания), акселератор полностью выключен, он перестает действовать, и
соответствующую цепную связь можно устранить из рассмотрения. Если же
X—> оо (бесконечная скорость реакции), тогда вообще нет запаздываний,
У и Z можно считать равными, и?две точки в блок-схеме совпадут.
Обратимся к предложенной" Самуэльсоном — Хиксом модели
мультипликатора-акселератора. Дискретная форма модели в «элементарном случае»
Хикса (см. 3.7) будет описываться уравнением
где
Ct = cYt_x и /, = »
226

Это уравнение приводит к конечно-разностному уравнению второго порядка.
Для получения схематического изображения необходимо модифицировать
схемы для непрерывных моделей. Операторы для запаздываний и
производных (L и D) заменяются различными комбинациями операторов сдвига
/.Модель Филлипса
т. Модель Гудвина
п. Модель Хикса
iv. Модель Калецкого
i
v Модель Филлипса
(Альтернативная блок - схема)
Переменные
А -независимые расходы-,
В-объем решений о капиталовложениях; К-основной капитал; Y-продукцу^
С- потребительские расходы; /-инвестиционные расходы; Z - спрос
Рис, 27
Е и обратного к нему Е'1. Запаздывание на один промежуток времени будет
равно Е^1, так как У t-i = E'1 Yt. Разность Yt и rt_i, выраженная через
оператор обратного сдвига, будет Yt — Yt—г = A — ?г)У1^Р
с запаздыванием представится выражением:
то есть
Следовательно, зависимости системы будут таковы:
Ct = cE~1Yt и It = v {E'1 - E~*fYt.
Все переменные имеют значения текущего момента времени. Они умножаются
в случае необходимости на соответствующие операторы сдвига. Модель пока-
1 См. приложение А, § 5 алгебра операторов.— Прим. ред.
227
15*

зана на рис. 27, //. В частном случае, если положим v = 0 и акселератор
перестанет действовать, цепной связью акселератора можно пренебречь.
Модель Гудвина, рассмотренная в разделе 7.3, включает те же
переменные, что^и модель Филлипса, но, кроме того, добавляется переменная (Б),
представляющая объем решений о капиталовложениях. Уравнение модели
таково:
где
С У / Я(*в) B (dY/dt) и Y =
Все переменные одинаково двигаются во времени, за исключением одного
случая с временным отставанием. Последняя зависимость4 записана для
запаздывания в обычной форме показательной функции [Y = Z X/(D + ЯI.
Но сам Гудвин дает соотношение Y = Z— e(dY/dt), которое эквивалентно
вышеприведенному, если 8 = 1Д = временной постоянной запаздывания.
В результате приходим к смешанному дифференциально-разностному
уравнению D) из раздела 7.3. Схема модели приведена на рис. 27, ///. Новым
здесь является нелинейная зависимость между В и dYldt, представленная
функцией ф. Форма этой функции обычно устанавливается эмпирически.
В качестве последнего примера приведем первоначальный вариант
модели Калецкого (см. 7.4). По сравнению с моделями Филлипса и Гудвина
в модели Калецкого имеется новая переменная К — величина основного
капитала. С другой стороны, спрос Z не отличается от продукции или
дохода Y. Это равносильно предположению, что в моделях Филлипса и Гудвина
К —> оо. Существенное новое состоит в том, что имеются уже две, а не одна
зависимости, действия которых складываются* Следовательно, существуют
два «сцепленных» сдвоенных уравнения, из которых следуют некоторые
прямые соотношения:
+ + и Я = аA-с)У-Ж,
где
Отсюда мы вновь приходим к смешанному дифференциально-разностному
уравнению G) из раздела 7.4. Схема модели показана на рис. 27, IV. Из нее
видно, что в модели Калецкого требуются уже три цепи — две, соединенные
в У (они очень похожи на цепи в предыдущих моделях), и одна новая,
присоединенная в В.
Схемы на рис. 27, /—IV сделаны по методу, предложенному Тастином
[14]. Существует и другая форма, разработанная инженерами для описания
электрических цепей и других замкнутых систем с обратными .связями,
встречающихся в технических задачах. Она показана на рис. 27, F, который
воспроизводит модель Филлипса (см. рис. 27, /). Теперь переменные показаны
на линиях блок-схемы. Их можно мыслить себе в виде потоков вдоль линий
(подобно электрическому току). Точка пересечения линий показана на
диаграмме светлым кружком. Здесь переменные складываются или вычитаются.
На блок-схеме показана также точка, в которой линия входит в черный
кружок и затем распадается на ряд отдельных линий. В этом случае одна
и та же переменная движется вдоль всех выходящих линий в неизменной
форме. Для указания того, где и как одна переменная сменяется другой,
или для характеристики функциональной зависимости переменных, на линиях
помещаются квадраты, где соответствующая зависимость показывается
при входе в квадрат. Таким образом, в каждый квадрат входит одна
переменная, и одна переменная выходит из него. Вторая переменная зависит от
первой, и выражение, стоящее внутри квадрата, показывает характер этой
зависимости. Эта вторая форма схематического представления моделей на
228

первый взгляд кажется менее понятной для экономиста. Поэтому в данной
главе мы будем пользоваться лишь первым вариантом. Заметим, однако, что
второй вариант обладает двумя преимуществами. Во-первых, он общепринят
при рассмотрении инженерно-технических задач и применялся Филлипсом
[9J к анализу экономических моделей. Во-вторых, его лучше приспособить
для представления более сложных моделей, чем рассматриваемые в данной
главе.
При сравнении моделей, изображенных на рис. 27, выявляется много
интересных моментов. Так, например, в модели Гудвина имеется нелинейный
элемент, а во всем остальном она сходна с моделью Филлипса.
Особенно поучительно изображение в форме блок-схемы модели Калецко-
го. Отличительные черты ее
заключаются в том, что капиталовложения
зависят прежде всего от уровня
выпуска продукции (а не от темпа его
изменения) и уж затем от величины
наличного основного капитала.
Первое отличие проявляется в
блок-схеме в модификации цепной связи
акселератора. Важнее второе
отличие, так как оно требует введения
дополнительной третьей цепной
связи. Место нового фактора во всей
системе (влияние величины основного
капитала на объем новых
капиталовложений) определяется
подключением новой цепи в точке В (объем
решений об инвестициях) к цепи,
характеризующей основную обратную
связь капиталовложений. Значение
этой особенности, возможно, более
ясно инженеру, пользующемуся для
проектирования замкнутыми
электрическими цепями, чем экономисту.
В самом деле, Калецкий сам
исключает именно эту черту из более
поздних вариантов своей модели
(см. 7.6).
Все рассмотренные модели
являются сильно укрупненными и
основываются исключительно на зависимости мультипликатор-акселератор и
некоторых тесно примыкающих к ним различиях между решениями об
инвестициях, фактическими затратами на капиталовложения и поставками
капитальных благ. Но даже и в этих пределах модель может стать достаточно
сложной — она будет описываться дифференциальными,
конечно-разностными и смешанными дифференциально-разностными уравнениями, которые
далеко не всегда легко решить. Мысль Калецкого о том, что поставки
товаров по капиталовложениям через размер основного капитала и его
воздействие на объем решений об инвестициях образуют вспомогательную обратную
связь системы, можно принять и отнести в равной мере и к личному
потреблению. Приняв эту предпосылку, можно на том же узком базисе построить
более обобщенную модель. Ее форма показана на рис. 28. Модель включает
две основные цепи — одну для мультипликатора, другую — для
акселератора. В точках, характеризующих объем решений о затратах денежных
средств (Вс и Вг), подключается вспомогательная цепь, отражающая влияние
уровня запасов (S и К). Решения о капиталовложениях, как и в модели
Калецкого, зависят от наличной величины основного капитала (К). В равной
мере решения потребителей о расходовании средств могут зависеть от таких
Рис. 28
229

факторов, как размер невыплаченных сумм по покупкам в рассрочку (S).
На рис. 28 некоторые квадраты заполнены — когда соответствующие
множители обычны или очевидны. Другие оставлены пустыми — их нужно
заполнить по выбору из стандартного списка множителей, производных,
интегралов и запаздываний. Возможно, что некоторые пустые квадраты
придется заполнить эмпирическими и нелинейными зависимостями.
Ясно одно — модель в форме блок-схемы, основанная на
мультипликаторе и акселераторе, достаточно сложна и без введения в нее дополнительных
факторов — правительственной политики, внешней торговли, налоговой
политики, цен и процентной ставки, — которые следует учесть, если модель
предназначена для приложения к реальной экономической
действительности. Блок-схема модели может разрастаться с угрожающей скоростью.
Поэтому постоянно необходимо компенсировать введение дополнительных
факторов в одну часть системы резким упрощением какой-нибудь другой
ее части. Это необходимо по крайней мере в первом приближении. Лишь
тогда возможно оценить влияние новых факторов на уже хорошо известную
систему. Например, модели Гудвина и Калецкого направляют внимание
на обратные связи капиталовложений и особенности последних, сводя к
простейшей форме обратные связи мультипликатора.
Задачи и упражнения
1. Показать, что модель Гудвина меньше похожа на модель Хикса, чем на
модель Филлипса. В каком смысле модель Филлипса является упрощенным
вариантом модели Гудвина?
2. Сравнить и противопоставить модель Хикса моделям,' показанным на рис.
26,6 и 27,1 (Я,-со).
3. Начертить блок-схему для дискретной модели Харрода—Домара (cms 3.6).
8.3. РЕАКЦИЯ ЛИНЕЙНОЙ МОДЕЛИ НА ВВОД СИНУСОИДАЛЬНЫХ
ИЗМЕНЕНИЙ
Обратимся теперь к свойствам линейной модели, связанным с
возможными изменениями синусоидального типа. Такого рода изменения не столь
ограничительны, как может показаться на первый взгляд. Синусоидальная
вариация в линейной модели определяется в отношении частоты и затухания
колебательных движений структурой модели, тогда как амплитуда и фаза
колебаний зависят от внешних условий (см. приложение Б). Если одна
переменная имеет синусоидальную вариацию, то все переменные
колеблются с одинаковой частотой и затуханием (р = а + ?со одинаково для всех
переменных), но с различными амплитудами и фазами. Более того,
зависимости линейной модели не ограничиваются постоянными множителями.
Производные, интегралы, временные отставания и запаздывания
показательной формы не изменяют частоты и затухания колебательного движения.
Поэтому их можно включить в ряд линейных зависимостей, что и делается
с помощью операторов.
Справедливо, что синусоидальная вариация, происходящая в линейной
системе с неизменным р = а + *<*>» представляет собой очень специальную
форму колебательного движения с симметричным восходящим и нисходящим
качаниями. С другой стороны, положив со = 0, мы включим в этот случай
и монотонное изменение по показательной кривой затухающего или
взрывного типа. Далее, колебательное движение не синусоидальной формы, но с
неизменным периодом 2jt/co можно анализировать «гармонически» с помощью
рядов Фурье, разложив его на основное синусоидальное колебательное
движение с частотой со и «гармоники» с последовательно возрастающей
частотой Bсо, Зсо,...).
Рассмотрим одну какую-либо зависимость линейной модели, одно звено
характеризующей ее схемы с замкнутой цепью. Одна переменная,
выход (выпуск) У, зависит от второй переменной Z, заданной величины
входа (затрат). Ниже приводятся примеры простых зависимостей между ними:
230

/17
1) Y — v—г- —зависимость акселератора;
dt
t
2) У = \ Zdt —процесс накопления;
о
о
3) Y — Z{t — Q) —фиксированное отставание продолжительностью 9;
4) У = Z — одинарное запаздывание формы показательной функ-
ции с временной константой 1Д;
5) У = тл о1 ) Z —двойное последовательное одинаковое запаздывание
формы показательной функции с совокупной
временной константой 1Д.
Заметим, что два последних выражения представляют собой частные
случаи зависимости, которая характеризуется дифференциальным
уравнением относительно У, a Z есть ввод, образующий правую часть уравнения:
Коль скоро ввод имеет синусоидальную форму, вариация будет
представлена векторным произведением Z = Aeieept (р = а + ico). Фактическая
динамика переменной характеризуется вещественной частью Z, то есть
выражением Aeat cos(co? + e). Так как модель линейна, то У будет иметь
синусоидальную вариацию с тем же^временным вектором ер*, но с
отличающимся вектором для амплитуды и фазы. Положим Y = Beift]evt. Задача
заключается в нахождении В и т\ по данным А и 8 и каким-либо
заданным значениям р — а+ш. Таким образом, ищется векторное отношение
которое не зависит от времени. Однако на него воздействует частное
значение р (частота и затухание) выбранного типа колебательного движения.
Отношение A) представляет собой комплексное число, которое изменяется
по величине вместе с комплексной переменной /> = а + гш. Следовательно,
его можно записать в виде функции F(p) комплексного переменного.
Положим, что мы нашли это комплексное число для данного
комплексного р:
F(p) = Q (cos ф + i sin ф) = Qei(P. B)
Подставим выражение^B) в A):
Be** = (Qelv) (Ae™) = QAell*+vK
Следовательно, переменная вывода (выпуска продукции) У имеет:
амплитуду B = qA,
фазу т] = 8 + ф.
Иными словами, в комплексном числе F(p) = Qei(v длина вектора q
представляет отношение амплитуд, а угол вектора ф —сдвиг фазы при
переходе синусоидальной вариации от Z к У. Поэтому F(p) называется
передаточной функцией зависимости У от Z.
При синусоидальной вариации с заданным р = а-\-ш в линейной
системе зависимость одной переменной У от другой Z выражается
так:
Y = F(p)Z,
где передаточная функция F(p) представляет комплексное число
Qei(P, в котором q показывает отношение амплитуд и ф —сдвиг фазы
от Z к У.
231

Если зависимость Y от Z задана в обычной аналитической форме
(как в вышеприведенных примерах 1 — 5), то передаточную функцию F(p)
можно написать сразу. Для этого нужно только записать D = p для
производных, /) = 1//? для интегралов и ввести множитель e~vQ для
временного отставания 0. Тогда в примерах 1 — 5 передаточная функция запишется
следующим образом:
и
2)
3)
*)
5)
Зависимость
Y=°w
t
У= \ Z dt
0
Y = Z(t — 6)
У % Z
D+X
f 2Х \а
V, D+2X )
Передаточная функция:
Y = vpZ
У % Z
Р+Х~
V- 1 \ *7
Любую из этих формул можно проверить на основании указанных
положений. Например, передаточную функцию D) можно записать так:
где
tg(p =
Следовательно, передаточная функция предполагает, что вариация на входе
Z = ea*cos(o? превращается в вариацию на выходе У = (Qeat) cos (wi — ф).
Но для запаздывания в виде показательной функции этот результат был
получен непосредственно в разделе 4.8 для случая У — ZK/(D-\-X).
Приведем еще один пример для иллюстрации получения передаточной
функции на основании изложенных принципов.
Пример
Примем У как среднее (сглаженное) значение Z на интервале длиной 2Т с
центром в t:
t+т
y=^ j zat.
t-T
t
Это не есть нарастающий итог \ Z dt, так что в данном случае неприменимы
операторные методы, пригодные для неопределенных интегралов. В самом деле, для такой
зависимости нельзя легко написать функцию F (р). Исключение представляет лишь
случай незатухающего колебания а = 0. При a = 0 вариация на входе будет A cos (coi —J— e),
а соответствующая вариация У на выходе:
t+T
t-T
= —тр cos (oat-f- e) sin (oT =
= qA cos(co?+e), где q =
Следовательно, передаточная функция будет иметь вид (при а = 0) для p±=i&:
Y = qZ, где Q = (sinco7')/oO1.
232

Таким образом, при сглаживании Z с помощью центрированной подвижной средней
длиной в 2Т\ фаза не изменяется, а амплитуда вариации уменьшается в отношении
Q=(sincoT)/@7\ При очень большом со, q мало. Высокочастотное (короткопериодовое)
колебание легко сглаживается.
Передаточную функцию F(p) для любых р = а + i со можно представить
как точку, характеризуемую выражением B), на диаграмме Аргана1. В
прямоугольных координатах точка Р будет (pcoscp, q sincp), в полярных (q, ф).
При изменении а и со точка Р перемещается по плоскости Оху. Изменение
Р можно представить в виде сети кривых или геометрических мест, очень
похожих на кривые безразличия в теории выбора потребителя. Одно
семейство кривых определяется изменением со (при неизменном а), причем одна
кривая соответствует каждому фиксированному значению а. Они
называются геометрическим местом точек (кривыми) вектора реакции. На каждой
такой кривой (при неизменном а) значения F(p) и, следовательно, q и ф
заданы для меняющегося со. Значит, при данном а кривая вектора реакции
установлена точно. Далее, при данном со определена и точка Р на этой
кривой, а следовательно, и отношение амплитуд (q = длине ОР) и сдвиг фазы
(ф-угол РОх) для зависимости Y от Z.
Например, передаточная функция для однократного запаздывания по
показательной кривой (с X = 1) будет
а соответствующая точка Р на диаграмме Аргана будет иметь координаты:
Кривая вектора реакции для а = 0 будет представлена кривой, описываемой
точкой Р [1/A + со2), — ю/A + со2)] при изменении о> от 0 до
бесконечности. Как видно из рис. 29, это — полукруг, представленный кривой (/).
Значения со для различных его точек отмечены на рис. 29 (со = %, 1, 2, 3, 4).
Кривая дает наглядное представление о соотношении амплитуд и сдвиге
фазы при прохождении регулярного колебания (а = 0) разной частоты
через запаздывание У в форме показательной функции по отношению к Z.
Вариация на входе A cos(co? + e) превращается на выходе в
qA cos (cat + е — ф),
1 Диаграммой Аргана называются две взаимно-перпендикулярные оси, на одной
из которых (обычно- ось х) представляются вещественные числа, а на другой (обычно
ось у) — чисто мнимые числа. Эти оси дают возможность графического изображения
комплексных чисел (см. приложение Б).— Прим. ред.
233

где q — длина ОР и ф — угол РОх. Для низкочастотных колебаний (с
большим периодом), например со = %, происходит лишь слабое затухание
амплитуд и небольшое изменение фазы. В случае высокочастотных (с коротким
периодом) колебаний, например со = 2, затухание амплитуды происходит
быстрее, и фаза имеет большее запаздывание (см. ОР и ОР' на рис. 29).
Кривая (//) на рис. 29 показывает кривую вектора реакции (а = 0) для
двойного запаздывания показательной формы с той же общей
продолжительностью временной константы AА = 1) (см. упражнение 4). ^х>щ
Наконец, передаточную функцию F(p) можно интерпретировать как
преобразование Лапласа (см. 4.6). Для иллюстрации приведем два частных
случая.
Пример (а)
Одинарное запаздывание показательной формы имеет вид Y = ZX/(D-\-X). Возьмем
единичное изменение Z и (как и в разделе 4.8) напишем соответствующее изменение
для У:
Y (t) = l — е~~М в форме нарастающего итога (кумулятивная кривая);
У ^) = Хе"^ при частотном распределении реакции во времени.
Пусть f(t) будет частотным распределением реакции во времени и F
(р)—соответствующим преобразованием Лапласа. В данном случае
и F(p) =
р+%-
Эти значения получаются из таблицы элементарных функций для преобразования
Лапласа, приведенной в разделе 4.6 (стр. 121). Следовательно, преобразование Лапласа
для функции f(t) есть передаточная функция запаздывания.
Пример (б)
) Z. Для
Z ф
(
единичного изменения Z реакция в форме нарастающего итога и распределенной
реакции во времени будет иметь вид:
Выражение / (f) = 4^2ie"*2^ имеет изображение (стр. 122):
которое представляет собой передаточную функцию запаздывания.
Тайим образом, приходим к следующему общему выводу (заметим, что
D=p):
Если У зависит от Z так, что f(t) есть распределение во времени
реакции Y на изменение единицы Z и, если F(p) есть преобразование
Лапласа функции f(t), то F(p) есть передаточная функция зависимости
при синусоидальной вариации (р = а + i<o).)
Применение этого вывода практически неоправдано в том случае, если
У и Z связаны простой зависимостью, так как F(p) можно написать сразу,
положив, например, D —р. Для более сложных случаев, возможно, удастся
f(t) представить в аналитической форме и затем написать F(p) как
соответствующее преобразование Лапласа. Однако вышеприведенный вывод полезен
в первую очередь для практически встречающихся случаев, когда реакция
с запаздыванием f(t) задана эмпирически. Как показано Тастином [14],
в этих случаях можно получить F(p) из f(t) численными или графическими
методами, то есть определить вид передаточной функции для данной
эмпирической зависимости.
Задачи и упражнения •
1. Непосредственным интегрированием Aeat cos ((ut-\-e) проверить, что Y = (\/p) Z
есть передаточная функция для У = J Z dt.
234

2. Рассмотреть уравнение ~d*Y/dt2 -f a (dY/dt)-{-bY = Z и показать, что решение
уравнения
при условии Y = dY/dt=zO в t = 0, будет иметь вид:
у (t) = —\1 (
P1-P2
где pi и /?2—корни уравнения р2-\-ар-\-Ь\=0. Получить затем частотное
распределение во времени / (t) и показать, что F (р) = 1/(р2-\-ар-\-р). Получить эту
передаточную функцию непосредственно из исходного соотношения.
3. Что можно сказать о передаточной функции F (р) для зависимости из,
предыдущего упражнения в случае, если р есть корень уравнения р2-\-ар-{-Ъ — 0? '
4. Начертить кривую вектора реакции (а=0) для двойного запаздывания
показательной формы
5. Показать, что при изменении а (© фиксировано) можно получить другое
семейство кривых для вектора реакции. Как связаны они с кривыми, рассмотренными
ранее? Почему можно ожидать, что эти два семейства кривых будут ортогональны
* (пересекаться в правых углах)?
6. Получить передаточную функцию F (р) для р=ш (а = 0) в случае, когда Y
есть подвижная средняя длиной 2Т, нецентрированная, но взятая для прошлого
периода. Показать, что отношение амплитуд характеризуется выражением q = (sin ®Т)/ш,
а запаздывание фазы равно соТ.
7. Показать, что если Zt представляет собой синусоидальную вариацию в
дискретной модели, то'
Yt=Zt_e=e~^ Zt
для отставания продолжительностью 6. Опираясь на это, доказать, что переход к
оператору сдвига позволяет применить рассмотренные в тексте методы к дискретным
моделям (E = eV). Указать пути применения их к модели типа Самуэльсона—Хикса.
8.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОБРАТНОЙ СВЯЗИ
Передаточная функция F(p) для характеристики зависимости двух
переменных (У зависит от Z) является основным построением в линейной
модели. Она представляет собой алгебраический вариант зависимости,
который может включать производные, интегралы, отставания и запаздывания
всех видов. Она выражает модификацию синусоидальной вариации,
переходящей с неизменяющейся частотой и затуханием (р = а + ?ю) от
переменной Z к переменной Y. Применение передаточной функции ко всей
замкнутой системе с обратной связью, как мы это теперь делаем, дает
возможность оперировать синусоидальными вариациями в линейной модели с
помощью обычной алгебры и комплексных чисел.
Рассмотрим теперь полностью замкнутую систему с обратной связью
и какую-либо переменную У в ней. После прохождения синусоидального
изменения через систему обратная связь У должна быть сопоставлена со
значением У на входе У — в той же самой точке и в тот же момент времени.
Все, что требуется, это — найти передаточную функцию этой обратной связи:
Обратная связь = F(p) значения на входе.
Как и в разделе 8.3, F(p) можем определить, используя уравнения
системы для устранения остальных переменных и сопоставления, таким
образом, обратной связи У и значения У на входе. Осложнения возникают лишь
в случае, если У представляет собой точку, в которой соединяются
различные обратные связи системы. Тогда необходимо уточнить, какую именно
из двух или более обратных связей мы рассматриваем, и принять во
внимание влияние других обратных связей на У. Для различных обратных связей
получим неодинаковые функции F(p). Но оказывается, что это не имеет
значения для приложения функции (см. следующий раздел),
235

Кроме того, возможно (либо для решения, либо для контроля) получить
передаточную функцию обратной связи из передаточных функций для всех
отдельных «звеньев» замкнутой схемы с обратной связью. Этот метод весьма
поучителен и полезен для приложений в частных случаях. На рис. 30, а
приведена блок-схема для простейшей
„ системы с одной завершенной обратной
связью. Выберем точку для Y. Пусть
Zx и Z2 будут двумя другими точками
обратной связи. Заменим зависимости
каждого звена их алгебраическими
выражениями, —передаточными функциями
F±(p), F2(p), Fz(p), полученными в
разделе 8.3. Обратная связь Y для любой
синусоидальной вариации системы
выразится в таком случае так:
Обратная связь Y=F3Z2 =FS(F2Z1) =
^F^F^F^) — {FXF2FZ) на значение Y
на входе. Значит, передаточная функция
обратной связи для всей системы будет
иметь вид:
Рис. 30
Таким образом, зависимости в
передаточной функции системы накапливаются,
следуя расположению стрелок на рис. 30.
Далее добавим в систему вторую
обратную связь (она может проходить
через другие, не указанные здесь
переменные), и предположим, что она
действует от Zx к Z2 с передаточной функцией F', то есть в том же
направлении, что и основная обратная связь, как это показано на рис. 30,6. Тогда
получим:
Обратная связь У = F3Z2 = Fs {F2ZX + F'Z^ = Fz (F2 + Ff) (FXY) =
= F1(F2JrF')F3 на значение Y на входе.
Передаточная функция обратной связи будет иметь вид
как и следовало ожидать.
Наконец, добавим вторую обратную связь, имеющую
противоположное направление, так что она будет действовать как обратная связь от Z2
к Zx и иметь передаточную функцию F' (рис. 30, в). Тогда:
Обратная связь У =zFsZ2,
где
и Z^
то есть где
или
и передаточная функция обратной связи примет следующий вид:
г» F\ F2F3
Г ~ 1 — F'F2 '
Таким образом, она включает эффект мультипликатора дополнительной
обратной связи F'.
236

Последний вывод может быть представлен в более общей форме, если
мы заметим, что F'F2 есть передаточная функция для всей системы
дополнительных обратных связей (Z1 —¦> Z2 —> Zx).
Эта обобщенная формулировка будет следующей:
Если F1(p) есть передаточная функция обратной связи какой-либо
системы и если в систему включается дополнительная группа
обратных связей с общей передаточной функцией для всей дополнительной
группы F2{p), то передаточная функция обратной связи всей новой
системы будет иметь вид:
Приложим этот результат к модели Филлипса, исключающей
независимые расходы (см. рис. 27, / или 27, F). Положим, что обратная связь
в цепи акселератора существует в точке Z. Если цепь мультипликатора
вообще не принимается во внимание, то передаточная функция будет
иметь вид:
'.М-
Теперь добавим в качестве дополнительной обратной связи цепь
мультипликатора. Передаточная функция для всей цепи выразится следующим
образом:
Следовательно, передаточная функция обратной связи (в цепи
акселератора в точке Z) будет иметь вид:
то есть
Задачи и упражнения
1. Показать, что если Fx (p) есть передаточная функция обратной связи в точке
У цепи акселератора, то добавление мультипликатора без запаздываний в цепь
следующим образом изменит вид передаточной функции:
2. Пользуясь результатами предыдущего упражнения, показать, что в простой
модели мультипликатора-акселератора (см. рис. 26) передаточная функция обратной
связи в цепи акселератора в точке У будет: а) для случая без запаздываний Р(р) =
z=vpl(\ — c); б) с временным отставанием 0 акселератора F (p) = vpe~pQ 1A— с);
в) с запаздыванием акселератора в форме показательной функции F (p) = [v/(l— с)] х
X [*/>/(/>+*)]•
3. Доказать для модели Филлипса (рис» 27,/), что передаточная функция
обратной связи в точке Z цепи мультипликатора будет иметь вид F (p) = F2 (р)/[1—Fx (/?)],
где F1 и F2 суть данные величины (см. текст). Почему в данном случае F (р)
отличается otF(p) в тексте данного раздела? ¦ .
8.5. СВОБОДНЫЕ ВАРИАЦИИ В ЗАМКНУТОЙ ЛИНЕЙНОЙ СИСТЕМЕ
Передаточные функции применяются прежде всего при определении
частоты и затухания (р = а + ?ю) свободной, или собственной, присущей
системе синусоидальной вариации, то есть самоподдерживающихся
изменений в линейной системе. Работа Фриша [5] является обобщением
первоначального опыта по анализу свободных колебаний.
237

В азделах 8.3 и 8.4 предполагалось, что синусоидальная] вариация
совершенно произвольна: р = а + ico могло принимать любые значения. Мы
не проводили различия между вынужденными и свободными, или
собственными колебаниями, так как это не имело значения. В частности, передаточная
функция обратной связи F (р) в точке У в завершенной системе принимала
различные значения в зависимости от изменения р. Для любого р, при
котором F (р) Ф 1, амплитуда и фаза У при наличии обратной связи отличались
от их значений на входе У. При этом частном значении р колебательное
движение не представляло собой самоподдерживающегося колебания, а таковым
соответствовали лишь значения р, при которых F (р) = 1. Эти-то собственные
колебания и представляют собой свободную вариацию системы.
Условие существования свободной вариации очень просто: F (р) = 1.
С алгебраической точки зрения это — уравнение относительно
комплексной переменной р = а + ico. Из этого уравнения можно найти одно или
несколько значений /?, каждое из которых соответствует свободной вариации
системы. Эта вариация может быть монотонной (со = 0) или колебательной
(со Ф 0); в последнем случае она может быть затухающей (а < 0), взрывной
(а > 0) или регулярной (а = 0). Для решения уравнения могут применяться
обычные алгебраические методы. Другой способ состоит в том, чтобы
действительную часть F (р) приравнять единице, а мнимую — нулю.
На блок-схеме кривая вектора реакции для F (р) покажет эффект
изменения аз для различных фиксированных а. Если какая-либо кривая из этого-
семейства кривых пройдет через точку А A, 0), то F (р) = 1,и на этой кривой
могут быть показаны значения а и со, при которых будет происходить
свободная вариация системы.
Для иллюстрации метода и получения^ результатов, в какой-то мере
известных, рассмотрим простейшую модель мультипликатора-акселератора (см.
рис. 26, а). В этой основной модели отсутствуют запаздывания, и мы
игнорируем независимые расходы (А = 0). Система, состоящая из двух замкнутых
цепей, соединяющихся в точке У (доход), описывается уравнением:
У = С + /, где С=сУ и I = v~.
Отсюда, приравнивая значения на входе и значения обратной связи, получаем:
у_ v\. dY
Дальнейшее углубление модели идет по линии введения различного рода
отставаний и запаздываний в цепь акселератора (но не мультипликатора).
Как видно из рис. 26, б, модель все еще остается простой. Но с помощью ее
уже можно показать сущность акселератора и важную роль введенного типа
запаздывания.
Основная модель рассматривается ниже в виде случая I. Затем вводим
три различных типа запаздываний: случай II — простое запаздывание по
показательной кривой; случай III — два последовательных равных
запаздывания и случай IV — фиксированное отставание. Нижеприводимая таблица
показывает, во-первых, соотношение значений на входе и при наличии
обратной связи и, во-вторых, соответствующую передаточную фуцкцию F (р)г
полученную с помощью обычных правил (см. также упражнение 2 раздела
8.4). Для упрощения записи F (р) используем дифференциальный оператор
D = dldt. Скалярный множитель обратной связи обозначим к = v/(l — с) =
= vis, то есть он представляет собой отношение силы действия акселератора
к предельной склонности к сбережению. Следовательно, к > 0, и значения к
могут быть достаточно большими.
При анализе непрерывных запаздываний единицу времени можно
выбрать так, чтобы >с = 1, то есть временная постоянная запаздывания
71=1/х = 1. За единицу времени берется запаздывание акселератора. Точно*
так же при анализе фиксированного временного отставания принимается
238

Случай
I. Запаздываний нет
II. Одинарное
запаздывание
показательного вида
III. Два равных
запаздывания .
показательного вида . . .
IV. Фиксированное
временное отставание
Соотношение значений
Вход
Обратная связь
Y = kDY
Y-k* BY
Y = kDY(t—6)
F(p)
kp
к %l
p+X
кРе-рв
0 = 1, так что за единицу времени берется фиксированное отставание
акселератора.
Случай I. Запаздываний нет. Свободная вариация (/? = а + ш) задается
) = kp = l, то есть р = 1/к. Следовательно*,
Is Л
к v
Свободная вариация системы не будет колебательным движением, она
характеризуется монотонным движением eat, где a = (s/v)>0. Как
и в модели Харрода — Домара, изменение системы монотонное и взрывное.
Случай II. Одинарное запаздывание показательного вида (х = 1).
Свободная вариация системы задается следующим образом:
Следовательно,
•51
О
—1
и со =
Свободная вариация системы вновь будет представлена неколебательным
движением видаеа', где а = 1/(&— 1). Обычно это движение будет взрывным
[k = (v/s) > 1, а>0], но при очень ^слабом акселераторе (v мало) оно
может быть и затухающим:
Случай III. Два равных запаздывания показательного вида [{к = 1),
Свободная вариация системы задана
то есть
откуда
При k = (v/s)>2, а это можно считать обычным случаем, оба значения р
вещественны и положительны. Для обоих видов свободной вариации системы
снова имеем со = 0 и а > 0. Обе вариации будут монотонными и
взрывными.
1 Здесь и далее вещественная часть F (р) приравнивается единице, а мнимая—
нулю (см. стр. 238).— Прим. ред.
•239

Весьма возможно, что k = v/s < 2. В этом случае значения р будут
комплексно сопряженными, то есть /? = a±ico, где
а = 2(Л-1) и ю =
Свободная вариация будет колебательным движением с частотой со (период
2я/со). При 1 </c = (tVs) < 2 колебание будет взрывным, при k = v/s <1 —
затухающим.
Введение двойного запаздывания делает возможной свободную
колебательную вариацию, которая может быть как взрывного, так и затухающего типа.
Как было показано в разделе 4.8, в действительности запаздывания, как
правило, не будут иметь простой формы показательной функции. Двойное
запаздывание более реалистично и может быть еще лучшим приближением к
фактическому распределению / (*), чем два последовательных запаздывания.
Тройные запаздывания и запаздывания более высокого порядка можно
исследовать аналогичном образом (см. упражнения 1 и 2), и их введение в систему
делает более вероятным колебательный характер свободной вариации
системы мультипликатора-акселератора (хотя оно может иметь и взрывной
характер).
Случай IV. Фиксированное временное отставание @ = 1). Уравнение
относительно р, характеризующее свободную вариацию системы F (р) =¦ 1,
будет теперь более сложным:
p = l. A)
Положим p = a-\-i(o, e"~i(u = cos со — i sin со и приравняем вещественную
и мнимую части уравнения A):
(a cos со + со sin со) е~а = у и a sin со — со cos со = 0. B)
Из второго уравнения системы B) определяем a = co/tgco и подставляем
в первое уравнение:
со _ , f I sin со \
tg со ~" ш V к со ) '
Значит, со выражается через к и а —через со, а затем и через /с —при
помощи следующих двух соотношений:
I \\\ == 1 Г\ к Л CL ТГ"! f 3^
tg СО ' СО tg СО ^ '
Заметим, что со = 0 является возможным решением, так что второе
уравнение системы B) будет автоматически удовлетворено, а из первого получим
[сае-а= 1. Это выражение представляет собой уравнение A)
после.подстановки вещественного корня р = а. Поэтому сначала ищется вещественное
решение уравнения A) (неколебательная свободная вариация), а затем находятся
значения а и со, удовлетворяющие C), которые характеризуют колебательное
свободное движение.
Решение находится графическим методом — точно так же, как это было
сделано для модели Калецкого в разделе 7.5. Решение такого типа показано
и в работе Тастина [14]. Для меньших значений к = (v/s) < 2,7 не
существует вещественных корней уравнения A). Основное решение будет представлять
собой низкочастотное колебание @ < со < я), которое в зависимости от
величины к будет медленно затухающим или взрывным. Период колебания
равен Bя/со) > 2, то есть более чем вдвое превышает продолжительность
фиксированного временного отставания. Для больших значений к = vis > 2,7
мы будем иметь два вещественных положительных корня уравнения A),
и основное решение представит собой монотонное взрывное свободное
изменение. Такой диапазон возможностей не представляется неожиданным при
растущей силе действия акселератора (и меньших склонностях к сбережению).
Но в каждом случае к основному решению добавляется и ряд
дополнительных, характеризующих колебания возрастающей частоты, то есть вначале
ряд значений со в пределах 2я < со < Зя, а затем значений со с интервалами
240

примерно в 2я. По мере увеличения значений к и возрастания частоты,
колебательные движения все в большей мере становятся взрывными. Все эти
дополнительные колебания [с периодом Bя/со) < 1] происходят в пределах
временного интервала отставания акселератора.
Широкий диапазон возрастающих взрывных колебательных движений
с высокой частотой и малым периодом характерен для решения экономической
модели с одним или более фиксированным отставанием во времени. Теперь
очевидно, что решения, включающие высокочастотные колебания, в
значительной мере являются фиктивными — они возникают из-за введения
жесткой и нереальной предпосылки о наличии фиксированного временного
отставания. Как только вводится распределенное запаздывание (или оно
аппроксимируется несколькими последовательными запаздываниями
показательного типа), основная свободная вариация (монотонная или колебательная,
затухающая или взрывная) остается, а побочные «обертона», то есть
высокочастотные колебания, исчезают.
Задачи и упражнения
1. Показать, что для рассмотренной в тексте модели акселератора при введении
тройного запаздывания показательного типа с общей временной константой У = 1/и —1
получается передаточная функция F(p) = k[p/(i/3p-{-lK]. Далее показать, что
свободная вариация системы описывается кубическим уравнением относительно р и что не
может быть более одного свободного колебательного движения.
2. Обобщить результат предыдущего упражнения на случай множественного
в форме показательной функции запаздывания произвольного порядка. Доказать, что
при последовательном введении четырех- или более кратного запаздывания
показательного вида могут возникнуть и другие свободные колебательные движения.
8.6. ИНЖЕНЕРНЫЙ ПОДХОД. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ СИСТЕМЫ
Изложенный выше метод использует инженерное понятие о передаточной
функции. Он предназначается для быстрого получения решения
экономической (или инженерной) модели, представленной линейной схемой из
замкнутых цепей. Частота и затухание всех свободных изменений системы находятся
при условии, что можно написать соответствующую передаточную функцию
F (р) и указать некоторые способы алгебраического решения уравнения
F(p) = 1. В линейную модель можно включить всевозможные зависимости.
Они могут быть представлены производными, интегралами, временными
отставаниями и запаздываниями, могут быть аналитическими или
эмпирическими. С помощью операторных методов все эти зависимости переводятся на
алгебраический «язык», и решение зависит только от алгебраических
операций.
Однако отметим и недостатки модели. Если модель достаточно сложна,
то нелегко найти общее решение уравнения F(p) = 1 или численно решить
его алгебраическими методами. Вышеприведенный метод скорее
подходит для получения частных решений моделей, а не решений в общей форме
с неустановленными численно параметрами [подобными k=(v/s)]. Но даже в
числовых построениях решение уравнений F(p) = 1 иногда можно получить
лишь графическими или эмпирическими методами. Далее, в модели можно
найти лишь частоту и затухание свободной вариации, общие всем
переменным линейной системы. Для определения амплитуды и фазы какой-либо одной
переменной необходимо проделать отдельный расчет при заданных
начальных условиях.
Весьма поучительно сравнить этот метод с «классическим» подходом,
то есть с приведением уравнений модели к одному уравнению относительно
выбранной переменной. Это уравнение может быть дифференциальным,
конечно-разностным или какого-нибудь смешанного вида. В случае
дифференциального уравнения метод передаточной функции не имеет каких-либо
преимуществ — уравнение F(p) = 1 будет точно таким же, как и
характеристическое уравнение дифференциального уравнения. Следовательно, с большими
или меньшими трудностями, но они решаются одинаково. В самом деле, с по-
16 р. Аллсн 241

мощью преобразования Лапласа—метода, разработанного также инженерами
и связанного с данным подходом к проблеме,— получается законченное
решение для частных случаев, то есть полное решение при точно определенных
начальных условиях. Это в основном тоже справедливо и для случая конеч-
ио-разностиых уравнений. Лишь в некоторых частных случаях конечное
решение приходится получать численным, постепенным, шаг за шагом,
решением самого уравнения.
Преимущества метода передаточной функции, как и вообще инженерного
подхода, заключаются в другом. Этот метод оправдывает себя даже в случае,
если приходится решать одно уравнение смешанной формы, как в примере IV
(см. 8.5). Однако в действительности нет необходимости добиваться
получения смешанного уравнения. Представление модели в виде блок-схемы и
переход с помощью преобразования Лапласа к алгебраической форме
зависимостей [F(p) = 1] позволяют получить решение численным или графическим
методом. Более того, из всего сказанного в конце раздела 8.3 очевидно, что
зависимости модели (например, запаздывания) не должны быть обязательно
представлены в аналитической форме.Они могут быть эмпирическими и
приспособлены к каждому дацному частному случаю.
Отметим два момента, совершенно очевидные для инженера, но менее
ясные для экономиста. Инженер не вводит в систему никакого вида
запаздывания или иной зависимости, так как знает, что тип и форма запаздывания
(безразлично, выражены ли они аналитически или эмпирически) изменяют
и природу решения. Экономист очень часто в большей мере стоит на
причинной точке зрения: он отмечает существование запаздываний,но обращает мало
внимания на их форму. Отчасти это происходит потому, что в качестве
исходных данных он пользуется временными рядами, пригодными лишь для
введения простых запаздываний в один или более временных интервалов.
Далее, инженер редко пытается добиться общего решения. Он
довольствуется получением частного решения (с помощью численных или
графических методов), обычно целого ряда частных решений данной задачи. Речь
идет о вычислительной работе, которую он стремится облегчить всеми
имеющимися в его распоряжении средствами. Экономисты нелегко воспринимают
такой подход, они воспитаны в традициях получения общих решений
проблемы. Обычно они склонны задавать такого рода вопросы: каковы пределы
значений v и s, дающих взрывные колебания дохода? Тогда для приложения
к реальному миру модель усложняется, наполняется большим эмпирическим
содержанием, ответы на общие вопросы становятся все менее возможными.
Поэтому и экономисту приходится переходить от общего к частному и
пользоваться методами и опытом инженера.
Вычислительная работа возможна лишь с помощью различных средств,
применяемых инженерами,— чертежной доски для получения графических
решений и в особенности различных механических и электронных
вычислительных машин-аналогов. Решения с помощью машин-аналогов были
получены для экономических моделей Гудвина и Калецкого [12] и [14]. Кроме
того, преимущество машин-аналогов состоит в том, что они не только
позволяют получать наглядные решения, но и дают возможность быстро
испытывать множество альтернативных гипотез [8], [10].
Нам остается рассмотреть еще основное ограничение метода
передаточных функций. Он применим пока еще лишь для исследования синусоидальных
изменений (включающих и монотонный рост по показательной кривой)
в линейной системе. Линейные модели обычно применимы для решения
инженерных задач, где все изменения в большей мере контролируемы. Иное
положение, конечно, с экономическими моделями. Характерная черта
экономических изменений, которые должна «объяснить» экономическая модель,
заключается в том, что колебания не симметричны (и потому даже приближенно
не являются синусоидальными), а их амплитуда не фиксируется внешними
факторами. В линейной же модели амплитуда колебания определяется либо
случайными, более или менее отдаленными историческими (начальными)
242

условиями, либо внешними факторами. Эти моменты приходится ввести
в модель для того, чтобы она полностью объясняла действительность.
Вследствие этого в экономической модели должны появиться нелинейные элементы.
Вопрос заключается в том, как и где их включить. Один возможный метод
сводится к тому, чтобы в основу положить линейную модель, с которой
относительно просто оперировать, а затем использовать ее в более широком
плане, включающем и нелинейные элементы (например, вводя гипотетические
и эмпирические верхние и нижние пределы или средние значения).
Примерами такого рода являются модели Самуэльсона—Хикса и Филлипса. Другой
метод — «встроить» в модель нелинейный элемент, так чтобы модель была
в достаточной мере независима от внешних условий. Именно так
конструировал свою модель Гудвин (см. рис. 27 ,Ж).
Второй метод может быть предпочтительнее, но он весьма затрудняет
решение. Об этом достаточно ясно говорят методы, примененные Гудвином
[7] для решения собственной модели. В нелинейной модели собственные ко-1"
лебаыия даже приблизительно не имеют синусоидальной формы.Но это не имеет
значения, ибо любое колебательное движение с фиксированным периодом
с помощью рядов Фурье можно разложить на синусоидальные компоненты
(прилож. Б.—Ред.) Однако в нелинейной системе эти синусоидальные
составляющие нельзя анализировать раздельно, так как у них изменяются
амплитуды и коэффициенты. Нелинейные системы из замкнутых цепей доступны для
анализа лишь в некоторых случаях, в частности с помощью методов Тастина
[13], примененных к модели ГудвинаБосуэллом[2]. Здесь открывается
широкое поле для разработки как инженерных, так и экономических проблем.
8.7. РЕГУЛИРОВАНИЕ В СИСТЕМАХ ЗАМКНУТЫХЩЕПЕЙ
Экономическая модель должна не только объяснять, но и указывать
неправильные действия и методы их исправления. Например, вследствие
сдвига в спросе,* изменение национального дохода может достичь уровня,
который считается «слишком низким», или могут обнаружиться
«нежелательные» колебания — в данном случае все зависит от выбранного критерия.
Положение можно «выправить», если увеличить национальный доход до
нужного уровня и сгладить колебания. Подобного рода проблема возникает и у
инженеров, например, при проектировании систем электрических цепей для
автоматического регулирования — приспособления к некоторым заданным
стандартам. Проблема регулирования существует одинаково как в
экономике, так и в инженерном деле.
Предположим, что в некоторой системе происходит свободная вариация
с недостаточно сильным затуханием, то есть а< 0 и мало (слабое затухание),
или а > 0 (взрывное колебание). Может потребоваться так отрегулировать
систему, чтобы затухание колебательного движения достигло определенной
нормы (например, а = —0,5). В то же время можно потребовать, чтобы
период всех колебательных движений не был слишком коротким. Одна
возможность сводится к видоизменению зависимостей системы, в частности
запаздываний. Этот метод едва ли практически применим в экономике
независимо от места его в инженерном деле. Другая возможность заключается во
введении в систему дополнительной цепи с обратной связью — механизм,
применяемый, в. частности, в теории электрических цепей. Тогда, если.
F\ (р) будет передаточной функцией обратной связи первоначальной системы,
&F2(p) — передаточной функцией полной дополнительной цепи, то из раздела
8.4 последует, что вся отрегулированная система будет иметь передаточную-
функцию обратной связи Fx(p)/[1 — F2(p)]. Выбор дополнительной цепи
и, следовательно, функции F2(p) делает возможным новое условие:
Flip) .
1+^2(/>) '
которое и определяет свободную вариацию р = а + ico требуемой формы,
243 16*

Для иллюстрации рассмотрим простейшую экономическую модель. Мы
умышленно выберем форму, которая допускает различные, но
непосредственно получаемые решения (см. упражнение 2). Тем самым мы сможем
практически проверить этот достаточно общий метод.
В рассмотренной в разделе 8.5 модели мультипликатора-акселератора
(случай III) акселератор имеет двойное запаздывание показательного вида.
Свободная вариация модели задается следующим уравнением:
=1- A)
Если 1 <& = и/5<2, свободная вариация будет представлять собой
взрывное колебание:
а = 2(А-1) и © = 2уг&B-А). B)
Для регулирования системы в модель, в дополнение к обычному доходу
У, вводится государственный спрос G, который официальная политика
ставит в зависимость от взятого с отрицательным множителем темпа
изменения дохода ( — g). Положим далее, что реакция государственной
политики на изменение дохода также имеет двойное запаздывание такой же
показательной формы, как и частный спрос на капиталовложения. Тогда
и передаточная функция дополнительной цепи (от Укби обратно к Г,
принимая во внимание также и множитель, см. рис. 31) будет иметь вид:
Из уравнений A) и C) следует, что свободная вариация регулируемой
системы определится следующим образом:
то есть
р определяется как корень уравнения
или
р= — 2A — Л:-ЬА:') ± 2i]/"l-A-
Выберем /с' = g/s в пределах А — 1 < Л' < fc и р комплексным, причем
( ) и о = 2^1 -A -fc+ /с'J. D)
Сопоставление регулируемой и первоначальной систем пойдет по линии
сравнения колебательных движений, определяемых D) и B). Очевидно, что
в заданных пределах к' можно выбрать так, что а будет равно требуемой
величине (например, а == —0,4), причем со не станет чрезмерно большим, а период
колебания 2я/со — слишком коротким.
244

Рис 31.
Возьмем следующий числовой пример: и = 0,4, s = 0,25, так что &=1,6.
Нерегулируемое взрывное колебательное движение B) будет а = 1,2 и
со = 1,6. Если а = —0,4 является критерием регулирования, то в этом
случае к'= 0,8 нужно подставить в уравнение D), которое дает регулируемое
(затухающее) колебание: а = —0,4 и со = 1,96.
Следовательно, g = k's = 0,8-0,25 = 0,2 будет
необходимым коэффициентом, характеризующим
государственный спрос G, то'есть последний должен
компенсировать 20% изменения дохода. Период
колебания в первоначальной системе Bя/1,6)
почти в 4 раза больше продолжительности
запаздывания акселератора, период колебания в
регулируемой системе Bя/1,96) — все еще превышает
его более чем втрое.
Если в схему вводится регулирующая цепь
(рис. 31), очевидно, что, при принятой форме
государственного спроса, G = — (g/v)I, и цепь
может быть взята от / к У со множителем, равным
(—glv). Действительно, данный государственный
спрос регулирует индуцированные частные
капиталовложения /. Когда сокращается доход У,
/ установится отрицательным, возмещение
основного капитала прекращается, и такое положение
компенсируется соответствующим увеличением государственного спроса
(например, общественными работами).
Задачи и упражнения
1. Показать, что не имеет значения, берется ли передаточная функция обратной
связи регулируемой системы в форме Fx (р)/[1— F2 (р)] (то есть обратная связь в
первоначальной цепи) или в форме F2(p)/[1— F1 (р)] (обратная связь в дополнительной цепи).
2. Показать, что рассмотренный в тексте случай регулирования модели
мультипликатора-акселератора эквивалентен уменьшению силы действия акселератора с и до
(v—g). В уравнение A) вместо к подставить (к— к') и непосредственно из B) получить
выражение D). '**
8.8. ПОЛИТИКА ЭКОНОМИЧЕСКОЙ СТАБИЛИЗАЦИИ
В разделах 7.8 и 7.9 мы применили к предложенной Филлипсом модели
мультипликатора-акселератора метод регулирования, основанный на
добавлении к системе одной или более цепей с обратной связью. Результаты
регулирования в этой модели удобно теперь рассмотреть с точки зрения метода
передаточной функции.
Основная модель мультипликатора-акселератора очень проста. Она
имеет одинарное запаздывание акселератора показательного вида (временная
постоянная равна 1/х) и такое же запаздывание производственного процесса
(временная постоянная равна 1А). Блок-схема приведена на рис. 27,/.
Передаточная функция получается непосредственно из схемы (как и в
разделе 8.4):
Следовательно, свободная вариация в нерегулируемой модели задана р,
удовлетворяющим условию
то есть
р2 + {х — К (vk — s)} p + kXs = 0.
В зависимости от значений параметров v и s для
мультипликатора-акселератора, к и X для запаздываний, оба корня могут быть вещественными или ком-
245

илексно-сопряженными. Свободная вариация будет представлять собой либо
два монотонных движения в форме показательных функций (затухающих или
взрывных), либо синусоидальное
колебание (опять-таки затухающее или
взрывное). Все эти варианты были подробно
изучены в разделе 7.7, где было показано,
что взрывное колебательное движение
является более вероятным. Например, если
5=0,25, 0 = 0,6, х = 1, JL = 4,
то уравнение будет иметь вид:
р2-0Ар-± 1 = 0.
Его решением будет
/? = 0,2 ±0,98г.
Это решение характеризует слабо
взрывное колебание (а=0,2) с периодом 2л/0,98,
то есть период превышает более чем в
6 раз продолжительность запаздывания
акселератора.
Система регулируется с помощью
введения государственного спроса G в до-
Рис. 32 полнение к нерегулируемому спросу Z.
G может различным образом зависеть от
дохода и его изменений. Кроме того, G берется с одинарным запаздыванием
в форме показательной функции (временная константа равна 1/р). В
случае комбинированного применения всех трех видов политики экономической
стабилизации (пропорциональной, интегральной и регулирования,
связанного с производной) G будет иметь вид
и для получения регулируемой системы (см. рис. 32) добавляются три
дополнительные цепи с обратными связями. Передаточная функция
обратной связи (в Z для данной модели) берется для всего комплекса из трех
дополнительных цепей [включая и цепь мультипликатора с передаточной
функцией сК/(р~\-Х)]:
р+Х
G
1—
сХ
р+Х
' (р+$)(р+Щ '
где G = fp + (l/p)fi + pfd получено в результате подстановки D — p и
\ =1/р в выражение, характеризующее G. Следовательно, регулируемая
система будет иметь передаточную функцию обратной связи следующего вида:
= l-V.Q») г='
Значение р для свободной вариации системы задается уравнением F(p) = 1,
которое в развернутом- виде запишется следующим образом:
-?±~
246

При такой записи очевидно, что влияние регулирования выражается
дополнительным членом с G. Не существует простых и общих методов
решения этого уравнения, если для дополнительных параметров |3, /р,
}г и fd регулирующего механизма не установлены конкретные числовые
значения. Но, коль скоро этим'параметрам приданы конкретные значения,
уравнение можно решить обычными алгебраическими методами
(преимущественно численными и графическими). Его решение и даст величину р
для свободной вариации регулируемой тем или иным способом модели.
Рассмотрим предыдущий числовой пример с добавлением
регулирования: 5 = 0,25, о = 0,6, р = 2, х = 1, Ь = 4, и /р = 2, Д = 2, /d = 0,55.
Следовательно, величина р для свободной вариации регулируемой
системы определится уравнением
то есть *
р4 + 6р3 + 20,6р2 + 34р + 16 = 0.
Решение графическим методом дает четыре корня р:
-0,74; -2,17; - 1,55 ± 2,76г.
Два первых корня соответствуют монотонным быстро затухающим изменениям
показательного вида. Но наиболее важная свободная вариация регулируемой
системы представлена синусоидальным колебательным движением, которое
определяется двумя другими корнями. Это сильно затухающее колебание
(а =—1,55) имеет период 2я/2,76, или продолжительность, более чем
вдвое превышающую запаздывание акселератора. Таким образом, в
результате регулирования первоначальное взрывное колебание (а = 0,2) перешло
в быстро затухающее (а = — 1,55).
Рассмотренная здесь модель имеет одинарное запаздывание
показательного вида акселератора и предложения. Анализ легко обобщить и на более
«реальный» случай с многократными запаздываниями, то есть двойными или
тройными запаздываниями показательного вида. Уравнение относительно р,
характеризующее свободную вариацию, будет иметь более высокий порядок.
У него будет и большее число корней, так что придется рассматривать и более
широкий диапазон вариантов свободной вариации. Но уравнение может быть
решено алгебраическими и графическими методами, способ решения задачи
остается прежним.
Решение этой задачи показывает простоту и эффективность метода
передаточных функций (и преобразования Лапласа). Зависимости линейной
системы и ее регулирующего механизма включают всевозможные изменения
во времени (производные, интегралы, запаздывания). Метод передаточной
функции заменяет их алгебраическими выражениями относительно
переменной р, характеризующей частоту и затухание свободной вариации системы.
Функции времени заменяются функциями частоты — характерная черта
преобразования Лапласа. Вследствие этого вся задача сводится к
алгебраическому решению одного обычного уравнения относительно одной
переменной. Само уравнение написать нетрудно. Его решение — чисто
алгебраическая задача. Хорошо известные численные и графические методы помогают
оправиться с ней в частных случаях. После первоначального быстрого
преобразования в функцию частоты решение сводится к довольно стандартным
вычислениям.
Но метод имеет также и свои границы. Он предназначен лишь для
определения частоты и затухания свободных изменений системы — наиболее
важной, но не единственной ее характеристики. Остается открытой проблема
определения амплитуды и фазы (и предельного уровня) любой из переменных
¦системы, например дохода У. В этом частном случае сама модель и фцрмы ее
(регулирования прорты — вся система описывается линейным дифференци-
247

альным уравнением относительно Y с постоянными коэффициентами.
Следовательно, снова в этом частном случае можно добиться численного решения
дифференциального уравнения со специфически определенными начальными
условиями с помощью преобразования Лапласа. Это и сделал Филлипс [9],
применив метод, описанный в разделе 7.9. Рассмотренный выше частный
случай регулирования представляет собой один из случаев Филлипса, полное
решение которых дает кривая d на рис. 9 из его работы.
Имеет свои границы и тип экономической модели, взятый здесь в
качестве примера экономического регулирования — предложенная Филлипсом
модель мультипликатора-акселератора. Эта модель, во-первых, в высшей
степени упрощена, во-вторых, она линейна. В силу этих причин она
непосредственно неприменима к анализу реальной экономики. Следовательно,
рассмотренное здесь воздействие регулирования экономической системы лишь
указывает путь политики экономической стабилизации, а вовсе не является
оперативным инструментом для применения на практике.
Совершенствование модели должно пойти двумя путями и, возможно,
в две стадии. На первом этапе сохраняются линейные свойства модели.
Но зависимости модели расширяются включением уже и других факторов,
в частности, внешней торговли, цен ресурсов, нормы процента. В то же время
аналитические и упрощенные формы некоторых зависимостей модели можно
заменить эмпирическими. Особенно это относится к запаздываниям [10, 11].
В результате уравнение относительно одной переменной (например, дохода)
уже не будет столь простым дифференциальным уравнением, и его нельзя
будет решить с помощью преобразования Лапласа. Однако весьма важно,
что по-прежнему можно написать передаточную функцию F(p), так что
вычислительная задача, связанная с получением частоты и затухания
свободной вариации системы, существенно не меняется.
Вторая стадия разработки — введение в модель важнейших элементов
нелинейности. Оно осуществляется введением либо эмпирических верхних
и нижних пределов значений переменных, либо нелинейных зависимостей
самой модели. Как только модель приобрела нелинейные свойства, ее
свободная вариация происходит в более «реалистичной» форме несинусоидальных
колебаний, амплитуда и фазы которых устанавливаются действием самой
модели. Изложенный выше метод передаточных функций теперь не помогает,
и приходится искать ему замену. В последнее время некоторые подходящие
методы были разработаны инженерами, и именно здесь открывается наиболее
широкое поле для дальнейших исследований.
Инженеры не создают абсолютно готовых методов, которые экономист
может просто перенять. Конечно, экономист должен усвоить и частично
заимствовать развитые инженерами методы регулирования управляющих систем
с замкнутыми цепями. Тастин [14] отмечает, что «одним из выдающихся
достижений современного инженерного дела является соединение точного
контроля с устойчивостью». Именно это и «сделало возможным разработку
новых и эффективных механизмов контроля почти во всех отраслях
промышленности — от радиоэлектроники до нефтеперерабатывающих заводов».
Экономисту, желающему создать практически применимые модели, нужно
многому поучиться у инженера. Ясны по крайней мере три следующих
положения: во-первых, важность введения в модель запаздываний и других
зависимостей в специфически определенной и подходящей форме; во-вторых,
необходимость осторожного и ограниченного введения нелинейных
элементов; в-третьих, связанное с этим перенесение центра тяжести с общего на
частное — с обобщенного анализа на обычную шаблонную вычислительную»
работу.

ГЛАВА 9
ОБЩЕЕ ЭКОНОМИЧЕСКОЕ РАВНОВЕСИЕ
9.1. РАВНОВЕСИЕ В СФЕРЕ ОБМЕНА
Излагаемая в этой главе теория общего равновесия производства и
обмена исходит из статических условий «чистой конкуренции», при которой
отдельный потребитель или фирма не в состоянии непосредственно влиять на
цены. Цены представляют собой параметры, заданные потребителям и фирмам.
Они определяются только рыночными условиями. Чистая конкуренция вовсе
не предполагает «свободного доступа» в любую группу производителей. Эта
категория — совершенно особая концепция, и условия «свободного доступа»
можно вводить или не вводить в модель, основанную на чистой конкуренции.
Нижеследующий анализ основан на трудах Вальраса и Парето,
продолженных и углубленных позднее Хиксом [6] и Самуэльсоном [11]. Эти работы
носят очень широкий всеобъемлющий характер: экономика рассматривается
в виде множества отдельных потребителей и производителей, и число
включаемых переменных совершенно не ограничивается. Опасность заключается
в том, что анализ может стать настолько общим, что он будет совершенно
бесплодным. Система общего равновесия замкнута в том смысле, что вся
совокупность переменных определяется заданными условиями. Чтобы убедиться
в совместности системы с состоянием равновесия, можно лишь сопоставить
число уравнений с числом неизвестных. Однако больше ничего неизвестно
о состоянии равновесия — мы ничего не знаем ни о его существовании, ни
о его единственности. Мы не получаем и никакого указания относительно
устойчивости равновесия в динамическом смысле.
Нужно вывести «общие законы действия системы цен при наличии
множества рынков» [6, стр. 6], «теоремы... обобщающие эмпирические факты,
которые могли бы быть опровергнуты лишь при идеальных условиях» [11, стр. 4].
Предположим, что в системе произошло какое-то изменение. В каком
направлении будут двигаться в этом случае переменные? Для ответа на подобные
вопросы обычно приходится рассматривать открытую систему как часть
полностью закрытой системы, в которой некоторые переменные являются
параметрами с произвольными значениями. Открытая система может быть лишь
объектом частичного анализа. Но она достаточно гибка для получения
«обобщающих теорем».
Вальрас провел анализ равновесия в сфере обмена в такой форме, что
к нему можно прибавить лишь некоторые второстепенные детали. Условимся
об обозначениях. Это весьма важно, когда приходится иметь дело со
множеством переменных. Строчными буквами, например х, будем обозначать
количество продуктов, проданных или купленных отдельными потребителями
или производителями; прописными буквами, например X,— совокупные
величины для всего рынка. Вводятся нижние индексы, соответствующие
товарам (г = 1, 2, ..., т) или отдельным потребителям (i = 1, [2, ..., п) или
производителям (/ = 1, 2, ..., N). В модели имеется т товаров (индекс г),
п отдельных потребителей (индекс i) и N фирм (индекс /). Таким образом,
Хг будет обозначать совокупность г-го товара на рынке, а хп —-покупку
г-го товара г-м потребителем.
Переходим к общему анализу сферы обмена. Пусть хн — заданный объем
г-го товара, первоначально имевшийся у г-го индивидуума, а хн —
соответствующий, но неизвестный объем его после обмена. Обозначим цену, по кото-
249

рой обменивается г-й товар, через рг. Так как нужно определить лишь
соотношения цен, удобно т-й товар взять в качестве масштаба или базисного
товара, (numeraire), а его цену —за ценностную единицу и положить рт = 1.
Общее число переменных будет
т(п-{-1) — 1,
то есть тп переменных хн для г = 1, 2, . .., т и i = 1, 2, .. ., п и (т — 1)
цен рг для г = 1, 2, ..., (т — 1).
Существует две совокупности условий равновесия. Одна из них
относится к покупкам-продажам индивидуумов, другая —к рыночным факторам.
I. Каждый индивидуум устанавливает свои покупки или продажи так,
чтобы максимизировать их «полезность» при условии балансирования
бюджета при заданных рыночных ценах. Для каждого индивидуума
предполагается порядковая (ordinal) функция полезности (соответствующая его
порядковому номеру):
ui = ui(xli, хи, . .., xmi) (* = 1, 2, ..., п)
с непрерывными частными производными:
uri = -^r- (г = 1, 2, .. ., т), (г = 1, 2, . .., п).
охп
Отношения ин для различных г не зависят от порядкового номера uv
Условием ut = максимуму при сбалансированном бюджете будет
Это означает, что отношения «предельных полезностей» uri (или
предельных норм заменяемости) равны заданным отношениям цен рТ. Так как
р?п = 1, то для каждого значения г от 1 до тп —1 и для каждого i от 1
до п условие будет иметь следующий вид:
II. Рыночное условие заключается в том, что цены товаров должны
быть совместны с равенством спроса и предложения (покупок-продаж)
каждого товара совокупности. Просто говоря, для каждого ;*-го товара
в отдельности должно соблюдаться равенство покупок и продаж:
2 (xH~xri) = 0. Одну из этих зависимостей можно, однако, получить из
других. Положим, что для (т —1) товаров
S(ri-^ri) = O, г = 1, 2, ..., (тгс-1).
Тогда, суммируя для каждого индивидуума условия балансирования
бюджета, получаем
О = 2 2 Pr (*ri - ~Xri) = 2 Pr { 2 (Xfi - *~ri)l = P
i i
i
то есть равенство 2 (xn ~~ xn) = 0 справедливо также и для r = m. Таким
образом, последнее рыночное условие для r = m можно исключить.
Тогда условия равновесия запишутся следующим образом:
Да). l^-wmi- I i = l, 2,..., n;
(б). Si'r(a;ri-^ri) = 0' i = l, 2, ...,n;
Г
II SKi-^ri) = 0, r = l, 2, ..., (m
250

В I (а) число уравнений равно (т — 1)/г, в I (б) = п, и в II равно
т—1. Всего имеется т(п-\-1) — 1 уравнений, то есть столько же,
сколько переменных. Система замкнута и совместна с условием равновесия
сферы обмена.
Всю систему можно разделить на открытые секторы и достичь
равновесия по отдельным этапам. Индивидуальный спрос характеризуется т — 1
уравнением I (а) и одним уравнением в 1F) для г-го индивидуума. Этих
т уравнений достаточно, чтобы определить переменные xri через цены
для г=1, 2, ..., т и заданного i. Рыночное равновесие описывается в
таком случае уравнением совокупного спроса и предложения, то есть
уравнениями П. Положим
так что Хг есть совокупный спрос, а Хг —совокупное предложение товара
г (г = 1, 2, ..., т), Хг задается, а Хг определяется путем индивидуального
спроса через цены рг. Следовательно, условие II будет просто:
ХГ = ТГ, г-1, 2, ...,,(т-1),
то есть получаем (т — 1) уравнение, в которое входит (т — 1) цен рг,
причем рт = 1. На рынке совокупность спроса отдельных лиц (в их отношении
к заданному начальному предложению), объединяясь, определяет рыночные
цены, совместные с равновесием.
Рыночные условия II подразумевают, что «цены должны уравнивать
спрос и предложение». Это не исключает возможности существования
отрицательных цен. Можно ли эти условия усилить, то есть должны ли
существовать неотрицательные цены, уравнивающие спрос и предложение? Ответ
отрицательный. В самом деле, как подчеркивает Цойтен [13], условие нужно
переформулировать: либо спрос равен предложению (неиспользуемые
ресурсы отсутствуют), либо цена товара равна нулю. Такая формулировка
облегчает применение методов, изложенных далее в главах 15 и 16.
Задачи и упражнения
1. Рассмотрим случай с двумя индивидуумами (i=*l, 2) и двумя товарами (X и Y).
Введем квадратичные функции полезности:
иг = aixl-\- 2h1x1y1 + Ьгу\\ и2 = я2*Ц-2М22/2+ Ь2уЬ
Написать условия равновесия обмена и выразить индивидуальный спрос xlf ylt х2 и у2
явно через отношение цен <рп двух товаров.
2. Показать, что в предыдущем упражнении рыночные условия сводятся к одному
кубическому уравнению относительно р. Написать выражение для произведения трех
корней р и показать, что при правдоподобных ограничениях, накладываемых на иг
и и2* это произведение положительно; отсюда показать, что при этих условиях
существует по крайней мере одно положительное значение р, совместное с равновесием
системы.
3. Показать, что для получения кубического уравнения относительно р в
предыдущем упражнении необходимо, чтобы аг—2h1pJ\~b1p2 и а2 — 2h2p-\-b2p2 не равнялось
нулю. Показать, что это условие соблюдается, если иг положительно для всех
значений хх и уг (не оба нули) и такое же условие соблюдено и для и2. Почему можно
с уверенностью принять "эту предпосылку? §
9.2. РАВНОВЕСИЕ ПРИ НЕИЗМЕННЫХ КОЭФФИЦИЕНТАХ ПРОИЗВОДСТВА
По-прежнему предполагаем, что имеется п индивидуумов (i = 1, 2, ...,
п), обладающих в начальный момент времени объемом хн каждого из т
товаров (г = 1, 2, ..., т) и предъявляющих конечный спрос на объем xri
товаров при данных отношениях ценрг (рт=1 для базисного товара). Условия
индивидуального спроса определены уравнениями 1(а) и 1F) предыдущего
раздела.
Кроме того, теперь принимается, что, помимо обмена товаров, на рынке
появляется в результате производства, то есть переработки первоначальных
251

ресурсов xri, дополнительное предложение. Для простоты мы не будем
рассматривать промежуточные продукты, а также те, которые являются как
предметами потребления, так и средствами производства. Совокупность т
товаров распадается на две неперекрывающиеся группы: к факторов
производства (s= 1,2,..., к) и т — к предметов потребления (t = к + 1, к + 2,
..., т). Нижний индекс г применяется ко всей группе т товаров. Когда же
две группы товаров рассматриваются отдельно, индекс s охватывает Л
факторов производства, а индекс t обозначает т — к предметов потребления.
Для всей рыночной совокупности положим, что
выражают спрос при данных ценах и предложение г-го товара. Тогда Хг
служит либо для обмена (г = ?), либо для употребления в качестве фактора
производства (г = s). Xr будет представлять собой либо объем спроса на
предметы потребления (полученные в результате обмена или расширения
производства), либо «резервированный» спрос на услуги факторов производства.
Для некоторых товаров (индекс ,s) ,XS<XS, и баланс сводится за счет
образования запаса фактора производства. Для других (индекс t) Xt^Xt и
дополнительный спрос покрывается расширением производства. Следовательно,
Рыночное предложение (факторов производства) = — (Xs — Xs), s=l7
2,..., к. _
Рыночный спрос (товаров) = Xt—Xt, ? = &+l, /с+ 2, ..., т.
И спрос, и предложение задаются как функции от цен рг.
Предполагается, что новое производство ведется при неизменных
технологических коэффициентах (при отсутствии комбинированного
производства, при постоянстве эффективности последовательных затратI. Пусть ast —
затраты s-ro фактора на производство единицы объема ?-го продукта
(потребительского товара), где ast—заданные постоянные величины для s=l, 2, ..., к
и t = Л+1, к+2, ..., т. Пусть Yr будет выпуск r-го товара в новом
производстве, так что У3<^ для факторов производства (s = 1, 2, ..., к)
и Yj>0 для предметов потребления (t = fc+1, fe+2, ..., т). Первое
техническое условие производства заключается в том, что при данных
технологических коэффициентах общие затраты какого-либо фактора s производства
составляют (—Ys) = IiastYt. Следовательно,
t
Далее мы предполагаем, что фирмы имеют «свободный доступ» во все
отрасли производства, так что при данных ценах расширение производства
обеспечивает равенство выручки и издержек (нулевую прибыль). Для ?-го
предмета потребления выручка | равна ptYt а издержки составляют
B Psasi)Yt. Следовательно, второе техническое условие производства таково:
Для полного описания системы нужно еще добавить рыночные
условия равенства спроса и предложения. Предложение факторов производства
равно — (Xs —Xs), а дополнительный спрос на продукцию факторов
производства есть (—У8). Спрос отдельных лиц на потребительские товары,
полученные в результате расширения производства, равен (Xt — Xt) для
?-го товара, а его предложение равно Yv Следовательно, условия
рыночного равновесия будут одинаковы для факторов производства и предметов
1 "Постоянство эффективности последовательных затрат" («constant returns to scale»),
или постоянные удельные затраты при изменении масштаба производства.— Прим, ред.
252

потребления:
;Yr = Xr-Jr, (r=l, 2, ..., my
Как и в разделе 9.1, одно из этих условий (например, для г = т)
можно получить из других условий (см. упражнение 1). Зависимое условие
нужно исключить. Тогда экономическая система в целом будет
описываться следующим образом:
г = 1, 2, ..., (т--1),
(б). 2 Рг(жк — ^ri) = 0, i = l, 2,..., л;
г
И(а). 2а81У, + Уз = 0, в=1, 2, ..., Л;
(б). 2pAi-A = 0, t = k+l, к + 2, ...,
S
III yr=S(«ri-^ri) = 0, r = l, 2, ..., (m-1).
Переменными являются яг1, Yr и /?г. Их число равно
тп + m + (т — 1) = m (п + 2) — 1.
Число уравнений определяется так:
Число уравнений
1(а) (тп-1)л
(б) л
И(а) к
(б) т-Л
III m-1
Итого /пл + т + (т—1),
то есть уравнений столько же, сколько переменных. Таким образом, система
замкнута и совместна с положением равновесия.
Один из путей постепенного достижения равновесия заключается в
следующем. Условия 1(а) и 1F) послужат для определения индивидуального
спроса хн через цены. Условия П(а), характеризующие техническую
сторону производства, выразят спрос на факторы производства (—Ys) через
величину выпуска продукции Yt. Условия И(б), которые выражают тот факт,
что «свободный доступ» подразумевает «цены конкуренции», необходимы для
определения цен на предметы потребления pt через цены факторов
производства ps. Рыночные условия для потребительских товаров, то есть уравнения
III для t = /с+1, к+2, ..., (т—1), дают выпуск продукции Yt сначала через
цены всех товаров, а затем только через цены факторов производства ps
(так как pt можно исключить, выразив их через ps). Теперь остаются лишь
рыночные условия "для факторов производства, то есть уравнения III для
5=1, 2, ..., к. В силу предыдущих зависимостей эти условия представляют
собой просто к уравнений относительно к цен на факторы производства, то
есть относительно ps. Именно рынок факторов производства связывает
воедино все зависимости системы, и здесь определяются рыночные цены,
отвечающие положению равновесия.
Задачи и упражнения
1. Написать 2 Рг B! (хгг —^п) —^г}, ГДе суммирование происходит по
г г
г = 1, 2, ..., т. Показать, что условия 1F), П(а) и II(б) превращают это выражение в нуль.
253

Пользуясь этим, доказать, что если условия III справедливы для г = 1, 2, ..., (т—1),
то они справедливы и для г~т.
2. Положим, что для imiwro-либо потребительского товара Xt=Xh то есть спрос
полностью удовлетворяется за счет обмена. Какое это окажет действие на уравнения
I — III? Будут ли они все же совместны с положением равновесия?
3. Введем в систему промежуточный продукт (индекс ы, на который не
предъявляется индивидуальный спрос, и начальные запасы его отсутствуют). Он производится
из ресурсов s с неизменными производственными коэффициентами, asu и, кроме того,
сам потребляется в производстве товаров t (также с неизменными коэффициентами
aui). Показать, что тогда к системе П(б) прибавляется еще уравнение ^\psaSVL—ри—0,
s
а к системе П(а)—-уравнение y?\autYt-\-Yu = 0. Показать, что таким способом просто
t
устанавливается цена и объем произведенного (и потребленного) дополнительного
товара.
9.3. ОБЩЕЕ РЫНОЧНОЕ РАВНОВЕСИЕ
В предыдущем разделе мы рассмотрели равновесие в сфере производства
и семена. Однако мы ограничивались случаем постоянства эффективности
последовательных затрат. Теперь можно снять это условие и обобщить
задачу, включив в нее и возможность ведения производства отдельными
предприятиями с различными техническими возможностями.
Снова предположим, что существуют п индивидуумов с начальными
ресурсами хн и спросом хн на товары (г = 1, 2, ..., т\ & = 1, 2, ..., п).
Условия равновесия заданы в Да) предыдущего раздела. Далее, теперь
мы предполагаем, что в число индивидуумов входят и предприниматели-
руководители производственных фирм. Сбалансирование бюджета,
заключавшееся прежде в равенстве расходов 2 Ргхн и доходов 2 Ргхп> получен-
Т Г
ных от первоначально имеющихся ресурсов, теперь необходимо изменить.
При предпосылке, что «свободный доступ» означает нулевую чистую
прибыль всех предпринимателей и фирм, условия 1F) предыдущего раздела
будут выдерживаться. Но в порядке дальнейшего обобщения предположим
теперь, что г-й предприниматель получает в качестве предпринимательского
дохода заданную фиксированную долю щ общей суммы прибыли R от
производства. Иными словами, мы считаем, что доход 1-го
предпринимателя увеличится на величину прибыли пгЯ. Доход каждого данного
индивидуума будет неизменным, но он зависит от неизвестного параметра R.
Сбалансированные бюджеты индивидуумов, заменяющие условия 1F),
будут иметь вид:
2 Рт (ХП —Яг) = Яг#> ГДе 2 Пг = 4 (l = 1, 2, . . . , п).
г г
Если г-й индивидуум не является предпринимателем, то для него
я* = о.
Предположим, что производство ведется Лг фирмами, которые
обозначаются индексом / (/=1, 2, ..., N), причем каждая фирма работает при
технических условиях, заданных функцией производства:
Здесь уг- означает (если оно положительно) объем r-то произведенного
товара или (если оно отрицательно) объем потребленного фактора
производства. Но могут также существовать товары —предметы потребления или
факторы производства, —для которых уг; = 0. Может случиться, что
отдельная фирма / не потребляет их в качестве факторов производства и не
производит их как предметы потребления. Предположим, что /;. имеет
непрерывные частные производные:
-ILL {
= 1' 2'
= 1, 2,
254

Отношения /г^ представляют собой предельные нормы заменяемости в
производстве.
Каждая фирма организует производство так, чтобы максимизовать
чистую прибыль Rj = 2 PrVrj ПРИ ограничениях, накладываемых функцией
г
производства и заданными рыночными ценами. Некоторые выражения в /?;
положительны (получения, z/r;- > 0), другие отрицательны (издержки, г/г;<0).
Условия в случае, когда R^ равно максимуму при ограничениях /;- = 0, будут
иметь вид:
Рт ~/m>' I /=1, 2, ..., TV.
Пропорции /1;- : /2j-: f3j: . . . : /mj- (/ дано) представляют предельные нормы
заменяемости ресурсов и (или) продуктов при производственных
возможностях, имеющихся у /-й фирмы.
Как и прежде (см. 9.2), условие рыночного равновесия сводится к
равенству спроса и предложения всех факторов производства и предметов
потребления. Пусть Yr = 2 уг.. Положительное Yr есть величина^
произведенной продукции, абсолютная величина отрицательного Yr — чистое
потребление фактора. Тогда рыночное равновесие будет соблюдено при Yr=Xr—Хг
для всех случаев, где Xr=2#ri и Xr= 2#ri. Итак,
г г
2 */г/ = 2 (хп-%п) (г = 1, 2, . .., те).
3 г
Кроме того, максимизируемая чистая прибыль^всех фирм должна
быть равна R:
г j j
Теперь нужно исключить одно лишнее у равнение.^Так как
г j г э г г
= 2 2 Рт (*п - *rt) = 2 «iR=л.
i r г
то последнее уравнение вытекает из остальных, и его^Гможно исключить.
Однако уравнение относительно R полезно, и его нужно сохранить. Вместо
него лучше исключить какое-либо другое уравнение. Легче всего
исключить уравнение, характеризующее одно из рыночных условий, например
условие для последнего или га-го товара:
2л J/mj = 2j (Xmi ~~ Xmi) •
3 i
Вся система будет в таком случае иметь вид:
т , ч ин Г г=1, 2, ..., (т-1),
Рг У. 1= 1, <4, . . . , П,
(б). 3jPT(xri-xri)=*ntR, ¦ i = l, 2, ..., n;
II (а) Г>"--/ { '• = 1'2'---'("г-1)'
" W--7T-^' 1 / = 1, 2, ...,iV;
(б). /,• (у1П ..-, Vmj) = 0, / = 1, 2, . . ., N;
Ш (а) 2 Уг/ = 2 (^ri -««), г - 1, 2, .... (те - 1);
2Г5

В этой системе переменными являются хн, yrj, рт и R.
Переменные Общее число
xri — спрос i-ro индивидуума на r-й товар или тп
ресурс г-го товара у г-го индивидуума
после обмена
уг. — количество произведенного или
потребленного г-го товара /-и фирмой mN
/?г —цена г-го товара (кроме последнего) в
условиях равновесия т—-1
/? —итог всей прибыли всех фирм 1
Итого переменных тп + mN + т — 1 + 1 =
( l
Столько же имеется и уравнений: тп — из 1(а) и 1F),
mN~m II(a) и 11F)
и m-из Ш(а) и Ш(б)
Система замкнута и совместна с положением равновесия.
Рассмотренное общее рыночное равновесие производства и обмена в
действительности тождественно равновесию в смысле Хикса [6]. Оно характеризует
полную замкнутую систему уравнений для определения объемов всех
произведенных, использованных и обмененных товаров—факторов производства и
равным образом предметов потребления,—а также величины всей полученной
прибыли и рыночных цен (по отношению к цене базисного товара, принятой за
масштаб измерения).
Состояния равновесия можно достичь и поэтапно, разделяя совокупную
закрытую систему на различные открытые секторы. Вот один из возможных
путей. Условия 1(а) и 1F) выражают индивидуальный спрос хн через цены
и R. Следовательно, и совокупный спрос на каждый товар Хг—ХТ выражается
через цены и R. Это относится как к факторам производства, так и к
предметам потребления. Условия П(а) и 11F) выражают продукцию фирм yrj
через цены. Таким образом, совокупное предложение каждого Уг товара
выражается через цены.
Подстановкой yrj в условие Ш(б) R выражается через цены. Наконец,
остаются рыночные условия Ш(а). Их m—1, и они выражены теперь через
m—1 соотношений рыночных цен. Эти условия означают, что на всех рынках
и для каждого из товаров (факторов производства и предметов потребления)
спрос равен предложению. Таких условий достаточно для определения
отношений рыночных цен.
Задачи и упражнения
1. Разделить список товаров на факторы производства (s=l, 2, ...,&) и
предметы потребления (t = k-{-i, k-\-2, . ..,m). Предположить, что для каждого
индивидуума a?Si>0 E = 1, 2, ..., к) и что хн=0 (г = Л:-|-1, &+2, ..., m). Объяснить это
и доказать, что система уравнений I — III не изменится существенным образом при
введении этой предпосылки.
2. Исследовать влияние на систему уравнений I — III равенства нулю R (и Rj)
и включения предпринимательских услуг в заданные ресурсы xri индивидуумов.
3. Фирма производит один потребительский товар Z, используя два вида
ресурсов 1иУ. Производственная функция f (x, t/, .z)—xy — az=0, где а — положительная
постоянная, х и у отрицательны (используемые ресурсы) и z положительно (выпуск
продукции). Показать, что условия производства, характеризуемые уравнениями П(а)
и П(б), дают следующее соотношение:
—хрх = — УРу = z = архРу,
где рх и ру — цены (pz = l).
4. К производственным условиям, указанным в предыдущем упражнении,
добавить уравнения 1(а) и 1F), которые включают двух индивидуумов и квадратичные
функции полезности. Первый индивидуум предлагает фактор X и не предъявляет
спроса на фактор У; второй предлагает фактор Y и не предъявляет спроса на
фактор X. Первый индивидуум предлагает также предпринимательские услуги. Оба
256

предъявляют спрос на товар Z, но не имеют в начале его запасов. Выразить
индивидуальный спрос через цены. Дать полное описание системы, добавив рыночные
условия III, и показать, как будут определяться цены.
5. В предыдущей задаче принять, что предпринимательские услуги (первый
индивидуум) являются свободной переменной и рассматриваются как фактор X.
Заменить производственную функцию функцией f (х, у, ?)=ху—«z2 = 0. Показать, что
условия производства будут тогда заданы выражениями:
1 1
—хрх= — уру = -2 z и рхРу = —.
Проверить, что i?.= 0.
6. Обобщить предыдущую задачу (предпринимательские услуги являются
свободной переменной) для производственной функции f (у1ч ..., г/п) = б и показать, что при
нулевых прибылях форма этой функции ограничена условием:
-° (
*-?)
Показать тогда, что при достижении положения равновесия (как оно определено выше)
масштаб производства не определяется на стадии «производства фирмы», то есть что
условия II определяют только отношения yrj для каждой фирмы /'. Сравнить с
результатами упражнения 2 и частным случаем равновесия из раздела 9.2.
9.4. ПОДСЧЕТ УРАВНЕНИЙ
Существенная особенность вышеописанной системы экономического
равновесия состоит в том, что число независимых условий в ней равно числу
неизвестных, подлежащих определению. Вопрос заключается в подсчете
числа уравнений и неизвестных, в
контроле их численного равенства,
В этом случае можно утверждать,
что система совместна с положением
равновесия, что она не является ни
переопределенной, ни недоопределен-
ной. Вообще условия включают
заданные величины, но форма связи
которых точно не установлена/Лишь в
частных случаях можно считать
уравнения, например, линейными или
квадратными относительно
переменных. Поэтому относительно общей
экономической системы можно лишь
сказать, что она совместна с
состоянием равновесия. В некоторых
частных случаях система может в
действительности и не иметь совсем
положения равновесия, то есть
уравнения не будут иметь вещественных
корней. В других случаях может
быть и много решений.
Все сказанное иллюстрируется
на рис. 33. Он показывает частные
случаи зависимости между
переменными X и У, описываемой
линейными, квадратными и кубическими
уравнениями. В каждом случае
система состоит из двух уравнений,
представленных двумя кривыми на
плоскости OXY. Система совместна Рис. 33
с положением равновесия, то есть
равновесие характеризуется значениями X и У, полученными из решения
уравнений, и соответствующими точками пересечения кривых. В частном
случае, показанном на рис. 33, а, существует только одно положение рав-
17 р. Аллеи
257

новесия — оно представлено единственной точкой Р пересечения кривых.
В другом частном случае (рис. 33, 6) равновесия в действительности вообще
не существует: система совместна с равновесием, но в данном случае
уравнения вовсе не имеют общих вещественных корней. Третий вариант показан
на рис. 33, в; в данном случае существует несколько положений равновесия,
представленных рядом точек пересечения кривых (Рг, Р2, ...).
Гораздо больше можно сказать, если по условиям задачи все уравнения
линейны или может быть допущена линейная аппроксимация для
определенной области значений переменных. Вообще этот случай рассматривается
нами в разделе 13.2, здесь мы резюмируем лишь результаты. Если уравнений
меньше, чем переменных, то имеются «излишние» переменные, и их численные
значения нельзя определить из уравнений. Если уравнений больше, чем
переменных, то существуют «излишние» уравнения, которые могут быть совместны
или несовместны с остальными. В случае совместности их можно получить
из остальных уравнений, а потому и исключить. Эта процедура нами уже
рассматривалась ранее. Несовместность уравнений указывает на ошибку в
формулировке задачи. Ошибку нужно исправить, а излишние уравнения
исключить.
Как правило, в системе линейных уравнений число уравнений равно
числу неизвестных, либо она может быть приведена к такой форме. В
обычном, «неособенном» случае существует решение относительно переменных
и притом единственное. Однако встречаются все же обстоятельства,
«особенный» случай, когда положение то же, что и при наличии «излишних»
уравнений или переменных. Это имеет место тогда, когда определитель,
составленный из коэффициентов уравнений, равен нулю. Всегда необходимо
принимать меры для избежания такой возможности.
Например, рыночные цены можно определить из системы уравнений,
в которой число уравнений равно числу искомых величин цен. В случае
линейных уравнений, как правило, существует единственный набор цен для
достижения равновесия. Однако при некоторых сочетаниях постоянных в
рыночных соотношениях может появиться «особенный» случай, и тогда нельзя
определить все цены или нельзя определить * их единственным образом.
Таким образом, при анализе экономического равновесия необходимо
подсчитать число уравнений. Но и в случае линейных уравнений этого недостаточно
для суждения о существовании решения, а тем более о его единственности.
Наконец, когда даже известно положение равновесия или допускается,
что оно существует, необходимо все же сказать что-то и о его устойчивости
и для различных открытых систем выяснить, что произойдет с одной
переменной, когда изменятся какие-либо другие переменные. Все это — проблемы
сравнительной статики, к рассмотрению которой мы переходим.
По-настоящему же проблема устойчивости может быть исследована лишь в полностью
динамической системе.
9.5. УСТОЙЧИВОСТЬ РЫНОЧНОГО РАВНОВЕСИЯ
В проблеме общего рыночного равновесия (т—1) рыночных цен (с рт
в качестве ценностной единицы, то есть при/?т=1) определялись с помощью
(т—1) уравнений вида:
Yr = Xr-Xr, г = 1, 2, ...,(то-1). A)
Здесь для г-го товара Yr=2iyrj-— чистая продукция (или чистое
потребление), суммированная по всем фирмам, и Хг—Хг=Ъ{хн—хн) — чистый
потребительский спрос (или чистая величина предложения факторов
производства), суммированный по всем индивидуумам. Это — уравнения III
из раздела 9.3. Каждое условие представляет собой равенство рыночного
спроса и предложения отдельного товара (факторов производства или
предметов потребления).
258

Пусть теперь ?г и Dr— предложение и спрос r-го товара на r-м рынке,
так что:
Предметы потребления: Sr = Yr, Dr = Xr — Xr.
Факторы производства: Sr = Xr — Xr, Dr= —Yr.
В том и другом случае превышение предложения над спросом будет иметь
одну и ту же величину
Sr-Dr = Yr-(Xr-Xr). B)
Рыночное условие A) просто констатирует, что Sr—Dr= О для каждого
товара^— предмета потребления или фактора производства.
Уравнение A) представляет собой уравнения относительно (т—1) цен,
так как предполагается, что выбор индивидуальными потребителями
(уравнения I из 9.3) и решения отдельных предприятий (уравнения II из 9.3)
дают совокупные величины Хг и Yr в виде функций от цен. Мы не
рассматриваем здесь вопросов, связанных с этими решениями, например их
устойчивости. Далее, не принимается во внимание т-е уравнение относительно
7гс-го товара, принятого за базисный товар. Это уравнение удовлетворяется
автоматически, если справедливы все остальные уравнения. Равным образом
если не удовлетворено какое-либо уравнение системы A), то есть рынок не
находится в состоянии равновесия при взятых ценах, то уравнение спроса-
предложения для базисного товара также больше не будет справедливым.
Любое нарушение равновесия на рынке отражается нарушением равновесия
на «рынке» базисного товара. Это обеспечивает необходимую гибкость
анализа сравнительной статики.
Всякое рассмотрение устойчивости рыночного равновесия выдвигает
проблемы экономической динамики. Какое-либо равновесие в ценах мы
назовем устойчивым, если за начальным изменением любой цены следует
возвращение цены к уровню равновесия. Все зависит от принятых динамических
условий. Мы показали это в разделе 1.8 на примере одного рынка. Для
различных динамических моделей мы получили и разные результаты.
Рассмотрим теперь модель Вальраса. В качестве динамической предпосылки примем,
что цена повышается с течением времени, если спрос превосходит
предложение при господствующей цене. В этом случае (см. 1.8) равновесие цен на одном
рынке будет устойчивым, если кривая предложения пересекает снизу кривую
спроса (см. рис. 2). Если S(p) и D(p) — функции предложения и спроса
соответственно, то условия устойчивости имеют вид:
-т- (S —- D) > 0 для такого р, что S — D = 0.
Превышение предложения над спросом (S—D) равно нулю при ценах
равновесия и становится положительным по мере того, как повышается*гцена.
Хикс [6] распространил это условие Вальраса на характеристику
устойчивости рыночного равновесия для взаимозависимых рынков. Если Sr
и Dr есть соответственно предложение и спрос r-го товара, представленные
как функции всех цен, то рынок, по* Хиксу, будет устойчив при
для отклонения от положения равновесия на каждом рынке (г = 1, 2, ...,
иг—1). Но при множестве цен на один товар это условие может быть
истолковано по-разному. В одном крайнем случае изменение цены рг может
происходить при неизменности всех остальных цен. Это означает, что равновесие
нарушено не только на r-м рынке (из-за изменения рг), но и на всех остальных
рынках. В другом крайнем случае изменение в рг компенсируется
соответствующими изменениями других цен, так что все рынки (за исключением
г-го и рынка базисного товара) сохраняют равновесие. В промежуточных
случаях некоторые цены остаются неизменными (и соответствующие рынки
не находятся в равновесии), а другие приспосабливаются так, что на соответ-
259 17,

ствующих рынках сохраняется равновесие. По Хиксу, совершенная
устойчивость равновесия цен имеет место, если условие d(ST—Dr)/dpr>0
справедливо при всех обстоятельствах — независимо от того, остаются ли
отличные от рТ цены постоянными или они приспосабливаются так, чтобы
сохранить равновесие на других рынках, либо же частично остаются
постоянными, а частично изменяются. Так как Хг задано, то в силу B) условие
совершенной устойчивости в смысле Хикса будет таково:
V т*=1 2 (т 1) C)
Условие должно быть справедливо во всех случаях. Безразлично,
изменяются ли другие цены или нет.
В данном случае d(Yr — Xr)/dpr есть полная производная,
характеризующая результат изменения как рг, так и тех прочих цен,
приспосабливание которых обеспечивает равновесие на других рынках. Это
изменение можно получить с помощью частных производных вида
d(Yr — Xr)/dps, причем каждая из частных производных берется в
положении равновесия, а потому является постоянной по величине. Запишем эти
постоянные при ценах равновесия следующим образом:
^ U /-уг -у" \ "*¦ Т МЛ. f
гз dps г г' dps др$
Таким образом, условие C) можно выразить через постоянные ars.
Пусть теперь ^ — изменяющаяся цена. Тогда первый рынок выведен
из состояния равновесия. Положим, что все остальные цены сохраняются
неизменными, так что соответствующие рынки также выведены из
положения равновесия. В силу условия C)
Точно так же а22, а23, • -. должны быть все положительны, так как
изменяющиеся цены мы выбираем произвольно. Далее, допустим, что когда
рх изменяется, то р2 варьирует так, что второй рынок находится в
равновесии. Остальные цены по-прежнему сохраняются неизменными, а
соответствующие им рынки выведены из положения равновесия. Тогда, в силу C),
-±- (Гх _ Xl) > О, когда -^- (У, - Xt) = 0.
Далее
и точно так же —— (Г2 — Х2) = а21 + а22
api
Приравнивание нулю второго из них дает dp2/dp±= — a21/a22 и
0
«22/
Так как a22 положительно, то в обозначениях, принятых в теории
определителей (см. 11.9), должно быть:
*21 2
То же самое условие справедливо и для любой пары цен и рынков, то
есть все такие определители второго порядка положительны. Далее, если
мы принимаем, что р2 и р3 при изменении рг варьируют так, чтобы
указанные два рынка находились в равновесии, то точно таким же образом
260

доказывается (см. упражнение 1), что
2
Я32
«23
Аналогично доказательство и для других определителей третьего порядка.
Эти результаты носят общий характер, Ьни справедливы для вариации
любого количества цен. Следовательно, условия совершенной устойчивости
рыночного равновесия в смысле Хикса будут иметь вид:
«и > 0;
п1
а»
ап
а21
пол
«12
«22
«32
а13
а23
«зз
для любого числа взятых товаров 1, 2, 3, ... на какой-то момент времени.
Самуэльсон [10, 11] подверг критике хиксианское понятие совершенной
устойчивости на том основании, что оно определено по аналогии со случаем
для одного рынка. Динамическая модель, удовлетворяющая этому критерию
устойчивости, построена лишь для такого простейшего случая. Общий случай,
включающий множество рынков, не рассматривался (по крайней мере явно)
сточки зрения динамической модели, характеризующей изменение во времени
взаимозависимостей системы цен. Анализ является, очевидно, неполным, и мы
вернемся к этой проблеме далее (см. 13.6). Неожиданное затруднение
возникает и потому, что ars и asr вообще различны, так как нельзя предположить,
что dXr/dp$ = dXs/dpr или что dYr/dps — dYs/dpr. Такая асимметричность
смущает, и Хикс [6] хорошо сознавал это. Он стремился устранить ее,
например, в потребительском спросе тем, что принимал «члены, характеризующие
доход», ничтожными по сравнению с величинами, выражающими эффект
замены.
Задачи и упражнения
1. Рассмотрим рынок из трех товаров. Пусть при изменении рг вариация р2 is p3
обеспечивает равновесие их рынков. Показать, что для совершения устойчивости
должно быть
#11 #12 #13
#21 #22 #23
«31 #32 #33
2. Хикс характеризует несовершенную устойчивость вышеприведенными
условиями C), когда рТ изменяется, а все остальные цены приспосабливаются к изменениям
рынков. Условия C) могут быть справедливы для некоторых, но не для всех
частичных приспособлений цен к состоянию равновесия. Как в этом случае изменятся
определители, составленные из «, выражаюшие условия устойчивости?
3. Исследовать условия несовершенной устойчивости для случая двух товаров
(кроме базисного). Показать, что
«22
«11 «12
а21 а22
так что а22 и определитель имеют один и тот же знак (не обязательно [плюс).
Распространить это на случай трех товаров (кроме базисного),
9.6. НЕКОТОРЫЕ ПРОБЛЕМЫ СРАВНИТЕЛЬНОЙ СТАТИКИ
Рассмотренное в разделе 9.3 рыночное равновесие представляло собой
статическую и закрытую систему. Можно было подсчитать число
уравнений системы и показать, что она совместна с равновесием. Это была важная,
но не слишком плодотворная процедура. Наиболее интересные проблемы
выдвигают сравнительная статика и динамика. Типичен следующий вопрос:
если в данных элементах произошли точно определенные сдвиги (например,
вкусов потребителей или технологии производства), как будут в таком случае
261

двигаться значения переменных в положении равновесия (например, цены
или объем покупок)? Цель сравнительного статического анализа состоит
в получении «обобщенных теорем». Но вывести их не так просто. Кроме того,
они не поддаются прямому истолкованию. Содержание сравнительной
статики вовсе не ограничивается голым утверждением, вроде такого: «покупки
возрастают при падении цен».
Часть трудностей связана с тем, что рассматривается закрытая система.
Так, например, на рынках определяются одновременно все цены. Нельзя
изменить одну цену и проследить влияние этого изменения на остальные
переменные. Цены представляют собой строго определенную систему, и одна
из них может изменяться только в том случае, если какой-либо рынок вышел
из состояния равновесия. Устраняется одно или несколько условий
равновесия, и система превращается из закрытой в открытую. Мы иллюстрировали
это уже при исследовании проблемы устойчивости в разделе 9.5, где рынок
базисного товара во всех случаях не находился в равновесии.
Далее, весьма важно подчеркнуть, что значительные результаты
метод сравнительной статики дает, лишь привлекая по существу
динамические условия устойчивости. Это явление Самуэльсон [11] назвал
«принципом соответствия». Рассмотрим его на примере единственного рынка
(см. 1.8). Цена Р и объем покупок-продаж X задаются в состоянии
равновесия следующим образом:
Пусть происходит сдвиг кривой предложения, скажем, вследствие
изменений в технологии производства. Пусть S(P, а) характеризует шкалу
предложения, где сдвиг представлен параметром а, причем (dS/да) >0.
Увеличение а означает повышение предложения. Значения Р и X в положении
равновесия выразятся тогда через а следующим образом:
I = B(P) = S(i>,o). A)
Продифференцируем A) по а:
da = dP da ~ dP da
то есть
dP dS 1 dX
1 da
dS
da
d
дР
dD
dP
•(S-D)
da да д da
Здесь (dS/да) > 0 и можно принять, что (dD/dp) < 0. В таком случае все
зависит от знака d(S — D)/dP. Теперь-то и вводятся условия
устойчивости. Например, в модели Вальраса для устойчивого равновесия
необходимо, чтобы d(S — D)/dP > 0. Поэтому в состоянии устойчивости
выражения для dP/da и dX/da дают:
да da
Повышение предложения уменьшает цену и увеличивает объем покупок-
продаж. В этом смысле покупки увеличиваются при падении цен.
Аналогичные результаты дает и сдвиг в спросе (см. упражнение 1).
Используя условия устойчивости Хикса, мы можем подойти точно
таким же методом и к исследованию равновесия на взаимосвязанных
рынках. При наличии двух товаров (кроме базисного) два условия
рыночного равновесия запишутся следующим образом:
YX^XX = -Xx и У2-Х2= -Х2, B)
где Хг и Х2 заданы, (Y1 — X1) и {Y2 — X2) представляют собой превышение
предложения над спросом, безразлично на факторы ли производства или
262

предметы потребления. Пусть (Уг — Хх) зависит от параметра а и цен р1
и р2. Положим, что [d(Y1 — XJ/da] > 0, так что увеличение а
соответствует повышению предложения или уменьшению спроса первого товара.
Вследствие этого цены равновесия, установленные условием B), будут
зависеть от а, то есть от изменений предложения или спроса первого
товара. Как и прежде, при ценах равновесия напишем для г, s = l, 2:
Дифференцируем B) по а:
(a) _ clPij
(б) а21 ^ + а22 *р- = 0.
v ' 21 da ' 22 о?а
Тогда из равенства (б) имеем
и подставляем его в (а):
™
да
da
Если равновесие устойчиво в смысле Хикса, то а22 и определитель оба
положительны. Следовательно, при увеличении а (повышение предложения
или сокращение спроса) dpjda < 0, a dp2/da имеет тот же знак, что и а21.
Цена первого товара падает при расширении предложения (или
сокращении спроса). Воздействие на цену второго товара зависит от соотношения
между двумя товарами, даваемого равенством
= —(У — X )
21 др± ^ 2 2'*
Если пренебречь «эффектом дохода», можно считать, что в таком случае для
двух заменяющих друг друга товаров а21 < 0, а для дополняющих
товаров а21 > 0. Следовательно, расширение предложения одного товара ведет
к падению цены заменяющего его товара и росту цены дополняющего его
товара. То же самое произойдет и в случае сокращения спроса на первый
товар.
Мы можем обобщить это и для случая нескольких товаров, когда на цены
всех товаров влияет изменение спроса или предложения одного из них. По-
прежнему остается верным (dpjda) < 0; «перекрестное же действие» dpjda,
dp3/da, ... (заменяемости-дополняемости) может быть более сложным. Мы
рассмотрим это в упражнениях 2 и 3.
Задачи и упражнения
1. Пусть для одного товара возрастание а характеризует расширяющийся спрос:
D(P, а) и (dD/da)>0. Показать, что изменение цены равновесия и объема покупок
будет определяться условиями:
dP
dP
da
dD
da
d
~dP
1
(S-D)
vt
dX
da
dD
~~da
Доказать, что расширение спроса при устойчивости равновесия вызовет повышение
цен, но что при росте S произойдет лишь увеличение покупок.
263

2. Имеется три рынка на товары (помимо базисного товара) и происходит
расширение предложения первого товара: д(У1—Хх)/^а>0. Показать, что
1
da ^ 32 da ^ 33 da
-=0.
Решить систему относительно трех изменений цен. Вывести отсюда, что
а dpz/da имеет такой же знак, как и определитель
«21 «23
и что то же условие
«31 «33
имеет место и для dp3/da, если равновесие устойчиво в смысле Хикса.
3. В предыдущем упражнении не принимать во внимание «эффект дохода» и
предположить, что третий товар слабо связан с остальными (а23*и «31 малы). На основании
этого доказать, что dp2/da имеет тот же знак, что и а21. Объяснить это. Исследовать
эффект вторичной заменяемости («замены заменителя»), который возникает, если а2з
и а31 значительны [6, стр. 74 и 318].
9.7. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ
Теперь анализ общего экономического равновесия вступает в такую
стадию, когда нужно сформулировать технические условия производства
или переработки продуктов. Из раздела 9.3 следует, что производство
находится в руках некоторого числа отдельных фирм, для каждой из которых
технические возможности просуммированы и представлены производственной
функцией формы f(x19 х2, ..., хт) = 0, где х суть затраты (отрицательные
величины) и выпуски (положительные величины). С другой стороны, в разделе
9.2 мы принимали, что производство в целом для всей экономики происходит
при постоянстве эффективности последовательных затрат (см. стр. 252) и имеет
неизменные технологические коэффициенты, то есть ars представлял объем
г-го фактора, расходуемого для производства единицы s-ro продукта (для раз •
ных г и s). Нет более столь резко различающихся формулировок общей
проблемы техники производства, как две приведенные, и это может служить
иллюстрацией диапазона имеющихся возможностей.
Для удобства обозначения положим, что х суть объемы затрат, или
.потребленных факторов, а у обозначают объемы выпусков, или произведенных
товаров. Все переменные положительны или по крайней мере
неотрицательны. Затем воспользуемся двумя вышеупомянутыми крайними
формулировками техники производства. Во-первых, возьмем для каждой фирмы
производственную функцию вида:
f(xv х2, ..., хт; у19 у2, ...,г/п) = 0 A)
и, во-вторых, примем для производства в целом постоянные технологические
коэффициенты:
» Х1п == а\пУп1
х2п = а2пуп; B)
Xml — aml2/l' Xm2 — am2^2> • • • > Xmn — атпУп*
где ars— объем затрат г-го товара (фактора производства) на производство
единицы s-ro товара в выпуске (произведенного товара). Таким образом,
общая сумма затрат составит:
Х1 — 2j ^ls» ^2 — 2j X2s'i * • • i Xm —
s=l s=l
Различия между этими формулировками сводятся к следующему:
A) относится к фирме, а B) — ко всему народному хозяйству; A)
предполагает непрерывную заменяемость затрат и выпусков, тогда как в B) связи
264

между затратами и выпусками принимаются жесткими и фиксированными;
A) учитывает изменение эффективности при изменении масштаба
производства, а B) предполагает эффективность производства постоянной.
Предпочтение той или иной формулировки или любой модификации их
вовсе не сводится к выбору между правильным и ошибочным. И этот выбор
нельзя сделать, сославшись только на окружающие факты. В реальном мире
технические условия настолько сложны, что любая их формулировка для
исследования неизбежно влечет за собой упрощение. Какая именно
упрощенная производственная функция будет принята, это вопрос экономического
удобства и математической аппроксимации. В реальной жизни техника
производства и соответствующие решения, принятые производителями, имеют
много различных особенностей, и их можно рассматривать с разных точек
зрения в зависимости от того, какие особенности мы считаем существенными,
а какие случайными. При экономической интерпретации любой анализ
удобно базировать на той или другой характерной черте производства. В
одних случаях может быть важно подчеркнуть возможности
взаимозаменяемости затрат и выпуска, в других — жесткие технологические связи
производственного процесса. Математическая формулировка явится тогда
приближением, основанным на явно упрощающих предпосылках. Такой может быть,
например, предпосылка о непрерывном изменении затрат и выпуска и
возможности их непрерывной взаимозаменяемости.
Рассмотрение вопроса о формулировке производственных функций
начнем с простого примера. Пусть имеется один продукт у и два вида затрат
хг и х2. Это допускает заменяемость факторов производства, а также фактора
производства и продукта, но не взаимозаменяемости продуктов. Однако легко
сделать обобщение в случае произвольного числа факторов производства и
видов продукции, включая и комбинированное производство и комплексное
использование различных видов затрат.
Первая формулировка отправляется от фирмы в качестве самостоятельно
принимающей решения единицы. На практике это может быть не «фирма»
в обычном смысле слова, а предприятие или группа предприятий или даже
цех завода. Затраты и выпуск принимаются непрерывно изменяющимися
и заменяемыми. Тогда производственную функцию A) можно записать так:
У = /0*1. xt).
Она имеет непрерывные частные производные
-^j— = /1(#х> Х2/ И ~faT ==J2\Xli x2Ji
которые представляют собой предельные величины продукции. Для
определения шкалы эффективности последовательных затрат в зависимости от
масштаба производства; возьмем факторы производства в постоянной
пропорции а1:а2, так что
y=f(Xa19 A,a2) = <p(X)t
где К характеризует масштаб производства. Если dy/dk постоянно, то
выпуск возрастает пропорционально увеличению объема затраченных
факторов производства, то есть налицо постоянство эффективности
последовательных затрат на единицу продукции. Меняющаяся эффективность задается
dy/dk, возрастающей (или убывающей) по мере увеличения к.
При графическом изображении производственная функция y = f(xv x2)
представляется трехмерной поверхностью, которую удобнее всего
изобразить как систему контуров или кривых постоянного выпуска продукции
на плоскости Оххх2, характеризующей затраты факторов производства:
f(x±J x2)^yx\ /(^А)==г/2; ...
для различных фиксированных выпусков продукции у±, г/2, ... . На рис. 34,а
нанесены три отдельные кривые постоянного выпуска продукции. В точке Рг
265

'Р
на одной из кривых (продукция ух) тангенс угла наклона касательной
отрицателен и численно равен [-—(dxjdx^ — fjf^, то есть отношению
предельных выпусков продукции, или предельной норме заменяемости
хг и х2. Шкала эффективности производства характеризуется темпом роста
выпуска продукции у по мере увеличения затрат пропорционально радиусу
ОР, проходящему через точку О.
Особый интерес представляет
частный случай, когда функция
производства есть однородная функция степени
г, так что увеличение затрат факторов
производства в одном и том же
отношении К влечет за собой увеличение
выпуска продукции в отношении Кг:
f (\т Ol /у \ \Ti I/r r \
/ I /w«A/-i у 1\Л>2% —• /\i I \<А/л у JL/nl.
Зависимость выпуска продукции
масштаба производства А,, заданная
становится в таком случае совсем
простой и не зависимой от фиксированных
пропорций, выбранных для затрат
факторов производства:
от
О
/Р
Уз где ух— выпуск продукции,
соответствующий К = 1 и первоначальным за-
й тратам факторов производства (агжа2).
шшт>ттттяяштяятшт_яттттттшт Эффективность последовательных затрат
У/ будет постоянной, не зависящей от
масштабов производства, при г = 1, то
^ есть когда производственная функция
cot есть линейная однородная функция.
рис 34 ^-Ри г > 1 эффективность возрастает
и при г < 1 убывает. При графическом
изображении кривых постоянной
продукции, принятой на рис. 34, а, однородная производственная функция будет
представлять систему кривых, каждая из которых есть расширение или
сокращение любой другой кривой посредством радиуса, исходящего из точки О.
При увеличении кривой постоянного выпуска продукции у1 в X раз
получается другая кривая постоянного выпуска продукции, для которой у2= Xryv
В частном случае линейной однородности (г = 1) фиксированный выпуск
продукции расширяется в том же самом отношении (у2 = Хуг), то есть
эффективность последовательных затрат будет постоянной.
Все это предполагает непрерывную заменяемость факторов при
производстве единственного продукта — безразлично, будет ли эффективность
последовательных затрат в данйой фирме величиной постоянной или
варьирующей в зависимости от масштаба производства. В качестве альтернативы можно
взять неизменные технологические коэффициенты, то есть форму B)
«производственной функции», опять-таки для данной фирмы. При наличии двух
факторов и лишь одного продукта «производственная функция» будет иметь
следующий вид1:
где а1ла2 — постоянные коэффициенты, объемы затрат двух факторов на
единицу выпуска продукции. Это выражение можно рассматривать как очень
специальную форму производственной функции у = f(xL, x2), когда мы при-
1 При неизменных технологических коэффициентах производственная функция
в данном случае будет иметь вид xi = aiyi и Х2 = п2у2, то есть без знака неравенства.—
Прим. ред.
266

нимаем, что затраты должны быть использованы только в пропорциях х± : х2=
= ах : а2 и не иначе. Любой излишек одного или другого вида затрат просто
пропадает зря, без какого-либо увеличения выпуска продукции. Тогда
«кривые» постоянного выпуска продукции принимают специальную форму,
показанную на рис. 34, б. Здесь выпуск в сущности ограничен комбинациями
затрат, расположенными на радиусе ОР. Производственная функция является
линейной однородной функцией: при увеличении хх и х2 в пропорции Я, у
также увеличивается в пропорции к. На рис. 34, б соотношения постоянного
выпуска продукции равны
у1:у2:у3: ... =ОР± :ОР2: ОР3: ... .
Но это не единственная интерпретация технических условий
производства (хх = агу иж2 = а2у). Возможно, что хг и х2 могут быть
взаимозаменяемыми, давая продукцию, варьирующую в соответствии с производственной
функцией (см. рис. 34, а), но в действительности фирма предпочитает
ограничиться данной пропорцией затрат аг: а2. Это означает, что вместо хх и #2,
произвольно варьирующих по кривой постоянного выпуска продукции, фирма
выбирает значения, соответствующие радиусу ОР. Тогда при дальнейшей
предпосылке, что производственная функция является линейной однородной,
технологические зависимости будут иметь вид хг = а1улх2 = а2у, где
направление ОР устанавливается отношением ах : а2. В этом случае нет видимой
причины, почему можно взять лишь единственную пару постоянных
технологических коэффициентов, то есть провести лишь единственный радиус через
семейство кривых постоянного выпуска продукции. Можно взять конечное
число и других технологических коэффициентов:
или х1* = а1*У> или я18 = а18у;...,
(о)
или х22~а22у, или х23=а2Ву
Каждый из этих технологических коэффициентов можно назвать
производственным процессом или способом получения продукта у из частной
фиксированной комбинации факторов производства хг жх2. Тогда xrs = ars у, гдеаГ8—
постоянный технологический коэффициент, показывающий использование г-го
вида затрат (в данном случае г = 1, 2) для производства у с помощью 5-го
способа. На рис. 34, а каждый способ соответствует единственному радиусу
типа ОР, проведенному через кривые постоянного выпуска продукции
линейной однородной функции производства. Та предпосылка, что фирма
производит при технических условиях C), предполагает линейную однородную
функцию производства (постоянство эффективности последовательных затрат)
и выбор между конечным числом технологических способов. В самом деле,
мы можем сделать следующий шаг, предполагая, что производство
развивается с помощью двух или трех технологических процессов одновременно
и выпуски складываются. Производственная функция C) не столь жестка,
как может показаться на первый взгляд. Гибкость достигается
комбинированием (сложением) различных технологических способов. При естественном
обобщении на случай включения многих факторов производства и продуктов,
эта концепция набора различных технологических способов, используемых
по отдельности или комбинированно, является основой «линейного
программирования» (или «анализа деятельности») фирмы, о которой речь будет идти
далее. Это представляет собой реальную альтернативу непрерывной
производственной функции вышеприведенного типа A).
Например, в модели с одним продуктом и двумя факторами производства
можно получить продукт, применяя четыре различных типа машин, каждый
из которых соответствует различной трудоемкости изделия. Тогда в нашем
распоряжении будет четыре технологических способа с постоянными
технологическими коэффициентами (соответственно производительности машины).
Фирма может выбрать один из этих способов или использовать их
комбинацию. Производственная функция будет иметь форму C); она включает четыре
267

пары коэффициентов, и выбор решения фирмы представит собой простое
упражнение по «линейному программированию».
9.8. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КАК МАТРИЦА
Вернемся опять к фирме, выпускающей один вид продукции (у) и
имеющей два вида затрат (хг и х2). Предположим, что решения фирмы ограничены
четырьмя технологическими способами или что фирма решает ограничить
свой выбор этими способами. Каждый способ описывается парой постоянных
коэффициентов, то есть пропорциями, в которых комбинируются различные
виды затрат. В случае линейной однородной функции производства
(постоянства последовательных затрат на единицу) эффективная производственная
функция будет иметь вид C) (см. раздел 9.7), или в данном частном случае:
Х21 = п^хУч Х22 =
Таким образом, имеется 8 постоянных коэффициентов ars (г = 1, 2; s —
= 1, 2, 3, 4), которые представляют объем r-го вида затрат на производство
единицы продукции с помощью 5-го способа.
Каждый способ полностью и просто характеризуется вектором из трех
элементов, то есть A, —als, —a2s) для s-ro способа, причем 1 показывает
величину выпуска; —аи и —a2s — соответствующие затраты на единицу
выпуска. Знак «+» указывает на выпуск, знак «—» указывает на затраты.
Совокупность технических условий фирмы будет характеризоваться в таком
случае матрицей
1
-ап
1
— «12
-«22
1
— «13
«23
1 -
-«14
— «24-
представляющей упорядоченную систему заданных элементов. Здесь строки
показывают товары (один для выпуска и два для затрат), а столбцы —
способы. Такая матрица называется технологией фирмы. В данном случае
возможен выбор из четырех способов, применяемых в отдельности или
комбинированно при постоянстве эффективности последовательных затрат.
Рис. 35
Технология показана на рис. 35. Выпуск единицы продукции мы можем
получить четырьмя способами, комбинируя затраты als, a2s для s = 1, 2, 3, 4.
Эти комбинации представлены четырьмя точками Р1У Q±, R±, Sx на плоскости
Охгх2, Выпуск двух единиц продукции получается с помощью любой
комбинации Bals, 2a2s), представленной четырьмя точками Р2, Q2, R2 и S2. По
свойству постоянства последовательных затрат на единицу продукции, Рг
268

и Р2 расположены на радиусе ОР так, что ОР2 = 2OPV Точно так же обстоит
дело и с другими способами. На рис. 35 четырьмя радиусами показаны для
четырех способов неизменные отношения соответствующих затрат. На этих
радиусах можно отметить частный набор точек Рг, Qx, i?x, S±,
характеризующих выпуск единицы продукции. Для получения любой другой величины
выпуска продукции нужно лишь пропорционально переместить этот набор
точек. Линия Рх Qx Rx Sx представляет собой кривую постоянного объема
производства при выпуске единицы продукции. Для получения >йе кривой
другого постоянного выпуска продукции нужно лишь пропорционально
растянуть или сократить первую кривую, так как последовательные затраты
постоянны. Вместо «непрерывной кривой» мы имеем четыре точки, соединенные
прямыми линиями, что указывает на возможность комбинирования способов.
Если четыре способа и независимы и «действенны» в том смысле, что
можно использовать каждый из них в отдельности, то тогда четыре точки Рг, (?х,
Rv Sx выпуклы по отношению к О (см. рис. 35). Например, если Qx будет
расположена вверх и вправо от РгВ1, тогда комбинация первого и третьего
процессов будет более «эффективна», чем Q±, ибо потребует меньше затрат на единицу
выпуска продукции. Из этого также следует, что комбинации «эффективных»
способов могут составляться лишь из смежных способов, изображенных на
рис. 35: можно взять комбинацию Рг и Q19 но не PtRi или Р^^ которые
представляют собой точки, расположенные вверх и вправо от линии PiQi. Далее,
возможную комбинацию способов представляют лишь комбинации затрат,
характеризующиеся точками, расположенными в пределах конуса,
ограниченного радиусами OP, OQ, OR и OS, но не комбинации, расположенные вне его.
Варьирование комбинаций факторов производства и видов продукции,
числа различающихся технологических способов, размера и соотношений
затраты-выпуск открывает очень широкие возможности выбора технологии
фирмы. Ниже приводятся простейшие примеры различных видов матриц,
могущих представить технологию фирмы при наличии не более двух факторов
производства и двух продуктов:
110 0 1110
0
0
1
— a«i — а99 —
а21
22
1
— а
24
о
1
— ап — а12 — а13 — а14
— а
21
— а22 — а23 —а
24
в)
1
0
1 О
Хл — ;
-аи -а
12
— а13 —а
13 — 4
— а21 —а22 — (
— а
24
В случае (а) нет комбинированного производства, и каждый из двух
продуктов производится двумя способами. В случае (б) с помощью двух
технологических способов производятся продукты комбинированно, именно хг при
втором способе и х2 единиц второго продукта при третьем способе
производятся на единицу первого. Случай (в) представляет собой еще один вариант:
второй продукт является выпуском двух способов (при втором способе как
продукт комбинированного производства) и затратой в третьем способе.
Такими двумя продуктами могут быть, например, холодильники и моторы
для них; моторы могут производиться вместе с холодильниками или отдельно
от них (например, как запасные части) или же могут поступать при третьем
способе (например, из запаса или от другой фирмы).
Легко представить технологию фирмы в совершенно общей форме:
'ал
А =
269

Все а представляют собой заданные постоянные — положительные, когда
товар представляет собой выпуск по относящемуся к нему способу, и
отрицательные, когда он является затратой. Многие а могут быть нулями — тогда
соответствующий товар вообще не выпускается при данном технологическом
способе. Если коэффициенты читать вдоль строки, то один и тот же товар
может в одних случаях быть выпуском, в других затратой, в третьих вообще не
участвовать в технологическом процессе. Аналогично при чтении вдоль
столбца может появиться комбинированное производство двух или более товаров
или комбинированное использование факторов производства.
Поэтому при рассмотрении фирмы может оказаться удобной и
плодотворной предпосылка о непрерывности производственной функции,
связывающей затраты и выпуск. Тогда становится возможным исследование
с помощью предельных категорий, которое может оказаться особенно
подходящим при долгосрочном анализе. С другой стороны, могут возразить, что
теория фирмы по самой природе своей краткосрочна, так как
предприниматель обладает ограниченным временным кругозором и что-то он всегда
должен принимать как неизменное. В самом деле, существует немного
доказательств того, что предприниматель склонен мыслить предельными
категориями, и еще меньше их имеется в пользу того, что именно так он и мыслит.
Предприниматель едва ли может рассчитывать на то, что в момент принятия
решения он будет располагать всеми необходимыми данными. Более вероятно,
что он оперирует прямыми вариантами простых и довольно жестких
процессов (см. работы Хэлла и Хитч [3] и Гордона [2]). В этом случае более
подходящей будет формулировка технологии в форме приведенной выше матрицы
А и анализ в абсолютных числах, а не в виде предельных выражений.
Можно возразить, что предпосылка ограниченности числа
технологических способов и постоянства технологических коэффициентов слишком жестка
и ограничительна. Нельзя выдвинуть серьезных возражений против
допущения о совершенной делимости элементов затрат и выпуска и против
постоянства" эффективности последовательных затрат для одного технологического
способа. Первая из этих предпосылок является удобным упрощением, а
затруднения при сохранении второй можно преодолеть путем выделения двух
или более способов в случае появления изменяющейся эффективности
последовательных затрат. Более серьезным является возражение против того, что
различные способы нельзя свести к малому числу и что их нельзя
комбинировать простым сложением затрат и выпуска. Но некоторые
упрощения неизбежны, и полезно оценить, какие из них являются наиболее
суровыми.
Нам осталось кратко рассмотреть еще одно обстоятельство. Анализ на
уровне индивидуальной фирмы (как в разделе 9.3) может оказаться слишком
детальным для данных целей. В качестве альтернативы возможно
рассмотрение крупных секторов экономики или всего процесса производства в целом
(как в разделе 9.2). И опять-таки формулировка технологии одной отрасли
производства, группы отраслей или «промышленности» в целом — это в
большой мере вопрос удобства с экономической и математической точек
зрения. Для долгосрочного анализа и для крупных секторов народного
хозяйства предпосылка о совершенно непрерывном изменении и заменяемости
кажется более разумной. Она ведет к анализу в предельных величинах
с непрерывной производственной функцией. С другой стороны, обобщение
в одной производственной функции, единственное между всеми затратами
и выпусками, может быть слишком широким для того, чтобы выделить
требуемые результаты.
Следовательно, и для производства в целом, по-видимому,
предпочтительнее принять технологию в форме вышеприведенной матрицы А, то есть взять
лишь ограниченное число «видов деятельности» или технологических способов,
связывающих различные товары в качестве затрат и выпусков, и ограничить
область действенных решений возникающими таким образом вариантами.
В зависимости от требования мы можем затем ограничить действительную
270

форму матрицы А. Следующая форма весьма проста и полезна:
— аЧ1 —с
Здесь каждая «деятельность», представленная столбцом матрицы А, есть
отрасль, производящая один и только один характерный для нее продукт.
Далее, если даже принять во внимание наличие многих нулевых элементов,
выпуск отрасли может быть как затратой нескольких других отраслей, так
и «конечным» продуктом. Эта формулировка подробнее развивается в
следующей главе. Ее недостатки очевидны: объединение разнообразных продуктов
в единственную группу, характеризующую выпуск отрасли; предпосылка
постоянства последовательных затрат на единицу продукции и неизменность
технологических коэффициентов; очевидное отсутствие всякой возможности
заменяемости. Сколь серьезны эти ограничения и перевешиваются ли они
преимуществами принимаемой ясной и простой формулировки, можно будет
решить лишь на основе некоторого опыта в технике применения модели.
В дальнейшем мы исследуем более тонкие и подробные формулировки задачи
на уровне фирмы и крупных секторов народного хозяйства.
В заключение этого методологического обзора следует еще раз
подчеркнуть важность экономической целесообразности и математической
аппроксимации. Вовсе не обязательно, чтобы теоретическое построение было
«реалистическим» в том смысле, что оно точно обосновывает путь практических
действий предпринимателя. Предельный анализ может оказаться вполне
подходящим для изложения и установления в наиболее ясной форме главных
результатов. С другой стороны, построение модели, предназначенной к
заполнению статистическими данными, в целях помощи фирмам в деле
принятия последними решений при полной информации их о существующем
положении, очевидно, должно базироваться на альтернативном анализе с помощью
технологической матрицы. Полезно использовать оба метода подхода — метод
предельных величин и анализ в абсолютных числах — и беспристрастно
судить о том, который из них принять.
Задачи и упражнения
1. Фирма производит продукт у с помощью двух факторов (хг и х2).
Производственная функция имеет вид x\x%—ay=Q. Показать, что у есть однородная функция
второй степени от i! и ж2.
2. Взять производственную функцию из предыдущего упражнения в форме
ххх%—ау* = 0 и показать, что у есть линейная однородная функция употребленных
факторов производства. Далее показать, что способ, в котором факторы применяются
в пропорции а : 1, является допустимым и описывается постоянными технологическими
коэффициентами, заданными вектором A, а, 1). Определить другие способы, совместные
с данной функцией производства, и затем построить допустимую технологическую
матрицу фирмы.
3. Технологическая матрица основана на производственной функции, имеющей вид:
/(*!» *2» ..., Хт\ уъ ?/2, ..., Уп)=0ш
Показать, что / должна быть однэродной в любой степени.

ГЛАВА 10
МЕЖОТРАСЛЕВЫЕ СВЯЗИ
10.1. АНАЛИЗ ЗАТРАТ И ВЫПУСКА ОТРАСЛЕЙ НАРОДНОГО ХОЗЯЙСТВА
Системы общего равновесия рынка слишком детализированы, для того
чтобы ими можно было пользоваться при решении практических задач.
В настоящей главе вместо этих систем применяется более широкий анализ,
при котором рассматриваются уже не фирмы, а отрасли хозяйства. Подобный
подход позволяет избежать многих трудностей; например, если для нас не
играет роли способ объединения самостоятельных единиц (то есть единиц,
способных принимать самостоятельные решения) в отрасли, то вполне
уместно допустить существование как чистой конкуренции1 (цены задаются извне),
так и свободного доступа (прибыль равна нулю). Достичь этого удается за
счет введения понятия «отрасль», неточного и являющегося грубым
приближением. По существу отрасли — это эмпирические совокупности,
построенные на основе какой-либо статистической классификации; выпуск отрасли,
например, состоит обычно не из одного продукта, как удобно было бы считать,
а представляет скорее комплекс основных и побочных продуктов.
Теория общего экономического равновесия при отраслевой разбивке
хозяйства впервые сформулирована Леонтьевым [5]. Она имеет глубокий
практический смысл и может быть непосредственно использована на практике
в виде анализа межотраслевых связей, то есть анализа как сети
межотраслевых потоков промежуточных продуктов, так и потоков конечных продуктов
к потребителям. Важнейшей особенностью этого анализа является
технологическая характеристика хозяйства, которая предполагается заданной в виде
производственной функции (см. стр. 271). Вместе с тем при анализе делаются
некоторые упрощающие предположения. В общем случае каждая из отраслей
использует несколько различных первичных факторов и производит
одновременно несколько видов промежуточных или конечных продуктов; кроме того,
значительное число продуктов вырабатывается более чем одной отраслью.
Для упрощения мы принимаем, что в каждой отрасли потребляется только
один вид первичных затрат (затраты труда), что каждая отрасль производит
только один вид продукции, а каждый продукт вырабатывается только одной
отраслью. Таким образом, имеются п отраслей и п различных продуктов,
причем каждый из продуктов производится только одной отраслью, но
потребляется в качестве промежуточного продукта любым числом отраслей.
Кроме того, для любой отрасли характерно наличие первичных затрат (труда)
и конечного (потребительского) спроса.
Основным объектом анализа является технологическая характеристика,
представленная в виде матрицы коэффициентов, аналогичной матрицам,
описанным в конце раздела 9.8. Тем самым мы вносим дополнительные
упрощения: во-первых, производство представляется в виде совокупности
отраслевых «процессов» с постоянными технологическими коэффициентами (само
по себе это не является столь уж большим отступлением от действительности)
и, во-вторых, для каждой отрасли принятый «процесс» является единствен-
1 Чистой конкуренцией современные англо-американские экономисты называют
конкуренцию, лишенную какой бы то ни, было примеси монополии, что предполагает два
условия: большое количество продавцов и покупателей и совершенную однородность
продукта.— Прим. ред.
272

ным и его 8с ie представляется возможной (этот вопрос нуждается
в дальнейшем i. лши; см. раздел 16.4). Таким образом, зависимость между
затратами и выщ ком проявляется в цростейшей форме—линейной связи, или
прямой пропорциональности. В сущности метод Леонтьева затраты — выпуск
представляет собой особый частный случай более общего метода линейного
программирования или анализа хозяйственной/деятельности,
рассматриваемого в главах 15 и 16; «программируемой» является здесь заданная
совокупность отраслевых процессов производства.
Анализ межотраслевых связей является статическим методом, поскольку
он представляет задачу общего экономического равновесия. Однако, изменяя,
например, структуру («ассортимент») конечного спроса или вводя в том или
ином виде динамические элементы, как это делает Леонтьев [6], можно легко
распространить подобный анализ и на случай сравнительной статики.
Объектом анализа в значительной части являются величины в
стоимостном (денежном) измерении; практически денежная единица представляет
собой единственную общую для всех отраслей (единицу измерения, дающую
возможность суммирования затрат и выпуска по отраслям. Однако
построение, естественно, распадается на количественную часть (продукция в
натуральном выражении) и на соответствующую систему цен. Применяются
следующие условные обозначения: 1) валовой выпуск отрасли обозначается
прописной буквой с соответствующим нижним индексом; 2) эти же буквы, но
строчные обозначают компоненты продукции отрасли и могут иметь двойные
нижние индексы. Цены товаров и ставка заработной платы для единственного
первичного фактора (труда) обозначаются строчными буквами: цены через /?,
ставка заработной платы через w.
10.2. МАТРИЦА МЕЖОТРАСЛЕВЫХ ПОТОКОВ
При анализе по методу затраты —выпуск основным является
охватывающая все хозяйство балансовая таблица или матрица межотраслевых потоков,
выраженных либо в количественной, либо в денежной форме. Поскольку
этот метод по существу является эмпирическим, да и предназначен он для
практического применения, поучительно было бы начать с рассмотрения
примеров стоимостных матриц фактических межотраслевых потоков.
В табл. 1 приведена матрица межотраслевых потоков для
Великобритании за 1935 г., построенная Варна [1], а также аналогичная матрица для
США за 1947 г., составленная на основе детальных расчетов Бюро статистики
труда и помещенная в книге Эванса и Хоффенберга [3]. Число групп отраслей
производства в каждой из этих матриц сокращено до 10, тогда как в
исходных матрицах число строк и столбцов было больше, и классификация
промышленности была более дробной.
Рассмотрим в качестве примера первую строку матрицы для
Великобритании. Весь валовой выпуск продукции сельского хозяйства и пищевой
промышленности составил в 1935 г. (в текущих рыночных ценах) 858 млн. ф. ст.
В первой строке таблицы показано распределение продукции этой отрасли.
Стоимость той части ее, которая пошла в качестве промежуточных продуктов
на потребление других отраслей, составила 23 млн. ф. ст., в том числе
потреблено: строительством — 2 млн. ф. ст., химической промышленностью —
4 млн. ф. ст., текстильной промышленностью — 8 млн. ф. ст., отраслью
«услуги» — 3 млн. ф. ст.; кроме того, осталась нераспределенной за
отсутствием статистических данных продукция на сумму 6 млн. ф. ст. Остальная
часть продукции отрасли охватывает конечный продукт, удовлетворяющий
конечный спрос: экспорт — 29 млн. ф. ст., капиталообразование (в данном
случае — увеличение запасов товаро-материальных ценностей) — 3 млн.
ф. ст., потребление государственных органов — 7 млн. ф. ст. и основная масса
G96 млн. ф. ст.) — личное потребление. Таким образом, первая строка
полностью характеризует распределение выпущенной продукции отрасли. В дан-
18 Р. Аллен 273

Матрица межотраслевых потоков для Англии (за 1935 г.) и США (за 1947 г.)
Отрасли хозяйства:
1. Сельское хозяйство и пищевая промышленность.
2. Угольная промышленность и энергетика.
3. Строительство, промышленность стройматериалов и лесная промышленность.
4. Химическая и резиновая промышленность.
5. Текстильная и швейная промышленность.
6. Бумажная, полиграфическая промышленность и другие отрасли.
7. Металлургия.
8. Машиностроение.
9. Производство металлоизделий.
10. Услуги.
А. Матрица для Англии за 1935 г. (в млн. ф. ст.)
Таблица 1
s^^ • Выпуск
Затраты ^*^>>.
^^
Поступило от
отраслей:
1
2
3
4
5
6
7
8
9
10
Не распределено . .
Итого ...
Распределение выпуска между отраслями
1
—
14
10
25
4
18
2
5
7
72
13
170
2
—
3
2
*
1
5
16
1
20
8
56
3
2
12
—
14
8
4
28
21
16
46
7
158
4
4
8
5
—
5
13
3
*
5
16
5
64
5
8
9
1
13
—
6
*
4
3
41
18
104
6
*
4
1
6
4
1
1
1
13
5
36
7
*
16
7
2
*
*
—
2
2
18
20
67
8
8
10
19
8
5
62
—
22
28
10
172
9
*
3
2
3
2
30
1
—
7
6
54
10
3
39
129
7
16
48
*
39
*
—
30
311
не

пределено
6
8
12
6
5
14
7
17
17
35
__
127
всего.
23
121
180
97
50
111
138
106
74
296
122
1318
ЭКС-
nODT
29
31
9
38
125
15
38
79
45
332
15
756
Конечное

лообразование
3
39
280
2
2
2
6
173
9
26
-3
544
потребление

государственные
органы
7
15
56
6
2
6
*
40
2
304
3
441
личное

потребление
796
129
53
73
298
69
5
79
32
1907
-5
3436
Весь
валовой
выпуск
858
334
577
217
476
208
188
477
162
2865
132
6 494
* Менее 0,г< млн ф. ст

^~\^^^ Выпуск
Затраты ^*\^^
Импорт
Государственные
органы
Первичные затраты
Всего валовая сумма
затрат
Распределение выпуска между отраслями
1
130
176
385
858
2
5
5
268
334
3
41
10
369
577
4
48
7
98
217
5
102
13
258
476
6
23
4
147
208
7
30
2
86
188
8
16
7
282
477
9
37
2
70
162
10
19
256
2280
2865
не

пределено
9
13
-18
132
всего
460
495
4225
6494
Продолжение
Конечное потребление

экспорт
52
808

лообразование
18
7
569

государственные
органы
8
2
450
личное

потребление
266
85
3788
табл. 1
Весь
валовой
выпуск
804
587
4 225
12108
^*^\^^ Выпуск
Затраты ^Vss\^^
Поступило от
отраслей:
1
2
3
4
5
6
7
8
Б.
Матрица для
[ США
за 1947 г. (в
сотнях млн.
долл.)
Распределение выпуска между отраслями
1
3
9
30
3
6
*
2
2
3
'5
*
*
1
1
3
3
3
—
17
4
4
22
15
4
19
8
4
—
5
5
2
*
27
2
1
12
—
4
*
1
б
1
2
5
6
2
—
2
1
7
*
3
4
11
*
—
1
8
*
2
10
12
4
3
47
—
9
1
3
2
1
3
18
5
10
49
49
67
28
2
41
2
19
не

пределено
4
14
20
11
26
14
44
всего
103
72
121
142
31
92
108
89

экспорт
30
4
5
17
13
4
8
34
Конечное

лообразование
-13
*
169
3
1
4
1
125
потребление

государственные
органы
13
2
56
4
3
3
*
17
личное

потребление
334
1
24
51
135
38
*
51
Весь
валовой
выпуск
467
79
375
217
183
141
117
316
¦ Менее 50 млн. долл.

Продолжение табл. 1
^*"^\^^ Выпуск i"
Затраты ^""\^
9
10
Не распределено . .
Итого . .
Импорт ......
Государственные
отэганы
Первичные затраты
Всего валовая сумма
Распределение выпуска между отраслями
1
, 6
80
22
160
28
21
258
467
2
4
4
17
*
И
51
79
3
10
67
22
168
3
15
189
375
4
2
23
зо„
98
9
17
94
217
5
*
14
21
82
5
12
84"
183
6
1
12
21
52
8
10
72
141
7
*
13
15
48
6
8
55
117
8
20
16
39
154
1
18
143
316
9
5
14
51
1
5
38
94
10
4
82
343
5
139
871
1358
не

пределено
15
70
219
1
22
18
261
всего
60
304
269
1393
66
278
1872
3609
Конечное потребление

экспорт
6
35
*
156
00 00 1
173

лообразование
8
40
-8
329
3
2
334

государственные
органы
2
63
*
162
13
35
301
511
личное

потребление
18
915
1569
13
313
21
1916
Весь
валовой
выпуск
94
1358
261
3609
93
637
2205
6543
* Менее 50 млн. долл.
Примечания.
По таблице А: Таблица взята с небольшими изменениями из книги Варна [1].
В строку «Государственные органы» включены только косвенные налоги за вычетом субсидий.
В столбец «государственные органы» включено только потребление государства без учета капиталообразования.
В столбец «капиталообразование» входят элементы основного капитала и сальдо изменений запасов товаро-материальных ценностей, включая
капиталообразование, осуществляемое государством. Изменения товаро-материальных ценностей исчислены приблизительно и отделены в таблице
книги Варна от столбца «не распределено».
По таблице Б: Таблица составлена (с укрупнением отраслей) на основе книги Эванса и Хоффенберга [3].
В строку «Государственные органы» включены все налоги и некоторые другие платежи.
В столбец «государственные органы» включено потребление и капиталообразование.
В столбец «капиталообразование» включены элементы основного капитала и сальдо изменений запасов товаро-материальных ценностей без учета
капиталообразования, осуществляемого государством.
Между этими таблицами имеется много других различий в объеме и определении классификационных рубрик; для уточнения этих различий нужно
обратиться к указанным двум источникам.
Ввиду округления отдельных элементов итоги суммирования по строкам или столбцам не обязательно совпадают с роставленными итоговыми цифрами.

ном случае основным видом потребления является личное потребление, хотя
имеют значение и другие категории потребления, объем которых относительно
невелик. Аналогичным образом истолковываются и элементы строк по другим
отраслям; в качестве примера можно рассмотреть седьмую строку. Общая
стоимость продукции металлургии (чугун, сталь и цветные металлы) в 1935 г.
составила 188 млн. ф. ст.; эта продукция распределена в виде
промежуточных продуктов преимущественно между отраслями «машиностроение»,
«производство металлоизделий» и «строительство». Некоторая часть продукции
этой отрасли экспортируется, и совсем небольшая доля расходуется
непосредственно на личное потребление и на капиталообразование.
Итогами столбцов таблицы являются те же приведенные выше величины
валового выпуска отраслей. Элементы первого столбца расшифровывают
затраты сельского хозяйства и пищевой промышленности: стоимость
материалов и услуг, полученных от других отраслей — 170 млн. ф. ст., стоимость
импортированных материалов — 130 млн. ф. ст., косвенные налоги (за
вычетом субсидий) составляют 176 млн. ф. ст. Остается добавленная стоимость»
этих отраслей, которая исчислена в сумме 385 млн. ф. ст. Она представляет
собой первичные затраты, или оплату первичных факторов (заработная плата
рабочих и служащих, прибыль). В данной таблице к первичным затратам
отнесена также и амортизация. Итог суммирования по вертикали элементов
первого столбца равен (если не учитывать погрешности округления) итогу
элементов первой строки, поскольку, по определению, вся сумма затрат
равна всему валовому выпуску, или 858 млн. ф. ст. Это же справедливо и для
строк и столбцов других отраслей; всякий раз по горизонтали
расшифровывается распределение выпуска, а по вертикали — затраты рассматриваемой
отрасли экономики.
Таблица заканчивается элементами правого нижнего квадранта,
представляющими реэкспорт, непосредственное личное потребление
импортируемых товаров и соответствующие косвенные налоги на стадии конечного
потребления.
Сумма всех элементов таблицы представляет собой совокупную стоимость
всех потоков по текущим рыночным ценам. Эта стоимость превышает
величину как валового национального продукта, так и национального расхода,
однако таблица позволяет вычислить и эти показатели национального дохода,
а также определить их соотношение с суммарной стоимостью потоков. Для
этого необходимо лишь воспользоваться итогами строк и столбцов правого
нижнего квадранта таблицы, начиная с ее нижнего правого угла.
Предпоследний элемент крайнего правого столбца таблицы D225 млн.
ф. ст.) соответствует валовому национальному продукту по факторным ценам,
то есть по стоимости первичных факторов. Общая стоимость ресурсов,
которыми располагает страна (валовой национальный продукт плюс импорт),
по рыночным ценам равна сумме трех предпоследних элементов этого же
столбца (804+587+4225), то есть 12 108 — 6494 = 5614 млн. ф. ст. Такая же
совокупная величина E614 млн. ф. ст.) получается в результате суммирования
четырех предпоследних элементов последней строки таблицы,
характеризующих имеющиеся в распоряжении ресурсы, или национальное потребление
и экспорт. Эта величина E614 млн. ф. ст.) представляет собой как сумму
оплаты первичных факторов и стоимости импорта, так и сумму государственного
и личного потребления, капиталообразования и экспорта, если каждая из
статей сосчитана по рыночным ценам. Это соответствует уже знакомому нам
тождеству производства продукта и потребления продукта — двух частей
баланса национального дохода.
Таблица распадается на четыре квадранта. Элементы верхнего левого
квадранта охватывают межотраслевые потоки, характеризующие
производство и распределение промежуточных Товаров и услуг; совокупная их
стоимость — 1318 млн. ф. ст. Правый нижний квадрант — это конечное
потребление, удовлетворяемое непосредственно за счет импортируемых товаров,
и соответствующие этому потреблению косвенные налоги; их общая сумма
277

равна 438 млн. ф. ст.1 Остальные два квадранта, верхний правый и нижний
левый, дважды отражают одну и ту же сумму F494—1318=5176 млн. ф. ст.).
В первом случае (правый верхний квадрант) она соответствует конечному
потреблению продукции отечественного производства, а во втором (левый
нижний квадрант) — стоимости первичных факторов и импортированных
продуктов, использованных отечественной промышленностью.
Следовательно, общий итог баланса A2 108 млн. ф. ст.) содержит (в млн. ф. ст.):
I. Межотраслевой оборот промежуточных товаров и услуг, не
включаемый в подсчет национального дохода 1 318
II. Реэкспорт и непосредственное потребление импортируемых товаров 438
III. Остальную часть итога ресурсов (сумма валового национального
продукта и импортированных товаров), взятую дважды, то есть
5176x2= . . . 10 352
Для замкнутого хозяйства, не имеющего внешней торговли, общая сумма
элементов таблицы равна сумме удвоенного валового национального продукта
и межотраслевого оборота промежуточных продуктов. Величина последнего
показателя зависит от принятого метода расчленения экономики на отрасли:
эта величина возрастает с увеличением дробности классификации отраслей.
10.3. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
Предположим, что имеется система, состоящая из п отраслей или видов
деятельности, причем каждая из отраслей производит один вид товара или
продукта, а каждый вид продукта вырабатывается единственной отраслью;
не существует ни доходов и потребления государства, ни внешней торговли.
Система статическая, и вопросы, связанные с капиталовложениями, не
рассматриваются.
Чтобы равновесие существовало, должны выполняться дэе группы
условий: условия первой группы определяют затраты и выпуск отраслей в
количественном выражении, условия второй группы — цены, денежные
поступления, издержки. Рассмотрим сначала количественные, или технические,
условия производства.
Материальный продукт, вырабатываемый r-й отраслью, обозначается
через Хг (г = 1,2, ..., п).} Этот продукт потребляется частично — в виде
промежуточного — другими отраслями, а частично — в виде конечного
продукта — непосредственно потребителями. Обозначим через xrs количество
продукта Хт, потребленное s-ж отраслью, а через хт количество этого же
продукта, выделенное для конечных потребителей. Величины xrs при s = 1, 2, ..., п
(s Ф г) и хт составляют элементы r-й строки матрицы межотраслевых потоков,
аналогичной табл. 1, однако характеризующей эти потоки в количественном,
а не в стоимостном выражении. Итог суммирования элементов строки равен
Хг, или валовому выпуску отрасли2.
Соответственно s-я отрасль получает промежуточные продукты от
других отраслей в количестве xrs при г = 1, 2, ..., п (г Ф s). Остальная часть
затрат отрасли — затраты первичного фактора, то есть затраты труда
различной квалификации, начиная от труда неквалифицированных рабочих
и вплоть до услуг предпринимателей, причем все затраты труда для удобства
объединены в виде одного фактора. Сумма трудовых затрат в целом по системе
обозначается через У, а затраты труда в 5-й отрасли — через ?s. Величины
затрат xrs при г = 1, 2, ..., п (г Ф s) и |s составляют s-й столбец матрицы.
1 Автор здесь суммирует элементы двух строк (импорт + государство) правого
квадранта. Незначительное расхождение итоговых сумм объясняется округлением
отдельных элементов (см. примечание к табл. 1).— Прим. ред.
2 При вфг это будет не «валовой», а «товарный» выпуск отрасли по терминологии
советской статистики.— Прим. ред.
278

Количества xrs при различных г и s играют двоякую роль: они являются
не только элементами матрицы, но и элементами балансовой таблицы. Здесь
важен порядок знаков в нижних индексах: xrs — продукт r-и отрасли,
потребляемый s-й отраслью, а следовательно, затраты s-й отрасли на продукты,
поступающие от r-и отрасли. xrs не равно xsr; элементы матрицы не
симметричны. xrs и xsr и не должны быть равны: первый элемент — продукт,
выпускаемый r-й отраслью, предназначенный для потребления в 5-й отрасли, а второй—
продукт, выпускаемый 5-й отраслью, предназначенный для г-ж отрасли, то есть
два совершенно различных продукта.
В матрице межотраслевых потоков, например в табл. 1, элементы xrs
при г, s = 1, 2, ..., п составляют верхний левый квадрант. Завершающими
элементами строк являются величины конечного спроса хг при г = 1,2, ..., п,
а столбцов — величины затрат первичного фактора ?s при s = 1, 2, ..., п.
В клетках левой главной диагонали матрицы проставляются нули, так как,
по условию, хтт = О при г = 1, 2, ..., тг; в нижнем правом углу также
проставляется нуль. Таким образом, матрица межотраслевых потоков имеет
следующий вид:
п строк
1 строка
xrs
Is
хТ
0
Хт
Y
п 1 Итоговый
столбцов столбец столбец
Строка итогов отсутствует по той причине, что элементы столбца
выражены в различных единицах измерения. Непосредственно из этого следует,
что при суммировании элементов по горизонтали должны быть получены
следующие итоги (г = 1, 2, ..., п):
^1. 2,
• A)
где 2 обозначает суммирование элементов, в которых s пробегает все значе-
S
ния от 1 до п.
Здесь необходимо упомянуть о технических условиях производства, то
есть о связи между величинами затрат и выпуска. Мы предполагаем, что
существуют неизменные коэффициенты, характеризующие зависимость между
элементами затрат отрасли и ее выпуском;
= bsXs (r,s = 1,2,
B)
Поскольку мы условились считать, что хтт = 0, то и атг = 0.
Постоянные величины а и Ъ называются коэффициентами затрат.
По-разному можно толковать предположение об их неизменности.
«Производственная функция» для s-й отрасли, изготовляющей продукт Х8, может
охватывать небольшое число альтернативных процессов, технологические
коэффициенты каждого из которых неизменны. Выбранный или применяемый
процесс отражается тогда уравнением B). Возможен и другой вариант —
непрерывная производственная функция, представленная линейным
однородным уравнением. Если заданы цены различных видов затрат и элементы
затрат комбинируются с целью минимизировать общую сумму издержек для
каждого уровня выпуска, то и в этом случае затраты в принятой комбинации
их элементов изменяются пропорционально выпуску (см. упражнения 1 и 2).
При этом а и b в уравнении B) остаются постоянными только для заданных
цен на элементы затрат.
279

Сделав подстановку в A) на основании B), получим, что
Xr = xr+^arsXs (г=1, 2, ...,п),
Эти уравнения обобщают технологические условия производства.
Для изучения второй группы условий равновесия следует рассмотреть
цены, денежную выручку и издержки. При чистой конкуренции и
свободном доступе прибыль каждой отрасли равна нулю, то есть выручка отрасли
(стоимость выпуска по ценам реализации) равна ее издержкам. Если цена
продукта равна рг (г=1, 2, ..., п) и если оу —ставка заработной платы,
то в таком случае условия равенства выручки и издержек для 5-й отрасли
выражаются уравнением
ИЛИ
! E=1, 2, ..., Г,).
Это уравнение обобщает условия цен для произх
Таким образом,,, полная система условий равноь ^_ л характеризуется
следующей совокупностью уравнений:
I(a). Xr-?,arsXs = xr (г = 1, 2, .... и);
S
(б). у=2*Л
s
П. Ps—HiP^rs^^s E=1, 2, ..., П).
г
Значения всех коэффициентов затрат а и Ъ нам известны. Далее,
система открытая, и некоторые ее параметры также должны быть заданы.
Например, можно принять в качестве заданных все цены продуктов отраслей рт
и ставку заработной платы w (см. упражнение 3). Однако удобнее задать
значения:
а) конечного спроса, или его ассортимента, хг (г = 1, 2, ..., п),
б) ставки заработной платы w на рынке труда (первичные затраты).
В системах уравнений I и II имеется 2п + 1 уравнений с 2п + 1
неизвестными: п величин выпуска Хг, общие затраты труда Y я п цен продуктов
отраслей рг. Эта система уравнений совместна с состоянием равновесия.
Существует одно довольно значительное различие между этой открытой
системой и более общими замкнутыми системами, рассмотренными в
предыдущей главе. Ни одно из уравнений систем I и II не является следствием
других уравнений, и ни одну из цен нельзя принять в качестве масштаба
и приравнять ее единице. В самом деле, если дана ставка заработной
платы w, то эта система позволяет определить не только соотношения между
ценами, но и абсолютные значения цен. Это различие объясняется тем, что
в данной системе должна быть задана ставка заработной платы, а это в свою
очередь устанавливает определенное значение каждой из цен. Если что-либо
и необходимо считать масштабом, то в этом случае таковым будет ставка
заработной платы.
Две указанные группы условий друг с другом не связаны и четко
разграничены; группа уравнений I определяет количественные соотношения,
а группа II — соотношения между денежными величинами, так что
уравнениями каждой из групп можно пользоваться самостоятельно, независимо
от уравнений другой группы. Если задана ставка заработной платы w, то п
уравнений группы II позволяют определить п цен равновесия продукта
отраслей, или pt. Последние представляют собой цены предложения, которые, если
280

открытая система превращается в замкнутую, могут быть сопоставлены вместе-
с заданным ассортиментом конечного потребления с функцией спроса.
Следовательно, если задан только ассортимент конечного спроса, можна
рассматривать уравнения I совершенно самостоятельно. Имеется п
уравнений 1(а), которые позволяют определить выпуск отраслей Хг при положении
равновесия. Единственное уравнение 1F) позволяет в таком случае вычислить
общее количество затрат первичного фактора (труда) Y.
Задачи и упражнения
1. Потребление двух факторов хх и х2 при производстве продукта у определяется
линейной однородной производственной функцией y=kf/ хгх2, где А:—постоянная. При
заданных значениях факторных цен р1 и р2 и заданном объеме производства продукта у
определить оптимальный (минимизирующий издержки производства) расход факторов х±
и х%. Показать, что при таком оптимальном использовании ресурсов
то есть соотношение между количеством [расходуемых факторов всегда остается
неизменным * ,гс это соотношение зависит от значений факторных цен р± и р2.
2. Распространить результаты, полученные при решении предыдущей задачи,
на сл^ " чюбой линейной однородной производственной функции; показать это
графически тх фак.оров) с помощью семейства кривых производственных функций,,
каждая соответствует постоянному определенному объему производства.
3. к с *nv словие равновесия, то есть уравнения I (а) и II при допущении,,
что все цены рт ь.^мвка заработной платы w заданы. Объяснить, почему это
допущение является неудобным.
10.4. МАТРИЦА МЕЖОТРАСЛЕВЫХ ПОТОКОВ В ДЕНЕЖНОМ ВЫРАЖЕНИИ
Матрица межотраслевых потоков, рассмотренная в предыдущем разделе,
является количественной, и единицы измерения для разных ее строк
неодинаковы. Суммирование элементов матрицы возможно лщпь по горизонтали,
так как элементы строки имеют общую единицу измерения; при таком
суммировании мы получаем условия, выраженные уравнениями I. Суммирование
по вертикали невозможна, и нет способа непосредственно ввести уравнения И,
отражающие условие равенства выручки отрасли и ее издержек производства.
Такую систему трудно составить по фактическим данным. На практике
матрица потоков строится в денежном выражении в виде табл. 1. В частности,
задаваемый конечный спрос представляет собой денежный расход, а не
количественный ассортимент товаров. Чтобы система, рассмотренная в предыдущем
разделе, нашла более широкое применение, а может быть, и стала более понятной,
ее элементы должны быть представлены в денежном выражении.
Если цены определены с помощью условий II равновесия, то все
элементы матрицы предыдущего раздела могут быть представлены в стоимостном
виде. Валовой выпуск r-й отрасли в денежном выражении (Vr= prXr)
распределяется следующим образом:
¦¦PTXr
vT=^p1xT (г, 5=1, 2, ..., п).
При ставке заработной платы w общая сумма заработной платы
(добавленная стоимость) W = wY и равна сумме добавленных стоимостей по
отдельным отраслям w?,s. Стоимостная матрица межотраслевых потоков имеет
следующий вид:
п строк
1 строка
vr
0
Vr
W
п 1 Итоговый
столбцов столбец столбец
Это построение совершенно аналогично табл. 1.
281

Соответствующим образом следует видоизменить и коэффициенты
затрат:
_ Vrs _ РгХгв _ Pr
ars - Vs - PsXs T p8 ars>
ft _ wls _ и& „ w h
Эти формулы можно истолковать так же просто, как и ранее: ars —
стоимость использованного продукта г-ж отрасли, а CS--оплата
потребленных первичных факторов, причем в обоих случаях на единицу
произведенного продукта 5-й отрасли. Коэффициенты затрат более не являются
величинами постоянными, они зависят теперь как от постоянных
технологических коэффициентов ars и Ь^ так и от цен.
Условия (I), получаемые в результате суммирования по горизонтали
элементов матрицы, идентичны для стоимостной и для количественной
матрицы:
(б) ^
s
Однако имеется и разница: в данном случае конечный спрос задается
не в количественном, а в денежном выражении. Тогда условия I определяют
стоимость выпуска отрасли V\ и общую сумму W оплаты первичных
факторов (добавленную стоимость).
Условия II, которыми валовая выручка каждой отрасли приравнивается
к ее издержкам, в этом случае определяются в результате суммирования
по вертикали элементов стоимостной матрицы межотраслевых потоков. Сумма
элементов 5-го столбца представляет собой общую сумму издержек 5-й отрасли:
которая должна равняться У3-сумме элементов соответствующей строки.
Следовательно, условия II выражаются следующими уравнениями:
(И) S«rs + Ps = l (* = 1. 2, ...,п),
Коэффициенты в уравнении II зависят от цен рг и ставки заработной платы w.
Совершенно так же, как и ранее, эти условия при заданном размере ставки
заработной платы определяют значения цен рт. Поскольку цены те же, что
и в предыдущем разделе, не имеет значения что в уравнениях I конечный спрос
задан не в количественном, а в денежном выражении; стоимость элементов
конечного спроса определяет количество продукции, и наоборот.
10.5. МАТРИЦА КОЭФФИЦИЕНТОВ ЗАТРАТ
Из матрицы межотраслевых потоков можно получить матрицу
коэффициентов затрат. Матрица количественных коэффициентов затрат имеет
следующий вид:
Г 0 а12 а13 ... а1п
а21 0 а23 ... а2п
h ... 6«J
1 В оригинале ошибочно дано ^. — Прим. ред.
282

Вместо arr (r = 1,2, ...,тг) мы условились проставлять нули.
Поскольку ars = xTJXs, матрицу количественных коэффициентов можно получить
из матрицы межотраслевых потоков делением элементов 5-го столбца на Xs.
Столбец конечного спроса такой операции не подвергается.
Различные коэффициенты а и Ъ имеют неодинаковые единицы измерения.
Значение коэффициента ars зависит от единиц измерения продуктов как
r-й, так и 5-й отрасли. Следовательно, непосредственное суммирование
элементов матрицы коэффициентов затрат невозможно ни по горизонтали, ни
по вертикали. Тем не менее из этой матрицы могут быть выведены условия I
и II раздела 10.3.
Если элементы каждого E-го) столбца приведенной матрицы умножить
на соответствующее значение Х$ (s = 1, 2, ..., тг), а затем произвести
суммирование по горизонтали, то в соответствии с условиями I (см. стр. 280) итог
по r-й строке будет равен Хг — хт и Y — по последней строке. Если элементы
каждой (r-й) строки умножить на соответствующее значение рг (г = 1, 2, ...
...,гс), а последней строки — нагг?, а затем произвести сложение по вертикали,
то в соответствии с условиями II итог по 5-му столбцу будет равен ps.
Аналогичная матрица стоимостных коэффициентов затрат ccrs и Ps
может быть получена из стоимостной матрицы межотраслевых потоков. В этом
случае
a Vs в стоимостной матрице межотраслевых потоков является итогом как
$-й строки, так и 5-го столбца. В табл. 2 приводятся матрицы стоимостных
коэффициентов затрат, полученные непосредственно на основе стоимостных
матриц межотраслевых потоков (см. табл. 1). В матрице стоимостных
коэффициентов затрат величина элементов уже не зависит от применяемых
единиц измерения. Каждый элемент (за исключением нулей, условно
проставленных нами по диагонали) представляет собой правильную дробь, а именно
долю в общей стоимости продукта, приходящуюся на закупки какого-либо
товара или на первичные затраты.
Суммирование по строкам матрицы стоимостных коэффициентов затрат
ars и Ps производится так же, как и в предыдущем случае, то есть после
умножения каждого из столбцов на соответствующее значение Vs. В результате
получаем условия I предыдущего раздела. Соответствующие условия II
имеют следующий вид:
Это значит, что суммирование по вертикали элементов матрицы стоимостных
коэффициентов затрат выполнить очень просто: итог по каждому столбцу
равен 1. Это можно проверить на эмпирических данных табл. 2.
Матрицу коэффициентов затрат можно записать и в следующем виде:
1 — а12 — а13 ... — а1п
— а23
*п
ап1 ап2 ап3
— Ъ1 —Ъ2 — Ъ3 ... — Ъ
U-i
В этой матрице все коэффициенты затрат имеют знак минус, а элементы,
расположенные на главной диагонали, приняты равными 1. Теперь матрица
приобрела такой вид, который характеризует «технологию» в том ее
понимании, как она описывалась в разделе 9.8. В матрице А каждая отрасль (или
вид деятельности) отражена столбцом, элементы которого положительны,
если они соответствуют выпуску, и отрицательны, если они соответствуют
затратам. Кроме того, для каждого столбца принята такая шкала, что выпуск
283

представлен элементом + 1, а затраты —их величиной, приходящейся на
единицу выпуска. Короче говоря, А представляет собой технологическую
матрицу условий производства в нашей задаче.
Задачи и упражнения
1. Показать, что в матрице стоимостных коэффициентов затрат (то есть с ars и ps)
суммирование по горизонтали выполняется в соответствии со следующей формулой!
Каков экономический смысл правой части этого уравнения?
2. Проверить правильность матриц табл. 2 путем суммирования по строкам
в соответствии с формулой, приведенной в предыдущей задаче.
3. Построить технологическую матрицу А стоимостных коэффициентов затрат аг&
и ps, полученных из стоимостной матрицы межотраслевых потоков. Каким правилом
следует руководствоваться при суммировании элементов матрицы А по столбцам
Таблица 2
Матрицы стоимостных коэффициентов затрат для Англии
(за 1935 г.) и для США (за 1947 г.)
(ars в стоимостных единицах)
Отрасли хозяйства:
1. Сельское хозяйство и пищевая промышленность.
2. Угольная промышленность и энергетика.
3. Строительство, промышленность стройматериалов и лесная промышленность.
4. Химическая и резиновая промышленность.
5. Текстильная и швейная промышленность.
6. Бумажная, полиграфическая промышленность и другие отрасли.
7. Металлургия.
8. Машиностроение.
9. Производство металлоизделий.
10. Услуги.
Структура затрат покупающей отрасли (Англия, 1935 г.)
Закупки на 1 ф. ст. выпуска продукции
^\^^ Закуплено
^4s>v^ отраслью
Поступило ^n.
от отрасли ^
1
2
3
4
5
6
7
8
9
10
Не распределено
Первичные затраты1
1
0
0,016
0,012
0,029
0,005
0,021
0,002
0,006
0,008
0,084
0,015
0,805
2
0,000
0
0,009
0,006
0,000
0,003
0,015
0,048
0,003
0,060
0,024
0,832
3
0,003
0,020
0
0,024
0,014
0,007
0,049
0,036
0,028
0,080
0,012
0,728
4
0,018
0,037
0,023
0
0,023
0,060
0,014
0,000
0,023
0,074
0,023
0,705
5
0,017
0,019
0,002
0,027
0
0,013
0,000
0,008
0,006
0,086
0,038
0,784
6
0,000
0,019
0,005
0,029
0,019
0
0,005
0,005
0,005
0,063
0,024
0,837
7
0,000
0,085
0,037
0,011
0,000
0,000
0
0,011
0,011
0,096
0,106
0,628
8
0,000
0,017
0,021
0,040
0,017
0,010
0,130
0
0,046
0,039
0,021
0,639
9
0,000
0,019
0,012
0,019
0,000
0,012
0,185
0,006
0
0,043
0,037
0,473
10
0,001
0,014
0,045
0,002
0,005
0,017
0,000
0,014
0,000
0
0,010
0,892
1 Включая импорт и государственные налоги.
284

Структура затрат покупающей отрасли (США, 1947 г.)
Закупки на 1 долл. выпуска продукции
^ч. Закуплено
^ч. отраслью
Поступило ^ч^^
от'отр&сли ^ч.
1
2
3
4
5
6
7
8
9
10
Не распределено
Первичные затраты1
1
0
0,006
0,019
0,063
0,007
0,012
0,000
0,004
0,014
0,171
0,047
0,657
2
0,000
0
0,043
0,066
0,001
0,001
0,006
0,008
0,001
0,046
0,045
0,783
3
0,008
0,008
0
0,046
0,010
0,012
0,060
0,041
0,028
0,178
0,058
0,552
4
0,087
0,036
0,020
0
0,023
0,023
0,010
0,000
0,011
0,106
0,137
0,547
5
0,145
0,009
0,007
0,065
0
0,024
0,000
0,003
0,001
0,079
0,114
0,553
6
0,005
0,013
0,035
0,040
0,013
0
0,015
0,005
0,003
0,082
0,149
0,635
7
0,001
0,030
0,034
0,092
0,000
0,001
0
0,011
0,002
0,111
0,128
0,590
8
0,000
0,008
0,032
0,037
0,011
0,010
0,150
0
0,064
0,052
0,123
0,513
9
0,001
0,007
0,032
0,019
0,003
0,027
0,186
0,053
0
0,055
0,152
0,459
10
0,036
0,036
0,049
0,021
0,001
0,030
0,002
0,014
0,003
0
0,060
0,748
1 Включая импорт и государственные налоги.
Примечание. Коэффициенты исчислены на основании табл. 1, причем для США более точные
цифры, чем в табл. 1. Вследствие округления элементов итог суммирования по
вертикали элементов столбца не обязательно равен единице.
10.6. РЕШЕНИЕ ДЛЯ СЛУЧАЯ ТРЕХ ОТРАСЛЕЙ
Ход решения уравнений для открытой системы Леонтьева достаточно
хорошо поясняется при п = 3. Выпуск определяется следующими
уравнениями (см. раздел 10.3):
Хг — а12Х2 — а13Х3 = x±J
Чтобы по заданному конечному спросу (жх, я2, хв) вычислить выпуск
каждой из отраслей (Хг, Х2, Х3), можно воспользоваться методами
элементарной алгебры, однако более краткое решение получается при
использовании определителей (см. 11.9 и 13.2).
Технологическая матрица имеет следующий вид:
А =
— а12 —
12
— 023
1 J
— «21 1
L — «31 — «32
Если мы обозначим через А определитель матрицы А, то
алгебраическими дополнениями элементов этого определителя будут:
1 — а2
-«32 1
Решение имеет следующий вид:
— а21 — щ
-«si 1
и т. д.
х2 + ^зА/' !
2^(l2l 22#2 + ^32*3)> ^
Аз = -д- (^13^1 + ^23^2 4" ^33^3/' J
A)
285

Общие затраты труда (первичные затраты) определяются из
уравнения 1F) раздела 10.3:
Приведенные значения выпуска отраслей и затрат труда в условиях
равновесия вычислены на основе заданного конечного спроса. Изменяя
ассортимент конечного спроса, мы, получаем различные результаты, что
можно назвать сравнительной статикой. Например, увеличение спроса на
автомобили прямо и косвенно влияет на выпуск стали. Если хх
увеличивается, а остальные элементы конечного спроса остаются неизменными, то
dY
дхл
1
дХ2
Совершенно аналогично решение для задачи в стоимостном выражении.
Если величины х, X и У заменить соответствующими стоимостными
значениями, уравнения A) и B) остаются в силе. Определитель матрицы
коэффициентов затрат тогда приобретает следующий вид:
— се
21
1 -<
— <х31 — а.
'32
где
= РТ д
; Ps Г
Значение определителя зависит уже не только от неизменных
технологических коэффициентов, но и от цен.
Способ определения цен равновесия не зависит от того, выражены ли
выпуск и затраты труда в количественной или в стоимостной форме. Для
определения этих цей необходимо решить систему уравнений (И)
раздела 10.3:
Л -
— а31р3 =
Р2 —
Следует обратить внимание на то, что в этой системе уравнений
коэффициенты транспонированы, то есть элементы строк заменены элементами
столбцов и наоборот. Решение этой системы уравнений имеет следующий вид:
Pi = ~j
А
w,
C)
Цены равновесия пропорциональны заданной ставке заработной платы w,
причем коэффициент пропорциональности для разных цен неодинаков
и зависит от значений коэффициентов затрат.
В формулах C), по которым исчисляются цены, коэффициенты затрат
труда (Ь) входят, лишь будучи умноженными на ставку заработной платы.
Обозначим Wi^wb^ w2 = wb2, w3 = wbs, где w^ w29 йу3 —издержки на
заработную плату в расчете на единицу продукции каждой из отраслей. Тогда
Pi = 4-
+ Л 1
D)
286

Аналогичные уравнения получаем из уравнения C) для р2 и р3. Формулы
решений A) и D) весьма схожи между собой, однако в них постоянные
коэффициенты транспонированы.
Важно также отметить сходство формулы исходных условий Aа) из
раздела 10.3 и формул решения A), если те и другие записать в
следующем виде.
Условия 1(а): хх
аналогичны этому).
Решение A): Х1 = ^^
аналогичны этому).
Коэффициенты правой части уравнений I (а) представляют собой
элементы определителя А, а коэффициенты решений A) — элементы определителя
Хг — а12Х2 — а13Х3
(два других уравнения
х3 (два других решения
А
А12
А
Аз
А
А
А22
А
Лз
А
А
^32
А
^33
А
Последний определитель хорошо известен—он является обратным для
определителя А (см. 12.7). Следовательно, при записи в общем виде решения
A) целесообразно не только составить матрицу коэффициентов затрат аг$у
но и построить обратную матрицу на основе определителя А и алгебраических
дополнений его элементов. Пример обратной матрицы приведен в табл. 6
книги Эванса и Хоффенберга [3]. Экономическое содержание элементов
обратной матрицы выясняется при рассмотрении решения A). Элемент Ars/A
представляет собой валовой выпуск г-ж отрасли, необходимый для единицы
конечного спроса на продукт 5-й отрасли; это справедливо для показателей,
выраженных как в количественной, так и в стоимостной форме.
Полученные результаты, хотя они выведены на примере трех отраслей,
действительны и для случая любого числа отраслей. Систематизированное
рассмотрение общего случая (в виде матричных уравнений) приводится
в разделе 13.7.
Задачи и упражнения
1. Сформулировать условия равновесия и найти решение для случая двух
отраслей (п = 2).
2. Матрица коэффициентов затрат для случая двух отраслей имеет следующий
12 . Показать, что обратной к ней является матрица:
вид: А =
1
1 — а12а21 1 —
«21
3. Доказать, что, хотя элементы определителя, составленного из стоимостных
коэффициентов затрат (ars), зависят от цен, величина этого определителя равна
величине определителя А.
4. Показать для случая трех отраслей, что p1 = w(dY/dx1); разъяснить
экономический смысл результата.
10.7. ЗАМКНУТАЯ СИСТЕМА ВАЛЬРАСА — ЛЕОНТЬЕВА
В рассматривавшейся до сих пор открытой системе мы задавали
исходные данные двух видов: конечный спрос по отраслям и издержки на
заработную плату в расчете на единицу продукции (учитывая ставку заработной
платы). Первая группа данных представляет собой спрос «домашних хозяйств»,
287

последние также определяют и количество труда, которое домашние
хозяйства могут выделить промышленности при заданном размере ставки
заработной платы. Для получения замкнутой системы необходимо лишь
дополнительно ввести еще одну отрасль производства — «домашние хозяйства»,
которая потребляет продукты других отраслей и удовлетворяет потребность этих
отраслей в затратах труда. При добавлении этой новой «отрасли» все товары
становятся промежуточными продуктами; ни конечный спрос, ни первичные
затраты особо не выделяются. Предполагается также существование чистой
конкуренции и свободного доступа, отсутствие государственных доходов
и расходов и внешней торговли, и не учитываются капиталовложения и все
другие элементы динамики.
Пусть народное хозяйство состоит из (п + 1) отраслей, каждая из
которых производит только один продукт, а каждый продукт вырабатывается
единственной отраслью. Выпуск г-ж отрасли пусть равен Хт (г = 1, 2, ...
...,п + 1). Последняя отрасль—домашние хозяйства; ее продукт Хп+1—труд,
используемый в остальных отраслях. Матрица межотраслевых потоков
состоит из элементов xrs1 то есть потребления продукта г-ж отрасли в 5-й отрасли,
причем элементы хтг условно принимаются равными нулю. В частности,
^r(n+i)— количество продукта г-ж отрасли, предназначенное для потребления
домашними хозяйствами (ранее оно именовалось конечным спросом),
a X(n+\),s —затраты труда в 5-й отрасли (ранее —первичные затраты).
В замкнутой системе первая группа условий равновесия имеет такой же
вид, как и в открытой системе, а именно условие точного равенства
использованных количеств продукта каждой отрасли и всего его выпуска. Оно
характеризуется уравнениями:
итогами суммирования по горизонтали элементов строк матрицы
межотраслевых потоков являются значения валового выпуска соответствующих
отраслей. В этой системе удобнее принимать элементы на главной диагонали
матрицы (хтт) равными не нулю, а (—Хг). При таком изменении матрицы условия
равновесия приобретают следующий вид:
3^ = 0 (г = 1, [2, ...,д + 1), A)
так что итоги суммирования элементов этой матрицы по горизонтали равны
нулю. Суммирование элементов по вертикали невозможно, поскольку
единицы измерения для разных строк неодинаковы.
Предположим, что и в этой системе имеются постоянные коэффициенты
затрат ars, задаваемые технологическими условиями:
xr8 = arsX8 (г, 5 = 1, 2, ...,гс+1). B)
Если мы условились, что хтг ~ — Хг, то при г = s, агг = — 1.
Новым здесь является, что #r(n+1> = ar(n+i) -^n+i' To есть предпосылка
о постоянной величине соотношения между потреблением домашними
хозяйствами продукта г-ж отрасли и общими затратами труда. Расход домашних
хозяйств на каждый вид товара составляет постоянную долю от их общего
дохода (если все величины измеряются количественно). Это — очень
ограничивающее допущение, которое мы рассмотрим позднее более подробно.
Подставим соотношения B) в уравнения A); тогда первая группа условий
равновесия приобретает следующий вид:
SarsXs = 0 (/- = 1,2, ...,72 + 1).
S
Вторая группа условий вводит и цены рг (г = 1, 2, ..., п + 1), где />п+1 —
ставка заработной платы, или цена труда. Для равновесия необходимо, чтобы
выручка каждой отрасли была равна ее издержкам. Выручка 5-й отрасли
288

составляет psXs, а издержки равны ^prxrs (где г Ф s). Следовательно,
г
при хп = -— Хг и агт = — 1, вторая группа условий равновесия
записывается в виде уравнений 2/?r#rs = 0, или же, используя B), в виде уравнений
г
Spr«rs=0 (s = i, 2, ..., л + 1);
при неизменных значениях технологических коэффициентов ars, условия
общего равновесия чрезвычайно просты:
I. 2«,Д, = 0 (г = 1, 2, .... л
s
И. S/>r«rs = O (*'=1, 2, ... п
Неизвестными здесь являются (я + 1) отраслевых выпусков продукции
Хг, которые встречаются только в уравнениях I, и тг + 1 цен рг, которые
встречаются только в уравнениях II. Однако простота этих условий
обманчива, и они выдвигают специфические трудности, не встречающиеся в открытой
системе.
Существо проблемы можно разъяснить на примере двух видов товара
(один продукт промышленности и труд). Условия равновесия таковы:
(I) -Xi + ДцХ^О, (II) -ft+ 0^ = 0,
апХг — Х2 = 0, а12рх — р% = 0.
На основании уравнений I можно записать:
^==ai2 = ^*
На основании уравнений II можно записать:
Следовательно, в системе равновесия задаются лишь соотношения
между выпусками отраслей (или между ценами), и система совместна (даже
при соблюдении этого ограничения) только в том случае, если коэффициенты
затрат удовлетворяют уравнению:
а12а21 = 1, то есть
— а
21
= 0.
Этот результат можно обобщить. Условия (I) и (II) представляют собой
линейные уравнения, однородные относительно неизвестных. Хотя число
уравнений равно числу неизвестных, на основе этих уравнений можно
получить только отношения между неизвестными, то есть получить значения п
неизвестных лишь в том случае, если произвольно устанавливается значение
одного из них. Однако даже для этого одно из уравнений должно быть
линейной комбинацией других уравнений системы, что налагает ограничение на
значения коэффициентов затрат —должен быть равен нулю определитель,
образованный из технологической матрицы (матрицы коэффициентов затрат).
Следует подчеркнуть также, что, хотя эти две системы уравнений (одна —
для выпусков отраслей, другая —для цен) совершенно самостоятельны, они
все же связаны между собой. Если коэффициенты затрат определяют
соотношения между выпусками отраслей, то они определяют и соотношения
между ценами. Следовательно, замкнутая система в лучшем случае определяет
структуру хозяйства, а не его масштаб. В открытой системе такого
ограничения не существует; здесь производство детерминировано как в отношении
структуры, так и в отношении масштаба деятельности. По сути дела, заданный
конечный спрос определяет объем выпуска, а фиксированная ставка заработ-
19 Р. Аллен 289

ной платы — масштаб цен. Эти вопросы рассматриваются также в
упражнении 1, а в общем виде —в разделе 13.7.
Рассматриваемую в настоящем разделе замкнутую систему можно назвать
системой Леонтьева, поскольку принято сделанное им предположение о
постоянстве коэффициентов затрат. Очевидно, однако, что форма этой системы
принадлежит Вальрасу. Это — простейший частный случай общего
экономического равновесия, рассмотренного в гл. 9 (см. также работу Гудвина [4]).
Как указывалось Камероном [2], эта система является одной из систем
общего равновесия Вальраса, в которой уже исчерпаны все возможности
дальнейшего «повышения экономичности».
Задачи и упражнения
1. Составить уравнения условий равновесия для случая трех отраслей (/1 = 3).
Показать, что соотношения Хг : Х2 : Х3 и р1: р2 : />3 можно исчислить только в том
случае, если равен нулю определитель технологической матрицы, составленной из
коэффициентов затрат:
[1 —«и — вхз!
— «21 1 —«23 •
— «31 —«32 1 J
Показать также, что трудности не устраняются и в том случае, если равны нулю
алгебраические дополнения элементов этого определителя, как, например,
1 — а12
— «31 1
2. Если в этом же случае (л=3) суммировать по горизонтали элементы
количественной матрицы межотраслевых потоков (xrs), то итоги суммирования равны нулю;
суммирование элементов по вертикали невозможно. Перестроить систему таким образом,
чтобы она основывалась на стоимостной матрице межотраслевых потоков, то есть
матрице, составленной из элементов vr8=prxrs. Показать, что в соответствии с двумя
группами условий равновесия итоги как строк, так и столбцов перестроенной матрицы
равны нулю.
3. Распространить изменения, сделанные в предыдущей задаче, на случай
технологической матрицы (матрицы стоимостных коэффициентов затрат). Показать, что
матрица составлена из элементов &rs=(pr/Ps)ars и что в соответствии с условиями
равновесия (II) итоги суммирования элементов матрицы по вертикали равны нулю.
Что можно сказать о результатах суммирования элементов матрицы по горизонтали?
|10.8. ДИНАМИЧЕСКАЯ СИСТЕМА ЛЕОНТЬЕВА
В изложенной выше системе межотраслевых связей капиталообразование
теоретически не принималось во внимание, а практически включалось в
заданный конечный спрос. Эта система статична и вместе с тем действует в
течение небольшого промежутка времени. Теперь мы расширим анализ путем
введения динамических процессов; естественно использовать принцип
акселерации, чтобы связать наличие капитальных благ с объемом выпуска либо
инвестиции с изменениями выпуска. Запаздывание во времени не
принимается во внимание (см., однако, упражнение 3); кроме того, мы предполагаем,
что капиталообразование производится в соответствии с планом. По сути
дела, эта система представляет собой систему подвижного равновесия.
Коэффициенты затрат ars определяются так же, как и выше: xrs =
= arsXs (г, s = 1, 2, ..., п). Величины xrs характеризуют поток текущего
производства: хгз — поток r-го продукта в 5-ю отрасль в течение какого-либо
периода (например, 1 года), причем он составляет неизменную пропорцию к
выпуску Xs s-й отрасли за этот же период. Вообще предполагается, что s-я
отрасль не потребляет производимого ею продукта, так что ass не
рассчитывается, а условно принимается равным (—1). Наряду с коэффициентами затрат
вводится новая система коэффициентов капиталоемкости fere,
определяемая уравнениями Srs = brsXs (r, s = 1, 2, ..., п), где6*гз— запас r-го товара
в s-й отрасли. Эти коэффициенты относятся к запасам капитальных благ
всякого рода, начиная от запасов материалов и продуктов и вплоть до
заводов и оборудования, в зависимости от характера продукта r-й отрасли.
290

В частности, определяются и значения Srr и ferr, так как они показывают
запас г-го продукта в той отрасли, которая его производит, то есть в г-й
отрасли.
Таким образом, две матрицы, составленные из постоянных и заданных
коэффициентов, в совокупности определяют структуру хозяйства: матрица
А — структуру межотраслевых потоков, матрица В — структуру
капитальных благ:
А==
6*1
Размерность коэффициентов а не изменилась, коэффициент аГ8 равен
количеству единиц r-го продукта, расходуемому (в течение заданного
периода) на выпуск в этом же периоде одной единицы 5-го продукта. Иной
является размерность коэффициентов b. Srs представляет собой запас г-го
товара, выраженный в единицах измерения, принятых для r-го товара в
какой-то момент времени; Xs—выпуск в течение некоторого периода,
выраженный в единицах измерения, принятых для 5-го товара. Следовательно, brs —
величина запаса r-го продукта (в соответствующих единицах измерения),
приходящаяся на единицу выпуска 5-го продукта за определенный период.
Например, если r-й продукт — сталь, а 5-й — автомобили, то brs равно
запасу стали (в тоннах), приходящемуся на один автомобиль, произведенный в
течение определенного периода.
Каждый из коэффициентов капитальных благ является постоянным
коэффициентом акселерации. Все величины Sra и Xs изменяются во
времени, и ври дифференцировании уравнения Sr8 = brgX8 мы получаем
(для случая непрерывных изменений):
Это означает, что
ГПрирост инвестиций в г-й
L продукт в 5-й отрасли
= ЬЛ X
ГПрирост выпуска]
[ 5-й отрасли J
В данном случае акселерация непрерывна, причем без запаздывания
(см. упражнения 1—3).
Теперь рассмотрена только первая группа уравнений системы
Леонтьева, то есть уравнений точного соответствия потребления и выпуска
продукции отрасли. Вторую группу уравнений (в ценностном выражении) можно
добавить в значительной степени аналогично тому, как мы делали ранее.
Обе системы, рассмотренные в разделах 10.3 и 10.7 — открытая и замкнутая, —
преобразуются в динамическую форму.
Открытая система. Пусть имеются п отраслей, для каждой из которых
задан конечный спрос хг (г = 1, 2, ..., я). Применительно к динамической
системе это значит, чтожг есть заданный во времени поток, то есть хТ является
заданной функцией времени. Таким образом, задается «ассортимент конечного
спроса», изменяющийся во времени определенным образом. Теперь условия
точного соответствия потребления и выпуска продукта какой-либо отрасли г
выражаются следующими уравнениями:
Одна часть продукта направляется конечным потребителям (первое
слагаемое), вторая становится текущими затратами других отраслей (второе
слагаемое), третья расходуется с целью капиталообразования в других
отраслях (третье слагаемое). Последняя величина может быть как положительной,
291
19*

так и отрицательной, в зависимости от того, например, происходит ли
увеличение запасов или их расходование. Далее вкратце мы указываем некоторые
трудности, возникающие в случае появления отрицательных слагаемых. Если
совместно использовать две системы структурных коэффициентов, то (при
1)
=1, 2, ..., п).
A)
Это — более общее выражение условий 1(а) раздела 10.3.
Замкнутая система, п-й отраслью считаются домашние хозяйства;
товары конечного потребления становятся затратами этой отрасли, а труд —
ее выпуском. Условие точного распределения отраслевого продукта
выражается для нее уравнением A), где хТ опущено1, то есть
0 (г = 1,2, .... п). B)
Это — более общее выражение условий I раздела 10.7.
В уравнениях A) или B) имеется п значений выпуска отраслей Хг
(г = 1, 2,..., гс), однако этот выпуск изменяется во времени, так что уравнения
включают не только объем выпуска, но и скорость его изменения во времени.
Это — системы линейных дифференциальных уравнений с постоянными
коэффициентами. Их решение содержит выпуск каждой отрасли как явную
функцию времени (изменение выпуска во времени), и оно должно включать
произвольные постоянные, устанавливаемые на основе первоначальных условий.
Поскольку эти уравнения первого порядка, в решение для каждого продукта
входит одна произвольная постоянная, для определения которой необходимо
знать начальный выпуск отрасли.
Для решения уравнений A)и B) применимы методы, рассмотренные в
главе 4 и очевидным образом расширенные. Уравнения для замкнутой системы
решаются проще, так как они являются однородными. Когда решения для
этих уравнений найдены, решение неоднородных уравнений для открытой
системы можно получить, прибавляя частный интеграл, учитывающий член хг,
заданный в виде функции времени. В следующем разделе приводится
решение для простейшего случая двух отраслей; решение для общего случая
приводится в разделе 13.9.
Очевидно, что характер движения Хг (для каждого из г — 1, 2, ...,.л)
может быть, а может и не быть колебательным, причем эти колебания могут
быть как затухающими, так и незатухающими. Рассматриваемая здесь
динамическая система основана на том же принципе акселерации и представляет
такой же диапазон возможностей, как и рассмотренная выше теория
экономических циклов. Эта система также подчинена обычным ограничениям, ее
необходимо соответствующим образом распространить на общий случай.
Запись dSTsldt = bTB(dXJdt) означает, что мы принимаем коэффициент
акселерации одинаковым при изменении выпуска как в сторону увеличения,
так и в сторону уменьшения, то есть что при уменьшении выпуска запасы
снижаются в той же мере, в какой они повышаются при увеличении выпуска.
В действительности же приходится учитывать нелинейный и несимметричный
характер акселератора, если не для товарных запасов, то по крайней мере
для сооружений и оборудования. Эти трудности рассматривались в главе 6,
а также исследуются Леонтьевым [6].
Задачи и упражнения
1. Изменить описанную в тексте динамическую Систему на систему дискретного
анализа, для чего принять, что акселератор имеет следующий вид: инвестирование
на создание запасов r-го продукта в 5-й отрасли равно коэффициенту brsi умноженному
1 хт входит в уравнение B) в качестве п-й отрасли.— Прим. ред.
292

на текущее изменение выпуска [Xs(t) — Xs(t— 1)]. Показать, что в замкнутой системе
условия равновесия выражаются последовательностью разностных уравнений первого
порядка:
Sfoe+frre) Xs(t)-%brsXs(t-l)=O (r=l, 2, ..., п).
S S
2. В систему предыдущей задачи ввести запаздывание, приняв, что
инвестирование зависит от прошлого изменения объема выпуска (на один период ранее), то есть
от [Xs(t—1)—Xs(t — 2)]; показать, что при этом получаются разностные уравнения
второго порядка:
3. В непрерывной системе, описанной в разделе 10.8, принять стоимость закупок
г-го продукта для средств производства в 5-ю отрасль в момент t равной
— Srs (t)z=brs x (Ожидаемая скорость изменения Xs).
Предположить, далее, что между моментом доставки оборудования и моментом
изменения объема выпуска имеется разрыв во времени, всегда одинаковый, величина
которого и принимается за единицу времени. Показать, что в замкнутой системе условия
равновесия выражаются в виде группы дифференциально-разностных уравнений:
10.9. РЕШЕНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ ДЛЯ СЛУЧАЯ ДВУХ ОТРАСЛЕЙ
В простейшем случае двух отраслей условия A) предыдущего раздела
выражаются уравнениями:
Y —n Y h x h dX* — г
Л1 «12-^2 И~5г l2~dT~~ X'
X, v 1 аХх 7 dX2
.х 1 + Х2 — о21--гг — Ь22-тГ=:а
A)
Эти уравнения отвечают случаю открытой системы. Замкнутая система
возникает при хх~ х2 = 0 (так как домашние хозяйства являются одной
из двух отраслей). Уравнения A) превращаются в однородные, их легче
решать, поэтому они и рассматриваются в первую очередь.
Замкнутая система. Попробуем применить метод, с успехом
использованный в главе 5.
Пусть
Хг = е-и и Х2 = &е-м.
Тогда
at
dt
где % и к — некоторые постоянные параметры, которые необходимо
выразить через структурные постоянные (коэффициенты а и Ь). Произведем
подстановку значений ^ и Х2 в A); сократим на е~^1 Ф 0 и получим два
уравнения для определения X и к:
откуда
— ка12 +Х(Ь1г + kb12) = 0
т,
Чтобы определить значение к, нам нужно знать значение К; в свою
очередь значение К находим на основе правой части уравнения B), кото-
293

рую можно представить в виде квадратного уравнения
A + ХЬп) A + П22) = (а12 - ХЬ12) (а21 - %Ь
или же
где
C)
У этого квадратного уравнения два вещественных и разных корня
так как Р2 > 4ау, что можно доказать следующим образом:
р2 = [(Ьп + a12b21) + F22 + а21612)]2«
= [(&ii + °>uhi) - (Ь22 + а21Ь12)]2 + 4 (bn + a12bn) (b22 + a2lb12).
Следовательно,
p2 - 4aY = [(bn + a12b21) - (b22 + a21b12)]2 +
+ 4(bn + a12b2l) (b22 + a2lbl2) - 4A - a12a21) (bnb22 - bl2b21) =
= i(bn + a12b21) ~(b22 + a2lbl2)Y +
Эта величина положительна, поскольку все коэффициенты а и b
положительны. Мы нашли две пары значений постоянных параметров % ж к.
Из уравнения C) получаем два вещественных и различных значения Кг и ^2,
а из уравнения B) —два соответствующих значения к:
к - 1+^&11 к = г+
1 «12 — ^1^12 ' 2 «12 —
Отсюда следует, что обе пары:
и
являются решениями уравнений A). Решением этого уравнения будет
и сумма двух попарных произведений — частных интегралов Хг и Х2,
умноженных на произвольные постоянные коэффициенты соответственно
Ах И А2.
Это — общее решение, поскольку в нем имеется необходимое число
произвольных постоянных (А± и А2), значения которых определяются по
начальным значениям выпуска отраслей (см. упражнение 2).
Решение D) нетрудно истолковать, однако это пока что не помогает.
С течением времени значения выпусков Хх и Х2 стремятся к нулю, если
\г и Х2 оба положительны, и беспредельно возрастают, если один из этих
корней отрицателен. Производство либо «затухает», либо «взрывается».
Этот неудобный для использования результат попросту является еще одним
проявлением особых свойств упрощенной замкнутой системы. Разгадка
заключается в том, что один из двух параметров, А,х или Х2, может оказаться
равным нулю. В статической замкнутой системе (см. 10.7), которую можно
получить, приравняв нулю все коэффициенты Ъ в уравнениях A), поддаются
определению не абсолютные значения Хх и Х2, а лишь их соотношение
Хг: Х2, и то только в том случае, если коэффициенты а удовлетворяют
294

дополнительному условию:
Предположим, что условие E) действительно и для динамической
модели. Тогда в уравнении C), служащем для определения Я, свободный
член y = 0, и один из корней % равен нулю, чему соответствует, исходя
из уравнения B), значение /с = 1/а12 = а21. Вторая пара значений К и к
будет следующей:
. F)
а Ь12Ь21—fenfe22 * а12—Я
Тогда решение D) принимает следующий вид:
где Л, и к — постоянные параметры, определяющие структуру экономики
и задаваемые уравнением F). Если X > О, выпуск каждой из отраслей
на основе уравнения G) является суммой двух слагаемых: постоянной
величины и величины, убывающей со временем. Этот результат более
осязаем. Значения конечного уровня продукции стремятся к
пределам Хг = Аг и X2 = Aja12, которые устанавливаются (с помощью
произвольной постоянной Аг) по начальным величинам выпуска отраслей.
Тем не менее соотношение между предельными выпусками Хг: Х2
равно а12, а этот коэффициент задается структурой системы. Данная
динамическая система является затухающей и устойчивой; соотношение между
конечными выпусками определяется структурой системы, а их абсолютная
величина — значениями начального выпуска отраслей.
Этот результат возможен лишь при ^положительном значении X в
уравнении F), а Я будет положительным в случае, если равен нулю один из двух
коэффициентов Ьп и Ь22, либо если оба эти коэффициента малы. Поскольку
вторым товаром является труд (продукт домашних хозяйств), то запасы
товара Х2 можно принять равными нулю, так что Ь22 = 0. Следовательно,
обычно К > 0.
Открытая система. В этом случае хг и х2 в уравнении A) —заданные
функции времени. Общее решение неоднородных уравнений A)
представляет собой общее решение однородных уравнений D), в интеграл которого
для каждого из двух неизвестных (Хх и Х2) добавлено еще одно слагаемое—
частный интеграл, определяемый видом функций хх и х2. Получить эти
частные интегралы возможно лишь в том случае, если известен характер
функций хг и х2. Приведем в качестве иллюстрации два примера.
I. Конечный спрос фиксирован и постоянен во времени:
Будем искать частные интегралы для системы уравнений:
(8)
1 а12А2 °11 ~~tfj °12 fa
Проверим, возможно ли решение Хх == Вг и Х2 = 2?2, где Вх и В2 — две
неизвестные постоянные, которые необходимо определить. Тогда
В1-а12В2 = с1 и -
что дает
С+Са __ D __
И По =
—I И По = —А •
1 — а12а21 1— а12а21
295

Отсюда общее решение (8) будет иметь вид:
где Ах и Л2 — произвольные постоянные, определяемые на основе заданных
начальных значений выпуска, а Хх и^2, кх и й2 — структурные постоянные,
заданные уравнениями B) и C).
При истолковании этого решения критическое значение имеют знаки
при А,х и Х2, а также при Вх и В2. Из уравнения C) следует, что
ч+*1=-1.
у.
а
Кроме того, Вх и В2 являются величинами положительными и
кратными 1/Y-
Обычно а < 0, например, когда запасы продуктов для собственного
потребления совсем отсутствуют или незначительны. Во всех случаях Р > 0.
Однако y = 1 — ai2a2i может быть величиной как положительной, так
и отрицательной. Необходимо рассмотреть два возможных варианта:
Знак величины
Вариант (а)
(l-ai2a2i>0)
Вариант (б)
(l-o12a2i<0)
В варианте (а) большая А, —величина положительная, а меньшая —
отрицательная. При наличии отрицательной К одно из слагаемых в
решениях для Хх и Х2 бесконечно возрастает с течением времени; второе
слагаемое является величиной затухающей. Следовательно, в этом варианте
система является «взрывной». С другой стороны, в варианте (б) оба к
положительны, и соответствующие слагаемые в решениях для Хх и Х>
являются затухающими; однако уровни, к которым стремятся значения
выпуска, то есть Вх и 2?2, отрицательны, а значит неприемлемы.
Следовательно, в варианте, который практически является единственно
возможным A — fli2#2i > 0), динамическая система является «взрывной»,
и выпуски отраслей неограниченно возрастают с течением времени.
Симметричная в обоих направлениях линейная акселерация, принятая в этой
модели, приводит снова к проблеме такого рода, которая была рассмотрена
в главе 6. Модель непосредственно не может быть применена к реальной
действительности, и приходится ввести понятие нелинейного и
несимметричного акселератора.
II. Конечный спрос с течением времени возрастает с заданной
относительной скоростью |л:
хх = схе&1 и х2 = с2е^.'
Будем искать частные решения для системы уравнений:
Хх — а12Х2 — Ъхх -
— а2ХХх
±
_ r plxt
-С2в
(9)
Проверим, возможно ли решение Хх = Вхе^ь и Х2 = 2?2е^, где Вхя В2 —
две неизвестные постоянные, которые необходимо определить, то есть
предположим, что выпуск каждой из отраслей будет возрастать с той же
относительной скоростью, что и конечный спрос. Подставим это решение
296

х и X2 в уравнение (9) и произведем сокращение на
Вг - а12В2 — }^Ъ11В1 - \хЬ12В2 = q,
Ф 0. Тогда
A—
откуда следует, что
152 (l-
Общее решение уравнений (9) имеет следующий вид:
Х2 = В2е
Полученные результаты во многом совпадают со случаем
фиксированного конечного спроса (см. упражнение 5). Обычно имеется лишь один
возможный вариант, при котором динамическая система является
«взрывной», и выпуск возрастает приблизительно по показательной кривой, а
относительная скорость роста выпуска та же, что и роста конечного спроса.
Задачи и упражнения
1. Показать, что квадратное уравнение для X, полученное на основе уравнения B),
можно записать в следующем виде:
(а21-ХЪ21) ( —1 —
причем определитель, очевидно, составляется из структурных постоянных
коэффициентов. *
2. Заданы начальные (при t = 0) уровни выпуска Х1 = Х10 и Х2 = Х20- Выразить
через Х10 и Х2о произвольные постоянные: а) в решении D); б) в решении G).
3. Почему в открытой системе с постоянным конечным спросом не обязательна,
чтобы 1 — а12а21 — 0, как это имеет место для закрытой системы? Рассмотреть вариант
1 — a12a2i = 0 в качестве примера, промежуточного между двумя примерами текста,
и изучить характер решения. Как определяются в этом варианте Вх и 2?2?
4. Пусть в открытой системе x1 = c1-\rd1ty x2 = c2~\-d2t. Найти частные интегралы
и исследовать общее решение.
5. Рассмотреть решение открытой системы (пример II в тексте). Принять а<0
и E>0 (как и ранее), 6и = 622 = 0 (отсутствие запасов продуктов для конечного
потребления). Показать, что имеется три варианта:
Знак величины
Вариант
(а)
Вариант
(б)
Вариант
(в)
а12а21
Вывести, что значения Хг и Я2 имеют противоположные знаки в вариантах (а)
и (б), а в варианте (в) оба положительны и что Вх и В2 положительны только
в варианте (а). Отсюда показать, что единственно возможной является «взрывающаяся»
система—вариант (а).
6. Пусть в открытой системе x1 = c11e^ltjrc12e[l2t1 x2 = c21elXlt-{-c22ell2t. Отыскать
частные интегралы и показать, что они представляют развитие постоянных типа Вх
и В2 в случае II (см. текст).
7. Составить уравнения для замкнутой системы с тремя отраслями и исследовать
характер решения, обращая особое внимание на возможность колебаний выпуска
отраслей (см. 13.9).
8. Рассмотреть систему с запаздываниями (см. 10.8, упражнение 3) для случая
двух отраслей, включающую смешанные дифференциально-разностные уравнения.
Положить a12 = a21r=0 и Ьг1 = Ь22 = 0 и истолковать эти частные случаи. Показать, что
Хг (t) и X2(t) удовлетворяют уравнению вида bl2b21 (d2/dt2) X(t-\-2) = X (t) или же
b12b21(d2/dt2)X(t) = X(t — 2). (Метод решения см. [9], русск. перев., стр. 101 — 106.)

ГЛАВА 11
МАТЕМАТИЧЕСКАЯ ЧАСТЬ. ВЕКТОРЫ И МАТРИЦЫ
11.1. ВВЕДЕНИЕ
Предметом этой и следующей глав является то, что довольно широко
может быть названо матричной алгеброй. Необходимо с самого начала
выяснить природу матричной алгебры и характер проблем, для решения которых
она пригодна. Тогда исчезнут некоторая таинственность, которая, кажется,
окружает этот предмет, и его некоторая сложность. Превосходное введение
в матричную алгебру, простое и ясное, можно найти в [51.
Элементарная алгебра имеет дело с выражениями, принимающими
вещественные численные значения. Эти выражения состоят из постоянных и
переменных величин, берущих свои значения из области вещественных чисел.
Постоянные величины могут быть определены численно, например 3 или ~\/~2,
но могут быть и неопределенны, например, а, Ь, с, ... Переменные величины,
обычно обозначаемые такими буквами, как xyyis.z, принимают численные
значения или из всей области вещественных чисел, или из более ограниченных
областей, таких, как область целых чисел или область рациональных чисел
(отношения целых чисел). В качестве примеров выражений, характерных
для элементарной алгебры, можно привести ]/а2 + Ь2 и ах + by. Если
постоянные а и Ъ определены, например а — 1, Ь = 2, то эти выражения получают
вид ]/~а2 + Ь2= |/5 и ах + Ъу = х + 2у. Второе выражение принимает
различные численные значения при различных значениях переменных хну.
X
У
х+2у
()
0
0
()
1
2
1
0
1
1
1
3
Неэлементарная алгебра разрушает эти узкие границы. Она имеет дело
с множествами, отличными от множества вещественных чисел, например
с комплексными числами (см. прилож. Б.—Ред.). Она оперирует не только
с «величинами», подобными массе или объему в физике, но и с более общими
понятиями— векторами», выражающими силу или скорость, которые имеют
величину и направление. Большая часть высшей алгебры, в частности
матричная алгебра, рассматривает не отдельные величины, а множества или группы
упорядоченных определенным образом элементов. Сами эти элементы могут
быть и вещественными числами, как это мы предполагаем здесь, но это отнюдь
необязательно; они могут быть и комплексными числами, или вообще
объектами любой природы, абстрактными, или какими-либо иными.
В качестве иллюстрации рассмотрим группировки элементов,
являющихся постоянными величинами, принимающими вещественные численные
значения. Набор из трех постоянных величин а, Ъ и с может быть расположен
в определенном порядке: а — на первом месте, Ъ — на втором и с — на
третьем. Это можно записать в виде (а, Ь, с) и сопоставить с точкой в
трехмерном пространстве. Вектор трех измерений является одной из таких
группировок; он может также рассматриваться как частный случай матрицы, которая
имеет только одну строку (или один столбец) из трех элементов.
Значительно более общим является набор из четырех постоянных а19 а2,
b^ji i2, которые могут быть размещены в виде блока из двух строк и двух
298

столбцов:
КМ*
И опять существенным является способ упорядочения. В данном случае этот
порядок таков, что первая строка, отмеченная индексом 1, содержит по
порядку ах и Ьг, и вторая строка упорядочена аналогично. Мы привели здесь
простой пример квадратной матрицы.
Очень важно проводить строгое различие между вектором или матрицей
как упорядоченными множествами элементов и отдельными величинами (или
выражениями), получаемыми из элементов. На основе вектора (а, Ь, с)
можно получить несколько выражений, например сумму элементов а + Ъ + с,
которая, так же как и сами элементы, имеет отдельное значение. Подобно
этому на основе написанной выше квадратной матрицы можно получить такие
выражения, как произведение элементов на главной (ведущей) диагонали
axb2 или так называемое перекрестное произведение четырех элементов
аф2-^ a2bx. Эти выражения имеют такой же характер, как и сами элементы
(например, вещественные числа), и к ним, так же как и к отдельным элементам,
применимы законы элементарной алгебры. Но из этого не следует, что и сами
векторы или матрицы также подчиняются алгебраическим законам
вещественных чисел или каким-либо другим.
Практическим испытанием матричной алгебры является выяснение того,
насколько она удобна и пригодна для разработки возникающих в различных
областях проблем. Одно дело — изобрести алгебраические обозначения и
ввести внутренне совместные законы действий. Совсем другая проблема —
найти поле применения алгебры, которое оправдывало бы усилия по освоению
новых обозначений и законов действий. Примером нового и полезного
развития алгебры являются комплексные числа. Другой пример —матричная
алгебра. На практике мы постоянно сталкиваемся с определенными
алгебраическими выражениями, например, axb2 — a2bx\ axxY + а2х2 + а3х3 и ах2 + 2hxy + by2.
Матричные обозначения и матричная алгебра являются результатом
стремления оперировать этими и многими другими подобными выражениями
общим, единообразным и удобным способом. Успешное применение
обозначений объясняется в основном тем, что с их помощью становится возможным
переход от простых случаев двух или трех измерений к общему случаю п
измерений.
Например, выражение axb2— а2Ъх само по себе очень простое, но вообще
его удобно рассматривать как «перекрестное произведение» квадратного
блока элементов:
ai\ /А
С
то есть как возникающее из квадратной матрицы
ь%у
Подобно этому выражение а1х1 +a2x2 + asxs лучше всего рассматривать
как полученное из двух наборов элементов, а именно: векторов (а2, <z2, a3)
я (хг, х2, х3); а выражение ах2 + 2hxy -j- by2 как результат соединения матрицы
Га А1
[h b\
и вектора (ху у).
Следовательно, матричная алгебра дает компактное обозначение, которое
позволяет оперировать с громоздкими выражениями и действиями. Более
того, это обозначение является общим и применимо не только тогда, когда
299

мы имеем дело с большим числом элементов, но и к неопределенному числу
элементов. Матричное обозначение позволяет переходить от случаев двух
или трех измерений к случаям, когда число измерений велико и точно
не установлено.
11.2. ЛИНЕЙНЫЕ УРАВНЕНИЯ И ПРЕОБРАЗОВАНИЯ
Характер проблем, для решения которых полезно использовать
матричную алгебру, хорошо иллюстрируется анализом системы линейных
уравнений и линейных преобразований. О системах уравнений уже
упоминалось в главе 9. Когда эти уравнения линейны, то в общем обозначении
их можно сформулировать следующим образом.
Одно линейное уравнение с одним неизвестным х имеет вид
ах = у, A)
где а и у заданы. Решением этого уравнения является х = у/а при
условии, что а Ф 0. Два линейных уравнения с двумя неизвестными хх и х2
имеют вид:
а~'"Л-"-*¦ = "у 1 B)
где величины а и у даны. Постоянные величины а можно расположить
в виде квадратного блока элементов (с двумя строками и двумя столбцами),
а величины у образуют упорядоченный столбец из двух элементов:
21
«
22
2/2
Решением этих уравнений является
1 — «122/2
Х2 =
при условии, что апа22 — а12а21 Ф 0.
Форма, в которой записано B), и обозначения, использованные для
блока и столбца данных величин, подсказывают и общий случай системы
линейных уравнений. Рассмотрим систему из т уравнений с п неизвестнымр!
величинами х1У x2i .. ., хп:
% А
а1пхп =
а22х2 + . ..
amlXl
атпХп = У
C)
Что нам дано, это, во-первых, блок из тхп элементов а, состоящий из т
строк и п столбцов, и, во-вторых, столбец из т элементов:
a «I а*
аъ
ао
хт\ ит2-
Уг
Ут
Наша задача состоит в том, чтобы найти значения всех х или сколько
вообще возможно из них, выраженные через известные величины any.
Как это делается, будет показано в разделе 13.2. Если не все у равны О,
то система C) называется неоднородной. В особом случае, когда все у
равны 0, система C) называется однородной системой уравнений. Слово
«однородная» понимается здесь в обычном смысле, именно в том, что
300

если все величины х умножить на одну и ту же постоянную, то
уравнения (и любое решение) не изменятся *. Одно решение однородной системы
получается автоматически (тривиальное. — Ред.): xl — x2=... = хп = 0.
Однако нас интересует другое решение, дающее отношения или
относительные значения переменных х.
Очевидно, что при обобщении системы B) с m = w = 2 в систему C),
где т и п точно не определены, обозначение становится громоздким
и алгебраические действия утомительными. Поэтому многое зависит от
удобной системы обозначений и разработки соответствующих средств
алгебры. Векторная и матричная алгебра позволяют записывать систему
уравнений в двух альтернативных формах, более компактных, чем C).
Первая форма записи получается только при помощи векторных
обозначений. Напишем
a. = (eis* a2S> •••> О (* = 1' 2' •••> п)
как векторы т измерений, составленные из столбцов коэффициентов и из
правых частей уравнений системы C). Тогда систему C), как будет
показано в разделе 11.8, можно написать так:
Это выражение означает, что, когда берется первый элемент в каждом
векторе, получается первое уравнение системы C); когда берется второй
элемент, получается второе уравнение и т. д. Чтобы записать систему C)
во второй форме, введем матрицу коэффициентов размерности тхп, то
есть составленную из т строк и п столбцов:
ап а12 ... аы
• • • а
2п
вектор п измерений
X = (Хр Х2, . . . > Хп)
и вектор т измерений
У = (Уи У* •••> Ут)-
Как будет показано, в этом случае система C) может быть записана
в очень компактной (матричной) форме2: Ах = у.
После того как разработана общая и компактная форма записи, всегда
можно получить и частные случаи. Например, пара уравнений B)
получается, когда матрица А является квадратной, второго порядка Bx2):
\ап а12]
La21 «22 J
а х и у суть векторы, состоящие из двух элементов. Рассмотренные нами
системы уравнений в общей форме C) и в частной форме A) и B) можно
1 Автор здесь имеет в виду следующее: если мы знаем какое-нибудь решение
(нетривиальное) #ь х2, ..., хп данной однородной системы, то из него можем получить
сколько угодно решений той же системы, умножая все хг известного решения на одну
и ту же постоянную. —Прим. ред.
2 Понятие матрицы, а также произведение матрицы А на вектор х определяются
в разделах 11.6 и 11.8. —Прим. ред.
301

исследовать и с другой точки зрения. Предположим, что у являются не
данными величинами, а новыми переменными, заменяющими все или
некоторые из первоначальных переменных х. В этом случае система уравнений
является линейным преобразованием от переменных х к переменным у.
В той форме, в которой система записана в C), значения у определяются
через х. В данном случае задача, соответствующая «решению» системы
линейных уравнений, состоит в том, чтобы «обратить» (перевернуть)
линейное преобразование или выразить х через у. Более компактно это
можно написать в следующей форме: линейное преобразование у = Ах
показывает, каким является у при данном х; обратное преобразование
х = А"ху показывает, каким является х при данном у. Все это можно
проиллюстрировать на очень простом примере. Импорт каучука составляет xi т
и оценивается в х2 ф. ст. Зная это, мы можем получить цену в фунтах
стерлингов за 1 т. Требуется перевести импорт в новые единицы — фунты и
пенсы — и получить цену в пенсах за 1 фунт. Если ввести новые переменные —
ух фунтов и у2 пенсов1: уг = 224(ЬХ и у2— 240#2, то получаем пару уравнений,
аналогичных B), где а12 = агх= 0. Средние цены равны:
— ф. ст. за 1 т
11.3. ВЕКТОРЫ
Рассматриваемые здесь векторная и матричная алгебра имеют дела
с вещественными числами. Все вещественные числа образуют множество F,
известное под названием поля. Вещественные числа служат двум целям:
они являются компонентами векторов и матриц и выступают как скаляры2
в действиях над ними. В частности, скаляр часто употребляется как
множитель; векторы и матрицы можно умножать на скаляр. Скаляр также может
получаться в результате определенных действий, например как произведение
векторов и матриц.
Понятие вектор с успехом используется при геометрической
интерпретации комплексных чисел (см. прилож. В.— Ред.). Это представляет случай
двух измерений, и многие полученные свойства специфичны только для этого
случая. Однако нетрудно развить идею двухмерного вектора как
упорядоченной пары компонентов (я, у), соответствующего точке Р с этими координатамиг
или линии ОР определенной длины и направления на плоскости Оху. В
случае трех измерений существует упорядоченная тройка компонентов (х, у, z),
соответствующая точке Р в пространстве Oxyz. Вообще в случае п измерений
имеется п упорядоченных компонентов, которые, хотя и нельзя представить
видимо, но можно мыслить как точку в я-мерном пространстве.
Общее и формальное определение вектора можно дать с помощью любого
множества элементов, удовлетворяющих точно определенным условиям или
правилам сложения и умножения на скаляр.
Здесь мы ограничиваемся рассмотрением одного особого типа векторов,
являющихся обобщением понятия упорядоченного набора компонентов,
взятых из поля F вещественных чисел. Короче говоря, в этом случае вектор
является набором пкомпонентов—вещественных чисел. Конечно, справедливо,
что это частный случай, однако это как раз тот случай, который почти
неизменно встречается на практике. В отличие от скаляра сам вектор не является
1 Здесь автор имеет в виду английскую большую, или длинную, тонну (long, или
wross ton), содержащую 1016 кг, а английский фунт содержит 453,6 г. Разделив 1016 кг
на 453,6 г, мы получим 2240 английских фунтов. 1 ф. ст. =20 шиллингов Х12 пенсов =
= 240 пенсов. Отсюда и получаются уравнения в тексте.— Прим. ред.
2 Всякое вещественное число называется скаляром. —Прим. ред.
302

вещественным числом, он—упорядоченный набор вещественных чисел.
Поэтому символ для обозначения вектора должен быть выбран таким, который
исключал бы отождествление его со скаляром. Здесь для обозначения
скаляра мы будем пользоваться буквами обычного шрифта, для обозначения
вектора применять буквы, написанные полужирным шрифтом.
Определение. Вектор размерности га является набором га компонентов
из поля F вещественных чисел и обозначается
а = К, а2, .... ап).
Рассмотрим вектор а определенной размерности га. Он может быть
интерпретирован как точка Р или как прямая ОР в геометрическом га-мерном
пространстве, направленная из начала координат в указанную точку Р. Точка Р
имеет координаты (alf a2, ..., aj,
отнесенные к фиксированным вза-
имноперпендикулярным
координатным осям. Если расстояния
между точками не определены и не.
принимаются вовнимание,то
га-мерное пространство называется
декартовым пространством. В
противном случае га-мерное
пространство называется эвклидовым
пространством.- Когда га = 2 и
вектор состоит только из двух
элементов, представление точки jP
или прямой ОР в двухмерном
пространстве логически вытекает из
рассмотрения комплексных чисел
(см. приложение Б). В этом
частном случае вектор также может
быть истолкован как комплексное
число. Когда га — 3, то вектор состоит из трех элементов и представляется
точкой jP (или прямой ОР) в трехмерном пространстве. В этом случае
понятие вектора обладает геометрической наглядностью, ибо можно фактически
начертить диаграмму. Например, на рис. 36 показаны три вектора ОРг, ОР2
и ОР3 размерности га = 3. Компонентами этих векторов являются
координаты точек Рг, Р2 и Р3 относительно координатных осей ОхгХоХ3. Когда
га > 3, то хотя и нельзя фактически сделать рисунка, но можно пользоваться
геометрической интерпретацией векторов как сопоставленных им точек или
j как направлецных отрезков прямых линий.
Однако всегда следует помнить, что вектор (как он определен здесь)
является алгебраическим понятием и что мы рассматриваем векторную
алгебру. Если изучению алгебраических понятий может помочь геометрическое
воображение га-мерного пространства, тем лучше. Однако геометрическая
интерпретация и геометрические аналогии не должны заходить слишком
далеко. Они достаточно хороши, когда га = 2, 3, то есть когда в действительности
можно сделать рисунок, но вообще рискуешь прийти на основе
геометрической интерпретации к ошибочным заключениям. Как частный случай
в векторной алгебре имеется нулевой вектор 0 = @, 0, ..., 0), играющий в ней
ту же роль, что и число нуль в алгебре вещественных чисел. Геометрическим
представлением нулевого вектора является начало координат 0 и в
декартовом и в эвклидовом га-мерном пространстве.
Имеется га особых векторов, которые называются единичными векторами:
8^A,0, ..., 0), в, = @,1, ..,,0), ...Геп = (О, 0, -.-. 1).
Считают, что эти векторы образуют «базис»1;всей системы векторов, базис
в том смысле, что любой вектор может быть выражен через эти единичные
векторы. Геометрически в га-мерном эвклидовом пространстве единичные
Рис. 36
303

векторы представляются точками на п координатных осях; расстояние
этих точек до начала координат равно 1. Единичный вектор 8Г имеет
1 на месте г, а остальные его компоненты равны нулю. Чтобы это
обозначить, удобно пользоваться дельтой Кронекера, которая определена так:
6rs = 0 (Г ф8) И 6rs = l (/' = *)
(то есть она равна нулю при всех г и s, кроме случаев г = s, когда она
равна 1. -—Ред.). Поэтому единичный вектор 8Г можно записать с
помощью дельты Кронекера следующим образом:
ег = (бг1, 6г2, ..., бгп) (г = 1, 2, ..., п).
11.4. ВЕКТОРНАЯ АЛГЕБРА
В алгебре комплексных чисел или двумерных векторов мы не
испытываем трудностей при определении равенства сложения и умножения
векторов на скаляр. Единственно неясным моментом является
формулирование соответствующего правила для умножения векторов. Если
умножение векторов оставить пока в стороне, то алгебра двумерных векторов
легко распространяется на векторы любого порядка. В своей простейшей
форме векторная алгебра построена таким образом, что два вектора
считаются равными, если равны по отдельности их элементы, а сумма двух
векторов получается сложением их соответствующих элементов. Умножение
вектора на скаляр производится путем умножения на скаляр каждого
элемента вектора. Эти простые условия можно выразить следующим
образом. Рассмотрим два вектора:
а = (а19 а2, ..., ап) и Ь = F1? 62, ..., Ьп).
Равенство и неравенство векторов. Равенство векторов определяется
следующим образом:
а = Ь, если аг = Ъг (г = 1, 2, ..., п),
а неравенство:
а > Ь, если аТ> ЬТ (г = 1, 2, ..., п).
Появляется некоторое осложнение, связанное с тем фактом, что хотя два
вектора могут быть не равны, они в то же время не удовлетворяют
данному определению неравенства векторов. Рассмотрим понятие «больше или
равно» («не меньше»). В этом случае для скаляров имеется очень простая
альтернатива: а>6 означает, что или а — Ъ, или а > Ь. В случае векторов
имеются другие возможности. Если а = Ь, то комедий элемент а равен
соответствующему элементу Ь; если а > Ь, то каждый элемент а больше
соответствующего элемента Ь. Теперь определим, что а больше или равен Ь,
если каждый элемент а больше или равен соответствующему элементу Ь.
Запишем это условие в двух обозначениях, отличающихся тем,
включается ли а = Ь или нет:
а^Ь, если аг>6г, допуская, что все аг = Ьг,
а> Ь, если аг>Ьг, не допуская, что все ar = fer,
где г = 1, 2, ..., п. Эти выражения отличаются только тем, что в первом
включен случай а = Ь, а во втором нет. Необходимо отметить, что а^Ь
вовсе не является объединением двух случаев а = Ь и а > Ь. Может быть
и так, что некоторые элементы а больше, а другие равны
соответствующим элементам Ь. Далее, несмотря на то что а^Ь включает широкий
круг векторов, было бы неправильно сказать, что а ^ b и а < Ь охватывают
все случаи. Имеется больше случаев, когда а и не равен и не неравен Ь.
Это бывает тогда, когда некоторые элементы а больше, а другие меньше
соответствующих элементов Ь.
304

Все эти случаи важны, когда а сравнивается с нулевым вектором:
а > 0, если аг > О,
а 2:0, если аг>0, доцуская, что все аг=0,
а>0, если яг>0, не допуская, что все <2г = 0,
где г=1, 2, ..., п. Положительный вектор а>0 достаточно ясен. Но
векторы а^О и а>0, которые можно назвать неотрицательными
векторами, имеют несколько более неясный смысл. Эта группа векторов
включает в себя неотрицательные элементы, то есть не только векторы с
положительными элементами, но и такие векторы, у которых некоторые
элементы положительны, а другие равны нулю. Эти неотрицательные векторы
имеют важное значение в экономических приложениях, особенно когда
изучается проблема цен (см. упражнение 2).
Сложение векторов. Определение очень просто:
Рассмотрим случай, когда и = 2. Пусть а, Ьиа + Ь представляются
соответственно векторами OPV ОР2 и ОР. В этом случае ОР получается
из ОРХ и ОР2 по правилу параллелограмма. То же самое мы имели бы
и для трехмерного пространства; можно вообразить это и для п-мерного
пространства. Определение сложения распространяется и на сложение трех
векторов (и на любое число векторов):
а+Ы-с = (а + Ь) + с = а + (Ь + с) = (а1 + Ь1 + с1, а2 + Ь2 + с2, ..., ап + Ьп+сп).
Для и = 3 это проиллюстрировано на рис. 36. Суммой векторов ОРг,
ОР2 и ОР3 является вектор ОР, полученный как направленная диагональ
параллелепипеда, построенного на векторах ОРХ, ОР2 и ОР3. Можно
«объединить» ОРг и ОР2 и получить ОР', или а + Ь, а затем сложить ОР'
и ОР3 и получить ОР, то есть (а + Ь) + с = а + Ь + с.
Умножение вектора на скаляр. Определение опять очень просто:
Хъ = (Хаг, Ха2, ..., Хап)
для любого скаляра X. Графически, если ОРХ представляет вектор а, то
вектор Ха. будет представляться отрезком ОР, имеющим то же направление,
что и ОРХ, но длина которого составит X длин отрезка ОРг. Если Я>1,
то ОР длиннее ОРХ, если 0< Х< 1, то ОР короче ОРХ. Если даже X < О,
то вектор Ха. все-таки определен; все его элементы по знаку
противоположны элементам вектора а, а точки Р и Рх будут расположены по разные
стороны от начала координат. Вектор —а, отрицательный по отношению
к данному вектору а, подходит под определение сложения векторов и
умножения векторов на скаляр:
а + (-а) = 0 и -а = (-1)а,
или, если выразить через элементы,
— а = ( — а19 —а2, ..., — ап).
Отметим, что порядок написания векторов не имеет значения: а + Ь =
= b + а — свойство коммутативности сложения, а нулевой вектор играет
такую же роль в процессе сложения, как нуль в обычной алгебре:
04 а = а.
Скалярное произведение векторов. Правило умножения двух векторов
(комплексных чисел) ограничивается случаем гс = 2. Оно вообще
оказывается бесполезным для определения произведения двух векторов,
результатом которого был бы еще один вектор системы. Однако имеется
совершенно другой тип произведения векторов; его результатом оказывается
20 р. Аллен ^05

не вектор, а скаляр. Это произведение связано с понятием «длины» вектора,
а потому имеет смысл только для евклидова пространства, в котором
определено «расстояние» между точками.
Рассмотрим случай двух векторов в двумерном пространстве. Пусть
а = (av а2) и b = (bv Ъ2) представляются соответственно векторами ОРХ и ОР2.
Определим
ab = а1Ь1 + a2fr2
как скалярное произведение векторов а и Ь. В частности,
где | а | = "]/~aJ + а\ является абсолютной величиной а или длиной ОР. Теперь
рассмотрим угол 9 между ОРХ и ОР2. Из элементарной тригонометрии
известно что
известно, что
Следовательно,
cos8 = TA1?r
Для векторов единичной длины (то есть когда |а| = |Ь| = 1) скалярное
произведение аЬ равно косинусу угла между этими векторами. Более
важным является случай, когда два вектора находятся друг к другу под.
прямым углом (ортогональны). Тогда cos 9 = 0 и скалярное произведение
выражается как
Выведенные нами алгебраические понятия и их геометрическую
интерпретацию легко распространить на трехмерное пространство. Для п-мерного-
пространства требуется новое определение алгебраических понятий.
Определение. Скалярным произведением двух векторов
а = (ах, а2, ..., ап) и Ь = FХ, 62, ..., Ьп)
является
Абсолютная величина (модуль), или длина |а| n-мерного вектора
определяется следующим равенством:
В n-мерном пространстве геометрическая интерпретация является проста
вопросом удобства, или, говоря более строго, алгебраические понятия,
и выражения, используемые для определения свойств евклидова
пространства, легко могут быть распространены на случай любого числа координат.
В д-мерном пространстве два вектора а и b представляются через ОРХ
и ОР2. Длина ОРг определяется как |а| = yraj + aj+ ... +а?г, а угол 9-
(между ОРг и ОР2) на основе выражения
Ь| уГ
Два вектора а и b ортогональны, а ОРг и ОР2 перпендикулярны, еслв
а. Ь = axbx + а2Ъ2 + ... + апЬп = 0.
Именно на этой основе можно построить алгебру и геометрию гс-мерного
пространства. Перед нами открываются широкий простор и возможности
развития в нескольких направлениях. В одном случае в качестве
отправной точки выбирают понятия длины, угла и т. п. (то есть увеличивают число»
измерений пространства,во сохраняют его основные геометрические свойства.—
Ред.). В другом случае полностью отказываются от этих понятий, а основой
306

становится идея взаимосвязанного пространства (или изучение более общих —
топологических — свойств пространства.— Ред.). Это приводит к предмету
топологии (или «анализу положения» по старой терминологии), которая
характеризуется следующим образом: «Эта отрасль математики изучает свойства
пространств, которые не зависят от их формы и размера. Таким образом, ее
предметом является не понятие длины, угла или прямой линии (straightness),
а свойство быть единым связным целым, свойство быть ограниченным,
свойство быть границей» (Chamber's Encyclopaedia, 1950). Такое развитие алгебры
используется в таких экономических приложениях, как линейное
программирование, поэтому его простые аспекты рассматриваются в следующих
разделах. Однако мы не будем заходить слишком далеко в этом направлении,
так как для нас более важно построить на основе чисто алгебраических свойств
векторов матричную алгебру. Тогда мы найдем, что скалярное произведение
векторов находит свое место и в более общей алгебре матриц.
Задачи и упражнения
1. Представить векторы B, 2, 2), B, 2, 1), B. 1, 1) и A, 1, 1) на рисунке в
трехмерном пространстве. Можно ли сказать, что первый вектор «больше», чем остальные.
2. Если р (рх, /?2, ..., Рп)—вектор цен, то можно выделить два случая: р^О
и р^О. Оба эти вектора в общем можно рассматривать как набор неотрицательных
цен. Какой из них обычно принимается при точном формулировании экономических
проблем?
3. Как применить правило параллелограмма к доказательству а+(—а) = 0?
4. Сформулировать и доказать следующие правила сложения векторов:
а) если а и Ь—векторы, то и а+b является вектором;
б) а+(Ь+с) = (а+Ь)+с;
в) а+Ь=Ь-|-а;
г) если а+Ь=а-|-с> т0 ь = с;
д) существует такой нулевой вектор 0, что
а+0=0+а=а;
е) для любого а существует такой отрицательный вектор (—а), что а + (—а)=:
= (-а)+а=0.
5. Сделать аналогичное для следующих правил умножения 'вектора на скаляр:
а) если а вектор, то и Яа—вектор для любого скаляра X;
б) 0а=0 и la = af
) Л() (Я)
)
в)
г)
)
)
д) (+ц) +1
6. Доказать следующие правила скалярного произведения векторов:
а) если а и b векторы, то ab—скаляр;
б) a-b=b-a;
в) a(b+c) = ab+ac.
7. Нормализованная форма вектора а определяется как Яа при условии, что
абсолютная величина |Ха| = 1. Показать, что («i/| а|, б2/| а|, ..., an/l a |) есть
нормализованная форма вектора а и что геометрически это вектор единичной длины
и одинакового с вектором а направления.
11.5. ЛИНЕЙНЫЕ КОМБИНАЦИИ ВЕКТОРОВ. ВЫПУКЛЫЕ МНОЖЕСТВА
Рассмотрим в двумерном декартовом пространстве два единичных
вектора 8i= A, 0) и 82= @,1), которые представлены точками Ах и А2, лежащими
на координатных осях на плоскости Оххх2. По правилам векторной алгебры
любой вектор х = (х19 х2) может быть выражен так:
где хх и х2— скаляры, являющиеся оба компонентами х и скалярными
множителями 8Х и 82. В этом случае говорят, что вектор х является линейной
комбинацией векторов 8х и 82. Любой вектор х является такой линейной
комбинацией. Говорят, что векторы ех и е2 образуют базис декартова двумерного»
пространства1— базис в том смысле, что двух векторов гх и е2 достаточно^
чтобы воспроизвести всю систему векторов двумерного пространства.
1 Или что двумерное пространство натянуто на единичные векторы ei и 8г.
Аналогично n-мерное пространство натянуто на п единичных векторов.— Прим. ред.
307 20*

С геометрической точки зрения то, что х является линейной комбинацией
базиса гг и 82, является просто выражением следующего факта. Векторы
базиса ех и е2 представлены OAi и ОА 2, образующими координатные оси и
единицы измерения в двумерном пространстве. Тогда любой вектор ОР является
суммой двух векторов, один из которых получается умножением ОАг на
хг, а другой—умножениемОА2 на х2. Другими словами, к точке Р можно
прийти, если отсчитать х± единиц в направлении OAV а затем х2 единиц в
направлении ОА2. Все, что мы сказали, легко распространяется на
декартово трехмерное пространство.
Вообще декартово /г-мерное пространство охватывается п единичными
векторами 8Х, 82, ..., еп, которые образуют базис пространства. Это значит,
что любой вектор х = (ж1, #2, ..., хп) является линейной комбинацией
базиса:
п
Х = 2 Хггг = ^181
i
2
r=i
Или в развернутом виде:
ж181 = х1A, 0, ..., 0) = ^, 0, ..., 0),
, ..., 0) = @, х2, ..., 0),
Xrfin = xn(°> °> ¦••» 1) = (°» 0, ..., Хп).
И, таким образом, получаем
п
2 х29 ..., 0)+
... + @, 0, ..., хп) = (xv х2% ..., хп) = х.
Рассмотрим теперь в декартовом га-мерном пространстве два вектора:
v<l>__/rU> Td) ГШ\ и хB)__/гB) г<2) гB)\
х — ^жх , х2 j .. ., хп ) и х — \А1 , х2 у • • • f лп ),
Линейной комбинацией векторов хA) и х<2) является вектор
KjX™ + X2xi2) для любых Klt k2.
Элемент r-й (или r-я координата. — Ред.) линейной комбинации есть
%,гх™ + Х2х{г2). Он получается сложением /--элементов хA) и хB), умноженных
соответственно на ^ и %2. Рассмотрим два частных случая линейной
комбинации векторов. Положительной линейной комбинацией векторов хA)
и х<2) является вектор
^xA) + VB>» где Х19 Я2>0;
выпуклой линейной комбинацией векторов хA) и хB) является вектор, для
которого сумму скаляров, Хх +^2 = 1» можно записать следующим образом:
I где
Способ образования этих комбинаций виден на рис. 37. Данные векторы
xd) и хB> представлены в виде направленных отрезков ОРХ и ОР2,
определяющих в w-мерном пространстве плоскость ОР±Р2.
На рис. 37 показана только двумерная плоскость (плоскость чертежа).
Ее нужно вообразить как л-мерную плоскость, образованную
координатными осями Оххх2 ... хп, которые не показаны на рисунке (и вообще не
могут быть представлены графически). Пусть ОР—выпуклая линейная
комбинация \xx^ + (l — \i)x^2\ где \i принимает значения от 0 до 1. Легко
показать на основании формул аналитической геометрии (см.
упражнение 2), что Р лежит на прямой линии, соединяющей Рг и Р2, и делит ее
в отношении fjt: A — |х). Следовательно, когда |i возрастает от 0 до 1,
Р движется от Р2 к Рг и ОР передвигается от ОР2 к OPV Рассмотрим
308

OQ — положительную линейную комбинацию:
где
Следовательно, 0() получается умножением ОР на положительное число.
Если множитель Х1 + А,2>1, то (? лежит на #Р дальше точки Р, как это
показано на рис. 37. Если 0<Х1 + Я,2<1, то в этом случае Q лежит
между О ж Р. Таким образом, для того чтобы получитьГ0(? при данных Кг
и Х2, надо сначала определить местонахождение ОР при ^ = Я1/(Я,1 + Х2),
а затем увеличением (или умножением) ОР в отношении (К1+'к2):1
получить OQ. При различных значениях Кг и Х2, OQ лежит в углу между
векторами ОР1 и ОР2 и имеет разную длину. Наконец, любая линейная
комбинация представляется вектором OR, лежащим где-нибудь в плоскости,
образованной ОРХ и.ОР^1.
Все эти определения и свойства легко распространяются на случай
любого числа векторов в я-мерном пространстве.
Определение. Линейной комбинацией данных векторов
хк = (х?\ xBk\ ..., xik)) (ft=l, 2, ..., m)
является
при любых значениях скаляров Xk. Линейная комбинация является
положительной, если все Xk>0, и выпуклЪй, если ^>0и, кроме того,
Геометрически линейная комбинация выражается через точки Д, Р2, ...,
Рт, соответствующие данным векторам гс-мерного пространства. Выпуклая
линейная комбинация представляется некоторой точкой Р на фигуре или
внутри фигуры (многогранника), определяемойPL, P2,..., Рт на
гиперплоскости, натянутой на эти векторы (если т < п). Положительной линейной
комбинацией является точка Q, лежащая на прямой линии, проведенной через
Q и Р и продолженной за Р (точка Р соответствует некоторой выпуклой
линейной комбинации данных векторов.— Ред.). Таким образом, Q лежит на
гиперконусе, образуемом ОР17 ОР2, ..., ОРт, или внутри него. Любая
линейная комбинация представляется точкой R в подпространстве (самое большее
т измерений), определяемом О, Рг, Р2, ..., Рт.
Теперь мы сосредоточим внимание на свойствах множества точек
Pfc(ft=l, 2, 3, ...)
/г-мерного пространства. Это точечное множество, обозначаемое нами через S,
может содержать конечное число точек; оно, например, может быть
составлено из угловых точек геометрического тела, ограниченного плоскостями в
трехмерном пространстве. S может быть и бесконечным множеством точек,
например если оно содержит все точки на поверхности сферы в трехмерном
пространстве. Мы не будем рассматривать тривиальный случай, когда S содержит
только одну точку. Если установлены координатные оси Охгх2 хп и
единицы измерения, любая точка Pk может рассматриваться как вектор,
имеющий координаты
Однако в данном случае это не существенно. Изучаемые свойства не зависят
от любого частного измерения пространства, и они не изменяются, если даже
пространство в некоторых направлениях расширяется или сокращается.
1 Таким образом, концы R всевозможных линейных;' комбинаций векторов ОРг
и ОР2 заполняют всю область угла, заключенную между этими векторами в
образованной ими плоскости. —Прим. ред.
309

Рассмотрим две точки Рг и Р2 множества S, которым соответствуют
векторы х*1) и х<2). Выпуклая линейная комбинация х = jix^1) + A — [х)х<2)
представляется некоторой точкой /\ которая лежит на отрезке прямой РХР2
и делит ее в отношении Р2Р : РРг = fi : A — |г). Когда [г увеличивается
(в пределах 0<[х<1), Р движется непрерывно от Р2 к Рг. Это свойство
не зависит от способа измерения пространства или от того, как пространство
может быть искривлено. Отношение jut : A — \i) и «прямизна» линии РгР2
вовсе не необходимы. Однако если \i возрастает от нуля до единицы, то точка
Р всегда движется по какому-то пути от Р2 к Pv Следовательно, точка Р
может быть выражена так:
и можно сказать, что Р находится «между» Рг и Р2 на некоторой линии в
пространстве. Ограниченная таким образом точками Рг и Р2 точечного
множества S, сама точка Р может принадлежать, а может и не принадлежать S.
Рис. 37
Множество S называется выпуклым, если все точки между любыми двумя
точками из S также принадлежат S. Выпуклое множество может быть
бесконечным, и его характерной чертой, если говорить просто, хотя и не очень точно,
является то, что оно «сплошное» и не имеет «входящих углов» («вмятин»).
Рассматривая выпуклое множество S, важно отличать его «граничные точки»
от «внутренней» части. Экстремальной точкой (extreme point) выпуклого
множества S называется такая точка, которая не лежит между какими-либо
двумя другими точками S; Р есть экстремальная точка S, если она не может
быть выражена как выпуклая линейная комбинация М-Рх+ A — Н^г каких-
либо двух точек Рг и Р2 из множества S. < Границы» множества S образуются
именно экстремальными точками1.
В двумерном пространстве все точки четырехугольника (рис. 38, а)
и круга (рис. 38, б) образуют выпуклое множество. В первом случае
экстремальными точками являются А, В, С и D, во втором — все точки окружности
круга. В то же время точки площади четырехугольника с вмятиной ABCD
(площадь, заштрихованная перекрестными линиями на рис. 38,<?) не образуют
выпуклое множество, так как этому множеству не принадлежат, например,
точки между А ж С.
Рассмотрим теперь любое множество *У, конечное или бесконечное.
Прибавим к нему все точки, лежащие между двумя любыми членами S. В
результате этого S «наполнится» в определенной степени, но не полностью, ибо
в расширенном таким образом множестве могут быть такие точки, что все
другие между ними не будут принадлежать полученному множеству. Этот
процесс прибавления к исходному множеству S всех промежуточных точек
можно продолжать до тех пор, пока S не дополнится до выпуклого множества,
1 Автор допускает неточность. «Границу» выпуклого множества образуют его
граничные точки. Граничной называется такая точка выпуклого множества, которая
не может быть центром сферы как угодно малого радиуса, все точки которой принадлежат
выпуклому множеству.— Прим, перев.
310

которое будет включать не только первоначальные точки Pk, но и все точки Р,
получающиеся как всевозможные выпуклые линейные комбинации точек Pk:
..+Хй+... =1),
то есть
х = ^хA) + ^2хB) + ... + Xkxik) +
Получающееся таким образом расширенное множество называется выпуклой
оболочкой («convex hull») первоначального множества.
Пусть выпуклая оболочка К данного точечного множества S содержит
все точки, являющиеся выпуклыми линейными комбинациями точек S, а
также и сами точки S. В широком смысле К является бесконечным выпуклым
множеством всех точек «внутри» конфигурации точек Рг, Р2, ... множества S.
Оно является «сплошным», не имеющим «входящих углов» (вмятин)
множеством, которое можно построить из множества S. Экстремальным
множеством Е (extremal) выпуклой оболочки К является множество
экстремальных точек К. Это экстремальное множество является «границами» К.
Следовательно, из множества S получается другое множество Е,
являющееся экстремальным множеством выпуклой оболочки множества S. Между S
и Е существует тесная связь. Ясно, что каждая точка Е должна также
принадлежать S. Рассмотрим, например, точку Р множества Е. Если точка Р
не входит в S, то она должна принадлежать выпуклой оболочке множества S,
являющейся линейной комбинацией точек S. Однако это исключено, ибо это
противоречит определению экстремальной точки. Следовательно, точка Р
должна входить в S. Также очевидно, что Е не должно совпадать с S: все
точки множества S не обязательно принадлежат Е, так как невыпуклость
множества S делает возможным нахождение его точек внутри, а не на
«границе» выпуклой оболочки.
Все вышеуказанное для случая двумерного пространства
иллюстрируется на рис. 38. Заштрихованные части фигур — это выпуклые оболочки.
Множество S четырех точек А, В, С и D на рис. 38, а является одновременно и
экстремальным множеством Е. Аналогично множество S всех точек на
окружности круга на рис. 38, б также рвляется экстремальным множеством Е. В
данном случае это бесконечное множество. Однако на рис. 38, в первоначальное
множество S четырех точек А, В, С иZ) образует выпуклую оболочку, которая
может быть образована и при помощи только трех точек, а оставшаяся точка
будет лежать внутри оболочки. В данном случае экстремальное множество Е
содержит только три точки А, В и С.
Таким образом, мы отправляемся от данного множества S, включаем
все выпуклые линейные комбинации точек S, получаем выпуклую оболочку К,
а затем находим экстремальное множество Е. Это позволяет устранить из S
все не «необходимые» члены, то есть такие точки, которые являются
выпуклыми линейными комбинациями других точек множества S. Если с самого
начала S не содержит таких точек, то оно само является экстремальным
множеством (extremal) собственной выпуклой оболочки. Однако обычно S содержит
такие точки, и они устраняются при приведении S к экстремальному
множеству Е выпуклой оболочки множества S.
Иногда удобнее использовать не точки Pk множества S, а линии OPk,
соединяющие эти точки с началом координат. В данном случае выпуклую
оболочку множества S можно рассматривать как «сплошной» пучок линий ОР,
где Р является выпуклой линейной комбинацией точек Pk. Эта выпуклая
оболочка называется выпуклым многогранным конусом, полученным из данного
множества S. При соединении точек экстремального множества Е с О
получается множество линий, которые образуют «границы» конуса1.
1 Это неточно. При соединении экстремальных точек с О получаются ребра
конура.— Прим. ред.
311

Задачи и упражнения
1. В двумерном пространстве даны два единичных вектора: ъ1^=ОА1, идущий
вдоль Охъ и е2 = ОА2, идущий вдоль Ох2. Показать, что уравнение прямой линии
АгА2 имеет вид хх-]-х2 = 1. Вывести, что точка x=x181+a:2e2» если она может быть
выражена как х=|хе1+A—\*)ъ2 для любого \i (при 0<[г<1), лежит на прямой
линии АгА2.
2. Развивая результат предыдущего упражнения, показать, что точка Р,
представляемая как конец вектора x = jxxA)-|--(l—\i) x<2), лежит на прямой линии между
Рг и Р2. На основе координат этих точек проверить, что Р2Р: РРг = \1: A —[л).
Истолкуйте Р как «среднюю взвешенную» из Рг и Р2.
3. Дано множество S конечного числа точек Р^ (Л: = 1, 2, 3, ...,п). Показать,
что если взять всевозможные положительные линейные комбинации точек Pki то
получится выпуклый многогранный конус, а если взять выпуклые линейные комбинации
этих точек, то получится выпуклая оболочка.
4. Множество ? в трехмерном пространстве состоит из четырех точек, которые
могут иметь или не иметь входящий угол (вмятину). Что будет выпуклой оболочкой
этого множества и экстремальным множеством? Если S является множеством всех
точек на поверхности сферы, то что будет его выпуклой оболочкой и экстремальным
множеством?
11.6. МАТРИЦЫ
Матрица любого размера является наиболее общим понятием,
необходимым для введения в новую алгебру. Если вспомнить изложенное в разделе
11.2 одно из применений матриц, а также то, как мы пользовались
«технологической матрицей», характеризующей производственные возможности
хозяйства (9.8 и гл. 10), нам станет очевидной основная идея применения матриц.
Однако прежде, чем переходить к основным проблемам развития матричной
алгебры, важно дать точное определение матрицы и придумать
соответствующее и удобное обозначение. Систематическое изложение матричной алгебры
дано в следующей главе; здесь же мы просто закладываем основы и даем
примеры матриц, которые позднее будут нами использованы.
По определению, данному далее, матрица является упорядоченным
расположением (а не отдельной величиной) множества элементов. Она
обозначается прописной полужирной буквой. Такое обозначение удобно тем, что
полужирный шрифт показывает, что мы имеем дело не с отдельной
величиной, а с комплексом величин, а прописная буква дает возможность отличить
матрицу от вектора.
Определение. Матрица т X п является множеством т X п
элементов из поля F вещественных чисел, расположенных в форме
прямоугольника с т строками и п столбцами. Эта матрица обозначается так:
и «12 ... «1
где г — 1, 2, ..., т обозначает строки, а 5= 1, 2, ..., п — столбцы.
Размерность матрицы, если она не очевидна, должна быть всегда
специально указана. Она определяется амплитудой значений, которые
принимают индексы г и 5. Матрица называется квадратной, если т = п, и
прямоугольной, если т Ф п. В последнем случае т может быть больше или
меньше п. Число строк (столбцов) квадратной матрицы называется ее порядком1.
В отличие от векторов, матрицы не имеют какой-либо геометрической или
диаграммной интерпретации, поэтому термины «квадратная» и
«прямоугольная» являются просто удобным выражением «вида» блока рассматриваемых
элементов. Можно воспользоваться и рядом других терминов. Например г
1 Ал лен и для прямоугольной матрицы сохраняет термин «порядок» («матрица
порядка т X л»). Однако в советской математической литературе термин «порядок»
относится только к квадратной матрице, а прямоугольная характеризуется просто
указанием числа строк и столбцов. Поэтому мы в переводе слово «порядок» при обозначении
прямоугольной матрицы т X п везде опускаем, заменяя его, в случаях необходимости^
термином «размерность».— Прим. ред.
312

элементы, подобные (а21, а32, ..., amm_i)> которые получаются, если по блоку
элементов идти вверх или вниз под углом 45°, могут быть названы
диагональными. В частности, если А—квадратная матрица, то совокупность элементов
(аи> «22» •••> апп) называется ее главной, или ведущей, диагональю.
Из бесконечного количества матриц на практике особенно важное
значение имеют следующие.
I. Нулевая матрица:
•0 0 ... 0"
0 = [0] :
о о
о
о о
о
размерности
Все элементы этой матрицы равны нулю, и если их число не очевидно»
то его необходимо уточнить, например 0 = [0]mXn- Если уравнение в
матричной форме в своей правой части содержит нуль, например А — KB = 0, то
этот нуль является нулевой матрицей соответствующей размерности. В
обычном уравнении нет сомнений насчет нуля в правой части уравнения.
В матричном уравнении нуль имеет размерность и должен быть точно
определен; он может быть любой размерности тхп.
II. Единичная матрица. Это — квадратная матрица любого порядка п
такого вида:
0 ... 01
0 1
о
0 0 ... 1
(г, 5 = 1, 2,
п),
где Srs —дельта Кронекера, которую мы определили в 11.3. Элементы
главной диагонали матрицы I равны 1, все остальные элементы равны 0.
Не существует какой-то единственной единичной матрицы I. Для каждого
порядка п х пу который должен быть специально указан или вытекает из,
текста, имеется своя единичная матрица.
Ш-. Диагональная матрица. Это — квадратная матрица любого порядка пу
являющаяся развитием единичной матрицы I:
\ о
о к
0 1
о
о о
(г, 5 = 1, 2, ..., /г).
Употребление строчной буквы % здесь можно оправдать, так как матрица
состоит из нулевых элементов, кроме элементов главной диагонали,
являющейся вектором ^ = (Х1, Я2, ..., А,п).
IV. Симметрические и кососимметрические матрицы. Квадратная матрица.
A=[ars] гг-го порядка называется симметрической, если
ara = a8r (для всех г и s),
(для всех г и s).
и кососимметрической, если
Следовательно, в симметрической матрице элементы по одну сторону от
главной диагонали совпадают цо абсолютной величине и знаку с
элементами, находящимися симметрично по другую сторону от главной
диагонали. В кососимметрической матрице соответствующие элементы равны по
абсолютной величине, но противоположны по знаку. Элементы arr главной
диагонали симметрической матрицы могут иметь любые значения, тогда как
такие же элементы кососимметрической матрицы должны равняться 0, так
313

как, по определению, агг = — агг, и, следовательно, агг = 0 (для всех г).
Приведем примеры:
0
1
.2
1
0
3
2'
3
0.
1
1
-1
0
-1
2
1
0"
1
3
»
ООП
О 0 0 и
— 1 О 0J
О 12
-1 0 3
-2 -3 О
Первые две матрицы являются симметрическими, а две остальные —
кососимметрическими.
V. Треугольная матрица. Это есть квадратная матрица n-го порядка,
имеющая следующую форму:
Т =
*
О а
ъ
-0 0 0
где звездочка * обозначает элементы, которые могут иметь любые значения.
Эта матрица подобна диагональной матрице, главная диагональ которой
состоит из элементов вектора а = (ах, а2, ..., ап), а нулевые элементы
находятся только по одну сторону от главной диагонали. Этот и
предыдущие случаи показывают важность характера расположения нулевых
и ненулевых элементов в матрице.
VI. Матрица Якоби. Это —пример образования матрицы из
совокупности функций нескольких переменных и их производных. Рассмотрим т
функций от п переменных:
ur = ur(xv х2, ..., хп) (г=1, 2, ..., т).
Пусть каждая из них имеет частные производные первого порядка по всем
аргументам. Образуем такую матрицу т х п:
дх± дх2
ди2 ди2
дх-± дх2
дхп
ди2
дхп
. дхг дх2
дхп
Это есть матрица Якоби данных функций. Как частный случай рассмотрим
функцию и = и(х±, х2, ..., хп), имеющую все частные производные первого
и второго порядка. Возьмем квадратную матрицу J порядка пхп, в которой
(г т т \ (г — 1 9 ¦ г)\
дхг
Ее можно записать как матрицу Н, где
н
L ^r ^s
сх &г2 " # # ^1 дхп
дхх дх2 дх\ " * дх2 дхп
дхх дхп дх2 дхп
Н является квадратной и симметрической матрицей, которую иногда
называют матрицей Гессе функции и(хг, х2, ..., хп).
314

VII. Ортогональная матрица. Определение этой матрицы будет дано
позже (см. 12.5). Здесь мы даем только пример ортогональной матрицы
второго порядка:
[cos0 sin 01
— sin0 cos0j "
Она имеет то свойство, что перекрестное произведение ее элементов равно
единице:
cos 0 • cos 0 — (— sin 0) sin 0 = cos2 0 + sin2 0 = 1,
и сумма квадратов элементов любой строки и любого столбца также равна
единице:
cos2 0 + sin2 0 = 1.
Употребление термина «ортогональная» обусловлено этими свойствами1.
Вместе с тем эта матрица применяется при повороте взаимно
перпендикулярных (ортогональных)
координатных осей. Например, если
{#, х%) — координаты точки Р отно- V
сительно координатных осей Оххх^
a (yv у2) — координаты этой точки
после поворота координатных осей
на угол 0, то, как видно из
рис. 39, новые и старые
координаты связаны следующим
образом:
у1 = хг cos 0 + #2 sin 0,
у2 = — хх sin 0 + х2 cos 0.
Матрицей коэффициентов в
правых частях этого
преобразования является вышеприведенная Рис. 39
ортогональная матрица.
VIII. Блочная матрица. Элементы некоторых матриц иногда
естественным образом распадаются на различные подматрицы, поэтому удобно
расчленить их на блоки и обозначить такую блочную матрицу компактным
символом. Например,
13
ап а12
Я 21 а22 ^23
0 0 0
0 0 0
L0 0 0
1 О
О 1
а,, а
«1
11 2 3
«22 «23
0 0 0
0 0 0
0 0 0
1 0
0 1
О
где A = [ars] (r = l, 2; * = 1, 2, 3), B = [6rs] (г=1, 2, 3; 5 = 1, 2), a О
и I — соответствующие квадратные нулевая и единичная матрицы @ порядка 3
и I порядка 2). Таким образом, исходная квадратная матрица пятого
порядка разбивается на четыре более простые матрицы: А —
размерности 2 х 3, В— 3 х 2, 0 порядка 3 и I порядка 2. Такое расчленение матрицы
на блоки не только упрощает запись, но часто облегчает анализ задачи.
1 Если строки (столбцы) матрицы рассматривать как векторы, то скалярное
произведение (см. 11.4) любых двух из них равно нулю, то есть эти векторы взаимно
ортогональны. Этим и объясняется происхождение названия «ортогональная матрица».—
Прим. ред.
315

Задачи и упражнения
1. К какому виду относятся следующие матрицы:
(а)
2
0
0
0
2
0
0
0
2
, (б)
1
0
0
0
0
1
0
1
0
, (в)
0
1
—1
—1
0
0
1
0
0
. (г)
1
/2
1
Уз
1 -
V2
1
/2.
в двумерном
Показать связь матрицы (г) с поворотом координатных осей на угол 45°
пространстве.
2. Скалярной матрицей называется такая диагональная матрица, у которой все
элементы (на главной диагонали) равны. Показать, какая матрица из предыдущега
упражнения является скалярной, и написать общий вид скалярной матрицы.
3. Дана единичная матрица I порядка /г. Пусть матрица E(rs) получена из I
перестановкой г-ж и s-й строк. Показать, что такая же матрица получается перестановкой
соответствующих столбцов и что матрица E(rs> симметрическая. Проиллюстрировать это
для случая /г = 3 и показать, что матрица (б) из упражнения 1 есть ЕB3).
4. Из единичной матрицы I порядка п получить: (а) матрицу H(rs) путем замены
нулевого элемента на пересечении г-ж строки и 5-го столбца на h; (б) матрицу К(г>
заменой элемента 1 в г-ж строке и r-м столбце на к. Проиллюстрировать это для
случая /г = 3, составить матрицы (а) НB,п и (б) КC).
5. Написать полностью блочную матрицу
Г а|Ь л
Li fo J •
где а есть вектор (аи а2) и b—вектор (blt b2,
Какого порядка вся матрица?
Какого порядка матрицы I и О?
11.7. ВЕКТОРЫ И МАТРИЦЫ
Существует очевидная двусторонняя связь между матрицами и
векторами: матрица строится на основе векторов (ее строк или столбцов),
а всякий вектор можно рассматривать как частный случай матрицы.
Первое требует небольшого пояснения. Матрица тхп,
A==Ks] (г = 1, 2, ..., го; s=l, 2, .. ., л),
строится из т векторов размерности п:
аг = (аг1, аг2, ..., аТп) (г = 1, 2, . ..,го).
Элементы этих векторов образуют строки А. Эта же матрица равным
образом может быть построена из п векторов размерности го, являющихся
столбцами матрицы:
as = Ks' tt2S> ---'О (*=1. 2, ..., п).
Расчленяя различным образом совокупность элементов матрицы, можно
обнаружить и другие виды связи матриц с векторами. Некоторые из них
полезны в частных случаях, например диагональная матрица а = (ar6rs)
(г= 1, 2, ..., п) получается исключительно из одного вектора а = (ах, а2, ...
..., ап), образующего главную диагональ матрицы а. Единичную матрицу
I порядка п можно рассматривать как совокупность единичных векторов:
е1 = A, 0, 0, ...,0); 82 = @, 1, О, ...,0); ...;8П = (О, 0,0, ...,1),
являющихся или ее строками, или столбцами. В данном случае
использование дельты Кронекера для обозначения особенно полезно. Матрицу I
обозначают через [6rs]. Она состоит из векторов
ег = (бг1, бг2, ..., бгп) = F1Г, б2г, ..., бпг);
вектор 8Г содержит нулевые элементы, за исключением 1 на г-м месте.
Однако другая связь приводит лишь к незначительному развитию
понятия вектора и к новому обозна/чению. Матрица A = [ars] имеет го строк
и п столбцов; тип могут быть любыми целыми числами. Если го = гс = 1,
то А сводится к одному элементу аш то есть является скаляром. Если
316

/гс = 1, но гг>1, то А состоит из единственной строки, и ее элементы
образуют n-мерный вектор (ап, а12, ...,а1п). ё
Может быть и другой случай. Если т>1 и гг = 1, то А состоит из
единственного столбца, полученного из m-мерного вектора (а1Х, а21, ..., аш1).
Обратно, любой и-мерный вектор
& = (av а2, ...,ап)
может рассматриваться как частный случай матрицы, имеющий двоякое
происхождение. Вектор а может являться матрицей, имеющей одну строку,
то есть матрицей lxw. Равным образом, этот вектор может быть
матрицей /г X 1» состоящей из одного столбца.
Следовательно, необходимо различать вектор-строку и вектор-столбец.
Если элементы одинаковы, то эти два вектора по существу совпадают
и отличаются только расположением. Чтобы различать их, введем новое
обозначение. Отметим, что из этих двух векторов в конечном счете важнее
вектор-столбец. Обозначается вектор-столбец, состоящий .из элементов
иг (г= 1, 2, , т), фигурными скобками:
Это —матрица из одного столбца mxl. Вектор-строка, состоящая из
элементов ag(s=l, 2, ...,тг) обозначается квадратными скобками:
а' = К] = К, a2, ,.*,aj.
Это—матрица из одной строки 1 X га. Эти два вектора могут содержать
различное число разных по значению элементов и быть совершенно
различными. Однако если т = п и соответственные элементы а матрицы-строки
и матрицы-столбца одинаковы, то а и а' являются альтернативными
расположениями одного и того же вектора.
Пользоваться обозначениями а и а' необходимо и в том случае, когда
т = п и имеется единственный данный набор п величин а. Необходимо
сказать несколько слов, предваряющих последующее изложение. Рассмотрим
матрицу А = [ars], m X п. Переставим взаимно строки и столбцы этой
матрицы, то есть, кдк говорят, транспонируем матрицу. Мы получим тогда
другую матрицу. Хотя она и состоит из прежних элементов, но их порядок
изменился. Новая матрица будет п X т и будет обозначаться (см. 12.5)
через А'. Чтобы показать транспонирование, к А приписывается сверху штрих.
Очевидно, что если т = п, то вектор-строка а' получается транспонированием
вектора-столбца а, и наоборот. Перестановка строк и столбцов в матрице а,
состоящей из одного столбца, дает матрицу а', имеющую одну
строку,матрица меняется с п X 1 на 1 X п. Следовательно, естественно с самого начала
пользоваться обозначениями а и а'7, соответствующими одному из действий
в матричной алгебре.
11.8. СОКРАЩЕННОЕ ОБОЗНАЧЕНИЕ СУММИРОВАНИЯ СИМВОЛОМ 2;
СКАЛЯРНЫЕ ПРОИЗВЕДЕНИЯ
Если для выражений, являющихся суммами элементов векторов и
матриц, использовать символ суммирования 2> то мы получим, по крайней
мере до определенного уровня, компактное и обобщенное обозначение.
Символ 2 не только полезен сам по себе. Он необходим и тогда, когда мы имеем
дело даже с более компактным матричным обозначением. Символ 2 зависит
от точного установления различных элементов с помощью нижнего индекса
или индексов. Рассмотрим, например, сумму п элементов а + Ъ + с +...+ А.
При такой форме записи мы больше ничего не можем сделать. Заменим эти
317

элементы на ах, а21 ..., ап; тогда их точное определение становится намного
проще. Эти элементы можно обозначить как as, где 5 = 1, 2, ..., /г, а их
сумму можно написать следующим образом:
2 as = ai + a2+ ...+ап.
s=l
Если не может возникнуть никакой неясности, то эту сумму записывают
просто как 2 as или Даже 2 <V Это обозначение удобно и гибко, но, чтобы
s
им пользоваться, необходим опыт. Например, общий постоянный множитель1
можно выносить за знак суммы:
2 (^as)== ^ 2 as (^ — постоянный множитель).
6 s
Однако нужно быть очень внимательным и не «вынести» за знак суммы
меняющиеся в действительности элементы. Например, выражение
несжимаемо, и оно не равно ни одному из следующих выражений:
S S S S
Преимущества этого обозначения становятся особенно очевидными, когда
мы переходим от простых рядов элементов к двойным рядам,
упорядоченным блокам элементов. В блодеу тхп элементов' матрицы
*и 2 • • • ат
ь. °* A)
общий член выражается как ars(r=l, 2, ...,тгг; 5=1, 2, ...,гс). В этом
случае сумму элементов первого столбца можно записать так:
т
2 аг1 = а1г + а21+ ... +а
ат1.
т п
Вообще, 2 агз является суммой элементов 5-го столбца, а 2 ar$— суммой
г=1 * s=l
элементов r-й строки.
Теперь давайте рассмотрим уравнения C) из раздела 11.2, образующие
систему линейных уравнений, или преобразований. Компактно эти т
уравнений можно записать так:
п
Е«,А = Уг (г = 1, 2, ...,т). B)
Пользуясь векторным обозначением, мы можем эту запись сделать еще
короче:
п
2Usas = y> C)
где as = (als, a2s, ..., aMS) и у = (г/г, г/2, ..., ут), то есть оба вектора яг-мерные.
Выражение в левой части C) является суммой векторов #sas; по правилам
сложения и скалярного произведения (см. 11.4) эта сумма сама
является т/г-мерным вектором. Так как равенство векторов в C) является равенством
1 Или множитель, не зависящий от индекса, по которому ведется суммирование;
в данном примере—не зависящий от s.—- Прим. ред.
318

их соответствующих т элементов (координат) по отдельности в двух векторах,
п
то уравнение для л-го элемента есть 2 arsxs = 2/г» и оно справедливо для
s=l
любого г, изменяющегося от 1 до w.
Особенно необходимо отметить применение в соотношении B) индексов г
и $. Если рассматривать одно уравнение системы, то г дано; например, в
случае второго уравнения г = 2. Левая часть уравнения является суммой п
членов, следующих в порядке изменения индекса 5, то есть от 1 до п.
Коэффициенты ars любого уравнения являются элементами одной строки
блока A). Различные уравнения системы B) получаются в результате изменения
г от 1 до т, и коэффициенты ars берутся из разных строк блока A).
Весьма распространенной в матричной алгебре характеристикой
уравнений B) является то, что один индекс (г) фигурирует в левой части уравнений
один раз, а другой индекс (s) — дважды. Первый индекс (г) называется
свободным индексом; он может принимать любые значения, а в данном случае любое
из ряда от 1 до т. Второй индекс (s), появляющийся дважды, «связан»
знаком суммы 2> и поэтому его называют условно связанным индексом или немым
(dummy subscript).
Применение связанных индексов в различных суммах произведений
элементов общепринято и имеет важное значение в матричной алгебре. В
частности, это относится к таким суммам произведений, которые называют
скалярными произведениями. Мы уже сталкивались с этим понятием ранее
(см. 11.4), когда рассматривали скалярное произведение двух векторов:
а- Ь =*=
a2b
2b2
anbn.
Если таким образом умножить любые два вектора, содержащие одинаковое
число элементов, то получим скалярное произведение. Теперь нам остается
только шире определить понятие скалярного произведения, пользуясь как
элементами векторов, так и элементами матриц. Рассмотрим несколько
случаев.
Определение. I. Два вектора (а1? а2,...,ап) и (хх, хг,..., хп), каждый
из которых содержит п элементов, образуют скалярное произведение:
2 as%3 = Q>&\ + ^2^2 + • • •
s=l
II (а). Матрица из т X n элементов
апхп
«21
«12
«22
«2П
- атх ат2 • • • атп-
и вектор (хг, х2, ..., хп) из п элементов образуют т скалярных произведений:
п
2 «rs^s = «ri;ri+ar2^2+---+«rn^n (г = 1, 2, ..., т).
II (б). Та же матрица и вектор (yl9 y2, ...,ym) из т элементов
образуют п скалярных произведений:
т
2
г=1
$ = 1, 2, ...,«),
III. Две матрицы, состоящие соответственно т тхк и кхп
элементов:
«11 «12 ••• «lft
«21 «22 ••• «2ft
¦~ «mi «тп2 • • • «mft J
b12 ... bin
L bkl bk2 • •
319

образуют тХп скалярных произведений, в которых строки первой
матрицы умножаются на соответствующие столбцы второй:
k
2 arpbps=arlbis+<ir2hs+*--+arkhs (r=U 2, ...,т; 5=1, 2, ..., п).
1
В пунктах I и II (а) связанным индексом является s, в пункте II (б) —
г, в III это есть р. В пункте I нет свободного индекса, в И (а) и II (б)
имеется по одному свободному индексу, а в III —два свободных индекса.
Свободный индекс можно установить так, чтобы он принимал любую
величину из соответствующего ряда чисел.
Для того чтобы приобрести опыт в применении знака 2 и> особенно,
скалярного произведения, необходимо всегда помнить о некоторых простых
и очевидных истинах. Например, поскольку величины а, 6, х являются
вещественными числами, то порядок записи их произведений несуществен.
Так,
2 ars xs = 2 xs ars> S У г ars = 2 ЯГ8 Уг\
2грР3Ер8гр
р р
Кроме того, индекс, который дважды фигурирует под знаком 2 и таким
образом порождает сумму, может обозначаться любыми подходящими
буквами, если область изменения его значений остается неизменной. Так,
если и s и t изменяются от 1 до п. По этой причине этот индекс и
называется условно связанным. Однако если изменить свободный индекс, то
изменится и значение скалярного произведения. Например, 2arsxs отлич-
8
но от 2ats#s (если гф*). Первое выражение это г-е, а второе t-e скаляр-
S
ные произведения в совокупности m различных скалярных произведений.
Равным образом совершенно различны выражения 2 ars xs и S ars xr* Пер-
8 г
вое выражение является суммой п членов, определенной для m значений
г, а второе — суммой m членов, определенной для п значений s. В
развернутом виде это будет:
п
2 anx,^anx1 + arixt+ ... +агпхп (г = 1, 2 тп),
m
2 aTsxr = aux1 + a2sXz+ ... +am,xm E = 1,2, .... л).
Г=1
Условились, и очевидно, что с точки зрения внешнего вида обозначений
удобно писать члены произведения таким образом, чтобы два вхождения
связанного индекса следовали друг за другом. Хотя порядок членов
произведения действительных чисел не имеет значения, удобнее писать arsx^
а не #sars; yTars, а не arsyr и arpbps, а не bpsarp. Это правило
соответствует данным выше определениям скалярного произведения.
Задачи и упражнения
1. Показать, что при /i = l скалярное произведение (III) сводится к скалярному
произведению матрицы m х к и вектора-столбца к х 1, то есть к скалярному
произведению II (а), т. е.
к
2 arp&p = ari
р=1
320

2. Аналогично показать, что при, т = 1 скалярное произведение, (III) включает
вектор-строку и сводится к скалярному произведению II (б).
3. Завершить изучение этих особых случаев, положив m=w = l, и показать, что
скалярное произведение (III) в таком случае сводится к скалярному произведению
двух ^-мерных векторов (I). Вывести, что скалярные произведения (I) и (И) являются
частным случаем более общего скалярного произведения (III) и что существенно
различение вектора-строки и вектора-столбца.
4. Проиллюстрировать применение двух связанных индексов в двойной сумме,
показав, что
п п п п п п
2j Zj ars^stxt = 2j arsB ^stXt) ~ ZJ Xt ( 2 arsbst)-
s=i *=1 s=l 2=1 t=l s=l
n
5. ^ arsxs содержит т линейных форм (г=1, 2, ..., m) с п переменными
s=l
n
x9 (s = l, 2, ..., n). Применить линейное преобразование #s=2 bstVt и показать, что
п п
линейные формы будут иметь вид 2 crtVti гДе crt = 2 ars^st- Показать также, что
и после преобразования остаются т линейных форм с п переменными.
11.9. ОПРЕДЕЛИТЕЛИ
Матрица А = [ars] является упорядоченным множеством элементов
(скаляров), комплексом величин, но не отдельной величиной. Как было
показано в разделе 11.1, из матрицы А можно получить различные
выражения, являющиеся отдельными величинами, то есть скалярами. Необходимо
всегда проводить различие между матрицей и любым скаляром, который
может быть получен из нее. Это, в частности, справедливо и в отношении
определителя — наиболее важного скаляра, получаемого на основе
(квадратной) матрицы. Определители хорошо известны из обычной алгебры; их
определение и свойства приводятся в любом учебнике по высшей алгебре, в работах
Феррара и Аллена [1, 4]. Здесь нам необходимо просто суммировать
основные положения теории определителей. Излагать подробно эту теорию было бы
нецелесообразно. Наше внимание должно концентрироваться здесь на новых
понятиях (матрица) и новой алгебре; поэтому, уделяя слишком много
внимания обычной алгебре, мы только запутали бы изложение. Могла бы
появиться опасность бессознательно соскользнуть к мысли, что матрица есть «что-то
подобное» определителю и что следует искать ее «величину». Матрица не
аналогична определителю и не имеет отдельного численного значения. Надо
запомнить такой простой факт: когда мы имеем дело с матрицами (как с
новыми понятиями), на их основе можно получить различные скалярные величины,
из которых важнейшее значение имеют определители, но сами матрицы не
являются скалярами1.
Определитель определен только для квадратной матрицы А = [ars]
(г и s = 1, 2, ..., гс), и его порядок (п) совпадает с порядком квадратной
матрицы (п X п). Существует несколько возможных способов установления
значения определителя, но, по-видимому, лучшим является даваемое ниже
определение по индукции. В этом случае определитель и-го порядка выражается
через определитель порядка п — 1 и т. д., пока мы не дойдем до определителя
первого порядка. Однако прежде, чем переходить к определению, мы введем
обозначения и сделаем ряд замечаний. Определитель матрицы А,
являющийся обычной величиной (вещественным числом), будем обозначать той же
буквой, но обычным шрифтом. Это позволит отличать определитель от матрицы,
обозначаемой полужирной буквой. Следовательно, А (обычный шрифт)
будет обозначать величину определителя, полученного из матрицы А
(полужирный шрифт). Условимся также, что, если для обозначения матрицы мы
1 Значениями матриц являются упорядоченные множества чисел.— Прим. ред.
21 р. Аллен 321

применяли квадратные скобки [ars], то для определителя мы будем
пользоваться прямыми параллельными линиями | аг$ |.
Следовательно, любой из символов
ап а12 ... aln
а21 а22 ... а2п
ап1 ап2 ... апп
обозначает величину определителя (скаляр), полученного на основе
матрицы А.
Рассмотрим теперь квадратную матрицу Ars порядка (п — 1) X (п\— 1),
полученную из матрицы А исключением r-й строки и s-ro столбца.
Определитель матрицы АГ8 называется минором элемента ars определителя А. Если
минор снабдить знаком (— l)r+s, то получится тесно связанное (и
альтернативное) с ним понятие алгебраического дополнения элемента аг$ определителя А.
Следовательно,
минор Mrs = | Ars |,
алгебраическое дополнение, ЛГ8 = (—- l)r+s | Ars |.
Например, минор и алгебраическое дополнение элемента а1Х в матрице А
совпадают. Их значение равно величине определителя, полученного из
матрицы А исключением первой строки и первого столбца. Поэтому Ars = (—1I+1х
X | Ars | = Мгв. Однако алгебраическое дополнение и минор элемента а12 (второй
элемент первой строки А), совпадая по абсолютной величине, противоположны
по знаку. В данном случае минор равен определителю, полученному из
матрицы А исключением первой строки и второго столбца.
^ Определение. Определитель А, полученный на основе матрицы А
порядка п, выражается через определители (алгебраические
дополнения) порядка (п — 1):
п
д "VI д
то есть этот определитель есть сумма элементов какой-либо строки этой
матрицы, умноженных на соответствующие алгебраические
дополнения. Это определение будет законченным, когда мы дойдем до
определителя первого порядка, являющегося величиной единственного
элемента, составляющего этот определитель.
Чтобы сделать это определение внутренне последовательным,
необходимо остановиться еще на одном вопросе. Определитель А был определен как
сумма произведений элементов r-й строки на их алгебраические дополнения.
В действительности эта сумма не зависит от выбора строки, а также от того,
берутся ли строки или столбцы.
Конечно, строго говоря, это последнее положение требует доказательства.
Этот результат вместе с нижеследующими свойствами определителей
доказывается в учебниках по алгебре; мы же этого здесь не делаем.
Свойство I. Алгебраическая величина определителя А в развернутом
виде является суммой всевозможных членов1, взятых с соответствующим
знаком и являющихся произведениями п элементов по одному из каждой
строки и каждого столбца определителя [4, стр. 8—И].
п п
Свойство II. А =2 ars^rs=2 ars^rs
s=l r—i
для любых т% 5=1, 2, ..., п.
Свойство III. Транспонирование (перестановка) строк и столбцов не
изменяет величину определителя:
1 Таких слагаемых будет п\, где символ п\ означает произведениеряда натуральных
чисел 1, 2,..., /г, называемое факториалом.— Прим. ред.
322

Свойство IV. Взаимная перестановка двух строк (двух столбцов)
в определителе изменяет только его знак. Например,
«и «19 .. . ал
ап1 ап2 .. . аг
Свойство V. Определитель, имеющий две одинаковые строки (или
два одинаковых столбца), равен нулю. Например,
ап а12 ... а±
а„л а„
= 0.
Свойство VI. При умножении строки (столбца) определителя на
скаляр X величина определителя изменяется в отношении X. Например,
алч ал
*21
аол а9
а2п
in и12
а19 ... а.
Хап1 ап2 . .. апп
Свойство VII. Если умножить каждый элемент одной строки (столбца)
определителя на скаляр X и прибавить к соответствующим элементам
другой строки (столбца), величина определителя не изменится. Например,
(«
и
. .. (а1п + Ха2п)
... а
In
На основе определения и свойств II и V определителя можно получить
следующее, наибрлее часто используемое свойство определителей, которое
называется правилом разложения определителей через алгебраические
дополнения:
fe=i fe=t
для любых значений r, s и ? (t Ф г, s) от 1 до п. В этом свойстве утверждаются
два факта. Если элементы строки (столбца) матрицы А умножить на их
собственные алгебраические дополнения и сложить полученные произведения,
то сумма дает величину определителя, или А— \ А |. Если же элементы строки
(столбца) умножить на алгебраические дополнения элементов другой строки
(столбца), то сумма полученных произведений будет равна нулю.
Задачи и упражнения
1. Найти величину определителей для каждой из матриц (см. 11.6,
упражнение 1).
323
21*

2. Если I является единичной, а а диагональной матрицей, образованной на основе
вектора (alt а2у ..., ап), показать, что |1| = 1 и \а.\ = а1а2 ... ап.
3. Показать, что
Может ли быть
1
2
1
2
1
2
1
1
2
1
2
1
~~2
1
а а
1 а
а а 1
4. На основе свойства V показать, что
= 0.
0 для любых каких-либо значений, помимо а =—~- ?
1
1
1
а
Ь
с
а*
с*
= (а—Ъ) (Ь—с)(с—а), и проверить
это непосредственным разложением и вычислением.
5. Показать, что определитель ортогональной матрицы (см. 11.6) равен
6. Показать, что
О
О
а2
О
= а1а2а3, и вывести,
что если в диагональной матрице нулевые элементы, находящиеся по одну сторону
диагонали, заменить на любые другие элементы, то величина определителя не
изменится. [См. треугольную матрицу из раздела 11.6 (V).]
7. Используя результаты предыдущих задач, показать, что |Н<гв)| = 1, где H(rs) —
матрица, определенная в разделе 11.6, упражнение 4.
8. Показать, что определители матриц (см. 11.6, упражнения 3 и 4)
9. Дана симметрическая матрица А
ГО 1 П
= 1 0 *
U * 1J
Показать, что А = \А\=2х—1. Вычислить все девять алгебраических дополнений
и показать, что матрица, составленная из элементов Ars, также является
симметрической. Показать также, что определитель этой второй матрицы (из элементов Ars)
равен А2. Какой из этих результатов будет справедлив для любой симметрической
матрицы?
10. Дана кососимметрическая матрица А== [ars] порядка пхп. Матрица А' получена
транспонированием строк и столбцов матрицы А, а матрица (—А) состоит из элементов,
противоположных по знаку элементам А. Показать, что А' = — А, и что (при п
нечетном)
|—А| = —|А| и, следовательно, |А| = 0*

ГЛАВА 12
МАТЕМАТИЧЕСКАЯ ЧАСТЬ. МАТРИЧНАЯ АЛГЕБРА
12.1. ВВЕДЕНИЕ; ОСНОВНЫЕ ПРАВИЛА АЛГЕБРЫ
Матричную алгебру приходится разрабатывать с начальных положений,
так как обычные правила арифметики и алгебры чисел, изучаемые в средней
школе, сами по себе не применимы к новым элементам, называемым
матрицами. Где же найти руководящую нить для построения новой алгебры?
Определители в данном случае не помогают; они являются вещественными
числами и подчиняются обычным правилам. Несколько больше могли бы
помочь комплексные числа: при определенных условиях над ними можно
производить обычные алгебраические действия. Вопрос стоит так: можно ли
то же самое сделать и в матричной алгебре? Ответ будет таков: несмотря на
попытки определить действия над матрицами так, чтобы матричная алгебра
по возможности была бы аналогична элементарной алгебре, все же между
ними имеются существенные различия.
Поэтому необходимо избегать переносить что-либо из элементарной
алгебры в матричную, если это полностью не оправдано. Рассмотрим,
например, действие умножения. «Умножение» двух матриц это не только не одно
и то же, но и даже не «нечто подобное» умножению двух чисел или двух
определителей. Произведение матриц еще должно быть определено, и определение
нужно выбрать. При выборе этого определения мы можем надеяться, что
будут выполняться обычные правила, однако мы не можем брать это без
доказательства. В действительности оказывается, что произведение матриц ведет
себя не очень хорошо. Например, выражение а'Аа является произведением
ектора а' на матрицу А и затем на вектор а. Произведение чисел обладает
свойством коммутативности, а именно числа могут перемножаться в любом
порядке, но в отношении матриц дело обстоит иначе. Если взять обратный
порядок множителей, то получится аАа', что представляет совершенно
различный результат, то есть произведение матриц в отличие от произведения
чисел не подчинено закону коммутативности.
В этой связи опять возникает дилемма. Если термины «произведение»
и «умножение» использовать для вновь определяемого действия над
матрицами, то будет очень легко впасть в ошибку и принимать произведение
матриц коммутативным. Может было бы лучше назвать это действие не умно-
жейием, а каким-нибудь порождающим меньше недоразумений термином,
например «соответствием» («conformation»). Однако с практической точки
зрения это нецелесообразно, так как «умножение матриц» — уже
установившийся термин, и его изменение вряд ли полезно, учитывая преимущества
сохранения признанной терминологии. Проще запомнить, что умножение
матриц подчиняется не всем обычным правилам, чем придумывать совершенно
новые названия.
Что представляют собой правила элементарной алгебры? При попытке
их установления, несомненно, нужно выяснить, насколько они условны,
а затем придать им более общую постановку. Алгебра вообще имеет дело
с множествами элементов, которые могут быть числами, как в элементарной
алгебре, но они могут быть также определенными объектами почти любой
природы, абстрактными или конкретными, например полиномами,
матрицами, преобразованиями. Следовательно, алгебра имеет дело с некоторым мно-
325

жеством элементов S — {а, Ь,с, ...}. Ее задача состоит в том, чтобы определить
действия над элементами а, Ь, с, ... из S.
Некоторые из этих действий унарного (unary) типа (с одним элементом
или с одной переменной.— Ред.). Они устанавливают правило перехода
{rule of translation) от одного элемента множества S к другому элементу из S.
Примерами таких действий являются извлечение квадратного корня из
вещественного числа, транспонирование матриц. Однако наиболее важны
действия бинарного типа, которые устанавливают правило комбинирования
(rule of combination) любых двух элементов S для получения другого
элемента S. Примером таких действий являются сложение и умножение. Если а и b
принадлежат S, то сумма а + Ъ определяется так, что она принадлежит S;
аналогично имеем и для произведения а X Ъ. В действительности, как мы уже
видели в случае комплексных чисел, большинство бинарных действий
определено так, что они могут быть отождествлены со сложением или умножением.
Определение бинарных действий сперва можно проиллюстрировать на
знакомом случае множества N = { 1» 2, 3, ...} положительных целых чисел.
В этом случае нахождение суммы и произведения можно дать при помощи
таблиц сложения и умножения, которые мы с таким трудом учили в школе:
+
1
2
3
1
2
3
4
2
3
4
5
3 ...
4 ...
5 ...
6 ...
X
1
2
3
1
1
2
3
2
2
4
6
3 ...
3 ; . .
6 ...
9 ...
Для множеств вообще бинарные действия можно определить
перечислением всех возможных случаев, составлением соответствующих таблиц
сложения и умножения, которые могут иметь совершенно необычную форму. Или
эти действия можно определить через другие действия и, таким образом,
через другие таблицы сложения или умножения. Рассмотрим множество трех
целых чисел S {О, 1, 2} и определим сложение и умножение таким образом,
что будем понимать под суммой и произведением двух элементов этого
множества остаток от деления обычных сумм и произведения на три.
В этом случае таблицы сложения и умножения будут кратки, сжаты
и иметь такой вид:
+
0
1
2
0
0
1
2
1
1
2
0
2
2
0
1
X
0
1
2
0
0
0
0
1
0
1
2
2
0
2
1
Ибо, например, 1+2 = 3, поэтому мы записываем 0 (остаток от деления
3 на 3 равен 0.— Ред.), и, поскольку 2x2 = 4, записываем 1.
Таблица 1, А содержит сводку законов или свойств действий сложения
и умножения чисел, однако они справедливы для элементов любого множества
S = {а, Ь, с, ...}. Эти законы полностью применимы к множеству
рациональных чисел (отношения целых чисел); они имеют силу и для более широких
множеств — вещественных чисел, а также множеств комплексных чисел.
Говоря о множествах рациональных, вещественных и комплексных чисел,
следует подчеркнуть, что они обладают свойством замкнутости в отношении
сложения, умножения и обратных им действий. По законам (А5) и (М5)
мы можем написать а — b = а + (— Ь) и а : b = а X b'1 (b Ф 0) и назвать
эти действия вычитанием и делением. Если мы произведем над рациональными
326

числами любое из этих четырех действий, то вновь получим рациональное
число и не выйдем за пределы множества.
Таблица 1
Законы алгебраических действий
А. Сложение и умножение в ?= { а, 6, с,;.. }
Закон
Замкнутость . .
Ассоциативность
Коммутативность
Идентичность г)
Обратимость . .
Сократимость . .
Дистрибутивность
(А1)
(А2)
(A3)
(А4)
а-
(А5)
Сложение (+)
а -\-Ь принадлежит
а^-(Ъ-\-с) = (а-\-Ъ)-
а-{-Ь = Ь-\-а
S имеет нуль, так
-0 = 0-\-а = а
S
-\-с
что
S имеет отрицательную вели-
чину —о, так что а-
(А5'
(D)
) если а -{-Ь = а-\-с,
а X (Ь-{-с) = а X &-f
то Ь = с
ах с и
(Ml) a
(М2) а
(МЗ) а
(М4) S
а X
(М5) S
а,
(М5')
то b
Умножение (х)
X b принадлежит S
X (Ъ X с) = (а X Ь) X с
X b = bX а
имеет единицу, так что
1 = 1 X а = а
имеет обратную величину
так что а х а~1 = а~1 х« =
если а X Ь = а X с (афО),
— с
= ах с+ЬX с
Б. Умножение на скаляр в S= {а, 6, с,... }
Скаляры из F= {A,, |x, v,... }
Замкнутость (S1) Х-а принадлежит S, (S2) 0-а = 0 и 1а = а
Ассоциативность (S3) Л • (и. • а) = (Ли.) • а
Дистрибутивность(S4) k-(a~\-b) = X'a-\-X-b, (S5) (A, + ti)-a = X-a-j-fi
1) Иначе, тождественность, то есть наличие во множестве элемента (нуля, единицы), который,
присоединяясь путем алгебраического действия (сложения, умножения) к какому-либо другому
элементу, оставляет последний тождественным, то есть не изменяет его.—Прим. ред.
Однако для других множеств элементов не все эти правила применимы.
Так, множество положительных целых чисел не имеет нуля и, следовательно,
отрицательных величин. Хотя оно имеет единицу, но обратных величин, кроме
самой единицы, не содержит. Для множества нечетных целых чисел теряет
силу и закон замкнутости, так как сумма двух нечетных целых чисел
является четным целым числом. Переходя к другим множествам элементов, как,
например, к матрицам, для которых определены сложение и умножение, мы
можем только сказать, что соблюдение законов (А1—5), (Ml—5) и (D)
желательно, но не обязательно. Мы хотели бы, чтобы все они соблюдались; если>
это нам не удается, мы стараемся так определить сложение и умножение
в этих множествах, чтобы выполнялось как можно больше законов.
Практически для матриц наиболее часто нарушается закон
коммутативности (МЗ) и обратимости (М5) произведения. Перемножать можно не всякие
матрицы. Когда же это возможно, то только в особых случаях существует
обратная величина, и очень редко произведение матриц является
коммутативным. Коммутативность умножения настолько укоренилась в нашем
сознании, что мы считаем вредным оставлять хотя бы крупицу ее и пишем, что
для матриц А X В Ф В X А. Особого внимания заслуживают правила
обратимости (А5) и (М5). В табл. 1 приведены также законы сократимости (пога-
шаемости), обозначаемые через (А5') и (М5'), поскольку в определенном
смысле они альтернативны по отношению к законам обратимости. С точки зрения
этих свойств наиболее важным действием является умножение. Если (М5)
выполняется, то ненулевой элемент а имеет обратную величину а, и,
следовательно, возможно деление на а (то есть умножение на обратную величину).
Благодаря этому выполняется и (М5') — правило деления на а. Однако
обратное утверждение не справедливо: закон сократимости (М5') может
соблюдаться, а обратной величины и, следовательно, деления не будет [(М5)
327

не выполняется]. Именно так обстоят дела с множеством целых
положительных чисел. Следовательно, мы можем или принять (М5) и иметь деление и
сокращение, или принять (М5') и иметь сокращение без деления.
Таблица 2
Основные алгебраические системы
Системы
Группа
Область
целостности *)
Полех)
Векторное
пространство
Линейная
алгебра1)
Действия
Умножение
Сложение и
умножение
Сложение и
умножение
Сложение и умг
ножение на
скаляр
Сложение,
умножение и
умножение на
скаляр
Законы» имеющие силу
(Ml, 2, 4, 5)
(Al-5), (D)
(Ml—4), (M5')
(Al-5), (D)
(Ml-5) .
(Al-5)
(Sl-5)
(Al-5), (D), (Sl-5)
(Ml, 2) и, возможно,
другие
Примеры
Неособенные линейные
преобразования
Неособенные матрицы
Целые числа
Полиномы с целыми
коэффициентами
Рациональные числа
Вещественные числа
Комплексные числа
m-мерные векторы
Матрицы т х п
Рациональные дроби
(отношения
полиномов).
Матрицы порядка п
1) Эти системы имеют структуру кольца, то есть как минимум выполняются законы (А 1—5),
(D) и (М1-2).
Закон (М5') является более слабой альтернативой по отношению к (М5).
Рациональные и вещественные числа удовлетворяют (М5), для целых чисел
справедливо только (М5'). Для матриц обычно не выполняется ни (М5), ни
более слабое (М5'). Для множества элементов, более сложных по своей
природе, чем числа, можно определить другие действия. Примером такого очень
широко используемого действия является введенное умножение на скаляр (мы
уже рассматривали умножение вектора на скаляр в разделе 11.4).
Вводимое нами действие состоит в следующем. Из множества S = {а, Ь,
с, ...} любых элементов берем, например, элемент а и умножаем его,
например, на скаляр Я из множества F = {Я, fi, v, ...}скаляров (обычные
вещественные числа). В результате получаем Х-а как элемент множества S. При этом
желательно, чтобы соблюдались законы (S1—5) (см. табл. 1,Б).
Современная алгебра имеет дело с различными по своей природе
алгебраическими системами, с множествами различных элементов, в которых
конкретные действия определены так, чтобы удовлетворять более или менее полно
законам, приведенным в табл. 1. Область алгебраических систем чрезвычайно
широка и разнообразна. Из табл. 2, в которой перечислены некоторые
алгебраические системы, читатель может получить представление об их области.
В этой таблице дается краткая характеристика и несколько примеров
наиболее важных типов алгебраических систем.
Две из этих системы мы уже использовали. Рассматривая векторы и
матрицы в разделах 11.3 и 11.6, мы вводили поле/1 вещественных чисел,
которыми пользовались как компонентами векторов и матриц и как скалярами. Для
328

этих целей мы могли бы использовать также и поле рациональных чисел
и поле комплексных чисел. Затем векторная алгебра конструировалась нами
таким образом, что удовлетворялись правила, необходимые для векторного
пространства (см., в частности, задачи 4 и 5 из раздела 11.4). Определенная
нами в предыдущей главе система векторов является одним из примеров
векторного пространства.
Задачи и упражнения
1. Множество рациональных чисел содержит все числа вида р/д, где р и q —
целые числа (положительные, отрицательные и нуль). Показать, что это множество
обладает свойствами замкнутости в отношении сложения, вычитания, умножения
и деления.
2. Показать, что свойство замкнутости теряет силу для множества: а) всех
целых чисел; б) четных целых чисел; в) нечетных целых чисел. Какие действия
явлются причиной этого в каждом случае?
3. Если выполняется закон коммутативности, то закон дистрибутивности
a (b-\-c)=ab-\-ac подразумевает также, что (b-\-c)a=.ab-\-ac. Будет ли это так,
если закон коммутативности не соблюдается?
4. Множество чисел х-\-у\^2 (х и у—рациональные числа) шире, чем поле
рациональных чисел, но уже, чем поле вещественных чисел. Показать, что это
множество также является полем.
12.2. ИЛЛЮСТРАЦИЯ ДЕЙСТВИЙ НАД МАТРИЦАМИ
Нижеследующие иллюстрации имеют своей целью показать область
применения матриц и практическое значение принятых определений
сложения и умножения матриц. Мы ограничиваем эти иллюстрации простейшими
случаями, рассматривая матрицы и векторы второго порядка. Это позволяет
в развернутом виде изложить все алгебраические действия.
Рассмотрим линейное преобразование с двумя переменными:
Это преобразование характеризуется квадратной матрицей А
Г* п ~\
L«21 «22 J
и векторами, один из которых содержит первоначальные переменные
(xv х2), а другой —новые переменные (у±, у2). Компактно A) можно
записать при помощи матричного обозначения и скалярных произведений
[xi 1
, мы получим два
Х2 J
скалярных произведения (а11ж1 + а12ж2) и (а21х1-{-а22х2I которые, как это
[Уг 1
следует из A), соответственно равны элементам вектора-столбца у==
L2/2 J
Этот процесс можно применить для определения произведения вектора
и матрицы и написать
Г «11 «12 1 Г Х1 1 Г («11*1+ «12^I | 2/х "I .
L «21 «22 J Х L Хг J """ L («21^1+ «22 ^2) J L 2/2 J '
или кратко Ах = у.
Как только мы дали это определение, линейное преобразование A)
принимает вид:
у = Ах. B)
Рассмотрим теперь два линейных преобразования: одно —от первоначальных
переменных х к новым переменным г/, а другое —от тех же
первоначальных переменных х к новым переменным z. Напишем их в развернутом
виде:
ух = axlxx + а12х2 и zx = Ьпхг + Ъпх2,
у2 = а21хх + а2 А и z2 = Ь21хх + Ъ22х2.
329

Матрицы этих преобразований будем обозначать соответственно через А
и В. Введем переменные и как суммы соответствующих у и z:
И ^2=
Теперь проблема сводится к тому, чтобы выразить введенные переменные и
через первоначальные переменные х, то есть получить «сложенное»
(«аддитивное») преобразование от переменных х к переменным и. Эта задача
решается просто:
ui = (ап + bn) xi + (ai2 + Ы я2,
и2 = («2i + Ы хг + (а22 + Ь22) х2.
Это преобразование характеризуется матрицей, состоящей из 2 X 2
элементов, которые являются суммой соответствующих элементов а и Ъ из матриц:
и В=
Поэтому естественно определить сумму двух матриц следующим образом:
p*ii а12 Г6и Ь1в1 Г(аи + 6ц) Ка+612)] Гсц с12\
[а21 а22 +[b21 Ь22\~[{а21 + Ь21) (а22 + b22) J *" [с21 с22\ '
то есть
А + В = С, где crs = ars + brs (г, 5=1, 2). C)
В матричном обозначении, как это сделано в C), процесс «сложения»
преобразований можно сформулировать следующим образом:
Если имеются линейные преобразования у = Ах и z = Bx, то тогда
линейным преобразованием к u = y + z является и = (А + В)х.
Рассмотрим далее два последовательных линейных преобразования
от переменных х к переменным у и от переменных у к переменным z.
Напишем их в развернутом виде, как в A):
Ух = «1А + «12^2 и zx = Ьг1уг + Ь12у2,
У 2 = Я2А + «22^2 И Z2 = &212/х + &22у2.
Задача состоит в том, чтобы выразить переменные z непосредственно через
переменные х, то есть получить преобразование от переменных х к
переменным z, которое можно рассматривать как «умножение» двух
первоначальных преобразований. Решение получается путем прямой подстановки
zi = 6ii К А + ^12^2) + 6i2 («2i^i + а22Я2)>
z2 = fe21 (а1гхг + а12х2) + Ъ22 (а21хг
или
Zl = F11а11 + ft12«2l)
z2 = F21ап + 622а21) х± + (Ь21а12 + Ъ22а22) х2.
Характеризующая это преобразование матрица состоит из скалярных
произведений элементов матриц А и В. Это подсказывает, как определить
произведение двух матриц:
21
2\ '
2i^n +b22a21) (b21a12
то есть
BA = C, где crs= S ftrpflpe (M=l, 2). D)
Процесс последовательного применения преобразований, или их
«умножения», теперь можно значительно короче выразить при помощи матричного
обозначения:
330

Если даны линейные преобразования у = Ах и z = By, то тогда
преобразованием от х к z явится z = (BA)x.
Рассмотрим, наконец, последовательные преобразования такого же
типа, как предыдущие, но проведенные в обратном направлении—не от
переменных х к у и затем от у к 2, а от переменных у к переменным х и от них
к переменным z. Напишем их в развернутом виде:
У\ = ai А
У г = а21Ж 1 + а22Х2 И Х2 = 62 А + ^22*2 •
Преобразование от переменных z к переменным г/ будет следующим:
Ух = (ai Ai + ai2*2i) *i + (ai A2 + а\Фгг) zv
2/2 = (tt2 Ai + a22&2l) Zl + (a21612 + ^22) Z2.
В этом случае определяется новое произведение матриц:
п a12l pn Ь12] |~KAi + a12b21) {a11b12 + a12b22)"\\d11 d12l
a21 tt22j L^2l ^22j L(a21^11 -Ta22^2l) («21^12 + a22&22)J |_d21 ^22j '
то есть
2
AB = D, где drs= 2 *rpbPs (r,s=l, 2). E)
p=i
Сформулируем это преобразование в матричной форме:
Если даны линейные преобразования у = Ах и х = Bz, то в таком
случае преобразованием от z к у является у = (AB)z.
Сложение матриц, соответствующее сложению линейных
преобразований, определяется C). В данном случае мы не сталкиваемся с трудностями;
в частности, порядок, в котором складываются матрицы А и В, не имеет
значения, так что и для матриц, как и для вещественных чисел, А + В =
= В + А, то есть сложение матриц обладает свойством коммутативности.
Умножение матриц, соответствующее последовательному применению
линейных преобразований, определяется D) и E). Однако эти два случая
существенно различаются. В одном случае мы имеем В А = С, где элементы матрицы С
определяются D); в другом случае АВ = D, где элементы матрицы D
определяются E). Два набора скалярных произведений D) и E) совершенно
различны, а следовательно, различны и две матрицы С = ВА и D = АВ-
В случае С = ВА скалярно умножаются строки матрицы В и столбцы
матрицы А, в случае D = АВ скалярно умножаются строки матрицы А и
столбцы матрицы В.
Умножение этих матриц не подчиняется закону коммутативности.
В этой главе мы рассматриваем матричную алгебру для общего случая
матриц т X п. Она основана на очень простом правиле сложения матриц C)
и менее простом (и некоммутативном) правиле их умножения D) и E). Может
иметь место также и специальный случай, когда умножаются вектор и
матрица, представленные в форме B). Как мы видим, сформулированные правила
возникли (мы рассматривали простой пример матриц второго порядка) в
результате применения линейных преобразований. Такое использование
матричной алгебры в более общей форме исследуется нами в следующей главе.
Задачи и упражнения
1. Пользуясь определением скалярных произведений, показать, почему правая
часть линейного преобразования A) выражается как Ах, а не как хА. Может ли
быть определено хА?
2. Дано линейное преобразование
от трех переменных #. к двум переменным у. Определить соответствующие А, х и у
и указать их размерность. Выразить преобразование как у = Ах.
3. Преобразование у = Ах из предыдущей задачи объединить с z = By, где
В—матрица порядка 2. Показать, что z = (BA)x, где ВА—матрица 2x3. Имеет лы
смысл произведение АВ?
331

4. То же самое преобразование у = Ах из предыдущей задачи объединить с x = Bz,
где В есть матрица порядка 3. Показать, что y = (AB)z, где АВ—матрица 2 х 3.
Имеет ли смысл произведение ВА?
12.3. РАВЕНСТВА, НЕРАВЕНСТВА МАТРИЦ, СЛОЖЕНИЕ МАТРИЦ
И УМНОЖЕНИЕ МАТРИЦЫ НА СКАЛЯР
Матричная алгебра является совокупностью правил действий над
матрицами в общей форме. Эти правила условны, и их можно выбирать. Однако те
правила, которые разработаны в действительности, далеко не произвольны.
При их разработке учитывались и законы элементарной алгебры и дриме-
нение матриц, уже кратко рассмотренное в разделе 12.2.
Простейшей частью нашей задачи, как это было и в векторной алгебре
(см. 11.4), является определение равенства, неравенства и умножения матриц
на скаляр. Эти правила являются естественным развитием соответствующих
правил, установленных для векторов.
Введем матрицы А = [ars], В = [Ьгз] и С = [crs] размерности т X п,
которыми будем пользоваться в последующем изложении.
Равенство и неравенство матриц. Определение равенства и неравенства
матриц соответственно таково:
А = В, если ars == fers,
и А > В, если ar$ > brs
для всех г и s (г = 1, 2, ..., т; $ = 1, 2, ..., п).
Для матриц, так же как и для векторов (см. 11.4), представляет
некоторую трудность определение соотношения «больше или равно». Здесь мы будем
иметь два обозначения:
А^В, если ars>brs, допуская, что могут все ars= fers,
А>В, если аГ8>ЬГз, не включая случая, когда все ars= brs,
для всех г и s (г = 1, 2, ..., т; s = 1,2, ..., п).
Выражение А^В включает А = В, А> В, а также случай, когда для
некоторых г и s ars>brs и ars= brs для других г и s. В выражении А>В
случай А = В исключается.
Как частный случай рассмотрим соотношение матрицы А и нулевой
той же размерности. Выражение А = 0 означает, что каждый элемент
матрицы А равен нулю, то есть А сама является нулевой матрицей..Выражение
А>0 означает, что матрица А положительна, то есть все ее элементы
положительны. Выражения А ^ 0 и А > О означают, что матрица А неотрицательна,
то есть она не содержит отрицательных элементов; некоторые ее элементы
положительны, а другие равны нулю. Вообще и в частности в экономических
приложениях чаще пользуются неотрицательными, а не положительными
матрицами, область применения которых весьма ограничена. Обычно в
матрице всегда имеются нулевые элементы, и вопрос состоит в том, являются ли
положительными другие элементы, так чтобы матрица была неотрицательной.
Сложение матриц. Определением сложения матриц является:
если crs = ara + brs
для всех г и 5 (г = 1, 2, ..., т; s = 1, 2, ..., п). Это определение очень просто
и согласуется с C) из раздела 12.2. Чтобы сложить две матрицы, нужно
сложить попарно их соответствующие элементы. Это определение легко
распространяется на случай более двух матриц. Однако необходимо подчеркнуть,
что складывать матрицы Аи В можно только в том случае, когда их
размерность совпадает. «Сложение» матриц различной размерности, таких, как
Г аи fli2l |Ai Ь12 &1з1
[а21 а22 J [b2l b22 b23] '
вообще не имеет смысла.
332

Приведем несколько простых примеров сложения матриц:
Пример (а)
Пример (б)
Г1 01 Г1 01 Г2 01 Г1 01
to lj + Lo IJ ~ Lo 2J-40 ij •
Пример (в)
Г 1 —2 1 _4- Г —4 21 = Г° °1=0пояка2
L — 2 1J L 2 — 1J L0 0 J
Пример (г)
Г1 2 3 1 Г4 5 6 1 Г 5 7 91
L4 5 6 J ^" L7 8 9 J L 11 13 15 J'
Умножение матрицы на скаляр. Определение опять очень просто:
для любого скаляра X. Каждый элемент матрицы А (а не только элементы
какой-нибудь одной строки или столбца) умножается на скаляр X. Скаляр X
может иметь любое значение — положительное и отрицательное (а также
равняться нулю. —Прим. ред.). Приведем несколько примеров:
2 -
1
1
' 2
1-
2
-
— 1
1
- 2
1 ^
2
-1
1 0] Гк 0
Сейчас мы рассмотрим несколько свойств и специальных случаев,
относящихся к вышеприведенным определениям. Некоторые из "них связаны
с правилами алгебры, которые мы перечислили в разделе 12.1. Все
доказательства очень просты, в чем читатель без труда убедится. В дальнейшем
изложении мы вновь будем пользоваться Матрицами A=[ars], B = [fcrs],
С = [crs], ..., все—размерности тхп.
I. Сложение матриц коммутативно. Закон (A3) из раздела 12Л:
каждая из полученных в результате сложения матриц равна С, где
II. Сложение более двух матриц. Сумма матриц А, В, С, ...
получается повторным применением правила сложения двух матриц:
III. Сложение матриц ассоциативно. Закон (А2) из раздела 12.1:
А + (В + С) = (А + В) + С;
каждая из полученных в результате сложения матриц равна D, где
IV. Повторное сложение матрицы А равносильно умножению матрицы
на целое положительное число X — N (iV = l, 2, 3, ...):
и т. д.
333

V. Умножение матрицы на скаляр подчиняется законам (S2 — 5) из
раздела 12.1:
0. А = 0; 1. А = А;
Вообще ЯА + М-В -f vC + ... есть матрица тх п с общим элементом
s + irs + r$ +)
VI. Сложение матрицы с нулевой матрицей не изменяет
первоначальной матрицы:
Следовательно, нулевая матрица играет роль нулевого элемента [закон (А4
из раздела 12.1].
VII. Вычитание двух матриц. Закон (А5) из раздела 12.1.
Определим сперва отрицательную матрицу как результат умножения
на скаляр ( — 1), то есть —А есть А, все элементы которой меняют знак
на противоположный:
-А = [(-аГ8)].
Теперь определим действие вычитания как сложение одной матрицы
с другой отрицательной (противоположной.— Ред.) по отношению к ней
о есть
В частности, А — А = А + ( — А) = 0, где 0 —нулевая матрица тхп. Этот
результат согласуется с определением равенства матриц, так как А — В = О
означает А = В.
Задачи и упражнения
1. Доказать свойства I — VII, обратив особое внимание на свойство V.
2. Проверить, что определение противоположной матрицы (—А) в VII
равносильно А + (—А) = 0 (см. правило (А5) из раздела 12.1).
3. Показать, что
Г1 0-1Г1 01Г2 01Г1 01 _Г1 0
2Lo ij Lo lJ-Lo 2j Lo ij —Lo i
Обобщить этот случай.
4. Написать А-|-В и А—В для
Г1 2 31
l= 4 5 6 и
|_7 8 9J
В =
5. Показать, что умножение матрицы на скаляр, или АА, сводится к повторному
сложению матриц, если А,-^-рациональное число вида p/q (p и q—целые числа),
12.4. УМНОЖЕНИЕ МАТРИЦ
Следующим этапом нашего изучения матричной алгебры является
определение действия умножения матриц. Это должно включать единичный
элемент, при умножении на который матрица остается неизменной. Если
окажется возможным дать такое определение умножения матриц, что матрица будет
иметь обратную величину, тогда можно будет говорить о делении как действии,
обратном умножению. Действие умножения характеризуется законами
(Ml—5) из раздела 12.1, а закон дистрибутивности (D) относится одновременно
к умножению и сложению. Как мы увидим, некоторые из этих законов не
действуют в матричной алгебре. Обратные алгебраические действия
(обратные матрицы и деление) мы рассмотрим в разделе 12.7.
334

Результаты рассмотрения линейных преобразований D) и E) в разделе
12.2 обеспечивают нам необходимый ориентир для определения умножения
матриц. В этом определении существенную роль будут играть скалярные
произведения (см. 11.8), образованные из элементов двух рассматриваемых
матриц. Выражение
k
И arpbPs (r=l,2, ...,ro; s = l, 2, ..., п)
состоит из т X п скалярных произведений (по одному для каждого г и s),
каждое из которых состоит из суммы к произведений (по одному для
каждого/?) элементов аиЬ. Индекс р является связанным, а индексы г и
s—свободными. Именно последние и порождают различные скалярные произведения.
Одну матрицу образуют элементы а, а другую —- элементы Ь:
А = [агр] и В = [ЬР8].
Важно отметить, что сперва нужно брать матрицу А, а потом матрицу В,
но не в противоположной последовательности.
При образовании скалярных произведений, а также произведения
матриц необходимо рассмотреть последовательно два обстоятельства.
Во-первых, нужно выяснить, позволяет ли размерность матриц А и В вообще
составить скалярные произведения. Скалярное произведение ^>]arpbvs (r =
= 1,2, ..., т; 5 = 1,2, ..., п) можно образовать только в том случае, если
А есть матрица т X к, а В —матрица к X п. Как мы видим, число
столбцов в первой матрице к должно равняться числу строк во второй матрице,
а т и п могут принимать любые значения; к соответствует связанному
индексу, а т и п — свободным индексам. Когда число столбцов в первой
матрице А совпадает с числом строк во второй матрице В, то можно сказать,
что А и В согласованы (conformable). Согласованные друг с другом
матрицы т X к и к X п образуют т X п скалярных произведений.
Второе обстоятельство, которое необходимо учитывать, это способ состав-
k
ления скалярных произведений. Скалярное произведение 2 arphps обра-
зуется из строки (r-й) матрицы А и столбца (s-to) матрицй В попарным
умножением двух соответствующих элементов и сложением получающихся
произведений. Существенно то, что берется строка первой матрицы А и столбец
второй матрицы В, но не как-либо иначе. Скалярное произведение
образуется, когда мы идем поперек матрицы А и вниз по матрице В; это можно назвать
правилом «поперек и вниз», или «строка на столбец».
Определение: А = [агр] согласовано с В = [bps], если число
столбцов в А равно числу строк в В: А размерности т X к и В размерности
к X п при любых т и п. В этом случае произведением АВ является
матрица С = [crs] размерности т X п, где crs является скалярным
произведением
к
2 arpbps>
p=i
к
то есть С = АВ означает, что crs=^arpbps.
p=i
Альтернативное выражение этого определения можно дать через
скалярные произведения векторов. Если А есть матрица т X к и В — матрица
к X п, то г, 5-й элемент произведения АВ является скалярным
произведением г-й строки А, или аг = (аг1, аг2, ..., ark), и 5-го столбца В, bs= (bls, b2s,
..., bks). Существенным является то, что эти векторы имеют одинаковое число
элементов, то есть матрица А имеет столько столбцов, сколько матрица В —
335

строк. В этом случае правило «поперек и вниз», или «строка на столбец»,
означает, что векторы поперек А объединяются с векторами вниз по В.
Прежде чем умножать матрицы, необходимо убедиться в том, что они
действительно согласованы друг с другом. Например, матрица АC X 2)
и матрица ВB X 2) соответственно согласованы, и их произведением
является матрица АВ размерности 3x2. Для краткости мы будем говорить, что
размерность 3 X 2 с 2 X 2 дает 3x2. Следующим шагом будет применение
правила «строка на столбец».
Способ получения произведения АВ легче всего уяснить, если написать
определение действия умножения в такой форме:
[
р=1
Любой элемент произведения получается «спариванием» строки А и
столбца В; если, например, это г, s-элемент, то он образуется из r-й строки А и
s-ro того столбца В. Например,

1
.0
1
0
1.
X
¦ о
-2
1"
0
[-2 2"
0 1
-2 0_
Левый верхний элемент произведения является скалярным произведением,
образованным первой строкой B, 1) матрицы А и первым столбцом @, -—2)
матрицы В:
2хО+1х(-2)= -2.
Аналогично получаются и другие элементы. Приведем еще несколько
примеров.
Пример {а)
1 01 Га ЪЛ
o lJ=Lc Л\-
2x2 с 2x2 дает 2x2; далее
а Ъ
Пример (б)
3 X 2 с 2 х 1 дает 3x1, но
не имеет смысла, так как 2 х 1 не согласуется с 3 х 2
Пример (в)
= 4 3 1 I
| 6 5 1 J
3x2 с 2x3 дает 3 х 3 и
г° * -ЧхГз 21—г—2 -2]
2 х 3 с 3 х 2 дает 2x2.
В произведении матриц роль единицы в определенном смысле играет
единичная матрица I = [6rJ разного порядка п. Однако необходимо иметь
в виду следующее усложнение. Пусть А—матрица т X п, а 1те и 1П обозначают
336

единичные матрицы соответственно порядка т я п. Тогда:
= A и А1П = А.
1П
Следовательно, матрица А не изменяется при умножении на единичную
матрицу I, однако порядок I меняется в зависимости от того, умножается ли
на нее матрица А слева или справа. В этом смысле закон (М4) из раздела 12.1,
строго говоря, не выполняется, так как не существует единственной единицы.
Эта трудность исчезает, когда матрица А' квадратная. В этом случае AI =
= IA = А, где I имеет тот же порядок, что и А.
Для того чтобы выяснить некоторые существенные моменты и выработать
правила матричной алгебры, исходя из раздела 12.1, мы сформулируем
несколько свойств умножения матриц, доказательство которых (оно не дается)
очень просто. Мы будем пользоваться матрицами А = [ars], В = [brs]
и С — [crsb Их размерность будет устанавливаться в контексте.
I. Произведение матриц вообще некоммутативно, то есть АВ Ф ВА,
исключая особые случаи (см. закон (МЗ) из раздела 12.1).
Различие между АВ и ВА может объясняться несколькими причинами.
Во-первых, одно из этих произведений может быть вообще не определено
(матрицы несогласованы). Далее, если даже определены оба эти произведения,
то АВ и ВА могут иметь разную размерность, а совпадение их размерности
не гарантирует равенства всех их элементов.
Пусть А — матрица т X к и В — матрица к X п, так что существует
АВ — матрица т X п. Рассмотрим разные возможные случаи.
1) т Ф п. В данном случае ВА не существует, так как при разных
значениях тип матрица В (к X п) не соответствует матрице А размера т X к
[см. выше, пример (б)].
2) т — п Ф к. В данном случае ВА существует, так как к X п с п X к
дает к X к. Однако АВ имеет порядок я, а В — порядок к, а мы знаем, что
квадратные матрицы разного порядка не равны между собой [см. пример (в)].
3) т = п = к. В данном случае матрица ВА существует, и ее порядок п
равен порядку АВ. Следовательно, АВ и ВА могут быть равны только в том
случае, если матрицы А и В квадратные, и их порядок совпадает. Однако
вообще они не равны, так как их элементы образуются разными способами и
поэтому отличаются друг от друга: • ,
[SrPU [Srpps]
р=1 р=1
Только тогда, когда А и В являются особыми квадратными матрицами,
АВ = ВА. Например, если взять матрицу А и единичную матрицу I с
одинаковым порядком п, то AI = IA = А (однако если А есть матрица тхп,
то нельзя сказать, что А1 = 1А, так как в первом случае порядок I должен
быть равен д, а во втором — т).
II. Произведение нескольких матриц достаточно проиллюстрировать
на примере трех матриц А, В и С. Чтобы получить произведение ABC
(с матрицами в такой и только такой последовательности), недостаточно,
чтобы три матрицы были согласованы попарно. Необходимо, чтобы А была
согласована с В, а АВ с С. Однако это условие очень просто: ABC
существует, если
А(*пхА), В(/сх/), С(/хй),
и тогда ABC будет матрицей (тхпI. В данном случае имеется два
свободных индекса (т и я, определяющие размерность ABC) и два связанных
индекса (к и /), а элементы матрицы ABC получаются в результате
двойного суммирования. Если ABC получается в последовательности (АВ)С,
1 Отметим, что существование ABC гарантировано, как уже заметил читатель,
попарным соответствием матриц А и В; В и С—Прим. ред.
22 Р. Аллен 337

то двойная сумма образуется следующим образом. Матрица АВ будет
(mxj), а ее общий элемент 2 ar*A>Q (г = 1, 2, ..., т\ д = 1, 2, ..., /);
i
p
пусть С имеет размерность (/Хтг), а общий элемент cqs (g=l, 2, .../;
5=1,2,..., /г). Следовательно, ABC будет размерности (т X га), а ее общий
элемент
2 2 *rpVv A)
а=1 р=1
Эту двойную сумму необходимо рассмотреть внимательно (см. упражнение 5).
У к
Она состоит из 2 cqs( 2 arpbpq)- В данном случае г и 5—свободные индексы.
g=l p=l
ft
Сумма к членов 2 arpbpq* когда г, свободный индекс, имеет / различных
значений, так как # = 1, 2, ...,/. Каждое из этих значений умножается
на соответствующий элемент cas, где д = 1, 2, ...,/E —свободный индекс),,
и полученные произведения суммируются по д = 1, 2, ...,/. Следовательно,
в A) имеется / членов, являющихся произведением единственного элемента с
на сумму к членов; в общем виде в A) будет kxj членов, образованных
в результате изменения р от 1 до к и q — от 1 до /.
III. Произведение матриц ассоциативно. (См. (М2) из раздела 12.1)*
Если матрицы А, В и С согласованы, тогда:
А(ВС)=:(АВ)С.
Мы уже получали (АВ)С, A), с общим элементом:
j к j к
2 ( 2 arpl>pq)cq8= 2 ljarpbpqCqs-
q=i p=i q=1 p=i
Аналогично получается и А (ВС) с общим элементом:
к j j к
2 агр ( 2 bpqcqs) = 2 2 arpbpqcqs-
1 g=l q=i p=l
IV. Матрицы обладают дистрибутивностью в отношении сложения
и умножения. (См. закон (D) из раздела 12.1). Если А согласована с В
и с С (так что АВ и АС существуют) и если В и С имеют одинаковую
размерность (так что В + С существует), то:
Если размерность А равна тхк, то и В и С должны быть одной
размерности к х п. Результативная матрица А(В + С), или АВ + АС, будет
размерности тхп.
V. Закон сократимости по отношению к матрицам вообще не применим
(см. закон (М5') из раздела A2.1)). Если АВ = 0, где 0 нулевая матрица
соответствующего размера, то из этого не следует, что или А = 0, или
В = 0. Достаточно привести пример:
Г1 11 Г 1 11 ГО 01
MxL-i -iJ=Lo oj=0'
хотя ни одна из матриц в левой части не является нулевой. Обобщая это
свойство матриц, отметим, что если А согласована с В и С и АВ = АС, то
из этого не сдедует В = С.
VI. Умножение матриц на нулевую матрицу. Трудность, с которой мы
только что встретились, не возникает, когда вопрос ставится в обратном
порядке. Произведение любой матрицы и согласованной с ней нулевой
338

матрицы дает нулевую матрицу:
АОПП = Omn = OmmA,
где индексы указывают размерность нулевых матриц. Когда А является
квадратной матрицей порядка п, достаточно только одной нулевой матрицы
(порядка п): АО = ОА = 0.
Вводя новые матрицы, являющиеся различными видоизменениями
единичной матрицы (см. упражнения 3 и 4 из раздела 11.6}, мы можем расширить
использование единичной матрицы I. Введем матрицу E(rs), полученную из I
перестановкой г-й и s-й строк; матрицу H(rs), полученную в результате замены
нулевого элемента в г-ж и s-u строках в матрице I на h, и матрицу К(г),
полученную из I заменой 1 в г-й строке и r-м столбце на к. Все эти матрицы
квадратные, но порядок их может быть различным в соответствии с характером
выполненных операций. При умножении этих матриц на данную матрицу А
размерности т X п мы получим результаты, приведенные в нижеследующей
таблице:
Матрица
E(rs)AI
IAE(U.)
Е(Г8)АЕ(Щ>)
H(rs)AI
IAH(uv)
H(rs)AH(ur)
K(r)AI
IAK(u)
• K(r)AK(w)
Результат: А
Переставлены г-я и s-строки
Переставлены столбец м и столбец v
Переставлены г-я и s-я строки, а также столбец и и
столбец V
s-я строка, умноженная на h, прибавлена к г-й строке
Столбец и, умноженный на Л, прибавлен к столбцу v
s-я строка, умноженная на &, прибавлена к г-й строке;
столбец w, умноженный на ht прибавлен к столбцу v
r-я строка умножена на к
Столбец и умножен на к
r-я строка и столбец и умножены на к
Характерной чертой полученных результатов является то, что
произведение матриц имеет форму PAQ, где Р — квадратная матрица порядка т
и Q — квадратная матрица порядка п. Можно произвести различное
«перекрестное сочетание» этих результатов, например E(rs)AK(W); интерпретация
вновь получаемых результатов будет совершенно очевидной. Можно составить
и расширенные произведения типа (K(r)E(rs))AH(MV), и снова их истолкование
очень ясно. Выполняем ли мы над матрицей А три вида действий вместе или
порознь, результат неизменно получается в форме PAQ. Этим мы
воспользуемся позже, в разделе 12.8.
Настало время обозреть достигнутые нами результаты. Пусть Smn—
множество всех матриц заданной размерности т X п. Как мы видели в
разделе 12.3, множество Smn не представляет особенностей в отношении
сложения и умножения матриц на скаляр, и в нем соблюдаются все
соответствующие законы из раздела 12.1. Короче говоря, подобно векторам, матрица
определенной размерности образует множество, являющееся векторным
пространством. Что касается действия умножения, то положение очень просто: если
т Ф /г, то в Smn умножение вообще невозможно; если т — п, то в Smn могут
умножаться все матрицы. Следовательно, Smn (m Ф п) является векторным
пространством, в котором определено сложение и умножение на скаляр, но
нет умножения.
339
22*

Умножение матриц можно произвести двумя путями. Рассмотрим, во-
первых, особое множество Snn квадратных матриц данного порядка п. Эти
матрицы ведут себя лучше, чем прямоугольные матрицы, и можно сразу же
отметить три момента. Snn по-прежнему остается векторным пространством,
поскольку в нем определено сложение и умножение матриц на скаляр. В
множестве Snn могут умножаться все матрицы, и оно является замкнутым в
отношении умножения. Наконец, множество Snn имеет единичный элемент I
порядка п. Для люббй матрицы А множества Snn: AI = IA = А. Большую
часть оставшихся разделов этой главы мы посвящаем изучению свойств
квадратных матриц.
Рассмотрим, во-вторых, множество S, охватывающее все матрицы любой
размерности. Это множество не является векторным пространством, так как
вообще в нем нельзя складывать две матрицы. Множество S не является также
замкнутым в отношении умножения, так как не все матрицы в нем
согласованы. Умножать можно только некоторые матрицы этого множества S и
интересно выяснить, в какой мере в этом случае оказываются справедливы законы
(М2—5). Мы уже видели, что закон ассоциативности (М2) выполняется и для
матриц, а закон коммутативности (МЗ) вообще неприменим. Закон
идентичности (М4) оказывается справедливым, как мы уже видели, только в
широком смысле. Однако практически этого вообще достаточно, так как единичная
матрица I соответствующего порядка всегда может быть введена в любое
произведение матриц, оставляя его неизменным. Например,
поскольку в каждом случае можно по мере надобности изменять порядок I.
И, наконец, закон обратимости (М5) вообще н!е применим.
Задачи и упражнения
1. Доказать свойства IV и VI.
2. В произведении АВ матрица А квадратная т х т, а В—матрица тх п.
Определено ли в данном случае ВА?
3. Показать, что закон дистрибутивности А (В+€)=АВ+АС можно применить
и к (В+С)А, но результат будет иным.
4. Образовать все возможные парные произведения из следующих матриц:
5. Используя матрицы из предыдущей задачи, образуйте произведение CDB
в виде матрицы 3x2. Показать, что каждый элемент произведения является
двойной суммой 22 crvdvo.bQs- Для выяснения количества членов и доказательства того,
V Q
что (CD)B=C(DB), написать эту сумму полностью.
6. Используя те же матрицы, напишите произведение ACDB в виде матрицы.
Можно ли получить произведения CDBA, CDAB и DBAC?
7. Если АВ = ВА, показать, что матрицы А и В должны быть квадратными
и иметь одинаковый порядок, но обратное вовсе не обязательно. Показать, что для'
матриц
¦
С! '1]
АВ = ВА=31. Проверить, что |А| = |В| = 3, |АВ| = 9.
8. Даны квадратные матрицы А, В, С, ... одинакового порядка. Показать, что
произведение любого количества этих матриц, взятых в любой последовательности,
всегда существует и является матрицей того же порядка.
9. Определить А2 = АА, А3 = ААА, где А—квадратная матрица. Проверить, что
АА2=а2А=А3 и доказать, что АтАп = Ат+л (тип целые числа).
Проиллюстрировать это для
А=
340
Г1 21
L3 4J •

Если
показать, что Вп=0 при /г>3.
Г«2 1 т
10. Даны матрицы А==
ГО 1 0]
в= о о 1L
L0 о oj
и В =
0 Ь
Найти С=АВ отсюда
написать С2 и С3 и вывести общее выражение для Сп (п—целое число).
11. Если А и В—квадратные матрицы одинакового порядка, показать, что
(А+ВJ=?АЧ-2АВ+В2; (А+В) (А—В)=?(А—В)
—В2.
Написать правильные выражения_для (A-j-BJ, (А+В)(А—В) и (А—В)(А-)-В).
12. Диагональная матрица % составлена из вектора Х = (Х1У Х2, ... Хп). Ее; и
A=[ars] —квадратная матрица порядка п, показать, что
Если к тому же X является скалярной матрицей (Хг=Х2^=... =А,П=Я), то показать,
что Х=Х1. Каким будет в этом случае произведение ХА? Используя полученные
результаты, показать, что если А и В—квадратные матрицы одинакового порядка,
то АВ ФВА, где В—диагональная, но не скалярная матрица, и АВ = ВА, где и А и В—
диагональные матрицы.
13. Если
[« *i *2 1 Г Ь ух г/2 1
а1 «11 «12 I » ^=| ^ ^1Х ^12 '
«2 «21 «22 J LP2 ^21 &22J
показать, что
где
АВ =
ау'+х'В*
а2
ау'+А*В*
а21
«22
и у', Р и В* определяются аналогично.
14 Умножение блочных матриц. Показать, что результат предыдущей задача
является частным случаем
[Ац А12 1
A2i A22 J
В
11
В
12
В22 ^
АцВ12+А12В22
при условии, что подматрицы вида Ап и Вп попарно согласованы. Этот результат
справедлив вообще. Истолковать умножение матриц по блокам как развитие
обычного правила умножения. Проиллюстрировать это, показав, что
Г1 Аа | [~iM=
и указать, какой порядок должны иметь Alf A2, Вх и В2, чтобы такое умножение
было возможно. Выразить аналогично
2|.
12.5. ТРАНСПОНИРОВАНИЕ[МАТРИЦ
Сейчас мы введем в матричную алгебру новое действие, с которым мы
не встречались в элементарной алгебре. Данная матрица т X п состоит из
т X п элементов, расположенных в т строках и п столбцах. Однако про-
341

стой перестановкой строк и столбцов эти же т X п элементов можно
расположить другим способом — в п строках и т столбцах. В результате такой
перестановки получится другая матрица размерности п X т. Эта матрица
называется транспонированной по отношению к исходной матрице.
Определение. Транспонированной к матрице А = [ars] размерности
т X п является матрица А' = [asr] размерности п X т.
Новое обозначение очень просто. Прибавление штриха к обозначению
любой матрицы показывает, что строки и столбцы транспонированы;
например, (АВ)' равно произведению матриц АВ, у которого транспонированы
строки и столбцы. Проиллюстрируем транспонирование матриц на
нескольких примерах.
Пример (а)
а41 21. а-[' ;
Пример (б)
fl]
а' = [1 2 3] (см. 11.7).
[3J
Пример (в)
Сейчас мы сформулируем несколько свойств и приведем несколько частных
случаев транспонирования матриц.
I. Матрица, транспонированная к транспонированной, является
исходной матрицей, то есть (А')'= А. Это свойство легко обобщить:
четное число операций транспонирования А дает А, нечетное число А'.
II. Транспонирование суммы. (А + В)' = А'+ В7, где А и В —
матрицы одинаковой размерности.
III. Транспонирование произведения. (АВ)' = В'А', где А —
матрицам X к согласована с В размерности к X п. Необходимо отметить,
что при транспонировании произведения изменяется
последовательность матриц, так как В' размерности п X к согласована с А'
размерности к X т и никак иначе. Произведение матриц АВ размерности
т X п получается из А, согласованной с В; транспонированная
матрица произведения (АВ)' получается из В', согласованной с А'.
IV. Транспонирование единичной матрицы. Если I — единичная
матрица порядка п, то 1' = I; мы это уже показали в цримере (в).
Очень удобны для транспонирования симметрические и кососимметри-
ческие матрицы (определенные в 11.6, пункт IV), являющиеся частными
случаями квадратной матрицы. Свойством симметрической матрицы А является
А = А'; кососимметрической: А = — А'.
Из многих интересных свойств транспонирования, связанных с
симметрическими и кососимметрическими матрицами, в качестве примеров приведем
следующее. Пусть А—любая квадратная матрица и А'—результат ее
транспонирования. Пусть, далее, В = АА', С = А + А'иБ = А — А'. Тогда
В' = (АА')' = (А')'А' = АА' = В,
D' = (A-A')' = A'-(A')' = A'-A= -(A-A')= -D.
Следовательно, для любой квадратной матрицы А матрицы АА' и А + А'
всегда симметрические, а А — А' всегда кососимметрические.
Задачи и упражнения
1. Доказать свойства II и III.
2. Обобщая свойство III, показать, что (АВС)' = С'В'А'. Обобщить и это.
342

3. Дана матрица
Г1 2 31
l= 4 5 6.
1.7 8 9j
Получить матрицу АА' и показать, что она симметрическая.
4. Показать, что если А является симметрической или кососимметрической
матрицей, то А2 = АА является симметрической матрицей.
5 Показать, что E(rs) = E(rs) (следовательно, E(rs)—симметрическая матрица)
и H(rs) = H(sr), где E(rs) и H(rs)—матрицы, определенные в разделе 12.4.
12.6. УМНОЖЕНИЕ ВЕКТОРОВ И МАТРИЦ
Когда векторы рассматриваются как матрицы, содержащие одну строку
или один столбец, то к ним полностью применимы все правила матричной
алгебры. В частности, по правилу умножений можно получить произведение
двух векторов и произведение вектора и матрицы любого порядка, если
только векторы и матрицы согласованы. Однако некоторые случаи умножения
векторов и матриц настолько полезны, что заслуживают специального
рассмотрения.
Рассмотрим несколько общих случаев.
I. Произведение двух векторов. Векторы должны быть одной
размерности п. Пусть x = {xs} и у = {г/Л векторы-столбцы и x' = [#s] и у' = [г/8]
векторы-строки (s = 1, 2, .. ., пI.
Пара векторов х' и у согласована, так как если считать их
матрицами, то их размерность соответственно будет 1 хп и пХ 1. Произведением
этих векторов является матрица порядка 1, состоящая из одного элемента,
то есть скаляр. Точно так же согласована пара у' и х и их произведение
снова оказывается скаляром. Применяя правило умножения, мы
обнаруживаем, что два произведения имеют одинаковое значение:
Скаляр (хгуг \- х2у2 + • • • + хпУп) является или произведением ху' или
произведением у'х; это — скалярное произведение, которое мы уже
рассматривали (см. 11.4), но здесь оно записано в новом обозначении. Как частный
случай х'х
п
l
то есть произведение данного вектора на транспониро-.
ванный равно сумме квадратов его компонентов.
II. Произведение матрицы и вектора-столбца. Рассмотрим матрицу
A=[ars] размерности тхп и тг-мерный вектор-столбец х = {#8}. В данном
случае г = 1, 2, ..., т, а 5 = 1, 2, ..., п. Матрицы А размерности тхп
и х размерности п х 1 согласованы, и их произведением является матрица
т X 1, то есть m-мерный вектор-столбец:
Ах =2 aTt
S=l
Если произведение обозначить
2, . .., m), то получим
2,
как вектор
у = Ах
{г/г} размерности m(r =
или
L Ут А
а9
'2п
а>«
а„
хЛ
1 Здесь, как и ранее (стр. 317), автор для обозначения вектора-столбца берет
¦фигурные скобки, а для вектора-строки—квадратные скобки.—Прим. ред.
343

что означает линейное преобразование:
п
2/r = S a>rsxs {r = U 2, ..., т)
от п переменных xs к т переменным уг.
Эта же пара матриц в обратном порядке: х и А не согласована, так
как их размерности соответственно wxl и тхп. Следовательно,
произведение хА вообще не существует.
III. Произведение матрицы и вектора-строки.
матрицу A = [ars] размерности тхп и m-мерный
В данном случае согласована пара матриц
Произведением этих матриц размерности 1X яг
1
Возьмем ту же самую
вектор-строку у' = [г/г].
у' и А (а не А и у'),
и тхп соответственно
р р рр
является матрица размерности 1 х п, или л-мерный вектор-строка
2
г=1
= 1» 2, . . . , П).
Если это произведение обозначить как вектор
то получим
или
у'А,
[#i? #2' • • • > Xn\ — I
что означает линейное преобразование
a21 a22
• • а
.. а
Хп
2п
2
г=1
= 1, 2, .. .,/г)
от m переменных уг к п переменным zs.
IV. Произведение матрицы, вектора-строки и вектора-столбца.
Рассмотрим ту же самую матрицу А = [ars] размерности тхп, гг-мерный
вектор-столбец x={#s} и 7га-мерную вектор-строку у7:=|уг| (г = 1, 2, ,.#,т7г;
5 = 1, 2, .. .,7г).
Произведение у'А получается в виде тг-мерного вектора-строки (см. III),
который можно умножить на тг-мерный вектор-столбец х. Таким образом,
произведение у'Ах является скаляром. Этот факт легко проверить, если
учесть размерность матриц в произведении у'Ах: размерность 1 х т с
размерностью тхп дает размерность 1 х тг, а размерность 1хп с
размерностью п х 1 дает размерность 1x1, то есть произведение является
скаляром.
Теперь нам осталось только найти величину скаляра у'Ах. Общим
элементом вектора-строки z'=y'A является zs=2
который умножается на общий элемент #s(s =
столбца х; y'Ax = z'x и, следовательно,
у'Ах =
2
8=1
B
T=i
n m
= 2 2 ar
S=l Г=1
Угагз E==1»2, ...,тг),
, 2, ..., тг) вектора-
xsyr =
...+ атпхпут.
344

Таким образом, одновременное умножение матрицы справа на вектор-
столбец и слева на вектор-строку дает в результате билинейную форму
(см. 13.5). Новшество, вносимое произведениями матриц и векторов, состоит
в том, что они представляют билинейную и квадратичную формы (см.
упражнение 4). Рассмотрим также несколько частных случаев,
относящихся к векторам особого вида.
V. Единичные векторы. Единичные векторы размерности п
выражаются как
= l, 2f
(бг1, бг2, ...,5rn)
где 6rs есть дельта Кронекера. Все элементы единичного вектора, крбме
одного, равного 1, равны 0. Теперь мы можем написать эти векторы как
вектор-столбец и вектор-строку:
б,
-'is
; = [бг8] = [6Г1, бг2, . . ., бгп].
Если говорить в терминах единичной матрицы, то вектор es есть 5-й
столбец, а вектор г'г является r-й строкой единичной матрицы I = [6rs].
Рассмотрим любой данный набор п величин xv х2, .. ., хп,
составляющих вектор-столбец х = {#8} и вектор-строку х' = [жг].
Каждый из этих векторов может быть разложен на сумму:
2
Таким образом, любой вектор w-мерного пространства можно выразить
через единичные векторы, на которые «натягивается» («span») это
пространство. Мы уже получали этот результат в разделе 11.5, когда
рассматривали линейную комбинацию векторов.
VI. Сумма элементов вектора. Рассмотрим векторы, содержащие п
элементов, равных 1:
Г 1
{1} =
1
и
= [1 1...1].
Умножение любого данного вектора x = {xs} или х' = [#г] на такие векторы
равносильно сложению элементов n-мерного вектора
VII. Сумма элементов строки или столбца матрицы. При помощи тех
же векторов {1} и [1] получается сумма элементов строк и столбцов
данной матрицы А = [ars] размерности тхп:
где {1} порядка п, а [1] порядка т. Следовательно, суммы элементов
строк матрицы А = [ars] размерности тхп образуют
вектор-столбец порядка т:
345

а суммы элементов столбцов А образуют вектор-строку порядка п
[2 ««]=[*] А.
Г
Например, если элементы обычной двойной (шахматной. — Ред.)
статистической таблицы рассматривать как элементы матрицы A=[ars], то
итоговый столбец таблицы получится как А{1}, а итоговая строка как [1]А.
VIII. Диагональные матрицы. Если вектор h = (X19 Я2, ..., Хп) порядка
п написать как главную диагональ матрицы, все остальные элемент^
которой равны 0, то получится диагональная матрица порядка п:
Х± О
О Х9
О 1
О
0 0
Kl
которую мы уже определили в разделе И.6, пункт III. Умножение такой
диагональной матрицы на любую квадратную матрицу А = [ars] порядка п
дает
Х1ап
Кппп J
то есть матрицу А, строки которой умножены последовательно на Xx
^2' • • •' ^п-
Умножение же любой квадратной матрицы A = [arJ порядка п на
диагональную матрицу дает матрицу А, столбцы которой умножены
последовательно на kv A,2, ..., %п:
А2а2
- ^iani ^2an2 • • • hnam
Задачи и упражнения
1. Даны векторы-столбцы х и у размерности п, так что произведение х'у = у'х
является скаляром. Чем являются произведения ху' и ух'? Можно ли получить любое
из этих четырех произведений, если размерности х и у различны?
2. Дан вектор-столбец х размерности и. Получить произведение хх' и показать, что
оно является симметрической матрицей.
3. Образовать все возможные парные произведения из следующих векторов
и матриц:
Г 31 ГО 1 -П Г1 2 31
-2 3], у= -2 , A- J 1 ], С= 4 5 6 .
J
Написать произведение х'Су как скаляр.
4. Дана квадратная матрица А порядка п. Объяснить, почему произведения Ах
и х'А можно написать только для га-мерного вектора х. Образовать далее произведение
х'Ах и истолковать его как скаляр (квадратичную форму) переменных х. Чем является
произведение x'lx, где I—единичная матрица порядка л?
5. Если х—вектор-столбец размерности п, то показать, что
х2
и х[1] =
х2
_хп хп
Чем являются произведения {1}[1] и [1] {1}?
Получить также и интерпретировать произведение [1]1{1}.
346

6. Даны диагональная матрица к порядка п и га-мерный вектор-столбец х.
Получить произведения %х и x'h. Найти также произведения Vx и х'Х, где к— вектор-
столбец, образованный из элементов главной диагонали А,, и показать, как они связаны
с Хх и хХ __ _
7. В случае VIII (см. выше) ХА и А % получены для квадратной матрицы А порядка п.,
Показать, что эти произведения могут быть определены с аналогичными результатами
для любой матрицы А размерности тхп. Какого порядка должна быть в таком
случае диагональная матрица X?
8. Проиллюстрировать использование единичной матрицы I, показав, что
х'х = 1х/х=х'1х=х'х1
п
и что общим значением этих произведений будет скаляр 2 х*—сумма квадратов эле-
s=l
ментов вектора х. Каким должен быть в каждом случае этой цепи равенств порядок I
12.7. ОБРАТНЫЕ МАТРИЦЫ. ВЕЛИЧИНА ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
Общей формой до сих пор рассматриваемых нами матриц была
прямоугольная. Размерность прямоугольной матрицы равна тХ п, причем вообще
т Ф п. В этом разделе наше внимание концентрируется на случае тгг = тг,
то есть мы будем рассматривать квадратные матрицы порядка п.
Отсутствие до сих пор в этой главе ссылок на определители также было
обусловлено общностью изучения матричной алгебры, так как
прямоугольная матрица (тФп) не имеет соответствующего определителя, по крайней
мере когда используются все ее элементы. Определитель по существу
является только одной из скалярных величин, получаемых из элементов
квадратной матрицы. Из элементов как квадратной, так и прямоугольной матрицы
можно получить и другие скаляры, например скаляр у'А х, что мы и сделали
в разделе 12.6. Однако определитель предполагает квадратную матрицу,
которую мы и будем изучать в этом разделе.
Квадратные матрицы А = [ars] порядка п разбиваются на два класса,
различающихся между собой по одному важному признаку.
Определение. Если А = | А| = |агв| есть определитель,
полученный из элементов матрицы А, то А называется особенной, когда А = О,
и неособенной, когда А Ф 0х. В последующем изложении
предполагается, что матрица А является неособенной (А Ф 0).
Алгебраическим дополнением, Ars, элемента ars в определителе А является
определитель порядка /г — 1, полученный из А порядка п исключением
r-й строки и 5-го столбца и приписыванием знака (—l)r+s (см. 11.9). Очевидно,
что алгебраических дополнений столько же, сколько элементов определителя,
и их можно упорядочить в матрицу [Ars] порядка п. Транспонируя эту
матрицу, мы получим матрицу, которую называют присоединенной к А:
22
Если каждый элемент этой матрицы [Ars\ разделить на величину
определителя А (А Ф 0), получится уже третья матрица, которая обозначается
через А.
Г А 1' 1
Определение: А~х= ~F —-^
г А А А
А А А
^12 Л22 ¦ • • лг
1 Эти матрицы называют иногда также соответственно вырожденными и
невырожденными.— Пр им. ред.
347

До сих пор это определение было совершенно произвольным; А является
особым видом матрицы, полученной из данной квадратной матрицы А. Мы
образовали матрицу из алгебраических дополнений определителя А,
транспонировали эту матрицу и, разделив каждый элемент транспонированной
матрицы на определитель А, получили матрицу А. Теперь нам нужно
интерпретировать А по существу, чтобы оправдать применение степени(—1). В
элементарной алгебре величина а является обратной к а и удовлетворяет
условию а X а = а X а = 1, так что а = 11а (а Ф 0). Это есть правило
(М5) из раздела 12.1. Как мы увидим, А играет такую же роль в матричной
алгебре.
В матричной алгебре имеются единичные элемёкты — единичные
матрицы I (квадратные) соответствующего порядка. Если А является
квадратной матрицей порядка п, а I — единичной матрицей такого же порядкаг
то матрица А" должна удовлетворять условию АА~1 = А~1А = I. Можно
показать, что А удовлетворяет этому условию и что А— единственная
матрица, удовлетворяющая этому условию. Приведем доказательство:
по правилу умножения (см^ 12.4);
р=1
А О ... О"
О А ... О
О 0 ... А
по правилу разложения определителя через алгебраические дополнения
(см. 11.9);
0 ... (Г
0 1 ... О
О 0 ... 1
по правилу умножения матриц на скаляр (см. 12.3). Аналогично
доказывается, что А"ХА = I, и матрица А удовлетворяет условию АА = А"ХА = I.
Чтобы доказать, что матрица А является единственной,
удовлетворяющей этому условию, предположим обратное, то есть что существует
такая матрица В, что АВ = 1. Тогда
А1 = А"Ч = А1 (АВ) = (А1 А) В = IB = В.
Следовательно, если АВ = I, то В = А. Аналогично если ВА= I, то В = А.
Следовательно, матрица А является обратной к А, единственной
матрицей, удовлетворяющей условию АА~1 = АА = 1. Как видно,
необходимо, чтобы А была квадратной и А Ф 0. Теперь можно рассмотреть
и деление как действие, обратное умножению. Если существуют два
произведения АВ и ВА, существуют и два способа деления В на А; один
из них ВА, а другой А"ХВ. Матрица А/1 определена единственным
образом (если А —квадратная матрица и А Ф 0), и она может быть до или
после умножена на В, то есть В может быть после и до разделена на А.
Следовательно, для квадратных матриц закон (М5) принимает такую
форму:
А обратная к А: АА~1 = А-1А= I.
Деление: А ЧВ Ф ВА.
Матрицы А и В должны быть квадратными и А Ф 0.
348

Теперь мы приведем некоторые полезные свойства обратных матриц,
которые помогают вычислениям в матричной алгебре.
I. Основное свойство: АА~1 = А"ХА = 1, то'есть произведение АА
коммутативно.
П. Обратная обратной матрицы: (А) = А.
Из1 имеем AA^I и (А) (А)^.
Поэтому А = AI = АА (А) = I (А*1) - (А).
III. Обратная матрица произведения: (АВ) = ВА~1, то есть
последовательность матриц в произведении—обратна.
Из I имеем А^А^В 48 = 1 и (АВ) (АВ) = I.
Следовательно, В1 А *=В1 А Ч=В А АВ (АВ)=B4B(АВI=
ВЧВ (АВ) = I (АВ) = (АВ).
IV. Обратная транспонированной матрицы: (А') = (А)'.
Из I имеем А~1А = 1. По свойству III из раздела 12.5,
A^A'A1)'
Отсюда следует: А'(А~1)' = (А"А)'= I' = I.
Следовательно, матрицы А' и (А)' обратны друг другу, то есть
V. Определители обратной матрицы. Обратная матрица А
и оба частных ВА и А~ХВ являются квадратными матрицами того же
порядка, что и А. Каждая из них имеет свой определитель, и можно
ожидать, что эти определители будут подчиняться правилам обычной
алгебры, то есть что
l^l-pb и |ВА-М = |А-В| = Щ.
Так оно и есть в действительности. Доказательство этого требует только
простого умения вычислять определители квадратных матриц. Отметим
прежде всего, что определитель единичной матрицы I равен единице:
1 =
1 0 ... О
О 1 ... О
О 0 ... 1
= 1.
Определитель обратной матрицы А получается из отношения АА~Ч=1.
Теперь для доказательства нам нужно, чтобы было справедливо следующее:
если АВ—произведение двух квадратных матриц, то |АВ| = |А| |В|.
Оказывается, что и это так. Формальное доказательство ([12], приложение)
этого свойства несколько трудно, и мы его не приводим. Заметим только,
что его справедливость основана на том факте, что умножение
определителей и матриц приводит к одинаковой форме скалярных произведений
(см. упражнение 1).
Следовательно, из | АА"1 = 11 j получаем, что
| А | | А1 = 1, то есть | А1 = -^гг •
Аналогично получаем:
Таким образом, хотя матрицы ВА и А-1В различны, их определители
равны —каждый равен |В|/|А|.
Значение численных элементов обратной матрицы, по определению,
можно получить путем вычисления алгебраических дополнений
определителя первоначальной матрицы, как мы это уже делали в разделе 10.6.
Приведем два примера.
349

Пример (а)
следовательно,
Пример (б)
l 2-|Ai = 2 Л12=0
0 2}А21=-2 Л22=1
А 1=
р -а-
по определению.
[12 3] Л1=1 А12=0
1= О 1 2 Ai=— 2 422=1
Lo о ij л31=1 iiM=-
2 433 =
следовательно,
Г1 -2 11
i-i= 0 1-2,
Lo о ij
по определению.
Из этих примеров видно, что матрица, обратная треугольной
(определение последней см. в разделе 11.6, пункт V), является также треугольной
матрицей (см. упражнение 9). Вычисление обратных матриц большого
порядка очень трудоемко. Вместо использования алгебраических дополнений А
иногда оказывается возможным найти такую матрицу В, для которой АВ = 1;
в этом случае В можно рассматривать как обратную матрицу, А. О другом
практическом методе вычисления обратной матрицы мы расскажем ниже
(см. 12.9).
Теперь мы найдем обратные матрицы для единичной матрицы I порядка
п, а также для различных матриц, получающихся на основе I. Поскольку
II = I, то I = I, то есть единичная матрица I является для себя и обратной.
Этот результат можно проверить и пользуясь алгебраическими дополнениями.
Если в I поменять местами r-ю и s-ю строки, то получится матрица Е(Г8)(см.
конец раздела 12.4), совпадающая со своей транспонированной, то есть Е(г8) =
= Е(Г8); это говорит о том, что при перестановке строк меняются местами и
соответствующие столбцы. Из определения также очень легко проверить (см.
упражнение 7), что Е[Д) = E(rS). Следовательно, подобноI, матрицаЩГ$)
является своей собственной транспонированной и обратной матрицей.
Следовательно,
где А — любая квадратная матрица порядка п. Все эти произведения
являются матрицей, полученной из А перестановкой г-й и 5-й строк и г-го и s-ro
столбцов.
Для того чтобы обобщить полученные нами результаты, введем
перестановочную матрицу Р* порядка п, все элементы которой равны нулю, за
исключением ровно одной единицы в каждой строке и столбце. Нетрудно видеть,
что Р* получается из I порядка п путем некоторой перестановки или
перетасовки строк. Если в исходной I переставлять таким же образом столбцы,
то получится матрица (Р*)', то есть транспонированная к Р*. Таких
перестановок существует очень много1, и Р* является удобным обозначением
всей совокупности матриц, связанных с единичной матрицей I [7, стр. 237].
Проиллюстрируем это на примере матриц третьего порядка. Переставим
в I строки и столбцы из последовательности A, 2, 3) в последовательности
1 Таких перестановок будет столько, сколько существует перестановок из п строкг
то есть /г!-— Прим. ред.
350

C, 1, 2):
р*_
0
1
.0
0
0
1
1-
0
0.
(Р*)'=
ГО 1 О
О О 1
Li о о J
Вообще говоря, Р* и (Р*)' различны. Но, по определению,
ГО 1 01
0 0 1
1 0 0
Таким образом, для Р* ее транспонированная и обратная матрицы
совпадают, но они не равны вообще (как это было в частном случае
перестановочной матрицы E(rs), см. упр. 8) самой матрице Р*. Цоскольку Р*(Р*)' = 1,
то (Р*)' «аннулирует» перестановку в исходной матрице I, выражаемую
матрицей Р*. Приведем несколько примеров. Возьмем ту же полученную
матрицу Р* и вектор-столбец х = {xv x%, х3}:
р*х = \х х х }
то есть Р* служит для перестановки элементов вектора х. Для любой
матрицы А порядка 3 получаем:
Р*А =
Как видно, в результате получается матрица А, у которой "соответственно
переставлены строки, столбцы и строки и столбцы. Развивая результаты,
полученные в разделе 12.4, последний пример можно обобщить следующим
образом:
Р*А = А (с переставленными строками),
А(Р*)' = А (с переставленными столбцами),
Р*А(Р*)' = А (с переставленными строками и столбцами).
Этот вывод справедлив для любой матрицы А порядка п и какой-либо
перестановки Р*. Рассмотрим частный случай, когда А = 1. В этом случае
Р*(Р*)' ==Р* 1(Р*)' есть I, у которой формально переставлены строки
и столбцы, что дает снова I. Следовательно,
Р*(Р*)' = 1 или (Р*)==(Р*)'.
Обратная и транспонированная матрицы Р* совпадают. Если строки ги
столбцы матрицы А переставлены одинаковым способом, то в результате
получится матрица
)' = Р*А(Р*)~1.
«31
«11
.«21
«32
«12
«22
«33
«13
«23 _
, А(Р
*)' =
«13
«23
«33
«11
«21
«31
«12
«22
«32.
, Р*А(Р
*)' =
«33
«13
«23
«31
«11
«21
«32
«12
«22.
Задачи и упражнения
1. Показать, что определители следующих трех матриц равны 3:
»-[•-; !]-"-[?JJ-4! "У-
Показать также, что АВ Ф ВА, но | АВ | = | ВА | = | А | х | В | =9. Отличаются ли между
собой произведения АС и СА?
Г 2 1 1
. о • Показать, что Л = 5. Вычислить все четыре
алгебраических дополнения и показать, что, по определению,
A-i=
351

—1
1
0
—1
1 0
1
Проверить, что АА=А*1А = 1, а I А1 = 1/4.
Г1 1 11 Г1
3. Дана матрица А= 0 1 0 . Показать, что А-1= 0 1 0| . Найти
I О О 1J I О
Г1 а Ь1
матрицу В *, обратную для матрицы В= О 1 О I .
L0 О 1J
4. Известно только, что А * удовлетворяет AA-1=:I. Предположить, что
существует матрица В, такая, что ВА = 1, и показать, что в этом случае В=А~1, то есть
доказать, что и А~1А=1.
5. Если А—квадратная матрица, определить, что (А~1J=АА. Показать, что
А2(А~1J = 1, и истолковать этот результат. Ввести понятие отрицательной целой
степени А-п, обратной к Ап. Наконец, показать, что для любых значений тип
(положительных или отрицательных целых чисел) AmAn = Am+n. Завершает ли А° = 1 всю
совокупность целых степеней матрицы А?
6. Основываясь на предыдущем упражнении, взять в качестве А диагональную
матрицу а и показать действия с целыми степенями а:
Гаг* 0 . . Л
i=l 0 aj*. . .
и т. д.
7. Дана матрица I порядка 3. Получить ЕB3) и, по определению, написать Е('23)
и Е(-2^). Обобщить этот результат.
8. Из единичной матрицы I порядка 3 получить шесть перестановочных матриц Р*
и показать, что три из них типа Е^, для которой P* = (P*)' = (P*)~i, а три
остальные таковы, что Р* Ф (Р*)' = (Р*)~1.
9. Дана треугольная матрица
Т =
Найти Т в виде
Получить произведение ТТ" и приравнять его к I. Показать, что 6Г= 1/яг и &12> ^13 и &гз
можно выразить через элементы а. Вывести отсюда, что матрица, обратная
треугольной, также является треугольной матрицей.
12.8. ЭКВИВАЛЕНТНОСТЬ И РАНГ МАТРИЦ
Сперва мы получим результаты, которые будут справедливы для любой
матрицы А = [я(Г8)] размерности т X п. Для удобства будем считать, что
m<n, то есть число столбцов в матрице не меньше, чем число строк. Если
в матрице А строк больше, чем столбцов, то можно получить
транспонированную матрицу А' иприйти к случаю яг< п.
Элементарными преобразованиями строк и столбцов матрицы мы
называем следующие:
а) перестановку двух строк (столбцов);
б) прибавление одной строки (столбца), умноженной на А, к
другой строке (столбцу);
в) умножение строки (столбца) на А.
Скаляры h и к могут принимать любые численные значения, за
исключением нуля. Назовем далее элементарной матрицу, которая получается
в результате элементарных действий над строками и столбцами единичной
матрицы I порядка п. Если мы применим элементарные преобразования
к строкам I, то получим элементарные матрицы:
а) E(rs), б) H(rS), в) К(Г),
которые определены в разделе 12.4. Здесь индексы г и s показывают номера
строк, над которыми производятся элементарные преобразования, и они
352

могут принимать любые значения: г, s = 1, 2, ..., п; г Ф s. Нужно отметить,
что элементарное преобразование (а) является частным случаем любой
перестановки или перетасовки строк, и, следовательно, E(rs) является частным
случаем перестановочной матрицы Р*. Однако перестановка двух строк
и перестановочная матрица E(rS) являются основными понятиями; любая
другая перетасовка строк является последовательной перестановкой двух
строк, а матрица Р* получается как произведение матриц Е(Г8). Например,
если п = 3 и строки переставлены в последовательности C, 1, 2), то в таком
случае Р* = ЕA2)ЕB3),а это означает, что сперва были переставлены вторая
и третья строки, а затем первая и вторая. Результаты, к которым мы пришли
в конце раздела 12.4, в упражнениях на умножение матриц, можно свести,
как будет вытекать из нижеследующих рассуждений, к одной простой
теореме. Сперва мы определим понятие эквивалентных матриц.
Определение. Если А получена из В с помощью некоторой
последовательности элементарных преобразований, то А эквивалентна В .
Из сущности элементарных преобразований (например, их можно
применять в любом порядке, и они обратимы) вытекают следующие важные
свойства:
I. А эквивалентна сама себе.
II. Если А эквивалентна В, то В эквивалентна А.
III. Если А эквивалентна В и В эквивалентна С, то А
эквивалентна С.
Эти свойства являются общими свойствами эквивалентности. Идея
перехода от А к эквивалентной матрице В состоит в том, чтобы получить более
простую матрицу. И, действительно, упрощение может быть очень
значительным.
Теорема. Матрицу А размерности т X п с помощью некоторой
последовательности элементарных преобразований можно привести к эквивалентной
ей матрице:
(Ir — единичная матрица порядка г), где г — некоторое фиксированное
число. Все матрицы, эквивалентные А, также Эквивалентны Dr.
Доказательство. Если А — нулевая матрица, то она уже имеет
требуемую форму. Любая другая матрица имеет ненулевой элемент (скажем, а),
который перестановкой строк и (или) столбцов можно расположить в первой
строке и первом столбце, то есть в верхнем левом углу. Затем, умножая
первую строку на соответствующий множитель 1/а, можно получить на этом
месте 1. Вычитая первую строку и первый столбец, умноженные на
соответствующие числа, из всех других строк и столбцов, мы получим, что первая
строка и первый столбец, за исключением 1 в левом верхнем углу, будут
состоять из нулей.
Следовательно, А станет эквивалентна
где С — размерности (т — 1) X (п — 1).
Аналогичные преобразования повторяются над С, пока А не станет
эквивалентной Dr. .
Проиллюстрируем это на нескольких примерах:
эквивалентна
112 3] Г1 0 01
0 0 0 эквивалентна 0 0 0 =DX.
0 0 Oj L0 0 Oj
23 р. Аллен 353

На первом этапе первая строка, помноженная на 2 и 3, вычитается
соответственно из второй и третьей строк. На втором этапе производится аналогичное
вычитание столбцов.
Пример (б)
О 1
А==|_3 -«-6
4 8
О
01
»-4
-4
2J
эквивалентна
8 —
1
0
4 21
О О
О 0J

эквивалентна
эквивалентна
2 —2 у
0
4
О
—4
О
— 3 —6
3 —
21
О
3

эквивалентна
rt о о о]
0 10 0 =]
[о о о oj
10 1 0
Lo о о
На первом этапе мы переставляем все строки, на втором первую строку,
;умноженную на 8/4, прибавляем к третьей строке, далее умножаем первую строку на х/4
и наконец первый столбец, умноженный на соответствующие числа, вычитаем из всех
других столбцов.
Пример (в)
эквивалентна
Г1 2 3"|
0 1 21
эквивалентна
эквивалентна
Порядок элементарных преобразований в данном случае очевиден. Интересно
отметить, что здесь (как, впрочем, и в других примерах и в общем случае) на
некоторой промежуточной стадии А становится эквивалентной треугольной матрице,
которая под главной диагональю содержит нулевые элементы.
Понятие эквивалентности матриц приводит нас к понятию ранга
матрицы. Исключая строки и (или) столбцы из матрицы А размерности т х п
(пусть для определенности /гг<п), можно получить различные подматрицы
размерности г X 5 (r<m, s< n).
Рассмотрим квадратные подматрицы различных порядков (наивысшим
может быть порядок т X т). Некоторые из них будут иметь нулевой,
другие — ненулевой определитель. Выберем из матриц, имеющих ненулевой
определитель, наивысшую по порядку.
Определение. Матрица А размерности т X п имеет ранг г, если
определитель по крайней мере одной из квадратных подматриц порядка
г не равен нулю, а определители всех квадратных подматриц более
высокого порядка равны нулю. Ранг матрицы будет г < игили п в
зависимости от того, какое из этих чисел (т или п) меньше.
В частности, если А — квадратная матрица порядка п, то г = п (если
А — неособенная матрица) и г < п (если А — особенная матрица).
Приведем пример.
Пример (г)
На основе определения ранг матрицы найти очень трудоемко:
0 1
— 3 —6
о
3
4 8—4
размерности 3x4. Ранг этой матрицы равен 2.
Из А можно получить четыре подматрицы порядка
определитель:
3, которые имеют нулевой
1
—6
8
0
3
—4
0
3
2
2
0
— 3
4
0
3
—4
0
3
2
2
0
— 3
4
1
— 6
8
0
3
2
2
=
з
Л
\
Л.
—6
я
О
= 0.
Из этой же матрицы можно получить восемь подматриц порядка 2, включая матрицу
Г о в I ' определитель которой равен 3^0. Следовательно, ранг А равен 2.
354

Требуются более простые способы нахождения ранга матрицы; понятие
эквивалентности матриц дает нам один из них. Прежде всего сформулируем
простую теорему:
Все эквивалентные матрицы имеют'одинаковый ранг и, обратно,
все матрицы, имеющие одинаковый ранг, эквиваленты.
Доказательство, Если А и В эквивалентны, то В получается из А
применением к А последовательности элементарных преобразований, ни одно
из которых не превращает ненулевой определитель подматрицы в нулевой
и наоборот. Следовательно, подматрицы матриц А и В имеют качественно
одинаковые определители (нулевые или ненулевые), и поэтому ранги А и В
равны. Далее, если матрицы А, В, ... эквивалентны матрице Dr ранга г,
то их ранг равен г. Обратно, если А и В имеют одинаковый ранг г, то в таком
случае каждую из них можно свести к эквивалентной матрице Dr. По
свойству III эквивалентности матриц, А и В эквивалентны. Следовательно, если
данная А приводится к эквивалентной матрице Dr, то ее ранг равен г. Мы
знаем, что ранг квадратной неособенной матрицы порядка п равен гс, поэтому
она эквивалентна Dn = I порядка п. Отсюда:
Все неособенные матрицы данного порядка п эквивалентны, и каждая
из них получается из I того же порядка п применением
элементарных преобразований.
Теперь наконец мы получили важное условие эквивалентности матриц.
Рассмотрим матрицу А размерности т X п. Применяя к А отдельные
элементарные преобразования, мы получим эквивалентные ей матрицы E(rs)A,
H(rS)A и К(Г)А. Последовательность таких элементарных преобразований
превращает А в эквивалентную ей матрицу РА, где Р{— некоторая матрица
порядка т, являющаяся произведением элементарных матриц. Аналогично
этому последовательность элементарных преобразований над столбцами А
превращает ее в эквивалентную матрицу AQ, где Q порядка п. Если
элементарные преобразования применяются одновременно к строкам и столбцам
А, она превращается в эквивалентную ей матрицу PAQ, где Р порядка т
и Q порядка п являются произведениями элементарных матриц. Поскольку
все неособенные матрицы, согласно вышесказанному, этого типа, то Р и Q
можно рассматривать просто как любые неособенные матрицы
соответствующего порядка. Следовательно:
Матрицы А к В размерности т X п эквивалентны, если и только
если В = PAQ, где Р порядка т и Q порядка п суть неособенные
матрицы.
Рассмотрим множество Smn всех матриц данной размерности т X п,
являющееся векторным пространством, в котором не определено
произведение (если тфп). Отношением эквивалентности для матриц А и В, то есть
В = PAQ, где Р и Q — неособенные матрицы, можно воспользоваться для
разбиения* Smn на подмножества. Это есть общее свойство отношения
эквивалентности, и способ разбиения в данном случае описать очень легко.
Возьмем любую матрицу А из множества Smn и найдем все эквивалентные ей
матрицы В = PAQ для различных неособенных матриц Р и Q. Мы получим одно
подмножество. Возьмем теперь другую матрицу из?тп, не относящуюся к
первому подмножеству, и найдем все эквивалентные ей матрицы. Мы получим
второе подмножество. Этот процесс продолжается, пока мы не исчерпаем все
множество Smn. Полученные нами подмножества называются классами
эквивалентности матриц т Хп. Так как эквивалентные матрицы имеют
одинаковый ранг, то все матрицы, принадлежащие к данному классу
эквивалентности, имеют одинаковый ранг. Классы эквивалентности, содержащие матрицы
ранга 0, 1,2, ..., можно обозначить соответственно через So, Sx, S2, ... . Часто
бывает полезно выделить для каждого класса матрицу-представителя,
которая бы выражала его каноническую форму. В данном случае лучшим
кандидатом является матрица Dr ранга г, являющаяся канонической формой класса
эквивалентности Sr, содержащего матрицы ранга г. Подытожим теперь
полученные результаты:
355 23*

Все матрицы размерности т X п образуют некоторое векторное
пространство Smn, в котором не определено произведение (если тфп). Две
матрицы А и В эквивалентны и имеют одинаковый ранг, если и только
если В = PAQ, гдеР «Q — неособенные матрицы. Векторное
пространство Smn можно разбить на классы эквивалентности SQ, S±, S2, ..., где
Sr содержит все эквивалентные матрицы ранга г и выражается
канонической формой
Lo
о
о
где 1Г есть единичная матрица порядка г.
Это все, что можно сказать о матрицах общей формы. Однако, когда мы
рассматриваем квадратные матрицы, можно обнаружить ряд специфических
свойств и особенностей. Этим мы займемся в следующем разделе.
Задачи и упражнения
1. Дана любая матрица А порядка 3. Вычислить РА, где
Р —
[ft О 01
0 0 1,
0 1 OJ
и показать, что РА равна матрице А, у которой первая строка умножена на к, а две
другие строки переставлены.
2. Показать, что если применять элементарные преобразования только к
строкам, то
эквивалентна
эквивалентна
1
0
-0
1
1
0
1-
2
0
0-
Указать, какие преобразования делаются на каждом этапе. Чему равен ранг
этих матриц?
2 -31
4 —6 I к эквивалентным матрицам D и по-
-6 9|
Г1 1 П Г 1 1
3. Привести 1 1 1 и 2 I.
Ь 1 1J L-3 -(
казать, что ранг каждой из матриц равен 1.
4. Показать, что О является единственной матрицей ранга 0.
5. Дана кососимметрическая матрица А ф О. Показать, что некоторые из ее
подматриц порядка 2 всегда будут неособенными, то есть иметь ненулевой определитель
и, следовательно, ранг А равен г > 2.
6. Дана матрица А
Г1 'а ЬЛ
= 0 1 с .
Lo о ij
Показать, какими различными элементарными
преобразованиями эту матрицу можно сделать эквивалентной I. В зависимости от
выбранных преобразований выразить А в форме PI, IQ и PIQ.
7. Показать, что
12 1 3 —51 Г1 —3 5 21
1—35 2 эквивалентна 0 7 —79
0 —7 7 9J [О 0 0 0J
и, следовательно, ее ранг равен 2.
Проверить, чго ранг матрицы А меньше 3, вычислив определители всех ее подматриц
порядка 3.
12.9. КВАДРАТНЫЕ МАТРИЦЫ
Из всего изложения матричной алгебры уже должно быть ясно, что
с квадратными матрицами обращаться легче, чем с прямоугольными, ибо
они в большей мере удовлетворяют системе алгебраических правил.
Простейшими из квадратных матриц являются неособенные, имеющие определитель,
отличный от нуля.
356

Все выводы в отношении ранга и эквивалентности любых матриц тХ п,
полученные в предыдущем разделе, справедливы и для частного случая
квадратных матриц данного порядка п. Так, любая квадратная матрица А
порядка п и ранга г эквивалентна квадратной диагональной матрице Dr,
содержащей на своей диагонали г элементов, равных 1, и п — г нулевых
элементов. В частном случае, если А — неособенная матрица ранга п, то она
эквивалентна единичной матрице I порядка п. В этом разделе мы будем
изучать дальше общие свойства квадратных матриц и частные свойства
неособенных матриц.
I. Квадратные матрицы вообще. Рассмотрим множество Snn всех
квадратных матриц порядка п. Это множество является векторным пространством,
замкнутым в отношении сложения и умножения на скаляр, в котором также
определено для всех матриц и произведение. В данном случае для умножения
матриц справедливы такие правила: замкнутость (Ml), ассоциативность
(М2), существование идентичности (единичного элемента) (М4) и
дистрибутивность (D). Выполнение этих правил является минимумом, вполне
достаточным для того, чтобы Snn классифицировать как линейную алгебру. Это
множество иногда обозначают Мп (Р)*гще п указывает порядок квадратных
матриц, a. F — поле (в данном случае вещественных чисел), из которого
берутся скаляры. Единственный «недостаток» этого множества, что оно
вообще не коммутативно в* отношении умножения и что в нем нет обратных
величин для всех его членов.
Отношение эквивалентности между квадратными матрицами А и В
выражается в виде В = PAQ, где Р и Q — некоторые неособенные матрицы
того же порядка, что А и В; оно позволяет разделить Snn на подмножества
*У0, Sl4 S2, •••? Sn классов эквивалентности. Класс Sr содержит все матрицы
ранга г, и его канонической (или представительной) формой является
диагональная матрица Dr. Класс Sn включает в себя все неособенные матрицы
порядка п, а его канонической формой является единичная матрица I.
Если вместо матрицы Q взять Р (а это всегда возможно, так как Р —
неособенная матрица), то мы получим частный случай отношения
эквивалентности между матрицами, а именно понятие подобных матриц.
Определение. Квадратные матрицы А и В называются подобными,
если В = РАР, где Р — неособенная матрица того же порядка,
что А и В.
Если неособенная матрица Р дана, то В = РАР дает единственное
отношение между любой квадратной матрицей А и ее подобным
«изображением» В. С этой точки зрения В можно назвать преобразованием А с помощью
данной матрицы Р, которое является единственным. С другой стороны, если
дана матрица А, то все матрицы В, подобные ей, получаются при разных
матрицах Р. Так как подобие матриц является частным случаем
эквивалентности, то все подобные матрицы имеют одинаковый ранг. Однако обратное
утверждение не справедливо: не все матрицы, имеющие одинаковый ранг,
подобны друг другу. Отношением подобия матриц можно воспользоваться
для дальнейшего подразделения классов эквивалентности ?0, дУх, аУ2» •••» Sn,
на которые разбивается множество Snn.
Важно отметить, что если бы произведение матриц было коммутативным,
то в выражении В = РАР матрицы Р и Р взаимно уничтожатся,
и матрицы А и В равнялись бы друг другу. Однако в матричной алгебре
матрицы вообще не коммутативны в отношении умножения, и поэтому
выражением В = РАР матрицы А и В могут быть описаны только как
подобные, но не как равные. Однако в отношении определителей, являющихся
скалярами, мы не испытываем подобного затруднения, и подобные матрицы
имеют равные по величине определители А и В. Доказательство элементарно:
в = j pap-1 | = | р 11 а 11 р-11 = i^-UAL = ^.
Следовательно, если неособенные матрицы подобны, то можно сказать, что
их «размер» одинаков в том смысле, что их определители равны. Что касает-
357

ся особенных матриц, подобных или нет, то их определители, как мы знаем,
равны нулю.
Подобные матрицы имеют очень разнообразное применение. Одно из
них связано с так называемой «диагонализацией» любой квадратной матрицы,
что мы рассмотрим в разделе 13.4.
II. Неособенные матрицы. Рассмотрим неособенную матрицу А порядка
п. Из всего, что мы пока знаем, можно сказать, что А имеет ненулевой
определитель А, ее ранг равен и, и она эквивалентна единичной матрице I порядка
п. Далее нам известно, что А имеет обратную себе матрицу А, то есть
произведение неособенных матриц удовлетворяет закону (М5), и возможно
деление. Может показаться, что множество всех неособенных матриц данного
порядка есть даже лучшая линейная алгебра, чем множество всех
квадратных матриц. Однако это не так. Выигрыш в отношении умножения
компенсируется потерями со стороны сложения, так как множество неособенных
матриц перестает быть замкнутым в отношении сложения: при сложении
двух неособенных матриц не обязательно получается неособенная матрица.
Наоборот, очень часто результатом такого сложения оказывается особенная
матрица. Приведем простой пример:
Г1 11 Г-1 0] ГО 1]
[о iJ + L о -1J~|_о ojs
Определитель каждой из матриц в левой части равен 1, а определитель
матрицы-суммы равен нулю.
Следовательно, множество неособенных матриц перестает быть
векторным пространством. Его значительно легче рассматривать с точки зрения
только одного бинарного действия — умножения матриц. В этом случае
множество неособенных матриц оказывается некоммутативной группой в
отношении умножения; за единственным исключением — закон коммутативности
(МЗ) — для него справедливы все правила умножения. Это множество иногда
называют полной линейной группой и обозначают Ln (F), где F — поле,
из которого берутся скаляры (в данном случае вещественные числа).
Когда рассматриваются неособенные матрицы, наибольшее внимание
концентрируется на матрице А, обратной А. При решении многих
практических задач приходится находить обратные матрицы очень большого
порядка, а это трудная вычислительная работа. Все, что мы можем сделать здесь,
это дать метод нахождения А, не прибегая к определению, на основе
которого искать обратную матрицу очень трудоемко. Предположим, что нам
известны элементарные преобразования, которые превращают матрицу А
в эквивалентную ей единичную матрицу I. Применяя эти же преобразования
к I, мы и получим матрицу А, обратную А. Приведем пример.
Пример (а)
°1
А = I 0 1 2 I эквивалентна I 0 1 2 1 эквивалентна
[1 2 3*1 Г1 0
0 12 эквивалентна 10 1
0 0 lj [О 0
В данном случае элементарные преобразования таковы: 1) вычитаем первый
столбец, помноженный на 2 и на 3, соответственно из второго и третьего столбцов;
2) второй столбец (полученный после первого преобразования), помноженный на 2,
вычитаем из третьего столбца. Применим те же преобразования к I:
[1 0 01 Г1 -2 —31 Г1
0 10 эквивалентна 0 1 01 эквивалентна I 0
0 0 lj [0 0 lj [о
Этот результат мы уже получили в разделе 12.7, пример (б).
III. Ортогональные матрицы. В разделе 11.6, пункт VII, мы приводили
пример линейного преобразования:
ух = хг cos 0 + х2 sin 0 и у2 = -— хг sin 0 + х2 cos 0
358

от двумерного вектора (хг, х2) к двумерному вектору (ylf у2). Характерной
чертой этого преобразования является то, что оба вектора представляют
одну и ту же точку пространства, если только имел место поворот
координатных осей на угол 0. Таким образом, это преобразование показывает
изменение координат любой точки пространства при повороте координатных осей
на угол 0. Следовательно, в результате такого преобразования все
расстояния и углы в пространстве остаются совсем незатронутыми. Эти свойства
пространства инвариантны относительно линейного преобразования.
Приведенное нами линейное преобразование является одним из примеров
ортогонального преобразования, а его матрица
[cos0 sin 01
— sin0 cos0J
есть частный случай ортогональной матрицы, являющейся одним из видов
неособенной матрицы. Теперь нам остается обобщить эти понятия.
Определение. Неособенная матрица А является ортогональной
только тогда, если матрицы, обратная ей и транспонированная,
совпадают, то есть
А-^А'.
Поэтому это условие можно выразить так:
Перечислим основные свойства ортогональной матрицы А = [ars] порядка п.
а) Определитель ортогональной матрицы Л = ± 1.
Доказательство. |А| | А'| = |1| = 1, так как АА' = 1 (по определению
ортогональной матрицы). Но поскольку и |А| и |А'| равны А, то Л2 = 1
ЙЛ = ±1.
б) Сумма квадратов элементов любой строки А равна единице:
в) Сумма элементов одной строки А, умноженных на соответствующие
элементы другой строки, равна нулю:
Докажем свойства (б) и (в). Напишем вектор аг = (а1, а2, ...,ап),
являющийся г-й строкой А, и рассмотрим произведение АА\ Элемент (г, г)
этого произведения есть скалярное произведение r-й строки А и г-го
столбца А', каждый из которых является вектором аг. Точно так же
элемент (г, s) есть скалярное произведение векторов аг и as. Но так как
АА' = 1, то диагональный элемент (г, г) равен 1, а внедиагональный
элемент (г, s) равен 0. Итак,
п
arar = 2а?* = 1
t=i
V. 2rA«
Последнее выражение означает, что если любые разные строки
ортогональной матрицы А рассматривать как векторы, то последние будут
находиться под прямым углом (ортогональны).
Два последних свойства справедливы и для столбцов ортогональной
матрицы. (Это легко доказать, если принять во внимание, что и А'А=1.—
Ред.)
Рассмотрим: теперь линейное преобразование у = Ах от /г-мерных
векторов х к гс-мерным векторам у, где А —ортогональная матрица. Это пре-
359

образование, так же как и матрица, называется ортогональным. Пусть
х19 х2, .... представляются точками Р1? Р2,... в /г-мерном евклидовом
пространстве, в котором определены понятия расстояния и угла:
Длина ОРг: OP\^xvx%.
Угол 9 между ОР± и ОР2: cos8 = -*)*** , ,
I Xl I I Х2 I
где \х1\2 = ОР1 = х1х2, и аналогично для |х2|2 (см. 11.4). Теперь
предположим, что у1э у2, ... представляются точками Qx, Q2, ... в другом
/г-мерном пространстве, полученном в результате преобразования у = Ах.
Напишем произведение двух векторов (см. 12.6):
у{у2 = (Ахг)' (Ах,) = х;А'Ах2 = x;ix2 = Х;х2,
так как А — ортогональная матрица, и поэтому А'А = 1. Но произведение
х[х2 равно скалярному произведению хх-х2, и аналогично у^у2 = У1*У2*
Следовательно, скалярные произведения — инвариантны в отношении этого
линейного преобразования: х1-х2 = у1-у2, а из этого сразу следует, что и углы
и расстояния—также инварианты в отношении ортогонального
преобразования:
и
Приведем пример.
Пример (б)
Матрица Р =
1
-/2"
/б /3
1 1
/2 /б
/б /3 .
ортогональная, так как РР' = /.
Легко также проверить свойства ортогональной матрицы*
Свойство а)
I р | —_J__ f * 1,2 1
V* /в
^_ i_j__ _
/2 Ч/б VT /6" /з"
/2 /18
Свойство б) Проверим, например, для первой строки Р:
4/2
Свойство в) Перемножим элементы двух первых строк Р:
1 \/ 1 \ ( 1 \/ 1 л / 1 >, / 1
1 j 1
IV. Неразложимые матрицы. Рассмотрим данную матрицу А порядка п
и данную перестановочную матрицу Р* (являющуюся, следовательно,
ортогональной). Предположим, что матрица А преобразуется с помощью
перестановочной матрицы Р* в следующую блочную форму:
О
*
где Ах —матрица порядка г (г < гг), и, следовательно, А2 —матрица порядка
п — г, а в верхнем правом углу находится блок любых элементов, обозна-
360

чаемый символом * и имеющий размерность гх(^-г). В этом случае
матрица А называется разложимой. Если же нельзя найти такой
перестановочной матрицы Р*, то матрица А называется неразложимой.
Следовательно, неразложимой является такая матрица, в которой
никакими перестановками строк и последующей соответственной
перестановкой столбцов нельзя получить в левом нижнем углу блок из нулевых
элементов. Любую другую (следовательно, разложимую) матрицу А
перестановкой строк и столбцов можно превратить в блочную матрицу, у
которой вдоль главной диагонали будут расположены неразложимые матрицы.
Для этого сначала нужно, как это сделано выше, превратить А в Art.
Если в этом случае матрицы Ах и А2 окажутся неразложимыми, то мы
получим желаемый результат. Если же хотя бы одна из них будет
разложимой, то ее в свою очередь можно разложить на отдельные блоки. Этот
процесс продолжается до тех пор, пока наконец А не превратится в
матрицу такого вида:
"А,
0
0
* :
A2j
0 1
i *
i *
|Аь.
где А1? А2, ..., Ak — неразложимые квадратные матрицы (в частном случае
это могут быть отдельные элементы), расположенные вдоль главной
диагонали. По одну сторону от диагонали в этой матрице расположены
нулевые элементы, а по другую —любые элементы (включая и нулевые.— Р)
Приведем пример разложимой матрицы 4x4:
0
0
0
1
3
1
0
4
2
2
1
3
1"
0
0
2
ТТТЮТ1Т1ЯТТТЯОГГГ* Я" "R
U.yj\5DjJaLUlcXKil.vjji в
0
1
0
0
1
2
0
0
2
3
1
2
3
4
0
1
Разложение достигается перестановкой второй и четвертой строк и второго
и четвертого столбцов. Блок Г. 2 1 неразложим, а блок [2 i ] можно
разложить дальнейшей перестановкой строк и столбцов. Если это сделать,
то первоначальная матрица А превратится в эквивалентную:
0
1
0
0
1!
2|
о!
01
2
о
1
0
з -
4
2
1
где I , 2 , 1 и 1 — неразложимые блоки, расположенные вдоль
главной диагонали.
Задачи и упражнения
1. Показать, что неособенную матрицу А =
run
010
LooiJ
можно получить элементарными
Г1-1-П
= 0 1 0
Lo о ij
преобразованиями из I. Найдя эти преобразования, доказать, что А =
2. Даны две квадратные матрицы А и В одинакового порядка, такие, что АВ = 0.
Показать, что если | А | ф 0, то В=0. Какие еще могут быть возможности? Ответив
на этот вопрос, показать, что если А и В—квадратные матрицы и такие, что АВ=0,
то или А=0, или В=0, или и А и В—особенные матрицы.
о „ | cos0 sin 9]
3. Показать, что есть ортогональная матрица, и проверить ее
L — sin в cos9J
свойства III*
361

4. Показать, что если А и В—ортогональные матрицы, то А', А и АВ—также
ортогональные матрицы.
5. Показать, что в определении подобных матриц последовательность матриц
в РАР может быть обратной, то есть вместо РАР можно записать РЧАР.
6. Если В=РАР', где А—квадратная матрица и Р—неособенная матрица,
показать, что те же элементарные преобразования (характеризуемые Р), примененные
к строкам и столбцам, превращают А в В.
1 1 .
7. Проверить умножением, что
/2
1
1
/2 /2 J
ГО I
Li o
/2
1
1
L/2 /2 J.
Г1 ОП ГО 11
= I q . , и вывести отсюда, что симметрическая матрица . ~ подобна
диагональной матрице 0 .
8. В одном из столбцов матрицы А порядка п на главной диагонали стоит h,
а на других местах этого столбца—нули. Показать, что матрицу А с помощью
перестановочной матрицы Р* можно преобразовать в
где At —матрица порядка п — 1. Почему этого нельзя сделать, если элемент h
находится не на главной диагонали? Сформулировать вывод, исходя из понятия
разложимой матрицы.
9. Показать, что матрица А из предыдущего упражнения эквивалентна
и что та же матрица, но с элементом h не на главной диагонали, также может быть
выражена эквивалентной матрицей такой же формы. Исследовать, исходя из этого,
границы преобразования с помощью перестановочной матрицы.

ГЛАВА 13
ПРИМЕНЕНИЕ ВЕКТОРНОЙ И МАТРИЧНОЙ АЛГЕБРЫ
13.1. ЛИНЕЙНАЯ КОМБИНАЦИЯ И ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
Понятия линейной комбинации и линейной зависимости применимы
к самым различным элементам совокупности {х^ х2, xz, ...}, если только
последние можно умножать на скалярные числа и складывать. Линейной
комбинацией элементов хх, ж2, х3, ... называется
X = /л ^г^Г'
г
где кг, А,2, Я3, ... —некоторые скалярные числа. Система {х^ #2, #3, ...}
является линейно зависимой, если хотя бы один элемент этой системы
представляет собой линейную комбинацию остальных. Понятия линейной
комбинации и линейной зависимости особенно важны, можно даже
сказать, существенно необходимы при рассмотрении систем векторов и матриц.
Как и в главе 11, векторами мы называем упорядоченные наборы т
вещественных чисел, отображаемых (относительно неподвижных осей
координат) точками в иг-мерном декартовом или евклидовом пространстве.
Рассмотрим систему п таких векторов, x(ft> = #<ft>, #(ft>, ..., х&\
представленных точками Pk (А:= 1, 2, ..., п). Векторы будут линейно зависимыми,
если можно подобрать такие скалярные числа ik, которые не все равны
нулю, что
Тогда если kt — последнее из ненулевых чисел X, то вектор х<*>
является линейной комбинацией предыдущих векторов системы
хШ=-хг2 ****>. B)
ft=l
Здесь A) и B) различными способами выражают одно и то же. Более
того, равенство B) можно записать для любого вектора x<ft> — при том лишь
условии, что соответствующее число Xk Ф 0. С другой стороны, если такие
числа подобрать нельзя и равенство A) возможно лишь в том случае,
когда все ^ = 0, то векторы линейно независимы, и ни один из них
не является линейной комбинацией остальных векторов системы.
Смысл линейной зависимости станет более ясным, если A) записать
в развернутом виде:
m ~г ^2^w "t" ^^m —
~г ^2*^w "t" • • • i
Тогда, если Хп Ф 0, то факт, что х<п) является линейной комбинацией
остальных векторов, в соответствии с уравнением B) описывается систе-
363

мой т уравнений:
+...)>
Соотношения A) и B) верны для каждого компонента в отдельности.
Рис. 40 является иллюстрацией для случая двумерных векторов.
Три точки Рх, Р2 и Р3 отображают на плоскости заданные векторы
хA) = (х{*\ а^), хB) = (я^2), х™) и хC) = (жA3), х™), отнесенные к осям Охх
и Ox2J на которых единичные координатные векторы е1 = A, 0) и 82 = @, 1)
отмечены точками Ах и А2. Как видно из рис. 40, Р3 является линейной
комбинацией векторов Рг и Р2. В соответствии с правилом
параллелограмма, ОР3 представляет собой сумму векторов OQX и OQ2, где точки Qx
и Q2 расположены соответственно
на отрезках ОРг и ОР2. Пусть
Тогда
или
Это — геометрический эквивалент
линейной комбинации
и, следовательно, соотношения
линейной зависимости
ос*
Рис. 40.
В данном случае линейная
зависимость системы трех векторов
характеризует то условие, что отрезки ОР^ ОР2 и ОР3 раздельны, то есть не
лежат на одной прямой. Однако линейная зависимость возможна и в том
случае, если две или все три точки лежат на одной прямой с точкой О.
Например, если OPi и ОР2 расположены на одном и том же луче прямой,
исходящем из точки О, то ОР2 = WPi, где Я — соотношение длин
отрезков. Тогда линейная зависимость выражается формулой ЪеA> — асB> = 0.
В этом случае не имеет значения, что в уравнении отсутствует третий
вектор: один из множителей X равен нулю, остальные два нулю не равны.
Из этого можно сделать вывод, что в двумерном пространстве линейная
зависимость существует между любыми тремя векторами. Очевидно также,
что два вектора в этом пространстве могут быть, а могут и не быть линейно
зависимы. Если ОРг и ОР2 расположены на одной прямой, то векторы
линейно зависимы, в противном случае линейно независимы. И, в самом деле,
в двумерном пространстве всегда можно подобрать два линейно независимых
вектора, в частности единичные координатные векторы О Ах и ОА%, —на
которые «натянуто» это двумерное пространство.
Эти результаты можно распространить да случай векторов в трехмерном
или многомерном пространстве. Во-первых, сформулируем следующее
определение: будем говорить, что векторное множество V «натянуто» на
некоторую систему п независимых векторов, если каждый из векторов множества
V является линейной комбинацией этих п векторов. Тогда:
364

Пусть V есть векторное множество в т-мерном пространстве.
Можно утверждать, что существуют системы т векторов, которые
линейно независимы и на которые «натянуто» множество V. Система,
состоящая из менее чем т векторов, также может быть линейно
независимой, но множество V на нее «натянуто» уже быть не может.
На систему, состоящую из более чем т векторов, множество V также
может быть «натянуто», но линейно независимой система уже
являться не может.
Существование системы т векторов, удовлетворяющих поставленным
условиям, доказывается тем обстоятельством, что множество V может быть
«натянуто» на линейно независимую систему единичных координатных
векторов eL, e2, ..., ет. Такая система твекторов, называется базисом множества
V. Система единичных координатных векторов представляет собой один из
базисов; существуют вообще и многие другие базисы.
Линейную зависимость применительно к матрице А = [ars] размерности
тхп можно рассматривать двояко: во-первых, по отношению к п столбцам
в w-мерном пространстве:
as = (als> a2s> • • • ' ams) (S = ly 2, ..., 7l)\
я, во-вторых, по отношению к т строкам в га-мерном пространстве:
а; = (аг1, аг2, ..., агп) (г=1, 2, ..., т).
Система п столбцов является линейно зависимой, если можно
подобрать такие числа Xs, из которых не все равны нулю, что
2*А = <>, C)
или, в развернутой записи,
Mil + ^12 + - • - + Кп1п = О»
Х2а22 •+- .. . + Кга2п — О,
Kaml + Vm2 + • - • + Катп = °-
Если каждый 5-й столбец матрицы А умножить на число \, а затем
произвести суммирование элементов по горизонтали, то результатом явится
столбец, все элементы которого (правые части) равны нулю. Если матрицу А
рассматривать как таблицу с двойным входом (как шахматную балансовую
таблицу) и каждый s-ik столбец этой таблицы соответственно умножить
на ^8, а затем произвести суммирование элементов по горизонтали, то
правый столбец (столбец итогов) будет состоять лишь из нулей; значит,
подобрав соответствующие числа —множители, можно добиться того, чтобы
суммирование элементов матрицы по горизонтали давало итоги, сплошь
равные нулю.
Соотношение C) можно записать более сжато в матричных
обозначениях. Пусть ^ — га-мерный вектор-столбец, элементы которого К±, Я2, ..., %n.
Тогда линейная зависимость между столбцами матрицы А выразится так:
А1 = 0 или ГА' = 0 (кФ 0). D)
Соответственно этому, условие существования линейной зависимости
между строками матрицы А заключается в том, что можно подобрать
такой вектор-столбец р, имеющий т элементов \iv \i2, ..., |лт, из которых
не все равны нулю, что
m
2Мтаг = 0, то есть А'|ш = 0 или ju/A = O (jx Ф 0).
365

Это соотношение соответствует C) и D) для столбцов матрицы.
Определение: В матрице А размерности т X п столбцы линейно
зависимы, если можно подобрать такой я-мерный вектор-столбец % Ф О, что
и строки линейно зависимы, если можно подобрать такой тгг-мерный вектор-
столбец |Л Ф О, что
На основании выводов, полученных при рассмотрении линейной
зависимости векторов, можно установить некоторые свойства матриц. Если
в матрице А число столбцов превышает число строк, то число столбцовых
векторов больше, чем их размерность т. Следовательно, между столбцами
при п > т должно существовать по меньшей мере одно соотношение линейной
зависимости. Предположим теперь, что п столбцов матрицы А являются
линейно зависимыми. Тогда один из столбцов этой матрицы является
линейной комбинацией других столбцов, то есть представляет собой сумму других
столбцов, умноженных на постоянные множители. Выполнив элементарное
преобразование — вычитание из одного столбца линейной комбинации
других (см. 12.8),— можно показать, что матрица А эквивалентна матрице В,
один из столбцов которой — нуль-столбец. Ранг матрицы В меньше, чем
/г, и так как эквивалентные матрицы имеют один и тот же ранг, то таким же
будет и ранг матрицы А. Аналогичные выводы можно сделать и для строк
матрицы А. Это иллюстрируется двумя примерами.
Пример (а)
Г1 2 21 Г1 2 01
Матрица А= 2 4 4 эквивалентна матрице 2 4 0, ранг которой равен 2»
L2 1 4J [2 1 0j
Здесь выполнено следующее преобразование: из • третьего столбца вычтен удвоенный
первый столбец. Три вектор-столбца матрицы А суть:
а1=A, 2, 2), а2=B, 4, 1), а3=B, 4, 4),
и они связаны между собой одним соотношением линейной зависимости
2а!—а3=0,
в котором множители X равны: Я-1 = 2, Х2=0, Х3=—1. Это попросту выражает то
обстоятельство, что элементы третьего столбца суть удвоенные элементы первого
столбца.^ В матрице А (порядок которой равен 3, а ранг 2) два столбца (первый
и второй) линейно независимы, а один столбец (третий) линейно зависим от них.
Пример (б)
[12 2— П Г1 2 0 01
2 4 4 —2 I эквивалентна матрице 12 4 0 0, ранг которой равен 2.
2 1 4 lj [2 1 0 0J
Четыре вектора-столбца ах = A, 2, 2), а2 = B, 4, 1), а3 = B, 4, 4), а4=(—1, —2, 1)
связаны между собой двумя соотношениями линейной зависимости:
2а!—а3 = 0 (Я,1=2, А,2=0, Я3=—1, Я4=0),
«1—а2—а4=0 (&! = !, Я2=—1, А,3 = 0, Я4= — 1).
Они выражают то обстоятельство, что элементы третьего столбца суть удвоенные
элементы первого столбца и что элементы четвертого столбца суть разности между
элементами первого и второго столбцов. Матрица А размерности 3x4. Поэтому ее столбцы
должны быть линейно зависимыми. И, в самом деле, ранг этой матрицы равен 2. Она имеет
только два линейно независимых столбца, а два другие столбца линейно зависимы от
первых двух.
Несомненно, имеется связь между существованием линейной
зависимости и рангом матрицы. Этот вопрос следует рассмотреть более подробно.
Пусть А — квадратная матрица п-го порядка, и ее ранг равен г< п.
Во-первых, если ее столбцы линейно зависимы, то матрица А эквивалентна матрице
В, все элементы одного столбца которой равны нулю, и ранг матрицы А, то
есть г, меньше, чем п. И обратно, если ранг матрицы А равен г<п, то между
366

столбцами этой матрицы существует линейная зависимость. Матрица А
содержит квадратную подматрицу А1? порядок которой равен г, причем
определитель этой матрицы | А21 =#= 0. Прибавим к матрице Аг строку и столбец,
взятые из матрицы А; получим квадратную подматрицу А2, порядка г + 1,
определитель которой | А21 =0, поскольку ранг матрицы А равен г. Возьмем
/•-мерный вектор h, элементами которого являются г + 1 алгебраических
дополнений элементов строки, добавленной для образования подматрицы
А2, и п — г — 1 нулевых элементов. Поскольку | А2| =0, то, разлагая
матрицу А2 по элементам добавленной строки, мы можем записать, что АХ =0.
Не все элементы вектора % равны нулю, так как одно из алгебраических
дополнений соответствует определителю |А1|=^0. Следовательно, столбцы
матрицы А линейно зависимы, что и следовало доказать.
Далее ясно, что в приведенном выше доказательстве именно
добавленный в матрицу А2 столбец линейно зависит от г столбцов матрицы Ах. В
качестве добавляемого столбца можно выбрать один из (п — г) столбцов матрицы
А. Следовательно, в матрице А имеется (п — г) столбцов, каждый из которых
линейно зависим от остальных г столбцов, несвязанных между собой
линейной зависимостью.
Хотя это предложение доказано для квадратной матрицы А, его легко
распространить на случай любой прямоугольной матрицы т X п (т Ф п),
где либо число столбцов превышает число строк, либо число строк превышает
число столбцов. Эти избыточные столбцы (или строки) должны представлять
собой линейные комбинации остальных столбцов (или строк). Полученные
результаты для квадратной матрицы мы попросту распространяем на
прибавляемые к этой матрице линейные комбинации ее столбцов или строк.
Следовательно:
Линейная зависимость между столбцами матрицы
Пусть матрица т X п имеет ранг г. Из этой матрицы всегда
можно выделить г линейно независимых столбцов, однако любая
система г+ 1 столбцов является линейно зависимой. Если г < п, имеется
по меньшей мере одна система линейно зависимых столбцов; если (нее
г = п, все столбцы матрицы линейно независимы.
Совершенно такой же результат можно получить и для строк матрицы.
Неособенная матрица предстает перед нами во всей своей простоте
и удобстве. Если квадратная матрица и-го порядка является неособенной,
то ее ранг г = п, и «лишних» строк или столбцов не имеется. Точнее говоря,
в неособенной матрице все столбцы и строки линейно независимы, и, наоборот,
лишь в матрице подобного вида не существует линейной зависимости между
столбцами или строками.
Для любого другого вида матрицы — будь то квадратная особенная
или же прямоугольная, имеющая неодинаковое число строк и столбцов, —
должна существовать линейная зависимость либо между столбцами, либо
между строками, либо и между столбцами и между строками. Вообще говоря,
в любом случае, когда число столбцов (строк) превышает ранг матрицы,
избыточные столбцы (строки) являются линейной комбинацией остальных.
Из матрицы ранга г всегда можно выделить квадратную подматрицу г-го
порядка с линейно независимыми строками и столбцами; все остальные
строки и столбцы являются линейно зависимыми.
Задачи и упражнения
1. Даны четыре трехмерных вектора. Отобразим их в виде точек в
пространстве и предположим, что последние являются вершинами объемного тела—тетраэдра.
Показать, что один из векторов может быть представлен в виде линейной
комбинации остальных трех. Рассмотреть особый случай, когда все четыре точки лежат в одной
плоскости или когда две или более из этих точек лежат на одной прямой с точкой 0.
2. Исследовать, существует ли линейная зависимость между строками или
между столбцами матрицы
[0 2 —1J
367
Р~4 21
5-6-1
|_0 2 —lj

12 1 3 —51
1—3 5 2
0—7 7 9J
3. Показать, что матрица А = I 1 —3 5 2| имеет одну линейно зависимую
[0 —7 7 9J
строку и два линейно зависимых столбца. Что можно сказать о транспонированной
матрице А'?
4. В матрице А размерности тхп между строками существует линейная
зависимость, множители в которой %lt Я2, ..., кт С^т Ф®)- Если матрица А преобразована
в эквивалентную матрицу В, последняя строка которой нулевая, то B = PAQ, где Р
и Q—соответствующие неособенные квадратные матрицы. Показать, что Q = I;
установить, какова форма матрицы Р.
5. В матрице А (размерности тхп) т<гс. Квадратная матрица В га-го порядка
получается в результате добавления п—m нулевых строк к матрице А. Показать,
что определитель |В| = 0 и что столбцы матрицы В линейно зависимы, а отсюда,
что линейно зависимы и столбцы матрицы А.
13.2. СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ И ЕЕ РЕШЕНИЕ
Система линейных уравнений в общем виде может быть записана
следующим образом (см. 11.2):
аих1
а21х1 + а22х2 + ... + а2пхп =
amlxl + am2x2 + . . .
или, в матричных обозначениях,
Ах = у,
где А = [ars] — матрица коэффициентов тхп, х — (х19 х29 ..., хп) — тг-мер-
ный вектор-столбец п переменных и y = (jjv 2/2> •••» У™) — вектор-столбец
заданных постоянных (правых частей) в т уравнениях.
Задача заключается в том, чтобы по заданным А и у отыскать
вектор х, то есть определить элементы х этого вектора — все или максимально
возможное их количество,— выразив их через заданные элементы матрицы А
и вектора у. Для простейшего случая двух уравнений с двумя
неизвестными это можно продемонстрировать на следующем примере:
ui + 122 = ?/! и
откуда
2 —а21а12
то есть
2/1 «12
Уг «22
«и У\
«2i Уг
«11 «12
а21 fl22
при записи с помощью определителей. Затруднения возникают только в том
случае, когда один (или более) из трех определителей равен нулю. Отсюда
ясно, что решение затруднено именно в тех случаях, когда вектор у = 0,
или матрица А (если она квадратная) является особенной, или при сочетании
обоих этих условий. Если у = 0, первые два определителя обращаются
в нуль; тождественно обращаются в нуль также элементы вектора х. Если
| А| = 0, третий определитель равен нулю, и х принимает бесконечные
значения. Если у — 0 и | А | = 0, все три определителя равны нулю, и элементы
вектора х неопределенны, так как они суть частные от деления нуля на нуль.
Положение еще более осложняется, если матрица А не является квадратной,
и число уравнений не совпадает с числом неизвестных.
Если имеется несколько линейных уравнений относительно нескольких
неизвестных с численными коэффициентами, методы решения элементарной
алгебры практически заключаются в поочередном исключении неизвестных
368

посредством отыскания значений отдельных переменных и подстановок этих
значений. Иногда это позволяет найти единственное решение, то есть
значения всех переменных. Иногда после использования всех уравнений остаются
избыточные переменные, и решение дает не абсолютные значения некоторых
неизвестных, а лишь выражает их через другие неизвестные. Это может
быть вызвано либо тем, что число уравнений меньше числа неизвестных,
либо тем, что некоторые уравнения являются линейными комбинациями
остальных. Иногда, после того как найдены значения всех неизвестных,
остаются избыточные уравнения, и возникает вопрос, совместны ли они
с использованными уравнениями. В этом случае затруднения возникают
по той причине, что некоторые уравнения могут оказаться несовместными
(или линейно независимыми) относительно других уравнений системы.
Очевидно, следовательно, что характер решения уравнения Ах— у
зависит от ранга матрицы А (например, от того, является ли квадратная матрица
А особенной) и от соотношений зависимости и совместности между
уравнениями системы. По-видимому, здесь большую роль играет понятие линейной
зависимости, сформулированное в разделе 13.1.
I. Однородные линейные уравнения: Ах = 0.
Это — случай, когда у = 0, то есть один из тех случаев, решение которых
должно представлять трудности. Уже заранее можно отметить два
обстоятельства. Всегда имеется решение х = 0, при котором все переменные равны
нулю; однако это решение является тривиальным, и им можно пренебречь.
С другой стороны, если найден вектор х, определяющий ненулевое решение,
тогда ненулевым решением оказывается и кх при любом значении к.
Следовательно, если существует ненулевое решение такой системы, оно никогда не
может быть единственным. Однородные уравнения не позволяют определить
абсолютных значений х; приходится искать лишь соотношения между
переменными либо, в общем случае, выражать некоторые переменные через другие.
Пусть в уравнениях Ах = 0 матрица А размерности т X п и ранга г.
Если столбцы этой матрицы линейно зависимы, то существует п чисел кг,
Х2, ..., Хп, из которых не все равны нулю, являющихся элементами вектора
А,, который удовлетворяет условию АХ, = 0. Следовательно, х = к является
решением системы уравнений. В этом можно вполне убедиться из
приведенных выше развернутых условий C) раздела 13.1; в однородных уравнениях
вместо неизвестных х подставлены удовлетворяющие их числа X, являющиеся
множителями (коэффициентами) в уравнении линейной зависимости столбцов
матрицы А. Следовательно, существование хотя бы одного уравнения
линейной зависимости между столбцами матрицы А влечет за собой существование
решения уравнений Ах = 0; множители в уравнениях линейной
зависимости представляют собой значения неизвестных, причем как для этих
множителей, так и для неизвестных определяются лишь соотношения между ними,
а не абсолютные их значения. Значит, в соответствии с выводами, сделанными
в разделе 13.1, условия существования какого-либо нетривиального решения
заключаются в том, чтобы г < п\ ранг матрицы А должен быть меньше числа
неизвестных (столбцов этой матрицы). Нетрудно установить следствия этого
условия. Если число уравнений меньше числа неизвестных (т < п), то г< т
иг<й во всех случаях; решения всегда существуют. Если же число
уравнений равно числу неизвестных (т = п)9 то А представляет собой
квадратную матрицу порядка п и г<и. Решение существует при г<п и |А| =0,
то есть матрица А должйа быть особенной. Необходимо исключцть случай
(при котором решение отсутствует) г — п, | А | Ф 0, А — неособенная
матрица. Если число уравнений превышает число неизвестных, возникает
аналогичное положение; в этом случае г< п < т, и необходимо исключить
случай, когда ранг матрицы А равен максимально возможному его значению п
(то есть числу переменных — или столбцов — этой матрицы).
Результат можно сформулировать таким образом:
Если Ах = 0 есть система т однородных уравнений с п
неизвестными, где А — заданная матрица т X п и ранга г, то условия суще-*
24 р. Аллен 369

ствования ненулевого решения для х заключаются в г <п. Если т <пг
решение всегда существует; прит> п решение существует в том
случае, если ранг матрицы А не равен максимально возможному его
значению, то есть если г <п.
Практически для отыскания одного или нескольких решений необходимо
из строк и столбцов матрицы А составить квадратную подматрицу г-го
порядка, определитель которой не равен нулю. Это дает г уравнений с г
неизвестными, а остальным п — г неизвестным придаются произвольные
значения. Уравнения являются неоднородными и (как показано ниже) имеют
единственное решение, в котором г неизвестных выражаются через остальные
п — г неизвестных. Тогда остальные п — г уравнений оказываются
совместными с полученным решением. Одним из важных случаев является система
п однородных уравнений с п неизвестными, если составленная для этой
системы квадратная матрица А порядка п имеет ранг (п — 1). В этом случае
одному из неизвестных придают произвольное значение, а остальные п — 1
неизвестных выражают через эту неизвестную; затем полученная система
уравнений позволяет установить отношения между неизвестными.
Мы можем продемонстрировать это на двух примерах, пользуясь теми*
же матрицами, что и в примерах (а) и (б) раздела 13.1.
Пример (а)
Г12 21
= 24 4
L2 14J
Матрица А = I 2 4 4 I имеет ранг, равный 2. Третий столбец матрицы А линейно
L214J я „
зависим от остальных столбцов. Поэтому зададимся произвольным значением х3 и на
основе первого и третьего уравнений определим хх и х2:
х1+2х2=--2х3 и 2х±+х2 =—4я3,
откуда
Второе уравнение совместно с этой системой, так как оно равносильно первому
уравнению. Следовательно, существует единственное решение, определяющее соотношения
между неизвестными:
х1:х%:х3= — 2:0:1.
Это — пример того случая, когда квадратная матрица А порядка п имеет
ранг (п — 1).
Пример (б)
х1+2х2+2хв—*4=0,
2 2 —1"]
4 4—2
14 1J
Г1
Матрица А=|2 4 4 —2| имеет ранг, равный 2. Последние два столбца матрицы
L2
линейно зависимы от двух первых; и в этом примере также можно опустить второе
уравнение как эквивалентное первому. Поэтому зададимся произвольными
значениями х3 и ж4 и на основе первого и третьего уравнений определим хг и х2\
откуда
Поскольку число неизвестных равно четырем, а ранг матрицы А равен 2, двум
из неизвестных должны быть приданы произвольные значения, после чего
определяются значения двух других.
II. Неоднородные линейные уравнения: Ах = у (у Ф 0).
В общем случае система состоит из т уравнений с п неизвестными.
Задается яг-мерный вектор-столбец правой части уравнений у; га-мернып
вектор-столбец х соответствует неизвестным переменным. Матрица А
размерности т X п, ее ранг г не превышает меньшего из двух чисел (т или п).
370

П(а). Случай неособенной матрицы. Наиболее важен и чаще всего
встречается случай системы уравнений, которой соответствует квадратная
неособенная матрица А порядка и ранга п. В этом случае число уравнений
совпадает с числом неизвестных, и | А | Ф 0. Здесь не имеется осложняющих
затруднений, и единственное решение может быть получено одним из нескольких
равносильных методов.
Метод исключения неизвестных. Одно из неизвестных мы можем явным
образом выразить через остальные неизвестные, а затем исключить
последовательно из уравнений системы путем подстановки полученного значения
этого неизвестного во все остальные уравнения. В результате этого процесса
по отношению к каждой неизвестной мы определим единственное решение
для последнего неизвестного, после чего, возвращаясь в обратном порядке
к предыдущим уравнениям, находим единственные значения остальных
переменных. Это — прямой метод, но он трудоемок.
Правило Крамера. Единственное решение можно отыскать с помощью
общей формулы:
w
2 arsArs
где As —матрица, образованная из матрицы А подстановкой вектора у
вместо 5-го столбца. Определители |Ав| и |А| разлагаются по элементам
5-го столбца, алгебраические дополнения которых в определителе |А|
суть |Ars| (r=l, 2, ..., п).
Для доказательства этой формулы умножим каждое из п уравнений
системы Ах = у на соответствующее алгебраическое дополнение А1$1 А2$, ...
..., ^4ns, а затем просуммируем полученные уравнения:
S B «rAJ*t = 2 VrK (s = l, 2,..., n).
*=1 r=l r=l
Тогда на основе правила разложения определителя:
п
2 anArs = О ПРИ s Ф *9
= |А| при s = t
Следовательно,
что и доказывает правильность формулы Крамера.
Нахождение матрицы, обратной к А. Если Ах = у, то, поскольку
| А | Ф 0, существует обратная матрица А; умножив на нее слева обе
части матричного уравнения Ах = у, получим
А1Ах = А1у
Произведение А"ХА = 1, а 1х = х; значит, решение системы есть
х = А""ху.
Таким образом, мы получаем единственное решение с помощью
умножения у на обратную матрицу А.
На практике следует пользоваться любыми приемами решения
уравнений с численными коэффициентами, позволяющими снизить до минимума
объем расчетов. Метод исключения переменных удобен только при малом
371 24*

числе уравнений. Применяя правило Крамера, необходимо вычислять
определители. Этот метод прост, но трудоемок. Путь от А к А, то есть метод
нахождения обратной матрицы, — также очень длительный процесс. В
некоторых случаях, как в приведенном ниже примере, для получения обратной
матрицы А можно применить к единичной матрице I ту же
последовательность элементарных действий, которые преобразовывают матрицу А в I.
Вообще же вычисление обратной матрицы производят в соответствии с
определенными алгоритмами на быстродействующих вычислительных машинах.
Технику нахождения обратной матрицы можно проиллюстрировать на
следующем примере.
Пример (в)
Для системы линейных уравнений
i—я2+#з = 26,
матрица А коэффициентов имеет следующий вид:
Эта матрица эквивалентна матрице:
-1 0 01
2 эквивалентна
0
1 — 1 0
1 0
1 2
Г-1 1 11
и= 1 -1 1 .
L 1 1 —ij
л це:
[ — 1 0 01 Г1 0 01
0 0 2 эквивалентна 0 10
0 2 0J [О 0 lj
эквивалентна матрице I.
Здесь произведены следующие элементарные преобразования: 1) ко второму
и третьему столбцам прибавлен первый столбец; 2) из первого столбца вычтены второй
и третий, умноженные на 1/2; 3) столбцы соответственно умножены на —1, V2, 1/2»
а затем два последние столбца обменены местами.
Проделывая те же преобразования над единичной матрицей I, мы последовательно
получаем следующие матрицы:
— 4- 0 1

эквивалентна
0 4г 4г
0 4г
4г -7г 0
Следовательно,
Т » '
4г — о
Решение системы уравнений:
11F). Особенные матрицы. Нам остается рассмотреть другие варианты,
когда матрица А квадратная, но особенная, или же А — прямоугольная
матрица. Построим расширенную матрицу В:
где к матрице А добавлен еще один столбец, элементы которого—правые части
уравнений. Матрица В размерности тх(п + 1) имеет ранг, равный либо г,
либо г + 1. Если последний столбец (столбец правых частей) линейно
зависим от столбцов матрицы А, то ранг матрицы В равен г, как и ранг матрицы
А; если линейно независим, то ранг В будет г + 1,
372

Система уравнений Ах = у может быть записана с перенесением у в
левую часть. Тогда она описывается уравнением
Bz = О,
где z есть (п + 1)-мерный вектор-столбец из элементов хх, х2, ..., хп, —1.
Это —система однородных уравнений, и, в соответствии с результатами A),
существование решения возможно лишь в случае линейной зависимости
между столбцами матрицы В. Но выполнение этого условия тоже оказывается
недостаточным. Решением (искомым вектором z) являются множители Я17
К2, ..., А,п, Яп+1из уравнения линейной зависимости. Поскольку важны только
соотношения между различными X, а не их абсолютные величины, то при
том условии, что Хп+1 Ф О, можно Яп+1 приравнять необходимой нам величине
—1. Это осуществимо лишь тогда, когда последний столбец матрицы В
(столбец у) линейно зависим от остальных столбцов, то есть если ранг матрицы В
равен г, одинаковый с рангом матрицы А. Следовательно, в первую очередь
вывод об отсутствии решения можно сделать, если ранг матрицы В равен
г + 1. Это значит, что столбец у линейно независим от столбцов матрицы
А, то есть что уравнения несовместны.
Во всех других случаях, если матрицы А и В имеют один и тот же ранг
г, решение может быть найдено. Различие между возможными вариантами
лишь в том, для какого числа неизвестных определяются абсолютные
значения, если мы придадим произвольные значения другим неизвестным,
Матрицы А и В дают квадратную подматрицу r-то порядка, определитель
которой не равен нулю. Это неособенное решение выражает единственные
значения соответствующих г неизвестных через остальные п — г
неизвестных. При этом используются только f уравнений. Однако остальные п — г
уравнений совместны с ними. Следует отметить, что г не превышает меньшую
из двух величин (тип). Только в случае неособенной матрицы г = т = п,
во всех других случаях либо г < т, либо г < п, либо действительны оба
неравенства. Если г < т, имеется «излишек» уравнений, что не вызывает
затруднений; при том условии, что матрица В имеет ранг г, эти «излишние»
уравнения являются линейными комбинациями других уравнений и совместны
с ними. Если г < п, имеется «излишек» неизвестных, что также не вызывает
затруднений, если мы придаем им произвольные значения и выражаем
выбранные нами г неизвестных через эти «излишние» неизвестные.
Таким образом, можно обобщить результаты для всех случаев, отличных
от случая неособенной матрицы. )
Система уравнений Ах = у, где матрица А размерности т X п
имеет ранг г, несовместна и не имеет решения, если ранг расширенной
матрицы В = [А | у] равен г + 1. Во всех случаях, когда ранг
матрицы В равен г, существует решение, в котором г соответственно
выбранных неизвестных определяются с помощью остальных п — г
неизвестных. Решение получается из г уравнений, а остальные п — г уравнений
не принимаются во внимание, поскольку они являются линейными
комбинациями г первых уравнений.
Два возможных варианта иллюстрируются следующим примером,
а остальные — упражнениями 6—8.
Пример (г)
Для системы уравнений
можно составить матрицы
Г1 1 1-1 Г1
: 1 _2 2 И В= 1
L2 -1 3J [2
373

ранг которых соответственно равен 2 и 3. Решения не существует, уравнения
несовместны. При сложении первых двух уравнений мы получаем
что несовместно с третьим уравнением.
Если изменить систему, а именно заменить постоянную в правой части третьего
уравнения (вместо 2 поставить 4), то система становится совместной, и третье
уравнение можно отбросить, как являющееся суммой двух других. Матрица В, правый
нижний элемент которой вместо 2 будет равен 4, будет иметь ранг 2, то есть такой же,
как ранг матрицы А. Тогда для первых двух уравнений можно получить решение:
Два неизвестных х1 и х2 выражаются через третье о?3, которому можно придать
произвольное значение. В этом случае квадратная матрица А порядка 3, а ранга 2, так
что имеется одно «излишнее» неизвестное и одно «излишнее» уравнение.
Задачи и упражнения
1. В примере (а) задаться произвольным значением а?2 и попытаться определить
значения хг и х3. По какой причине этого сделать не удается?
2. Проверить, существуют ли решения, и найти их для систем уравнений
2*1+4*.+4*,+*4=0,
2xi
=0,
Сравнить полученные решения с решениями примеров (а) и (б) в тексте.
3. Найти решение примера (в) в тексте методом исключения неизвестных
и с помощью формулы Крамера.
4. Доказать, что решение уравнения Ах=у методом умножения на обратную матрицу
(х=Ау) равносильно применению правила Крамера.
5. Показать, что
а — b — с
26
2с
2а
6 — с — а
2с
2а
26
с—а — 6
Исходя из этого, решить систему уравнений
(a — b — c) x + 2ay-\-2azz=0,
2bx-\-(b — c. — a) 2/+26z = O,
2сх-\-2су+(с— a — b) z=0.
6. Исследовать систему
2х1-\-4х2-1гх3 = —1,
«1+2*8+2*3 = 1.
Показать, что как матрица коэффициентов, так и расширенная матрица имеют один
и тот же ранг 2. Определить значение х3 и показать, что х± можно выразить через #2
и наоборот. Что произойдет, если:
а) правая часть второго уравнения будет равна не —1, а другому числу?
б) правая часть третьего уравнения будет равна не 1, а другому числу?
7. Показать, что решение системы уравнений
одинаково с решением предыдущей задачи.
Чем это можно объяснить?
374

8. Рассмотреть систему уравнений
*3 =1
и показать, что она эквивалентна неособенной системе трех уравнений с тремя
неизвестными, решение которого: х1 = 1, *2 = —1» а?3 = 1. Сравнить эту систему уравнений
с системой из упражнения 6.
13.3. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
Преобразованием называется отображение одного множества объектов
на другое множество объектов. Для линейного преобразования наиболее
общим является следующее определение: отображение одного множества
векторов на другое множество, при котором линейная комбинация векторов
первого множества отображается подобной же линейной комбинацией
векторов второго множества. Здесь мы рассматриваем лишь векторы,
представляющие собой упорядоченные наборы п вещественных чисел, или же точки
в гс-мерном декартовом пространстве. Возьмем некоторый базис этого
пространства (систему единичных координатных векторов); положение точек
определяется относительно неподвижных осей координат. Тогда линейное
преобразование аналитически описывается особой матрицей преобразования:
у = Ах, где А = [ars] размерности т X п. Это — преобразование ^-мерных
векторов х = (х19 х2, ..., хп) в m-мерные векторы у = (ух, у2, ..., ут), или
перевернутая система уравнений раздела 13.2 (то есть система, в которой
поменяли местами правую и левую части. — Ред.).
При решении системы уравнений задача заключается в том, чтобы
по заданному у найти х. Для обратного линейного преобразования задача
ставится таким же образом — выразить х через у. Решение первой задачи
нужно только истолковать по-иному.
I. Неособенное преобразование. Квадратная матрица А порядка п имеет
ранг п; обратной к ней является матрица А. Количество переменных в
системе х и в системе у совпадает. Тогда преобразование, обратное у = Ах,
будет х = А~ху.
На практике обратное преобразование можно осуществить путем
построения обратной матрицы А, или методом исключения переменных, или же
с помощью формулы Крамера (см. 13.2).
Пример (а)
2/1=—
»II
Здесь у=Ах, где матрица А= 1 —1 1 и А-1=
Г-1 1 П
= 1-1 1
L 1 1 -iJ
как это пока-
зано в примере (в) раздела 13.2. Следовательно,
111
a?i = y B/2+2/з)» ^2 = Y^3+yi^ ^з=-у B/1 + 2/г)-
Li ?л Ci
Зтот же результат можно получить также непосредственно из исходной системы
уравнений.
Линейное преобразование можно истолковать геометрически и применить,
например, к теории выпуклых множеств. Точечное множество в я-мерном
пространстве может быть конечным, как множество вершин /г-мериого
многогранника, а может быть и бесконечным, как множество точек некоторой
375

хг
D
кривой или поверхности. Сопоставим точке, координированной относительно
осей Оххх2 xnJ га-мерный вектор х = (хг, х2, ..., хп) и выполним линейное
преобразование у = Ах.
Тогда данное точечное множество преобразуется в новое множество
координированное относительно осейОуху2... уп в другом n-мерном
пространстве. Такое преобразование устанавливает взаимно однозначное соответ-
' ствие между точечным множеством в
одном пространстве и точечном
множеством в другом пространстве.
Вершины (углы) многогранника в
пространстве х преобразуются в
вершины другого многогранника в
пространстве у, а кривые или
поверхности в пространстве х соответственно
изменяются в другие кривые или
поверхности в пространстве у. При
преобразовании одного пространства
в другое, в зависимости от характера
матрицы А, возможны различные ви^
ды «растяжения» или «смещения»
пространства. Это легко
продемонстрировать для двумерного
пространства наследующих примерах, в
которых мы пользуемся хорошо нам
знакомой квадратной матрицей второго
порядка.
Пример (б)
О
Уг1
0
У,°2х, Уг
л . „ _ ..„
А
, г»
п
Уг
Уг'
0
А<*
,+2х2
Уг=хг
D
С
У/
Гк 0-|
х, то есть у1 =
и у^—
Рис. 41.
Эта матрица относится к классу
диагональных матриц К, описанному в
разделе 12.4. При ее использовании
квадрат в пространстве Ох±х2 преобразуется в
прямоугольник в пространств^ Оу\Уъ, как
это показано для к=2 на рис. 41.
Аналогичным образом круг может быть преобразован в эллипс. Если &>1 (и Xi>0), то
при преобразовании отмечается смещение вправо и «растяжение» в горизонтальном
направлении.
Обратное преобразование имеет следующий вид:
X"~~
или же x1 = (ilk)y1, х2 = у2. Преобразуем на основе этой матрицы (при Л = 2)
окружность с радиусом 1, центр которой лежит в точке B,2):
Этой окружности в пространстве у соответствует кривая
или
которая является эллипсом.
Пример (в)
у=
х, то есть уг
376
и г/2==

Здесь матрица преобразования—треугольная матрица вида Н (см. 12.4).
Применив это преобразование по отношению к квадрату в пространстве Охгх2 (при Л = 2),
получим ромб в пространстве Оуху2, как это показано на рис. 41. Круг и в этом
случае преобразуется в эллипс, главная ось которого расположена теперь под углом
к оси абсцисс. Если й> 1 (и я2>0), то преобразование приводит к смещению вправо,
которое не является постоянным, но увеличивается пропорционально высоте над осью
абсцисс.
Выполним обратное преобразование:
х=[0 "~1 у, или же x1r=y1—hy2 и х2 = у27
по отношению к той же окружности
При k = 2 кривая, полученная в пространстве у, описывается уравнением
или
Можно показать, что эта кривая—эллипс1.
Очень удобное неособенное преобразование достигается с помощью*
ортогональной матрицы (см. 12.9). Если матрица А ортогональная, так
что АА' = 1 и А = А', преобразование у = Ах называется ортогональным
преобразованием. В этом случае обратному преобразованию соответствует
х = А-1у = А'у.
Если матрица А ортогональна, то матрица А' также ортогональна, а
следовательно, и обратное преобразование будет ортогональным.
Частный случай ортогонального преобразования в двумерном
пространстве описывается уравнениями
ух = хх cos 8 + х2 sin 0,
у2= —хг sin 0 + #2 cos 6.
* а Г cos 9 sin 01
Матрица этого преобразования А = Л I.
[ — sin 0 cos 0J
С геометрической точки зрения это соответствует повороту осей
координат против часовой стрелки на угол 0 (переход от одной системы
прямоугольных координат Ох±х2 к другой Оуху2). При этом все фигуры
не претерпевают никаких изменений ни по форме, ни по размерам
(см. рис. 39). Точки соответствующих точечных множеств в пространстве х
и в пространстве у совершенно одинаково ориентированы относительно
ДРУГ друга; просто, одно точечное множество вращают до тех пор, пока
оно не совместится со вторым. В частности, в противоположность
преобразованию, изображенному на рис. 41, ни одно из расстояний между точками
этим не затрагивается. С алгебраической точки зрения квадрат расстояния
от точки О до любой точки в пространстве х равен (? = sj + a?. Осуществив
обратное преобразование, мы получим
xi = У\ cos 0 — 2/2 sin е> #2 = Уг sin
а по отношению к формуле для определения Q:
Q - (У1 cos 0 - уг sin 0J + (Vl sin 0 + у% cos 0J = у\ + у\.
Следовательно,
и расстояние от начала не изменилось по сравнению с исходным. Этот
вывод нетрудно обобщить (см. упражнение 7).
1 Так как дискриминант из коэффициентов А, В, С при старших членах уравнений
кривой больше нуля: 6 =
А В
В С
1 — 2
г2 5
377
= 1 > 0. — Прим. ред.

Можно доказать, наоборот, что любое ортогональное преобразование
Г cos 9 sin0]
в двумерном пространстве имеет матрицу А = , где угол 0
L — sin 6 cos 0J
выбран надлежащим образом; в этой матрице могут лишь быть умножены на
{ — 1) строка, или столбец, или строка и столбец. Для доказательства
рассмотL^2l ^22J
рим матрицу А = I, которая ортогональна, что означает (см. 12.9):
La aj
A)
B)
0. C)
На основании равенства A) элемент аг1 по абсолютной величине должен
быть меньше 1, так что в интервале @, я) можно подобрать единственный
угол 0, удовлетворяющий условию an = cos0, а отсюда a12 = sin0 (или
a12= — sin0, в соответствии с одним из упомянутых выше вариантов).
Аналогично этому, основываясь на равенстве B), можно подобрать такой
единственный угол <р, что a21 = sinq), a22 = cos<p. Из условия C) мы имеем
(опять-таки не принимая во внимание всех возможных вариантов знаков
при sincp и coscp), что
cos 0 sin ф + sin 0 cos ф = О,
или
что соответствует 0= — ф.
Г cos0 sin 01
Следовательно, А есть матрица или один из ее знако-
L — sin0 cos0j
различных вариантов.
В соответствии с этим, в двумерном пространстве любое ортогональное
преобразование попросту представляет собой поворот осей, и все расстояния
(и форма фигур) при преобразовании не изменяются (инвариантны).
Инвариантность расстояний между точками и форм фигур есть общее
свойство ортогональных преобразований в пространстве с любым числом
измерений. Это свойство, установленное в пункте III раздела 12.9, может
быть сформулировано следующим образом:
Если у = Ах есть ортогональное преобразование, так что А~1==
= А', то в результате преобразования инвариантными остаются как
скалярные произведения векторов (то есть х^Ха = Ух'Уг)* так и Рас~
стояния между точками и углы.
В частности, не изменятся и расстояния точек от начала координат:
г г
Алгебра линейных преобразований попросту представляет собой
алгебру соответствующих матриц. Она несложна, если эти матрицы квадратные
и неособенные; можно всегда вычислить величину определителя такой
матрицы и составить для нее обратную матрицу. Легко распространить на общий
случай выводы, сделанные в разделе 12.2 для двумерного пространства.
Например, если х = Ау и y = Bz суть два неособенных линейных
преобразования, то можцо установить непосредственную зависимость между х и z:
х = A (Bz) = (АВ) z.
Это — линейное преобразование, матрица которого АВ. Аналогичные
операции можно проделать и по отношению к обратным преобразованиям:
если у = А-1х и z = В^у, то
z = В^А-Чс = (AB)-Xx;
это есть преобразование, обратное х = (AR)z.
378

II. Особенные преобразования. Если матрица линейного преобразования
является либо прямоугольной, либо квадратной и особенной, задача состав-
ления обратной матрицы усложняется. Выводы, сделанные в случае П(б)
из раздела 13.2, применимы и здесь, но толковать их следует по-иному.
Рассмотрим преобразование у = Ах, где А — квадратная матрица
порядка п и ранга г < п. Количество переменных х равно количеству
переменных у. Однако то обстоятельство, что матрица А является особенной (г < я),_
препятствует непосредственному выполнению обратного линейного
преобразования. Нетрудно истолковать смысл этого преобразования: задавшись
любыми произвольными значениями х, мы получим единственную систему
соответствующих значений у. Каждой заданной точке в пространстве х здесь
соответствует как раз одна точка в пространстве у. Для обратного
преобразования приходится придать какие-либо значения г/-ам и попытаться найти
соответствующие х; это равносильно отысканию точки в пространстве х,
соответствующей заданной точке в пространстве у. Оказывается, что
осуществить это невозможно, по крайней мере для всех п измерений.
Матрица А ранга г имеет квадратную неособенную подматрицу порядка
г. Последняя соответствует г некоторых х (скажем, хг, х2, ..., хг) и г
некоторых уравнений и некоторых у (скажем, уг, у2, ..., ут). Если мы зададимся
какими-либо г значениями у, то можно получить г единственных значений х,
что весьма соответствует случаю I, изложенному выше, — неособенному
преобразованию. Геометрически точка в х-м пространстве г измерений (в п-
мерном пространстве) соответствует некоторой точке в у-м пространстве
г измерений, и наоборот. Остается нерешенным следующий вопрос: как
поступить с «избыточными» (п — г) переменными (#г+1, #г+2, ..., хп и г/„+1, уг+2, ...,
уп), то есть с «избыточными» измерениями в пространствах х и у?
«Избыточным» п — г переменным х приходится придавать произвольные
значения, что мы, по существу, и делали, определяя х19 х2, ..., хп по
выбранным г уравнениям линейного преобразования. «Избыточные» переменные у
можно не принимать во внимание или же придавать им определенные
значения. В последнем случае эти значения должны быть такими, чтобы
расширенная матрица В = [A j у] имела ранг г. Тогда излишние уравнения системы,
описывающей преобразование, будут совместны с остальными. Вместе с тем
если «излишним» у приданы такие значения, при которых матрица В = [A j у]
имеет ранг г + 1, то в таком случае они не совместны с полной обратимостью
преобразования. Короче говоря, чтобы осуществить обратное преобразование
по отношению ко всем п измерениям, должны быть наложены ограничения
на принятые нами значения у и, кроме того, некоторым х следует придать
произвольные значения. Это иллюстрируется следующим примером.
Пример (г)
Матрица этой системы уравнений
[ 1 i"j
имеет ранг 2.
Г1 1 П
1= 1 —2 2
L2 -1 3J
Правая часть последнего уравнения является суммой правых частей двух первых
уравнений. Чтобы выразить х через у, следует задать значения игреков. Можно
задаться любыми значениями ух и у2, но для того, чтобы три уравнения были совместны,
необходимо, чтобы 2/3 = 2/i+2/2- В этом случае третье уравнение попросту можно
отбросить, так как оно не вносит ничего нового. Если же мы придадим любое другое
значение ys, то третье уравнение окажется несовместным с первыми двумя, и его снова
можно отбросить. Но уже не потому, что оно вытекает из них, а потому, что им
нельзя воспользоваться. Следовательно, чтобы можно было использовать все три
уравнения, должно соблюдаться следующее соотношение или ограничение значений у:
379

Однако дайке в этом случае можно найти только два значения х, а третьему
приходится придавать произвольное значение. Решение двух первых уравнений
* B+У4*) *(
является лишь той формой, в которой и можно выразить обратное линейное
преобразование. Здесь можно задаться любым произвольным значением х3, а избыточная
переменная г/3 либо отбрасывается вовсе, либо принимается равной 2/з = 2/1+2/2» благодаря
чему она становится совместной с остальными.
Во многом аналогичен описанному и тот случай, когда матрица А
прямоугольная размерности т X п, причем ее ранг г ниже или равен меньшей
из двух величин (т или /г). Если т < п, то имеются «избыточные» переменные
х, которым мы при обратном преобразовании должны придать произвольные
значения. Если т> п, то имеются «избыточные» переменные у, которые мы
должны отбросить или определенным образом связать с другими у. С
геометрической точки зрения каждой точке в w-мерном пространстве х можно
сопоставить одну и только одну точку в m-мерном пространстве у. Однако
обратного соответствия между точками в пространстве х и заданными точками
в пространстве у можно добиться лишь для ограниченного числа (г)
измерений или для всех измерений — при наложении некоторых ограничений.
При изучении алгебры особенных линейных преобразований требуется
большая осторожность. Необходимо проверять размерность или порядок
соответствующих матриц, так как в общем случае обратное преобразование
может оказаться невозможным. Например, если х = Ау и у == Bz, то можно
написать х = (AB)z только в том случае, если матрица А и матрица В
согласованные. Если матрица А размерности т X к, а матрица В размерности
kxriy то только в таком случае существует матрица АВ размерности тхп.
Это значит, что т переменных х можно преобразовать в п переменных z
с помощью к промежуточных переменных у. Однако в общем случае такое
обратное преобразование невозможно.
Задачи и упражнения
1. Показать/ что при линейном преобразовании у = ЕA2)х, где ЕA2) — матрица
сдвига, описанная в разделе 12.4; лишь меняются местами оси координат а форма
и размеры фигур остаются неизменными.
2. Показать, что для системы уравнений
2/3
обратной является система
^2=2/2—Ун
#3 = 2/3—2/2-
п
Обобщить полученные результаты для кумулятивных функций вида уп = 2 ХЬ
k=i
и разностей уп и уп_г и истолковать эти результаты.
3, Рассмотреть приводимое ниже линейное преобразование и установить, какие
ограничения необходимо наложить на у. Отбросить один из у и построить обратное
преобразование. Сверить с результатом упражнения 8 из раздела 13.2:
4, Выразить z через заданные х, если известно, что
и Н = ~2
380

Проверить полученный результат, перемножив матрицы.
5. Показать, чтоу=АВ~1г и z=BA"xy, если у = Ах, z = Bx, где А и В
—квадратные неособенные- матрицы. Что можно сказать о следующих вариантах: а) матрица А
или матрица В особенная; б) одна из этих матриц прямоугольная?
Г-1 2 -2
=| 2-1 -2
31 2 2 1 J
6. Показать, что матрица А =-5-1 2 —1 —2 I есть
31 2 2 1 J
ортогональная, и проверить, остаются ли неизменными расстояния между точками
в пространствах х и у при ортогональном преобразовании у=Ах.
7. Показать, что при ортогональном преобразовании в двумерном пространстве
расстояние между любыми двумя точками остается неизменным.
13.4. ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ КВАДРАТНОЙ МАТРИЦЫ
Понятие характеристического уравнения для квадратной матрицы с
большой пользой применяется в алгебре матриц. Здесь излагаются лишь основные
идеи, а также частные случаи применения характеристических
уравнений для симметрических матриц и квадратичных форм (см. книгу Тролла
и Торнхейма [15, стр. 142—146]).
Пусть А = [arsj представляет собой квадратную матрицу п-то порядка,
а I — единичная матрица такого же порядка. Характеристической
матрицей для А называется матрица
А-Я1 =
~аи — X а12 ... а1п
021 «22 — ^ • • • а2п
где Я — любой множитель или параметр.
Определитель | А — Я11 матрицы, если его написать в развернутом виде,
представляет собой многочлен степени п относительно Я, коэффициенты
которого составлены из элементов матрицы [аГ8]. Член, имеющий наивысшую
степень относительно Я, равен (—1)ГТ\ а свободный член равен | А|. Труднее
выразить в общем виде коэффициенты при АЛ", Яп~2, ...ит. д. (см.
упражнение 3). Если мы приравняем этот характеристический многочлен нулю,
получим уравнение степени п относительно Я, корни которого Я1? Я2, ..., Яп могут
быть как вещественными числами, так и попарно сопряженными комплексными
числами. Мы получаем таким образом характеристическое уравнение
квадратной матрицы А, и его корни называются характеристическими, или
скрытыми, корнями, а иногда собственными значениями матрицы А.
Определение. Характеристическим уравнением квадратной
матрицы А гс-го порядка называется уравнение
| А — XI j = О,
характеристические корни (или собственные значения) которого
будут Ях, Я2, ..., Яп.
Если Хг — характеристический корень этого уравнения, так что
| А — ХГ1\ = О, то матрица А — ЯД является особенной. Следовательно
(см. 13.1), ее строки и столбцы линейно зависимы, и можно подобрать тдкую
систему чисел, из которых не все равны нулю, что если представить их
в виде вектора-столбца
kr = {fclr, k2r, ..,, knr} (kr Ф 0),
то
(А-Яг1)кг = 0.
Вектор kr называется собственным вектором, соответствующим
собственному значению Яг.
381

Свободным членом характеристического уравнения является |А|. Если
матрица А неособенная, то | А| Ф О, и ни один из характеристических
корней не равен нулю. Если же матрица А особенная, то по меньшей мере один
из характеристических корней равен нулю. Развивая эту мысль, мы должны
доказать, что если ранг матрицы А равен г, то имеется г ненулевых и п — г
нулевых характеристических корней.
Пример (а).
Г 2 -1 -П
Матрица А=| —1 2 —II особенная,
L-1 -1 2\
ее ранг равен 2. Характеристическое уравнение этой матрицы после упрощений
приводится к многочлену Л3—6А,2Ц-9А,=0, корни которого равны 3, 3 и 0. Существование-
одного нулевого корня свидетельствует о том, что ранг матрицы А на единицу меньше 3-
При рассмотрении этого вопроса мы воспользуемся понятием подобных
матриц. Будем рассматривать только квадратные матрицы п-то порядка.
Матрицы А и В называются подобными, если можно подобрать такую
неособенную матрицу Р, что В = РАР. Идея доказательства заключается в том,
чтобы установить подобие матрицы А и некоторой диагональной матрицы X,
а затем показать, что диагональные элементы матрицы X суть
характеристические корни матрицы А. Выполнить это довольно сложно; в самом деле,,
не всегда осуществима такая «диагонализация» матрицы А. Приведем
доказательство для частного случая, взятое из книги Мёр док а [10].
Одну из посылок доказать легко: если матрица А ранга г подобна
диагональной матрице X, диагональные элементы которой суть (Х1у Х2, ..., Хп)г
то тогда эти элементы представляют собой характеристические корни
матрицы А, причем г из них отличны от нуля. Это доказательство распадается
на две части.
I. Подобные матрицы имеют один и тот же ранг и одинаковые
характеристические корни.
Доказательство. Для подобных матриц А и В (ранг которых одинаков,,
см. раздел 12.9) В = РАР-1, и поскольку Р1Р~1 = РР1 = I, то
Далее, [Р^ 1/|Р|, так что
что и требовалось доказать.
II. Характеристическими корнями диагональной матрицы X являются
ее диагональные элементы Xv Х2, ..., Хп.
Доказательство. Матрица (к —XI) также является диагональной, по ее
диагонали расположены элементы (А-х — X), (Х2—Х), ...,(ХП —Я). Значит,,
характеристическим уравнением этой матрицы будет
что и требовалось доказать. _
Из I и II следует, что если матрицы А и % (обе ранга г) подобны,,
то матрица А имеет те же характеристические корни, что и матрица X, то
есть (Х1у Х2, ...,Хп). Но ранг матрицы X равен г только в том случае,,
если г и только г чисел X отличны от нуля.
Задача состоит в том, чтобы «диагонализовать» матрицу А. Рассмотрим
здесь только один частный случай - матрица А симметрическая, так что
А' = А. Тогда все характеристические корни матрицы А оказываются
вещественными числами. Это представляет значительное упрощение, поскольку
отпадают трудности, связанные с наличием комплексных элементов во
взятых нами матрицах. Доказывается этот вывод следующим образом. Пусть
382

симметрическая матрица А имеет характеристический корень Я = +р
а сопряженный ему обозначим через А/ = а— ф. Тогда |А — Я. Ж ] = 0.
Составим матрицу:
которая является квадратной матрицей, составленной из вещественных
чисел. Эта матрица особенная, поскольку из |А — АЛ| = 0 следует, что
|В| = 0. Значит, в соответствии с пунктом I раздела 13.2, Вх = 0 для
некоторого ненулевого вектора х, а значит, х'Вх = х'0 = 0. Вместе с тем
х'Вх = х' (А - a IJ х + х' Р21х.
Легко* видеть, что первое слагаемое правой части, будучи квадратичной
формой, неотрицательно; второе слагаемое Р2х'1х = Р2х'х, разлагая по
элемента^ вектора х, можно представить в виде $2(х1 + %1+ • • • + #п). Значит,
если х есть ненулевой вектор, то х'Вх = 0 только в том случае, если равны
нулю как первое слагаемое, то есть |А —aI| = 0, так и второе слагаемое,
то есть р = 0. Следовательно, Х = а и представляет собой вещественное
число, что и требовалось доказать.
Обозначим вещественные характеристические корни симметрической
матрицы А через А,х, А,2, ..., %п и построим, используя их, диагональную
матрицу. Тогда можно сделать следующий важный вывод:
Для любой симметрической матрицы А можно подобрать такую
ортогональную матрицу Р, что Р~АР представляет собой диагональную
матрицу Л,, построенную на характеристических корнях матрицы А.
Из P~1AP = h следует, что А = РЯР 1, и что матрица А подобна
диагональной матрице Л,; наша задача тогда решена. Доказывается приведенное
выше положение следующим образом.
Пусть ненулевой вектор хг является собственным вектором,
соответствующим характеристическому корню Яг-матрицы А, то есть (A—Xr I)xr = 0.
Следовательно,
Axr = hrxr (r = l, 2, ...,л)> A)
Составим из векторов хг (г = 1, 2, ..., га), взятых в качестве столбцов,
матрицу Р. Тогда п уравнений A) представятся одним матричным
уравнением
АР = РХ,
или
PAP = P'PL B)
Транспонируем обе части уравнения B); поскольку матрицы А и X
симметрические, то есть А' = А и V = h, получаем
Р'АР^Р'Р. C)
Следовательно, правые части уравнений B) и C) равны между собой:
а это возможно только в том случае, если РР' = I, или Р' = Р. Значитг
матрица Р ортогональная, и уравнение B) можно представить в виде:
что и требовалось доказать.
Всю совокупность полученных результатов можно теперь объединить
в следующем предложении:
383

Симметрическая матрица А тг-го порядка и ранга г имеет п
вещественных характеристических корней, образующих диагональные
элементы диагональной матрицы X, подобной матрице А:
А = РЛА, где Р — некоторая ортогональная матрица;
г характеристических корней отличны от нуля, an — г нулевые.
Продемонстрируем это на следующем примере.
Пример (б).
Матрица А = I — 1
-1
::1
2J
— 1 —1
2 —1 | симметрическая, ее ранг равен 2;
-1 2!
характеристические корни этой матрицы [см. выше, пример (а)] равны 3, 3 и О*
Рассмотрим матрицу Р, ортогональность которой доказана в примере (б) раздела 12.9:
, так что Р'=Р х =
1
/2
1
>/2
0
1
/6
1
/6
2
1
/з
1
/з
1
/6 /3 J
1
/2
1
/в
1
i
/2
1
/6
1
0
2
1
Дважды выполнив операцию умножения матриц, т. е. умножив последовательно Р г
на А, а затем результат на Р, получим
[3 ° ° I
0 3 0 =А,.
0 0 0 J
Эта диагональная матрица образована из характеристических корней ^матрицы А*
Значит, матрица А преобразована в подобную ей диагональную матрицу X ас помощью
операции
где Р—приведенная выше ортогональная матрица. Отметим, что характеристическому
корню 3 соответствует тако,й собственный вектор х = (а?1? хг, х3), что
Г-1 -1 -IT
(А—31)х= — 1 —1 —1 х=0.
L-1 -1 -ij
После операции умножения каждый из элементов полученной матрицы
оказывается равным —(^1+^2+^3M следовательно, он должен быть равен нулю. Значит,
х = A, —1,0) и х=A, 1, —2) являются собственными векторами матрицы А. Нужно
искать два значения собственных векторов, так как существуют два
характеристических корня, равные 3 (кратность равна двум). Возьмем два приведенных выше
значения собственных векторов, элементы которых пропорциональны соответственно
элементам первого и второго столбцов матрицы Р. Третьему характеристическому корню
матрицы А (нулю) соответствует собственный вектор A, 1, 1), элементы которого
пропорциональны элементам третьего столбца матрицы Р.
Значительный интерес представляют и квадратные матрицы другого
вида, все элементы которых неотрицательны (А>0). Такими матрицами часто
пользуются в экономике. Пусть неотрицательная матрица А является и
неразложимой — в том смысле, как это понимается в пункте V раздела 12.9. Тогда
матрица (XI — А) или характеристическое уравнение для матрицы А,
обладает рядом свойств, установленных Дебрэ и Герштейном [4]. Если Хт—
наибольший из характеристических корней матрицы А, то он и наибольший из
корней уравнения | XI — А | = 0, первый член которого равен АЛ
Следовательно ,^если X > Хт, то | XI — А | > 0. Дебрэ и Герштейн первыми сумели
показать, что все главные квадратные подматрицы матрицы | X I — А|, то есть
такие подматрицы, в которых опущены столбцы и строки одних и тех же
номеров, имеют положительные значения определителей в том и только в том
случае, если X > Хт. Далее, обратная матрица (XI — А) положительна в том
и только в том случае, если X > Хт.
384

Задачи и упражнения
1. Найти характеристические корни матриц
1 — 1
-:.]¦
1
0
1
2
0
1
—
1
2
1
2
1
~2
1
2. Показать, что характеристические корни симметрической неособенной матрицы
А= равны 1 и —1 и что, следовательно, она подобна матрице Я= .
На этом основании показать, что ортогональная матрица Р в равенстве А =
имеет следующий вид:
Р=
1
/2
1
V2
1
3. Пусть A = [ars] — любая квадратная матрица третьего порядка. Показать, что
| А-М |= -
«и
«21
Pi —
«12
«22
Т"
i-«2
«22
«32
2П~ «
«23
«33
33>
«11
«31
«13
«33
где
А|.
Представить полученный результат в общем виде для квадратной матрицы А
любого порядка п.
4. Матрица А является ортогональной (АА' = 1). Показать, что
=0, а следовательно,
—а(А — Я,1) = А —J-I.
Доказать, что если |А — ЯД|=О, то справедливо и
если X—характеристический корень ортогональной матрицы, то характеристическим
корнем является и 1Д.
13.5. КВАДРАТИЧНЫЕ ФОРМЫ
Мы часто пользовались линейными формами, представляющими собой
сумму членов, каждый из которых — произведение одной из переменных
xv x2, . .., хп на постоянный коэффициент. В системе линейных уравнений
левая часть каждого уравнения — линейная форма; используются линейные
формы и при линейных преобразованиях. В общем виде линейная форма
описывается следующим уравнением:
п
L = 2 атхт = aix\ + а2х2 + - • • -г апхп*
где ат — постоянный коэффициент, а хг — переменная величина. Обозначим
вектор-столбец величин ат через а и хт через х. Тогда
представляет собой сжатую запись линейной формы.
Предположим теперь, что ат — не постоянные коэффициенты, а
переменные второй системы, которую мы обозначим через у. В таком случае мы
получаем простейший случай так называемой «билинейной формы»:
2Уъ + • • • + ХпУп = Х'У = У'Х-
25 р. Аллеи
385

Эта форма называется «билинейной» потому, что имеется две системы
переменных, и форма линейна относительно каждой из них. Если же первая
система переменных тождественна со второй (то есть х = у), то мы имеем
дело с частным случаем билинейных форм:
Это простейший случай «квадратичной формы» относительно переменной х.
В более общем виде билинейные и квадратичные формы включают
члены, являющиеся всеми попарными произведениями двух переменных
обеих систем, как-то: хху2 или хгх2, взятыми с различными постоянными
коэффициентами. Если мы имеем матрицу постоянных коэффициентов A=[ars]
размерности тхп и две системы переменных, записанных в виде векторов-
столбцов х={хг} и y = {ys} (r=l, 2, ..., т, и 5 = 1, 2, . ..,тг), то
билинейная форма в общем виде описывается уравнением:
# = 22 arsxrys = апх{уг + а12хху2 + ... + alnxxyn +
+ «22^2 + • • • + ЯгЛ
В частном случае, если т — п и первая система переменных
тождественна второй, мы получаем квадратичную форму в общем виде:
Q — 2j2j arsXrXs ~ пПХ1 ~Ь <*>\ъХ\Хг + • • • + а1пХ1Ха ~Ь I
|
-р a2jX^x2 -у а22Х'2 ~\~ • . . "т &2ц,х2,хп i f v /
аппх2п.
Здесь А = [ars] — квадратная матрица га-го порядка, а переменные
образуют вектор-столбец х={хг} также /г-ro порядка.
Легко заметить (см. упражнение 1), что мы без потери общности можем
принять ars — asr для всех г и s. Тогда матрица A=[ars] симметрическая.
Поэтому для всякой квадратичной формы Q матрицу коэффициентов А = [ars]
можно считать симметрической; величину определителя матрицы А, то есть
-4 = | А|, назовем дискриминантом формы Q. Приведем три простейших
примера квадратичной формы для двух переменных х± и х2:
Пример (а)
О
Q=*f+a?l, А =
О 1
Пример (б)
1 О
О —1
4 х *2' A~L0 -1J ' А~
Пример (в)
= 1.
= —1.
Г 1 —П л
L=[-l lJ'A=
-t -\ -•
Эти три примера показывают, какие возможны варианты изменений
знака квадратичной формы Q при изменении значений переменных хх и х2.
При хг — х2 = 0 во всех случаях Q = 0, и этот тривиальный вариант
исключается, если мы примем, что вектор х=(^17 х2) Ф 0. Поэтому мы принимаем, что
х Ф 0 и что ни ж1, ни х2 не равны оба нулю. В примере (а) квадратичная форма
Q может принимать только положительные значения, в примере (б) — как
положительные, так и отрицательные в зависимости от абсолютных значений
хх и х2. Более затруднителен случай квадратичной формы Q в примере (в),
386

где матрица А особенная, то есть А = 0. Так как в этом примере
то очевидно, что Q может принимать положительные (при хх Ф х2) или
нулевые (при хг = х2) значения, но ни в коем случае не отрицательные. Значит,
в примере (в) квадратичная форма Q является неотрицательной в отличие
от примера (а), где она положительна.
Следовательно, при исследовании знака квадратичной формы Q полезно
«дополнить квадрат» и попытаться преобразовать Q в сумму квадратов.
Рассмотрим другие примеры:
Пример (г)
Q = xl + 2x1-2x0*
А=| . ~ —неособенная матрица.
Тогда
Q = (xl-2x1x2+xl)+xl
то есть
Q = (*i-*iJ+*L
а эта квадратичная форма может принимать только положительные значения. От
примера (в), где форма Q была квадратом одной величины и могла принимать
положительные и нулевые значения, форма Q настоящего примера отличается тем, что
представляет собой сумму двух квадратов и может быть только положительной.
Это наводит на ту мысль, что если матрица А является неособенной, то форма Q
может быть представлена в виде суммы двух квадратов; если же А—особенная
матрица, один из квадратов исчезает. И, действительно, дело обстоит именно так.
Вместе с тем «сумму» двух квадратов (при неособенной матрице А) следует
понимать как «алгебраическую сумму» (то есть как «сумму или разность»). Например
Q = х\—х\—2ххх2 = (х1 — <г2J—2^1
является примером квадратичной формы Q, матрица которой неособенная, так что
форма может принимать как положительные, так и отрицательные значения.
Развивая далее эти идеи, необходимо иметь общую запись билинейной
формы A) и квадратичной формы B) в виде матричных уравнений.
Приводимые ниже результаты получены путем непосредственного применения
-правила умножения матриц. В общем виде билинейная форма описывается
уравнением
Я = х'Ау, C)
где векторы-столбцы х и у представляют две системы соответственно из т
и п переменных и где А = [ars] — матрица т X п из постоянных
коэффициентов. Частным случаем этой формы является квадратичная форма общего
вида:
<? = х'Ах, D)
где х — вектор-столбец (тг-го порядка) переменных, а А — квадратная
матрица га-го порядка. Можно убедиться в том, что матрицы уравнений C)
и D) согласованные: х'Ау являются произведением трех матриц, размерность
которых соответственно 1 Хш, т X п и п X 1; в результате умножения
получается скалярная величина В.
Представляет интерес частный случай, когда матрица А —• единичная
матрица I п-го порядка. На основании C) можно написать
Я=х'1у = х'у,
что соответствует форме:
в = ^i2/i + я2г/2 + • • • + хпуп.
На основании же уравнения D) можно написать
387 25*

что соответствует форме
Q=x\ + x\+...+x\.
Эти формы мы уже встречали выше.
Квадратичная форма Q — скалярная функция переменной х. Если путем
линейного преобразования мы переходим от системы переменных х к системе
у, равной ей по числу переменных, то Q преобразовывается в функцию г/,
причем она остается также квадратичной формой относительно новых
переменных. Нетрудно построить матрицу коэффициентов этого преобразования.
Пусть линейное преобразование х = Су применено по отношению к
уравнению (? = х'Ах:
<? = (Су)'А(Су) = у'С'АСу, E)
то есть (? = у'Ву, где В = С'АС.
Это — преобразованная квадратичная форма. Новая матрица В подобна
исходной матрице А и ранг матрицы В равен рангу матрицы А.
Матрица А квадратичной формы Q является симметрической. Поэтому
все характеристические корни этой матрицы суть вещественные числа. Это
значит, что можно применить результат, полученный в разделе 13.4: матрица
А оказывается подобной диагональной матрице 'к, диагональными
элементами которой являются характеристические корни матрицы А. Для этого
воспользуемся ортогональной матрицей Р:
так как для ортогональной матрицы Р = Р'.
Если мы применим преобразование х = Ру или обратное преобразование
у = Р хх = Р'х по отношению к квадратичной форме Q, то, в соответствии
с уравнением E), получаем
<? = у'Ву, где B =
то есть
Все п характеристических корней (^, Я2, . .., Х^) матрицы А являются
вещественными, но не обязательно различными, а некоторые из них
могут быть равны нулю. Если ранг матрицы А равен г</г, то существует
п — г нулевых и г ненулевых (включая кратные) характеристических корней.
Основным выводом для квадратичных форм является возможность
преобразовать всякую квадратичную форму D) в сумму квадратов F).
С помощью некоторого ортогонального преобразования х = Ру
любую квадратичную форму Q = х'Ах можно представить в виде
суммы квадратов:
Q = у'Ъу = XlV\ + \у\ +...+ 1пу1
Коэффициенты К являются характеристическими корнями матрицы
А, а у — переменные, находящиеся в определенной зависимости от х
(выраженной уравнением у = Р'х). Если ранг матрицы А равен г</2,
то тогда Q представляет собой сумму г квадратов с ненулевыми
коэффициентами при них.
Приведем пример квадратичной формы относительно трех переменных.
Пример (д)
Здесь применимы результаты, полученные в примере (а) раздела 13.4. Матрица
Г 2-1-П
формы Q есть А=| —1 2 —11. Она ортогонально эквивалентна матрице
Г 2-1-П
= -1 2-1
L-l -I 2J
388

Соответствующее преобразование описывается уравнением х = Ру или у = Р'х где
Р —та же матрица, что и в примере (а) раздела 13.4:
111
) или *а = —— У1 + -—у2 + — Уз,
" 2 1 '
ИЛИ Х3= - |
Произведем подстановку:
то есть
В этом случае ранг матрицы А равен 2, а ее характеристические корни 3, 3 и 0;
квадратичная форма Q является суммой двух квадратов.
Возможны разные выражения квадратичной формы Q в виде суммы квадратов.
И, в самом деле, даже в столь простом численном примере, который приведен здесь,
можно «дополнить» форму до других квадратов, причем значительно быстрее:
\ 1 2 2 2 3J 4
= ( х _-1^2__1
V 1 г 2
Значит,
Это—другой вариант выражения квадратичной формы Q. Операция «дополнения
до квадратов» практически производится в тех случаях, когда форма задана с
численными коэффициентами; выводы, полученные для; ортогонального преобразования,
показывают, что подобная операция возможна в любом случае.
Приведение квадратичной формы к сумме квадратов применяется
главным образом с целью определения знака формы Q. Пусть форма (относительно
п переменных) Q = х'Ах, причем | А| ФО, то есть матрица А неособенная.
Тогда Q равна точно сумме п квадратов:
Все переменные у не могут одновременно быть равными нулю, какими
бы мы ни задались значениями х (если только не все х равны нулю). Переход
он у их осуществляется посредством ортогонального преобразования х = Ру,
обратное преобразование имеет вид у = Р'х. Каждому значению х можно
сопоставить одно значение у, и наоборот. Так как у = 0 соответствует х = 0,
нулевое значение у не может соответствовать ненулевым значениям х.
Следовательно, знак формы Q зависит от знаков характеристических корней
матрицы А, то есть Ях, Я2, ..., Яп. Если все эти корни положительны, то
всегда положительна и форма Q, и наоборот.
Квадратичная форма называется положительной определенной, если
она принимает только строго положительные значения при любых значениях
переменных (если не все из них равны нулю). Если матрица А неособенная,
то для того, чтобы квадратичная форма была положительной определенной,
необходимо и достаточно, чтобы положительными были все
характеристические корни матрицы А.
389

Остается исследовать тот случай, в котором матрица А особенная и ее
ранг г < п. В этом случае п — г характеристических корней матрицы А
нулевые; форма Q равна сумме лишь г квадратов, и в нее входит только г из
переменных ух, у2, ..., уп, полученных из системы переменных х. Всегда
можно подобрать такие значения х, из которых не все нулевые, чтобы г
переменных у были равны нулю, но не все остальные у были бы равны нулю.
Следовательно, даже если г ненулевых значений характеристических корней
матрицы А являются положительными, и квадратическая форма Q — сумма г
положительных квадратов, всегда можно подобрать такие значения х, при
которых форма Q обращается в нуль. Отсюда следует, что должно строго
соблюдаться условие, установленное для существования положительной
определенной формы Q, то есть все решительно характеристические корни
матрицы А должны быть положительными. Случай особенной матрицы А,
имеющей несколько характеристических корней, равных нулю, должен быть
категорически исключен.
Важно подчеркнуть разницу между положительными определенными
и неотрицательными квадратичными формами Q. Форма Q > О тогда и только
тогда, когда матрица А имеет п положительных характеристических корней,
исключая тот случай, когда матрица А особенная и некоторые из ее
характеристических корней равны нулю. Условие почти (но не полностью)
удовлетворяется, если матрица А особенная, причем имеет г положительных и п — г
нулевых характеристических корней. Тогда форма Q является
неотрицательной (positive semi-definite), принимающей наряду с положительными
и нулевые значения.
Для того чтобы все характеристические корни матрицы А были
положительными, члены левой части характеристического уравнения | А — УЛ. | = О
должны быть знакочередующимися. Это значит, что должны быть
положительными определители всех диагональных квадратных подматриц матрицы
А, начиная от подматрицы первого порядка и вплоть до подматрицы га-го
порядка (см. упражнение 5). Результаты, полученные для положительной
определенной квадратичной формы, можно сформулировать следующим
образом.
Квадратичная форма Q — х!Ах относительно п переменных является
положительной определенной, если она принимает положительные
значения при любых значениях переменных (из которых не все равны
нулю). Это имеет место тогда и только тогда, когда положительны все
п характеристических корней квадратной и симметрической матрицы
п-го порядка А = [ars]; последнее равносильно соблюдению следующих
неравенств:
> 0,
а12 а22 .
... а.
Отрицательная определенная квадратичная форма Q принимает только
отрицательные значения при любых значениях переменных (не все из
которых равны нулю). Это можно сформулировать иначе: (—0 > 0, то есть (—Q)
является положительной определенной формой. В приведенных выше
неравенствах величины определителей для отрицательной формы должны быть
знакочередующимися (первый из них отрицательный).
Дальнейшие результаты мы можем получить, исходя из установленного
теперь основного свойства. Важнейшим из них является условие, согласно
которому квадратичная форма относительно п переменных является
положительной определенной (или отрицательной определенной), если переменные
линейно зависимы:
а'х = аххх
390

где а — заданный вектор постоянных коэффициентов (не все из которых
равны нулю). Используя это уравнение для того, чтобы выразить одно
переменное через остальные, мы приводим Q к квадратичной форме относительно
п — 1 переменных. Необходимое условие заключается в том, что Q после его
приведения будет положительной (или отрицательной) определенной
формой. Как уже показано [1], это условие можно выразить с помощью
определителей следующим образом:
Квадратичная форма Q = х'Ах относительно п переменных является
положительной определенной при условии существования линейной
зависимости (описываемой уравнением а'х = 0), если
0
«1
а2
ах
«и
«12
2
«22
О
do do
13
а2 а12 а22 а23
а
«
13 а23 аЗЗ i
«3
и
«1
а2
ai
«и
«12
а2 ..
«12 ••
Й22 ••
• «п
• «1«
При этих же условиях квадратичная форма Q является отрицательной
определенной, если знаки указанных определителей чередуются (первый
определитель положительный).
Мы можем указать здесь еще одно свойство квадратичных форм, которым
мы воспользуемся далее (см. 18.2). Пусть форма (? = х'Ах является
положительной определенной, так что А — неособенная симметрическая матрица
(характеристические корни которой положительны). Применим неособенное
преобразование у = Ах или х = А~1у, при котором любым заданным
значениям переменных х (из которых не все равны нулю) соответствовала бы
единственная совокупность переменных у (из которых не все равны нулю).
Тогда
Q = (А" !у)' А (А^у) = у' (А)' (АА) у = у'А^у,
так как, ввиду симметричности матрицы А, АА х = 1 и (А~г)' = А *. Отсюда
следует, что:
Если форма х'Ах является положительной определенной, то
положительной определенной является и форма у'А^у.
' Предположим теперь, что Q = 22 arsxrxs является положительной опре-
r s
деленной при условии:
= «А
• • • + апХп =
Составим выражение
для любого А,, то есть
где х —система п+1 переменных (X, хг, х2, . .., жЛ), а матрица В
представляет собой окаймленную матрицу А, то есть матрицу, к которой
присоединены строка и столбец коэффициентов а, как это сделано в приведенных
выше определителях. Дополнительные условия для Q быть положительной
определенной состоят в том, что форма R есть положительная
определенная при любом значении х, если не все х равны нулю и если ^]агхг~0.
г
Выполним преобразование у = Вх или х = В-1у и заметим, что если
то
Уо = Ь ъгХг
г
391

Следовательно, как и выше, R может быть представлено в виде
результата преобразования
где у = @, у1ч y2J ...,г/п), и переменные у могут принимать любые
значения (но не нулевые для всех у). Форма R положительная определенная,
и, поскольку первое переменное системы у есть нуль, эту форму можно
написать в виде ^j^j(Brs/B)yrys. Здесь В есть |В| и Brs — алгебраическое
г s
дополнение элемента ars в матрице В; суммирование производится по
элементам, в которых каждое из ут и ys пробегает п значений. Значит, можно
сделать следующий вывод:
Если 22агз^Л> О и Sttr^r^O' mo в шаком случае для любых
Г S Г
значений у (где не все у нулевые)
где | В | — определитель, образованный из матрицы A = [ars]
окаймлением коэффициентами а.
Аналогичные результаты можно получить и для отрицательных
определенных квадратичных форм.
Задачи и упражнения
1. Квадратичная форма Q— 2 ^]arsxrxs несимметрична (ars Ф asr). Показать, что
Г S
эту форму можно представить в виде симметрической] формы Q = 2 2 asrxrxs> гДе
г s
ars=asr — 1/2(ars~\-asr) = asr. На этом основании установить, что матрицу формы Q
всегда можно сделать симметрической. Проверить правильность этого предложения
на примере:
[I 1 -)
1 *
Ранг этой матрицы р!авен 1, а характеристические корни 0 и 2. Показать, что с
помощью ортогонального преобразования:
2/1 = —^-(^1 — ^2), У2=^—^(
форма Q может быть представлена в виде одного полного квадрата.
3. Q = 2xxx2 является квадратичной формой относительно двух переменных.
Составить матрицу этой формы, определить характеристические корни матрицы и показать,
что с помощью ортогонального преобразования, приведенного в предыдущей задаче,
форма Q может быть представлена в виде разности двух полных квадратов.
Установить, что ни эта и ни предыдущая квадратичные формы не являются
положительными определенными.
4. Показать, что форма Q = x\-\-xl~\-xl—х^х3—х2х3 является положительной
определенной: а) путем отыскания характеристических корней матрицы этой формы,
б) путем приведения ее затем к сумме трех полных квадратов.
5. Q = x'Ax есть квадратичная форма относительно трех переменных. Написать
характеристическое уравнение матрицы А в виде
(см. 13.4, упражнение 3) и показать, что все характеристические корни (A,lf Х2 и Я3)
положительны в том и только в том случае, если положительны все коэффициенты
рг, р2 и р3. Показать, что это равносильно условию:
> О,
«12
«22
«23
«23
«33
Каким образом этот результат можно обобщить?
392

6. Форма х'Ау является билинейной. Перейти к новым переменным и и v
посредством преобразований х = Си и y = Dv и показать, что u'Bv — преобразованная
билинейная форма, где B = C'AD. Каким условиям должна отвечать размерность каждой из
матриц? При каких условиях вместо матрицы С можно взять матрицу D?
13.6. УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ РЫНКА
Теперь становится возможным окончательно связать между собой
свободные звенья в условиях Хикса, касающиеся устойчивости равновесия
рынка (см. 9.5). Пусть имеется т товаров и последний из них базисный, или
единичный, его цена принимается за единицу; остальные цены рг(г=1,
2, ...,т —1) определяются при состоянии равновесия рынка из условия
равенства спроса и предложения:
Sr-Dr = Yr-(Xr-Xr) = 0 (гс.1,2 (го-1)), A)
где Yr и Хг суть функции цен, а Хг задано.
Равновесие является устойчивым, если каждая из цен, в какой-либо
момент получившая возмущающее отклонение, с течением времени стремится
возвратиться к значению в положении равновесия. Следовательно, понятие
«устойчивость» применимо лишь к точно определенной динамической системе.
В разделе 9.5, где рассматривалась модель Хикса [7], это не было сделано,
и мы попытались идти кратчайшим путем. Теперь же необходимо
исследовать динамику цен на взаимосвязанных рынках.
По Вальрасу, динамическая модель в случае единственного рынка
(см. 1.8) описывается следующим уравнением:
^-yHS-D). B)
Если спрос и предложение описываются линейными формами {D — a-\-ap,
S~$-\-bp), решение уравнения B) есть
где р0 — начальное отклонение цены от уровня равновесия, а р —
отклонение от него в любой последующий момент времени. По этой формуле можно
определить цену и при любой другой форме кривых спроса и предложения,
но лишь приближенно, в случае небольших изменений формы. Здесь а и b —
тангенсы углов наклона касательных к кривым спроса и предложения
в точке равновесия относительно оси абсцисс. Чтобы равновесие было
устойчивым, в точке равновесия должно соблюдаться условие
Модель Вальраса можно распространить и на взаимосвязанные рынки,,
как это сделал Самуэльсон [12]. Тогда мы заменяем уравнение B)
следующим:
^ ,(m-l)), • C)
= l 2
где, в соответствии с уравнением A), (Sr — Dr) зависит от каждой из цен
и равно нулю при равновесии. Постоянные коэффициенты \ir
характеризуют скорости приспособления цен на различных рынках. Предположим,
что (по крайней мере приближенно для небольших отклонений от
состояния равновесия) Sr и Dr можно считать линейными формами в каждом
из уравнений для цен, так что
m-l
Sp-Z>r = C + S "rsPs ('=1. 2, ...,(/И-1)),
[8=1
где С —постоянная и ars —значение в точке равновесия (d/dps) (Sr—- Dr) =
dYd dX/d Тогда в динамической модели условия равновесия C),
393

выражаемые с помощью отклонений рг от цен равновесия, описываются
следующей системой уравнений:
d -Vr^arsPs (' = 1. 2, ...,(*-!)).
dt
Рассмотрим частный случай (не являющийся ограничением), при
котором, благодаря надлежащему выбору единиц измерения времени и
количества товаров, все скорости приспособления, или fxr, равны 1. Тогда
-^r + 2<Ws = 0(r=l, 2, ...,(п»-1)): D)
На основе этих уравнений определяется характер изменения рг во
времени.
Решение в случае единственного рынка позволяет предположить, что
рт = Ате-и (г=1, 2, ...,(т-1)),
где К есть неизвестный параметр, который необходимо найти, а Аг —
постоянные коэффициенты, определяемые на основе начального возмущения.
Произведем подстановку в уравнение D):
e-Mr,Le = 0 (г = 1, 2, ..., С»-1)),
где 6rs — дельта Кронекера. Этой системе однородных уравнений должна
удовлетворять некоторая совокупность ненулевых значений Л8, при
которой (как это указано в разделе 13.2)
\а —
12
= 0. E)
Соответствующие значения X определяются из E), то есть из
характеристического уравнения матрицы A = [ars]; m— 1 характеристических
корней Хг, Х2, ..., ^7П_Х могут быть как вещественными, так и комплексными.
Каждый из характеристических корней является возможным значением X,
так что, суммируя различные частные решения, взятые с произвольными
постоянными коэффициентами при них, получаем общее решение
уравнения D):
m-l
Pr= S ЛГ8е-^ (г = 1, 2,..., (m-l)). F)
Здесь Л,— корни уравнения E), а ЛГ8 — произвольные постоянные,
заданные начальными условиями.
В динамической модели взаимосвязанных рынков, описываемой
уравнением A), состояние равновесия является устойчивым, если цены в
соответствии с уравнением F) изменяются таким образом, что каждая рг~>0
при t—> оо. Для этого все вещественные характеристические корни ks должны
быть положительными, а попарно сопряженные комплексные корни должны
иметь положительные вещественные части. Отрицательный вещественный
корень вводит в уравнение F) монотонно возрастающее «взрывное»
слагаемое, а пара сопряженных комплексных корней с отрицательной
вещественной частью—слагаемое, соответствующее взрывному колебательному
процессу.
В общем случае матрица А не является симметрической, так как
ars = dYr/dps — dXr/dps не равно asr = dYjdpr — dXs/dpr. При этом немногое
известно о характеристическом уравнении E) и о его корнях. В частном
случае предположим, что ars = asr и, следовательно, матрица А является
симметрической. Тогда условия существования устойчивости принимают
394

более простой вид, так как в соответствии с разделом 13.4 все корни
уравнения E) являются вещественными числами; чтобы состояние равновесия
было устойчивым, корни должны быть также и положительными. Отсюда
следует (см. 13.5), что квадратичная форма (? = х'Ах, дискриминант
которой ^4=|ars| симметричен, является положительной определенной и что,
следовательно,
ап > О,
«22 «23
а13
Таковы, по Хиксу, условия существования совершенной устойчивости.
Следовательно, если только матрица A = [ars] симметрическая, условия
Хикса необходимы и достаточны для устойчивости этой модели Вальраса
(это эквивалентно тому условию, чтобы вещественные части всех X были
положительными). Тогда при состоянии равновесия
_ dYr дХг
а™ ~ dPs dPs '
и Хикс [7] превратил матрицу [ars] в симметрическую, отбросив в
выражениях для Yr и Хг члены, касающиеся дохода. Это не более чем
приближение, допустимое при определенных обстоятельствах. Если же
симметрия отсутствует, например в результате влияния дохода в той части
модели, которая определяет спрос, то условия Хикса по-прежнему могут
являться необходимыми и достаточными для устойчивости, если матрица
А = [аГ8] обладает свойством Метцлера: для всех г и s (г Ф s) ars < 0,
arr > 0, а это значит, что все товары в массе заменимы (being gross
substitutes); см. работу Метцлера [9]. Вслед за Хиксом, Самуэльсоном
и Метцлером дальнейшим изучением этой задачи занимались несколько
исследователей; см., например, работу Ньюмэна [11].
Задачи и упражнения
1. Разложить характеристическое уравнение E) в форме многочлена:
и выразить р через определители, образованные из матрицы A = [ars].
2. Пусть А—симметрическая матрица. В характеристическом многочлене
предыдущей задачи приравнять коэффициенты р суммам или произведениям т—1
вещественных корней Я1? Я2» ..., Ящ-1- Чтобы состояние равновесия было устойчивым, все
числа X должны быть положительными. Объяснить, какими свойствами при этом
обладает матрица А.
13.7. СТАТИЧЕСКАЯ СИСТЕМА ЛЕОНТЬЕВА
Матричные обозначения дают возможность представить в сжатом виде
системы межотраслевых потоков Леонтьева (см. гл. 10). В замкнутой системе
Леонтьева имеются тг + 1 отраслей. Последняя отрасль — домашние
хозяйства, предоставляющие трудовые услуги в качестве своей продукции,
а затратами в ней является личное потребление товаров. Пусть #rs
—количество продукта Хг, или продукции г-й отрасли, направленное в s-ю отрасль.
Из элементов xrs можно составить матрицу межотраслевых потоков
(д + 1)-го порядка:
Т = [*„].
Условимся считать хгг — 0 при г = 1, 2, ...,(w + l), так что элементы
главной диагонали матрицы Т нулевые. Суммируя элементы матрицы Т
по горизонтали, мы получаем вектор валового выпуска Х = {ХГ}. И
наоборот, если условимся считать хгг= — Хг, то итоги построчного
суммирования элементов матрицы Т представят собой нуль-вектор.
395

Примем, что количественные коэффициенты затрат суть величины
постоянные:
и, по условию,
агг = 0.
Тогда из этих коэффициентов можно построить матрицу
коэффициентов затрат (гс+1)-го порядка:
A* = [ars]
и технологическую матрицу (в том смысле, как она понимается в
разделе 9.8):
1
— а
21
al
1
... —а
... —а9
Юг +
¦ а(п+1I
Тогда условия равновесия, которые отображают точное распределение
выпуска продукции каждой отрасли по категориям потребления, а также,
что в каждой отрасли поступления равны ее издержкам, описываются
уравнениями:
(I) АХ = О и (II) р'А==О, A)
где р — {рг} — вектор цен. Эти два условия совершенно самостоятельны;
условие (I) определяет выпуск отраслей, а условие (II) —цены. Каждое
условие описывается системой однородных линейных уравнений, имеющих
нетривиальное решение только в том случае, если матрица А является
особенной, и ее ранг равен г</г + 1. Обычно ранг матрицы равен г = п,
и в этом случае уравнения A) позволяют определить лишь соотношения
между выпусками отраслей и между ценами (см. упражнение 3).
Абсолютные же значения выпуска и цен поддаются определению только в том
случае, если известны выпуск одной из отраслей (например, затраты труда)
и одна из цен (например, ставка заработной платы).
Если мы задаемся некоторыми значениями элементов одной (или более)
строки и столбца матрицы Т, система превращается в открытую систему
Леонтьева. Как правило, в матрице межотраслевых потоков открытой
системы Леонтьева определяются абсолютные значения элементов последней
строки матрицы (затраты труда) и последнего столбца (потребление
домашних хозяйств). Матрица при этом приобретает следующий вид:
, Г Xrs\Xr 1
"LTToj
при г, 6 = 1, 2, .. .,/г. Порядок матрицы Т по-прежнему равен га+1,
однако элементы последней строки отображают известные затраты труда
по отраслям (?s), а последний столбец — заданный конечный спрос (хг).
Матрица коэффициентов затрат А* = [ars] и технологическая матрица
А = 1 —А* суть 7г-го порядка. Вместе с тем к последней матрице можно
присоединить строку коэффициентов затрат труда (— feg) = — (gs/Xs)
E = 1, 2,...,w):
-Ь'
где Ь' =
Теперь условия равновесия (I) описываются матричными уравнениями:
(I) АХ = х и (II) p'A = w'. B)
396

Далее:
Общие затраты труда Y — WX.
Национальный доход Z = р'Х = w'X.
Это —условия I и II из раздела 10.3, написанные с помощью матричных
уравнений. Кроме технологической матрицы А-то порядка, условия B)
включают также следующие векторы п-то порядка (столбцевые или строчные):
X = {Хг} — валовой выпуск,
р = {#.} — цены,
х = {хг} — конечный спрос,
w = w{bs} — заработная плата на единицу продукции.
Наряду с технологической матрицей А, заданными величинами для
открытой системы являются как конечный спрос х, так и заработная плата
на единицу продукции w. Последняя зависит от коэффициентов затрат труда
bs и от ставки заработной платы w. Для определения общих затрат труда
У необходимо знать только коэффициенты затрат труда.
С помощью уравнений B) определяются неизвестные — валовой выпуск
X и цены р. Можно определить также общие затраты труда Y и
национальный доход Z. Если матрица А является неособенной — а обычно это так,
если технологическая матрица замкнутой системы (п + 1) -го порядка имеет
ранг г = п, — то уравнение B) имеет единственное решение:
A~iY и' w'A V b'A^iv 7 w'A~1y (Ч\
Условия B) друг с другом совершенно не связаны, как это вытекает
из решения C). Выпуск X, а также затраты труда У выражаются через
заданный конечный спрос х. Цены р определяются на основе заданных
значений заработной платы на» единицу продукции w. Значения выпуска
продукции, затрат труда, цен и национального дохода исчисляются после
получения матрицы А, обратной по отношению к технологической матрице А.
Задачи и упражнения
1. В решении для открытой системы Леонтьева валовой выпуск и цены
необходимо выразить через определитель А=|А| и алгебраические дополнения его элементов;
показать, что решение имеет вид (при /• = !, 2, ..., п)
s s
2. Будем считать АХ = х линейным преобразованием, позволяющим перейти от
валового выпуска к конечному спросу, а Х = А-1х—обратным преобразованием. Какой
вид имеет соответствующее линейное преобразование для перехода к ценам?
3. Пусть в замкнутой системе Леонтьева, включающей п-\-1 отраслей, матрица
А имеет ранг п и подматрица Апп, полученная из матрицы А вычеркиванием
последней строки и последнего столбца, является неособенной. Обозначим через с вектор
последнего столбца (взятого без последнего элемента) матрицы А. Решить систему
первых п уравнений АХ = 0, представив вектор-столбец выпуска первых п отраслей
в виде A^cXn+i» где Xn+i—выпуск последней отрасли. Если (л + 1)-я «отрасль» есть
«домашние хозяйства», показать, что, таким образом, выпуск каждой отрасли
выражается через ставку заработной платы.
4. В открытой системе Леонтьева обозначим через х и w диагональные матрицы,
диагональными элементами которых являются соответственно конечный спрос и
заработная плата на единицу продукции, взятые по отраслям. Показать, что (г, s)-ii
элемент матрицы U = wA~1x будет wrxsAsr/\ А |, где Asr—алгебраическое дополнение
(s г)-го элемента в определителе А = \А\. Показать далее, что вектор построчных сумм
элементов матрицы U есть {wrXr}, а сумм элементов столбцов есть [psxB]. Показать,
что матрица LJ может выполнять роль матрицы межотраслевых потоков в системе
«счетов национального дохода», где национальный доход принимается .равным сумме
«добавленных стоимостей» по отраслям, равной сумме конечных расходов по отраслям
экономики [2].
397

13.8. МАТРИЦЫ МЕЖОТРАСЛЕВЫХ ПОТОКОВ
Матрица межотраслевых потоков Т = [xrs], в которой мы условились
считать хгг — — Хг, обладает тем свойством, что итог суммирования по
горизонтали элементов каждой строки равен нулю. Это есть выражение
первого условия равновесия, то есть точного соответствия переданных в
другие отрасли количества продукции отрасли и ее выпуска. Однако
суммирование элементов столбцов матрицы Т невозможно, так как эта матрица —
количественная, и различные элементы столбца имеют разные единицы
измерения. Если мы считаем цены рт заданными или определяем их с помощью
второго условия равновесия, то стоимостная матрица межотраслевых
потоков имеет следующий вид:
V = [",.] =
где^условлено считать
При построчном суммировании элементов матрицы V итог по-прежнему
равен нулю, поскольку условие равновесия заключается в том, что стоимость
валового выпуска каждой отрасли VТ в точности соответствует стоимости
потребленной для разных целей продукции этой отрасли. Однако, кроме
этого, нулевые итоги получаются и при суммировании элементов матрицы V
по вертикали. Это выражает второе условие равновесия, согласно которому
цены должны быть таковы, что выручка каждой отрасли равна ее издержкам.
Следовательно, если применяются цены, соответствующие состоянию
равновесия, уже само получение нулевых итогов суммирования элементов матрицы
V по строкам и по столбцам включает выполнение обеих групп уравнений
равновесия.
Мы можем определить технологию экономики и по-иному, заменив
матрицу А = I — А* другой матрицей, элементы которой не технологические
(количественные ars), а соответствующие стоимостные коэффициенты затрат:
Если (см. упражнение 1) X есть вектор валового выпуска в стоимостном
выражении, то в таком случае первое условие равновесия (итоги построчного
суммирования элементов матрицы V равны нулю) представляется точно
в таком же виде, как и при количественном выражении элементов, а именно
Подобные же изменения в определениях можно внести и в открытую
систему Леонтьева. Если выразить в стоимостной форме А, X и х, то условия
равновесия описываются следующими уравнениями:
АХ = х, откуда Х = А"хх,
а общая сумма заработной платы равна Ь'А^х. Следует отметить также, что
расширенная технологическая матрица стоимостных коэффициентов затрат
имеет следующий вид:
А1
В = • •
-Ь'
В этой матрице сумма элементов каждого столбца равна нулю [см. 10.4,
уравнение (II)]. Именно эта форма имеет особое значение при практическом
применении открытой системы.
Понятия матрицы межотраслевых потоков, использованные в системе
Леонтьева, далее развили и расширили Стоун [13] и Гудвин [6]. Пусть
в замкнутом хозяйстве имеется п видов деятельности (отраслей хозяйства),
которые можно считать, а можно и не считать отраслями промышленности.
398

Обозначим через xrs продажу r-то продукта s-му виду деятельности в
количественном выражении и через vrs — pTxrs — в стоимостном выражении, где
рг — цена продукта г-ж деятельности.
Условимся считать, что
ягг = -Хг и vrr=.-prXr= -Fr,
где Хг и Vт — валовая продажа продукции г-ж деятельности, выраженная
соответственно в количественной и стоимостной форме/ Соответствующие
количественные и стоимостные матрицы межотраслевых потоков имеют вид:
T=[zM], V = [or,l (r, s = l,2, ...,п).
Технологические коэффициенты хозяйства представляют собой
отношения закупок какой-либо одной отраслью (продукции других отраслей)
к валовой продаже ее собственной продукции. Эти коэффициенты можно
выразить в количественной форме (см. упражнение 2) или же, как это
сделано здесь, только в стоимостной форме. Предположим, что имеются
неизменные технологические коэффициенты, определяемые следующим образом:
ara = Vf-s (r, * = 1, 2, ...,п),
то есть как отношения стоимости закупок s-й отраслью (продукции /*-й
отрасли) к валовой стоимости всех продаж продукции 5-й отрасли. Условимся
считать vrr — —Fr, то есть
arT = vf-=-i (г = 1,2, ...,п).
Составим матрицу
— а12...— а
1п
— а21 1 ... -а2п
в сжатом виде полностью характеризующую технологические условия
хозяйства.
Можно без труда вывести связь между матрицей межотраслевых потоков
V и технологической матрицей А. Обозначим через v диагональную матрицу,
составленную из элементов валовой стоимости продаж (VT) n отраслей.
Тогда в соответствии с правилом умножения матриц:
Для хозяйства, рассматриваемого как единое целое, можно установить
два совершенно независимых одно от другого условия:
I. Итог валовой стоимости продаж продукции какой-нибудь отраслью
в точности равен стоимости закупок продукции этой отрасли другими
отраслями.
II. Для каждой отрасли выручка от продажи равна издержкам
(стоимости закупок). Следовательно, условия равновесия выражаются следующим
образом:
Условия I — итоги суммирования элементов матрицы V по горизонтали
равны нулю, то есть
V{l} = 0,
ИЛИ
Av{l} = 0,
или
АХ = О,
399

поскольку элементами вектора v{l} являются Fr, и можно считать, что это —
вектор X, то есть вектор валовых продаж (по стоимости). Это — знакомое
нам условие Леонтьева для замкнутой системы в стоимостном выражении.
Условия II — итоги суммирования элементов матрицы V по вертикали
равны нулю, то есть
[1]V = O,
ИЛИ
[l]Av = 0,
или
[l]Avv х = 0 (v — неособенная матрица),
или
[1]А = 0.
Это попросту является ограничением, налагаемым на технологическую
матрицу А; при суммировании элементов столбца итог должен быть равен
нулю.
Замкнутую систему мы можем преобразовать в открытую, задавшись
элементами одной строки и одного столбца матриц межотраслевых потоков
Т и V. Предположим, что для этого выбраны последняя строка и последний
столбец, так что нам известны закупки п-и отрасли. Тогда технологическая
матрица А может быть сведена к матрице (п — 1)-го порядка, а вектор X
валовой продажи продукции п — 1 отраслей — к вектору (п — 1)-го
порядка. Оказывается, что (см. упражнение 3)условие/1 описывается теперь
уравнением:
АХ = Вектор заданных закупок п-я отрасли. Это — знакомые нам
условия для открытой системы Леонтьева, когда закупки п-й отраслью
истолковываются как потребление домашних хозяйств.
Задачи и упражнения
1. В замкнутой системе Леонтьева преобразовать матрицу стоимостных
коэффициентов затрат А* = [.аГ8],'имея в виду, что ars = vrs/Vs. Показать, что условия
равновесия (точное соответствие потребления и выпуска продукции по каждой отрасли)
описываются при этом уравнением АХ = О, где А = 1 — А*, а X — вектор валового
выпуска отраслей в стоимостном выражении.
2. Рассмотреть стоимостную матрицу межотраслевых потоков Y — [vrs] для
замкнутого хозяйства, если постоянные технологические коэффициенты заданы в
количественном выражении: ars = xrs/Xs. Показать, что V = pAx, где А — матрица,
составленная (как и ранее) из коэффициентов количественных затрат ars; p—диагональная
матрица, построенная из элементов вектора цеп р, и х~диагональная матрица,
построенная из элементов вектора валовых продаж X. Вывести, что при этом условия
равновесия для хозяйства описываются теми же уравнениями, что и для замкнутой
системы Леонтьева, а именно:
3. Если матрица В =
-О 0 ... О а1П
О 0 ... О а2п
Г А* ! О -]
то показать, что А-'ГВ= - т-х-
L ам ; и J
|_0 0 ... О — 1J
где А —технологическая матрица га-го порядка, А* — матрица (п — 1)-го порядка,
полученная из матрицы А вычеркиванием строки и столбца n-й отрасли, и ап —некоторый
вектор (п — 1)-го порядка. Рассмотреть условия для замкнутой системы АХ = О (как
в предыдущей задаче) и показать, что они сводятся к следующим:
А*Х* = Закупки n-й отрасли,
где X* —вектор продаж продукции /г — 1 отраслей.
4. Продолжить анализ, произведенный в двух предыдущих задачах, показав, что
условие для замкнутой системы, то есть р'А —О, превращается в условие:
р*'А* = Заработная плата на единицу продукции, где опущенная п-п отрасль
понимается как деятельность домашних хозяйств.
400

5. Истолковать количественную матрицу межотраслевых потоков T=[xrs] не для п
отраслей Хозяйства, а для п категорий юридических лиц, между которыми существуют
хозяйственные отношения, как-то: домашние хозяйства, торгово-промышленные
предприятия, правительство. Таким путем указать возможность применения матрицы
в системе «счетов национального дохода». (См. Стоун и Аттинг [14].)
13.9. ДИНАМИЧЕСКАЯ СИСТЕМА ЛЕОНТЬЕВА
Статические условия равновесия для замкнутой системы Леонтьева
описываются уравнением АХ = 0, где А = 1 — А*, а А* = [ars] отображает
структуру межотраслевых потоков хозяйства; ars суть неизменные
коэффициенты затрат. В более всеобъемлющей динамической системе (см. 10.8)
добавляется вторая матрица В = [brs], которая характеризует структуру
капиталов хозяйства; brs — коэффициенты основного капитала (запас на
единицу выпуска). В динамической модели условия точного соответствия
потребления продукции и ее выпуска вместо уравнений B) раздела 10.8
теперь определяются следующим матричным уравнением:
= Ь -jj- , A)
где Х = {ХГ}, как и ранее, представляет собой вектор-столбец валового
выпуска и где
dX (dXy^y
~dT~~ \~dfj
есть вектор-столбец скоростей изменения выпуска отрасли (г = 1, 2, . ..,тг).
Чтобы решить систему A) дифференциальных уравнений первого
порядка, испытаем решение
где к = {кг} — вектор-столбец постоянных величии и К — скаляр, который
необходимо найти. Тогда dX/dt— —k%e~^f; после сокращения на е~№ Ф 0
система уравнений A) превращается в следующую:
Ak=-?JBk,
то есть
(А + ХВ)к = 0. B)
Матрица
1 + А,Ьи — ai2 + Х612 ... — а1п + ХЬЪ
а21 "Г ^^21 1 "Т ^^22 • * * а2п ~^' ^21
есть общий случай характеристической матрицы (см. 13.4).
Условия B) заключаются в том, что вектор-столбец п-то порядка
приравнивают нулю; всего система имеет п уравнений, и этого достаточно,
чтобы определить Я и соотношения между элементами кг вектора к. В
уравнении B) не все элементы кг нулевые, откуда следует, что
| А + ХВ | = 0. C)
Это —уравнение п-\\ степени относительно Я, коэффициенты которого
определяются значениями структурных коэффициентов ars и brs.
Уравнение C) имеет п корней (Я1? Я2, .. ., Яп). Поскольку матрицы А и В не
являются симметрическими, не следует ожидать, что все значения Яч
окажутся вещественными числами. Некоторые значения этих корней могут
оказаться попарно сопряженными комплексными числами, что соответствует
колебательному характеру динамики выпусков отдельных отраслей.
Рассмотрим корень Я, = Я3 уравнения C). Матрица (А+Я3В) является
особенной, поскольку |А + Я8В| = 0; предположим, что ее ранг равен п—1.
26 Р. Аллеи 401

Тогда в соответствии с разделом 13.2 уравнение B) определит
соотношения между элементами вектора к, то есть между кг. Собственному
значению Ks соответствует собственный вектор k;s = {/crs}, то есть некоторая
система krs, заданных в виде соотношений kls: к28: ... : kns через Xs
и структурные коэффициенты ars и brs (см. упражнение 2). Следовательно,
одним из частных решений уравнения A) является X = kse~A*'. При
5=1, 2, . ..,тг имеется п таких решений; общее решение есть сумма всех
частных решений, взятых с произвольными постоянными коэффициентами:
s=l
то есть
Хг = А1кг1е~Ы + А2кг2е~Ы+ ... +АпкГпе~К* (г=1, 2 п). D)
В уравнении D) As суть произвольные постоянные, определяемые из
начальных условий. С другой стороны, К и к суть постоянные структурные
параметры, заданные коэффициентами ars и brs уравнений A); X — корни
уравнений C); после того как найдены Я, на основе уравнения B)
находятся элементы /crs, соответствующие каждому ks.
Отдельные слагаемые решения D) могут включать как вещественные,
так и комплексные (сопряженные) значения X. Если Хг есть вещественное
число, то первый член затухает с течением времени при ^>0 и
неограниченно возрастает при Хг < 0. Если Лх и Х2 суть сопряженные
комплексные числа а ± i(o, то два первых слагаемых в совокупности
характеризуются частным решением следующего вида:
Akre~at cos (at — е),
где А и е — произвольные постоянные. Это вводит колебательный элемент
в изменение Хг во времени; период колебаний здесь равен 2я/со. Колебания
затухают, если а > 0, и неограниченно возрастают по амплитуде, если а < 0.
Особое внимание следует уделить предельным значениям выпуска, когда
время t стремится к бесконечности, то есть доминирующему слагаемому
решения D). Это слагаемое соответствует корню Хш, «вещественная» часть
которого является минимальной. Выпуск каждой отрасли затухает или
неограниченно возрастает в зависимости от того, является ли
вещественная часть корня Хт положительной или отрицательной. Выпуск изменяется
колебательно, если Хт не является вещественным числом, и монотонно,
если Хт вещественно. Предельная динамика ХТ при бесконечно большом
значении t приближенно описывается следующим уравнением:
Xr = Amkrme-bmt,
если %т — вещественное число; или же
Xr = Amkrme-^t cos (©m* - е),
если ^ — комплексное число, Хт = ат+шт. Отсюда следует, что (если
^-—вещественное число)
л.Т аъ л.8 Ksm
Следовательно, в конечном счете относительные темпы прироста выпуска
одинаковы для всех отраслей, причем соотношения между выпусками
различных отраслей неодинаковы; темп роста и эти соотношения определяются
структурой системы.
В статической системе (см. 13.7) решение, определяющее выпуски
отраслей (в их соотношении) при состоянии равновесия, существует только
в том случае, если матрица А является особенной, |А| = 0. Если это верно
и для динамической системы, то (как в разделе 13.4) слагаемое, не
зависящее от величины корня X уравнения C), равно нулю, и Ы0 является
402

одним из корней уравнения C). В решении D) примем Кг = 0, так что
первое слагаемое в уравнении, определяющем Хг, есть постоянная
величина А1кг1. Тогда динамика Хг будет представлять затухающее или взрывное
колебательное изменение относительно постоянного уровня. Если процесс
затухающий (наименьшее по абсолютной величине из остальных значений Я—
положительно), то предельное значение выпуска равно постоянной величине
А1кг1. Очевидно, для этого параметры кг должны быть положительными.
Для динамического варианта открытой системы составляется та же
система дифференциальных уравнений A); к ней лишь добавляют в правой
ее части вектор конечного спроса х = {хг}- Каждый из элементов хт является
заданной функцией времени. И в этом варианте решение имеет вид
уравнения D), в котором добавлены частные решения, определяемые из
специфической формы временной функции, принятой для вектора х. Например,
пусть х = се^, где с = {сг} является вектором заданных постоянных
элементов, и где [х —заданный скаляр, так что относительный темп прироста
конечного спроса одинаков по всем отраслям (см. 10.9, вариант II). Тогда
дифференциальные уравнения A) примут вид:
требуется отыскать частное решение этого уравнения. Испытаем, не является
ли им решение Х = Се^, где С = {?>}—- вектор постоянных величин, который
должен быть найден. Произведя подстановку, получим
АС =
или
где заданную матрицу (А — |хВ) мы считаем неособенной. Тогда общее
решение имеет следующий вид:
и выпуск каждой отрасли изменяется с некоторым отклонением
(затухающим или взрывным, колебательным или монотонным) относительно члена,
выражающего тенденцию, которая возрастает с той же относительной
скоростью, что и конечный спрос.
Задачи и упражнения
1. Матрица [Л8Г], построенная на основе матрицы A=[ars] и представляющая
собой транспонированную матрицу алгебраических дополнений элементов матрицы А
называется присоединенной к матрице А. Показать, что если А — особенная матрица
(то есть | А | = 0), то произведение матрицы А на любой столбец присоединенной
матрицы представляет собой пулевой вектор-столбец.
2. Рассмотреть систему однородных линейных уравнений (A-f-Л8В) к = 0
относительно переменных к = {Лг} в том случае, если матрица (A-j-A,sB) особенная, то есть
ее определитель равен нулю. Воспользоваться результатом предыдущей задачи, чтобы
показать, что левая часть обращается в нуль, если элементы вектора к
пропорциональны элементам любого столбца матрицы, присоединенной к (A + A,SB).
3. Воспользоваться результатами двух предыдущих задач, чтобы показать, что
ранг матрицы, присоединенной по отношению к особенной матрице, равен 1 и что
лишь один столбец такой присоединенной матрицы является линейно независимым.
4. Рассмотреть открытую динамическую систему АХ = В (dX/dt)-\-c, где с = {сг}
есть постоянный во времени конечный спрос. Найти частные решения, а затем написать
и общее решение.
5. Рассмотреть динамическую модель, основанную на акселераторе без
запаздывания во времени, путем дискретного анализа (см. 10.8, упражнение 1). Показать, что
возможна такая модель открытой системы, в которой вектор валового выпуска Х$
задается системой разностных уравнений:
где С — квадратная матрица постоянных коэффициентов затрат и структуры элементов
капитала, а К — вектор, зависящий от конечного спроса. Исследовать, при каких
условиях конечные выпуски равны Х=A — С) К.
26*

ГЛАВА 14
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ИГР
14.1. ЭКОНОМИЧЕСКИЕ ПРИМЕНЕНИЯ ТЕОРИИ ИГР
Решение многих экономических проблем сводится к определению
наилучшего положения, подчиненного только некоторым ограничениям,
вытекающим из условий самой проблемы. Так, например, индивидуальный
потребитель максимизирует полезность при условии сбалансированности своего
бюджета. Задача часто может быть выражена альтернативно, как достижение
максимального или минимального, в каком-то смысле, положения; фирма
может, например, максимизировать выпуск продукции при данных
издержках или минимизировать издержки при данном выпуске. Существо дела
в том, чтобы решение было просто и приводило бы к максимуму или
минимуму. С такой ситуацией мы встречаемся на конкурентном рынке, где может
быть большое число покупателей и большое число продавцов; каждый
индивидуум старается достичь максимума собственной прибыли, и на его действия
не оказывают влияния действия других индивидуумов. Задачи при наличии
монополии или монопсонии, то есть при ситуации с единственным продавцом
и большим числом покупателей и обратной, равным образом сводятся к
задачам на максимум.
Однако в других экономических ситуациях встречаются совершенно
иные проблемы. Особое внимание на них было обращено в работе Неймана
и Моргенштерна [8]. Такие ситуации возникают там, где имеется конфликт
интересов) который должен быть разрешен. Наиболее известными из них
являются двусторонняя монополия (монополия — монопсония), где имеется
только один покупатель и только один продавец, и дуополия или олигополия,
где два или ограниченное число продавцов торгует с большим числом
покупателей. Более сложные ситуации подобного рода возникают, если образуются
объединения или коалиции лиц, участвующих в столкновении интересов,
например, в том случае, когда ставки заработной платы определяются
союзами или объединениями рабочих и предпринимателей. Решение такой
проблемы не является просто решением какой-либо задачи на максимум или
минимум. Оно поднимает более сложные вопросы о стратегиях, которых
придерживаются участники, и соответствующая математическая формулировка
бывает часто, но не всегда, минимаксного типа. Так, если на рынке имеется
только два продавца А и 5, то А должен планировать свои действия при
некоторых предположениях о том, что будет предпринимать В, и наоборот. При
рассмотрении. любой линии поведения или стратегии продавец А может
попытаться определить наихудшие для него действия В; А тогда выбирает
наилучшую (дающую максимальный выигрыш) стратегию, принимая во
внимание наихудший для него (то есть приводящий к минимальному
выигрышу) ответ со стороны В. В свою очередь, В, принимая свои решения, также
учитывает, что может сделать А. .Таким образом, действия каждого
участника основываются на принципе минимакса, и в их решения входят как
элементы максимизации, так и минимизации. Вопрос заключается в том,
существует ли какой-либо исход, совместимый с действиями участников, то есть
согласуется ли минимаксное положение для А с минимаксным положением
для В,
Теория игр исследует подобные математические проблемы. Если в игре
участвуют два игрока, то каждый из них имеет ряд доступных ему, согласно
404

правилам игры, стратегий и старается максимизировать свой выигрыш
(измеряемый, например, в деньгах) в результате многих партий или свое
ожидание1 выигрыша в одной партии. Имеет ли игра какой-нибудь
оптимальный или устойчивый исход (stable outcome), зависит от того, совпадает ли
минимаксное положение, к которому стремится один из игроков, с таким же
положением для другого игрока.
Таким образом, теория игр имеет отношение к рассмотрению
экономических проблем. Однако теорию можно формулировать только в
математических терминах, далеко не простых, и, может, нет необходимости в
использовании такого «кузнечного молота» только для того, чтобы «расколоть орех»
проблемы дуополии. Но оказалось, что определенная группа экономических
проблем, которая включает взаимосвязь технических отношений (например,
производственных), может быть удовлетворительно изложена с помощью
аппарата математической теории игр. К ним относятся отношения затрат
и выпуска, изложенные в главе 10. Более общие экономические проблемы,
известные как линейное программирование или анализ видов деятельностиу
представляют одну из главных областей экономического применения теории
игр. Интересно отметить, что к этому же классу относится целый ряд технико-
экономических проблем, которые встречает статистик, когда ему при
принятии решения приходится соизмерять точность выводов с производимыми
затратами, или когда он пытается минимизировать максимальный риск, к
которому приводит то или иное решение. Подобно экономисту, статистик может
достичь цели путем элементарных рассуждений, но, вртречаясь с более
сложными проблемами, он будет вынужден воспользоваться математической
теорией игр. Развитие линейного программирования (анализа видов
деятельности) экономистами и теории статистических решений — статистиками
происходило одновременно, но почти независимо, с помощью однотипного
математического аппарата.
14.2. ИГРА ДВУХ УЧАСТНИКОВ С НУЛЕВОЙ СУММОЙ И ЕЕ ПЛАТЕЖНАЯ МАТРИЦА
Игры, рассматриваемые теорией игр, могут включать элемент
случайности, но, в основном, они являются играми мастерства, в которых стратегии
(то есть выбор способа действия) являются их частью. Практически в эту
группу попадают и простые игры и очень сложные. В качестве известных
в обиходе примеров можно привести игру «крестики и нолики», шахматы
и бридж.
Предварительно необходимо сформулировать некоторые определения
и отличительные особенности.
Игра — это совокупность правил и процедур, относящихся к партии,
которым подчиняются ее участники. Партией называется конкретная
реализация игры, практическое применение правил, приводящее к
определенному результату.
Ход — момент в игре, когда один из партнеров встречается с
альтернативами2, выбор — вариант, действительно избранный в партии. Платежи
делаются по окончании каждой партии в соответствии с ее исходом, причем
безразлично, выражаются ли «платежи» в денежной сумме или подсчитывают-
ся набранные в партии очки или фишки. Если в игре участвует больше двух
игроков, то возможны платежи каждого из них любому другому игроку.
Простая иллюстрация этих положений дается далее в упражнении 1 к этому
разделу.
1 Речь идет о математическом ожидании выигрыша, см. далее, стр. 409, сноска.—
Прим. ред.
2 Аллен в определении и в приводимых им примерах (но не везде) считает ходом
момент, когда оба игрока встречаются с альтернативой. В соответствии с принятой в
советской и переводной литературе терминологией, мы считаем далее ходом момент игры,
когда один из партнеров встречается с альтернативой. Таким образом, далее числом
ходов считается сумма ходов А и ходов В.— Прим. ред.
405

Здесь мы рассматриваем лишь такие игры, в которых участвуют только
два игрока, А и Вл причем выигрыш одного партнера равен проигрышу
другого и, следовательно, сумма платежей всегда равна нулю. В результате
партии такой игры двух лиц с нулевой суммой игрок А получает чистую
сумму а от игрока Z?, а игрок В получает чистую сумму Ь=—а от игрока А.
Здесь а может быть положительно (А выиграл) или отрицательно (В выиграл).
В действительности происходит только одна передача — платеж от А к В
или наоборот. Такой тип игры имеет более общий характер, чем это может
показаться на первый взгляд. Например, бридж является игрой двух лиц
с нулевой суммой. Хотя имеется четыре партнера, но они играют попарно,
то есть имеется два «игрока», где под каждым из них нужно понимать
команду из двух участников.
Более того, игры двух лиц с нулевой суммой бесконечно разнообразны.
Число ходов может меняться от одного до любого конечного числа или может
быть бесконечным, равно как и число возможных при каждом ходе вариантов.
Объем информации (например, знание при каждом ходе о выборе
противника, сделанном при предыдущих ходах), имеющейся в распоряжении
каждого игрока, может различаться. В большей или меньшей степени в игру
могут входить элементы случая. Например, сдача карт или подбрасывание
монеты устанавливают, какой игрок делает первый ход. Общим для игры
двух лиц с нулевой суммой является наличие конфликта интересов между
двумя игрокам и тот факт, что в конечном счете то, что теряет один,
выигрывает другой игрок.
Игра, состоящая из нескольких ходов, может быть названа развернутой
или экстенсивной игрой (extensive game). Может случиться, что игра имеет
конечное число ходов и конечное число вариантов при^каждом ходе. В таком
случае игра конечна, и все доступные игрокам «стратегии» могут быть
перечислены. Однако это вовсе необязательно: существуют игры, в которых
число ходов неограниченно и число «стратегий» бесконечно. Настоящее
изложение, фактически, охватывает конечные игры; хотя они и важны, но не
только эти игры представляют интерес.
Теория игр тесно связана с теорией выпуклых множеств (см. 11.5).
В общих чертах здесь создается следующая ситуация. Если мы нашли,
согласно минимаксному принципу, некоторое число решений игры, то их
выпуклая оболочка представляет собой бесконечное множество решений игры.
Задача заключается в нахождении полного выпуклого множества решений.
Литература по математической теории игр приведена в конце книги, в
библиографии к настоящей главе.
Цель этой главы состоит в том, чтобы дать более простое изложение
главных результатов теории игр. Лучшими введениями в теорию игр
являются книги Мак-Кинси [6] и Кемени, Снелла и Томпсона [1J. В популярной
и увлекательной форме изложены первоначальные сведения по теории игр
в работе Вильямса [11]. В книге Льюса и Райфа [4], кроме игр двух лиц
с нулевой суммой, рассмотрены игры и многих других типов. Во всех этих
работах внимание больше обращено на изложение концепций и методов,
чем на математические детали.
Будем рассматривать конечную игру, то есть игру с конечным числом
ходов и конечным числом альтернатив при каждом ходе. Тогда, можно
сказать, что у игрока А есть выбор из т стратегий в партии, и эти стратегии
могут быть перенумерованы числами от 1 до т (г = 1, 2, ..., т). Таким же
образом, у В имеется выбор из п стратегий (s = 1, 2, ..., п). Когда игроки
А и В выберут свои стратегии, то вся партия игры автоматически
определится по правилам игры. Каждая стратегия должна составить план,
в соответствии с которым при каждом ходе и при каждой возможной
совокупности обстоятельств игрок делает свой выбор. Число различных
стратегий типу игроков может быть очень велико, и на практике оно
обычно бывает велико, но конечно. Поэтому всегда возможно перечислить
стратегии для каждого игрока.
406

Когда в игре имеется только два хода (по одному для каждого партнера),
перечисление стратегий довольно просто. При своем ходе А имеет для выбора
конечное число альтернатив; занумеруем их числами г = 1, 2, ..., т. В свою
очередь, В имеет конечное множество альтернатив для выбора,
перенумерованных числами s = 1, 2, ..., п. Как только А и В выбрали свои номера
стратегий г и s, партия игры определится. Однако, как это будет ясно из
упражнения (ж) настоящего раздела, перечисление стратегий для игроков А и В
(т для А и п для В), может быть сделано независимо от того, какое может
быть (конечное) число ходов. В любой игре возможны затруднения при
практическом перечислении всех различных стратегий; но возникающие здесь
трудности чисто практического, а не теоретического характера.
Пусть игра будет сыграна при стратегии с номером г, выбранной
игроком Л, и стратегии s, выбранной игроком В. Партия в таком случае
определена, и в результате ее будет произведен соответствующий платеж. Пусть ars
обозначает сумму, полученную А от В. Здесь ars определено для любых г я s
и может быть положительным, отрицательным или равным 0. Всего имеется
т X п различных способов разыграть партию, и для каждого из них —
определенный платеж ars (г =•¦ 1,2, ..., т; s = 1, 2, ..., п).
Эти суммы можно записать в виде платежной матрицы для игрока А:
*12
Имеется также платежная матрица для игрока В: В = [brs], где brs =.
= —ars. Нет необходимости рассматривать ее самостоятельно, так как В=—А.
Легко объяснить строение платежной матрицы. Каждая строка
элементов отображает выбор стратегии игроком А. Всего в матрице имеется т строк,
по одной для каждой стратегии А, и аналогично п столбцов, по одному столбцу
для каждой стратегии игрока В. Когда игроки А и В выбирают свои
стратегии, то тем самым определяются одна строка и один столбец в матрице А,
и элемент ars на их пересечении представляет собой сумму, полученную
игроком А в результате партии, проведенной согласно выбранным стратегиям.
Пример (а).
Рассматривается игра с двумя ходами, в которой каждый из игроков А и В
называет число 1 или 2, не зная о выборе своего противника. А получает 1 фунт
•стерлингов от Ву если названные числа различны; А платит 1 фунт игроку #, если
эти числа совпадают. Платежная матрица для игрока А имеет вид:
-["I -1J ¦
Пример (б).
Для игры предыдущего примера рассматривается измененная платежная
матрица:
А-Г2 Ч
L3 -2J '
согласно которой, например, если А и В оба называют 1, то Л получает от В 2 фунта.
Пример (в).
Игра с двумя ходами состоит в том, что при первом ходе игрок А называет одно
из трех чисел: 1, 2 или 3; при втором ходе В тянет карты из колоды до тех пор,
пока не вытянет туза. Перенумеруем стратегии игрока В в соответствии с мастью
этого туза: 1 — пики, 2—черви, 3—бубны, 4—трефы.
Определим платежную матрицу следующим образом:
407

согласно которой, например, партия заканчивается вничью (без платежа), если А
назовет 1 и В вытянет туза пик.
Пример (г).
Две лошади участвуют в скачках. Пари определяются ставками и выигрышами
лошадей B к 1 за первую лошадь и 2 к 1 против второй лошади) * которые
определены заранее. Игрок А ставит 1 фунт на одну из лошадей, но он совершенно
не знает степени их готовности к состязаниям. Игрок В представляет собой
комбинацию всех сил, определяющих результат скачек (например, букмекер, владельцы
и жокеи). Платежная матрица игрока A («punter») будет:
Пример (д).
Меховое пальто, оцененное в 100 фунтов, можно за 1 фунт застраховать от
пожара. Игрок А (владелец пальто) выбирает между двумя стратегиями:
1 ... Страховать; 2 ... Не страховать.
В роли игрока В, который решает быть (стратегия 1) или не быть (стратегия 2)
пожару, выступают силы природы.
Платежная матрица для А будет:
— 100 0
Пример (ё).
Игра Морра («Могга») широко распространена в Италии. В варианте игры,
называемом two-finger Могга (двухпальцевая Морра), игрок А показывает один или два
пальца и называет вслух число пальцев (тоже один или два) которое, по его
предположению, назовет игрок В. Одновременно с ним совершенно так же поступает
игрок В. Каждый игрок имеет четыре стратегии, которые могут быть перенумерованы:
1 ... A, 1), 2 ... B, 1), 3 ... A, 2), 4 ... B, 2), где первый номер в скобках
обозначает число показанных, а второе — число названных игроком пальцев. Если только
один игрок угадывает правильно, то он получает выигрыш, равный сумме числа
показанных игроками пальцев; если ни один не угадывает или правильно угадают
оба, то платежи не производятся. Платежная матрица для этой игры имеет вид
0—3 2 0-
3 0 0—4
-2003
0 4—3 0
Пример (ж).
Игра имеет три хода, I, II и III.
I. В выбирает одно из двух чисел 1 и 2; выбранное число назовем р.
II. Не зная р, А выбирает число q из 1 и 2;
III. Не зная р и q, В выбирает число г из 1 и 2.
Можно представить, что при третьем ходе или В забывает, какое число р он
выбрал при первом ходе, или что «игрока» В представляют два индивидуума, каждый
из которых не знает выбора, сделанного его напарником. Платеж при расчете
представляет сумму (p-\-q~\-r), которую выигрывает игрок А, если q равно г, и игрок В,
если q не равно г.
У игрока А имеются две стратегии:
1 ... B = 1), 2 ... (?=2).
У игрока В — четыре стратегии:
1 ... Ср = 1, /- = 1), 2 ... (р — 2, г==1),
3 ... (/>=1, г = 2), 4 ... (р=2, г = 2).
Платежной матрицей для игрока А будет матрица
4 —4 —5
_ г з 4 —4 —5 ]
'- | __4 -5 5 6J '
Задачи и упражнения
1. Определить игру «крестики и нолики», то есть указать ходы и возможные
выборы при каждом ходе. Показать, что партия состоит из неопределенного, но
конечного числа ходов. Построить схему платежей.
2. Сколько «ходов» в игре бридж? Сколько выборов в партии этой игры?
3. Написать платежную матрицу для игрока В в примере (а) этого раздела.
1 То есть при ставке игрока А на первую лошадь, выигрыш составляет
половину ставки; при ставке на вторую лошадь, выигрыш равен удвоенной ставке.—
Прим. ред.
408

4. При думать описание игры в два хода с платежной матрицей:
Г1 2 0 1
L2 -1 3J '
5. Условия примера (г) этого раздела распространить на случай трех лошадей,
предполагая, что пари заключаются на условиях 1:1; 2 против 1 и 3 против \.
Показать, что матрица:
Г П-1 -11
-1 2 -1
L-1 -1 sj
будет платежной матрицей для этой игры.
6. Обобщить условия примера (е) на случай «three-finger Morra» (трехнальце-
вая Морра) и показать, что в этом случае платежная матрица будет 9x9.
14.3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ИГРЫ; ЧИСТЫЕ
И СМЕШАННЫЕ СТРАТЕГИИ
Если игра с платежной матрицей А = [ars] (г = 1, 2,..., т; s — 1, 2,..., п)
играется один раз, то ars — это выплата игроку А в соответствии с
выбранными игроками стратегиями:. Если игра играется большое число раз (N),
то определим Е как среднюю сумму выплат игроку А или математическое
ожидание игры1. Тогда величина Е зависит от системы стратегий,
выбираемых игроками в следующих одна за другой партиях. Общая цель игрока А
при повторении партий состоит в таком выборе своих стратегий, чтобы
сделать Е как можно больше. Напротив, целью В является сколь возможно
уменьшить величину Е путем выбора системы своих стратегий. При выборе
стратегий каждый игрок должен принимать в расчет действия своего
противника настолько, насколько он может это сделать. Конечно, никакой
игрок не может непосредственно влиять на выбор другого игрока.
Игрок А следует чистой стратегии в повторяющихся партиях, если
в каждой партии он выбирает из всех доступных для него альтернатив одну
и ту же стратегию. Если оба игрока следуют чистым стратегиям, то любая
партия такова же, как и всякая другая. В каждой партии А следует своей г-й
стратегии, В применяет свою 5-ю стратегию, и платеж для А равен ars.
Следовательно, ожидание Е также равно аг$1 и оно мажет быть понимаемо,
как функция двух переменных, каждое из которых принимает только целые
значения:
Е(г, $) = аг< (г= 1, 2, ..., ти; s= 1, Г2, ..., п).
Игрок А выбирает г с целью сделать Е как можно больше, после
принятия во внимание возможных выборов s игроком В. Таким же образом,
В выбира'ет s и пробует учесть выбор г со стороны А для того, чтобы
сделать Е возможно меньше. Вопрос состоит в том, возможно ли так
одновременно выбрать г и s, чтобы они были для каждого игрока оптимальны
(устойчивы) с точки зрения минимаксного принципа и совместны и чтобы
каждый игрок выбцрал бы именно ту стратегию, которая для него
предсказана в своих рассуждениях другим игроком. Если дело обстоит так,
то игра имеет решение в чистых стратегиях. Будет показано, что это имеет
место только в специальных случаях. Однако, даже если существуют такие
стратегии г и s, такое решение не представляет особого интереса, так как
игра, в которой результат и течение каждой партии совершенно
идентичны, будет скучна.
Более сложный вопрос относится к игре, в которой каждый игрок
принимает в последовательных партиях различные стратегии. Мы говорим,
1 Строгое определение величины Е как математического ожидания выигрыша для
игрока предполагает употребление понятия «вероятность». Аллен везде говорит просто
об «ожидании» (expectation) и только в редких случаях употребляет термин
«математическое ожидание», но без связи с понятием вероятности. В тексте мы переводим
«expectation» через «математическое ожидание».— Прим. ред.
409

что игрок следует смешанной стратегии, если он меняет выбор стратегии
от одной партии к другой, согласно некоторой системе. Эта «система»
(«pattern») понимается не как особая последовательность стратегий, выбираемых
в партиях в этом порядке, это скорее случайный порядок выбора стратегий
в заданных пропорциях. Например, если «система» предписывает игроку
применять первую стратегию в одном из десяти случаев, то из этого следует,
что в среднем первая стратегия должна* выбираться в одной десятой части
сыгранных партий, но вовсе не означает, что в каждой десятой партии
применяется первая стратегия. Математическое ожидание Е тогда усложняется,
и оно зависит от того, какие стратегии комбинируются или «смешиваются»
игроками. Задать Е как функцию от двух переменных возможно только
в простейшем случае игры с двумя стратегиями для каждого игрока. Этот
случай заслуживает детального рассмотрения до того, как будет рассмотрен
общий случай (см. 14.7).
Пусть каждый игрок имеет две стратегии (г, $ = 1, 2), и платежная
матрица будет второго порядка:
a12l
«22 J #
Оба игрока придерживаются смешанной стратегии, и свои стратегии они
выбирают с разной вероятностью (относительной частотой). Пусть игрок А
выбирает стратегию 1 с вероятностью х\ следовательно, стратегия 2 будет
выбираться им с вероятностью A — х). Пусть вероятность выбора игроком
В своих стратегий будет соответственно у и A — у). Мы предполагаем, что
между выборами стратегий в каждой партии игроками А ж В нет никакой
взаимосвязи. Тогда в длительной серии из N партий четыре комбинации пар
стратегий встретятся с численностями, которые можно представить
следующей матрицей1:
Г xyN z(l-y)N "I
[(l-x)yN (l-x)(l-y)N\'
Следовательно, в xyN партиях из N партий платеж равен а1г и так
далее для остальных пар стратегий. Средний платеж, получаемый
игроком А в результате партии, или математическое ожидание игры тогда
будет:
Е(х, у) = а11ху+а12хA-у) + апA—х)у + а22A-х){1-у). A)
Он является функцией от двух переменных хну, каждое из которых
может принимать значение от 0 до 1, то есть 0<ж, г/<1. Уравнение A)
можно записать и в таком виде:
Е(х, у)^{аи — а12-а21+а22)ху--(а22--а12)х--(а
Когда аи — а12 — а21 + а22 ф 0, то можно записать
Е{х, у) = а(ж-а)(у-
где
«11 —«12—«21+«22
«22 — «12
«11 — «12 — «21+ «22 "
1 Ал лен избегает употреблять термин «вероятность», говоря вместо этого о
«пропорции» и «отношениях». Мы вводим в перевод и «вероятность» и «относительную
частоту» как эмпирическое выражение вероятности («статистическая вероятность»).
Нетрудно видеть, что х, A — а?), ?/, A — у) представляют собой относительные частоты
отдельных стратегий в серии партий.— Прим. ред.
410

Это обычная квадратичная (гиперболическая) функция. Когда ап — а12—-
— ап + а22 = 0, функция Е (#, у) превращается даже в еще более простую,
линейную форму:
Е (х, у) = а22 - (а22 - а12) х - (а22 - а21) у. C)
Пример (а).
г 1 1~|
Пусть А=| i —1| » тогда
Пример (б).
Пусть А=[* __*] ' тогда *(*• У)=-4(^-5/4
Пример (в).
Пусть А = | __2 2 J , тогда Я (я, г/) = а?—4г/+2.
Величина Е нами определена как средняя величина платежа, полученного
игроком А на протяжении большого числа партий рассматриваемой игры. Для игрока А
она является математическим ожиданием выигрыша в каждой отдельной партии.
В качестве иллюстрации к такому истолкованию величины Е рассмотрим игры на
скачках, приведенные в примере (г) раздела 14.2.
Здесь
-¦[i
Если игрок А ставит 1 фунт на первую лошадь с относительной частотой х
в большом числе скачек, и если первая лошадь выигрывает скачку с относительной
частотой г/, тогда среднее значение выигрыша для игрока А будет:
Е(х, у) = 1^-я.A-у)-уA-
Предположим, что рассматривается только одна скачка, и вероятность на
выигрыш у первой лошади оценивается числом у. Пусть игрок А делит свой 1 фунт,
ставя х на первую лошадь и A — х) на вторую. Тогда его ожидание выигрыша
выражается той же величиной Е(х, у).
Задачи и упражнения.
fl [ -л
\ '
Чем отличается эта игра и ее математическое ожидание от игры примера (а)
этого раздела?
2. Составить платежную матрицу второго порядка, для которой Е (#, у) =
= а(аг+а) (г/+Р)+6, где параметры а, аир положительны. Показать, что ап должно
быть больше, чем другие три элемента этоД матрицы.
3. Показать, что элементами платежной матрицы второго порядка являются
/?A, 1), ЕA, 0), Е@, 1) и #@, 0). Для случая, рассмотренного в предыдущем
упражнении, показать что условие b > 0 определяет игру, в которой А всегда выигрывает вне
зависимости от действий В.
4. В задаче о скачках (пример (г)) рассмотреть незначительно измененную
платежную матрицу
и
Каковы в этом случае условия ставок? Написать функцию Е(х, у) и объяснить,
в каком смысле верно, что в этом случае букмекер обычно выигрывает.
5. В примере (д) в разделе 14.2 предположить, что вопрос о страховании мехового
пальто встает на протяжении ряда периодов N. А страхует пальто в х N случаях, а
вероятность гибели от огня для каждого периода равна у. Показать, что средний убыток для
А будет:
Е{х, у)=х+Шу—Шху.
Каков будет убыток, если А страхует в каждом периоде и если А совсем не
страхует? Какова должна быть вероятность пожара, чтобы убыток в обоих случаях был
одинаков? Объяснить результат.
6. Игра имеет платежную матрицу 2 X п. Показать, что математическое
ожидание Е в том случае, когда А смешивает свои стратегии, а игрок В играет согласно своей
411

чистой стратегии, можно записать в виде Е(х, s), где 0 < х < 1 и &г = 1, 2,..., п.
Выразить Е через элементы платежной матрицы и проиллюстрировать на материале примера
(ж) в разделе 14.2. -
14.4. МИНИМАКС, СЕДЛОЭЫЕ ТОЧКИ И РЕШЕНИЯ ИГР
При некоторых обстоятельствах, математическое ожидание игры
является функцией двух переменных, то есть Е(х, у), где х — это выбор
игрока А, и у — выбор игрока В. Функция Е(х, у) может быть
представлена поверхностью в трехмерном пространстве, как это сделано графически
на рис. 42, а. Изменение
высоты поверхности показывает
изменение математического
ожидания игры для А в
зависимости от различных выборов
разных х и г/. Такое
представление математического
ожидания возможно для игры с
платежной матрицей 2 X 2 в
смешанных стратегиях.
Переменные х к у непрерывны, но
ограничены областью 0 < х, у < 1 „
Итак, только часть
поверхности, показанная на рис. 42,а,
для которой 0<Сх, у<.1, имеет
отношение к рассматриваемой
задаче. Подобное графическое
представление возможно также
для игры с платежной
матрицей т X /г, если противники
придерживаются чистых
стратегий. В этом случае
переменные х я у принимают только
некоторые дискретные
значения, то есть
х — г = 1, 2, . . ., т и
4 0 V}
и поверхность в
рассматриваемой проблеме превращается в
совокупность дискретных точек.
Цель игрока А состоит в
том, чтобы, выбирая х и
учитывая возможные действия
игрока В, подняться по поверхности как можно выше. Цель игрока В состоит
в том, чтобы держаться на поверхности возможно ниже. Игра имеет
решение, если одновременно можно сделать совместные и устойчивые выборы
стратегий х и у. Легко показать, что здесь мы встречаемся с минимаксной
проблемой, то есть вопрос идет о максимизации среди множества
минимальных величин и наоборот. Ключ к нахождению решения лежит в
необходимости для А определить наихудшее для него (минимальное), что при
каждом его выборе может сделать В, и тогда сделать свой наилучший
(максимальный) выбор, то есть выбрать наименее невыгодную возможность.
Рассмотрим поверхность на рис. 42,а, предполагая, что х ж у
непрерывные переменные. Особенностью этой поверхности является существование
линий А А' и ВВ' или линии гребня (ridge line) и линии стока (trough line),
пересекающихся в седловой точке Р. Всякое движение от точки Р в
направлении Ох по поверхности ведет вниз; всякое движение в направлении Оу
ведет вверх. Седловая точка — это точка максимума по х и минимума по у.
\\г

Для заданного х, Е(х, у) изменяется в зависимости от у> и может быть найден
min Е(х, у); он дается точкой на линии стока ВВ\ Тогда при движении вдоль
У
линии ВВГ можно найти х, при котором ттЕ(х, у) является наибольшим;
У
это приводит в точку Р, где имеет место max min Е(х, у). Таким же образом,
х у
при заданном у, Е(х, у) изменяется по мере изменения х; max Е(х, у) дости-
X
гается на линии гребня А А', и х, дающий min max E(x, у), соответствует снова
у ' х
точке Р. Если х* и у* являются значениями переменных в точке Р, тогда
эта седловая точка удовлетворяет следующим условиям:
max min E(x, y) = min maxi?(#, у) = Е(х,* у*). A)
х у ух
Поверхность на рис. 42,а изображена для 0 < х, у < 1 их* = у* = у .
Эти условия могут быть истолкованы на примере игры с математическим
ожиданием Е(х, у). Игрок А, фиксируя величину х (свой выбор), определяет
наихудший для него выбор у, который может быть сделан игроком В, то есть
min E(x, y)Jr лежащий на линии стока ВВ'. Затем он выбирает тот х, кото-
у
рый дает наибольшее значение для min Е(х, у) на ВВ', то есть выбирает
у
координату х точки Р на линии ВВ', в которой достигается max min E(x, у).
х у
Вне зависимости от того, как играет его противник, игрок А не может
получить меньше, чем сумму, определяемую высотой поверхности в точке Р.
Другими словами, какой бы х ни выбирал А, его противник может снизить
его платеж до платежа, указываемого высотой в толчке на линии ВВ'. Это
вынуждает А выбирать на линии стока ВВ' точку как можно выше, что он
может сделать путем выбора х. Следовательно, он выбирает координату х
так, чтобы попасть в точку Р, где его выигрыш от игры равен max min E(x, у),
х у
то есть высоте поверхности в точке Р. Игрок В идет по этому же пути, но
пытается снизить Е и помешать своему противнику повысить величину Е.
Какой бы у игрок В ни выбрал, его противник может увеличить платеж до
высоты поверхности в точке, лежащей на линии гребня АА'. Поэтому В
держится как можно ниже на линии стока и выбирает у так, чтобы попасть
в точку Р, где платеж равен min max Е(х, у). Тот факт, что Р есть седловая
у х
точка, означает, что оба игрока достигают одной и той же точки на
поверхности; это и есть совпадающий, устойчивый выбор х* и у*. Игра имеет
решение, и ^сумма, ожидаемая игроком А, будет:
Е(х*9 2/*) = max min Е (х, у) = min max E (х> у).
х у ' ух
Важно сделать ясным существо этого решения. На поверхности Е(х, у)
имеется седловая точка (#*, у*), где выполняются условия A). Игрок А
выбирает ж* среди всех доступных для него альтернатив х потому, что в этом
случае он может быть уверен в получении Е(х*, у*) в результате игры
независимо от стратегий, выбранных его противником. Он может получить
больше, если противник ошибется, но он не может получить меньше. В свою
очередь, игрок В выбирает у* среди разных доступных ему у, потому что
он может быть уверен в том, что его платеж противнику будет не больше
?*(#*, у*) вне зависимости от действий противника. Игрок В может проиграть
меньше, если его противник недостаточно хитер, но он не заплатит больше.
В соответствии с правилами рационального поведения предполагается, что
оба игрока хорошо осведомлены о характере функции Е(х*, у*), и А
выбирает х*, а В выбирает г/*. В этом смысл того, что игра имеет решение.
Теперь предположим, что внутри рассматриваемой области
переменных поверхность не имеет седловой точки Р. В этом случае можно было бы
сказать, что игра не имеет решения, так как нет единой точки на поверх-
413

ности, к которой стремились бы оба игрока. Но если область изменения
переменных ограничена и рассматривается только часть поверхности, то
из несуществования седловой точки внутри рассматриваемой области не
следует, что игра не имеет решения, так как точка, определяющая решение
(в которой оба игрока придут к соглашению), может лежать на границе
области. Такой случай показан на рис. 42,6, где поверхность Е(х, у)
представляет плоскость. Точка Р, лежащая на поверхности в одном из углов
рассматриваемой области, действительно представляет собой седловую точку,
принадлежащую области допустимого изменения переменных х и у. Любое
допустимое перемещение от Р в направлении Ох (вдоль по РВ) ведет вниз
по поверхности, а перемещение в направлении Оу (вдоль по РА) — вверх.
Если (я*, у*) — переменные в точке Р, то справедливы минимаксные
соотношения A). Максимум и минимум ищутся просто в рассматриваемой
ограниченной области переменных 0<.#, г/<1.
В качестве предварительной, специальной проблемы рассмотрим игру
с любой платежной матрицей А размерности т X га, предполагая, что игроки
выбирают только свои чистые стратегии. Тогда математическое ожидание Е
для игрока А принимает следующий частный вид:
Я (г, s) = ars (г=1, 2, ...,го; «=1,2 л).
Здесь Е является функцией двух переменных г и s, каждое из которых
принимает только дискретные значения (из области целых чисел). Функция Е
в этом случае отличается от математического ожидания Е как функции двух
переменных для игры 2 X 2 в смешанных стратегиях; в простом случае
игры с матрицей 2x2 чистые стратегии соответствуют значениям х = О
и 1; у = 0 и 1. Однако результат в вышеприведенной форме A) верен для
чистых стратегий в игре с платежной матрицей любой размерности. Решение
или устойчивый исход существует среди чистых стратегий, если матрица А
имеет такую седловую точку, что:
max min ? (г, s) = min max E (r\ s) = E(r*, s*) /o\
r s s r V '
для некоторого г* из г — 1, 2,..., т и некоторого s* из s = 1, 2,..., /г.
Решение состоит в том, что А играет, придерживаясь чистой стратегии г*, а В
разыгрывает чистую стратегию s*. Согласно минимаксному принципу, это
лучшее, что игроки могут сделать. Графическое представление будет
аналогично предыдущему, за исключением того, что в последнем случае мы имеем
дело не с непрерывной поверхностью, а с дискретным множеством точек
(г от 1 до т и s от 1 до п). Высоты точек задаются самими элементами
матрицы А, и седловая точка ищется среди них.
Если такое решение существует, то есть, если А имеет седловую точку
в том смысле, как мы установили, и только для чистых стратегий, тогда
в дальнейшем рассмотрении нет необходимости. Смешанные стратегии не
потребуются. Но вовсе не обязательно, чтобы в чистых стратегиях седловая
точка вообще существовала; наоборот, в общем случае нет седловой точки
для А. Имеет смысл искать седловую точку среди смешанных стратегий
предварительно. Вполне возможно, что она существует, и тогда вопрос
исчерпан. Если нет, то в общем случае решения надо искать в смешанных
стратегиях.
Тот факт, что в чистых стратегиях игра может вообще не иметь
устойчивости, виден из такого простого примера платежной матрицы:
А=1Л з
Если А начинает со стратегии 1, В выбирает стратегию 2 для того, чтобы
уплатить игроку А только 1. Но тогда А переходит на стратегию 2, чтобы
получить от игрока В платеж в 3 единицы. Это приводит В к выбору
стратегии 1, и он снижает свой платеж до двух. Процесс продолжается, и
соглашение не устанавливается.
414

Пример (а).
Рассмотрим игру примера (в) из 14.2. с платежной матрицей:
А
10 — 2 —1 3]
2 3 1 2 .
3 4 0 — 4\
Игрок А выбирает г = 1, 2 или 3. При каждом выборе игроком А чистой
стратегии наихудшее, что может для него случиться, показывает минимальный элемент в
соответствующей строчке матрицы А, показанный курсивом. Если А выбирает г = 1,
худшее для него состоит в том, что он проиграет две единицы; если он выберет г = 2, он
выигрывает по крайней мере 1; если он выбирает г = 3, он может заплатить даже четыре
единицы. Поэтому А планирует выбрать г = 2 и ожидает, что его противник примет
стратегию 3, чтобы снизить получения игрока А до 1. Игрок В выбирает s = 1, 2, 3 или 4
и для каждого из этих выборов определяет наибольшее, что, возможно, ему придется
заплатить своему противнику, то есть максимум в столбцах. Этими максимумами являются
соответственно в четырех столбцах числа: 3, 4, 1 и 3. Поэтому В планирует выбрать
5 = 3, чтобы ограничить свой платеж единицей, и ждет, что противник выберет вторую
из своих стратегий, чтобы сохранить выигрыш одной единицы: Естественно, это приводит
к решению г* = 2 и s* = 3. Игроки могут условиться заранее об этих стратегиях, и А
будет получать от В в каждой партии сумму, равную 1.
При помощи обозначений, примененных в B), эти рассуждения можно изложить-
следующим образом. Для игрока А и какого-нибудь выбранного г:
mini? (г, s) =—2, 1 или —4 в соответствии с г=1, 2, или 3.
s
Поэтому max mini?(r, s) = i?B, 3) = 1. Аналогично находим maxi?(r, s) = 3, 4, 1
г s г
или 3 в соответствии с s=l, 2, 3 или 4. Условия B) удовлетворяются при г* = 2, s* = 3.
Пример (б).
Рассмотрим игру «двухпальцевая Морра», описанную в примере (е) раздела 14.2,.
для которой платежная матрица будет:
0—3 2 0п
3 0 0—4
—2.0 0 3
0 4—3 0_
Здесь, как это показано в матрице А числами, напечатанными курсивом,
mini? (г, s) = — 3, —4, —2 или 3 для г=1, 2, 3 или 4.
S
Таким образом, maxmini?(r, s) = EC, 1)=—2. Но minmaxE(r, s) = i?(l, 3) = 2r
Г 8 8 Г
что следует из рассмотрения максимальных в столбцах А элементов.
Условия B) не выполняются. Для случая, когда играются чистые стратегии,
нет решения игры. Действительно, игра Морра ни в коем случае не является
скучной игрой. Если А выберет стратегию 3, он может проиграть две единицы, если В
выберет стратегию 1. При других своих выборах он может проиграть больше.
Наоборот, если В выберет стратегию 3, он также может проиграть 2, когда А выберет
стратегию 1; В может проиграть и больше, если выберет другую стратегию. Эта игра
открывает полный простор для маневрирования стратегиями.
Задачи и упражнения.
1. Показать, что игра с платежной матрицей . . не имеет решения
- Г2 М
в чистых стратегиях, в то время как у игры с платежной матрицей такое
решение есть.
Каково это решение во втором случае?
2. Показать, что нет решения в чистых стратегиях в игре со скачками, пример
(г) из 14.2.
Объяснить этот результат.
3. Показать, что игра в упражнении 4 к разделу 14.2 не имеет решения в
чистых стратегиях»
21
4. Если I —1 0 есть платежная матрица, показать, что игра имеет в чистых
Г *
—1
L 1
L j
стратегиях два решения—игрок А имеет две оптимальные стратегии. Рассмотреть,
что случится, когда В ошибется (то есть сыграет неоптимально), и показать, что одна
из оптимальных для А стратегий «более оптимальна», чем другая.
5. Для платежной матрицы A = [ars] и чистых стратегий,' показать, что решение
существует, если минимум в строке совпадет с максимумом в том столбце, которому
принадлежит рассматриваемый минимум.
415

Выразим это условие так: г* и s* определяют решение игры, если:
ar*s*<av*s (s=i> 2 »)•
6. Если Е(ху у) — ( х—— ) —( у — — ) -\-— , показать, что поверхность имеет
седловую точку х* = ~, ?/* = у в геометрическом смысле, но не имеет ее в смысле
условий A) этого раздела. Какую форму принимают условия A) в этом случае?
Указать, что Е может быть математическим ожиданием для игрока В (вместо игрока А)
и в этом случае точка а?* = --, t/* = -— является седловой точкой игры.
14.5. РЕШЕНИЕ ДЛЯ ПЛАТЕЖНОЙ МАТРИЦЫ 2x2
Игра имеет платежную матрицу А = и играется в смешанных
La21 a22j
стратегиях. А играет первую из своих стратегий в пропорции х к общему
числу партий, а В играет первую свою стратегию в пропорции г/.
Математическое ожидание игры для А дается уравнением A) раздела 14.3.
Е
Рис. 43.
Рассуждения раздела 14.4 теперь значительно упрощаются, так как
Е(х\у) имеет специальную форму. Исключая частный случай (а=0)?
который на ^'время можно игнорировать, функцию Е можно записать в виде
Е(х, у) = а(х-а)](у-$) + Ъ9 A)
где значения постоянных даны равенствами B) в разделе 14.3. Поверхность,
представленная уравнением A), всегда имеет одну седловую точку при
х = а и г/ = р,иее форма показана на рис. 431. Это частный случай линей-
1 Рисунок, данный в книге Аллена, заменен здесь другим — более наглядным,
принадлежащим Э. Б. Ершову.— Прим. ред.
416

чатой поверхности, образованной прямыми линиями. Во всех сечениях
поверхности плоскостями под прямым углом к оси Ох получаются прямые
линии, а сечение через точку Р является горизонтальной прямой линией РМ
(Е = Ъ). На рис. 43 видно, что, когда заданное значение х увеличивается,
прямая линия в сечении сначала возрастает в направлении Оу, при х = а
прямая проходит через Р и становится горизонтальной (прямая РМ)\ для
больших х прямая становится понижающейся в направлении Оу. Поэтому,
если игрок А фиксирует для х значение, равное а, он получает Е = Ъ (в
среднем.— Ред.), что бы игрок В ни делал; при любом другом х платеж для А
может оказаться меньше. Таким же образом, рассмотрение прямых линий
в сечениях поверхности плоскостями, образующими прямой угол к оси Оу,
показывает, что игрок В платит ? = Ь, если он фиксирует у = [},
независимо от того, что делает А, но он может заплатить больше, выбирая для у
любое другое значение. Оба игрока поступают правильно, останавливаясь
на х* = а, г/* = р. Эти стратегии определяют решение игры, и А получает
от В сумму, равную Ъ. Все это предполагает, что нет ограничений в
отношении выбора значений х и у.
Однако в отношении хну имеются ограничения; каждое из этих
переменных принадлежит отрезку от 0 до 1. Если 0<а, Р<1, тогда все
в порядке, седловая точка для функции Е, определенной формулой A),
принадлежит допустимой части поверхности, и игра имеет решение. В
противном случае, седловая точка попадает вне эффективной части поверхности,
и предлагаемое решение должно быть отвергнуто. Внимание тогда должно
быть сконцентрировано на границах этой области, где один или оба игрока
принимают чистые стратегии (х = О или .1 и у = 0 или 1). Представляется
естественным ожидать такой же ситуации, как на рис. 42, б, то есть что
изогнутая поверхность (или плоскость при а = 0) будет иметь седловую точку
в углу границы. Действительно, так оно и бывает. Учитывая, однако,
должным образом ограничения в отношении переменных х и у, нам необходимо
отказаться теперь от геометрического подхода и дать определения и условия
в алгебраической формулировке. Такая форма облегчит их
распространение на общий случай (см. 14.7). Прежде всего нет необходимости вести
рассуждения для частного случая, когда математическое ожидание для игры
с платежной матрицей 2x2 задано в форме A). Какая бы форма Е ни была
принята, может быть приведено следующее определение:
Определение: Если величины х* и г/* могут быть найдены так,
что для любых хжу @<?, г/<1):
& \xi У )<>&\X | у*)^?Ь(Х , y)j \6)
тогда (ж*, г/*) является седловой точкой для ?\ игра имеет
устойчивый исход или решение (ж*, у*) с оптимальными стратегиями х*
и у* (соответственно для игроков А и 5), и Е(х*, у*) называется
ценой (value) игры для игрока А.
Условие B) является прямым переводом геометрических свойств
седловой точки на алгебраический язык. Интерпретация этих условий в
терминах игры достаточно проста. Игрок А выбирает х* среди своих
смешанных стратегий, так как тогда он получает по меньшей мере Е(х*, г/*I,
какая бы стратегия у ни выбиралась его противником, и так как он может
получить меньше, если выберет другое значение для х, а его противник
будет играть согласно стратегии у*. Игрок В выбирает у* по аналогичным
причинам.
Условия B) могут быть связаны с минимаксными свойствами Е (х, у):
Е(х, у) имеет седловую точку (х*, г/*) тогда и только тогда, когда
maxminZ? (я, y) — minmaxE(x, y) = E(z*, у*) . C)
х у ух
1 Автор не указывает здесь и в других местах этой главы, что его рассуждения
относятся к средним из ряда партий.—Прим. ред.
27 р. Аллен 417

при условии, что минимаксные значения для х и у [существуют
в области 0<#, г/< 1.
Доказательство состоит из двух частей:
Во-первых, предположим условия C) выполненными. Следовательно,
Е(х*, г/*) = max min Е (ж, у) является максимальным значением (при х = х*)
х у
для mini? как функции от х\ эта величина есть mini?(я*, у). Таким
у У
образом, по определению минимума:
E{x*t y*) = minE(x*, y)<E(x*, у)
у
для любого
Таким же образом Е(х*, y*) = maxi?(#, г/*) >Е(х, у*) для любого
)
Следовательно: Е(х*, ?/)<#(#*, у*)<Е(ху*) для любых хну
(х, г/<1), то есть выполнены условия B) для (#*, у*) как седловой
точки функции Е.
Во-вторых, предположим, что Е имеет седловую точку, и условия B)
удовлетворены. Тогда выбираем х, который делает Е(х, у*)
максимальным, и у, который делает Е(х*, у) минимальным:
тьхЕ{х,у*)<Е{х*9у*)<ттпЕ(х*,у).
х у
Но по определению максимума и минимума:
min max Е (ж, у) < max 2? (я, у*) и max min Е(х, у) > min E(x*y).
уХ X X у у
Следовательно:
min max E (#, у)кЕ(х*, ^*)<maxmin?'(^, у). D)
ух х у
С другой стороны, по определению максимума и минимума:
max2?(z, y)>E(x, y)>minE(x, у)
х у
для любых х и у @<х, у<1).
Выбранный х делает максимальным штЕ(х, г/), как функцию от х>
У
а у делает maxi?(#, у) минимальным, как функцию от у:
X
min max E (#, г/) > max min/?(#,]/). E)
у х . » х г/
Неравенства D) и E) выполняются одновременно только в том случае,
если знак неравенства в них изменить на знак равенства, то есть, если
max min Е (ж, у) = min max E (х, у) = ?(ж*, г/*),
х у ух
а это и есть условия C). Это завершает доказательство.
То обстоятельство, что Е(ж, у) берется в частном виде (I),
используется теперь впервые для того, чтобы установить частный случай
минимаксной теоремы:
Игра с платежной матрицей 2x2 всегда имеет решение. Ценой
игры является:
(#, у),
где х*, у* суть оптимальные стратегии.
О Е(
д у у р
Во-первых, предположим афО для Е(х, у) = а(х>-а)(у—$) + Ь и что
аир принадлежат отрезку от 0 до 1. Тогда: Е(х, Р) = ?"(а, |5) = i?(a, у)
для всех хну @<#, г/<1). По определению, #* = а и j/* = P являются
оптимальными стратегиями, и цена игры есть 2? (а, Р) = Ь. Этот случай
седловой точки изображен на рис. 43.
418

Во-вторых, во всех других случаях легко показать, что оба игрока
следуют чистым стратегиям. Например, предположим, что а > О, а, Р>1
Тогда:
Я (О, 1) = аа(Р-1) + 6,
Е(х, 1)= -а(х-а)ф-1) + Ь = ааф-1) + Ъ-а($-1)х<Е@, 1),
?@, у) = ааф-у) + Ъ = аа{$-1) + Ь + ааA-у)>Е@1 1)
для любых х и у @<х, у<1).
Итак, Е(х, 1)<Е@, 1)<СЕ(О, у) для любых х и у @<я, */<1).
Согласно определению, #* = 0, г/*==1 являются оптимальными стратегиями;
в этом примере Л разыгрывает свою вторую, а В — свою первую
стратегию. Решение такого рода возникает для всех других аир вне области
@<а, Р<1) и также в случае, когда а = 0 (см. упражнение к этому
разделу). Это завершает доказательство.
Требуется остановиться еще на одном положении. Игра с платежной
матрицей 2x2 всегда имеет решение, но это не исключает возможности
существования многих решений. Могут встретиться случаи, в которых игра
имеет более одного решения, и тогда она имеет бесконечное множество
решений. Это показано в примере (в) и в упражнениях 3 и 4 к
настоящему разделу; в дальнейшем такой случай будет исследован в примере (б)
раздела 14.7.
Пример (а).
А=Г^1 _1J ; E(xt y)=—?fx——J Гг/—~J, как в примере (а) из
раздела 14.3. Решением игры является а?* = г/*=— ,и цена игры равна нулю. Каждый
игрок смешивает свои стратегии, придерживаясь их одинаково часто.
Пример (б).
А=Г3 __2J ; Е(х, 2/) = — 4 (х—— jf у—- Л , как в примере (б) из раздела
14.3. Решением игры является х* = 19 г/* = 0, потому что:
ЕA, 0) = 1, Е(х, 0) = 3*—2 = 1—3A—*)<1,
то есть
Е(х, 0)<ДA. 0)<^A, у) для 0<х,
Цена игры равна 1, и каждый игрок применяет чистую стратегию, А выбирает свою
первую, а В свою вторую стратегию.
Пример (в).
' А= [J J] ; Е(х, у)=«у-2«+1 = 1-*B-у).
На основании общих соображений ви^но, что А должен играть свою вторую
стратегию (х* = 0), так как она дает ему больше, чем его первая стратегия, чтобы
игрок В ни делал. Но каков выбор игрока В? Легко показать, что он может
выбирать любую стратегию (O«Jy*<!l), так как если А играет согласно второй стратегии,
он проигрывает во всех случаях одну и ту же сумму. Формально, легко показать, что
Е(х, у*)<Е@, у*)=Е{0, у)
для любого у* @ < у* < 1).
Имеется бесконечное число решений. Цена игры равна 1, и она единственна.
Имеется, однако, «лучший оптимум» для В (вторая стратегия), так как, если В
выбирает эту стратегию, он получит больше, при условии, что игрок А совершает ошибку,
то есть, если А вообще применяет свою первую стратегию.
Задачи и упражнения.
1. Исследовать игру с платежной матрицей 2x2, для которой Е(ху у) явл^дороя?
линейной функцией. Показать, что а?* = 0, у*=1 является решением, когда <*%<$*> a,\%
и «22 > a2i- Показать, что чистые стратегии также являются решениями и щ>&
других значениях величин аГ8.
2. Показать, что игра с платежной матрицей I 3 имеет следующее реше*.
ние в смешанных стратегиях:
2 1
** = * для А и 2/* = *2" ДЛЯ В'
419 27,

что
3. Если А= . , показать, что Е(х, y) = l — 2zfy—- J, и вывести,
в решении игры первый игрок следует чистой стратегии, в то время как второй
имеет бесконечное число смешанных стратегий. Имеется ли «наилучший оптимум»?
4. Распространить результаты примера (в) этого раздела и предыдущего
упражнения, исследуя случай платежной матрицы А.= х Й2 со строкой равных
элементов. Если а^>а1 и а>а2» показать, что #* = 0 и 0<г/*<1. Если величина а лежит
между «! и а2» показать, что решение (цена игры и оптимальная стратегия для
игрока А) остается таким же, за исключением того, что область значений у* более
ограничивается. Существует ли бесконечное число решений также и при а<^аи
а<а2?
14.6, ГРАФИЧЕСКОЕ РЕШЕНИЕ ДЛЯ ИГР С ПЛАТЕЖНОЙ
МАТРИЦЕЙ 2 х п
Для того чтобы упростить процесс решения игры с платежной
матрицей 2x2, можно прибегнуть к графическому методу. Этот же способ можно
применить и в более общем случае, когда игра имеет платежную матрицу
2 X /г, и уже становится труднее рбойтись чисто алгебраическими методами.
До тех пор, пока матрица имеет только две строки, выбор А может быть
представлен переменной #@<#<1), определяющей пропорцию, в
которой игрок выбирает первую из своих двух стратегий. Графический метод
позволяет находить оптимальную смесь стратегий х*> сначала для игрока А,
а затем отдельно для игрока В. Достаточно нескольких примеров для
иллюстрации его применения.
Пример (а).
А выбирает свои стратегии в пропорции х : A—х). Если В выбирает свою первую
стратегию, то (из первого столбца матрицы) математическое ожидание для А будет:
Е=— х+A—х) = 1—2х.
Если В выбирает свою вторую стратегию, то, в соответствии со вторым столбцом
матрицы,
Е=х—A —х) = 2х—1.
Каждое из этих уравнений может быть изображено графически отрезком прямой
линии в области 0 <! х <; 1 на плоскости ОхЕ. Они показаны на рис. 44
соответственно как отрезки АгА[ и А2А'2] в этом случае линии пересекаются в точке Р, где
вг
в',
Рис. 44.
х = — и Е = 0. Цель А состоит в выборе х так, чтобы сделать Е как можно больше.
При данном х на рис. 44 показаны две величины Е, которые А может получить, если
В выбирает свои чистые стратегии; промежуточные значения величины Е получаются,
когда В смешивает свою стратегию. Меньшая из этих двух величин показывает
минимум, который А может получить, выбирая стратегию х. Следовательно, при
изменении х @<я<1), ломаная линия А2РА[ показывает платеж, который А безусловно
может получить. Он выбирает х так, чтобы достичь наивысшей точки на линии А2РА[,
то есть х* = -77 при Е = 0 в точке Р.
Мы можем таким же образом проанализировать игру Ву пользуясь линиями
ВлВ\ и Вфъ (которые соответствуют стратегиям игрока А) на плоскости ОуЕ (см.
рис. 44). Линия ВгВ[ выражается уравнением ? = 1—2у при условии, что А следует
420

своей первой стратегии. Если А применяет свою вторую стратегию, то
рассматривается линия В2В'2у уравнение которой Е = 2у—1. Ломаная линия BXQB2 представляет
наибольший проигрыш игрока В при различных выборах у. В выбирает у так, чтобы
достичь низшей точки линии BxQB2t то есть у* = — при Е=0 в точке Q. Следова-
тельно, решение игры есть х* = у*=—, и цена игры равна нулю.
?
Пример (б)#
-1]
А=
Линии, которые должно нанести для игроков А и Ву будут:
=1—х, А2А'2 Е=1—2х,
=y-lt В2В'2 Е=1,
АгА'г
где отрезок АгА[ представляет математическое ожидание для А в случае, когда А
смешивает свои стратегии в пропорции х к 1—х, а Б следует только своей первой
Е
1
О
1 х
4
Рис. 45.
Е
о

в8
и* —J
в,
в', у
-4
Рис. 46.
Рис. 47.
стратегии, и т. д. Эти линии показаны на рис. 45. Очевидно, что А будет
придерживаться своей второй стратегии, то есть х* = 0% и что В может играть так, как ему
нравится @<!2/*<;i), поскольку х* определяет высшую точку линии А2А'2, и нет
самой низкой на Вф2 точки. В этом случае имеется бесконечное число решений,
421

Пример (в):
в отиошЗТ к(Т1
-Г1 2
L2 -1
ПредпОлагая'
он
«вой стратегии
Линия
ожидание
Стратегии игрока В
1
2
Эти линии изображены на рис. 46. А выбирает х* для наивысшей точки ломаной
линии А2РА'3. Значения ** = - и Я = 1 получаются графически или решением
последних двух уравнений. Затем рассмотрим
действия игрока В. Из рис. 46 ясно, что для него
никогда не будет необходимости в пользовании
своей первой стратегией, так как, независимо
от действий А, он может сделать свой платеж
Е меньше, применяя одну из своих двух
других стратегий или их комбинацию.
Следовательно, в действительности В выбирает между
двумя стратегиями, представленными
столбцами:
и графический анализ (см. упражнение 2 к
этому разделу) покажет, что он разыграет эти
стратегии с равными численностями и? = 1.
По отношению к исходной матрице А игра
имеет решение, в котором А смешивает две
2 1
свои стратегии в пропорции -^ к -^ (то есть
о о
играет первую в два раза чаще), В не
придерживается вообще своей первой стратегии, а обе
другие применяет с равными численностями.
Цена игры равна 1.
Пример (г).
Рис. 48.
3 2—4
-2 5 —1
Если А смешивает свои стратегии в отношении х к A—х), то:
]¦
Стратегии игрока В Линия
А2А'2
AZA'Z
44Л;
Ожидание
# = 5:г — 2
Е=5—Ъх
Е=— Зя — 1
Из рис. 47 находим, что А выбирает а:*=='о" Для наивысшей точки ломаной линии
АхРА'ъ, для которой Е=.—-— . Эти величины могут быть получены решением
уравнений для отрезков АХА[ и А3А'3. Следовательно, А выбирает свои стратегии в отношении
1 7 ;
К
Для В стратегии 2 и 4 не эффективны. В выбирает между двумя другими
стратегиями, заданными столбцами:
Г 3 -4
Тогда графический анализ показывает, что В играет эти две стратегии в отношении
3 ^ „ И „ / 1Г\
¦g- к -g- и что Е=—^ . Игра имеет цену, равную ( — -g- \ , и оптимальны естратегии со-
422

стоят в том, что А применяет свои стратегии в пропорции 1: 7, а В придержива
ется своей первой и третьей стратегии в пропорции 3 : 5.
Графический метод в применении к игре с платежной матрицей 2 X п
изображен весьма схематично на рис. 48. На нем показано изменение
математического ожидания Е для игрока А для каждой смешанной стратегии
(я, 1 — х), когда х изменяется в пределах от 0 до 1. Имеется п прямых
линий, по одной для каждого выбора чистой стратегии игроком В.
Минимальное ожидание для А изменяется в зависимости от # в
соответствии с ломаной Р(?/??..., состоящей из нижних отрезков линий, как это
показано на рис. 48. Согласно минимаксному принципу, высшая точка (или
точки) на ломаной дает оптимальную величину (или величины) для х. В общем
случае существует или ряд оптимальных я, которому соответствует
горизонтальный отрезок (RS на рис. 48), или единственное оптимальное значение х,
задаваемое вершиной системы отрезков рассматриваемых линий. Как
частный случай, возможно, что единственная оптимальная точка расположена
в начале или конце отрезка, то есть в точке х = 0 или х = 1. В этом
случае А применяет при устойчивом исходе свою чистую стратегию.
Такой же метод применяется для игр с платежной матрицей т X 2.
Чертеж тогда позволяет установить отношение у : A — у), в котором игрок В
смешивает свои стратегии. Возможно, хотя это не очень практикуется,
применить трехмерные диаграммы для решения игр с платежными матрицами
3 X п или т X 3. Прямые линии на рис. 48 тогда становятся плоскостями
в трехмерном пространстве. Оптимальные смешанные стратегии (для игрока
•с тремя стратегиями) задаются или частью горизонтальной плоскости, или
отрезком горизонтальной линии, или наивысшей точкой,— все это в
трехмерном пространстве.
Задачи и упражнения.
Г2 1 1
1. Если А= ~ „ I » решить игру [графически и затем проверить решение,
данное в примере (б) раздела 14.5.
2. Показать графически, что решение игры с А= . ~ I содержит у* = ~ .
Каковы х* и цена игры? См. пример (в) в тексте раздела.
3. Показать графически, что если А = о Л I , то решение будет ж*=-— ,
L —^ —1J о
3 11
#*=-5-, и цена игры равна —-q-. См. пример (г) в тексте раздела.
о о *
4. Исследовать графически случай А= . . , в котором имеется бесконечное
число решений. См. упражнение 3 к разделу 14.5.
5. Показать графически, что игра с А=| —1 0| имеет бесконечное число ре-
¦[-! 3
шений. См. упражнение 4 к разделу 14.4.
6. Исследовать игру в примере (ж) раздела 14.2 графическим способом. В каком
смысле можно сказать, что выбор стратегий игроком В не играет никакой роли?
14.7. ОБЩИЙ СЛУЧАЙ ИГРЫ ДВУХ1УЧАСТНИКОВ НУЛЕВОЙ СУММОЙ
Теперь мы рассмотрим общий случай игры с платежной матрицей тхп.
Гибкое применение матричных и векторных обозначений (см. главы 11 и 12)
облегчит наше изложение.
Пусть платежная матрица будет А= [ars] (r = l, 2,..., т; s = 1, 2..., п).
Игрок А выбирает между т стратегиями, и он может смешивать их по
своему желанию в последовательности партий. Пусть он придерживается
своих стратегий с относительными частотами хи х2, ..., хт, где все
переменные хг неотрицательны и их сумма равна 1, Иначе говоря, х19 х2,..., хт—
положительные правильные дроби, некоторые из них (но не все) могут быть
равны нулю, если имеются стратегии, которые А вообще не применяет.
В особом случае все хг, кроме одного, могут быть равны нулю, и этот один х
423

должен тогда равняться 1; это есть случай чистой стратегии, когда игрок
выбирает одну из своих стратегий во всех партиях. Во всех других имеет
место смешанная стратегия.
Заданная смешанная стратегия для игрока А тогда представлена
вектором
•^11 Хо9 ... * Х~у,*
подчиненным существенным ограничениям:
хг>0
(г=1, 2, ..., т) и
г=1
A)
Это включает и специальный случай чистой стратегии:
хг=1 и #Г' = 0 (г' = 1, 2, ..., т\ г'фг).
В соответствии с выбором г существуют т чистых стратегий. В матричных
обозначениях вектор х может быть изображен как вектор-столбец или как
вектор-строка:
L
х'= К] =
%
ОС.
Штрих в обозначении х' показывает, как обычно, транспозицию строк и
столбцов.
Таким же образом В выбирает между п стратегиями в соответствии
с вектором (у19 у2,..., уп), координаты
которого подчинены условиям,
аналогичным A). Этот вектор может быть
обозначен в форме вектора-столбца
у = {уё} или в форме вектора-строки
У'= IVsl (* = 1, 2,..., /г).
Если А применяет смешанную
стратегию х = {хг} ж Б — смешанную
стратегию у = {i/s}, то математическое
ожидание игры для А будет:
т п
2 2 B)
Символ Е (х, у) теперь показывает*
что величина Е является функцией
двух векторов х и у, причем afa
функция выражается через двойную сумму
B), включающую элементы х и у. В
матричном обозначении равенство B)
может быть записано (см. раздел 13.5)
как билинейная форма:
Рис. 49.
Е(х, у) = х'Ау,
C)
Размерности этих трех перемножаемых
матриц равны соответственно A X т), (т X п) и (п X 1), и их
произведение дает скаляр Е (см. 12.6).
Важно рассмотреть множество всех векторов х ={хг},
удовлетворяющих условиям A). Обозначим это множество через X, тогда «х из X»
обозначает один допустимый вектор х из полного множества X. Таким же
образом множество всех векторов {^}, удовлетворяющих условиям, подобным
условиям A), обозначается через У. Когда т=3, вектора х = {хг} (г = 1Г
2, 3) могут быть показаны точками (xvx2, x3) в пространстве трех
измерений. Множество X тогда заключает в себе все трчки, для которых 0
424

ж2>0, х3>0 и хг + х2 + х3 = 1. Это суть точки, которые лежат на
части плоскости хг + х2 + #3 = 1» отсекаемой координатными
плоскостями. На рис. 49 это показано частью плоскости, А^А^А^ где
ОАг = ОА2= ОА3 — 1. Любая точка треугольника представляет собой систему
стратегий игрока А; точки А19 А2 или А3 представляют чистые стратегии;
все другие точки представляют смешанные стратегии. Для т > 3 множество
X векторов х может мыслиться как множество точек, лежащих на сегменте
гиперплоскости в пространстве т измерений.
Величина Е, заданная равенством C), определена для каждого вектора х
из X и каждого вектора у из У. Основная цель игрока А состоит в том, чтобы,
выбирая х из X, сделать Е как можно больше, принимая во внимание
действия противника, выбирающего у из У. Игрок В таким же образом
стремится сделать Е как можно меньше. Полная теория таких игр зависит от
следующего определения, взятого непосредственно из раздела 14.5:
Определение: Если векторы х* и у* могут быть найдены так,
что для каждого х из X и у из У
Е(х, у*)<Я(х*, у*)<#(х*, у),
то есть
х'Ау* < (х*)' Ау* < (х*)' Ау,
то тогда (х*, у*) является седловой точкой для J?, игра имеет
устойчивый исход или решение (х*, у*), и и = 2?(х*, у*) есть цена игры
для игрока А.
Когда х* принимается в качестве оптимальной стратегии для А, то это
подразумевает, что оптимальный способ игры для А состоит в том, чтобы
придерживаться своих т стратегий с частотами Xj*, #2*,..., х^, где х* есть
вектор (#!*, #*2,..., Хт)- Определение показывает, что А выбирает х*
потому, что в этом случае он может получить по меньшей мере i?(x*, у*), чтобы
ни делал его противник, в то время как всякий другой выбор х делает
возможным для его противника удержать выигрыш А на уровне ниже Е(х*, у*).
Отсюда следует (это было доказано в разделе 14.5): Е(х, у) имеет седло-
вую точку (х*, у*) тогда и только тогда, когда
maxminZ?(x, у) = minmax E (х, у) = 2?(х,* у*).
х у ух
Основные положения теории завершаются затем минимаксной теоремой:
Билинейная форма Е(х, у) = х'Ау такова, что
max min ^(х, у) и minmaxi?(x, у)
х у ух
существуют и равны.
Специальный случай этой теоремы доказан в разделе 14.5, но общее
доказательство здесь не приводится. Доказательства, данные фон Нейманом и
Моргенштерном [8], Вальдом [10, стр. 52—54], сложны. Существуют
различные более простые доказательства. Одно из них опирается на применение
теоремы Броуера о неподвижной точке преобразования в топологии; это
доказательство найдено было Нэшем и приведено в прилож. 2 к [4].
Упрощенное алгебраическое доказательство дано Лумисом в [3]. Минимаксная
теорема является частью общематематического фундамента теории игр| и
минимаксных теорий решений, имеющих разнообразные применения. Ее
значение для теории игр определяется следующим предложением:
Игра двух лиц с нулевой суммой с ожиданием 2?(х, у) всегда
имеет решение х*, у* — седловую точку для Е(х, у). Игрок А имеет
не менее одной оптимальной стратегии (х* из X) и игрок В также
имеет не менее одной оптимальной стратегии (у* из У). Цена игры
есть v, равное ?(х*, у*), то есть общему значению для max min E(x, у)
х у
и min max E(x, у).
у х
425

В некоторых случаях существует более одной оптимальной стратегии,
но тогда их существует бесконечное число, хотя цена игры по-прежнему
единственна. В таких примерах она достигается каждым из игроков при всякой из
бесконечного числа оптимальных стратегий. Этот дополнительный пункт
мы уже показали на простых случаях. Он не исключается приведенными
выше основными результатами.
Теперь мы установим некоторые свойства решения игры. На первый
взгляд они могут показаться формальными, если не бесполезными.
Фактически же они являются основой практических правил, без которых едва ли
возможно решать встречающиеся на практике игры с вполне определенными
числовыми платежными матрицами в тех случаях, когда каждый игрок имеет
больше двух стратегий. Решение игры или даже нахождение и проверки
цены игры требуют огромной работы на практике, и свойства, подобные
следующим, составляют существенную часть методов решения игры.
Первое из свойств относится к платежным матрицам, и мы показываем,
как его можно использовать для облегчения вычислений (например, для
того чтобы избавиться от отрицательных элементов в матрице А).
Второе свойство дает важный способ проверки оптимальности
стратегий, если найдена или даже угадана цена игры.
Третье свойство используется|в связи со вторым и относится к
обстоятельствам, при которых одна стратегия вообще не играется в оптимальном
положении. Вот эти свойства.
Свойство I. Если х* и у* являются оптимальными стратегиями
для игроков в игре тхп с платежной матрицей А, то они также
оптимальны для игры с платежной матрицей (сА + В), где с
—положительный скаляр и В—матрица размерности га х и, имеет все
элементы, равные скаляру Ъ. Если v есть цена исходной игры, то цена
второй игры равна (cv + b).
Свойство II. Если игра имеет цену' v, то х* и у* являются
оптимальными стратегиями для игроков тогда и только тогда, когда:
а) ?(х*, y)>v для каждого у из У,
Е (ху*) < v для каждого х из #,
и, следовательно, тогда и только тогда, когда
п т
б) 2 <t>rSy*<v< 2 arsx*
s=l r=l
для всех г = 1, 2, ..., га и s== 1, 2, ..., п.
Свойство III. Если игра имеет цену v и оптимальные стратегии
х* и у*, то для любого г и s (г=1, 2, ..., га; s = l, 2, ..., п):
п
неравенство 2 arSy* < v предполагает #* =.0 и
8=1
га
неравенство 2 arsx* > v предполагает у? = 0.
г=1
Условия свойств II и III могут быть выражены в матричном
обозначении:
И(а) (х*)'Ау>и для каждого у из У,
(х)'Ау*<а для каждого х из X,
11F) Ау*<а{1}<А'х*,
где {1} есть вектор-столбец, состоящий из га или п элементов, каждый из
которых равен единице.
426

III. В неравенстве Ау*<у{1} предполагается, что ели для одного
какого-либо элемента левая часть строго меньше правой, то
соответствующая координата вектора х* равна нулю, аналогично и для неравенства
Доказательства этих свойств основываются на определении решения
игры и для иллюстрации мы приведем здесь доказательство свойства II (а).
Во-первых, пусть даны оптимальные стратегии х* и у*. По
определению:
Е(х, y*)<i; = #(X*, у*)<Я(х*, у)
для каждого х из X и у из У, что и требовалось доказать.
Во-вторых, пусть дано Е (х, у*)< v<CE(x*, у) для каждого х из X
и у из У. Положим х = х* и у = у*: Е(х*, у*)< а<#(х*, у*), то есть
v = E(x*, у*). Тогда Е(х, у*)<#(х*, у*)<?(х*, у) для каждого х из X
и у из У, то есть (х*, у*) является по определению седловой точкой
функции Е, а х* и у* — оптимальные стратегии. Что и требовалось доказать.
Один частный случай является достаточно важным, чтобы привести
его наряду с более общими свойствами:
Свойство (IV). Если платежная матрица игры квадратная и кососим-
метрическая, тогда стратегия, являющаяся оптимальной для одного игрока,
будет оптимальной и для другого, и цена игры равна нулю.
Кососимметричность платежной матрицы А показывает, что в игре
имеет место симметрия между двумя игроками. Если переменить роли
игроков и рассмотреть матрицу платежей, получаемых игроком В, то новая
платежная матрица будет равна (—А'), Эта матрица, по определению косо-
симметрической матрицы, равна исходной матрице А. Платежные матрицы
игроков совпадают, и естественно ожидать, что совпадут и их оптимальные
стратегии. Совершенно независимо от этого, игра может быть названа
справедливой, если ее цена равна нулю: когда игроки выбирают оптимальные
стратегии, то в результате ни один игрок не выигрывает у другого. В этом
смысле почти все виды игр, в обычном значении этого слова, включая
большинство салонных, являются справедливыми. В частности, для игр,
симметричных по отношению к участникам, следует ожидать, что они также будут
справедливыми. Например, для описанной в 14.2, пример (е), игры «двух-
пальцевая Морра» платежная матрица является кососимметрической:
О -3 2 0 1
3
-2
0
0
0
4
0
0
-3
-4
3
0
Игра симметрична для игроков; естественно предположить, что она
справедлива. Именно это и утверждает свойство IV.
На основании свойства II (б) можно доказать, что каждый игрок имеет
в этом случае одну и ту же оптимальную стратегию z*, и цена игры равна О1.
Можно также привести некоторые соображения для игр, не
являющихся справедливыми (v Ф 0). Пусть v > 0, так что в результате игрок В
при устойчивом исходе проигрывает игроку А некоторую сумму. Почему
вообще В будет играть? Действительно, если он знает решение игры, то
не видно основания, по которому он должен был бы играть. Но здесь
возможно существование компенсирующего соглашения, возможен обратный-
платеж от игрока А игроку В в каждой партии рассматриваемой игры.
Встает вопрос: какой платеж делает игру справедливой? Исчерпывающий
ответ дается свойством A). Если А в каждой партии платит сумму,
равную v, игроку В, тогда платежная матрица в действительности равна (А — В)г
где все элементы матрицы В равны v. Цена игры в этом случае будет (и — v) =
= 0. Обратный или компенсирующий платеж v от игрока А игроку^ В
1 Нами опущено доказательство свойства IV, приведенное автором.— Прим. ред.
427

делает игру справедливой; В, если он искусен, может играть совершенна
спокойно и без убытка для себя.
Задачи и упражнения.
1. Вектор х принадлежит к множеству X, определенному условиями (I)
настоящего раздела. Когда его размерность равна 2, показать, что х является точкой
на плоскости Охгх2 и что X включает все точки, лежащие на отрезке прямой линии/
соединяющем лежащие на координатных осях точки Аг и А2у для которых ОА1 = ОА2 =
= 1, то есть х есть вектор (х, 1—х) при 0<><;1.
2. Если вектор х имеет размерность 3, показать, что множество X включает все
точки треугольника АгА2А3, изображенного на рис. 49. Рассмотреть и истолковать
случай, когда точки лежат на сторонах треугольника. Показать, что в общем случае
х является вектором^!, аг2,1—xt—х2), определяемым двумя такими переменными хи
х2, что точка (х19 х2) принадлежит треугольнику ОАгА2.
3. Пусть хA) и хB)—два вектора из Х\ показать, что вектор x=-r-(xA>-f х<2)>
также принадлежит множеству X и пояснить это на рис. 49. Обобщить это утверждение
для любого числа векторов из X, сформулировав его в терминах выпуклых линейных
комбинаций (см. раздел 11.5).
4. Игра имеет платежную матрицу 2хтг. Показать, что если (жA), 1—яш) и {xi2)r
1—яB)) — пара оптимальных стратегий для игрока А, то стратегия (я, 1—х) также
является оптимальной стратегией, если х лежит между ха) и #<2). Вывести, что если
существуют две различные оптимальные стратегии, то тогда существует и бесконечное
множество оптимальных стратегий. Обобщить вывод для матриц тхп, пользуясь
линейной выпуклой комбинацией.
5. Доказать свойство I.
6. Вывести свойство П (б) из свойства II (а) и затем доказать свойство III.
7. Показать, что игра не может иметь двух различных цен, то есть цена игры
имеет единственное, значение, даже когда существует бесчисленное число
оптимальных стратегий.
14.8. РЕШЕНИЯ КОНКРЕТНЫХ ИГР
Когда хотя бы один из участников игры имеет только две стратегии,,
то есть когда игра имеет платежную матрицу 2 X п или т X 2, игра всегда
может быть решена при помощи приемов, описанных в разделах 14.5 и 14.6^
Как это следует из минимаксной теоремы, игра т X п всегда имеет
решение, либо единственное, либо (в худшем случае) бесконечное множество.
Следовательно, объект поиска существует, и проблема состоит в том, как
его найти.
Введение понятия математического ожидания 2?(х, у) при
практическом решении этой задачи, вероятно, не принесет пользы, так как с функцией
двух векторов х и у, имеющей вид двойной суммы, вообще нелегко
обращаться. Практическая методика нахождения решения должна быть создана
на иных путях и разбита на две стадии. Рассмотрим платежную матрицу А =
= [ars] размерности т X п. На первой стадии матрица уменьшается за
счет удаления излишних строк и столбцов (соответствующих стратегиям,
никогда не применяемым). Полученную матрицу можем далее, опираясь
на свойство 1 из раздела 14.7, привести к более удобному виду (например,
избавиться от отрицательных и дробных чисел) и, наконец, проверить
матрицу на седловую точку, предполагая, что игроки применяют в устойчивом
исходе только чистые стратегии. Если существует такая седловая точка, то
решение найдено, и ничего больше не надо делать. В противном и более
общем случае, необходимо переходить ко второй стадии нахождения реше-
. ния. Идея здесь состоит в том, чтобы перебрать теми или иными средствами
всевозможные мыслимые случаи оптимальных стратегий для каждого игрока
и проверить их, опираясь на цену игры. Вот теперь на сцену появляются
свойства II, III и IV раздела 14.7. Не следует отказываться ни от одной
возможности найти решение, даже непосредственная догадка хороша. Ибо
очень простым способом, при помощи свойства П(б), можно проверить,
является ли какая-либо пара предлагаемых стратегий оптимальными
стратегиями, и таким образом принять ее или отбросить.
Первая стадия нахождения решения нуждается в детальной разра-
428

«ботке. Должны быть даны определения излишних строк и столбцов в
матрице А и способ их выявления. Рассмотрим строки матрицы А. Строка
может быть исключена как ненужная, если над ней доминирует другая
строка в том смысле, что каждый элемент доминирующей строки больше
или равен соответствующему элементу исключаемой строки. У игрока А
никогда не будет основания для того, чтобы применять стратегию,
соответствующую избыточной строке, как в чистом виде, так и в комбинации с
другими стратегиями. Пользуясь другой стратегией, то есть доминирующей
строкой, игрок А всегда может добиться лучшего или такого же
результата. Например, если А = Г. ~\ | , то первая строка может быть
исключена, и игроку А должно ограничиться рассмотрением только второй, или
доминирующей, стратегии. Очевидным обобщением является случай, когда
одна строка может быть исключена, если над ней доминирует некоторая
выпуклая линейная комбинация других строк. Эта комбинация получается
умножением соответствующих строк на положительные дроби, дающие
в сумме единицу.
Например, если дана матрица:
-1 1"
1 1 0
то комбинация (сумма) половины второй и половины третьей строки дает
смешанную стратегию, для которой, при различных чистых стратегиях игрока В,
получения А будут соответственно равны 1, —1/2 и 1. Эти платежи больше
или равны элементам первой строки, а потому первая строка А может
быть исключена, так как над ней доминируют две другие строки. Таким же
образом можно рассмотреть столбцы матрицы А с той только разницей, что
теперь игрока В интересуют меньшие элементы. Следовательно, столбец
матрицы А может быть исключен как избыточный, если над ним доминирует
другой столбец или выпуклая линейная комбинация других столбцов, в том
смысле, что элементы исключаемого столбца больше или не меньше
соответствующих элементов рассматриваемой комбинации. Следующие примеры
иллюстрируют эти положения:
Пример (а).
А Г 3 2-4 61
A=L_2 5 -I 2j-
Вычеркнуть второй и четвертый столбец, над которыми доминирует третий. Реше-
Г 3 —41
яие игры находится по матрице ~ . , если добавить нулевые относительные
частоты для второй и четвертой стратегии игрока В. Как в примере (г) и на рис. 47
раздела 14.6, оптимальные стратегии игроков будут
Пример (б)
•а цена игры г>= —^- •
о
L ^ — А О J
Вычеркнуть первый столбец, так как над ним доминируют два других:
±B) + |@) и
Решение получается из I . ~ • Оптимальные стратегии суть:
а цена игры и = 1, как и в примере (в) раздела 14,6.
429

Пример (в)
[О 2-1 31
2 3 1 2
3 4 0 —4J
Можно вычеркнуть первые два столбца, над которыми доминирует третий, и третьн>
строку для оставшейся матрицы, над которой доминирует вторая. Наконец, в матрице
[ 4 о ВТ0Р0И столбец и первая строка также исключаются, и остается
единственный элемент 1. Цена игры есть 1, существует седловая точка и применяются только
чистые стратегии из исходной матрицы А: вторая для игрока А и третья для игрока В~
Пример (г)
1
3
1
3
1
3
1
3
1
3
0
2
3
1
3
1-
3
1
~6
1
3
1
А =
Исключить вторую строку, над которой доминирует комбинация (с равными
частотами) третьей и четвертой строки. Решение следует находить по оставшейся
квадратной матрице 3x3.
Следующий этап первой стадии нахождения решения состоит в
упрощении матрицы А при помощи свойства 1 раздела 14.7. Прежде всего мы можем,
избавиться от отрицательных элементов в А, для чего найдем наибольший
по абсолютной величине отрицательный элемент и прибавим его
абсолютную величину ко всем элементам матрицы. В упрощенной таким способом
матрице наименьшим элементом будет нуль; соответствующая этой матрице
игра имеет те же оптимальные стратегии, что и исходная, а ее цена равна
цене исходной игры плюс постоянная величина, прибавленная ко всем
элементам матрицы. Далее умножением на подходящий скаляр с можем
уничтожить в матрице все дробные элементы, не меняя оптимальных стратегий,,
а только увеличивая цену игры в с раз. Не всегда необходимо добиваться
исключения всех отрицательных и дробных элементов матрицы А, так как
решение может быть получено и без этого. Но можно сделать это всегда,
когда потребуется.
Игра в вышеприведенном примере (г) настоящего раздела служит
хорошей иллюстрацией такого приема. Если А (без второй строки) умножить
на 3 и если затем прибавить 1 к каждому ее элементу, то полученная
матрица будет иметь следующий вид:
О О"
О
4
и для игры с такой матрицей легко найти решение. Исходная игра имеет те>
же оптимальные стратегии, что и игра с полученной платежной матрицей.
Кроме этого, если цена исходной игры равна и, то новая цена может быть
найдена на основании того факта, что цена упрощенной игры равна (Зи + 1).
На заключительном этапе первой стадии матрицу игры можно
проверить на седловую точку, то есть определить, имеет ли игра решение в
области чистых стратегий. Целесообразно это сделать до каких-либо
преобразований матрицы А; или же можно попытаться найти такое решение для
частично или полностью упрощенной (в смысле лишних строк и столбцов,
дробных и отрицательных элементов) матрицы. Рассмотрим с этой точки зрения
пример (в) настоящего раздела. Минимальные элементы в строках А равны
соответственно -—1, 1, —-4, а максимальные элементы в столбцах будут 3, 4,
1, 3. Следовательно, в соответствии с методом, изложенным в конце разде-
430

ла 14.4, цена игры и равна 1, игрок А применяет только свою вторую,
а игрок В — только свою третью чистую стратегию. Этот же результат
мы получили раньше путем исключения из матрицы А излишних строк
и столбцов.
Немногие игры имеют решение в области чистых стратегий. Но все
игры должны быть проверены на седловые точки на первой стадии поиска
решения, что дает возможность больше не рассматривать чистые стратегии
и экономит труд на второй стадии.
Это иллюстрируется следующим примером.
Пример (д).
Рассмотрим проблему закупки угля, сформулированную в примере A5) из книгш
Вильямса [11]. Вы имеете следующие данные о количестве и ценах угля,
необходимого зимой для отопления вашего дома:
Зима
Мягкая
Обычная ....
Холодная ....
Количество
угля, т
4
5
6
Средняя цена,
ф. ст. за 1 m
7,0
7,5
8,0
Эти цены относятся к текущим покупкам угля в течение зимы. Летом, однако, уголь
может быть куплен по цене 6 фунтов за тонну, и у вас есть место для хранения запаса
до 6 тонн. Вы обдумываете три стратегии, выбирая между тремя вариантами запасов
в 4, 5 или 6 тонн, заготовляемых летом. При этом вы предполагаете докупить недостающее
количество (если потребуется) по зимним ценам. Весь уголь, который сохранится до конца
зимы, вами в расчет не принимается, так как вы предполагаете оставить ваш дом и не
сможете поэтому распоряжаться оставшимся углем. Платежная матрица (в фунтах) тогда,
будет иметь вид:
Зима
Летний запас (в т) 4
мягкая
4
5
6
~~24
-30
-36
обычная
-4
-30
-36
холодная
-40 "
-38
-36*.
«Игра» имеет седловую точку и решение (отмечено звездочкой). Ваша оптимальна»
стратегия состоит в покупке 6 тонн угля летом. В «игре» против природы, подобной этой,
предполагается, что игрок не знает о том, какую «стратегию» выбирает природа. В этой
задаче решением игры является стратегия полного страхования на случай холодной?
зимы. Но это не предполагает, что вы должны поступать именно так. Напротив, вы
можете, рассчитывая на нормальную зиму, купить пятитонный запас и уменьшить издержки.
Тогда, если зима будет холодная, вы потеряете по сравнению с «решением» игры.
Применяемый на второй стадии практического поиска решения общий
метод иллюстрируется достаточно хорошо случаем игры с платежной
матрицей 3x3* Игры большего размера имеют только больше переменных
и больше соотношений между ними, но в них нет ничего принципиально
нового.
Платежная матрица игры 3 X 3 — это матрица А= [ars] (г = 1, 2, 3;
s = 1, 2, 3). Пусть цена игры будет v, и пусть (х19 х2, х3) и (у±, y2J у3) будут
оптимальные стратегии для двух игроков. Тогда, согласно свойству II (б)
раздела 14.7, семь неизвестных (иксы, игреки и v) подчинены восьми
соотношениям:
«32^3 > v «2i2/i + Й22У2 + ЯгзУз < v
а13хг + a23x2 + a33x3 > v . a31yi + a32y2 + a33y3 < у
Кроме того, еще имеются ограничения, требующие неотрицательности
всех хт и ys. Смысл соотношений ясен. Выражение (апхг + а21х2 + а31а:з)
является математическим ожиданием выигрыша игрока А, когда он при-
431

меняет свою оптимальную стратегию (х19 х2, х3), а игрок В — свою первую
чистую стратегию. Следовательно, поскольку А придерживается своей
оптимальной стратегии, вне зависимости от того, какую чистую стратегию
выбирает В, выигрыш для А должен быть не менее г;. Это остается справедливым,
как бы игрок В не смешивал свои стратегии. Точно таким же образом,
если В применяет свою оптимальную стратегию, то несущественно, какую
-стратегию выбирает А в том смысле, что В никогда не проигрывает
больше, чем и. В этом состоят ограничения при любых мыслимых оптимальных
стратегиях и любой мыслимой цене игры. Эти условия должны
автоматически выполняться.
Положение таково, что имеется больше соотношений, чем переменных,
и среди соотношений есть неравенства. Но проблема состоит не в том, чтобы
перечислить уравнения и затем решить их. Напротив, это не является нашей
ближайшей целью; не все соотношения являются уравнениями, но если бы
это было так, их подсчет показал бы, что уравнений «слишком много».
Проблемы такого типа встречаются в линейном программировании,
и существуют вычислительные методы (например, симплексный меход) для
нахождения решения. Они будут рассмотрены в разделе 15.8.
В качестве временной меры мы предлагаем здесь более грубый и
легкий метод решения. Когда переменные связаны неравенствами, их
возможные значения попадают в частично перекрывающие друг друга области.
В геометрической интерпретации это обозначает, что, когда переменные
изображаются точками в пространстве, точки не лежат обязательно на
линиях, плоскостях и так далее, но они попадают и внутрь (или вне)
некоторых областей, определяемых этими линиями, плоскостями и так далее.
Решение ищется все же в виде одной точки или множества точек, но
определяется не пересечением линий, плоскостей и так далее; оно скорее является
общей частью определенных пересекающихся областей. Однако, на что
можно надеяться, это, что некоторые (но не все) границы областей служат
для определения решения, то есть некоторые (но не все)
соотношения-неравенства могут быть обращены в равенства и, в результате их решения,
будет найдено решение игры. Существенное отличие этой идеи от обычных
методов решения систем уравнений состоит в том, что мы должны из всех
возможных соотношений в форме неравенств сделать выбор таких, которые
мы превращаем в уравнения. Другие же ограничения рассматриваются
нами в форме строгих неравенств. Весь вопрос заключается в том, какие
именно соотношения должны быть записаны в виде уравнений.
Имея это в виду, можно с новых позиций посмотреть на решение
(оптимальную стратегию для игрока А) в случае игры с матрицей 2 X тг, который
проиллюстрирован, например, на рис. 48. Если оптимальной стратегией
для А является (хг, х2), тогда имеется одно уравнение (хг + х2 = 1) и п
неравенств относительно х1 и х2. Положим хг = х и х2 = 1 — х, в результате
получим п неравенств относительно одного переменного х и цены игры v.
Любые два из них, записанные в виде уравнений, служат для определения
величины х и и, но они могут противоречить другим из п соотношений или
х может оказаться отрицательным. Графический метод, использованный
на рис. 48, состоит в том, что все соотношения записывают как уравнения,
затем изображают их в виде прямых линий, показывающих изменение и
в зависимости от х, лежащего между 0 и 1, выбирают наименьшее и для
каждого х и, наконец, определяют х для наибольшего из этих
минимизированных и. Если игра имеет единственное решение, х находится решением
двух уравнений и чертеж показывает, какими именно.
Метод, подсказанный этим направлением мысли, состоит в выуживании
из полной системы соотношений некоторых из них, затем в решении их,
как уравнений, и контроле результата с помощью других неравенств. Метод
можно сформулировать в терминах подматриц, образованных из платежной
матрицы и их определителей. В результате он сводится к применению
правила Крамера для решения подгрупп уравнений. Простое изложение этого
432

метода для случая 3 X 3 дано в [11, стр. 91—98]. Примененный здесь метод
является прямым подходом к решению вопроса, какие соотношения
записываются в виде уравнений, и он выявляет важность свойства III, описанного
в разделе 14.7. Метод можно объяснить на примере восьми ^ соотношений
между семью переменными, полученными для игры с платежной ^
матрицей 3 X 3.
Сначала запишем все восемь соотношений в виде уравнений, решим
любые семь из них относительно входящих в них переменных, проверим
неотрицательность переменных хг и ys и посмотрим, удовлетворяется ли
также восьмое уравнение. Если это так, то решение получено. Если не так,
то переходим к следующему приему. Выберем какое-либо соотношение
и запишем его как строгое неравенство, а другие семь как уравнения. Если
одно из соотношений между я'ами выполняется как строгое неравенство,
то соответствующий ys равен нулю, что следует из свойства III раздела 14.7.
Теперь мы имеем семь уравнений относительно шести переменных (нулевой
ys будет исключен), и процесс повторяется. В конце концов, рассматривая
некоторую совокупность уравнений, найдем решение относительно тех
переменных, которые не должны быть равны нулю по свойству III.
Изложенный метод иллюстрируется далее на реальном примере в разделе
14.9.
Мы можем пока продолжить дальнейшее изложение практических
методов поиска решения, основанных на неравенствах свойства II (б) и условиях
свойства III. Если соотношение между переменными х имеет место в форме
«больше v» (S^s^r > v)i тогда соответствующий ys равен нулю, то есть,
г=1
если оптимальная стратегия игрока А в сочетании с s-й чистой стратегией
игрока В дает платеж для А, больший и, тогда игрок В не пользуется этой
стратегией для своей оптимальной смеси. Для соотношений переменных
п
ys в форме «меньше и» (^jarsys < v) справедливо аналогичное утвержде-
ние. Если эти случаи исключены, то остается множество соотношений между
я'ами и между i/'ами, в которых левые части равны v. Это относится к
оптимальным хг и у$, которые не равны нулю, то есть к стратегиям, которые
применяются в устойчивом исходе. Таким образом, если А применяет свою
оптимальную смешанную стратегию, тогда любая чистая стратегия,
проводимая В, дает платеж игроку А, равный точно и, при условии, что эта
чистая стратегия является одной из стратегий, включаемых В в его
оптимальную смесь. В этом смысле, пока А играет как следует, безразлично, как
играет В. Аналогично, когда В придерживается своей оптимальной
стратегии, безразлично, как играет А, выбирая чистые стратегии для своего
оптимального смешивания. Это приводит к простейшему способу контроля
оптимальности любых предлагаемых стратегий для того и другого игрока. Если
взять оптимальную смесь стратегий для игрока А и оценить ее для каждой
из чистых стратегий, применяемых В в своей оптимальной смеси, то в каждом
случае в результате получим одинаковый платеж игроку А. Аналогично
этот же платеж (v) мы найдем, оценивая оптимальную смесь для В для
каждой из чистых стратегий, применяемых игроком А.
Задачи и упражнения
Г 121
1. Если А= —1 0 , показать, что вторая строка' излишня. Затем решить
L 13j
игру и"сравнить с упражнением 4 (к 14.4) и упражнением 5 (к 14.6).
2. Путем исключения избыточных строк и столбцов, показать, что игра с матрицей
ГО 3 37
ГО 3 -31
l= 3 9 —6
I 3 —1 2j
имеет цену p^-j > а оптимальные стратегии Го, у , ~Л для Ли@,~, -|Л для J5.
А=
28 Р. Аллен 433

3. Упростите матрицу предыдущего упражнения, исключив отрицательные"
элементы. Решите преобразованную игру, а затем по цене последней найдите цену исход-
ной игры ( v = — J.
4. Решите игру с А
Г-1 1 П
= 1-1 1,
L 1 1 -iJ
исключая сначала положительные
элементы. Это наводит на мысль, что v = -k является ценой игры.
5. Взять А в той же форме, как в предыдущем упражнении, но порядка п.
Пользуясь свойством II (б), из 14.7, покажите, что стратегия (—, —,..., — j
является оптимальной для каждого игрока, т. е. все численности равны. Почему вы
могли ожидать этого? Выведите, что цена игры равна
'3 О (П
1 .
6. Игра имеет матрицу А=
!-•¦
. Упростите А, избавившись от
отрицательных и дробных элементов и исключив лишний столбец. Решить графически
полученную игру с матрицей. Cx2) и показать, что оптимальная стратегия для J5 будет/
/* 3 2 \
( 0, -г , -Е" ) • Какова оптимальная стратегия для игрока А?
имеет седловую точку.
-3 3 —1 01
7. Показать, что игра с А=| 1 2 0 1 I
_ 3-2-4 -lj
Вывести, что при устойчивом исходе игроки выбирают чистые стратегии и что*
игра справедлива.
-г
8. Показать на примере платежной матрицы А =
1
—2
О ™ -
2 -—•
-г
' 4-
1 —1
, что
возможны'многочисленные седловые точки. Каково решение игры, и как оно может быть
истолковано? Какой компенсирующий платеж должен игрок А делать игроку В в
каждой партии?
14.9. ИЛЛЮСТРИРУЮЩИЕ ПРИМЕРЫ^
Следующие примеры поясняют описанные выше практические приемы
решения заданной игры. Все они относятся к играм, у которых
оптимальный исход лежит в области смешанных стратегий. Все они также являются
играми, которые интересно играть; некоторые из них «справедливы»,
другие, хотя и не являются справедливыми, содержат какую-либо приманку
для игроков. Типичным случаем последних является игра на скачках.
Пример (а).
Матрица А
Г12 3Т
= 231
L3 12J
известна статистикам под названием латинского квадрата
C-го порядка). Каждая цифра A, 2, 3) встречается по разу в каждой строке и в
каждом столбце. Матрица симметрична, ее не нужно упрощать, так как в ней нет ни
отрицательных, ни дробных элементов, она не имеет седловой точки, и
соответствующие переменные, определяющие оптимальные стратегии, должны быть найдены из
следующих условий, относящихся к хг:
434

и подобных же соотношений между ys. Поэтому оптимальные стратегии игроков
совпадают.
Рассматривая приведенные четыре соотношения как уравнения, находим: х1=х2=
Следовательно, в устойчивом исходе смешанная стратегия для каждого игрока
задается вектором С -~- , -^ , -х- j , то есть стратегии имеют равные относительные
частоты, и цена игры равна 2.
Пример (б).
—3 О ОН
Матрица А=
3 1
не является ни симметрической, ни кососимметри-
ческой. Следовательно, можно ожидать, что игроки принимают различные стратегии.
Пусть цена игры будет v\ она, вероятно, будет положительной.
Упростим матрицу А, умножая ее на 2 и затем прибавляя 2 к каждому ее эле-
Г8 2 21
416
L6 5 0J
менту1. Игра с матрицей I 4 1 6 I имеет такие же оптимальные стратегии, как и исход-
L6 5 Oj
ная игра, а ее цена равна v = 2(y+l). Полученная игра не имеет седловой точки.
Соответствующие переменные удовлетворяют соотношениям:
8*i+4*2+6*3 >v
2*1+*2+5*3>v
2*!+6*2>v
Рассмотрим все эти соотношения как уравнения и, решив систему четырех
уравнений, записанных слева, получим:
13 3 7
*i= —, *2=Т, *з=^, v=^,
что неприемлемо, так как *х < 0. Теперь будем считать одно из соотношений строгим
неравенством. Испытаем неравенство
8*1+4*2+6*3 >v,
с которым связано i/i = 0. Теперь уравнения будут
3 = 1 #2 + 2/3=1»
Последние два уравнения из уравнений относительно ys дают^г/2=—¦~>2/з=- >
что неприемлемо, так как другие уравнения относительно ys; при этих значениях
г/2 и уг не удовлетворяются. Уравнения несовместны. Любой другой выбор одного
соотношения приводит к такому же отрицательному результату.
На следующем этапе берем два соотношения в форме строгих неравенств.
Предшествующая попытка наводит на мысль попробовать испытать в качестве строгого
неравенства одно из соотношений для ys> например берем:
и уг =
и *! =
Рассмотрим оставшиеся соотношения как уравнения:
*2+*з = 1 2/2+2/3=1»
*2+5*3=v
1 Нахождение решения игры значительно упрощается, если исключить первый
столбец матрицы А, над которым доминирует второй. —Прим. ред.
* У Аллена здесь ошибка: последнее уравнение относительно ys должно быть
1 4
5i/2=v. Отсюда f/2=TVJy3=|v' Но это не меняет вывода автора, что полученные
решения для у2 и yz не удовлетворяют другие уравнения, а потому эта проба, и при
устранении ошибки Аллена, не приводит к решению игры. —Прим. ред.
435 28*

Они совместны, и их решением является:
1 1 3 2
*2 = у> *з=-2> ^^У ^^У v==3'
Следовательно, решение исходной игры состоит в том, что оптимальной страте-
/ 1 1 Ч ( 3 2 \
тией для А является (О, -^, -^ j и (О, -г-, -^-J для #. Цена игры и находится
из уравнения: v = 2(v-{-l) = 3, то есть р=-—. Игра становится «справедливой», если
в каждой партии игрок А платит 1/2 игроку В.
Пример (в).
Игрок А ставит на три лошади; выплаты в случае победы каждой лошади
Г 1 -1 -11
относятся к ставке как 1:1, 2:1 и 3:1. Платежная матрица I —1 2 —1 может быть
L-1 -1 3J
упрощена прибавлением 1 к каждому ее элементу. Получим диагональную матрицу:
Г2 0 01
0 3 0.
L0 0 4J
Если цена исходной игры равна v, то цена для игры с матрицей А равна (г>+)
Оптимальные стратегии для этих двух игр одни и те же. Запишем соотношения между
хт в виде уравнений:
и точно такую же систему уравнений запишем для ys. Системы этих уравнений дают
совпадающее решение для хг и ysi
х- =— • х = =—• х— =—. У + 1-—
Игра на скачках имеет цену v=—j~ ; тот, кто ставит на лошадь, в итоге
проигрывает, а выигрывает «букмекер». Для того чтобы достичь такого оптимального
результата (иначе можно проиграть большую сумму), надо ставить на лошадей в
смешанной стратегии ( ^, ^» То ) • лУчше всего разделить ставку между тремя
Ч^ хо хо хо у
лошадьми в пропорции 6:4:3.
«Устроители», определяющие соотношение ставок, также знают, что шансы
лошадей на победу соответственно равны То» То и То • Зная соотношение 6:4:3 между
шансами на победу устроители тотализатора, если бы они стремились быть совершенно
справедливыми, установило бы следующие условия ставок:
7:6; 9:4 и 10:3.
В действительности же эти условия A:1, 2:1, 3:1) были несколько менее
благоприятны для игроков:
6 ' 1 ^ 4 ' 1
что и давало букмекеру возможность выигрыша.
Не всегда шансы бывают таковы, что v получается отрицательным, и букмекер
выигрывает. Например, как заметил Г. Мортон, в канун розыгрыша Большого
Национального приза 1954 года условия ставок при оптимальном их распределении дали бы
игрокам выигрыш в 4% от суммы ставок, и в итоге букмекеры имели бы верный
проигрыш в этом размере.
Пример (г).
Платежной матрицей для игры «двухпальцевая Морра» (смотри пример (е) из
раздела 14.2) является матрица
0—3 2 0
3 0 0—4
— 2003
0 4—3 0
436

Матрица косо симметрическая, игра справедлива (цена нулевая), и игроки имеют
одинаковые оптимальные стратегии. Это упрощает соотношения.
Именно получаем:
2*3 >,
и такие же соотношения между ys.
Все пять соотношений, рассматриваемые как уравнения, несовместны. Тогда
возьмем одно из соотношений в форме строгого неравенства. Пусть это будет 3*2—2*3>0,
так что #1 = 0 и, следовательно, из-за симметрии между переменными ж^О. В таком
случае останутся соотношения:
4*4=— 3*4=0,
которые дают *2 = -=-, *3=^^-, *4=0. Следовательно, стратегия Г 0, — , -у , 0 J
является оптимальной стратегией для того и другого игрока. Однако это решение
не единственно. Выделим как строгое неравенство —4*2+3*з>0, Так что 2/4=0 и,
следовательно, *4=0.
Получим тогда уравнения:
3*2—2*з=0,
—3*!=2*х=0,
которые дают
B з \
0, -р- , -jr- , 0 J является другой оптимальной стратегией для
каждого игрока. Так как любая выпуклая линейная комбинация оптимальных
стратегий также является оптимальной стратегией, то из того факта, что найдены два
решения, следует, что существует бесконечное множество решений, то есть стратегия
@, *, 1 — *, 0) является оптимальной стратегией при любом х из области *1ь^х^*1т
Результат, полученный в конце раздела 14.8, может быть проверен на этом
примере. Предположим, что игрок А придерживается смешанной стратегии
/ 29 41 Л
\* 70 ' 70 ' ^ ) ' К0Т0Рая является одной из его оптимальных смесей. Тогда, при
условии, что В применяет только одну вторую или одну третью стратегию, игра
является ничейной (цена игры равна 0):
-3-0+0- Щ+0- §+4-0=0,
2-0+0- g+0-g-3-0=0,
Но если В применит отдельно первую или четвертую стратегии, которых нет среди
его оптимальных смесей, тогда А выигрывает:
»•«+»• I-»-я+»-«-п.
0.0-4. 5+3.^1
Следовательно, даже, если А заранее объявит, что он собирается делать (например,
играть вторую и третью стратегии в пропорции 2:3), В никак не может повлиять
на исход игры. Стало быть, если В придерживается второй и третьей стратегии,
смешивая их в любых пропорциях, то он всегда вынуждает ничейный исход. Если В
437

уклоняется от оптимальной комбинации и применит или первую или четвертую
стратегии, он проигрывает игроку А *.
Для играющего в эту игру решение совсем не является очевидным с самого начала.
Полезный для него совет заключается в том, что он должен играть только вторую
и третью стратегии (то есть показывать два пальца, а называть один, или показывать
один палец, а называть два) и использовать вторую стратегию 14 или 15 раз, а третью 21
или 20 раз в каждых 35 партиях.
Пример (д).
Рассмотрим проблему инвестиций, при формулировке которой мы использовали
пример 16 из [11].
У вас есть долг, который необходимо уплатить по истечении года, и 1000 фунтов,
которые можно использовать сейчас. Вы советуетесь с вашим маклером о возможностях
вложения этой суммы в три вида акций, и он говорит, что доходы за год (дивиденды
и повышение стоимости капитала) зависят от оценки экономических перспектив на год
и, вероятно, будут такими, как элементы следующей платежной матрицы (в фунтах):
Акции
Ценные бумаги ....
Акции отраслей,
производящих
вооружение
Акции прочих отраслей
Перспективы
хорошие
40
0
150

удовлетворительные
30
100
50
плохие
20
250
-50
Как играть на бирже, чтобы получить наибольший доход?
Допустим, что вы руководствуетесь минимаксным принципом и по отношению к
состоянию экономики принимаете во внимание наихудшее, что может случиться. Вы решаете
«игру» против экономических сил, задаваемых платежной матрицей. Всего имеется восемь
соотношений между семью переменными. Переменные хъ х2, х3 определяют пропорции
вложений; переменные уи у2, Уз характеризуют состояние экономики и v — ваш
доход. Находить решение можно в соответствии с изложенными выше практическими
приемами (см. упражнение 5 к этому разделу). Но нужно заметить, что над первой
строкой матрицы доминируют различные комбинации двух других строк и она может
быть удалена из платежной матрицы. Остается матрица
Г0 100 2501
L.150 50 -50 J '
Теперь применим графический метод решения, данный в разделе 14.6 (см. упражнение 6
и указание к нему). Тем или другим методом вы найдете, что комбинация @, 1/2, 1/2)
является вашей оптимальной стратегией, и что цена игры равна 75 фунтов. Поэтому вы
решаете вложить ваши 1000 фунтов равными суммами в акции отраслей, производящих
вооружение, и в акции прочих отраслей, и совсем не вкладывать деньги в ценные бумаги.
Если год окажется хорошим или удовлетворительным, вы продадите акции и получите
прибыль в 75 фунтов. Если год будет плохой, то есть «стратегия» экономического
состояния не будет находиться в соответствии с минимаксным принципом, вы заработаете
больше, а именно 100 фунтов. Существуют даже большие возможные выигрыши; так, если год
будет «хорошим», акции прочих отраслей принесут доход в 150 фунтов, если год
«плохой», то 250 фунтов дадут акции вооружения. Однако.для получения таких доходов,
вам необходимо знать или предугадать, каким же будет год. Не имея такой информации,
вы вкладываете деньги в акции вооружений и акции прочих отраслей в пропорции 50 : 50
и обеспечиваете верных 75 фунтов дохода.
1 Этот вывод автора правилен, если В применяет первую или четвертую
стратегию с относительной частотой г/, величина которой лежит в пределах строгого
2 3
неравенства -=-<г/<— . Если же В следует первой или четвертой стратегии с отно-
2 3
сительной частотой, соответственно, -=• или -=- (граничные значения для оптималь-
о /
ной стратегии), то В ничего не проигрывает, и цена игры по-прежнему равна 0.—
Прим. ред.
438

Задачи и упражнения
1. Показать, что для игры,
Г1 2
имеющей платежной матрицей латинский квадрат
четвертого порядка А =
цена игры г; = —
41
1
2
3J
2. Обобщить результат предыдущего упражнения и показать, что
- является
ценой игры, для которой платежной матрицей служит латинский квадрат порядка п X п.
3. В игре «двухпальцевая Морра» игрок А знает, что его противник применяет
только вторую и третью стратегии, и тогда сам ограничивается также этими двумя
стратегиями. Показать, что полученная игра с платежной матрицей ~ о не пР0ТИВ0Речит
тому положению, что стратегии (о, х, 1 — а?, 0) (при 2/5 <! х <; 3/7) являются
оптимальными для игроков.
4. Игра «трехпальцевая Морра» имеет платежную матрицу 9X9. Показать, что
оптимальной стратегией для каждого игрока является @, 0, 5/12, 0, 4/12, 0, 3/i2,0, 0).
Объяснить это решение и сравнить с решением для игры «двухпальцевая Морра».
5. Решить пример (д) настоящего раздела, в котором имеется восемь
соотношений между семью переменными.
6. Взять матрицу А или 2 X 3 из вышеприведенного примера (д), решить игру
графическим методом раздела 14.6 и получить единственное решение х : A — х) = 1 : 1.
7. Если
10—1—3 1 31
1 о 3—3—1
-1 -2 3, 1 -1 '
0 3—31 — 1J
показать, что
при устойчивом исходе игрок А должен играть свои четыре стратегии с равными
относительными частотами и что игра справедлива. Затем показать, что у игрока В
оптимальная стратегия не единственная.
8. Рассматривается игра, в которой для определения исхода каждой партии
используется элемент случая. Сначала подбрасывается не имеющая изъяна монета, и
определяется, выпал герб или решка. Зная результат подбрасывания монеты, игрок А
называет число р, равное 1 или 2, а игрок В — число q, также равное 1 или 2. Если p=q,
то платеж не производится; если рфд, то сумму (р -ф- д) получает А, если выпал герб,
и В, если выпала решка. Показать, что каждый игрок имеет четыре стратегии и
платежная матрица игры имеет вид:
0 А
2
2
—к- 0
—
" 2
<• -!
3^
2
о 4
о — ~ ~-
Пользуясь сходством А с платежной матрицей игры «двухпальцевая Морра»,
найдите решение рассматриваемой игры.
9. Рассмотрите платежную функцию А(х, у)=к( х—— j (-^—у ) , где переменные
хжу непрерывны и где А выбирает х и В выбирает у из отрезка @, 1). Покажите
возможности существования игры с бесконечным множеством стратегий. На основе
минимаксного принципа покажите, что а?=?4, г/=% является оптимальным выбором для
игроков. Объясните далее, каким образом игра с двумй стратегиями у каждого игрока,
имеющая платежную матрицу . , может рассматриваться как частный случай такой
игры.

ГЛАВА 15
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
15.1. ПРОСТОЙ ПРИМЕР ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим задачу о питании с экономической точки зрения, как это
сделал Штиглер [15]. Потребитель покупает ряд продуктов питания: хлеб,
мясо, молоко и т. п. Как это обычно предусматривается теорией поведения
потребителей, в определении производимых им закупок играют роль,
например, рыночные цены, уровень его дохода, а также «предпочтение»,
оказываемое им различным продуктам. Чем же вызывается такое предпочтение?
Частично его вкусами и привычками в потреблении (а также привычками его
соседей). Однако частично оно может также являться отражением его
потребности в питательных веществах (по калорийности, содержанию белков,
витаминов и т. п.).
В настоящей задаче мы рассматриваем этот вопрос только с точки
зрения питательной ценности продуктов; нас не интересует, например, то
обстоятельство, что потребитель покупает масло, а не маргарин, потому что
ему больше нравится вкус масла или потому, что Джонсы тоже покупают
масло. Рассматриваемая проблема есть задача на преобразование: продукты,
купленные по рыночным ценам, преобразуются или превращаются в
источник питательных веществ. К этой задаче возможен двоякий подход: с одной
стороны, пищевой рацион потребителя должен иметь определенную
калорийность и содержать определенное количество граммов белка и т. п., с другой
стороны, при покупке продуктов по заданным рыночным ценам покупатель
стремится минимизировать общую стоимость рациона при заданной
питательной ценности последнего. Известные «технологические данные» задачи суть
показатели питательной ценности единицы каждого вида продуктов; это
не что иное, как функция преобразования, которую мы здесь принимаем
в форме системы постоянных коэффициентов. Зная эти коэффициенты, можно
получить нормальный рацион всевозможными способами, покупая продукты
в различных количествах. Допустимым решением является любой такой
набор покупаемых продуктов. Задача считается решенной и оптимальное
допустимое решение — полученным, если стоимость найденного набора
покупаемых продуктов оказывается минимальной.
Рассмотрим простой пример для двух продуктов: Хг (хлеб) и Х2 (сыр),
которые характеризуются двумя показателями питательной ценности —
калорийностью (в калориях) и содержанием белка (в граммах). ИзвестнвР
следующие данные: 1 фунт хлеба дает 1000 калорий и содержит 25 г белка,
1 фунт сыра — 2000 калорий и 100 г белка. Минимально необходимая суточ-
Цена (пенсов за
Калорий (тыс.)
Белков (единиц;
ница = 25 г)
фунт)
1 еди-
.Единица
Xi(хлеб)
6
1
1
440
продукта
Х2 (сыр)
21
2
4
Суточная
потребность
3
4

ная норма равна 3000 калорий и 100 г белка. По рыночным ценам 1 фунт
хлеба стоит 6 пенсов, 1 фунт сыра — 1 шиллинг 9 пенсов (или 21 пенс). Эти
данные можно упорядоченно записать в виде таблицы (стр. 440),
предварительно введя более удобные единицы измерения (тысячу калорий; единицу,
равную 25 г белка; 1 фунт хлеба или сыра). Тогда задача формулируется
следующим образом. Найти значения суточных покупок хх и х2 (в фунтах),
минимизирующие выражение
при условии
я1 + 2#2>3, /^ч
хх>0, х2>0. 4
Минимизируемая суточная стоимость питания z есть линейная функция
переменных хх и хх. Ограничивающие соотношения суть неравенства,
выражающие требование, чтобы питательная ценность продуктов была по
меньшей мере равна норме. При этом переменные могут принимать только
неотрицательные значения.
Это — задача линейного программирования. Линейность проявляется
здесь дважды: требуется минимизировать линейную функцию
неотрицательных переменных при условии удовлетворения некоторых линейных
неравенств. Поскольку в задаче имеются неравенства, при ее решении
приходится отказаться от методов, применяемых в математическом анализе для
нахождения условных экстремумов. По сути дела, методы математического
анализа не помогают даже в том случае, если ограничивающие
соотношения A) представлены в виде равенств, как в следующей задаче: требуется
минимизировать выражение
z = 6хх -
при условии, что
= 4.
B)
Трудность заключается в том, что система уравнений B) содержит
слишком много ограничений; любые два из трех уравнений системы дают
«решение». Например, можно определить минимум z при условии выполнения
одного ограничения хх + 2х2 = 3. Подставим в уравнение z — 6хх + 21#2
значение хх = 3—2х2 из этой же системы уравнений:
и минимум выражения z (при неотрицательных хЛ получится при х2 = 0,
а значит хх = 3. Следовательно, минимальная стоимость питания составит
18 пенсов в сутки, если покупать 3 фунта хлеба, а сыра не покупать вовсе*
При таком «решении» достигается (в соответствии с использованным нами
одним ограничением) требуемая калорийность питания C000 калорий
в сутки), но не удовлетворяется суточная потребность в белках A00 г), что
легко проверить — рацион питания содержит лишь 75 а белков. С другой
стороны, два ограничивающих условия сами по себе также дают
«решение». Из системы уравнений хх + 2х2 = 3 ж хх + 4#2 = 4 мы получаем
хх = 2 и х2 = г/2. При этом решении удовлетворяются оба требования
(в отношении калорийности и содержания белка), но совершенно не
принимается во внимание стоимость рациона.
Приведенную нами простую задачу линейного программирования A)
можно решить графически (рис. 50). В плоскости Оххх2 прямая А А'
соответствует уравнению хх + 2х2 = 3, а прямая ВВ' — уравнению хх + 4#2 = 4.
Наличие неравенств в задаче A) свидетельствует о том, что допустимые
решения образуют множество точек (х19 х2) на заштрихованной области
441

рис. 50. Остается выбрать ту из точек заштрихованной области, которая
соответствует минимальной стоимости рациона питания. Нанесем на рис. 50
(пунктиром) прямые, соответствующие постоянной стоимости рациона:
= COIlSt.
2 =
Это — параллельные прямые, и тангенс угла их наклона относительно
оси абсцисс равен (—2/7). Стоимость питания, характеризуемая такой прямой,
тем меньше, чем ближе прямая к точке О. Следовательно, стоимость
питания является минимальной в Р, точке пересечения прямых АА' и ВВ'.
Оптимальным допустимым решением будет:
хх = 2, #2 = 4' z = 22 Т (МИШШУМ) •
Если мы ежедневно покупаем 2 фунта хлеба и г/2 фунта сыра,
удовлетворяется потребность организма в питательных веществах, причем
стоимость питания будет
минимальной, а именно 22V2 пенса в сутки.
В решении этой задачи
потребность в калориях и в белке
удовлетворяется полностью, причем в
состав рациона входят оба
продукта. Это совпадение объясняется
тем, что угол наклона прямых,
характеризующих постоянную
стоимость, является промежуточным:
он больше угла А'Ахг, но меньше
угла В'Вхг. Однако при изменении
цен продуктов или их питательной
ценности могло бы случиться, что
угол наклона прямых,
характеризующих постоянную стоимость,
не окажется более между накло- .
нами прямых А'А и В 'В. Различ-
ные варианты таких изменений
рассматриваются в упражнениях
1-3.
Очевидно, что на рис. 50 решением может оказаться и точка В (если
цена сыра относительно высока) или точка А' (если относительно дорог хлеб);
в каждом из этих случаев" одно из требований может и перевыполняться.
По-видимому, существуют также задачи, имеющие бесконечное множество
оптимальных решений. Цены и питательная ценность продуктов могут быть
такими, что прямые постоянной стоимости параллельны прямой А А' (или
ВВ')\ тогда решением явится любая точка, лежащая на отрезке А'Р (или
соответственно РВ). Следовательно, можно сделать следующие общие выводы:
1) областью допустимых решений является заштрихованная площадь
на рис. 50;
2) оптимальные допустимые решения, являющиеся искомыми
решениями задачи, соответствуют точке (или бесконечному множеству точек),
расположенной (или расположенным) где-нибудь на границе (на рис. 50
соответствуют ломаной АГРВ) области допустимых решений.
Такого рода решения следует искать во всех задачах линейного про-
гр аммир ов ания.
Задачи и упражнения
1. Рассмотрим задачу A) в тексте, приняв, однако, что цена 1 фунта сыра
составляет: а) 24 пенса, б) 30 пенсов. Показать, что:
в варианте (а) имеется бесконечное множество оптимальных наборов покупаемых
продуктов, в которых количество сыра изменяется от нуля до Уг фунта; в варианте (б)
стоимость питания минимальна, причем сыр вовсе не входит в рацион, а хлеба покупают еже-
442

дневно 4 фунта; при этом требования в отношении питательной ценности продуктов
перевыполняются при минимальной стоимости.
2. Аналогичным образом рассмотреть задачу A) в тексте и ее решение, если цена
1 фунта сыра снижена до: а) 12 пенсов; б) 9 пенсов. Показать, что решения этих
вариантов задачи совпадают с решениями для случая, когда цена сыра останется на уровне
21 пенса, но хлеб подорожает до: а) 10% пенсов за фунт; б) 12 пенсов за фунт.
3. Сформулировать задачу A) в тексте, если цены хлеба и сыра соответственно
равны pi я р2 (цены считаются заданными, но численные значения их не установлены).
Показать, что в оптимальном решении покупается только хлеб, если р± < 1/4ср2, и только
сыр, если/?1 > хАр2. Показать также, что оба продукта входят в набор, если lUp2 < Pi <
< УгРъ, и что имеется множество решений, если pi — 1/&P2 или pi=V2p2.
4. Показать, что аналогичные варианты решений появляются и в том случае, если
изменяются не цены на продукты, а содержание в них калорий и белков.
5. Рассмотреть задачу питания, приведенную в тексте главы, в которой продукты
остаются теми же (хлеб и сыр), однако учитывается и потребность в третьем питательном
веществе — в углеводах. Суточная потребность в углеводах составляет 400 г. 1 фунт
хлеба содержит 250 г, а 1 фунт сыра — 50 г углеводов. Сформулировать новую задачу
линейного программирования, где требуется минимизировать стоимость пищевого
рациона; решить ее графически. Сравнить полученное решение с решением для случая двух
показателей питательной ценности (содержание калорий и белка). Показать, что область
допустимых решений на графике в зависимости«от величины «технологических
коэффициентов» может быть обозначена отрезками одной прямой, двух прямых или же всех
трех прямых. Если одна из прямых не ограничивает область решений) то показать, что
требования по соответствующему показателю питательной ценности автоматически
удовлетворяются в любом допустимом варианте набора покупаемых продуктов.
6. Вернемся к задаче питания, приведенной в тексте раздела. Пусть число
показателей питательной ценности по-прежнему равно двум, но для составления
нормального рациона такой же питательности добавляется третий продукт, скажем мясной фарш
или же макароны. Калорийность 1 фунта этого продукта равна 2000 калорий,
содержание белка — 75 г, цена — 18 пенсов. Сформулировать задачу линейного
программирования, если минимизируется стоимость питания. Какой вид принимает в этом случае
диаграмма и графическое решение?
7. Ниже излагается упрощенный вариант транспортной задачи, рассматриваемой
в сборнике [9]. Суда совершают рейсы между портами Р и Q, и переменными являются
количества рейсов (путь в оба конца) в месяц, проделанных при различных условиях:
хх — число рейсов, в которых груз перевозится в обоих направлениях;
о?2 — число рейсов, в которых груз перевозится только из Р в Q, а обратный рейс —
без груза;
х3 — число рейсов, в которых суда совершают переход из Р в Q порожняком, а
возвращаются с грузом;
#4 — число рейсов без груза в оба конца.
Продолжительность в месяцах каждого из вариантов рейса соответственно
составляет *i, ?2, *з и ?4- Ежемесячно необходимо перевезти из Р в Q количество груза,
равное &i, а из Q в Р— равное Ь2, Единицей измерения количества перевозимого груза служит
грузоподъемность одного судна. Требуется (при неотрицательных х) минимизировать
число судов z, занятых на перевозках между портами Р и Q, то есть минимизировать
при условии
i = min
h-
Что означает знак «^» в ограничивающих условиях; можно ли без потери
общности заменить его знаком равенства? С какой целью введена переменная #4?
Можно ли приравнять ее нулю?
8. В другой простой транспортной задаче требуется минимизировать стоимость
перевозки некоторого однородного продукта из портов Рх и Р2 в порты Qx и Q2-
Всего груза в порту Рх имеется аъ а в порту Р2—груза я2; необходимо Ьг продукта
перевезти в порт Qj, a Ь2—в Q2. Переменные х суть количества грузов, перевозимые
между портами по каждому маршруту:
Перевозки
Из порта Рг . .
» » Р2 . 1
Всего . .
В порт
Qi
хп
*21
h
Q2
*12
*22
ь2
Всего перевозится
а2
ai+a2 = &i + &2
443

Стоимость перевозки единицы продукта по каждому из маршрутов равна
(г, 5=1, 2). Показать, что отыскиваются такие неотрицательные значения х, что-
при условии
2 *>¦•=*• (s=1' 2>-
г
Показать, что одно из четырех ограничивающих уравнений можно отбросить, по*-
скольку оно является линейной комбинацией трех остальных.
15.2. ПРОСТОЙ ПРИМЕР: ДВОЙСТВЕННАЯ ЗАДАЧА
Задача питания, рассмотренная в предыдущем разделе, представляет
собой пример на нахождение мицимума. В простейшем варианте она имеет
следующий вид:
Требуется минимизировать zx = 6хх + 21#2
при условии
хх>09 х2>0.
A)
С формально алгебраической точки зрения всякая задача подобного
рода на нахождение минимума двойственна — ей соответствует задача на
нахождение максимума. Составить двойственную задачу очень важно, хотя
она, несомненно, вовсе не является очевидной1. Для задачи A) двойственная
ей задача получается следующим образом. Пусть из хлеба и сыра
необходимо составить суточный рацион питания, калорийность которого 3000
калорий, а содержание белка 100 г. Примем те же, что и раньше, единицы
измерения A000 калорий и 25 г белка); пусть ^и ^2 — наша оценка (в пенсах
за единицу) полезности каждого из этих показателей. Тогда общая
(условная) оценка рациона питания равна ? — 3?х + 4?2; мы будем стремиться
максимизировать ?. Однако стоимость 1 фунта каждого продукта не может
превышать рыночной его цены (для хлеба — 6 пенсов, для сыра — 21 пенс).
Если 1 фунт хлеба содержит 25 г белка и 1000 калорий, то оценка его
питательного содержания, то есть \х + ?2, не может превышать 6 пенсов.
Аналогично этому для сыра оценка питательных веществ, равная 2\х + 4g2,
не может превышать 21 пенса. Следовательно, двойственную задачу можно
сформулировать таким образом:
Найти такие оценки единицы питательных веществ ?х и
?2>
при условии
B)
12>0. ,
Задача питания имеет двойственные формы A) и B). Связь между этими
задачами проста и легко распространяется на задачи линейного программи-
1 Поиски минимума и максимума в исследовании одной и той же проблемы с одними
и теми же лежащими в основе данными по существу составляют пару двойственных
задач. Однако автор в большинстве случаев наименование двойственной задачи придает
только второй по порядку рассуждения задаче (в данном случае задаче максимизации).
Первую задачу мы далее называем прямой задачей.— Прим. ред.
444

рования всех других типов. В задаче A) минимизируется z, и
ограничивающие соотношения переменных входят в форме «больше или равны» (>);
в задаче B) максимизируется ?, и ограничивающие соотношения
переменных представлены в форме «меньше или равны» (<С) некоторой величине,
В условиях обеих задач имеется матрица технологических коэффициентов
(показателей питательной ценности продуктов) [1/|? однако в
ограничениях задачи B) коэффициенты транспонированы по сравнению с
задачей A). В задаче A) цены F и 21) являются коэффициентами
минимизируемой функции, а показатели потребности C и 4) — ограничивающими
соотношениями; в задаче B) положение обратное.
Нам остается лишь показать, что обе двойственные задачи имеют одно
и то же решение — в том смысле, что минимум функции z в задаче A) равен
максимуму функции ? в задаче B). Решение задачи A) следующее:
1 1
#1 = 2; #2==т; 2 = 22-^ (минимальная стоимость рациона питания).
Графически или тем же методом, что в упражнении 1, находится
следующее решение задачи B):
3 9 1
\х = —- ; 12 = —; ? = 22 у (максимальная оценка заданного питательного
рациона).
Один и тот же расход, а именно 22х/2 пенса в сутки, мы получаем как при
оптимальном ассортименте покупаемых продуктов B фунта хлеба и 1/2
фунта сыра), так и при оптимальной оценке полезности единицы питательных
веществ A1/2 пенса за 1000 калорий и 4V2 пенса за 25 г белка).
Все вышесказанное вытекает из чисто алгебраических соображений.
Однако прямая и двойственная ей задача линейного программирования
должны иметь и экономическое истолкование; в самом деле, существование
экономической двойственности легко обнаружить и в общем случае. Так,
в задачах на распределение ограниченных ресурсов в производстве
функцию издержек производства можно получись (при заданных ценах
ресурсов), либо минимизируя издержки для заданной программы, либо
максимизируя выпуск при заданной общей сумме издержек. Двойственными
аспектами одной и той же задачи являются распределение ресурсов и оценка их.
Если для ресурсов не существует рыночных цен, то необходимо их создать,
ввести систему условных или расчетных цен. Этому указанию придется
следовать в дальнейшем.
В задаче A) требуется найти минимальную стоимость входящих в рацион
продуктов питания при заданных рыночных ценах на эти продукты и при
соблюдении ограничений в отношении потребности в питательных
веществах. Оценки питательного содержания не устанавливаются, хотя именно
они (а не продукты) лежат в основе задачи. Введем теперь условные оценки
показателей питательной ценности: gx пенсов за 1000 калорий и ?2 пенсов
за 25 г белка. Тогда возникает двойственная задача B), где требуется
максимизировать условную оценку рациона заданной питательной ценности при
соблюдении ограничений, согласно которым расходы в расчете за единицу
продукта не могут превышать его заданной рыночной цены. Цель первой,
прямой задачи заключается в том, чтобы закупаемые продукты были
возможно более дешевыми, удовлетворяя вместе с тем ^требованиям в
отношении питательной ценности, а цель сопряженной двойственной задачи — в том,
чтобы при заданных рыночных ценах на продукты получить рацион
наиболее высокопитательный.
Задачи и упражнения
1. Решить двойственную задачу B) графическилГметодом (см. рис. 50) и указать
основные различия между геометрическими методами решения прямой и
двойственной задач.
)л . 2. Исследовать характер изменений графического "решения задачи B), если мы
будем менять цены так как это делалось в упражнениях 1—3 предыдущего раздела.
445

3. Составить и истолковать двойственную задачу, приведенную в упражнении 6
раздела 15.1. Решить ее графически (на плоскости) и показать, что добавление третьего*
продукта не вносит ничего нового по сравнению с решением задачи 1 данного раздела.
4. Объяснить, почему нельзя решить графически на плоскости двойственную
задачу 5 раздела 15.1. Показать, что эта двойственная задача аналогична прямой задаче 6
раздела 15.1.
5. Показать, что двойственную транспортную задачу 7 раздела 15.1 можно
сформулировать следующим образом:
Найти неотрицательные |х и |2» максимизирующие функцию
при условии
Дать экономическое истолкование этой двойственной задаче.
15.3. ПРИВЕДЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
К РЕШЕНИЮ ИГРЫ
В задаче о питании в случае двух продуктов и двух показателей
питательной ценности (количество калорий и содержание белка) данные можно»
записать в общем виде с помощью буквенных обозначений. Тогда прямая
и двойственная задачи будут основываться на следующих данных:
Цена (в пенсах за
единицу) ....
Калорий (единиц)
Белков (единиц) . .
Единица продукта
Pi
ап
Ч\
х2
Р2
«12
Я22

Потребность
h
Эти задачи можно сформулировать так:
Прямая задача Двойственная задача
Минимизировать Максимизировать
z =
при условии
а1 А
при условии
х2>0.
?2>о. J
Допустимые решения для х и | удовлетворяют; неравенствам
системы A); оптимальное допустимое решение удовлетворяет также условиям
максимума или минимума.
Рассмотрим игру с двумя участниками и нулевой суммой, платежная;
матрица которой —квадратная пятого порядка:
0
0
-«11
-«21
А
0
0
-«12
— «22
А
«и
«12
0
0
— Ь1
«21
«22
0
0
— Ь2
-Pi
-А
ь,
0 -
446

Поскольку эта матрица кососимметрическая, то из раздела 14.7
следует, что игра справедлива (цена игры равна нулю) и что оптимальной
для обоих игроков является одна и та же смешанная стратегия г/ =
= (У1» 2/г» Уз» У& У&)> Тогда в соответствии со свойством II раздела 14.7:
11 «12^3 + «22^4 — РгУь < °»
IV - а2хУх - а22у2 + Ь2уь < О,
V Р\УХ + РъУ* — ЪхУъ "" &2#4 < 0. ^
Нули в правой части неравенств объясняются тем, что [игра
справедлива (цена игры равна нулю).
Пусть уъф0. Но в соответствии со свойством (III) раздела' 14.7 знак
неравенства (<) в условии (V) системы неравенств (З)^означал бы, что для
обоих игроков у5 = 0. Следовательно, условие V [выражается равенством:
(V) РхУх + р2у2 — Ъхуъ — Ъ2уь = 0.
Введем новые переменные:
1 Уъ ' 2 2/5 ' б1 1/5 f &2 уъ
Тогда система неравенств C) превращается в следующую систему:
III '
IV
V рххг + p2x2 = 6^ + Ь212.
Здесь неравенства I —IV суть ограничения прямой и двойственной задач»
линейного программирования A). Поскольку вероятности у смешанной
стратегии по самому своему существу неотрицательны, то неотрицательны
и переменные х и ?; этого требует также и система A). Чтобы завершить
выявление связи между задачей линейного программирования A) и игрой B),
нам необходимо лишь истолковать условие (V).
Введем переменные z = рххх + р2х2 и ? = Ь?г + Ь2|2 для любых
стратегий, примененных двумя игроками, не обязательно оптимальных. Тогда
условие (V) является утверждением, что если игроки применяют
оптимальные стратегии, то z = ?. Естественно предположить, что, если
стратегии не являются оптимальными, z превышает ?, то есть что z превышает
(или по меньшей мере равен) свое оптимальное значение (то есть минимум),
и что ? становится меньше (или по крайней мере равен) своего
оптимального значения (то есть максимума). И действительно дело обстоит именно
так, хотя это нелегко доказать математически (см. 15.4 и 15.5). Если же
мы будем считать это предложение доказанным, то условие (V) можно
истолковывать следующим образом. При оптимальной стратегии игры
значение выражения z = рххх + р2х2 становится минимальным, а значение ? =
^ &i?i + ^2^2 достигает максимальной величины, причем эти значения равны
между собой.
Следовательно, решение игры B) является решением как прямой, так
и двойственной ей задачи линейного программирования A). Можно сделать
следующий вывод:
Игра, характеризуемая платежной матрицей B), имеет
оптимальное решение:
(Уи У2У Уз, Уы Уъ)'
Если уь Ф 0, то хх = ух1уь и х2 = yjyb есть решение прямой задачи
линейного программирования A), а \x = yjyb и ?2 = уJyb — решение
двойственной ей задачи,
447

В прямой и двойственной задачах A) минимум z равен максимуму ?•
Этим мы достигаем двоякого результата. Во-первых, мы показываем, что
прямая и двойственная задачи имеют одно и то же решение. Во-вторых,
решение каждой из этих задач, можно получить на основе решения игры,
характеризуемой некоторой заданной платежной матрицей.
Для этого уъ должно быть отличным от (нуля. Если г/5 = 0' игра по-
прежнему имеет решение, однако прямая и двойственная задачи линейного
программирования решения не имеют. Это различие заставляет нас лишь
сделать следующее добавление к полученному выводу: либо прямая и
двойственная задачи A) имеют одно и то же решение, либо обе они не имеют
решения.
Пример
В задаче питания (см. 15.1 и 15.2) прямая и двойственная ей задача линейного
программирования описываются следующими численными системами (при
неотрицательных значениях х и |).
Минимизировать Максимизировать
6+21 С ЗБ + 4Б |
|
при условии ^+2x2^3, ii+?2<6, [ D)
2|1+4?2<21.J
р
6, [
<21.J
Платежная матрица соответствующей игры имеет вид:
"О 0 1 1 — 6 "
0 0 2 4 —21
— 1—2 0 0 3
— 1—4004
6 21 —3 —4 О
E)
Решение задач D) можно получить на основе матрицы E), и наоборот.
Необходимо лишь связать вероятности оптимальной стратегии уъ у2, Уз, Уы Уъ матрицы E)
с переменными х и \ системы D):
На этом простом примере можно продемонстрировать оба метода1 решения.
Первый метод решения. Решив систему D) с помощью графических] методоо,
описанных в разделах 15.1 и 15.2, получаем решение:
#х=2; S2=2~; 2i=="» ^2=="'
= 22-~- •
А
Значит, в решении системы E) должно соблюдаться соотношение:
13 9
Ух : 2/2 : Уъ ' У* ' 2/5=2 : у : у : у : 1#
Чтобы получить абсолютные значения у, необходимо лишь принять во внимание,
что г/i+2/2+2/з+2/4+2/5 = 1; это — важнейшее свойство всякой стратегии. Нетрудно
установить, что мы получаем абсолютные величины у, умножая на 2/19 элементы
приведенного выше соотношения. Следовательно, решением игры E) явится
смешанная стратегия D/i9, V19, 3/i9» 9/i9> V19); цена игры равна нулю, игра справедлива.
Второй метод решения. Найти решение игры E) можно с помощью метода,
описанного в разделе 14.8. Если (уъ у2, у3, г/4, уъ) является оптимальной стратегией
для каждого из игроков, причем цена игры равна нулю, то:
2/i+ 2/2+ 2/з+ 2/4+ 2/5 = 1,
2/з+ 2/4— 6i/5<0,
22/3+42/4—2l2/5< 0,
— 2/1— 2jfc + Зг/5<0,
— 2/1— 4г/2 + 4
1г/2 — 31/з-4г,4
448

Проверим, можно ли заменить все неравенства равенствами при положительных
значениях г/. В данном случае это возможно. Решаем совместно второе и третье
уравнения:
3 9,
Уз '-У*- 2/5=у :Y
Решаем совместно четвертое и пятое уравнения:
2/1:2/2 :2/5 = 2: у : 1,
Затем определяем абсолютные значения у, используя полученные соотношения
совместно с первым уравнением системы; эти значения равны D/i9, 1/i9, 3/i9> 9/ю> 2/ig)-
Если это и есть решение игры E), то полученные значения у должны удовлетворять
последнему уравнению системы. Легко проверить, что это действительно так.
Следовательно, мы получили решение игры E). На его основе получаем решения системы A):
13 9
хг = 2; х2=у; gx = y; l2=~2 •
Первые две величины минимизируют z (z = 221/2 пенсов), вторые максимизируют
С (? = 22Va пенсов).
Задачи и упражнения
1. Записать упражнение 5 раздела 15.1 с помощью буквенных обозначений:
Минимизировать z=
при условии
Затем сформулировать двойственную задачу с теми же постоянными
коэффициентами. В примере, приведенном в тексте данного раздела, матрица коэффициентов [arsl
квадратная, а в данной задаче прямоугольная. Какое влияние это оказывает на
симметричность прямой и двойственной задач?
2. Построить платежную матрицу игры, соответствующую предыдущей задаче
линейного программирования. Показать, что это — квадратная матрица, порядок
которой равен 6. Почему матрица игры продолжает оставаться квадратной, хотя матрица
коэффициентов [ars\ является прямоугольной?
3. Найти решение игры, приведенной в предыдущем упражнении, но с численными
коэффициентами, взятыми из упражнения 5 раздела 15.1 Таким путем проверить
правильность общего решения этого упражнения. Решить также двойственную задачу и
сравнить полученный результат с решением упражнения 4 раздела 15.2, где
графическое решение оказалось невозможным.
4. Сформулировать в буквенных коэффициентах прямую и двойственную задачи
упражнения 6 раздела 15.1; построить платежную матрицу соответствующей игры.
Показать, что эта матрица аналогична матрице упражнения 2 настоящего раздела.
15.4. ОБЩАЯ ПРЯМАЯ И ДВОЙСТВЕННАЯ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Задачу питания для случая двух продуктов и двух показателей их
питательной ценности, рассмотренную в разделе 15.3, можно обобщить на
случай т показателей питательной ценности и п продуктов. В этом случае
мы получаем общую форму линейного программирования, отвечающую
различным экономическим и другим задачам. Простые примеры таких
задач см. в работах Дорфмана, Солоу и Самуэльсона [7] и Кемени, Снелла
и Томпсона [8].
Общая прямая и двойственная задачи линейного программирования
описываются следующими соотношениями:
I Минимизировать z = рххг + р2х2 + .. . + рпхп
при условии
аг1хг + а12х2 + ... + а1пхп > b19
а2Ххх -г а22х2 +...¦+- а2пхп > Ъ2,
29 р. Аллен 449

amlxl + am2X2, + • • •
хг>0, x2>0, . .., xn>0.
II Максимизировать
5 *
при условии
«11^1 + ^2l52 + • • • + атЛт<
? + ^ + + ^ Pa*
lni
El>0,
Задача питания —лишь один пример применения таких систем; тогда
коэффициенты а суть «технологические показатели» т питательных свойств
для п продуктов, Ъ — потребности в каждом из т питательных свойств7
р — цены каждого из п продуктов, х — переменные количества покупаемых
продуктов и z — минимизируемая стоимость. В других] задачах
истолкование постоянных и переменных величин будет иным.
Более сжатая запись задач линейного программирования достигается
при использовании матричных обозначений:
Минимизировать Максимизировать
при условии при условии
Ах>Ь,
х>0.
При такой формулировке заданными являются следующие элементы
условий:
А = [aTS] матрица технологических
коэффициентов т х п
Ь = {6Г} вектор m-го порядка;
p = {ps} вектор яг-го порядка.
г= 1,2, ..., т
5=1, 2, . . . , П
Транспонированные элементы соответственно обозначаются А', Ь' и р'*
Решением прямой задачи является вектор х гс-го порядка, а
двойственной — вектор | /гг-го порядка. Для всех допустимых решений
выполняются ограничения (неравенства); в оптимальных допустимых решениях
удовлетворяются также условия максимума (или минимума). В частном
случае задачи питания решением является вектор х количеств покупаемых
продуктов, минимизирующий стоимость рациона питания, или вектор %
условных оценок единицы питательных свойств, максимизирующий общую
условную оценку рациона.
Результаты, полученные выше при анализе простого примера в раздела
15.3, дают основание ожидать, что прямая и двойственная ей задача имеют
одно и то же решение, то есть что минимум z совпадает с максимумом ?. Это
действительно так, если только исключена возможность отсутствия решения.
Следовательно, основная теорема двойственности формулируется
следующим образом:
Прямая и двойственная задачи линейного программирования либо
имеют общее решение, либо вовсе не имеют решения.
Математическое доказательство этой теоремы вовсе не легко; частный
очень простой пример из раздела 15.3 является не более, чем ее
иллюстрацией. Одно из доказательств теоремы, которое принадлежит Гейлу, Куну
и Таккеру, приведено в [9, гл. XIX]; это доказательство основано на
теории игр и разработано применительно даже к более широкому классу задач
450

линейного программирования, чем приведенные в настоящем разделе.
Другой способ доказательства, принадлежащий Чарнесу приведен в книге
Чарнеса, Купера и Гендерсона [2, лекция VIII]; это доказательство
базируется на работах Данцига и симплексном методе решения задач линейного
программирования (см. 15.8). Вероятно, простейшее из существующих
доказательств предложено Дано [4].
15.5. ЭКВИВАЛЕНТНОСТЬ ОБЩИХ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ И ИГРЫ С ДВУМЯ УЧАСТНИКАМИ
И НУЛЕВОЙ СУММОЙ
Теперь можно обобщить результаты, полученные в разделе 15.3, где
решение простой задачи линейного программирования было сведено к
решению некоторой задачи игры. Этот метод разработан Данцигом и приведен
в [9, гл. XX]; он кладет в основу сформулированную выше основную
теорему двойственности. Метод основан на следующем положении.
Всякая задача линейного программирования (минимизировать
выражение z = р'х при условии Ах>Ь и х>0) совместно с
двойственной ей задачей (максимизировать выражение ? = Ь'| при
условии А|<р и !>0) может быть сведена к некоторой игре с двумя
участниками и нулевой суммой; и обратно, всякая игра с двумя
участниками и нулевой суммой может быть представлена в форме
некоторой задачи линейного программирования.
Во-первых, докажем прямую посылку. Предположим, что решение
задачи линейного программирования существует, так что й минимум z и
максимум ? равны одной и той же величине М. При допустимых значениях х
и g удовлетворяются обе системы неравенств:
Ах>Ь и А'1<р.
Запишем эти неравенства в развернутом виде:
апх± + а12х2
а21хх
... + alnxn
... + агихп
ат1хг
nlm < рп.
A)
При оптимальных допустимых значениях переменных z = ? = М,
Следовательно, z— ? = 0:
РА + Р2Х2 + - - • + Рпхп — (&i5i + b?2 + ... + Ьт1ы) = 0. B)
Введем в систему A) «фиктивную» переменную и (и — 1) и преобразуем
неравенства так, чтобы в правой части каждого из них появились нули,
и все неравенства имели в правой части «<0». Тогда A) и B) в
совокупности образуют систему:
I • • • а2пХп
¦Ь^и^О, v
=0.
451
29*

В соответствии со свойством II раздела 14.7, система C) означает,
что элементы решения
(х„ я2, .. ., zn, lv ?2, ..., ?m, u), D)
пропорциональны вероятностям оптимальной стратегии игры, платежная
матрица которой кососимметрическая:
п строк E=1, 2, . .., п)
0
— ars
Ps
asr
0
-W
-Ps
br
0
m строк (r = 1, 2, .. ., m)
1 строка
j
п т 1
столб- столб- стол-
цов цов бец
E = 1, 2, . .., п) (г = 1,2, .. ., т).
Эту блочную матрицу можно записать более сжато:
О А' - р"
-А О Ь
р' -Ь' О
E)
Цена игры равна нулю, о чем свидетельствуют кососимметричность
матрицы E) и нулевые значения правых частей неравенств системы C). Оба
игрока имеют одну и ту же оптимальную стратегию, однако элементы D)
только пропорциональны элементам стратегии, так как необходимо изменить
шкалу их так, чтобы сумма абсолютных величин была равна 1. Вместе с тем
система C) является однородной относительно всех переменных, так что
изменение шкалы абсолютных значений роли не играет. Последнее условие
системы C) есть равенство, поскольку мы предположили существование
решения задачи A) и поскольку ифО. Следовательно, если задача
линейного программирования имеет решение, то игра с платежной матрицей E)
имеет оптимальную стратегию с ненулевым последним элементом и, и задача
линейного программирования и задача игры соответствуют друг другу.
Можно снять сделанное нами здесь ограничение, допустив как отсутствие
решения задачи линейного программирования, так и возможность нулевого
значения последнего элемента оптимальной стратегии игры. Это завершает
доказательство. Обобщим полученные результаты: задача линейного
программирования связана с игрой, имеющей платежную матрицу E).
Оптимальная стратегия этой игры должна существовать и определяется
вектором D). Если и = О, задача линейного программирования решения не имеет.
Если и Ф О, можно пропорционально изменить абсолютные значения
элементов решения D) так, чтобы и = 1; тогда значения жи|и явятся решением
прямой и двойственной ей задачи линейного программирования.
Во-вторых, докажем обратную посылку теоремы. Пусть игра
характеризуется платежной матрицей С = [crs] порядка т X п. Если первый
(максимизирующий) игрок применяет смешанную стратегию (z±, z2,..., zn)>
т
то математическое ожидание его выигрыша есть М = min ^,crszr, и игрок
S Г=1
m
стремится максимизировать М. Поэтому
для каждого s.
В матричных обозначениях это записывается следующим образом:
Cz>M{l},
452

или
Сх>{1}, где х = -Цг.
Всегда можно преобразовать это выражение так, чтобы выполнялось
неравенство М > 0 (например, прибавляя к каждой сг$ постоянную
величину). Мы налагаем следующие ограничения: (I) z>0, а поэтому и х>0;
т т
(II) 2*г = 1» а поэтому 2жг == 1/^» или же Шх = 1/ЛГ. Когда один
г=1 г=1
из игроков достигает максимума М, он применяет оптимальную стратегию.
Тогда минимизируется [1]х = ИМ. Следовательно, оптимальная стратегия
игры определяется вектором х, при котором минимизируется
м
при условии
х>0.
Это — задача линейного программирования с технологической
матрицей С и двумя заданными (единичными) векторами. Оптимальная стратегия
второго (минимизирующего) игрока приводит ко второй задаче линейного
программирования — двойственной. Это завершает доказательство.
Значение полученного результата заключается в том, что метод решения
игровой задачи одновременно позволяет решить и задачу линейного
программирования, и наоборот, метод решения задачи линейного
программирования дает возможность решить также и игровую задачу. Далее, как
указали Дорфман, Самуэльсон и Солоу [7], любую задачу игры можно
представить в виде задачи линейного программирования, а последнюю, в свою
очередь,— в виде игры, матрица которой кососимметрическая. Таким
образом, любую игру можно преобразовать в игру с кососимметрической
матрицей, то есть в справедливую игру, с одинаковыми оптимальными
стратегиями обоих игроков. Это является значительным преимуществом.
Остается разработать более универсальный метод решения задач
линейного программирования и, следовательно, задач из области игр. Таким
методом является симплексный метод, который по сути дела представляет собой
итеративный метод практического выполнения вычислительных операций
на автоматических вычислительных машинах. Как указывается в [9],
возможны и другие методы, однако, по-видимому, из существующих в
настоящее время вычислительных методов симплексный метод пока является
наилучшим.
Задачи линейного программирования и задачи игры эквивалентны
с точки зрения формальной алгебры, что позволяет расширить возможности
решения подобных задач. Однако эти задачи не обязательно эквивалентны
с точки зрения их интерпретации. Два участника игры и не помышляют
о том, чтобы решать своей игрой задачи линейного программирования.
Если же ставится задача линейного программирования, как, например,
задача питания, это вовсе не значит, что на самом деле имеется игра с двумя
участниками. Правда, в этой задаче можно считать первым «игроком»
потребителя, минимизирующего стоимость питания, а его противником, вторым
«игроком», природу, столь скупо отпускающую необходимые питательные
вещества. Однако такое толкование настолько далеко выходит за рамки
понятия «игры», что является искусственным.
453

15.6. ПРЕОБРАЗОВАНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ДЛЯ ВЫЧИСЛИТЕЛЬНЫХ ОПЕРАЦИЙ
Объем вычислительных операций при практическом решении задачи
линейного программирования может оказаться очень большим. Поэтому
важно внимательно и упорядоченно расположить данные и подготовить их
для обработки на быстродействующих вычислительных машинах. Общая
задача линейного программирования рассмотрена в разделе 15.4: требуется
максимизировать или минимизировать некоторую линейную функцию
неотрицательных переменных при условии удовлетворения некоторой системы
линейных неравенств. Первый шаг состоит в том, чтобы представить задачу
в несколько иной форме: линейная функция неотрицательных переменных
должна максимизироваться при условии удовлетворения системы линейных
уравнений. Всякую задачу можно подвергнуть такому преобразованию:
вначале задачу на минимум (если такой ее характер предусмотрен)
превращаем в задачу на максимум, а затем вводим «добавочные переменные»,
обращая таким образом неравенства в уравнения. Сущность этого метода в
достаточной степени можно проиллюстрировать на простом примере (см. 15.3)
двух переменных и двух неравенств; общий случай рассматривается в
упражнениях 2 и 3.
Решим следующую задачу линейного программирования:
Минимизировать выражение
при условии
хх > О, #2 > 0.
Во-первых, введем обозначения сх= — рг и с2= — /?2, так что требуется
уже максимизировать
Далее, введем новые переменные: Хх = х19 Х2 — х2, Х3 — неотрицательную
переменную разность (ДцА^ + а12^2) — bt и Х4—аналогичную разность
КА + а22^г) — ьъ- Тогда
а11^1 + а12^2 — ^3 = &1»
а21К1 + а22Х2 — Я4 = Ь2.
Наконец, представим z = с^ + с2Х2 в более общем виде z = с^ + саД,а +
+ с3А,3 + с4^4' где с3 = с4 = 0. Тогда задача линейного программирования
представится в следующем виде:
Максимизировать
z = схХг + с2
при условии
Требуется максимизировать линейную функцию четырех
неотрицательных переменных (коэффициенты при двух из них равны нулю) при
условии удовлетворения системы двух линейных уравнений относительно
этих же переменных. Из четырех переменных две суть первоначальные,
а остальные две —добавочные, условные переменные, введенные для
удобства вычислений. Последние мы назовем вспомогательными или
дополняющими (slack) переменными. Матрица технологических коэффициентов, ранее
454

квадратная второго порядка, теперь превращается в матрицу типа 2x4:
г ап -1 О"!
,1 «22 © —1 J *
Рассмотренную нами общую задачу линейного программирования можно
записать следующим образом:
Максимизировать
при условии
A)
где А —соответственным образом расширенная матрица т х п
технологических коэффициентов, Ь — вектор m-го порядка потребностей и
имеющихся ресурсов, с —вектор гс-го порядка, характеризующий поставленную
цель или максимизируемую функцию, и Л, —искомый вектор неизвестных
/г-го порядка. Если учесть, каким способом мы увеличили число
переменных, то можно считать т < га, как это и принято далее. В основном
выводе, принадлежащем Гейлу и доказанном простым способом Дано [4],
утверждается, что в решении (оптимальном) задачи A),. если оно
существует, имеют положительные значения не более чем т (из общего их
числа п) переменных Я.
Удобнее (по крайней мере для вычислений) представить A) в
линейной форме относительно векторов ттг-го порядка с п коэффициентами.
Расширим матрицу А, добавив справа столбец Ь: тогда матрица А станет
т х (л+ 1). Обозначим через p<s> (s = 1, 2, ..., п) и р m-мерные столбцы
этой матрицы коэффициентов:
Л11
... а
1»
Чп
B)
Тогда задача линейного программирования может быть представлена
в следующем виде:
найти неотрицательные значения A,s>0 E = 1, 2, ... п),
максимизирующие выражение
при условии
^pd) 4- Я2рB> + ... + ^пр(п) = р. D)
В уравнениях C) и D) также можно применить знак 2» т0 есть
максимизировать
п
при условии
8=1
При такой постановке задачи мы пользуемся векторами m-го и w-ro
порядка, где т < п. Эти векторы изображаются точками в двух
пространствах—соответственно т- и w-мерном. Эти «геометрические» термины все
время применяются в дальнейшем, и мы можем воспользоваться теорией
выпуклых множеств. Следует проводить четкое различие между двумя
пространствами.
455

I. Пространство условий или требований ттг-мерное, то есть низшей
размерности (т < тг). Точки этого пространства рA\ рB\..., р<п) и р
определяются технологическими коэффициентами (матрица А) и потребностями Ь
в матрице B). Все это—известные данные задачи, входящие в уравнения D).
II. Пространство решений тг-мерное, то есть высшей размерности
(п > т). Кроме точки с = (cv с2,...у сп), соответствующей
максимизируемой линейной функции C), это пространство содержит точки X = (Xi, Яг,.-,
Лп), элементы которых — искомые переменные. Эти элементы являются
переменными в выражении C), а также коэффициентами при заданных векторах
в уравнении D).
Всякая точка Я, удовлетворяющая уравнению D), называется
допустимым решением задачи; она не обязательно максимизирует функцию C).
Такое допустимое решение, которое максимизирует функцию C),
называется оптимальным допустимым решением; именно такую точку мы и
стремимся найти. Общий метод решения заключается в том, чтобы сначала
сосредоточить внимание на множестве всех допустимых решений, а затем — на тех
допустимых решениях, которые оптимальны. Мы увидим далее, что
множество допустимых решений есть выпуклое множество и что оптимальное
решение следует искать среди экстремальных точек этого множества. Таким
образом, здесь непосредственно применима теория выпуклых множеств.
Удобно пользоваться следующими терминами. Связь переменных
решения Я с заданными векторами (или точками) р в уравнении D) можно
определить, сказав, что Xs есть вес вектора (или точки) p<s> (в m-мерном
пространстве) в решении Я. Поскольку Я8>0, решение может иметь некоторые p(s>
с положительными и некоторые с нулевыми весами, что соответствует
положительным и нулевым значениям переменных в решении. Оказывается, что
важно различать положительные и нулевые веса.
Число переменных и число ограничений. В канонической форме (I) задач
линейного программирования имеется п переменных и т ограничивающих
уравнений; таким образом, максимум линейной функции п переменных
должен быть найден при условии удовлетворения т линейных уравнений»
Общую задачу линейного программирования (см. 15.4) можно
сформулировать относительно N переменных при М ограничениях (линейных
неравенств). Предположим, что все ограничивающие соотношения являются
неравенствами, а уравнений среди них не имеется. Тогда эта задача,
приведенная к канонической форме, будет иметь п = М + N переменных (из
них М дополняющих переменных) и т = М линейных уравнений (см.
упражнение 2). Следовательно, в канонической системе т < п. Это
предложение справедливо и для двойственной задачи (см. упражнение 3).
То обстоятельство, что т < п, то есть что пространство решений имеет
большую размерность, чем пространство условий, важно потому, что при
этом значения переменных в допустимых решениях должны удовлетворять
числу уравнений, меньшему чем число переменных. В соответствии с этим
задача линейного программирования, приведенная к канонической форме,
обычно имеет множество — причем даже бесконечное множество —
допустимых решений.
Однако может оказаться, что это не так, если в представленной в общем
виде (см. 15.4) задаче линейного программирования (с N переменными,
подчиняющимися М ограничениям) некоторые или все ограничивающие
соотношения уже с самого начала являются уравнениями, а не
неравенствами. Тогда после приведения задачи к канонической форме может
оказаться, что т/г>тг, и допустимые решения определяются из системы
уравнений, число которых не меньше, чем число переменных (см. упражнение 4).
В этом случае, если уравнения совместны, возможно существование только-
одного допустимого решения, а если несовместны — даже полное отсутствие
допустимых решений.
Обобщим сказанное: если в общей задаче линейного программирования
все ограничения выражаются неравенствами, то в канонической ее форма
456

число ограничивающих уравнений т меньше числа переменных п, и
существует бесконечное множество допустимых решений. Обычно дело обстоит
именно тДк. Однако, если в исходной задаче некоторые или все
ограничивающие соотношения суть уравнения, тогда может случиться, что т>/г.
Это имеет место лишь в редких случаях.
Задачи и упражнения
1. Привести к канонической форме A) двойственную задачу с двумя переменными
(см. 15.3) и показать, что при этом число переменных увеличивается до четырех (в том
числе две дополняющие переменные), а число ограничивающих уравнений равно двум.
2. Общая задача линейного программирования состоит в том, чтобы найти N
переменных х, минимизирующих функцию z = р'х при условии выполнения М ограничений
Ах > Ь. Привести эту задачу к канонической форме с п переменными и т уравнениями.
Если все М исходных ограничений выражены неравенствами, показать, что т = М
и п= М + iV, а следовательно, что т < п.
3. Двойственная задача из предыдущего упражнения состоит в том, чтобы найти М
переменных §, максимизирующих функцию ? = Ь'§ при условии выполнения N
ограничений А'|<р. Привести задачу к канонической форме с п1 переменными,
подчиненными тг уравнениям, и показать, что т' =iV и п' = М + N, если все исходные
ограничения являются неравенствами.. Доказать, что прямая и двойственная ей задача
линейного программирования, выраженные в канонической форме, имеют одинаковое
число переменных, но различное число ограничивающих уравнений.
4. Пусть в общей задаче линейного программирования (задача 2 настоящего раздела)
с N переменными некоторые из исходных М ограничений выражены уравнениями.
Показать, что после приведения к канонической форме может случиться, что т > л,
рассматривая следующие возможные варианты:
а) M — N и все ограничения суть уравнения (т=п);
б) Af>iV и N ограничений суть уравнения (т — п);
в) М > N и более чем N ограничений суть уравнения (т > п).
15.7. НЕКОТОРЫЕ СВОЙСТВА ВЫПУКЛЫХ МНОЖЕСТВ
Изложим здесь важнейшие результаты теории выпуклых множеств,
рассмотренной в разделе 11.5. Кроме того, поскольку к ней относится и
понятие линейной зависимости векторов и точек, разобранное в разделе 13.1,
приведем сначала основные результаты, полученные в этой области.
Линейная зависимость
Пусть в яг-мерном пространстве имеется п точек р^1), р<2> ,...,р<п) (п > т).
Любая система к этих точек (например, к первых точек) является линейно
зависимой, если можно подобрать такие коэффициенты [is, из которых не
все равны нулю, что
2ц3р(8) = о.
8=1
Если линейная зависимость существует, то одна из точек
(соответствующая ненулевому значению fis) может быть представлена в виде линейной
комбинации остальных точек. Например, если |Lii ф 0, то
s=2
В противном случае система точек является линейно независимой; это
значит, что ни одна из точек не является линейной комбинацией остальных.
Основной результат выражается следующим положением:
(А). Изпточек р*1), р<2> ,..., р<п> в т-мерном пространстве линейно
независимыми могут быть не более чем т точек.
Следовательно, если число точек равно т + 1, то по крайней мере одна
точка должна быть линейно зависимой от остальных, представляя собой
линейную комбинацию остальных точек. Однако линейная зависимость
может существовать даже между т точками.
Пусть система именно т точек, например рA>, р<2> ,..., р<т>, является
линейно независимой. Эта система образует базис га-мерного пространства
457

т в том смысле, что всякую другую точку этого пространства можно
представить в виде линейной комбинации точек р<*>, р<2> ,..., р<т>. Система,
состоящая из большего числа точек, уже не есть базис, поскольку она не является
линейно независимой. Не будет базисом и система, состоящая из меньшего
числа точек, так как невозможно линейно выразить через них все остальные
точки. Примером базиса, к тому же очень удобным, является совокупность т
единичных точек на осях координат, которым можно сопоставить единичные
координатные векторы ег (г = 1, 2,..., т):
A,0, 0,...,0); @,1,0, ...f0);...
В дальнейшем мы с большой пользой применяем следующее
положение, вытекающее из основного результата. Выделим из п точек p(s> E = 1,
2,..., п) систему т линейно независимых точек, например первые т точек,
или р<г> (г = 1, 2,..., т). Тогда каждую точку из p<s> можно представить
в виде линейной комбинации т точек р(г>. Обозначим коэффициенты этой
линейной комбинации через xrs. Тогда можно сделать следующий вывод:
(Б). Если система точек р<г) (г = 1, 2, . .., т) в т-мерном
пространстве является линейно независимой, то всякую точку
p(s) E = 1,2, . .., п) в этом пространстве можно представить в виде
т
где хГ8 суть некоторые коэффициенты (г = 1, 2, . .., иг; s = 1, 2, . . . ,я).
Следует подчеркнуть, что это верно не только при s > иг, но и в том
случае, если s есть одно из первых иг значений, и p<s> является одной из
точек линейно независимой системы. В этом случае все значения #rs = 0,
кроме хгг = 1.
Свойства выпуклых множеств
I. Если в т-мерном пространстве заданы точки р и p<s> ($ = 1, 2, . . .
. . ., п), то точки ^ = (Ях, Я2, . .., Я,п), которые неотрицательны
(Я0), удовлетворяют уравнению
2^рр
s=i
и составляют гс-мерное выпуклое точечное множество Г.
Далее, если 2?A>, Е&\ . .. суть экстремальные точки множества Г,
то в применении теории выпуклых множеств к линейному
программированию предполагается, что множество экстремальных точек является
конечным, и их число равно к. Тогда выпуклое множество Г есть выпуклая
многогранная оболочка (полиэдр), порожденная множеством Е^1\ Е&\ ...,?(fe>.
Допустимые решения задачи линейного программирования изображаются
точками выпуклой оболочки Г.
Доказательство. Пусть №) и Л/2> суть две различные точки
множества Г, неотрицательные и удовлетворяющие условию:
2 *4V>=p, 2
s=l s=i
Следовательно, при любом [i @<[л<1)
S
8=1
Значит, если точки Л/1) и М2> принадлежат к множеству Г, то к этому
же множеству принадлежит и точка |А^A> + A — [*>) ^BI и, следовательно,
множество Г выпуклое.
1 Ибо она удовлетворяет двум вышеуказанным условиям (см. выше).—Прим. ред.
458

И. Линейная функция /(^), определенная в некоторой точке к
выпуклого множества Г, имеет максимум в экстремальной точке
этого множества.
Далее, если функция / (к) имеет максимум только в одной
экстремальной точке ЕA), этот максимум является единственным; если же / (h)
максимизируется в нескольких экстремальных точках Еш, ЕB\ . . ., то в таком
случае имеется бесконечное множество максимумов, во всех точках
выпуклой оболочки подмножества (части множества Г), порожденной
точками ЕA), ЕB\ .... Эти два случая соответствуют существованию
единственного оптимального допустимого решения и бесконечного множества
оптимальных допустимых решений задачи линейного программирования.
Доказательство. Будем считать fCk) линейной функцией, как это
имеет место в линейном программировании. Предположим, что функция
f(k) имеет максимум в точке Я, которая не является экстремальной. Тогда,
по определению экстремальных точек, ЕA), ЕB), .. ., E(ft> принадлежат
к некоторому выпуклому множеству,
h k
X = 2 Ит^(г) Для некоторой системы \хг>0, 2 Мт^-
г—1 г=1
Следовательно, поскольку /(Ji) есть линейная функция,
max/(*,) = 2 AГ/(Я<«) </(ЯA)J ^
если в экстремальной точке Еа) достигается наибольшее значение /.
Следовательно, max / (h) < / B?A)).
Здесь возможен лишь знак равенства, и / (к) имеет максимум в
экстремальной точке Еа). Те же соображения показывают, что если существует
несколько экстремальных точек Еа\ Е(*\ .. ., имеющих одно и то же
наибольшее значение /, то все эти значения суть максимумы /(^), причем
максимум достигается и в любой точке Л,, являющейся выпуклой
линейной комбинацией этих экстремальных точек.
III. Точка ^ = (Хх, Х2, ...,А,П) является экстремальной для
множества Г тогда и только тогда, когда точки p<s>, имеющие
положительные веса (A,s>0), составляют линейно независимую систему,
выделенную из множества p(s) (s= I, 2, ¦. ., п). Остальные p{s} имеют
нулевые веса (A,s = 0).
Далее, в соответствии с положениями (А) и (Б) для линейной
зависимости экстремальная точка множества Г имеет не более чем т
положительных весов и не менее чем (п — т) нулевых весов; если число
положительных весов равно в точности т, то всякую точку p(s> можно представить
в виде:
р2
где р<г) (г = 1, 2, ..., т) имеет т положительных весов.
Доказательство. Пусть %, есть экстремальная точка множества Г,
имеющая к положительных весов Ях, Х2, . ¦., Xk; остальные X нулевые. Так как
точка к принадлежит к множеству Г, то, в соответствии с пунктом 1,
2 4p(s) = p> все 4>о. A)
s=l
Предположим, что точки рA>, рB\ ..., p(ft) —линейно зависимы, так что
S f*sP(s) = O, B)
s=i
где не все значения fxs равны нулю.
459

Теперь выберем постоянную с, столь малую, что и А,8 + Фа и ks — c\i^
(подобно Xs) будут положительны для s = l, 2, . .., к. На основе
уравнений A) и B):
s (к+ф.) p(s)=р чи s (*•.- ф.) p(s)=р.
s= 1 s= 1
Следовательно, и Vv = X + c\i и A,(a) = h —qi также принадлежат к
множеству Г. Однако
1 — * Qi <1> _L_ * а B)
что невозможно, поскольку ^ — экстремальная точка множества Г. Значит,
линейная зависимость между рA), рB), ...,р(Ь) невозможна; эти точки
линейно независимы, что и требовалось доказать.
Докажем обратное предложение. Пусть точки рA), рB), . . ., p(/i\
соответствующие к положительным весам точки X множества Г, суть линейна
независимы. Предположим, что % — выпуклая линейная комбинация двух
точек Vv и Л/2) множества Г:
Точки К, Vv и V2) в совокупности имеют лишь к положительных
весов (остальные веса — нулевые), и поскольку все эти точки принадлежат
к множеству Г, то
S^sp(s)=p. 2 W=p и 2я?у«=р.
s=l s=i s=l
k k
Следовательно, 2 (К - W1}) P(s) = 0 и 2 (К - Wf)) P(s> = °» что ПРИ
s=i s—1
линейно независимых p(s) возможно лишь в случае, если
Значит, ^ не может быть выпуклой линейной комбинацией ^двух
других точек множества Г, то есть % является экстремальной точкой этого
множества, —что и требовалось доказать.
15.8. СИМПЛЕКСНЫЙ МЕТОД
Представим рассмотренную нами общую задачу линейного
программирования в таком виде, как это Сделано в разделе 15.6.
Требуется отыскать неотрицательные значения Xs>0 E = 1,2, . .., тг),
максимизирующие выражение
z^c^ + cJb + ... + сп%п A)
при условии
= p. B)
Допустимое решение удовлетворяет условию B), но не должно
обязательно максимизировать также и выражение A). В соответствии со
свойством 1 раздела 15.7, такие решения образуют выпуклое множество Г.
Множество Г имеет экстремальные точки Е{1\ ЕB\ ...,i?(fe>, и
оптимальное допустимое решение, максимизирующее выражение z в соответствии
со свойствами B) того же раздела, совпадает с одной или с большим
числом экстремальных точек Е{1\ Ei2\ .. ., Eik). Следовательно, чтобы
решить задачу линейного программирования, необходимо сосредоточить
внимание на экстремальных точках, порождающих множество Г. При этом
нужно иметь в виду две возможности: либо максимум достигается только
в одной экстремальной точке, которая в этом случае есть единственное
460

решение задачи; либо максимум достигается в нескольких экстремальных
точках, и в этом случае существует бесконечное множество решений во всех
точках % выпуклой оболочки, порожденной этими несколькими
экстремальными точками.
Свойство III раздела 15.7 заставляет обратить внимание на еще одну
особенность экстремальных точек множества Г, а именно на число
положительных весов вектора h = (А,х, Я2, ..., Хп) экстремальной точки. Это
число может быть меньше т\ тогда имеющие положительные веса векторы
р(Г) (г = 1, 2, ..., к) будут линейно независимы (к<т). Более полезен
другой случай, когда число положительных весов равно как раз т: тогда
линейно независимые значения р(г) (г = 1,2, ...,яг) образуют базис т-мер-
т
ного пространства, и всякое p(s) можно представить в виде p(s) = 2 яГ8р(г>.
r=l
Предположим, что нами найдено допустимое решение задачи,
представляющее собой экстремальную точку множества Г, которая имеет т
положительных весов, то есть решение
л = (л1? л2, ..., лт, 0, 0, ..., 0),
где кг > 0 (г = 1, 2, ..., т). Тогда значения р(г) — линейно независимы, и
т
Р== LJ ^гР \Лг ^ ^/ \у)
г=1
И
т
n(s> = ^ х п(г) (s 12 иЛ (&\
r=i
Выражение z принимает при этом соответствующее (не обязательно
максимальное) значение:
т
о — Z^ c~hT* (О)
Введем переменные
т
S r=l Г rS
После этого будем искать новое допустимое решение в одной из
экстремальных точек множества Г. Для этого выбрасываем р(г), где г выбрано
из значений 1, 2, ...,т, и включаем p(s), где s берется из числа значений
(ттг + 1), (тгг + 2), ...,?г. Подстановка должна быть такой, чтобы значение
переменной z превысило значение z0. Таким образом, перебирая одну
за другой все экстремальные точки множества Г, мы приближаемся к
максимуму 2, то есть к оптимальному допустимому решению (или к одному из
бесконечного числа таких решений).
Задача^ состоит в следующем: как выбрать г, подлежащее исключению,
и 5, подлежащее включению. Пусть 0 —некоторый постоянный
коэффициент. На основе уравнений C) и D) можно записать, что
т т
р = 2 *гР<г> - 0р<г) + Qp(s) = S (К - &О р<г) + 0p<s>- (?)
В качестве 0 возьмем 0 = Xr/#rs, так что г-ж член в уравнении G)
исчезает, и остается только т членов. При условии, что lkT — 0#rg>O
и 0>О, совокупность коэффициентов уравнения G) представит новое
допустимое решение, и, в соответствии с уравнениями E) и F), новое
значение z определяется уравнением:
m
К = 2 ст СКТ - Qxrs) + 0cs = z0 + 0 (cs - zs). (8)
r=i
461

Следовательно, если 8 > 0 и cs > z8, то, судя по уравнению (8),
проделанная нами подстановка позволила получить улучшенное решение
(zo > 2о)- Значит, выбирать г и s нужно так, чтобы
6==^Г>0' Xi~Qxis>° и cs-zs>0, (9)
где i — любое число в ряду A,2, ...,т), кроме г. При выборе г и s
должно удовлетворяться два условия:
1) По крайней мере одно cs—- zs (s = m-{-1, тгг + 2, ..., п) должно быть
положительным; при этом выбирается s для наибольшего cs — zs > 0, и
удовлетворяется последняя часть условий (9).
2) По крайней мере одно из xrs (г = 1, 2, . .., т) должно быть
положительным; при этом г выбирается (из числа г, для которых xrs
положительно) так, чтобы минимизировать Q = Xr/xrs и удовлетворить два первых
ограничения системы (9).
При этих условиях мы получаем улучшенное решение, исключив р<г>
и включив p<s) в исходную систему линейно независимых точек
р(г) (г = 1, 2, .. ., т). Более того, новая система также линейно независима,
так как она снова соответствует экстремальной точке множества Г. Чтобы
удостовериться в этом, предположим, что точки пронумерованы так, что
мы исключаем р^1) и добавляем р^т+1>, то есть что г = 1, 5 = /?г+1. Тогда,
в соответствии с уравнением D), если новая система р<2>, р<3>, . . ., p(m+i)
линейно зависима, то
p2
r=i
И
p2
r=2
Вычтем первое равенство из второго:
Но исходная система была линейно независимой, и р*1) не может
представлять собой линейную комбинацию остальных точек системы, как теперь
указано. Невозможно и #i(m+i) = 0, так как г = 1 выбиралось из числа
положительных #r(m_|-i). Значит, новая система не представляет собой
линейно зависимую систему; она линейно независима.
Следовательно, можно прийти к выводу, что, если удовлетворяются
условия A) и B), то в таком случае можно улучшить первоначальный выбор Л*
и значение z0; мы получаем новое допустимое решение, также
соответствующее экстремальной точке множества Г, и большую величину z0.
Полученное решение явится отправной точкой для повторения тех же операций.
Весь процесс итерации от выбранной исходной точки может быть повторен
сначала; при этом возвращения к ранее полученным решениям никогда не
происходит, так как значение z на каждом шаге возрастает. Если не считать
рассматриваемого далее случая вырождения, необходимость в прекращении
процесса может возникнуть лишь по той причине, что на каком-то шаге
перестают удовлетворяться условия A) и B). А это значит, что максимальное
допустимое решение уже получено. Нетрудно заметить, что либо перестает
удовлетворяться условие B), и все значения #rs<0, так что величина z
становится бесконечной, либо перестает удовлетворяться условие B), и все
cs —zs<0, в этом случае фиксируется некоторый конечный максимум 2,
то есть экстремальная точка % является искомым оптимальным допустимым
решением.
Итеративный метод неприменим на практике лишь в том случае, если
на каком-то шаге допустимое решение % имеет менее т положительных
462

весов. Это — случай вырождения. Выход из этого затруднения
(позволяющий применять симплексный метод во всех без исключения случаях)
предложен Чарнесом [1] и приводится в книге Чарнеса, Купера и Гендерсона [2].
Отметим, наконец, что любая двойственная задача линейного
программирования также может быть приведена к канонической «симплексной»
форме уравнений A) и B). Следовательно, двойственную задачу также
можно решать симплексным методом. Однако ясно, что прямая и ее
двойственная задачи столь тесно между собой связаны (например, значение
максимума в одной совпадает со значением минимума в другой), что можно
рассчитывать при однократном применении этого метода получить сразу
решения обеих задач. И, действительно, дело обстоит именно так, что
иллюстрируется на частном примере, приведенном в разделе 15.9. При
использовании симплексного метода Ь этом примере на последнем шаге, когда
достигнут некоторый конечный максимум, все cs — zs < 0.
Противоположные по знаку величины (то есть ze—cs), полученные окончательно для
дополняющих переменных, являются оптимальными значениями
переменных в решении двойственной задачи.
15.9. РЕШЕНИЕ СИМПЛЕКСНЫМ МЕТОДОМ ПРОСТОЙ ЗАДАЧИ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Практическое применение симплексного метода можно
продемонстрировать на простом примере; возьмем для этой цели двойственную задачу,
решенную уже графически в разделе 15.2 и в форме соответствующей задачи
теории игр — в разделе 15.3. Теперь мы получим такое же решение с
помощью симплексного метода: однако последний обладает тем преимуществом,
что позволяет решать и более сложные задачи линейного программирования,
не поддающиеся графическому решению и не приводимые к теории игр.
Более сложная задача решается симплексным методом в книге Чарнеса,
Купера и Гендерсона [2], Там же рассматриваются некоторые аспекты
практического его применения, благодаря чему становится ясно, что
симплексный метод предназначен для систематизированного решения задач с
помощью вычислительных машин.
Требуется при неотрицательных значениях 6i и ?2 максимизировать
выражение
?= 3^ +46, -max,
при условии
6х + ?2<6,
2Б1 + 4Б1<21.
Чтобы применить симплексный метод, необходимо привести задачу
к канонической форме (см. 15.9), для чего введем две дополняющие
переменные. Тогда число переменных увеличится до четырех: Xx = 6i» ^2 — ^
причем Я3 и А,4 — дополняющие переменные. В новой задаче требуется
отыскать неотрицательные Xs (s = 1, 2, 3, 4), максимизирующие выражение
при условии
^2+^3 = 6'
Здесь пространство условий является двумерным и содержит пять
заданных точек:
"110 6
463

Пространство решений является четырехмерным и содержит точки
являющиеся возможными решениями задачи. В этом же пространстве
расположена также заданная точка с = C, 4, 0, 0), которая определяет
максимизируемую функцию z.
Все допустимые решения к, удовлетворяющие двум ограничивающим
уравнениям, образуют в четырехмерном пространстве выпуклое
множество Г. В качестве исходного допустимого решения необходимо выбрать
некоторую экстремальную точку множества Г, имеющую два
положительных и два нулевых веса. В качестве такого решения удобно взять X = @, 0,
6, 21), которая несомненно удовлетворяет поставленным условиям; точки
рC) = [1] и рD) = joj^ имеЮщИе положительные веса, линейно
независимы. В самом деле, эти точки соответствуют единичным координатным
векторам двумерного пространства, они образуют простейший базис этого
пространства, все другие точки которого можно представить в виде
линейной их комбинации. Именно поэтому данное решение и выбрано в качестве
исходного допустимого решения.
Теперь построим шаг за шагом следующую симплексную таблицу.
А
В
С
РC)
РD)
zs
cs—zs
рC)
рB>
г
Cs-Zs
р<»
рB)
0
0
0
4
3
4
i
6
21
3
4
21
4
to| со
9
2
P<*>
3
1
2
0
3
1
2
1
2
2
1
1
0
3
0
p<2>
4
1
4
0
4
0
1
4
0
0
1
4
0
pC)
0
1
0
0
0
1
0
0
0
2
-1
2
-2
P<4>
0
0
1
0
0
1
4
1
4
1
-1
1

1
2
1
2
1
2~
Рассмотрим сектор А, то есть первый сектор таблицы, являющийся
исходным допустимым решением. Первые две строки соответствуют точкам
(здесь р<3> и р<4>), имеющим положительные веса в К = @, 0, 6, 21); эти
положительные веса проставлены в столбце %. Остальные четыре столбца
соответствуют точкам р*1), р<2\ р<3> и р<4>. Против этих строк и столбцов указана
соответствующая величина с = C, 4, 0, 0). Важнейшей частью сектора А
являются элементы двух строк р<3> и р<4") и четырех столбцов р*1), р<2>, р<3>
464

и р<4>. Это — коэффициенты xrs уравнения D) раздела 15.8. Они
показывают, каким образом точка, изображаемая каждым из столбцов,
представляется линейной комбинацией выбранного нами базиса рC> и р<4>. Например,
или
По сути дела это — элементы заданной матрицы задачи (см.
упражнение 1). В остальных двух строках сектора А проставлены вычисленные
в соответствии с уравнением F) раздела 15.8 значения: во-первых,
выражения
*s = сзхз$ + сAs (s = 1, 2, 3, 4)
и, во-вторых, cs — zs.
Чтобы перейти к сектору В, заменим в строках одно из р<3> и рD> на
одно и-з р*1) и р<2>. Чтобы выбрать необходимый вариант замены:
1) найдем наибольшее положительное значение (cs — rs); оно равно 4;
следовательно, включению подлежит р<2>;
2) на основе столбца рB> найдем наименьшее из значений 9 (то есть
13/ж32 или "kjx^) для положительных значений xrs. Эти значения
соответственно равны 6/х и 21/4. Следовательно, исключению подлежит строка р<4>.
Сектор В составляет р<3> и р<2>, новая пара линейно независимых точек,
имеющих положительные веса в новом допустимом решении h. Элементы i
определяются на основе уравнений 7 раздела 15.8; здесь % = @,21/4, 3/4, 0).
Положительные веса проставлены в столбце X сектора В. Затем находим
коэффициенты xrs уравнения D) раздела 15.8 и проставляем их в таблицу.
Например,
РA)
или
уравнению удовлетворяют значения х31 = х/2, х21 = х/2 (см.
упражнение 2). Затем тем же методом, как и раньше, вычисляем значения
элементов строк zs и cs — zs.
Сектор С является результатом дальнейшего применения того же
процесса. Пару точек рC) и р<2>, являвшуюся базисом в решении В, заменяем
новым базисом рA> и р<2>. Сначала включаем р*1) на основе наибольшего
положительного значения (с8—zs) в секторе В, а по сути дела единственного
{cs — zs), оставшегося положительным. Затем исключаем р<3> на основе
наименьшего из двух значений 0 = Я3/х31 = SU : */г и в = А,2/аг21 = 21/4 • х/2.
Следовательно, 9 = 3/2, и на основе уравнения G) раздела 15.8 вычисляем
новую величину %, = C/2, 9/2, 0, 0). Остальные элементы сектора С
получаются тем же методом, что и ранее.
Мы закончили решение, так как все (cs — zs) < 0, и получен конечный
максимум выражения z. Максимальное допустимое решение есть % = C/2,
9/2, 0, 0), при котором
= 22.
Это есть решение, полученное в разделе 15.2, а именно: ?г = 3/2,
|2 = 9/2 и ? = 22х/2. Следует отметить, что задача, двойственная
рассмотренной, то есть задача питания (см. 15.1), имеет решение, которое можно
получить из симплексной таблицы. Это решение представляют элементы послед-
ней строки (с^ — 23), взятые с обратным знаком, после того как основные
и дополняющие переменные обменены местами. Для этой задачи % = B,V2,
0, 0), то есть хг = 2, х2 = 1/2, откуда следует z = 22V2.
30 Р. а л лен 4&5

Задачи и упражнения
1. Два вектора и ,« линейно независимы; точки A, 0) и @, 1)
образуют базис двумерного пространства. Любую точку (xlf х2) можно представить в виде
линейной их комбинации. Показать, что эта комбинация отыскивается с помощью
следующего уравнения:
2. Базисом двумерного пространства может служить любая пара линейно
независимых векторов второго порядка, а не только пара векторов, принятая в качестве
базиса в предыдущей задаче. Примем за базис векторы и . Любая точка
(xlf x2) является их линейной комбинацией:
Показать, что при отыскании такой комбинации] необходимо воспользоваться
уравнениями:
|1 . 1
3. Решить задачу питания (см. 15.1) непосредственно симплексным методом. Тем
самым получить решение и ее двойственной задачи. Сверить этот результат с
непосредственным решением указанной двойственной задачи.
4. Решить симплексным методом модифицированные задачи питания —
упражнение 5 раздела 15.1 и упражнение 4 раздела 15.2. Сверить результаты с решениями
соответствующих задач из теории игр (упражнение 3 раздела 15.3).
5. В транспортной задаче (см. упражнение 7 раздела 15.1) показать, что пять
заданных точек в двумерном пространстве условий суть:
5;!!
Сколько пар здесь линейно независимых и сколько линейно зависимых?
6. Рассмотрим частный случай транспортной задачи (см. упражнение] 7
раздела 15.1):
Минимизировать выражение
при условии х\ -\- #2=10, х\ -f a?3=20.
Показать непосредственным расчетом, что 2 = 15 для любых допустимых
значений a?i, X2 и х3. Попытаться решить задачу: а) графически, б) на основе решения-
соответствующей игровой задачи, в) симплексным методом. Рассмотреть также двойственную
задачу. Разъяснить проделанные операции и истолковать задачу с точки зрения
необходимой численности судов для перевозки и продолжительности различных рейсов.
7. В транспортной задаче (см. упражнение 8 раздела 15.1) рассмотрим частный
случай, для которого количества грузов, перевезенных между портами, и стоимости
перевозки единицы груза соответственно представляются следующими матрицами:
Ui *м 10 и Г
L 6 6 112J L
Показать, что в этой задаче требуется минимизировать линейную функцию четырех
неизвестных при условии соблюдения трех ограничивающих линейных уравнений.
Каковы в этом случае результаты применения симплексного метода? Сравнить с
результатом предыдущей задачи. Более общий анализ см. в статье Данцига (гл. XXIII)
в сборнике под редакцией Купманса [9].

ГЛАВА 16
ПРОГРАММИРОВАНИЕ ПРОИЗВОДСТВЕННЫХ ОТРАСЛЕЙ
И РАСПРЕДЕЛЕНИЕ ОГРАНИЧЕННЫХ РЕСУРСОВ
16.1. ВВЕДЕНИЕ. ОБЩЕЕ ЭКОНОМИЧЕСКОЕ РАВНОВЕСИЕ
Возвратимся вновь к рассмотрению основного стержня экономической
теории: общехозяйственных статических и динамических моделей. В главе 9
экономическое равновесие охарактеризовано широко, а в главе 10 — очень
специально; теперь следует слить воедино эти внешне различные методы
подхода. Модель Вальраса (см. гл. 9) учитывает всю совокупность
возможных взаимосвязей в задаче, которую Роббинс [17] назвал главной
экономической задачей: использование ограниченных ресурсов для достижения
определенных хозяйственных целей. Однако все это имело слишком общий
характер. Даже при изобретательности, присущей Хиксу или Самуэльсону,
удалось получить немного практически ценных результатов. Правда, подсчет
числа уравнений показывает, что решения возможны, но не доказывает
существования таких решений, по крайней мере решений с
неотрицательными ценами и количествами.
Преодолеть эти недостатки можно с помощью двух приемов: берется
линейная система, и уравнения в ней заменяются линейными неравенствами.
Это не очень серьезное ограничение, так как линейность означает
постоянство технологических коэффициентов, а вовсе не влечет линейности
функций спроса или издержек, необходимость же в неравенствах возникает так
или иначе, например для цен, р>0.
В линейной системе Вальраса (см. 9.2) технологические коэффициенты
приняты постоянными. Для удобства рассмотрения введем здесь еще
одно упрощение: будем считать фиксированным предложение Xs каждого
из к факторов производства (s = 1, 2,..., к) и т предметов потребления
(t = 1, 2,..., wi), причем начальные запасы принимаются нулевыми.
Уравнения (I) и (III) раздела 9.2 устанавливают функции Xt рыночного спроса
на предметы потребления, причем каждая из них зависит от цен на все эти
товары. Обозначим постоянные технологические коэффициенты через ast,
цены факторов производства через л8, цены предметов потребления через рг
Остается рассмотреть две системы линейных уравнений (И) раздела 9.2:
а) 2astXf = Xs (*=1, 2....Л),
б) 2*tsasf=ft (*=1, 2, ...9т).
Так как Xt выражаются через цены, а Xs задаются, то эти уравнения
определяют рыночные цены.
Как указал Цойтен (см. стр. 251), если область решений ограничена
условием неотрицательности цен (jts>0, pt > 0), то уравнения
приходится заменить неравенствами. Система (а) должна означать, что «расход
ресурсов не может превышать заданного их количества», в то время как
ранее «расход ресурсов в точности должен был соответствовать заданному
их количеству». Аналогично этому система (б) ставит условие нулевых или
отрицательных прибылей, а не обязательно только нулевых прибылей.
Следовательно,
а) %astXt<X8 (*=1, 2, ...f ft),
467 30*

б) 2 «.«.«> A («=1, 2 m).
S
В развернутом виде эти системы линейных неравенств запишутся
следующим [образом:
а) а11Х1 + а12Х2 + ... + а1тХт<Х1> б) а^ + а21п2 + ... + aklnk>pv
Далее, как показано в теории игр (см. свойство III из раздела 14.7),
строгое неравенство для 5-го фактора в системе (а) означает, что этот фактор
используется не полностью и что его цена ns должна быть равна нулю.
Аналогично этому строгое неравенство для t-ro товара в системе (б) означает,
что прибыль должна быть отрицательной, а выпуск Xt — нулевым. Именно
в этом и заключается различие между свободными и дефицитными
факторами, между применяемыми и неприменяемыми производственными
способами.
Однако в 1-аком случае линейная система Вальраса сходна с задачей
линейного программирования, имеющей прямую и двойственную системы
неравенств, и можно доказать основной вывод, который не сумели
установить Вальрас и его последователи: если удовлетворяются простейшие
условия (непрерывность функций спроса при любых сочетаниях цен), то
существуют решения системы, представляющие собой один или несколько
наборов неотрицательных цен. Простое доказательство этого приводится в
главе 13 книги Дорфмана, Самуэльсона и Солоу [7]; оно основано на понятиях
прямой и двойственной задач линейного программирования. Это —
модифицированный вариант первоначального доказательства, принадлежащего
Вальду [18]. Более общий характер имеет доказательство, предложенное
Эрроу и Дебрэ [1].
Следует отметить два обстоятельства. Во-первых, линейная система
Вальраса обязательно имеет соответствующие решения; случай «отсутствия
решений» исключен. По-прежнему возможно существование множества
решений, представляющих собой различные системы неотрицательных цен.
Чтобы решение было единственным, условия должны быть более строгими;
как показали Дорфман, Самуэльсон и Солоу [7], эти условия связаны со
свойством «явной предпочтительности» функций рыночного спроса. Второе
обстоятельство заключается в том, что доказательство существования
решения в таком виде, как оно сформулировано здесь, относится к линейным
системам. Однако можно полагать, что решения существуют и для других
систем с непрерывными производственными функциями, предельными
продуктами и т. п. Нахождение общехозяйственного равновесия в условиях
конкуренции — не пустое упражнение; для него существуют решения,
определяемые с помощью методов линейного программирования. Первое
успешное выполнение этого принадлежит Вальду.
Теперь найдено надлежащее место и для системы Леонтьева (см. гл. 10).
Это — линейная система с неизменными соотношениями между затратами
и выпуском, и она незамедлительно позволяет получить результаты,
пригодные для практического применения. Необходимо лишь несколько ее
упорядочить, например, в вопросе очевидной невозможности
взаимозаменяемости в производстве. Ни линейная система Вальраса, ни линейная система
Леонтьева не являются задачами линейного программирования, но они
несомненно связаны с последним. Теория игр и линейное программирование
(см. глг. 14 и 15) будут далее использованы применительно к вопросам общего
экономического равновесия и к динамическим задачам.
Пытаясь решить методами линейного программирования широкую
экономическую задачу распределения ограниченных ресурсов для достижения
468

определенных производственных целей, мы рассматриваем следующие
элементы задачи:
1. Технологические характеристики производственных возможностей,
обычно выражаемые в линейной форме в виде постоянных коэффициентов,
из которых можно составить матрицу.
2. Имеющиеся в распоряжении точно определенные ресурсы, обычно
выражаемые в форме вектора количеств разных первичных факторов;
расход факторов не должен превышать этих количеств.
3. Цели производства, точно определенные в количестве конечных
продуктов и других требуемых товаров; наряду с этим устанавливается
оптимальная методика выбора наиболее эффективного варианта
распределения ресурсов при заданных технологических условиях.
Здесь особенное значение придается технологическим аспектам задачи,
и создается впечатление, что не уделяется внимания рассмотрению функции
рынка (спроса.— Ред.), рыночных цен и прибылей. Однако, составив прямую
задачу линейного программирования на основе технологических данных,
мы можем затем составить и исследовать двойственную задачу, а именно
в последней ищутся цены и прибыль. В этом случае становится ясной
функция рыночных цен и прибылей как руководящий принцип эффективного
распределения технических ресурсов и как способ установления
степени централизации или децентрализации при комбинировании отраслей
производства. Таким образом, линейное программирование имеет очевидное
и непосредственное отношение к экономике социализма и к планированию
коллективистского хозяйства [14]. Суть дела в следующем: в какой бы мере
механизм ценообразования ни обусловливал возможность децентрализации,
всегда кому-то приходится принимать некоторые технические решения
и выбирать между различными вариантами. Наряду с этим могут
приниматься и другие решения, например государством.
Следовательно, применение методов линейного программирования
в вопросах общего экономического равновесия создает необходимую увязку
между технологией и рыночным механизмом (хотя и кажется, что внимание
уделяется только чисто техническим аспектам). Преимущество линейного
программирования заключается в том, что в нем допускаются неравенства,
неизбежные в любой «реальной» задаче, а недостаток — в упрощении
технологических условий, которое неминуемо, если задачу, взятую из
практики, приходится решать с учетом ограниченных вычислительных
возможностей [4].
Имеется множество различных областей применения линейного
программирования, начиная от транспортных задач и материально-технического
обеспечения вооруженных сил и кончая техническими решениями в рамках
фирмы. Далее рассматривается частный случай применения линейного
программирования к вопросам межотраслевых связей — распределение
производственных ресурсов и распределение программы производства между
отраслями при условии общего экономического равновесия. В
последующих главах рассматривается применение линейного программирования
к теории фирмы и к теории поведения потребителя.
16.2. АНАЛИЗ ПРОИЗВОДСТВЕННЫХ ОТРАСЛЕЙ: ПОНЯТИЯ
И ОПРЕДЕЛЕНИЯ
Применение линейного программирования к анализу производства
в широком смысле легче всего истолковать с экономической точки зрения,
если сначала дать четкие определения понятиям «товары» и «отрасли
производства» («activity»). Наилучшие определения приведены в сборнике
Купманса [11, гл. III].
Товары определяются так же, как это сделано в главе 9 настоящей
книги. К товарам относятся:
469

1. Первичные факторы (например, сырье или труд), имеющиеся в
распоряжении в виде наличных ресурсов вне рассматриваемой системы.
2. Промежуточные продукты, производимые и потребляемые в
пределах системы.
3. Конечные продукты, производимые в пределах системы; их выпуск
и является целью системы.
Следовательно, первичные факторы входят в число заданных ресурсов,
конечные продукты — в число требуемых продуктов или целей, а
промежуточные продукты, как-то чугун или хлопчатобумажная пряжа, не относятся
ни к той и ни к другой категории. Осложнение состоит в том, что некоторые
из первичных факторов сами по себе могут быть необходимой конечной
целью, например труд, затрачиваемый непосредственно для удовлетворения
конечного спроса. При разрешении этого затруднения целесообразно
считать, что либо ни один из первичных факторов не относится к
«потребностям», либо все они относятся к «потребностям».
Возьмем совокупность т товаров (г = 1, 2,..., т). Обозначим через хТ
выпуск каждого из этих товаров (г = 1, 2,..., пг); хт —чистый выпуск,
который может быть положительным, отрицательным или нулевым. Если
хт > 0, то г-й товар есть конечный продукт, удовлетворяющий конечный
спрос; если хт < 0, то г-й товар потребляется, он представляет фактор
производства, полностью расходуемый; если же хг = 0, то это —
промежуточный продукт, целиком производимый и потребляемый в пределах системы.
Производственными отраслями (activities) называются сочетания
товаров, из коих некоторые затрачиваются в неизменных пропорциях для
производства других товаров—выпускаемых, причем между затратами и
выпуском сохраняются постоянные пропорции (см. 9.8). Производственная
отрасль — понятие количественное; она ийеет некоторый уровень, а
следовательно, может иметь единицу объема или единичный уровень.
Единичный уровень 5-й производственной отрасли выражается вектором яг-го
порядка:
где элемент ars представляет собой количество (или доля потока) г-го
товара, включенное в единицу объема s-ro производства. Если аГ6<0,
то r-й товар относится к числу продуктов, затрачиваемых в данном
производственном способе, а если ars > 0, то — к числу выпускаемых продуктов.
Между всеми элементами вектора сохраняются неизменные пропорции, ибо
элементы ars суть постоянные и заданные величины. Если ars = 0, то г-й
продукт не участвует в s-м производстве, а если и участвует, то лишь в
качестве промежуточного продукта.
Мы делаем два допущения, основанные на общих свойствах векторов.
Во-первых, возможно сложение двух производственных отраслей без
изменения их структурных коэффициентов, выполняемое по правилам сложения
векторов. Это значит, что если аг1 и аг2 характеризуют выпуск r-го товара
в двух производственных отраслях АA) и АB), то при их объединении будет
производиться (аг1 + аг2) этого товара. Такое свойство описывается
уравнением:
А<8> + А<" = {агз} + {аг(} = {(art + art)}. A)
Во-вторых, уровень производственной отрасли определяется скалярным
числом X, на которое умножается вектор единичного уровня. С возрастанием
уровня в такое же число раз увеличиваются затраты и выпуск по всей сово^
купности товаров. Для любого X > О это можно записать в следующем виде*
ЬАC> = Ч«гЛ = {КЛ- B)
470

В этих допущениях предполагается, что затраты пропорциональны
выпуску как при объединении производственных отраслей, так и в рамках
одного производства. Далее, если при непрерывном изменении множителя К
непрерывно изменяется и уровень производственной отрасли, то последняя
обладает свойством совершенной делимости; затраты и выпуск по всем
товарам изменяются одновременно и непрерывно. В свете соображений,
приведенных в разделе 9.8, можно сказать, что более серьезные ограничения
накладывает первое допущение; на практике производственные способы
могут и не быть аддитивными в принятом здесь простом смысле.
Совокупность двух уравнений A) и B) определяет любую комбинацию
(положительную и линейную) ряда к производств:
к к к
2 4A<S) = 2 К {ars} = (B KarS)} (К > °)- C)
s=i s=i s=l
Сумма 2^s^(S) и сама является производственной отраслью; это —
столбец т величин затрат и выпуска, взятых в постоянных соотношениях.
Несомненно, имеется множество таких отраслей с различными
неотрицательными Я8 и с различными А(8\ входящими в комбинацию. Если дан
полный ряд таких производств, то их можно расчленить на основные
(базисные) отрасли и на отрасли, представляющие собой комбинации основных.
В системе производств совокупность базисных отраслей охватывает
такие производства, которые не представляют собой комбинации
(положительной и линейной) других отраслей системы. Пусть имеется п таких
базисных способов:
IS
Из их элементов можно составить матрицу А, которая определяет
технологию системы:
«11
«21
a .
, A<2) =
«12
«22
_«m2_
ail
a21
«12
«22
(I
... aln
... a2n
• • • amn-
Тогда любое производство, как базисное, так и всякое другое, можно
записать с помощью уравнения C) в виде положительной линейной
комбинации отраслей А*3) с теми или иными (неотрицательными)
коэффициентами Я8. Такое общее определение производственной отрасли SA,SA<S)
является весьма широким по охвату, ибо некоторые из коэффициентов к
могут быть нулевыми, а другие могут принимать любые положительные
значения.
Технологическая матрица А — матрица т X /г. Элементы строки
матрицы А суть затраты или выпуск некоторого товара в п базисных
отраслях. Элементы столбца матрицы А суть затраты или выпуск т товаров для
некоторой базисной отрасли. Матрица охватывает все возможные
технологические варианты. Например, рассмотрим различные способы получения
выпуска х1 первого товара. В первой строке матрицы А может оказаться
несколько положительных элементов, и выпуск хА можно получить в
результате применения любого соответствующего этим! элементам производства,
взятого в отдельности или в сочетании с другими такими же отраслями.
Значит, хг является первым элементом вектора ^,к8А^\ где знак
суммирования относится ко всем столбцам, первый элемент которых положителен.
471

Можно менять как соотношения между коэффициентами Я, изменяя таким
путем распределение ресурсов между производственными отраслями, так
и абсолютные величины этих коэффициентов, меняя таким образом
масштаб производства. В то же время, наряду с выпуском первого товара, могут
производиться и другие товары, так как в числе столбцов As, первый
элемент которых положителен, могут быть столбцы, имеющие один, два или
несколько других положительных элементов (кроме первого).
Иллюстрация этого дается в упражнении 4.
Анализ производственных отраслей имеет дело с производством или
переработкой в столь же широком их понимании, как и в разделе 9.8.
Технологическая матрица А должна показать, какие имеются в распоряжении
альтернативные варианты способов производства, почему один вариант
предпочитают другому, и какое последует переключение процессов при
любом заданном изменении условий экономической задачи. Здесь мы
оставляем открытыми все вопросы, относящиеся к принятию решений
администрацией; это не предполагает отказа от выбора между альтернативными
технологическими вариантами, с которым приходится иметь дело
руководителю.
Понятно, сколь велика область применения и интерпретации
технологической матрицы А. Так, например, она может характеризовать
питательные свойства единицы разных пищевых продуктов в задаче питания (см.
15.1). Или она может быть применена для решения различных
транспортных задач; например, при перевозке однородного продукта между портами Р
и Q можно считать, что имеется два «товара», то есть продукт в порту Р
и тот же продукт в порту Q, и перевозка из порта Р в порт Q есть
«производство», которое затрачивает первый продукт, а выпускает второй.
Задачи и упражнения
1. Товары и связанные с ними отрасли, рассматриваемые в настоящем разделе,
относятся к «открытой» системе, где затрачиваемые ресурсы поступают извне системы,
а конечные продукты передаются внешним потребителям. Показать, что технологическая
матрица А в такой же мере применима и к «замкнутой» системе, причем элементы ars по-
прежнему могут быть положительными, отрицательными или нулевыми (в зависимости
от характера использования r-го товара в 5-м производстве), но что все товары, для
которых 2гг = 0, являются промежуточными. Выпуском какой производственной отрасли
явятся в этом случае человеко-часы работы?
2. Рассмотреть подход, при котором труд считается r-м товаром открытой системы,
и общее количество затраченного труда (—хг) равно постоянному общему количеству
имеющихся в распоряжении ресурсов труда хг. Удобно ли ввести производственную
отрасль «отдых», выпуском которой является «досуг», а затратами «труд»? Не следует ли
считать первичным фактором только неквалифицированный труд, а квалифицированный
труд считать «выпуском» производственной отрасли «обучение»?
3. Если в открытой системе r-й товар является первичным фактором, ресурсы
которого ограничены (— хТ -< хг), то каким путем следует отобразить «свободные блага»,
имеющиеся в распоряжении данной системы? Будут ли результаты одинаковыми, если:
1) считать ресурсы хт бесконечно большими или 2) вовсе не принимать во внимание г-й
товар, если его ресурсы неограниченны?
4. Пусть матрица А, все элементы первой строки которой (характеризующей
производство первого товара) положительны, имеет следующий вид:
А =
""* Истолковать смысл этой матрицы и показать, что может производиться либо только
первый товар, либо первый товар совместно со вторым, либо первый товар совместно со
вторым и третьим. Показать, что всю совокупность возможных вариантов производства
единицы первого товара можно представить в виде одной комбинации производственных
отраслей с переменными множителями %i, Яг, и Я3, подчиняющимися ограничению Ях+
-f- A,2 -j- Я3=1. Составить уравнение чистого выпуска (положительного, нулевого или
отрицательного) каждого из трех остальных товаров и рассмотреть, при каких
условиях они будут представлять затраты, а при каких — выпуск.
472

16.3. ПРЕДСТАВЛЕНИЕ ОТКРЫТОЙ СИСТЕМЫ ЛЕОНТЬЕВА
В ВИДЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ПРОИЗВОДСТВЕННЫХ ОТРАСЛЕЙ
Открытая форма статической модели межотраслевых связей Леонтьева
описана в разделе 13.7. Пусть имеется п отраслей промышленности и
хозяйства и видов товаров, в том числе один первичный фактор (труд). Известными
данными являются следующие характеристики Ьтих отраслей (г = 1, 2,...,/г):
А = I—А*, где А* = [ars] есть матрица коэффициентов затрат
гс-го порядка (и принято, что элементы аГТ = 0);
b = {br} — вектор коэффициентов затрат труда;
х = {хг} — вектор конечного спороса на товары, выпускаемые
отраслями промышленности и хозяйства;
w = {wr} — вектор отраслевых издержек на заработную плату
в расчете на единицу продукции.
Если w есть заданная ставка заработной платы за единицу первичного
фактора (скалярная величина), то между Ь и w существует следующая связь:
Переменными являются:
X = {Хг} — вектор валового выпуска отраслей;
Р = {Рг\ — вектор цен на товары, выпускаемые отраслями.
Матрица А — квадратная матрица га-го порядка, все векторы также п-то
порядка.
|А 1
...
размерности (п + 1) X п. Все элементы последней строки этой матрицы, или
коэффициенты затрат труда, суть величины отрицательные. Остальную часть
матрицы составляют строки и столбцы, каждая (или каждый) из которых
имеет только один положительный элемент, а именно 1. Каждая отрасль
(производство) выпускает только один товар, отличающийся от товаров,
вырабатываемых другими отраслями; все товары, кроме выпускаемого,
являются для данной отрасли затратами или вовсе не фигурируют в ней.
Каждый товар производится в соответствующей отрасли единственным
способом; в других отраслях он может быть затратами.
Для этой системы условия равновесия выражаются уравнениями:
(I) АХ = х и (II) A'p = w,
к которым следует добавить X > 0 и р > 0, поскольку неотрицательны
и выпуск отраслей и цены. Условие (II) есть транспонированное уравнение
р'А = w' (в таком виде это условие было записано в разделе 13.7).
На основании переменных X и р можно вычислить две скалярные
величины. Общие затраты первичного фактора труда равны У = Ь'Х.
Обозначим общую сумму заработной платы через z = wY. Тогда:
Общая сумма заработной платы z — н?Ь'Х = w'X
есть линейная функция переменных, выражающих объемы выпусков X.
Вектором переменных цен р можно воспользоваться для расчета общего
конечного, спроса в стоимостном выражении.
Общая стоимость конечного спроса ? = х'р.
Теперь систему Леонтьева можно представить как частный случай
прямой и обратной задачи линейного программирования:
(I) z = -w'X (II) ? = х'р
при условии АХ = х при условии A'p = w
и Х>0; и р>0.
Следует подчеркнуть, что z и ? не максимизируются и не
минимизируются — их просто выражают через векторы X и р. Причина отсутствия
в задаче условий оптимизации выясняется при рассмотрении характера
ее решения. Разгадкой является число переменных и число уравнений в сис-
473

темах (I) и (II): как в прямой, так и в обратной задачах линейного
программирования число переменных равно п; число ограничивающих
уравнений также равно п. Следовательно, поскольку уравнения линейные,
а матрицу А мы считаем неособенной, то в таком случае допустимое решение,
если оно вообще существует (при Х>0, р > 0), является единственным.
Значит, не остается места для максимизации или минимизации z или ?, и не
может быть оптимального допустимого решения. Из ограничивающих
уравнений возможно получить единственное решение для X и р и вообще, в
соответствии с этим, только одно значение z или ?. Это совпадает с общими
рассуждениями из раздела 16.1, если допустить, что при распределении ресурсов для
удовлетворения конечного спроса в системе Леонтьева нет необходимости
выбирать оптимальный вариант. В системе Леонтьева невозможен выбор или
взаимозаменяемость производств; в формулировке задачи вовсе исключен
вопрос, почему то, а не другое производство выбрано для изготовления
данного продукта.
Однако зависимости (I) и (II) — это прямая и двойственная задачи
линейного программирования; они имеют общее и единственное решение.
Остается лишь найти решения обеих задач и показать их тождественность.
Решение получаем с помощью матрицы А*, обратной матрице А:
(I) Х = Ах, (II) р = (А')"^или же p'^w'A.
Таким образом, вектор переменного валового выпуска X выражается через
вектор конечного спроса х, а вектор переменных цен р—через вектор
отраслевых издержек на заработную плату в расчете на единицу
продукции w. Связующим элементом обоих решений является то обстоятельство,
что общая сумма заработной платы z и суммарная стоимость конечного
спроса ? равны между собой. Это и выражает тот факт, что (I) и (II) суть
прямая и двойственная задачи линейного программирования. Найдем значение
целевой функции, общее для обоих решений:
Общая сумма заработной платы z = w'X = w'A*.
Общая стоимость конечного спроса ? = х'р = р'х = w'A^x.
Первичный фактор — это труд, конечный спрос — это спрос
потребителей, предоставляющих свой труд; в состоянии равновесия доходы
потребителей и их расходы равны между собой.
Здесь впервые иллюстрируется мысль, высказанная в конце раздела
16.1. Открытую систему Леонтьева можно представить и в виде только
одной задачи линейного программирования — задачи A). При этом весь
валовой выпуск выражается через конечный спрос (X = А"хх), а общая
сумма заработной платы равна z = w'A^x. Здесь вовсе не принимаются
во внимание рыночные цены или расходы потребителей. Однако эти
элементы используются при составлении двойственной задачи; так оно всегда
и бывает. В этом случае также задаются и значения рыночных цен р = (A'^w.
Эти цены таковы, что результаты между собой уравниваются, то есть общая
стоимость конечного [спроса равна w'Ax или общей сумме заработном
платы,
16.4. ЗАМЕНЯЕМОСТЬ В ОТКРЫТОЙ СИСТЕМЕ ЛЕОНТЬЕВА
При построении открытой системы Леонтьева делаются два следующих
допущения. Во-первых, мы считаем, что каждая отрасль производит
единственный продукт, отличающийся от продуктов других отраслей, причем
затраты пропорциональны выпуску. Изменить что-либо здесь невозможно;
это — упрощение практического характера, которое помогает описать тип
рассматриваемого хозяйства. Второе допущение имеет иной характер: оно
состоит в том, что в каждой отрасли существует только один
производственный способ. Каждая из отраслей отображается в технологической матрице
только одним столбцом. По-видимому, это исключает всякую возможность
взаимозаменяемости производственных способов или по крайней мере изба-
474

вляет от необходимости выяснения, почему выбран тот или иной процесс,
а не другие возможные процессы.
Руководствуясь рис. 34 и 35, второе допущение мы можем
сформулировать следующим образом: либо на процесс производства в отрасли наложено
технологическое ограничение — соблюдения фиксированного соотношения
между затратами и выпуском (рис. 34, б), либо из определенного и
конечного числа имеющихся вариантов производственного процесса выбирается
один вариант (рис. 35), либо, наконец, выбирается один вариант
производства, для которого между затратами и выпуском сохраняется
фиксированное соотношение, и прямая, отображающая этот процесс, пересекает
кривые — геометрические места точек постоянного объема продукции,
полученные из непрерывной (линейной и однородной) производственной функции
(рис. 34, а). Поскольку нет необходимости в выборе варианта — и если
затраты считаются пропорциональными выпуску,— то совершенно
несущественно, что именно скрывается за понятием об единственном процессе,
существующем в какой-либо отрасли. Вместе с тем этот вопрос можно
исследовать при более четкой алгебраической его формулировке.
Рассмотрим прямую задачу линейного программирования для системы
Леонтьева (о выпуске товаров), не принимая во внимание двойственную
задачу (о ценах). Кроме того, запишем уравнения в виде, включающем общие
затраты труда У, а не общую сумму заработной платы z. Тогда
АХ = х и -Ь'Х=--У A)
суть (п + 1) уравнений системы, технологическая матрица которой имеет
г А]
вид .... Элементы этой матрицы являются коэффициентами левой части
уравнений. Если задан конечный спрос х = (хг, х2,..., хп), то эти
уравнения позволяют определить вектор валового выпуска X и общие затраты
труда У. В частности, У линейно выражается через х:
У-Ь'А^х. B)
Предположим теперь, что по-прежнему заданы х2, х3, ... , хп, но не хг,
конечный спрос на первый товар. Тогда систему A) можно записать в
следующем виде:
Максимизировать хх = Хг — а12Х2 — ... — а1пХп
при условии — а21Хг + Х2 — ... — а2пХп = х2,
— ап1Х1 — апА — - . •
C)
В этой задаче линейного программирования уже включено условие
максимизации. В ней имеется п ограничений, которые позволяют выразить
элементы вектора X через У. Следовательно, хг представляет максимизируемую
функцию от У; если существует допустимое решение задачи, то максимум
хх ограничен лишь наличными ресурсами труда, в противном случае он мог
бы возрастать до бесконечности. В конечном счете мы выражаем все элементы
вектора X через заданные элементы конечного спроса х21 х3, ... , хп;
максимизируемая величина хх также определяется через эти же заданные элементы.
Решение задачи C) весьма сходно с решением системы A). Разница в
основном заключается в постановке задачи — в одном случае [задача C)] хг
не задано, а максимизируется, а в другом [задача A)] хг является заданным.
В частности, определяемая нами величина У совершенно так же, как и в B),
линейна относительно всех элементов конечного спроса; разница состоит
в том, что хг в качестве максимизируемой величины выражается через х2,
аг3, ... , хп> а не является заданной, как остальные элементы.
475

Форму C) можно представить в более общем виде, для того чтобы ее
применить к тому случаю, когда технологические коэффициенты ars= xrs/Xs
/ П C)
и bs— x
n+ltS
у у фф rs rss
/Xs не являются постоянными. Перепишем задачу C), пользуясь
s n+ltSs
переменными хТ8, представляющими собой количество r-го товара,
затраченное в 5-й отрасли. Приняв хгг= О, получим:
Максимизировать
при условии
e1 = X1-S xu
Xr-%xrs = zr (r = 2,3, .... i»)
2л
s==l
^_J TI+1jS *
s=l J
(n + 1)-й товар есть труд, являющийся затратами во всех отраслях; однако
соответствующей отрасли не имеется, а значит, не имеется ни #п+1, ни ХЛ+1.
Если технологические коэффициенты постоянны, то задача линейного
программирования D) полностью совпадает с задачей C). С другой стороны,
задача D) остается задачей на условный максимум даже в том случае, когда
технологические пропорции между затратами и выпуском не являются
постоянными. Этот вопрос следует рассмотреть более подробно.
Для валового выпуска Хг первого товара требуются затраты хг1
остальных товаров (г = 2, 3,... , п) и затраты труда яя+ь г. Допустим, что существует
производственная функция, линейная и однородная:
1 = Л (^21'
Xn+1, l)'
так что
при всяком X > 0. В частном случае примем X =
21_ Х3\ ХП1
то есть fx (а21, а31, ..., ап1, 6Х) = 1, где а и 6, как и ранее, суть
технологические коэффициенты. Разница состоит в том, что эти коэффициенты —
переменные, а не постоянные величины. В системе Леонтьева, где
технологическая матрица имеет вид ~-г; , коэффициенты— величины постоянные,
они являются элементами первого столбца матрицы: элемент первой
строки—это «1», далее следуют ( — а21), ( — а31), ..., ( — ап1), ( — Ьг). Теперь же
становится возможной взаимозаменяемость затрат, тогда как в системе
Леонтьева она не допускалась.
Перепишем задачу D), используя производственные функции типа E)
для всех п товаров.
Максимизировать
Xl == /l \X1V ^21' • • • > Хп+1, 1/ 2лш Xls
при условии
I— 2л х
s=i
/r \xi
п+1, г
) 2л xrs "" Хт V — 2, 3, . . . , П)
s=i
и
2л Хп+1, » —
s=l
F)
476

где, чтобы упростить запись, хгт (равный нулю) также представляется в
производственной функции в виде «переменной». Нужно определить значения
п(п + 1) переменных xrs, где г = 1, 2, ... , (п + 1) и s = 1, 2, ... , п.
Функция этих переменных максимизируется при условии выполнения п
ограничений. Заданными являются пвеличин, значения элементов хг(г = 2, 3 ,... , п)
и У.
Решая задачу с помощью методов дифференциального исчисления,
можно показать, что для максимизации хг нужны не значения п(п + 1)
переменных xrs, а значения тг2 соотношений crs = xrs/xn+ltS (для г = 1, 2, ... , п,
s = l,2, ... , п). Далее, величины этих соотношений определяются
независимо от заданных значений х2, х3, ... , хп я Y. Доказательство этого можно
найти в статье Самуэльсона в сборнике под ред. Купманса [11, гл. VII].
Отсюда следует, что, какие бы ни задавались значения х21 х3, ... , хп
и У, и какое бы максимальное значение ни принимала величина хг,
соотношения
С — ХТ8 ___. arS
TS *П+1, 8 bs
в оптимальном решении задачи F) остаются постоянными. При решении этой
задачи мы исходим сначала из переменных технологических коэффициентов.
Однако, когда достигнуто оптимальное решение, технологические
коэффициенты становятся постоянными, какие бы значения ни принимали величины
хг и У. Следовательно, задача F) имеет то же решение, что и система
Леонтьева, которая с самого начала считает технологические коэффициенты
постоянными.
Наконец, хотя в задаче F) мы считаем У заданным, так же как
#2» жз> ••• » хп> в оптимальном решении мы можем исключить это допущение
с помощью соотношения зависимости, которое, как и в системе Леонтьева,
должно существовать между значениями У и хг, х2, ... , хп (первая величина
максимизируется, остальные заданы). Это соотношение — линейное
уравнение B).
Значит, можно сдел:ать вывод, что в системе Леонтьева и в ее решении
допустима взаимозаменяемость затрат в соответствии с непрерывной
производственной функцией, линейной и однородной (при пропорциональности
между затратами и выпуском). Тот же вывод получается и в случае
единственно возможного заданного способа (технологические коэффициенты
которого постоянны), и в случае, если этот процесс есть один из числа многих
возможных. Суть дела в том, что в системе Леонтьева не рассматривается
необходимость принятия решений (например, фирмой) и, таким образом,
заменяемость является случайной.
16.5. ПРЕДСТАВЛЕНИЕ ТЕХНОЛОГИЧЕСКИХ ВОЗМОЖНОСТЕЙ
Приведенное выше понятие технологии (см. 16.2) является весьма
широким. Задана матрица технологических коэффициентов А — [ars] размерности
т X п. Имеется т товаров, отображаемых строками матрицы А, и п
базисных производств, отображаемых ее столбцами. Элементы строки матрицы А
представляют собой различные количества некоторого товара, затрачиваемые
или выпускаемые в соответственных производственных отраслях. Элементы
столбца матрицы А показывают, какие товары затрачиваются и выпускаются
при единичном уровне соответствующего базисного производства. Все
сказанное в одинаковой степени относится к самым разнообразным системам,
например к фирме, к некоторому сектору народного хозяйства, к народному
хозяйству в целом (если оно рассматривается как открытая система).
Матрица отображает специфические технологические возможности в рамках
системы, что последняя собой ни представляла бы, и не более того.
Пусть х = {хг} (г = 1, 2, ... , т) есть вектор выпуска, получаемого при
комбинировании базисных производств, взятых с уровнями % = {A,s}
(s = 1, 2, ... , тг), где As>0. Тогда технологическое преобразование уровней
477

X к выпуску х попросту описывается уравнением
х = АХ (Х>0) A)
или, в развернутом виде,
Х2 = «21^1 + й22^2 + • • • + a2n^n» I /2)
Любая технологическая возможность в рамках системы описывается
уравнением A) или системой уравнений B). Они отображают всю
совокупность допустимых распределений для задачи линейного программирования,
ограничениями которой является соотношение A).
Не надо забывать о результатах предположения линейности, или
пропорциональности. Если увеличить вдвое уровень каждой из
производственных отраслей, то в соответствии с уравнением A) удваивается и выпуск
каждого из товаров; это справедливо и для любого другого изменения уровней
в одинаковой пропорции для всех способов. Поэтому целесообразно
проводить различие между относительным распределением ресурсов и масштабом
производства. Единичную комбинацию базисных производственных отрас-
лей можно характеризовать вектором jx = {ц8}, где \i$ > 0 и^|*8=1;
« 8=1
соответствующий выпуск описывается уравнением х = Afi. С изменением
элементов \is изменяется относительное распределение ресурсов, хотя всегда
уровень остается единичным. Масштаб производства учитывается затем
с помощью коэффициента х, одинакового для всех производственных
отраслей. Тогда любое распределение или состояние производства будет задано
уравнением
X = х {\i8}, х = АХ = хА {ц8}.
Различие между относительным распределением ц и масштабом
производства х проводится во всех случаях без исключения. Например, если
эксплуатируется только первая базисная производственная отрасль, то
относительное распределение задается постоянным вектором (л = A, 0, ... , 0),
масштаб производства — уровнем Хг использования этой отрасли:
х = АХ = Хх
где X = (Xlf 0, ... , 0).
В зависимости от того, производится ли товар (выпуск), потребляется
ли он (затраты) или вовсе не участвует в рассматриваемой отрасли,
коэффициенты ars могут быть положительными, отрицательными или нулевыми.
Аналогичным образом в соответствии со своим знаком истолковываются
элементы вектора выпуска х. В общем можно считать, что в любой реальной
системе имеется один (или несколько) видов конечных продуктов, которые
невозможно получить извне системы и для которых яг> 0, и один (или
несколько) видов первичных факторов, поступающих извне системы, для
которых хт < 0. Могут быть также и промежуточные продукты, для которых
хг — 0; эти продукты не поступают извне системы и не производятся для
потребления за пределами сис/гемы. С другой стороны, первичный фактор
вполне может не только поступать извне системы, но и являться выпуском
некоторых производственных отраслей, а • конечный продукт не только
производиться для потребления за пределами системы, но и затрачиваться
в некоторых отраслях. Это попросту означает, что любая строка матрицы А
478

может включать как положительные, так и отрицательные коэффициенты.
Вместе с тем характерным для реальной системы можно считать еще одно
свойство: непременно имеется хотя бы один первичный фактор, который
только потребляется (и никогда не производится). Таким фактором можно
считать «труд» или, по крайней мере, «неквалифицированный труд», если
«квалифицированный труд» рассматривается как продукт такого вида
деятельности как «обучение». В соответствующей строке матрицы А все
коэффициенты отрицательны. По аналогии предположим существование хотя бы одного
конечного продукта, который может производиться, но не потребляется ни
в одной отрасли, так что в соответствующей строке матрицы А все
коэффициенты положительны (или равны нулю).
Указанные свойства технологической матрицы соответствуют частным
случаям. Они удобны для применения матрицы А в реальных системах, но
не требуются с математической точки зрения, и можно построить системы,
для которых данные свойства не характерны. Для удобства и простоты
(но не более того) сделаем здесь следующие допущения:
Допущение I. Должен существовать один товар (будем считать его
первым), который в качестве конечного продукта направляется для потребления
за пределы системы, не поступает в качестве первичного фактора извне
системы и не является затратами ни в одном из производств, так что als>0
ж хг>0.
Допущение II. Должен быть один товар (будем считать его
последним), который поступает в качестве первичного фактора извне системы и
является затратами во всех производственных отраслях, так что ams<0
и хт<0.
Во всех этих рассуждениях мы не принимаем во внимание тривиального
случая к = О, когда не эксплуатируется ни одно из производств; в противном
случае хг и хттакже могли бы быть равны нулю. Следовательно, когда в A)
мы пишем А,>0, это следует понимать следующим образом: все Я8>0,
причем некоторые из A,s>0.
Более общий анализ, основывающийся на других и не столь строгих
ограничениях, приведен в сборнике Купманса [11, гл. III]. Одно из таких
частных допущений рассматривается и иллюстрируется упражнениями
4 и 5.
Графическое изображение технологических возможностей,
возникающих при преобразовании A), полезно во всех случаях, но особенно если число
товаров т не превышает трех. Пусть имеются два пространства, в которых
могут быть отображены (соответственно) точки к и х. /г-мерное пространство
производственных отраслей содержит точки к — (А,1Э Я2, ... , А,п), каждая из
которых отображает определенную комбинацию производственных отраслей;
так как % > 0, то мы должны взять только положительную область этого
пространства. Еще более полезно га-мерное пространство товаров, точки
которого х = (хг, х2, ... , хт) отображают некоторую совокупность выпусков.
Рассматривается все это пространство, так как элементы х могут быть как
положительными (выпуск), так и отрицательными (затраты). Однако мы
допускаем существование только положительных хх is. только отрицательных
хт, что является значительным упрощением. Тогда преобразование A)
оказывается «отображением» пространства отраслей на пространство
товаров, и сразу же можно применить топологические приемы (см. 11.5). Однако
в настоящем анализе мы стараемся избежать наиболее специальных
математических вопросов; ограничимся рассмотрением случаев т = 2, 3 и
графическим изображением двух- и трехмерного пространства товаров. Более
общие результаты формулируются без доказательства по аналогии с
полученными для случая т = 3.
Рассмотрим случай двух отраслей и двух товаров (т — п = 2):
А =
479
22J "

Пусть два базисных производства описываются матрицами АA)= пп
L a21 J
АB)= | 1Я~]. По сделанному нами допущению, элементы ап и а12 неотрица-
тельны, а а21 и а22 отрицательны. Поскольку единичньщ уровень каждой
из производственных отраслей выбирается произвольно, весьма удобно
принять а21= а22= —1, то есть единичным считать такой уровень
производства, которому соответствует единица затрат «труда». Тогда
неотрицательные элементы ап и а12 характеризуют выпуск конечного продукта хх
на единицу «труда» в двух базисных производствах. В пространстве товаров
Оххх2 построим точки АA)= (аи,—1) и АB)= (а12,— 1). Эти точки
отображают выпуск при единичном уровне первого или второго производств. Любая
комбинация (тоже единичная) этих базисных отраслей, описываемая
системой уравнений
^а^ + а A-,), }@<11<1),
отображается точкой Р, расположенной на отрезке прямой, соединяющей
точки Аа) и АB> на рис. 51. Чтобы учесть масштаб производства,
результаты для единичного уровня можно умножить на любой коэффициент
к (к > 0). На рис. 51 это означает, что любая точка луча ОАау отображает
выпуск первого производства при различных его уровнях и аналогично для
луча ОА{2)— выпуск второго производства, а точки луча ОР —
комбинацию этих двух производств. Таким образом, любой возможный выпуск
х — АХ = кА{\х, 1 — \х} отображается некоторой точкой на луче ОР,
который может вращаться относительно точки О в секторе, ограниченном
лучами ОАа) и OAi2) и включающем эти лучи. Следовательно, все множество
допустимых точек х = АХ лежит внутри или на гранях конуса OAa)Ai2).
В соответствии со сделанными предположениями, вершиной этого конуса
является точка О, и расположен он в квадранте х{> 0, х2< 0. Этот конус —
графическое отображение множества допустимых распределений ресурсов
или допустимых производственных отраслей, причем допустимые решения
понимаются так же, как и в линейном программировании.
В упражнении 6 показано, что при сделанных предположениях
невозможен случай двух товаров и трех или более производственных отраслей
(т = 2, п > 2). Но так или иначе задача с двумя товарами не представляет
большого интереса: ведь один из этих товаров — «труд», а второй —
единственный конечный продукт. Более важен случай трех товаров (т?г = 3),
который дает трехмерное графическое изображение пространства товаров.
Количество производств при этом может быть равно двум и более.
В случае трех товаров и двух производств (т = 3, п = 2) мы имеем:
а21 а22 ,
«31 a32j
= \а2
a3lJ
, А<2) =
где, согласно сделанным предположениям, яп> 0 и а12> 0, а31< 0 и азг < 0.
Этот случай иллюстрируется на рис. 52, причем уровни производств и здесь
считаются единичными при а31= а32 = —1.
В пространстве Охгх2х3 построим две точки Аа) и ЛB); тогда любое
возможное распределение отображается точкой х внутри двумерного конуса
OA(l)Ai2) или на его грани. Допустимые точки х = АХ опять лежат внутри
или на грани двумерного конуса с вершиной в точке О, размещенного уже
в трехмерном пространстве. Сечение конуса плоскостью xs= —1 (что
соответствует единичному уровню производства, или выпуску при затрате
единицы «труда») также показано внизу на рис. 52. Это сечение — отрезок
прямой, соединяющей точки Аа) и АB), которые в соответствии со сделанными
допущениями лежат где-то правее вертикальной оси (х2).
480

В случае трех товаров и трех производственных отраслей (т = п = 3):
Гап а12 а13~|
А = а21 а22 а23 ,
La3i аз2 a3sJ
, A<3> = U3
Графическое изображение этого случая показано на рис. 53. И в этом
случае ап, а12, а13>0, и, согласно выбранным единичным уровням, а31=
= а32 = я33= —1- Три точки Аа\ А{2) и ЛC), находящиеся в пространстве
Ох±х2х3 и на сечении конуса
плоскостью #3= —1, составляют двумерный
треугольник. Ни одна из этих
точек (например, АC)) не может лежать
на отрезке прямой, соединяющем две
другие точки. В противном случае
производственная отрасль АC) оказалась
бы комбинацией отраслей АA> и А<2);
она не была бы базисным производством
и не заслуживала бы включения в
Рис. 51.
Сечение плоскостью
Рис. 52.
матрицу А. Если не считать этого ограничения, точки Аа\ АB) и А(ЗУ
могут находиться в любом месте плоскости #3= —1, вправо от
вертикальной оси (х2). Допустимые точки х = Ah лежат внутри или на гранях
трехмерного конуса ОАШАB)А{Ю с вершиной в точке О.
Если число производств превышает три, так что в матрице А имеется
более трех столбцов, или более трех базисных производственных отраслей
АA\ АB), А<3>, ... , то положение весьма сходно с изображенным на рис. 54.
Чтобы учесть дополнительные базисные производства, необходимо лишь,
чтобы точки Аа\ Ai2\ ЛC), ... в секущей плоскости х3= —1 представляли
собой плоский многоугольник и были бы экстремальными точками выпуклого
множества. Это требуется, если производственные отрасли должны быть
базисными, и ни одна из них не является комбинацией остальных.
Следовательно, для случая трех товаров (т = 3) все множество
технологически возможных вариантов распределения ресурсов отображается
точками в трехмерном пространстве, лежащими внутри или на гранях конуса
с вершиной в точке О; этот конус «порожден» многоугольником в плоскости
х3= —1. Плоский многоугольник (в секущей плоскости х3= —1)
представляет собой выпуклое множество, экстремальные точки которого ЛA\ А^2\
ЛC>,... . Образованный этим многоугольником конус имеет почти те же
пропорции, и его можно называть выпуклым конусом. Можно установить четкое
31 Р. Аллен
481

различие между внутренними и граничными точками как выпуклого
множества, так и выпуклого конуса. Поверхность конуса состоит из одной или
нескольких граней, то есть плоских треугольников, аналогичных
треугольнику ОА({ЫB\ и прямых вида ОА^\ разделяющих эти грани»
Совершенно ясно, что все эти рассуждения можно распространить на
случай более чем трех товаров, и очевидно, что вся теория выпуклых
множеств и соответствующих им выпуклых конусов может быть здесь применима
Выпуклый конус
Сечение плоскостью Ху*-1
Рис. ЪЪ9
Сечение плоскостью x^-i
Рис. 54.
(см. 15.7). Для случая т товаров технологически допустимые варианты
распределения отображаются допустимыми точками х = АХ, лежащими внутри
или на гранях т -мерного выпуклого конуса. Обозначим этот конус через:
(А); он имеет вершину в точке О и одну или более граней, которые в общем
случае имеют (т—1) измерений, но могут иметь и меньшую размерность.
Исследовать тип конуса (А) всегда можно с помощью секущей плоскости
—1; сечение является выпуклым (т—1)-мерным множеством.
х
Задачи и упражнения
1. Рассмотреть более широкую область видов конуса (А), образующихся в том
случае, если мы отказываемся от допущения (I), но по-прежнему сохраняем
допущение (II). Показать, что если матрица А второго порядка, то конус может быть похож на
изображенный на рис. 55 и что это влечет за собой «расточительные» производства
(затраты имеются, а выпуск отсутствует).
2. Распространить условия предыдущей задачи на случай матрицы А третьего
порядка, пользуясь при этом рис. 53. Показать, что в таком случае будут существовать
производственные отрасли, в которых для выпуска товара х\ затрачивается (кроме труда)
товар #2, и обратно. Доказать, что и х\ и Х2 могут быть конечными продуктами, но оба
они должны поступать извне такой системы. В каком смысле подобная система является ч
«нереальной»? Рассмотреть альтернативную возможность такого ограничения множества
точек X в пространстве производств, чтобы хотя бы один из товаров х\ или хч нельзя
было получить извне системы.
482

3. Отказаться от допущений (I) и (II) и показать, что если матрица А второго
порядка, то конус (А) может принимать всевозможные формы, в том числе «сплошную»
форму (то есть охватывать собой всю плоскость) и три формы, изображенные на рис. 56.
Распространить это доказательство на случай матрицы А третьего порядка. ^^
4. Вместо допущений (I) и (II) сделать два следующих допущения:
а) не существует такого вектора Л, ^> О, что х = Ah = 0;
б) не существует такого* вектора X > О, что х = Ah > 0.
Здесь символ «>» исключает возможность равенства всех элементов вектора нулю.
Показать, что эти допущения налагают менее строгие ограничения, чем допущения (I)
и (II), а именно что они удовлетворяются в случае выполнения (I) и (II), но не наоборот.
(См. сборник Купманса [11, гл. III].)
5. Сделав те же допущения, что и в
предыдущем упражнении, истолковать
допущение (а) в предыдущей задаче как
«производственный процесс необратим» и
допущение (б) как «нельзя сделать что-либо из
ничего». Показать, что если матрица А второго
порядка, то допущение (а) исключает
вариант рис. 56, б, а допущение (б) — вариант
рис. 56, в, так что при выполнении обоих
допущений возможен только вариант
рис. 56, а. Сравнить с рис. 51 и 55.
а»?
X,
\
Л
-г \
\
Ч
Рис. 55.
РисЛ 56.
6. Показать, что если размерность матрицы А есть 2 X 3, то невозможны ни
допущения (I) и (II), ни допущения упражнения 4.
7. Вычертить рисунки, аналогичные рис. 53, если
а) А =
Г 12 3 11 Г 1 2 1]
2 0 3 L б) А= 2 1 1 .
L —1 —1 —ij L —1 —1 —ij
8. Вычертить конусы (А) и их сечения плоскостью ха = —1, если
2 2 1
а) А==
-1 —1 —1
б) А =
2
3
— 1
1 1
1 2
-1 —1
и сопоставить их с рисунками к предыдущему упражнению. В каком смысле можно
утверждать, что первое базисное производство в этих матрицах явно более «эффективно», чем
остальные базисные отрасли производства?
16.6. ЭФФЕКТИВНОЕ РАСПРЕДЕЛЕНИЕ ПРИ НЕОГРАНИЧЕННЫХ
РЕСУРСАХ ПЕРВИЧНЫХ ФАКТОРОВ
До настоящего момента мы рассматривали только чисто технологические
свойства системы, описываемой уравнением х = АЪД>0). Но даже при
этом вопрос не сводится лишь к «подсчету числа уравнений». Например, в
частном случае при т=п (число производственных отраслей равно числу това-
483
31*

ров) и неособенной матрице А, уравнение х = Ак можно превратить в
обращенное уравнение к = А"хх. Но это не гарантирует неотрицательность
элементов вектора к для любых заданных значений выпуска и не позволяет
выявить соответствующие друг другу значения элементов векторов х и к.
В более общем случае (т Ф п) даже возможность обращения уравнения
х = АЛ, не является очевидной. С точки зрения технологии задается выпуклый
конус возможных точек к в положительном секторе пространства
отраслей, а также соответственный выпуклый конус возможных точек х в
пространстве товаров; размерность точек различна. Теперь остается перейти
от технологически допустимых к экономически оптимальным или
эффективным решениям. В задачах линейного программирования наряду с
ограничениями добавляется некоторый критерий максимизации или
минимизации, в соответствии с которым мы преобразуем допустимые решения в
решения оптимальные. Нечто подобное требуется и здесь: критерий
оптимизации или намеченная цель должны характеризоваться не только с чисто
технологической точки зрения.
Сначала сделаем общее замечание. Сформулированные выше свойства
выпуклых множеств (см. 15.7) заставляют предположить, что
оптимальные или эффективные варианты распределения ресурсов следует искать на
ограничивающей поверхности (гранях) яг-мерного конуса (^1), построенного
на основе технологического преобразования х = Ак. Эта поверхность в
общем случае состоит из граней, имеющих размерность (т—1) или меньше.
Например, если т = 3, то она состоит из плоских треугольников и
разделяющих (или связывающих) их одномерных ребер — образующих. Следует
сделать некоторые уточнения относительно характеристики граней,
составляющих поверхность конуса (А).
В случаях трехмерного пространства (см. рис. 53 и 54) существенным
является следующее. Если число товаров равно трем, то грань типа OA^AW
является двумерной; ее можно рассматривать как открытую, если к ней не
причислены ребра ОЛ<1> и ОА^2К и как замкнутую, если она включает эти
ребра. В первом случае (открытая грань) линии, подобно ОАМ и ОА<2\
следует также считать гранями; эти грани одномерны, причем они являются
открытыми, если к ним не причислена точка О, и закрытыми, если точка О
присоединена к ребру. Легко составить алгебраическое описание грани.
Если конус изображен рис. 54, то:
ап а12 а13 а14П
а21 а22 а23 а24 .
а31 а32 а33 a34j
а31 а32 а33 а34_
Весь конус (А) определяется четырьмя столбцами (А^1), А<2>, А<8) и АD))
матрицы А и уравнением х = Ак. Грань OAa)Ai2) точно таким же образом
определяется! двумя столбцами АA) и АB); она отображает все множество
возможных вариантов распределения при использовании только двух первых
базисных производств.! Следовательно, грань (F) = ОАа)А™ определяется
уравнением
где F =
ап ал
Эта грань является замкнутой или открытой в зависимости от того,
причислены ли к ней сами базисные производства Аа) и Ai2\ то есть от того,
допустимы ли значения к == {к1У 0) или к = @, к2). Аналогично этому
определяется и одномерная грань (F) = ОАа):
: = FA, (Л>0), где F =
484
B)

Следует отметить, что в уравнении A) h есть вектор, состоящий из двух
элементов, тогда как в уравнении B) к представляет одноэлементное
скалярное число. Этот результат очевидным образом обобщается на случай любого
числа товаров т.
Рассмотрим сначала простую задачу эффективного распределения
ресурсов. Будем считать, что не налагается ограничений на количество
первичных факторов, которые можно получить извне системы, например не
ограничиваются ресурсы «труда», которые можно использовать. Если не
ощущается потребности в самом первичном факторе, то есть если этот фактор не
относится к необходимым требованиям системы, то в таком случае он является
свободным благом и вообще не заслуживает рассмотрения. Следовательно,
чтобы случай был «реальным», мы будем в дальнейшем считать, что все
первичные факторы — желательные товары и фигурируют в числе потребностей
системы. Кроме того, для удобства примем, что технологическая матрица А
не включает промежуточных продуктов или же что матрица сокращена
с целью освободиться от таких продуктов.
С технической точки зрения задача ставится следующим образом.
Технология системы описывается матрицей А размерности т X п.
Существует потребность в каждом из т товаров; некоторые из этих
товаров — первичные факторы, могущие быть полученными извне системы в
неограниченном количестве, а другие — конечные продукты, которые получить
таким образом невозможно.
Пространство товаров является m-мерным, и так как требуются все без
исключения товары, то при отображении потребностей используются все
размерности пространства.
Теперь остается определить поставленную цель и на этой основе
выбрать — из всего множества допустимых точек конуса (-4) —. те точки,
которые являются оптимальными или эффективными.
Определение. Допустимое распределение ресурсов х = Ah
является эффективным, если увеличение выпуска одного товара,
входящего в х, возможно лишь при условии уменьшения выпуска другого
товара.
Как и ранее, «выпуск» понимается здесь в прямом смысле — как
«выпуск для конечного спроса». Следовательно, в эффективной точке х выпуск
одного конечного продукта может быть увеличен только при условии
сокращения выпуска другого конечного продукта или за счет увеличения каких-
либо затрат. В последнем случае ограничивается применение затрачиваемого
товара в его собственном желательном качестве (для непосредственного
удовлетворения конечного спроса.— Ред.),например, если для производства
требуется больше труда, то уменьшается возможность «досуга».
Проанализируем теперь случай трех товаров и трех (или более) отраслей.
Конус (А) технологически допустимых точек показан на рис. 53 и 54.
Поверхность конуса (А) состоит из замкнутых двумерных граней типа ОАA)АB);
эти же грани могут рассматриваться как открытые, но тогда поверхность
конуса должна включать и одномерные грани, аналогичные лучу ОАа\
Назовем нормалью к конусу (А), восстановленной к нему в точке х, такой
луч прямой, который направлен вовне конуса и ортогонален к поверхности
конуса в точке х. Следовательно, нормаль определена только для точек
поверхности конуса (А). В каждой точке двумерной грани можно восстановить
только одну нормаль. Нормаль же к одномерной грани не определяется
однозначно; так, в некоторой точке грани ОАB) может быть восстановлено
бесчисленное множество нормалей к этому ребру, расположенных между
нормалями к граням ОАа)АB) и OAi2)Ai3\
Точка х конуса (А) является эффективной в том и только в том случае,
если в пределах конуса (А) нет неотрицательного направления изменения;
это значит, что при любом изменении должен уменьшиться выпуск какого-то
продукта. Следовательно, в точке х должна быть нормаль, направленная
положительно. Если же такая нормаль существует, то любое движение от
485

точки х в пределах конуса (А) должно быть направлено.под прямым углом
к нормали или под углом, большим чем прямой, а значит, всегда не
в положительном направлении. Следовательно:
Точка х конуса (А) является эффективной в том и только в том
случае, если эта точка расположена на поверхности конуса {А) и
нормаль в ней направлена положительно.
Теперь рассмотрим двумерную грань конуса (А) типа OAA)Ai2\ Если
точка в пределах этой грани (а не на одном из ее ребер) имеет положительно
направленную нормаль, то одинаковая положительно направленная
нормаль будет и в любой другой точке в пределах грани и на ее ребрах. Поэтому
если эффективна какая-либо одна точка открытой грани, то эффективна и вся
замкнутая грань в целом. Аналогично этому нормаль к одномерной грани
(ребру) типа ОА{2) может быть расположена во всей области между норма-
лями к соседним граням О А а)А{2) и OAi2)AiB\ Даже если нормали к
последним граням и не направлены положительно, то какая-то промежуточная
нормаль, расположенная между ними, все же может оказаться
положительно направленной, то есть точка на ребре ОАB) будет эффективна, и, таким
образом, все другие точки этого ребра окажутся тоже эффективными.
Отсюда следует, что нужно искать не столько отдельные эффективные
точки конуса (А), сколько эффективные грани этого конуса. На рис. 53
имеется одна эффективная грань ОАа)А{2), к которой причислены и ее
ребра ОАа) и ОАB\ На рис. 54 имеются две эффективные грани ОА{1)А{2)
и ОАB)А™\ включая их ребра ОАа\ ОАB} и OAi3\ Далее, каждый из этих
конусов можно повернуть таким образом, чтобы ни одна из двумерных
граней не была эффективной и чтобы эффективным был только один из лучей типа
ОАа); следовательно, эффективные точки могут быть представлены
одномерной гранью.
Остается выразить все эти соображения алгебраически. В случае трех
товаров технологическая матрица для любого п > 3 имеет следующий вид:
[а1г а12 . . . alnl.
а21 а22 .. . а2п
«31 «32 ... «3nJ
В соответствии с уравнениями A) и B) одномерная грань ОАа) и двумерная
грань OAa)Ai2) соответственно описываются матрицами
*21
и F =
C)
Аналогичным образом определяется и любая другая грань. Пусть р =
^(Pi» P2» Рз) — любой положительный вектор или положительное направление;
нам нужно знать только соотношение рх: р2'- р3 (конечно, все элементы р1У
Ръ> Рз должны быть положительными, р > 0). Пусть эффективным является
ребро ОАа); тогда оно имеет положительно направленную нормаль р.
Значит, вектор р должен быть ортогональным вектору (аи, а21, а31), но
расположен под прямым или тупым углом к любому другому направлению в конусе
(А) и, в частности, к линиям ОА{2), ОА{2) и т. д., направления которых
характеризуются соответственно векторами (а12, а22, а32), («13, «2з> «зз) и т- Д-
Далее, косинус угла между р и (а1Ъ а21, а31) пропорционален РхаХ1-\~ р2«21+
+Рз«з1' а это выражение должно быть равно нулю (как косинус прямого угла).
Углы между вектором р и другими ребрами суть прямые или тупые; их
косинусы определяются аналогичными выражениями и должны быть
неположительны по знаку. Следовательно, ОАа) является эффективной гранью, если
Piam + Р2а*п + Рз«зп < 0.
486

Предположим теперь, что OAa)Ai2)— эффективная грань, так что
существует положительно направленная нормаль р, которая расположена под
прямым углом к ребрам ОАа) и ОА{2) и под прямым или тупым углом ко всем
другим полулучам ОАC\... . Тогда
зп32 = 0»
Piai3 + Ргагз + Рзазз < 0, [ E)
Системы D) и E) суть алгебраические условия эффективности граней,
соответственно одномерных и двумерных. Все левые части соотношений
неположительны (<0), а те, которые относятся к лучам, принадлежащим
эффективной грани, суть равенства (= 0). Все эти соотношения можно
сокращенно записать с помощью матриц:
p'F = O и р'А<0 (р>0), F)
хде F есть подматрица матрицы А^ для грани, как выше в C). Если для F)
можно подобрать положительный вектор р (р > 0), то грань является
эффективной.
Этот анализ выполнен для случая трех товаров (ттг= 3). Однако
результат, выраженный в форме уравнений F), имеет общий характер; это
доказано в сборнике Купманса [11, гл. III]. Для любой технологической
матрицы А размерности т X п имеют место следующие услодия эффективного
распределения ресурсов.
Алгебраическая формулировках
Замкнутая грань (F) конуса (А) является эффективной в том
и только в том случае, если существует такой положительный вектор
р, что
p'F = O и р'А<0 (р>0),
где F есть подматрица матрицы А, характеризующая исследуемую
грань.
Графическая формулировка:
Замкнутая грань (F) конуса (Л), то есть грань, к которой
присоединены ее пограничные ребра, является эффективной в том и только
в том случае, если в открытой грани (F),ne включающей эти ребра,
существует хотя бы одна эффективная точка, то есть в том и только
в том случае, если существует положительно направленная нормаль р
к открытой грани. Направление р является единственным, если
размерность грани (F) равна (т—1), и не является единственным, если
эта размерность меньше, чем (т—1).
Теперь задача решена полностью. Допустимые варианты распределения
ресурсов в производстве отображаются всем множеством точек х= Ah
конуса (А). Эффективные варианты распределения (при принятом выше
определении эффективности) отображаются точками эффективных граней конуса
(А), а последние характеризуются приведенными выше условиями.
Очевидно, что могут существовать одна или несколько эффективных граней,
размерность которых равна (т—1) или меньше; это иллюстрируется рис. 53
и 54.
Практически задача состоит в том, чтобы найти вектор р,
удовлетворяющий условиям F). Здесь нам помогает сечение конуса (А) плоскостью
х3= —1, изображенное для случая трех товаров (т = 3) на рис. 53 и 54.
Конус в целом можно вообразить себе, смотря вниз на многоугольник
сечения из точки О, которая расположена над секущей плоскостью. Нужно
отыскать нормаль р = (р1э р2, р3) для каждой грани, например для каждой
стороны или вершины многоугольника сечения. Значения соотношений
487

Pv j?2: Рз находим из уравнений системы D) или E), а знаки элементов р1г
р2 и р3 проверяются с помощью неравенств этих систем. Если все элементы р
оказываются положительными, то грань является эффективной. Можно
поочередно рассмотреть каждую сторону или вершину сечения; если она
имеет положительно направленную нормаль в плоскости сечения, то грань,
идущая от нее к точке О, может иметь положительно направленную нормаль.
Это зависит от того, в какую сторону поворачивается нормаль из плоскости
сечения, когда переходим к рассмотрению грани конической поверхности.
Упражнения 1 и 3 позволяют попрактиковаться в отыскании р для граней
реальных конусов.
Задачи и упражнения
1. Рассмотреть технологическую матрицу задачи 7(а) к разделу 16.5. Показать, что
р = B, 1, 6) является нормалью к грани ОЛа)А^\ р =* (—3, —2, —9) к грани O4<2U<3>
и р = A, 1, 4) к грани ОЛA)Л<3) конуса (А). На этом основании показать,,
что эффективные варианты распределения ресурсов в производстве отображаются
точками двух граней конуса (А).
2. Показать, что конус (А), построенный на основе технологической матрицы
упражнения 1F) раздела 16.5, имеет только одну эффективную грань.
3. Показать, что ни одна из трех двумерных граней конуса (А), построенного на
основе технологической матрицы упражнения 8(а) раздела 16.5, не имеет положительно
направленной нормали. Доказать, что эффективной является только образующая ОАа\
4. Исследовать случай матрицы А размерности 3X2, конус которой дан на
рис. 52. Показать, что в зависимости от положения лучей Аа) и Ai2) эффективными
являются либо вся грань ОА{Х)А<2), либо только одна из образующих ОАа> или ОА{2>.
16.7. ЦЕНЫ И ДВОЙСТВЕННАЯ ЗАДАЧА
В задаче, приведенной в разделе 16.6, эффективное производство
зависело от существования положительного вектора р, удовлетворяющего
условиям F), в развернутой форме записанным в виде системы D) или E). Такой
вектор в пространстве товаров должен быть нормалью к эффективной грани
конуса (А), отображающего технологические возможности, описанные
уравнением х = Ak. На следующем этапе мы должны интерпретировать вектор
р уже как вектор цен и затем связать задачу раздела 16.6 с ее двойственной
задачей.
Компоненты положительного вектора р считаются
внутрипроизводственными или расчетными оценками; точно устанавливаются не их абсолютные
значения, а только соотношения между ними. Эти оценки пока еще не
связаны с рыночными ценами; в самом деле, понятие рынка не определено, и.
его может вовсе не быть. Рассмотрим случай трех товаров и предположим,
что конус (А) имеет эффективную двумерную грань ОА^ А^2\ Тогда
существует единственное соотношение элементов рг: р2: р3, являющихся
расчетными оценками, при котором выполняются условия E) раздела 16.6.
Выражение (р1а11+р2а21+ р3а31) есть чистая прибыль при этих оценках при
единичном уровне производства А^; элементы а могут быть как
положительными, так и отрицательными (это соответствует товарам, выпускаемым и
расходуемым), так что при вычислении чистой прибыли выручка
сопоставляется с издержками. Аналогично этому выражение (Pia12 + р2а22 + Рз^зг)
есть чистая прибыль для единичного уровня производства А&К В
соответствии с условиями E) раздела 16.6 прибыль в обоих случаях равна
нулю.Следовательно, обе отрасли (А^ is. A^) дают нулевую прибыль, так же как
любая комбинация этих отраслей, то есть любое эффективное распределение
на грани 0ЛA>Л<2>. Остальные соотношения системы E) раздела 16.6
показывают, что все другие производственные отрасли, то есть А(г\ А^\ ...,
или любая комбинация с участием этих способов, дают нулевую или
отрицательную прибыль.
Полученный результат можно обобщить на случай т товаров. Здесь
эффективная грань имеет либо (т — 1)-ю, либо меньшую размерность (в
последнем случае система оценок не определяется однозначно). Для любой
488

эффективной комбинации производств расчетные оценки таковы, что чистая
прибыль равна нулю; для любой другой комбинации производств прибыль
отрицательна (или в лучшем случае равна нулю). Следовательно, расчетные
оценки можно определить следующим образом:
При системе расчетных оценок р (р > 0), которая может быть,
а может и не быть единственной, ни одна из производственных
отраслей, включенных в технологическую матрицу А, не дает положительной
прибыли, а всякая эффективная отрасль дает по этим оценкам нулевую
прибыль.
Расчетные оценки служат показателями эффективности распределения
ресурсов. Вообще говоря, верно то, что при эффективных вариантах
распределения прибыль равна нулю, а при других — отрицательна. Однако,
поскольку могут быть многочисленные системы оценок, а значит, могут иметь
место и различные варианты эффективных распределений, следует учитывать
возможность существования не только отрицательной, но и нулевой прибыли,
помимо рассмотренных возможностей эффективного производства. Вместе
с тем во всех случаях можно утверждать, что убыточные отрасли (дающие
отрицательную прибыль) не являются эффективными.
Теперь можно истолковать расчетные оценки с экономической точки
зрения как нормы замены. Рассматриваемая здесь замена заключается в
переходе от одного эффективного варианта распределения к другому, причем
точки, отображающие оба варианта, расположены на одной и той же
эффективной грани конуса (^4). Для замены должна быть выбрана (т—1)-мерная
грань; так, если т = 3, возможность замены существует на двумерной
грани, но не на одномерной грани; на последней возможны изменения только
в масштабе производства, но не в относительном распределении. Пусть hA)
и Л/2) суть два варианта эффективного распределения на грани (F), и пусть
х<4> = F^1* и х<2> = FXB> суть соответствующие выпуски. Поскольку (F)—
эффективная грань, то, в соответствии с условиями F) раздела 16.6,
Следовательно,
Рассмотрим случай, когда изменяется выпуск лишь двух первых
товаров. Тогда
или
В соответствии с определением эффективности, если х™ > х(*\ то х™ < х™
и наоборот. Поэтому соотношение в правой части уравнения A)
положительно и является показателем нормы заменяемости выпуска двух
товаров. В случае небольших изменений соотношение оценок можно считать
предельной нормой заменяемости, однако вовсе нет необходимости
рассматривать предельные категории. Отсюда соотношения оценок рг: /?2: • • •: Рт
суть нормы замены выпусков различных товаров на эффективной грани (F).
Если число эффективных граней равно двум или более, то при переходе
от одного варианта эффективного распределения к другому возможны
разрывы. Расчетные оценки для одной грани одинаковы, но изменяются
(прерывно) при переходе с одной грани на другую, так что не существует
установленной нормы замены при переходе от совокупности эффективных
значений выпуска на одной грани к аналогичной совокупности на другой
грани.
489

Следовательно, если задана технологическая матрица А и критерий
эффективности распределения, то при решении технологической задачи
распределения ресурсов мы получаем системы расчетных оценок, которые
позволяют отличить эффективный вариант распределения от неэффективного.
Может существовать либо единственное соотношение между оценками, либо
несколько таких соотношений. Если окажется, что произведено
неэффективное распределение (не были приняты во внимание выводы расчетных
оценок), то в хозяйстве возникает «чистый убыток», который поддается
измерению. (По этому вопросу см. [6].)
При вычислении оценок приходится строить обратную матрицу.
Рассматриваемая эффективная грань (F) описывается подматрицей матрицы А,
то есть матрицей F тх(т — 1). Транспонированная матрица F' будет
(т — 1)хт, и ее ранг можно принять равным (т — 1). Эту матрицу
всегда можно представить в виде- [B:|J], где В — неособенная квадратная
матрица (т— 1)-го порядка, а Р — вектор-столбец. Например, если
матрица F строится на основе первых (гп— 1) производственных отраслей
матрицы А, то
""1 Л21 ••• ат-1,1
12 а22 • • • ат-1, 2
*т-1, т-
Соотношения между оценками находятся из уравнения p'F = O, то есть
F'p = O, что соответствует системе (т—-1) линейных уравнений
относительно (т — 1) соотношений между оценками. Обозначим через q вектор
ЛР1, Р2_ Рт-г\
4 \ Рт ' Рт ' * " ' Рт J '
так что уравнение F'p = O превращается в
Bq = (— Р)
и, значит, B)
Следовательно, для вычисления соотношений между оценками требуется
построить матрицу, обратную по отношению к В.
Например, в случае трех товаров (ттг = 3) и эффективной грани OAiVAi2\
для определения соотношения между оценками pt: p2: ps мы воспользуемся
двумя уравнениями системы E) раздела 16.6:]
рхап + р2а21 + р3а31 = О,
, = 0.
И
Отсюда вычисляем соотношение Рх'-Рг'Рз- Знаки оценок следует
подобрать таким образом, чтобы выполнялись неравенства системы E)
раздела 16.6.
Теперь можно рассмотреть решение этой задачи с помогцью
линейного программирования. Необходимо подчеркнуть одно обстоятельство.
Если принять два допущения, а именно: 1) технологическая матрица А
обусловливает пропорциональность затрат выпуску, 2) имеются
неограниченные ресурсы первичных факторов, то это означает, что можно найти
относительное распределение ресурсов и соотношения между оценками,
490
Тогда уравнения B) превращаются в следующие:

но не масштаб производства и не абсолютный уровень оценок.
Определяются лишь относительные значения элементов 1ир, а не масштаб
производства. Отсюда следует, что если эту задачу рассматривать как
задачу линейного программирования, то в ней не будет условия
максимизации или минимизации в обычном понимании, ибо для максимизации
линейной функции типа z~b"k потребуется определить не только
относительное распределение ресурсов между производственными отраслями,
но и масштаб производства.
Будем искать такую подматрицу F технологической матрицы А, чтобы
уравнение x = Fi, представляло эффективные варианты распределения в
рамках более широкой области возможных вариантов распределения х== А X
при ?о>0. Если матрица А размерности тхп, то F обычно тх(т — 1).
Значит, допустимые векторы распределения % размерности тг, но
эффективные h —только размерности (т— 1); не все базисные производства
включаются в эффективное распределение. Матрицу F находим на основании
некоторого положительного вектора оценок р размерности т и уравнения
F'p = O (при одновременном выполнении условия А'р<0). Прямая и
двойственная задачи линейного программирования заключаются в нахождении
векторов Я и р, удовлетворяющих условиям:
F^ = x и F'p = O,
% > О, р > 0. C)
Это частный (сокращенный) случай более обычной задачи линейного
программирования:
Минимизировать z = Ъ"к Максимизировать ? = х'р ^
при условии Fh>x, при условии F'p<b, [ D)
%>0. р>0. J
Здесь Ь —некоторый заданный вектор в пространстве
производственных отраслей; в настоящем контексте истолковать его значение нельзя.
Однако достаточно в D) приравнять Ь = 0, и мы получим задачу C);
см. также упражнение 4.
Задачи и упражнения
Г 1 2 11
1. Конус (А), построенный на основе технологической матрицы А = 2 1 11,
L-1 -1 -ij
имеет одну эффективную грань 0АаК4™ (см. упражнение 2 раздела 16.6). Записать
систему соотношений E) раздела 16.6 в виде
Показать, что из первых двух уравнений следует р1: р2: р3 = 1 '• 1 : 3 и что для
удовлетворения третьего неравенства знаки р19 р2 и р3 должны быть положительными.
Г 2 3 П
2. Матрица А= 2 0 3 1. Найти оценки для эффективных граней ОАA)АB)
и О4A)Л<з>.
3. Какая система или какие системы оценок могут быть установлены для
эффективного распределения, если
2 2 1-1
> > i •
-1 -1 -ij
4. Истолковать задачу линейного программирования D), приняв х за вектор
минимально требующегося выпуска, a b за вектор чистой прибыли, которая не может
быть превышена в различных базисных производственных отраслях. Показать, что
при этом z и ? следует считать совокупной чистой прибылью. Почему D) лишено
смысла при сделанных допущениях пропорциональности затрат выпуску и
неограниченности ресурсов, кроме одного случая, а именно Ь=0?
491

16.8. ЭФФЕКТИВНОЕ РАСПРЕДЕЛЕНИЕ ПРИ ОГРАНИЧЕННЫХ
РЕСУРСАХ ПЕРВИЧНЫХ ФАКТОРОВ
В разделах 16.6 и 16.7 были получены важные результаты для случая,
когда не существует ограничений, налагаемых на имеющиеся в
распоряжении ресурсы первичных факторов. Было показано, что возможные варианты
распределения ресурсов отображаются в пространстве товаров точками,
расположенными внутри или на поверхности выпуклого конуса (А),
построенного на основе технологической матрицы А. Эффективным вариантам
распределения соответствуют определенные точки — или, вернее, грани — на
поверхности конуса (А). Эти варианты находятся с помощью системы
расчетных оценок; убыточные варианты распределения (прибыль отрицательна)
исключаются как неэффективные, а все множество эффективных вариантов
распределения характеризуется условием нулевой прибыли при подсчете
затрат и выпуска по указанным оценкам. Введение ограничений на
имеющиеся в распоряжении ресурсы первичных факторов не изменяет этого
положения; оно лишь позволяет определить не только эффективное
распределение ресурсов, цо и оптимальный масштаб производства, и добавляет в
соответствующую задачу линейного программирования условие
максимизации (или минимизации).
Теперь т товаров делятся на две группы: первичные факторы, не
являющиеся сами по себе предметом конечного спроса и чистый выпуск которых
#р<0, и конечные продукты, чистый выпуск которых ж;>0. Пусть ?р —
количество первичного фактора, которое можно получить извне системы,
и это количество задано и положительно. Тогда
( — хР)<Ър или #р>( — Ер).
Если хр = —?р, то ресурсы используются полностью, и отыскивается оценка
(расчетная) этого фактора. Если же хр > (— ?р), то некоторая часть ресурсов
остается неиспользованной, первичный фактор является «свободным
благом», и следует ожидать, что его оценка равна нулю.
И в этом случае для удобства рассуждений предположим, что нет
промежуточных продуктов (или что матрица А сокращена с целью освободиться
от них). Это не исключает возможности xf = О (в отличие от xf> 0) для
некоторых вариантов распределения ресурсов и для определенного конечного
продукта. Может случиться, что возможное производство одного или
нескольких конечных продуктов экономически невыгодно.
Рассмотрим графически два случая, когда имеется три производства
и три товара. В первом случае мы получаем два конечных продукта х1 и х2
при затрате одного первичного фактора xs (труд). Можно так выбрать
единицы для измерения количества х3, что его ресурсы ?3 будут равны 1,а
значит, что я3>—1- Как и ранее, единичные уровни производственных отраслей
можно выбрать так, чтобы элементы последней строки технологической
матрицы были равны (—1):
an a12 а13
«21 Л22 «23
-1 -1 -1
где все элементы а можно считать положительными. Конус допустимых
вариантов распределения (Л), если не учитывать ограничений, налагаемых
на х3, имеет ту же форму, что на рис. 53,— разница лишь в том, что все
точки А^\ А^ и А^ расположены в положительном квадранте пространства
Оххх2. Достижимыми вариантами распределения называются такие
варианты, точки которых в пределах конуса допустимых распределений (А)
попадают в пространство между заданными неизменными границами, в данном
случае #3>—1. Следовательно, конус достижимых вариантов {А) попросту
представляет собой первоначальный конус, усеченный плоскостью х3= —1,
как это показано на рис. 57. Требуется найти эффективные точки или гра-
492

ни конуса достижимых вариантов (А), причем эффективность понимается
так же, как и ранее (см. 16.6), с тем лишь исключением, что она применяется
уже только к конечным продуктам. Значит, х является эффективным, если
увеличение выпуска одного конечного продукта достигается лишь за счет
уменьшения выпуска другого конечного продукта.
Из рис. 57 становится ясно, что при эффективном распределении
лимитирующий первичный фактор должен использоваться полностью, х3 =—1;
в противном случае выпуск обоих конечных продуктов может быть увеличен,
благодаря использованию большего количества этого первичного фактора.
Следовательно, эффективные точки расположены на гранях двумерной
выпуклой фигуры А^А^А^ и должны размещаться на отрезке прямой,
таком, как отрезок A^AW на рис. 57, имеющем отрицательный наклон
но отношению к осям хг и х2 (см. упражнение 1). В такой эффективной точке
пространства Оххх2 существует положительно направленная нормаль,
определяющая вектор оценок (р1г р2) конечных продуктов. Значит, существуют
оценки рг и р2, положительные и характеризующие норму замены
(эффективных) выпусков продуктов хх и х2. Далее, если х± и х2 являются эффективными
выпусками (из всего множества достижимых значений выпуска), то
максимизируется величина
? = PlXl + />2#2
{способ доказательства этого см. в упражнении 2). Это — условие
максимизации, добавляемое к задаче линейного программирования C) раздела 16.7;
оно определяет цены (оценки) конечных продуктов и максимизирует
возможную выручку от их продажи по указанным оценкам.
Во втором случае (см. рис. 58) имеется один конечный продукт хх
и два первичных фактора х2 и х3, причем единицы измерения выбраны
таким образом, чтобы ограничения описывались неравенствами х2>— 1
и #3>—1. Элементы двух последних строк технологической матрицы А
отрицательны, и единичный уровень каждого из производств может быть
выбран так, чтобы больший элемент (по абсолютной величине) из двух
отрицательных элементов каждого столбца матрицы А был равен (—1). Тогда два
последних элемента каждого столбца матрицы А представляют собой, во-
первых, —1 и, во-вторых, некоторую величину, между 0 и —1; при этом
элемент (—1) может находиться как в последней, так и в предпоследней строке.
Например, в случае, иллюстрированном рис. 58, он является третьим сверху
в столбце AW и вторым сверху в столбцах AW и "
«11 «12 «13
«21 -1 -1
— 1 а32 а33
где ап, а12, а13 > 0 и 0 > д21, а32, а33 > —1.
Теперь конус достижимых решений (А) представляет собой конус
допустимых решений, усеченный в двух направлениях плоскостями х2 = —1
и xs——1. Этот конус показан в трехмерном пространстве на рис. 58;
приведены также его сечения плоскостями х2=—1 и х3=—1 (то есть два
усеченных «конца» конуса). Очевидно, эффективные точки конуса (А) следует
искать на ребрах усеченных концов конуса, где достигаются предельные
значения одного или обоих первичных факторов, то есть (рис. 58) на ломаной
AWCB^B^WAW. В рассматриваемом случае при выпуске только одного
конечного продукта условие эффективного распределения попросту сводится к
причем эффективные точки ищутся на той части поверхности конуса (А),
которая определяется уравнениями х2 = —1 и хь = —1. Это — частный
случай задачи «максимизирования ?», поскольку в настоящей задаче ? = pxxv
Единственный вариант эффективного распределения отображается на рис. 58
493

точкой ВB\ где х1 = max, х2 = —1 njx3 > —1- Это наиболее очевидно при
рассмотрении сечений конуса плоскостями х3= —1 и х2= —1, на которых
выбирается точка с максимальным xv Один из первичных факторов (xs > —1)
является свободным благом, его оценка равна нулю; второй используется
в максимально имеющемся количестве. Эксплуатируется только одна
производственная отрасль АB\ и имеется только один дефицитный первичный
фактор х2.
Выпуклый усеченный конус
Р)
Выпуклый усеченный конус
Д
В
C)
г
0)
Сечение- плоскостью
Рис. 57.
Сечение плоскостью
\в
Сечение плоскостью
Рис. 58.
Теперь в достаточной мере ясны общие результаты для технологической
матрицы А любого порядка; они наиболее полно изложены в сборнике Куп-
манса [11, гл. III]. Точки эффективного распределения для случая
ограниченных ресурсов размещаются на тех участках поверхности усеченного
(достижимого) конуса (А) в пространстве товаров, которые соответствуют
предельным, имеющимся в распоряжении количествам одного или
нескольких первичных факторов. За оценками (расчетными) сохраняется прежняя
их функция; убыточные варианты распределения исключаются, а
эффективные варианты характеризуются нулевой прибылью. Соотношения между
оценками конечных продуктов по-прежнему равны нормам замены между
эффективными выпусками этих продуктов. Кроме того, имеется и
условие максимизации, которое добавляется к задаче линейного
программирования, а именно максимизировать ? = р/Х/, где ? — выручка от
продажи конечных продуктов по оценкам (расчетным). Тем самым
определяется и масштаб производства, а значит, и абсолютные значения оценок.
Следует особо подчеркнуть одну сторону результатов, полученных для
общего случая. В эффективном варианте распределения некоторые
первичные факторы используются до предела, а другие — нет. Имеются
дефицитные факторы, оценки которых положительны; могут быть также свободные
факторы, оценки которых равны нулю. Эффективное распределение (на
эффективной грани) представляет собой комбинацию нескольких производ-
494

ственных отраслей; следовательно, при эффективном распределении
некоторые отрасли мы используем, а другие — нет. В этой задаче, где нет
конечного спроса на первичные факторы как таковые, можно сказать, что, как
правило, число эксплуатируемых производств равно числу дефицитных
первичных факторов. Поэтому число эксплуатируемых производств (которое
не превышает общего числа базисных производств п) меньше, чем общее число
первичных факторов, поступающих извне, или равно ему; здесь «меньше
чем» возникает в том случае, если имеются некоторые свободные факторы,
не используемые до предела, а «равно» — если все первичные факторы
являются дефицитными и используются до предела. Это правило несколько
видоизменяется в определенных «вырожденных» случаях, когда число
используемых производственных отраслей может быть меньше числа дефицитных
факторов; см. основной вывод из раздела 15.6.
Система расчетных оценок устанавливается на основе технологических
условий задачи. Ключом к более широкому истолкованию системы оценок
являются их свойства: они характеризуют нормы замены, а также
определяют относительные уровни прибыли для различных производственных
отраслей. Расчетные оценки эквивалентны рыночным ценам, если существует
рынок и если условия конкуренции таковы, что они приводят к
отождествлению рыночных цен и норм замены. В другом крайнем случае, в
планируемом народном хозяйстве или «государстве всеобщего благосостояния»,
«плановики» центрального планового органа руководствуются расчетными
оценками (и минимальными размерами прибылей, которые вытекают из этих
оценок) при решении задач о распределении ресурсов, и пользуются ими в
качестве средства децентрализации принятия решений. Более того, поскольку
проблема представляет собой задачу линейного программирования с
условием максимизации, то для нахождения эффективного распределения
ресурсов и системы расчетных оценок применительно к таким задачам линейного
программирования разработаны вычислительные алгоритмы.
Задачи и упражнения
1. Вычертить рис. 57 для случаев, когда число товаров по-прежнему равно трем,
а число производственных отраслей больше трех. Рассмотреть возможные варианты
расположения точек ЛA), ЛB), ... . Показать, что эффективные варианты
распределения ресурсов могут отображаться: а) единственной точкой, как-то ЛA); б) одним
отрезком прямой, как-то ЛA)ЛB); в) ломаной линией, состоящей из нескольких
отрезков прямых, как-то Аа)АB)А3.
2. Пусть на рис. 57 Р есть любая точка на эффективном отрезке ЛA)ЛB),
a Q—любая другая достижимая точка, для которой х3=—1. Показать, что нормаль
(Ри Ръ) к Aa)Ai2) перпендикулярна к PQ, если Q также является эффективной
точкой и расположена на том же отрезке ЛA)ЛB), что и Р, и что эта нормаль
расположена под прямым или под тупым углом к PQ при любом другом местонахождении
точки Q. Обозначим через хг и х2 выпуск в точке Р, а через хх и х2 в точке Q.
Доказать, что если обе эти точки являются эффективными и лежат на отрезке
>d(i)/d^} то
Pi х»—Хо
¦?-±- = —-—re = норма замены,
Р2 Хг — Хг
и что если точка Р эффективная, а точка Q нет, то
Pi (Xl — ^l) ~\~P2 (X2 — Х2) ^ 0«
На этом основании показать, что t,^^ Р\Хг-\-р2х2^Р\Хг-\-p%x2i то есть что ? есть
максимум.
3. Вычертить конус (Л) достижимых вариантов распределения ресурсов и его
сечений соответствующими плоскостями, как на рис. 58, если
' 2 3 2"
-1-1-1
_. 2_
Проанализировать эффективные варианты распределения. Показать, что при
эффективном распределении ресурсов оба первичных фактора используются до предела.
495

16.9. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ; МОДЕЛЬ РОСТА
НЕЙМАНА
Анализ, проведенный в предыдущих разделах, применим только при
статических, или стационарных, условиях к хозяйству со свободной
конкуренцией или к планируемому хозяйству. В этих разделах мы не рассматривали
монополистическое хозяйство. Что еще более важно, анализ не ставил
задачей динамическую трактовку проблемы. Однако анализ можно провести
шире, чтобы на его основе изучать любые аспекты состояния равновесия
в развивающемся народном хозяйстве, а также осветить важнейшие
особенности общей динамической модели.
Сама концепция технологической матрицы А является чисто
статической; элементы ars отображают вневременные значения выпуска и затрат,
то есть потоков в единицу времени в стационарном хозяйстве. Рассмотрим
теперь частный случай последовательности временных интервалов равной
продолжительности; t-и интервал длится от (t — 1)-го момента до t-ro
момента времени (? = 1, 2, . . ., Г). При этом п базисных производственных
отраслей (каждая для т товаров), составляющих матрицу А, необходимо
приурочить к определенным моментам времени; это значит, что
производственные отрасли должны обозначаться уже не A(s), a A(s)B), где
5 = 1, 2, ..., п, ? = 1, 2, . .., Т. Может случиться, что производство
останется неизменным (то есть не изменятся коэффициенты затрат и выпуска)
при переходе от одного периода к другому; или структура производств
может изменяться во времени. В том и в другом случае теперь требуется
не вообще комбинация производственных отраслей вида 2 ^A(s\ a
s=l
п Т
нация всех этих отраслей во времени: 2 2 ^sf^C>@ пРи всех ^^^0.
8=1 f=l
Коэффициент X8t — уровень 5-го производственного способа в t-й период
времени.
Производственную отрасль Ais) (t) удобнее всего представить себе
следующим образом: на начало интервала, или в (t — 1)-й момент,
производятся ряд затрат, вслед за чем, в конце интервала, или в t-й момент,
происходит ряд выпусков товаров. Тогда можно пользоваться только
неотрицательными значениями коэффициентов затрат и выпуска, и каждый
товар фигурирует и в числе затрачиваемых и в числе выпускаемых
продуктов (причем не исключена возможность нулевых коэффициентов).
Обозначим:
Г*ы 1 Г
Затраты в момент A(,s) = пш . Выпуски в момент В<в> = |
(*—1) I ' г I
l-^mstJ
где 5=1, 2, .. ., щ *=1, 2, ..., Т; arst>0; brst>0. Из этих векторов
можно составить две матрицы, характеризующие технологию ?-го периода:
затраты в момент (? — 1): A/ = [ars*l;
A)
выпуски в момент t: Bt = [brst].
Уровень 5-го производства в ?-м интервале задается коэффициентом
Xst. Составим вектор it = {k$t} п-й размерности E = 1,2, . . ., п). Задачу
динамического линейного программирования можно сформулировать следующим
образом: выбрать такой характер изменения %t во времени, при котором
максимизируется (или минимизируется) линейная целевая функция
где вектор c( = {cs,} га-й размерности E = 1, 2, ..., п) является заданным.
Кроме ограничения kt>0, в этой задаче будут и другие ограничения.
496

Последние представляют собой развитие соответствующих соотношений для
стационарного состояния, подобных АА, = х. Очевидная система
соотношений для каждого товара в отдельности, аналогичных A), связывает затраты
t-ro периода с выпуском (t — 1)-го периода, причем затраты и выпуск
фиксируются в один и тот же момент времени (?—1). Для г-го товара
имеем:
п
затраты t-ro периода = 2 ars/^sf
s=i
n
выпуск (t — 1)-го периода = 2 brs,U-i)^sXt-iy
s=i
Следовательно, чистые затраты т*-го товара к моменту начала t-то
интервала составляют
то есть
Ограничения определенным образом лимитируют этот вектор чистых
затрат. Так, если максимальные чистые затраты (поступление извне системы),
допустимые в течение каждого интервала, обозначить через xt = {xri}
(г = 1, 2, ..., т), то прямая и двойственная задачи линейного
программирования динамического типа представятся в следующем виде:
Максимизировать 2=2 с^* Минимизировать ? = 2 xtPt
t t I
при условии Atkt — Bf_1X,f_1<xi при условии AJpf — BJ__1p^_1 >cf j" ( ^
и Pi>0. ]
Это —задача программирования во времени ? = 1, 2, ..., Г. Такую
задачу можно составить для распределения во времени инвестиций
оборотного капитала, то есть стоимости затрат в течение какого-либо периода
за вычетом стоимости выпуска за предыдущий период.
Подобные задачи линейного программирования, а также задачи более
общего вида, в которых допускаются непрерывные изменения, обобщены
Данцигом [5]. Некоторый интерес представляют и применяемые в них
вычислительные методы, потому что ограничения B), взятые для
различных ?, приводят к очень большим матрицам, составленным, исходя из A),
для ? = 1, 2, ..., Т. Если в качестве начального условия приравнять В^х
нулю при ? = 1, то ограничения для fkt в B) выразятся в следующем
виде:
где все матрицы А и В размерности т X п. Если к представляет все
множество % во времени, ах — все множество х во времени, то для большой
разложимой матрицы (см. 12.9) вида
-Вх|
0 I
0
А2
-в2
1 °
1 °
| Аз
1
32 р. Аллен 497

ограничения выражаются так:
А
Вычисления упрощаются благодаря тому, что ненулевые элементы
сосредоточены вокруг главной диагонали. Обычно блоки ненулевых элементов
переплетаются между собой по строкам и по столбцам, так что один и тот
же товар появляется в различные периоды, а в одной производственной
отрасли затрачиваются товары, выпущенные в разные периоды. По сути дела
если такого переплетения не имелось бы, то задача динамического линейного
программирования распадалась бы на ряд независимых задач для
последовательных периодов.
Все это предусмотрено в модели экономического роста, разработанной
Нейманом [16]. Эту модель нельзя назвать «применением» линейного
программирования, так как она возникла (в 1937 г.) гораздо раньше, чем
последнее. Однако Нейман первым использовал линейную модель
производства с линейными неравенствами и подчеркнул важность двойственной
задачи, Кемени, Моргенштерн и Томпсон [9] недавно обобщили эту модель,
включив в нее, например, в качестве частного случая динамическую модель
Леонтьева. Примем, что в задаче B) xt = 0 и ct = 0; тогда условия
максимизации (или минимизации) исчезают и заменяются — для растущего хозяйства —
целевой функцией минимаксного типа. Предположим далее, что
технология (матрицы Aj и Bt) не изменяется во времени, так что задача линейного
программирования B) преобразуется в следующую:
(I) A^-BVi<0, ^>0, 1
; C)
При истолковании задачи C) применительно к народному хозяйству
делаются следующие широкие и общие допущения: во-первых, народное
хозяйство представляет собой замкнутую систему, где затраты
пропорциональны выпуску; во-вторых, система располагает неограниченными первичными
ресурсами (земля, неквалифицированный труд). Это влечет за собой ряд
выводов. Например, трудовые услуги представят выпуск такой отрасли,
затраты которой — потребление (в фиксированных пропорциях) товаров,
нужных для поддержания существования (а если необходимо, и для обучения)
рабочих. Далее, пропорциональность затрат выпуску и неограниченность
ресурсов с технологической точки зрения означают (см. 16.6 и 16.7), что
масштаб производства и уровень цен не поддаются определению. Отыскиваются
лишь соотношения между элементами 1( и р(.
Условия (I) задачи C) гласят тогда, что затраты t-ro периода не могут
превышать выпуска предыдущего периода; это — технологические условия.
Добавляем еще одно весьма знакомое нам условие: если неравенство (I)
задачи C) является строгим, то товар является свободным благом, и его
оценка равна нулю. Условия (II) задачи C) выражены в оценках (расчетных);
и они устанавливают, что чистая прибыль каждого производства всегда
неположительна. Добавляем знакомое уже нам условие: если прибыль для
производственной отрасли s отрицательна, так что в условии (II) задачи C) следует
применить знак неравенства «>», а не знак равенства «=», то 5-я отрасль
не эксплуатируется, и Х5 = 0.
Введем теперь требования для расширяющегося хозяйства с постоянным
темпом роста. Пусть а — постоянный коэффициент роста, где а = 1 + (>7100),
a r есть постоянный прирост в процентах за каждый период (г%). Тогда
kt - ^и1= а- Двойственной характеристикой в системе оценок будет
процентная ставка на капитал. Пусть Р — постоянный коэффициент роста
капитала по формуле сложных процентов [р = 1 + (q/100)] и процентная ставка
на капитал за один период равна Q. Тогда pt : pf_i= Р, так как проценты
взимаются за время между началом и концом каждого периода.
Запишем задачу линейного программирования C) в расширенной форме:
а) Технологические условия aAh<Bh, h0
498

причем знак « < » для любого товара означает, что соответствующая оценка
равна нулю.
б) Ценностные условия РА'р > В'р, р > О,
причем знак « > » для какого-либо производства означает, что его уровень
равен нулю. В этих задачах уровни производственных отраслей Л, и оценок р
задаются только в виде отношений. Исключим возможность тривиального
случая X = р = 0; тогда неравенства Х>0 и р>0 должны пониматься
в смысле «все элементы неотрицательны, причем некоторые из них
положительны». Условия можно записать в развернутом виде следующим образом:
(I) Технологические условия
а 2 &г*К = 2
s=l " s=l
(II) Условия оценок
т
arS/>r=2 ^rs/
2
s=l
т
2
г=1
2
г=1
m
Р 2 агяРг> 2
Для некоторых г,
r = 0 для остальных г.
K>° Для некоторых 5,
остальных s.
D)
Пусть >о и р суть векторы любых уровней производства и оценок,,
не обязательно являющиеся решением задачи D). Обозначим через ф
соотношение билинейных форм
m n
Il1
2 2
Теперь векторы I ир мы используем только для решения задачи
программирования D), а функцию ф —для выбора решений % и р.
Рассмотрим технологические условия (I) задачи D). Они
устанавливают, что:
2 brs
а ~
некоторых г (рг > 0)
2 ar
s=l
то есть что
2
а <
2 «r
s=l
для остальных r(pr = 0),
2
499
32*

2 brs%s
Обозначим -^ = <x + ar, где ar = 0 при pr > 0, ar>0 при рг = 0.
8=1
Тогда
m n
2 pr(s arsxs) 2 2 arsKPr
r=l s=i r=l s=l
Второе слагаемое здесь неотрицательно; оно обращается в нуль при
рг = рг, так как либо ar = 0 (рг>0), либо рг = 0.
Следовательно, <p(A>, p)_><p(A*, p) = a, и функция ф(^, р) имеет
минимальное значение (а) при р = р.
Аналогичным образом можно проанализировать условия (II), из которых
следует, что:
то есть функция cp(h, р) имеет максимальное значение (Р) при % = Ju
Таким образом, решение {к, р) задачи D) следует искать в седловой точке:
функции ф(Х/, р) для любых неотрицательных к и р. Решение этой задачи
сводится к решению задачи теории игр. Нейман показал [16], что может быть
несколько решений для отношений между элементами векторов % и р, но
что все решения дают единственную пару равных значений а и р. Он
предположил, что все элементы матрицы А + В положительны, то есть что
каждый товар появляется (в виде затрат или в виде выпуска) в каждом
производстве. Такое допущение налагает серьезные ограничения. Его несколько
ослабили Кемени, Моргенштерн и Томпсон [9], допустив существование более
одной пары одинаковых значений аир.
Отсюда следует также, что а есть максимально возможный с
технологической точки зрения коэффициент роста, который определяется по тому
товару, для которого коэффициент роста минимален. Ведь если а есть
некоторый другой возможный коэффициент роста, которому соответствует любой
другой вектор Я, то:
Почленно умножим это соотношение на соответствующие элементы
вектора р и сложим полученные произведения:
т п т п
a S S ars\Pr< S 2 hsksPr,
r=i s=l r=l s=l
то есть
<х<ф(?, р)<ф()о, p) = a.
Аналогично этому р есть соответствующий минимальной процентной
ставке коэффициент возрастания капитала, возможный при системе оценок,
приносящих отрицательную или нулевую прибыль в каждом из
производств. Короче говоря, хотя для этой замкнутой системы равновесия
развивающегося хозяйства и не установлены условия минимизации или
максимизации, но получаемое решение соответствует минимаксу в теории игр, где a —
максимально возможный коэффициент роста, а р — коэффициент,
соответствующий минимально возможной процентной ставке.
Условия и свойства решения можно теперь суммировать в следующей
последовательности (см. замечания Чемперноуна [3]).
500

I. Свободные товары: согласно технологическим условиям задачи,
затраты любого товара не могут превысить выпуск этого товара в
предыдущем периоде; однако если затраты последующего периода меньше,
чем выпуск предыдущего периода, то товар является свободным
благом, и его оценка равна нулю.
II. Неприменяемые (убыточные) производственные отрасли:
согласно условиям, налагаемым на оценки (расчетные), ни одно из
производств не может иметь положительной прибыли; однако если
производство дает отрицательную прибыль, то оно не применяется.
III. Коэффициент роста системы во времени является
максимально возможным с технологической точки зрения; он
устанавливается по тому товару, темп роста производства которого является
минимальным во всей данной системе.
IV. Процентная ставка для системы является минимально
возможной при оценках, дающих неположительную прибыль для любого
производства; зндчит эта ставка устанавливается по самым прибыльным
отраслям системы.
V. Свойство равновесия заключается в том, что темп роста
(максимальный) равен процентной ставке (минимальной); эта пара
значений определяется единственным образом.
Здесь рассмотрена основная проблема длительного хозяйственного
равновесия в условиях монотонного роста во времени. Мы анализировали
замкнутую систему, где затраты пропорциональны выпуску и ресурсы первичных
факторов неограниченны. Поэтому такой анализ можно считать не более
как основой, на которой будет строиться анализ более «реальных» задач,
например учитывающих предпочтение, оказываемое потребителем
отдельным товарам, или возможность замены товаров, или задач, возникающих,
в частности, при переходе к проблемам динамики отклонений от длительного
состояния равновесия или изменений в рамках последнего.
Вместе с тем в настоящем анализе весьма рельефно отображены некоторые
важнейшие особенности экономического равновесия, как-то: функция
расчетных оценок и выбор производственной отрасли, в зависимости от того,
является ли прибыль нулевой или отрицательной (см. [7], в частности,
стр. 386—388). Если рассматриваемая модель представляется в виде
задачи линейного программирования, то технологической задаче эффективного
распределения ресурсов соответствует двойственная задача оценок и
прибыли. Фон Нейман был первым исследователем в этой области (см. [12]).
Оценки выполняют лишь расчетную функцию; они могут превратиться в
рыночные цены при соответствующих условиях конкуренции или же могут быть
использованы «плановиками» в централизованной или децентрализованной
системе, направленной ко «всеобщему благосостоянию». Можно лишь
сказать, что, какова бы ни была система, если таких расчетных оценок не
существовало бы, то их следовало бы изобрести.

ГЛАВА 17
ТЕОРИЯ ФИРМЫ
17.1. ПРЕДЕЛЬНЫЙ АНАЛИЗ: ВЗАИМОЗАМЕНЯЕМОСТЬ ФАКТОРОВ
В ПРОИЗВОДСТВЕ
Теперь мы располагаем математическим инструментарием для
детального анализа процесса производства в рамках фирмы. Понятие «фирма»
весьма простое, дело лишь в том, каким образом его определяют; в какой бы
отрасли производства мы ни рассматривали фирму, она представляет собой
некоторую организационную единицу, в рамках которой принимаются
эффективные решения. На практике «фирмой» может быть предприятие, завод,
компания. Вместе с тем «фирмой» можно считать и некоторую группу
предприятий или компаний, объединенную с целью эффективного управления,
то есть организацию типа «Юнилевер» или национализированной отрасли
промышленности. Однако, каковы бы ни были организационные формы, в
настоящей главе мы предполагаем, что существует некоторая единица,
принимающая решения относительно отдельного производства и рассматриваемого
(короткого или длительного) периода времени, и что эту единицу мы
условились называть фирмой.
Анализ деятельности фирмы следует противопоставить анализу
производственной системы в целом, ибо это анализ «микроэкономического» типа.
Можно попытаться анализировать деятельность некоторого сектора
хозяйства, не охватывающего собой народное хозяйство в целом, но более
крупного, чем одна фирма. Это вряд ли уместно; не существует
самоочевидной промежуточной градации между фирмой и народным хозяйством в
целом. Чтобы получить приближенное решение, фирмы обычно группируют
(на статистической основе) в «отрасли промышленности». Но даже тогда вовсе
не очевиден ответ на вопрос, «сколько фирм составляет отрасль
промышленности?». Этот вопрос может не иметь значения (и даже смысла), если во всех
фирмах ^организация и технология производства одинаковы, то есть если
каждая фирма — это отрасль промышленности в уменьшенном масштабе.
В то же время вопрос может быть поставлен таким образом, что на него будет
чрезвычайно трудно ответить, для этого придется изучать ожидаемые
результаты и условия доступа.
Как указывалось в разделе 9.8, теорию фирмы можно развивать либо
с помощью предельных категорий, вытекающих из «классического» или
традиционного подхода, либо в крупном плане с помощью линейного
программирования и анализа производственной отрасли. Эти подходы являются
скорее взаимодополняющими, а не взаимоконкурирующими; в зависимости от
постановки задачи можно пользоваться любым из них. В настоящей главе
используются оба метода. Однако, во всяком случае, анализ проводится
применительно к короткому (или умеренно длительному) периоду времени, ибо
организационная структура фирмы считается в известной степени
стабильной, а принимаемые решения относятся к более или менее ограниченному
отрезку времени.
При традиционном предельном анализе внимание в основном уделяется
вопросам взаимозамены между собой факторов, или продуктов, или
взаимозамены факторов и продуктов. Чтобы выделить проблему взаимозаменяемости
факторов, рассмотрим сначала задачу, где фигурирует фирма с одним
продуктом и несколькими факторами. Для иллюстрации большинства
возникающих вопросов достаточно наличия двух факторов. Производственная
502

функция при этом такова:
y = f{xvx2),
где у есть продукт, а хх и х2 — используемые факторы. В графической
форме эту функцию можно представить в виде семейства кривых
постоянных объемов продукции (см. 9.7). Пусть частными производными в любой
точке (хг, х2) являются выражения fr = dy/dxr и frs~d2y/dxrdxs (г, 5=1, 2).
Построим симметрическую матрицу
о/,/,
- /2 /l2 /22 -»
Обозначим через F величину определителя этой матрицы, а через Fr и Fr8
алгебраические дополнения соответственно элементов /г и frs.
Предположим, что в условиях чистой конкуренции фирма покупает
факторы производства на соответствующем рынке по заданным ценам рх и р2
и продает продукт по заданной рыночной цене я. Тогда задача состоит в
том, чтобы найти такую комбинацию (хх и х2) используемых факторов
и такой объем производства (у), при которых максимизируется чистый
доход:
R=*ny — (рххг + р2х2), где у = / (хх, х2).
Необходимым условием максимума будет dR/dx1 = dR/dx2 = 0, откуда
ЯЛ-Pi =
я/г--/последовательно, расходуемые количества факторов (х1шх2) получаются
как функции цен (рг, р2 и Jt) из уравнений
а масштаб производства (г/) —на основе функции y=^f{x1,x2).
Первая часть уравнения A) показывает, что для достижения состояния
равновесия соотношение между расходуемыми количествами факторов
должно быть таким, чтобы предельная норма замены (соотношение
предельных продуктов /х: /2) была равна заданному соотношению цен. Тогда
объем производства, то есть уровень затрат хг и х2, а значит, и уровень
выпуска y = f(x1,x2), определяется с помощью второй части уравнения A),
записанной в следующем виде:
/?1 = я/1, р2 = я/2. B)
Это значит, что объем производства продолжает увеличиваться до тех
пор, пока стоимость каждого из предельных продуктов1 при расчете его
по заданной цене не окажется равной цене соответствующего фактора.
Достаточные условия максимизации /?, или так называемые условия
устойчивости, заключаются в том, что для любого отклонения, при
котором <?R = 0, дифференциал второго порядка d2R < 0:
d*R = /u dx\ + 2/12 dr1 dx2 + f22 dx\ < 0,
если
dR = /x dxx + /2 dx2 = 0.
На основании выводов, полученных для квадратичных форм (см.
раздел 13.5), это условие выражается следующим образом:
о h и
/l /11 /12
i i i
/2 /12 /22
C)
1 То есть стоимость прироста продукта при увеличении расхода первого или
второго фактора на единицу.—Прим. ред.
503

Состояние равновесия, характеризуемое уравнениями A) и B) при
условии выполнения неравенства C), может быть достигнуто за два этапа.
Во-первых, пусть наряду с ценами факторов рг и р2 задан и объем выпуска у.
Тогда расходуемые количества факторов (хх и х2) устанавливаются таким
образом, чтобы минимизировать издержки производства С ==/Va + РЛ при
условии выполнения f(^x2) = y (где у задано). С помощью множителей
Лагранжа (см. упражнение 1) хх и х2 представляются в виде функций
переменных у, ^и р2:
J± = J? = k и f{xvxt) = y. D)
Тогда издержки производства С также будут функцией переменных у,
рх и р2. И в этом случае на основе уравнения D) предельная норма
замены приравнивается соотношению цен рг:р2- На втором этапе на основе
заданной цены продукта я выпуск у определяется так, чтобы
максимизировать чистый доход (яу — С). Сравнение уравнений A) и D) показывает,
что нужно лишь в D) принять значение множителя к равным я. Тогда
условие устойчивости снова будет описываться неравенством C).
Преимущество анализа, проводимого в два этапа, заключается в том,
что можно составить выражение для функции издержек и для
соответствующих предельных и средних издержек, а также определить их отклонения при
изменении значений у, рх и р2. Мы получаем нужные выражения,
поочередно дифференцируя уравнение D) по ух, рх и р2 (см. упражнения 2 и 3). Во-
первых, мы находим, что дС/ду = А, = я при оптимальном выпуске.
Следовательно, при состоянии равновесия предельные издержки равны цене
продукта. Однако нет необходимости, чтобы эта одинаковая величина
предельных издержек и цены продукта была также равна и средним издержкам
(см. упражнение 4).
Далее, по мере изменения рх (при фиксированных у и р2), спрос на
факторы изменяется в соответствии со следующими нормами замены:
%F
dPl "" X F "" %F ^ v#
Это — следствие того, что выполняются условия устойчивости C). Значит,
по мере снижения цены одного фактора его потребление увеличивается, а
потребление второго фактора уменьшается. В процессе производства эти два
фактора являются взаимозамещающими; факторы могут быть
взаимодополняющими лишь в том случае, если их имеется более двух.
На рис. 59 изображен первый этап определения состояния равновесия.
Кривая производственной функции для постоянного объема продукции
f(xlf x2) = у строится на основе условий задачи. Имеется ряд параллельных
прямых постоянных издержек {р^^ р2х2 = С для различных уровней С),
и требуется найти самую нижнюю из них (где С является минимальным).
Если кривая постоянного объема продукции выпукла относительно точки О,
то расход факторов в состоянии равновесия отображается координатами
точки Р — точки касания прямой постоянных издержек АХА2 и кривой
постоянного объема продукции. Условие касания состоит в том, что предельная
норма замены равна соотношению цен. На рис. 59 показан также результат
увеличения выпуска у (точка касания перемещается из Р в 0, снижения
цены фактора рх (точка касания перемещается из Р в R) и обоих изменений
сразу (точка касания перемещается из Р в S). Соответствующие изменения
спроса на каждый из факторов (хх и х2) определяются непосредственно
по чертежу.
Представляет интерес частный случай пропорциональности затрат
выпуску. Производственная функция в этом случае описывается линейной
504

однородной формой, так что, согласно теореме Эйлера1, как она приведена
в [1], соотношение
удовлетворяется для любой точки. Следовательно, на основе B) в точке
равновесия:
Щ' = Pixi + Р*Х2>
и стоимость продукта в точности равна стоимости затрат обоих факторов.
Значит, максимизированная величина чистого дохода R равна нулю. При
любом другом расходе факторов, не отвечающем их отношению в точке
равновесия, получается отрицательная прибыль. Такой результат, а именно
О
Рис. 59.
«совмещение» предельных продуктов и нулевой прибыли, всегда имеет
место в состоянии равновесия, если затраты пропорциональны выпуску.
При других формах производственной функции этот результат сохраняет
силу только для некоторых особых точек равновесия.
Однако при более глубоком рассмотрении оказывается, что случай
пропорциональности затрат выпуску вряд ли применим к теории фирмы. На
первом этапе анализа мы обнаруживаем, что (см. упражнение 5) функция
издержек обладает следующим свойством:
дС С «
ду У
то есть предельные издержки и средние издержки равны между собой и
постоянны при различных значениях выпуска. Когда же на втором этапе
анализа мы вводим цену продукта я; (равную X), то оказывается возможным
только один вариант — величина я должна быть задана равной общему
и постоянному значению средних и предельных издержек. Если заданное
значение я отвечает этому условию, то любое значение выпуска у удовлетворит
задаче, то есть объем производства фирмы (при пропорциональности затрат
выпуску) оказывается неопределенным.
Задачи и упражнения
1. Если выражение С=^р1х1-\-р2х2 минимизируется при] условии f(xlt x2) = y (где
у задано), то, составив форму Z = C — X{f (хъ х2)—у}, будем минимизировать Z.
Показать, что условия минимизации являются следующими:
есть
1 Теорема Эйлера гласит, что если /(a?i, a?2) есть однородная форма п степени, то
(#i, хъ) = аохп -)- aixi71'^^ -\- ... + апхп, то имеет место формула #i(d/i/d#i)+
+ X2(df2/dx2) = nf, Эта формула получается непосредственно путем дифференцирования
формы /(a?i, X2) по xi и затем по а?2.—• Прим. ред.
505

2. Дифференцируя по у уравнения D), получаем
, an
¦-=о.
Решение этой системы с помощью правила Крамера дает dxJdy^FJF и дх2/ду=
=zF2IF. Использовать первое из уравнений этой системы и условия равновесия и
показать, что дС/ду=%.
3. Продифференцировав уравнения D) по plt получим систему уравнений,
аналогичную системе предыдущей задачи. Решить эту систему и показать, что dxJdp-i —
= (l/b)(Fu/F) и dx%/dPl = (l/X)(F1%!F).
4. Показать, что средние издержки равны л—R/y, где R есть
максимизированный чистый доход; доказать, что средние издержки равны предельным только
в том случае, если максимизированный чистый доход равен нулю.
5. Если производственная функция есть линейная однородная форма, показать,
что при состоянии равновесия должно быть
Доказать, что предельные издержки равны средним при любом значении выпуска yt
а значит, что каждая из этих величин постоянна и не зависит от изменения у.
17.2. КОМБИНИРОВАННОЕ ПРОИЗВОДСТВО
До сих пор мы предполагали при анализе, что фирма производит только
один вид продукта; комбинированное производство было исключено для того,
чтобы можно было сконцентрировать внимание на взаимозамене факторов
производства. Рассмотрим теперь общий случай, когда фирма производит
любое число видов продукции и потребляет любое число видов факторов.
Здесь возможны всякие варианты взаимозамены факторов и продуктов. Как
и ранее, мы предполагаем, что технологические условия отображаются одной
непрерывной производственной функцией, имеющей непрерывные
производные. Один из способов выражения производственной функции есть (как
в разделе. 9.7) уравнение
4 („ ~ <г и и и \ П
где г видов факторов (х) затрачивается на производство $ видов продукции
(у). В простом случае, рассмотренном в разделе 17.1, г =±= 2, s = 1. Но даже
такой случай нельзя считать общим, так как он не учитывает той
возможности, что один и тот же товар может затрачиваться в одних производственных
комбинациях и выпускаться — в других. Так или иначе, желательно ввести
единую систему обозначений товаров, при которой затраты рассматриваются
как отрицательный выпуск. Запишем производственную функцию в виде
•f (/у» /у /у» \ ____ Г\
J \t*'li •*'2* • • • » щ*'п) — и)
где выпуск каждого из п товаров равен хг (г = 1, 2, ..., п). Если хг > 0,
то товар выпускается; если хг < 0, то это есть фактор производства или
затраты. Обозначим частные производные через fr = df/dxr и frs=d2f/dxrdxs
и построим симметрическую матрицу
"о и U ¦•• /« '
/1 /11 /12 • • • tin
/2 /12 /22 • • • /2п
. Тп Jin Т2га ' • • /п
Величина определителя этой матрицы есть F, a Fr и Frs суть
алгебраические дополнения элементов /г и frs этого определителя.
506

Изложим теперь анализ Хикса [7].
Пусть в условиях чистой конкуренции цены товаров (разных видов
продукции и факторов производства) задаются фирме извне и равны
рг (г= 1, 2, ..., п). Фирма выбирает комбинацию затрат и выпуска
различных товаров, максимизирующую прибыль:
при условии / (хх, я2, ..., хп) = 0.
Отметим, что в форме R имеются как положительные члены
(соответствующие продуктам), так и отрицательные (соответствующие факторам),
то есть R — разность между выручкой и издержками. Состояние равновесия
лучше всего определить, если использовать множитель Лагранжа К и
максимизировать выражение
для п переменных хг (г = 1, 2, ..., п). Необходимые условия равновесия
будут dz/dxr = 0, откуда
pr = kfr (r=l,2, ..., л),
В этой системе имеется п -\-1 уравнений относительно п +1
переменных (хг и К),
Достаточные условия максимизации в отличие от минимизации чистого
дохода R заключаются в том, что должно быть d2z < 0 при любом
отклонении, удовлетворяющем уравнению производственной функции. Поскольку
d2z =¦ — taZ2/, то такие условия отображаются неравенством
если
Этим условиям должны удовлетворять любые отклонения от состояния
равновесия. Принятые здесь условия устойчивости должны гарантировать
возможность существования некоторого состояния равновесия (максималь-
цого) при любой системе цен:
S Hfrslrls > 0 при условии 2/г?г = 0,
г s г
где не все ? равны нулю (они отображают отклонения от точки равновесия
в разных направлениях). Здесь применимы выводы, сделанные (в
разделе 13.5) относительно определенных положительных квадратичных форм;
значит, условиями устойчивости является отрицательность определителя F
и всех его главных миноров F. Другой способ записи этих условий,
который обычно более удобен, приведен в конце раздела 13.5 и связан
с использованием обратной матрицы F:
2ЕтМз>0. B)
Г S
Здесь не все у равны нулю; Frs — алгебраическое дополнение элемента /rs
в определителе F.
Состояние равновесия для фирмы описывается системой A) при
выполнении условий устойчивости B). Значения переменных хг определяются
как функции всех цен рг (как функции спроса для факторов производства
и функции предложения для продуктов). Можно изучить влияние
заданного изменения цен, продифференцировав уравнения A) по каждой из
507

изменяющихся цен и учитывая условие B). Это —задача из области
сравнительной статики. Предположим, что изменяется только одна из цен
(например, рх). Продифференцируем уравнения A) по р± и расположим
уравнения в следующем порядке:
у. dxs_J_
1л 'is дрх ~ К '
C)
Уравнения C) представляют собой линейную систему относительно
переменных A/%)(дк/дрх) и dxs/dp1 E= 1, 2, ...,/г), и решить ее можно
с помощью правила Крамера. Значение первой переменной не требуется,
а значения остальных переменных определяются из dxs/dpi = (l/'k)(Fls/F).
Обобщим этот результат на случай изменения любой из цен (рг):
^ = -W <'.—1.2.....П). D)
Это уравнение показывает влияние изменения одной из цен на спрос
и предложение каждого из товаров.
Остается использовать условия равновесия для определения или
ограничения знаков выражений D). Представим теперь уравнения B) в виде
где не все у равны нулю. Это можно сделать, потому что, в соответствии
с A), X есть величина положительная. В частности, если нулевыми
являются все у, кроме уг, то
^>0 (г=1,2, ...,п). F)
Еще одно уравнение можно составить с помощью определителя F
и условий равновесия A), не используя условий устойчивости. Если
элементы первой строки определителя F умножить на алгебраические
дополнения элементов (r-\-i)-& строки и эти попарные произведения сложить,
то в соответствии с правилом разложения определителя такая сумма равна
нулю. Значит, на основании A) и D)
Отсюда следует, что
или
где 2' есть знак суммирования для всех s Ф г.
s
Истолкуем теперь полученные результаты. Во-первых, условия
равновесия A) показывают, что для любых двух товаров (например, г = 1, 2)
dx2 __../1. —. J?L
dxx /2 P2
508

где dxA и dx2 суть отклонения затрат этих двух товаров (от состояния
равновесия), соответствующие технологическим возможностям
производственной функции. Соотношение цен двух продуктов (хг > О, х2 > 0)
в состоянии равновесия равно предельной норме замены этих продуктов
в процессе производства (при неизменных затратах факторов). Соотношение
цен двух факторов (хх < 0, х2 < 0), как и прежде, равно предельной
норме их замены (при неизменном выпуске продуктов). Соотношение цен
фактора хг < 0 и продукта х2 > 0 равно соотношению между dx2, или
изменением выпуска продукта, и d( — x1), или дополнительным расходом
фактора; иными словами, в состоянии равновесия отношение цен
соответствует предельному продукту единицы потребляемого фактора.
Во-вторых, неравенство F) определяет непосредственное влияние
изменения цены какого-либо товара на спрос или предложение этого же товара.
Для продукта хт > 0 мы получаем дхг/дрг > 0, то есть при повышении цены
предложение увеличивается. Для фактора хг < 0 получаем д( — хг)/дрг < 0,
то есть при повышении цены спрос сокращается.
Наконец, «перекрестное» (взаимное) влияние отклонений цен
определяется уравнением D) при условии выполнения неравенств E) и G). Здесь
выявляется влияние изменения цены одного из товаров на спрос или
предложение других товаров. Так как F —матрица симметрическая и, таким
образом, Frs = F8r, то «перекрестные» влияния также симметричны, то есть
dxjdpr=-dxrldps. Тогда неравенство G) показывает, применительно
к dxjdpr(s Ф г), что изменение цены одного товара рг влияет на спрос
и предложение других товаров таким образом, что отрицательные величины
превышают положительные. Значит, если рг возрастает, то в отношении
других товаров1 либо уменьшается предложение (если товар —продукт),
либо увеличивается потребление (если товар — фактор). Как показал Хикс,
можно считать, что в общем случае продукты и факторы производства
в основном оказывают взаимозаменяющее влияние: при повышении цены
фактора уменьшается предложение продуктов, а при повышении цены
продукта увеличивается потребление факторов. Этому можно
противопоставить то обстоятельство, что в пределах группы продуктов и в пределах
группы факторов более существенную роль играет взаимодополняемость:
при росте цены продукта увеличивается предложение продуктов группы,
при росте цены фактора сокращается потребление группы факторов.
В частном случае пропорциональности затрат выпуску объемы затрат
и выпуска всех видов товаров могут быть увеличены в одно и то же
число раз, так что если f(x±, х2, ..., жп) = 0, то f(\ixly \\х2, ..., [ажл) = 0
при любом \х > 0.
Функция /—однородная (нулевой степени), и, в соответствии с теоремой
Эйлера,
= 0. (8)
Следовательно, на основании A) можно утверждать, что в состоянии
равновесия
Стоимость продуктов в точности равна стоимости факторов и
распределяется между ними в соответствии с их предельной производительностью;
максимизированный чистый доход равен нулю.
Вместе с тем уравнение (8) сохраняет силу для всех точек. Его можно
продифференцировать:
то есть 2яг/Гз= -fs (*=!> 2,..., п). (9)
1 В зависимости от назначения товара г. — Прим. ред.
509

Для интерпретации этого уравнения можно воспользоваться
определителем F. Если каждую из строк этого определителя (начиная со второй)
умножить соответственно на х±, х2, ... , хп и почленно прибавить к элементам
первой строки (О, /х, /2, ... , /п), то, согласно (8) и (9), мы получим строку
нулевых элементов. Значит, F = 0, Это очень важно: ведь условия
устойчивости требуют, чтобыF Ф 0. При/1 = 0 эти условия не удовлетворяются,и мы
не сумеем определить на основании уравнения D) влияния изменений цен.
Цены должны принимать некоторые заданные значения, и ни одну из
них нельзя изменить, не нарушив состояние равновесия. Это аналогично
результату, полученному в конце раздела 17.1 для простого случая одного
продукта. Если деятельность фирмы рассматривается применительно к
небольшому периоду времени, то в течение этого периода какой-то элемент
деятельности можно считать фиксированным, и не будет соблюдаться
пропорциональность затрат выпуску. Можно определить и изменять положение
равновесия (при выполнении условий устойчивости); будет существовать
излишек (максимум) чистого дохода, являющийся доходом именно от
фиксированных факторов. Если же деятельность фирмы рассматривается
применительно к длительному периоду времени, то в том случае, когда все элементы
изменяются и затраты пропорциональны выпуску, подобный анализ терпит
неудачу или становится непригодным.
Задачи и упражнения
1. Производственная функция / (xlt х2, ..., хп) = 0 не является единственной;
технология фирмы столь же хорошо описывается любой функцией от /, то есть
ф{/(#1* Х2> ¦••» а?п)}::=0» если только ф(/) = 0 при / = 0. Показать, что, если / заменить
на ф (/), это не отразится ни на уравнениях равновесия A), ни на условиях
устойчивости B).
2. Показать, что в частном случае условий устойчивости E)
т т
2 2^при т<п-
п
Воспользоваться уравнением V Ps~^~-=0> как в G), и показать, что
s=l
m
2 Y PrPsP-
-*—* *-л ' дрг
r=l s=m-|-l
Если товары с индексом r=l, 2, ..., т суть факторы, а с индексом s = m-\-ir
m-f-2, ..., п — продукты, истолковать это соотношение в широком его понимании как
условие увеличения предложения для группы продуктов при снижении цен для
группы факторов.
3. Фирма производит один вид продукта (у), затрачивая при этом п различных
факторов (a?lf x2, ..., хп); производственная функция описывается уравнением
/ (х1у х2, ..., а?п, у)—-О, где все переменные положительны. Пусть заданы цены
факторов и выпуск продукта у (но не цена этого продукта). Найти необходимые условия
равновесия (при минимальных издержках), истолковать их и сравнить с A).
4. В предыдущей задаче продифференцировать уравнения равновесия по одной
цене, приняв остальные цены и объем выпуска (у) фиксированными. Составить
выражение для dxs/dpr, то есть изменение спроса на 5-й фактор при увеличении цены
r-го фактора. Найти условия устойчивости и показать, что они обеспечивают
выполнение неравенства дхг/дрг < 0, но не решают вопросов, будет ли верным dxs/dpr > О
(взаимозаменяемость факторов) или dxs/dpr < 0 (взаимодополняемость факторов).
Сравнить с примером, рассмотренным в разделе 17.1.
17.3. ПРЕДЕЛЬНЫЙ АНАЛИЗ И ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
ДЕЯТЕЛЬНОСТИ ФИРМЫ
Предельный анализ, проведенный в разделе 17.2, построен таким
образом, что он применим обычно при определенных условиях, характерных для
чистой конкуренции, и, в частности, если фирма по заданным рыночным
510

ценам может получить неограниченное количество факторов. Как показали
Мейкоуэр и Бомоль [8], этот анализ можно построить по-иному, исходя из
того, что имеющиеся в распоряжении ресурсы факторов ограничены
некоторыми лимитами. Все виды факторов приобретаются по заданным
рыночным ценам, но налагается ограничение, по крайней мере в отношении
имеющихся у фирмы денежных средств или кредита, предоставленного ей
для финансирования операций. Кроме основного ограничения, касающегося
денежных средств, некоторые количественные ограничения могут налагаться
и на наличные ресурсы отдельных факторов, например на принадлежащие
фирме и фиксированные факторы, такие, как земельный участок илА
здания. При расширенном анализе учитываются заданные ресурсы фирмы. Эту
теорию можно еще более обобщить, распространив ее на случай
несовершенной конкуренции и на разнообразные типы экономической мощи
монополистической конкуренции, как это сделано в известных работах Чемберлина
[3] и Робинсон [10].
Преимущества предельного анализа состоят в том, что он дает четкое
ясное представление об операциях фирмы в условиях возможного изменения
любого из элементов этой деятельности; это позволяет получить различные
результаты общего характера. Технология фирмы описывается одной
непрерывной функцией — производственной функцией. На тип этой функции не
налагается ограничений; в частности, не является обязательным допущение
о пропорциональности затрат выпуску или какое-либо другое точно
определенное предположение.
Однако и при предельном анализе возникают трудности как
умозрительного, так и математического порядка. Одно из возражений против его
применения состоит в том, что решения, принимаемые фирмой, по самой своей
сущности относятся к коротким промежуткам времени и что поэтому
предположение о совершенно непрерывном характере варьирования или
заменяемости не является подходящей базой для теоретических построений.
Другое возражение сводится к тому, что предельный анализ в прошлом
предназначался для изучения более «примитивных» производств, например
сельскохозяйственных, и что примеры для этого анализа по-прежнему весьма
широко берутся из этих областей. Высказывается мнение, что высокоразвитые
промышленные процессы являются гораздо более сложными и менее
гибкими, чем это предполагается при предельном анализе. В последнем случае
вопрос сводится не к тому, чтобы выбрать оптимальную комбинацию
нескольких факторов, как-то: земли, оборудования и труда разных
профессий и квалификации, а скорее к выбору какого-либо определенного процесса
с относительно негибкой сопутствующей ему формой организации,
например специализированные рабочие, работающие на специализированном
оборудовании. Непрерывность и всеобъемлющий охват производственной
функции кажутся неудовлетворительным средством анализа деятельности
современной промышленной фи^мы.
Недостаточно ответить на такие возражения, сказав,что в конце концов
все изменяется и что целесообразно изучить возможные решения для
длительного периода времени. Ведь, как показано в конце раздела 17.2, при
сделанных логических предположених для длительного периода времени
(пропорциональность затрат выпуску и линейная однородная форма
производственной функции) применение предельного анализа терпит неудачу.
Масштаб операций, проводимых фирмой, становится неопределимым.
Следовательно, предельный анализ является одним из способов
описания принятия решений о направлении деятельности фирмы, причем способом
упрощенным и приближенным. Судить о нем следует по тому, насколько
успешными или неудачными оказываются попытки решения задач,
поставленных для сравнительно короткого периода времени. Этот анализ дает
четкое и ясное изложение деятельности фирмы, но он не претендует ответить
на все возникающие вопросы о поведении фирмы. Можно попытаться найти
и другие методы анализа, дополняющие, а не заменяющие предельный ана-
511

лиз; именно здесь особенно уместными кажутся методы линейного
программирования и анализа производственных отраслей.
Основой применения линейного программирования к теории фирмы
является определение технологии более конкретным и более подробным
образом, чем с помощью производственной функций, используемой при
предельном анализе. И, в самом деле, при линейном программировании мы
подчеркиваем технологические аспекты решений, принимаемых фирмой. Этот
метод исходит из той предпосылки, что фирма рассматривает лишь
ограниченное число самостоятельных технологических вариантов производственного
процесса. Для короткого периода времени может оказаться целесообразным
рассмотрение фирмой только немногих таких вариантов; для более
длительного периода число вариантов может быть довольно большим, но все же
ограниченным. Применяется не всякий процесс; напротив, основная цель — это
показать, почему один способ выбирают, а другой отвергают. Гибкость
вводят посредством допущения, что любой способ может быть применен на
различных уровнях производства и что разнообразные способы могут
комбинироваться в различных сочетаниях.
Таким образом, метод линейного программирования в изложенном выше
виде оказывается весьма подходящим для принятия решений в рамках
фирмы. С помощью этого метода легко решается задача, которая представляет
трудности при предельном анализе: случай больших (а также и малых)
изменений затрат и выпуска при ограниченных ресурсах имеющихся в
распоряжении факторов (например, возможность приобретения факторов
ограничена размером наличных денежных средств или кредита). Уделяя большое
внимание технологии, этот метод представляет собой необходимое связующее
звено между вопросами, интересующими экономиста, и вопросами,
привлекающими к себе внимание предпринимателя и инженера. Точно так же как
система межотраслевых связей, предложенная Леонтьевым, наилучшим
образом применима к народному хозяйству в целом и к проблемам широкого
масштаба, например к мероприятиям, проводимым правительством, так
наиболее плодотворной сферой применения линейного программирования
является более ограниченная область решений, принимаемых в рамках фирмы.
Как и в предельном анализе, в технику линейного программирования
необходимо вносить упрощения, причем упрощения самые коренные,—
хотя бы для того, чтобы свести объем вычислительных работ к приемлемому
уровню. Обычным упрощением является предположение о
пропорциональности затрат выпуску при любом производственном процессе, так что
технология фирмы описывается, как в разделе 9.8, матрицей А = [ars] для т
товаров (факторов или продуктов), обозначаемых нижним индексом г =
= 1, 2, ... , т, и для п процессов, обозначаемых индексом s = 1, 2, ... , п.
Элементы столбца матрицы А характеризуют постоянные пропорции, в которых
затрачиваемые и выпускаемые товары фигурируют в одном процессе.
Элементы строки матрицы А характеризуют появление какого-либо одного
товара в различных процессах и качестве затрат или выпуска. Предположение
о линейности, или о пропорциональности затрат выпуску, является отчасти
вопросом достаточно дифференцированного расчленения процессов; если
в «процессе» выявляются кажущиеся отклонения от пропорциональности^,
это может быть вызвано тем, что его следует расчленить на несколько
большее число базисных процессов.
В задаче линейного программирования, рассматривающей операции
фирмы, кроме технологической характеристики, требуются конкретные
данные об имеющихся в распоряжении фирмы ресурсах и об условиях
размещения ее продуктов. Ресурсы факторов могут быть предоставлены в
распоряжение в фиксированном количестве или же они могут свободно приобретаться
на рынке. Например, можно допустить, что фирма располагает заданным
количеством рабочей силы и оборудования или же что она нанимает рабочих
и арендует оборудование по заданным рыночным ценам; можно также
допустить и то и другое. Может оказаться, что предложение продуктов должно
512

строго отвечать заданному ассортименту в неизменных пропорциях или же
продукты могут и свободно продаваться на рынке, например по заданным
ценам. Все это должно быть четко оговорено.
В задаче линейного программирования об операциях фирмы известными
являются следующие данные: во-первых, технические условия деятельности
(технологическая матрица А); во-вторых, условия о наличии имеющихся
в распоряжении ресурсов и о сбыте продуктов. Существует множество
различных типов задач; они отличаются по характеру заданных условий. Мы
не стремимся исчерпывающим образом рассмотреть все многообразие задач
линейного программирования. Мы попытаемся привести лишь ряд
иллюстраций постановки и решения таких задач в рамках фирмы. Приведенные здесь
примеры принадлежат к такому типу задач, которые, будучи
соответствующим образом модифицированы, по идее могут быть использованы для
эмпирического анализа решений, принимаемых фирмой.
17.4. ТЕХНОЛОГИЯ ФИРМЫ
Задача линейного программирования для фирмы зависит от того, какую
форму имеет матрица А = [ars] типа т X п, характеризующая, по
предположению, технологию фирмы. Это — не только вопрос придания элементам
а матрицы определенных значений, положительных для выпуска,
отрицательных для затрат. По существу, здесь играет роль число и тип товаров,
а также количество и тип базисных процессов, составляющих технологию.
В общем случае имеется т товаров и п процессов; тип — конечные числа,
которые, однако, могут быть большими.
Если для фирмы определена матрица А, то сразу же можно
воспользоваться техникой анализа, описанного в главе 16,— анализа с помощью
конуса (А) допустимого распределения ресурсов. Если X = (А^Дз, ... , Хп) —
вектор уровней п процессов, то вектор х = (хх, х2, ... , хт) выпуска или
затрат т товаров определяется уравнением
х = АХ,
то есть
2j
s=l
A)
где xr — выпуск (или затраты, если элемент отрицателен) г-го товара.
Например, выпуск 7*-го товара равен аг1к1, если применяется только один
процесс (первый), и (ппк1+ аг2Х2), если применяются два процесса (первый
и второй). Если знаки коэффициентов аг1 и аг2 противоположны, то товар
производится в одном процессе и затрачивается во втором.
При построении матрицы А = [ars] необходимо выбрать две системы
единиц измерения: единицы измерения количества товаров и единичные
уровни для процессов. С первыми мы в достаточной мере знакомы; это, например,
человеко-годы труда, тонны добытого угля. Менее очевиден смысл единичных
уровней процессов. Так, первый столбец матрицы А представляет собой
вектор (ап, а21, а31, ... , #mi), характеризующий постоянные пропорции между
затратами и выпуском в первом процессе. Значения элементов а будут
известны только в том случае, если установлен уровень процесса; например,
а могут быть затратами на 1 т угля или же коэффициентами использования
100 человеко-лет труда. Значит, и строки и столбцы матрицы А можно
нормировать тем или иным образом путем выбора определенных единиц
измерения. Например, можно (как это часто делается) установить единичный уровень
s-ro процесса таким образом, что выпуск одного какого-либо выбранного
продукта будет равен « + 1» или затраты одного из факторов будут равны « — 1».
Даже после выбора единичных уровней процессов можно установить
наиболее удобную единицу измерения каждого из товаров, например такую,
33 Р. Аллен 513

чтобы общая сумма имеющихся в распоряжении ресурсов этого товара была
равна единице.
Полезно рассмотреть простые примеры, которые можно изобразить
графически. Если имеется только три товара, то матрицу А размерности 3 X п
и конус (А), описываемый уравнением A), можно изобразить в трехмерном
пространстве товаров. На рис. 53 и 54 представлены возможные случаи
соответственно трех и четырех процессов. Не будет очень серьезным
ограничением, если считать, как это принято на рисунках, что один товар (хг) всегда
выпускается, второй (х3) всегда затрачивается, а третий (х2) иногда
выпускается, а иногда затрачивается. Частными случаями этого примера являются
«2 продукта и 1 фактор» (продукты — товары х1 и х2) и «1 продукт и 2
фактора» (факторы — товары х2 и х3).
Рассмотрим в графической форме случай одного продукта и двух
факторов, как это сделано в разделе 9.8. Выберем единичные уровни процессов
таким образом, чтобы выпуск каждого процесса был равен +1. Тогда
1 1 ... 11
«21 а22 • • • а2
La31 а32 • • • аЗ
1 1 ... 11
— а21 — а22 ... — а2п
где ars= —ars, что позволяет нам пользоваться для обозначения затрат не
отрицательными элементами а, а положительными элементами а. Принятые
уровни процессов характеризуются вектором п-то порядка к = (Хг, Х2,;...*, А,п).
Следовательно, общий выпуск продукта (первого товара) равен
а соответствующие затраты двух факторов суть положительные величины:
*2=2a2A и ^3=2a3sV B)
s s v '
Для каждого из заданных значений Xs значения х2 и х3, определяемые
уравнениями B), могут быть нанесены.на график в виде координат точки Р
в двумерном пространстве Ох2х3 (рис. 60). Таким путем можно изобразить
все допустимые комбинации; исключив из множества допустимых
комбинаций все неэффективные комбинации, можно отобрать эффективные варианты
распределения ресурсов.
Рассмотрим болееЪнимательно единичный выпуск продукта: хх= 2Я8 = 1.
Такой выпуск может явиться результатом какого-либо одного процесса,
и в этом случае затраты отображаются на рис. 60 точками Рг, Р2, jP3, ... ,
где координаты точки Ps суть (a2^, a3s); они определяются уравнениями B)
при Ks = 1 и остальных X, равных нулю. Предположим, что все процессы
различны (взаимонезависимы), так что ни одна из этих точек не совпадает
с другой. Единичный выпуск можно получить также посредством двух
процессов (например, первых двух), взятых в соотношении \i : A—jut), где
Кх= \i и Х2= 1—|х суть уровни в системе B). Тогда затраты отображаются
на рис. 60 точками прямой РгР2\ аналогичным образом отображаются
затраты для любой другой комбинации какой-либо пары процессов. Теперь
исключим неэффективные комбинации; можно отказаться от таких одиноч-
йых процессов, как Ръ, и от таких пар процессов, как РгР3 (рис. 60). Ведь,
например, процесс Р'ъ есть комбинация процессов Р2 и Р3, которую можно
предпочесть процессу Рб, ибо для получения единицы продукта факторы
потребляются в том же соотношении, что и в последнем процессе, нов меньших
количествах. Наконец, единицу продукта можно получить и в результате
сочетания трех и более процессов; однако ни одна из таких комбинаций не
является эффективной, их можно сразу исключить. Например, комбинации
первых трех процессов отображаются множеством точек, лежащих на рис. 60
внутри треугольника РгР2Р3, однако точку на прямой Р{Р2 или Р2Р3 (где
совмещаются только два процесса) всегда следует предпочесть любой из внут-
514

ренних точек треугольника. Значит, допустимой комбинацией,
позволяющей получить единицу продукта, является любая комбинация факторов,
отображаемая на рис. 60 точкой в пределах многоугольника РгР2Р3Р^Ръ,
однако эффективными будут лишь комбинации, отображаемые точками на
выпуклой ломаной линии РгР2Р3Р^. Все это совпадает с положениями
раздела 9.8 и теории выпуклых множеств (см. 11.5).
Если затраты пропорциональны выпуску, то сразу же выясняется способ
отображения любого уровня выпуска, исходя из единичного. При выпуске
не единицы продукта, а х± продуктов, соотношения затрат факторов будут
Рис. 60.
Рис. 61.
точно такими же, как для точек на ломаной Р1Р2Р3Р/к, но объем затрат
увеличивается (то есть удаляется от точки 0) в отношении xt: 1. Дело попросту
сводится к построению фигур, подобных РХР2Р3Р^ но увеличенных или
уменьшенных в соответствующее число раз. Так, на рис. 61 для хх— 2
комбинации затрат определяются ломаной Q±Q2QsQ^ причем OQS = 20Ps
(* = 1, 2, 3, 4).
Теперь получены фигуры, весьма напоминающие кривые
производственных функций для постоянных объемов продукции. Это — семейство
ломаных типа РХР2Р3Р± для постоянных объемов продукции, и каждой ломаной
соответствует определенный уровень выпуска продукта хх. Разница — а она
очень важна — заключается в том, что область возможных комбинаций
факторов заключена внутри некоторых границ, общих для всего семейства
ломаных (на рис. 61 — внутри конуса ОАг Л4), и что допустимы лишь
линейные комбинации установленных пропорций между затратами и выпуском
(то есть процессов). Если рассматривать процессы матрицы А, то первый этап
состоит в исключении некоторых процессов вообще (в случае, изображенном
на рис. 60,— пятого процесса); затем устанавливается, что эффективными
являются только сочетания некоторых пар оставшихся процессов.
Эффективные пары процессов отображаются на рис. 61 парами соседних лучей
(ОА1Ч ОА2), (ОА2, ОА3), {ОА3, ОАА). Значит, матрица А чрезвычайно
ограничивает условия эффективного использования факторов: эффективным
является либо один процесс, либо комбинация двух смежных процессов. Это —.
частный случай применения понятия эффективных граней, изложенного^
в разделе 16.6.
Следует отметить, что замещение кривых постоянного объема продукции
ломаными постоянного объема не о?н*а^ает перехода от непрерывных
изменений к прерывным. Правда, при новой формулировке действительно
существует элемент прерывности, например рассматривается только
конечное число процессов, которые могут применяться или каждый
самостоятельно, или соседние попарно, так что линии постоянного выпуска имеют
«переломы» в таких точках, как Р2 и Р3 (см. рис. 61). Хотя и может отмечаться
конечное число резких изменений норм замены факторов, но эта замена может
быть непрерывной во всей области (для единицы выпуска) от Рх до Р4, если:
515
33*

идти через точки Р2и Р3. В самом деле, по-прежнему сохраняются в силе
предположения о непрерывности изменения уровня любого процесса, а также
непрерывности изменения пропорции, в которой берутся два
комбинируемых процесса.
Частный пример, в котором технология фирмы включает три товара
(один продукт и два фактора), можно распространить на общий случай с
помощью рисунка, аналогичного рис. 61. Допустим, что ни один из п
процессов не зависит или не совпадает ни с одним из остальных процессов и что
неэффективные процессы исключены. Следовательно, если P1P2,P3^P4L, ..,
суть точки единичного выпуска на лучах ОАг, ОА2, ОА3, ОА±, ... ,
отображающих процессы, то ни одна из этих точек не расположена на прямой,
соединяющей две другие точки, ни одна из точек не совпадает с другой
точкой и ни одна из точек не расположена выше и правее прямой, соединяющей
две другие точки. Процессы могут быть расположены в таком порядке, что
эффективное распределение ресурсов достигается только в результате
какого-либо одного процесса или сочетания двух соседних процессов. Это
соответствует свойству кривых постоянного объема производства (при
предельном анализе), по которому их наклон увеличивается при уменьшении
ординаты точки кривой, и они выпуклы относительно начала координат.
Так как здесь рассматривается только технология, то пока еще не
предлагается критерий ни для выбора процесса или пары процессов, ни для
выбора уровня процессов. Эти критерии зависят от других условий задачи.
17.5. ДВЕ ИЛЛЮСТРАТИВНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Первая намеченная к рассмотрению задача из области деятельности
фирмы по существу принадлежит Дорфману [4]. Кроме технологической
характеристики фирмы, представленной матрицей А, в задаче ставятся
следующие условия: во-первых, фирма располагает т фиксированными
факторами в заданных количествах; во-вторых, продукты (а также все остальные
затрачиваемые факторы) могут покупаться и продаваться по заданным
рыночным ценам. Принимая решения, фирма не учитывает фиксированные
факторы при сопоставлении выручки и издержек; принимается, что эти факторы
представляются в распоряжение по тем ценам, какие могут быть получены
при вышеуказанных условиях.
Факторы и продукты фигурируют в п процессах, характеризуемых
столбцами матрицы А, которые считаются взаимонезависимыми, причем
неэффективные процессы исключены. В настоящей задаче можно еще более упростить
матрицу А. В этой матрице установлены затраты т фиксированных факторов
при единичном уровне каждого процесса (каким бы образом ни выбирался
этот уровень), а также соответствующие объемы выпуска и затрат переменных
факторов. Эти объемы можно подсчитать по заданным ценам и суммировать
для того, чтобы получить чистый доход для рассматриваемого процесса при
единичном его уровне. Пусть вектор г = {rs} характеризует этот чистый
доход для п процессов (s = 1, 2, ... , п). Технологической матрицей А удобно
пользоваться, предварительно переменив знаки элементов (чтобы затратам
соответствовали положительные элементы). Матрицу можно ограничить
т строками фиксированных факторов с добавлением строки чистых доходов
А 1
г'
Здесь А = [ars] есть матрица неотрицательных затрат т фиксированных
факторов в п процессах (г = 1, 2, ... , т\ s = 1, 2 , ... , п).
Задача заключается в максимизации общей суммы чистого дохода фирмы
при ограничении затрат т фиксированных факторов заданными количествами
й при заданных значениях чистого дохода п процессов при единичном их
уровне. Приводимые ниже два примера иллюстрируют постановку задачи
516

и ее решение. Хотя эти примеры относятся к сельскохозяйственным товарам
(которыми обычно проще всего пользоваться для изложения), но они в
равной мере применимы и к промышленным процессам.
Пример (а).
Два вида продуктов (зерно и свинина) производятся с использованием двух
фиксированных факторов (труд и земля) в соответствии со следующей технологической
характеристикой:
Труд
Земля
Зерно
Свиньи
человеко-месяц
акр
100 т
100 голов
50
5
1
У
-1
25
50
-1
0
75
60
-1
1
2
В первом процессе конечным продуктом являются свиньи, зерно используется
в качестве промежуточного продукта для откорма свиней. Во втором процессе
производится только зерно, в третьем продуктами являются и зерно и свиньи.
Имеющиеся в распоряжении ресурсы соответствуют следующим количествам
фиксированных факторов: 50 человеко-месяцев труда и 52% акров земли. Цена зерна — 20 ф.
ст. за 1 т, цена свиней — 20 ф. ст. за голову. Тогда чистая выручка для каждого из
процессов (при выбранных здесь единичных их уровнях) соответственно равна 1000, 2000
и 3000 ф. ст. Изменим масштаб технологической матрицы, приняв такие единичные уровни
процессов, чтобы выручка в каждом случае составляла 2000 ф. ст. Тогда задача может
быть представлена в следующем виде1:
Коэффициенты затрат
[100 25 501
10 50 40
Выручка (тыс. ф. ст.)
2 2 2
Ресурсы
50 человеко-месяцев
52 у акров
Пусть эти три процесса применяются с уровнями, характеризуемыми вектором
>, = (Xi, Хг, Я3). Задача состоит в том, чтобы найти такой неотрицательный вектор %, при
котором максимизируется выручка (тыс. ф. ст.)
при условии
< 52 ~ .
A)
Эту задачу линейного программирования можно решить графически (рис. 62).
Поскольку продукты всех трех процессов выражены в одинаковых стоимостных
единицах (равных 2000 ф. ст.), то геометрическое место точек постояннаго объема
производства, упомянутое в разделе 17.4, можно построить так, как это сделано на рис. 62, а.
Если по осям координат отражаются затраты труда и земли, то геометрическое место точек
единичного объема определяется точками Р± с координатами A00, 10), Р2 B5, 50) и Р3
E0, 40). Из графика видно, что точка Р3 расположена выше прямой РгРг, значит, при
указанных ценах на зерно и на свиней третий процесс не применяется. Тогда Х3 — 0,
и задача упрощается: нужно выбрать лишь две величины %\ и А,2. Остается определить,
в каком соотношении и при каком уровне применяется комбинация первых двух
процессов. Это можно сделать на рис. 62, а, построив ряд геометрических мест точек
постоянного объема продукции; здесь проведены две такие линии, а именно: PiP2,
соответствующая единичному уровню B000 ф. ст.), и, скажем, QiQ2j соответствующая 1,25 единичного
уровня B500 ф. ст.). Пусть точка Q имеет координаты E0, 52*4), то есть использование
фиксированных факторов ограничено, согласно A), областью заштрихованного на
рисунке прямоугольника. Задача состоит в том, чтобы в пределах этого прямоугольника найти
точку, лежащую на линии наибольшего объема производства. Это будет точка Q, которая
делит отрезок Q1Q2 в отношении 4:1. Значит, решение задачи: %i = 0,25, Х2 = 1,0,
получаемое из условий 100A,i -f- 25А,2 = 50 и 10 А* + 50 Хг = 5234; см. A).
Максимальная выручка равна z = 2(Xi -j- ^2 + h3) == 2500 ф. ст., что соответствует уровню
постоянного объема производства Q1Q2.
1 Для этого коэффициент затрат в первом процессе удваиваем, во втором
оставляем без изменения и в третьем умножаем на 2/3.—Прим. ред.
517

Тем не менее если установлено, что Х3 = 0, то можно (руководствуясь указаниями
раздела 15.1) построить еще более простой график, показанный на рис. 62, б. По осям
координат откладываются уровни Х± и Яг
двух применяемых процессов. Прямые
АР и ЯР, пересекающиеся в точке Р,
/А3
а
SO WO 150
Затраты труда
(человека - месяцы)
я,
, рщ ,
отображают ограничения A),
представляемые уравнениями:
52
= 50 и
Положение точки,
соответствующей решению, ограничено
заштрихованным участком; требуется найти
максимальное значение z = 2(А* -f- Яг).
Пунктирные линии на рис. 62, б
отображают уравнения
= COnst ( Y Z J
для все возрастающих значений
постоянной (максимизируемой) величины.
Решение ясно; ему соответствует точка
Р, так что
Ях=0,25, Я2 = 1,0Д3 = 0, 2 = 2500 ф. ст.
Решение можно представить в
общем виде (см. таблицу ниже).
Сразу же можно составить задачу
линейного программирования,
двойственную по отношению к задаче A),
введя в нее расчетные оценки (рх и/>2 в
ф. ст.) двух фиксированных факторов—
труда и земли. Снова исключаем третий
процесс. Тогда задача представится в
следующем виде:
Минимизировать
при условии
B)
Чтобы получить решение, ограничивающие соотношения будем считать
равенствами. ;;Тогда
_320 __600
Л—19 ' А""ЙГ"
При этих расчетных оценках, то есть при 16,8 ф. ст. за человеко-месяц труда
и 31,6 ф. ст. за акр земли, расчетная стоимость имеющихся в распоряжении ресурсов
является минимальной (?=2500 ф. ст.), и каждый из процессов приносит нулевую при-
Распределяемые ресурсы:
тпуд
. земля
Продукция:
зерно
свиньи
Выручка
Единица
измерения
человеко-месяц
акр
т
голова
ф. ст.
Первый
процесс
25
4
-25
50
500
Второй
процесс
25
50
100
2000
Итого
50
4
75
50
2500
518

быль, как это видно из ограничивающих уравнений задачи B). Решение, представленное
выше в табличной форме, можно в таком случае подсчитать по расчетным оценкам. При
этом получаем стоимостную матрицу (фунты стерлингов):
Затраты
Труд ....
Земля ....
Выручка . .
Оценка
16,8 ф. ст. за человеко-месяц
31,6 ф. ст. за акр
Первый
процесс
421
79
500
Второй
процесс
421
1579
2000
Итого
842
1658
2500
Более того, соотношение между этими расчетными оценками равно норме замены
(в денежном выражении) двух факторов при постоянном объеме продукции. Для
доказательства в приведенной выше таблице количественных показателей увеличим на 100 ф. ст.
уровень первого процесса и уменьшим на эту же сумму уровень второго процесса. Тогда
изменения в распределении ресурсов будут следующие:
Труд ....
Земля ....
Единица
измерения
человеко-месяцы
акры
Первый
процесс
+5,0
+0,5
Второй
процесс
-1,25
-2,5
Итого
+3,75
-2,0
Следовательно, норма замены труда землею равна 3,75 : 2,0, а это равно
соотношению расчетных оценок F00 : 320).
Решение зависит как от конкретных лимитирующих объемов фиксированных
факторов E0 человеко-месяцев, 52У2 акров), так и от конкретных цен на продукты B0 ф. ст.
за 1 т зерна, 20 ф. ст. за одну свинью). Обычно решение изменяется при изменении
ресурсов, цен, или тех и других одновременно. Более того, изменение решения не обязательно
сводится'к сдвигам в удельном весе двух процессов (A,i : ^)ик изменению уровня
выручки (z). Вполне может потребоваться и отказ от того или иного процесса; в самом деле,
третий процесс может стать эффективным и быть введен в действие.
Пусть, например, лимитирующие ресурсы факторов составляют 150
человеко-месяцев и 12У2 акров, а цены на продукты остаются без изменения. Тогда (см* рис. 62, а),
точка Q переместится в Q', и решение отобразится точкой Qii
^=1,25, Я2=0, 2=2500 ф. ст.
Все ресурсы направляются в первый процесс (где экономится земля). Земля
используется полностью (все 1234 акров), но из имеющихся в распоряжении ресурсов труда
{150 человеко-месяцев) расходуется только 125 человеко-месяцев. Продукт представляет
собой 250 голов свиней, стоимость которых 5000 ф. ст., однако для их откорма придется
закупить на рынке 125 т зерна, общей стоимостью 2500 ф. ст. Тогда решение
двойственной задачи B) в расчетных оценках будет:
^ = 200, /?2 = 0, ?=2500 ф. ст.
Оценка дефицитного фактора (земли) возрастает до 200 ф. ст. за 1 акр, тогда как
оценка труда становится равной нулю.
Возьмем другой пример: мы можем изменить соотношение между ценами на свиней
и зерно; оказывается, что такое изменение приводит к еще более значительной ломке
решения. Пусть цена зерна остается равной 20 ф. ст. за 1 т, а цена свиней упадет до
15 ф. ст. за голову. Тогда можно показать (см. упражнение 3), что ни один из трех
процессов не исключается как неэффективный и что при тех же имеющихся в распоряжении
лимитирующих ресурсах труда и земли выбирается в действительности вариант
производства, представляющий собой комбинацию второго и третьего процессов. Снижение
цены свинины приводит к тому, что по сравнению с приведенным выше решением
производство зерна возрастает, а свинины уменьшается. Важно, однако, что это достигается
путем перехода от первого процесса к третьему, то есть к процессу, который ранее вообще
не входил в число эффективных.
При изучении рассмотренных выше случаев, а также упражнений 2—5,
обнаруживается связь между числом применяемых процессов и дефицитностью факторов
производства (см. 16.8). Обычное решение приводит к тому, что применяется комбинация двух
процессов из трех, а ресурсы обоих факторов используются до предела, то есть оба
фактора являются дефицитными, и их расчетные оценки положительны. Однако может слу-
519

читься, что ресурсы труда настолько велики, что (при заданных значениях цен на
продукты) применяется лишь первый процесс, производство концентрируется только на
свинине; или альтернативно может случиться также, что велики ресурсы земли и
производится только зерно (применяется второй процесс). Эти варианты иллюстрируются
выше и в упражнениях 2 и 5. Особенность этого положения в том, что применяется только
один процесс и ресурсы только одного фактора расходуются до предела; другой же
фактор не является дефицитным, и расчетная его оценка равна нулю. Наконец, имеется еще
одна нерассмотренная возможность — своего рода «вырожденный» случай. Существуют
некоторые сочетания имеющихся в распоряжении ресурсов факторов, когда оба эти
ресурса расходуются до предела, но применяется только один из процессов, например, если
точка Q будет расположена на рис. 62, а в Q± (см. также упражнение 5). Лучше всего
считать это частным случаем, который возникает лишь тогда, когда наличные ресурсы
факторов в точности соответствуют их затратам в одном из процессов.
Пример (б). Производится один вид продукта (зерно), для чего три
фиксированных фактора (труд, земля и тракторы) используются в соответствии со следующей
технологической матрицей:
Труд
Земля
Тракторы
Зерно
человеко-месяц
акр
тракторо-месяц
100 т
25
50
20
-1
5
100
4
-1
4
125
0
-1
Первый процесс высоко механизирован, высока и его трудоемкость. В двух
других процессах мала трудоемкость и меньшие затраты рабочего времени тракторов.
Заданная цена зерна равна 10 ф. ст. за 1 w, так что при единичном уровне каждого
процесса выручка составляет 1000 ф. ст. Имеющиеся в распоряжении фиксированные
ресурсы факторов определяются следующими данными:
Коэффициенты затрат
125 5 41
50 100 125
20 3Vt Oj
Выручка
1 1 1
Ресурсы
10 человеко-месяцев
110 акров
10 тракторо-месяцев
г(тыс. ф. ст.)
1
Если применяемый уровень в трех процессах характеризуется вектором
Л» = (Л.1, А,2, Я3), то задача линейного программирования состоит в том, чтобы отыскать
неотрицательное значение Я,, при котором максимизируется выручка
при условии
50^ + 100^+125^3 < НО,
C>
20^+3 ~Л2< 10.
С помощью симплексного метода (см. 15.8) получаем следующее решение:
^ = 0,2, Х2 = 1,0, Х3 = 0, z = 1200 ф. ст.
Максимальную выручку, или 1200 ф. ст., дает сочетание первых двух процессов
Распределение ресурсов:
труд
земля
тракторы
Продукция:
зерно
Выручка .
Единица
измерения
человеко-месяц
акр
тракторо-месяц
т
ф. ст.
Первый
процесс
5
10
4
20
200
Второй
процесс
5
100
4
100
1000
Итого
10
но *
72Г
120
1200
520

Для этого решения характерно то обстоятельство, что применяются лишь два»
процесса из трех. При этом только два фактора из трех являются дефицитными, и их
ресурсы используются до предела: третий фактор (тракторы) не является дефицитным,
затрачивается лишь 71/2 тракторо-месяцев из имеющихся в распоряжении 10. Этот
вопрос еще более разъясняется с помощью задачи, двойственной для [3]. Ее можно*
записать следующим образом:
Минимизировать ? = 10^
при условии
>1000,
ърг+юор2+г-^р3> looo,
4/>1-fl25/?2>1000. J
Расчетные оценки (ф. ст. за единицу) трех факторов таковы, что стоимость
имеющихся в распоряжении ресурсов этих факторов минимизируется при том условии, что»
по каждому из процессов издержки должны быть не меньше, чем выручка. Решив
задачу C) с помощью симплексного метода, одновременно получаем и решение
двойственной задачи D): '
л=-
200
80
3 = 0, ? = 1200 ф. ст.
Нулевая расчетная оценка тракторов отражает то обстоятельство, что они
представляют собой свободный фактор, то есть ресурс, используемый не до предела.
Расчетные оценки таковы, что первые два ограничения системы задачи D) превращаются в
уравнения, то есть при этих расчетных оценках два применяемых процесса дают нулевую
прибыль. Третье ограничение выражается неравенством 4р± -f- 125/?2 > 1000, и третий
процесс, который не применяется, является убыточным. Подсчет по этим оценкам
одновременно позволяет выявить и тот фактор, который не является дефицитным, и
убыточный процесс, который не применяется.
Расчетные оценки таковы, что соотношение между ними соответствует норме замены
труда и земли при постоянном объеме продукции (см. упражнение 7). С помощью
расчетных оценок решение, приведенное выше в количественной форме, можно записать
в виде стоимостной матрицы (в ф. ст.):
Затраты
Труд
Земля
Тракторы ....
Оценка
22,2 ф. ст. (человеко-месяц)
8,9 ф. ст. (акр)
Выручка
Первый
процесс
111
89
1
200 •
Второй
процесс
111
889
i
1000
Итого
222
978
i
1200
1 Ресурсы не используются до предела, поэтому расчетная оценка этого фактора
равна нулю.
На плоскости нельзя графически решить задачу линейного программирования (&
или двойственную ей задачу D), если только мы не догадываемся о характере решения
или не знаем что-либо о нем заранее. В качестве разумной догадки примем, что тракторы
являются недефицитным фактором; исключим их 'из задачи линейного
программирования C), отбросив третье ограничение.Тогда можно построить на графике геометрические
места точек постоянного объема производства и нанести пределы имеющихся ресурсов
двух факторов (труда и земли). Результаты этого показаны на рис. 63, «, где ломаная
Р\Р2Р3 есть линия единичного уровня продукции A000 ф. ст.), a Q1Q2Q3—линия выпуска
при уровне 1,2 единицы продукции A200 ф. ст.). Решение, при котором выручка
максимизируется и равна 1200 ф. ст., соответствует точке Q — сочетанию первых двух
процессов в соотношении 1 : 5. Это совпадает с полученным ранее решением. Можно сделать
и другое также разумное предположение, что третий процесс не применяется; тогда в
задаче C) запишем Я3 = 0. Здесь снова можно воспользоваться графическим методом
решения, предложенным в разделе 15.1; полученный результат показан на рис. 63, б. Из нега
видно, что третий фактор (тракторы) не используется до предела; как и ранее, находим,
что Ki = 0,2, А,2=1>0 и решение отображается точкой Р.
521

<?7
Влияние изменений заданных наличных ресурсов трех факторов на решение в общем
случае определяем следующим образом: в ограничения задач C) и D) вносим новые
заданные значения ресурсов, а затем снова решаем эти задачи симплексным методом. Если,
однако, третий фактор (тракторы) можно
сразу исключить как свободный или
же если третьим процессом можно
пренебречь как неприменяющимся, то
характер возникающих изменений можно
проследить и по рис. 63. Рассмотрим
сначала только два первых процесса,
то есть предположим, что в задаче C)
Я3=0, и отобразим их уровни на
рис. 63, б. Имеются три прямые,
изображающие ограничения (если последние
представляются уравнениями); они
перемещаются параллельно самим себе
вверх и вправо, по мере того как
возрастают объемы факторов. Так, если
заданные ресурсы труда возрастают с
10 до,* скажем, 15 человеко-месяцев, то
линия АР смещается вправо, за линию
А'Р\ представляющую заданные
ресурсы третьего фактора A0 тракторо-
месяцев). Тогда новое решение
отображается точкой Р'. Труд становится
свободным благом, а земля и тракторы—
дефицитными факторами. В
соответствии с C) знчея
10 20 30
Затраты труда,
(человека - месяцы)
. соответст
и л2
определявии с C) значения
ются уравнениями
50Х1+100Я2=110 и
откуда
А,!=0,35, л2=0,93, z=1270 ф. ст.
Прибыль несколько
увеличивается, если тракторы используются до
предела, а ресурсы труда имеются в избытке.
Другой пример: пусть заданная
площадь земельного участка равна не
110 акрам, а больше, так что линия ВР
смещается вверх. Если площадь участка
составляет 200 акров, то прямая ВР
настолько сместится, что точка Р пересечения прямых ВР и АР будет
расположена на оси ординат; ресурсы труда и земли по-прежнему будут использоваться
до предела, но будет применяться уже только второй процесс. Его уровень будет равен
2 единицам, и z = 2000 ф. ст. Это — «вырожденный» случай использования двух
дефицитных факторов и применения только одного процесса. Если площадь земельного
участка увеличить еще более, то дефицитным останется только труд, и по-прежнему
применяется исключительно второй процесс с уровнем 2 единицы при z = 2000. Этот
случай снова является иллюстрацией общего положения, что, за исключением отдельных
или «вырожденных» случаев, число применяемых процессов равно числу дефицитных
факторов—здесь соответственно один процесс и один фактор или два процесса и два
фактора из трех возможных.
0,25
Рис. 63.
Задачи и упражнения
1. В примере (а) текста принять имеющиеся в распоряжении ресурсьГфакторов
равными 150 человеко-месяцами 12% акрам. Вычертить рисунок, аналогичный рис. 62, б,
и найти решение новой задачи.
2. В примере (а) принять имеющиеся в распоряжении ресурсы факторов равными
311/4 человеко-месяцев и 75 акров. Показать на рис. 62, а, что точка Q смещается за
линию ОАч и что решение отображается точкой Q2. Доказать, что применяется только один
производственный процесс и что только один фактор (труд) является дефицитным.
3. Цены на продукты, заданные в примере (а), изменяются и будут следующие:
20 ф. ст. за 1 т зерна, 15 ф. ст. за свинью. Имеющиеся в распоряжении ресурсы остаются
без изменения. Показать, что третий процесс уже не придется отбрасывать как
неэффективный и что решением является комбинация второго и третьего процессов. Показать,
что, несмотря на снижение цены на свинину, откорм некоторого количества свиней все
же продолжается. Проверить это на рис. 62, а. Какой вид принимает рис. 62, б?
4. Примем цены такими же, как в предыдущей задаче, наличные ресурсы труда
установим в 50 человеко-месяцев, но будем изменять площадь имеющегося в распоряже-
522

нии земельного участка. Сколько земли потребуется, если применять только третий
процесс (производство зерна и откорм свиней)? Сколько земли потребуется, если применять
исключительно второй процесс (производство только зерна)?
5. Если цены приняты такими же, как в примере (а), то показать, что
«вырожденный» случай двух дефицитных факторов и одного применяемого процесса возникает при
наличии ресурсов, равных 125 человеко-месяцам и 12% акрам земли.
6. Решить задачу C) примера (б) в тексте данного раздела с помощью симплексного
метода. В процессе этого же решения получить и решение двойственной задачи D).
7. При решении вышеприведенного примера (б) показать, что норма замены труда
и земли (при постоянном объеме продукции) равна соотношению оценок факторов (то
есть 2 : 5).
8. Исключим третий фактор в примере (б) и воспользуемся рис. 63, а. Рассмотреть
различные варианты, возникающие при изменении заданных ресурсов труда и земли.
Показать, что в общем случае имеют место либо два применяемых процесса и два
дефицитных фактора, либо один применяемый процесс и один дефицитный фактор. При каких
сочетаниях возникает «вырожденный» случай одного процесса и двух дефицитных
факторов?
17.6. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ДЛЯ ФИКСИРОВАННЫХ ФАКТОРОВ И ЗАДАННЫХ ЦЕН
НА ПРОДУКТЫ
Задача, примеры решения которой приведены в разделе 17.5, может быть
поставлена в общем виде. Пусть фирма использует т фиксированных
факторов, причем их ресурсы характеризуются вектором b = {&r}, г = 1, 2, ... , т.
Пусть далее существуют п процессов; при заданных ценах продуктов (и
переменных факторов) и при единичных объемах производства по каждому из
этих процессов, чистая выручка характеризуется вектором г = {rs}, где
s = 1, 2, ... , п. Если А — матрица т X п коэффициентов затрат *
фиксированных факторов в различных процессах, то исходные данные задачи
могут быть представлены в следующем виде:
Коэффициенты затрат: Ресурсы:
A = [ars] Ь = {6Г}
Выручка
»'=['•.]
Вектор h = {Xs} (s = 1, 2, ... , п) характеризует уровни применяемых
процессов, а вектор р = {рг} (г = 1, 2,..., т) — расчетные оценки т
фиксированных факторов. Рассматриваемая задача состоит в том, чтобы
найти неотрицательные векторы % и р, удовлетворяющие условиям прямой
и двойственной задач линейного программирования:
Максимизировать выручку z = г"к Минимизировать издержки ? = b'pi ,,ч
при условии АЛ, < Ь. при условии А'р > г. J
Прямая задача линейного программирования поддается
непосредственному истолкованию: фирма выбирает такую комбинацию процессов, при
которой максимизируется выручка от продажи продуктов (за вычетом затрат
на закупку переменных факторов), при том условии, что затраты
фиксированных факторов не превышают заданных их ресурсов. Тогда двойственную
задачу получаем автоматически: существуют такие расчетные оценки
фиксированных факторов, что подсчет имеющихся в распоряжении ресурсов
по этим оценкам дает минимальную величину — при том условии, что
прибыль (расчетная) не является положительной величиной ни в одном из
процессов. Соотношения между такими оценками можно истолковать как
нормы замены соответствующих факторов при заданном уровне выручки
(см. 16.7).
После того как из прямой и двойственной задач линейного
программирования найдены значения переменных Xs и рТ, столбцы матрицы А
коэффициентов затрат можно умножить на элементы А,8, а строки — на элементы рг. В
результате будет получена стоимостная матрица решения, пример которой
523

приведен в разделе 17.5. Суммы элементов строк равны стоимости
ограниченных ресурсов факторов (если эти ресурсы используются полностью), суммы
элементов столбцов — выручке по различным процессам (если последние
применяются, и получаемая в них прибыль равна нулю).
Легче всего разобраться в решении и получить его с помощью
симплексного метода, если в задачу включим, как в разделе 15.6, т «дополняющих
переменных» и соответствующую совокупность фиктивных процессов, или
«псевдопроцессов», или «имеющихся в распоряжении свободных процессов»..
Составим матрицу
в.[
размерности т х (т + п),
где I — единичная матрица т-то порядка. Аналогичным образом к векторам
ги! п-го порядка соответственно прибавим m нулевых элементов и m новых
переменных. Тогда
v = (г„ г2, .. ., гп, О, .. ., 0) и х = (Х19 Х2, ..., ln, \iv ..., \im)
суть два вектора (ш + га)-го порядка, причем первый вектор задан, а второй:
характеризует переменные уровни для п первоначальных процессов и m
«псевдопроцессов». |3адача состоит в том, чтобы найти неотрицательные
векторы х и р, позволяющие:
Максимизировать z = v'x Минимизировать ? = Ь'р|
при условии Вх = Ь. при условии В'р > v. | ^
Отметим, что в прямой задаче имеется m ограничивающих уравнений
относительно (т + п) переменных х, а двойственная содержит (т + п)
ограничивающих неравенств относительно т переменных р. Если найдено
решение прямой задачи (например, с помощью симплексного метода), то
одновременно получается и решение двойственной задачи.
Остается истолковать найденное решение для х, то есть значения
элементов X и [х вектора в их связи с расчетными оценками р. Рассмотрим 5-й
процесс, уровень которого Х3. Если оказалось, что Х8 = 0, то в оптимальном
варианте процесс не применяется; если Xs > 0, то процесс применяется.
Пусть в векторе х число положительных X равно N, а нулевых есть (п—N).
Следовательно, число применяемых процессов iV<n. Рассмотрим теперь
г-ж фиксированный фактор, наличные ресурсы которого равны br. Если
оказалось, что \ir = 0, то на самом деле не применяется «псевдопроцесс»
или «свободный процесс», ресурсы этого r-го фактора используются
до предела, и его расчетная оценка рг положительна. Если же мы найдем,
что |хг > 0, то «свободный процесс» применяется, ресурсы фактора не
используются до предела, и его расчетная оценка рг равна нулю. Пусть число
нулевых \i в векторе'х, равное числу положительных р в векторе р, есть М;
тогда число положительных \х в векторе х или нулевых р в векторе р есть
(т — М).
В общем случае (см. 16.8) М — N, то есть число применяемых процессов
равно числу дефицитных факторов, ресурсы которых используют до предела,
по положительным расчетным оценкам. Как показано в разделе 17.5,
возможны, однако, такие случайные сочетания заданных ресурсов, что число
применяемых процессов окажется меньше числа дефицитных факторов.
Первый случай — общий, или обычный, второй — «вырожденный».
Известные данные задачи представляются либо в виде матрицы А и
векторов Ь и г в A), либо в виде матрицы В и векторов b и v в B). Нетрудно так
сформулировать условия построения матрицы и векторов, чтобы
технология была правильно составленной (то есть чтобы в ней не было
несамостоятельных или неэффективных процессов) и чтобы была бы исключена воз-
524

можность «вырожденной» задачи. Для выполнения первого условия ранг
матрицы В должен быть равен т, или числу строк, а матрицы • • • равен
(т-\-1), или тоже равен числу строк. Для выполнения второго условия, то
есть для пресечения «вырожденного» случая, ранг матрицы В, в которой
любой столбец замещен вектором Ь, также должен быть равен т. Это значит,
что вектор имеющихся в распоряжении ресурсов Ь не должен быть зависим
ни от одного из (т—1) столбцов матрицы В, в частности ни от одного из
(т—1) столбцов матрицы А; таким образом, исключается случайное
«совпадение» вектора ресурсов с вектором затрат в каждом из (т—1) процессов.
Например, если т = 2, как в примере (а) раздела 17.5, то исключается
возможность случайного совпадения (см. рис. 62, а) вектора ресурсов OQ с
одним из векторов процессов — ОАХ или ОА2. Этот вопрос довольно подробно
рассматривает Дорфман [4].
Решение задачи линейного программирования A) дает как значения к
для применяемых процессов (а следовательно, и для продуктов,
продаваемых по рыночным ценам), так и р — расчетные оценки фиксированных
факторов. Решение обычно меняется при каком-либо изменении исходных
данных, то есть А, Ь или г. Возможны столь многообразные изменения
исходных данных, что целесообразно попытаться классифицировать эти
изменения.
Во-первых, могут пропорционально измениться наличные ресурсы
всех фиксированных факторов (то есть элементы вектора Ь) или же все
значения выручки процессов при единичном уровне последних (то есть г).
Из A) ясно, что при любом положительном множителе к влияние изменения
характеризуется следующей таблицей:
Данные
А,
А,
А,
кЬ,
Ь, 1
кЪ,
(А, Ь,
111
кт =
г)
1
изменены на
4, Ь,
А, Ь,
гг
Ь, г
г
Решение (Я,, р
кХ,
я.,
а,
изменено на
Р
fcp
fcp
Пропорциональное увеличение ресурсов всех факторов приводит к
возрастанию в такое же число раз уровней всех процессов (и выпуска всех
продуктов). Пропорциональное увеличение выручки за единицу по всем
продуктам (то есть в рыночных ценах) вызывает увеличение в такое же число
раз расчетных оценок на все фиксированные факторы. Пропорциональное
увеличение рыночных цен или расчетных оценок равносильно снижению
в такое же число раз коэффициентов затрат в технологической матрице. Так,
если ресурсы всех факторов удвоились, то тогда вдвое больше будет
произведено всех продуктов; таким же будет результат, если имеющиеся в
распоряжении ресурсы не изменились, но все коэффициенты затрат уменьшились
вдвое.
Во-вторых, могут измениться ресурсы только одного фактора, например
Ьх (первого фактора). В общем случае решение (к, р) изменится; это
изменение затронет не только общий уровень производства, но и удельные веса
применения отдельных процессов и соотношения между расчетными
оценками. Такое же влияние оказывает и пропорциональное изменение (в
противоположном направлении) элементов первой строки матрицы А; так,
уменьшение в два раза коэффициентов затрат первого фактора во всех
процессах равносильно увеличению вдвое его наличных ресурсов. Аналогичные
525

результаты получаются и в случае изменения выручек единичного уровня
в одном процессе или при равносильном ему пропорциональном изменении:
элементов одного столбца матрицы А.
В-третьих, возможны изменения относительных величин коэффициентов:
затрат внутри какой-либо строки или какого-либо столбца матрицы А.
Это не равносильно какому-либо изменению имеющихся ресурсов или
выручки за единицу. Но в результате в общем случае опять-таки изменяются
удельный вес применения отдельных процессов и соотношения между
расчетными оценками факторов. Такое изменение можно назвать технологическим
изменением. С экономической точки зрения изменение относительных затрат
отдельных факторов в разных процессах происходит здесь в результате
какого-то технологического сдвига, а не вызвано просто изменением
наличных ресурсов или прибыльности различных процессов. ;
В.одном отношении результаты весьма схожи с результатами,
получаемыми при предельном анализе: предложение продуктов фирмой изменяется
в зависимости от заданных наличных ресурсов факторов производства и от
рыночных цен на продукты. Разница в том, что теперь мы не только
изменяем пропорции применения различных процессов, но полностью
переключаемся от одного процесса к совершенно другому. Возможные варианты
иллюстрируются простым примером. Пусть в примере (а) раздела 17.5 фирма
выбирает только между двумя первыми процессами, причем ресурсы труда
равны Ъх человеко-месяцев, земли — Ъъ акров, а рыночные цены составляют
Я] ф. ст. за 100 т зерна и я2 ф. ст. за 100 голов свиней.
Коэффициенты затрат Ресурсы
_ Г50 251 Ъх
А==[ 5 50 J Ъ2
Выручка С я2 — ^ Я1 ) ni
Задача линейного программирования состоит в том, чтобы найти
неотрицательные ^ и ^?, максимизирующие выручку, при условии
z = (зт2 — / 2*^1) ^i ~h я^л»21
Для этой задачи можно построить диаграмму, аналогичную рис. 62,6.
Координаты точки Р определяются из вышеуказанных ограничений в форме-
уравнении:
¦ _ 2Ь1- Ь2 . __ Юба-А _
Л1~~ 95 ' 2~ 475 * W
Для отыскания максимального z воспользуемся семейством
параллельных прямых
(я2 — 1/2я1) Хх + лгК2 = const. D):
Чтобы применялись оба процесса и решение задачи соответствовало бы
уравнению C), должны выполняться два условия:
(I) Точка Р должна находиться в положительном квадранте (Хх и Х2.
положительны), так что, согласно C):
что ограничивает (хотя и в широких пределах) область изменения
соотношения 62: 6rj
(II) Наклон прямых D) должен быть промежуточным между
наклонами прямых, представляемых ограничивающими уравнениями:
То < ^ <А
526

или
Это — границы (причем довольно широкие) области соотношения n2:nv
Будем считать, что выполняются неравенства E) и F), так что
применяются оба процесса; если уровни этих процессов соответствуют C), то
выпуск равен:
Зерно (единица = 100 т) Х2-Х/Л = 25&a~Q12fel ,
Oh h
Свиньи (единица = 100 голов) К± = —*9~ 2 .
На объем выпуска влияют только наличные ресурсы Ьг и 62,
отношение между которыми ограничено областью неравенства E). Откорм
свиней ведется в любом случае, а выпуск зерна может быть как
положительным Г 95 < -^" < 2 j , так и отрицательным Г jg < ^" < 95 ) • Если
участок земли велик (отношение Ъ2: Ъх большое), то производится достаточное
количество зерна как для откорма свиней, так и для продажи. Если
избыточны ресурсы рабочей силы (отношение b2: Ьг мало), то производимого
зерна недостаточно для откорма свиней, и зерно приходится покупать.
Пока соотношение цен на зерно и на свиней находится в пределах
амплитуды F) и пока применяются оба процесса, величина этого
соотношения не имеет значения. Если же соотношение цен является критическим,
то приходится решать, какой процесс применять. Если п2/л1 < 3/5, так что
свинина продается по низкой цене, то применяется только второй процесс
(производство зерна). Если я2/ях > 5/2 (цена зерна относительно низка),
то применяется только первый процесс (откорм свиней). При
промежуточных значениях соотношения цен производятся и зерно и свинина. Более
того, если существуют и другие процессы, например третий процесс
[см. пример (а) раздела 17.5], то цены могут оказаться такими, что
по сравнению с двумя рассмотренными процессами предпочтение будет ,
отдано этому третьему процессу.
Задачи и упражнения
1. Фирма располагает лишь одним фиксированным фактором (например, трудом),
и существует несколько процессов, включающих продукты и переменные факторы,
которые продаются и приобретаются по рыночным ценам. Показать, что применяется только-
один процесс — тот, в котором на единицу выручки используется наименьшее
количество фиксированного фактора.
2. Предприятие характеризуется следующей простой технологией:
Труд
Земля
Пшеница
Сено
чеяовеко-месяцы
акры
100 т
100 т
~ 25
50
-1
- 0
10
100
0
л
то есть имеются два независимых процесса — производство пшеницы и производство-
сена. Ресурсы составляют 50 человеко-месяцев труда и 260 акров земли, а цены за 1 m
пшеницы и сена заданы и равны соответственно 20 и 10 ф. ст. Решить задачу графически
и показать, что ресурсы обоих факторов используются до предела и что производятся
и пшеница и сено. Во сколько раз цена пшеницы должна быть выше цены сена, чтобы
производилась только пшеница? Насколько мала она должна быть, чтобы производилось
только сено?
3. Показать, что для задачи производства зерна и свинины (в тексте) двойственной
является следующая: найти неотрицательные оценки, при которых минимизируется
С = bi/>i -f- b2jt?2 при условии
Jt2—у я1э
527

-Отсюда определить зависимость расчетных оценок факторов от цен на продукты. При
каких ценах на продукты один из факторов имеет нулевую расчетную оценку, то есть
один фактор используется неполностью и производится либо только зерно, либо
только свинина?
4. В задаче линейного программирования A) доказать, что в общем случае
отношение расчетных оценок двух дефицитных факторов равно норме замены этих
факторов (при постоянном уровне выручки).
17.7. ПАРАДОКС РИКАРДО
В разделе 17.6 задача линейного программирования для фирмы
представлена в простой форме; ее можно расширить в ряде направлений. При одном
из этих направлений мы выделяем из фиксированных факторов и из
продуктов фирмы группы переменных факторов, которые можно получить по
заданным рыночным ценам, то есть факторов нанимаемых (арендуемых) в
противоположность факторам фиксированным. При этом налагается ограничение
на количество нанимаемых факторов, например оно может быть ограничено
суммой кредита, которым располагает фирма. Исходные данные задачи
предоставляются в следующем виде.
Коэффициенты затрат Ресурсы
Фиксированные факторы Г Ах 0 ~| Ь
Нанимаемые (арендуемые) факторы | О А2 J
Издержки по найму факторов: [01 с'] С
Выручка от продажи продуктов [r^ | г^]
В задачу входят тг фиксированных,факторов и пх процессов, или имеется
матрица Ах размерности тг X щ. Далее, имеются т2 нанимаемых факторов,
которые могут включать некоторые или все виды фиксированных факторов;
нанимаемые факторы используются в разных комбинациях в п2 процессах,
так что матрица А2 размерности т2 X п2. Строчные векторы издержек по найму
факторов и выручки от продажи строятся на основе заданных рыночных цен.
Фирма располагает кредитом, равным С. Матрица коэффициентов затрат
(т1 + щ) X (пх + п2) относится к классу разложимых (см. 12.9). Один из
частных случаев возникает тогда, когда фиксированные и нанимаемые
факторы представляют собой одну и ту же совокупность т факторов, так что
в п процессах, применяемых фирмой, могут использоваться как
фиксированные, так и нанимаемые факторы в любом их сочетании. Тогда А1 = А2,
и матрица коэффициентов затрат будет 2т X 2/г.
Задача линейного программирования заключается в следующем: найти
неотрицательные уровни отраслей производства, характеризуемые вектором
% = {'кх! %2}, размерности (щ + и2)-ой, максимизирующие
при условии
Решение находится тем же способом, что и ранее.
Дальнейшее усложнение в том же направлении заключается в том, что
рыночные цены нанимаемых факторов (или продаваемых продуктов)
принимаются не неизменными, а изменяющимися заданным образом в
зависимости от спроса на эти товары. Одна из форм такой задачи, показывающая
несовершенство конкуренции на рынке нанимаемых факторов, получается
в следующем случае. Примем, что имеются т факторов, которыми фирма
располагает в заданных количествах; определенное дополнительное
количество этих факторов фирма нанимает по некоторым заданным ценам, второе
дополнительное количество — по другим, более высоким ценам и т. д.
Исчерпав имеющиеся у нее ресурсы факторов, фирма по-прежнему может полу-
528

чить их дополнительно на рынке нанимаемых факторов, но в некоторых
определенных количественных совокупностях — «блоках» и по все
возрастающим ценам каждого блока. Задача линейного программирования в этом
случае соответствует приведенному выше типу, ее матрица коэффициентов
затрат имеет следующий вид:
~А
0
0
0
А
0
0
0
А
Заданные п процессов мы можем выполнить с помощью фиксированных
факторов, используя совершенно равносильно первый «блок» нанимаемых
факторов и т. д. Матрица будет km X кп, где к — число «блоков» факторов;
эта матрица относится к классу разложимых.
Главная особенность задачи линейного программирования, усложненной
в соответствующих направлениях с тем, чтобы модель отвечала эмпирическим
данным, заключается в том, что получающаяся технологическая матрица будет
иметь большое число строк и столбцов. Увеличение размера матрицы до
порядка, скажем, превышающего четвертый, вызывает трудности
вычислительного характера. Если все же приходится производить вычисления, например
с помощью симплексного метода, то разница здесь заключается только в
неодинаковой трудоемкости и продолжительности расчетов для матрицы 20-го
порядка и матрицы 100-го порядка. Поэтому некоторый практический
интерес представляет разложимость матрицы, то есть наличие в ней нулевых
блоков, ибо это облегчает вычислительную работу.
Приводимый ниже простой пример иллюстрирует задачу линейного
программирования с технологической матрицей разложимого типа. В нем
проводится разделение факторов на фиксированные и нанимаемые; при
дальнейшем усложнении учитывается также расчленение периода производства
на меньшие периоды. На основе этой задачи можно показать (как в
разделе 17.6), каким образом изменение заданных рыночных цен влияет на характер
решения. Этот пример — вариант задачи, рассмотренной Мейкоуэр [9].
Возьмем следующие исходные данные для фирмы (все цифры годовые):
Коэффициенты затрат
Собственные факторы
Рабочая сила
(человек)
Машины (штук)
Наемные факторы
Рабочая сила
(человек)
Машины (штук)
Издержки по найму
факторов (ф. ст.)
Выручка от продажи
продуктов (ф. ст.)
Ч
10
5
0
- 0
[ о
[6500
Процессы
12
2
0
0
0
6500
а2
10
5
0
0
0
6400
h
12
2
0
0
0
6400
0
0
10
5
6750
6500
0
0
12
2
6700
6500
Л
0
0
10
5
6750
6400
Ресурсы:
в2
0
0
12
100
60
6700J 33 500
6400]
Продукт изготовляется посредством двух процессов; первый из них
(а или А) является капиталоемким1, а второй (Ъ или В) — трудоемким.
Процессы изготовления продукта различаются также своей продолжительностью
(при сохранении соотношений между затрачиваемыми факторами): в
краткосрочном процессе, обозначенном нижним индексом 1», выпуск продукта
происходит в том же году, что и затраты, в длительном (нижний индекс «2») —
в следующем году. Наконец, все четыре процесса дублируются с учетом
использования наемных факторов, причем имеющийся в распоряжении кредит
1 Точнее, «машиноемким».— Прим. ред.
34 р. Аллен
529

ограничен суммой 33 500 ф. ст. Цены наемных факторов заданы: 500 ф. ст.
за человеко-год и 350 ф. ст. за машино-год. Цена продукта, а также выбор
единичных уровней процессов таковы, что выручка краткосрочного процесса
равна 6500 ф. ст. В длительном процессе продукта производится больше, его
стоимость по ценам реализации составляет 7040 ф. ст., но получение этих
денег состоится только в будущем году. Эквивалентная сумма для текущего
года при учете (дисконтировании) этой стоимости из 10% годовых равна
6400 ф. ст.; эта сумма и проставлена в строке «выручка».
При таких исходных данных и с помощью уже описанного графического*
метода решения мы определяем, что все производство следует вести с
применением первого способа (краткосрочный, капиталоемкий, при
использовании собственных ресурсов фиксированных факторов). Уровень процесса
равен 10 единицам, так что рабочая сила используется полностью, а машины —
неполностью. Это уже знакомый нам частный случай одного дефицитного
фактора и одного применяемого процесса. Выручка фирмы (максимизированная)
равна 65 000 ф. ст. Следует обратить внимание на то обстоятельство, что
способ построения модели (наем факторов в твердом соотношении.— Ред.)
исключает возможность использования избыточных собственных машин
с помощью наемных рабочих.
Рыночными ценами (заданными) являются цены продукта, наемного*
рабочего E00 ф. ст.), машины C50 ф. ст.) и процентная ставка A0%). Если
изменяется любая из этих величин, то меняется и решение задачи линейного
программирования; можно ожидать, что тогда вместо первого процесса
производство будет переключено на один из других процессов или на какую-либа
их комбинацию. Изменение решений фирмы в отношении выбора процессов
может быть исследовано на различных примерах. Изменение цен на факторы
рассматривается в упражнении 3; сейчас же мы сосредоточим внимание на
влиянии изменения цены продукта и процентной ставки.
I. Увеличение цены продукта на 10%. Вектор выручки от продажи
приобретает следующий вид:
[7150 7150 7040 7040 7150 7150 7040 7040].
Здесь по-прежнему применяется первый процесс с максимальным
использованием ресурсов труда. Но, кроме того, прибыльными являются
и процессы с наемными факторами; их можно применять в пределах
предоставляемого кредита. Чистая выручка от применения четырех процессов
с наемными факторами при единичном их уровне соответственно равна
400, 450, 290 и 340 ф. ст.1. Очевидно, и это можно проверить на графическом
решении, что применяется второй из этих процессов, то есть процесс Вг.
Следовательно, решение будет следующее: применять процесс ах при уровне
10 до исчерпания собственных ресурсов труда (собственные машины
используются неполностью) и процесс В± при уровне 5, до предела используя
кредит, имеющийся у фирмы. Тогда выручка от реализации составит 107 250 ф.-ст.,
а стоимость найма факторов 33 500 ф. ст.; чистый доход (максимизированный)
равен 73 750 ф. ст. Это более чем на 10% превышает ранее указанный размер
прибыли 65 000 ф. ст., так как теперь фирма применяет наемные факторы
и пользуется представляемым кредитом. Новый введенный процесс является
краткосрочным, трудоемким, использующим наемные ресурсы и
присоединяется дополнительно к старому процессу (краткосрочному,
капиталоемкому и использующему собственные ресурсы).
И. Уменьшение процентной ставки с 10 до 4%. Вектор выручки от
реализации приобретает следующий вид:
[6500 6500 6769 6769 6500 6500 6769 6769],
ибо приведение (дисконтирование) стоимости продукта длительного процес-
1 Эти числа суть разности между элементами последней строки матрицы,
увеличенными на 10%, и предпоследней строки (для процессов Ai, Bi, А%, Въ).— Прим. ред.
530

са G040 ф. ст.) к эквивалентной сумме текущего года теперь производится
из процентной ставки 4%; поэтому эквивалентная сумма текущего года будет
равна 6769 ф. ст. Решение теперь предусматривает полное использование
собственных ресурсов труда (машины по-прежнему используются
неполностью), однако уже с помощью процесса а21 а не аг. Из-за снижения
процентной ставки становится более прибыльным длительный процесс (но, как и
ранее, капиталоемкий). Однако, кроме того, становятся прибыльными два
процесса с использованием наемных факторов, а именно два длительных
процесса, А2 и В2, чистая выручка по которым соответственно равна 19 и 69 ф. ст.
Решение состоит в применении процесса В2 в полном размере
предоставляемого кредита. Следовательно, решение заключается в применении процесса
а2 при уровне 10 до полного исчерпания ресурсов труда и процесса В2 при
уровне 5, при котором имеющийся кредит используется полностью. Выручка
равна 101 535 ф. ст., издержки 33 500 ф. ст., прибыль 68 035 ф. ст. Увеличение
прибыли по сравнению с исходной F5 000 ф. ст.) частично объясняется
использованием фиксированных факторов для более прибыльного длительного
процесса, частично — использованием представляемого кредита. Новое
решение представляет комбинацию двух процессов: один — длительный,
капиталоемкий, использующий собственные факторы, второй — длительный,
трудоемкий, использующий наемные факторы. Это является полным уходом
от старого процесса (краткосрочного, капиталоемкого, использующего
собственные факторы). См. также упражнение 2.
Нужно отметить следующую главную особенность полученных
результатов. Первоначальное положение фирмы характеризовалось высокой
процентной ставкой, что вызывало применение краткосрочных процессов, и
низкой ценой машин относительно цены труда (см. упражнение 5), что
соответственно приводило к выбору капиталоемких процессов. Более того, цена
продукта не оправдывала пользование доступным фирме кредитом, при
найме факторов фирма только проиграла бы. Поэтому применялся лишь
один процесс — краткосрочный, капиталоемкий, использующий
собственные факторы. При снижении процентной ставки мы можем ожидать
переключения производства на длительный процесс. Как при росте цен на продукцию,
так и при снижении процентной ставки можно ожидать, что окажется
возможным использование наемных факторов в пределах предоставляемого
фирме кредита. К первоначальному процессу, использующему собственные
факторы, добавляется новый процесс, включающий наемные факторы. Не
является самоочевидным лишь один вариант, показанный здесь, по
крайней мере в качестве возможного, а именно, что дополнительный процесс
может оказаться трудоемким, а не капиталоемким, как первоначальный
процесс.
Следовательно, мы показали, что если фирма работает при
ограниченном кредите, получаемом для найма факторов, то вследствие повышения
цены продукта возможно более интенсивное применение трудоемких
процессов. Для устранения этого цены арендуемых машин должны быть
снижены, а не повышены, как это можно было бы предположить, учитывая
повышение цены продукта. Это и есть парадокс Рикардо, который исследоваЛ
Хайек [6]. Аналогично этому снижение процентной ставки может привести
к увеличенному использованию ресурсов труда и к относительно меньшему
использованию машин, а не к повышенному применению <эборудоваиия„
как это могло бы показаться ввиду снижения процентной ставки.
Анализ таких случаев, как парадокс Рикардо, может производиться
и с помощью предельного анализа [8]. При предельном анализе должны быть
учтены ограниченность ресурсов фирмы и, особенно, предел доступного
кредита, ибо это необходимо для возникновения парадокса Рикардо. Однако
весь этот анализ гораздо естественнее и легче провести с помощью линейного-
программирования. Парадокс Рикардо связан не столько с предельными
изменениями, сколько с выбором между различными вариантами
производственных процессов, при котором учитываются ограничения, например
531 34*

кредита, открытого фирме. Здесь мы имеем пример надлежащего
применения линейного программирования, когда этот метод проявляет себя с
наилучшей стороны.
Задачи и упражнения
1. Пусть в первоначальном варианте задачи фирмы, приведенном в тексте,
возможность выбора ограничена двумя первыми процессами. Применить графический метод
решения задачи линейного программирования и показать, что выбор следует остановить
на первом процессе.
2. Показать, что в (II) снижение процентной ставки с 10 до 6% приводит к
переключению с процесса а± на длительный процесс а 2. Почему все еще невыгодно
использование предоставляемого кредита? Насколько должна снизиться процентная ставка,
чтобы вызвать переход к длительному процессу или чтобы стало прибыльным
производство с помощью наемных; ресурсов?
3. Решить задачу, если цена аренды машины снизилась до 300 ф. ст., а цена
наемного рабочего не изменилась. Какое влияние окажет при этом увеличение на 10% цены
продукта?
4. Пусть в первоначальном варианте задачи имеется 50 собственных машин.
Показать, что при этом ресурсы машинного времени используются до предела. Составить
двойственную задачу линейного программирования (включив в нее только два первых
процесса) и решить ее относительно цен факторов.
5. Показать, что в первоначальной постановке задачи производительность труда
в 1,5 раза выше производительности машин, что превышает соотношение между ценами
труда и машин A,43). Показать также, что отношение обоих показателей обратно тому,
которое имеет место в задаче 3. Истолковать решение настоящей задачи.
6. Любое изменение цены продукта, цен факторов и процентной ставки приводит
к изменению соотношения между элементами двух строк матрицы задачи: строки «издерж-
ои по найму;факторов» и строки «выручка от продажи продуктов» (стр. 528). На этой
генове показать, каким образом возникает решение о переходе от одного процесса к дру-
кому. Показать*также, что изменение процентной ставки влияет на соотношения между
элементами столбцов матрицы; определить влияние этих изменений на решения фирмы.
17.8. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ДЛЯ СЛУЧАЯ НЕИЗМЕННОЙ
1 СТРУКТУРЫ СПРОСА
В приводимой ниже задаче, отличающейся отфадачи раздела 17.6,
исходными данными являются технология и имеющиеся в распоряжении
фирмы ресурсы фиксированных факторов; при этом вместо условия продажи
продуктов по заданным рыночным ценам ставится иное условие, а именно
что продукты требуются рынком в определенных неизменных пропорциях.
Это условие определяет соотношения между объемами выпуска различных
продуктов; в задаче же требуется максимизировать уровень производства.
Простейший способ решения такой задачи линейного
программирования заключается в введении добавочного процесса или «псевдопроцесса»,
который распределяет продукцию по процессам в соответствии с
технологией при соблюдении заданных пропорций. Технология фирмы дается
матрицей А = [ars] размерности (& + т) X п, где первые к строк соответствуют к
фиксированным факторам, а остальные т строк — т продуктам, и п
столбцов соответствуют п альтернативным производственным процессам. В матрице
А затраты удобнее представить положительными элементами. С добавлением
«псевдопроцесса» получаем матрицу
В==[А|с],
где с есть вектор, состоящий из к нулевых элементов (первых) и следующих
за ними т элементов. Он представляет неизменные пропорции спроса на
продукты (например, шкала этих элементов может быть такова, что спрос на
один из продуктов будет равен единице). Вектор Ь характеризует заданные
ресурсы, то есть в нем имеется к заданных величин фиксированных
факторов и т следующих за ними нулевых элементов. Если h есть вектор уровней
п + 1 процессов, то задача линейного программирования будет состоять
в том, чтобы максимизировать Яп+1; это можно представить как максимизацию
выражения z = s'n+A, где sn+1 — единичный вектор, последний элемент
которого равен единице. Следовательно, задача состоит в следующем:
532

Максимизировать
при условии
A)
Что касается ограничивающих условий в задаче A), то первые к
ограничений суть неравенства, характеризующие пределы расхода
фиксированных факторов; остальные т ограничений — уравнения, и они выражают факт
полного размещения на рынке продукции при соблюдении заданных
соотношений между их количествами.
т уравнений в задаче A) определяют характерную особенность решения.
Каждое из этих уравнений есть линейная форма относительно Я1? Я27 ... , Яп,
приравненная какому-то числу, кратному Яп+1; множители — показатели
кратности — суть элементы вектора с. Эти уравнения определяют Хп+г и т—1
элементов Хг, Я2,... , Хп через остальные (п—т + 1) элементов к. Если
применяются все п процессов или если с самого начала исключены неприменяемые
процессы, то п > т, то есть число процессов по меньшей мере равно числу
продуктов. Тогда к неравенств в ограничивающих условиях, которые не
содержат А,п+1, приводятся к к неравенствам относительно /г—т + 1
элементов Я. Чтобы максимизировать Кп+1, необходимо преобразовать в
уравнения возможно большее число этих неравенств. Наибольшее число неравенств,
которое можно преобразовать в уравнения надлежащим выбором значений
переменной Я, равно п—т + 1; остальные неравенства остаются
неравенствами «меньше, чем». Однако каждое уравнение соответствует дефицитному
фактору, а каждое неравенство «меньше, чем» — свободному фактору.
Следовательно, в общем случае число дефицитных факторов равно п — (т—1),
или на т—1 меньше числа применяемых производственных процессов.
Этот вывод очень важен. В предыдущей задаче (см. 17.6) число
дефицитных факторов в общем случае было равно числу применяемых процессов.
Уменьшение на т—1 числа дефицитных факторов в данной задаче вызвано
ограничениями в рыночном спросе. Заданные т—1 соотношений между т
продуктами означают, что из числа применяемых процессов п—(т—1)
являются взаимонезависимыми (их число равно числу дефицитных факторов),
тогда как остальные т—1 процессов выполняют ограничивающие условия
спроса. Чтобы практически использовать этот вывод, проще всего выразить
его следующим образом: когда технологическая матрица сокращена путем
исключения неприменяемых процессов и недефицитных факторов, то число
строк равно [п — (т—1)] (число факторов) плюс т (число продуктов), то есть
всего п + 1; число столбцов также равно п + 1, или числу применяемых
производственных процессов п плюс один процесс потребления.
Следовательно, технологическая матрица, преобразованная в ходе решения,
становится квадратной.
Двойственная задача составляется относительно k + m цен на факторы
и продукты, образующих элементы вектора р:
Минимизировать
при условии I , B)
I
Выражение, минимизируемое в задаче B), есть стоимость
фиксированных факторов по оценкам (расчетным); это условие нам уже знакомо.
Первые п ограничений задачи B) являются неравенствами, левые части которых
«>0». Эти неравенства выражают то обстоятельство, что чистые издержки
по каждому процессу (то есть издержки за вычетом выручки от продажи
продуктов) не являются отрицательными, то есть что прибыли не являются
положительными. Последнее ограничение носит чисто формальный характер;
оно гласит, что стоимость набора продуктов, требующихся в определенных
533

соотношениях, равна единице. Это условие попросту устанавливает масштаб
цен р, и его обычно можно отбросить при рассмотрении только соотношений
между ценами. Если расчетная оценка фактора в B) оказалась нулевой, то
это значит, что в ограничениях задачи A) ресурсы фактора используются не
до предела. Если же оказываетсяj что в A) процесс применяется, то в
ограничениях B) прибыль равна нулю.
Раз определены уровни процессов % и цены р, столбцы технологической
матрицы А можно умножить на соответствующие Я, а строки — на
соответствующие р; в результате получим стоимостную матрицу решения. Она
показывает стоимость каждого фактора или продукта, израсходованного или
произведенного в каждом процессе. Согласно ограничениям задачи A),
сложение элементов тех строк, которые характеризуют расход факторов,
дает стоимость лимитирующих объемов соответствующих факторов (если
они используются полностью), а строк продуктов — выручку от продажи
соответствующих продуктов. Согласно ограничениям задачи B), сумма
элементов каждого столбца равна нулю, то есть в каждом из примененных
процессах прибыль равна нулю.
Совершенно так же, как в разделе 16.7, соотношения между ценами,
определяемые B), равны нормам замены между факторами и продуктами, если
только задача обладает достаточной гибкостью для необходимых
изменений. Теперь возможны три типа замены: между двумя факторами, между
двумя продуктами, между фактором и продуктом. В общем случае для товаров
г и s результат выражается следующим соотношением:
рг Увеличение xs
ps Уменьшение хг
[прочие х (продукты и факторы) не изменены].
Здесь хг и xs — общий расход товаров (он положителен для факторов
и отрицателен для продуктов). Проставив нужные знаки, получаем
результаты для частных случаев.
I. Два фактора:
р- Увеличение расхода s-ro фактора тт Y
¦?-L- = ^т - - т — = Норма замены между факторами
ps Уменьшение расхода r-го фактора r MJ v F
(прочие факторы и все продукты неизменны).
II. Два продукта:
рг Уменьшение выпуска s-to продукта тт
J1J- = -ту ———- = Норма замены между продуктами
ps Увеличение выпуска r-го продукта r «j ±* «j
(прочие продукты и все факторы неизменны).
(III) Один фактор и один продукт:
рг _ Увеличение выпуска s-to продукта _
ps Увеличение расхода r-го фактора
= Производительность г-го фактора при изготовлении
5-го продукта
(прочие факторы и продукты неизменны).
В качестве иллюстрации приведем два простых примера.
Пример (а)
Технологию предприятия, производящего *зерно и свинину с использованием двух
фиксированных факторов (рабочая сила и земля), примем такой же, как в примере (а)
раздела 17.5; введем лишь дополнительное условие, согласно которому рыночный спрос
на зерно и на свинину характеризуется отношением с : 1.
Исходные данные следующие:
Труд
Земля
Зерно
Свиньи
Технология
человеко-месяцы
акры
100 т
100 голов
~ 50
5
1
~2
-1
25
50
-1
0
75
60
-1
1
j
0^
0
с
1
Ресурсы
h
0
0
534

Задача линейного программирования состоит в максимизации Я4 при условии:
5021!+ 25Я*+ 75^з < &i,
БХг+ 50Л2+ 60Я3
Решить эту задачу можно, например, симплексным методом (см. 15.8). Если можно
догадаться или предположить, что третий процесс не применяется (Х3 = 0), то доступно
и простое графическое решение, аналогичное
показанному на рис. 62, 6. Решение должно *
состоять из двух этапов. *
Во-первых, ограничения, включающие
предельные значения факторов, суть
Область допустимых решений отображается
заштрихованной площадью на плоскости ОХгХ2
(рис. 64). Прямая АР соответствует
ограничению ресурсов труда, если это
ограничивающее условие считать уравнением; прямая ВР
таким же образом ограничивает ресурсы
земли. Любая точка на одной из этих прямых
соответствует полному использованию
соответствующего фактора. Координаты точки Р, в
которой ресурсы обоих факторов используются
до предела, определяются решением этой
системы уравнений: Я1 = B61 — Ь2)/95 и Я2 = A062 —
&!)/475. Тогда наклон прямой ОР (тангенс угла
с осью ОХХ) равен 1/5 A062 — Ь1)/BЬ1 — b2).
'Во-вторых, остальные ограничения суть
уравнения, из которых получаем
Х2—
Х4:—Х1 =
Следовательно, нужно максимизировать %х при условии Xt = (l/с) (X2 — 1/2Xi), то есть
А-2 , 1
_А —с+— = const.
Ах г
Будем искать наивысшую точку области допустимых решений на прямой OQ
(см. рис. 64), наклон которой равен с-{-1/2. Решением задачи являются %i и Я2
координаты точки Q, которая расположена на прямой АР (труд дефицитен), если
с+1/2< 1/5 (ЮЬ2—Ь1)/BЬ1 — fe2), и на прямой ВР (земля дефицитна), если с-|-1/2>
> 1/б (Ю62 — Ь1)/BЬ1 — b2). Значит, применяются оба процесса, но только один из
факторов используется до предела наличных ресурсов. Однако лишь один из
процессов является независимым, ибо условия спроса устанавливают неизменное
отношение Х2:Хг равное с-|-1/2; это соответствует дефицитности только одного фактора.
Если с мало, дефицитным является труд; больший спрос предъявляется в таком
случае на свиней, которые требуют значительных затрат труда. Напротив, если больший
спрос предъявляется на зерно (с велико), то дефицитной является земля.
В примере, изображенном на рис. 64, Ьг — 50 человеко-месяцев, 62 = 521/2 акров,
с = 1.
Спрос на свиней достаточно велик по сравнению со спросом на зерно, что
делает труд дефицитным фактором. Уровни производства равны Х1 = */7 и Х2 = 6/7.
Двойственная задача линейного программирования (относительно четырех
расчетных оценок) представляется в следующем виде:
Минимизировать
при условии
Третье ограничение (относительно с, р3 и /?4) опущено, поскольку оно
предназначается лишь для установления удобного масштаба цен. При решении числен-
у Рз—Р* > 0.
535

ного примера, иллюстрированного рис. 64, получаем следующее соотношение цев
(см. упражнение 3):
Это решение снова показывает, что в данном случае ресурсы земли не
используются до предела. Норма замены свиней на зерно определяется отношением 62,5 :25Г
или 5:2. Производительность труда при производстве зерна равна 1 :25 (то есть
4 т зерна за 1 человеко-месяц), а при откорме свиней 1:62,5 (то есть 1,6 свиньи
за 1 человеко-месяц). Если одна из цен установлена, то из приведенных соотношений
можно получить остальные цены; так, если цена зерна определилась в 10 ф. ст.
за 1 т> то свинья стоит 25 ф. ст., а рабочий получает 40 ф. ст. в месяц.
Яснее всего характер решения выявляется с помощью стоимостной матрицы
в фунтах стерлингов (где выпуску соответствуют положительные элементы), построен
ной с использованием расчетных,оценок (цена зерна принята равной 10 ф. ст. за 1 т):
Используемые факторы:
труд
земля
Продукция:
зерно
свиньи
Оценка единицы
40 ф. ст./человеко-
месяц
—
10 ф. ст./т
25 ф. ст./гол.
Первый
процесс
-1143
1
-286
-1429
Второй
процесс
-857
1
857
—
Итого
-2000
1
571
1429
1 Не является дефицитной; используется -=- -\—=- = 45-=- акра < 52— акра.
Ill Cl
Уровни производства равны (см. выше):
и fi
-=-, А,2 = -s~«—Прумеч. ред.
Пример (б). Следующий пример основан на задаче, составленной Камероном [2].
Имеется один фиксированный фактор (труд, имеющиеся в распоряжении ресурсы его>
составляют 300 человеко-месяцев). С помощью трех процессов получаются три
продукта (свежая и копченая рыба, дрова); спрос на эти продукты (в тоннах)
определяется соотношением 2:1:1. Исходные данные следующие.
Труд
Свежая рыба
Копченая рыба
Дрова
Технология
человеко-месяцы
т
т
т
Ресурсы
7
1
0
0
1
2
-1
3
1
4
0
0
-1
0
2
1
1
300
0
0
0
Следует подчеркнуть, что во втором процессе (копчение рыбы) потребляются!
рыба и дрова, производимые в двух других процессах. Задача линейного
программирования состоит в следующем:
Максимизировать А,4
при условии
-т- Я3<!300
X1+2X2+2%i0\ Я2+Я4 ; 2 3+4
Исходя из последних трех уравнений, определяем соотношения между К:
ввиду чего первое ограничение (неравенство) превращается в
30Х2 < 300.
X4=h2 максимизируется при Х2 = 10, когда ресурсы труда используются до предела..
Имеется один дефицитный фактор и один независимый процесс (и два зависимых,
процесса): ^ = 40, Я2 = 10, Я3 = 40.
Двойственная задача состоит в минимизации рг
при условии
1р Л
536

Последнее ограничение (определяющее масштаб цен) снова опускается. Соотношения
между ценами получаем, рассматривая эти три выражения как уравнения (все
процессы применяются с нулевой прибылью):
л:л:л = Л=4:28:63:1.
Эти соотношения определяют производительность труда и нормы замены между
продуктами. Если» задаться ценой дров, равной 5 ф. ст. за 1 т, то это обусловит
значения цен остальных продуктов, что позволяет построить стоимостную матрицу
в фунтах стерлингов:
Используемый фактор:
труд
Продукты:
свежая рыба
копченая рыба
дрова
Оценка
20 ф.
ст./человеко-месяц
140 ф, ст./т
315 » » »
5 » » »
Первый
процсес
-5600
5600
—
—
Второй
процесс
-200
-2800
3150
-150
Третий
процесс
-200
—
—
200
Итого
-6000
2800
3150
50
Задачи и упражнения
1. В простой технологической матрице упражнения 2 из раздела 17.6 заданные
ресурсы снова примем равными 50 человеко-месяцам и 260 акрам. Будем считать,
что спрос на пшеницу и сено (в тоннах) выражается неизменным соотношением 1 : с.
Показать, что ресурсы труда или земли используются неполностью, если
соответственно с>5/з или с<6/3. Интерпретировать решение. Найти расчетные оценки
и истолковать их.
2. В примере (а) в тексте настоящего раздела рассмотреть случай с-|-1/2=
= 1/бA0&2—&i)/B&i — Ь2)\ интерпретировать полученные результаты. Можно ли назвать
этот случай нетипичным или «вырожденным»?
3. Решить задачу, двойственную по отношению к примеру (а), то есть определить
оценки, если Ь1 = 50, 62 = 521/2, с=1. Приняв />4=1, исключим р3 и получим:
минимизировать ?
при условии С
Построить графическое решение на плоскости Оргр2 и( установить, что
Pi • Р2 * Рз ' Р&=== 1:0 : 25 : 62,5.
4. В примере (б) в тексте настоящего раздела показать, что норма замены рыбы
равна 28 т копченой за 63 т свежей и что производительность труда составляет
примерно 0,14 т свежей рыбы и 0,06 т копченой рыбы за 1 человеко-месяц.
17.9. ПРИМЕР СПЕЦИАЛИЗАЦИИ
Задача линейного программирования с неизменной структурой спроса
будет рассматриваться далее (см. 18.7) в более широкой постановке. Она
применяется во многих случаях; в настоящем разделе приводится один из
них, иллюстрирующий задачу специализации, которую подвергла анализу
Мейкоуэр [9].
Рассмотрим фирму, применяющую простую технологию: производятся
раздельно два продукта, в каждом из двух процессов производится один
продукт и расходуются два фиксированных фактора; спрос на продукты
задан в определенном соотношении:
Технология
ап а12 0
«21 Я22 0
-1 0 с
0-11
Ресурсы
о
о
537

В задаче линейного программирования требуется: найти
неотрицательные Я, которые максимизируют Х3 при условии:
«11^1 ~Н «12^2 ^ ^1 И «21^1 ~Ь «22^2 ^ ^2>
Aj == ^^3 ^ 2 === ™3"
В случае, если числовые значения исходных данных известны, получаем
решение задачи графически с помощью чертежа, аналогичного рис. 64.
В общем случае один из двух факторов является дефицитным, а ресурсы
второго не используются полностью. Рассмотрим теперь вторую фирму с такой
же технологией, но располагающей иными ресурсами (Ь3 и fc4) двух
фиксированных факторов. И в этом случае мы получаем решение с одним
дефицитным и одним неполностью используемым фактором. Вполне возможно, что
в этих фирмах дефицитными окажутся разные факторы, то есть что первая
фирма не использует до предела ресурсы одного, а другая — второго
фактора. Возникает вопрос: не могут ли фирмы прийти к какому-то соглашению,
имеющему целью улучшить совокупные результаты деятельности? В
данном случае не столь важно, какую частную форму примет это соглашение;
это может быть договоренность относительно производства и совместного
(а не раздельного) предложения продуктов рынку в соотношении последних
с : 1. Это может быть и процесс взаимного обмена, если, например, две
фирмы размещены в различных географических районах. Здесь важно лишь то,
что фиксированные фактбры'не могут перебрасываться и что предложение
продуктов производится совместно в соответствии со следующей
объединенной технологией:
Технология Ресурсы
Факторы первой фирмы
Факторы второй фирмы
П родукты
Объединенная задача линейного программирования в данном случае
X, максимизирующие Я5 при
«11
«21
0
0
-1
0
«12
«22
0
0
0
-1
0
0
«11
«21
-1
0
0
0
«12
«22
0
-1
0
0
0
0
с
1
b
h
b
b
0
0
состоит в том, чтобы найти неотрицательные
условии:
^ + ^ < Ъ и
«Л^З + #12^4 < ^3 И «21^3 + «22^4 ^ ^4»
^1 + ^3 = СК И ^2 + К = ^5-
Последние уравнения C) служат для исключения Я4 и кь:
A)
B)
C)
и ^ =
Теперь имеются три X (Я17 Я2, Я3), которые надлежит найти из четырех
неравенств A) и B), определяющих лимитирующие ресурсы факторов в двух
фирмах. Конкретный способ нахождения X зависит от типа решения задачи
линейного программирования. Однако в общем случае три из четырех
соотношений A) и B) считаются уравнениями (ресурсы факторов используются
до предела), а одно остается неравенством. Поэтому решение задачи
совместной работы двух фирм в общем случае предусматривает один неполностью
используемый фактор; одна из фирм использует оба фактора до предела,
а вторая имеет один дефицитный и один неполностью используемый фактор.
Это явится улучшением по сравнению с результатами, полученными при
раздельной работе фирм, ибо тогда у каждой фирмы имелись бы неполностью
используемые ресурсы.
Такое решение соответствует общему случаю. В частных случаях
улучшения может и не быть. С другой стороны, иногда лимитирующие ресурсы
538

факторов могут случайно в точности совпасть с заданным соотношением спроса
на продукты — тогда ресурсы всех факторов полностью используются при
совместной, но не при раздельной работе. Это можно наглядно
продемонстрировать на числовом примере.
Пример
Каждая из двух фирм применяет технологию, описанную в упражнении 2 раздела
17.6: пшеница и сено производятся с использованием труда и земли. Лимитирующие
факторы различны; одна фирма имеет больше земли, другая—больше труда. Рынку
требуются равные количества пшеницы и сена. Рассмотрим положение при совместной
работе фирм.
Труд
Земля
Труд
Земля
Пшеница
Сено
Технология
человеко-месяцы
акры
человеко-месяцы
акры
100 т
100 т
' 25
50
0
0
л
0
10
100
0
0
0
1
0
0
25
50
—1
0
0
0
10
100
0
—1
о-
0
0
0
1
1
Ресурсы
50
260
62
220
0
0
Графическое решение задачи показано на рис. 65, где к± и Яг — уровни
производства для первой, а Х3 и Х4 — для второй фирмы.
Во-первых, предположим, что фирмы работают раздельно и продают продукты по
заданным (например, по одинаковым) ценам, как это принято в разделе 17.6. Тогда
решения для случая раздельной работы фирм отобразятся точками Р и R на рис. 65:
D)
Выпуск (в тоннах) распределяется между фирмами следующим образом:
Первая
фирма
Вторая
фирма
Итого
Пшеница
Сено . .
120
200
200
120
320
320
Здесь не налагается ограничений на соотношения спроса между продуктами; лишь
случайно общее предложение сена как раз равно предложению пшеницы.
Предположим, далее, что фирмы работают раздельно, причем спрос на оба вида
продукции определяется соотношением 1:1. Эта задача рассмотрена ранее в разделе
17.8, ее решение на рис. 65 отображается точками Q и S:
22
E)
и выпуск (в тоннах) распределяется между фирмами следующим образом:
Первая
фирма
Вторая
фирма
Итого
Пшеница
Сено ..
143
143
147
147
290
290
Разница между D) и E) заключается в том, что в D) равенство общих количеств
сена и пшеницы возникло чисто случайно, тогда как в E) это условие налагается на общую
продукцию обеих фирм и на продукцию каждой фирмы в отдельности.
В задаче о совместной работе общий выпуск продуктов обеими фирмами должен
отвечать соотношению 1:1, в то время как каждой фирме разрешается
специализироваться в своем направлении. Вопрос заключается в следующем: можно ли путем
совместных действий получить решение D), а не решение E)? Ответ здесь будет положительным.
539

Можно показать, что величины D) удовлетворяют условиям задачи при совместной
работе, то есть условиям A) — C), и проверить, что это и есть решение последней задачи.
В данном примере оказывается, что если фирмы работают раздельно, как в E), то они
имеют неиспользуемые ресурсы — одна фирма землю, вторая труд; при совместной работе
они могут полностью использовать свои ресурсы, как в D). Выпуск и пшеницы и сена
увеличивается одинаково на 30 т.
Случайный характер этого результата (а также и характер результатов,
получаемых в общем случае) виден из рис. 65. При раздельной работе возможности фирм
ограничены точками Q и S; %± и Х3 отображают выпуск фирмами пшеницы, а %2 и Я4 — сена.
Если фирмы обьединятся и станут принимать решения совместно, то первая фирма может
перейти из точки Q в точку Р, используя больше земли, а вторая — из точки S в точку R,
используя больше труда. При этом общее
предложение продуктов должно
соответствовать соотношению 1 : 1. В данном примере
обе фирмы случайно могут добиться своей
цели — полностью использовать ресурсы;
это — результат того, что заданное
соотношение спроса на продукты A:1) совпадает
с совместными результатами производства
при полном использовании ресурсов. В более
общем случае одна из фирм (скажем, первая)
достигает полного использования ресурсов
(точка Р), тогда как второй это не вполне
удается (она не достигает своей цели —
точки R). Даже при совместной работе вторая
фирма продолжает неполностью
использовать труд. Однако положение существенно
улучшилось; первая фирма не имеет
неиспользуемых ресурсов, а во второй
значительно уменьшилось неполное использование
труда. Обе фирмы имеют возможность
специализировать свое производство при совместном
удовлетворении спроса. Это — истолкование
условий A)—C), сформулированных выше
для общего случая.
Задачи и упражнения
1. Решить с помощью симплексного
метода задачу для случая совместной работы
с приведенными выше численными данными и
показать, что это решение совпадает с D).
2. Составить и решить двойственную
задачу для приведенного численного примера
и проверкой установить, что в решении нет
неиспользуемых ресурсов.
3. Изменить численные данные задачи,
приняв в качестве неизменной пропорции
спроса с = 4/6 вместо с = 1. Показать, что
при раздельной и при совместной работе ре-
Рис. 65. шения будут следующими (в тоннах):
Раздельная работа
первая
фирма
вторая
фирма
Совместная работа
первая
фирма
вторая
фирма
Пшеница
Сено . .
133
167
126
157
259
324
120
200
154
143
274
343
Показать, что если фирмы принимают совместные решения о размерах выпуска,
то лишь у второй фирмы имеются неиспользуемые полностью ресурсы (труд).

ГЛАВА 18
ТЕОРИЯ СТОИМОСТИ
18.1. ПОЛЕЗНОСТЬ. ПОРЯДКОВАЯ ИНТЕРПРЕТАЦИЯ ПОЛЕЗНОСТИ
Будем рассматривать поведение индивидуального потребителя. Пусть
имеется п потребительских товаров (хи х2, ... ,хп) и потребление
индивидуума характеризуется вектором:
х = (хг, х2, ..., хп)
и, следовательно, точкой Р в гг-мерном пространстве товаров. Примем, что
уровень удовлетворенности индивидуума или полезности есть функция его
потребления:
и = и(%, х2, . ..,зя), A)
где и — непрерывная функция, имеющая непрерывные производные
первого и второго порядка. Вместе с тем связь между уровнем полезности и
и вариантом потребления х здесь — порядковая, то есть
рассматривается в порядковом (качественном, ordinal) смысле; иначе говоря, функция
и(х19 х2, ... , хп) лишь одна из многих функций, характеризующих
полезность, и для этого может быть использована любая другая функция, в
которой элементы потребления] следуют в том же порядке. Это значит, что
функция и определена с точностью до возрастающего (монотонно) преобразования:
Полезность = ср (и), B)
где ф — любая функция, удовлетворяющая условию <р'(и) > 0.
Например:
аи-\-Ь\ аи2; a log и (а>0).
Все эти функции могут описывать порядковую полезность.
Функция полезности A) отображается гиперповерхностью в (лг + 1)-
мерном пространстве, то есть образованном из п измерений пространства
товаров и одного дополнительного измерения, добавленного для уровней
полезности, которое можно назвать «вертикальным». «Высоты» точек
гиперповерхности характеризуют полезность каждого из сочетаний товаров при
потреблении. Изогипсы («горизонтали») гиперповерхности — это ^-мерные
геометрические места точек Р заданных уровней полезности в пространстве
товаров; совокупность их составляет карту безразличия индивидуума.
Таким образом, если число товаров равно всего двум, то функция
полезности и = и(х19 х2) отображается поверхностью в трехмерном пространстве,
отнесенной к осям координат Оххх2и. Карта безразличия представит собой
семейство двумерных кривых в плоскости Оххх2 пространства товаров:
и(хх, х2) = const
для различных параметров этих кривых — постоянных уровней
полезности.
Форма порядковой функции полезности B) в общем случае определяется
выбранным типом функции ф. Форма поверхности полезности (при п = 2)
или гиперповерхности полезности (гс> 2) также зависит от выбранного типаф;
«высоты» точек поверхности можно менять как угодно произвольно, но
всякое изменение потребления, которому соответствует увеличение «высоты»
541

(полезности) на какой-либо одной поверхности или гиперповерхности, будет
характеризоваться увеличением «высоты» и на любой другой поверхности.
Поэтому форма «горизонталей» совершенно не зависит от порядкового места
вариантов потребления: «горизонтали» одной поверхности или
гиперповерхности (то есть геометрические места точек одинаковой полезности) будут
«горизонталями» и любой другой поверхности или гиперповерхности.
Изменяется лишь постоянный уровень полезности, сопоставленный каждой
«горизонтали». Следовательно, карта безразличия индивидуума не зависит
от свойства порядкового места полезностей; она не изменится, какую бы <р
ни взяли в качестве функции B). И обратно, если для индивидуума задана
карта безразличия, являющаяся семейством геометрических мест точек,
отображающих равноприемлемые (безразличные) сочетания товаров, то
сразу же можно составить порядковую функцию полезности B). Необходимо
лишь сопоставить упорядоченную совокупность уровней полезности с
семейством геометрических мест точек безразличия и описать эту совокупность
некоторой функцией и = и(хг, х2, ... , хп); тогда одинаково хорошо можно
воспользоваться любым возрастающим (монотонно) преобразованием ц>(и)„
Следовательно, понятие порядковой полезности можно выразить в двух
альтернативных и равносильных формах: либо в виде функции полезности
и = и (хг, х2, ... , хп), подчиненной монотонному преобразованию <р(м),
где ф'(^) > 0; либо в виде карты безразличия, представленной
u(xi, х2, ... , хп) = const или семейства кривых. Ограничения, налагаемые
на тип функции и или на карту безразличия, могут быть добавлены в
дальнейшем; например, обычно допускается, как мы укажем позднее, что кривые
безразличия монотонно убывают вниз и выпуклы относительно начала
координат, по крайней мере для относящихся к рассматриваемым
областям изменения переменной х. Карта безразличия таким же образом связана
с полезностью, как геометрические места точек (кривые) постоянного объема
производства связаны с производственной функцией.
При любом варианте потребления (хх, х2, ...,хп) существуют две
первые производные функции полезности и:
иг — faT и \Х1> Х2> • * • ' хп) и urs ~~ дх.дх U *'*'1' ^2' # " * ' Хп'
г,
= 1, 2,
Построим матрицу:
О их и2
и2 и21
22
2п
и
п1
ип
которая определена при любом варианте потребления (ггх, х
U Е
Так как urs~usr, то U есть симметрическая
й
2,
р (х 2 п
rssr, р матрица. Ее можно считать
неособенной, и значение определителя принять равным C7=[U|. Эта
матрица (и+1)-го порядка; ее общий элемент можно обозначить через
0 1 2 )
ur
()
(r, 5 = 0, 1, 2,
п), если условиться, что
= О и
Производные иг и мгв,' а значит и матрица U, зависят от типа
функции ф, взятой в общем ее выражении B). Важно изучить, каково влияние
выбора функции ф. Первые частные производные равны:
Аф(и) = Ф>К, C)
так что отношения между иг не зависят от типа функции ф. Нельзя иТ
назвать «предельной полезностью» r-го товара. Однако соотношение ur: us
есть величина определенная, не зависящая от характера функции ф, и ее*
542

можно назвать предельной нормой замены между r-м и s-м товарами: .
dxs __ иг
dxr us
для любых изменений (дхг и дх$) при движении по кривой безразличия.
Вторые частные производные равны:
дХгдх& Ф (и) = q/ (u)ura + ф" (и) urus. D)
Их значения зависят от принятой формы функции ф; даже знак второй
частной производной не инвариантен. В равной мере и матрица U зависит
от принятой формы ф. Это не столь важно, если на величину определителя
JJ= | U | и различных миноров или алгебраических дополнений этого
определителя не влияет выбор типа функции ф. При любом типе ф
определитель принимает следующую форму:
u)urus}\ (г, * = 0, 1, 2, ...,п).
Это следует из C) и D), если принять по соглашению, что цоо = О. Такой
определитель можно представить в виде суммы двух определителей, если
каждый элемент расчленить на два его слагаемых, но единственная часть
этой суммы, которая не обращается в нуль —это | ф' (и) urs |, ибо во втором
определителе две строки или два столбца имеют пропорциональные
элементы. Следовательно,
Ф = |ф'(«)"г81 = {ф'(")Г1|«гз1- E)
Из E) следует, что, если отвлечься от положительного множителя
(ф' (u)}n+1' т0 определитель U = | urs | будет одинаковым для всех типов
порядковой функции полезности. Это же можно сказать и о любом минора
или алгебраическом дополнении определителя U.
В частном случае, если функция полезности в общем виде
представляется выражением ф(м) = ам + 6, где а и Ъ — постоянные (а > 0), то,,
согласно C) и D),
¦щ. ф (") = а»г и щш,' № = aw«-
Все соотношения между первыми и вторыми частными производными
инвариантны; кроме постоянного (положительного) множителя а, задаются
значения иг и urs. В этом случае можно говорить о «предельной полезности»
иг и об определенных знаках ее производных urs; например, если гггг<0,
то иг можно считать «убывающей предельной полезностью». Это — тот
случай, когда и определено с точностью до линейного преобразования (аи + &),
то есть можно выбирать только единичный и нулевой уровень и. Именно этот
случай соответствует (см. 18.5) «измеримой» или «количественной»
полезности. Это — весьма особый частный случай, не включаемый в понятие
порядковой (качественной) полезности.
Это — основа теории поведения потребителя в условиях безденежного
хозяйства. Здесь ничего не говорится о том, предпочитает ли потребитель
(или предъявляет спрос) наличные деньги или облигации; данная теория
не связана с теорией предпочтения ликвидности (см. гл. 2). Моришима [16]
показал, что при определенных допущениях эту теорию можно
распространить и на денежное хозяйство. Обычная, порядковая, функция полезности
и(хх, х2, ... , хп) для п потребительских товаров усложняется до вида:
ф{и(ж!, x2t ...,жп); q(PnP2, . .., рп, М, В, ръ, L)},
где Рп Р*1 •-• 1 Рп — цены товаров, М и В — количества наличных денег
и облигаций, имеющихся у потребителя, ръ —цена облигаций и L — индекс
будущего уровня жизни, желательного для потребителя. Здесь q —
вероятность достижения в будущем уровня жизни L, зависящая от
финансовых ресурсов потребителя в настоящий момент (М и В) и от существующих
543

цен. В более широкой функции полезности ф, опять-таки являющейся
порядковой, показатели, натуральные и денежные, разделяются. Важнейшее
допущение состоит в том, что предельная натуральная норма замены между
двумя реальными благами не зависит от денежных характеристик (цен,
имеющихся количеств наличных денег и облигаций). Моришима развивает на этой
основе теорию поведения потребителя, которая включает в себе традиционную
(безденежную) теорию и связана с понятиями предпочтения ликвидности.
Например, Моришима показывает, что если с увеличением процентной ставки
возрастают сбережения, то уменьшается спрос на товары в вещественном их
выражении (за исключением малоценных товаров) и возрастает спрос на
наличные деньги и облигации (не говоря уже о влиянии замены).
Задачи и упражнения
1. Показать, что U = | U | есть квадратичная форма относительно переменных «г,
коэффициенты которой зависят только от значений вторых производных urs. Для случая двух
товаров записать этот определитель в виде:
2. Приняв V2 и2 за мерило полезности, то есть ср(и) = У2 и2, причем функция и
задана, покажите, что определитель Ф = un+1U. Написать это выражение в развернутом
виде для случая двух товаров.
3. Пусть в качестве другого показателя полезности принят log и. Показать, что
при этом Ф = U/u71*1, Сравнить это с результатом, полученным для предыдущей
задачи.
18.2. СПРОС ПОТРЕБИТЕЛЯ
Пусть индивидуальный потребитель, порядковая функция полезности
для которого есть и — и(хи х2, ... , хп), имеет заданный денежный доход М
и может купить на рынке п товаров по заданным ценам рг, /?2> ••• > Рп-
Задача состоит в определении такого варианта его спроса количеств (хи х2,... ,»#п),
при котором полезность становится максимальной, то есть максимизируется
и, или, в равной мере, ф(ю). Решение является условным максимумом;
значения переменных х определяются с целью максимизации и при условии
Введя множитель Лагранжа Я, преобразуем это выражение:
max {и — К B Ртхт — М)).
Следовательно,
= l, 2, ..., гг),|
A)
Уравнения A) суть условия равновесия для потребителя; их число
достаточно для выражения Я и п величин спроса на товары (хг, х2, ... , хп)
через заданные цены и доход потребителя.
Если цены и доход считать параметрами, то условия A) определяют
спрос на количества товаров как функции цен р и дохода М.
Пропорциональное возрастание всех цен/? и дохода М (и уменьшение в такое же число
раз величины К) не изменяет A), то есть спрос потребителя остается прежним.
Функции спроса однородны (нулевой степени) относительно переменных.
Это — характерная особенность задачи: рассматриваются только
соотношения цен и дохода. Ничего не изменится, если, например, удвоить все цены,
а также денежный доход потребителя. Рассмотрим альтернативный вариант
задачи: примем один товар (n-й) за базисный (за единицу измерения) и
приравняем рп единице. Тогда спрос потребителя будет выражаться функциями
относительно (п—1) цен и дохода, и эти функции не являются однородными,
так как рп = 1 определяет уже относительные значения цен (и дохода).
544

Выше мы для удобства математических расчетов ввели параметр X.
Согласно условиям A), при состоянии равновесия его значение равно
единому (общему) значению соотношений иг : рг, то есть
Pi
Рг
Рп
В той же мере, в какой иг можно считать «предельными полезностями»,
которые пропорциональны ценам в состоянии равновесия, X можно назвать
«предельной полезностью денег». Она также является функцией цен
и дохода. Говоря более строго, условие равновесия (для порядковой
функции полезности) состоит в том, что всякая предельная норма замены
(ur:us) равна соответствующему отношению цен (pr-Ps)- Тогда предельная
норма замены одного из товаров и денег (иг: X) равна отношению цен
(Р,:1).
Уравнения A) суть необходимые условия максимизации и.
Достаточные условия заключаются в том, что:
= 3 2 ursdxrdx8 <0
r=l s=l
при
2
r=l
Последнее следует из условия 2 Prxr= M. Поскольку в состоянии
равновесия рг пропорционально иг9 приведенные выше условия представляются
в следующем виде:
п п
d2U = 2 2 Urs dxr dxs < О
при
r=i s=l
du = 2 ur
B)
Это —условия «устойчивости» в том ее понимании, которое
сформулировал Хикс [9]. Чтобы обеспечить во всех случаях нахождение истинного
максимума вне' зависимости от заданных цен и дохода, эти условия должны
соблюдаться для любых отклонений (dxr), из которых не все равны нулю,
от всякого положения (х1У х2, ..., хп).
Условия («2) обусловливают определенную отрицательную форму
для некоторой квадратичной формы при соблюдении ограничивающего
соотношения, то есть
для всех 1Г (не все из которых равны нулю) при 2wr?r = 0. Эти усло-
г
вия сформулированы в разделе 17.5. Они заключаются в следующем:
0
«1
щ
ui
«11
«21
щ
«12
«22
>o,
0 иг и2 и3
Mi un и12 и13
щ и21 и22 и23
и3 и31 и32 и33
C)
то есть в том, что главные миноры определителя U = | U | будут
знакочередующимися. Эти условия не зависят от того, какая выбрана форма
функции полезности ц>(и) (см. упражнение 3).
35 р. Аллен
545

Чтобы придать этим условиям более удобную форму, воспользуемся
результатами, полученными в конце раздела 13.5. Они касаются связи
соответствующей квадратичной формы с обратной матрицей U. При этом
для любых значений ут и г/8, из которых не все равны нулю, условия
устойчивости выражаются следующим образом:
|8М8<0. D)
Здесь Urs — алгебраическое дополнение элемента иг$ в определителе
(п + 1)-го порядка U = | U |.
Следует отметить, что выражения C) и D) — различные способы
представления всей совокупности условий устойчивости. Одно частное условие,
выбранное из всей этой совокупности, может быть получено на основе
двух последних неравенств C):
^я<0 (г = 1, 2, ...,и).
Его можно получить также из D), приняв нулевыми значения всех у,
кроме уг. Но это —только одно из многих условий, заданных в
развернутом виде неравенствами C), а также и D).
Задачи и упражнения
1. Показать, что если функция полезности есть м = 1/2 (a11xl-\-2a12x1x2-\-a22zt), то
спрос определяется через цены (р19 р%) и доход (М) с помощью следующих уравнений:
Доказать, что линейной будет зависимость спроса от М, но не от рг и jo2. Каким
будет значение X для состояния равновесия? Рассмотреть условия монотонного
убывания кривых спроса.
2. Если функция полезности является такой же, как и в предыдущей задаче,
показать, что условием устойчивости является выполнение неравенства а>ъъР\—
—2a12PiP2Jrai\Pl<^^ ПРИ любых рх и р2. Вывести, что при этом Яц<0, я22<0»
ai2<Caiia22« Показать, что кривые спроса явятся тогда монотонно убывающими.
Объяснить, почему условие отрицательности аХ1 и а22 вызывает «нереальность»
квадратичной функции полезности.
3. Показать, что условия устойчивости C) не связаны с порядковым свойством
полезности и.
18.3. ВЛИЯНИЕ ДОХОДА И ВЛИЯНИЕ ЗАМЕНЫ
Функции спроса для индивидуума, то есть зависимость каждого из
значений х от цен и дохода, задаются условиями равновесия:
иг = Хрг и ^ргхг = М (г==1, 2, ..., п). A)
Эти (тг + 1) уравнений мы можем продифференцировать по любой из
переменных или по всем переменным М и рг(г=1, 2 ..., п), определив
таким образом отклонения спроса при. изменениях цен и дохода.
Во-первых, рассмотрим случай увеличения дохода М при неизменных
ценах. Продифференцируем уравнения A) по М и расположим полученные
уравнения в надлежащем порядке:
546

Произведем подстановку pr = (l/X)ur\ тогда они приобретают
следующий вид:
2 и dx$-X
UsdM"A"
B)
Эту систему уравнений можно решить с помощью правила Крамера,
относительно значений {— A/Х)(дХ/дМ)} и п переменных dxJdM. Для
системы B) матрицей коэффициентов будет U; величина ее определителя равна
C7 = |U|, а алгебраические дополнения элементов последнего суть Ur и Urs.
Решением системы B) является
зм'
и
= 1, 2,..., п)
C)
и аналогичное выражение для { — A/Х)(дХ/дМ)}, которое нам не требуется.
В условиях устойчивости предыдущего раздела (см. 18.2) ничего не
говорится о знаке величины Z78. Следовательно, изменение спроса, вызванное
увеличением дохода и определяемое уравнением C), может быть как
положительным, так и отрицательным. С возрастанием дохода спрос на
некоторые товары увеличивается, на другие (малоценные) —уменьшается.
Далее, рассмотрим повышение одной цены (скажем, рх), причем
остальные цены и доход остаются неизменными. Продифференцируем уравнения
A) по рх и произведем подстановку pr = (l/X)ur:
п).
D)
)
Из системы уравнений D) с помощью правила Крамера можно
определить значения п переменных dxjdp1 и переменной ( — i/X)(d'k/dp1)^
которая нам не требуется:
|Ьв-Х«1$ + *%. (—1,2,...,»).
Вместо р± можно выбрать любую цену рг\ тогда, произведя
соответствующие подстановки в C), получим результат в общем виде:
где
и
(г, s = l, 2, ...,»).
E)
F)
Согласно E), изменение цены одного товара влияет на спрос, причем
оно состоит из двух слагаемых: одно из них есть dxJdM, а второе
обозначено через Xrs и определяется F). Этот результат впервые получил
Слуцкий [29], а позднее —Хикс и А л лен [8].
Первое слагаемое в уравнении E) —это влияние дохода. Увеличение
цены рг соответствует снижению реального дохода, а следовательно —
уменьшению спроса на все товары, для которых (dxJdM) > 0, и
увеличению спроса на все малоценные товары, для которых (dxJdM) < 0. Чтобы;
исключить это влияние, а значит выделить только другое влияние (влия-
547
35*

ние замены), рассмотрим увеличение dpr цены рг, сопровождаемое
компенсирующим увеличением дохода dM = xrdpr. Спрос на любой товар при
таком увеличении цены изменяется следующим образом:
Следовательно, в соответствии с E), компенсированное изменение спроса
равно:
Это — влияние замены; оно показывает результат относительных
изменений цен, то есть вызванную ими взаимозамену товаров при
потреблении. Направленность изменения спроса на товар xs при компенсированном
изменении цены рг определяется знаком выражения Xrs, даваемым F).
Если Xrfe > 0, то с возрастанием цены рг спрос на xs увеличивается; два
товара взаимозаменяемы. Если Xrs < 0, то с ростом цены рг спрос х$
уменьшается; товары взаимодополняемы.
Теперь вступают в силу условия устойчивости D) из раздела 18.2.
Их можно записать в следующем виде:
Для любых значений z/, из которых не все равны нулю,
В частности, приравняв нулю значения всех г/, кроме i/r, получим:
Xrr<0 (r = l, 2, ...,п). (8)
Кроме того, имеет место еще одно соотношение, которое всегда
соблюдается, независимо от выполнения условий устойчивости:
Здесь элементы первой строки определителя U умножены на
алгебраические дополнения соответствующих элементов другой строки (расположенной
через г строк после первой) этого определителя, и, согласно правилу
разложения определителей, сумма таких произведений всегда равна нулю.
Следовательно,
2Xrs/>s = 0 (r = l,2,...,n). (9)
s
Если условия устойчивости удовлетворяются, то значения слагаемых
замены, Xrs, ограничены соотношениями G) — (9). Это позволяет сделать множество
выводов, важнейшие из которых следующие:
Поскольку U есть симметрическая матрица, то Urs — Usr и, значит,
Xrs = Xsr, то есть соотношения замены между двумя товарами
симметричны. Согласно (8), непосредственное влияние компенсированного изменения
цены суть (dx,Jdpr) = Xrr < 0, то есть спрос на товар уменьшается с
увеличением цены на него. Это касается компенсированного увеличения цены,
сопровождаемого соответствующим увеличением дохода. Отсюда не следует,
что некомпенсированное повышение цены также вызывает сокращение
спроса. И в самом деле, в соответствии с уравнением E):
Здесь ( —Xrr) есть величина положительная, однако и { — дХг/дМ)
может оказаться положительной величиной: если товар малоценен и,
преобладающим может быть влияние дохода, то (дхг/дрг)>0. Это —хорошо
известный парадокс Гиффена\ при повышении цены малоценного товара
548

возможно увеличение, а не уменьшение спроса на этот товар (например,
при низком уровне дохода).
Что же касается «перекрестных», взаимных влияний компенсированных
изменений цен, то здесь можно сказать только одно: критерием
взаимозаменяемости или взаимодополняемости двух товаров является знак
выражения Xrs. Согласно (9):
^j'XrsPs=(-Xrr)pr>0,
S
где 2' означает суммирование по эфг. Все Xrs (при заданном г, s Ф г)
S
могут оказаться положительными, но не все отрицательными. Все товары
могут быть взаимозаменяющими, но исключено, чтобы все они были
взаимодополняющими. В любой системе товаров существует предел
взаимодополняемости.
Важное значение ограничений G), в которых используются все
условия устойчивости, становится очевидным при рассмотрении спроса на
группу товаров, когда цены на все товары изменяются в одинаковое число
раз. Рассмотрим в качестве одной группы товаров первые по порядку т
товаров; пусть dp есть пропорциональное изменение цены, так что
dp = (dpr/pr) (г =* 1, 2, ..., то). Обозначим через vr = prxr расходы на г-я
т
товар и через и = 2 vr расходы на все товары группы. Тогда, если
изменяется цена только r-то товара [{dpr/pr) = dp], то
dvs = •?*- dpr = рs ^ dpr = (согласно E)),
s дрг ГТ s opr ri v \ //'
( ~ «. дх» i ~ v
= ( — Ро%г ь~П- + Рч^
то есть
Если цены на все товары изменяются пропорционально, то, суммируя
все такие уравнения со значениями индексов г и s, пробегающими от 1 до
гс, и обозначив через v = 2 vn можно написать:
m m
r=i s=\
Это есть уравнение для группы товаров; оно имеет в точности такой же
вид, как уравнение для единичного товара, входящего в группу. Более
того, слагаемое, представляющее замену для группы при
пропорциональном повышении цен, равно:
Этот результат получим, если в неравенстве G) считать значения m первых
у-ов ценами, а остальные г/ —нулевыми. Слагаемое замены отрицательно,
совершенно так же, как Хгг для одного товара, и совокупный спрос (в
стоимостном выражении) по группе снижается, если имеет место
пропорциональное (и компенсированное) повышение цен. Именно в этом смысле
группу товаров можно рассматривать как один товар так, как это делал
Хикс [9].
Задачи и упражнения
1. Представить уравнение E) в виде уравнения- эластичности:
Ру дх& pyXr f M dxs
xs дрг М \ xs дМ
549

Показать, что коэффициент слагаемого, учитывающего влияние дохода, является
здесь долей дохода, затраченной на приобретение рассматриваемого товара (после
изменения цены), и рассмотреть следствия, связанные с парадоксом Гиффена.
2. Если имеются только два товара, показать, что единственный член
«перекрестной» замены Хг2 является положительным и, следовательно, взаимодополняемость
товаров невозможна. В какой степени возможна взаимодополняемость в случае трех
товаров?
3. На основе ограничения G) показать, что при любых ценах (из которых не
т п
все равны нулю) и при любом т^п справедливо неравенство ^] 2 Xrsprp8<0.
r=l s=i
т п
Затем воспользоваться уравнением (9) и доказать, что ^ 2 Xrsprps>0. Объяс-
r=l s=m+l
нить, каким образом полученный вывод показывает, что если все товары разбить на
две группы, то одна группа заменяет другую, и взаимодополняемости между
группами быть не может.
4. Рассмотреть задачу питания (для двух продуктов и двух показателей
питательности), сформулированную в разделе 15.3 и иллюстрированную рис. 50, а именно:
минимизировать z = Pixi-\~P2x2
При УСЛОВИИ
Показать, что количества покупаемых продуктов (х± и х2) при изменении цен остаются
неизменными (оба положительны) до тех пор, пока (пц/пц) > (Pi/Ръ) > («21/^22) (если для
удобства рассуждений считать, что а1га22 >a12a2i)« Минимальное значение z зависит от
цен. Доказать, что при уменьшении рг (р2 фиксировано) z уменьшается, но xi не
изменяется, пока рг не достигнет критического значения, затем хг скачком изменяется
до более высокого значения. Истолковать это как влияние замены при одном
критическом значении [pi = (a2il<h&} Ръ[> см. [17].
18.4. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ
Если число товаров равно двум, то спрос потребителя определяется
путем максимизации и(х1ч х2) при условии выполнения уравнения бюджета
рхх ~\- х2 = М, где р — цена первого товара (относительно цены второго
товара, принятой за единицу), а М —доход. Условия равновесия состоят в
следующем:
их = ри2 и рхг + х2 = М.
Здесь х1 и х2 заданы как функции двух переменных: относительной цены р и
дохода М. Для существования устойчивости должно быть d2u < 0 для любого
изменения, при котором du = 0.
Карта безразличия — это семейство кривых Aи /2, /3, ...) в плоскости
Охгх2; уравнение каждой такой кривой есть и{хх> х2) = const, причем
постоянная принимает разные заданные значения. Уравнение бюджета
pxt + х2 — М отображается прямой бюджета A±A2i имеющей наклон (—р)
и отсекающей на осях координат отрезки
ОАХ = — и 0А2 = М.
Отрезок, отсекаемый на оси ординат, отображает доход потребителя;
величина ОАХ увеличивается со снижением цены р. Условия равновесия
состоят в том, что прямая бюджета касается кривой безразличия — наклоны (—р)
и (—иг/и2) равны между собой —в точке Р, координаты которой — закупки
товаров в состоянии равновесия. Для устойчивости должно выполняться
условие d2a < 0 при любом движении от точки Р вдоль касательной к
кривой безразличия {du = 0); это значит, что касательная пересекает более
низкие кривые безразличия, и что кривая безразличия в точке Р выпукла
относительно начала координат. Все это показано на рис. 66.
550

С изменением р и М изменяются и параметры линии бюджета АХА2—
либо наклон (изменение/?), либо точка пересечения с осью ординат
(изменение М), либо обе величины. При этом точка равновесия Р изменяет свое
положение на карте безразличия, и отклонения ее координат показывают
соответствующие изменения спроса (х± и х2). Если М увеличивается
(при фиксированной р), то АХА2
смещается параллельно самой
себе, и Р движется по кривой
дохода РВ, составленной из тех точек
различных кривых безразличия,
касательные в которых
параллельны (имеют заданный наклон
(—¦/?)). Если р уменьшается (при
фиксированномМ), то прямая АХА2
поворачивается относительно
точки А2 таким образом, что точка Аг
смещается вправо. Точка Р
движется по кривой цен PC у в точках
которой вращающаяся прямая
бюджета является касательной к
кривым безразличия. Основным
выводом, который удалось
получить Слуцкому, является то обстоятельство, что движение точки Р вдоль
кривой PC есть результат совместного действия двух смещений: смещения Р
вдоль линии бюджета (влияние замены) и смещения Р вдоль кривой РВ
(влияние дохода). Два товара должны быть взаимозаменяющими, так что (при
О
ос,
Рис. 66.
Рис. 67а.
Рис. 676.
снижении р) влияние замены должно вести к увеличению ^ик
уменьшению х2. Однако рост дохода приводит обычно к увеличению и хх и #2, и при
движении по кривой PC в направлении возрастания хх возможно как
увеличение, так и уменьшение х2.
Все это касается бесконечно малых изменений. Наряду с этим,
целесообразно тем не менее графически изобразить характер изменений, и при
конечных малых изменениях. Это сделано на рис. 67. Пусть цена
изменяется от р до (р — А/>) при фиксированном М; тогда прямая бюджета
поворачивается из положения А2Р в положение A2Q, точка равновесия
смещается из Р в Q, то есть с кривой безразличия 1г на кривую безразличия /2.
На рис. 67а прямая A'JP параллельна прямой A2Q и проходит через точку Р.
Поскольку прямая A'JP является бюджетной, ей соответствует определенная
цена товара (р—Ар) и доход, достаточный для покупки прежних
количеств товаров (координаты точки Р) по этой цене. Сокращение дохода (по
сравнению с М) равно А'гА2 = ххАр, где хх — количество первого товара,
покупавшееся в точке Р. Прямая A'JP является касательной к какой-то
промежуточной кривой безразличия 1[; касание происходит в точке Л,
координаты которой характеризуют покупки товаров после снижения цены на Ар9
551

компенсированного соответствующим уменьшением дохода ххкр.
Следовательно, изменение цены (при фиксированном доходе) приводит к изменению
спроса, показанному в виде перемещения от Р к Q. Это перемещение
(приблизительно) представляет собой сумму влияния замены (перемещение от Р к R)
и влияния изменения дохода (перемещение от R к Q). Такое истолкование
выводов Слуцкого — применительно к конечным изменениям — является
приближенным, но наглядным; оно совпадает с изложением как Слуцкого
[29], так и Хикса (в его приложении к [9]).
Однако опасно пользоваться на чертеже конечными смещениями для
отображения бесконечно малых изменений при предельном анализе. Как
показал Мозак [18], Хикс в основном тексте своей книги, в
противоположность упомянутому приложению к ней, воспользовался другим методом
графического изображения. На рис. 676 то же перемещение от точки Р
к точке Q расчленено на две части: от Р к Q по кривой безразличия (влияние
замены), а затем от R к Q по кривой дохода (влияние дохода). Это
перемещение можно с таким же успехом изобразить при обратной последовательности
влияний: вначале от Р к S по кривой дохода, а затем от S к Q по кривой
безразличия. Здесь суть дела в том, что эти два перемещения различны, и
каждая из частейнового перемещения отличается от истолкования, данного выше
(см. рис. 67а). Приближенное изображение конечных отклонений вносит
неясность. В пределе же для бесконечно малых величин все изображения
дают одинаковые результаты. В частности (см. упражнение 2), влияние
замены на рис. 67а, отражаемое смещением по линии бюджета А'2Р,
в пределе будет таким же, как на рис. 676 смещение точки Р по кривой
безразличия; компенсированное изменение цены равносильно изменению
цены при постоянном и.
Если число товаров равно трем, то изображение в трехмерном
пространстве возможно, но его трудно истолковать. Картой безразличия при этом
будет семейство поверхностей в пространстве, отнесенных к осям координат
Оххх2х3. Уравнение бюджета (если цена третьего продукта принята равной
единице) есть ргхг + р2х2 + х3 = М; оно отображается плоскостью бюджета
в трехмерном пространстве. Эта плоскость отсекает на осях координат
отрезки ОАг = М/рх, ОА2 = М1р2 и ОА3 = М; они позволяют определить
влияние изменений двух относительных цен (рх и р2) и дохода (М). Спрос
потребителя характеризуется координатами точки Р, в которой плоскость
бюджета является касательной к поверхности безразличия. Если М
изменяется (рх и р2 фиксированы), то Р движется по трехмерной кривой дохода,
являющейся геометрическим местом точек на поверхностях безразличия;
касательные плоскости в этих точках параллельны между собой. Если
изменяется одна относительная цена рх (р2 и М фиксированы), то Р движется по
кривой цен — геометрическому месту точек касания плоскости бюджетаг
вращающейся вокруг прямой А2А31 и поверхностей безразличия. Именно
эту кривую, а также соответствующую кривую для цены р21 трудно
зрительно представить и истолковать. Трудность заключается не только в том,,
каким образом отделить влияние замены от влияния дохода, но и в том,
чтобы учесть зависимость взаимодополняемости, которая (как и
взаимозаменяемость) может возникнуть при переходе от двух к трем товарам.
Задачи и упражнения
1. Если число товаров равно двум, а функция полезности есть и (а?х, а^)> т<>
условия устойчивости (d2w<0 при <2м = 0) представляются в виде
О их и2
их ихх и12
и2 и12 и22
Если тангенс угла наклона касательной к кривой безразличия численно равен
—dx2/dxx)= их/и2, выразить — (—dx2/dxx) через производные от и и объяснить
знак этого выражения с помощью условий устойчивости. Отсюда показать, что для
существования устойчивости кривая безразличия должна быть выпуклой относительно*
начала координат.
552

2. Применить метод, изложенный в разделе 18.3 (для случая п товаров), для
нахождения изменения спроса, если одна цена изменяется при и = const. Показать,
что (dxs/dpr) = Xrs и что это изменение эквивалентно компенсированному изменению
цены. (См. [18].)
3. Если число товаров равно двум, показать, что парадокс Гиффена возникает
при (—дх1/др)<С,0 и дх±/дМ<0, то есть если на рис. 66 обе кривые РВ и PC
направлены вверх и влево. Вычертить карту безразличия, форма которой
соответствует этому (необычному) случаю.
18.5. ИЗМЕРИМОСТЬ ПОЛЕЗНОСТИ
Вышеприведенный анализ был основан на том предположении, что
решения индивидуума имеют целью максимизировать порядковую функцию
полезности,' или достигнуть как можно более высокой кривой на его карте
безразличия в пространстве товаров. Здесь обойден один вопрос,
представляющий некоторый интерес. Порядковое понятие полезности можно
обосновать на какой-либо единственной аксиоме, например, на том, что любую
совокупность вариантов потребления можно расположить в единственном
и непротиворечивом (совместном) порядке возрастающего предпочтения.
Предположим, что индивидуум предпочитает вариант В варианту А, вариант
С — варианту В, что он отдает равное предпочтение вариантам D и С, что
он предпочитает вариант Е варианту D, и т. д. Для совместности требуется,
чтобы варианту С отдавалось предпочтение перед вариантом А, варианту D —
перед вариантом А и В и т. д. Уровни полезности будут следующими:
иа<иь < uc = ud< ие. A)
Если будем рассматривать соответствующие точки в пространстве
товаров, то точки С и D окажутся расположенными на одном и том же
геометрическом месте точек (гиперповерхности, поверхности или кривой)
безразличия, которое ниже того, на котором расположена точка Е, но выше того, на
котором расположена точка В (и еще выше того, на котором расположена
точка .4).
Однако из этой основной аксиомы еще не следует, что существует
функция полезности и, по отношению к которой может производиться только
монотонное преобразование <р (гг), то есть что в пространстве товаров
действительно имеется система геометрических мест точек безразличия (кривых,
поверхностей, гиперповерхностей). Это есть вопрос «возможности суммирования»,
возникающий при таком подходе к порядковой полезности, как у Слуцкого
[29] или Хикса и Аллена [8]. Основная аксиома позволяет определить
безразличное направление отклонения от любой точки (сочетания товаров),
характеризуемой предельной нормой замены; эта аксиома дает построение
всего геометрического места точек безразличия только в том случае, если
направления для отдельных точек можно «объединить» в такое
геометрическое место. Для этого предельные нормы замены должны отвечать некоторому
«условию суммируемости»: не существует явной экономической причины,
почему они должны — или не должны — отвечать этому условию. Тем не
менее свойство транзитивности для предпочтения или безразличия,
представленное выражением A), можно сформулировать в виде аксиомы,
обеспечивающей «суммируемость» и, следовательно — существование
упорядоченной функции полезности и карты безразличия. По этому вопросу см. [6].
При другом подходе, которому следовали Самуэльсон [25], [26] и Хаут-
эккер [11], пользуются понятием «выявленного предпочтения»,
основывающимся (в идеальном случае) на наблюдениях за поведением потребителя
при смене вариантов потребления. Для обеспечения «суммируемости»
формулируется «усиленная аксиома» транзитивности: если выявлено
предпочтение А по сравнению с В, В по сравнению с С, ... , У по сравнению с Z,
то в таком случае выявлено и предпочтение А по сравнению с Z. Z,
находящемуся в конце цепочки предпочтений, не может быть отдано предпочтение
по сравнению с -4, находящимся в начале этой цепочки. Корлетт и Ньюмэн
553

ЛЗ] обобщили это положение. Понятие выявленного предпочтения
представляет полезное дополнение простого допущения порядковой функции
полезности и карты безразличия.
Гораздо более значителен вопрос о том, можно ли считать порядковую
полезность также и измеримой и, если да — то при каких условиях. По этому
вопросу имеется обширная литература, математический характер которой все
более усиливается. Нижеследующее изложение представляет не более чем
набросок в простейшей математической трактовке одного из направлений его
разработки. Оно основано на беседах с д-ром Г. Мортоном, д-ром С. А. Озга
и другими коллегами по работе в Лондонской школе экономики и на
изложении этой проблемы в соответствующих работах [1, 5, 15 и 21].
Вопрос ставится следующим образом: можно ли соответственным
образом расширить основную аксиому упорядоченных предпочтений, чтобы
порядковая полезность стала измеримой? В своем предварительном докладе
(«Interim Report») по этому вопросу Робертсон [23] спрашивает: почему слово
«порядковый» не может влечь за собой «не только идею наличия
упорядоченности, но и сопутствующее значение наличия упорядоченности методичного
вида, то есть такой, при которой между каждыми двумя упорядоченными
точками имелось бы делимое пространство?» (стр. 129 его работы). Несомненно,
априори нет основания для согласия с такой точкой зрения или поспешного
отказа от нее.
Согласно основной аксиоме упорядоченных предпочтений совокупность
вариантов потребления располагается в соответствии с их возрастающей
полезностью, как это сделано в A). Добавим теперь вторую аксиому:
приращения полезности, или ступени предпочтения, также могут быть упорядочены,
то есть (иь — ма), {ис — мь), ... могут быть, как и иа, иЪ1 ис, ... , расположены
в порядке возрастания разности предпочтения. В частности, можно выбрать
такой вариант В, находящийся в списке упорядоченных предпочтений между
вариантами А ж С, что приращение (иь — иа) оценивалось бы наравне с
приращением (ис — иъ):
иь — иа = ис — иь, или ub = |(Me + wc). B)
Когда мы к основной упорядоченности A) добавляем положение,
подобное B), то полезность становится измеримой, при условии только, что
начальная точка и единица измерения произвольны. Ибо равенством B) утверждается,
что В находится точно посредине, а не где-то в промежутке между А и С,
и уровень полезности иь является средней арифметической между иа и ис.
Описанное положение можно иллюстрировать на численном примере
гипотетических вариантов потребления индивидуумом чая и кофе:
Комбинация
товаров
Потребление, фунтов
в неделю
чай
кофе
Порядковая
полезность
Показатель (мера) полезности,
полученный на основании:
оценки
приращений
оценки
вариантов, связанных
с риском
1
А
В
С
D
Е
F
2
2
2
2
3
2
4
3
_
1
2
3
2
4
1
2
I 3
4
5
5
1
2
2,5
3
4
6
1,5
2
2,5
3
5
Применяя только упорядочение предпочтений (на основе первой аксиомы),
предположим, что все шесть комбинаций потребления расположены, как
это показано, в порядке возрастания предпочтений, причем вариантам С
554

ш D оказывается одинаковое предпочтение. Один ряд уровней полезности
(порядковых) приведен в четвертом столбце таблицы. Это — только одна из
многих возможных систем, другой может быть следующая (вместо и берется
In и):
О 0,69 0,92 1,10 1,39.
Предположим теперь, что можно упорядочить и приращения полезности
(вторая аксиома). Чтобы определить шкалу измерения, произвольно выберем
для этой цели два варианта В ж Еж примем иь = 2 и ие = 3. Сделаем
следующие допущения:
I. Увеличение потребления на 1 фунт кофе против варианта В B фунта чая
и 1 фунт кофе) оценивается одинаково с таким же увеличением потребления
кофе против варианта С B фунта чая и 2 фунта кофе). Это значит, что два
последовательных приращения полезности (от В к С и от С к ?) равны:
ис — иь = ие — ис, или ис = у (иь + ц) = 2,5.
Следовательно, ис = ad = 2,5.
II. Увеличение потребления на 1 фунт кофе против варианта А B фунта
чая) оценивается одинаково с увеличением потребления на 2 фунта кофе
против варианта В B фунта чая, 1 фунт кофе). Приращения от А к В и от
В к Е оцениваются одинаково:
иъ — иа = ие — иъ, или иа = 2иь —ве = 1.
III. Увеличение потребления на 1 фунт чая против варианта А B фунта чая)
оценивается одинаково с увеличением потребления на 2 фунта чая против
варианта С B фунта чая, 2 фунта кофе). Приращения от А к D и ог С к F
оцениваются одинаково:
u>d — ua = uf-ucJ или uf = ue + ud — ua = 4.
Следовательно, если известны три ранжирования (I, II, III) или оценки
приращений полезности, и заданы точки шкалы иь и ие, то однозначно
получаем показатели полезности, приведенные в пятом столбце таблицы. Если
выбрать другие точки шкалы, то иными будут и цифры в этом столбце — но
только в том смысле, что величина любого показателя зависит от начала
отсчета и от единицы измерения.
Трех оценок достаточно для измерения пяти определенных уровней
полезности. Подобная цроцедура будет успешной при любом числе уровней
полезности — конечно, при том условии, что соответственно возрастает число
оценок приращений. Важным пунктом второй аксиомы (как и первой)
является необходимая совместность оценок. Например, приращения
потребления на 1 фунт чая против варианта А, на 2 фунта кофе против варианта
А и на 2 фунта чая против варианта С должны оцениваться одинаково —
в каждом из этих случаев приращение полезности равно 1,5 единицам.
Двух аксиом согласного упорядочения предпочтений достаточно для
того, чтобы появилась возможность измерить полезность. Одна аксиома
касается упорядочения исходных предпочтений, вторая — упорядочения их
приращений. Если и представляет уровень полезности, то первая аксиома
гласит, что и есть порядковая функция, в общем случае имеющая форму
<р(м), где ф—монотонная (возрастающая) функция. Тогда вторая аксиома
гласит, что и есть количественная функция (и измеримо), и в общем случае
ее форма есть (аи + |3), где аир — постоянные, показывающие начало
отсчета и единицу измерения. Упорядоченная полезность определима с
точностью до монотонного (возрастающего) преобразования, количественная
полезность — с точностью до линейного преобразования.
Следует отметить, что и в точных науках для построения шкалы
измерения требуются те же две постоянные. Так, высоту полета самолета можно
измерить в футах над уровнем Лондонского аэропорта, или в метрах над
уровнем аэродрома Ле-Бурже. Даже если кажется, что необходима только одна
555

постоянная (например, при измерении веса в фунтах или граммах), то это>
вызывается лишь тем, что существует уже какая-то естественная точка
отсчета (например, нулевой вес).
Обе аксиомы раздельны, и не обязательно нужно дополнять второй
аксиомой первую. Любую из них можно испытать или проверить путем
наблюдений. Можно считать, что первая аксиома успешно прошла испытания;
ее можно проверить путем наблюдения, по крайней мере в принципе.
Вторая аксиома вызывает сомнения в большей мере. Например, при любой
проверке эквивалентности оценок двух приращений — таких, как в II,—
приходится, во-первых, гипотетический вариант В сравнивать с фактически
существующим вариантом А, и затем, во-вторых, сравнивать вариант В
с другим гипотетическим вариантом Е. С точки зрения эмпирических
наблюдений сомнительно, можно ли таким образом нагромождать одно сравнение
гипотетических вариантов на другое. По-видимому, позиция Робертсона
может быть защитима только при слепом доверии к нему.
Другой и совершенно иной подход открывается при рассмотрении
поведения потребителя не с точки зрения сравнения альтернативных, но
совершенно определенных вариантов, а с точки зрения принятия решений в
условиях неопределенности. Введение элементов учета риска предоставляет
возможность избежать оценки одного гипотетического варианта путем его
сравнения с другим таким же вариантом, и вернуться к данным, поддающимся
наблюдению.
Пусть А, В, С, ... суть варианты потребления, каждый из которых
считается несомненным или достоверным событием. Согласно основной аксиоме*
эти варианты можно расположить в порядке возрастания предпочтенияг
как в A). Предположим теперь, что индивидуум также столкнулся с
перспективой двух или более вариантов А, В, С, D, ... , вероятность которых
различна, как это бывает при покупке лотерейного билета. Простейшая
форма такой перспективы — это, когда существует вероятность р добиться
одной ситуации А и вероятность A—р) добиться второй ситуации С. Здесь
р есть субъективная вероятность, собственная оценка индивидуумом его
шансов добиться варианта А. Эта оценка может совпадать, а может и не
совпадать с действительной вероятностью варианта, какова, например,
вероятность выигрыша в лотерее. Введем понятие:
Ожидаемая полезность перспективы = риа + A — р) ис, C)
где иа и ис суть полезности достоверных событий А ж С. Выражение C) есть
«ожидание» в математическом или статистическом его понимании, это —
так называемое «нравственное ожидание» математика XVIII в. Даниила
Бернулли. К основной аксиоме упорядоченных предпочтений достоверных
событий добавим вторую аксиому, согласно которой при ситуациях,
связанных с риском, индивидуум ведет себя так, чтобы максимизировать
ожидаемую полезность перспективы C). Тогда для измеримости и будет достаточным
сопоставить ожидаемые полезности и приравнять друг другу математические
ожидания для ситуаций, связанных с риском, оцениваемых одинаково.
Рассмотрим вариант J9, расположенный между вариантами А и С в порядке
предпочтительности достоверных событий. Перспективу совокупности
вариантов А и С с вероятностями р и A—р) можно считать более
предпочтительной, одинаково предпочтительной или менее предпочтительной, чем
достоверное событие В. Все зависит от величины р. Выберем такое значение /?,
чтобы для индивидуума были безразличны перспективы А и С и вариант Bt
Раз определено значение р и установлены значения иа и ис (например, для
шкалы измерения), то сразу же становится известной иь.
Это можно иллюстрировать с помощью численного примера приведенной
выше таблицы. Для построения шкалы снова примем иь = 2, ие = 3. Сделаем
следующие допущения:
556

а) Для индивидуума безразлично получение по варианту С B фунта
чая, 2 фунта кофе) как достоверного события и перспектива варианта В
{2 фунта чая, 1 фунт кофе) или Е B фунта чая, 3 фунта кофе) с равными
вероятностями. Иными словами, ему безразлично, если ему, по сравнению
стем, что он имеет, предложат с равной вероятностью увеличение или
уменьшение потребления кофе на 1 фунт. Если вероятность р = Уг. то ожидаемая
полезность перспективы C)
или
uc = ud = 2,5.
б) Для индивидуума безразличен выбор между вариантом В B фунта
чая, 1 фунт кофе) как достоверным событием и перспективой вариантов А
(только 2 фунта чая) или Е B фунта чая, 3 фунта кофе), взятых с шансами
.2:1. Это значит, что он согласен рискнуть своим 1 фунтом кофе, если имеются
шансы 1 : 2 получить 3 фунта кофе. В выражении для ожидаемой полезности
примем р = 2/3; тогда
2 1
иЪ=~зиа+-зие> или На = 1,5.
в) Индивидууму безразличен выбор между вариантом В как
достоверным событием и перспективой вариантов А (только 2 фунта чая) и F D фунта
чая, 2 фунта кофе), вероятности которых относятся как 6 : 1. Это значит,
что если отношение вероятности достичь более высокого уровня потребления
к вероятности варианта А превышает 1 : 6, то это компенсирует индивидууму
риск потери имеющегося у него 1 фунта кофе. Примем в выражении
ожидаемой полезности р = 6/7. Тогда:
иь = ~иа+уиг или м/ = 5-
Таким путем строятся показатели полезности, приведенные в последнем
«столбце F) таблицы (стр. 554).
Эти две аксиожы (упорядоченных достоверных событий и
максимизации ожидаемой полезности перспектив) достаточны для того, чтобы сделать
полезность измеримой. Однако показатели полезности будут иными, чем
когда за вторую аксиому принимаем предпосылку упорядоченности
приращений полезности. Только если предположить, что индивидуум одновременно
упорядочивает и приращения полезностей достоверных событий, и ожидаемую
полезность перспективных вариантов, то показатель полезности каждого
варианта потребления в обоих случаях будет одним и тем же — при условии,
что индивидуум последователен в оценках. Однако он вполне может
оказаться непоследовательным в своем упорядочении приращений и
упорядочении ожидаемых полезностей перспектив. Высокое значение ^ = 5в столбце
показателя полезности вариантов, связанных с риском (см. выше таблицу),
возникает из-за малой вероятности A : 6) получить в лотерее желаемый
высокий уровень потребления F. Возможно, что индивидуум «склонен к риску»
{«любитель лотереи — «lottery-minded»), и его мнения о приращениях
полезности при достоверных вариантах потребления дадут величину uf= 4. См.
также упражнение 2 настоящего раздела.
Для графической иллюстрации этого положения (см. рис. 68) будем
считать, что разные расходы потребителя могут быть расположены в порядке
возрастания их предпочтительности, в соответствии с величиной
требующегося для этого недельного дохода (х ф. ст.). Тогда переменная х может
служить в качестве одного из показателей порядковой полезности.
Количественная мера полезности может быть получена на основании аксиомы
упорядоченных приращений, например в форме
557

wo-
20
(А)
(В)
где аир — некоторые постоянные точки на шкале. Это — кривая (^4) на
рис. 68, где шкала (начало координат и единица измерения) определена
следующим образом: и = 0 при х = 0, и = 100 при х = 20. С другой
стороны, количественная мера полезности, исчисленная на основе аксиомы
упорядоченных перспектив вариантов, связанных с риском, может быть
представлена выражением и = hx2(\i—#), где X и \х являются постоянными, снова
определяющими шкалу (единицу измерения и начало отсчета, см.
упражнение 3 настоящего раздела). Таким образом построена кривая (В) на рис. 68;
и здесь и = 0 при х — 0 и и = 100 при х = 20. Два показателя полезности,.
отображаемые кривыми (^4) и (#),
совершенно различны. Для кривой (А}
предельная полезность уменьшается,
для кривой (В) — это не имеет места
(за исключением больших значений х).
Можно лишь сказать, что одну кривую-
получаем из другой посредством
некоторого монотонного (возрастающего)
преобразования.
Преимущества меры полезности,
получающейся из вариантов,
связанных с риском, состоят в том, что можна
предусмотреть (при идеальных
условиях) эмпирическую ее проверку и что в
мире неопределенности такой
показатель может найти широкое поле
применения. При этом следует не упускать
одного: эта мера полезности зависит от
сделанного выше неявного допущения
о том, что субъективные оценки
вероятности можно охарактеризовать и
вычислить. Однако на практике можег
оказаться, что субъективная вероятность не поддается наблюдению. Уже-
одно то обстоятельство, что индивидуума спрашивают о том, как он
оценивает шансы — или что за ним наблюдают — может заставить его изменить
сделанную ранее субъективную оценку вероятности. Он может стесняться
своей «склонности к риску».
Метод измерения полезности для связанных с риском вариантов может1
быть развит далее. Вовсе нет надобности утверждать в качестве аксиомы или
гипотезы (принимаемой после успешной эмпирической проверки), что решения
потребителя совместны с принципом максимизации ожидаемой полезности.
Вместо этого можно придумать более фундаментальную систему аксиом,,
касающихся поведения потребителя как математическое следствие, из
которых может быть выведена максимизация полезности. Весь этот метод основан
на работах Рамсея [22] и Неймана и Моргенштерна [20]; ему следовали
также Маршак [13], [14], Самуэльсон [27] и другие. Точную формулировку
аксиом дали Герштейн иМилнер [7]. Важнейшей из них является так
называемая «аксиома независимости»: если достоверным событиям А и В отдается
одинаковое предпочтение, то так же обстоит дело и с перспективными
вариантами рА + A—р)С и рВ + A—р)С, где С — любой вариант. Далее, как
показали Сэвидж [28] и Маршак [15], вовсе не обязательно предполагать,,
что субъективные оценки вероятностей известны; на основе этих аксиом
можно построить шкалу для измерения и полезности, и субъективной
вероятности, причем и та и другая будут совместны с решениями
потребителя, основанными на принципе максимизации ожидаемой полезности.
Здесь единственный критерий — правильно ли, а также подходящим ли
образом описывают аксиомы поведение потребителя.
Общий вывод состоит в следующем: порядковая концепция полезности,
основанная на простой аксиоме упорядоченных предпочтений, остается той;
Рис. 68.
558

основой, на которой базируется анализ спроса потребителя. Всякий может
добиться измеримости полезности, приняв допущение об упорядоченности
приращений, хотя при этом он неизбежно довольно далеко отойдет от
фактов, поддающихся наблюдению на практике. Любому также открыт путь для
определения показателя полезности в стохастическом или вероятностном ее
понимании; такой показатель применим во всех случаях, когда индивидууму
приходится иметь дело с недостоверными событиями и когда он оценивает
возможные варианты потребления на основе личной или субъективной
вероятности этих событий.
Задачи и упражнения
1. Вторая аксиома для вероятностных вариантов подразумевает, что
упорядоченность ожидаемых полезностей является согласованной. Продемонстрировать это на
численном примере вышеприведенной таблицы и показать, что перспектива вариантов В
и Е, взятых с равными вероятностями, должна оцениваться одинаково с перспективой
вариантов А и F, взятых с вероятностями, отношение которых равно 5 : 2.
2. В том же численном примере изменить предпосылку (в) таким образом, чтобы
шансы перспективных вариантов А и F изменились от 6 : 1 до 3 : 1. Показать, что при
этом щ = 3,5 а не 5.
3. На кривой (В) рис. 68 построить следующие точки. Примем и@) = 0, мB0) = 100.
Сравним (по их полезности) достоверное событие х = 10 с перспективой х = 20 или
х = 0 с вероятностями соответственно р и A — р). Для случая безразличия обоих
вариантов примем р= 3/8. Отсюда получим мA0) = 37,5. Затем сравним перспективу х = 20
или х = 10 с достоверным событием х = 16, приняв для состояния безразличия/? = 0,6288
Отсюда получим мA6) = 76,8. Показать, что эти четыре точки (# = 0, а?= 10, #=16,
х = 20) лежат на кривой, описываемой уравнением ы=1/во #2D0 — х).
18.6. СПОСОБЫ ПОТРЕБЛЕНИЯ И ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Анализ спроса потребителя (см. 18.2) и аналогичный ему анализ
деятельности фирмы (см. 17.2) находят свое место в более широком комплексе
вопросов общего равновесия рынка. Значение такого анализа, при котором
рассматривается большое число отдельных фирм и потребителей, состоит в том,
что при этом возможна непрерывная замена взаимоконкурирующих и
взаимодополняющих товаров в производстве и потреблении. Недостаток его —
в излишней детализации, при которой «за деревьями не видно леса». Чтобы
упростить анализ, насытить его практическим содержанием, очевидным
образом напрашивается объединение производителей и потребителей в крупные
группы; соответствующим образом группируются и товары. Одновременно
допускают упрощения характера рассматриваемой функции, например
предположение линейности, или пропорциональности затрат выпуску. Такие
допущения кажутся вполне разумными, если дело касается производства, но
в гораздо меньшей степени, если речь идет о потреблении. Эмпирические
факты, касающиеся потребительского спроса, хорошо согласуются,
по-видимому, с соотношениями взаимоконкуренции и взаимодополняемости продуктов
потребления: здесь представлялось бы неуместным допущение о
пропорциональности, при которой товары покупаются в неизменных пропорциях.
И все же в вопросах потребления также необходимо сделать какое-то
коренное упрощение. В замкнутых системах равновесия, как-то в системе
Леонтьева (см. 10.7) и Неймана (см. 16.9) упрощение можно довести до
крайнего случая — все потребление брать огулом, объединить в одной «отрасли»
(«activity»), в которой потребительские товары считаются затратами
(взятыми в фиксированных соотношениях), а трудовые услуги — выпуском. При
этом четко выявляется взаимозависимость производственных отраслей в
экономике, однако это достигается за счет игнорирования аналогичных связей
между различными отраслями потребления. Здесь требуется не такая широкая
шкала, а метод, где больше внимания уделялось бы потреблению.
Напрашивается сам собой метод линейного программирования, который позволяет
вводить очень большое число переменных и, несмотря на это, задачи
поддаются решению. Методы анализа, которыми пользовались Леонтьев и фон Нейман,,
являются частными случаями линейного программирования, разработанными
/ 559

применительно к народному хозяйству в целом. Теперь мы предлагаем
ограничить число выделяемых групп производителей и потребителей и применить
более привычные формы линейного программирования. Излагаемый далее
метод анализа многим обязан работам Мейкоуэр [12]; здесь также уместно
привести некоторые примеры, составленные Камероном [2].
Основная идея заключается в рассмотрении фирмы (или
группы-производителей), с одной стороны, и группы потребителей — с другой, причем
рамки анализа ограничены определенными группами товаров,
вырабатываемых фирмой и покупаемых потребителями, которые являются фактическими
или возможными клиентами фирмы. Производственные аспекты изучались
в главе 17; остается более подробно проанализировать аспекты потребления.
Нужно рассмотреть два вопроса: группировку индивидуальных потребителей
и отбор отдельных «укрупненных» товаров. Последнее является весьма
серьезным упрощением. Как показано в разделе 18.3, предположение о том, что
цены товаров, входящих в группу, изменяются пропорционально, является
достаточным для того, чтобы трактовать эту группу товаров как единый
«составной» товар, который подчиняется тем же закономерностям, что и
отдельный товар. Более того, при группировке товаров можно их объединять
вместе с взаимодополняющими предметами потребления, так что соотношения
между «составными» товарами обычно отвечают простейшему типу
взаимозаменяемости.
Первый вопрос вызывает более существенные затруднения; здесь
приходится сравнивать субъективные оценки полезности. Мы не пытаемся решить
эту задачу, а уходим от ее рассмотрения, предполагая попросту, что для
группы потребителей имеется карта безразличия в отношении различных
продуктов фирмы или группы производителей, и что нечто измеряемое (для удобства
называемое «полезностью») может быть сопоставлено с последовательностью
упорядоченных геометрических мест точек безразличия. Это — не экскурс
в экономику всеобщего благосостояния; мы не предполагаем наличия карты
безразличия общества, для всех потребителей и для всех товаров, а лишь
то1, что имеется карта для потребителей определенных товаров,
производимых фирмой. На практике «полезность» можно измерить с помощью рыночных
цен; во всяком случае, ее оценивают с помощью определенных расчетных
оценок, так что, по существу, «полезность» принимается как некая величина
меры удовлетворенности.
Карту безразличия можно представить в форме матрицы, характерной
для линейного программирования. Это преобразование аналогично (если
производство фирмы отображается чертежом на плоскости) тому, что мы
кривые постоянного объема производства заменяем ломаными линиями,
состоящими из отрезков прямых. Предполагаем существование конечного числа
базисных способов потребления. В каждом таком способе потребительские
товары, взятые в фиксированных пропорциях, считаются затратами, но
выпуска нет. Это весьма напоминает «псевдоотрасли» или «свободные отрасли»,
применяемые в симплексном методе для удобства исчисления. Мы допускаем,
что существует пропорциональность и что уровень способа может изменяться
непрерывно. Далее, мы принимаем, что способы могут объединяться линейно
и непрерывно, причем снова делается допущение аддитивности, то есть, что
объединение производится согласно правилам сложения векторов (см. 16.2).
Наконец, путем подходящего подбора шкалы фиксированных пропорций
устанавливается единичный уровень каждого способа, и каждому единичному
уровню способа приписывается уровень полезности. Тогда
пропорциональность означает, что в одном каком-либо способе показатель полезности
возрастает пропорционально уровню этого способа.
Если число потребительских товаров равно двум (хг и х2), то карту
безразличия мы можем графически изобразить на плоскости, отнеся ее к осям
Охххг (рис. 69). Рассмотрим случай четырех способов потребления и
представим неизменные затраты двух товаров с помощью матрицы, в которой
единичный уровень каждого способа выбран таким образом, чтобы шкала соответ-
560

ствующей полезности дала и = 1.
Коэффициенты затрат: А =Гаи а™
|_а21 «22
Уровень полезности (и): 1=1 1 1
Единичный уровень полезности на карте безразличия отображается
четырьмя точками Рг с координатами (а1г, а2г), где г = 1, 2, 3, 4, и любыми их
попарными комбинациями. Мы предполагаем, что ни одна из точек Рг не
совпадает с другой и не лежит на прямой, соединяющей две другие точки; это
обеспечивает взаимонезависимость способов, то есть их включение в базисную
систему. Мы предполагаем также,
что ни одна из точек Рг не лежит
выше и вправо от прямой,
соединяющей две другие точки; это
исключает неэффективные и не
применяемые способы.
Геометрическое место точек единичной
полезности (или безразличия) имеет
форму, показанную на рис. 69.
Точки пронумерованы в порядке
РгР2Р3Р^ и выбор ограничен
либо одним способом, либо
сочетанием двух соседних способов.
Иные геометрические места точек
безразличия, для других уровней
полезности, получаем, растягивая
или стягивая фигуру РХР^Р9Р^
вдоль радиуса, идущего к точке О.
На рис. 69 показана линия
Q Уровень полезности для
3 Карта,
изображенная на этом рисунке,
соответствует семейству равносторонних гипербол, описываемых уравнением
х±х2 = к2. Непрерывные кривые безразличия показаны пунктиром; для
уровня и= 1 они заменены отрезками прямых, кьк-то PtP2i Р2Р3и P3PV
Следовательно, в этом частном, но довольно типичном случае коэффициенты
затрат удовлетворяют условию: а1га2г= 1.
Норма замены между двумя товарами при заданном уровне полезности
определяется без труда. Если применяются r-й и s-й способы, то
р
которой и = 3/2.
Рис. 69.
Норма замены =
= fllr~~gl8
Это — уменьшение хх по расчету на единичное увеличение х2 при переходе
от г-го способа к s-му (см. упражнение 2 настоящего раздела). В случае,
продемонстрированном на рис. 69, имеется только три различные нормы
замены, характеризуемые, соответственно, наклонами прямых РХР2, Р^Р3
и ^3^4— прямых, отражающих попарные комбинации способов. Такое
положение верно и для любого другого заданного уровня полезности. В этом
состоит одно из важнейших отличий ломаных линий от непрерывных кривых
карты безразличия, получаемой при предельном анализе. Оба эти отображения
позволяют непрерывно изменять сочетания товаров, однако, при анализе
способов потребления, возможность изменений ограничена отдельными
отрезками прямых, и число норм замены является конечным, тогда как при
предельном анализе норма замены определяется в пределе и изменяется
непрерывно.
Задачи и упражнения
1. Как истолковать, с точки зрения полезности для потребителей, сочетания
товаров, лежащие на рис. 69 выше OAi? ниже ОА$.
36 р. Аллен
561

2. Если число товаров равно двум, показать, что любая комбинация первых двух
способов, взятых при единичном уровне полезности, может быть представлена
уравнениями:
ос1 = \1а11 + A—\1)а12, x2 = \ia21 + (\ — \i) a22 @<jx<1).
Показать также, что предельное изменение получается, если \i считать переменной, что
дает: (—dxi/dx2) = («u — «12)/(а22 — «21) = норме замены х\ и а?2 для двух способов.
Истолковать этот результат в соответствии с рис. 69.
3. Для случая 3 товаров и п способов составить матрицу коэффициентов затрат
3 X л. Вычертить карту безразличия в трехмерном пространстве и показать, что
одна из поверхностей (например, соответствующая единичному уровню полезности)
состоит из совокупности плоских фигур, каждая из которых образована тремя точками
множества Pi, Р2»~> Рп- Показать также, что все семейство геометрических мест
(поверхностей) точек безразличия определяется и ограничивается конусом, вершиной которого
является точка О, Истолковать полученный результат с точки зрения выпуклых множеств
и конусов.
4. Показать, что если число товаров равно трем, как в предыдущем примере, то на
карте безразличия точки (и способы) упорядочены таким образом, что выбирать можно
лишь между каким-либо способом, комбинациями двух соседних или трех соседних
способов; все остальные комбинации приводят к менее предпочтительным результатам.
Показать, что и в этом случае существует конечное число различных норм замены.
18.7. ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ,
КАСАЮЩАЯСЯ ТЕХНОЛОГИИ ПРОИЗВОДСТВА И ВКУСОВ ПОТРЕБИТЕЛЕЙ
(СТРУКТУРЫ СПРОСА)
В этой задаче рассматриваются фирма и потребители, покупающие
производимые ек* продукты. Фирма выпускает т продуктов, пользуясь при этом
к фиксированными факторами и применяя технологию, состоящую из п
базисных производств. Потребители имеют h базисных способов потребления,
в каждом из которых в фиксированных соотношениях потребляется т
продуктов. На основе этих данных можно построить матрицу (к + т) х (n + h)
технологии производства и вкусов потребителей (структуры спроса):
А =[<!„],
где
г=1, 2, ...,& для факторов,
r = fc+l, k + 2, ...,к + т для продуктов,
5=1, 2, ..., п для производственных процессов,
s = n-\-l, п + 2, ..., n + h для способов потребления.
Коэффициенты ars положительны для затрат и отрицательны для
выпуска продуктов.
Левая часть матрицы А отображает технологию производства фирмы
(s = 1, 2, ..., /г), правая часть—вкусы потребителей или структуру спроса
(s = /г + 1, тг + 2, ..., n+h). Верхняя часть матрицы А состоит из строк
факторов (г = 1, 2, ..., к), в блоке спроса (правая часть) элементы верхних
строк — нулевые. Это соответствует предпосылке, согласно которой
факторы сами по себе не нужны потребителям. Нижние строки матрицы А— строки
продуктов (г = А + 1,Л + 2, ..., к + т); в блоке технологии производства
элементы в своем большинстве отрицательны, в блоке спроса — все
положительны (или равны нулю).
Остальными исходными данными задачи являются,, во-первых, ресурсы
фиксированных факторов, которыми располагает фирма, и, во-вторых,
уровни полезности, связанные с различными способами потребления и в
каждом отдельном случае зависящие от выбора единичного уровня. Эти данные
записываются в виде двух векторов:
Ь = {Ъг Ь2 ... bk 0 0 ... 0} (к + т)-то порядка
с = {0 0 ... 0 сх с2 ... ch} (п + !г)-то порядка,
где Ъ — ресурсы факторов, ас — уровни полезности. Нужно отметить, что
ресурсы продуктов всегда равны нулю; продукты полностью используются
562

при потреблении. Аналогично этому, уровни полезности для
производственных процессов всегда равны нулю, производство не есть конечная цель.
Следовательно, исходные данные задачи представляются в таком виде:
Технология и вкусы Ресурсы
A = [«rs] Ь
Полезность: с'
Постановку задачи можно иллюстрировать на частном примере, хотя
характер последнего для многих целей является достаточно общим. Пусть
имеется 2 фактора и 2 продукта, 3 производственных процесса и 3 способа
потребления. Исходные данные располагаются следующим образом:
Технология и вкусы
Полезность:
Производство
«п
«21
-«31
_—«41
0
«12
«22
-«32
— «42
0
Потребление
«13
«23
— «зз
— «43
0
0
0
«34
«44
Сл
0
0
«35
«45
С
Ресурсы
0
0
«36
«46-
с
h
Ъг
0
0
Если считать все а, Ъ и с фиксированными (причем обычно все они
положительны), то можно так выбрать единичные уровни и единицы измерения
для процессов производства, способов потребления и для товаров, что,
например, все бис будут равны единице, причем остаются достаточные
возможности для того, чтобы элементы первых трех столбцов и последних двух строк
матрицы были равны + 1 или — 1. Преобразование, в результате которого
Ь и с становятся равными единице, называется нормированием
соответствующих строк и столбцов.
Чтобы завершить составление прямой и двойственной задач линейного
программирования, составим вектор % размерности (п + /г),
характеризующий переменные уровни способов потреблениям вектор р размерности (к + т)
для соответствующих цен. Задача линейного программирования заключается
в максимизации достигаемых уровней полезности, то есть в максимизации
z = с"к. Требуется найти такой неотрицательный вектор X, чтобы полезность
При УСЛОВИИ
Первые к ограничений из общего их числа (к + т) выражают
лимитирующие ресурсы факторов. Последние т ограничений — это уравнения,
правая часть которых (согласно определению вектора Ь) равна нулю; они
отражают требование полного потребления всех производимых продуктов.
Двойственная задача линейного программирования состоит в том, чтобы
найти неотрицательный вектор р, минимизирующий стоимость ресурсов
при условии ; B)
Минимизируемая переменная ? есть стоимость фиксированных факторов
по расчетным оценкам. Первые п из (п + К) ограничений выражают тот факт,
что в каждом производственном процессе эта стоимость по меньшей мере равна
выручке (прибыль неположительна). Остальные ограничения обусловливают
такой выбор масштаба цен на продукты, чтобы уровень полезности каждого
способа потребления был численно равен стоимости потребленных товаров.
Задача линейного программирования, касающаяся технологии
производства и вкусов потребителя (или структуры спроса), является расширенным
563 36*

вариантом задачи о фирме, рассмотренной в разделе 17.8. Последнюю можно
теперь считать частным случаем задач A) и B), в котором существует только
один способ потребления, то есть продукты потребляются в определенных
фиксированных соотношениях. Сформулированное выше расширение задачи
позволяет предусмотреть любое число способов потребления, а значит,
взаимозаменяемость товаров не только в производстве, но и в потреблении.
Здесь снова применимы общие замечания, сделанные в разделе 17.8,
нужно лишь определенным образом их расширить. Предположим, что в
задаче A) уже исключены неупотребляемые производственные процессы и
способы, так что применяется п производственных процессов и h способов
потребления. Можно считать, что /г< т; нет нужды применять большее число
базисных способов потребления, чем имеется видов потребляемых продуктов.
Тогда т уравнений из числа ограничений задачи A) определяют т — h
уровней производственных процессов Ях, К2, ..., кп и h уровней способов
потребления, входящих в z через уровни остальных п — т + h производственных
процессов. В А: неравенств задачи A) войдут только уровни Ях, А,2, •••> ^п
производственных процессов, и поэтому они могут быть приведены к
неравенствам относительно п — т + h уровней из них. При максимизации z можно
(надлежащим выбором переменных К) превратить в уравнения возможно
большее число из п — т + h неравенств. Следовательно, в общем случае п — т +
+ h факторов из к являются дефицитными, а остальные — свободные блага.
Число дефицитных факторов нат — h меньше, чем число применяемых
производственных процессов; уменьшение вызвано ограничениями, налагаемыми
на потребление, где предусмотрено h систем фиксированных отношений (то
есть применяемых способов потребления) между т товарами. Этот вывод,
исключениями из которого всегда могут быть «вырожденные» случаи, почти
тот же, который получен был ранее (см. 17.8).
Практически этот вывод можно использовать тогда, когда матрицу
технологии производства и структуры спроса в ходе решения сокращают,
исключая все недефицитные факторы и все неприменяемые процессы и способы.
Число дефицитных факторов, или п — т -+- /г, сложенное с числом продуктов
т, дает число строк преобразованной матрицы п + /г. Но это же — и число
столбцов: имеется п применяемых производственных процессов и h способов
потребления. Следовательно, когда в ходе решения матрица технологии
производства и вкусов потребителей сокращается, то она оказывается
квадратной.
Назначение расчетных оценок задачи B) обычно: фактор является
свободным, если его оценка равна нулю: во всех применяемых процессах прибыли
нулевые (в противоположность неположительным). Столбцы матрицы
технологии и вкусов А можно умножить на элементы вектора Л,, а строки — на
элементы вектора р, в результате получим стоимостную матрицу:
Эта матрица — квадратная, как и сокращенная матрица А; в самом деле,
нулевые элементы вектора р исключают в исходной матрице А строки
недефицитных факторов, а нулевые элементы вектора % — столбцы неприменяе-
мых процессов производства и способов потребления. В силу свойства
ограничений задачи A), при суммировании элементов матрицы V по строкам мы
приходим к стоимости ресурсов фиксированных факторов и к нулевой
стоимости продуктов. В силу ограничений задачи B), при суммировании
элементов матрицы V по столбцам производственных процессов получаем нули
(нулевая прибыль), а по столбцам способов потребления — уровни полезности.
Далее, отношения между расчетными оценками, определенными из B),
равны разным нормам замени между товарами. В производстве возможны
три типа норм замены (как это показано в разделе 17.8), а здесь вводится
еще один тип замены — замена товаров при потреблении. Отношение между
ценами двух продуктов равно норме замены этих товаров как при
производстве, так и при потреблении.
564

Прямая A) и двойственная B) задачи линейного программирования в
совокупности определяют производство, потребление и расчетные оценки,
выраженные через известные исходные данные: матрицу технологии производства
и вкусов потребителей (структуры спроса) А, ресурсы b и карту безразличия
для потребителей с. С изменением исходных данных меняется и решение,
причем самым различным образом, так что здесь снова полезен метод
классификации изменений исходных данных, вкратце обрисованный в разделе 17.6.
Если ресурсы одного из факторов (скажем, bi) увеличиваются в к раз, то
совершенно такие же результаты получим, уменьшая все элементы первой
строки матрицы А в А: раз. До тех пор пока в решении требуется найти уровни
способов потребления и расчетные оценки, не имеет значения — увеличены ли
ресурсы дефицитного фактора или уменьшены его затраты на единицу
продукта в каждом производственном процессе. Аналогично этому, если вкусы
потребителей изменились так, что уровень полезности одного из способов
потребления (скажем, сх) увеличился в к раз, то такой же результат получаем
при уменьшении в к раз всех элементов одного столбца матрицы А
(соответствующего первому способу потребления). В частности, если ресурсы всех
факторов и уровни полезности всех способов потребления увеличены в к раз,
что равносильно уменьшению всех элементов матрицы А в к раз, то из A)
и B) очевидно, что все уровни способов потребления и все расчетные оценки
также возрастут одинаково в к раз.
С этой точки зрения, удобно выразить все изменения данных с помощью
матрицы технологии производства и вкусов потребителей А. Изменение всех
элементов строки матрицы А в одинаковое число раз соответствует изменению
имеющихся в распоряжении ресурсов; аналогичное изменение элементов
столбца этой матрицы отражает изменение вкусов потребителей. Остается
рассмотреть вопрос непропорционального изменения элементов строки или
столбца матрицы А. Такое изменение можно назвать изменением в технологии
производства или в структуре вкусов (спроса) потребителей.
Значит, сосредоточив внимание на матрице А, можно так выбрать единицы
измерения для к факторов, что ресурсы каждого из них будут равны
единице, то есть что вектор Ь будет включать к единичных и т нулевых элементов.
Аналогично этому, можно так выбрать единичные уровни способов
потребления, что вектор с будет состоять из п нулевых элементов, за которыми
следуют h единичных элементов. Это — нормированная форма задачи.
Задачи сравнительной статики бывают следующего типа: как изменяются
производство и потребление и расчетные оценки при заданных изменениях
ресурсов? уровней полезности? технологии производства? структуры вкусов
потребителей? Когда прямая A) и двойственная B) задача линейного
программирования нормированы, все такие задачи сравнительной статики
сводятся к прослеживанию влияния различных изменений на матрицу А.
Иллюстративные примеры, приведенные в следующем разделе, должны
продемонстрировать способы решения численных задач линейного
программирования. Они показывают также метод решения задач сравнительной
статики. Если задача формулируется в общем виде, то она имеет столь большое
число различных типов изменений, что почти невозможно всеобъемлюще
рассмотреть характер решения в каждом случае и ответить на все вопросы,
возникающие при сопоставлении статических вариантов. Здесь необходимы
некоторые упрощения, как это сделано в упражнении 2 настоящего раздела.
В приводимых ниже иллюстративных примерах упрощениями являются
рассмотрение лишь малого числа факторов и продуктов — производственных
процессов и способов потребления,— а также задание численных величин,
характеризующих технологию производства и спрос потребителей.
Задачи и упражнения
1. Интерпретировать задачу линейного программирования A), если: а) ненулевыми
являются элементы правого верхнего угла матрицы А (первые к строк, последние h
столбцов); б) все элементы вектора b отличны от нуля; в) все элементы вектора с отличны от
нуля. Показать, что производство продуктов не обязательно совпадает с потреблением
565

(могут изменяться их запасы) и что прибыль по производственным процессам может быть
и величиной положительной.
2. Задача линейного программирования A) охватывает очень многие случаи,
особенно если ее расширить, как это сделано в предыдущей задаче. Рассмотреть, сравнить
и противопоставить один другому следующие варианты упрощения задачи:
I). Имеется только один спссоб потребления, то есть один «составной» товар для
потребления.
(II) Имеется только один фиксированный фактор, как-то: ресурсы труда или
денежного кредита.
(III) Ни один продукт не затрачивается, а выпускается только в одном
производственном процессе; в каждом производственном процессе выпускается только один
продукт.
3. Показать, что случаи (I) и (II) предыдущей задачи являются прямой и
двойственной задачами, и что при (I) максимизируется полезность, а при (II) минимизируется
стоимость факторов.
4. Показать, что в случае (III) задачи 2 число продуктов равно числу процессов п
и что они могут быть расположены так, чтобы появилась отрицательная единичная
матрица (—1) п-то порядка в левом нижнем углу матрицы А. Показать, что в двойственной
задаче это упрощение заключается в следующем преобразовании ограничивающих
соотношений: стоимость единицы равна цене продукта для применяемых процессов и больше
цены продукта для остальных процессов.
5. Пусть число факторов и число способов потребления одинаковы (т), а в
верхнем правом углу матрицы А имеется отрицательная единичная матрица (—I) m-го
порядка. Истолковать этот случай и установить связь его со случаем замкнутой экономики,
где трудовые услуги являются выпусками процессов, а потребительские товары —
затратами.
18.8. НЕКОТОРЫЕ ИЛЛЮСТРАТИВНЫЕ ПРИМЕРЫ
Основные примеры, иллюстрирующие методы решения задачи линейного
программирования, касающейся технологии производства и структуры
вкусов, являются расширением задач, приведенных в разделе 17.8. Другой и еще
более простой пример представляет собой упражнение 1 настоящего
раздела. Хотя рассматриваемые задачи взяты снова из области
сельскохозяйственного производства и рыбного промысла, примененный метод в равной
мере пригоден и для процессов промышленного производства.
Пример (а).
Производятся зерно и откорм свиней: фиксированными факторами являются
земля и труд. Спрос потребителей имеет место в разных пропорциях в соответствии
с матрицей технологии и заданными ниже условиями.
Труд
Земля
Зерно
Свиньи
Полезность
Технология и
- 50
5
V.
L —1
0
25
50
—1
0
0
спрос
0
0
1
1 г1
1
0-1
0
2
'г "
1
50
52
0
0
Ресурсы
человеко-месяцев
V2 акра
Задача линейного программирования состоит в том, чтобы найти
неотрицательные А,, максимизирующие полезность:
при условии
566

Следует обратить внимание на то, что комбинации товаров в способах
потребления соответствуют случаю «равносторонней гиперболы», изображенному на рис. 69.
Каждое геометрическое место точек безразличия состоит только из одного отрезка
прямой, и существует только одна норма замены:
2—1
-у
= 2,
*го есть 200 т зерна компенсируют уменьшение откорма свиней на 100 голов.
Ограничения этой задачи линейного программирования распадаются на две пары, A) и B),
каждая из которых легко решается.
Из уравнений B) получаем: q
3 л 1 , 2
2 3 3
C)
Тогда максимизируемую величину
можно выразить через Хг и к2:
=1^+1^ = max.
D)
Допустимы только те Хх и А,2, при
которых %3 > 0 и Я4 ^ 0, так что на
основании C) получаем:
3
2,0
15
as
0,25
0,5
0,75
и точка с координатами (AiA2) на
плоскости 0X^2 (рис. 70, а) должна
лежать между двумя лучами OQ и
OR, соответственно описываемых
уравнениями:
Прямая OQ отражает случай А,3 = 0
(первый способ потребления не
применяется). Второй способ
потребления не применяется в случае,
отображаемом прямой OR. Между
этими лучами проводится ряд
параллельных прямых, описываемых
уравнением 1/2^1+1/з^2 = const;
согласно D), наша задача—попасть
на возможно более высокую из
этого ряда прямую.
Нам уже знакомы
ограничения A); они отражают лимиты
ресурсов (соответственно) земли и труда. Точка с координатами
должна быть расположена в пределах фигуры ОАРВ, где:
X
Рис. 70.
Xa) на рис. 70, а
труда используются полностью),
Прямой АР соответствует: 50Я1+25Я2 = 50 (ресурсы
Прямой ВР соответствует 5ах-|-50а2 = 52 — (ресурсы земли используются полностью).
А
Следовательно, решение задачи линейного программирования отображается точкой Р,
которая лежит на пересечении прямых АР и ВР и одновременно расположена на
самой высокой из параллельных прямых, проведенных на участке допустимых
решений. Решением будет:
3=^2» ^4=="б~» 2 = 12 максимум).
При этом ресурсы распределятся подобным же образом, как в примере (а) в тексте
раздела 17.5, но, кроме того, получается следующее распределение чистого продукта
между способами потребления:
567

Зерно (то)
Свиньи (голов) ....
Чистый
продукт
75
50
Потребление
первый
способ
42
42
второй
способ
33
8
Группа потребителей потребляет часть продуктов в равных количествах D2 т
зерна и 42 головы свиней), а часть—в заданном неравном соотношении C3 т зерна
и 8 голов свиней).
В этом случае порядок матрицы остается в решении прежним, то есть матрица
решения—четвертого порядка. Возможны и другие случаи, когда порядок матрицы
уменьшается до третьего, при этом только один фактор является дефицитным и
применяется только один способ потребления. В этом случае решение отображается
точкой пересечения одной из прямых OQ или ОР с одной из прямых АР или ВР. Такие
случаи иллюстрируются далее в задачах 2 и 3 этого раздела.
Пример (б).
Свежая рыба, копченая рыба и дрова производятся при использовании
единственного фиксированного фактора (труда). Технология производства и фиксированные
соотношения спроса отображаются следующей схемой.
Труд
Свежая рыба
Копченая рыба
Дрова
Полезность
Технология и спрос
человеко-месяцы i
т 1
» 1
» 1
- 7
—1
0
0
0
1
2
—1
3
0
V*
0
0
—1
0
0
4
0
1
1
От
0
2
lj
1
Ресурсы
300
0
0
0
Задача линейного программирования состоит в максимизации
при условии:
Из уравнений F) получаем:
11
Я4 = -т-Я1—Y
= 0 и ЗЛ*—
1 1
"<Г^а; слеД°вательно> 2 = -7-
E)
F)
Значит, максимизируется %г при неотрицательных Я4 и Л5, то есть при условии
2A и Я2!>0. Произведем подстановку значения Х3 в E):
4800
Так как максимизируется Я17 решение есть л2 = 0 и ^i = -jto" » что
удовлетворяет условиям Хх > 2Х2 и Я2 > 0. Остальные X можно найти на основе
вышеприведенных результатов; полное решение будет следующим:
Исходная матрица технологии и спроса—размерности 4x5, так что в решении
можно получить квадратную матрицу только тогда, когда исключается (по крайней
мере) один процесс производства или способ потребления как неприменяемый. В
фактически полученном решении удалось добиться большего: исключены два столбца, из
них один по производственному процессу (Я2 = 0) и один по способу потребления
(ЛБ=0). В то же время исключен и один товар (копченая рыба), ибо она не произ-
56S

водится. Полученная квадратная матрица—третьего порядка, и решение приобретает
следующий вид:
Свежая рыба (т) . . .
Дрова » ...
Труд (человеко-месяцы)
Производство
первый
процесс
42,5
297,4
третий
процесс
10,6
2,6
Потребление^
42,5
10,6
—
1 В соответствии с первым способом потребления.
Пример (в).
Предыдущую задачу мы можем изменить, исключив производственный процесс-
заготовки дров и предположив, вместо этого, что имеется наличный запас дров;
(подобно труду). Рассмотрим следующую схему:
Технология и спрос
Ресурсы
Труд
Дрова
Свежая рыба
Копченая рыба
Полезность
человеко-месяцы
т
ь
»
- 7
0
—1
- 0
0
1
3
2
—1
0
0
0
1
1
1
01
0
3
1/2-
1
300
b
0
0
Здесь Ь—постоянная величина (заданные ресурсы дров), которой можно
придавать различное значение и отмечать влияние этого значения на характер решения.
Следует отметить, что матрица в этой задаче квадратная, так что можно ожидать,,
что в решении либо применяются все процессы производства и способы потребленияг
и оба фактора являются дефицитными, либо применяется только один способ
потребления, и только один фактор является дефицитным.
Задача линейного программирования состоит в том, чтобы найти
неотрицательные Я, максимизирующие z=A,3+^4 ПРИ условии:
< 300 и
=0 и -
G)
Из (8) следует, что А,8=1/в(8А,а—Ю, А>4=2/б (А*—ЗА,2) и 2 = 1/5(^1 + 2X2). Значит,
максимум достигается в том случае, когда точка решения расположена на самой
высокой из параллельных прямых, описываемых уравнением А,].+2Я2 = const, в
пределах конуса OQR, где, как показано на рис. 70,6, OQ описывается уравнением Я2 = 1/8Х1
(при Х3 = 0), а О R—- у равнением Х2 = 1/з^1 (ПРИ ki = 0). Из G) следует, что решения
для Я-i и Х2 должны, в соответствии с лимитами факторов, лежать внутри участка
ОЛРВ, где прямая АР описывается уравнением 7Xi+X2 = 300, а прямая ВР
параллельная оси OXi на высоте ОБ = г1ф. Координаты точки S суть Хг = 450/11, А,2 = 150/11,
а точки Т: Хг = 800/19, А,2=Ю0/19. Из рис. 70, б ясно, что характер решения зависит
от значения b следующим образом:
I. Ъ > 450/11; решение соответствует точке S:
150
-^t-JV«' 0k JL f^Vy a At/V/ » ^ь
II. 300/19 < Ь < 450/11 решение соответствует точке Р (расположенной между S
и Т): Ях = 1/21(900— &), A^Veb, Я3= 1/35 A96—300), Я4= D50—116) D/105).
III. Ь< 300/19; решение соответствует точке Т: ^1 = 800/19, Я2 = 100/19, Я3=0,
Х4=200/19.
В случае (I) дрова избыточны, и их ресурсы не используются до предела, то
есть применяется только один способ потребления (Яз) и является дефицитным только
один фактор (труд); производятся оба продукта, причем несколько больше внимания
уделяется копчению рыбы. В случае (III) положение аналогично этому, лишь
дефицитными являются дрова, ресурсы труда не используются полностью, и применяется
569

тот способ потребления, в котором спрос на свежую рыбу превышает спрос на
копченую рыбу. Случай II является не столь крайним, а промежуточным: он отвечает
положению, при котором оба фактора являются дефицитными, и потребление
происходит в соответствии с обоими способами.
В примере (а) получится задача из области сравнительной статики, если
заменить численные значения технологических показателей (затрат —
выпуска) и вкусов (спроса) потребителей буквенными обозначениями:
Технология
Труд
Земля
Зерно
Свиньи
Полезность
и
-
-
спрос
«11
«21
Vl
— 1
0
«12
«22
—1
0
0
0
0
1
1
1
¦
р-1
1
Ресурсы
1
1
0
0
Все четыре коэффициента а положительны, а > 1 и р < 1. Можно
изменить эти параметры и выявить влияние таких изменений на решение задачи.
Приводимая матрица нормирована. Единицы измерения для труда и
земли установлены так, что ресурсы факторов равны единице. Единицы
измерения для зерна и свиней выбраны так, что в первом способе потребления
расходуется по единице каждого из этих продуктов. Единичные уровни двух
производственных процессов установлены таким образом, что выпуском
каждого из процессов является единица каждого продукта (соответственно,
свиней и зерна). Единичные уровни потребления взяты такими, что каждому из
них соответствует единичная полезность.
В настоящей задаче мы не рассматриваем изменения соотношений
выпуска товаров, эти соотношения фиксированы в численном их значении с помощью
подматрицы 2 ~~ . Это имеет целью сосредоточить внимание на измене-
L —1 О J
ниях наличных ресурсов факторов и на структуре потребительского спроса,
выражаемых, соответственно, элементами а и а, р. Так, если значения ап и а12
уменьшены в одинаковое число раз, то результат будет таким же, как при
увеличении наличных ресурсов труда. С другой стороны, если изменится
соотношение между ап и а12, то естественным результатом явится изменение
производительности труда в двух производственных процессах.
Пример (г).
В задаче линейного программирования, исходные данные для которой указаны
выше, требуется найти неотрицательные Я, максимизирующие 2 = Я3+Я4 при условии
«11^1 + «12^2 <^ 1 «21^1 + «22^2 < 1»
Решение показано на рис. 70, а, где:
Прямой АР соответствует «11A,1-j-a12A,2=:l (ресурсы труда используются полностью)
Прямой ВР соответствует «21^1 + ^22^2 = 1 (ресурсы земли используются полностью)
Точке Р соответствуют координаты %1 = fl22~"~gl2 , Х2 = gll~~g21 (ресурсы труда и
земли используются полностью)
Прямой OQ соответствует г-2-=-з--|~"о" (Я3=0)
Л,1 р ^
л о
Прямой OR соответствует ^=-^ (Я4=0), и тангенс угла наклона параллель-
ных прямых (позволяющих найти максимум z) равен:
1 R 3
P
Здесь А =
а1\
«22
570
1-р
и порядковые номера двух факторов выбираются

таким образом (а это всегда можно сделать), чтобы А > 0, то есть, чтобы:
«11 ^ «21 «11 .. «12
«12 «22 «21 «22 "
Решение отражается точкой Р, в которой ресурсы обоих факторов используются
до предела, и применяются все четыре процесса производства и способа потребления,
если только удовлетворяются все следующие условия:
Точка Р в положительном квадранте: — > 1 > —
«21 «22
Точка Р расположена между OQ и OR: -5-+¦«¦> — ~ > ~о~
Р Z 6^22 — «12 "
Тангенс угла наклона параллельных прямых является промежу- (9)
точным между соответствующими величинами для прямых АР и ВР:
!р_А
1 ^ 2 2_ N.«21
«12 1—Р «22*
Если не выполняется хотя бы одно из этих условий, то решение отражается
точкой пересечения одной из пары линий (OQ и OR) с АР (или ВР); так, при пересечении
2 3
OR я ВР получаем: Х1=——-г-~—, ^2 = -^—Т~о—• В этом случае только один
21 ) 22 21 + 22
фактор является дефицитным, и применяется только один способ потребления, например
дефицитной является земля, а продукты потребляются в соотношении 1:1.
Двойственная задача линейного программирования состоит в том, чтобы найти
неотрицательные р, минимизирующие
при условии:
\ > Pi""% Р3
До тех пор пока удовлетворяются условия (9), значения к\ и Я2 отвечают
координатам точки Р, а все р положительны. Они находятся по следующим формулам:
2 — «12 л _«11 — «21
Pl=
1-р а-1
=5= ^4=^Н?
A0)
Из соотношений A0) можно узнать все параметры решения, например уровни
потребления к3 и А*» максимум полезности 2, минимум стоимости по расчетным
оценкам ?, объем выпуска обоих продуктов и т. д. Представляют интерес нормы замены:
—= ^ = единственная норма замены между продуктами в процессе потребления
/>4 а—1
= норма замены между факторами
— = -т-1 z—о «22 — «2i I = производительность труда в производстве зерна
Рз А \ -1 — Р /
(аналогичным образом производительность труда выражается и при другом процессе
производства).
Будем исходить теперь из решения A0), предполагающего полное использование
ресурсов факторов. С помощью уравнений A0) можно проследить влияние любого
изменения параметров а или аир; нужно только не забывать, что нарушение
любого из условий (9) приводит к неполному использованию ресурсов одного из
факторов и к тому, что перестает применяться один из способов потребления.
Рассмотрим два следующих изменения из множества возможных их вариантов.
Увеличение имеющихся в распоряжении ресурсов труда, или пропорциональное
уменьшение аг1 и «12. Непосредственным результатом, исходя из A0), является
увеличение Xi и уменьшение Я2, то есть выпуск (производство) свинины (Хх) возрастает,
571

а зерна ( %2—Т^1) С0КРаЩается- Это увеличение ресурсов может быть настолько»
большим, что нарушится второе условие (9), при еще большем увеличении нарушится
и первое условие (9). В этот момент Я2 = 3/2А,1, и выпуск зерна будет равен выпуску
свинины. Дальнейшее возрастание наличных ресурсов труда не изменяет выпуска
продуктов; ресурсы труда начинают использоваться не до предела, а потребление
продуктов устанавливается в фиксированном соотношении 1:1. На рис. 70, а это
значит, что положение конуса OQR осталось неизменным, но положение точки Р
изменилось—она сместилась ниже прямой OR.
Изменение структуры вкусов или спроса таким образом, что возрастает
полезность сочетания а: р. Это соответствует уменьшению в одинаковое число раз
значений аир, при котором увеличивается норма вамены ? . На основании A0) такое
изменение непосредственно не ведет к изменению %г и Я2, а значит—и выпуска зерна
и свинины. Изменение вкусов не влияет на производство. Его влияние следует искать
в ценах и в максимуме достигаемой полезности (а также в минимуме стоимости).
Опять на основании тех же уравнений A0) отношение между р3 и />4 возрастает
пропорционально норме замены, ибо зерно дорожает ввиду увеличения спроса на
комбинацию а : р (а> 1, р< 1). Далее, падает соотношение между рх и р2, и земля
(интенсивно используемая при производстве зерна) начинает оцениваться выше. Если аир-
уменьшились намного, то перестает выполняться последнее условие (9). Когда это
происходит, Х± уменьшается, а Л2 увеличивается настолько, что -г-2^-—_|_i/2; ресурсы
Ах р
труда перестают использоваться до предела, и потребление устанавливается в
предпочтительном соотношении а : р. Расчетная оценка труда рх становится равной нулю.
На рис. 70, а это значит, что положения точки Р и прямых OQ и ОТ? неизменны,
а лишь уменьшаются численно (по абсолютному значению) наклон параллельных
линий, служащих для нахождения максимума z; когда этот наклон становится
равным или меньше наклона прямой ВР, то точка, отображающая решение,
перемещается из Р в точку пересечения OQ и ВР.
Задачи и упражнения
1. Решить задачу линейного программирования, в которой требуется
максимизировать полезность. Исходные данные следующие:
Технология и вкусы (спрос) Ресурсы
Труд
Земля
Пшеница
Сено
Полезность
г 25
50
—1
- 0
0
10
100
0
—1
0
0
0
1
1
1
о -
0
2
i/2 -
1
50
•260
0
0
человеко-месяцев
акров
Единица измерения пшеницы и сена—100 т. Показать, что дефицитным является
только труд и что применяется только первый способ потребления. Как малы должны
быть ресурсы земли, чтобы она стала дефицитным фактором?
2. В предыдущей задаче принять ресурсы равными 30 человеко-месяцам и 75
акрам. Решить задачу линейного программирования и показать, что только один
фактор дефицитен. Что можно сказать о соотношении применяемых способов потребления?
3. В примере (а) правый нижний угол матрицы записать в виде . R I , где
параметры а>1, Р<1. Решить задачу, выразив % через аир. Показать, что точка
Р на рис. 70,а должна быть расположена внутри конуса OQR (оба фактора являются
дефицитными, применяются оба способа потребления) только в случае а/р > 3/2.
Отсюда показать, что при а/р < 3/2 дефицитным является только один фактор [см.
пример (г) в тексте этого раздела].
4. Составить и решить задачу линейного программирования, двойственную по
отношению к задаче примера (а):
Pi'Pt'Ps- j04=28 :J5 : 950 : 1900.
f5. Составить и решить задачу линейного программирования, двойственную
относительно задачи примера (в), вначале—при 6 = 45 т, затем—при 6 = 30 т.
Истолковать полученные соотношения цен с точки зрения норм замены.
6. В примере (г) текста рассмотреть влияние пропорционального уменьшения
а21 и а22 или, следовательно, увеличения наличных ресурсов земли.
7. В этом же примере (г) каков смысл и каково влияние следующих изменений:
(I) пропорционального увеличения ап и я21;
(II) пропорционального увеличения а12 и а22;
(III) изменения соотношения величин а1Х и а12;
(IV) изменения соотношения величин аир?

ГЛАВА 19
ПРОБЛЕМА УКРУПНЕНИЯ
19.1. СУЩНОСТЬ ПРОБЛЕМЫ УКРУПНЕНИЯ (aggregation)
Если экономические модели предназначаются для объяснения или
прогнозирования, то они должны быть увязаны с эмпирическими данными. При
существующих методах и технике вычислений модели должны включать
относительно небольшое число синтетических показателей — таких, как
национальный доход, потребление и капиталовложения, или затраты и выпуск широких
групп материалов и продуктов. Это безусловно верно для моделей народного
хозяйства в целом, например для модели, применяемой в теории
экономических циклов Хикса (см. гл. 6), или для модели затраты — выпуск Леонтьева
{см. гл. 10). Это также справедливо и для тех моделей (например, моделей
линейного программирования), в которых рассматривается деятельность
отрасли промышленности или крупного, предприятия. В большинстве
случаев модель должна рассматривать лишь несколько макросоотношений
между немногими макроэкономическими переменными.
Макроэкономические модели, например рассмотренные в первых главах
книги, вполне правомерны, если можно допустить, хотя бы приближенно,
что между синтетическими переменными существует непосредственная
и простая связь. Однако такое допущение не удовлетворяет экономиста,
который понимает, что связи между синтетическими показателями являются
совокупными результатами множества решений, принимаемых потребителями
и фирмами. Поэтому естественным является стремление глубже изучить
макроэкономические связи и понять, каким образом из отдельных решений
создаются устойчивые зависимости между синтетическими показателями —
если они вообще действительно создаются.
При таком подходе картина совершенно меняется. Экономическая теория
любой модели рассматривает уже микрослагаемые, соответствующие
решениям, принятым, например, отдельными потребителями или фирмами;
макросоотношения являются здесь производными построениями. Укрупнение
должно представлять собой совершенно определенный переход от
микросоотношений к соответствующим макросоотношениям. Этот переход может
оказаться (что часто и бывает в действительности) чрезвычайно грубым. Если,
например, индивидуальный спрос на чай является функцией дохода
потребителя, цены чая и многих других связанных с ним товаров, то по аналогии
рыночный спрос на чай характеризуется такой же функцией — но уже
национального дохода, цены чая и общего индекса цен. Другие варианты перехода
могут быть связаны с более тонкими соображениями, экономическими и
статистическими. В этом случае модель основывается на экономической теории,
имеющей вид множества микросоотношений между микроэкономическими
переменными, но выражается она в виде совокупности
экономико-статистических макросоотношений |между синтетическими переменными. Метод
укрупнения чрезвычайно важен, как с точки зрения экономического, так и
статистического осмысливания имеющихся данных.
Здесь возникает множество вопросов. Какое именно укрупнение
требуется? В примере рыночного спроса на чай укрупнение может проводиться по
группам потребителей, по различным видам и сортам чая, а также по
времени — по пересчету тех «дней», когда принимались индивидуальные решения,
в месяцы или кварталы, за которые даются эмпирические данные. Далее,
каким образом связать между собой синтетические переменные, если они уже
573

имеются? Это может определиться теми предпосылками, которые заложены
в исходной экономической теории; так, если в функциях индивидуального
спроса эластичность от цен для спроса на чай принята постоянной, то и в
функции рыночного спроса эластичность спроса в зависимости от цен также
можно считать постоянной. Какова связь между коэффициентом (осереднен-
ным) макросоотношения и соответствующими коэффициентами
(экономическими) в исходных микросоотношениях? Например, эластичность в
зависимости от цен для рыночного спроса на чай можно считать средней из эластич-
ностей от цен для отдельных индивидов. Правильно ли такое допущение?
Если правильно, то какого именно вида средней величиной является
синтетический показатель? Несомненно, что такие вопросы затрагивают самые основы
построения экономических моделей. Необходимость ответа на них понимали
экономисты и в прошлом, например Тинберген [9], [10], но лишь недавно
было предпринято систематическое их исследование. Причину этого нетрудно
видеть. В этих вопросах ни экономические, ни статистические аспекты не
преобладают. Экономисту ничего не удается сделать без помощи статистика;
статистик располагает несколькими шаблонными ответами, но ему нужно
получить от экономиста больше указаний, чем обычно. В отдельных
направлениях проделана некоторая работа, например разработаны экономические
основы индексов «стоимости жизни». Однако на более общие вопросы
ответов нет, что свидетельствует о недостаточно систематическом рассмотрении
индексных показателей как в экономических курсах, так и в теории
статистики.
По вопросам теории укрупнения имеется очень скудная литература.
Чуть ли не впервые эти вопросы были серьезно рассмотрены в серии статей
Клейна и других авторов, помещенных в журнале «Эконометрика» в 1946 г.
Значительный интерес к этим вопросам проявляют французские
эконометрики [5] и [6]. Однако систематизированное рассмотрение впервые появляется
в монографии Тейла [8]. Настоящее изложение в значительной степени
основано на первой в этой области работе Тейла.
В настоящей главе рассматривается только один частный случай
проблемы, когда с помощью укрупнения из совокупности микросоотношений
получается единственное макросоотношение. Тейл [8] исследует и сложные
случаи — получения из совокупности микросоотношений системы
взаимосвязанных макросоотношений; однако здесь такие цели не преследуются. Даже
рассматриваемый простой частный случай является серьезной экономической
задачей, которая не относится к чистой математической экономии и не
сводится к простому добавлению статистического критерия значимости. В самом деле,
мы исключили бы эту задачу из настоящей книги — в которой не
рассматриваются технические приемы эконометрики — если бы она не представляла
серьезного интереса с экономической точки зрения. Задача заставляет нас
возвратиться к самому началу, к исходным рассуждениям.
Сначала рассмотрим вопрос совместности трех элементов задачи:
микросоотношений, укрупнения переменных, макросоотношения. При одном из
методов укрупнения, сторонником которого является и Клейн [1], [2],
считаются заданными некоторые микросоотношения, основанные на
экономической теории, и точное макросоотношение соответственного вида. Вопрос
ставится следующим образом: какой способ укрупнения микроэкономических
переменных в макроэкономические переменные совместен с такой постановкой?
Попытка найти совместный с этим подход к укрупнению рассматривается
далее в следующем разделе как метод [I].
При другом подходе к Совместности, которого, по-видимому,
придерживается Мэй [3], [4], считаются точно определенными микросоотношения
и способ укрупнения. Вопрос заключается в том, существует ли при этом
точное макросоотношение между синтетическими показателями, и, если
существует,— то какой вид оно имеет. При таком подходе вскоре возникают
трудности. Тейл [8] показал, что не при всех условиях удается добиться
совместности; по сути дела, в обычном случае, нельзя даже ожидать суще-
574

ствования совместности. Это заставило Тейла отказаться от требования
совместности; вместо этого он использует статистический критерий в своем
«методе аналогии». Здесь вопрос ставится следующим образом: если заданы
микросоотношения и способ укрупнения, то можно ли с помощью
статистических методов подобрать подходящее макросоотношение определенной
формы? Это рассматривается далее как метод (II).
Следует помнить, что при методе (I) основное внимание уделяется
совместности некоторого точного макросоотношения с заданными
микросоотношениями, достигаемой путем выбора надлежащего способа укрупнения.
С другой стороны, метод (II) основан на статистическом подборе
макросоотношения между заданными синтетическими переменными, полученными
исходя из заданных микросоотношений.
Анализ упрощается, если в исходной теории считать микросоотношения
линейными и если для макросоотношения (которое мы считаем заданным или
выбранным в качестве статистического подбора) ограничиться также линейной
формой. Это допущение можно считать либо важным частным случаем, либо
удобной аппроксимацией при малых изменениях переменных. Кроме того, мы
ограничимся анализом случая линейного укрупнения, то есть такого
укрупнения, при котором макроэкономические переменные линейно синтезируются
из микроэкономических переменных. Синтетические показатели могут быть
как простыми, так и взвешенными (в статистическом смысле), но
микроэкономические переменные входят в них только в линейной форме. Короче
говоря, наш анализ рассматривает переход от линейных микросоотношений к
линейному макросоотношению с помощью линейного укрупнения.
Задачи и упражнения
1. Показать, что вопрос совместности трех элементов задачи может рассматриваться
и с третьей точки зрения: можно допустить, что между определенными синтетическими
переменными существует макросоотношение заданной формы, и задаться вопросом —
какие микросоотношения будут совместны с этим.
2. Показать, что эта третья точка зрения уместна при эмпирическом подходе, когда
считается, что между определенными синтетическими показателями существует
определенная связь. Какая микроэкономическая теория подходит к этому представлению?
19.2. ПРОСТОЙ ПРИМЕР: УКРУПНЕНИЕ ПО ИНДИВИДУАЛЬНЫМ ПОТРЕБИТЕЛЯМ
В микроэкономической теории спрос индивидуального потребителя
на определенный товар (например, чай) задается функцией (линейной) ряда
переменных: дохода потребителя, цены чая, цен всех связанных с ним
товаров. Требуется построить соотношение для рыночного спроса на чай, если
рынок представляет собой совокупность п индивидуальных потребителей.
Во всех задачах на укрупнение важно с самого начала уяснить себе,
каким образом микроэкономические переменные и микросоотношения
«сжимаются» в соответствующие макроэкономические переменные и
макросоотношения. В данной задаче имеется п микросоотношений спроса, по одному
на каждого потребителя; их надо «сжать» до одного макросоотношения
рыночного спроса. Труднее определить, как трактовать переменные. Если допустить,'
что все потребители приобретают товар по одним и тем же ценам, то, значит,
«сжимать» в этом отношении нечего, и одинаковые цены легко поддаются
обработке (см. упражнение 1 и 2 настоящего раздела). Остаются такие
переменные, как доход, размер и состав семьи, которые для различных
потребителей неодинаковы. Именно, эти микропеременные и нужно заменить
синтетическими переменными: совокупным доходом, общей численностью
народонаселения, показателями их распределения по группам потребителей. В
настоящем примере переменной величиной для различных потребителей
считается только доход.
Пусть имеются п линейных уравнений спроса, по одному для каждого
потребителя:
Ув^ЯвРз + К (*=1, 2, ...,И), A)
575

где ys — спрос на чай 5-го потребителя, доход которого равен ц8. Параметры
as и ks характеризуют, соответственно, наклон прямой линии1, графически
выражающей это микросоотиошение, и величину отрезка, отсекаемого такой
прямой на оси ординат. Особый интерес представляет параметр а$; это —
предельная склонность индивидуума к потреблению чая.
&-!' На этом закончим рассмотрение микросоотношений, даваемых
микроэкономической теорией оценки. Остальное зависит от применяемого
метода укрупнения.
Метод (I). Допустим, что макросоотношение есть линейное соотношение
между совокупным спросом у и совокупным доходом ii:
где а я к суть макропараметры, соответственно характеризующие наклон
прямой и отсекаемый ею отрезок на оси ординат. Вопрос заключается в
следующем: каким способом следует производить укрупнение? Относительно у
трудностей не существует: совокупный спрос y=22/s- Задача касается п
» S
микроэкономических переменных, обозначающих доходы отдельных
индивидуумов. Эти доходы необходимо объединить (тем или иным образом) в одну
макроэкономическую переменную совокупного дохода. Суммирование
уравнений A) дает:
В этом уравнении утверждается очевидное положение, что общий спрос
зависит от всех индивидуальных доходов. Пока еще не произошло «сжатия» \is
*в (г. Требуемое «сжатие» достигается с помощью только одного способа
укрупнения. Обозначим через а = A/п) 2 as среднее значение наклонов микро-
s
прямых, то есть среднюю предельную склонность к потреблению чая для
всей совокупности потребителей. Теперь установим, что укрупнение
индивидуальных доходов производится по формуле \х = A/а) 2 ^sM's» то есть
s
берется сумма индивидуальных доходов ц3, взвешенных по предельной
склонности к потреблению чая каждого индивидуального потребителя as. Тогда
уравнение совокупного спроса:
у = а\к + к,
где
и fc=
при условии
B)
явится точным линейным макросоотношением, определяющим совокупный
спрос на чай и полученным из п микросоотношений A).
Уравнение B) просто истолковать; это именно то макросоотношение,
которое нам требуется. Макронаклон а, или совокупная предельная склонность
к потреблению, является средней из индивидуальных микронаклонов, или
из индивидуальных склонностей к потребленною. Отсекаемый на оси ординат
макроотрезок к есть сумма индивидуальных микроотрезков ks. Затруднение
относительно B) состоит в том, что взвешивание доходов на основе
индивидуальных предельных склонностей к потреблению не является «естественным»
1 Автор здесь и далее под «наклоном прямой» подразумевает не сам угол наклона,
а тангенс угла наклона прямой с осью х-в> каковым тангенсом и является параметр as.—t
Прим. ред.
576

способом укрупнения. Большие веса придаются тем потребителям, которые
в наибольшей степени увеличивают свои закупки при росте дохода. Еще более
вызывает неуверенность относительно взвешенной укрупненной переменной
то обстоятельство, что синтетический показатель дохода \х присущ только
рассматриваемому товару (чаю). «Правильный» совокупный доход будет иным
для другого товара (например, сахара или мыла), ибо иными будут
предельные склонности к потреблению, которыми мы будем пользоваться в качестве
весов. Говоря строго теоретически, существует столько же показателей
совокупного дохода |Л, сколько имеется товаров. Практически же положение
может оказаться не столь плохим, поскольку различные показатели будут,
вероятно, изменяться одинаковым образом (например, во времени).
Метод (И). Допустим, что принят простой метод укрупнения:
Вопрос заключается в следующем: можно ли вообще составить линейное
макросоотношение между у и \х, и если да, то каковы параметры этого
уравнения? Сразу же выясняется одно обстоятельство. Только случайно можно
получить на основе микросоотношений A) точную линейную зависимость
между у и [х. Искомое макросоотношение является не точным, а осередненным;
следовательно, оно относится к определенному периоду времени (скажем,
1 = 1,2, ..., 7"), а не просто к какому-то одному моменту времени. Должен
быть задан характер изменения во времени величин ys и \is в течение этого
периода, а значит — и характер изменения совокупных показателей у и |i.
Для такого периода времени мы получим ряд точек с координатами (у, \х),
и с помощью какого-либо статистического способа, как-то способа
наименьших квадратов, можно подобрать соответствующую линейную функцию
у = а\х + к + и, где и — остаточный член или возмущение. Это — максимум
того, чего можно добиться.
Подбор с помощью способа наименьших квадратов производится
косвенным образом. Рассмотрим зависимость между изменениями индивидуальных
доходов [xs и изменениями совокупного дохода fi=^(x8 для рассматривае-
s
мого периода времени (t = 1, 2, ..., Т). Выразим эту зависимость в форме
уравнения регрессии, построенного с помощью способа наименьших квадратов:
где As и Ks — коэффициенты, полученные в процессе подбора уравнения
регрессии и зависящие от характера изменения во времени \is и (Л. Поскольку
2 H<s = Щ то из этого следует 2 А = 1 и ^>]Ks = 0. Средняя арифметиче-
S S S
екая остаточного члена us будет равна нулю, дисперсия будет минимальной,
и он не связан корреляционной зависимостью с ц; здесь важно лишь то, что
для рассматриваемого периода времени среднее значение us равно нулю.
Произведя суммирование уравнений A) и подстановку значений \is, получим:
а это уравнение имеет требуемый вид: у = а\л -\-%кк + и. Значит, уравнение
где
C)
37 p. Аллен 577

является осередненным (статистическим) макросоотношением, определяющим
совокупный спрос на чай, если пользоваться простыми укрупненными
показателями спроса (у) и дохода (|х). Среднее арифметическое значение остаточного
члена возмущения и для рассматриваемого периода равно нулю.
Результат C) можно сравнить с тем результатом, которого можно было
бы ожидать — и который был в самом деле получен с помощью первого
метода решения задачи. При условии простого (невзвешенного) укрупнения обычно
требуется найти недостающее соотношение совокупного спроса. Оно не
только является осередненным (а не точным), но и его коэффициенты не те,
которых можно было бы «естественно» ожидать. Мы могли бы достичь соответствия:
в динамике, вычислив средние значения а=а=A/п) 2 as и к=^]к8. По сути
S S
дела, макронаклон а есть средневзвешенная микронаклонов as, и веса (As)
зависят от характера изменения переменных во времени. Совокупная
предельная склонность к потреблению чая не является простой средней
арифметической индивидуальных предельных склонностей к потреблению; это —
взвешенная средняя, с весами, изменяющимися от одного периода времени к
другому. Вычисление макроотрезка, отсекаемого на оси координат, является
еще более затруднительным, ибо на значение к влияет не только характер
изменения переменных во времени, но также и значения как отсекаемых
микроотрезков, так и микронаклонов.
Ясно, что простое укрупнение (II) вносит в макросоотношение
совокупного спроса систематическую ошибку укрупнения, которая не имеет ничего
общего со статистической систематической ошибкой исчисления в рассматриваемом
периоде времени. Полезно выявить значение ошибки укрупнения. Она
выявляется при нахождении корреляционной зависимости между
предельными склонностями к потреблению as (для всех индивидуальных потребителей
на рынке) и коэффициентами (соответственно А8 или К8) в уравнении
регрессии индивидуального дохода \is относительно совокупного дохода (i.
Определим значения ковариации1:
"Cov (а$ As) •= — 2 (as ~~ a) (Aa j ( поскольку средняя арифметическая
(поскольку i
и Cov (as #s) = ™ 2 (as~~ U)KS Г поскольку средняя арифметическая
\ 2 as Ks (ПОСКОЛЬКУ ^ #s = °) ¦
x) Ковариацией распределения двух признаков х и у какой-либо совокупности
из N единиц или первым моментом произведения называется в статистике
выражение A/iV) 2 ху, где х и у суть отклонения от средних величин соответствующих
признаков. Ковариация входит как составная часть в формулу коэффициента корреляции
r = (i/NexOy)y 2 ХУ> гДе °х и <*у СУТЬ средние квадратические отклонения соответственно
признаков X и Y. — Прим» ред.
578

Таким образом, макропараметры уравнения C) можно представить
в следующем виде:
а = 2 as^s = a + n Gov (as As) \
|
Уравнения D) показывают, насколько макронаклон и отсекаемый
макроотрезок для совокупного спроса могут отличаться от «естественных»
значений, соответственно от а и 2^s' из-за систематической ошибки
укрупнения по рынку.
Рассмотрим группу потребителей, отличающихся высокой предельной
склонностью к потреблению чая (as > а). Пусть индивидуальные доходы этих
потребителей быстро возрастают при увеличении совокупного дохода во
времени. Тогда As > О может оказаться весьма большим. При этих условиях
между as и As существует положительная корреляционная зависимость,
Cov (asAs) > 0 и а > а. Макронаклон совокупного спроса на чай выше, чем
этого можно было ожидать, то есть больше, чем средняя арифметическая
отдельных микронаклонов. Совокупная предельная склонность к
потреблению может оказаться больше, чем средняя склонность к потреблению
отдельных потребителей.
Следовательно, в заключение можно сказать, что при методе (I)
макропараметры аи к всегда являются «правильными» (а = а, к = 2*8)» доходы
s
при их укрупнении взвешиваются таким образом, что мы всегда получаем
этот результат. С другой стороны, при простом укрупнении, принятом в
методе (II), макропараметры могут оказаться «правильными» только в результате
статистической случайности.
Задачи и упражнения
1. Составить уравнения индивидуального спроса на чай следующего вида:
У9=а&8+ЬвР+кл E=1, 2, ..., и),
где р—цена чая, одинаковая для всех потребителей. При помощи метода (I) показать,
что если |А определяется так, как это сделано в данном разделе, то у=а\л-\-Ьр-{-к
есть точное макросоотношение, и что
а = а; Ь = пЬ; E*=2*s.
S
2. Пользуясь в предыдущей задаче методом (II), покажите, что способ и
результаты, приведенные в данном разделе, применимы, если макроуравнение
подобрано (с помощью простого укрупнения) для п микросоотношений, имеющих вид
(Vs—Ь8р) = а8ц8-\-к8. Истолковать полученный результат.
3. Отрасль промышленности, состоящая из п фирм, производит единственный
продукт; согласно микроэкономической теории, потребность s-u фирмы в каком-либо
факторе производства (скажем, в рабочей силе) задается уравнением y$ = aszs^-
-\-Ics E = 1, 2, ...,/г), где х8—выпуск продукта фирмой. Показать, каким образом
в целом для отрасли можно построить макросоотношение у = ах-\-к. Показать также,
каким образом можно включить в анализ цену фактора, одинаковую для всех фирм.
19.3. ПРОСТОЙ ПРИМЕР: УКРУПНЕНИЕ ПО ТОВАРАМ
В настоящем разделе снова используется микроэкономическая теория
оценки, однако здесь требуется укрупнение иного рода: спрос единственного
индивидуума на т различных товаров укрупняется для определения
совокупного спроса этого потребителя в отношении группы товаров. Такой
группой могут быть < напитки», куда входят различные виды и сорта чая, кофе,
какао, безалкогольных напитков и т. д.; группа может быть еще более широкой,
579 37*

например — все продукты питания или даже все товары в целом. Поскольку
в каждом уравнении спроса мы имеем дело с одним и тем же значением дохода
потребителя (которое легко поддается обработке, см. упражнение 2
настоящего раздела), то приходится сводить и укрупнять такие переменные, как
цены на товары. Пусть т микроотношений (спроса индивидуального
потребителя на различные товары) необходимо «сжать» в одно макросоотношение
совокупного спроса. Имеется т переменных цен, по одной для каждого
товара; путем укрупнения или осереднения необходимо их «сжать» в одну
групповую цену. В настоящем примере принято следующее упрощение: считается,
что в каждое микроотношение входит цена только одного товара (товара,
спрос на который изучается), а не целый комплекс цен.
Имеются т линейных соотношений спроса, по одному для каждого товара:
(г=1, 2, ...,го), A)
где уТ— спрос потребителя на г-й товар (например — на некоторый сорт
чая) при цене этого товара, равной рг. Параметры ЪТ и кг, соответственно,
отражают наклон и отрезок на оси ординат, отсекаемый прямой, графически
отображающей это уравнение. Коэффициент Ъ показывает предельное влияние
цены на спрос; он равен эластичности спроса от цены, если угж рг —
измерены по логарифмической шкале.
Требуется объединить m значений уг в совокупный спрос у, a m значений
рг— в совокупную или среднюю цену р всех товаров. Если это не
затрудняется различием единиц измерения, то можно суммировать уг и рг для различных
товаров. Такой подход правилен, если эти товары представляют собой,
например, разные виды или сорта чая; вполне разумно^ использовать — в качестве
переменных макросоотношения — совокупный спрос на чай (в фунтах)
и среднюю цену чая (пенсов за фунт). Результаты в точности совпадают с
полученными ранее, то есть с уравнением B) из раздела 19.2 для
соответствующего взвешенного укрупнения цен с помощью метода (I) и с уравнениями C)
и D) для простого укрупнения с помощью метода (II). С формальной точки
зрения, укрупнение по товарам и укрупнение по потребителям —
эквивалентные операции. Они различаются только в отношении истолкования и
практического применения.
Если же группа товаров является смешанной, то единицы измерения
и цены не однородны, и складывать их нельзя. Эта трудность в основном
практическая, и ее преодолевают с помощью обычных технических приемов
построения индексов. Однако наличие этой трудности подсказывает возможность
обобщения результатов, которые имеют общий характер и вполне очевидны,
но лучше всего представляются в следующей связи.
Обычная практика построения индексов количества (или цены)
устанавливает отношение каждого количества (или цены) к базисной (или эталонной)
величине. Для г-го товара:
Индекс количества = — ; Индекс цены = ^ .
Уго Pro
Мы можем получить средние значения этих индексов, применяя или
не применяя взвешивание. Если применяются индексы Ласпейреса
(взвешенные по базисному значению), то:
2-»? 2*.*
у = — = — (индекс количества),
B)
(индекс цен),
г
580

где весами, wr0 = pr0 yr0, служат базисные стоимости спроса соответствующего
товара. Здесь у и р можно считать результатами простого (невзвешенного)
укрупнения неоднородных товаров, заменяющими г/=2^г и P^Sa- Для
г г
случая однородных товаров.
Микросоотношения A) можно построить по-иному:
..... (r = l, 2, ...,m), C)
#ro /'ro
где br понимается как эластичность спроса от цен в базисной точке
(см. упражнение 3 настоящего раздела). Требуется на основе т
микросоотношений C), с помощью средневзвешенных индексов типа B), построить
одно макросоотношение следующей формы:
У = Ър + к.
Произведем преобразование переменных:
5>»
В таком случае микросоотношения C) представятся в виде:
где
Тогда можно непосредственно применить результаты B) и C) из раздела
19.2, и простое укрупнение B) опишется уравнениями:
г г
Пользуясь методом (I), мы получаем следующий результат: точное
макроуравнение у = Ьр-\-к получается в том случае, когда р отображается
не простым (Ласпейресовским) индексом B), а взвешенным в дополнение
к обычным весам wr0, также и по показателям эластичности спроса от
цены (ЬТ). Пользуясь методом (II), в результате простого (Ласпейресовско-
го) осереднения мы получаем макроуравнение у==.Ър-\-к только с помощью
статистического подбора для некоторого периода времени, причем даже
в этом случае параметры Ъ и к включают систематическую ошибку
укрупнения.
Распространение на общий случай, подсказываемое этим практическим
применением техники вычисления индексов, заключается в том, что простое
укрупнение (например, р=2.Рг) можно заменить любым укрупнением по
г
неизменным весам:
Р = 2 WrPn
г
где веса ауг(г = 1, 2, ...,т) являются неизменными и задаются заранее.
Необходимо лишь осуществить следующее преобразование переменных:
Pr = Wrpr.
Тогда укрупнение микросоотношений yr = (br/wr) pr + кг (г = 1, 2, ..., ш)
производится с помощью переменной /?=2^- Эта операция уже рассмат-
ривалась при изложении метода (II).
Задачи и упражнения
1. Составить микросоотношения Уг = Ьгрг-{-кг, где уг—логарифм спроса на г-й
товар, а рг—логарифм цены этого товара. Тогда параметр Ъг — эластичность спроса
от цены. Показать, что здесь, как и в тексте данного раздела, применимы простое
укрупнение и подбор макросоотношения у^Ър-^-к, но только р равно взятому m раз
логарифму средней геометрической цен; аналогичным образом выражается и у.
Истолковать параметр Ь.
581

< 2. Показать, что макросоотношение совокупного спроса t/ = ajji-|-bp-|-& можно
получить из микросоотношения г/г — ar\i-\-brpr-\-kr, где \i—доход потребителя.
Истолковать fl=mac точки зрения предельных склонностей к потреблению.
3. Пусть микросоотношения спроса представлены в виде уравнений C) в тексте
раздела. Вывести, что значение эластичности спроса от цены изменяется в
зависимости от цены, причем в базисной точке (цена равна рг0, количество у,0) оно равно br.
4. Для производства заданного выпуска продукта фирма использует т видов
затрат (факторов производства). Когда цена г-го фактора равна рг (г = 1, 2, ..., т),
потребность в нем составляет yr = brpr-f-kr. Показать, что можно построить
макросоотношение у — Ьр-\-к, где у—общие затраты фирмы, а ^ — средняя цена
затрачиваемых факторов.
19.4. ПРОТИВОРЕЧИЯ МЕЖДУ МИКРО- И МАКРОСООТНОШЕНИЯМИ
В настоящем разделе следствия простого укрупнения рассматриваются
на примере укрупнения по потребителям (см. 19.2). Аналогичными будут
и результаты укрупнения по товарам.
п микросоотношений вида ys = as\is + ks (s== 1, 2, ..., п) слиты в одно
макросоотношение вида у = а\х-\-к + и, статистически подобранное для
некоторого периода времени (г/= 2ys> !x==:2fJts)- Во-первых, устанавливается
S S
зависимость во времени между \is и \i в соответствии с уравнением
регрессии:
B4.-1. 2^s = o). (i)
s s
Затем определяются макропараметры:
B)
Их значения обусловлены значениями не только микропараметров as и /cs,
но и коэффициентов As и Ks, которые появляются при подборе уравнений
регрессий к линии движения переменных в течение определенного периода
времени.
При пользовании таким макросоотношением возникают трудности
двоякого рода. Во-первых, неверно, что значение какого-либо макропараметра
зависит только от значений соответственных микропараметров. Из B)
очевидно, что значение к зависит от соответственных &s, но также и от
несоответственных as в микросоотношениях. В настоящем простом
примере лишь случайно оказалось, что значение а зависит только от
aQ] не так обстоит дело в более сложных вариантах, рассматриваемых
ниже. Во-вторых, на значения макропараметров оказывает влияние и
характер изменения переменных во времени, отражающийся в коэффициентах
регрессии As и Ks уравнения A). Если рассматривать другой период
времени, или если переменные изменяются иным образом, то в общем случае
значения макропараметров также будут иными. Это отражается членами,
характеризующими в B) систематическую ошибку укрупнения.
Можно ожидать, что эти затруднения приведут к противоречиям
в прогнозах, основанных на применении микро- и макросоотношений.
Рассмотрим этот вопрос более подробно. Пусть приращение |jis равно
Д|ха (s = l, 2, ..., я), и в результате таких приращений синтетический
показатель \х увеличится на Л[Л=2 ^l^s' Определить влияние этих измене-
S
ний на совокупный спрос у = 2j Vs можно ДвУмя способами. В одном из
s
них используются микросоотношения:
582

Во втором воспользуемся макросоотношением (опуская остаточный член):
= aA\i = a
В общем случае C) и D) не тождественны; между ними существует
противоречие.
Это частично обусловлено тем обстоятельством, что а, а значит, и А2у
зависят от характера изменений в рассматриваемом периоде времени, тогда
как Агу от таких изменений совершенно не зависит. Даже если все as
фиксированы (а значит, фиксировано и Д^), то различный характер
изменения доходов потребителей во времени может изменить а, а
следовательно — значение Д22Л предсказанное на основе макроуравнения. Этот
вопрос необходимо исследовать. Возьмем частный, но важный случай, при
котором каждое |ы8 изменяется, точно или приближенно, пропорционально \i.
При возрастании или уменьшении совокупного дохода пропорционально
изменяется доход каждого из индивидуальных потребителей (хотя доля
его может быть неодинаковой для различных потребителей).
Следовательно, пропорцию для 5-го потребителя определяют К$ = О и As Ф 0 в уравнении
регрессии A). В среднем га рассматриваемый период времени пропорция для
5-го потребителя задается формулой A):
As — ^ir (так как средняя арифметическая us = 0).
Таким образом, пропорция изменения дохода отдельного потребителя
относительно совокупного дохода определяется значением среднего дохода
потребителя |ы3 за данный период времени. Поэтому, исходя из B):
а = |г2аЛ- E)
8
Влияние рассматриваемого периода времени на значение а сказывается
только через посредство средних доходов; этот результат кажется довольно
обоснованным. Если распределение потребителей по уровням доходов не
меняется, то выбор периода времени слабо влияет на совокупную предельную
склонность к потреблению а. В оценке значения а, полученной укрупнением
индивидуальных предельных склонностей к потреблению, лицам с высоким
доходом придается больший вес, чем лицам с малым доходом.
Предположим далее, что приросты индивидуальных доходов
пропорциональны их уровням; это кажется достаточно реальным допущением. Тогда:
AfcLe4t (,в1,2,...,п),
»*. I*
и, в соответствии с C), D) и E),
Aj2/ = 4t 2 as\is = aAfx = А2у.
Здесь противоречие отсутствует. В рассматриваемом случае в
значительной мере удается избежать, по-видимому, трудностей, связанных с
применением укрупнения для прогнозирования. Поставленный ранее вопрос
приводится в таком случае к следующему: действительно ли индивидуальные доходы
изменяются во времени пропорционально совокупному доходу? Это кажется
вероятным, по крайней мере приближенно, для устойчивых периодов
времени. С помощью' уравнения E) мы получаем «уравновешенную» («well-
behaved») совокупную предельную склонность к потреблению, где
индивидуальные предельные склонности к потреблению взвешены по средним доходам
потребителей.
583

Тейл [8, стр. 24—25] приводит данные, свидетельствующие о том, что
распределение по уровням доходов становится более широким (у лиц с
высоким доходом последний повышается в большей степени) в периоды подъема
по сравнению с периодами депрессии. Если это действительно так, то
индивидуальные доходы не изменяются пропорционально совокупному доходу:
в'периоды подъема высокие доходы возрастают в большей степени, чем низкие.
Тогда допущение Ks — О неправильно. В самом деле, выражение
должно увеличиваться с ростом [г, если доход s-ro потребителя высок, и
уменьшаться — если он низок. Следовательно, Ks < 0 для лиц с высоким доходом
и Ks > О — с низким. Найдем среднее значение \is = As\i + Ks + us для
состоятельного потребителя в течение некоторого периода времени (при Ks < 0);
здесь \xs < ^ts|i, то есть вес при as в формуле B), определяющей значение а,
равен
Предельные склонности к потреблению состоятельных потребителей
вдвойне влияют на совокупную склонность к потреблению, во-первыхг
потому, что средний доход этих потребителей выше, и, во-вторых, потому,
что их доходы в большей степени изменяются во времени.
С другой стороны, доходы некоторых индивидуумов (например, рантье)
могут оставаться неизменными даже при увеличении или уменьшении
доходов других лиц. Для таких индивидуумов равно нулю уже не Ks, a ^4S.
Предельные склонности к потреблению этих лиц ни в коей мере не влияют
на совокупную предельную склонность к потреблению. Более того, если
рассматриваются доходы в их реальном, а не в денежном выражении, то
значения As для рантье могут оказаться отрицательными. При определении
совокупной предельной склонности к потреблению с помощью уравнения B)
«веса» отличаются тем необычным свойством, что они могут быть
отрицательными. Если имеются отрицательные «веса», то совокупная предельная
склонность к потреблению может не только отличаться от средней арифметической
индивидуальных склонностей к потреблению — она может оказаться больше
или меньше любой из них.
Обратимся теперь к другому аспекту противоречий между Агу и А2уг
заключающемуся в C) и D). Распределение Afxs по потребителям может быть
любого вида; оно должно лишь отвечать условию 2 ДМ'в ~ ^fx. Соответствен-
s
но, Агу может изменяться самым различным образом, даже если Afi и А2у
фиксированы. Только в случае очень специальных условий противоречие
невозможно при любом распределении заданного прироста совокупного
дохода. Можно было бы думать, что этого удается добиться при значении
ковариации Cov (asAs) = Cov (asKs) = 0, ибо тогда а я к принимают cboit
«лучшие» значения, соответственно по B) аи 2^s- Однако это не так: ва
S
избежание противоречия, по-прежнему требуется соблюдение
дополнительного условия (равномерное распределение приращений дохода между
потребителями); см. задачи 2 и 3 к настоящему разделу.
В самом деле, при простом укрупнении чрезвычайно трудно избежать
всех без исключения противоречий. Противоречие между макро- и
микросоотношениями невозможно при любом распределении прироста дохода
в том и только в том случае, если:
а8 — а (для всех 5=1, 2, ...,п),
то есть если предельная склонность к потреблению будет одинаковой для
всех потребителей. Это можно доказать следующим образом. Во-первых,,
если as-=-a для всех s, то Co\(asAs) = 0 и, согласно B), макропараметр а
584

также равен а. Значит, и Агу и А$ равны аД(л; противоречия здесь нет.
Во-вторых, если противоречия не существует, то 2asi^M's:==a 2 Afis» неза-
S S
висимо от того, каким бы образом ни распределялись A(Lts. Пусть А[х1 =
= — Api2 =^= 0 и Д[Л8 = О (s>2). В этом случае условие отсутствия
противоречия заключается в том, что
(a1 — a2)A\i1 = 0, то есть что ах — аг.
Аналогично этому равны и все остальные as, то есть as = a для всех s.
Это завершает доказательство.
Полученный результат кажется не особенно полезным: ведь в
макроэкономической модели, построенной путем простого укрупнения,
противоречий удается избежать в том и только в том случае, если каждый
потребитель имеет одинаковую предельную склонность к потреблению. Однако
остается еще вывести важное следствие этого результата. Предположим,
что укрупнение доходов не обязательно является простым (невзвешенным),
но что допустимо взвешивание по специально подобранным и
фиксированным заранее весам. Тогда надлежащим подбором весов всегда
удастся избежать" противоречий в макроэкономической модели. Пусть
|х= ^]ws\is при постоянных весах ws. Преобразуем переменные индивиду-
8
ального дохода так, как мы поступили в конце раздела 19.3:
И-^ад, E = 1, 2, ..., п),
так что из микросоотношений:
простым укрупнением получаем совокупный доход y = a\i + k, где fx =
= 2 1*8= 2 ^sf*s- Противоречия не имеется в том и только в том случае, если:
8 S
-2i-= const (для всех 5 = 1, 2,..., и).
ws
Веса uys должны быть пропорциональны as. Это можно записать в
следующем виде:
w == —
S ~a '
так что макропараметр a = (t/n)^>](as/ws) = a. Значит, для избежания про-
S
тиворечия необходимо принять следующее укрупнение по постоянным
весам:
и макросоотношение, как это и требуется, будет иметь вид у —
s
Укрупнение по формуле F) Тейл [8] называет совершенным укрупнением.
Это — единственный вид взвешивания, применение которого при
прогнозировании устраняет все противоречия между макросоотношением
(статистическим или осередненным) и индивидуальными микросоотношениями. Это
макросоотношение обладает также требующимися свойствами, например
совокупная предельная склонность к потреблению является средней
арифметической индивидуальных предельных склонностей к потреблению.
Следовательно, в конечном счете мы возвращаемся к тому, чего удалось
достигнуть с помощью метода A). Теперь установлено, что частный случай —
укрупнение по формуле F) — дает точное макроуравыеггае; далее, от такого
укрупнения нельзя отказаться, если мы хотим, чтобы в макроэкономической
585

модели не имелось противоречий. Хотя такое укрупнение и не является
«естественным», это — единственный вид укрупнения, при котором достигается
отсутствие противоречий в макромодели при любых обстоятельствах.
В простом случае, когда значения индивидуального спроса на товар
объединены в одно уравнение зависимости между совокупным спросом и
совокупным доходом, результаты могут быть выражены и истолкованы следующим
образом:
I. Точное уравнение совокупного спроса получается при укрупнении
доходов, взвешенных пропорционально индивидуальным предельным
склонностям к потреблению;
II. Уравнение совокупного спроса при простом укрупнении
определяется статистически, и его параметры в общем случае зависят от
характера изменения доходов во времени в течение рассматриваемого
периода;
III. При простом укрупнении существует только один случай,
в котором никогда не встретятся противоречия в прогнозировании
между соотношениями индивидуального и совокупного спроса, это — тогда,
когда все индивидуальные предельные склонности к потреблению равны
между собой;
IV. Единственная система взвешивания по постоянным весам для
определения совокупного дохода, которая не дает противоречия при
прогнозе, это — взвешивание по весам, пропорциональным индивидуальным
предельным склонностям к потреблению, то есть как в п. I.
Для совершенного укрупнения доходов, позволяющего избежать
любых противоречий, требуется взвешивание по индивидуальным склонностям
к потреблению; при таком способе система весов для различных товаров
неодинакова. Здесь важно то обстоятельство, что противоречия при прогнозе
совершенно исключены. Даже при простом укрупнении возможны такие
частные случаи, когда на основе макросоотношения мы получаем тот же прогноз
{по крайней мере приблизительно), что и на основе индивидуальных
микросоотношений.
Задачи и упражнения
1. Если отрасль промышленности состоит из п фирм имеющих различные
выпуски продукции, то спрос на некоторый фактор производства определяется так, как
это сделано в упражнении 3 из раздела 19.2. Показать, что этой модели присуще
отсутствие противоречий, если выпуск каждой фирмы изменяется во времени
пропорционально общему выпуску отрасли. Является ли такая ситуация вероятной?
2. В примере, рассмотренном в тексте данного раздела Gov(as^4s) = 0, так что
•а = а. Показать, что Ait/=A22/ только в том случае, если 2 as^\Jis=:(^/n) 2 us 2 ^8t
8 S S '
то есть только тогда, когда все Ajis равны между собой.
3. Доказать положение, обратное предыдущему, то есть задаться Afxs=(l/n) Aji
{для всех s) и показать, что Д^—ДгЗ/, если Gov (asA$) = 0.
4. Показать, что условие а8=а (для всех s) является более строгим, чем условие
Cov (asA8) = 0; для этого установить, что Cov(as^s) = 0 при а8—а, но не наоборот.
5. Показать, что в случае совершенного укрупнения доходов некоторые
индивидуальные доходы могут появиться в совокупном доходе в виде отрицательных
слагаемых (например, когда товар является слишком малоценным для одних и
слишком дорогим для других потребителей).
19.5. УСЛОЖНЕНИЕ ПРОСТЫХ ПРИМЕРОВ
Простота примеров, рассмотренных в разделах 19.2 и 19.3, вызвана тем,
что, во-первых, в каждом микроуравнении имеется только одна независимая
переменная (доход или цена), и, во-вторых, что ни одна независимая
переменная не встречается более чем в одном микроуравнении. Откажемся от этих
ограничений: от первого — в настоящем разделе, от второго — в двух
последующих разделах. Теперь каждое из микроуравнений, а также полученное
из них единственное макроуравнение, включает несколько независимых пере-
586

менных; при этом приобретают важность различные перекрестные влияния,
ранее исключавшиеся.
Предположим, что индивидуальные потребители на самом деле
представляют семьи различного размера, и что размер семьи можно отобразить каким-
то единым показателем, характеризующим спрос этой семьи на
рассматриваемый товар (например, с помощью какой-то шкалы эквивалентности).
Обозначим через
(* = 1, 2, ...,П) A)
спрос 5-го потребителя, если его доход равен |j,s, а размер семьи vs.
Требуется найти макроуравнение г/= ац, + frv + к, где \х — некоторый
совокупный доход, а V —некоторый показатель общей численности населения.
Метод (I). Пусть суммирование уравнений A)
.дает точное макроуравнение, которое означает, что и \i и v суть
взвешенные синтетические показатели рассмотренной выше формы. В самом деле:
у = ар + bv + fe,
где
при условии
B)
является точным макроуравнением, получаемым из микроуравнений A).
Метод (II). При простом укрупнении {y=^]ys, |*в2^в и v==2vs)
осередненное макросоотношение y = aii + bv + k + u приходится подбирать
для некоторого периода времени, для которого заданы динамика ys, \i$
и vs, а значит и движение г/, |л и v. Подберем уравнения регрессии:
C)
где
Значения шести коэффициентов регрессии зависят от характера
движения переменных во времени. Произведем подстановку в уравнение A)
на основе C), просуммируем по s и получим осередненное
макросоотношение для случая простого укрупнения:
где
а = 2 asAas + 2 Ь8АЬ8 =~а -f n Cov K-Aas) + n Cov (Mbs)
8 S
* = 2 «As + 2 bs5be = b + n Cov (a8fias) + n Cov Fs5b8)
* = 2 К + 2 «Да, + 2 *Дь. - 2 К + п Cov (asKas) + п Cov (ЬДЬ8)
8 8 S S
587

Здесь и — отклонение, имеющее нулевую среднюю арифметическую и не
связанное корреляционной зависимостью во времени с \л и v. Ковариационные
члены в правых частях уравнений D) представляют систематическую ошибку
укрупнения в макропараметрах. Их значения определяются точно так у$е, как
это делалось выше (см. упражнение 1 настоящего раздела).
Все это уже нам знакомо. Укрупнение по методу (I) является простым,
но не «естественным». Осередненные макропараметры, получаемые с помощью
метода (II), зависят от значений микропараметров, а также от «истории»
переменных в течение выбранного периода времени. Пользуясь этим способом,
обычно получаем противоречивые прогнозы. Существуют ситуации, когда
противоречиями можно пренебречь, например, если индивидуальные доходы
изменяются пропорционально изменениям совокупного дохода, а размер
семьи — пропорционально общей численности населения. Однако
единственная возможность избежать противоречий во всех случаях — это вычисление ц
и v как взвешенных синтетических показателей, причем веса определяются
уравнениями B); это — способ безупречного укрупнения (perfect aggregation)
обеих переменных.
Новой особенностью здесь являются взаимные влияния подобранных
макропараметров уравнений D). Значение предельной склонности к
потреблению а зависит не только от индивидуальных предельных склонностей
к потреблению (as), но и от коэффициентов &s, характеризующих влияние
размера семьи на индивидуальный спрос. Перекрестное влияние в уравнениях D)
отображается членом
Здесь сумма весов при bs равна нулю B^bs~ 0) и» казалось бы, можно
s
считать, что перекрестные влияния всегда малы. На самом деле это далеко
не так. Если окажется, что коэффициент регрессии Abs является
положительным для семей с большим коэффициентом влияния размера семьи на спрос
(&s), а для семей с малым bs— отрицательным, то перекрестные влияния
могут быть значительными.
Этот результат легко обобщается для системы микроуравнений:
(*=1, 2, ..., /l),
укрупняемых в макроуравнение:
у == ахг + Ьх2 + сх3 + ... + Л.
Укрупнение осуществляется просто; необходимо лишь произвести
суммирование всех п уравнений по всем и по каждому из х-в. Результаты
укрупнения в точности совпадают с приведенными выше B), C) и D) — лишь в
каждом случае число слагаемых будет больше. В частности, в системе D)
окажется больше слагаемых, отражающих взаимные влияния одного параметра
на другой. Это рассмотрено Тейлом в его теореме 1 [8]. Такой случай
иллюстрируется приведенными ниже задачами.
Задачи и упражнения
1. Определить значения членов, отображающих ошибку укрупнения в
уравнении D), показав, что
Cov(<v4as) = — ^ Mae —— а и Cov (bsAbs) = — ^
2. Если #s = aspis+bs^s+cs<vs+&s есть спрос семьи, имеющей доход \is и
состоящей из Xs взрослых и vs детей, то каким образом можно получить уравнение
совокупного спроса г/ = а|ы-f-&Я+cv -f- Л:? Истолковать полученный результат.
3. Ряд товаров входит в некоторую группу товаров (г = 1, 2, ..., п), остальные
не входят. Если спрос индивидуального потребителя на товары определяется
уравнением yr = arpr-\-brqr-\-kr (г=*1, 2, ..., п), то правильно ли будет характеризовать спрос
этого потребителя на товары всей группы в целом укрупненным уравнением у=ар-\-bq\-k,
где р—гиндекс цен рг для группы товаров (г = 1, 2, ..., п), а q—индекс цен qr для
другой группы товаров (г = 1, 2, ..., п).
588

4. Показать, что результаты решения упражнения 3 из раздела 19.2 (о
потребности отрасли промышленности в рабочей силе), можно ^распространить на случай
выпуска отраслью (и входящими в нее фирмами) более чем 'одного вида продукции.
5. Рассмотреть упрощения в уравнениях D) при Gov (bsAbs) — Gov (asBas) — 0;
проанализировать этот случай аналогично тому, как это сделано в разделе 19.4.
В частности, рассмотреть случай простых форм уравнений регрессии C): jxs = ^4asl[XH-Ms
и vs = Bbsv+vs.
19.6. СУММИРОВАНИЕ ПО ПОТРЕБИТЕЛЯМ И ПО ТОВАРАМ
Откажемся теперь и от второго ограничения (см. 19.5), то есть от
предположения, что ни одна независимая переменная не встречается более чем
в одном микроуравнении. Серьезность этого ограничения можно видеть
из того, что в микроэкономической теории сирое индивидуума на какой-либо
товар обычно считается функцией цен на многие товары, а спрос фирмы на
фактор производства — функцией цен многих факторов. Короче говоря, в
общем случае цена одного товара (или фактора производства) входит в
уравнения спроса на многие товары (факторы).
Приводимые ниже примеры свидетельствуют о том, насколько в задачах
на укрупнение важно представить уравнения и переменные в такой форме,
чтобы очевидным был характер «сжатия» микроуравнений в макроуравнения,
и особенно характер укрупнения или осереднения микропеременных в
макропеременные. Первые два примера относятся к промежуточному случаю.
В третьем примере мы знакомимся с весьма полезным вариантом
укрупнения — двойным суммированием одновременно по потребителям и по
товарам. Этот пример приводит к общему случаю, рассматриваемому в следующем
разделе.
Пример (а).
Спрос индивидуального потребителя на группу товаров.
В случае, рассмотренном в разделе 19.3, было введено упрощение — спрос на
каждый товар считался зависящим от цены только этого товара; таким образом
исключались все перекрестные взаимодействия цен товаров, столь важные в
микроэкономической теории стоимости. Теперь можно дополнительно ввести эти
перекрестные влияния. Индивидуальный спрос на г-ж товар равен:
(г=1, 2, ..., т)
+ ... A)
Имеется т таких микросоотношений, и каждое включает весь комплекс цен на т
товаров (хотя некоторые значения Ь могут быть нулевыми, если цены на отдельные
товары не влияют на спрос рассматриваемого товара). В уравнении A) слагаемые,
включающие цены товаров, выписаны столбцом, чтобы показать, каким образом
осуществляется укрупнение. Индивидуальный спрос на все товары группы
определяется одним макросоотношением:
где i/= 2 2/г и Р есть некоторая средняя цен pv p2, ..., рш. Здесь, по сути дела,
г
т
имеются две суммы весьма различного характера: У=2 Уг охватывает т микросоот-
г=1
т
ношений A), тогда как р= V, р (или какой-либо другой взвешенный вариант
0=1
средней) относится к каждому из микросоотношений в отдельности. Поэтому для
определения макропараметра b (который характеризует эластичность спроса от цен)
требуется двойное суммирование, ибо Ъ исчисляется на основе микропараметров brQi
где г и q пробегают значения 1, 2, ..., т. Этот параметр можно рассматривать как
одну величину, характеризуемую квадратной матрицей m-го порядка
Ьц &21 • • • ЪшЛ
Ь\гп '
589

При осереднении мы получаем не только влияние цен т различных^ товаров,
но и все перекрестные влияния цен в каждом из индивидуальных уравнений спроса.
Матрица b очень удобйа для упорядоченной записи микропараметров. Элементы
столбца этой матрицы дают параметры спроса на один товар, элементы строки—
соответствующие параметры для уравнений спроса на разные t товары.
Пример (б).
Спрос фирмы на группу затрачиваемых факторов производства.
При производстве к продуктов некоторая фирма затрачивает т факторов. Спрос
фирмы уг на г-й фактор производства зависит от объемов выпуска всех
продуктовая (#=1, 2, ..., к) и от всех цен факторов производства рг (г=1, 2, ..., т):
(r=l, 2, ..., т)
... + •-. B)
arkxh+ ...'
Эти т микросоотношений необходимо укрупнить в одно макросоотношение
у = ах-\-Ър-\-к,
где у—общие затраты фирмы, х—некоторый индекс объемов выпуска, р—некоторый
индекс цен потребляемых факторов производства. Производятся следующие суммиро-
т k
вания: у= ^ yr no m микросоотношениям, х = У] xq (средняя может также быть
r=l q=l
какой-нибудь взвешенной) по к переменным выпуска в каждом микросоотношении
m
и р= ^ Pq (средняя может также быть какой-нибудь взвешенной) по т переменным
0=1
цен в каждом микросоотношении. Макропараметр а, отражающий влияние объема
выпуска на спрос факторов производства, это та величина, которая соответствует
прямоугольной матрице микропараметров ку^т и которую можно надеяться
получить из этой матрицы:
а21 ... ат1
а
12
_alk a2k ••• amk
Макропараметр Ъ соответствует квадратной матрице b лг-го порядка точно-
такой же формы, как в примере (а). Каждое из микросоотношений B) дает элементы
одного столбца матрицы а и одного столбца матрицы Ь-
Пример (в).
Рыночный спрос на группу товаров.
Усложним пример (а) следующим образом: в каждое уравнение спроса введем
доход индивидуального потребителя, который одинаков для каждого потребляемого им
товара, затем просуммируем по п потребителям (s = l, 2, ..., п) и по т товарам
(г = 1, 2, ..., т), имеющимся на рынке. Тогда число микросоотношений спроса равно
тхп(т товаров, п потребителей):
г = 1, 2, ..., т\
<? — 1 2 п )
..-1,2,...,» У C)
Рыночный спрос определяется одним макросоотношением:
)
yz=a\i-{-bp+k.
Чтобы установить совокупный спрос, необходимо в данном случае двукратное
суммирование: 2/= 2 S ^rs' Для П0ЛУчения каждой из макропеременных (\i и р) суммирова-
r s
иие по-прежнему производится однократно: H'=2^s по п потРебителям, P~^PQ
s Q
по т товарам. Чтобы показать, какие микропараметры соответствуют тому или иному
макропараметру, заменим двойное суммирование по г и по s единым суммированием
по ?, где индекс i пробегает значения от 1, 2, ... до т х п (то есть суммирование
производится по всем потребителям и всем товарам). Каждое из т х п микросоотноше-
590

ний C) определяется нижним индексом г. Тогда параметр а соответствует вектору-
строке микропараметров, имеющему тхп элементов: а=[в{]. Эти
элементы—предельные склонности к потреблению каждого из т товаров каждым из п потребителей.
Параметр Ь соответствует прямоугольной матрице тх(тхп) микропараметров:
b=[ibQ], где i = l, 2, ..., тхп и Q = l, 2, ..., т. Каждое микросоотношение C)
отображается в матрице b одним столбцом из т элементов.
Функцию потребления кейнсианского типа, применяемую в простых мак-
родинамических моделях, можно записать в этих обозначениях следующим
образом:
Где у __ совокупное потребление и \i — некоторый совокупный доход. Здесь
предполагается отсутствие запаздывания во времени и обычная линейная
форма уравнения. Можно считать, что,это уравнение есть частный случай
более общего:
у^ар + Ьр + к, D)
Где р — некоторый индекс цен потребительских товаров, причем р считается
заданным. Если уравнение D) основывается на соответствующей
микроэкономической теории решений индивидуального потребителя, то приведенный
выше пример (в) относится именно к этому случаю, и D) есть макросоотиоше-
ние, полученное из т X п микросоотношений C).
Это кажется достаточно удовлетворительной основой построения функции
потребления — до тех пор, пока учитываются результаты, полученные
в настоящей главе (и расширенные далее в разделе 19.7). При простом
укрупнении ([х == 2 M's и Р ^ Sj^q или же ПРИ взвешивании по соответствующей
s Q
формуле Ласпейреса) уравнение D) оказывается осередненным, и параметры
(a, fc, к) отражают как перекрестные влияния, так и влияние динамики
индивидуальных доходов и цен. В общем случае также имеет место противоречие
между уравнениями C) и D), используемыми для прогноза значения у.
Единственный случай простого укрупнения, свободного от всех
противоречий, в котором уравнение D) принимает «наилучшую» форму (а равно средней
арифметической предельной склонности к потреблению), это — случай
равенства между собой всех соответственных микропараметров. Это
подразумевает одинаковую предельную склонность к потреблению для всех
потребителей, лежащую в основе уравнения D). В противном случае приходится
делать дополнительные допущения для рассматриваемого периода времени>
например, что все индивидуальные доходы изменяются во времени
пропорционально национальному доходу. С другой стороны, если мы
отказываемся от простого укрупнения и допускаем возможность какого-либо
суммирования по постоянным весам для \i и р, то тогда, в поисках совершенного
укрупнения, мы приходим к взвешиванию по микропараметрам (например,
(I взвешивается по индивидуальным предельным склонностям к потреблению).
Совершенно очевидно, что в результате простого укрупнения
нельзя получить точно уравнение D). Другие альтернативы заключаются в том,
"чтобы, пренебрегая микроэкономической теорией, рассматривать функцию
потребления D) как исходное построение; либо же, наоборот,
придерживаться микроэкономической теории и избегать макросоотношений типа D),
считая их лишь грубым приближением или характерными для некоторых
особых частных случаев в отдельные периоды времени. Оба эти варианта
выхолащивают сущность. Экономисту нужны простые макросоотношения; он желает,
кроме того, чтобы они были хорошо обоснованы микроэкономической теорией.
Задачи и упражнения
1. Показать, что результат, полученный в примере (а), можно применить к спросу
одной фирмы на группу факторов производства (затрат). Сравнить этот пример с
упражнением 4 из раздела 19.3 и с примером (б) в тексте этого раздела.
2. Показать, что пример (б) может быть использован для определения спроса на
группу товаров со стороны потребителя, располагающего к различными источниками
дохода.
591

3. В примере (б) будем считать уг(г=1, 2,..., т) соответствующим группе
затрачиваемых факторов производства (не охватывающей все виды факторов); пусть уг зависит,
кроме уже включенных переменных, и от цен p's E = 1, 2,..., п) других затрачиваемых
факторов. Показать, какой метод укрупнения позволяет получить уравнение
и истолковать смысл этого макросоотношения.
4. Сформулировать задачу по определению совокупного спроса отрасли
промышленности на группу т факторов производства (г=1, 2,..., т), если отрасль состоит из п
фирм E=4, 2,..., п). Предположить вначале, что каждая фирма производит один
продукт, и показать, что эта задача аналогична примеру (в). Распространить на случай к
продуктов, причем макросоотношение приобретет вид у=а\хх -\- ачх% •=(- ... -f- а^х^ -\-
-|- const. Можно ли еще более упростить это уравнение — свести его к виду у = ах-\-
-\- bp -\- const?
19.7. ОБЩИЙ СЛУЧАЙ: ОДНО МАКРОСООТНОШЕНИЕ
Пусть заданы микросоотношения для каждого из входящих в группу
потребителей или товаров или и для тех и других одновременно. С помощью
укрупнения требуется получить одно макроуравнение. Все соотношения —
линейные; предполагается отсутствие запаздываний во времени или
укрупнения во времени. Пусть нижний индекс i обозначает одно микросоотношение,
так что 2 означает требуемое укрупнение микросоотношений. Вообще 2
г г
означает двойное суммирование, например суммирование по т товарам и п
потребителям. Формулировка задачи зависит от того, каким образом
микропеременные укрупняются в макропеременные, входящие в макросоотношения,
и от метода вычисления соответствующих макропараметров. Пример (в)
из текста раздела 19.6 иллюстрирует это положение и подсказывает способ
записи задачи.
Составим микросоотношения для различных i:
Уг ^ га\\х\\ + ia21X21 + . . . + iamlXml
"Т" iainXln "Т" ia2nX2n ~Ь • • • 'Г iamnXmni
то есть
т п
Уг= S 2А.*г. + *1- A)
Г=1 8=1
Имеется тХп микропеременных (#rs), и ЛК)бое из них в общем случае
входит в каждое из микросоотношений. Если не считать постоянное
слагаемое fe|, то в каждое микросоотношение входит соответствующий набор
тУ^п микропараметров dars). Если какая-либо микропеременная не
появляется в микросоотношении, то это значит, что соответствующий
микропараметр принят равным нулю; однако в общем случае должны быть в
наличии все члены.
Целью укрупнения является получение одного макросоотношения:
2
r=l
B)
Суммирование производится следующим образом. Во-первых, просуммируем
y~^jVi по всем микросоотношениям; в общем случае это суммирование
г
п
является двойным. Затем определим макропеременные хг= 2 хп Для каж-
s=l
дого г (г = 1, 2, . .., т); это суммирование — однократное, или
суммирование по столбцу вниз в каждом микросоотношении A).
592

Важнейший момент —это выявление способа получения т
макропараметров аТ в B) на основе комплекса макропараметров гаГ8, входящих в A).
Однако установлены возможности существенного упрощения этого
комплекса. В получаемых результатах гаГ8 никогда не появляется
самостоятельно, обособленно, а лишь в виде суммы 2 Av получаемой путем выде-
i
ления микропараметра, который находится в одной и той же «клетке»
каждого из микросоотношений, и последующего суммирования по всем
микросоотношениям, Следовательно, можно определить производные
микропараметры, по одному для каждого микропеременного xrs:
а = У\ .а (г = 1, 2, ...,т* 5=1, 2, ,.,,«),
г
Макропараметр аг (коэффициент при хг) можно сопоставить с простой
совокупностью соответственных производных микропараметров,
образующей вектор-столбец:
-2г1-
Larn J
Каждое микросоотношение A) дает один столбец расширенной и-строч-
ной матрицы микропараметров:
[iars\ =
При построчном суммировании элементов этой матрицы получаем
вектор аг. Желательное свойство операции укрупнения состоит в том, чтобы
значение макропараметра аг зависело исключительно от значений
соответственных микропараметров, суммированных в аг. Это — желательное, но, как
мы увидим далее, не всегда реализуемое свойство.
Чтобы получить из A) уравнение B) первым методом, просуммируем
все уравнения A):
т n
г r=l 6=1 i
Это эквивалентно B), если только укрупнение проводится согласно
формуле: -
Хг:
ат
где ar = 7r
C)
и макропараметры в этом случае равны:
Параметры уравнений C) и D) известны для каждого г (г = 1, 2, ...,?п).
Веса микропеременных, позволяющие получить макропеременные хг в C),
пропорциональны соответственным (производным) микропараметрам,
являющимся элементами вектора аг. Конечно, взвешивание варьирует для
различных параметров; имеется столько же разных систем взвешивания, сколько
имеется макропараметров в макросоотношении B). Макропараметр аг,
даваемый уравнением D), имеет требуемую форму; он получается из соот-
38 р. Аллен
593

ветствепных (производных) микропараметров аг и оказывается простой
средней арифметической п элементов вектора аг.
При методе (И) приходится пользоваться простым укрупнением или же
любой формой укрупнения по неизменным весам. Если заранее не выбрана
специфическая форма укрупнения C), то макросоотношение B) удается
получить только путем статистического подбора во времени. Все
микропеременные представляют собой заданные временнйе ряды, и в общем случае
результат зависит от характера их изменения во времени. Пользоваться
при этом нужно уже описанными приемами. Тейл [8] математически
доказал правильность этого метода даже при более широкой, чем здесь,
постановке вопроса. Построим уравнения регрессии:
где
(г=1, 2, ..., m; 5 = 1, 2, ..., п),
И
s=l
= 0
В уравнении E) все коэффициенты (^4 и К) зависят от характера
исходных временнйх рядов. Статистически подобранные значения
макропараметров уравнения B) равны:
т п
г r=\ в—1
Этот результат мало что добавляет к результатам, полученным в более
простых случаях (см. 19.5) за исключением того, что в большей степени
учитывается разнообразие перекрестных влияний. Можно снова проверить,
обладают ли найденные значения макропараметров в F) желательными
свойствами. Оказывается, что эти условия не соблюдаются в двух отношениях:
во-первых, желательно, чтобы значения аг определялись только
соответственными микропараметрами а,*; на самом же деле они обычно определяются
всеми микропараметрами, одинаково соответственными и несоответственными.
Во-вторых, значение аг зависит и от конкретного характера временного ряда,
использованного для исчисления; об этом свидетельствует наличие в
выражении для аг коэффициентов регрессии А, получаемых из уравнения E).
Этим же объясняется и то обстоятельство, что прогнозы на о.снове осе-
редненного макросоотношения B) обычно противоречат результатам,
получаемым на основе микросоотношений A). Имеются особые случаи, например,,
особый характер изменения переменных во времени, при которых
противоречий можно избежать. Однако полностью избежать любых противоречий
удается в том и только в том случае, когда ars = dr (по всем $) для каждого г =
= 1,2, ..., т. Это равносильно взвешиванию совокупностей по формуле C), то
есть способу укрупнения по методу (I), который позволяет получить точное
макросоотношение заданной формы. Безупречное укрупнение—это взвешивание
по формуле C). Оно обладает тем двояким свойством, что дает точное и
требуемое макросоотношение, а также что оно является единственным видом
взвешивания по фиксированным весам, при котором удается избежать всех
противоречий в макроэкономической модели.
Задачи и упражнения
1. Показать, что макросоотношения A) могут быть скорректированы таким
образом, что разные микропеременные хг будут представлять собой суммы различного числа
594

(пг) микропеременных и что они при этом представляются в следующем виде:
3 2
Г=1 S=i
Показать также, что уравнение A) в тексте раздела по-прежнему остается характерным
для общего случая, при тг=тах пг> причем столбцы дополняются фиктивными или
псевдопеременными (имеющими нулевые коэффициенты).
2. Показать, что примеры (а) и (б) из текста раздела 19.6 представляют собой
частные случаи приведенной здесь общей формулы. Какими будут в этих примерах
значения нижнего индекса г?
3; Группа т пекарей (г=1, 2,...., ш) поставляет хлеб п (s = 1, 2,..., п)
потребителям; г-ж пекарь устанавливает цену хлеба, равную рг\ доход 5-го потребителя равен \is.
Показать, каким образом можно укрупнить микросоотношения спроса на хлеб:
m
t/rs=arsu.s+ 2 rsbQpQ+krs>
Q=l
чтобы получить совокупный спрос на хлеб: y=a\i~\-bp-\-k, где 2/=2 2^s
г s
ji=2h-s» P—^jPq- Сравнить с примером (в) из текста раздела 19.6.
S Q
4. Показать, что пример (в) из текста раздела 19.6 и предыдущее упражнение
суть частные случаи рассмотренного выше общего случая, для чего
микросоотношения примера (в) записать в виде:л
+ г«п|Л7г+ ФтРт-
Показать, что только один из коэффициентов fas(s = l, 2,..., п) отличен от нуля. Что
это за коэффициент и каков его смысл?
5. Записать пример (в) из текста раздела 19.6 таким образом, как это сделано в
предыдущем упражнении, применить простое укрупнение и воспользоваться уравнениями E)
и F) для определения макропараметров уравнения y = a\i -f bp + к. Исследовать
зависимость совокупной предельной склонности к потреблению от индивидуальных эластич-
ностей спроса от цен.
6. В предыдущем упражнении ввести различие между товарами, соответственно
являющимися предметами роскоши и предметами первой необходимости. Если r-й товар
является предметом роскоши, принять krs < 0 и считать также отрицательной
постоянную в уравнении регрессии для рТ (поскольку в периоды промышленного подъема рг,
вероятно, быстро возрастет). Показать, что при определении макропараметра А: предметы
роскоши, вероятно, должны иметь повышенный вес, и что вся группа таких товаров
в целом тоже, вероятно, будет обладать свойствами «предмета роскоши».;
19.8. ТЕОРИЯ ЭКОНОМИЧЕСКОГО БЛАГОСОСТОЯНИЯ
Следует тщательно проводить различие между вопросами укрупнения
потребительского спроса — по потребителям, по товарам, или одновременно
по потребителям и по товарам — от вопросов, возникающих в теории
экономического благосостояния. Из приводимого выше анализа ясно, что
совокупный спрос определяется после того, как каждый потребитель принял решение
(например, поставив перед собой цель максимизации полезности). Хотя
распределение доходов потребителей и имеет значение, но проблема сравнения
общих уровней полезности различных потребителей здесь не ставится. В то
же время в теории экономического благосостояния необходимо каким-то
путем укрупнить или сравнить полезности для отдельных потребителей до
того, как начаты поиски оптимальной ситуации (например, максимального-
благосостояния общества). Краткое рассмотрение этой второй проблемы
укрупнения является подходящим завершением настоящей главы. Этот вопрос
рассматривается кратко — частично по той причине, что ему посвящена
обширная литература (библиография избранных работ приведена ниже),,
а частично потому, что математика играет в трактовке этой проблемы
сравнительно небольшую роль.
595 за*

Теория экономического благосостояния отличается от анализа спроса
потребителя также и тем, что в первом случае не выдвигается никаких
посылок о характере рынка. Например, мы не предполагаем существования чистой
конкуренции между потребителями, при которой рыночные цены можно
считать параметрами. Напротив, одна из целей теории экономического
благосостояния — это исследовать, можно ли чистую конкуренцию считать
оптимальным условием (социальным), и если можно — то в каком смысле. Далее,
в этой теории рассматриваются оптимальные условия, например, в отношении
распределения доходов, налоговой или таможенной политики, как это делает
Хотеллинг [17].
По-видимому, наиболее простой и прямой подход — это явное
предположение, что индивидуальная полезность количественно измерима и затем
суммировать полезности для всех индивидуальных потребителей. При таком
суммировании можно воспользоваться соответствующей системой
взвешивания по той причине, что, хотя все потребители могут считаться равноправными,
некоторые из них в оценке полезности более близки между собой, чем
другие. Значит, можно сформулировать понятие функции благосостояния
общества W = S^C/^, где полезность иг для i-то индивидуума берется
г
с весом wi% W является здесь функцией всех затрат и выпусков, количеств
различных потребительских товаров и предложений услуг. Поэтому оптимум
(общественный) отыскивается путем максимизации функции W при условии
подчинения ограничениям, установленным в задаче.
Против такого метода можно выдвинуть два возражения. Во-первых,
как очевидно из раздела 18.5, индивидуальную полезность можно считать
измеримой (с точностью до линейного преобразования) только в ситуациях,
связанных с риском. Во-вторых, что более важно, даже если попросту сделать
допущение о существовании количественно измеримых полезностей, то все же
нельзя логически оправдать их соединение. Как подчеркивал Кеннеди [19]
и другие авторы, полезность неделима — нельзя сложением двух полезностей
получить третью (см. упражнение 1 и 2 из настоящего раздела).
Если согласиться с этими возражениями, то возникает важный вопрос —
как избежать суммирования полезностей в теории экономического
благосостояния. Имеются по меньшей мере две возможности. Одна — это составить
перечень возможных в народном хозяйстве ситуаций; предположить, что
каждый член общества способен расположить их в некотором порядке,
отвечающем его предпочтениям (например, в порядке последовательности функции
качественной полезности); наконец, принять систему прямого или
комиссионного (многостепенного) голосования, позволяющего свестимножествоиндиви-
дуальных порядков к одному, общественному. Наивысшая ситуация, то
есть та, которая занимает первое место в общественном списке, явится
оптимальной в общественном понимании этого слова.
Здесь трудность заключается в том общеизвестном факте, что, даже если
каждый член выборного органа или общества является «разумным
существом», «последовательным» в своих оценках, то это не обязательно
справедливо для решений, принимаемых большинством голосов. И это вовсе не
маловероятная возможность. Пусть три индивидуума A-й, 2-й, 3-й) столкнулись
с тремя ситуациями (^4, J5, С). Пусть каждый индивидуум расположит эти
ситуации в каком-то последовательном порядке, например:
Индивидуум
1-Й
2-й
3-й
Порядок предпочтения
А, В, С
В, С, А
С, Л, В
Последовательность здесь попросту означает от обстоятельство, что если
ситуацию А предпочитают ситуации В, а ситуацию В — ситуации С, то ситуа-
596

цию А должны предпочитать ситуации С1. Пусть эти три индивидуума
являются комиссией, которая устанавливает предпочтительность ситуаций для
общества большинством голосов, поочередно рассматривая каждую пару ситуации.
Индивидуумы,
Сравниваемая ситуация голосующие
за против
Отдается предпочтение А перед 5 1,3 2
» » В » С 1,2 3
» » С » А 2,3 1
Значит, общественные предпочтения здесь несовместны; комиссия из трех
человек является «неразумной». Она предпочитает ситуацию С ситуации А
после того, как отдавалось предпочтение ситуации А перед В и ситуации В
перед С, Именно такое положение возникает, когда, например, какой-либо
штат США положительно решает в порядке референдума вопрос о проведении
некоторого общественного мероприятия и в то же время выбирает
губернатором лицо, являющееся противником этого мероприятия, или наоборот.
Здесь, очевидно, существует столкновение интересов, аналогичное
рассмотренному в теории игр (глава 14). Это заставляет предположить, что
решения вопросов теории экономического благосостояния можно искать с помощью
теории игр; это было отмечено Эрроу [12].
Другой подход к теории экономического благосостояния — это подход
Самуэльсона [22], сторонниками которого были также Бергсон [14] и Лан-
ге [20]. Здесь в первую очередь исходят из того простейшего принципа, что
«большее» всегда предпочтительнее «меньшего». В отношении производства
это дает преобразованное соотношение (производственную функцию) затрат
и выпуска; в отношении индивидуального предложения и спроса это
позволяет приравнять предельную норму заменяемости или отношение
предельных полезыостей — соответствующему нормативному коэффициенту
преобразования в производственной функции. В результате мы получаем систему
уравнений с их числом, меньшим, чем число переменных, на (к — 1), где к —
число индивидуумов (см. упражнения 5, 6 и 7 настоящего раздела).
Следующий этап — составить недостающие (к — 1) уравнений на основе
отдельного рассмотрения понятия общественного благосостояния. Калдор
[18] и Хикс [16] исходят исключительно из одного принципа, согласно
которому улучшение имеется только тогда, когда кто-то выигрывает, и никто не
проигрывает из-за перемен (при том условии, что допускается выплата
компенсации). Тем не менее Самуэльсон [22] стремится найти функцию
благосостояния общества, дредставляющую собой вектор к функций
индивидуальной полезности:
W=W (Ult Ut,...,Uk);
W—порядковая функция, подобно всем функциям индивидуальной полезности
11г (i = 1, 2, ..., к); она устанавливает последовательный совместный
общественный порядок всех возможных ситуаций. Самуэльсон описывает функцию
W, как характеризующую «некоторое этическое убеждение — убеждение
благожелательного деспота, или законченного эгоиста, или всех
доброжелательных людей». Для определения W требуется сделать ряд допущений,
что часто и делается. Например, каждая 11г должна зависеть от
потребления индивидуумом товаров и от предложения им услуг; расходы, вызванные
лишь «очевидным» желанием не отставать от соседей), исключаются.
Недостающие (к — 1) уравнений составляются, исходя из условия
максимизации W при условии подчинения ограничениям, налагаемым остальными
уравнениями системы (см. упражнение 8 настоящего раздела). В теории эко-
1 Автор говорит здесь о понятии транзитивности, которое имеет частое применение:
если А больше В, а. В больше С, то А больше С (или «лучше», «тяжелее» и т. д.).
Свойство транзитивности является одним из свойств конечных множеств,— Прим. ред.
597

номического благосостояния для оптимума требуется только то, чтобы W
была заданной функцией, хотя бы и порядковой (то есть определимой с
точностью до монотонно возрастающего преобразования). Не обязательно,
чтобы отдельные Ui считались когда-либо равными или сопоставимыми; еще
менее требуется, чтобы их можно было суммировать или укрупнять в какую-
нибудь форму типа W = 2 wi&i- Экономист, работающий в области теории
экономического благосостояния, не обязательно должен быть утилитаристом,
хотя и утилитарист может работать в этой области.
Задачи и упражнения
1. Количественная полезность является измеримой с точностью до линейного
преобразования, то есть U*=zolu-{- p, где и — один из показателей полезности, а а и
Р — произвольные постоянные. Показать, что от влияния р можно избавиться, суммируя
только приращения полезности. Каким образом единица измерения полезности
устанавливается с помощью а? Сравнить эту ситуацию с измерением температуры.
2. Вместо того чтобы суммировать полезности, как в выражении2^г» рассмотреть
возможность трактовки полезностеи как векторов Ui с последующим «сложением» этих
векторов, аналогичным сложению сил в механике. Является ли это полезным для
концепции функции благосостояния общества W? (См. [20]).
3. Показать, что несовместимость результатов голосования, проведенного
комиссией (в приведенном выше примере), можно рассматривать и с иной точки зрения:
согласованный порядок для общества можно получить, если комиссия ограничится
сопоставлением двух пар ситуаций из трех (поскольку третье «решение» может оказаться
несовместным с двумя предыдущими); однако, рассматривая разные пары ситуаций, мы
можем получить различные варианты общественного порядка для общества.
4. В простом примере голосования показать, что несовместность вызвана тем, что
каждую ситуацию один из индивидуумов считает наиболее предпочтительной, а
другой — наименее предпочтительной, то есть порядок предпочтений образует «латинский
квадрат». Построить другой аналогичный пример.
5. Рассмотрим случай к индивидуумов (i = 1, 2,..., к) и т (г = 1, 2,....,m)
товаров, которые могут как затрачиваться, так и выпускаться. Обозначим через ХТ = ^] хгт
г
общий выпуск (или затраты, если Хт величина отрицательная), где xir — количество
для i-ro индивидуума. Показать, что технологические условия производства
(построенные по принципу, что «большее» предпочтительнее, чем «меньшее»), дают функцию
f(Xl9X%, ...,Xm) = 0.,,
6. В предыдущей задаче обозначим индивидуальную (порядковую) полезность
через ^ = ^г(жг1» xi2* •••> xim)- Показать, что если руководствоваться тем же
принципом, то
dUi dUi df df . . o , . o , , ч
•^—L : = '¦ ¦ : ' для г = 1 2, ..., к и r, 5 = 1, 2, ..., m (r^s).
7. В предыдущем упражнении число переменных xir равно km. Показать, что
на основе упражнения 6 можно составить ? (т — 1) независимых уравнений, а на
основе упражнения 5—одно уравнение, то есть что общее число уравнений на (к—1)
меньше, чем km.
8. Если ограничения предыдущей задачи свести к F (Ult U2, ..., #"&)==()» то
показать, что условие, W = W (и±, ?72> •••» #ь)=тах, позволяет составить точно (к — 1)
„ - dW dW dF dF ,. • „ o
независимых уравнении следующей формы: т : тт = тт : ~тт (i, / = 1, 2, ...
dW
..., к\ гф]). Ланге [20] называет ^ npedeAbnou общественной значимостью i-ro
индивидуума.

ПРИЛОЖЕНИЕ А
АЛГЕБРА ОПЕРАТОРОВ
1. ОПЕРАТОРНЫЕ МЕТОДЫ
Операторные методы широко применяются в прикладной математике.
При этом часто не задумываются над строгим обоснованием этих методов,
считая, что правильные результаты, полученные с их помощью,
свидетельствуют о целесообразности их применения. Основная идея этих методов
состоит в том, что преобразование функции, числа и т. д., то есть преобразование
элемента некоторого множества в другой элемент того же или иного множества
обозначается определенным символом, а затем некоторым разумным образом
проводятся алгебраические действия над этим символом, взятым отдельно
от относящейся к нему переменной. Например, если результат
дифференцирования функции у(х) обозначить через Dy = dy/dx, тос символом/)
оказывается возможным обращаться в известном смысле как с числом. В операторных
методах Dy принимается как D, умноженное на у; в таком случае D можно
отделить от у и трактовать его как алгебраическую величину.
Операторные методы применялись в тексте книги -во многих случаях:
для решения линейных дифференциальных и линейных разностных уравнений
с постоянными коэффициентами (см. 4.5, 5.5), в частности, при исследовании
распределенных запаздываний A.9, 4.8, 7.7). Операторный метод оказался
весьма полезным при изучении систем с замкнутыми контурами (см. гл. 8).
Мы будем рассматривать операторы дифференцирования D,
неопределенного интегрирования/)**1, операторы сдвига Е и Е~г, применявшиеся при
решении конечно-разностных уравнений, и разностные операторы Д и V.
В настоящем приложении мы рассмотрим вкратце практические
правила действия над этими операторами, большею частью не останавливаясь
ла их обосновании, если оно не оказывается вполне элементарным.
2. ОПЕРАТОРЫ D И ГГ1
Рассмотрим функцию у = у(х); мы будем считать, что она обладает
производными любого порядка в рассматриваемой области изменения аргумента.
Введем символ D для обозначения операции однократного
дифференцирования «d/dx»:
Повторное дифференцирование будет обозначаться с помощью целых
степеней оператора D:
Вообще
где /г —любое целое положительное число. Введенный нами оператор
является пока лишь удобным способом записи производных различных
599

порядков. Например, дифференциальное уравнение -т-f- — г/=sin юж можно
теперь записать в виде D2y — у —sin соя.
Сейчас мы введем правила алгебраических действий над операторными
выражениями; на основании этих правил мы сможем, например, левую
часть написанного дифференциального уравнения преобразовать следующим
образом:
Мы увидим, что алгебраическое преобразование операторных выражений
очень полезно при интегрировании линейных дифференциальных уравнений.
Необходимо оговорить, что за символом D или за выражением
относительно D всегда должна следовать переменная или ряд переменных, для
того чтобы это выражение имело смысл.
На операторные выражения распространяются коммутативный закон
сложения и дистрибутивный закон умножения по отношению к сложению,
что можно проверить непосредственно:
Коммутативный закон: D2-\-D — D + D2, так как
Дистрибутивный закон: D(D-\-l) — D2-\-D, так как
Введем произведение целой положительной степени оператора на число
с помощью равенства:
Сумму таких произведений мы определим равенством:
(u{iDn + axDn^+ ... +an_1D + an)y
dny . dP-ty . , dy
Выражение в круглых скобках называется операторным многочленом.
Пусть F (D) и Ф(?)) — два операторных многочлена с постоянными
коэффициентами. Рассмотрим простейший случай, когда оба эти многочлена —
первой степени:
Рассмотрим выражение
(atD + aJi
где у — произвольная функция, обладающая производными всех нужных
порядков. Это выражение мы условимся истолковывать так: сначала
к функции у применяется оператор Ь0О-гЬг^ то есть составляется
выражение bo(dy/dx)Jrb1y, а затем к полученной сумме применяется оператор
Нетрудно проверить, что
(a0D + a,) (b0D + Ьх)у = (b0D + Ъх) (a0D + аг) у.
600

Вообще, для произвольных операторных многочленов F (D) и Ф(Д)
применим переместительный закон умножения:
Непосредственной проверкой легко убедиться в справедливости
ассоциативного закона умножения:
{F(D)Ф (/>)} ? (D) у = F{D) {Ф (Z))? (D)} у.
Заметим, что переместительный закон не применим в случае, когда
оператор прилагается к произведению двух функций:
D (yz) = yDz -f zDy Ф yDz Ф yzD,
где последнее выражение бессмысленно, так как за оператором не следует
никакая функция. Равным образом
так как и здесь за D и D2 не следует какая-либо функция.
Пусть а —постоянная. Тогда имеют место формулы (следствия обычных
правил дифференцирования):
D {ay) = aDy
Введем теперь оператор Z)'1, обратный к D. Естественно определить
D~xy как неопределенный интеграл от функции у:
Действительно, при таком определении мы получаем (так как
интегрирование обратно дифференцированию):
то есть
Введем целые отрицательные степени оператора D с помощью равенств:
и т. д.
Если положить по определению D0 — 1, то правило DmDn = Dm+n окажется
верным для любых целых т и п.
Алгебраические правила распространяются, таким образом, на все
целые — положительные и отрицательные степени Z), например:
- -D + TT-D + tr1'
так как
Это является основой алгебры оператора D и его обратной величины
Z). Нужно подчеркнуть, что допустимы только целые степени J9, однако
этого достаточно для последовательного дифференцирования и
интегрирования любой переменной у,
601

3. ПРАВИЛА ПРИМЕНЕНИЯ ОПЕРАТОРНЫХ ВЫРАЖЕНИЙ К НЕКОТОРЫМ
ЭЛЕМЕНТАРНЫМ ФУНКЦИЯМ
Пусть F(D)y обозначает результат нескольких дифференцирований,
интегрирований и рациональных действий, произведенных над функцией у
и некоторыми постоянными. Понятно, что F(D) есть в таком случае
рациональная функция от ?), которую можно представить в виде отношения
двух операторных многочленов. Пусть у и z — две функции, a F±(D)
и F2(D) — два операторных многочлена, связанные соотношением:
Тогда z = [F1(D)/F2i(D)]y, так как результат применения
к [Fx(D)lFt(D)\y дает F1(D)y.
При интегрировании линейных уравнений чаще всего приходится
применять оператор F (Z)), являющийся отношением двух операторных
многочленов, к показательной функции, многочлену, синусу или косинусу,
а также к произведениям названных функций. Мы приведем здесь
основные формулы и проверим их справедливость на нескольких примерах.
I. Применение операторной рациональной дроби к показательной
функции. Основная формула имеет вид:
.. A)
Более общая формула имеет вид:
F{D)ye"x = e«xF(D + a)y ...f B)
где ^ — произвольная функция, дифференцируемая нужное число раз.
Из последней формулы следует, в частности, важный результат,
использованный нами при изложении теории линейных дифференциальных
уравнений с постоянными коэффициентами.
Рассмотрим линейное однородное уравнение:
Пусть а есть Q-кратный корень характеристического уравнения F(a) = 0.
Покажем, что в этом случае уравнение F(D)y = 0 имеет частные решения:
еах, хе™, х2еах, ..., х<*-* еах.
В самом деле,
и (если D заменить D-fa): F(D + a) = DQQ)(D + a). Поэтому, если у =
то по формуле B):
F (D) xkeax = eax F(D + a)xk =
= еах /)°Ф (D + a)xk = е™Ф (D + a) DQxk = 0,
ибо
DQxk = 0,
«ели А = 0, 1, 2, ...,q — 1. Заметим, что линейную независимость этих
решений нетрудно доказать обычным способом (см. гл. 4).
Рассмотрим теперь несколько примеров применения формул A) и B).
Пример (а)
ф2_1)е«х = (а2_1)еа*.
Проверка:
Пример (б)
602

•Это означает, что
а2—Г
в чем нетрудно убедиться непосредственным вычислением.
Пример (в)
Действительно,
уеах ~
2— 1) у,
II. Применение операторной рациональной дроби к многочлену.
Пусть у—-многочлен относительно х. Если F(D) — операторный
многочлен, то вычисление выражения F(D)y не представляет труда.
Если F(D) — рациональная дробь, ее нужно разложить на
элементарные рациональные дроби, представив F(D) в виде линейной
комбинации дробей вида 1/(?> + Я-). Затем каждую элементарную дробь
этого вида мы записываем в виде jjztk =т(^ + г)
иРазлагаемвбиномиальный ряд по возрастающим степеням D. Идея метода заключается
в том, что все производные высших порядков (выше, нежели степень
многочлена) исчезают, и раскрытие формулы в действительности приводит
к конечному числу членов.
Пример (г)
(D2— 1) (ах* + Ьх+с) =-^5- {ах* + Ьх+с) — (ах* + Ьх + с)=
Пример (д)
—jr^—— (ax2-\-bx-{-c). Преобразуем операторную дробь:
2
Поэтому
Проверка:
(?2__i) ( — ах2 — Ъх — с — 2а)=
чтх) получается таким же образом, как и в предыдущем примере (г).
Пример (е)
Преобразуем операторную дробь следующим образом:
D (/)+!) ==jD+1 IT'
Поэтому
= 2 B*+3—2) — (л2+3о;) = 2+л—а;2.
603

III. Применение операторной рациональной дроби к функциям sincoa?
и cos сох. Имеются формулы:
F (D2) sin (ox = F(—со2) sin юх, )
F (D2)cos(x>x = F (—<xJ)cos ax. J ^ '
В этих формулах F(D2) есть рациональная функция относительно D2,
то есть рациональная функция, содержащая лишь четные степени
оператора D. Если нечетная степень оператора появляется в числителе
рациональной дроби F(D), то она применяется к sin сох или cos сох
непосредственно. Если же нечетная степень оператора имеется в знаменателе, она
переводится в числитель приемом, примененным ниже в примеped (и)»
Пример (ж)
(D2 + 1) cos (дх = A — о2) cos ш\
Проверка:
(D2 + 1)cosco# = _y cos ax -|- cos (ax = —(o2cos(Da:-[-coscoa; = (l—со2) cos war.
Пример (a)
1 . sin соя
ncox-^-—-.
Это равенство эквивалентно следующему:
в справедливости которого нетрудно убедиться.
Пример (и)
2D + 1
cos co*
f 1 , 1 Л
1+co
со sin (ax cos cox
COS COX \ 1 .
)sin
\ 1
J со
Следовательно,
2D4-1 Tsin сож , cos core 4- со sin (ox
___C0S(Ba;=___+—__—
Это может быть проверено непосредственно, если показать, что BD-\-l)cos(dx равно
D (D + 1), примененному к полученному решению.
4. ИНТЕГРИРОВАНИЕ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим линейное дифференциальное уравнение с постоянными
коэффициентами п-то порядка:
dny , dn~xy , , dy . , t ч
tx
Это уравнение можно записать в операторной форме:
Здесь
где pv p2, ..., рп — вещественные или комплексные корни
Соответствующее однородное уравнение имеет вид:
Будем искать решение этого уравнения в виде y = evx. В силу равенства
F(D)y=zF (D) ev* = F (p) e*>x
604

{см. формулу A)],выбудет решением, если F(p) — 0. Предполагая
отсутствие кратных корней, получаем п линейно-независимых частных решений
6pfc*(/c=l, 2, ...,п). Следовательно, общее решение однородного
уравнения есть
21
где Аг, А%, ..., ^ — произвольные постоянные.
Найдем теперь какое-либо частное решение исходного неоднородного
уравнения F(D)y = f(x). Напишем формальное решение:
Найдем теперь какоелибо частное решение исход
уравнения F(D)y = f(x). Напишем формальное решение
где для получения частного решения правую часть следует вычислять по
изложенным выше правилам (I), (II), (III) предыдущего раздела, если f(x)
фсть показательная функция, многочлен, синус или косинус, а также
произведение этих функций. Приведем два примера.
Пример (а)
(d2y/dx2) — г/= sin сод:,
или, в операторной форме,
(D2 — 1) t/ = sin ых.
Так как
то общее решение однородного уравнения есть
где Ах и А2 — произвольные постоянные.
Ищем теперь частное решение неоднородного уравнения; используя формулу C)
получаем:
— 1 . sin coa;
Общее решение неоднородного уравнения имеет вид:
_„ sin а>х
Пример (б)
Рассмотрим дифференциальное уравнение, определяющее изменение переменной
Y, запаздывающей по отношению к переменной Z, причем запаздывание непрерывно
распределено по показательной функции со скоростью реакции X, а изменение Z
задается синусоидальной функцией (см. 4.8)
где, как указано выше,
Z=eat cos (at.
Общее решение однородного уравнения есть Y = Ae~^\ где А — произвольная
постоянная. Ищем частное решение неоднородного уравнения.
Применяя B), получаем:
Применяя C), получаем:
[(Qsin^ + (^ + ^)cosco^] = A eat cos (of-s),
где
Y и tge
605

Итак, общее решение имеет вид:
Y = Ae~xt + A ea'cos(©*—е).
Если при ? = 0 У = 0, то постоянная А= cose, и решение примет вид:
У = А е* (ы-е) -A Cos ze-%t .
5. ОПЕРАТОРЫ Е И Е~К
Рассмотрим функцию ух, заданную для дискретных значений ж = 0,.
1, 2, .... Тогда функция при этих значениях аргумента будет обозначена
таким образом:
2/о» У\-> Уы • • • > Ух1 «...
Введем оператор правого сдвига Е. Он обозначает процесс продвижения,
от ух к ух+1 и выражается равенством:
и оператор левого сдвига Е'1, обозначающий противоположный процесс
равенством:
Ух-г^Е^Ух-
Оператор Е'1 является обратным к оператору Е:
то есть
Введем целые степени этих операторов:
Е*уя = Е(Еух) = ЕухЛ = ух.„
Е-*ух = Е-1 (E-iyx) = Е-*ум = у,.,.
Вообще,
Епух = ух+п,
где п — любое целое, положительное или отрицательное число.
Введем многочлены от операторов Е и Е'1. Легко проверить, что
правила алгебраических действий над этими многочленами такие же, как,
и над многочленами от оператора D. Например:
= Е\ так как
и
, так как
Рассмотрим выражение F(E)yx, где F (Е) есть рациональная функция
от оператора Е. Нетрудно установить следующие формулы, выражающие-
правила применения оператора F (Е) к показательной функции <хж и к
произведению произвольной функции на показательную:
F{E)yxa = aF{aE)yx. } l p
Пример (а)
(Я2— 1)а*=(а2—1)а*.
Проверка:
(?2—\)ах=Е2ах—<zx=ax+z—^^(a2
606

Пример (б)
Это означает:
в чем нетрудно убедиться непосредственно.
Пример (в)
(?2 _ 1) ухах=а
Проверка:
(?¦-1) уха*=Е^^-уха!*=ух+&**
Заметим, что если г/Л есть многочлен относительно х, целесообразно
разложить его по факторнальным многочленам вида:
Имеет место простая формула:
Действительно,
*»> = Ея(*--1)(ж-2) ... (х-п
или
Оператор сдвига тесно связан простым соотношением с разностным
оператором А и может быть им замещен в операциях с конечными разностями.
К рассмотрению разностного оператора мы и переходим.
6. РАЗНОСТНЫЙ ОПЕРАТОР А.
Рассмотрим снова функцию ух, заданную дискретным рядом значений
х— 0, 1, 2, ... . Введем разностный оператор Д равенством:
Целые положительные степени этого оператора определим, как
последовательные применения этого оператора:
Д21Ь = А (АУх) = А (Vx+i - Ух) = Ух** — 2Ухч + Ух*
А3ух = к(А2ух) = Ухя-Зу^ + Зу^-ух и т. д.
Вообще, для всякого целого положительного п: Апух = А(Ап~1ух) и таким
образом:
&ПУх = Ух+п-СпУх+п-1 + С1ух+п_*-С1Ух+п_г+ ... +(-1)П»яэ
где
суть коэффициенты бинома.
Правила алгебраических действий над оператором А совпадают с
правилами действий над операторами D и Е. Например, А(А + 1) = А2 + А,
что нетрудно проверить, применяя правую и левую часть к произвольной
функции:
(А2 + А) ух = А2^ + Аух = (ух+2 - 2г/х+1 + ух) + (ух+1 - ух) = ух+2- Vx*
Операторы Е и А связаны простым соотношением:
607

В самом деле,
АУх = Ух+1 - Ух = Еу* -Ух = (Е.-1) ух
и также: Eyx = yxtl —Аух + ух = (А + 1) ух. В операторных выражениях
нетрудно переходить от оператора Е к оператору Д и наоборот.
Вот несколько примеров:
= (А +1)^ Ух = А*Ух + 2Аух + ух = yXi2;
-1)*ух = Е*ух - 2ЕУх + ух = z/x+2 - 2г/ж+1 + уя;
i? (Е +1) уя = (Д +1) (Д + 2) г/х = А2^ + ЗАух + 2ух = ух^ + ухЛ.
Вообще,
Иногда применяют вычисление разностей «назад». Введем соответствующий
оператор V равенством:
Также:
V2?/x = V(Vi/J = V (Уя-1 -ух) = ух_2-2ух_1 + ух и т. д.
Операторы V л Е'1 связаны соотношением:
V=?1-l и JB-1
Соотношение, связывающее А и V, получим из равенства ЕЕ~г = 1, заменив
Е через А + 1 и Е~г через V + 1:
Таким образом, операторы А+1 и V + 1 являются взаимно-обратными.
Кроме того,
Таким образом,
V=-i?"xA и A--EV.
7. РЕШЕНИЕ ЛИНЕЙНЫХ РАЗНОСТНЫХ УРАВНЕНИЙ
Рассмотрим линейное разностное уравнение с постоянными
коэффициентами:
<Wx*n + а1Ух+п-1 + • • • + «n-lPx+l + ап^Я = ф («),
где г/х и ф (ж) — неизвестная и заданная функции, определенные при
равноотстоящих значениях ж = 0,1,2, ... .Если ввести операторный многочлен:
F {Е) = а0Еп + а^-1 + ... + ап^Е + ап9
то уравнение запишется в виде:
Пусть pv p2, ..., рп — вещественные или комплексные корни уравнения
F(p) = 6 (предполагается, что кратных корней это уравнение не имеет).
Тогда:
= ao(E-Pl)(E-p2) ... (Е-рп).
Рассматриваемое разностное уравнение можем записать также с помощью
разностного оператора А, воспользовавшись соотношением ? = Д + 1:
608

Ищем решение соответствующего однородного уравнения:
F(E)yx = 0
в виде показательной функции: ух = рх. По формуле D) имеем:
Поэтому рх будет решением однородного уравнения, если F (р) = 0. Таким
образом, мы получаем п линейно-независимых частных решений рх
(к =*1,2, . ..,гс). Общее решение однородного уравнения получает вид:
у-
fc=l
где Аг, А2, ... , Ап произвольные постоянные.
Частное решение неоднородного уравнения
получим, применяя к обеим частям уравнения оператор l/F(E):
; А
Заметим, что исходное разностное уравнение может быть записано
в эквивалентной форме, если произвести замену аргумента х-{-п = х'.
Опуская штрих, запишем уравнение в виде:
ЧУх + ахУх-1 + • • • + апУх-п = Ф (х - Л) •
Обозначим ф (х — n) = f(x) =?~п<р(ж). Разностное уравнение принимает вид:
(а0 + axE-i + ... + апЕ'п) yx=f (z),
то есть
E-nF{E)yx = f(x).
Его частное решение есть:
/(г) F)
Решения E) и F), конечно, совпадают в силу соотношения f(x) = E~n(f(x).
Если / (х) есть показательная функция или произведение показательной
на некоторую другую, правые части E) и F) вычисляются сразу с помощью
формул D).
Если f(x) есть многочлен относительно ж, можно рекомендовать перейти
от оператора Е к оператору А:
1 _ 1
F(E) "~ F(b+i) '
Затем полученная операторная дробь разлагается на элементарные, каждая
из которых разлагается в ряд по возрастающим степеням А. Таким образом,
задача сводится к вычислению последовательных разностей целых степеней
аргумента х, х2, ж3, .... Например:
Нетрудно заметить, что все разности функции хп порядка выше п равны
нулю. Поэтому результат применения бесконечного операторного ряда
к многочлену содержит лишь конечное число членов. Два примера,
иллюстрирующие описанный метод, рассмотрены в разделе 5.5.
39 р, А л лен

Алъб. Л. Вайнштейн
ПРИЛОЖЕНИЕ В
НЕОБХОДИМЫЕ СВЕДЕНИЯ О КОМПЛЕКСНЫХ ЧИСЛАХ
1. ОСНОВНЫЕ ПОНЯТИЯ
Комплексное число z есть число вида z = х + iy, где i определяют
формально, как число, дающее в квадрате «—1», то есть i — ]/" — 1 и i2=— 1,
а х и у любые вещественные числа. Число х называется вещественной частью
комплексного числа z, &iy — его мнимой частью. Иногда применяют
обозначения: х = R(z), у = I(zI. Если в комплексном числе величина у = О, то z = x,t
то есть получаем вещественное
*число, если х = О, то z = iy или
«чисто мнимое» число.
Комплексное число может
быть изображено точкой на
плоскости: число х + iy изображается
точкой с абсциссой х и с ордина-
. той у. Вещественные числа
изображаются точками на оси абсцисс,
чисто мнимые — точками на оси
ординат (которая называется
поэтому мнимой осью).
Модулем комплексного числа
z = х + iy называется
расстояние точки плоскости, соответствую-
рис. 71. Щей комплексному числу, от
начала координат. Он обозначается
\\ \ y\yf
Аргументом комплексного числа z называется угол Э между
соответствующим этому числу вектором и положительным направлением оси Ох,
отсчитываемый от положительного направления оси Ох против направления
движения стрелки часов и выражаемый в радианах. Он обозначается
символом arg z (см. рис. 71), т. е. 9 = arg (ж + ^г/). Два комплексных числа
z\— #i+ Щ\ и z<*r^ #2+ гУг считаются, по определению, равными, если равны
порознь их вещественные части и коэффициенты при мнимых частях:
2! = 22, если хг = х2 и Ух — Уг*
Два комплексных числа назьшаются взаимно сопряженными, еслг их
вещественные части равны, а мнимые отличаются только знаком: zx = х + iy
и z2-=x—iy.
2. АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ
Сложение и вычитание комплексных чисел zl=x1
производится по следующей формуле:
iyx и z2= x^-\- iy2
Это правило можно распространить на любое число комплексных чисел.
1 R — начальная буква французского слова «Reel» (действительный,
вещественный), / — начальная буква французского слова «Imaginaire» (мнимый). Соответственно
английские слова «Real» и «Imaginary».
610

Умножение двух комплексных чисел zx и z2 производится по правилу
перемножения двучленов. Их произведение z определяется формулой:
z = zxz2 = (хх + iyx) (х2 + iy2) = (ххх2 - уху2) + i (хху2 + ухх2).
Деление двух комплексных чисел определяется как действие, обратное
умножению. Таким образом, частным комплексных чисел zx и z2 мы назовем
такое комплексное число z, что zz2 = zx. Если z1= хх+ iyx и z2= х2+ iy2,
то частное
Сумма и произведение сопряженных комплексных чисел — вещественны:
z+~z=(x + iy) + (x— iy) = 2х\ z-~z = {x + iy) (x - iy) = ж2 + у2.
Если комплексным числам 2]= хг-\- iy\ и z2 = x2-\- iy2 сопоставить
векторы, то сумма или разность комплексных чисел в геометрической
интерпретации представится как сумма или разность этих векторов, полученная по
правилу параллелограмма, построенного на слагаемых векторах или на
уменьшаемом и вычитаемом векторе. В геометрической интерпретации
вектор, изображающий произведение zxz2, получается поворотом вектора zx
против часовой стрелки на угол, равный argz2 и растяжением его в \z2\ раз.
Вектор, изображающий частное zx/z2, в геометрической интерпретации
получается поворотом вектора, изображающего число zx, по часовой стрелке
на угол argz2 и сжатием его в \z2\ раз.
3. ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Вещественная часть и коэффициент при мнимой части произвольного
комплексного числа могут быть выражены через его модуль и аргумент (см. рис.
71):
х = г соа0г у = г sin 0.
Поэтому всякое комплексное число х + iy можно записать в
тригонометрической форме в следующем виде:
z = r (cos Q + i sin 6).
При перемножении двух комплексных чисел в тригонометрической форме
их модули перемножаются, а аргументы складываются; при делении
комплексных чисел в такой форме их модули делятся, а аргументы вычитаются:
z=z1z2 = r1 (cos Qx+i sin81)-r2(cos02+isin02)=r1r2r[cos@1+02)+i'sin@1+82)],
Сумма и произведение сопряженных комплексных чисел, как было
указано, вещественны. В тригонометрической форме это дает:
z -f z = г (cos 0 + i sin 0) + г (cos 0 — i sin 0) = 2r cos 0,
2-z = r (cos0 + i sin0)«r(cos0 — ?sin0) = r2.
Степень п комплексного числа z в тригонометрической форме может
быть представлена в виде:
zn = rn (cos 0 + i sin 0)n = rn (cos Q+i sin 0)(cos Q+i sin 6) (cos0-Msin0) =
n
= rn (cos nQ+i sin w0).
Эта формула справедлива при любом значении п: целом, дробном,
положительном, отрицательном. При дробном п необходимо учитывать
многозначность результата. При г=1 предыдущее равенство превращается ъ
формулу Муавра:
(cos Q+i sin 0)n = cos nQ + i sin n0.
611 39*

4. ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Из анализа известны формулы Эйлера, связывающие
тригонометрические и показательные функции:
eixj^e-ix # eix__e-ix
cosz = —=? ; sinz = - .
Умножая обе части второго равенства на i и складывая, получаем
фундаментальную формулу Эйлера:
С помощью формулы Эйлера любое комплексное число с модулем г
и аргументом 0 может быть записано в показательной форме:
z — r (cos в + i sin 0) = reiB.
При 0=±я/2 получаем: & = eijt/2 и — i = e-i
Правила умножения и деления комплексных чисел можно записать
теперь следующим образом. Если 21 = r1ei0i и z2 = r2eie2, то
Умножение комплексного числа на i эквивалентно прибавлению я/2
к аргументу этого числа:
zi =
5. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И СВОЙСТВА ИХ КОРНЕЙ
Алгебраическим уравнением га-й степени называется уравнение вида:
где в левой части Рп (х) — многочлен п-й степени относительно #,
коэффициенты которого вещественны и а0 Ф 0.
Корнем алгебраического уравнения называется всякое комплексное
число (в частном случае вещественное), обращающее левую часть
уравнения в нуль при подстановке его вместо аргумента. Корни уравнения
Рп(х) = 0 называют также корнями многочлена Рп(х).
Квадратное уравнение с вещественными коэффициентами в общем виде:
- ах2 + Ъх + с = 0,
где старший коэффициент а > 0. Решение
~1'2~ 2а
Корни уравнения, в зависимости от дискриминанта трехчлена Ъ2 — 4ас
могут быть следующие:
Дискриминант
Ь2 > 4 ас
Ь2=4 ас
Ь* < 4 ас
Корни
вещественные и различные
вещественные совпадающие
комплексные сопряженные
Графическое изображение
трехчлена
парабола с осью, параллельной осп у
пересекает ось х в двух точках
парабола касается оси х
вся парабола находится над осью х
В любом случае имеют место формулы Виета:
Ъ с
612

Кубическое уравнение с вещественными коэффициентами имеет вид:
где старший коэффициент а —положителен.
По теореме Безу можно разложить левую часть кубического
уравнения следующим образом:
ах3 -4-bx2 + cx + d = a(x — хг) (х — х2) (х — х3), где xv x2 и х3
суть корни кубического уравнения.
Могут быть следующие комбинации корней при решении кубического
уравнения:
три различных вещественных корня
один вещественный корень и два сопряженных комплексных
два или три совпадающих вещественных корня.
Формулы Виета для кубического уравнения:
Х1 ~Ь Х2 ~\~ Х3 = — ~? » ^1^2 + Ж А ~Ь ХъХ3 == "J" » Х1Ж2^3 = ~ •
Каждое алгебраическое уравнение /г-й степени можно представить
в виде произведения линейных множителей:
Рп (х) = аохп + а1хп-1+...+ап_1х + ап = ао (х-хг) (х-х2) ... (;г-яп) = 0,
где числа х±, х2, ...,хп суть корни многочлена Р(х).
Таким образом, всякий многочлен п-я степени или алгебраическое
уравнение п-й степени имеет ровно п корней. Если среди корней
уравнения (х19 х2, ...,жп) окажутся q равных чисел, то это число называется
Q-кратным корнем уравнения Рп(х) — 0. Корень кратности единица
называется простым корнем.
Если уравнение Рп (х) = 0 с вещественными коэффициентами имеет
комплексный корень a+ij} кратности q, to он имеет и сопряженный
корень а —ф той же кратности. Произведение двух линейных множителей,
соответствующих двум сопряженным корням, можно преобразовать
следующим образом:
[х-(а+ г"Р)] [*На-*Р)] = [(я-аЖР] [(*-<*) - *Р1 = (»- aJ+$2 = x*+px+q,
где х2 + рх + q — вещественный квадратный трехчлен. Поэтому каждый
многочлен с вещественными коэффициентами может быть разложен на
вещественные множители первой и второй степени:
Рп(х) = а0(х — хг)(х — х2) ... (x — xh)(x2 + px + q) ... (x2 + rx + s),
где х1У х2, ..., xh — вещественные простые корни, а каждый квадратный
трехчлен в правой части имеет пару сопряженных комплексных корней.
Отсюда следует, что всякий вещественный многочлен нечетной степени
имеет, по крайней мере, один вещественный корень.
Для алгебраического уравнения четной степени количество
[положительных и отрицательных корней определяется знаком ап
Знак ап
«»>о
ап<0
Количество
положительных корней
четное
нечетное
отрицательных
корней;
четное
нечетное
613

6. КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ
Если переменная у меняется по закону у = sin t или у = cos t, где t
обозначает время, то мы говорим, что переменная у совершает
гармонические колебания. Период колебаний этой функции равен 2л, так как
( 2) ( 2)
) ( )
Гармонические колебания в общем случае описываются функцией:
). . A)
Эта функция называется гармоникой. В ней величина А > 0 называется
амплитудой колебаний, со обозначает число колебаний в единицу времени
или частоту колебаний, а е — фазой. Чтобы задать гармонику, нужно
задать три параметра —ее амплитуду, частоту и фазу. Период колебания Т
гармоники связан с ее частотой соотношением:
При Л = 1, 8 = 0 и Г==2я, функция A) превращается в
вышеприведенную у = cost.
Гармоника имеет максимумы в те моменты, когда со? + 8 = 2шг, где
/г —любое целое число, то есть при тг = — 1, 0, 1, ... .
2я+е # е 2л—е
йГ~; "~^Г; со ; '••
Любая гармоника A) может быть представлена в виде суммы
(наложения) двух колебаний — синусоидального и косинусоидального г — с одной
и той же частотой, равной частоте исходной гармоники, но с различными
амплитудами:
A cos (cot + e) = A (cos cat • cos 8 — sin art- sin г) = A cos e cos oat —A sin e sin <ot ==
= a cos at + b sin oo?,
где
a = A cos 8, b = — A sin 8.
Обратно, сумму синусоидального и косинусоидального колебания одной
и той же частоты можно записать в виде одной гармоники:
a cos (ot + b sin at = A cos (<ot + e),
где
A~Ya2 + b2; a = .4 cos e; —6 = A sins.
Гармонические колебания описанного типа имеют постоянную амплитуду
(А = const). Но А может также изменяться во времени, то есть само быть
функцией t. Наиболее интересными для описания экономических процессов
являются колебательные движения с устойчивым нарастанием или
затуханием колебаний. Для их описания берут произведение гармоники на
положительный множитель eat, и тогда колебания будут описываться косинусоидой
B)
1 Синусоидальное и косинусоидальное колебания различаются между собой
только фазой, ибо cos ? = sin (t-\-n/2), то есть косинусоидальное колебание всегда
может быть представлено в виде синусоидального. Поэтому Аллен в тексте книги
всегда говорит только о синусоидальных колебаниях.
614

Отсюда получаются следующие виды колебательных (осцилляторных)
процессов при t—> оо (рис. 2):
а
а<0
а>0
а=0
У
стремится к нулю
неограниченно
возрастает
периодически
колеблется около оси t
Характер колебательного
(осцилляторного) процесса
затухающий
взрывной
регулярный (гармоника)
а)а<0
Вышеприведенная функция характеризуется четырьмя параметрами:
А— начальная амплитуда,
Т — 2я/со — период (условный)г затухающих или нарастающих колебаний,
со — частота колебаний
(в радианах),
а — коэффициент
затухания,
е —фаза колебаний,
которая задается
моментом t максимума
функции: t = — е/(о.
Гармоника A) представляет
простейший колебательный
процесс, обладающий
определенной симметрией:
продолжительность размаха в одну сто- .
рону равна продолжительности
размаха в другую сторону;
скорость процесса при
возрастании и убывании независимой
переменной меняется по
одинаковому закону.
Описание экономических
явлений требует более сложных
периодических функций из
достаточно широкого класса.
Если F(t) есть
непрерывная периодическая функция с
неизменным периодом r = 2jt/co,
имеющая конечное число
максимумов и минимумов на
каждом конечном отрезке, то она рис 72.
может быть представлена, по
теореме Фурье, в виде тригонометрической суммы или так называемого
ряда Фурье функции F (t): \
F(t) ^ -тг
cos n
sin n(dt
n=l
1 Мы говорим «условный» период, так как функция B) не является, строго говоря,
периодической, ибо нет числа Т, обладающего свойством: у@ = 2/(*+?1)> где t—любое
значение аргумента.
615

где
т
an*=-jr \ F(t)cosn(otdt (гс = О, 1,2, ...),
о
т
bn = -^r\ F(t)sinnatdt (ra = O, 1, 2, ...).
о
Стоящий в правой части функции F(t) ряд Фурье можно написать
в виде бесконечной суммы гармоник A), объединив два слагаемых,
описывающих гармонические колебания одной частоты (см. стр. 614):
ап cos n (ot + bn sin (nat) = An cos (ncot -f- en)
где
Тогда
= -у" + 2 Лп COS (/UD* + 8Л),
п=1
то есть всякую периодическую функцию, удовлетворяющую условиям теоремы
Фурье, можно представить как сумму, постоянного слагаемого и
бесконечного числа гармоник A), в которой частота первого слагаемого равна
той же основной частоте (ш) периодической функции, а остальные частоты
кратны ей.
7. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ КОЛЕБАТЕЛЬНОГО ПРОЦЕССА
Если взять комплексную показательную функцию (вектор)
вещественного аргумента t такого вида:
то гармоника A) У = A cos(co?+?) представит собой вещественную часть
этой функции. Это следует из формулы Эйлера (см. стр. 612):
W (t) = Ле*<®'+е> = A cos ((ot + e) + A i sin (go* + e).
Если W(t) записать в виде произведения:
то Aeie есть начальный вектор И^@), а множитель ei@* можно истолковать
как поворот начального вектора на угол cat к моменту t, то есть, другими
словами, как равномерное вращение начального вектора с угловой
скоростью со в направлении, противоположном направлению вращения часовой
стрелки. Гармоника A cos (at + e) в каждый момент t есть проекция
равномерно вращающегося вектора на вещественную ось.
На рис. 73 вещественная ось —линия АА'\ начальный [вектор W@)
изображается отрезком ОР, составляющим угол е с вещественной осью ОА.
Гармоника Acos((dt + e) есть проекция равномерно вращающегося
вектора ОР на вещественную ось ОА. Ее график приведен в правой части
рис. 73.
Затухающий или взрывной колебательный процесс, описываемый
функцией
616

можно рассматривать как вещественную часть функции:
W (t) = Лва'е^Н-8) = 4е*ве<а+*®>« = Aeieept 4
где р = <х+ш (так называемый характеристический показатель колебаний).
Здесь AeiB — W @) есть начальный вектор. Умножение этого вектора
на зависящий от времени множитель e<a+iG))' = ешеш можно истолковать
как равномерное вращение начального вектора в положительном
направлении с угловой скоростью о и его одновременное удлинение
(укорочение), пропорциональное eat. Конец вектора Y описывает на комплексной
плоскости спираль, скручивающуюся или раскручивающуюся в зависимости
от знака коэффициента затухания а.
я/
А
^<
0
м
\
)
г
У1
/X Г\
\ /Л /л
Рис. 73.
Таким образом, значение функции Aeat cos (tot + &) в момент t можно
истолковать как вещественную часть произведения векторов Ае1ее(а+1®I =
= Aeieept, где два параметра .А и е (вектор Аегг) характеризуют начальное
положение, а два других (а и со), входящие в вектор ер*, описывают
последующее движение вектора во времени: eat служит для характеристики
растяжения или сжатия вектора (иУ), а еш — для опережения вектора (и У)
с угловой скоростью со. В частном случае, когда о) = е = 0, мы получаем:
то есть неколебательное монотонное изменение (затухающее или взрывное)
в форме показательной функции.
8. ДИФФЕРЕНЦИРОВАНИЕ, ИНТЕГРИРОВАНИЕ И КОМБИНИРОВАНИЕ
КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
Рассмотрим гармонику:
у = Л cos (<ut + г).
Скорость колебательного процесса определяется производной, то есть
Таким образом, скорость колебательного процесса изменяется также
по гармоническому закону, но фаза скорости на четверть периода обгоняет
фазу исходной гармоники, а амплитуда скорости = соЛ.
Рассмотрим теперь затухающий или взрывной колебательный процесс:
у = Aeat cos (tot + е),
(JLZ
= Aeat l/a2 + со2
= QAeat [cos г) cos
cos Ш + e)
sin((o* + eI =
e) — sin r\ sin (tot + e)] = qAeat cos (tot + e + Л)»
617

где
g = |/a2 + oJ и r] =
Вторая производная имеет вид
-^f- = QMe«< cos (ю* + е + 2г)).
Производная /г-го порядка выразится аналогичной формулой:
где D —оператор дифференцирования, a DnY представляет собой
вещественную часть производной DnAeieept.
Применение оператора дифференцирования D к выражению W (t) = Ае1ее&
эквивалентно умножению этого выражения на характеристический
показатель p = a+i(o: (dW/dt) = рАе{ее& = pW и в общем виде DnW = pnW. Эта
формула имеет смысл и в случае целого отрицательного п.
Колебательный процесс, запаздывающий на неизменный промежуток
времени 0 единиц относительно процесса Y (t) = Aeat cos(co? + e), будет:
Y (t — Э) = 4еа«-8> cos [со (t — 0) + е] = e-*>*Aeat cos (cot + & — а>0).
Если взять вектор W (t) = Ае1ее&, то запаздывающий вектор будет:
W (t — 0)=4eie^f-0> = Aeie. е^г • е-?9 = e-^W @,
то есть запаздывание процесса на 0 эквивалентно умножению вектора W(t)
на е~р0, a Y(t — 0) будет вещественной частью запаздывающего вектора
или Уу-в) = е-«Ые^ cos (co* + e —co0). Итак:
Затухающий (или взрывной) колебательный процесс г/ (t) = Леаг cos (со? + б)
можно рассматривать как вещественную часть комплексной функции:
где р(р = а-\-ш) есть характеристический показатель колебательного
процесса.
Последовательное дифференцирование функции W(t) сводится к
умножению ее на соответствующую степень характеристического показателя р:
DnW = pnW, а запаздывание процесса на 0 эквивалентно умножению этой
функции на e~Qp.
Комплексное представление колебательных процессов полезно при
исследовании наложения двух процессов с одинаковыми частотами и
коэффициентами затухания. Пусть имеется любое число колебательных
процессов:
yn = Aneat cos (at+ en) (n= 1,2,3, ...),
которые могут иметь различные начальные амплитуды и фазы. Их суммак
то есть результат наложения колебаний, описываемых г/п, выразится так:
У = S Уп = 2 К&1 cos (at + en).
j n n
Эта сумма является вещественной частью функции W(t), а последняя равна:'
W (t) = S wn (*)
где ^lei8 = 2 Aneien.
n
Следовательно, начальный вектор Aeie суммарного колебательного
процесса является суммой начальных векторов слагаемых процессов.
Суммарный комплексный колебательный процесс получается умножением этого
начального вектора на е!>1 = еаеш, то есть имеет ту же частоту и тот же
618

коэффициент затухания, что и слагаемые процессы. В случае двух
колебательных процессов Y = Y1 + Y2 = {A1eiei + A2i^)e^.
На рис. 74 изображен простейший случай — сложение двух гармоник.
Соответствующие комплексные гармоники изображены в виде их начальных
векторов] ОРХ и ОР2. Начальный вектор суммарного процесса есть
векторная сумма ОР = ОРг + ОР2, то есть направленная диагональ параллелограмма,
построенного на слагаемых векторах.
Рис. 74.
На рис. 74 слагаемые гармоники представлены пунктирной и
штриховой линиями, а их сумма—сплошной кривой.
Если у = Aeat cos (<nt + е) есть колебательный процесс с
характеристическим показателем р = а+ш, то запаздывающий процесс y(t — Э),
производные любого порядка, а также сумма процессов этого вида будут также
колебательными процессами с тем же характеристическим показателем,
то есть с той же частотой (ю) и коэффициентом затухания (а).

ПРИЛОЖЕНИЕ В
РЕШЕНИЯ И УКАЗАНИЯ К ЗАДАЧАМ И УПРАЖНЕНИЯМ
1.2 1. Получить из A): а=Х—аР, Р=-Х"—ЬР, и подставить в B). X и Р
* должны быть положительны; отсюда — ^Р^а- 2. Решение: />*=/?ос'»
где с= j~ ' >0. Необходимо различать два случая: (-&)>(-«) и (—&)<
<»(—а). 3. Модель получится такая же, как в тексте но в ней а и b
взаимно переставлены; решение Pt = Po ( — J имеет затухающее
колебание, если S круче D. 4. Подставить Pt = Xo+kit в E) и найти Яо и Ai
приравниванием нулю отдельно коэффициента при t и постоянного члена.
1.3 1. Написать с= /—Ц—- и определить знак с. Если —&>—а,
(стр. 26) ъ_а (-fli)
то 6<я и с= будет положительно; если —6<—а, то с будет отри-
цательно. 2. Дифференциальное уравнение: —j^—yp, где у=^-г—. При
истолковании этого случая рассмотреть непрерывное запаздывание (типа
показательной функции) на стороне спроса, как в 1.9, упражн. 2. 3.
Дифференциальное уравнение: -~-=у/>, где у=^—т~- Коэффициенты аг и Ьг
Cut Ci-y — Oi
характеризуют скорость реакции спроса и предложения.
3 15 117
1.6 1. Pt—O; 1; —-5-; —57 > ЕТо » ••• Здесь D круче, чем S; отклонения
(ctd 32)
v F' ; цены имеют затухающие колебания, медленно сходящиеся к нулю. 2. pt =
9 105 1161
=0; 1; —5- ; -777 ; ^тт;; •••» т. е. отклонения знакочередующиеся, взрыв-
о Ь4 51Z
ного характера.
1.7 1. Когда (—&)<(—я), как в тексте, то (&—л)>0. Когда (—&)>—я,
(стр. 36) тогда (Ь — а)<0, и с>1 при всех положительных X, т. е. имеет место
взрывной (случай. 3. При 1 = 0 />f = постоянной, независимо от запасов.
I есть pt=ipt_1; II есть pt — 2pt-i—Pt-2- Каждая из моделей дает pt = Po,
если начальная цена po=Pi- При X -> оо, Pt-i = cpt_2 в обоих случаях
(полагая коэффициент при -г- равным нулю ), т. е. простая паутино-
образная модель. 4. Почти то же, что в модели I, см. выше, упражн. 1.
Если _(— Ь) < (— а), то (Ь — я) >0 и — А, F—я)< 0, следовательно,
(Ро — Р)е""^ь~а^ стремится к нулю. Если (—&)>(—а), то —Х(Ь—я)>0
и е-ЯХЬ-а)* ^ ^ 6> При я==0 /,(^)== const. Модель III есть -^ = 0;
IV есть -г-^-=0 при начальном условии --^-=0. При X -> оо [получается
дифференциальное уравнение, как ранее в модели 1.3. Ср. с дискретным
. случаем в вышеприведенных упражнениях 2 и 3.
6Y 1
1.9 1. Положить У=0 в -т— =—^- (У—Zo) и показать, что касательная
(стр. 45) л Т
есть ОЛ. 2. Здесь а+аР = ^ц-^(р + &Р), т. е. D (а + аР) + Х (а+аР) —
)=О и т. д. Уравнение A.3) получается при а = а0 и Х = — .
4. У дано уравнением ^- + ^-^-+4Я2У=4Х% с У = -^=0 при ^=0.
' 620

Решение (см. далее 4.8): У = {1 — (l-\-2kt) e~2%t} Zo, кривая подобна ///
на рис. 3, но касательна к Ot в точке О. 5. Обратить внимание на то, что
интеграл (8) есть сумма двух частей: в одной Z(t—t)=Z0(t<;*); в
другой Z(*—т) = 0 (x>t).
2.2 1. Подставить линейные функции С, I и L в уравнения У—С=1
(стр. 52) и L = M, определяющие условия равновесия, и решить их относительно Y
и i. Смысл постоянных: Ъ—изменение инвестиций при повышении нормы
процента, с—возрастание потребления на рубль прироста дохода, Хг и Я2—
увеличение сбережений соответственно на рубль увеличения дохода и на
единицу снижения нормы процента. 2. Продифференцировать У и i из
предыдущего упражнения по Р и взять отношение производных. Классический
случай: Яг=О; особый случай Кейнса: A,i = 0.
2.4 1. Ожидаемые сбережения = Yt^ — С (У^-i) Ф Yt—C (y*-i) = / ft),
(стр. 56) 2. Равны ожидаемые сбережения и капиталовложения, а не фактические.
4. Условие устойчивости: SI круче, чем LM, или
(_6) " (к2)
2.6 1. Разложение в ряд Тейлора функции С (У) для малых (Y—Yo)
(стр. 60) дает
Подставить выражение С (У) в равенство У—С(У) = А и принять во
внимание, что У0—С (Y0) = A0. Тогда получим требуемую формулу
Преобразуем это равенство следующим образом:
или
Отсюда при малом (У—Уо) получаем требуемую формулу. 2. Средняя
Q
склонность к потреблению (сбережению) =^г • Если C=y-\-cY, то
среден V
няя склонность к потреблению будет =-^- —с-\—~г.
2.7 2. (Yt—Yt-i) есть запаздывание дохода: доход заработанный минус
(стр. 64) доход расходуемый У^_х—С{У^г) составляет планируемые сбережения.
3. Наклон OS есть ^j =— . Он уменьшается по мере возрастания s.
dY — A
4. Линейный случай: —т—\-A — c)Y=A с частным решением Y = -z .
Отсюда для у=Y—Y: ~~--\-(\ — с)у=0, что после интегрирования при-
^4
водит к y=const'e~A-c)'. 5. В доказываемое неравенство Fo<^—^— под-
А А
ставить выражение у0 из G). Получаем — < -.—— . Преобразовав это
1 ?_ 1~~с
1 + г
неравенство, имеем —сг<0, что справедливо при с>0 и г>0.
3.3 1. В (II) написать Z=Y—7^- и скорректировать в соответствии
<СТР- 78> a dZ dY
с (I). 3. Написать Z=Y—-——; —-=——. Следовательно, A) равно-
J. •"" С dt CLl
сильно D): -—= of Z епЛ . 5. Тенденция роста: Y = Yoert. При
y=Y—У уравнение D) дает y=yoeQt, как в тексте. Пропорциональные
отклонения будут: т)= "Z , и D) дает -q = r]o*(Q~~r)'- Первые можно
показать графически на натуральной шкале в виде отклонений от тенден-
621

ции роста; вторые — на полулогарифмической шкале, как отклонения
от прямой линии тенденции.
/TV
3.4 3. Непрерывная показательная форма запаздывания —г—=—x(Y—Z),
(стр. 81) . dt
где k = Xs и Z =— . Обратить внимание, что прямая О А является
касательной к кривой /// в точке О на рис. 3; см. 1.9, упражн. 1.
3.5 2. В момент *=0, Y0 = 0 и -=-- = Ы. Тогда D) дает -—. (хо—•*) AM,
(сто 82)
что обычно >0. Следовательно, У есть касательная к Ot, но выпукла
книзу в точке О. 3; Выражение I, данное в задаче, есть операторная запись
уравнения A). Операторная запись уравнения C) есть DY=—А, (Y—Z),
откуда получаем выражение Y через операторы Y= Z.
U-\- Л
где
Это уравнение превращается в D), когда y -* оо (т. е. когда нет
запаздывания потребления).
3.6 1. Условие для реализации плана капиталовложений: (а) Дискрет-
(стр. 87) ная модель без запаздываний (рассматриваемое упражнение) sY{ =
= y(Yf—Yt-i)- (б) Дискретная модель с запаздываниями (см. выше, 3.6):
sYt-x=v(Yt~Yj-i). (в) Непрерывная модель без запаздываний (см. выше 3.3):
sY = v —r—. В каждом из этих случаев существует гарантированный теми
dt
роста, q/ > q при условии 5>0 и г>>5. 2. Если #<5, то гарантирован-
1 s
ный темп роста в (а) упражн. 1 есть q' = <0, ср. q=—> 1 в (б)
s
и (в).
3.7 2. В D) подставить с2=0, 5 = 1—с=0 или с = 1. Zi~vZt_Y-\-A имеет
решение Zt — -z {-const v* -> ^ (о<1). Это есть рост дохода при
равновесии, а не уровень дохода. Обратить внимание, что уровень стати-
(А \
— J бесконечно велик при s=0. 3. Тот же
результат, но v уменьшается до (v—са), пока о>с2. Если и<с2, тогда Zt
попеременно меняет знак.
3.8 1. Из неравенства v > с2+A + V^sJ следует, что чем ниже s, тем мень-
(стр. 92) ше может быть v. Если подставить в указанное неравенство с2=0>
5 = 0,04 и s = 0,25, то должно быть соответственно v > 1,44 и v > 2,25.
Положительная величина с2 просто увеличивает критическое значение v
на такую же величину. 2. Если 5 = 0, то один корень R есть нуль, а
другой будет положительным в том случае, если v—с2>1. Кривая на рис. 8
пройдет через точку О. 3. Подставить в уравнение C) из 3.7 частное
решение yt при г/0=— ?? » -*4f = А> (!+**)* и выражение i? из 3.8.
Тогда получится тождество. 4. На рис. 8 видно, что для кривой R3
ординаты точек ее между qx и q2—отрицательны (Д<0).
3.9 2. Л = 5>0 при г=0; Я—^^оо, когда г—^±оо. Следовательно,
(стр. 95) кривая пересекает Or один раз слева от О. Если она пересекает Or снова,
то могут быть две дальнейшие точки пересечения, либо обе слева, либо
обе справа от точки О. Отсюда вытекают три варианта.
4.1 1. Если -т—= const, то это значит, что Y=Y0-j-a#, т. е. объект дви-
(стр. 98) гается с постоянной скоростью а. Если Y есть народный доход или
продукция за сс-й год, то ~т—=const означает, что годовое, приращение
постоянно, a Y есть объем народного дохода или продукции в последнем
d2Y
я-ом году. Если = const, то это означает, что ежегодный прирост уве-
CLX
личивается пропорционально количеству лет, нрошедших от начала от-

счета. 2. Здесь х кратно — и Yx устанавливается по индукции: если Ух~
—V' —><?, т. е. A+— J —> ег. Следовательно, Узс = УоеГ:х:.
Отсюда ^=
4.2 3. Частное решение данного неоднородного уравнения будет У =
(стр. 102) *+*
4.3 1. — С y— J=«x ПРИ аф^\ отсюда получается решение У —
ах
(стр/106) =-5 \-А. Если а = 1, то дифференциальное уравнение превращается
в -— = 1, так что Y—x-\-A. 2. Проверить решение путем
дифференцирования. 3. Воспользоваться соотношением sin (ах+&) = cos ( ах-\-Ъ—^ ) ''>
х-\-Ь—?j- ) . 4. У= \ f (x) dx4-А. 5. Продиффереи-
2 У J ,
cos
цировать уравнение у=Ае~х и подставить у и -~- в заданное уравнение;
получится тождество. 6. Дополнительную функцию взять из упражн. 5.
Проверить частные решения: (I) Y = x и (II) У = sin x. Решения монотонно
приближаются: (I) — к постоянно возрастающей тенденции, (II)—к
колебательной тенденции. 7. Тенденция будет У= \ f (x) dx как частная линия
движения У. Изменение по сравнению с тенденцией постоянно.
4.4 1. Характеристическое уравнение дает рг—а2=0 или j3=ia. Неза-
(стр. 112) висимо от знака а один член всегда будет взрывной. 2. Дополнительную
функцию взять из упражн. 1. Проверить частные решения: Y = x и У = е"х.
3. у = (А1-\-А2х) е~х с А1 = А2~1, что получается из начальных условий.
4. Дополнительная функция из задачи 3. Проверить в качестве частного
решения Y = x(l — е~х); найти постоянные (Л1 = Л2=У0) из начальных
условий. 5. -^ = ±у-тЛе±хsin (z-e); -0-=F2 ^ + 2У=0' 6- Л==1'
8 = 0; то же самое для обоих начальных условий, так к"ак из (I) следует,
что У = — при а:=—. 7. Подставить у — ие 2 в F); тогда —-^-=0,
что дает и-=Ах-\-А2х. 8. Если (—а) < (—6), то характеристическое
уравнение будет я2=я (а—Ь)>0, т. е. имеет место взрывной случай, как в уп-
d2p
ражн. 1. Если (—а) = (—6), —^|-==0 и р = Л1+^2*« 9- Колебания будут
^|-
4
только тогда, когда Х<—^(б—а). Правая часть здесь положительна
(а < 0, Ь>0), но может быть совсем мала, например, если численная велм-
лл d*D , dY , v dD d2/) dD л ^
чина a велика. 10. =A:-^-= лрУ=д-^-, т. е. —-т- q—=0.
Характеристическое уравнение: X2—qX=O; отсюда ^=0 и Л2=5 и решение
J9 = Ах-\~A2eQt. Постоянные Аг и Л2 определяются по начальным уело-
it к
виям: Л! = 2>0 Уо и А2= — Уо. Подставляя выражения Аг и А2 в D,
получаем требуемое решение для D.
4.5 1. Однородное уравнение второго порядка без члена, содержащего у,
(стр.117) имеет решение у=А1-\-А2еах. Из начальных условий получаем А1 = у0^-~
и А2=— . Цодставляя Ах и А2 в г/, получаем частное решение, ука-
dy
занное в задаче. 2. Подставив -г— =z(a:) в левую часть (I), получим левую
часть (II) уравнения. 3. Подстановка решения Y = (ax-\-b) ex в (8) дает
линейное уравнение относительно всех х: хBа — 1)+26-|-а=^0. Приравняй
нулю коэффициент при х и свободный член, находим] а, Ь и частное
решение У =— Bя— 1) е*. 4. Характеристическое уравнение будет куби-
623

ческое, распадающееся на два множителя: {р—1) (р2—2/?+2) = 0. Корни:
Pi = i; Р2,з= 1± i = a±l'P- Общее решение: Аеах cos (ш:—8)+ Bepix=
= ex{Acos(x — е)+?}. Доминирующей частью будет в*, т. е. у имеет
монотонный и колебательный взрывной элемент. 5. Доминирующим
членом будет член с вещественным корнем характеристического уравнения.
4.6. 1. Изображение у' (t) получается по правилу (II) при л = 1. 2. «Ин-
(стр. 122) тегрировать по частям» формулу упражн. 1, заменяя у через у' и у".
3. Второй интеграл вычисляется по частям, третий—по формуле
f xneaxdx = — xneax—— ? хп~Чах dx\ четвертый [ e~(p+G>)* dt вычисляется,
как первый. 4. Формулы в упражнении суть формулы «интегрирования
по частям». Из первой формулы исключить \ e-Pf cos Ш dt и получить
значение \ е~Р' sin cat dt, а из второй таким же образом получить
оо
\ е-?* cos at dt. 5. Дифференцирование дает \ е~РЧ cos (dt dt = ^ 2.2 -.
оо
Отсюда \ e-P'(sino)^—сог cos cof) ^ =-—-^—г—-со
И J32+C02
1 ^
И
О
7. В определенном интеграле может появиться любая переменная, так что
оо оо р
у (р)= \ e~vxy (т) dr, и, следовательно, ^ ( — J = \ е ® у (т) dr. 8. Ори-
о о
гинал е~®г должен иметь изображение по правилу (IV): у{р — (—Ъ)} =
= у{р-\-(д) или —т:—• Функция г/(f) = —— имеет изображение у(р) =
= п+1 . Если функцию 2/@ умножить на еа*, то по предыдущему она
будет иметь изображение у(р—а), т. е. ее изображение имеет вид:
(p—a)n+i •
4.7 2: Из уравнений у = 0 и —~=0 при ? = 0 получаем Ах~—^ , Л2 =
1 11
<стр. 127) =— и частное решение 2/ = ^—ггв'+ire"*. ^' Вспомогательные уравне-
ния: (I) <р+1)«»(р) = -??{± ; (Ц) {Р+1J?(Р)=*?±± {р + 2). Раз-
ложим (I) на элементарные рациональные дроби: у (р)=—g- , 2 .
Отсюда по стандартным формулам получается решение (I): y=t(l — е~г).
Из (II) имеем (р+ 1)«у(р) = - />8+2^-2/'-1 ^^^
и по стандартным формулам B), Bа) и D) предыдущего
раздела получаем искомый оригинал-решение. 4. Вспомогательное уравнение:
2
Отсюда по стандартным формулам получается решение y-=.i-\-e 2 cos ^.
4,8 1. (ZK+9^ZJ+27^2JD-{-27X3)y = 27^Z. Характеристическое уравнение
(стр.131) имеет трехкратный корень p1 = p2=zp3=z —ЗА,. Испытать решение
Y=(A-\-Bt-\-Ct2)e~sxt, частное решение Y=ZQ. А, В к С определяются из
начальных условий. 2. Характеристическое уравнение имеет два корня
624

(—^i) и ( — Яо). Воспользоваться начальными условиями для решения
ЛLW П'z- 4< Для Решения Дифференциального урав-
{
нения (8) ——\-XY = Xeat cos со* можно взять общее решение
соответствующего однородного уравнения в виде y=Be~~*tt. Частное решение
уравнения (8) можно получить операторным методом (см. приложение А) в виде
Y = Qeat cos (со* — ф),
где о = # — < 1. Общее решение будет
cos (at — ф).
Постоянная /? находится из начальных условий: У = 0 при ? = 0, отсюда
В =—осовф; Итак, решение уравнения (8) будет: Y = Qeat cos (a>*—ф) —
— q cos фе""^', т. е. такое же, как полученное ранее в тексте, см. A0).
4.9 2. Заменить два члена в D): у (р) = \--, —г^+..., что дает
(стр.135) P—Pi (P-Pir
y(t) = (Ax-\-Ait)e x +••• Аналогично получаем для двух одинаковых пар
сопряженных комплексных корней. Когда внутренние и вынужденные
колебания совпадают, то получается резонанс со взрывным элементом,
подобным (Лх+Лг*). 3. Решение: у = ^^2 +Acos(t — е), т. е. вынуж^
денные + внутренние колебания. Резонанс возникает, когда со —> 1 и у —> со.
5.1 1. я г/х A2/x А2^ А3ух А42/х А62/х 3. а: уж А^ А2г/Х...
(стр.139) 0 0 1 14 36 24 0 0 1 ~2 4
1 1 15 50 60 24 0 я —1 2 —4
2 16 65 110 84 2я 1 —2
3 81 175 194 Зя —1
4 256 369
5 625
1 /1 Л2 Z' 1 \3
5.2 2. Частное решение: г/х =~-ух_х = Г — ) t/x_2 = ( -у ) 2/х-з= ••• =
(стр.143) , 2 ^2У V2A\-
= ( — \ ; при а:=0, 1/^ = 1. Общее решение: yx=yJ ~J . 3. у2=
= 2/i—Уо'» 2/з= —2/о; 2/4= —«fi; г/б= —(г/i — 2/o)i 2/e = 2/o- Каждое решение?/
повторяется через 6 интервалов.
5-3 1. A
(стр. 47) +2
. 2. Д1пж = 1п(ж + 1) —lnar==ln-^i^ = ln^l + -i-) . 3.
= 2cos a Г а;+-^-J -sin-^-. 5.
= sina
X X
=2 (ж-flJ-- ^х2 = (х-\-\J. Из предыдущей задачи следует, что если
о о
AY^^-flJ, то Yx = ^rx(x+l)Bx+l) + A, ГдеЛ=У0=0.
Воспользоваться результатом предыдущей задачи 4. 7. Для нахождения частного
ния п
ax+i
решения подставить Ух = [хазс. Тогда \iax— я^ха:)С~1 = ах или fi= и
Ух \-Аах. Случай а —а есть пример резонанса. 8. Принять Yx =
= Н'1Ж+И'2 за частное решение и подставить в данное уравнение, из
которого определить цг и jx2: ц1 = —^—и \i2= aa~rPJ ~"^ . Отсюда У (х) —
= С??_2" —м^. \2 • Общее решение Уд.=У (ajj+^a^, что и требовалось
доказать. 9. Уравнение этого упражнения получается, если в предыдущем
принять а=1, р=0, а=:2. Частное решение получается У (#) = —(х-\-2).
40 р. Аллеи 625

Y
10. Решение уравнения будет: Yx=: ——-—A — ax+1). Заменяя 1 — а =
имеем: Ух = ~^ [1— A —r)^+i].
5.4 1
(стр.* 152) *• Характеристическое уравнение дает X2—-т- = 0и
/ 1 Лх /* 1 "\ж
общее решение однородного уравнения ух=А1( — ) -\-А2(—1)х ( — ) . Изна-
чальных условий получаем А1—-^- и Аг-=Ту Следовательно, yx=f--O x
х{1 + ( — 1)ЖЬ 2. Характеристическое уравнение: X2—а2 = 0; Я,!=+ат
Х2=(— 1) я. Отсюда получаем искомое общее решение. Решение —
затухающее, если я<1. 3. Корни характеристических уравнений: A)-^-и 2, моно-
11 11
тонное, взрывное; (II) -уи -г-,монотонное, затухающее; (III) — и --г
монотонное, затухающее. 4. Характеристическое уравнение имеет корни Хи 2 =
= —_J-i--j-. Решение: 2/=^lr:x:cos(9a? — е), где r= , tg 0 = 1 и 9 = — .
Период =-7г~=8. Корни второго характеристического уравнения: Яь 2 =
= —— _f- i— . Решение аналогично, г равно по-прежнему , а 9 = -^-
и период =-5-. 5. Характеристическое уравнение дает Xlj2=-.-r-±~— у
откуда г = 1, т. е. регулярное колебательное решение, и 9 = -~-, следовательно,
период равен 6. 6. Характеристическое уравнение дает Яь 2 = II______L__L____' .
1) При я = _Ь 2, Я,!, 2=—-тг 5 ^!= — 1, Я2=+ 1. Одно решение 2/х = Я^,
второе решение ух = хХх = х. Общее решение ух = ( — l)x At-\-Ax, т. е.
изменяется линейно. 2) Если а2 < 4, получаются два комплексных сопряженных
а У А —а2
решения: Alt 2= —^i*-1—о ' ГДе Г= Т" е* УДУТ имсть место
колебания постоянной амплитуды. 3) Если а2 > 4, то Я1? 2 = — ( —а _|- }/~а2 —4),
т. е. получаются два^вещественных и отрицательных корня X. 7. Подста-
- вить частные решения: (I) Y = u.ax и (II) Y = \ix-\-v. В первом случае
yx_i = (iax~1; Ух_2 = [гах~2. Подставить в неоднородное уравнение, найти ц.,
и тогда придем к искомому решению (I). То же проделать и с частным
решением (II). 8. Если Я = 0, то fe = 0, и уравнение C) в тексте
превращается в уравнение первого порядка. Если ^ = 1, один член в решении E)
будет аддитивной постоянной. 9. Характеристическое уравнение Л2 — аХ— '
— р=-0. Колебательный характер щ будет при комплексных корнях,
т. е. при а2-|-4р<0. 10. Характеристическое уравнение будет первого
порядка X—а=0, а решение будет Uf = uoa*. 11. Характеристическое
уравнение: X2 — (a-\-b)X-{-b=O. Колебательный характер будет при а2+4х
х ( -|—1 J 6-)-62<0. В случае, указанном Оркуттом, а = 1.
5.5 1. Характеристическое уравнение имеет корень Я, = 1. Разница с реше-
(стр. 156) нием примера (б) в тексте в знаке постоянного члена. Здесь он знако-
устойчив, а в примере текста он—знакочередующийся. Так как >^2>1T
то, при А ф 0,(]/2)" безгранично увеличивается и решение будет коле-
бательным, взрывным. Период колебания = —— = 8. 3. Подставить в
заданное уравнение Y — \ix и найти \i. Получаем [х=-=
или У = ——-г-7>—| -т- х. Если этот знаменатель равен 0, то поло-
жить У —\хх2 и подставить опять в заданное уравнение. Тогда, приняв во вин-
мание 81+2-,+За,+ ...+»ап = 0 °
626

и отсюда решение У = гт^ п^ ; i—т— х%- &. Характеристическое
1 + 2 + 3++
уравнение имеет трехкратный корень Я = а. Отсюда частные решения будут
ах, хах и х<2)ах (а не ж2ах, см. 5.3), где х{2) — х (х—1). Общее решение имеет
вид (Ах-\~А2х-\~ Azx (х—\)) ах. Распространить этот способ на разностные
уравнения любого порядка, применяя #C\ #D), .... 5. Поступить, как
в случае кратного корня, ибо при 9 —> О, sin 9 —> 0; при 9 -> я, cos 9 —¦> — 1
Так как Хх = г cos 9 и X2 = ffrcos9, то решение будет (А1-\-А2х) (— /¦)*"
6. Поступить, как в 6.4 (второй случай)*
5.6 1. Характеристическое уравнение: Я2 — с A — q) X—cq = O. Отсюда
-|-4cq>0, а потому оба корня вещественны. Так как первый член
отрицателен, то отрицательный корень будет большим по абсолютной
величине и он будет определять знакопеременный характер решения, как
в простой паутинообразной модели. 2. Характеристическое уравнение то же,
что и в предыдущей задаче; 0<с = — < 1. При q>0 оба корня
вещественны, наибольшим будет положительный корень. При q = 0, 2ц = 0
и А,2=с, т. е. рх =РоС*, как в простой паутинообразной модели. При q= 1
L
^i, 2 = i Yc и Pt = c2 {^i+^2 (— 1)'}. Решение будет затухающим и зна-
4
копеременным. 3. ПриЯ>т ,с<—1 и доминирующим членом будет
О — CL
Щ=с—У^с2 —1<—1. Отсюда pt будет знакочередующимся и взрывным.
(Ь—а)<0, если (— Ь) >( — а), т. е ^ понижается и круче, чем Z>, что
нереалистично. 4. Модель II из 1.7, упражн. 2, имеет характеристическое
уравнение \i2 — B-\-Ха) |х-]~A-|-ХЬ)=0, колебательный характер будет при
4^
5.7 1. Отставание на два промежутка времени, равносильно единому
(стр. 164) запаздыванию. 2. Характеристическое уравнение: X2—A—с2) X — с2 = 0.
Отсюда Xx = l; Я2= — с2, т. е. доминирующий член есть yt -> постоянной,
определяемой начальными условиями. Проверить: любая постоянная Yt
удовлетворяет уравнению, и сбережения равны нулю. 3. Решение yt =
= A1X[-\-A2Xl дает Аг-{-А2 = у0 и AtX1~\-A2X2=y1, откуда получаем
требуемые значения для Ах и А2. Хг есть положительная дробь, и"первый член
АгХ^ является доминирующим, т. е. знак Ах определяет, стремится ли
yt -> 0 через положительные или отрицательные значения, (— Х2) является
положительной и вообще малой величиной, а потому знак ух более важен,
нежели знак t/0.
6.1 1. Л>0 при всех г, когда уравнение R~0 имеет комплексные
(стр. 169) корни; R >0 для всех положительных г, когда уравнение R — 0 имеет два
вещественных отрицательных корня. Трудности представляет случай
Л=0 с двумя положительными корнями; здесь г меньше, чем меньший
из корней, при котором еще Я>0. 2. Колебательное движение будет,
когда w—v— с2 заключено в пределах (l — Y^J<w < (l+|/7J. Отсюда
пределы: (I) 0,5 О < 2,5; (II) 0,7<i><1,5. 3, Да, входит в группу (I)
При у=с2, w=0, и уравнение B) в тексте превращается в конечно-
разностное _уравиение_ первого порядка. 4. Колебания будут, если
1 — Vs<Y®< 1 + YS> т. _е. если Ys> 1 — V'w или если Y~s > Yw — 1.
Следовательно, s>(l— ]/шJ для колебаний, например, для о>=0,75
5>0,018. 5. Когда 5 = 0, то w=l и колебаний нет. Если5^1 — с=0,
то с = 1 и конечно-разностное уравнение B) в тексте превращается в
требуемое данной задачей.
6.2 1. Решая характеристическое уравнение B) при данных иъ s и с2,
(стр.173) получаем, что Л^О^б |и А2= — 0,01. Отсюда решение уравнения C)
будет yt = A1@,96)t-\-A2 (-~0,01)t -> 0, движение затухающее, yt медленно
стремится к нулю (ш<0). 2. Решая первую часть неравенства, имеем
*—Y$<0. как и должно быть, если s правильная положительная дробь.
1 — *<1 всегда при s>О.»[3начение w при наименьшем периоде равно
1 — s, которое находится в области (II). Самый короткий период =-т^~ ,
где cos дт = 1^ 1^=1^6775 = 0,51/3. Отсюда Qm =-|-, и самый короткий
период равен 12. 3. Характеристическое уравнение имеет'веществениые корни
627 40*

1 и до. Возможны только решения I Ь и IV (см. текст). 4. Характеристическое
уравнение имеет два равных вещественных корня. Если a/ = (l-|-yrsJ, то
X=l-\-}f-s; если w — (\ — У^J, то Я=1—Ys- Отсюда и искомое
решение, даваемое в тексте задачи. 5. Из предыдущего упражнения следует,
что при w = (l±:yrsJ множителем в формуле для yt явится (l ± YsYi
т. е. в одном случае (при знаке минус в двучлене) положительная дробь,
меньшая 1, и в другом (при знаке плюс)—большая 1. 6. В уравнение A)
текста подставляем yt=Yt—У* = 11*У*> a вместо У*, Yt-\ и Yf_2 их
выражения через Уо и q по формуле Yt=YQ A + q)'. Регулярные
колебания в yi*. отклонения от тенденции постоянной амплитуды; в r\t:
отклонения в % от тенденции постоянной амплитуды (т. е. фактические
отклонения возрастают по амплитуде вместе с тенденцией).
6.5 1. При 5 = 0,25, условие E) для возникновения колебаний дает
* —<1+^<3, откуда А<2. Условие F) для затухания колебаний:
1 к
к < -^-. 2. s> (из неравенства F)). 3. Производство для запасов,
замещения ранее уничтоженных запасов. Характеристическое уравнение
B) из 6.2 будет X2 — 2сХ-{-с=з0, его корни: c±i j/~c(l — с); г==|^с<1.
Следовательно, колебания yt будут затухающие. 4. Положить Yt = Cf-\-
+ Л, У*-1 = С*-1 + ^-1 и таким образом У<—У*_! выразить через У и Д.
Затем исключить (Rf — Rt-i)> подставив его значение, равное и (Yt i—
У) + ЛУA)У+А
6.6 1. Характеристическое уравнение B) из 6.2 при ад=1 будет:
(стр.182) Я2—B—s)X+l = O1 откуда а = 2—s и 6 = 1. Из (8) в 6.2 следует, что
при w=lf г = 1 и cos 6 = 1 k-s.
6.8 л гж л Jt 2л . _/-
(стр. 186) * При ~2~ пеР1ЮД=="~0~==4' затухание при г = у — а/,
являющемся обычно малой дробью, если только г; совсем невелико, а
запаздывание потребления значительно. 2. Кривая / (X) будет иметь максимум
ниже 0А,. 3. Приравниваем нулю производную от /(Я), т. е. решаем
уравнение /' (Х) = ЗА,2—2А,—иу = О. Получаем Х=—(l^ }^l-f Зад). При
А,=-^-A-)-уЛ1+Зш), вторая производная положительна, т. е. это реше-
о
ние соответствует минимуму. Подставляем величину А,=— (l-f-l/4 + to)
в функцию /(Я)==А,3 — X2—wk-^w и получаем ее минимальное выражение,
указанное в задаче. При ш==~27~> минимум будет равен = .
6.9 1. Первая производная g (К) дает Я2=1 и h=jz !• Вторая производ-
(стр. 189) пая равна (—2до2Ат3). Если ш2> 0, то максимум будет при Л= 1, он равен 0.
Минимум будет при А,= —1. При w2<0 максимум будет при Я=—1,
минимум—при %= +1» т. е. максимум и минимум поменяются
местами. 3. Подставить Х=—1 в характеристическое уравнение B) и решить
его относительно до2. Левая часть должна делиться на А.+1, а в частном
должно появиться искомое выражение. 4. При s=0 уравнение B)
удовлетворяется значением Х=1 и, наоборот, при Х = 1, 5 = 0. При Х—1 в yt
появляется аддитивная постоянная. Так как левая часть B) должна
делиться на (X — 1), то получаем (учитывая, что при Я=1 5=0): к2—wxX—
— w2=0 (ибо. w = w1+w2). Его корни: к = —- (wx ± 1/гш|+4ш2). 5.
Характеристическое уравнение для zt будет, как в упражн. 4: X2—wxX—ш2=0.
Аддитивная постоянная исчезает, когда берется разность zt. 6.
Подставить в уравнение D) текста w = wx-\-w2- 7. В уравнение D) подставить
w = Wi-\~w2- При s = 0 получается упражн. 4. Для wt>0 и ш2>0
кривая / (X) подобна уравнению C) в 5.7 (см. рис. 10); кривая g (X) есть
гипербола, подобная той, которая на рис. 15. 8. Подставьте w = w1Jrw2
в уравнепие A) и получится уравнение, требуемое в задаче. 9. Первая
производная от F (X) (см. предыдущее упражнение) равна ЗА,2—2Хх
X (-k-w-\- с J=0, откуда А,х = 0 и Л2=—^ —ш+с J . Так как вторая произ-
2/1 *\
водная от F (X) при Х = -^ f—до + с ) = ш, т. е. равна положительной
величине, следовательно, X соответствует минимуму.
628

7.2 2. Если К<К, то начальная точка лежит между А и В (умерен-
(стр. 196) ный дефицит) или слева А (более значительный дефицит). Первый шаг
к точке В, тогда цикл BCDA ... 3. Независимые затраты (потребление,
капиталовложения) могут войти в член, выражающий технический
прогресс.
7.5 1. Если а и к малы, то Ь = а-{-к будет также мало, a In b отрицатель^
(стр.205) но и велико по абсолютной величине. Следовательно, А —а— In b > 1,
и будут существовать два вещественных корня q (рис. 21). 2. Рис. 22
(для ^4>1) показывает, что самое меньшее значение со>2я. 3. А = 0,405
(In 1,1 = 0,0953). Из рис. 32 видно, что, при со = —, / (©) я- A. a=ln b-\-
-^- 3sm -~-
=-0,0946-и
"
^—0,1. 4. 6=0,7 (In0,7 =—0,357), А = 0,857. со здесь меньше, чем
в упражн. 3, следовательно, период будет больше, а а ближе к нулю.
7.6 1. После подстановки в уравнение E) текста / = /ое°' получается
(стр. 207) о о о Q+P лг
х г ' условие q = ae4—р или ew= у ' г . Условие касания прямой и кривой
— равенство наклонов прямой и касательной к кривой: е°=— или q = —In a.
Подставляя в первое уравнение, имеем Л = р—1па=1 в качестве условия
касания. При А < 1 или Р < In а вещественных корней нет, а будут только
комплексно-сопряженные. 2. P = XY-^-\i для постоянного X и \i.
Уравнение A) будет Xy+jLi = ^i^; D) будет В = аA — с) (ХУ+ц)+...; E) не
изменится, кроме постоянных. 3. Если ср есть среднее запаздывание,
взвешенное по с, т. е. Y (t — ф)=—' ^~~с— ЗУ . В таком случае A)
превращается в Y (t) = ' ~г~У'*~— . Отсюда уравнение, непосредственно
предшествующее E), становится /(?-(-9)=... выражению в 7(^ + ф), т. е.
/ (* + & — ф)=... выражению в I (t). Запаздывание в E) уменьшилось от 0
до 6—ф.
7.7 1. Уравнение C) для этого случая может быть записано так:
(стр. 213) 1 f х \
-T-D2Y-\-( s-\--z—xi> ) DY-\-k$Y = (D-\-%) А. При А,—>оои Л-постоянной,
К \^ К у
DA = 0, и это уравнение превратится в DY—qY = —q — . Интегрирующий
s
множитель для этого уравнения будет |и = е^ = е~0/. Тогда общий
- t
интеграл находится по формуле У = е ^ \ Q\idt, где Р=—q и Q =
О
А
= — о — . Подставляя эти выражения из дифференциального уравнения
s
в формулу, получаем: У=eQt д ( —q— j e~Qi dt=—q — eQt
b
A A yds s
= —eQ (e~Q—1)=—A — eQ ), где o= . Если к—>оо, то o = —.
s v ' s v ^ y.v — s v v
Уравнение Харрода — Дома pa при q=— и постоянном А будет DY — @У=0
[см. B) в 3.3]. 2. Подставить в решение примера (б) в тексте Л=—1
и заменить радианы градусным измерением, а затем применить формулу
приведения sin (х—90°) = —cos х. 3. В D) положить PiP2 = 0,2± iO,98. \
7.9 5. Уравнение предыдущего упражнения при заданных параметрах
(стр. 223) будет ?зу_1_18?2У+48/)У+288У = 64(/)+2)Л с устойчивым уровнем^ ,
как в примере (а). Корни уравнения />3+18/?2+48у?+288 = 0,
определенные графически: jt>= 16,13; —0,935 ± i4,12. У (t) имеет сильно затухающий
монотонный член и умеренно затухающее колебание (а= —0,935) с периодом
629

¦т-ттг ^1,5. Колебание слабее затухает по сравнению с примером (а) в тексте.
6.' D*Y + i8D*Y+A8D2Y-\-288DY+25SY = №D(D+2)A с устойчивым
уровнем У = 0, как в примере (б) текста. Корни будут: р=—1; —16,06;
—0,47 ii' 3,96. Y (t) имеетдва монотонно затухающих члена и умеренно
затухающее колебание (а =—0,47) с периодом =1,6, т. е. колебание
о, У о
затухает слабее, чем в примере (б).
(стр. 234)
t
¦j
Aeat cos (Ш -f-е) dt = вещественной части Qe"l^Z=—Z.
Р
Интегрирование производится по частям. 2. / (t)=Yf (t) = (ePl'+eP2').
Pi—Ръ
Преобразование Лапласа дает (см. изображения элементарных функций):
F{P)=
так как из соотношения следует D=p. 3. Случай резонанса. 4. F(p)=z
= . 2 = .... .2 для p = io)(a=0). Отсюда получается геометрическое
1 —со2 2о) _
место точек с координатами . . 2 2 и —. . 2.2 . При изменении о
t
1 С
получается кривая III на рис. 29. 6. Y = ^- \ Zdt. Подставить
t-2x
Z—A cos (Ш -\- г) и проинтегрировать.
8.4 1. Цепь с мультипликатором без запаздывания имеет передаточную функ-
(стр. 237) цию Ръ(р) = с. 3. В заданной точке F (р) различна в соответствии с целью,.
для которой она вычисляется. Но F(p)=!l дает то же самое уравнение;
здесь Fx (p)-\-F<2,{p) — \ получается и в тексте и в этом упражнении.
8.5 1. Кубическое уравнение относительно р не может иметь больше одной
(стр. 241) пары сопряженных комплексных корней, т. е. самое большее одно
колебательное решение. 2. Для двух колебательных решений необходимо, по
крайней мере, уравнение четвертой степени относительно р.
8.7 . F^ (p) F2 (p)
(стр. 245) *• 4 р / \ Ф л___р / \» но то же самое р полечится при подстановке
вместо той или другой единицы (см. 8.4, упражн. 3). 2. При мощности
акселератора (v — g) соотношение A) имеет коэффициент JL=k — k'
S S
вместо к. B) становится
а = 2(к—к' — 1), @=2 У (к—к') B —
а это эквивалентно D).
9.1 1. Для первого индивида уравнения будут:
(стр. 251)
а) ^[^Р~Ъ~ ИЛИ
б)
Решая эти два уравнения, получаем
Общее решение будет
где JDi = ai — 2hip-\-bip2 (i = l, 2, ...). 2. Первое уравнение из (II) сводится
к х1-\-х2 = х1-\-'х2» При подстановке результатов упражн. I получаем для
630

первого товара
9.2
(стр. 253)
9.3
{стр. 256)
(ЬгР-hj
Другое уравнение удовлетворяется автоматически. Так как Рх и Рг
являются квадратическими функциями, то уравнение относительно р должно
быть 4-го порядка. Но коэффициент при члене с /?4 равен нулю, а
коэффициент при р*7 вообще говоря, не нуль, т, е. уравнение будет кубическое.
Произведение его корней, как это известно из высшей алгебры, равно
Постоянный член _ а1а2(х1 -\-x2)-\-a2h1y1-\-a1h2y2
"Коэффициент при р* "~ к1Ъ2х1+кф~х2+Ъ1Ъ2(у1-\-'~у2)
если аи а2, Ьъ Ь2—отрицательны, hx и h2—малы. В таком случае по
крайней мере один корень >0
_ г г г г г г г
—xri) — 2 Ps^s — 2 Pt^t* Первое слагаемое равно 0 в силу A6), сумма второго
s t
и третьего равна нулю в силу (Па) и (Нб). Суммируя условия
сбалансирования бюджета A6), получаем
г г г г г
т. е. если соблюдается (III) для г = 1, 2, ...,(т—1), то оно будет также
справедливо и для г=т. 2. Одно F^=0, и одно из уравнений (III)
снимается; таким образом, одним уравнением и одной переменной будет меньше;
совместно с положением равновесия. 3. ри и Yu появляются только
в двух добавочных уравнениях, которые служат для установления этих
переменных при подстановке р и У" из других уравнений.
3. (Па) дает — хрх=—уру = архру; (Нб) дает xy—az. Отсюда г=архру.
4. Спрос первого индивида (u1^=a1x\-\-2h1x1zxJrb1z\):
-КРх)
; ух = 0; zx = (
где Р1 = а1 — 2h1px~\-b1px. Аналогично для второго индивида:
Рыночные условия (х^=хх—х, у—у2—у) суть два уравнения относительно
цен (р). 5. Уравнения (И): — = — =— 2az и xy = az2. Отсюда
Рх Ру
1
Таким образом, R=xpx~\-ypy~\-z—§.
9.5 1. Напишем условия устойчивости для трех товаров:
(СТР' 261) (D— (Г1-Х1) = «11 + «12 ^l+aJ-^
dpx dpi dpx
Найдем -^ и
арх
из уравнений B) и C) и подставляем в A):
а1г а12 а13
«21 а22 а23
«31 «32_«33
«22 «23
«32 «33
для совершенной устойчивости должно быть
> 0. Знаменатель здесь положителен. Значит,
«11 «12 «13
«21 «22 «23
«31 «32 «33
>0. 3. ОТНО-
631

шения детерминантов положительны, это требуется соотношением:
р
9.6 2. Проще всего воспользоваться определителями (см. далее, 11.9 и
(стр. 263) 13.2). Если A = \qrs\ и Ars суть алгебраические дополнения, та
1^ и т- д- При заданном
^ п>0, Л>0 (устойчивость по Хиксу), ^ < 0 и —^ имеет
знак ( —^i2)- 3. Пренебречь я23, «3i» принять «Зз>° (устойчивость); таким
образом, -р2 соответствует знаку а21. Но если а23 и а31 велики и имеют один
dp» ^
и тот же знак, тогда -—¦ может быть отрицательным, даже если а21
положительно. Аналогично будет, если а23 и а31— противоположного знакаг
и а21— отрицательно.
9.8 1. На единицу продукта затраты: первого фактора а17 второго а2.
(стр.271) Тогда имеем уг (единица продукта) = °^. При у = уг1 получаем, чта
» = У1*«. 2. Vl= /^ ; ^
х2 =
/ = Яг/!. 3. Если /—однородная функция степени г:
2, , w, Xy1? Я?/2, ..., Яг/п)=Хг/=О. Следовательно, одна из переменных
есть однородная линейная функция от других.
10.3 1. Задача сводится к нахождению минимума функции У=рлХ1-\-р2х2ч
(стр. 281) _/¦ у ,
если У x1x2=-j- (pi, p2, у и /:—заданные величины).
! i = j&r>Y=:Pi Щ + Р*хг- Дифференцируем по х2.
отсюда ^2=jPl jgj и 4=5^2 ^2==С22/' ГДе С2 = Т /й ; ^^Щ^
2. Для линейной однородной производственной функции все кривые
постоянной продукции подобно проведены относительно радиуса от
начала 0 (см. 9.7).
3. Условия (I) суть соотношения между выпуском и конечным
спросом; (II) подразумевает, что заданные цены и ставки заработной платы
должны быть совместны с техническими условиями производства.
10.5 1. Правая часть уравнения (Vr—vr) представляет собой часть продук-
(стр. 284) ции отрасли г, потребленную другими отраслями (см. итог выпуска,
распределенный по отраслям в табл. 1). 2. Воспользуйтесь итогами из
табл. 1. 3. Итоги суммирования по столбцам равны нулю.
10.6 1. Выпуск при равновесии определяется совокупностью следующих
(стр. 287) двух уравнений:
2=х2.
Решая эти уравнения, получаем решение (значения выпуска):
1
L — a12a2l * 2 1 — a12a21 '
аналогично находятся решения для рг и р2.
2. Л= 12 =1 — а12а21;
А11 = 11 А12=а21 и т. д. (см. упражн. 1). 3. Воспользуйтесь результатом
(см. 11.9 далее), умножая строки или столбцы детерминанта на
постоянные множители (здесь цены). 4. Цена товара, деленная на ставку
заработной платы, равна приросту занятости, деленному на прирост конечного
спроса.
632

10.7 1. Попробуйте решить пару уравнений для Хх и Х2 при произволь-
(стр. 290) ном Х3. Результаты будут несовместны, если только определитель третьего
порядка не будет равен нулю. Если определители второго порядка также-
нули, то Хх и Х2 неопределенны. 2. Суммирование матрицы по
горизонтали и по вертикали дает нуль. 3. Из (I) ^PlarsV8=0, т. е. суммирование
элементов матрицы по горизонтали дает нуль, когда элементы столбцов
умножены на Fx, F2, ...
10.9 1. Если раскрыть указанный в упражнении определитель, то придем
д. v V
(стр.297) к квадратному уравнению B) относительно X. 2. Ах= 2 10 —^,
к2—#!
д. % jf
, так как t = 0. Аналогично для G) при Л1 =
А2 =
кг—к2
3. 1 — а12а21=0 представляет условие однородной (замкнутой) * системы,
а не какой-либо иной. Примите 1 — а12а21=0, т. е. а12=1/а21, так что
В\ — а12В2 = с1яВ1—а12В2=—с2/а21. Следовательно, В1 : В2 дано только
при условии, что c1=z — c2/a21. 4. Испытайте решение Xi = Bl-{-B11t,
X2 = B2-\-B22t и найдите все В. 6. Испытайте решение Х1 = /?11еМ1' +
+В12е»2*, Х2=В21е^+В22еа2г и найдите все В. 8. а12=а21 = 0:
производство товаров без затрат; Ьп = Ь22—0: нет запасов товаров в производстве;
&12 Ф 0, Ь21 Ф 0: запасы одного товара необходимы для производства
другого.
11.4 1. Вектор B, 2, 2)>A, 1, 1). Остальные соотношения вида >
(стр. 307) 2. р>0; это характеризует случай, когда цены неотрицательны, но по
крайней мере одна положительна. Первый вектор р ^ не пригоден как
допускающий возможность исчезновения всех цен. 3. ОР и ОР' равны па
величине и противоположны по направлению, т. е. диагональ сжимается
в точку О (начало координат), которая представляет нулевой вектор.
Если ОР есть а, тогда ОР' есть (—а).
11.5 1. Из аналитической геометрии известно, что уравнение прямой АхАг
(стр. 312) x1-{-x2 = i. Точка (х±, х2) лежит на этой линии между Аг и А2, если
х2 = 1 — хъ где О^;?!^!. Требуемый результат получится, если положить
#1 = H(O<fA<l). 2. Р имеет координаты
Таким образом
т. е.
Р2Р:РРх = у,:A-\х)
11.6 1. Матрица (а)—диагональная и скалярная (см. упражн. 2); (б) — сим-
(стр. 316) метрическая, полученная из единичной перестановкой второй и третьей
строк (см. упражн. 3); (в) — кососимметрическая матрица; (г) —
ортогональная. Если в формулах, выражающих новые оси прямоугольных
координат через старые (r/1=x1co^6+a:2sin 6; у2 = хг sin 9-j-#2 cos 6), вместо 9
подставить угол 45°, то матрица коэффициентов в формулах перехода
к новой системе координат совпадает с матрицей (г) этой задачи. 2.
Общий вид скалярной матрицы будет Я1 = Л[6Г8], где I — единичная
матрица. Матрица (а) представляет скалярную матрицу. 3. Единичная
матриг 1 0 Оп
О 10.
L о о 1 J
, то получил
[10 0-] г 1 0 0 и Г <*! а2 Ьг b2 bs ~i
h 1 0 и К3= 0 105. 10000
ooiJ Loo*J LoioooJ
ца 3-го порядка 0 10. Если переставить в ней вторую и третью
L 0 0 1 J
строки (столбцы), то получим симметрическую матрицу (б) первого
упражнения
I — второго порядка, 0—размерности 2x3.
п п
11.8 5. Линейные формы будут иметь вид У! ars У! &S^=V V arsbstyt.
(стр. 320) ь~1 (=i s=i &
п
Коэффициенты при yt будут ^ arsbst=zCrb T- е- мы получим m линейных
s=i
форм с п переменными.
11.9 1. (а) 8; (б)-1; (в) 0; (г) I; 2. (J) =1.1.1... 1 = 1; | а \ = а1 \ an.i 1 =
(стр. 323) =а1а2\ ап_2| = а1а2 . . . ап. 3. Если прибавить к элементам первого столбца
633

12.1.
стр. 329)
12.2
(стр. 331)
12 3
(стр. 334)
12.4
1стр. 340)
(строки) элементы двух других столбцов (строк), то получится
определитель с первым столбцом (строкой) из нулей. Второй определитель равен
1 — 3a2-f-2a3 = (l-l-2a) A — аJ. Он обращается в нуль при а ——^ и а — \.
4. При а = Ь величина определителя =0, значит, (а — Ъ) является
множителем в выражении определителя. Аналогично и для других множителей-
двучленов. 5. По определению перекрестное произведение элементов
ортогональной матрицы равно 1, но этому же должен равняться и
определитель, построенный по ортогональной матрице. 6. Разлагаем определитель D,
заданный в упражнении, по элементам первого столбца. Получаем D =
Л =а1а2а3. Отсюда видно, что прочие элементы определителя не
U а3
оказывают влияния на его величину. 7. Если этот определитель разложить
по элементам первого столбца или первой строки, то результат равен 1.
8. | Ers | — определитель, образованный из единичной матрицы, в которой
взаимно переставлены r-я и s-я строки. На основании свойства IV, в
результате такой перестановки величина определителя меняет только знак. Для
|КГ| разложение будет давать везде 1, кроме элемента arr = &. Поэтому
и величина этого определителя будет равна к. 9. Разлагая определитель А
матрицы А, получаем 2х— 1. Определитель, составленный из
алгебраических дополнений всех девяти элементов первого определителя, будет
—х2 х — 1 х
х — 1 1 1 =4я2—4x + i = Bx — IJ, то есть | Ars |=42. Но это будет
х 1—1
иметь место только для определителя 3-го порядка. 10. Воспользуйтесь
сформулированными ранее свойствами (II) и (VI).
1.
Pi
| Р2 =
4%
есть рациональное число; аналогично для
других действий. 2. (а) Результат деления целых чисел выходит из области
целых чисел; (б) результат деления целых четных чисел не принадлежит к
области этих же чисел; кроме того, это множество не имеет единицы,
(в) Результат сложения, вычитания и деления не принадлежит к области
целых нечетных чисел. 3. При отсутствии закона коммутативности а F—j— с) =
= ab-\-ac и F + с) а~Ъа-\-са ф ab-\-ac. 4. Сумма и произведение таких
чисел суть числа той же формы; аналогично для вычитания и деления.
1. хА не определяется, нет скалярных произведений. 2. Матрица А
размерности 2x3, х—трехмерный вектор. 3. АВ не определяется. 4. ВА не
определяется.
Г1 0
Левая часть равна
Г2 01
U 2J
Г1 1 I"!
A+B = 10 1 1 1 и А — В = 2
0
0-1Г1 On
iJ Lo i.
__4 —3 -2
— 1 0 1
[23 4^
.Т. (р членов); при X=p/q, q(plq) А=рА и т. д.
, то есть правой части
. 5. При Х = р: рА =
2. ВА не определено, так как т ф п. 3. (В+С) А = ВА-|-СА, но
ВА Ф АВ, СА ф АС (за исключением особых случаев). 4. Можно
образовать следующие произведения: AC, AD, ВА, CD, BD, например, АС =
г_з _з -ят Г34 401 Г 458 5661
= I * ,l\\ DB= 71 86 . 5. CDB= 1055 1298 .
L 8 10 12J 1.94 118J L1652 2030 j
6. ACDB= получается либо умножением А на CDB из
упражнения 5, либо умножением АС на DB из упражнения 4. CDBA
и DBAC могут быть определены, но не CDAB
умножая снова на В, получим В3 = 0. 10. С = а2Ь
Сп=
1 ЛС"^"+УЛ. 11.
Затем,
+( + )==А2+АВ+ВА-}-В2 и т. д. 13. Применить обозначение для
блочных матриц из 11.6 (VIII); проверить, что произведения вида х'Р
634

12.5
(стр. 342)
12.6
(стр. 346)
12.7
(стр. 351)
12.8
(стр. 356)
12.9
(стр. 361)
умножить АВ на квадратную матрицу 3-го порядка в блочпой
согласованы
форме
1. Доказательство свойства (III): (АВ)' = В'А'
Элемент на месте (гр) в В' есть bpr.
Элемент » » (ps) » А' есть asp
Следовательно, (гз)-й элемент в В'А'== 2] &prasp = (Г5)-й элемент в (АВ)'.
1Г1 4 7] Г14 32 501
X 2 5 8 = 32 77 122
[3 6 9J |_50 122 194 J
3. АА'=|4 5 6 | х | 2 5 8 | = | 32 77 122 |= симметрической матрице.
194
1. ху' = [(xrys)] порядка п; ух' — транспонировано по отношению к ху\
На вторую часть задачи—ответ положительный: можно получить ху' и ух'
размерности пхт или тхп. 2. хх' ~[(xrxs)] есть симметрическая матрица
гс-го порядка. 3. Например, х'С = [14 16 18]; затем х'Су=28. 4. х'Ах=
=22
г s
{1} [1] =
[1 1 ... 1
1 1 ... 1
l" 1'..." 1.
; [1] {1}—п (скаляр).
[1] I {1}=[1] {1} = п, см. также x'lx из упражнения 4. 6.
= I (А,2#2)
х'к = [(к1х1) (к2х2) ...]; Vx=x'>,= 2 Xrxr, что является суммой элементов
вХхив х'Х. 7. h должно быть порядка твЦ; порядка га в Ah. 8.
Порядок I будет соответственно 1, п и 1.
ВА= л ; АС = СА= . Определи-
тель каждого произведения матриц равен 9. 2. |А|=6—1 = 5; Аг1 — Ъ,
Г 3 —1-1
I——=— 3
'- А 5 *
Г1 -а -61
L= 0 1 О
|_0 0 1 J
А
An
- А
ж, —|
¦^1
А
А22
~А.
5 5
— 1 2
_ 5 Т -
. 4. Написать А'1=1
; IA
[А-1==В
1
1=4
1 5
= и т. д.
2. Первое: из 2-й строки вычитается первая и из третьей вычитается
первая, умноженная на 3/2. Второе: берется V4 первой строки. 3. Каждая
приводится к матрице
Элементарные преобразования
оставляют всегда по крайней мере один ненулевой элемент, исключая тот
случай, когда отправляются от 0. 5. Выделить ненулевой элемент и
соответствующий ему отрицательный элемент; присоедините два элемента из
диагонали, чтобы получить субматрицу о с 0ПРеДелителем» величина
которого равна а2 ф 0.
1. Вычесть первый столбец из второго и третьего, чтобы привести
матрицу А к I, а затем I — к А. 2. 0 = А~10 = А~1АВ = 1В = В,
если А—неособенная матрица. Аналогично А = 0, если В—неособенная.
Но если и А и В—особенные матрицы, то АВ может тем не менее
равняться 0, в то время как ни А, ни В не будут нулем.
_Г cos 6 sin9"l TcosQ —sin9"|_
L—sine cosej Lsine cosej
г 1 1
3. AA'
4. Воспользоваться равенством АА' = ВВ'=1. 7.
У 2 l/\
нальная матрица; значит, ее транспонированная матрица и ее обратная ма-
71/2
— 1 1
есть ортого-
635

13.1
(стр. 367)
13 2
(стр. '374)
13 3
(стр.' 380)
13.4
(стр. 385)
13.5
(стр. 392)
трица—те же самые. 8. Матрица Ал получена путем той owe самой
перестановки строк, как и столбцов, так что элементы главной диагонали А
остаются на главной диагонали в Ая, а элементы вне главной диагонали
так и остаются вне ее.
1. Сложить векторы, как на рис. 37, и применить метод рис. 40.
2. Покажите прежде всего, что ранг матрицы равен(—3); следовательно, нет
линейной зависимости (определитель не равен 0). 3. Ранг матрицы равен 2.
Транспонированная матрица также ранга 2, но имеет две зависимые строки
и один зависимый столбец. 4. Применить H(rs) из 12.4.
1. Только значение х2 = 0 совместно с уравнениями. Первая
совокупность: матрица системы имеет ранг 3 и лг( = 3)<и(=4). Решение
существует: хг=—2х3\ а?2=а?4=0 (при заданном х3). Противоположное в
примере (б). Вторая совокупность: матрица имеет ранг 3 и лг( = 4)>п ( = 3).
Решения нет. Последнее уравнение несовместно, ср. пример (а). 4.
Выразить А через алгебраические дополнения А, по определению. 5. Вычтем
из второго столбца первый и из третьего—второй, получаем
а — Ъ—с а-\-Ъ-\-с 0
26 —а—Ъ — с а-\-Ь-\-с
2с 0 —а — Ь — с
Раскладывая по элементам первой строки, находим (а-\-Ь-\-сK. Решение
только в случае а-\-Ь-\-с — 0. Тогда подставить с=—(а-\-Ь) и решить.
6. Третье уравнение то же самое, что и первое. Отбросьте его и положите
а?3=1и #1+2а;2-|-1=0. (а) Решение изменится по величине, но будет той
же формы, (б) Расширенная матрица будет иметь ранг 3, решения нет;
третье уравнение будет несовместно с первым. 7. Здесь даются только два
уравнения из задачи 6. Отбрасывание первого (или третьего) уравнения
системы из задачи 6 не изменяет решения. 8. Отбросьте первое или третье
уравнение, и получится неособенная система. Подставьте решение задачи 3
в добавочное уравнение {хг-{-х2-\-х3=1) для получения решения xt=lr
2= — 1, а?
у
=1.
3. Отбросьте уг или у3; они связаны соотношением г/х = 2г/3 пРи
совместности. 4. z=
то есть z± =
1. Определитель для нахождения корней первой матрицы |А—АД| =
I ^ I
, отсюда характеристические корни: Х = 0 и 2. Вторая мат-
1 L Л
рица, характеристическое уравнение:
Отсюда X = 1 и 1 ± -у=. 3. Pi равно сумме определителей первого порядка
(главная диагональ) от А; р2 равно сумме определителей второго порядка того
же типа. 4. Транспонируйте А (А—XI)' = (А—XI) А' = —тг ( A'—yl ) .
Таким образом, —j- А (А—М)' = (а' — i I^' = A' -~1.
[0 1"!
4 0|—неособенная. 4. Матрица
,_•¦
имеет положительные характеристические корни 1 и 1 ± —г=- (см. 13.4,
У ^
упражн. 1). 5. Сумма корней равна рг\ сумма попарных произведений
корней равна рг\ произведение корней равно р9. Все р положительны, если
636

корни положительны, и обратно. Выразите затем р, как в упражн. 3 из
раздела 13.4.
13.6 1 и 2. См. 13.4, упражн. 3, и 13.5, упражн. 5.
<стр. 395)
13.7 1. Применить правило Крамера, см. 13.2. 2. p'A = w' с обратным пре-
(стр. 397) образованием p/ = w'A как вектор-строка или A'p=w с обратным
преобразованием p = (A)'w, как вектор-столбец. 4. Сумма элементов r-й строки
матрицы U = 2 WsXs ~T==wr^r равна добавленной стоимости в r-й отрасли,
8
см. упражн. 1. Аналогично сумма элементов 5-го столбца матрицы V = psx8
равна стоимости элементов 5-го конечного расхода. Итог потоков равна
2 wrXr=^\ psxs равна национальному доходу,
г s
13.8 2. Показать, что vrs=prxr8 = prarsXs = (rs)-My элементу в рАх. Первое
<стр. 400) уСЛовие: У,[суммируемое по строкам, сводится к нулю, т. е. к рАх {1}=0.
Умножая слева на р-1, получаем АХ = 0. Второе условие получаем аналогично
из [1]рАх = 0, умножая справа на х. 3. А+В имеет нулевые элементы
в последнем (п-м) столбце. В матричном уравнении АХ = 0 прибавить ВХ
к каждой стороне.
13.9 1. Если |А| = 0, то несущественно, умножаем ли мы элементы строки
(стр. 403) А на ее собственные алгебраические дополнения или на алгебраические
дополнения другой строки; результат будет равен нулю в любом случае
(см. правило разложения в 11.9). 4. Испытайте решение Х = С, где С есть
вектор, который нужно найти. В этом случае показать, что С==А~1с.
5. Частное решение есть Xt—X (постоянно во времени), где X есть
Х = СХ+К, то есть Х = A — С) К. Это будет конечным выпуском, если
вариация затухает.
14.2 5. Заметьте, что шансы п : 1 указаны числами п на главной диаго-
(стр. 408) налы; другие элементы (—1) представляют потерю ставки. 6. Каждый
из игроков имеет 9 стратегий: A, 1) B, 1) C,1) A,2) B, 2) C,2) A, 3)
B, 3) C, 3). Платежная матрица 9x9 будет следующего вида:
[0-3-42 ...1
3 Q 0 0 ....
(стр. 411) *• ^ = 4 ( х—к~ ) ( У—о" )• По сравнению с примером (а) в тексте,
в этой игре условия для игроков Л и В поменялись: А получает от В 1 ф.
ст. при тождественности названных чисел и платит 1 ф. ст., когда названы
разные числа. 2. Так как Е (я, у) = аху-\-а$х-\-аау-\-аа$-{- Ь, то,
сопоставляя это выражение с общей формулой Е (х, у) в тексте, получаем
соотношения а = ап— «i2+«22J оф = а12 — а22; аа = а21 — а22\ яар = а22> что ПРИ
Р <<
пi2+22J ф 12 22; 21 22\ р
положительных а, а и Р приводит к «22<a2i<«n и а22<12<п
3. Чистые стратегии х = 1, г/ = 1 имеют 2? A, 1) = а(а+1) (8 + 1) + 6> О
7 / 4 N\ / 4 \ 1
и т. д. 4. Ставки: 2 : 1 и 1 : 1. Е=^ ( X~~~Y ) ( у—7 )—Т ' ПослеДний
член в Е отрицателен, что гарантирует выигрыш «букмекеру» (см. далее
11 '"IN
14.5), например, при а?=:—,г/=~- показать, что ?<0 ( Е=—-д- ) .
5. В соответствии с формулой для Е (х, у) при матрице .~„ 0
(см. пример (д) из 14.2), средний платеж для А будет — х—lOOy-j-lOOzi/,
следовательно, средний убыток равен х-{-100у—ЮОху. Когда х=1 (всегда
страхуется), то Е1 — 1\ когда х = 0 (совсем не страхуется), то ?2=100г/.
Для того чтобы Е1=^Е2, вероятность быть пожару, г/, должна быть
равна 0,01, или пожар должен случаться в 1% всех случаев. 6. А — [аг$]
для г = 1, 2; *=1, 2, ..., п.
Е(х, s) = xau-{-(I — x)a2s.
В случае примера (ж) из раздела 14.2 матрица А=Г r~~^~
тогда Е(х, s) = lx — A(s = l); 9х — 5E = 2); 5 —9л; E = 3); 6 — 11s E = 4).
14-4 \щ Решение: платеж 1 фунта игроку А; первая стратегия для А и вто-
(стр. 415) рая для В. 2. Если игрок ставит па одну лошадь, то скачка может всегда
637

расстроить планы. 4. А придерживается первой или третьей стратегии,
а В играет в соответствии с первой стратегией и платит I фунт игроку А.
Если случится, что В выберет вторую стратегию, то А выиграет,
придерживаясь третьей стратегии, «более оптимальной» (платеж 3 фунта вместо 2).
/1 1 \
6. Поверхность имеет седловую точку в Р ( -?-, — ) , но с АА', как линией
стока, и ВВ' как линией гребня вместо
другого—перевернутого—положения (рис. 42, а). Е имеет знак не тот, который нужен для игрока А—для А
нужно (—Е),—но благоприятный для игрока В г).
14.5 1. Е есть C) из раздела 14.3. 2. Е=Cх—2) Bу—1) + 1; цена игры = 1.
(стр 419) 1
3. #* = 0, Tj-^> 2/*"^ ^' Чена игры = 1. Если Л играет необдуманно и
применяет вообще первую стратегию, то В выигрывает, концентрируя игру на
первой стратегии (г/* = 1), которая и есть «наилучший оптимум». 4. Примем
> (или переставим столбцы в А)
если a>a2>«i :** = 0, то 0<г/*<1 Е = а,
если а2>а>а1 :#* = 0, то — <^*/*<С1 Е = а,
а2—й1
если «2>ai> a :х* = г/* = 1 Е = ал
(стр.423) 2* ж*=="з"' 2/*=-2->Я=1, как в примере (в)текста. 4. z*=0, y<t/*<l,
Я = 1. 5. Нанести J^B; (? = 2—у); #2#2 (Я=—у); ?3#з (?=3—2г/).
Исключите 2?2#2> то есть Л не следует второй стратегии. В таком случае
[1 2 1
. график
дает 0<>*<;i, 22 = 1. 6. График для игрока А включает четыре линии
в плоскости ОЕх. Первая и четвертая линии дают #* = -—, Е=-—^-. Но
линии, проходят близко от х = -—, так что выбор вариантов игры В влечет
только неощутимые различия.
14.7 1. Вектор (ж, 1 — х) для 0О<;1 есть отрезок линии АХА2 (см. 11.5).
(стр. 428) В игре 2 х п выбор А устанавливается переменной х, а не вектором х.
2. Плоскость есть х1-\-х2-\-'х3 = 1, то естьаг3=1—хг — х2. Для стороны АХА2
(д;3—0) х есть (jcj, 1—#!, 0) и игрок А смешивает только первую и вторую
стратегию. 3, 4. Если хA> и х<2) удовлетворяют A), то ему же
удовлетворяет х. Если Рх и Р2 содержатся в. А1А2А3, то в нем содержится и
промежуточная точка Р (рис. 49). Вообще любая выпуклая линейная
комбинация точек из X также содержится в X. 7. Примените свойство (I). Если
игра имеет две цены, иг и v2, взять с=— . А. и с А имеют одну и ту же
г>2
цену, и таким образом, с = 1.
14.8 2. Первая строка излишняя, так как над ней доминирует комбинация
(стр. 433) (средняя) из двух других. Так как игрока В (столбцы) интересуют меньшие
элементы, то первый столбец также не нужен, ибо над ним доминирует
есть мат-
Г6 9 31 20 Г~~2 ° °1
последний. 3. А=|9 15 0 , цена игры = -?г - 4. 0 —2 0
L9 5 8j 3 LOO —2J
2
рица преобразованной игры, ее цена i?=——. Отсюда цена исходной
о
2 1 2
игры= ~—(—1) = -q- • Свойство (Пб) дает —2хг >—— и т. д. Возь-
о о о
мите все знаки одинаковые: х1=^х2=х3=— (и аналогично для у). В исход-
о
ной игре решение содержит одинаковые численности партий, и цена ?? = -—.
Г2 2] 3
6. Привести к матрице 16с ценой 2 (v -J-1); найти графически у* = -^- .
Г2 21
16 '
LsoJ
1) Если нормальный чертеж перевернуть снизу вверх, то вогнутые и выпуклые
поверхности поменяются местами и прежнее благоприятное положение для игрока А
станет благоприятным для В.—Прим. ред.
638

Оптимальная стратегия для А после исключения первой стратегии будет
(О, —» у ) • 7- Минимумы строк: —3, 0, —4. Максимумы столбцов:
3, 3, 0, 1. Следовательно, чистые стратегии 6}дут: вторая для А и третья
для В, и игра справедлива (v = 0). 8. Четыре седловые точки ( цена i;=-— J .
Любая комбинация первой и третьей стратегии для А и второй и
четвертой для В есть решение. Игра справедлива, если А платит В в качестве
компенсации -^ .
14.9 1. См. пример (а) в тексте. Можно предположить, что оптимум для
Р' ' каждого игрока ( — , -г , -г-, -т~ ) » и цена игры = ^-. Испытайте это, при-
„ / 1 1 1 1 \ '
менив игру ^1 т»Т'Т' Т; к кажД°и из чистых стратегии А:
д w 1 о ч/ 1 х v" i_ Л v — . тт т тт
X /ч . —1~ lj /Ч —^ |~* О /ч . -| т: /Ч . ~с\" г\'
4. Цена игры = 0. Испытайте предложенную оптимальную стратегию для В
против каждой чистой стратегии А (как в упражн. 1), найдите цену игры
v = 0 для третьей, пятой и седьмой стратегий; т. е. В применяет
стратегии А. 5. Соотношения:
1+2+з 21 + 2/2+2/з
40*! +150*3 > v 40^+301/2 + 201/3 < *
30*! +100*2+50*3 > * ЮОуа + 250г/3 < ^
20*!+ 250*2—50*з> у 150г/х +50i/2—50г/3< г;
Успешные пробы дают: 20*!+250*2—50*3>у (г/3 = 0)
40г/!+ 30г/2+20г/зО (^ = 0)
Оптимальные стратегии: ( ^» "о"» "о" ) и ( "/"' "» ^ ) » ^ = 75. 6. Провести
на графике три линии: ?" = 150A—*); ? = 50(* + 1); iS = 50F* — 1) и получить
х~— и Е = 7Ь. 7. Испытайте р=0 и игру Л ( х' Т ' X' Т" ) ПРОТИВ
каждой из чистых стратегий В и покажите, что для каждой из них
результат равен нулю. 8. Например, А играет A,1), В играет B, 1) с платежом,
который равен половине суммы 3 (выпадение герба при бросании монеты) и 0
(выпадение решетки). 9. А (*, у) = — 1 (х—у — 0); А(х, г/) = 1 (* —1, у = 0);
А(х, ?/) = ! (* = 0, у = 1); и А(ху у)= — 1 (х=у = \). Это дает платежную
Г 1 1
матрицу | Ч —1J "
15,1 1. (а) Необходимо минимизировать 2 = 6*1+24*2=6(*1 + 4*2)-
Министр. 442) мальное значение г, удовлетворяющее второму из неравенств A), будет
1
при *!+4*2 = 4, которое при 0<*2<-^-, удовлетворит и первому неравен-
ству из A) : *! + 2*2> 3. Между тем условие *1+4*2=4 допускает
бесконечное число решений. Можно решать графически: (а) тангенс угла наклона
параллельных прямых (постоянной стоимости), когда функция стоимости
2 = 6*!+ 24*2, равен ( —— j = (тангенсу угла наклона ВР). Оптимальный
набор—любая точка ВР. (б) Минимизации подлежит выражение 2 = 6*! +
+30*2 = 6 (*! + 5*2). Последнее минимально при *2=0 и *! = 4
(выполнение требования по содержанию белка), ибо всякая замена единицы *]
единицей *2 влечет за собой повышение калорийности вдвое, содержания
белка —вчетверо, а стоимости сыра—впятеро по сравнению с заменяемой
единицей (хлебом). Графическое решение (б): тангенс угла наклона
параллельных линий численно =—-< тангенса наклона РВ. Оптимум [будет
в точке В. 2. (а) Минимизировать необходимо z = 6*i + 12*2 = 6(*i+2*2),
а последнее будет минимально при первом из условий A), когда *г + 2*2=3,
1
причем если *2 > -к-, то одновременно будет удовлетворяться и второе из
неравенств A). Таким образом, минимум стоимости будет при любой
покупке сыра *2, большей 0,5 фунта, если вес купленного хлеба будет
равен 3—2*2- Графическое решение: параллельные линии (постоянной
стоимости) при цене 12 пенсов или цене хлеба 10— пенсов, если другой
639

продукт неизменяется в цене, будут хх-\-2х2 — const. Аналогично и в
случае (б). 3. Минимизации подлежит выражение z = рххх + р2х2 при тех же
ограничивающих условиях. Если р1 — — р2, то z = p1(z1-\-4x2)\ т0 есть
минимум будет при ^+4^2 = 4 при любом 2 ' Если Pi=-w р2 или zt =
1 А
= Pi
), то минимум будет при любом *2>у и д:1+2х2=3. 5.
Добавить дополнительную строку к данным таблицы (стр. 440):
Углеводов E0 г) 5 1 8
и присоединить к соотношениям A) еще одно: 5^ ~|-ат2 >-8 и
соответствующую третью линию на рис. 50. Заштрихованная площадь будет лежать
выше и правее всех трех линий. Точка Р будет все же решением.
6. Добавить дополнительный столбец к данным таблицы (стр. 440) для х3
(мясной фарш): 18
2
3
Задача сводится к минимизации: z=6x1-\-21x2-\-18x3.
Ограничивающие неравенства: х^-{-2х2-{-2х3^3 и Xi-\-4x2-{-3x3^ 4. Для графического
решения требуется построение в трех измерениях. 7. Ответы на вопросы
в конце задачи зависят от того, могут ли суда быть нагружены частично
или нет; также, если задача должна быть обобщена. 8. Одно из
ограничивающих условий (хп+х12 = а1; х21-\-х22 — а2; xll-\-x2x — bl и х12-\-х22 = Ь2)
следует из других, так как al-\-a2 = b1-\-b2.
15.2 1. Нанести линии ?i-|-g2=6 и 2?1-f-4?2=21 на плоскости 0|i?2.
|(стр. 445) Допустимые решения будут лежать внизу и налево от этих линий, и
оптимум есть максимальное положение на параллельных линиях 3?14-4|2 =
3 9
= const. Решение как пересечение линий будет: |i= —к- ; ?2= ~о~ » 5 =
= 3?г-И?2=22-2-. 2- Например, в упражн. 1 (а) в 15.1 будет: ?г + ?2=6;
2?i+4|2 = 24; 3|г+4?2=тах. Вторая линия будет выше, она пересекает
сначала 0?2, давая решение: ?i = 0; ?2 = 6; ? = 24. Удовлетворять будет
любой рацион в пределах @—0,5 фунта сыра, 4—2 фунта хлеба) с 4
единицами белка по оценке 6 пенсов. Потребность в калориях удовлетворяется
при этом с избытком; значит, калории не имеют оценки. 3. Двойственная
задача: ? = 3?14-4|2=иШх; подчинено ограничениям ?i+?2<6; 2^ +
+4?2<21 и 2%х -f 3?2 < 18. Графически: три линии дают то же решение,
что и задача 1 этого раздела. 4. Двойственная задача: ? = 3g1-j-4g2+
+8?3=max; подчинено ограничениям 5i + ?2+5?3<6 и 2?1-Н?2+?з<.21.
Для решения требуется построение в трех измерениях, так же как в
задаче 6 раздела 15.1. 5. ?х и |2 можно истолковать как количество месяце-
су до в с грузом (ср. порожняком).
15.3 1. Двойственная задача: ? = &i?i + &2?2+&3i3==max; подчинено усло-
<стр. 449) виям: flii4i+«2ii2+«3i?3 <^и «i2?i+«22&H-«32?3 < />2. Прямая задача имеет
три ограничивающих соотношения в двух измерениях; двойственная
задача— два ограничивающих соотношения в трех измерениях.
2. Матрица =
- о
0
-«11
— «21
— «31
- Pi
гры =
0
0
— «12
— «22
— «32
P2
' 0
0
—1
—1
— 5
_ 6
«ii
«22
0
0
0
-*1
0
0
— 2
— 4
— 1
21 -
1
2
0
0
0
-3
«21
«22
0
0
0
1
4
0
0
0
4
«31
«32
0
0
0
-*a
5
1
0
0
0
— 8
—Pi
—/>2
bl
b2
Ьг
0 .
— 6 -
—21
3
4
8
0 .
640

15.6
(стр. 457)
15.9
(стр.466)
16.2
(стр.472)
16.5
(стр. 482)
16.6
(стр. 488)
Оптимум ( -^д-, 19"' Т§*г 9"• ' ~19У ' ^ЛЯ линеиного программиро-
вания задачи 5 из 15.1: #1 = 2, #2=-^- . Двойственная задача из 15.2,
упражн. 4 дает ?i=^r , h =-y-, 1з=°-
4. z =
«11*1 + «12*2 + «13*3 >
«21*1+ «22*2+ «23*3 > &2
Матрица =
" 0
0
0
— «и
— «21
- Pi
0
0
0
— «12
—«22
Р%
0
0
0
— «13
— «23
Рг
«12^1+«22^2 </>2
«11
«12
«13
0
0
— Ъ1
«21
«22
«23
0
0
-ъ2
^ гг
—Pi
—Рг
— Рз
bi
Ьг
0
1. ? = Ь1[х1+Ь2И'2 = 1йах. Ограничивающие условия:
=р19 а12\1г + а22Ц2+^ = Р2-
2. М дополняющих переменных в w=M-f-iV, m = M неравенств
становятся уравнениями. 3. В двойственной задаче N дополняющих
переменных в группе n'=M-{~N, m' = N неравенств превращаются в
уравнения. Прямая и двойственная задачи имеют одно и то же число переменных
(M-{-N). Число уравнений (и дополняющих переменных) М—в прямой
задаче и N — в двойственной.
2 = а:2. 3.
[1] = [
Таким образом, Х1-\-Х2 — х1 и
В последнем секторе симплексной таблицы столбец X есть
строка для с8—zs есть ( 0, 0, ^~ , ^~ )• 4.
Двойственная задача легче: ? = ЗА,х+4А,2-1-8А,з=тах. Ограничивающие условия:
^1+^2+5^3+^4=6 и 2^+4^2+^3+^6 = 21. Пространство условий двух
измерений о 4. 1 О 1 21 « Исходные векторы рD) и рE) с весами 6 и 21.
3 9 3
1 = -тг » ^2=-9~i Я3=А,4=Я5=0. Таким образом, gx = —- ;
= 0 (см. упражн. 4 из 15.2). В задаче программирования
последняя строка для с8—z8 есть ( 0, 0, 0, —2, ^~ J . Следовательно,
а?! = 2, ж2=-^-. 5. Опустить р<4)= I . В таком случае любая пара из
110 1 бУДет линейно зависима; также * с любой из других, если
только &i=?0, Ь2ф0 и ЬхфЬ2. 6. Бесконечное число решений: ж2 = 10—хх
и ^з=20—хг для любого хх (О^х^Щ. Двойственная задача: ^ — Ю^^-
"~|2 = тах. Ограничивающие условия: ii + |2 = l- Это определяет %х и
—- и ^ = 15. Методы решения терпят неудачу (излишни). 7. z=
Окончательно:
g
12 = —
11 + 12+21+4*22 = nun; #u+*i2 = 2; xlir\-x21 = 6 и 12[22
Примем х11 = 'к. Тогда хг2=2—X; я21 = 6—Я и я22=4-|-^- 2=50 независимо
от к. Получается бесконечное число решений @<А<2). Симплексный
метод неприменим (не нужен).
1. Например, х2~—Я1+2А,2+-Х3 = 1 — 2^+^ (Ях и Я2 суть положи-
тельные дроби). Выпуск, если X2>B^i —1).
1. Сравнить рис. 55 с рис. 61. Производственные отрасли (способы)
в конусе (А) между ОА<2) и вертикалью: оба товара суть затраты (не
выпуск). 8. Точка ЛA> выше и по крайней мере так же далеко вправо, как
и другие, то есть при единице затраты труда может быть получено от
первого способа больше, не жертвуя х±.
1. ОЛA)ЛB), ОАа)А<3) эффективны (ибо в данном случае первое из
соотношений D) есть равенство, второе также равно нулю, а третье
меньше 0). 2. Только OAa)Ai2) эффективна. 3. р1 = A, 0, 2) является нормалью
а 41 Р. Аллен
641

к ОАЮА<*>, р2=(—1, 2, 2)—к 0ЛA>Л<3). Положительное р, например, р=
= V ~2~ ' ~2~ ' 2 J лежит между рх и р2. 4. На рис. 52 ОЛA)ЛB) изображена
эффективной. Если ЛB) лежит налево от Лш, то в таком случае будет
эффективным только ОАаК
16.7
<стр,491)
<\ if\ |_ га л . Jr 1
Рз ^з ' ^з
= 1:1:3. *
2. Для <Х4AЪ1B) : 2р1-{-2р2—/?3=0,
о„ _ q что дает (из первых
л Уравнений) />х :/?2: />3=2:1:6
^1 + /2 /з
Аиалсгичио для OA^Ai3} (из 1-го и 3-го уравнений) : рх : р2: ^3=1 : 1:4.
3. См. 16.6, унражн. 3.
16.8 3. Эффективное размещение в точке, подобной С на рис. 68, но ле-
(стр. 495) жащей между Ai2y и ЛC) и между Bi2y и 5C), то есть на грани ОЛB)ЛC),
где х2 = хг=—1, и оба фактора используются до предела.
17.1 1. Относительный минимум функции будет: dZ/dx1 = O и dZ/dx% =0.
(стр.505) Или: dC/dx1 — Xf1 = p1 — 'kf1 = Q и dC/dx2-—tkf2 = p2—Xf2 = 0. Отсюда условия
минимума: рг — Vi = P2—Х/г = О. 2. Напишите D) : / = г/; Pi = hf1; />2 = Я/2-
Продифференцируйте по г/, имея в виду, что л (а также хх и х2) зависит
от у. Тогда дС/ду=р1дх1/ду-\-р2дх2/ду = Х(/1дх1/ду-{-/2дх2/ду) — %1 так
как выражение в скобках равно 1 на основании первого уравнения
системы в задаче [результат дифференцирования уравнения D) по у]. 5. В
соотношение y=fiX1-\~f2x2 (теорема Эйлера) поставить/1 = -т—/?1 и/2=
1 1С
=z-r-р2. Получаем г/ = — (рхХх-\-р2х2) = — . Заметьте, что дС/ду = Х, см.
упражн. 2 этого раздела.
17.2 1. Производные от ф (/) суть ф'(/)/г и ф' (/) /rs+ф" (/) /r/s- Отноше-
(стр. 510) ния первых производных заданы в виде /х: /2 :... . Подставьте в F,
разбейте каждую строку (после первой) на две части, одна из которых
(будучи пропорциональной первой строке) обращает определитель в нуль.
Следовательно, F имеет только многократное {ф' (/)}n+1.
3. C = 2przr==max для
/(*!, х2, ..., хп) = 0.
Найти значения переменных х, максимизирующие z — C—Я/ при заданных р
и у. Тогда dz/dxr — O дает pr = Xfr, которое имеет тот же вид, что и A),
но только для факторов. 4. Анализ и результаты аналогичны уравнениям
C) в тексте.
17.5 1. Принять Я3=0 и построить АР и ВВ по уравнениям 100Я1-|-25Я,2==
(стт) 522) 1
v F* =150 и 10^-1-50^2=12-^-. Эти линии пересекутся ниже Окг. Решение
ограничивается площадью, лежащей под первой линией, то есть, где она
пересекает линию ОХг (Я1 = 1,5Д2 = 0).
Г 200 25 60 1 50 чел-час.
3. А=[ 20 50 48 J 52,5 акра
тыс. ф. ст. 2 2 2
Рис. 62, а теперь показывает геометрическое место точек постоянной
продукции с двумя эффективными частями РгР2Р3 и Q между ОА2 и OAS. Так
как применяется третий процесс OA3J то производится свинина. Рис. 62, б
при Х1=0 имеет две линии:
5 95
3 = 50; таким образом, X2z=—1X3=-~
4. Изменяйте постоянную в правой части второго уравнения в
упражнении 3 (рис. 62, б). Если земельная площадь составит 40 акров, то Я2 = 0
и будет применяться только третий процесс; если 100 акров, то Я3=0
и будет применяться только второй процесс. 5. Решение будет в точке Qx
на рис. 62, а\ применяется только первый процесс, и оба фактора
используются полностью. 6. Одна дополняющая переменная (при обращении
642

17.6
(стр. 527)
третьего ограничивающего условия в уравнение) имеет ненулевое значение,
равное 2,5. 7. При увеличении первого процесса и уменьшении второго
на 100 ф. ст. получаем изменение:
Факторы
Труд (чел.-мес.)
Земля (акры) . .
Первый
процесс
+2,5
+5
Второй
процесс
-0,5
-10
Итого
+2
—5
Соотношение 2 : 5 равно отношению оценок факторов. 8. Два дефицитных
фактора и два применяемых процесса, если отношение земли (акры)
к труду (чел.-месяцы) будет между 125:4 и 50:25. Другими словами,
если имеется (больше земли (дефицитен труд), то применяется только
третий процесс (А3), и аналогично, если будет меньше земли. Исключение:
отношение земли к труду равно точно 125 : 4 или 100 : 5, или 50 : 25
(вырожденные случаи).
1. Единичные уровни для выручки 1 ф. ст.; А = [а11а12 ] (вектор-
строка). Задача состоит в максимизации *=2 ^s Для 2 alsks <^ &•
S S
ние: а1т есть минимум строки А, кт= и другие X суть нули.
а17]
2. А =
тыс. ф. ст.
25
1
100
1
50 чел.-мес.
260 акров
. Будет
Решение: ^ = 2,4, А,2=2,0. Факторы используются полностью при
производстве 200 т пшеницы и 160 т сена. Если цены будут Юр ф. ст. для
\^- ю"
пшеницы и 10 ф. ст. для сена, то в таком случае А=| Р
— 100
производиться только пшеница (л2=0), если тангенс угла наклона
по абсолютной величине (см. рис. 62, б), то есть /?>2,5 (цена пшеницы =
= 25 ф. ст. за тонну). Аналогично, при 5 ф. ст. за тонну, производится
только сено. 3. Если Яг^-^-я^ две прямые,
17.7 .
(стр. 532)
50/?1+5^а=Я2—2Ki и 25р1 + 50р2 = я1,
пересекутся ниже Орг. При решении /?2=0, земля используется
неполностью, производится только свинина. Аналогично при я2 ^ -р- ях, реше-
D
ние />i = 0, труд используется неполностью, производится только зерно.
10 12"] 100 человек z = X1-)-^2 = max
2J 60 машин при условии:
6500 ф. ст.
^+2^ < 60
Графическое решение: Хх = 10, Х2=0. 2. Ставка процента в размере 6%.
= 6640 J
J
меньшей,
неприводит к дисконтированной сумме выручки
жели стоимость наемных или арендуемых факторов. Если процентная
ставка будет 100 г%, то переключение на длительный процесс произойдет,
если ~ТХ— >6500, то есть процентная ставка должна быть <;8,3%.
Переключение на наемные факторы будет иметь место, если
ф
>6700, та
есть когда ставка «<5,1%. 3. Строка стоимости наемных факторов:
[0000 6500 6600 6500 6600]
643 41*

18.1
<стр. 544)
18.2
<стр. 546)
18.3
(стр. 549)
Любое переключение на наемные факторы есть переключение на процессы
А, но не В. При увеличении цены продукта на 10%, произойдет
переключение на Аи—дополнительный процесс, подобный первоначальному. 4.
В задаче 1 измените второе ограничивающее условие на 5Я,1-)-2Я2<^50.
Показать, что машины используются полностью, несмотря на то что
по-прежнему ^ = 10, Я2=0. Двойственная задача: ? = 100/?i-|-50»2 = imn
3 1
при ограничениях Юр1-\-5р2'^1; 12р1-\-2р2^> 1. Решение: р1=-~, р2=— .
5. Отношение цен в двойственной задаче (см. пред. упр. 4) дает отношение
производительности труда к производительности машины: рг: /?2=—: —- =1,5.
В первоначальной (прямой) задаче труд относительно недооценен, а потому
происходит переключение на трудоинтенсивные процессы. Обратный
случай в задаче 3 этого раздела.
Точка Р:Х1 = 112; Я2=2,
'Х2 5
то есть ~5Г~==-о"
(как на рис. 64).
Другие ограничивающие соотношения (—Xt-{-X3 = 0 и —Х2-\-сХ3=0) дают
-т^- = с, и ищется,максимум ХХ = Х3. Положение на рис. 64 (земля не
используется до предела, и цена земли равна нулю) получается, если с< —- .
о
2. Совпадение OQ с ОР (рис. 64) случайно, нетипично. 4. Норма замены =
~Р2 ' 7?з = 28 : 63. Производительность*труда = рх: р2 = Ь : 28=0,14 т свежей
рыбы за 1 чел .-час, и аналогично производится расчет для копченой рыбы.
2. ф(м) = -7г-1г2; ф'(м) = м; ф"(м) = 1. Для двух товаров:
17.8
(стр.
537)
1.
А =
" 25
50
—1
-0
10
100
0
—1
0"
0
1
с
50 чел.-мес.
260 акров
0
0
0
ии2
1ШЦ + И1
ии2
о
их
и2
и2
Все остальные определители будут равны нулю (вследствие
пропорциональности столбцов). 3. Так же, как в предыдущей задаче, но при ф(м) = 1пм;
1. Из A) иг=Хрг. Дифференцируя заданную функцию полезности,
получаем а11х1-\-а12х2=Хр1; а12х1-\-а22х2 = Хр2 при условии ^ргхг=:М или
г
/>i#i + Р2Х2~М. Решая эти три уравнения относительно хи х2 и X, получаем
Хг = (М/Р) («22.Pl — «12^2)> х2==(М/р) («ц/>2 — «12^1)» Х = (М/Р) («11^22—«12I
где Р = а22р\—2а12р1р2-\-а1гр1. Дифференцируем хг и х2: дх1/др1 =
= —(M/P2){pl(a11a22^-al2) + (a22p1 — a12p2J}. Таким образом, дх1/др1<С.О9
если, конечно, axla22>a\2. 2. Р, как в предшествующей задаче 1. Из
первого условия C) имеем:
0 их и2
«И
и2
0
Хрг
Я/>2
Хрх
«И
«21
Хр2
«12
«22
= Х2
0
Pi
Р2
Pi
«11
«21
Рч
«12
«22
так как их = Хрх и11 = а11 и12=и21 = а12=а21
и2 = Хр2\ и22 = о22 ]
Следовательно, Р<0и, в силу свойств квадратичных форм, аХ1 (и а22) <0
и a11a22>af2. Замечание: при этих условиях и19 и2 и X отрицательно
(см. задачу 1), то есть «предельная полезность» отрицательна. 3. Применить
формулу E) из 18.1.
2. На основании (8) и (9) для случая трех товаров X12p2-\-Xlsp3^>0;
%i2Pi-\-X23p3>0; X13pi-\-X23p2^>0. Только одна из величин Х12, Х231 Х13
отрицательна;5не может быть более одной пары взаимно дополняемых товаров.
4. Примите, что рх уменьшается, а р2 неизменно. Когда рх проходит
критическое значение | рх = —— р2 ), покупки перемещаются от Р к В на
_\ «22 У
рис. 50 (то есть х2 становится равным нулю). Это есть замена второго
товара первым. В противном случае покупаемые количества остаются
неизменными.
644

18.4
(стр. 552)
иг и2
^22
Кривая безразличая более полога к правой части, то есть она выпукла
к точке О. 3. (— dx^jdp) и дхг/дМ отрицательны: хг уменьшается при
уменьшении цены (вдоль PC) и для возрастающих доходов (вдоль РВ),
то есть траектории имеют в Р наклоны в обратном направлении. Линии
безразличия должны сближаться вместе и быть крутыми для малых хх\
гораздо более обособленными и ровными для больших хг.
18.6 1. Сочетания выше ОАг: х2 находится в избытке, или хг слишком малсу
(стр. 561) по сравнению с потребностями. 2. dx1 — (a11 — а12) d\i и dx2=—(^22—^21) Ф-
Отсюда ( —-—^ \ дается тангенсом угла наклона Р^Р2 на рис. 69. 4. Конеч-
Ч ®х2 у
ное число частей плоскостей, каждая только с одним наклоном (нормой
замены) для данной пары товаров.
18.7 1. Некоторые факторы потребляются непосредственно (желаемые сами
(стр. 566) по себе); некоторые продукты потребляются не полностью, а в пределах
установленного образования запасов; некоторые производственные процессы
обладают сами по себе «полезностью». 2. (I), как в 17.8: максимальная
полезность от одного способа потребления; (II), как в 17.8, пример (б), на
с несколькими способами потребления: двойственной задачей будет
минимизация стоимости единственного фактора; (III) А в нижнем левом секторе
имеет главную диагональ из (— 1) и остальные элементы—нули.
1
18.8 1. На диаграмме (рис. 70, a): z=—A + 2)
(стю 572)
v р- ; др 25А,! + 10А,2 = 50 (труд используется полностью)
ВР 50^4-100^2 = 260 (земля используется полностью)
OQ Х2 = Х1 (^4=0, только первое соотношение потребления)
OR X2 = X1/^(iz=0, только второе соотношение потребления)
Решение: %1=zX2 = %s=-y , Х4 = 0, где АР пересекает OQ. Таким образом,
только труд полностью используется, применяется лишь первое
соотношение потребления. Ср. 17.8, задача 1. Если земли —=— = 214 акров или менее,
то земля также дефицитна. 2. Р лежит ниже OR (рис. 70, а),
земля—дефицитна, труд используется неполностью. ВР параллельна линиям z = const,
и разные X неопределенны в областях: -г<!-^-<1; Я3^0Д4^0. 5. При
4 Аг
Ь = 45 имеем рг: р2: р3 : /?4— 1: 0 : 7 : 15 (нужно пересчитать по шкале, исходя
из />з+^4=1)- При 6 = 30 имеем Pi=y Рз и Р2=-7^Aрь— 15/>3); если
1
^3+^4=^ и 3/>з+-тг Р±— 1 также применяется, то в таком случае
рх: р2 : р3 : />4==3 : 13 : 21 : 84. 6. Хг уменьшается относительно Х2 до тА =
= -5--j-~6~ • С этого момента только отношение а/|3, и земля не используется.
Р ^
Р идет выше OQ (рис. 70, а). 7. (I) и (II): пропорциональное снижение
производительности земли и труда в первом (втором) производственном
процессе. (III): относительное изменение производительности труда двух
> производственных процессов. (IV): Изменение в структуре спроса (вкусов).
Проанализировать влияние, как это сделано в тексте и в упражнении 6*
19.1 2. См. Тейл [8], стр. 5 — 6.
(стр. 575)
19.2 3. Из метода (I), а = а=\ у. as ) п и А:=У, kSi если только х =
(стр. 579) Ч^-1 У/ ^
= — V. asxs равно взвешенной средней продукции фирм, причем веса
а *-*
равны предельным склонностям применения рассматриваемого фактора.
Если цена фактора есть psi то индивидуальный спрос будет описываться
уравнением ys — asxs-\-b$ps-\-kSi а совокупный: у = ах-\-Ьр-\-к1 где Ь = пЪ*
19.3 1. Ъ есть совокупный показатель эластичности от цен по отношению
(стр. 581) к индексу цен в форме средней геометрической. 2. Как в 19.2, упражн. 1 и 2.
Предельная склонность к потреблению группы товаров есть сумма предель-
1/г 41 Р. Аллен 645

иых склонностей к потреблению составляющих ее товаров. 3. -EZ-
Ут
= Ът -^- /-^- в базисной точке.
Pro I УгО
/
Pro I УгО
19.4 1. См. доказательство обратного у Тейла [8], стр. 25. 3. &хУ =
(стр. ) _( __ 2 а& Л др, = адр,; Д2г/ = аА[1. Эти выражения равны, если а=~а,
S
то есть если Cov (asAs) = Q. 4. Cov(asAg) = 0, когда fls=const, но также
и при других обстоятельствах.
19.5 1. Воспользуйтесь соотношениями: V^as = l, Vibs=0. 3. Индекс q
(стр. 588) s в
охватывает цены товаров из группы и вне группы; если группа включает
товары не взаимозависимые, то только цены товаров вне группы. 5. а
зависит только от as и b—только от bs; можно избежать противоречий в
частном специальном случае, если доход возрастает пропорционально средней
из уровней дохода.
19.6 1. Предположите фирму, имеющую единственную (заданниую) про-
(стр. 591) дукцию. 2. Принять xq (q=i, 2, ..., к) как сумму дохода из разных
источников. 4. См. пример (б) в тексте, распространенный путем суммирования
по всем фирмам.
19.7 1. i = l, 2, ..., m по всем^ товарам или затратам. 2. См. [8], стр. 29.
стр. 594) 4. Если yi относится к r-му товару, ^-индивидууму, то тогда \а8 Ф 0 есть
предельная склонность к потреблению товара.
19.8 5. Истолковать условие какХ1 = тах для данного Хт (? = 2, 3, ...,т).
>?тр. 598) 6. Условие есть ?/"г = тах. для f (Х1у Х2, ..., Хт)=0. 7. Для каждого i
диг dUi df df
условия упражнения 6 суть : -т—- = ¦ ' :« ' и аналогично для дру-
гих пар товаров. Существуют только (т—1) независимых отношений;
другие из них вытекают. Проверьте для 3 и 4 товаров. 8. Только (к — 1)
независимых уравнений, как в упражн. 7.

БИБЛИОГРАФИЯ
К введению
1. Allais М., L'Utilisation de ГОиШ Mathematique en Economique, Econometrica,
1954, № 22, p. 58—71.
2. Allen R. G. D., Mathematical Analysis for Economists, Macmillan, 1938.
3. Hersteinl. N., Some Mathematical Methods and Techniques in Economics,
Quarterly Journal of Applied Mathematics, 1953, № 6, p. 249—262.
4. H i с к s J. R., A Contribution to the Theory of the Trade Cycle, Oxford, 1950.
5. Koopmans Т. С, Activity Analysis of Production and Allocation, Wiley, 1951.
6. Leontief W. W., The Structure of American Economy, 1919—1939, Oxford, second
ed., 1951.
7. Leontief W. W., Ed., Studies in the Structure of the American Economy, Oxford,
1953.
8. Leontief W. W., Mathematics in Economics, Bulletin of the American
Mathematical Society, 1954, № 60, p. 215—233.
9. Samuelson P. A., Foundations of Economic Analysis, Harvard, 1947.
10. Samuelson P. A., Economic Theory and Mathematics — An Appraisal, American
Economic Review, 1952, № 42, p. 56—66.
11. Samuelson P. A. and others, Mathematics in Economics, Review of Economics
and Statistics, 1954, № 36, p. 359—386.
12. S t i g 1 e r G. J., The Mathematical Method in Economics, in Five Lectures on
Economic Problems, Longmans, 1949.
13. T i n t n e r G., Mathematics and Statistics for Economists, Constable, 1954.
К главе I
1. В aumol W. J., Economic Dynamics, Macmillan, 1951, Ch. 7.
2. E v a n s G. C, Mathematical Introduction to Economics, McGraw-Hill, 1930, Ch. IV.
3. E z e к i e 1 M., The Cobweb Theorem, Quarterly Journal of Economics, 1938, № 52,
p. 255—280.
4. Goodwin R.M., Dynamical Coupling with Especial Reference to Markets Having
Production Lags, Econometrica, 1947, № 15, p. 181—204.
5. H a n s e n В., A Study in the Theory of Inflation, Allen and Unwin, 1951.
6. Hooton F. G., Risk and the Cobweb Theorem, Economic Journal, 1950, № 60,
p. 69-80.
7. К о у с к L. M., Distributed Lags and Investment Analysis, North-Holland, Amsterdam,
1954, Ch. II.
8. Leontief W. W., Verzogerte Angebotanpassung und Partielles Gleichgewicht,
Zeitschrift fur Nationalokonomie, 1934, № 5, p. 670—676.
9. Leontief W. W\, Econometrics in A Survey of Contemporary Economics, ed. by
Howard S. Ellis, Vol. I, Blakiston, 1948.
10. Phillips A. W\, Stabilisation Policy in a Closed Economy, Economic Journal,
1954, № 64, p. 290—323.
11. Phillips A. W., Some Notes on the Estimation of Time-Forms of Reactions in
Interdependent Dynamic Systems, Economica, 1956, № 23, p. 99—113.
12. Samuelson P. A., The Stability of Equilibrium: Comparative Statics and
Dynamics, Econometrica, 1941, № 9, p. 97—120.
13. Samuelson P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. IX.
14. W о 1 d H. O. A., Dynamic Systems of the Recursive Type, Sankhya, 1951, № 11,
p. 205-216.
15. W о 1 d H. O. A. and J и г е е n L., Demand Analysis, Wiley, 1953.
К главе 2
1. Alexander S. S., Issues of Business Cycle Theory Raised by Mr. Hicks, American
Economic Review, 1951, № 41, p. 861—878.
647 41*

2. F о r t D. M., A Theory of General Short-run Equilibrium, Econometrica, 1945, № i3?
p. 293-310.
3. И a h n F. H., The Rate of Interest and General Equilibrium Analysis, Economic
Journal, 1955, № 65, p. 52—66.
4. H i с к s J. R., Mr. Keynes and the «Classics», Econometrica, 1937, № 5, p. 147—159.
5. Hicks J. R., A Contribution to the Theory of the Trade Cycle, Oxford, 1950, Ch. II,
III and XI.
6. L ange 0., The Theory of the Multiplier, Econometrica, 1943, № 11, p. 227—245.
7. Metzler L.A., Three Lags in the Circular Flow of Income in Income, Employment
and Public Policy, Norton, 1948.
8. Modigliani F., Liquidity Preference and the Theory of Interest and Money,
Econometrica, 1944, № 12, p. 45—88.
9. Smithies A., Process Analysis and Equilibrium Analysis, Econometrica, 1942,
№ 10, p. 26-38.
10. S о 1 о w R., A Note on Dynamic Multipliers, Econometrica, 1951, № 19, p. 306—316.
11. Turvey R. and В г е m s H., The Factor and Goods Markets, Economica, 1951,
№ 18, p. 57—68.
12. Turvey R., Some Notes on Multiplier Theory, American Economic Review, 1953,
№ 43, p. 275—295.
К главе З
1. Alexander S. S., Mr. Harrod's Dynamic Model, Economic Journal, 1950, № 60,
p. 724—739.
2. Alexander S. S., Issues of Business Cycle Theory Raised by Mr. Hicks, American
Economic Review, 1951, № 41, p. 861—878.
3. В a u m о 1 W. J., Notes on Some Dynamic Models, Economic Journal, 1948, № 58,
p. 506—521.
4. В a u m о 1 W. J., Formalisation of Mr. Harrod's Model, Economic Journal, 1949, № 59,
p. 625—629.
5. В a u m о 1 W. J., Economic Dynamics, Macmillan, 1951, Ch. 4, 10, 12.
6. G 1 a r к J. M., Business Acceleration and the Law of Demand, Journal of Political
Economy, 1917, № 25, p. 217—235.
7. Domar E. D., Capital Expansion, Rate of Growth, and Employment, Econometrica,
1946, № 14, p. 137-147.
8. Frisch R., The Interrelation between Capital Production and Consumer-Taking,
Journal of Political Economy, 1931, № 39, p. 646—654.
9. Goodwin R.M., Secular and Cyclical Aspects of the Multiplier and the Accelerator,
in Income, Employment and Public Policy, Norton, 1948.
10. Ham berg D., Full Capacity vs. Full Employment Growth, Quarterly Journal
of Economics, 1952, № 66, p. 444—449.
11. H a r г о d R. F., The Trade Cycle, Oxford, 1936, Ch. 2.
12. H a r г о d R. F., Towards a Dynamic Economics, Macmillan, 1948, Lecture Three.
13. Hicks J. R., A Contribution to the Theory of the Trade Cycle, Oxford, 1950, Ch. IV,
V, VI.
14. К n о x A. D., The Acceleration Principle and the Theory of Investment: A Survey,
Economica, 1952, № 19, p. 269—297.
15. Lundberg E., Studies in the Theory of Economic Expansion, King, 1937, Ch. IX.
16. Phillips A. W., Stabilisation Policy in a Closed Economy, Economic Journal, 1954,
№ 64, p. 290-323.
17. P i 1 v i n H., Full Capacity vs. Full Employment Growth, Quarterly Journal of
Economics, 1953, № 67, p. 545—552.
18. Samuelson P.A., Interactions between the Multiplier Analysis and the Principle
of Acceleration, Review of Economic Statistics, 1939, № 21, p. 75—78.
19. Samuelson P.A.,A Synthesis of the Principle of Acceleration and the Multiplier,
Journal of Political Economy, 1939, № 47, p. 786—797.
20. Smithies A., Process Analysis and Equilibrium Analysis, Econometrica, 1942,
№ 10, p. 26—38.
21. Yeager L.B., Some Questions about Growth Economics, American Economic Review,
1954, № 44, p. 53—63.
К главе 4
1. Allen R.G. D., Mathematical Analysis for Economists, Macmillan, 1938, Ch. XVI.
2. В a u m 0 1 W. J., Economic Dynamics, Macmillan, 1951, Ch. 12.
3. Carslaw H. S. and Jaeger J. C., Operational Methods in Applied Mathematics,
Oxford, First Ed., 1941, Second Ed. 1948, Ch. I.
4. Domar E. D., The «Burden of the Debt» and the National Income, American
Economic Review, 1944, № 34, p. 798—827.

5. Gardner M. F. and Barnes J. L., Transients in Linear Systems, Wiley, 1942.
6. Jaeger J. C, An Introduction to the Laplace Transformation, Methuen, 1949, Ch. I.
7. P i a g g i о Н. Т. Н., An Elementary Treatise on Differential Equations, Bell, 1920,
Ch. III.
К главе 5
1. В aumol W. J., Economic Dynamics, Macmillan, 1951, Ch. 9—11.
2. В a u m о 1 W. J., Topology of Second Order Linear Difference Equations with Constant
Coefficients, Econometrica, 1958, № 26, p. 258—285.
3. Durell C. V., and Robson A., Advanced Algebra, Bell, 1937, Ch. XI.
4. G a r d n e r M. F. and Barnes J. L., Transients in Linear Systems, Wiley, 1942,
Ch. IX.
5. Goldberg S., Introduction to Difference Equations, Wiley, 1958.
6. H i с к s J. R., A Contribution to Theory of the Trade Cycle, Oxford, 1950.
7. Milne W. E., Numerical Calculus, Princeton, 1949, Ch. XI.
8. Orcutt G. H.,A Study of the Autoregressive Nature of the Time Series used for Tin-
bergen's Model of the Economic System of the United States, 1919—1932, Journal
Royal Statistical Society, Series B, 1948, № 10, p. 1—45.
9. Solow R., A Note on Dynamic Multipliers, Econometrica, 1951, № 19, p. 306—316.
К главе 6
1. Alexander S. S., The Accelerator as a Generator of Steady Growth, Quarterly
Journal of Economics, 1949, № 63, p. 174—197.
2. Alexander S. S., Issues of Business Cycle Theory Raised by Mr. Hicks, American
Economic Review, 1951, № 41, p. 861—878.
3. В a u m о 1 W. J., Notes on Some Dynamic Models, Economic Journal, 1948, № 58,
p. 506—521.
4. В a u m о 1 W. J., Topology of Second Order Linear Difference Equations with Constant
Coefficients, Econometrica, 1958, № 26, p. 258—285.
5. Bennion E. G., The Multiplier, the Acceleration Principle, and Fluctuating A utono-
mous Investment, Review of Economic Statistics, 1945, № 27, p. 85—92.
6. Duesenberry J.S., Hicks on the Trade Cycle, Quarterly Journal of Economics, 1950,
№ 64, p. 464—476.
7 Fisher G. H., Hicks'Elementary Case Economic Model for the United States, 1929—
1941, Journal of the American Statistical Association, 1952, № 47, p. 541—549.
8. H a n s e n A. H., Fiscal Policy and Business Cycles, Norton, 1941, Ch. 12.
9. H a n s e n A. H., Business Cycles and National Income, Norton, 1951, Ch. 11.
10. Hicks J. R., A Contribution to the Theory of the Trade Cycle, Oxford, 1950, Ch. VI
and Appendix.
11. Lundberg E., Studies in the Theory of Economic Expansion, King, 1937, Ch. IX.
12. Metzler L. A., The Nature and Stability of Inventory Cycles, Review of Economic
Statistics, 1941, № 23, p. 113—129.
13. Samuelson P. A., Interactions between the Multiplier Analysis and the Principle
of Acceleration, Review of Economic Statistics, 1939, № 21, p. 75—78.
14. S a m u e 1 s о n P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. XI.
К главе 7
1. Frisch R. and Holme H., The Characteristic Solutions of Mixed Difference and
Differential Equations, Econometrica, 1935, № 3, p. 225—239.
2. Goodwin R.M., The Non-linear Accelerator and the Persistence of Business Cycles,
Econometrica, 1951, № 19, p. 1—17.
3. Kalecki M.,A Macrodynamic Theory of Business Cycles, Econometrica, 1935, № 3,
p. 327-344.
4. Kalecki M., Studies in Economic Dynamics, Allen and Unwin, 1943.
5. Kalecki M., Theory of Economic Dynamics, Allen and Unwin, 1954.
6. Le Corbeiller Ph., The Non-linear Theory of the Maintenance of Oscillations,
Journal of the Institution of Electrical Engineers, 1936, № 79, p. 361—378.
7. Phillips A. W., Stabilisation Policy in a Closed Economy, Economic Journal,
1954, № 64, p. 290—323.
8. Phillips A. W., Stabilisation Policy and the Time-Form of Lagged Responses,
Economic Journal, 1957, № 67, p. 265—277.
9. Strotz R.H., McAnulty J. C. and Naines J. В., Goodwin's Non-linear Theory of the
Business Cycle: An Electro-Analog Solution, Econometrica, 1953, № 21, p. 390—411.
10. Tizard R. H., Note on Initial Conditions in the Solution of Linear Differential
Equations with Constant Coefficients, Econometrica, 1956, № 24, p. 192—197.
11. T us tin A., The Mechanism of Economic Systems, Heinemann, 1953.
649

К главе 8
1. Allen R. G. D., The Engineer's Approach to Economic Models, Economica, 195S
№ 22, p. 158—168.
2. Bothwell F. E., The Method of Equivalent Linearization, Econometrica, 1952.
№ 20, p. 269—283.
3. Brown G.S. and Campbell D. P., Principles of Servomechanisms, Wiley, 1948.
4. Carslaw H. S. and Jaeger J. C, Operational Methods in Applied Mathematics,
Oxford, second ed., 1948.
5. Frisch R., Propagation Problems and Impulse Problems in Dynamic Economics,.
in Economic Essays in Honour of Gustav Cassel, Allen and Unwin, 1933.
6. G a r d n e r M. F. and Barnes J. L., Transients in Linear Systems, Wiley, 1942.
7. Goodwin R.M., The Non-linear Accelerator and the Persistence of Business Cycles^
Econometrica, 1951, № 19, p. 1—17.
8. Phillips A. W., Mechanical Models in Economic Dynamics, Economica, 1950,
№ 17, p. 283—305.
9. P h i 1 1 i p s A. W., Stabilisation Policy in a Closed Economy, Economic Journal,
1954, № 64, p. 290—323.
10. Phillips A. W., Some notes on the Estimation of Time-Forms of Reactions in
Interdependent Dynamic Systems, Economica, 1956, № 23, p. 99—113.
11. Phillips A. W., Stabilisation Policy and Time-Form of Lagged Responses,
Economic Journal, 1957, № 67, p. 265—277.
12. S m i t h O. J. M. and Erdley H. F., An Electronic Analogue for an Economic
System, Electrical Engineering, 1952, № 71, p. 362—366.
13. T u s t i n A., A Method of Analysing the Effect of Certain Kinds of Non-linearity in
Closed Cycle Control Systems, Journal of the Institution of Electrical Engineers, 1947,.
№ 94, Part 2 A, p. 152—160.
14. Tustin A., The Mechanism of Economic Systems, Heinemann, 1953.
К главе 9
1. В о w 1 e у A. L., Mathematical Groundwork of Economics, Oxford, 1924, Ch. II, V.
2. Gordon R.A., Short Period Price Determination in Theory and Practice, American
Economic Review, 1948, № 38, p. 265—288.
3. Hall R. L. and Hitch C. J., Price Theory and Business Behaviour, Oxford
Economic Papers, 1939, № 2, p. 12—45.
4. H i с к s J. R., Leon Walras, Econometrica, 1934, № 2, p. 338—348.
5. Hicks J. R., Theorie mathematique de la Valeur, Hermann, 1937.
6. Hicks J. R., Value and Capital, Oxford, 1946, Ch. IV—VIII and Appendix.
7. Metzler L.A., Stability of Multiple Markets: the Hicks Conditions, Econometrica f
1945, № 13, p. 277—292.
8. P are to V., Manuel d'economie politique, Giard et Briere, Paris, 1909, Appendix.
9. Pareto V., Economie mathematique, Encyclopedic des Sciences Mathematiques,
Librarie Gauthier-Villars, Paris, 1911.
10. Samuelson P. A., The Relation between Hicksian Stability and True Dynamic
Stability, Econometrica, 1944, № 12, p. 256—257.
11. Samuelson P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. IX.
12. Walras L., Elements d'economie politique pure, Lausanne, 1874.
13. Zeuthen F., Economic Theory and Method, Longmans, 1955, Ch. 10—13 (англ»
пер. с датского издания 1942 г.)
К главе 10
1. Вагпа Т., The Interdependence of the British Economy, Journal Royal Statistical
Society, Series A, 1952, № 115, p. 29—77.
2. Cameron В., The Construction of the Leontief System, Review of Economic Studies,
1951, № 19, p. 19—27.
3. E v a n s W. D. and Hoffenberg M., The Inter-Industry Relations Study for
1947, Review of Economics and Statistics, 1952, № 34, p. 97—142.
4. Goodwin R.M., Static and Dynamic Linear General Equilibrium Models in Input-
Output Relations: Proceedings of a Conference on Inter-Industrial Relations held at
Driebergen, Holland, Stenfert Kroese, Leiden, 1953.
5. Leontief W. W., The Structure of American Economy, 1919—1939, Oxford, 1951.
6. Leontief W. W., Ed., Studies in the Structure of the American Economy, Oxford,.
1953, Ch. 1—3.
7. Leontief W. W., Domestic Production and Foreign Trade, Proceedings American
Philosophical Society, 1953, № 97, p. 332—349.
8. Stone J. R. N. and Utting J. E. G., The Relationship between Input-Output
Analysis and National Accounting, in Input-Output Relations: Proceedings of a
Conference on Inter-Industrial Relations held at Driebergen, Holland, Stenfert Kroese,
Leiden, 1953.
650

К главе 11
1. Allen R. G. D., Mathematical Analysis for Economists, Macmillan, 1938, Ch. XVIII.
2. Birkhoff G. and MacLane S., A Survey of Modern Algebra, Macmillan, 1941,
ch. VII.
-3. D u r e 1 1 C. V. and R о b s о n A., Advanced Algebra, Bell, 1937, ch. XVI.
4. Ferrar W. L., Algebra, Oxford, 1941, ch. I, II, VI.
5. Kemeny J. G., Snell J. L. and Thompson G. L., Introduction to Finite
Mathematics, Prentice-Hall, 1957, ch. V.
6. Murdoch D. C, Linear Algebra for Undergraduates, Wiley, 1957, ch. 1—2.
7. Thrall R. M. and Tornheim L., Vector Spaces and Matrices, Wiley, 1957, ch. 1.
К главе 12
1. Aitken A. C, Determinants and Matrices, Oliver and Boyd, 1949, Ch. I, III.
2. Birkhoff G. and MacLane S., A Survey of Modern Algebra, Macmillan, 1941,
Ch. VIII, X.
3. Debreu G. and Flerstein I. N., Non-negative Square Matrices, Econometrica,
1953, № 21, p. 597—606.
4. Ferrar W. L., Algebra, Oxford, 1941, Ch. VI—IX.
5. Ferrar W. L, Finite Matrices, Oxford, 1951, Ch. I—IX.
6. Frazer R. A., Duncan W. J. and Collar A. R., Elementary Matrices,
Cambridge, 1947, Ch. I, HI.
7. К e m e n у J. G., Snell J. L. and Thompson G. L., Introduction to Finite
Mathematics, Prentice-Hall, 1957, Ch. V.
8. Littlewood D. E., University Algebra, Heinemann, 1950, Ch. I, II.
9. M u r d о с h D. С, Linear Algebra for Undergraduates, Wiley, 1957, Ch. 2, 3.
10. T h r a 1 1 R. M. and Tornheim L., Vector Spaces and Matrices, Wiley, 1957,
Ch. 2, 3.
11. Tintner G., Econometrics, Wiley, 1952, Appendices.
12. Wade T. L., Algebra of Vectors and Matrices, Addison-Wesley Press, 1951, Ch. 1, 5, 6, 9.
К главе 13
1. Allen R.G.D., Mathematical Analysis for Economists, Macmillan, 1938, Ch. XVIII.
2. В а г п а Т., The Interdependence of the British Economy, Journal Royal Statistical
Society, Series A, 1952, № 115, p. 29—77.
3. Birkhoff G. and MacLane S., A Survey of Modern Algebra, Macmillan, 1941,
Ch. X.
4. Debreu G. and Herstein I. N., Non-negative Square Matrices, Econometrica,
1953, № 21, p. 597—606.
5. Ferrar W. L., Algebra, Oxford, 1941, Ch. X—XIII.
6. Goodwin R. M.,( Static and Dynamic Linear General Equilibrium Models, in Input-
Output Relations: Proceedings of a Conference on Inter-Industrial Relations held at
Driebergen, Stenfort Kroese, Leiden 1953.
7. Hicks J. R., Value and Capital, Oxford, 1946, Ch. VIII and Appendix.
8. Leontief W. W., Ed., Studies in the Structure of the American Economy, Oxford,
1953, Ch. 3
9. Metzler L. A., Stability of Multiple Markets: the Hicksian Conditions, Economet-
rica, 1945, № 13, p. 277—292.
10. Murdoch D. C, Linear Algebra for Undergraduates, Wiley, 1957.
11. Newman P. K., Some Notes on Stability Conditions, Review of Economic Studies,
1958.
12. S a m u e 1 s о n P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. IX.
13. Stone J. R. N., Simple Transaction Models, Information and Computing, Review
of Economic Studies, 1951, № 19, p. 67—84.
14. S t о n e J. R. N. and U 11 i n g J. E. G., The Relationship between Input-Output
Analysis and National Accounting, in Input-Output Relations: Proceedings of a
Conference on Inter-Industrial Relations held at Driebergen, Stenfert Kroese, Leiden, 1953.
15. T h r a 1 1 R. M. and Tornheim L., Vector Spaces and Matrices, Wiley, 1957,
Ch. 2—3 and 5—7.
К главе 14
1. Kemeny J. G., Snell J. L. and Thompson G. L., Introduction to Finite
Mathematics, Prentice-Hall, 1957, Ch. VI.
2. К u h n H. W. and Tucker A. W., Ed., Contributions to the Theory of Games,
Princeton, Vol. I, 1950; Vol. II, 1953.
3. Loomis L. H., On a Theorem of von Neumann, Proceedings National Academy of
Sciences, U. S. A., 1946, № 32, p. 213—215.
651

4. L u с e R. D. and R a i f f a H., Games and Decisions, Wiley, 1957.
5. McDonald J., Strategy in Poker, Business and War, Norton, 1950.
• 6. M с К i n s e у J. С. С, Introduction to the Theory of Games, McGraw-Hill, 1952.
7. Neumann J. von, Zur Theorie der Gesellschaftsspiele, Mathematische Annalen.
1928, № 100, p. 295—320.
8. Neumann J. von and Morgenstern 0., Theory of Games and Economic
Behaviour, Princeton, First Ed., 1944; Third Ed. 1954.
9. V a j d a S., The Theory of Games and Linear Programming, Methuen, 1956.
10. W a 1 d A., Statistical Decision Functions, Wiley, 1950.
11. Williams J. D., The Compleat Strategyst, McGraw-Hill, 1954.
К главе 15
1. Charnes A., Optimality and Degeneracy in Linear Programming, Econometrica,
1952, № 20, p. 160—170.
2. Gharnes A., Cooper W. W. and Henderson A., An Introduction to Linear
Programming, Wiley, 1953.
3. Ghipman J., Computational Problems in Linear Programming, Review of
Economics and Statistics, 1953, № 35, p. 342—349.
4. D a n 0 S., Linear Programming in Industry: Theory and Applications, 1958.
5. Dantzig G. В., The Programming of Interdependent Activities: Mathematical
Model, Econometrica, 1949, № 23, p. 200—211.
6. Dorfman R., Application of Linear Programming to the Theory of the Firm,
California, 1951.
7. Dorfman R., Samuelson P. A. and S о 1 о w R. M., Linear Programming
and Economic Analysis, McGraw-Hill, 1958, Ch. 1—4, 16.
8. К e rn e n у J. G., S n e 1 1 J. L. and Thompson G. L., Introduction to Finite
Mathematics, Prentice-Hall, 1957, Ch. VI.
9. KoopmansT.C, Ed., Activity Analysis of Production and Allocation, Wiley, 1951.
10. Lomax K. S., Allocation and Programming in Modern Economics, Manchester
Statistical Society, 1952, 1—48.
И. М с К i n s e у J. С. С, Introduction to the Theory of Games, McGraw-Hill, 1952,
Ch. 14.
12. Morton G., Food Consumption Levels — Some International Comparisons, London
(Ph. D. thesis, 1950, unpublished).
13. Morton G., Notes on Linear Programming, Economica, 1951, № 18, p. 397—411.
14. Newman P., Some Calculations on Least-cost Diets using the Simplex Method,
Bulletin of Oxford Institute of Statistics, 1955, № 17, p. 303—320.
15. S t i g 1 e r G. J., The Cost of Subsistence, Journal Farm Economics, 1945, № 27, p.
303-314.
16. V a j d a S. and others, Symposium on Linear Programming, Journal Royal
Statistical Society, Series B, 1955, № 17, p. 165—203.
17. V a j d a S., The Theory of Games and Linear Programming, Methuen, 1956, Ch. IV—XI.
18. W a u g h F. V. and Burrows E.L.,A Short Cut to Linear Programming,
Econometrica, 1955, № 23, p. 18—29.
19. Wood M. K. and Dantzig G.B., The Programming of Interdependent Activities:
General Discussion, Econometrica, 1949, № 17, p. 193—199.
К главе 16
1. Arrow К. J. and D e b r e u G., Existence of an Equilibrium for a Competitive
Economy, Econometrica, 1954, № 22, p. 265—290.
2. Cameron В., The Construction of the Leontief System, Review of Economic Studies,
1951, № 19, p. 19—27.
3. Champernowne D. G., A Note on J. v. Neumann's Article, Review of
Economic Studies, 1945, № 13, p. 10—18.
4. Chipman J., Linear Programming, Review of Economics and Statistics, 1953, № 35,
p. 101-117, 342-349.
5. Dantzig G. В., Programming of Interdependent Activities: Mathematical Model,
Econometrica, 1949, № 17, p. 200—211.
6. Debreu G., The Coefficient of Resource Utilisation, Econometrica, 1951, № 19,
p. 273—292.
7. Dorfman R., Samuelson P. A. and Solow R. M., Linear Programming and Economic
Analysis, McGraw-Hill, 1958, Ch. 9—10, 13.
8. Georgesc u-R о e g e n N., Fixed Coefficients of Production and Marginal
Productivity Theory, Review of Economic Studies, 1935, № 3, p. 40—49.
9. Kemeny J.G, Morgenstern O. and Thompson G. L., A Generalisation
of the von Neumann Model of an Expanding Economy, Econometrica, 1956, № 24,
p: 115-135.
10. К e m e n у J. G., Snell J. L. and Thompson G. L., Introduction to Finite
Mathematics, Prentice-Hall, 1957, Ch. VII.
652

И. К о о р m a ns Т. С, Ed., Activity Analysis of Production and Allocation, Wiley, 1951.
12. К u h n H. W. and Tucker A. W., John von Neumann's Work in the Theory of
Games and Mathematical Economics, American Mathematical Society, 1958, № 64,
C II), p. 100—122.
13. L e о n t i e f W. W., The Structure of American Economy, 1919—1939, Oxford, 1951.
14. M i s e s L., Economic Calculation in the Socialist Commonwealth, in Hayek F. A.,
Ed., Collectivist Economic Planning, Routledge, 1935.
15. Morgenstern 0., Ed., Economic Activity Analysis, Wiley, 1954.
16. Neumann J. von, A Model of General Economic Equilibrium, Review of Economic
Studies, 1945, № 13, p. 1—9 (пер. с немецкого, 1937 г.)
17. R о b b i n s L. C, The Nature and Significance of Economic Science, Macmillan, 1932.
18. W a 1 d A., On Some Systems of Equations in Mathematical Economics, Econometrica,
1951, № 19, p. 368—403 (пер. с немецкого, 1935 г.)
19. Wong Y. К. and Morgenstern 0., A Study of Linear Economic Systems,
Weltwirtschaftliches Archiv, 1957, № 79, p. 222—239.
К главе 17
1. A 1 1 e n R. G. D., Mathematical Analysis for Economists, Macmillan, 1938, Ch. XIX.
2. Cameron В., The Determination of Production, Cambridge, 1954.
3. Chamberlin E. H., The Theory of Monopolistic Competition, Harvard, 1933.
4. Dorfman R., Application of Linear Programming to the Theory of the Firm,
California, 1951.
5. Dorfman R., Samuelson P. A. and Solow R. M., Linear Programming and Economic
Analysis, McGraw-Hill, 1958, Ch. 6, 7.
6. H ay ek F. A., The Ricardo Effect, Economica, 1942, № 9, p. 127—152.
7. H i с k s J. R., Value and Capital, Oxford, 1946, Ch. VI, VII and Appendix.
8. Makower H. and В a u m о 1 W. J., The Analogy between Producer and Consumer
Equilibrium Analysis, Economica, 1950, № 17, p. 63—80.
9. Makower H., Activity Analysis and the Theory of Economic Equilibrium,
Macmillan, 1957.
10. Robinson J., The Economics of Imperfect Competition, Macmillan, 1933.
11. Samuelson P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. IV.
12. S h e p h a r d R. W., Cost and Production Functions, Princeton, 1953.
К главе 18
1. A 1 с h i a n A. A., The Meaning of Utility Measurement, American Economic Review,
1953, № 43, p. 26—50.
2. С a m e г о п В., The Determination of Production, Cambridge, 1954.
3. Corlett W. J. and NewmanP. K., A Note on Revealed Preference and the
Transitivity Condition, Review of Economic Studies, 1952, № 20, p. 156—158.
4. Dorfman R., Samuelson P. A. and Solow R. M., Linear Programming
and Economic Analysis, McGraw-Hill, 1958, Ch. 14 and Appendix A.
5. Ellsberg D., Classic and Current Notions of «Measurable Utility», Economic
Journal, 1954, № 64, p. 528—556.
6. Georgesc u-R о e g e n N., The Pure Theory of Consumer's Behavior, Quarterly
Journal of Economics, 1936, № 50, p. 545—593.
7. Herstein I. N. and M i 1 n e r J., An Axiomatic Approach to Measurable Utility,
Econometrica, 1953, № 21, p. 291—297.
8. Hicks J. R. and Allen R. G. D., A Reconsideration of the Theory of Value,
Economica, 1934, № 1, p. 52—76 and 196—219.
9. H i с k s J. R., Value and Capital, Oxford, 1946, Ch. I—III and Appendix.
10. H i с k s J. R., A Revision of Demand Theory, Oxford, 1956.
11. Houthakker H. S., Revealed Preference and the Utility Function, Economica,
1950, № 17, p. 159—174.
12. Makower H., Activity Analysis and the Theory of Economic Equilibrium,
Macmillan, 1957.
13. Marschak J., Rational Behaviour, Uncertain Prospects and Measurable Utility,
Econometrica, 1950, № 18, p. 111—141.
14. Marschak J., Why «Should» Statisticians and Businessmen Maximise «Moral
Expectation» in Second Berkeley Symposium on Mathematical Statistics and
Probability, California, 1951.
15. Marschak J., Scaling of Utilities and Probabilities, in Shubik M., Ed.:
Readings in Game Theory and Political Behaviour, Doubleday, 1954.
16. Morishima M., Consumer's Behaviour and Liquidity Preference, Econometrica,
1952, № 20, p. 223-246.
17. Morton G., Food Consumption Levels — Some International Comparisons, London
(Ph. D. thesis, unpublished).
42 p. Аллен 653

18. М о s a k J. L., On the Interpretation of the Fundamental Equation of Value Theory,.
in Lange O., Mclntyre F. and Yntema Т. О., Editors.: Studies in Mathematical
Economics and Econometrics, Chicago, 1952.
19. M о s t e 1 1 e r F. and N о g e e P., An Experimental Measurement of Utility, Jour-
nal of Political Economy, 1951, № 59, p. 371—404.
20. Neumann J. von and Morgenstern 0., Theory of Games and Economic-
Behaviour, Princeton, second ed., 1947.
21. О z g a S. A., Measurable Utility and Probability, Economic Journal, 1956, № 66, p.
419—430.
22. Ramsey F. P., Truth and Probability, in the Foundations of Mathematics, Kegan
Paul, 1931, p. 156—198.
23. R о b e r t s о n D. H., Utility and All That, Manchester School, 1951, p. 111—142.
24. Robertson D. H., Utility and All What?, Economic Journal, 1954, № 64, p. 665—678.
25. Samuelson P. A., Consumption Theory in Terms of Revealed Preference, Econo-
mica, 1948, № 15, p. 243—253.
26. Samuelson P. A., The Problem of Integrability in Utility Theory, Economical
1950, № 17, p. 355—385.
27. Samuelson P. A., Probability, Utility and the Independence Axiom, Economet-
rica, 1952, № 20, p. 670—678.
28. Savage L. J., The Foundations of Statistics, Wiley, 1954.
29. S 1 u t s к у E., Sulla teoria del bilancio del consumatore, Giomale degli Economisti
e Rivista di statislica, 1915, № 51, p. 1—26.
Aggregation Theory
К главе 19
1. К 1 e i n L. R., Macroeconomics and the Theory of Rational Behavior, Econometrica,
1946, № 14, p. 93—108.
2. К 1 e i n L. R., Remarks on the Theory of Aggregation, Econometrica, 1946, № 14,
p. 303-312.
3. M ay K., The Aggregation Problem for a One-Industry Model, Econometrica, 1946,
№ 14, p. 285-298.
4. May K., Technological Change and Aggregation, Econometrica, 1947, № 51, p. 51—63.
5. N a t a f A., Sur la Possibility de Construction de Certains Macromodeles, Econometrica,
1948, № 16, p. 232-244.
6. R о у R., Les Elasticites de la Demande relative aux Biens de Consommation et aux
Groups de Biens, Econometrica, 1952, № 20, p. 391—405.
7. Shou Shan Pu, A Note on Macroeconomics, Econometrica, 1946, № 14, p. 299—302.
8. T h e i 1 H., Linear Aggregation of Economic Relations, North-Holland, Amsterdam,
1954.
9. Tinbergen J., Statistical Testing of Business Cycle Theories, Geneva, 1939.
10. T i n b e r g e n J., Econometrics, Allen and Unwin, 1951, Ch. 2.
11. Wolff P. de, Income Elasticity of Demand, a Micro-Economic and a Macro-Economic
Interpretation, Economic Journal, 1941, № 51, p. 140—145.
Welfare Economics
12. Arrow K. J., Social Choice and Individual Values, Wiley, 1951.
13. В a u m о 1 W. J., Welfare Economics and the Theory of the State, Longmans, 1952.
14. В е г g s о n A., A Reformulation of Certain Aspects of Welfare Economics, Quarterly
Journal of Economics, 1938, № 52, p. 310—334.
15. Dorfman R., Samuelson P. A. and S о 1 о w R. M., Linear Programming
and Economic Analysis, McGraw-Hill, 1958, Ch. 14.
16. Hicks J.R., The Foundations of Welfare Economics, Economic Journal, 1939, № 49,
p. 696-712.
17. Hotelling H., The General Welfare in Relation to Problems of Taxation and of
Railway and Utility Rates, Econometrica, 1938, № 6, p. 242—269.
18. К a 1 d о r N., Welfare Propositions in Economics, Economic Journal, 1939, № 49,
p. 549-552.
19. Kennedy C, Concerning Utility, Economica, 1954, № 21, p. 7—20.
20. Lange O., The Foundations of Welfare Economics, Econometrica, 1942, № 10, p.
215—228.
21. L i t t 1 e I. M. D.9 A Critique of Welfare Economics, Oxford, 1950.
22. Samuelson P. A., Foundations of Economic Analysis, Harvard, 1947, Ch. VIII.
23. Scitowsky Т.,A Note on Welfare Propositions in Economics, Review of Economic
Studies, 1941, № 9, p. 77—88.
24. Theil И., Models and Welfare Maximisation, Weltwirtschaftliches Archiu, 1954,
№ 72, p. 60—81.
654

Из литературы, цитируемой
Chamberlin A7).
Hansen F).
К е m e n у и др. A1,12,14,15,
Kuhn and Tucker A4)
Leontief и др. A, 10, 13).
Luce and Raiffa A4)
Me Kinsey A4, 15).
Milne E).
Slutsky A8).
Vajda A4, 15).
Williams A4).
Алленом (см. библиография), изданы в русском переводе
следующие работы1.
Чемберлин Э. X., Теория монополистической
конкуренции, ИЛ, М., 1959. Перев. с 7-го издания
(Аллен ссылается на 1-е издание).
Хансен Э., Экономические циклы и
национальный доход, ИЛ, М., 1959.
Кеме&и Дж. Г., С?нелл Дж. Л., Томпсон Дж. Л.,.
Введение в конечную математику, ИЛ, М., 1963.
Кун Г. У. и Таккер А. У., Линейные
неравенства и смежные вопросы, ИЛ, М., 1959.
Леонтьев В. и др., Исследования структуры?
американской экономики, Госстатиздат, М., 1958.
Лью с Р. Д., Райфа X., Игры и решения; ИЛ,
М., 1961.
16).
Мак-Кинси Дж., Введение в теорию игр, Гос-
физматиздат, М., 1960.
Милн Вильям Эдмунд, Численный анализ,
ИЛ, М., 1961.
Слуцкий Е. Е., К теории сбалансированного
бюджета потребителя, «Экономико-математические
сборники», вып. I, Академиздат, М- 1963 (печ.).
Вайда С, Теория игр и линейное
программирование, Приложение к сборнику Куна Г. У. и Так-
кера А. У., Линейные неравенства и смежные
вопросы (см. выше).
Вильяме Дж. Д., Совершенный стратег или
букварь по теории стратегических игр, «Советское
радио», М., 1960.
1 Цифры в скобках означают главы, к которым относится данная работа и в
которых дается ее оригинальное название. — Прим. ред.
42*

ИМЕННОЙ УКАЗАТЕЛЬ
Александер (Alexander S. S.) 63 , 83 , 92
Аллен (Allen R. G.) 17 , 97 , 321 , 547 , 553
Аттинг (Utting J. Е.) 401
Варна (Ваша Т.) 18 , 273 , 276
Беннион (Bennion E. G.) 182
Бергсон (Bergson A.) 597
Бернулли (Bernouilli D.) 556
Бомоль (Baumol W. J.) 18 , 83 , 106 , 178 , 511
Босуэлл (Bothwell F. Е.) 243
Броуер (Brower) 425
Вальд (Wald A.) 425 , 468
Вальрас (Walras L.) 18 , 37 - 39 , 249 , 259 ,
262 , 287 , 290 , 393 , 395 , 467 , 468
Вильяме (Williams J. D.) 406 , 431
Валд (Wold H. О. А.) 29
Ган (Hahn F. Н.) 14 , 50 , 52
Гейл (Gale D.) 450 , 455
Гендерсон (Henderson A.) 451 , 463
Герштейн (Herstein I. N.) 384 , 558
Гиффен (Giffen R.) 548
Гольдберг (Goldberg S.) 15
Гордон (Gordon R. А.) 270
Горман (Gorman W.) 14
Гудвин (Goodwin R. М.) 18 , 25 , 31 , 176 ,
192 — 193 , 196 — 199 , 226 — 230 , 242 , 243 ,
290 , 398
Дано (Dano S.) 15 , 451 , 455
Данциг (Dantzig G.B.) 451 , 466 , 497
Дебрэ (Debreu G.) 384 , 468
Домар (Domar E. D.) 18 , 66 , 75 , 77 , 78 ,
83 , 106 , 159 , 161 , 213 , 225 , 230 , 239
Дорфман (Dorfman R.) 15 , 18 , 449 , 453 , 468 ,
525
Дьюзенберри (Duesenberry J. S.) 18 , 176
Егер (Jaeger J. G.) 78 , 119 , 121 , 122
Калдор (Kaldor N.) 597
Калецкий (Kalecki M.) 192 — 193 , 199 ,
200 , 202 , 205 — 207 , 227 — 230 , 240 , 242
Камерон (Cameron В.) 290 , 560
Кан (Kahn) 89
Карслоу (Garslaw H. S.) 119 , 121
Кейнс (Keynes J. M.) 13 , 48 , 50 , 52 , 53 ,
56 , 192
Кемени (Kemeny J. G.) 15 , 406 , 449 , 498 , 500
Кеннеди (Kennedy G.) 596
Кларк (Clark J. M.) 73
Клейн (Klein L. R.) 18 , 574
Корлетт (Corlett W. J.) 553
Крамер (Cramer G.) 371 , 372 , 374 , 375 ,
432 , 506 , 508 , 547
Кронекер (Kronecker L.) 304 , 313 , 316 ,
345 , 394
Кун (Kuhn H. W.) 450
Купер (Cooper W. W.) 451 , 463
Купманс (Koopmans Т. С.) 18 , 466 , 469 ,
477 , 479 , 483 , 487 , 494
Лагранж (Lagrange J. L.) 507 , 544
Ланге О. 597 , 598
Лаплас (Laplace P. S.) 117 — 119 , 122 — 124 ,
127 , 129 , 130 , 132 — 134 , 166 , 208 , 209 ,
213 , 215 — 218 , 220 , 221 , 234 , 242 , 247 ,
248
Ласпейрес (Laspeyres) 580
Ле Корбейль (Le Corbeiller) 199
Леонтьев В. В. 18 , 30 , 272 , 273 , 278 ,
285 , 287 , 290 — 292 , 395 — 398 , 400 , 401 ,
468 , 473 — 477 , 498 , 512 , 559 , 573
Лумис (Loomis L. H.) 425
Лундберг (Lundberg E.) 70 , 73 , 75 , 177
Лыос (Luce R. D.) 15 , 406
Маршалл (Marshall A.) 37 — 39
Мак-Кинси (McKinsey J. C.) 406
Мак-Манус (McManus M.) 15
Мак-Эналти (Me Anulty J. C.) 199
Маршак (Marschak J.) 558
Мёрдок (Murdoch D. C.) 15 , 382
Мейкоуэр (Makower H.) 14 , 16 , 18 , 511 ,
529 560
Метцлер (Metzler L. A.) 177 , 395
Мид (Meade J.) 14
Милнер (Milner J.) 558
Модильяни (Modigliani F.) 52 — 54
Моргенштерн (Morgenstern O.) 404 , 425 ,
498 , 500 , 558
Моришима (Morishima M.) 543 , 544
Мортон (Morton G.I4 , 18 , 554
Мозак (Mosak J. L.) 552
Мэй (May K.) 574
Нейман (Neumann J.) 404 , 425 , 498 , 500 ,
501 , 558 , 559
Нейнс (Names J. B.) 199
Нокс (Knox D.) 14
Ньюмэн (Newman P. K.) 15 , 395 , 553
Нэш (Nash J. F.) 425
Озга (Ozga S. A.) 554
Папандру (Papandreou A. G.) 52 , 54
Парето (Pareto V.) 249
Патэнкэн (Patinkin D.) 52
Пиаджё (Piaggio H. T.) 97
Райфа (Raiffa H.) 15 , 406
Рамсей (Ramsey F. P.) 558
Роббинс (Robbins L. C.) 14 , 467
656

Робертсон (Robertson D. H.) 70 , 554 , 556
Робинзон (Robinson J.) 511
Самуэльсон (Samuelson P. A.) 15 , 18 , 73 , 85 ,
87 , 88 , 90 , 160 , 167 , 176 , 178 , 191 — 193 ,
195 , 226 , 243 , 249 , 261 , 262 , 393 , 395 ,
449 , 453 , 467 , 468 , 477 , 553 , 558 , 597
Слуцкий Е. 547 , 551 — 553
Смизи (Smithies A.) 52 , 90
Снелл (Snell J. L.) 15 , 406 , 449
Солоу (Solow R.) 15 , 18 , 164 , 449 , 453 , 468
Стоун (Stone J. R.) 398 , 401
Стротц (Strotz R. H.) 199
Сэвидж (Savage L. J.) 558
Таккер (Tucker A.) 450
Тастин (Tustin A.) 199 , 226 , 228 , 234 , 240 ,
243 , 248
Тейл (Theil H.) 574 , 575 , 584 , 585 , 588 ,
594 , 646
Терви (Turvey R.) 14 , 18
Тизард (Tizard R. H.) 215 , 216
Тинберген (Tinbergen J.) 574
Тинтнер (Tintner G.) 17
Тогнетти (Tognetti C.) 15
Томпсон (Thompson G. L.) 15 , 406 , 449 ,
498 , 500
Торнхейм (Tornheim L.) 15 , 381
Тролл (Thrall R. M.) 15 , 381
Феррар (Ferrar W. L.) 321
Филлипс (Phillips A. W.) 14 , 18 79 , 80 , 88 ,
95 , 191-193 , 196 , 208 , 210 , 212 , 213 , 215 ,
222 , 223 , 226 — 230 , 237 , 243 , 245 , 248
Фишер (Fisher G. H.) 174
Фолдс (Foldes L. ) 15
Форт (Fort D. M.) 54
Фриш (Frisch R.) 73 , 202 , 204 , 237
Фурье (Fourier J.) 230 , 243 , 615 , 616
Хайек (Hayek F. A.) 531
Хансен (Hansen A. H.) 18 , 73
Харрод (Harrod R. F.) 18 , 66 , 72 , 73 , 75 ,
77 , 78 , 83 , 85 — 87 , 91 , 106 , 159 , 161 ,
213 , 225 , 230 , 239
Хаутэккер (Houthakker H. S.) 553
Хикс (HicKs J. R.) 18 , 52 , 55 , 57 , 62 , 65 ,
73 , 85 , 87 — 90 , 92 , 160 , 167 , 168 , 176 —
178 , 187 , 191 — 193 , 195 , 226 , 227 , 230 ,
243 , 249 , 256 , 259 , 260 - 264 , 393 , 395 ,
467 , 507 , 545 , 547 , 549 , 552 , 553 , 573 ,
597
Хитч (Hitch C. J.) 270
Хольм (Holme H.) 202 , 204
Хотеллинг (Hotelling H.) 596
Хоффенберг (Hoffenberg M.) 273 , 276 , 287
Хэлл (Hall R. L.) 270
Цойтен (Zeuthen F.) 251 , 467
Чарнес (Charnes A.) 451 , 463
Чемберлин (Chamberlin E. H.) 511
Чемперноун (Champernowne D. G.) 500
Шумпетер (Schumpeter J. A.) 63 , 196
Штиглер (Stigler G. J.) 440
Эйлер (Euler L.) 110 , 505 , 509 , 612
Эванс (Evans W. D.) 273 , 276 , 287
Эрроу (Arrow K. J.) 468 , 597

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аддитивная постоянная (additive constant)
73 , 115 , 119 , 144 , 156
призвольная (arbitrary) 103 , 117 , 144 ,
145
Акселератор (accelerator) 56 , 57 , 66 , 73 , 75 ,
76 , 78 — 83 , 86 , 87 , 93 — 95 , 106 , 158 ,
161 , 169 , 176 , 178 , 182 , 191 , 193 ,
196 — 198 , 200 , 201 , 207 , 212 , 213 , 223 ,
225 , 230
— взрывная сила (explosive power of) 92
— взрывное действие (explosive operation
of) 77 , 201
— мощность (power of) 73 , 74 , 91 , 93 ,
159 , 160 , 174
— линейный (non-linear) 177 , 192 , 196 ,
*• 292 '
— с запаздыванием (lagged of) 74 , 87
— сила действия (power of) 186 , 209 , 210 ,
238 , 240
Алгебраические дополнения (co-factors)
286 , 287 , 322 , 348 , 350 , 371 , 508 , 543 ,
546
Амплитуда колебания (amplitude of
oscillation) 110 , 112 , 130 , 131 , 134 , 151 ,
161 , 172 , 180 , 181 , 231
Анализ дискретный (period analysis) 21 ,
22 , 30 , 40 , 55 , 71 , 83 , 88 , 93-95 ,
158 , 160 , 161 , 191 , 292
— непрерывный (continuous) 21 , 30 , 35 ,
41 , 48 , 73 , 83 , 88 , 93 — 95 , 161 , 162 ,
191
— общего экономического равновесия
(general equilibrium) 18
— предельный (marginal) 510 , 511
— производственных отраслей (способов)
(activity) 469 , 472
— частичный (partial) 52
— экономического регулирования
(analysis of economics regulation) 19
Аппроксимация линейная (linear
approximation) 27
Ассортимент товаров , количественный (bill
of goods) 281
Баланс межотраслевых связей
(inter-industry relations) 281
Балансовая таблица (double table) 281
Безразличия , карта (indifference map) 541 ,
542 , 550 , 552 — 554 , 560 , 562
— кривая (curve) 550 - 552 , 561
Блага инвестиционные (investment goods)
191
— капитальные (capital) 57 , 71 , 72 , 88 ,
193 , 195 , 196 , 208 , 290
Блок-схема (schematic diagram) 224 — 226 ,
229 , 230 , 236
Векторная алгебра (algebra of vectors) 302 ,
304
Вектор единичный (unit vector) 303 , 308 ,
312 , 345
— неотрицательный (non-negative) 305
— нормализованный (normalised) 307
— нулевой (zero) 303 , 307
— ортогональный (orthogonal) 306
— отрицательный (negative) 307
— положительный (positive) 305
— реакции (response) 233 — 235
— собственный >(eigenvector) 381 , 384
Вектор-столбец (column vector) 329 , 343 ,
344 , 346 , 351 , 365 , 366 , 373 , 401 , 426
Вектор-строка (row vector) 317 , 344 , 345 ,
424
Взаимодополняемость (complementarity)
504 , 509 , 510
Возмущение начальное (unitial disturbance)
25 , 172 , 174 , 181 — 183 , 197 , 394
Временная постоянная запаздывания
(time-constant of lag) 40 , 42 , 43 — 45 , 74
— — итоговая (total) 131
«Выпуклая оболочка» («convex hull of set»)
311 , 312
Выпуклое множество (convex set) 307 , 310 ,
457 — 459 , 481 , 515
Выпуклые множества и грани (convex cones
and facets) 482 - 488
Вырождения случай (generate case) 463 ,
520 , 522
Движение взрывное (explosive path) 211
— затухающее (damped) 211
Дискретная форма акселератора (period
accelerator) 74
Доминирующий корень (dominant root)
149 , 164 , 170
— член (term) 102 , 111 , 114 , 117 , 144 , 149 ,
153 , 160 , 163 , 164
Зависимость линейная (linear dependence)
363 — 367
«Зависимость» Харрода («relation» of Har-
rod) 72
Задача двойственная (dual problem) 444 —
450 , 456 , 465 , 469 , 474 , 488 , 497 , 523
533 , 540 , 565 , 566 , 571
— питания (nutrient ) 443 , 444 , 448 — 450 ,
465
— эконометрическая (econometric) 30
Закон ассоциативности (associative rule)
327 , 340 , 601
— дистрибутивности (distributive) 327 , 334 ,
338 , 340 , 600
— замкнутости (closure) 327
— идентичности (identity) 327
— коммутативности (commutative) 372 ,
331 , 340 , 600
— обратимости (inverse) 327 , 340
— сократимости (cancellation) 327 , 338
Запаздывание (lag) 35 , 40 , 48 , 55 , 61 , 68 ,
69 , 83 , 88 , 90 , 94 , 131 , 135 , 163
— акселератора (accelerator) 93 , 207 , 211 ,
221 , 239
— формы показательной функции
(exponential) 42 , 44 , 73 , 74 , 79 , 134 , 234
— двойное (тройное) (double , triple) 31 , 46 ,
129 , 131 , 135 , 213 , 222 , 240 , 244 , 247
658

Запаздывание дискретное (period) 65
— /г-кратное экспоненциальное (ra-fold
exponential) 131
— многократное (multiple) 29 , 129 , 160 , 222
— непрерывно распределенное
(continuously distributed) 42 , 45 , 79 , 81 , 88 ,
127 , 160 , 192
— однократное (одноинтервальное) (one-
period) 28 , 29 , 39 , 49 , 68 , 128 , 129
— потребления (consumption) 93
— предложения (on supply) 22 , 25 , 37 ,
196 , 211 , 221
— распределенное (distributed) 29 , 40 , 41 ,
64 , 74 , 87 , 89 , 93 , 95 , 160 , 161 , 169 , 191 ,
241 , 599
— — геометрически 40 , 44
— спроса (on demand) 22 , 36 , 37
— Филлипса (of Phillips) 88
Затраты первичные (primary input) 275 —
277
Затухание (damping) 132 , 134 , 151 , 157 ,
161 , 179 , 189
Значения собственные (eigenvalue) 381
Игра конечная (finite game) 406
— Морра (Могга) 408 , 415 , 436 , 438
— с нулевой суммой (zero-sum game) 405 ,
406 , 423 , 446 , 451
— экстенсивная (extensive) 406
Изменение «взрывное» («explosive»
variation) 102 , 104 , 108 , 111 , 112 , 114 , 149 , 169
— «затухающее» («damped») 102 , 104 , 108 ,
130 , 149 , 152 , 169
Изображение функции (преобразование
Лапласа) (Laplace transform) 118 , 119 ,
122 — 124 , 130 , 133
'Индекс свободный (free subscript) 319
— связанный условно (dummy subscriptK19
Интенсивность затухания (degree of
damping) 170
Итерация (iteration) 24 , 32 , 44 , 84
Капиталовложения индуцированные
(induced investment) 71 — 74 , 77 , 78 , 81 , 84 ,
89 , 90 , 93 , 167 , 183 , 186 , 225
— концентрированные (скученные)'
(humped) 184
— независимые (autonomous) 58 — 60 , 63 , 67 ,
68 , 71 , 75 , 77 , 80 , 81 , 84 , 89 , 167 , 168 ,
177 , 179
— непредвиденные (unintended) 66 , 69 ,
81 , 179
— распределенные (distributed) 93 , 187
— чистые (net) 71 , 193
Капиталообразование (capital formation)
274 - 276
Колебание (колебательное движение)
взрывное (explosive oscillation) 23 , 24 , 34 ,
85 , 89 , 110 , 117 , 154 , 159 , 160 , 172 — 174 ,
178 — 181 , 186 , 204
— внутреннее (собственное) (inherent)
132 — 135 , 180 — 182
— вынужденное (forced) 133 — 135 , 176 , 181 ,
182
— затухающее (damped) 25 , 34 , 39 , 110 ,
111 , 114 , 152 , 154 , 157 , 159 , 160 , 172 —
174 , 178 — 181 , 186 , 188 , 189 , 195
— регулярное (regular) 23 , 24 , 38 , 110 ,
114 , 158 , 169 , 173 , 178 , 180 , 195
— — с неизменной амплитудой (of fixed
amplitude) 111
— синусоидальное (sinusoidal) 132 , 133
Комплексная переменная (complex variable)
118 , 131 , 133
Корни вещественные (real roots) 115 , 125 ,
148 , 153 , 170
равные (real and equal) 107 , 148 , 203
различные (real and different) 107 ,
114 , 148 , 203
— скрытые (latent) 381
— комплексные сопряженные (conjugate
complex) 107 , 109 , 111 , 114 , 125 , 132 ,
148 , 150 , 153 , 155 — 159 , 164 , 170 — 172 ,
185 , 210 , 218
Коэффициенты затрат (input coefficients)
279 , 282 , 496 , 517 , 525 , 526
— инвестиций (investment) 73 , 74 , 81 ,
85 , 88 , 90 , 168 , 174 , 183 , 205
— инвестиционные ослабленные (reduced)
168 , 183
— капиталообразования (capital) 290
— производства , неизменные (fixed
production) 251
— спроса (demand) 24
— — и предложения (demand and supply)
23 , 25
— структурные (structural) 172 , 292
— технологические (technical) 264 , 267 ,
270 — 272 , 289 , 467 , 476
Крамера правило (Cramer's rule) 371 ,
372 , 375 , 432 , 506 , 508 , 547
Кронекера дельта (Kronecker delta) 304 ,
313 , 316
Линейное преобразование (linear
transformation) 375
Линия гребня (ridge line) 412
— стока (trough) 412 , 413
Макроэкономика динамическая
(macro-dynamic economics) 17
Макроэкономические переменные (macro-
economic variables) 47
Марковский процесс , простой (simple Маг-
koff process) 152
Матрица (matrix) 325 — 362
— блочная (partitioned) 315 , 316 , 340
— Гесса (Hessian) 314
— диагональная (diagonal) 313 , 314 , 316 ,
324 , 346 , 352 , 357 , 376 , 382 — 384 ,
388
— единичная (unit) 313 , 315 , 316 , 324 ,
336 , 339 , 340 , 342 , 345 — 348 , 350 , 352 ,
353 , 356 , 358 , 372 , 381
— квадратная (square) 299 , 312 — 315 , 321 ,
329 , 337 , 339 , 340 , 341 , 346 - 349 ,
352 , 354 , 356 , 357 , 361 , 367 , 369 , 370 ,
374 , 375 , 385 , 386 , 426 , 564.
— кососимметрическая (skew-symmetric)
313 , 324 , 342 , 343 , 356 , 426 , 447 , 453
— коэффициентов затрат (of input
coefficients) 282 , 283 , 287 , 289 , 290 , 374 ,
396 , 528 , 529
Матрица межотраслевых потоков
(transactions) 273 , 274 , 279 , 282 , 283 , 288 , 395 ,
398 , 399
— стоимостная (value) 281 — 284 , 290
398
— неособенная (non-singular) 354 — 359 ,
362 , 367 , 371 , 387 , 474
— неразложимая (indecomposable) 360 , 361
— нулевая (zero) 313 , 315 , 338 , 339 , 353.
— обратная (inverse) 287 , 347 , 348 — 351 ,
358 , 372 , 375 , 378 , 384 , 490 , 546
659

Матрица ортогональная (orthogonal) 315 ,
324 , 358 — 362 , 377 , 383 — 385 , 388
— особенная (singular) 354 , 403
— перестановочная (permutation) 350 — 353 ,
362
— платежная (pay-off) 405 , 407 — 411 , 414 ,
416 , 418 - 420 , 422 , 423 , 425 — 428 , 431 ,
435 , 438 , 439 , 446 - 449 , 452
— подобная (similar) 357 , 358 , 362 , 382 ,
384
— присоединенная (adjoint) 403
— прямоугольная (rectangular) 312 , 340 ,
347 , 379
— разложимая (decomposable) 361
— симметрическая (symmetric) 313 , 324 ,
342 , 343 , 362 , 382 — 385 , 395 , 506 ,
509 , 542 , 548
— скалярная (scalar) 316
— согласованная (conformable) 335
— технологических коэффициентов
(технологическая) (of technical
coefficients or technology) 271 , 284 , 285 ,
289 , 290 , 312 , 396 , 397 , 399 , 440 ,
453 — 455 , 471 , 472 , 475 — 477 , 479 ,
485 — 487 , 489 - 492 , 494 , 496 , 516 ,
517 , 520 , 525 , 529 , 533 , 537
— транспонированная
(транспонирование) (transpose) 341 , 342 , 403 , 490
— треугольная (triangular) 314 , 324 , 350 ,
352 , 377
— характеристическая (characteristic) 381 ,
401
— эквивалентная (equivalent) 353 , 355 ,
356 , 362 , 368
— элементарная (elementary) 352
— Якоби (Jacobian) 314
Матричная алгебра (matrix algebra)
298 - 301 , 307 , 312 , 319 , 325 , 331 , 332 ,
334 , 337 , 341 , 343 , 363
Метод операторный (operator method) 116 ,
117 , 599
Множитель Лагранжа (Lagrange
multiplier) 507 , 544
Модель Вальраса (Walrasian model) 259 ,
262 , 393 , 395 , 467
— Гудвииа 192 , 193 , 196 , 197 , 227 — 230 ,
242 , 243
— динамическая (dynamic) 22 — 24 , 27 ,
. 29 , 36 , 38 , 39 , 47 , 54 , 55 , 57 , 61 , 65 ,
71 , 86 , 87 , 91 , 92 , 158 , 192 , 225 , 259 ,
261 , 393 , 467
— — денежная (monetary) 54
— — дискретная (period) 24 , 235
Леонтьева 498
— — непрерывная (continuous) 37
— дискретная (period) 28 , 30 , 94 ,
175
— Калецкого 192 , 193 , 199 , 200 , 202 ,
205 , 207 , 227 — 230 , 240 , 242
— Кейнса 48 , 53 , 54.
— «классическая» («classical») 53 , 54
— Леонтьева , открытая (Leontief's open)
278
Модель макроэкономическая (macroe-
. conomic) 45 , 47 , 48 , 56 , 87 , 105 , 199
— Модильяни (Modigliani) 52 — 54
— мультипликатора (multiplier) 91 , 92 ,
106 , 161 , 208 , 212 - 214 , 217 — 219 , 223
— мультипликатора-акселератора
(multiplier-accelerator) 79 , 91 , 161 , 162 ,
174 - 177 , 183 , 208 , 212 , 213 , 217 ,
220 — 222 , 226 , 237 , 238 , 244 , 245 , 248
— — — без запаздываний (with no lags)
81 , 225 * '
— — — Самуэльсона — Хикса (Samuel-
son—Hicks) 87 , 160 , 226
— — — с концентрированными
капиталовложениями (with humped
investment) 167
— мультипликатора , динамическая
(dynamic multiplier) 61 , 158
Филлипса (Phillips') 79 , 94 , 196
— непрерывная (continuous) 25 , 27 , 29 ,
30 , 65 , 80
— Папандру (Papandreou) 54
— паутинообразная (cobweb) 21 , 22 , 25 ,
27 , 28 , 31 , 39 , 55 , 65 , 105 , 111 , 156 ,
157 , 160
— рекурсивная (recursive) 29
— роста Неймана (Neumann growth)
496
— Самуэльсона — Хикса (Samuelson—
Hicks) 85 , 88 , 91 , 178 , 192 , 195 ,
243
— — — дискретная 87
— с распределенными
капиталовложениями , общая (general model with
distributed investment) 183 , 189
— с трехкратным запаздыванием (with
triple lag) 69
— Филлипса (Phillips') 192 , 208 , 212 ,
226 - 230 , 237 , 243
— Филлипса непрерывная (continuous) 88
— Харрода — Домара (Harrod-Domar) 87 ,
159 , 213 , 225 , 230
— Хикса , простая (simple Hicks) 90 ,
227 - 393
— экономического регулирования
Филлипса (Phillips model of economic
regulation) 208
Мультипликатор (multiplier) 47 , 56 , 57 ,
59 , 60 , 63 , 65 — 67 , 71 , 72 , 73 , 75 , 78 ,
82 , 86 , 87 , 92 , 94 , 158 , 161 , 177 , 178 ,
181 , 182 , 196 , 199 , 223
— динамический (in its dynamic form) 72 ,
77 , 80 , 81
— — с непрерывным ' запаздыванием
(dynamic accelerator with a
continuous lag) 79
— Кана (Kahn) 63 , 89
— Лундберга (Lundbergian) 69
— Робертсона (Robertsonian) 69
— с запаздыванием (lagged) 207
— статический (static) 58 , 60 , 61 , 64 , 75 ,
79 , 82 , 89 , 94 , 208 , 209 , 224
Мультипликатор-акселератор (multiplier-
accelerator) 160
Норма замены (заменяемости) (rate of sub*
stitution) 489 , 495 , 534 , 536 , 561
предельная (marginal) 266 , 489
Оператор (operator) 42 , 115 , 131 , 132 , 145 ,
154 , 161 , 225 , 226 , 599 - 603 , 605 — 609
Оператор дифференциальный 73
— разностный (difference) 154 , 155 , 607
— 608
— сдвига (shift) 154 , 599 , 606 - 607
Определитель (determinant) 321 , 323
Оригинал (в преобразовании Лапласа) 118 ,
121 , 122 , 125 , 126 , 130
Отрасли базисные (basic activities) 471 , 480
660

Отрасли производственные (activities) 470 ,
471 , 480 , 484 , 488 , 489 , 491 , 496 ,
498
— свободные или «псевдоотрасли»
(disposal or dummy activities) 560
— (способы) единичного уровня (unit
level) 560
— убыточные (unprofitable) 489
— эффективные (efficient) 489 , 561
Отставание , отставание с фиксированной
продолжительностью отставания
(fixed-time delay) 22 , 40 , 43 , 44 , 79 , 94 ,
160 , 161 , 192 , 205
— простое однократное (одноинтерваль-
ное) (simple delay of one period) 22 , 64
Оценка (цена) расчетная (accounting price)
445 , 488 , 489 , 492 , 494 , 495 , 501 ,
518 — 521 , 523 — 525 , 533 , 534 , 564
— условная (imputed) 445
Ошибка укрупнения (aggregation bias) 578
Парадокс Гиффена (Giffen effect) 548 ,
550 , 553
— Рикардо (Ricardo) 528 , 531
Партия (в игре) (play) 405 , 407 , 435 , 439
Переменная вещественная (real variable)
118
— вспомогательная или дополняющая
(slack) 454
— синусоидальная (sinusoidal) 131 , 132 ,
161
— фиктивная («dummy») 451
Период колебания (period of oscillation)
110 , 112 , 172 , 174 , 182 , 204
Подматрица (sub-matrix) 341 , 354
Поле (field) 302 , 303
Полезностей соединение (utility
aggregation) 596
Полезность измеримая (measurable
utility) 596
— количественная (cardinal) 596
Политика интегральной экономической
стабилизации (integral stabilisation
policy) 213
— пропорциональной экономической
стабилизации (proportional stabilisation
policy) 213 , 217
— экономической стабилизации ,
ориентирующаяся на производные
(derivative stabilisation) 213 , 219
Потребление независимое (autonomous
consumption) 60 , 61 , 167
Предельная склонность к потреблению
(marginal propensity to consume) 58 —
60 , 64 , 68 , 75 , 79 , 87 , 89 , 93 , 158 , 163 ,
164 , 173 , 174 , 183 , 583 — 585
— — к расходованию (to spend) 68
— — к сбережениям (to save) 59 , 62 ,
76 , 79 , 92 , 93 , 106 , 159 , 173 , 174 ,
183 , 184 , 189 , 238
— утечка денежных средств (marginal
leakage) 79 , 81
Предпочтения выявленные (revealed
preferences) 553
— ликвидности (liquidity) 50 , 51 , 56 , 65
— общественные (social) 597
— упорядоченные (ordered) 553 , 554 , 557
Преобразование Лапласа (изображение)
(Laplace transform) 117 — 120 , 122 —
124 , 127 , 129 , 130 , 132 — 134 , 166 ,
209 , 213 , 215 — 218 , 220 , 221 , 234 ,
242 , 247 , 248
Преобразование матриц (of matrices) 375
Принцип акселерации (acceleration
principle) 71 — 73 , 290
— соответствия (correspondence) 262
Продукт конечный (final product) 479 , 517
Пространство векторное (vector space) 328 ,
329
— декартово , двумерное и трехмерное
(Cartesian space of two or three
dimensions) 307 , 308
— эвклидово (Euclidean space) 303 , 306 , 307
Равновесие (equilibrium) 21 — 24 , 56 , 58 ,
60 , 65 , 67 , 80 , 143
— макроэкономическое (macro-economic)
54
— неустойчивое (unstable) 32 , 38
— общее (general) 52 , 56 , 249 , 264
— при росте в геометрической прогрессии
(progressive) 91
— статическое (static) 24 , 156
— устойчивое (stable) 38
Разложение в ряд Тейлора (Taylorexpan-
sion) 27
Размах наблюдений (range of observation)
30
Ранг матрицы (rank of matrix) 352 , 354 ,
366 , 369 , 370 , 389
Распределение вероятностей (probability
distribution) 30
Расходы (затраты) независимые (autonomous
expenditure) 59 — 62 , 68 , 75 , 77 , 78 ,
83 , 89 — 94 , 158 , 167 , 168 , 176 , 179 — 183 ,
191 , 196 , 208 , 215 , 216
Решение взрывное (explosive solution) 144 ,
147 , 150 , 155
— допустимое (feasible) 440 , 456 , 459 — 461 ,
475
— затухающее (damped) 144 , 147 , 150 , 155
— оптимальное допустимое (optimal
feasible) 474
— разностного уравнения , дискретное
(discrete solution of a difference
equation) 139 - 153 , 155 , 157 , 158 , 164 - 166
— — — непрерывное (continuous) 139 ,
165 , 166
Ряд авторегрессивный временной (auto-
regressive time series) 152
Сбережения непредвиденные (unintended
saving) 66 , 87
Сдвиг (shift) 26 , 31
— фазы (phase) 231 , 233
Симплексный метод (simplex method) 460 ,
463 , 520 , 524 , 535
Система Вальраса — Леонтьева замкнутая
(Walras-Leontief closed system) 287
— Вальраса , линейная (linear Walrasian)
467 , 468
— замкнутая (closed) 292 , 293 , 297 , 498 , 501
— Леонтьева , динамическая 290
замкнутая 395 , 400 , 401 , 473
— — линейная 468
— открытая , в том числе Леонтьева
(Leontief's open) 291 , 295 , 297 , 396 —
398 , 400 , 474 , 475
Скаляр (scalar) 302 — 304 , 316
Скалярное произведение векторов (inner
product) 305 — 307 , 317 — 321 , 335
«Скачки» («spurts») 63
Скорость реакции (speed of response) 35 ,
37 , 38 , 41 , 43 — 45 , 62 , 65 , 73 , 74 , 79 — 81 ,
661

83 , 90 , 128 , 131 , 197 , 208 , 210 , 214 ,
215 , 219 , 220 , 226 , 605
Сложение векторов (addition of vectors) 305
— матриц (of matrices) 332
Случай «взрывной» («explosive» case) 104
— «затухающий» («damped») 104
— резонанса (— of resonance) 135
Спрос конечный (final demand) 474 , 475
— независимый (autonomous) 81
Стратегия смешанная (mixed strategy) 409 ,
410 , 423 , 424 , 434 , 437
— чистая (pure) 409 , 414 , 419 , 420 , 423 , 430
«Структурная» постоянная («structural»
constant) 110 , 149 , 151 , 167 — 169
173 , 174 , 161 , 183 , 204 , 210 , 215 , 293 ,
296
Схема авторегрессивная (autoregressive
scheme) 152 , 153
Сходимость (convergence) 65 , 164 , 169 ,
Счета национального дохода (national
income accounts) 397
Темп роста Харрода гарантированный
(«warranted» rate of growth) 77 , 78 , 83
Тенденция (trend) 100 , 102 , 104 , 108 , 110 , 143
Теорема минимаксная (minimax theorem)
418
Теория «заемных средств» (loanable funds
theory) 50
— игр (of games) 18 , 404 — 406
— ожиданий (of expectations) 18
— принятия решений (of decision taking)
18
— роста Харрода — Домара (Harrod—
Domar growth) 75 , 77 , 78 , 106 , 158
в дискретной форме (in period
form) 83
— Самульэсона — Хикса (Samuelson —
Hicks) 191
— стоимости (of value) 541
— Филлипса (Phillips') 191
— фирмы (of firm) 18 , 502 , 505 , 512
— экономических циклов (trade cycle) 18
175
Хикса (of Hicks) 18 , 167 , 177
— экономического благосостояния
(welfare economics) 18 , 595 , 596 , 598
Топология (topology) 307
Точка внутренняя (interior point) 482
— граничная (boundary) 482
— допустимая (feasible) 480 , 481
— поворотная (turning) 114
— равновесия (equilibrium position) 27 ,
30 , 31 , 37 , 38 , 55 , 551
— седловая (saddle point) 412 — 414 ,
416 — 418 , 424 , 428 , 430
— экстремальная (extreme) 310 , 311
— эффективная (efficient) 486 , 492 , 493 ,
495
Укрупнение (aggregation , aggregation
problem) 18 , 47 , 48 , 573
Умножение матриц (multiplication of
matrices) 334 , 343
на скаляр (by scalar) 328 , 333 , 334
Управляющие системы с замкнутой цепью
(closed-loop control systems) 224 , 243
Уравнение вспомогательное (subsidiary
equation) 119 , 120 , 123 , 126 , 127 , 130 ,
133 , 158 , 216
— характеристическое (auxiliary) 107 ,
108. 111 , 113 — 117 , 125 , 127 , 129 ,
131 — 133 , 148 — 150 , 152 — 156 , 158 —
160 , 162 - 164 , 170 , 184 , 186 , 187 , 189 ,
190 , 602
— — квадратной матрицы 381
Устойчивость рыночного равновесия
(stability of market equilibrium) 36 ,
258 , 259 , 393
Фаза колебаний (phase of oscillation) 134 ,
151 , 161 , 178 , 180 , 181
Факториал л(п) (factorial x(n)) 144
Факторы дефицитные (scarce factors) 494 ,
495 , 522 — 524 , 530 , 533 , 535 , 538 ,
569 - 572
— (множители) затухания (damping) 109 ,
— первичные (primary) 470 , 483 , 492 — 494
— производства (production) — 21 , 259.
264 - 266 , 269 - 271
— свободные (free) 494
Функция благосостояния общества (social
welfare function) 597
— времени , временная (function of time)
21 , 58 , 106 , 118 , 127 , 133 , 134
— дополнительная (complementary) 100 ,
101 , 142 , 155 , 158
— женератриса (generating) 166
— передаточная (обратной связи)
(transfer , feed-back) 231 — 237 , 235 — 237 ,
241 , 246 - 248
— полезности (utility) 250 , 541 , 542 , 545 ,
546 , 552
порядковая (ordinal) 543 , 544 , 534 ,
597
— потребления (consumption function) 57 ,
59 , 67 , 74 , 87 , 94 , 161
— — с запаздыванием (lagged) 90
— предложения (supply) 259
— производственная (production) 256 , 257 ,
264 — 268 , 272 , 279 , 281 , 475 , 476 ,
503 — 507 , 509 — 511 , 515 , 597
— разрывная (discontinuous) 118
— сбережений (saving) 57 , 59 , 83
— синусоидальная (sinusoidal) 110 , 114 ,
118 , 151 , 153 , 180 , 605
— спроса (demand) 47 , 259 , 544
— статистических решений (statistical
decision function) 405
— ступенчатая (step) 21 , 118 , 216
— частоты и затухания (of frequency and
damping) 134
Цена игры (value of game) 420 , 422 , 427 ,
429 — 431 , 447 , 452
— предложения (supply price) 280
— равновесия (equilibrium price) 21 , 22 ,
30 , 111 , 112 , 259 , 263 , 280
Частота колебаний (frequency of oscillation)
202
Эйлера теорема (Euler's theorem) 505 , 509
— формула 110
Экономика замкнутая (closed economy) 48
Эластичность спроса от цены (price-
elasticity of demand) 582
— стохастические (stochastic) 18
Эффект «мультипликатора» («multiplier»
effect) 224
— «резонанса» («resonance») 182
— «Эхо» («echo») 94
Элементы знакочередующиеся (alternating
elements) 186
662

ОГЛАВЛЕНИЕ
Альб. Л. Вайнштейн. Вступительная статья 5
Предисловие автора к первому изданию . 13
Предисловие автора ко второму изданию 15
Введение 17
Глава 1. Паутинообразная модель и другие простые динамические модели . . 21
1.1. Обозначения 21
1.2. Паутинообразная модель 22
1.3. Простая непрерывная модель 25
1.4. Общие свойства моделей 27
1.5. Эконометрическая задача . 30
1.6. Углубление паутинообразной модели 31
1.7. Модель со включением запасов 32
1.8. Устойчивость рыночного равновесия 36
1.9. Запаздывания в динамических моделях 39
Глава 2. Кейнс и классические модели: мультипликатор 47
2.1. Макроэкономические переменные и зависимости ......... 47
2.2. Формулировка кейнсианского предпочтения ликвидности 50
2.3. Общее равновесие. Модель Модильяни 52
2.4. Динамическая денежная модель 54
2.5. Макроэкономические модели в «реальном» выражении 56
2.6. Статический мультипликатор 58
2.7. Модель с динамическим мультипликатором 61
2.8. Зависимость между сбережениями и капиталовложениями 65
2.9. Рынки товаров и факторов производства 67
Глава 3. Принцип акселерации 71
3.1. Независимые и индуцированные капиталовложения 71
3.2. Акселератор 73
3.3. Теория роста Харрода — Домара 75
3.4. Модель мультипликатора Филлипса 79
3.5. Модель Филлипса с мультипликатором-акселератором 81
3.6. Теория роста Харрода — Домара в дискретной форме 83
3.7. Модель Самуэльсона — Хикса, включающая мультипликатор и аксе- »
лератор 87
3.8. Возможность равновесия при росте в геометрической прогрессии ... 91
3.9. Распределенные капиталовложения. Дискретный и непрерывный анализ 93
Глава 4. Математическая часть. Линейные дифференциальные уравнения ... 96
4.1. Дифференциальные уравнения 96
4.2. Основные выводы; начальные условия и произвольные постоянные . . 98
4.3. Линейные дифференциальные уравнения первого порядка 102
4.4. Линейные дифференциальные уравнения с постоянными коэффициентами
второго порядка 107
4.5. Линейные дифференциальные уравнения с постоянными коэффициентами
произвольного порядка 113
4.6. Преобразование Лапласа 117
663

4.7. Интегрирование линейных дифференциальных уравнений с постоянными
коэффициентами методом преобразования Лапласа 123
4.8. Непрерывно распределенное (экспоненциальное) запаздывание . . . 127
4.9. Применение р = а-\-ш 131
Глава 5. Математическая часть. Линейные разностные уравнения 136
5.1. Разностные уравнения 136
5.2. Дискретное решение разностного уравнения Основные результаты
и свойства 139
5.3. Линейные разностные уравнения первого порядка 144
5.4. Линейные разностные уравнения второго порядка 148
5.5. Линейные разностные уравнения общего вида 153
5.6. Экономические иллюстрации 156
5.7. Отставания, распределенные запаздывания и мультипликатор-акселе
ратор 160
5.8. Непрерывные решения разностных уравнений 165
Глава 6. Теория экономического цикла Самуэльсона — Хикеа 167
6.1. Простая модель мультипликатора-акселератора с концентрированными
капиталовложениями 167
6.2. Подробное решение простой модели 170
6.3. Интерпретация решения 173
6.4. Приложение к теории экономического цикла 175
6.5. Циклы в движении запасов 177
6.6. Колебания независимых капиталовложений 179
6.7. Более общая модель с распределенными капиталовложениями .... 183
6.8. Исследование концентрированных (скученных) капиталовложений 184
6.9. Анализ распределенных капиталовложений 187
Глава 7. Теория экономического цикла Гудвина, Калецкого и Филлипса ... 191
7.1. Введение 191
7.2. Простой вариант модели Гудвина 193
7.3. Дальнейшее развитие модели Гудвина 196
7.4. Ранний вариант модели Калецкого 199
7.5. Решение дифференциально-разностного уравнения 202
7.6. Модели Калецкого. Позднейшие варианты .• 205
7.7. Модель экономического регулирования Филлипса 208
7.8. Политика экономической стабилизации 213
7.9. Некоторые иллюстрации политики экономической стабилизации . . . 217
Глава 8. Экономическое регулирование. Управляющие системы с замкнутой
цепью 224
8.1. Схематическое представление экономических моделей 224
8.2. Представление некоторых экономических моделей в форме блок-схем 226
8.3. Реакция линейной модели на ввод синусоидальных изменений .... 230
8.4. Передаточная функция обратной связи 235
8.5. Свободные вариации в замкнутой линейной системе 237
8.6. Инженерный подход. Линейные и нелинейные системы 241
8.7. Регулирование в системах замкнутых цепей 243
8.8. Политика экономической стабилизации 245
Глава 9. Общее экономическое равновесие 249
9.1. Равновесие в сфере обмена 249
9.2. Равновесие при неизменных коэффициентах производства 251
9.3. Общее рыночное равновесие 254
9.4. Подсчет уравнений 257
9.5. Устойчивость рыночного равновесия 258
9.6. Некоторые проблемы сравнительной статики 261
9.7. Производственные функции 264
9.8. Производственная функция как матрица 268
664

Глава 10. Межотраслевые связи 272
10.1. Анализ затрат и выпуска отраслей народного хозяйства 272
10.2. Матрица межотраслевых потоков 273
10.3. Открытая модель Леонтьева 278
10.4. Матрица межотраслевых потоков в денежном выражении 281
10.5. Матрица коэффициентов затрат 282
10.6. Решение для случая трех отраслей 285
10.7. Замкнутая система Вальраса — Леонтьева « . 287
10.8. Динамическая система Леонтьева 290
10.9. Решение динамической системы для случая двух отраслей 293
Глава 11. Математическая часть. Векторы и матрицы 298
11.1. Введение 298
11.2. Линейные уравнения и преобразования 300
11.3. Векторы .' 302
11.4. Векторная алгебра 304
11.5. Линейные комбинации векторов. Выпуклые множества 307
11.6. Матрицы 312
11.7. Векторы и матрицы 316
11.8. Сокращенное обозначение суммирования символом 2; скалярные
произведения 317
11.9. Определители 321
Глава 12. Математическая часть. Матричная алгебра 325
12.1. Введение; основные правила алгебры 325
12.2. Иллюстрация действий над матрицами 329
12.3. Равенства, неравенства матриц, сложение матриц и умножение
матрицы на скаляр 332
12.4. Умножение матриц 334
12.5. Транспонирование матриц 341
12.6. Умножение векторов и матриц 343
12.7. Обратные матрицы. Величина определителя матрицы 347
12.8. Эквивалентность и ранг матриц 352
12.9. Квадратные матрицы 356
Глава 13. Применение векторной и матричной алгебры 363
13.1. Линейная комбинация и линейная зависимость 363
13.2. Система линейных уравнений и ее решение 368
13.3. Линейные преобразования 375
13.4. Характеристическое уравнение квадратной матрицы . 381
13.5. Квадратичные формы 385
13.6. Устойчивость состояния равновесия рынка . . .* 393
13.7. Статическая система Леонтьева 395
13.8. Матрицы межотраслевых потоков 398
13.9. Динамическая система Леонтьева 401
Глава 14. Элементарная теория игр / 404
14.1. Экономические применения теории игр 404
14.2. Игра двух участников с нулевой суммой и ее платежная матрица] . . . 405
14.3. Математическое ожидание игры; чистые и смешанные стратегии . . . 409
14.4. Минимакс, седловые точки и решения игр 412
14.5. Решение для платежной матрицы 2x2 416
14.6. Графическое решение для игр с платежной матрицей 2 X п 420
14.7. Общий случай игры двух участников с нулевой суммой 423
14.8. Решения конкретных игр 428
14.9. Иллюстрирующие примеры 434
Глава 15. Линейное программирование 440
15.1. Простой пример задачи линейного программирования 440
15.2. Простой пример: двойственная задача • . . . . 444
15.3. Приведение задачи линейного программирования к решению игры 446
665

15.4. Общая прямая и двойственная задачи линейного программирования 449
15.5. Эквивалентность общих задач линейного программирования и игры
с двумя участниками и нулевой суммой 451
15.6. Преобразование задач линейного программирования для
вычислительных операций 454
15.7. Некоторые свойства выпуклых множеств 457
15.8. Симплексный метод 460
15.9. Решение симплексным методом простой задачи линейного
программирования 463
Глава 16. Программирование производственных отраслей иТ распределение
ограниченных ресурсов 467
16.1. Введение. Общее экономическое равновесие 467
16.2. Анализ производственных отраслей: понятия и определения .... 469
16.3. Представление "открытой системы Леонтьева в виде задачи линейного
программирования производственных отраслей 473
16.4. Заменяемость в открытой системе Леонтьева 474
16.5. Представление технологических возможностей 477
16.6. Эффективное распределение при неограниченных ресурсах первичных
факторов 483
16.7. Цены и двойственная задача 488
16.8. Эффективное распределение при ограниченных ресурсах первичных
факторов 492
16.9. Динамическое программирование; модель роста Неймана 496
Глава 17. Теория фирмы 502
17.1. Предельный анализ: взаимозаменяемость факторов в производстве . . 502
17.2. Комбинированное производство 506
17.3. Предельный анализ и линейное программирование деятельности фирмы 510
17.4. Технология фирмы 513
17.5. Две иллюстративные задачи линейного программирования 516
17.6. Задача линейного программирования для фиксированных факторов
и заданных цен на продукты 523
17.7. Парадокс Рикардо 528
17.8. Задача линейного программирования для случая неизменной
структуры спроса 532
17.9. Пример специализации 537
Глава 18. Теория стоимости 541
18.1. Полезность. Порядковая интерпретация полезности 541
18.2. Спрос потребителя 544
18.3. Влияние дохода и влияние замены 546
18.4. Графическое изображение 550
18.5. Измеримость полезности 553
18.6. Способы потребления и линейное программирование 559
18.7. Задача линейного программирования, касающаяся технологии
производства и вкусов потребителей (структуры спроса) 562
18.8. Некоторые иллюстративные примеры 566
Глава 19. Проблема укрупнения 573
19.1. Сущность проблемы укрупнения (aggregation) 573
19.2. Простой пример: укрупнение по индивидуальным потребителям . . 575
19.3. Простой пример: укрупнение по товарам 579
19.4. Противоречия между микро- и макросоотношениями 582
19.5. Усложнение простых примеров 586
19.6. Суммирование по потребителям и по товарам 589
19.7. Общий случай: одно макросоотношение 592
19.8. Теория экономического благосостояния 595
Приложение А. Алгебра операторов 599
1. Операторные методы 599
666

2. Операторы D и D 599
3. Правила применения операторных выражений к некоторым элементарным
функциям 602
4. Интегрирование линейных дифференциальных уравнений с постоянными
коэффициентами . . * 604
5. Операторы Е и Е'1 606
6. Разностный оператор А 607
7. Решение линейных разностных уравнение 608
Приложение Б. Альб. Л. Вайиштейн. Необходимые сведения о комплексных числах 610
1. Основные понятия 610
2. Алгебраические действия • 610
3. Тригонометрическая форма комплексного числа 611
4. Показательная форма комплексного числа ... 612
5. Алгебраические уравнения и свойства их корней 612
6. Колебательные процессы .... 614
7. Комплексное представление колебательного процесса 616
8. Дифференцирование, интегрирование и комбинирование колебательных
процессов 617
Приложение В. Решения и указания к задачам и упражнениям 620
Библиография 647
Именной и предметный указатели 656

Р. Аллен
МАТЕМАТИЧЕСКАЯ
экономия
Редактор А. И. Латышев
Художник А. Г. Антонова
Технический редактор
Л. М. Харьковская
Сдано в производство 26/IX 1962 г.
Подписано к печати 26/III 1963 г.
Бумага 70Х 108i/i6=20,9 бум. л.
57,3 печ. л. Уч.-изд. л. 57,6 Изд.
«No 8/0102. Цена 3 р. 61 к. Зак. 461.
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1-й Рижский пер., 2
Московская типография № 5
Мосгорсовнархоза
Москва, Трехпрудный пер., 9

ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.
11
53
62
156
211
Строка
13 св.
2 »
11 сн.
1 сн.
16—17 сн.
Напечатано
в которой
(©)
Wo = l/l-c)
*<2+Y(l-Q)b+YQ =
(/г>—]ЛJ<Г<> —s
Комплексные (а±Ш) а>0
Следует читать
в котором
и
P0P/Q0Po=ll(i-c)
\2 + y(i-Q)X+yQ = 0
Комплексные (aiiw)
(Vv— /sJ<r<» — s a>0
Зак. 461