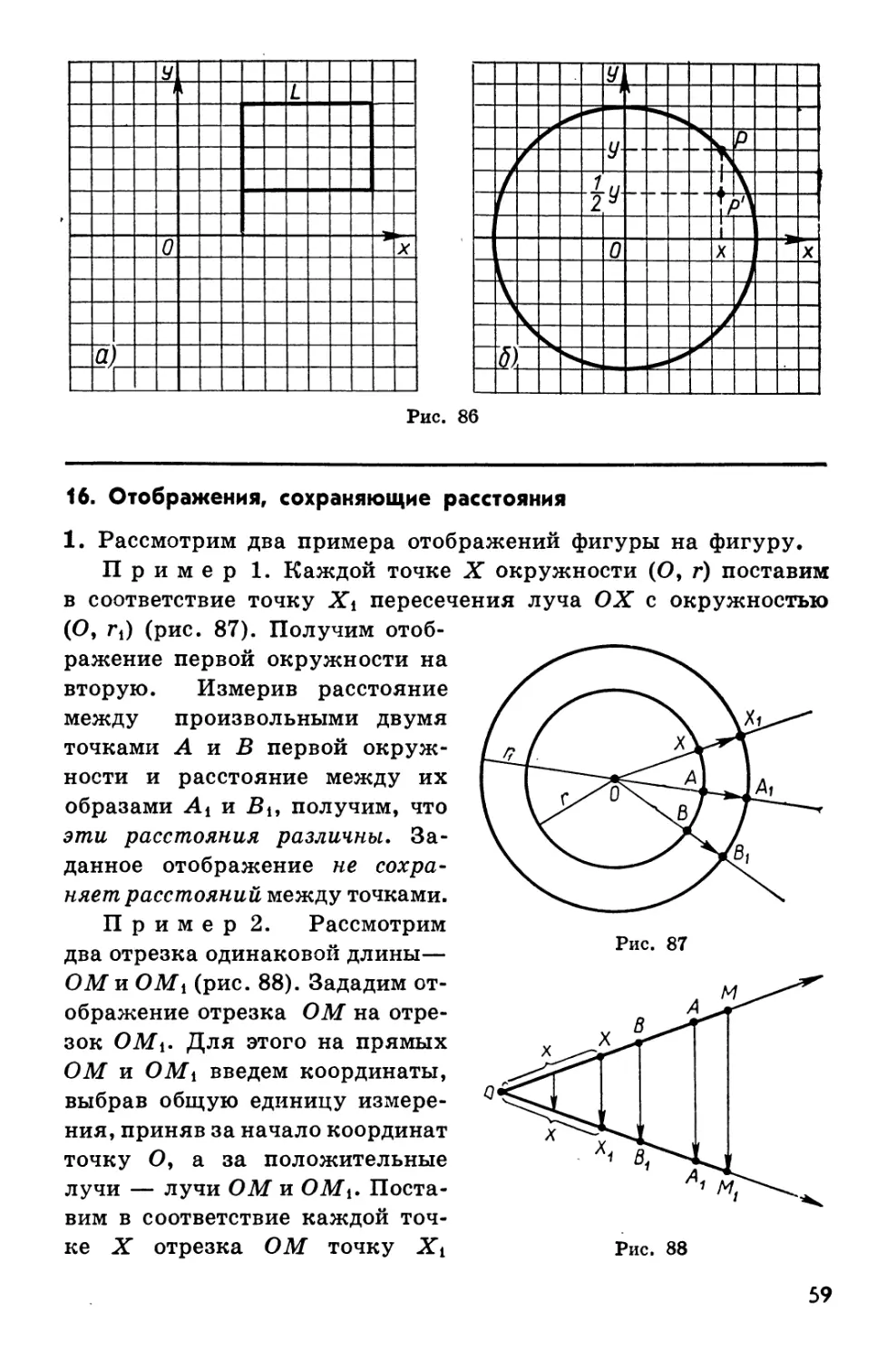
Текст
Α. Η. Колмогоров,
Α. Φ. Семенович,
Р. С. Черкасов
ГЕОМЕТРИЯ
6-8
УЧЕБНОЕ ^%"JC КЛЛССОВ
ПОСОБИЕ ДЛЯ %J ^Л СРЕДНЕЙ ШКОЛЫ
Под редакцией
А. Н. КОЛМОГОРОВА
Допущено
Министерством просвещения СССР
Издание 3-е, доработанное
МОСКВА
«ПРОСВЕЩЕНИЕ»
1981
22. 151 я 72
К 60
Переработка учебного пособия
выполнена с участием А. М. Абрамова.
60601—176
К инф. письмо 4306020400
103(03)—81 1
© Издательство ♦Просвещение», 1370 г.
(Ё; Издааельстио «Про^е^ение», 1981 г., с изменениями.
ОГЛАВЛЕНИЕ
6 класс
ГЛАВА I. НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
1. Что такое геометрическая фигура? 8
2. Основные понятия, принимаемые без определений 12
3. Величины и числа . . . 13
4. Основные свойства расстояний , , 14
5. Взаимное расположение трех точек на прямой.
Неравенство треугольника 18
6. Отрезок и луч 20
7. Координаты на прямой 23
8. Ломаная 23
9. Плоскость. Планиметрия 2Э
10. Область 33
11. Многоугольник 37
12. Полуплоскость. Угол 40
13. Взаимное расположение двух окружностей ... 44
14 ^ψ. Из истории геометрии 47
Дополнительные задачи к главе I » , 50
ГЛАВА II. КОНГРУЭНТНОСТЬ ФИГУР И ПЕРЕМЕЩЕНИЯ
§ 1. Конгруэнтность
15. Отображения фигур 54
16. Отображения, сохраняющие расстояния .... 59
17. Конгруэнтные фигуры 63
18. Измерение углов 66
§ 2. Перемещения
19. Поворот 70
20. Центральная симметрия · 75
з
21. Осевая симметрия 78
22. Построение треугольников 83
§ 3. Симметрия фигур
23. Оси симметрии окружности 89
24. Оси симметрии отрезка 91
25. Оси симметрии угла и равнобедренного треугольника 94
26. Расстояние от точки до прямой. Свойство
биссектрисы угла 97
27 'ψ. Симметричные фигуры 101
§ 4. Окружность
28. Угловая величина дуги окружности 105
29. Взаимное расположение прямой и окружности . . 107
30. Задачи на построение 110
Дополнительные задачи к главе II 114
7 класс
ГЛАВА III. ПАРАЛЛЕЛЬНОСТЬ И ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
§ 1. Параллельные прямые
31. Параллельность прямых и центральная симметрия 119
32. Аксиома параллельных .... 121
33 Ύ. Неевклидова геометрия. Геометрия и физика 124
§ 2. Параллельный перенос
34. Отношение эквивалентности 127
35. Направления 129
36. Параллельный перенос 132
37. Углы между направлениями 137
38. Сумма углов многоугольника 139
Дополнительные задачи к главе III 142
ГЛАВА IV. МНОГОУГОЛЬНИКИ
§ 1. Треугольники
39. Элементы, определяющие треугольник 146
40. Соотношения между сторонами и углами
треугольника 150
§ 2. Четырехугольники
41. Параллелограмм 153
42. Условие и заключение теоремы 156
43. Прямоугольник 162
44. Ромб 165
4
45. Квадрат 167
46. Теорема Фалеса *"э
47. Трапеция 1*1
§ 3. Площади многоугольников
48. Общие сведения о площадях фигур 174
49. Площадь параллелограмма 178
50. Площадь треугольника 180
51. Площадь трапеции 183
52. Площадь многоугольника . 184
Дополнительные задачи к глазе IV 185
ГЛАВА V. ВЕКТОРЫ
53. Композиция перемещений 191
54 *ψ. Общий способ задания перемещений . . . 19Г>
55. Что такое вектор? 197
56. Векторы и способы их задания 199
57. Противоположный вектор. Сумма векторов . . . 202
58. Законы сложения векторов. Вычитание векторов . 204
59. Умножение вектора на число 208
60. Законы умножения вектора на число 210
61. Координаты вектора 213
Дополнительные задачи к главе V 217
ГЛАВА VI. ПОДОБИЕ
§ 1. Подобие и гомотетия
62. Подобные фигуры 219
63. Гомотетия 223
64. Свойства гомотетии 228
65. Пропорциональные отрезки 231
66 ^ψ. Преобразования подобия 234
§ 2. Подобные многоугольники
67. Признаки подобия треугольников 237
68. Теорема Пифагора 245
69. Подобные многоугольники 248
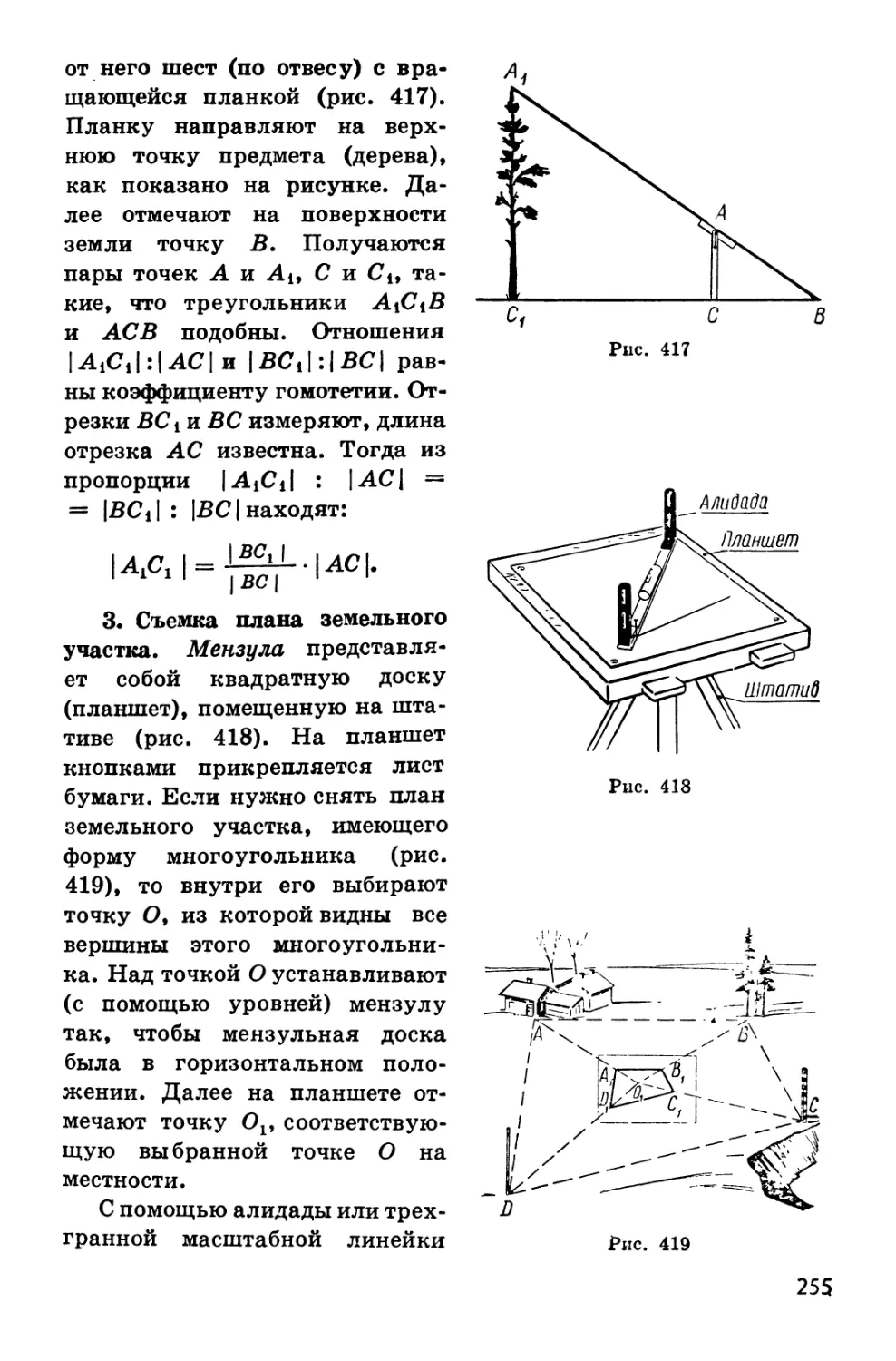
70. Измерительные работы 253
Дополнительные задачи к главе VI 25Э
8 класс
ГЛАЗА VII. ПОВОРОТЫ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 1. Повороты и их композиции
71. Способы задания поворотов 262
72. Угловые величины. Их измерение в радианах 265
73. Композиция поворотов с общим центром .... 267
5
§ 2. Тригонометрические функции
74. Синус и косинус 269
75. Некоторые тождества для функций синус и косинус. 273
76. Таблицы синусов и косинусов 275
77. Тангенс 278
78. Соотношения между сторонами и углами
прямоугольного треугольника 279
Дополнительные задачи к главе VI) · 283
ГЛАВА VIII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ
§ 1. Теоремы косинусов и синусов
79. Теорема косинусоз 285
80. Формулы для вычисления площади треугольника . 288
81. Теорема синусов 290
§ 2. Некоторые применения подобия и формул тригонометрии
82. Применение подобия к решению задач .... 291
83. Измерительные работы 298
84 ^ψ. Решение треугольников 299
Дополнительные задачи к главе VIII 302
ГЛАВА IX ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОУГОЛЬНИКИ
§ 1. Треугольники и четырехугольники
85. Вписанный угол 305
86. Вписанные и описанные треугольники 309
87 ^ψ. Вписанные и описанные четырехугольна ι . . 312
§ 2. Правильные многоугольники
88. Построение правильных многоугольников .... 315
89. Формулы для вычисления стороны и площади
правильного многоугольника 317
§ 3. Длина окружности и площадь круга
90. Длина окружности 320
91. Площадь круга 325
Дополнительные задачи к главе IX 327
ГЛАВА X. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
§ 1. Прямые и плоскости в пространстве
92. Расположение плоскостей в пространстве . . , 329
93. Параллельные прямые в пространстве . . 331
94. Перпендикулярность прямой и плоскости .... 333
§ 2. Многогранники
95. Прямая призма 335
96. Пирамида 338
97 ψ. Общие свойства объемов , 342
§ 3. Фигуры вращения
98. Цилиндр 343
99. Конус 346
100. Шар 348
Дополнительные задачи к главе X 350
Задачи на повторение по курсу 6—8 классов . . . 352
Ответы и указания . , . 331
Приложения
О логическом строении геометрии 373
Формулы геометрии 377
Язык теории множеств в геометрии 380
Формулы тригонометрии —
Греческий алфавит —
Перечень обозначений, встречающихся в учебнике . . 381
Предметный указатель , · 3^2
6
КЛАСС
ГЛАВА
НАЧАЛЬНЫЕ ПОНЯТИЯ
ГЕОМЕТРИИ
В первых пяти классах вы уже
занимались геометрией, знакомились со
многими геометрическими фигурами и
их свойствами; вам известны
некоторые определения геометрических
понятий и некоторые доказательства.
Теперь вы получаете специальную
книгу, в которой излагаются первые
разделы систематического курса геометрии.
Естественно, что в ней будет уделено
внимание и повторению уже
известного материала. Но при этом почти все
известные вам понятия будут точно
определены, а некоторые предложения,
принятые ранее без обоснований,
будут доказаны. О том, как развивалась
геометрия и когда возник интерес к
логической строгости в изложении
геометрии, вы можете прочесть в конце
первой главы.
1. Что такое геометрическая фигура!
1. Отрезки, окружности,
треугольники — все это известные вам
геометрические фигуры. Вам знакомы
также фигуры, изображенные на
рисунке 1.
Что же такое «геометрическая фигура»? Начнем с
примера.
Рассмотрим окружность, радиус которой 1,5 см (рис. 2). Она
состоит из всех точек плоскости, находящихся от центра О на
расстоянии 1,5 см. Например, \АО\ = 1,5 см (эта запись
читается так: расстояние \АО\ равно 1,5 сантиметра). Если точка
Μ не принадлежит этой окружности, то \МО\ Φ 1,5 см.
Радиус окружности, изображенной на рисунке 3, обозначен
через г. Для любой точки X этой окружности \ХО\ = г. Если
точка Μ не принадлежит окружности, то \МО\ Φ г.
Итак, любая окружность состоит из всех точек плоскости,
которые находятся от центра на расстоянии, равном
радиусу этой окружности. Поэтому и принимают следующее
определение.
Определение. Множество точек плоскости, находящихся
на данном положительном расстоянии от данной точки этой
плоскости, называется окружностью.
Окружность с центром О и радиусом г будем обозначать так:
Окр (О, г).
Мы определили окружность как некоторое множество точек.
Каждая геометрическая фигура тоже множество точек. В
геометрии принимают следующее определение понятия
«геометрическая фигура».
Рис. 1 Рис. 3
9
Рис. 4
Определение.
Геометрической фигурой называется любое
множество точек*.
2. Окружность определена как
множество точек, обладающих
указанными свойствами. При
определении других геометрических фигур
поступают так же: указывают
свойства точек, из которых состоит
определяемая фигура.
Дадим, например, определение
круга. Нетрудно заметить, что
точки круга радиуса г лежат в одной
плоскости и удалены от центра О на
расстояние, меньшее или равное г
(рис. 4).
Определение. Множество
точек плоскости, расстояние от
каждой из которых до данной точки
этой же плоскости не больше
данного положительного расстояния,
называется кругом.
Круг с центром О и радиусом г
будем обозначать так: Кр (О, г).
3. Вы знаете много предметов,
имеющих форму шара. Поверхность шара называется сферой*
Например, Земля приближенно имеет форму шара (рис. 5),
а ее поверхность можно считать сферой, точки которой
находятся приблизительно на расстоянии 6400 км от ее центра.
Определение. Множество точек пространства,
находящихся на данном положительном расстоянии от данной точки,
называется сферой.
Определения сферы и окружности очень похожи.
Единственное отличие состоит в том, что в определении окружности
рассматриваются лишь точки, принадлежащие плоскости, а в
определении сферы — точки пространства.
В геометрии множество всех точек называют пространством.
Каждая геометрическая фигура есть подмножество
пространства.
Рис. 5
* Пустое множество также принято считать геометрической фигурой.
to
Вопросы и задачи
1°. 1) Назовите известные вам геометрические фигуры*.
2) Назовите какие-либо предметы, имеющие форму: а)
прямоугольного параллелепипеда; б) шара; в) цилиндра.
2. Постройте окружность с данными центром О и радиусом 4 см.
Отметьте на полученном рисунке (не пользуясь ни циркулем,
кж масштабной линейкой): 1) точки А, В и С такие, что
\ОА\ < 4 см, \0В\ < 4 см, \0С\ < 4 см; 2) точк* D, Ε и F
такие, что \0D\ = 4 см,|ОЕ| = 4 см, \0F\ =4 см; 3)
точки L, Μ и ЛГ такие, что \0L\ >4 см, \ОМ\ >4 см,
\ON\ >> 4 см; 4) запишите с помощью знаков 6 и ί : а)
точка А не принадлежит окружности (О, г); б) точка D
принадлежит окружности (О, г); в) точка L не принадлежит
окружности (О, г).
3°. 1) Принадлежит ли окружности ее центр?
2) Принадлежит ли кругу его центр?
4. Запишите с помощью знаков 6 и £, принадлежат или не
принадлежат данному кругу точки, отмеченные на
рисунке 4.
5. Даны точки А, В и С. Перечислите все геометрические
фигуры, которые содержатся в фигуре: 1) {А, В}; 2) {А, В, С}.
6г Постройте окружность радкуса 3 см. Можно ли найти на этой
окружности такие точки Μ и Ν, для которых: 1) \ΜΝ\ = 2 см;
2) \ΜΝ\ = 3 см; 3) \ΜΝ\ = 6 см; 4) \ΜΝ\ = 7 см?
7°. Сколько существует окружностей дан:-ore pa£*yca г с
заданным центром О: 1) на плоскости; 2) в пространстве?
8°. Приближенно Землю можно считать шаром. 1) Назовите
известные вам из географии названия окружностей с центром
в це:-:тре Земли. 2) Назовите окружности, изображенные на
глобусе.
9*. Орбиты спутников Зеллли часто близки к круговым.
Предполагая, что спутники движутся по круговым орбитам с центром
в центре Земли, ответьте на следующие вопросы. 1) Можно
ли запустить 1000 спутникоз Земли так, чтобы их орбиты не
пересекались? 2) Можно ли вывести на разные орбиты два
спутника Земли так, чтобы их орбиты имели одинаковый
радиус и не пересекались?
* Болео сложные задачи отмечены звездочками. Задачи, номера которых
отмечены нуликом, рекомендуются для усгного решения.
11
10. Постройте две окружности с общим центром О и
радиусами Г! и г2 (п <С г2). Выделите штриховкой фигуры, состоящие
из таких точек X, для которых: 1) \ОХ\ ^ г2; 2) |ОХ| ^ г^·
3) г, ^ |ОХ| <г2.
2. Основные понятия, принимаемые без определений
В предыдущем пункте были даны определения окружности,
круга, сферы, геометрической фигуры. Рассмотрим, как
строятся определения.
Определяя понятие «окружность», мы пользовались
понятиями «множество», «точка», «плоскость», «расстояние». Вообще,
при определении любого понятия употребляются другие
понятия, которые должны быть уже известны. Но нельзя дать
определения всем понятиям. Поэтому некоторые из них приходится
принимать без определений. Такие понятия называются основ-
ними. Все другие понятия определяются.
В нашем курсе геометрии в качестве основных
геометрических понятий приняты следующие четыре понятия: 1) точка;
2) прямая; 3) плоскость; 4) расстояние от одной точки до
другой.
Кроме этих специально геометрических понятий, будем
пользоваться и некоторыми общематематическими понятиями.
Например, в пункте 1 мы уже воспользовались понятием
«множество» (оно относится к числу основных понятий всей
математики). В следующем пункте мы будем говорить о величинах и
числах, которые тоже являются общематематическими понятиями.
Вопросы и задачи
11°. Назовите несколько геометрических понятий, которым
даются определения.
12°. Назовите основные геометрические понятия, которые были
использованы при определении: 1) геометрической фигуры;
2) окружности; 3) круга.
13. Начертите смежные углы ЛОВ и ВОС. Какой фигурой
является пересечение этих углов? объединение этих углов? Дайте
определение смежных углов.
14°. Сформулируйте определение вертикальных углов. Какие
геометрические понятия используются в этом определении?
12
15°. Сформулируйте определение шара.
16. Какие фигуры можно получить как пересечение: 1) двух
кругов; 2) двух окружностей; 3) окружности и круга?
17*. Фигура называется ограниченной, если существует круг,
содержащий эту фигуру. Являются ли ограниченными
фигурами: точка, круг, отрезок, прямая, угол, треугольник, луч,
квадрат? Приведите другие примеры ограниченных и
неограниченных фигур.
3. Величины и числа
Вы уже знакомы с натуральными, целыми и дробными числами.
Встречались также и с различными величинами — длинами,
площадями, объемами.
Приведем два примера.
1) Расстояния между точками, длины отрезков, ломаных и
кривых линий — это величины одного и того же рода. Их
выражают в сантиметрах, метрах, километрах и т. д.
2) Длительности промежутков времени тоже величины
одного и того же рода. Их выражают в секундах, минутах, часах
и т. д.
Величины одного и того же рода можно сравнивать между
собой и складывать:
1 м > 90 см, 350 м + 650 м = 1 км;
3000 с<1ч, 2ч+3ч=5ч;
1 кг > 720 г, 500 г + 500 г = 1 кг.
Но бессмысленно спрашивать, что больше — 1 метр или
1 час, и нельзя сложить 1 метр с 30 секундами.
Длительность промежутков времени и расстояния — величины разного
рода. Складывать и сравнивать величины разного рода
нельзя.
Величины можно умножать на положительные числа и нуль.
В результате умножения величины а на неотрицательное число
χ получается величина Ъ = ха того же рода. Приведем
несколько примеров.
5 · 20 см = 100 см = 1 м,
0,01 · 20 см = 0,2 см = 2 мм,
0 · 20 см = 0 см.
13
Приняв какую-либо величину е за единицу измерения,
можно с ее помощью измерить любую другую величину α того же
рода. В результате измерения получим, что а = хе, где χ —
число. Это число χ называется числовым значением величины а
при единице измерения е. Числовое значение величины зависит
от выбора единицы измерения. Если, например, длина комнаты
имеет числовое значение 5,6 при единице измерения в один метр
(е — 1 м), то эта же длина имеет числовое значение 560 при
единице измерения в один сантиметр (е = 1 см).
Пусть числовые значения величин а и Ъ при одной и той же
единице измерения е равны χ и у, т. е. а = хеу Ъ = уе. Если
X
Ъ Φ 0, то отношение — называют отношением величины а к Ь.
у
Вопросы и задачи
18°. Назовите известные вам единицы измерения длины, площади,
времени, массы.
19. Расположите величины в порядке возрастания: 1) 2 м, 305 см,
24,2 дм, 2416 см; 2) 1050 кг, 1,5 т, 10,52 ц; 3) 90 мин,
3000 с, 2 ч.
20°. Составьте задачи, при решении которых необходимо: 1)
сравнивать величины; 2) складывать величины; 3) умножать
величины на числа.
21. Найдите числовое значение величины а = 3 см, если за
единицу измерения принят: 1) миллиметр; 2) метр; 3) километр.
22°. Как изменится числовое значение величины, если единицу
измерения ее: 1) уменьшить в 10 раз? 2) увеличить в 100 раз?
23. Найдите отношение следующих величин: 1) 2 км к 40 м;
2) 2 τ к 50 кг; 3) 100 кв. м к 4 га; 4) 3 ч к 15 мин.
24. В одной морской миле 1,852 км. 1) Сколько километров в:
а) 3 милях; б) 12 милях; в) 200 милях? 2) Сколько миль
в 1 км?
25. В одной версте 1066,8 м. 1) Сколько километров содержат
а верст? 2) Сколько верст в 1 км?
4. Основные свойства расстояний
1. Вы уже умеете измерять расстояния. Каждым двум точкам
соответствует вполне определенная величина — расстояние от
одной точки до другой. Сформулируем свойства расстояний.
14
Рис. 6
• В
•С
а)
А'
А
В
о)
β)
Рис;
7
С
С
в
\ I Расстояние от одной точки до другой
больше нуля, если эти точки
различны, и равно нулю, если они совпадают:
\АВ\ >0, если А ф В, и \АВ\ = О,
если А = В.
Расстояние от точки А до точки В
(рис. 6) равно 3 см. А каково расстояние
от точки В до точки А? Конечно, тоже
3 см.
2 | Для любых точек А и В расстояние
от А до В равно расстоянию от В до А:
\АВ\ = \ВА\.
Отметьте точки А, Б, С. Измерьте
расстояния \АВ\, \АС\Ч \ВС\ и сравните
сумму \АВ\ + \ВС\ с расстоянием \АС\.
Как бы вы ни выбирали точки А, Б и С,
обнаружится, что расстояние \АС\
меньше или равно сумме \АВ\ + \ВС\ (рис. 7).
3 | Для любых точек А, В, С расстояние \ АС\меньше или
равно сумме расстояний \АВ\ и \ВС\:
\АС\ < \АВ\ + \ВС\.
Свойства 1, 2 и 3 принято называть основными свойствами
расстояний.
2. Основные свойства расстояний практически можно
проверить лишь приближенно и на отдельных примерах. В
геометрии считают, что они соблюдаются точно. В нашем курсе
геометрии эти свойства принимаются без доказательства.
С помощью основных свойств расстояний можно доказывать
другие предложения. Докажем, например, что
4 В для любых точек А, В, С расстояние \АС\ больше или равно
разности расстояний \АВ\ и \ВС\:
\АС\ > \АВ\ - \ВС\.
Доказательство. По третьему свойству
расстояний имеем:
\АВ\ < \АС\ + \ВС\.
Уменьшив обе части этого неравенства на \ВС\9 получим:
\АВ\ - \ВС\ < \АС\9
т. е.
\АС\ > \АВ\ — \ВС\.и *
* Знак В означает, что доказательство закоичено.
15
Предложение, истинность-'
которого доказывается путем
логических рассуждений на
основе принятых ранее
предложений, называется
теоремой. Предложение 4 в нашем курсе геометрии — теорема.
В пункте 2 уже объяснялось, что нельзя дать определения
всем геометрическим понятиям. Некоторые понятия необходимо
принять за основные. Таково же положение с геометрическими
предложениями. Чтобы начать их доказывать, необходимо иметь
какие-то предложения, на которые можно опираться при
доказательствах. Эти основные предложения, принимаемые без
доказательства, называются аксиомами.
Например, в нашем курсе геометрии являются аксиомами
свойства расстояний. За аксиому принимается и предложение:
5 I Через любые две точки проходит одна и только одна пря-
I мая *.
На основе этой аксиомы (ее называют аксиомой прямой)
можно доказать следующую теорему.
б| Теорема. Две прямые имеют не более одной общей точки.
Доказательство. Пусть даны две прямые а и Ъ.
Предположим, что они имеют более одной общей точки — точки
Μ и N (рис. 8). Тогда через две точки Μ и N проходила бы не
одна, а две прямые — прямые а и Ъ. Но это противоречит
предложению 5. ■
Вопросы и задачи
26. При измерении расстояний были получены следующие
результаты: |ХУ| —5 дм, \АВ\ =7 дм, \CD\ = 1 дм. 1)
Запишите эти результаты, если за единицу измерения принять:
а) метр; б) сантиметр. 2) Запишите числовые значения этих
расстояний, если за единицу измерения принять миллиметр.
27. Известно, что \АВ\ =8 см, \ВС\ =4 см. 1) Может ли при
этом условии расстояние \АС\ оказаться равным: а) 20 см;
б) 4,5 см; в) 12 см; г) 4 см; д) 3 см; е) 6 см? 2) Укажите еще
какие-либо возможные значения расстояния |^С|.
* Другая формулировка аксиомы прямой приведена на странице 30.
Заметим также, что, говоря далее «дне ι очки», «три прямые» и т. д., буде.л, как
правило, считать, что рассматриваемые точки, прямые и т. д. различны.
16
28. Расстояние \АВ\ равно 2 см. 1) Каким может быть расстоя-
* ние |АХ"|, где X — произвольная точка окружности (В, 3 см)?
2) Существует ли такая точка С этой окружности, что точки
А, В и С лежат на одной прямой?
29. Ниже приведено несколько равенств и неравенств. Укажите
те из них, которые: 1) верны для любых точек Χ, Υ, Z; 2) для
любых Χ, Υ, Ζ неверны; 3) верны для некоторых Χ, Υ, Ζ.
а) |ΧΖ|<|ΧΥ|+- \ΥΖ\; е) \ΥΖ) <0;
б) \ΧΥ\^\ΖΧ\ + \ΖΥ\; ж) \ΥΖ\>0;
в) \ΥΖ\>\ΧΥ\ + \ΧΖ\; з) \ΧΖ\ — \ΥΖ\>\ΧΥ\;
г) |ΧΖ|>|ΧΥ| + |ΥΖ|; и) \ΧΥ\ + \ΥΖ\^\ ΧΖ\;
д)|ХУ|=|УХ|; к) | ΧΥ\ = \ΥΖ\ = \ΖΧ\.
30. Запишите в принятых обозначениях: 1) точка Μ принадлежит
прямой АВ; 2) точка С не принадлежит прямой АВ.
31°. Прочитайте следующие записи: 1)Α£(!ΓΡ); 2) В g (TN)',
3) МЦАВУ, 4) N t{CD).
32°. 1) Сколько существует прямых, содержащих: а) одну данную
точку; б) две данные точки; в) три данные точки?
2) Сколько линий может проходить через две данные точки?
33°. Могут ли две прямые иметь: 1) только одну общую точку;
2) только две общие точки? Ответ обоснуйте.
34. Сколько прямых определяются тремя точками? (Покажите
возможные случаи на рисунках.)
35. Покажите, что число точек попарного пересечения трех
прямых может равняться 0,1, 2 или 3.
36*. Сколько точек пересечения могут иметь четыре попарно
пересекающиеся прямые? Для каждого возможного случая
сделайте рисунок.
37*. Докажите, что четыре точки могут определять одну, четыре
или шесть прямых (рис. 9).
38*. Докажите, что для любых η точек А\, Аг, ..., Ап существует
круг, которому принадлежат все эти точки.
17
5. Взаимное расположение трех точек на прямой.
Неравенство треугольника
Отметив на прямой три точки, вы увидите, что одна из них
лежит между двумя другими. Например, точка В лежит между
точками А и С (рис. 10). Среди геометрических
понятий,'которые выбраны за основные, нет понятия «лежать между».
Его можно определить, пользуясь понятиями «расстояние»
и «точка». Из рисунка 10 видно, что расстояние \АС\ равно
сумме расстояний \АВ\ и \ВС\. Это выполняется всегда,
если точка В лежит между точками А и С. Дадим теперь
определение.
Определение. Точка X лежит между точками А и В>
если эти точки различны и \АХ\ -f \ХВ\ = \АВ\*.
Рассматривая рисунки 10 и 11, естественно предположить,
что: 1) если три точки принадлежат одной прямой (рис. 10),
то одна из них лежит между двумя другими; 2) если три точки
не принадлежат одной прямой (рис. 11), то ни одна из них
не может лежать между двумя другими.
Эти два предложения мы примем без доказательства и
сформулируем короче:
Рис. 10
три точки принадлежат одной
прямой тогда и только тогда,
когда одна из них лежит
между двумя другими,
С помощью предложения 7
докажем следующую теорему.
8 | Теорема (неравенство
треугольника). Для любых точек
А, В и С, не
принадлежащих одной прямой, расстояние
\АС\ меньше суммы
расстояний \АВ\ и \ВС\.
Рис. 11
Рис. 12
* В житейской практике выражение
«лежать между» употребляется и для трех
точек, не лежащих на одной прямой.
Например, двигаясь по дороге, изображенной
на рисунке 12, мы скажем, что пункт В
лежит между пунктами А и D, а пункт D
лежит между пуньтамн Ρ и С, что не
соответствует принятому в геометрии
определению.
18
Доказательство. Пусть точки А, Б и С не лежат
на одной прямой (см. рис. 11). По третьему свойству расстояний
\АС\ <\АВ\ +\ВС\, т.е. либо | АС\< \ АВ\ + \ВС\, либо
\АС\ = \АВ\ + \ВС\.
Но равенство | АС \ = | АВ | -f | ВС | выполняться не может.
В самом деле, это равенство означает, что точка В лежит между
точками А и С. Но тогда (по предложению 7) точки А, В и С
принадлежали бы одной прямой. Это противоречит условию. Итак,
\АС\ < \АВ\ + \ВС\. в
Вопросы и задачи
39°. Точка X лежит между точками А и В. Верно ли, что точка X
лежит между точками В и А1
40°. Верно ли, что если точка X не лежит между точками А и Б,
то эти три точки не лежат на одной прямой?
41°. Какие геометрические понятия использованы для определения
понятия «лежать между»?
42. Лежит ли одна из точек А, В и С между двумя другими, если:
1) \АВ\ = 5 см, \АС\ = 3 см, \ВС\ = 2 см;
2) \АВ\ = 4 см, \АС\ = 6 см, \ВС\ = 2 см;
3) \АВ\ = 5 см, \АС\ = 4 см, \ВС\ = 6 см?
Постройте эти точки.
43. Покажите на рисунках, как расположены три точки Р, Q
ий, если: 1) \PQ\ + \QR\ = \PR\ ; 2) \PR\ + \QR\ = \PQ\;
3) |ДР| = \RQ\-\PQ\.
44°. На рисунке 13 даны точки А, В и С, лежащие на одной прямой.
Какие из записанных ниже равенств и неравенств верны:
1) \АВ\ + \ВС\ = \АС\
2) \АС\ + \АВ\>\ВС\
3) |ВС| + |АС|>|АВ
4) |АВ| + |БС|>|АС|
5) | АС | — | ЕС | > | АВ
6) \АС\ — |АВ| = |ВС|?
45. 1) Могут ли для трех точек Χ, Υ и Ζ быть верными равенства:
а) \XY\ = 9 см, \ΧΖ\ = 3 см, \ΥΖ\ = 5 см;
б) \ΧΥ\ = 12 см, \ΧΖ\ = 6 см, \ΥΖ\ = 6 см;
в) \ΧΥ\ = 5 см, \ΧΖ\ = 18 см, \ΥΖ\ = 12 см;
г) \ΧΥ\ = 7 см, \ΧΖ\ = 8 см, \ΥΖ\ = 12 см?
2) В каких из этих случаев данные точки лежат на одной
прямой?
Рис. 13
19
46. Расстояние от дома до школы 2 vm, а от дома до станции5 км.
1) Может ли расстояние от школы до станции равняться:
а) 2 км; б) 3 км; в) 6 км; г) 8 км? 2) Укажите наибольшее
и наименьшее из возможных расстояний от школы до станции.
(Сделайте для этих случаев рисунки.)
47*. На рисунке 14 указаны длины стержней, соединенных
шарнирами. 1) Для каждого из этих шарнирных механизмов укажите
наибольшее и наименьшее расстояния, на которые можно
раздвинуть концы А и В стержней. Покажите на рисунках
шарнирные механизмы в этих крайних положениях. 2) Может
ли расстояние \АВ\ принимать все промежуточные значения
между найденными наибольшим и наименьшим
расстояниями?
6. Отрезок и луч
1. На рисунке 15, а изображен отрезок АВ. Этому отрезку
принадлежат точки А и В и все точки, лежащие между ними.
Никакие другие точки отрезку АВ не принадлежат. Поэтому можно
дать следующее определение отрезка.
Определение. Отрезком
АВ называется множество,
состоящее из двух точек А и В
Μ
А
6)
В
Рис. 15
и точек, лежащих между ними.
Точки А и В называются
концами отрезка АВ, а
расстояние | АВ\ — длиной отрезка АВ.
Точки отрезка, лежащие
между его концами, называются
внутренними точками отрезка.
Например, точки X и Μ (см.
рис. 15, а) — внутренние точки
отрезка АВ.
20
Ρ
Μ
α
Рис. 16
Рис. 17
Рис. 18
уже получившими опреде-
Все точки, лежащие между
А и Б, принадлежат прямой АВ
(предложение 7). Поэтому
отрезок АД есть подмножество
прямой АВ, т. е. [АБ] с: (АВ)
(рис. 15, б). Говорят также, что
прямая АВ содержит
отрезок АВ, или отрезок АВ
лежит на прямой АВ.
2. Вы знаете, что каждая
точка произвольной прямой
задает два луча с началом в этой
точке. Теперь разъясним смысл
понятия «луч», пользуясь
только основными геометрическими
понятиями, а также понятиями
ления.
На горизонтальной прямой ρ (рис. 16) одни точки лежат
правее точки О, а другие —левее. Можно заметить, что если
одна из точек прямой ρ лежит правее, а другая — левее точки
О, то точка О лежит между ними. Например, точка О лежит
между точками Μ и Ν, Ρ и Q и т. д. Вообще,
любая точка О прямой ρ разбивает множество отличных от
О точек этой прямой на два непустых подмножества, таких,
что точка О лежит между любыми двумя точками,
принадлежащими разным подмножествам.
"Объединение каждого из этих множеств с точкой О
называется лучом с началом О.
Чтобы задать луч, надо указать его начало и любую точку
этого луча, отличную от начала. Например, луч АВ (рис. 17)
можно назвать и лучом АС, и лучом AD, и т. д. Поэтому на
изображении луча АВ точку В обычно не выделяют (рис. 18).
Луч с началом А, содержащий точку В, обозначают \_АВ).
Дуч АВ является подмножеством прямой АВ, т. е. [АВ) а (АВ).
Вопросы и задачи
48. Пользуясь обозначениями 6 и i, запишите, какие из
указанных на рисунке 19 точек принадлежат и какие не
принадлежат отрезку АВ,
21
щС 49°. Расстояние между точками
А и С равно 10 см. Принад-
• ? * 'β }) лежит ли точка В отрезку
АС, если: 1) \АВ\ = 7 см,
FlIC 19 |ЯС|=Зсм;2) |АВ|=2см,
\ВС\ =9 см; 3) \АВ\ =
Μ Α Β =6,5 см, |ВС|=3,5 см;
-а · · · 4) \АВ\ = \BC\1
рис 20 ^0°. Принадлежат ли точки А, В
и С одному отрезку, если:
1) \АВ\ = 5 см, \АС\ = 4 см, \ВС\ = 6 см;
2) | АВ\ = 5 см, |АС| = 3 см, \ВС\ = 2 см;
3) \АВ\ = 5 см, \АС\ = 7 см, |ДС| = 2 см?
51°. Могут ли два отрезка иметь: 1) только одну общую точку;
2) только две общие точки?
52. Даны различные точки А, В, С и D. Сколько имеется
различных отрезков, оба конца которых принадлежат фигуре,
состоящей из точек: 1) А, В и С; 2) А, В, С и D?
53. Точка X является внутренней точкой отрезка АВ. Докажите:
1) |АХ| < \АБ\] 2) \АВ\ > \ВХ\.
54. 1) Сформулируйте определение середины отрезка.
2) На отрезке CD длиной 18 см взята точка А, такая, что
\СА\ =4 см. Вычислите расстояние между серединами
отрезков: a) CD и СА; б) CD и AD; в) СА и AD.
55. На рисунке 20 изображена прямая α с отмеченными на ней
точками М, А, В. Укажите на этом рисунке фигуру,
состоящую из таких точек X, что: 1) точка А лежит между
точками Μ и X; 2) точка В лежит между точками Μ и X; 3) точка
λ" лежит между точками Μ и А.
56. Запишите в принятых обозначениях: 1) точка Μ принадлежит
лучу О А; 2) отрезок АВ является подмножеством луча АВ;
3) луч ОВ является подмножеством луча АВ; 4) отрезок CD
является подмножеством прямой CD.
57. 1) Какой фигурой является пересечение лучей АВ и ВА1
2) Покажите на рисунках, какой фчгурой может быть: а)
пересечение двух лучей, лежащих на прямой; б) объединение
двух лучей, лежащих на пряллой.
53. Даны два луча, АВ и ВА. Какой из этих лучей содержит
точку М, отличную от точек А и В, если известно, что:
1) \АВ\ + \ВМ\=\АМ\\ 2) \МА\ + \АВ\ = \МВ[;
3) \АМ\ + \ВМ\ = \ЛВ\?
22
59*. Какие основные геометрические понятия были использованы
при определении: 1) отрезка; 2) луча?
60*. Докажите, что если две точки отрезка АВ принадлежат
отрезку СД то эти отрезки лежат на одной прямой.
61*. Объясните, почему звенья выдвижной антенны приемника
лежат на одной прямой.
62**. Докажите, что если различные точки А и В, отличные от
точки О, принадлежат одному лучу с началом О, то либо точка
А лежит между точками О и В, либо точка В лежит между
точками О и А.
7. Координаты на прямой
1. При выбранной единице измерения расстояния выражаются
числами. Часто бывает удобно сами эти числа называть
расстояниями.* Выберем, например, за единицу измерения
расстояние |ίλΕ| (рис. 21). Можно сказать, что расстояния \ΧΖ\9
I XY\ и | ΥΖ\ равны соответственно 3, 4 и 5. (Отрезок ОЕ
называется единичным.)
2. Отметим на луче ОА произвольную точку Μ (рис. 22, а).
При выбранной единице измерения | ОЕ | длина отрезка ОМ
выражается определенным числом: | ОМ\ = хм. Число хм есть
координата точки Μ на луче ОА. Обратно, по заданному числу χ
можно найти на луче ОА одну-единственную точку М, такую
Хм
OEM A
а)
Ρ 1 Μ
-н 1 1——· · 1 1 1 1—*-
В 0 Ε Α
δ)
Рис. 21 Рис. 22
* В задачах практического характера будем обязательно указывать
единицы измерения расстояний (метр, сантиметр и т. д. в зависимости от характера
задачи).
23
что ^расстояние \ОМ\ равно числу х. Сформулируем это важное
свойство луча.
10 I Для любого неотрицательного числа χ на заданном луче су-
I ществует одна и только одна точка, расстояние от которой
| до начала луча равно х.
3. В 5 классе вы познакомились с координатами на прямой.
Для того чтобы ввести координаты на прямой р, выбираются
точка О этой прямой — начало координат и единичный отрезок
(отрезок ОЕ, рис. 22, б). Один из двух лучей с началом О (на
рис. 22, б этот луч отмечен стрелкой) называется
положительным, а другой — отрицательным. Тогда для каждой точки
прямой ρ можно указать вполне определенное число, которое
называется координатой этой точки: начало координат (точка О)
имеет координату 0 (нуль); произвольная точка А
положительного луча имеет координату хА = \ОА\, точка В
отрицательного луча имеет координату хв =— \ОВ\. Например, хЕ = 1,
Хл = 5, хв = —3 (см. рис. 22).
Таким образом, каждой точке прямой ρ соответствует
определенное число — координата этой точки. Верно и обратное:
для любого числа χ на координатной прямой существует одна
и только одна точка, имеющая координату х.
4. Зная координаты двух точек прямой, можно найти
расстояние между ними.
11 | Теорема. Расстояние между двумя точками
координатной прямой равно модулю разности координат этих точек:
\АВ\ = \хв-хА\.
▼* Доказательство. Рассмотрим три случая: 1)
начало координат О лежит между точками А и В; 2) точка А лежит
между точками О и Б; 3) точка
В лежит между точками О и А.
Пусть точка О лежит между
точками А и В и хА < О (рис.
23, а). Тогда хв > 0. В этом
случае
\АВ\ - \АО\ + \ОВ\ =
= —хЛ + Хв = Хв — Ха =
= \хв — ха |.
г)
♦Значком ψ выделен необязатель-
Рис. 23 ный материал.
А
β
δ)
0
д)
А
ш
£
β
ш
0 Ε В
0 Ε А
А В
ρ ξ
24
Если же χα > 0, то χβ < 0 (рис. 23, б) и
\АВ\ = \АО\ + \ОВ\ = хА — хв = |*в — *л |.
Доказательство теоремы для второго и третьего случаев
аналогично (см. рис. 23, β и г).Τ
Вопросы и задачи
63. 1) Постройте точки данной прямой р, удаленные от точки
А 6 ρ на расстояние: а) 1 см; б) 2 см.
2) Сколько существует на прямой ρ точек, удаленных от
точки А 6 ρ на данное расстояние с?
64. Отметьте на прямой пять точек — О, А, В, С, D. Введите на
этой прямой координаты и найдите координаты отмеченных
точек, пользуясь масштабной линейкой.
65. На координатной прямой отмечены точки А (—7), В(—5),
С(1), D{5). 1) Укажите расстояния от этих точек до начала
координат. 2) Вычислите расстояния |АВ|, |АС|, |AD|, \BC\,
\BD\, \CD\.
66. Найдите расстояние \АВ\ при помощи масштабной линейки
с отломанным концом (рис. 24).
67. 1) Вычислите длину отрезка, если координаты его концов
равны: а) 2 и —3; б) 3 и 10; в) —4 и —9; г) — 7 и 15; д) —3, 7
и 7,3; е) 6,8 и —12.
2) Найдите координату середины отрезка АВ, если известны
координаты его концов: а) А (2), В(—3); б) А (3), В (10);
в) А (-4), В(-3).
68. Координаты точек А и В прямой равны соответственно
— 7 и 9. Какие координаты может иметь точка С прямой АВ,
если известно, что: 1) точка С лежит между точками А и В;
2) точка С не лежит между точками А и В1
69. Координаты концов отрезка CD равны соответственно 2 и 5.
Какими станут координаты концов отрезка CD, если он
переместится вдоль координатной прямой:
1) влево на 2 единицы;
2) вправо на 5 единиц;
3) влево на 5 единиц; А в
/i..|....j.- ■; И j ■■■.,!.,.■ , ■■■ lll.l,'fill И1Ц11 III
4) вправо на 3 единицы; ) 5 6 7 s 9
5) влево на а единиц; 1 |
6) вправо на а единиц? Рис. 24
25
8. Ломаная
1. На рисунке 25 изображена
ломаная AiA2A3AAAb. Она является
объединением отрезков ΑιΑ2, А2А3, А3АА>
А4А5. Эти отрезки называют звеньями
ломаной.
Другие примеры ломаных
приведены на рисунке 26. Ломаные,
изображенные на рисунках 26, а, б, г,
простые. Несоседние по порядку звенья
простой ломаной не имеют общих
точек. Ломаные, изображенные на
рисунках 26, б, д, не являются простыми.
Простой ломаной ΑχΑ2 ... Ап (где
η > 2) называется объединение
отрезков ΑιΑ2, Α2Α3, ..., Αη_ιΑη, среди
которых соседние по порядку не лежат
на одной прямой, а несоседние не
имеют общих точек.
Точки Αι, Α2, ..., Ап называют
вершинами, точки Ai и Ап называют
концами ломаной ΑιΑ2 ... Ап.
2. Сумма длин всех звеньев
ломаной называется ее длиной.
12|Теорема (о длине ломаной).
I Длина простой ломаной больше
I расстояния между ее концами.
Докажем эту теорему для
ломаных, состоящих из трех звеньев
(рис. 27).
Дано: AiA2A3A4c — простая
ломаная.
Доказать:
\А,А2\ + \А2А3\ + \AM>\AiAA\.
Доказательство. По
третьему свойству расстояний (с. 15)
\AlA3\+ \AM^\AiAA\. (1)
Точки Аи А2, А3 не лежат на одной
прямой (эти точки — концы соседних
звеньев ломаной). По неравенству треугольника (п. 5)
\АМ <\AiA2\+\A2A9\. (2)
Заменим в неравенстве (1) слагаемое | ΑΧΑ3| суммой |-44A21 +
+ |А2А3|, которая в силу неравенства (2) больше ] ΑιΑ%\. При
такой замене левая часть неравенства (1) увеличится. Поэтому
| А,А2| + \А2А,\ + \А3А,\ > \АХА4\. ш
Аналогично можно провести доказательство теоремы и для
ломаной с любым числом звеньев.
3. На рисунке 28 приведены примеры замкнутых ломаных.
Замкнутые ломаные, изображенные на рисунках 28, α, β, г,
простые. Замкнутые ломаные, изображенные на рисунках 28, б
и 5, не простые.
Объединение простой ломаной А^А2 ... Ап (п > 2) и
отрезка АпА\ называется простой замкнутой ломаной, если
соседние (в круговом порядке) отрезки не лежат на одной прямой,
а несоседние не имеют общих точек.
Замечание. Говоря далее о ломаных, мы всегда
будем иметь в виду простые ломаные (замкнутее или
незамкнутые).
Вопросы и задачи
70°. На рисунке 29 изображены
различные фигуры, являющиеся
объединениями отрезков. Какие из них
являются простыми ломаными?
71. Отметьте в тетради точки так, как
показано на рисунке 30, и постройте
несколько простых ломаных,
вершины которых находятся в этих
точках.
α) δ) в) г) д)
56ГВ9
е) ж) з) и) и)
Л) М) Н) 0) П)
Рис. 29
27
в)
Рис. 30
72°. Приведите примеры ломаных из
окружающей обстановки.
73. На модели куба покажите ломаные:
1) все звенья которых лежат в
одной плоскости; 2) звенья которых
не лежат в одной плоскости.
74. Какое наименьшее число звеньев
может иметь ломаная, два звена
которой лежат на одной прямой?
Начертите такую ломаную.
75. Постройте ломаную ABCDE,
выполните необходимые измерения и
вычислите ее длину.
76. Звенья ломаной КРТМ имеют
длины: \КР\=\ см, |РГ|=2 см,
\ТМ\ = 3 см. Может ли расстояние
\КМ\ оказаться равным: 1) 0,5 см;
2) 6 см; 3) 1 см; 4) 7 см?
(Постройте такую ломаную, если это
возможно.)
77. Какую длину может иметь отрезок
АВ, концы которого соединены
ломаной, имеющей звенья длиной:
1) 3 см, 2 см и 5,5 см; 2) 3 см, 4 см
и 5 см? (Ответ запишите в виде
двойного нерааенства.)
78. Докажите, что длина ломаной ЛВС
меньше длины ломаной АМС
(рис. 31, а).
79. Докажите, что длина ломаной ABC
меньше длины ломаной АМТС
(рис. 31, б).
80. Докажите, что длина ломаной АМС
больше длины ломаной АТКС
(рис. 3?).
Μ
δ)
81°. Какие из фигур, изображенных на рисунке 29, являются
простыми замкнутыми ломаными?
82°. Какое наименьшее число звеньев может быть у замкнутой
ломаной?
83. Покажите, что точки Μ и Т, А и В можно соединить ломаной,
не пересекающей данную окружность (рис. 33). Можно ли
соединить такой ломаной точки А и Т; В и Ml
84**. 1) Сколько существует двузвенных ломаных, вершинами
которых являются точки, изображенные на рисунке 30, а
сторонами— отрезки с концами в этих точках?
2) Сколько таких трехзвенных ломаных?
85*. Дан квадрат ABCD. 1) Покажите, что существуют 5 простых
замкнутых ломаных, все вершины которых — вершины этого
квадрата. 2) Покажите, что существуют 20 простых
незамкнутых ломаных, все вершины которых являются вершинами
квадрата ABCD.
9. Плоскость. Планиметрия
Вы уже имеете представление о плоскости. В пространстве
много различных плоскостей. Например, грани куба (рис. 34)
лежат в шести различных плоскостях.
На рисунке 35 изображены некоторые «кривые»
поверхности — сферическая, цилиндрическая и др. На любой из этих
поверхностей всегда найдутся такие две точки А и Б, что прямая
АВ не будет полностью содержаться в этой поверхности. Для
Рис. 34 Рис. 35
29
Рис. 36
плоскости это не так (рис.
36). Плоскость обладает
следующим свойством:
13 В прямая, проходящая че-
\рез любые две точки
[плоскости, содержится в
\этой плоскости.
Фигура называется
плоской, если она является
подмножеством некоторой
плоскости, т. е. «лежит в
плоскости». Например, окружность и
круг по определению
являются плоскими фигурами. Сфера
и шар — фигуры неплоские.
На рисунке 37
изображен параллелепипед.
Ломаная AKHD — плоская
фигура, а ломаная АВСЕ —
неплоская.
Из приведенного выше свойства плоскости (предложение 13)
следует, что прямая — плоская фигура. Значит, и отрезок, и
луч тоже плоские фигуры.
Часть геометрии, в которой изучаются свойства и взаимное
расположение фигур, лежащих в одной плоскости, называется
планиметрией*. Весь этот учебник (за исключением главы X
и части главы I) посвящен планиметрии. Далее будем
считать, что все рассматриваемые точки, прямые и другие фигуры
лежат в одной плоскости.
Замечание. С применением таких понятий теории
множеств, как «множество», «принадлежит», «пересечение», вы уже
знакомы. В геометрии употребляются и другие выражения.
Например, если точка А принадлежит прямой ρ, то говорят: «точка А
лежит на прямой р» или: «прямая ρ проходит через точку А».
Выражения «лежит на», «проходит через» и т. п. надо уметь
формулировать на языке теории множеств и записывать с
помощью знаков 6, <£, cz, ς£. Например, аксиома прямой на
языке теории множеств формулируется так: для любых двух точек
плоскости существует прямая, их содержащая.
* От латинского planum (равнина, плоскость) и греческого μετπα (мерю).
30
Особо отметим принятое по традиции в
геометрии употребление глагола
♦пересекаться». На рисунках 38,39, 40
изображены пары отрезков, пересечение которых
состоит из одной точки. Но в геометрии
только в одном случае говорят, что эти
отрезки пересекаются,— в том случае,
когда эти отрезки имеют только одну
общую внутреннюю точку (рис. 38).
Также считают, что:
1) отрезок и прямая пересекаются,
если прямая содержит одну и только
одну внутреннюю точку отрезка (рис. 41);
2) прямые а и Ъ пересекаются, если
они имеют одну и только одну общую
точку (рис. 42).
Вопросы и задачи
86°. Назовите известные вам: 1) плоские
геометрические фигуры; 2) неплоские
геометрические фигуры.
87. Покажите на моделях: 1) ломаную, все
звенья которой расположены в одной
плоскости; 2) ломаную, не все звенья
которой расположены в одной
плоскости.
88. Покажите не моделях примеры плоских
поверхностей и поверхностей, не
являющихся плоскими.
89. Даны три точки А, В и Ct не лежащие
на одной прямой. Лежат ли β одной
плоскости: 1) прямые АВ, АС и ВС;
2) отрезки АВ, АС и ВС?
90. Укажите, какие из следующих
предложений верны:
1) объединение двух отрезков есть
плоская фигура;
2) двузвенная ломаная есть плоская
фигура;
к
В
Рис. 43
Рис. 44
Μ
L
Рис. 45
D
93.
3) трехзвенная ломаная есть
плоская фигура;
4) трехзвенная замкнутая
ломаная есть плоская фигура;
5) четырехзвенная замкнутая
ломаная есть плоская фигура;
6) объединение двух лучей с
общим началом есть плоская фигура;
7) объединение трех лучей с
общим началом есть плоская
фигура.
Принадлежат или не
принадлежат указанные на рисунке 43
точки заданным прямым? Ответ
запишите в принятых
обозначениях.
1) Прочитайте записи:
а) А6[ЯС]; е) [АБ) cz (CD);
б) Μ^ίΑΒ); ж) [CO) # [М#);
в) К6 (AD): з) (А, В}с[СЛ];
г) LilMNl; M)[MJV]qt[lTZ).
д) Ρ 6 [OF);
2) Пользуясь обозначениями,
принятыми для отрезков, лучей,
прямых, и знаками 6 , i, с:, Ф%
запишите следующие предложения:
а) отрезок ML есть
подмножество прямой XY;
б) отрезок АВ есть подмножество отрезка ML;
в) точка L принадлежит прямой XY;.
г) точка Μ не принадлежит отрезку АВ;
д) отрезок MB есть подмножество луча ML;
е) луч AL есть подмножество луча ML;
ж) отрезок MB не является подмножеством луча BL.
На рисунке 44 изображены две пересекающиеся пр9\^лъ\е ρ
и q с отмеченными на них точками. Запишите в принятых
обозначениях следующие предложения:
1) объединение лучей DE и АС есть прямая р;
2) объединение лучей FA и АВ есть луч FA;
з) пересечение лучей FA и АВ есть луч АВ;
4) объединение отрезков ED и АС есть отрезок ЕС;
32
5) пересечение отрезков EDm АС есть отрезок AD;
6) пересечение лучей CD и AD есть отрезок АС.
94. На рисунке 45 изображена прямая а с отмеченными на ней
точками. Назовите следующие фигуры: 1) [JETM]U[iAf];
2) 1КМ-] П \_LM]; 3) [JTZ] f] [£M]; 4) [#£) П C^M);
5)[iTL)n[iVi).
95. Покажите, выполнив соответствующий рисунок, что
пересечением двух отрезков может быть: 1) пустое множество;
2) точка; 3) один из данных отрезков; 4) отрезок, отличный
от данных.
96. Покажите на рисунках, какой фигурой может быть
объединение двух отрезков, лежащих на одной прямой.
97. Может ли объединение двух различных кругов быть
кругом?
98. Может ли пересечение двух различных кругов быть кругом?
99. Укажите ошибки в записях:
1) (AB)c=.\_CD); 2) [АБ]#(АВ); 3) ,ΙΜΝ)ζ(ΜΝ);
4)ic(MA); 5) IPQ1 ςέ IQPJ, 6) [АЯ]((CD).
100. 1) Начертите две фигуры, объединение которых — круг, а
пересечение — треугольник.
2) Начертите две фигуры, объединение которых —
треугольник, а пересечение — круг.
10. Область
Окружность разбивает множество не принадлежащих ей
точек плоскости на два множества (рис. 46). Точки одного
из этих множеств находятся от центра на расстояниях,
меньших радиуса окружности; точки
другого— на расстояниях, больших ее
радиуса.
Рассматривая рисунок 47,
можно заметите, что каждое из этих
множеств обладает следующими двумя
свойствами:
1) любые две точки множества
можно соединить содержащейся в нем
ломаной или отрезком; Рис. 46
33
2) вместе с любой своей точкой
множество содержит хотя бы один круг
с центром в этой точке.
Любое множество точек, обладающее
этими двумя свойствами, называется
областью.
Множество точек М, для которых
\ОМ\ < г, является областью. Ее
называют внутренней областью
окружности (О, г). Множество точек JV, для
которых |OJV| > г, также область.
Она называется внешней областью этой
окружности (см. рис. 46).
Итак, множество точек, не
принадлежащих окружности, можно
представить в виде объединения двух
областей. Само же это объединение областью
не является: отрезок (или ломаная) с
концами А и В пересекает данную
окружность (рис. 48). Это же можно
сказать иначе:
окружность разбивает множество не принадлежащих ей
точек плоскости на две области.
м
о
\
I
/
Рис. 48
На рисунке 49 приведены другие примеры областей.
Обратите внимание на то, что граница области (на рисунке границы
областей выделены штриховой линией) не содержится в
области. Так, множество точек Μ плоскости (см. рис. 46), для
которых \ОМ\ < г, есть область, но объединение этого
множества с его границей областью не является. В самом деле, для
круга не выполняется второе свойство области. Например,
точка А принадлежит кругу (О, г) (рис. 50), но не существует
круга с центром в точке А, который бы целиком лежал в
данном круге.
ψ Замечание. Определять геометрическую фигуру как
множество точек стали не так давно. В течение многих веков
геометры представляли себе дело иначе. Прямые или
окружности считали чем-то самостоятельным, не состоящим из точек.
Терминология, исходящая из таких представлений, сохраняется
по традиции и в настоящее время.
34
Вы могли убедиться в том, что
подход к фигурам как к множествам точек
удобен. Он позволяет дать простые и
ясные определения окружности, круга,
отрезка, луча, простой ломаной,
простой замкнутой ломаной, а также многих
других геометрических понятий.
Теоретико-множественный подход
иногда приводит к необходимости
различать фигуры, которые с более наивной
наглядной точки зрения неразличимы.
Как, например, различить на глаз
круг, ограниченный данной
окружностью, и внутреннюю область этой
окружности или шар и внутреннюю
область ограничивающей его сферы? Если
представить себе шар в виде
апельсина, то, чтобы представить себе
его внутреннюю область, потребуется
снять с него «кожуру», которая совсем
не имеет толщины.
Отвлечение от непосредственных
возможностей эксперимента
характерно уже для первых шагов
геометрии. Еще древнегреческие геометры
представляли прямую совсем не
имеющей толщины, но зато
простирающейся в обе стороны неограниченно, а
точку — совсем не имеющей
протяженности. Только для этих идеальных
прямых и точек могут с полной
точностью соблюдаться такие
геометрические положения, как, например,
аксиома прямой, в силу которой через две
точки проходит одна и только одна
прямая, ψ
Вопросы и задачи
101. 1) На сколько областей разбивают плоскость: а) две
окружности (рис. 51); б) три окружности (рис. 52)?
2)* На сколько областей могут разбивать плоскость: а) две
окружности; б) три окружности?
102· На сколько областей разбивают плоскость фигуры, которые
являются объединением лучей (рис. 53)?
103. Даны три точки А, В и С, не лежащие на одной прямой. На
сколько областей разбивает плоскость: 1) замкнутая ломаная
ABC; 2) объединение прямых АВ, ВС и АС1
104. Покажите, что фигуры, изображенные на рисунке 49,
являются областями.
105. 1) Объясните, почему не является областью: а) отрезок;
б) простая замкнутая ломаная; в) множество точек, не
принадлежащих внутренней области окружности.
2) Верно ли, что объединение внутренних областей любых
двух окружностей есть область?
106. На сколько областей могут разбивать плоскость: 1) две
прямые; 2) три прямые?
Рис. 53
36
^ш
t
шшш
11. Многоугольник
1. Простая замкнутая ломаная раз-
бывает множество не
принадлежащих ей точек плоскости на две
области — внешнюю и внутреннюю
(одна из этих областей на рисунке 54
заштрихована). Внешняя область
характеризуется тем, что существует
прямая, все точки которой принад- Рис. 54
лежат этой области; во внутренней
области таких прямых нетДсм. рис.
54). Сама ломаная не содержится
ни в одной из этих областей. Она
является их общей границей.
Определение. Объединение
простой замкнутой ломаной и ее
внутренней области называется мно- Рис. 55
гоугольником.
Точки многоугольника, не принадлежащие его границе,
называют внутренними точками этого многоугольника, точки его
границы — граничными точками. Вершины ломаной, о которой
говорится в определении многоугольника, называют вершинами
многоугольника, а ее звенья — сторонами многоугольника.
Сумму длин всех сторон многоугольника называют его периметром.
По числу вершин (сторон) многоугольники делятся на
треугольники, четырехугольники, пятиугольники и т. д. При
обозначении многоугольника перечисляют его вершины в порядке
их следования. Например, четырехугольник, изображенный на
рисунке 55, можно обозначить ABCD, BCDA, CDAB и т. д.
Отрезок, соединяющий две несоседние вершины
многоугольника, называется его диагональю. Например, отрезки АВ, CDf
EF — диагонали многоугольников (рис. 56).
Рис. 56
37
г) д) ε)
Рис. 57
α) δ) 6)
Рис. 58
2. Определение. Фигура называется выпуклой, если
она содержит любой отрезок, концы которого принадлежат
гтой фигуре.
Например, фигуры, изображенные на рисунках 57, а, г, 9,
выпуклые, а фигуры, изображенные на рисунках 57, б, в, е,
невыпуклые.
Любой треугольник является выпуклой фигурой.
Многоугольники с числом сторон, большим трех, могут быть как
выпуклыми, так и невыпуклыми (рис. 58).
Фигуру, состоящую из одной точки, и пустое множество тоже
считают выпуклыми фигурами.
Вопросы и задачи
107. Начертите треугольник, четырехугольник, пятиугольник.
Выполните необходимые измерения и вычислите периметры
построенных многоугольников.
38
108°. Какая зависимость существует между числом η вершин и
числом ρ сторон многоугольника?
109. Верно ли, что любая ломаная разбивает плоскость на две
области?
110. Сколько вершин может иметь многоугольник, если он
является пересечением: 1) двух углов; 2) двух
треугольников?
111*. Покажите на рисунках, какие фигуры могут быть
пересечением двух треугольников.
112°. Назовите известные вам выпуклые фигуры.
113°.Является ли выпуклой фигурой: 1) отрезок; 2) луч; 3)
фигура, состоящая из трех точек?
114°. Является ли выпуклой фигурой: 1) треугольник; 2)
четырехугольник?
115°. Является ли выпуклой фигурой: 1) круговое кольцо (рис. 59, а);
2) круг без одной своей точки — центра круга; 3) плоскость
без одной своей точки; 4) полукруг (рис. 59, б)?
116. Может ли объединение двух кругов быть выпуклой
фигурой?
117. Покажите на рисунках, что объединение двух выпуклых фигур
может быть как фигурой выпуклой, так и невыпуклой.
118*. Докажите, что пересечение двух выпуклых фигур есть
фигура выпуклая.
119. Начертите невыпуклый многоугольник и объясните, почему он
является невыпуклым.
120°. Какое наименьшее число вершин может иметь: 1) выпуклый
многоугольник; 2) невыпуклый
многоугольник?
121. На какое наименьшее число
треугольников можно разбить выпуклый п-угольник
лучами, общее начало которых находится
в одной из вершин многоугольника
(п > 3)?
122. Верно ли, что любой многоугольник
содержит все свои диагонали?
123*. Существует ли многоугольник: 1) число
диагоналей которого равно числу его
сторон; 2) число диагоналей которого
больше числа его сторон? р 5д
39
12. Полуплоскость. Угол
А 1. Произвольная прямая ρ разбивает
множество не принадлежащих ей
точек плоскости на две области (рис. 60).
Точки Ау Б, С, например,
принадлежат одной области, а точки D, Е> К —
другой.
Каждая из полученных областей
является выпуклой фигурой, так как
вместе с любыми двумя точками она
содержит и соединяющий их отрезок.
Например, отрезок DE содержится в
одной области. Итак,
14 I любая прямая разбивает множество не принадлежащих ей
I точек плоскости на две выпуклые области.
Если точки Аи В принадлежат одной и той же области,
ограниченной прямой р, то . существует соединяющий эти точки
отрезок или ломаная, которые не пересекают прямую р. Если
же точки принадлежат различным областям, то отрезок с
концами в этих точках (так же как и любая ломаная, их
соединяющая) пересекает прямую ρ (см. рис. 60).
Определение. Объединение прямой ρ и одной из
ограниченных ею областей называется полуплоскостью с границей р.
Полуплоскость с границей ρ принято обозначать так: [р, С),
где С — произвольная точка этой полуплоскости, не
принадлежащая прямой р.
2. Два луча с общим началом разбивают плоскость на две
области (рис. 61).
Определение. Объединение двух лучей с общим
началом и одной из ограниченных ими областей называется
углом.
—4 Два луча О А и ОВ с общим
началом определяют два угла. Каждый из
них называется углом АОВ (или углом
ΒΟΑ) и обозначается Ζ. АОВ (Δ.ΒΟΑ).
Лучи ОА и ОВ называются сторонами
угла АОВ, точка О — его вершиной.
Тот из двух углов, который хотят
рассматривать, на чертеже обычно
Рис. 61 выделяют дугой.
40
Рис. 62
Рис. 63
Рис. 64
Центральный yeonJ\OB
Если лучи О А и QB не лежат на одной прямой (рис. 62),
го один из углов со сторонами ОА и ОВ является выпуклым
углом, другой — невыпуклым. На рисунке 62 выпуклый угол
отмечен одной дугой, невыпуклый — двумя дугами.
Вы знаете, что угол называется развернутым, если его
стороны составляют прямую
(рис. 63).
3. Пользуясь известными
вам геометрическими
понятиями, а также понятиями
пересечения и объединения
фигур, можно определить
некоторые другие фигуры.
Угол АОС, изображенный
на рисунке 64, является
суммой углов АОВ и ВОС.
Вообще, объединение двух
углов, имеющих общую
вершину, называется суммой этих
углов, если их пересечением
является луч.
Угол с вершиной в
центре окружности называется
ее центральным углом
(рис. 65, а). Пересечение круга
и его центрального угла
называется сектором (рис. 65, б).
Пересечение окружности и
ее центрального угла
называется дугой
окружности (рис. 65, в).
Два луча О А и ОВ с
общим началом в центре О рис. 65
41
окружности определяют два
центральных угла. Две точки А и В
окружности определяют на ней две
дуги. Чтобы отличить эти
дуги, на каждой из них отмечают
по промежуточной точке
(отличной от концов дуги) и говорят о
дугах АСВ и ADB (рис. 66, а). Эти
дуги принято обозначать так: kjACB
и yyADB.
Отрезок, соединяющий две точки
окружности, называется хордой этой
окружности. Хорда, проходящая
через центр окружности, называется
ее диаметром (рис. 66, б). Хорду
и диаметр окружности называют
также хордой и диаметром круга,
ограниченного этой окружностью.
Пересечение круга и
полуплоскости, граница которой содержит
хорду этого круга, называется
сегментом (рис. 66, б).
Вопросы и задачи
124°. Укажите полуплоскости [т, А), [п, А), [т, В), [п, В)
(рис. 67).
125. В одной или в разных полуплоскостях с общей границей ρ
лежат две точки А и В, если: 1) отрезок АВ не имеет с
прямой ρ общих точек; 2) отрезок АВ имеет с прямой ρ
только одну общую точку, не совпадающую с концом
отрезка; 3) точки А и В можно
соединить ломаной, не имеющей
общих точек с прямой р! (Для
β· ^ν л ^*^ каждого случая выполните ри-
J «д сунки.)
126. Даны две прямые т, η и две точ-
7π п4 ки А и Б (см. рис. 67). Сде-
Рис. 67 лайте чертеж и отметьте штри-
42
ховкой пересечение и объединение полуплоскостей: а) [м, А)
и [л, А); б) [п, А) и [т, В); в) [т, В) и [л, В).
127- Покажите, выполнив рисунки, какие можно получить фигуры
при пересечении: 1) двух полуплоскостей; 2) полуплоскости и
круга; 3) полуплоскости и окружности.
128. Даны прямая ρ и точка А (А( р). Какой фигурой является
множество таких точек X плоскости, что отрезок АХ: 1) имеет
общие точки с прямой р; 2) не имеет общих точек с этой
прямой?
129°-Является ли областью: 1) угол; 2) полуплоскость?
130°. Назовите геометрические понятия, которые были
использованы при определении: 1) угла; 2) центрального угла; 3)
сектора; 4) сегмента.
131. (АВ) Π {CD) = О. По этому условию выполните рисунок и
запишите в принятых обозначениях образовавшиеся
выпуклые углы.
132°. Покажите на рисунке 68 объединение и пересечение углов:
1) АОВ и COD; 2) АОВ и АОС.
133. Установите, верны ли следующие предложения: 1) два угла,
сумма которых есть развернутый угол, являются смежными
углами; 2) два угла с общей вершиной, объединение
сторон которых есть две прямые, являются вертикальными
углами.
134. Запишите, пересечением каких полуплоскостей, заданных
на рисунке 67, является: 1) каждый из вертикальных углов:
a) Z.1 и Z.3, б) Δ.2 и /14; 2) каждый из смежных углов:
a) Z.1 и ZL2, б) ZL3 и ZL4.
135. Углы АОВ и ВОС имеют общую сторону ОВ. Верно ли, что
объединение этих углов является их суммой?
136. Пересечение двух углов — луч. Верно ли, что объединение
этих углов — их сумма?
137. Сколько дуг и сколько центральных
углов определяют две прямые,
проходящие через центр данной
окружности?
138. Концы отрезка КМ лежат на
сторонах угла АОВ. Для каких углов
АОВ будет выполняться
требование: 1) [МК] cz Δ.ΑΟΒ;
2) [МК] gtsLAOBl Рис# 68
43
139*. Во внутренней области угла АОВ дана точка М. Какой
фигурой является множество таких точек X, что отрезок MX
имеет общую точку хотя бы с одной стороной угла?
13. Взаимное расположение двух окружностей
На рисунке 69, а изображены две окружности (Oi, r{) и (02, г2).
Эти окружности не имеют общих точек, т. е. не пересекаются.
Сравнив расстояние h между центрами Οι и 02 с радиусами
окружностей, заметим, что А > π + г2.
r,-r2<h < r1+r2
δ)
Рис. 69
44
Представьте теперь, что первая окружность передвигается
так, что расстояние h между центрами Οι и Оо уменьшается.
Когда расстояние между центрами станет равным сумме
радиусов (А = π + г2), окружности будут иметь только одну
общую точку. О таких окружностях говорят, что они касаются
внешним образом у а их общую точку называют точкой касания
(рис. 69, б).
При дальнейшем уменьшении расстояния h окружности
будут пересекаться, т. е. иметь две общие точки (рис. 69, в). При
этом г{ — г2 < h < η + г2 (считаем rt > г2).
В случае, когда h = rt — г2, окружности имеют лишь одну
общую точку — точку касания (рис. 69, г). Все точки
окружности меньшего радиуса, кроме точки касания, будут
расположены во внутренней области окружности большего радиуса.
В этом случае говорят, что окружности касаются внутренним
образом.
При дальнейшем уменьшении расстояния между центрами,
т. е. при условии h < г{ — г2 (рис. 69, д), окружности не
пересекаются, т. е. не будут иметь общих точек, причем окружность
меньшего радиуса расположена во внутренней области
окружности большего радиуса. В частности, при h = О центры
окружностей совпадут (рис. 69, е). Окружности, имеющие общий центр,
называются концентрическими. Итак, в зависимости от
соотношений между Γι, г2 и h
15 I dee окружности могут не иметь общих точек, могут иметь
I одну или две общие точки.
Вопросы и задачи
140. Каково взаимное расположение двух окружностей, если
расстояние между их центрами 4 см, а радиусы
соответственно равны: 1) 1 см и 3 см; 2) 3 см и 5 см; 3) 2 см и 1 см;
4) 3 см и 7 см; 5) 1 см и 4 см; 6) 4 см и 4 см?
141. Отметьте в тетради такие точки А и В, что \АВ\ =5 см·
Постройте точку X, если известно, что: 1) \АХ\ = 3 см,
\ВХ\ =4 см; 2) \АХ\ =2 см, \ВХ\ =3 см; 3) \АХ\ =
= 6 см, \ВХ\ = 1 см. Сколько таких точек можно построить
в каждом из этих случаев?
142. Начертите окружность (О, г) и постройте точки,
принадлежащие этой окружности и находящиеся на данном расстоя-
45
нии α: 1) от данной вне этой окружности точки М; 2) от
данной на этой окружности точки В. Сколько таких точек можно
построить?
143. Постройте две окружности, каждая из которых проходит
через центр другой. 1) Сколько общих точек имеют эти
окружности? 2) Чему равно расстояние между их центрами?
144. Постройте точки, находящиеся на расстоянии а от данной
точки А и на расстоянии Ъ от другой данной точки В. При
каком условии такие точки существуют?
145. Постройте окружность, которая касается данной
окружности (О, 2 см) в данной точке и имеет радиус, равный: 1) 1 см;
2) 2 см; 3) 3 см. Сколько окружностей можно построить
в каждом из этих случаев?
146. 1) Постройте окружность, которая касается данной
окружности (О, г) в данной на ней точке М. Сколько таких
окружностей можно построить?
2) Постройте окружность данного радиуса г, которая
касается данной окружности (Οι, Γι) в данной на ней точке М.
Сколько решений может иметь эта задача?
147. 1) Постройте окружность, которая проходит через данные
точки А и В (\АВ\ = 2 см) и имеет радиус: а) 3 см; б) 4 см;
в) 1 см. Сколько окружностей можно построить в каждом
из этих случаев?
2) Постройте несколько центров окружностей, проходящих
через точки А и В. Какое можно высказать предположение
о множестве центров всех таких окружностей?
148. На прямой ρ даны точки А и В, \АВ\ = h. 1) Сколько
существует в каждой из полуплоскостей с границей ρ таких
точек X, что |АХ\ = а, \ВХ\ = Ы 2) В каком случае точка X:
а) принадлежит прямой р; б) не принадлежит прямой р?
Рис. 70
46
149*. Даны три окружности: Окр (Οι, Γι), Окр (Ог, Гг), Окр (Оз, Гз).
Выразите расстояния |О1О21v |O2O31 и ΙΟ1Ο31 через радиусы.
г\, г2, г3 (рис. 70, а, б, в).
150**. Докажите, что если две окружности (Οι, Т\) и (Ог, Гг)
касаются, то точка касания принадлежит прямой, проходящей
через центры этих окружностей.
151*. Постройте окружность, касающуюся двух данных
концентрических окружностей. Какой фигурой является множество
центров всех таких окружностей?
14 у. Из истории геометрии
1. Геометрия возникла из нужд практики. Большое число
правил для решения практически важных задач можно найти
уже в древнегреческих папирусах и древневавилонских
клинописных текстах. Древние египтяне умели вычислять площади
прямоугольника, треугольника и трапеции. Площадь круга
« 8
они считали равной площади квадрата со стороной — диамет-
ра. Это довольно точное приближение с ошибкой 0,6%. Наряду
с этим приводилось значительно более грубое приближение для
длины окружности, которую предлагалось считать равной
утроенному диаметру (ошибка около 5%). Египтяне знали, что
треугольник, стороны которого пропорциональны числам 5, 4
и 3, имеет прямой угол. По-видимому, веревочный треугольник
с таким отношением сторон служил для разбивки прямых углов
на местности при делении полей (рис. 71). Вавилоняне в связи
с задачами астрономии умели измерять углы в градусах и
минутах.
Но все это были отдельные практически найденные рецепты,
иногда точные, а иногда лишь приближенные. Сами египтяне и
вавилоняне такого различия, по-видимому, не делали. Не было
ни точных определений, ни отчетливых доказательств.
2. Геометрия как наука систематическая, развивающаяся
при помощи строгих логических
рассуждений, возникла в VI—III вв. до нашей
эры в Древней Греции. Что же позволило
греческим математикам построить
стройное здание науки геометрии? Для этого
им пришлось понять, что при
определении и изучении геометрических фигур Рис. 71
47
следует отвлечься от некоторых свойств,
присущих окружающим нас реальным
телам. Они решили заниматься свойствами
точек, совсем не имеющих размеров,
свойствами линий, совсем не имеющих
толщины, и т. д. Их не смутило то
обстоятельство, что «геометрическую
точку», не имеющую размеров, или прямую,
не имеющую толщины, нельзя увидеть и
«потрогать». Поговорим об этом
несколько подробнее.
На практике люди имеют дело с
телами, имеющими конечные размеры.
Кусок оконного стекла — тело, имеющее
длину, ширину и толщину. Лишь
отвлекаясь от его толщины, мы можем считать
его моделью геометрической
поверхности (рис. 72). Кусок проволоки,
конечно, тоже тело, но его поперечное сечение очень мало по
сравнению с длиной. Отвлекаясь от размеров поперечного сечения
проволоки, мы получаем представление о геометрической
линии (рис. 73). Лишь представив себе тело, все размеры которого
очень малы, и решившись совсем отвлечься от этих размеров,
приходим к понятию геометрической точки.
Из геометрических линий проще всего представить себе
наглядно отрезок, соединяющий две точки: достаточно натянуть
между этими точками шнурок, чтобы получить хорошую модель
отрезка. Отрезок можно продолжить в двух противоположных
направлениях. Лишь представив себе его уже продолженным
неограниченно, «до бесконечности», получаем наглядное
представление о прямой. При этом мы отвлекаемся от того
обстоятельства, что на практике такое продолжение отрезка «до
бесконечности» неосуществимо.
Мы видим, что геометрические понятия являются
отвлеченными, или, как принято говорить, абстрактными понятиями
(абстракция — «отвлечение»). Реальные тела имеют не только
определенную форму и размеры, но и массу, могут быть сделаны
из железа, из дерева и т. д. Отвлекаясь от всех их свойств,
кроме формы и размеров, приходят к представлению о
геометрическом теле. Отвлекаясь от тех или иных размеров тел, приходят
к представлениям о геометрических поверхностях и линиях и,
48
наконец, к представлению о геометри- п *_
ческой точке. Но геометры нашего
времени предпочитают обратный путь: Рис. 74
линии, поверхности, тела и вообще
геометрические фигуры они считают
множествами точек.
Можно спросить себя: для чего все ft\
это делается? Зачем нужно это отвле- .^Ч *
чение? Ответ заключается в том, что
только для абстрактных
геометрических фигур можно сформулировать
ряд простых и весьма важных
предложений.
Например, в геометрии через лю- -—- t ^—
бые две отличные друг от друга точки φ jf
проходит одна и только одна прямая.
В чертежной практике через две дан- Рис. 75
ные на чертеже точки одна определенная
прямая проводится достаточно уверенно только в том случае,
когда точки расположены не слишком близко (рис. 74). А
представьте себе, что в классе московской школы поместили одну
над другой по вертикали две точки на расстоянии 10 см (рис. 75).
С точки зрения геометрии соединяющая их прямая пройдет
сквозь Землю и выйдет на земную поверхность в определенной
точке. Практически мы не можем указать такую точку
совершенно точно. Она будет находиться в южной части Тихого
океана, но где именно, можно указать лишь приближенно.
3. Первый систематический курс геометрии (не дошедший
до нас) был написан Гиппократом Хиосским во второй половине
V в. до нашей эры. В III в. до нашей эры достижения
древнегреческих геометров были объединены в знаменитом сочинении
Евклида «Начала».
Евклид стремился дать определения всем геометрическим
понятиям. Понятий, признанных основными и не подлежащих
определению, он совсем не выделяет. Естественно поэтому, что
как раз определения самых простых понятий у него иногда
весьма расплывчаты. Показательны, например, определения:
«линия — длина без ширины», «прямая линия — такая, которая
одинаково расположена по отношению ко всем своим точкам».
Евклид перечисляет аксиомы, на которых он считает
возможным обосновать всю геометрию. С современной точки
4?
зрения некоторые его доказательства содержат пробелы. Совсем
безукоризненное «аксиоматическое» построение геометрии —
дело ученых конца XIX и начала XX в., когда разными
авторами было дано несколько таких изложений геометрии,
опирающихся на разные системы аксиом. (Одна из возможных
систем аксиом сформулирована в приложении на страницах 373,
374.)
Но шаг в этом направлении, сделанный Евклидом, был едва
ли не самым значительным.
Дополнительные задачи к главе I
152. В пунктах А, В и С находятся радиостанции местной связи;
\АВ\ = 12 км, \ВС\ = 15 км, \АС\ = 21 км. Радиус
уверенного приема станции, находящейся в пункте А, равен 9 км,
станции, находящейся в пункте В,— 12 км, и станции в пункте
С—18 км. Взяв масштаб (1 см — 3 км), изобразите на чертеже
зоны уверенного приема: 1) каждой станции; 2) двух
станций— А и В; 3) станций В и С; 4) всех трех станций; 5) хотя
бы одной станции.
153. Расстояние между точками А и В равно 2 см. Покажите на
чертеже фигуру, состоящую из таких точек X, что: 1) \АХ\ =
= \ВХ\ =0,5 см; 2) |АХ\ = \ВХ\ = 1 см; 3) |АХ|<1,5см,
\ВХ\ < 1,5 см; 4) \АХ\ > 1,5 см, \ВХ\ > 1,5 см. Назовите
полученную фигуру.
154. Постройте пересекающиеся окружности (Οι, Γι) и (02, г2). На
полученном рисунке покажите следующие фигуры:
1) Окр (О,, г,) П Окр (02, г2); 4) Кр (О,, г,) U Кр (02, г2);
2) Кр (0lf г,) П Окр (02, г2); 5) Окр (О,, г,) U Окр (02| г2).
3) Кр (О,, г,) П Кр (02, г2);
155. Покажите, что отношение двух величин не зависит от выбора
единицы измерения, т. е. если Х\ и х2 — числовые значения
величин а и Ъ при единице измерения е\, а у\ и ι/2 — числовые
значения этих же величин при единице измерения е2, то
х\ : *2 = У\ : г/2.
156. Точка А лежит внутри круга (О, г), расстояние \ОА\ равно а.
Докажите, что круг (Аг г — а) содержится в круге (О, г).
50
,
I
в
I
0
I
£
I
I
D
1
a
1
—J
Гпс. 70
Рис. 77
157. На рисунке 76 изображена сеть дорог, соединяющих
населенные пункты Л, В, С, D, Е, F и G, и указаны длины этих дорог
в километрах. Назсвем «расстоянием» между двумя пунктами
длину кратчайшего пути между этими пунктами, проходящего
по сети дорог. 1) Найдите «расстояния»: а) \ЛВ\; б) \ВС\;
в) \CD\; г) \ED\. 2) Проверьте, выполняются ли для этих
< расстояние» основные свойства расстояния? 3) Какие точки
лежат между точками А и В; А и Е; А и D1
158. Покажите, что пять точек могут определять 1, 5, 6, 8 или
10 прямых.
159. Точка С лежит между точками А и В, а точка X— между
точками А и С. Докажите, что точки А, В, С и X лежат на одной
прямой.
160. Точки А, В, С и D не лежат на одной прямой. Докажите, что
\AD\ < \АВ\ + \ВС\ + \CD\.
161. На прямой ρ взяты точки А и В. Покажите на этой прямой
фигуру, состоящую из таких точек X, что: 1) \АХ\ = |ВХ|;
2) |АХ|<|АВ|;3) \АХ\ - \ВХ\ = \АВ\; 4) \АХ\^>\ВХ\.
Назовите полученные фигуры.
162. 1) Приняв за начало координат точку О, луч ОС за
положительный, а отрезок ОЕ за единичный, найдите координаты точек
А, В, С и D (рис. 77). Найдите числовые значения расстояний
|АС|, \BD\, \OA\ и \CD\ при единице измерения |0£?|.
2) Найдите координаты точек О, В, С и D и числовые
значения расстояний \АС\, \BD\, \OA\ и \CD\t если принять
точку А за начало координат, луч AD за положительный, а
отрезок АЕ — за единичный отрезок.
163. Найдите координату середины отрезка с концами А (х) и В (ζ/).
164. На рисунке 78 изображены различные фигуры, являющиеся
объединением отрезков. Какие из этих фигур являются:
51
абвгдеж^ииклмьшп
рстуфхцчшщъыьзюя
Рис. 78
1) простыми ломаными; 2) простыми замкнутыми
ломаными?
165. Существует ли замкнутая ломаная, длины звеньев которой
равны: 1) 2 см, 3 см, 4 см, 10 см; 2) 3 см, 3 см, 4 см, 4 см;
3) 4 см, 5 см, 0,5 см? Ответ обоснуйте (постройте такую
ломаную, если это возможно).
166. 1) Покажите, что существует трехзвенная ломаная длиной За,
содержащая все вершины квадрата со стороной а. Докажите,
что число звеньев и длину такой ломаной нельзя уменьшить.
2) Покажите, что существует семизвенная ломаная длиной 7а,
содержащая все вершины куба с ребром а. Докажите, что
число звеньев и длину такой ломаной нельзя уменьшить.
167. Верно ли предложение: 1) объединение двух областей есть
область; 2) пересечение двух областей является областью?
168. Покажите, что любой выпуклый η-угольник можно получить
как пересечение η полуплоскостей.
169. 1) Докажите, что сумма длин диагоналей любого выпуклого
четырехугольника меньше его периметра, но больше
полупериметра. 2) Верно ли предложение 1) для любого
невыпуклого четырехугольника?
170. Докажите, что число диагоналей η-угольника равно — .
Δ
171°. Какие геометрические понятия были использованы при
определении: 1) простой замкнутой ломаной; 2) многоугольника?
172. Начертите такие два треугольника, что их объединение —
четырехугольник, а пересечение — отрезок.
173°. Сформулируйте определение: 1) касающихся окружностей;
2) пересекающихся окружностей; 3) непересекающихся
окружностей; 4) концентрических окружностей.
174. Как расположены окружности (Οι, Γι) и (02, г2), если:
1) |0,02| =5, п= 2, г2 = 3;
2) |0,02| =7, г,= 3, г2=3;
3) |0,02| =7, г, = 10, г2 = 3;
4) |Οι02| =3, п= 2, г2=5?
52
175°- На рисунке 79 изображено
несколько фигур. Их называют: 1) кольцо
(рис. 79, а); 2) восьмерка (рис. 79, б).
Сформулируйте определения этих
фигур.
176.^_ Докажите, что множество точек кру- α) δ)
га (О, г), не принадлежащих окружно- рИСш 79
сти (О, г), есть область.
177- На сколько областей могут разбивать плоскость: 1) прямая
и окружность; 2) луч и окружность?
178. Может ли пересечение двух углов быть фигурой: 1)
выпуклой; 2) невыпуклой?
179. 1) Найдите множество центров окружностей, касающихся
данной окружности (О, г) в данной точке А.
2) Постройте окружность данного радиуса г, которая
касается двух данных окружностей (Οι, Γι) и (Ог, г2), если эти
окружности: а) не пересекаются, б) касаются, в)
пересекаются.
180. Стороны АВ, ВС и АС треугольника ABC равны
соответственно 4 см, 5 см и 6 см. Постройте три окружности, центры
которых находятся в вершинах треугольника ABC и каждая
из окружностей касается внешним образом двух других.
181. Окружности (Ои Г\), (Ог, г2) и (03, г3) имеют общую точку
касания М, первые две из этих окружностей имеют в этой
точке внутреннее касание. 1) Найдите расстояния |O1O2Iv
|0203| и |Οι03|. 2) Докажите, что точки Ои 02, 03иМ лежат
на одной прямой.
8
ГЛАВА II
КОНГРУЭНТНОСТЬ ФИГУР
И ПЕРЕМЕЩЕНИЯ
г
4\
• ι ι
1
F
0 λ
: l, \
Ί I
§ 1. Конгруэнтность
15. Отображения фигур
1. Из курса алгебры вы знакомы с
понятием отображения множества на
множество. Фигура — множество
точек. Поэтому можно рассматривать
отображения одной фигуры на другую.
Пример 1. Пусть L и Ij — две
окружности с ©бщим центром О
(рис. 80, а). Будем считать, что каждой
точке X первой окружности
соответствует та точка Х{ второй, которая лежит
на луче ОХ. Например, точке А
соответствует точка А и точке В — точка
Б ι (это записывают так: А ->- Aiy
В -> Bt).
Итак, каждой точке первой
окружности соответствует одна точка
второй. При этом каждая точка второй
окружности поставлена в соответствие
некоторой точке первой окружности.
Множество всех точек,
соответствующих точкам окружности L, —
окружность Li. Мы получили отображение
окружности L на окружность Lle
Обозначим это отображение
буквой /. Точку Χι второй окружности,
соответствующую точке X первой
окружности, называют образом точки X
при отображении / и пишут: Xt =
54
= / (X). Если фигура G — часть
окружности L, то фигуру Gi9 состоящую
из образов всех точек фигуры G,
называют образом фигуры G при Αι
отображении / и пишут: Gi = / (G).
Например, κ^ΑιΧι =/(υΑΙ), Lt =
= / (L) (см. рис. 80, α).
Пример 2. Зададим
отображение окружности (О, г) на ее диаметр
АВ (рис. 80, б). Каждой точке X
окружности поставим в соответствие
точку Χι — точку пересечения прямой АВ и перпендикуляра,
проведенного через точку X к этой прямой (точку Χι называют
основанием перпендикуляра). Тогда каждой точке окружности
соответствует одна точка отрезка АВ. (Например, точка А
отображается на себя, точка С отображается на точку F
и т. д.) При этом каждая точка диаметра АВ является образов
хотя бы одной точки окружности. Значит, мы задали
отображение окружности на ее диаметр АВ. Образом
окружности при рассмотренном отображении является отрезок
АВ.
Между этими двумя примерами отображений есть важное
различие. В первом примере каждая точка Χι окружности Li
является образом только одной точки окружности L. Поэтому
по точке Χι можно найти точку X, для которой точка Χι
является образом при отображении /. Такое отображение называется
обратимым. Отображение одного множества на другое
обратимо, если каждый элемент второго множества является
образом только одного элемента первого множества. Для любого
обратимого отображения имеется отображение, ему обратное.
Если Χι — образ точки X при отображении /, то образ точки Χι
при отображении g, обратном /, — точка X. Например,
отображение g, обратное / (пример 1), задано на рисунке 81.
Отображение, заданное во втором примере, необратимо: точка F
является образом двух различных точек С и D (рис. 80, б).
Такое отображение не имеет обратного.
2. В приведенных двух примерах рассмотрены отображения
одной фигуры на другую. Рассмотрим теперь отображения,
при которых образом фигуры является она сама, т. е.
отображения фигуры на себя.
Пример 3. Любую фигуру, в том числе и плоскость,
55
можно отобразить на себя с
помощью тождественного
отображения Е, при котором каждая
точка X этой фигуры
отображается на себя:
Ε (X) = X.
Пример 4. Пусть С —
точка внутренней области
окружности (рис. 82, α), Χ —
произвольная точка этой
окружности. Образом точки X будем
считать вторую точку
пересечения прямой СХ с этой
окружностью — точку Χι.
Получили отображение
окружности на себя. В самом
деле, каждой точке окружности
соответствует единственная
точка этой же окружности
(например, точке Μ соответствует
точка Μι). И каждая точка
окружности является образом единственной точки этой же окружности
(например, точка Х\ есть образ точки X). Рассмотренное
отображение обратимо.
Пример 5. Введем координаты на прямой ρ и каждой
точке Μ (χ) прямой ρ поставим в соответствие точку Μι
прямой р, которая имеет координату χ + 2. Тогда каждая точка
прямой ρ отобразится на определенную точку этой же прямой р.
Например, точка А (3) отобразится на точку At (5), точка
В (—6) — на точку JSi (—4); начало координат О отобразится
на точку С (2). И каждая точка прямой будет образом некоторой
точки этой же прямой. Например, точка В (—6) является
образом точки К (—8) и т. д. Значит, имеем отображение прямой ρ
на себя. Это отображение тоже обратимо.
ψ Пример 6. Каждой точке X отрезка АВ (рис. 82, б)
поставим в соответствие основание перпендикуляра,
проведенного через точку X к отрезку CD. При этом А -> Аи В ->■ Б,,
Μ -> Μι и т. д. Каждая точка X отрезка АВ отобразится на
определенную точку Χι отрезка CD. Но среди точек отрезка CD
56
Рис. 82
есть такие точки, которые не являются образами точек отрезка
АВ при заданном отображении (обозначим его через /).
Итак, образы всех точек отрезка АВ составляют только
отрезок ΑιΒι (но не весь отрезок CDI). Значит, / отображает
отрезок АВ на отрезок А^В\. Можно сказать также: «/
отображает отрезок АВ β отрезок CD>>> но нельзя говорить: «отрезок
АВ отображается на отрезок CD», ψ
Вопросы и задачи
182. На рисунке 83 задано отображение / ломаной AXBCD на
отрезок A\D\\ каждой точке X ломаной соответствует та
точка отрезка, которая лежит на луче ОХ, Ответьте на
следующие вопросы и запишите ответы в принятых обозначениях
(например, f(A) = A\, А-+А\). 1) Какая точка является
образом точки А? точки X? точки L? 2) Какая точка ломаной
отображается на точку Μι? на точку L\l на точку Di? 3) Образом
какой точки является точка А\1 точка Χι? точка С\1 4)
Является ли отображение / обратимым?
183. На рисунке 84 задано отображение
квадрата ABCD на отрезок A\D\i
каждой точке X квадрата
соответствует основание перпендикуляра,
проведенного через точку X к
прямой A\D\. 1) На какую точку
отрезка отображается точка С? точка D1
точка А? 2) Образом какой точки
является точка Hi? точка Pi? 3)
Обратимо ли это отображение?
184. Постройте образы нескольких
точек при отображении: 1)
отрезка АВ на отрезок CD (рис. 85, а),
если соответствующие точки отрез-
. ков лежат на лучах с началом М;
2) луча ОМ на луч ON (рис. 85, б),
если соответствующие точки этих
лучей лежат на окружности с
центром О и 0-^0; 3) замкнутой
ломаной ABC на окружность (О, г)
(рис. 85, в), если соответствующие
точки лежат на лучах с началом О. Αι ρι Ηι
4) Обратимы ли эти отображения? рИСш S4
Рис. 83
€
А
I
Л
X
N
1
Ы ι ι
Μ
»
«
<
1
1 \
к
F
' \
С
D
LJ
57
190.
185. Две окружности касаются: 1)
внешним образом; 2) внутренним
образом. Покажите, выполнив рисунки,
как можно отобразить одну из этих
окружностей на другую.
186. На данной окружности отметьте
точку М. Укажите образ этой точки
при: 1) тождественном отображении
этой окружности; 2) симметрии
относительно центра окружности.
187. Задайте (выполнив рисунок)
отображение, отличное от
тождественного, при котором отображается на
себя: 1) отрезок АВ; 2) замкнутая
ломаная ABC; 3) квадрат ABCD;
4) окружность (О, г).
188. При каких из указанных ниже
отображений координатная прямая
отображается на себя:
1) А(х)->А1(2х);
2) А(х)
3) А{х)-+Аг{х2)\
4) А(х)-^А1(х — 1);
5) ilW^Ajfi);
6) Α (χ) -> Αλ (—χ)?
189*. 1) Укажите при помощи стрелок
все отображения фигуры {А, В, С}
на себя (например, тождественное
отображение этой фигуры
записывается так: А->А, В->В, С->С).
2) Для одного из этих отображений укажите обратное.
1) На координатной плоскости задана фигура L (рис. 86, а).
Каждой точке Р{х, у) поставлена в соответствие точка:
а) Р'(Ъх, Зу); б) Р'(—2х, —2у). Постройте образы фигуры L
при этих отображениях.
2) На координатной плоскости задана окружность (рис. 86, б).
Каждой точке Р(х, у) окружности поставлена в соответствие
точка Р'(х, — у). Постройте образ данной окружности при
этом отображении.
аф
58
Ά
)
У.
ι
0
{
L
—^
χ
δ)
Ψί
Υ~
У
■h
0}
,0"
^
>
г-
φ
ί\
• Λ
W
-ΓΤ"
1
χΤ
\j
Α
_L
t
/
л
-*
—ι
χ]
Рис. 86
16. Отображения, сохраняющие расстояния
1. Рассмотрим два примера отображений фигуры на фигуру.
Пример 1. Каждой точке X окружности (О, г) поставим
в соответствие точку Χι пересечения луча ОХ с окружностью
(О, г4) (рис. 87). Получим
отображение первой окружности на
вторую. Измерив расстояние
между произвольными двумя
точками А и В первой
окружности и расстояние между их
образами Αι и Βί9 получим, что
эти расстояния различны.
Заданное отображение не
сохраняет расстояний между точками.
Пример 2. Рассмотрим
два отрезка одинаковой длины—
ОМ и ОМ ι (рис. 88). Зададим
отображение отрезка ОМ на
отрезок О Mi. Для этого на прямых
ОМ и ΟΜι введем координаты,
выбрав общую единицу
измерения, приняв за начало координат
точку О, а за положительные
лучи — лучи ОМ и ΟΜχ.
Поставим в соответствие каждой
точке X отрезка ОМ точку Χι Рис. 88
Рис. 87
59
отрезка ОМи имеющую ту же координату, что и точка X.
Получим отображение отрезка ОМ на отрезок ОМ\. Для любых
двух точек А и В отрезка ОМ расстояние между образами А^
и В\ этих точек равно |АВ|.
ψ В самом деле, по теореме 11
\АВ\ = \хв — ха]·
Но образы Αι и Б4 точек А и В имеют те же самые координаты,
что и точки А, В. Следовательно,
l-Ai-Btl = \χΒχ — ха, I = \хв — ха I = \АВ\. γ
Если отображение фигуры L на фигуру ii таково, что
расстояние между образами А4 и Βι любых двух точек А и В
фигуры L равно расстоянию | АВ|, то говорят, что это отображение
сохраняет расстоян ия.
2. Отображения, сохраняющие расстояния между точками,
обладают рядом свойств, которыми не обладают другие из
рассмотренных нами отображений. Так, мы видели, что если
отображение фигуры на фигуру не сохраняет расстояния, то
образом ломаной, например, может оказаться окружность, а не
ломаная (см. ркс. 85, в), образом квадрата — не квадрат, а отрезок
(см. рис. 84). Напротив, при любом отображении,
сохраняющем расстояния, каждая фигура отображается на фигуру того
же названия, т. е. образом отрезка является отрезок, образом
круга — круг, образом прямой — прямая и т. д.
Отображения, не сохраняющие расстояния, могут быть
необратимыми (см. пример 2, п. 15). Для отображений,
сохраняющих расстояния, имеет место следующая теорема.
ί5 9 Теорема. Отображения, сохраняющие расстояния, об-
I ратимы. Обратные к ним отображения тоже сохраняют рас-
1 стояния.
γ Доказательство. Пусть / — отображение,
сохраняющее расстояния, X и Υ — две различные точки и
f(X) = Хи f(Y) = Y±.
Так как точки X и Υ различны, то | ΧΥ\ > 0 (по первому
свойству расстояний). Но |ΧΊΥΊ| =\ΧΥ\ (так как
отображение / сохраняет расстояния). Значит, | ΧιΥι\ > О, т. е. точки Х4
и Υι различны.
Итак, при отображении / две различные точки не могут
иметь один образ, т. е. это отображение обратимо и, значит,
имеет обратное отображение.
60
Отображение, обратное к Д тоже сохраняет расстояния.
В самом деле, если точки Χι и Yt — образы 'точек X и Υ при
отображении Д то при отображении, обратном к Д образами
точек Χι и Υ^ являются точки X и Υ соответственно. А так как /
сохраняет расстояния, то \ΧΥ\ = | -ΧΊΥΊ|. у
Вопросы и задачи
191. На рисунках 89 и 90 заданы отображения ломаных на
отрезок. 1) Какие из этих отображений обратимы? 2)
Выполняются ли для этих отображений равенства: |ΑΧ| = |ΑιΧι|,
\ΧΥ\ = |ΧιΥι|? 3) Сохраняются ли при этих отображениях
расстояния?
192. Задано отображение
фигуры L на фигуру L\.
Произвольной точке X
фигуры L соответствует
симметричная ей
относительно оси / точка фигуры L\
(рис. 91).
1) Назовите образы точек
А, Я, С.
2) Образами каких точек
являются точки Q, Х\, К1
3) Какому отрезку
соответствует отрезок КМ1
отрезок КХ\1
4) На какие фигуры
отображаются: точки Ρ и В;
отрезок ВС; ломаная
РАВС1
5) Верно ли равенство
\ХР\ = \XxQ\l
Сохраняются ли при этом
отображении расстояния?
6) Покажите, что это
отображение обратимо.
Укажите образы нескольких
точек и фигур при
отображении, обратном
данному. Рис. 91
61
193. На рисунке 92 задано отображение
отрезка АВ на отрезок CD. 1) Какая
точка является образом точки У? На
какие фигуры отображаются отрезки
XY и AY1 2) Образами каких фигур
являются отрезки DX\ и CD1 3)
Является ли рассматриваемое
отображение обратимым? 4) Сохраняются ли
при этом отображении расстояния?
194. Дан угол MON. Каждой точке
стороны ОМ соответствует та точка
стороны ON, которая лежит на
окружности с центром О; вершина угла
отображается на себя (см. рис. 85, б).
1) Отображение какой фигуры на
какую здесь задано? 2) На какой отрезок
отображается отрезок OY1 Образом
какого отрезка является отрезок OL1
3) Сохраняются ли при этом
отображении расстояния? 4) Покажите, что
это отображение обратимо. Укажите
образы нескольких точек и фигур
при отображении, обратном данному.
195. Каждой точке полуокружности соответствует точка ее
диаметра (рис. 93). Точки А и В отображаются на себя. 1)
Отображение какой фигуры на какую здесь задано? 2) Обратимо ли это
отображение? 3) Сохраняются ли при этом отображении
расстояния? (Проверьте измерением.)
196. Верны ли предложения: 1) любое обратимое отображение
сохраняет расстояния; 2) любое сохраняющее расстояния
отображение обратимо?
197*. 1) Укажите все сохраняющие расстояния отображения
фигуры, состоящей из точек А, В и С на себя, если: а) \АВ\ = 3,
\ВС\ = 4, \АС\ = 5; б) \АВ\ = \ВС\ = 4, \АС\ = 5;
в) \АВ\ = \ВС\ = \АС\ =5.
2) Для каждого из найденных отображений укажите
отображение, ему обратное.
198. Сохраняют ли расстояния следующие отображения
координатной прямой на себя: 1) Р(х)-+Р'(2х); 2) Р(х)-+Р'(—х);
3) Р(х)-+Р'(х + 2); 4) РМ^Р'Н-З)?
17. Конгруэнтные фигуры
В младших классах вы говорили, что две фигуры равны,
если их можно наложить друг на друга так, чтобы они совпали.
Так, например, фигуры ii и i2, L2 и L3 (рис. 94) равны.
Геометрическая фигура есть множество точек. Два
множества называются равными лишь в том случае, когда они состоят
из одних и тех же элементов или оба не имеют элементов.
Например, множество Μ = {α, 7, 1, b} равно множеству М\ =
= {а, &, 1, 7}. Иначе говоря, равные множества — это одно
и то же множество. Но фигуры, изображенные на рисунке 94,
не являются равными множествами. Они не состоят из одних
и тех; же точек. Поэтому сказать, что такие фигуры «равны», было
бы неточно. Мы будем говорить, что эти фигуры конгруэнтны.
Дадим определение конгруэнтных фигур. Для этого выясним,
какими свойствами обладают фигуры, которые «можно наложить
друг на друга так, чтобы они совпали».
Пусть, например, треугольник ABC можно «наложить»
на треугольник AiBiCi так, чтобы они «совпали» (рис. 95).
Скопируем треугольник ABC на кальку. Наложим эту кальку
на треугольник ΑιΒιΰχ. Тогда копия
каждой точки X треугольника ABC
«совпадет» с определенной точкой Χι
треугольника AiBiCi.
Значит, для каждой точки X
треугольника ABC можно указать
соответствующую ей точку Xi
треугольника AYBiCi. Получаем отображение
треугольника ABC на треугольник
AiBxCi. Нетрудно заметить, что при
этом произвольные две точки Μ и N
треугольника ABC отображаются на
такие точки М4 и Nl треугольника
AiBiCly что расстояния | MN\vl \ Μ{Ν{\
равны. Итак, треугольник ABC можно
отобразить на треугольник Ai£tCi с
сохранением расстояний между
точками.
Следовательно, понятие
«конгруэнтные фигуры» можно определить с
помощью понятия «отображение».
63
Определение. Фигура конгруэнтна данной фигуре L,
если L можно отобразить на нее с сохранением расстояний.
Если фигура L2 конгруэнтна фигуре Li9 то будем писать:
L2 = L{.
Рассмотрим еще один пример конгруэнтных фигур. Как
показано выше (пункт 16, пример 2), если длины отрезков ОМ и
OiMi равны, то существует сохраняющее расстояния
отображение одного из этих отрезков на другой. Следовательно,
[Oiilfj]^ [_ОМ].
В дальнейшем будем пользоваться следующими свойствами
отношения конгруэнтности фигур:
1) каждая фигура конгруэнтна себе (свойство
рефлексивности):
L ^ L\
2) если фигура L2 конгруэнтна фигуре Lu то и фигура L{
конгруэнтна фигуре L2 (свойство симметричности):
если L2 ~ L\y то L^ ^ L2
(поэтому говорят, что две фигуры конгруэнтны друг другу,
не обращая внимания на порядок, в котором они названы);
3) две фигуры, конгруэнтные третьей, конгруэнтны
(свойство транзитивности):
если L{ ^ L2 и Ι/ο = L3, то L{ ^ L3.
Сказанное можно сформулировать короче:
17 || отношение конгруэнтности фигур рефлексивно, симметрия-
I но и транзитивно.
у Докажем первое свойство. Пусть L — некоторая фигура.
Каждой ее точке X поставим в соответствие эту же точку X.
Получим тождественное отображение фигуры L на себя. Оно
сохраняет расстояния, так как для любых точек А и В имеет
место равенство \АВ\ = \АВ\. Значит, L ^ L.
Второе свойство конгруэнтности фигур непосредственно
следует из теоремы 16.
Объясним замысел доказательства третьего свойства. Если
фигура Li конгруэнтна фигуре L2i то копию фигуры L{ можно
наложить на фигуру L2 (см. рис. 94). Затем эту же копию мож-
64
но наложить и на фигуру L3, так как L2 = L3. Поэтому фигуру
Li можно отобразить на фигуру L3 с сохранением расстояний,
т. е. Li ^ Z,3. V
Вопросы и задачи
а)
199°. Какие фигуры называются конгруэнтными?
200. Запишите в принятых обозначениях: 1) фигура Τ
конгруэнтна фигуре Т\) 2) отрезок АВ конгруэнтен отрезку CD;
3) луч АС конгруэнтен лучу BD.
201. Пусть отображение / сохраняет 1 .д
расстояния и f(A) = P, f(B) = Q,
f(C) = R. 1) Найдите расстояния
\PQ\, \QR\, \PR\, если \AB\ =7, A)
\BC\ = 7, \AC\ = 12. 2) Назовите
подмножества фигуры {P,Q,R},
конгруэнтные фигурам {А, В}, {А, С},
{В, С}.
202°. Конгруэнтны ли две фигуры,
симметричные относительно: 1) данной
прямой; 2) данной точки?
203. Какие из фигур, изображенных на
рисунке 96, конгруэнтны?
204. Начертите какую-либо фигуру и
постройте фигуру, ей конгруэнтную.
(Для построения можно
воспользоваться линейкой, циркулем,
угольником, калькой.)
205*. На рисунке 97 задано отображение
/ фигуры {С, D, Е} на фигуру
{А, В}; \АВ\ = \CD\ = \DE\ =
= | СЕ |. Верно ли, что: 1)
отображение / сохраняет расстояния; 2)
фигуры {С, D, Е) и {А, В)
конгруэнтны; 3) фигуры {А, В) и {С, D),
{А, В} и {Е, С} конгруэнтны?
206°. Может ли фигура, состоящая из
двух точек, быть конгруэнтной
фигуре, состоящей из трех точек? рИСш 97
65
207· Отметьте на плоскости три точки А, В, С. Постройте при
помощи циркуля фигуру {D, Ε, М}, конгруэнтную фигуре
{Л, В, С}.
208*. Начертите два конгруэнтных треугольника ABC и А\В\С\
и отметьте точку X, принадлежащую первому из них.
Постройте образ точки X при каком-либо отображении первого
треугольника на второй, сохраняющем расстояния.
209**. Начертите два конгруэнтных квадрата ABCD и КМРТ и
отметьте точку X, принадлежащую первому из них. 1) Постройте
образ точки X при сохраняющем расстояния отображении
первого квадрата на второй, если: а) А->К, В-+М; б) С-+Р,
В-+Т. 2) Сколько образов точки X может быть построено при
различных отображениях первого квадрата на второй с
сохранением расстояний?
210*. Докажите, что два отрезка различной длины не конгруэнтны.
211*. Докажите, что две окружности различных радиусов не
конгруэнтны.
212*.Три точки А, В и С не лежат на одной прямой. Точки А\, В\
и С\ — различные точки одной прямой. Докажите, что фигуры
{А, В% С} и {А\, В\, С\) не конгруэнтны.
18. Измерение углов
1. Вы уже умеете измерять углы в градусах. Рассмотрим
некоторые свойства величин углов.
1) Как известно, каждый угол можно разделить пополам,
т. е. представить его в виде суммы двух конгруэнтных углов.
Углы можно делить и на большее число частей. Так, проведя
сначала биссектрису угла АОС> а. затем биссектрисы углов АОВ
и ВОС, получим четыре конгруэнтных
А/ угла, сумма которых — угол АОС
/ χ (рис. 98). Справедливо такое общее ут-
/ / 5- верждение:
/ / ^^ 18|любой угол можно разделить на η
// \s^ с I конгруэнтных углов (п — произ-
УаУ^—"-""" | вольное натуральное число).
A* q Разделим развернутый угол на 180
конгруэнтных углов. Величину каждо-
Рис. 98 го из этих углов называют градусом
66
(обозначается так: 1°). За величину
угла, являющегося суммой целого числа
k углов в один градус, принимают k°.
Например, величина развернутого
угла равна 180°.
Величины углов, не являющихся
суммой целого числа углов в один
градус, выражают через градусы
приближенно. При измерениях углов, требующих высокой точности
(например, в астрономии или навигации) пользуются и более
мелкими единицами измерения. Такими единицами являются одна
минута (Г) и одна секунда (1"). Минутой называют — часть
* 60
градуса. Минута — это величина каждого из 60 углов,
полученных при делении угла в один градус на 60 конгруэнтных углов.
Разделив в свою очередь угол в одну минуту на 60
конгруэнтных углов, получим углы величиной в одну секунду:
1' = !. 1°, 1" = 1.1'=— 1°.
60 60 3600
2) На рисунке 99 изображены конгруэнтные углы:
/LAOB ^ /-DEF.
Измерив эти углы, мы получим, что они имеют одну и ту же
величину:
АОВ = DEF.
Вообще,
I82I ^βα угла конгруэнтны тогда и только тогда, когда их вели-
I чины равны.
3) Пусть угол АОС является суммой углов АОВ и ВОС
(рис. 100). Тогда:
АОС = АОВ + ВОС.
V
Рис. 101
67
θ I
Рис. 102
а)
Рис. 103
1831
Справедливо предложение:
величина суммы двух углов равна сумме величин этих
углов.
4) Построим с помощью транспортира угол с данной
стороной, имеющий заданную величину а (на рис. 101, α α = 80°, на
рис. 101, б а = 230°). Очевидно, при любом значении а можно
построить два таких угла. Это утверждение'сформулируем
следующим образом:
184| от любого луча можно отложить два угла заданной ве-
I личины.
2. Прямым углом называется угол, конгруэнтный своему
смежному. Величину прямого угла часто обозначают буквой d.
Так как величины конгруэнтных углов равны, а сумма смежных
углов — развернутый угол, то 2d = 180° и, следовательно,
d = 90°.
При пересечении двух прямых образуются четыре выпуклых
угла (отличных от развернутого). Пусть один из этих углов
прямой (рис. 102). Тогда, как это легко проверить, и другие
три угла тоже прямые.
Если при пересечении двух прямых образуются четыре
прямых угла, то такие прямые называются взаимно
перпендикулярными. Говорят также, что каждая из этих прямых есть
перпендикуляр к другой. Для построения перпендикуляра к данной
прямой р, проходящего через данную точку О, пользуются
чертежным угольником (рис. 103, а и б). Проводя такие
построения, можно наглядно убедиться в справедливости
утверждения:
19 1 через любую точку плоскости проходит один и только один
I перпендикуляр к данной прямой.
68
Вопросы и задачи
213°. Сформулируйте определение
биссектрисы угла.
214. При помощи транспортира и линейки
постройте углы, величины которых
равны: 1) 70°; 2) 110°; 3) 229°; 4) 330°.
215. Угол величины 45° разделили на η
конгруэнтных углов. Запишите величины этих углов: 1) в
градусах; 2) в градусах и минутах; 3) при единице измерения,
равной d, если η равно 2; 3; 6; 10.
216. Запишите следующие величины в порядке их возрастания:
67°42'; 0,75 d; 67°45".
217. Выполните указанные действия:
1) 45°30,45" + 44°29Ί 5"; 2) 83°05'30" + 22°45'55";
3) 93°35'20" — 45°40Ί 5"; 4) 102°43Ί 5" — 50°50'30";
5) 3 - 20Ί5'30"; 6) 4 · 30°25'15"; 7) 144°50'22" : 3.
218. Докажите, опираясь на свойства величин углов:
1) сумма величин смежных углов равна 180°;
2) величины вертикальных углов равны.
219. При помощи транспортира измерьте величины всех
выпуклых углов, образовавшихся при пересечении двух прямых
(рис. 104). Сколько углов достаточно измерить, чтобы
ответить на поставленный вопрос?
220. Начертите произвольный отрезок АВ. 1) Постройте с
помощью транспортира треугольник ABC, если: а) А = 45°,
В = 75°; б) А = 30°, В = 60°. Измерьте угол С. 2) Сколько
различных треугольников можно построить по этим данным?
221. Постройте прямую, перпендикулярную к данной прямой а
и проходящую через данную точку В, если: 1) В 6 о; 2) В $ а.
222. Докажите, что если один из четырех выпуклых углов,
образованных двумя пересекающимися прямыми, имеет
величину 90°, то и величины трех других углов равны 90°.
223- Докажите, что угол между биссектрисами двух смежных
углов равен 90°.
224°. Сформулируйте определения тупого и острого углов.
225. Как известно, азимутом (магнитным) данного направления
называется угол между осью магнитной стрелки и данным
направлением. Азимуты отсчитываются от направления на
север по часовой стрелке от 0° до 360°. Например, азимут
направления ОМ—острый угол в 70° (рис. 105, а).
69
I 5F" ίΑΜ",ρον£^τ
Волоколамск \ 1 /
Ioz-n.^,^ Крюково! J
MOCKBAraL-. ^
II / / «эбарыбино
II /^МалоярослдвецоСерпухов Л Кашира
^Александров II
Петушки ||
Куровское ||
sBocxpeceHCK
\Луховицы
Рис. 105
На рисунке 105, б дана схематичная карта Подмосковья.
1) Определите азимуты направлений от Москвы на Загорск,
Клин, Воскресенск, Каширу, Серпухов, Крюково, Можайск.
2) Чтобы определить по карте маршрут перехода,
необходимо найти азимуты каждого из направлений этого маршрута.
Сделайте это, используя карту Подмосковья, для маршрутов:
а) Кубинка — Малоярославец; б) Кубинка — Волоколамск;
в) Крюково — Пушкино; г) Барыбино — Подольск.
§ 2. Перемещения
19. Поворот
Нарисуем на листе бумаги какую-либо фигуру L и отметим
точку О (рис. 106, а). Положим на лист бумаги лист кальки,
покрывающий фигуру L и точку О. Проколем оба листа в
точке О булавкой. Скопируем на лист кальки фигуру L и повернем
Рис. 106
70
Рис. 107 Рис. 108
кальку вокруг точки О (рис. 106, б). Тогда копия фигуры L
займет на плоскости новое положение L^ Говорят, что фигура
Σ{ получается из фигуры L при помощи поворота вокруг
центра О. Каждой точке X фигуры L при этом повороте
соответствует некоторая точка Χι фигуры Lu и каждая точка фигуры L^
является образом некоторой точки фигуры L. Получаем
отображение фигуры L на фигуру L{.
Легко заметить, что при повороте кальки вокруг точки О
копии всех точек фигуры L перемещаются в одном и том же
направлении (все против часовой стрелки или по часовой
стрелке) на угол одной и той же величины (эту величину называют
углом поворота). Иначе говоря, для любых двух точек X и Υ
фигуры L и их образов Χι и Υι
ΧΟΧι = ΥΟΥι = α,
причем углы ХОХ{ и ΥΟΥ{ отложены от лучей ОХ и ΟΥ
соответственно в одном и том же направлении (на рис. 107, а
показан поворот против часовой стрелки на 60°, а на рис. 107, б —
поворот на 60° по часовой стрелке).
При повороте с центром О на угол а фигура L отобразится
на ту же фигуру £lf что и при повороте вокруг точки О на угол
360° — а, но в противоположном направлении (рис. 108). Один
из углов α или 360° — α не превышает 180°. Таким образом,
любой поворот на угол, больший 180°, является поворотом
на угол, меньший 180°. Поэтому можно ограничиться
рассмотрением поворотов на углы, не превышающие 180°.
Итак, поворот фигуры задается указанием: 1) центра О,
2) угла поворота α (0° ^ а ^ 180°) и 3) направления поворота.
Если центр О, угол α и направление поворота заданы,
то точка Х{ — образ точки X — строится так: от луча
ОХ в заданном направлении откладывается угол ХОА величи-
71
д ны α (рис. 109) и на луче О А нахо-
V χ дится точка Хи лежащая на расстоя-
\ нии \ОХ\ от центра О.
\ Описанный способ получения образа
^-"•*^^^ х"4? X точки X применим к любой точке пло-
^"Тдп * · скости. Что же получится, если за
ог^Д фигуру L принять всю плоскость? Полу-
I чится отображение всей плоскости на се-
\\4) бя, которое называют поворотом с цент-
\ ром О на угол а в заданном направлении.
* Действительно, каждая точка плос-
Рис 109 кости будет иметь образ, полученный
указанным способом. И для любой
точки М\ плоскости "найдется такая точка М, образом которой
при этом повороте является Mt. Получить эту точку Μ очень
просто: надо построить образ точки М\ при повороте вокруг
центра О на тот же угол а в направлении, противоположном
направлению данного поворота (см. рис. 109). Дадим теперь
определение поворота.
Определение. Поворотом с центром О на угол а
(0° ^ α <J 180°) в заданном направлении называется
отображение плоскости на себя, при котором точка О отображается на
себя, а любая другая точка X —на такую точку Хи что:
1) расстояния \ОХ\ и \OXY\ равны;
2) угол ХОХ1 имеет величину а и отложен от луча ОХ в
заданном направлении.
Поворотом на 0° считают тождественное отображение
плоскости.
Примем без доказательства следующее важное свойство
поворота:
20 | пРи повороте расстояния сохраняются.
Наглядная убедительность этого предложения ясна из
сказанного в начале пункта. В самом деле, расстояния между
копиями произвольных точек X и Υ плоскости — точек Χι и
Yi — при повороте кальки вокруг точки О, конечно, не
меняются (см. рис. 106,6). Значит, \Χ{Υ{\= \ΧΥ\.
Ранее было сказано (теорема 16), что отображение,
сохраняющее расстояния, имеет обратное. Отображение, обратное
повороту, есть поворот с тем же центром О и на тот же угол,
но в противоположном направлении.
/2
Далее мы познакомимся с другими отображениями
плоскости на себя, сохраняющими расстояния (в п. 21 рассматривается
осевая симметрия, а в п. 36 — параллельный перенос). В
геометрии такие отображения плоскости играют важную роль и
поэтому получили специальное название — перемещения.
Определение. Отображение плоскости на себя,
сохраняющее расстояния, называется перемещением.
21 I Теорема. При перемещении любая фигура отображается
I на конгруэнтную ей фигуру.
Доказательство. При перемещении любая пара
точек X и Υ фигуры L отображается на такую пару точек -ΧΊ и
Υι фигуры L{ (Li — образ фигуры L), что | XiYl\.^= \ XY\
(перемещение сохраняет расстояния!). Это и означает, что 1ч = L. ■
Вопросы и задачи
226. Заданы центр поворота О и точка М. Постройте образы
точки Μ при поворотах с центром О на углы 30°, 60°, 120°, 180°.
(Направление поворота — против часовой стрелки.)
227°. На какую фигуру отображается при повороте: 1) прямая,
проходящая через центр поворота; 2) окружность, центр которой
совпадает с центром поворота; 3) угол с вершиной в центре
поворота?
228. 1) Постройте образ данного отрезка АВ при повороте вокруг
центра О на данный угол а.
2) Постройте образ данного угла ABC при повороте на
данный угол α вокруг данного центра О, лежащего вне угла.
229- Стороны АО и ВО треугольника АОВ конгруэнтны, АОВ = а.
Постройте образ этого треугольника при повороте вокруг
центра О: 1) на угол α в направлении против часовой стрелки;
2) на угол α в направлении по часовой стрелке; 3) на угол
α = 100° в направлении по часовой стрелке.
230. Постройте образ данного прямого угла при повороте
вокруг вершины угла на 45° против часовой стрелки. Отметьте
штриховкой: 1) объединение данного и построенного углов;
2) пересечение этих углов.
231. Постройте несколько центров поворотов, при которых
данная точка А отобразится на другую данную точку В,
232. Какие фигуры, составленные из конгруэнтных полукругов
(рис. 110), при некотором нетождественном повороте
отображаются на себя?
233. Укажите центры и углы поворотов, при которых фигуры, изо-
73
a)
б)
%>
б)
А?
А
А,
Ав^
*S
У
0/
Чл
^
А5
δ)
Рис. 111
С
сх
О
о
(
Р,
^_у
г)
Рис.
110
ГУЛ
я
J^fe
е;
ж)
Рис. 112
браженные на рисунке 111, а,
отображаются на себя.
234. Докажите, что многоугольник
ΑιΑ2ΑζΑ4Α5Α6Α7Α8 (рис. 1116)
при некоторых поворотах с
центром О отображается на себя.
Найдите углы этих поворотов.
235. Укажите пары конгруэнтных
отрезков и углов,
изображенных на рисунке 111, б.
236. Начертите несколько фигур,
каждая из которых при
некотором нетождественном
повороте отобразится на себя. Для
каждой из этих фигур укажите
центр поворота и возможные
углы поворота.
237*. Сколько существует
перемещений, отображающих одну
данную фигуру на другую
данную фигуру, если этими
фигурами являются: 1) точки; 2)
лучи; 3) прямые; 4)
конгруэнтные окружности; 5) отрезки?
238. На лучах ОМ и 0\МХ выбраны
такие точки А и А\, что \ОА | =
= |ΟιΑι|. Докажите, что при
любом перемещении,
отображающем луч ОМ на луч 0\Ми
образ точки А — точка А\ш
239. Постройте образы точек А, В,
С, D, Ε при перемещении,
отображающем луч ОМ на луч
0\М\, а полуплоскость α на
полуплоскость αϊ (рис. 112).
74
240. Ниже заданы отображения плоскости. Покажите, что ни одно
из них не является перемещением.
1) f\(A) = В, f\(B) = A, остальные точки плоскости
отображаются на себя (А Φ В),
2) /2(0) = О, произвольная точка X плоскости отображается
на такую точку Х\ луча ОХ, что |0^i| = k \OX\ (k — любое
положительное число, не равное единице).
3) Образом произвольной точки X плоскости является
основание перпендикуляра, проведенного из точки X к прямой р.
241. Приведите примеры фигур, для которых существует
несколько поворотов, отображающих эти фигуры на себя.
20. Центральная симметрия
При α Φ 0° и αφ 180° существуют два поворота с заданным
центром О на угол а: один в направлении по часовой стрелке,
а другой — против часовой стрелки. Но при α = 0° такой
поворот лишь один — ото тождественное отображение плоскости.
Особый случай мы получим и при α = 180°. Существует
лишь один луч с началом О, образующий с данным лучом ОМ
угол 180°, — это луч ΟΜι прямой ОМ, противоположный
лучу ОМ (рис. 113). На луче ОМА имеется лишь одна точка Xi9
удаленная от О на расстояние \ОХ\. Следовательно, образ
любой точки плоскости при поворотах с центром О на угол 180°
не зависит от направления поворота, и, значит, существует
лишь один поворот с заданным центром на 180°.
Из построения видно (см. рис. 113), что образ произвольной
точки X плоскости при этом повороте — это такая точка -ΧΊ,
что центр О — середина отрезка ΧΧι. Как вы уже знаете,
такие точки IhIj называют симметричными относительно
точки О. Поворот на 180° называется центральной симметрией.
Симметрию с центром О обозначают Z0.
Рассмотрим свойства центральной симметрии.
22 | Центральная симметрия есть перемещение.
Справедливость этого свойства сразу следует из
предложения 20. Свойством 22 мы будем часто пользоваться при
доказательствах конгруэнтности фигур. Докажем, например, уже
известное вам предложение:
вертикальные углы конгруэнтны.
Как известно, вертикальные углы АОВ и COD (рис. 114)
симметричны относительно точки О,
75
Μ,
о
χ
-ΦΑ/
Рис. 113
Рис. 114
Центральная симметрия
является перемещением и,
значит, отображает любую фигуру
на конгруэнтную ей фигуру.
Поэтому
/-АОВ ^ /-COD.M
22М Отображение, обратное
центральной симметрии, есть
\та же центральная
симметрия.
Доказательство.
Пусть X — произвольная точка
плоскости. Если точка Χι
симметрична X относительно центра
О, то точка X симметрична Х\ относительно той же точки О
(рис. 113). Поэтому при отображении, обратном симметрии Ζ0,
произвольная точка плоскости отображается на симметричную
ей относительно центра О точку. Это означает, что отображение,
обратное симметрии ZQ, есть та же центральная симметрия ZQ. ■
2221 Любая прямая, проходящая через центр симметрии, ото-
| бражается при этой симметрии на себя.
Доказательство. Пусть центр О симметрии
принадлежит прямой р. Возьмем на прямой ρ любую другую
точку М. При симметрии Ζ0 прямая ОМ отображается на прямую,
проходящую через образы точек О и М. Но О отображается
на себя, а М — на точку М\ прямой ρ (см. рис. 114).
Поэтому прямая ρ — (ОМ) отображается на прямую ОМи т. е. на
себя. ■
Фигура, которая при симметрии относительно некоторого
центра О отображается на себя, называется
центрально-симметричной (говорят также, что эта фигура имеет центр
симметрии). Из доказанного только что предложения следует, что
прямая — фигура центрально-симметричная.
Вопросы и задачи
242. Отметьте на плоскости точку О и точки At В, С. 1) Постройте
точки Μ = Ζ0(Α), Ρ = Z0(B), D = Z0 (С). 2) Укажите на этом
же рисунке точки Z0 (Μ), Z0 (P), Z0(D), Z0{0).
243°. 1) Какая точка плоскости при центральной симметрии
отображается на себя?
76
2) Какие прямые при центральной симметрии отображаются
на себя?
3) Центральная симметрия задана парой соответствующих
точек: А —>А\. Как найти в этом случае центр симметрии?
244°. Какой фигурой является образ: 1) прямой АВ при симметрии
относительно точки О 6 (АВ); 2) луча ОС при симметрии
относительно центра О; 3) угла ABC при симметрии
относительно точки В1
245. 1) Постройте отрезок, симметричный отрезку АВ
относительно данного центра О, если: а) О 6 (АВ); б) О i (АВ).
2) Постройте прямую, симметричную данной прямой АВ
относительно данного центра О $ (АВ).
3) Отметьте штриховкой образ данной полуплоскости с
границей АВ при симметрии Ζ , если: а) О 6 (АВ); б) О </■ (АВ),
246°. Какая фигура называется центрально-симметричной?
Приведите примеры центрально-симметричных фигур.
247. 1) Имеет ли центр симметрии отрезок, прямая, луч,
окружность, объединение двух пересекающихся прямых?
2) Существуют ли треугольники (четырехугольники,
пятиугольники), имеющие центр симметрии?
3) Существуют ли фигуры, имеющие несколько центров
симметрии?
248. Какие из фигур, изображенных на рисунке 110, имеют центр
симметрии?
249. Постройте фигуры, центрально-симметричные фигурам,
данным на рисунке 115. В каждом случае центр симметрии
выберите сами.
250. Образ треугольника PQR при симметрии Ζ0—треугольник
ABC (рис. 116). 1) Найдите расстояния \QR\, \AB\, \QP\,
если известно, что \АС\ =8, \RP\ =6, \ВС\ =6. 2) Какой
угол конгруэнтен углу ABC; углу QRP1 3) Найдите расстояния
α) δ) β) β)
Рис. 115
77
в
/ % \ т Q
А М С 0 ^
Рис. 116
\AQ\, \NC\ и \АР\, если известно, что \0С\ = 1, а точки Μ
и N — середины отрезков АС и QP соответственно.
251. Даны прямая а и точка В i α. Постройте несколько таких
точек М, что образ точки В при симметрии с центром Μ
лежит на прямой а.
252. Найдите величины углов αϊ, а2, βι и β2, если α = 35°, β = 40°
(рис. 117).
253. Точка О — середина отрезка АА\. Пользуясь только
циркулем, постройте образ точки В при симметрии Ζ0 , если:
1) В6[АА,]; 2) Βί [ΑΑ,].
254*. Докажите, что биссектрисы вертикальных углов лежат на
одной прямой.
255*. Докажите конгруэнтность: 1) двух окружностей равных
радиусов; 2) двух полуплоскостей, имеющих общую границу.
256*. Отрезки А\ВХ и А2В2 имеют общую середину О. 1) Докажите
конгруэнтность отрезков А\А2 и В\В2, А\В2 и А2В\. 2)
Докажите, что середины отрезков А\А2 и В\В2 лежат на одной
прямой с точкой О.
21. Осевая симметрия
1. Вы уже знаете, что две точки
X и Χι называются
симметричными относительно прямой р,
если эта прямая перпендику-
~р лярна отрезку XXi и проходит
через его середину (рис. 118).
Будем также считать, что
каждая точка прямой ρ
симметрична самой себе относительно этой
прямой.
Ν Ρ
Рис. 117
1
м=м1
<
>х
A=Ai
Рис. 118
78
vVVv
A
4
•£Ш
.л
V ν
"ΤΊ
j t
Τ
»
•
i x i
ι
β
Ι θ °i
\ A .. 1
1 <
г
Г л
1
<
>
1
i, ^,
►
1 I
I 5' ι
α) δ)
Рис. 119 Рис. 120
Определение. Симметрией с осью ρ называется
отображение плоскости на себя, при котором каждая точка плоскости
отображается на точку, ей симметричную относительно прямой р.
Симметрию с осью ρ называют также осевой симметрией.
Обозначают осевые симметрии обычно буквой S, а если нужно
указать и ось ρ симметрии, то пишут: Sp.
2. Рассмотрим свойства осевой симметрии.
23 ^Осевая симметрия является перемещением.
Доказательства этого свойства мы не приводим. Его
справедливость можно усмотреть из наглядных соображений. Для
этого представим себе плоскость в виде листа, изготовленного
из твердого материала (рис. 119). Тогда симметрию с осью ρ
можно представить как результат вращения в пространстве
этого листа вокруг прямой ρ на угол 180° (рис. 120). Очевидно,
что расстояния между точками плоскости при этом вращении
не меняются.
231| Отображение, обратное осевой симметрии, есть та же осевая
| симметрия.
Доказательство. Пусть X — произвольная точка
плоскости. Если точка Х\ симметрична X относительно прямой
р, то точка X симметрична Χι относительно этой же прямой
(см. рис. 118). Поэтому при отображении, обратном симметрии
Sp9 произвольная точка плоскости отображается на
симметричную ей относительно прямой ρ точку. Это означает, что
отображение, обратное осевой симметрии, есть та же осевая симметрия.я
23:1 При симметрии с осью р: а) любая прямая, перпендикуляр-
| пая оси симметрии, отображается на себя; б) полуплоскос-
1 ти с границей ρ отображаются друг на друга.
Μ
χ,
Рис. 121
α9
Доказательство, а) Пусть
ос прямая а перпендикулярна оси ρ
(рис. 121). Если X — произвольная
точка прямой а, то точки X и Х{ = Sp (X)
при симметрии Sp отображаются друг
—- на друга (по определению
симметричных точек). Следовательно, Sp (α) =α. ■
γ б) Обозначим полуплоскости с
границей ρ через а4 и а2. Пусть Χ £ α4
и X $ ρ (см. рис. 121). Если точка Х{
симметрична точке X относительно
прямой р, то прямая ρ проходит
через середину отрезка XXи т. е. пересекает этот отрезок.
Следовательно, точка Χι (образ точки X при
симметрии Sp) принадлежит полуплоскости а2. Кроме того, каждая
точка Μ полуплоскости а2 является образом точки Mi =
= Sp (M), принадлежащей полуплоскости α4. Поэтому
Sp (α4) = α2.ψ
3. Задача. Построить при помощи циркуля точку,
симметричную данной точке X относительно оси р.
Решение. Обозначим точку Sp (X) через Х{. Для
построения Χι удобно воспользоваться свойствами осевой
симметрии.
Отметим на прямой ρ две произвольные точки А и В
(рис. 122). Так как осевая симметрия сохраняет расстояния и
Sp (A) = A> Sp (В) = В (по определению осевой симметрии),
то \АХ\ = \АХ{\, \ВХ\ = \ΒΧι\. Следовательно, точка Χι
должна лежать и на окружности с центром А радиуса | АХ\9 и
на окружности с центром В радиуса |-В-ХГ|. Эти окружности
пересекаются в двух точках (см. п. 13), одна из которых —
точка X. А так как точка Х{ должна принадлежать
полуплоскости, которая не содержит X, то
образом X является вторая точка
пересечения построенных
окружностей. Итак, для построения точки
Хх = Sp (X) надо:
1) отметить на прямой ρ две
произвольные точки А и В;
2) построить окружности с цент-
Рис. 122 рами А и 5, проходящие через X.
80
Точка пересечения этих окружностей, отличная от точки X,
искомая. Очевидно, что построение выполнимо с помощью
одного только циркуля. Задача решена.
Вопросы и задачи
257. Запишите в принятых обозначениях: 1) точка У
симметрична точке X относительно прямой р; 2) отрезок АВ
симметричен отрезку CD относительно прямой Л; 3) луч ОМ
симметричен лучу 0\М\ относительно прямой р\ 4) фигура L
симметрична фигуре L\ относительно прямой с.
258°. 1) Точка А симметрична точке А\ относительно оси I. Верно
ли, что точка А\ симметрична точке А относительно этой же
оси?
ч2) Фигура Τ симметрична фигуре Ρ относительно оси I.
Верно ли, что фигура Ρ симметрична фигуре Τ относительно
той же оси?
259°. Как расположена относительно оси а точка X, если:
о 1) Sa(X) = X; 2) Sa(X)^Xl
260°. 1) Какие точки при осевой симметрии S отображаются на
себя?
2) Какие прямые при осевой симметрии Sp отображаются
на себя?
261.. 1) Осевая симметрия задана парой соответствующих точек:
S(A) = В. Как построить ось этой симметрии?
2) Две пересекающиеся прямые а и Ъ симметричны
относительно оси I. Как расположена относительно оси I точка О
пересечения этих прямых?
262. На рисунке 123 изображены различные фигуры. Постройте
образы этих фигур при симметрии Sa.
Рис. 123
81
263.
264.
265.
Фигуры, изображенные на рисунке 124 (квадрат, звезда, круг,
полуплоскость), отображаются на себя при некоторых осевых
симметриях. Укажите оси этих симметрии.
1) Докажите конгруэнтность треугольников ONB и ОМА
(рис. 125).
2) Укажите пары конгруэнтных отрезков и углов,
изображенных на рисунке 125.
Четырехугольник ABCD симметричен относительно
прямой АС. 1) Найдите длины сторон
ВС и AD этого четырехугольника,
если \АВ\ = 1 см, \CD\ = 2 см.
2) Найдите величины углов ADC и
BCD, если СВА = а, ВС А = β.
266*. Каждая точка Р(х,у) . плоскости
отображается на точку: 1) Р\(—xt —у);
2) Р2(х, —у)] 3) Р3(—х, У). Покажите,
что эти отображения являются
перемещениями.
267. На плоскости задана прямая I.
Пользуясь только циркулем, постройте
образ при симметрии St : 1) точки Μ
(Μ $ I); 2) окружности (О, г).
268. Дан отрезок АВ и две точки С и D
такие, что \СА\ = \СВ\ и \DA\ =
= |Ζλδ|. Докажите, что точки А и В
симметричны относительно
прямой CD.
269*. Как проверить, пользуясь только
циркулем, лежат ли три данные точки
на одной прямой?
270. Окружности (О, г) и (Οι, Г\) имеют
две общие точки А и В. Пользуясь
только циркулем, постройте
окружности, симметричные данным
относительно оси АВ.
271*. Данная окружность (О, г) пересекает
сторону ВА данного угла ABC в
точках Μ и Т. Пользуясь только циркулем,
постройте окружность, симметричную
данной относительно оси ВС.
ч>'·'/,
//,
у/,
Рис. 124
82
272*. Во внутренней области прямого угла BOD взята точка X
и построены точки X\=SB0 (X) и X2=SD0 (X).
Докажите, что точки Х\, ОиХг лежат на одной прямой.
273**. Даны прямая ρ и две точки А и В, лежащие в одной
полуплоскости с границей р. Найдите на прямой ρ такую точку С,
для которой сумма расстояний \АС\ и \СВ\ будет
наименьшей.
Рис. 126
22. Построение треугольников
1. Рассмотрим произвольный
треугольник ABC. Сторону ВС и угол А
треугольника ABC называют
противолежащими друг другу. Противолежащими
являются также сторона АС и угол В,
сторона АВ и угол С (рис. 126). Углы А и
С называют прилежащими к стороне АС.
(Назовите углы, прилежащие к
стороне АВ, к стороне ВС.)
Длины сторон треугольника ABC
обозначают обычно через а, Ь, с (а = \ВС\9
Ь = | АС\, с = | АВ\). Для краткости эти
длины а, Ь, с называют также и
сторонами треугольника ABC.
Величины углов ВАС, ABC и АСВ
часто обозначают через А, В и С или а,
β и γ соответственно. Для краткости их
называют также и углами треугольника.
Отрезок биссектрисы угла
треугольника от его вершины до противолежащей
стороны называется биссектрисой тре- q
угольника. Отрезок, соединяющий
вершину треугольника с серединой
противолежащей стороны, называется медианой
треугольника. Отрезок, соединяющий
вершину треугольника с основанием
перпендикуляра, проведенного из этой
вершины к прямой, содержащей
противолежащую сторону, называется высотой
треугольника. На рисунках 127—129 с
изображены биссектриса 1а, медиана та
Рис. 127
Рис. 128
Рис. 129
83
α χ и высота ha 'треугольника ABC,
проведенные из вершины А.
Для краткости длину
биссектрисы (медианы, высоты)
треугольника называют также
просто его биссектрисой
(медианой, высотой).
Длины сторон и величины
углов треугольника принято
называть его основными
элементами. У треугольника ABC
шесть основных элементов: а, &, с»
У\ /Ч /X
А, -В, С. Длины биссектрис,
медиан, высот треугольника тоже называют его элементами
(но не основными).
Длину отрезка (и величину угла) можно задать
геометрически, начертив конгруэнтный ему отрезок (угол). В задачах на
построение фигур так часто и поступают.
2. Решим несколько задач на построение.
Задача 1. Построить треугольник ABC no трем
сторонам а, Ъ и с (рис. 130, а).
Ρ е ш е н и е. 1) Построим отрезок АВ длины с (рис. 130, б).
2) Так как | АС | = Ъ и | ВС \ = а, то С принадлежит
пересечению окружностей (А, Ъ) и (В, а). Построим эти окружности
и обозначим одну из точек их пересечения через С.
3) Соединим точку С отрезками с точками А и В.
Треугольник ABC искомый.
Окружности (А, Ъ) и (В, а) будут пересекаться только тогда,
когда \а — Ъ\ <с <а + Ь (см. пункт 13). Поэтому задача
имеет решение только в том случае, если \а — & | < с < α + &.
Выбирая различные положения отрезка АВ на плоскости,
получим бесконечное множество треугольников, имеющих
заданные три стороны. Но все эти треугольники конгруэнтны.
Справедлив следующий признак конгруэнтности
треугольников:
24 I если три стороны одного треугольника конгруэнтны трем
I сторонам другого треугольника, то такие треугольники кон-
I груэнтны.
Поэтому говорят, что решение задачи 1 с точностью до
конгруэнтности единственно.
84
3 а д а ч а 2. Построить угол
с заданной стороной OiXiy
конгруэнтный данному углу XOY.
Решение. 1) Построим
окружности с центрами О и 04
радиуса г (рис. 131). Обозначим
точки их пересечения со
сторонами угла XOY и лучом OlXl
через А, В и А{.
2) Построим окружность с
центром Ai радиуса \АВ\.
Обозначим точки пересечения
окружностей с центрами 0{ и А{
через В^ и В2.
3) Проведем лучи 0{В{ и
04Β2. Углы AjOjBj и ААВа
искомые (это следует из
конгруэнтности треугольников ОАВ,
ΟιΑιΒι и 0{А{В2 по трем
сторонам).
Задача 3. Построить
треугольник по двум сторонам
Ъ, с и углу а между ними
(рис. 132, а).
Решение. 1) Проведем
произвольный луч АХ (рис.
132, б).
2) Построим угол XAY
величины а.
3) На луче АХ отложим
отрезок АС длины Ь.
4) На луче AY отложим
отрезок АВ длины с.
5) Проведем отрезок ВС.
Треугольник ABC искомый.
Выбирая различные
положения луча АХ и выполняя
описанное построение, мы получим
бесконечное множество тре- А
угольников. Но все эти
треугольники конгруэнтны. Справедлив
следующий признак
конгруэнтности треугольников:
25 I если две стороны и угол
между ними одного
треугольника конгруэнтны двум
сторонам и углу между
ними другого треугольника,
то такие треугольники
конгруэнтны.
Итак, все треугольники,
имеющие заданные две стороны
и угол между ними,
конгруэнтны. Поэтому говорят, что
задача 3 имеет с точностью до конгруэнтности единственное
решение.
Задача 4. Построить треугольник по стороне а и двум
прилежащим к ней углам β и у (рис. 133, а).
Ρ е ш е н и е. 1) Построим отрезок ВС длины а (рис. 133, б).
2) Построим угол СВХ величины β.
3) Построим угол ВС Υ величины γ, расположенный в той
же полуплоскости с границей ВС, что и угол СВХ.
Если лучи ВХ и С Υ пересекутся, то построенный
треугольник искомый.
С точностью до конгруэнтности задача имеет одно
решение. Справедлив следующий признак конгруэнтности
треугольников:
26 1 если сторона и два прилежащих к ней угла одного
треугольника конгруэнтны стороне и двум прилежащим к ней углам
другого треугольника, то такие треугольники конгруэнтны.
Вопросы и задачи
274. 1) Постройте биссектрисы и медианы данного треугольника.
2} Постройте высоты данного треугольника: а)
остроугольного; б) прямоугольного; в) тупоугольного.
275. Даны конгруэнтные треугольники ABC и DEM.
1) Известно, что [АВ] ^ [DE], [AC] ^ [DM]. Укажите углы
треугольника ABC, конгруэнтные углам D, Ε и М.
2) Известно, что ADEF ^ AABC, ZJD ^ /.A, /JE ^ /-B.
Какие стороны этих треугольников конгруэнтны?
86
3) Докажите, что каждая биссектриса (медиана, высота)
треугольника ABC конгруэнтна некоторой биссектрисе
(медиане, высоте) треугольника DEF, конгруэнтного
треугольнику ABC,
276. Можно ли построить треугольник, стороны которого равны:
1)13 см, 2 дм, 8 см; 2) 1 м, 1 м, 0,5 см; 3) 45 см, 45 см, 1 м;
4) 1 дм, 5 см, 5 см?
277. Постройте треугольник по трем данным сторонам a, b и с,
если: 1) а = 4 см, Ъ = 3 см, с = 2 см; 2) а = 4 см, Ъ = 3 см,
с = 5 см; 3) а = 4 см, Ъ = 3 см, с = 6 см.
278. Постройте треугольник по двум сторонам 6, с и углу а,
заключенному между ними, если: 1)6=5 см, с = 4 см, а = 72°;
2) 6 = 3 см, с = 4 см, а = 108°.
279. Постройте треугольник по стороне с и двум углам α и β,
прилежащим к этой стороне, если: 1) с = 5 см, α = 30°, β = 50°;
2) с = 5см, α= 100°, β = 30°.
280. 1) Сколько можно построить
треугольников, конгруэнтных данному
разностороннему треугольнику ABC,
при условии, что данный
отрезок будет их общей стороной?
2) Докажите, что любые два из таких
конгруэнтных треугольников
симметричны относительно некоторой оси.
281°. Из металлического прутка нужно
сделать деталь, имеющую форму
равнобедренного треугольника.
Одна из сторон треугольника
должна иметь длину 250 см, а другая
100 см. Какой должна быть длина I
прутка, чтобы это можно было
сделать?
282. Дано: \АВ\ = \ВС\, \AD\ = \DC\
(рис. 134).
Доказать: 1) AABD ^ ACDB;
2) (AC)-L(BD).
283. Дано: [ВС] ^ [AD], ?=1
(рис. 135).
Доказать: ААВС ^ AADC.
284. Дано: [AD) — биссектриса угла
ВАС, \АВ\ = \АС\ (рис. 136).
Рис. 135
Рис. 136
87
Доказать: 1) AABD ^ AADC;
2) {BC).L(AD).
285. Дано: \ВЕ\ = \EC\; \AE\ = \ED\
(рис. 137).
Доказать: \CD\ = \AB\;
BAE = CDE.
Рис.137 286. Дано: [ВС] д* [СА]\ /.A^ZJB
(рис. 138).
Доказать: \ААХ\ = \BB{\,
Δ.ΑΧ^Δ.Β{.
287*. Постройте треугольник по двум
сторонам и углу, лежащему против
одной из них, если:
1) а = 6 см, Ъ = 4 см, α = 70°
2) а = 4 см, Ъ = 6 см, α = 70°
3) а = 6 см, Ъ = 3 см, β = 40°
4) & = 3,5 см, с = 6,5 см, ν = 110°.
ι 288*. Диагонали четырехугольника ABCD
• в точке пересечения О делятся
пополам. Докажите: 1) ААОВ ^
^ ADOC; 2) AAOD ^ АВОС;
3) каждая из диагоналей
четырехугольника делит его на два
конгруэнтных треугольника.
289*. Длины всех сторон
четырехугольника ABCD равны, его диагонали
В пересекаются в точке О. Докажите,
рИСш 139 что треугольники АОВ, ВОС, COD
и DOA конгруэнтны.
290. По преданию, древнегреческий математик Фалес* первым
решил задачу о вычислении расстояния от берега до корабля.
Для этого он измерил расстояние \АВ\ и угол ABC (рис. 139),
а затем, произведя на суше некоторые построения и
измерения, вычислил расстояние |АС|. Какие построения и
измерения мог провести Фалес для решения этой задачи? На чем
основывалось это решение?
1 .-"wlc^-jr^irirzri^-Tir^iirj:
'-£Ξ0
- -
~^-
v___-
^—~у
^-\-—r^^r^rr^r^
щ\С~— — ■—
—-^ \ ~~"_
\- --■-
\
\
V
з ___5~~
* Фалес Милетский (639—548 гг. до н. э.) прославился также
предсказанием солнечного затмения (585 г. до н. э.). По-видимому, открытия Фалеса
производили очень сильное впечатление на современников; его имя — первое
из имен ученых, известных и поныне.
88
§ 3. Симметрия фигур
23. Оси симметрии окружности
На рисунке 140 изображены
фигуры (отрезок, окружность, треугольник,
квадрат), каждая из которых
симметрична себе относительно некоторой
оси. О таких фигурах говорят, что они
имеют ось симметрии.
Существуют фигуры, имеющие
несколько осей симметрии. Например,
квадрат, как мы докажем позднее,
имеет четыре оси симметрии (рис. 141).
Прямая имеет бесконечно много осей
симметрии. Во-первых, она сама
является своей осью симметрии.
Во-вторых, осью симметрии этой прямой
является любая прямая, ей
перпендикулярная (рис. 142).
Докажем следующую теорему.
27|Те.орема. Окружность симмет-
щрична относительно любой прямой,
I проходящей через ее центр.
Доказательство. Пусть
прямая ρ проходит через центр
окружности (О, г) (рис. 143). Осевая
симметрия сохраняет расстояния
(предложение 23). Но при любом отображении,
сохраняющем расстояния, окружность
отображается на окружность того же
радиуса. А так как при симметрии Sp
центр окружности (О, г) отображается
на себя (О £ р), то и окружность (О, г)
отображается на себя, т. е. она
симметрична относительно прямой ρ Μ
Следствие. Точки пересечения
двух окружностей симметричны
относительно прямой, содержащей их
центры.
м<
Μ
τρι
I
Рис. 145
В самом деле, пусть X и Х\
—точки пересечения окружностей (О, г) и
(Οι, π) (рис. 144). При симметрии Sp
каждая из окружностей (О, г) и (Οι, rt)
отображается на себя (теорема 27).
Значит, точки пересечения этих
окружностей при симметрии Sp отображаются
друг на друга, т. е. точки X и Х{
симметричны относительно прямой р. ■
28|Теорема. Диаметр,
перпендикулярный хорде, делит ее и
стягиваемые ею дуги пополам.
Доказательство. Пусть
диаметр MN перпендикулярен хорде АВ
(рис. 145). По определению осевой
симметрии точка, симметричная точке А
относительно прямой MJV, лежит на
перпендикуляре к прямой MN,
проходящем через А. Кроме того, точка
Smn (А) лежит на данной
окружности (О, г) (теорема 27). Но такой точкой
является только точка В.
Следовательно, SMn (A) = В и SMn(B) = А.
Поэтому прямая MN является осью
симметрии хорды АВ и каждой из дув
АМВ и ANB. Значит, диаметр MN
делит хорду АВ и эти дуги пополам. ■
Вопросы и задачи
291. 1) Сколько осей симметрии данной окружности проходит
через данную точку?
2) Сколько осей симметрии может иметь объединение двух
окружностей?
\J 292. Докажите, что диаметр окружности
есть наибольшая из хорд этой
окружности.
293. Центр окружности, пересекающей
стороны данного угла, лежит на
биссектрисе этого угла (рис. 146).
Докажите конгруэнтность отрезков ОМ
Рис. 146 и OK, MN и KL.
90
294. Окружности (Οι, Γι) и (02, г2) пересекаются в точках А и В.
Докажите, что прямые 0\02 и АВ перпендикулярны.
295. Две окружности имеют общий центр, [АВ]—хорда
окружности меньшего радиуса, С и D — точки пересечения прямой
АВ с окружностью большего радиуса. Докажите: 1) \АС\ =
= \BD\; 2) \ВС\ = \AD\.
296. Как разделить дугу данной окружности пополам?
297. Постройте хорду данной окружности, серединой которой
является данная точка.
298. Докажите, что диаметр, который делит пополам хорду, не
проходящую через центр, перпендикулярен этой хорде.
299*. Докажите, что две хорды окружности, пересекающиеся в
точке, отличной от центра окружности, не могут обе делиться в
точке пересечения пополам.
300*. Фигура L является объединением двух окружностей.
Докажите: 1) если фигура L имеет бесконечно много осей
симметрии, то центры этих окружностей совпадают; 2) если
фигура L имеет в точности две оси симметрии, то радиусы
этих окружностей равны.
24. Оси симметрии отрезка
Рассмотрим оси симметрии отрезка. Каждый отрезок имеет
две оси симметрии. Одна из них — прямая, содержащая этот
отрезок, другая — серединный перпендикуляр к отрезку, т. е.
прямая, перпендикулярная этому отрезку* и проходящая через
его середину.
Действительно, прямая АВ является осью симметрии
отрезка АВ, так как при симметрии Sab каждая точка отрезка АВ
отображается на себя.
Если ρ — серединный перпендикуляр отрезка АВ, то (по
определению симметричных точек) точки
А и В симметричны относительно
прямой ρ (рис. 147). Значит, серединный
перпендикуляр отрезка является его осью
симметрии.
А
* Говорят, что прямая (отрезок, луч) АВ
перпендикулярна отрезку (лучу) ΜΝ, если (АВ) J.
1 (ΜΝ). Рис. 147
a
91
Рис. 148
29|Теорема. Множество точек
плоскости, равноудаленных οι
концов отрезка, есть серединный
перпендикуляр к этому отрезку.
Доказательство. 1)
Сначала докажем, что если точка
плоскости равноудалена от концов отрезка,
то она принадлежит серединному
перпендикуляру этого отрезка.
На прямой АВ имеется
единственная точка, равноудаленная от точек
А и В, — это середина Μ отрезка АВ
(рис. 148). Она принадлежит
серединному перпендикуляру отрезка АВ.
Рассмотрим теперь точку X,
равноудаленную от концов отрезка АВ
и отличную от М. Так как \АХ\ =
= \ВХ\ и \МА\ = \МВ\, то точки А
и В симметричны относительно
прямой MX (см. построение симметричных
точек, п, 21). Значит, прямая MX есть
ось симметрии точек А и Б, т. е. (MX)—
серединный перпендикуляр
отрезка АВ.
2) Теперь докажем обратное: если
точка принадлежит серединному
перпендикуляру отрезка, то она
равноудалена от его концов.
Пусть ρ — серединный
перпендикуляр отрезка АВ, a Y — произвольная
точка прямой ρ (рис. 149). Тогда
точки А и Б симметричны относительно
прямой р. Поэтому отрезки ΑΥ и BY
симметричны друг другу относительно
оси р. Следовательно, \YA\ = \YB\,
е. точка Υ равноудалена от концов отрезка АВ.ш
Задача. С помощью линейки и циркуля построить
серединный перпендикуляр данного отрезка АВ.
Решение. Для построения серединного перпендикуляра
отрезка АВ достаточно найти две точки этого перпендикуляра.
Построим окружности с центрами А и В одного и того же радиу-
Рис. 149
Рис. 150
т.
92
са, большего половины |АБ|. Эти
окружности пересекаются (п. 13).
Точки пересечения Μt и Μ2 равноудалены
от концов отрезка АВ (рис. 150).
Значит, точки Mi и М2 лежат на
серединном перпендикуляре отрезка АВ, т. е.
прямая ΜιΜ2 искомая.
Рассмотренный способ построения
серединного перпендикуляра отрезка
применим и для построения середины
отрезка с помощью циркуля и
линейки. Этим же способом можно
воспользоваться и при построении
перпендикуляра к данной прямой р, проходящего
через данную точку Μ (рис. 151, 152).
Вопросы и задачи
301°. Сколько осей симметрии имеет:
1) отрезок; 2) луч; 3) прямая?
302. Постройте серединный
перпендикуляр к данному отрезку АВ% выполняя вспомогательные
построения: 1) в различных полуплоскостях; 2) в одной
полуплоскости с границей {АВ).
303. Постройте к данной прямой а перпендикуляр, проходящий
через точку М: 1) лежащую на данной прямой; 2) не
лежащую на данной прямой.
304. Даны прямая МТ и не принадлежащие ей точки А и В.
Постройте на этой прямой точку, равноудаленную от точек А и В.
Сколько решений может иметь задача?
305. 1) Постройте точки, принадлежащие данной окружности и
равноудаленные от данных точек А и В. Сколько таких точек
можно построить?
2) Найдите множество точек, принадлежащих кругу и
равноудаленных от данных точек А и В,
306. Постройте центр данной окружности, если на чертеже этот
центр не отмечен.
307. Найдите множество центров поворотов, при которых данная
точка А отображается на другую данную точку Б.
308. Найдите множество вершин равнобедренных треугольников,
построенных на данном отрезке как на его основании.
Μ
д Ρ
Рис. 151
Ж"/
Μ /j
β ρ
Рис. 152
93
309*. Стороны АВ и CD, а также углы А
и D четырехугольника ABCD
конгруэнтны. Докажите конгруэнтность углов
В и С.
Рис. 153. 310. Даны две точки А и В. Какую фигуру
образует множество таких точек X,
что: 1) \АХ\ Φ \ВХ\\ 2) \АХ\ ^ \ВХ\; 3) \АХ\ < \BX\1
311**. Населенные пункты А и В расположены по одну сторону от
трассы железной дороги (рис. 153). В каком пункте этой
трассы следует построить платформу С при условии, что: 1)
расстояния \АС\ и \ВС\ должны быть равны; 2) сумма
расстояний \АС\ и \ВС\ должна быть наименьшей; 3) разность
расстояний \АС\ и \ВС\ должна быть наибольшей?
25. Оси симметрии угла и равнобедренного треугольника
30|Теорема. Прямая, содержащая биссектрису угла, явля-
щется осью симметрии этого угла.
Доказательство. Обозначим через ρ прямую,
содержащую биссектрису ВМ угла ABC (рис. 154). Рассмотрим
симметрию Sp.
При этой симметрии луч ВМ отображается на себя, а угол
АВМ — на угол со стороной ВМ, лежащий в полуплоскости
а2 и конгруэнтный углу АВМ. Но АВМ = СВМ (по
условию луч ВМ — биссектриса угла ABC). В полуплоскости
<х2 с границей ВМ существует
единственный угол со стороной ВМ,
конгруэнтный данному углу (п. 18,
предложение 184). Поэтому образом луча В А
при симметрии Sp является луч ВС, а
образом луча ВС — луч ВА.
Следовательно, угол ABC при симметрии Sp отобра·
Рис. 154 жается на себя.·
С помощью теоремы 30 легко
обосновать построение биссектрисы угла,
которое сводится к построению оси
симметрии данного угла (рис. 155).
Следствие 1. Прямая,
содержащая биссектрису угла при вершине
равнобедренного треугольника, является осью
Рис. 155 симметрии этого треугольника.
94
Доказательство. Обозначим
через ρ прямую, содержащую
биссектрису ВМ угла В при вершине
равнобедренного треугольника ABC (рис. 156).
Пользуясь теоремой 30, получаем, что при
симметрии Sp образом луча ВА является
луч ВС, а образом луча ВС — луч ВА.
По условию \АВ\ = \ВС\. Поэтому
Sp (A) = С, Sp (С) = А.
Кроме того, по определению осевой
симметрии Sp (В) = В (так как В 6 р).
Следовательно, при симметрии Sp
равнобедренный треугольник ABC отображается , на себя.·
Следствие 2. Биссектриса угла при вершине
равнобедренного треугольника является также его медианой и
высотой (рис. 156).
31|Теорема. Две стороны треугольника конгруэнтны тог-
Ida и только тогда, когда конгруэнтны противолежащие
им углы.
Доказательство. Надо доказать два предложения:
1) если две стороны треугольника конгруэнтны, то
конгруэнтны и противолежащие им углы; 2) если углы
треугольника конгруэнтны, то конгруэнтны и противолежащие этим углам
стороны.
Первое из этих предложений вытекает из следствия 1: углы
А и С симметричны относительно прямой ВМ (рис. 156) и,
следовательно, конгруэнтны.
Докажем второе предложение. Пусть углы А п С
конгруэнтны (рис. 157). Проведем серединный перпендикуляр ρ к
отрезку АС и рассмотрим симметрию Sp. При этой симметрии лучи
АС и СА> а также точки А и С отображаются друг на друга.
А так как по условию угол А
конгруэнтен углу С, то образом луча АВ при
симметрии Sp является луч СВ, а
образом луча СВ — луч АВ.
Точка В пересечения лучей АВ и С В
отображается при симметрии Sp на точку
пересечения образов этих лучей, т. е. на
себя.
Следовательно, отрезки АВ и СВ
симметричны и поэтому конгруэнтны.· Рис. 157
?5
Вопросы и задачи
312.
313.
314.
315.
316.
317.
318.
1) Сколько осей симметрии может иметь угол?
2) Постройте при помощи циркуля и линейки биссектрису
данного угла.
Докажите, что разносторонний треугольник не имеет осей
симметрии.
Сколько осей симметрии имеет равносторонний треугольник?
Докажите, что каждая биссектриса равностороннего
треугольника является также его медианой и высотой.
1) Постройте равнобедренный треугольник, симметричный
относительно данной прямой а.
2) Как можно построить равносторонний треугольник, осью
симметрии которого является данная прямая?
Докажите конгруэнтность: 1) медиан; 2) биссектрис; 3)
высот равнобедренного треугольника, проведенных к его
боковым сторонам.
Высота, проведенная из вершины равнобедренного
треугольника, отсекает от него треугольник, периметр которого 18 см.
Вычислите длину высоты, если периметр данного
равнобедренного треугольника равен: 1) 24 см; 2) 30 см; 3) 20 см.
319. Найдите длины основания и боковой
стороны равнобедренного
треугольника, если известно, что две его стороны
имеют длины: 1) 3 см и 7 см; 2) 20 см
и 10 см; 3) 7 см и 8 см.
320. Дано: \АВ\ = \ВС\, BAD = ВСЕ
(рис. 158). .
Доказать: ABDE равнобедренный.
321. Постройте равнобедренный
треугольник: 1) по основанию а и боковой
стороне Ь; 2) по боковой стороне Ъ и
высоте /г, проведенной к основанию;
3) по основанию а и высоте ht
проведенной к основанию.
322. Через внутреннюю точку данного угла
проведите прямую, отсекающую от
сторон этого угла конгруэнтные от-
Рис. 159 резки.
96
323. Докажите, что если все углы треугольника конгруэнтны, то
этот треугольник равносторонний.
324. Как можно воспользоваться шарнирным механизмом,
имеющим звенья равной длины (рис. 159), для построения: 1)
биссектрисы данного угла; 2) середины данного отрезка; 3)
центра данной окружности?
325*. Докажите, что если треугольник отображается на себя при
некотором нетождественном повороте, то этот треугольник
равносторонний.
А·
26. Расстояние от точки до прямой.
Свойство биссектрисы угла
Рассмотрим произвольные прямую ρ и точку А $ р.
Основание перпендикуляра, проведенного через точку А к прямой р,
называется проекцией точки А на прямую р. Например, точ-
κηΟ,Οιη02 — проекции точек А, А4и А2 на прямую ρ (рис. 160).
Проекция любой точки, принадлежащей прямой р, на эту
прямую есть сама эта точка. Множество проекций всех точек
отрезка АВ на прямую ρ называется проекцией отрезка АВ на
эту прямую. Например, отрезок ОВх — проекция отрезка АВ
на прямую р.
Прямая, пересекающая прямую ρ
и не перпендикулярная ей,
называется наклонной к прямой р. На рисунке
161 прямая АО — перпендикуляр к
прямой р, а прямая АВ — наклонная
к прямой р. Иногда для краткости
отрезки АО и АВ называют
соответственно перпендикуляром и
наклонной, проведенными из точки А к
прямой р.
32|Теорема. Расстояние от точки
до ее проекции на прямую меньше
расстояния от этой точки до любой
другой точки данной прямой
(кратко говорят: перпендикуляр короче
наклонной).
Дано: О — проекция точки А
на прямую р, В 6 ρ, Β Φ О (рис. 161).
Доказать: \АО\ < \ АВ\. Рис. 161
м ι
Αι*
0ζ 0
Рис. 160
97
jf/ А Доказательство. В случае
А 6 Ρ теорема очевидна.
Пучсть A i р. Построим точку Ai =
= Sp (А) и проведем прямую Α Α ι.
Так как*В 6 ρ и В Φ О, то Б £ (АА4).
Тогда по неравенству треугольника
(п. 5) имеем:
L=0Kp(0,r) \AAi\< \AB\ + \ВА,\. (1)
с %^Л
l = [bc]
Осевая симметрия сохраняет
расстояния. Поэтому \АВ\ = \A\B\ и
Ъ \АО\=\А{0\. Значит, \АА,\=2 \АО\
и неравенство (1) можно переписать в
виде:
2IAOI <2 \АВ\.
\ L \ф 9 Отсюда
V-^^У β А \АО\<\АВ\.Ш
Рнс· 162 Итак, расстояние от точки А до ее
проекции на прямую ρ есть наименьшее из расстояний от точки
А до точек прямой р. Это расстояние называют расстоянием
от точки А до прямой р.
Вообще, если фигура L содержит точку В, самую близкую
из точек фигуры L к данной точке А, то расстояние \АВ\
называется расстоянием от точки А до фигуры L (рис. 162).
33 I Теорема. Множество точек выпуклого угла, равноуда-
I ленных от его сторон, есть биссектриса этого угла.
Доказательство. 1) Докажем сначала, что если
точка Μ принадлежит биссектрисе ON угла АОВ, то она
равноудалена от сторон ОА и ОВ (рис. 163), т. е. докажем равенство
расстояний ME и MD (точка Ε — проекция точки Μ на
прямую ОА, а точка D — проекция точки Μ на прямую ОВ). Для
этого достаточно доказать, что эти отрезки симметричны
относительно прямой ON.
Рассмотрим симметрию S с осью ON. Так как точка Μ
принадлежит оси симметрии, то S (М) = М. При симметрии S
луч ОА отображается на луч ОВ (по условию ΙΟΝ) —
биссектриса угла АОВ). Поэтому перпендикуляр ME к прямой ОА
отображается на перпендикуляр MD к прямой ОБ, проходящий
через точку М. Образом точки пересечения луча ОА и прямой
98
Μ
В 3
Рис. 163
ЕМ при симметрии S является точка
пересечения образов этих фигур, т. е.
S (Е) = D. Итак,
S (М) = М, S (Е) - D.
Значит, расстояния \МЕ\ и \MD\
равны. Первая часть теоремы доказана.
2) Докажем теперь обратное: если
точка Μ выпуклого угла АОВ равноудалена
от сторон этого угла, то она
принадлежит его биссектрисе.
Обозначим проекции точки Μ на
стороны угла АОВ через Ε и D (рис. 164).
По условию \МЕ\ = \MD\. Рассмотрим
треугольник MED. Так как |АГЕ|= \MD\9
то этот треугольник равнобедренный и,
следовательно, MED = EDM. А так как
OEM = ODM = 90°, то OED = ODE. Это
означает, что треугольник OED также
равнобедренный и | ОЕ \ = \ OD |. Итак,
\ЕМ\ = \MD\ (по условию),
\ОЕ\ = \OD\ (по доказанному).
Поэтому точки Ε и D симметричны относительно оси ОМ
(см. п. 21) и углы АОМ и ВОМ, симметричные относительно
этой оси, конгруэнтны, т. е. луч ОМ — биссектриса угла АОВ. ■
Рис 164
Вопросы и задачи
326. 1) Постройте проекции вершин данного треугольника ABC
на прямые АВ, ВС и АС. (Рассмотрите различные случаи:
треугольник ABC может быть остроугольным, прямоугольным
и тупоугольным.)
2) Постройте проекцию данного отрезка АВ на данную
прямую а. (Рассмотрите различные случаи: отрезок АВ лежит
на прямой а, пересекает эту прямую и не имеет с ней общих
точек.)
327. 1) Могут ли два различных отрезка иметь одну и ту же
проекцию на данную прямую?
99
2) Проекцией какой фигуры на данную
прямую может быть точка?
328. Дан отрезок АВ. Какой фигурой
является множество, состоящее из таких
точек X, что проекция отрезка АХ
на прямую АВ — отрезок АВ1
329. Измерьте расстояния от точек А, В,
С, D: 1) до прямой а; 2) до луча MN;
3) до отрезка PQ (рис. 165).
330. Докажите, что наклонная,
проведенная из данной точки к данной
прямой, больше проекции наклонной на
эту прямую.
331. Докажите, что гипотенуза
прямоугольного треугольника больше его катета.
332*. Внутри треугольника ABC взята
точка М. Докажите, что сумма
расстояний от этой точки до вершин
треугольника больше суммы расстояний от этой
точки до сторон треугольника.
333. Какую фигуру образуют точки, каждая
из которых равноудалена от двух
пересекающихся прямых?
334. Пользуясь планом местности (рис.166),
измерьте возможно точнее расстояния
от точек А, В и С до озера (масштаб
плана 1 : 10 000).
335. 1) Внутри угла дана точка М.
Постройте точки этого угла, равноудаленные
от сторон и отстоящие от точки Μ на
заданное расстояние г.
2) Постройте точки данного
выпуклого угла ABC, равноудаленные от его
сторон и от концов данного
отрезка EF (точки Ε и F лежат на различных
сторонах данного угла).
336*. Докажите, что расстояние от точки Μ
до окружности (О, г) равно \МА\
(рис. 167).
337. Двор имеет треугольную форму. Где
нужно вкопать столб для подвески
светильника, чтобы одинаково были
освещены углы двора?
338*. На рисунке 168 показан план
местности. Укажите кратчайший
маршрут, которым следует пройти от
пункта С до: 1) пруда; 2) рощи;
3) железнодорожной станции.
339. 1) Дано: \ОА\ = \ОВ\, (ОМ)±(АВ)
(рис. 169). Доказать: \МА\ = \МВ\.
2) Дано: \ОА\ > \ОВ\, (ОМ)±(АВ)
(рис. 169). Доказать: \МА\ = \МВ\.
27 Τ - Симметричные фигуры
Окружность, отрезок, угол и равнобедренный треугольник
имеют оси симметрии. Существуют ли другие перемещения, кроме
осевой симметрии, отображающие эти фигуры на себя?
1) Любое перемещение, отображающее на себя окружность
(О, г), является либо осевой симметрией, ось которой проходит
через центр О (рис. 171), либо поворотом с центром О на
произвольный угол (в частности, таким перемещением является
симметрия с центром О и тождественное отображение Е).
Заметим, что и поворотов, и осевых симметрии, отображающих
окружность на себя, бесконечно много.
2) Существуют 4 перемещения,
отображающие на себя отрезок АВ
(рис. 172): две осевые симметрии —
относительно прямой АВ и серединного
перпендикуляра к отрезку АВ, а
также симметрия с центром в середине
данного отрезка и тождественное
отображение.
3) Как показано в пункте 25,
любой угол имеет одну ось симметрии.
Других перемещений, отображающих
угол на себя (за исключением
тождественного отображения), не существует*.
4) Равнобедренный треугольник
имеет хотя бы одну ось симметрии
* Это верно для углов, не являющихся
развернутыми.
В Μ А
Рис. 170
• \ I {—\ ·
А В
Рис. 172
101
(п. 25). Если этот треугольник не
является равносторонним, то
существует единственное нетождественное
перемещение, отображающее данный
треугольник на себя. Это
перемещение — симметрия, ось которой
содержит биссектрису угла при вершине
равнобедренного треугольника.
Равносторонний треугольник
имеет три оси симметрии — это
серединные перпендикуляры к сторонам
этого треугольника (рис. 173).
Повороты с центром в точке пересечения
серединных перпендикуляров на
углы 0е и 120° (в направлении по
часовой стрелке и против) также
отображают равносторонний
треугольник на себя.
Если фигура отображается на
себя при повороте с центром О на
ЗС0°
угол , то говорят, что эта фи-
η
гура обладает симметрией
вращения порядка п, а точка О называется
центром вращения порядка п.
Можно сказать, что равносторощшй
треугольник обладает симметрией
вращения порядка 3, а отрезок —
Рис. 177 Рис. 178
Рис. 179
симметрией вращения порядка 2.
Пятиконечная звезда (рис. 174)
обладает симметрией вращения
порядка 5 (докажите это), а фигура,
изображенная на рисунке 175, имеет
симметрию вращения порядка 4, однако эта
фигура не имеет осей симметрии.
Как и многие другие
математические понятия, понятие симметрии фигур
цоявилось в результате наблюдений
над объектами окружающего мира.
Например, рассматривая изображения
растений и живых организмов
(эти изображения можно считать
плоскими фигурами), легко
убедиться, что многие из них с большой
степенью точности обладают той или
иной симметрией. Так, лист клена (рис.
176) обладает осевой симметрией.
Различными видами симметрии обладают
цветы (рис. 177, а, б), многие живые
организмы — морские звезды (рис. 178),
бабочки (рис. 179). Симметрией
вращения порядка 6 и осевыми симмет-
риями обладают снежинки (рис. 180).
С симметрией мы часто
встречаемся в искусстве, технике, быту.
Например, симметричны фасады многих
зданий (рис. 181) и их виды сверху.
Симметричны узоры на коврах, узоры
бордюров, многие виды механизмов, например колесо или
шестеренка.
Рис. 180
Рис. 181
Вопросы и задачи
340°. Какими симметриями обладают фигуры, изображенные на
рисунке 182?
341. Постройте фигуру, имеющую центр вращения пятого порядка.
342. Постройте фигуру, которая не имеет осей симметрии и
обладает симметрией вращения порядка 6.
103
343. Приведите несколько примеров живых
организмов и растений, обладающих
какой-либо симметрией.
344°. Приведите несколько примеров
симметричных фигур, встречающихся в
архитектуре, технике, быту.
345. Вырежьте ножницами какой-либо узор
на сложенном вдвое листе бумаги.
Разверните лист. Покажите ось
симметрии и симметричные относительно
этой оси фигуры.
346. На рисунке 183 изображен узор,
полученный при перегибании листа бумаги
и вырезании фигуры. Попробуйте
изготовить этот узор
самостоятельно.
347. Постройте какую-либо симметричную
красивую фигуру, состоящую из
отрезков и дуг окружностей.
348. Восстановите изображение фигуры L,
если известно, что точка О является
центром вращения этой фигуры
шестого порядка и сохранилась часть
изображения этой фигуры (рис. 184).
349. От луча ОА\ откладываются
углы AiOAo, A2OA3l ...,An_l OAn, вели-
360' _
чины которых равны . Фигу-
Рис. 183 Рис. 184
pa L\ — произвольное
подмножество угла А\ОА2,
фигуры Lo, .llf L n—образы
фигуры L\ при поворотах
с центром О на различные
360°
углы, кратные .
Докажите
те, что объединение фигур
L], L2, ..., Ln — фигура,
обладающая симметрией
вращения порядка п. (На рис. 185
выполнено построение для
л = 8.)
Рис. 185
§ 4. Окружность
28. Угловая величина дуги окружности
34|Теорема. Два центральных угла окружности
конгруэнтны тогда и только тогда, когда конгруэнтны
соответствующие им дуги.
Для того чтобы доказать эту теорему, надо доказать два
предложения: 1) если два центральных угла окружности
конгруэнтны, то конгруэнтны и соответствующие им дуги; 2) если
конгруэнтны две дуги окружности, то конгруэнтны и
соответствующие им центральные углы. Докажем первое из этих
предложений (второе примем без доказательства).
Доказательство.
Обозначим точки пересечения сторон
данных центральных углов с
окружностью (О, г) через Ai9 В\
(рис. 186). Имеем:
и Ао9 By
А{ОА, = ΑγΟΒχ + ΒιΟΑ,,
В{ОВ2 - В{ОА2 + А2ОВ2.
Но Α{ΟΒι — А2ОВ2 (по условию).
Поэтому AiOA2 = BiOB2 = а.
Рис. 186
105
Рассмотрим поворот с центром О на угол а. При этом
повороте точка О, а значит и окружность (О, г) отображаются на
себя, угол ΑιΟΒι — на угол А2ОВ2 (величины этих углов
равны). Отсюда следует, что образом дуги ΑιΒ{ является дуга А2В2.
А так как поворот есть перемещение, TO^AtBi ^^уА2В2.Ш
Определение. Угловой величиной дуги окружности
называется величина соответствующего ей центрального угла этой
окружности.
Угловая величина дуги AB обозначается так: АВ.
Как известно, два угла конгруэнтны тогда и только тогда,
когда равны их величины (п. 18). Отсюда и из теоремы 34
получаем:
две дуги окружности конгруэнтны тогда и только тогда,
когда угловые величины этих дуг равны.
Вопросы и задачи
350. Как разделить окружность на четыре конгруэнтные дуги?
351. С помощью циркуля (способом проб) разделите данную
окружность: 1) на семь конгруэнтных дуг; 2) на пять
конгруэнтных дуг.
352. Дана окружность (О, г). Пользуясь одной линейкой,
постройте: 1) хорду этой окружности, конгруэнтную данной хорде АВ
той же окружности; 2) дугу окружности (О, г), конгруэнтную
данной дуге этой окружности.
353. Две окружности имеют общий центр О; [АВ] —хорда
окружности большего радиуса, пересекающая вторую окружность
в точках С и D. Докажите, что /-АОС ^ ZJBOD,
354. Сколько градусов содержат центральные углы,
соответствующие дуге АВ, которая составляет: 1)-—; 2) —; 3) — ; 4) —
5 о 10 16
часть окружности? Запишите с помощью обозначений
угловую величину дуги АВ в каждом из этих случаев.
355. Разделите окружность на четыре дуги, угловые величины
которых пропорциональны числам 1, 4, 8 и 11. В каком
отношении находятся величины центральных углов,
соответствующих этим дугам?
356. Окружность разделена двумя точками на две дуги. Какова
угловая величина каждой из этих дуг, если: 1) угловая
величина одной из них на 30° больше угловой величины дру-
106
гой; 2) угловые величины этих дуг пропорциональны
числам 1 и 3?
357. 1) Постройте равносторонний треугольник, вершины
которого лежат на данной окружности.
2) Постройте с помощью линейки и транспортира
правильную пятиконечную звезду.
358. 1) Какова угловая величина дуги, которую описывает конец
часовой стрелки: а) за 2 ч; б) за 1 ч 30 мин; в) за 15 мин?
2) Сколько минут содержит угол, на который поворачивается
минутная стрелка за 1 мин?
359. 1) Докажите, что две дуги окружности конгруэнтны тогда и
только тогда, когда конгруэнтны стягивающие их хорды
(предполагается, что величины обеих дуг либо не превышают
180°, либо больше 180е).
2) Докажите, что две дуги, лежащие на различных
окружностях равных радиусов, конгруэнтны тогда и только тогда,
когда их угловые величины равны.
360. На окружности даны три точки А, С и Ζλ Постройте при
помощи циркуля Дугу АВ, конгруэнтную дуге CD.
361. Разделите дугу окружности пополам, если центр этой
окружности недоступен.
362*. Какую фигуру образует: 1) множество середин хорд данной
окружности, перпендикулярных данному диаметру этой
окружности; 2) множество середин хорд данной окружности,
имеющих длину а (а <С г)1
363. 1) Хорда делит окружность на две дуги, угловые величины
которых пропорциональны числам 4 и 5. Под каким углом
видна эта хорда из центра окружности?
2) Под каким углом была бы видна из центра Земли дуга
экватора длиной: а) 1 км; б) 2 м? Длину экватора принять
за 40 000 км.
29. Взаимное расположение прямой и окружности
Различные случаи взаимного расположения прямой и
окружности показаны на рисунках 187, а, б, е. Прямая, имеющая
с окружностью только одну общую точку, называется
касательной к этой окружности, а их общая точка — точкой касания.
Если прямая и окружность имеют две общие точки, то говорят,
что прямая и окружность пересекаются.
107
Для того чтобы ответить на вопрос, сколько общих точек
имеют данные прямая ρ и окружность (О, г), требуется
сравнить расстояние h от центра О окружности до прямой ρ с
радиусом г этой окружности.
Возможны три случая: 1) h > г; 2) h = г; 3) h < г.
Рассмотрим эти случаи.
1) Если расстояние от центра окружности до прямой боль-
ше радиуса окружности, то прямая и окружность не имеют
общих точек.
В самом деле, если h > г (см. рис. 187, а), то ближайшая
к центру О точка прямой ρ (а значит, и любая точка этой
прямой!) не может принадлежать окружности (О, г), так как она
находится от центра на расстоянии, большем г. ■
2) Если расстояние от центра окружности до прямой рае-
но радиусу окружности, то прямая и окружность имеют одну
и только одну общую точку.
В самом деле, если h = г (см. рис. 187, б), то ближайшая
к центру О точка прямой ρ находится на расстоянии, равном
радиусу окружности, и, значит, принадлежит окружности.
Все остальные точки прямой ρ находятся от центра О на
расстоянии, большем радиуса окружности, и, следовательно,
окружности не принадлежат. ■
3) Если расстояние от центра окружности до прямой
меньше радиуса окружности (h < г), то прямая и окружность
имеют ровно две общие точки (рис. 187, в).
Доказательство этого утверждения сложно, поэтому мы
его опускаем. Итак,
35 I окружность и прямая могут не иметь общих точек, иметь
I одну или две общие точки.
Докажем теоремы о касательной к окружности.
108
Рис. 188
36 i Τ е о о е м а. 1) Если прямая
перпендикулярна к радиусу
окружности и проходит через его конец,
лежащий на окружности, то она
касается этой окружности.
2) Если пряная касается
окружности, то она перпендикулярна
радиусу этой окружности,
проведенному в точке касания.
Первая часть теоремы уже
доказана. Действительно, в этом случае
(рис. 188) расстояние h от центра
окружности (О, г) до прямой ρ равно
радиусу г. Поэтому, как показано
выше, прямая ρ и окружность (О, г)
имеют единственную общую точку. Это
и означает, что прямая ρ —
касательная к окружности (О, г).
Докажем вторую часть теоремы.
Дано: ρ — касательная] к окружности (О, г) в точке А.
Доказать: ρ ± (ОА) (рис. 189).
Доказательство. Допустим, что прямые ρ и ОА
не перпендикулярны и [ОБ] — перпендикуляр к р. Тогда по
теореме 32 расстояние от точки О до прямой ρ равно \ОВ\.
Так как по предположению А Ф В, то \ОВ\ < \ОА\, т. е. h <
< г. Но, как показано выше, в этом случае прямая ρ
пересекает окружность (О, г). Получили противоречие с условием:
ρ касается окружности (О, г). Значит, наше допущение
неверно и ρ j_ (OA). ■
Рис. 189
Вопросы и задачи
364°. Даны окружность (О, г) и прямая а. Каково взаимное
расположение этих фигур, если известно, что расстояние от точки О
до прямой а: 1) больше г; 2) меньше г; 3) равно г?
365. На сторонах данного угла АОВ постройте точки, находящиеся
на данном расстоянии а: 1) от вершины угла; 2) от точки М,
лежащей во внутренней области угла АОВ.
366. Постройте окружность данного радиуса г, которая касается
данной прямой а в данной на ней точке М.
109
367. Постройте касательную к данной окружности, проходящую
через данную точку этой окружности.
368. 1) Постройте окружность, касающуюся сторон данного угла.
2) Постройте окружность, которая касается сторон данного
угла, причем одной из них в данной точке.
369. Найдите множество центров окружностей, касающихся
сторон данного угла.
370. Две окружности касаются друг друга в точке А. Существует
ли прямая, касающаяся обеих этих окружностей и
проходящая через А?
371. Постройте окружность, касающуюся всех сторон данного
треугольника.
372. Известно, что \АО\—наименьшее из всех расстояний от
точки А до точек прямой ρ (А $ р). Докажите: (АО) А-р.
30. Задачи на построение
Вы уже решали довольно много задач на построение — задачи
на построение треугольников по заданным элементам, задачи на
построение образа данной фигуры при осевой симметрии,
фигуры, центрально-симметричной данной, и т. д. Решение этих
задач, как правило, начиналось сразу с построения.
Однако при решении более сложных задач на построение
сразу найти требуемое построение трудно. Предварительно проводят
анализ задачи. Предполагают задачу уже решенной и
составляют предположительный чертеж взаимного расположения данных
элементов (точек, прямых, окружностей и т. п.) и искомых. На
этом чертеже пытаются найти вспомогательные элементы,
которые могли бы помочь построению искомых, а сами могли бы
быть построены при помощи данных. В случае успеха такого
анализа задачи ее решение становится очевидным. В виде
первого примера рассмотрим задачу.
Задача 1. Построить прямоугольный треугольник по
гипотенузе и катету.
Решение. Проведем анализ. Предположим, что
треугольник, удовлетворяющий условиям задачи, построен (рис. 190).
Отметим на полученном чертеже элементы, данные в условии.
Рассматривая полученный рисунок, мы видим, что вершины
В и С можно построить, отложив отрезок ВС заданной длины а.
Третья вершина А: 1) лежит на перпендикуляре к прямой БС,
проходящем через С, и 2) находится от точки В на расстоянии,
равном длине отрезка АВ, т. е. лежит на окружности (Б, с).
110
Отсюда следует, что для решения
задачи (рис. 191) достаточно построить:
1) отрезок ВС длины а;
2) перпендикуляр ρ к прямой ВС,
проходящий через точку С;
3) окружность (Б, с);
4) точку А пересечения этой
окружности с прямой р.
Треугольник, вершинами которого
являются точки А> В, С, искомый.
Треугольник, удовлетворяющий
условиям задачи, существует лишь при
условии с > а (объясните почему). При
этом условии задача имеет решение.
Это решение (с точностью до
конгруэнтности) единственно. Справедлив
следующий признак конгруэнтности
прямоугольных треугольников:
37 \если гипотенуза и катет одного
прямоугольного треугольника
конгруэнтны гипотенузе и катету
другого треугольника, то такие
прямоугольные треугольники
конгруэнтны.
Задача 2. Построить
касательную к данной окружности, проходящую
через данную точку.
Решение. Данная точка А
может: 1) принадлежать внутренней
области данной окружности (О, г) (| О А | <
< г); 2) лежать на окружности (О, г)
(|ОА| = г) и, наконец, 3) лежать во
внешней области данной окружности
(|ОА| > г). Рассмотрим эти три
случая отдельно.
1) | О А | < г (рис. 192, а). В этом
случае расстояние от центра О окружности
до любой прямой, проходящей через
точку А, меньше радиуса г (перпендикуляр
короче наклонной!). Значит, любая пря-
a)
Рис. 193
мая, проходящая через данную точку А,
пересекает данную окружность (п. 28).
В этом случае искомой касательной не
существует.
2) \ОА\ = г (рис. 192, б). В этом
случае точка А лежит на окружности (О, г).
По теореме 36 искомая касательная
должна быть перпендикулярна прямой ОА.
Но существует единственная прямая,
проходящая через точку А и
перпендикулярная прямой ОА. Значит, в рассматриваемом случае
решение единственно. Для построения касательной достаточно
провести прямую ОА и построить прямую р,
перпендикулярную прямой ОА и проходящую через точку А. Прямая ρ —
искомая.
3) \ОА\ > г (рис. 193, а). Проведем анализ. Допустим, что
искомая касательная AM построена. Отложим на прямой ОМ
отрезок MB длины г (рис. 193, а). Тогда точки О и В
симметричны относительно прямой AM. В самом деле, (ОМ) j_ (AM)
(теорема 36,2). Кроме того, по построению \ОМ\=\ВМ\.
Поэтому отрезки АО и АВ симметричны относительно прямой AM и,
следовательно, \ОА\ = \АВ\. Тем самым мы показали: а)
точка В принадлежит и окружности (О, 2г), и окружности (А, | О А |);
б) точка касания Μ — середина отрезка ОВ — принадлежит
окружности (О, г) и прямой ОВ. Построив точку Μ искомой
касательной, нетрудно построить и саму касательную:
достаточно провести прямую AM. Теперь можно перейти к построению.
Построим окружности (О, 2г) и (А, |ОА|) (рис. 193, б). Зти
112
окружности имеют две общие точки (п. 13). Обозначим их через
JSi и В2. Проведя прямые ОБ4 и ОВ2, найдем точки пересечения
этих прямых с окружностью (О, г) — точки Mi и М2. Прямые
АМи АМ2 — касательные к окружности (О, г).
Таким образом, в этом случае задача имеет два решения:
из точки, лежащей во внешней области окружности, можно
провести две касательные к этой окружности. Отрезки AMt и АМ2
этих касательных конгруэнтны. В самом деле, при симметрии с
осью ОА точка А отображается на себя, точки касания М4 и М2
отображаются друг на друга (см. рис. 193, в).
Вопросы и задачи
373. Постройте прямоугольный треугольник: 1) по гипотенузе с и
катету Ь; 2) по катетам а и Ь; 3) по катету а и прилежащему
острому углу β; 4) по гипотенузе с и острому углу а; 5) по
катету а и высоте h, проведенной к гипотенузе.
374. Постройте равнобедренный треугольник: 1) по боковой
стороне Ъ и высоте h, проведенной к этой стороне; 2) по
основанию а и высоте h, проведенной к одной из боковых сторон.
375°. Сколько касательных, проходящих через данную точку А,
можно провести к данной окружности (О, г)?
376. Постройте касательную к данной окружности, проходящую
через данную точку.
377*. Какую фигуру образует множество точек, для любой из
которых касательные, проведенные к данной окружности,
имеют одну и ту же длину а?
378. Постройте окружность, которая отсекает от сторон данного
угла отрезки длины а.
379*. Даны окружность (О, г) и прямая а — касательная к этой
окружности. Постройте окружность, которая касается: 1)
данной окружности и данной прямой в данной на этой прямой
точке М; 2) данной прямой и данной окружности в данной
на этой окружности точке М.
380*. Две окружности (Oi, rj) и (02, г2) касаются внешним
образом. 1) Найдите такую точку М, что касательные,
проведенные из нее к данным окружностям, имеют равные длины.
2) Какую фигуру образует множество точек М, таких, что
касательные к данным окружностям, проведенные из этих
точек, имеют равные длины?
113
Дополнительные задачи к главе II
381. Фигура L состоит из всех точек полуокружности с центром О,
за исключением точек А и В (рис. 194). Произвольной точке X
этой фигуры поставлена в соответствие точка Х\ прямой р,
лежащая на луче ОХ. Проверьте, что тем самым задано
отображение фигуры L на прямую р. Обратимо ли это
отображение?
382. Приведите примеры обратимых отображений фигуры на
фигуру, при которых расстояния между точками: 1)
сохраняются; 2) не сохраняются.
383. Фигура L состоит из точек А, В, С и D; \АВ\ = \ВС\ =
= \CD\ = |-AD|. 1) Покажите, что существуют четыре
отображения этой фигуры на себя, сохраняющих расстояния.
2) Для одного из этих отображений укажите отображение,
ему обратное.
384. Отрезки АВ и CD имеют одинаковую длину. Приведите
пример отображения отрезка АВ на
отрезок CD: 1) сохраняющего
расстояния; 2) не сохраняющего расстояния.
В морской практике принято
определять направления в румбах. Румб —
это угол между направлением оси
магнитной стрелки и выбранным
направлением. Румбы отсчитываются как
от северного, так и от южного
конца магнитной стрелки от 0° до 90°.
При этом указывается, какой из
четырех четвертей — СВ, ЮВ, ЮЗ, СЗ —
принадлежит угол (рис. 195, а).
Например, для направления I румб равен
СВ 45е, а для направления III румб
равен ЮВ 60°.
На схеме (рис. 195, б) стрелками
показаны направления движения кораблей
в некотором районе. Определите эти
направления в румбах.
Докажите: 1) любые два луча
конгруэнтны; 2) любые две прямые
конгруэнтны; 3) любые две полуплоскости
конгруэнтны.
Л4
385.
386.
387. Ученику требуется начертить в тетради фигуру,
конгруэнтную фигуре, изображенной на картинке. Как это можно
сделать?
388°. Какие фигуры, изображенные на рисунке 78, имеют: 1) центр
симметрии; 2) ось симметрии?
389. Точки Οι и Ог, принадлежащие фигуре L, являются центрами
симметрии этой фигуры; расстояние |Οι02| равно 1.
Докажите, что существуют такие две точки фигуры L, расстояние
между которыми равно: а) 2; б) 3; в) 1 000 000.
390. Известно, что при некотором перемещении точка А
отобразилась на точку А\, точка В— на точку В\. Как можно
построить образ точки X при этом перемещении, если:
1) Χζ(ΑΒ); 2) X UAB)1
391. 1) Докажите, что отрезок имеет только один центр
симметрии.
2) Докажите, что окружность имеет только один центр
симметрии.
392. Докажите, что фигура, являющаяся объединением двух
кругов равных радиусов, имеет центр симметрии. Имеет ли центр
симметрии пересечение этих кругов?
393. Каждой точке Р(х, у) плоскости поставлена в соответствие
точка: 1) Р'{-х-\, -у - 1); 2) Ρ' (χ, 1-ι/); 3) Р'(]-х,у).
Покажите, что каждое из этих отображений является
перемещением.
394. Дан угол АОВ и точка Μ внутри этого угла. Постройте точки
M\=SA0{M) и M2 = SB0(Mi). Докажите, что величина
угла М\ОМ2 не зависит от положения точки М.
395. Сколько осей симметрии может иметь фигура, если она
является объединением: 1) окружности и точки; 2) окружности
и прямой?
396. Две точки А\ и А2 симметричны относительно оси р.
Постройте с помощью одной линейки точку, симметричную данной
точке В относительно прямой р, если известно, что В £ (А1А2).
397. Даны взаимно перпендикулярные прямые а и Ъ,
пересекающиеся в точке О, и точка М, не лежащая ни на одной из этих
прямых. Постройте точки М{ = Sa(M), M2 = Sb{Mx), М3 =
= Sa (M2) и т. д. Сколько различных точек при этом будет
построено?
398. Докажите, что при любом повороте с центром О
окружность (О, г) отображается на себя.
115
399. Дан угол в 54°. С помощью циркуля и
линейки разделите его на три
конгруэнтных угла.
400. Дан угол в 17°. Как можно при
помощи циркуля и линейки построить угол:
1) 10°; 2) 22°; 3) 1 Г?
401. Постройте объединение фигуры,
заштрихованной на рисунке 196, и
фигуры, являющейся образом этой
фигуры при повороте на 45° вокруг центра
данной окружности в направлениях
по часовой стрелке и против.
402. Постройте центр и угол поворота, если
даны точки А и А\ (образ А при
этом повороте) и известно, что центр
поворота принадлежит данной
прямой а.
403. Даны две концентрические
окружности (рис. 197). Докажите, что
расстояние между ними равно |АВ|*.
404. Как можно найти расстояние между
двумя окружностями, изображенными
на рисунках 198, а, б?
405. Какой фигурой может быть множество
точек, равноудаленных от сторон угла?
406. Точка Μ равноудалена от сторон угла
АОВ. Следует ли из этого, что
точка Μ лежит на биссектрисе этого угла?
(Сделайте рисунок и покажите на нем
возможные положения точки М.)
407. Постройте фигуру, которая является
объединением данной фигуры (рис. 199)
и фигуры, ей симметричной
относительно оси s.
408. Для нахождения центра детали,
имеющей форму круга, применяется
прибор, который называется центроиска-
телем. 1) Объясните, как можно найти
* Расстоянием между фигурами Zj и L2
называется наименьшее из расстояний |ХУ|, где
X <Е Llt Υ е L2.
Рис. 199
0)
в
центр круга при помощи центроиска-
теля, изображенного на рисунке 200, а.
(Вершина прямого угла находится в
середине отрезка АВ.) 2) Объясните,
как можно воспользоваться этим
прибором для построения биссектрисы
данного угла.
409. -Объясните, почему механизм из трех
звеньев, изображенный на рисунке
200, б, будет жестким (т. е. не
шарнирным) даже в том случае, когда все три
его звена соединены шарнирами.
410. Докажите, что если диаметр делит
дугу, стягиваемую хордой, пополам, то
он перпендикулярен этой хорде.
411. Докажите, что сумма высот любого
треугольника меньше его периметра.
412. Докажите, что сумма медиан любого
треугольника меньше его периметра,
но больше полупериметра.
413. 1) Внутри треугольника ABC взята
точка М. Докажите, что периметр
треугольника АМВ меньше периметра
треугольника АСВ.
2) Докажите, что расстояние между
любыми двумя вершинами замкнутой
ломаной не больше половины суммы
длин ее звеньев.
414. Найдите расстояние от точки А,
лежащей внутри окружности (О, г), до этой окружности.
415. 1) Докажите, что если через концы хорды данной
окружности провести перпендикулярные ей хорды, то их длины
будут равны.
2) Можно ли через точку, лежащую во внутренней области
окружности, провести три хорды равной длины?
416. Постройте прямоугольный треугольник, если даны его катет
и отрезок, длина которого равна сумме длин другого катета
и гипотенузы.
417. 1) Внутри острого угла взята точка М. Постройте треугольник
KLM, имеющий возможно меньший периметр, вершины
К и L которого лежат на сторонах данного угла.
117
2) Даны прямая а и точки Α £ α, ЗД α. Постройте на
прямой а такую точку X, что сумма расстояний |АХ| и |ХВ|
равна длине данного отрезка.
418. Через данную точку А, лежащую во внутренней области
окружности (О, г), проведите хорду наименьшей длины.
419. 1) Постройте четырехугольник ABCD по четырем сторонам
так, чтобы луч АС был биссектрисой угла А.
2) Луч АС является биссектрисой угла А четырехугольника
ABCD; периметры треугольников АСВ и ACD равны.
Докажите, что эти треугольники конгруэнтны.
420. 1) Из точки Μ проведены касательные к окружности (О, г);
точки касания — Αι и А2. Докажите: а) (АХА2) -L (МО);
б) ^АхМО ^ /LA2MO.
2) Точки А и В принадлежат прямой I, а точки Ρ и Q
расположены вне этой прямой. Найдите на прямой I такую точку X,
что QXB = 2АХР. (Рассмотрите два случая: точки Ρ и Q
лежат по одну сторону от прямой /и по разные стороны от этой
прямой.)
ГЛАВА
III
ПАРАЛЛЕЛЬНОСТЬ
И ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
7
КЛАСС
§ 1, Параллельные прямые
31. Параллельность прямых
и центральная симметрия
1. Определение. Прямые а п Ь
называются параллельными, если они
лежат в одной плоскости и не
имеют общей точки или совпадают.
По определению любая прямая а
параллельна себе: а \\ а. Из
определения сразу следует, что если а || &, то и
Ъ || а.
38 |Теорема (о центрально-симме-
\ тричных прямых). Если две прямые
центрально-симметричны, то они
|параллельны.
Дано: Ъ = Ζο (α).
Доказать: а \\ Ь.
Доказательство.
Предположим противное: прямые α и & не
параллельны. Это значит, что они
различны и имеют общую точку С (рис. 201).
Эта точка С не может совпадать с
центром симметрии О, так как тогда прямые
а и Ъ отобразились бы при симметрии ZQ
каждая на себя, а не друг на друга.
Обозначим через С χ образ точки С
при симметрии Ζο . Точки С и С ι
различны, так как С Φ О. Точка С по
предположению принадлежит прямым а и
Ь. Поэтому ее образ С χ принадлежит
/\
/ \
/ \
/ \
/ I
\ /
Рис. 201
119
образам этих прямых, т. е. прямым Ъ и а. Получаем, что две
различные прямые а и Ъ имеют две общие точки С и Ci9 что
противоречит аксиоме прямой. Следовательно, предположение, что
прямые α и & не параллельны, неверно. Значит, а \\ Ь. Ш
Следствие. Через любую точку проходит хотя бы
одна прямая, параллельная данной прямой.
Доказательство. Пусть даны прямая ρ и точка А.
Возможны два случая:
1) А 6 р. В этом случае искомой прямой является прямая р.
2) A i р. Отметим на прямой ρ точку С и найдем середину О
отрезка АС (рис. 202). Обозначим через q образ прямой ρ при
симметрии Ζ0. По теореме 38 прямые ρ и q параллельны.
Прямая q состоит из всех точек, симметричных точкам
прямой ρ относительно точки О. Поэтому она содержит, в
частности, и точку А, симметричную С. Значит, q — искомая прямая. ■
2. Теорема о
центрально-симметричных прямых является одним из
признаков параллельности прямых. Докажем
теперь другой признак параллельности
прямых.
39 | Теорем а. Если две прямые
перпендикулярны одной и той же
прямой, то эти прямые параллельны.
Дано: a j_ p, b j_ ρ, α Φ Ъ.
Доказать: а \\Ъ.
Доказательство.
Предположим, что прямые α и & пересекаются в
точке Μ (рис. 203). Тогда через точку Μ
проходят два перпендикуляра к прямой р,
что противоречит предложению 19.
Значит, наше допущение неверно.
Прямые а и Ъ параллельны. ■
Рис. 202
ι \
I \
/ \
πα
Рис. 203
Вопросы и задачи
421°. Назовите различные случаи
взаимного расположения двух прямых на
плоскости.
422°. Верно ли, что любые две прямые
пространства либо параллельны, либо
пересекаются?
120
423°. 1) Какие прямые (отрезки) при центральной симметрии
отображаются на себя?
2) Могут ли две различные центрально-симметричные
прямые иметь общую точку?
424°. Каково взаимное расположение прямых а и Ъ, если:
1) а = Z0(b); 2) а = Z0(a) и Ъ = Z0 (6)?
425. 1) Постройте прямую, симметричную данной прямой а
относительно данного центра 0(0^ а).
2) Постройте прямую, параллельную данной прямой а и
проходящую через данную точку. Какими инструментами можно
это сделать?
426. Даны треугольник ABC и точка М. Постройте прямые,
проходящие через точку Μ и параллельные прямым АВ, ВС и АС.
427. Постройте четырехугольник, противоположные стороны
которого попарно параллельны.
428°. Прямые а и Ъ касаются окружности в диаметрально
противоположных точках Ми Г. Каково взаимное расположение этих
прямых?
429. Каково взаимное расположение прямых а и Ъ, а и с, Ъ и с,
если: 1) а_1_с, Ь_1_с; 2) а_1_ Ъ, c_L b; 3) a-Lb, c_La?
430. Какие прямые при осевой симметрии Sp отображаются на
параллельные им прямые?
431. Все углы четырехугольника прямые. Докажите, что его
противоположные стороны попарно параллельны.
32. Аксиома параллельных
1. Мы доказали, что через любую точку можно провести хотя
бы одну прямую, параллельную данной прямой. Сколько на
самом деле существует таких прямых? Мы знаем, что их не
менее одной. Примем без доказательства следующее предложение.
40 I Аксиома параллельных. Через данную точку прохо-
I дит не более одной прямой, параллельной данной прямой.
Следствие 1. Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и другую.
Доказательство. Пусть a\\bnc[\a = A (рис. 204).
Если бы прямая с не пересекала прямую 6, то через точку А
проходили бы две прямые (а и с), параллельные прямой Ь. Это
противоречит аксиоме параллельных. Значит, прямая с
пересекает прямую Ь. Ш
121
Рис. 204
-л-.
Рис. 206
Следствие 2. Перпендикуляр и
наклонная к одной и той же прямой
пересекаются.
Доказательство. Пусть
прямая а — перпендикуляр, а прямая Ъ —
наклонная к прямой с (рис. 205). Через
точку В пересечения прямых Ъ и с
проведем перпендикуляр ρ к прямой с.
Тогда прямая ρ параллельна прямой а (п. 31).
Значит, прямая Ъ не может быть
параллельна прямой а, так как в противном
случае через точку В проходили бы две
прямые (Ъ и р), параллельные прямой а,
что противоречит аксиоме параллельных.
Итак, прямые а и Ъ пересекаются. ■
Следствие 3. Если прямые а и Ъ
параллельны прямой с, то прямые а и Ъ
параллельны.
Доказательство. Допустим
противное: прямые а и Ъ не параллельны,
т. е. пересекаются в некоторой точке Ρ
(рис. 206). Тогда через точку Ρ будут
проходить две прямые (а и 6),
параллельные прямой с. Но это противоречит
аксиоме параллельных, и, следовательно, наше
предположение неверно. Поэтому а \\ Ъ.Ш
2. В пункте 3 была доказана
теорема о параллельности
центрально-симметричных прямых. Верно и обратное
предложение.
41 | Теорема. Если две прямые
параллельны, то они
центрально-симметричны.
Доказательство. Пусть а || Ъ.
Докажем, что существует точка О,
относительно которой эти прямые
симметричны.
Возьмем на прямых а и Ъ по одной
точке — А и Αχ (рис. 207). Обозначим
середину отрезка ΑΑι через О.
122
При симметрии Zq точка А отобразится на точку А и прямая
а отобразится на прямую Z0 (а), проходящую через точку At
ji параллельную (по теореме 38) прямой а. По аксиоме
параллельных такая прямая едииствениа. Но по условию Ъ \\ а и,
кроме того, Ai ζ b. Значит, образом прямой а при симметрии
Z0 может быть только прямая Ь. Итак, Zo (а) = Ь, т. е. прямые
а и Ъ центрально-симметричны. ■
Вопросы и задачи
432. Докажите, что через любую точку плоскости проходит одна
и только одна прямая, параллельная данной прямой.
433. Можно ли провести прямую, параллельную каждой из
пересекающихся прямых а и fe?
434. Даны прямые а, Ъ и с. Верно ли, что: 1) а \\ а; 2) если а \\ Ь,
то Ъ || а; 3) если а || Ь и а || с, то Ъ \\ с; 4) если а±.Ъ и Ъ_1_с,
то a_Lc; 5) если а пересекает Ъ и Ъ пересекает с, то прямые
а и с пересекаются?
435. Обладает ли отношение параллельности, заданное на
множестве прямых, свойствами рефлексивности, симметричности и
транзитивности?
436. Даны прямые а, Ъ и с. Каково взаимное расположение
прямых α и с, если а \\ Ъ и прямая Ъ пересекает прямую с?
437. Докажите, что прямая, перпендикулярная одной из сторон
острого угла, пересекает вторую его сторону.
438. Прямые α и Ъ параллельны, а прямая с
пересекает их (рис. 208). Докажите*:
а) 7 = 3; 6)1 =8; в) 6 = 7; г) 3 = 5;
д) 4 = 6; е) 7 = 2; ж) 5 = 8; з) 2=ί
и) 2 + 8= 180°; к) 7 + ?= 180°.
439. Две прямые а и Ъ пересечены
прямой с (рис. 208). Докажите, что а \\ Ъ,
если:
а) Т = 8; б) 5 = 8; в) 4 +1> = 180°;
г) 6 = 7; д)1 +7= 180^.
* Такие углы, как 1 и 8, 7 и 2, ..., принято
называть соответственными углами. Углы 2 и 4, 8 и 5
называют внутренними накрест лежащими при
параллельных а и Ь и секущей с.
123
Рис. 208
На рисунке 209 показаны способы
построения параллельных прямых
при помощи: 1) угольника и
линейки; 2) рейсшины. Объясните,
почему построенные прямые
параллельны.
Сколько центров симметрии имеет
фигура, являющаяся: 1)
объединением двух параллельных прямых;
2) объединением трех прямых, две
из которых параллельны; 3)
объединением двух прямых.
Противоположные стороны
четырехугольника ABCD попарно
параллельны. Найдите величины углов и
длины сторон этого
четырехугольника, если А = 30°, \АВ\ = 2 см,
\ВС\ =4 см.
33 γ. Неевклидова геометрия.
Геометрия и физика
Пользуясь уже известными вам
предложениями геометрии, можно
доказать, что принятую нами аксиому
параллельных А («через данную точку
проходит не более одной прямой,
параллельной данной прямой») можно
заменить другими утверждениями,
равносильными аксиоме А. (Равносильность
утверждений Ρ и Q означает: из Ρ
вытекает Q, а из Q вытекает Р.) Например,
в качестве такого утверждения
может быть принято предложение
«перпендикуляр и наклонная
пересекаются» или более точно: «если прямая а
перпендикулярна прямой с, а прямая
Ъ пересекает прямую с, но ей не
перпендикулярна, то прямые а и Ъ
пересекаются» (рис. 210, а).
Сам Евклид принимал в качестве
аксиомы параллельных такое предложе-
ние: «Если прямая падает на две прямые и образует
внутренние односторонние углы, в сумме меньшие двух прямых, то при
неограниченном продолжении этих двух прямых они пересекутся
с той стороны, где углы меньше двух прямых» (рис. 210, б).
Многим математикам, работавшим после Евклида, аксиома
параллельных в том или ином ее виде казалась с наглядной
точки зрения недостаточно убедительной. Поэтому было
потрачено много усилий на ее доказательство. Но все предлагаемые
доказательства оказывались несостоятельными.
Для дальнейшего развития науки особенно плодотворными
оказались попытки доказать аксиому параллельных «от
противного», или, как говорят иначе, «приведением к абсурду».
Допускали отрицающее А предложение В («допускали
противное»): если точка Ρ не лежит на прямой а, то через Ρ проходят
по крайней мере две прямые & и с, параллельные прямой а
(рис. 211).
Из этого допущения извлекали многочисленные следствия
в надежде прийти к противоречию: если бы такое противоречие
появилось, то «противоположное допущение» было бы неверно и
предложение А было бы доказано.
Но противоречия никак не удавалось обнаружить. Вместо
этого получалась длинная цепь предложений, часто отличных
от тех, которые имеются в евклидовой геометрии, но которые
тем не менее складывались в стройную теорию. Например, из
аксиомы А вытекает, что сумма углов треугольника равна 2d
(см. доказательство в п. 38), а из В следовало, что эта сумма
всегда меньше 2d, причем разность Δ = 2d — К — R — L
пропорциональна площади S треугольника KLR: Δ = kS, где
k — некоторая положительная константа.
Особенно полно такую, по его словам, «воображаемую
геометрию» развил русский математик Николай Иванович
Лобачевский (1792—1856). Он впервые открыто высказал
убеждение, что геометрия эта непротиворечива и потому с чисто
логической точки зрения равноправна евклидовой. Несколько позже
Лобачевского (но независимо от него) опубликовал аналогичную
работу венгерский математик Янош Бойяй (1802—1860).
В XIX в. были построены и другие системы геометрии,
отличные от евклидовой. Например, в геометрии Римана (1820—
1864) совсем нет параллельных. В этой геометрии два
перпендикуляра к прямой непременно пересекаются (рис. 212).
Приведенное в нашем учебнике доказательство невозможности та-
125
кого положения вещей (см. п. 31) не
действует в геометрии Римана.
С созданием новых геометрий, отличных
от евклидовой, получил более полное
освещение вопрос об отношении геометрии,
развиваемой чисто логически из
определенных допущений (аксиом), к свойствам
окружающего нас реального пространства.
В пункте 14 уже было сказано, что в геометрии мы
приписываем геометрическим фигурам свойства, которые в применении
к реальным телам наблюдаем только приближенно. Геометрия
представляет собой математическую модель реальных
пространственных отношений. Модель эта правильна в том смысле, что
она с хорошим приближением отражает свойства доступной
нам части реального пространства.
Η С развитием науки и измерительной техники оказалось, что
выводы евклидовой геометрии остаются правильными со
значительно большей точностью, чем это могли проверить на
практике ученые прошлых времен. Например, К. Ф. Гаусс (1777—
1855), одновременно с Лобачевским пришедший к мысли о
возможности неевклидовой геометрии, измерил с большой
точностью углы треугольника, образованного вершинами трех
немецких гор, и, сложив, эти углы, не обнаружил значимого
отклонения от 2d.
Но современная физика не абсолютизирует пригодность
евклидовой геометрии в очень больших космических масштабах
или в очень малых масштабах элементарных частиц. В обоих
случаях остается возможность, что данные физики окажутся
в лучшем согласии с какой-либо геометрией, отличной от
евклидовой.
Вопросы и задачи
443. Докажите равносильность предложений А и В:
(В) если прямая а перпендикулярна прямой с, а прямая Ъ
пересекает прямую с, ко ей не перпендикулярна, то
прямые а и Ь пересекаются;
(А) через любую точку проходит не более одной прямой,
параллельной данной прямой.
444. 1) Приведите примеры теорем, при доказательстве которых
используется аксиома параллельных.
л
126
2) Приведите примеры теорем, доказательства которых не
опираются на аксиому параллельных.
445**. Докажите, не опираясь на аксиому параллельных, что угол,
смежный с углом А треугольника ABC, больше каждого из
углов J5 и С.
§ 2. Параллельный перенос
34. Отношение эквивалентности
Вы знакомы с понятием отношения между элементами
множества. Известны, например, отношения параллельности и
перпендикулярности между прямыми, отношение конгруэнтности
между фигурами. В алгебре вы познакомились с отношениями
неравенства (строгого и нестрогого) между числами. Вы знаете
также, как употребляются знаки перечисленных отношений:
а || &, a _l_ &, Li ^ i2, х < г/, х < г/.
Утверждение, что предметы χ и у связаны некоторым
отношением R, записывают так: xRy. В рассмотренных выше
примерах отношением R было отношение параллельности,
перпендикулярности, конгруэнтности, строгого и нестрогого
неравенства.
Как в алгебре, так и в геометрии вы встречались со
следующими свойствами отношений.
1) Отношение R рефлексивно на множестве М, если для
любого χ из Μ выполняется условие: xRx.
2) Отношение R симметрично, если из xRy следует, что
yRx (т. е. если χ и у связаны отношением R, то у и χ тоже
связаны этим отношением).
3) Отношение R транзитивно, если из xRy и yRz следует,
что xRz.
Отношение может обладать или только одним из этих
свойств, или двумя из них, или же всеми тремя свойствами
(или не обладать ни одним из них). Проверьте следующую
таблицу, где знак «+» означает, что отношение обладает
указанным свойством, а знак «—» означает, что оно этим свойством
не обладает.
Рефлексивность . . .
Симметричность . . .
Транзитивность . . .
=
+
+
+
-L
1+1
~
+
+
+
<
+
<
+
+
127
Среди рассмотренных отношений
имеются два, которые обладают всеми тремя
свойствами: рефлексивностью,
симметричностью и транзитивностью. Таковы
отношения параллельности и конгруэнтности.
Отношения, обладающие свойствами
рефлексивности, симметричности и транзитивности,
Рис. 213 называются отношениями эквивалентности.
Τ Если множество Μ каким-либо способом разбито на попарно
не пересекающиеся классы, то отношение «χ и у принадлежат
одному и тому же классу» есть отношение эквивалентности.
Верно и обратное: если между элементами множества Μ
задано отношение эквивалентности, то множество Μ разбивается
на попарно не пересекающиеся классы эквивалентных
элементов, т. е. отношение эквивалентности для элементов χ и у будет
выполняться в том и только в том случае, когда χ и у
принадлежат одному и тому же классу. Это формулируют и иначе:
каждое заданное на множестве Μ отношение эквивалентности
определяет разбиение множества Μ на классы эквивалентности.
Например, отношение параллельности между прямыми
плоскости определяет разбиение множества всех прямых плоскости
на классы. Каждый из этих классов состоит из прямых,
параллельных друг другу (рис. 213). Эти классы — пучки
параллельных прямых. Другой пример таких классов — направления,
которые будут определены в следующем пункте.ψ
Вопросы и задачи
446°. Является ли отношение конгруэнтности, заданное на
множестве отрезков, отношением эквивалентности?
447. Заданы отношения: 1) многоугольники L и L\ имеют
одинаковую площадь; 2) отрезки χ и у симметричны относительно
данного центра О; 3) прямые а и Ь имеют общую точку.
Ответьте на следующие вопросы: является ли данное
отношение рефлексивным, симметричным или транзитивным
отношением? Является ли оно отношением эквивалентности?
448. Задайте несколько отношений эквивалентности.
449. Ученик сформулировал определение параллельных прямых
следующим образом: «Прямые а и Ъ параллельны, если они
лежат в одной плоскости и не имеют общих точек». Верно ли,
что при таком определении отношение параллельности
прямых является отношением эквивалентности?
128
35. Направления
С понятием «направление» вы уже / '—*^θ
встречались. Однако оно не было
разъяснено. Сделаем это сейчас. Начнем с
того, что разъясним смысл выражений
«два луча одинаково направлены» (или
короче — «сонаправлены») и «два
луча противоположно направлены».
а) Пусть лучи АВ и CD лежат на
различных параллельных прямых*. Проведя
через точки А и С прямую, получим две
полуплоскости с границей АС. Если лучи
АВ и CD лежат в одной из этих
полуплоскостей, то они называются сонаправ-
ленными (рис. 214, а). Если лучи АВ и CD
лежат в разных полуплоскостях, то они
противоположно направлены (рис. 214, б).
б) Пусть лучи АВ и CD лежат на одной
прямой. Эти лучи называются сонаправ-
ленными, если один из них содержится в
другом (рис. 215, а). Если же ни один из
лучей АВ и CD не содержится в другом,
то они называются противоположно
направленными (рис. 215, б).
Сонаправленность лучей АВ и CD
обозначим так: [АВ) ft [CD). Если лучи АВ и CD
противоположно направлены, то будем писать: [АВ) \\ [CD).
Рассматривая рисунок 216, а, можно заметить, что
отношение сонаправленности лучей обладает свойствами
рефлексивности, симметричности и транзитивности:
1) lAiBx) ft DA,B,);
2) если [ΑιΒΛ ff [А2Д2), то [А2Б2) ft DAi^i);
3) если ΙΑ&ύ ft ίΛ2Β2) и [А2В2) \\ [А3Я3), то
1АХВХ) ft LA3B3).
Значит, отношение сонаправленности лучей есть отношение
эквивалентности.
Любой луч определяет множество сонаправленных с ним
лучей (рис. 216, б). Говорят, что все эти лучи задают одно и
* Бели лучи (отрезки) АВ и CD лежат на параллельных прямых, то будем
говорить, что эти лучи (отрезки) параллельны.
D
Л
А
С
А
•
С
а)
А
С
•
В
D
В
В
δ)
Рис. 215
129
A)
О)
Βι+ то же направление*.
Направление можно задавать с помощью
#2^ одного луча и говорить о
направлении этого луча.
Вт 42 Ι Τ е о ρ е м а (о
симметричности противоположно
направленных лучей). Два
противоположно
направленных луча симметричны
относительно середины
отрезка, соединяющего их на-
чала.
Доказательство.
Рассмотрим противоположно
направленные лучи АВ и ΑιΒι,
не лежащие на одной прямой
(рис. 217). Пусть точка О —
середина отрезка Α Αχ.
При симметрии с центром О
точка А отображается на
точку Ai. Прямая АВ
отображается на прямую, проходящую
через точку А\ и параллельную
(теорема 39) прямой АВ, т. е. на
прямую А\В\. Полуплоскость α
(см. рис. 217) отображается на
полуплоскость а4. Поэтому луч
АВ отображается на луч прямой
AiBi, с началом в точке А19
лежащий в полуплоскости at. Но
этим условиям удовлетворяет
Рис. 217 лишь луч ΑιΒι. Значит, луч
АВ отображается при
симметрии с центром О на луч A iBi.
Если прямые АВ и AiBi совпадают, доказательство
аналогично. ■
Верно и такое утверждение: два центрально-симметричных
луча противоположно направлены.
* Понятию, направления можно дать и явное определение: множество
чей, каждый из которых сонаправлен с одним и тем же лучом, называется
правлением.
лу-
на-
130
Вопросы и задачи
450°. Прямые АВ и CD параллельны. 1) Ка- 4 / Ρ
кие лучи, изображенные на рисун- ' ^
ке 218, сонаправлены? 2) Какие лучи
противоположно направлены?
451°. Дан луч АВ. 1) Сколько различных ,
лучей, сонаправленных с лучом АВ,
имеют свое начало в данной точке М?
2) Сколько существует лучей, противоположно
направленных лучу АВ и имеющих свое начало в данной точке М?
452. 1) Постройте два сонаправленных луча МА и KB: а) не
лежащих на одной прямой; б) лежащих на одной прямой.
2) Постройте два противоположно направленных луча МС
и KD: а) не лежащих на одной прямой; б) лежащих на одной
прямой.
3) Запишите с помощью принятых обозначений: лучи МА
и KB сонаправлены, лучи МС и KD противоположно
направлены.
453. 1) Сонаправленные лучи АВ и CD лежат на одной прямой.
Какой фигурой может быть: а) объединение этих лучей;
б) их пересечение?
2) Противоположно направленные лучи AM и BD лежат на
одной прямой. Какой фигурой может быть: а) объединение
этих лучей; б) их пересечение?
Покажите возможные случаи на рисунках и запишите ответы
в принятых обозначениях.
454°. Сколько существует лучей, сонаправленных с данным лучом?
455. Сколько различных направлений можно задать лучами,
которые: 1) лежат на данной прямой; 2) лежат на двух данных
пересекающихся прямых; 3) содержат стороны данного
треугольника?
456°. Является ли отношение противоположной направленности
отношением рефлексивным, симметричным и транзитивным
на множестве лучей плоскости?
457. Дан луч ОМ. Постройте луч, центрально-симметричный лучу
ОМ относительно центра Р: 1) лежащего на прямой ОМ;
2) не лежащего на прямой ОМ. .
458. 1) Докажите, что два противоположно направленных луча,
лежащих на одной прямой, центрально-симметричны. Как
найти центр симметрии этих лучей?
131
2) Докажите, что при центральной симметрии каждый луч
плоскости отображается на противоположно направленный
луч. т
459*. 1) Сколько пар параллельных сторон может иметь: а)
выпуклый четырехугольник; б) выпуклый пятиугольник; в)
выпуклый шестиугольник?
2) Может ли многоугольник с нечетным числом сторон иметь
центр симметрии?
36. Параллельный перенос
1. Вы уже знакомы с такими перемещениями, как осевая
симметрия и поворот (в частности, центральная симметрия).
Сейчас рассмотрим еще один вид перемещений — параллельный
перенос.
Отметим на плоскости две точки А и А4 (рис. 219). Проведем
луч АА{. Он задает на плоскости некоторое направление. Пусть
X — произвольная точка плоскости. Построим луч ХМ
заданного направления и отложим на нем отрезок XX\ длины | ΑΑι|.
Точке X поставим в соответствие точку Х\. Тогда каждой
точке X плоскости будет соответствовать определенная точка Χι и
каждая точка Υ\ плоскости будет образом некоторой точки Υ.
Получим отображение плоскости на себя — параллельный
перенос.
Определение. Параллельным переносом называется
отображение плоскости на себя, при котором каждая точка X
отображается на такую точку Хи что:
1) луч XXι имеет заданное направление;
2) отрезок XXχ имеет заданную длину.
Направление луча ΧΧι называют направлением
параллельного переноса. Параллельный перенос обычно обозначают
буквой Т. Тождественное отображение Ε плоскости на себя по
определению также считают параллельным переносом. Этот
параллельный перенос не имеет направления.
Чтобы задать параллельный перенос, достаточно задать
какую-либо точку плоскости и ее образ. Действительно, если
образом точки А при параллельном переносе Τ является
точка Α ι, то эти точки определяют и направление параллельного
переноса, и расстояние lAAJ. Тогда для любой точки X можно
построить ее образ Х{ = Τ (X) (см. рис. 219).
2. Сформулируем два свойства параллельных переносов.
132
43 I Параллельный перенос является
I перемещением.
у Доказательство. Пусть А
и В — две произвольные точки
плоскости; Αι и Bi — их образы при
параллельном переносе (рис. 220). Надо
доказать, что ΙΑι-ΒιΙ = \АВ\.
Обозначим через О середину
отрезка ΑΒι. По определению
параллельного переноса расстояния IAAJ и \ВВ{\
равны, а лучи АА^ и ВВ{ сонаправле-
ны. Поэтому лучи ΑΑι и В^В
противоположно направлены и,
следовательно, симметричны относительно точки
О (теорема 42).
При симметрии Ζ0 точка А
отображается на точку Бь а луч В^В — на
луч АА^. Точка В луча В{В
отобразится на ту точку луча AAif которая
находится от точки А на расстоянии
| ΒιΒ\9 т. е. наточку Αι (так как | АА{\ =
= \ΒιΒ\). Таким образом, точки А и В
при симметрии Ζ0 отображаются на
точки Bi и Αι соответственно. По
теореме 22ι \ΑΒ\= | ΑιΒιΙ-ψ
Из этого свойства следует, что при
параллельном переносе каждая
фигура отображается на конгруэнтную ей
фигуру.
44 I Образом прямой при параллельном
переносе является параллельная ей
прямая (рис. 221, а), а образом
луча — сонаправленный ему луч
J (рис. 221, б),
ψ Доказательство. Так
как параллельный перенос есть
перемещение, то образом прямой ρ
является некоторая прямая рА (см. п. 16).
Докажем, что ρ ι \\ρ.
Выберем на прямой ρ две
произвольные точки А и В (рис. 222).
Обозначим их о5разы при параллельном переносе через Αι и
В{. Тогда В^ и А{ являются образами точек А и В
соответственно при симметрии относительно середины О отрезка ΑΒχ
(см. предыдущее доказательство). Следовательно, Zq (ρ) = ρ ι-
При центральной симметрии любая прямая отображается
на параллельную ей прямую (п. 31), а луч — на
противоположно направленный луч. Поэтому прямые рА и ρ параллельны, а
лучи АВ и BiAi противоположно направлены. Но так как
1АВ)\\1В,А,)9 получаем: [АВ) \\ [Α,Β,). γ
Если требуется построить образ фигуры при параллельном
переносе., отображающем данную точку А на другую данную
точку Αι, то можно избежать откладывания отрезков заданной
длины. Второе свойство параллельного переноса позволяет
свести построение к проведению параллельных прямых (это
особенно удобно при пользовании рейсшиной или угольником,
скользящим вдоль линейки). На рисунке 223 показано, как
строится образ точки X, не лежащей на прямой АА{, а на
рисунке 224 построен образ точки X, принадлежащей прямой АА^
(сначала строится образ точки Б, не принадлежащей
прямой АА{).
3. С помощью свойств параллельного переноса докажем
следующую теорему.
45 I Теорема (о параллельных отрезках).Отрезки двух парал-
I лельных прямых, заключенные между двумя другими па-
1 раллелъными прямыми, конгруэнтны.
Дано: (АВ) || (CD), (AC) \\ (BD) (рис. 225).
Доказать: [АВ~] ^ [CD].
Доказательство. Рассмотрим параллельный
перенос 7\ отображающий точку А на точку С. При этом переносе
прямая АВ отображается на параллельную ей прямую,
проходящую через точку С, т. е. на прямую CD. Прямая BD
отображается на себя.
<^
Рис. 223 Рис. 224 Рис. 225
134
A
1
Ao
A
4
Рис.
Рис.
В
■_«——>_ч
■
Ι
So
226
~t
4-
227
Образом точки Б (точки пересечения
прямых АВ и BD) при параллельном
переносе является точка D (точка
пересечения прямых CD и BD). Итак,
Τ (А) = С9Т (В) = D. Значит, при
переносе. Τ отрезок АВ отображается на
отрезок CD. Следовательно, эти отрезки
конгруэнтны. ■
Следствие. Точки одной из двух
параллельных прямых находятся на одном
и том же расстоянии от другой из них
(рис. 226).
Это расстояние называется
расстоянием между данными параллельными
прямыми.
4. Сформулируем еще одну теорему.
46|Теорема. Любое перемещение, которое каждый луч
отображает на сонаправленный ему луч, является
параллельным переносом.
у Доказательство. Пусть перемещение F
отображает любой луч на сонаправленный ему луч. Возьмем на
плоскости произвольную точку А и обозначим через Αχ ее образ при
перемещении F: Ах = F (А).
Выберем произвольную точку X, отличную от А (рис. 227).
По условию теоремы перемещение F отображает луч АХ на
сонаправленный ему луч с началом в точке А г, образ точки X —
такая точка Xt этого луча, что \АХ\ = \Α^Χι\ (F —
перемещение).
Итак, если Xi=F (X), то [АХ) \\ [_А,Х,) и | АХ\ - | А,Х,\.
Поэтому при переносе, отображающем точку А на X, точка
Αι отображается на точку Xla
Следовательно,
I-A-Ail = \XXi\ (теорема 43),
[-A-Ai) ft ΙΧΧχ) (теорема 44).
По определению переноса это означает, что перемещение F —
параллельный перенос.
В начале проведенного рассуждения мы предположили, что
-Αι Φ А. Доказательство теоремы в случае Αί = А проведите
самостоятельно. Τ
135
Вопросы и задачи
460°. Можно ли задать параллельный перенос указанием: 1) его
направления; 2) расстояния от точки до ее образа при этом
переносе?
461. Даны точки А, В и С. Постройте образ точки С при
параллельном переносе, отображающем: 1) точку А на В; 2)
точку В на А. Рассмотрите два случая: а) Α £ (ВС); б) А $ (ВС).
462. Дайте обоснование построений, приведенных на рисунках
223 и 224.
463. Задайте параллельный перенос и постройте образы при этом
переносе: 1) отрезка; 2) луча; 3) прямой; 4) окружности;
5) треугольника; 6) угла.
464°. При каком условии существует параллельный перенос,
отображающий один из отрезков на другой?
465. Существует ли параллельный перенос, при котором: 1) одна
сторона треугольника отображается на его другую сторону;
2) одна из сторон квадрата отображается на его другую
сторону?
466°. Приведите примеры фигур, которые можно отобразить на
себя с помощью параллельного переноса.
467*.Дан треугольник ABC. 1) Постройте сначала АА\В\С\ —
образ этого треугольника при переносе Τι (известно,
что Т\ (А) = В), а затем АА2В2С2— образ полученного
треугольника при переносе Т2, отображающем В на С. 2)
Докажите, что треугольники ABC и А2В2С2 конгруэнтны. 3)
Существует ли параллельный перенос, отображающий треугольник
ABC на треугольник A2B2C2I
468. 1) Даны две параллельные прямые а и Ъ. Сколько
существует параллельных переносов, отображающих одну из этих
прямых на другую?
2) Даны два сонаправленных луча. Сколько существует
параллельных переносов, отображающих один из этих лучей
на другой?
469°. При каких перемещениях каждый луч отображается: 1) на
противоположно направленный луч; 2) на сонаправленный
луч; 3) на себя?
470°. 1) При некотором перемещении луч АВ отображается на
сонаправленный ему луч CD. Следует ли из этого, что такое
перемещение есть параллельный перенос?
136
2) При некотором перемещении луч ·Α
АВ отображается на противоположно
направленный ему луч CD. Следует ли :=l_j=t—_ζ=£Ξ:ζ=ΞΞΞΞΞ:
из этого, что такое перемещение есть _;~ ~ : __
центральная симметрия? ~" L_ "
471. Докажите, что сумма расстояний от
точки, лежащей в полосе между
данными параллельными прямыми, до ·"
этих прямых величина постоян- Рис. 228
ная.
472. Докажите, что параллельный перенос, отображающий
точку А на В, отображает прямую АВ на себя.
473. 1) На стороне ОА острого угла АОВ постройте точку,
расстояние от которой до другой стороны равно т(т = 1,5 см; 2 см).
2) Постройте окружность данного радиуса, которая касается
сторон данного угла.
474. Найдите множество точек плоскости, удаленных от данной
прямой ρ на данное расстояние а.
475**. Населенные пункты А и В расположены по разные стороны
от реки с параллельными берегами (рис. 228). Как нужно
расположить перпендикулярный берегам мост, чтобы получить
кратчайшую дорогу из А в В?
476°. Назовите перемещения, при которых каждая прямая
отображается на параллельную ей прямую.
477. Верно ли предложение: если перемещение F каждую
прямую плоскости отображает на параллельную ей прямую, то
F—параллельный перенос?
478*. Докажите, что перемещение, отображающее каждый луч
плоскости на противоположно направленный ему луч,
является центральной симметрией.
37. Углы между направлениями
Возьмем два направления.
Произвольная точка О плоскости является началом п
одного луча ОА первого и одного
луча ОВ второго направления (рис. 229).
Отметим какую-нибудь другую точку 0А
и лучи ΟίΑι и 0YBi тех же направлений.
Рассмотрим параллельный перенос, при О
котором точка О отображается на точку Рис. 229
137
Οί. Образом луча О А при этом переносе является сонаправленный
ему луч (п. 36) с началом в точке Oi9 т. е. луч OiAu а образом
луча ОБ — луч OiBi. Поэтому выпуклый угол АОВ отображается
на выпуклый угол Α^ΟιΒγ и, следовательно, АОВ = AiOiB\.
Итак, какую бы точку О плоскости мы ни взяли, величина
выпуклого угла, образованного лучами ОА и ОВ двух данных
направлений, окажется одной и той же. Эту величину называют
углом между направлениями. Считают также, что каждое
направление образует с самим собой угол в 0°.
Отметим, что проведенное выше рассуждение приводит к
выводу: два выпуклых угла с соответственно сонаправленными
сторонами конгруэнтны.
Обратите внимание, что углом между направлениями
названа величина, а не фигура. Два луча ОА и ОВ образуют два угла
АОВ. Углом между лучами ОА и ОВ называют величину
выпуклого угла АОВ. Угол между направлениями равен углу между
любыми лучами этих направлений, если лучи имеют общее начало.
Вопросы и задачи
479°. На рисунке 230 даны две параллельные прямые,
пересеченные третьей прямой. Укажите углы, стороны которых со-
направлены.
480. Дан угол АОВ. Постройте угол, стороны которого сонаправ-
лены (противоположно направлены) сторонам угла АОВ, а
вершина находится в данной точке М: 1) лежащей на
стороне угла; 2) не лежащей на стороне угла.
481. Точка В лежит между точками А и С. Найдите угол между
направлениями, которые заданы лучами: 1) [АВ) и [ВС);
2) [АВ) и [СВ).
482. Проведите лучи АВ и CD и постройте угол с вершиной в
данной точке М, величина которого равна углу между
направлениями этих лучей.
Докажите, что два выпуклых угла,
стороны которых противоположно
направлены, конгруэнтны.
Даны два выпуклых угла, две стороны
которых сонаправлены, а две другие —
противоположно направлены.
Докажите, что сумма величин этих углов
равна 180°.
483.
484.
Рис. 230
138
485°. Чему равен угол между
направлениями: 1) на юг и на запад; 2) на юг и на
север; 3) на восток и на юго-восток?
486. 1) На рисунке 231 укажите все углы,
величины которых равны а, (АС) || (FE).
2) Найдите угол между
направлениями, заданными лучами: а) ВС и DE;
б) ВС и DF; в) ВА и DR; г) BR и DE.
487*. Докажите конгруэнтность двух острых
(тупых) углов, стороны которых
взаимно перпендикулярны.
38. Сумма углов многоугольника
Пусть [АБ] и \_AF~]— стороны выпуклого многоугольника
(рис. 232). Лучи АВ и AF образуют два угла. Тот из них, в
котором содержится данный многоугольник, называется углом
этого многоугольника. Угол, смежный с углом многоугольника,
например угол BAG, называют его внешним углом*.
Докажем сначала теорему о сумме углов треугольника.
47§Теорема. Сумма углов треугольника равна 180°.
Дано: Z.1, Z_2, Z13—углы
треугольника ABC.
Доказать: Ϊ + 2 + 3 = 180°.
Доказательство. Проведем
через вершину С прямую MN,
параллельную прямой АВ. Продолжим стороны АС
и ВС (рис. 233).
Лучи AF и CF9 а также лучи АВ и CN
сонаправлены. Из сонаправленности этих
лучей следует, что 1 = 4 (п. 37).
Аналогично доказывается, что 3 = 6.
Так как углы 2 и 5 вертикальные, то
2=5. Значит,
1+2 + 3 = 4> 5+ 6.
* Для краткости величины углов
многоугольника (и величины его внешних углов) также называют
углами (внешними углами) многоугольника. Рис. 233
139
Рис. 231
Но углы 4, 5 и 6 в сумме составляют
развернутый угол MCN. Поэтому
/ч /\ /\
1 + 2 + 3 - 180 . ■
Следствие 1. £слн оди« аз углов
треугольника прямой или тупой, то два
другие — острые.
Следствие 2. Каждый угол рае-
постороннего треугольника равен 60\
Следствие 3. Внешний угол
треугольника равен сумме двух углов
треугольника, не смежных с ним (рис. 234).
Доказательство. По
свойству смежных углов BCD + С = 180°.
По теореме о сумме углов
треугольника (А + В) + С = 180°.
В равных суммах вторые слагаемые
(С) равны. Значит, BCD = А + Б. ■
48 1 Теорема. Сумма углов выпуклого
I п-уголъника равна 2d (п—2).
Доказательство. Возьмем
какую-либо точку О внутри данного
тг-угольника (рис. 235) и соединим точку О
отрезками с его вершинами. Все эти
отрезки содержатся в данном многоугольнике,
так как он выпуклый. Поэтому такие
отрезки разобьют многоугольник на η
треугольников с общей вершиной О.
Сумма всех углов полученных
треугольников равна 2dn (имеется η
треугольников, сумма углов каждого из них
равна 2d). Значит, сумма углов
многоугольника и углов с вершиной О равна 2dn.
Сумма углов с вершиной О равна 4d.
Следовательно, чтобы найти сумму углов
выпуклого тг-угольника, достаточно из
2dn вычесть 4d, т. е. эта сумма равна
2d(n—2).M ц
В частности, сумма углов
четырехугольника равна Ы.
491 Теорема. Сумма внешних углов выпуклого много-
I угольника, взятых по одному при каждой вершине,
I равна 4 d.
Доказательство. Построим при каждой вершине
многоугольника по одному внешнему углу (рис. 236).
Сумма каждого угла многоугольника и смежного с ним равна 2d.
Сумма всех углов многоугольника и всех его внешних
углов (по одному при вершине) равна 2dn. Поэтому сумма
внешних углов выпуклого η-угольника равна 2dn — 2d (η — 2), т. е.
равна 4d. ■
Замечание. Теорема о сумме углов многоугольника
верна и для невыпуклых многоугольников. Например, сумма
углов невыпуклого пятиугольника (рис. 237) равна сумме всех
углов трех треугольников, т. е. 6d. Но 6d = 2d (η — 2) при
η = 5.
Вопросы и задачи
488. Вычислите величины углов треугольника, если известно, что
они пропорциональны числам: 1) 1, 2, 3; 2) 3, 7, 8; 3) 1, 1, 3.
489. Докажите, что если два угла одного треугольника
соответственно конгруэнтны двум углам другого треугольника, то
и третьи их углы конгруэнтны.
490. Через вершины треугольника ABC проведены прямые,
параллельные противоположным сторонам. Найдите углы
треугольника, образованного этими прямыми, если А = 25°,
В = 68°.
491. Укажите аксиомы и теоремы, которые применялись при
доказательстве теоремы о сумме углов треугольника.
492. Может ли внешний угол треугольника быть меньше его
внутреннего угла?
493. 1) Дайте определения тупоугольного, прямоугольного и
остроугольного треугольников.
2) Установите вид треугольника (по углам), если один из его
углов: а) равен сумме двух других углов; б) больше ее;
в) меньше ее.
494. Какой вид имеет треугольник, если сумма любых двух углов
его больше 90°?
141
Μ д д/ 495*. Два угла треугольника равны 60° и 72°.
Вычислите меньшие из углов,
образованных двумя прямыми,
содержащими: 1) высоты треугольника; 2) бис-
— сектрисы треугольника.
496. Внешний угол равнобедренного тре-
Рис. 238 угольника равен 100°. Вычислите углы
этого треугольника.
497. Докажите, что треугольник не может иметь два острых
внешних угла.
498. Какой вид имеет треугольник, если один из его внешних
углов: 1) острый; 2) равен внутреннему углу?
499. Дано: (MN) \\ (KL) (рис. 238). Доказать: ABC = NAB + BCL.
500. Найдите сумму углов: 1) десятиугольника; 2)
двенадцатиугольника; 3) тридцатиугольника; 4) 96-угольника.
501. Сколько сторон имеет многоугольник, если сумма его углов
равна: 1) 1080°; 2) 1620°; 3) 3960°; 4) 1800°?
502. Сколько сторон имеет многоугольник, если каждый угол
этого многоугольника равен: 1) 144°; 2) 150°; 3) 170°; 4) 17Г?
503. Докажите, что не существует многоугольника, у которого:
1) больше четырех прямых внешних углов; 2) больше трех
тупых внешних углов.
504. Может ли сумма углов многоугольника равняться: 1) 9180°;
2) 3600°; 3) 2040°; 4) lid; 5) 18d?
505*. Придумайте доказательство, отличное от имеющегося в
пункте 38: 1) теоремы о сумме углов треугольника; 2) теоремы
о сумме углов выпуклого многоугольника.
Дополнительные задачи к главе III
506. Известно, что образ прямой а при симметрии Z0 — прямая Ь.
Докажите, что Z0(b) = α.
507. Сколько центров симметрии может иметь фигура,
являющаяся объединением: 1) двух прямых; 2) трех прямых?
508. При столярных и плотничьих работах для разметки
параллельных прямых и срезов под данным углом употребляется малка
(в прорези одной деревянной планки шарнирно прикреплена
вторая планка, рис. 239, а). Объясните, на чем основано
применение малки.
142
Рис. 239
Рис. 240
509. При столярных работах для разметки на поверхности бруска
прямой, параллельной краю бруска, применяется рейсмус.
При движении рейсмуса вдоль края бруска металлическая
игла намечает прямую, параллельную краю бруска (рис. 239, б).
Объясните, на чем основано применение рейсмуса.
510. Найдите множество точек, удаленных на данное расстояние а
от: 1) отрезка; 2) луча.
511. Постройте прямую, параллельную данной прямой и
высекающую на двух данных окружностях хорды одинаковой длины.
512. Населенные пункты А и В разделены двумя реками (рис. 240,
считаем, что берега рек параллельны). Как нужно
расположить перпендикулярные берегам мосты, чтобы получить
кратчайшую дорогу из А в В1
513. Постройте окружность данного
радиуса, касающуюся двух пересекающихся
прямых. Сколько решений имеет
задача?
514. Даны угол АОВ и прямая,
пересекающая стороны данного угла. Постройте
отрезок данной длины, концы
которого лежат на сторонах данного
угла и который параллелен данной
прямой.
515. Как изменится сумма всех углов
многоугольника ABCD, если от него
«отрезать»: 1) треугольник ΕAF (рис. 241);
2) четырехугольник АВКЕ (рис. 242)?
516. Найдите число сторон многоугольника,
сумма углов которого равна сумме
всех его внешних углов. Рис. 242
143
517. Сколько сторон имеет многоугольник,
если все его внешние углы тупые?
518. Вычислите сумму всех острых углов
пятиконечной звезды (рис. 243).
519. Имеет ли объединение двух
конгруэнтных дуг окружности ось симметрии?
_ _ 520. Какое множество точек образуют се-
Рис. 243 r 7
редины всех хорд данной
окружности: 1) параллельных данной прямой;
2) перпендикулярных данной прямой?
521. Диаметр данной окружности — сторона равностороннего
треугольника. 1) Найдите угловые величины дуг, на которые
стороны треугольника рассекают полуокружность. 2)
Докажите, что расстояние между точками пересечения сторон
треугольника с окружностью равно радиусу этой окружности.
522. Постройте касательную к данной дуге АВ в данной на
ней точке С, не находя центра окружности, содержащей эту
Дугу-
523. Из одной точки проведены к · данной окружности две
касательные. Найдите угловые величины дуг, на которые делят
окружность точки касания, если величина угла между
касательными равна: 1) 100°; 2) 90°; 3) 60°.
524. Полосой называется непустое пересечение двух
полуплоскостей с различными параллельными границами, отличное от
прямой и полуплоскости.
1) Сколько осей симметрии имеет полоса?
2) Имеет ли полоса центр симметрии? Какую фигуру
образует множество всех центров симметрии полосы?
3) Существуют ли параллельные переносы, при которых
полоса отображается на себя?
525. 1) Даны две параллельные прямые и точка, принадлежащая
полосе, образованной этими прямыми. Постройте окружность,
касающуюся данных прямых и проходящую через данную
точку.
2) Постройте окружность, которая касается двух данных
параллельных прямых и окружности, расположенной между
ними.
526. 1) Постройте окружность данного радиуса, проходящую
через данную точку и касающуюся данной прямой.
2) Постройте окружность данного радиуса, касающуюся
данной окружности и данной прямой.
144
527. Постройте равносторонний треугольник так, чтобы одна из
его вершин находилась в данной точке, другая — на данной
прямой, а третья — на данной окружности.
528. Докажите, что если непустая фигура при некотором
(нетождественном) параллельном переносе отображается на себя,
то эта фигура — неограниченная (определение ограниченной
фигуры см. на с. 13).
529. Представив себе лист клетчатой бумаги бесконечным,
получим фигуру, являющуюся объединением бесконечного
множества «горизонтальных» и «вертикальных» прямых. При
каких перемещениях эта фигура отображается на себя?
530. Фигуры L\ и L2 имеют общий центр симметрии. Докажите,
что пересечение и объединение этих фигур также являются
центрально-симметричными фигурами.
531. 1) Докажите, что если прямые а и b являются осями
симметрии фигуры, то прямая, симметричная а относительно прямой
Ъ, тоже является осью симметрии этой фигуры.
2) Докажите, что если точки А и В— центры симметрии
фигуры L, то и точка С, симметричная точке В относительно А,
тоже является центром симметрии этой фигуры.
ГЛАВА
ιν
МНОГОУГОЛЬНИКИ
А
/
А
ь
Рис. 244
Рис. 245
С
С
Рис.
ζ
Рис
246
А
\
247
\
§ 1. Треугольники
39. Элементы, определяющие
треугольник
1. Стороны а = \ВС\, Ъ = \СА\, с =
= \АВ\ и углы α — САБ, β — ABC,
γ = БСА* треугольника (рис. 244)
называют основными элементами
треугольника.
Вы уже решали задачи на
построение треугольника по трем его основным
элементам (п. 22). Были рассмотрены
три задачи.
Задача 1. Построить
треугольник по стороне а и двум прилежащим
к ней углам β и у (рис. 245).
Задача 2. Построить
треугольник по двум сторонам а, Ъ и углу γ
между ними (рис. 246).
Задача 3. Построить
треугольник по трем его сторонам а, Ь> с
(рис. 247).
Как известно, в этих случаях три
элемента определяют треугольник с
точностью до конгруэнтности.
Например, любые треугольники с данными
элементами α, β, γ конгруэнтны. По-
* Напомним, что для краткости длины
сторон и величины углов многоугольника называют
просто его сторонами и углами.
46
этому говорят, что каждая из задач
1—3 имеет не более одного решения.
Выясним теперь, при каких
условиях эти задачи имеют решение.
Первая задача имеет решение, если
сумма данных углов β и γ меньше 180'.
ψ Действительно, проведем луч СК, со-
направленный лучу ВМ (рис. 248). Тогда
KCD = β (см. п. 37), КСВ + β = 180°
(углы КСВ и KCD — смежные), γ + β < 180° (по условию).
Значит, КСВ > γ, и поэтому луч CN отличен от луча СК.
Прямая CN, пересекающая одну из параллельных прямых
С К, пересекает и вторую — ВМ (следствие 1 из аксиомы
параллельных). Точка пересечения прямых CN и ВМ лежит в
полуплоскости, содержащей лучи ВМ и СК, так как луч CN лежит
внутри угла КСВ. Итак, лучи ВМ и CN пересекаются, и,
значит, третья вершина искомого треугольника может быть
построена. Следовательно, если β + У < 180°, то задача имеет
решение, ψ
Вторая задача имеет решение, если у < 180°.
Третья задача имеет решение при условии \а—Ъ\ <с <
< а + Ъ (при выполнении этого условия окружности (А, Ъ) и
(Б, а) имеют общие точки, не лежащие на прямой АВ, см. п. 13).
2. Рассматривая всевозможные тройки основных элементов,
можно сформулировать еще три задачи на построение
треугольника по его основным элементам.
Задача 4. Построить треугольник по двум сторонам а>
Ъ и углу а, противолежащему одной из них (рис. 249, а).
,ос
о)
147
Решение. Построим сначала две вершины искомого
треугольника. Для этого на луче АХ построим отрезок АС
(рис. 249, б): | АС\ = &, а затем от луча АХ отложим угол XAY>
такой, что XAY = а.
Для построения искомого треугольника ABC остается
построить его третью вершину. Эта вершина должна лежать на
луче AY (так как Υ АХ = а) и на окружности (С, а) (так как
\СВ\ = а). Построив эту окружность, найдем ее точки
пересечения с лучом ΑΥ. Возможны три случая.
1) Окружность (С, а) пересекает луч ΑΥ в двух точках —
Bi и В2 (см. рис. 249, б). В этом случае задача имеет два
решения (треугольники ABiC и АВ2С не конгруэнтны).
2) Окружность (С, а) может иметь с лучом AY только одну
общую точку В (рис. 250, а, б). Задача имеет одно решение.
3) Окружность (С, а) может не иметь общих точек с лучом
AY (рис. 250, в). В этом случае задача не имеет решений.
Задача 5. Построить треугольник по стороне а,
прилежащему к ней углу β и
противолежащему ей углу а (рис. 251).
Так как В = 180°— α — β, то
решение этой задачи сводится к первой
задаче. Поэтому задача 5 имеет не более
одного решения. Решение существует, если
а + β < 180°.
Задача 6. Построить треугольник
по трем его углам α, β и γ.
Из теоремы о сумме углов
треугольника видно, что задача разрешима
только в случае α + β + У = 180°. Если это
Рис. 252 условие выполнено, то задача имеет бес-
Рис. 251
148
конечно много решений: одна из сторон может быть задана
произвольно (рис. 252).
Другие тройки основных элементов не приводят к новым
задачам. Например, задача на построение треугольника по
элементам 6, α и β уже рассмотрена (задача 5): даны сторона,
прилежащий к ней угол и угол, ей противолежащий.
Вопросы и задачи
532°. Какие тройки основных элементов определяют треугольник?
533. Длины двух сторон некоторого треугольника равны а и Ь.
Какую длину может иметь его третья сторона?
534°. Величина одного из углов некоторого треугольника равна а.
Какую величину может иметь один из других углов этого
треугольника?
535. Даны пары основных элементов треугольника: 1) а, Ь; 2) Ъ, А]
3) А, С; 4) Ъ, с. Укажите еще какой-либо его основной элемент,
чтобы полученная тройка элементов определяла треугольник.
536. Постройте треугольник: 1) по стороне 2 смг прилежащему
к ней углу 40° и противолежащему ей углу 60°; 2) по
сторонам 4 см и 5 см и углу, противолежащему большей из этих
сторон, равному 40°; 3) по сторонам 4,5 см и 5 см и углу,
противолежащему одной из этих сторон, равному 120°; 4) по
сторонам 4 см и 5 см и углу, противолежащему одной из
этих сторон, равному 90°.
537. Постройте треугольник: 1) по данной стороне,
прилежащему к ней и противолежащему ей углам; 2) по двум
сторонам и углу, противолежащему одной из них.
538. Постройте треугольник: 1) по высоте, проведенной к
основанию, и двум боковым сторонам; 2) по стороне а, высоте ha
и медиане та; 3) по стороне Ъ, высоте ha и медиане та .
539*. Какой вид имеет треугольник, если две его медианы являются
биссектрисами?
540*. Какой вид имеет треугольник, если две его медианы являются
высотами?
541*. Постройте треугольник по двум боковым сторонам и разности
углов при основании.
149
40. Соотношения между сторонами и углами треугольника
50 | Τ е о ρ е м а. 1) Против большей стороны треугольника'
лежит больший угол.
\2) Против большего угла треугольника лежит большая
сторона.
1) Дано: \ВС\ > \АВ\ (рис. 253).
Доказать: А > С.
Доказательство. Отложим на стороне ВС отрезок
BD, конгруэнтный отрезку АВ. Так как по условию \ВС\ >
> | АВ\, то точка D — внутренняя точка отрезка ВС. Соединим
точки А и D отрезком. Треугольник ABD равнобедренный.
Поэтому BAD = BDA. По следствию 3 теоремы 47 BDA = С +
+ DAC. Значит BDA > С и
BAD > С.
Но угол BAD составляет часть угла А. Поэтому
А >С. Ш
2) Д а н о: А > С.
Доказать: \ВС\ > \АВ\.
Доказательство. Длина отрезка АВ не может быть
больше длины отрезка ВС, так как в этом случае по предыдущей
теореме С > А, что противоречит условию.
Длина отрезка АВ не может быть и равной длине отрезка
ВС, так как треугольник ABC был бы равнобедренным и
величины углов А и С были бы равны.
Итак, длина отрезка АВ не больше и не равна длине
отрезка ВС. Значит, она меньше длины отрезка ВС. Поэтому
\ВС\ > \АВ\. ш
Задача. Доказать, что катет
прямоугольного треугольника, лежащий
против угла в 30°, равен половине
гипотенузы.
Доказательство. Построим
треугольник ACD, симметричный тре-
Рис. 253 угольнику ABC относительно оси АС, и
150
рассмотрим треугольник ABD (рис. 254).
Все углы этого треугольника
конгруэнтны, и поэтому он равносторонний.
Значит, \AB\=\BD\. Но \BC\=\DC\
(по построению). Следовательно,
\АВ\ = \BD\ - 2 \ВС\.
Отсюда
\вс\
±\лв\.
\30°
Рис. 254
Вопросы и задачи
542°. Какая сторона является наибольшей в
тупоугольном треугольнике?
543. Докажите, что против наименьшей из
сторон треугольника всегда лежит
острый угол.
544. В треугольнике ABC сторона АВ
наибольшая. Какие углы этого
треугольника острые? Каким может быть угол С?
545. Каким должен быть угол α при
вершине равнобедренного треугольника,
чтобы длина его боковой стороны
была: 1) меньше длины основания;
2) больше длины основания?
546. Дано:. ΔΛ ш ZJ1, ZJi s* Z_4 (рис. 255).
Доказать: 1) Z_B s* Z.D; 2) [ВС] s*
s* [AD].
547. Постройте равнобедренный
треугольник: 1) по основанию и высоте,
проведенной к боковой стороне; 2) по
основанию и углу при вершине.
548. Дано: [АВ] ~ [ВС], [BD] ^ [BE],
[ВО] _1_ [АС] (рис. 256). Укажите
конгруэнтные треугольники.
549. Дано: ААВС равносторонний, [BD] ^
^ [СЕ] (рис. 257). Какого вида
треугольник DEA1
550. Докажите, что если катет прямоугольт
ного треугольника равен половине
Рис. 255
Рис. 256
151
гипотенузы, то один из его углов
равен 30°.
551. Найдите расстояния \BD\, \AD\, \DjQk\
и \АВ\ (рис. 258), если известно, что
\АС\ = Ъ, \ВС\ = а, ВАС = 30°.
552. Разделите с помощью циркуля и линейки
прямой угол на три конгруэнтных угла.
553*. Даны шесть множеств: множество А\
состоит из разносторонних треугольников,
А2 — из равнобедренных, Аз — из
равносторонних треугольников, А4 — из
остроугольных, А-0 — из тупоугольных, Аб — из
прямоугольных треугольников. Укажите
пары этих множеств, пересечение
которых пусто.
§ 2. Четырехугольники
Рис. 259
Четырехугольники могут быть выпуклыми
(рис. 259) и невыпуклыми (рис. 260).
Разобьем множество выпуклых
четырехугольников на непересекающиеся подмножества по
числу пар параллельных сторон:
1) четырехугольники, имеющие по две
пары параллельных сторон (рис. 261, а);
2) четырехугольники, имеющие
только по одной паре параллельных сторон
(рис. 261, б);
3) четырехугольники, у которых нет
параллельных сторон (рис. 261, б).
Свойства четырехугольников
рассматриваются ниже.
L
а)
Рнс. 260
S)
Рис. 261
152
Рис. 262
Рис. 263
41. Параллелограмм
Определение. Четырехугольник,
имеющий две пары параллельных
сторон, называется параллелограммом.
На рисунке 262 изображен
параллелограмм ABCD. Отрезки M{N{ и M2N.2,
перпендикулярные его противоположным
сторонам, называются высотами
параллелограмма.
51 |Теорема. Середина диагонали па-
Ί раллелограмма является его
центром симметрии.
Доказательство. Пусть
точка О — середина диагонали АС
параллелограмма ABCD (рис. 263), тогда точки А и С
симметричны относительно О.
При симметрии с центром О прямая АВ отображается на
параллельную ей прямую (п. 31), проходящую через точку
С, т. е. на прямую CD (по определению параллелограмма
(АВ) || (CD)). Прямая СВ при этой симметрии отображается
на прямую AD.
Следовательно, при симметрии Z0 образами прямых АВ и
С В являются соответственно прямые CD и AD. Точка В —
точка пересечения прямых АВ и СВ. Поэтому ее образ при
симметрии Z0 есть пересечение образов прямых АВ и СВ, т. е. точка D:
Z0 (В) = D.
Итак, при симметрии с центром О вершины А, В, С, D
отображаются соответственно на вершины С, D, А, В.
Значит, и параллелограмм ABCD при симметрии ZQ
отображается на себя, следовательно, середина диагонали
параллелограмма (точка О) есть центр симметрии этого
параллелограмма. ■
Следствие 1. Противоположные стороны
параллелограмма попарно конгруэнтны.
Следствие 2. Противоположные углы
параллелограмма попарно конгруэнтны.
Следствие 3. Сумма углов, прилежащих к одной
стороне параллелограмма, равна 2d.
Доказательство. А + В + С + D = 4d (п. 83).
А = С, В = D (следствие 2). Значит, А + В = 2d. ■
153
Следствие 4. Диагонали
параллелограмма делятся точкой их
пересечения пополам.
Доказательство. Вершины
А и С (а также Вий)
центрально-симметричны относительно точки О (рис. 264).
Значит, отрезки АО и СО, ВО и DO
конгруэнтны, т. е. точка О — середина
диагоналей АС и BD. Ш
Вопросы и задачи
554. 1) Могут ли все углы параллелограмма
быть острыми?
2) Может ли только один из углов параллелограмма быть
.прямым?
555. Диагональ параллелограмма образует с двумя его сторонами
углы в 30° и 50°. Вычислите все углы этого параллелограмма.
556. 1) Докажите, что диагональ параллелограмма делит его на
два конгруэнтных треугольника.
2) Докажите, что вершины А и С параллелограмма ABCD
равноудалены от прямой BD.
557. 1) Параллелограмм одной из его диагоналей делится на два
треугольника, периметр каждого из них 6 см. Вычислите
длину этой диагонали, если периметр параллелограмма равен 7 см.
2) Параллелограмм, периметр которого равен 50 см,
разделен диагоналями на четыре треугольника. Разность
периметров двух из этих треугольников равна 5 см. Вычислите
стороны параллелограмма.
558. Стороны параллелограмма равны 3 см и 5 см. Может ли
диагональ этого параллелограмма равняться: 1) 10 см; 2) 8 см;
3) 4 см?
559. Существует ли параллелограмм, две диагонали и сторона
которого равны соответственно: 1) 4 см, 10 см и 6 см; 2) 8 см,
10 см и 9 см; 3) 8 см, 10 см и 10 см?
560. 1) Биссектриса одного из углов параллелограмма делит
пересекаемую ею сторону на отрезки в 4 см и 5 см. Вычислите
периметр этого параллелограмма.
2) Длины сторон параллелограмма равны 3 см и 5 см.
На какие отрезки делит большую сторону биссектриса острого
угла этого параллелограмма?
.154
Рис. 265
Рис. 266
561. Докажите, что биссектрисы двух
противоположных углов
параллелограмма параллельны.
562*. При пересечении биссектрис углов
параллелограмма образовался четырех- А
угольник. Докажите: 1) этот
четырехугольник является
параллелограммом; 2) все углы этого
четырехугольника прямые.
563. Дано (рис. 265): ABCD—
параллелограмм, \АМ\ = \CN\. Доказать:
MBND— параллелограмм.
564. Дано: ABCD — параллелограмм,
\АМ\ = \CN\ (рис. 266).
Доказать: MBND—параллелограмм.
565. Постройте параллелограмм, если
даны: 1) две стороны и угол между ни- β
ми; 2) диагонали и угол между ними; £\
3) сторона, диагональ и угол между
диагоналями; 4) две высоты,
проведенные из одной вершины, и сторона.
566. Постройте треугольник по двум
сторонам и медиане, проведенной к третьей
стороне.
567**. Постройте центр симметрии
параллелограмма, вершины которого
недоступны.
568. Какими элементами может быть задан Рис. 268
параллелограмм?
569*.Дано: ABCD—параллелограмм, [АЕ] ^ [AF] ^ [CK]^[CN]
(рис. 267). Доказать: Е, F, N, К—вершины параллелограмма.
570. Дано: ABCD—параллелограмм, [AM] ± [BD], [CN] _L [BD]
(рис. 268). Доказать: 1) [AM] ~ [CN]; 2) [BN] ~ [DM];
3) AMCN — параллелограмм.
571. Докажите, что сумма расстояний от любой внутренней точки
параллелограмма до прямых, на которых лежат его стороны,
постоянна для данного параллелограмма. Чему она равна?
572*. Постройте параллелограмм: 1) по острому углу и двум
высотам; 2) по высоте и двум диагоналям.
155
42. Условие и заключение теоремы
1. Часто теоремы формулируют в виде условных предложений,
т. е. предложений вида «Если ..., то ...». Напомним,
например, теорему (см. п. 31):
«Если прямые ρ и q центрально-симметричны, то они
параллельны* (1).
Обозначим через А и В предложения:
«Прямые ρ и q центрально-симметричны» (А),
«Прямые ρ и q параллельны» (В).
Предложения А и В — это предложения с переменными
(р и q), и сами по себе они не истинны и не ложны. Все зависит
от того, какие значения придать переменным. Но
предложение (1) верно (оно доказано в пункте 31). В этом предложении
утверждается, что при любых значениях переменных (прямых
ρ <и q), для которых верно предложение А, верно и
предложение В.
Предложение (1) можно кратко записать в виде:
А => В
(читается: из А следует В; стрелка здесь — знак следования,
с употреблением которого вы уже познакомились в курсе
алгебры).
В условном предложении А =>- В предложение А называется
условием, а предложение В — заключением.
Рассмотрим теперь предложение
В => А,
где заключение В теоремы (1) превратилось в условие, а
условие А теоремы (1) — в заключение. Подробно оно
формулируется так:
Если прямые ρ и q параллельны, то они
центрально-симметричны (1').
Предложение (1') также верно (см. п. 32). Эту теорему
называют теоремой, обратной к теореме 1.
Вообще, предложением, обратным к предложению Ρ =>- Q*
называется предложение Q =>- Р.
В нашем случае предложение, обратное к теореме вида
Ρ =>- Q, оказалось верным. Это не всегда так, как показывает
следующий пример. Рассмотрим предложение: }
Если углы вертикальные, то они конгруэнтны. (2)
156
Здесь условием является предложение
«Углы вертикальные» (С),
а заключением — предложение
«Углы конгруэнтны» (D).
Предложение С =^ D, как вы знаете,
истинно, но обратное предложение (если
углы конгруэнтны, то они вертикальные)
ложно. Действительно, легко указать
конгруэнтные углы, не являющиеся
вертикальными (рис. 269).
. 2. В тех случаях, когда верны оба рис 270
условных предложения Ρ =^ Q и Q =>- Р,
говорят, что условия Ρ и Q равносильны, и пишут: Ρ фф Q
(читается: «Р равносильно Q» или «Р верно тогда и только
тогда, когда верно Q»; двойная стрелка здесь — знак
равносильности предложений).
В рассмотренном выше первом примере предложения А и В
равносильны. Предложения С и D не равносильны: из С
следует D, но из D не следует С.
Предложения «Четырехугольник ABCD есть
параллелограмм» (Е) и «Противоположные стороны четырехугольника
ABCD конгруэнтны и параллельны» (F) равносильны.
Действительно, как показано в предыдущем пункте, Ε =>- F.
Докажем обратное.
521Теорема. Если две противоположные стороны четырех-
\ угольника конгруэнтны и параллельны, то такой
четырехугольник есть параллелограмм.
Доказательство. Пусть стороны ВС и AD
четырехугольника ABCD (рис. 270) конгруэнтны и параллельны;
точка О — середина диагонали АС. Тогда точки А и С
симметричны относительно точки О. Так как по условию (ВС) \\ (AD),
то лучи СВ и AD противоположно направлены и, значит,
симметричны относительно О. Но \ВС\ = \AD\. Следовательно,
при симметрии Zo точки В и D отобразятся друг на друга.
Мы видим, что отрезки АВ и CD симметричны относительно
центра О и поэтому параллельны. Итак, противоположные
стороны четырехугольника ABCD попарно параллельны
((ВС) || (AD) по условию, (АВ) \\ (CD) по доказанному), т. е.
этот четырехугольник есть параллелограмм. ■
Теорему 52 часто называют признаком параллелограмма.
Докажем другой признак параллелограмма.
I
157
53 I Теорема. Если противоположные
стороны четырехугольника попарно
конгруэнтны, то этот четырехуголь'
ник есть параллелограмм.
Доказательство. Пусть | АВ | =:
\CD\ и |ЯС| = \AD\ (рис. 271).
Проведем диагональ АС и обозначим ее
середину через О. При симметрии Zo точки А и С отображаются
друг на друга (О — середина [_АС~]). Найдем образ точки В.
Центральная симметрия сохраняет расстояния. Поэтому
точка В отображается при симметрии Zj на такую точку В\ что
\АВ\=\СВ'\, \СВ\ = \АВ'\иВ' Φ В. Но этим условиям
удовлетворяет только точка D. Значит, В' = Ζ о (В) = D.
Аналогично получаем, что Z0 (D) = В. Итак, прямые АВ и CD,
AD и ВС центрально-симметричны и поэтому параллельны
(теорема 39). Следовательно, четырехугольник ABCD —
параллелограмм.■
Отметим, что предложение, обратное теореме 53, также верно
(см. следствие 1 теоремы 51, доказанной в п. 41).
ψ 3. Отношения следования и равносильности предложения
словами выражают многими способами; некоторые из них
указаны в следующей таблице:
В случае Ρ =>- Q говорят:
В случае P^Q говорят:
а) если верно Р, то верно и Q,
б) Q есть следствие Р,
в) Ρ есть достаточное условие для Q,
г) Q есть необходимое условие для Р.
а) предложения Ρ и Q
равносильны,
б) Ρ верно тогда и только тогда,
когда верно Q,
в) Ρ есть необходимое и достаток-
ное условие для Q.
Здесь для вас новы обороты речи со словами «достаточно» и
«необходимо». Иногда эти слова путают одно с другим, хотя,
казалось бы, их смысл ясен.
Пусть верно предложение: из Ρ следует Q. Тогда: а) для
того чтобы утверждать, что верно Q, достаточно знать, что
158
верно Р; б) если известно, что верно предложение Р, то
обязательно (с необходимостью) выполняется и условие Q.
' Так, например, теорему 52 можно сформулировать иначе:
для того чтобы четырехугольник являлся параллелограммом,
достаточно, чтобы его противоположные стороны были
попарно конгруэнтны. Так как верна и обратная теорема (для того
чтобы четырехугольник был параллелограммом, необходимо,
чтобы его противоположные стороны были конгруэнтны),
справедлива теорема:
для того чтобы четырехугольник был параллелограммом,
необходимо и достаточно, чтобы его противоположные стороны
были попарно конгруэнтны, γ
Вопросы и задачи
573. Сформулируйте в виде условного предложения: 1) теорему
«параллельные прямые центрально-симметричны»; 2)
теорему о симметричности противоположно направленных
лучей!
574°. Какие предложения называются взаимно-обратными?
575°. Сформулируйте предложения, обратные данным, и
установите, какие из них истинны, а какие ложны. 1) Если
четырехугольник— параллелограмм, то сумма его углов, прилежащих
к одной стороне, равна 180°. 2) Если два угла центрально-
симметричны, то они конгруэнтны. 3) Если точка
равноудалена от концов отрезка, то она лежит на его серединном
перпендикуляре. 4) Если точка лежит на биссектрисе угла,
то она равноудалена от сторон этого угла. 5) Если две точки
симметричны относительно некоторой прямой, то они
равноудалены от этой прямой. 6) Если прямая является осью
симметрии круга, то она проходит через центр этого круга.
7) Если прямая является осью симметрии отрезка, то она
проходит через середину этого отрезка.
576°. 1) Приведите примеры двух истинных взаимно-обратных
предложений.
2) Сформулируйте два взаимно-обратных предложения, одно
из которых истинно, а другое — ложно.
577. Приведите примеры теорем, в формулировке которых
встречаются слова «тогда и только тогда».
159
578. Верны ли предложения: 1) прямые а и Ъ параллельны тогда
и только тогда, когда они центрально-симметричны; 2) две
фигуры конгруэнтны тогда и только тогда, когда существует
поворот, отображающий одну из них на другую; 3)
различные прямые а и Ъ перпендикулярны тогда и только тогда,
когда Sа(Ь) = Ъ] 4) диаметр перпендикулярен хорде, не
проходящей через центр окружности, тогда и только тогда,
когда он проходит через середину хорды?
579. Верно ли предложение: выпуклый четырехугольник является
параллелограммом, если: 1) две противоположные стороны
его конгруэнтны; 2) две противоположные стороны его
параллельны; 3) диагонали точкой их пересечения делятся
пополам; 4) сумма углов, прилежащих к одной из его сторон,
равна 180°; 5) две его противоположные стороны центрально-
симметричны; 6) диагонали его конгруэнтны?
580. Постройте параллелограмм по двум сторонам и диагонали.
581. Верны ли следующие предложения: 1) чтобы углы были
смежными, достаточно, чтобы две их стороны были
противоположными лучами; 2) чтобы треугольник был
прямоугольным, достаточно, чтобы сумма двух его углов была
равна 90°; 3) чтобы четырехугольник был
параллелограммом, достаточно, чтобы его диагонали делились в точке их
пересечения пополам; 4) чтобы два угла были конгруэнтны,
достаточно, чтобы они были вертикальными?
582. 1) Сформулируйте условие, достаточное для того, чтобы
точка была равноудалена от сторон угла.
2) Проверьте, является ли найденное вами условие
необходимым.
583. Сформулируйте некоторые известные вам теоремы с
помощью понятий необходимости и достаточности.
584. Верны ли следующие предложения: 1) чтобы углы были
смежными, необходимо, чтобы две их стороны были,
противоположными лучами; 2) чтобы треугольник был
прямоугольным, необходимо, чтобы он имел два острых угла;
3) чтобы четырехугольник был параллелограммом,
необходимо, чтобы его диагонали были конгруэнтны; 4) чтобы два
угла были конгруэнтны, необходимо, чтобы они были
вертикальными?
585. Укажите условия, необходимые для того, чтобы: 1)
четырехугольник был параллелограммом; 2) два луча были со-
160
направлены; 3) два треугольника были конгруэнтны; 4)
треугольник был равносторонним.
586. Сформулируйте необходимое и достаточное условие для
того, чтобы: 1) некоторая точка X плоскости была
равноудалена от двух данных точек А и В; 2) прямые а и Ъ были
параллельны.
587°. Какие из перечисленных ниже предложений верны: 1)
чтобы треугольник был равносторонним, необходимо и
достаточно, чтобы два угла его были конгруэнтны; 2) чтобы
четырехугольник был параллелограммом, необходимо и
достаточно, чтобы его противоположные углы были попарно
конгруэнтны; 3) чтобы точка была равноудалена от двух данных
точек А и В, необходимо и достаточно, чтобы она делила
отрезок АВ пополам; 4) чтобы два конгруэнтных отрезка
были центрально-симметричны, необходимо и достаточно,
чтобы они были параллельны?
588. Укажите несколько необходимых и достаточных условий
для того, чтобы четырехугольник был параллелограммом.
589. Какие слова — «достаточно», «необходимо», «необходимо и
достаточно» — можно поставить вместо многоточия в
следующих предложениях, чтобы получить верные предложения:
1) чтобы произведение двух чисел равнялось нулю..., чтобы
каждое из них равнялось нулю; 2) чтобы сумма двух целых
чисел была четным числом..., чтобы каждое из слагаемых
было четным; 3) чтобы четырехугольник был
параллелограммом..., чтобы две стороны его были параллельны; 4)
чтобы два четырехугольника были конгруэнтны..., чтобы
соответствующие стороны их были равны?
590**. Рассмотрите шесть условий:
1) [АВ] || [CD]; 3) \АВ\ = \CD\; 5) А = С;
2) [ВС] || [AD]; 4) \ВС\ = \AD\; 6) В = D.
Покажите, что: а) каждое из этих условий необходимо для
того, чтобы четырехугольник ABCD был параллелограммом;
б) ни одно из этих условий не является достаточным для
того, чтобы четырехугольник ABCD был параллелограммом;
в) объединяя их попарно, получим девять необходимых и
достаточных условий для того, чтобы четырехугольник ABCD
был параллелограммом.
161
43. Прямоугольник
В младших классах прямоугольник определяли как
четырехугольник, все углы которого прямые. Следовательно, понятие
«прямоугольник» было определено с помощью понятий
«четырехугольник» и «прямой угол».
Одному и тому же понятию можно дать различные
определения. Например, прямоугольник можно определить как частный
вид параллелограмма с помощью понятий «параллелограмм» и
«прямой угол».
Определение. Параллелограмм, у которого все углы
прямые, называется прямоугольником.
Оказывается, в определении прямоугольника через понятие
«параллелограмм» не обязательно указывать, что все четыре
угла параллелограмма должны быть прямыми. Можно дать
более «экономное» определение.
Действительно, если один из углов параллелограмма ABCD,
например угол А, прямой (рис. 272), то и три остальные угла
прямые: угол В прямой, так как А + В = 180°, угол С прямой,
так как В + С = 180° (п. 41). Но тогда и угол D прямой.
Поэтому определение прямоугольника можно сформулировать и
так: параллелограмм, имеющий прямой угол, называется прямо-
угольником.
Так как прямоугольник является частным видом
параллелограмма, то он обладает всеми свойствами параллелограмма (п. 41).
Кроме того, прямоугольник обладает и другими свойствами.
54 I Теорема. Серединный перпендикуляр к стороне прямо-
| угольника является его осью симметрии.
Дано: ABCD — прямоугольник, \_AM~] ^ [AfD], (MN) ±
± (AD) (рис. 273).
Доказать: (MN) — ось симметрии
прямоугольника ABCD.
Доказательство. Рассмотрим осевую симметрию
Smn- Из условия следует, что точки А и D симметричны
относительно оси MN.
Но прямая MN является также серединным
перпендикуляром отрезка ВС. В самом деле:
(ВС) || (AD) (по условию),
поэтому (ВС) j_ (ΜΝ).
162
Кроме того, \BN\ = \АМ\ и \NC\ =
= | MD | (теорема 45). А так как \АМ\ =
= \MD\9 то |Atf| = |Ж7|.
Следовательно, точки Б и С
симметричны относительно оси MN.
Итак, при симметрии с осью MN
А -> D, Б -> С, С -> Б, D -> А.
Поэтому и прямоугольник ABCD
отображается на себя. Значит, прямая MN
есть ось симметрии прямоугольника
ABC DM
Следствие!.. Прямоугольник
имеет две оси симметрии.
Следствие 2. Диагонали прямо-
угольника конгруэнтны.
Доказательство. Точки D и
Б симметричны точкам А и С
относительно оси MiV (рис. 274). Значит, отрезки
АС и DB симметричны относительно
оси MN. Поэтому [АС] ^ [£>£].■
Вопросы и задачи
591. Покажите, что четырехугольник, имеющий два прямых
угла, не обязательно является прямоугольником.
592. Укажите перемещения, при которых прямоугольник
отображается на себя.
593. Даны два конгруэнтных прямоугольника. Сколько
существует различных перемещений, при которых один из них
отображается на другой?
594. 1) Можно ли построить четырехугольник, не являющийся
прямоугольником, диагонали которого были бы конгруэнтны
между собой?
2) Докажите, что параллелограмм, диагонали которого
конгруэнтны, является прямоугольником.
595. Укажите свойства, которыми обладает прямоугольник, но
не обладает параллелограмм, не являющийся
прямоугольником.
Рис. 274
163
596.
597.
598.
599.
600.
601.
602*.
Биссектриса одного из углов прямоугольника делит
пересекаемую ею сторону на отрезки равной длины. Найдите
периметр этого прямоугольника, если длина меньшей стороны
прямоугольника 15 см.
Периметр прямоугольника равен 12 см. Найдите сумму
расстояний от произвольной внутренней точки прямоугольника
до его сторон.
Постройте прямоугольник: 1) по двум сторонам, имеющим
общую вершину; 2) по стороне и диагонали; 3) по
диагонали и углу между диагоналями; 4) по диагонали и сумме
прилежащих сторон.
1) Докажите, что медиана прямоугольного треугольника,
проведенная к гипотенузе, равна половине гипотенузы.
2) Сформулируйте и докажите обратную теорему.
Какой фигурой является множество вершин прямых углов
всех прямоугольных треугольников с данной
гипотенузой АВ1
Как найти на прямой I такую точку С, что угол АСВ— прямой
(А и В— данные точки)?
Постройте прямоугольник, все вершины которого лежат на
данной окружности, причем две из них — в данных точках.
603. Объясните, на чем основано
устройство центроискателя, изображенного
на рисунке 275.
604*. Пользуясь только чертежным
угольником: 1) постройте оси симметрии
двух данных точек; 2) разделите
данный отрезок пополам; 3) удвойте
данный отрезок.
605*. Из вершин А и В треугольника ABC
проведены высоты. Докажите, что
вершины А, В и основания построенных
высот принадлежат одной окружности.
Где находится центр этой окружности?
Чему равен ее радиус?
606*. Точка А лежит вне данного круга
(рис. 276), [ВС]—диаметр. С
помощью одной линейки постройте
перпендикуляр к прямой ВС, проходящий
Рис. 276 через А.
Рис. 275
• Я
164
44. Ромб
Определение. Параллелограмм,
все стороны которого конгруэнтны,
называется ромбом.
Кроме общих свойств
параллелограмма (см. п. 41), ромб обладает и
другими свойствами.
55|Теорема. Прямая, содержащая диагональ ромба, явля-
I ется его осью симметрии.
Доказательство. Рассмотрим симметрию Sac
(рис. 277). Точки АиС при этой симметрии отображаются на себя
(эти точки лежат на оси), а точки В и D — друг на друга, так
как они равноудалены от точек А и С на одно и то же
расстояние.
Итак, при симметрии относительно оси АС
А -> А, В -+ D, С -> С, D -> Б.
Следовательно, при симметрии Sac ромб ABCD
отображается на себя.Я
Следствие 1. Диагонали ромба делят его углы пополам.
Следствие 2. Диагонали ромба взаимно
перпендикулярны.
Доказательство. Ось симметрии перпендикулярна
прямой, соединяющей точки, симметричные относительно этой
оси. Значит, (АС)± (BD)M
Вопросы и задачи
607. Докажите: 1) четырехугольник, у которого все стороны
конгруэнтны, является ромбом; 2) параллелограмм, у которого
две смежные стороны конгруэнтны, есть ромб.
608. Докажите, что четырехугольник ABCD, для которого
прямые АС и BD являются осями симметрии,— ромб.
609. Докажите, что параллелограмм является ромбом тогда и
только тогда, когда его диагонали взаимно
перпендикулярны.
610. Верны ли предложения: 1) четырехугольник является
ромбом тогда и только тогда, когда его диагональ делит
противоположные углы пополам; 2) параллелограмм является ром-
165
бом тогда и только тогда, когда он имеет ось симметрии,
проходящую через противоположные вершины; 3)
четырехугольник является ромбом тогда и только тогда, когда его
диагонали взаимно перпендикулярны?
611. 1) Какие свойства ромба следуют из существования у него:
а) осей симметрии; б) центра симметрии?
2) Укажите перемещения, при которых ромб отображается
на себя.
612°. 1) Какие определения можно дать ромбу?
2) Сколькими элементами определяется ромб? Укажите
такие элементы.
613. 1) Вычислите периметр ромба, один из углов которого
равен 60°, а длина меньшей диагонали 8 см.
2) Может ли длина стороны ромба равняться половине
длины его диагонали?
3) Может ли диагональ ромба быть: а) перпендикулярна его
стороне; б) конгруэнтна его стороне?
614. Существует ли точка, равноудаленная: 1) от всех вершин
ромба; 2) от всех сторон ромба?
615. Докажите, что если все стороны параллелограмма
конгруэнтны, то конгруэнтны и его высоты, проведенные из одной
вершины. Сформулируйте обратное предложение. Верно ли
оно?
616. Постройте ромб: 1) по стороне и диагонали; 2) по
диагоналям; 3) по стороне и углу; 4) по диагонали и углу; 5) по
диагонали и высоте.
617. Сторона ромба ABCD равна 2 см, D=120° (рис. 278).
1) Найдите расстояния |АМ|, |MD|, \BD\. 2) Докажите, что
треугольник MBN равносторонний.
618. 1) Как проверить, является ли вырезанный из картона
четырехугольник ромбом?
2) Швея выкроила из материи четырехугольник, который
должен быть ромбом. Как проверить правильность
изготовления выкройки (не пользуясь никакими
инструментами?
619*. С помощью одной двусторонней
линейки (т. е. линейки с двумя
параллельными краями) постройте: 1) ось
симметрии двух данных точек А и В
(ширина линейки меньше |^£|);
Рис. 278 2) биссектрису угла; 3) прямую,
перпендикулярную данной прямой.
620*. Точки Mi, M2r Мз, М4 — середины
сторон ромба ABCD (рис. 279).
1) Докажите, что четырехугольник
М1М2М3М4 — прямоугольник. 2)
Докажите, что точки В и D лежат на
одной прямой с серединами отрезков
а) М\М2 и МЪМА; б) М\М3 и МгМ4.
45. Квадрат
Определение. Квадратом
называется прямоугольник, у которого все
стороны конгруэнтны.
Из определений квадрата и ромба
следует, что квадрат (рис. 280)
является ромбом, у которого все углы прямые. Так
как квадрат является и
параллелограммом, и прямоугольником, и ромбом, то
он обладает всеми их свойствами. В
частности, серединные перпендикуляры к
сторонам квадрата и прямые, содержащие
диагонали квадрата, являются его осями
симметрии (рис. 281). Следовательно,
имеются четыре осевые симметрии,
отображающие квадрат на себя.
Существуют и другие перемещения,
отображающие квадрат на себя. Это
повороты вокруг центра квадрата на
углы 0°, 180° и 90° (в направлениях по
часовой стрелке и против часовой
стрелки).
Вопросы и задачи
621°. Дайте определение квадрата с помощью понятия: 1)
«параллелограмм»; 2) «ромб»; 3) «четырехугольник».
622. Докажите: 1) ромб, у которого один из углов прямой,
является квадратом; 2) прямоугольник, у которого две смежные
β М2 С
А М4 Π
Рис. 279
Ρ ' q
d , ύ
Рис. 280
Рис. 281
167
623е
624°
625.
626'
627.
628.
стороны конгруэнтны, является квадратом; 3)
четырехугольник, у которого все стороны конгруэнтны и один из углов
прямой, является квадратом.
. Какими особыми свойствами обладает квадрат по сравнению:
1) с прямоугольником, не являющимся квадратом; 2) с
ромбом, не являющимся квадратом?
. Длина проекции одной из сторон квадрата на его диагональ
равна Ь. Найдите длину диагонали.
Постройте квадрат: 1) по его стороне; 2) по его диагонали.
.Два конгруэнтных квадрата имеют общую сторону. Укажите
все такие перемещения, которые отображают один из этих
квадратов на другой.
Верны ли предложения: 1) если диагонали четырехугольника
взаимно перпендикулярны и конгруэнтны, то такой
четырехугольник— квадрат; 2) если диагонали четырехугольника
взаимно перпендикулярны и точкой их пересечения делятся
пополам, то такой четырехугольник — квадрат?
Как проверить (не производя измерений), является ли
вырезанный из бумаги или ткани четырехугольник квадратом?
629. 1) Через вершины В и D квадрата
ABCD проведены параллельные
прямые, пересекающие стороны AD и ВС
соответственно в точках F и Е.
Докажите: a) \BF\ = \DE\; б) AABF s*
£ё ADEC; в) отрезок FE делится
диагональю АС пополам.
2) Дано: ABCD — квадрат, \АЕ\ =
= \BF\ = \СК\ = \DL\ (рис. 282).
Доказать: EFKL — квадрат.
3) Дано: ABCD — квадрат, \АЕ\ =
= \CF\ (рис. 283). Доказать: BEDF —
ромб.
630*. Постройте квадрат: 1) по двум
данным вершинам; 2) по серединам двух
противоположных сторон; 3) по
серединам двух прилежащих сторон; 4) по
центру и двум точкам на одной из
Рис. 283 сторон.
Рис. 282
46. Теорема Фалеса
56 Ι Τ е о ρ е м а (Фалеса). Если на одной стороне угла от-
I ложитъ последовательно несколько конгруэнтных отрезков
I и через их концы провести параллельные прямые, пересе-
I кающие вторую сторону угла, то они отсекут на второй сто-
I роне угла отрезки, конгруэнтные между собой.
Доказательство. Рассмотрим на стороне ОХ угла
ΧΟΥ два отрезка АВ и ВС (рис. 284). Пусть \_АВ~\ ^ [ВС] и
(АА{) || (ВВ{) \\ (СС{). Через точки А и В проведем прямые,
параллельные прямой ΟΥ. Точки их пересечения с прямыми BBt
и СС{ обозначим через Μ и N.
Заметим, что [АВ] ^ [ВС] (по условию). Углы ВАМ и
CBN, ABM и BCN тоже конгруэнтны (п. 37). Следовательно,
конгруэнтны треугольники ВАМ и BCN и поэтому [AM]^[BiV].
Четырехугольники АМВ^ и BiBNCi — параллелограммы
(по построению). Поэтому [AM] ^ [AjBj] и [BiV] ^ [Bid]
(п. 41). Учитывая конгруэнтность отрезков AM и BN,
получаем: \_А^Ву\ ^ [BiCi]. Точно так же доказывается, что [ΑιΒ4] ^
- [CiDi] ц т. д. ■
Задача. Разделить данный отрезок ОА на пять
конгруэнтных отрезков.
Решение. Проведем через точку О луч ОМ (рис. 285)
и отложим на нем последовательно пять конгруэнтных
отрезков:
[OB,-] ^ lBtB2l ~ ... ~ ίΒ,Β,Ι
Проведем прямую АВЪ и через точки Ви В2, В3, В4 прямые,
параллельные этой прямой. По теореме Фалеса эти прямые
разделят отрезок ОА на пять конгруэнтных отрезков.
Рис. 284 Рис. 285
169
В Определение. Средней линией
треугольника называется отрезок,
соединяющий середины двух сторон
треугольника.
57|Теорема. Средняя линия тре-
I угольника параллельна третьей его
I стороне, а длина ее равна половине
Рис- 286 I длины этой стороны.
Дано: ABC — треугольник, \AD\ = \DB\, \BE\ = \ЕС\
(рис. 286).
Доказать: 1) IDE] || [АС]; 2) \DE | = - |АС|.
Доказательство. 1) Через точку Z> проведем
прямую, параллельную стороне АС. Эта прямая (по теореме Фале-
са) разделит отрезок ВС пополам, т. е. пройдет через точку Е.
Значит, IDE} — средняя линия треугольника ABC. По
построению IDE] || [АС].
2) Проведем (EF) \\ (АВ). По теореме Фалеса прямая EF
разделит отрезок АС пополам: \AF\ = \FC\ = — \АС\.
Но IDE] ^ \_AF] (ADEF — параллелограмм).
Следовательно, |ΙλΕ| = — |АС|.И
2
Вопросы и задачи
631. Разделите данный отрезок: 1) на три конгруэнтных отрезка;
2) на четыре конгруэнтных отрезка.
632. Данный отрезок разделите на два отрезка, длины которых
пропорциональны числам: 1) 1г 2; 2) 2, 3.
633. Проекции двух сторон остроугольного треугольника ABC
на прямую АС имеют длины 6 см и 4 см. Какую длину имеют
проекции медиан этого треугольника на ту же прямую?
634. Одна из сторон треугольника разделена на шесть конгруэнт*
ных отрезков. Как разделить (возможно более простым
способом) две другие стороны этого треугольника: 1) на два
конгруэнтных отрезка; 2) на три конгруэнтных отрезка?
635. Докажите, что если на каждой стороне угла
последовательно отложить отрезки равной длины и через соответствующие
концы отрезков, считая от вершины, провести прямые, то
эти прямые параллельны.
170
&
636. 1)° Найдите периметр треугольника,
вершины которого — середины сторон
данного треугольника, имеющего
периметр р.
2) Длины диагоналей данного
четырехугольника тип. Найдите периметр
четырехугольника, вершины которого —
середины сторон данного
четырехугольника. Вычислите этот периметр,
если m = 3 дм и л = 8 см.
637*. Каждая из сторон треугольника ABC разделена на три
конгруэнтных отрезка, и точки деления соединены отрезками
(рис. 287). Найдите периметр образовавшейся на этом
рисунке звездочки, если периметр треугольника ABC
равен р.
638**. Докажите, что три медианы треугольника проходят через
одну точку, делящую каждую из медиан в отношении 2: 1
(считая от вершины).
639. Постройте треугольник, если заданы середины его сторон.
640. Внутри угла ABC дана точка Ζλ Проведите через точку Ό
прямую так, чтобы отрезок ее, отсекаемый сторонами угла:
1) делился в точке D пополам; 2) делился в точке D в
отношении 1 : 2.
641. Докажите, что каждый треугольник можно разрезать на две
части, из которых можно составить параллелограмм.
642*. Докажите, что вершины треугольника находятся на равном
расстоянии от прямой, на которой лежит средняя линия
этого треугольника.
643.* Даны три точки, не лежащие на одной прямой. Покажите на
рисунке, как будет расположена прямая, равноудаленная от
этих точек. Сколько существует таких прямых?
644*. Как можно воспользоваться свойствами средней линии
треугольника для измерения на местности расстояния между
двумя пунктами, разделенными препятствием?
47. Трапеция
Определение. Четырехугольник, две стороны которого
параллельны, а две другие не параллельны» называется
трапецией.
171
^
δ)
LL
К
δ)
Рис. 288
Ν
Параллельные стороны трапеции
называются ее основаниями, а
непараллельные — боковыми сторонами (рис. 288, а).
Боковые стороны трапеции могут
оказаться конгруэнтными, тогда трапеция
называется равнобедренной (рис. 288, б).
Трапецию, один из углов которой
прямой, называют прямоугольной (рис. 288, в).
Любой отрезок ΜΝ (рис. 288, а),
перпендикулярный основаниям трапеции,
называется ее высотой. Отрезок,
соединяющий середины боковых сторон трапеции,
называется средней линией трапеции.
58|Теорема. Средняя линия
трапеции параллельна основаниям, а длина
ее равна полусумме длин оснований.
Дано: ABCD — трапеция, [AD] ||
|| [Ж7], |А#| = |#В|, \СЕ\ = \ED\
(рис. 289).
Доказать: 1) [#£] || [AD];
2) \НЕ\ = 1^1+1^1,
2
Доказательство. 1)
Проведем через середину Η стороны АВ
прямую НК, параллельную основаниям AD и
ВС. Она (по теореме Фалеса) пройдет через середину отрезка CD,
т. е. через точку Е. Следовательно, средняя линия НЕ трапеции
параллельна ее основаниям. Первая часть теоремы доказана.
2) Проведем диагональ BD и обозначим точку ее пересечения
со средней линией через М. Тогда точка Μ — середина отрезка
BD (по теореме Фалеса), а отрезки Μ Η и ME — средние линии
треугольников ABD и BCD. Следовательно,
\МЕ\ = - \ВС\, \МН\ = - |AD|,
2 2
\МЕ\ + \МН\ =1|БС| +- |AD| = -(\BC\ + \AD \).Ш
АЛ. Λ
Рис. 289
\НЕ\
Вопросы и задачи
645. Докажите, что у трапеции не может быть: 1) трех прямых
углов; 2) трех острых углов.
172
646. Докажите, что перпендикуляр, проведенный к основанию
равнобедренной трапеции через его середину, является осью
симметрии этой трапеции.
647. Докажите, что в равнобедренной трапеции конгруэнтны:
1) диагонали; 2) углы при основании.
648. Сколько элементов определяют трапецию?
649. Постройте трапецию ABCD {[AD] || [ВС]) по следующим
элементам:
1) \AD\ = 12 см, \АВ\ = 6 см, \CD\ = 8 см и А = 35°;
2) \AD\ = 10 см, \АВ\ =5 см, \CD\ = 6 см и |BD|=8cm;
3) \AD\ = 12 см, \ВС\ = 2,8 см, D = 35° и А = 40°;
4) \AD\ = а, \ВС\ = Ь, \АС\ = с и \АВ\ = d.
650. Докажите: 1) сумма боковых сторон трапеции больше
разности оснований; 2) сумма диагоналей трапеции больше суммы
оснований; 3) разность оснований больше разности боковых
сторон; 4) диагонали трапеции точкой их пересечения не
делятся пополам.
651. Постройте равнобедренную трапецию ABCD ([AD] \\ [ВС])
по следующим элементам: 1) \AD\, \AB\, А; 2) \AD\,
\ВС\, \АВ\; 3) \AD\, \AB\, \АС\; 4) \AD\, \BC\ и
высоте h.
652. Докажите: 1) если углы при основании трапеции
конгруэнтны, то трапеция равнобедренная; 2) если диагонали
конгруэнтны, то трапеция равнобедренная.
653. Дан четырехугольник. Середины его сторон последовательно
соединены отрезками. Определите вид полученного
четырехугольника, если данный четырехугольник: 1) не трапеция и
не параллелограмм; 2) трапеция; 3) параллелограмм
(отличный от ромба и прямоугольника); 4) прямоугольник
(отличный от квадрата); 5) ромб (отличный от квадрата);
6) квадрат.
654. Высота, проведенная из вершины тупого угла равнобедренной
трапеции, делит большее основание на части, имеющие длины
5 см и 2 см. Вычислите среднюю линию этой трапеции.
655. 1) Длина средней линии трапеции равна 10 см. Одна из
диагоналей делит ее на два отрезка, разность длин которых
равна 2 см. Вычислите длины оснований этой трапеции.
2) Длины оснований трапеции равны 4 см и 10 см. Найдите
длины отрезков, на которые делит среднюю линию этой
трапеции одна из ее диагоналей.
173
656. 1) Основания трапеции имеют длины 8,2 и 14,2 см. Найдите
расстояние между серединами диагоналей.
2) Меньшее основание трапеции имеет длину 6,2 см,
расстояние между серединами диагоналей равно 4 см. Найдите длину
большего основания.
657*. Как разрезать трапецию: 1) на две части, чтобы из них
можно было сложить параллелограмм; 2) на две части, чтобы
из них можно было сложить треугольник; 3) на три части,
чтобы из них можно было сложить прямоугольник?
658*. Докажите, что прямая, проходящая через точку пересечения
диагоналей равнобедренной трапеции и точку пересечения
продолжений боковых сторон, перпендикулярна основаниям
трапеции и делит их пополам.
§ 3. Площади многоугольников
48. Общие сведения о площадях фигур
1. В 5 классе вы уже пользовались формулами для вычисления
площадей некоторых фигур — прямоугольника, треугольника,
круга. В этом параграфе мы приведем более подробные сведения
,о площадях.
За единицу измерения площадей принимают площадь
квадрата, сторона которого равна единице длины. Например, за
единицу измерения площадей можно принять площадь
квадрата, длина стороны которого 1 м (1 см, 1 км). Площадь такого
квадрата называют квадратным метром (квадратным
сантиметром, квадратным километром).
Площади являются величинами, и, как все величины одного
и того же рода, их можно складывать между собой и умножать
на положительные числа (п. 3). При сложении двух площадей
и умножении площади на число получаются площади.
Площади будем обозначать заглавной латинской буквой S.
Единицу измерения длин обозначим е> а площадь квадрата со
стороной длины е обозначим е%- и примем за единицу измерения
площадей.
Любую площадь S можно выразить через единицу
измерения площадей в виде S = ke2y где k — числовой множитель.
Это число k — числовое значение площади S при единице
измерения е2. Пусть, например, за единицу измерения площадей
принят квадратный сантиметр (т. е. е2 = 1 см2). Тогда площадь
174
S = 5 см2 имеет числовое значение 5 при единице
измерения 1 см2.
Если две площади Si и S2 выражены через общую единицу
измерения е2 в виде
St = ае\ S2 = Ъе\
то отношение Si : S2 равно отношению числовых значений а и Ь:
Si : S2 = а : &.
В следующих пунктах этого параграфа мы научимся
находить площади различных многоугольников, опираясь на
основные свойства площадей, которые примем без доказательства:
1) конгруэнтные многоугольники имеют равные площади;
2) если многоугольник составлен из неперекрывающихся
многоугольников, то его площадь равна сумме площадей
этих многоугольников.
Предложение «многоугольник Ρ составлен из
неперекрывающихся многоугольников» означает, что: а) Р является
объединением этих многоугольников и б) никакие два из этих
многоугольников не имеют общих внутренних точек. Примеры таких
разбиений многоугольников приведены на рисунке 290.
2. Применим свойства 1 и 2 к выводу формулы площади
прямоугольника. Рассмотрим случай, когда основание и высота
прямоугольника равны целому числу единиц длины е:
а = me, h = пе.
β этом случае прямоугольник составляется из тп^ квадратов
со стороной е (рис. 291). Эти квадраты конгруэнтны и,
следовательно (по свойству 1), имеют одну и ту же площадь в2. Тогда
(по свойству 2) искомая площадь S равна:
S = тпе2.
QJ
il
-с;
a=me
Рис. 291
175
2 см
4 см
Рис. 292
ί \^ΓΎΛ n^KL I
Ml Τ N
И N
ι/ κι
/IN
Ml
MM
N И
1Ή и ι
НИ
HJJJJMiff
~тЫ.
—^Η—r^—
Вычисляя по обычным
правилам алгебры, имеем:
ah = (те) (пе) = тле2 = S.
Вообще, разумно условиться,
что длины α и & можно «умножать»
друг на друга, получая при этом
площадь. В данном случае это
«произведение» равно площади
прямоугольника с основанием а и
высотой h. Например, принято писать:
5 см · 7 см = 35 см2.
Полученная выше формула
площади прямоугольника верна не
только для целых, но и для всех
положительных а и й. Обычно ее
записывают короче:
S = ah.
Из этой формулы сразу следует,
что площадь квадрата равна
квадрату его стороны, S = а2.
3. По первому свойству площадей любых два конгруэнтных
многоугольника имеют равные площади, т. е. равновелики.
Обратное неверно: два равновеликих многоугольника не
обязательно конгруэнтны. Например, квадрат со стороной 2 см
и прямоугольник со сторонами 1 см и 4 см (рис. 292)
равновелики (площадь каждой из этих фигур равна 4 см2), но не
конгруэнтны.
4. Измеряя площади при помощи палетки, вы уже
познакомились с тем, как можно оценивать с недостатком и избытком
площадь фигуры, имеющей криволинейную границу. На
рисунке 293 в круге помещается полностью 120 квадратов
площади е2. Объединение же всех 172 квадратов на этом рисунке
полностью содержит круг. Поэтому для площади S данного
круга имеем неравенства:
120е2 < S < П2е2.
Приближенно можно принять:
0 120 + 172 2 i ла«
S « е2 = 146ez.
Рис. 293
В действительности эта площадь равна пг2 ж 154е2
176
Вопросы и задачи
659. Практическая работа. 1) Произведите необходимые
измерения и вычислите площадь участка прямоугольной
формы. 2) Произведите необходимые измерения и
вычислите площадь поверхности пластинки прямоугольной формы.
660. Практическая работа. Вырежьте из бумаги два
конгруэнтных прямоугольных треугольника и сложите из них:
1) равнобедренный треугольник; 2) прямоугольник; 3)
параллелограмм, отличный от прямоугольника. Почему
площади всех получившихся фигур равны?
661. 1) Вычислите площадь поля в гектарах, если поле имеет
форму прямоугольника с размерами: а) 2 км X 1 км;
б) 500 м X 500 м; в) 100 м X 150 м; г) 0,8 кмХ1,2 км.
2) Известно, что периметр прямоугольника, каждая из
сторон которого измеряется целым числом сантиметров, равен
12 см. Вычислите площадь этого прямоугольника. В каком
случае площадь прямоугольника будет наибольшей?
662. Основание прямоугольника в два раза больше его высоты.
Покажите на рисунке: 1) как разрезать этот прямоугольник
на две части так, чтобы из них можно было составить
прямоугольный треугольник; 2) как разрезать его на две части
так, чтобы из них можно было составить равнобедренный
треугольник; 3) как разрезать его на три части так, чтобы из
них можно было составить квадрат.
663. Участок земли имеет площадь 100 га. Найдите числовое
значение этой площади, если за единицу измерения принять:
1) квадратный километр; 2) квадратный метр; 3) ар.
664. Как изменится площадь прямоугольника, если: 1) основание
и высоту его увеличить в два раза; 2) основание и высоту
уменьшить в три раза; 3) основание увеличить в четыре
раза, а высоту уменьшить в четыре раза; 4) основание
увеличить в шесть раз, а высоту уменьшить в два раза?
665. Длина комнаты 5,4 м, а ширина 4,2 м. В комнате два окна
шириной 1,2 м и высотой 1,6 м. Освещенность комнаты
считается нормальной, если площадь (световая площадь) окон
составляет 20% от площади пола. Нормально ли освещение
комнаты?
666. Практическая работа. Произведите необходимые
измерения и вычислите световую площадь своего класса. Вычис-
177
в
F
Ε
К
/Я
L
*ч
v\
XT
A
Ρ О
Рис. 295
b=fe
Рис. 296
И
Л/
Л
I
QJ
'
1
0)
II
-^ »-
лите отношение световой площади к
площади пола и выразите его в
процентах.
667. Дано: Е, F, К и L — середины сторон
квадрата ABCD (рис. 294). Сравните
площадь четырехугольника MNOP с
площадью квадрата ABCD.
668*. Дано: ABCD — квадрат (рис. 295), Е,
F, Kt L, Μ, Ν, О и Р — точки,
делящие каждую сторону на три равные
части. Докажите, что площадь четырех-
2
угольника QRST равна — площади
квадрата ABCD.
669*. Докажите, что площадь квадрата,
построенного на катете
равнобедренного прямоугольного треугольника,
вдвое больше площади квадрата,
построенного на высоте, проведенной
к гипотенузе.
670*. Постройте квадрат, площадь которого
в два раза больше площади данного
квадрата.
671*. Пользуясь формулой S = лг2,
проверьте, насколько хорошо
приближение S= 146e2 для площади круга,
вычисленной по рисунку 293.
672**. Докажите, опираясь на свойства
площадей, что при любых положительных
рациональных числах ρ и q
прямоугольник с основанием а = ре и
высотой Ъ = qe имеет площадь pqe2.
Указание. См. рисунок 296, где ρ =
= — и q
3 ч
49. Площадь параллелограмма
59 1 Теорема. Площадь параллелограмма равна произве-
I дению его основания на высоту.
Дано: а — основание параллелограмма ABCD, h — его
высота.
178
Рис. 297
Доказать: S = ah.
Доказательство. В случае, когда один из углов
параллелограмма прямой, теорема уже доказана (в этом случае
параллелограмм является прямоугольником). Пусть один из
двух углов (например, угол А, рис. 297). прилежащих к
основанию AD параллелограмма ABCD, острый.
Проведем через вершины В и С перпендикуляры к прямой
AD. Получим прямоугольник BCFE, вершины F и Ε которого
лежат на луче AD. Точка F при этом всегда лежит вне отрезка
AD. В положении точки Ε могут встретиться три различных
случая (рис. 297, а, б, в). Во всех случаях
^ABCF = ^AB^D + SD0F = &BCFE "Τ" ^ J
Но Δ DCF ^ Δ ABE. Значит,
Άβε'
(i)
^d:f — ^abe*
Поэтому из равенства (1) следует, что
Но SBrFE=\BC\
Поэтому
Итак,
'ABCD
^'A BCD — ^BCFE*
\ВЕ\
= \ВС\ -\ВЕ\ =\AD\ -\ВЕ\ = а - h.
SABCD = ak-
Вопросы и задачи
673. Постройте параллелограмм, произведите необходимые
измерения и вычислите его площадь.
674. Стороны параллелограмма равны 4,2 см и 5,6 см. Высота,
проведенная к большей стороне, равна 3,3 см. Вычислите
площадь и вторую высоту этого параллелограмма.
179
675. Стороны параллелограмма равны 8 см и 10 см, одна из
высот равна 6 см. Вычислите площадь и вторую высоту
параллелограмма. Сколько решений имеет задача?
676. Стороны параллелограмма равны 8 см и 10 см. Одна из
высот равна 9 см. Вычислите вторую высоту параллелограмма.
Сколько решений имеет задача?
677. Постройте параллелограмм, отличный от прямоугольника,
и покажите, как его разрезать на части так, чтобы из них
можно было сложить прямоугольник.
678. Докажите, что прямая, проходящая через центр симметрии
параллелограмма, разбивает его на две равновеликие части.
679. Площадь параллелограмма равна 24 см2. Точка пересечения
его диагоналей удалена от прямых, на которых лежат
стороны, на 2 см и 3 см. Вычислите периметр этого
параллелограмма.
680. Постройте два неконгруэнтных равновеликих
параллелограмма с общей стороной.
681. Постройте ромб. Выполните необходимые измерения и
вычислите его площадь.
682. 1) Выведите формулу, выражающую площадь S ромба через
его диагонали т и п.
2) Выведите формулу для вычисления площади S квадрата
по его диагонали с.
683. 1) Вычислите площадь ромба, диагонали которого имеют
длины: а) 2,5 дм и 3,6 дм; б) 8,8 м и 9,5 м.
2) Вычислите площадь ромба, если сторона его равна 6,2 см,
а один из углов равен 30°.
684. Вычислите диагонали ромба, если известно, что их длины
пропорциональны числам 2 и 3, а площадь ромба равна 12 см2.
685*. Найдите площадь S параллелограмма, периметр которого
равен т, а точка пересечения диагоналей находится на
расстоянии t от каждой из его сторон.
50. Площадь треугольника
60 I Теорема. Площадь треугольника равна половине про-
I изведения его основания на высоту.
Дано: а — основание треугольника ABC, h — его высота
(рис. 298).
Доказать: SABC = ^.
180
Доказательство. Проведем
через вершины В и С прямые,
параллельные сторонам АС и АВ. Получим
параллелограмм ABDC, который
состоит из двух треугольников — А АВС и
ABDC. Диагональ параллелограмма
делит его на два конгруэнтных
треугольника, и поэтому площадь каждого из
этих треугольников равна половине
площади параллелограмма ABDC. Так как
J ABDC
ah, то
S
ABC
ah
2*
Формулу для вычисления площади
треугольника можно прочитать иначе:
площадь треугольника равна
произведению его средней линии на высоту.
Следствие. Площадь
прямоугольного треугольника равна половине
произведения его катетов.
Задача. Построить прямоугольник, равновеликий
данному треугольнику и имеющий с ним общее основание.
Решение. Пусть дан треугольник АВС (рис. 299). Его
площадь равна половине произведения основания на высоту,
или, иначе, произведению основания на половину высоты. А
площадь прямоугольника равна произведению его основания на
высоту. Значит, если взять прямоугольник с основанием,
равным основанию треугольника, и с высотой, равной половине
высоты треугольника, то он и будет равновелик треугольнику.
Отсюда ясно построение искомого прямоугольника (рис. 299).
Вопросы и задачи
686. Две стороны треугольника равны 18 см и 24 см. Высота,
проведенная к первой из них, равна 22 см. Вычислите площадь
треугольника и высоту, проведенную ко второй данной сто*
роне.
687. Вычислите площадь остроугольного треугольника, если его
высота, проведенная к основанию, равна 6 см, а проекции
боковых сторон на это основание равны 12 см и 4 см.
688. Какую фигуру образуют вершины равновеликих
треугольников, имеющих общее основание АВ?
18!
689. Как можно разрезать треугольник на
три части так, чтобы из них можно
было сложить прямоугольник,
имеющий то же основание, что и данный
треугольник?
690. Докажите, что диагонали
параллелограмма разбивают его на четыре
равновеликих треугольника»
Рис. 300 691. Постройте параллелограмм,
равновеликий данному треугольнику.
692*. Дайте несколько различных доказательств теоремы о площади
треугольника.
693. Найдите зависимость ллежду площадью S данного
треугольника и площадью S\ треугольника, отсеченного от него любой
из средних линий.
694*. Дан треугольник, площадь которого равна 6 см2. Стороны
его разделены пополам, и точки деления последовательно
соединены отрезками. Стороны получившегося треугольника
вновь разделены пополам, и также построен треугольник.
Вычислите площадь последнего треугольника.
695. Практическая работа. Вычислите площадь, занятую
школьным садом и огородом (рис. 300). Произведите
необходимые построения и измерения. Масштаб 1 : 5000.
696. Выведите формулу для вычисления площади
равнобедренного прямоугольного треугольника по его гипотенузе с.
697. Вычислите площадь четырехугольника, диагонали которого
взаимно перпендикулярны и равны 6 см и 8 см.
698*. Выпуклый четырехугольник ABCD называется дельтоидом,
если \АВ\ = \ВС\ и \AD\ = \DC\. Выведите формулу,
выражающую площадь дельтоида через его диагонали тип.
699. Треугольник и параллелограмм имеют равные основания и
высоты. Как относятся их площади?
700. Длины двух сторон треугольника равны 4 см и 3 см. Какой
может быть его площадь?
701*. Какой вид должен иметь треугольник со сторонами а и Ь,
чтобы его площадь была наибольшей? Вычислите площадь
такого треугольника.
702*. 1) Какой из всех параллелограммов с диагоналями, равными
4 см и 8 см, имеет наибольшую площадь? Вычислите ее.
2) Какой из всех параллелограммов со сторонами, равными
4 см и 8 см, имеет наибольшую площадь? Вычислите ее.
182
51. Площадь трапеции
61 | Теорема. Площадь трапеции
равна произведению полусуммы ее
оснований на высоту.
Дано: ABCD — трапеция, α и с — ее
основания, h — высота (рис. 301). А
Доказать: S
а +с
ABCD
h.
Доказательство. Проведя диагональ АС, получим
два треугольника. Примем за основание треугольника ABC
отрезок АВ, а за основание треугольника ACD — отрезок CD.
Высоты этих треугольников равны высоте трапеции h. Поэтому
ch
S --·
°ABC — о»
&ACD — "Г*
Тогда площадь трапеции (по второму свойству площадей)
равна:
с _а+сь о
о _ah ch%
°ABCD— 2 "Г 2>
'ABCD
Следствие. Площадь трапеции равна произведению
средней линии на высоту.
Вопросы и задачи
703. Вычислите площадь трапеции, основания которой 12 см и
16 см, а высота 15 см.
704. Вычислите площадь трапеции, большее основание которой
38 см, высота 14 см, а проекции боковых сторон на основание
равны высоте трапеции.
705. Докажите, что площадь трапеции, диагонали которой взаимно
перпендикулярны, равна половине произведения длин
диагоналей.
706. Диагонали трапеции взаимно перпендикулярны и равны 3,6 дм,
6 дм. Вычислите площадь этой трапеции.
707. Докажите, что прямая, проходящая через середину средней
линии трапеции и пересекающая основания, делит эту
трапецию на две равновеликие части.
708. Покажите, как можно разделить трапецию прямыми на η
равновеликих частей (п = 3; 4).
183
709. Вычислите площадь прямоугольной трапеции, основания
которой равны 2 см и 4 смг а один из углов 45°.
710. Вычислите площадь равнобедренной трапеции, основания
которой равны 5 см и 7 см, а один из углов при основании
равен 45°.
711. Вычислите площадь трапеции, основания которой равны 9 см
и 7 см, а одна из боковых сторон образует с основанием угол
в 30° и равна 8 см.
712*. Дана трапеция. Постройте равновеликие ей: 1)
параллелограмм (отличный от прямоугольника); 2) прямоугольник.
52. Площадь многоугольника
Чтобы вычислить площадь многоугольника, можно разбить
его на треугольники, не имеющие общих внутренних точек,
и найти сумму их площадей. Такое разбиение выпуклого
многоугольника можно осуществить,
проведя, например, диагонали из
одной его вершины (рис. 302, а). Иногда
удобно пользоваться другими
разбиениями (рис. 302, б, в).
δ)
Вопросы и задачи
713. Выполните необходимые измерения и
вычислите площади фигур,
изображенных на рисунке 303.
714. Практическая работа. 1)
Произведите необходимые построения и
измерения и вычислите площадь
участка земли, изображенного на плане
(рис. 304, а). 2) Пользуясь палеткой,
вычислите площадь озера (рис. 304, б).
Найдите ту же площадь приближенно,
заменив контур озера
многоугольником. 3) Вычислите площадь «живого
сечения реки» * (рис. 304, в).
* «Живое сечение реки» — вертикальное
сечение, плоскость которого перпендикулярна
берегам реки.
184
Рис. 303
715. Выполните необходимые построения
и измерения и по полученным данным
вычислите площадь четырехугольника
(рис. 305), если никакие построения и
измерения внутри этого
четырехугольника проводить нельзя.
716. Практическая работа.
Разметьте на местности участок земли,
имеющий форму многоугольника,
произведите необходимые измерения и
вычислите площадь этого участка.
717. Постройте треугольник, равновеликий
данному четырехугольнику.
Дополнительные задачи к главе IV
718. Существует ли треугольник, сумма
любых двух углов которого меньше
120°?
719. Постройте треугольник, если известны
его периметр, угол при основании и
высота, проведенная к этому
основанию.
720. Можно ли произвольный треугольник
разрезать на два остроугольных
треугольника?
721. Может ли треугольник иметь более
трех осей симметрии?
Масштаб 1:1000
а)
Масштаб 1:1000
δ)
Масштаб 1:i000
в)
Рис. 304
Рис. 305
185
722.
723.
724.
725.
Постройте треугольник по основанию а и высотам h\ и йг,
проведенным к боковым сторонам.
Сколько можно построить параллелограммов с вершинами
в трех данных точках?
Постройте трапецию по ее основаниям α и & и двум
диагоналям тип.
Постройте четырехугольник, если даны его стороны а, Ь, с, d
и диагональ Z.
726. Постройте четырехугольник, если даны
его диагонали тип, угол α между
ними и сторона а, лежащая против этого
угла.
727. Существует ли многоугольник, число
диагоналей которого: 1) в два раза
больше числа сторон; 2) в два раза
Рис. 306 меньше числа сторон; 3) в три раза
меньше числа сторон?
728. Укажите несколько условий,
достаточных для того, чтобы четырехугольник
являлся: 1) прямоугольником; 2)
трапецией.
729. Какой вид имеет четырехугольник,
если проекции его сторон на каждую
из диагоналей конгруэнтны?
730. Пользуясь данными, указанными на
рисунках (конгруэнтные отрезки
отмечены одинаковым числом черточек,
параллельные прямые отмечены
одинаково направленными стрелками),
докажите, что:
1)
2)
3)
Ш =1 (рис. 306);
\FC\ 2 '
\ВН\
\HF\
\CF\
\СВ\
\HF
I FC
_1
= 1 (рис 307);
(рис. 308).
731.
Рис. 308
Постройте квадрат: 1) по сумме
диагонали и стороны; 2) по разности
диагонали и стороны.
186
732. Постройте равновеликие: 1)
прямоугольники; 2) ромб и прямоугольник
(отличные от квадрата).
733. Покажите на чертеже, как можно
разрезать прямоугольник со
сторонами 6 см и 2 см на две части так,
чтобы из них можно было составить
прямоугольник со сторонами 3 см и
4 см.
734. Разрежьте квадрат на части, из кото»
рых можно составить квадратную
рамку.
735. Данную фигуру (рис. 309) разрежьте
на части так, чтобы из них можно было
составить квадратную рамку.
736. Каждая из сторон квадрата KLMN
разделена на два отрезка длиной а
и & и выполнены построения,
указанные на рисунке 310. Докажите, что
площадь заштрихованного квадрата
(рис. 310, а) равна сумме площадей
двух заштрихованных квадратов
(рис. 310, б).
737. Найдите площадь четырехугольника,
вершинами которого являются
середины сторон данного выпуклого
четырехугольника, имеющего площадь S.
738. 100 выпуклых четырехугольников
имеют общие середины сторон. Докажите,
что эти четырехугольники
равновелики.
739. Одна из сторон параллелограмма
равна а, другая Ъ. Какие значения
может принимать площадь S этого
параллелограмма?
740. Выведите формулу для вычисления
площади фигуры, изображенной на
рисунке 311, если известно, что (АВ) \\
II (DE) || (CF), \АВ\ = \DE\, \AF\ =
= \FE\ и (CF)±(AE).
Рис. 309
Μ,
V77/
УУУл
ι
Ш
к,
5)
Рис. 310
Л/,
187
741. Докажите, что площадь фигуры, изображенной на рисунке
312, равна | {\BD\ · \СК\ + \АЕ\ · \ОК\) (известно, что
(BD) || (АЕ) и (CUT)-_L (АЕ)).
742. Дано: ABCD — параллелограмм, Ε 6 [BD], (ТзГЬ) || (ВС),
(MN)\\(AB) (рис. 313).
Доказать: AKEN vxEMCL — параллелограммы; SAKEN=SEMCL.
743. Участок земли имеет форму параллелограмма. Покажите на
рисунке, как можно разбить его на два участка так, чтобы их
площади были пропорциональны числам 3, 4, а линия деления
была бы параллельна основанию.
744. Через вершину ромба проведите две прямые, делящие ромб
на три равновеликие части.
745.
746.
747.
748.
749.
Рис. 313
750.
Рис. 314
Через вершину параллелограмма
проведите прямые, разбивающие этот
параллелограмм на: 1) 4; 2) 5
равновеликих частей.
Постройте треугольник, равновеликий
данному параллелограмму.
Диагонали равнобедренной трапеции
ABCD ((AD) || (ВС)) пересекаются в
точке О. Докажите, что треугольники
АВО и CDO конгруэнтны.
От участка земли, имеющего форму
трапеции, нужно отделить
треугольный участок так, чтобы его площадь
была равна площади оставшейся
части. Как это можно сделать?
Участок земли, имеющий форму
трапеции, требуется разделить на четыре
равновеликие части, каждая из
которых должна быть трапецией. Как это
можно сделать?
Дано: ABCD — трапеция, |СЛГ| =
= \KD\, (KE)±.(AB) (рис. 314).
Доказать: 1) 8 Авк = ~S AB:D)
2) SABCD= \AB\ ■ \EK\.
Найдите множество вершин
параллелограммов, равновеликих данному
параллелограмму ABCD и имеющих
общее основание длины а.
188
Μ
Рис. 315
С
в
Рис. 316
Рис. 317
>в
в
А
752. Через данную точку проведите
прямую, рассекающую данный
параллелограмм на две равновеликие части.
753. Какие значения может принимать
площадь параллелограмма, если его
диагонали равны тип?
754. Какие значения может принимать
площадь ромба, если: 1) его сторона
равна а; 2) высота равна hi
755. Через точку пересечения двух
окружностей проведите прямую так, чтобы
отрезки, отсекаемые на этой прямой
окружностями, были конгруэнтны.
756. Найдите площадь фигуры, которая
является объединением
равностороннего треугольника, имеющего
площадь S, и его образа при повороте на
60° вокруг центра этого треугольника.
757. Площадь равнобедренного
треугольника равна S. Найдите площадь
фигуры, которая является пересечением
этого треугольника и его образа при
симметрии относительно оси,
параллельной основанию и делящей
высоту, проведенную к этому основанию,
в отношении 1 :2, считая от
основания.
758. Окружность касается трех сторон
треугольника ABC (рис. 315), \ВС\ = а,
\СА\ = Ь, \АВ\ = с. Выразите длины отрезков касательных
х, у, ζ через а, Ъ, с.
759. Внутри равностороннего треугольника взята точка М.
Докажите, что сумма расстояний от точки Μ до сторон
треугольника есть величина постоянная, не зависящая от положения
точки М.
760. Через точку Е, расположенную внутри угла ВАС, проведите
прямую так, чтобы она отсекала от угла ВАС треугольник
наименьшей площади.
761. Через точку Ε (рис. 316) проведите прямую так, чтобы она
имела общие точки с параллельными лучами ВА и CD и
отсекала бы фигуру наименьшей площади.
189
762. На сторонах АВ и АС треугольника ABC взяты такие точки
,. .. \АМ\ \AN\ , п \ВС\
Μ и /V, что -1 = L = #. Докажите, что отношение——
I АН I I AL· I | iWiV |
111
тоже равно ft, если k принимает значение: 1) —; 2) —; 3) —;
4) — (р и g — натуральные числа).
763. Докажите, что множество всех вершин прямоугольников,
имеющих общую диагональ, есть окружность, для которой
эта диагональ является диаметром.
764. Постройте окружность данного радиуса R, которая касается
данной прямой I и данной окружности (О, г).
765. Через данную точку Μ проведите прямую, которая
находится на данном расстоянии I: 1) от данной точки А; 2) от данной
окружности.
766. Отрезок данной длины движется так, что концы его скользят
по сторонам прямого угла. При каком положении этого
отрезка площадь отсекаемого им треугольника будет
наибольшей?
767. На рисунке 317 изображено шарнирное устройство: одна из
сторон параллелограмма CDMN — сторона CD — неподвижно
закреплена, а к стороне MN жестко прикреплена
горизонтальная планка АВ. Объясните, почему при всех возможных
положениях стороны NM планка АВ будет сохранять
горизонтальное положение.
768. Найдите множество середин отрезков данной длины а, концы
которых принадлежат сторонам данного прямого угла.
769. На бильярдном столе прямоугольной формы лежат два шара.
Укажите несколько направлений ударов, при которых первый
шар попадет во второй (положение шаров выберите
самостоятельно).
ГЛАВ
.ν
ВЕКТОРЫ
53. Композиция перемещений
1. Проведем на плоскости две взаимно
перпендикулярные прямые χ и у.
Отметим произвольную точку Μ
плоскости и построим ее образ Μι при
симметрии с осью χ (рис. 318). Затем
построим точку Μ2 — образ точки Μ4 при
симметрии с осью у. Точке Μ поставим
в соответствие точку Мг. Любой
другой точке плоскости поставим в
соответствие точку, полученную в
результате аналогичного построения. Таким
образом, последовательно выполняя
симметрии Sx и Sy9 получаем новое
отображение плоскости на себя. Что
это за отображение?
Обратимся к рисунку 318. Углы
1 и 2 симметричны относительно оси х,
а углы 3 и 4 — относительно оси у.
Поэтому 1 = 2, 3 = 4. Так как пря-
мые χ и у перпендикулярны, то 2+3 =
= 90°. Значит Л + *2 + 3 + 4 = 180°,
т. е. угол МОМг развернутый.
Следовательно, точки М, О и Μ2 лежат на
одной прямой.
Отрезки МО и MtO симметричны
относительно оси х> а отрезки ΜιΟ и
Рис. 318
191
МгО— относительно оси у. Поэтому \МО\ = \MtO\9 |М40| =
= \М20\ и, следовательно, |МО| = \М20\. Таким образом,
отрезок ММ2 делится точкой О пополам, т. е. точки Μ и М2
симметричны относительло точки О.
Итак, в результате последовательного выполнения осевых
симметрии Sx и Sy получаем повое отображение — центральную
симметрию ZQ.
Результат последовательного выполнения отображений
называют композицией этих отображений. Значит, композицией
двух осевых симметрии с перпендикулярными осями χ и у
является центральная симметрия с центром в точке пересечения
этих осей.
Композицию симметрии Sx и Sy записывают так: Sy о Sx.
Обратите внимание на порядок: отображение, которое
выполняется первым, пишется справа. Например, предложение
«композиция Sx и Sy есть Z0» записывают следующим образом:
£у ° &х = Ζ о·
2. Рассмотрим другой пример — композицию осевой
симметрии Sp и этой же осевой симметрии Sp. Найдем образ
произвольной точки Μ при композиции Sp о Sp. Для этого надо найти
точку Mi = Sp (Μ), а затем точку М2 = Sp (Mi). Точка М2
и будет образом точки Μ при композиции Sp о Sp (рис. 319).
Но Sp (Mi) = Μ, т. е. любая точка Μ при композиции
Sp о Sp отображается на себя. Следовательно, Sp о Sp = Ε
(Ε — тождественное отображение плоскости).
В рассмотренных случаях композиция перемещений
оказалась перемещением не случайно. Справедлива такая теорема:
62ι Ι Теорема. Композиция перемещения есть перемещение.
у Доказательство. Рассмотрим перемещения Fi и
F2. По определению перемещений и Fi9 и F2 отображают
плоскость на себя. Значит, и в резуль-
м φ Λ; тате их последовательного выполне-
/V ния (т. е. при композиции F2 о F{)
' \ образом плоскости является сама
ι | ρ эта плоскость. Поэтому остается до-
! | казать, что F2 о F{ сохраняет рас-
1 ! | стояния.
\ J j Пусть А и В — произвольные
\м точки плоскости. Обозначим их об-
I разы при перемещении Fi через Ai
Рис. 319 и Бь Образы точек Αι и В{ при
192
перемещении F2 обозначим через А2 и
В2. Тогда точки А2 и 52 — образы точек
А и В при композиции F2cFi.
При перемещении расстояния
сохраняются, поэтому | AijBiI = \AB\ и \А2В2\ =
= |ΑιΒι|. Следовательно, \А2В2\ = \АВ\,
т. е. композиция F2 ° F{ сохраняет
расстояния, ψ
3. Из доказанной теоремы следует,
что композиция параллельных
переносов есть перемещение. Выясним, каким
видом перемещений является эта
композиция.
Возьмем дзе произвольные точки Μ
и N. Построим их образы М2 и Ν2 при
композиции переносов Τ{ и Τλ (рис. 320)*
М{ = Τ, (Μ), Ni = rt (Ν)\ Μ, = Τ* (Mt), Ν, = Τ2 (NJ.
Тогда
Μ2 = (Γ2ο Γι) (Μ) и Ν2 = (7\ о 71,) (iV).
Рассматривая рисунок 320, можно заметить, что лучи ММ2
и NN2 сонапразлены, а расстояния | ММ21 и | NN2 | равны.
Поэтому можно предположить, что композицией
параллельных переносов 7\ и Т2 является перенос, отображающий точку
Μ на М2. Это предположение оказывается верным.
62о| Теорема. Композиция параллельных переносов есть па-
I раллелъный перенос.
ψ Доказательство. Рассмотрим произгольный луч h
плоскости. Пусть А4 = Τι (А) и h2 = T2 (hi) (рис. 321). Тогда
луч А2 — образ луча h при композиции Т2 о ΤΊ.
Так как при параллельных переносах каждый луч
отображается на сонаправленный ему луч, то
At ft b и А2 ff A4.
* Так как перенос можно задать указанием
произвольной точки А плоскости и ее образа В, то на
рисунке удобно задавать рассматриваемый перенос
направленным отрезком (стрелкой) АВ. Именно так
заданы переносы на рисунке 320. Понятно, что
перенос может быть задан направленным отрезком с
началом в любой точке плоскости.
Рис. 320
Рис. 321
193
jfr В силу транзитивности отношения со-
направленности лучей (п. 35) получаем,
Μ ^ ^77 "^М2 что Λ2 ft h. Итак, композиция
переносов Т2 о Т\ отображает каждый луч
плоскости на сонаправленный ему луч и по
теореме 62 является перемещением. Но перемещение,
обладающее таким свойством, есть параллельный перенос (см. п. 36).
Значит, композиция параллельных переносов есть
параллельный перенос, γ
Чтобы задать параллельный перенос Т2 ° ΤΊ, достаточно
указать образ произвольной точки Μ при этом переносе. Поэтому,
бзяв произвольную точку Μ плоскости и построив ее образ
М2 = (Т2 о Ti) (Μ), получим, что Т2 о ΤΊ — перенос,
отображающий точку Μ на М2 (рис. 322).
а
m
9
Вопросы и задачи
770. На рисунке 323 показано
построение образа L2
фигуры L при композиции
L
^ м\
а\
Рис. 323
'< 1
л/1
61
Рис. 324
h
• 3^
и S m (n _L m). 1) Разъясните,
как выполнено это
построение. 2) Назовите вид
перемещения, при котором
фигура L отображается на
фигуру L2.
771. Даны две параллельные
прямые /пили две точки
А и В. 1) Постройте точки
Al = Sm(A), A2 = Sn(Ai).
Б, = Sm (В), В2 = Stl (В{).
2) Каким перемещением
является композиция:
a) Sm о Sn; б) Sn о SJ
Указание. Сравните:
1) расстояния |ААг| и
|ЯВ2|; 2) направления
лучей АА2 и ВВ2.
772. На рисунках 324, 325, 326
показано построение об-
194
раза Ζ/2 фигуры
композиции двух
L при
осевых
ζ
X
Рис.
b
326
Ζ
симметрии Sa и Sh с
параллельными осями а и 6.
1) Разъясните, как
выполнено это построение. 2)
Назовите вид перемещения,
при котором фигура L
отображается на
фигуру Ь2.
773. Выполняется ли переместительный закон для композиции двух
симметрии с параллельными осями?
774. На рисунке 327 показано построение образа L2 фигуры L при
композиции двух центральных симметрии с различными
центрами Οι и 02. 1) Каким перемещением является композиция:
а) Ζοι ° Ζο2> б) Ζο2 ° ZoJ 2) Верно ли, что ZQ^ZQ=ZQ^ о Z^?
775°. Пусть Fi — произвольное перемещение, F2— перемещение,
обратное F\. Найдите композицию: 1) F\ о F2; 2) F2 oFj.
776°. Назовите перемещение, обратное: 1) осевой симметрии;
2) центральной симметрии; 3) повороту.
777. Задайте параллельные переносы Т\ и ЗГ2, композиция которых
является тождественным отображением плоскости на себя:
Т2 ό Τλ = Ε. .
778. Приведите примеры композиций трех перемещений, которые
являются тождественным отображением плоскости.
779. 1) Каким перемещением является композиция Z0° SQl если
Оба?
2) Верно ли, что Sa о ZQ = Z0 ° Sa{0 6 а)?
780. 1) Покажите, что квадрат ABCD (рис. 328) отображается на
себя при композициях поворота R с центром О на угол 90° по
рх
i
>',
Рис.
г А
327
I
•о,
Рис. 328
195
часовой стрелке и симметрии SQ;
поворота R и симметрии Sh.
Какими перемещениями являются эти
композиции?
2) Покажите, что равносторонний
треугольник ABC (рис. 329)
отображается на себя при композиции
перемещений Sn о Sm. Каким
перемещением является эта композиция?
Выполняется ли для этой композиции
переместительный закон?
781*. 1) Докажите, что композиция двух
центральных симметрии есть
параллельный перенос (рис. 330).
2) Докажите, что композиция двух
осевых симметрии Sx ° Sv с
пересекающимися осями есть поворот Я,
где центр поворота — точка О
пересечения осей симметрии, а
угол поворота α равен удвоенной
величине угла между осями χ и у
(рис. 331).
3) Докажите, что композиция двух
осевых симметрии Sx о Sy с
параллельными осями есть параллельный
перенос (рис. 332).
782. Скользящей симметрией
называется композиция осевой симметрии
и параллельного переноса в
направлении, параллельном оси
симметрии. Задайте скользящую
симметрию и постройте образ данного
треугольника ABC при этом
перемещении.
54ψ. Общий способ задания
перемещений
Задача. Даны два луча 0{АХ и 02А2.
Найти перемещение, которое
отображает луч ΟιΑι на луч 02А2.
Решение. Рассмотрим
параллельный перенос 7\
отображающий точку Oi на точку
02 (рис. 333). Пусть луч 02А'—
образ луча ΟιΑι при этом
переносе. Ясно, что существует
поворот R (на угол А202А' с
центром 02), отображающий
луч 02А' на луч 02А2.
Композиция Fi = R о Τ и является
искомым перемещением (см.
рис. 333, а).
Но существует и другое
перемещение, отображающее луч
OiA1 на луч 02А2. В самом
деле, осевая симметрия S с осью
02А2 отображает луч 02А2
на себя. Поэтому перемещение F2 = S о Fi9 отличное от
перемещения F\9 тоже является решением задачи (см. рис. 333, б).
Можно доказать, что других перемещений, отображающих
луч OiAi на луч 02А2, кроме этих двух, нет.
Пусть а! — полуплоскость с границей OtAi.
Рассмотренные два перемещения F{ и F2 отличаются друг от друга тем,
что они отображают полуплоскость а{ на разные полуплоскости
а2 и а2 с границей 02А2. Справедлива такая теорема:
63 I Для любой пары лучей 0\А{ и 02А2 и примыкающих к ним
I полуплоскостей^ и а2 существует единственное перемеще-
I кие, отображающее луч О\А{ на луч 02А2, а полуплоскость аг
I на полуплоскость се2.
Итак, перемещение полностью задается указанием образов
одной точки, лучом с началом в этой точке и примыкающей к
нему полуплоскости*.
55. Что такое вектор?
На этот вопрос нельзя дать очень простой ответ. Дело в
том, что в геометрии и в физике векторами называют весьма
различные вещи. Но у объектов, которые называют в школьной
геометрии и в физике векторами, есть много общего — это
объекты, которые можно задавать при помощи указания их
направления и абсолютной величины (модуля).
* В прилагаемой в конце учебника системе аксиом этот факт принимается
за аксиому.
Ϊ97
Рис. 334
F,
А
♦<rj
Рис. 335
1) Первым примером могут служить
направленные отрезка. На рисунке 334
изображено несколько таких отрезков с
общим началом. Каждый из них полностью
определяется указанием его направления
и его длины.
2) В физике сила, приложенная к
данной точке (рис. 335), тоже
полностью определяется своим направлением и
1—I модулем, измеряемым в ньютонах.
F, 1 с Так как в обоих этих случаях кроме
направления и модуля надо задавать на-
чальную точку (точку приложения силы),
то говорят, что направленные отрезки и
силы являются «приложенными» или
«закрепленными» векторами.
3) Примером «свободных» векторов
могут служить параллельные переносы, так
как каждый параллельный перенос
полностью определяется своим направлением
и общим расстоянием, на которое он перемещает любую точку
плоскости. Это расстояние и есть модуль переноса. (На
рисунке 336 все направленные отрезки задают один и тот же
параллельный перенос.)
▼ 3 физике примером свободного вектора может служить
скорость поступательного движения твердого тела.
На рисунке 337 изображен подъемный кран, движущийся
по рельсам прямолинейно. Все его точки имеют одну и ту же
Рис. 336
т^Л^шМ Ш\1
40м _С/
к//^^,.
С
Рис. 337
198
скорость. Изображением этой скорости можно считать любую
из стрелок, указанных на рисунке, независимо от начальных
точек (точек приложения) этих стрелок. Поэтому говорят,
что скорость всего крана при таком движении есть свободный
вектор.
Позднее вы познакомитесь в курсе физики и с другими
примерами векторов, или, как говорят, «векторных величин».у
56. Векторы и способы их задания
В соответствии со сказанным в предыдущем пункте
параллельные переносы в нашем курсе получают и другое название —
их называют векторами и обозначают строчными буквами со
стрелкой: а, Ь9 с, ..., х, ... Тождественное отображение
плоскости (параллельный перенос на нулевое расстояние) называют
нулевым вектором и обозначают 0.
Как уже говорилось, параллельные переносы (векторы)
удобно изображать с помощью направленных отрезков. Если
различные направленные отрезки АВ, CD, XY, ... (рис. 338)
задают один и тот же вектор, то пишут:
a=AB = CD==XY==...
Все это разные обозначения одного и того же вектора.
Точно так же О, АА, ВВ, ... — разные обозначения нулевого
вектора.
Рассмотрим пример. На рисунке 339 изображен
параллелограмм ABCD. Векторы АВ и DC равны, так как
направленные отрезки АВ и DC задают один и тот же параллельный,
перенос. Векторы ВС и DA не равны
щий В на С, не совпадает с переносом
А, так как их направления различны.
Расстояние \АВ\ называют длиной
вектора а = АВ и обозначают | АВ | или
—►
I а |. Направление, заданное лучом АВ,
называют направлением вектора АВ.
Нулевой вектор не имеет направления.
Векторы АВ и CD называют сона-
правленными, если сонаправлены
лучи АВ и CD (рис. 340). Если же
лучи АВ и CD противоположно направ- Рис. 338
перенос, отображаю-
отображающим D на
199
вш
η
Рис. 339
Рис. 340
Рис. 341
лены, то и векторы АВ, CD называют
противоположно направленными (рис. 341).
Ненулевые векторы а и Ъ называются
коллинеарными, если их направления
совпадают или противоположны.
Нулевой вектор считается коллинеарным
любому вектору.
Если известно одно из изображений
вектора а — направленный отрезок АВ
(рис. 342), то легко построить и любой
другой направленный отрезок, задающий
тот же вектор и имеющий заданное
начало X. Для этого по определению
параллельного переноса надо построить
луч ХМ, сонаправленный лучу АВ,
и отложить на нем отрезок XY длины
| АВ |. Направленный отрезок XY —
искомый. Построение направленного
отрезка XY, такого, что XY = а,
называют откладыванием вектора а от точки X·
Рис. 342
Вопросы и задачи
783. 1) Укажите способы задания вектора.
2) Заданы точки А, В, С, Μ и N.
Постройте образы этих точек при
параллельных переносах: a) MN; б) ΝΜ.
784. Запишите все переносы, которые вершину А
параллелограмма ABCD отображают на вершину этого же
параллелограмма.
785°. Какие из векторов, заданных на рисунке 343: 1) равны;
2) одинаково направлены; 3) противоположно направлены;
4) коллинеарны?
786. Сколько существует переносов, которые отображают: 1)
вершину параллелограмма ABCD на точку пересечения его
диагоналей; 2) точку пересечения диагоналей этого
параллелограмма на его вершину?
787. Сколько различных векторов задают упорядоченные пары,
составленные из вершин параллелограмма ABCD1
200
"Ι Η 1Ν1И111J Η1
1/И Μ/
Тал П7Т 7Ί /ί ι ι
И U HthfrH
rLL r г 11
III (pI 11 IgI УI 111 FB
Рис. 343
В С А
г\
Ώ А
а)
Рис. 344
/Г^
1
/
Ь)
7\
Ί
7
ζ?
788. Диагонали
параллелограмма ABCD пересекаются
в точке О. 1) Какие
упорядоченные пары,
составленные из точек А, В, С,
D и О, задают один и тот
же вектор? 2) Сколько
различных векторов
задаются упорядоченными
парами, составленными
из этих точек?
789. Перенос отображает
точку (0Г 0) на точку (—2, 2).
На какие точки
отображает этот перенос точ-
ки А(Ъ, 2), Б(-3, 2),
С(1, 1), D(5, 4), Е{\, -1),
F(-5, -4)?
790. Один и тот же или
различные векторы
определяют следующие
упорядоченные пары точек
координатной плоскости:
1) (2, 3), (3, 2) и (3, 2),
(2, 3); 2) (2, 3), (3, 2) и
(-2, 3), (-3, 2); 3) (2, 3),
(3, 2) и (0, 0), (1, -1)?
791. Задайте вектор а и
отметьте точки К, D, М. Отложите вектор а от каждой из этих
точек.
792. На рисунках 344, а и б изображены: 1) трапеция ABCD;
2) куб ABCDA\B\C\D\. Сколько различных векторов
задают упорядоченные пары точек, составленные из
вершин этих фигур?
793. Известно, что AB=CD и АфВ. Докажите, что: 1) (АВ) \\ {CD);
2) \АВ\ = \CD\.
794. От произвольно выбранной точки О плоскости отложите
векторы, противоположные векторам АВ, RS, PQ, EF и KL
(см. рис. 343).
795. Докажите, что если АВ = CD, то АС = BD.
201
\ллд/
АСЕ
Рис. 345
796*. Точки О, А и В различны. Докажите, что равенство О А = ВО
справедливо тогда и только тогда, когда точка О является
серединой отрезка АВ.
797*. На рисунке 345 изображена ломаная со звеньями равной
длины и прямыми углами между смежными звеньями.
Представьте себе, что эта ломаная простирается неограниченно
вправо и влево. Докажите, что такая фигура отображается
на себя при переносах BD и АЕ.
57. Противоположный вектор. Сумма векторов
При отображении, обратном параллельному переносу а
(рис. 346), все точки плоскости перемещаются в одном и том же
направлении, противоположном направлению переноса а, на
одно и то же расстояние. Это означает, что отображение,
обратное переносу, есть перенос, и поэтому
его тоже можно назвать вектором.
Пользуясь словом «вектор», говорят также, что
этот вектор противоположен вектору а, и
обозначают его —а. Например, вектор,
противоположный вектору АВ, есть
вектор В А:
—АВ = ВА.
Перенос с, являющийся композицией
переносов а и 6, называют также суммой
—► —► _^
векторов а и Ь. При этом вместо знака
композиции употребляют знак суммы и
пишут: с — а + Ь (вместо записи с =6 о а).
Например, сумма любого вектора а и
—►
противоположного ему вектора —а равна
нулевому вектору:
а + (—а) = 0.
В пункте 53 было показано, как
можно задать композицию данных перено-
Рис. 347
202
Μ Ι" |α ι /α
J Τ I Г
1 4J i 1
\s\M \\\/\\\νή\\\\\
Щ\ liN/f щ\\\ \И
Г If I ' π
1 Ы I I I Ы 1 m Ы 1 Ы Ι ι
Рис. 349
сов (рис. 347). Это правило мы можем теперь
сформулировать так: чтобы отложить сумму векторов а + Ъ от точки А,
достаточно отложить 1) от точки А вектор а = АВ и 2) от
точки В вектор Ъ = ВС. Тогда а + Ъ = АС
Записав векторы а и b иначе (α = АВ, Ъ = .ВС), получаем
правило треугольника, по которому находится сумма
векторов:
АВ + БС = АС.
Вопросы и задачи
798°. На рисунке 348 укажите векторы а-\-Ъ, с -\- d, Ъ -\- с, f -\- ft.
799. Суммой каких двух векторов, заданных на рисунке 348, явля-
—► —► —>~
ется вектор /, вектор с, вектор AD1
—► —► —► -ν
800. Даны векторы а и Ъ (рис. 349). Найдите вектор а + Ь.
801. Диагонали параллелограмма ABCD пересекаются в точке О.
Верны ли равенства: 1) АВ + аЬ = АС; 2) AB + BD = BC;
3) OC + OD = AO + BO; 4) АС + ВА=--СВ) 5)OD + OS=,
= ОА + ОС; 6) Б/Г + Α?= AD + ВС?
802. От произвольной точки О отложите векторы а и Ь (рис. 350).
Найдите суммы α -|- Ъ и 6 + α·
-Λ
α
b
о)
δ)
α
>/
г)
д)
ь
e)
Рис. 350
203
Рис. 351
352
Рис. 353
803. Даны три вектора а, Ъ, с (рис. 351).
Найдите суммы (а + Ь) + с и а + (Ъ + с).
804. Даны точки Л(-1, 2), В(2, 3), С(1, 1) и
D(3, 5). 1) От начала координат
отложите сумму векторов АВ и CD. 2)
Найдите суммы векторов: а) АВ + DC;
б) АВ + ВС; b)AC + BD; г) AD + ВС.
835. Радиусы ОА, ОВ и ОС окружности (О, г)
образуют углы в 120°. 1) От точки О
отложите векторы: χ = АО + ОВ, у =
= ОВ + ОС, 2 = ОС + ОА, ϊ=(ΟΑ +
+ ОВ) + ОС. 2) Выразите через г длины
векторов х, у, ζ и t.
G06. От точки О отложите векторы:
1) (ОА + ОВ) + ОС; 2) ОА + (ОВ + ОС)
(рис. 352).
S07. Найдите суммы векторов:
1) (ОВ + ОС); 2) (OD + OA);
3) {АС + DB) (рис. 353).
808. Задайте три вектора а, Ъ, с, таких, что:
1) (а + Ь) + с*=Ь; 2) (а +~Ь) + с = 0.
809. На рисунке 354 изображен квадрат;
(СЕ) || (BD). Докажите:
1) AC + CE = AD+BC;
2) (АО + OD) + DC = AC;
3) (ОА+ОС) + (ОВ + OD) = 0;
4) (АВ + ВС) + CD = АВ + СЕ;
5) АС + ВА = ВС.
58. Законы сложения векторов.
Вычитание векторов
Сочетательный закон:
Рис. 354
(а±Ъ) + с = а + (Ь-гс).
£ Доказательство. Отложим
вектор а от некоторой точки А: а = АВ. Век-
204
А (а+7)+Г=5+(ь+с)
Рис. 355
тор Ъ отложим от точки В, а
вектор с —от точки С (рис. 355): Ь = ВС,
с = CD. Пользуясь правилом
треугольника, получим:
а + ~Ъ =АС,
(а + Ь) + с = AC +CD = AD;
Ь + с = #D,
а+(Ь+сТ = АВ+^В= AD.
Следовательно,
(о + 6) + с = о + (6 + с). ■
—► —►
Так как суммы векторов (a -f- Ъ) +
-f- с и а + (6 + с) равны, то их
можно записывать без скобок:
(о + ft) + с = о + (6 + ί) = о +"6 + ~с.
642| Переместительный закон: а + Ъ = Ь + а.
Доказательство. Проведем доказательство для
—► —»·
случая неколлинеарных векторов а и Ъ (рис. 356). При
откладывании их от точки А (а = АВ, b=AD) получим, что
точки А, В и D не лежат на одной прямой. Построим четвертую
вершину С параллелограмма со сторонами АВ и AD. Имеем:
а = АВ = DC, Ъ = AD — ВС. По правилу треугольника
АВ + ВС = АС,
AD + DC = AC,
а + Ъ
Ь + о
откуда и следует, что
a + b = b + а*Ш
Доказанное свойство позволяет выполнять сложение двух
—► —►
неколлинеарных векторов α и & по «правилу параллелограмма»:
векторы а и Ъ откладываются от одной точки А (рис. 356) и
* В случае коллинеарных векторов требуется другое доказательство (см.
задачу 826).
205
строится параллелограмм со сторонами
АВ и AD. Тогда АС = а + ~Ь.
64з| Закон поглощения нулевого векто-
щра: а + О = а.
Доказательство. Отложим
—> *
вектор а от произвольной точки .А:
а = АБ. Тогда
а + 0 = АВ+ББ=АБ=о'. ■
Рассмотрим теперь вычитание векторов. Для любых двух
векторов а и Ъ существует вектор с, сумма которого с вектором
Ъ есть вектор а. Такой вектор называется разностью векторов
—► —►
а и Ъ.
-* -»· -► -►
Разность векторов α и & (обозначается а —Ъ) равна вектору
—► -*—►—►—► —►
а + (—Ь): а — Ь = а + (—&)·
Докажем это, опираясь на законы сложения векторов.
Применяя сочетательный закон, свойство противоположных
векторов ((—Ъ) + Ъ = 0) и закон поглощения нулевого
вектора, получим: (а + (—&)) + b = а + ((—Ъ) + Ь) = а + 0 = а. ■
Если векторы а и & отложены от одной точки О (рис. 357),
то для нахождения разности а — Ъ удобно пользоваться таким
правилом: О А — О В = В А.
Вопросы и задачи
—► -*■
810. Найдите сумму векторов α и & по правилу параллелограмма
и по правилу треугольника (рис. 349, а, б, д).
811. Докажите сочетательный закон сложения векторов, пользуясь
рисунком 358.
812*. Докажите, что для любых перемещений F\t F2 и F3 (F3 о р2) 0
о р, =F2 o(F2 о ρ,).
813. А, В, С, D и Ε — произвольные точки плоскости. 1) Выразите
через векторы а = АВ, Ь = ВС, с = CD, d = DE векторы
AD, BD и АС. 2) Выразите через α, Ъ, с, d векторы AD, BD,
ЁА, ВС, СЕ.
814. Докажите: 1) АВ + ВС + СА = 0; 2) АВ + ВС + DA = ~DC;
3) АВ + BD + ВС + DB = AC.
206
815. Найдите векторы: 1) AB + EF;
2) XY + PQ + RS;
3) ΟΤ+MN+Ts (см. рис. 343).
816. На рисунке 359 изображен
параллелограмм ABCD, (CE)\\{BD). Докажите:
1) лЬ + ВО = AD + BC;
2) ~АВ + ВС + CD = ~АВ + СЕ;
3) АС -|- BD + СВ = DB + СЕ + ВС.
817. На рисунке 360 заданы векторы
АВ = а, ВС = Ъ, CD = d. Выразите
векторы СА, DB и DA через а, Ъ и <2.
818. От произвольно выбранных точек
плоскости отложите векторы а — Ъ, β
Ъ — α и —а — Ъ (векторы а и Ъ заданы +
на рис. 349).
819. Задайте векторы α и & и найдите векто-^
ры: 1) а— Ъ; 2) Ъ — а; 3) —а—Ъ.
820. В каком случае выполняются равенства:
1) a—b=b — a; 2) 2—Ь = —а—Ы
821. Отметьте точки А, В, С, D и отложите
от точки О векторы: 1) АС — АВ;
2) ΑΌ - АС; 3) DB - DA;
4) АВ + СА+ВС; 5) AB — CD + CA
\
А
Рис. ЗСО
-7/
822
823.
Pic. 361
Выразите через векторы а, Ъ и d векторы: 1) DC; 2) DB;
3) СА; 4) ΒΑ (рис. 360).
Упростите выражение: 1) (АВ -f- AC) -f-
+(ВА + СВ); 2) AB-DB-CA-DA; 3) (АВ - ВС) -
-(CD + AD) + (C^- CD).
824*. От пристани к противоположному берегу реки отправляется
катер со скоростью 40 км/ч. Скорость течения реки 5 км/ч.
В каком направлении (покажите его на рисунке) следует
плыть катеру, чтобы приплыть в ближайшую точку
противоположного берега реки?
207
825. Груз спускается на парашюте со скоростью 3 м/с. Ветром
его относит в сторону со скоростью 2 м/с. Под каким углом
к вертикали будет спускаться груз при этих условиях? (Угол
найти построением.)
826**. Докажите: если векторы а и Ъ коллинеарны (рис. 361), то
а + b = b -\- а.
59. Умножение вектора на число
1. Зададим какой-либо вектор а и найдем сумму a -f- a -f- a
(рис. 362). Такую сумму естественно обозначить За и назвать
произведением вектора а на число 3. Длина вектора За равна
—►
длине вектора а, умноженной на число 3. Направление вектора
-*· —►
За совпадает с направлением вектора а.
—*·
Произведением вектора α на число —1 естественно назвать
—► —►
вектор —а, противоположный вектору а (рис. 363).
Произведением вектора α на отрицательное число, например на —3,
естественно считать такой вектор AM, длина которого равна
произведению |—3| ■ |ά|, а
направление противоположно направлению
вектора α (рис. 364).
Сформулируем общее определение.
Определение. Произведением
ненулевого вектора а на число χ φ О
называется вектор, длина которого
равна произведению длины вектора
а на модуль числа х9 а направление
совпадает с направлением вектора
а при χ > 0 и противоположно
направлению а при χ < 0.
Произведение вектора α на число
χ обозначается через ха (числовой
множитель пишется слева). По
определению
|.га| = |*| ■ |а|.
Рис. 362
Рис. 363
■δα
Μ
Рис. 364
208
Выше не рассмотрены случаи а = 0 и χ = 0. Для этих
случаев принимаются дополнительные определения:
χ · 0 = 0 для любого числа х,
0 · а = 0 для любого вектора а.
65|Теорема. Ненулевые векторы а и Ъ коллинеарны
тогда и только тогда, когда существует такое число х,
—V —*·
что Ъ = χα.
Доказательство. 1) Докажем сначала, что если су-
—► —► —► —►
ществует такое число х, что Ь = ха, то векторы α и Ъ
коллинеарны. Но это очевидно; по определению произведения вектора
—> —►
на число векторы а и ха имеют либо одинаковые (если χ > 0),
либо противоположные (если χ < 0) направления.
2) Докажем теперь обратное утверждение: если ненулевые
—► —►
векторы α и & коллинеарны, то существует число х, такое, что
—► —*■
Ъ = ха.
По определению коллинеарных векторов направления
векторов а и Ъ либо совпадают, либо противоположны. Если векто-
—►
ры а и Ъ направлены одинаково, то Ъ = ха при χ = '—-. Если
\а\
же направления векторов α и & противоположны, то Ь=ха
Ι&Ί _
при χ == Чг-. В
1*1
Вопросы и задачи
827. Задан вектор е = ОЕ. Найдите вектор а, если 1) а — 2е;
2) а = Ъе\ 3) а = 0,5<Г; 4) а = —3,5е[ 5) а*= Ае + Зе.
828. Дан вектор а. Найдите векторы 2а, —За, —1,5а, — а.
829. При каких значениях числа k векторы а (а ф 0) и &а: 1) со-
напразлены; 2) противоположно направлены; 3) равны?
830. При каких значениях числа k верны соотношения:
1) \kc\ < |с|; 2) |ftc| > |с|; 3) \kc\ = \с\, где <Г—
ненулевой вектор?
831. Задайте векторы а и Ъ и найдите векторы:
1) а— Ь; 2)а"&; 3) 2а-ЗЬ.
209
J" Ί Ы
A\ U
II 1 1 \ \ nil I N
1 Μ I U Ή
τ Ν Ν Ι
МП LM гч
ШИП ΓΝ
Мл Π
Рис. 365
832. Укажите, при каких значениях числа
k вектор kc-\-c (с φ 0): 1) имеет
то же направление, что и вектор с;
2) имеет направление, противополож-
—►
ное направлению вектора с; 3) равен
нулевому вектору.
833. На рисунке 365 задано несколько векторов. Какие из этих
векторов коллинеарны, какие неколлинеарны?
834. Даны точки О(0), А (0,5) и В(— 1). Найдите такое число х, что
1) ОА = хОВ; 2) ОБ = хОА; 3) ВА = хОА;
4) ВА = хВО; 5) ОВ = хВА; 6) АО = хВА.
835*. Верно ли утверждение: любые два вектора а и Ъ
коллинеарны тогда и только тогда, когда существует такое число х,
—*■ —►
что Ъ = ха\
—► —►
836*. Докажите, что если ненулевые векторы а и Ь коллинеарны,
то число χ такое, что Ъ = ха, единственно.
837*. Докажите, что три точки А, В и С принадлежат одной прямой
тогда и только тогда, когда существует число ft, для
которого АВ = kAC.
60. Законы умножения вектора на число
Определив сумму векторов и произведение вектора на
число, мы определили тем самым две операции — сложение
векторов (любым двум векторам соответствует третий вектор —
их сумма) и умножение вектора на число (любым вектору а и
числу χ соответствует вектор ха). Основные законы сложения
векторов были сформулированы выше (п. 57). Перечислим
теперь основные законы умножения вектора на число.
66
66
66
6641
(ху)а = х(уа) (сочетательный закон).
ха-{-уа= (х-\-у)а (первый распределительный закон).
ха + хЬ = х(а + Ь) (второй распределительный закон).
χ · 0 = 0 · α = б.
210
τφ а) Свойство 664 непосредственно вытекает из определения
умножения вектора на число.
б) Сочетательный закон. Предположим сначала, что
а Φ О, χ Φ О, у Φ 0. Чтобы доказать равенство векторов (ху) а
и χ (уа), достаточно доказать, что они имеют одну и ту же
длину и общее направление. Равенство их длин доказывается
простой выкладкой:
I(ху)а| = |ху| \а\ = |*| \у\ |а|,
\х (уа)\ = |*| \уа\ = |*| \у\ \а\.
Направления этих векторов также совпадают. В самом деле,
векторы (ху) а и χ (уа) имеют направление вектора а (если χ
и у имеют одинаковые знаки) или направление,
противоположное вектору а (если знаки χ и у различны).
Если же а = 0 (или χ = 0, или же у = 0), то
(ху) а = 0 и χ (уа) = 0.
в) Первый распределительный закон.
Если а = 0, то
*0 + уО = (Г + (ί = 0, (х + у) 0 = (Г.
Поэтому хО + уО = (х + у) 0 = 0.
Если д: = 0 или ι/ = 0, доказательство также очевидно.
Будем считать теперь, что а ф 0, χ Φ 0 и у Φ 0. Для то-
го чтобы доказать равенство векторов (д: + у) а и ха + ДО»
докажем, что и длины, и направления этих векторов совпадают.
Возможны два случая: 1) числа χ и у одного знака, 2) числа
χ и у имеют разные знаки. Докажем утверждение для
первого случая (второй разбирается аналогично).
Так как χ и у — одного знака, длина вектора (х + у) а
равна \х + у\ · \а\:
\(х +у)1\ = \х +у\ М. (1)
Найдем длину вектора ха + уа. Она равна (д: + у) \а\ (если
χ > 0 и у > 0) или (—χ — у) \а\ (если χ < 0 и у < 0).
Отсюда следует, что
\ха+уа\ = |х +у\ · |а|, (2)
211
Рис. 366
Сравнивая (1) и (2), получаем: длины векторов (ха + уа) и
(х + у) а равны.
Рассмотрим теперь направления векторов ха + уа и
(* + У) а- Если х > 0 и у > О, то направление вектора ха + ί/α
совпадает с направлением вектора а (рис. 366, а). Если же
л: < 0 и у < 0, то вектор ха + уа сонаправлен с вектором —а
(рис. 366, б). Но это же можно сказать и о векторе (х + у) а
(рис. 366, в, г). Значит, направления векторов ха + уа и
(х + у) а совпадают.
Так как выше мы показали, что и длины этих векторов оди-
—► —► —►
наковы, то векторы ха + уа и (х + у) а равны.
г) Второй распределительный закон имеет очень большое
значение: на нем основано все изложение следующей главы,
посвященной подобию фигур. Для доказательства рассмотрим
несколько случаев.
1-й случай, х — натуральное число.
По определению произведения вектора на число и
определению суммы векторов имеем:
ха + хЪ = (α + α + - + Q) + (Ь + Ь + - + &)-
х раз х раз
Применяя сочетательный и переместительный законы сложения
векторов, получим:
ха + хЪ = (а +1) + (а + Ъ) + ... + (а +-~Ь) = х (а + Ь).
х раз
2-й случай, х = —, где η — натуральное число.
η
Так как распределительный закон для натурального х и
сочетательный закон умножения уже доказаны, мы можем
написать:
212
η Ι— α + — ~b\ = nl— a) + n(1-l)) = ~a-\-~b.
Но равенство
n—a-\- — b) = a-\-b
\ га ra J
и означает, что векторы — a -j fr и — (а + Ь) совпадают.
га га га
1 "*" 1 "*" 1 ~*" -**
Следовательно, — а Н & = — (α + Ъ).
η η η
3-й случай, χ — любое рациональное неотрицательное число:
т _ __
х = —, где m и я — натуральные числа, или χ = 0. Поль-
зуясь тем, что при л: = m и я; = — закон верен, получим:
га
χα + xb = т (—а) + т(—b) = т(— а н— & ι =
= т — (а +Ъ) = — (а + 6).
га га
При χ = 0 имеем:
0а + 0Ь -0+0-0-0 (а +"&).
4-й случай, χ — рациональное отрицательное число.
Заметим вначале, что произведение (—1) · а есть не что
иное, как вектор—а, противоположный вектору а. Легко
проверить, что (—а) +(—Ь) есть вектор, противоположный век-
—► —*>
тору а + b (проверьте!). Поэтому
(-1) а + (-1) Ь = -Са + Ъ) - (-1) (а + Ь).
Если —д: — любое рациональное отрицательное число, то
χ = (—1) | л: |, и, пользуясь доказанным выше, см. иункт 3, по-
лучаем: ха + xb = (—1) \х\ - а + (—1) \х\ · b = (—1) X
х(\х\а+\х\Ъ) =(-1) \х\(а + Ь) - χ (а + Ъ).
Распределительный закон верен и в случае действительного
числового множителя, не являющегося рациональным. Не
владея теорией таких чисел, вы не можете это доказ&яъ. Но
наглядный смысл этого утверждения прост. Любое действительное
число χ с любой заданной точностью может быть заменено
приближенным рациональным числом х0. Для х0 равенство
х0~а + х0 Ъ = х0 (a + ~S)
доказано. Естественно, что равенство, «приближенно верное»
при любой степени приближения, верно и для х.у
213
Вопросы и задачи
838. Какие законы действий над векторами выражаются
равенствами:
1) Ь + 0 = Ь; 2) с + d = d + с]
3) (c + d)+~b = c + (d + b);
4) Ос = kO; 5) Ос = 0; 6) (st)6 = s (tb); 7) sa + ta = {s + t) a;
8) sb + seT= s (b + c)?
839. Упростите выражения (назовите законы действий над
векторами, которые при этом вы применяете):
1) За + (-6) - 2а + 36; 2) -2 (2,5а + 0 -~6) + 3 ·~0 + 5а;
3) 3 (5а -f 26) + 4 (—За + 6);
4) ^ ((£ - 26) + 5а) - |(6а - 96).
61. Координаты вектора
Вектор, длина которого принята за единицу измерения длин,
—► —►
называют единичным. Обозначим через i и у единичные векторы,
отложенные от точки О в положительных направлениях на осях
χ и у прямоугольной системы координат (рис. 367). Рассмотрим
произвольный вектор с = ОС. Проведем через точку С прямые
СС к и ССу> параллельные соответственно осям у и х. Векторы
ОС к = сх и i, а также ОСу = су и у коллинеарны.
Следовательно, по теореме 65 существуют такие числа сх и су> что сх
и с
cxi
V·
По правилу параллелограмма имеем: ОС = сх + су.
Значит, с = cxi + cy у.
Если вектор с представлен в виде
cxi + cyj9 TO говорят, что вектор с
разложен по векторам inj. Векторы сх=
У\
с,
1
Ту
7
0
i
с/
1 у/
' Гл
1
ffl
£*
Л
<М и с„
cv у называются
составляло. 367
ющими вектора с по осям л: и ι/.
Коэффициенты сх и су разложения вектора
с по единичным векторам £ и у называ-
214
ются координатами вектора Ί в данной системе координат*.
Задача. Доказать: 1) каждая координата суммы
векторов а и Ъ равна сумме соответствующих координат этих
векторов', 2) каждая координата произведения вектора а на число
k равна произведению соответствующей координаты этого
вектора на число k.
Τ Доказательство. Пусть
α =aj + ау7, Ъ = bj + bj.
Пользуясь законами сложения векторов и умножения
вектора на число, получим:
а +1 = (a J + ау7) + (bj + Ьу1) =
= (ах + ЬХ)1 + (ау +Ьу)~].
—► —►
Значит, координаты вектора а + Ь равны ах + Ьх и ау-\-Ъу,
что и требовалось доказать.
Легко доказать и второе предложение:
k (a J + a J) = (kax) I + (kav) £ ψ
Вопросы и задачи
840. Разложите по векторам в\ и в2 векторы (рис. 368): ОА, ОВ,
ОС, ОА + ОВ, ОВ + ОС, ОС + ОА, ОА+ОВ + ОС.
841. На координатной плоскости даны
точки А(1, 2), В (5, 6), С (7, 8) и
Ζ)(5, 12). 1) Разложите векторы АВ и
CD по единичным векторам i и /.
2) Найдите координаты векторов АВ
и CD. Указание. Задачу
рекомендуется решать на клетчатой бумаге.
842. На координатной плоскости даны
точки А (6, 2), В (2, 5) и С (10, 11). По-
У\
5
Ц-
3
2
1
^
ό
\
\
5
Р]
1 2
ИС.
А
368
В
С
5 i
* χ
* Обратите внимание: обозначения составляющих сх и су вектора с по осям
координат отличаются от обозначений соответствующих координат вектора с
только стрелками (составляющая вектора — вектор, а координата — число).
Заметим также, что числа сх и су — уже известные вам координаты точки О
215
ία
к!
с ζ
Рис. 369
Рис. 370
стройте составляющие векторов АВ и
ВС по осям χ и ι/.
843. Может ли: 1) составляющая
ненулевого вектора равняться 0; 2) обе
составляющие ненулевого вектора
равняться 0?
844. а = Зе, Ъ = —2£. Запишите в виде
хе векторь! За, 5Ь, а + 6, 2а + 3&.
845. На одной из сторон угла отложены
векторы О А = а, АВ = 2а. Через точ-
ма A v\ В проведены две
параллельные прямые, пересекающие вторую
сторону угла в точках С и D (рис. 369).
Известно, что ОС = Ь. 1) Выразите
через вектор Ь векторы CD и OD.
2) Выразите через векторы α и Ъ
векторы ас, я5, ad и са.
846. Дано: |АМ| = |МБ|, |МЕ| = \ЕС\9
(МН) || (AF) (рис. 370).
Доказать: ВН = HF = FC.
847. Разложите по векторам АВ = а и
AD = b векторы AM, ΜΗ, AF
(рис. 371), если \АН\ = \HD\,
\BF\ = \МС\ =- \ВС\.
С84С*.Дано: \AD\ = \DC\, \BE\ = \ED\
(рис. 372). Доказать: \ВС\ = ЗВМ.
849*. Дано ABCD — параллелограмм,
|ОЯ| = \HD\ (рис. 373). Доказать:
CF = 2FD.
850. Разложите по векторам а \л Ь векторы
BD, АС, ВН, АН, AF (см. рис. 373),
где а = АВ, Ь = AD.
Рис. 373
216
Дополнительные задачи к главе V
851. Упростите выражение: 1) АВ + ВМ + МК; 2) (АВ + MB)+
+ ВС + ОМ; 3) МВ + АС + ВМ; 4) —ОА-ОС + ОВ — СО.
852. На плоскости даны точки Μ и N. Докажите, что сумма
ΜΝ + MX + XN не зависит от выбора точки X.
853. Докажите, что для любых векторов χ и у:
2) ||*|-Μ|<|*-ίΓ|<|*|-|ί/Ί·
854. Даны векторы х, у, г. Отложите от данной точки векторы:
1) х + у-г; 2)±(х — у) + ±{у — г)— -х-,
3) (х + У) - 4(у + г) + у; 4) 5(х-^у) + 2(у - 2х) +1;
5) 3 (х + 2у) - 2 (2 + Зу) - 2 (ж + у).
855. Решите уравнения относительно вектора х: 1) а-\-5х = Xе,
2)^(α-2ί) + 3(χ-|α) = α; 3) 2(а + ±х) - 3(& - ί) =
= α— &.
856. Докажите, что если АС = 2АВ, то точка В — середина
отрезка АС.
857. Дан параллелограмм ABCD, точка О — его центр. Докажите,
что РА+РВ+^РС + рЬ = 4Р0, где Р — произвольная
точка плоскости.
858. Какой вид имеет четырехугольник ABCD, если известно, что:
1) AD = ВС; 2) векторы AD и ВС коллинеарны?
859. Точка Μ — середина отрезка АВ, О — произвольная точка
плоскости. Докажите, что ОМ = — (ОА + ОВ).
860. 1) Точка Μ принадлежит отрезку АВ, \АМ\ : \МВ\ =2:1.
Докажите, что ОМ = —ОА -\- —ОВ (О — произвольная точка
3 3
плоскости).
2) Докажите с помощью векторов теорему: медианы
треугольника пересекаются в одной точке, причем точка
пересечения делит каждую медиану в отношении 2:1, считая от
вершины.
217
861. Докажите с помощью векторов теорему о средней линии
треугольника.
862. Отложите от точки (1, 0) вектор а, если известны его коорди-
наты: 1) (2, 4); 2) (3, -4); 3) (-2, -3); 4) (-4, 2).
863. В координатной плоскости XOY задайте векторы а и Ь.
1) Найдите составляющие этих векторов по осям координат.
2) Найдите составляющие векторов а-\-Ъ и а — & по осям
координат. 3) Докажите, что составляющая суммы (разности)
векторов равна сумме (разности) соответствующих
составляющих этих векторов по той же оси.
864. Докажите единственность разложения векторов по двум не-
коллинеарным векторам в\ и £2.
865. Точки А и В симметричны относительно точки О. Докажите,
что MB = 2МО — ΜΑ, где Μ—произвольная точка
плоскости.
866. Докажите с помощью векторов, что Ζ 0 ° ZQ = 2О2О1.
867. Докажите, что отрезок АВ — множество таких точек X
плоскости, что ОХ = kOA + (1 — k) OB, где 0 ^ k ^ 1 (О —
произвольная точка плоскости).
868. 1) Докажите, что прямая АВ — множество таких точек
X плоскости, что ОХ= kOA + (\ — k)OB, где fc 6 R, а О —
произвольная точка плоскости.
2) Докажите, что луч АВ состоит из таких точек X плоскости,
что ОХ = kOB + (1 — k)OA, где k > 0.
869. Фигура L состоит из всех точек координатной плоскости,
имеющих координаты (т, п), где т и η — целые числа.
Докажите, что перенос а отображает фигуру L на себя тогда и
только тогда, когда α = &ιί + &27, где k\ и &2—целые числа.
ГЛАВА
ПОДОБИЕ
§ 1. Подобие и гомотетия
62. Подобные фигуры
К понятию конгруэнтности фигур мы
гфишли, рассматривая предметы
одинаковой формы и размеров. Однако
часто встречаются предметы
одинаковой формы, но разных размеров.
Таковы корабль и его модель, карты,
выполненные в разных масштабах
(рис. 374, 375), фотоснимки,
напечатанные с одного негатива при разных
увеличениях, и т. п. Все это примеры
подобных фигур.
Рассмотрим еще один пример. На
рисунках 376 и 377 изображены два
треугольника — ААВС и AAiBiC{.
Отношение длин сторон второго
треугольника к длинам соответствующих
сторон первого равно двум:
\AibL = I Б»с11 = l АЛ l = 2
\АВ\ \ВС\ \АС\
Мы увидим вскоре, что существует
отображение первого треугольника на
второй, при котором любые точки X
и Υ треугольника ABC (а не только
его вершины) отображаются на такие
точки Xi и Yu что
\XiYi\ = 2 \XY\.
219
35 J4- 35 36
Рис. 374
В этом случае говорят, что при таком отображении расстояния
изменяются в одном и том же отношении k = 2, а
треугольник ΑιΒχΟι подобен треугольнику ABC, причем коэффициент
подобия равен двум.
Определение. Фигура 14 подобна данной фигуре L, если
L можно отобразить на нее так, что при этом расстояния
изменяются в одном и том же отношении к.
Это число k называют коэффициентом подобия.
Если фигура L2 подобна фигуре Lu то пишут L2 °^ L{ или
(когда хотят указать коэффициент подобия k) L2 ^ £ι·
2
Например, запись ΑΑχΒχΟι со дАБС означает, что
треугольник ABC можно отобразить на треугольник AtBfii так,
что IXiYil =2 \XY\, где Х{ и У4 — образы произвольных
точек X и Υ треугольника ABC (см. рис. 376 и 377).
Из определения подобных фигур сразу следует, что
конгруэнтные фигуры подобны (коэффициент подобия равен
единице). Рассмотрим другие свойства отношения подобия
фигур.
1) (Рефлексивность.) Каждая фигура подобна себе
(коэффициент подобия равен единице).
220
Л 34 55 36
Л J4 35 36
Рис. 375
2) (Симметричность.) Если фигура L2 подобна фигуре 1^ с
коэффициентом подобия k, то фигура Li подобна L2 с
коэффициентом —:
к k
L2 сч) Lx =ф- Lx сч) L2.
ψ Доказательство. Так как фигура L2 подобна
фигуре Lu то существует такое отображение / фигуры L4 на фигуру
Z2» что если X и Υ — произвольные две точки фигуры i4, a
точки Xt и Yi — их образы, то |ΧΊΥι| = k \XY\. Расстояние
I X\Y\ I не равно нулю, так как | ΧΥ\ Φ О и k Φ 0.
Следовательно, Xt Φ Yu т. е. любые две точки фигуры Ζ,4 при отображении /
переходят в различные точки фигуры L2. Поэтому отображение /
обратимо. При обратном ему отображении расстояния
изменяются в — раз. В самом деле, если |/ (X) f (Y)\ = k Ι-ΧΤΊ, то
k
\XY\= i \f(X)f(Y)\. Τ
Рис. 377
221
3) (Транзитивность.) Если фигура Li подобна фигуре L
с коэффициентом ku а фигура L2 подобна фигуре L{ с
коэффициентом ft2, то фигура L2 подобна фигуре L с коэффициентом
k = kik2:
kt kt ktk2
(Lx oo L, L2 cxd ^i) => L2 oo L.
У Доказательство. Пусть А и В — две произвольные
точки фигуры L. Так как Lx со L> то существует отображение
/ι фигуры L на фигуру Lu такое, что
Ι-ΑιΒιΙ = fti 1-АЯ I
(Αι и В ι — образы точек А и В при отображении Л)·
Так как L2 со Li9 то существует такое отображение f2
фигуры L{ на фигуру L2, что
\А2В2\ = ftaliliBil
(А2 и В2 — образы точек At и Б4 при отображении /2).
Рассмотрим композицию f2 и ft — отображение /2 ° /ι· При
этом отображении фигура L отображается на фигуру L2. Кроме
того,
\А2В2\ = k2 I-A1B1I = ft2 (ft ι 1-АЯ I) = ft2fti | АЯ|.
Значит, фигура i2 подобна фигуре Ζ, причем коэффициент
подобия равен h\k2. γ
Итак,
£ 7 I отношение подобия фигур рефлексивно, симметрично и тран-
I зитивно.
Вопросы и задачи
870°. Приведите примеры подобных фигур.
871°. Подобны ли любые две конгруэнтные фигуры?
872. 1) Конгруэнтны ли любые две подобные фигуры? При каком
условии подобные фигуры конгруэнтны?
2) Постройте какие-нибудь две подобные, но не
конгруэнтные фигуры.
k k
873. О двух фигурах L\ и L2 известно, что L\ 00 L2 и L<i 00 L\.
Можно ли по этим данным найти значение ft?
874. 1) План одного и того же земельного участка начерчен в
двух видах: первый план имеет масштаб 1 : 100, а второй —
222
1 : 1 000. Чему равны коэффициенты подобия этих планов?
2) Макет плотины выполнен в — натуральной величины.
Затем с этого макета сделали второй, уменьшив его размеры
в четыре раза. Каков коэффициент подобия плотины и
второго макета плотины?
875. 1) Расстояние между Москвой и Ленинградом по железной
дороге равно приблизительно 650 км. Какой масштаб надо
выбрать, чтобы изображение железной дороги поместилось
на листе тетради?
2) Найдите расстояние между Джанкоем и Севастополем,
Севастополем и Симферополем (см. рис. 374), если
масштаб равен 1 : 5 000 000.
876. Дана фигура, состоящая из трех точек А, В и С, не лежащих
на одной прямой. Постройте фигуру, подобную данной, с
коэффициентом подобия, равным: 1) 3; 2) — .
Ζ77. Зададим следующее отображение прямой а на прямую Ъ\
каждой точке Ρ (х) прямой а поставим в соответствие
точку P\(kx) прямой Ъ (k — постоянное число). Докажите, что
при этом отображении расстояния между точками
изменяются в отношении \k\.
878. Известно, что при отображении отрезка АВ на отрезок А\В\
расстояния изменяются в одном и том же отношении 3.
Постройте образ точки X отрезка АВ при этом отображении.
879*. Докажите: окружности (О, г) и (О, 2г) подобны с
коэффициентом 2. Указание. Поставьте в соответствие каждой
точке X окружности (О, г) точку Х\ окружности (О, 2г), такую,
что точки О, X и Х\ лежат на одном луче с началом О.
880*. Докажите подобие любых двух: 1) треугольников; 2)
квадратов, если отношение их сторон равно двум.
881. Любая прямая подобна сама себе с любым коэффициентом
подобия k > 0. Укажите другие фигуры, обладающие этим
свойством.
63. Гомотетия
В предыдущем пункте было дано определение подобных
фигур. Рассмотрим теперь один из способов построения таких
фигур. Как, например, построить многоугольник, подобный
данному многоугольнику ABCDE с коэффициентом подобия
к = 2?
223
Возьмем произвольную точку О (рис. 378) и отложим от нее
векторы OAi = 20А, ОВ{ = 20В и т. д. Многоугольник
AxBiCiDiEu как вы убедитесь в дальнейшем, и будет искомым.
При этом построении мы воспользовались отображением
X -> Хи при котором каждая вершина многоугольника
отображалась на определенную точку плоскости по указанному
правилу.
Если каждой точке X плоскости (а не только точкам
многоугольника ABCDE) поставить в соответствие такую точку Хи
что OXi = 20Х, то получим отображение плоскости на себя.
На рисунках 379—381 приведены примеры отображений
плоскости на себя, при которых каждая точка X плоскости
отображается на такую точку Хи что ΟΧ ι — ЮХ (k = 3,
k = I, k = —2).
2
Задача построения фигуры, подобной данной, привела ι;
новому отображению плоскости на себя, которое называют
гомотетией.
Определение. Гомотетией с центром О и коэффициентом
к Φ О называется отображение плоскости на себя, при котором
образом произвольной точки X является такая точка Х19 что
όχι = kox.
Гомотетию g центром О и коэффициентом k обозначают Н(
224
Рис. 378
Рис. 379
Рис. 380 Рис. 381
Говоря о гомотетиях с каким-либо определенным центром,
букву О в обозначении опускают. Если речь идет о какой-
либо одной гомотетии, ее обозначают просто буквой Н.
Отметим два частных случая. При гомотетии с
коэффициентом 1 каждая точка отображается на себя. Значит,
тождественное отображение может рассматриваться как гомотетия с
любым центром и коэффициентом k = 1.
При гомотетии с центром О и коэффициентом — 1* каждая
точка X отображается на точку Хи для которой (λΧΊ = —ОХ9
т. е. на точку, центрально-симметричную точке X. Значит,
гомотетия с коэффициентом —1 есть центральная симметрия
но1 = ζο-
По определению гомотетии с центром О и коэффициентом k
точка О отображается на такую точку Οί9 что ΟΟι = ЮО — 0.
Значит, Oi = О, т. е. при гомотетии ее центр отображается
на себя.
* Обратите внимание на то, что коэффициент гомотетии может быть и
отрицательным числом, в то время как коэффициент подобия фигур — число
положительное.
225
х,=н*Ю
Xi = Hn(X)
Рис. 382 Рис. 383
Непосредственно из определения следует также, что если
к > О, то точки X и Χι = Η (Χ) лежат на прямой ОХ по
одну сторону от центра гомотетии (при k > О векторы ОХ
и OXi = ЮХ сонаправлены, рис. 382).
Если k < 0, то точки X и -ΧΊ = Η (Χ) лежат на прямой
ОХ по разные стороны от центра гомотетии (при k < 0
векторы ОХ и OXi = k OX противоположно направлены,
рис. 383).
68|Теорема. Отображение, обратное гомотетии с
коэффициентом k, есть гомотетия с тем же центром и коэффициен-
1
том —.
k
Доказательство. Пусть
Я* (X) = Xim
По определению гомотетии
OXt - k OX.
Из этого равенства следует:
ОХ = - ОХ1У
а это означает, что
X = Н}(Х,).П
Из теоремы 68 следует: если фигура Ζ ι гомотетична фигуре L
с коэффициентом k (т. е. существует такая гомотетия Но, что
Но (L) = Li), то фигура L гомотетична фигуре Li с коэффици-
1
ентом —.
k
225
Вопросы и задачи
882°. Как построить точку, гомотетичную данной точке X, если
даны центр О и коэффициент k гомотетии?
883. Отметьте на плоскости точки О, А, В и С.
1) Постройте точки А\, В\ и С\ такие, что: а) ОА\ = ЗОА;
б) ОВ{ = —20В) в) ОСх =- ОС.
з
1 ι 1
2) Постройте точки А2 = Я03 (А), Б2 = Н03 (Б), С2 = Я03 (С).
884°. Найдите значение ft, при котором: 1) гомотетия Нк0 являет-
j_
ся перемещением; 2) Hq(X) = Н£ {X).
88$. Найдите коэффициенты &ι, 62, из, ^4, fes, если известно,
что А1 = Н^(А), Вх = Нк0<(В), Cx = Hkd(C), Dx = Hk0<(D),
Ex = Hk0*(E) (рис.384).
886. Известно, что фигура L\ — образ фигуры L при гомотетии
Н£. Можно ли получить фигуру L как образ фигуры Lx при
некоторой гомотетии? Найдите центр и коэффициент згой
гомотетии.
887. Как расположены точки А и А\ = Нк0 (А) относительно
центра гомотетии Н£ , если: 1) k > 0; 2) k < 0; 3) 0 < &<1;
4) fc> 1?
888. Укажите центры и коэффициенты гомотетий, обратных гомо~
j_
тетиям Н2А, Я^3, Яс2 , Нд1.
889. Постройте фигуру, гомотетичную: 1) данной окружности;
2) данному отрезку; 3) треугольнику; 4) четырехугольнику
(центр и коэффициент гомотетии выберите самостоятельно).
890*. Докажите, что любая гомотетия является обратимым
отображением плоскости на себя.
891*. Покажите, что композиция двух гомотетий Нк* и Нк с
общим центром есть гомотетия с тем же центром и
коэффициентом &1&2-
892**. Из результата задачи 891 вытекает,
что композиция гомотетий с общим
центром переместительна. Покажите
на примере, что, вообще говоря, для
гомотетий с произвольными
центрами это не так. Рис. 384
шпини
D,B<E..Cl0BAA1CDiA
ι I г il Ι Ι Ι ι ι Л
227
64. Свойства гомотетии
69ιΙ Гомотетичные фигуры подобны*.
Доказательство. Обозначим через Χι и Υι образы
произвольных точек X и Υ при гомотетии Hq. По определению
гомотетии ΟΧ ι = ЮХ> ΟΥ ι = kOY (рис. 385). Для любых трех
точек О, Xiy Yi
XXYX = ΟΥ\ — OXi.
Значит,
χ\γι = ΟΥ! — dx4 = ftdy — kox
k (ΟΥ — OX)-=kXY.
По определению умножения вектора на число | Χ{Υ\ | =
= |ft| |.ΧΎ|. Следовательно, при гомотетии с коэффициентом k
расстояния между точками изменяются в одном и том же
отношении \k\. А это и означает, что каждая фигура при гомотетии
отображается на подобную ей фигуру. ■
69
69
При гомотетии с положительным коэффициентом
каждый луч отображается на сонаправленный с ним луч
(рис. 386, а). При гомотетии с отрицательным
коэффициентом каждый луч отображается на противоположно
направленный с ним луч (рис. 386, б).
При гомотетии любая прямая отображается на
параллельную ей прямую, отрезок— на параллельный ему
отрезок, угол — на конгруэнтный ему угол.
* Отметим, что из этого свойства вытекает, что многоугольники А^В^С^О^Е^
и ABCDE, рассмотренные в пункте 62, действительно подобны.
Рис. 385
228
Эти свойства мы принимаем без доказательства.
694| Если три точки О, А и А\ принадлежат одной прямой,
I то существует единственная гомотетия с центром О,
I отображающая точку А на Αχ.
Доказательство. Для задания гомотетии
достаточно задать ее центр и коэффициент. По условию центр
известен — это точка О. Найдем коэффициент гомотетии с центром
О, отображающей точку А на А\.
По определению гомотетии О Αι = ЮА. Этим равенством
число k определяется однозначно. В самом деле, \k\ = ^.
Если О лежит между точками А и Аи то k = — —. Если же точ-
\ОА\
АЛ ГЛ L I О А. I
ки А и Αι принадлежат одному лучу с началом О, то k = ' и . ■
|<М|
Итак, для задания гомотетии достаточно указать ее центр,
произвольную точку А и ее образ А\. Теперь рассмотрим, как
строится образ произвольной точки плоскости при таком
способе задания гомотетии.
Пусть точка В — произвольная точка плоскости, не
принадлежащая прямой ОА (рис. 387, а). Проведем прямые ОБ и
АВ. Затем построим прямую ААМ, параллельную прямой АВ.
Точка Βι = (ΑιΜ) f| (OB) — образ точки В при гомотетии Н.
Действительно, образ точки В при гомотетии Η —
некоторая точка прямой ОВ (так как эта прямая при гомотетии Η
отображается на себя). Кроме того, прямая АВ отображается на
прямую, ей параллельную (свойство 633) и проходящую через
точку At (так как Η (А) = А{). Поэтому точка Η (В)
принадлежит и прямой ОВу и прямой ΑιΜ> т. е. Η (В) = Bim
α) δ)
Рис. 387
229
В случае, когда точка В принадлежит прямой ОА,
построение приведено на рисунке 387, б. (Сначала строится образ
точки С i (ОА).)
Вопросы и задачи
893°. Как изменяются (увеличиваются или уменьшаются)
расстояния между точками при гомотетии, если: 1) |fc|>1,
2) μ| <ΐ; з) μ| = ι?
894. Можно ли найти центр гомотетии, если известны: 1) только
одна пара соответствующих точек; 2) две пары
соответствующих точек, не лежащих на одной прямой?
895°. 1) В каких случаях расстояния между точками при гомотетии
не изменяются?
2) Сохраняется ли при гомотетии параллельность прямых?
896°. Каков коэффициент подобия фигур L\ и L, если L\
гомотетична L с коэффициентом гомотетии: 1) 2,5; 2) —3;
3) ml
897. Лучи ОА и 0\А\ гомотетичны. Каково взаимное
расположение прямых ОА и ΟιΑι? Где может находиться центр и каков
коэффициент гомотетии, отображающей луч ОА на луч 0\А\,
если эти лучи: 1) противоположно направлены; 2)
одинаково направлены?
898°. Могут ли быть гомотетичными: 1) две пересекающиеся
прямые; 2) два луча, лежащие на пересекающихся прямых;
3) два луча, не лежащие на одной прямой?
899. Верны ли предложения: 1) если фигуры подобны, то они
гомотетичны; 2) если фигура L конгруэнтна фигуре L\ и
фигура L\ гомотетична фигуре L2, то фигура L подобна
фигуре L2) 3) если фигура L гомотетична фигуре L\ и фигура L\
конгруэнтна фигуре L2, то фигура L подобна фигуре £г?
900. Гомотетичны ли фигуры L и L\ (рис. 388)? Если эти фигуры
гомотетичны, укажите центр и коэффициент гомотетии,
Г
I
I
""■J"·"
' i
/
Г7
I
I
I
и)
|
I
/\
>
г
I ! ' L
I !z >>
L^^l
Χ
ч
1 ' ι
! I
I
д)\
Г
6)
ί
ι
4
\
!
Ι
!
Ι
мм
j I
Ί ! ι
υ
ι
|
Ι ,'>)Ι
ι
I '
ι \L,
I
I' :
! 1
ι ι
1
!/
—1 s\\
N
\
ΖΛ
/
&
/
Рис. 388
230
отображающей L на L\. Если такой гомотетии не существует,
приведите доказательство.
901. Постройте центр гомотетии Η по данным точкам X и У,
X, = Н{Х) и У,=Д(У).
902*. Докажите: при гомотетии с положительным коэффициентом
каждый луч отображается на сонаправленный луч.
903**. Докажите, что композиция двух гомотетий есть либо
гомотетия, либо параллельный перенос.
65. Пропорциональные отрезки
Отрезки АВ и CD называются пропорциональными отрезкам ΑίΒι
и C\D{> если пропорциональны их длины:
\АВ\ =\AlBll
\cd\ KVM*
701 Теорема. Параллельные прямые, пересекающие сторо-
I ны угла, отсекают на них пропорциональные отрезки.
Дано: (ΑΑι) \\ (ВВ,) (рис. 389).
Доказать: '\ОА,\ : \ОА\ = \ОВ{\ : \ОВ\.
Доказательство. Рассмотрим гомотетию с
центром О, при которой точка А отображается на точку В. При этой
гомотетии прямая О Αι отображается на себя, а прямая AAi —
на параллельную ей прямую, проходящую через точку В, т. е.
на прямую ВВ{ (по условию (АА{) \\ (ВВО). Поэтому образ
точки Ai — точка В χ. Но при гомотетии с коэффициентом k
расстояния между точками изменяются в отношении \k\.
Значит,
\ОВ\ = \k\ · \ОА\ и \ОВА = \k\ · Ю-Ail,
откуда
\ОВ\ : \ОА\ = \ОВ{\ : \ОА,\ (1)
и
\ΟΑι\ : \ОА\ = \ΟΒι\ : \ОВ\. ■
Следствие 1. Если (ΑΑι) || (ΒΒι),
mo ΙΟ-Ail : \ОА\ = \АХВХ\ : \АВ\ (см.
рис. 389).
Доказательство. Из
равенства (1) следует:
I ОВг \ г =\ОВ\ г
\ОАх\ \ОА\ * Рис. 389
231
Отсюда
\ОВ{\ — \ОА1\ _ \ОВ\—\ОА\
\ОАг\ ~ \ОА\
| АХВХ | =\АВ\
\ОАг\ \ОА\'
Из последней пропорции получаем, что
\ΟΑι\ \Λ1Βί\ ш
\ОА\ \АВ\
Следствие 2. Прямая,
параллельная стороне треугольника и пересе-
Рис 390 кающая две другие его стороны, отсекает
от него треугольник, стороны которого
пропорциональны сторонам данного тре-
-1 / оплч \СА\ \СВ\ \АВ\
и угольника (рис. 390):' - = ■ ■ = J .
-£· 1 * \CD\ \CH\ \DH I
—£ 1 Задача. Даны отрезки, длины
которых а, Ъ, с. Построить отрезок длины х,
чтобы выполнялась пропорция а : Ъ =
= с : χ (такой отрезок называют
четвертым пропорциональным к трем данным).
Решение. Для построения
искомого отрезка на сторонах угла (рис. 391)
отложим отрезки ОА, ОВ и ОС такие,
Рис. 391 что \ОА\ = а, \ОВ\ = Ъ, \ОС\ = с.
Через точку В проведем прямую ВН
параллельно прямой АС. Получим отрезок ОХ, отсекаемый прямой
ВН на луче ОС. Отрезок ОХ искомый (докажите это).
Вопросы и задачи
904. Даны два отрезка: \АС\ = 6 см и \BD\ = 12 см. 1) Найдите
отношение длин этих отрезков. 2) Изменится ли отношение
длин взятых отрезков, если длины их будут выражены в
дециметрах (в миллиметрах)?
905. Данный отрезок АВ разделите в данном отношении т : п.
Рассмотрите случаи: 1) т и η заданы отрезками; 2) т и η
заданы числами, например: т = 5, η = 3.
I AM I 1
906. Точка Μ делит отрезок АВ в отношении ——-= —. 1) Най-
I AM I I ВМ I _% Л
дите отношения -и- . 2) Вычислите длины отрезков
AM и MB, если длина отрезка АВ равна 9 см.
232
907. Отрезок разделен на две части в
отношении 3:8. Меньшая его часть
короче большей на 3,5 см. Найдите
длину каждой части отрезка.
908. Вычислите длину отрезка DM
(рис. 392, а), если известно, что
(АС) || (DM), ||£|={. \АС\=9см.
909. Прямые а и Ъ пересечены тремя
параллельными прямыми (рис. 392, б).
Вычислите длины отрезков DE и EF,
если \АВ\ = 1 см, \ВС\ = 2 см,
\DF\ = 6 см.
910. 1) Известны стороны треугольника
ABC: |ЛВ|=6 см, |ВС|=8 см,
\АС\ = 9 см. Через точку Μ
проведена прямая ΜΝ, параллельная
стороне ВС (рис. 392, в). Вычислите:
а) стороны треугольника ΑΜΝ, если
\АМ\ = 4 см; б) отношение
периметров треугольников ΑΜΝ и ABC, если
\АМ\ : \МВ\ =2:3.
2) Стороны треугольника ABC
известны: \АВ\=А см, |ВС|=6 см,
\АС\ = 8 см. Через точку Μ стороны
АВ(\АМ\=3 см) проведены
прямые, параллельные сторонам АС и
ВС (рис. 392, г). Вычислите: а)
периметр треугольника ΑΜΝ\ б) периметр
треугольника МВК.
911. Сторона АВ треугольника ABC
делится точкой D на два отрезка: \AD\ =
= 8см и \DB\ = 4 см. Найдите
отношение расстояний от точек D и В до
стороны АС этого треугольника.
912. Стороны угла COD пересечены
прямыми а и Ъ (рис. 393). Параллельны
ли эти прямые, если:
1) |ОА| =4 см, \АС\ = 2 см, 0
\ОВ\ =3 см, \OD\ = 4,5 см;
2) \0B\ = 4 см, \0А\ = 2 см, |BD| = 2 см, |АС| = 1 см;
3) \0С\ = 6 см, \0А\ = 4 см, |BD| = 1,5 см, \0D\ = 3,5 см?
913. Даны три отрезка а, Ъ, с. Постройте отрезок:
чч аЬ лч °с г>ч be
1)* = -; 2)х = -; 3)* = -.
с Ь а
914*. Докажите, что биссектриса BD внутреннего угла
треугольника ABC делит противоположную сторону на отрезки,
пропорциональные сторонам ВС и ВА треугольника.
915*. Докажите, что точка пересечения биссектрисы угла
разностороннего треугольника с его стороной лежит между
точками пересечения с этой стороной высоты и медианы
треугольника.
66 Τ · Преобразования подобия
Вы уже знакомы с композицией перемещений (п. 54). Можно
рассматривать и композиции отображений плоскости на себя,
не являющихся перемещениями. Рассмотрим, например,
гомотетию Но и поворот R с центром Αί9 переводящий точку В ι
в В2 (рис. 394). Образами точек -А, Б, С, ... при гомотетии Но
являются соответственно точки Аи Biy Си ··· Точки Aiy B2>
С2, ... — образы точек Ai9 Вь Си ... при повороте R. Тогда
образами точек А> В, С, ... при композиции R о Но будут
соответственно точки Аи В2, С2, ...
При гомотетии Но расстояния между точками изменяются
в отношении \k\. При повороте расстояния сохраняются.
Значит, при композиции гомотетии Но и поворота R расстояния
между точками изменяются в отношении \k\. Однако такая
композиция не является гомотетией, так как она отображает
прямую АВ на непараллельную ей прямую А{В2.
234
Итак, существуют отображения плоскости на себя,
отличные от гомотетии, при которых расстояния между точками
изменяются в одном и том же отношении.
Определение. Отображение плоскости на себя, при
котором расстояния между любыми двумя точками изменяются
в одном и том же отношении к > О, называется
преобразованием подобия.
Число k называется коэффициентом преобразования подобия.
Частными видами преобразований подобия являются
перемещения (k = 1) и гомотетии (п. 63).
Этот вид преобразования подобия характеризуется тем,
что любая прямая, содержащая точку и ее образ, проходит через
одну и ту же точку плоскости — центр гомотетии.
Преобразование подобия отображает любую фигуру L на
подобную ей фигуру Lit В самом деле, при этом преобразовании
расстояния между любыми двумя точками фигуры L изменяются
в отношении k (k — коэффициент преобразования подобия).
Верно и обратное: если фигура Lt подобна фигуре L, то
существует преобразование подобия, отображающее фигуру L
на фигуру Lu
Поэтому можно дать другое определение подобных фигур.
Фигура Li подобна фигуре L, если существует
преобразование подобия, отображающее фигуру L на фигуру Lt.
Рассмотрим некоторые свойства преобразований подобия.
711| Преобразование подобия с коэффициентом k обратимо, при-
I чем обратное отображение есть преобразование подобия
I с коэффициентом — .
Доказательство. Пусть А п В — различные точки
плоскости, Ai и Bi — их образы. Тогда | AiBil = k \АВ\ Φ 0.
Следовательно, Ai Φ Bi и потому преобразование подобия
обратимо и, значит, имеет обратное. При обратном
преобразовании точки Ai и Bi отображаются на точки А и В. Но | АВ\ =
= — |AiBi|. Значит, это обратное отображение есть преобра-
k
зование подобия с коэффициентом—. ■
k
71г| Композиция двух преобразований подобия Р4 и Р2 с коэф-
■ фициентами kx и k2 есть также преобразование подобия
I с коэффициентом k = kik2.
Доказательство. При преобразовании Pi
расстояния изменяются в отношении ki > 0, а при преобразова-
235
нии Ρ2 — в отношении k2 > 0. Значит, при композиции Р2 оР,
расстояния изменяются в отношении k = ktk2 и,
следовательно, J?2 ° -Pi есть преобразование подобия с
коэффициентом k = kik2* ■
В частности, композиция гомотетии с коэффициентом k
и перемещения есть преобразование подобия с коэффициентом,
равным \k\.
Оказывается, для последнего предложения верно и обратное:
721 каждое преобразование подобия есть композиция переме-
I щения и гомотетии.
Доказательство. Пусть F — произвольное
преобразование подобия с коэффициентом k. Рассмотрим
композицию преобразования F и гомотетии Η с коэффициентом — и
k
произвольным центром О. Тогда отображение Η о F плоскости
на себя является преобразованием подобия с
коэффициентом й · — = 1, т. е. HoF есть некоторое перемещение Р.
k
Итак,
HoF = Р.
Поскольку отображения Η о F и Ρ совпадают, то совпадают
и композиции Н' о (Н о F) и Η' ο Ρ (где Н' — отображение,
обратное Я), т. е.
#' о (Н о F) = Н' о Р.
Отсюда
(Я'о Н) о F = Н' о Р9
Ε о F = Я' о р,
Ρ = Я' о Р.
Но отображение плоскости на себя, обратное гомотетии Я*'
есть гомотетия Я*.
Следовательно, Ρ = Hk о р. Итак, произвольное
преобразование подобия с коэффициентом k мы представили в виде
композиции перемещения и гомотетии с коэффициентом k.
Утверждение доказано. ■
Вопросы и задачи
916°. Верно ли, что соответствующие углы подобных фигур
конгруэнтны?
917. Назовите такие фигуры, которые подобны самим себе при
любом коэффициенте подобия.
236
918. Назовите несколько фигур,
гомотетичных самим себе при любом
коэффициенте гомотетии.
919. Верно ли, что если два угла подобны, то
они и конгруэнтны?
920. Даны два конгруэнтных квадрата.
Постройте третий квадрат, конгруэнтный
одному из данных и гомотетичный
другому.
921. Равнобедренный треугольник ABC
подобен равнобедренному треугольнику А\В\С\ с
коэффициентом подобия 2 (рис. 395). Как можно отобразить второй
треугольник на первый при помощи гомотетии и
перемещения?
922. Прямоугольный треугольник ABC подобен треугольнику
А{В\С\ с коэффициентом подобия 2. Отобразите первый
треугольник на второй при помощи композиции гомотетии
с центром С и перемещения.
923. Отобразите квадрат ABCD на квадрат EFTH с вершинами
в серединах сторон квадрата ABCD при помощи гомотетии
и перемещения.
924. Может ли быть композиция Ρ ° Hk0 перемещением (Р —
преобразование подобия)?
925. Может ли композиция преобразования подобия и
перемещения быть перемещением?
§ 2. Подобные многоугольники
67. Признаки подобия треугольников
73 | Теорема. Если три стороны одного треугольника
пропорциональны трем сторонам другого треугольника, то такие
треугольники подобны.
Дано: |i4,Bi|: \АВ\ = \ВХСХ\ : \ВС\ = \А,СХ\ : \АС\.
Доказать: /\A{B{Ci сЧ) ААВС (рис. 396).
Доказательство. Рассмотрим гомотетию Но с
произвольным центром О и коэффициентом k = |Αι2?ι| : \АВ\.
Эта гомотетия отобразит треугольник ABC на подобный ему
треугольник А0В0С0 (рис. 396):
237
AA0B0C0 oo ААВС, (1)
причем
\A0B0\=k \AB\9 \B0C0\=k\BC\9 \A0C0\=k\AC\. (2)
По условию
\AiBi\=k\AB\9 IJJtCil =ft |ВС|, \А,С,\=к\АС\. (3)
Из равенств (2) и (3) следует:
\AiBi\=\A0B0\9 \BiCl\=\B0C0\, \AiCi\=\A0C0l (4)
Поэтому
AAiBfii ~ AA0B0C0, (5)
а так как конгруэнтные фигуры подобны, можно записать:
Δ-AiBiCi оо АА0В0С0. (6)
Но AA0BQCQ счэ ААВС, и, следовательно, в силу
транзитивности отношения подобия фигур
AAiBiCt оо ААВС. В
74 | Теорема. Если две стороны одного треугольника
пропорциональны двум сторонам другого треугольника и углы
между этими сторонами конгруэнтны, то такие
треугольники подобны.
Τ Дан о: \AiBi\i \АВ\ = \Bid\i \ВС\, В\ = ζΓ (рис. 397).
Доказать: АА1В1С1 <*> ААВС.
Доказательство. Рассмотрим гомотетию Но с
произвольным центром О и коэффициентом k = |AiSi| : \АВ\.
Эта гомотетия отобразит треугольник ABC на подобный ему
треугольник А0В0С0:
АА0В0С0 оо ААВС, (1)
238
Рис. 397
причем
\A0B0\ = k\AB\, \BQC0\ = k \ВС\, Во = В. (2)
По условию
\AlBi\=k\AB\9 l-Bidl =* I ВС I, Bt = В. (3)
Из равенств (2) и (3) следует:
lAiBd = \А0В0\9 \Bid\ = \В0С0\, Во = В,. (4)
Из равенств (4) вытекает:
AAiBid ^ АА0В0С0,
а так как конгруэнтные фигуры подобны, то
AAiBid счэ АА0В0С0. (5)
Из соотношений (5) и (1) в силу транзитивности отношения
подобия фигур следует, что
AAiBid <s> ΑΑΒΟ.Ύ
75 I Теорема. Если два угла одного треугольника
конгруэнтны двум углам другого треугольника, то такие треугольники
подобны.
Hk0
▼ Дано: Ах = А, В{ = В.
Доказать: AAiBid со д ABC (рис. 398).
Доказательство. Рассмотрим гомотетию
с произвольным центром О и коэффициентом k = Ι-AiBil : | АВ\.
Эта гомотетия отобразит треугольник ABC на треугольник
АовоС0 (рис. 398). Значит,
АА0В0С0 cv AABC, ■ (1)
причем
\А0В0\ = k \АВ\ и А0 = АУ В0 = В
(2)
(так как при гомотетии величина угла сохраняется, см. п. 63).
239
β.
Рис. 398
Кроме того, по построению и условию
U,B,| =ft \АВ\, Ai = А, Б, = В. (3)
Из равенств (2) и (3) следует:
\A,Bi\ = \А0В0\, Αι = А0, В, = В0. (4)
Поэтому
ΔΑ^Α ^ АА0Б0С0 (5)
и, значит,
AAiBiCi cnp ΑΑ<β0Ο0. (6)
Из соотношений (6) и (1) в силу свойства транзитивности
отношения подобия фигур следует, что
AAjBjCi с\> ААВС. Ύ
Вопросы и задачи
926°. Подобны ли любые два равносторонних треугольника?
927. В разностороннем треугольнике проведены его средние
линии. Среди всех образовавшихся треугольников укажите
подобные.
928°. Что можно сказать о соответственных углах подобных
треугольников? Назовите по рисунку 398 пары соответственных
углов подобных треугольников ABC и А\В\С\.
929. Подобны ли два треугольника, если их стороны имеют длины:
1) 4 см, 5 см, 6 см и 8 мм, 10 мм, 12 мм;
2) 3 см, 4 см, 6 см и 9 см, 15 см, 18 см;
3) 1 дм, 2 дм, 2 дм и 1 дм, 1 дм, 0,5 дм?
930. 1) Стороны одного треугольника 4 дм, 3,6 дм и 1,5 дм.
Вычислите стороны другого треугольника, подобного данному»
если отношение их соответственных сторон равно 1,6.
240
2) Стороны данного треугольника
8 см, 6 см и 5 см. Меньшая сторона
второго треугольника, подобного
данному, 2,5 см. Вычислите другие
стороны второго треугольника.
931. 1) Стороны данного треугольника
3,5 см, 4 см, 8 мм. Большая сторона
второго треугольника, подобного
данному, 6 см. Вычислите стороны
второго треугольника.
2) Стороны треугольника 12,6 м,
16,5 м и 18,0 м. Вычислите стороны
треугольника, подобного данному,
если меньшая сторона этого
треугольника конгруэнтна большей
стороне данного треугольника.
932. Известно, что \АВ\ = 16,2 см,
|БС|=24,3 см и \АС\= 32,7 см.
Вычислите стороны треугольника
А\В\С\ подобного данному, если
сторона А\В\ этого треугольника
соответствует стороне АВ первого
треугольника и: 1) больше этой стороны
на 10,8 см; 2) меньше этой стороны
на 5,4 см.
933. 1) Сформулируйте признаки подобия
равнобедренных треугольников.
2) Сформулируйте признаки подобия
прямоугольных треугольников.
934. Подобны ли прямоугольные
треугольники, если в одном из них
имеется угол в 42°, а в другом — угол
в 48°?
935. На рисунке 399, а, б, в, г
параллельные прямые показаны одинаково
направленными стрелками. Найдите на
этих рисунках подобные
треугольники и объясните, почему они подобны.
936. По данным рисунка 400, а, б, в, г
найдите подобные треугольники и
объясните, почему они подобны.
в)
В 937. Используя рисунок 401, где (АС) \\
|| (А\С\) || (А2С2), напишите пропорции,
начинающиеся с отношений:
JAJ1. 2) μ·£|. „ IJ.B1.
1
4)1^1; 5)i^i
938. Прямая, параллельная стороне
данного треугольника ABC, делит другую
сторону в отношении 1 : 5 (считая от
вершины). Вычислите длины сторон
отсеченного треугольника, если длины
сторон данного треугольника равны:
1) 9 см, 12 см, 18 см; 2) 15 см, 21 см,
24 см.
939. Подобны ли равнобедренные треуголь-
В ники, если они имеют: 1) конгруэнтные
тупые углы; 2) по прямому углу; 3)
конгруэнтные острые углы?
940. Из вершины прямого угла данного
треугольника проведена высота.
Сколько пар подобных треугольников
образовалось на этом чертеже?
941*. Можно ли любой остроугольный или
тупоугольный треугольник, не
имеющий равных сторон, рассечь прямой,
β проходящей через вершину, на два
подобных треугольника?
942. Подобны ли два треугольника, если все
их средние линии соответственно
пропорциональны?
943. На одной из сторон данного угла А
отложены отрезки |АВ|=5 см и
| -АС | = 16 см. На другой стороне
В1 этого же угла отложены отрезки
|AD|=8 см и |AF| = 10 см.
Подобны ли треугольники ACD и ABF1
Ответ обоснуйте.
944. Стороны угла АОВ пересечены двумя
параллельными прямыми CD и C\D\
Рис. 401
(рис. 402) так, что \ОС\ =
= 8 см, | ССХ | = 6 см,
\OD\ = 12 см. Вычислите
\DDX\ и \CXDX\, если
\CD\ = 9 см.
945. На стороне АС
треугольника ABC дана точка D
такая, что ABD = АСВ.
Вычислите длины сторон
треугольника ABD, если:
1) \АВ\ = 8 см, \ВС\ =
= 12 см, \АС\ = 18 см;
2) \АВ\ = 12 см, |БС| =
= 5 см, \АС\ = 13 см.
946. Чтобы определить на
местности расстояние между
двумя точками А и Б, из
которых точка В
недоступна, можно выполнить
построение, план которого
показан на рисунке 403.
Определите расстояние |^-£|,
если \АС\ =150 м, [DF] \\
II [AS], |DF|=16 м и
\CD\ =30 м.
947. На рисунке 404 показано,
как можно определить
ширину реки |AD|f построив
на местности два подобных
треугольника — ААВС и
0 П* Л^В
Рис. 402
С
Рис. 403
Рис. 405
243
ADFC. Определите \AD\, если \ВС\ = 50 м, \FC\ = 16 м
и |DC| = 17 м.
948. Наблюдатель, находящийся в точке А (рис. 405), видит конец
шеста точку С и верхнюю точку D мачты расположенными
на одной прямой. Какова высота мачты, если \AF\ =60 м,
\АВ\ =6 ми |ВС| =3м?
949. Практическая работа. Измерьте высоту какого-либо
сооружения (моста, высокого здания, телевизионной вышки
и т. п.), находящегося в окрестностях школы.
950. Выполните на местности измерительные работы по
определению расстояния между двумя точками, одна из которых
недоступна.
951. Докажите, что в подобных треугольниках отношение двух
соответственных сторон равно отношению двух
соответственных: 1) высот; 2) биссектрис; 3) медиан.
952. Выполняются ли свойства рефлексивности, симметричности
и транзитивности для отношения: 1) гомотетичности фигур;
2) подобия фигур?
953. Длина основания треугольника ABC равна а. Прямая,
проведенная параллельно основанию, делит боковую сторону в
отношении т '. η (считая от вершины). Выразите через а, т
и η длину отрезка этой прямой, заключенного между
сторонами треугольника. Вычислите длину этого отрезка, если:
3 5
1) а = 25 см, т : η =— ; 2) а = 4,8 см, т : η = —;
3) а = 12,6 см, т : п = 0,75.
68. Теорема Пифагора
Докажем очень важную теорему, позволяющую по двум
сторонам прямоугольного треугольника вычислить третью.
7б|Теорема (Пифагора). Квадрат гипотенузы
прямоугольного треугольника равен сумме квадратов его катетов:
с2 = а2 + Ъ2.
Для доказательства нам понадобится следующее
предложение: квадрат катета равен произведению гипотенузы на
проекцию этого катета на гипотенузу. В обозначениях рисунка 406, а:
а2 = с · ас. (1)
Треугольники ABC и CDB (рис. 406, а) подобны, так как
углы С nD прямые, а угол В — общий. Поэтому с : а = а : ас,
откуда по свойству пропорций вытекает справедливость (1).
244
*♦
By
Ay
0
β
-4i
Лг
В
С
Ir *
δ)
*c>
b2 = с ■ &„
Рис. 406
По соотношению (1) имеем: а2 = с ·
Складывая эти два равенства, получаем:
а2 + &2 = с (а^ + ^} = С2 и
Теорема Пифагора имеет -много применений. Докажем,
например, следующее предложение:
77 I Теорема. Расстояние между точками А(х\, у\) и В(х2, уг)
I координатной плоскости вычисляется по формуле:
\АВ\= V (*2 - XiY + (У2 - »ι)2.
Пусть прямая АВ не параллельна ни одной из осей
координат. Тогда Χι Φ х2 и у{ Φ у2. Проведем через точки А и В
прямые, параллельные осям координат (рис. 406, б). Получим
прямоугольный треугольник ABC. По теореме Пифагора
имеем: \АВ\ = }/ | АС\2 + \ ВС|2.
Из прямоугольников АСВХ Ах и ВСАуВу находим, что
\АС\= \АХВХ\, \ВС\ = \АуВу\. По теореме 111 АХВХ\ = \x2—Xi\,
|АуВу| = | у2 — у 11. Следовательно,
\АВ | = У\х2-Х{\* + \у2-у{\2 = У(х2-хх)*+(у2-У1)*.
Справедливость теоремы 77 в случае Xi = х2 или у{ — yt
очевидна. ■
Вопросы и задачи
При решении задач на зависимости между элементами
прямоугольного треугольника будем пользоваться обозначениями,
приведенными на рисунке 406, а.
954. Докажите: 1) h = -; 2) - = -; 3) А2 = ас - Ьс.
955. Высота прямоугольного треугольника делит гипотенузу
на отрезки, длины которых: 1) 2 см и 3 см; 2) 15 мм и 24 мм.
Вычислите: а) длину этой высоты, б) длины катетов.
956. Дано: ас = 3 см, Ъс = 2 см. Вычислите с, а, 6, А.
245
957. Выразите Ьс и α, через
α и ft.
958. Биссектриса прямого угла
делит гипотенузу в
отношении ρ : g. В каком
отношении делит гипотенузу
основание проведенной к ней
высоты?
959. Постройте отрезок х, если:
\)x=Vab\ 2) x^V2bc\
3)χ=γψ где α, b-
данные отрезки.
960. Сформулируйте и докажите
(предположив противное)
теорему, обратную теореме
Пифагора.
961. 1) В прямоугольном
треугольнике ABC a = 38 см,
& = 16 см. Вычислите
площадь каждого из
заштрихованных прямоугольников
(рис. 407, а, б, в).
2) В прямоугольном
треугольнике ABC a = 36 см,
с = 45 см. Вычислите
площадь заштрихованных
треугольников (рис. 408).
962. Стороны треугольника
пропорциональны числам 13, 12
и 5. Докажите, что такой
треугольник прямоугольный.
А в
Рис. 408
963. Вычислите стороны ромба,
если его диагонали равны
4,6 см и 6,4 см.
964. Выразите площадь
равностороннего треугольника
через его сторону а.
965. Внутри круга дана точка.
Какая из всех хорд круга, Рис. 409
проходящих через эту
точку, имеет наименьшую длину и какая — наибольшую?
966. В окружности радиуса г проведена хорда. 1) Найдите ее
расстояние от центра окружности, если длина хорды равна а.
Произведите вычисления, если: а) г =14 см, а = 8 см;
б) г = 8 см, а= 14 см. 2) Выразите длину хорды через ее
расстояние Л от центра.
967. Радиус круга равен 25 см. В этом круге проведены две
параллельные хорды длиной 14 см и 4 см. Вычислите
расстояние между хордами.
968. Вычислите расстояния \АС\, \АЕ\ и \СЕ\ (рис. 409).
969. Вычислите расстояния от начала координат до точек:
1) (0; 15); 2) (18,0); 3) (3; 4); 4) (5; 12).
970. Вычислите расстояние между двумя точками координатной
плоскости: 1) А (0, 0), В (2; 4); 2) А(1; 3), В (2; 4); 3)А(-1; 2),
В (4; -3).
971. Из точки А, находящейся вне прямой MN, проведены к этой
прямой две наклонные. Одна из них имеет длину 13 см, а ее
проекция на эту прямую равна 5 см. Вычислите длину
второй наклонной и ее проекцию на прямую MN, если эта
наклонная составляет с прямой MN угол: 1) в 30°; 2) в 45°.
972. Дано: а = 9 см, 6= 12 см. Вычислите: с, А, ас, Ьс.
973. Дано: а = 12 см, с = 13 см. Вычислите: &, А, ас , Ьс.
974. Вычислите катеты прямоугольного треугольника, если
биссектриса прямого угла делит гипотенузу на отрезки k и /.
Проведите вычисления при &=12сми/=5 см.
975. Две окружности радиусов 3 см и 5 см касаются внешним
образом. Вычислите длину отрезка их внешней общей
касательной, заключенной между точками касания.
976. К окружности (О, г) проведена из точки Μ касательная.
Найдите формулу, выражающую зависимость между
расстояниями \ОМ\, \МА\ =т (А — точка касания) и радиусом г.
247
977. Расстояние между центрами окружностей радиусов 6 см
и 2 см равно 10 см. Вычислите длину: 1) отрезка общей
внешней касательной; 2) отрезка общей внутренней
касательной.
978. Докажите, что в одном круге (или в конгруэнтных кругах):
1) хорды равной длины равноудалены от центра; 2) из двух
неконгруэнтных хорд хорда большей длины ближе к центру.
979. Каждая из двух конгруэнтных окружностей радиуса г
проходит через центр другой. Выразите через г длину их общей
хорды.
980. Две конгруэнтные и взаимно перпендикулярные хорды
окружности точкой их пересечения делятся каждая на
отрезки в 10 мм и 16 мм. Вычислите радиус окружности.
981. Могут ли длины всех сторон прямоугольного треугольника
выражаться: 1) четными числами; 2) нечетными?
Рис. 411
69. Подобные многоугольники
1. В пункте 66 было доказано,
что два треугольника подобны,
если стороны одного из них
пропорциональны сторонам
другого. В случае многоугольников
с числом сторон, большим трех,
пропорциональности их
соответственных сторон уже
недостаточно для подобия этих
многоугольников. Например,
квадрат не подобен ромбу, один из
углов которого острый, хотя
их стороны пропорциональны
(рис. 410).
Недостаточно для подобия
многоугольников и равенства их
соответственных углов.
Например, квадрат не подобен
прямоугольнику, не все стороны
которого конгруэнтны.
Достаточное условие подобия
двух многоугольников сфор-
248
мулировано в следующей теореме, которую приведем без
доказательства.
78 I Теорема. Если стороны одного многоугольника соответст-
I венно пропорциональны сторонам другого многоугольника и
I соответственные углы этих многоугольников конгруэнтны,
I то такие многоугольники подобны.
2. Докажем теорему о периметрах подобных
многоугольников.
79 1 Теорема. Отношение периметров подобных многоуголь-
I никое равно коэффициенту подобия этих многоугольников.
Доказательство. Так как многоугольники
подобны (рис. 411), то
1-AiBil = k \AB\9 \Bid\ = k \BC\9 ..., \EiAt\=h\EA\.
Сложив почленно эти равенства, находим:
1-AiBil + IBidl + ... + |£i-Ail =
= k(\AB\ + \BC\ + ... + \EA\),
т. е. Рг — kP> где Рг и Ρ — периметры данных многоуголь*
ников.
Итак Рг : Ρ = k. Ш
3. Рассмотрим отношение площадей подобных фигур.
Пусть прямоугольник имеет стороны в 5 см и 3 см. Его
площадь равна:
S = 5 · 3 см2 = 15 см2.
Если другой прямоугольник подобен первому с
коэффициентом подобия k, то его стороны равны 5k см и 3k см, а площадь
Si равна:
Si = 5k - 3k см2 = k2 · 15 см2 = k2S.
Мы видим, что отношение площадей S{ и S равно квадрату
коэффициента подобия.
801 Теорема. Отношение площадей подобных многоугольни-
I кое равно квадрату коэффициента подобия.
Доказательство. 1) Рассмотрим сначала подоб-
k
ные треугольники. Если Δ AiBiCi о* Δ АВС> то существует
отображение ААВС на Δ AiBiCi9 при котором расстояния
между точками изменяются в k раз. Образ высоты CD
треугольника ABC при этом отображении — высота CiZ>i
(рис. 412).
249
Имеем:
l-Ai^il
Отсюда
k \AB\,
k \CD\.
SA = ±(k\AB\).(k\CD\) =
= k>(±\AB\.\CD\\ = k*SA,
Δ,
sA = k\
доказанному выше получим:
Найдем теперь площадь многоугольника L^
Для треугольников
теорема доказана.
2) Теперь рассмотрим
произвольные подобные
многоугольники L и Σ\Λ Пусть
многоугольник L разбит на
треугольники Δι, Δ2, ...» Δ„
(см. рис. 413, где η = 4). Так
к
как L <*> Lu то существует
отображение многоугольника L
на Li9 при котором
расстояния между точками
изменяются в k раз. Обозначив образ
треугольника Ат при этом
отображении через Δ/Λ, по
Sdl)
+ SA[ +
+ - + **Дя = ν (sAi + sA
Итак, S (LJ : S (L) = A2. ■
+
= fc2
k>sAt + k>sA +
+ SA ) = fc2S (X).
Вопросы и задачи
982°. Верно ли, что: 1) любые два конгруэнтных многоугольника
подобны; 2) все квадраты подобны?
983. Верны ли предложения: 1) параллелограммы с
соответственно равными углами подобны; 2) любые два ромба подобны?
250
984.
985.
Могут ли два подобных, но
не конгруэнтных
многоугольника иметь: 1) по
конгруэнтной стороне; 2) равные
периметры?
Постройте равносторонний
треугольник и проведите
прямую, параллельную одной из
сторон, так, чтобы
коэффициент подобия данного и
отсеченного треугольника был равен: 1)
А
0
Рис. 414
2)
»!·
986.
987.
988*.
989.
990.
991.
992.
993.
994.
Постройте два подобных прямоугольника с коэффициентом
подобия, равным: 1) 0,3; 2) 3.
Постройте два подобных ромба с коэффициентом подобия,
2
равным: 1) 0,5; 2) —.
В прямоугольнике ABCD \АВ\ = а и \ВС\ = b (a > &).
Отрезок EF проведен так, что полученный прямоугольник
BCEF подобен данному. Найдите стороны
прямоугольника ADEF. Произведите вычисления для случаев: 1) а = 8 см,
6 = 6 см; 2) а = 6,4 см, Ъ = 4,8 см.
В ящик плотно сложены коробки, имеющие форму
прямоугольного параллелепипеда. (На рис. 414 показан вид
сверху.) Подобны ли показанные на этом рисунке малые
прямоугольники прямоугольнику ΑΒΟΏΪ
Разрежьте тетрадный лист бумаги на несколько конгруэнтных
частей прямоугольной формы так, чтобы полученные после
разрезания малые прямоугольники были подобны взятому
листу.
Наименьшие стороны двух подобных многоугольников
относятся как 2 : 5. Вычислите периметр большего из этих
многоугольников, если периметр меньшего из них 42 см.
Стороны одного треугольника 1,2 м, 2,4 м и 3 м. Периметр
подобного ему треугольника 11 м. Вычислите стороны
второго треугольника.
Отношение периметров двух треугольников равно 0,625.
Стороны меньшего из этих треугольников 4 дм, 5 дм, 7 дм.
Вычислите стороны большего треугольника.
В двух подобных многоугольниках меньшие стороны 35 см и
21 см, а разность их периметров 40 см. Вычислите периметр
каждого многоугольника.
251
995. Найдите отношение площадей двух квадратов, если
отношение сторон этих квадратов равно: 1) 2:3; 2) |/~2 : \ Ъ\
3) 1 : 1,5; 4) k : L
996. Как относятся стороны двух квадратов, если отношение
площадей этих квадратов равно: 1)4:9; 2) 3 : 4; 3) 0,5 : 2;
4) Ρ : <7?
997. Как изменится площадь многоугольника, если каждая из его
сторон: 1) увеличится в η раз; 2) уменьшится в k раз (а
величины углов не изменятся)?
998- Одна из сторон треугольника разделена на три
конгруэнтные части, и через точки деления проведены прямые,
параллельные другой стороне. Найдите отношения площади
данного треугольника к площадям треугольников,
отсеченных построенными прямыми.
999. Как прямоугольник со сторонами 2 см и 5 см рассечь прямой
на два подобных прямоугольника?
1000. Стороны параллелограмма имеют длины а и 6. Постройте
прямую, отсекающую от данного параллелограмма
подобный ему параллелограмм.
1001. 1) Докажите, что два выпуклых четырехугольника
конгруэнтны, если у них имеется одна пара равных соответственных
углов и все соответственные стороны равны.
2) Сформулируйте условие подобия выпуклых
четырехугольников.
1002. Соответствующие стороны двух подобных многоугольников
относятся как—-. Площадь первого многоугольника равна S.
о
Найдите площадь второго многоугольника. Произведите
вычисления при S = 24 см2 для случаев, когда:
!)£- = !; 2)^ = 0,5; 3)-^=^; 4)^=1
' Ь 9 ' Ь ' Ь у% Ь 5
1003. Периметры двух подобных многоугольников относятся как
3 : 5. Площадь большего многоугольника равна 40 м2.
Вычислите площадь второго многоугольника.
1004. Постройте квадрат, площадь которого равна: 1) четвертой
части площади данного квадрата; 2) половине его площади.
1005. Площади двух подобных треугольников равны Si и S2.
Основание первого из них а\. Найдите высоту первого, основание
и высоту второго треугольника. Вычислите при Si = 64 см2,
S2 = 24 см2, а\ = 4 см.
252
70. Измерительные работы
1. Поперечный масштаб. Численным масштабом называют
отношение расстояний между двумя любыми точками на чертеже
(плане, карте) к расстоянию между соответствующими им
точками в натуре. Если, например, расстояние на карте между
точками А{ и Bt равно 1 см, а расстояние между
соответствующими им точками А и Б на местности равно 10 км, то численный
масштаб этой карты равен | ΑιΒι\ : \АВ\ = 1 см : 1 000 000 см =
- 1 : 1 000 000.
Значит, численный масштаб — это коэффициент подобия
участка на местности и его изображения на карте.
Линейный масштаб — это отрезок с нанесенными на него
делениями и надписью, указывающей, какой отрезок
соответствует каждому делению в натуре. На рисунке 415 изображен
линейный масштаб, соответствующий численному масштабу
1 : 1 000 000.
Для определения расстояния между двумя пунктами А и В
по карте нужно одну ножку измерительного циркуля
поставить в точку А, другую — в В. Затем, не меняя раствора
циркуля, следует поставить его ножки так, чтобы одна из них
находилась справа от 0 на каком-нибудь крупном делении, а
другая — слева от 0 на мелком делении (или в самой точке 0).
Тогда по линейному масштабу можно определить расстояние
между пунктами А и В в натуре.
Для увеличения точности измерений расстояний по карте
(или плану) используют поперечный масштаб (рис. 416).
В линейном масштабе левый крайний отрезок (масштабная
единица или основание масштаба) делится на 10 равных частей.
Чтобы измерять отрезки с точностью до сотых частей
масштабной единицы, строят прямоугольник ABCD (рис. 416, а) и
на его основании АВ наносят линейный масштаб. Боковые
стороны прямоугольника делят на 10 конгруэнтных частей и
проводят через точки деления отрезки, параллельные (АВ).
На стороне DC откладывают последовательно масштабную
1:1000 000
10 0 10 20 30 ^0 50км
liniliiiil 1111!
Рис. 415
253
9 7 5 3 ЮЕ
щи
I
t
J
л
1 llliii
"ft
11
mm
\q
N
a)
Рис. 416
5,
δ)
единицу и полученные точки соединяют с соответствующими
делениями линейного масштаба АВ. Отрезок DE делят на 10
равных частей и обозначают, как на рисунке (отметки 0, 1,
2, 3, ... сдвинуты на одну влево по сравнению с
соответствующими отметками на отрезке ОА). Точки отрезков DE и АО с
одинаковыми отметками соединяют отрезками. Поперечный
масштаб готов.
Рассмотрим треугольник ОЕ0, изобразив его для удобства
отдельно (рис. 416, б). Параллельные прямые отсекают от него
подобные треугольники. Из подобия треугольников следует,
что^^! : 10JE71 = 1 : 10, |А2В2|: \0Е\ = 2 : 10, \А3В3\:\0Е\ =
= 3 : 10, ..., | A9BQ\ : \0Е\ = 9 : 10.
Следовательно, расстояние |AiBi| равно 0,01 масштабной
единицы, |А2Б2| —0,02 масштабной единицы и т. д.
Используют поперечный масштаб следующим образом.
Раствор циркуля, перенесенный с карты, накладывают так, чтобы
острия обеих ножек находились на одной горизонтали, причем
одно острие — в точке пересечения горизонтали с вертикалью,
правее прямой ОЕ (на рис. 416 — в точке N)9 а другое — на
этой же горизонтали, левее прямой ОЕ (в точке М). Получили:
\NM\ = \NQ\+ \QP\ + \РМ\. Но \NQ\ = 3, \PQ\ = 0,08,
\РМ\ = 0,4.
Следовательно, \NM\ = 3,48 масштабной единицы.
2. Определение высоты предмета, а) Для определения высоты
предмета (например, дерева) ставят на некотором расстоянии
254
от него шест (по отвесу) с
вращающейся планкой (рис. 417).
Планку направляют на
верхнюю точку предмета (дерева),
как показано на рисунке.
Далее отмечают на поверхности
земли точку В. Получаются
пары точек А и Ai9 С и Ci9
такие, что треугольники А\С\В
и АСВ подобны. Отношения
|iliC||:|AC|H \BCt\i\BC\
равны коэффициенту гомотетии.
Отрезки ВС ι и ВС измеряют, длина
отрезка АС известна. Тогда из
пропорции |AtCi| : \АС\ =
= |BCil : \BC\ находят:
|ii1C1| = -L5^LL-|-ACl·
iiii |вс | ι ι
3· Съемка плана земельного
участка. Мензула
представляет собой квадратную доску
(планшет), помещенную на
штативе (рис. 418). На планшет
кнопками прикрепляется лист
бумаги. Если нужно снять план
земельного участка, имеющего
форму многоугольника (рис.
419), то внутри его выбирают
точку О, из которой видны все
вершины этого
многоугольника. Над точкой О устанавливают
(с помощью уровней) мензулу
так, чтобы мензульная доска
была в горизонтальном
положении. Далее на планшете
отмечают точку 019
соответствующую выбранной точке О на
местности.
С помощью алидады или
трехгранной масштабной линейки
через точку 0lf проводят лучи
в направлениях на вехи,
поставленные в вершинах
многоугольника, план которого
снимается. Измерив расстояния от
точки О до вершин
многоугольника, откладывают их в
выбранном масштабе на
соответствующих лучах, вычерченных
на планшете. Получают точки
А\9 Ви Си Ό{ (рис. 419),
соответствующие вершинам данного
на местности многоугольника.
Многоугольники ABCD и
Ai-BiCiJDi подобны.
Коэффициент подобия равен выбранному
масштабу.
Интересна с точки зрения
геометрии возможность при
помощи мензулы снимать планы
почти без измерения
расстояний на местности. Достаточно
измерить одно расстояние —
базис.
Пусть, например, измерив на
местности базис АВ (рис. 420),
мы нанесли его в надлежащем
масштабе на планшете в виде
отрезка ΑχΒγ и хотим нанести
на планшет положение вех С,
D и Е. Для этого ставим
мензулу в точке А, ориентируем
планшет так, чтобы луч АХВ^
проходил через точку Б, и визируем
вехи С, D, Е, проводя на
планшете из точки Αι
соответствующие лучи (рис. 421). Потом
переносим мензулу в точку J5,
ориентируем планшет так, чтобы
луч В{А{ проходил через точку А
(рис. 422), и визируем вновь
4D
I
I
h
Рис. 424 Рис. 425
вехи С, D, Ε. На рисунке 422 видно, как в результате
получаются на планшете изображения точек С, D, Е.
▼ Существует еще много приемов съемки без измерения на
местности расстояний, кроме измерения базиса. С ними
интересно ознакомиться на практике. Рассмотрим одну из
возникающих здесь задач. Пусть мы нанесли на плане точки А9 В
и С (рис. 423), причем точка С нанесена засечками из точек А
и Б, подойти же к ней нельзя. Веха, поставленная в точке D,
видна, из точки В, но не видна из точки А. Поставив мензулу
в точку Б, мы ориентируем ее так, чтобы луч Βι-Αι проходил
через точку А9 и проводим на планшете прямую χ = (Bi-D)
(рис. 424). Перенеся мензулу в точку D, можно найти ее
положение «засечками на себя», как это показано на рисунке 425.
Сначала ориентируют планшет так, чтобы нанесенная ранее
прямая χ проходила через точку В на местности, а затем
проводят прямую у = (CCi). Пересечение прямых χ и у даст
на планшете изображение Ζ>ι точки D, в которой мы находимся.
Выполнив на местности измерения базиса и
соответствующих углов, можно находить площади участков,
воспользовавшись для этого известными формулами площади
треугольника. Τ
4. Пантограф. Для построения фигуры, гомотетичной данной,
служит прибор пантограф (рис. 426).
Возьмем параллелограмм ABCD (рис. 427), сторонами
которого служат металлические стержни, скрепленные шарнирно.
На продолжении стержня ВС в точке Ε закрепим острие
карандаша. В точке F пересечения АЕ и CD на стержне CD
укрепим иглу с тупым концом.
257
Рис. 426
Теперь будем изменять положение нашего шарнирного
параллелограмма ABCD, не меняя положения вершины А.
Докажем, что точки A, F и Ε будут оставаться на одной
прямой. Пусть ABfiiDi — новое положение параллелограмма
ABCD.
A ABE ^ AFCE,
откуда
\АВ\ : \CF\ = \ВЕ\ : \СЕ\ = \АЕ\ : \FE\9 (1)
ААВ{Е{ ** АР{С{Е{,
откуда
\ABi\ : IC^il = \BiEi\ : \С,Е{\ = \AE{\: ΙΛ^ιΙ. (2)
Но
IBi^il = \BE\9 |C4Ei| = |C£|, lilBtl = |AB|, (3)
так как эти отрезки меняют только положение, а не длину.
Поэтому из соотношения (2) получаем: | АВ \: \ CiFi | = | BE |: | СЕ |.
Сравнивая это соотношение с (1), заключаем, что IC.FI = \CiFi\.
Отсюда следует, что точка F{ является новым положением
точки F и, значит, точки А9 F и Ε при изменении положения
параллелограмма ABCD
остаются на одной прямой.
На основании (1) и (2),
учитывая равенства (3), находим
также, что | AEt \: \ FiEx\ = \AE\:
:\FE\9 откуда \АЕ,\ : \AF{\ =
= \АЕ\ : \AF\.
Поэтому точкам F и F{
соответствуют при гомотетии с
центром А точки Ε и 2?t.
Коэффициентом этой гомотетии
является отношение |J3i?| : \ЕС\.
258
В СЕ
Рис. 427
Таким образом, если острием иглы обводить контур
некоторой фигуры, то острие карандаша нарисует контур фигуры,
гомотетичной данной.
1 Дополнительные задачи к главе VI
I 1006. Постройте треугольник, подобный данному треугольнику
I ABC, сторона которого, соответствующая стороне ВС, кон-
I груэнтна данному отрезку.
I 1007. Постройте треугольник по данному углу, отношению сторон,
I образующих этот угол, и данной: 1) медиане, проведенной
I к третьей стороне; 2) высоте, проведенной к третьей сто-
I роне.
I 1008. Постройте треугольник по двум данным углам и высоте, про-
I веденной из вершины третьего угла.
I 1009. Постройте прямоугольный треугольник: 1) по данному отно-
I шению его катетов и гипотенузе; 2) по данному катету,
отношению второго катета к гипотенузе; 3) по высоте, проведен-
I ной к гипотенузе, и отношению катетов.
1010. На каждом из оснований трапеции ABCD построены вне тра-
I пеции равносторонние треугольники. Докажите, что прямая,
I соединяющая вершины треугольников, не лежащие на осно-
I ваниях трапеции, проходит через точку пересечения диагона-
I лей трапеции.
I 1011. На каждом из оснований трапеции ABCD построены вне тра-
I пеции квадраты. Докажите, что эти квадраты гомотетичны,
I причем центр гомотетии — точка пересечения диагоналей
I трапеции.
I 1012. На рисунке 428 изображен сегмент. 1) Выразите формулой
I зависимость между I — длиной хорды, й — «стрелкой» (вы-
I сотой) сегмента и г — радиусом. 2) Вычислите радиус, если
I I = 8 см, h = 3 см.
1013. Докажите, что сумма квадратов диагоналей параллелограм-
I ма равна сумме квадратов его сторон.
I 1014. Найдите величины углов равнобедрен-
I ного треугольника, если известно, что
биссектриса угла при его основании
отсекает треугольник, подобный
данному.
I 1015. Диагонали четырехугольника перпен-
I дикулярны. Докажите, что сумма рис# 428
259
10 ΠΓ
Γι
6 fh
4- rr
2 rr
I
11111
Juc-LL
к
1 li
jlcpjy^
til1
г
.IT
I
\i
,/?
'o
£
» 77
4J
,r
'Г
/0 5 J
70
20 J0
a;
40'
50
50
70
квадратов противоположных его
сторон равна сумме квадратов двух
других его сторон.
1016. Докажите, что разность квадратов
двух сторон треугольника равна
разности квадратов их проекций на
третью сторону.
1017. Четырехугольник
ABCD—прямоугольник, О—произвольная точка
плоскости. Докажите: \ОА\2+\ОС\2 =
= \ОВ\2+ \OD\2.
Постройте отрезок длины х, если:
1018.
1) * = Κα2 + Ь2; 2) * = Υ а? — Ь2;
где а и Ъ — длины данных отрезков
(а > 6).
1019. Докажите, что разность квадратов
расстояний от точек перпендикуляра к
отрезку АВ до концов этого отрезка
есть величина постоянная.
1020. Найдите множество точек, сумма
квадратов расстояний от которых до
концов данного отрезка постоянна.
1021. Какую фигуру образуют середины хорд данной окружности,
конгруэнтных данному отрезку? Постройте эту фигуру, если
дана окружность и одна из хорд.
1022. Постройте отрезок длины х: 1) х =
ab
a -f- с
2) х =
а2+С2— 62
(а, 6, с — длины данных отрезков).
1023. На рисунке 429, а изображены масштабная линейка с
сантиметровыми делениями и поперечным масштабом. 1)
Объясните, почему такая линейка позволяет измерять расстоя-
260
ния с точностью до 0,1 мм. 2) Найдите по этому рисунку
расстояния \EF\, \AB\, \CD\ и \KL\ с точностью до 0,1 мм.
1024. На рисунке 429,6 изображен пропорциональный
(делительный) циркуль, позволяющий делить отрезки на
конгруэнтные части и выполнять построения подобных фигур.
Объясните, на чем основано устройство такого циркуля.
1025. Какими тремя последовательными натуральными числами
могут выражаться стороны прямоугольного треугольника?
1026. Может ли композиция двух гомотетий быть перемещением?
1027. Приведите пример фигуры, которая подобна себе с любым
коэффициентом подобия k = 2n, где η — целое число, но
не подобна себе ни при каком другом коэффициенте.
δ
КЛАСС
ГЛАВА
VII
ПОВОРОТЫ
И ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
Рис. 430
Рис, 481
§ 1. Повороты и их композиции
71. Способы задания поворотов
Вы уже знаете (п. 19), что поворот
определяется заданием:
а) его центра О,
б) угла поворота а,
в) направления поворота.
Угол поворота а при этом
считается заключенным в пределах
0° < α < 180°.
Поворот на 0° — это тождественное
отображение плоскости:
Ε (X) = X.
Для любого центра О повороты на
180° в обоих направлениях совпадают
и являются центральной симметрией
относительно центра поворота.
Мы познакомимся теперь с другой
системой задания поворотов,
преимущества которой выяснятся постепенно.
Выберем какое-либо направление
поворота в качестве положительного,
а противоположное направление будем
считать отрицательным.
Положительным обычно считают направление
поворота против часовой стрелки.
Например, поворот на 80° против
часовой стрелки будем называть поворотом
на 80°, поворот же на 80° по часовой
стрелке — поворотом на минус 80°
262
(рис. 430). При таком соглашении поворот полностью
определяется заданием: 1) центра О; 2) угла поворота α (—180°^
< α < 180°).
Угол поворота теперь считается направленной величиной,
числовое значение которой может быть как положительным;
так и отрицательным или нулем. Поворот с центром О на угол α
обозначается Щ. Например, повороты, указанные на
рисунке 430 стрелками, обозначаются Д*°° и Л~80°.
Удобно, однако, рассматривать повороты и на углы,
лежащие вне пределов от —180° до 180°. На рисунке 431 показано,
почему поворот на —20° совпадает с поворотом на 340°:
Поворот мы рассматриваем теперь как результат вращения.
Чтобы наглядно представить себе вращение, положите на лист
бумаги лист кальки и проколите оба листа булавкой в
некоторой точке О. На листе бумаги заранее начертите какую-либо
фигуру. Скопируйте эту фигуру на кальку и после этого
вращайте кальку вокруг точки О. Точка О будет оставаться
неподвижной, любая же другая отмеченная на кальке точка будет
двигаться по окружности. Если вначале она занимала на
плоскости положение X, то после вращения на 340° против
часовой стрелки она займет положение Χγ (рис. 431). Тот же
результат получится и при вращении по часовой стрелке на 20°.
Поэтому мы и считаем, что записи Нио° и i?~20D являются просто
разными обозначениями одного и того же поворота. Тот же
поворот можно получить при помощи вращения бесконечным
числом способов. В самом деле, в результате вращения на 360°
по часовой стрелке (или против часовой стрелки) все
нанесенные на кальку точки возвращаются на прежние места, поэтому
поворот на 340° можно получить и в результате вращения на
углы: —20° + 360° = 340°, —20° + 360° ■ 2 = 700°, ..., —20°—
_360° = —380°, —20° — 360° · 2 = —740°, ...
Вообще, поворот R* получается в результате вращения не
только на угол а, но и на угол α + 360° ■ η, где η — любое
целое число.
Итак, если β = α + 360° · η (η — целое, и —180° < α <
^ 180°), то поворотом на угол β называется поворот Ra. (По-
* Рассматривая повороты с каким-либо одним заданным центром, можно
опустить обозначение центра: вместо В!£ писать просто Ла.
263
где —180° ^ α ^ 180°, был определен ра-
р1200° _ d120°+3603-3 _ д!20э
i?720°= Е300°'2 = Ε
T5-1200J D-120°-360°.3 D-120°
Γί = Γί = Γί ·
Рассматривая приведенные выше примеры поворотов на
определенный угол, мы рассуждали так, как это принято в
физике при изучении вращательного движения. В курсе
геометрии мы не исследуем движения (процесса, проходящего во
времени), а интересуемся только перемещениями. Но
использованные нами представления из области кинематики (раздел
механики, занимающийся описанием различных видов
движения) помогают понять определение и свойства поворотов.
Вопросы и задачи
1028. Отметьте на листе бумаги центр поворота О и некоторую
точку М. Найдите образ точки Μ при повороте на
следующие углы: 1) 35°; 2) 70°; 3) 125°; 4) 160°; 5) —145°;
6) —110°.
1029. Два наблюдателя, стоящие по разные стороны от
велосипеда, заметили, что колеса этого велосипеда вращаются в
направлении по часовой стрелке. Может ли это быть?
1030°. На рисунке 432 стрелкой показано направление вращения
одной из шестерен. Какие из шестерен будут при этом
вращаться в положительном и какие — в отрицательном
направлении?
1031. Точка Μ отображается на точку М\ при повороте вокруг
центра О: 1) на 40°; 2) на 70°; 3) на 130°. Укажите другие
значения углов поворота, при которых точка Μ
отображается на эту же точку М\.
1032. Точка Μ отображается на
точку М\ при повороте
вокруг центра О: 1) на —130°;
2) на —40°; 3) на —90°.
Укажите другие значения
углов поворота, при
которых точка Μ отображается
Рис. 432 на эту же точку.
ворот на угол а,
нее.) Например,
264
1033. Представьте в виде йа(-180° ^ а ^ 180°) следующие
повороты: 1) д380°; 2) Д750; 3) RU60'; 4) ВГ2Ж; 5) Д2000';
6)Д1080'; 7) Л220';
1034. Запишите с использованием обозначения Да(—180° ^Ξ α ^
^180°) повороты на угол: 1) 660°; 2) —570°; 3) —1000°;
4) 890°; 5) 740°; 6) 1100°; 7) 1500°.
1035. При каких значениях числа k справедлива запись:
1) ДР = ДР+360°·*; 2) Д3 = дР+™°·*?
72. Угловые величины. Их измерение в радианах
1. В предыдущем пункте мы рассматривали новый вид угловых
величин — углы поворота. Как и другие угловые величины,
углы поворота можно измерять в градусах. Градусная мера
угла поворота может равняться любому действительному числу.
Вспомним все виды угловых величин, с которыми имели дело.
1) Величина угла α (геометрической фигуры) заключена в
пределах 0° < α < 360°.
2) Угол а между направлениями лежит в пределах
0° < α < 180°.
3) Угол α между прямыми лежит в пределах 0° ^ а ^ 90°.
(Углом между пересекающимися прямыми называется
величина меньшего из углов, образуемых этими прямыми; угол между
параллельными прямыми считается равным 0°.)
4) Угловая величина α дуги окружности может принимать
значения 0° < а < 360°.
5) Вращательное движение в физике характеризуется
любыми угловыми величинами, принимающими любые
действительные значения, т. е. — оо < а < оо.
Таково же положение с поворотами в геометрии. Однако
здесь имеется важное различие. Например, вращения на 50°
и на 410° как физические процессы различны. Но в результате
они дают один и тот же поворот
2. Вы знакомы с различными единицами измерения
угловых величин: это градус, минута, секунда, прямой угол
(а = 90°). При измерении угловой величины дуги за
единицу измерения принимается угловая величина дуги, длина
которой равна радиусу. Эта единица измерения угловых
величин называется радианом.
265
Чтобы выразить радиан в градусах, вспомним формулу
длины окружности радиуса R:
С = 2лД.
Длина дуги в один градус равна:
в а градусов равна:
1= -?-aR.
180
(1)
= — Л, а длина дуги
360 180
(2)
Дугу длины I = R мы получим, если в формуле (2) поло-
180 π
жим а = —. Поэтому радиан выражается в градусах по
π
формуле
ι /180\°
1рад=(-].
(3)
Приближенно 1 радиан равен 57°18\
Из формулы (3) получаем выражение градуса в радианах:
1о 3l
= — Рад.
180
(4)
Приближенно 1° равен 0,01745 радиан.
Формула для длины дуги при радианном измерении
угловой величины дуги принимает особенно простой вид: длина I
дуги окружности радиуса R в χ радиан равна *:
I = xR. (5)
Радианное измерение угловых величин оказывается во многих
вопросах математики и физики особенно удобным.
В следующей таблице указаны числовые значения
величин некоторых углов, если за единицу измерения приняты
градус, прямой угол, радиан.
Единицы
измерения
Градус
Прямой угол
Радиан
Числовые значения величин углов
30
1
3
π
6
45
1
2
π
4
90
1
π
2
180
2
π
270
3
3
— π
2
360
4
2π
* Заметьте, что эта формула проще формулы (2).
266
Вопросы и задачи
1036. Радиус окружности равен 10 см. Вычислите длину дуги,
угловая величина которой равна: 1) 45°; 2) 18°.
1037. Вычислите длину дуги окружности, радиус которой равен
50 см, если: а) угловая величина этой дуги в градусах
равна 144°; б) угловая величина дуги в радианах равна 0,1.
1038. Найдите радианную меру дуги, угловая величина которой
равна: а) Г; б) 45°; в) 75°; г) 225°.
1039. Найдите угловую величину дуги в градусах, если ее радиан-
я 2 π
ная мера равна: 1)1; 2) 0,1; 3) 0,3; 4) —; 5) —π; 6) —;
« 3 ό 9
7) ±ш
' 12
1040. В морской практике углы между направлениями
измеряются в румбах. При таких измерениях окружность делится на
32 румба. Вычислите: 1) сколько градусов в одном румбе;
2) сколько румбов в одном градусе.
73. Композиция поворотов с общим центром
Рассмотрим повороты R20° и Д30° с общим
центром О. В результате
последовательного их выполнения получится поворот
вокруг точки О на 50°. Например,
точка А (рис. 433, а) при повороте R20°
отобразится на точку Αι, а при повороте
530° точка Αι отобразится на точку
«я·",. А2 = R30
R50\A).
R*
А2: Αι = R™ (А);
чит, R30\R20\A)) =
(А,). Зна-
Рис. 433
267
χϊ** чх
'Χ'
χ
Рис. 434 Рис. 435
Напомним, что результат последовательного выполнения двух
отображений fug обозначается g°f и называется композицией
отображений /и g (п. 54). В нашем примере композиция поворотов
Д и J? оказалась поворотом Д , т. е. Д о Д' =
__ р20°+30°= „50°
Вообще, при любых углах поворота а и β:
Дэ о Да = Да+Р.
Например,
Д130ОоЛ80О=Д80'+|3°а=Д210,= Д-150,(рис. 433, б),
Л2М,,Л'40,= Й№+»=Л»=£ (рис. 433, в),
Л-^оЛ'^Я5^'-5»'»^-30, (рис. 433, г),
Л-5'0' о R~m° = Д-780'+(-5.0',= д-.290» = д-2.0> = д.50> ^ 433, д).
Так как всегда α + β = β + α. то Лр . йа = Λα+β =
= Rao Др, т. е. композиция поворотов с общим центром пере-
местительна: J?p о J?a = Ra о Я15.
Τ В случае различных центров это не так. Например, при
композиции двух центральных симметрии Ζ0 = Л1^0" и
Z0 = i?^80° получаются различные перемещения (рис.
434, 435): . -- -
1 ^ ° К = 20iOa, Ζ0ι о Ζ0ί = 20lO„ Z0a о Ζ0ι Φ Ζ0ι ο Ζ0>. Τ
Вопросы и задачи
1041. Найдите угол сс(—180° ^ α ^ 180°) поворота, являющегося
композицией поворотов с общим центром на: 1) 25° и —60°;
2) -35° и 180°; 3) 70° и 20°; 4) 245° и 135°; 5) -170° и —20°;
6) 90° и 45°.
263
1042. Найдите все значения а, для которых: R70' 0 i?a = R30°;
2) i?70° о Да = Л35 ; 3) Я70 о Да = Д70 ; 4) R70' «Ла=£;
5) Да о Д90° = Д80°; 6) Ra с i?-20° = i?I80°; 7) Ra ° Д^ = л*.
1043. Каким перемещением является композиция двух
центральных симметрии с общим центром М?
1044. Найдите поворот, для которого Rl{R%3Q) = X, где Χ—
любая точка плоскости (короче: Да° К* = Е). Сколько
решений имеет задача?
1045. Композицией каких трех поворотов на один и тот же угол a
является поворот на 90°?
1046. Композицией каких двух поворотов на один и тот же
угол α является поворот на 180°?
1047. Сколько существует различных поворотов (с общим
центром), для которых Да о Ra о Ra = El
1048°. Обладает ли композиция поворотов с общим центром
свойством сочетательности?
1049. При каких значениях k (и любых α и β) верно равенство:
3а4-Р+/г-360э
5а МН/г.180°
1) R*о Др == д»ч-р+*·™- ; 2) й%йр- ЯГ ' Pi"*,10υ ?
1050**. Найдите такое наименьшее число п, что композицией η
поворотов на 19° является поворот: 1) на 10°; 2) на 20°.
§ 2. Тригонометрические функции
74. Синус и косинус
Окружность с центром в начале координат и радиусом,
равным 1, будем называть единичной окружностью.
Отметим на единичной окружности
точку Р0 (1, 0). При повороте Ro точка
Р0 отображается на точку Ра, которая
тоже принадлежит единичной
окружности (рис. 436).
Поставим в соответствие каждому углу
а определенное число уа — ординату
точки Ра. Эту ординату называют синусом
угла α и обозначают sin α, т. е. уа = sina.
Тем самым мы определили функцию,
называемую синусом. Рис. 436
269
^ jf—
P^o°/\
Pso°[^\
4\ /Ί
P \^ /
Ί2θ\ /
P1C J^-,
150 p^
180°
l
-R30°
/W _/
G/
^\-180°-150o-120° у
к со
/J
/90°-60°-30° 0
-/
$ a
X 120 150° 180°_
30* 60° 90\
ОС
Рис. 437
A sin α
Po-180°-WO~120O'90° -60°-30°
30°
30° 60° 90° 120° 150°180 <*
Рис. 438
Областью определения функции sin (читается: синус)
является все множество угловых величин. А областью значений —
промежуток [—1, 1], так как ординаты точек J?a, лежащих на
единичной окружности, могут принимать значения от —1 до 1.
Аналогично поставим в соответствие каждому углу а
абсциссу ха точки Ра. Эту абсциссу называют косинусом угла а
и обозначают cos α, т. е. *а= cos а. Получим функцию,
называемую косинусом. Областью определения функции cos
(читается: косинус) является все множество угловых величин, а
областью значений — промежуток [—1, 1].
2. На рисунках 437 и 438 показаны значения функций sin
и cos для данных на этом рисунке углов. При увеличении угла α
от 0° до 90° значения функции sin увеличиваются от 0 до 1,
а значения функции cos уменьшаются от 1 до 0.
На тех же рисунках показаны графики функций sin и cos
для углов, принадлежащих промежутку [—180°, 180°]. При
любом целом η поворот на угол β = а + 360° · η совпадает с
поворотом на угол а. Поэтому Ра+Шо,п = Ра при любом целом
п. Значит, *а+360..я = ха, уа+ж,,п = уа, т. е.
sin (α + 360° · η) = sin α,
cos (α + 360° · η) = cos α.
270
(1)
sinoc к
Рис. 439
COSOC 1
7]
Рис. 440
Любой угол β можно представить в виде β = α + 360° · п9
где η — целое число, а α находится в пределах —180° ^ а ^
^ 180°. Поэтому достаточно изучить поведение функций sin
и cos на промежутке [—180°, 180°].
Равенства (1) означают, что функции sin и cos «периодиче-
ские> с «периодом» 360°. Подробнее вы займетесь свойствами
периодичности тригонометрических функций в 9 классе.
Наличие у синуса и косинуса периода в 360° позволяет представить
себе, как выглядят графики этих функций и за пределами
промежутка [—180°, 180°] (рис. 439 и 440).
Вопросы и задачи
1051. Постройте окружность, уравнение которой Xх + У2 = 4.
1) Лежат ли на этой окружности точки: а) А (2, 0); б) -8(1, 1);
в) С (—2, 0); г) D(—1, 1)? 2) Запишите координаты каких-
либо четырех точек, лежащих на этой окружности.
1052. Какие координаты будет иметь точка, симметричная точка
Μ (0,8; 0,6) относительно: 1) начала координат; 2) оси у;
3) оси jc?
1053. На окружности, уравнение которой x2 + y2=^, дана
точка М(х\, у\). Постройте эту окружность и укажите возмож-
271
ное положение точки М, если известно, что: 1) xt = 0,3;
2) ух = 0,3; 3) χι = ух; 4) х, = -у,; 5) |х, | = 0,5;
6) Ιί/. |=0,5.
1054. Укажите координаты точки единичной окружности: 1) <Р9о°*
2) Р1в0.; 3) Р_90л 4) Р_180.; 5) Р270 ; 6) Р_270,.
1055. Чему равны синус и косинус следующих углов: 1) 90°; 2) 180°;
3) -90°; 4) -180°; 5) 270°; 6) -270°?
1056. Существует ли такой угол а, для которого: 1) sin α = 0;
2) sin α = — 1; 3) sin α = ; 4) sina=—; 5) sina = ;
5 2 6
6) sin a = —2? Постройте этот угол, если он
существует.
1057. Определите знак синуса угла: 1) 122°; 2) 90°30'; 3) — 103°;
4) 270°; 5) 450°; 6) -725°; 7) 1100°.
1058. На миллиметровой бумаге постройте окружность
единичного радиуса, отметьте на ней точки: -Ρ2ο» ^45 » ^60=» ^во3·
Найдите значения sin 20°; sin 45°; sin 60°; sin 80°.
1059. Запишите в порядке возрастания: sin 20°; sin 45°; sin 90";
sin 30°; sin 60°; sin 70°.
1060. Существует ли угол α, для которого: 1)cosa = —1;
2 5 11
2) cos a = 0; 3) cos a = —; cos a = ; 5) cos a = —;
3 4 12
6) cos a = —2? Постройте этот угол, если он существует.
1061. Определите знак косинуса угла: 1) 170°; 2) —91°; 3) 0о20г;
4) 290°; 5) —640°; 6) 530°; 7) 3660°.
1062. На миллиметровой бумаге постройте окружность
единичного радиуса, отметьте на ней точки Р20 ; Р45\ -^бо > ^scr
и найдите значения cos 20°; cos 45°; cos 60°; cos 80°.
1063. Запишите в порядке возрастания: cos 20°; cos 45°; cos 90°;
cos 30°; cos 60°; cos 70°.
1064. Существует ли угол α, для которого: 1) sin a = cos a;
2) sin a = —cos a?
1065. Отложите на координатной плоскости вектор ОА,
координаты которого равны: 1) (1, 0); 2) (0, 1); 3) (—1, 0);
4) (—1, 1); 5) (1, —1); 6) (1, 1). Найдите величину угла,
образованного вектором ОА с положительным
направлением оси х.
1066. Отложите от начала координат вектор, имеющий
координаты: а) (|, θ); б) (0, 5); в) (2, -2); г) (-3, 2); д) (4, 3).
1067. Отметьте на координатной плоскости хОу точки М, А,
272
В, С и найдите составляющие векторов ОМ, ОА, ОВ, ОС по
осям χ и у,
1068. Координаты вектора а равны 3 и —4. Постройте
составляющие вектора а по осям координат.
1069. Даны составляющие вектора а по осям координат: αν —
= —2i, ay = 3;. Постройте вектор а.
1070. Выразите координаты вектора через тригонометрические
функции угла а, образованного этим вектором с
положительным направлением оси х, если даны координаты этого
вектора: 1) (0, 2); 2) (2, 0); 3) (—f. |)г 4) (2, -2); 5) (1,1).
75. Некоторые тождества для функций синус и косинус
Если точка Ра единичной окружности не лежит на осях
координат, то точки Ра, О и Q (проекция точки Ра на ось х) являются
вершинами прямоугольного треугольника (рис. 441). По
теореме Пифагора получаем:
«г + у\ = к
sin2a + cos2a = 1. (1)
В случае, когда точка Ρ лежит на одной из осей координат
(ха = 0, уа = ±1 или уа = 0, ха = ±1), координаты точки
Ρ также удовлетворяют соотношению (1).
Перейдем к выводу других формул. Заметим сначала, что
точка <Р180о_а является образом точки Ра при симметрии
относительно оси у (рис. 442). Поэтому ординаты этих точек
совпадают, а их абсциссы противоположны:
*180э-а = Ха*
#180 -а = Уа'
Рис. 441
Рис. 442
273
Рис. 443
%0
У
с/
\4£
0
уа
Ι χ
Рис. 444
Рис. 445
Значит,
cos (180° — α) = —cos α,
sin (180° — α) = sin α.
(2)
Точки Ρα и Ρ_α симметричны
относительно оси χ (рис. 443). Поэтому,
(п. 73)
Х-а =
У-а =
Следовательно,
cos (—α) =
sin (—α) =
*α.
—Уа*
cos α,
—sin α.
(3)
При повороте на 90° (рис. 444),
точка Рп отображается на точку Ροη0, .
^_^ а уи ~t~Ct
Поэтому (см. рис. 444)
X,
90°-f-a
"Уа·
У,
90°+а Ха'
Значит,
cos (90° + °0 = —sin a,
sin (90° + a) = cos a.
(4)
Точки Pa и P90o_a симметричны
относительно оси Ζ, содержащей
биссектрису угла хОу (рис. 445). Поэтому
Значит,
*9(Γ-α Уа9
Уы°-а = Ха"
cos (90° — a) = sin a,
sin (90° — a) = cos a.
COS a sin a
(5)
274
Замечание. Из первой формулы (5) вытекает, что
график функции sin получается из графика функции cos
параллельным переносом вдоль оси α вправо на расстояние,
соответствующее углу 90° (рис. 446).
Вопросы и задачи
1071. Вычислите значение cos α, если: 1) sin α = 0,6, 0° < α <C 90°;
2) sin α = 0,96, 90° < α < 180°; 3) sin α = 0,8, 0°< α < 90э;
4) sin α =-ί 90° < α < 180°; 5) sin a=¥L, 0° < α < 180°.
3 2
1072. Вычислите значение sin α, если: 1) cos α = —, 0° < α < 90°;
2) cos α = —0,5, 90° < α < 180°; 3) cos α = 0,6, 0°<α<90°;
4) cos α = — \, 90°< α <180°; 5) cos α =ίΑ, 0°<α<180°.
1073. Упростите выражение: 1) 1 —cos2 α; 2) sin2 α— 1; 3) ;
1—sin2a
4) sin2 a + cos2 a — 1; 5) 2 sin2 a + cos2 a — 1; 6) sin a X
X (1 — cos2 a); 7) 2 — sin2 a — cos2 a; 8) (1 — sin a) (1 + sin a).
1074. Выразите через значение тригонометрической функции
положительного угла, меньшего 90°: 1) sin 100°; 2) sin 160°;
3) cos 170°; 4) sin 95Ί6'; 5) sin 103°45'; 6) cos 124Ί5'.
1075. Выразите через значения тригонометрических
функций положительных углов, меньших 90°: 1) sin (—70°);
2) cos (—70°); 3) sin (—20°); 4) cos (—20°); 5) sin (—45°);
6) cos (—45°).
1076*. Докажите, что: 1) sin (a + 180°) =—sin a; 2) cos(a+180°) =
= —cos a; 3) (cos a — sin a) (cos a + sin a) = 1 — 2 sin2 a;
4) sin (90° — a) cos (180° — a) = —cos2 a;
5) cos (90° — a) sin (180° — a) = sin2 a.
76. Таблицы синусов и косинусов
Значения синусов и косинусов углов а, где 0° ^ а ^ 90°,
находят по таблицам. В школе употребляются четырехзначные
математические таблицы.
Заметим сначала, что равенства
sin (90° — a) = cos a,
cos (90° — a) = sin a,
275
известные из пункта 75, позволяют находить значения синусов
и косинусов, пользуясь лишь одной таблицей.
Рассмотрим примеры нахождения значений синуса и
косинуса по их аргументам.
Синусы
А
70°
71°
72°
73е
74°
0'
0,9397
9455
9511
9563
9613
60'
16
9403
9461
9516
9568
9617
54'
12'
9409
9466
9521
9573
9622
48'
18'
9415
9472
9527
9578
9627
42'
24'
9421
9478
9532
9583
9632
36'
30'
9426
9483
9537
9588
9636
30'
1 36'
9432
9489
9542
9593
9641
24'
42'
9438
9494
9548
9598
9646
18'
48'
9444
9500
9553
9603
9650
12'
1 54'
9449
9505
9558
9608
9655
6'
60'
0,9455
9511
9563
9613
9659
0'
19°
18°
17°
16°
15°
А
1'
1
1
l\
l\
1
ν
2'
2
2
2
2
2
2'
3'
з\
з\
з\
2\
2\
3'
Косинусы
Пример 1. Найти sin 70°36'.
Находим число градусов в крайнем левом столбце таблицы,
число минут — в верхней части таблицы. На пересечении
соответствующей строки и столбца находим искомое число:
sin 70°36' = 0,9432*.
Пример 2. Найти sin 74°55\
В таблице находим синус угла, ближайшего к данному:
sin 74°54' = 0,9655. Затем в столбцах поправок (в правой
стороне таблицы) находим поправку на 1'. Эта поправка равна 0,0001.
Учитывая, что при возрастании угла от 0° до 90° синус
также возрастает, найденную поправку прибавляем. Таким
образом,
sin 74°55' = 0,9655 + 0,0001 = 0,9656.
Пример 3. Найти cos 16°12'.
Число градусов ищем в правой стороне таблицы (в
столбце А4), число минут — в нижней строке таблицы. На пере-
* В записях табличных данных вместо знака приближенного равенства
(=г) обычно пишут знак равенства (=).
276
сечении соответствующих строки и столбца находим искомое
число:
cos 16°12' = 0,9603.
Пример 4. Найти cos 18э50'.
По таблицам находим значение косинуса угла, ближайшего
к данному: cos 18°48' = 0,9466. В столбце поправок находим
поправку на 2'. Эта поправка равна 0,0002. Учитывая, что при
возрастании аргумента от 0° до 90° значения косинуса убывают,
найденную поправку надо вычесть. Поэтому
cos 18°50' = 0,9464.
По этим таблицам можно решать и задачи, обратные
рассмотренным: по данным значениям синуса и косинуса
некоторого угла находить этот угол.
Пользуясь формулой 2 из пункта 74 и формулами 2—5 из
пункта 75, нахождение синуса (косинуса) любого угла можно
свести к нахождению синуса или косинуса угла, лежащего в
пределах от 0° до 90°.
Примеры.
1) sin (—72°) =± —sin 72° = —0,9511;
2) cos (—108°) = cos (90° + 18°) = —sin 18° = —0,3090;
3) sin 430° = sin (360° + 70°) = sin 70° = 0,9397;
4) cos 550° = cos (2 · 360° — 170°) = cos (—170°) =
= cos (180° — 10°) = —cos 10° - —0,9848.
Вопросы и задачи
1077. Найдите по таблицам значения синусов и косинусов
следующих углов: 1) 40°; 2) 14°36'; 3) 25°54'; 4) 40°56'; 5) 80°03';
6) 89°50'; 7) 0°54'; 8) 105°; 9) 160°; 10) 170°; 11) —40°;
12) —110°; 13) —1000°; 14) 1100°.
1078. Найдите по таблицам величину острого угла х, зная синус
или косинус этого угла: 1) sin х = 0,0175; 2) sin x = 0,5015;
3) sin χ = 0,5814; 4) cos x = 0,0670; 5) cos x = 0,5673;
6) cos χ = 0,9047.
1079. Вычислите без помощи таблиц: 1) sin 30° + cos 60°;
2) sin 90° —sin 180°; 3) sin 90° + cos 90°; 4) sin (—180°) +
+ cos (—90°).
277
77. Тангенс
1. Отношение
называется тангенсом угла а и
обозначается tg a.
Функция tg определена для тех углов а, для которых cos а Φ
Φ 0. Ha промежутке [—180°, 180°] имеются два угла, для
которых cos а = 0, — это углы 90° и —90°. Следовательно, tg a
не определен при α = 90° и а = —90°.
Значения функции tg а для углов а от 0° до 90° даны в
четырехзначных математических таблицах. Описание таблиц
«Тангенсы» содержится в объяснительном тексте к ним.
Τ На рисунке 447 показано, как строится график тангенса
для углов а, если —90° < а < 90°. В силу подобия треуголь-
бОЖ
Q-n
ников OEQa и ОМаРа имеем:
0 Ж 60°с< 90° а
Рис. 447
\ОЕ\
РаМа\
\ОМ„\
sin a
cos a
= tga.
Но IOJE71 = 1, и,
следовательно, \EQa\ = tga. T
2. Рассмотрим прямую Ζ,
проходящую через начало
координат (рис. 448). Ее
уравнение: у = kx. Коэффициент k
называется угловым
коэффициентом этой прямой.
Пусть Μ — произвольная
точка прямой I. Ее координаты
равны: χ = \ОМ\ cos а и у =
= \ОМ\ sin α. Координаты
точки Μ удовлетворяют
уравнению этой прямой. Поэтому
\ОМ\ sin a = k \OM\ cos a.
Отсюда
sin a
cos a1
т. е.
Рис. 448
k = tg a.
278
Прямые с уравнениями у=кхиу=кх-\-Ь параллельны
(см. рис. 448), так как их угловые коэффициенты равны. Верно
и обратное: если угловые коэффициенты двух прямых равны, то
эти прямые параллельны.
Вопросы и задачи
1080. 1) Вычислите без помощи таблиц: a) tg 45°; б) tg (—45°);
в) tg 0°; г) tg 30°; д) tg 60°; е) tg 180°.
2) Не прибегая к таблицам, укажите наименьшее
положительное значение а, при котором: a) tg α=1; б) tg α= —1.
1081. Докажите, что: 1) tg(—α) = —tg α; 2) 1 + tg2 α = ——.
cos2 α
1082. Найдите по таблицам значения тангенса угла: 1) 5°; 2) 25°;
3) 35°42'; 4) 46°56'; 5) 80°03'; 6) 89°50'.
1083. Найдите по таблицам острый угол х, если: 1) tg χ = 0,3227;
2) tg χ = 0,7846; 3) tg χ = 1,4632; 4) tg χ=6,152; 5) tg x=
= 17,89; 6) tg x= 156,3.
1084. 1) Найдите угловой коэффициент прямой: а) 2х—ι/ + 3 = 0;
б) 4х + Ау — 5 = 0; в) у = 5х — 7; г) у = х\ д) у = 5.
2) Параллельны ли прямые, заданные уравнениями: а) 4х +
+ Ау = 5; и у = х + 1; б) Ах + Ау = 5 и у = — 2 — х?
3) Постройте прямую, уравнение которой: а) х=2; б) у = Ъ;
в) у = 0,5*; г) у = X) д) у = —х; е) 2х + Ъу = 0.
78. Соотношения между сторонами
и углами прямоугольного треугольника
Рассмотрим прямоугольный треугольник ABC с катетами
а, & и гипотенузой с. Выберем прямоугольную систему
координат так, как показано на рисунке 449. Пусть Ρ — точка
пересечения луча АВ с единичной
окружностью, Рх и Ρу — проекции этой
точки на оси координат. Тогда по
определению синуса и косинуса
\ОРх\ = cos X, \ОРу\ = sin А. Из
подобия треугольников АРРХ и ABC
получаем:
. = LFP^J = йпА = s.n λ
с | АР | 1
У1
А
0
ι
с/
РЛ
h I
3
a
с х
Рис. 449
279
ν b \ΛΡΧ\ cos A 7
— =J —' = = cos Α.
с \АР\ 1
Отсюда:
. ^ sinA a
tgA= —- = -.
cos A
Треугольник, как вы знаете, определяется тремя
элементами. В прямоугольном треугольнике один элемент — прямой
угол — всегда известен. Поэтому прямоугольный треугольник
определяется двумя другими основными элементами, из которых
хотя бы один является его стороной.
Выпишем некоторые из формул, связывающие элементы
прямоугольного треугольника:
А + В = 90°; (1)
(2)
(3)
а2
sin A =
cos A =
+ г>2
а
с
Ъ
с
• = с2;
ήηΒ =
cos В
ъ
с
=
»
а и
с
(4)
tg-A = 7-, tgS=-. (5)
b a
Формулы 3—5 можно прочитать так:
Синус острого угла прямоугольного треугольника равен
отношению противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника равен
отношению прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника равен
отношению противолежащего катета к прилежащему.
Решим несколько задач на вычисление элементов
прямоугольного треугольника по двум его известным элементам.
Задача 1. Дано: а, Ъ. Требуется найти: А, Б, с.
1) tg А = — (формула 5); величину угла А находим из
b
таблиц.
2) В = 90° — А (формула 1).
3) с = —^ (формула 3).
sin A
Задача 2. Дано: а, с. Требуется найти: А, В, Ъ.
1) sin А = — (формула 3); величину угла А находим из
с
таблиц.
280
2) В = 90° — А (формула 1).
3) Ъ = с sin Б (формула 3).
Задача 3. Дано: а, А. Требуется найти: В, &, с.
1) В = 90° — А (формула 1).
2) & = a tg Б (формула 5).
3) с = —^ (формула 3).
sin Л
Задача 4. Дано: а, В. Требуется найти: А, &, с.
1) А = 90° — В (формула 1).
2) Ъ = α tg Б (формула 5).
3) с = —— (формула 3).
sin A
Задача 5. Дано: с, А. Требуется найти: В* а, 6.
1) В = 90° — А (формула 1).
2) α = с sin А (формула 3).
3) Ъ = с cos А (формула 4).
Вопросы и задачи
1085. Формулу a=btgA можно прочитать так: катет
прямоугольного треугольника равен другому катету,
умноженному на тангенс угла, противолежащего первому катету. Про-
читайте формулы: 1) Ъ = с cos А; 2) а = с sin A;
3) с = —-; 4) с = —-.
sin A cos А
1086. Найдите, не прибегая к таблицам, значения: 1) sin 30°;
2) sin 45°; 3) sin 60°; 4) sin 90°; 5) cos 45°; 6) cos 60°;
7) tg 30°; 8) tg 45°; 9) tg 60°.
1087. Постройте прямоугольный треугольник. Выполните
необходимые измерения и вычислите значения тригонометрических
функций его углов.
1088. Вычислите неизвестные стороны и углы прямоугольных
треугольников по следующим данным:
1) по двум катетам:
а) α = 2,61, & = 3,80; б) α =13,6, Ь = 8,23?
в) α =4,35, &=1,45; г) а =156, & = 133;
281
Рис. 450
2) по гипотенузе и катету:
а) с = 65, a = 63; б) с = 6,91, a = 5,28;
в) с = 113, Ь = 112; г)с = 0г140г & = 0,1;
3) по катету и противолежащему ему углу:
а) α = 63,7, А = 85°25'; б) a = 18,0, А = 17°;
в) Ъ = 1,74, В = 24°05'; г) Ъ = 2,95, В = 25°36';
4) по катету и прилежащему к нему углу:
a) a = 6,37, В = 29°42'; б) α = 380, Б = 34°29';
в) Ъ = 528, А = 49Ί 5'; г) Ъ = 3,92, А = 65Ί 4Г;
5) по гипотенузе и острому углу:
а) с = 4,67, А = 65Ί 5'; б) с = 62,8, А = 23°32';
в) с = 0,798, Б = 45°30'; г) с = 9,42, В = 68°04'.
1089. Найдите расстояние от наблюдателя, находящегося на
высоте 30 м, до автомашины, которая видна наблюдателю под
углом 20° (рис. 450).
1090. Пользуясь рисунком 451, объясните, как можно
определить угол подъема α дороги, зная пройденное по дороге
расстояние / и высоту подъема h.
1091. Найдите угол подъема шоссейной дороги, если на
расстоянии 200 м высота подъема
составила 6 м.
1092. Горная железная дорога на
одном из перегонов поднимается на
1 м на каждые 60 м пути. Найдите
угол подъема дороги на этом уча-
282
1093. На какую высоту h поднялся пешеход, прошедший / км по
прямой дороге, поднимающейся под углом α к горизонту?
Вычислите Л, если: 1) /=1,5 км, α = 4°30'; 2)а = 3 км,
а = 8°18'.
1094. Насыпь, поперечное сечение которой представляет собой
равнобедренную трапецию, имеет у основания ширину 12 м.
Высота насыпи 3 м. Какова ширина верхней части насыпи,
если угол откоса равен 39°?
Дополнительные задачи к главе VII
1095. Композицией какого наименьшего числа поворотов на 70°
является поворот на 10°?
1096. При каких значениях ft:
1) Ra = Ra+90°'k; 2) Ra = да+45°·*?
1097. При каких значениях ft:
1) ЛаоД4= Д«+Р+«°·*. 2) RaoRt= д«+3+бов.*?
1098. 1) На единичной окружности найдите такие точки Ра,
V2 1 1
для которых a) sin a = f-^~; б) sin α = —; в) cosa = ~;
ч 1
г) cos a = .
2) В каждом из этих случаев (см. задачу 1): а) укажите
наименьшие положительные значения а; б) запишите все
множество углов поворотов, соответствующих точкам Ра .
1099. 1) Какие значения может принимать сумма: а) sinx + 1;
б) cos χ + 0,5; в) sin2 χ + cos2 xl
2) Какие из следующих равенств воз-
ч 2γτηη Лч .
можны: а) cos a = » о) sina^=
ι 1 ч πι1 Λ- η2,
= т -\— ; в) cos a = —!— , где т
m m2 — nl
и п — положительные числа?
1100. Укажите знак разности:
1) sin 31° — sin 30°; 2) sin 26° —
- sin 27°; 3) cos 30° - cos 31 °;
4) cos 27° — cos 26°.
1101. При каких значениях ft:
1) sin a = sin fa + —ft ];
2) cos a = cos/a + —ft j?
Рис. 452
233
1102. Докажите, что если А, В и С — углы треугольника, то:
1) sin A = sin (В + С); 2) cos A = —cos (Вί + С).
1103. Чтобы измерить высоту объекта, основание которого
доступно, измеряют базис \АС\ и угол α прямоугольного
треугольника А\ВС\ (рис. 452). Докажите, что Η = \АС\ tga + Л,
где h — высота угломерного инструмента.
1104. В момент времени, когда высота солнца .равна а,
измерили длину тени от мачты. Она оказалась равной а м.
Выразите через α и α высоту мачты. Вычислите высоту мачты,
если: 1) а = 15 м, α = 47°; 2) а = 18 м, α = 43°30'.
ГЛАВА VIM
МЕТРИЧЕСКИЕ СООТНОШЕНИЯ
В ТРЕУГОЛЬНИКЕ
§ 1. Теоремы косинусов и синусов
79. Теорема косинусов
В конце предыдущей главы были
получены соотношения между сторонами
и углами прямоугольного треугольника.
Перейдем к изучению соотношений
между сторонами и углами
произвольного треугольника.
81 |.Теорема (косинусов). Квадрат
стороны треугольника равен
сумме квадратов двух других сторон
без удвоенного произведения этих
сторон на косинус угла между
ними:
а2 = Ь2 + с2 — 2Ъс cos А.
Доказательство. Угол А
треугольника ABC может быть
острым, тупым или прямым. Рассмотрим
каждый из этих случаев.
1) Угол А острый. Проекция
вершины С (обозначим ее через D) на
сторону АВ может занимать три положения.
Точка D может лежать: а) между
точками А и В (рис. 453, а); б) по одну
сторону с точкой В от точки А
(рис. 453, б), и, наконец, в) точка D
может совпасть с точкой В (рис. 453, в).
Обозначив проекции отрезков АС
A/
L
"лсх
by/
be
с
he
V
Oc\
D
" I
β A
B=D
и ВС на сторону АВ через Ъс и ас, а высоту CD через Лс, в
случаях а) и б) по теореме Пифагора получим:
а2 = ft* + а*, (1)
(2)
Ъ2 = Ъ% — Ъ*.
с с
Эти равенства справедливы и в случае в) (ас = О, Ьс = с).
Выразим а2 через &с и с. Заметим, что ас равно либо с — Ьс
(см. рис. 453, а), либо Ъс — с (см. рис. 453, б), либо 0 (см. рис.
453, в). Но в каждом из этих случаев
а2 = (с — bcf = с2 — 2сЪс + Ъ2С. (3)
Подставляя выражение h2 (см. (2)) и а2 (см. (3)) в равенство
(1), получим:
а2 = Ь2 _ Ъ2 + с2 _ 2сЪс+ Ь2 = Ь2 + с2 _ 2с&^
Но Ъс = Ъ cos А. Следовательно,
а*
Ь2 + с2 — 2Ьс cos А.
2) Угол А тупой (рис. 454). Проведем через вершину С
перпендикуляр CD к прямой АВ и рассмотрим прямоугольные
треугольники BCD и ACD. По теореме Пифагора получаем:
а*
Ь2 — U2
hc + аС9
Ъ2 - Ь\.
(4)
(5)
Выразим ас через Ъс и с:
а2 = (Ъс + с)2 = Ь2 + 2сЪс + с2. (6)
Подставим выражение Щ (см. (5)) и а\ (см. (6)) в
равенство (4):
а2 = h] + а2 = (Ъ2 — Ъ2С) + (Ь2 + 2сЪс + с2) =
= &2 + 2с&, + с2.
286
Рис. 454
Но Ьс = Ь cos (180° — А) = — Ь cos А.
Поэтому а2 = &2 + с2 — 2bc cos А.
3) Угол А прямой (рис. 455). В этом
случае cos A = 0. Пользуясь теоремой
Пифагора, получаем:
аз = ь2 + с2 = б2 + с2 — 2Ьс cos А. В
Формула
а2 = &2 + с2 — 2&с cos а (7)
позволяет вычислять длину одной из
сторон треугольника по данным длинам двух
других сторон и величине угла, лежащего
против неизвестной стороны.
С помощью теоремы косинусов можно также по данным
сторонам треугольника найти его утлы. В самом деле, из
равенства (7) следует:
tf + c2 — а1
1)=А
Рис. 455
COS α =
2bc
Вопросы и задачи
1105. Запишите, пользуясь теоремой косинусов, квадрат
стороны с треугольника ABC, если: 1)γ = 60°; 2) γ = 30°;
3) γ = 45°.
1106. Пользуясь формулой α2 = b2 + с2 — 2bc cos α, исследуйте
как изменяется сторона а при возрастании угла α от 0° до
180° (при постоянных значениях Ъ и с).
1107. При каких значениях угла α квадрат стороны треугольника,
лежащей против этого угла: 1) меньше суммы квадратов
двух других сторон; 2) равен сумме квадратов двух других
сторон; 3) больше суммы квадратов двух других сторон?
1108. Не вычисляя величины углов треугольника, укажите вид
каждого из треугольников (относительно углов), если его
стороны равны: 1) 7; 8; 12; 2) 0,3; 0,4; 0,5; 3) 15; 15; 15;
4) 8; 10; 12.
1109. Вычислите неизвестную сторону треугольника ABC по
следующим данным: 1)α = 7, &=10, ν = 56°29'; 2) а = 2,
с = 3, β = 123Ί7'; 3) Ь = 0,4, с = 1,2, а = 23°28,i
287
1110. Докажите, что сумма квадратов диагоналей
параллелограмма равна сумме квадратов его сторон.
1111. Вычислите больший из углов треугольника ABC, если:
1) а = 3, Ь = 4, с = 6; 2) а = 40, Ъ= 13, с = 37; 3) а = 13,
Ъ = 5, с = 12; 4) а = 19, Ъ = 80, с = 63.
1112. Выразите диагонали параллелограмма через стороны а,
Ъ и его угол α и вычислите их при: 1) а = 12 дм, Ъ = 15 дм,
α = 52°; 2) α = 3,5 дм, Ъ = 3,5 дм, α = 100°.
80. Формулы для вычисления площади треугольника
Одна из формул для нахождения площади треугольника
известна: S = —. Выведем другую формулу.
82 I Теорема. Площадь треугольника равна половине произ-
I ведения двух его сторон на синус угла между ними:,
S = — Ъс sin α.
2
Доказательство. Обозначим высоту CD
треугольника ABC через hc (см. рис. 453). Выразим hc через сторону Ъ и
синус угла а. Для этого надо рассмотреть несколько случаев.
Но во всех этих случаях hc = Ъ sin α:
hc = b sin α (см. рис. 453, α, 6),
hc = b sin (180° — a) = b sin α (см· рис. 454),
hc = b = b sin a (a = 90°) (см. рис. 455).
Подставляя в формулу
S=-chc
2 с
выражение hc, получим:
S = — bc sin a. ■
2
у Древнегреческий математик Герон Александрийский (I в.
н. э.) получил замечательную формулу для вычисления
площади треугольника по его трем сторонам:
S =Vp(p — a)(p — b)(p — c),
где ρ — половина периметра треугольника.
Дадим вывод этой формулы.
288
Пусть α, Ь, с — стороны треугольника, а α, β, γ —
величины его углов. Обозначим через ρ полупериметр этого
треугольника:
а -1- b -I- с
р =—!——·
2
По теореме косинусов
cos а = —! .
2Ъс
Из формулы S — —be sin α находим:
2S
since = —.
be
Подставляя найденные выражения sin α и cos α в формулу
sin2 α + cos2 α = 1, получим:
/2S\2 /frg + c8 — α2 \8_ t
Отсюда, применяя формулу разности квадратов, имеем:
~2 _ 4Ь2с2 — (б2 + с2 — в2)'2 _ ((6 + с)а — а2) (а2 — (Ь — с)2; _
~~ 16 ~~ 13
а -\- b -\- с b -\- с — а а -\- b — с a j-c — b
"~ 2 2 2 2 ~~
= Р(Р — а)(р — Ь)(р—с)\
S = Vp(p-a)(p-b)(p-c). т
Вопросы и задачи
1113. Пользуясь формулой S = — α6 sin у, исследуйте, как
будет изменяться площадь треугольника ABC при
возрастании γ от 0° до 180° (а и & постоянны). При каком значении
γ площадь треугольника ABC будет наибольшей?
1114. Вычислите площадь равнобедренного треугольника,
боковая сторона которого равна 10 м, а угол при вершине равен
75°20'.
1115. Вычислите площадь треугольника ABC, если: 1) а= 125 м,
Ь = 160 м, γ = 52°; 2) Ъ = 20 см, с = 35 см, α = 79°06'.
289
1116. Докажите, что площадь параллелограмма равна
произведению длин его смежных сторон на синус угла между ними.
1117*. 1) Докажите, что площадь параллелограмма равна
половине произведения его диагоналей на синус угла между ними.
2) Вычислите площадь параллелограмма, если известны его
диагонали d\ и d2 и угол α между ними: a) d\ = 10, d2 = 15,
α = 57°; б) dx = 12, d2 = 42, α = 49°.
1118. Вычислите площадь ромба: 1) по его стороне а = 7,5 см и
острому углу а = 22°10Г; 2) по его диагонали т = 4,5 см и
углу α = 150°, лежащему против этой диагонали.
1119*. По формуле Герона вычислите площадь треугольника, если
его стороны равны 32 см, 18 см и 22 см.
81. Теорема синусов ,
83|Теорема. Стороны треугольника пропорциональны си-
I нусам противоположных углов.
Доказательство. Рассмотрим треугольник ABC
со сторонапи а, &, с и углами α, β, γ.
По теореме 82 из предыдущего пункта
S = — be sin a = — ас sin β = —ab sin γ.
2 2 r 2 r
Отсюда
be sin α = ас sin β и ас sin β = ab sin γ.
Значит, b sin α = α sin β и с sin β = b sin γ, а так как синус
каждого из углов α, β, γ не равен нулю, то
abbe
= и = .
sin a sin β sin β sin у
Следовательно,
a b с
= -7-7Г = " · ■
sin α sin p sin γ
Теорема синусов позволяет по двум данным сторонам и углу,
лежащему против одной из них (или по стороне и двум углам),
вычислять остальные элементы треугольника.
Вопросы и задачи
1120. Вычислите стороны и углы треугольника, если:
1) а = 109, β = 33°24', у = 66°59';
2) с = 16, α = 143°08', β = 22°37';
290
3) a = 20, 6=13, α = 67°23';
4) α = 37, с = 59, у = 23°20'.
1121. Выведите формулу, по которой может быть вычислен один
из неизвестных элементов треугольника ABC, если
известны элементы: 1) а, & и γ; 2) а, & и а; 3) а, & и с.
1122. Диагональ параллелограмма длиной т образует со
сторонами этого параллелограмма углы α и β. Выразите длины
сторон параллелограмма через т, а и β.
1123. Две силы Ρ и Q приложены к материальной точке. Угол
между их направлениями а. Найдите величину
равнодействующей.
1124. Вычислите составляющие силы Р= 5,2 Н, если эти
составляющие перпендикулярны друг другу и одна из них составляет
с направлением силы Ρ угол α = 46°.
1125*. Докажите: площадь четырехугольника равна половине
произведения его диагоналей на синус угла между ними.
§ 2. Некоторые применения
подобия и формул
тригонометрии
82. Применение подобия
к решению задач
1. Во многих задачах на
построение данные в условии задачи
можно разбить на две такие
группы, что одна определяет форму,
а другая — размеры искомой
фигуры.
Для решения таких задач
сначала строят фигуру, подобную
искомой. Затем, используя
сведения о размерах, строят искомую
фигуру. Рассмотрим примеры.
Задача 1. Построить
треугольник ABC no углам а
и β и биссектрисе 1С (рис. 456, а).
Решение. Проведем
анализ. Предположим, что задача
решена и треугольник ABC
(рис. 456, б) искомый. Рис 456
291
Углы α и β определяют множество
треугольников, подобных искомому
треугольнику ABC. Если, например, через
произвольную точку Αι луча С А провести
прямую ΑιΒι параллельно стороне АВ, то
получим один из треугольников (AAiBiC),
подобных искомому, так как А4 = a, J3± =
= β. Такой треугольник построить можно,
взяв сторону A{Bi произвольной длины.
Заметим теперь, что треугольник AtBtC
подобен искомому треугольнику, но его
биссектриса не равна 1С. Поэтому для
решения задачи остается построить
треугольник, подобный треугольнику AiBfi
и имеющий биссектрису 1С. Для этого
достаточно построить отрезок CD длины 1С
и через точку D провести прямую,
параллельную прямой ΑιΒι.
Выполнив указанные построения (рис. 456, б), получим
треугольник ABC. Этот треугольник искомый. В самом деле,
стороны углов А и Аг соответственно сонаправлены. Поэтому
(п. 37)
Аналогично
А = А{ = а.
В = В{ = β.
Кроме того, по построению луч CD — биссектриса угла С
треугольника АВС> причем \CD\ = lc.
Задача 2. В данный остроугольный треугольник вписать
квадрат так, чтобы две его вершины лежали на основании, а две
другие — на боковых сторонах этого треугольника.
Решение. Проведем анализ. Допустим, что искомый
квадрат MNPQ построен (рис. 457, а). Тогда квадрат,
гомотетичный искомому (с центром гомотетии в точке А), построить
нетрудно: проведем прямую M0N0> перпендикулярную прямой
АС, и построим квадрат со стороной M0/V0.
Две вершины построенного квадрата лежат на стороне АС,
а третья вершина — на боковой стороне АВ треугольника ABC.
Остается построить квадрат, который обладает этими же свой-
292
ствами и, кроме того, его четвертая вершина лежит на стороне
ВС. Этим требованиям удовлетворяет квадрат с вершиной в
точке Ρ (см. рис. 457, а).
Перейдем к построению. Построим квадрат со стороной Μ0Ν0
и проведем через точку Р0 и вершину А прямую АР0. Эта
прямая пересечет сторону ВС в некоторой точке Р. Построим
прямоугольник PNMQ. Этот прямоугольник является квадратом
(он гомотетичен квадрату M0N0P0Q0), две его вершины лежат
на основании, а две другие — на боковых сторонах этого
треугольника. Следовательно, квадрат MNPQ искомый.
Эту задачу можно решить и другим способом.
Обозначим длину стороны искомого квадрата через ху
длину основания данного треугольника через Ъ и длину
соответствующей высоты через А. Из подобия треугольников ABC
и NBP (рис. 457, б) получаем:
1 — h
χ h — χ
Выполнив преобразования, находим:
Ь + h _ Ь_
h χ
Отрезок, длина которого равна х, может быть найден
построением четвертого пропорционального (см. п. 65).
Составленное уравнение позволило нам найти неизвестную
величину, что и привело к решению задачи. Этот метод решения
задач на построение называется алгебраическим методом.
Задача 3. Ε двум данным окружностям построить общую
касательную.
Ψ Решение. Пусть даны две окружности различных
радиусов, расположенные, как показано на рисунке 458. Заметим,
что эти окружности гомотетичны и центр гомотетии лежит на
прямой 001. Действительно, проведем радиусы этих
окружностей ОА, 0{А{ и ΟιΑ2, лежащие на параллельных прямых. При
гомотетии, переводящей окружность (О, г) в окружность (Οι, г4),
точка О отображается на точку Ои а прямая О А — на
параллельную ей прямую 0\А[. Точка пересечения окружности
(О, г) и прямой О А при этой гомотетии отображается на точку
пересечения их образов. Отсюда получаем, что при этой
гомотетии точка А отображается на точку Αι или А2. Поэтому центр
гомотетии, отображающей окружность (0>г) на окружность (Оиг{),
293
Рис. 458
лежит и на прямой OOiy и на прямой ААХ (или АА2)·
Следовательно, центр Ρ (или Q) этой гомотетии может быть построен —
это точка пересечения прямых 001 и Α Αχ (или прямых 001
и АА2).
Заметим теперь, что прямая, проходящая через точку Ρ (или
Q), при гомотетии с центром Ρ (или Q) отображается на себя, а
окружность (О, г) — на окружность (0lt /ί). Следовательно,
касательная, проведенная из точки Ρ к одной из данных
окружностей, является касательной и к другой окружности, т. е.
является их общей касательной. Таким образом, решение задачи
свелось к построению касательной к одной из данных
окружностей из точки Ρ (или из точки Q). Это построение уже
известно (п. 30).
В зависимости от взаимного расположения данных
окружностей и их радиусов задача может иметь четыре решения (две
внутренние и две внешние касательные, рис. 458), три, два,
одно решение или ни одного. Τ
2. Рассмотрим пример решения задачи на доказательство.
Задача 4. Доказать, что медианы треугольника
пересекаются в одной точке и делятся в ней в отношении 2 : 1,
считая от вершины*.
Доказательство. Разделим медиану ААХ в
отношении 2:1 и точку деления обозначим через М, т. е.
|AAf| : IAfi4.il =2:1 (рис. 459). Тогда достаточно доказать,
* Точка пересечения медиан треугольника называется его центром тяжести.
294
что Μ 6 ΙΒΒιΊ, Μ 6 [CCi], и выполня- β
ется равенство:
\АМ\ _\ВМ\ _ \СМ\ _2
\МАХ\ ~~ \МВХ\ ~~ \МСХ\ ~ 1*
Рассмотрим гомотетию Н-0^5.
Образом точки А при этой гомотетии
является точка Α ι. а а, и
Образом отрезка АВ является парал-
„ Рис. 459
лельныи ему отрезок, имеющий вдвое
меньшую длину (п. 63). Отсюда следует, что образ отрезка АВ
совпадает со средней линией АХВГ треугольника ABC
(поскольку лучи АВ и ΑιΒι противоположно направлены).
Следовательно, образом точки В является точка В\.
Поэтому Μ 6 IBBi] и \ВМ\ : \МВ{\ =2:1.
Рассуждая аналогично, получаем, что образом стороны АС
является средняя линия A iC4 и потому Μ 6 [СС4] и
\СМ\ : \Md\ =.2:1. ■
Вопросы и задачи
1126. Постройте треугольник, подобный данному, площадь
которого составляет: 1) половину площади данного
треугольника; 2) четвертую часть площади данного треугольника.
1127. Постройте ромб по данному отношению диагоналей и
данной стороне.
1128. Постройте параллелограмм по отношению диагоналей, углу
между диагоналями и стороне.
1129. Постройте трапецию: 1) по двум углам, прилежащим к
одному основанию, этому основанию и отношению его к
высоте; 2) по отношению ее оснований, двум углам при одном
из этих оснований и высоте.
1130. В данный равносторонний треугольник впишите другой
равносторонний треугольник так, чтобы стороны его были
перпендикулярны сторонам данного треугольника.
1131. В данный треугольник впишите прямоугольный
равнобедренный треугольник так, чтобы вершины его лежали на сторонах
данного.
1132. В данный ромб впишите квадрат, вершины которого лежат
на сторонах ромба.
295
1133*. В данный сегмент впишите прямоугольник с данным
отношением сторон т : η так, чтобы две вершины
прямоугольника лежали на хорде, а две другие — на дуге сегмента.
1134. В данный сектор впишите квадрат так, чтобы две его
вершины лежали на радиусах, а две другие — на дуге сектора.
1135. В данный треугольник впишите прямоугольник с данным
отношением сторон так, чтобы две вершины
прямоугольника лежали на боковых сторонах треугольника, а две
другие— на его основании.
1136. Постройте треугольник, подобный данному, и такой, что
его вершины лежат на сторонах данного треугольника.
1137*. Найдите множество точек, отношение расстояний которых
до сторон данного выпуклого угла равно т : п.
1138*. Найдите множество точек, делящих в данном отношении
отрезки прямых, параллельных данной прямой и
заключенные между сторонами данного угла.
1139*. Через точку внутри угла проведите прямую так, чтобы
отрезок прямой, отсекаемый сторонами угла, делился этой
точкой в данном отношении.
1140. В данный угол впишите окружность, проходящую через
данную внутри угла точку.
1141. В окружности (О, г) проведена хорда. Проведите два радиуса
этой окружности так, чтобы они делили эту хорду на три
конгруэнтных отрезка.
1142. Постройте общие касательные к двум данным окружностям
разных радиусов, если эти окружности: 1) не имеют общих
точек; 2) имеют внешнее касание; 3) пересекаются.
1143. На рисунке 460 изображен измерительный прибор,
позволяющий с точностью до 0,1 t^M. измерять толщину
различных изделий. Разъясните устройство этого прибора.
1144. На рисунке 461 изображен измерительный прибор,
позволяющий определять величину зазора между двумя
стенками детали, внутренний диаметр трубок и т. д. Объ-
Рис. 460
296
ws/λ
W^'
ясните, на чем основано устройство этого
прибора.
1145. На рисунках 462 и 463 показано, как можно
отрезок АВ разделить в данном отношении
т : η (внутренним и внешним образом).
Объясните этот способ.
1146. На рисунке 464 показано, как можно
разделить на равные части различные бруски,
планки, используя для этого
разграфленную доску. 1) Укажите, на основании какой
теоремы геометрии можно установить
справедливость этого приема. 2) Покажите, как
можно при помощи этого устройства
разделить данный брусок АВ в отношении 1 : 2;
1:3; 2:3.
1147. На рисунке 465 показано, как можно
разделить ширину доски на равные части,
используя линейку с имеющимися на ней
равными делениями. Из какой теоремы геометрии следует
справедливость такого приема? Как можно, пользуясь такой
линейкой, разделить ширину доски в отношении 2:1; 3:1;
3:2; 1:4?
Рис. 461
\AD\_m
\DB\~ η
\AD\_ т
\BD\~ η
Рис. 462
Рис. 463
/f//;w/s/^ww/////Mu
Рис. 464
Рис. 465
297
1148. Разметьте на местности участок, имеющий форму
многоугольника. Снимите план этого участка в выбранном
масштабе и определите по плану площадь участка.
83. Измерительные работы
1. Измерение высоты предмета. Пусть требуется измерить
высоту предмета, основание которого недоступно (рис. 466).
Воспользуемся следующим приемом. На прямой, проходящей
через основание Μ предмета ВМ> выберем две точки Ао и Со.
Измеряем базис |.АоСо| = Ъ и углы BAD = а и BCD = β
(А 6 (CD), (CD) || (АоСо)).
По теореме синусов из треугольника ABC имеем:
|АВ| _ | AC \ sin β _ *>8ίηβ
11 sin В sin (α-β)"
Из прямоугольного треугольника ABD имеем: | BD | =
= | АВ | sin α.
гл ι nni & sin α · sin β
Следовательно, \BD\ = --*-.
sin (α — β)
А так как \ВМ\ = \BD\ + Л, то
\ВМ\= &sinasinP +h.
1 ' sin (α — β)
2. Измерение расстояния до недоступной точки. Расстояние
от точки А до недоступной точки В на местности можно найти,
пользуясь признаками конгруэнтности треугольников. Проще
это сделать, если воспользоваться признаками подобия
треугольников или формулами тригонометрии.
Для этого на местности выбирают точку С, измеряют
отрезок АС и углы А и С (рис. 467). Затем на листе бумаги строят
в каком-нибудь масштабе отрезок AiC4 и ZLAi^Z_A,
/L С{ £ё Ζ- С. Получают Δ А^В^С^
По второму признаку
подобия Δ ABC ~ Δ AiBiCi (п. 67).
β Поэтому \АВ\: \А{В{\ =
= \АС\: 1-AiCil. Из этой
пропорции находим \АВ\\
1 ' ИА1
λ^Ά
Μ
ссу
Рис.
h
/4(7
466
h
!о
298
Для измерения расстояния | АВ \
можно применить и иной способ.
Измерив расстояние \АС\ =
= Ъ и углы ВАС = а, ВС А = у
(см. рис. 467), находим (по
теореме синусов):
\АВ\ =1АС18^У =
sin В
frsin у & sin v
~~ sin (180°—(α + ν)) ~~ sin (α + у) '
Рис. 467
Рис. 468
Вопросы и задачи
1149. На рисунке 468 изображен
четырехугольник ABCD и
указаны длина его стороны
\AD\ = а, величины углов
A, BDA, BDC, CBD.
Найдите расстояние \ВС\.
1150. По одну сторону реки отмечены две точки А и В, Вычислите
расстояние между точками С и D, находящимися по другую
сторону реки, если \АВ\ = а = 3784 м, ВАС = α =87°25'г
BAD = β = 47°32,| ABC = δ = 46°34,| ABD = у = 84°35'.
1151. Практическая работа. Выполните на местности одну
из измерительных работ (измерение высоты предмета,
основание которого недоступно, измерение расстояния до
недоступной точки и т. п.).
84 Τ - Решение треугольников
В пункте 78 были рассмотрены задачи на построение
треугольников по трем элементам. Теперь мы рассмотрим эти же
задачи с вычислительной точки зрения. По трем элементам
Треугольника будем вычислять оставшиеся три.
Задача 1. Дано: а, &, у. Требуется вычислить с, α, β.
Решение.
с2 = а2 + Ь2 — 2аЪ cos γ;
b2 -f- с2 — 2bc cos а, поэтому cos а
β = 180° — (а + γ).
Ь2 + с2
2bc
299
Пример 1. Вычислить длины сторон и величины углов
треугольника: если а = 49,4; Ъ = 26,4; γ = 47°20\
Решение.
с2 = (49,4)2 + (26,4)2 — 2 · 49,4 - 26,4 - 0,6778 = 1369,
с = 1/Ί369 = 37,0;
697 + 1369 — 2440 374 Л л м
cosa = ! = « — 0,191;
2· 26,4 37,0 1954
угол α тупой, по таблицам находим угол 180° — ос.
180° — а = 79°, а = 180° — 79° = 101°.
β = 180° — (101° + 47°20') = 31°40'.
Задача 2. Дано: α, β, у. Требуется вычислить &, с, а.
Решение.
а = 180° - (β + γ);
a b , a sin ββ α с a sin γ
"» О =■ ; ; - — — , С = ; .
sin a sin β sin a sin a sin у sin a
Пример 2. Вычислить длины сторон и величины углов
треугольника, если а = 17Α, β = 44°30', у = 64°.
Решение.
а = 180° — (44°30' + 64°) = 71°30';
, 17,4-0,7009 .ОЛ 17,4-0,8988 ла к
k = ~ 12,9; с = —■ » 16,5.
0,9483 0,9483
Задача 3. Дано: а, 6, с. Требуется вычислить α, β, у.
Решение.
£2 _1 с2 а2
а* = Ь2 -{- с2— 26ccosa, поэтому cosa
2Ьс
b . 0 b sin a
-, отсюда sin β =
sin a sin β α
γ = 180° —(a + β).
Пример 3. Вычислить величины углов треугольника,
если а = 24, Ъ = 13, с = 15.
Решение.
169 + 225 — 576 182 7 Л , „„„
cos a = ! = = « —0,4667,
2 · 13 · 15 390 15
угол α тупой, следовательно, a = 180° — 62°11' = 117°49\
. Q 13. sin 117 49' 13sin62 11' 13 · 0,8845 п .„п
sin β = = = ! « 0,4790.
r 24 24 24
β = 28°37'.
у = 180D — (117°49' + 28°37') = 180° — 146°26' = 33°34'.
300
^Задача 4. Дано: α, &, α. Требуется найти β, γ и с.
Напомним, что еще в пункте 22 мы обнаружили, что
соответствующая задача на построение может с точностью до
конгруэнтности иметь одно или два решения или же совсем не иметь
решений. Естественно, что это обстоятельство надо учитывать
при вычислениях.
Решение.
а Ь . η Ь sin α
= , поэтому sin ρ = .
sin α sin β α
Приходится различать три случая:
1) Ъ sin α > α; 2) b sin a = a; 3) b sin a < a.
1) В первом случае решений нет (sin β не может быть
больше единицы).
2) Во втором случае β = 90°, у = 90° — а, с = b cos a.
Решение единственно.
3) Пусть b sin a < а. Тогда существуют два угла, синусы
которых равны sm — один из этих углов острый, а другой
а
тупой. Приходится различать два случая:
3') а > Ъ\ 3") а < Ъ.
3') Если a ^ by то α ^ β (теорема 50), а так как у
треугольника не может быть двух тупых углов, то β — острый угол и
решение единственно.
3") Если а < Ь, то существуют два угла βι и β2 (β2 = 180°—β4),
b sin a
синусы которых равны .
a
В этом случае задача имеет два решения:
Vx = 180° — a — β1τ cx = n ·
γ2 = 180°-α-β2,
sin a
о о «sin γ2
sin a
Π ρ и м е ρ 4 (a ^ &). Вычислить длину стороны и
величины углов треугольника, если а = 12, 6 = 10, a = 40 .
Решение.
. о 10sin40° 5-0,6428 Л кос_
sin β = = : = 0,5357,
12 б
так как 12 > 10, то β = 32°23';
γ = 180° — 40° — 32°23' = 107с37';
12 · sin 107 37' л- 0
с = = 17,8.
0,6428
301
Π ρ и м е ρ 5. (α < &). Вычислить длину стороны и
величины углов треугольника, если а = 3, Ъ = 5, β = 6°19'.
Решение.
sin β = -sin6°19' = i · 0,11 = 0,1833;
3 з
так как 3 < 5, то β! = 10°33', β> - 169°27'.
Vi = 180° — α — β! = 163°08\ γ2 - 180° — α — β2= 4°14'.
3 · sin 163'08' _ 7 q. _ 3 ■ sin 4 14' __« Π1
0,11 ί 0,11
Вопросы и задачи
1152. Решите треугольник по двум сторонам и углу, заключенному
между ними, если:
1) о = 28, с = 42, β = 124°;
2) о= 13, & = 20, γ =75°0Γ;
3)с = 143, Ь = 260, а = 82°07';
4) о = 325, с = 728, β = 97°53'.
1153. Решите треугольник по стороне и двум углам, если:
1) а = 13, α = 52°08\ β = 67°23';
2)6 = 8,5, а = 8Г12', β = 24ΊΓ.
1154. Решите треугольник по трем сторонам, если:
1)о = 37, Ь=13, с = 40;
2) а = 44. Ъ = 37, с = 15.
1155. Решите треугольник по двум сторонам и углу, лежащему
против одной из них, если:
1)α = 34, & = 93, Α = 14Ί5',·
2) с = 24, & = 83, С = 26°45'.
1156. Решите треугольник по стороне и двум углам, если:
1) а = 4, β = 24°57', γ = 57°30';
2) а = 37, β = 86°03', γ = 50с56'.
Дополнительные задачи к главе VIII
1157. Диагональ прямоугольника равна т, угол между
диагоналями а. При каком значении α площадь прямоугольника
наибольшая?
302
1158. Диагонали параллелограмма равны тип, угол между
диагоналями а. При каком значении α площадь этого
параллелограмма будет наибольшей? Какой вид имеет параллелограм/л
в этом случае?
1159. Вычислите наибольший из углов треугольника ABC, если
даны три его стороны: 1) α = 3, Ъ = 4, с = 6; 2) а = 40,
Ъ = 13, с = 37; 3) а = 16, Ъ = 12, с = 20.
1160. Две силы Ρ = 100 Η и Q = 200 Η приложены к
материальной точке под углом α = 50° друг к другу. Определите
величину равнодействующей R и углы, которые она составляет
с направлениями Ρ и Q.
1161. В равнобедренный треугольник ABC
вписаны два квадрата (рис. 469).
Основание ВС треугольника равно а,
величина угла А равна а. 1) Найдите
отношение площадей вписанных
квадратов. 2) Произведите вычисления,
р,сли: а) α = 60°; б) α = 45°.
1162. В треугольник, основание которого
равно а, а высота, проведенная к
основанию, равна А, вписан
прямоугольный равнобедренный
треугольник так, что гипотенуза параллельна
основанию треугольника, а вершина
прямого угла лежит на этом
основании. Найдите площадь вписанного
треугольника. Вычислите эту площадь,
если а = 30 см, h = 10 см.
1163. В данный параллелограмм впишите
ромб так, чтобы стороны ромба
были параллельны диагоналям
параллелограмма, а вершины ромба
лежали на сторонах параллело- рис 470
грамма.
1164. В треугольник ABC вписан квадрат
(рис. 470). Найдите площадь
квадрата, если \АС\ =а и высота
образует с боковыми сторонами углы α
и β. Вычислите эту площадь, если:
1) а = 6 см, а = 30°, β = 40°;
2) а = 4,5 см, а = 70°, β = 20°. Рис. 471
Рис. 469
С
303
1165. На рисунке 471 изображен план участка, выполненный в
масштабе: 1:1000. Произведите необходимые измерения
и вычислите площадь участка.
1166. Докажите, что для любого треугольника справедливо
соотношение а = Ь cos С + с cos В.
1167. Докажите, что для любого треугольника
и 111
а : Ъ : с = — : — : —.
ha hb К
1168. Постройте треугольник, если известны три его высоты.
1169. В данный сектор впишите прямоугольник с данным
отношением сторон т : η {т — 2, η = 3).
ГЛАВА ΙΛ
ВПИСАННЫЕ И ОПИСАННЫЕ
МНОГОУГОЛЬНИКИ
§ 1. Треугольники
и четырехугольники
85. Вписанный угол
1. Выпуклый угол, вершина которого
принадлежит окружности, а стороны
пересекают ее, называется вписанным
углом. Например, угол ABC (рис.
472) вписанный. Он опирается на
дугу АС.
84|Теорема.Величина вписанного
угла равна половине угловой
величины дуги, на которую он
опирается.
Доказательство.
Рассмотрим три случая расположения центра
окружности относительно данного
вписанного угла.
1) Центр окружности лежит на
стороне вписанного угла (рис. 473, а).
Вы знаете, что величина
центрального угла равна угловой величине
соответствующей ему дуги (п. 28).
Проведем отрезок ОА и рассмотрим
центральный угол АОС. Он является
внешним углом треугольника BOA. По
свойству внешнего угла треугольника
АОС = ОВА + ОАВ.
Но ОВА = ОАВ, так как треугольник
АОВ равнобедренный (| О В \ = \ О А \ = Я),
Рис. 472
Рис. 473
а углы ОВА и ОАВ — углы при
основании равнобедренного треугольника.
Следовательно,
АОС = 2АВС. (1)
По свойству центрального угла (п. 28)
АОС = АС.
Из равенств (1) и (2) следует, что
ABC
(2)
±АС.
2
Для первого случая теорема доказана.
2) Центр окружности лежит
внутри вписанного угла (рис. 473, б).
Проведя луч ВО у представим данный угол
в виде суммы двух углов — ABD и
ВВС.
АвЬ = ABB + ВВС.
Общая сторона ВВ этих углов проходит
через центр окружности. '
Значит, по доказанному
АВВ= ~^AD>
ВВС = ^ DC.
Отсюда
ABC = ABB + ВВС =
= -АВ +
2
- ВС = - АС.
2 2
Теорема доказана и для второго случая.
3) Центр окружности лежит вне вписанного угла (рис. 473, в).
Для этого случая доказательство проведите самостоятельно.
Следствие. Вписанный угол, опирающийся на диаметр,
прямой.
2. Рассмотрим задачу на построение отрезка, среднего
геометрического между двумя данными отрезками.
Определение. Отрезок χ называется средним
геометрическим (или средним пропорциональным) между
отрезками т и τι, если выполняется равенство т : χ = χ : η.
Задача. Построить отрезок, средний геометрический
между двумя данными отрезками тип (рис. 474, а).
306
a)
δ)
Решение. Мы знаем, что высота
прямоугольного треугольника,
проведенная к гипотенузе, разбивает этот
треугольник на два подобных треугольника
(пункт 68). Это свойство
прямоугольного треугольника позволяет найти
решение.
В самом деле, рассмотрим
прямоугольный треугольник ABC и проведем его
высоту CD (рис. 474, б). Тогда:
ABCD ~ ACAD.
Следовательно,
\вр\ =\ср\
\CD\ \AD\
Таким образом, высота
прямоугольного треугольника является средним
геометрическим между полученными
отрезками гипотенузы. Отсюда вытекает,
что для решения задачи достаточно
построить прямоугольный треугольник по
его гипотенузе с = т + п, зная при этом,
что его высота должна пройти через
общую точку отрезков тип. Выполним
это построение.
1. На произвольной прямой отложим
отрезок АВУ равный сумме данных отрезков тип.
Обозначим общую точку данных отрезков через D (рис. 474, в).
2. Через точку D проведем прямую, перпендикулярную
прямой АВ.
3. На отрезке АВ как на диаметре построим окружность.
Обозначим через С одну из точек пересечения этой окружности
с построенной прямой.
4. Рассмотрим треугольник, вершинами которого являются
точки А, С и В. Этот треугольник прямоугольный (угол С
вписанный, опирающийся на диаметр). Его высота h является
средним геометрическим между данными отрезками тип.
Решение единственно. Всякий другой треугольник,
отвечающий заданным условиям, например треугольник ABCi (см.
рис. 474, в), конгруэнтен треугольнику ABC и высоты этих
треугольников равны.
Рис. 474
307
Вопросы и задачи
1170. Окружность разделена на пять конгруэнтных дуг:
kjAB ^ kjBC & куСО ^ё kjDE ^ kjEA. Вычислите величины
вписанных в эту окружность углов ВАС, BAD, BAE, CAE
и DAE.
1171. Хорда АВ делит окружность на две дуги АМВ и АТВ.
Вычислите величины вписанных в эту окружность углов
АМВ и АТВ, если: 1) АМВ : АТВ = 2 : 3; 2) АМВ : АТВ =
= 4:5.
1172. Углы АМС и АТС вписаны в одну и ту же окружность. Что
можно сказать о величинах этих углов?
1173. Центральный угол на 35° больше вписанного угла,
опирающегося на ту же дугу. Вычислите величину каждого из этих
углов.
1174. Хорда делит окружность на две дуги. Под какими углами
видна хорда из точек окружности, если угловые величины
этих дуг относятся как: 1) 5:4; 2) 7:3?
1175. 1) Постройте центр данной окружности с помощью одного
чертежного угольника.
2) Конгруэнтные углы ABC и ADC опираются на отрезок АС,
и их вершины лежат по одну сторону от прямой АС.
Докажите, что точки А, В, С и D принадлежат одной
окружности.
1176. Постройте отрезок, средний геометрический между двумя
данными отрезками тип.
1177. Постройте прямоугольный треугольник, если известно, что
его высота, проведенная к гипотенузе, делит ее на отрезки
в 2 см и 3 см.
1178*. Дана прямая а и точка D, лежащая вне этой прямой. На
прямой а даны отрезок АВ и точка Μ—середина этого
отрезка. Через точку D проведите прямую, параллельную
прямой а, пользуясь только линейкой, не имеющей делений.
1179. Докажите, что величина угла, образованного касательной и
хордой, имеющими общую точку на окружности, равна
половине угловой величины дуги, лежащей внутри этого угла.
1180*. Докажите, что величина угла между двумя касательными
к окружности, проведенными через одну точку, равна
полуразности угловых величин дуг, заключенных между его
сторонами.
308
1181*. Докажите, что величина угла с вершиной внутри круга
равна полусумме угловых величин двух дуг, из которых одна
заключена между сторонами этого угла, а другая — между
продолжениями сторон.
1182*. Докажите, что величина угла между двумя секущими,
пересекающимися вне круга, равна полуразности угловых
величин большей и меньшей дуг, заключенных между его
сторонами.
86. Вписанные и описанные треугольники
1. Многоугольник, все вершины которого принадлежат
окружности, называется вписанным в эту окружность, а
окружность — описанной около этого многоугольника (рис. 475).
85 I Теорема. Около любого треугольника можно описать ок-
I ружность, и притом только одну. Центр этой окружности —
I точка пересечения серединных перпендикуляров к сторо-
| нам треугольника.
Доказательство. 1) Центр О окружности,
описанной около треугольника ABC, должен быть удален от всех
вершин треугольника на одно и то же расстояние R (рис. 476).
Значит, в частности, должно выполняться
равенство \ОА\ = \ОВ\. Поэтому точка О
должна принадлежать серединному
перпендикуляру к отрезку АВ. Так как | О А \ =
= \ОС\9 то центр Одолжен принадлежать
серединному перпендикуляру к отрезку
АС. Указанные серединные перпендикуляры
пересекаются. Их точка пересечения О
равноудалена от всех вершин треугольника и, Рис. 475
значит, является центром описанной
окружности. 2) Точка О принадлежит также и
серединному перпендикуляру к отрезку ВС,
так как \ОВ\ = \ОС\. Значит, серединные
перпендикуляры к сторонам треугольника
пересекаются β одной точке — центре
описанной окружности. ■
Центр окружности, описанной около
треугольника, лежит внутри его, если он
остроугольный (рис. 477, а), и вне — если Рис. 476
309
Θ β
7—^ ft β)
Рис. 477
тупоугольный (рис. 477, б). Центр окружности, описанной
около прямоугольного треугольника, является серединой его
гипотенузы (рис. 477, в).
2. Многоугольник, все стороны которого касаются
окружности, называется описанным около этой окружности, а
окружность — вписанной в этот многоугольник (рис. 478).
86 Ι Τ е о рема. Во всякий треугольник можно вписать ок-
I ружность, и притом только одну. Центр этой окружности —
| точка пересечения биссектрис треугольника.
Доказательство. 1) Центр окружности, вписанной
в данный треугольник, должен быть равноудален от всех его
сторон (рис. 479). Поэтому он должен быть равноудален от
сторон АВ и АС, а также от сторон АВ и ВС. Значит, центр
принадлежит биссектрисе угла А, а также биссектрисе угла В.
Указанные биссектрисы пересекаются. Их точка пересечения
равноудалена от всех сторон треугольника и, значит,
является центром вписанной окружности. 2) Обозначим точку
пересечения биссектрис AD и BE через О. Она удалена от всех
Рис.478 Рис. 479
310
сторон треугольника на одно и то же расстояние. Поэтому
точка О принадлежит и биссектрисе угла С. Значит, биссектрисы
углов треугольника пересекаются в одной точке. ■
Вопросы и задачи
1183. 1) В данный треугольник впишите окружность.
2) Постройте окружность, описанную около данного
треугольника.
1184. 1) В данную окружность впишите равносторонний
треугольник.
2) Около данного равностороннего треугольника опишите
окружность.
1185. Вычислите радиус окружности, описанной около
прямоугольного треугольника, если отношение его катетов равно ОД
а высота, проведенная к гипотенузе, равна 12 см.
1186. В прямоугольном треугольнике катеты равны 12 см и 16 см.
Вычислите радиус: 1) вписанной в него окружности; 2)
описанной окружности.
1187. Вычислите радиус окружности, вписанной в равносторонний
треугольник, высота которого ft (ft = 1 см; 2,5 см).
1188. Докажите, что сумма диаметров вписанной и описанной
около прямоугольного треугольника окружностей равна сумме
его катетов.
1189. Какой вид имеет треугольник, если: 1) центры вписанной и
описанной около него окружности совпадают; 2) центр
описанной окружности лежит на его стороне; 3) центр вписанной
окружности лежит на одной из его высот; 4) центр
описанной окружности лежит на одной из его высот или на
продолжении высоты?
1190*. Постройте окружность, касающуюся трех данных прямых,
попарно пересекающихся и не проходящих через одну
точку.
1191**. Впишите в данную окружность треугольник, подобный
данному.
1192. Докажите, что площадь треугольника равна произведению
его полупериметра на радиус вписанной окружности.
1193*. Докажите, что радиус R окружности, описанной около
треугольника, может быть вычислен по формулам:
1) R = -^; 2) R = Н£.
' 2hc 4S
311
87 Τ . Вписанные и описанные четырехугольники
В пункте 86 было доказано, что
около любого треугольника можно
описать окружность и в каждый
треугольник можно вписать окружность. Для
четырехугольников эти свойства не
выполняются. Конечно,
четырехугольники, около которых можно описать
окружность, существуют (рис. 480, а).
Но не каждый четырехугольник можно
вписать в окружность (рис. 480, б)
и не каждый четырехугольник
описанный (рис. 480, в).
87 | Τ е о ρ ем а,.Сумма
противоположных углов вписанного
четырехугольника равна 2d.
Доказательство. Пусть
четырехугольник ABCD вписан в
окружность (О, г). Тогда по теореме о
вписанном угле
-BCD, C=-DAB
2 2
А =
Следовательно,
А + С =.-
1
(рис. 481).
- BCD + - DAB
2 2
(BCD-{-DAB).
Рис. 481
Но объединение дуг BCD и DAB есть
окружность. Следовательно, сумма
величин углов А и С равна угловой
величине полуокружности, т. е.
A +C=2d.M
Итак, для того чтобы около
четырехугольника можно было описать
окружность, необходимо, чтобы сумма его
противоположных углов была равна 2d.
Это условие и достаточно для того,
чтобы четырехугольник был вписанным.
Докажем это.
312
38|Теорема. Если сумма двух
противоположных углов
четырехугольника равна 2d, то около этого
четырехугольника можно описать
окружность.
Доказательство.
Рассмотрим четырехугольник ABCD, у
которого сумма углов В и D равна 2d:
В + D = 2d.
Проведем через вершины А, В и С
четырехугольника окружность. Для
доказательства теоремы необходимо
показать, что четвертая вершина D не
может лежать внутри этой окружности
или вне ее.
Допустим, что точка D лежит внутри
окружности (рис. 482, а). Тогда
В + D = 2d (по условию теоремы),
В + Ε = 2d (по теореме 87).
Отсюда следует: D = Е, что
невозможно (внешний угол треугольника
EDC не может быть конгруэнтным его
внутреннему углу Е). Значит,
допущение неверно: точка D не может лежать
внутри построенной окружности.
Аналогично доказывается, что
вершина D не может лежать и вне этой
окружности (рис. 482, б).
Итак, вершина D не может лежать
ни внутри окружности, ни вне ее.
Следовательно, точка D должна лежать на
этой окружности, т. е. около четырехугольника ABCD можно
описать окружность. ■
89 I Теорема. Суммы противоположных сторон описанного
I четырехугольника равны.
Доказательство. Пусть стороны четырехугольника
ABCD касаются окружности (О, г) соответственно в точках ЛГ,
Р, Q, N (рис. 483). Тогда по свойству касательных, проведенных
313
Рис. 483
из одной точки (п. 30), имеем:
\АМ\ = \ANU \ВМ\ = \ВР\, \CQ\ = \CP\, \DQ\ =\DN\.
Сложив эти равенства почленно, получим:
\АВ\ + \CD\ = \AD\ + \ВС\. ■
Итак, необходимое условие того, чтобы в четырехугольник
можно было вписать окружность, получено. Оказывается, что
для выпуклых четырехугольников это условие и достаточно.
901 Теорема. Если суммы противоположных сторон вы-
I пуклого четырехугольника равны, то в этот четырехуголь-
I ник можно вписать окружность.
Вопросы и задачи
1194. Постройте квадрат: 1) вписанный в данную окружность;
2) описанный около данной окружности; 3) по радиусу
описанной окружности; 4) по радиусу вписанной окружности.
1195. Можно ли описать окружность около четырехугольника
ABCD, углы которого соответственно равны: 1) 90°, 90°, 60°,
120°; 2) 70°, 130°, 110°, 50°; 3) 45°, 75°, 135°, 105°?
1196. Можно ли описать окружность около четырехугольника
ABCD, углы которого относятся как числа: 1) 2, 3, 4, 3;
2) 7, 2, 4, 5?
1197. Докажите: 1) любая трапеция, вписанная в окружность,
равнобедренная; 2) любой параллелограмм, вписанный в
окружность,— прямоугольник; 3) любой ромб, вписанный в
окружность,— квадрат.
1198. Можно ли вписать окружность в четырехугольник, стороны
которого, взятые последовательно, относятся как числа:
1) 2, 2, 3, 3; 2) 2, 5, 3, 4; 3) 3, 5, 3, 1?
1199. Постройте прямоугольник по радиусу описанной около него
окружности и углу между диагоналями.
1200. Постройте ромб по радиусу вписанной в него окружности
и стороне.
1201*. Впишите в данную окружность прямоугольник, подобный
данному.
1202*. Общая хорда двух пересекающихся окружностей длиной m
служит для одной из них стороной равностороннего
вписанного треугольникам для другой — стороной вписанного
квадрата. Вычислите расстояние между центрами окружностей,
если m = 2 см.
314
§ 2. Правильные многоугольники
88. Построение правильных многоугольников
Рис. 484
1. Разделим окружность на η (η > 2) конгруэнтных дуг. Это
можно сделать, построив последовательно центральные углы,
величина каждого из которых равна (рис. 484). Соединим
πόα
следовательно точки деления хордами. Получим л-угольник,
вписанный в эту окружность. При повороте вокруг цент-
360° „ -
ра окружности на угол а = построенный η-угольник отоб-
п
ражается на себя. Значит, все стороны полученного л-уголь-
ника и все его углы конгруэнтны.
Определение. Многоугольник, у
которого все стороны конгруэнтны и
все углы конгруэнтны, называется
правильным.
Правильный многоугольник можно
построить и таким образом. -
Разделим окружность на η
конгруэнтных дуг (п > 2). Через точки деления
проведем касательные к этой
окружности (рис. 485). Образованный при
этом многоугольник (его вершинами
служат точки пересечения касательных,
проведенных через соседние точки
деления) будет правильным.
2. Вы знаете, что около
правильного треугольника и около квадрата
(правильного четырехугольника) можно
описать окружность. Оказывается, это
верно для любого правильного
многоугольника.
91 | Теорема. Около всякого
правильного многоугольника можно
описать окружность.
Доказательство. Построим
биссектрисы двух соседних углов А
и В этого многоугольника (рис. 486).
Они пересекутся, так как 1+2 < 2d. Рис. 486
Рис. 485
315
Точку О пересечения этих биссектрис
соединим отрезками с остальными
вершинами данного многоугольника.
Так как углы А и В конгруэнтны,
то конгруэнтны и их половины: Z_l^ Z-2.
Значит, треугольник АОВ
равнобедренный и [ОА] & [ОБ].
Рассмотрим треугольники АОВ и ВОС.
Рис. 487 Отрезок ОВ — их общая сторона, [АВ] ^
^ [ВС] (по условию), Z.2 ^ /JZ ЦВО) —
биссектриса угла В). Следовательно, ААОВ ^ АВОС, откуда
[ОБ] ^ [ОС]. Итак, [ОА~\ ^ [ОБ] ^ [ОС]. Рассматривая теперь
треугольники АОВ и COD, АОВ и Ζ>0£ и т. д., приходим
к выводу:
\ОА\ = |ОБ| = |ОС| = ... = \OL\.
Отсюда следует, что все вершины данного многоугольника
лежат на окружности с центром О. ■
3. Докажем, что во всякий правильный многоугольник
можно вписать окружность.
92 8 Τ е о ρ е м а. Во всякий правильный многоугольник можно
^вписать окружность.
Доказательство. Проведем через центр О
окружности, описанной около правильного я-угольника ABC ... Μ,
перпендикуляры к его сторонам (рис. 487). Обозначим их
основания через Аь Бь Сь ..., М^ При повороте вокруг центра О
на угол многоугольник и окружность (О, г) отображаются
η
на себя (объясните почему). Поэтому точка Αι отобразится на
точку Bi, точка Б4 — на точку С4 и т. д. Точка М{ отобразится
на точку Αι, Следовательно, |OA4| = |OBi| = |OC4| = ... =
= |Oiifi| и, значит, точки Al9 Бь Си ···> Mi лежат на одной
окружности с центром О. А так как по построению (ОAi) J_
J_ (АВ), (ОВι) _L (ВС), ..., то любая сторона данного
многоугольника касается этой окружности. ■
Центры вписанной и описанной около правильного
многоугольника окружностей — одна и та же точка. Эта точка (ее
называют также центром правильного многоугольника)
является центром поворотов, отображающих этот правильный
многоугольник на себя.
316
Отрезок OAi (см. рис. 487) перпендикуляра, проведенного
из центра правильного многоугольника к его стороне,
называется апофемой правильного многоугольника (апофема является
радиусом вписанной окружности).
Вопросы и задачи
1203. Вычислите: 1) внутренние, 2) внешние углы правильного
л-угольника (п = 3, 4, 5, 6, 8, 10, 12).
1204. Найдите число сторон правильного многоугольника, если
1) его угол равен: а) 135°; б) 150°; в) 140°; 2) его внешний
угол равен: а) 36°; б) 24°; в) 60°.
1205. Докажите, что центральный угол правильного
многоугольника конгруэнтен его внешнему углу.
1206. Постройте правильный л-угольник по стороне (п = 5, 6, 8).
1207. Впишите в данную окружность правильный л-угольник (п=3,
4, 6, 8, 12).
1208. Опишите около данной окружности правильный л-угольник
(п = 3, 4, 6, 8).
1209*. При каких перемещениях отображается на себя: 1)
правильный пятиугольник; 2) правильный шестиугольник?
1210*. 1) Сколько осей симметрии имеет правильный п-угольник?
2) Сколько существует поворотов, отображающих на себя
правильный л-угольник?
3) Каждый ли правильный многоугольник имеет центр
симметрии?
89. Формулы для вычисления стороны и площади
правильного многоугольника
Сторона ап правильного я-угольника находится по формуле
ап = 2 Д sin ,
η
где R — радиус описанной около этого
/г-угольника окружности.
В самом деле, пусть [ АВ] — сторона
правильного η-угольника, вписанного в
окружность радиуса R (рис. 488), и (ОМ) J_
1 (АВ). Тогда
^\ 1 ^ 1 360° 180°
АОМ = 2АОВ = -· — = — ·
317
Из прямоугольного треугольника АОМ:
\АМ\= \АО\ sin АО Μ = R sin —
Но \АВ\ = 2 \АМ\.
18 ОJ
Итак, ап = 2R sin . ■
η
Следствие 1. αύ = R.
Действительно,
180
6
Следствие 2. а4 = Л ^2
180°
а6 = 2Л sin
2i?sin 30r = 2R · - -=Л.
2
а4 = 2Д sin -^- = 2Д sin45°=i?K2.
а3 =
93
Следствие 3. αό
180°
2R sin
3
- R J/3.
2i?sin60J =i?K3.
Рис. 490
Теорема. Площадь правильного
многоугольника равна половине
произведения его периметра на радиус
вписанной окружности.
S= -Pr,
2
где Ρ — периметр многоугольника, а г — радиус вписанной в
него окружности.
Доказательство. Разобьем правильный п-угольник
на η треугольников, соединяя отрезками вершины я-угольника
с центром вписанной окружности (рис. 489). Эти треугольники
1
конгруэнтны. Площадь каждого из них равна — апг,
сторона правильного я-угольника.
Площадь S многоугольника равна — апг
Следовательно, S = — Рг. ■
где ап —
п, но апп = Р.
94|Теорема. Площадь Sn правильного η-угольника равна:
0 1 D2 . 360
Sn = — nR2 sin ,
п 2 η
где R — радиус описанной окружности.
Доказательство (рис. 490).
ьаов = 110 А |· | ОБ | · sin AOB.
318
Ho \OA\ = \OB\ = R, AOB = . Поэтому
η
0 1 D2 . 360°
^vin» = -й 81П .
A0B 2 η
Так как правильный η-угольник является объединением
неперекрывающихся треугольников, конгруэнтных треугольнику
АОВ9 то
rs, 1 по · 360° —
S„ = — nR2 sin . ■
Вопросы и задачи
1211. 1) Выразите радиус окружности, описанной около
правильного л-угольника, через сторону ап этого многоугольника, если
η равно: а) 3; б) 4; в) 6.
2) Выразите сторону а п правильного л-угольника через
радиус г вписанной окружности, если л равно: а) 3; б) 4; в) 6.
1212. Выразите радиус г вписанной окружности через радиус Я
описанной около правильного л-угольника окружности.
1213. 1) Из заготовки цилиндрической формы выточен болте
квадратной головкой наибольших размеров. Каково расстояние
между противоположными гранями этой головки, если
диаметр заготовки равен: а) 20 мм; б) 8 мм!
2) Из заготовки, имеющей форму правильной
шестиугольной призмы, изготовлен цилиндр наибольшего диаметра.
Вычислите диаметр цилиндра, если расстояние между
противоположными боковыми ребрами заготовки равно: а) 16 мм;
б) 12 мм.
1214. В окружность радиуса 6 см вписан правильный треугольник,
на стороне которого построен квадрат. Вычислите радиус
окружности, описанной около этого квадрата.
1215*. При каких значениях л сторона правильного л-угольника:
1) больше радиуса описанной окружности; 2) равна радиусу
описанной окружности; 3) меньше радиуса описанной
окружности?
1216*. 1) Три конгруэнтные окружности, касающиеся между собой
попарно, касаются внешним образом окружности радиуса Л.
Вычислите радиусы этих окружностей, если R = 2 см.
2) Докажите, что для любой окружности (О, R) при любом
319
η > 2 можно построить п окружностей радиуса г, каждая из
которых касается двух окружностей радиуса г и окружности
(О, R). Выразите г через Д.
1217*. Выразите через сторону ап наименьшую диагональ
правильного л-угольника. Вычислите эту диагональ, если:
1) ап = 1 см, η = 5; 2) ап = 5 см, /г = 6.
1218*. Через середины двух смежных сторон квадрата, вписанного
в окружность радиуса R, проведена хорда. Какова длина
этой хорды, если:
1) R = 2 см; 2) R = Зсм?
1219. Вычислите площадь правильного л-угольника, вписанного
в окружность радиуса R = 8 см, если:
1) η = 3; 2) η = 4) 3) η = 5.
1220. Вычислите площадь правильного /г-угольника, описанного
около окружности радиуса г=А см, если: 1) η = 3;
2) л = 4; 3) л = 5.
1221. Стороны двух правильных одноименных многоугольников
равны а и &. Как относятся: 1) периметры этих
многоугольников; 2) площади многоугольников?
1222. В окружность вписаны и около нее описаны правильные
л-угольники. Вычислите для л = 3, 4, 6 отношение: 1) их
периметров; 2) их площадей.
1223*. Докажите, что площадь правильного л-угольника, вписанного
в окружность радиуса R, может быть вычислена по формуле
0 Ion 180° „
Ьп — — JrnJti cos , где Fn — периметр многоугольника.
1224. Вычислите радиус окружности, вписанной в треугольник,
если стороны его равны: 1) 3 см, 4 см, 5 см; 2) 10 см,
6 см, 5 см.
§ 3. Длина окружности и площадь круга
90. Длина окружности
1. В пункте 8 было дано определение длины ломаной. Строгое
определение длины произвольной кривой линии основано на
понятии предела числовой последовательности, которое
изучается в курсе алгебры и начал анализа 9 класса. Однако вы
знакомы с формулами длины окружности:
С = 2nR = nD
320
и длины I дуги окружности в α градусов:
I = π R = π — D.
180 360
Вы знакомы и с приближенным
значением числа «пи»:
π « 3,14159.
Сейчас будет рассказано, как можно
оценить это число «пи» с любой наперед
заданной точностью, исходя из прос- Рис. 491
того допущения (рис. 491): длина
окружности больше периметра любого вписанного в нее
многоугольника и меньше периметра любого описанного вокруг нее
многоугольника.
Рассмотрим окружность диаметра D = 1. Ее длина равна π.
Обозначим периметр вписанного в такую окружность
правильного п-угольника через рп, а периметр описанного — через qn.
Тогда по сделанному допущению
Рп < π < <1п-
Вот результаты вычислений, способ которых объяснен ниже:
η
6
12
24
48
96
Рп
3,00000
3,10595
3,13301
3,13475
3,14134
Чп 1
3,46414
3,21554
3,16005
3,14665
3,14284
Уже неравенства р96 < π < q96 позволяют оценить число
«пи» с довольно большой точностью. Именно при помощи
96-угольников Архимед (II в. до н. э.) получил свои оценки:
з^0<жз1.
71 7
у 2. В приведенной выше таблице даны значения рп и qn
для номеров η вида
η = 3 · 2ту (1)
где т = 1, 2, 3, 4ι 5.
Объясним, как вычисляются рп и qn для этой таблицы.
(При этом будем пользоваться формулами (3) и (4), вывод кото-
321
рых дан ниже отдельно, чтобы не затруднять объяснение
деталями вычислений.)
1) Ясно, что
Рп = η · αΛ, qn = η · Ья, (2)
где ап — сторона правильного вписанного /г-угольника, а Ъп —
описанного. Значит, задача вычисления рп и qn сводится к
вычислению ап и Ъп.
2) Для вычисления ап используем формулу удвоения: -
1
г
а2п = -]/ 2-2|Л-<#
(3)
где а2п — сторона правильного вписанного 2я-угольника.
Сторона а6 правильного вписанного шестиугольника равна
радиусу. Поэтому при D = 1
а« = —·
По формуле удвоения (3) далее последовательно вычисляются
αϊ 2, Л-J4» β48 И α96"
3) По α„ вычисляются Ъп при помощи формулы
Ья = α« : 1/Ί-α«·
(4)
Теперь по формулам (2) вычисляются значения рл и qn
для таблицы.
Из формулы (4) получаем:
Рп _ пап __ а
Qn
пЬ„
v^<-
(5)
Увеличивая п> можно сделать ап сколь угодно малым, а
\\ — ап сколь угодно близким к единице. Так как рп и qn
являются нижней и верхней оценкой для числа
«пи», то это и значит, что при помощи
неравенств
Рп < π < Qn
число «пи» оценивается при достаточно
большом η со сколь угодно большой
точностью.
3. Докажем теперь формулу (3).
Пусть [АБ] — сторона правильного
η-угольника, вписанного в окружность
Рис. 492 (О, R) (рис. 492). Проведем перпендику-
322
ляр ОС к прямой АВ. Дуга АВ делится в
точке С пополам (п. 23). Поэтому хорда АС
есть сторона правильного вписанного
2/г-угольника.
Выразим ее длину а2п = \АС\ через
длину стороны ап = | АВ | данного п-уголь-
ника и радиус R описанной окружности.
Из треугольника АСО по теореме
косинусов находим:
Рис. 493
|АС|2 = |ОА|2 + \ОС\2 — 2 \ОА\ · \ОС\ cos АОС.
(6)
Из прямоугольного треугольника AOD имеем: | О А | cos АОС =
= |ОJ01. Кроме того, \ОА\ = \ОС\ = Д. Поэтому равенство (6)
примет вид:
|АС|2 = 2R2 — 2R \OD\. (7)
По теореме Пифагора из треугольника AOD находим:
\OD\=\f\AO\*-\AD\*=yR2-feiJ=yR2_4t
Подставляя значение \OD\ в равенство (7), получим:
о|„=2Л«-2л1/ла—^.
Огя = У 2Д2 — 2R у В? — ^·
(8)
Если рассматривать окружность диаметра D = 1, то
формула удвоения (8) примет вид формулы (3), которой мы и
воспользовались выше.
4. Докажем формулу (4).
Пусть ап= \АВ\ —сторона правильного тг-угольника,
вписанного в окружность (О, R) (рис. 493). Через Ъп = |CZ>|
обозначим сторону правильного η-угольника, описанного около
этой окружности.
Рассмотрим прямоугольные треугольники ONC и ОМА.
Они подобны. Поэтому \NC\i \ МА\ = |OJV| : \ОМ\,
т. е.
^ : ^ = R:\OM
323
Но
Поэтому
2 2 V 4Д2
Отсюда
^ = *
ι/^З (9>
Если рассматривать окружность диаметра D = 1, то
формула (9) примет вид формулы (4), которой мы и воспользовались
при объяснении метода вычисления рп и qn для] заполнения
таблицы, ψ
Вопросы и задачи
1225. Как изменится длина окружности, если: 1) радиус
увеличится в η раз; 2) радиус уменьшится в η раз?
1226. Вычислите длину окружности, если радиус ее равен:
1) 12,5 см; 2) 6 дм.
1227. Вычислите радиус окружности, длина которой равна:
1) 78,5 см; 2) 12,56 дм.
1228. Чтобы найти толщину дерева (диаметр), можно измерить его
обхват (длину окружности). Вычислите толщину дерева,
обхват которого равен: 1) 2 м; 2) 1,5 м.
1229. Сторона равностороннего треугольника равна 3 см.
Вычислите длину окружности: 1) вписанной в этот треугольник;
2) описанной около него.
1230. Сторона квадрата равна 4 см. Вычислите длину окружности:
1) вписанной в него; 2) описанной около него.
1231- Постройте окружность, длина которой равна: 1) 12 см;
2) 18 см (построение приближенно).
1232. Минутная стрелка Кремлевских курантов имеет длину 3,6 м.
Какова длина дуги, которую описывает конец стрелки в
течение: 1) 5 мин; 2) 1 ч?
1233. Вычислите длину дуги окружности радиуса г = 5, если угло-
вая величина дуги равна: 1) 30°; 2) 40°; 3) —.
5
1234*. Выведите формулу, выражающую зависимость между
разностью длин двух окружностей, ограничивающих кольцо,
и толщиной кольца.
324
1235. Радиусы двух концентрических окружностей равны 10 см
и 26 см. Вычислите длину отрезка наибольшей длины, все
точки которого принадлежат этому кольцу.
1236. Вычислите длину дуги земного экватора величиной в 1 мин
(радиус земного экватора приближенно равен 6400 км).
1237. Две дуги разных окружностей имеют одну и ту же длину.
Вычислите отношение радиусов этих дуг, если угловая
величина одной из них 25°, а другой — 45°.
91. Площадь круга
Сравнивая площади Sn вписанных в круг правильных
многоугольников, можно заметить, что при возрастании числа их
сторон площади увеличиваются, оставаясь при этом меньше
площади круга (рис. 494, а). Площади Sn описанных около
этого же круга правильных многоугольников при возрастании
числа их сторон уменьшаются, но остаются больше площади
этого круга (рис. 494, б). Вычисляя площади правильных
вписанных (описанных) многоугольников, можно находить
приближенные значения площади круга с
недостатком (с избытком).
Площадь правильного я-угольника
равна половине произведения его периметра
на радиус вписанной в него окружности
(п. 89). При возрастании числа его сторон
периметр Ρ стремится к длине окружности
2nR, а площадь Sn — к площади круга
Ίφ·
Поэтому
'кр
- · 2лД
2
R
nR\
Итак,
'кр
ДД2
Площадь сектора, дуга которого
содержит 1°, равна — площади круга. Поэтому
360
площадь сектора, дуга которого
содержит α градусов, находится по формуле:
~ 7iR2a
325
круга, диаметр которого равен:
1239.
1240.
1241.
1242.
Вопросы и задачи
1238. Вычислите площадь
1) 4 см; 2) 10 м.
Как изменится площадь круга и длина его окружности, если:
1) диаметр уменьшить в четыре раза; в η раз; 2) радиус
увеличить в три раза; в η раз?
Выразите площадь круга через длину его окружности.
Вычислите площадь сечения провода, если его диаметр
равен: 1) 3 мм; 2) 0,2 мм.
Произведите необходимые измерения и вычислите
площади фигур, изображенных на рисунке 495 (масштаб
1 :10).
1243. Вычислите площадь поперечного
сечения дерева, если его обхват (длина
окружности) равен: 1) 88 см; 2) 5 дм.
1244. Из квадратного листа жести
вырезали круг наибольшей площади.
Какая часть листа ушла в отходы?
1245. Вычислите площадь сектора, радиус
г которого равен 6 см, а величина
Рис. 495
угла равна: 1) 24°; 2) 30°; 3)
1246.
1248.
Рис. 496
Постройте круг, площадь которого
была бы равна: 1) 4 см2; 2) 16 м2
(построение приближенно).
1247*. Вычислите радиус окружности,
которая делит круг радиуса г на две
равновеликие фигуры — кольцо и
круг.
Докажите, что сумма площадей
полукругов, построенных на
катетах прямоугольного треугольника,
как на диаметрах, равна площади
полукруга, построенного на
гипотенузе.
1249*. Докажите, что сумма площадей двух
заштрихованных луночек (рис. 496)
равна площади прямоугольного
треугольника.
326
Дополнительные задачи к главе IX
1250. Две окружности с центрами в точках О и Οι пересекаются
в точках А и В. Через точку А проведены диаметры этих
окружностей АА\ и АВ\. Докажите, что точки А\, В и В\
лежат на одной прямой.
1251. Постройте фигуру, состоящую из точек, из которых данный
отрезок АВ виден под данным углом а.
1252. Докажите, что из всех треугольников: 1) имеющих общее
основание и равные углы при вершине, наибольшую площадь
имеет равнобедренный треугольник; 2) вписанных в данную
окружность, наибольшую площадь имеет равносторонний
треугольник.
1253. Докажите, что из всех четырехугольников, вписанных в
данную окружность, наибольшую площадь имеет квадрат.
1254. Угловая величина дуги сегмента равна 120°, а длина этой
дуги равна /. Вычислите длину окружности, вписанной в этот
сегмент.
1255. Докажите, что площадь любого описанного многоугольника
равна— Рг, где Ρ — периметр этого многоугольника, а г —
радиус вписанной окружности.
1256. Докажите, что "|/"оЬ ^ , где а и Ъ — длины данных
отрезков.
1257. Две окружности пересекаются в точках А и В. Через точку
В проведена произвольная прямая, пересекающая данные
окружности в точках X и У. Докажите, что угол ΧΑΥ не
зависит от выбора этой прямой.
1258. Постройте треугольник, вписанный в данную окружность,
если известны точки пересечения с окружностью продолжений
биссектрисы, медианы и высоты треугольника, проведенных
из одной и той же вершины.
1259. Проведены два диаметра окружности. Постройте хорду,
которая делится этими диаметрами на три конгруэнтных
отрезка.
1260. Докажите, что площадь кольца равна площади круга,
диаметр которого — хорда окружности (Οι, Γι), касающаяся
окружности (02, Гг). (Окружности (Οι, Γι) и (Ог, Г2)
ограничивают данное кольцо, Γι > Гг.)
1261. Даны прямая АВ и две окружности (О, г) и (Οι, Г\).
Проведите к данным окружностям секущую, параллельную (АВ),
327
так, чтобы сумма длин хорд этих окружностей равнялась р.
1262. Постройте треугольник по стороне а, углу а и высоте Ла.
1263. Постройте равносторонний треугольник, вершины которого
лежат на трех данных параллельных прямых.
1264. Постройте квадрат, если даны точки А, В, С и D, лежащие
на его сторонах (по одной на каждой стороне).
1265. В окружность вписан равнобедренный треугольник ABC с
углом В при вершине, равным 36°. Из точки А проведена
биссектриса угла А, пересекающая окружность в точке D.
Докажите, что отрезок BD — сторона правильного
пятиугольника, вписанного в эту окружность.
1266. Пользуясь только циркулем и линейкой, в данную
окружность впишите правильный десятиугольник.
1267. Около правильного многоугольника со стороной а описана
окружность, в многоугольник вписана другая окружность.
Вычислите площадь образовавшегося кольца.
1268. Правильный многоугольник вращается вокруг своего
центра. При каких значениях угла поворота α этот п-угольник
совмещается с самим собой?
1269. Точка О лежит на серединном перпендикуляре к отрезку
АВ. При вращении плоскости вокруг центра О отрезок АВ
заметает кольцо с центром О. Докажите, что площадь
кольца не зависит от расстояния от точки О до прямой АВ.
ГЛАВА XV
НАЧАЛЬНЫЕ СВЕДЕНИЯ
ИЗ СТЕРЕОМЕТРИИ
В этой главе приведены некоторые
сведения из стереометрии — той
части геометрии, в которой изучаются и
неплоские фигуры.
§ 1. Прямые и плоскости
в пространстве
92. Расположение плоскостей
в пространстве
Вы знаете, что любые две отличные
друг от друга точки пространства
определяют одну и только одну содержащую
их прямую. А как определить
положение плоскости в пространстве?
На рисунке 497 видно, что
плоскостей, содержащих две данные точки А
и Б, много. Взяв одну из этих
плоскостей, все остальные можно получить
из нее вращением вокруг оси АВ.
Чтобы выделить какую-либо из них,
надо фиксировать еще одну точку С,
не лежащую на оси АВ. Эти
наблюдения убеждают в справедливости
следующих предложений:
95 | ТРи не лежащие на одной прямой
точки пространства определяют
одну и только одну содержащую их
плоскость;
Рис. 497
ί^Ί Α. /
riztj ^=7
Рис. 498 Рис. 499
96 I прямая и не принадлежащая ей точка определяют одну и
I только одну содержащую их плоскость.
Рассмотрим теперь взаимное расположение двух плоскостей
в пространстве. Плоскости пола и потолка класса дают
наглядное представление о параллельных плоскостях. Плоскость
пола и плоскость стены дают представление о пересекающихся
плоскостях. Их пересечение — прямая.
Определение. Плоскости α и β называются
параллельными, если они не имеют общих точек или совпадают.
Сформулируем теперь основное предложение о возможных
случаях расположения двух плоскостей:
97 I две плоскости или параллельны, или пересекаются по пря-
I люй(рис. 498).
Отношение параллельности плоскостей обозначается тем же
знаком, что и отношение параллельности прямых (||). Подобно
отношению параллельности прямых оно транзитивно:
98 I две плоскости, параллельные третьей, параллельны меж-
I ду собой (рис. 499).
▼ Из определения параллельных
плоскостей следует, что отношение
параллельности между плоскостями симметрично
и рефлексивно. Таким образом,
отношение параллельности между плоскостями
является отношением эквивалентности.
Поэтому все множество плоскостей
пространства разбивается на пучки
параллельных плоскостей: любые две
плоскости одного пучка параллельны друг
другу, а плоскости из разных пучков не
Рис. 500 параллельны. Τ
330
LZJ
r~j
Отметим следующее предложение:
если две плоскости параллельны, а третья им не параллельна9
то эта третья плоскость пересекает две первые по двум
параллельным прямым (рис. 500).
Вопросы и задачи
1270. Почему штативы фотоаппаратов, геодезических приборов
имеют три опорные ножки? Почему стол, имеющий четыре
ножки, не всегда устойчив?
1271. Можно ли утверждать, что плоский выпуклый
многоугольник лежит в данной плоскости, если известно, что этой
плоскости принадлежит: 1) одна его точка; 2) две его точки;
3) три его точки; 4) три вершины многоугольника?
1272. Докажите, что плоскость и не лежащая в ней прямая не
могут иметь более одной общей точки.
1273*. Докажите, что через две пересекающиеся прямые
проходит одна и только одна плоскость.
1274. Две прямые одной плоскости параллельны двум прямым
другой плоскости. Верно ли, что такие плоскости всегда
параллельны? Воспользуйтесь моделью.
1275. Две пересекающиеся плоскости пересечены третьей
плоскостью. Могут ли линии пересечения этих плоскостей быть:
1) параллельными; 2) непараллельными; 3)
непересекающимися и непараллельными? Рассмотрите модели.
93. Параллельные прямые в пространстве
Определение параллельных прямых вам хорошо знакомо:
прямые а и Ъ называются параллельными, если они лежат в одной
плоскости и не имеют общих точек или же совпадают.
Для прямых, лежащих в одной плоскости,
была доказана транзитивность отношения параллель- а
ности (см. п. 32). Свойство транзитивности верно
и для прямых в пространстве (рис. 501):
991 две прямые, параллельные третьей, парал-
I лельны между собой.
Τ Так как, кроме того, отношение параллельности
прямых симметрично и рефлексивно, то это
отношение есть отношение эквивалентности. Рис. 601
С
331
Множество всех прямых,
параллельных какой-либо одной
прямой в пространстве,
называется связкой* параллельных
прямых. Множество всех прямых
пространства разбивается на
связки параллельных. Из курса
черчения вы знакомы с
употреблением связок параллельных
прямых при параллельном
проектировании фигур
пространства на плоскость (рис. 502). ψ
Вопросы и задачи
1276°. Укажите несколько
примеров параллельных прямых
из окружающей
обстановки. Приведите примеры
прямых, которые не
пересекаются, но и не
параллельны. (Такие прямые
называются скрещивающимися.)
1277°. Верно ли предложение:
если две прямые в
пространстве не пересекаются,
то они параллельны?
1278°. Может ли прямая быть
параллельна: 1) только
одному ребру куба; 2) только
двум; 3) только трем?
1279°. На рисунке 503 изображен
прямоугольный
параллелепипед. Назовите прямые
связки параллельных,
содержащих ребра этого
параллелепипеда.
* Слово «связка» употребляется
для отличия от «пучков» параллельных
прямых на плоскости.
Рис. ZL
94. Перпендикулярность прямой
и плоскости
1. Рассмотрим прямую О А (рис. 504).
В каждой плоскости, проходящей через
эту прямую, проведем к ней через
точку О перпендикуляр. Оказывается, что
все эти перпендикуляры лежат в одной
плоскости. Наглядно в этом легко
убедиться на модели, изображенной на
рисунке 505.
Определение. Прямая
перпендикулярна плоскости, если она
пересекает плоскость в какой-либо точке и
перпендикулярна всем лежащим в этой
плоскости прямым, проходящим через
эту точку.
Перечислим основные свойства
отношения перпендикулярности между
прямой и плоскостью.
1001 Через любую точку пространства
Ί проходит одна и только одна
прямая, перпендикулярная данной
\ плоскости.
Все прямые, перпендикулярные
данной плоскости, параллельны между
собой (рис. 506).
10ΐ|^£ρβ3 каждую точку пространства
Ί проходит одна и только одна пло-
I скостьу перпендикулярная данной
прямой.
Две плоскости, перпендикулярные
данной прямой, параллельны между
собой (рис. 507).
Τ Прямые, перпендикулярные
данной плоскости, образуют связку
параллельных прямых.
Из последних двух предложений вытекает, что плоскости,
перпендикулярные данной прямой, образуют пучок
параллельных плоскостей, ψ
2. Расстояние между полом и потолком комнаты
измеряется вдоль какой-либо вертикальной прямой.
/о(
Λ
/
/
/а
•
<
Рис.
1 1
J I
i\
α
'В
507
А
J
У
X
ι/
/
А /
/
/
/
/
У
Рис. 508
333
Этот способ основан на следующих геометрических фактах:
\02\прямая, перпендикулярная плоскости а, перпендикулярна
Ш любой другой плоскости, параллельной а;
103| длины отрезков, отсекаемых двумя параллельными плос-
I костями на их общих перпендикулярах, равны.
Например, на рисунке 508 \АВ\ = |ΑιΒι| = |Α2Β2Ι·
Длина отрезка, отсекаемого двумя параллельными
плоскостями α и β на любом их общем перпендикуляре, есть
расстояние между этими плоскостями.
Вопросы и задачи
1280°. Покажите на моделях из окружающей обстановки
перпендикуляры к одной и той же плоскости. Что можно сказать
о взаимном расположении этих перпендикуляров?
1281°. Прямые АВ и CD перпендикулярны плоскости а.
Существует ли плоскость, содержащая эти прямые?
1282°. Как расположены две плоскости, перпендикулярные одной
и той же прямой?
1283°. По рисунку прямоугольного параллелепипеда (см. рис. 503)
укажите: 1) грани, перпендикулярные ребру: а) АА\\ б) АВ;
в) В\С\) 2) ребра, перпендикулярные грани DCC\D\.
1284°. На рисунке 509 изображена треугольная пирамида; углы
DCA, DCB, АСВ прямые. Каким ребрам перпендикулярны
грани ACD, DCB, ACB, ADB1
1285°. Верны ли следующие предложения: 1) прямая
перпендикулярна плоскости, если она перпендикулярна двум
различным прямым, лежащим в этой плоскости; 2) две прямые,
перпендикулярные одной и той же прямой, параллельны?
1286. 1) Как на практике (с помощью отвеса) можно проверить
вертикальность установки столба?
2) Как с помощью уровня может быть проверена
горизонтальность установки подставки для прибора?
1287. Ребро куба равно а. Чему равно
расстояние от одной из вершин куба:
1) до его граней; 2) до других его
вершин?
1288. Диагональ основания куба равна а.
Чему равно расстояние между
противоположными гранями куба?
1289. Измерьте расстояние между проти-
Рис 509 воположными стенами класса.
334
§ 2. Многогранники
95. Прямая призма
1. На рисунке 510 изображена прямая пятиугольная призма.
На ее примере познакомимся с тем, как получают другие
прямые призмы (рис. 511).
Рассмотрим две параллельные плоскости и на одной из них
возьмем многоугольник ABCDE. Через его вершины проведем
прямые, перпендикулярные плоскости. Эти прямые пересекут
вторую плоскость в точках Аи В{, Си D{ и Е^ Можно доказать,
что многоугольники ABCDE и A^iCiDiEi конгруэнтны. Они
называются основаниями призмы. В силу предложений 100 и 103
отрезки ААи BBU CCU DD{ и ЕЕ{ конгруэнтны. Эти отрезки
называются боковыми ребрами призмы. Высотой призмы
называется отрезок, заключенный между ее основаниями и
перпендикулярный им. (Высотой призмы называют и длину этого
отрезка.)
Можно также доказать, что четырехугольники ABBiAi9
BCCiBi9 CDDiCu DEEiDi и ΕΑΑ{Ει являются
прямоугольниками. Это боковые грани прямой призмы. Боковые грани и
основания призмы называются ее гранями. Стороны граней
называют ребрами призмы, а концы ребер — ее вершинами.
Прямая призма, в основании которой лежит
параллелограмм, называется прямым параллелепипедом. Если же в
основании прямой призмы лежит прямоугольник, то она
называется прямоугольным параллелепипедом (рис. 512).
Прямоугольный параллелепипед, все ребра которого конгруэнтны между
собой, называется кубом. Длины трех ребер прямоугольного
параллелепипеда, имеющих общую вершину, называют
измерениями этого параллелепипеда.
£>
Рис. 611
335
/Γ~7|
II 1^1
l| 1 ь Ι
а
Рис. 512
Рис. 513
Задание. Постройте на листе бумаги два
симметричных относительно оси ΜΝ многоугольника (на рис. 513
построены пятиугольники), так, чтобы одна сторона
многоугольника была параллельна прямой ΜΝ. Затем постройте
прямоугольники, как на рисунке: |АВ2| = |АВ|, \В2С2\ = \ВС\,
\C2D2\ = \CD\, \D2E2\ = \DE\. В результате вы получите
развертку прямой пятиугольной призмы. Если согнуть ее
надлежащим образом по сторонам прямоугольников, то
получится поверхность прямой пятиугольной призмы.
2. Площадь боковой поверхности призмы есть сумма
площадей прямоугольников, являющихся ее боковыми гранями.
Обозначим через h высоту призмы и через а, &, ..., / — стороны
основания (рис. 514). Так как боковые грани прямой призмы —
прямоугольники, площадь боковой поверхности прямой
призмы равна:
«бок = ah + bh + ... + fh - (α + b +...+/) h = Ρ - Λ,
где Р — периметр основания призмы.
Итак,
^бок = Ph.
Площадь боковой поверхности прямой
призмы равна произведению периметра основания
призмы на ее высоту.
Площадь поверхности* прямой призмы
равна сумме площади боковой поверхности и
удвоенной площади основания:
£цр —
'бок
+ 2S,
ОСИ"
Рис. 514
* Иногда вместо слов «площадь поверхности призмы»
гоьорят «полная поверхность призмы».
336
3. В младших классах вы уже вычисляли объем
прямоугольного параллелепипеда по формуле
V = abc9 (1)
где а, & и с — соответственно длина, ширина и высота
параллелепипеда. Формулу (1) можно записать в виде
V = Sh (2)
(S = аЪ — площадь основания, h — высота призмы). Формула
(2) верна для любой прямой призмы.
Объем прямой призмы равен произведению площади ее основа-
ния на высоту.
Вопросы и задачи
1290. 1) Начертите треугольную и четырехугольную призмы.
2) Начертите развертку правильной треугольной призмы.
1291°. 1) Сколько граней имеет неочиненный шестигранный
карандаш?
2) Какой многоугольник служит основанием призмы,
имеющей η граней?
1292°. Какова зависимость между числом боковых граней прямой
призмы и числом сторон ее основания?
1293. Какое наименьшее число граней (ребер, вершин) может
иметь прямая призма?
1294°. Какими фигурами являются грани прямого
параллелепипеда, все измерения которого равны?
1295. 1) Существует ли призма, число ребер которой равно: а) 8;
б) 15; в) 13; г) 12?
2) Сколько вершин, граней и ребер имеет п-угольная
призма?
1296. Основанием прямой призмы служит прямоугольный
треугольник с катетами 5 см и 6 см. Высота призмы 8 см.
Вычислите площадь поверхности и
объем призмы.
1297. Основанием прямой призмы
служит ромб с диагоналями
6 см и 8 см, высота призмы
12 см. Вычислите площадь
боковой поверхности и объем
призмы.
1298. На рисунке 515 изображен
сарай с двускатной крышей, дли- Рис. 515
337
.г
sl£
гп
8 м
,— — *-
л с,
1<У
Рис. 517
Рис. 518
1300.
на которого 12 м. Остальные размеры указаны на рисунке.
Вычислите: 1) площадь кровли сарая; 2) емкость
чердачного помещения; 3) емкость всего сарая.
1299. Найдите расстояние от вершины А до вершины С\
прямоугольного параллелепипеда, зная его измерения а = 3 м,
& = 4м и с = 5 м (рис. 516).
Практическая работа. Сделайте развертку прямой
призмы, основание которой — прямоугольный треугольник
с катетами 3 см и 4 см, а высота равна 4 см. Согните и
склейте ее так, чтобы получилась модель призмы (сообразите,
где нужно оставить выступы для склеивания).
Практическая работа. Возьмите модель прямой
треугольной призмы. Выполните необходимые измерения и
вычислите площадь поверхности призмы.
1302*. Выполните необходимые измерения и вычислите по двум
ортогональным проекциям прямой треугольной призмы на
горизонтальную и вертикальную плоскости (рис. 517): 1)
площади боковых граней; 2) площадь основания.
1303. Из листа картона, размеры которого 240 мм X 160 мьа,
вырезали по углам квадраты со стороной 40 мм и из
получившейся фигуры (рис. 518), загнув края, склеили открытую
сверху коробку. Вычислите площадь дна, площадь всех
боковых стенок этой коробки и ее объем.
1301.
96. Пирамида
1. На рисунке 519 изображены пирамиды. Как можно
получить пирамиду? Возьмем какой-нибудь многоугольник ABC ...
Вне плоскости этого многоугольника возьмем точку S
(рис. 520, а). Соединим ее отрезками со всеми вершинамц
338
Рис. 519
многоугольника (рис. 520, б). Треугольники SAB, SBC и т. д.
называются боковыми гранями пирамиды, многоугольник
ABC ... — называется основанием, а точка S — вершиной
пирамиды.
Поверхность пирамиды состоит из многоугольника
(основания пирамиды) и треугольников (боковых граней). В
зависимости от вида многоугольника, лежащего в основании
пирамиды, различают треугольные, четырехугольные,
пятиугольные и т. д. пирамиды.
Высотой пирамиды называется отрезок перпендикуляра,
проведенного через вершину пирамиды к плоскости ее основания
(концами этого отрезка являются вершина пирамиды и
основание перпендикуляра). Отрезок SO (рис. 521) — высота
пирамиды. (Высотой пирамиды называют и длину этого отрезка.)
Пирамида называется правильной, если основанием ее
является правильный многоугольник, а вершина проектируется
в центр основания. Высота боковой грани правильной
пирамиды, проведенная из вершины пирамиды, называется апофемой
пирамиды. Например, отрезки SM и SN (рис. 522) — апофемы.
Все апофемы правильной пирамиды конгруэнтны между собой.
Рис. 620 Рис. 521
339
Прямые призмы и пирамиды являются
частными видами многогранников. Другие
примеры многогранников приведены на
рисунке 523. Поверхность каждого из
многогранников состоит из
многоугольников.
2. Площадь одной боковой грани
правильной я-угольной пирамиды равна
—anh6oK, где ап —сторона основания,
h
бок
апофема пирамиды. Так как все
боковые грани правильной пирамиды
конгруэнтны, то площадь боковой поверхности пирамиды равна:
■ ah6oKn
anhr,
Ρ- h6o
где Р — периметр основания пирамиды.
Итак,
^бок ^ Т^*1
бок·
Если известна апофема А0С11 основания пирамиды, то
поверхность правильной пирамиды находится по формуле:
1
ς» *"бок ι *"осн
°пир — 0 "Г
' Ρ С*бОК + Kdl)·
Объем любой пирамиды равен одной трети произведения
площади ее основания на высоту:
V = — SocA
Рис. 523
340
Вопросы и задачи
1304. Начертите треугольную и четырехугольную пирамиды.
1305. Сколько ребер и сколько граней имеет η-угольная
пирамида?
1306. Вычислите площадь поверхности и объем каждой из
правильных пирамид, изображенных на рисунке 524.
1307. Вычислите объем правильной: 1) треугольной; 2)
четырехугольной; 3) шестиугольной пирамиды, сторона основания
которой равна а и высота h(a = 15 см, h = 20 см).
1308. Выразите объем правильной четырехугольной пирамиды
через ее боковое ребро Ъ и радиус R окружности, описанной
около основания.
1309. Выразите площадь поверхности и объем правильной
четырехугольной пирамиды через ее высоту h и радиус г
вписанной в основание окружности.
1310. На модели треугольной пирамиды выполните необходимые
измерения и вычислите площади ее боковых граней,
площадь основания и объем этой пирамиды.
1311. На модели четырехугольной пирамиды, в основании которой
лежит прямоугольник, выполните необходимые измерения и
вычислите площади боковых граней, площадь основания и
объем этой пирамиды.
1312. Начертите развертку треугольной пирамиды, в основании
которой лежит равносторонний треугольник, а все боковые
ребра имеют одну и ту же длину. Изготовьте из этой
развертки модель пирамиды.
α) δ) в)
Рис. 524
341.
97 Т. Общие свойства объемов
Познакомимся с постановкой задачи измерения объемов
(сравните эту задачу с задачей измерения площадей, см. п. 49).
Единицей измерения объема будем считать объем куба с дли-
ной ребра е, где е — единица измерения длины. Этот объем
обозначается е3. Любой объем V выражается через эту единицу
измерения в виде V = υ · е3, где ν — числовое значение объема V
при данной единице измерения е3. В дальнейшем, считая
единицу измерения выбранной, будем говорить о числовых
значениях объемов. Задача состоит в том, чтобы каждому
многограннику (а по возможности и некоторым другим фигурам)
поставить в соответствие определенное число V (L) > О,
обладающее такими свойствами:
1) если фигурыLluL2 конгруэнтны, то их объемы равны:
V (Li) = V (i2);
2) если многогранник L является объединением
многогранников 1>г и L2y не имеющих общих внутренних точек, то
Рис. 525
342
объем многогранника L равен сумме объемов
многогранников Lx и L2:
V (L) = V (Li) + V (i2);
3) если фигура L есть часть фигуры Ьг (т.е. подмножество
Lx), to объем фигуры Ь не превышает объема фигуры L±:
V (Ζ) < V (i,);
4) объем куба Е с длиной ребра е равен единице:
V (Е) = 1.
Можно доказать, что при заданной единице длины е эта зада-
ча для многогранников имеет одно-единственное решение. Только
одним-единственным образом можно каждому
многограннику L поставить в соответствие числа V (L) с соблюдением
требований 1—4. Покажем это для прямоугольного
параллелепипеда, длина, ширина и высота которого выражаются
рациональными числами а, Ь, с. Приведя числовые значения длины,
ширины и высоты параллелепипеда к общему
знаменателю я, запишем их в виде
а = —, Ь = —, с = —.
η η η
Этот параллелепипед составлен из т = pqr кубов с ребром—в
(на рис. 525 ρ = 10, q = 11, г = 9).
Так как куб с ребром е составляется
из п3 таких кубов, числовое значение
объема каждого из них есть 1 : п3.
Следовательно, числовое значение
объема всего параллелепипеда есть
V = pqr — = ~ · — - — = α · b · с.
η? η η η
§ 3. Фигуры вращения
98. Цилиндр
Наглядное представление о цилиндре
можно получить, вращая
прямоугольник вокруг одной из его сторон
(рис. 526). Основания цилиндра —
конгруэнтные между собой круги. Боковая
поверхность — кривая поверхность,
называемая цилиндрической (рис. 527).
У/Л
_,:л
Рис. 526
Рис. 527
343
Рис. 528
Если развернуть боковую
поверхность цилиндра, то получится
прямоугольник, длина основания
которого равна длине окружности
основания цилиндра, а высота — высоте
цилиндра. Следовательно, развертка
цилиндра состоит из прямоугольника
и двух кругов (рис. 528).
Зная радиус основания
цилиндра и его высоту, можно вычислить
площадь поверхности цилиндра.
Заметим, что площадь основания
равна лД2, площадь обоих
оснований 2лД2.
Площадь боковой поверхности
цилиндра равна площади
прямоугольника, основание которого равно 2лД,
а высота h, т. е. равна
2лД · h.
Следовательно, площадь поверхности цилиндра равна:
Яцил = 2лД2 + 2nRh = 2nR (R + h).
Объем цилиндра равен произведению площади его основания
на высоту:
Уиил = Sh = nR2h.
ψ Доказательство этой формулы дается в 10 классе. На
примере цилиндра покажем, как оценивать с любой требуемой
точностью объем произвольной фигуры. На рисунке 529 показано,
что цилиндр с диаметром основания и высотой е помещается
полностью в объединении 88 χ 10 = 880 кубов с ребром е : 10 и
содержит в себе объединение 60 · 10 = 600 непересекающихся
таких же кубов. Поэтому числовое значение объема этого
цилиндра заключено в пределах:
0,6 = °°° < V < -^ = 0,88.
1000 1000
Выбирая кубы с ребром е : η (при достаточно большом гс),
можно было бы оценить объем взятого цилиндра со сколь угодно
большой точностью, ψ
344
Рис. 529
Вопросы и задачи
1313. 1) Как изменится площадь боковой поверхности цилиндра,
если: а) высоту его увеличить в два раза; б) радиус его
основания увеличить в три раза?
2) Как изменится объем цилиндра, если?~а) высоту его
увеличить в два раза; б) радиус его основания увеличить в три
раза?
1314. Начертите развертку цилиндра, размеры которого
выберите сами.
1315. Вычислите площадь поверхности и объем цилиндра по
следующим данным: 1) диаметр основания равен 12 см, высота
3,5 см; 2) радиус основания 18 см, высота 2,5 дм.
1316. Выразите объем цилиндра через его высоту h и длину С
окружности основания.
1317. Вычислите объем резервуара, имеющего цилиндрическую
форму, если: 1) его высота равна 8 м, а длина окружности
основания 30 м; 2) радиус окружности его основания равен
3,5 м, а высота равна диаметру основания.
345
1318*. Сравните объемы трех цилиндров: два из них получаются
вращением прямоугольника со сторонами 6 см и 10 см вокруг
каждой из двух смежных сторон, а третий — вращением
квадрата, периметр которого равен периметру этого
прямоугольника, вокруг стороны.
1319. На модели цилиндра проведите необходимые измерения и
вычислите: 1) площадь боковой поверхности; 2) площадь
поверхности; 3) объем модели.
99. Конус
Наглядное представление о конусе можно получить, вращая
прямоугольный треугольник вокруг одного из его катетов
(рис. 530). Катет SO при этом будет высотой конуса. Второй
катет ОА описывает круг, который называется основанием
конуса. Гипотенуза SA описывает боковую
поверхность конуса. Отрезок SA
называется образующей конуса.
Развертка конуса состоит из сектора,
радиус которого есть \SA\> и круга,
лежащего в основании конуса (рис. 531).
Площадь боковой поверхности конуса,
равная площади сектора SAB,
находится по формуле
лХ2а
7бок. кон
3G0
где L — длина образующей SA, a —
величина (в градусах) угла ASB.
Дуга АВ имеет длину (см. п. 93).
TiLa
180"
/ =
Поэтому
'бок. кон —
nLza
360
nLa L , L_
180 " 2 "" 2
Рис. 531
Но длина I дуги АВ есть длина
окружности основания конуса. Если
радиус основания конуса Rf то i = 2nR
и, следовательно,
346
>бок. ком = J Τ- — 2яД
= ziRL9
^бок.кон = nRL.
Площадь поверхности конуса равна S60K -f-
+ S0C||I и, значит,
SK0!1 = яЯ£ + лД2 = яй (I + Л),
SK0:I = nR(R + L).
Объем конуса равен одной трети
произведения площади его основания на
высоту:
VK0U = | nR*h.
Рис. 532
Формула объема конуса выглядит почти так же, как
формула объема пирамиды. Это не удивительно, так как конус похож
на пирамиду с основанием в виде правильного многоугольника
с достаточно большим числом сторон (рис. 532).
Вопросы и задачи
1320. Как изменится площадь боковой поверхности конуса, если:
1) длина его образующей увеличится в три раза; 2) радиус
его основания уменьшится в три раза?
1321. Постройте развертку конуса, размеры которого выберите
сами.
1322. Может ли длина образующей конуса равняться: 1) его
высоте; 2) радиусу окружности основания? Ответ обоснуйте.
1323. Вычислите высоту конуса, если его образующая 13 см,
диаметр основания 10 см.
1324. Вычислите площадь поверхности и объем конуса по
следующим данным: 1) образующая равна 1,6 дм и радиус
основания 4 см; 2) образующая равна 15 см и высота 10 см; 3)
высота равна 2,4 дм, а радиус основания 15 см.
1325. Прямоугольный треугольник с катетами 40 см и 20 см
вращается вокруг большего из катетов. Вычислите объем и
площадь поверхности полученного при вращении конуса.
1326. Как изменится объем конуса, если: 1) его высота увеличится
в η раз, а радиус окружности основания не изменится; 2)
радиус окружности основания увеличится в η раз, а высота не
изменится?
347
1327. Вычислите объем вырытой в земле конической воронки,
образующая которой равна 2м,а длина окружности 8 м.
1328. Практическая работа. На моделях правильной
пирамиды, цилиндра, конуса произведите необходимые
измерения и вычислите площади поверхностей и объемы этих тел.
100. Шар
Множество точек пространства, находящихся от данной точки
О на расстоянии, не большем данного расстояния г(г>0),
называется шаром с центром О радиуса г.
Наглядное представление о шаре можно получить, вращая
полукруг вокруг его диаметра (рис. 533). Отрезок,
соединяющий две точки поверхности шара (сферы) и проходящий
через его центр, называется диаметром шара.
В сечении шара любой плоскостью получается круг (рис. 534).
Если секущая плоскость проходит через центр шара, то в
сечении получается круг, радиус которого равен радиусу
шара. Такой круг называется большим кругом.
Окружностями больших кругов на глобусе, например, являются
экватор и меридианы.
Боковые поверхности конуса и
цилиндра — кривые поверхности. Но их
можно, «разгибая», превратить в плоские
(т. е. положить на плоскость, развернуть).
Поверхность шара, оказывается, никаким
«разгибанием» нельзя сделать плоской.
Поэтому формулу для площади шара
невозможно найти, пользуясь разверткой.
Эта формула (как и формула объема
шара) будет выведена в 10 классе, а пока
мы воспользуемся готовыми результатами.
Площадь поверхности шара равна
учетверенной площади большого круга:
Stll = 4лД2 или Sm = nD2,
где R — радиус шара, D — диаметр шара.
Объем шара вычисляется по формуле:
Рис. 533
Рке. 534
3
348
Вопросы и задачи
1329. Полукруг, радиус которого равен г, вращается вокруг
своего диаметра. 1) Выразите через г площадь поверхности и
объем шара, полученного при этом вращении. 2) Вычислите
площадь поверхности и объем этого шара, если г равно:
а) 4 см; б) 2,5 см; в) 16,8 мм; г) 1 дм.
1330. Вычислите площадь поверхности и объем шара, диаметр
которого равен q, если: 1) g = 0,5 м; 2) q = 8 м.
1331. Практическая работа. Вычислите объем и площадь
поверхности детали или специально изготовленной модели,
имеющей форму шара, выполнив предварительно
необходимые измерения.
1332. Найдите отношение объемов двух шаров, радиусы которых
Γι и Г2. Вычислите это отношение, если: 1) Γι = 5 см, Гг =
= 3 см; 2) Γι = 6,8 см; Гг = 1,6 см.
1333. Как относятся площади поверхностей двух шаров, радиусы
которых Γι и Г2? Вычислите это отношение при: 1) Г\ = 7 см,
г2 = 5 см; 2) Γι = 5,4 см, Гг = 0,7 см.
1334. Как относятся радиусы двух шаров, если отношение
объемов этих шаров равно: 1) 1:8; 2) 8:27; 3) 3:5; 4) 0,8?
1335. Принимая, что Земля имеет форму шара с радиусом 6400 км,
вычислите: 1) сколько квадратных километров занимает
площадь поверхности Земли; 2) сколько квадратных километров
Земли занимает суша, если она составляет около 30%
всей поверхности Земли; 3) чему равна длина земного
экватора.
1336. Вычислите массы шаров диаметром 10 см, изготовленных из
свинца, стали, меди, алюминия. (Необходимые для решения
задачи дополнительные данные найдите в справочнике.)
1337. Сколько дробинок диаметром 2 мм можно изготовить
из 1 кг свинца?
1338. Медный цилиндр, диаметр основания и высота которого
равны 8 см, переплавлен в шар. Каков диаметр полученного
шара?
1339. Шар вложен в цилиндрическую коробку так, что он
касается цилиндрической поверхности, дна и крышки этой
коробки. Вычислите: 1) объем шара и объем
цилиндрической коробки; 2) площадь поверхности шара и площадь
полной поверхности цилиндрической коробки, если известно,
что диаметр дна коробки равен 18 см.
349
CSt\
.1
Φ18^
Рис. 535
1340. Вычислите объем и площадь
поверхности полушара радиуса г, если:
1) г= 12 м; 2) г = 7 м.
1341. Резервуар, наибольшая глубина
которого равна 4 м, имеет форму
полушара. Какова вместимость этого
резервуара?
1342. Найдите объем детали, осевое
сечение которой имеет форму полушара
с приставленным в центральной части
большого круга цилиндром (рис. 535).
Дополнительные задачи к главе X
1343. Ребро куба имеет длину а. Найдите длину кратчайшего пути
по граням куба из точки А в С\ (рис. 536). Сколько имеется
таких путей?
1344. Покажите, что куб можно разрезать на три четырехугольные
пирамиды.
1345. Вообразите, что лучи света перпендикулярны экрану. Какой
может быть тень: 1) прямоугольника (отличного от
квадрата); 2) квадрата; 3) куба?
1346. Представьте себе, что вы смотрите на куб вдоль его
диагонали. Нарисуйте, что вы увидите (для проверки возьмите
модель куба и посмотрите на нее вдоль диагонали).
1347. Боковые грани деревянного куба с ребром 10 см покрыли
краской, а затем этот куб разрезали на кубики с ребром
2 см. Сколько получилось кубиков: 1) с двумя окрашенными
гранями; 2) с одной окрашенной гранью; 3) не имеющих
окрашенных граней?
1348. Решите предыдущую задачу при условии, что окрашены все
грани куба.
1349. Какие размеры может иметь
прямоугольный лист бумаги, если известно,
что из него можно вырезать
развертку куба с ребром 4 см?
1350. Какие из данных фигур (рис. 537)
являются развертками куба?
1351. Какие из данных на рисунке 538
фигур являются развертками
прямоугольного параллелепипеда?
Рис 536 1352. Открытый бак, имеющий форму ку-
350
1
2
5
г
9
—
в
! I
з\
4
7
Ри
10
2. 537
д
11
ба с ребром а, стоит на плоскости, наклоненной под углом α
к горизонту (рис. 539). Какой наибольший объем воды может
вместить бак в таком положении? Вычислите этот объем,
если: 1) а = 1г5 м, α = 30°; 2) а = 1г5 мг α = 10°.
1353. Вычислите объем правильной треугольной пирамиды,
боковое ребро которой равно т, а плоские углы при вершине
пирамиды прямые.
1354. Вычислите объемы и площади поверхностей геометрических
J
5
4
6
Рис. 538
351
Рис. 539
^ьг=
[6 см
15см
S
>г
см|
5)
у^Ь/
10 см
*^
0J
тел, представляющих собой
комбинацию: 1) двух конусов (рис. 540, а);
2) цилиндра и двух конусов
(рис. 540, б), 3) цилиндра и двух
полушаров (рис. 540, в); 4) конуса и
полушара (рис. 540, г). Необходимые
размеры указаны на чертеже.
1355. 1) Вычислите массу
дюралюминиевого пустотелого шара, внешний
диаметр которого равен 2 м, а
толщина стенок 3 см (плотность
дюралюминия 2,8 г/см).
2) Утонет ли такой пустотелый шар
(см. задачу 1355, 1)), если его
погрузить в воду? А если внутри шара
находится груз в 200 кг?'
1356. Диаметр Луны составляет 0,25
диаметра Земли. Вычислите: 1) какую
часть площади поверхности Земли
составляет площадь поверхности Луны;
2) какую часть объема Земли
составляет объем Луны.
Задачи на повторение по курсу 6—8 классов
1357.
1360.
Начертите две фигуры, объединение
которых — треугольник, а
пересечение— отрезок.
1358. Начертите два треугольника,
пересечение которых: 1) пустое множество,
2) точка, 3) отрезок, 4) треугольник,
5) четырехугольник, 6) пятиугольник,
7) шестиугольник.
1359. Сколько вершин может иметь
многоугольник, являющийся объединением
двух квадратов?
В озеро впадает река (рис. 541). По реке и озеру курсирует
моторная лодка. Скорость ее больше скорости течения реки.
На озере течения нет. «Расстояния» между пунктами на
берегах реки и озера будем оценивать по времени,
необходимому для того, чтобы моторная лодка пришла из одного
352
пункта в другой. Какие из свойств
расстояний (1, 2и 3) будут выполнять- ^ \ς^
ся для такого выбора «расстояния»
при любом выборе пунктов А, В и С
на берегах реки и озера? Что можно
сказать о таком «расстоянии», если
г ' Рис. 541
пункты выбираются только на берегу
озера?
1361. Точка Μ принадлежит треугольнику ABC. Докажите, что
сумма расстояний точки Μ до вершин треугольника больше
его полупериметра, но меньше периметра.
1362. В плоскости даны две точки А и В. Какой фигурой является
множество таких точек Μ зтой плоскости, для которых:
1) \МА\ < \МВ\; 2) \МА\ > \МВ\; 3) \МА\ = \MB\1
1363. Дан угол ABC. Какой фигурой является множество таких
точек Μ этого угла, для которых: 1) расстояние от точки Μ
до стороны ВА больше расстояния точки Μ до стороны ВС;
2) расстояния от точки Μ до сторон угла не равны?
1364. В выпуклом четырехугольнике найдите точку, сумма
расстояний которой от вершин четырехугольника наименьшая.
1365. Внутри выпуклого многоугольника, все стороны которого
конгруэнтны, взята точка М. Докажите, что сумма
расстояний от точки Μ до прямых, на которых лежат стороны
многоугольника, не зависит от положения точки М.
1366. Постройте равносторонний треугольник, вершины которого
лежат на трех данных прямых.
1367. Дайте определения следующих фигур как пересечений двух
или трех других известных вам фигур: 1) треугольника; 2)
параллелограмма; 3) прямоугольника; 4) ромба; 5) квадрата;
6) трапеции.
1368. Докажите, что: 1) у любого выпуклого четырехугольника,
имеющего ось симметрии, точка пересечения диагоналей
лежит на этой оси; 2) у любого четырехугольника, имеющего
центр симметрии, этот центр совпадает с точкой пересечения
диагоналей.
1369. Какой вид имеет выпуклый четырехугольник, если: 1)
серединные перпендикуляры к его противоположным сторонам
совпадают; 2) биссектрисы его противоположных углов
лежат на одной прямой?
1370. Луч АС — биссектриса угла А четырехугольника ABCD,
В = Ъ. Докажите, что ААВС ^ AADC.
353
. Через точку пересечения диагоналей параллелограмма
проведены две прямые, пересекающие противоположные
стороны параллелограмма. Докажите, что полученные
четыре точки пересечения являются вершинами
параллелограмма.
1372. Докажите, что два отрезка, концами которых
соответственно являются середины противоположных сторон и середины ι
диагоналей четырехугольника ABCD, пересекаются и де-'
лятся точкой пересечения пополам. ·}
1373. Докажите, что площадь треугольника, две стороны
которого равны т и п, не больше 0,5 тп.
1374. Докажите, что площадь четырехугольника ABCD не больше
0,25 (\AB\ + \CD\)(\BC\ + \BD\).
1375. Докажите теорему, обратную теореме Фалеса.
1376. Вычислите площадь ромба, если его сторона равна 4 см, а
один из углов равен: 1) 80°; 2) 30°.
1377. Длины сторон параллелограмма, отличного от
прямоугольника, равны 4 см и 10 см. На отрезки какой длины делит
сторону параллелограмма биссектриса: 1) его острого угла;
2) его тупого угла?
1378. Прямая, параллельная основанию треугольника, делит его
на две равновеликие части. В каком отношении эта прямая
делит боковые стороны треугольника?
1379. Дана трапеция с основаниями а и Ь. Выразите через а и Ь
длину отрезка, параллельного основаниям и проходящего
через точку пересечения диагоналей.
1380. Постройте прямую, на которой две данные окружности
высекают хорды данной длины.
1381. Докажите, что средние линии четырехугольника в точке
своего пересечения делятся пополам.
1382. Докажите, что наибольшая из площадей треугольников, впи-
3r2l/~^
санных в окружность радиуса г, равна —*-Л .
4
1383. Докажите, что наибольшая из площадей четырехугольников,
вписанных в окружность радиуса г, равна 2г2.
1384. Данный отрезок разделите на две части в отношении 1 :|/!£
(Воспользуйтесь тем, что отношение квадратов катетов
равно отношению их проекций на гипотенузу.)
1385. Проведите прямую, параллельную одной из сторон данного
треугольника, так, чтобы площадь треугольника делилась
этой прямой пополам.
354
1386. На гипотенузе и катетах прямоугольного треугольника
построены правильные треугольники. Докажите, что площадь
треугольника, построенного на гипотенузе, равна сумме
площадей треугольников, построенных на катетах.
1387. На гипотенузе и катетах прямоугольного треугольника как
на сходственных сторонах построены подобные
многоугольники. Докажите, что площадь многоугольника, построенного
на гипотенузе, равна сумме площадей многоугольников,
построенных на катетах.
1388. Постройте квадрат, равновеликий данному треугольнику.
1389. В плоскости α даны две точки А и В. Какой фигурой
является множество проекций точки А на прямые, проходящие
через точку В и лежащие в плоскости а?
1390. Какой фигурой является множество середин хорд данной
окружности, проходящих через данную точку?
1391. Дана окружность (О, г), которая касается двух
параллельных прямых. Через точку Μ этой окружности проведена
к ней третья касательная, которая пересекает две первые
прямые в точках А и В. Докажите, что: 1) произведение
\МА\ · \МВ\ не зависит от выбора точки М; 2) это
произведение не изменится, если две параллельные касательные
заменить двумя другими параллельными касательными.
1392. Через точку М, лежащую вне данной окружности (О, г),
проведены к этой окружности секущие. Какой фигурой является
множество середин всех образовавшихся хорд?
1393. Докажите, что: 1) продолжения боковых сторон трапеции
и прямая, проходящая через середины ее оснований,
пересекаются в одной точке; 2) прямая, проходящая через точку
пересечения продолжений боковых сторон трапеции и точку
пересечения ее диагоналей, проходит через середины
оснований.
1394. Докажите теорему: если через точку, взятую внутри круга,
проведены какая-нибудь хорда и диаметр, то произведение
длин отрезков хорды равно произведению длин отрезкоз
диаметра.
1395. Докажите, что произведение длин отрезков хорд,
проходящих через точку, взятую внутри данной окружности,
постоянно для всех хорд.
1396. Из точки, лежащей вне окружности, проведены к ней
касательная и секущая. Докажите, что квадрат касательной
равен произведению всей секущей на ее внешнюю часть.
355
Найдите множество точек, равноудаленных от двух данных
прямых, если эти прямые: 1) параллельные; 2)
пересекающиеся.
1398. Найдите множество точек, находящихся на данном
расстоянии а: 1) от данного угла; 2) от границы данного квадрата.
1399. Найдите множество точек, находящихся на данном
расстоянии: 1) от данной окружности; 2) от данного круга.
1400. Проведите прямую, перпендикулярную основанию
треугольника, так, чтобы площадь треугольника делилась этой прямой
пополам.
1401. Даны параллелограмм ABCD и произвольная точка О.
Докажите, что ОА+ОС = ОВ +1эЬ.
1402. Что можно сказать о векторах а и Ъ, если для них
выполняются следующие равенства:
1) |а+"Ь| = |а-&|; 2) \а +"Ъ| = |с| + \~Ь\;
3) \а + Ь\ = \а\ - \Ь\; 4) \а-Ь\ = |а| + |Ь|?
1403. Докажите, что в параллелограмме ABCD найдется
единственная такая точка О, что ОА + ОВ + ОС + OD = 0.
1404. Дан правильный шестиугольник ABCDEF. Докажите, что
AB + AC + AE + AF = 2AD.
1405. Точка О является точкой пересечения медиан треугольника
ABC. Докажите, что ОА+ОВ + ОС=0.
1406. Постройте треугольник: 1) по двум углам и радиусу
вписанной окружности; 2) по двум его углам и периметру.
1407. В данный треугольник впишите треугольник, ему подобный,
так, чтобы вершины построенного треугольника лежали на
сторонах данного (на каждой стороне по одной).
1408. Сколько центров гомотетии имеют: 1) два конгруэнтных
круга; 2) два неконгруэнтных круга? (К ответам дайте
соответствующие рисунки.)
1409. Докажите, что отношение длины стороны треугольника к
синусу противолежащего угла равно длине диаметра
описанной около треугольника окружности.
1410. Какие из названных ниже отношений являются отношениями
эквивалентности: 1) конгруэнтность фигур; 2) подобие
фигур; 3) гомотетичность фигур; 4) перпендикулярность
прямых; 5) параллельность прямых; 6) сонаправленность лучей;
7) противоположная направленность лучей; 8)
коллинеарность двух векторов?
356
1411. Противоположные стороны шестиугольника ABCDEF
попарно параллельны и равны. Какую часть площади этого
шестиугольника составляет площадь треугольника АСЕ1
1412. В круге радиуса R проведены две параллельные хорды, каж
дая из которых стягивает дугу в α радиан. Вычислите площадь
части круга, заключенную между этими хордами.
1413. Площадь равностороннего треугольника, вписанного в круг,
равна а2. Выразите через а радиус круга.
1414. В угол 60° вписаны две окружности, касающиеся сторон угла
и друг друга. Вычислите отношение их радиусов.
1415. По данным, приведенным ниже, вычислите: 1) какую часть
площади поверхности Земли составляет площадь
поверхности каждой из планет (если принять, что планеты имеют
форму шара и за единицу измерения диаметра планет принят
диаметр Земли), 2) какую часть объема Земли составляет
объем каждой из планет.
1. Меркурий . . 0,39 5. Сатурн .... 9,4
2. Венера .... 0,97 6. Уран 4,2
3. Марс 0,53 7. Нептун .... 3,9
4. Юпитер ... 11,26 8. Плутон .... 1
1416- Укажите отображения, при которых полуплоскость
отображается на себя.
1417. Какими перемещениями отображается на себя: 1) фигура,
являющаяся объединением двух конгруэнтных кругов;
2) правильный п-угольник?
1418. Какими перемещениями может быть отображена на себя
плоскость, из которой «выколоты»: 1) точка; 2) две точки?
1419. 1) Каким перемещением может быть композиция двух
центральных симметрии?
2) Каким отображением может быть композиция двух
гомотетий?
1420. Укажите перемещения, при которых: 1) прямая
отображается на себя, а полуплоскости с границей ρ отображаются
друг на друга; 2) одна и только одна точка плоскости
отображается на себя; 3) не существует ни одной точки
плоскости, отображающейся на себя.
1421. Укажите известные вам отображения плоскости на себя, при
которых каждая прямая отображается на параллельную ей
прямую.
1422. Докажите, что любое перемещение плоскости является
либо поворотом, либо переносом, либо скользящей
симметрией (см. задачу 782).
357
ОТВЕТЫ И УКАЗАНИЯ
Глава I. Начальные понятия геометрии
3. 1) Не принадлежит; 2) принадлежит. 5. 1) {А}, {В}, {А, £}, 0. 6. Можно
в случаях 1), 2), 3). 7. 1) Одна; 2) бесконечное множество. 8. 1) Экватор,
меридианы. 9. 1) Можно; 2) нельзя. 12. 1) Точка; 2), 3) точка, расстояние и
плоскость. 17. Ограниченными фигурами являются точка, круг, отрезок,
треугольник и квадрат. 21. 1) 30. 22. 1) Увеличится в 10 раз; 2) уменьшится в
100 раз. 23. 1) 50; 4) 12. 24. 1) а) 5,556 км; б) 22,224 км; в) 370,4 км,
2) ^0,540 мили. 25. 1) 1,0668 а км; 2) ^ 0,937 версты. 26. 1) a) | XY | = 0,5 м;
| АВ | = 0,7 м; | CD |= 0,1 м. 27. Может в случаях б), в), г), е). Указание.
Воспользуйтесь предложениями 3 и 4. 28. 1) 1 см ^ | АХ | ^ 5 см. 2)
Существуют две такие точки. 29. Равенства или неравенства всегда верны в случаях
а), б), д); в случаях г), е), з) всегда неверны; в других случаях могут быть как
верными, так и неверными. 32. 2) Бесконечное множество. 33. 1) Могут;
2) не могут. 34. Одна или три. 36. Могут иметь: одну, четыре или шесть
точек пересечения. 38. Указание. Центром такого круга может служить
любая из данных точек. 39. Верно. 40. Неверно. 42. 1), 2) Да. 45. 1) Могут в
случаях б), г). 46. 1) а), г) — не может; 2) наименьшее расстояние — 3 км,
наибольшее — 7 км. 47. 1) Наибольшее значение | АВ | равно 8. Наименьшее значение
| АВ\ равно: а) 2; б) 5; в) 1. 49. В6 (АС\ в случаях 1) и 3); в случае 2) В£ \АС\\
в случае 4) В 6 [АС] лишь при условии | АВ \=\ ВС \— 5 см. 50.
Принадлежат в случаях 2) и 3). 52. 1) Три; 2) шесть. 53. Указание.
Воспользуйтесь равенством | АХ | + | ВХ \ — | АВ |. 54. 1) Можно, например, дать такое
определение: серединой отрезка называется точка этого отрезка,
равноудаленная от его кондов. 2) а) 7 см; б) 2 см; в) 9 см. 57. 1) [АВ) β [ΒΑ) = [АВ~\\
2) а) лучом, отрезком, точкой или пустым множеством. 58. 1) Луч АВ; 2) луч
В А; 3) точка Μ принадлежит и лучу АВ, и лучу В А, 5Θ. 1) Точка и
расстояние; 2) прямая, точка и расстояние. 60. Указание. Воспользуйтесь
предложением 5. 62. Указание. Воспользуйтесь предложениями 7 и 9. 65.
1) | АО | = 7, | DO | = 5; 2) | АВ | = 2. 67. 1) а) 5; 2) а)—0,5. 68. 1) —7 <
< хс < 9; 2) хс < —7 или хс > 9. 69. 5) (2 — а) и (5 — а); 6) (2 + а) и
(5 + я). 74. Четыре. 76. Может в случаях 1) и 3). 77. 1) 0,5 см < \АВ\ <
< 10,5 ем; 2) 0 см < | АВ \ < 12 см. 82. Три. 89. 1), 2) Да. 90. Предложения
2), 4) и 6) верны; предложения 1), 3), 5) и 7) не верны. 92. 2) б) [АВ] d [A//J;
г) Μ ^ [АВ\. 97. Да. 98. Да. 101. 1) а) На три области; б) на шесть областей.
2) а) На три или четыре области, б) на 4, 5, 6, 7 или 8 областей. 102. Данные
353
лучи разбивают плоскость на три области (рис. 53, а), на две области (рис. 53,
б), на четыре области (рис. 53, в), на одну область (рис. 53, г). 105. 1) Не
выполняется второе свойство области. 2) Неверно (если, например, две окружности
не имеют общих точек и ни одна из них не лежит внутри другой, го объединение
их внутренних областей областью не является). 106. 1) На три или четыре
области, 2) на четыре, шесть или семь областей. 113. 1), 2) Да; 3) нет. 114. 1) Да;
2) не обязательно. 115. Полукруг — фигура выпуклая. 116. Может. 118.
Указание. Воспользуйтесь определениями пересечения множеств и выпуклой
фигуры. 120. 1) Три; 2) четыре. 121. η — 2. 122. Нет. 123. 1) Существует, это
пятиугольвик. 125. В случаях 1) и 3) точки А и В лежат в одной полуплоскости;
в случае 2) — в разных полуплоскостях. 128. 1) Полуплоскость с границей р,
не содержащая точки А; 2) та из областей с границей р, которая содержит
точку А. 133. 1) Да. 136. Не всегда. 137. 12 дуг и 12 центральных углов. 138. 1)
Для выпуклого угла АОВ; 2) для невыпуклого угла АОВ. 139. Угол со
сторонами ОА и ОВ, отличный от данного. 140. 1) Имеют внешнее касание; 2), 5) и 6)
пересекаются; 3) не пересекаются; 4) имеют внутреннее касание. 142. 1) Две,
одну или ни одной точки. 143. 1) Две. 144. Задача имеет решение, если \ а — Ь |^
^ | АВ|^ а + Ь, и не имеет решений, если | АВ|> а + Ь или | АВ\ < \а — Ь\ш
145. В случаях 1) и 3) — две окружности, в случае 2) — одну. 146. 1)
Бесконечное множество. 2) Одно или два решения. 148. Если \ а — Ь| < | АВ\ < а + Ь,
го в каждой из полуплоскостей с границей ρ существует одна точка X {X dp),
удовлетворяющая поставленным условиям. Если | АВ \ — \а — Ь\ или | АВ| =
= а + Ь, го точка X принадлежит прямой р. Если | АВ |> а + Ъ или | АВ\ <
< \а — Ь|, то тогда таких точек не существует. 149. | 0203 \ — г2 — г3,
I Ог03\ = п + г3 (рис. 70, а); | ОхОг\ = гх + г2, | 0203| = г2 + г3, | Οχ03| =
= *Ί + г3 (рис. 70, б); | Οι02\ = гй — г2, | 0203| = г2 + г3, | Ох03\ = гх — г3
(рис. 70, в). 150. Указание. Воспользуйтесь предложением 7 и условием
касания окружностей. 151. Окружность (О, — ), где О — общий центр
данных окружностей, г, и г2 — их радиусы. 153. 1) 0; 2) точка; 3) пересечение
внутренних областей окружностей (А; 1,5 см) и (В; 1,5 см); 4) пересечение
внешних областей окружностей {А\ 1,5 см) и (В; 1,5 см). 155. Указани е. Если
а = xvex h«! = ke2t то а = {kxx)e2. 157. 3) Точки F и С лежат между А и В. 158.
Указание. Рассмотрите различные случаи: на одной прямой лежат пять
точек, четыре точки и т. д. 160. Указание. Воспользуйтесь неравенством
треугольника. 161. Искомой фигурой является: 1) точка; 2) отрезок; 3) и 4) луч.
165. 1) и 3) Не существует; 2) существует. 167. 1) Неверно; 2) неверно. 169. 1)
Указание. Воспользуйтесь неравенством треугольника. 171. 1) Точка,
прямая, отрезок; 2) простая замкнутая ломаная, внутренняя область простой
замкнутой ломаной. 173. 1) Две окружности называются касающимися, если
их пересечение — точка. 174. 1) Окружности касаются внешним обравом.
175. 2) Объединение двух окружностей, касающихся внешним образом,
называется восьмеркой. 177. 1) На три или четыре. 181. 1) \Ολ02\ = | гх — г2|,
I 0203| = \г2± г3|, | O^gl = | гх ± г3|.
Глава II. Конгруэнтность фигур и перемещения
182. 1) f(A) = Ац 2) D -+Dx\ 4) да. 183. 1) С -+ Dx\ 2) например, f (К) =
= Hi, f (L) = Hi. Множес1во точек, образами которых является точка Hlt —
з:9
отрезок KF. 3) Нет. 184. 4) Да. 188. Координатная прямая отображается на
себя при отображениях: 1); 2); 4); 6). 189. Указание. 1) Существует
шесть отображений фигуры {А, В, С} на себя. 2) Например, отображение,
обратное отображению А -> В, В -> С и С -> А, таково: А ->■ С, С -* В, В -> А.
191. 1) Отображение, заданное на рисунке 89, обратимо; отображение,
заданное на рисунке 90, необратимо. 2) Не выполняются. 192. 1) Точки Я,
М, R. 2) Образами точек Р, X, А. 3) Отрезку АВ, отрезку АХ, 4) На точку Q,
на отрезок MR, на ломаную QKMR. 5) Да. 6) Например, при отображении,
обратном данному, образом отрезка KQ является отрезок РА, точки К — точка А9
ломаной QKMR — ломаная Ρ ABC, 193. 1) Точка Υγ, на отрезки ΧλΥχ и DYX.
2) Отрезков АХ и АВ. 3) Да. 4) Нет. 194. 1) Отображение луча ОМ на луч ON,
2) На отрезок OYlf отрезка О А. 3) Да. 195. 1) Отображение полуокружности на
ее диаметр. 2) Да. 3) Не сохраняются. 196. 1) Нет. 2) Да (см. теорему 16). 197.
Указание. 1) В случае а) существует одно такое отображение
(тождественное); в случае б) два, а в случае в) шесть. 198. Расстояния
сохраняются при отображениях 2), 3), 4). 200. 2) [АВ]^ [CZ>]. 201. 1)
IPQ | = 7. 202. Конгруэнтны. 205. 1), 2) Неверно, 3) верно. 206. Не
может. 208. Указание. Пусть [АВ] ->■ [ΑιΒ{]. Тогда при помощи
циркуля можно построить точку Хх треугольника AiBiClt для которой | ΑλΧλ\ =
= \АХ\, \В1Х1\ = | ВХ |. 209. 1) См. указание к предыдущей задаче. 2) В
зависимости от выбора точки X может быть построено восемь, четыре или одна
точка, являющиеся ее образом. 210. Указание. На отрезке меньшей
длины нельзя найти две точки, расстояние между которыми равно длине большего
отрезка. 212. Указание. Для решения задачи предположите, что
существует отображение, сохраняющее расстояния, воспользуйтесь свойствами
этого отображения и предложением 7. В результате будет получено противоречие
с условием. 213. Биссектрисой угла называется луч с началом в вершине
этого угла, делящий его на два конгруэнтных угла. 215. — · 45° = 22,5° =
d 1 d
= 22°30' = —; — . 45° = 7,5° = 7°30' = —. 217. 1) 90°; 2) 105°51'25";
4 6 12
3) 47с55'05"; 4) 51°52'45"; 5) 60°46'30'; 6) 121°41'; 7) ^48°16'48". 219.
Достаточно измерить один угол. 220. 2) Два треугольника. 222. Указание.
Сумма величин смежных углов равна 180°. 227. 2) На себя. 3) На угол,
конгруэнтный данному. 232. Фигуры, изображенные на рисунке 110, а, б, г, е.
233. В случае квадрата углы поворотов равны 0°, 180° и 90° (в направлении по
часовой стрелке и против). Центр поворота — точка Н. 237. 1) 3), 4) Бесконечное
множество; 2) два; 5) четыре (если длины отрезков равны) или ни одного (если
их длины различны). 238. Указание. Воспользуйтесь определением
перемещения и предложением 10. 239. Указание. Воспользуйтесь
определением перемещения и результатом задачи 238. 240. 1) Указание. Если
\ АС\ Φ \СВ\, то | АС\ Φ |/ι(Α)/х (С)|. 241. Например, прямая и плоскость.
243. 1) Центр симметрии. 244. 1) Прямая АВ\ 2) луч, противоположный
лучу ОС\ 3) угол, вертикальный с углом ABC. 247. 1) Прямая имеет бесконечно
много центров симметрии; луч не имеет центра симметрии; у отрезка и
объединения двух пересекающихся прямых один центр симметрии. 2) Указание.
Многоугольник с нечетным числом сторон не имеет центра симметрии. 3)
Существуют. 248. Фигуры, изображенные на рисунке 110, а, б иг. 250. 1) | QR\ = 6,
| АВ\ - 6, | QP\ = 8. 2) /_АВС ^ /_QRP. 3) | АО\ = 9, | NC\ = 6, | АР\ =
360
= 18. 252. β, = a, = 105°, β2 = 40°, α2 - 35°. 255. Указание.
Покажите, что данные фигуры центрально-симметричны. 256. Указание.
Рассмотрите симметрию с центром О. 257. 2) [АВ] = Sh(\CD]). 258. 1) Верно.
259. 2) X £ а. 260. 2) Прямые, перпендикулярные оси р, а также сама
прямая р. 261. 2) О £ /. 272. Указание. Угол ХхОХ2 развернутый.
273. Указание. Рассмотрите точку, симметричную точке А относительно
прямой р. 276. 1), 2) Можно. 280. 1) Четыре треугольника. 281. Не меньше
600 см. 282—286. Указание. Воспользуйтесь признаками
конгруэнтности треугольников. 288. Указание. Четырехугольник ABCD симметричен
относительно центра О. 289. Указание. Рассмотрите симметрии
относительно прямых АС и BD. 291. 1) Одна или бесконечно много. 2) Одну, две
или бесконечно много. 293. Указание. Рассмотрите симметрию
относительно прямой, содержащей биссектрису данного угла. 294. Указание.
Рассмотрите симметрию относительно прямой Ох02. 297. Указание.
Воспользуйтесь теоремой 28. 298. Указание. Проведите прямую, проходящую
через центр окружности и перпендикулярную данной хорде. 299. Указание.
Воспользуйтесь результатом задачи 293. 300. Указание. 1)В результате
допущения, что центры окружностей различны, получается противоречие с
условием. 301. 1) Две; 2) одну; 3) бесконечно много. 304. Возможны такие
случаи: искомая точка единственна, множество решений — данная прямая МТ,
задача не имеет решений. 307. Серединный перпендикуляр к отрезку АВ.
308. Серединный перпендикуляр к данному отрезку за исключением
середины этого отрезка. 310. 1) Множество точек плоскости, не принадлежащих
серединному перпендикуляру к данному отрезку АВ. 314. Три. 318. 1) 6 см;
2) 3 см; 3) 8 см. 327. 1) Могут. 328. Прямая, перпендикулярная прямой АВ
и проходящая через точку В. 331. Указание. Воспользуйтесь теоремой
32. 333. Таким множеством является объединение двух пересекающихся
прямых» содержащих биссектрисы углов, образованных данными
прямыми. 336. Указание. Докажите, что для любой точки Ν Φ Μ окружности
\ΜΝ\ > |ΛΓΑ|. 337. Указание. Воспользуйтесь свойствами серединного
перпендикуляра к отрезку. 341. Указание. Постройте угол в 72".
Постройте произвольную фигуру, содержащуюся в этом угле, и образы этой
фигуры при поворотах вокруг вершины построенного угла на углы в 72° и 144°
по часовой стрелке и против. 348. Указание. Искомая фигура обладает
симметрией вращения порядка 6, поэтому, чтобы восстановить ее изображение,
достаточно знать часть этой фигуры, содержащуюся в угле 60° с вершиной О.
о m
349. Указание. При повороте с центром О на угол 360 · — фигура Lx
η
отображается на фигуру Lm+lt L2— на Lm+2 и т. д. 352. Указание.
Воспользуйтесь свойствами центральной симметрии. 353. Указание.
Проведите прямую р, перпендикулярную прямой АВ и проходящую через общий центр
окружностей. Затем рассмотрите симметрию Sp. 354. 1) АВ = 72°. 356. 1) 165°,
195°. 358. 1) а) 60°. 2) 360 мин. 362. 2) Окружность. 363. 1) 160°. 2) а) 0,054';
б) 0,0648". 366. Указание. Воспользуйтесь теоремой 36. 375.
Указание. Рассмотрите различные случаи: 1) А лежит во внутренней области
окружности; 2) А 6 Окр (О, г); 3) А лежит во внешней области окружности.
380. 2) Прямая, которая касается окружностей в их общей точке, исключая
эту точку касания. 381. Отображение обратимо. 387. Можете воспользоваться
361
калькой и копировальной бумагой; только копировальной бумагой. 388. 1)
Фигуры «Ж», «И*, «Н», «О, «X». 389. Указание. Точка Оэ = ZQ (02)
принадлежит фигуре L и |020:ί| = 2. 390. Указание. Если Х\ — образ
точки Х% то \АЛХ{\ = |АХ|, hBi-STiI = \ВХ\. 391. Указание. 1) При любом
перемещении, отображающем отрезок на себя, косны этого отрезка
«отображаются на -его концы. 2) При перемещены як, отображающих на себя «окружность,
ее центр отображается ыа себя. 392. Указание. Рассмотрите симметрию,
центр которой — середина отрезка Ох02 {Ох и «02 — центры данных кругов).
394. Указание. М}ОМ2 = 2АОВ. 395. 1) Одну или бесконечно много;
2) одну или две. 397. Будет построено четыре точки (считая М). 399.
Указание. 54° = 90° — 36°, 18°= 54° : 3 = 36° : 2. 400. Указание, а) 17°Х
X 11 = 187°, 10° = 17° — 7°. 406. Указание. Рассмотрите различные
случаи: данный угол может быть острым, прямым, тупым, развернутым или
большим развернутого. 409. Указание. Выясните, сколько решений
имеет задача на лостроение треугольника или четырехугольника, если
известны длины его сторон. 412. Указание. Воспользуйтесь
предложениями 4 и 8. 413. 1) Указание. Продолжите отрезок AM до пересечения со
стороной ВС и воспользуйтесь неравенством треугольника. 417. 1)
Указание. Рассмотрите образы точки Μ при симметриях относительно прямых,
содержащих стороны данного угла.
Глава III. Параллельность и параллельный перенос
422. Нет; прямые могут не лежать в одной плоскости. 428. 1) Прямые,
проходящие через центр симметрии; отрезки, имеющие центр симметрии своей
серединой. 424. 1) α || b. 2) Прямые α и Ь либо пересекаются, либо совпадают.
428. а || Ь. 430. Прямые, перпендикулярные или параллельные прямой р.
431. Указание. Воспользуйтесь признаком параллельности прямых.
433. Нет. 434. 1), 2), 3) Да. 436. Прямые α и с пересекаются. 438, 439.
Указание. Рассмотрите симметрию Zq , где О — середина отрезка прямой с,
заключенного между прямыми а и Ъ. 440. Указание. Воспользуйтесь
результатом задачи 439. 441. 1) Бесконечное множество; 2) ни одного, один
или бесконечное множество. 442. В = D = 150°, С = 30°, | AD\= 4 см, | CD\ =
= 2 см. 446. Да. 449. При таком определении отношение параллельности не
рефлексивно. 451. 1), 2) Один. 453. 1) Лучом. 2) а) Прямой АВ или
подмножеством этой прямой, состоящим из точек, не являющихся внутренними точками
отрезка АВ; б) отрезком, точкой или пустым множеством. 454. Бесконечное
множество. 455. 1) Два; 2) четыре; 3) шесть. 456. Нет: свойства рефлексивности
и транзитивности не выполняются. 459. 1) а), б) Ни одной, одну или две; в) ни
одной, одну, две или три. 2) Нет. 460. 1), 2) Нет. 464. Если отрезки параллельны
и конгруэнтны. 465. 1) Нет; 2) да. 467. 2) Указание. Воспользуйтесь
теоремой 43 и транзитивностью отношения конгруэнтности. 3) Да. 468. 1)
Бесконечное множество; 2) один. 469. 1) При центральной симметрии; 2) только при
параллельном переносе; 3) при тождественном отображении. 470. 1) Нет. Например,
при симметрии SAB луч АВ отображается на оонаправленный луч. 2) Нет.
476. Центральная симметрия и параллельный перенос. 477. Нет. 481. 1) 0°;
2) 180°. 483. У казани е. Рассмотрите центральную симметрию, отображающую
вершину первого угла на вершину второго. 485. 1) 90°; 2) 180°; 3) 45°. 488. 1) 30°,
362
60°, 90°; 2) 30°, 70°, 80°; 3) 36°, 36°, 103°. 49Э. 25°, 68° и 87°. 491. Аксиома
параллельных, теорема о конгруэнтности зглэв с сонаправленными сторонами и
свойство величины суммы углов. 49& 1) Треугольник, все углы которого острые,
называется остроугольным. 2> а) Прямоугольный; 6>) тупоугольный. 494.
Остроугольный. 495. 1) 48°, 60°, 72°. 496. 50?, 50°, 80*> или 80°, 80°г 20°. 498. 1)
Тупоугольный; 2) прямоугольный. 590. 1) 16d; 2) 20d; 3) 56rf; 4> 188d. 501. 1) Восемь;
2) одиннадцать; 3) двадцать четыре; 4) двенадцать. 502; 1) Десять; 2) двенадцать;
3) тридцать шесть; 4) сорок, 504. 1), 2),. 5)· Да. 3), 4) Нет. 597. 1) Один или
бесконечное множество. 515·» В обоих случаях увеличится на 2d. 516. Шесть. 517.
Три. 518. 2d. 519. Да. 5201 1) Диаметрч перпендикулярный данной прямой
(концы диаметра не принадлежал искомому множеству). 52L. 1) 60°, 60°, 60°.
523. 1) 230° и 80°. 524. 1) Бесвонечюое множество* 2) Имеет; множество центров
образует прямую. 3) Да. 527. Указание. Рассмотрите образ данной
прямой при повороте вокруг данной точки на угол в 60°. 530. Указание.
Воспользуйтесь тем, что образ объединения (пересечения) фигур £х и L2
при» перемещении — объединение (пересечение) образов этих фигур.
Глава IV. Многоугольники
533. Больше \ а — &|, но меньше & + Ъ. 535. 2) В, Спела с. 539. Треугольник
равносторонний. 540. Треугольник равносторонний. 541. Указание.
Постройте вспомогательный треугольник по двум боковым: сторонам и углу
между ними, равному разности углов при основании искомого треугольника. 543.
Указание. Предположение, что против меньшей стороны лежит тупой или
прямой угол, приводит к противоречию. 544. Углы А и В острые, С > 60°.
545. 1) 60° < α < 180°; 2) 0° < α < 60°. 551. | BD\ = —. 553. Аг {] А2 =
Аг{] А3 = А3{] А5 = А3{] А6 = А, [] А, = A,{]AQ=A5{]AG = 0. 554. 1), 2) Нет.
555. 80е и 100°. 557. 1) 2,5 см; 2) 15 см и 10 см. 558. 1), 2) Нет; 3) да. 559. 1) Да;
2), 3) нет. 560. 1) 28 см или 26 см; 2) 3 см и 2 см. 561. Эги биссектрисы
симметричны относительно центра симметрии параллелограмма. 562. Указание.
1) Воспользуйтесь результатом задачи 551. 2) Воспользуйтесь следствием 3
теоремы 51. 568. Например, двумя дгсагоналячии и стороной. 58§*. Указание.
Рассмотрите центральную симметрию, отображающую паралшелогралш ABCD
на себя. 575* Истинны предложения, обратные предложениям 3 и 6. 579. 1),
2), 4), 6) Нет; 3), 5) да. 581. 1) Hen 2), а), 4) да, 584. 1), 2} Да; 3), 4) нет. 585.
2) Например, существует параллельный перенос, отображающий один луч
на другой; 4) угол треугольника равен 60°. 586. 1) Точка X принадлежит
серединному перпендикуляру к отрезку АВ; 2) существует такая тачка О, что Zj (α) =
= Ь. 587. Верны предложения 2 и 4. 589. 1), 2) Достаточно; 3), 4) необходимо.
593. Если стороны каждого из. этих прямоугольников не равны,, то существует
4 перемещения. 594. 1) Да. 595. Например^ «диагонали конгруэнтны». 596.
90 см. 597. 6 см. 599. 1) Указание. Достройте прямоугольный треугольник
до прямоугольника. 600. Окружность (за исключением тачек А и В). 601—603.
Указание. Воспользуйтесь результатом задачи 600. 606. Указание.
Высоты треугольника пересекаются в одной точке. 610. 1), 3) Нет; 2) да. 613.
1) 32 см; 2) нет; 3) а) нет, б) да. 614. 1) Нет, если только угол ромба не является
прямым; 2) да. 617. | АМ\ = 1 cm,|MD| = 1 см, | BD\= 2 см. 623. 1) Например,
363
диагонали квадрата перпендикулярны. 626. Указание. Существует 8
перемещений. 627. 1), 2) Нет. 629. Указание. Можно рассмотреть
перемещение, отображающее квадрат ABCD на себя. 630. 4) Указание.
Существуют повороты, отображающие квадрат на себя. 633. 1 см, 8 см и 7 см.
636. 2) т -\- п; 38 см. 637. Периметр звездочки равен р. 640. Указание.
Через точку D проведите прямую, параллельную стороне угла. 653.
Полученный четырехугольник является: 1), 2), 3) параллелограммом; 4) ромбом;
5) прямоугольником; 6) квадратом. 654. 5 см. 655. 1) 12 см и 8 см; 2) 5 см и
2 см. 656. 1) 3 см; 2) 14,2 см. 661. 2) Площадь прямоугольника равна 5 см2,
8 см2 или 9 см2. 663. 1) 1; 2) 1 000 000; 3) 10 000. 664. 1) Увеличится в 4 раза;
2) уменьшится в 9 раз; 3) не изменится. 665. Нет. 670. Ук а з а н и е. Стороной
искомого квадрата является диагональ данного. 674. 18,48 см2; 4,4 см. 675. 48 см2
тп
или 60 см2 или 7,5 см. 676. 7,2 см. 679. 20 см. 682. 1) S = —. 683. 2) 19,22 см2.
mt
684. 4 см и 6 см. 685. S = —. 686. 99 см2, 16,5 см. 687. 48 см2. 688. Объединение
2
S с2
двух прямых, параллельных прямой АВ. 693. Sx = —. 694. 37,5 мм2. 696. S = —.
тп
697. 24 см2. 698. S = —. 699. 1) 1 : 2. 700. Площадь треугольника меньше или
аЪ
равна 6 см2. 701. S= —. 702. 1) Ромб. 2) Прямоугольник. 703. 210 см2. 704. 336 см2.
706. 10,8 дм2. 709. 6 см2. 710. 6 см2. 711. 32 см2. 718. Нет. 719. Указание.
Постройте вспомогательный треугольник, сторона которого равна периметру,
а высота — высоте искомого треугольника. 720. Нет. 727. 1), 2) Да; 3) нет.
η (η — 3)
Указание. Число диагоналей гс-угольника равно . 729. Такой
4 2 а -\-b-c Ь + с — а
четырехугольник — ромб. 756. — S. 757. — S. 758. ζ= , χ = ,
о 3 2t 2
а -\- с — b
у— и 759. Указание. Соедините точку Μ с вершинами данного
треугольника. 760. Отрезок искомой прямой, заключенный между сторонами
угла, должен делиться точкой Ε пополам. 761. Указание. Искомая прямая
должна проходить через точки С и Е. 766. Площадь отсекаемого треугольника
максимальна, если отрезок перпендикулярен биссектрисе данного угла.
Глава V. Векторы
771. 2) Параллельным переносом. 773. Нет. 774. 1) Параллельным переносом.
2) Нет. 776. 1) Sp; 2) Z0 . 779. 1) Sb (b 1 α, Ο 6 Ь). 786. 1) Четыре. 787. Девять.
788. 2) Тринадцать. 790. 1), 2) Векторы различны; 3) один и тот же вектор. 792.
2) Двадцать семь. 795. Указание. Рассмотрите два случая: точки А, В,
С и D лежат на одной прямой или нет. 801. Верны равенства 1), 2), 3), 5) и 6).
805. 2) |*| = \у\ = \1\ = г, |7| = 0. 813. 1) AD = а + ~Ь + "с, BD = Ь*+ ?,
'АС = α + ?. 820. 2) ~а = "θ. 829. 1) к > 0; 2) k < 0; 3) k = 1. 830. 1) |k|< 1;
364
2) 1*1 > 1; 3) |A| = 1. 832. 1) ft > -1; 3) ft = -1. 834. 1) χ = _-; 3) *=3.
835. Нет. 836. Указание. Если χγα = х2а, то (хг — х2)а = α Так как
а ф 0, то *! = дг2. 840. ОА = 2^+ 4^, ОА + ОВ = 6^ + 9^. 843. 1) Да;
2) нет. 845. 2) BD = ЗЬ — 3<Г. 851. 3) АС. 853. Указание. Воспользуйтесь
свойствами расстояний. 855. 2) χ = α. 857. Указание. Воспользуйтесь
правилом параллелограмма. 858. 1) Четырехугольник ABCD — параллелограмм;
2) четырехугольник ABCD — параллелограмм или трапеция. 859.
Указание. Воспользуйтесь правилом параллелограмма и свойством диагоналей
параллелограмма. 860. 2) Указание. Сначала покажите, что если О —
\ОА\ —> 1 —> _> —>
точка медианы АА1 и ——— =2, то РО = — (РА + РВ + PC), где Ρ —
I G^il 3
произвольная точка плоскости. 861. Указание. Пусть Ε и F — середины
сторон АВ и АС треугольника ABC. Докажите, что EF = — ВС. 864. У к а-
-*■ -*■ —► -> —► -*.
з а н и е. Если л: = ж^ -\- Ухе2 и χ = х2е1 + ^г» то д^ = дг2, */х = ί/2· 866·
Указание. Докажите, что если Х2 = (Ζ0 ο Ζ0 ) X, то ХХ2 = 20^2·
Глава VI. Подобие
872. 1) Нет. 874. 1) Второй план подобен первому с коэффициентом 1/10.
877. Указание. Воспользуйтесь формулой | АВ | = \хА — хв \.
880. Указание. Воспользуйтесь теоремой о средней линии треугольника.
881. Луч, полуплоскость, угол. 891. Указание. Воспользуйтесь
определением гомотетии. 892. Указание. Рассмотрите композицию двух
центральных симметрии с различными центрами. 897. Центр Q — любая точка
прямой ΟΟν за исключением точек Ot и О. 898. 1), 2) Нет; 3) могут. 899. 1) Нет.
1 2
904. 1) | АС\ : \ BD\ = 1 : 2; 2) нет. 906. 1) —, —; 2) 3 см, 6 см. 907. 2,1 см;
3 3
5,6 см. 908. 6 см. 909. 2 см, 4 см. 910. 1) а) 6 см, —5,3 см. 911. 2 : 3. 914.
Указание. Рассмотрите подобные треугольники ABD и ADXC, где Dt — точка
пересечения прямой АВ с прямой, проходящей через С и параллельной BD.
916. Да. 919. Да. 924. Да, если коэффициент подобия Ρ равен —. 925. Да, если
I k I
Ρ сохраняет расстояния. 929. 1), 3) Подобны; 2) не подобны. 930. 1) 6,4 дм;
5,76 дм; 2,4 дм или 2,5 дм, 2,25 дм, 0,9375 дм; 2) 4 см, 3 см. 931. 1) 5,25 см; 1, 2 см;
2) 18 м; —23,6 μ; ^25,7 м. 932. 1) 27 см; 40,5 см; 54,5 см; 2) 10,8 см; 16,2 см;
21,8 см. 934. Подобны. 938. 1) 3 см, 2 см, 1,5 см; 2) 4 см, 3,5 см, 2,5 см. 939. 1),
2) Подобны; 3) подобны лишь в том случае, если оба угла взяты при вершинах
треугольников или при их основаниях. 940. Три пары. 941. Нельзя. 942.
Подобны. 944. 9 см; 15,75 см. 945. 1) 8 см, —5,3 см, —3,6 см; 2) 12 см, — 4,6 см,
та
«11,1 см. 946. ^80 м. 947. —36 м. 948. —30 м. 953. ■—; 1) 7,5 см;
т -\- η
2) 1,5 см; 3) 5,4 см. 956. с = 5 см, а = УТЬ см, Ь = /Ϊ0 см, h = /б" см.
а2 Ь2
957. аг= г , Ьс = г · 958. р2: д2. 962. Указание. Воспользуи-
365
тесь теоремой, обратной теореме Пифагора. 963. =3,9 см. 964. S = (LjL—.
4
966. 1) h = ^4/'2 ~ g3 ; 2) а = 2 /г2 — А2. 967. =48,9 см или =0,9 см.
969. 1) 15; 2) 18; 3) 5; 4) 13. 970. 1) 2 /5; 2) уТ; 3) 5 >Л2". 971. 1) 24 см, =21 см;
2) =17 см, 12 см. 972. 1) с = 15 см; а, = 5,4 см, Ьс = 9,6 car, A = 7,2 см.
£ (£ -J- Л Kk 4-1)
973. & = 5 см, «.as 11,1 см, к = 4,6 см; Ь.= 1,9 см. 974. / , r ϊ
с с >^2-ь /2 К*2 + *2
=6,5 см, =15,7 см. 975. =7,7 см. 976. \ОМ\ = /го2 + г3. 977. 1) =9,2 см;
2) 6 см. 980. =13,3 мм. 981. 1) Могут; 2) не могут. 983. Не верны. 984.
а2— Ь*
1) Могут; 2) не могут. 988. 6, ; 1) 6 см; 3,5 см; 2) 4,8 см; 2,8 см. 989. Не
а
подобны. 992. 2 м, 4 м, 5 м. 993. 6,4 дм, 8 дм, 11,2 дм. 994. 60 см, 1С0 см.
995. 1) 4 : 9; 4) k2 : J2. 996. 3) 1 : 2; 4) У ρ : Yq. 997. 1) Возрастет в η2 раз.
b2S 2S.
2) Уменьшится в k2 раз. 998. 9 : 1; 9 : 4. 1002. —; 4) =66,7 см2. 1005. Л, =~- —,
α2 αγ
α2 = \гтг2> h2 = ~^——· 32 CM'» ~2,5 см; = 19,6 см. 1010. Указание.
У si ^1
Докажите гомотегичносгь построенных равносторонних треугольников
относительно точки пересечения диагоналей трапеции. 1012. 1) —Z2 == 2rh — Л2,
4
/2 h
откуда г = — + —'» 2) ~4,2 см. 1015. Указание. Выразите квадраты
Sh 2
длин сторон многоугольников через квадраты длин отрезков их диагоналей.
Глава VII. Повороты и тригонометрические функции
1026. Для одного наблюдателя направление вращения будет положительным,
для другого — отрицательным. 1030. Первая и третья шестерни вращаются в
отрицательном направлении, вторая шестерня — в положительном. 1031.
1) 40° + 360°гс; 3) 130° + 360°гс, где η £ Ζ. 1032. 1) —130° + 360°гс, где п£ Ζ.
1033. 1) Я20'; 2) Д3°э; 3) Я20°; 4) Я90°; 5) RTm^\ 6) Я°°; 7) Я"140'. 1034. 1) Я"60;
2) Я150°; 3) Я80°; 4) Я170'; 5) Я20°; 6) Я20°; 7) Я60°. 1035. 1) При любых целых
значениях k\ 2) при любых четных значениях k. 1036. 1) =7,85 см. 2) =3,14 см.
1037. а) =125,6 см; б) 5 см. 1038. а) =0,01745; б) =0,785; в) =1,309;
г) =3,927. 1039. 1) =57°18'; 2) =5°44'; 3) =17°12'; 4) 60°; 5) 120°;
6) 20°; 7) 15°. 1040. 1) 11,25°; 2) =0,09. 1041. 1) Я"60' о Я25° = Я~35"';
2) Я18(Г о Я~35Э = Я1455; 3) Я20° о Я70° - Я90°; 4) Я135° о Я245° = Я3803 = Я20';
5) Я-2(Г о Я~170° = Я"190' = Я170°; 6) Я45° о Я90° = Я135°. 1042. 1) -40° +
+ £360°; 2) —35° f £360°; 3) Α·330°; 4) —70° + £360°; 5) —10° + £360°; 6) 20°+
-Ь (2k + 1) 180° (где k — любое целое число). 1043. Тождественным
отображением плоскости на себя. 1044. гл — £180° (k £ Ζ). Задача имеет бесконечное
множество решений. 1045. 1) Яа о Ra о Ra = R90\ если α = 30° + 120е*
{k 6Z). 1046. Яа о Яа = Я1ь0\ если а = 90° + 180е £ (k £ Ζ). 1047. RV20k (k 6 Ζ).
366
1048. Указание. Следует показать, что (Да о Д0) . RV = да 0 (Д** о Rv).
1049. 1) При А 6^5 2) при любых четных значениях k. 1050. Указа-
н и е. 1) Я19°·190 = дИЧ-аимо = βιο°. 2) л19-.20= л20°+зб0°= Л20°в 1052в ц ,_0>8;
—0,6); 2) (—0,8; 0,6); 3) (0,8; —0,6). 1054. 1) (0, 1); 2) (—1; 0); 3) (0, —1);
4) (-1, 0); 5) (0, -1); 6) (0, 1). 1055. sin 90° = 1, cos 90* = 0; sin (-90°) =
= —1, сое (—90°) = 0; sin 180° = 0, cos 180° = —1; sin 270° = —1, cos 270° =*·
= 0; sin (—270°) = 1. 1056. 1), 2), 3), 5) Углы а, соответствующие указанным
значениям sin α, существуют (точки Ра на единичной окружности могут быть
построены). 1057. 1), 2), 5), 7) Положителен; 3), 4), 6) отрицателен.
1059. sin 20° < sin 30° < sin 45° < sin 60° < sin 70° < sin 90°. 1060. 1), 2), 3),
5) Углы, соответствующие указанным значениям cos α, существуют. 1061. 3), 4),
5), 7) Положителен; 1), 2), 6) отрицателен. 1063. cos 90° < cos 70° < cos 60° <
< cos 45Ό < cos 30° < cos 20°. 1064. Да, существуют. Например: 1) α = 45°;
2) α = 135°. 1070. 1) χ = 2 cos 90°, у = 2 sin 90°; 2) χ = 2 cos 0°; у = 2 sin 0°;
3) χ = iQL cos 135°, у = iQL sio 135°; 4) χ = 2 ^2 cos (— 45°), у = 2 /2 sin(—45)°;
5) χ = Υ2 cos 45°, у = }/Tsin 45°. 1071. 1) 0,8; 2) —0,28; 3) 0,6;
4) — Ώ^Σ s —0,943; 5) ± 1UL zz± 0,707. 1072. 1) Ώ^Σ ~ 0,943; 2) 1^.^
3 2 3 2
~ 0,866; 3) 0,8; 4) KA =: 0,745; 5) L?_ =; 0,707. 1073. 1) sin2 a; 2) — cos2 a;
3 2
3) 1 (если a ^ 90° + 180°*, k 6 Z); 4) 0; 5) sin2 a; 6) sin3 a; 7) 1; 8) cos2 a.
1074. 1) sin 100° = cos 10° = sin 80°; 2) sin 160° = cos 70° = sin 20°;
3) cos 170° = —cos 10° = —sin 80°; 4) sin 95°16' = sin 84°44' = cos5°16';
5) sin 103°45' = sin 76°15' = cos 13°45'; 6) cos 124°15' = —cos 55°45' =
= —sin 34 15'. 1075. 1) sin (—70") = —sin 70' = —cos 20°; 2) cos (—70°) =»
= cos 70° = sin 20°; 3) sin (—20°) = —sin 2C° = —cos 70°; 4) cos (—20°) =
= cos 20° = sin 70°; 5) sin (—45°) = —sin 45° = —cos 45°; 6) cos (—45°) =
= cos 45° = sin 45°. 1080. 2) а) а = 45°; б) а = 135°. 1081. Указание.
Воспользуйтесь свойствами функций sin α и cos α. 1084. 1) a) 2; б) —1; в) 5;
г) 1; д) 0. 1088.
1 а
б
в
г
2 а
б
в
г
а
2,61
13,6
4,35
156
63
5,28
15
0,098
Ь
3,80
8,23
1,45
133
16
4,55
112
0,100
с
4,61
15,9
4,59
205
65
6,97
113
0,140
А
34°29'
58°49'
71°23'
49°33'
75°45'
49°15'
7°36'
44°25'
В
55°31'
31°11'
18°37'
40°27'
14°15'
40°45'
82°24'
45°35'
367
Продолжение
3 а
б
в
г
4 а
б
в
г
5 а
б
в
г
а
63,7
18,0
3,89
6,16
6,37
380
613
8,49
4,24
25,1
0,559
3,52
Ъ
5,11
58,9
1,74
2,95
3,63
261
528
3,92
1,95
57,6
0,569
8,74
с
63,9
61,6
4,26
6,83
7,33
461
809
9,35
4,67
62,8
0,798
9,42
А
85°25'
17°
65°55'
64°24'
60°18'
55°31'
49°15'
65°14'
65°15'
23°32'
44°30'
21°56'
В
4°35'
73°
24°05'
25°36'
29°42'
34°29'
40°45'
24°46'
24°45'
66°28'
45°30'
68°04'
1089. ~88 м. 1091. ^1°43'. 1092. ^0°57'. 1093. I sin а\ 1) ~ Ш м; 2) ^433 м.
1094. ^4,6 м. 1095. 31. 1096. 1)-* = 4л; 2) k = 8п (п 6 Z). 1097. 1) k =-8л;
30°; 60°; 120°;
2) k = 6л (и 6 Z). 1098. 2) а) 45е
б) 45° + 360°гс,
30° + 360е щ
60° + 360°л,
120° + 360°л,
1099. 1) а) 0 < sin χ + 1 < 2;
135° + 360°л;
150° + 360°л;
—60° + 360° п;
—120° + 360°л (η ζ Ζ).
б) —0,5 < cos χ + 0,5 < 1,5;
+ cos2 x = 1; 2) равенство а) возможно. 1101. Например: 1), 2)
η 6 Ζ. 1104. a tg α. 1) ss 16 м; 2) ~ 17 м.
в) sin2 x -f
k = 4л, где
Глава VIII. Метрические соотношения в треугольнике
1105. 1) с2 = а2 + Ь2 — аЬ; 2) с2 = а2 + Ь2 — аЬ /З; 3) с2 = а2 + Ь2 — }^2аЬ.
1106. При возрастании угла α от 0° до 90° значение α возрастает, так как cos α
при этом убывает, оставаясь положительным. При дальнейшем возрастании
угла α от 90° до 180° значения cos α убывают от 0 до —1. Следовательно,
значение а при этом продолжает возрастать. 1109. 1) с =г 8,5; 2) Ъ ==; 4,4; 3) а =s 0,8.
1111. 1) =;117°1Г; 2) ~93°42'. 1112. 1) ^24,3 дм и = 12,1 дм; 2) ^ 5,4 дм;
^ 4,5 дм. 1113. При возрастании угла у от 0° до 90° площадь треугольника
возрастает. При дальнейшем возрастании угла у от 90° до 180° площадь
треугольника убывает. Наибольшее значение площади получим при γ = 90°.
1114. яг 48,4 м2.1115. 1) ~ 7880 м2; 2) ss 344 см2. 1118. 1) ss 21,2 см2; 2) =s 2,7 см2.
1119. ~ 190,5 см2. 1120. 1) Ь ~ 61; с ~ 102, α = 79°37'; 2) а ~ 39; Ь я; 25,
368
V 25 14°15'; 3) β 25 35°52'; γ 25 75°45'; с 25 21; 4) α 25 14°23'; β 25 142°17';
m sin
L122.
sin (α -
α sin α sin ftt
л п -- л msina τηβίηβ
b 25 91,3.1122. -———— и -——f—u 1124.25 3,6Н; 25 3,7 Η. 1149. | ВС\=
sin (a + β) sm (a + β)
, 0 v . , , Ων—. Замечание. Решением этой задачи
sin (αχ + β^ sm (a + β)
можно воспользоваться при вычислении расстояния до недоступных точек на
местности. (В рассмотренном случае, если точка С невидима из точки В,
расстояние между точками Б и С не может быть найдено измерением.)
1150. \CD\ = a l/ sin2v . sin26 _? sin Υ sin 6 cos (α-β)
V sin2 (β + γ) "Τ" sin2 (a + δ) sin (a + β) sin (β + у) ·
Указания. 1) При решении задачи применяются теоремы косинусов и
синусов. 2) При проведении вычислений следует учитывать, что значения углов
β + γ, α + δ, α — β уже известны. 1152. 1) b 25 62,1; a 25 21°55'; γ ~ 34°05';
2) с 25 20,8; β 25 67°δ1'; α 25 37°08/; 3) θ2 279; γ 25 30°30'; β 25 67°23';
4) b 25 837; α 25 22°37'; γ - 59°30'. 1153. 1) & 25 15; с 25 14; γ 25 60°29';
2) α 25 20,5; с 25 20; ν - 74°37'. 1154. 1) α 25 67°23/; β 25 18°55'; у ~ 93°42';
2)α2 107°57'; β 25 53°08'; у ~ 18°55'. 1157. α = 90°. 1158. α = 90°, ромб.
1159. 1) 25ll7°19\ 1160. R 25 275 Η; 16°; 34°. 1161. 1) 4 (Ι + tg a)2.
α2Α2
1162. , 36 см2.
(α + 2Λ)2
Глава IX. Вписанные и описанные многоугольники
1170. 1) 36°; 72°; 108°; 72°; 36°. 1171. 1) 108° и 72°; 2) 100° и 80°. 1172. АМС =
= АТС или АМС + ЛТС =180°. 1173. 35° и 70°. 1174. 1) 100° или 80°;
h
2) 54° или 126°. 1185. 12,3 см. 1186. 1) 4 см; 2) 10 см. 1187. —. 1189. 1) Тре-
3
угольник равносторонний; 2) треугольник прямоугольный; 3), 4) треугольник
равнобедренный. 1190. Указание. Задача имеет 4 решения. 1195. 2), 3) Мож-
но. 1196. 1) Можно. 1198. 1), 3) Можно. 1202. — (3 dz ]^3). 1203. 1), 2) 60°,
6
120°; 90°, 90°; 108°, 72°; 120°, 60°; 135°, 45°; 144°, 36°; 150°, 30°. 1204. 1) а) 8;
б) 12; в) 9; 2) а) 10; б) 15; в) 6. 1210. 1) η осей симметрии; 2) η поворотов
(включая тождественный); 3) центр симметрии имеют только правильные мно-
гоугольники с четным числом сторон. 1211. 1) а) JLL— ; б) -J-J1—; в) а6;
О Δ
2) а) 2г/3· б) 2г; в) 2г^3. 1212. г= Л cos . 1213. 1) а) 25 14,1 мм;
3 η
б) 25 5,7 мм. 2) а) 25 13,8 мм; б) 25 10,4 мм. 1214. 3 /б см 25 7,3 см. 1215. 1) При
180°
Rsin~V 180*
η < 6; 2) при η = 6; 3) при η > 6.1216. 2) г = ——. 1217. 2aa cos ,
180 п
1-sin
η
1) 1,62 см; 2) 8,66 см. 1218. R УТ; 1) 25 3,46 см; 2) 25 5,20 см. 1219.
180°
а) 25 83 см2; б) 128 см2; в) 25 152 см2. 1220. S = nr2 tg ; а) 25 83,1 см2;
а
369
a a3 1 V5" VT 113
6) 64 см8; в) = 58,1 cm*. 1221. 1)-; 2) -. 1222. 1) —, JL±, LL- 2) —.-.—.
b b2 222 424
1226.1) ss 78,5 см; 2) ss 37,7 дм. 1227. 1) ~ 12,5 см; 2) ^ 2 дм. 1228. 1) =s 64 см;
2) ^48 см. 1229. 1) ss 5,4 см; 2) = 10,9 см. 1230. 1) ss 12,6 см; 2) =s 17,8 см.
3232. 1) ss 1,9 м; 2) ss 22,6 м. 1233. 1) τζ 2,62; 2) ss 3,49; 3) π. 1234. ^ — C2 =
= 2πΖ, где Ct — длина внешней окружности, С2 — длина внутренней окружг
ности, I — толщина кольца. 1235. 48 см. 1236. ss 1,85 км. 1237. 1,8.
1238. 1) ^ 12,6 см2; 2) ss 78,5 м2. 1239. 1) Уменьшится в 16 раз (в п2 раз);
уменьшится в 4 раза (в η раз); 2) увеличится в 9 раз (в п2 раз), увеличится в
С2
3 раза (в η раз). 1240. —. 1241. 1) 7,1 мм2; 2) 0,03 мм2. 1243. 1) ^616 см2;
4π
2) ^2,0 дм2. 1244· ss 0,21. 1245. 1) ss 7,5 см2; 2) ss 9,4 см2; 3) 5=11,3 см2.
1250. Указание. Надо доказать, что А1ВВ1 = 180°. 1251. Указание.
Искомое множество точек — две дуги, общей хордой которых является данный
отрезок. Чтобы построить каждую из этих дут, достаточно найти хотя бы одну
из ее точек, отличную от точек А и В. 1265. Указание. Следует
доказать, что хорда BD стягивает дугу BD, угловая величина которой равна 72°.
πα2 π | ΑΒ \2
1267. —. 1269. Указание. Это следует из того, что S Л,има = .
А кольца л
Глава X. Начальные сведения из стереометрии
1270. Три различные точки всегда лежат в одной плоскости. Этим объясняется
устойчивость «треножников», возможная неустойчивость стола и других
устройств, имеющих четыре опорные точки. 1271. 1), 2), 3) Нельзя; 4) можно.
1272. Указание. Доказательство ведется методом от противного.
1273. Указание. Для доказательства возьмите две точки на одной из
данных прямых и одну точку на второй прямой. Докажите, что проходящая
через эти точки плоскость единственна и что она содержит обе данные прямые.
1277. Высказывание неверное. 1278. Нет. Указание. Если прямая
параллельна одному из ребер куба, то она параллельна и еще трем другим его ребрам.
1281. Прямые АВ и CD параллельны. Следовательно, существует плоскость,
проходящая через эти прямые. 1282. Плоскости параллельны. 1285. Не всегда.
1287. 1) 0 или а. 2) а, а /2", а /з". 1288. {LlA. 1291. 1) 8. 2) Многоугольник,
имеющий η — 2 стороны. 1293. Пять граней, девять ребер, шесть вершин.
1295. 1) б) Существует (пятиугольная призма); а), в) не существует. 1296. S ζζ,
ж 180,5 см2, V = 120 см3. 1297. S6oK = 240 сма, V = 288 см3. 1298. 1) ss 114 м2;
2) ^125 м3; 3) ^413 м3. 1299. —7,1 м. 1303. 128 см2; 192 см2; 512 см2. 1305. 2л
ребер, η + 1 граней. 1307. 1) a%h V* ·. 2) ^; 3) **¥*.. 1308. **-ур=1?т
12 2 2 о
4
1309. S = 4г (г + ]/Л2 + г2); V = — r*h. 1315. 1) =: 358 см2; is 396 см3;
о
C2h
2) ^48,6 дм2; is25,4 дм3. 1316. . 1318. Vx = 600 π см3; V2 = 360π см3;
4π
V3 — 512л см3; V2 < V3 < Vx. 1322. He может. (Рассмотрите соответствующий
прямоугольный треугольник.) 1323. 12 см. 1324. 1) S zz 251 см2, V ~ 260 см3;
370
2) S s 920 см2, V ss 1204 см2; 3) S ss 20,4 дм; F ss 5,7 дм3. 1325. V ss 16 755 cil3,
S ss 4067 см2. 1327. ss 2,6 м3. 1329. 2) a) sj 201 см2, ss 268 см3; б) ss 78,5 cm-.
=ξ65,4 см3; в) ss 3550 мм2, ss 19 860 мм3; г) ss 12,6 дм2, =s 4,2 дм3. 1330. 1) S =з
г?
-0,79 м2, У ss 0,065 м3; 2) S ~ 201 м2, К а; 268 м3. 1332. —; 1) ж 4,63;
г2
2) гг 76,77. 1333. -^; 1) =s 1,96; 2) ss 59,5. 1334. 1) —; 2) —; 3) =s 0,840;
J2 2 3
4) ss 0,928.1335. 1) ~ 5,10 · 10s км2; 2) =s 1,5 . 108км2; 3)40 · 108м. 1337. Οκο,το
1750 дробинок. 1338. ~Э,2 см. 1339. 1) ~ 3050 см3, ^4580 см3; 2) г; 1020 см2,
ss 1530 см2.1340. 1) =г 3619 м8, =s 1357 м2; 2) ss 718 м3, ^462 м2. 1341. ss 134 ινΑ
а3
1347. 1) 20; 2) 60; 3) 45. 1348. 1) 36; 2) 54; 3) 27. 1352. — (2 — tg а).
2
1356·Х) Γδ: 2) й-
Задачи на повторение по курсу 6—8 классов
1360. Свойства 1 и 3 выполняются. Свойство 2 не выполняется. 1362. 1)
Область, содержащая точку А, границей которой является серединный
перпендикуляр к отрезку АВ. 2) Область, содержащая точку В,
границей которой является серединный перпендикуляр к отрезку АВ. 3)
Серединный перпендикуляр к отрезку АВ. 1363. 1) Этим свойством обладают
точки угла DBC, не лежащие на луче BD, где \_BD) — биссектриса данною
угла. 2) Все точки данного угла, не лежащие на его биссектрисе. Π ρ и-
м е ч а н и е. Рассматриваются только углы, меньшие развернутого. 1369.1)11 ря-
г 2аЪ
моугольник. 2) Ромб. 1377. 1), 2) 4 см и 6 см. 1378. 1 : (]/2 — 1). 1379. -.
a -f- о
1380. Указание. Пусть длины данных хорд равны а и Ь. Расстояние между
центрами данных окружностей \Ολ02\. Задача решается методом параллель-
а +ь
ного переноса и имеет решение, если \ Οι02\ ^ . 1382. Указание.
Решение задачи сводится к доказательству того, что указанный вписанной
треугольник является равносторонним. 1383. Указание. Решение
сводится к доказательству того, что указанный вписанный четырехугольник —
квадрат. 1386. Указание. Доказательство основано на теореме Пифагора
и теореме об отношении площадей подобных многоугольников. 1387.
Указание. Доказательство следует из теоремы Пифагора и из того, что площади
многоугольников относятся как квадраты сторон. 1389. Окружность,
построенная на отрезке АВ как на диаметре. 1390. 1) Окружность (если данная точка
не центр данной окружности). 1391. Указание. Во всех случаях это
произведение равно г2. 1392. Дуга окружности, построенной на отрезке ОМ как ьа
диаметре, расположенная во внутренней области данной окружности (О, /).
1398. 2) У к а з а н и е. Пусть сторона квадрата равна а и данное расстояние т.
а а а
Рассмотрите случаи: 1) т = —; 2) т < —; 3) т > —. (В последнем случаэ
л л л
искомые точки не содержатся во внутренней области данного квадрата.)
37!
1399. Пусть радиус окружности равен г и данное расстояние т Φ 0. 1) а) Две
окружности, концентрические с данной (если т < г), б) Окружность,
концентрическая с данной (если т > г), в) Окружность, концентрическая с данной и
одна точка — центр окружности (если т = г). 2) Окружность,
концентрическая с окружностью (О, г), радиус которой равен т + г. 1402. Для
каждого случая верны следующие высказывания: 1) а) хотя бы один из векто-
—► —►
ров нулевой; б) направления векторов а и b взаимно перпендикулярны; 2) а)
хотя бы один вектор нулевой; б) направления векторов совпадают; 3) а) век-
—► —► ->
тор Ь нулевой; б) оба вектора нулевые; в) векторы а и Ъ противоположно на-
—► —► -*■
правлены, причем \а\ > \Ь\\ 4) а) хотя бы один вектор нулевой; б) векторы а
и Ь противоположно направлены. 1406. 1) Указание. Сначала по данным
двум углам строится треугольник, подобный искомому. Центр вписанной в
этот треугольник окружности принимается за центр гомотетии, и выполняется
построение искомого треугольника по заданному радиусу вписанной в него
окружности. 2) Указание. Для построения можно применить
гомотетию. 1407. Указание. Около данного треугольника описать треугольник,
ему подобный, так, чтобы каждой из сторон описанного треугольника
принадлежала только одна вершина данного треугольника. В общем случае задача
имеет бесконечное множество решений. 1411. —. 1412. Л2 (π — α + sin α).
2α Ar —
1413. — у 3. 1414. 3. 1415. Указание. При решении рекомендуется
о
применять логарифмическую линейку. При этом учесть, что площади
поверхностей двух шаров относятся как квадраты их диаметров и объемы — как кубы
диаметров. 1416. Тождественное отображение, параллельные переносы,
осевые симметрии, гомотетии. 1417. 1) Центральной симметрией, двумя
осевыми симметриями, тождественным отображением. 2) Поворотами на угол
360°
а ■== k, где k — целое число, η осевыми симметриями. 1418. 1) Поворотами
η
на угол α (—180° < α < 180°); с центром в «выколотой» точке; осевыми
симметриями относительно осей, проходящих через «выколотую» точку. 2)
Центральной симметрией с центром в середине отрезка, концами которого являются
«выколотые» точки; двумя осевыми симметриями; тождественным отображением.
ПРИЛОЖЕНИЯ
О логическом строении геометрии
Логически строгий курс геометрии строится следующим
образом:
1. Перечисляются основные геометрические понятия,
которые вводятся без определений.
2. При их помощи даются определения всех остальных
геометрических понятий.
3. Формулируются аксиомы.
.4. На основе аксиом и определений все дальнейшие
геометрические предложения доказываются.
В применении к планиметрии первые два пункта этой
программы в основном выполнены. Были названы три основных
понятия планиметрии: «точка», «прямая», «расстояние».
Большинству понятий, рассматриваемых далее в курсе
планиметрии («окружность», «круг», «отрезок», «луч» и т. д.), были даны
определения. Отметим, что при изложении планиметрии имеют
в виду какую-либо одну плоскость. Рассматриваются только
принадлежащие ей точки. Поэтому по определению плоскость
есть множество всех рассматриваемых точек*.
Существенный пробел в отчетливости определений допущен
в п. 18, где вводится понятие «величина угла». Смысл этого
понятия здесь лишь поясняется на простейших примерах.
Следовало бы точно определить смысл равенства АОВ = а° (при
любом действительном числе а, лежащем в пределах О < а <
< 360).
Но в 6 классе было бы невозможно это сделать, так как
первые представления о действительных числах даются только в
* В стереометрии понятие «плоскость» появится в качестве одного из
основных понятий.
373
7 классе. Но и независимо от этого затруднения строгое
изложение теории измерения углов неизбежно очень громоздко*.
Для выполнения третьего пункта программы следует
перечислить аксиомы, на основе которых можно построить
логически строгое изложение планиметрии. Этот список приводится
далее. Следует только заметить, что при построении
планиметрии пользуются также правилами логики и свойствами
множеств как известными. После того как в одной из аксиом
будет сказано, что расстояние от точки до точки есть
неотрицательное действительное число, пользуются также
изучаемыми в алгебре свойствами действительных чисел.
Полное осуществление четвертого пункта программы
потребовало бы последовательного, без пропусков,
доказательства на основе аксиом всех геометрических истин, с которыми
вы познакомились по учебнику. Это заняло бы много места.
Все логически строгие курсы элементарной геометрии
довольно трудны для изучения. Поэтому нам пришлось без
доказательства принять еще ряд предложений, которые могли бы
быть доказаны как теоремы на основе сформулжрованных ниже
двенадцати аксиом. Предлагаемая система аксиом лишь одна
из возможных. Она соответствует принятой в нашем учебнике
системе изложения. Двенадцать аксиом этой системы
разделены на пять групп.
I. Аксиомы принадлежности
А к с и о м а Ιι· Каждая прямая есть множество точеке
Аксиома 12. Для любых двух точек существует одна
и только одна содержащая их прямая.
Аксиома 13. Существует хотя бы одна прямая; каждой
прямой принадлежит хотя бы одна точка.
II. Аксиомы расстояния
Расстояния между точками мы будем считать числами. С
практической точки зрения это значит, что мы уже выбрали единицу
измерения расстояний.
* В некоторых учебниках в обход этой трудности понятие «величина угла»
причисляется к числу основных геометрических понятий, как это сделано в
нашем учебнике в применении к понятию расстояния.
374
Аксиома lit. Любым точкам А и В поставлено в
соответствие неотрицательное действительное
число |АВ|, называемое расстоянием от
точки А до точки В. Расстояние \АВ\ равно
нулю тогда и только тогда, когда точки А
и В совпадают.
Аксиома II2. Расстояние от точки А до точки В равно
расстоянию от В до точки А: \АВ\ = \ВА\.
Аксиома II3. Для любых точек А, В и С расстояние от А
до С не больше суммы расстояний от Λ до Б
и от В до С: \АС\ < \АВ\ + \ВС\.
III. Аксиомы «оредиа
Аксиома IIIt. Три точки принадлежат одной прямой тогда
и только тогда, когда одна из них лежит
между двумя другими.
Аксиома III2- Любая точка О прямой ρ разбивает
множество отличных от О точек прямой ρ на два
непустых подмножества так, что точка О
лежит между любыми двумя точками,
принадлежащими разным подмножествам.
Аксиома III з- Для любого неотрицательного
действительного числа а на заданном луче с началом О
существует одна и только одна точка,
расстояние от которой до начала О равно числу а.
Аксиома 1И4. Любая прямая разбивает множество не
принадлежащих ей точек плоскости на две
непустые выпуклые области.
IV. Аксиома лодвнжностм
Аксиома IV. Для любой пары лучей 0{А{ и 02А2 и
примыкающих к ним полуплоскостей а4 и
а2 существует единственное перемещение,
отображающее луч О^А^ на луч 02А2, а
полуплоскость а { на полуплоскость а2.
V. Аксиома параллельных
Аксиома V. Через любую точку А плоскости ρ проходит
не более одной прямой, параллельной
данной прямой р.
375
Замечания. 1. В формулировки аксиом вошли, помимо
основных понятий, такие геометрические понятия: «лежать меж ν
ду», «луч», «область», «полуплоскость», «перемещение»,
«параллельные прямые». Напомним, что эти понятия были определены
в пунктах 4, 6, 10, 12, 19 и 31 соответственно.
2. Аксиомы расстояния П4_3 сохраняются без изменений
в стереометрии (геометрии пространства). Сохраняются они и
в некоторых «неевклидовых» геометриях, например в геометрии
Лобачевского, о которой говорится в п. 33. Из задачи 157 вы
можете получить первое представление о том, что свойства
Πι_3 сохраняются и для некоторых других «расстояний». В
современной математике любое множество, на котором
определено «расстояние» со свойствами 111_у, называют «метрическим
пространством». Существует целая теория таких «прост|ранств».
3. Содержание всех приведенных выше двенадцати аксиом
вы найдете в тексте учебника в виде принятых без
доказательства допущений. Различие состоит в том, что в основном тексте
учебника таких допущений значительно больше. Например,
приняты без доказательства такие предложения: а) при повороте
расстояния сохраняются, т. е. поворот есть перемещение
(предложение 20), при осевой симметрии расстояния сохраняются, т. е.
осевая симметрия есть перемещение (предложение 23). Эти
предложения можно было бы доказать при помощи аксиомы
подвижности. Но и обратно, приняв эти предложения без
доказательства, можно доказать аксиому подвижности в качестве теоремы.
О такой условности различия между аксиомой и теоремой было
уже сказано в п. 33, где сообщалось о том, что аксиому
параллельности V можно заменить постулатом Евклида.
4. Первые одиннадцать аксиом выполняются и в геометрии
Лобачевского. Чтобы получить полную систему аксиом
планиметрии Лобачевского, надо аксиому V заменить на
следующую:
V*. Через точку, не лежащую на прямой, проходят по
крайней мере две прямые, параллельные этой прямой.
5. В заключение напомним пример, показывающий
возможность различного выбора аксиом: аксиому параллельных V
можно заменить на постулат Евклида, сформулированный в
п. 33.
376
Формулы геометрии
(всюду S обозначает площадь, V — объем).
, .
Название формул
Площадь
прямоугольника
1 Площадь квадрата
Площадь
параллелограмма и ромба
Площадь
треугольника
Формула Герона
(площадь треугольника)
Площадь
треугольника
Площадь
прямоугольного треугольника
Теорема косинуссв
Теорема синусов
Сумма углов
треугольника
Площадь трапеции
Формулы
S = ab
S = а2
S = ah
ah
S = —
2
S=V p(p — a)(p-b)(p — с)
ab
S = — sin ν
2 r
ab
2
c2 = a2 _|_ b2 _ 2ab cos γ
a b с
sin α sin β sin γ
A+B+C= 180°
a + b
S = —— Λ
1 2
1
Обозначения
α, Ь — длины сторон
1
а — длина стороны
а — длина основания,
h — высота, проведенная
к этому основанию
а — длина основания,
h — высота, проведенная
к этому основанию
ρ — полупериметр,
а,Ь, с — длины сторон
а, Ь — длины сторон,
у — величина угла
между
сторонами а и b
α, b — длины катетов
α, Ь, с— длины сторон
треугольника,
γ — величина угла,
лежащего против
стороны с
а, Ь, с — длины сторон,
α, β, γ— величины
углов
треугольника
А, В, С — величины
углов
треугольника
a, b— длины оснований,
h — высота
377
Продолжение
Площадь трапеции
(другой вид формулы)
Площадь
правильного многоугольника
Стороны правильных
многоугольников
Уравнение
окружности с центром в начале
координат
Длина окружности
Длина дуги
окружности
Площадь круга
Площадь сектора
Площадь поверхно-
j сти куба
Объем куба
Объем
прямоугольного параллелепипеда
S = ch
1
S= -rP
2
ап = 2R sin
η
α3 = r ]/3,
α4 = Я V 2,
α0 = R
χ* + y2 = R2
С = π£>,
С = 2лД
π Ra
~~ 180
S = nR\
s = —■
4
7iR2a
S=
360
S = 6a2
V = a*
V = abc
с — длина средней
линии,
h — высота
г — радиус вписанной
в многоугольник
окружности,
Ρ — периметр
ап — длина стороны,
R — радиус описанной
окружности,
η — число сторон
многоугольника
R — радиус окружности
С — длина окружности,
D — диаметр,
R — радиус
1 — длина дуги,
R — радиус,
α — угловая величина
дуги
R — радиус,
D — диаметр
R — радиус круга,
α — угловая величина
дуги
S — площадь
поверхности,
а — длина ребра куба
а—длина ребра куба
а, Ь, с — измерения
параллелепипеда
378
Продолжение
Площадь боковой
поверхности
параллелепипеда
Площадь боковой
поверхности правильной
призмы
Объем
параллелепипеда, призмы
Площадь боковой
поверхности цилиндра
Площадь поверхности
цилиндра
Площадь боковой
поверхности правильной
пирамиды
Объем пирамиды
Площадь боковой
поверхности конуса
Площадь поверхности
конуса
S0ok - Ph
S6ok = Ph
V = «оснЛ
«бок = 2Л*Л
S = 2лД (h + R)
1
бок 2
1
У = — sn, h
3 осн
S6ok = *RL
S = лД (L + R)
Ι ι
Объем конуса V = —nR2h
Площадь
поверхности шара
Объем шара
S = 4лД2,
S = л2>2
4
V = — лД3,
3
V = — л£3
6
бок— площадь боковой
поверхности,
Ρ — периметр
основания,
h — высота
Ρ — периметр
основания,
h — высота
Sqch — площадь
основания,
h — высота
Д — радиус основания,
// — высота
S — площадь
поверхности,
R — радиус основания
h — высота
Ρ — периметр
основания,
т — апофема (высота
боковой грани)
S . — площадь
основания,
h — высота
R — радиус основания,
L — длина образующей
R — радиус основания,
L — длина образующей
R — радиус основания,
h — высота
R — радиус,
D — диаметр
R — радиус,
D — диаметр
379
Язык теории множеств в геометрии
На языке теории
множеств
1. Точка X принадлежит
прямой АВ, или прямая АВ
содержит точку X.
2. Точка X не принадлежит
прямой АВ, или прямая
АВ не содержит точку X.
3. Точка X принадлежит
отрезку АВ.
4. Точка X не принадлежит
отрезку АВ.
5. Отрезок АВ есть
подмножество прямой 'р.
6. Отрезок АВ не является
подмножеством прямой р.
На языке геометрии
Точка X лежит на прямой
АВ, или прямая АВ
проходит через точку X.
Точка X не лежит на
прямой АВ, или точка X лежит
вне прямой АВ, или
прямая АВ не проходит через
точку X.
Точка X лежит на отрезке
АВ.
Точка X лежит вне
отрезка АВ, или точка X не
лежит на отрезке АВ.
Отрезок АВ лежит на
прямой р.
Отрезок АВ не лежит на
прямой р.
Формулы тригонометрии
1) sin2 α -f- cos2 a = 1;
2) sin (180° — a) = sin a;
3) cos (180° — a) = —cos a;
4) sin (—a) = —sin a;
5) cos (—a) = cos a;
В
обозначениях
Χ 6 (АВ)
X g (AB)
χ e iAB]
XI LAB]
LAB] czp
LABlqtP
6) sin (90° + a) = cos a;
7) cos (90° + a)= —sin a;
8) sin (90° — a) = cos a;
9) cos (90° — a) = sin a;
10) tg a = !^.
Греческий алфавит
Буквы Название букв
Aa
Ββ
Гу
Δδ
Ε ε
Ζζ
Ηη
ΘΟί)
Ιι
Κκ
Λλ
Μμ
альфа
бета
гамма
дельта
эпсилон
дзэта
эта
тета
йота
каппа
ламбда
мю
Буквы
Νν
US
Оо
Пл
Рр
Σσ
Ττ
Γυ
Φ φ
χχ
ψψ
Ω ω
Название букв
НЮ
КСИ
омикрон
ПИ
ро
сигма
тау
ипсилон
фи
хи
пси
омега
380
Перечень обозначений, встречающихся в учебнике
(АВ)
ίΑΒ)
[АВ]
\АВ)
А АВС
Окр (О, г)
Кр (О, г)
Ζ ABC, Ζ Β
— прямая АВ.
— луч АВ.
— отрезок АВ.
— расстояние от точки А до точки В.
— треугольник ABC.
--- окружность с центром О и радиусом г.
— круг с центром О и радиусом г.
— угол ABC, угол В.
ABC, В — величина угла ABC, величина угла В.
^ABC,\JAF— дуга ABC, дуга АВ.
ABC, АВ — угловая величина дуги ABC, дуги АВ.
[р, А) — полуплоскость с границей р, содержащая точку А.
JL — знак перпендикулярности прямых (лучей отрезков).
|| — знак параллельности прямых (лучей, отрезков).
= — знак конгруэнтности фигур.
Ε — тождественное отображение плоскости на себя.
Sp — симметрия с осью р.
#0 — поворот с центром О и углом поворота а.
Z0 — симметрия с центром О.
Τ — параллельный перенос.
ff — знак сонаправленности лучей (векторов).
fj — знак противоположной направленности лучей (векторов).
а, АВ — вектор а, вектор АВ.
\а\, \АВ\ — длина вектора а, длина вектора АВ.
О — нулевой вектор.
Hq — гомотетия с центром О и коэффициентом k.
оо — знак подобия фигур.
о — знак композиции отображений.
^АВС — площадь треугольника.
S (L) — площадь фигуры L.
V — объем.
ζ — знак принадлежности элемента данному множеству.
d — знак отрицания принадлежности элемента данному множеству.
СГ — знак включения одного множества в другое данное множество.
д£ — знак отрицания включения одного данного множества в другое.
0 — пустое множество.
(J — знак объединения множеств.
Р) — знак пересечения множеств.
ζφ. — следует.
<=^ — равносильны (эквивалентны).
381
Предметный указатель
Аксгома
— параллельности
— прямой
Аксиомы планиметрии
Апофема пирамиды
Биссектриса треугольника
— угла
Вектор
— нулевой
Векторы коллинеарные
Величина угла
Внешняя область многоуголь-
16
121
16
373
Зо9
83
66
198
199
200
66
ника 37
окружности 34
Внутренняя область много-
угольника
— — окружности
Высота параллелограмма
— пирамиды
— призмы
— трапеции
— треугольника
Гомотетия
Градус
Грань пирамиды
— призмы
Диагональ
Диаметр
Длина дуги
— ломаной
— окружности
Достаточное условие
Дуга
Касательная к окружности
Квадрат
Композиция перемещений
Конус
Координаты вектора
— на прямой
Косинус
Коэффициент гомотетии
— подобия
Круг
Куб
Ломаная
— простая
замкнутая
37
34
153
339
335
172
83
224
66
339
335
37
42
266
26
320
158
41
107
167
192
346
213
23
270
224
220
10
335
26
26
27
Луч
Медиана треугольника
Между (лежать)
Многоугольник
— вписанный
— описанный
— правильный
Наклонная
Направление
Необходимое условие
Неравенство треугольника
Объем
Окружность
— вписанная
— описанная
Оси симметрии
Откладывание вектора
Отношение рефлексивное
— симметричное
— транзитивное
— эквивалентности
Отображение
— обратимое
— обратное
— тождественное
Отрезок
Параллелепипед
— прямой
— прямоугольный
Параллелограмм
Параллельные прямые
Параллельный перенос
Перемещение
Перпендикулярные прямые
Пирамида
Площадь
Поворот
Полуплоскость
Построение биссектрисы угла
— касательной к окружности
— образа точки при гомотетии
осевой симметрии
21
83
18
37
309
309
315
97
130
158
18
342
9
309
309
79
198
127
127
127
128
54
55
55
56
20
335
335
335
153
119
132
73
68
338
174
71
40
155
111
223
80
переносе 132, 134
повороте 71
центральной
симметрии 75
382
Построение окружности,
вписанной в треугольник
описанной около
треугольника
— параллельных прямых
— перпендикуляра к прямой
— серединного
перпендикуляра отрезка
— среднего
пропорционального отрезка
— угла, конгруэнтного
данному
— четвертого
пропорционального отрезка
Преобразование подобия
Призма прямая
Признаки конгруэнтности
треугольников
— параллельности прямых
— подобия треугольников
Проекция (точки, отрезка) на
прямую
Произведение вектора на
число
Пропорциональные отрезки
Пространство
Противоположно направленные
лучи
Прямая
Прямоугольник
Радиус (круга, окружности)
Развертка конуса
— призмы
— цилиндра
Расстояние
— от точки до фигуры
Ромб
Свойства объема
— площади
Сегмент
Сектор
Симметрия осевая
— центральная
Синус
Сложение векторов
Сонаправленные лучи
Средняя линия трапеции
треугольника
Сумма векторов
310
310
119
93
92
307
85
232
234
335
83
120
237
97
207
231
10
129
12
162
9,10
344
336
344
12
98
165
340
175
42
41
78
75
270
205
129
172
170
202
Сфера
Тангенс
Теорема
— косинусов
— обратная
— Пифагора
— синусов
— Фалеса
Трапеция
— равнобедренная
Треугольник вписанный
— описанный
Угловой коэффициент
прямой
Угол
— внешний (многоугольника)
— вписанный
— выпуклый
— между направлениями
— — прямыми
— поворота
— прямой
— развернутый
— треугольника
— центральный
Умножение вектора на число
Уравнение прямой
Фигура
— выпуклая
— невыпуклая
— симметричная
— — относительно оси
— — — центра
Фигуры гомотетичные
— конгруэнтные
— подобные
— равновеликие
Хорда
Центр (круга, окружности) 9
— гомотетии
— поворота
— симметрии
Цилиндр
Четырехугольник
— вписанный
— описанный
Шар
20
278
16
285
156
245
290
169
171
172
309
310
278
40
139
305
41
137
265
71
68
41
139
41
208
278
10
38
38
101
89
76
226
64
218
176
42
, ю
224
71
75
343
152
312
313
348
383
СВЕДЕНИЯ О ПОЛЬЗОВАНИИ УЧЕБНИКОМ
№
1
2
3
4 т
5
Фамилия и имя
ученика
Учебный
год
Состояние учебника |
в начале
года
в конце
года
Андрей Николаевич Колмогоров
Александр Федорович Семенович
Ростислав Семенович Черкасов
ГЕОМЕТРИЯ
Учебное пособие для б—8 классов средней школы
Спец. редактор Г. Г. Маслова. Редакторы Т. А. Бурмистрова и С. В. Пазельс-
кий. Художник С. С. Водчиц. Художественный редактор Ε. Η. Карасик.
Технический редактор Н. А. Биркина. Корректоры Т. А. Кузнецова, Н. И.
Новикова
ИБ № 5586
Сдано в набор 21.03.80. Подписано к печати 14.08.80. 60x90Vie.ByM. кн.-жур. № 2. Гарн. шк. и журн.
рубл. Печать высокая. Усл. печ. л. 24+0,25 форзацы. Уч.изд. л: 20,88+0,44 форзацыГТираж
3 500 000 экз. Заказ 354. Цена 35 коп.
Ордена Трудового Красного знамени издательство «Просвещение» Государственного комитета
РСФСР по делам издательств, полиграфии и книжной торговли. Москва, 3-й проезд Марьиной
рощи, 41.
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Росглавполиграфпро-
ма Государственного комитета РСФСР по делам издательств, полиграфии и книжной торговли.
Саратов, ул. Чернышевского, 59.
с
\
Ч » ^21 Ϊ-3 · U ·. L-j "ОСИ
с 1мме р' ι
О-це тр говорота
на О 71^2\Ζ)449
*-А ι «-Β τ lr ""ОСИ СИГ -
С
метрии
О -центр поворота
на 0°, rJ20°
В
α
α + b =
b
сГ+ b =
ЗАКОНЫ СЛОЖЕНИЯ ВЕНТОРОЗ
О + Ь= Ь+ α (переместительный занон)
α + (b + c) = ^α 4- Ь) + С (сочетательный зачон)
сГ+0= (Г
ЗАКОНЫ УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО
' (ху)а = x(ycf) 'сочетательный занон)
ха + уа = (х+ Ja (первый распределительный закон)
xa + xb=X(a+b) (второй оаспределительный занон)
Оа=хО=Ъ
в
СООТНОШЕНИЯ
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИНЕ
с
α = csinA= с cosB, a=btgA
sinA = u cosA = -B, tgA = -°
с с b
a
СООТНОШЕНИЯ
В ПРОИЗВОЛЬНОМ ТРЕУГОЛЬНИНЕ
b с
в
(теорема синусов)
sin A sin В sin С
, , - о οι а (теорема
2 = Ь2+ С2- 2bccosA
косинусов)
S - 0,5absinC
'
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСНИХ
ФУННЦИЙ НЕНОТОРЫХ УГЛОВ
\
\
' *
О
^
1 !
О
1
Уз
2
1
Уз
2
У5
2
1
Уз
2
1
Vi!
1
о
О
-1
О
ЛАТИНСКИЙ АЛФАВИТ
ι 1
Печатные
оуквы
1 " ■ "J
\ А а \
\в ь\
\С с\
\D d\
\Е el
ΓΙΟ g
h
I i
\Jj
К к
L I
Mm
Рукописные буквы
4
/ j
Название
букв
а
бэ
це
A3
э
эф
же
аш
и
йот
(жи)
а
эль
эм
1
Печатные
буквы
1
V л
\о о
г Ί
\Qq\
\R r\
\S s\
\τ ι
II
"
\Ww\
\xx<
1 y'
1 *~
Ι Л~>
Рукописные буквы
1
\
Название
букв
эн 1
0
пэ
ί ку
эр ι
1 эс
1 тэ
1
1 у
вэ
1 дубль-вэ
икс
игрек
зэт
А.Н. Колмогоров
А.Ф. Семенович <
Р.С.Черкасов •-"v*. .^