М. И. Скворцов
СИСТЕМАТИЧЕСКИЕ
ПОГРЕШНОСТИ
В СУДОВОЖДЕНИИ
УДК 656.61.052 :681.02.088
Скворцов М. И. Систематические погрешности
в судовождении. — М.: Транспорт, 1980. — 168 с.
(Б-чка судоводителя).
В книге излагается методика обработки ре-
зультатов измерений, не рассматривавшаяся в ра-
нее изданной литературе: свойства систематиче-
ских погрешностей, их влияние на точность изме-
рений и оценок искомых величин, способы отыска-
ния эффективных оценок искомых величин. Изло-
жено применение этих способов к обработке ре-
зультатов навигационных измерений, содержащих
систематические погрешности. Даются практиче-
ские рекомендации, как решать, с учетом влияния
систематических погрешностей, конкретные задачи
судовождения: определение и учет поправок на-
вигационных приборов, учет влияния ветра на
путь и скорость судна, учет течения, определение
места судна, корректировка и оценивание точно-
сти счисления. Приводятся примеры решения за-
дач и таблицы, упрощающие вычисления.
Книга рассчитана на судоводителей транс-
портного, промыслового и экспедиционного фло-
тов; может быть использована в качестве учебно-
го пособия на курсах повышения квалификации
командного состава флота, аспирантами и курсан-
тами морских учебных заведений.
Ил. 29, табл. 15, библиогр. 69 назв.
31806-202
С ~049(01)-80~ 202'80 3605040000
© Издательство «Транспорт», 1980
ВВЕДЕНИЕ
Количественный и качественный рост транспортного и
промыслового флотов, расширение районов плавания судов,
их оснащение современными навигационными приборами
и электронными вычислительными машинами (ЭВМ) ста-
вят перед судовождением ряд задач и проблем, злободнев-
ность которых еще недавно не ощущалась столь остро, как
теперь, а также таких задач, которые раньше не решались
вовсе или решались упрощенно, но с применением совре-
менной вычислительной техники могут получить полное
и точное решение. К их числу относится, в частности, проб-
лема систематических погрешностей измерений.
Одним из основных требований, предъявляемых к су-
довождению, является точность. О ней судят по величине
погрешностей измерений и получаемых при их обработке
конечных результатов. Существуют два пути уменьшения
этих погрешностей: совершенствование технических средств,
какими выполняются измерения, и совершенствование ме-
тодов измерений и обработки их результатов. Свойства
систематических погрешностей таковы, что первый путь
либо вовсе не позволяет достичь их уменьшения, либо дает
желаемый эффект только ценой значительного усложнения
применяемых технических средств. Второй путь нередко
оказывается более простым и эффективным.
В судовождении постоянно приходится иметь дело с из-
мерениями, систематические погрешности которых превос-
ходят по величине случайные погрешности. Однако в на-
стоящее время как при обработке результатов измерений,
так и при оценивании точности получаемых результатов
применяются преимущественно алгоритмы, основанные на
предположении о пренебрежимо малой величине система-
тических погрешностей. Задача обработки результатов из-
мерений , отягощенных систематическими погрешностями,
является одной из насущных проблем современного судо-
вождения. С ней приходится встречаться в той или иной
степени каждому, кто выполняет измерения и занимается
3
обработкой их результатов. Предлагаемая вниманию чи-
тателя книга призвана оказать помощь в решении возни-
кающих при этом практических задач.
Академик А. Н. Крылов в статье «Теория и практика»
[34, с. 759] пояснял: «Оба слова греческие, по-русски бли-
же всего, не вполне, передаваемые словами: обсуждение
и действие. Отсюда ясно общее соотношение между теорией
и практикой. Можно обсуждать не действуя, но гораздо
хуже действовать без обсуждения.
Теория без практики мертва или бесплодна, практика
без теории невозможна или пагубна».
Многие вопросы теории систематических погрешностей
должного освещения в литературе еще не получили. По-
этому, памятуя только что приведенные слова А. Н. Кры-
лова, автор счел своим долгом посвятить ее основам гл. 1.
Предполагается, что читатель знаком с такими основными
понятиями навигации и теории вероятностей, как навига-
ционный параметр, его градиент, изолиния, линия положе-
ния, вероятность, случайная величина. Но если попытаться
обойтись без математического аппарата алгебры матриц
и теории случайных функций, то изложение окажется
очень долгим и малопонятным. Поэтому в § 1.1 приведены
краткие пояснения тех понятий, которые используются
в дальнейшем. Вместе с тем автор стремился по возможности
строить изложение так, чтобы основное содержание книги,
выводы и практические рекомендации были понятны и тем,
кто предпочитает обходиться возможно более простым мате-
матическим аппаратом.
Совершенно ясно, что обработка результатов измерений,
содержащих систематические погрешности, должна осно-
вываться на знании свойств этих погрешностей. Поскольку
этот вопрос еще не получил освещения в литературе, ему,
а также определению основных понятий уделено особое
внимание.
Автор выражает глубокую признательность академику
АН УССР Б. В. Гнеденко, контр-адмиралу А. Н. Мот-
рохову, профессорам Е. П. Чурову, Ю. В. Кемницу,
В. А. Коугия, Р. А. Скубко, доцентам П. П. Скородумову,
В. С. Болдыреву, Д. Н. Рубинштейну и особенно В. Т.
Кондрашихину, на разных этапах работы оказавшим ему
большую помощь, а также проф. Г. Г. Ермолаеву, выпол-
нившему нелегкий труд рецензирования рукописи, за кри-
тику, добрые советы и пожелания.
4
ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
М (X),	— математическое ожидание случайной величины
(вектора) X.
D(X), Dx —дисперсия случайной величины X.
Апт — || аи || пт — матрица, имеющая п строк и т столбцов.
aij — элемент матрицы, находящийся в /-й строке,
в /-м столбце.
Xml= II xj II — вектор (матрица, имеющая т строк и один
столбец).
Кх — корреляционная матрица вектора X.
i — номер измерения.
п — число измерений.
j — номер искомой величины.
т — число искомых величин.
г — номер систематической погрешности.
s — число систематических погрешностей.
Ui — результат i-го измерения, исправленный все-
ми учитываемыми поправками.
Д/ — истинная остаточная погрешность /-го измере-
ния.
су — среднее квадратическое отклонение, средняя
квадратическая погрешность.
х — оценка искомой величины х.
су(1) — средняя квадратическая погрешность измере-
ния, вес которого принят равным единице.
Hi — отклонение уравновешенного значения изме-
ряемой величины от результата измерения.
Глава i
ОСНОВЫ ОБРАБОТКИ
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
§ 1.1 МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Случайная величина и ее числовые характеристики.
Случайной величиной называется такая величина, которая
в результате опыта может принять то или иное значение,
причем заранее неизвестно, какое именно. Основными чис-
ловыми характеристиками случайной величины X служат
математическое ожидание и дисперсия.
Математическое ожидание случайной величины анало-
гично понятию среднего арифметического значения. Пусть
выполнено п измерений какой-либо постоянной величины,
например пеленга на ориентир с неподвижного судна.
Тогда среднее арифметическое из наблюденных значений
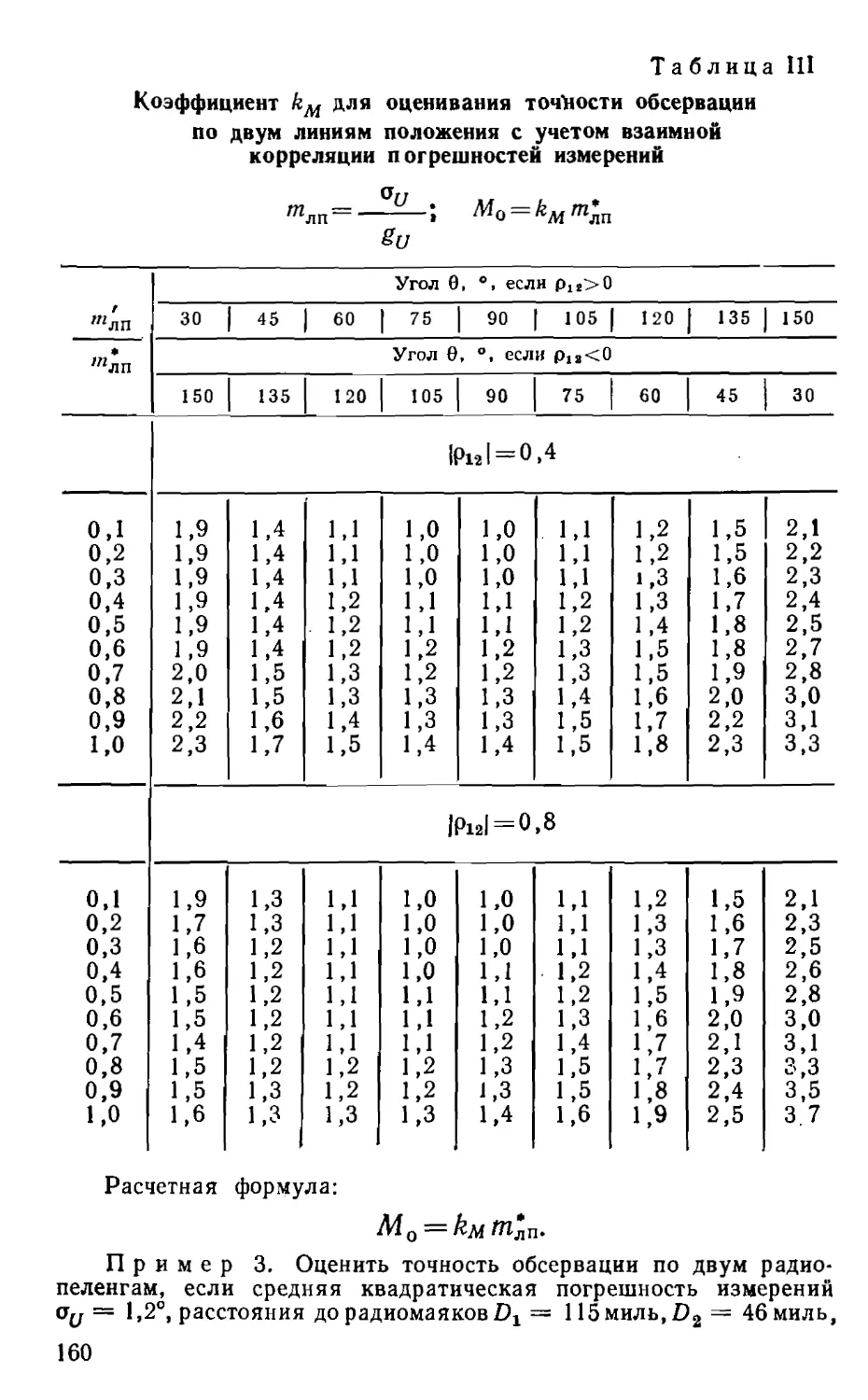
будет равно
Хср =	.	(1.1)
п
Предположим, в тх случаев результат измерений был
равен в т2 случаев он оказался равен х2 и т. д. Тогда,
учитывая, что тг + т2 + ... + mk = п, формула (1.1)
примет вид
у _ т1х1 + т2х2+	+	__
Аср------------------------—
п
—---Х1 I л2 ~г i-------
n n	n
Но величины p* = pl = и т. д. представляют собой’
частости случаев, когда результаты измерений приняли
значения х19 х2 и т. д. Следовательно, формулу (1.1) можно
записать в виде
k
Хср Рх х1~\~ Р2	••• рь xk =	Pi 0 *2)
Если речь идет не об уже выполненных измерениях, а о
возможных результатах опыта, который предстоит выпол-
нить в будущем, то для случайной величины дискретного
6
типа (могущей принимать только конечное число значений)
место частостей должны занять вероятности, а вместо сред-
него арифметического мы должны говорить о математиче-
ском ожидании случайной величины X:
k
M(X)=^Pixb	(1.3)
/=1
где k — число всех возможных значений случайной вели-
чины X;
pi — вероятность события, что эта случайная величи-
на примет значение х(.
Формула (1.3) есть определение понятия математиче-
ского ожидания дискретной случайной величины. Анало-
гично определяется понятие математического ожидания слу-
чайной величины непрерывного типа, но там суммирование
заменяется интегрированием, а вероятность — элементар-
ным приращением вероятности (дифференциалом f (х) dx
интегральной функции распределения):
M(X)=+J xf(x)dx,	(1.4)
— оо
где f(x)— дифференциальная функция распределения
вероятностей случайной величины X. *
W Дисперсией D (X) случайной величины X называется
математическое ожидание квадрата ее отклонения от ма-
тематического ожидания:
D (X) = М [(X - Мх)21.	(1.5)
Средним квадратическим отклонением называется квад-
ратный корень из дисперсии:
ох = Г^(Х).	(1.6)
Корреляционным моментом (ковариацией) Rxy слу-
чайных величин X и У называется математическое ожида-
ние’произведения их отклонений от математических ожи-
даний:
Rxy = М [(X - Мх) (У - Afy)L (1.7)
Коэффициентом корреляции (ковариации) рху слу-
чайных величин X и У называется отношение их корреляци-
7
онного момента к произведению средних квадратических
отклонений:
Абсолютная величина коэффициента корреляции не мо-
жет быть больше единицы. Если коэффициент корреляции
равен нулю, то случайные величины X и Y называются вза-
имно некоррелированными.
Основные свойства математических ожиданий функций
случайных величин:
1.	Математическое ожидание неслучайной величины рав-
но этой неслучайной величине:
М (с) = с.	(1.9)
2.	Математическое ожидание суммы (разности) двух
случайных величин равно сумме (разности) их математиче-
ских ожиданий:
М (X ± У) = М (X) ± М (У).	(1.10)
3.	Математическое ожидание произведения двух неза-
висимых случайных величин равно произведению их мате-
матических ожиданий:
М (ХУ) - М (Х)М (У).	(1.11)
4.	Математическое ожидание произведения неслучайной
величины с на случайную величину X равно произведению
неслучайной величины с на математическое ожидание слу-
чайной величины:
М (сХ) = сМ (X).	(1.12)
Основные свойства дисперсий случайных величин:
1.	Дисперсия неслучайной величины равна нулю:
D (с) = 0.	(113)
2.	Дисперсия произведения неслучайной величины на
случайную величину равна произведению квадрата не-
случайной величины на дисперсию случайной величины;
D (сХ) = сЮ (X).	(1.14)
3.	Дисперсия суммы (разности) случайных величин
X и У равна
D (х ± У) = D (X) + D (У) ± 2рЛу(Тх(Ту. (1.15)
8
В частном случае, когда X и Y являются взаимно некорре-
лированными случайными величинами (и только тогда),
формула (1.15) принимает вид
D(X±Y)=D(X)+D(X).	(1Л6)
В другом предельном частном случае, когда рху = + 1
(случайная величина Y прямо пропорциональна случайной
величине X, причем коэффициент пропорциональности по-
ложителен), формула (1.15) принимает вид
D (X ± У) = (ах ± *г)2.	(1.17)
Оценкой X случайной величины X называется любое
приближенное значение этой величины, отыскиваемое в
виде функции результатов измерений. Операция отыска-
ния оценки X называется оцениванием случайной величи-
ны X.
Оценка X называется несмещенной, если ее математиче-
ское ожидание равно математическому ожиданию случай-
ной величины, т. е. если
М (X —X) = 0.	(1.18)
Оценка X называется эффективной, если ее дисперсия
не превышает дисперсии любой другой оценки случайной
величины X:
М 1(Х — X)2] = min.	(1.19)
Когда мы говорим, что задачей обработки наблюдений
является отыскание наиболее точных значений искомых
величин, то обычно это означает, что мы стремимся найти
несмещенные и эффективные оценки этих величин.
Случайная функция. Если величина X случайным обра-
зом меняется при изменении аргумента /, ее называют слу-
чайной функцией аргумента t и обозначают символом Х(/).
Величина X (/,), соответствующая некоторому фиксирован-
ному значению /г- аргумента /, есть случайная величина.
Она называется сечением случайной функции, соответст-
вующим данному значению аргумента t.
Математическим ожиданием случайной функции X (/)
называется неслучайная функция Мх (0 аргумента /,
которая при любом значении t равна математическому
ожиданию соответствующего сечения случайной функции:
Мх (/) = MIX (/)].	(1.20)
9
Случайная функция, математическое ожидание которой
при любых значениях аргумента t равно нулю, называется
центрированной случайной функцией.
bu Дисперсией случайной функции называется математиче-
ское ожидание квадрата отклонения случайной функции от
ее математического ожидания. Она также является неслу-
чайной функцией аргумента
Da(/) = D [X (/)] = о>(/) - М{[Х (/) - Мх(/)]2}. (1.21)
Корреляционной функцией /2) случайной функ-
ции X (/) называется корреляционный момент сечений слу-
чайной функции, соответствующих значениям и /2 аргу-
мента /; она является неслучайной функцией аргументов
и /2:
Ях(4. /2) = М{[Х &) - ЭД] [X (^ - Мх (/2)]}. (1.22)
Нормированной корреляционной функцией px(/i, /2)
называется отношение корреляционной функции к произ-
ведению средних квадратических отклонений сечений слу-
чайной функции (т. е. коэффициент корреляции между дву-
мя сечениями случайной функции):
р t )=	(1,23)
Структурной функцией Sx(Ai> ^2) случайной функции
X (/) называется математическое ожидание квадрата раз-
ности сечений случайной функции, соответствующих зна-
чениям и /2 аргумента /; она также является неслучайной
функцией аргументов и /2:
Sx(/i, /2) = Л4{1Х (/2) - X О2}.	(1.24)
Интеграл от случайной функции X (/) по аргументу t
является случайной функцией аргумента Л Математиче-
ское ожидание интеграла от случайной функции равно ин-
тегралу от ее математического ожидания. Корреляционная
функция интеграла от случайной функции равна результа-
ту двукратного интегрирования корреляционной функции
исходной случайной функции по аргументам 4 и /2. Если
t
Y(t) = ^X(t)dt,	(1.25)
о
10
TO	t
=	=	(1.26)
О
G G
Ry (tu Q = J f Rx (4. 4) ^4 dt2. (1.27)
о о
Элементарной случайной функцией называется случай-
ная функция вида
X(t) = Zf(t),	(1.28)
где Z — обычная случайная величина, не являющая-
ся функцией аргумента /;
/(/) — неслучайная функция аргумента /.
Теорема о каноническом представлении случайных функ-
ций [48]: любая случайная функция, дисперсия которой ко-
нечна, сколь угодно большим числом способов и со сколь
угодно малой погрешностью может быть представлена в
виде суммы ее математического ожидания и конечного чис-
ла элементарных случайных функций:
Х(/) = Л4х(4+22г4(4 + 6(4,	(1.29)
г— 1
где Zb ..., Ze — взаимно некоррелированные случайные
величины с математическими ожидани-
ями, равными нулю;
6 (/) — остаточный член канонического разло-
жения (является случайной функцией
аргумента /).
Случайная функция Х(/) называется стационарной,
если все ее вероятностные характеристики (математичес-
кое ожидание, дисперсия, корреляционная функция и т. д.)
не изменятся, при прибавлении ко всем значениям аргу-
мента t одного и того же произвольного числа т (например,
корреляционная функция не изменится, если от аргумен-
тов tr и /2 перейти к аргументам tr + т и /2 + т).
Математическое ожидание и дисперсия стационарной
случайной функции суть постоянные числа. Корреляцион-
ная и структурная функции являются функциями только
одного аргумента т, где т = /2 — tr — разность значений
/2 и аргумента t.
11
Имеют место важные соотнощения:
Ях(0) = DXi	(1.30)
Sx(t) = 2 [7?х(0) - Rx (т)1.	(1.31)
Если X (/) — стационарная случайная функция, при-
чем Y (/) есть ее интеграл по аргументу /, то в силу четности
корреляционной функции Rx (т) дисперсия случайной
функции Y (/) равна
t
Dr(/) = 2 J(/—г)7?х(т)б/т.	(1.32)
О
Интервалом корреляции называется такое значение т0
промежутка т, при котором абсолютная величина коэффи-
циента корреляции между двумя сечениями X (т) и X (/ +
+ т) случайной функции остается больше некоторого за-
данного уровня, например | р (т) | > 0,05. Если т > т0,
то сечения X (/) и X (t + т) можно считать практически не-
коррелированными случайными величинами.
Матрицей называется упорядоченная совокупность чи-
сел (элементов), записываемая в виде таблицы:
аи ... а-ц... а17П
А ^пт II aij II		ац..	• ^im	(1.33)
	^nl •	• * ^nj •	•• &пт	
Обозначение Апт показывает, что матрица А имеет п
строк и т столбцов; обозначение [| аи || — что элемент,
находящийся в z-й строке, в у-м столбце, есть
Матрица, имеющая и строк и один столбец, называет-
ся вектором (матрицей-столбцом). Каждый из элементов
(компонентов) вектора снабжается только одним индексом,
показывающим, в какой строке матрицы он расположен,
например
к
L = Lnl^\\U = I,
(1.34)
I
п
12
Две матрицы А и В считаются равными тогда, и толь-
ко тогда, когда число строк первой равно числу строк второй,
число столбцов первой равно числу столбцов второй
и когда любой элемент первой матрицы равен соответст-
вующему элементу второй матрицы, т. е. при любых i и /
выполняется равенство
ai} = Ьц.	(1.35)
Таким образом, выражение
Апт = Впт	(1.36)
является сокращенной записью п X т равенств вида (1.35).
Элементы ап, а22, • матрицы (1,33), у каждого из ко-
торых первый индекс, обозначающий номер строки, и вто-
рой индекс, обозначающий номер столбца, совпадают, на-
зываются диагональными, а диагональ, на которой они
расположены, —главной диагональю. Если матрицу А по-
вернуть вокруг главной диагонали, то получится матрица,
которую называют транспонированной по отношению к ма-
трице А и обозначают символом /1Т:
=	=11 “л || =
«и ••• ат
&12 ^22 *•* ап2
(1.37)
&1т @2т •••
Сложение двух матриц А и В определено тогда и толь-
ко тогда, когда число строк матрицы А равно числу строк
матрицы В и число столбцов матрицы А равно числу столб-
цов матрицы В. Суммой этих матриц называется матрица,
составленная из сумм соответствующих элементов матриц
А и В:
#11 + ^11 ••• aij -\~bij + Ь1т
&ni ! bni... anj-j- bnj ... #nniH bum
Аналогично определяется и вычитание матрицы В из
матрицы А:
^пт Впт = || (tZ/j- bjj) || пт,	(1.39)
13
Матрица, все элементы которой равны нулю, называется
нулевой и обозначается символом 0 или 0nm:
АПт Апт = ОП7П = 0»	(1.40)
Произведением матрицы А — ||	|| на число с назы-
вается матрица, каждый из элементов которой получен ум-
ножением соответствующего элемента матрицы А на число с:
сАпт = Аптс = || саи || nm.	(1.41)
Если число столбцов матрицы Апт равно числу строк
другой матрицы Bmqy то произведением АВ этих матриц
называется матрица Cnq9 определяемая по правилу: чтобы
найти элемент с^, находящийся в i-й строке, в /-м столб-
це матрицы С, надо каждый из элементов z-й строки матри-
цы А умножить на соответствующий элемент /-го столбца
матрицы В и полученные произведения сложить (рис. 1.1):
Cij =	+ ••* +	(1-42)
Необходимо иметь в виду, что даже если возможны произ-
ведения как АВ, так и ВА, в общем случае ВА =/=АВ (при
перестановке сомножителей произведение матриц}£ме-
няется).
Произведение двух матриц равно транспонированному
произведению транспонированных сомножителей, взятых
в обратном порядке:
АВ .= (Bl4t)t.	(1.43)
Другие формулы, выражающие основные свойства сумм и
произведений матриц:
А + (В + С) = (А + В) + С; А + В = В + А; (1.44)
А (ВС) = (АВУС; (А + В) С = АС + ВС. (1.45)
Рис. 1.1. Умножение матриц: СПд =
~ АптВтд
Матрица, разделен-
ная горизонтальными и
вертикальными линиями
на несколько частей, на-
зывается блочной (кле-
точной), а матрицы, на
которые она разделе-
на, — блоками^ (клетка-
ми). Если существует
произведение АВ мат-
14
риц А и В, то можно разбить их на блоки таким образом,
что станет возможным отыскание произведения по обще-
му правилу умножения матриц (см. рис. 1.1), обращаясь
с блоками так, будто это числа. Для этого надо следить,
чтобы выполнялось условие, при котором умножение бло-
ков возможно: число столбцов в первом сомножителе обя-
зательно должно быть равно числу строк во втором сомно-
жителе. В частности, если
Ckl I Fkm
____i____
G/a [ f^hm
I-lq j Slr
T । U
1 mg । umr
(1.46)
то
| CL+FT \CS + FU
I GL + HT [ GS + HU
(1.47)
Матрица, число n строк которой равно числу столбцов,
называется квадратной матрицей порядка п. Квадратная
матрица Апп = ||	|| называется симметрической, если
ее элементы, расположенные симметрично относительно
главной диагонали, равны между собой, т. е. при любых
i и / соблюдается равенство
аг; = а,г.	(1.48)
Из этого	определения видно, что	симметрическая	матрица
равна своей транспонированной матрице:
А = Лт.	(1.49)
При умножении двух	симметрических (только	симметриче*
ских!) матриц в обратном порядке их произведение не ме-
няется:
АВ = ВА.	(1.50)
Диагональной называется квадратная матрица, все эле*
менты которой, не лежащие на главной диагонали, равны
нулю. Очевидно, что любая диагональная матрица явля-
ется симметрической.
Единичной называется диагональная матрица, все диа-
гональные элементы которой равны единице. Она обозна-
чается символом Е или, если надо указать, что ее порядок
15
равен /г, символом Епп. Произведение любой матрицы А на
единичную матрицу равно исходной матрице А:
^ппАПт ~	АптЕтт	Апт. (1.51)
Для каждой квадратной матрицы существует ее опреде-
литель (детерминант) — число, отыскиваемое по общим пра-
вилам вычисления определителей [9, с. 146—148; 14,
с. 223—229]. Если в матрице Апт выбрать k произвольных
строк и столько же произвольных столбцов и образовать
из элементов, стоящих на их пересечении, квадратную ма-
трицу, то определитель этой матрицы называется минором
Л-го порядка матрицы А. Рангом матрицы А называется
максимальный порядок минора этой матрицы, отличного от
нуля. Очевидно, что ранг матрицы Апт не может быть боль-
ше, чем минимальное из чисел п и т. Важно знать также,
что ранг произведения нескольких матриц не превосходит
минимального из рангов отдельных сомножителей.
Квадратная матрица, ранг которой равен ее порядку
(т. е. такая, определитель которой отличен от нуля), назы-
вается неособенной. Для каждой неособенной матрицы Апп
существует матрица Л-1, называемая обратной по отноше-
нию к матрице Л и отыскиваемая из уравнения
ЛЛ"1 - Е или Л'М = Е.	(1.52)
Операция отыскания матрицы, обратной по отношению
к матрице Л, называется обращением этой матрицы. Если
матрица Л — симметрическая, то и матрица Л-1 также
будет симметрической. Наиболее простым является обраще-
ние диагональных матриц. Пусть дана такая матрица С,
причем для упрощения записи z-й отличный от нуля эле-
мент, находящийся в z-й строке, в z-м столбце, обозначен
символом q:
сх 0 ... О
с — Hi linn	0 с2... 0	(1.53)
О 0 ... сп
Тогда матрица С-1 = || рг || пп будет также диагональной,
причем ее z-й отличный от нуля элемент рг, находящий-
ся в z-й строке и в z'-м столбце, равен
р. = 1/с. = cf1.	(1.54)
16
Квазидиагональной называется блочная матрица вида
К =
Кг 0 ... О
О ха...о
(1.55)
о о ...кт
где Ki, К2,
ные элементы — нули,
триц следует, что
Кт — квадратные матрицы, а все осталь-
Из правила умножения блочных ма-
к-2 =
к;1 О ...О
о к~г... О
(1.56)
О 0	... Кт1
Большой интерес представляет частный случай обраще-
ния квазидиагональной матрицы
Чо’л} (1'57)
когда все диагональные элементы квадратной матрицы Ki —
очень большие (практически бесконечно большие) числа,
а недиагональные элементы конечны. Тогда
Случайной называется матрица, элементами которой
являются случайные числа. Математическим ожиданием
М (U7) случайной матрицы W называется матрица, каждый
из элементов которой равен математическому ожиданию
соответствующего элемента матрицы W.
Пусть X = || Xj || П1 — случайный вектор; А — вектор,
компонентами которого являются отклонения элементов
случайного вектора X от их математических ожиданий:
А = II А/ II m = II - М (xj) || = X - М (X), (1.59)
где М (...) — символ математического ожидания. Рассмо-
трим матрицу ААТ. Ее элемент, расположенный в z-й стро-
ке и в /-м столбце, представляет собой произведение А^Ау,
17
диагональными элементами будут квадраты А?, А*, ...» А*
отклонений компонентов случайного вектора X от их мате-
матических ожиданий.
Корреляционной матрицей Кх случайного вектора X
называется матрица
Кх - М (ДДТ) = м [(X — Мх) (X - Л4Х)Т1. (1.60)
Из этого определения видно, что корреляционная матри-
ца есть симметрическая квадратная матрица. Ее диагональ-
ными элементами являются дисперсии компонентов х19
х2, хп случайного вектора X. Элемент, расположенный
в Z-й строке и в /-м столбце корреляционной матрицы, пред-
ставляет собой корреляционный момент случайных вели-
чин Xt И Xj.
Если G = Gmn —^некоторая неслучайная матрица и
зависимость между случайными векторами Хт1 и Ynl
устанавл ивается выражением
X = GY,	(1.61)
то имеют место важные равенства
М (X) = GM (У);	(1.62)
Кх- М (ДхАх) = М [6Ду(СДу)т1 =
= GM (ДуAy) GT = GKyG*,	(1.63)
где Дх= X — М (X); Ду= Y — М (У); Ку— корреля-
ционная матрица вектора У.
§ 1.2 ОСНОВНЫЕ СВОЙСТВА
ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Основной способ познания человеком количественных
закономерностей, свойственных окружающему его реаль-
ному миру, — измерение. Судовождение не является ис-
ключением: чтобы знать, где находится судно, каковы на-
правление и скорость его перемещения, где оно окажется
через некоторый промежуток времени, надо выполнять
измерения.
Абсолютно точных измерений, которые давали бы ис-
тинные, безошибочные значения измеряемых величин, не
существует.Как бы тщательно ни выполнялись измерения,
18
какие бы точные приборы и системы для этого ни применя-
лись, всем им неизбежно присущи некоторые погрешности.
Истинной погрешностью измерения называется разность
между результатом измерения и истинным значением изме-
ряемой величины:
AfHCT — ^Лизм ^Л'иСТ»	(1*64)
где i — номер измерения;
6\*изм — результат измерения;
t/iHcT — истинное значение измеряемой величины.
Истинная погрешность никогда не бывает известна абсо-
лютно точно (для этого надо было бы знать истинное зна-
чение измеряемой величины, что невозможно). Но, пользу-
ясь методами теории вероятностей и математической ста-
тистики, можно оценивать ее основные вероятностные ха-
рактеристики (математическое ожидание, дисперсию и сред-
нее квадратическое отклонение, коэффициент корреляции
между погрешностями двух разных измерений) и таким
образом составлять суждение о точности измерений. Од-
ним из основных путей такого исследования является пред-
ставление истинной погрешности в виде суммы более про-
стых составных частей — элементарных погрешностей.
Элементарные погрешности можно делить по разным
признакам и соответственно получать разные их классифи-
кации. Мы рассмотрим лишь основные.
Происхождение погрешностей измерений. Каждый из
материальных факторов, участвующих в процессе измере-
ний, является источником особых, специфических погреш-
ностей. Соответственно по происхождению они подразде-
ляются на погрешности объекта, обусловленные отличиями
реального объекта измерений от его модели, на которой ос-
нованы способы измерений и обработки их результатов;
инструментальные, порождаемые прибором, которым вы-
полняются измерения; внешние, обусловленные влиянием
среды, где выполняются измерения и распространяется из-
мерительный сигнал; личные (только при неавтоматических
измерениях), обусловленные свойствами человека, выпол-
няющего измерения. Иногда выделяют в особую разновид-
ность методические погрешности, «обусловленные методом
измерений». Но ясно, что, с одной стороны, ни одна из по-
грешностей не^может рассматриваться в отрыве от метода
измерений; с другой — говорить о методе' измерений без
упоминания о средствах, которыми он реализуется, не име-
19
ет смысла. Поэтому любая погрешность может рассматри-
ваться как методическая, происходящая от неполного соот-
ветствия модели измерений натуре (по меткому выражению
ученого XVIII в. И. X. Ламберта — от «предположений
о совершенной правильности того, что правильно лишь при-
ближенно»).
Обычные и необычные погрешности. Существуют такие
погрешности, которые неизбежно встречаются в любых из-
мерениях, и такие, которых можно избежать. По признаку
неизбежности следует делить элементарные погрешности на
обычные (неизбежные), свойственные всем измерениям без
исключения, и необычные, или грубые (иногда их называют
промахами), случающиеся лишь в некоторых измерениях.
Такое деление позволяет акцентировать внимание на раз-
личиях в методах борьбы с обычными и необычными погреш-
ностями.
Промахи не являются неизбежными; основными при-
чинами их возникновения бывают невнимательность на-
блюдателя, сбои в работе измерительных приборов (напри-
мер, не замеченный своевременно выход гирокомпаса из ме-
ридиана или рассогласование вследствие кратковременного
прекращения электропитания принимающих приборов, рез-
кое изменение поправки гидродинамического лага вследст-
вие попадания постороннего предмета в приемное отверстие),
аномальное состояние внешней среды (магнитная буря)
и т. д. Основное внимание должно обращаться на их преду-
преждение, а если такая погрешность все же возникла,—
на ее своевременное обнаружение и исключение из резуль-
татов измерений.
Важной особенностью грубых погрешностей является
то, что какая-либо зависимость между возможными вели-
чинами этих погрешностей и вероятностями возникновения
погрешностей такой величины отсутствует (грубым погреш-
ностям не свойственны законы распределения вероятно-
стей). Поэтому они не обладают свойством ограниченности:
любая из них может быть сколь угодно велика в пределах,
в которых определен результат измерения. Это обстоятель-
ство служит основанием для обнаружения грубых погреш-
ностей: если выполнено несколько измерений одной физи-
ческой величины, и результат одного из них необычно силь-
но отличается от остальных, то это измерение считается про-
махом; его результат отбрасывается (не принимается во вни-
мание при дальнейшей обработке результатов измерений).
20
Основной статистической характеристикой грубых по-
грешностей является вероятность события, заключающего-
ся в том, что такая погрешность в некотором измерении про-
изойдет; главная задача исследования — выяснение зави-
симостей этой вероятности от факторов, характеризующих
условия измерений, и изыскание мероприятий, ведущих к ее
уменьшению.
Неизбежных погрешностей, как видно из названия, из-
бежать нельзя: они свойственны всем измерениям без ис-
ключения. Изучение свойств и способов уменьшения их
величины и влияния на точность конечного результата,
ради которого выполняются измерения, является основным
содержанием теории погрешностей измерений.
Любой неизбежной погрешности присущ закон распре-
деления вероятностей: каждому возможному значению этой
погрешности соответствует вероятность такого события,
что в результате измерения погрешность не превзойдет за-
данной величины (это свойство часто называют свойством
ограниченности возможной величины погрешностей).
Случайные, систематические и зависимые погрешности.
Лишь очень редко мы имеем дело с одним-единственным из-
мерением. Гораздо чаще выполняется подряд несколько из-
мерений. Так, для определения места судна в море надо вы-
полнить не менее двух измерений; для повышения точности
результатов — измерения выполняются сериями, и к по-
следующей обработке принимают среднее арифметическое
их результатов, и т. д. Мы будем рассматривать некоторую
совокупность измерений, например, составленную всеми
измерениями, выполненными для определения места суд-
на, или несколькими измерениями одного навигационного
параметра, используемыми для вычисления его среднего зна-
чения, и т. п. По свойствам неизбежных элементарных по-
грешностей в совокупности измерений они делятся на слу-
чайные, систематические и зависимые.
Случайными погрешностями, согласно ГОСТ 16263—70
[18], называются погрешности, при повторных измерениях
одной и той же величины изменяющиеся случайным обра-
зом; систематическими— остающиеся постоянными или
изменяющиеся закономерно. Как понимать выражения —
«изменяющиеся случайным образом», «изменяющиеся зако-
номерно»? ГОСТ ответа не дает. Однако в современной ли-
тературе по теории погрешностей измерений все без ис-
ключения авторы, обычно не оговаривая этого особо, счи-
21
тают случайные погрешности удовлетворяющими условиям
А. Н. Колмогорова [27]:
1.	Математическое ожидание любой случайной погреш-
ности равно нулю: если — случайная погрешность z-ro
измерения, то при любом z
K(6f) = 0.	(1.65)
2.	Дисперсия любой случайной погрешности конечна:
М (6?) = о?,	(1.66)
где <тг Ф 0; crf оо.
3.	Корреляционный момент двух разных случайных по-
грешностей равен нулю (следовательно, и коэффициент их
взаимной корреляции тоже равен нулю): если i=/=j, то
М (6Д-) = 0.	(1.67)
Таким образом, чтобы следовать установившейся тради-
ции, надо принять следующее определение: случайными
погрешностями называются элементарные погрешности,
в рассматриваемой совокупности измерений образующие
систему взаимно некоррелированных случайных величин,
математические ожидания которых равны нулю, а диспер-
сии конечны.
Из формул (1.16) и (1.67) следует важный вывод: дис-
персия суммы случайных погрешностей равна’'сумме их
дисперсий; если ах, а2, ..., оп — средние квадратические
отклонения слагаемых погрешностей, — среднее квадра-
тическое отклонение их суммы, то
ст2 =/ ст? + ст! + ... + а*.	(1.68)
Систематической погрешностью будем называть такую
элементарную погрешность, которая в рассматриваемой
совокупности измерений может быть выражена в виде ]
U = Ur (ah pZ) ...),	(1.69)
где Sir — величина r-й систематической погрешности
в z-м измерении рассматриваемой совокуп-
ности измерений;
— случайная величина, в рассматриваемой со-
вокупности измерений принявшая некоторое
конкретное, фиксированное значение (бу-
дем называть ее амплитудой r-й систематиче-
ской погрешности).
/г (...) — неслучайная функция параметров, характе-
ризующих условия измерений, именуемая
координатной функцией [48, § 6.21;
осг, Рь • •• — значения, которые приняли эти параметры
при /-м измерении;
Если fr (a>t, Pi, ...)	+ 1, то мы имеем дело с постоян-
ной (повторяющейся) систематической погрешностью, ве-
личина которой во всех измерениях одинакова. Очевидно,
что для таких погрешностей понятия «амплитуда погреш-
ности» и «погрешность» совпадают.
Простым и наглядным примером систематических по-
грешностей является радиодевиация. Ее зависимость от
радиокурсового угла на радиомаяк выражается формулой
f (?) = А + В sin q + С cos q + D sin 2q + E cos 2q,
где q — радиокурсовой угол;
Л, ..., E — коэффициенты радиодевиации.
Она представляет собой сумму пяти систематических
погрешностей. Величина А есть постоянная систематиче-
ская погрешность измерений радиопеленгов; величины В,
С, D, Е — амплитуды систематических погрешностей, за-
кономерно изменяющихся при изменении радиокурсового
угла; величины sin q, cos q, sin 2q, cos 2q — координатные
функции.
Компенсация систематических погрешностей. Для умень-
шения систематических погрешностей результаты измере-
ний исправляются поправками (примеры — поправка ги-
рокомпаса, инструментальная поправка и поправка индек-
са секстана, поправки высоты светила за наклонение ви-
димого горизонта, за астрономическую рефракцию). Если
^гизм — результат f-го измерения, — поправка, слу-
жащая для компенсации r-й систематической погрешности,
то результат, исправленный поправками, вычисляется по
формуле
=	2 Д^г-	(1-70)
Г —1
Идеальным было бы назначать поправки таким образом,
чтобы они в точности были равны исключаемым погрешно-
стям, взятым с обратными знаками. Но это невозможно:
любая поправка представляет собой результат, полученный
23
из некоторых предыдущих измерений (поправка компаса —
разность истинного и измеренного пеленгов створа, радио-
девиация — разность принимаемого за истинный визуаль-
ного курсового угла и радиокурсового угла на радиомаяк,
и т. д.). Поэтому она всегда известна с некоторой погреш-
ностью, обусловливаемой погрешностями измерений, из ко-
торых определена. Кроме того, многие погрешности сами
не остаются постоянными, а изменяются случайным обра-
зом с течением времени, являются случайными функциями
времени (типичный пример — изменение по времени погреш-
ности показаний гирокомпаса). Поэтому приходится в ка-
честве поправок пользоваться оценками компенсируемых по-
грешностей, взятыми с обратными знаками. Из формул
(1.69) и (1.70) видно, что поправка, вводимая в результат
/-го измерения для компенсации r-й систематической по-
грешности, должна отыскиваться в виде
Д^г = -СЛ(^, Рь ...),	(1.71)
где Сг — оценка амплитуды r-й систематической погреш-
ности, найденная из некоторых выполненных ранее изме-
рений.
Остаточные систематические погрешности. Те погреш-
ности, которыми отягощены результаты измерений после
исправления поправками, называются остаточными. Из
выражений (1.69)—(1.71) видно, что величина r-й остаточ-
ной систематической погрешности в результате /-го изме-
рения равна
ziT = Ъг +	- Cr - t) fr (аг, Pi, ...).	(1.72)
Величину — Сг назовем амплитудой r-й остаточной систе-
матической погрешности и обозначим символом zT. Кроме
того, для упрощения записей впредь значение координат-
ной функции r-й систематической погрешности в /-м изме-
рении будем обозначать символом fiT:
fir = fr («п Pi,	(1.73)
Тогда выражение (1.72) примет вид
Ztr = zrfir.	(1.74)
Ясно, что как амплитуда zr остаточной систематической
погрешности, так и сама эта погрешность ziT являются слу-
чайными величинами — уже хотя бы потому, что оценка
£г, как функция результатов некоторых предыдущих изме-
24
рений, неизбежно содержащих случайные погрешности, за-
ведомо является случайной величиной.
Как бы тщательно мы ни старались компенсировать си-
стематические погрешности поправками, сделать это аб-
солютно точно никогда не удается: и после введения по-
правок результат измерений содержит остаточные систе-
матические погрешности, которые, следовательно, являют-
ся неизбежными погрешностями.
Обычно стремятся поправки, которыми исправляются
результаты измерений, назначать таким образом, чтобы ве-
личина £г была несмещенной оценкой амплитуды ис-
ключаемой систематической погрешности. Если это важ-
нейшее требование соблюдено, то, как видно из выражений
(1.18), (1.10), (1.12), математические ожидания амплитуды
любой остаточной систематической погрешности и той ве-
личины, которую эта погрешность примет в результате лю-
бого измерения, оказываются равными нулю:
М (zr) - М (zir) = 0.	(1.75)
Как непосредственно следует из выражений (1.14) и
(1.6), дисперсия и среднее квадратическое отклонение г-й
остаточной систематической погрешности z-ro измерения
равны
D Ы = tfffr;	(1.76)
a&r) =	(1.77)
где ог — среднее квадратическое отклонение (от нуля)
амплитуды г-й систематической погрешности. Поскольку
символом a (zir) обозначается среднее квадратическое от-
клонение от математического ожидания, равного нулю,
величину о (z/r) часто называют средней квадратической
величиной г-й систематической погрешности z-ro измерения,
или, еще проще, — средней квадратической погрешностью.
Вспомним, что отношение произведения двух отличных
от нуля чисел к произведению их абсолютных величин мо-
жет принимать только два значения: + 1, если оба эти чис-
ла имеют один знак, или —1, если их знаки различны.
Следовательно, коэффициент корреляции между значения-
ми г-й остаточной систематической погрешности в z-м и
в £-м измерениях одной совокупности равен
Формула (1.78) выражает наиболее существенную осо-
бенность систематических погрешностей: если каким-либо
образом стала известна величина такой погрешности в од-
ном измерении рассматриваемой совокупности, при кото-
ром fr (аь рг, ...) у= О, то однозначно определена^ее ве-
личина и в любом другом измерении той же совокуп-
ности.
Пример 1.1. После компенсации радиодевиации истинная
величина коэффициента D радиодевиации равна +' 1,5°. При
определении остаточной радиодевиации эта величина была найде-
на из наблюдений неточно; при расчете таблицы радиодевиации она
была принята равной + 2,1°. Чему окажутся равными вызывае-
мые этой причиной остаточные погрешности измерения радиопелен-
гов на радиокурсовых углах ^ = 45°, <?2 = 75°, q3 = 90 , <?4 = 105°?
Решение.
Поскольку sin (2 • 45°) = + 1,0; sin (2 • 75°) = 4- 0,5;
sin (2 • 90°) = 0; sin (2 . 105°) = — 0,5, эти остаточные погреш-
ности измерения радиопеленгов будут равны соответственно:
= — 0,6°; z2 = — 0,3°; z3 = 0; z4 = + 0,3°. Если стало извест-
ным, что на курсовом угле 75° погрешность оказалась равной
—0,3°, то сразу можем сказать, что на курсовом угле 45° она будет
равна — 0,6°; на курсовом угле 105° ее величина окажется равной
4- 0,3° и т. д.
Совсем иной характер имеют случайные погрешности из-
мерений. Если нам стало бы известным, что случайная по-
грешность первого измерения оказалась равной, предпо-
ложим,+0,4°, то это нисколько не увеличило бы информа-
ции о том, какой она окажется, например, при втором из-
мерении: она с одинаковой вероятностью может оказаться
положительной или отрицательной; может случиться, что
ее величина будет равна + 0,6°, но она может оказаться
равной и — 0,3°: величина случайной погрешности второго
измерения не зависит от величины, которую она приняла
в первом измерении. Аналогично, отсутствует какая-либо
зависимость между величинами случайных погрешностей
первого и третьего, второго и третьего измерений и т. д.
Следствием взаимной независимости случайных погреш-
ностей является еще одно важное их свойство. Предполо-
жим, мы выполнили п измерений некоторой постоянной ве-
личины X, причем измерения отягощены только случайны-
ми погрешностями, так что
Ui - X + 6Р
(1-79)
Пусть измерения равноточны, т. е. = й2 = ... = ап =
= о(1) ; за оценку искомой величины X принято среднее
арифметическое из результатов измерений:
X =	(1.80)
п /=1
Тогда, как видно из выражений (1.14) и (1.68), средняя квад-
ратическая погрешность оценки X окажется равной
т. е. точность среднего арифметического из п результатов
равноточных измерений постоянной величины в Уп выше
точности единичного измерения. Это свойство часто назы-
вают свойством взаимной компенсации (следовало бы гово-
рить — частичной компенсации, поскольку она никогда не
бывает полной) случайных погрешностей в среднем ариф-
метическом из результатов измерений. Оно является след-
ствием только тех свойств случайных погрешностей, ко-
торые выражаются формулами (1.65)—(1.67). Его «доказа-
тельства», якобы основанные на свойствах нормального рас-
пределения погрешностей [43, с. 23], представляют собой
пример логической ошибки (в любом учебнике по теории
вероятностей встречается предупреждение, что нормаль-
ность распределений нескольких случайных величин не
влечет за собой их взаимной некоррелированности).
Если бы измерения содержали одни случайные погреш-
ности, то решение проблемы повышения точности оказа-
лось бы очень простым: выполнил вместо одного четыре
измерения — и точность результата повысится вдвое; уве-
личил число измерений в 25 раз — получил пятикратное
повышение точности, и т. д. Но в действительности так не
бывает. Мешают систематические погрешности.
Систематические погрешности свойством взаимной ком-
пенсации в среднем арифметическом не обладают. Нагляд-
нее всего это видно на примере постоянной систематиче-
ской погрешности, одинаковой во всех измерениях совокуп-
ности. Действительно, для этого случая, воспользовавшись
выражениями (1.15) и (1.78) или непосредственно выраже-
ниями (1.72), (1.74), (1.77), подставив туда Дг = +1,
27
нетрудно убедиться, что погрешность Среднего арифметгГ
ческого окажется в точности равна погрешности единич-
ного измерения; увеличение числа измерений точности
результата не повышает.
Мы видим, что наиболее существенное отличие между
случайными и систематическими погрешностями заключа-
ется в величине коэффициента корреляции. Коэффициент
корреляции между величинами случайных погрешностей
двух разных измерений одной совокупности равен нулю,
а систематической погрешности — единице (+ 1 или — 1).
Существуют погрешности, занимающие промежуточное
положение между случайными и систематическими, у ко-
торых абсолютная величина коэффициента корреляции
лежит между нулем и единицей. Их называют зависимыми.
Примером зависимых погрешностей может служить сумма
остаточных систематических и случайных погрешностей
(ее называют сложной погрешностью). Пусть
(1.82)
где 6; — случайная погрешность; положим для простоты,
что при любых г, /, i справедливы равенства M (zrZi) =0;
М (zT8t) = 0, т. е. величины zT и zh zr и 6, являются взаим-
но некоррелированными случайными величинами. Тогда
среднее квадратическое отклонение (от нуля) сложной по-
грешности /-го измерения окажется равным
<^ = 1/ S п?/Л + а(2б0,	(1.83)
Г Г=1
где а(С/) — среднее квадратическое отклонение случайной
погрешности.
Корреляционный момент /-й и &-й сложных погрешно-
стей равен
R^it ДА) = 2	(1-84)
их коэффициент корреляции при i Ф k равен
fir hr
Р(Ab Д/.) =	-----f=1_	5 — = . (1.85)
1/ 2 °? ffr	V 2 °?
г Г = 1	Г г=1
Воспользовавшись неравенством Буняковского—Коши [9,
с. 157], получим, что
0<|p(Az, Afe)|< + 1.	(1.86)
Расположив погрешности измерений в порядке возра-
стания абсолютной величины коэффициента корреляции
между их значениями в двух любых измерениях одной сово-
купности, увидим, что случайные и систематические по-
грешности являются предельными членами этого ряда, со-
ответствующими предельным значениям коэффициента кор-
реляции, равным нулю или единице. Четких границ, кото-
рые отделяли бы одни погрешности от других, не сущест-
вует: случайные и систематические погрешности являются
предельными частными случаями зависимых.
Говорить о том, что та или иная погрешность является
случайной, зависимой или систематической, имеет смысл
только тогда, когда одновременно указывается, в какой
совокупности измерений рассматриваются ее свойства. Од-
на и та же погрешность в одной совокупности измерений
может проявлять свойства случайной, а в другой — систе-
матической. Это обстоятельство отмечалось еще Гауссом
[15, с. 17]. Приведем другой пример. Погрешность опреде-
ления инструментальной поправки любого прибора оди-
накова во всех измерениях, результаты которых исправле-
ны этой поправкой, т. е. является систематической. Но
если для определения места судна измерено несколько на-
вигационных параметров разными приборами (высота све-
тила секстаном, навигационный параметр гиперболиче-
ской РНС судовым приемоиндикатором, глубина моря эхо-
лотом и т. д.), то в этой совокупности измерений те же по-
грешности окажутся взаимно независимыми случайными
величинами, т. е. будут проявлять свойства случайных по-
грешностей.
Нельзя отождествлять термины «случайная погрешность»
и «погрешность измерений, являющаяся случайной вели-
чиной». Случайными называются не всякие погрешности,
являющиеся случайными величинами, а лишь те из них,
которые в рассматриваемой совокупности измерений вза-
имно некоррелированы. Систематические погрешности —
случайные величины, хотя случайными погрешностями не
являются. Применение к их изучению математического ап-
парата теории вероятностей и математической статистики
не только допустимо, но и необходимо; возможно создание
29
общей теории системати-
ческих погрешностей.
Можно предполо-
жить, что встречающе-
еся во многих пособиях
противопоставление слу-
чайных погрешностей,
как обладающих свой-
ствами случайных вели-
чин, систематическим по-
грешностям, как якобы
этими свойствами не об-
ладающим, л стало след-
ствием несовершенства
терминологии, приво-
дившего к невольной
подмене понятий (отож-
погрешность» и «погреш-
Рис. 1.2. Классификация погрешностей
измерений
дествлению понятий «случайная
ность, являющаяся случайной величиной»). С этой точки
зрения термины, предложенные Гауссом, были более удачны-
ми. Он подразделял погрешности измерений на правильные
(regulare, regelmafJige) и неправильные (irregulare, unregel-
mapige). Но мы и впредь будем пользоваться современной
терминологией, регламентированной ГОСТ 16263—70. Клас-
сификация погрешностей по трем признакам: по проис-
хождению, по отношению к поправкам и по взаимной кор-
реляции в совокупности измерений показана на рис. 1.2.
Каноническое представление погрешностей измерений.
Из сопоставления выражений (1.28) и (1.69) видно, что си-
стематические погрешности измерений представляют собой
элементарные случайные функции параметров, характе-
ризующих условия измерений. Это обстоятельство, уже от-
меченное в печати [13], приводит к важным выводам.
Будем рассматривать истинную погрешность измерения
Агист как случайную функцию параметров, характеризую-
щих условия измерений. Если ее дисперсия конечна, то,
в соответствии с теоремой о каноническом представлении
случайных функций (см. § 1.1), она может быть сколь
угодно большим числом способов представлена суммой ко-
нечного числа элементарных случайных функций (т. е.
систематических погрешностей) и остаточного члена 6г-
AfncT^AfncT(abPb...)= t ^fir + Si (J’87)
Г —1
30
таким образом, чтобы дисперсия остаточного члена была
меньше любого наперед заданного положительного числа
(т. е. с любой наперед заданной точностью).
Обычно нас удовлетворяют не любые представления по-
грешностей измерений в виде (1.87), а лишь те из них, ко-
торые отвечают некоторым дополнительным требованиям.
Пусть £/ — значение коэффициента в разложении (1.87)
истинных погрешностей одной совокупности измерений;
& — значение того же коэффициента в разложении по-
грешностей другой совокупности измерений.
Если с удовлетворяющей нас точностью выполняется
равенство
(1.88)
то это означает принципиальную возможность, найдя из
результатов первых измерений оценку этого коэффи-
циента, компенсировать r-ю систематическую погрешность
в измерениях второй совокупности введением поправок
вида (1.71). Но, ограничивая таким образом число членов
канонического разложения (1.87), мы уже не можем счи-
тать остаточный член бг пренебрежимо малым. В итоге
приходим к каноническому представлению истинных оста-
точных погрешностей измерений в виде
Дг (аг, ₽г>...) = 2 &~Ъ) fir +	1 fir + 6г. (1.89)
r—1	r=l
Величину 6£ остаточного члена разложения (1.89) мож-
но было бы назвать остаточной погрешностью. Но этот тер-
мин^ у же”применяется для обозначения другого понятия.
Поэтому будем называть ее архиостаточной погрешностью
i-го измерения. Если корреляция между величинами 6Z
в двух любых измерениях одной совокупности отсутст-
вует, то их можно называть случайными погрешностями из-
мерений, в общем же случае^они являются^взаимно зависи-
мыми.
I В любом случае величина 6г- является случайной функ-
цией параметров,характеризующих^условия измерений,
и также может быть представлена в виде (1.89) суммы си-
стематических погрешностей и остаточного члена. Таким
31
образом, называть случайные и зависимые погрешности
элементарными можно только условно, подобно тому, как
в физике объекты, состоящие из протонов, нейтронов и
электронов, условно называются атомами (неделимыми).
Столь же условно выражение «измерения, свободные от си-
стематических погрешностей». Его можно понимать только
в переносном смысле, для обозначения предположения, что
истинные остаточные погрешности в рассматриваемой со-
вокупности измерений обладают свойствами, мало отличаю-
щимися от свойств случайных погрешностей.
Сложная структура случайных погрешностей любых
измерений проявляется ощутимо всякий раз, как обнару-
живается новый, дотоле неизвестный источник систематиче-
ских погрешностей. Тогда оказывается, что вновь открытые
систематические погрешности являются составными ча-
стями тех погрешностей, которые раньше считались слу-
чайными, т. е. элементарными. Этот процесс выявления все
новых систематических погрешностей является одной из
необходимых предпосылок повышения точности измерений.
Чем больших успехов мы добиваемся на этом пути, тем
большую практическую значимость приобретает теория си-
стематических погрешностей.
Нами рассмотрены самые простые свойства погрешно-
стей измерений. При рассмотрении других свойств, как и
способов обработки результатов измерений, приходится
встречаться с соотношениями, запись которых в обычных
алгебраических обозначениях оказывается весьма громозд-
кой и мало наглядной. От этих недостатков свободен аппарат
алгебры матриц. Выражения, в обычных обозначениях за-
нимающие несколько страниц, тут записываются одной
строкой. Мы будем пользоваться простейшими соотноше-
ниями алгебры матриц, изложенными в § 1.1; основные
результаты будем стараться формулировать так, чтобы
суть была понятна и тому читателю, которого матричные
выражения не интересуют.
Вектор истинных остаточных погрешностей совокуп-
ности измерений
А = 11 Mini =
(1.90)
имеет п строк, соответствующих измерениям рассматривае-
мой совокупности, и один столбец, единственным элемен-
том z-й строки которого является истинная остаточная по-
грешность z-ro измерения, равная
А. = и. _ [у.ист,	(1.91)
где Ut — результат z-ro измерения, исправленный всеми
учитываемыми поправками.
Обозначим символом Z вектор амплитуд остаточных си-
стематических погрешностей, символом F — матрицу зна-
чений координатных функций, символом б — вектор архи-
остаточных погрешностей совокупности измерений:
Z = || zr || sl; F = || fir ]| ns; 6 = || 6f || nl. (1.92)
Тогда n равенств вида (1.89) можно записать одной форму-
лой:
А = FZ + б.	(1.93)
Если поправки, вводимые в результаты измерений, яв-
ляются несмещенными оценками компенсируемых погреш-
ностей, т. е. выполнено требование (1.75), то математиче-
ское ожидание вектора А равно нулю;
М (А) = 0.	(1.94)
Корреляционная матрица вектора А:
Кд = М (ААТ)	(1.95)
имеет z’-м диагональным элементом дисперсию z-й остаточ-
ной погрешности; ее элемент, стоящий в z-й строке и в £-м
столбце, есть корреляционный момент остаточных погреш-
ностей Af и Aft.
Все практически применяемые способы математической
обработки результатов измерений основываются на пред-
положении, что до того, как она начинается, корреляцион-
ная матрица Кд вектора остаточных погрешностей уже из-
вестна, хотя бы с точностью до постоянного множителя.
Как ее оценить? Для этого существует два пути.
1. Статистическое оценивание погрешностей измерений,
наблюденных в специально организованном эксперименте.
Истинная остаточная погрешность каждого измерения оце-
нивается как разность его результата, исправленного все-
ми учитываемыми поправками, и эталонного значения изме-
ряемой величины (результата более точного измерения),
принимаемого за истинное. Затем приходится делать пред-
2 зак. 1363	33
положение, что истинная остаточная погрешность являет-
ся стационарной случайной функцией времени, номера из-
мерения или какого-либо другого параметра и, рассчитав
наблюденные значения коэффициента корреляции между
погрешностями разных измерений, распространять полу-
ченные результаты на все однотипные измерения,, которые
предстоит выполнять в сходных условиях в будущем.
Этот путь оправдан только тогда, когда допустимость
подобной экстраполяции доказана теоретически или экс-
периментально. Он неудобен, если надо оценить корреля-
ционную матрицу вектора неоднородных измерений. Во-
прос об оценивании корреляционной матрицы эталонных
измерений остается открытым; по существу мы не получа-
ем решения поставленной задачи, а лишь откладываем его.
2. Косвенное оценивание корреляционной матрицы, ос-
нованное на представлении истинной остаточной погреш-
ности в виде (1.89) суммы остаточных систематических и
архиостаточной погрешностей. Учитывая, что обычно нет
причин, которые могли бы повести к взаимной корреляции
величин zT и 6г-, приложение формул (1.44), (1.45) и (1.59)—
(1.63) ведет к выражению
Кь = М (ДДТ) = FKzF' + Кв, (1-96)
где Kz=Al(ZZT)— корреляционная матрица вектора Z ам-
плитуд остаточных систематических по-
грешностей;
Кб Д1(66т)— корреляционная матрица вектора 6 ар-
хиостаточных погрешностей.
Некоторые возможности оценивания корреляционных
матриц Kz и Кб будут рассмотрены ниже. В частном слу-
чае, когда амплитуды zT и г^двух любых остаточных погреш-
ностей взаимно некоррелированы и, кроме того, корреля-
ционную матрицу Кб можно полагать диагональной, для
оценивания элементов матрицы Кд можно пользоваться
выражениями (1.83), (1.84).
§ 1.3 свойства оценок искомых
ВЕЛИЧИН И ВЕКТОРА ОТКЛОНЕНИЙ
Уравнения поправок. При обработке наблюдений ча-
сто встречаются случаи, когда измеряются не сами иско-
мые величины непосредственно, а некоторые другие величи-
ны, являющиеся функциями искомых, Например, при оп-
34
ределении места судна искомыми являются его географиче-
ские координаты, измеряются же навигационные парамет-
ры— пеленги, расстояния до ориентиров и т. д., завися-
щие от места судна на земной поверхности, т. е. являющие-
ся функциями географических координат (такие измере-
ния называются косвенными).
Точный вид зависимости между искомыми и измеряе-
мыми величинами известен редко. Обычно приходится до-
вольствоваться ее аппроксимацией (приближенным выраже-
нием) некоторой функцией, которая на наш взгляд удов-
летворительно описывала бы реально существующие соот-
ношения. Так, мы считаем траекторию перемещения цент-
ра тяжести судна, идущего постоянным курсом, локсодро-
мией, хотя в действительности, вследствие качки, рыска-
ния судна на курсе, непостоянства ветра и течения, она
представляет собой значительно более сложную кривую
линию.
В общем случае зависимость между искомыми величина-
ми £2, ..., и результатом /-го измерения, исправлен-
ным всеми учитываемыми поправками, можно выразить
в виде
Фг- ...,	..., U) = Ui - Д/ + д; = Ui - Дн (1.97)
где Фг (...) — функция, которой аппроксимируется эта за-
висимость;
Д/ А/ - А";
А/ — истинная остаточная погрешность /-го измере-
ния;
А/ — погрешность аппроксимации.
Обычно, ради простоты, величину Аг называют истин-
ной погрешностью /-го измерения. Но в действительности
ее структура более сложна: помимо собственно погрешности
измерения А/ она содержит также погрешность аппрокси-
мации Af. Каждая из этих слагаемых может быть пред-
ставлена в виде суммы элементарных погрешностей, кото-
рые, в зависимости от того, какая совокупность измерений
рассматривается, проявляют свойства систематических, слу-
чайных или зависимых погрешностей.
Если т — число искомых величин, то, чтобы их найти,
необходимо иметь не менее т уравнений, связывающих ис-
комые и измеренные величины. Если число измерений рав-
2*	35
йо числу искомых величин, то их оценки отыскиваются из
уравнений вида
Фг(Г1Д2,-Л7-Лт)=^.	(1.98)
При определении места судна выражение (1.98) представ-
ляет собой уравнение навигационной изолинии, соответст-
вующей измеренному значению Z-ro навигационного пара-
метра. Применяются как аналитические решения системы
уравнений (1.98), так и графические (обсервованное место
помечается в точке пересечения навигационных изолиний).
Чтобы повысить точность оценок искомых величин,
обеспечить возможность обнаружения промахов и апосте-
риорного (от латинского a posteriori — после опыта) оце-
нивания их точности, число измерений увеличивают сверх
минимально необходимого. Тогда число уравнений (1.98)
превысит число искомых величин; они оказываются несовме-
стимыми (если число навигационных изолиний больше двух,
то они не пересекаются в одной точке, а образуют фигуру
погрешностей). Возникает задача уравнивания погрешно-
стей— отыскания таких поправок vlt ..., vit ..., vn к ре-
зультатам измерений, которые привели бы систему урав-
нений к согласию (привели бы к изолиниям, пересекающим-
ся в одной точке); получим уравнения, которые принято
называть уравнениями поправок:
ф{(11...Г„...,1то)=*Л + й- (1.99)
Ясно, что это можно сделать сколь угодно большим числом
способов (но нас интересует не любое возможное решение,
а такое, которое доставляет несмещенные и эффективные
оценки искомых величин).
Другая трудность заключается в том, что нередко урав-
нения (1.99) оказываются нелинейными относительно ис-
комых величин; тогда найти общее их решение невозможно.
Поэтому прибегают к их линеаризации. Для этого каждую
искомую величину выражают как сумму ее произвольного
приближенного значения £упр и искомой поправки х/.
(1.100)
Если обозначить символом Ц разность измеренного зна-
чения навигационного параметра и значения функции
Ф (linp, •••» Lnp)» соответствующего приближенным зна-
чениям искомых величин,
Ц = Ui Ф( (£1пр> •••> £jnp> •••> ?mnp)j (1.101)
символом atj — первую частную производную этой функ-
ции по переменной при = |;Пр>
то, разложив функцию Фг- (...) в ряд Тейлора и ограничив-
шись членами первой степени, получим z-e уравнение по-
правок в виде
а;1Х1+  + aijxj+ ...+aimxm — Ц =	(1.103)
Величины а/2, •••» аи, •••> aim называются коэффи-
циентами уравнения поправок при искомых величинах, ве-
личина li — свободным членом уравнения поправок, вели-
чина Vi— отклонением уравновешенного значения измеряе-
мой величины от результата измерения (часто ее называют
просто z-м отклонением, иногда — невязкой). При опреде-
лении места судна уравнение вида (1.103) есть уравнение
линии положения, которой приближенно заменяется на-
вигационная изолиния.
Подобным образом, обозначив символом Xj разность ис-
тинного значения искомой величины и ее приближенного
значения
Xj =	(1.104)
из уравнений (1.97), (1.101) можно получить еще одно важ-
ное соотношение
l[ Ч- Ч~ Ч- Ч- Ч- (1.105)
которое называют уравнением погрешностей.
Общие свойства оценок искомых величин. В дальней-
шем, помимо примененных в выражении (1.96), будем поль-
зоваться следующими обозначениями матриц:
| = ||	|| ml — вектор истинных значений искомых ве-
личин;
£пр= II Ъпр II mi — вектор произвольных приближенных
значений искомых величин;
Х = II mi — вектор разностей — ^пр;
£ = II Ъ II mi — вектор оценок искомых величин;
37
X = II Xj li ml — йёктор искомых поправок к произволь-
ным приближенным значениям иско-
мых величин;
L = II Ц || ni — вектор свободных членов уравнений по-
правок;
А = 11 вц II пт — матрица коэффициентов при неизвест-
ных в системе уравнений поправок.
Тогда система из п уравнений поправок (1.103) может
быть записана в виде одного матричного уравнения
АХ — L = V;	(1.106)
выражениям же (1.100) и (1.105) будут соответствовать
матричные равенства
1 = Впр + Х;	(1.107)
L = АХ + А-	(1.Ю8)
Предположим, каждая из искомых величин отыскива-
ется в виде некоторой линейной функции свободных чле-
нов уравнений поправок:
xi = ghh + gizh + **• + gjdi +	+ gjnln^ (1.109)
или, что то же самое, вектор X — в виде
X = GL,	(1.110)
где G = П || тп — матрица линейного преобразования.
Еще Гаусс показал [15, с. 94—96], что если мы считаем,
что оценки вида (1.109) могут быть эффективными, то это
равносильно предположению, что вектор А есть нормаль-
ный вектор (т. е. каждая из истинных погрешностей Af есть
нормально распределенная случайная величина). Однако
это ограничение не слишком нас стесняет: распределения
погрешностей измерений, которые приходится выполнять
в судовождении, обычно близки к нормальному, а оценки
искомых величин, как правило, отыскиваются в виде
(1.109).
Нетрудно убедиться, что эти оценки будут несмещенны-
ми, если выполнено условие (1.75), т. е. измерения тщатель-
но исправляются всеми учитываемыми поправками, и,
кроме того, матрица G удовлетворяет требованию
GA=E.	(1.111)
38
Действительно, тогда, в соответствии с выражениями (1.44),
(1.45), (1.108) и (1.94),
М (Г— g) = M (X — X) - М (GL — X) = М (GAX +
+ G& — X) = М (X + G& — X) = GM (А) = 0. (1.112)
Заметим, что X — неслучайный вектор (истинные зна-
чения искомых величин — неслучайные величины). По-
этому из выражения (1.108) следует важный вывод о кор-
реляционной матрице вектора L:
Kl = Ks,	(1.113)
где Хд = М (ААТ) — корреляционная матрица вектора ис-
тинных остаточных погрешностей измерений.
Из формул (1.63) и (1.96) следует выражение для кор-
реляционной матрицы вектора оценок искомых величин:
Кх = GXa(? - GFKzFKF + GKt>G\ (1.114)
Если нас интересует влияние, которое оказывает на
точность оценок искомых величин некоторая конкретная,
г-я систематическая погрешность, то, положив, что s = 1
и что соответственно
Kz = <fr F = Fr,	(1.115)
получим
Kx(ry = tfGFrFrG\	(1.116)
где ог — среднее квадратическое отклонение амплиту-
ды г-й систематической погрешности;
Fr — вектор значений ее координатной функции
в совокупности измерений.
Матрица Kxtr) есть корреляционная матрица вектора
погрешностей в оценках искомых величин, обусловленных
влиянием г-й остаточной систематической погрешности из-
мерений. Поскольку ранг матрицы FT равен единице, ясно,
что ранг матрицы Кх^у также равен единице, т. е. погреш-
ности оценок искомых величин, происходящие от влияния
любой из систематических погрешностей, линейно зависи-
мы. По аналогии с терминами, применяемыми в отношении
двумерной случайной величины (например, при определе-
нии места судна), можно сказать, что если погрешности оце-
нок искомых величин, происходящие от влияния случай-
ных погрешностей измерений, характеризуются’/и-мерным
средним квадратическим гиперэллипсоидом погрешностей
39
(или, что то же самое, системой из т взаимно независимых
векториальных погрешностей), то погрешности оценок ис-
комых величин, происходящих от влияния любой система-
тической погрешности, характеризуются одной векториаль-
ной погрешностью системы оценок искомых величин.
Формулу (1.116) можно переписать в виде
Кх(г) = СГС1	(1.117)
где Cr = <yrGFr. Это приводит к следующему правилу оце-
нивания влияния любой конкретной систематической по-
грешности на точность оценок искомых величин: подверг-
нув вектор Fr тому же преобразованию (1.110), каким из
вектора L отыскивается вектор X оценок искомых величин,
и умножив результат на + о> или на — аг, получим иско-
мую векториальную погрешность Сг вектора оценок ис-
комых величин. Применение этого правила к задаче оце-
нивания точности определения места судна будет рассмо-
трено в § 3.4.
Случайные погрешности измерений всегда ведут к по-
грешностям оценок искомых величин; их влияние неустра-
нимо. Систематические же погрешности, как бы велики они
ни были, в некоторых ситуациях не ухудшают точности оце-
нок искомых величин. Из выражения (1.116) видно, что
это происходит, если соблюдается равенство
GFr = 0.	(1.118)
Примеры известны. Если место судна определяется по
высотам трех светил, измеренным навигационным секста-
ном, и разность азимутов светил близка к 120°, или по вы-
сотам четырех светил при разности азимутов двух любых
соседних светил, близкой к 90°, то любая, даже очень боль-
шая, но одинаковая во всех измерениях погрешность в на-
клонении видимого горизонта не ухудшит точности обсер-
вации. Если курсовой угол на один радиомаяк близок к 0
или 180°, а на другой — к 90°, то точность обсервации не
ухудшается погрешностью в коэффициенте D радиодевиа-
ции, и т. д. Такой выбор условий измерений или способа
обработки их результатов, при котором некоторые конкрет-
ные систематические погрешности не влияют на точность
оценок искомых величин, называется методом исключения
систематических погрешностей. К сожалению, он далеко
не всегда применим и эффективен. Но речь об этом впереди,
40
Свойства вектора К Мы уже говорили, что г!ри чйсле
измерений, превышающем число искомых, влияние погреш-
ностей измерений ведет к несогласию их результатов: пра-
вые части уравнений поправок (1.103) в нуль не обращают-
ся, а выражают собой отклонения уравновешенных значе-
ний измеряемых величин от результатов измерений. В су-
довождении эти отклонения нередко можно непосредствен-
но наблюдать. Так, невязки счисления выражают несогласие
измерений, выполненных при определении места судна, с
измерениями, по которым велось счисление; при определе-
нии места судна, если число линий положения больше двух,
образование фигуры погрешностей свидетельствует о вза-
имном несогласии результатов измерений навигационных
параметров, и т. д.
’ Вектор отклонений V служит основой апостериорного
оценивания точности измерений. Для этого в первую оче-
редь надо знать, как он зависит от погрешностей измерений.
Из уравнения (1.106), учитывая соотношения (1.108), (1.110),
(1.93) и (1.111), нетрудно получить:
V = АХ — L = (AG — £) L = (AG — £) (ЛХ + А) =
= AGAX + AG& — АХ — А = (ЛС — £) А =
= (AG — E) (FZ + 6).	(1.119)
Случайные погрешности при п>т всегда ведут к несо-
гласию результатов измерений (хотя бы один из компонен-
тов вектора V будет отличен от нуля). Систематические же
погрешности в некоторых ситуациях не вызывают несогла-
сия измерений; тогда, очевидно, вектор V не может служить
основанием для суждения о величине систематических по-
грешностей. Из выражения (1.119) ясно, что это происхо-
дит при условии
(AG — E)Fr = 0.	(1.120)
Пример 1.2. Если выполнено п прямых равноточных измере-
ний одной постоянной величины, оценка которой отыскивается как
среднее арифметическое из результатов измерений, причем измере-
ния содержат постоянную (одинаковую во всех измерениях) си-
стематическую погрешность, то эта погрешность не может вызывать
несогласия измерений. Действительно, в этом случае i-e уравнение
поправок имеет вид
aix—li=vij
где йг = 4-1;
li=Xi — результат ьго измерения
41
Вектор свободных членов уравнений поправок есть
Формулу среднего арифметического можно представить в виде
п
+ х2 • • • 4~ хп
п	п
Следовательно, матрица G есть матрица вида
G = Gln
2
п
п п
В этом можно убедиться, выполнив по общему правилу (см. рис. JJ)
умножение матриц; получим
~ - 11	1
X = х = GL =	Ху 4~ х2 + • * • 4~ хп*
п п	п
Матрица коэффициентов уравнений поправок есть
— II Uni —
Произведя умножение матриц, получим
	1	1	1
	п	п	п
	1	1	1
	-	- -	
Д6 =	п	п	п
1	1	1
п	п	п
откуда
AG-E--
1	1	1
— — 1	—	...	—
п	п	п
А
п п	п
п п	л
42
Рассматривается влия-
ние постоянной,одинаковой
во всех измерениях, систе-
матической погрешности,
т е.
Еще раз воспользовав-
шись правилом умножения
матриц, увидим, что любой
член матрицы (AG — Е) Fr
равен
Рис. 1.3. Случай, когда постоянная
погрешность измерения пеленгов не
вызывает несогласия их результатов:
----- линии истинных пеленгов;----ли-
нии пеленгов, содержащих погрешность е
+ — -1=п — -1=0,
п п
что и требовалось доказать.
Пример 1.3. Если
место судна определяется
по пеленгам нескольких
ориентиров и все ориенти-
ры и судно находятся на
одной окружности, то по-
стоянная (одинаковая во
всех измерениях) погреш-
ность измерений пеленгов
не может вызвать несогла-
сия измерений (образования
фигуры погрешностей). Это
видно из рис. 1.3.
Пример 1.4. Если
радиомаяки расположены
на одной прямой (рис. 1.4)
и линия курса судна ей
параллельна (близкие си-
Рис. 1.4. Случай, когда погрешность
в коэффициенте D радиодевиации ие
вызывает образования фигуры по-
грешностей
туации часты в практике судовождения), то при определении ме-
ста судна по радиопеленгам погрешность в коэффициенте D радио-
девиации не вызывает образования фигуры погрешностей. Действи-
тельно, расстояние от истинного места судна до точки, в которой
линия ложного радиопеленга пересечет перпендикуляр к прямой,
на которой расположены радиомаяки, равно
h sin 2q	2h
d = '-------------- AD =-------AD,
57,3° sin q cos q	57,3°
(1.121)
43
где h — расстояние от истинного места корабля до линии, на
которой расположены радиомаяки;
q — курсовой угол на радиомаяк;
ДО — погрешность в коэффициенте D радиодевиации, гра-
дусы.
Это расстояние не зависит от курсового угла на радиомаяк, следо-
вательно, все ложные линии радиопеленгов при отсутствии других
погрешностей пересекутся в одной точке.
Можно показать, что при п> т условия (1.118) и
(1.120) несовместны: если какая-либо систематическая по-
грешность не ведет к искажению оценок искомых величин,
то она обязательно вызовет несогласие результатов изме-
рений; если же систематическая погрешность не вызывает
несогласия результатов измерений, то она обязательно
ведет к искажению оценок искомых величин. При определе-
нии места судна этот вывод получает следующую интерпре-
тацию: если некоторая систематическая погрешность не
ухудшает точности обсервации, то она обязательно ведет
к образованию фигуры погрешностей; систематическая
погрешность, не ведущая к образованию фигуры погреш-
ностей, неминуемо ухудшает точность обсервации. Следо-
вательно, если в измерениях возможны значительные систе-
матические погрешности, то малые размеры фигуры
погрешностей нельзя считать признаком высокой точности
обсервации.
Обработка результатов измерений преследует две ос-
новные цели:
1. Отыскание наиболее точных оценок искомых вели-
чин, т. е. оценок, которые были бы несмещенными, для че-
го должно удовлетворяться требование (1.111), и эффек-
тивными, т. е. такими, чтобы диагональные элементы кор-
реляционной матрицы Кх, определяемые выражением
(1.114), были минимальны.
2. Оценивание точности полученных оценок искомых
величин, т. е. корреляционной матрицы Кх, определяемой
выражением (1.114).
Приступим к рассмотрению способов достижения этих
целей, имея в виду, что только аналитические описания поз-
воляют выявить и понять все их особенности. Для кратко-
сти будем применять, помимо общепринятых, также со-
кращенные названия рассматриваемых способов («способ А »,
«способ В» и т. д.).
44
§ 1.4 СПОСОБЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ
Способ наименьших квадратов (способ Л). Этот способ
основан на предположениях, что результаты измерений
содержат только случайные погрешности, т. е. выполнены
условия (1.65)—(1.67), и что распределения этих погреш-
ностей нормальны. В теории способа доказывается, что
при этих допущениях требования несмещенности и эффек-
тивности оценок искомых величин приводят к матричному
уравнению
АТРАХ - ArPL,	(1.122)
где
(1.123)
\ с2 /
с — произвольный множитель.
Из уравнения (1.122) отыскивается вектор X поправок
к произвольным приближенным значениям искомых вели-
чин:
X	= (A'PA^A'PL.	(1.124)
Корреляционная	матрица вектора оценок	искомых ве-
личин оценивается по формуле
7<х = <г(2Х)(Лт/’Д)-1,	(1.125)
где а(1) —	средняя	квадратическая погрешность	измере-
ния, вес которого принят равным единице.
При априорном оценивании корреляционной матрицы
Кх в формулу (1.125) подставляется величина а(Х), оце-
ненная по результатам некоторых предыдущих измерений.
Для апостериорного оценивания вычисляется вектор от-
клонений:
V = АХ — L;	(1.126)
оценивается дисперсия погрешности измерения, вес которо-
го принят равным единице:
которая и подставляется в формулу (1.125).
Предположение (1.67) означает диагональность корре-
ляционной матрицы что значительно упрощает вычис-
ления. В частности, для обращения корреляционной ма-
45
трицы оказывается достаточным воспользоваться пра-
вилом (1.54). Поскольку эта матрица может быть известна
с точностью до постоянного множителя, поступают еще про-
ще: руководствуясь только соображениями удобства вы-
числений, выбирают произвольный множитель с и рассчиты-
вают веса измерений:
(1.128)
где щ — средняя квадратическая погрешность i-го изме-
рения. Вес pi представляет собой i-й диагональный элемент
матрицы Р; все ее недиагональные элементы априорно
(и обычно произвольно) полагаются равными нулю.
Последствия, к которым ведут эти упрощения, проде-
монстрируем для частного случая, когда число искомых
величин равно двум и уравнения поправок имеют вид
а^х + Ьг\у — Ц = vit
Соответственно матрица коэффициентов при неизвест-
ных в уравнениях поправок может быть записана в виде
А =
ai
^2
&П Ьп
Учтя, что матрица Р полагается диагональной, что ее
1-й отличный от нуля элемент на главной диагонали есть pit
и применив общее правило умножения матриц (см. рис. 1.1),
получим:
Р1 Pi Рп
АТР =
Pi Ь± р^Ъ*... Рп Ьп
Применив это правило еще раз и воспользовавшись обоз-
начениями Гаусса для сумм, найдем:
АгРА [раЬ]
I [pab] [pbb]
где [раа] = р±а\ + р2а22 + ... + рпа2п\
[pab] = pja^ + p2azb2 + ... + рпапЬп'>
[pbb] = р±Ы + р2Ь22 + ... + рпЬ%.
46
Совершенно аналогично получим
ЛТРЛ = | [ра1} |,
I) [ры\ ||
где [pal] =	+ p^l^ + ... + pnanln\
[pbl\ = Pib^ + p2b2l2 + ... + pnbnln.
Выражение (1.122) оказывается сокращенной, матрич-
ной записью следующей системы уравнений, которую при-
нято называть системой нормальных уравнений:
[раа] \x + [pab] \y = [pal]A
[pab] + [pbb] Ay = [рЫ]. J
Формула (1.127) для апостериорного оценивания диспер-
сии погрешности измерения, вес которого принят равным
единице, приобретает следующий простой вид:
(1.130)
где	[pvv] = p1vl + piV2 + -+pn vn.
Решение системы нормальных уравнений, обращение ма-
трицы АТРА и оценивание элементов корреляционной ма-
трицы вектора оценок искомых величин удобно вы-
полнять по схеме Гаусса. Эти действия, к которым сводит-
ся практическое применение способа наименьших квадра-
тов, подробно описаны в многочисленных пособиях, в том
числе адресованных судоводителям [2, 29, 43, 49, 66],
поэтому на них останавливаться не будем. Вследствие своей
относительной трудоемкости они применяются в повседнев-
ной практике судовождения пока редко, за исключением
простейших приложений — вычисления среднего арифме-
тического результатов измерений, вычисления коэффици-
ентов девиации по ее значениям, наблюденным на восьми
равноотстоящих курсах, и т. д. Но стремительное совершен-
ствование ЭЦВМ, их внедрение во все области человече-
ской деятельности быстро меняет наши представления о
трудоемкости вычислений. Возможно, через несколько лет
применение алгоритма способа наименьших квадратов ста-
нет доступным каждому судоводителю. В частности, он
реализован в навигационной вычислительно-управляющей
системе МВУ-3 [42].
47
В повседневной практике судовождения широкое при-
менение получили графические и графоаналитические ин-
терпретации способа наименьших квадратов, приводящие
к тем же, что и он, оценкам искомых величин, но более про-
стые и удобные. Их создание есть заслуга главным образом
П. А. Гельвиха и Н. Г. Келля; популяризации, приложе-
нию к задаче отыскания обсервованного места в фигуре по-
грешностей и развитию приближенных, но более простых,
удобных в практике судовождения графических построений
много внимания уделяли моряки В. В. Каврайский,
Н. Н. Матусевич, А. П. Ющенко, А. Д. Козлов, Г. П. По-
пеко, В. Т. Кондрашихин и др.
Применение любого из этих способов начинается с вы-
числения среднего квадратического смещения и веса линии
положения:
(1.131)
(1.132)
где Si — градиент навигационного параметра;
с — произвольный коэффициент, выбираемый исходя
из соображений удобства вычислений.
Если место судна определяется по трем линиям положе-
ния, то обсервованная точка А, адекватная результату ана-
литического применения способа наименьших квадратов,
при равноточных линиях положения (рис. 1.5) совпадает
с точкой пересечения противомедиан треугольника погреш-
ностей (прямых, симметричных медианам относительно бис-
сектрис). При неравновесных линиях положения сначала
надо каждую из сторон треугольника погрешностей разде-
лить в отношении, рав-
ном отношению весов
прилегающих линий по-
ложения; соединив по-
лученные точки с про-
тиволежащими вершина-
ми, провести уравнове-
шенные квазимедианы, а
затем симметричные им
относительно биссектрис
уравновешенные проти-
вомедианы; точка их пе-
48
ресечения есть искомое
обсервованное место.
В четырехугольнике
погрешностей (рис. 1.6)
надо разделить каждую
из сторон в отношении,
равном отношению квад-
ратов средних квадрати-
ческих погрешностей
прилегающих линий по-
ложения; точки, ле-
жащие на противопо-
ложных сторонах четы-
Рис. 1.6. Отыскание обсервованного
места способом А в четырехугольнике
погрешностей
рехугольника, соединить прямыми линиями и в их пере-
сечении пометить искомую точку А. Если число линий по-
ложения больше четырех, приходится прибегать к центро-
графическому приему отыскания обсервованной точки или
к построению полигона весов и полигона переносов. Как
способ наименьших квадратов, так и эквивалентные ему
графические и графоаналитические приемы приводят к
обсервованной точке, находящейся всегда внутри фигуры
погрешностей.
Совершенно ясно, что условия, на которых базируется
теоретическое обоснование способа наименьших квадратов,
в действительности всегда соблюдаются лишь приближенно.
Как это влияет на точность оценок искомых величин? Ког-
да его применение можно считать оправданным, а когда
нельзя? Рассмотрим возможные отступления реальных по-
грешностей измерений от этих условий.
Распределения вероятностей реальных погрешностей
измерений хотя нередко и близки к нормальному, но в об-
щем случае с ним не совпадают. Однако и при отличии ре-
ального распределения от нормального оценки искомых ве-
личин, доставляемые способом Л, обладают следующими
свойствами:
1)	поскольку преобразование (1.124) удовлетворяет ус-
ловию (1.111), они являются несмещенными;
2)	дисперсии этих оценок меньше или по крайней мере
не больше дисперсий любых других оценок искомых ве-
личин, отыскиваемых в виде (1.110) (теорема Гаусса—Мар-
кова);
3)	оценка (1.127) дисперсии погрешности измерения,
вес которого равен единице, является несмещенной и, при
49
выполнении некоторых дополнительных условий относи-
тельно свойств распределения погрешностей измерений,
эффективной (теорема Р. Рао).
Таким образом, отличия распределения погрешностей
измерений от нормального нельзя считать серьезным пре-
пятствием к применению способа наименьших квадратов.
Значительно более суровые ограничения накладываются
условием (1.67). Случаи, когда оно выполняется и корре-
ляционную матрицу Дд можно считать заведомо диагональ-
ной (например, при определении места судна по измерени-
ям разнородных навигационных параметров), редки. Зна-
чительно чаще оно не выполняется. В частности, если обра-
ботке подвергается совокупность измерений, содержащих
соизмеримые со случайными остаточные систематические
погрешности, то, как видно из выражений (1.85), (1.86).
недиагональные элементы корреляционной матрицы Дд
могут отличаться от нуля весьма ощутимо. Рассмотрим,
к каким последствиям это ведет.
Если выполнено требование (1.75), то, поскольку усло-
вие (1.1Н) тоже выполняется, оценки искомых величин
и теперь окажутся несмещенными. Но они в общем случае
не будут эффективными. Оценка (1.127) дисперсии погреш-
ности измерения, вес которого принят равным единице,
будет несмещенной только в тех случаях, когда координат-
ные функции всех систематических погрешностей удовлетво-
ряют условию (1.120). Но даже если выполнено и это ус-
ловие, оценка (1.125) корреляционной матрицы вектора оце-
нок искомых величин будет смещенной. Чтобы найти ее не-
смещенную оценку, надо, помимо случайных, учесть влия-
ние также и систематических погрешностей. Для этого мож-
но воспользоваться формулой (1.114) или, если рассматри-
вается влияние только одной систематической погрешно-
сти, — правилом (1.117).
Пример 1.5. Выполнено п прямых равноточных измере-
ний одной постоянной величины (допустим, пеленга на ориентир с
неподвижного судна). Измерения содержат только случайные по-
грешности и постоянную (одинаковую во всех измерениях) остаточ-
ную систематическую погрешность е (погрешность поправки ком-
паса), среднее квадратическое отклонение которой о£. Оценить точ-
ность среднего арифметического.
Поскольку тут условие (1.120) выполнено (см. пример 1.2), фор-
мула (1.127) даст несмещенную оценку 7т0) дисперсии случайной
погрешности единичного измерения. С учетом того, чтоД> = +
+ 1, правило (1.117) приведет к следующей оценке средней квадра-
50
тической погрешности среднего арифметического, выражающей
вли яние систематической погрешности измерений:
1 п
(г) П /э=1
Учтя также влияние случайных погрешностей измерений,
получим
Если бы измерения содержали одни случайные погрешности, то
увеличение, их числа позволяло достичь сколько угодно высокой
точности среднего арифметического. Когда же они содержат еще
и постоянную систематическую погрешность, то при безграничном
увеличении числа измерений средняя квадратическая погрешность
среднего арифметического приближается к средней квадратической
величине постоянной систематической погрешности.
Переходя к рассмотрению других способов обработки
результатов измерений, отметим, что все они могут рассма-
триваться как разновидности и усовершенствования способа
наименьших квадратов. Но, чтобы различать эти способы,
им присвоены разные наименования. О способе же А, учи-
тывая многолетние традиции его применения, можно гово-
рить как о традиционной трактовке способа наименьших
квадратов. Поскольку в способах В и D число искомых ве-
личин расширяется по сравнению со способом А, впредь
те величины, которые были искомыми в этом способе (на-
пример, при определении места судна — обсервованные ко-
ординаты), будем называть «основными».
Способ исключения систематических погрешностей (спо-
соб В). Этот способ отличается от способа А тем, что в урав-
нения поправок, помимо «основных» искомых величин,
включаются искомые амплитуды поправок, служащих для
компенсации подлежащих исключению систематических по-
грешностей. Тогда, учитывая выражения (1.70), (1.71)
и (1.101), уравнение поправок (1.103), составленное по
результатам i-ro измерения, приобретает вид
^2 + ••• + aijXj + ••• + aim xni +
+ ai,	+ ••* + ty, m+r *m+r + ••• +
, m-f-s xm+s	(1.133)
51
гдеап,..., aim— коэффициенты при «основных» искомых
величинах, совершенно идентичные тако-
вым в способе А;
^z,m4-r = fr (ab Ро •••);
хт+г — искомая амплитуда поправки, предназна-
ченной для компенсации r-й систематиче-
ской погрешности.
Последующие действия (составление и решение системы
нормальных уравнений, оценивание корреляционной ма-
трицы вектора оценок искомых величин) осуществляются
по стандартным предписаниям способа наименьших квад-
ратов; при этом полагается, что Кд есть корреляционная
матрица только тех погрешностей, амплитуды которых
не включены в число искомых величин.
Покажем, что при обработке наблюдений способом В
систематические погрешности, как бы ни были они велики,
не ухудшают оценок «основных» искомых величин. Дейст-
вительно, как видно из сравнения выражений (1.110) и
(1.124), при обработке наблюдений способом А матрица
G есть
G = (АТРА)~МТР£;
если применяется способ В, то
G = (Д^РДвНДЬР,
где Ав — матрица коэффициентов при неизвестных в урав-
нениях поправок. Эта последняя, как ясно
из выражения (1.133), может быть представле-
на как блочная матрица:
Дв= II А : — Р||,
где А — матрица коэффициентов при «основных» иско-
мых величинах;
F — матрица значений координатных функций тех
систематических погрешностей, амплитуды ко-
торых включены в число искомых величин.
Аналогично, в виде блочных матриц, могут быть пред-
ставлены также вектор X оценок искомых величин и матри-
ца линейного преобразования G:
где %! — вектор «основных» искомых величин;
Х2 — вектор поправок к произвольным значениям
амплитуд, включенных в число искомых ве-
личин.
Это означает, что векторы и Х2 находятся посредством
следующих преобразований вектора свободных членов:
X, = GrL; Х2 = G2L.
Если мы хотим проверить, выполняется ли условие
(1.118), то нас должны интересовать свойства матрицы GF.
Ее, в свою очередь, можно представить как корень матрич-
ного уравнения
AbPAbGF = A^PFJ	(1.134)
Учитывая блочную структуру матрицы Ав, справедливы
равенства:
Представим, наконец, и матрицу GF как блочную ма-
трицу:
Тогда, в соответствии с правилом (1.47) умножения
блочных матриц, уравнение (1.134) может быть записано
в виде системы из двух матричных уравнений:
Лт PAYX—Лт PFY2 = ATPF\
—F* PAYX + FT PFY2 = — FT PF.
(1.135)
Заметим, что столбец коэффициентов при искомой ма-
трице Y2 в левой части этой системы равен взятому с обрат-
ными знаками столбцу свободных членов. Поэтому, если,
воспользовавшись условием (1.35) равенства двух ма-
триц, записать систему линейных уравнений, эквивалент-
ную системе (1.135), и решить ее по правилу Крамера, то,
в соответствии с общими свойствами определителей [9,
с. 147, 149; 14, с. 227, 241], все элементы искомой матрицы
окажутся равными нулю. Но это означает выполнение
условия (1.118) для «основных» искомых величин.
Итак, при обработке наблюдений способом В система-
тические погрешности, амплитуды которых включены в
число искомых величин, как бы они ни были велики, не ис-
кажают оценок «основных» искомых величин (отсюда и про-
изошло название — «способ исключения систематических
погрешностей»). Видимо, это обстоятельство побудило не-
которых авторов рекомендовать его как универсальный спо-
соб, пригодный во всех случаях [22, 23].
Способ упоминался еще Гельмертом [16, с. 19]; его раз-
новидностями являются предложенные Гауссом способы
организации измерений и обработки их результатов, иног-
да именуемые способами замещения, компенсации погреш-
ностей по знаку и противопоставления [37, с. 167—168].
Некоторые их разновидности хорошо знакомы судоводите-
лям, например измерение наклонения видимого горизон-
та с поворотом наблюдателя на 180° и расчетом среднего
из двух отсчетов, чем исключается постоянная систематиче-
ская погрешность прибора; измерение высоты светила через
зенит для исключения погрешности в наклонении видимо-
го горизонта и т. д.
Если исключению подвергается только одна системати-
ческая погрешность, то при определении места судна способ
В получает простую и наглядную геометрическую интер-
претацию. Пусть (рис. 1.7) линии положения /, //, 111,
IV образовали фигуру погрешностей, причем ничем иным,
кроме влияния некоторой конкретной систематической по-
грешности, это объяснено быть не может. Задавшись про-
извольным значением zT амплитуды исключаемой система-
тической погрешности,
вычислим поправки
\UiT = zTfT (at, pi, ...)
к результатам измере-
ния каждого из нави-
гационных параметров и
проложим смещенные
линии положения Г,
1Г, 11Г, IV', соответ-
ствующие изменившим-
ся значениям навигаци-
онных параметров. Пря-
мые, соединяющие одно-
in
т
Рис. 1.7. Графический прием исклю-
чения систематической погрешности
из фигуры погрешностей
54
именные точки (13 и 13*, 23 и 23', 24 и 24') первоначал^
ной и вновь полученной фигуры погрешностей, соответ-
ствуют навигационным параметрам вида 4/^- = fTjUi —
— friUj. Поэтому их называют изоразностными линиями
положения. Очевидно, что они свободны от влияния исклю-
чаемой систематической погрешности (лишь исключаемой,
но могут быть отягощены другими систематическими по-
грешностями, иным образом зависящими от параметров,
характеризующих условия измерений). При отыскании
обсервованной точки В внутри фигуры погрешностей, об-
разованной изоразностными линиями положения, следует
считать, что последние отягощены только случайными по-
грешностями. Если размеры фигуры велики, то это озна-
чает, что предположение, будто причиной образования пер-
воначальной фигуры погрешностей было главным образом
влияние исключаемой систематической погрешности, не
сбылось, и, следовательно, применение способа В не оп-
равдано.
В отличие от точки А, доставляемой способом А,
которая всегда лежит внутри первоначальной фигуры по-
грешностей, точка В может оказаться находящейся и вне
этой фигуры.
Если исключается постоянная систематическая погреш-
ность, то способ сводится к простым геометрическим по-
строениям, изложенным во всех учебниках навигации и
мореходной астрономии: исключение систематической по-
грешности в поправке компаса при определении по пелен-
гам нескольких ориентиров [67, с. 152—154], погрешности
в наклонении видимого горизонта при определении места
по высотам нескольких светил [32, с. 293] и т. д. Он может
применяться и в более сложных случаях.
Так, в печати неоднократно отмечалось, что при опре-
делении места судна по радиопеленгам погрешность ко-
эффициента D радиодевиации часто превышает по величине
все другие погрешности [21, 57]. Чтобы ее исключить, надо,
получив большую фигуру погрешностей и убедившись, что
она не может быть объяснена другими причинами, задать-
ся произвольным значением АО поправки к коэффициенту О
радиодевиации и изменить каждый из радиопеленгов на
величину АО sin 2q, где q — отсчет радиокурсового угла
на радиомаяк. Проложив линии измененных таким образом
радиопеленгов и соединив прямыми линиями соответствен-
ные вершины старой и новой фигур погрешностей, в их
55
пересечении найти обсервованное место, свободное от влия-
ния погрешности в коэффициенте D радиодевиации.
Ряд других графических и аналитических вариантов
способа для разных конкретных ситуаций, в том числе не-
мало красивых, изящных, неожиданных, предложили
Н. Н. Матусевич, М. М. Лесков, М. И. Гаврюк [39, 35, 67].
Отметим основные особенности способа В,
1.	Оценки искомых величин, к которым он приводит,
не зависят от тех значений амплитуд, исходя из которых вы-
числялись поправки, первоначально введенные в результаты
измерений. Результаты измерений могут вовсе не исправ-
ляться этими поправками: оценок искомых величин это не
изменит. Полученная при предыдущих наблюдениях ин-
формация о значениях амплитуд этих поправок нами не
используется, мы ею пренебрегаем. Таким образом, приме-
нение способа В равносильно утверждению, что все на-
блюдения, выполненные ранее для определения этих ам-
плитуд, не заслуживают никакого доверия.
2.	Если при применении способа А некоторая система-
тическая погрешность не вызывает несогласия результатов
измерений, то включение амплитуды этой систематической
погрешности в число искомых величин при обработке наблю-
дений способом В приведет к тому, что главный определитель
системы нормальных уравнений окажется равен или почти
равен нулю; система окажется неразрешимой. Если при
определении места судна применяется графический ана-
лог способа В, то в этой ситуации изоразностные линии
положения окажутся взаимно параллельными или почти
параллельными; точка их пересечения лежит настолько
далеко от первоначальных линий положения, что верить
ей нельзя. Например, если применить общеизвестный прием
исключения постоянной систематической погрешности пе-
ленгования в ситуации, показанной на рис. 1.3, то получит-
ся результат, изображенный на рис. 1.8.
3.	Возможно найти такие оценки искомых величин, ко-
торые будут обладать дисперсиями меньшими или, по край-
ней мере, не большими, нежели оценки, доставляемые лю-
бым из рассмотренных способов А и В; оценки, доставляе-
мые способами Л и В, не являются эффективными. Дейст-
вительно, пусть ха — оценка искомой величины х, достав-
ляемая способом Л; хв— оценка, доставляемая способом
В. Полная погрешность любой оценки х есть сумма состав-
56
ляющих, обусловленных
влиянием, во-первых,
случайных и, во-вторых,
систематических погреш-
ностей измерений. При
х = ха минимальна дис-
персия первой составля-
ющей; при х = хв мини-
мальны (равны нулю)
дисперсии погрешностей
в оценке х, обусловлен-
ных влиянием исключа-
емых систематических
погрешностей. Посколь-
ку дисперсии слагаемых
полной погрешности
оценки х возрастают
пропорционально квад-
рату ее удаления от оце-
нок ха и хв соответст-
венно (рис. 1.9), ясно,
что можно найти такую
оценку хс, дисперсия
полной погрешности ко-
торой была бы меньшей
или по крайней мере не
большей, нежели дис-
персии полных погреш-
ностей оценок, достав-
ляемых способами А и
В. Очевидно, что она
должна находиться где-
то между оценками А и
В. Как ее найти? Рас-
смотрим способы, даю-
щие ответы на этот воп-
Рис. 1.8, Случай неопределенности
Рис. 1.9. Графики полной погрешно-
сти оценки х и ее составляющих:
1 — полная погрешность; 2 — составляю-
щая, обусловленная влиянием случайных
погрешностей; 3 — составляющая, обуслов-
ленная влиянием исключаемой системати-
ческой погрешности измерений
рос.
Обобщенный способ наименьших квадратов (способ С).
Поскольку остаточные систематические погрешности ве-
дут к недиагональности корреляционной матрицы Кд, т. е.
к невыполнению условия (1.67), естественным является
применение способа, этим условием не ограниченного, —
57
обобщенного способа наименьших квадратов. В матричных
обозначениях он описывается формально теми же выраже-
ниями (1.123)—(1.127), что и классический способ наи-
меньших квадратов. Единственное его отличие от послед-
него заключается в том, что корреляционная матрица Дд
вектора истинных остаточных погрешностей измерений
теперь уже не полагается априорно диагональной, т. е.
при обработке наблюдений учитывается взаимная корре-
ляция погрешностей измерений. Если корреляционная
матрица Кд априори известна, хотя бы с точностью до по-
стоянного множителя, то обобщенный способ наименьших
квадратов приводит к несмещенным и эффективным оцен-
кам искомых величин. Эти оценки будут эффективными и в
том случае, когда причиной недиагональности корреля-
ционной матрицы Кд являются остаточные систематиче-
ские погрешности, которыми при обработке наблюдений спо-
собом А мы пренебрегали.
Поскольку корреляционная матрица Дд не полагается
диагональной, для ее обращения теперь требуются значи-
тельно более сложные действия, нежели простое вычисле-
ние весов измерений по формуле (1.128); усложняются и
вычисления коэффициентов и свободных членов нормаль-
ных уравнений. Сложность и большой объем вычислений
приводят к тому, что реализация обобщенного способа наи-
меньших квадратов практически осуществима только при
использовании ЭВМ. В некоторых частных случаях воз-
можны упрощения, позволяющие уменьшить объем вы-
числений. Таков, например, вариант способа, разработан-
ный В. Т. Кондрашихиным [30; 29, § 18] и названный им
способом наименьшей квадратичной формы. Он основан на
предположении, что измерения отягощены, помимо слу-
чайных, только постоянной (одинаковой во всех измерениях)
систематической погрешностью.
Чтобы применение способа С стало возможным, матрица
/<д должна быть априори известна, хотя бы с точностью до
постоянного множителя. Ее можно оценивать, например,
пользуясь выражением (1.96), но и для этого должны быть
известны хотя бы отношения дисперсий случайных и ам-
плитуд остаточных систематических погрешностей. Как
оценить эти отношения, способ С непосредственного ответа
не дает.
Способ последовательного уточнения оценок искомых
величин (способ/)). В современной литературе он часто на-
58
зывается фильтром Калмана. Но справедливость этого йй-
звания вызывает сомнения. Идея была высказана еще Га-
уссом: по результатам вновь выполненных измерений отыс-
кивать такие оценки искомых величин, которые были бы
эквивалентны результату совместной обработки как вновь
выполненных, так и всех предыдущих измерений. Ее пер-
вым воплощением стал разработанный Бесселем способ двух-
группового решения нормальных уравнений, разновид-
ностью которого является фильтр Калмана. Графоанали-
тический вариант с названием «объединение распределений»
был опубликован советским ученым П. А. Гельвихом в
1928 г., за двадцать с лишним лет до работы Калмана.
Этот факт может быть неизвестен иностранным авторам, но
советским надо бы о нем знать. Более удачные названия
способа — «последовательное уточнение» и «комплексиро-
вание измерений» предложены А. Е. Сазоновым иЮ. М. Фи-
липповым [50, 51].
Суть способа может быть пояснена следующим приме-
ром. Пусть сначала было выполнено k прямых равноточных
измерений (назовем их измерениями первой группы) не-
которой постоянной величины X; результаты измерений
оказались равны хи ..., х,, ..., хк. Затем выполнено еще п
измерений (измерений второй группы) той же искомой ве-
личины; результаты измерений были х[, ...,х/,..., х«. Если
измерения содержат только случайные погрешности, то
несмещенной эффективной оценкой искомой величины бу-
дет среднее арифметическое из результатов измерений:
т; (*i+ • • • +*/ + - • • +*fe) + (xl + • • * +х/+ • • • +^n)
А =-------------------------—---------------; (1.13b)
k-}-n
несмещенная эффективная оценка ее дисперсии равна
<Т?1)
k-^-n

(1.137)
где Иц) — дисперсия погрешности единичного измере-
ния.
Теперь предположим, что, не дождавшись измерений
второй группы, мы нашли оценку искомой величины Хс по
59
результатам измерений только первой группы (назовем ее
счислимой) и оценили ее дисперсию:
=	+	(1.138)
К
О-139)
Как, зная только оценки Хс и Dxc и выполнив измерения
второй группы, найти такие оценки X и Dx, которые бы-
ли бы эквивалентны результатам (1.136), (1.137) совмест-
ной обработки измерений и первой, и второй группы?
Из формул (1.138) и (1.139) можно найти число измере-
ний k и сумму результатов измерений, по которым могли
бы быть получены оценки Хс и Dxc:
(1.140)
Х1 + ... + Xi + ... + хк = kX~. (1.141)
Вычислив разности результатов измерений второй груп-
пы и счислимого значения искомой величины:
Zic = Хс, Z2© = ^2 Xc*t Znc = Хп Xct
введем обозначение
ATPLC = Zlc + Z2C + ... + Znc;
оценку искомой величины будем искать в
XD = Xc + (k + и)'1 ДТРАС.
Подставив сюда величины Хс и Ат PLC из выражений
^1.138)—(1.144), получим, что оценка Хв равна
v +»»>
D k	п -\-k
(Л-Н) (-«1+ ••+*h)+* W+ ... + *£)— л(хх+... + хл)
(1.142)
(1.143)
виде
(1.144)
k (n-}-k)
(xi+...+%A)+W+ •••+4)
(1.145)
fl —|— k
Сравнив итог (1.145) с выражением (1.136), видим, что
оценка XD эквивалентна результату совместной обработ-
60
кн первой и второй групп измерений. Впредь будем имено-
вать оценки искомых величин, полученные из некоторых пре-,
дыдущих измерений (измерений первой группы), счисли-
мыми. Их примером могут служить координаты счислимого
места судна на момент обсервации.
Преимущества алгоритма, выраженного формулами
(1.140)—(1.144), становятся очевидными, как только мы
предположим, что искомая величина X — не постоянная,
а случайно изменяющаяся по времени. Пусть на основании
каких-то предыдущих наблюдений мы можем прогнозиро-
вать ее счислимую оценку Хс на любой наперед заданный
момент времени и оценить дисперсию £>хс этой оценки.
Если в этот момент будет выполнено еще хотя бы одно из-
мерение, мы сможем, пользуясь формулами (1.140)—(1.144),
найти ее эффективную оценку, эквивалентную результату
совместной обработки всех измерений — как предыдущих,
так и вновь выполненного. Приняв полученную оценку за
счислимую, мы будем готовы повторить ту же процедуру,
как только будет выполнено еще одно измерение, и т. д.,
т. е. осуществлять последовательное уточнение оценок.
С течением времени счислимые оценки искомых величин
«стареют», их точность ухудшается. Но каждое новое из-
мерение позволяет их уточнять. Если искомых величин не-
сколько и выполняются не только прямые, но и косвен-
ные измерения, то матричная запись способа принимает
вид выражений, сходных с формулами (1.40)—(1.44):
В2 = АТРА-,
X = (Bj + Вз)-1 ЛтР£с;
(1.146)
(1-147)
(1.148)
(1.149)
(1.150)
(1.151)
Kt =	+ В2)Л
где £с — вектор счислимых значений искомых величин;
— ег0 корреляционная матрица;
с — произвольный коэффициент, выбираемый ис-
~ ходя из соображений удобства вычислений;
0(1) — оценка дисперсии погрешности измерения,
вес которого принят равным единице.
61
Остальные обозначения — те же, что применялись раньше.
Особо подчеркнем: подобно тому, как в правой части выра-
жения (1.143) фигурируют не результаты измерений второй
группы непосредственно, а разности их и счислимого зна-
чения искомой величины, теперь при вычислении свобод-
ных членов уравнений поправок в формулу (1.101) долж-
ны подставляться функции Ф, (glc, g2c, £mc) не произ-
вольных приближенных, а счислимых значений искомых
величин. Чтобы об этом напоминать, вектор свободных чле-
нов уравнений поправок в формуле (1.149) обозначен сим-
волом Вс, а не L, как раньше.
Полезна следующая интерпретация алгоритма (1.146)—
(1.151). Пусть по результатам измерений второй группы со-
ставлены уравнения поправок вида (1.103), свободные чле-
ны которых вычислены исходя из счислимых значений ис-
комых величин. Число п этих уравнений равно числу вновь
выполненных измерений, Кд — корреляционная матрица
вектора погрешностей этих измерений. Дополним эти урав-
нения системой из п уравнений поправок вида
Xj = vn+}	(1.152)
со свободными членами, равными нулю, которые формаль-
но будем считать выражающими результаты некоторых во-
ображаемых измерений первой группы (прямых измере-
ний счислимых значений искомых величин). Конечно, та-
кие уравнения имеет смысл составлять для поправок толь-
ко к тем счислимым оценкам искомых величин, точности
которых не пренебрежимо малы; следовательно, п <1 т.
Корреляционную матрицу вектора погрешностей этих во-
ображаемых измерений будем считать идентичной корре-
ляционной матрице вектора погрешностей счислимых
оценок искомых величин, для которых составлены урав-
нения поправок вида (1.152). Если теперь обозначить сим-
волом Pq блочную матрицу

Р 0
0 Bi
(1.153)
символами: Ad— матрицу коэффициентов при неизвест-
ных, Vd — вектор отклонений системы уравнений попра-
вок (1.103), (1.152) и подставить их и вектор Lc вместо ма-
триц Р, Д, V и L в формулы (1.123)—(1.127), то это приве-
дет к тем же оценкам искомых величин, что алгоритм
62
(1.146)—(1.151). При этом число п в формуле (1.127)
следует считать обозначающим общее число измерений, как
реально выполненных, так и воображаемых. Ясно, что если
число вновь выполненных измерений невелико, то достав-
ляемая формулой (1.127) оценка дисперсии измерения, вес
которого принят равным единице, окажется грубой; тогда
предпочтительнее воспользоваться априорной (найденной
по результатам предыдущих измерений) оценкой величины
Применяя способ D к обработке результатов измере-
ний, остаточные систематические погрешности которых
могут быть велики, надо иметь в виду следующие сообра-
жения. Выполнив любые измерения, мы всегда с наиболь-
шей возможной тщательностью (за исключением случаев,
когда обработка наблюдений ведется способом В) исправ-
ляем показания приборов всеми учитываемыми поправка-
ми и лишь затем приступаем к дальнейшим вычислениям.
Те измерения, из которых в свое время были найдены
учитываемые теперь значения поправок, будем называть
измерениями первой группы, а амплитуды этих поправок —
счислимыми значениями амплитуд. Вновь выполненные
измерения будем считать измерениями второй группы, вклю-
чим поправки к счислимым значениям амплитуд в число ис-
комых величин и применим к их отысканию алгоритм после-
довательного уточнения оценок искомых величин. При
этом уравнения поправок, выражающие результаты ре-
ально выполненных измерений, имеют тот же вид (1.133),
что и в способе В, с тем лишь отличием, что теперь резуль-
таты измерений должны исправляться поправками, рас-
считанными исходя из счислимых, а не из произвольных зна-
чений амплитуд. Эти уравнения дополняются столькими
уравнениями (1.152), сколько амплитуд поправок включе-
но в число искомых величин. Корреляционную матрицу
погрешностей этих уравнений следует полагать иден-
тичной корреляционной матрице счислимых значений ам-
плитуд, а корреляционную матрицу Кд в выражении
(1.147) — корреляционной матрице Ко вектора 6 остаточ-
ных погрешностей, не включенных в число искомых ве-
личин.
Отметим основные особенности такого применения спо-
соба D.
1.	Он доставляет несмещенные оценки искомых величин,
дисперсии которых меньше или, по крайней мере, не больше,
63
нежели дисперсии оценок, доставляемых способом Л, спо-
собом В, или любых других оценок, отыскиваемых в виде
(1.110).
2.	Если последовательному уточнению подвергаются
оценки не всех искомых величин, а только амплитуд попра-
вок, вводимых в результаты измерений (полагают, что по-
лученные из предыдущих измерений оценки остальных ис-
комых величин имеют пренебрежимо малую точность), то
при однократном применении способ D приводит к тем же
оценкам «основных» искомых величин, что и способ С (вви-
ду сложности доказательство этого утверждения приводить
не будем). Но и тогда применение способа D более пред-
почтительно, нежели способа С.
Во-первых, способ D непосредственно доставляет оцен-
ки не только «основных» искомых величин, но и ампли-
туд поправок, которые должны вводиться в результа-
ты последующих измерений для компенсации системати-
ческих погрешностей. Если применяется способ С, для
этого требуются дополнительные вычисления. Во-вторых,
для применения способа С, как мы уже говорили, должны
быть известны, хотя бы с точностью до постоянного мно-
жителя, корреляционная матрица или матрицы Къ и Дг.
Рекомендаций, как их оценить, способ С не дает. Применяя
же способ D, мы, оценивая корреляционную матрицу век-
тора оценок искомых величин, оцениваем вместе с тем,
как один из ее блоков, и корреляционную матрицу K'z
вектора оценок амплитуд поправок, включенных в число
искомых величин, — тех самых амплитуд, которые при
следующем применении способа будут выступать как счис-
лимые значения искомых величин. Что же касается корре-
ляционной матрицы До вектора архиостаточных погреш-
ностей, то в тех случаях, когда она может считаться диа-
гональной, ее можно оценивать по несогласию результатов
измерений (по отклонениям v). Таким образом, мы полу-
чаем все необходимое для того, чтобы, выполнив новые из-
мерения, опять применить к их обработке способ D.
3.	Способы А и В являются предельными частными слу"
чаями способа D. Первый соответствует предположению,
что все поправки, вводимые в результаты измерений, из-
вестны со столь высокой точностью, что любое последую-
щее уточнение оценок их амплитуд не имеет смысла. Он
аналогичен ситуации, в которой при определении места суд-
на измерения навигационных параметров имеют столь низ-
кую точность, что мы пренебрегаем обсервацией и про-
должаем счисление, не корректируя его, от последней
счислимой точки. Способ В, наоборот, соответствует слу-
чаю, когда поправки, вводимые в результаты измерений
для компенсации систематических погрешностей, счи-
таются известными со столь малой точностью, что всеми
измерениями, выполненными ранее для их определения,
можно пренебречь, подобно тому, как мы пренебрегаем счис-
лимым местом, точность которого несоизмеримо ниже точ-
ности обсервованной точки.
4.	В отличие от способа В, при применении которого
включение амплитуд поправок в число искомых величин
может повести к ухудшению точности оценок искомых
величин по сравнению со способом А или даже к неопределен-
ности, применение способа D, при котором включение но-
вых неизвестных в число искомых величин сопровождает-
ся присоединением к системе уравнений поправок новых
уравнений вида (1.152), не может повести к ухудшению точ-
ности оценок искомых величин (дисперсии их погрешностей
уменьшатся или, по крайней мере, не увеличатся). Способ
D соответствует условию, что мы не намерены пренебре-
гать ни предыдущими, ни вновь выполненными измерения-
ми и стараемся полностью использовать всю доставляемую
ими информацию.
Отметим еще два существенных достоинства способа D:
его применение становится возможным, когда выполнено
хотя бы одно новое измерение; он очень удобен для реали-
зации в ЭЦВМ. Если в «памяти» ЭЦВМ будет храниться
вектор оценок всех величин, которые при судовождении
могут оказаться искомыми: координат текущего места
судна, проекций скорости течения, коэффициентов изме-
нения скорости судна от влияния ветра, волнения моря
и других факторов, амплитуд поправок всех навигацион-
ных приборов, а также его корреляционная матрица, то
любое новое измерение будет приводить к уточнению оце-
нок всех искомых величин и всех элементов этой корреля-
ционной матрицы. Может показаться парадоксальным:
каким образом выполненное только что измерение, пред-
положим, высоты светила может послужить поводом для
корректировки коэффициентов радиодевиации, определен-
ных четыре месяца тому назад, если радиопеленгатор уже
месяц как не включался? Но если учесть взаимную связь
3 з^к. 136?	65
всех оценок, то удивительного в этом нет: высотная линия
положения показала, что учитываемый вектор течения не
совсем точен, и предыдущая невязка была частично обус-
ловлена погрешностью в поправке компаса, определенной
3 ч тому назад; в свою очередь, уточнение поправки компа-
са заставило пересмотреть и оценку поправки лага, уточнен-
ную позавчера при определении места по визуальным пе-
ленгам, и т. д., пока цепь уточнений не дойдет до поправки
прибора, которым выполнялись измерения почти одновре-
менно с последними измерениями радиопеленгов, и до ко-
эффициентов радиодевиации.
Однако при более тщательном рассмотрении окажется,
что многие из недиагональных элементов корреляционной
матрицы вектора оценок искомых величин, выражающих
взаимную связь оценок, исчезающе малы. Соответственно
пренебрежимо малыми будут и поправки к счислимым зна-'
чениям большинства искомых величин. Исключение со-
ставят только те из них, у которых зависимость от оценок,
включенных в уравнения поправок, составленные по ре-
зультатам последних реально выполненных измерений, не
пренебрежимо мала. Этим обстоятельством можно вос-
пользоваться для уменьшения объема вычислений и облег-
чения требований к объему оперативной памяти ЭВМ:
пусть она включает в число искомых величин лишь те, по-
правки к счислимым значениям которых не могут заведомо
оказаться пренебрежимо малыми. При неавтоматизирован-
ной же обработке наблюдений мы вынуждены в угоду упро-
щению расчетов пренебрегать и теми зависимостями, ко-
торыми, строго говоря, пренебрегать не следовало бы (на-
пример, при определении места судна — зависимостями
невязки не только от погрешностей в учете течения, но и
от погрешности в учете поправки лага, от систематических
погрешностей измерения навигационных параметров ит. д.).
Алгоритмы, к которым приводят эти упрощения, рассмо-
трены в следующих главах.
Глава 2
НАВИГАЦИОННЫЕ ИЗМЕРЕНИЯ
§ 2.1 ЗАДАЧА ОБНАРУЖЕНИЯ
СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Развитие теории информации и ее приложения к изме-
рениям — информационной теории измерений — позволи-
ло установить связь между точностью измерений и количе-
ством информации, приносимой их результатами. Грубо
она выражается так: чем точнее измерения, тем, при прочих
равных условиях, большее количество информации содер-
жат их результаты. Справедливо и обратное соотношение:
чем большее количество информации используется при об-
работке результатов измерений (конечно, тут подраз/ме
вается должным образом организованное использование),
тем, при прочих равных условиях, более точными будут
оценки искомых величин. В первую очередь речь должна
идти о той априорной информации (иногда ее называют те-
заурусом) о процессе измерений и его погрешностях, кото-
рой мы располагаем, приступая к измерениям. Выражение
«априорная информация» условно: в действительности она
сама является обобщенным итогом некоторых предыдущих
измерений.
Исторически одной из первых попыток получения та-
кой информации была задача обнаружения систематиче-
ских погрешностей. Традиционная ее формулировка тако-
ва: пусть выполнено п измерений некоторых физических
величин; при обработке их результатов найдены оценки
искомых величин и по формуле (1.103) вычислены откло-
нения и2, ..., viy ..., vn. Как узнать, свободны или нет
результаты измерений от систематических погрешностей?
Во всех современных пособиях по математической ста-
тистике излагается критерий Аббе, предназначенный для
обнаружения систематических погрешностей в результа-
тах прямых равноточных измерений некоторой постоянной
физической величины, или его модификации. Он основан
на предположении, что разности результатов следующих
одно за другим (последовательных) измерений менее под-
вержены влиянию систематических погрешностей, нежели
непосредственно сами результаты измерений. По формуле
3*	67
(1.127) вычисляется оценка oft) дисперсии погрешности
единичного измерения; вычисляются величины
<21>
Величина Dr есть оценка дисперсии разности погрешностей
последовательных измерений. Поскольку, согласно фор-
муле (1.16), дисперсия разности погрешностей, если они
взаимно некоррелированы, равна сумме дисперсий этих
погрешностей, ясно, что для равноточных измерений при
отсутствии систематических погрешностей величина г долж-
на быть близка к единице. Если так и есть, то делается вы-
вод об отсутствии систематических погрешностей, в про-
тивном случае — об их наличии. Но возникают сомнения.
Во-первых, существуют погрешности, удовлетворяющие
условию (1.120); они не могут вызывать несогласия резуль-
татов измерений (например, при прямых равноточных изме-
рениях постоянной физической величины этим свойством
обладает постоянная погрешность, одинаковая во всех из-
мерениях). Ясно, что ни критерий Аббе, ни любой другой
критерий, основанный на исследовании свойств вектора
отклонений, не в состоянии их обнаружить. Поэтому даже
в тех случаях, когда их существование применением кри-
терия не обнаружено, делать вывод об отсутствии система-
тических погрешностей недопустимо. Во-вторых, остаточ-
ные систематические погрешности неизбежны; они немину-
емо содержатся в любых измерениях. Поэтому и второй
альтернативный вывод, что испытуемая совокупность изме-
рений не свободна от систематических погрешностей, три-
виален и никакой новой информации не несет.
Видимо, сама традиционная постановка задачи (сущест-
вуют или нет систематические погрешности в данной сово-
купности измерений?) не корректна. Следует исходить из не-
избежности этих погрешностей; нас должно интересовать
не то, существуют ли они, а как велики и как зависят от
условий измерений. Итак, впредь будем формулировать
задачу следующим образом. Пусть рассматриваются изме-
рения некоторого данного вида. Обнаружить, отличаются
ли в их результатах заметно от нуля амплитуды система-
тических погрешностей, зависимость которых от условий
измерений характеризуется некоторой заданной коорди-
68
натной функцией fr (af, pf, ...), или эти амплитуды прене-
брежимо малы?
Приступая к решению этой задачи, надо иметь в виду
следующие обстоятельства. В соответствии с теоремой о ка-
ноническом представлении случайных функций вектор ис-
тинных погрешностей любой конечной совокупности изме-
рений с любой наперед заданной точностью и сколь угодно
большим числом способов может быть формально представ-
лен в виде суммы элементарных случайных функций, т. е.
систематических погрешностей: при этом в качестве коор-
динатных функций могут выбираться любые функции пара-
метров, характеризующих условия измерений, лишь бы
ранг матрицы F = || fir || П5 был равен числу s координатных
функций. Иначе говоря, в любой конечной совокупности
измерений можно формально обнаружить систематические
погрешности, зависимости которых от условий измерений
выражаются любыми наперед заданными координатными
функциями. Практический же смысл имеет выделение толь-
ко таких систематических погрешностей, амплитуды кото-
рых обладают некоторой устойчивостью при переходе от
одной совокупности измерений к другой, что является не-
обходимым условием возможности их компенсации вве-
дением поправок в результаты измерений. Таким образом,
исследованию должны подвергаться не одна, а возможно
большее число совокупностей измерений, и надо искать та-
кие координатные функции, при которых амплитуды систе-
матических погрешностей меньше изменяются при переходе
от одной совокупности измерений к другой.
Любая из удовлетворяющих этому требованию коорди-
натных функций есть лишь приближенная модель реально
существующих соотношений. Пока условия измерений су-
щественно не изменились, ее неточность малозаметна. Но
значительное изменение этих условий может повести к ощу-
тимому ухудшению точности оценок искомых величин и
возрастанию абсолютной величины отклонений и; это по-
служит признаком того, что точность первоначальной мо-
дели, уже перестала нас удовлетворять. Таким образом,
исследования координатных функций надо вести при воз-
можно большем диапазоне значений каждого из параметров,
характеризующих условия измерений.
Получить аналитические выражения координатных функ-
ций непосредственно из результатов измерений невозмож-
69
но. Поэтому приходится идти по пути последовательных
приближений: от построения математической модели (ги-
потезы о виде координатных функций) на основе теоретиче-
ского анализа явлений переходить к ее практической про-
верке, затем — к построению более совершенной модели
и т. д. Основным признаком, свидетельствующим о необ-
ходимости корректировки модели, является обнаружение
зависимости отклонений v от факторов, характеризующих
условия измерений. Тут многое зависит от наблюдатель-
ности, пытливости, любознательности и трудолюбия прак-
тиков, повседневно занимающихся измерениями и обработ-
кой их результатов.
Поучительный пример представляет построение и уточ-
нение модели ветрового дрейфа. Формула, предложенная
проф. Н. Н. Матусевичем, привлекала своей простотой и в
небольшом диапазоне отношений скорости кажущегося
ветра к скорости судна хорошо себя оправдывала. Но
вскоре судоводители-практики обнаружили, что величина
коэффициента дрейфа (т. е. взятая с обратным знаком оцен-
ка амплитуды систематической погрешности) не остается
постоянной, а зависит от курсового угла кажущегося ве-
тра и отношения его скорости к скорости хода судна. Бо-
лее точные результаты давала формула К. К. Федяевского.
Но и она оказалась не свободной от недостатков. С. И. Де-
мин, основываясь на обстоятельном анализе результатов
аэродинамических испытаний моделей судов и натурных
экспериментов, создал еще более совершенную математиче-
скую модель явления. Однако и она, возможно, потребует
дальнейшего уточнения (см. §3.1).
Проверка гипотез о виде координатных функций нераз-
рывно связана с задачей оценивания амплитуд соответст-
вующих систематических погрешностей. Можно идти по
пути включения этих амплитуд в число искомых величин,
т. е. вести обработку измерений способами В или D
(см. § 1.4). Другой путь, позволяющий несколько умень-
шить объем вычислений, основан на исследовании вектора
отклонений.
Пусть при обработке результатов измерений найдены
оценки искомых величин и вычислены отклонения у. Пусть
V = II vi II ni — вектор отклонений; возникло предполо-
жение, что одной из причин несогласия результатов изме-
рений были систематические погрешности, амплитуды ко-
70
торых не включены в число искомых величин; F= || fir || ns—
матрица значений их координатных функций. Как вид-
но из выражения (1.119), для оценивания вектора Z ампли-
туд этих погрешностей надо составить систему уравнений
поправок, матричная запись которой имеет вид
(AG — Е) FZ V = (Е — 4G) 6.	(2.2)
Тут роль матрицы коэффициентов при неизвестных играет
матрица (4G — Е) F, роль вектора свободных членов —
вектор отклонений V. Далее остается, составив и решив си-
стему нормальных уравнений (см. § 1.4), найти вектор Z.
Нетрудно убедиться, что эта оценка идентична той, к ко-
торой приведет способ В, если сразу включить вектор Z
в число искомых величин. Незначительность изменений век-
тора Z при переходе от одной совокупности измерений к
другой свидетельствует об удачном выборе координатных
функций; в противном случае надо искать и испытывать
другие их аппроксимации.
Если в выражении (2.2) пренебречь членом 4G, то мат-
ричная запись системы уравнений поправок принимает
более простой вид
FZ + V = — 8	(2.3)
(в компонентах вектора отклонений V отыскиваются состав-
ляющие, пропорциональные значениям координатных функ-
ций). Этот приближенный способ решения задачи применя-
ется очень часто; к нему, в конечном итоге, сводится вся
современная практика определения поправок, предназна-
ченных для компенсации систематических погрешностей.
Так, получив при ряде обсерваций несколько невязок при-
мерно одного направления и заподозрив, что это является
следствием погрешности в учете течения (погрешности счис-
ления, нарастающей пропорционально времени), штурман,
поделив суммарную невязку на время, за которое она на-
росла, получает поправку к вектору скорости учитываемо-
го течения, представляющую собой решение системы урав-
нений вида (2.3), и проверяет затем приемлемость этой ги-
потезы последующими обсервациями.
Особого внимания заслуживают те из систематических
погрешностей, которые не могут вызывать несогласия ре-
зультатов измерений. Они могут обнаруживаться или по
аномальным погрешностям оценок искомых величин, кото-
71
рые не могут быть объяснены другими причинами, или срав-
нением результатов измерений с эталонными, принимае-
мыми за истинные. Если и эта возможность отсутствует (на-
пример, при исследовании эталонных измерений), остается
только один путь — применение косвенных методов исследо-
вания (анализ всех факторов, могущих порождать эти по-
грешности, и возможного влияния каждого из них на точ-
ность измерений).
Типичный пример представляет погрешность измерения
высот светил навигационным секстаном, возникающая вслед-
ствие асимметрии наклонения видимого горизонта. В райо-
нах атмосферных и океанических фронтов, где велики гори-
зонтальные составляющие градиентов температуры и влаж-
ности воздуха, заметно отличается от нуля и горизонталь-
ная составляющая градиента земной рефракции; зависи-
мость наклонения видимого горизонта от азимута имеет
вид
d (Л) = zQ + cos (Л — Л о) = г0 + г2 cos Л +
+ z3 sin Л,	(2.4)
где z0 — постоянная составляющая наклонения види-
мого горизонта;
zb z2, г3 — амплитуды переменных составляющих.
Так же зависит от азимута и погрешность измерения вы-
соты светила секстаном с искусственным горизонтом, по-
рождаемая заклоном гировертикали (отклонением ее глав-
ной оси от отвесной линии на угол z± по азимуту Ло). Если
высоты светил измеряются для определения места судна,
то коэффициенты при искомых величинах в f-м уравнении
поправок равны -- cos Ль ai2 sin Лг-; условие (1.120)
удовлетворяется, и, следовательно, погрешность вида (2.4)
не может вызвать несогласия результатов измерений. При
отсутствии других погрешностей это ведет к тому, что все
линии положения, не образуя фигуры погрешностей, пере-
секутся в одной точке, отстоящей от истинного места суд-
на на расстоянии zY по пеленгу Лп. Поскольку при любых
азимутах наблюдений d (Л) + d (А ± 180°) = 2z0, ясно,
что эта погрешность не может быть обнаружена также ни
измерениями наклонения видимого горизонта наклономе-
ром, ни измерением высот светил секстаном через зенит.
Но если измерять зенитное расстояние видимого горизон-
та теодолитом с небольшого острова, лежащего вдали от
берегов, то асимметрия наклонения будет обнаружена.
7?
Решение задачи обнаружения систематических погреш-
ностей в только^ что изложенной ее трактовке доставляет
информацию о виде координатных функций и о математиче-
ских ожиданиях амплитуд систематических погрешностей;
для тех погрешностей, координатные функции которых были
найдены ранее, амплитуды поправок (т. е. взятые с обрат-
ными знаками оценки амплитуд систематических погреш-
ностей) могут оцениваться способами/) или В, рассмотрен-
ными в § 1.4. Чтобы надлежащим образом использовать эту
информацию, надо располагать и другими статистическими
характеристиками систематических погрешностей.
§ 2.2 ОПРЕДЕЛЕНИЕ И УЧЕТ ПОПРАВОК
ПРИБОРОВ
На первый взгляд все кажется простым: сначала, вы-
полнив некоторые измерения, мы определяем поправки при-
боров, а потом, через несколько часов, дней, а иногда и ме-
сяцев исправляем ими результаты вновь выполненных из-
мерений (часто эту вторую операцию называют учетом по-
правок приборов). Но в общем случае следует говорить об
определении не самих поправок непосредственно, а их ам-
плитуд — взятых с обратными знаками амплитуд компен-
сируемых систематических погрешностей. Такими ампли-
тудами являются, в частности, коэффициенты девиации,
радиодевиации, дрейфа, изменения скорости судна от влия-
ния ветра и волнения моря и т. д. Непосредственное опре-
деление поправок является частным случаем: если fir = 1,
то понятия «амплитуда систематической погрешности»^
«систематическая погрешность» совпадают.
Основным содержанием учета поправок является пред-
сказание (прогнозирование) величин погрешностей на лю-
бой наперед заданный момент времени, назначение попра-
вок, равных взятым с обратными знаками прогнозам по-
грешностей, и оценивание точности прогноза. Например,
в предвычислении поправки хронометра или часов на мо-
мент измерений высот светил объединены два действия:
предсказание погрешности измерителя времени и назначе-
ние поправки, обратной предсказанной погрешности. Ког-
да мы считаем, что погрешность с течением времени не из-
меняется (например, вычислив таблицу девиации магнит-
73
Moro компаса, пользуемся ею до очередного определения),
это — тоже одна из разновидностей прогноза, и нас; ко-
нечно, должна интересовать его точность. При предсказа-
нии следует учитывать статистические характеристики из-
менчивости прогнозируемой величины по времени. С этой
точки зрения погрешности, с которыми приходится встре-
чаться в судовождении, можно подразделить наследующие
типы.
1-й тип. Амплитуда рассматриваемой систематической
погрешности является заведомо постоянной величиной (не
существует причин, которые могли бы приводить к ощути-
мым ее изменениям с течением времени).
Таковы, например, погрешности, обусловленные неточ-
ностью установки некоторых приборов на судне. Если ось
О—180° азимутального кольца репитера гирокомпаса, уста-
новленного на пелорусе, не параллельна диаметральной
плоскости судна, или курсовая черта котелка магнитного
компаса развернута относительно диаметральной плоскости
судна, то систематическая погрешность измерения пеленгов
не равна погрешности измерения курса судна. Если поправ-
ка компаса определяется как разность эталонного («истин-
ного») и измеренного пеленгов на какой-либо ориентир, то
в измерении курса судна возникает погрешность, равная
углу разворота репитера гирокомпаса (котелка магнитного
компаса) относительно диаметральной плоскости судна. Ее
изменения, обусловленные деформациями корпуса судна,
ничтожно малы; эту погрешность можно считать заведомо
постоянной до тех пор, пока репитер (котелок магнитного
компаса) не будет заменен другим или не будет развернута
шейка пелоруса (нактоуза магнитного компаса).
Практически постоянными можно считать также коэф-
фициенты ветрового дрейфа и изменения скорости судна от
влияния ветра при фиксированном водоизмещении судна,
если математическая модель явления достаточно точна (по-
грешности аппроксимации пренебрежимо малы); коэффи-
циент пропорциональности между приращением скорости
судна и отклонением водоизмещения от расчетного при фик-
сированной частоте вращения гребного вала; параметры,
характеризующие эксцентриситет оси вращения алидады
секстана с верньерным отсчетным устройством, и т. д. Как
увидим ниже, свойством постоянства обладают и некоторые
составляющие других погрешностей, изменяющихся с те-
чением времени.
74
Исчерпывающими статистическими характеристиками не-
изменной во времени нормально распределенной системати-
ческой погрешности являются оценка ее математического
ожидания и оценка дисперсии этой оценки. Применяя спо-
соб последовательного уточнения оценок искомых величин
(см. § 1.4, способ £>), в принципе можно, безгранично уве-
личивая число наблюдений, оценивать амплитуды погреш-
ностей, обладающие свойством неизменности по времени,
со сколь угодно высокой точностью. Однако, поскольку лю-
бая из этих погрешностей наблюдается не изолированно, а в
сумме с другими погрешностями, свойством неизменности не
обладающими, реализация этой возможности является
делом не простым, требующим громоздких вычислений, прак-
тически осуществимых только на ЭЦВМ с достаточно боль-
шим объемом оперативной памяти. По той же причине до-
биваться особо высокой точности и нет необходимости:
поскольку погрешность суммы нескольких величин решаю-
щим образом зависит от погрешности наименее точного сла-
гаемого, надо стремиться лишь к тому, чтобы погрешность
каждого слагаемого не превосходила значительно погреш-
ностей других слагаемых («принцип равного вклада»,
«соображения практической целесообразности»); наиболь-
шую заботу следует уделять уменьшению погрешностей
менее точных слагаемых.
В отношении погрешностей и амплитуд погрешностей,
обладающих свойством неизменности по времени, наиболее
употребительны два способа действий.
1. Соответствующей регулировкой прибора погреш-
ность сводится до величины, не превосходящей допуска,
устанавливаемого в соответствии с принципом равного
вклада (соображениями практической целесообразности).
В дальнейшем остаточная погрешность считается пренебре-
жимо малой (поправка для ее компенсации не определяется
и в результаты измерений не вводится); средняя квадрати-
ческая погрешность прогноза полагается равной средней
квадратической погрешности регулировки прибора. Так
поступают, например, с упомянутой выше непараллель-
ностью оси 0—180° репитера гирокомпаса (курсовой черты
магнитного компаса) диаметральной плоскости судна.
2. Поправки (амплитуды поправок) определяются в спе-
циально организованном эксперименте и впредь учитываются
до следующего их определения. Средняя квадратическая
погрешность прогноза полагается равной средней квадра-
75
тической погрешности определения поправки. Так посту-
пают, например, с инструментальными погрешностями* сек-
стана и ряда других приборов.
2-й тип. Рассматриваемая систематическая погрешность
(амплитуда систематической погрешности) может считать-
ся практически стационарной случайной функцией вре-
мени. Такие погрешности возникают, когда чувствительный
элемент измерительного прибора или физическая система,
являющаяся источником погрешностей, испытывает слу-
чайные отклонения (флуктуации) относительно некоторого
среднего состояния (положения равновесия), причем при
каждом таком отклонении возникают силы, моменты сил
или другие подобные факторы, действующие в направле-
нии возвращения системы к положению равновесия. Ти-
пичными примерами являются: погрешность измерения
курса судна гирокомпасом; наклонение видимого горизон-
та; составляющие вектора скорости течения в фиксирован-
ной точке моря; погрешности измерения радионавигацион-
ного параметра при приеме пространственных радиоволн.
Если рассматривается нормальная стационарная слу-
чайная функция, то исчерпывающими ее статистическими
характеристиками являются математическое ожидание и
корреляционная функция. Корреляционная функция (или
дисперсия и нормированная корреляционная функция)
характеризует изменчивость случайной функции во времени,
что надо учитывать как при оценивании точности опреде-
ления поправок, так и при предсказании погрешностей.
Будем пользоваться обозначениями, введенными в § 1.1:
X (t) — стационарная случайная функция времени, Мх —
ее математическое ожидание, ох — дисперсия, (у) =
= &хрх СО — корреляционная функция, рх (т) — норми-
рованная корреляционная функция, т0 — интервал корре-
ляции.
Пусть перед нами стоит задача оценить математическое
ожидание случайной функции; эта оценка отыскивается как
среднее арифметическое из результатов ряда измерений:
Так поступают, например, определяя среднее значение по-
грешности показаний гирокомпаса, относительно которого
происходят ее случайные отклонения, или рассчитывая
76
среднее арифметическое из ряда измеренных значений ра-
дионавигационного параметра для уменьшения влияния
ионосферных погрешностей при определении места судна.
Как велика может быть погрешность этой оценки?
Для простоты будем считать, что измерения выполняют-
ся через равные промежутки временит; обозначим символом
(То дисперсию случайной погрешности единичного изме-
рения. Тогда, как следует из определений (1.20)—(1.23)
и выражения (1.15), дисперсия оценки (2.5) окажется рав-
ной
a^ = -^-tn + 2(n—1)Px(x) + 2(n—2)Рх (2т) +••• +
+ 2рх(пт-т)] + ^_	(2.6)
л	п
Предсказанию стационарных случайных функций по-
священа обширная литература. Но сложность математиче-
ского аппарата затрудняет ознакомление с нею. К наи-
более популярным, удачно сочетающим в себе простоту и
краткость изложения, относится, по-видимому, брошюра
А. Н. Ефимова [24]. Мы рассмотрим три простейших способа
предсказания, не требующие сложных вычислений.
1.	Прогноз по последнему значению (ступенчатая экст-
раполяция). За прогноз на любой последующий момент вре-
мени /0 + т принимается последнее из измеренных значений
X (t0) случайной функции:
л (t0 + т) = X (to).	(2.7)
Этот способ предсказания применяется в штурманской прак-
тике очень часто: во всех случаях, когда до следующего
определения поправки компаса мы пользуемся последним ее
наблюденным значением, когда исправляем измеренные вы-
соты светил поправкой за наклонение видимого горизонта,
измеренной наклономером перед измерением высот; когда
учитываем течение, определенное по невязкам обсерваций,
И т. д.
Как видно из выражений (1.15) и (1.23) или непосредст-
венно из (1.31), дисперсия погрешности такого прогноза
равна
4('о + т) 2<^ [1 - Рх(т)] + аб2,	(2.8)
где его — средняя квадратическая погрешность измерения
случайной функции.
77
2.	Прогноз по математическому ожиданию. В качест-
ве прогноза на любой момент времени Zo + т принимается
оценка математического ожидания случайной функции:
X (Z0 + t) - Мх,	(2.9)
например, показания гирокомпаса исправляются поправ-
кой, вычисленной как среднее арифметическое из ряда по-
правок, определенных при длительных наблюдениях с не-
подвижного судна (у причала). Если, как и в формуле
(2.6), (Jj—средняя квадратическая погрешность оценки
математического ожидания, то, как следует из определения
(1.21), дисперсия погрешности такого прогноза равна
Оу(/о + т) ==СТ^+°ГЙ-	<2Л0)
3.	Статистический прогноз по одной точке. Он основан
на следующих соотношениях. Пусть X, Y — случайные
величины, Мх и Му—их математические ожидания,
ох и оу — дисперсии, рХу — коэффициент корреляции.
Если случайная величина X приняла некоторое конкретное
значение Х1( то условное математическое ожидание случай-
ной величины Y (определяемое при условии, что случай-
ная величина X приняла значение Хг) равно
ov
MY/x-MY+—	(2.11)
°х
В теории вероятностей выражение (2.11) называется
уравнением регрессии Y на X. Его физический смысл по-
Рис. 2.1. Регрессия случайной величи-
ны У на X
78
ясняет рис. 2.1, где по
оси абсцисс откладыва-
ются значения случай-
ной величины X, по оси
ординат — значения слу-
чайной величины У, кре-
стиками помечены точки,
соответствующие сов-
местным реализациям
случайных величин X и
У; прямая АВ — линия
регрессии, уравнение
которой — выражение
(2.11). Если известно, что
случайная величина X
приняла значение Хх, то
естественно ожидать, что случайная величина Y примет
значение, более близкое к условному математическому
ожиданию Му/х, нежели, например, к значению Му.
Среднее квадратическое отклонение случайной величины Y
от условного математического ожидания MyjX равно
OyjY 1 —рху-	(2.12)
Теперь вернемся к предсказанию случайной функции.
Будем считать, что случайная величина X есть сечение
X (t0) случайной функции X (f), соответствующее моменту
времени /0 последнего ее измерения, случайная величина
Y — сечение X (/0 + т), соответствующее моменту времени
/0 + т прогноза. Учитывая, что вследствие стационарности
случайной функции имеют место равенства
Му ~ МХ, Пу — Ov, Рху — Рх (т),
выражение (2.9) примет вид
X (/0 + т) = Мх + рх (т) [X (/0) - Мх]. (2.13)
Дисперсия погрешности этого прогноза равна
пН^о + т)	- Р1(т)1.	(2.14)
Как видно из выражений (2.7) — (2.14) и рис. 2.2, ста-
тистический прогноз по одной точке при т — 0 совпадает
с прогнозом по последнему значению; по мере того как про-
межуток времени т приближается к интервалу корреляции
т0, он приближается к прогнозу по математическому ожи-
данию. Прогноз по последнему значению при неболь-
ших т более точен, нежели прогноз по математическому
ожиданию, но ошибки измерений могут делать это преиму-
щество весьма незначительным; через некоторое время оно
и вовсе пропадает. Статистический прогноз по одной точке
всегда более точен, нежели любой из первых двух.
Существуют способы предсказания случайных функций,
основанные на использовании результатов не только послед-
него измерения, но и ему предшествовавших («по предысто-
рии случайного процесса»). Однако они требуют значитель-
но более сложных вычислений и дают заметный выигрыш
точности только при небольших промежутках времени т.
Когда величина т приближается к интервалу корреляции
79
Рис. 2.2. Сравнение прогнозов:
а — прогноз; б — его среднее квадратическое отклонение;
1 — по последнему значению; 2 — по математическому ожиданию; 3 — стати-
стический прогноз по одной точке
т0, любой из этих прогнозов приближается к прогнозу по
математическому ожиданию, а его дисперсия — к дисперсии
этого прогноза.
Представим случайную функцию X (/) в виде суммы ма-
тематического ожидания и отклонения от математического
ожидания (центрированной случайной функции с матема-
тическим ожиданием, равным нулю):
X (0 = Мх + [X (О -Мх] = Мх+ X (/).	(2.15)
Соответственно погрешность любого прогноза можно
рассматривать как разность двух случайных величин: от-
клонения прогноза от математического ожидания и откло-
нения мгновенного значения случайной функции от ее ма-
тематического ожидания:
Д [X (tQ + т)] = X (/0 + т) - X (/0 + т) =
= [X (/0 + т) - Мх\ - X (/0 + т).	(2.16)
Если предсказание выполняется первым или вторым
способом (по последнему значению или по математическо-
му ожиданию), то до тех пор, пока не будет сделан очеред-
ной прогноз, первое слагаемое в правой части формулы
80
(2.16) остается неизменным и во всех измерениях, выпол-
ненных в течение этого времени, выступает как системати-
ческая погрешность. Его дисперсия равна о% + о? для
первого способа предсказания и для второго способа.
Второй член в формуле (2.16) выражает влияние слу-
чайной изменчивости погрешности по времени; его диспер-
сия при первом и втором способах прогноза равна ох-
Если все измерения рассматриваемой совокупности изме-
рений выполнены в течение столь небольшого промежутка
времени т, что практически можно считать р (т) = + 1, то
эта погрешность за время измерений не успевает заметно
измениться, и во всех измерениях ее можно считать прак-
тически одинаковой, т. е. систематической. Такова, на-
пример, погрешность в учитываемой поправке гирокомпа-
са, которой исправляются несколько пеленгов на ориенти-
ры, измеренных в течение нескольких минут, или погреш-
ность наклонения видимого горизонта в высотах светил,
измеренных навигационным секстаном в течение 5—10 ми-
нут. Если промежутки времени между очередными измере-
ниями рассматриваемой совокупности превышают интер-
вал корреляции, то значения, которые принимает эта по-
грешность в двух следующих одно за другим измерениях,
оказываются взаимно некоррелированными случайными
величинами, т. е. случайными погрешностями. В промежу-
точных ситуациях, когда р (т) =# 0, но т< т0, надо учиты-
вать взаимную корреляцию значений этой погрешности в
результатах измерений.
Чтобы применять рассмотренные способы предсказания
и оценивать точность прогноза, надо знать корреляционную
функцию прогнозируемой случайной функции. Информация
о корреляционных функциях погрешностей измерений, ко-
торые мы еще только собираемся^ выполнять, неизбежно
носит характер прогноза, т. е. той априорной информации,
о которой говорилось в начале главы (хотя и является ре-
зультатом обработки некоторых выполненных ранее изме-
рений). Конечно, нет оснований полагать, что корреляцион-
ные функции погрешностей измерений, выполненных на
разных судах и в разных условиях, будут одинаковыми.
Однако, как показывают теоретический анализ и практиче-
ский опыт, даже при довольно больших ошибках в пара-
метрах корреляционной функции, прогноз, ее использую-
щий, будет более точен, чем в случае, когда этой инфор-
мацией пренебрегают.
81
Способы оценивания корреляционных функций погреш-
ностей уже выполненных измерений описаны во многих
литературных источниках, в том числе адресованных су-
доводителям [8], [29]. Но сведений о результатах таких
исследований пока опубликовано очень мало.
Корреляционные функции большинства случайных функ-
ций, с которыми приходится встречаться в судовождении,
с достаточной для практических приложений точностью
аппроксимируются одним из следующих выражений:
RxW = ^e~^^	(2.17)
Rx (t) = Охе~а Iт I cos |3т;	(2.18)
/?х(т) = al е~а 1 т 1 (cos |3т-’г — sin |3 | т | V (2.19)
\ ₽ /
Значения параметров о, а, 0 этих корреляционных
функций для нескольких основных навигационных пара-
метров приведены в табл. 2.1.
3-й тип. Рассматриваемая систематическая погрешность
представляет собой первый интеграл по времени от некото-
рой практически стационарной случайной функции. При-
меры: погрешность в учитываемой поправке хронометра,
погрешность измерения курса двухрежимным гирокомпа-
сом в режиме гироазимута [54], погрешность счисления,
возникающая вследствие погрешностей в учете течения.
Здесь вновь рассматривается прогноз, на сей раз —
прогноз интеграла от случайной функции времени. За на-
чало счета времени выберем момент последнего измерения.
Пусть истинное значение прогнозируемой величины выра-
жается формулой
Y(t) = Y0+^X(t)dt,	(2.20)
о
где — результат последнего измерения.
X (/) — случайная функция времени;
Представим случайную функцию X (Z) в виде (2.15) сум-
мы математического ожидания и отклонения от математиче-
ского ожидания (центрированной случайной функции), а
математическое ожидание — в виде канонической суммы
' (2:21)
Г = 1
82
Таблица 2.1
Параметры корреляционных функций погрешностей
навигационных измерений
Навигационный параметр, прибор (система)	ст	а	3	Формула	Литератур- ный источник
Курс по гироком- пасу типа «Курс»	0,6°	0,75 ч-1	5,3 ч-1	(2-18)	[29], [56]
Разность фаз, РНС «Декка»: днем ночью	5—10 деле- ний точной шкалы 15—35 де- лений	0,05—2,0 мин-1	0,02—2,0 МИН—1	(2.18)	[25], [26]
Разность расстоя- ний, РНС «Ло- ран-С»: поверхностные сигналы пространствен- ные сигналы	1,4—2,5 мкс 3—10 мкс	0,05 мин"1 0,02 мин"1	0,02 мин-1 0,01 мин—1	(2.18) (2.18)	
Радиопеленг при расстоянии до ра- диомаяка: до 100 миль более 100 миль: днем ночью	0,8 — 1,0° 0,8° до 4,0°	0,37 мин-1 0,14 мин"1 0,10 мин-1	0,35 мин-1 0,12 мин-1 0,08 мин-1	(2.18)	[29]
Наклонение види- мого горизонта	0,6-1,О'	0,29 ч-1	0,52 ч-1	(2.18)	[29]
Составляющая век- тора скорости те- чения (по меридиа- ну, по параллели) В океане	0,1—0,5 уз	0,1— 0,6 ч“х	0,3— 0,7 ч-1	(2.19)	[45], [7]
83
где — амплитуда, fr (а, Р, ..., /) — координатная функ-
ция. Например, если X (t) — составляющая вектора ско-
рости приливного течения по меридиану или по параллели,
то символами ... будут обозначаться амплитуды ее
суточной, полусуточной и т. д. составляющих, а символом
fr (а, Р, /) — косинус или синус соответствующего ар-
гумента.
Естественно отыскивать оценку математического ожи-
дания в виде, аналогичном выражению (2.21):
Mx(t) = 2 tfr (а, Р,/),	(2.22)
Г=4
где — оценка амплитуды £г.
Обычно так и поступают; в примере с приливным тече-
нием оценки £2> ••• СУТЬ гармонические постоянные при-
ливного течения. Эти оценки представляют собой резуль-
таты обработки каких-то предыдущих наблюдений и пото-
му неизбежно отягощены некоторыми погрешностями. Ос-
таточная погрешность оценки случайной функции X (/)
оказывается равной
s	о
Ах (0= 2 гг/г(а, р,...,	(2.23)
Г=1
где zr = f — £г.
Пусть прогноз (можно называть его также счислимым
значением) случайной функции Y (t) отыскивается в виде
У(0 = Уо+	t)dt\
Г = 1	0
(2.24)
тогда его погрешность равна
s * \
Д?(0 = А?о + J fr (а, Р......../) dt - $ X (/) dt. (2.25)
1 о	о
Если к оценкам ..., f предъявляется требование,
чтобы они были несмещенными оценками соответствующих
амплитуд (обычно оно удовлетворяется), то, как следует из
формулы (1.26), оценка Y (t) будет также несмещенной:
математическое ожидание погрешности Ау (/) прогноза
(2.24) равно нулю.
84
Мы окажемся недалеко от истины, если будем считать
все слагаемые в правой части выражения (2.25) взаимно не-
коррелированными случайными величинами и выразим дис-
персию погрешности прогноза в виде
где
Dy(t)=DYD +D. (0+1М0>
(2.26)
(2.27)
(2.28)
Оценивая дисперсию Dx (t), ограничимся простейшим
случаем, когда fr (а, Р, /) — + 1, т. е. будем рассма-
тривать влияние постоянной, неизменной по времени со-
ставляющей погрешности суточного хода хронометра, или
скорости ухода гироазимута, или вектора учитываемой ско-
рости течения. Как непосредственно следует из выражений
(2.27) и (1.14), дисперсия соответствующей составляющей
погрешности прогноза равна
D. (О = о* t\	(2.29)
т. е. средняя квадратическая погрешность прогноза нара-
стает пропорционально времени. 0
Будем полагать случайную функцию X (/) практически
стационарной. Тогда, как следует из выражений (2.28)
и (1.32), дисперсия D2 (t) погрешности прогноза может быть
оценена по одной из следующих формул:
а)	если корреляционная функция (т) аппроксими-
руется выражением (2.17), то
2о2 г
£>2(0 = —г	+
а2 I
б)	если корреляционная функция 7?х(т)
руется выражением (2.18), то
£>2(0 =
2О2	(
----— 1at
а2 + Р2 [
Р2—а2
а2+Р2 +
(2.30)
аппроксими-
+ 8 -м [(а2— ₽2) cosp/—2а0 sin р/] ;.	(2.31)
а2+р2	I
85
в)	если корреляционная функция (т) аппроксими-
руется выражением (2.19), то
2о2	Г В2 —За2	,	За2-₽2	_f й, ,
£) (/)=----*-	|2а/ + 2 , Я2-	+	„2~Тяг е	“'cosp/Ч-
2V/ а2 + ^2	[ а2 + Р	а2+р
। а (а2— Зр2) t .
J----1---L—- e-at sin
P(a2 + P2)
(2.32)
В большинстве практических приложений со вполне
удовлетворительной точностью можно пренебрегать все-
ми членами, кроме первого, в скобках выражений (2.30) —
(2.32), и пользоваться приближенной формулой
аа(/) = Гад) = ^хГ^	(2.33)
т. е. полагать погрешность прогноза нарастающей пропор-
ционально квадратному корню из времени прогноза. Ко-
эффициент k выражается через параметры корреляционной
функции:
при ее аппроксимации формулой (2.17) — в виде
(2-34)
при ее аппроксимации формулой (2.18) — в виде
k=]/(2.35)
V a2 + ₽2	V
при ее аппроксимации формулой (2.19) — в виде
(2.36)
Из сопоставления формул (2.29) и (2.33) видно, что
при небольшом времени t прогноза большее влияние на его
точность оказывают погрешности, обусловленные случай-
ными отклонениями случайной функции X (/) от ее матема-
тического ожидания (в наших примерах — случайными
флуктуациями суточного хода хронометра или ухода гиро-
азимута, случайной изменчивостью вектора скорости тече-
ния по времени). Чем больше время прогноза, тем больший
относительный вес приобретают погрешности в оценке Мх
математического ожидания случайной функции X (/), вли-
яние которых описывается выражением (2.29); тем больше
внимания надо уделять точности этой оценки.
86
Предположим, суточный ход хронометра (поправка к со-
ставляющей по меридиану или параллели учитываемого
вектора скорости течения) определяется как частное от де-
ления разности двух наблюденных поправок хронометра
(проекций вектора суммарной невязки счисления) на про-
межуток времени между наблюдениями:
Мх = у	(2.37)
Какова точность этой оценки?
Полагая, что погрешности первого и второго измерений
функции Y (/) являются взаимно некоррелированными слу-
чайными величинами, и исходя из соображений, аналогич-
ных изложенным выше, получим
=y	<2-38)
где Ор о2— средние квадратические погрешности первого
и второго измерений случайной функции Y (t). Если пре-
небречь этими погрешностями и аппроксимировать диспер-
сию О2(0 выражением (2.33), то среднюю квадратическую
погрешность оценки математического ожидания Мх слу-
чайной функции X (/) можно оценивать формулой
=	<2.39)
где/ — промежуток времени между наблюдениями, по
которым она вычислялась.
Поясним сказанное примером, представляющим интерес
не своей практической значимостью (в наше время судово-
дители имеют возможность определять поправку хрономе-
тра хоть каждый день), а тем, что он позволяет рассмотреть
простейшую, одномерную модель более сложных задач
(возникающих, например, при определении вектора ско-
рости течения навигационным способом и его учете при
дальнейшем счислении пути судна).
Пример 2.1. У современного механического морского хро-
нометра величина kvx составляет 0,3—0,5 с • сут-0-6. Предпо-
ложим, у некоторого хронометра она равна 0,5 с • сут“0*6.
1. С какой точностью будет определен суточный ход хрономет-
ра за 10 сут, если средняя квадратическая погрешность определе-
ния поправки хронометра равна 0,2 с?
87
По формулам (2.38) и (2.33)
оо= V0,22+0,22+0,52-10=0,16 с-сут-1.
2. С какой средней квадратической погрешностью будет извест-
на поправка хронометра: а) через 4 сут? б) через 10 сут после
последнего определения его поправки?
По формулам (2.26), (2.29) и (2.33):
а)	при t ~ 4 сут
ои = У0,22+(0,16-4)2Н-0,52 • 4«1,2 с;
б)	при t = 10 сут
ои = У0,22+(0,16.10)2+0,5М0	2,3 с.
Если рассматриваются измерения, выполненные в те-
чение сравнительно короткого промежутка времени, пока
прогнозируемая погрешность не могла существенно изме-
ниться, то во всех таких измерениях она выступает как по-
стоянная систематическая погрешность, дисперсия которой
равна дисперсии прогноза. Таковы, например, погрешность
поправки хронометра в исправленных ею моментах изме-
рений нескольких высот светил, разделенных промежутка-
ми времени до нескольких часов; погрешность счислимого
места судна в течение нескольких минут, пока длятся изме-
рения навигационных параметров при определении места
судна, и т. д.
4-й тип. Погрешность и амплитуды погрешностей, кото-
рые остаются практически постоянными в течение сравни-
тельно коротких промежутков времени, пока длятся рас.
сматриваемые измерения, но изменяются случайным обра-
зом в течение более длительных промежутков времени-
проходящих от определения до учета поправок приборов,
Причины таких изменений очень многообразны: у меха-
нических измерительных приборов — необратимые изме-
нения консистенции смазки и износ соединений подвижных
частей, усталостные изменения упругости пружин при дли-
тельных вибрациях, изменения конфигурации отдельных
элементов приборов вследствие ударов при неосторожном
обращении; у электрических и электромагнитных — изме-
нение сопротивления изоляции при ее старении, происхо-
дящие с течением времени необратимые изменения сопро-
тивлений, индуктивностей, взаимной индуктивности, ем-
костей отдельных элементов приборов. Обрастание подвод-
ной части корпуса судна ведет к изменению поправки лага;
88
изменение магнитной широты, прием на судно железных
грузов и грузов в железной упаковке — к изменению ко-
эффициентов девиации магнитного компаса; изменение осад-
ки судна, намокание при дожде и загрязнение изоляторов
антенн и лееров — к изменению коэффициентов радиоде-
виации, и т. д.
В результате таких изменений определенные ранее по-
правки и амплитуды поправок становятся все менее точны-
ми, «стареют». Изменения погрешностей редко бывают од-
носторонними. Чаще погрешности разных знаков и разной
величины накладываются друг на друга; происходит их
взаимная компенсация, вследствие чего изменение по вре-
мени дисперсии остаточной систематической погрешности
(амплитуды остаточной погрешности) характеризуется вы-
ражением, аналогичным формулам (2.27), (2.33):
(0 =	+ k*t.	(2.40)
Недостатка в наблюдениях, из которых могло бы опре-
деляться значение коэффициента kz, характеризующего ско-
рость «старения» поправок (амплитуд поправок) приборов
каждого типа, нет. Регулировке любого прибора всегда пред-
шествует определение его погрешностей. По их разностям
с погрешностями, для компенсации которых служили по-
правки, определенные после предыдущей регулировки,
нетрудно рассчитать частное значение коэффициента kz
для данного конкретного случая. Среднее значение этого
коэффициента для однотипных приборов, установленных
на разных судах одного типа, является существенной ха-
рактеристикой устойчивости погрешностей данного при-
бора, качества этого прибора. Однако, к сожалению, дан-
ные таких наблюдений, за редкими исключениями, не со-
бираются, не обобщаются, не систематизируются и не пуб-
ликуются. Примерами инициативного, творческого отно-
шения к решению этой важной проблемы являются статьи
Н. Степанова [55] и Г. Дралова [21].
Использование основного свойства систематических по-
грешностей — их взаимной зависимости в одной совокуп-
ности измерений — позволяет компенсировать происходя-
щие с течением времени изменения погрешностей исправ-
лением таблиц поправок, составленных по выполненным ра-
нее наблюдениям. Судоводители старших поколений пом-
нят, как во времена, когда основным курсоуказателем на
судах служил магнитный компас, цо наблюдениям девиа-
ции на нескольких курсах исправлялась составленная ра-
нее таблица девиации. В девиационных таблицах для это-
го помещалась специальная таблица. Способ основан на
том обстоятельстве, что наиболее подвержены «старению»
коэффициенты В и С девиации; соответствующее изменение
девиации на произвольном компасном курсе выражается
формулой
Л6 = &В sin КК + ДС cos КК,	(2.41)
которая в полярной системе координат представляет собой
уравнение окружности, проходящей через полюс. Инвер-
сией такой окружности является прямая линия. Поэтому,
если рассчитать инверсированные приращения
=	(2-42)
До
и отложить каждое из них на полярной диаграмме, напри-
мер на маневренном планшете, по направлению КК, то все
полученные точки расположатся на одной прямой линии.
Чтобы откорректировать таблицу девиации, надо рас-
считать разности Л6 наблюденных и табличных значений
девиации на нескольких компасных курсах, по формуле
(2.42) вычислить инверсированные разности и отложить их
на полярной диаграмме (если Л6 отрицательна, то инвер-
сированная разность тоже считается отрицательной, т. е.
ее абсолютная величина
Рис. 2.3. Построение полярной диа-
граммы инверсированных девиаций
90
откладывается от центра
по направлению КК ±
± 180°). Погр ешности
измерений, а также из-
менения коэффициентов
A, D и Е ведут к тому,
что точки ложатся на
диаграмме (рис. 2.3) с
разбросом. Проведя меж-
ду ними согласную пря-
мую, надо измерить ра-
диус-векторы ее точек
для компасных курсов,
кратных 10°; по формуле
(2.42) выполнить обрат-
ную инверсию, и рас-
считанные таким обра-
зом приращения девиации придать табличным значениям.
В годы Великой Отечественной войны, когда гирокомпасы
на судах транспортного флота не устанавливались, для
полного определения девиации подчас не было ни времени,
ни возможности, а от судовождения при плавании по фар-
ватерам между минными полями требовалась особо высокая
точность, этот способ не раз оказывал судоводителям нео-
ценимую помощь.
Подобным образом может корректироваться и таблица
радиодевиации. Но тут наибольшим изменениям подверже-
ны коэффициенты D и Е [57], поэтому при построении по-
лярной диаграммы полярный угол должен приниматься
равным удвоенному радиокурсовому углу. Не представля-
ет особой сложности разработка аналогичных способов
исправления и любых других таблиц поправок, применяе-
мых в судовождении.
Располагая современной вычислительной техникой, при-
менять эти способы нет необходимости. Наилучших резуль-
татов следует ожидать от применения способа последова-
тельного уточнения оценок искомых величин (в данном слу-
чае — амплитуд поправок), рассмотренного в § 1.4 (способ
D). При этом для оценивания точности априорной информа-
ции может служить формула (2.40).
Поправка гирокомпаса. Это одна из важнейших по-
правок приборов в судовождении; об ее учете следует ска-
зать особо. До сих пор живут традиции, сложившиеся лет
40 тому назад, когда наибольшее распространение имели
гирокомпасы с проволочным подвесом чувствительного
элемента. Неприятной особенностью такого прибора явля-
ется возможность закручивания проволочного подвеса при
пуске или остановке гирокомпаса, что ведет к существен-
ному изменению математического ожидания его погреш-
ности. Поэтому считалось правилом заново определять по-
правку прибора после каждого его пуска. Обычно это де-
лалось при выходе из гавани и потом при каждой возмож-
ности (при пересечении створов, по пеленгам небесных све-
тил и т. д.); каждый раз последнее из наблюденных значе-
ний поправки учитывалось до следующего определения.
Это — рассмотренный выше способ предсказания по по-
следнему значению.
Современные гирокомпасы типов «Курс», «Амур» и т. п.
имеют жидкостный подвес чувствительного элемента. Не
существует причин, которые могли бы приводить к сущест-
91
венному изменению математического ожидания погрешно-
сти такого гирокомпаса «от пуска к пуску». Математиче-
ское ожидание (среднее значение, относительно которого
происходят флуктуации, случайные отклонения мгновен-
ного значения) погрешности отличается большим постоян-
ством: при грамотной эксплуатации гирокомпаса его изме-
нения в течение нескольких месяцев и даже лет не превос-
ходят 0,1—0,2°. Поэтому вполне оправдан прогноз погреш-
ности вторым способом, по математическому ожиданию.
Как видно из выражения (2.9), начинать надо с оценива-
ния математического ожидания (среднего значения) по-
грешности гирокомпаса. Наблюдения удобно вести с не-
подвижного судна, при стоянке у причала или на якоре:
тогда результаты наблюдений не будут искажаться погреш-
ностями корректора. Поправка компаса определяется по пе-
ленгам на отдаленный ориентир или небесное светило (ис-
тинный пеленг должен быть известен с погрешностью, не
превосходящей 0,Г) каждые 10—15 мин в течение 2—3 ч,
после чего рассчитывается ее среднее арифметическое зна-
чение. Если пеленг во время измерений существенно не
изменился, то пренебречь систематическими погрешностя-
ми измерений (происходящими вследствие эксцентрисите-
та пеленгатора, непараллельности оси 0—180° репитера диа-
метральной плоскости судна, погрешностей эталонного пе-
ленга и т. д.) нельзя; вместо выражения (2.6) будем пользо-
ваться формулой
<т& = krt + аг2 + О2	(2.43)
М л 1 сист 1	о’	4	'
где Осист — дисперсия суммы систематических погрешно-
стей. Значения коэффициента k для случая, когда проме-
жуток времени между последовательными измерениями ра-
вен 10 минутам, приведены в табл. 2.2.
Таблица 2.2
Значения коэффициента k при т=10 мин, а —0,75 ч~\
Р-5,3 ч-1
п	1	2	3	4	5	10	20
k	1,0	0,78	0,55	0,35	0,20	0,06	0,03
Пример 2.2. Измерения проводились каждые 10 мин в те-
чение 3 ч (т. е. п = 19); ох ^0,5°; оСист = 0,2°;	= 0,2°. Тогда
92
по формуле (2.43) получим = 0,22 « 0,2°; тут наибольшее влия-
ние оказывают систематические погрешности измерения пеленгов.
По формуле (2.10) средняя квадратическая погрешность прогноза
окажется равной = "}/0,52 + 0,22 = 0,55°.
Если при тех же условиях предположим, что при плавании суд'
на к учету принимается результат последнего определения поправки
гирокомпаса (прогноз по последнему значению), то, как видно из
формулы (2.8), непосредственно после определения поправки сред-
няя квадратическая погрешность прогноза будет равна примерно
0,3°; через 30—40 мин она возрастет до 0,7—0,8°.
Преимущества прогноза по математическому ожиданию
в данном случае очевидны. Они станут еще более велики,
если от погрешностей мгновенного измерения (например,
пеленга) мы перейдем к рассмотрению средней за длитель-
ное время погрешности измерения курса при плавании по
счислению. Так, если длительность плавания по счислению
t = 4 ч, то влияние изменяющейся по времени составляю-
щей погрешности измерения курса, как видно из выраже-
ний (2.28), (2.33) и (2.35), будет исчезающе мало (среднее
квадратическое отклонение средней за 4 ч погрешности из-
мерения курса не превысит 0,1°). Среднее квадратическое
отклонение суммарной погрешности окажется равным: при
прогнозе по математическому ожиданию около 0,2°; при
прогнозе по последнему значению — около 0,5°.
Из всего сказанного ни в коем случае нельзя делать вы-
вод, что, определив однажды среднее значение поправки ги-
рокомпаса, можно успокоиться и при последующем пла-
вании судна вовсе ее не определять. Такой вывод нельзя не
назвать опрометчивым. Поправку гирокомпаса в море на-
до определять регулярно, и чем чаще, тем лучше. Но де-
лать это не для того, чтобы принимать к учету каждое вновь
определенное значение поправки, забыв о всех предыдущих,
а главным образом для своевременного обнаружения воз-
можных неисправностей прибора, сказывающихся на его
поправке, а также для последовательного уточнения учи-
тываемой поправки. Это можно делать, например, следую-
щим образом. Рассчитав среднее арифметическое из деся-
ти последних результатов надежных определений поправ-
ки компаса, найти разность этого значения и учитываемой
поправки гирокомпаса; придать одну пятую этой разности
к учитываемой поправке компаса:
АГХуч = ДГХ5Ч+ Ф 2	• (2-44)
93
Глава 3
СЧИСЛЕНИЕ ПУТИ СУДНА
И ЕГО КОРРЕКЦИЯ
§ 3.1	ВЛИЯНИЕ ВЕТРА НА ПУТЬ
И СКОРОСТЬ СУДНА
Учет влияния ветра и волнения моря на путь и ско-
рость судна является не только необходимой предпосылкой
точности счисления, но и основой выбора оптимального
по избранному критерию (обычно — по времени) маршрута
перехода в соответствии с прогнозом погоды. Как известно
[52], [53], уже при первых экспериментальных плаваниях
судов приближенно оптимальными маршрутами через Ат-
лантический океан сокращение времени перехода состав-
ляло в среднем 2—3%.
Выберем жестко связанную с судном систему прямоуголь-
ных координат (рис. 3.1) таким образом, чтобы ось Ох
была горизонтальна, параллельна диаметральной плоскости
и направлена к носу судна, а ось Оу горизонтальна и на-
правлена в сторону правого борта. Введем обозначения:
Кр — вектор относительной скорости (скорости пе-
ремещения судна относительно водной среды);
Vp—скорость относительного перемещения;
ccj — угол дрейфа;
VpCosa— скорость судна (продольная проекция вектора
относительной скорости)1;
W — вектор скорости относительного («кажущего-
ся») ветра, — вектор скорости потока возду-
ха, обдувающего надводную часть корпуса
судна, определяемый в системе координат,
жестко связанной с судном;
W — скорость кажущегося ветра;
— курсовой угол кажущегося ветра.
1 Здесь и далее в этом смысле употребляется термин «скорость
судна» вместо устаревшего термина «скорость хода».
94
Как известно, вектор
U скорости истинного
ветра (определяемый в
системе координат, не-
подвижной относительно
земной поверхности) из-
меняется с изменением
высоты над поверхно-
стью моря; соответству-
ющие изменения испы-
тывает и вектор W. Но
мы упрощаем модель яв-
ления, считая вектор U
всюду постоянным. Кро-
ме того, пренебрегаем
турбулентностью пото-
ка, случайными измене-
Рис. 3.1. Составляющие вектора отно-
сительной скорости
ниями вектора U во времени и в пространстве. Чтобы
уменьшать возникающие при этом погрешности, следует
измерять скорость и направление кажущегося ветра всегда
в возможно более высоко расположенной точке, где вызы-
ваемые надстройками возмущения ветрового потока мини-
мальны, в течение времени осреднения, не меньшего 100 с;
выполнять не одно, а серию таких измерений, и по ним вы-
числять среднее значение W вектора скорости кажущегося
ветра.
Дрейф. Применяемые ныне способы косвенного оцени-
вания угла ветрового дрейфа самоходного судна исходят из
следующих основных допущений:
вектор W считается не зависящим от высоты над по-
верхностью моря и неизменным по времени;
можно отвлекаться от вызываемых качкой и рысканием
судна изменений приложенных к нему сил, т. е. рассматри-
вать задачу как статическую.
Тогда зависимость между проекциями на ось Оу сумм
сил, приложенных к надводной и подводной частям корпуса
судна, выражается уравнением
^C,oPoSnV^^-CypSH№2,	(3.1)
где j)0 — плотность воды;
р — плотность воздуха;
95
Sn, — площади проекций на диаметральную пло-
скость подводной и надводной частей корпу-
са судна;
СУо» Су — коэффициенты поперечных составляющих гид-
родинамических (аэродинамических) сил,
приложенных к подводной (надводной) части
корпуса судна.
Следует различать математическую модель дрейфа —
формулу или систему формул, выражающих зависимость
угла ветрового дрейфа от аргументов qw, W, Vp, и способ
реализации этой модели. Все предложенные до сих пор мо-
дели дрейфа различаются только выражениями, которыми
аппроксимируются зависимости коэффициента Су0 от угла
дрейфа и коэффициента Су от курсового угла кажущегося
ветра. Способы реализации этих моделей можно разделить
на две группы. К первой группе относятся те, в которых
для решения уравнения (3.1) относительно угла дрейфа
используются значения коэффициентов CyQ и Су, наблю-
денные в модельном эксперименте, при продувках сдвоен-
ных моделей подводной и надводной частей судна в аэро-
динамической трубе [65, ч. 10], [19], [20]. Они позволяют
получить правильное представление о характере зависи-
мости угла дрейфа от факторов, его определяющих, но при
распространении полученных ими результатов на натуру
возможны значительные систематические погрешности, обус-
ловленные приближенностью подобия модели натуре и пре-
небрежением неравномерностью ветрового потока. В спо-
собах второй группы [38], [60] зависимости, исследованные
на модели с точностью до постоянных коэффициентов, ис-
пользуются для определения этих коэффициентов из на-
блюденных в натуре значений углов дрейфа.
Перепишем уравнение (3.1) в виде
C;/0V?, = ^W*C;/.	(3.2)
^пРо
Введем обозначения:
АТ — разность средних осадок судна: фактиче-
ской и принятой за исходную для расче-
тов, м;
L — длина судна по ватерлинии, м;
Sn(H), SH(H) — площади проекций подводной и надводной
частей корпуса при осадке, принятой за
исходную, м2.
9(5
Тогда приближенно
=	(3.3)
Sn	Sn (н)
где
= Sn(H) + SH(H) L	(3.4)
*$п (н) *$н (н)
Величина отношения SH<H) : Sn(1I) для данного судна яв-
ляется постоянной; коэффициент нетрудно подсчитать,
пользуясь чертежом продольной проекции судна. В виде,
аналогичном формуле (3.3), можно выразить и изменение
отношения SH/Sn при приеме палубного груза.
Пренебрегая изменением коэффициента Су0, происходя-
щим вследствие изменения удлинения подводной части
корпуса при отклонении осадки от расчетной (оно может
быть учтено введением дополнительного поправочного ко-
эффициента), можно считать величину Су0 функцией толь-
ко угла дрейфа, а величину Су — функцией только кур-
сового угла кажущегося ветра:
Суо = cofo (а)>	(3*5)
Су = СЛ Ы,	(3.6)
где с0, q — постоянные коэффициенты.
С. И. Демин предложил [19] за один из аргументов при
предвычислении угла ветрового дрейфа принимать не отно-
сительную скорость Vp, а ее продольную проекцию (ско-
рость судна) У*. Это безусловно целесообразно, поскольку
по принципу устройства величину Vp непосредственно из-
меряют только забортные лаги. Остальные же относитель-
ные лаги, если они правильно сконструированы и установ-
лены, должны измерять величину она же определяется
и на мерной линии. Поскольку
Vp = Vx sec а,	(3.7)
учтя выражение (3.5), (3.6) и считая отношение плотностей
воздуха и воды величиной постоянной, получим уравнение
(3.2) в виде
kf0 (а) sec2 а = (1 -k. ДТ) К (qw),	(3.8)
где k — коэффициент, постоянный для всех однотипных
судов. Таким образом, проблема сводится к решению сле-
дующих частных ^задач.
4 Зак. 1363	97
1.	Предложить наилучшие аппроксимации зависимо-
стен f0 (а) и (qw).
2.	Из результатов модельных или натурных экспери-
ментов найти значения коэффициента k и функций f0(a),
fi (<7w0-
3.	Когда они известны и аргументы W, Vx, qw заданы,
решив уравнение (3.8), найти искомый угол дрейфа а.
Формулы, которыми аппроксимируются функции f0 (а)
и (qw) в моделях дрейфа, предложенных разными авто-
рами, приведены в табл. 3.1, где символами х, хх, х2 обоз-
начены искомые коэффициенты.
Таблица 3.1
Приближенные выражения /0 (а) и f± (qw)
Автор	Аппроксимации функций	
	Ь(а)	ММ
Н. Н. Матусевич	х а	sin qw
К- К. Федяевский	*1 а+х2а3	fi (4w>
Г. В. Соболев	х (а + ^т <*2)	fi
С. И. Демин	(*1+х2 tg а)2	sin qw
Примечания: 1. Коэффициент kT вычисляется на основании тео-
ретических соображений по размерениям судна.
2. Функция fj (qw) получена осреднением результатов продувок
моделей судов нескольких типов.
Приближение Д (qw) = sin qw, принятое Н. Н. Ма-
тусевичем и С. И. Деминым, является грубым: такая за-
висимость поперечной составляющей полной аэродинамиче-
ской силы от курсового угла кажущегося ветра свойствен-
на судну, надводная часть корпуса которого представляет
собой тело вращения с вертикальной осью симметрии (ко-
нус, цилиндр, полусфера). Предложение К. К. Федяев-
ского более удачно; по его данным, относительная величина
отклонения функции fi (qw) для судов разных типов от
осредненной функции f'(qw) не превышает 10%. Значе-
ния функции fi (qw) по К. К. Федяевскому приведены
в табл. 3.2 (см. ниже).
Однако ограничиваться этим приближенным решением
не следует. Поскольку постройке любого современного суд-
96
на предшествует продувка его модели в аэродинамической
трубе, при вычислении таблиц дрейфа надо использовать
полученные там значения функции fi(qw)- В качестве при-
мера в табл. 3.3 (см. ниже) приведены значения этой функ-
ции для танкера «Крым» [58].
Из соображений симметрии ясно, что f0 (а) должна быть
нечетной функцией угла а (при положительном угле дрей-
фа поперечная проекция гидродинамической силы направ-
лена в сторону левого борта, при отрицательном — в сто-
рону правого борта; при а = 0 она равна нулю). Этому
требованию должна удовлетворять и ее аппроксимация.
Например, взяв число т достаточно большим, с любой на-
перед заданной точностью можно представить функцию
/о (а) тригонометрической суммой
/о (а) = *1 sin а + х2 sin 2а + ... + хт sin та. (3.9)
Если пользоваться современной вычислительной техни-
кой, то ни оценивание коэффициентов х2, ..., хт по ре-
зультатам модельных или натурных экспериментов, ни
затем решение уравнения (3.8) и вычисление угла а не
представят существенных трудностей. Но пока такая тех-
ника отсутствовала, вполне естественным было желание
возможно более упростить вычисления и выразить угол а
в виде явной функции аргументов W, qw, Vx или Vp. Так
возникли аппроксимации, представленные в табл. 3.1.
Многие модельные и натурные эксперименты показали,
что формула Н. Н. Матусевича дает удовлетворительное
приближение только при малых углах дрейфа, не превос-
ходящих 5—6°. Формулы К. К. Федяевского и особенно
С. И. Демина более удачны; последняя дает хорошее при-
ближение при углах дрейфа, доходящих до 20—25°. Но тре-
бование нечетности не удовлетворяется; это приводит к
заметным погрешностям предвычисления малых углов дрей-
фа.
Испытания моделей судов нескольких типов [3] показа-
ли, что при любых а от 0 до 180° функция f0 (а) вполне
удовлетворительно аппроксимируется выражением
f0 (а) = sin 2а cos а + с2 sin2 а + с3 sin4 а, (3.10)
где q, с3, с3 — коэффициенты, зависящие от формы обво-
дов подводной части корпуса судна. Если считать, что
/о (а) = ci sin a cos а + с2 sin2 а,	(3.11)
4*	99
то при углах а, достигающих 25е, погрешности вычисления
угла дрейфа, происходящие от неточности аппроксимации,
не превосходят нескольких десятых долей градуса’. Урав-
нение (3.8) принимает вид
tg а + х2 tg2 а = Л (?uz),	(3.12)
где
IV/ 2
(3.13)
г х
Решение уравнения (3.12) приводит к формуле
—+	4" ^х2^1 (Ям)	/о 1Д\
a = arctg-------------------
Коэффициенты %! и х2 являются постоянными числами,
одинаковыми для всех однотипных судов. Они могут вы-
числяться по результатам испытаний модели судна или
оцениваться способом наименьших квадратов по натурным
наблюдениям углов ветрового дрейфа. Уравнение поправок,
выражающее результаты Лго наблюдения, имеет вид
а^х + Ь^у — Ц =
Выражения для свободного члена и коэффициентов при
искомых величинах в этом уравнении легко найти из соот-
ношения (3.14) по общим правилам (1.101), (1.102): если
хс, Ус — значения коэффициентов х и у, найденные по ре-
зультатам предыдущих измерений, то
Л=(1-МЛ)-4-/1М;
V*l
Г1 = Ух^ + 41/сР{;
«ic = arctg
2</е
аг = — 57,3-----;
2^^ + ^—П Хс
ь. = —57,3----?	с——-------:
2^+2^cFi+xc-rixB
Ц = CCj ®г'С-
Конечно, выполнение этих хотя и простых, но трудо-
емких вычислений на каждом судне было бы неоправдан-
ным. При современном развитии средств связи и обработки
100
информации целесообразна централизованная обработка
результатов выполненных на судах наблюдений в учреж-
дениях, располагающих современной вычислительной тех-
никой. Конечные результаты должны представляться в
форме, удобной для практического использования, напри-
мер в виде комплекта таблиц, выражающих угол а как фук-
цию курсового угла qw и отношения W : Vx.
Если скорость судна невелика и к тому же переменна
(например, при выполнении маневра швартовки), то учет
влияния ветра на путь судна через угол дрейфа становится
неудобным. Возникает необходимость предвычисления ско-
рости дрейфа С той же относительной точностью (око-
ло 10—15%), с какой удовлетворяется приближенное ра-
венство
Wo (а) = sin а,	(3.15)
можно считать скорость дрейфа зависящей только от ско-
рости и курсового угла истинного ветра и не зависящей от
скорости судна. Действительно, при условии (3.15) урав-
нение (3.12) принимает вид
vx tg а = Vy = х3 /(1-МП	(3-16)
где х3 — постоянный коэффициент, зависящий от типа
судна;
Uy — поперечная проекция вектора скорости истин-
ного ветра.
При отношениях коэффициентов с\ : с2 : с3 выражения
(3.10), свойственных моделям судов, исследованным в рабо-
те [3], и углах дрейфа от 30 до 150° относительная погреш-
ность аппроксимации скорости дрейфа формулой (3.16) не
превышает 10%. Отыскание коэффициента х3 из натурных
наблюдений скорости дрейфа способом наименьших квад-
ратов сводится к следующим вычислениям. Если пометить
индексом i данные, относящиеся к Z-му наблюдению, и вве-
сти обозначения
а, = /(1 -^)АТ/[/аг;
h = vyi,
(3.17)
(3.18)
то
А3 — .	, >
[раа]
(3.19)
О:
[pvo]
(л — 1) [раа] ’
(3.20)
101
где pi = afj) : a/;
[pal\ = p^! + p2a2Z2 + ... + pnantn;
[paa] = pxa\ + p2a% + ... + pna%;
^i-^3 Zj,
[fiv] = p^f + p^2 + ... + Pn^n]
o(1) — произвольный коэффициент, выбираемый ис-
ходя из соображений удобства вычислений;
— средняя квадратическая погрешность z-ro из-
мерения скорости дрейфа
Изменения скорости судна от влияния ветра и волнения
моря. Скорость судна в свежую погоду определяется тремя
факторами. Во-первых, чтобы уменьшить заливание палу-
бы и силу ударов волн, избежать повреждений судна и гру-
за, приходится ограничивать мощность главных двигате-
лей или частоту вращения движителей. Статистической
характеристикой каждой ступени такого преднамеренного
снижения скорости является вероятность события, что при
данных курсовом угле и средней высоте волн будет предпри-
нято снижение скорости на данную ступень. Во-вторых,
вследствие испытываемого судном дополнительного сопро-
тивления движению гребной винт становится «тяжел»; при
той же мощности главных двигателей частота вращения
движителей становится меньшей, нежели при штиле, или,
наоборот, для поддержания той же частоты вращения тре-
буются большая мощность и больший расход топлива. В-
третьих, при той же частоте вращения движителей скорость
судна будет иной, нежели при штиле,—происходит так на-
зываемое гидродинамическое изменение скорости. Все три
фактора подвергались за последнее десятилетие обстоятель-
ным исследованиям. Особого интереса заслуживают резуль-
таты, полученные в ЦНИИМФе. В значительной мере они
освещены в обобщающем труде [62]. Поэтому остановим свое
внимание только на третьем факторе, как на типичном при-
мере систематической погрешности.
Как и прежде, будем обозначать скорость судна симво-
лом Ух; кроме того введем следующие обозначения:
— скорость судна при штиле и тех же, что теперь,
частоте вращения движителей, осадке, диффе-
ренте и состоянии подводной части корпуса
судна;
102
ДУи\в— гидродинамическое изменение скорости, обус-
ловленное влиянием ветра и волны;
Р (Ух) — УПОР» создаваемый движителями (функция ско-
рости судна);
7?1(УЖ, а) — сопротивление воды движению судна (функ-
ция скорости судна и угла дрейфа);
/?2(^, 1У) — продольная проекция суммы приложенных к
надводной части корпуса аэродинамических сил;
/?3(в) — средняя величина дополнительного сопротивле-
ния движению судна от волнения моря.
Тогда при установившемся] движении судна имеют место
равенства
Д^.в=Ух-Уш;	(3.21)
Р (Уш + Д Vw,b) = R. (У ш + Д Уц7.в, а) + /?2 (qw, W) +7?з(в).
(3.22)
При штиле qw = О, W = Уш, /?3(в) = 0; уравнение (3.22)
примет вид
р (Уш) = (Уш) + /?2 (о, Уш).	(3.23)
Решение системы уравнений (3.21)—(3.23) относительно
искомой величины АУ^,П представляет собой общий путь
предвычисления изменений скорости судна от влияния ветра
и волнения моря. При углах дрейфа, доходящих до 10°,
можно пренебречь зависимостью силы сопротивления воды
от угла дрейфа, т. е. считать (У*, а) = /?! (У*). Возни-
кающая при этом погрешность будет величиной второго по-
рядка малости [3], [58]. Ограничиваясь также первыми
членами разложения функций Р (У*) и (У*) в степенные
ряды, получим
=	№)-я2(0, Уш)+Яз(В);
(3-24)
решим это уравнение относительно искомой величины Д У^,в-
АТ,	^2 {^W* ^)—^2 (0, УШ) +Я3 (в)
ZX к Wt в — --------------------
дР дЪ
dV ~ дУ
103
С удовлетворительной точностью можно считать, что
Я2 (^, Ю = cjz (qw) IT2;	(3.26)
Я2 (О, Уш) = сх/2 (0)П;	(3.27)
= (3-28)
(329)
где с19 с2 — коэффициенты^ которые при неизменной
осадке судна практически постоянны;
Сх (7г) — значение коэффициента продольной сос-
тавляющей полной аэродинамической силы
при курсовом угле кажущегося ветра qw\
Сх (0) — то же, при qw = 0.
Выражая величины ДУ и в узлах, a IT — в метрах
в секунду, получим выражения для изменений скорости
судна от влияния ветра:
д V w == kw----------------- (3.30)
и волнения моря:
=	(3.31)
где kw, kB — коэффициенты, зависящие только от осадки
судна (при одинаковых осадках их можно считать одина-
ковыми у всех однотипных судов).
Подобно функции /i(7r), функция f2(qw) должна опре-
деляться из результатов аэродинамических продувок мо-
дели надводной части корпуса судна. У современных судов
ее значения, соответствующие одинаковым курсовым уг-
лам кажущегося ветра, различаются не очень сильно. По
этому в случаях, когда данные аэродинамических иссле-
дований модели судна отсутствуют, в качестве паллиатив-
ной меры можно пользоваться приведенными в табл. 3.2
значениями этой функции, полученными осреднением опуб-
ликованных в печати результатов продувок нескольких
моделей судов двухостровного типа, или приведенными в
104
Таблица 3.S
Значения функции f J (qw) по К. К- Федяевскому
и осредненной функции 3,78 fl (qw)
	fi (?if)	3-78 f* (?U7)		f*l (w)	3,78 f’ (<7u/)
0	0	+3,78	90	1,00	0
10	0,10	+3,93	100	0,99	—0,60
20	0,25	+4,23	ПО	0,96	—1,10
30	0,45	+4,03	120	0,88	—1,80
40	0,62	+3,80	130	0,77	—2,70
50	0,76	+3,30	140	0,62	—3,15
60	0,88	+2,60	150	0,46	—3,55
70	0,95	+1,90	160	0,27	—3,60
80	0,99	+1,10	170	0,11	—3,40
90	1,00	0	180	0	—3,10
Таблица 3.3
Значения функций fa (qw) и 3,78 f2 (q^r)
для танкера «Крым»
	Zi (?Ц?)	3.78 h (<7u?)	»U7°	Л (?uz)	3.78 f, (?U7)
0	0	+3,78	90	1,00	+0,08
10	0,04	+3,65	100	0,97	+0,02
20	0,14	+3,45	110	0,94	—0,25
30	0,38	+3,25	120	0,86	—0,90
40	0,60	+3,00	130	0,76	—1,55
50	0,77	+2,70	140	0,63	—2,10
60	0,87	+2,20	150	0,49	—2,25
70	0,94	+1,75	160	0,33	—2,40
80	0,99	+1,25	170	0,16	-2,35
90	1,00	+0,08	180	0	—2,20
табл. 3.3 результатами продувок модели танкера «Крым»
[58]. Возникающая при этом погрешность в учете влияния
ветра будет заведомо меньшей, нежели при полном пренеб-
режении этим влиянием.
В формулу (3.31) входит средняя величина 7?3(в) допол-
нительного сопротивления движению судна от волнения
моря. Простых формул для ее вычисления, которые дава-
ли бы удовлетворительную точность, пока не предложено.
Из более сложных, но зато дающих лучшую точность мето-
105
дик ее вычисления особого внимания заслуживают предло-
женные Л. С. Шифриным [63], [64] и В. Б. Липисом [36].
Оценивание коэффициентов kw и kB по результатам на-
турных наблюдений изменений скорости судна в свежую
погоду может выполняться по стандартным рекомендаци-
ям способа наименьших квадратов. Как и для вычисления
коэффициентов дрейфа, следует считать целесообразной
организацию централизованной обработки наблюденных
данных в учреждениях, располагающих современной вы-
числительной техникой.
Почему в моделях дрейфа, предложенных Н. Н. Мату-
севичем, К. К. Федяевским и другими авторами, угол дрей-
фа, а в формуле (3.30) также и потеря скорости от влия-
ния ветра выражаются как функции курсового угла и ско-
рости кажущегося ветра, а не истинного? Это естественно,
поскольку аэродинамические силы, приложенные к
надводной части корпуса судна, непосредственно зависят от
кажущегося ветра, такие выражения более просты; они
облегчают оценивание искомых коэффициентов по резуль-
татам натурных наблюдений и удобны в случаях, когда
надо оценить угол дрейфа и потерю скорости судна в не-
который настоящий момент времени, ибо на судне непосред-
ственно наблюдается кажущийся ветер, а не истинный.
Но при предварительных расчетах, например, при выборе
оптимального маршрута с учетом прогноза погоды, такая
форма выражения неудобна: для каждого намечаемого
курса надо найти курсовой угол и скорость кажущегося
ветра, а для этого надо знать, какова будет скорость судна
с учетом потерь от влияния ветра и волны; последние же
сами являются искомыми. Это затруднение можно устра-
нить, составляя таблицы изменений скорости и углов дрей-
фа не только в традиционной форме функций кажущегося
ветра, но и в виде функций истинного ветра.
Если рассматривать развитое (установившееся) вол-
нение, то все статистические характеристики ветровых
волн можно считать однозначными функциями скорости ис-
тинного ветра; соответственно изменения скорости от влия-
ния ветра и волны, как и угол дрейфа, также окажутся од-
нозначными функциями курсового угла истинного ветра и
отношения его скорости к скорости судна. Задачу придется
решать способом последовательных приближений; при
вычислениях на ЭЦВМ это не представит существенных
трудностей.
106
§ 3.2 ОПРЕДЕЛЕНИЕ СКОРОСТИ
СУДНА И ПОПРАВКИ ЛАГА
Применяемые ныне способы обработки наблюдений,
выполняемых при испытаниях ходовых качеств морских
судов, не свободны от ряда существенных недостатков. Поль-
зуясь этими способами, приходится для исключения влия-
ния изменяющегося по времени течения делать на каждом
режиме по три, четыре или даже пять пробегов, что ведет
к неоправданным затратам времени и моторесурсов. Исклю-
чение влияния ветра вовсе не предусматривается, что вы-
нуждает существенно ограничивать условия, при которых
допустимо проведение испытаний. При обработке наблю-
дений производится уравнивание лишь части погрешно-
стей измерений; апостериорное оценивание точности полу-
денных результатов не предусматривается. Неоднократно
предпринимались попытки освободиться хотя бы от части
этих недостатков применением способа наименьших квад-
ратов [17, 68], но коренного улучшения при этом достигну-
то не было.
До сих пор обработка наблюдений базируется на весьма
трудоемких ручных вычислениях с использованием лога-
рифмической линейки, не обеспечивающей должной точно-
сти, или, в лучшем случае, арифмометра. Схемы вычис-
лений не предусматривают контроля их правильности для
своевременного обнаружения промахов. Учитывая, что
полученными на мерной линии результатами приходится
потом пользоваться многие месяцы, это совершенно недо-
пустимо. При современном развитии средств вычислитель-
ной техники, которыми во все более нарастающих масшта-
бах оснащаются как пароходства, так и непосредственно
сами суда, ручная обработка наблюдений является ничем
не оправданным анахронизмом. Централизованная обра-
ботка в организациях, располагающих современными
ЭЦВМ, позволит, помимо устранения перечисленных не-
достатков, собирать и обобщать данные испытаний, отно-
сящиеся к однотипным судам, что, в свою очередь, является
предпосылкой к применению способа последовательного
уточнения оценок^искомых величин и дальнейшему повы-
шению точности; (получаемых результатов. Необходима
разработка алгоритмов машинной обработки результатов
наблюдений и формализованных схем представления наблю-
денных данных для упрощения их ввода в ЭЦВМ.
107
Впредь будем говорить об обработке наблюдений, вы-
полненных на визуальной мерной линии. Все другие спосо-
бы определения ходовых качеств судна (с использованием
РЛС, высокоточных РНС ит. д.) отличаются только измере-
ниями, выполняемыми для определения продольной проек-
ции вектора абсолютной скорости перемещения судна; по-
этому все ниже сказанное будет справедливо и для них.
Заметим, что при испытаниях ходовых качеств судов ве-
тер и течение выступают как источники систематических
погрешностей. Следовательно, мы имеем дело с одним из
частных случаев обработки наблюдений, отягощенных сис-
тематическими погрешностями. Чтобы при этом применить
современные способы обработки наблюдений, надо в пер-
вую очередь выразить зависимость между измеренными и
искомыми величинами в виде уравнений поправок. Усло-
вимся о правиле знаков. Обозначим символом i номер
пробега. Всем пробегам, выполненным (хотя бы и на разных
режимах) в одном направлении, будем приписывать не-
четные номера; пробегам, выполненным в обратном направ-
лении, — четные. Продольную проекцию вектора скорости
течения, имеющую то же направление, что нечетные про-
беги, будем считать положительной, противоположно на-
правленную — отрицательной.
Номер режима будем обозначать символом /. Для каж-
дого режима зададимся приближенным значением Vjc ско-
рости судна (например, тем, которое соответствовало на-
значенной на этом режиме частоте вращения движителей
при предыдущих испытаниях). Скорость судна, соответству-
ющую при штиле заданной на режиме частоте вращения дви-
жителей, будем отыскивать в виде
Vj = V}c + Al/,..	(3.32)
На мерной линии компасный курс судна назначается
так, чтобы истинный курс отличался от направления ство-
ров на 90°, т. е. диаметральная плоскость судна была пер-
пендикулярна линиям створов. Рассчитанная как частное
от деления расстояния между створами (длины пробега)
на время пробега скорость Vi есть средняя за время пробе-
га величина продольной проекции абсолютной скорости
(скорости перемещения судна относительно земной поверх-
ности). Введем обозначения:
Ni — средняя за время пробега частота вращения
движителей,* об/мин;
108
Nj3 — заданная на /-м режиме частота вращения дви-
жителей, об/мин;
AVrz — средняя за время i-ro пробега величина изме-
нения скорости судна от влияния ветра, уз;
vTi — средняя за время пробега величина продоль-
ной проекции скорости течения, уз;
fdV\
— —значение частной производной скорости судна
по частоте вращения движителей при Nj = 'Nj3t
уз- (об/мин)"1.
Пренебрегая изменением скорости судна от волнения мо-
ря (при значительном волнении, когда это изменение замет-
но, испытания не проводятся), выразим зависимость меж-
ду искомыми величинами и результатами наблюдений, вы-
полненных на t-м пробеге для определения скорости судна:
Vjc +	+ у; (/Vi-Л^з) + AVw< + (-	- Vit (3.33)
где (—1/+1 — величина, принимающая значение +1 при
нечетных и —1 при четных пробегах. Воспользовавшись вьь
ражением (3.30) и представив величину коэффициента kw
как сумму его значения kwc, найденного по результатам
предыдущих испытаний однотипных судов, и поправки
А/г^, определяемой теперь, получим уравнение поправок
в виде
^/2^2	( l)^1	~	(3.34)
ац = +1;	= А V/, х2 = Ай^;	(3.35)
«;2=~[Г7с-3,78/2(^) F?];	(3.36)
Vjc
li = Vi - Vjc - (A/f - tf>3) -	(3-37)
Величину Yj, входящую в выражение (3.37), можно вычис-
лить, пользуясь паспортной диаграммой ходовых харак-
теристик судна или таблицей соответствия скорости судна
частоте вращения движителей, составленной по результа-
там предыдущих испытаний, или по приближенной форму-
ле, вытекающей из известной формулы В. И. Афонасьева:
V> = 0,9-^.	(3.38)
Nj3
109
Заметим попутно, что в брошюре [1] описана устарев-
шая, не обеспечивающая должной точности, методика на-
блюдений за суммирующими счетчиками числа оборотов
гребного вала и счетчиками пройденного расстояния лага
(авторы предлагают замечать отсчеты счетчиков в начале
и конце пробега по командам «товсь», «ноль», передавае-
мым с мостика; при этом любая задержка в подаче или при-
еме команды ведет к погрешностям измерений). Более совер-
шенная методика изложена в пособии [59]: по команде «На-
чать (окончить) замеры» наблюдатели у счетчика лага, вы-
ждав, когда показание счетчика будет кратно 0,1 мили,
каждый самостоятельно пускает (в конце пробега останав-
ливает) свой секундомер, записывает отсчет лага, показа-
ние секундомера и время по судовым часам; в машине се-
кундомеры пускаются (останавливаются), когда отсчет
суммирующего счетчика будет кратен 10 оборотам. Средние
за время пробега скорость нарастания отсчета лага1 * Jit и
частота вращения движителей Nt вычисляются по фор-
мулам
Лгй =3 600= 600^4	(3.39)
4k	4k
(3.40)
где tik> fik — отсчет секундомера, зафиксированный
fe-м наблюдателем;
poAik, poCik — разность отсчетов счетчика (лага,
числа оборотов), при которых пушен
и остановлен секундомер;
п — число наблюдателей.
Напишем уравнение, выражающее зависимость между
искомыми величинами и результатами наблюдений, вы-
полненных на i-м пробеге для определения поправки лага:
+ <3-41’
1 Не следует отождествлять ее со скоростью по лагу, которая
равна скорости нарастания отсчета лага, умноженной на коэффи-
циент лага: чтобы это подчеркнуть, и введено несколько необычное
обозначение Л*.
ПО
Отсюда легко получить следующее уравнение поправок:
^^3 + (-iy+1vTi-/i2 = Vi2, (3.42)
где ai3 = Jli : 100;	(3.43)
li2 = К* — х3 = Лл;.	(3.44)
Представив зависимости между искомыми и измерен-
ными величинами в виде уравнений поправок (3.34) и (3.42),
мы получаем возможность аппроксимировать продольную
проекцию скорости течения не только степенной функцией
номера пробега, как в традиционных способах, но и любы-
ми другими функциями номера пробега или времени, в ча-
стности — тригонометрическими суммами (это важно при
испытаниях в районе, где наблюдаются значительные при-
ливные течения). Например, можно положить
^тг = *4 + Х5 si*1 05 (Л — Го) + хв cos со (Тi — То) (3.45)
или
Utz = Х4 +'х6 (Ti — то) + хв (Ti — Т0)2 + х7 (Л — То)3.
(3.46)
где хБ, xQ, x^ — искомые коэффициенты:
Ti — средний момент времени /-го пробега;
Го— произвольный момент времени, принятый
за начало счета;
со — угловая частота полусуточного или суточ-
ного прилива.
Подставив, например, выражение (3.45) в (3.34), получим
уравнение поправок в виде
“h <2i2-^2 4“ <2/4X4	4“	=	(3*47)
где au = (—1/+1; ai3 = (-I/+1 sin co (Tf - Го); (3.48)
czie = (-1/+1 cos co (Ti - Го).	(3.49)
Аналогичный вид примет уравнение (3.42). Одни и те же
искомые коэффициенты х4, х6, хб могут включаться в число
искомых величин в уравнениях поправок, составляемых по
результатам пробегов на разных режимах (если только ин-
тервалы времени между режимами не слишком велики).
Это позволит ограничиваться меньшим, чем в традиционных
способах, числом пробегов на каждом режиме (например,
111
делать по два пробега на режиме вместо трех, кагсрекомен-
дуется теперь) без ущерба для точности аппроксимации
течения и той точности, с какой будут найдены оценки ис-
комых величин.
Повышению точности оценок искомых величин может
способствовать использование других измерений, вы-
полняемых на мерной линии, и добавочных соотношений.
Так, при испытаниях нередко производится измерение кру-
тящего момента на гребных валах или упора гребных вин-
тов [17, §9, 10]. Если рассматривать конкретный греб-
ной винт фиксированного шага, установленный на конкрет-
ном судне, то при небольших углах дрейфа крутящий мо-
мент на гребном валу есть функция двух аргументов: ско-
рости хода VXi и частоты вращения Nt. Будем отыскивать
крутящий момент, соответствующий заданной на /-м режи-
ме частоте вращения гребного вала Nj3 и той скорости хо-
да Vjt которую будет иметь судно при штиле, в виде
Mj = Mjc + AMj,	(3.50)
где Mjc — счислимое (полученное при предыдущих испы-
таниях или вычисленное по результатам модель-
ных экспериментов) значение крутящего момен-
та;
AMj — искомая поправка.
Тогда зависимость между искомыми и измеренными на
i-м пробеге величинами выразится уравнением
Mi = Mjc 4- ДМ; 4- Ц; (Уя{ - У;с) + Vj (Nf - Nj3), (3.51)
где Mt — средняя величина крутящего момента по из-
мерениям на i-м пробеге;
р,;, vj — частные производные крутящего момента по
скорости судна и по частоте вращения гребно-
ного вала при V = Vjc, N = Nj3.
Заметим, что Vxi = Vi — (—l)i+1 uTj. Учитывая также
выражение (3.32) и (3.38), получим еще одно уравнение по-
правок
ai3xa + аЬ~г — li3 = Vi з.	(3.52)
где al2 = p.;ai2; х2 = &kw;	(3.53)
а1Л = +1; x3 = ДМ;;	(3.54)
/|3 = М|^М;0 (Hj'Yj	Wi	Nj3)	(3.55)
112
Значения частных производных ц, и Vj можно вычислить,
пользуясь паспортной диаграммой ходовых характеристик
судна или общими зависимостями, изучаемыми теорией греб-
ного винта.
К дополнительным соотношениям между искомыми ве-
личинами, которые могут быть использованы для повыше-
ния точности их оценок, относится известная формула
В. И. Афонасьева. Ею весьма поучительным образом вос-
пользовался для обработки наблюдений, выполненных при
испытаниях теплохода «Нефтесиндикат СССР» на прилив-
ном течении, академик А. Н. Крылов [33]. Позже в печа-
ти высказывались предложения об использовании аналогич-
ных зависимостей между авансом и отношением крутящего
момента к квадрату частоты вращения гребного вала или
между авансом и отношением мощности на валу к кубу
частоты вращения гребного вала. Но к простым и удоб-
ным способам обработки наблюдений они не привели.
Обобщив формулу В. И. Афонасьева, можно высказать
утверждение, что отношение авансов на двух разных режи-
мах при штиле, неизменных осадке и состоянии подводной
части корпуса судна есть некоторая функция отношения
частот вращения движителей:
(3.56)
Предположим, что при тех же заданных частотах вра-
щения движителей, как на /-м и /г-м режимах, выполнялись
наблюдения и на ряде предыдущих испытаний. Пусть VjC
и Vkc — средние значения полученных при этих предыду-
щих испытаниях скоростей судна, приведенных к стандарт-
ным условиям, причем именно эти скорости были введены
в качестве приближенных значений искомых величин в фор-
мулу (3.37) для вычисления свободных членов уравнений
поправок (3.34). Тогда, как следует из выражения (3.56),
с той же точностью, как это было раньше, должно удовлет-
воряться равенство
VkcSVj-V^Vk = 0,	(3.57)
что приведет к еще одной системе уравнений поправок ви-
да
QjiAVj + akAVk = vjk,	(3.58)
где	= Vkc*, ^kj ~	Vjc*	(3.59)
113
Составлению системы нормальных уравнений должно
предшествовать оценивание корреляционной матрицы по-
грешностей измерений. В качестве примера рассмотрим
оценивание элементов этой матрицы для измерений, резуль-
таты которых выражаются уравнениями поправок вида
(3.34). Тут надо учесть влияние погрешности, с которой из-
вестна длина пробега, погрешностей измерения времени
пробега и определения средней частоты вращения движи-
телей, остаточной погрешности аппроксимации продоль-
ной проекции вектора скорости течения формулой (3.45)
или (3.46). Соответствующий диагональный элемент кор-
реляционной матрицы Кд следует считать равным
Кп =	+ (^гУ <й+°3т,	(3.60)
\ ti )	\ Mi /
где о! — дисперсия погрешности, с которой известна дли-
на пробега;
о? — дисперсия погрешности измерения продолжи-
тельности пробега;
on — дисперсия погрешности определения средней
за пробег частоты вращения гребного вала;
oJT — дисперсия остаточной погрешности аппрокси-
мации продольной проекции скорости течения
формулой (3.45) или (3.46).
В измерениях, выполненных на i-м и на й-м пробегах,
общими являются погрешности длины пробега и аппрок-
симации продольной проекции скорости течения; соответ-
вующий элемент корреляционной матрицы Кд следует
полагать равным
Kth=-!- oS+(- 1)'+Мтрт(т),	(3.61)
ti th
где рт (т) — значение нормированной корреляционной
функции погрешности, с которой аппроксимируется фор-
мулой (3.45) или (3.46) средняя за время пробега величина
продольной проекции вектора скорости течения, соответ-
ствующее промежутку времени т между средними момен-
тами i-ro и ft-го пробегов.
Требованию наиболее полного использования всей имею-
щейся информации лучше всего отвечает обработка наблю-
дений способом!) (см. § 1.3). При этом корреляционная
матрица погрешностей уравнений поправок вида (3.58) мо-
жет оцениваться апостериорно по результатам предыду-
114
щих испытаний, с последующей экстраполяцией на вновь
проведенные испытания. Поскольку при испытаниях суд-
на на нескольких режимах общее число искомых величин
в системе уравнений поправок (3.34), (3.42), (3.52), (3.58)
может достигать десятка, а число уравнений поправок —
нескольких десятков, общий путь составления и решения
системы нормальных уравнений приводит к большому объ-
ему трудоемких вычислений, практически осуществимых
только на современных ЭЦВМ. Первые опыты машинной
обработки выполненных на мерной линии наблюдений дали
обнадеживающие и весьма интересные результаты. Следу-
ет надеяться, что в недалеком будущем она получит широ-
кое распространение. Там же, где такая возможность пока
отсутствует, вычисления приходится вести по сокращенной,
упрощенной схеме.
Если обрабатывать результаты выполненных на разных
режимах наблюдений раздельно, пренебречь влиянием вет-
ра и аппроксимировать продольную проекцию вектора ско-
рости течения степенной функцией номера пробега, напри-
мер, при трех пробегах на режиме положить
= х4 + (i — 1)х5,	(3.62)
то решением системы уравнений поправок вида (3.34), сос-
тавленных по трем пробегам одного режима, будет
AV/ = J-(/u + 2Z21 + /31),	(3.63)
где 1ц = Vi — VjC — yj (Nt — N}3); аналогично и реше-
ние трех уравнений вида (3.42)
Ал, = 1™+21™+1™.,	(3>64)
а13~!~^а23~1~а33
где II2 = Vt — JIt\ ais = JIt : 100.	(3.65)
Оценки скорости хода при штиле и поправки лага, к
которым приводят эти формулы, с точностью до величин
второго порядка малости совпадают с оценками, доставляе-
мыми традиционными способами обработки наблюдений.
Но вычисления будут проще, поскольку их придется вести
с величинами, имеющими меньшее число значащих цифр.
Принято считать, что об отсутствии грубых погрешностей
в наблюдениях можно судить по графику продольной про-
115
екции скорости течения: при двух пробегах на режиме пря-
мая, соединяющая нанесенные на графике точки, должна
быть примерно параллельна оси абсцисс; при трех пробегах
точки должны располагаться на одной прямой и т. д. Такое
представление не совсем правильно: эти критерии позво-
ляют судить об отсутствии грубых погрешностей только в
вычислениях, но не в наблюдениях. Но и такой контроль
несомненно полезен.
Традиционные способы обработки наблюдений преду-
сматривают вычисление продольной проекции скорости
течения только по наблюдениям, выполненным для опреде-
ления скорости судна. Но ее можно и нужно вычислять и по
наблюдениям, выполненным для определения поправки
лага. Из уравнения (3.34), пренебрегая влиянием ветра,
получим
=	ДУ7-);	(3.66)
из уравнения (3.42)
= (-l)f+1 (Цг - зАл7).	(3.67)
Теперь можно строить графики продольной проекции ско-
рости течения, вычисленной двумя способами: по формуле
(3.66) и по формуле (3.67); это позволит судить об отсутствии
грубых погрешностей в вычислении не только скорости суд-
на, но и поправки лага. Сравнение же величин, вычислен-
ных по формулам (3.66) и (3.67), позволит обнаруживать
и некоторые (не все) грубые погрешности в наблюдениях.
Пример 3.1. По результатам предыдущих испытаний ча-
стоте вращения гребного винта 120 об/мин соответствовала скорость
судна 12,09 уз; у у = AV: AW = 0,083 уз/(об/мин). Результаты вновь
выполненных на мерной линии наблюдений приведены в табл. 3.4;
расчеты скорости судна и поправ-
ки лага — в табл. 3.5 и 3.6.
Точки на обоих графиках
продольной проекции скорости те-
чения (рис. 3.2) располагаются
на прямых линиях, что свиде-
тельствует об отсутствии грубых
погрешностей в вычислениях. Но
значительные различия между ве-
личинами и v”it доходящие до
0,46 уз, говорят о неточности на-
блюдений (ее причиной явилось
неисключенное влияние ветра на
скорость судна).
Таблица 3.4
Результаты наблюдений
на мерной линии
i	vt, уз	TVp об/мин	лг. мили/ч
1	12,36	122,0	11,87
2	12,10	119,1	12,23
3	12,47	118,5	12,13 I
116
Расчеты скорости судна
Таблица 3.5
i	vi	д w£ = =Ni-N*	Ъ AJVf	V>c + +?AW£	~(Vjc + +?Д*/)	41,J- + 2Z.+Z.)	
1	12,36	+2,0	+0,17	12,26	+0,10		—0,09
2	12,10	—0,9	—0,07	12,02	+0,08	+0,19	+0,11
3	12,47	—1,5	—0,12	11,97	+0,50		+0,31
Vj = V/c + &Vj = 12,09 + 0,19 = 12,28 уз.
Таблица 3.6
Расчеты поправки лага
i	: 100	z; = v;- -*z	°1 + "F + aa	/, + 2/, + Z,	Ал	агзДЛ	гт VTi
1	0,1187	+0,49				+0,14	+0,35
2	0,1223	-0,13	0,487	+0,57	+1,2%	+0,14	+0,27
3	0,1213	+0,34				+0,14	+0,20
Суда морского промыслового и транспортного флотов
проводят испытания ходовых качеств и определение поправ-
ки лага на мерной линии редко. Необходим постоянный
контроль стабильности поправки лага и соответствия ско-
рости хода частоте вра-
щения движителей при
последующем плавании
судна. Это — одна из
задач коррекции счис-
ления, которой будет
посвящен § 3.4.
Рис. 3.2. Графики продоль-
ной проекции скорости тече-
ния:
1 — по формуле (3.67); 2 — по
формуле (3.66)
117
§ 3.3 СЧИСЛЕНИЕ ПУТИ СУДНА
Как бы ни были велики успехи науки и техники в обес-
печении возможности определения места судна в любой точ-
ке Мирового океана и в любой момент времени, как бы точ-
ны ни были обсервации, заменить счисления они не могут.
Во-первых, обсервации в лучшем случае дают возможность
судить о месте судна в любой настоящий момент време-
ни, но предвидеть, где оно окажется в будущем, позволяет
только счисление. Во-вторых, нередко погрешности счис-
ления понижают точность обсерваций, например обсерваций
по разновременным измерениям навигационных парамет-
ров и по навигационным искусственным спутникам Земли.
В-третьих, необходимой предпосылкой повышения точно-
сти обсерваций является применение оптимальных спосо-
бов обработки результатов измерений, которые существен-
ным образом основаны на использовании данных счисле-
ния (см. § 1.4). С полным основанием можно утверждать,
что без точного счисления невозможны ни точное судовож-
дение вообще, ни точные обсервации в частности.
Если счисление ведется по показаниям компаса и отно-
сительного лага, то погрешности счисления слагаются из
погрешностей измерения направления и скорости переме-
щения судна относительно водной среды и погрешностей
учета течения. Эти погрешности не остаются постоянными.
Изменение каждой из них во времени может быть описано
как случайный процесс, который в течение сравнительно
короткого промежутка времени, пока длится счисление,
не прерываемое обсервациями, можно считать практически
стационарным.
В § 2.2 уже упоминалось, что истинная погрешность из-
мерения курса судна в любой момент времени может быть
представлена как сумма двух составляющих: погрешности,
с которой известно математическое ожидание (среднее
значение) поправки гирокомпаса, и случайного отклоне-
ния ее мгновенного значения от математического ожидания.
Первая в течение всего времени, пока не будет произведена
корректировка учитываемой поправки компаса, остается
практически постоянной, т. е. проявляет свойства система-
тической погрешности; вторая испытывает случайные из-
менения по времени. Подобным образом и погрешность по-
правки лага может быть представлена как сумма постоян-
ной (систематической) составляющей и изменяющегося по
118
времени отклонения от
среднего значения. Рас-
смотрим их влияние на
точность счисления.
Постоянная погреш-
ность измерения курса
Д/Сх приводит к тому,
что все линии курсов,
проложенные на карте
(рис. 3.3), будут развер-
Рис. 33. Влияние постоянной погреш-
ности измерения курса
нуты относительно их верного положения на один и тот
же угол Д/Сх. Из равенства фигур, образованных проло-
женными на карте и истинными линиями курсов, сле-
дует, что погрешность счисления перпендикулярна вектору
Sreti генерального плавания и равна
Сх = ^%5ген,	(3.68)
о?, о
где ДЛ^ — погрешность измерения курса, градусы.
Обозначив символом а/<1 среднюю квадратическую по-
грешность в оценке математического ожидания поправки
гирокомпаса (см. § 2.2), получим выражение для оценива-
ния соответствующей векториальной погрешности счисле-
ния:
nh=-^SI№,	(3.69)
где Зген — генеральное плавание (модуль вектора Зген),
мили.
Постоянная погрешность в учете поправки лага приво-
дит к тому, что все пройденные расстояния прокладывают-
ся на карте с одной и той же относительной погрешностью;
фигура, образованная проложенными на карте линиями
курсов, будет подобна истинной и так же ориентирована
в пространстве (рис. 3.4). Соответствующая векториальная
погрешность счисления направлена вдоль вектора Зген и
равна
m2=-^-Srea,	(3.70)
2	100% гев	v
где аДл — средняя квадратическая погрешность в оценке
математического ожидания поправки лага, %.
119
Обратим внимание нй
следующее обстоятель-
ство. Вектор SreH пред-
ставл я ет собой геомет-
рическую сумму векто-
ров перемещений судна
на частных курсах. По-
этому, если надо оце-
нить векториальную по-
грешность счисления,
происходящую вследст-
вие постоянной погреш-
Рис. 3.4. Влияние постоянной по-
грешности в поправке лага
ности измерения курса, то можно поступать следующим
образом.
Векториальные погрешности счисления на частных кур-
сах оценим, пользуясь формулой (3.69); затем условно пред-
ставим каждую из них вектором, направление которого сов-
падает с повернутым на 90° по часовой стрелке направле-
нием линии курса. Нетрудно убедиться, что если геометри-
чески сложить полученные векторы и приписать их сумме
два взаимно противоположных направления (±), то по-
лучится тот же результат, что при непосредственном оцени-
вании векториальной погрешности по формуле (3.69), если
подставить туда генеральное плавание. Этот прием назовем
векторным (линейным) сложением векториальных погреш-
ностей. Его можно рассматривать как обобщение формулы
(1.17) на случай двумерных погрешностей. Аналогично мож-
но оценивать и влияние систематической погрешности в
поправке лага, но заменяя при этом векториальную погреш-
ность счисления на очередном частном курсе вектором, на-
правленным вдоль линии курса.
Случайные отклонения погрешности курсоуказания от
ее среднего значения приводят к погрешности счисления,
перпендикулярной линии курса и равной
t
Cs = \Vp(t)zK(t)dt,
о
(3.71)
где Vp (/) — скорость судна;
гк(/) — мгновенное отклонение погрешности гироком-
паса от среднего значения.
Рассматривая простейший случай, когда скорость хода
и заданный рулевому курс полагаются постоянными, можно,
120
пользуясь выражениями (2.33) и (2.35), оценить соответ-
ствующую векториальную погрешность счисления:
ms=^kVT, (3.72)
где k — коэффициент, вычисляемый по формуле (2.35).
Если считать = 0,6°, а = 0,75 ч~х, 0 = 5,3 ч“х,
Ур = 15 уз, то после 4 ч плавания она будет равна 0,2 мили.
Аналогично можно оценить погрешности неавтоматического
счисления, возникающие вследствие неучитываемого рыс-
кания судна на курсе; если отсутствует систематическое
зарыскивание на ветер или уваливание под ветер, то они
тоже невелики.
Отклонения погрешности курсоуказания от ее среднего
значения, происходящие в моменты времени, удаленные
один от другого более чем на час, практически взаимно не-
зависимы. Следовательно, если время плавания частными
курсами измеряется часами, то взаимно независимыми
можно считать и обусловленные этой причиной погрешно-
сти счисления, накапливающиеся на каждом из частных
курсов; векториальные погрешности, их характеризую-
щие, следует складывать квадратически. Правила такого
квадратического сложения, являющегося геометрической
интерпретацией сложения корреляционных матриц (см.
§1.1) и обобщения формулы (1.16) на двумерные случайные
величины, подробно освещены в ряде пособий [43, с. 61—62;
61, гл. 4; 66, с. 131—135], поэтому на них останавливаться
не будем.
Погрешность в учете ветрового дрейфа, подобно рассмот-
ренным выше погрешностям, может быть представлена в
виде суммы систематической и случайной составляющих.
Приняв за основу одну из моделей дрейфа, описанных в
§3.1, нетрудно оценить соответствующие погрешности счис-
ления.
При современном оснащении морских судов гироком-
пасами и относительными лагами наибольшее влияние на
точность счисления оказывают погрешности в учете тече-
ния. Успехи науки и техники в создании абсолютных лагов
и средств определения места судна не могут освободить мо-
реплавателей от необходимости пользоваться прогнозами
течений, хотя бы потому, что без них невозможны предвари-
тельные расчеты плавания судна. Мореплаватель должен
J2J
быть снабжен такими пособиями, которые давали бы ему
возможность решать следующие частные задачи:
предсказывать направление и скорость течения в любой
точке моря (океана) на любой заданный момент времени;
оценивать возможные отклонения фактического течения
от прогноза и погрешности счисления, к которым эти откло-
нения могут приводить.
Для предсказания течений могут применяться способы,
аналогичные рассмотренным в § 2.2: по последнему значе-
нию (учитывается вектор скорости течения, определенный
навигационным способом по невязкам обсерваций), по ма-
тематическому ожиданию (учитывается вектор течения,
выбранный из пособия), статистический прогноз по одной
точке. Чтобы применять эти способы и оценивать точность
прогноза, необходимо располагать сведениями об основных
статистических характеристиках течения.
Первой и важнейшей из этих характеристик является
оценка математического ожидания (среднего значения) век-
тора скорости течения как функция географических коор-
динат (места точки на земной поверхности), глубины гори-
зонта, сезона (месяца), поля ветра и (для приливных тече-
ний) астрономических факторов. Насколько позволяет изу-
ченность течений, сведения такого рода, приводимые в по-
собиях (атласах, таблицах течений и т. п.), запросам море-
плавания удовлетворяют.
Но необходимы и другие характеристики, подобно то-
му, как при предсказании скалярной случайной функции
надо знать, помимо ее математического ожидания, еще дис-
персию и корреляционную функцию. Таких сведений из
современных пособий мореплаватель, к сожалению, не полу-
чает. Так называемые «розы течений», приводимые во многих
атласах, практически бесполезны. Нельзя считать удач-
ными характеристиками и средние квадратические откло-
нения направления и скорости течения (если, как нередко
бывает, среднее квадратическое отклонение скорости пре-
вышает среднюю скорость течения, то понятие среднего
квадратического отклонения направления оказывается ли-
шенным смысла).
Характеристиками, аналогичными дисперсии и сред-
нему квадратическому отклонению случайной величины,
для случайного вектора служат корреляционная матрица
компонентов или эквивалентный ей средний квадратиче-
ский эллипс отклонений; корреляционной функции аиа-
122
логична многомерная корреляционная функция компонен-
тов случайного вектора, которая должна характеризовать
как временную, так и пространственную его изменчивость.
Учитывая сложность задачи, понятно стремление ее упро-
стить. В частности, если считать поле вектора скорости те-
чения приближенно стационарным и локально изотропным,
то, поскольку географические координаты движущегося
судна являются однозначными функциями времени, можно
выразить эти корреляционные функции в параметриче-
ской форме, как функции одного аргумента т—промежут-
ка между двумя моментами времени, в которые рассматри-
вается вектор скорости течения.
Погрешности счисления, порождаемые ошибками в уче-
те течения, относятся к 3-му типу погрешностей (см. §2.2)
и описаны выражением (2.20). Но там рассматривались од-
номерные (скалярные), погрешности, теперь же мы имеем
дело с двумерными (векторными).
Представим полную погрешность учета течения как гео-
метрическую сумму двух векторов:
отклонения Дит1 принятого к учету вектора скорости
течения (выбранной из пособия его оценки) от математиче-
ского ожидания вектора скорости течения;
отклонения ДиТ2 мгновенного значения вектора факти-
ческого течения] в данной точке океана в данный момент
времени от его математического ожидания.
Первая из этих погрешностей происходит главным об-
разом вследствие кратковременности и эпизодичности на-
блюдений, из которых выводятся приводимые в пособиях
оценки вектора скорости течения, вследствие неучитываемых
в прогнозах длительных, с периодами, измеряемыми меся-
цами и годами, изменений интенсивности океанских тече-
ний, смещений их главных струй и других подобных явле-
ний. Пусть судно плавает в районе, где приливные явления
незначительны, при отсутствии резких изменений поля вет-
ра. Тогда за сравнительно короткий срок, пока длится счис-
ление, не прерываемое обсервациями, рассматриваемую
погрешность Дут1 можно считать практически постоянной.
Если ат1, 6Т1 — главные полуоси среднего квадратиче-
ского эллипса, характеризующего эту постоянную погреш-
ность учета течения, то, аналогично формуле (2.29), по-
грешность счисления за промежуток времени t может быть
123
оценена так же ориентированным в пространстве средним
квадратическим эллипсом с главными полуосями
йс(т)1 = Wi ^с(т)1 =	(3.73)
Отклонение ДуТ2 вектора мгновенной скорости течения
от его математического ожидания есть проявление случай-
ной изменчивости, турбулентности морских течений; оно
испытывает случайные изменения (флуктуации) во вре-
мени и ведет к случайно изменяющимся по времени погреш-
ностям счисления. Последние удобно характеризовать,
обобщая формулу (2.33), средним квадратическим эллипсом
отклонений с главными полуосями
^с(т)2	tу &с(т)2	(3.74)
где ят2, 6т2 — главные полуоси среднего квадратического
эллипса отклонений вектора мгновенной
скорости течения от его математического
ожидания;
k — коэффициент, вычисляемый по формуле
(2.36);
t — время плавания по счислению.
Представление о порядке погрешностей дает следующий
пример.
Пусть аТ2 = Ьт2 = 0,3 уз; а =0,3 ч-1; Р = 0,4 ч~г. Тогда по формуле
(2.36) получим k = 2,2 ч°«5; ka^2 = kbT2 = 0,66 миль • ч"0-6;
средняя квадратическая погрешность счисления составит: 0,9 мили
за 1 ч плавания; 2,1 мили за 5 ч; 3,2 мили за 12 ч.
При пользовании формулой (3.74) удобно вместо вели-
чин аТ2, 6Т2 и коэффициента k пользоваться уже вычислен-
ными произведениями &ат2 и &6Т2. Следует надеяться, что
сведения о размерах полуосей и ориентировке такого при-
веденного эллипса отклонений, характеризующего слу-
чайную изменчивость течений, равно как и полуосей ат1,
6Т1 эллипса, характеризующего постоянные погрешности
учета течения, будут публиковаться в атласах и других по-
собиях по течениям. Пока же этого нет, к оцениванию этих
эллипсов можно подойти, исходя из следующих соображе-
ний.
«Розы течений», которыми отображается изменчивость
течений в современных атласах и других пособиях, сос-
тавлены в основном по результатам анализа невязок счис-
124
Ления судов, плававших в данном районе океана. Пользу-
ясь элементарными формулами теории вероятностей (оце-
нивание математических ожиданий и корреляционных мо-
ментов случайных величин по их наблюденным значениям),
нетрудно рассчитать параметры среднего квадратического
эллипса, эквивалентного «розе течений». Опыт такой харак-
теристики, предпринятый А. Е. Кошкаревым для одного
из районов Тихого океана по данным атласа [4], представ-
лен на рис. 3.5 (стрелкой показана рассчитанная по тем же
данным оценка математического ожидания вектора скорос-
ти течения). Для сравнения на рисунке показана и «роза
течений», по которой эллипс рассчитан.
Теперь сделаем следующие предположения:
а)	«роза течений» отображает распределение по восьми
главным и четвертным румбам средних (за промежуток
времени от одной обсервации до другой) значений векто-
ра скорости течения, определенных навигационным спосо-
бом (по невязкам обсерваций) плававшими в данном районе
судами (результатов инструментальных измерений тече-
ний накоплено еще немного, и отображения в пособиях они
пока практически не получили);
б)	промежуток времени от одной обсервации до другой
составлял в среднем 12 ч (от вечерних сумерек до утренних
или от утренних до вечерних), но мог доходить и до 24 ч;
Рис. 3.5. Статистические характеристики вектора скорости течения:
а — «роза течений»; б — средний квадратический эллипс отклонений
125
в)	вклад постоянных и случайно изменяющихся по вре-
мени погрешностей учета течения в образование невязки при
этом времени плавания примерно одинаков; погрешностя-
ми обсерваций в первом приближении можно пренебречь.
Если обозначить символами apt &р главные полуоси сред-
него квадратического эллипса, эквивалентного «розе тече-
ний», то в соответствии с перечисленными предположения-
ми можно считать приближенно, что
аТ1 = 0,7ар; 6Т1 = 0,7&р;
kaT2 = 2,5ар; kbT2 = 2,5&р.
Так, для примера, показанного на рис. 3.5, получим:
ат1 = 0,22 уз; &Т1 = 0,19 уз;
/гаТ2 = 0,8 мили-ч-0,5; kbTi = 0,7 мили-ч”0*5.
Ясно, что условность предположений ведет к тому, что
эти оценки можно считать лишь весьма приблизительными.
Более точные оценки, а заодно и оценки средней точности
обсерваций в данном районе океана можно получить толь-
ко путем непосредственной обработки массива наблюденных
невязок. Пока же такие данные отсутствуют, приближенно
можно считать, что в районах океана с незначительны-
ми течениями размеры полуосей аТ1, дт1 среднего квадра-
тического эллипса постоянных погрешностей учета тече-
ния не превышают 0,1—0,2 уз. В областях сильных течений
эллипс вытянут по направлению течения; его большая по-
луось может достигать 0,3—0,4 уз. Большая полуось kaT2
эллипса,характеризующего случайно изменяющиеся погреш-
ности учета течения, может достигать 0,8—1,5 мили-ч-0,5.
Решая задачу статистического прогноза течения по од-
ной точке, надо располагать оценкой корреляционной функ-
ции рт (т) компонентов среднего за время плавания по счис-
лению (от одной обсервации до другой) вектора скорости
течения. Для определенности положим это время равным
опять 12 ч. При аппроксимации формулой (2.19) параметры
этой корреляционной функции, вычисленные по данным
наблюдений [691 для одного из районов северо-западной
части Тихого океана, оказались в среднем следующими:
а = 0,15 ч-1, Р = 0,1 ч-1.
Пусть (рис. 3.6)_утп — вектор скорости течения, выбран-
ный из пособия; утп — определенный по невязкам обсер-
126
Рис. 3.6. Статистический прогноз те-
чения по одной точке
ваций. Прогноз ит век-
тора скорости течения
через промежуток вре-
мени т после последней
обсервации можно най-
ти, подобно формуле
(2.13), отложив от точки
А отрезок d=pr (O.StjH-
+ т)&, где b — длина
отрезка Л В; тх — про-
межуток времени между обсервациями, по которым найден
вектор течения vTH; (0,5тх + т) — значение нормирован-
ной корреляционной функции, соответствующее аргумен-
ту 0,5тх + т.
Изучение изменчивости течений есть весьма сложная и
трудоемкая задача, требующая длительных наблюдений:
в каждой избранной точке океана направление и скорость
течения должны измеряться неделями и месяцами; для
изучения пространственной изменчивости должны вестись
синхронные наблюдения как минимум в нескольких точках.
Изменчивость течений и, соответственно, параметры кор-
реляционных матриц (эллипсов) и корреляционных функ-
ций, ее характеризующих, в разных точках океана различ-
ны. Следует надеяться, что по мере накопления результатов
исследований они будут отображаться в адресованных мо-
реплавателям пособиях по течениям.
Рассмотренные нами погрешности счисления можно раз-
делить на следующие основные группы:
нарастающие пропорционально времени (порождаемые
постоянными погрешностями в учете течения);
нарастающие пропорционально квадратному корню от
времени (обусловленные временной и пространственной из-
менчивостью вектора скорости течения, случайными откло-
нениями погрешностей курсоуказания и измерения ско-
рости хода судна от их средних значений);
нарастающие пропорционально генеральному плаванию
(порождаемые постоянной погрешностью измерения кур-
са судна, постоянной погрешностью в поправке лага).
Поскольку преобладают по величине погрешности в уче-
те течения и, кроме того, при редких и незначительных
изменениях курса и скорости судна, что характерно для
транспортных судов, генеральное плавание практически
127
пропорционально времени плавания по счислению, ради-
альную среднюю квадратическую погрешность счисления
за время t можно аппроксимировать формулой
Mt = V^t + k2t\ ,	(3.75)
оценивая значения коэффициентов kr и k2 по невязкам счис-
ления, наблюденным при плавании в некотором данном
районе океана однотипных судов в сходных условиях.
Если постоянные погрешности учета течения или время
плавания по счислению невелики, то, пренебрегая вторым
членом в подкоренном выражении формулы (3.75), можно
положить
Mt = KcVt.	(3.76)
Значение коэффициента К с находится в пределах от
0,8 миль-ч"0’5 при плавании в районах с незначительны-
ми и хорошо изученными течениями до 2,0 миль-ч-0,5 в
районах со значительной изменчивостью течений и в шторм.
§ 3.4 ОПРЕДЕЛЕНИЕ МЕСТА СУДНА
И КОРРЕКЦИЯ СЧИСЛЕНИЯ
Общие основы обработки результатов измерений и оце-
нивания точности оценок искомых величин были рассмот-
рены в гл. 1. Теперь обратим внимание натспецифику их
приложения к задаче определения места судна, отдавая при
этом предпочтение наглядной геометрической интерпрета-
ции рассмотренных ранее зависимостей и простейшей оцен-
ке точности места — радиальной средней квадратической
погрешности.
Определение места судна по двум линиям положения
Пусть измерения навигационных параметров привели к ли^
ниям положения I и II (рис. 3.7); gr и g2 — градиенты на-
вигационных параметров. Погрешности и Д2 измерения
первого и второго навигационных параметров вызовут сме-
щения’первой и второй линий положения, равные соответ-
ственно
Anx = A_; Дп2 = А_.	(3.77)
Si	g2
Выбрав косоугольную систему координат так, чтобы ее
начало'(точка О) совпало с истинным местом судна, ось Ох
128
места по двум линиям положения
была направлена вдоль
одной линии положения,
а ось Оу—вдоль другой,
получим следующие ко-
ординаты обсервованной
точки Ко:
х = ДП1 = Д1 .
sin 0 sin 6
= Дд2 = Д2
sin 0 g2 sin 0 ’
(3.78)
где 0 — угол между гра-
диентами навигацион-
ных параметров.
Если результаты из-
мерений тщательно ис-
правляются всеми учитываемыми поправками, т. е. выпол-
няются условия (1.65) и (1.75), то М (х) = М (у) = 0: ма-
тематическое ожидание обсервованной точки совпадает с
истинным местом судна, — обсервованная точка является
несмещенной оценкой истинного места судна.
Истинной погрешностью обсервации называется ради-
ус-вектор г, начало которого — истинное место судна О,
а конец — обсервованная точка 7<о. Квадрат модуля ис-
тинной погрешности обсервации равен
г2__х2_|_^2—2ху cos 9 = —-— f—+ ——2 A1 cos9\
sin20	gl gig2 /
(3.79)
дисперсия модуля, в соответствии с определениями (1.14),
(1.22) и (1.23), равна
D (г) = М (г*) = -J- (4+4- -2Р12 — cos 4 (3-8°)
sm2 0 \ gf gf	gj g2 )
где оъ о2 —средние квадратические погрешности изме-
рений первого и второго навигационных па-
раметров;
Р12 — коэффициент корреляции погрешностей из-
мерений.
Радиальной средней квадратической погрешностью 7ИО
обсервации называется квадратный корень из дисперсии
5 Зак. 1363	129
модуля истинной погрешности обсервации (т. е среднее
квадратическое отклонение модуля радиуса-вектора г):
M0 = or = KD(r) = -L ’I/ -4 + ^--2Р12~ cos0.
sin 9 F gl gl	glg2
(3.81)
Введя обозначения средних квадратических смещений
линий положения
т1 = —; т.г = — ,	(3.82)
gl	g2
получим формулу (3.81) в виде
Л40 = —у—— К ml + ml~2p12m1m2cosQ;	(3.83)
sin О
обозначив символами llt /2 векториальные погрешности
точки 7<0—средние квадратические отклонения (от нуля)
координат х и у:
gi sin 0
^2
/1 = ]/Л1(х2) = А—21
sin 0
/2 = ГВД) = ^—
Sin 0 g-2Sin0
(3.84)
получим еще одно выражение для величины Мо:
Мо = //!2^/22-2Р12/1/2 cose.	(3.85)
Отметим своеобразие того влияния, которое оказывают
на точность обсервации случайные и систематические по-
грешности измерений. Случайные погрешности измерений
первого и второго навигационных параметров взаимно
некоррелированы: если погрешность измерения первого
параметра оказалась равной, предположим, 6П то ничего
нельзя сказать ни о знаке, ни о величине погрешности из-
мерения второго навигационного параметра. Точки пере-
сечения линий положения, соответствующих разным со-
четаниям погрешностей и 62» беспорядочно располагают-
ся вокруг точки О. Изолинии, соответствующие равным
значениям плотности вероятности совместного распределе-
ния погрешностей и 62> представляют собой эллипсы.
Поэтому говорят, что квадратическое сложение двух век-
ториальных погрешностей G и /2> выражающих влияние
130
случайных погрешностей измерений, приводит к среднему
квадратическому эллипсу погрешностей обсервованной
точки (рис. 3.8, а).
Если рассматривается влияние некоторой конкретной,
r-й систематической погрешности измерения навигационных
параметров, то вызываемые ею смещения линий положе-
ния будут равны
Дп(г) 1 = zr; Дя(г) 2 = — zr; (3.86)
gl	g2
смещение второй линии положения пропорционально сме-
щению первой линии положения:
Ди(г)2=-^Дн(г) ь	(3.87)
gzflr
где flr, f2r, gi, g2 — величины, которые для данной обсер-
вации и для данной систематической погрешности остают-
ся постоянными. Точки пересечения линий положения, со-
ответствующих разным значениям случайной амплитуды
zT остаточной систематической погрешности, располагают-
ся на одной прямой — линии действия г-й систематической
погрешности. Поэтому можно говорить, что влияние, кото-
рое оказывает на точность обсервации r-я систематическая
погрешность, характеризуется одной векториальной по-
грешностью обсервованной точки (рис. 3.8, б).
Рис. 3.8. Влияние на точность обсервации:
а — случайных погрешностей измерений; б — систематической погрешности
5*	131
Теперь вернемся к формуле (3.81). Предположив, что
измерения содержат только случайные погрешности и что
соответственно oj = сгсл1, сг2 = сгСл2; Р12 = 0» получим вы-
ражение для оценивания влияния случайных погрешно-
стей:	________________
1	ГТ 2	гу 2
М0(СЛ) =-*-]/	+	(3.88)
sine |/ g?	gi
Предположив, что измерения содержат одну r-ю систе-
матическую погрешность, и учтя соотношения (1.72)—(1.78),
получим выражение для векториальной погрешности /(г),
характеризующей влияние г-й остаточной систематической
погрешности измерения навигационных параметров:
1/ А1+4г ~2 —-cos 0 •	<з-89>
sine V gj gl g!g2
Эту формулу можно вывести и непосредственно из вы-
ражения (1.117). Рассматривая конкретные способы опре-
деления места судна, ее можно существенно упростить. Так,
если оценивается влияние постоянной систематической по-
грешности на точность определения места судна по пелен-
гам двух ориентиров, то
1(г) =----+	— 20^ cose = —,
( )	57.3° sine	12	57,3° sine
(3.90)
где Од — средняя квадратическая величина постоянной
(одинаковой во всех измерениях) систематиче-
ской погрешности измерения пеленгов;
d — расстояние между ориентирами.
В традиционном изложении теории определения места
судна, когда влиянием систематических погрешностей из-
мерений пренебрегают, принято считать, что при одинако-
вых углах между градиентами навигационных параметров
более точные линии положения приводят к более точным
обсервациям. Если же рассматривать влияние систематик
ческих погрешностей, то оказывается, что более точная ли-
ния положения иногда ухудшает точность обсервации. Это
утверждение, на первый взгляд кажущееся парадоксальным,
наглядно подтверждает рис. 3.9, на котором сплошными
показаны линии безошибочных пеленгов, пунктиром —
линии пеленгов, отягощенных постоянной систематической
132
погрешностью Лп; /Со —
обсервация по ориенти-
рам А и В; /Со — обсер-
вации по ориентирам А
и С; г± и г2— истинные
погрешности этих обсер-
ваций. Формула (3.90)
подтверждает: посколь-
ку расстояние между
ориентирами?! и С боль-
ше, нежели между ори-
ентирами А и В, обсер-
вация по ним будет ме-
нее точна, чем по ориен-
тирам А и В, хотя, ко-
нечно, измерение пелен-
га на ориентир С даст бо-
лее точную линию поло-
жения , чем пеленгова-
ние ориентира В.
Для оценивания точ-
ности обсервации с уче-
том влияния как случай-
ных, так и систематиче-
ских погрешностей изме-
рений существует два
пути, приводящих к
Рис. 3.9. Ситуация, когда более точ-
ная линия положения ведет к менее
точной обсервации
идентичным результа-
там. Первый — оценив по формуле (1.85) коэффициент
корреляции погрешностей измерений, воспользоваться за-
тем одной из формул (3.81), (3.83), (3.85). Второй путь—
оценив сначала по формуле (3.88) влияние случайных по-
грешностей измерений и по формуле (3.89) влияние каждой
из систематических погрешностей, оценить затем их сово-
купное влияние:
/s
М?(сл)+ 2	,	(3.91}
где s — число систематических погрешностей.
Оценки входящих в формулы (3.81) — (3.89) характе-
ристик осл, о>, р12 погрешностей одновременных или
почти одновременных измерений некоторых основных
навигационных параметров приведены в табл. 3.7>
133.
Т а б л и ц а 3.7
Статистические характеристики
остаточных погрешностей в совокупности одновременных измерений однородных
навигационных параметров
Навигационный параметр, прибор	Единицы из- мерения	Элементарные погрешности			Полная погрешность	
		преобладающие системати- ческие		случайные стсл	О	Р1 2
		hr	i °r			
Пеленг; гирокомпас, РЛС	о	4-1	0,5-1,6	0,2—0,3	0,6—1,7	<Н0,7±0,8)
Пеленг; магнитный компас	о	4-1	0,7—2,0	0,4—1,0	0,9—1,9	+(0,64-0,8)
Высота светила, навигационный секстан	t	4-1	0,5—1,0	0,3—0,9	0,6—1,4	+(0,6±0,8)
«Декка», ПИРС-1: днем ночью	фазовый цикл то же	—	—	—	0,05 0,1	+(0,24'0,3) +(0,24-0,8)
«Лоран-С», КПИ-4 (по огибаю- щей импульсов): поверхностные волны пространственные волны	мкс мкс	—				1,4—2,5 3,0—10,0	+0,3 +0,4
«Омега», ILA-101: днем ночью	фазовый цикл то же	—	—	—	0,04 0,06	±(0,24-0,8)
Радиопеленг, радиопеленгатор	о	+1 sin2g cos2g	0,4—0,6 0,5—1,5 0,4—0,6	0,3—1,0	0,8—2,0	±(0,14-0,8)
составленной по данным
В. Т. Кондрашихина [29,
с. 245—246] и Ю. К. Ба-
ранова [5, с. 20]. Пред-
ставление о взаимной
корреляции погрешно-
стей измерения радиопе-
ленгов, к которой ведут
систематические погреш-
ности коэффициентов ра-
диодевиации, дает рис.
3.10.
В простейшем слу-
чае, когда gx = g2 = 1
(рассматривается обсер-
Рис. ЗЛО. Взаимная корреляция по-
грешностей измерения радиопеленгов
на курсовых углах q\ и q2 при сгСл =
= 0,4°; (Та = 0,4°; О в — Ос =0,2°;
(Те = 0,4° (показаны изоли-
нии равных значений коэффициента
корреляции)
вация по высотам двух
светил), flr = hr = +1
(рассматривается влия-
ние одинаковой в обеих
линиях положения си-
стематической погреш-
ности), причем оу = о2—
= о (измерения равноточны), выражение (3.91) принимает
вид известной формулы проф. В. В. Каврайского:
Мо
sin2 0
о2
повт
г
COS2 —
2
(3.92)
где о'повт — дисперсия повторяющейся остаточной систе-
матической погрешности. Другие частные случаи формул
(3.81), (3.91) детально рассмотрены в книге В. Т. Кондра-
шихина [29].
Наглядное представление о зависимости погрешностей
определения места судна, порождаемых имеющими одина-
ковые дисперсии случайными и повторяющимися систе-
матическими погрешностями измерений, от угла 0 между
градиентами навигационных параметров дает рис. 3.11.
Формула (3.92) объясняет некоторые факты, которых
классическая теория погрешностей объяснить не в состоя-
нии. Так, судоводителям хорошо известно, что обсервации
по пеленгам двух ориентиров, расстояния до которых при-
мерно одинаковы, при угле 0 между направлениями на
135
ориентиры, близком к 150°, значительно менее точны, не-
жели при 0 = 30°, хотя согласно классической формуле
(3.88) они должны бы быть равноточны. Еще недавно неко-
торые бывалые моряки, замечая это противоречие, сове-
товали при плавании проливами избегать определений по
ориентирам, расположенным на противоположных бере-
гах, поскольку между ними «может отсутствовать геодези-
ческая привязка». Но если учесть, что при измерении пе-
ленгов преобладают по величине повторяющиеся система-
тические погрешности (рис. 3.12), то формула (3.92) под-
тверждает: при одинаковых расстояниях до ориентиров и
0 = 150° обсервация по пеленгам может оказаться в 3,7 ра-
за менее точной, неже-
ли при 0 = 30°.
Таблицы для оцени-
вания точности обсерва-
ций по двум линиям по-
ложения с учетом влия-
ния случайных и систе-
матических погрешно-
стей измерений приведе-
ны в приложении.
Обсервация по трем
и более линиям положе-
ния. Как оценить вли-
яние систематических
погрешностей измерений
на точность обсервации,
если число линий поло-
жения больше двух? Об-
щий путь оценивания
погрешностей в оценках
искомых величин, при-
годный во всех случа-
ях, выражен формулами
(1.114)—(1.117). В при-
ложении к оцениванию
точности обсервации при
любом числе линий по-
ложения он получает
следующую геометриче-
скую интерпретацию.
Пусть (рис. 3.13) /, П9
Рис. 3.11. Зависимость погрешностей
обсерваций от угла 0:
1 — порождаемых случайными погрешно-
стями измерений; 2 — порождаемых по-
стоянной систематической погрешностью
Рис. 3.12. Влияние повторяющейся си-
стематической погрешности измерений
пеленгов на точность обсервации:
/ — при 6=30°; 2 — при 0—150°
136
Ill—линии положения,
соответствующие изме-
ренным значениям на-
вигационных парамет-
ров; применение некото-
рого алгоритма (хотя
бы способа А в любой
его геометрической ин-
терпретации) привело к
обсервованной точке А.
Чтобы оценить влияние
некоторой, например г-й,
систематической погреш-
ности на точность об-
Рис. 3.13. Оценивание влияния г-й
систематической погрешности на точ-
ность обсервации
сервации, изменим каждый из навигационных парамет-
ров на величину orffr, где fir — значение координатной
функции этой систематической погрешности, соответствую-
щее условиям измерений Z-го навигационного параметра;
проложим соответствующие измененным таким образом
значениям навигационных параметров линии положения
//',	и к ним применим тот же алгоритм, каким
по исходным линиям положения получена обсервованная
точка Л. Если А' — точка, к которой он приведет, то, как
ч—►
видно из выражения (1.117), отрезок 1Т = А А' есть векто-
риальная погрешность обсервованной точки, обусловлен-
ная влиянием r-й систематической погрешности измерений.
Заметим кстати, что, применив это правило к обсервации
по двум линиям положения и выразив результат числом,
мы получим формулу (3.89).
Учет влияния систематических погрешностей сущест-
венным образом изменяет представления об относительной
точности обсерваций. Предположим, место судна определя-
ется по трем или четырем линиям положения. Если выбрать
из них две такие, точка пересечения которых, рассматри-
ваемая как самостоятельная обсервация, обладает наимень-
шей радиальной средней квадратической погрешностью по
сравнению с любой другой комбинацией исходных линий
положения, и оценивать влияние только случайных по-
грешностей измерений, то окажется, что добавление к ним
одной или двух из оставшихся линий положения умень-
шает радиальную среднюю квадратическую погрешность
обсервации не более чем на 20—30%.
6 Зак. 1363
137
Выгода от увеличения числа линий положения свыше
двух, обеспечивающих наилучшую точность обсервации,
состоит не столько в повышении точности определения мес-
та судна, сколько в обеспечении возможности обнаружения
промахов или (иногда, не всегда) аномально больших сис-
тематических погрешностей в результатах измерений. Ес-
ли же рассматривается влияние не только случайных, но
и систематических погрешностей, то выигрыш от добавле-
ния третьей или четвертой линий положения может оказать-
ся значительно более существенным. Так, при определении
места судна по пеленгам в ситуации, показанной на
рис. 3.14, из всех возможных комбинаций по две линии
положения наилучшую точность обеспечит обсервация по
ориентирам А и В. Если отношение средних квадратичес-
ких отклонений повторяющейся систематической и случай-
ных погрешностей измерения пеленгов близко к двум, что
обычно при использовании гирокомпаса, то измерение
третьего пеленга на ориентир С уменьшает радиальную
среднюю квадратическую погрешность обсервации в 1,8
раза — почти вдвое.
В § 1.4 мы уже говорили, что если число взаимно неза-
висимых измерений (при определении места судна — число
взаимно непараллельных линий положения) превышает
число «основных» искомых величин, то могут применяться
четыре способа обработки результатов измерений (отыска-
ния обсервованной точки в образованной линиями положе-
ния фигуре погрешностей), которые мы обозначили, как
способы А, В, С и D. При автоматизированной обработке
информации с использованием цифровых вычислительных
машин нет принципиальных препятствий к тому, чтобы
всегда применялся до-
ставляющий эффектив-
ные оценки искомых ве-
личин способ D.
При неавтоматизиро-
ванной же обработке ин-
формации далеко не по-
следнее место занимают
соображения простоты
применяемых алгорит-
мов и трудоемкости вы-
числений, гвследствие’че-
го обычно предпочита-
Рис. 3.14. Обсервация по пеленгам
трех ориентиров
138
ются способ А или способ В (их геометрические экви-
валенты были рассмотрены в § 1.4). Если при выборе
между способами А и В большую точность обсервован-
ного места рассматривать как выигрыш, а меньшую как
проигрыш, и считать величину выигрыша (соответственно
проигрыша) пропорциональной уменьшению (увеличению)
радиальной средней квадратической погрешности обсер-
вации по сравнению с другим альтернативным спосо-
бом, то достоинством способа А можно считать меньшую
долю риска: если, выбрав способ Л, мы проиграем, то
проигрыш будет не так велик, как тот, который возмо-
жен при неудачном выборе способа В. Достоинством
же 'способа В является предоставляемая им возможность
определить не только место судна, но и амплитуду поправ-
ки, предназначенной для компенсации исключаемой в этом
способе систематической погрешности. Количественным
критерием для выбора между способами А и В может слу-
жить отношение радиальных средних квадратических по-
грешностей доставляемых ими обсервованных точек. Таб-
лица для оценивания этих погрешностей, составленная для
частых в практике судовождения обсерваций по трем рав-
новесным линиям положения (по высотам трех светил, по
визуальным пеленгам трех равноудаленных от судна ориен-
тиров и т.д.), и пример пользования ею приведены в при-
ложении.
Рассмотрение таблицы показывает, что применение спо-
соба В может оказаться целесообразным, когда одна из сис-
тематических погрешностей измерения однородных нави-
гационных параметров заметно преобладает по величине
над остальными систематическими и над случайными по-
грешностями. Если к тому же каждый навигационный па-
раметр измеряется по несколько раз и к прокладке прини-
мается среднее арифметическое из результатов измерений,
то это преобладание становится еще более заметным. При-
знаком, его подтверждающим, является сохранение конфи-
гурации и размеров фигуры погрешностей в нескольких
выполненных одна за другой обсервациях при полной уве-
ренности в правильности опознания ориентиров. Кос-
венными признаками, позволяющими судить о допусти-
мости применения способа В, являются углы пересечения
изоразностных линий положения и величина образованной
ими фигуры погрешностей. Если углы пересечения изораз-
ностных линий положения малы, то от применения способа
6*	139
В лучше воздержаться. Большая величина образованной
изоразностными линиями положения фигуры погрешностей
свидетельствует о том, что предположение о пренебрежимой
малости случайных погрешностей измерений и всех других
систематических погрешностей, кроме исключаемой, лежа-
щее в основе способа, не подтвердилось, и его применение
нельзя считать оправданным.
Заметим, что если п — число исходных линий положе-
ния, то число взаимно независимых изоразностных линий
положения равно п — 1. Если число исходных линий по-
ложения равно трем, то изоразностные линии положения
всегда пересекутся в одной точке; возможность контроля
правильности измерений и геометрических построений по
величине фигуры погрешностей будет отсутствовать. Поэто-
му результаты, полученные из трех исходных линий поло-
жения способом В, следует подвергать особо тщательной
проверке (лучше всего —повторными обсервациями по дру-
гим комбинациям ориентиров, применяя для вычисления
поправок только что найденное значение амплитуды исклю-
чаемой в способе В систематической погрешности).
Большое влияние на точность обсервации оказывает вы-
бор ориентиров. Если ориентиры примерно равномерно
распределены по азимутам (не находятся все в одной по-
ловине горизонта), то обсервованная точка, к которой при-
водит способ В, лежит внутри образованной исходными
линиями положения фигуры погрешностей, т. е. недалеко
от точки, доставляемой способом А; дилеммы выбора меж-
ду этими способами не возникает или она не столь остра,
как в случаях, когда это условие не соблюдено. Представ-
ление о том, как это влияет на точность обсервации, дает
следующий пример.
- Пусть место судна определяется по трем примерно рав-
ноточным линиям положения (по высотам трех светил или
по пеленгам на ориентиры, расстояния до которых пример-
но одинаковы) при углах между соседними градиентами
навигационных параметров в первом случае 0Х = 02 = 60°
и во втором случае 0Х = 02 = 120°. Тогда при отношении
средних квадратических отклонений случайных и повторяю-
щейся систематической погрешностей измерений, близком
к 0,5, радиальная средняя квадратическая погрешность
второй обсервации будет меньше первой в 1,8 раза (если
учитывать влияние одних случайных погрешностей, то обе
обсервации представляются равноточными).
140
Ё случаях, когда обсервованные точки, к которым при-
водят способы А и В, далеки одна от другой, выигрыш в
точности обсервации при применении способа D по сравне-
нию с любым из первых двух может достигать 30%. Но
если применять алгоритмы, изложенные в §1.4, то этот
выигрыш достигается ценой значительного увеличения тру-
доемкости вычислений. Однако существуют способы их
существенного упрощения. Проф. В. В. Каврайский в од-
ной из своих последних работ, к сожалению, оставшейся
неопубликованной, высказал предположение, что в част-
ном случае, когда рассматривается влияние только одной
повторяющейся систематической погрешности, преобладаю-
щей по величине над остальными, вектор эффективных оце-
нок искомых величин должен отыскиваться как линей-
ная комбинация векторов, доставляемых способами А и В,
вида
XD = Хл + X (Хв - Ха),	(3.93)
где X — некоторое положительное число, не большее еди-
ницы (точка D лежит между точками Л и В на прямой, их
соединяющей). Потом удалось доказать справедливость это-
го утверждения при любом числе искомых величин и лю-
бом числе измерений (доказательства, ввиду его сложности,
приводить не будем). Эта идея, дополненная соображени-
ем М. М. Лескова о том, что эффективная оценка исключае-
мой систематической погрешности должна отыскиваться
как среднее весовое из двух ее оценок — найденной из пре-
дыдущих наблюдений и доставляемой способом исключе-
ния [35, с. 44—45], легла в основу способа отыскания об-
сервованного места, предложенного В. В. Вейхманом [12]
и затем развитого В. Т. Кондрашихиным [28]. Один из ва-
риантов таблиц готовых ответов для вычисления коэффи-
циента X и оценивания точности обсервованного места при-
веден в приложении.
Коррекция счисления. Общий алгоритм последователь-
ного уточнения оценок искомых величин, позволяющий
при каждом новом измерении получать эффективные оцен-
ки всех искомых величин, в том числе и элементов счисле-
ния (счислимого места, поправок приборов, угла ветрового
дрейфа, изменения скорости хода от влияния ветра и вол-
нения моря, вектора скорости течения), был изложен в
§ 1.4. Но его применение в полном объеме практически воз-
можно только в автоматизированных навигационных сис-
141
Кс	темах. Тут мы рассмбт-
рим два его упрощенных
t У	варианта, наиболее важ-
ных при неавтоматизиро-
Ко ванном судовождении.
а	Последовательное
уточнение счислимого
Рис. 3.15. Уточнение счислимого ме- места судна. Еще недав-
ста	но считалось, что опре-
делив место судна, всег-
да надо начинать последующее счисление от обсервованной
точки. Но факты убеждают, что далеко не всегда обсерва-
ция точнее счислимого места; нередко бывает наоборот. В
общем случае, когда точности счислимого места и обсерво-
ванной точки сравнимы, эффективные оценки искомых ве-
личин доставляет алгоритм последовательного уточнения
счислимого места. Если распределения счислимой и об-
сервованной точек являются практически круговыми (их
эллипсы погрешностей близки к окружностям), его приме-
нение сводится к очень простым вычислениям и построени-
ям.
Пусть (рис. 3.15) Ко—обсервация, Кс— счислимое
место судна на тот же момент времени; Мо, Мс — их ради-
альные средние квадратические погрешности. Вычислив
веса этих точек:
z*2	zi2
р0 = —, рс = — ,	(3.94)
Fo Mg Ис Mg ’	' ’
где d — произвольный коэффициент, назначаемый исходя
из соображений удобства вычислений, и отложив от точки
Кс отрезок
Ь =—^—d,	(3.95)
Ро + Рс
где d — длина отрезка КсКо (невязка обсервации), полу-
чим уточненное счислимое место /Су; его радиальная сред-
няя квадратическая погрешность
Му= - С—.	(3.96)
V Ро+Рс
Если через некоторый промежуток времени t будет по-
лучена еще одна обсервация, то, оценив радиальные сред-
142
ние квадратические погрешности: счисления — по форму-
ле (3.76) и счислимого места — по формуле
MC=VM*+M?,	(3.97)
мы получим возможность опять применить тот же алгоритм
и т. д.
Пример 3.2. В 04 ч. 32 мин начали счисление от обсерво-
ванной точки, радиальная средняя квадратическая погрешность ко-
торой была Л4о1 = 1,3 мили. В 08 ч. 40 мин опять определили место
судна, получив невязку 147°—3,6 мили; радиальная средняя квадра-
тическая погрешность обсервации Л4О2 = 3,0 мили. Радиальная
средняя погрешность счисления аппроксимируется формулой (3.76);
Кс = 0,8 мили . ч-0-5. Уточнить счислимое место.
По формуле (3.76): Mt =	= 1,6 мили; по формуле (3.97):
Мс = Moi + М* = 2,1 мили. Приняв с = 2,1 мили, получим
веса: счислимого места рс = 1, вновь выполненной обсервации р0—
= 0,5.
В соответствии с формулой (3.95) последующее счисление надо
начинать от точки, находящейся от счислимого места по направле-
нию 147°, на расстоянии,
0,5’’
равном---------
F 1,0 4-0,5
3,6 = 1,2 мили.
Поправка лага. Суда транспортного, промыслового,
экспедиционного флотов обычно не имеют возможности
производить определение поправок лага на мерной линии
так часто, как следовало бы, чтобы всегда знать ее с точно-
стью, соответствующей современным требованиям к точно-
сти судовождения [2, с. 41. Между тем ее изменения от од-
ного посещения судном мерной линии до другого могут
быть значительными. Поэтому приходится довольство-
ваться ее определением по расстояниям, проходимым суд-
ном между обсервациями. Как известно, оно сводится к
следующему (рис. 3.16). Пусть^счисление велось с учетом
поправки лага Алс и течения, выбранного из пособия. Если
Сх — продольная (вдоль диаметральной плоскости, т. е.
линии курса судна) проекция невязки, то разность опре-
Рис. 3,16. К уточнению поправки лага по обсервациям
ЦЗ
деленной по обсервациям и учитываемой поправки лага
равна
Лло—Ллс=	100%,	(3.98)
5Л
где 5Л — пройденное по лагу расстояние. Если рассматри-
ваются не две, а ряд обсерваций, то величину Сх в формуле
(3.98) следует полагать равной продольной проекции гео-
метрической суммы невязок.
Считая распределения погрешностей обсерваций прак-
тически круговыми и обсервации равноточными, среднюю
квадратическую погрешность определения поправки лага
этим способом можно оценивать приближенной формулой
Oa,,Q)=^/(^)-+aV.	(3.99)
где V — скорость судна';
7И0 — радиальная средняя квадратическая погреш-
ность обсервации;
t — промежуток времени между обсервациями,
по которым определяется поправка лага;
aDTx — средняя квадратическая погрешность среднего
т за время t значения продольной проекции ско-
рости течения.
Пример 3.3. Скорость судна равна 15 уз, его место опре-
деляется с радиальной средней квадратической погрешностью
0,4 мили, средняя квадратическая погрешность в учете продольной
(вдоль диаметральной плоскости судна) составляющей вектора ско-
рости течения равна 0,3 уз. При t = 4 ч средняя квадратическая
погрешность определения поправки лага составит примерно 2,1% —
точность явно неудовлетворительная.
Как показывает теоретический анализ, не более точны
и другие предложенные в последние годы способы опреде-
ления поправки лага (по обсервациям с изменением курса
судна на угол, меньший 180°, по пеленгам и расстояниям
до другого судна, курс и скорость которого полагаются по-
стоянными).
Чтобы наилучшим образом использовать хотя бы эти
малоточные результаты, и тут следует прибегать к способу
последовательного уточнения искомых величин (в данном
случае — поправки лага), например в его простейшей фор-
ме, после каждого определения поправки лага изменяя учи-
тываемую поправку лага на некоторую долю вычисляемой
Ж
по формуле (3.98) разности вновь определенного и учиты-
ваемого ее значений:
Алс(л-1) = ^^cU) “Ь k (Дл0 Алс0-)),	(3.100)
где j — номер шага итерации (уточнения учитываемого зна-
чения поправки лага).
В соответствии с общими выражениями (1.146)—(1.151)
коэффициент k следует вычислять по формулам
°Дл(с)	аДл(о)
k= Рг	(3.101)
Р1+Р2
где Одд(С)— средняя квадратическая погрешность учиты-
ваемой поправки лага;
^дл(о) — средняя квадратическая погрешность послед-
него ее определения, оценка которой выражена
формулой (3.99).
Если предположим, что такое уточнение поправки лага
осуществляется систематически, при каждой представив-
шейся возможности, и что вследствие постепенного «старе-
ния» учитываемая поправка лага постоянно известна со сред-
ней квадратической погрешностью около 0,5—1,0%, то при
прочих условиях предыдущего примера величину коэффи-
циента k следует принимать равной примерно 0,1.
§ 3.5 НЕИЗБЕЖНЫЕ ПОГРЕШНОСТИ,
ПРОМАХИ И АВАРИЙНЫЕ СИТУАЦИИ
Предупреждение навигационной аварийности есть одна
из наиболее насущных проблем современного судовождения.
Катастрофы танкеров «Торри Каньон» (март 1967 г.) и
«Амоко Кадис» (март 1978 г.), нанесшие непоправимый
ущерб природной среде, привлекли к этой проблеме вни-
мание широкой международной общественности. Не может
не тревожить и большое общее число происходящих еже-
годно аварий (статистические данные публикуются регу-
лярно; мы на них останавливаться не будем). По данным
польского исследователя Т. Ольховы, до 67% всех аварий
происходит вследствие ошибок ориентирования и предви-
дения [47]. Очевидно, тут речь идет о промахах (грубых
погрешностях) в работе судоводителей.
145
В § 1.2 уже говорилось, что в отличие от неизбежных
(случайных, зависимых, систематических) погрешностей,
промахи не являются неизбежными: их можно предупреж-
дать, а если такая погрешность все же возникла — заме-
тить; заметив — исключить из результатов наблюдений.
Промахам не присущи законы распределения вероятностей
и свойство ограниченности; их величина может быть сколь
угодно большой. Основной статистической характеристи-
кой грубой погрешности является вероятность события,
что в рассматриваемом измерении такая погрешность про-
изойдет.
Источниками промахов могут быть не только наблюда-
тель, но и внешняя среда и прибор, посредством которого
выполняются измерения. Так, в радионавигационных сис-
темах промах может возникнуть в опознании сигнала(по-
верхностный, пространственный), по которому производят-
ся измерения, и в устранении многозначности фазовых из-
мерений (опознании номера дорожки). Вероятность устра-
нения многозначности, являющаяся одной из важнейших
характеристик радионавигационной системы и условий из-
мерений [11], есть не что иное как вероятность события,
что промах не возникнет. Как известно, в современных ра-
дионавигационных системах вероятность промаха при ус-
транении многозначности отнюдь не мала: она достигает
5% днем и 40—45% ночью.
Справедливо считать промах явлением, аналогичным
сбою, отказу в работе технических средств и рассматривать
проблему промахов как проблему надежности судовожде-
ния. Следует четко различать смысл терминов «точность
судовождения» и «надежность судовождения». Когда мы
говорим о точности судовождения, то подразумеваем ха-
рактеристики неизбежных погрешностей измерений и ре-
зультатов их обработки (дисперсии, средние квадратические
отклонения и т. д.). Предметом заботы надежности судо-
вождения должны служить промахи и их вероятности.
Промахи представляют собой значительно большую уг-
розу безопасности судовождения, нежели неизбежные по-
грешности. Пусть место судна известно неточно, пусть да-
же очень неточно. Если судоводитель это сознает (оценил
точность счислимого места), то большая ошибка места суд-
на не будет для него неожиданной; он заранее примет пред-
писываемые Уставом службы на судах и рекомендуемые
хорошей морской практикой меры предосторожности и
146
продумает варианты действий для разных возможных
вариантов опасной ситуации, к которой может повести боль-
шая погрешность счислимого мёста; аварии не произойдет.
Это подтверждается опытом многих лучших мореплава-
телей старших поколений, которые без гирокомпаса, эхо-
лота, радиолокатора, при значительно худшей, нежели те-
перь, точности судовождения плавали без аварий. Промах
же, своевременно не обнаруженный, остается неосознан-
ным. Меры предосторожности не приняты — судно неожи-
данно оказывается в аварийной ситуации, к чему судово-
дитель ни психологически, ни организационно не подго-
товлен.
Точность и надежность судовождения суть хотя и раз-
ные, но тесно между собою связанные его свойства: при не-
которых условиях неизбежные погрешности могут созда-
вать предпосылки для возникновения промахов. Так, срав-
нительно небольшие, изменяющиеся случайным образом
неизбежные погрешности счисления, постепенно накапли-
ваясь, за сутки—двое, а иногда и за несколько часов при-
водят к существенной погрешности счислимого места. Суд-
но подходит к берегу; вахтенный штурман пытается опоз-
нать ориентиры. Погрешность счислимого места в течение
сравнительно небольшого промежутка времени, отделяю-
щего одну обсервацию от другой, остается практически по-
стоянной, выступает как систематическая. Если интервал
между участками берега со сходными очертаниями (такие
встречаются нередко — общеизвестны, например, Босфор
и Ложный Босфор, залив Советская Гавань и бухта Фаль-
шивая) или между ори-
ентирами со взаимно по-	А/
хожими характеристика-
ми примерно равен по-
грешности счислимого
места (рис. 3.17), то соз-
даются условия, при ко-
торых легко может про-
изойти один из самых
опасных промахов—про-
мах в опознании ориен-
тиров. Примеры тому об-
щеизвестны [31, 46, 47]. Рис. 3.17. Промах в опознании ориен-
Последовательное вы- тиРов:
/ — истинное место судна; 2 — место по
прокладке
полнение судоводителем
147
ряда элементарных действий (будем называть их шагами),
при котором каждое последующее исходит из результатов
предыдущего (последовательное нанесение на карту несколь-
ких счислимых точек или такой ряд действий: измерение
навигационных параметров, исправление их поправками,
прокладка результатов на карте) аналогично системе после-
довательно включенных элементов; промах при любом ша-
ге влечет за собой промах в конечном результате. Вероят-
ность события, что конечный результат не будет содержать
грубой погрешности, равна
Роп = п (1 —Р/)>	(3.102)
где п — число шагов;
Pi — вероятность промаха при r-м шаге.
Пример 3.4. Место судна определяется по двум линиям
положения; для этого надо выполнить как минимум восемь элемен-
тарных действий (опознание первого и второго ориентиров, измере-
ние первого и второго навигационных параметров, исправление их
поправками, прокладка двух навигационных изолиний на карте).
Промах в любом из них влечет к промаху в обсервации. Если вероят-
ность промаха при каждом шаге равна 0,02 (в действительности она
бывает и выше), то по формуле (4.1) вероятность промаха в обсерва-
ции составит 15%; в среднем каждая шестая-седьмая обсервация
будет неверной.
Но безопасности судовождения угрожает не каждый
промах сам по себе, а тот, который своевременно не был
обнаружен. Основой обнаружения промахов является дуб-
лирование измерений, вычислений, графических расчетов,
сопровождаемое сличением их результатов. Если промаха
не произойдет хотя бы в одном из взаимно друг друга конт-
ролирующих действий (будем называть их инстанциями), то
возникнет аномальное несовпадение их результатов; факт
промаха будет обнаружен. Судоводитель должен тщательно
проверить правильность всех измерений и расчетов; если
и тогда причина промаха не будет обнаружена, то, зная,
что место судна ненадежно, он своевременно может при-
нять необходимые меры предосторожности.
Рассмотрим простейший случай однократного дублиро-
вания каждого элементарного действия. Промах останется
необнаруженным, если результаты друг друга дублирую-
щих действий, хотя и будут неверными, но совпадут в пре-
делах допусков, установленных для неизбежных погрешно-
148
стей. Обозначим вероятность этого события символом рсвп.
Она не так мала, как может показаться на первый взгляд,
например, при опознании ориентиров, когда результатов
может быть только два («да» или «нет»), или в случаях, когда
взаимно друг друга дублирующие действия не являются
независимыми (оба измерения выполняются одним лицом,
которое оба раза повторяет одну и ту же ошибку). Таким
образом, при однократном дублировании вероятность со-
бытия, что факт промаха в контролируемом действии не
будет обнаружен, равна
Pi = РАрВ/Арсвп,	(3.103)
где рА — вероятность промаха в первой инстанции;
Рв/а — вероятность промаха во второй инстанции при
условии, что в первой он произойдет;
Рсвп — вероятность совпадения результатов.
Пример 3.5. При условиях примера 3.4, но при однократном
дублировании каждого действия и независимости результатов вза-
имно друг друга контролирующих действий (что достигается макси-
мальной добросовестностью и самокритичностью наблюдателя), ког-
да Рв/а = Рв* положим осторожно рсвп = 0,5; тогда вероятность
события, что при очередном шаге будет допущен необнаруженный
промах, равна 0,02%; вероятность промаха в обсервации будет
равна всего 0,16%. Если место судна определяется не по двум, а по
трем линиям положения, что даст дополнительный контроль, эта
вероятность будет еще ниже.
Не касаясь технических, инженерно-психологических
и организационных аспектов проблемы предупреждения
промахов (конструктивная и эксплуатационная надежность
приборов, рациональная конструкция их шкал и удоб-
ное расположение, меры против рассеивания внимания су-
доводителя, против вредного влияния его усталости, недо-
сыпания и т. д.), обратим основное внимание на мероприя-
тия, относящиеся к квалификации судоводителя, его про-
фессиональным навыкам. Из них наиболее важна привычка
к постоянному,^неукоснительному самоконтролю правиль-
ности всех без исключения наблюдений и расчетов:
произведя наблюдение (сняв отсчет прибора), выполнить
действие повторно и сличить результаты;
измерения, выполненные одним прибором, проверять
показаниями другого (курс’по основному компасу — кур-
сом по другому курсоуказателю, пройденное расстояние
по лагу — расстоянием, рассчитанным по скорости хода и
времени, и т. д.);
149
правильность расчетов контролировать повторным их
выполнением, как правило, — другим способом;
работу автопрокладчика контролировать ручной гра-
фической прокладкой; счислимое или обсервованное место —
сличением глубины по карте с глубиной, измеренной эхо-
лотом; место корабля, определенное одним способом —
контрольной обсервацией по другим ориентирам или дру-
гим способом (не следует увлекаться однообразными обсер-
вациями с измерениями однородных навигационных пара-
метров при неизменной комбинации ориентиров, в особен-
ности при использовании радионавигационных систем,
которым свойственна неоднозначность отсчета);
правильность путеисчисления в целом проверять изме-
рением контрольных пеленгов, расстояний, глубин, наблю-
дением за предупредительными и опасными створами и т. д.
Опознанию ориентиров, неукоснительной проверке его
правильности по всем их признакам следует всегда уделять
самое серьезное внимание. При этом учитывать возмож-
ность возникновения «стереотипа ложного представления»
[47, § 11]; для контроля первоначальных предположений
использовать все доступные способы и средства, к которым
в первую очередь относятся измерение расстояний до бе-
рега радиолокационной станцией и глубин эхолотом.
Основным способом взаимного контроля счисления и
обсерваций служит анализ невязок счисления. Вектор не-
вязки за промежуток времени t между двумя следующими
одна за другой обсервациями равен
С=72—7i —С(0,	(З.Ю4)
где гъ г3 — векторы истинных погрешностей первой и вто-
рой обсерваций;
С (/) — вектор истинной погрешности счисления за
промежуток времени между обсервациями.
Первый вопрос, возникающий при анализе, — считать
ли невязку обычной, обусловленной неизбежными погреш-
ностями счисления и определения места судна, или необыч-
ной, обусловленной промахом в одном из этих действий?
Простейший ответ дает сличение величины невязки с кри-
терием kMH) где k — коэффициент, о котором речь будет
впереди, 7ИН — оценка среднего квадратического отклоне-
ния невязки. Как видно из формулы (3.104), если обсерва-
150
цииАне содержат систематических погрешностей, последнее
равно
мн = ГМоа1+Моа2+Л4?,	(3.105)
где Л101, Л4о2 — радиальные средние квадратические по-
грешности первой и второй обсерваций;
- радиальная средняя квадратическая по-
грешность счисления за промежуток вре-
мени между обсервациями.
Если невязка не превышает величины kMH, она счита-
ется обычной, и, в зависимости от соотношения точностей
счислимого места и обсервации, дальнейшее счисление про-
должается от счислимой точки, обсервации или осреднен-
ного места. В противном случае невязка считается обуслов-
ленной промахом со всеми вытекающими отсюда послед-
ствиями (в первую очередь — причину промаха обязатель-
но надо найти и устранить). Как правильно выбрать коэф-
фициент k? При анализе обсервации мы можем совершать
ошибки двух видов.
1. Принять обычную невязку, обусловленную неизбеж-
ными погрешностями, за промах. Событие, что мы совершим
такую ошибку, противоположно событию, что обычная не-
вязка не превзойдет величины kMa. Вероятность последне-
го, ph (С <foVfH), зависит от величины коэффициента k и
соотношения полуосей суммарного эллипса погрешностей;
при нормальном распределении погрешностей измерений
ее можно оценить, пользуясь табл. 1-в Мореходных таблиц
[41]. Итак, вероятность ошибки первого вида равна
1-рк(С <kM^	(3.106)
при k = 2 она лежит в пределах от 1,8 до 4,6%; при k =
= 3 — в пределах от 0,0 до 0,3%.
2. Промах можем принять за обычную невязку. Такая
ошибка возникнет, если совместно произойдут два события:
а)	промах в счислении или в одной из обсерваций;
б)	невязка будет принята за обычную.
Вероятность рпр первого из них может быть подсчитана
по формулам (3.102), (3.103); вероятность второго равна ph.
Таким образом, вероятность ошибки второго вида равна
Рг = PvpPk-	(3.107)
151
Какая из этих ошибок опаснее? Если обычную невяз-
ку судоводитель примет за промах, он должен проверить
как счисление, так и обсервации; такая дополнительная
проверка ничего, кроме пользы, не принесет. Значитель-
но опаснее ошибка второго вида, когда промах будет при-
нят за обычную невязку. Поэтому нецелесообразно прини-
мать значение коэффициента k больше двух: если величина
невязки превышает 2Л4Н, лучше посчитать ее аномально
большой, тщательно проверить все наблюдения и расчеты,
предпринять необходимые меры предосторожности, неже-
ли оставить большую величину невязки без внимания и
обсуждения.
Анализ невязок нескольких следующих одна за другой
обсерваций позволяет обнаруживать промахи и аномально
большие систематические погрешности как в счислении,
так и в определении места судна. Перечисленные ниже при-
знаки проявляются отчетливее, если обсервации следуют
одна за другой примерно через одинаковые промежутки вре-
мени.
1.	После ряда относительно малых невязок возникла
большая, за которой опять следуют малые. Большая не-
вязка, возникшая в момент перехода от одной комбинации
ориентиров, по которым определяется место судна, к дру-
гой, или в момент изменения способа измерений, свидетель-
ствует о значительной систематической погрешности в из-
мерениях навигационных параметров, предшествовавших
большой невязке, или следовавших за ней, или и тех, и
других. Если комбинация ориентиров и способ измерений
неизменны, такая ситуация может возникнуть вследствие
скачкообразного изменения систематической погрешности
показаний одного из приборов. Распознанию причин может
способствовать определение места по другим ориентирам
или другим способом.
2.	Преобладание невязок одинакового или примерно
одинакового направления, закономерное изменение направ-
ления и величины невязок в нескольких обсервациях, вы-
полненных одним способом при неизменной комбинации ори-
ентиров, но отсутствие такой закономерности в обсерваци-
ях, выполненных разными способами или по разным комби-
нациям ориентиров, свидетельствует о систематической по-
грешности обсерваций (измерения навигационных парамет-
ров или опознания ориентиров).
152
3.	Преобладание невязок одинакового или примерно
одинакового направления, сохраняющееся при изменении
способа определения места судна или комбинации ориенти-
ров, свидетельствует о систематической погрешности счис-
ления (учета течения, учета поправок приборов).
Промах, своевременно не обнаруженный, близ берега,
навигационных опасностей, других судов может повести
к возникновению предаварийной ситуации, последняя —
перерасти в аварийную. Предупреждению и своевременно-
му обнаружению промахов, как необходимым предпосыл-
кам предупреждения навигационной аварийности, каждый
судоводитель должен уделять неослабное внимание.
ЗАКЛЮЧЕНИЕ
Подводя итоги рассмотрения проблемы систематических
погрешностей, в первую очередь обратим внимание на важ-
нейшее значение операций определения и классификации
понятий. Деление, погрешностей на обычные (неизбежные)
и необычные (промахи) приводит к выводу о необходимости
существенных различий в методах их изучения и в опреде-
лении целей борьбы с ними. Неизбежные погрешности
должны изучаться как случайные величины; целью явля-
ется уменьшение этих погрешностей и их влияния на точ-
ность конечных результатов, ради которых производятся
измерения. Промахи следует рассматривать и изучать как
случайные события; целью является предупреждение
(уменьшение вероятности) промахов, а если промах все же
случится — своевременное его обнаружение и исключение
из результатов измерений.
Предупреждение промахов оказывается весьма сущест-
венным аспектом надежности измерительных и управляющих
комплексов и систем, в частности — систем «человек—ма-
шина». Эта проблема лежит на стыке теории измерений,
теории управления, теории надежности, эргономики, ин-
женерной психологии. Поскольку промахи являются одной
из основных причин навигационных аварий, до сих пор ве-
дущих к человеческим жертвам и значительным материаль-
ным потерям, их изучению и предупреждению следует уде-
лять неослабное внимание.
Представление о систематических погрешностях как о
случайных величинах, ведущее свое начало еще от Гаусса,
но пока не получившее должного развития, открывает путь
к их изучению методами теории вероятностей и математи-
ческой статистики, к становлению одной из основ аддитив-
ной теории погрешностей — теории систематических по-
грешностей. Введение понятия остаточных систематических
погрешностей обнаруживает сущность поправок, вводимых
в результаты измерений, как взятых с обратными знаками
оценок исключаемых ими погрешностей, — оценок, к ко-
торым должны предъявляться требования несмещенности
154
и эффективности. Оказывается, что остаточные системати-
ческие погрешности представляют собой элементарные
случайные функции параметров, характеризующих усло-
вия измерений. Это, в свою очередь, влечет за собой ряд вы-
водов об их свойствах и отличиях от случайных погрешно-
стей, из которых важнейшими являются следующие.
Случайные погрешности измерений всегда искажают
оценки искомых величин и, если число измерений превышает
число искомых величин, ведут к несогласию результатов
измерений. Систематические же погрешности могут при
•некоторых условиях не искажать оценок искомых величин
и (при других условиях, несовместных с первыми) не вы-
зывать несогласия измерений (в частности, при определе-
нии места судна — не приводить к образованию фигуры
погрешностей). Следовательно, если в измерениях возмож-
ны значительные систематические погрешности, то хоро-
шее согласие результатов измерений не может считаться
признаком высокой точности оценок искомых величин (ма-
лые размеры фигуры погрешностей — признаком высокой
точности обсервации).
Поскольку систематические погрешности неизбежны и
не всегда ведут к несогласию измерений, задача их обна-
ружения в традиционной формулировке (путем анализа
вектора отклонений установить, свободны или нет изме-
рения данной совокупности от систематических погрешнос-
тей) лишена практического смысла. Она должна преследо-
вать другие цели: выявление вида координатных функций
систематических погрешностей, а когда координатные
функции известны — оценивание амплитуд и дисперсий
остаточных систематических погрешностей. Задача учета
поправок, вводимых в результаты измерений, есть по свое-
му существу задача предсказания амплитуд систематических
погрешностей; к ее решению следует привлекать аппарат
теории случайных функций.
Основным методом обработки результатов измерений,
содержащих "систематические погрешности, следует считать
способ последовательного уточнения оценок искомых ве-
личин. При этом последовательному уточнению подлежат
счислимые значения амплитуд поправок, вводимых в ре-
зультаты измерений. Способ наименьших квадратов’в’его
традиционной трактовке представляет собой частный*слу-
чай способа последовательного уточнения, соответствую-
щий предположению о пренебрежимой малости остаточных
155
систематических погрешностей. Способ .исключения систе-
матических погрешностей есть другой предельный частный
случай, соответствующий предположению о том, что опре-
деленные ранее амплитуды поправок, служащих для ком-
пенсации систематических погрешностей, не заслуживают
никакого доверия.
Как в теории систематических погрешностей, так и в ее
практических приложениях существует немало задач и
проблем, пока решенных лишь в первом приближении или
вовсе не решенных. К ним относятся, в частности, экспери-
ментальные исследования устойчивости поправок и ампли-
туд поправок во времени; продолжение статистических ис-
следований погрешностей измерения навигационных пара-
метров; исследования частостей и причин промахов в изме-
рениях, вычислениях и принятии решений судоводителя-
ми; разработка мер для уменьшения вероятностей прома-
хов и способов их своевременного обнаружения и т. д.
Судовождение принято считать не только наукой, но
искусством. Рассказы, предания и легенды о самых искус-
ных, удачливых штурманах и капитанах кораблей переда-
ются из поколения в поколение, на них воспитывается
молодежь. Их опыт учит, что познание тайн морской сти-
хии, искусство в управлении судном, высокое мастерство
судовождения никогда не приходят сами по себе и не дости-
гаются только опытом, стажем, числом пройденных миль.
Они добываются неустанным трудом, изучением наук, твор-
ческим приложением накопленных знаний к повседневной
практике.
Одним из существенных показателей профессиональ-
ного мастерства судоводителя издавна считалось искусство
выполнять измерения и обрабатывать их результаты. Ко-
ренные качественные преобразования технического оснаще-
ния судов, вызванные научно-технической революцией и
являющиеся ее проявлением, еще более увеличивают роль
измерений. По мере повышения точности измерений, с од-
ной стороны, и требований к точности судовождения — с
другой, неизбежно все большую остроту приобретает проб-
лема систематических погрешностей. Автор надеется, что
книга поможет читателю ощутить ее сложность, усмотреть
пути решения и извлечь некоторую пользу для практики.
ПРИЛОЖЕНИЕ
ВСПОМОГАТЕЛЬНЫЕ ТАБЛИЦЫ
ДЛЯ ОЦЕНИВАНИЯ ТОЧНОСТИ ОБСЕРВАЦИЙ
В таблицах приняты следующие условные обозначения:
Мо — радиальная средняя квадратическая погрешность обсер-
вации;
М0(СЛ) — радиальная средняя квадратическая погрешность обсер-
вации — оценивается влияние только случайных погреш-
ностей измерений;
/сист — векториальная погрешность обсервации (оценивается
влияние постоянной систематической погрешности изме-
рений);
Я2дП — среднее квадратическое смещение более точной линии
положения;
т*п — среднее квадратическое смещение менее точной линии
положения;
сгСл — среднее квадратическое отклонение случайных погреш-
ностей измерений;
(ТСИст — среднее квадратическое отклонение постоянной (повто-
ряющейся) систематической погрешности измерений;
р12 — коэффициент корреляции погрешностей измерений двух
навигационных параметров;
gt gu — градиент навигационного параметра;
g, gu — модуль градиента;
О — угол между градиентами навигационных параметров.
Градиенты основных навигационных параметров:
g =	(°/милю —если D в милях; °/кб—если D в кб)—
пеленг, радиопеленг;
g = 1 миля/милю, кб/кб — расстояние до ориентира;
g— 2 sin -^1миль/милю (со — угол между направлениями на
ориентиры)— разность расстояний;
(О
g = 12,3 sin мкс/милю;
g = sin -у- фаз. циклов/милю (X — линейный эквива-
лент фазового цикла в милях);
g= 17милю — высота светила.
Среднее квадратическое смещение линии положения:
Шди --	
8и
Если измеряются однородные навигационные параметры и из-
мерения равноточны, то отношение средних квадратических сме-
157
щений линий положения обратно отношению градиентов:
тлп1  g2
тлп2
Таблицы I и II предназначены для оценивания точности обсер-
вации по двум линиям положения при раздельном учете влияния по-
стоянной (повторяющейся) систематической и случайных погреш-
ностей измерений. Расчетные формулы:
Afo (сл) ~ ^лп (ел)’, ^(сист) = ^лп (сист)»
Af 0 = рГА1оа(сл) + /(сист).
Пример 1. Оценить точность обсервации по высотам двух
светил, если 0 = 45°; осл в 0,3'; осист = 0,5'.
Из табл. 1 по тл п 1т*л п = 1,0 и 0 = 45° выбираем ^=2,0;
из табл. II по тлп/щ*п = 1,0 и 0 =45° выбираем ki = 1,1; М0(СЛ) =
= 2,0 • 0,3 = 0,6 мили; /сист = 1,1 -0,5 =0,6 мили;
Мо = V 0,6а + 0,62 = 0,9 мили.
Пример 2. Оценить точность обсервации по пеленгам
двух ориентиров, если расстояния до них D± = 115 кб, Р2 = 46 кб,
разность пеленгов 0 = 30°, средние квадратические погрешности
измерений осл = 0,3°; осист = 0,4°.
Вычисляем m^n/m*n=D2/D1 = 0,4; для менее точной линии
положения gg = 57,3°/D1 = 0,5°/кб; соответствующие средние квад-
ратические смещения линии положения равны: т*л = 0,3/0,5 =
= 0,6 кб; т*ист = 0,4/0,5 = 0,8 кб. По коэффициентам и
kl, выбранным из табл. I и II
/Ио(Сл) = 2,2 •	= А3 кб; Аист = 1,4 • 0,8 = 1,1 кб;
Мо = V 1,За + 1,12 = 1,7 кб.
Таблица III предназначена для оценивания точности обсерва-
ции по двум линиям положения с учетом взаимной корреляции по-
грешностей измерений. Для оценивания коэффициента корреляции
р12 можно пользоваться табл. 3.7, рис. 3.9 или формулой
S
2 аг ?1Т f2Г
где
— дисперсия амплитуды г-й систематической погрешности;
Аг» Аг — значения координатной функции, соответствующие усло-
виям измерений первого и второго навигационных пара-
метров.
158
Таблица t
Коэффициент для оценивания точности обсервации
по двум линиям положения (учет влияния случайных
погрешностей измерений)
тлп = °Л » ^О(СЛ) =^мтлп
ёи
тлп	Угол 0, °								
	30	45	60	75	90	105	120	135	150
тлп									
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	2,0 2,0 2,1 2,2 2,2 2,3 2,4 2,6 2,7 2.8	1,4 1,4 1,5 1,5 1,6 1,6 1,7 1,8 1,9 2,0	1,2 1,2 1,2 1,2 1,3 1,3 1,4 1,5 1,6 1,6	1,0 1,1 1,1 1,1 1,2 1,2 1,3 1,3 1,4 1,5	1,0 1,0 1,0 1,1 1,1 1,2 1,2 1,3 1,3 1,4	1,0 1,1 1,1 1,1 1,2 1,2 1,3 1,3 1,4 1,5	1,2 1,2 1,2 1,2 1,3 1,3 1,4 1,5 1,6 1,6	1,4 1,4 1,5 1,5 1,6 1,6 1,7 1,8 1,9 2,0	2,0 2,0 2,1 2,2 2,2 2,3 2,4 2,6 2,7 2,8
Таблица II
Коэффициент ki для оценивания точности обсервации по
двум линиям положения (учет влияния постоянной
систематической погрешности измерений)
__ асист .	__, „»
тлп — _	1 (сиси —
ёи
тлп	Угол 0, °								
	30	45	60	75	90	105	120	135	150
т лп									
0,1	1,8	1,3	1,1	1,0	1,0	1,1	1,2	1,5	2,2
0,2	1,7	1,2	1,1	1,0	1,0	1,1	1,3	1,6	2,4
0,3	1,5	1,2	1,0	1,0	1,0	1,2	1,4	1,7	2,5
0,4	1,4	1,1	1,0	1,0	1,1	1,2	1,4	1,9	2,7
0,5	1,2	1,0	1,0	1,0	1,1	1,3	1,5	2,0	2,9
0,6	1.1	1,0	1,о	1,1	1,2	1,3	1,6	2,1	3,1
0,7	1,1	1,0	1,0	1,1	1,2	1,4	1,7	2,2	з,з
0.8	1,0	1,0	1,1	1,1	1,3	1,5	1,8	2,4	3,5
0.9	1,0	1,0	1,1	1,2	1,3	1,6	1,9	2,5	3,7
1.0	1,о	1,1	1,2	1,3	1,4	1,6	2,0	2,6	3,9
159
Таблица III
Коэффициент kM для оценивания точности обсервации
по двум линиям положения с учетом взаимной
корреляции погрешностей измерений
(Jr т
^лп =--------»	тлп
ёи
№лп	Угол 0, °, если р12>0								
	30	45	60	75 |	90 |	1 105 |	1 120 |	1 1351	| 150
/ллп				Угол 0	, °, если pi2<0				
	150	135	120	105 |	90 |	75 |	60 |	45 1	30
	IPi2I = 0,4								
0,1	1,9	1,4	1,1	1,0	1,о	1,1	1,2	1,5	2,1
0,2	1,9	1,4	1,1	1,0	1,0	1,1	1,2	1,5	2,2
0,3	1,9	1,4	1,1	1,0	1,0	1,1	1,3	1,6	2,3
0,4	1,9	1,4	1,2	1,1	1,1	1,2	1,3	1,7	2,4
0,5	1,9	1,4	1,2	1,1	1,1	1,2	1,4	1,8	2,5
0,6	1,9	1,4	1,2	1,2	1,2	1,3	1,5	1,8	2,7
0,7	2,0	1,5	1,3	1,2	1,2	1,3	1,5	1,9	2,8
0,8	2,1	1,5	1,3	1,3	1,3	1,4	1,6	2,0	3,0
0,9	2,2	1,6	1,4	1,3	1,3	1,5	1,7	2,2	3,1
1,0	2,3	1,7	1,5	1,4	1,4	1,5	1,8	2,3	з,з
	|Pi2I = 0,8								
0,1	1,9	1,3	1,1	1,0	1,0	1,1	1,2	1,5	2,1
0,2	1,7	1,3	1,1	1,0	1,0	1,1	1,3	1,6	2,3
0,3	1,6	1,2	1,1	1,0	1,0	1,1	1,3	1,7	2,5
0,4	1,6	1,2	1,1	1,0	1,1	1,2	1,4	1,8	2,6
0,5	1 ,5	1,2	1,1	1,1	1,1	1,2	1,5	1,9	2,8
0,6	1,5	1,2	1,1	1,1	1,2	1,3	1,6	2,0	3,0
0,7	1,4	1,2	1,1	1,1	1,2	1,4	1,7	2,1	3,1
0,8	1,5	1,2	1,2	1,2	1 ,з	1,5	1,7	2,3	3,3
0,9	1,5	1,3	1,2	1,2	1,3	1,5	1,8	2,4	3,5
1,0	1,6	1,3	1,3	1,3	1,4	1,6	1,9	2,5	3.7
Расчетная		формула:							
				Мо = kM m*n.					
Пример 3. Оценить точность обсервации по								Двум '	радио*
пеленгам, если средняя квадратическая погрешность измерении									
ау = 1,2 , расстояния до радиомаяков D± :						= 115 миль, D2 = 46 миль,			
160
Таблица IV
Способ А: коэффициенты kM и при обсервации по трем равноточным линиям положения
Угол 0lt°	Угол 02,°													
	0		30		60		90		120	|		150		180	
	М	kl	м	1 ki 1	м		Л1	kl	Л1	1 1	Л1	ki	Л1	kl
30	2,45	1,04	1,55	1,09	1,23	1,24	1,22	1,53	1,55	2,04	2,44	2,02	2,46	1,99
60	1,42	1,15	1,23	1,24	1,15	1,33	1,22	1,40	1.41	1,16	1,55	0,29	1,42	1,15
90	1,22	1,41	1,22	1,53	1,22	1,40	1,22	1,00	1,23	0,41	1,23	0,41	1,22	1,00
120	1,41	2,00	1,55	2,04	1,41	1,16	1,23	0,41	1,15	0,00	1,22	0,41	1,41	1,15
150	2,44	3,84	2,44	2,02	1,55	0,29	1,23	0,41	1,22	0,41	1,54	0,29	2,43	1,96
Таблица V
Способ В: коэффициенты и kz при обсервации по трем равноточным линиям положения
	Угол 02,°													
Угол 01(°	0		30		60		90		120		150		180	
	kM 1 1	kz	м		fe м		м		м	feF	kM	^F	kM 1	
30	.					9,27	8,37	4,95	3,87	3,63	2,24	3,06	1,30	2,83	0,71	2,83	0,70
60	—	—	4,95	3,87	2,59	1,74	1,90	1,04	1,64	0,71	1,56	0,60	1,63	0,71
90	—	—	3,63	2,24	1,90	1,04	1,42	0,71	1,25	0,60	1,25	0,60	1,41	0,71
120			—	3,06	1,30	1,64	0,71	1,25	0,60	1,15	0,58	1,25	0,60	1,63	0,71
150	—	—	2,83	0,71	1,56	0,60	1,25	0,60	1,25	0,60	1,55	0,60	2,80 I	0,70 1
Таблица VI
Способ D: отношение К коэффициенты kM и Kz при обсервации по трем равноточным
линиям положения
Угол 6lte	Угол в,, °														
	30°			60°			90°			120е			150°		
	к		kz		м	&Z	к	L. М			Axz М	kz	к	k Л1	
тЛП(СИСТ) * ШЛП(СЛ) 0’5
30	0,00	1,64	1,00	0,02	1,37	0,99	0,05	1,43	0,98	0,13	1,82	0,93	0,33	2,58	0,82
60	0,02	1,37	0,99	0,08	1,32	0,96	0,19	1,38	0,90	0,33	1,49	0,82	0,41	1,55	0,77
90	0,05	1,43	0,98	0,19	1,38	0,90	0,33	1,29	0,82	0,41	1,24	0,77	0,41	1,24	0,77
120	0,13	1,82	0,93	0,33	1,49	0,82	0,41	1,24	0,77	0,43	1,15	0,76	0,41	1,23	0,77
150	0,33	2,58	0,82	0,41	1,55	0,77	0,41	1,24	0,77	0,41	1,23	0,77	0,41	1,55	0,77
180	0,33	2,59	0,82	0,33	1,49	0,82	0,33	1.29	0,82	0,33	1,49	0,82	0,33	2,56	0,82
тлп(сист) : тЛП(СЛ) °’7
30	0,01	1,73	1,00	0,03	1,49	0,98	0,09	1,59	0,95	0,23	1,99	0,88	0,49	2,64	0,71
60	0,03	1,49	0,98	0,14	1,44	0,93	0,31	1,47	0,83	0,49	1,53	0,71	0,58	1,56	0,65
90	0,09	1,59	0,95	0,31	1,47	0,83	0,49	1,32	0,71	0,58	1,24	0,65	0,58	1,24	0,65
120	0,23	1,99	0,88	0,49	1,53	0,71	0,58	1,24	0,65	0,60	1,15	0,64	0,58	1,24	0,65
150	0,49	2,64	0,71	0,58	1,56	0,65	0,58	1,24	0,65	0,58	1,24	0,65	0,58	1,55	0,65
180	0,50	2,65	0,71	0,50	1,53	0,71	0,50	1,32	0,71	0,50	1,52	0,71	0,50	2,62	0,71
^ЛТЦСИСТ) : тлП(СЛ)~1,0
30	0,01	1,89	0,99	0,06	1,71	0,97	0,17	1,85	0,91	0,37	2,23	0,79	0,67	2,71	0,58*
60	0,06	1,71	0,97	0,25	1,63	0,87	0,48	1,59	0,72	0,67	1,56	0,58	0,74	1,56	0,51
90	0,17	1,85	0,91	0,48	1,59	0,72	0,67	1,36	0,58	0,74	1,24	0,51	0,74	1,24	0,51
120	0,37	2,23	0,79	0,67	1,56	0,58	0,74	1,24	0,51	0,75	1,15	0,50	0,74	1,24	0,51
150	0,67	2,71	0,58	0,74	1,56	0,51	0,74	1,24	0,51	0,74	1,24	0,51	0,74	1,55	0,51
180	0,67	2,71	0,58	0,67	1,56	0,58	0,67	1,35	0,58	0,67	1,56	0,58	0,67	2,68	0,58
тЛП(СИСТ> : ^ЛЩСЛ) 1’5
30	0,03	2,24	0,98	0,13	2,12	0,93	0,31	2,26	0,83	0,57	2,53	0,65	0,82	2,77	0,43
60	0,13	2,12	0,93	0,43	1,90	0,76	0,68	1,71	0,57	0,82	1,60	0,43	0,86	1,56	0,37
90	0,31	2,26	0,83	0,68	1,71	0,57	0,82	1,38	0,43	0,86	1,25	0,37	0,86	1,25	0,37
120	0,57	2,53	0,65	0,82	1,60	0,43	0,86	1,25	0,37	0,87	1,15	0,36	0,86	1,24	0,37
150	0,82	2,77	0,43	0,86	1,56	0,37	0,86	1,25	0,37	0,86	1,24	0,37	0,86	1,55	0,37
180	0,82	2,77	0,43	0,82	1,60	0,43	0,82	1,38	0,43	0,82	1,59	0,43	0,82	2,73	0,43-
тлп(сист) : тлп(сл)
30	0,05	2,63	0,97	0,21	2,52	0,89	0,44	2,58	0,75	0,70	2,70	0,54	0,89	2,79	0,33
60	0,21	2,52	0,89	0 ,57	2,09	0,66	0,79	1,78	0,46	0,89	1,61	0,33	0,92	1,56	0,29
90	0,44	2,58	0,75	0,79	1,78	0,46	0,89	1,40	0,33	0,92	1,25	0,29	0,92	1,25	0,29
120	0,70	2,70	0,54	0,89	1,61	0,33	0,92	1,25	0,29	0,92	1,15	0,28	0,92	1,25	0,29
150	0,89	2,79	0,33	0,92	1,56	0,29	0,92	1,25	0,29	0,92	1,25	0,29	0,92	1,55	0,29
180 )	0,89	2,79	0,33	0,89	1,61	0,33	0,89	1,39	0,33	0,89	1,60	0,33	0,89	2,76	0,33
курсовые углы На радиомаяки qY = 70б, q2 = 130°, отношения
средних квадратических погрешностей амплитуд радиодевиации те
же", что на рис. 3.9.
Вычисляем т'л п /ш* п =D2/Di = 0,4; для менее точной линии
положения gy = 57,372?! = 0,5 7милю; среднее квадратическое
смещение линии положения /п*п = 1,2/0,5 = 2,4 мили. На рис. 3.9
Р12 = — 0,4; из табл. III для р “ — 0,4, 0 — 60° находим kM —
= 1,3;
Л40 = ймтл*п = 3,1 мили.
Таблицы IV — VI предназначены для оценивания точности обсер-
ваций, полученных способами А,В и D по трем равновесным линиям
положения, отягощенным постоянной (повторяющейся) систематиче-
ской и случайными погрешностями. В них используются, помимо
перечисленных выше, следующие условные обозначения:
^1» 02 — углы между направлениями среднего и двух других
градиентов;
oz — средняя квадратическая погрешность, с которой в спо-
собах В и D определяется поправка, служащая для ком-
пенсации постоянной систематической погрешности;
X — отношение, в котором надо разделить отрезок между
точками, полученными способами 4 и В, чтобы найти
обсервованную точку по способу D.
Расчетные формулы:
способ А
Af0 (СЛ) —	^(сл)*» ^(СИСТ) = tfl(CMCT) » о =
— Мо(сл) + ^(сист);
способ В
Мо	СГсл»
способ D
М q =	ГЩсл))	^СИСТ*
П р и м е р 4. Место судна определяется по высотам трех све-
тил; преобладает постоянная систематическая погрешность измере-
ний, оСист = 0,6'» среднее квадратическое отклонение случайных
погрешностей измерений осл = 0,4'; 02 = 02 = 60°.
Способ А: 2И0(сл) = 1,15 * 0,4 = 0,46 мили; /сист = 1,33 X
X 0,6 = 0,8 мили; Мо = 0,92 мили.
Способ В: Мо = 2,59 • 0,4 = 1,03 мили; ог = 1,74 • 0,6 =
= 1,0'.
Способ D: X = 0,43; Мо = 1,9-0,4 = 0,76 мили;
о2 = 0,76 • 0,6 = 0,45'.
Пример 5. Место судна определяется по пеленгам трех
ориентиров, расположенных на примерно одинаковых расстояниях
от судна; углы между направлениями на ориентиры 02 = 02 =
= 120°, поправка гирокомпаса известна со средней квадратической
погрешностью осист= 0,4°; среднее квадратическое отклонение
случайных погрешностей измерения пеленгов осл = 0,6°.
164
Обсервованные точки, найденные способами А и Й, совпадают.
Применяя способ А, мы считаем причиной образования треуголь-
ника погрешностей случайные погрешности пеленгования. Поправ-
ка гирокомпаса корректировке не подлежит. Ее средняя квадрати-
ческая погрешность останется прежней (<т~ = 0,4°).
Пусть найденная способом В дополнительная поправка к тому
значению поправки компаса, которое учитывалось ранее, оказалась
равна А2/С(^). Из табл. V выбираем: k~, = 0,58. Следовательно,
средняя квадратическая погрешность поправки компаса, найденной
способом В, равна — k~, асл — 0,58-0,6 = 0,35°.
Z Z
Из табл. VI по осист: осл = 0,7 находим X = 0,60; k~ = 0,64.
Следовательно, чтобы найти эффективную оценку мгновенного зна-
чения поправки компаса, надо изменить поправку компаса, которая
учитывалась ранее, на величину 0,60 А2^(В)* Средняя квадратиче-
ская погрешность этой оценки равна /г£ОсисТ = 0,64 • 0,4 = 0,25°.
Решая вопрос о том, какую поправку компаса учитывать в даль-
нейшем, надо иметь в виду сказанное в § 2.2 о трех способах прог-
ноза.
СПИСОК ЛИТЕРАТУРЫ
1.	Авербах Н. В., Баранов Ю. К- Определение ма-
невреных элементов морского судна и поправки лага. М., Транспорт,
1970, 85 с.
2.	Автоматизация судовождения. Под ред. А. А. Якушенкова.
М., Транспорт, 1967. 364 с.
3.	Анисимова Н. И. Позиционные гидродинамические
характеристики судов при произвольных углах дрейфа. — Судо-
строение, 1968, № 5, с. 4—8.
4.	Атлас поверхностных течений северо-западной части
Тихого океана. Л., УНГС, 1959. 13 с.
5.	Б а р а н о в Ю. К. Использование радиотехнических
средств в морской навигации. М., Транспорт, 1978. 224 с.
6.	Безобразов А. И. Автокорреляция ошибок ра-
дионавигационного приемоиндикатора СПР-1. — Тр. ЦНИИМФ,
1966. вып. 73, с. 84—98.
7.	Беляев Б. Н., Болдырев В. С. Применение те-
ории случайных функций к изучению морских течений. — Океаноло-
гия, 1963, т. III, вып. 6, с. 953—961.
8.	Б е н д а т Дж., П и р с о л А. Измерение и анализ слу-
чайных процессов. М., Мир, 1974. 464 с.
9.	Бронштейн И. Н., Семендяев К. А. Справоч-
ник по математике. М., ГИТТЛ. 1954. 608 с.
10.	Б у х а н о в с к и й И. Л. Навигационные ошибки. М.,
Морской транспорт, 1960. 141 с.
11.	Б ы к о в В. И., Никитенко Ю. И. Судовые ра-
дионавигационные устройства. М., Транспорт, 1976. 399 с.
165
12.	В ейхман Ё. В. Нахождение вероятного места прй
определении места по трем звездам. — Мор. флот, 1966, № 8, с.
19—21.
13.	Власов В. Д. Интерпретация систематических ошибок
геодезических измерений как элементарных случайных функций. —
Известия ВУЗ, Геодезия и аэрофотосъемка, 1969, вып. 5, с. 63—70,
14.	Выгодский М. Я. Справочник по высшей математи-
ке. М., Наука, 1977. 871 с.
15.	Гаусс К . Ф. Избранные геодезические сочинения. Т. I.
М., Геодезиздат, 1957. 152 с.
16.	Г с л ь м е р т Ф. Р. Уравновешивание по способу наи-
меньших квадратов. М., 1914. 320 с.
17.	Г и р с И. В., Ру се цк ий А. А., Нецве-
та ев Ю. А. Испытания мореходных качеств судов. Л., Судо-
строение, 1977. 191 с.
18.	ГОСТ 16263—70. Метрология. Термины и определения. М.,
Г КС, 1970.
19.	Д е м и н С. И. Предвычисление угла дрейфа судна. —
Информационный сборник ЦНИИМФ, 1966, вып. 155, с. 16—43.
20.	Д е м и н С. И. Результаты продувки подводной части
модели теплохода «Ленинский комсомол» в аэродинамической тру-
бе. — Тр. ЦНИИМФ, 1968, вып. 91, с. 64—76.
21.	Д р а л о в Г. Радиодевиация и причины, изменяющие ее.—
Мор. флот, 1958, № 12, с. 5—8.
22.	Д ь я к о н о в В. Ф., Черниев Л. Ф., Демин А. П.
Применение способа наименьших квадратов для решения задач
судовождения. — Судовождение, 1974. вып. 14, с. 67—73.
23.	Д ь я к о н о в В. Ф., Черниев Л. Ф., Де-
мин А. П. Об определении места судна по трем звездам и плане-
там. — Судовождение, 1974, вып. 15, с. 19—35.
24.	Е ф и м о в А. Н. Предсказание случайных функций.
М., Знание, 1976. 64 с.
25.	3 у р а б о в Ю. Г. Определение взаимной корреляции
ошибок измерений в фазовых РНС. — Тр. ЦНИИМФ, 1970, вып.
124, с. 14—25.
26.	3 у р а б о в Ю. Г. Статистические характеристики радио-
навигационной информации приемоиндикатора «ПИРС-1>. — Тр.
ЦНИИМФ, вып. 97, 1968. с. 24—35.
27.	Колмогоров А. Н. К обоснованию метода наимень-
ших квадратов. — Успехи математических наук, 1946, т. I, вып. I
(11) с. 57—70.
28.	К о н д р а ш и х и н В. Т. Определение места судна по
высотам трех светил. — Мор. флот, 1967, № 3, с. 12—14.
29.	К о н д р а ш и х и н В. Т. Теория ошибок и ее приме-
нение к задачам судовождения. М., Транспорт, 1969. 256 с.
30.	К о н д р а ш и х и н В. Т. Уравнивание косвенных вза-
имозависимых измерений способом наименьшей квадратичной фор-
мы.— Тр. ЦНИИМФ, 1966, вып. 69, с. 19—38.
166
31.	Короткий И. М. Аварии и катастрофы кораблей.
Л., Судостроение, 1977. 296 с.
32.	Красавцев Б. И. Мореходная астрономия. М.,
Транспорт, 1968. 408 с.
33.	Крылов А. Н. Некоторые замечания об обработке про-
грессивных испытаний судов.— Собр. трудов. Т. IX, ч. 2. М.—Л.,
1949, с. 132—143.
34.	Крылов А. Н. Теория и практика.— В кн.: Воспоми-
нания и очерки. М., Изд. АН СССР, 1956, с. 759—760.
35.	Л е с к о в М. М., Г а в р ю к М. И. Ошибки навига-
ционных определений. М., «Транспорт», 1964, 136 с.
36.	Л и п и с В. Б. Расчет дополнительного сопротивления
судна на нерегулярном волнении. — Тр. ЦНИИМФ, 1977, вып. 221,
с. 43—61.
37.	М а л и к о в С. Ф., Тюрин Н. И. Введение в метро-
логию. М., Стандарты, 1966. 247 с.
38.	М а т у с е в и ч Н. Н. Методы определения угла ветро-
вого дрейфа малых кораблей.— В сб.: Материалы по дрейфу и рыс-
кливости кораблей при ветре и волне. М.—Л., Гидрометеоиздат,
1946, с. 48—135.
39.	М а т у с е в и ч Н. Н. О некоторых систематических
ошибках измерений и методы исключения их влияния. — Записки
по гидрографии, 1946, №3, с. 87—102.
40.	Монин А. С., К а м е н к о в и ч В. М., Корт В. Г.
Изменчивость Мирового океана. Л., Гидрометеоиздат, 1974. 262 с.
41.	Мореходные таблицы МТ—75. Изд. ГУНИО МО,
1975, 322 с.
42.	Навигационная вычислительно-управляющая си-
стема МВУ-3. М., Транспорт, 1971. 64 с.
43.	Н и к о л а е в А. В. Оценка точности плавания судов
флота рыбной промышленности. М., Пищевая промышленность,
1977. 143 с.
44.	Новые технические средства судовождения. Под ред.
А. А. Якушенкова. М., Транспорт, 1973. 264 с.
45.	О з м и д о в Р. В. Горизонтальная турбулентность и
турбулентный обмен в океане. — Тр. Института океанологии АН
СССР, 1961. с. 52
46.	П е т р о в М. К- Предупреждение посадки судов на мель.
М., Морской транспорт, 1956. 175 с.
47.	Пономарев В. Е. Человек и безопасность судовож-
дения. М., Транспорт, 1976. 152 с.
48.	П у г а ч е в В. С. Введение в теорию вероятностей. М.,
Наука, 1968. 368 с.
49.	Р ы б а л т о в с к и й Н. Ю. Математическая обработка
задач судовождения. Л., Морской транспорт, 1959. 191 с.
50.	С а з о н о в А. Е., Филиппов Ю. М. Комплекси-
рование навигационных измерений. Л., Судостроение, 1966. 56 с.
»	51. Сазонов А. Е., Филиппов Ю. М. Строгое по-
следовательное уточнение счислимого места в случае разновремен-
ных линий положения. — Судовождение, 1962, вып. 2, с. 65—69.
52.	С а й ф у л л и н Б. И. Результаты экспериментального
плавания судов оптимальными путями в северной части Атлантиче-
ского океана. — Информационный сборник ЦНИИМФ, 1967,
вып. 167, с. 3—12.
167
53.	Сайфуллин Б. И. Статистическая оценка результа-
тов экспериментального плавания иаивугоднейшими путями. —
Информационный сборник ЦНИИМФ, 1967, вып. 185, с. 11—22.
54.	Симановский Б. Г. Средства промыслового судо-
вождения. М., Пищевая промышленность, 1976. 223 с.
55.	С т е п а н о в Н. Эффективность использования техниче-
ских средств судовождения в морях Дальневосточного бассейна.—
Мор. флот, 1966, № 3, с. 16—17.
56.	С т е ф у т и н С. А. Статистическое исследование гиро-
компаса в судовых условиях. — Информационный сборник
ЦНИИМФ, 1967, вып. 188, с. 39—42.
57.	Т о п а л о в В. П. Определение места судна по радиопе-
ленгам. М., Транспорт, 1975. 63 с.
58.	Трещевский В. Н., Волков Л. Д.» Корот-
кий А. И. Аэродинамический эксперимент в судостроении. Л.,
Судостроение, 1976. 190 с.	'
59.	Ф а т ь я н о в А. И. Практическое руководство по вы-
верке и определению поправок штурманских приборов. М.» Транс-
порт, 1976. 303 с.
60.	Ф е д я е в с к и й К. К. Простой приближенный способ
определения угла дрейфа самоходного судна. — В сб.: Материалы
по дрейфу и рыскливости кораблей при ветре и волне. М.—Л.,
Гидрометеоиздат, 1946, с. 32—47.
61.	Филиппов Ю. М., Сазонов А. Е. Теоретиче-
ские основы автоматизации судовождения. Л., Судостроение, 1971.
312 с.
62.	Ш а п а е в В. М. Гидрометеорологические условия и мо-
реплавание. М., Транспорт, 1975. 248 с.
63.	Ш и ф р и н Л. С. Приближенный расчет дополнитель-
ного сопротивления судна на регулярном волнении.—Судострое-
ние, 1973. № 12, с. 5—7.
64.	Ш и ф р и н Л. С. Моделирование на ЭВМ дополнитель-
ного сопротивления судна в условиях морского волнения. — Судо-
строение, 1975, № 1, с. 13—17.
65.	Ш у л е й к и н В. В. Физика моря. М., изд. АН СССР,
1953. 989 с.
66.	Ю щ е н к о А. П. Способ наименьших квадратов. Л.,
Морской транспорт, 1956. 164 с.
67.	Ю щ е н к о А. П., Лесков М. М. Навигация. М.,
Транспорт, 1972. 360 с.
68.	А е г t s s е n G. The regression method of analysis of
measured mile trials. — «Transport» (Belg.), V. 7, 1967—69, № 5.
69.	Data of the oceanographic observations. Maizuru marine
observatory. 1972. 846 c.
ОГЛАВЛЕНИЕ
Введение................................................. 3
Основные условные обозначения ........................... 5
Глава 1. Основы обработки результатов измерений ...	6
§ 1.1.	Математические основы теории систематических
погрешностей............................................. 6
§ 1.2.	Основные свойства погрешностей измерений ...	18
§ 1.3.	Свойства оценок искомых величин и вектора от-
клонений 	51
§ 1.4.	Способы обработки результатов измерений .... 45
Глава 2. Навигационные измерения.........................67
§2.1.	Задача обнаружения систематических погрешно-
стей 	67
§ 2.2.	Определение и учет поправок	приборов......73
Глава 3. Счисление пути судна и его коррекция .... 94
§ 3.1.	Влияние ветра на путь и скорость судна .... 94
§ 3.2.	Определение скорости пути судна и поправки
лага	107
§ 3.3.	Счисление пути судна......................118
§ 3.4.	Определение места судна и коррекция счисления 128
§ 3.5.	Неизбежные погрешности, промахи и аварийные
ситуации................................................145
Заключение..............................................154
Приложение..............................................157
Список литературы.......................................165
МАРК ИВАНОВИЧ СКВОРЦОВ
Систематические погрешности в судовождении
Рецензент Г. Г. Ермолаев
Редактор И. Я. Мартьянова
Технический редактор С. В. Ахмеджанова
Корректоры; О. Ю. Голотынина, Т. А. Мальцева
ИБ № 1656
Сдано в набор 10.08.79.	Подписано в печать 08.04.80.	Т-02093
Формат 84ХЮ8'/э2. Бум. тип. № 2. Гарнитура литературная. Высокая печать.
Уел. печ. л. 8,82. Уч.-изд. л. 9,29. Тираж 6000 экз. Заказ 1363. Цена 45 коп.
Изд. № 1-3-1/11 № 9659.
Издательство «ТРАНСПОРТ», 107174, Москва, Басманный туп., 6а________________
Московская типография № 4 Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли,
г. Москва, 129041, Б. Переяславская, д. 46