А.М.БОГОМОЛОВ, В.Н.САЛИЙ
АЛГЕБРАИЧЕСКИЕ
ОСНОВЫ ТЕОРИИ
ДИСКРЕТНЫХ
СИСТЕМ
МОСКВА
НАУКА•ФИЗМАТЛИТ
1997
ББК 22.14
Б74
УДК 512.5

Издание осуществлено при поддержке
Российского фонда фундаментальных
исследований по проекту 97-01-14099
Богомолова. М., С а л и й В.Н. Алгебраические основы теории
дискретных систем.—М.: Наука. Физматлит, 1997.—368 с.—ISBN 5-02-015033-9.
Наряду с дискретной математикой современная прикладная алгебра является
одним из главных инструментов теории систем. В книге выделен алгебраический
материал, который наиболее широко используется в этой области: булевы алгебры
и алгебры отношений, полугруппы и решетки, многоосновные и частичные алгебры,
категории, функциональные системы, универсально-алгебраические конструкции.
При этом в качестве основных моделей конечной системы рассматриваются ориен-
тированный граф и детерминированный автомат.
Может служить справочным пособием для научных работников, аспирантов и
инженеров, а также для студентов университетов и высших технических учебных
заведений.
Ил. 121. Библиогр. 90 назв.
Рецензент
доктор физико-математических наук А.А. Разборов
Научное издание
БОГОМОЛОВ Анатолий Михайлович
САЛИЙ Вячеслав Николаевич
АЛГЕБРАИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ДИСКРЕТНЫХ СИСТЕМ
Редактор Ф.И. Кизнер
Корректор О.Ф. Алексеева
ИБ № 41866
ЛР № 020297 от 27.11.91. Подписано в печать 08.09.97. Формат 60 x 90/16.
Бумага офсетная. № 1. Печать офсетная. Усл. печ. л. 23. Усл. кр.-отт. 23.
Уч.-изд. л. 25,3. Тираж 1000 экз. Заказ № 2313	С-030.
Издательская фирма «Физико-математическая литература» РАН
117071 Москва В-71, Ленинский проспект, 15
Отпечатано в Московской типографии № 2 РАН
121099 Москва Г-99, Шубинский пер., 6
„ 1602040000-030
Б—053(02)—97—61‘98- Наука, I полугодие
© А.М.Богомолов, В.Н.Салий,
1997
ISBN 5-02-015033-9
ОГЛАВЛЕНИЕ
Предисловие .......................................................... 4
Введение ............................................................. 5
Г л а в а 1. Множества и отношения .................................. 13
§	1.1.	Булевы алгебры ...................................... 13
§	1.2.	Алгебры отношений ................................... 30
§	1.3.	Отношения эквивалентности............................ 50
§	1.4.	Упорядоченные множества.............................. 68
Г л а в а 2. Алгебраические	системы ................................. 91
§	2.1.	Основные конструкции универсальной алгебры .......... 91
§	2.2.	Полугруппы.......................................... 116
§	2.3.	Группы и кольца..................................... 136
§	2.4.	Решетки............................................. 157
§	2.5.	Функциональные системы.............................. 182
§	2.6.	Частичные и многоосновные алгебры. Кагтегории ...... 203
Г л а в а 3. Графы.................................................. 227
§ 3.1.	Основные алгебраические конструкции................. 227
§ 3.2.	Неориентированные графы ............................ 246
§ 3.3.	Специальные пути в ориентированных графах .......... 265
§ 3.4.	Направленные графы ................................. 284
Г л а в а 4. Автомдтм	................................ 307
§ 4.1.	Гомоморфизмы и конгруэнции ......................... 307
§ 4.2.	Некоторые оптимизационные задачи для автоматов ....	325
§ 4.3.	Алгебраические свойства автоматов общего вида ...... 340
§ 4.4.	Представление языков в автоматах.................... 355
Список литературы................................................... 365
ПРЕДИСЛОВИЕ
Наряду с дискретной математикой современная прикладная
алгебра является одним из главных инструментов математической
кибернетики. Булевы алгебры и алгебры отношений, полугруппы
и решетки, многоосновные и частичные алгебры, категории,
универсально-алгебраические конструкции,—с этим постоянно
приходится сталкиваться читателю научной и технической лите-
ратуры. В последние годы зарубежные издательства выпустили
большое число книг, в которых систематически излагаются
основные сведения о тех или иных из указанных разделов
абстрактной алгебры и которые ориентированы на пользователя,
работающего со сложными дискретными системами. На русском
языке было издано лишь написанное в 1970 г. пособие Г. Биркгофа
и Т. Барти «Современная прикладная алгебра» (М.: Мир, 1976).
Авторы предлагаемой книги ставят перед собой цель в какой-то
степени восполнить создавшийся в отечественной литературе су-
щественный пробел. Основываясь на своем опыте исследователь-
ской и преподавательской работы, а также учитывая высказанные
специалистами пожелания, они выделили тот алгебраический
материал, который наиболее широко используется в теоретических
и прикладных работах по теории систем. Авторы стремились изло-
жить этот материал по возможности просто, но без тяжелых мате-
матических потерь. Для иллюстраций привлечено большое число
примеров прикладного характера, заимствованных из оригиналь-
ных работ, в частности, по технической диагностике. При этом
в качестве основных моделей конечной системы рассматриваются
ориентированный граф и конечный детерминированный автомат.
Все содержащиеся в книге математические предложения снабжены
подробными доказательствами, разбор которых поможет читателю
творчески освоить идеи и методы прикладной алгебры. В списке
литературы указаны работы, непосредственно использованные при
написании текста.
Книга предназначена для научных работников, аспирантов и
инженеров, работающих в областях, связанных с исследованием
дискретных систем. Она может служить также пособием для сту-
дентов соответствующих специальностей, обучающихся в универ-
ситетах и высших технических учебных заведениях.
Авторы выражают искреннюю благодарность доктору физико-
математических наук А.А. Разборову за сделанные им ценные
замечания.
4
ВВЕДЕНИЕ
Для сокращенной записи рассуждений будем использовать
следующую символику, не вдаваясь в связанные с ней формальные
детали. Ниже для каждой группы обозначений слева даются
символьные выражения, справа—их значения.
р или q р & Q Т р =» Q Р Q Р -о 9 Зх 3!х Vx 0 а е А а £ А {а} {х|П(х)} а := b а >b Ц-li 6 1} ISI	«р или q (или оба)», «р и д», «неверно, что р», «если р, то д», «из р следует д», «р равносильно д», «р тогда и только тогда, когда д», «р равносильно д по определению». «существует по крайней мере один х такой, что», «существует единственный х такой, что», «для всех х», «для любого х». пустое множество, «ц является элементом множества А», «а не является элементом множества А», множество, состоящее из единственного элемен- та а, множество, состоящее из таких элементов х, для которых истинно утверждение П(х), «а равняется b по определению», «а присваивается значение Ъ», «элементу а сопоставляется элемент Ь», совокупность объектов, индексированных элемен- тами множества I, количество элементов в конечном множестве 5.	
Остановимся	коротко на основных алгебраических	конст-
рукциях, изучаемых в данной книге.
1. Алгебры. Пусть п—натуральное число. (Алгебраической)
п-арной операцией на непустом множестве А называется функция
от п переменных, заданная на множестве А и принимающая
значения в этом множестве.
Для п = 1, 2, 3 имеются специальные названия операций:
унарная, бинарная, тернарная.
5
Иногда возникает необходимость зафиксировать какой-нибудь
специальный элемент данного множества А. В этом случае говорят,
что в А задана нульарная операция; символом ее служит
обозначение указанного элемента. Алгеброй называется пара (А,
F), где А—непустое множество {носитель), a F—некоторая
совокупность заданных на нем операций.
У всех рассматриваемых нами алгебр множество операций F
будет конечным: F = {/г /2, Такие алгебры записываются
в виде А = (A, fx, f2,	где символы операций считаются
расположенными в порядке убывания их арностей. Последователь-
но выписывая эти арности, получаем тип алгебры: (п{,
п2, ..., nJ. Две алгебры, имеющие одинаковый тип, называются
однотипными.
Изоморфизм алгебры А = (А, Д,	на °ДНОТИПНУЮ
ей алгебру В = (В, g^, g2, ..., g^)—это взаимно однозначное
соответствие <р: А -» В такое, что:
а2, ..., ап)) = g. (ip(aj, ?(а2), ..., р(а„))
i	i
для i = 1, 2, ..., т.
Если изоморфизм существует, то говорят, что алгебры А
и В изоморфны и пишут: А а В. С абстрактной точки зрения
изоморфные алгебры не различаются, хотя по внешним признакам
они могут быть разительно непохожими.
П р и м е р 1. Пусть (R+, •, \ 1)—множество всех поло-
жительных чисел, рассматриваемое вместе с умножением (би-
нарная операция), обращением *	~ (унарная операция) и
фиксированным элементом 1 (нульарная операция). Эта алгебра
имеет тип (2, 1, 0).
Такой же тип у алгебры (R, +, -, 0), где R—вся числовая
прямая с бинарной операцией + (сложение), унарной операцией
х |—»-х (смена знака) и нульарной операцией—фиксированием
числа 0.
Следующие равенства:
log (ху) = log х + log у,
log (х-1) = - log х,
log 1	=0
показывают, что функция <р(х) = log х (по любому основанию)
является изоморфизмом алгебры R+ на алгебру R (заметим, что
соответствие х >—»log х взаимно однозначно отображает R+ на R).
Основные алгебраические конструкции и конкретные алгебры
будут рассмотрены в дальнейшем в главе 2.
6
2. Графы. Графам специально посвящена глава 3. Однако
поскольку они будут встречаться в примерах и раньше, введем
необходимые для этого понятия.
Под (ориентированным) графом понимается пара G =
= (V, а), где V— конечное непустое множество, а—некоторый
набор пар вида (u, у), и, v G V. Элементы множества V
называются вершинами графа G, элементы множества а называ-
ются его дугами. Если (и, у)—дуга графа, то говорят, что вершина
и является ее началом, а вершина v—концом. Дуги, у которых
начало и конец совпадают, называются петлями.
Графы с небольшим числом вершин удобно представлять в
виде рисунков: вершины изображаются точками (или кружками,
квадратиками и т.п.), а дуги изображаются стрелками, соединя-
ющими—от начальной к конечной—соответствующие вершины.
Графы используются в качестве функциональных моделей
дискретных систем, при этом вершины соответствуют элементам
системы, а дуги—связям между элементами.
Пример!. Рассмотрим систему, состоящую из пяти
блоков, функциональная схема которой заимствована из [17] и
приведена на рис. 1. Эта схема интерпретируется каждым из двух
графов, изображенных на рис. 2.
Желание (или необходимость) по-разному изображать один и
тот же граф, а также присваивать новые имена его вершинам,
заставляет искать принцип идентификации графов, более широ-
кий, чем тождественное совпадение. Так возникает понятие
изоморфизму.	?
Графы Gj = (Ej, с^) и G? = (V2, a2) называются изоморф-
ными (обозначение: G{ st G2), если между их вершинами (т. е.
между множествами и V2) можно установить взаимно
однозначное соответствие <р:	-» V2 таким образом, чтобы из
вершины и в вершину v в графе Gl вела дуга тогда и только
тогда, когда в графе G2 дуга соединяет вершину <р(и) с вершиной
р(у).
Графы могут быть использованы при диагностике дискретных
систем.
Предположим, что для пары (и, у) элементов системы
существует проверка, состоящая в воздействии на первый элемент
и и в ответе, снимаемом со второго элемента v. Для проверки
работоспособности системы проводится некоторое число однократ-
ных проверок указанного вида. Диагностический граф для данного
набора проверок (теста) определяется следующим образом: верши-
ны его соответствуют элементам системы, а дуги—проверкам,
входящим в состав теста. Результаты тестирования фиксируются
в виде пометок на дугах.
ПримерЗ. Пусть известно, что в системе, схема которой
представлена на рис. 1, имеется отказ одного или двух блоков.
Для обнаружения неисправностей проведены проверки (1, 2),
(3, 1), (3, 5) и (4, 5). При этом, по определению, результат
5	1	проверки есть 0, если оба участвующих блока
о	о	исправны, и 1, если один из блоков неиспра-
0/\1 \о вен’ а ДРУгой исправен. В случае двойного
/ \ /	\ отказа результат проверки может быть О
</	V	ь или 1. Предположим, что указанный тест
4	3	2 описывается диагностическим графом, изобра-
Рис. 3 женным на рис. 3. Зная, что число отказов
не превышает двух, однозначно устанавлива-
ем: отказавшим является блок 3.
В приложениях наряду с ориентированными графами при-
меняются и неориентированные графы—когда для любой дуги
(и, у) существует встречная дуга (у, и). В этом случае, изображая
граф, пару стрелок (и, у), (у, и) заменяют одной неориентирован-
ной линией (чаще всего отрезком), которую называют ребром и
обозначают символом неупорядоченной пары (и, у}. Когда
одновременно встречаются графы разных типов, для них вводят
специфические названия: орграф, диграф и т.п. В примерах,
обсуждаемых в первых двух главах, мы будем пользоваться общим
термином «граф», поскольку из контекста всегда будет ясно, о
каких именно графах идет речь.
3. Автоматы. Математической моделью функционирования
дискретной системы является конечный детерминированный ав-
томат. По определению, это пятерка объектов А = (S, X, Y,
д, А), где S, X, Y—конечные непустые множества соответственно
состояний, входных и выходных сигналов, д—отображение
множества S XX в множество S, называемое функцией переходов,
8
a A—отображение множества SxX в множество У, называемое
функцией выходов.
Автомат А «работает» в дискретной временной шкале по
следующему правилу: если s G S—состояние автомата А в
данный момент и на его вход подан сигнал х G X, то в следующий
момент времени автомат перейдет в состояние d(s, х) и даст на
выходе сигнал А($, х). Автомат А может быть задан таблицей,
состоящей из двух подтаблиц—переходов и выходов. Строки обеих
таблиц помечаются элементами множества S, а столбцы—симво-
лами входного алфавита X. На пересечении строки $ и столбца
х в подтаблице переходов помещается элемент <5(s, х) G 5, а в
подтаблице выходов—элемент A(s, х) G У.
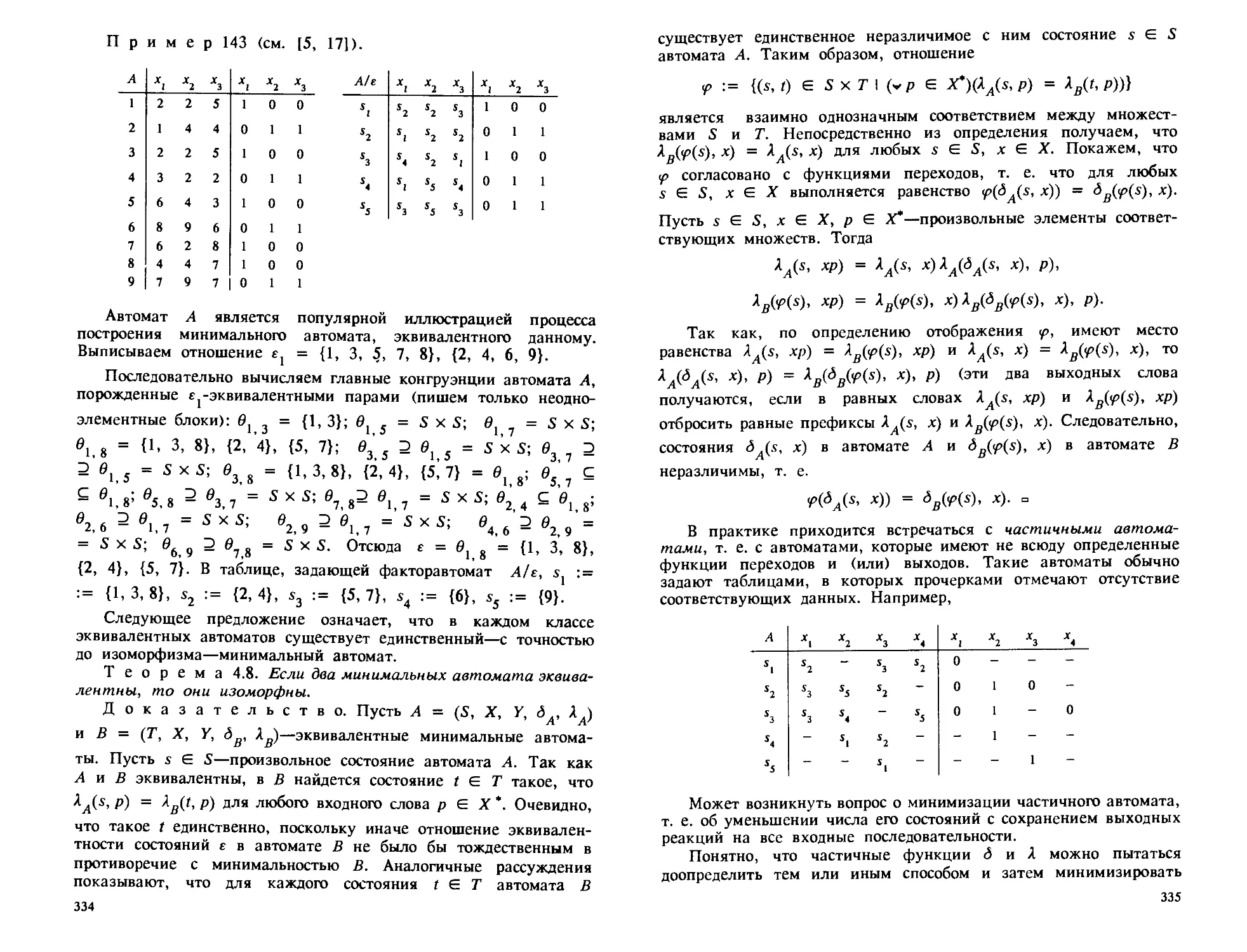
П р и м е р 4. Пусть задан автомат А, в котором S =
= {sr s2, sy $4}, X = {xr х2}, У = {0, 1} и функции <5 и А
заданы следующей таблицей.
А	Х1	x2	X1	x2
S1	s2	S1	0	1
s2	s3	s2	1	0
s3	s3	s2	1	0
s4	s4	s3	0	1
Из этой таблицы видно, например, что автомат А, находясь
в состоянии s2, под воздействием сигнала х[ перейдет в состояние
$3 и выдаст выходной сигнал 1.
Автомат А[ = (Sp Ар У, Aj) называется изоморфным
автомату А, = (S,, X , У , д , А А (обозначение: A es АА, если
существует тройка взаимно однозначных соответствий <р‘.	-»
-» S2, Ц>: Х{ -» Ху %: У -» У2 таких, что £>(<5j(s, х)) =
= д (<p(s), V'W) и %(A.(s, х)) = A_(p(s), У»(х)) Д'18 любых s G
G х 6 Ху
Часто рассматриваются автоматы с общим входным и общим
выходным алфавитами, такие автоматы называются сравнимыми.
В этом случае изоморфизм автомата А} = (Sy X, У, <5 , А}) на
автомат А2 = (S2, X, У, ду А2) определяется как взаимно одноз-
начное соответствие <р: Sj -» Sy удовлетворяющее равенствам
х)) = &2(<p(s), х), Aj(s, х) = X2(<f>(s), х) для любых
s е Sp х е х.
Изоморфные автоматы считаются разными копиями одного и
того же абстрактного автомата.
Обозначим через X * множество всех последовательностей
конечной длины (слов), образованных из элементов множества X,
9
называемого алфавитом. В множество X * включают и пустое
слово е, не содержащее ни одной буквы.
Под длиной Ipl слова р G X* понимается количество
содержащихся в р букв.
Функции переходов и выходов автомата А = (S, X, Y,
д, А) можно расширить на произвольные входные слова согласно
индуктивным (по длине слов) формулам:
d (s, е) = s,	<5(s, рх) = <5(<5($, р), х),
A(s, е) = е,	A(s, рх) = A(s, p)A(<5(s, р), х).
Здесь s G S, х & X, р & X *—произвольные элементы соот-
ветствующих множеств, а умножение в У*, которое присутствует
в правой части четвертой формулы, понимается как приписывание
к первому слову второго (операция конкатенации).
Индукцией по длине слова q легко доказываются равенства:
<5(s, pq) = <3(<5(s, р), q), A(s, pq) = A(s, p)A(<5($, p), q).
Значение продолженной функции переходов д($, р) определяет
состояние автомата, в которое он переходит из состояния $ под
действием входного слова р. Значение продолженной функции
выходов А($, р)—это выходное слово, которое выдает автомат в
результате указанного перехода.
Таким образом, автомат является моделью устройства, которое
осуществляет некоторое отображение множества входных слов
X * в множество выходных слов У *.
Одним из употребляемых способов описания автомата является
построение его диаграммы—графа с помеченными дугами. Верши-
ны этого графа соответствуют состояниям
автомата, и из вершины $. в вершину Sj
проводится дуга с метками (xly), если
d(s., х) = s., A(s., х) = у. На рис. 4
представлена диаграмма автомата А из
примера 4.
Автомат называется автономным, если
его входной алфавит состоит из единствен-
ного символа: X = {х}. Пусть А = (S,
X, У, <3, А)—некоторый автомат. Для фик-
сированного входного сигнала х. G X че-
рез <У, Л. обозначим ограничения функций
<5 и А на множестве S х {х,}. Автономные автоматы вида
А. = (S, {х.}, У, д., Ар назовем автономными компонентами
автомата А. Диаграммы автономных автоматов представляют собой
графы с дугами, помеченными символами выходного алфавита У.
ю
Произвольный автомат можно задавать также и набором
графов, представляющих его автономные компоненты. На рис. 5
дано такое описание автомата А из примера 4.
Рис. 5
Может оказаться, что в некоторых ситуациях выходные
реакции автомата неизвестны или не представляют интереса, а
объектом исследования является доступная наблюдению эволюция
его внутренних состояний под воздействием входных сигналов.
Тогда удобно в качестве модели такого поведения использовать
автомат без выхода, или полуавтомат А' = (S, X, б), где все
символы несут тот же смысл, что и в исходном автомате А.
Полуавтомат А' называется редуктом автомата А. Полуавто-
маты описывают таблицами, в которых отсутствует часть,
связанная с выходными сигналами, а также диаграммами и
графами автономных компонент (без меток на дугах).
Рис. 6
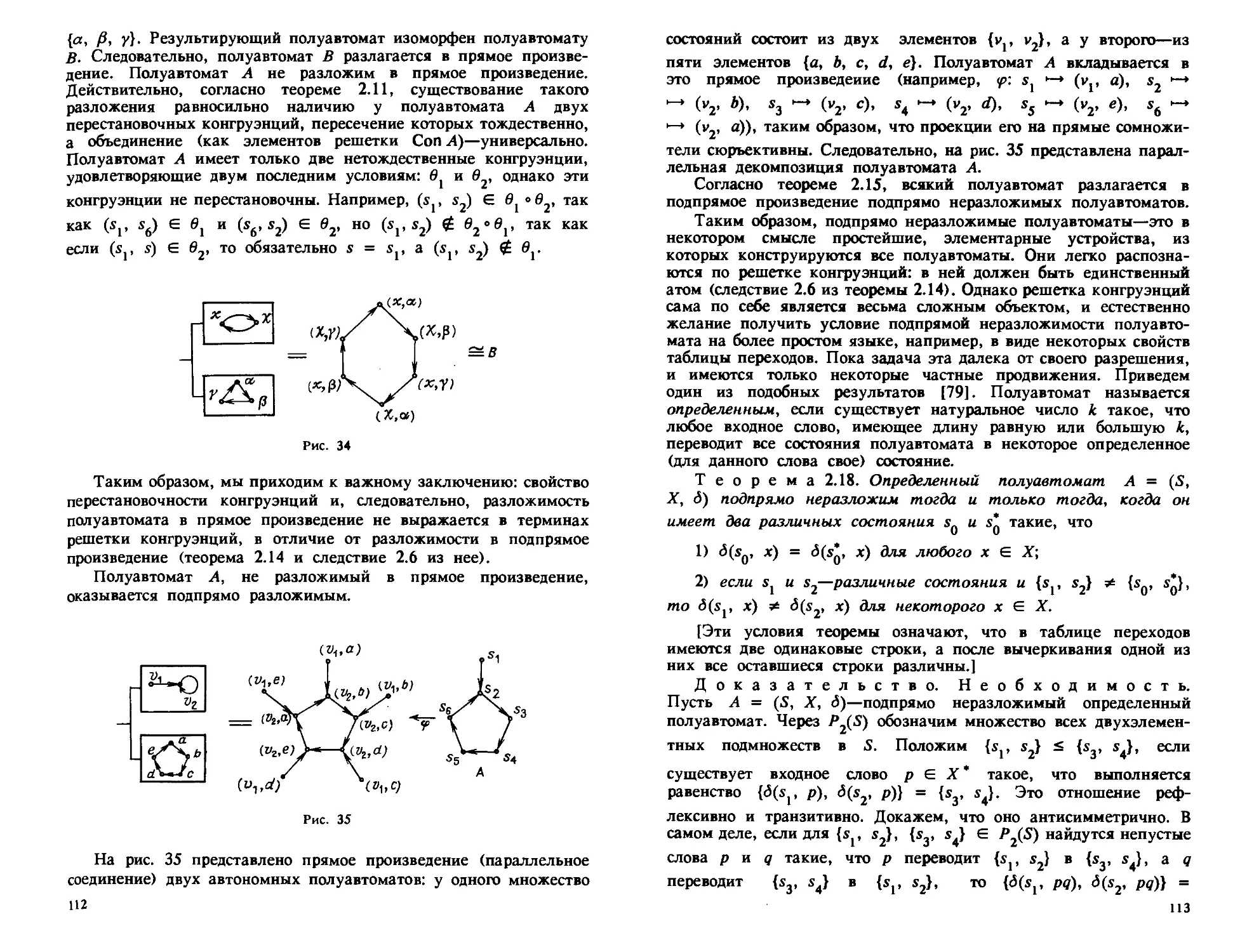
t Кроме того, каждому полуавтомату А можно сопоставить граф
О(Л) следующим образом. Вершины графа соответствуют состо-
яниям полуавтомата, и из вершины s. в вершину проводится
дуга, если существует такой входной сигнал х 6 X, что
п
<5(s„ x) = s.. Этот граф получается из диаграммы полуавтомата
снятием меток входных сигналов со всех дуг, и устранением
возможных при этом кратных дуг. Если, например, из вершины
s. в вершину s. было две дуги с метками Xj и х2, то после снятия
меток будет идти одна дуга. В качестве иллюстрации на рис. 6
приведены графы всех семи возможных типов автономных
полуавтоматов с тремя состояниями.
ГЛАВА 1
МНОЖЕСТВА И ОТНОШЕНИЯ
§ 1.1. Булевы алгебры
Под булевой алгеброй понимается непустое множество В, на
котором заданы две бинарные операции—объединение V и
пересечение А, одна унарная операция, обозначаемая штрихом
' и называемая дополнением, и две нульарные операции, т.е.
выделены два элемента: ноль 0 и единица 1.
Предполагается, что в этой алгебре типа (2, 2, 1, 0, 0)
выполняются следующие тождества:
I.
X V X = X, X А X = X
(законы идемпотентности для объединения и пересечения);
II.
X V у = у V х, X Л у = у Л X
(законы коммутативности);
III.
х V (у V z) = (xV у) V z,
(законы ассоциативности);
IV.
X Л (у Л z) = (х Л у) Л Z
х V (х Л у) = X, х Л (х V у) = X
(законы поглощения);
V.
X Л (у V z) = (х Л у) V (х Л z), х V (у Л z) = (х V у) Л (х V z)
(законы дистрибутивности);
VI.
х V 0 = х, хЛО = 0, xVl = l, хЛ 1 = х
(законы, описывающие особые свойства нуля и единицы по
отношению к объединению и пересечению);
13
VII.
х V х' = 1, хЛх' = О
(законы дополнения)',
VIII.
(х')' = х
(закон инволютивности дополнения)',
IX.
(х V у)’ = х' Л у', (х Л у)' = х' V у'
(законы Де Моргана).
Определение булевой алгебры, кажущееся с первого взгляда
громоздким и весьма специальным, на самом деле явилось
результатом глубокого проникновения в существо многих внешне
не схожих явлений и процессов, абстрактное описание которых
позволило обнаружить далеко идущие аналогии.
Рассмотрим некоторые примеры, которые помогут приобрести
необходимую интуицию для понимания общих булевых свойств.
На множестве из двух элементов F и Т (от английских слов
false—ложь и true—истина) определим бинарные операции логиче-
ского сложения + и логического умножения • следующими
таблицами:
F т
F	т
т	т
F Т
F	F
F	Т
Положим далее
F' = Т и Т' = F,
вводя тем самым унарную операцию, которую назовем допол-
нением.
Теорема 1.1. Алгебра
({F, Т},	, F, Т)
является булевой алгеброй.
Доказательство. Нужно показать, что в рас-
сматриваемой алгебре выполняются булевы тождества I—IX, если
в них заменить V на + , Л на •, сохранить знак ' и соответственно
заменить 0 на F и 1 на Т. Проверка истинности каждого тождества
сводится к вычислению левой и правой его части при всевозмож-
ных конкретных значениях переменных (F или Т) и сравнением
получаемых результатов. Удобнее всего это делать составлением
таблиц, описывающих последовательные этапы вычислений. Про-
верим, например, справедливость закона дистрибутивности V.
Этапы вычислений представлены в следующей таблице.
14
х у z	JH-Z	x(jh-z)	ху	xz	(xy)+(xz)
F	F	F F	F	Т F	Т	F F	Т	Т Т	F	F TFT Т	Т	F Т	Т	Т	F	F	F	F	F T	F	F	F	F T	F	F	F	F T	F	F	F	F F	F	F	F	F T	T	F	T	T T	T	T	F	T
Как видно из таблицы, значения левой части х(у + z) и правой
части (ху) + (xz) совпадают при соответствующих значениях
переменных,—этим доказано, что логическое умножение распре-
делительно относительно логического сложения. Аналогичным
образом могут быть проверены все остальные тождества, о
Булева алгебра ({F, Т}, +, •, ', F, Т) называется двоичной
булевой алгеброй логики.
По разным причинам обозначение логических элементов
буквами F и Т может быть не совсем удобным.
Условимся в дальнейшем вместо буквы F писать символ 0, а
вместо Т—символ 1. Тогда двоичная булева алгебра логики будет
записываться в виде В2 = ({0, 1}, +, •, ', 0, 1). Операции
двоичной булевой алгебры тесно связаны с логическими связками:
сложение—с дизъюнкцией, умножение—с конъюнкцией, а допол-
нение—с отрицанием. Как нетрудно заметить, логическое значение
дизъюнкции (конъюнкции) двух высказываний равно сумме
(произведению) их логических значений, а логическое значение
отрицания некоторого предложения равно дополнению его логиче-
ского значения. В этом контексте булевы законы выражают
естественные свойства логических действий над высказываниями.
Наряду с основными операциями двоичной булевой алгебры в
ней рассматривают и некоторые производные от них операции.
К числу важнейших производных операций относятся:
1)	импликация
х -» у := х' + у;
2)	эквивалентность
х ** у := (х' + у)(х + у');
3)	сложение по модулю 2
X ф у := (х'у) + (ху').
Пусть S—некоторое непустое множество. Множество А назы-
вается подмножеством множества 5 (обозначение: А С S), если
каждый элемент множества А является элементом множества S.
Среди всех подмножеств в 5 выделяются само множество 5
и его пустое подмножество 0.
15
Для любого подмножества А имеют место включения 0 £
С А С S.
Подмножества множества S, отличные от S, называются
собственными подмножествами.
Желая подчеркнуть, что А является собственным подмноже-
ством в S, будем использовать в записи знак строгого включения:
А С S.
Для рассуждений, связанных с множествами, удобно ис-
пользовать язык диаграмм Эйлера—Венна. Будем изображать
данное фиксированное множество S в виде прямоугольника, а его
подмножества—частями этого прямоугольника. Область, представ-
ляющую то подмножество, которое в данный момент интересует
нас, отметим штрихами. На рис. 7 первая диаграмма соответствует
самому множеству S, вторая—его пустому подмножеству, а
третья—произвольному собственному подмножеству А. Обозначим
через P(S) совокупность всех подмножеств произвольного задан-
ного множества S. Пусть А, В G P(S), т. е. А С S и В С S.
Объединением подмножеств А я В называется подмножество,
обозначаемое A U В, элементами которого являются элементы
множества 5, входящие хотя бы в одно из подмножеств А и В.
Таким образом, xGAUBroxGA или х G В.
________£
0
Рис. 7
Пересечение подмножеств А и В определяется как такое
подмножество А П В, которое состоит из элементов, одновременно
входящих в А я В, т. е. xGAC\B:*>xGA&xG В. Если
А П В = 0, то говорят, что подмножества А и В не пересека-
ются.
_ Дополнение подмножества А С S—это такое подмножество
А множества S, которое состоит из элементов, не входящих в А,
т. е. х G А :о х £ А. Диаграммы для объединения, пересечения
и дополнения представлены на рис. 8.
див	Ап8	А
Рис. 8
Сопоставляя каждой паре подмножеств А я В множества S
их объединение A U В, мы определяем тем самым на Р(5)
бинарную операцию, которая называется объединением. Анало-
гично соответствие (А, В) >—» А П В задает на P(S) бинарную
16
операцию—пересечение, а функция А •—»А определяет унарную
операцию—дополнение.
Пусть	—некоторый набор подмножеств множества S, т.е.
Л С P(S).
Будем говорить, что множество замкнуто относительно
операции объединения подмножеств, если ему принадлежит
объединение любых двух входящих в него подмножеств:
A G^4 & В G .4 => A U В G ,4.
Аналогично, замкнутость набора ^4 относительно операции
пересечения определяется формулой:
A G,d &. В G е4 А Г\ В G ^4.
Замкнутость набора подмножеств ^4 относительно дополнения
определяется формулой:
A G ^4 =* А 6 ^4.
Если некоторая совокупность подмножеств <j4 £ P(S) замкнута
относительно теоретико-множественных операций объединения,
пересечения и дополнения и содержит в своем составе пустое
подмножество 0, а также само множество S, то система
(е4, U, А, 0, S) называется алгеброй множеств.
Очевидными примерами алгебры множеств будут (P(S),
U, А, ”, 0, S), а также ({0, S}, U, А, 0, S), называемые
соответственно тотальной и тривиальной алгебрами множеств.
Пусть А—собственное непустое подмножество в S. Тогда
совокупность f0, A, A, S}, как нетрудно убедиться, замкнута
относительно объединения, пересечения и дополнения, содержит
подмножества 0 и S и, следовательно, тоже будет алгеброй
множеств.
Т е о р е м а 1.2. Всякая алгебра множеств является
булевой алгеброй.
Доказательство. Нужно показать, что в алгебре
(<j4, U, А, 0, S) выполняются следующие тождества:
Г.
X и X = X, X А X = х-,
II'.
X и У = У и X, X А У = У А X;
III'.
X и (У и Z) = (X и У) и Z, X А (У A Z) = (X А У) A Z;
IV'.
X и (X А У) = X, X А (X и У) = Х\
17
V.
X П (У U Z) = (X П У) и (X n Z), XU (УП Z) =
= (X U У) n (X и Z);
VI'.
X и 0 = X, X П 0 = 0, X и S = S, X n S = X;
VII'.
X их = S, X П X = 0;
VIII'.
IX'.
X U У = X П У, X П У = X U У.
Большая часть из соотношений Г—IX' описывает очевидные
свойства теоретико-множественных операций. Истинность каждого
тождества проще всего проверяется построением отдельных
диаграмм для левой и правой частей с последующим сравнением
результатов. На рис. 9 приведем диаграммы, подтверждающие
справедливость первого из тождеств IV', а на рис. 10—диаграммы
для первого из тождеств IX'; аналогично диаграммы могут быть
построены и для всех остальных тождеств. Совпадение финальных
диаграмм для левой и правой частей доказывает соответствующее
тождество, о
X U У	ХЛ(хиГ)	X
Рис. 9
X и у
X ПУ
Наряду с основными операциями алгебры множеств в ней
рассматривают и некоторые производные от них операции. К
числу важнейших относятся:
18
разность А - В := А П В,
симметрическая разность А &В := (Л Г) В) U (А Г) В).
Их диаграммы приведены на рис. 11. Ясно, что А ьВ =
= (А —В) U (В-А).
Ш
Рис. 11
В алгебре множеств обычно используются следующие легко
проверяемые свойства указанных производных операций:
1)
X - (У- Z) = (X - У) U (X П Z),
2)
X - (У П Z) = {X - У) и (X - Z),
3)
X - (У и Z) = (X - У) A (X-Z),
4)
X &(Y<Z) = (ХдУ) aZ,
5)
X дУ = У дХ,
6)
(х дУ) n z = (х n z) д(упг).
Операции объединения и пересечения могут быть расширены
на целые совокупности подмножеств.
Пусть {Л;.| i Е 1}—некоторый набор подмножеств множества
S. Положим
и А. := {х е s| (зг е Г)(х е л.)} ,
i G 1
т.е. объединение U Л. состоит из таких элементов множества S,
i е 1 ‘
которые входят хотя бы в одно из объединяемых подмножеств.
Аналогично
п л. := {х е s| (vi е о(х е л.)} ,
i е 1 1	'
19
т. е. пересечение П А. состоит из таких элементов множества
i G /
S, которые входят во все подмножества A., i 6 I. Вместо
U А. и Г) А. пишут также U {Л. I i е 1}, Г) {A. I i G I}.
Очевидно, что U {A. I i = 1, 2, и} = Al U A2 U ... U An в
обычном понимании объединения.
Аналогично: Г) {А(. I i = 1, 2, ..., п} = Л] П П ... Л А^.
Отметим обобщенные законы Де Моргана:
U А. = П А., П А. = U А .
iGI iG 7 i G 7 iG7
Проверим, например, справедливость первого из них:
s е и А. о - е и ал о - ((э i е i)(s е а )) о
ig7 1 I	7	'
o(v i g !)(-> (s е а.)) о (v i е i)(s ел.) о 5 е п а.,
'	'	iei ‘
—множества U А. и ЛА. состоят из одних и тех же элементов,
i G I i G 7
и, следовательно, совпадают.
Пусть А—некоторое подмножество множества S. Определим
на S функцию хА со значениями в двоичной булевой алгебре
В2, полагая:
ZA(s) := J’
если s 6 А ,
в противном случае.
ХА называется характеристической функцией подмножества А в
S. Для s G S элемент %л(«) G В2 представляет собой логиче-
ское значение высказывания «элемент s принадлежит подмноже-
ству А».
Пусть X(S) обозначает совокупность характеристических функ-
ций всех подмножеств множества S. На множестве X(S) поточечно
определяются операции +, •, ':
(%! +z2Xs) := *1<S) +	'X2)(s) '•= %i(s) 'X2(s)>
%'(s) := [/(s)]'
для любых xr Z2, % e X(S) и s e S.
T еорема 1.3. Для характеристических функций подм-
ножеств множества S имеют место следующие соотношения:
п ХА = хв А = В,
ХА и в ~ ХА + Хв-,
3)	ХА п в = ХлХв,
20
4)
5)	Х0($) = 0 для любого s G S,
6)	Zs(s) = 1 для любого s G S.
Доказательство. Докажем, для примера, первое
соотношение. Равенство = %в означает, что каждый элемент
множества S принадлежит подмножеству А тогда и только тогда,
когда он принадлежит и подмножеству В. Следовательно,
подмножества А л В состоят из одних и тех же элементов, а это
равносильно их совпадению.
Для проверки второго соотношения строим цепочку рав-
носильных высказываний:
и B(s) = 1 о s G A U В о (s G А или s G В) о
° (Хл(«) = 1 или = 1) о
° Хл(«) + XB(s) = 1 о (XA+XB)(s) = 1>
из которой следует, что функции г . .. _ и г . + на одних и
тех же элементах принимают значение 1. Значит, на одних и
тех же элементах они принимают и значение 0. Поскольку других
значений у них нет, то они совпадают:
ХА и в = ха + хв'
Свойство 3) доказывается аналогично свойству 2), а свойства 5)
и 6) очевидны, о
Пусть множество S конечно и содержит п элементов.
Фиксируя порядок элементов: S = {$р	..., s^}, мы можем
записать характеристическую функцию произвольного подмноже-
ства А С S в виде n-мерного двоичного вектора, полагая его i'-ю
компоненту равной т. е.
ХА := <Xa(SJ’ ^2)> -W
Понятно, что каждый двоичный вектор над S представляет
характеристическую функцию подходящего подмножества А С S.
Операции сложения, умножения и дополнения над двоичными
векторами выполняются покомпонентно так же, как и над
характеристическими функциями. Нуль-вектор 0 соответствует
функции Хгя , a Xv изображается вектором 1, состоящим из одних
единиц.
Таким образом, мы получаем удобный способ кодирования
подмножеств конечного множества двоичными векторами. При
этом, вследствие теоремы 1.3, теоретико-множественными опе-
рациями U, П,— над подмножествами соответствуют логические
операции +, •, ' над двоичными векторами.
21
П р и м е р 5. Пусть S = {Sp s2, s3J. Выпишем все под-
множества множества S и соответствующие им двоичные векторы.
Подмножества	Векторы	Подмножества	Векторы
0	(0, 0, 0)	{Sp s2}	(1, 1,0)
{Sj}	(1, 0, 0)	{SpS3}	(1,0, 1)
{$2^	(0, 1, 0)	{S2, s3}	(0, 1, 1)
{*3}	(0, 0, 1)	S	(1. 1. 1)
Пусть 0 < иг < п. В n-элементном множестве S имеется С™
различных m-элементных подмножеств (т.е. столькими способами
можно выбрать т элементов из п имеющихся элементов). Тогда
общее число подмножеств в S будет
С° +	С1	+ ... + С"	= (1	+ 1)"	= 2”,
п	п	П '	'
—здесь в первом переходе использована формула бинома Ньютона.
Столько же будет и различных n-мерных двоичных векторов
над S.
Пусть В = (В, V, л, 0, 1) и В* = (В*, V, л, 0, 1)—
две булевы алгебры. Конечно, соответствующие операции в них
могут иметь разные обозначения, но в принципе это не
существенно. В соответствии с общим определением изоморфизма
алгебр, взаимно однозначное соответствие <р между множествами
В к В* будет изоморфизмом булевой алгебры В на булеву алгебру
В*, если оно сохраняет все операции, т.е. если тождественно
выполняются соотношения:
1)
v у) = <р(х) V <р(у),
2)
р(х л у) = >р(х) л <р(у),
3)
<?(*’) = [?(*)]',
4)
/>(0) = о,
5)
Р(1) = 1.
Заметим, что в левых частях тождеств операции выполняются в
алгебре В, а в правых частях—в алгебре В*.
П р и м е р 6. Двоичная булева алгебра В2 изоморфна
тривиальной алгебре множеств.
По определению, В2 = ({0, 1}, +, •, ', 0, 1), где 0' = 1,
Г = 0, а операции + и • задаются соответственно таблицами:
22
•	0	1
О_____1^
О	1
1	1
о о
о 1
о
1
Пусть S—непустое множество.
о
1
Тривиальная алгебра множеств на
нем—это_система ({0, S}, U, Г), —, 0, S). Заметим, что
0 = S, S = 0, а теоретико-множественные операции U и Г)
имеют следующие таблицы:
п
0
S
и
0
S
0 S
0
S
0 S
0
0
s
s
0
s
Теперь видно, что если в В2 заменить 0 на 0 , 1 заменить
на
S, а вместо операций +, •, ', писать соответственно U, Г), , то
получается тривиальная алгебра множеств. Таким образом,
изоморфизмом является соответствие р: 0 •-» 0, 1 •-» S.
На этом примере особенно наглядно видно, что изоморфные
алгебры отличаются друг от друга лишь обозначением элементов
или операций, представляя собой по существу различные копии
одного и того же объекта.
П р и м е р 7. Из теоремы 1.3 следует, что тотальная
алгебра множеств (P(S), U, Г), —, 0, S) изоморфна алгебре
(X(S), +, •, ', %0, %s) всех характеристических функций на S.
Изоморфизмом является соответствие, сопоставляющее каждому
подмножеству А С S его характеристическую функцию % . В
частности, если S конечно и содержит п элементов, то
(P(S), U, Г), —, 0, S) изоморфна алгебре всех и-мерных
двоичных векторов с логическими операциями сложения . +,
умножения -, дополнения ' и выделенными векторами 0 и 1.
Понятие изоморфизма позволяет существенно увеличить коли-
чество конкретных примеров булевых алгебр.
Особую роль в классе булевых алгебр играют алгебры
множеств. Оказывается, имеет место следующая теорема Стоуна.
Т е о р е и а 1.4. Всякая булева алгебра изоморфна подхо-
дящей алгебре множеств. □
Несколько позже эта теорема будет доказана для интересу-
ющего нас конечного случая. Сейчас отметим ее практическое
значение: элементы произвольно заданной булевой алгебры
(В, У, Л, 0, 1) можно считать подмножествами некоторого
множества S, интерпретируя операции V, Л, ', соответственно
как теоретико-множественные операции U, Г), ~ и отождествляя
элемент 0 с пустым подмножеством 0, а элемент 1 с самим
множеством S. В частности, производя булевы вычисления, можно
пользоваться языком диаграмм.
Ненулевой элемент а булевой алгебры В = (В, У, Л, ',
О, 1) называется атомом, если для любого х G В выполняется
23
одно из равенств а л х = а или а л х = 0. Например, в
тотальной алгебре множеств атомами будут одноэлементные
подмножества, а в булевой алгебре n-мерных двоичных векторов
множество атомов составляют п штук «координатных» векторов,
т. е. векторов, имеющих только одну ненулевую компоненту.
Будем говорить, что элемент а булевой алгебры В содержит
атом а, если а л а = а.
Лемма 1.1. В конечной булевой алгебре каждый ненулевой
элемент содержит по крайней мере один атом.
Доказательство. Пусть В = {ар а2, ..., ап} и
a е В, а * 0. Следующий алгоритм обнаруживает атом, содер-
жащийся в а.
Шаг 1. а^ := a, k := 1.
Шаг 2. Найти л а,. Если а. Л а, = 0 или а. Л а, = а„, то
• 0 к	Ок	ОкО
переход к шагу 3, иначе—к шагу 4.
Шаг 3. Если к = п, то конец. Иначе к := к + 1, переход к
шагу 2.
Шаг 4. aQ := aQ Л а*. Если к = п, то конец, иначе к :=
= к + 1, и переход к шагу 2.
После окончания работы алгоритма в aQ будет записан атом,
содержащийся в а. В самом деле, алгоритм пропускает через aQ
конечную (длины < п) последовательность ненулевых элементов
а, а л а., а л а. л а., ..., последний из которых а = а л
*i	*i ‘1
Ла. Л ... Л а. обладает тем свойством, что а Л х = 0 или
*i
а Л х = а для любого х G В. Кроме того, аЛа=аЛа=
= а л (а л а. л ... л а.) = ала. л ... л а. = а, т. е. а содер-
1	t	1	‘к
жится в а. о
Приведем пример работы алгоритма.
Пусть S = {1, 2, 3, 4}, и пусть 16 элементов булевой алгебры
(P(S), U, П, 0, S) представлены в следующих обозначениях:
0	а9’	{4}	= а8’	{2, 3}	=	а13’	{1,2,4}	=	а7,
{1}	= а1б’	{1,	2} = а4,	{2,4}	=	а6>	{1,3,4}	=	а1’
{2}	= а5’	{1,	3} = а14,	{3, 4}	=	а2,	{2, 3, 4}	=	а3,
{3}	а15'	{1,	4} = а12,	{1, 2, 3} =	а10’	{1, 2, 3, 4} =	а1Г
Найдем атом, содержащийся в элементе а = а$. Вычисления
сведены в таблицу, заполняемую по строкам, в которых
последовательно записываются значения для aQ л ак при соответ-
ствующем aQ. Согласно предписанию из шага 4, происходит
24
переход в следующую строку, обозначенную новым значением
для aQ, и увеличение к на 1. Вместо для наглядности пишем
О (элемент 0 булевой алгебры выявляется, например, по таблице
операции л: в соответствующей элементу 0 строке нет отличных
от него элементов).
а1	а2	а3	а4	а5	а6	а7-	а8	а9	а10	а11	а12	а13	а14	а15	а16
а3 а2
а2	а2	а2	0	0	а8
Og	а8	а8	О	0	а8	а8	О	О	О	О
Таким образом, а8 = {4} является одним из атомов, содер-
жащихся в а3 = {2, 3, 4}.
Через А обозначим множество всех атомов данной булевой
алгебры, а через А (а)—множество всех атомов, содержащихся в
ее элементе а.
Например, Л(0) = 0, Л(1) = А.
JI е м м а 1.2. Всякий ненулевой элемент конечной булевой
алгебры равен объединению всех содержащихся в нем атомов:
а = V а.
а е А(а)
Доказательство. Пусть В—конечная булева
алгебра. Сначала покажем, что 1 = V а. В самом деле, положим
a G А
v = а. Предположим, что а # 1. Тогда а' # 0 и, значит, по
a G А
лемме 1.1 А(а') * 0. Пусть aQ G А(а'), т. е. aQ Л а' = aQ.
Так как aQ Л а = aQ Л [ v а 1 = V (а0 Ла) = aQ Л aQ = aQ,
'а G А ' a 6= А
то а0 = а0 Л а0 = (а0 Л а) Л (aQ Л а') = aQ Л (а Л а') = aQ Л 0 =
= 0, что невозможно. Итак, элемент 1 является объединением
всех атомов булевой алгебры В.
Берем теперь в В произвольный ненулевой элемент а. Имеем:
а = аЛ1 = аЛ / V a) = v (а л a) =
е А ) а е А
= V (а Л а) = V а.
а е А(а)	а Е А(а)
Докажем теорему Стоуна для конечного случая, где она
допускает следующее усиление.
Теорема1.5. Всякая конечная булева алгебра изомор-
фна подходящей тотальной алгебре множеств.
Доказательство. Пусть В = (В, У, А, О, 1)—
конечная булева алгебра. Покажем, что она изоморфна булевой
25
алгебре (Р(А), U, Г), —, 0, А), где А—множество всех атомов
из В. Сопоставим каждому элементу a G В множество А(а) всех
содержащихся в нем атомов. Покажем, что это отображение
<р: В -» Р(А) и является искомым изоморфизмом.
1)	Отображение <р является взаимно однозначным соответ-
ствием между множествами В и PG4). В самом деле, если
<р(а) = <р(Ь), то а = V а = V а = V а =
a G А(а) а 6 <р(а) a G y>(Z>)
= V а = Ь, и, значит, <р взаимно однозначно. Далее, пусть
a G А(Ь)
X—произвольное подмножество множества А, т. е. какой-то набор
атомов булевой алгебры В. Положим х = V а. Тогда
аех
<р(х) = А(х) = X , т. е. <р отображает В на Р(А).
2)	<р сохраняет операцию объединения, т. е. <р(а V Ь) =
= <р(а) U <р(Ь). В самом деле, для любого атома a G А имеем
a G <р(а V Ь) о а = а Л (а V Ь) = (а Л а) V (а Л Z>) о (а — а Л а
или а = а Л Ь) о (а 6 <р(а) или а 6 о а G <р(а) U <р(Ь).
Следовательно, множества <р(а V Ь) и <р(а) U <р(Ь) состоят из одних
и тех же элементов и поэтому совпадают.
3)	<р сохраняет операцию пересечения, т. е. <р(а Л Ь) =
= <р(а) Г) <р(Ь). В самом деле, а G <р(а Л Ь) о а = а Л (а Л Ь) =
= (а Л а) Л (a hb)oa=aha& а = а Л b о a G <p(d) &а G
G <р(Ь) о a G <р(а) П <р{Ь). Отсюда <р(а л Ь) = <р(а) Г) <р(Ь).
4)	<р сохраняет операцию дополнения, т. е. <р(а’) = <р(а).
Действительно, a G <р(а') а = а л а' а Л а = (а Л а') Л а =
= а Л (а' Л а) = «лО = О<>а£ <р{а) о а £ р(а).
5)	у>(0) = 0, <р(У) = А.
Таким образом, конечная булева алгебра В изоморфна булевой
алгебре всех подмножеств множества, образованного атомами
булевой алгебры В. =
Отсюда получаются два простых следствия.
Следствие 1.1. Если конечная булева алгебра имеет
п атомов, то общее число элементов в ней равно 2п. =
Следствие 1.2. Две конечные булевы алгебры с
одинаковым числом элементов изоморфны. =
Из теоремы 1.5 следует, что любая конечная алгебра множеств
изоморфна некоторой тотальной алгебре множеств. Однако сама
она, разумеется, не обязана быть тотальной. Например, если А
является собственным непустым подмножеством какого-то множе-
ства 5, где ISI > 2, то подмножества, 0, A, A, S образуют
четырехэлементную алгебру множеств, которая будет тотальной
лишь в том случае, когда S состоит из двух элементов.
Пусть S—непустое множество и А С S. Характеристическая
функция % подмножества А отображает S в двоичную булеву
алгебру J?2 таким образом, что %А принимает значение 1 на
26
элементах, входящих в подмножество Л, и 0 на элементах, не
принадлежащих этому подмножеству. В сложных дискретных
системах суждение о принадлежности того или иного элемента
данной подсистеме может не быть столь категоричным: мы не
всегда имеем исчерпывающую информацию на этот счет и
вынуждены ограничиваться лишь некоторой степенью правдопо-
добия, не поддающейся даже вероятностной оценке. Фор-
мализацией отсутствия точных представлений в указанных
ситуациях является понятие нечеткого подмножества.
Нечетким подмножеством в S называется любая функция
р: S -* [0, 1], заданная на S и принимающая значения на
числовом отрезке [0, 1]. Число д(а) истолковывается как мера
уверенности в суждении о принадлежности элемента а 6 S
нечеткому подмножеству р.
Характеристические функции подмножеств множества S можно
считать очень частным случаем нечетких подмножеств. Отожде-
ствляя их с соответствующими им подмножествами, можно
сказать, что в число нечетких подмножеств данного множества
входят все его обычные подмножества. Совокупность всех нечетких
подмножеств множества 5 обозначим через M(S). Фиксируя
некоторый порядок элементов конечного «-элементного множества
S = {а,, а., ..., а }, нечеткие множества можно записать в виде
1 1	2 П
«-мерных векторов с компонентами из отрезка [0, 1]. Двоичные
векторы, как уже отмечалось, соответствуют обычным подмноже-
ствам множества S.
Над нечеткими множествами можно ввести операции, обоб-
щающие теоретико-множественные конструкции.
Объединением нечетких подмножеств /г и v называется
нечеткое подмножество V v такое, что
(и V v)(a) := max (u(a), v(a))
для любого a G S.
Формулой
(и л v)(a) := min («(a), v(a))
определяется пересечение нечетких подмножеств р и v.
Нетрудно проверить, что введенные таким образом операции
удовлетворяют булевым тождествам I—V. Например, первый закон
дистрибутивности превращается в соотношение
min [х, max (у, z)] = max [min (х, у), min (х, z)],
истинное для любых трех чисел х, у, z (а не только для точек
отрезка [0, 1]).
Среди всех нечетких подмножеств на S выделяются подмно-
жества и р^, совпадающие с характеристическими функциями
соответственно пустого подмножества 0 и самого множества S.
Для них очевидна справедливость булевых законов VI.
27
Однако ввести операцию дополнения, удовлетворяющую буле-
вым свойствам VII и IX, для нечетких_множесгв невозможно. То,
что обычно называется дополнением fi для нечеткого подмноже-
ства д, определяется равенством:
Д(а) := 1 - р(а)
для любого а 6 S.
Это определение сохраняет закон инволютивности VIII:
Д(я) = 1 - Д(а) = 1 - [1 -fi(a)] = fi(a),
но булевым дополнением оно не является.
Таким образом, алгебра нечетких подмножеств (M(S), V,
л, д ) имеет тип булевой алгебры (2, 2, 1, 0, 0) и
обладает всеми ее свойствами, выводимыми из тождеств I—VI,
VIII. Алгебра M(S) бесконечна даже в случае конечного множе-
ства S.
Нечеткие подмножества сравниваются друг с другом отно-
шением включения: р. < v тогда и только тогда, когда д(а) <
< v(a) для любого а 6 S.
Включение обычных подмножеств является частным случаем,
поскольку
А С В о хА Хв-
Отметим часто используемые в M(S) соотношения:
fi Л v = р о р < v о fi V v = V.
Они следуют из очевидных числовых неравенств:
min (х, у) = х о х < у о шах (х, у) = у.
В реальных дискретных системах средства проверки принад-
лежности элемента той или иной подсистеме могут иметь
различные (например, пороговые) ограничения чувствительности.
Изменяя эту чувствительность, мы изменяем представление и о
самой системе. Эти соображения приводят к следующему понятию
уровневой детерминизации для нечетких множеств.
Пусть fi G M(S) и е—положительное число, не превосходя-
щее 1.
Под е-детерминизатором нечеткого подмножества р понима-
ется нечеткое подмножество
такое, что
е
1
0
Wa) :=
при р(а) > £,
в противном случае.
На
самом деле, конечно,
представляет собой характеристиче-
скую функцию некоторого подмножества в S. Это подмножество
тоже называется е-детерминизатором для р. Оно состоит из таких
элементов множества S, степень принадлежности которых к
^и, г
28
данному нечеткому подмножеству /л выражаемся числом, не
меньшим, чем е.
Если множество 5 имеет п элементов и нечеткие подмножества
в 5 представлены «-мерными числовыми векторами, то вектор
получается из вектора д заменой каждой его компоненты,
е
ие меньшей чем е, единицей, а всех остальных компонент—ну-
лями.
Пример8. Рассмотрим функциональную схему некото-
рого устройства, представленную на рис. 12 (см. [46] , с. 128).
Предположим, что каждый элемент устройства допускает лишь
определенный уровень загрузки, при превышении которого элемент
отказывает. Схему можно представить в виде сети из нечетких
элементов, приписывая каждому из них соответствующим образом
нормированный предельно допустимый уровень загрузки. Тогда
наше представление о принадлежности каждого из десяти
имеющихся элементов данной схеме описывается нечетким
множеством, пусть например, таким:
/ 1	2	34	567	8	9	10 \
“ |Д30 0,60 0,25 0,95 1,00 1,00 0,35 0,80 0,70 0,75) ’
В первой строке перечислены элементы, а во второй строке
указана степень их «участия» в схеме. При уровне детерминизации
£ = 0,75 получаем:
/1	2	3	4	5	6	7	8	9	10\
V.0,75 “^0	00	1	1	1	0	1	0	1)’
и функциональная связь между элементами при соответствующей
загрузке предстает в виде схемы, изображенной на рис. 13.
29
Рис. 13
При е = 0,25 получаем полное соответствие теоретической
схеме функционирования устройства.
§ 1.2.	Алгебры отношений
Пусть А и В—некоторые произвольные непустые множества.
Декартовым произведением множества А на множество В
называется множество А х В, элементами которого являются
всевозможные пары (а, Ь), где первый элемент берется из
множества А, а второй—из множества В. Две такие пары
считаются равными, если у них совпадают и первые, и вторые
элементы:
(а, Ь) = (с, </):<> а = с & b = d.
П р и м е р 9. Если А - {0, 1, +} и В = {д, □, *, +}, то
А х В = {(0, Д), (0, □), (0, *), (0, +), (1, д), (1, □),
(1. *), (1. +)> (+> *). (+, □). (+> *), (+, +))•
Несложными рассуждениями устанавливается справедливость
следующих соотношений:
1)	(A U В) X С = (А X С) U (В X С),
А X (В U С) = (А X В) U (А X С);
2)	(А П В) X С = (А X С) П (В X С),
А х (В П С) = (А х В) Cl (А X С);
3)	(А - В) X С = (А X С) - (В X С),
Ах (В-С) = (А х В) - (А х С);
4)	ACB&CCjD=»AxBCCxZ>.
Мы оставляем их проверку в качестве упражнения.
30
Декартово произведение S х S называется декартовым квад-
ратом множества S.
Бинарным отношением между множествами А и В называется
всякое подмножество декартова произведения А X В, т. е. любой
элемент множества Р(А х В) всех подмножеств множества
А х В.
Если 1Л1 = т, 1.81 = п, то декартово произведение А х В
будет состоять из тп различных пар. Подсчеты, проведенные в
конце § 1.1, показывают, что в этом случае 1Р(Л х 8)1 = 2т”,—
это и есть общее число всевозможных бинарных отношений
между множествами А и В.
Бинарные отношения будем обозначать строчными греческими
буквами. Если (a, b) G р, то говорят, что элемент а находится
с элементом b в отношении р.
Среди всех отношений между множествами А и В выделяются:
пустое отношение 0, оно не содержащее ни одной пары;
универсальное отношение, содержащее все возможные пары, т. е.
само декартово произведение А х В. Для любого отношения
р G Р(А х 8) имеют место включения
0 £ р С А х В.
Есть два удобных способа представления отношений между
элементами конечных множеств:
1) с помощью двоичных булевых матриц;
2) с помощью графов.
Пусть А = Ц, а2,...,ат}, В = {Z>p Ь2, ..., Ьп}, р £ лх В.
Построим матрицу М(р) размерности т х п следующим образом.
Строки этой матрицы пометим элементами множества А, распо-
ложенными в некотором фиксированном порядке, а столбцы
аналогично пометим элементами множества 8. Затем положим в
качестве элементов матрицы М(р):
если (a., bp G р,
в противном случае.
Здесь 0 и 1—элементы двоичной булевой алгебры В2. Таким
образом, элемент [М(р)] „ представляет собой логическое значение
высказывания: «пара (a., bp принадлежит отношению р», или,
что то же самое, «элемент а. находится в отношении р с эле-
ментом Ь».
ПримерЮ. Пусть А = {0, 1, +}, В = {д, □, *, +},
и задано отношение
р = {(0, д), (0, □), (1, д), (1, *), (1, +), (+, +)}.
0
Тогда
31
II1	1	0	°||
М(р)	=1	0	1	1
IIО	О	О	1II
(считается, что порядок элементов в Л и В задан при их
перечислении).
Очевидно, что различным отношениям между множествами А
и В соответствуют различные двоичные булевы матрицы. Подчер-
кнем, что порядок элементов в А и В в этом случае раз и
навсегда фиксирован. Каждая двоичная булева т х n-матрица М
представляет в точности одно отношение р(М) между Л и В,
именно:
р(М) := {(a., bj) е Л х В I М.} = 1}.
Из способа построения булевой матрицы М(р), соответствую-
щей отношению р, и отношения p(Af) по заданной двоичной
булевой матрице М со строками и столбцами, нумерованными
элементами двух конечных множеств, получаем:
р(М(р)) = р, М(р(МУ) = М.
Пусть снова р Q А х В. Определим (ориентированный) граф
G(p) следующим образом. Множество вершин этого графа будут
составлять элементы множества Л U В, и при этом из вершины
а. проводится дуга в вершину b в том и только том случае, если
(а., А.) ер.
Пример 11. Построим граф G(p), соответствующий
отношению р из примера 10. Он представлен на рис. 14.
Очевидно, что если р
Далее, если граф G таков,
# ст, то G(p) и G(ct)—разные графы,
что его вершинами являются элементы
множества Л U В, а дуги соединяют только элементы множества
/\	□	4- х-ч Л с элементами множества В, то такой
граф представляет в точности одно отно-
/ шение />(3) с л х В, а именно:
У	p((z) := {(a., Z>.) G Л х В I в G имеется
0	1	' 7
Рис. 14
дуга из а. в Ь.}.
Поскольку отношения между множествами
Л и В представляют собой не что иное, как подмножества
множества Л х В, то для них определены все теоретико-множе-
ственные операции. Частным случаем теоремы 1.2 из § 1.1
является
Т еорема 1.6. Совокупность Р(А х В) всех бинарных
отношений между множествами А и В, рассматриваемая вместе
с теоретико-множественными операциями объединения, пересе-
чения и дополнения и с выделенными пустым и универсальным
32
отношениями, т. е. система (Р(А X В), U, Г), , 0, А х В)
является булевой алгеброй. □
Теоретико-множественные операции над отношениями естест-
венно интерпретируются на языке двоичных булевых матриц.
Пусть ^тХп—совокупность всех двоичных булевых т х п-
матриц. В этом множестве вводятся операции сложения +,
пересечения Л и дополнения определяемые соответственно
поэлементным (в Л2) выполнением логических операций сло-
жения, умножения и дополнения:
(M + N)..:= М.. + N.', (М Л N)..:= М..  N..; (М').} := (АГ.)'.
Заметим, что матричный аналог логического умножения называ-
ется иначе и обозначается другим символом (эта операция
слишком не похожа на обычное матричное умножение). Выделим
в множестве матриц ^тхп нуль-матрицу О (все ее элементы
равны 0), и универсальную матрицу I (все ее элементы
равны 1).
Т еорема 1.7. Пусть А и В—конечные множества,
содержащие соответственно тип элементов. Тогда отобра-
жение М: Р(А X В) -* ^тХп. сопоставляющее каждому отно-
шению р С А х В соответствующую ему булеву матрицу,
обладает следующими свойствами'.
1)
М(р) = М(а) р = а,
2)
М(р U ст) = М(р) + 1И(ст),
3)
М(р П ст) = М(р) Л М(а),
4)
М(р) = [Л/(р)]',
5)
М(0) = О,
6)
М(А X В) = I,
т. е. алгебры (Р(А X В), U, О,-, 0,Ах В) и (^тХп> +> л> >
О, Г) являются изоморфными булевыми алгебрами.
Доказательство. 1) Это свойство становится
очевидным, если считать, что строки и столбцы каждой булевой
т х «-матрицы помечены соответственно элементами множества
2 А.М.Богомолов, В.Н.Салий	33
А и множества В, перечисленными в некотором фиксированном
порядке: А = {ар а2, ат}, В = {ftp b2,...,bj.
2)	Покажем, что в т X n-матрицах М(р U ст) и М(р) +
+ ЛГ(ст) единицы расположены на одних и тех же местах (тогда
на остальных позициях будут нули, и матрицы совпадают). Имеем:
[М(р U ст)] у = 1 о (a., b.) S р U ст о
о ((a., ftp е р или (а., ftp G ст) о
о ([ЛГ<р)]у = 1 или [М(ст)]у = 1) о
о [М(р)].. + [ЛГ(ст)1 = 1 о [М(р) + ЛГ(ст)] = 1.
V	Ч	Ч
3)	Здесь действуем по аналогии со случаем 2), учитывая
свойства теоретико-множественной операции пересечения и опе-
рации пересечения булевых матриц:
[М(р П ст)].. = 1 о (a., ftp е р П ст о (а„ ftp £
е Р & (a., b.) G ст о [М(р)].. - 1 & [М(ст)].у = 1 о
о [M(p)]z/- [ЛГ(ст)].у = 1 о [М(р) Л	= 1.
4)	К цели ведет следующая цепочка равносильных предло-
жений:
[М(р)].. = 1 о (a., ftp G р о (a., bp £ р [М(р)].. =
= 0 о [М(р)]'.. = 1 о ([М(р)])'.. = 1.
Истинность утверждений 5) и 6) очевидна. =
Специфическая структура множества А х В позволяет ввести
отличные от теоретико-множественных операций способы полу-
чения новых отношений из заданных.
Пусть р Р(А х В) и ст G Р(В х С). Произведением отно-
шения р на отношение ст называется отношение между множест-
вами А и С, обозначаемое р ° ст и такое, что:
(а, с) €Е р о ст :<» (э ft G В)((а, ft) G р & (b, с) G ст).
Другими словами, вхождение пары (а, с) в отношение р ° о
равносильно существованию «посредника» ft 6 В, с которым а
находится в отношении р и который сам находится с с в
отношении ст.
Умножение отношений можно проиллюстрировать с помощью
графов.
Пример 12. Пусть отношение р С А X В такое же, как
в примере 10, а отношение ст С В X С, где С = {a, (i, у],
зададим списком принадлежащих ему пар: ст = {(=, /3), (*, а),
34
(+, a), (+, у)}. Тогда в отношение р ° о будут входить следующие
пары (их элементы связывает двухзвенный путь—сначала по
p-дуге, а затем по ст-дуге):
рост = {(0, 0), (1, a), (1, у), ( + , а), (+, у)}.
На рис. 15 p-дуги показаны сплошными линиями, и ст-дуги—
пунктирными.
Пусть А * 0. Тождественным от-	д
ношением, или отношением равенства —
на А называется отношение Д. С	„ и>
Л	—
С А X А такое, что	1
\—"-А' ' Р
(а, Ъ) е АЛ ;о а = Ъ.	\
—---Y
Другими словами, А^ состоит из
всевозможных пар с одинаковыми эле-
Рис. 15
ментами.
Тождественному отношению на п-
элементном множестве А соответствует тождественная (еди-
ничная) булева п х п-матрица Е:
Е..
v
1,	если i = /,
О	в противном случае.
Множество дуг графа G(A) состоит из петель при каждой вершине.
Следующая теорема описывает основные свойства операции
умножения бинарных отношений.
Т е о р е м а 1.8. 1) Умножение отношений ассоциативно:
для любых р е Р(А X В), о е Р(В X С) и те Р(С X D)
Р ° (ст о т) = (Р ° ст) о т;
2) тождественные отношения являются нейтральными эле-
ментами относительно умножения: для любого р е Р(А х В)
р°Лв = р и Ал »р = р.
Доказательство. 1) Формально в приводимой
цепочке рассуждений используется ассоциативность логической
связки конъюнкции и правила ее взаимодействия с квантором
существования (можно просто следить за содержательным смыслом
переходов):
(a, d) е р ° (ст о т) о (э Ъ е В)((а, Ь) е р & (b, d) е ст о т) о
о (э Ъ е в)((а, Ъ) & р&(эс е С)((5, с) е ст & (с, d) е т)) о
о (э Ь е в)(з с е С)((а, b) е р & (b, с) е а & (с, d) е т) о
(э с е С)(э Ъ е в)((а, Ъ) е р & (Ъ, с) е ст & (с, d) е т) о
2*
35
о (a c G С)((а, с) G р ° а & (с, d) & т) о (a, <Z) G (р » ст) » т.
Таким образом, отношения р ° (ст«т) и (р «ст) °т состоят из одних
и тех же пар, и, следовательно, совпадают.
2) Имея в виду, что (х, у) G А означает х “ у и что
(х, х) G А—тождественно истинное высказывание, получаем для
р е Р(А х В):
(a, b) G р ° о (э с G А)((а, с) 6 р & (с, Ъ) G Ад) о
о (a, b) G р & (b, b) G &в о (a, b) G р.
Отсюда р°^в = Р- Аналогично ДА«р = р. =.
Умножение отношений тесно связано с операцией умножения
для двоичных булевых матриц. Пусть	и N G —
*	*	т*п	пхр
двоичные булевы матрицы соответственно размерности т х п и
п х р. Их произведением называется матрица М ° N размерности
т х р такая, что
п
2 Mtl N
/=1
где умножение и сложение выполняются в двоичной булевой
алгебре В2, т. е. являются логическими операциями.
Т е о р е м а 1.9. Если р С А х В и а С в х С, где А,
В, С—конечные множества, то имеет место равенство
М(р ° ст) = М(р) ° М(а)
для представляющих указанные отношения булевых матриц.
Доказательство. Используются свойства ло-
гических операций и определение булевой матрицы, представля-
ющей отношение:
[М(р о ст)] lk = 1 о (аск) S р ° а о
о (э Ъ е. В) ((a, b ) S р & (Ъ, с ) е ст) о
/ 1 / / *
О G В)([М(р)].. = 1 & [М(ст)]	= 1) О
/	Ч	1К’
о 2 [М(р)].. • [М(ст)].Л = 1 О [M(p)oM(CT)]tt = 1. о
/
Для р С S X S определим рп := р «р ° ... ор.
п
Полагают также: р° := А.
36
Унарная операция обращения определяется для отношений
следующим образом: для р С А х В обратным называется
отношение р-1 С В х А такое, что:
(Z>, а) е р~х :о (a, b) G р.
Матрица ЛТ(р-1) транспонирована по отношению к М(р)
(строки становятся столбцами, а столбцы строками), т. е.
М(р := [ЛГ(р)]т, а граф G(p~l) получается из графа G(p)
обращением всех дуг.
Те орема 1.10. Операция обращения отношений обла-
дает следующими свойствами:
1)
(Р-1)’1 = Р.
2)
(р о ст)-1 = СТ-1 о р-1
для всех р С Ах В, a Q ВхС.
Доказательство. Первое свойство очевидно,
если обратиться к графовой интерпретации отношения.
Второе свойство доказывается следующими рассуждениями:
(с, a) G (р о ст)-1 о (а, с) € р J ст о
о (э b G В)((а, J) 6 р & (b, a) G а) о
о (ab G В)((с, Ь) G ст-1 & (b, a) G р'1) о (с, а) G ст-1 вр-1. =
Следствием теоремы 1.10 является равенство
«')" -
Отметим некоторые связи умножения и обращения отношений
с теоретико-множественными операциями.
Т е о р е м а 1.11. Для любых отношений р, ру, р2 G
G Р(А X В) и а, Стр ст2 G Р(В х С) справедливы следующие
утверждения:
1)
р « (cfj и (?2) = р ° CTj и р ° ст2, (pt и р2) о а = рх о a U р2 ° ст;
2)
р ° (ст И ст ) С р о а Пр» а , (р П р_) о ст С р о ст И р, ° ст;
1	1	XI	Xх	1	X
3)
Pl с р2 & СТ1 с ст2 =* р!°CTj £ р2°<72;
37
4)
(pY U р2) 1 = р/ U р2‘;
5)
(Р1 Л р2)~' = р;1 Л р"1;
6)
Р1 Р2 * Р~1 £ Р~2-
Доказательство.
1)	Используется дистрибутивность конъюнкции относительно
дизъюнкции и взаимодействие квантора существования с дизъ-
юнкцией:
(а, с) е р о (o-j U <т2) о (э b 6 В)((а, Ь) 6 р & (b, с) 6 tZj U <т2) о
о (э J 6 Ь) &р & ((Ь, с) е ст1 или (Ь, с) е <т2)) о
*(э J 6 В)(((а, Z>) G р & (Ь, с) 6 <7j) или
((а, Б) 6 р & (Ъ, с) е <т2)) о
* (э i 6 В)((а, А) 6 р & (Ь, с) 6 стр или
(a JG В)((а,	€ р & (Б, с) G СТ2) о
о (а, с) Ер « cTj или (а, с) £р « а2 » (а, с) 6р «<т( Up» ст2-
Вторая формула в этом пункте доказывается вполне ана-
логично.
2)	Вначале доказательство проводится как и в случае 1):
(а, с) е р о (CTj Л ст2) о (а Ь 6 В)((а, Ь) 6 р & (b, с) G Л <т2) о
О (а Ъ 6 в)((а, Ь) 6 Р & (Й, с) 6 <7j & (b, с) 6 <т2) о
* (э J £ В) [((<2, Ъ) 6 р & (b, с) 6 <7j) &
& ((a, Z>) G р & (Ь, с) е <т2)] =»
[На этом этапе доказательства равносильность формул нарушается:
наличие Ъ и Ъ с нужными свойствами не гарантирует существо-
вание элемента Ъ, удовлетворяющего предыдущей формуле.]
=> (aiG В)((д, b) G р & (Ь, с) 6 Ст|) &
& (э Б G В)((а, Б) 6 р & (Б, с) G ст2) <*
о (а, с) 6 р °	& (а, с) G р с ст2 о (а, с) G р ° Л р « ст2.
38
Итак, всякая пара, принадлежащая отношению р« (CTj Г) <т2),
входит в отношение р « Г) р ° а2, т. е.
р о (Oj Г) ст2) С р о (Tj Про а2.
Чтобы показать, что равенство в доказанной формуле в общем
случае не имеет места, рассмотрим простейший пример: А = {а},
В = {5р b2}, С = {с}, р = {(а,	(а, Ъ2)} = А х В,	=
= {(йр с)}, а2 = {(Ь2, с)}. Тогда CTj П а2 = 0, а значит, и
pofc?! Л ст2) = 0. Но р»^ = {(а, с)} и р»а2 = {(а, с)},
откуда р°сг1 Л р о ст2 = {(а, с)} # 0.
3)	Пусть р{ С р2, cTj С а2 и (а, с) Е ру Тогда для
некоторого Ъ 6 В будет: (а, J) G Pj 4 (b, с) Е Стр Отсюда
(а, Ъ) G р2 & (й, с) Е ст2, т. е. (а, с) е р2 ° а? Соотношения
4)—6) достаточно очевидны. □
Бинарное отношение р £ S х 5 между элементами одного
множества называется однородным. При этом говорят, что р
является отношением в множестве 5. В n-элементном множестве
2
имеется 2” различных отношений.
Совокупность Р(5 х 5) всех отношений в множестве 5
представляет собой богатую алгебраическую структуру: кроме трех
теоретико-множественных операций в P(S х 5) можно выполнять
еще умножение и обращение. Заметим, что в общем случае
операция умножения отношений является лишь частичной—она
определена далеко не всегда, а операция обращения, хотя и
применима к любому отношению, имеет своим результатом
отношение в общем случае между другими множествами.
Алгебры множеств и двоичная булева алгебра являются
примерами конкретных реализаций абстрактного понятия булевой
алгебры. Аналогично и алгебра однородных отношений представ-
ляет собой частное воплощение одной общей конструкции, которая
в последнее время все чаще встречается в литературе, ориен-
тированной на приложения в области дискретных систем [85].
Абстрактной алгеброй отношений называется алгебра
(R, V, л, о, ', -1, 0, 1, е) типа (2, 2, 2, 1, 1, 0, 0, 0), где
(/?, V, л, ', 0, 1)—булева алгебра, для которой имеют место
тождества I—IX из § 1.1, а операции умножения «, обращения
1 и выделенный дополнительно элемент е таковы, что выполня-
ются следующие тождества:
X.
X ° (у ° z) = (X о у) о Z
(закон ассоциативности для умножения),
39
XI.
х° е = е° х = х
(закон нейтральности элемента е),
XII.
X о (у V z) = (х о у) V (х о z), (X V у) 0 Z = (X 0 z) V (у 0 z)
(законы дистрибутивности умножения относительно объединения),
XIII.
(л'1)-1 = х
(законы инволютивности для обращения),
XIV.
(х V у)-1 = х-1 V у-1
(закон обращения объединения),
XV.
(X о у)-1 = у-1 о X-1
(закон обращения произведения),
XVI.
(х-1 о (х о у)') Л у = О
(закон Шредера).
Теорема 1.12. Система (P(S х S), U, П, °, ", -1, 0,
А х А, А) является алгеброй отношений.
Доказательство. Согласно теореме 1.6 система
(P(S х S), U, П, ", 0, А х А)—булева алгебра. Законы X, XI
выполняются для однородных отношений вследствие теоремы 1.8.
Тождества XII и XIV—это формулы 1) и 4) из теоремы 1.11.
Истинность законов XIII и XV установлена в теореме 1.10.
Остается убедиться в справедливости закона Шредера, т. е.
доказать, что для любых отношений р, ст 6 P(S х S) имеет место
равенство (р-1 ° (р ° ст)) П ст = 0. Предположим противное, т. е.
что для некоторых отношений р, ст G P(S х S) пересечение
(р-1 о (р о ст)) П ст не пусто. Тогда найдется пара (а, с) е. S х S
такая, что (а, с) G ст и (а, с) 6 р-1° (р ° ст). Из последнего
соотношения следует существование элемента b 6 S такого, что
(а, Ь) 6 р-1, т. е. (6, а) G р и одновременно (6, с) 6 р <> ст. Но
так как (6, a) G р и (а, с) G ст, то (6, с) 6 р ° ст. Пришли к
противоречию: отношения р ° ст и р ° ст не должны иметь общих
пар по определению дополнения. Таким образом, предположение
(р 1 о (р о ст)) П ст * 0 привело к противоречию, и, следователь-
40
но, тождество XVI истинно для бинарных отношений на множестве
S. □
Алгебру отношений образует любой набор отношений в
некотором фиксированном множестве, замкнутый относительно
теоретико-множественных операций, умножения и обращения и
содержащий пустое, универсальное и тождественное отношения
на этом множестве. Все такие алгебры отношений называются
конкретными алгебрами отношений. К сожалению, не всякая
абстрактная алгебра отношений изоморфна подходящей конкретной
(см. [4, 85]).
Из теорем 1.7 и 1.9 следует, что и двоичные булевы матрицы
размерности п х п образуют алгебру отношений, она изоморфна
алгебре всех отношений на некотором фиксированном п-элемен-
тном множестве. Именно, имеет место
Т е о р е м а 1.13. Алгебра	+> А, °, ',Т, О, I, Е)
является алгеброй отношений. □
Сделаем несколько замечаний к теореме 1.13.
Во-первых, число элементов в алгебре отношений *^пХп> т. е.
количество всевозможных двоичных булевых п х n-матриц, равно
2
2” ,—столько же, сколько отношений в n-элементном множестве.
Далее, напомним, что унарная операция транспонирования
Т
сопоставляет каждой матрице симметричную ей относительно
главной диагонали матрицу и Е обозначает тождественную булеву
п X п-матрицу.
Полезно переписать тождества XI—XVI в матричных обозна-
чениях:
ХГ.
М ° Е ~ Е о М = М,
Х1Г.
M°(N + Р) = М° N + М*Р, (М + N) <> Р = М ° Р + N ° Р,
XIII'.
(М^ = м,
XIV'.
(М + N)T = МТ + NT,
XV'.
(M°N)T = NT°MT,
XVI'.
(МГ ° (М °N)') Л N = О.
41
Отметим, что закон Шредера в алгебре отношений P(S х S)
допускает запись в виде включения р-1 ° (р ° а) С и. Действитель-
но, если ни одна из пар, входящих в отношение р-1 « (р « ст), не
содержится в ст, то значит, все они содержатся в дополнении ст,
и обратно. Далее, если для двоичных булевых матриц считать
М < N тогда и только тогда, когда каждый элемент первой
матрицы не превосходит соответствующего элемента второй
матрицы (имея в виду, что 0 < 1 в В?), то тождество XVI'
сводится к неравенству:
Мто (М° N)' < N'.
Пусть р Q А х В и а е А. Срезом отношения р через
элемент а называется множество
р(а) := {й 6 В I (a, b) 6 р}.
Другими словами, срез через элемент а—это совокупность
вторых элементов пар отношения р, первым элементом в которых
является а, т. е. множество всех элементов, с которыми элемент
а находится в отношении р. Срез через подмножество X Q А
определяется как объединение срезов через все элементы этого
подмножества:
р(Х):= U р(а).
аЕХ
Первой проекцией отношения называется совокупность первых
элементов составляющих его пар, а второй проекцией называется
совокупность вторых элементов этих пар:
рГ|Р := {а 6 Л1 (ai Е 5)((а, b) G р)},
ргуэ := {й € В I (a a G Л)((ст, Й) € р)}.
Если отношение р задано матрицей М(р), то строка этой матрицы,
соответствующая элементу а, будет характеристической функцией
среза р(ст) в В. В графе G(p) срезом р(а) является совокупность
всех вершин, в которые входят дуги из вершины а. Первая
проекция отношения р в матрице М(р) распознается как множество
меток ненулевых строк, а вторая проекция—как совокупность
элементов множества В, помечающих ненулевые столбцы. В графе
G(p) первая проекция для р выделяется как множество вершин,
из которых исходит хотя бы одна дуга, а вторая проекция—как
множество концов всевозможных дуг этого графа.
Теорема 1.14. Для любых отношений р, р^ р2 6
G Р(А X В), a G Р(В X С) и подмножеств Хр Х2 С А спра-
ведливы следующие утверждения'.
42
1)
р(0) = 0, р(А) = pr2p, р-1(5) = pfjp;
2)
Р(Хх U Х2) = р(Хр U р(Х2);
3)
р(^ Л Х2) С р(Хх) Л р(Х2);
4)
\ £ Х2 => р(Х,) С р(х2);
5)
(рх U р2)(Х) = Р1(Х) U р2(Х);
6)
(Рх Л р2)(Х) с Р1(Х) Л р2(Х);
7)
pt С р2 => рх(Х) С р2(Х);
8)
Р1 С р2 => prjPj £ ргхр2 & рг2р1 £ рг2р2;
9)
(роСТ)(Х) = СТ(р(Х));
10)
prjp-1 = рг2р, рг2р“1 = prjp;
11)
p^fpocr) = р-1(рг1ст), рг2(роСТ) = ст(рг2р).
Доказательство. Сразу отметим как вполне
очевидные свойства 1), 4), 7), 8), 10).
Логическая структура доказательства формулы 2) такая же,
как при доказательстве формулы 1) из теоремы 1.10:
b S р(Х U У) о (э а А)(а G X U Y & (a, b) £ р) <=>
о (э а 6 Л)((а G X или a £ У) & (а, А) 6 р) о
« (э а е А)((а X & (a, b) G р) или (a G У & (a, b) G р)) о
о (эй 6 А)(а 6 X & (a, i) G р) или
(э a G Л)(а G Y&(a, b) G р) о
о (й£р(Х) или йбр(У)) о bG (X) U р(У),
—множества р(Х U У) и р(Х) U р(У) состоят из одних и тех же
элементов, и, следовательно, совпадают.
Логическая схема доказательства свойства 3) та же, что и в
случае 2) теоремы 1.9. Приведем пример, показывающий, что
43
равенства в общем случае нет. Пусть А = {ар а2}, В = {й},
Х{ = Ц}, Х2 = {а2}, р = {(ар Ь), (а2, й)} = А х В. Тогда
р(Х{ Г) Х2) = р(0) = 0,
р(Х{) П р(Х2) = {*} П {й} = {Ь} = В * 0.
При доказательстве свойств 5) и 6) рассуждения вполне
аналогичны тем, которые были проведены при доказательстве
соответственно 2) и 3). Вот простой пример, когда левая и правая
части в 6) не совпадают:
А = {ар а2}, В = {й}, р{ = {(ар й)}, р2 = {(«2, й)}, X = А.
Для доказательства свойства 9) используется определение
умножения для отношений, свойства логических связок и квантора
существования:
с G (р ° сг)(Х) о (э а 6 Л)(а 6 X & (а, с) G р ° а) о
о (э а 6 А)(а 6 X & (в й 6 В)((а, й) 6 р & (Ь, с) 6 а)) о
о О а 6 Л)(э й 6 В)(а G X & ((а, й) 6 р & (й, с) 6 сг)) о
<=> (з й 6 В)(й 6р(Х) & (й, с) е а) о с 6 сг(р(Х)).
Отсюда (р ° а)(Х) = а(р(Х)).
Остается доказать равенства 11). Равенство рг2 (р ° а) =
= сг(рг2р) следует из 1) и 3). Последовательно применяя 10),
теорему 1.9, а также 1), 9), 1), получаем:
рг^осг) = рг2(р°сг)“1 = рг2(сг-1 °р~1) = (с-1 °р-1)(С) =
= /ЛаЛО) = Р~1(РГ1СГ)-
Теорема доказана, о
Бинарное отношение р С А х В называется 1-полным, если
pi^p = А и 2-полным, если рг2р = В. В матричной интерпре-
тации 1-полнота для р означает, что в матрице М(р) нет нулевых
строк, а 2-полнота равносильна отсутствию в М(р) нулевых
столбцов. В графе 1-полного отношения р из каждой вершины
исходит по крайней мере одна дуга, а 2-полнота по графу G(/>)
проверяется наличием в каждой вершине входящей дуги. Отно-
шение, одновременно 1- и 2-полное, называется полным.
Отношение р С А х В, по определению, однозначно, если для
любого а 6 А срез р{а) содержит не более одного элемента,
другими словами, если тождественно истинна следующая формула
(при х G А, ур у2 G В):
44
(х, у{) G р & (х, у2) 6 р =>	= У2.
Однозначное 1-полное отношение р между множествами А и
В называется отображением множества А в множество В или
функцией, заданной на Л и принимающей значения в Я. В этом
случае применяется запись р: А -» В.
Отношение р тогда и только тогда будет отображением, когда
каждый срез его р(а) состоит в точности из одного элемента. Этот
элемент называется р-образом элемента а и обозначается через
р(а), т. е. применяется обычная функциональная символика.
Для поэлементного задания отображения используют запись
вида а •—»р(а), например, х >—» sin х или р •—»М(р).
Отношение р С А х В называется обратно однозначным, если
однозначно обратное ему отношение р-1, что равносильно
тождественной истинности формулы
(хр у) 6 р & (х2, у) 6 р =>	= х2.
Однозначность конечного отношения р распознается по матрице
М(р) наличием в каждой ее строке не более одной единицы.
Аналогично обратная однозначность для р равносильна наличию
не более одной единицы в каждом столбце матрицы М(р).
В графовой интерпретации однозначность отношения р рав-
носильна тому, что в графе G(p) из каждой вершины выходит
не более одной дуги, а обратная однозначность означает, что в
каждую вершину входит не более одной дуги.
Если р—отображение, то в каждой строке матрицы М(р) стоит
точно одна единица, а из каждой вершины графа G(p) исходит
точно одна дуга.
Говорят, что р С А х В взаимно однозначно, если оно
однозначно и обратно однозначно.
Взаимно однозначное отображение р: А -» В называют вло-
жением множества А в множество В. Употребляют также термины:
инъективное отображение, инъекция. Наложение множества А на
множество В—это 2-пол ное отображение р: А -» В. Синонимами
наложения являются: отображение А на В, сюръективное
отображение, сюръекция.
Полное взаимно однозначное отношение р между множествами
А и В называется взаимно однозначным соответствием между
А и В; принята также терминология—биективное отображение,
биекция. Матрица М(р) для конечного биективного отображения
р является квадратной перестановочной матрицей: в каждой
строке и в каждом столбце ее стоит точно одна единица.
Язык алгебры отношений позволяет по-новому увидеть смысл
введенных понятий.
Именно, имеет место
45
Теорема 1.15. Пусть р £ А х В. Каждая из следующих
формул равносильна указываемому для нее свойству :
1)	ЛА	£ Р	Г1		(1—полнота),
2)	Ал	£ Р~1	°Р		(2—полнота),
3)	р 1 ор	£ Ал			(однозначность),
4)	р ор-1	£ Аа			(обратная однозначность),
5)	р ор-1	= Аа	& р1 ор =	Ал	(биективность).
Д	ока	з а т	е л ь с т в	О.	
1)	В графовой		интерпретации		1-полнота означает, что из
каждой вершины а 6 А исходит по крайней мере одна р-дуга.
Возвращаясь по этой же дуге, т. е. проходя по р-1-дуге, получаем,
что каждая пара (а, а) входит в произведение р °р-1, и значит,
Ал С р-р-1.
2)	Доказывается аналогично.
3)	Определение однозначности может быть записано в следу-
ющем виде:
(уг X) е р-1 & (х, У2) е Р => yt = у2, ИЛИ
(Уг У2) 6 р-1ор => (ур у2) е дд)
что и означает включение р-1 ° р £ Afi.
4)	Доказывается аналогично 3).
5)	Биективность—это одновременное выполнение свойств 1)—
4). Если Ал £ pop 1 (1-полнота) и р °р-1 £ Д^ (обратная
однозначность), то р°р-1 = Ал как множества, состоящие из
одних и тех же элементов. Аналогично из 2) и 3) следует
равенство р-1 °р = Ад. =
Следствие 1.3. Если <р: А -> В и у: В -» С—отоб-
ражения, то их произведение А -» С также является
отображением. При этом <р ° у будет инъективным (.соответ-
ственно сюръективным, биективным), если инъективны (соот-
ветственно сюръективны, биективны) сомножители <р и tf>.
Доказательство. Если <р и у»—отображения, то
<р 1 о р С Дд и у»-1 ° у» £ Дс. Тогда (р ° у»)-1 о (р о у») =	(у»-1 о
О р О (р ° у») = р^»(р^ор)ор С у» * О Д# оу» = у» 1 о у, С Д
и, значит, <р ° у» однозначно. Аналогично доказывается сохранение
46
свойств инъективности, сюръективности и биективности при
умножении. =
Совокупность всех отображений множества А в множество В
обозначим через F(A х В). Следующий результат показывает, что
свойства инъективности и сюръективности тесно связаны с
некоторыми специальными уравнениями для отображений.
Теорема 1.16. Если f—отображение множества А в
множество В, то:
1) уравнение f°x = Ал разрешимо в F(B х А) тогда и
только тогда, когда f инъективно',
2) уравнение x°f= &в разрешимо в F(B х А) тогда и
только тогда, когда f сюръективно.
Доказательство. 1) Пусть отображение / инъ-
ективно. Тогда / обратно однозначно, и значит, /°/-1 £ А., а
в силу 1-полноты А С /о/-1 (теорема 1.15). Таким образом,
fof~x — А . Но у-1 не принадлежит множеству F(B х А), если
рг^У-1 * В, т. е. если рг2/ * В. В этом случае произвольно
выберем точку aQ G А и положим
У-1(7>), если b G рг_у,
К d f
aQ,	если Ь £ рг2/.
Очевидно, что g е F(B х А) и что f°g- А^.
С другой стороны, пусть fog = Ал и /(at) = У(д2) для
некоторых Др д2 G А. Тогда
а1 = ЛЛ(а1> = <7о*)(а1) =	=
= (f'g)(«2) = Ал(д2) = а2,
откуда следует, что / инъективно.
2) Пусть отображение / сюръективно. По теореме 1.15,
/-1 о/ С Дп (однозначность) и An С У-1 «у (полнота). Следова-
О	о
тельно, у-1 ° f = Ад. Конечно, pi^y-1 = В, но, вообще говоря,
У 1 не будет однозначным. В таком случае для каждого b G В
в f \b) выберем (не сомневаясь, что это можно сделать)
произвольный элемент а*. Положим, далее, g(b) := а*. Так как
У Г) У-1(52) = 0 при # />2 (в силу однозначности /), то
* g(b2) при b{ & Ъ2, т. е. g однозначно. Поскольку
рг^ — В, то g & F(B х А).	При этом для любого b G В
47
имеем (g°f)(b) = /(gfbf) = f(a*) = b, ибо a* G f~l(b). Итак,
g°/ =
С другой стороны, пусть g«/ = Дя и A 6 В—произвольный
элемент. Тогда b = &B(b) = (gof)(b) = /(g(6)), и значит, b 6
G рг2/, откуда рг2/ = т- е- / сюръективно. □
Отображения непустого множества S в себя называются его
преобразованиями. Из теоремы 1.15 видно, что
F(S х S) = {/ G P(S х S) I A £ /о/-1 & f~l of С Д}.
Совокупность полных взаимно однозначных преобразований
множества 5 обозначим через K(S х S). Из теоремы 1.15 получаем:
K(S х S) = {<f> G P(S x S) I p ° p 1 = Д = <f> 1 ° <f>}.
Согласно следствию 1.36 из теоремы 1.15 множество F(S х S)
замкнуто относительно умножения. Очевидно, что Д G
G F(S х S). Множество K(S х S) замкнуто не только относительно
умножения, но и относительно обращения (если <р—биекция, то
и	—тоже биекция). Поэтому элементы множества K(S х S)
называются обратимыми преобразованиями множества S.
Следующий результат находит многочисленные применения.
Т е о р е м а 1.17. Для преобразования f конечного множе-
ства S следующие условия равносильны:
1)	/ отображает S на S (т. е. f сюръективно);
2)	/ взаимно однозначно (т. е. f инъективно);
3)	/ обратимо (т. е. f биективно).
Доказательство. Если множество 5 имеет п
элементов, то граф G(f), соответствующий преобразованию /, имеет
п вершин и п дуг: из каждой вершины исходит точно одна дуга.
Из 1) следует 2). Пусть / отображает 5 на 5. Если / не
взаимно однозначно, то в G(f) имеется вершина, в которую входят
как минимум две дуги. Получается, что п дуг имеют больше чем
п концов—приходим к противоречию.
Из 2) следует 3). Если / взаимно однозначно, то в каждую
вершину входит самое большее одна дуга. Это означает, что п
дуг графа G(f) имеют точно п различных концов. Следовательно,
в каждую вершину графа входит дуга, т. е. / отображает S
на S.
Из 3) следует 1) и 2). Обратимые преобразования множества
5 взаимно однозначны и отображают 5 на 5. □
Примеры отображений п [(п + 1)/2] (целая часть) и
2
п •—> п на множестве натуральных чисел показывают, что для
бесконечных множеств свойства сюръективности и инъективности
преобразований независимы, так что в отличие от теоремы 1.16
теорема 1.17 не является теоремой алгебры отношений.
48
Конструкция декартова произведения может быть обобщена и
на большее, чем 2, число множеств. Именно для п > 3 полагаем:
А, х А. х ... х А , х А := (А. х Л_ х ... х А ,) х А
1	2	п-1 п v 1	2	п-1' п
(рекурсивная формула).
Если А^ = Л2 = ... = Ап = А, то говорят о п-й декартовой
степени множества А и пишут: Ап.
Элементы декартова произведения Аг х А2 х ... х Ап записы-
ваются в виде (а,, а~,.... а ), где а. G А., и называются
1 L	П'	I	I
упорядоченными п-системами (или упорядоченными п-ками).
По определению, при п > 3 получаем:
(й1> аГ ап) = «аГ аТ - an-J' а>
Отсюда следует, что две упорядоченные и-ки равны тогда и только
тогда, когда у них равны соответствующие компоненты.
Пусть п > 1. Под п-арным отношением между множествами
Лр А2, ..., Ап понимают всякое подмножество декартова произве-
дения А, х Л_ х ... х А , т. е. любой элемент множества
1 L	П
Р(А, х А. х ... х А ) всех подмножеств множества А, х А- х ...
... хЛд. Частным случаем теоремы 1.2 из § 1.1 является
Теорема 1.18. Совокупность х А2 х ... х Лд) всех
п-арных (п > 1) отношений между множествами Лр А2, ...
..., Ап, рассматриваемая вместе с теоретико-множественными
операциями объединения, пересечения и дополнения, а также
вместе с выделенным пустым (0) и универсальным (Л( х
х А2 х ... хЛд) отношениями, является булевой алгеброй. =
Понятие проекций бинарного отношения обобщается на случай
произвольного и-арного (и > 1) отношения р С А{ х А2 х ...
... х Ап следующим образом. Если 1 < k < п и < i < ...
... < ik—некоторые числа из множества {1, 2, ..., и}, а
< i2 < ... < j—остальные числа этого множества, то
i{i2 ... [^-проекцией отношения р называется отношение (при
к = 1—множество)
Рг, i tP := Uai > ai..ai) G Ai xAi x ••• x A. I
U" *	1	2 lk	'1 l2	lk
(3(a , a , ..., a ) 6 A xA x ... x A )((a a ..., a ) Gp)}.
A J2 Jn-k A A	Jn-k 1	2 n
При n = 2 и к = 1 получаются первая и вторая проекции
бинарного отношения.
49
§ 1.3.	Отношения эквивалентности
Здесь мы определим важнейшие с прикладной точки зрения
типы отношений между элементами фиксированного непустого
множества S.
1.	Отношение р £ S х S называется рефлексивным, если
каждый элемент х Е S находится в этом отношении сам с собой,
т. е.
р рефлексивно :о (vx £ S)((x, х) G р).
Алгебраическим эквивалентом условия рефлексивности является
включение: А С р. Матрица М(р), представляющая рефлексивное
отношение р, характеризуется т^м, что все элементы ее главной
диагонали равны 1. На графе G(p) рефлексивность отношения р
выражается наличием петли в каждой вершине.
2.	Отношение р £ S х S называется антирефлексивным, если
никакой элемент х Е S не находится сам с собой в отношении
р, т. е.
р антирефлексивно :о (v х Е S)((x, х) £ р).
Алгебраическим эквивалентом условия антирефлексивности явля-
ется равенство: А П р = 0. Матрица М(р) антирефлексивного
отношения р характеризуется тем, что все элементы ее главной
диагонали равны 0. На графе G(p) антирефлексивность отношения
р характеризуется отсутствием петель.
3.	Отношение р £ S х S называется симметричным, если
пары (х, у) и (у, х) при х, у Е S одновременно принадлежат
или не принадлежат отношению р. В компактной форме это
выражается так:
р симметрично :<» (* х, у Е S)((x, у) £ р => (у, х) Е р).
Алгебраическим эквивалентом условия симметричности является
включение р~1 £ р. Оно, как легко видеть, влечет равенство
р 1 = р. На языке двоичных булевых матриц симметричность
отношения р означает симметричность матрицы М(р), т. е.
выражается равенством [М(р)]г = М(р). В графовой интерпре-
тации свойство симметричности означает, что всякая дуга имеет
встречную дугу между теми же вершинами (петли считаются
двухсторонними дугами).
4.	Отношение р £ S х S называется антисимметричным,
если при х # у, где х, у Е S, разве лишь одна из пар (х, у)
или (у, х) входит в р. Это требование логически выражается
следующим образом:
р антисимметрично :<> ((v х, у Е S)((x, у) Е р &
& (у, х) Е р => х = у).
50
Алгебраическим эквивалентом условия антисимметричности явля-
ется включение р П р~1 С А. В графе G(p) антисимметричность
представляется как отсутствие встречных дуг (кроме петель). В
матричной интерпретации свойство антисимметричности означает,
что если вне главной диагонали матрицы М(р) имеется 1, то на
симметричном ей месте (относительно диагонали) стоит 0.
5.	Отношение р Q S х S называется транзитивным, если для
него выполняется условие:
(*х, у, z 6 S)((x, у) G р & (у, z) 6 р => (х, z) 6 р).
Алгебраическим эквивалентом транзитивности является включение
р°р С р. В графе G(p) транзитивность равносильна следующему
условию: если из вершины х в вершину z имеется двухзвенный
путь, то из х в z ведет дуга. Для матричного эквивалента условия
транзитивности: М(р)-М(р) £ М(р) не существует простой эле-
ментарной проверки.
6.	Отношение р С S х S называется полным, если из любых
двух элементов множества S по крайней мере один находится в
отношении р с другим, т. е.
р полно :о (vx, у 6 $)((х, у) 6 р или (у, х) 6 р).
Алгебраическим эквивалентом полноты является равенство
р U р-1 = S х S. В графе G(p) полнота означает, что любые две
вершины соединены дугой (без учета ориентации). В матричной
интерпретации свойство полноты проверяется тем, что если в
М(р) имеется 0, то на симметричном ему месте относительно
главной диагонали стоит 1. В частности, все элементы главной
диагонали равны 1.
Ограничением отношения р С S х S на непустом подмноже-
стве S* С S называется отношение р| , := р Г) (S* х S*) = р*.
S
В отношение р* входят те и только те пары из р, оба элемента
в которых принадлежат подмножеству S*. Матрица М(р*)
получается из матрицы М(р) вычеркиванием строк и столбцов,
помеченных элементами множества S, не входящими в S*. Граф
G(p*) состоит из вершин графа G(p), соответствующих элементам
подмножества S*, и дуг графа G(p), соединяющих эти вершины;
таким образом, G(p*) является подграфом графа G(p).
Почти очевидна следующая
Теорема 1.19. Пусть S*—непустое подмножество
множества S. Если отношение р Q S х S обладает каким-нибудь
из следующих свойств: рефлексивность, антирефлексивность,
симметричность, антисимметричность, транзитивность, пол-
нота,—то это свойство выполняется (на S*) и для ограни-
чения р* = р\ .. а
51
Отношение т в множестве S называется отношением толе-
рантности (кратко: толерантностью), если оно рефлексивно и
симметрично:
т—толерантность :» Д С т & т-1 = т.
Совокупность всех толерантностей на множестве S обозначим
через T(S). Нетрудно видеть, что множество T(S) замкнуто
относительно объединения, пересечения и обращения отношений.
Например, если х^ и т2—толерантности, то
(Т1 и = т;1 и г-1 = Tj и т2,
и значит, отношение х^ U т2 симметрично, и, кроме того, оно
рефлексивно:
Д £ С т( и т2.
В T(S) входят также отношения S х S, Д и, по соглаше-
нию, 0.
Дополнение сохраняет свойство симметричности, но превраща-
ет рефлексивное отношение в антирефлексивное. Так что если
т—толерантность, то т U Д тоже будет толерантностью.
Более сложно обстоит дело с операцией умножения.
Т е о р е м а 1.20. Произведение Г1°Т2 отношений толе-
рантности х^ и х^ тогда и только тогда является отношением
толерантности, когда г и т2 перестановочны:
Тот = Т о Т
1 12	2 *Г
Доказательство. Необходимость.
Пусть Тр т2,	° т2 е T(S). Тогда т"1 =	т"1 = т2 и ° т2)-1 =
= Tj от2> Применяя формулу 2) из теоремы 1.10 § 1.2, получаем:
Т1°Т2 = (Т1 ° Т2>-1 =	= Т2 ° V
Достаточность. Пусть и т2—перестановочные
толерантности. Так как Д С г Д С т2, то Д = Д ° Д С
С т »т2 (здесь использована формула 3) из теоремы 1.11 § 1.2),
и, значит, отношение х ° т_ рефлексивно. Поскольку т 1 = т и
IX	11
Ъ1 = Т2’ Т0
(T1°T2)_1 = (Т^1) = Т2оТ1 = Т1ОТ2)
и, следовательно, т1 ° т2 симметрично, о
Из теоремы 1.19 следует, что всякое ограничение толерант-
ности является толерантностью на соответствующем множестве.
52
Совокупность {Л.I i 6 /} подмножеств множества S называется
его покрытием, если U А. = S. Покрытия множества тесно
связаны с толерантностями на нем.
Пусть т С S х S—отношение толерантности на S. Предклас-
сом толерантности т, или t-предклассом, называется всякое
подмножество А С S такое, что А х А С т, т. е. любые два
элемента подмножества А находятся в отношении т. Тривиальным
примером т-предкласса является всякое одноэлементное подмно-
жество {s}, s 6 S. Очевидно, что совокупность всевозможных
предклассов толерантности т образует покрытие множества S.
Больший интерес представляют классы отношений толерант-
ности.
Классом толерантности т называется такой т-предкласс,
который не включается ни в какой другой т-предкласс.
Пусть S—конечное множество, (а, Ь)—произвольная пара его
элементов, находящихся в отношении толерантности т С S х S.
Рассмотрим всевозможные т-предклассы, содержащие оба указан-
ных элемента, т. е. содержащие предкласс {а, Ь}. Какой бы
длинной ни была цепочка включений
{а, Ь} = Ло С А^ С Л2 С ... С С ...
таких т-предклассов, в силу конечности множества S она рано
или поздно оборвется. Последнее в ней подмножество будет уже
т-классом.
Более тонкие рассуждения позволяют установить, что и в
общем случае (т. е. не обязательно для конечного S) имеет место
Теорема 1.21. Пусть т—отношение толерантности
на множестве S. Тогда для любых двух элементов, находящихся
в отношении г, существует по крайней мере один содержащий
их 't-класс. о
Следствие 1.4. Пусть С{, С2, ..., Ст—всевозможные
классы толерантности т. Тогда т = U (С. х С.). о
Представление толерантности т в виде объединения декартовых
квадратов т-классов называется ее разложением на квадраты. О
таком разложении говорят, что оно неприводимо, если в нем нет
«лишних» квадратов, т. е. если в правой части нельзя исключить
ни одного из декартовых квадратов, не нарушая при этом
равенства.
П р и м е р 13. Пусть задана толерантность т на множестве
S = {1, 2, 3, 4, 5, 6} в виде графа. В силу симметричности
отношения т в графе G(r) у каждой дуги есть встречная дуга, и
такие пары дуг на рис. 16 заменены одной неориентированной
дугой. Кроме того, опущены петли (в каждой вершине). Классами
толерантности т будут Cj = {1, 2, 3}, С2 = {2, 3, 5}, С3 =
53
4
= {2, 4, 5}, С4 = {3, 5, 6}. Покрытие т = U (С. х С.) избы-
1=1
точно, так как любая пара, входящая в декартов квадрат
1	С2 х Су содержится в одном из остальных
Л	квадратов. В то же время разложение
/ \	т = (Ct х CJ U (С3 х С3) U (С4 х С4) уже непри-
А~	водимо: например, пара (1, 1) содержится только
J \J \ в Cj х Ср пара (4, 4)—только в С3 х Су а пара
4	5	6 (6, 6)—только в С. х С..
4	4
Рис. 16 Базисом толерантности т на конечном множе-
стве S называется всякий набор т-классов, опреде-
ляющий неприводимое разложение т на квадраты.
Так, в предыдущем примере единственный базис толерантности т
состоит из ее классов Ср Су Су Следующий пример показывает,
что толерантность может иметь несколько базисов, причем с
Поим
различным числом входящих в них классов.
П р и м е р 14. В соответствии с соглашениями, принятыми
в примере 13, зададим толерантность на восьмиэлементном
множестве неориентированным графом без петель, изображенным
на рис. 17. Тогда классы I—V, VII образуют ее шестиэлементный
базис, а классы I, III, IV, VI, VII—пятиэлементный базис.
Пусть #(т)—некоторый базис отношения толерантности т на
Фактормножеством множества S по т-базису
$?(т) называется множество S/&В(т), элементами
которого являются т-классы, входящие в базис
<ёв(т), и всевозможные (не только попарные!)
непустые пересечения классов. Понятие фактор-
множества по базису толерантности бывает
особенно полезным в тех случаях, когда этот
базис состоит из небольшого числа классов.
Если т имеет единственный базис й?(т), то
вместо 5/Й?(т) будем писать й?/т.
е р 15. Пусть толерантность т на множестве
5 = {1, 2, 3, 4, 5, 6, 7, 8, 9} задана двоичной булевой мат-
рицей
М(г) =
1
1
1
1
1
1
1
1
1
1111
1111
1111
1110
110 1
1110
110 1
10 0 1
110 1
1111
1111
110 1
10 0 0
0 111
10 0 0
0 10 1
0 0 10
0 10 1
54
Единственным т-базисом является совокупность &В(т) подмно-
жеств Cj = {1, 2, 3, 4, 6}, С2 = {1, 2, 3, 5, 7, 9}, С3 =
= {1, 2, 5, 8}. Находим пересечения: С4 = С’1 Г> С2 =
= {1, 2, 3}, С$ = С] П С3 = {1, 2) = Cj П С2 П C3, C6 =
= C2 П C3 = {1, 2, 5}. Фактормножество S/т состоит из шести
элементов. К этому примеру мы еще вернемся в § 4.2.
Отношение е в множестве 5 называется отношением эквива-
лентности (кратко: эквивалентностью), если оно рефлексивно,
симметрично и транзитивно:
е—эквивалентность :о Д С е & е-1 = е & е «е = е.
Совокупность всех эквивалентностей на множестве S обозначим
через E(S). Очевидно, что E(S) С T(S): всякая эквивалентность
является толерантностью. Множество E(S) замкнуто относительно
пересечения и обращения отношений. Например, если	е2—
эквивалентности, то
Д С £j & Д С е2 => Д С £j Г1 е2,
(е. Г) е_)"1 = е?1 Г) eZ1 = е. П е_,
(ei п е2) ° (ei п - <eioei) n (ei05) п	п
П (е2 о е2) С (£1 о £1) П (е2 « е2) С £j « е2,
и, следовательно, £j Г1 е2 рефлексивно, симметрично и тран-
зитивно. В E(S) входят отношения Д и S х S, пустое отношение
в число эквивалентностей не включается.
Теорема 1.22. Произведение £j ° е2 отношений эквива-
лентности и е2 тогда и только тогда является отношением
эквивалентности, когда £] и е2 перестановочны: £] ° е2 =
= е2 ° еГ
Доказательство. Необходимость.
Если £р е2, г1 °е2 е E(S), то все эти отношения входят в T(S),
т. е. являются толерантностями на множестве S. В этом случае,
как было показано в теореме 1.19,	= е2°ег
Достаточность. Если £j и £2—перестановочные
эквивалентности, то е1°е2 будет толерантностью (теорема 1.19).
Убедимся в транзитивности этого отношения:
(ei ° е2) ° (ei ° e2> = ei ° (е2 ° ei) ° е2 = ei ° (£i ° ег) ° е2 =
= (*! ° ^1) ° (е2 ° е2) = «4 ° е2- =
55
Из теоремы 1.19 следует, что всякое ограничение эквивален-
тности является эквивалентностью на соответствующем множестве.
Решение часто возникающей задачи дает
Теорема 1.23. Наименьшим отношением эквивалент-
ности, содержащим заданное отношение р С 5 х S, является
отношение
00
е(р) = U (р U р"1)".
п=0
Доказательство. При п - 0 получаем, что
(р U р-1)0 = А, так что А С е(р). Этим показана рефлексив-
ность. Далее,
(е(р)Г1 =
00
и (р
л=0
U р"1)"
и [(р и р"1)"]"1
л=0
= и [(р и р-1)-1]" = и (р 1 и р)п = е(р),
п=0	п=0
и значит, е(р) симметрично. Покажем транзитивность:
е(р) »е(р) = U (р U р-1)" о U (р U р~1)т =
п=0	т=0
= U U (р Up-1)wo(p Up 1)й = U (р Up 1)n+w = е(р).
л=0 т=0	п+т=0
Таким образом, е(р) является эквивалентностью.
Пусть теперь е—некоторая эквивалентность, содержащая р.
Тогда
р С е =* р 1 Се 1 = £ => р U р 1 С е =>
=> (р U р"1)" Ce"Ce=>U(pU р-1)" С е.
л=0
Следовательно, е(р) содержится в любой эквивалентности,
содержащей отношение р. □
Следствие!.5. Наименьшим отношением эквивален-
тности, содержащим данные эквивалентности и е2 на
множестве S, является отношение
е1 V е2 := К*’ У) е х (э n G 2V)(3	•••> хп е $)((*> xi) е ej &
&(Х1,Х2)	62	(Хп-1 ’ Хг) ei & (хп> У) е2^’
Доказательство. Очевидно, что наименьшая
эквивалентность, содержащая и е2, будет наименьшей эквива-
56
лентностью, содержащей теоретико-множественное объединение
е. U е_. Но тогда она совпадает с отношением
1	X
00	со
и ((Bj и е2) и (£1 и e2)_1)n = U U е/.
п=0	п=0
00	’
Покажем, что £j V е2 = U (Ej (J е2)" По определению, пара
п=0
(х, у) входит в отношение £j V е2, если существует цепочка
Хр х2, ..., хп элементов множества 5 с условиями (х, Xj) G Ер
(х,, х_) G е„ ..., (х ,,х )6е„ (х ,у)£е, (здесь число и можно
считать нечетным — в противном случае к цепочке приписывается
хп+1 = у и добавляется очевидное (у, у) G е2). Но тогда
(х, у) 6 Ej ° е2 ° ... ° Ej ° е2 С (е U е2)" С и (Ej U е2)п,
п=0
т. е.
е V в С и (е. U е,)п.
1 z п=0 1	2
Установим обратное включение. Заметим, что Ej V е2—
эквивалентность. Действительно, для любого х G 5 имеем
(х, х) G Cj,(x, х) G е2 и, значит, А С g v в2, т. е. имеет
место рефлексивность. Затем, если (х, у) 6 Ej V е2, т. е.
(х, Xj) G Ер (Хр х2) G е2, ..., (хп, у) 6 е2> то, используя сим-
метричность Ej и е2, получаем, что
(у, у) G Ер (у, xn) 6 е2...(х2, Xj) 6 е2, (хр х) 6 ер
(х, х) G е2,
откуда (у, х) 6 Ej V е2, т. е. отношение £j V е2 симметрично.
Объединением цепочек, ведущих от х к у и от у к z, строим
цепочку от х к z, чем доказывается транзитивность для
Ej V е2> Итак, Ej V е2—эквивалентность, содержащая Ej и е2>
Тогда U (е. U е_)п С в V в Отсюда е. V е, = U (в. U £,)". =
п=0	п=0
Следствие 1.6. Если Ej и —перестановочны, то
£1 V 62 = £! ° £2-
Доказательство. Если (х, у) G Ej V е2, то при
е1 ° е2 = е2 ° е1 полУчаем что (х> У} е ej ° е2> а обратное
включение очевидно, о
57
Совокупность {A.I i G 1} подмножеств множества S называ-
ется его разбиением, если:
1) U А = S; 2) А. П А = 0 при i # j.
Другими словами, разбиение множества — это его покрытие
попарно непересекающимися подмножествами. Подмножества, об-
разующие разбиение, называются его блоками.
Разбиения множества тесно связаны с эквивалентностями на
нем.
Пусть е £ S х S—отношение эквивалентности на S. Посколь-
ку е представляет собой толерантность, то можно говорить об
е-классах.
Т е о р е м а 1.24. Если е—отношение эквивалентности на
множестве S, то его классами (как толерантности) являются
в точности срезы е(а), где а& S.
Доказательство. По определению, е(а) =
= {> 6 SI (а, А) 6 е}, т. е. е(а)—это совокупность таких эле-
ментов множества S, с которыми а находится в отношении е.
Так как е рефлексивно, a G е(а) для любого a G А, т. е. все
срезы вида е(а), a G А, будут непустыми подмножествами в 5.
Используя симметричность и транзитивность отношения е, для
любых Ь, с G S получаем:
Ь, с G е(а) => (a, b) G е & (а, с) G £ => (5, а) G £ &
& (а, с) G £ => (b, с) G е,
откуда следует, что £(а)—предкласс отношения е. Пусть
£(а) С А, где А—некоторый £-класс, и b G А. Так как
aG е(а) С А, то a G А. По определению £-класса, (a, b) G е,
откуда b G £(а), и, следовательно, А £ е(а). Значит, е(а) = А.
Мы показали, что все срезы вида е(а) являются £-классами.
С другой стороны, если А—некоторый £-класс и a G А, то
А £ £(а), так как каждый элемент b G А находится в отношении
£ с элементом а. Собственное включение между £-классами
невозможно, так что А = е(а). =
Следствие 1.7. Если е—отношение эквивалентности
на множестве S и a, b G S, то е(а) = е(Ь) о (a, b) G е. =
Теорема 1.25. Если е—отношение эквивалентности на
множестве S, то е-классы образуют разбиение П(е) этого
множества. И обратно, если П—некоторое разбиение множе-
ства S, то отношение
£(П) := {(a, b) G S х 5 I а лежит в том же П-блоке, что и Ь}
является эквивалентностью на S. При этом е(П(е)) = е,
П(Е(П)) = п.
Доказательство. Пусть е—эквивалентность на
множестве S. Тогда £-классы образуют покрытие этого множества.
58
Допустим, что е(а) П е(й) # 0. Тогда найдется элемент
с 6 S такой, что (а, с) 6 е и (й, с) 6 е. Из симметричности
и транзитивности отношения е получаем, что (а, Ь) 6 е.
Следствие 1.7 из теоремы 1.24 приводит к равенству е(а) =
= е (й). Таким образом, разные е-классы не пересекаются. Мы
получили, что е-классы образуют разбиение множества S.
Обозначим его через П(е).
Пусть теперь П—некоторое разбиение множества S и отно-
шение е(П) определено, как в условии теоремы. Рефлексивность
и симметричность этого отношения очевидны. Если элемент а
лежит в одном П-блоке с элементом Ь, а элемент Ь находится в
одном П-блоке с элементом с, то, поскольку разные П-блоки не
пересекаются, получаем, что элемент а будет в одном П-блоке с
элементом с. Таким образом, е(П) есть также и транзитивное
отношение. Равенство е(П(е)) = е утверждает, что если по
отношению эквивалентности е мы построим разбиение П(е),
блоками которого являются е-классы, а затем рассмотрим
отношение «принадлежать одному П(е)-блоку», то согласно
следствию 1.7 из теоремы 1.24, снова вернемся к е. Аналогично
убеждаемся в справедливости равенства П(е(П)) = П. Теорема
доказана. □
Отношение эквивалентности е С S х S имеет единственный
базис, и он состоит из всех е-классов. Поэтому множество S
однозначно факторизуется по е. Именно, фактормножеством
множества S по эквивалентности е будет множество S/e,
элементами которого являются всевозможные е-классы.
Если П—некоторое разбиение множества S, то под фактор-
множеством S/П понимают фактормножество 5/П(е) по эквива-
лентности, соответствующей этому разбиению. Элементами
множества S/П будут, следовательно, П-блоки.
Говорят, что эквивалентность е С S х S разделяет подмно-
жество A Q S, если в каждый е-класс входит не более одного
элемента из S, т. е.
е разделяет А :<> е П (А х А) = Д .
А
В частности, е разделяет элементы a, b 6 S, если (а, Ь) £ е.
Если е разделяет подмножество А С S и при этом в каждом
е-классе есть элемент из А, то А называется трансверсалом для
е. Трансверсал включает по одному представителю из каждого
е-класса, в нем столько же элементов, сколько в фактормножестве
S/e.
Отображение nate: S -» S/e, s •—»e(s), сопоставляющее каж-
дому элементу множества S класс отношения эквивалентности
е С S х S, содержащий этот элемент, называется естественным
отображением множества S на фактормножество S/e (понятно,
что nate сюръективно). Таким образом,
(nat e)(s) := e(s).
59
Пример 16. Пусть /: А * В—некоторое отображение.
Ядром его называется отношение
Кег/ := {(ар aj G А х А1 /(а^ = /(а2)}.
Другими словами, пара , а2) входит в ядро Кег / тогда и только
тогда, когда элементы а[ и а2 имеют один и тот же /-образ.
Конечно, Кег / является эквивалентностью на множестве А. Пусть
А*—некоторый трансверсал для Кег /. Понятно, что А* находится
во взаимно однозначном соответствии с множеством рг2 /.
Обозначим это соответствие через <р. Тогда для a G А* будет
у>(а) = /(а), и значит, y>((Ker= /(а), поскольку все эле-
менты в Кег/-классе, содержащем а, имеют тот же /-образ, что
и элемент а. Отсюда для любого х G S получаем
p((nat Кег /)(х)) = у>((Кег /)(х)) = /(х),
т. е.
/ = nat Кег / о <р.
Имея в виду это соотношение, говорят, что диаграмма, изобра-
женная на рис. 18, коммутативна.
Пример! 7. С каждым базисом $?(т) отношения толе-
рантности т С S х S связано отношение эквивалентности е ^(т),
которое определяется следующим образом.
Пусть ^S(t) = {Вр В2, ..., Вт}. Полагаем:
е^(т) := {(a, b) G S x S I (v i)(a G В. о b G B.)}.
А
nat Kerf
A/Kerf
Рис. 18
pr2f Другими словами, элементы а и b счита-
ются эквивалентными, если они входят в
одни и те же базисные множества. Полу-
ченное отношение, очевидно, будет экви-
валентностью. Можно считать, что
Вр В2,..., Вт—это некоторые свойства, по
которым проводится классификация эле-
s. Тогда эквивалентность двух элементов
обладают одинаковым набором указанных
ментов множества
означает, что они
свойств. Рассмотрим в этом смысле толерантность т из примера
15. Ее
С1 =
единственный базис состоит из подмножеств
{1, 2, 3, 4, 6},
С2 = {1, 2, 3, 5, 7, 9}, С3 = {1, 2, 5, 8}.
Следовательно, разбиение, определяю-
щее эквивалентность е = е(т) будет
иметь своими блоками подмножества
{1, 2}, {3}, {4, 6}, {5}, {7, 9}, {8}.
Наглядно это разбиение представляется
диаграммой на рис. 19. Заметим, что
6 перечисленных е-классов составляют
60
фактормножество S/e, имеющее лйшь один общий элемент {1, 2}
с шестиэлементным же фактормножеством S/т.
Рассмотрим некоторые эквивалентности, связанные с графами,
именно, те, которые определяются теми или иными свойствами
графов.
П р и м е р 18. Отношение изоморфности графов является
отношением эквивалентности.
Граф = (Ур а{) называется изоморфным графу G2 =
= (V2, а2), если существует взаимно однозначное соответствие
(изоморфизм) <р: Fj -* V2 такое, что (и, v) G о (у>(д),
р(у)) 6 а2 для любых и, v G V{.
Каждый граф изоморфен себе: изоморфизмом является тожде-
ственное отношение Д на множестве вершин графа. Пусть
<р—изоморфизм графа Gj на граф G2, и пусть <р(и) = и',
<p(v) = v' для и, v 6 Ур Тогда и = у>-1(д'), v = F-1(v'), где
и', v' €= У2. Таким образом, из соотношения для получаем:
(д', v') 6 а2 о (<р~\и’), y>-1(v')) G «!
для любых и', v' G У2, т. е. <р~1—изоморфизм графа G2 на граф
Gp Для доказательства транзитивности отношения изоморфности
графов предположим, что отношение Ц>: У2 -» У3 является изо-
морфизмом графа G2 на граф G3 = (У3, а3). Произведение
<р о ip будет взаимно однозначным соответствием между множест-
вами yt и V. Так как (д', v') €= а2 о (^(д'), V’(v')) G а3 ДДЯ
д', v' €= У2, то для любых д, у G У1 имеем
(д, у) е Oj о (у>(д), y>(v)) е а2 о
«• (^(у>(и)), HpW)) G а3 О ((у>°^)(“)> (F’V’X»’)) G а3,
откуда заключаем, что <р будет изоморфизмом графа Gl на
граф G3. Таким образом, совокупность всех ориентированных
графов разбивается на классы изоморфности; входящие в такой
класс графы попарно изоморфны, и ни один из них не имеет
изоморфного ему графа в друп^ч классе.
Пример! 9. Пусть G = (У, а)—некоторый ориенти-
рованный граф. Говорят, что вершина у достижима из вершины
и за к шагов, если существует последовательность вершин
д = дп, и,, и~, ..., и. = у
О 1’	2 к
такая, что Д^ G « при всех i = 1, 2, ..., к.
61
Через Vk(u) обозначим множество вершин, достижимых из
вершины и за к шагов и не достижимых из нее за меньшее число
шагов.	t
Положим также У0(и) = {и}. Пусть в графе G существует
такая вершина uQ, из которой достижима (за подходящее число
шагов) любая другая вершина. Тогда подмножества вида У^(и0)
образуют разбиение множества V. Действительно, каждая верши-
на, по условию, входит в некоторое У^(д0), так что
V = U V,(u и в то же время очевидно, что У.(и ) И
к>0	‘
Г) У.(и0) = 0 при i * j. Для графа, показанного на рис. 20, и
его вершины 0 имеем:
Уо = {0}, У, = {1, 2, 3}, У2 = {4, 5, 10}, У3 = {6, 7},
У4 = {8, 9}-
Рассмотренное разбиение вершин графа по их расстоянию от
некоторой начальной вершины будет использовано в дальнейшем
при построении кратчайших путей в графе (см. § 3.3).
Рис. 20
П р и м е р 20. Продолжим рассмотрение вопросов, связан-
ных с достижимостью вершин в графах. Верщины и и р, по
определению, взаимно достижимы в графе G = (У, а), если
каждая из них достижима из другой. Обозначим отношение
взаимной достижимости через е. В обозначениях предыдущего
примера
е := {(u, р) 6 У X У1 (э к, I)(v G У^(и) & и G У^(р))}.
Отношение е очевидным образом рефлексивно и симметрично. Не
вызывает сомнений и его транзитивность: если вершина р
достижима из вершины и, а вершина w достижима из вершины
р, то, пройдя по соответствующим дугам сначала из вершины и
в вершину р, а затем из вершины р в вершину w, получим, что
вершина w достижима из вершины и.	,
Классы отношения е называются слоями графа G. Разбиение
на слои применяют, например, при построении эйлеровых путей
в графах. Мы вернемся к этим задачам в гл. 3. Слоями графа,
изображенного на рис. 21, являются подмножества {1, 2, 5, 6},
{3} и {4, 7, 8}.
62
Пример 21. Стоками в графе
G = (У, а) называются его вершины,
из которых не исходит ни одна дуга.
Говорят, что вершина и имеет сток
V, если v — сток, достижимый из
5	6	7	8 вершины и. Эквивалентность а :=
Рис- 21	:= {(u, v) е Ух V I и и у имеют одни
и те же стоки} используется при
построении одновыходных подсистем в комбинационных устрой-
ствах без обратных связей (см. § 3.4).
Рассмотрим некоторые эквивалентности, связанные с автома-
тами. Как и в случае графов, начнем с изоморфизмов.
Пример 22. Отношение изоморфности автоматов является
отношением эквивалентности. Автомат А{= (5р Ху Ур бр Лг)
называется изоморфным автомату А^ = (S2, Ху У2, <52> Л2),
если существует тройка биекций <р: Sj -» Sy ip: Х^ -» Ху
%: У -» У2 такая, что
х)) = <52(y>(s), ip(x)),
х)) = A2(y>(s), ^(х))
для любых s G Sp х G Ху
Каждый автомат А = (S, X, У, б, Л) изоморфен себе: изо-
морфизм осуществляет тройка тождественных отношений
Дх’ ДУ
Пусть <р, ip, х—биекции, задающие изоморфизм автомата А[
на автомат Ау и пусть <p(s) = s’, tp(x) = х', х(У) = У' для
s 6 5р х 6 Ар у G Ур Тогда s = y>-1(s'), х = ip~l(x’),
у =	где s' 6 S2, х' 6 Ху у' G У2- Из формул, опре-
деляющих изоморфизм, получаем;
^«‘(s'), У~ЧХУ) = У’-1(<52(5'’ *'))’
Л, «‘(s'), Ч>~ЧХ'У) = x~l (A2(s’, х'))
для любых s' G Sy х' G Ху Следовательно, тройка биекций
у>-1, ip~l, х1 осуществляет изоморфизм автомата А^ на автомат
Ар
Для доказательства транзитивности отношения изоморфности
автоматов предположим, что тройка биекций р:	-» Sy
а: Х^ Ху т: У2 -* У3 определяет изоморфизм автомата А2 на
63
автомат Л, = (S,, X,, У,, <5,, Л,). Произведения <Р°р, 4>°а,
X °т будут биекциями между множествами Sj и S3, Х{ и
Х3, Kj и У3 соответственно. Так как p(d2(s', х')) = <53(p(s'),
сг(х')) и t(A2(s',x')) = A3(p(s')> О(*У)> то
(<P°p')(^l(s’	*))) = p(<52(*’(s)>V’W)) =
= <530>(р(«))» ^W)) = &3((<P°p)(s), (^ °о)М),
(X	х)) = TfxCA^s, х))) = r(A2(?(s), V>(x))) =
= Цр№)), <Ш))) = Л3((у>ор)(«), (у>°сг)(х))
для любых s G Sp х е X . Отсюда заключаем, что тройка
биекций <f>°p, У’°сг, х°т осуществляет изоморфизм автомата
на автомат А3.
П р и м е р 23. Состояния s, / е S автомата А называются
эквивалентными (s = t или (s, f) G e), если под воздействием
любого входного слова р G X * автомат А, находящийся в этих
состояниях, выдает одинаковые выходные слова:
s = t :<»• (*р е X’)(A(s, р) = Л((, р)).
О неэквивалентных состояниях s, t говорят также, что они
различимы в данном автомате и пишут s ж t. Очевидно, что
е-эквивалентность (неразличимость) состояний в автомате в самом
деле является отношением эквивалентности. Для его построения
разработаны специальные методы. Состояния s, t называются
к
к-эквивалентными ((s, t) 6 или s = t), если для любого
входного слова р 6 X * длины не более к при переходах из этих
состояний выдаются одинаковые выходные слова:
к
s = t :о (»р 6 Х*)(1р1 к => (Л(х, р) = X(t, р))).
Нетрудно понять, что при к - 1, 2, ... получается убывающая
цепочка эквивалентностей £t □ е2 Э ..., каждая из которых
содержит отношение е, так как если два состояния эквивалентны,
то они ^-эквивалентны при любом к. В силу конечности множества
S будет конечным и множество E(S) эквивалентностей на нем.
Следовательно, указанная цепочка оборвется на каком-то месте:
Е, □ Е_ □...□ £ , И ТОГДа £	= £.
12	т	т
П р и м е р 24. Понятие эквивалентности (неразличимости)
состояний можно распространить и на случай двух разных
сравнимых автоматов. Именно, если s G S—состояния автомата
64
A = (S, X, Y, d,, A.), a t G T—состояние автомата В =
'	A A'
= (T, X, Y, <5И, Л„), то полагаем:
'	D D'
s = t :o (V p G X*)(l/s, p) = XB(t, p)).
Класс сравнимых автоматов {Л., i G 1} называется исклю-
чительным, если при i * j любое состояние автомата Л отличимо
от любого состояния автомата А..
Автомат А, по определению, эквивалентен автомату В, если
каждое состояние автомата А эквивалентно некоторому состоянию
автомата В, и наоборот, каждое состояние автомата В эквивален-
тно некоторому состоянию автомата А. О неэквивалентных
автоматах говорят, что они различимы. Содержательно эквива-
лентность двух автоматов А и В означает, что работу первого
автомата А, начатую в любом из его состояний, может
воспроизвести второй автомат В при соответствующем выборе его
начального состояния, и наоборот. При этом внутренняя логика
работы этих устройств может быть совершенно различной,
существенным является лишь выдача одинаковых выходных слов
на одни и те же входные слова. В этом существенное отличие
эквивалентности автоматов от их изоморфизма. Изоморфные
сравнимые автоматы, очевидно, эквивалентны, но обратное в
общем случае неверно.
Рассматриваемые ниже два автомата [17] эквивалентны, но
имеют разное число состояний.
А	Х!	Х2	X!	X2
S2 S3	S!	S2 S3	Sl S2	S1	0	1 1	0 1	0
в	xi x2	xi x2
*1 *2	f2 f2	fl	0	1 1	0
В подтаблице
состояниям «2
выходов автомата А строки, соответствующие
и «3, совпадают, а в таблице переходов они
становятся одинаковыми при взаимной замене s2 и $ . Ясно, что
«2 и «3 эквивалентны в автомате А. Аналогичные соображения
показывают, что оба эти состояния эквивалентны состоянию в
автомате В, а эквивалентно Следовательно, автоматы А и
В эквивалентны.
В классе эквивалентных автоматов естественно искать пред-
ставителей с наименьшим возможным числом состояний. Этот
процесс минимизации будет рассматриваться в § 4.2.
П р и м е р 25. Будем говорить, что состояние t достижимо
из состояния s в автомате А, если существует входное слово
р G X , переводящее автомат А из состояния s в состояние t,
3 А.М.Богомолов, В.Н.Салий
65
т. е. если <5(s, р) = t. Если в этом определении допустить и
пустое слово е, то каждое состояние будет достижимым из себя:
<5(s, е) = s. Состояния s и t, по определению, взаимно дости-
жимы в автомате А, если они достижимы друг из друга. Отношение
взаимной достижимости обозначим через к. Таким образом:
к := {(s, Г) е S х SI (эр е X *)(<$(«, р) = Г) &
& е Х*)(<5(/, q) = s)}.
Нетрудно убедиться в том, что к—отношение эквивалентности на
множестве состояний автомата А. Классы этого отношения
называются слоями автомата А. Автомат называется сильно
связным, если любые два его состояния взаимно достижимы, т. е.
если отношение к универсально на нем: к = S х S. Сильно
связные автоматы представляют большой теоретический и практи-
ческий интерес, в частности, в вопросах технической диагностики.
Например, имеет место
Т е о р е м а 1.26. Пусть А и В—сильно связные сравнимые
автоматы. Если в автомате А имеется хотя бы одно
состояние, эквивалентное некоторому состоянию автомата В,
то А и В—эквивалентны.
Доказательство. Пусть S = {«р s2, ...,	—
множество состояний автомата А и Т = {<,, Г_, ..., t }—множе-
1 Г 2’ п'
ство состояний автомата В. Не нарушая общности, будем считать,
что Sj — Гр Выберем произвольное состояние s. е S. Так как
А—сильно связный автомат, то существует слово р G X*,
переводящее автомат из состояния s в состояние s., т. е.
<5(Sp р) = s.. При этом <5(Zp р) = t. для некоторого
j, 1 < j < п. Пусть q 6 X*—произвольное слово. Тогда:
РЧ) = ^(Sp р) А(<5(«р р), ч) = Л(«р Р) A(s., q),
Л(*Р РЧ) = ^Op P) Л(д(Гр p), q) = Л(Гр p)X(t., q).
Поскольку A(Sp pq) = Л(Гр pq) и A(sp p) = Л(Гр p), to
X(s., q) = X(t., q) для любого слова q 6 X *. Значит, s. = t..
Таким образом, каждое состояние автомата А эквивалентно
подходящему состоянию автомата В. Аналогично устанавливается,
что и для каждого состояния автомата В найдется эквивалентное
ему состояние автомата А. Отсюда заключаем, что автоматы А
и В эквивалентны, о
Следствие 1.8. Если автоматы А и В сильно связны
и различимы, то в автомате А нет состояний, эквивалентных
состояниям автомата В. о
66
Следствие!.9. Всякий набор попарно неэквивалент-
ных сильно связных сравнимых автоматов является исклю-
чительным классом, о
П р и м е р 26. Пусть {Л. = (S., X, Y, <5., A.)l i =
= 1, .... п}— некоторый класс сравнимых автоматов. Условие
исключительности этого класса формально представляется в
следующем виде:
(vi # J)^s е s.)(vr е s.)(3p е X*)(A.(S, р) * X.(t, Р)).
Как видим, для проверки этого условия вовсе не обязательно
знать, какие конкретные выходные сигналы выдает каждый
автомат класса в ответ на данный
входной сигнал. Важно только знать,
различны ли эти выходные сигналы для
разных автоматов или нет. Для проверки
выполнимости условия исключительности
или более слабых его следствий исполь-
зуются так называемые векторы раз-
К личимости [6]. Рассмотрим устройство,
представленное на рис. 22.
Пусть на вход автоматов At, А?, ...
..., Ап одновременно подается сигнал
х G X. Под его воздействием на выходе
автомата А. появляется сигнал у.,
1 < I < п. Комбинационная схема К
перерабатывает вектор (ур у2, ..., уп) в
n-мерный вектор R = (Гр г2, ..., rj с компонентами из множе-
ства {1, 2, ..., п} по следующему правилу:
Г1
= 1,
max г. + 1, если у # у. при всех j < i - 1,
г. :=	7	7
'	г,	если у. = у. при некотором j < i— 1.
Например, вектору (у3, у2, уу уу ур у2) будет соответствовать
вектор (1, 2, 1, 1, 3, 2). Векторы, получаемые с выхода комби-
национной схемы К, называются векторами различимости.
Следующий результат показывает, что векторы различимости
представляют собой некоторый способ кодирования эквивалентно-
стей на конечных множествах с фиксированным порядком
элементов.
Т е о р е м а 1.27. Пусть количество (и) автоматов в
рассматриваемом классе не превосходит количества символов в
выходном алфавите Y. Тогда векторы различимости находятся
во взаимно однозначном соответствии с эквивалентностями на
множестве {1, 2, ..., л}.
3*	67
Доказательство. Если R = (г^ г2, г )—век-
тор различимости, то отношение
е[Л] := {(i, j) I г. = г.}
будет эквивалентностью на множестве {1, 2,	п}. Покажем,
что разным векторам соответствуют разные отношения. Для этого
воспользуемся специальной записью эквивалентности е[Л]. Имен-
но, сначала выпишем блок соответствующего ей разбиения,
содержащий номера компонент, равных Номера пишем в
порядке возрастания. Все компоненты вектора R с этими номерами
равны 1. Затем выписываем тоже в порядке возрастания номера
компонент, равных 2, и так далее. Ясно, что вектор R однозначно
восстанавливается по отношению е [Л], так что если е [Л] =
= £ [/?'], то R = R'. С другой стороны, пусть е—некоторая
эквивалентность на множестве {1, 2, ..., л}. Следующий алгоритм
строит соответствующий ей вектор различимости.
Шаг J. к := 1, j, := 1.
’ 'к
Шаг 2. г. := к для всех i G е(/*).
Шаг 3. Если e({/j, /2, ..., /*}) = S х S, то конец, иначе
к := к + 1 и переход к шагу 4.
Шаг 4. jk := min {/^ /2, ..., и переход к шагу 2. о
Пусть, например, эквивалентность е на восьмиэлементном
множестве имеет три блока:	{1, 3, 6},	{2, 4, 7},	{5, 8}.
Сначала получаем R [е] = (1,	—, 1, —, —, 1,—	, —).	Чер-
точками здесь отмечены еще не известные компоненты. Затем
выбираем min {1, 3, 6} = 2 и	получаем	еще	три	компо-
ненты: R [е] = (1, 2, 1, 2, -,	1, 2, —).	Еще	один	выбор:
min {1, 2, 3, 4, 6, 7} = 5, и процесс заканчивается: R [е] =
= (1, 2, 1, 2, 3, 1, 2, 3).
В построенном векторе R [е] компоненты, равные 1, можно
заменить, скажем, на компоненты, равные 2 — на у2, и т.д.
(по условию теоремы выходных сигналов достаточно). И в этом
случае /?[е] будет одним из векторов, снимаемых с выхода
комбинационной схемы К, т. е. вектором различимости. =
В § 1.4 мы продолжим изучение векторов различимости.
§ 1.4.	Упорядоченные множества
Отношение £ на множестве S называется отношением
квазипорядка, если оно рефлексивно и транзитивно. Будем кратко
называть это отношение квазипорядком. Таким образом:
£—квазипорядок :<»ДС£&£°£С£.
68
Из теоремы 1.19 следует, что всякое ограничение квазипорядка
является квазипорядком.
Т е о р е м а 1.28. Пусть £ £ S х S—отношение квази-
порядка на множестве S. Тогда его симметричная часть
е = £ П £-1 является эквивалентностью на этом множестве.
Доказательство. Так как Д £ £, то Д =
= Д-1 £ £-1, откуда Д £ е. Этим показана рефлексивность.
Далее,
£ —1 = (С А Г1)-1 = Г1 А (Г1)"1 = t п Г1 = е,
и, значит, £ симметрично. Применяя формулы 2) из теоремы 1.11
(§ 1.2), получаем
е°£ = (С A	А Г1) £ A П А
А Г1 °C'1 £ А Г1 “Г1 = А (С °C)'1 £
£ С А г1 = Е,
т. е. е транзитивно. □
Симметричная часть квазипорядка называется его ядром.
П р и м е р 27. Пусть G = (V, а)—некоторый граф. Расс-
мотрим на множестве его вершин отношение достижимости (см.
пример 19 из § 1.3).
<5 := {(и, у) е V X VI v достижима из и}.
Если считать, что каждая вершина достижима из себя за О
шагов, то <5 становится отношением квазипорядка. Его ядро
<5 П <5-1 есть отношение взаимной достижимости е (см. пример
20 из § 1.3).
Рассмотрим теперь отношения порядка. Отношение ш на
множестве S называется отношением порядка, если оно реф-
лексивно, транзитивно и антисимметрично:
ш—порядок на 5 :<» Д£ш&шош£ш&шПш 1 £ Д.
Всякий порядок является (антисимметричным) квазипорядком.
Пусть 5—непустое множество, и ш—отношение порядка на
нем. Пара (S, ш) называется упорядоченным (или частично
упорядоченным) множеством. Из теоремы 1.19 § 1.3 следует, что
ограничение ш* порядка ш £ S х S на непустом подмножестве
S* £ S является порядком на S*. Пара (S*, ш*) называется
упорядоченным подмножеством упорядоченного множества
(5, ш). В этой ситуации для ограниченного порядка обычно
используют те же обозначения, что и для исходного, и пишут
(5*, а>).
В качестве первых примеров упорядоченных множеств укажем:
69
(N, <)—множество всех натуральных чисел с естественным
для них порядком;
(N, I)—то же множество с отношением делимости (xly:ox—
делитель числа у);
(P(S), £)—совокупность всех подмножеств некоторого множе-
ства S с отношением включения между подмножествами.
П р и м е р 28. Контуром в ориентированном графе G =
= (У, а) называется последовательность дуг вида
(vp v2), (v2, v3), ...» (у„_р y„), (vn, V1),
в которой все вершины vp v2> ..., vn различны. Число n считается
длиной контура. Контур длины 1—это петля, т. е. тривиальный
контур.
Обращаясь к примеру 27, получаем следующий результат.
г Теорема 1.29. Отношение достижимости в графе
G = (V, а) тогда и только тогда является порядком на
множестве его вершин, когда этот граф не содержит нетриви-
альных контуров.
Доказательство. Необходимость.
Пусть Vj -* v2 -»...-» vn -* Vj—некоторый нетривиальный кон-
тур в графе G. Тогда для любого v., 1 < i < п, будет иметь
место (ур v.) 6 <5 О <5-1 (взаимная достижимость). Следователь-
но, д П д-1 * А, и условие антисимметричности для отношения
достижимости <5 нарушено. Таким образом, если <5—порядок, то
в графе G нет нетривиальных контуров.
Достаточность. Отношение достижимости <5 явля-
ется квазипорядком в любом графе. Пусть G—бесконтурный граф,
и разные вершины и и у в нем взаимно достижимы, т. е.
(и, у) 6 <5 П <5-1. Тогда существуют бесконтурные пути Р
из и в у и Р2 из у в и. Среди входящих в эти пути вершин
есть общие, например, и и у. Пусть и,—первая в порядке
прохождения пути Р вершина, которая не входит в состав пути
Р2, а ик—первая после нее вершина пути Рр принадлежащая
Р2. Тогда «_1^>1и^2и|_1 будет нетривиальным контуром в орграфе
G. о
Проверка выполнимости аксиом порядка во многих случаях
упрощается, если эти аксиомы представить в элементарной записи,
т. е. в записи, выраженной через элементы.
Условимся в общем случае вместо (а, Ь) 6 а> писать а < Ь,
и читать это выражение следующим образом: «а меньше или
равно Ь», «а не больше Ь», «а содержится в Ь», «а включается в
Ь», или соответственно в другом порядке: «Ь больше или равно
а», «Ь не меньше а», «Ь содержит а», «Ь включает а». Тот же
70
смысл придается записи: b > а. Если имеют место соотношения
а < Z> и а * Ь, то будем употреблять знак строгого неравенства:
а < b или b > а.
В этих обозначениях упорядоченное множество—это пара
(S, <), где S—непустое множество, <—бинарное отношение на
этом множестве такое, что тождественно выполняются условия:
1) х < х (рефлексивность),
2) x<y&y<z=>x<z (транзитивность),
3)х<у&у<х=>х = у (антисимметричность).
Таким образом, чтобы доказать, например, что (P(S), £)
является упорядоченным множеством, нужно убедиться в очевид-
ной справедливости утверждений:
1) X С X,
2) X С Y&YQZ=>XQZ,
3)ХСУ&УСХ=»Х=У
для любых подмножеств X, У, Z С 5.
Для упорядоченного множества (N, <) общее обозначение
порядка совпадает с уже имеющимся в нем, и аксиомы порядка
переходят в хорошо известные соотношения между числами.
Истинность предложений: xlx, xly & ylz * xlz («делитель
моего делителя—мой делитель»); хIу & ylx => х = у в множестве
N не вызывает сомнений.
П р и м е р 29 (факторизация квазипорядка по его ядру).
Пусть £—отношение квазипорядка на множестве S. Согласно
теореме 1.28 его ядро е = £ (1 £-1 является эквивалентностью
на S. Для произвольных элементов х, у 6 S положим
е(х) < е(у) :«• (х, у) G $.
Отношение < упорядочивает фактормножество S/e. Чтобы пока-
зать это, сначала заметим, что в формуле, определяющей
отношение <, выбор конкретных представителей в е-классах не
играет роли. Действительно, если (х, х') 6 е, (у, у') G е и
(х, у) G £, то (х', х) 6 £, (х, у) G £ и (у, у') 6 £, откуда, в
силу транзитивности, (х', у') G £. Отношение < рефлексивно и
транзитивно ввиду рефлексивности и транзитивности квазипоряд-
ка £.
Если е(х) < £(у) и в(у) < е(х), то, по определению,
(х, у) G £ и (у, х) 6 £, т. е. (х, у) G £ (1 £-1 = е- Следова-
тельно, е(х) = е(у), и отношение < антисимметрично. =
Если ш—отношение порядка на множестве S, то, как легко
проверить, обратное отношение ш~1 также будет порядком на S.
Упорядоченное множество (S, ш~1) называется дуально (или
двойственно) упорядоченным по отношению к (S, ш). В
(S, ш ) элемент х меньше элемента у тогда и только тогда,
когда х больше чем у в (S, ш).
71
Рассмотрим экстремальные элементы в упорядоченных множе-
ствах. Наименьшим элементом упорядоченного множества
(5, <) называется его элемент 0 (ноль), удовлетворяющий в
(5, <) тождественному неравенству: 0 < х. Очевидно, что каждое
упорядоченное множество имеет не более одного наименьшего
элемента: если Oj и 02—наименьшие элементы в (5, <), то
Oj < 02 и 02 < Oj одновременно, откуда следует, что = 02,
в силу антисимметричности.
Наибольший элемент 1 (единица) определяется в (S, <)
тождественным неравенством: х S 1. Очевидно, что каждое
упорядоченное множество имеет не более одного наибольшего
элемента.
В упорядоченном множестве (Р(5), С) наименьшим элементом
будет пустое подмножество 0, а наибольшим—само множество 5;
упорядоченные множества (N, <) и (N, I) наибольшего элемента
не имеют, а наименьшим элементом будет число 1. Элемент а
упорядоченного множества (S, <) называется минимальным, если
в (5, <) нет элементов, строго меньших, чем а. Аналогично,
элемент а называется максимальным в (S, <), если в этом
упорядоченном множестве нет элементов, строго больших, чем а.
Т е о р е м а 1.30. В конечном упорядоченном множестве
каждый элемент содержит некоторый минимальный элемент и
содержится в некотором максимальном элементе.
Доказательство. Пусть s—произвольный эле-
мент конечного упорядоченного множества (5, <). Если s не
минимален, то найдется такой элемент s G 5, что s >	Если
Sj не минимален, то можно найти «2 G 5 такой, что > «2.
И так далее. Получаем убывающую цепь s =	> Sj >
> «2 > ... Поскольку множество 5 конечно, эта цепь тоже
конечна. Ее последний элемент sn = а будет минимальным в
(5, <). В силу транзитивности, а < s, т. е. мы нашли минималь-
ный элемент, содержащийся в s. Для нахождения максимальных
элементов рассуждения вполне аналогичны, при этом строится
возрастающая цепь. =
Следствие!. 10. Если конечное упорядоченное мно-
жество имеет только один минимальный (максимальный)
элемент, то этот элемент будет наименьшим (наибольшим)
элементом. =
Если упорядоченное множество имеет наименьший элемент 0,
то 0 будет единственным минимальным элементом этого множе-
ства. Точно так же наибольший элемент 1 (если он есть) является
единственным максимальным элементом.
В общем случае упорядоченное множество может иметь
несколько минимальных и (или) максимальных элементов, а
может не иметь их совсем.
72
П р и м е р 30. Пусть множество 5 имеет не менее двух
элементов и Р'(5) обозначает совокупность всех собственных, т. е.
отличных от 5, непустых подмножеств в 5. Тогда одноэлементные
подмножества {s}, s 6 5, и только они, будут минимальными
элементами в упорядоченном множестве	С). Максималь-
ными же элементами будут, очевидно, дополнения {«} одноэле-
ментных подмножеств. Таким образом, (Р'(5), £) имеет много
минимальных и много максимальных элементов, но в этом
упорядоченном множестве, конечно, нет ни наименьшего, ни
наибольшего элемента.
Рассмотрим диаграммы и графы упорядоченных множеств.
За длину конечной убывающей цепи а{ > а2 > ... > ап
принимается уменьшенное на единицу число элементов в ней.
Высотой элемента в конечном упорядоченном множестве
называется наибольшая из длин убывающих цепей, начинающихся
с этого элемента. Высота элемента а обозначается через Л (а).
Например, любой минимальный элемент .имеет высоту 0.
Очевидно, что в упорядоченном множестве (N, <) будет
Л(и) = п - 1 для любого п 6 N. В (N, I) высоту элемента п
определить не так просто. Например, Л(12) = 3, поскольку длину
3 имеют все максимальные цепи делителей, начинающиеся с 12,
именно, 12 : 6 : 3 : 1, 12 : 6 : 2 : 1, 12 : 4 : 2 : 1 (здесь :
есть I-1).
а а
В общем случае можно показать, что если п = р^ р^2...
а
... pkk (каноническое разложение по степеням простых чисел), то
h(n) = а. +	+ ... + а..
'•'12	к
Если, например, X—конечное n-элементное подмножество
множества 5, то в упорядоченном множестве (Р(5), С) будет
Л(Х) - п, так как максимальную убывающую цепь от X до
0 можно построить, отбрасывая по одному элементу из X.
Пусть а, b—элементы упорядоченного множества (5, <). При
помощи неравенств в (5, <) определяются интервалы разных
типов:
[а, Л]	:=	{х	6	SI	а	<	х	<	Ь},
(а, Ь)	:=	{х	6	SI	а	<	х	<	Ь},
[а, Ь)	:=	{х	6	SI	а	<	х	<	Ь},
(a, Z>]	:=	{х	£	51	а	<х < £>},
аЛ	:= {х £ 51 а < х},
а?	:= {х 6 51 х < а}.
Интервалы аЛи av называются соответственно верхним конусом
и нижним конусом для элемента а.
73
Говорят, что в упорядоченном множестве (S, элемент b
является верхним соседом элемента а (или что b покрывает а),
если а < Ъ и при этом [а, Л>] = {а, £>}, т. е. если не существует
х G S такого, что а < х < Ь. В этом случае элемент а
называется нижним соседом для элемента Ь.
Верхние соседи наименьшего элемента 0 называются атомами
упорядоченного множества, а нижние соседи наибольшего элемента
1 называются коатомами.
Пусть наибольшая из высот элементов упорядоченного мно-
жества (S, <) равна п. Диаграмма этого упорядоченного множе-
ства строится следующим образом. На п + 1 горизонтальных
прямых, пронумерованных снизу вверх числами 0, 1, 2, ..., п,
располагаются элементы данного множества в соответствии с их
высотой, они изображаются точками. Затем, последовательно
поднимаясь по уровням, каждый элемент соединяем прямолиней-
ными отрезками с его нижними соседями. Полученный рисунок,
на котором горизонтали не изображаются, называется диаграммой
упорядоченного множества (S, <). При построении диаграммы
имеется произвол в расположении элементов одинаковой высоты.
Желательно их размещать так, чтобы диаграмма была по
возможности простой, например, минимальной по числу самопе-
ресечений. На рис. 23 изображены диаграммы следующих
упорядоченных множеств: а) первые 6 натуральных чисел с
естественным порядком; б) эти же числа, упорядоченные делимо-
стью; в) (P(S), £) для трехэлементного множества S = {1, 2, 3}.
> 6
‘ 5
" 4
'3
2
- 1
Рис. 23
Диаграмма наглядно представляет структуру упорядоченного
множества и связи между его элементами. На ней сразу видны,
например, минимальные и максимальные элементы, легко выде-
ляются все цепи между фиксированными элементами, и т. д. В
упорядоченном множестве (5, <) элемент а меньше элемента b
(т. е. а < Ь) тогда и только тогда, когда на его диаграмме имеется
восходящая ломаная от а к Ь.
Диаграмму упорядоченного момента нельзя считать графом:
этому препятствует уровневая фиксация элементов (вершин).
Поэтому полезно рассматривать еще и модифицированную диаг-
рамму упорядоченного множества—граф, получаемый из диаграм-
74
мы путем ориентации ее отрезков от меньшего к большему
элементу. Модифицированная диаграмма содержит в себе всю
информацию об исходной диаграмме, но, кроме того, является
графом, что дает новые возможности для изучения представляе-
мого ею упорядоченного множества. На рис. 24 показаны графы,
соответствующие упорядоченным множествам, диаграммы которых
представлены на рис. 23.
Рис. 24
{1,3}	{1,2,3}
В упорядоченном множестве (S, <) вершина а меньше
вершины b (т. е. а < Ь) тогда и только тогда, когда вершина b
достижима из вершины а в графе, соответствующем этому
упорядоченному множеству, т. е. отношение порядка совпадает
с отношением достижимости в графе. Вследствие теоремы 1.29
графы упорядоченных множеств не имеют контуров, в том числе
и тривиальных. Однако не любой бесконтурный граф может
рассматриваться как граф упорядоченного множества. Действитель-
но, если элемент b является верхним соседом для элемента а в
упорядоченном множестве (S, <), то в соответствующем графе
от вершины а к вершине b возможен только один путь: это дуга
(а, Ь). Этим запрещаются почти контуры: графы, получаемые
из контуров изменением ориентации одной дуги.
Очевидно, что граф для дуально упорядоченного множества
(S, ш-1) получается из графа, соответствующего упорядоченному
множеству (S, ш), изменением ориентации всех дуг. При этом,
в частности, источники (минимальные элементы) превратятся в
стоки (максимальные элементы) и наоборот.
Отображение <р: А -» В упорядоченного множества (А, в
упорядоченное множество (В, <) называется изотопным, если
для него тождественно выполняется условие
х < у =» <р(х) < <р(у).
Взаимно однозначное изотонное отображение <р: А -» В, удовлет-
воряющее дополнительно условию обратной изотонности:
/>(х) < <р(у) * х < у,
называется вложением упорядоченного множества (Л, <) в
упорядоченное множество (В, <). Взаимно однозначное соот-
ветствие между элементами упорядоченных множеств (A, S),
75
(В, <), являющееся изотонным и обратно изотонным отобра-
жением, называется изоморфизмом.
Для упорядоченных множеств рассматривают также антиизо-
тонные отображения—изменяющие порядок на противоположный.
Они определяются тождественным соотношением:
х < у =* у>(х) > <р(у).
Примером антиизотонного отображения является дуальный изо-
морфизм или антиизоморфизм упорядоченного множества
(А, <) на упорядоченное множество (В, <)—так называется
изоморфизм упорядоченного множества (А, <) на дуальное к
(В, <) упорядоченное множество.
Легко видеть, что два конечных упорядоченных множества
тогда и только тогда изоморфны, когда их можно изобразить
одной и той же диаграммой без обозначения элементов. Другим
критерием изоморфности конечных упорядоченных множеств
является изоморфность их графов. Граф дуально изоморфного
упорядоченного множества получается из графа данного упорядо-
ченного множества сменой ориентации всех дуг.
На рис. 25 показаны все пять существенно различных (т. е.
попарно не изоморфных) упорядоченных множеств с тремя
элементами. Для каждого из них приведена диаграмма и
соответствующий ей граф.
0< О »О О >0 >0
4	5
Рис. 25
Аналогом теоремы Стоуна из теории булевых алгебр является
следующий результат.
Т еорема 1.31. Всякое упорядоченное множество вкла-
дывается в упорядоченную включением совокупность всех под-
множеств подходящего множества.
Доказательство. Пусть (S, <)—произвольное
упорядоченное множество. Докажем, что отображение
/>: 5 -* P(S), s ~ sv,
сопоставляющее каждому элементу s G S нижний конус, соот-
ветствующий этому элементу, будет искомым вложением.
Покажем, что взаимно однозначно. Действительно, на-
поминая, что := {х G S I х < s}, получаем:
y>(s) = <p(f) => sV =	=> t G sV & s ё =>
=>t<s&s<t=>s = t,
76
так что неравным элементам $ и t должны соответствовать
неравные подмножества <p(s) и <f>(f).
Покажем, что изотонно и обратно изотонно. В самом деле,
s < t о sV С Л о y>(s) с у>(0. о
Доказанная теорема позволяет элементы любого упорядочен-
ного множества (S, <) интерпретировать как подмножества
некоторого множества (самого множества S), а отношение S—как
теоретико-множественное включение между этими подмножест-
вами.
Элементы a, b упорядоченного множества (S, S) называются
сравнимыми, если а < Ъ или Ъ < а. В противном случае а и b
несравнимы, и это обозначается как а II Ь.
Упорядоченное множество, в котором любые два элемента
сравнимы, т. е. тождественно истинно предложение «х £ у или
у < х», называется линейно упорядоченным. Диаграмма такого
упорядоченного множества представляет собой цепь.
П р и м е р 31. Лексикографическое упорядочение последо-
вательностей. Пусть X—конечное множество (алфавит), на
котором задан некоторый линейный порядок: < х^< ... < хд.
В множестве X * всех конечных последовательностей (слов) над
алфавитом X введем отношение S следующим образом:
1) е < р для любого р е X * (здесь е—пустое слово);
2) х х ... х = р < q = хо хо ... хо , если р является на-
«, «2 «
чальным фрагментом слова q, может быть, совпадая с q, или
ха < Хр для некоторого i < г, в то время как ха = х@ при
всех j < i.
Нетрудно проверить, что этот принцип «первого различия»
линейно упорядочивает множество X *. Полученный порядок
называется лексикографическим или словарным (именно так
упорядочиваются слова в словарях).
Линейно упорядоченные подмножества упорядоченного множе-
ства (S, <) называются его цепями. Например, упорядоченные
множества (N, <) и (R, <) сами являются цепями. В упорядо-
ченном множестве (N, <) цепь образуют, например, все степени
некоторого фиксированного числа. Частным случаем цепей явля-
ются встречавшиеся уже убывающие цепи. Всякую конечную цепь
можно считать убывающей или возрастающей в зависимости от
способа перечисления ее элементов.
В приложениях часто используется следующая теорема
Шпильрайна.
Т е о р е м а 1.32. Всякое упорядоченное множество вкла-
дывается в подходящее линейно упорядоченное множество.
77
Доказательство проведем для конечного случая. Пусть упоря-
доченное множество (S, <) имеет п элементов. Построим
диаграмму этого упорядоченного множества и перенумеруем
его элементы, двигаясь снизу вверх по уровням и слева направо
на каждом уровне. Тогда каждый элемент s е S получит
некоторый индивидуальный номер <p(s) G {1, 2, ..., и}. Если
а < b в (S, <), то элемент а расположится на диаграмме ниже
элемента b (от а к b имеется восходящая ломаная), и,
следовательно, номер <р(а) будет строго меньше номера у>(5). Таким
образом, <р вкладывает упорядоченное множество (S, <) в
начальный отрезок натурального ряда ({1, 2, ..., и}, <). =
Теорему Шпильрайна формулируют и по другому: всякий
порядок может быть продолжен до линейного порядка на том же
множестве.
Обращаясь к диаграммам б) и в) рис. 23, получаем следующие
линейные порядки, продолжающие упорядоченности на соответст-
вующих упорядоченных множествах:
б) 1<2<3<5<4< 6,
в) 0 < {1} < {2} < {3} < {1, 2} < {1, 3} < {2, 3} <
< {1, 2, 3}.
В полученных линейно упорядоченных множествах сох-
ранились все порядковые соотношения между парами элементов,
существовавшие в первоначальных упорядоченностях, но появи-
лось и много новых (между ранее несравнимыми элементами).
Говорят, что в конечном упорядоченном множестве (S, <)
выполняется цепное условие Жордана—Дедекинда, если все
максимальные (т. е. неуплотняемые) цепи между двумя произ-
вольными фиксированными элементами а < Ъ имеют одинаковую
длину.
В графе упорядоченного множества (S, <) цепное условие
Жордана—Дедекинда означает, что все пути между двумя
фиксированными вершинами имеют одну и ту же длину, т. е.
составлены из одинакового количества дуг.
Т е о р е м а 1.33. В конечном упорядоченном множестве
с 0 тогда и только тогда выполняется цепное условие
Жордана—Дедекинда, когда в нем для любых двух соседних
элементов х < у имеет место равенство: h(y) = h(x) + 1.
Доказательство. Необходимость.
Пусть в конечном упорядоченном множестве (S, <) с О
выполняется условие Жордана—Дедекинда и элемент у является
верхним соседом для х. Высота h(y) элемента у будет длиной
любой максимальной цепи от 0 до у, в частности и той, которая
проходит через х. Так как между х и у в этой цепи нет других
элементов, получаем, что h(x) + 1 = Л(у).
Достаточность. Пусть а < b в упорядоченном
множестве, удовлетворяющем условию теоремы. Если а =
=	< flj< ... < ап = b—произвольная максимальная цепь
78
между а и Ь, то каждый элемент а. является верхним соседом
элемента а _р 1 < z S и, и, значит, Л(а.) =	+ 1. Сле-
довательно, любая максимальная цепь между а и Ъ имеет ту же
длину п. о
На основании теоремы 1.33 выполнимость цепного условия
Жордана—Дедекинда легко проверяется по диаграмме упорядо-
ченного множества: ее отрезки в этом случае соединяют элементы
только соседних уровней. Простейший пример, где это требование
нарушается,—упорядоченное множество (решетка N$), изображен-
ное на рис. 46а (см. с. 164).
Условие Жордана—Дедекинда тесно связано с задачами о
кратчайших путях в графе (см. § 3.3).
Пусть S*—некоторое подмножество упорядоченного множества
(S, <). Элемент а 6 S называется нижней гранью подмножества
S*, если а < х для всех х 6 S*, и верхней гранью для S*, если
а > х при всех х 6 S*. Под наибольшей нижней гранью
подмножества S в упорядоченном множестве (S, <) понимается
наибольший (если он существует) элемент в множестве всех
нижних граней для S*. Аналогично определяется наименьшая
верхняя грань подмножества S*: это наименьший элемент (если
он существует) в множестве всех верхних граней для S*.
Очевидно, что любое подмножество S* С S имеет не более
одной наибольшей нижней грани и не более одной наименьшей
верхней грани. Эти элементы обозначают соответственно Inf S*
(инфимум) и Sup S* (супремум), и называют также точными
(нижней и верхней соответственно) гранями подмножества S*.
Говорят, что множество S образует относительно порядка <
полную нижнюю (верхнюю) полурешетку, если любое его
непустое подмножество имеет точную нижнюю (верхнюю) грань.
Упорядоченное множество (S, <), одновременно являющееся
полной нижней и полной верхней полурешеткой, называется
полной решеткой. Полная нижняя полурешетка (S, обяза-
тельно имеет наименьший элемент—им будет Inf S, а в полной
верхней полурешетке необходимо присутствует наибольший эле-
мент—это Sup 5. Полная решетка обладает обоими этими
экстремальными элементами.
Упорядоченное множество (5, <) называется решеткой, если
каждое его конечное подмножество имеет точную нижнюю и
точную верхнюю грани. Понятно, что упорядоченное множество
будет решеткой уже тогда, когда точными гранями обладает
каждое его двухэлементное подмножество. Вместо Inf {х, у} и
Sup {х, у} будем писать соответственно inf (х, у) и sup (х, у).
Очевидно, что каждая конечная решетка полна.
Нижняя (верхняя) полурешетка—это упорядоченное множе-
ство, в котором для любых двух элементов х, у существует
79
inf (x, у) (соответственно sup (x, у)). Непосредственно из опреде-
лений следует, что если упорядоченное множество (Л, является
решеткой (соответственно нижней или верхней полурешеткой) и
упорядоченное множество (В, изоморфно ему, то (5, также
будет решеткой (соответственно нижней или верхней полурешет-
кой). При этом свойство полноты, разумеется, сохраняется.
Упорядоченное множество, дуально изоморфное нижней (вер-
хней) полурешетке, является верхней (нижней) полурешеткой.
Следовательно, класс всех решеток замкнут относительно дуаль-
ных изоморфизмов.
Рассмотрим некоторые примеры.
Пример 32. Всякое линейно упорядоченное множество
является решеткой, так как в нем при х < у будет, очевидно,
inf (х, у) = х и sup (х, у) = у.
Таким образом, решетками будут упорядоченные множества
(N, <) и (R, <), где inf (х, у) = min (х, у), sup (х, у) =
= max (х, у). Обе эти решетки неполны: например, множества
N и R не имеют точной верхней грани.
Пример 33. Упорядоченное множество (N, I)—решетка,
поскольку для любых х, у S N имеем: inf (х, у) = НОД (х, у)
(наибольший общий делитель), sup (х, у) = НОК (х, у) (наимень-
шее общее кратное).
Решетка (N, I) тоже не является полной: ни одно бесконечное
подмножество в ней не имеет точной верхней грани.
П р и м е р 34. Для любого множества 5 упорядоченное
множество (Р(5), С) представляет собой полную решетку: для
произвольного набора подмножеств {X. I i е /} множества 5, как
нетрудно убедиться, имеет место
Inf {X. I 1 £ 1} = Г) X., Sup {X. I i 6 /} = U X..
1^.1	1^.1
Имея в виду этот ключевой пример, в решетках общего вида
Inf {х; I i €Е 1} называют пересечением семейства элементов
{х(. I i G /}, a Sup {х. I i 6 /}—объединением этого семейства
элементов.
Пример 35. Из трехэлементных упорядоченных множеств
(рис. 25) только одно—линейно упорядоченное — является
решеткой. В четырех других случаях легко указать
л двухэлементные подмножества, вообще не имеющие
/ X. нижних и (или) верхних граней. При этом диаграммы
с р.	3) и 4) на рис. 25 представляют соответственно
верхнюю и нижнюю полурешетки.
Упорядоченное множество, изображенное на рис.
а	26, иллюстрирует другие «нерешеточные» ситуации:
о	элементы а	и b имеют три общие верхние грани
(с, d и 1),	но среди них нет наименьшей, а у
Рис. 26 элементов с	и d среди трех общих нижних граней
(а, b и 0) нет наибольшей.
80
Следующая теорема очень часто используется в приложениях.
Теорема 1.34. Упорядоченное множество (S, <) тогда
и только тогда является полной решеткой, когда:
1) оно имеет наибольший элемент 1;
2) для любого его непустого подмножества X существует
точная нижняя грань (пересечение) InfX.
Доказательство. Необходимость.
Пусть (5, <)—полная решетка. Тогда каждое непустое подмно-
жество X С 5 имеет точную нижнюю грань InfX и точную
верхнюю грань Sup X. В частности, существует Sup 5, и, как
легко понять, Sup 5=1.
Достаточность. Покажем, что в условиях теоре-
мы каждое непустое подмножество X С 5 имеет точную верхнюю
грань Sup X. Положим
Хд: = {a S 5 I (vx S X) (х < а)}.
Подмножество Хд является совокупностью всех верхних граней
для X. Очевидно, что 1 6 Хд, так что Хд# 0. По условию
существует элемент aQ = Inf Х.д Этот элемент и будет точной
верхней гранью подмножества X. В самом деле, пусть х—
произвольный элемент из X. Тогда х < а для любого а 6 Х.д
Следовательно, х является нижней гранью подмножества Х.д Но
aQ—это наибольшая из нижних граней этого подмножества.
Значит, х < «0 для всех элементов х 6 X, т. е. aQ 6 X? Так
как aQ < а для любого а 6 Хд то aQ представляет собой
наименьший элемент множества Х,д т. е. наименьшую из верхних
граней подмножества X. Итак, aQ — Sup X, откуда заключаем,
что (5, <)—полная решетка, о
Следствие 1.11. Конечное упорядоченное множество
тогда и только тогда является решеткой, когда:
1) оно имеет наибольший элемент;
2) для любых двух его элементов существует точная нижняя
грань (пересечение).
Таким образом, полные решетки — это в точности полные
нижние полурешетки с наибольшим элементом, а конечные
решетки — это конечные нижние полу решетки с наибольшим
элементом.
В практических ситуациях проверка наличия точных нижних
граней у подмножеств упорядоченного множества обычно не
вызывает затруднений, в то время как отыскание точных верхних
граней, как правило, требует нетривиальных усилий. Теорема 1.34
и следствие 1.11 являются эффективными критериями решеточ-
ности порядка.
81
Пример 35. Упорядоченное множество (E(S), С) всех
эквивалентностей на данном множестве 5 является полной
решеткой. Действительно, для любого набора эквивалентностей
{е. I i е 1} их пересечение Г) е. тоже будет эквивалентностью,
i G /
обладая свойствами рефлексивности, симметричности и тран-
зитивности (см. § 1.3). Ясно, что это наибольшая из эквивален-
тностей, содержащаяся во всех е„ i G I. Декартов квадрат
S X S является наибольшим элементом в E(S).
П р и м е р 36. В примере 14 § 1.3 для конечного класса
сравнимых автоматов рассматривались векторы различимости
диагностической задачи. Пусть п—число автоматов в классе, и
оно не превосходит количества символов выходного алфавита.
Введем на множестве R(ri) векторов различимости следующее
отношение [6]:
tz b :о (V г, /) (Ь. = Ь. => а. = а.).
Теорема 1.35. Отношение < упорядочивает множество
векторов различимости. При этом (R(n), является решет-
кой, дуально изоморфной решетке эквивалентностей на п-эле-
ментном множестве.
Доказательство. В теореме 1.27 § 1.3 между
множеством R(ri) векторов различимости и множеством Е(п)
эквивалентностей на множестве {1, 2, ..., п} было установлено
взаимно однозначное соответствие, при котором вектору a €Е
€Е R(n) сопоставляется эквивалентность е [а] := {(г, f) I а. = а^.
Следующие рассуждения приводят к цели:
a S i о (Vi, j)(b. = b. => а(. = а?) о
° (v г» Z)((i> f) G е ДО =* (*• f) G е М) °
О £[Ь] £ £[д] О е[<2] D e(Z>).
Таким образом, отношение < является порядком, дуально
изоморфным теоретико-множественному включению на Е(п). Так
как (Е(п), С)—решетка (см. пример 35), то и (R(ri), —решет-
ка. Соответствие а «♦ е [а] устанавливает между ними антиизо-
морфизм. □
На рис. 27 приведен неориентированный граф, вершины
которого помечены элементами множеств Е(4) и R (4). При этом
отношения эквивалентности обозначаются соответствующими им
разбиениями, для которых указываются только неодноэлементные
блоки. При повороте графа на 90° по часовой стрелке получается
диаграмма решетки (Л(п), 5), а при повороте против часовой
стрелки—диаграмма решетки (£(4), С). Данный граф превраща-
ется в граф решетки (£(4), С) ориентацией всех ребер слева
направо, и в граф решетки (Л(4), <) при их противоположной
ориентации. Таким образом, рис. 27 представляет векторы
82
различимости диагностической задачи для четырех автоматов и
разбиения четырехэлементного множества.
Рис. 27
Рассмотрим теперь решетку подавтоматов полуавтомата. Пусть
А = (5, X, б)—полуавтомат. Подмножество 5* С S называется
устойчивым в А, если (* $ 6 S)(s 6 S* => (v х 6 X)(d(s,
х) 6 S*)), т. е. когда никакими входными сигналами нельзя
вывести полуавтомат из состояний класса 5*. В любом полуавто-
мате множество состояний S и его пустое подмножество 0
устойчивы.
Пусть 5*—устойчивое подмножество в полуавтомате А =
= (S, X, д). Полуавтомат А* = (5*, X, б*) называется подавто-
матом полуавтомата А, если д* является ограничением функции
д на множестве 5* X X. (Заметим, что правильнее было бы
говорить о «подполуавтоматах», однако мы для простоты речи
используем термин «подавтомат».) В дальнейшем будем писать
А* = (5*, X, б).
Каждый полуавтомат А имеет по крайней мере два подавто-
мата. Во-первых, сам полуавтомат А является своим подавтоматом,
а во-вторых, подавтоматом будет и так называемый нулевой
подавтомат 0 := (0, X, 0) с пустыми множеством состояний
и функцией переходов.
83
Ненулевые отличные от полуавтомата А его подавтоматы
называются собственными. Совокупность всех подавтоматов полу-
автомата А обозначается символом Sub А.
Если Л) = (Sp X, <5) и А2 = (52> X, <5)—подавтоматы полу-
автомата А, то положим
Л, < л2 3, с sr
Очевидно, что введенное отношение упорядочивает множество
Sub А. Поскольку упорядоченное множество (Sub А, С) имеет
наибольший элемент (им является, очевидно, сам полуавтомат А)
и для любых двух подавтоматов Л) и А^ существует наибольший
содержащийся в них подавтомат, именно, inf (.Ар А^) =
= (Sj О S2, X, д), то, согласно теореме 1.34, (Sub Л, <) будет
решеткой. Это и есть решетка подавтоматов автомата А.
П р и м е р 37. Нарисуем диаграмму решетки подавтоматов
для каждого типа автономных полуавтоматов с тремя состояниями,
графы которых приведены на рис. 6 (см. введение). В каждом
случае будем строить решетку устойчивых подмножеств, выделяя
их в решетке всех подмножеств трехзлементного множества,
изображенной на рис. 28.
Рис. 28
На рис. 29 представлена решетка Sub А для полуавтомата А
типов I (устойчивы все подмножества множества 5), II (устойчивы
0, {1}, {3}, {1, 2}, {1, 3}, S), III (устойчивы 0, {3}, {1, 2}, S).
На рис. 30 приведена диаграмма решетки Sub А для полуавтомата
А типов IV (устойчивы подмножества 0, {!}, {1, 2}, {1, 3}, S),
V (устойчивы 0, {!}, {1, 2}, 5), VI (устойчивы 0, {1, 2}, 5),
VII (нет нетривиальных устойчивых подмножеств).
Множество всех состояний полуавтомата А, достижимых из
состояния s, обозначим через S(s). В частности, s G S(s).
Очевидно, что подмножество S(s) устойчиво при любом s е S.
Подавтомат вида Л($) = (S(s), X, б) называется главным подав-
томатом полуавтомата А.
84
I
III
и
Рис. 29
Рис. 30
По свойствам решетки подавтоматов полуавтомата можно
судить о некоторых особенностях его функционирования. Отметим
несколько фактов такого рода.
Полуавтомат А называется примитивным, если он не имеет
собственных подавтоматов: Sub Л = {О, А}.
Т е о р е м а 1.36. Полуавтомат примитивен тогда и
только тогда, когда он сильно связен.
Доказательство. Пусть s , s2—произвольные
состояния примитивного полуавтомата А. Вследствие примитив-
ности Л^) = А, и, значит, s2 6 S(Sj), т. е. $2 достижимо из
Следовательно, полуавтомат Л сильно связен.
Предположим теперь, что Л—сильно связный полуавтомат и
что Л* = (S*, X, д)—его ненулевой подавтомат. Если s G S*,
то, конечно, S(s) С S* в силу устойчивости подмножества 5*. Из
сильной связности следует, что S(s) = 5. Итак, S* = 5, откуда
вытекает, что Л* = Л. Таким образом, полуавтомат Л примити-
вен. а
Следствие!.12. Автономный полуавтомат прими-
тивен тогда и только тогда, когда его граф представляет
собой цикл, о
Следствие!.13. Атомами решетки подавтоматов
полуавтомата являются его сильно связные подавтоматы, и
только они.
Доказательство. Атомы решетки Sub Л—это
верхние соседи нулевого подавтомата 0, т. е. такие ненулевые
85
подавтоматы, которые сами являются примитивными полуавтома-
тами. о
Следствие!.14. Атомами решетки подавтоматов
автономного полуавтомата будут в точности его циклы. а
Ненулевой полуавтомат называется связным, если пересечение
любых двух его ненулевых подавтоматов отлично от 0.
Теорема 1.37. Для ненулевого полуавтомата А следу-
ющие условия равносильны:
1)	А—связный полуавтомат',
2)	решетка подавтоматов Sub А содержит в точности один
атом;
3)	полуавтомат А имеет точно один сильно связный
подавтомат.
Доказательство. Из условия 1) следует условие
2), поскольку единственной нижней гранью для двух различных
атомов любой решетки является 0. Из условия 2) следует условие
1), так как в случае, когда конечная решетка содержит точно
один атом, пересечение любых двух ее ненулевых элементов
отлично от 0. Условия 2) и 3) равносильны ввиду следствия 1.13
из теоремы 1.36. о
Следствие 1.15. Автономный полуавтомат связен
тогда и только тогда, когда его граф содержит точно один
цикл, о
Теорема 1.38. Решетка подавтоматов полуавтомата
А линейно упорядочена тогда и только тогда, когда, каковы бы
ни были два различных состояния полуавтомата А, одно из
них достижимо из другого.
Доказательство. Необходимость.
Пусть Sub А—цепь. Предположим, что в полуавтомате А суще-
ствуют различные состояния s{,s2, не достижимые друг из друга.
Тогда главные подавтоматы Л^) и Л($2) будут несравнимыми
элементами решетки Sub А,—противоречие с линейностью порядка
в Sub Л.
Достаточность. Если состояние достижимо из
состояния s2, то A(Sj) S Л($2), так что в полуавтомате А,
удовлетворяющем условию теоремы, главные подавтоматы обра-
зуют цепь. Но поскольку любой подавтомат представляет собой
объединение всех содержащихся в нем главных подавтоматов,
получаем, что все подавтоматы полуавтомата А—главные, о
Следствие!.16. Решетка подавтоматов автоном-
ного полуавтомата линейно упорядочена тогда и только тогда,
когда граф этого полуавтомата является циклом или циклом
с входящей в него цепью, »
В § 2.4 -мы покажем, что для любого полуавтомата А
существует полуавтомат В с двумя входными сигналами, решетка
подавтоматов которого изоморфна решетке подавтоматов полуав-
томата А, т. е. Sub В st Sub А.
86
Обратимся теперь к решетке конгруэнций полуавтомата. Пусть
А = (5, X, д)—некоторый полуавтомат. Эквивалентность в на
множестве 5 называется конгруэнцией полуавтомата А, если она
устойчива относительно функции переходов д в том смысле, что
для любых состояний Sj 6 S и любого входного сигнала
х G X выполняется условие
(sp s2) G в =>	х), <5(s2, х)) G в
(т. е. если состояния и s2 находятся в одном 0-классе, то
состояния, получаемые из них под действием входного сигнала
х, тоже окажутся в одном 0-классе). В любом полуавтомате
конгруэнциями будут тождественное отношение Д и универсальное
отношение 5x5.
В § 4.2 нам понадобится следующий простой, но важный факт.
Т е о р е м а 1.39. Отношение эквивалентности (нераз-
личимости) состояний в автомате А' = (5, X, У, д, А) явля-
ется конгруэнцией его редукта А = (5, X, <5).
Доказательство. По определению,
(sr s2) G е (*р G Х*)(А(^, р) = l(s2, р)).
Пусть х G X и р G X*—соответственно произвольный входной
сигнал и произвольное входное слово. Если (Sj, s2) G е, то,
используя формулы из введения (с. 10), получаем:
A(sp x)A(d(sp х), р) = А (хр хр) = A(s2, хр) =
= A(s2, x)A(<5(s2, х), р) = A(sp x)A(d(s2, х), р).
Слова в алфавите У в начале и конце формулы равны, и оба
они начинаются с буквы А(Хр х). Значит, равными будут и слова,
полученные отбрасыванием этой буквы:
A(<5(s1( х), р) = X(d(s2, х), р).
В силу произвольности слова р СОСТОЯНИЯ	х) И д($2, х)
неразличимы в автомате А', т. е. (<5(5^ х), d(s2, х)) G е. о
Заметим, что ^-эквивалентность состояний (т. е. их не-
различимость входными последовательностями длины меньшей или
равной к) в автомате А' = (S, X, У, д, А) в общем случае не
является конгруэнцией редукта А = (5, X, <5) ни при каком
фиксированном к.
П р и м е р 38. Отношение взаимной достижимости состо-
яний будет конгруэнцией в любом автономном полуавтомате
(отождествляются элементы каждого цикла), но в общем случае
отсутствует устойчивость относительно функции переходов.
87
Совокупность всех конгруэнций полуавтомата А обозначим
через Con А. Так как теоретико-множественное пересечение
0 А 02 двух конгруэнций снова является конгруэнцией и
5 х 5—тоже конгруэнция, то, согласно следствию 1.11 теоремы
1.34, упорядоченное множество (Con Л, £)—решетка.
П р и м е р 39. Пусть полуавтомат А = (5, X, <5), где
5 = {Sp s2, s3> s4J, X — {Xp.Xj}, функционирует согласно
диаграмме, представленной на рис. 31. Этот автомат без выходов
является редуктом автомата из примера 4 (см. введение).
Устойчивыми относительно входного сигнала будут разбиения
Д, {2, 3}, 02: {3, 4}, 6^. {1, 2, 3}, 6^. {2, 3, 4}, 5x5:
{1, 2, 3, 4} (здесь мы отождествляем эквивалентности с соответ-
ствующими разбиениями и указываем только неодноэлементные
блоки). Устойчивостью относительно х2 обладают разбиения
Д, 0р 0*: {1, 2}, 0Д и S х S. Диаграмма решетки СопЛ
изображена на рис. 31 справа.
П р и м е р 40 (решетка конгруэнций цикла). Пусть граф
автономного полуавтомата А представляет собой цикл длины
п: 1 -» 2 -» ... -» п -» 1. Если d—делитель числа п, т. е.
п = dk, то разбиение 0rf с блоками {1, 1 + d, ..., 1 + d(k - 1)},
{2, 2 + d, ..., 2 + d(k ' 1)}, .... [d, d + 1, ..., d + d(k - 1)}
согласовано с движением по циклу и, значит, является конгру-
энцией полуавтомата А. Несложные рассуждения показывают,
что любая конгруэнция цикла имеет вид для некоторого
делителя d числа п. При этом = 5 х 5 и вп = Д. Каждый
класс конгруэнции содержит к = n/d элементов, так что если
d^ < dp то Э ,—решетка Con А антиизоморфна решетке
L(n) делителей числа п. Но поскольку решетка L(n) антиизомор-
фна сама себе (антиизоморфизмом является соответствие d «♦
«♦ n/d), то получаем, что решетка конгруэнций цикла длины п
изоморфна решетке делителей числа п. На рис. 32 изображены
88
решетки конгруэнций циклов длиной п = 4, 6, 12, 36. При
этом 6^ обозначает конгруэнцию, соответствующую делителю
d - п/к. Она имеет d классов, в каждом из которых содержится
к элементов. На первой из диаграмм р обозначает простое число.
Рис. 32
Полуавтомат А, имеющий больше одного состояния, называется
простым, если у него нет конгруэнций, отличных от тождест-
венной и универсальной, т. е. если решетка Con Л двухэлемен-
тна.
Пусть А = (S, X, <5)—некоторый полуавтомат. Если А* —
= (5*, X, б)—его подавтомат, то отношение в* = (5* х 5*) U Д^
(эквивалентность с единственным неодноэлементным классом 5*),
как нетрудно заметить, будет конгруэнцией полуавтомата А. При
этом, если Л* и А*—различные собственные неодноэлементные
подавтоматы в Л, то различными будут и определяемые ими
конгруэнции: 0* * в*. Конечно, в общем случае не любая
конгруэнция полуавтомата Л имеет вид в* для некоторого
собственного в Л подавтомата. Следующее предложение показы-
вает, что простые полуавтоматы «почти примитивны».
Т е о р е м а 1.40. Простой полуавтомат с не менее чем
тремя состояниями содержит самое большее один собственный
подавтомат, причем этот подавтомат имеет точно одно
состояние.
Доказательство. Пусть Л—простой полуавто-
мат, 151 > 3, и Л*—собственный подавтомат в Л. Если
множество состояний 5* подавтомата А* содержит более одного
элемента, то отношение в* = (S* х S*) U Д^ будет, как нетрудно
заметить, отличной от Д и 5 х 5 конгруэнцией полуавтомата Л.
Следовательно, каждый собственный подавтомат в Л имеет точно
одно состояние. Пусть теперь Л! и Л2—различные подавтоматы
в Л.
89
Так как по доказанному I5J = IS21 = 1, то ISt U 521 <
< ISI. Поэтому подавтомат А*, являющийся объединением А и
А2 в решетке Sub А, будет собственным подавтоматом полуавто-
мата А, содержащим два состояния, что, как мы видели,
невозможно, о
Следствие 1.17. Автономный полуавтомат тогда и
только тогда является простым, когда: 1) он имеет два
состояния', или 2) граф его переходов представляет собой цикл
простой длины.
Доказательство. Покажем необходимость. Из
теоремы 1.40 получается, что простой автономный полуавтомат
А с п > 3 состояниями может быть только циклом. В примере
39 мы установили, что Con Л a L(n), где L(n)—решетка
делителей числа п. Значит, п—простое число. Покажем достаточ-
ность. Понятно, что любой полуавтомат с двумя состояниями
будет простым. Если граф автономного полуавтомата А—цикл
простой длины, то Con А—двухэлементна, о
В § 4.2 мы покажем, для каждого полуавтомата А существует
полуавтомат В с четырьмя входными сигналами, такой, что
Con А = Con В. Конгруэнции автоматов общего вида будут
рассмотрены в § 4.3.
ГЛАВА 2
АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
§ 2.1. Основные конструкции универсальной алгебры
Во введении мы определили алгебру как пару (A, F), где
А—непустое множество (носитель), и F = {f{, f2, fm}—ко-
нечный набор операций на этом множестве, причем под п-арной
(п > 0) операцией понимается отображение /: Ап -» А, а нульар-
ная операция фиксирует некоторый элемент носителя. В списке
F операции считаются расположенными в порядке убывания их
арностей: nt > «2 > ... > пт, а вектор (п^ п2, ..., пт) называется
типом алгебры (A, F). В дальнейшем будем обозначать алгебры
полужирными латинскими прописными буквами А, В, С, ..., ив
случае необходимости будут вводиться соответствующие индексы
и другие знаки, например, А{, А*, А..
Отношение изоморфности алгебр является эквивалентностью
на классе всех алгебр данного типа: действительно, оно реф-
лексивно (изоморфизмом алгебры на себя является тождественное
отображение), симметрично (если <р—изоморфизм алгебры А иа
алгебру В, то у>-1 будет изоморфизмом алгебры Л на А) и
транзитивно (если р: А -» В, Ц>: В -* С—изоморфизмы, то их
произведение <р ° у. А -» С—тоже изоморфизм). Классы отно-
шения изоморфности называются абстрактными алгебрами, их
свойства изучает универсальная алгебра. Конструкции и методы
универсальной алгебры находят все более широкое применение в
исследованиях дискретных систем.
Пусть А = (А, / , /2, ..., fm)—некоторая алгебра. Подмноже-
ство А* называется устойчивым в А, если оно замкнуто
относительно всех операций алгебры в том смысле, что
а , а2, ..., ап G А* => /(«Др а2, ..., а^) 6 А* для произвольной
n-арной операции f алгебры А. Ограничивая все операции алгебры
А на устойчивом подмножестве А*, мы получаем подалгебру
А* = (А*, / , /2, ..., f ), причем за ограниченными операциями
91
циями сохраняются исходные обозначения. Совокупность всех
подалгебр алгебры А обозначим через Sub А. Понятно, что сама
алгебра является своей подалгеброй. Подалгебры, отличные от
самой алгебры, называются собственными. Если в алгебре А есть
хотя бы одна нульарная операция, то элемент, фиксируемый ею,
должен входить во все подалгебры, так что пересечение любого
семейства подалгебр в этом случае будет непустым (конечно,
такое может случиться и при отсутствии нульарных операций).
Когда в алгебре А нет нульарных операций, в число ее
подалгебр формально вводят пустую подалгебру: это алгебра с
пустым носителем и пустыми операциями, тем самым пустое
подмножество объявляется устойчивым. Если {Л* I i 6 1}—произ-
вольное семейство устойчивых подмножеств алгебры А = (A, F),
то, как нетрудно проверить, их пересечение Г) А*, тоже будет
i е I 1
устойчивым. Подалгебра с носителем Г) Л* называется пересе-
tei 1
чением подалгебр А* = (Л*, J). Она представляет собой наиболь-
шую из подалгебр, содержащихся во всех подалгебрах Л*,
i €Е I, т. е. точную нижнюю грань семейства {Л* I i €Е 1} в
упорядоченном множестве (Sub Л, С). Таким образом, вследствие
теоремы 1.34 из § 1.4, (Sub Л, С) является полной решеткой.
Это решетка подалгебр алгебры Л. Коатомы этой решетки
называются максимальными подалгебрами алгебры Л.
Пусть X—некоторое подмножество алгебры Л, точнее носителя
этой алгебры. Пересечение всех подалгебр, содержащих X,
является подалгеброй, это подалгебра, порожденная множеством
X. Если множество X порождает всю алгебру А (т. е. не
содержится ни в какой собственной подалгебре), оно называется
системой порождающих (или образующих) алгебры А. Например,
носитель Л алгебры А является системой порождающих для Л.
Об алгебре, имеющей конечную систему порождающих, говорят,
что она является конечно порожденной. Система порождающих
алгебры Л, не содержащаяся ни в какой другой системе
порождающих этой алгебры, называется базисом.
Сужение носителя алгебры А = (Л, F) приводит к появлению
подалгебр, уменьшение же множества F ее операций дает новые
алгебры, называемые редуктами. Таким образом, редукт данной
алгебры—это алгебра с тем же носителем, операциями которой
являются некоторые операции исходной алгебры. Понятно, что
редукт имеет уже другой тип.
Пусть А = (Л, F) и В  (В, F)—две однотипные алгебры.
Будем считать для простоты, что соответствующие операции в
А тл В имеют одинаковое обозначение. Гомоморфизмом алгебры
А в алгебру В называется отображение у>: Л -» В такое, что для
92
любых flp а2, ап 6 А и n-арной операции / €Е F выполняется
равенство:
а2... апУ) = /(рЦ), р(а2), .... У»(а„)).
При этом пишут: <р: А -* В.
Гомоморфизмы классифицируются по свойствам их как отоб-
ражений. Инъективный и сюръективный гомоморфизмы называ-
ются соответственно вложением и наложением. Гомоморфизм,
являющийся взаимно однозначным соответствием, — это изо-
морфизм.
Гомоморфизмы алгебры А в себя называются ее эндо-
морфизмами, их совокупность обозначается через End А. Под
автоморфизмами алгебры А понимают ее изоморфизмы на себя.
Множество всех автоморфизмов алгебры А обозначается символом
Aut А.
Простые рассуждения показывают, что произведение гомо-
морфизмов одного класса является гомоморфизмом того же класса.
Если <р—гомоморфизм алгебры А в алгебру В, а А*—подалгебра
в А, то ограничение <р* отображения <р на подалгебре А* будет
гомоморфизмом алгебры А* в В. Если <р: А -» В—наложение,
то алгебра В называется гомоморфным образом алгебры А.
Теорема 2.1. Пусть X—система порождающих алгеб-
ры А = (A, F) и <р, V'—гомоморфизмы этой алгебры, ограни-
чения которых на множестве X совпадают: у>1	= ip\ . Тогда
Л	Л.
<р =
Доказательство. Положим Ао := X,
Л+1 := Ak U аТ 1 f е F’ av а2> ап е V
Тогда А С А С ... С А, С ... и U А. является устойчивым
01	*	(=0 ‘
подмножеством в алгебре А. Поскольку X не содержится ни в
00
какой собственной подалгебре, получаем, что U А. = А. Пусть,
<=0 '
далее, х , х2, ..., хп G X. Тогда для любой n-арной опера-
ции / G F
<p(f{xv х2, ..., хп)) = f(<p(xx), ip^xj, ..., у>(хп)) =
= fMxJ, ip(x2), ..., ЩХ")) = У(/(хх, х2, ..., хп)),
и, следовательно, <р и ip совпадают на Ар Индукцией по к
получаем, что у>1	= ipl для любого к = 0, 1, ..., и, значит,
At	Ак
<Р = 1р. а
93
Следующее предложение утверждает, что гомоморфный образ
и гомоморфный прообраз подалгебры являются подалгебрами
соответствующих алгебр.
Теорема 2.2. Если	—гомоморфизм алгебры А -
- (A, Е) в алгебру В - (В, Е) и А* = (А*, F), В* = (В*, F)—
подалгебры соответственно в А и в В, то <р(А*) :=
:=	Е) и <р~1(В*) := (<р~\в*), Е) являются подалгеб-
рами соответственно в Вив А.
Доказательство. Пусть Ь{, Ь2, ..., bn G <р(А*) и
f G F—произвольная n-арная операция. Тогда Ь{ = ^(а^,
Ъ2 = у>(я2), ..., Ьп = у>(яп) для некоторых а{, а2, ..., ап е А и
/(йр b2, ..., bn) = /(<р(а{), <р(а2).<р(ап))	= <р(/(а{, а2, ап)) G
G <р(А*), поскольку /(яр а2, ..., я^) G Л*. Следовательно, под-
множество у>(-4*) устойчиво в алгебре В. Если же Яр я2, ...
..., ап е <р~{(В*), то у>(я2), ..., <р(ап) G В*, и тогда
р(/(яр я2, ..., яп)) = f(<p(aj, ^(aj. <р(ап)) G В*,
откуда /(Яр я2, ..., ап) G р-1(В*) и, значит, <р~{(В*) устойчиво
В А. а
Отношение эквивалентности 6 на множестве А называется
конгруэнцией алгебры А = (A, F), если оно устойчиво относи-
тельно всех операций этой алгебры, т. е. для любых элементов
Яр я2, ..., ап, Z>p Z>2, ..., bn G А и любой n-арной операции
f 6 F
(Яр е 6 & (я2, ь2) е в & (ап, Ьп) е в =>
=>	а2, ..., яп), f(bv ь2,..., ЬПУ) е в.
Таким образом, если в—конгруэнция алгебры А и ^(я^ =
- в^), в(а2) = в(Ь2), ..., в(ап) = в(Ьп), то
av ..., яп)) = 6(f(bv ь2,bn)).
Совокупность всех конгруэнций алгебры А обозначим через
Con А. Понятно, что декартов квадрат А х А является конгру-
энцией алгебры А = (А, Е). Эта конгруэнция называется универ-
сальной, а все остальные—собственными конгруэнциями. Так как
всякая конгруэнция рефлексивна, то тождественное отношение
А содержится в каждой конгруэнции. Очевидно, что A G
6 Con А; это наименьший элемент упорядоченного множества
(Con А, С). Нетрудно понять, что пересечение О в. любого
семейства конгруэнций само является конгруэнцией и притом
наибольшей из всех конгруэнций, содержащихся в каждой
в., i G I. Из теоремы 1.34 § 1.4 следует, что (Con Л, С)—полная
решетка. Это решетка конгруэнций алгебры А. Алгебра А
называется простой, если решетка Con А состоит всего из двух
элементов: Con А = {А, А х А}.
Т е о р е м а 2.3. Наименьшая эквивалентность, содержа-
щая две заданных конгруэнции алгебры А, сама является
конгруэнцией этой алгебры.
Доказательство. Пусть 0^ 62—конгруэнции ал-
гебры А - (A, F). Согласно теореме 1.23 из § 1.3, наименьшая
эквивалентность, содержащая и 62, выражается формулой
в = U (0( °02)\ Предположим, что элементы а^, а2, ..., а ,
/с=0
Ь{, Ъ2, ..., bn 6 А таковы, что (a., b.) G 6 для i = 1, 2, ..., п.
Тогда для некоторого натурального числа к найдутся элементы
V х2, ..., хк, уг у2, ..., ук, zp z2, ..., zk такие, что
(av Xj) е & (хр x2) e 62 &...& (xk, bj e e2,
(a2, yt) e er & (yr y2) e e2 &...& (yk, b2) e e2,
(an, Z1) e & (V z2) e 02 & ...& (zk, bn) e e2
(можно выровнять цепочки по длине, вставляя нужное число пар
с одинаковыми элементами: и 02 рефлексивны).
Пусть f G F—произвольная n-арная операция. В силу ус-
тойчивости отношений 0j и 62
(f(av а2, ..., ап), /(хр ур ..., z^) G &
&	*1.. Z1)’	f(x2' у2’~’ z2)) е в2 &-
...& (f(xk, ук,..., zk), f(b{, ь2,..., bn)) e 62.
Отсюда (f(al, a2, ..., an), f(b{, b2, .., b )) €E в, и, значит, в—кон-
груэнция алгебры А. =
Следствие 2.1. Произведение двух конгруэнций тогда
и только тогда является конгруэнцией, когда сомножители
перестановочны.
Доказательство. Пусть 0^ в2 G Con А. Отно-
шение ° в2 тогда и только тогда будет эквивалентностью, когда
0j 0 в2 = в2 ° 0j (теорема 1.22). При этом 0 #2 оказывается
95
наименьшей эквивалентностью, содержащей 0( и &2 (следствие 1.6
§ 1.3). Теперь ссылаемся на теорему 2.3. о
Пусть а и b—различные элементы алгебры А. Наименьшая
из конгруэнций, содержащих пару (а, Ь), обозначается через
в(а, Ь) и называется главной конгруэнцией, порожденной парой
(а, Ь). Таким образом,
в(а, Ь) = Г) {0 е Con A I (a, b) е 0}.
Роль главных конгруэнций показывает
Теорема 2.4. Всякая конгруэнция 0 является теорети-
ко-множественным объединением содержащихся в ней главных
конгруэнций:
0 = U {0(<а, b) I (а, Ь) е 0}.
Доказательство. Очевидно, что если (a, b) G
е 0, то в (a, b) С 0. Так как (a, b) G в(а, Ь), то 0 С U{0(tz,
b) I (a, b) 6 0} С v {в(а, Ь) I {а, Ь) 6 0} С 0, где V {в(а, b) I
(a, b) G 0}—это решеточное объединение всех главных конгру-
энций, содержащихся в 0, т. е. наименьшая из конгруэнций,
содержащих все 0(я, Ь), где (a, b) 6 0. Следовательно, 0 =
= U {в(а, b)l (a, b) е 0} о
Согласно теореме 1.19 из § 1.3, ограничение конгруэнции 0
алгебры А = (A, F) на любом подмножестве А* С А является
эквивалентностью. Если к тому же А* устойчиво в А, т. е.
(Л*, F)—подалгебра, то 0 сохраняет свойство устойчивости относи-
тельно всех операций из F на А*. Тем самым доказана
Теорема 2.5. Ограничение конгруэнции на подалгебре
является конгруэнцией этой подалгебры, о
Говорят, что алгебра А обладает свойством продолжаемости
конгруэнций, если для любой ее подалгебры А* и любой
конгруэнции г] G Con А* найдется конгруэнция 0 G Con А такая,
что 0* = 01л« = т]. Не всякая алгебра обладает этим свойством—
примеры мы приведем далее.
Связь между конгруэнциями и гомоморфизмами устанавливают
теорема 2.6 и следствие 2.2 из теоремы 2.7.
Т е о р е м а 2.6. Если <р—гомоморфизм алгебры А, то его
ядро Кег <р является конгруэнцией этой алгебры.
Доказательство. Пусть <р: А -» В—гомомор-
физм алгебры А = (A, F) в некоторую алгебру В. Напомним
(см. § 1.3), что
Кег <р := {{a, b) G А х А I <р(а) =
Покажем, что эта эквивалентность устойчива относительно
всех операций алгебры А. Пусть а^ а2, ..., а ,	b2, ...
..., bn 6 A—произвольные элементы, и f 6 F—любая из n-арных
96
операций алгебры А. Если (a., b.) G Кег у?, то <р(а.) = <р(Ь.),
i •= 1, 2, ..., п, и, используя тот факт, что <р—гомоморфизм,
получаем
а2, ..., ап)) = /(рЦ), р(а2), ..., <р(ап)) =
=	ч>(Ь2)... р(\)) = <p(f(bv ь2,..., Ьп)),
откуда
(f{av а2,..., ап), f(bv b2. bj) е Кегу>
и, значит, Ker <р е Con А. □
Пусть А = (A, F)—некоторая алгебра, в—конгруэнция на ней,
а{, а2, ..., ап G А—произвольные элементы, / G F—произволь-
ная n-арная операция. В фактормножестве А/в положим
6(а2), ..., в(ап)) := 0(f(av а2, ..., ^)).
Заметим, что выбор конкретных элементов а^, а2, ..., ап в
соответствующих 0-классах не имеет значения: если (a., b.) G
G в, то 0(а.) = 0(b.), i = 1, 2, ..., п, и, в силу устойчивости
отношения в относительно всех операций алгебры А, получаем
W в(Ь2), ..., в(Ьп)) = /(©(ар, в(а2)... 6(апУ) =
= 0(f(a а ...,а)) = O(f(b Ь ..., Ь )).
1	ft	1	ft
Таким образом, для любой операции f G F можно определить
в A/в одноименную операцию (для нульарной операции, фикси-
рующей в А элемент а®, будем считать, что в А/0 она фиксирует
элемент в(а^)), и, следовательно, на A/в вводится структура
алгебры того же типа, что и А. Эта алгебра называется
факторалгеброй алгебры А по конгруэнции в и обозначается
А/в.
Теорема 2.7. Пусть А = (A, F)—некоторая алгебра
и в—конгруэнция на ней. Тогда-.
1) естественное отображение
nat в: А -* A/в, а •—♦ в(а),
является гомоморфизмом алгебры А на факторалгебру А/0;
2) ядром этого гомоморфизма является конгруэнция в.
Доказательство. Используя определение опе-
раций в факторалгебре, имеем:
(па^Х/Ц, а2, ..., ап)) = 6(f(av а2, ..., ап)) =
= f(0(ai), 0(а2), ..., 0(ап)) =
= /((nat в)(а1), (nat в)(а2), .... (nat в)(ап)).
Отсюда заключаем, что nat 0—гомоморфизм.
4 А.М.Богомолов, В.Н.Салий	97
Далее,
(a, b) 6 Ker nat в о (nat в)(а) = (nat 6)(6) о
о 0(a) = 6(b) о (a, b) S 0,
и, следовательно, Ker nat 6 = 6. о
Следствие 2.2. Всякая конгруэнция алгебры являет-
ся ядром подходящего гомоморфизма этой алгебры. =
Полученное следствие вместе с теоремой 2.6 означает, что
конгруэнциями алгебры являются в точности ядра ее гомо-
морфизмов.
Гомоморфизмы алгебры, сохраняя ее структурные свойства,
пренебрегают в той или иной степени индивидуальными особен-
ностями ее элементов, «не различая» некоторые из них. Можно
сказать, что гомоморфный образ алгебры в общем случае дает
огрубленное представление об ее структуре.
Важнейшая роль следующей теоремы заключается в том, что
она позволяет обозреть все гомоморфные образы данной алгебры
ее внутренними средствами: любой гомоморфный образ изоморфен
подходящей факторалгебре.
Т е о р е м а 2.8 (теорема о гомоморфизмах). Пусть <р—го-
моморфизм алгебры А на алгебру В. Тогда алгебра В
изоморфна факторалгебре Л/Кегу>.
Доказательство. Пусть А = (A, F) и В =
= (В, F). Через 6 обозначим ядро гомоморфизма т. е.
6 = Кегу>. Согласно теореме 2.6, 0 6 Con Л. Положим
г. А/6 -» В, 0(a) — >р(а).
Прежде всего заметим, что выбор элемента а в 6(a) несущественен:
если ~а 6 6(a), то ф(а) = р(а).
Покажем сначала, что отображение i устанавливает взаимно
однозначное соответствие между множествами А/6 и В. Действи-
тельно,
z(0(a)) = i(6(a)) о <р(а) = <р(а) =>
=» (а, а) €Е Кегу> = 6 =» 6(a) = 6(a),
т. е. <р взаимно однозначно. Так как <р отображает А на В, то
для любого b G В найдется а 6 А такой, что <р(а) = Ь. Но тогда
i(6(a)) = <р(а) = Ь, так что i сюръективно.
Остается доказать, что i—гомоморфизм. В самом деле, если
йр а2, ..., ап 6 А и / G F—произвольная n-арная операция, то
i(f(6(a(), 0(а2), ..., 0(ап)) = i(6(f(av а2, ..., а*))) =
= <P(f(av аг ..., а^) = f(p(ax), ^(aj, ..., ^(а^) =
= f(i(6(ax)), i(0(a2)), ..., i(6(an))),
т. e. i сохраняет операцию f. о
98
Оказывается, что решетка конгруэнций факторалгебры вкла-
дывается в решетку конгруэнций исходной алгебры. Именно, имеет
место
Т е о р е м а 2.9 (теорема о соответствии). Пусть 6—конг-
руэнция алгебры А = (A, F). Решетка конгруэнций факторал-
гебры А/в изоморфна интервалу [0, А х Л] решетки Con Л.
Доказательство. Рассмотрим отображение <р
решетки ([0, ЛхЛ], С) в решетку (ConЛ, С), полагая
;= {(0(a), 0(й)) е А/6 х А/6 I (a, b) S tj}
для произвольной конгруэнции г) G Con Л. Очевидно, что <f>(rf)
является эквивалентностью на фактормножестве А/6. Пусть
f 6 F—произвольная n-арная операция и (0(я.), в(Ь.)) 6 </>(у),
i = 1, 2, ..., п. Тогда (a., b.) €Е rj, i = 1, 2, ..., п, и, значит,
(f(a а , ..., а ), f(b, b , ..., й )) S 7),
1	II	1	ц
так как г]—конгруэнция алгебры Л.
Из определения эквивалентности ф(т]) получаем, что
(6Ща{, а2, ..., ац), 6^, Ь2, ..., й())) 6 у>(^).
Поскольку
6(J(ai, а2, ..., ап)) = f^aj, 6(а2), ..., 0(^))
И
6(f(b{, ъ2,.... Ьп)) = /(6(Ь{), 6(Ь2), ..., 6(Ьп)),
то
Щ6(^ е(а2), ..., 6(апУ), f(6(bx), 6(b2), ..., 6(bn))) 6 <p(rj),
и, таким образом, <р(т/)—конгруэнция факторалгебры А/6. Пока-
жем, что <р взаимно однозначно. Действительно, если <р(г]{) =
= Для ’/р ’/г е [6, ЛхЛ], то для любых a, b €Е Л
(а, й) S Т]1 о (6(a), 6(b)) £ >р(т]х) = р(>72) О (а, й) S t]2,
откуда t]l = т)2.
Докажем теперь сюръективность отображения. В самом деле,
пусть Н G Con А/6. Положим
т) := {(а, й) 6 Л х Л I (6(a), 6(b)) S Н}.
Очевидно, что rj—эквивалентность на множестве Л, причем
® £ >7, так как если (a, b) G 6, то 6(a) = 6(b) и, значит,
(^(а), 6(b)) е Н, откуда (а, й) 6 тр Пусть (а., й.) G i], i =
= 1> 2, ..., п. Тогда (6(а^, 6(b^)) G Н, i = 1, 2, ..., п. Посколь-
4*
99
ку Н—конгруэнция на факторалгебре А/в, то для любой и-арной
операции f G F имеем
(fWaJ, в(а2), .... в(ап)), /(©(*,), в(Ь2), ..., в(Ьп))) е Н.
Отсюда
(d(f(av а2,	%)), d(f(bv Ь2, .... й,))) е Н,
и, следовательно, (/(Пр а? ап), f(b{, b2,	b*)) е у. Таким
образом, t] G Con А. При этом = Н.
Остается показать, что отображение <р изотонно и обратно
изотонно.
Пусть п,, w е Con Л и в С п,, 0 С По определению
конгруэнций	<р (*?2) тождественно выполняются соотно-
шения:
(a, b) G о (в(а), в(Ь)) G
(a, b) G г]2 о (6(а), в(Ь)) G <р(у2).
Отсюда сразу получается, что
° <р(пх) £
Таким образом, упорядоченные множества (СопЛ/0, С) и
([0, ЛхЛ], С)—изоморфны, о
Прямым произведением однотипных алгебр А = (A, F) и
В = (В, F) называется алгебра С = (А х В, F), операции в
которой определяются следующим образом:
/((“,. »,)• (“2' »2>.<“„•	».» '= №• а2....%)' «».• »2> •• ».»
для любых Пр а2, ..., ап G А, Ь}, Ь2, ..., Ьп G В, и произволь-
ной n-арной операции f G F. Таким образом, элементами прямого
произведения являются всевозможные пары (а, Ь), а&А, ЬЕВ,
а операции выполняются покомпонентно. Прямое произведение
алгебр А и В обозначается через А X В.
Пример 4.1. Пусть А = (А, У, Л, ', 0, 1) и В =
= (В V, Л, ', 0, 1)—две булевы алгебры. По определению,
Ах В = (Ах В, V, Л, ', 0, 1), где
(ар Ъ^) v (а2, b2) := (flj v а2, by v i2),
(Пр Ъх) Л (а2, Ь2) := Л а2, \ Л Ь2),
(а, Ь)' := (а', Ь'),
О := (0, 0), 1 := (1, 1).
100
Поскольку операции выполняются покомпонентно, в А х В имеют
место все тождества I—IX, входящие в определении булевой
алгебры (см. § 1.1). Следовательно, прямое произведение булевых
алгебр само является булевой алгеброй.
Если алгебры А	и	В	конечны	и,	например, IAI = т,
IВI	=	п, то	алгебра	А	х В	содержит	тп	элементов.
Отображения
я :	А	х В	-* А, (а,	Ь)	а,
л у	А	х В	-* В, (а,	Ь)	•—»Ь,
называются проекциями прямого произведения А X В на сом-
ножители. Ясно, что JTj и л2—сюръективные отображения.
Т е о р е м а 2.10. Проекции прямого произведения на сом-
ножители являются гомоморфизмами:
л.: А X В -» А, л - А X В -* В.
1	it
Доказательство. Пусть ах, а?, ..., ап G А, Ьх,
by ..., bn е В—произвольные элементы, и f е F—некоторая
n-арная операция. Тогда
bj, (а2, Ь2), ..., (ап, bj» =
=	а2, ..., ап), f(bv by .... bj) =
= аг....... %) =	Ъх), лх{а2, Ь2), .... лх(ап, bj).
Аналогичные соотношения имеют место для отображения Лу □
Подалгебры прямого произведения алгебры А на себя (т. е.
прямого квадрата А х А) называются устойчивыми (стабиль-
ными) отношениями на А. Например, конгруэнция—это не что
иное, как подалгебра прямого квадрата, являющаяся эквивалент-
ностью.
Говорят, что алгебра С разлагается в прямое произведение,
если С = А х В, где А и В—неодноэлементные алгебры.
Например, алгебра, имеющая количество элементов, выражаемое
простым числом, не разлагается в прямое произведение.
Теорема 2.11. Алгебра А = (A, F) тогда и только
тогда разлагается в прямое произведение, когда на ней
имеются нетождественные перестановочные конгруэнции 0^
в2 такие, что 0 Г) в2 = А и V в2 = А X А.
Доказательство. Необходимость.
Пусть А а Ах х Ау Для простоты будем считать, что А и есть
Ах X Ау Тогда отношения = Кег^ и в2 = Кегл2 и дают
нужную пару конгруэнций. Прежде всего, вх, в2 е Con А, так
101
как л, и jt2—гомоморфизмы (см. теоремы 2.10 и 2.6). Пусть
(a, b), (с, d) е А—произвольные пары. Тода
((a, i), (а, d)) е 0, = Кег л,. ((а, d), (с, </)) е е2 = Кег л,,
откуда ((a, b), (с, d)) е 0,0 0,, и’ след°вательно’ =
= А X А. Аналогично, 0	= А X А. Так как 0, и 0,
оказались перестановочными, то их произведение »0, будет
наименьшей содержащей их конгруэнций: 0, V 0, = 0, ° 0, =
= А X А.
Далее,
((а, Ь), (с, d)) е 0, П е2 => ((а, Ь), (с, d)) е 0, =
= Кегл, & ((о, b), (с, d)) е в2 = Кегл, =*
=> а = с & b = d => (а, с) = (b, d),
т. е. 0, Г) 0, = А.
Достаточность. Предположим, что на алгебре
А = (A, F) имеются конгруэнции и 0,, удовлетворяющие
условиям теоремы. Покажем, что А = А/8{ х А/б?. Рассмотрим
отображение
<р". А -* А/вх X А/62, а н- (0,(а), 0,(а)).
Если <р(а) = <р(Ь), то 0,(о) = 0,(£) и 0,(o) = 02(i), т- е-
(a, b) G 0, А в2 = А, и, значит, а - Ь\ следовательно, отобра-
жение взаимно однозначно. Пусть вх(а), 02(й)—произвольные
классы соответствующих конгруэнций. Так как 0, и 0, переста-
новочны, 0, о в2 =	V в2 = А X А. Значит, найдется элемент
с е А такой, что (а, с) G и (с, b) G 62> т.е. 6j(c) = 0j(a)
и в2(с) = 62{Ь). Тогда <р(с) = (в^с), 02(с)) = (0/а), в2(Ъ)), и
следовательно, <р отображает А на А/вх X А/в2. Наконец,
учитывая, что вх и в2—конгруэнции, для любой л-арной операции
f G F получаем
>p(f(av а2, ..., aj) = (0^, «2,	%)),	а2’ ап^ =
=	вх(а2)... (0^^)), /(02(й1), 02(а2), ..., 02(%))) =
= f((ex(ax), в2(ах)), (0,(0,), 02(о2)). (0^,6^)) =
= /(^(а,). <р(а2)' -> (Р(й„))>
—таким образом, отображение <р является гомоморфизмом. □
102
Рассмотренная конструкция прямого произведения двух алгебр
допускает весьма широкое обобщение. Для наших целей доста-
точно расширить его на произвольное конечное число сомножите-
лей.
Прямым произведением однотипных
i = 1, 2, ..., к называется алгебра А =
алгебр А. = (A., F),
к
П A., F , где
/((а1> а2' "•> ак)' (а1> а2’ ак)' (Й1’ а2' ак)^ :
••= <f(^r ...<)>	4 •••>	•••’ *4 а1...
для произвольных элементов G A., i = 1, 2, ..., к, j = 1,
2, ..., п, и любой n-арной операции f G F. Будем писать
А = А} х Л2 х ... х А^. При к - 2 получается уже известное
определение прямого произведения двух алгебр.
Следующая теорема дает сведение к первоначальной конст-
рукции.
Т е о р е м а 2.12. Имеет место изоморфизм
А} X А2 X А3 = (Л X А2) X А3
для любых трех однотипных алгебр
А. = (A., F), i = 1, 2, 3.
Доказательство. Искомым изоморфизмом, оче-
видно, является отображение
<р: Ау X Л2 X А3 -* (А^ X А2) х А3, (а, Ь, с) •—»((а, Ь), с). □
Индукцией по числу прямых сомножителей получаем
Следствие 2.3.
А, X А- X	... X А,	= (... (Л,	X А.)	X ...) X А,.	□
12	Л 4	4 1	27 'к
Т е о р е м а 2.13. Всякая конечная алгебра разлагается в
прямое произведение не разложимых в прямое произведение
алгебр.
Доказательство. Понятно, что рассматриваются
лишь такие конечные алгебры А = (A, F), которые разлагаются
в прямое произведение двух алгебр. Предположим, что доказы-
ваемое утверждение справедливо для всех алгебр, носители
которых имеют меньше чем 1Л1 элементов. Если А = А} х А2,
где IAI > 1, i = 1, 2, то IAI < 1Л1, i ° 1, 2. По предполо-
жению, А = В X В- X ... X В , Ж = С, X С, X ... X С ,
112	т' 2	1	2	п
103
где В., С. не разложимы в прямое произведение, i •= 1, 2, т,
j *= 1, 2, ..., п. Согласно следствию 2.3,
А = В, X В- X... ХВ X С, X С, X.... X С . =
1 z	т 1 z	п
В качестве конкретного примера применения теоремы 2.13
приведем
Следствие 2.4. Всякая конечная булева алгебра раз-
лагается в прямое произведение двоичных булевых алгебр.
Доказательство. Покажем, что среди всех
булевых алгебр не разложима в прямое произведение только
двоичная булева алгебра В2. В самом деле, пусть В—некоторая
булева алгебра с носителем В, имеющая более двух элементов.
Тогда в ней существует элемент а <£ {0, 1}. Положим
ва := {(х, у) е BI х Л а = у Л а].
Очевидно, что ва—эквивалентность. Далее,
(х, у), (z, t) 6 ва => х Л а = у Л а & z Л а = t Л а =>
=> (х Л z) Л а = (х Л а) Л (z Л а) = (у Л а) Л (t Л а) =
= (у Л t) Л а & (х V z) Л а = (х Л а) V (z Л а) =
= (у Л а) V (/ Л а) = (у V t) Л а => (х Л z, у Л /),
(х v z, у v t) е еа,
т. е. ва устойчива относительно объединения V и пересечения
Л. Кроме того,
(х, у) е Qa => х Л а = у Л а => (х Л а)' = (у Л а)’ =>
=> х' V а' = у’ V а' => (х' V а') Л а = (у' V а') Л а =>
=> х' Л а = у' Л а => (х', у') G &а,
и, значит, ва устойчива относительно дополнения. Конгруэнции
6а и & а' УД°влетв0Ряют условиям теоремы 2.11, т. е. задают
некоторое разложение булевой алгебры В в прямое произведение.
В самом деле,
(х, у) G 9^ П =>хЛа = уЛа&хЛа'=уЛа'=>х = хЛ1 =
= х Л (а V а') = (х Л а) V (х Л а') = (у Л а) V (у Л а') = у,
и значит, в Г| в = А.
а а
Для произвольных элементов х, у G В рассмотрим элементы
и = (х Л а) V (у Л а') и v = (х Л а") V (у Л а). Имеем: и Л а =
104
= х Л а, и Л а' = у Л а', т. е. (х, у) G 0а ° 0а,; v Л а' = х Л а',
v Л а = у Л а, т. е. (х, у) G 0а, ° Отсюда 0а ° 0а, = В X В =
= в ,00 . о
а а
Рассмотрим подпрямые произведения алгебр. Пусть А. =
= (A., F), i = 1,	к,—однотипные алгебры. Подалгебра А =
k
= (A, F) прямого произведения А, называется подпрямым
;-1
произведением алгебр A., i - 1, ..., к, если ограничения л*
к
проекций л.: А. -* А. на подалгебре А являются сюръ-
/=1
ективными отображениями.
Так как носитель А подалгебры А представляет собой i-арное
отношение между множествами А{, А2, ..., Ак, то указанное
условие означает, что рг А = A., i •= 1, ..., к.
В отличие от прямого произведения подпрямое произведение
к
алгебр A., i = 1, ..., к, выделяется неоднозначно: в А. может
1	1-1	1
быть несколько (и даже много) подалгебр, удовлетворяющих
нужному свойству для проекций. Поэтому подпрямое произведение
не имеет символьного обозначения.
Говорят, что алгебра А разлагается в подпрямое произведение
алгебр Л , А^, ...., Ак, если А допускает изоморфизм на
некоторое подпрямое произведение А* этих алгебр, причем ни
одна из проекций л*: А -* А. не является изоморфизмом.
Алгебра, не разложимая в подпрямое произведение, называется
подпрямо неразложимой.
Множество нетождественных конгруэнций вр #2, ..., 0к алгеб-
к
ры А называется разделяющим, если П 0. = А.
Теорема 2.14. Алгебра тогда и только тогда разла-
гается в подпрямое произведение, когда на ней существует
разделяющее множество конгруэнций.
Доказательство. Необходимость.
Пусть алгебра А изоморфна подпрямому произведению А* алгебр
Ар А2, ..., Ак, причем ни одна из проекций л*: А* -* А. не
является изоморфизмом. Положим 0. = Кегл*, i = 1, ..., к.
Согласно теореме 2.6, все 0. будут конгруэнциями алгебры А* и
притом нетождественными, так как л* по условию не инъективны.
105
к
При этом Г) в. = А, так как для любых элементов а =
i=i
= (ар а2, и Ь = (йр Z>2, алгебры Л* ймеем:
(а, Ь) е П в. => (v i)(n*(a) = л*(Ь)) => (v i)(a. = b.) а = b.
1=1
Следовательно, {в. I i = 1,к}—разделяющее множество конгру-
энций на А*. Так как алгебра А изоморфна алгебре А*, то и на
А существует разделяющее множество конгруэнций.
Достаточность. Пусть {в. Iz= 1, ..., Л}—разде-
ляющее множество конгруэнций на алгебре А = (A, F). Покажем,
что А разлагается в подпрямое произведение факторалгебр А/6.,
к
i = 1, ..., к. В прямом произведении А/0. выделим подмно-
i=i
жество А* = {(б^а), 62(а), ..., 0^(а)) I a G А}. Это подмножество,
как нетрудно убедиться, устойчиво и, следовательно, определяет
в прямом произведении некоторую подалгебру А*. При этом,
конечно, л.(А*)=А/6., i = 1, ..., к, так что А*—подпрямое
произведение алгебр А/в? i = 1, ..., к. Положим
А - А*, а (в^а), 0/а), ..., ^(а)).
Это сюръективное отображение является гомоморфизмом, так как:
а2, .... ал)) =
ат аЛ в2^а1' а2’	%))’ Wai’ а2’ ап»> =
= (f(W< вх(а2), .... вх(апУ), f(02(ax), в2(а2),.... <?2(ап)), ...
= /((^(а,), 02(в1), .... вк(ах)), (0х(а2), б2(а2), .... ^(а2)), ...
-> (е1(%)>	вк^ =
для любой n-арной операции f G F и произвольных элементов
Цр а2, ..., ап 6 А. (Заметим, что в приведенной цепочке равенств
символ / выступает для обозначения одноименной операции в
106
алгебре А, в ее факторалгебрах и в прямом произведении.)
Поскольку
р(а) = <р(Ь) => (г1)(е((а) = 0.(Ь)) =>
к
=> (v i))((a, Ъ) €	=> (a, b) G Г) 0. = Д => а = Ъ,
i=l
то <р—изоморфизм алгебры А на подпрямое произведение А*
алгебр A., i = 1, к. Осталось показать, что ни одна из
проекций л*: А* -* А. не является изоморфизмом. Так как
0. * Д, то найдутся элементы а, Ь G А такие, что (a, b) G 0.,
к
но а * i. Из условия Г) 0. = Д получаем, что (а, Ь) £ 0. для
i=i	1
некоторой конгруэнции 0. из нашего множества конгруэнций.
Тогда <р(а)	<р(Ь) (эти векторы отличаются /-й компонентой:
0.(а) * 0.(Ъ)). Но
л(р(я)) = е((а) = 0.(Ь) = я.(р(й)),
и, значит, проекция л* не инъективна. □
Следствие 2.5. Алгебра подпрямо неразложима тог-
да и только тогда, когда пересечение всех ее нетождественных
конгруэнций является нетождественной конгруэнцией, о
Следствие 2.6. Конечная алгебра А подпрямо нераз-
ложима тогда и только тогда, когда решетка Con А ее
конгруэнций—одноатомная, т. е. содержит в точности один
атом, о
Следствие 2.7. Подпрямо неразложимая алгебра не
разлагается в прямое произведение. □
П р и м е р 42. В доказательстве следствия 2.4 из теоремы
2.13 было установлено, что любая булева алгебра, содержащая
более двух элементов, разложима в прямое произведение.
Применяя следствие 2.7 из теоремы 2.14, получаем, что
единственной подпрямо неразложимой булевой алгеброй является
двухэлементная булева алгебра В^.
Впоследствии мы увидим, что следствие 2.7 не допускает
обращения: неразложимая в прямое произведение алгебра вполне
может быть разложима в подпрямое произведение.
Следующее предложение является частным случаем теоремы
Биркгофа, утверждающей, что каждая алгебра разложима в
подпрямое произведение подпрямо неразложимых алгебр.
Т е о р е м а 2.15. Всякая конечная алгебра разложима в
подпрямое произведение конечного числа подпрямо неразложимых
конечных алгебр.
107
Доказательство. Пусть А = (A, F)—конечная
алгебра, разложимая в подпрямое произведение, и пусть а, b—
произвольные ее элементы, а * Ь. Так как пересечение всех
нетождественных конгруэнций алгебры А является тождественной
конгруэнцией (следствие 2.5 из теоремы 2.14), то найдется
в G Con А такая, что в * А и (a, i) С 9. Упорядоченное
множество ({9 6 Con ЛI (а, Ь) £ 0}, С) будет, следовательно,
непустым упорядоченным подмножеством решетки (Con A, G). В
силу конечности, в этом упорядоченном множестве существуют
максимальные элементы. Пусть &а ь—один из них. Рассмотрим
интервал [0 ь, Ах А] решетки Con А. Если &а С в С
С Л х Л, , то (a, b) G в в силу максимальности ва ь среди
конгруэнций, не содержащих пару (а, Ь). Но тогда главная
конгруэнция в(а, Ь), порожденная парой (а, Ь), содержится во
всякой конгруэнции 6 из указанного интервала, отличной от
в .. Следовательно,
(Z, о
п{9 6 Con л1 в . с 9 с лхл} * 9 ,,
1	a, b	‘ а, b
и, значит, ([&а b, А X Л], С)—одноатомная решетка. Согласно
теореме о соответствии (теорема 2.9) решетка конгруэнций фак
торалгебры А/ва ь изоморфна решетке ([ва b, А X Л] , С), и, в
силу следствия 2.6 из теоремы 2.14, алгебра At&a ь подпрямо
неразложима. Поскольку, очевидно, П {&а ^la, b 6 Л} = А,
вследствие теоремы 2.14 алгебра А разлагается в подпрямое
произведение подпрямо неразложимых алгебр А1&а . □
Исследуем полуавтоматы как алгебры. Пусть Л = (S, X, <5)—
некоторый полуавтомат и х. G X—произвольный входной сигнал.
Сопоставляя ему функцию
д:. S -* S, s •—» <5(s, х.),
определяем на множестве 5 унарную операцию. Это дает
возможность рассматривать полуавтомат Л как унарную (т. е.
только с унарными операциями) алгебру Л = (S, <5р
д , ..., <3 ), где т = 1X1.
С другой стороны, если (S, f , f^, ..., /т)—некоторая конечная
унарная алгебра, то ее можно считать полученной путем
описанной процедуры из полуавтомата Л = (S, X, <5), где X =
= {Хр х ..., х^}—произвольный алфавит с т символами, и
d(s, х.) := /(.(s) для всех s G S, i = 1, ..., т. Алгебра с одной
унарной операцией называется унаром. С нашей точки зрения
автономные полуавтоматы—это не что иное, как конечные у нары.
Теорема 2.16. Подавтоматы, гомоморфизмы и конг-
руэнции полуавтомата—это в точности подалгебры, гомо-
108
морфизмы и конгруэнции соответствующей этому полуавтома-
ту унарной алгебры.
Доказательство. То, что S*—устойчивое под-
множество в полуавтомате А = (S, X, б), записывается тожде-
ственным по s 6 S* и х. G X соотношением 6(s, х(.) G S*. Но
в алгебре А, соответствующей полуавтомату А, оно равносильно
соотношению 6(.(s) G S*, означающему устойчивость подмножест-
ва S* относительно всех операций.
Гомоморфизм полуавтомата А = (S, X, б) в сравнимый с ним
полуавтомат В = (Т, X, б)—это отображение <р: S -• Т такое,
что:
p(<5(s, х(.)) = 6(p(s), х.)
для любых s 6 S, х. G X Но
?(<5(s, х.)) = 6(p(s), х.) о p(6.(s)) = d.{<p{s)),
где д.—унарная операция, определяемая на S входным сигналом
х.. Равенство же у>(б .(s)) = d.(<p(s)) означает, что <р—гомоморфизм
унарной алгебры А, соответствующей полуавтомату А.
Совпадение конгруэнций полуавтомата А и соответствующей
ему унарной алгебры А очевидным образом вытекает из схемы:
(v s, s 6 S)((s, s) G в) =>
(v x(.)((6(s, x.), 6( s, x )) G в) о в G Con A,
(v <5.)((<5.O), 6.( s)) G 6) о в G Con A. D
Факторавтоматом полуавтомата A = (S, X, б) по конгру-
энции в называется полуавтомат A/в = {S/в, X, б), где
6(6(s), х) := 0(6(s, х))
для любых s G S, х G X. (Заметим, что точнее было бы говорить
о «факторполуавтомате», но это привело бы к утяжелению
терминологии,—аналогичная оговорка была нами сделана при
определении подавтомата.)
Понятно, что алгебра, соответствующая факторавтомату А/в,
есть не что иное, как фактор по конгруэнции в алгебры,
соответствующей полуавтомату А.
109
Прямым произведением сравнимых полуавтоматов А. =
к
называется полуавтомат f] А. =
= (S,, х, <5),
= П х>
1-1, .... к,
<5 , где
6((s1, s2, sk), х) := (6(s1, х), 6(s2, х),	6(s*, х))
для любых s* 6 S., i - 1, к, х 6 X.
Подпрямым произведением сравнимых полуавтоматов
А. = (S., X, б), i - 1, к, по определению, является подавто-
к
мат А = (S, X, б) прямого произведения А. такой, что
pr(JS = S. для всех i - 1, ..., к.
Таким образом, все рассмотренные алгебраические конструкции
для полуавтоматов совпадают с соответствующими конструкциями
для конечных унарных алгебр, сопоставляемых этим полуавтома-
там. Следовательно, все ранее полученные алгебраические
результаты в подходящих формулировках справедливы для полу-
автоматов. Но, естественно, возникают и некоторые специфические
свойства.
Т е о р е м а 2.17. Пусть А = (S, X, б)—некоторый
полуавтомат и А* = (3 , X, б)—любой из его подавтоматов.
Тогда всякая конгруэнция полуавтомата А* может быть
продолжена до конгруэнции на А, т. е. является следом на А*
подходящей конгруэнции полуавтомата А.
Доказательство. Пусть в* 6 Con А*. Положим
в := в* U Д„ Очевидно, что в является эквивалентностью на
U-□
множестве 5 и все ее неодноэлементные классы—это неодноэле-
ментные в*-классы. Следовательно, если s * s и (s, s) Е б, то
s, s 6 S* и (s, s) 6 в*. Отсюда (6(s, х), б( s, х)) 6 в* С в,
так что в & Con Л, в П (S* х S*) = в*, о
Свойство продолжаемости конгруэнций присуще далеко не всем
алгебрам.
П р и м е р 43. Пусть А = {е, а, Ъ, с}—носитель алгебры
А с одной операцией ° («умножение»), которая определяется
таблицей:
о	е	а	ь	с
е	е	а	ь	с
а	а	а	а	а
ь	ь	а	ь	е
с	с	а	е	е
по
Подмножество А* = {е, a, b} С А замкнуто относительно умно-
жения и, значит, определяет некоторую подалгебру. Эквивалент-
ность в*: {е}, {а, Ь} является конгруэнцией этой подалгебры, но
на всей алгебре не существует конгруэнции в, следом которой на
А* была бы в*. Действительно, в противном случае было бы
(a, i) ё fl* С в, (с, с) е в, но элементы а - ас и е • Ьс
лежат в разных в*-классах и, следовательно, в разных 6-классах.
Прямое произведение полуавтоматов, применимое только к
сравнимым автоматам, можно содержательно интерпретировать как
их параллельное соединение: на общий вход подается сигнал
и—одновременно и независимо—во всех полуавтоматах происходит
переход в соответствующее состояние.
Подпрямое произведение представляет собой, грубо говоря,
подавтомат параллельного соединения, в котором «задействованы»
все состояния каждого из данных полуавтоматов.
Если полуавтоматы А я В сильно связны, то любой подавтомат
прямого произведения А х В будет подпрямым произведением
полуавтоматов А я В. Представление полуавтомата в виде
подпрямого произведения называется его параллельной деком-
позицией, а в виде прямого произведения—полной параллельной
декомпозицией.
Изучение следующего примера отчетливо показывает особен-
ности этих декомпозиций полуавтоматов.
Пример 44. Рассмотрим автономные полуавтоматы
4 = ({Sj, Sj, s3, s4, s5, s6}, {x}, 6) я В = ({Гр t2, ty ty ts, <6),
{x}, б), графы которых представлены на рис. 33, и там же
приведены их изоморфные решетки конгруэнций. При этом в
полуавтомате А
вх‘ V’ <S3>’ {s4}’ {s5>’ e2:	<S2> S3’ s4’ s5’ S6}’
а в полуавтомате В
Ц, ty t5}, {t2,t4,t6}, 02: Ц, <4}, {t2, t5}, {ty <6).
Рис. 33
На рис. 34 показано параллельное соединение (т. е. прямое
произведение) двух автономных полуавтоматов: у одного из них
множество состояний {к, %}, а у второго множество состояний
ill
[a, p, у}. Результирующий полуавтомат изоморфен полуавтомату
В. Следовательно, полуавтомат В разлагается в прямое произве-
дение. Полуавтомат А не разложим в прямое произведение.
Действительно, согласно теореме 2.11, существование такого
разложения равносильно наличию у полуавтомата А двух
перестановочных конгруэнций, пересечение которых тождественно,
а объединение (как элементов решетки Con А)—универсально.
Полуавтомат А имеет только две нетождественные конгруэнции,
удовлетворяющие двум последним условиям: и 0^, однако эти
конгруэнции не перестановочны. Например, (s^ s2) G «в2, так
как (s , s6) G и (s6, s2) G #2, но (Sp $2)	так как
если (s , s) G 02, то обязательно s = Sp a (Sp s2) £ 0p
Рис. 34
Таким образом, мы приходим к важному заключению: свойство
перестановочности конгруэнций и, следовательно, разложимость
полуавтомата в прямое произведение не выражается в терминах
решетки конгруэнций, в отличие от разложимости в подпрямое
произведение (теорема 2.14 и следствие 2.6 из нее).
Полуавтомат А, не разложимый в прямое произведение,
оказывается подпрямо разложимым.
На рис. 35 представлено прямое произведение (параллельное
соединение) двух автономных полуавтоматов: у одного множество
112
состояний состоит из двух элементов fy, v2), а у второго—из
пяти элементов {a, b, с, d, е}. Полуавтомат А вкладывается в
это прямое произведение (например, <р: •—» (vp а), $2 •—»
(v2, b), s3 — (у2, с), s4 — (у2, d), ss — (v2, е), Sf) —
» (у2, а)), таким образом, что проекции его на прямые сомножи-
тели сюръективны. Следовательно, на рис. 35 представлена парал-
лельная декомпозиция полуавтомата А.
Согласно теореме 2.15, всякий полуавтомат разлагается в
подпрямое произведение подпрямо неразложимых полуавтоматов.
Таким образом, подпрямо неразложимые полуавтоматы—это в
некотором смысле простейшие, элементарные устройства, из
которых конструируются все полуавтоматы. Они легко распозна-
ются по решетке конгруэнций: в ней должен быть единственный
атом (следствие 2.6 из теоремы 2.14). Однако решетка конгруэнций
сама по себе является весьма сложным объектом, и естественно
желание получить условие подпрямой неразложимости полуавто-
мата на более простом языке, например, в виде некоторых свойств
таблицы переходов. Пока задача эта далека от своего разрешения,
и имеются только некоторые частные продвижения. Приведем
один из подобных результатов [79]. Полуавтомат называется
определенным, если существует натуральное число к такое, что
любое входное слово, имеющее длину равную или большую к,
переводит все состояния полуавтомата в некоторое определенное
(для данного слова свое) состояние.
Теорема 2.18. Определенный полуавтомат А = (S,
X, д) подпрямо неразложим тогда и только тогда, когда он
имеет два различных состояния sQ и s* такие, что
1) <5($0, х) = с5($*, х) для любого х G Х\
2) если и s2—различные состояния и {$р $2) * {s0, s*},
то d(Sp х) * <5(s2> х)	некоторого х G X.
[Эти условия теоремы означают, что в таблице переходов
имеются две одинаковые строки, а после вычеркивания одной из
них все оставшиеся строки различны.]
Доказательство. Необходимость.
Пусть А = (S, X, д)—подпрямо неразложимый определенный
полуавтомат. Через P2(S) обозначим множество всех двухэлемен-
тных подмножеств в S. Положим {Sp $2} < {s3> sj, если
существует входное слово р G X* такое, что выполняется
равенство {<5(Sp р), d(s2, р)} = {^3, s4). Это отношение реф-
лексивно и транзитивно. Докажем, что оно антисимметрично. В
самом деле, если для {$р $2}, {$3, G P2(S) найдутся непустые
слова р и q такие, что р переводит {Sp s2} в {$3, $4}, a q
переводит {s3, s4) в Ц, s2), то {<5(Sp pq), d(s2, pq)} =
113
= {Sp s2}. Следовательно, существуют слова сколь угодно боль-
шой длины, переводящие {s , s } в себя. Вследствие определен-
ности полуавтомата А это невозможно (Sj * s2), и, значит,
{Sp s2} = {s3, s4}. Итак, рассмотренное отношение является
отношением порядка на множестве	Покажем, что в
упорядоченном множестве (P2(S), <) есть наибольший элемент.
Так как P2(S) конечно, оно имеет максимальные элементы. Пусть
{Sp s2}, {s3, s4)—различные максимальные элементы. Тогда
<5(Sp х) = d(s2, х) и d(s3, х) = 6(s4, х) для любого х G X. В
самом деле, допустив, например, что <5(Sp х) * d(s2, *) Д'151
некоторого х G X, мы получили бы в силу максимальности
элемента {Sp s2) равенство: {<5(Sp х), d(s2, х)} = {Sp s2), кото-
рое сохранялось бы при повторной подаче на вход сигнала х. В
силу определенности полуавтомата это невозможно.
Теперь рассмотрим на полуавтомате А две конгруэнции
6(Sp s2) и e(s3, s4). Очевидно, что их пересечение совпадает с А,
а это противоречит подпрямой неразложимости полуавтомата А.
Мы показали, что в упорядоченном множестве (P2(S), S) есть
наибольший элемент. Обозначив его через {s0, s^}, и получаем
выполнимость условий 1) и 2) для полуавтомата А.
Достаточность. Пусть в определенном полуавто-
мате А выполняются условия 1) и 2). Так же, как при
доказательстве необходимости, введем порядок на множестве
Р2(5) всех двухэлементных подмножеств множества S. Тогда
{sQ, s*) будет наибольшим элементом в этом упорядоченном
множестве.
Покажем, что конгруэнция 6(sQ, s*) является наименьшей из
нетождественных конгруэнций полуавтомата А. В самом деле,
пусть в—произвольная нетождественная конгруэнция на А.
Выберем какие-нибудь различные в-конгруэнтные состояния
Sp s2 G 5. Так как {sQ, s*}—наибольший элемент в (P2(S), ^), то
{sp s2J < {sQ, s*}, и, значит, найдется непустое слово р G X*
такое, что {<5(sp р), <5(s2, р)} = {s0, s*}. Но тогда (s0, s*) G в,
откуда 6(s0, $*) £ в. Таким образом, решетка Con А имеет
единственный атом. Согласно следствию 2.7 из теоремы 2.14,
полуавтомат А подпрямо неразложим, о
Полное описание [90] подпрямо неразложимых автономных
полуавтоматов дает
114
Теорема 2.19. Подпрямо неразложимыми автономны-
ми автоматами являются те и только те, графы которых
изоморфны графам, изображенным на рис. 36 (n > 1, р—
простое число, а > 1).
Рис. 36
Доказательство. Необходимость.
Пусть автономный полуавтомат А = (S, <5) подпрямо неразложим.
Тогда пересечение любых двух его нетождественных конгруэнций
отлично от А.
Пусть граф переходов полуавтомата А состоит из одной
компоненты. Могут представиться два случая:
1) Единственный цикл графа одноэлементен. Тогда А—
определенный полуавтомат, и из теоремы 2.18 следует, что граф
имеет вид на рис. 36б.
2) Цикл графа переходов полуавтомата А неодноэлементен.
Если —нециклическое состояние, a —циклическое и при этом
c5(s,) = sn = <5(s ), то главные конгруэнции 0(s , sA и 6(sn, s )
1z U	L	1 L	U л'
имеют тождественное пересечение. Следовательно, полуавтомат А
не имеет нециклических состояний и его граф представляет собой
цикл. Предположим, что длина цикла п не является степенью
простого числа. Тогда п можно представить в виде произведения
двух взаимно простых чисел: п ш pq, причем р * 1, q * 1. В
решетке делителей числа п получаем р Л q = 1, и значит, в
решетке Con А будет 0^ Л 0п^ = А. Следовательно, длина
цикла не разложима в произведение двух взаимно простых чисел,
т. е. является степенью простого числа. Соответствующий граф
изображен на рис. 36в.
Пусть граф полуавтомата А несвязен. Предположим, что в
графе больше двух циклов. Если среди них есть два неодноэле-
ментных, то для конгруэнций и в2 имеет место: П 0^ = А ,
где имеет единственным неодноэлементным классом один цикл,
а б2—другой. Если неодноэлементный цикл только один, то
конгруэнции 0^ и в2 имеют тождественное пересечение, при этом
0 отождествляет элементы этого цикла, а 0 отождествляет два
1	Л
одноэлементных цикла. Если, наконец, все циклы одноэлементны,
то выбрав три из них, построим конгруэнции и ®23’ п₽и этом
115
в12 отождествляет элементы первого и второго циклов, а
в23—второго и третьего циклов. Понятно, что 612 П в23 = А.
Итак, граф переходов полуавтомата А имеет в точности два цикла,
причем один из них одноэлементен.
Пусть и второй цикл одноэлементен. Тогда ни одна из двух
компонент связности графа не может иметь больше одного
элемента: если и —циклические состояния, и <5(s3) = Sp
$3 * Sp то 0(sp s2) О в($р s3) = А. Следовательно, граф сос-
тоит из двух петель (рис. 36а).
Если один из циклов содержит не менее двух элементов, то,
согласно случаю 2) связного графа, он должен иметь длину ра,
где р—простое число. Соответствующий граф изображен на рис.
36г.
Достаточность. Решетки конгруэнций полуав-
томатов, изображенных на рис. 36, все являются цепями: в случае
а) цепь Con А содержит два элемента, в случае б) в ней п
элементов, в случаях в) и г) в ней а + 1 элемент. Так что во
всех вариантах Con А— одноатомная решетка и А—подпрямо
неразложимый полуавтомат, о
§ 2.2. Полугруппы
Группоидом называется алгебра с одной бинарной операцией.
В конкретных случаях для обозначения операции и результи-
рующих элементов применяется специальная символика. В общих
рассуждениях о группоидах чаще всего используют мультипли-
кативную или аддитивную запись. В первом случае результат
операции, примененной к элементам х и у группоида, обозначается
ху, а сама операция называется умножением, во-втором—здесь
операцию называют сложением—пишут х + у. Мы будем в
основном использовать мультипликативную символику и термино-
логию.
Пусть А = (Л, •)—некоторый группоид. Если множество
А—конечно, то операцию группоида удобно задавать «таблицей
умножения». Строки и столбцы этой таблицы помечены элемен-
тами множества А = {а^ а2, ..., а^}, на пересечении строки а(.
и столбца а. помещается элемент, являющийся произве-
дением а.а..
Пример 45. Турниром называется ориентированный
граф, в котором для любых двух вершин и, v имеется точно одна
из двух возможных дуг: (u, у) или (у, и).
116
Пусть Т = (V, а)—некоторый турнир. Определим на множе-
стве V операцию, полагая:
и,	если	(и, v)	G	а,
uv=vu:=	;	(
у,	если	(у, и.)	G	а
для любых и, у 6 V. Получается группоид (V, ).
На рис. 37 изображен турнир с четырьмя вершинами, справа
приводим таблицу умножения соответствующего ему группоида.
V1 v2 v3 v4
V1	V1
v2	V1
v3	v3
v4	v4
V1	v3	v4
v2	v3	v2
v3	v3	v4
v2	v4	v4
Элемент а группоида A = (A, •) называется идемпотентом,
если аа = а. Например, в группоиде, сопоставляемом турниру в
примере 45, все элементы идемпотентны. Такой группоид
называется идемпотентным группоидом. Среди идемпотентов
группоида А выделяются некоторые, представля-
ющие особый интерес.
Элемент е G А называется левой единицей / I \
группоида А, если еа = а для любого а 6 А.
Тождественная выполнимость равенства ае = a
выделяет правую единицу е группоида. В груп-
поиде может существовать несколько левых еди- Рис- 37
ниц или несколько правых единиц, однако
справедливо следующее простое предложение.
Теорема 2.19. Если в группоиде есть левая единица е
и правая единица е, то е = е и этот элемент является
двусторонней единицей, т. е. еа = ае = а для любого элемента
а группоида.
Доказательство. В самом деле, ее = е, так как
е—левая единица, и ее = е, так как е—правая единица, отсюда
е = е. □
Аналогично определяются левый нуль группоида—как элемент
О со свойством Оа = а для любого a G А и правый нуль:
аО = 0 для всякого а 6 А. Если в группоиде есть левый нуль и
есть правый нуль, то они совпадают, и этот элемент является
двусторонним нулем. Единицы и нули группоида легко распозна-
ются по его таблице. Например, в строке, соответствующей левому
нулю, мы встретим только этот элемент.
Пусть <р: А -* В—гомоморфизм группоида А = (А, •) в
группоид В = (В, •), т. е. <р—отображение из Л в В, сохраня-
ющее операцию: <р(ху) = <р(х)<р(у) для любых х, у G А. Тогда
образом идемпотента a G А будет идемпотент <р(а) G В, так как
1Р(а)1Р(а) = <р(аа) = <р(а).
117
Если <р—сюръективный гомоморфизм (наложение), то гомоморф-
ный образ левой, правой или двусторонней единицы, левого,
правого или двустороннего нуля группоида А будет соответственно
левой, правой или двусторонней единицей, левым, правым или
двусторонним нулем группоида В.
Принципиальное значение имеет
Т е о р е м а 2.20. Всякий группоид вкладывается в груп-
поид с двусторонней единицей (с двусторонним нулем).
Доказательство. Если в группоиде А =
= (А, •) нет двусторонней единицы, то присоединим к А новый
элемент е и доопределим умножение, полагая ае •= еа :«= а для
любого а е А и ее := е. В полученном группоиде Ае =
= (A U {е}, •) элемент е будет двусторонней единицей. Требо-
ваниями а • 0 = 0 • а := 0 для любого а е А и 0’0	0
присоединяют к А двусторонний нуль. □
Группоид А = (А, •) называется коммутативным, если в
нем выполняется тождество ху = ух (любые два элемента
перестановочны). Например, группоид из примера 45 всегда
коммутативен. Критерием коммутативности конечного группоида
является симметричность его таблицы относительно главной
диагонали.
Группоид А = (А, •) называется полугруппой, если умно-
жение в нем ассоциативно, т. е. в А выполняется тождество
ассоциативности: x(yz) = (xy)z для всех х, у, z е А. Проверка
ассоциативности группоида является очень трудоемкой процедурой.
Например, если \АI = и, то для проверки истинности указанного
□
тождества нужно рассмотреть п случаев различного выбора
значений для элементов из А. Признанным эффективным
средством проверки ассоциативности конечного группоида является
так называемый тест Лайта. В его основе лежит следующее простое
наблюдение.
Лемма 2.1. Если a(xb) = (ах)Ь и a(yb) = (ау)Ь для всех
а, Ь е А, то а((ху)Ь) = (а(ху))2> для всех а, b G А в группоиде
А = (А, •).
Доказательство. В самом деле,
а((ху)2>) = a(x(yb)) = (ax)(yb) = ((ах)у)Ь = (а(ху))Ь. »
Следствие 2.8. Пусть X—некоторое порождающее
множество группоида А = (А, •). Если a(xb) = (ах)Ь для
любых a, b G А, х G X, то А—полугруппа.
Доказательство. Так как любой элемент груп-
поида А представим в виде некоторого произведения элементов
порождающего множества X, то, вследствие леммы 2.1, в А будет
a(bc) - (ab)c для любых а, b, с 6 А. □
118
Пусть X = {Xj, х2, xm}—некоторая система порождающих
конечного группоида А = (А, •), где А = {а^ а2, ап}. Для
каждого х S X при помощи таблицы умножения группоида А
составляются две таблицы:
X	а1	а2	ап	X	ха1	ха2 	' хап
aix	(<V)a!	(а1Х)а2 .	• (а1х>ап	а1	at(xat)	а1(ха2> .	 а1(хап>
а2х	(а2х)а1	(а2х)°2 '	 (а2х)ап	а2	a2(xai)	а2(ха2) .	 ^п)
апх	<апх)а1	(апх)а2 	' (апх^ап	ап	ап(ха!)	an<xa2> '	 ап<-хап)
Если при любом х G X построенные для этого элемента
таблицы совпадают, то группоид А ассоциативен. Тест особенно
эффективен для группоидов, имеющих базис из небольшого числа
элементов.
Пример 46. Пусть группоид с носителем А = {1, 2,
3, 4, 5} задан таблицей умножения
	1	2	3	4	5
1 2 3 4 5	1114	4 1	2	3	4	4 1	3	2	4	4 4	4	4	1	1 4	5	5	1	1
Подмножество X = {3, 5} порождает А, поскольку 1 •= 5-5,
2 = 3-3, 4 = 3-5. Составим проверочные таблицы для элемента
3. Первая таблица получается переписыванием строк таблицы
умножения в порядке 1, 3, 2, 4, 5, а вторая таблица получа-
ется переписыванием столбцов таблицы умножения в порядке
1, 3, 2, 4, 4:
3	1	2	3	4	5	3	1	3	2	4	4
1 3 2 4 5	1114	4	1 1	3	2	4	4	2 1	2	3	4	4	3 4	4	4	1	1	4 4	5	5	1	1	5	1114	4 1	3	2	4	4 1	2	3	4	4 4	4	4	1	1 4	5	5	1	1
Построенные таблицы совпадают. Аналогично убеждаемся, что
обе таблицы для элемента 5 совпадают. Таким образом, данный
группоид ассоциативен.
Индукцией по числу множителей устанавливается
Т е о р е м а 2.21. Произведение нескольких элементов
полугруппы не зависит от расстановки скобок. □
119
Теорема дает возможность писать произведение любого числа
элементов полугруппы без скобок:	а^... ап—это вполне
определенный элемент, который может быть вычислен в любой
конкретной расстановке скобок. Индукцией по числу множителей
доказывается
Теорема 2.22. В коммутативной полугруппе тождест-
венно выполняется равенство
а,а- .... а = а ,,ха ... а , ч,
12 п <р(1) <р(2)	(р(и)
где <р—биекция на множестве {1, 2, ..., п}, т. е. произвольная
перестановка индексов. □
Подалгебра полугруппы называется подполугруппой. Очевидно,
что гомоморфный образ полугруппы является полугруппой. В
частности, факторполугруппа по любой конгруэнции ассоциативна.
Поскольку в прямом произведении алгебр операции выполняются
покомпонентно, то прямое произведение и любое подпрямое
произведение полугрупп будут полугруппами.
Для полугрупп в конкретной интерпретации справедливы все
результаты, установленные в § 2.1 для алгебр общего вида.
Из теоремы 2.20 вытекает
Теорема 2.23. Всякая полугруппа вкладывается в
полугруппу с двусторонней единицей (с двусторонним нулем).
Доказательство. Присоединяя к полугруппе
единицу е (или ноль 0), нужно убедиться в том, что в полученном
группоиде умножение будет ассоциативным. Проверять нужно
лишь те тройки, в состав которых входит новый элемент.
Например, (ea)b = ab = e(ab) и т.д. Еще проще убедиться в том,
что присоединение нуля сохраняет ассоциативность (все произве-
дения, в которые входит 0, равны 0). а
Если необходимо подчеркнуть, что в рассматриваемой полу-
группе есть (двусторонняя) единица е, то этот элемент выделяют
в качестве специальной нульарной операции, т. е. рассматривают
полугруппу как алгебру (Л, •, е) типа (2, 0). Такие алгебры
называются моноидами.
Таким образом, моноид—это алгебра А = (Л, •, ё) типа
(2, 0), в которой выполняются тождества.
1) x(yz) = (xy)z; 2) хе = ex - х.
Второе тождество называют свойством нейтральности элемен-
та е относительно умножения.
Появление новой операции вносит своеобразие в алгеб-
раические конструкции для моноидов по сравнению со случаем
полугруппы. Так подмоноид данного моноида А = (Л, •, е)—это
не просто его подполугруппа, т. е. подмножество, замкнутое
относительно умножения, а подполугруппа, содержащая элемент
е. Гомоморфизм моноида А в моноид В = (В, •, е)—это
отображение <р: А -* В, сохраняющее не только умножение, но
и нейтральный элемент, т. е. должны выполняться два условия:
1) <Р(ху) = <р(х)<р(у),	2) <р(е) = е.
120
Простые рассуждения показывают, что гомоморфный образ
моноида является моноидом, что прямое произведение и любое
подпрямое произведение моноидов тоже будет моноидом.
Если А = (Л, •, е)—моноид, то его редукт А* = (А, •)
является полугруппой. Это полугрупповой редукт моноида.
Заметим, что Л* содержит все элементы моноида А: единица е
лишь перестает быть нульарной операцией, особо выделенным
элементом. Но вследствие этого может расшириться число
подалгебр и число гомоморфных образов. Конгруэнции же
полугруппового редукта—это в точности конгруэнции моноида.
Переформулируем общее определение конгруэнции алгебры на
случай полугруппы. Эквивалентность 0 на полугруппе А =
= (Л, •) называется конгруэнцией этой полугруппы, если
(a, b) G в & (с, </) =» (ас, bd) G 0
для всех а, Ь, с, d Е А.
Непустое подмножество / полугруппы А — (Л, •) называется
ее левым идеалом, если ai €= I для любых a G Л, i G I. Правый
идеал определяется как непустое подмножество / G А такое, что
ia G I для всех a G A, i G I. Подмножество, одновременно
являющееся левым и правым идеалом, называют двусторонним
идеалом полугруппы.
Если в полугруппе есть хотя бы один правый нуль, то любой
набор правых нулей этой полугруппы образует в ней левый идеал.
Аналогично правым идеалом полугруппы будет любая непустая
совокупность ее левых нулей. Если полугруппа обладает нулем
О, то одноэлементное ее подмножество {0} является двусторонним
идеалом.
Операцию умножения полугруппы А = (А, •) можно распро-
странить на множество Р(А) ее подмножеств, полагая:
ВС := {6cl b G В, с G С}
для любых В, С G Р(А). Это глобальное умножение в А. С
помощью глобального умножения характеристическое свойство
левого (правого) идеала / записывается в виде включения
AI £ I (соответственно /АС/). Двусторонний идеал / на этом
языке выделяется условием AI U IA С /, С каждым двусто-
ронним идеалом / полугруппы А = (А, •) связывается отношение
Qj := Дл U (/ х /).
Это эквивалентность на множестве А, единственный класс которой
совпадает с подмножеством / С А. Нетрудно понять, что 0^
является на самом деле конгруэнцией полугруппы А. Она
называется идеальной конгруэнцией (конгруэнцией Риса, рисов-
ской конгруэнцией). Факторполугруппа по обозначается All и
121
называется идеальной или рисовской. Идеальная факторполугруппа
является полугруппой с нулем: нулем в ней будет ^-класс I.
Рассмотрим некоторые важнейшие примеры полугрупп (боль-
шинство из них обладают нейтральным элементом и могут
рассматриваться как моноиды).
П р и м е р 47. Редукт (P(S х S), °, Д) алгебры отношений
на фиксированном множестве S является моноидом: умножение
отношений ассоциативно, а тождественное отношение Д является
нейтральным элементом (см. § 1.2). Это моноид всех отношений
на данном множестве. Подмоноидами этого моноида будут:
(Р(5 х S), °, Д)—моноид всех преобразований множества S или
симметрический моноид на S и (K(S X S, °, Д)—моноид всех
биекций множества S. Мы их рассмотрим в дальнейшем.
Заметим, что совокупность E(S) всех эквивалентностей на
множестве 5 хотя и содержит Д, тем не менее не образует
подмоноида в моноиде всех отношений на S, так как произведение
эквивалентностей не обязательно будет эквивалентностью (см.
§ 1.3), поэтому £(5) не замкнуто относительно умножения.
П р и м е р 48. Алгебра = («л^л, •, £) двоичных буле-
вых матриц размерности п х п является моноидом, изоморфным
моноиду всех отношений на л-элементном множестве. Совокуп-
ность всех матриц М G у которых первая или любая другая
фиксированная строка состоит только из нулей, образует в
правый идеал, а матрицы с нулевым первым или любым другим
фиксированным столбцом образуют левый идеал. Соединение в
матрицах этих двух особенностей приводит к двустороннему
идеалу полугруппы М^.
Двоичные булевы матрицы образуют моноид и относительно
сложения. Нейтральным элементом в этом случае будет нулевая
матрица О. Аддитивный моноид (UZ , +, О), очевидно, изоморфен
редукту (P(S х S), U, 0) алгебры отношений на л-элементном
множестве S.
П р и м е р 49. Пусть X—некоторое конечное множество
(алфавит). Через X* обозначается совокупность всех конечных
последовательностей, составленных из элементов алфавита, эти
последовательности называются словами. Произведением двух слов
р, q G X * считается их конкатенация pq—когда к слову р
приписывается справа слово q. Поскольку конкатенация ас-
социативна, то (X*, •)—полугруппа. Это свободная полугруппа,
порожденная множеством X. В понятие «свободная» вкладывается
тот смысл, что два слова считаются равными только в случае их
графического совпадения: одни и те же буквы в одном и том же
порядке-без учета каких-либо других соотношений или условий.
В X * вводится нейтральный элемент—пустое слово е, не
содержащее ни одной буквы. Ясно, что ре - ер - р для любого
122
p G X*, и ее “ е. Подмножества множества X * (с включением
в него пустого слова е) называются языками. Выделяя пустое
слово, говорят, что (X *, •, ё)— свободный моноид над X.
Пусть п—некоторое натуральное число. Слова р G X *, длина
которых не меньше п, образуют в X* двусторонний идеал 7
Идеальная факторполугруппа X* /1 состоит из всех слов
р G X*, у которых I pl < л и еще одного—«длинного» слова,
обозначим его символом ». Произведение PjP2’ имеющее длину
меньше л, в X* и в Х*Ип одно и то же, но если IРхРгI — п,
то р,р_ = о© в X* /1 независимо от того, какими были р, и
гг 2	п	1
Р2< Легко представить себе технические устройства, работающие
с входными (или выходными) словами ограниченной длины и не
различающие слова, имеющие бблыпую длину.
Пусть L G X *—некоторый язык. Положим:
6L := {(р, q) G X*xX*l(Vu,v G X*}(upv G L^uqv G L)}.
Очевидно, что 6L—эквивалентность на множестве X *. Пусть
(р, г) G 6L, (q, s) G &L и и, v G X *—произвольные слова.
Тогда
u(pq)v G L о up(qv) G L о ur(qv) G L о
о (uf)qv G L о (ur)sv G L о u(rs)v G L,
и, следовательно, (pq, rs) G 6^
Конгруэнция называется синтаксической конгруэнцией
свободной полугруппы X * относительно языка L. Множество
Cont^(p) := {и, v G Х*\ upv G L} называют L-контекстом
слова р. Синтаксическая конгруэнция &L не различает слова с
одинаковым L-контекстом:
(р, q) G BL о Cont£(p) = ContL(<z).
П р и м е р 50. Пусть А = (А, •)—произвольная полугруп-
па и a G А—некоторый ее элемент. Положим ап := аа... а для
п раз
натурального п, и а° := е, если полугруппа А содержит единицу
е. Совокупность всевозможных степеней элемента а образует в
А подполугруппу, поскольку атап = ат+п (здесь использована
теорема 2.21). Это циклическая полугруппа, порожденная элемен-
том а. Она является, как легко заметить, наименьшей из
123
подполугрупп полугруппы А, содержащих элемент а. Обозначим
ее через А(а). Циклические полугруппы очевидным образом
коммутативны. Циклическим моноидом является, например, ад-
дитивный моноид (N, +, 1) натуральных чисел: он порождается
элементом 1. В аддитивной записи вместо слова «степень»
употребляют термин «кратное» и вместо а” пишут па :=
= а + а +...+ а, Оа := 0.
п раз
Если все степени элемента а в полугруппе А = (Л, •)
различны, то циклическая полугруппа А(а) бесконечна. В этом
случае она изоморфна упомянутому моноиду (N, +, 1). Изо-
морфизмом является соответствие <р'. а1 п. Действительно, оно
взаимно однозначно и <р(атап) = <р(а'п+п) = т + п = <р(ат) +
+ <р(ап) для любых т, п 6 N.
Может оказаться, однако, что, просматривая последователь-
ность степеней элемента а, мы обнаружим следующую ситуацию:
а = а2
„т т+1
а , а
п —
а = а .
где 1 < т < п. Тогда все дальнейшие степени элемента а будут
совпадать с одним из элементов ат, am+l, ..., ап~1,—циклическая
полугруппа А(а) оказывается конечной. Наглядно ее можно
представить в виде графа, вершинами которого являются элементы
этой полугруппы, а дуги соответствуют парам (ак, ak+i),
к = 1, 2, ... Число т - 1 называется индексом, а число п - т—
периодом элемента а. Другими словами, период—это длина цикла,
а4	а индекс—длина «хвоста» в графе,
уч	изображающем циклическую полугруп-
а g2 <£/ s пу А(а). На рис. 38 показан случай,
°-	./ когда индекс равен 2, а период равен
4. В этой циклической полугруппе
as	7	3
имеет место соотношение а = а .
Рис. 38	т.
Количество элементов в конечной
полугруппе называется ее порядком.
Таким образом, сумма индекса и периода циклической полугруппы
равна ее порядку.
Теорема 2.24. Всякая конечная полугруппа содержит
по крайней мере один идемпотент.
Доказательство. Пусть А = (А, •)—конечная
полугруппа и a G А—некоторый ее элемент. Тогда циклическая
полугруппа А(а) тоже конечна. Пусть к и I—соответственно ее
индекс и период. Тогда ak+l+l = ak+l. Среди I последовательных
чисел к + 1, к + 2, ..., к + I есть точно одно, кратное I. Пусть
это будет s. Тогда элемент а является идемпотентом. Действитель-
но, отправляясь по циклу из вершины а5 и пройдя s шагов, мы
124
снова придем в эту вершину, совершив s умножений элемента
с	S	S	S S
а на а. т. е. а = а а-... а = аа.о
s раз
На рис. 38, например, к - 2, I - 4, s - 4, и а4—идемпотент.
Практическое значение имеет и вытекающее из теоремы 2.24
Следствие 2.9. Если в конечном группоиде нет
идемпотентов, то он неассоциативен. =
Например, латинские квадраты, представленные на приведен-
ных ниже таблицах, являются таблицами умножения неас-
социативных группоидов.
ских полугрупп (моноидов) (F(S х S), о) (и соответственно
(F(S х S), °, А)).
Для случая дискретных систем наиболее важными являются
конечные полугруппы (моноиды) преобразований и, в частности,
полугруппы (моноиды) преобразований конечных множеств.
Пусть S = {Sj, s2, ..., sn). Преобразование f: S -» S может
быть представлено в виде двустрочной таблицы
Ml	•••
f __ I	z	rt
f /(^) - Z4)J’
называемой подстановкой на множестве S. Если порядок элемен-
тов множества 5 фиксирован, подстановки можно записывать в
виде n-мерных векторов с компонентами из S, т. е.
/ =	Л*2). .... /(*„))•
Произведению преобразований соответствует произведение сопо-
ставляемых им подстановок. Схема умножения подстановок на
множестве 5 выглядит следующим образом:
П р и м е р 51. Подстановки л{ = (2, 3, 3) и л^ =
= (1, 1, 2) на множестве S = {1, 2, 3} порождают семиэлемен-
тную полугруппу: л , л , л, = л л = (3, 3, 3), л. = л.л. =
1 X О	11	IX
125
= (1, 2, 2), л5 = л^л4 = (2, 2, 2), %6 =	= (2, 2, 3),
л1 =	= (1, 1, 1).
Как уже отмечалось в § 1.2, преобразования конечного
множества удобно описывать их графами. На рис. 39 показаны
графы всех элементов полугруппы преобразований из примера 51.
Рис. 39
Каждой полугруппе преобразований конечного множества 5
можно сопоставить полуавтомат А = (5, X, <5), где X—некоторая
система образующих данной полуг-
згч	руппы, a <5 (ж, л) := л(х) для любых
s G S, л G X. Диаграмма полуав-
^1 л2 2	3 томата, соответствующего полугруп-
пе из примера 51, представлена на
Рис- 40	рис. 40.
Граф G(f) преобразования / ко-
нечного множества S состоит в общем случае из нескольких
компонент связности. Каждая компонента в свою очередь
представляет собой ориентированный цикл (контур) и некоторый
набор корневых деревьев—связных бесконтурных графов с
ориентацией в сторону выделенной вершины (корня). Корнями
этих деревьев являются вершины данного контура. Одноэлемент-
ные циклы (петли) соответствуют неподвижным точкам преоб-
разования /, т. е. таким s £ 5, что /(s) = s. Понятно, что граф
каждого преобразования на л-элементном множестве можно
интерпретировать также как граф переходов подходящего авто-
номного полуавтомата с л состояниями.
Спецификацией преобразования f = (/(Sj), /($2), •••’Л\)) на-
а а	а
зывается л-мерный вектор [/] :=	’, s^, ..., s^"), где а. пока-
зывает, сколько раз элемент s. €= S входит во вторую строку
подстановки, представляющей /, или, другими словами, сколько
дуг графа G(f) входит в вершину s.. Отсюда а. = I I для
всех i = 1, л.
Два преобразования /р /2 £ F(S х 5) называются графически
эквивалентными, если изоморфны их графы: G(JX) з С7(/2).
Рассматривая рис. 41, можно убедиться, что в общем случае
совпадение спецификаций двух преобразований никак не связано
126
с их графической эквивалентностью. Здесь для преобразований
fv fr f3 имеем: Gf/,) = G(f2), GtfJ 1 G(f3), но
Рис. 41
Подстановка, соответствующая взаимно однозначному преоб-
разованию конечного множества 5, называется перестановкой на
5. Подстановка тогда и только тогда является перестановкой,
когда в ее второй строке нет повторяющихся элементов. Специ-
фикацией любой перестановки будет вектор ($J,	..., А).
Теорема 2.25. Для преобразований fi и f конечного
множества S равенство L/j] = [/21 имеет место тогда и только
тогда, когда на S существует перестановка <р такая, что
/2 = <P°fv
Доказательство. Необходимость.
а а	а
Пусть [/J = (Sj1, $2 ,	и /2 =	Заметим, что
поскольку <р—взаимно однозначное преобразование конечного
множества, то \<р~'(Л)1 = IAI для любого А £ S. Тогда
|^’(\)| = =
= l/^(S.) I = а.
и, значит, [f2] = [/J.
Достаточность. Пусть [/J = I/2J. Это означает,
что для любого s. G 5 множества /. '(s.) и / !(s) имеют
одинаковое число элементов. Пусть <р.—некоторое взаимно
однозначное соответствие между f~l(s.) и \s.). Положим
127
п
<р = U <р., при этом некоторые <р. могут оказаться пустыми.
/=1
Очевидно, что <р—взаимно однозначно отображает S на 5. Если
s е 5—произвольный элемент, то s £	для некоторого
s е 5. Тогда p(s) = <p.(s) G	и, значит, (^>°/j)(s) =
= ДСП*)) = si = /2^)>т-е- 4 =	°
На рис. 42 изображены графы преобразований, взятых по
одному из каждого класса графической эквивалентности на
множестве всех преобразований четырехэлементного множества.
Их можно интерпретировать также как графы всех существенно
различных (т.е. попарно неизоморфных) автономных полуавтома-
тов с четырьмя состояниями.
Большое значение имеет следующий результат.
Т е о р е м а 2.26. Всякий моноид изоморфен некоторому
моноиду преобразований, т. е. вкладывается в симметрический
моноид на подходящем множестве.
Доказательство. Пусть А = (А, •, е)— неко-
торый моноид. Определим отображение
<р: А -» F(A х Л), а •—»
где Ад(х) = ха для любого х 6 А. Преобразование А : А -* А
называется правым сдвигом моноида А, соответствующим элементу
a G А.
128
Отображение у? взаимно однозначно:
Аа = Xb => (V х 6 А)(ха = Ад(х) = A^(x) = xb) => а = еа = eb = Ь,
и, значит, из а # i следует, что х
<р сохраняет умножение:
^(*) = x(^) = (ха)й = Ал(Ла(х)) = (Ла°Мх)
для всех х G А, так что <p(ab) =	= ^a°^b = p(a)°W^)-
^-образом нейтрального элемента е является тождественное
преобразование Д:
Цх) = хе = х = Д(х)
для всех х G А, и, значит, <р(е) =	= Д.
Таким образом, моноид А = (Л, •, ё) вложен в симметри-
ческий моноид (£(Л х Л), °, Д). □
Вложение моноида в симметрический моноид, описанное в
доказательстве теоремы 2.26, называется представлением данного
моноида правыми сдвигами.
Ядро Ker / = f преобразования /: 5 -» 5 представляет
собой эквивалентность на множестве S (см. § 1.3). Следовательно,
Д £ Кег/ £5x5. Преобразования / с тождественным ядром
Ker f = Д являются взаимно однозначными отображениями мно-
жества 5 в себя, а когда 5 конечно, то они являются биекциями
этого множества.
Представляет интерес и противоположный случай: Кег/ =
= 5 х 5. В этом случае / имеет только одно значение: fix) - s
для всех х G 5 и некоторого фиксированного х G 5. Такие
преобразования множества 5 называются его постоянными или
константными преобразованиями.
Теорема 2.27. Постоянные преобразования, и только
они, являются правыми нулями симметрической полугруппы
(F(S х 5), °). Они образуют в этой полугруппе левый идеал.
Доказательство. Пусть f—постоянное преобра-
зование множества 5 такое, что рг^ = {ж}. Тогда для любых
f G F(S х 5) и х G 5 получаем
</°4)(х) = W» = 5 =
и, значит, f ° / = f.
С другой стороны, пусть f*—некоторый правый нуль в
F(S х 5), т. е. f°f* = f* для каждого / G F(S х 5). Возьмем
произвольные элементы a, b € 5. Тогда для любого х G 5
имеем
5 А.М.Богомолов, В.Н.Салий	129
/*(а) =/VeW) = «в °/*)(*) =	= f*(fb(x)) = f*(b),
т. e. f\a) = f*(b) для любых a, b 6 S.
Второе утверждение теоремы непосредственно следует из
первого. □
Теперь обратимся к автоматам. Эндоморфизмами полуавтомата
А = (S, X, <5) называются его гомоморфизмы в себя, т. е.
преобразования /: S -* S, удовлетворяющие условию
W, X)) = <5(/(s), х)
для любых 5 G S, х G X.
Если р G X* и х G X—произвольное входное слово и
произвольный входной сигнал, то для эндоморфизма / полуавто-
мата А получаем
f(d(s, рх)) = f(d(d(s, р), х)) = d(/(d(s, р)), х),
откуда следует, что /(<5(s, р)) = <5(/(х), р) для любого р G X*.
Совокупность всех эндоморфизмов полуавтомата А обозначается
через End А.
Т е о р е м а 2.28. Эндоморфизмы полуавтомата образу-
ют подмоноид симметрического моноида на множестве состо-
яний этого полуавтомата.
Доказательство. Очевидно, что тождественное
преобразование Д^ является эндоморфизмом полуавтомата А =
= (S, X, <5). Нужно показать, что произведение эндоморфизмов
будет эндоморфизмом. Пусть /, g G End А. Тогда при любых
s G S и х G X получаем
(f°g)(d(s, х)) = g(/(d(s, х))) = g(d(f(s), х)) =
=	x) = d((f°g)(s), x),
т. e. / о g G End A. о
Моноид (End A, °, Д) называется моноидом эндоморфизмов
полуавтомата А. Теорему 2.26 о представлении произвольного
моноида преобразованиями в конечном случае существенно
усиливает
Теорема 2.29. Всякий конечный моноид изоморфен
моноиду эндоморфизмов подходящего полуавтомата.
Доказательство. Пусть 5 = (S, •, е)— конеч-
ный моноид. Рассмотрим полуавтомат А = (S, S, д), где
<5: S х S -* S, (s, х) •—» xs. Таким образом, носитель S моноида
S является одновременно множеством состояний и входным
алфавитом полуавтомата А, а функция переходов такова, что
входной сигнал s G S переводит состояние s G S в произведение
xs, вычисляемое в моноиде S. Докажем, что S = End А.
130
Каждый правый сдвиг Ад моноида S является эндоморфизмом
полуавтомата А. Действительно, для произвольных s, х е S
получаем
Afl(<5(s, х)) = Afl(x5) = (xs)a = x(sa) = d(sa, х) = <5(Afl(s), х),
так что А G End А.
а
Каждый эндоморфизм полуавтомата А является правым
сдвигом моноида S. В самом деле, если f G End А, то для любого
х е 5 имеем
/(х) = /(хе) = f(d(e, х)) = d(f(e), х) = х/(е) = А^х),
т- е- f -
Соответствие $ •—» А$ является изоморфизмом моноидов S и
End А. В теореме 2.26 было доказано, что это соответствие
вкладывает моноид S в симметрический моноид F(S х S). Теперь
мы видим, что область значений этого вложения совпадает с
множеством End А С F(S х S), которое в силу теоремы 2.28
замкнуто относительно умножения (суперпозиции) и содержит
тождественное преобразование Д. □
Полуавтомат А называется сильно жестким, если он не имеет
нетождественных эндоморфизмов, т. е. если End А - {Д}.
Теорема 2.30. Сильно жесткий автономный полуав-
томат тривиален, т. е. имеет одно состояние. Для любого
натурального п существует сильно жесткий автомат с двумя
входными сигналами и п состояниями.
Доказательство. Пусть А = (S, д)—автоном-
ный полуавтомат; д здесь рассматривается как преобразование
множества S. Эндоморфизмами полуавтомата А, по определению,
будут преобразования /, перестановочные с <5:
/6 End Л о (Vs 6 S)(f(d(s)) = d(f(s))) о f°d = d°f.
Если д = Д, то любое преобразование множества 5 будет
эндоморфизмом полуавтомата А, т. е. End А = F(S х S). По-
нятно, что F(S х S) “ {Д} лишь для одноэлементного S. Если
<5 # Д, то само преобразование <5 является нетождественны»*
эндоморфизмом полуавтомата А, и, значит, А не может быть
сильно жестким.
Рассмотрим полуавтомат А = (S, X, <5), где S = {$р s2, ...
..., sn), X = {Xj, х2), а функция переходов <5 такова, что
<5(s, х^ = для любого s G S, а автономная х2—компонента
представляет собой цикл -* s2 -*...-* sn -» . Если /—эндо-
морфизм полуавтомата А, то
/(^) = f@(sv х^) =	х^ =
Следовательно, для любого i > 2 будет
S’	131
f(Si) = /0(st, x2x2 ... x2)) =	x2x2...x2) =
i-l	i-l
= 6(svx2x2...X2) = s..
i-l
Итак, f(s) - s для любого s G S, t. e. f “ Д, и, значит,
полуавтомат А сильно жесткий, о
Большое влияние на свойства эндоморфизмов полуавтомата
оказывает отношение достижимости в этом полуавтомате.
Т е о р е м а 2.31. Если два эндоморфизма полуавтомата
одинаково воздействуют на некоторое состояние ж, то они
одинаково воздействуют и на любое состояние, достижимое
из s.
Доказательство. Пусть А = (S, X, <5)—про-
извольный полуавтомат, /, g—его эндоморфизмы и /($0) = ^(х0)
для некоторого состояния $0 G 5. Если состояние s достижимо
из sQ, т. е. существует входное слово р G X * такое, что
<5(s0, р) = ж, то
/(s) = /(<5(s0, р)) = d(f(sQ), р) = <5(£(s0), р) =
= $(<5(*0, Р)) = g(s)- °
Под начальным состоянием полуавтомата будем понимать
такое его состояние sQ, из которого достижимо любое другое
состояние этого полуавтомата.
Следствие 2.10. В полуавтомате, имеющем началь-
ное состояние sQ, каждый эндоморфизм однозначно определя-
ется своим значением в sQ. а
Следствие 2.11. Если в полуавтомате А = (S,
X, <5) есть хотя бы одно начальное состояние, то lEnd-AI <
< ISI, т. е. эндоморфизмов не больше, чем состояний, о
Следствие 2.12. В сильно связном полуавтомате А
с п состояниями существует не более чем п различных
эндоморфизмов, о
Взаимно однозначные эндоморфизмы полуавтомата называются
его автоморфизмами.
Т е о р е м а 2.32. Каждый эндоморфизм сильно связного
полуавтомата является его автоморфизмом.
Доказательство. Согласно теореме 1.17 из § 1.2
достаточно установить, что каждый эндоморфизм f сильно связного
полуавтомата А = (5, X, <5) сюръективен, т. е. отображает мно-
жество S на себя. Пусть s—произвольное состояние полуавтомата
132
А. Так как А сильно связен, найдется слово р G X * такое, что
<5(/(s), р) = ж. Тогда для состояния s* = <5(s, р) получаем:
f(s*) = /(<5(s, р)) = <5(/(s), р) = s. Следовательно, рг2/ = S. »
Полукольцом называется алгебра А = (А, +, •) типа (2, 2),
где (А, +) и (А, •)—полугруппы, первая из которых комму-
тативна, и выполняются два дистрибутивных закона (левый и
правый):
х(у + z) = ху + XZ, (х + y)z = XZ + yz.
Если в полугруппе (А, •) есть единица, то говорят, что
А—полукольцо с единицей.
Коммутативное полукольцо—это полукольцо с коммутатив-
ным умножением.
П р и м е р 52. Полукольцом с единицей является редукт
(Р(5 х 5), U, °) алгебры отношений на фиксированном множестве
5: умножение отношений дистрибутивно относительно их объеди-
нения (теорема 1.11 § 1.2), обе операции ассоциативны, единицей
будет тождественное отношение Д.
Пример 53. Редукт (В, V, Л) любой булевой алгебры—
коммутативное полукольцо с единицей, ею будет элемент 1. В
частности, (Р(5), U, Г))—коммутативное полукольцо всех подм-
ножеств множества 5 с единицей 5. Вообще, полукольцом
множеств называется любая совокупность подмножеств некоторого
множества, замкнутая относительно теоретико-множественных
операций объединения и пересечения.
Пример 54. Пусть X *—свободный моноид над конечным
алфавитом X. Совокупность Р(Х*) всех языков над X образует
полукольцо относительно теоретико-множественного объединения
U и глобальной конкатенации:
LxL2 = {pq е X * I р 6 Lx & q G LJ
для любых Lx, L2 с х*. Единицей в этом полукольце будет язык
{е}, где е—пустое слово. Заметим, что L • 0 = 0 • L = 0 для
любого языка L G Р(Х*).
Пусть А = (А, +, •)—некоторое полукольцо. Матрицей раз-
мерности т х п над полукольцом А называется прямоугольная
таблица, имеющая т строк и п столбцов, заполненная элементами
полукольца А. Обычным образом (поэлементно) вводится сложение
матриц одинаковой размерности:
(М + АГ).. := М.. + N...
v 'ч У У
Здесь справа стоит операция + полукольца.
133
Если М имеет размерность т х р, a N имеет размерность
р х п, то произведением матриц М и N называется матрица MN
размерности т х л такая, что:
р
(MN) := J «, Лу.
к=1
где умножение и сложение в правой части выполняется в
полукольце Л. В § 1.2 эти операции были введены для двоичных
булевых матриц—матриц над полукольцом (В2, +, •).
Т е о р е м а 2.33. Совокупность всех квадратных мат-
риц фиксированной размерности п над данным полукольцом
образует полукольцо относительно сложения и умножения
матриц.
Доказательство. Проверка ассоциативности сло-
жения и умножения матриц над произвольным полукольцом, а
также законов дистрибутивности ничем не отличается от доказа-
тельства одноименных свойств для числовых матриц—над полу-
кольцом действительных чисел (R, +, •).
Пример 55. Полукольцо («Л^л, +. двоичных булевых
п х л-матриц изоморфно полукольцу (Р(5 х 5), U, °) всех отно-
шений на л-элементном множестве. Булевыми матрицами назы-
ваются матрицы над произвольной булевой алгеброй. Обозначим
через M^(B) совокупность всех л х л-матриц с элементами из
булевой алгебры В = (В, V, А, ', 0, 1). Для М, N G M^(B)
положим:
(М ANY. := М.. Л N..,	(М')., := М'.., (МТ)„ := М.„
v	'ij	ij ij v 'ij	ij v 'ij	ji
а также О.. := 0, / := 1 для любых г, /. Через Еп обозначим
единичную л х л-матрицу. Тогда (Мл(В), V, А, °, ', т, О,
I, Е ) оказывается алгеброй отношений (см. следствие из теоремы
1.35% 1.4).
Пример 56. Пусть А = (5, X, <5)— произвольный полу-
автомат. Сопоставим ему матрицу М(А) размерности л х л, где
л = 151, следующим образом. Строки и столбцы этой матрицы
помечены состояниями полуавтомата А, на пересечении строки
s. и столбца s. выставляется подмножество множества X, состоящее
из всех таких входных символов х G X, что d(s., х) = Sj.
Матрица переходов М(А) полностью описывает функционирование
полуавтомата и является одним из способов его задания. Ниже
134
даны таблица переходов
и матрица переходов полуавтомата А с
четырьмя состояниями и
четырьмя входными сигналами.
	X1	x2 x3 x4
S1 s2 s3 s4 {*3} 0 М(л) =	{x2}	s2	s3	S1	s3 s3	s3	s3	s3 s4	S1	s4	s4 S1	s4	s4	S1 {x,}	{x2, x4}	0 0	X	0 0	0	{Xj, x3, x4} 0	0	{x2, X3}
Заметим, что М.. П М.к — 0 при j * к и любом i. Кроме того,
U М.. = X для любого i.
Матрицу переходов можно рассматривать как матрицу над
полукольцом (Р(Х *), U, •) всех языков в алфавите X. Используя
операцию умножения матриц над полукольцом Р(Х *), можно
строить последовательные степени матрицы переходов М данного
полуавтомата А. При этом, как нетрудно убедиться, элемент
Л
матрицы М , стоящий на пересечении строки i и столбца /,
является множеством всех входных слов длины к, переводящих
состояние ж. в состояние ж. в полуавтомате А.
Матрицу переходов полуавтомата можно воспринимать и как
матрицу над полукольцом (Р(Х), U, П),—см. § 4.1.
Пример 57. Пусть G = (V, а)—некоторый граф. Мат-
рицей смежности его называется двоичная булева матрица
М = M(G) размерности л х л, где л = IVI, представляющая
отношение а С V х V (совокупность а всех дуг графа, очевидно,
является отношением на множестве V его вершин). Так как
, .2	2
матрица М соответствует квадрату а = а °а отношения а, то
=
1 означает, что существует вершина v G V, для которой
(у., v) G а и (у, у.) G а,
т. е. что вершина у. достижима из
вершины у. за 2 шага. Аналогично матрица Мк представляет
собой отношение достижимости вершин за к шагов в графе G.
135
§ 2.3.	Группы и кольца
Пусть А = (А, •, е)—некоторый моноид. Элемент a G А
называется обратимым слева, если ха “ е для подходящего
х G А, и обратимым справа, если ау “ е для подходящего
у G А. Упомянутые элементы х и у называют соответственно
левым и правым обратными для а. Если для а существует элемент
b G А такой, что ab - ba - е, то b называется (двусторонне)
обратным для а, а сам элемент а—(двусторонне) обратимым
элементом.
Теорема 2.34. Если элемент а моноида обратим слева
и обратим справа, то для него существует обратный элемент
Ь, и при этом Ь является единственным левым обратным,
единственным правым обратным и единственным (двусторонне)
обратным для а.
Доказательство. Пусть х—произвольный ле-
вый, а у—произвольный правый обратный для а. Используя
ассоциативность умножения, получим
х - хе “ х(ау) - (ха)у = еу - у.
Положим b = х - у. Тогда ab = Ьа - е, т. е. Ъ—(двусторонне)
обратный для а элемент. Из приведенных выше выкладок следует,
что для а нет других левых, правых или двусторонне обратных
элементов. □
Группой называется моноид, в котором каждый элемент
обратим. Согласно теореме 2.34, каждый элемент а группы имеет
в точности один обратный элемент, обозначим его через а-1.
Отображение а •—» а 1 является, следовательно, унарной опе-
рацией. Это операция обращения в группе. Таким образом, группу
можно рассматривать как алгебру А = (Л, •, -1, е) типа
(2, 1, 0), в которой выполняются следующие тождества:
1)	x(yz) - (xy)z (ассоциативность),
2)	хе = ех = х (нейтральность элемента е),
3)	хх-1 = х-1х = е (обратимость).
Вопрос о том, является ли данный конечный моноид
А = (А, , е) группой, решается просмотром его таблицы умно-
жения: элемент е должен встречаться в каждой ее строчке и
каждом столбце. Впрочем, как показывает следующая теорема,
достаточно ограничиться изучением главной диагонали этой
таблицы.
Теорема 2.35. Конечный моноид А = (А, •, е) тогда
и только тогда является группой, когда он имеет единственный
идемпотент е.
Доказательство. Если А—группа и е—некото-
рый ее идемпотент, то
е = ее = е(ее-1) = (ее)е-1 = ее-1 = е.
136
С другой стороны, если е—единственный идемпотент моноида
А = (А, •, е), то для любого элемента a G А порожденная им
циклическая полугруппа А(а) содержит элемент е. Пусть,
например, ак =е. Тогда ак 1а = е = аак \ т. е. ак 1—обрат-
ный для а элемент в А. □
Понятие группы тесно связано с вопросом о разрешимости
уравнений в полугруппах. Именно, имеет место
Теорема 2.36. Для любых элементов а, b группы
уравнения ха = b и ay = b однозначно разрешимы. С другой
стороны, полугруппа, в которой разрешимы все уравнения
указанных типов, является группой.
Доказательство. 1) Так как (Ьа !)а =
b(a~la) = be = b и a(a~xb) = (aa~)b = eb = Ь, то элементы
ba~i и а~1Ь оказываются решениями соответственно уравнений
ха “ b и ау = Ь. Если с—произвольное решение для ха “ Ь, то
са = b и, умножая обе части этого равенства справа на а-1,
получаем, что с = Ьа~\ Аналогично, а~^Ь будет единственным
решением для ау = Ь.
2) Пусть в полугруппе А = (А, •) при любых a, b G А
разрешимы уравнения ха = b и ау = Ь. Тогда, в частности,
разрешимы уравнения ха - а и уа = а. Пусть е—некоторое
решение уравнения ха — а, т. е. еа “ а, а с—произвольное
решение уравнения ау - Ь. Тогда еЬ = е(ас) = (еа)с - ас - Ъ,
и, следовательно, е—левая единица полугруппы А. Аналогично,
всякое решение уравнения уа = а будет правой единицей этой
полугруппы. Тогда элемент е является двусторонней единицей
полугруппы А. Решая теперь уравнения ха w е и ау = е,
обнаруживаем, что каждый элемент a €= А обратим слева и
обратим справа, и, согласно теореме 2.34, двусторонне обра-
тим. □
Пример 58. Группой является алгебра (R*, •, -1, 1)—
множество отличных от нуля действительных чисел с обычным
умножением, обращением и числом 1 в качестве нейтрального
элемента. В этой группе выполняется тождество коммутативности
ху = ух. Коммутативные группы называют также абелевыми.
Для абелевых групп часто используют аддитивную запись:
бинарная операция обозначается знаком + и называется сло-
жением, унарная операция (противоположение) обозначается
знаком - и вместо термина «обратный» говорят «противоположный
элемент», нейтральный элемент фиксируется символом 0.
Пример 59. Аддитивная группа действительных чисел
(R, +, —, 0) содержит в качестве подгруппы аддитивную группу
целых чисел (Z, +, —, 0).
Подгруппа группы—это такое подмножество ее носителя,
которое замкнуто относительно всех трех групповых операций,
т. е. является подполугруппой, содержит нейтральный элемент, и
вместе с каждым своим элементом содержит ему обратный
137
(противоположный) элемент. Например, совокупность всех не-
отрицательных целых чисел является подмоноидом группы
(Z, +, —, 0), но не ее подгруппой (нет противоположных
элементов).
Как уже отмечалось во введении, отображение log: R+ -* R,
х •—» log x, является изоморфизмом мультипликативной группы
положительных чисел на аддитивную группу всех действительных
чисел.
Понятно, что гомоморфный образ группы—это группа и что
свойство коммутативности сохраняется при гомоморфизмах.
Интересно отметить, что если А = (Л, •, -1, е) и В —
= (Л, •, -1, е)—две группы, то уже гомоморфизм <р полу груп-
пового редукта (Л, •) на полугрупповой редукт (В, •) будет
групповым гомоморфизмом <р’. А -» В. Это следует из того, что
свойства «быть нейтральным элементом» и «быть обратным для
данного элемента» выражаются через операцию умножения (при
этом важна, конечно, и сюръективность отображения <р).
Прямое произведение (абелевых) групп является (абелевой)
группой.
Пример 60. Примером некоммутативной группы являет-
ся группа всех невырожденных числовых матриц фиксированной
размерности п х л, рассматриваемая с операциями умножения и
обращения матриц и с единичной п х л-матрицей в качестве
нейтрального элемента.
П р и м е р 61. Групповой бинарной операцией на множе-
стве Р(5) всех подмножеств произвольного множества 5 оказыва-
ется_симметрическая разность множеств: А д В := (А Г) В) U
U (Л А В). Здесь нейтральным элементом является пустое
подмножество 0, а обратным для каждого элемента является он
сам (А д А = 0 для любого А С S).
Эквивалентность в на группе А = (А, •, -1, е) называется
конгруэнцией этой группы, если:
(а, Ь) е в & (с, d) G в => (ас, W) е в,
(a, b) е в => (а-1, b~') 6 в
для любых а, Ь, с, d G А.
Конгруэнции группы находятся во взаимно однозначном
соответствии с ее специальными подгруппами, которые мы сейчас
определим. Подгруппа Н группы А называется нормальной, если
хНх 1 = Н для любого элемента х группы А. Здесь слева в
определяющем равенстве производится глобальное умножение,
вместо подмножества {х} пишется, как это принято, сам элемент
х. В любой группе нормальными подгруппами будут сама группа
и единичная подгруппа {е}. В абелевой группе каждая подгруппа
нормальна.
138
Теорема 2.37. Для любой конгруэнции 6 на группе
А = (Л, •, -1, е) класс Н = 0(e) является нормальной под-
группой в А. При этом если б^е) = ^2(е) для б^,в2 G Con Л,
то 0j = 62- Обратно, если Н—нормальная подгруппа группы
А, то Н = 0(e) для подходящей конгруэнции в на А.
Доказательство. Пусть х—произвольный эле-
мент группы А и a G 0(e), где 0 G Con Л. Тогда (хах-1,
хех-1) G 0, так как (а, е) G в. Но хех- = е, так что
хах-1 G 0(e), т.е. х0(е)х С 0(e). Обратное включение: если
а 6 0(e), то х-1ах 6 0(e), а тогда а = х(х-1ах)х-1 6
е х0(е) х-1, откуда 0(e) С х0(е)х-1 для любого х G А.
Пусть 0р 02 G Con Л и 0j(e) = 02(е). Возьмем произволь-
ную пару (а, b) G 0 . Тогда имеем:
(a, b) €= 0j => (аЬ 1, ЬЬ ^) €= 0^ => ab 1 €= 0^(е) = б2(е) =>
=* (ab \ е) £ 0j =* ((ab 1)^’, е^)	(а’ е ®2’
откуда 0j С 02> Аналогично, 02 С 0(, так что 0j = 02.
Пусть Н—нормальная подгруппа группы А = (А, •, -1, е).
Положим
вн := {(a, b) е А X AI аН = ЬН}.
Очевидно, что 0н—эквивалентность на множестве А. Получаем:
(a, b) S вн & (с, d) & вн => аН = ЬН & сН = dH =>
=> (ас)Н = а(сН) = a(dH) = а[</(</-1Я</)] = a[(dd~X)Hd] =
= a(Hd) = (aH)d = (bH)d = b(Hd) = b[(dHd~l)d] =
= bldH^'d)] = b(dfT) = (bd)H => (ac, bd) 6 0^,
и, значит, вн устойчива относительно умножения.
Далее, так как Н—подгруппа, то Я-1 = Я (здесь под Я-1
понимается совокупность всех элементов, обратных элементам из
Я). Тогда
(а, Ь) аН = ЬН => (аЯ)-1 = (6Я)-1 => Ha~l = НЬ~Х =>
=> (а~ХНа)а~Х = (b~XHb)b~X => а~ХН = b~XH => (a-1, b~X) 6 0Я,
и, следовательно, вн устойчива относительно обращения. □
139
Пусть А—группа и в—конгруэнция на ней. Этой конгруэнции,
согласно теореме 2.37, взаимно однозначно соответствует некото-
рая нормальная подгруппа группы Н. Факторгруппу А/в обозна-
чают через А/Н и называют факторгруппой группы А по
нормальной подгруппе Н.
Из определения нормальной подгруппы Н группы А следует,
что хН = Нх для любого элемента х € А. Учитывая это
замечание, получаем из теоремы 2.37
Следствие 2.13. Конгруэнции на любой группе пере-
становочны.
Доказательство. Пусть 0р 02—произвольные
конгруэнции группы А = (Л, •, -1, е) и	ff2—соответству-
ющие этим конгруэнциям нормальные подгруппы, т.е.
= {(•*. У) G А X AI хЯ) = yHj,
в2 = {(х, у) G А X Al хН2 = yH^j.
Пусть а, с 6 А и (а, с) 6 0^0^ Тогда найдется элемент
b G А такой, что (zz, й) е 0 и (/>, с) 6 02- Это означает, что
Н^а = Н{Ь и ЬН2 = сН2. Рассмотрим элемент ab~Xc. Так как
Н}(аЬ~Х) =	= Н^е, то ab 1 6 ^(е) = Н}. Аналогично,
(Ь~Хс)Н2 = Н2 = еН2, откуда b~Xc 6 $2(е) = ^2' Следователь-
но,
(ab~xc)H2 = a((i-1c)H2) = аН2,
и, значит, (a, ab~Xe) G 02, и кроме того, Н^(аЬ~Хс) =
= {Н^{аЬ~хУ)с = Н^с, и, следовательно, (ab~Xc, с) € 02. Таким
образом, (zz, с) G #2°^. Мы показали, что	=	для
любых вр 02 G Con А. о
Так как для перестановочных эквивалентностей 0р 02 произве-
дение 01 ° 02 является наименьшей эквивалентностью, содержащей
и 02, то, согласно теореме 2.21 § 2.1,	°02 будет наименьшей
конгруэнцией группы А, содержащей конгруэнции 0 и 02- Как
устроена нормальная подгруппа Н, соответствующая конгруэнции
0^ °02? Чтобы выяснить это, заметим сначала, что Я-1 = Н для
любой подгруппы группы А и что Н^Н2 = Н2Н^ для любых двух
ее нормальных подгрупп. Тогда получаем:
(Н^Н^ = н{н2нхн2 = (Я1Я1)(Я2Я2) = Я1Я2,
140
<W‘ =	= н2нх = НХН2,
т. е. подмножество НХН2 С А замкнуто относительно умножения
и обращения, и содержит нейтральный элемент е, поскольку е
входит и в Нх и в Н2. Значит, НХН2—подгруппа группы А. Так
как х(Я Я )х-1 = хН (х~Хх)Н х~Х = (хН х-1)(хЯ-х-1) = Н Н., то
подгруппа НХН2 оказывается нормальной подгруппой группы А.
Очевидно, что Я^2 Д°лжна содержаться в любой подгруппе,
порожденной объединением /7Х U Н2. Итак, получаем, что если
конгруэнции &х и в2 группы А определяются ее нормальными
подгруппами Нх и Н2, то нормальная подгруппа НХН2 соответ-
ствует конгруэнции ° 62, т. е. для любых двух нормальных
подгрупп Н, и Н_ имеет место равенство: 0., »0„ = 0., ... Из
1	2	л л	л л
12	12
проведенных рассуждений вытекает
Теорема 2.38. Совокупность всех нормальных подгрупп
произвольной группы А образует относительно теоретико-мно-
жественного включения решетку, изоморфную решетке Con Л
конгруэнций этой группы. В этой решетке inf (Яр =
= Нх С\ Н2 и sup (Я(, Я2) = Я}Я2 для любых двух нормаль-
ных подгрупп Я Я2 группы А.
Доказательство. Единственным моментом, тре-
бующим некоторых пояснений, является равенство inf (Я1,
Я2) = Я А Я2. Его справедливость следует из того, что
пересечение Нх А Я2 нормальных подгрупп Нх и Я2 само будет
нормальной подгруппой. Действительно, для любого элемента
х S А получаем:
х(Я[ А Я2)х-1 С хНхх~1 А хЯ2х-1 = А Я2 =
= е(Нх А Я2)е = х(х-1(Я1 А Я2)х)х-1 С Х(НХП Я2)х-1,
откуда х(Нх А Я2)х-1 = Я( А Я2> о
Продолжим рассмотрение некоторых групп частного вида.
П р и м е р 62 (см. пример 50 § 2.2). Пусть А = (А, •,
-1, е)—произвольная группа и а 6 А. Если п—натуральное
число, то под а~п будем понимать произведение а~ 1а~1 ... а-1
(п раз). Без труда доказываются обычные правила действий со
степенями: а’па’1 = ат+п, (а'п)п = атп (здесь т, п—произволь-
ные целые числа). Легко видеть, что совокупность всех степеней
элемента является подгруппой группы А. Это циклическая группа,
141
порожденная элементом а. Обозначим ее через А(а). В аддитивной
записи для натурального числа п полагают (—п)а := п(—а), и
вышеуказанные правила действий со степенями для кратных
приобретают следующий вид:
та + па = (т + п)а, п(та) = (тп)а.
Примером бесконечной циклической группы является адди-
тивная группа целых чисел (Z, +, —, 0). Она порождается
числом 1. Пусть п > 1—натуральное число. Через Z^ обозначим
множество {0, 1, п - 1} остатков от деления натуральных
чисел на п. В Z^ определяется сложение по модулю п:
результатом действия а +п Ь для a, b Е Z^ считается остаток
от деления обычной суммы а + b на п. Относительно введенной
операции сложения +п множество Z^ образует группу. Ее
нейтральным элементом является 0, а противоположным для
х ё Z будет число п - х.
Т е о р е м а 2.39. Всякая бесконечная циклическая группа
изоморфна аддитивной группе Z целых чисел. Конечная
циклическая группа порядка п изоморфна аддитивной группе
Z остатков от деления на п.
п
Доказательство. Пусть А(а)—бесконечная цик-
лическая группа, порожденная элементом а. Положим
<Р'. А(а) -* Z. ап п. Отображение <р устанавливает взаимно
однозначное соответствие между элементами групп Л(а) и Z.
Кроме того, <р(атап^ = <р(ат+п) = т + п = <р(ат) + <р(ап),
т. е. <р является полугрупповым гомоморфизмом. Этого достаточно,
чтобы утверждать, что <р—изоморфизм группы А(а) на
группу Z.
Пусть теперь Л(а) = {е, а, а2, ..., а”-1}. Рассмотрим отобра-
жение р: а1 >—> I. Оно устанавливает взаимно однозначное
соответствие между множествами А (а) и Z^. Покажем, что <р
является гомоморфизмом относительно бинарной операции, т. е.
что <р(а‘ак) = ^(а') +n В самом деле,
откуда и следует требуемое равенство для <р. Еще раз напомним,
что изоморфизм полугрупповых редуктов двух групп является
изоморфизмом самих этих групп. □
142
Ниже приведена таблица сложения циклической группы Z4 по
модулю 4.	+4	0	1	2	3
	0	0	1	2	3
	1	1	2	3	0
	2	2	3	0	1
	3	3	0	1	2
Пусть S—некоторое непустое множество, K(S х S)—совокуп-
ность всех его биекций, т. е. взаимно однозначных сюръективных
преобразований. В моноиде (K(S х S), °, Д) каждый элемент /
обратим: обратным элементом для него является обратное
преобразование/-1 := {(b, d) 6 5 х SI (а, Ь) е /}. Таким обра-
зом, алгебра (K(S х S), ° -1, Д) оказывается группой. Это
симметрическая группа на множестве S. Если множество 5
конечно, то, как уже отмечалось, его взаимно однозначные
преобразования можно записывать в виде перестановок
, _ Р1 "2	- Sn
1 ~ /(*,)	/(S2)	•••	/(Sn)
\
или в виде векторов f =	/(s2), •••> Л\))» если ПОРЯД°К
элементов в S фиксирован: S =	s2, .... s;;}.
Граф G(f) для f G K(S x S) состоит в общем случае из
нескольких компонент связности, каждая из которых представляет
собой цикл.
Симметрическая группа SP на n-элементном множестве
содержит п! элементов—это количество всевозможных перестано-
вок из п символов.
Пример 63. Симметрическая группа состоит из
шести элементов, зададим их векторами: тг) = (1, 2, 3),
я2 = (1, 3, 2), я3 = (2, 1, 3), л4 = (2, 3, 1), л5 = (3, 1, 2),
= (3, 2, 1). Таблица умножения группы представлена ниже.
О	Л1	л2	л3	л4	л5	л6
Л1	Л1	л2	л3	л4	л5	л6
л2		Л1	л4	л3	л6	л5
л3	л3	л5	Л1	л6	л2	л4
л4	л4	л6	^2	л5	Л1	л3
л5	л5	л3	л6	Л1	Л4	
л6	л6	л4	л5	л2	л3	Л1
143
Группой преобразований называется любая подгруппа некото-
рой симметрической группы.
П р и м е р 64. Пусть р(Хр х2, ..., ху— некоторый число-
вой многочлен от п переменных. Для перестановки л е SP
положим
рл(х,, х_, ..., х ) := р(х х ..., х ,
1 4 Г 2’	’ п' 1 4 л(1)	л(2)’	’ л(пу
Если р71 = р, будем говорить, что л не изменяет данный
многочлен р. Если перестановки л и л* не изменяют р, то их
произведение лл тоже обладает этим свойством. Многочлен,
инвариантный в этом смысле относительно перестановки л, будет
инвариантным и относительно обратной перестановки л-1. Отсюда
следует, что перестановки, не изменяющие данный многочлен р,
образуют подгруппу симметрической группы SP . Эта группа
преобразований называется группой инерции многочлена
р(х , х_, ..., х ). Например, если р(х , х_, х ) = (х - х.) х
1 X >1	1X01 xz
х (Xj — х3)(х2 — х3), то для шести элементов симметрической
группы <7'3 (пример 63) получаем:
л
р '(х,, х2, х3) = р(хр х2, х3),
Л
р 2(Х[, х2, х3) = р(хр х3, х2) =
= (•«! -	- *2) = ~P(XV Xr xj'
Л
Р 3(хг *2’ Хз) = Р(Х2’ V Лз) =	х2* Хз)’
Л
р 4(Х[, х2, х3) = р(х2, Х3, Xj) = p(Xj, х2, х3),
рл5(хг х2, х3) = р(х3, Хр х2) =р(хг х2, х3),
л
р 6(*г х2, х3) = р(х3, х2, Xj) = -р(Хр х2, х3).
Таким образом, группа инерции многочлена р(Хр х2, х3) состоит
из трех перестановок:
/1 2	3\	/1	2	3\	/1	2	3\
л 1 г	з]’	л4 _ ,2	з	1]’	71 s	~ |з	1	iy
Т е о р е м а 2.40. Всякая группа изоморфна подходящей
группе обратимых преобразований.
Доказательство. Пусть А = (А, , -1, ё)—не-
которая группа. В теореме 2.26 § 2.1 было описано представление
моноида (А, , е) правыми сдвигами—преобразованиями множе-
144
ства А, имеющими вид х •—» ха, где а е А. Покажем, что
правые сдвиги группы являются обратимыми преобразованиями
множества А. В самом деле,
Aq(Z>) = Лд(с) => ba = са => b = (Z>a)a-1 = (са)а-1 = с,
и, значит, Ха взаимно однозначно. Далее, для произвольных
а, х G А получаем
Ха(ха~1) = (ха~1)а = х,
т. е. Ха—сюръективно. Таким образом, отображение у. a1—
является вложением группы А в симметрическую группу
К(А X А). □
Пусть А = (S, X, <5)—некоторый полуавтомат. Через Aut А
обозначим совокупность всех его автоморфизмов, т. е. таких
биекций f: S -* S, что /(d(s, х)) = <5(/(s), х) для любых
s G S, х е X.
Теорема 2.41. Автоморфизмы полуавтомата образу-
ют подгруппу симметрической группы на множестве состояний
этого полуавтомата.
Доказательство. По определению, автоморфиз-
мы полуавтомата А = (S, X, <5)—это его биективные эндо-
морфизмы, так что Aut А = End А Г) K(S X S'). Поскольку
End А и K(S X S) являются подмоноидами симметрического
моноида F(S X S), то и Aut А—подмоноид в F(S X S). Осталось
показать, что если f 6 Aut А, то /-1 6 End А, поскольку уже
/-1 е K(S X S). Но, в самом деле, для любых s G S, х G X
имеем:
X)) =	(&(/(/~\s)), X)) =	X))) =
=	х),
откуда /-1 6 Aut А. □
Теорему 2.40 о представлении группы обратимыми преобразо-
ваниями в конечном случае существенно усиливает
Т е о р е м а 2.42. Всякая конечная группа изоморфна
группе автоморфизмов подходящего полуавтомата.
Доказательство. Пусть (S, •,	\ е)—произ-
вольная конечная группа. Как показано ранее, моноидный редукт
(S, •, е) может быть реализован как моноид эндоморфизмов
полуавтомата А = (S, S, <5), где <5(s, х) = xs для любых
s & S, х & S. При этом для любых двух состояний a, b G S
будет иметь место соотношение b = (Z>a-1)a = <5(а, Сле-
довательно, в полуавтомате А любые два состояния взаимно
достижимы, т. е. А—сильно связный автомат. Все эндоморфизмы
145
полуавтомата А являются его автоморфизмами (теорема 2.32
§ 2.2), т. е. End Л = AutA. □
Полуавтомат А называется жестким, если он не имеет
нетождественных автоморфизмов, т. е. если AutA = {А}.
Т е о р е м а 2.43. Для любого натурального числа п
существует жесткий автономный полуавтомат с п состо-
яниями.
Доказательство. Пусть S =	s2, ..., s^},
п > 2. Положим <5(Sj) = s( и <5(sz) = l для i > 2. Граф
переходов полуавтомата А = (S, <5) представляет собой петлю (в
вершине «р с входящей в нее цепью sn -* s j	Пусть
f—произвольный автоморфизм построенного полуавтомата А. Тогда
/(sl) = /(^(si)) = ^(/(si))> откуда /(Sj) = 5р так как в полуав-
томате А есть только одно состояние, переходящее в себя под
действием входного сигнала. Далее, = f(s{) = /(<5(s2)) =
= <5(/(s,)), и, следовательно, f(sA = s, или f(sA = s_. Первое
равенство противоречит взаимной однозначности преобразования
/, так как мы уже имеем = /(Sj). Поэтому имеет место
/($2) = «2- Аналогичные рассуждения показывают, что /($3) =
= «3, и так далее. Таким образом, / = Д, и в полуавтомате А
нет нетождественных автоморфизмов. □
Напомним, что полуавтомат А = (S, X, <5) называют про-
стым, если Con А = {Д, S х S}. Следующая теорема [74] харак-
теризует группы автоморфизмов простых полуавтоматов.
Т е о р е м а 2.44. Циклические группы простого порядка,
и только они, являются группами автоморфизмов простых
полуавтоматов.
Доказательство. Необходимость.
Пусть f—нетождественный автоморфизм простого полуавтомата
А = (S, X, <5). На множестве S рассмотрим отношение
:= {(a, b) е S х SI (3 k е Z) (b = fk(a))}, где
	А,	если	к = 0,	
fk =	f °f ° ... °f, к раз	если	к >	0,
		если	к <	0.
Отношение является конгруэнцией полуавтомата А, поскольку
для него выполняются все необходимые для этого условия:
a)	s = Д(х) = f°(s) (рефлексивность);
б)	b = /\а) & с = fl(b) => с = fk+l(a) (транзитивность);
к	—к
в)	b = f (а) => а = f (b) (симметричность);
146
г)	(а, b) е (а к е Z) (Ь = /*(а)) => <3(2>, х) = д(/к(а), х) =
= fk(d(a, х)) => (<5(а, х), <5(Z>, х)) G (устойчивость).
Так как А—простой полуавтомат, то О? = Д или =
= S х S. Но равенство = Д немедленно влечет равенство
/ = Д. Так как /, по предположению,—нетождественное преоб-
разование, то остается одна возможность: = S х S.
Пусть g—произвольный автоморфизм полуавтомата А и
sQ—некоторое фиксированное состояние. Поскольку = S х S,
к
то найдется целое число kQ такое, что g(sA = f °(s0). Положим
к	U	Л У	к
h := f °°g~\ тогда h(sQ) = (f 0 ° £-1)O0) = S~X(f °Oo)) =
= £-1(#(s0)) = sQ. Следовательно, hl(sQ) = s0 Для любого
I G Z. Это означает, что e,(sA = {s„}, и, значит, в, t SxS.
В силу простоты полуавтомата А получаем = Д, откуда
следует, что h = Д. Таким образом, Д = h =f °°g~l, и,
к
следовательно, g = f °, т. е. каждый элемент группы Aut А
является степенью элемента /, поэтому группа Aut А циклическая.
Автоморфизм f выбирался произвольно из AutA — {Д}. Значит,
группа AutA порождается любым своим элементом, отличным от
Д. Это возможно лишь в том случае, когда порядок этой
циклической группы—простое число.
Достаточность. Пусть (S, •, -1, е)—цикличес-
кая группа простого порядка р. По теореме 2.42 эта группа
изоморфна группе автоморфизмов полуавтомата А = (S, S, <5),
где <5(s, х) = xs для любых s G S, х 6 S. Покажем, что
полуавтомат А простой. Допустим, что в—нетождественная
конгруэнция полуавтомата А. Тогда существуют два различных
состояния а и b таких, что (a, b) G в. Состояния е = а~1а =
= <5(а, а-1) и $0 = а~хЬ = <5(/>, а-1) (они различны) должны
содержаться в одном 0-классе. Поскольку мы имеем циклическую
группу простого порядка р, то S = {е, sQ, Sq, ..., (каждый
отличный от е элемент порождает группу). Теперь получаем:
(е, s0) ее => (<5(е, s0), <5(>0, sQ)) е в => Оо, е е => (е, $ G в =>
=* (<5(е, s0),	s0)) е в => (s0, s30) е в => (е, ф G в => ...
...=>(£>,
так что в = S х S. Следовательно, полуавтомат А простой, а
147
Пример 65. Автоморфизмом графа G = (V, а) называ-
ется его изоморфизм на себя, т. е. такое взаимно однозначное
соответствие /: V -» V, что (и, v) G а о (/(u), /(v)) G сс для
любых и, v G V. Очевидно, что последовательное выполнение
двух автоморфизмов также будет автоморфизмом и что тождест-
венное отображение А и отображение /~1, обратное для
автоморфизма /, являются автоморфизмами. Следовательно, мно-
—>	—'►
жество Aut G всех автоморфизмов произвольного графа G образует
группу. Эта подгруппа симметрической группы на множеств? v
называется группой автоморфизмов графа. Можно показать 155],
что любая конечная группа изоморфна группе автоморфизмов
подходящего графа. Граф называется асимметрическим, если у
него нет нетождественных автоморфизмов. Переводя на язык
графов рассуждения, проведенные в доказательстве теоремы 2.43,
получаем, например, асимметричность графа, состоящего из петли
в вершине У[ и входящей в эту вершину цепи vn -» v j -* ...
... -» Vj (рис. 43<z). На рис. 43 приведены графы с тривиальной
группой автоморфизмов, в случае б) изображен асимметрический
неориентированный граф с наименьшим возможным числом
вершин.
а	5
Рис. 43
Говорят, что группа перестановок Р транзитивна на множе-
стве S, если для любых a, b G S найдется перестановка
л G Р такая, что л(а) = Ь. Граф с транзитивной группой
автоморфизмов называется симметрическим. Например, всякий
цикл является симметрическим графом. Очевидно, что в симмет-
рическом графе любые два максимальных пддграфа изоморфны.
(Максимальным подграфом данного графа G называется граф,
получаемый из графа G удалением одной вершины и всех дуг,
которым она принадлежит.)
Пусть группа А = (А, •, -1, е) представлена обратимыми
преобразованиями некоторого множества 5, т. е. задано некоторое
вложение <р'. А -» K(S х 5) этой группы в симметрическую группу
на множестве 5. Будем говорить в этом случае, что А действует
на множестве S. Если <ра—преобразование множества S, соответ-
ствующее при данном представлении элементу а группы А, и
х G 5, то вместо <ра(х') будем писать ха. Тогда, очевидно, хе = х
и х(а{а2) = (ха{)а2 для любых х G 5 и а{, а2 G А.
148
Пусть s е S—некоторый фиксированный элемент. Стабилиза-
тором точки s называется подмножество St (s) := {a G
£ Al sa = s}, состоящее из таких элементов группы А, для
которых s является неподвижной точкой (здесь элементы группы
А воспринимаются как обратимые преобразования множества S).
Нетрудно убедиться в том, что St (s) будет подгруппой группы
А при любом s 6 S. Для каждого элемента s е S можно
определить А-орбиту :
orb (s) := {хе SI (За 6 А)(х = sa)}.
Т е о р е м а 2.45. Если группа А действует на множестве
S, то всевозможные A-орбиты образуют разбиение лА(3) этого
множества.
Доказательство. Так как se = s, то s е
е orb (s), и, следовательно, Л-орбиты образуют покрытие мно-
жества S. Далее, если х е orb (s), то х = sa для некоторого
элемента а группы А, откуда s = ха 1, т. е. s е orb (х).
Следовательно, orb (х) = orb (s). □
Отсюда получается, что различные орбиты не имеют общих
элементов. Если существует всего одна Л-орбита, говорят, что
группа Л транзитивно действует на множестве S.
Пример 66. Пусть Л—некоторая группа и Н—какая-
нибудь подгруппа в ней. Правые сдвиги А -» Л, а •—» ah, где
h f= Н, определяют действие подгруппы Я на множестве Л. В
этом специальном случае Я-орбиты называются (правыми)
смежными классами группы Л по подгруппе Н. При этом
orb (a) = аН для любого элемента а группы Л. Если группа Л
конечна, то все ее смежные классы по данной подгруппе Н имеют
одинаковое число элементов—столько же, сколько элементов в
Н (если оЛ[ = оЛ2, то = h2, т. е. разным элементам
подгруппы Я соответствуют разные элементы в смежном классе
аН). Количество Я-орбит называется индексом подгруппы Я в
группе Л и обозначается (Л : Я). Таким образом, мы получаем
следующую теорему Лагранжа.
Т е о р е м а 2.46. Порядок конечной группы делится -ia
порядок ее любой подгруппы: 1Л1 = 1Я1(Л : Я). □
Следствие 2.14. Пусть конечная группа А действу-
ет на множестве S. Тогда 1Л1 = lSt(s) I lorb(s) I для любого
s е s.
Доказательство. Покажем, что lorb(s) I ш
= (Л : St(s)). Для этого каждому смежному классу a St(s)
сопоставим элемент sa G orb(s), где а 6 Л. Если saj = sa2, то
sa{a~l = s, откуда следует, что a{a~l е St(s), и, значит,
ajSt(s) = a2St(s). Таким образом, указанное соответствие взаимно
однозначно. Сюръективность его очевидна. Следовательно, количе-
149
ство смежных классов по подгруппе St(s) равно числу элементов
в подмножестве orb(s). о
В комбинаторике часто используется так называемая лемма
Бернсайда:
Т е о р е м а 2.47. Пусть конечная группа А действует на
множестве S. Тогда количество A-орбит может быть вычисле-
но по формуле
= 777 2 ISt(s)L
s е s
Доказательство. Заметим прежде всего, что
если orb(s) = orb(0, то lSt(s) I = ISt(O I для любых s, t e S.
Действительно, в этом случае sa = t для некоторого а G А,
откуда s = ta~x. Далее, для произвольного h G St(s) имеем
sh = s => (ta~x)h = ta~1 => t(a~xha) = t => a~xha G St(Z).
Сопоставляя каждому h G St(s) элемент a~xha G St(Z), получаем
взаимно однозначное соответствие между подгруппами St(s) и
St(Z). Выберем теперь в каждом блоке разбиения ял(5) множества
S на Л-орбиты по одному элементу:	s^, ..., Используя
следствие из теоремы 2.46, получаем:
1 1 "
777 2 ISt^)' = 777 2 ist(5.)i iorb(5.)i =
s е 3	1=1
1 "
= 7-77 У 1Л1 - п = 1л.(5)1. о
\А\	'
1=1
Кольцом называется алгебра R = (Л, +,	0) типа (2, 2,
1, 0) такая, что: 1) редукт (R, +, -, 0) представляет собой
абелеву группу, 2) редукт (Л, •) является полугруппой, 3)
справедливы законы дистрибутивности: х(у + z) = ху + xz,
(х + у) z = xz + yz.
Кольцо называется коммутативным, если коммутативна
операция умножения: ху = ух, и называется кольцом с единицей,
если в полугруппе (R, •) есть нейтральный элемент.
П р и м е р 67. Первыми очевидными примерами колец
служат кольцо R всех действительных чисел и его подкольцо Z,
образованное целыми числами. Оба они коммутативны и обладают
единицей (число 1). Кольцо четных целых чисел уже не будет
кольцом с единицей.
П р и м е р 68. Некоммутативное кольцо с единицей обра-
зуют всевозможные числовые матрицы фиксированной размерности
150
п х п. Этот пример является конкретной иллюстрацией следую-
щего общего факта, вытекающего  из теоремы 2.33.
Т е о р е м а 2.48. Совокупность всех квадратных мат-
риц фиксированной размерности п над данным кольцом R
образует кольцо относительно сложения и умножения матриц.
Пример 69. Конечное коммутативное кольцо Z^ с еди-
ницей образуют остатки от деления натуральных чисел на данное
натуральное число п, рассматриваемые относительно бинарных
операций сложения и умножения по модулю п.
Ниже приведены таблицы сложения и умножения в коль-
це z6.
+6	0	1	2	3	4	5
0 1 2 3 4 5	0	1	2	3	4	5 1	2	3	4	5	0 2	3	4	5	0	1 3	4	5	0	1	2 4	5	0	1	2	3 5	0	1	2	3	4
6	0	1	2	3	4	5
0 1 2 3 4 5	0	0	0	0	0	0 0	1	2	3	4	5 0	2	4	0	2	4 0	3	0	3	0	3 0	4	2	0	4	2 0	5	4	3	2	1
Пусть R—произвольное кольцо. Для любых a, b е R положим
а - b := а + (-/>). Элемент а - b называется разностью элемен-
тов а и Ь. Отметим некоторые простейшие свойства колец.
Л е м м а 2.1. Во всяком кольце выполняются тождества'.
а) хО = Ох = О, б) х(-у) = -(ху) = (-х)у,
в) х(у - z) = ху - xz, (х - y)z = xz - yz.
Доказательство. Используются свойства груп-
повой операции сложения и дистрибутивность умножения относи-
тельно сложения.
а)	ху + 0 = ху = х(у + 0) = ху + хО => 0 = хО
(здесь к обеим частям равенства ху + 0 = ху + хО прибавили
-(ху)). Аналогично Ох = 0.
б)	х(—у) + ху = х[(-у) + у] = хО = 0 => х(-у) = “(*У)«
Аналогично (~х)у = — (ху).
в)	х(у — z) = х[у + (—z)] = ху + х(—z)= ху + [-(xz)] = ху — XZ.
Аналогично (х - y)z = xz - yz. □
Заметим, что в кольце Zfi произведение 2 • 3 равно нулю,
хотя оба сомножителя отличны от нуля. Такие элементы кольца
называют делителями нуля. Легко видеть, что кольцо Z^ тогда
и только тогда будет кольцом без делителей нуля, когда п—простое
число. Не имеют делителей нуля также кольца R и Z.
Идеалом кольца R = (R, +, •, -, 0) называется его под-
кольцо I, являющееся двусторонним идеалом полугруппы (/?,•)•
Само кольцо R и его нулевое подкольцо {0} дают очевидные
151
примеры идеалов. Все другие идеалы кольца (если они есть)
называются его собственными идеалами.
Из определения идеала следует, что пересечение Г) I
любых двух идеалов кольца не пусто (оно содержит, например,
элемент 0) и само является идеалом.
Пусть а—произвольный элемент кольца R. Тогда подмножество
1(a) = RaR будет в R идеалом. Это главный идеал кольца R,
порожденный элементом а. Очевидно, что 1(a)—наименьший идеал
кольца R, содержащий элемент а. Конгруэнции кольца находятся
во взаимно однозначном соответствии с его идеалами. Именно,
имеет место
Т е о р е м а 2.49. Для любой конгруэнции в кольца
R = (Л, + , •, —, 0) класс I = 0(0) является идеалом кольца
R. При этом если 0{(О) = 02(О) для в^, 6 Con Л, то
0[ = 02. Обратно, если I—идеал кольца R, то I = 0(0) для
подходящей конгруэнции в на R.
Доказательство. Пусть 0—произвольная конг-
руэнция кольца R. Тогда для любых a, b 6 0(0) получаем:
a, b G 0(0) => (а, 0) G 0 & (Ь, 0) G 0 (а + Ь, 0) G 0 => а + b G 0(0),
а €Е 0(0) => (а, 0) & 0 => (—а, 0) G в => —а G 0(0),
откуда следует, что 0(0)—подгруппа группы (R, +, -, 0). Далее,
если a G R, i G 0(0), то (ai, <z0) G 0, т. е. (ai, 0)6 0, и
значит, ai & 0(0). Аналогично ia 6 0(0). Следовательно, 0(0)—
двусторонний идеал полугруппы (R, •). Пусть 0^ 02 6 Con Л.
Конгруэнция кольца, очевидно, является конгруэнцией его груп-
пового редукта (R, +, -, 0). Согласно теореме 2.37, из
0j(O) = 02(О) следует равенство в{ = 02-
Пусть I—произвольный идеал кольца R. Тогда он является
(нормальной) подгруппой абелевой группы (R, +, -, 0) и
двусторонним идеалом полугруппы (R, •). Рассмотрим групповую
конгруэнцию 0у := {(a, b) 6 RxR\a + I = b + /}. Если
(a, b) 6 0; и (с, J) 6 0;, то
ас + I = ас + а! = а(с + Г) = a(d + Г) = ad + al = ad + I =
= ad + Id = (а + I)d = (b + I)d = bd + Id = bd + I,
т. e. (ac, bd) 6 0;. Следовательно, 0 оказывается конгруэнцией
кольца R. □
Пусть R—кольцо и 0—конгруэнция на нем. Этой конгруэнции,
согласно теореме 2.49, взаимно однозначно соответствует некото-
рый идеал кольца R. Факторкольцо R/в обозначают через R/I
и называют факторкольцом кольца R по идеалу I.
152
Пусть /[, /2—идеалы кольца R. Тогда Ц + /2 является
наименьшей подгруппой аддитивной группы кольца, содержащей
идеалы I , К. Так как R(J + I ) = RI + RI QI. + Л и
аналогично (1{ + /2)Л Q 1{ + /2, то Ц + /2 оказывается наи-
меньшим идеалом кольца R, содержащим идеалы 1{ и /2. Отсюда
и из теоремы 2.38 следует
Теорема 2.50. Совокупность всех идеалов произволь-
ного кольца R образует относительно теоретико-множествен-
ного включения решетку, изоморфную решетке Con R
конгруэнций этого кольца. В этой решетке inf(/j, /2) =
= /j Г) /2 и sup(/1, /2) = /j + /2 для любых двух идеалов
/	/2 кольца R. о
Следствие 2.15. Конгруэнции на любом кольце пере-
становочны.
Доказательство. Пусть 0^ G Con R. Этим
конгруэнциям соответствуют некоторые идеалы I , /2 кольца R.
Отношения и являются конгруэнциями аддитивной группы
кольца R. В этой абелевой группе наименьшей конгруэнцией,
содержащей 0 и #2, будет в =	°в^ = 02°01, котоРая опреде-
ляется (нормальной) подгруппой I = /j + /2, т. е. в = в/ =
— {(a, b) 6 R х Л1 а + I = b + /}. Но так как I = 1} + /2 пред-
ставляет собой идеал кольца R, то в оказывается конгруэнцией
кольца R. Таким образом, для любых 0^ 6^ €Е Con Л получаем:
9,°в^ = sup(0., 0-) = sup (в-, 9) = 9°9. а
П р и м е р 70. Булевым кольцом называется кольцо с
единицей, в котором каждый элемент является мультиплика-
тивным идемпотентом, т. е. выполняется тождество х = х.
Примером такого кольца может служить Z2—кольцо остатков от
деления на 2. Структуру булева кольца задают на множестве
Р(5) всех подмножеств непустого множества 5 операции симмет-
рической разности А и пересечения Г) подмножеств. Обе эти
ситуации представляют собой частные случаи следующего общего
факта.
Теорема 2.51. Пусть В = (В, V, л, ', 0, 1)—произ-
вольная булева алгебра. Положим а ф Ъ := (ал 5') V
V (а' л 5) для любых a, b 6 В. Множество В с операциями
фа л является булевым кольцом.
Доказательство. Докажем сначала ассоциатив-
ность операции ф. Используя свойства булевых операций,
получим:
а ф (Ь ф с) = (а л (Ь ф с)') v (а' л (Ь ф с)) =
153
= (а л ((Z> л c') v (Ь' л с))') V (а' л ((Ь л с') V (Ь' л с))) =
= (а л (/>' v с) л (Ь л с')) V (а' л ((Ь л с') V (Ь' л с))) =
= (а л />' л с') v (а' л Z> л с') V (а' л Ь' л с) V (а л Ь л с) =
= (а л Ь' л с') v (а! л Ъ л с') v ((а' v J) л (а v 6') л с) =
= (((а л />') v (а' л />)) л с') v (((а л />') v (а' л />))' л с) =
= ((а ф Ъ) л с') v ((а ф Ь) л с) = (а ф Ь) ф с.
Нейтральным элементом относительно операции ф является
элемент 0. Противоположным для каждого элемента а G В будет
сам элемент а, так как а ф а = 0. Таким образом, моноид
(В, ф, 0)—абелева группа. Операция пересечения л ассоциативна
и коммутативна и, кроме того,
(а ф Ь) л с = ((а л Z>') v (а' л Ь)) л с =
= (а л Ь' /\ с) v (а' л Ь /\ с) =
= (а л с л (/>' v с')) V ((а' v с') Л Ъ л с) =
= ((а л с) л (Ь л с)') V ((а л с)' л (Ь л с)) = (а л с) ф (Ь л с).
Наконец, х л х = х для любого х 6 В. о
Таким образом, каждой булевой алгебре В описанная в теореме
2.51 конструкция соотносит булево кольцо R(B). Оказывается,
имеет место и обратное соответствие. Предварительно—
JI е м м а 2.2. В любом булевом кольце имеют место
тождества:
х + х = 0, ху = ух.
Доказательство. В самом деле, (х + х) +
+ (х + х) = хх + хх + хх + хх = (х + х) (х + х) = х + х, а
так как 0—единственный аддитивный идемпотент кольца, то
х + х = 0. Далее, х + у = (х +	у)2	= х2	+ ху	+ ух + у2 =
= х +	у	+ ху + ух, откуда ху +	ух	= 0 =	ху +	ху и, значит,
ху = ух. о
Т е	о	р е м а 2.52. Пусть	R	= (R,	+, •,	0, 1)—булево
кольцо	с	единицей 1. Положим a	v b :=	а + b	+ ab, а л Ь : =
:= ab, а' : = 1 + а для любых a, b G R. Тогда алгебра В =
= (Л, V, л, ', 0, 1) является булевой алгеброй.
Доказательство. Нужно доказать, что в алгебре
В выполняются тождества I—IX из § 1.1, определяющие булеву
алгебру. Из леммы 2.2 и определения операций в В следует, что
операции v и л идемпотентны и коммутативны, а операция л
ассоциативна. Операция v также ассоциативна:
a v (b v с) = а + (b v с) + a(b v с) = а + (Ь + с + Ьс) +
+ а(Ь + с + be) = (а + b + ab) + с + (а + b + ab)c = (a v b) v с.
154
Проверим справедливость законов поглощения:
а л (a v Z>) = а(а + b + ab) = а + ab + ab = а,
и аналогично имеет место
a v (а л Ь) = а.
Для законов дистрибутивности имеем
а л (b v с) = а(Ь + с + be) = ab + ас + abc =
= ab + ас + (aZ>)(ac) = ab v ас = (а л b) v (а л с)
и аналогично
а v (Ь л с) = (a v Ь) Л (а v с).
Проверим действия с 0 и 1:
av0 = a + 0 + o0 = a, а л 0 = оО = О,
flvl = a+ l+el=fl + l+ a=l, а л 1 = al = а.
Элемент 1 + а является дополнением для а:
а л (1 + а) = tz(l + а) — а + а = О,
av(l+a) = a+ l + a + a(l + a) = 1 + а + а = 1.
Дополнение здесь инволютивно:
a" = (1 + a)' = 1 + 1 + a = а.
Наконец, покажем выполнение законов Де Моргана:
(a v b)' = 1 + (a V b) = 1 + а + b + ab = (1 + а)(1 + Ь) = а' л Ь',
(а л by = 1 + ab = (1 + а) + (1 + Z>) + (1 + a)(l + Z>) = a' v Ь'. =
Таким образом, каждому булеву кольцу R описанная в теореме
2.52 конструкция соотносит булеву алгебру B(R). Нетрудно
заметить, что Л(Л(В)) = В и Л(В(Л)) = R, т. е. что кольцо,
построенное по булевой алгебре, соответствующей булевому кольцу
R, совпадает с R, и что булева алгебра, соответствующая булевому
кольцу, полученному из булевой алгебры В, совпадает с В.
Выражая этот факт, говорят, что между булевыми алгебрами и
булевыми кольцами имеет место двойственность.
Прямое произведение двух колец и R^ обычно называют
их прямой суммой и обозначают через ф R^. Типичное
разложение кольца с единицей в прямую сумму получается по
следующей схеме.
Т е о р е м а 2.53. Пусть i—мультипликативный идемпо-
тент кольца с единицей R, перестановочный со всеми его
элементами. Тогда R изоморфно прямой сумме своих главных
идеалов КП и 1(1 - г).
155
Доказательство. Пусть R = (R, + , •, —,
О, 1)—кольцо с единицей 1, а элемент i G R таков, что
z2 = i и ix = xi для любого х G R. Тогда элемент 1 - i тоже
является мультипликативным идемпотентом: (1 — z')(l — i) =
= 1 — i — i + i = 1 — i,—и тоже перестановочен со всеми элемен-
тами кольца: х(1 - i) = х — xi = х — ix = (1 — i)x. Кроме того,
i(l — i) =	i - i = 0. Рассмотрим отношение	в := {(х,	у) е
G R х R	\ xi = yi}.	Очевидно, что в.—эквивалентность на	мно-
жестве R. Далее,
(х, у), (z,	f) G в. =>	xi = yi & zi = ti => (х +	z)i = xi + zi =
=	yi + H =	(У + t)i & (xz)i = (xi)(zi)	= (yi)(ti) =	(yt)i,
t. e. 0. устойчиво относительно сложения и умножения. Кроме
того, используя лемму 2.1, получаем:
(х, у) G 0. => xi = yi => — (xi) = —(yi) =* (~x)i = (—y)i =*
=> (“*, -У) 6 0..
Таким образом, 0. е Con Л. Аналогично 0 G Con Л. Пока-
жем, что 0. и удовлетворяют условиям теоремы 2.11 § 2.1.
Действительно,
(х, у) G 0. Г) 0{_. => xi = yi & х(1 - i) = у(1 — z) => х =
= х • 1 = x[z + (1 — z)] = xz + х(1 — i) =
= yi + y(l-i) = y^ (x, у) g a,
так что 0. Г) = А- Далее, для произвольных х, у G R
рассмотрим элементы и = xi + у(1 - I) и v = х(1 — z) + yz.
Тогда, в силу того что z(l — i) = 0, имеем:
ui = xz, zz(l - z) = y(l - z), t. e. (x, y) G
v(l — i) = x(l — z), vi = yz, t. e. (x, y) G
Отсюда следует, что в.<>01_. = RxR = 6	<>6.. Как было
показано в теореме 2.11 § 2.1, прямое разложение кольца теперь
осуществляется соответствием: х •—» (в((х), &l_i(x)), или х •—»
•—» (xz, х(1 — i)) для любого х G R. Элементы вида xz образуют
в R главный идеал /(z), а элементы вида х(1 - z)—главный идеал
/(1 - z). □
С л е д с т в и е 2.16. Всякое конечное булево кольцо раз-
лагается в прямую сумму колец Z2>
156
Доказательство. В булевом кольце, содержа-
щем более двух элементов, имеется элемент i, отличный от 0 и
1. По свойствам булева кольца, он является идемпотентом и
перестановочен со всеми элементами. Согласно теореме 2.53, этот
элемент определяет прямое разложение данного кольца. Так что
единственным неразложимым в прямую сумму булевым кольцом
является Z2. Теперь ссылаемся на теорему 2.13. □
Сравнивая доказательства теоремы 2.53 и следствия 2.4 из
теоремы 2.13, следует отметить разительное сходство рассуждений,
связанных с конгруэнциями в. и Оно объясняется тем, что
центральные (т. е. перестановочные со всеми элементами) иде-
мпотенты кольца образуют в нем булево подкольцо, а булевы
кольца—это фактически булевы алгебры в кольцевой интерпре-
тации.
§ 2.4.	Решетки
Пусть (S, <)—решетка, т. е. упорядоченное множество, в
котором для любых двух элементов a, b е 5 существует точная
верхняя грань sup (а, Ь) и точная нижняя грань inf (а, Ь). Тем
самым на множестве 5 определены две бинарные операции:
(а, Ь) •—» sup (а, Ь) и (а, Ь) •—» inf (а, Ь). Полагая a v b :=
:= sup (a, Z>), а л b := inf (а, Z>), получаем алгебру L = (S, V, л)
типа (2, 2), где операции v и л называются соответственно
объединением и пересечением. Таким образом, решетку можно
рассматривать и как специальное упорядоченное множество, и как
алгебру. Это позволяет вводить для решетки конструкции и
понятия как порядкового, так и алгебраического происхождения,
что приводит к богатой и многообразной в своих приложениях
теории.
Прежде всего выясним, какие алгебры типа (2, 2) являются
решетками в смысле описанной выше процедуры перехода от
упорядоченного множества к алгебре. Из самого определения
точных граней следует идемпотентность и коммутативность
операций	v	и	л.	Например, х v	х = sup (х, х) = х или
х л у =	inf	(х,	у)	=	inf (у, х) = у л	х. Простые рассуждения
доказывают ассоциативность х v (у v z) = (х v у) v z и
х л (у л z)	=	(х	л	у) л z. Например, если х л (у л z) =
= inf (х,	inf	(у,	z))	=	и, а (х л у) л z	= inf (inf (х, у), z) = v, то,
используя свойства точных нижних граней, получаем:
и < X,
и < inf (у, z)
и < х,
и < у,
и < Z
и < inf (х, у),
и < z
=> и < inf (inf (х, у), z) = v.
Аналогично, v < и, откуда, в силу антисимметричности порядка,
и = V.
157
Важную роль в теории решеток играют и следующие законы
поглощения, которые связывают операции sup и inf: inf (х,
sup (х, у)) = х, sup (х, inf (х, у)) = х. Они почти очевидны: так
как х < sup (х, у) для любого у, то всегда inf (х, sup (х, у)) =
= х. Двойственные рассуждения доказывают второе равенство.
Рассмотренные свойства и являются характеристическими для
операций inf и sup решетки.
Будем говорить, что алгебра (L, V, Л) типа (2, 2) ас-
социирована с решеткой, если на множестве L можно задать
порядок < таким образом, чтобы упорядоченное множество
(L, <) было решеткой и при этом чтобы операция sup в этой
решетке совпала с заданной на L операцией V, а операция inf—с
заданной операцией Л.
Т е о р е м а 2.54. Алгебра (L, V, Л) типа (2, 2) тогда и
только тогда ассоциирована с некоторой решеткой, когда в ней
выполняются следующие тождества'.
I.	(1) х v х = х, (2) х Л х = х (идемпотентность)',
II.	(1) х v у = у v х,	(2) х Л у = у Л х (коммута-
тивность)',
III.	(1)	х v (у	v	z) = (х V у)	v	Z,
(2)	х Л (у	Л	z) = (х Л у)	Л	z (ассоциативность)',
IV.	(1)	х л (х	v	у) = х, (2)	х	v (х л у) = х (законы
поглощения).
Доказательство. Необходимость условий теоре-
мы, т. е. выполнимость законов I—IV для операций sup и inf
решетки, уже доказана в предварительных рассуждениях. Покажем
достаточность. Пусть в алгебре (L, V, Л) истинны тождества
I—IV.
Рассмотрим на множестве L отношение ф := {(х, у) 6
G L х L\ х л у = х}. Условие 1(2) обеспечивает рефлексивность
отношения ф, условия Ш(2) и 11(2) обеспечивают его транзи-
тивность и антисимметричность. Например:
(х, у) £ и & (у, х) £ w => х Л у = х & у Л х = у => х = х Л у =
= у Л X = у.
Таким образом, (L, ф) является упорядоченным множеством.
Теперь, как обычно, вместо (х, у) £Е ф будем писать х < у.
Докажем, что (L, <)—нижняя полурешетка, в которой
inf = л. В самом деле,
11(2)	П1(2)	1(2)
(х Л у) Л X = X Л (х Л у) = (х Л х) Л у = X Л у => X Л у < X,
111(2)	1(2)
(хЛу)Лу = х л (у л у) = X Л у => X л у < у.
158
Это означает, что х л у является нижней гранью для х и у.
Если t—другая нижняя грань для х и у, то имеем
Z<x&Z<y=>ZAx=Z&ZAy=Z=>
Ш(1)
=> t Л (х Л у) = (t Л х) Л у - t Л у - t,
откуда t < х л у. Значит, элемент х л у—точная нижняя грань
для х и у.
Оказывается, что отношение порядка < можно определить и
другим способом. Именно, со := {(х, у) е L х LI х V у = у}.
Действительно,
(х, у) 6 И => X Л у = X => X V у =
11(1)	П(2)	IV(1)
= (х Л у) V у = у V (х Л у) = у V (у Л х) = у,
а с другой стороны,
IV(2)
X V у = у => X Л у = х Л (х V у) = х => (х, у) 6 W.
Итак, x<yoxVy = у.
Теперь рассуждениями, аналогичными тем, которые были
проведены выше при доказательстве равенства inf (х, у) =
= х л у, получаем, что в (L, <) для любых элементов х, у
существует точная верхняя грань sup (х, у) и что этот элемент
совпадает с х V у. о
Таким образом, переход от алгебраической формы задания
решетки к ее порядковой интерпретации и обратно осуществляется
формулой:
хЛ у = xox<yoxVy = у.
Тождества I—IV под теми же номерами входят в определение
булевой алгебры (см. § 1.1). Следовательно, если мы имеем булеву
алгебру В = (В, V, л, ', 0, 1), то ее редукт (В, v, л) является
решеткой. При этом тождества VI булевой алгебры показывают,
что элементы 0 и 1 будут соответственно наименьшим и
наибольшим ее элементами. Другими словами, булевы алгебры —
это некоторые специальные решетки. Какие именно, мы увидим
позднее.
Из теоремы 2.54 извлекается следующее любопытное
Следствие 2.17. Группоид (S, •) тогда и только
тогда ассоциирован с (верхней или нижней) полурешеткой, когда
он является идемпотентной коммутативной полугруппой.
Доказательство. Необходимость.
Если (5, <)—нижняя полурешетка, то операция inf в ней
идемпотснтна, коммутативна и ассоциативна.
Достаточность. Если группоид (5, •) удовлетво-
ряет трем указанным условиям, то отношение ш = {(х, у) G
159
G S X SI ху = x}, как показано при доказательстве теоремы 2.54,
задает на нем структуру нижней полурешетки, в которой
inf (х, у) = ху. Аналогичные рассуждения показывают, что
(S, •) можно рассматривать и как верхнюю полурешетку, где
sup (X, у) = ху. О
Полурешетки, т. е. идемпотентные коммутативные полугруп-
пы, играют самостоятельную роль в приложениях.
П р и м е р 71. Пусть G = (V, а)—произвольный неори-
ентированный граф. Ребро, соединяющее вершины и, v G V,
будем обозначать {и, у}—это слившаяся пара дуг (и, у) и (у, и).
На множестве S = V U a U {0} определим умножение (см.
[66]):
ху = ух :=
X,	если	х = у,
У,	если	х G у G а
{*, у},	если	{х, у} G а,
0 в остальных случаях.
Группоид (S, •) оказывается полурешеткой. Граф G однозначно
восстанавливается по ее диаграмме как нижней полурешетки:
ребрам соответствуют элементы высоты 1, а вершинам—элементы
высоты 2. При этом элементы и, у являются единственными
верхними соседями для элемента {и, у}. Это кодирование графа
полурешеткой сводит проблему изоморфизма графов к проблеме
проверки изоморфизма полурешеток. На рис. 44 показаны граф
G и диаграмма соответствующей ему нижней полурешетки как
упорядоченного множества. Ниже приведена таблица умножения
этой полурешетки.
О-------------о
VZ 62
Рис. 44
0	V1	v2	v3	е\	е2
0	0	0	0	0	0	0
Vj 0 Vj 0	0	0
г2	°	0	v2	е2	0	е2
v3	0	0	е2	v3	0	е2
0	i?j	0	0	<?j	0
е2	0	0	е2	е2	0	е2
160
Для решеток как алгебр обычным образом определяются
понятия подрешетки, гомоморфизма, изоморфизма, конгруэнции,
прямого и подпрямых произведений.
Следующий набор примеров показывает различие между
соответствующими порядковыми и алгебраическими конструк-
циями для решеток. На рис. 45а элементы решетки, помеченные
черными кружками, образуют в ней упорядоченное подмножество,
являющееся решеткой. Но оно не будет подрешеткой данной
решетки, поскольку не замкнуто относительно операции объедине-
ния. На рис. 456 показано изотонное отображение (порядковый
гомоморфизм) четырехэлементной решетки на трехэлементную
цепь, не сохраняющее ни объединения, ни пересечения. Рисунок
45в представляет изотонное отображение (порядковый гомо-
морфизм) той же решетки на двухэлементную цепь, сохраняющее
только пересечения. Перевернув этот рисунок, получим пример
изотонного отображения, сохраняющего только объединения. На-
конец, на рис. 45г изображено порядковое вложение одной решетки
в другую, не сохраняющее решеточных операций.
Рис. 45
С другой стороны, всякое отображение одной решетки в
другую, сохраняющее хотя бы одну из решеточных операций,
изотонно, т. е. будет порядковым гомоморфизмом. Например, если
отображение <р сохраняет объединение, то х < у => х V у =
= У =* <р(х) v ¥>(У) = <?(х v У) = <Р(У) =* Z’ W - и зна-
чит, <р изотонно. Однако понятие «изоморфизм» означает одно и
то же для решеток как упорядоченных множеств и как алгебр.
Т е о р е м а 2.55. Две решетки изоморфны как алгебры
тогда и только тогда, когда они изоморфны как упорядоченные
множества.
Доказательство. Необходимость.
Пусть <р—изоморфизм решетки (L, V, Л) на некоторую другую
решетку. Так как отображение <р взаимно однозначно и изотонно,
то остается убедиться в его обратной изотонности. Но, в самом
деле,
<р(х) - <Р(У) => <?(х) = <?(х) Л <Р(У) = Л у) => х =
= х Л у => х < у.
Достаточность. Пусть (Л, <) и (В, <)—две
решетки и <р—взаимно однозначное, изотонное и обратно изотон-
6 А.М.Богомолов, В.Н.Салий
161
ное отображение А на В, т. е. порядковый изоморфизм. Возьмем
произвольные элементы х, у G А. В силу изотонности отобра-
жения <р элемент <р(х Л у) решетки В будет нижней гранью для
элементов />(х) и <р(у). Пусть b—также нижняя грань для <р(х) и
<р(у) в (/?, <). Так как <р—биекция, то в Л найдется единственный
элемент а = <р \b). Но тогда
р(а) < <р(х) &	< <р(у) =>а<х&а<у=>
=>а<хЛу=>Ь = <р(а) < <р(х) Л <р{у).
Таким образом, <р(х К у) будет точной нижней гранью для пары
{<р(х), /’(у)}, т. е. <р(х Л у) = <р(х) К Двойственно доказы-
вается равенство <р(х V у) = <р(х) V <р(У)- °
Система аксиом I—IV, определяющая решетки, обладает тем
свойством, что если в каждой аксиоме взаимно заменить знаки
V и Л, то общая совокупность полученных тождеств совпадает
с исходной. Отсюда вытекает
Принцип двойственности для ре-
шеток. Если некоторый класс решеток можно задать
системой аксиом, не изменяющейся при взаимной замене знаков
V и Л во всех аксиомах, и в этом классе истинна формула
Ф(\/, Л), то в нем истинна и двойственная формула, получа-
ющаяся из Ф взаимной заменой знаков У и Л.
Пусть решетка (L, V, Л) имеет наименьший элемент 0 и
наибольший элемент 1, и пусть a G L. Дополнением элемента а
называется элемент b 6 L такой, что а Л b = О, а V b = 1.
Решетка, в которой каждый элемент имеет по крайней мере одно
дополнение, называется решеткой с дополнениями. Например,
всякая булева алгебра будет решеткой с дополнениями: допол-
нением произвольного элемента х в ней является элемент х'.
П р и м е р 72. Пусть А = (S, X, д)—полуавтомат, и кон-
груэнции , 6? G Соп А задают его параллельную деком-
позицию, т. е. и $2 нетождественны и Г) = А. Эта
параллельная декомпозиция называется простой, если
V 02 = S х S в решетке Соп Л. Таким образом, простые
параллельные декомпозиции полуавтомата находятся во взаимно
однозначном соответствии с парами его конгруэнций (в, в*), где
в, в* * А и в*—дополнение для в в решетке Соп А. Например,
всякая полная параллельная декомпозиция полуавтомата будет
простой. Но, как показывает пример 44 из § 2.1, полуавтомат
может иметь простую параллельную декомпозицию, но не иметь
полной. Пусть в—нетождественная конгруэнция полуавтомата А.
Существует ли нетождественная конгруэнция в* G Соп А такая,
чтобы пара (в, 0*) определяла простую параллельную деком-
позицию для А? Если в с нужным свойством существует, то
162
единственна ли она? Ответ на оба вопроса мы получаем,
анализируя устройство решетки конгруэнций Соп А данного
полуавтомата А.
Рассмотрим полуавтоматы А = (S, X, д) и В = (Т, X *, д),
заданные следующими таблицами переходов (см. [76]):
6А	X X N) X CM 4* О to	*	* X1	x2
S1 s2 s3 s4 sS s6 s7 s8	Sj	s5	s7	s4	tj s2	s6	s8	s3	f2 Sj	s7	s5	s2	t3 s2	s8	s6	S1	f4 s2	S1	s2	s8	f5 s2	s2	S1	s7	f6 S1	s3	S4	s6 S1	s4	S3	s5	f5	f2 f6	fl fl	f6 f2	f5 f3	f4 f4	f3
Нетрудно проверить, что конгруэнции 0р , $2}, {$3, $ },
{s5, s6), {sr s8) и Oy {sr s8}, {s2, s6}, {s3, s7), {s4, s5) задают
простую параллельную декомпозицию полуавтомата А. Однако
конгруэнция в  {s , s~, s,, s }, {s_, s.., s_, s„} вместе c 0, onpe-
деляет более экономную (по числу состояний) и к тому же полную
декомпозицию этого полуавтомата (конгруэнции 0, и 0 переста-
и
новочны, что устанавливается перемножением соответствующих
этим отношениям двоичных булевых матриц). На полуавтомате
В рассмотрим три конгруэнции, которые сразу зададим их
двоичными булевыми матрицами М[г М% и Му Легко вычисляем,
что М1 и М^ задают простую параллельную декомпозицию
полуавтомата В, а М^ и М^—полную параллельную декомпозицию
этого полуавтомата (ММ * ММ, но М М = ММ). Кроме
i £	XI	10	01
того, параллельная декомпозиция, определяемая матрицами М^ и
m3,	также	полна.			
	W1	=	1 1 0 0 0 0 1 1 0 0 0 0 0 0 1 10 0 0 0 1 10 0	, M2 =	10 0 10 0 0 10 0 10 0 0 1 0 0 1 10 0 10 0
			0 0 0 0 1 1 0 0 0 0 1 1		0 10 0 10 0 0 1 0 0 1
6'
163
мз
На рис. 46 изображены
венно пятиугольником N5
b = М2, с = Му i = Т X
элементами решетки Con В.
Рис. 46
10 10 10
0 10 10 1
10 10 10
0 10 10 1 •
10 10 10
0 10 10 1
гки, которые называются соответст-
1И Пентагоном) и ромбом М$ (или
диамантом). Конгруэнции, рас-
смотренные для полуавтоматов
А и В, как раз и приводят к
этим решеткам: если в пяти-
угольнике Ns положить 0 = Д$,
С а = в^, b = в2 с = 6^, i =
= SxS, то получаем в точ-
ности решеточные связи в
Con А, а конкретизация элемен-
тов ромба Му задаваемая ра-
венствами 0 = Aj., а = М^,
Т, описывает соотношения между
Обе решетки N и М^ являются решетками с дополнениями,
но дополнения в них определены неоднозначно: в N элемент с
имеет два сравнимых дополнения а < Ь, а в М$ каждый из трех
элементов а, Ь, с будет дополнением для двух других. Отсюда и
вытекает неоднозначность простых параллельных декомпозиций
полуавтоматов А и В.
Вопросы, аналогичные тем, которые возникают при изучении
параллельных декомпозиций полуавтоматов, привели к выделению
двух важнейших классов решеток.
Решетка L называется модулярной (или дедекиндовой), если
для любых х, у, z G L выполняется условие
х < у => х V (у Л z) = у Л (х V z),
называемое модулярным законом.
Заметим, что при х < у в любой решетке х V (у Л z) <
< у Л (х V z), так что смысл модулярного закона—в требовании
противоположного неравенства. Очевидно, что всякая подрешетка
модулярной решетки сама модулярна.
Т е о р е м а 2.56. Решетки конгруэнций групп и колец
модулярны.
Доказательство. Согласно теореме 2.38 § 2.3
решетка конгруэнций группы изоморфна решетке нормальных
подгрупп этой группы. В решетке нормальных подгрупп
164
Л Н2 = Hr П Н2 и V Н2 =	Следовательно, мо-
дулярность этой решетки равносильна выполнимости в ней
включения У Г) XZ С Х(У Г) Z) при X Q У. Но, в самом деле,
если t G У Г) XZ, то t G У и t - xz, где х G X С у и
z G Z. Так как z = x~lt G У, то t = xz, где х G X и
z G У (Т Z, откуда и следует требуемое включение.
Решетка конгруэнций кольца изоморфна решетке его идеалов
теорема 2.46 из § 2.3). Идеалы кольца, в свою очередь, образуют
юдрешетку в модулярной решетке (нормальных) подгрупп адди-
тивной группы кольца, о
Пятиугольник N5 дает пример немодулярной решетки:
а < Ь, но а V (Ь л с) = а, в то время как b л (а V с) = Ь. Этот
пример является ключевым: можно показать, что решетка
модулярна тогда и только тогда, когда в ней нет подрешеток,
изоморфных решетке N$. Этот критерий модулярности решетки
особенно часто используется в прикладных задачах. Из него
следует, в частности, что в конечной модулярной решетке
выполняется условие Жордана—Дедекинда для цепей: если в
решетке L две максимальные цепи между фиксированными
элементами а < b имеют разную длину, то интервал [а, А]
содержит подрешетку, изоморфную N .
Модулярный закон равносилен тождеству
X V ((х V у) Л z) = (х V у) Л (х V z).
Действительно, так как всегда х < х V у, то, заменяя в
модулярном законе у на х V у, получаем указанное тождество.
С другой стороны, если в решетке выполняется это тождество,
то она модулярна, поскольку при х < у, т. е. при х V у = у,
тождество превращается в заключение импликации, выражающей
модулярный закон. Отсюда следует, что любой гомоморфный образ
модулярной решетки модулярен, прямое и все подпрямые
произведения модулярных решеток являются модулярными решет-
ками.
Решетка называется дистрибутивной, если в ней выполняется
тождество х Л (у V z) = (х Л у) V (х Л z), называемое дист-
рибутивным законом.
Заметим, что в любой решетке имеет место неравенство
х Л (у V z) > (х Л у) V (х Л z), так что смысл дистрибутив-
ного закона состоит в требовании противоположного неравенства.
Всякая булева алгебра является дистрибутивной решеткой. Пяти-
угольник	дает пример недистрибутивной решетки:
b Л (а V с) = Ь, но (Ь Л а) V (Ь Л с) = а. Отсюда и из крите-
рия модулярности решетки заключаем, что всякая дистрибутивная
решетка модулярна. Другой пример недистрибутивной решетки—
это ромб М^. а Л (b V с) = а, но (a A b) V (а А с) = 0.
Эти примеры являются ключевыми: можно показать, что решетка
165
дистрибутивна тогда и только тогда, когда в ней нет
подрешеток, изоморфных решеткам N5 и М^. Этот критерий
дистрибутивности решетки особенно часто используется в прило-
жениях.
П р и м е р 73. Всякая цепь (линейно упорядоченное мно-
жество) является дистрибутивной решеткой. Это сразу следует из
критерия дистрибутивности. Но можно и непосредственно про-
верить истинность тождества
min (х, max (у, z)) = max (min (х, у), min (х, z)),
выражающего дистрибутивный закон в цепях (здесь а Л b =
= min (a, b), а V b = max (а, Ь)).
П р и м е р 74. Дистрибутивна и решетка (N, I) натураль-
ных чисел, упорядоченных отношением делимости. Здесь
т Л п = НОД (т, п), т V п = НОК (т, п). В терминах наи-
большего общего делителя и наименьшего общего кратного
дистрибутивный закон выглядит следующим образом: НОД (х,
НОК (у, z)) = НОК (НОД (х, у), НОД (х, z)). Запишем х, у, zb
каноническом представлении по степеням простых чисел:
х = Р[ р.‘, у = Р[ рz = П р.‘ (считаем, что показатели
i=l	i=l	i=l
степеней могут равняться нулю, если соответствующего простого
числа нет в данном разложении). Тогда
’ min (а , max (в , у ))
НОД (х, НОК (у, Z)) = П Pi ‘
48 1
* max (min (а , в ), min (а , у))
НОК (НОД (X, у), НОД (х, Z)) = П Pi ' '	' ' •
/8 1
Числа а , [5., у.—являются элементами естественно упорядоченной
цепи неотрицательных целых чисел. Для них выполняется
дистрибутивный закон в интерпретации примера 73, откуда сразу
вытекает дистрибутивность решетки (N, НОД, НОК).
П р и м е р 75. Поскольку пересечение подмножеств дистри-
бутивно относительно их объединения: X Г) (У U Z) =
= (X П У) U (X Г) Z),—то решетка (P(S), U, О) всех подмно-
жеств произвольного множества 5 дистрибутивна.
В решетке (P(S), U, О) выполняется и другой дистрибутивный
закон: X U (У П Z) = (X U У) Г) (X U Z). Оказывается, это
общее свойство всех дистрибутивных решеток.
Лемма 2.2. В каждой дистрибутивной решетке имеет
место закон дистрибутивности объединения относительно
пересечения:
х V (у л z) = (х V у) Л (х V z).
166
С другой стороны, каждая решетка, в которой выполняется
указанное тождество, дистрибутивна.
Доказательство. Используя тождества I—IV,
определяющие решетку, а также стандартный дистрибутивный
закон, получаем:
х V (у Л z) = [х V (х Л z)] V (у Л z) = х V [(х Л z) V (у Л z)] =
= X V [(х V у) Л z] = [(х V у) Л х] V [(х V у) Л z] =
= (х V у) Л (х V z).
Вывод стандартного дистрибутивного закона из тождества, приве-
денного в формулировке леммы, получается повторением преды-
дущих выкладок с взаимной заменой знаков V и Л—по
алгебраическому принципу двойственности для решеток. □
П р и м е р 76. Дистрибутивной решеткой является решетка
Sub А подавтоматов произвольного полуавтомата А = (S, X, д).
Она изоморфна решетке устойчивых подмножеств в полуавтомате
А, а устойчивые подмножества образуют подрешетку решетки
(P(S), U, О), поскольку теоретико-множественное объединение и
теоретико-множественное пересечение устойчивых подмножеств
устойчивы.
Неоднозначность дополнений, обсуждавшаяся в примере 72 в
контексте параллельных декомпозиций полуавтоматов, в дистри-
бутивных решетках невозможна.
Т е о р е м а 2.57. В дистрибутивной решетке с 0 u 1
каждый элемент имеет самое большее одно дополнение.
Доказательство. Пусть, в дистрибутивной ре-
шетке с 0 и 1 элементы b и с являются дополнениями для
некоторого элемента а. Тогда Ь = ЬЛ1=ЬЛ (а V с) =
— (Ь л а) v (Ь л с) = О v (Ь л с) = (а л с) v (b л с) =
= (а v Ь) л с = 1 л с = с. □
Следствие 2.18. Каждая булева алгебра является
дистрибутивной решеткой с дополнениями. С другой стороны,
каждая дистрибутивная решетка с дополнениями может расс-
матриваться как булева алгебра.
Доказательство. Тождества I—VII, входящие в
определение булевой алгебры, характеризуют ее как дистри-
бутивную решетку с наименьшим элементом 0, наибольшим
элементом 1, в которой дополнением для произвольного элемента
х служит элемент х'. С другой стороны, пусть (L, V, Л)—
дистрибутивная решетка с дополнениями. Согласно теореме 2.57,
каждый ее элемент а имеет в точности одно дополнение,
обозначаемое через а'. Тогда соответствие х ►—» х' представляет
собой унарную операцию на множестве L. В алгебре
(L, V, л, ', 0, 1) будут выполняться тождества I—VII булевой
алгебры. Проверка истинности тождеств VIII (инволютивность
дополнения) и IX (законы Де Моргана) также не вызывает
затруднений. Действительно, элемент (х')' является дополнением
167
для элемента х'. Но дополнением для х' будет и х, так что
(х')' = х в силу единственности дополнения. Чтобы убедиться в
справедливости первого закона Де Моргана IX, нужно показать,
что элемент х’ Л у' есть не что иное, как дополнение для
х V у, и затем воспользоваться единственностью дополнений.
Имеем:
(х V у) Л (х' Л у') = ((X V у) Л х') Л у'= ((х Л х') V (у Л х')) Л у' =
= (0 v (у л х’)) л у' = (у л х') л у' = (у л у') л х' = 0 л х' = О,
(х V у) V (х' Л у') = (х V (х' Л у')) V у = ((х V х') Л (х V у')) V у =
= (1 Л (х V у')) V у = (X V у') V у = X V (у' V у) = X V 1 = 1.
Двойственные рассуждения доказывают второй закон Де
Моргана IX. □
П р и м е р 77. Пусть G = (У, а)—произвольный ориенти-
рованный или неориентированный граф. Его подграфом называется
граф G* = (V*, а*), где V* С V, и а* = а| ,—ограничение
отношения а на подмножестве V*. Совокупность всех подграфов
графа G обозначим через Sub G. Понятно, что подграфы графа
G находятся во взаимно однозначном соответствии с подмноже-
ствами множества V. Будем писать G* < G*, если G^ является
подграфом в G*. Тогда G* < G% о С и, следовательно,
упорядоченные множества (Sub G, <) и (Р(У), —) изоморфны.
Отсюда получаем, что (Sub G, <)—дистрибутивная решетка с
дополнениями, т. е. булева алгебра. Ее наименьшим элементом
будет пустой подграф; наибольшим элементом будет сам граф
G; пересечение G* Л G^ имеет множеством вершин У^ О У^ и
множеством дуг а* Г) а*. Дополнением подграфа G * будет
подграф, множество вершин которого дополняет У* до всего У.
В объединении G* V G^ множеством вершин является У^ U У^,
а множество дуг состоит из всех дуг графа G, соединяющих
вершины из У^ U У^.
Просматривая список аксиом булевой алгебры (тождества I—IX
из § 1.1), можно заметить его избыточность. Действительно, в
любой решетке один из дистрибутивных законов V влечет за
собой второй закон. Инволютивность дополнения VI и законы Де
Моргана IX выводятся из I—VII. Законы идемпотентности I
вытекают из законов поглощения IV (например, применяя к
выражению х Л (х V (х Л х)) второе тождество IV, получаем
х, а вследствие первого тождества IV оно равно х Л х, и значит,
х Л х = х).
168
В настоящее время существует несколько очень коротких
неизбыточных списков тождеств для определения булевой алгебры,
но в отличие от стандартных условий I—IX, направленных на
нашу интуицию, связанную с алгеброй множеств и диаграммами
Эйлера—Венна, эти короткие аксиоматики носят формальный
характер. Вот, например, как выглядит минимальная самодвойст-
венная (не меняющаяся при взаимной замене знаков V и Л, а
также 0 и 1) система аксиом (см. [49]) всего из шести тождеств
(вместо девятнадцати классических):
А.	а)	(х	V	у)	Л	у	=	у,	б)	(х	Л у)	V у = у;
В.	а)	х	Л	(у	V	z)	=	(у	Л	х)	V	(z л	х),
б)	х	V	(у	л	z)	=	(у	V	х)	Л	(z V	х);
С.	а)	х	Л	х'	=	0,	б) х V х' = 1.
Рассматривая булеву алгебру как дистрибутивную решетку с
дополнениями, мы можем использовать терминологию и резуль-
таты теории упорядоченных множеств. Если В—булева алгебра,
то как уже отмечалось, отношение х<у:<»хЛу = х
(ox V у = у) превращает ее в упорядоченное множество,
которое является дистрибутивной решеткой с дополнениями.
Элементы 0 и 1 булевой алгебры становятся соответственно
наименьшим и наибольшим ее элементами, inf (х, у) = х Л у,
sup (х, у) = х V у для любых х, у G В, а дополнение х'
элемента х—это единственный элемент со свойствами
х Л х' = 0, х V х' = 1. Атомы булевой алгебры оказываются
верхними соседями нуля, т. е. атомами в смысле упорядоченности
<, их дополнения будут нижними соседями единицы, т. е.
коатомами упорядоченного множества {В, <). Обычным образом
строится диаграмма конечной булевой алгебры. При этом высотой
элемента а будет количество Л(а) содержащихся в этом элементе
атомов.
Операция дополнения обладает свойством антиизотонности
относительно порядка: х < у => х' > у'. Это следует из опреде-
ления порядка и закона Де Моргана:
х < у => х Л у = х => х' V у' = (х Л у)' = х' => х' > у'.
Представление элемента а булевой алгебры в виде объедине-
ния входящих в его состав атомов: а = V {ala < а} (см. § 1.1),
называется дизъюнктивной нормальной формой элемента а.
Применяя закон Де Моргана, получаем, что а = Л {а'1а <
< а'}, где а'—коатомы булевой алгебры, содержащие элемент а.
Такое представление называется конъюнктивной нормальной
формой элемента а. Идеалом булевой алгебры В называется ее
непустое подмножество J, которое:
1)	включает в себя 0;
2)	замкнуто относительно объединения V (т. е. если
а, Ъ G J, то а V b G J);
169
3)	вместе с каждым своим элементом а содержит все элементы
из В, содержащиеся в а. Часто это условие заменяют ему
равносильным: если а & J н х & В, то а Л х G J.
Например, множество aV всех элементов булевой алгебры,
содержащихся в данном элементе а, является идеалом. Это
главный идеал, порожденный элементом а. Если J—идеал
конечной булевой алгебры, то все элементы из J содержатся в
элементе V J = sup J, который также принадлежит J по свойству
2) идеалов, так что J = (sup J)V,—в конечной булевой алгебре
все идеалы главные. Пример неглавного идеала—совокупность всех
конечных подмножеств в алгебре всех подмножеств P(S) беско-
нечного множества 5.
Сама булева алгебра является своим идеалом. Это несобст-
венный идеал. Все остальные идеалы называются собственными.
Очевидно, что идеал будет собственным тогда и только тогда,
когда он не содержит элемента 1.
Следующее предложение показывает, что идеалы булевой
алгебры находятся во взаимно однозначном соответствии с ее
конгруэнциями.
Теорема 2.58. Если в—конгруэнция булевой алгебры
В, то класс := 0(0) является идеалом, причем
в = {(cz, 5)1 (в х G v х = b v х)}.
Обратно, если J—какой-либо идеал в В, то отношение
в{ := {(а, 5)1 (в х е J)(a V х = 5 V х)}
будет конгруэнцией, причем 0^(0) = J.
Доказательство. Пусть 0 G Соп В. Положим
:= 0(0). Тогда: 1) 0 е в силу рефлексивности 0; 2) если
а,	5 G J$,	то	(а,	0)	G	0, (5, 0)	G	0,	откуда (а	V	5,	0)	=
=	(а V	5,	0	V	0)	G	в,	т.	е. а V	5	G	J&; 3) если	a	G	и
х	G В, то	(а,	0)	G	0,	(х, х)	G	0,	откуда (а	Л	х,	0)	=
=	(а Л	х,	0	Л	0)	G	в,	т.	е. а Л	х	G	Ja. Следовательно, Ja—
и	и
идеал. Наконец, если (а, 5) G 0, то (а Л 5', 0) = (а Л 5',
5 Л 5') G 0, (0, а' Л 5) = (а' Л а, а' Л 5) G в, откуда а Л 5',,
и, значит, a tb = (а Л b') V V (а' Л 5) е J&. При этом
а V (a ib) = 5 V (a tb) (это свойство симметрической разности
непосредственно усматривается из ее диаграммы в Р(5)).
Обратно, пусть J—идеал булевой алгебры В, и отношение
dj определено как в условии теоремы. Рефлексивность этого
отношения следует из условия 0 G J, симметричность очевидна,
а транзитивность обеспечивается V-замкнутостью идеала J: если
а V x=5VxH5Vy=cV у для некоторых х, у G J, то
170
x v у G J и a v (x v у) = (a v x) v у = (b v x) v у =
= (b V у) V x = (с V у) V x = с V (x V у). Таким обра-
зом, Oj—эквивалентность.
Пусть (a, b), (c, ci) G Oj, t. e. aVx = bVx, cVy =
= d V у для некоторых x, у G J. Тогда x V у G J, и получаем:
(a v c) v (x v у) = (a v x) v (c v у) = (Z> v x) v (t/ v у) =
= (b У d) v (x v y),
(a Л c) v (x	v y)	= ((a л c) v x)	v у = [(a v x) л (c v x)] v у =
= ((Z> v	x) л	(c v x)J v у =	[(Z> v x) v у] л [(c v x) v y] =
=	[(Z> V x)	V y]	A [(c V y) V x]	= [(Z> V X) V у] A [(</ V y) V x] =
= [(Z> V	X) V	у] A [(</ V X) V y] = [(Z> V x) A (d V x)] V у =
= [(i л d) v x] v у = (b л d) у (x v y),
a V x = b V x => а' л x’ = b‘ A x' => (a' л x') V x = (b' л x') V x =>
=* (a1 v x) л 1 = (V v x) л 1 =* a' v x = b' v x,
t. e. Oj устойчиво относительно всех операций булевой алгебры.
Равенство 0ДО) = J получается следующим образом. Если
a G 0ДО), то а V х = х для некоторого х G J. Следовательно,
используя свойство 3) идеалов, имеем a = a Л (a V х) =
= а Л х G J, так что 0^(0) С J. Если же a G J, то из тождеств
a V а — а = а V 0 получаем, что a G 0^(0), откуда
/ С 0j(0). =
Если 0—конгруэнция булевой алгебры В, то факторалгебра
ВЮ обычно обозначается через В/J, где J—идеал, соответству-
ющий в смысле теоремы 2.58 конгруэнции 0.
Двойственным для понятия идеала булевой алгебры является
понятие фильтра. Фильтром булевой алгебры В называется ее
непустое подмножество F, которое:
1)	содержит единицу 1;
2)	замкнуто относительно пересечения Л (т. е. a, b G F =>
=> а Л b G Я;
3)	вместе с каждым своим элементом а содержит все элементы
из В, содержащие а.
Условие 3) часто заменяют следующим ему равносильным:
если aGFnxGB, тоа V х G F.
Например, множество аЛ всех элементов булевой алгебры,
содержащих данный элемент а, является фильтром. Это главный
фильтр, порожденный элементом а. Все фильтры конечной
булевой алгебры главные. Примером неглавного фильтра является
171
совокупность дополнений всевозможных конечных подмножеств в
алгебре всех подмножеств P(S) бесконечного множества S.
В общем случае, если J—идеал булевой алгебры В, то его
глобальное дополнение F = J' := {a' G Bl a G J} является
фильтром. Это фильтр, присоединенный к идеалу J. Сама булева
алгебра является своим фильтром. Это несобственный фильтр.
Все остальные фильтры называются собственными. Очевидно, что
фильтр будет собственным тогда и только тогда, когда он не
содержит элемента 0. Фильтрами булевой алгебры являются в
точности классы ее конгруэнций, содержащие единицу 1.
Таким образом, идеалы булевой алгебры—это прообразы нуля
при ее гомоморфизмах, а фильтры—это прообразы единицы.
В конечных дистрибутивных решетках общего вида атомы не
имеют такого значения, как в булевых алгебрах. Например, в
любой конечной цепи всего один атом. Гораздо большую роль
играют неразложимые в объединение элементы.
Ненулевой элемент а конечной решетки L называется
неразложимым, если для любых х, у Е L из а = х V у следует
а = х или а = у. Из этого определения следует, что в конечной
булевой алгебре неразложимыми элементами будут в точности
атомы. В конечной цепи неразложимы все ненулевые элементы.
В решетках N5 и М^, изображенных на рис. 46, неразложимы
элементы а, Ь, с.
Следующее простое наблюдение используется при построении
конкретных конечных решеток.
Лемма 2.3. В конечной решетке каждый ненулевой эле-
мент может быть представлен в виде объединения нераз-
ложимых элементов.
Доказательство. Если элемент а неразложим,
то а = а V а. Пусть а = al V а2, где а[ * а * а^. Если а[
и а2 неразложимы, то цель достигнута, в противном случае
представляем а^ и (или) а^ в виде объединения строго меньших
элементов, и т. д. В силу конечности решетки этот процесс
разложения элементов в объединение закончится, и исходный
элемент а будет представлен в виде объединения неразложимых
элементов, о
Множество всех неразложимых элементов решетки L обоз-
начим через Irr L.
Пусть (S, <)—произвольное упорядоченное множество. Под-
множество J С s называется полуидеалом в (5, <), если вместе
с каждым своим элементом а оно содержит все элементы из 5,
содержащиеся в а.
Лемма 2.4. Полуидеалы любого упорядоченного множе-
ства (S, <) образуют подрешетку решетки (Р(5), U, П).
Доказательство. Достаточно показать, что тео-
ретико-множественное объединение и теоретико-множественное
пересечение любых двух полуидеалов будут полуидеалами. Пусть
172
7p 72—произвольные полуидеалы упорядоченного множества
(S, <). Для любых а, х G 5 имеем: х < а & а & U 72 =>
=> х < а & (a G или a G 72) => (х < а & a G 7р или
(х < а & a G /р =» х G Jj или х G J=> х € U J^. Сле-
довательно, Jj U /2—полуидеал. Аналогично проводится доказа-
тельство для пересечения JГ) 72 (пустое подмножество тоже
считается полуидеалом). □
Следствие 2.19. Полуидеалы любого упорядоченного
множества образуют дистрибутивную решетку относительно
теоретико-множественного включения. □
На множестве Irr L неразложимых элементов конечной решет-
ки L индуцируется порядок, являющийся ограничением на этом
множестве порядка, заданного в L.
Т е о р е м а 2.59. Каждая конечная дистрибутивная ре-
шетка L изоморфна решетке полуидеалов упорядоченного мно-
жества IrrT, ее неразложимых элементов.
Доказательство. Пусть L—конечная дистрибу-
тивная решетка. Через J(L) обозначим решетку полуидеалов
упорядоченного множества (IrrT,, <). Очевидно, что для любого
a G L множество J(a) := {х G IrrT, I х < а}, состоящее из
неразложимых в L элементов, содержащихся в а, является
полуидеалом в (IrrT,, <). Заметим, что 7(0) = 0, по соглашению,
считается полуидеалом.
Покажем, что отображение
<р: L -♦ 7(7,), а >-> 7(a),
будет изоморфизмом упорядоченных множеств (L, <) и
(7(7,), С). Согласно лемме 2.3, а = V 7(a) для любого a G L.
Отображение <р взаимно однозначно. В самом деле,
<р(а) = <р(Ъ) => 7(a) = 7(5) => а = V 7(a) = V 7(5) = 5.
<р отображает L на 7(7,). Действительно, пусть 7—произвольный
полуидеал упорядоченного множества (7(7,), С). Положим
a = V 7. Тогда х < а для любого х G 7, так что х G 7(a), и,
значит, 7 С 7(a). Обратно, пусть х G 7(a). Если 7 = {ар
а2, ..., ар, то
z к \ к
х = хла = хл v а. = v (х л а.) =
\	i=i	‘
= (х л ар v (х л а2) v ... v (х л ар.
Но элемент х неразложим в L. Следовательно, х = х Л а. для
подходящего i. Значит, х < a. G 7. Поскольку 7—полуидеал,
173
получаем, что х G J. Таким образом, J(a) С J. Мы показали,
что для любого полуидеала J G J(L) будет J = <р(у J).
<р сохраняет порядок. В самом деле, для любых a, b G L
имеем:
а < b => <р(а) = J(a) С J(b) = <p(b) => а = V J(a) s V j(b) = b,
т. е. а < b о <р(а) С <р(Ь). Таким образом, решетки L и J(L)
изоморфны. □
Из доказанного и теоремы 2.55 получаем
Следствие 2.20. Две конечные дистрибутивные ре-
шетки и Z<2 тогда и только тогда изоморфны, когда
изоморфны упорядоченные множества IrrZ^ и 1гг£,2 их нераз-
ложимых элементов. □
Применим полученные результаты к решетке Sub А подавто-
матов произвольного полуавтомата А = (5, X, д'). Напомним, что
главным подавтоматом полуавтомата А называется всякий подав-
томат A(s), порожденный в А некоторым фиксированным состо-
янием s G 5.
Лемма 2.5. Ненулевой подавтомат А* полуавтомата А
тогда и только тогда является неразложимым элементом
решетки подавтоматов Sub А, когда А*—главный подавтомат.
Доказательство. Необходимость.
Пусть А* = (S*, X, д)—неразложимый элемент решетки Sub А.
Если 5* = {«j, s2, ..., s^}, то в решетке Sub Л будет А* =
= 4(Sj) V A(s2) V ... V A(sfc) = A(sx) V [A(s2) V ... V А($р]. В силу
неразложимости, А* = Af^), и тогда все доказано, или А* =
= А($2) V ... V А(«р. После нескольких шагов получаем, что
А* = A(s.) для некоторого состояния s. G 5*. Таким образом,
А*—главный подавтомат.
Достаточность. Пусть A(s)—главный подавтомат
полуавтомата А, порожденный состоянием s G S. Тогда для
любых Ар А2 G Sub А имеем:	A(s) = Aj V А2 => s G
G U 52 => s G 5( или s G => A(s) < А{ или A(s) < А?
С другой стороны,
A(s) = А1 V А2 => Aj < A(s) & А2 < A(s).
Следовательно, A(s) = Aj или A(s) = А2, т. е. подавтомат A(s)
является неразложимым элементом решетки Sub А. □
Как было выяснено в примере 76, решетка подавтоматов
любого полуавтомата дистрибутивна. Оказывается, имеет место
(см. [51]).
Т е о р е м а 2.60. Всякая конечная дистрибутивная ре-
шетка изоморфна решетке подавтоматов полуавтомата с двумя
входными сигналами.
174
Доказательство. Пусть L—конечная дистрибу-
тивная решетка и Irr L—множество всех ее неразложимых
элементов. Сначала построим множество S. Каждому минималь-
ному элементу а упорядоченного множества (1ггД <) взаимно
однозначно соотнесем элемент sQ(a). Пусть а—не минимальный
элемент. Тогда в (1ггД <) у него есть нижние соседи:
aQ, Пр ...,	к > 1. Сопоставим элементу а точно к различ-
ных элементов: sQ(a), s^a), ..., sk l(a). Проделав указанные
действия для каждого a G Irr L, закончим построение множества
S.
Полуавтомат A(L) = (5, X, д) с двумя входными сигналами
х(, х2 будет работать по следующим правилам:
1)	если а—минимальный элемент в (IrrZ, <), то
<5(s0(a), Xj) = s0(a) = d(s0(a), x2);
2)	если a—не минимальный элемент в (IrrZ,, <), то состояния
$0(а), Sjfa), ...,	относительно входного сигнала х2 образуют
цикл:
*0<а) - s/a) -•••- sk_x(a) - sQ(a);
3)	если	a—не	минимальный элемент в (Irr L, <) и
а0, Пр ...,	j—его нижние соседи, то
<5(s.(a), х2) = х0(й.), О < i < к - 1.
По построению, все главные подавтоматы полуавтомата A(L)
имеют вид Л($0(а)), a G Irr L. Напомним, что главные подавто-
маты—это в точности неразложимые элементы решетки подавто-
матов данного полуавтомата (лемма 2.5).
Отображение <р: A(sQ(a)) а является изоморфизмом упоря-
доченных множеств ({Л($0(а))1 a G IrrZ,}, <) и (IrrZ, <).
В силу следствия из теоремы 2.59, дистрибутивные решетки
L и Sub А(Е) изоморфны.
П р и м е р 78. На рис. 47 последовательно изображены:
конечная дистрибутивная решетка L, в которой неразложимые
элементы выделены черными кружками, диаграмма упорядочен-
ного множества (IrrZ, <), диаграмма полуавтомата A(L), полу-
чающегося из L применением конструкции, описанной в теореме
2.60.
Любая дистрибутивная решетка (L, V, л) является комму-
тативным полукольцом: обе операции ассоциативны, а пересечение
л коммутативно и дистрибутивно относительно объединения V.
Следующая теорема Биркгофа аналогична теореме Стоуна для
булевых алгебр.
175
*1

Рис. 47
Теорема 2.61. Всякая дистрибутивная решетка изо-
морфна подходящему полукольцу множеств.
Доказательство для общего случая, как и в теореме Стоуна,
мы не будем проводить, а для конечных дистрибутивных решеток
нужное представление дает теорема 2.59. =
Одним из важных практических следствий, вытекающих из
теоремы 2.61, является то, что при изучении конкретных
дистрибутивных решеток можно пользоваться языком диаграмм
Эйлера—Венна, интерпретируя элементы решетки как подмноже-
ства некоторого множества, а решеточные операции можно
отождествлять с соответствующими теоретико-множественными
операциями.
В § 1.1 были определены нечеткие множества. Они получаются
как частный случай следующей более общей конструкции.
Пусть 5—непустое множество, L—полная дистрибутивная
решетка (в приложениях чаще всего используются конечные
решетки). Под L-множествами, или L-нечеткими множествами,
на S понимают отображения а: 5 -* L. Если L = {0, 1},
получаются характеристические функции подмножеств множества
5; если L—отрезок [0, 1] числовой прямой в естественной
упорядоченности, то Z-множества на 5—это в точности нечеткие
подмножества множества 5. Совокупность всех Z-множеств на 5
обозначим через P^S).
В PL(S) поточечно вводятся операции объединения и пересе-
чения:
(а V Р)(х) := а(х) V ft(x), (а Л ft)(x) := а(х) Л /3(х).
Наименьшим элементом решетки (/*^(5), V, Л) будет харак-
теристическая функция пустого подмножества—это Z-множество
с постоянным значением 0. Наибольшим элементом будет
характеристическая функция самого множества 5, т. е. Z-множе-
ство с постоянным значением 1. Оставим для их обозначения
соответственно 0 и 5.
176
Если решетка L дистрибутивна, то дистрибутивной оказывается
и решетка P£(S).
В случае, когда L—булева алгебра, булевой алгеброй будет и
PL(S), если дополнение L-множества а определить условием:
а'(х) := [а(х)]'.
Напомним, что дополнение, обычно вводимое для нечетких
множеств (см. § 1.1)—это совсем другая операция: в решетке
([О, 1], <) нет операции дополнения, так что приведенная выше
формула в этом случае неприменима.
Определим теперь L-отношение, или L-нечеткое отношение,
на множестве S как отображение f: S X S -* L. Если L—двоичная
булева алгебра, то L-отношения на множестве S—это в точности
характеристические функции обычных отношений на S.
Когда нет необходимости специально выделять решетку L,
говорят о решеточных отношениях на данном множестве (правиль-
нее было бы говорить о решеточно-значных отношениях). Когда
L—булева алгебра, говорят о булевых (или булевозначных)
отношениях на данном множестве.
Кроме обычных для L-множеств операций в множестве
х S) всех L-отношений на множестве S вводят еще две
специальные операции: умножение и обращение. Если /, g £
£ PL(S X S), то полагают:
(/°g)(x, z) : = V (Дх, у) Л g(y, z))
yes
для любых х, z £ S. Здесь нужна полнота решетки L: в правой
части вычисляется точная верхняя грань бесконечного в общем
случае подмножества решетки L. Обратное L-отношение для
/ £ PL(S х S) вводится формулой:
/-1(х, у) : = /(у, х)
при любых х, у £ S.
Кроме 0 и S х S выделим в PL(S х S) характеристическую
функцию тождественного отношения, сохранив для него обозна-
чение:
* / х (1, если х - у,
(Л'> У) •	|q, если х у.
Очевидно, что f ° А = А ° / = / для любого / £ PL(S х S).
Если L—двоичная булева алгебра, то введенные операции
превращаются в операции умножения и обращения отношений,
записанные в терминах характеристических функций.
Если множество S конечно и имеет п элементов с фиксирован-
ным порядком их перечисления: S — {Sj, s^, ..., s^}, то L-отно-
шение / на множестве S удобно задавать матрицей M(f)
размерности п х и, проставляя на пересечении строки i и столбца
177
j элемент /(s., s\) решетки L. Тогда, как нетрудно убедиться,
произведению f°g будет соответствовать произведение матриц
M(f)M(g) над полукольцом (Z, V, Л), а Z-отношению/-1 будет
т
соответствовать транспонированная матрица [М(/)] .
Т е о р е м а 2.62. Если L—полная булева алгебра и S—не-
пустое множество, то система (PL(S х X), V, Л, °, ',	', 0,
S х S, А) является алгеброй отношений.
Доказательство. Специального внимания за-
служивает лишь тождество Шредера: [/ 1 °(/°g)'] Л g = 0 для
любых /, g е. PL(S х X),—все остальные постулаты алгебры
отношений проверяются без труда. Для любых a, b G X прямым
вычислением получаем:
I/-1 0 (/°g)'l(a, b) = V \f~’(а, х) л (/°g)'(x, 6)] =
х е S
= V [/(х, а) Л ((/°g)(x, />))'! =
х е $
= v г/(х, а) Л ( v (/(х, у) л g(y, д))\'1 =
X е s L \ у е S	/ J
= V Г/(х, а) I Л (/'(х, у) V g'(y, £>))Ч =
X е 5 [	I, У е 5	) J
=	V	л	[/(X,	а)	Л	(f'(x, у)	V g'(y, Л))]	=
х е S у е S
=	Л	V	[/(х,	а)	Л	(/(х, у)	V g'(y, Л))]	<
у е S х е S
< V |/(х, а) Л (/'(х, а) V g'(a, Л))] =
х е S
= V	(/(х, а) Л g'(a, £>))=/' V	/(х, а)'] Л g'(a, b).
х е S	\ х е S )
Следовательно,
(I/ ' ° (/°g)'l Л g)(a, b) = If 1 ° (f° g)'](a, b) Л g(a, b) <
< V /(x, а)) Л g'(a, d)) Л g(a, b) = 0,
откуда получается требуемое равенство Шредера. о
Следствие 2.21. Алгебра (М,(, V, Л, •, ', Т, О, I,
Efi) булевых матриц фиксированной размерности п х п явля-
ется алгеброй отношений. =
В алгебре отношений, как в любой решетке, вводится порядок:
178
х < у :о х V у = у (о х Л у = х).
Его важнейшие свойства, а также некоторые другие часто
используемые соотношения устанавливает
Т е о р е м а 2.63. В любой алгебре отношений истинны
следующие предложения:
1)	х Л у = 0 о х < у';
2)	О-1 = О, I-1 = 1;
3)	х < у => х-1 < у-1;
4)	(х Л у) 1 = х 1 Л у
5)	(х-1)- = (X')-1;
6)	х у => х ° z < y°z & z ° х < z ° у;
7)	(х Л у) о Z < (х о z) Л (у ° Z), X ° (у Л z) < (х ° у) Л (х о z).
Доказательство. Пусть А—произвольная алгеб-
ра отношений с носителем S.
1)	Пусть х Л у = 0. Тогда
х = х Л 1 = х Л (у V у') = (х Л у) V (х Л у') =
= 0 V (х Л у') = х Л у',
откуда х < у'. Если х < у', то
х Л у = (х Л у') л у = х Л (у' Л у) = х Л 0 = 0.
2)	Для любого элемента х G S получаем:
О-1 v х = О-1 V (х-1)-1 = (0 V х-1)-1 = (х-1)-1 = х =* О-1 < х,
и, значит, О-1—наименьший элемент в А, откуда О-1 = 0.
Аналогично, с использованием тождества (х V у) 1 =
= х-1 V у-1 устанавливается, что I-1—наибольший элемент в
А, т. е. 1 1 = 1.
3)	Для любых х, у G S имеем:
X < у => у = X V y => у’1 = (х V у)~1 = х~1 V у-1 => х~1 < у~1.
4)	Применяем уже установленное свойство 3):
X Л у < X & X Л у < у => (х Л у)-1 < х~1 & (х Л у)’1 < у-1 =>
=> (х Л у)-1 < х-1 Л У-1,
х-1 Л у-1 < х-1 & х~’ Л у-1 < у-1 =* (х-1 Л У-1)-1 £
< X & (х 1 Л у”1)”1 <у* (х-1 Л у1)-1 X Л у => х-1 Л у-1 <
< (х Л У)-1.
В силу антисимметричности порядка, (х Л у)-1 = х1 Л у-1.
179
5)	Используя тождество (х V у) 1 = х 1 V у 1 и свойства
2.4, получаем:
х-1 V (х')-1 = (х V х')-1 = I-1 = 1,
х-1 V (х')"1 = (х л х')-1 = О-1 = О,
и, значит, элемент (х')-1 является дополнением для х1. В силу
единственности дополнений, (х')-1 = (х *)'.
6) Применяется тождество (х V у)-1 = х-1 V у-1 и дис-
трибутивность умножения относительно сложения. Например,
х < у => у = X V у => у ° z = (х V у) ° Z = (х ° z) V (y°z)=>
=> х ° z < y°z.
7) Является непосредственным следствием свойства 6). о
Следующий общий результат широко используется при реше-
нии уравнений в различных алгебрах отношений.
Т е о р е м а 2.64. Уравнение а ° х = Ь разрешимо в алгеб-
ре отношений тогда и только тогда, когда ему удовлетворяет
элемент xQ = (а~1°Ь')'. При этом xQ является наибольшим
решением указанного уравнения.
Доказательство. Тождество Шредера [х-1 °
°(х°у)'] Л у = 0, ввиду свойства 1) из теоремы 2.63, можно
переписать в виде х '°(х°у)' < у'. Применяя антиизотонность
дополнения, имеем у < [х 1о(х°у)']'. Пусть с—произвольное
решение уравнения а ° х — Ь, т. е. а ° с = Ь. Согласно тождеству
Шредера, с < (а ’° (а ° с)')' =
дестве Шредера х = а-1, у
(а 1 ° д’)' = x(J. Полагая в тож-
= Ь', имеем а°(а~1°Ь')' < Ь,
т. е. а ° xQ <
Ь. В силу антисимметричности порядка, а ° xQ = b,
Рис. 48
и, значит, х0 = (а 1 ° Ь')' является решением
уравнения а ° х = Ь. о
Пример 79. Рассмотрим матричное
уравнение АХ = В, где
	а b а		b 0 1	
А =	у 0 с	, В =	1 р Ъ	
	1 /3 0		уса	
а булева	алгебра,	которой принадлежат эле-		
менты обеих матриц, представлена диаграммой				
на рис. 48.
180
Последовательными вычислениями получаем:
	а	У	1		0	1	0		с
АТ =	Ь	0	0	, в' =	0	b	0	, АТВ' =	0
	а	с	0		с	У	а		0
Хо = (АТВ'У =
у а
ь 0
1 а
а
1
b
лх0 = В.
а а
Ъ О
а 0
Таким образом, уравнение АХ = В разрешимо, и матрица
XQ является его наибольшим решением. Другим решением будет,
например, матрица
у а а
О 0 у
1 а Ь
X
1
Поэлементное сравнение показывает, что Xl < XQ.
Пусть L—булева алгебра и S—непустое множество. Назовем
L-отношение f S х S) однозначным, если для любых
х, Ур у2 е S, yf * у2, выполняется условие /(х, yt) Л /(х, у2) = 0.
Обратная однозначность L-отношения f выражается равенством
/(х., у) Л /(х_, у) = 0 для любых х., хэ, у е S, X. * х_, что
равносильно однозначности обратного L-отношения /-1.
Однозначность L-отношения / над конечным множеством S
распознается по матрице M(f) тем, что в каждой ее строке любые
два разных элемента имеют нулевое пересечение. Аналогично,
обратная однозначность для / равносильна тому, что нулевое
пересечение имеют любые два разных элемента каждого столбца
в матрице M(f). Говорят, что / S P^(S х 5) взаимно однозначно,
если оно однозначно и обратно однозначно. Нетрудно заметить,
что когда L—двухэлементная булева алгебра, введенные понятия
превращаются в одноименные свойства обычных отношений на
множестве S.
Согласно определению порядка в алгебре отношений, неравен-
ство f < g для f, g е PL(S х S) означает, что /(х, у) <
< g(x, у) при любых х, у е S. Переписав условие однозначности
L-отношения / в виде /(х, у^ Л /(х, у2) # 0 => у1 = у2, или
/ — 1(у1, х) л /(х, у2) # 0 => у1 = у2, замечаем, что оно оказы-
вается равносильным неравенству f~l ° f < А. Аналогично, алгеб-
раическим эквивалентом обратной однозначности будет
неравенство /°/ -1 А. Как видим, соответствующие наблюдения
для обычных отношений (см. теорему 1.15), являются частными
случаями этих общих замечаний.
181
§ 2.5. Функциональные системы
Под функциональной системой понимается алгебра, носителем
которой является некоторое множество функций.
Примерами функциональных систем могут служить симмет-
рический моноид и симметрическая группа, булева алгебра
характеристических функций подмножеств некоторого множества.
Другие возможности показывает
П р и м е р 80. Пусть 5—некоторое непустое множество и
п > 1. Через ^n(S) обозначим совокупность всех «-местных
функций на нем, т. е. отображений вида fi Sn -* 5. Определим
в Fn(S) операцию подстановки, для любых /,	..., fn е Fn,
х,, х_, ..., х G 5 полагая
12	П
:= f(f^xv xv •••> \)...fn<xv •••> *„))•
Тем самым Fn(S) превращается в алгебру типа (п + 1). Операцию
подстановки будем обозначать символом ст:
ст^ /г •••• Л) == Шг 4)’
Рассмотрим ситуацию, описанную в этом примере, с абстрак-
тной точки зрения.
Алгебра А = (А, ст) типа (.п + 1) называется сверхассоциа-
тивной системой, если в ней выполняется тождество сверхас-
социативности:
ст(х, ст(уг zr ..., zn), ..., ст(уп, zt.zn)) =
= o(o(x, y{, ..., yj, z{, ..., zj.
Говорят, что сверхассоциативная система А имеет полный набор
селекторов, если существуют е2, ..., еп е А такие, что
истинны тождества
а(е,, х,, ..., х ) = х., 1 < к < п;
' к’ V ' п'	к'	’
а(х, е,, ..., е ) = х.
v Г	п7
Элементы ек называются селекторами.
Теорема 2.65. Совокупность Гп($) всех п-местных
функций на непустом множестве S с операцией подстановки
является сверхассоциативной системой с полным набором
селекторов.
182
Доказательство. Проверку сверхассоциативнос-
ти для простоты записи проведем при п = 2. Пару (хр х2)
обозначим через х. Нужно доказать, что для любых /, g^, g^,
Л2 е F2(S) и лю^ого х е S х S выполняется равенство
hi^S2(hv h2)))(x) = ((f(g{, gJKh', Л2))(х).
Отдельно вычисляем левую и правую часть и проверяем
совпадение финальных выражений:
(ftg^, h2), g2(h}, Л2)))( х ) = /((^(Лр Л2))( х ), (g/Лр Л2))( х )) =
=	(Aj( х ), Л2( х )), g/h^ х ), Л2( х ))),
((f(gv £2))(Ар А2))( х ) = (f(g{, g2))(Aj( x ), Л2( x )) =
= /(^(AjC x ), Л2( x )), g2(Aj( x ), Л2( x ))).
Селекторами в Fn(S) будут функции
е,(х,, х_, х ) := х,,	1 < к < п. □
к4 Г 2 п' к
Следующая теорема [68, 88] сводит вопрос об изучении
сверхассоциативных систем к функциональным системам, рассмот-
ренным в примере 80.
Теорема 2.66. Всякая сверхассоциативная система
типа (п + 1) допускает вложение в подходящую функциональную
систему (F^S), а).
Доказательство. Полезно рассмотреть сначала
один важный частный случай. Пусть А = (А, ст)—сверхас-
социативная система типа (п + 1) с полным набором селекторов
вр ..., еп. Построим ее вложение в алгебру (Fn(A), ст). Произволь-
ному элементу а е А сопоставим функцию Ап -* А, полагая
/ (Ь., ..., b ) := а(а, Ь., ..., Ь )
J Г	п' v ’ Г ’ п'
для любых Z>p ..., А. Отображение а >—♦ f взаимно одно-
значно:
Л = а - а(а^ •••, е ) = / (е,, ..., е ) = f.(e,, ..., е ) =
а 'о	v Г п' Jа> г п' 'Г п7
= а(Ь, ег ..., еп) = Ь.
Нужно показать, что отображение а fa является гомоморфиз-
мом, т. е. что
....S?
i /г	1	п
183
для любых а, Ь,, b , с,, .... с G А. Но, в самом деле, исполь-
1 П 1 п
зуя сверхассоциативность, получаем
Л(а, Ь , .... Ь /С1.С«) := а(а(а’ \)’ С1’	с«) =
I п
= а(а, a(bv ср ..., cj, ..., а(Ьп, ср ..., cj) :=
.= a(a,fb(cv...,cn), ...,/д(С1,...,сп)): =
1	п
1	п
1	п
В общем случае сверхассоциативная система А = (А, а) может
не иметь полного набора селекторов, и тогда базисное множество
функциональной системы, представляющей А, приходится расши-
рить. Именно, положим 5 = A U {<?}, где е (£ А. Произвольному
элементу а Е А сопоставим функцию ft Sn -* S, полагая
fa(bv •••’ V :=
а(а, b,, ..., b ), если b,,...,b е А;
v ’ 1’ ’ п'	г ’ п ’
а,	если b = ... = b = е;
е в остальных случаях.
Отображение а >—♦ f взаимно однозначно:
fa = fb~ а = С> = 4^’ С> = Ъ-
Для доказательства того, что построенное отображение явля-
ется гомоморфизмом, нужно рассмотреть три случая.
а)	Ср ..., с Е А. Здесь проводятся те же рассуждения, что и
в случае системы с полным набором селекторов.
б)	с = ... = с = е. В этом случае
/. а . Дс, ..., е) := ст(а,) : =
Ja(a, ft)' 7	' ’ Г n7 a' 1’ n7
:= fa(fb (e,	e), ..., fb (e, ..., e)) = (a(fa, fb , ..., fb ))(<?, ..., c).
I	n	In
в)	В остальных ситуациях
f . .	, (с , ..., с ) := е = (a(f , f,,..., с ). □
a(a. b , b )' I n7	v va b Jb''K Г n7
In	in
Пусть A = (A, a)—произвольная алгебра типа (n + 1). В
множестве Ап определим бинарную операцию (умножение)
формулой
(а., ...,	а ) (Ь.,	..., Ь )	:= Ма., Ь.,	..., Ь ),	..., а(а , Ь.,	...,	b ))
v 1	п' v 1 И7 v v Г 1	’ П7’	’	' п 1’	’ п77
для любых а,, ..., а , Ь.у .... b 6 А.
I’	’ и’ 1’	’ и
Теорема 2.67. Группоид (Ап, •) тогда и только тогда
будет полугруппой, когда (А, ст)—сверхассоциативная система.
Доказательство. Пусть а^, ..., ап, Ь^, ..., Ьп,
Ср ..., сп—произвольные элементы. Тогда
(al,...,an)((bl,...,bn)(cl,...,cn)) =
= (аг	•••>	•••>	..., сп)) =
= (ст(ар ст(Ар с,, ..., сп), ..., а(Ьп, ср .... с^)), ...
а(ЬГ СГ сн>’ <Ьп> СГ
((Стр .... an)(ip ..., \))(С1.с„) =
= (ст(«р Ар ..., bj, .... а(ап, bv .... in))(cp .... с,) =
= (ст(ст(«р Ар .... Ьп), Ср ..., сп), ..., ст(ст(стп, Ар ... Ьп), Ср .... с^)).
Согласно тождеству сверхассоциативности, ст(ст(яр Ар ..., А^),
Ср ..., сп) = ст(аг ст(Ар Ср ..., сп).а(Ьп, с{.cj) для любого
k = 1, 2, ..., п. Таким образом, если (А, а)—сверхассоциативная
система, то группоид (Ап, •) ассоциативен. С другой стороны,
если (Ап, •)—полугруппа, то в силу произвольности элементов
Яр ..., ап, Ар ..., А , Ср ..., с;1 е А получаем сверхассоциативность
операции ст. □
Пусть 2L = {0, 1}. Функции /: 2?" -» В называются п-мес-
х	X	Z
тными булевыми функциями. Элементами 2?” являются всевоз-
можные n-мерные двоичные векторы. Каждый такой вектор можно
рассматривать как двоичную запись некоторого числа. Следова-
тельно, 2?” представляет собой не что иное, как числовое
множество {0, 1,..., 2”- 1}, элементы которого закодированы их
двоичными изображениями. Согласно теореме 2.67, функциональ-
ной системе F = F (BJ «-местных булевых функций соответ-
ствует полугруппа (2^, •), элементами которой являются п-мерные
векторы / = (/р /2, с компонентами из Fn. Для краткости
положим
/(а) := (//я), /2(я), ...,/п(я))
для любого я е 2?".
185
Теорема 2.68 (см. [561). Отображение, сопоставляю-
щее каждому f G Fnn подстановку
~	( О 1	•"	2" - 1 )
U(0) л1) - 7(2"-ij’
где f(i)—десятичное число, соответствующее двоичному набору
f(i), является изоморфизмом полугруппы	•) на симметри-
ческую полугруппу на множестве {1, 2,	2” — 1}. При этом
отображении подмножество
Гпп := (g& Fnn: (?a,b G B")(a # b => g(a) * g(b))}
будет прообразом группы перестановок множества {0, 1, ...
..., 2” - 1}.
Доказательство. Инъективность отображения
f ♦ / очевидна.
Пусть р—произвольное преобразование множества {0, 1, ...
..., 2” — 1}. Для каждого 0 < I < 2” — 1 элемент <p(i) представим
в двоичной записи: p^typ^i) ... <pn(i). Упорядоченный набор
(<р.(0), <Pj(V), ...,<рр.п — 1)), где 1 < j < п, однозначно определяет
некоторую булеву функцию f G Fn, и, следовательно, f =
=	е ?п П Очевидно, что f = <р. Таким образом,
рассматриваемое отображение сюръективно. Покажем, что оно
является гомоморфизмом. Используя определение умножения в
полугруппе (F п, •), получаем:
(7'5)(O =	..., gn), ..., °(fn(gv £„)))(*) =
= ^(KO),..., fn(g(i))) = 7(5(0)-
откуда
7 ' g = 7° g-
Итак, отображение f * / в самом деле является изоморфизмом.
При этом подмножество Г” С Fn ” отображается на множество
всех перестановок множества {0, 1, ..., 2" — 1} и, следовательно,
образует группу, изоморфную симметрической группе SP п. □
Пусть А = (Л, ст)—сверхассоциативная система типа (и + 1).
Возьмем произвольный элемент a G А и, как в доказательстве
186
теоремы 2.66, сопоставим ему n-арную операцию на множестве
А:
fa(bi..bn> := Ь1........ Ьп>
для любых Z>p b е А. Получается алгебра {A, /а) типа (п).
Алгебры такого вида, получаемые из функциональных сверх-
ассоциативных систем, используются при организации контроля в
логических схемах.
П р и м е р 81. На множестве В2 = {0, 1} можно задать
шестнадцать различных функций от двух переменных, представ-
ленных в следующей таблице:
4 4
4 4
4 4 4 4 4 4 4о 4i 4z 4з 4« 4$
о о
О 1
1 о
1 1
оооооооо
0	0	0	0 1	1 1	1
0	0	1	1 0	0 1	1
0	10	10	10	1
iiiiiiii
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 10 10 10 1
Некоторые из этих функций имеют индивидуальное название
и специальное обозначение. Их можно трактовать также как
бинарные операции на множестве В2- Наиболее известными
являются:
КОНЪЮНКЦИЯ ДИЗЪЮНКЦИЯ	/1(хг х2) = /7(*1, х2) = Xj	Л х2' v х2,
импликация	/1з(хг х2) =	-* х2,
эквивалентность	— Xj	« х2,
сложение по модулю	2	х2) = xt	Ф х2
штрих Шеффера	/14(х1 ’ Х2^ = *1	1 Х2,
стрелка Пирса	/8(хг х2) = X]	1	Х2’
постоянные функции	/0(Х1, х2) = 0,	
	Л5^х1’ х2> = 1	
Функции /Ах,, хА = х. и /Ах., х ) = х_ представляют со-
□	1	1	3	1	*>
бой селекторы.
Функциональная сверхассоциативная система F2 = F^B^)
двуместных булевых функций порождает 16 группоидов, получа-
ющихся фиксированием в тернарной операции подстановки первого
аргумента. Операцию в группоиде естественно обозначать симво-
лом определяющей его функции.
Группоиды (F2, Л) и (Fj, V), соответствующие конъюнкции
и дизъюнкции, являются изоморфными полурешетками. Изо-
морфизмом будет отображение /.	* /*, 0 < i < 15. Оно явля-
187
ется взаимно однозначным преобразованием множества F^, и
(f. Л f)’ = /(! V f. (закон Де Моргана).
Группоид (Л,, -»), порождаемый импликацией, неассоциативен
(например, (/б “* Л) “*/7 =/9 “*/7 =/7> но /6 “* (7, “* /7) = /6 “*
-»/=/). Он также некоммутативен (например, /_ -»f = / ,
1010	V 1	1 0
но -»/0 = /14). Элемент / = 1 является в этом группоиде
правым нулем (f. -»/ = / для всех i) и левой единицей
(f , -» f. = f. для всех z). Так как /.-♦/. = / тогда и только
тогда, когда f. < f. в поточечном сравнении, то естественный
порядок для двуместных булевых функций оказывается выражен-
ным через операцию рассматриваемого группоида.
Совокупность Fn =	всех ^-местных булевых функций
является булевой алгеброй относительно операций
(71 V /2)(х,, х2, ..., xt)	:=	^(Хр	х2,	....	Х() + /2(Хр	х2,	..., хп),
(/1 Л /2)(Хр х2, ..., х()	:=	^(Хр	х2,	...,	х()-/2(хр х2, ...,	х(),
/'(Хр х2, ..., Х()	:=	|7(Хр	х2,	...,	х()]',
0(х17 хэ, х )	:=	О,
v 1	2 /г
1(Хр Х2, ..., хн) := 1,
где в правых частях действия выполняются в двоичной булевой
алгебре = (В2, +, •, ', 0, 1). Как и в каждой булевой
алгебре, в F вводится порядок по формуле
Л - }2 Л Л 6 = Л Л V }2 =
Наименьшим элементом в Fn	постоянная функция 0, а
наибольшим элементом—постоянная функция 1.
Булева алгебра F конечна и, как было показано в § 1.1,
каждый ее элемент равен объединению всех содержащихся в нем
атомов (такое представление называется дизъюнктивной нормаль-
ной формой этого элемента). И в то же время каждый ее элемент
равен пересечению всех содержащих его коатомов (такое пред-
ставление называется конъюнктивной нормальной формой этого
элемента).
Учитывая определение порядка в F , получаем, что атомами
этой булевой алгебры будут функции вида:
1, если (/»,,/»_,...,/») = а,
v г 2’ te
О в остальных случаях,
/ (b , b , ..., />):=(
(Г Г 2 /Г
188
где а = (яр а2, ап)—некоторый n-мерный двоичный вектор.
Например, в F атомами будут функции f , / , f и f (пример
Z	1 Z 4 о
81).
Положим х1 := х, х° := х'. Тогда
а а	а
/а(хгх2, ...,хн) = X/ Л X/ Л ... Л хп\
тт	а а	а
Действительно, конъюнкция Л х^ Л ... л х^ принимает зна-
чение 1 только при
а	а	а
х.1 = х< = ... = х п = 1.
1	2	п
а
Если а. = 0, то х.' = х'„ откуда х. = 0; если а. = 1, то
а.
Х.‘ = X. И X. = 1.
I	I I
Заметим еще, что f < f тогда и только тогда, когда
/(Яр а2, ..., я^) = 1. Теперь из проведенных рассуждений получа-
ется
Теорема 2.69. Каждая п-местная булева функция, от-
личная от 0, однозначно представима в дизъюнктивной
нормальной форме
а а	а
/(хр х2, ..., х() = V (х/ Л х22 Л ... Л х^),
°2..........................=	1
где объединение справа берется по всем таким двоичным наборам
(я,, яэ, ..., я ), что /(я,, я., ..., я ) = 1. о
v 1	2 п'	v Г 2 п'	'
Булева алгебра F^B^ имеет 2” атомов: это количество
всевозможных n-мерных двоичных векторов, и, следовательно, в
ней 2 элементов (следствие из теоремы Стоуна, § 1.1).
Дуальными атомами (коатомами) в Fj(B2) будут дополнения
атомов При этом для Ь., Ь-, ..., b G. В- имеем:
a r	1’ 2’ и 2
[0, если (Ь,, Ь., ..., Ь ) = я,
_ j 7	' г 2’ н'
11 в остальных случаях.
а’ а'	а'
= х.1 V х 2 V ... V х ". В самом деле,
12	п	«	,
а'
V ... V х ” принимает значение 0 только
а'	а'
с" = 0. Если я. = 0, то х.' — х., откуда
а'
х. = 0. Если я. = 1, то х.' = х'. и, значит, х. = 1. Понятно,
i	iii	i
что f < f тогда и только тогда, когда /(я., я_, ..., я ) = 0.
а'	\ L п
Из этих рассуждений следует
’ ьг..., bj
Тогда / ,(х , х_, ..., х )
а 1 z	п
а'	а’
ДИЗЪЮНКЦИЯ Xj1 V Х22
при Xj1 — Х2 = ... =
189
Теорема 2.70. Каждая п-местная булева функция, от-
личная от 1, однозначно представима в конъюнктивной
нормальной форме
Лхг х2, ..., хп) = л (х“‘ V х“2 V ... v х“Л),
Лв(’ “г •••• V = 0
где пересечение справа берется по всем таким двоичным наборам
(ар а2, ..., ап), что /Ц, а2, .... ап) = 0. о
П р и м е р 82. Укажем нормальные формы для некоторых
двухместных булевых функций (см. пример 81). Имеем:
/0(Х1> х2)	=	0 =	Ц	V	х2)	Л (Xj V х')	Л	(х{	V	х2)	Л	(х{ V	х'),
•^1(х1’ Х2)	Х| Л	Х2	(Х|	V х2) Л (Xj	V	х2)	Л	(Xj	V	х2),
/6(xr х2)	=	Xj®	х2 = (xj Л	х2) V (xt Л	х2) =	(xt	V х2)	Л (х'	V	х2),
/7(Хр х2)	=	х, V	х2	=	(xj	Л х2) V (Xj	Л	х2)	V	(Xj	Л	х2),
/8(х1> х2^ ~ Х1 ^х2~ Х1 Л х2 = (Х1 V Х2> Л (Х1 v Х2^ Л (Х1 V Хг)’
А)(Х1 ’ Х2^	Х1**Х2 (Х1 Х2^ V (Х1 Х2^ (Х1 V Х2^	(Х1 V х2)’
/. ,(х., хэ) = х. -»хэ = (х.' Л х') V (х.' Л х_) V (х. Л X,) = X.' V х_,
10' 1 Xz IX	1 X	1 Xz	IX	IX
•^14^Х1 ’ Х2^ Х1' х2 (Х1	Х2^ V (Х1	Х2^ V (Х1	Х2^ ~ Х1 V Х2’
/15(х1> х2) = 1 = (Х1 л х2) V (Х1 Л х2) V <Х1 Л х2> V (Х1 Л Х2>'
Заметим, что в приложениях операции V и л булевой алгебры
F (В.) часто обозначают символами + и • соответственно, и это
более естественно, поскольку эти операции получаются перене-
сением на Fn(B2) логических операций сложения и умножения
из В2. В этой символике дизъюнктивная и конъюнктивная
нормальные формы булевой функции записываются соответственно
как
а а а
f(xv Х2, ..., Хп) =	2	Х1'Х22-Хп
а2...<9 = 1
и
г1-»	g а	а
/(хгх2, ...,хп) = П (х^+х^ + .-. + х^),
л*. •••’<9 = о
190
или в еще более короткой форме
Л	Л
/(хгх2,...,хп)	2 П xi‘ П Ё xi-
f(av а2, .... aj = 1 i=l Ла(, а^, .... aj = 0 1=1
В частности, в F2(B2) получаем (см. пример 82):
X. ф X =	х'х_	+	х.х'	=	(х.	+ х_)(х'	+ х/),
1 X	IX	IX	1	XI	X
X, J х2 = х[х± = (Xj + xp(Xj + х2)(х{ + х2),
х -* X = х,'х' + х'х_ + Х.Х- = х' + х_,
1 X	IX	IX	IX 1	X
Xj 1х2	=	XjX2	+	XjX2	+ Х]Х2	=	Xj +	Х2>
Одной из самых известных областей применения булевых функций
является теория релейно-контактных схем.
Как следует из теорем 2.69 и 2.70, всякая булева функция
от п переменных может быть представлена с помощью дизъюнк-
ции, конъюнкции и отрицания—это логические синонимы для
объединения V, пересечения л и дополнения '. Указанные три
логические операции допускают естественную трактовку в терми-
нах электрических сетей.
Будем обозначать переключатели в сети буквами х, Xj,
х2, ... Если Xj и х2—переключатели, то параллельное их
соединение пропускает ток тогда и только тогда, когда хотя бы
один из этих переключателей включен, а последовательное их
соединение пропускает ток тогда и только тогда, когда включены
оба переключателя. Кроме того, переключателю х можно сопо-
ставить противоположно действующий переключатель х', включа-
ющийся при выключении х и выключающийся при включении х.
Таким образом, булевым выражениям х + х_, х.х_ и х' можно
1 X 1 X
соотнести элементарные электрические схемы, изображенные на
рис. 49.
Рис. 49
Поскольку, согласно теоремам 2.69 и 2.70, каждая булева
функция может быть выражена через дизъюнкцию, конъюнкцию
и отрицание, стоящее у переменных, ей можно сопоставить
некоторую электрическую схему, в которой переключатели,
помеченные одним и тем же символом переменной, срабатывают
одновременно (например, все они подключены к одному реле).
191
П р и м е р 83. Построить схему освещения с тремя перек-
лючателями Хр х2, х^, действующими так, что включение х.
выключает работающее освещение и включает его в противном
случае, t: - 1, 2, 3. Пусть /(Хр х2, х3) = 0 при выключенном
освещении и /(Хр х2, х3) = 1 при включенном освещении.
Положим /(0, 0, 0) = 1. Тогда для функции /(хр х2> х3) полу-
чается следующая таблица значений:
Х|	х2	хз	Л*гх2’хз)
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0
Представим функцию /(Хр х2> х3) в конъюнктивной нормаль-
ной форме:
Ахг х2, х3) =
= (х' + х2 + х3)(х' + х2 + x3)(Xj + х'2 + X3)(Xj + х2 + х^).
Электрическая схема, соответствующая этому представлению,
изображена на рис. 50.
Рис. 50
Число используемых в схеме переключателей можно сократить,
преобразуя выражение для /(Хр х2> х3). Именно,
/(Хр х2, х3) = [х^ + (х2 + х^)(х2 + х3)]	+ (х2 + х3)(х2 + х3)].
(Порядок действий в булевых выражениях такой же, как и в
числовой алгебре: в выражении а + Ьс сначала выполняется
умножение, а потом сложение.) Упрощенная схема показана на
рис. 51.
В современных устройствах роль переключателей играют целые
электронные блоки, реализующие те или иные логические
компоненты схемы. Каждый такой блок (вентиль) имеет некоторое
число входов и реализует значения вполне определенной булевой
192
функции от соответствующего числа переменных. На рис. 52
приведены простейшие вентили, представляющие отрицание (такой
вентиль называется инвертором), n-местную дизъюнкцию (ИЛИ-
вентиль) и n-местную конъюнкцию (И-вентиль).
Рис. 52
Из теорем 2.69 и 2.70 следует, что любая булева функция
может быть представлена вентильной схемой, элементами которой
являются инверторы, И-вентили и ИЛИ-вентили.
Законы Де Моргана влекут за собой равенства
*1 + х2 = (х[х'2У, х{х2 = (х^ + хр’,
позволяющие ограничиться инверторами и И-вентилями, соответ-
ственно инверторами и ИЛИ-вентилями (рис. 53).

Рис. 53
На самом деле, при построении вентильных схем можно
обойтись лишь вентилями одного типа. В роли таких универсаль-
ных элементов выступают вентили НЕ-И и HE-ИЛИ, реализу-
ющие соответственно штрих Шеффера xJ I х2 и стрелку Пирса
Xj 1 х2 (рис. 54).
(^ хг)'
•*2
+ ^г)'
Рис. 54
Нетрудно заметить, что xJlx2 = (х^)' и xJ | х2 =
= (Xj + х2)', этим и объясняются названия вентилей. Далее,
х' = xlx, х.х = (х. 1х )1 (х 1х_), х. + х_ = (х, Iх,)I(х_Iх_), так
1 Z	1 х 1 X 1 X	1 1z х Xz
что все сводится в конечном счете к вентилю НЕ-И (рис. 55).
7 А.М.Богомолов, В.Н.Салий	193
Рис. 55
Аналогично производится замена инвертора, И-вентиля и
ИЛИ-вентиля вентилями НЕ-ИЛИ.
Одним из важнейших типов функциональных систем являются
алгебры Поста. Пусть F((S)—совокупность всех п-местных
функций на непустом множестве S. Каждую функцию
/ 6 Fn(S) можно представить как реализованную некоторой
комбинационной схемой, на п входов которой подаются значения
переменных Хр х2,	х;|, а с выхода снимается значение функции
/(Хр х2,	х(1).
00
Положим F(S) := U F (S). Множество F(S) представляет
м=1
собой совокупность всех функций от любого возможного числа
переменных, заданных на S и принимающих значения в 5. В
множестве F(S) вводятся следующие четыре унарные операции,
соответствующие элементарным действиям на входах комбина-
ционных схем. (см. [41]). Полагаем
(£0(Хр х2, ...,xt) := /(х2, х3, ...,xt, xt),
(т/)(Хр х2, ...,х() := /(х2, хр х3, ...,хп),
(<5/)(Хр х2, ..., х^) := /(хр Хр х2, ..., хп_(),
считая, что операции г, <5 тождественны на одноместных
функциях:
(£/)(*) := (т/)(х) := (<5/)(х) := /(х).
Далее
(V/)(x., х_, ..., х , х ,:= /(х_, х_, ..., х , х А
\ Р 2’	’ п n+l'	2	3 /Г /г+1'
для любого И > 1.
Операция £ осуществляет циклическую перестановку аргумен-
тов, операция т переставляет первые два аргумента. Операция
д отождествляет первые два аргумента, а операция V добавляет
фиктивный аргумент. На рис. 56 показаны соответствующие
преобразования на входах комбинационной схемы, реализующей
функцию /(Хр х2, ..., х().
194
Рис. 56
Пусть / 6 F((S), g G	Бинарная операция подстановки
функции g в функцию / определяется формулой
(f * g)(x,, х_, .... х , х ,,..., х ,	.) : =
v i> 2’	’ ш’ in+1 т+п-1'
'= f(g(x,, Хэ, .... X ), X	X ,	.).
р 2’ ’ п|/’ т+1 ’	ш + п-17
Таким образом, f*g 6 ^1п+п_^). Операция подстановки соот-
ветствует композиции комбинационных схем, представленной на
рис. 57. Функциональная система Р$ = (F(S), *, т, <5,
называется алгеброй Поста многоместных функций на множестве
S. В частности, если 5 =	= {0, 1}, получается алгебра Поста
Рис. 57
булевых функций.
Подалгебры алгебры Поста обычно называются замкнутыми
классами функций, они образуют решетку Sub Р$.
Замкнутый класс, по определению, является предполным, если
он представляет собой коатом (дуальный атом) решетки Sub Р...
О
Системы порождающих алгебры Р называют полными системами
О
функций на множестве S. Следующая теорема справедлива для
произвольных алгебр.
1*	195
Т е о р е м а 2.71. Если А—конечно порожденная алгебра,
то каждая ее собственная подалгебра содержится в некоторой
максимальной подалгебре.
Доказательств.о. Пусть алгебра А = (Л, F)
имеет конечную систему порождающих X, и пусть {Л.1 i е 1}—
произвольная цепь собственных подалгебр алгебры А. Положим
А. = ил.. Если .... а е Л_, то найдется подалгебра
О . _ r Z	1	2 П О
I G I
A., j G. I, такая, что а., а-,..., а е Л., и тогда для любой
л-арной операции f е F получим, что f(a{, а2, ..., ап) е
е А. С Aq. Следовательно, AQ—подалгебра алгебры Л. Если
Л = Л, то X С л . Но тогда найдется подалгебра Л,, k е I,
и	и	к
содержащая все элементы множества X (здесь нужна конечность
этого множества), и, значит, Л* = Л, что противоречит выбору
алгебр Л , z е I. Итак, объединение в решетке Sub Л любой цепи,
не содержащей элемента Л, дает элемент, отличный от Л.
Пусть А*—произвольная собственная подалгебра алгебры Л.
Рассмотрим некоторую максимальную цепь (т. е. не содержащу-
юся ни в какой другой цепи) {Л.I i G. 1} собственных подалгебр,
в состав которой входит Л* (существование такой цепи обес-
печивается так называемой леммой Цорна; мы опускаем детали).
Согласно доказанному, Л = U Л. будет собственной подалгеброй
i е I 1
в Л, содержащей подалгебру Л . Предположим, что Ло не является
максимальной подалгеброй. В этом случае найдется собственная
подалгебра В алгебры Л такая, что Ло С В. Это невозможно,
поскольку тогда цепь {Л. I i 6 /} U {В} в качестве своей собст-
венной части содержала бы максимальную цепь {Л.I 1: G Г}, о
Следствие 2.22. Подмножество X конечно порожден-
ной алгебры А тогда и только тогда является системой
порождающих алгебры А, когда X не содержится ни в одной
максимальной подалгебре этой алгебры, о
В применении к алгебрам Поста следствие 2.22 носит название
стандартного критерия полноты системы функций.
Следствие 2.23. Если конечно порожденная алгебра
А имеет п максимальных подалгебр, то каждая система
порождающих этой алгебры содержит подсистему, состоящую
не более чем из п элементов и тоже порождающую А.
Доказательство. Пусть X—произвольная систе-
ма порождающих алгебры Л и Л^Л^ ...,Л—полный список
максимальных подалгебр этой алгебры. Согласно следствию 2.22,
X не содержится ни в одной из подалгебр А., 1 < i < п. Значит,
существуют элементы х^ х2, ..., xj( G X такие, что х. А.,
196
1 < i: < n. Подсистема XQ = {xp x2, ..., x^} будет порождать
алгебру А, так как она не содержится ни в какой ее максимальной
подалгебре, о
Из теоремы 2.69 (или теоремы 2.70) следует, что алгебра
Поста булевых функций F(B2) является конечно порожденной:
все булевы функции выразимы через конъюнкцию, дизъюнкцию
и отрицание. Конечно, например, полная запись дизъюнктивной
нормальной формы функции в терминах операций алгебры Поста
г, д, V и * весьма громоздка, но получение ее принципиальных
трудностей не вызывает.
П р и м е р 84. Рассмотрим функцию	= xi ® *2'
Согласно теореме 2.69, х1 ф х2 = (х}' Л х2) V (х} Л х2). Для удоб-
ства обозначим: К(х{, х2) = х} Л х2, ^(Xj,x2) = х} V х2,
N(x) ~ х'. Тогда получаем: х' Л х2 = К * N, х} Л х'2 =
= т(тК * N), Xj ф х2 = t(t(D ♦ (К * N)) * (т(тК * N))).
Решение проблемы полноты для конечно порожденных алгебр
Поста сводится к явному описанию предполных классов функций
в этих алгебрах. Покажем, как это делается в алгебре Поста
булевых функций F(B2).
Функция / G F ;(В2) называется функцией, сохраняющей ноль,
если /(0, 0, ..., 0) = 0. Аналогично определяется функция, сох-
раняющая единицу. Функция / е F (В2), по определению,
самодвойственна, если [/(х,', х', ..., х')]' = /(х,, х,, ...» х ).
1 L tV	х 1 I tv
Функция f е	называется монотонной, если из
(ар а2, ..., ап) < (6р Ь2, ..., Ьп) (порядок в булевой алгебре в”
определяется покомпонентным сравнением) следует, что
f(a , а, ..., а ) < f(b , А, ..., b ).
'v 1’ 2’	’ п' 1’ 2 п'
Полиномом Жегалкина от переменных х , х2, ..., хп называется
булева функция вида
ф а. . . х. х. ... х. ,
z. .	. v I I ...I II I
(1,1, .... I ) i 2 т I 2 т
М 2 т7
представляющая собой сумму по модулю 2, составленную из
конъюнкций всевозможных наборов переменных х}, х2, ..., х^,
причем коэффициент а. . показывает, входит или не входит
1 2 т
соответствующая конъюнкция в запись полинома. Поскольку число
конъюнкций в полиноме Жегалкина равно 2”, а каждый
коэффициент а. . может равняться 0 или 1, получаем, что
1 2 т
2П
всего имеется 2 различных полиномов Жегалкина. Но именно
197
столько элементов имеет и совокупность F^B^ всех «-местных
булевых функций. Отсюда следует
Т е о р е м а 2.72. Всякая булева функция однозначно пред-
ставима в виде полинома Жегалкина. о
Функция / е F^B^) называется линейной, если ее можно
представить в виде
f(xvx2, = aQ®axxx®...®anxn,
т. е. если линейным является ее полином Жегалкина.
П р и м е р 85. Среди двуместных булевых функций (см.
пример 81) / — / сохраняют 0, функции с нечетными номерами
сохраняют 1. Монотонными функциями являются /0, fx, fy f , /15-
Линейность функции f(xx, х2) проверяется методом неопределен-
ных коэффициентов: в равенстве f(x., х ) = а фа х фа х, при
различных значениях Хр х2 вычисляется левая часть, а справа
получаются соотношения между неизвестными aQ, ах, а^. Линей-
ными ФУНКЦИЯМИ будут /0 = 0, /3 = Хр /5 = Ху = Xj ф Ху
f9 = 1 ф Xj ф Ху /10 = 1 Ф Ху fX2 = 1 ф Хр /15 = 1. Само-
двойственных функций в F2(B2) две: это селекторы /3 = и
/ = Ху Введенные классы булевых функций обозначим следу-
ющим образом: TQ—сохраняющие О, —сохраняющие 1, 5—са-
модвойственные, М—монотонные, L—линейные. Следующая
теорема Поста показывает значение этих классов.
Т е о р е м а 2.73. Алгебра Поста булевых функций имеет
в точности пять предполных классов: Т , Тр 5, М и L.
Доказательство. Нужно доказать, что каждый
из указанных классов является максимальной подалгеброй алгебры
Поста (F(2?2), *, £, т, d, V) и что других максимальных подал-
гебр у нее нет.
Очевидно, что класс TQ замкнут относительно постовских
операций, т. е. является подалгеброй. Чтобы показать, что эта
подалгебра максимальна, достаточно установить, что подмножество
X = TQ U {/ ], где f—любая булева функция, не входящая в
TQ, порождает всю алгебру F(B2).
Пусть /(Хр х2, ..., хп)—произвольная функция, не сохраняющая
константу 0, т. е. /(О, 0, ..., 0) = 1. С помощью этой функции
построим в X отрицание х'. Возможны два случая:
а)	/(1, 1, ..., 1) = 0. Тогда функция g(x) := /(х, х, ..., х)
как раз и будет отрицанием: g(x) = х'.
198
б)	/(1, 1,	1) - 1. Так как функция /6(х1>х2) =
= х( ф х2 сохраняет 0, она входит в состав X. Тогда
Л(х) = (/6 * /)(х, х) = /(х, х, х) ф х = 1 ф х = х'. Таким
образом, подалгебра, порожденная множеством X, содержит
конъюнкцию, дизъюнкцию (эти функции сохраняют 0) и отрица-
ние. Согласно теореме 2.69, эта подалгебра совпадает с F(B2).
Рассуждения для класса вполне аналогичны.
Проверка замкнутости класса S самодвойственных функций не
представляет труда. Например, если f,g& S, то
[(/ * £)(х,', х' ..., X ', X ' , ,, X '	,)]' =
iv Г 2’ ш m+Г m+n-V
—	х', ..., х'), х х '	,)]' =
’ tw m+1’	’ zn+n-17
= l/((g(x. , Х_, ..., X ))', X ',..., X '	,)]' =
. р 2’ т" ’ ш+г ’ т+п-1'
= f(g(xv х2, ..., хм), хт+1, ..., xM+n_j) =
= (/* g)(xr х2, ..., хт, xm+v ..., xw+n_j).
Пусть X = S U {/}, где /(Хр х2, ..., х^)—произвольная неса-
модвойственная функция. Поскольку X содержит отрицание
(х'—самодвойственная функция), нужно получить конъюнкцию
(или дизъюнкцию). Так как / не самодвойственна, найдется набор
(<71, а2, ..., ап) е В" такой, что f(av а2, ..., aj = f(a[, а'2, ..., cQ.
Возможны два случая:
a)	f(av а2, ап) = 0. Функция яЦ, х2, х3) = хух2 +
+ XjX3 + х2х3 самодвойственна:
[g(x', х2, х')]' = (х'х' + х'х' + х^х')' = (х'х2)(х'х')(х'х') =
= (xj + Х2^Х1 + Х3^Х2 + х3> = <Х1 + х1х2 + х1х3 + Х2Х3^Х2 + Х3> =
= X X + X X + XXX + X X = X X + X X + X X- = g(x , X , X )
IX 1 «Э 1X0 X О IX 10 X О	1X0
(здесь использованы законы Де Моргана и тот факт, что
XjX2x3 < XjX2). Тогда в подалгебру, порожденную множеством X,
входит и конъюнкция, ибо XjX2 = g(XpX2, 0) = g(XpX2,
f(av a2, ..., afi)) = ^((^g) *f(ar a2, , an))- Как уже отмечалось,
конъюнкция и отрицание порождают всю алгебру В(В2).
б)	/(<7р <z2, ...,	= 1. С помощью самодвойственной функции
g(x., хэ, х,) = (х + х )(х. + х,)(х_ + х-) получаем дизъюнкцию:
1 X	1 Xz 1	□ X
199
+ х2 = g(xv x2, f(av а2.an)). Дизъюнкция и отрицание
порождают всю алгебру
Замкнутость класса М относительно операций т, 6 и V
следует из очевидных соотношений:
(хр х2, ..., хп) < (ур УГ .... Уп) => (х2> .... хп, xj < (у2, Уп, ух) &
& (х2,	х3> .... хп) < (у2,ух,уу ...,уп),
(хр х2, .... хп_{) < (уру2, • ••> Уп—Х) =>
=* (*1>Х1’Х2..Xn-J =* (yvyvy2.....Уп-J'
(х1> Х2, ..., хп, хп+1) < (yv У2, ..., Уп, уп+х) =>
=* <Х2’ х3.хп’ ХП+Р * (уг у3’ уп’ yn+J-
Пусть /, g е М И (хр х2, хт, хт+1, ..., Хт+п_х) <
~ (УР у2, ..., ут, У„(+1,..., Ут+п_х). тогда g(xp х2,..„ хт) <
— ЖУр У2, ут) и
(/* g)(xp х2, ..., хп1, хт+1,=
=	х2, хт), хт+1,	хт+п_{) <
^f(g(yvy2, ->Ут)>У„1+1..
Пусть X = М U {/}, где /—произвольная немонотонная функ-
ция. Поскольку конъюнкция и дизъюнкция монотонны, нужно
показать, что в алгебре, порожденной множеством X, содержится
отрицание х’. Так как / немонотонна, найдутся наборы
а = (а{, а2, ап) и b = (Лр Z>2, ..., ZQ такие, что а < Ь, но
/( а) > /( Ь). В диаграмме решетки В2 выделим какую-нибудь
максимальную цепь, соединяющую элементы а и Ь, например,
а = а° < а1 < ... < ак = Ь. Здесь каждый элемент, начиная со
второго, является верхним соседом предыдущего, и следовательно,
отличается от него лишь заменой на одном месте 0 на 1. Вычисляя
/(а), /(а ),...,/(а ) = /(Ь), получим, что для каких-то двух
соседних наборов а11, а1 будет /(а1-1) > /(а1), 1 S i < к.
Пусть
а1'1 = (с1,с2,...,с/_р0,с.+1.с(),
а1 = (сг с2, ..., С]_х, 1,с.+ р...,с().
200
Положим g(x) .= f(c , с , ..., с , х, с , ... с ). Тогда #(0) =
к аг	J к	J Т 1	fl
=	> f(a‘) = #(1). Поскольку g(0), #(1) е В2, получаем,
что g(0) = 1 и g(l) = 0, т. е. g(x) = х'.
Замкнутость класса L линейных функций очевидна для
унарных постовых операций т, <5, V. Пусть /(Ур у2, •••
п	m
->Уп) = Ф ау и g(x х .........х ) = Ф b х . Тогда
"	1=о ' '	1	m i=0	‘
х2,..., хт, х)п+1,..., хш+п_1) =
= /(g(xr х2, ..., хт), хт+1.xm+n_t) =
/ т	\
— f ф Ьх., х	. =
. . i i т+г m+n-l
\ J=1	/
«1 \
= ап ф а. | Ф Ь. х. ф а~х ,, ® ... ® а х ,	,,
0	1	„ i /	2 ш+1	п т+п-1
\ i=0	/
— получается линейный полином Жегалкина.
Пусть X = L U {/}, где /—произвольная нелинейная функ-
ция. Тогда в ее полиноме Жегалкина найдется член, содержащий
не менее двух переменных. Пусть это будут х} и х2. Так как /
не является тождественным нулем (О G L), то существует набор
(Яр а2, ау ..., я/() G В2 такой, что /(Яр а2, а^, ..., я/() = 1. Тогда
g(x., х ) = f(x,, х , а,, ..., а} будет иметь вид
к Al	к Al J	*1
g(Xp х2) = XjX2 ф ах{ ф Ьх2 ф с,
где а, Ь, с G В2—некоторые константы. Тогда
g(Xj ф Ь, х2 ф а) ф ab ф с = (xt ф Ь)(х2 ф я) ф а(хх ф Ь) ф
Ф Ь(х2 фа)фс®аЬфс = х^.
Поскольку класс L содержит отрицание: х' = 1 Ф х, получаем,
что X порождает всю алгебру
Таким образом, Г , Т , S, М и L являются предполными
классами (максимальными подалгебрами) алгебры Поста булевых
функций F(B2). Осталось показать, что других предполных классов
нет. Пусть А—некоторый замкнутый класс, не содержащийся ни
в одном из предполных классов TQ, Т S, М, L. Тогда среди
функций класса А найдутся функции /2, /3, /4, /5, не
принадлежащие соответственно классам TQ, Ту 5, М, L. С
201
помощью функций /*, /2, /3 строятся константы 0 и 1.
Используя их и функцию f5, получаем отрицание х'. Наконец,
О, 1, х' вместе с /4 дают конъюнкцию х^. Класс А совпадает
с Подробности можно посмотреть в [59]. □
Следствие 2.24 (стандартный критерий полноты для
систем булевых функций). Система булевых функций полна
тогда и только тогда, когда она не содержится целиком ни в
одном из классов TQ, Т{, S, М и L. □
Из следствия 2.24 вытекает, что всякий базис алгебры Поста
F(B2) содержит не более пяти элементов. Этот результат усиливает
Т е о р е м а 2.74. Всякий базис алгебры Поста булевых
функций содержит не более четырех элементов.
Доказательство. Пусть f(x{, х2, ..., х^) £ Т ,
т. е. не сохраняет ноль. Возможны два случая:
а)	/(1, 1, ..., 1) — 1. Тогда /(х^ х2, ..., х ) не самодвойствен-
на:
/(О, 0..0) = 1 = /(1, 1. 1) = /(О', О', ..., О').
б)	/(1, 1. 1)	= 0. Тогда / Й Гг / Й М.
В случае а) алгебру F(B^ будет порождать подмножество
X = {У1,/2,/4,/5}, где fl=f$TQ,	f(£S, f4 (£ M,
f5 L. В случае б) алгебру F(B2) порождает подмножество
X = {У1,/3,/5}, где /1 = У (£ 7^, /1 g Т1( /3 g S, fl £ М,
f5 t L. о
Пример 86. Рассмотрим функции Z1 = 1, /2 = 0,
/4(х1,х2, х3) = х{ ф х2 ф х3, fS(x{, х2) = х^. Приведенная ни-
же таблица показывает, что эти функции порождают алгебру
F(B2) и что ни одну из них исключить нельзя. Знаки + и -
обозначают вхождение или невхождение функции в соответству-
ющий класс. Получаем четырехэлементный базис.
/’
/2
/4
f5
S М L
Трехэлементный базис образуют двухместные функции
У1(*1> *2)	*1*2’	*2^ *i ® *2’	’ *2^ = 1’ ДеЙСТ-
202
вительно, /15 не сохраняет 0, /6 не сохраняет 1, все три функции
несамодвойственны, / немонотонна, нелинейна. В то же время
</6,/15) с L, (/,./„) С Т, П И,	С Т„.
Примерами двухэлементных базисов являются подмножества
{х', XjX2} и {х', xt + х2}, а одноэлементных—{xt 1х2} и
{Xj 1 х2}.
§ 2.6. Частичные и многоосновные алгебры. Категории
Во многих практических случаях процедуру получения из
заданного набора объектов некоторого нового объекта не удается
описать с помощью алгебраических операций, понимаемых в
смысле § 2.1. Чаще всего этому препятствует одно из следующих
двух обстоятельств:
1)	невозможность применить упомянутую процедуру к произ-
вольному по составу набору объектов;
2)	разнородность рассматриваемых объектов, неестественность
объединения их в одно множество.
Попытки дать абстрактное описание подобных ситуаций
привели к понятиям частичной алгебры и многоосновной алгебры.
П р и м е р 87. Пусть G = (V, а)—ориентированный граф
с множеством вершин V и отношением смежности а. Для
и, v G V положим:
(и, если (и, v) G а,
uv := vu := 1
1 v, если (v, и) G а.
Если граф G является турниром, т. е. (и, v) G а, либо
(v, и) G а для любых и, v G V, то получим группоид (V, •)
(см. пример 45). В общем же случае введенная операция
определена не для любых пар (и, v) G V х V, т. е. является
частичной, и (У, •) естественно назвать частичным группоидом.
Пример 88. Структурным автоматом с заданными т
входами и п выходами называется система
с = (S, X, X AL X ... X X , Y, X Y X ... X Y , <5, А),
v ’	1	2	т' 1	2	п '
где S—конечное непустое множество внутренних состояний,
X,, Х„, .... X —конечные входные алфавиты, У,, У,, ..., У —конеч-
1 ’ 2	’ т	1	2 я
ные выходные алфавиты, <5: S х (А^ х Х2 X ... X Хт) -* 5—
функция переходов и А: 5 X (A^ X Х^ X ... X Хт) -»
-» yt X У2 X ... X У(—функция выходов.
Пусть С обозначает класс всевозможных структурных автома-
тов. Для описания композиций элементов этого класса введем
одну бинарную и счетное множество частичных унарных операций.
203
Параллельным соединением элементов
к=1
I = 1,2,
называется элемент
«<=.• с2) = S, X S2, П Х‘ X
к=1
П £ >я
к=1
где
<5((srs2), (х1,*2)) := (^(s,,?), <52(s2, х2)),
A((srs2), (x*,x2)) := (A^.x1), *2(s2, x2))
для любых (s], s2) G x S2, (x1, x2) G X1. X J”[ A"2. Ha
рис. 58 показано параллельное со-
единение g(clt с2) двух структурных
автоматов и с2. Пусть к, I—нату-
ральные числа. Операция fk отождест-
вляет /-й выходной узел автомата с к-м
входным узлом. Операция / 1 определе-
на лишь на таких элементах с, у
Рис. 58
которых число входных каналов не меньше к, число выходных
каналов не меньше /, и при этом Х^ = (совпадение алфавитов).
В зависимости от конструктивных особенностей схемы, в которую
входит данный элемент, указанное отождествление может проис-
ходить без образования обратной связи или с ее образованием.
Рассмотрим первый случай. Говорят, что l-й выходной узел не
зависит от &-го входного узла, если для определения сигнала в
l-м выходном узле не требуется знать сигнал в к-м входном узле,
т. е. если для любых .$ G 3, х,, х' G X,,
’ к’ к к’
(х, , Х_, ..., X, ,,Х,	X ) G
' Г 2’	’ к-г к+1 ’	’ т'
е X, х Ап х ... х х, , х X, , х ... х X
1	2	к-l к+1	т
имеет место равенство
рг,А(х, (х,, х_, ..., х, ,, х,, х,х )) =
I v v Г 2’	к-\ к k+l ’ т”
= рг.Л($, (х., х_, ..., х, ., х\ х, х )).
/ '	' 1	2	’ Л-1’ к' к+1 ’	т''
204
В случае указанной независимости полагаем:
Л/с);= № *1 * *2 х - X xt_, х XJ+1 X ... X хт,
r,xr2x...xr,_, Х^Х.^ХУ,.^,.^,),
где для любых s G 5,	(х^ х2, ..., х^_^, х^+1, хт) G
G X х AL X ... X X, х X, х ... х X , по определению,
1	/С 1	л т1	/А1
<3, ,($> (х., хп, ...» х. х..х )) : =
k,lv v 1	2	Л-1’ Л+1	т77
:= d(s, (х., хэ, х. Л, (s, (х., х„, х. ., е, х. .., х )),
' ’ ' Г 2	’ Л-1	/' ’ ' Г 2 к-l Л+Г т77
Л+1’	т77’
*к,1 (ХГ х2’ Xk-v xk+l’ хт^
= рГ12...(/-1)(/+1)...п^’ (Л1’ Х2' Хк-Г*1 (s’ (*]> х2’ •	Хк-\' в'
к+1 т" к+\	т''
На рис. 59 изображен элемент f 2(с).
Теперь рассмотрим основные понятия теории частичных алгебр.
Пусть S—непустое множество, п—натуральное число. Частичной
п-арной операцией в 5 называется
однозначное бинарное отношение
f С S1' х S. Если рГ|/ = S", то опе-
рация / называется полной или
просто операцией. Частичная алгебра
типа (п,, п~, ..., п ), где п, >
'Г 2 »г	1
> л > ... > пт—натуральные
числа,—это система Л = (S, f[rf2, .где1 < / < т,—
частичная n.-арная операция в S.
Пусть Л = (Л,/1(/2, ...,/((|) и В = (В, gv g2, ..., gm)— две од-
нотипные частичные алгебры. Отображение <р: А -» В называется
гомоморфизмом, если для всех 1 < i < т и (а^, а2, ...
..., а ) G pFj/. выполняются условия:
i
р{а2), ..., р(ап )) £ рг^.,
i
р(/(а а ..., а )) = g^a ), <р(а ), ..., р(а )).
I к	Il	I	А	Лл	II
i	i
Под вложениями частичных алгебр понимают их инъективные
гомоморфизмы. Гомоморфизм р: А -» В, по определению, явля-
205
ется сильным, если для всех 1 < i: < т и (ар а2, ...
•••» а ) G рг./.	из (<р(а ), <р(а),..., <р(а )) G pr g следует,
IЬ	1	«	1	> I
что (OpOj, ...,а ) G prj /.. Сильные биективные гомоморфизмы
называют изоморфизмами. Нетрудно убедиться в том, что
произведение гомоморфизмов (сильных гомоморфизмов) является
гомоморфизмом (сильным гомоморфизмом).
Пусть А = (A, F)—частичная алгебра. Подмножество
В Q А называется устойчивым в А, если оно замкнуто
относительно всех операций алгебры А, т. е. если из b , Ь2, ...
..., Ъп е В и (Z>p Ь2, ..., bn) е рг}/ следует, что f(b{, b2, ...
..., Л(|) G В,—для любой n-арной частичной операции f G F. В
этом случае говорят, что В образует подалгебру в А. Ее
операциями являются ограничения на В операций частичной
алгебры А.
Другой, не менее естественный тип подалгебр возникает, если
рассматривать подмножества В частичной алгебры А = (Л, F),
наделенные частичными операциями, являющимися ограничения-
ми на В операций частичной алгебры А. Такие подалгебры
называют относительными подалгебрами в А. Каждое подмно-
жество частичной алгебры является носителем ее относительной
подалгебры, но носителем подалгебры может быть только ус-
тойчивое подмножество.
Наконец, слабая подалгебра частичной алгебры А = (А,/^,
f2,...,fiti) определяется как однотипная с А частичная алгебра
А* = (А*,	*, f2 *, fm *) такая, что А* С Ли/.* С / для всех
1 < i < т. Таким образом, если а2, ..., a G А* и
I
а ) G рг /. *, то	а ) G рг, /. и /.	.
2	’ н '	1'1	4 Г 2’ п 7 к 1'i Ji v 1’ 2*
i	i
..., a ) = f.(a,, a,, ..., a ).
и ' 'А Г 2’ и '
i	i
T e о p e м a 2.75. Пусть A = (A, f{, f2, ..., f —частич-
ная алгебра. Частичная алгебра А* = (Л*, /, *, /2 *, ..., f *), где
А* С А, тогда и только тогда будет слабой подалгеброй,
подалгеброй, относительной подалгеброй в А, когда соответ-
ственно выполняются условия:
1)	тождественное вложение А^. является гомоморфизмом
из А в А;
2)	тождественное вложение А 4. является сильным гомо-
А
морфизмом из А в А;
206
3)	если <р—гомоморфизм частичной алгебры В = (В, F) в
А и Р^2<Р — то *Р—гомоморфизм из В в А*.
Доказательство. 1) Пусть А*—слабая подалгеб-
ра в Л и (ара^ а ) G рг/.*. Тогда
{
(^4*(а1)>	***’	)) *"	а2' ***’ ап
г	i
И
A »(f. *(а., а )) = /. *(а1, а_, а ) =
A v/ 4 1	2 п >' i v г 2 п '
i	i
= f.(av а2, ап ) = //Д^а/, Дл’(«2). •••>	)),
i	i
т. е. Дл’—гомоморфизм. Доказательство обратного утверждения
также не представляет труда.
2) Очевидно, что если А*—подалгебра в Л, то Д^.: А* -» А
будет сильным гомоморфизмом. Обратно, пусть Д^.—сильный
гомоморфизм из Л* в Л и а2, ..., а^ G Л*, (а^ а2, ...
ап > е ₽Г1 А’ Тогда	длЧ«2)’	Aa-(« , )) е РГ, <•>
/ <
откуда (а , а , ..., а ) G prf /. *. Далее,
i
f.*(a,, а-, а ) = Д *(а., аэ, ..., а )) =
'/'12’ п ' A v/ ' 1’ 2’ п 7/
i	i
=	Дл*(а2)’ •••’ &А’(ап )) = Ма1’ а2’ •••’ ап^’
i	i
т. е. /. * является ограничением частичной операции /. на
устойчивом подмножестве А*.
3) Пусть Л* = (Л*, / *,/2*, ...,f *)—относительная подалгеб-
ра частичной алгебры Л = (Л,/,/2, ...,/ ) и —гомоморфизм
частичной алгебры В = (В, g{, g2, g j в Л, причем pr^> С
С л*. Если (Лр Ь2, ...,	) G pFj g.,	то, по определению,
(^(*,)>	<р(Ь2), ..., <р(Ьц )) е рг, <p(g.(bv ь2,ьц )) = /.(^(л,),
г	i
...,	)). Поскольку Л*—относительная подалгебра, полу-
i
чаем, что
(^(*,)> ^(^2)> •••> V>(\)) G РГ/
207
f' 'X</’(bl), Ф(.Ь2)’ Ф(Ьп )) = f&lbj, <p(b2), ..., <p(bn )) =
i	i
= Ч>ЩЬГ b2, ..., bn )).
I
Следовательно, <p—гомоморфизм частичной алгебры В в А*. С
другой стороны, пусть выполняется условие 3). Рассмотрим
относительную подалгебру частичной алгебры А, имеющую
операциями будут ограничение /.| м
1 А
из А на подмножестве А*. Если
носителем
1 < i < т,
(ap а2, ...,
при этом
А*. Ее
операций
ап ) е рг1^1Л>)’ т0 конечно> <av а2’ •••> ап ) е Pri Л и
(/.I ,.)(«,> а2' ап > = Ца\’ аГ ап ОтСЮДа полУ-
I Д 1	fl	I 1 л	П
чаем, что тождественное вложение Д^* является гомоморфизмом
частичной алгебры (Л*,/| в,/| в, ...,
1 а' 1 а'
будет гомоморфизмом и в (Л*, / *, /
Но тогда Д^*
Пусть (яр а2, ..., ап ) G р^ /. и а2, ..., ап ) G А*. Тогда
(Яр а2, ..., ап ) G рГ]	и, значит, (яр ау ..., ап ) =
= (\.(ai)> дл-(а2)’ •••’ АА*(ап)) е pri4>и при этом
f.(av а2, ...,	) = /*(д4.(а1), Дл.(я2),	Дл.(«„ )) =
=	..., ап^)) = /.(Яр я2, ..., ап^).
Таким образом, /* = /,| ., так что А*—относительная подалгебра
1	1 А
в т4. □
Пример 89. Пусть неполностью описанный полуавтомат
А = (S, X, д) задан таблицей переходов
<5
\ Х2
S3
Рис. 60
и диаграммой на рис. 60. На рис. 61
изображены: я) единственный собственный
ненулевой подавтомат, б) все относительные
подавтоматы с двумя состояниями, в) два из
тридцати двух слабых подавтоматов с тремя
состояниями.
Совокупность подалгебр каждого вида, как
нетрудно заметить, замкнута относительно
208
произвольных пересечений и потому образует полную решетку.
При этом решетка относительных подалгебр изоморфна решетке
всех подмножеств носителя данной частичной алгебры (каждое
подмножество является носителем точно одной относительной
подалгебры), а решетка слабых подалгебр в общем случае
необозрима: каждое подмножество оказывается носителем, как
правило, многих слабых подалгебр. Таким образом, объектом
содержательного изучения может служить лишь решетка Sub А
подалгебр данной частичной алгебры А.
а.	6	В
Рис. 61
Пусть А—частичная алгебра и X С. А. Наименьшая подалгебра
В с условием X С в называется подалгеброй, порожденной в
А подмножеством X,	при этом X	называется	множеством
порождающих для В.	Из определения следует,	что если	X
порождает частичную алгебру А = (A, f f2, ..., f ), то для всех
a G А при а £ X	существуют 1	< i < т	и (а^, а2,	...
..., а ) G рг,/. такие, что а = f,(a,,	..., а ).
п.' г /	’	'Л г 2’	’ п '
I	i
Пусть А = (A, F) и В = (В, F)—однотипные частичные
алгебры. Их прямым произведением называется частичная алгебра
А X В := (А X В, F) того же типа такая, что для любой п-арной
операции f G F и любых a. G A, b. G В, 1 < i < п, по
определению,
((йг bj, (а2, Ь2), (ап, bn)) G рг/ :«•
:«• (а{, а2, ап) G prj & (b{, Ь2, ..., bfi) G р^ f
и при этом
f((av bj, (а2, Ь2), ..., (ап, bj) ;= (/{а{, а2,	ац),/(Ь{, Ъ2, ..., Ь;)).
Очевидно, что проекции Лр А х В -* А, (а, Ь) а, и л2:
А X В -* В, (а, Ь) >—» Ь, будут гомоморфизмами прямого произ-
ведения А х В соответственно на Л и на В.
Эквивалентность в на частичной алгебре А — (A, F) называ-
ется конгруэнцией, если для любой n-арной операции / G F и
любых (йр а2, ..., ап), (Ар Ь2, ..., bn) G ргг/ из (a., b.~) G в,
1 < i < п, вытекает, что (/(а{, а2, ..., ап), f(bx, b2, ... bfi)) G в.
209
Конгруэнция в называется сильной, если из (ах, а2, ...
..., an) е рг}/	и	(а., Ь.) ев, I < i < п, следует, что
(Ь,, Ь„, ..., Ь ) е рг,/ для любых Ь,, Ь-, ..., b е А. Например,
' 1	2 /г	1	1	2 П
разбиение {1}, {2, 3} определяет конгруэнцию на частичном
полуавтомате А из примера 89, но эта конгруэнция не будет
сильной: входной сигнал х} не воспринимается полуавтоматом А
в состоянии Sy Имея конгруэнцию в на частичной алгебре
А = {A, F), в фактормножестве А/в вводят одноименные час-
тичные операции, полагая
(в(в1), е(а2).0(ап))	е рг/
:о (3 Ьх, Ь2, ..., Ьп е Л)(У 1 < i < п)((а., Ь.) е в &
& <М2......bn) е ₽Г1П
и при этом
f(e(ax), е(а2), ..., в(ап)) := 6(f(av а2, ..., aj).
Частичная алгебра А/в := (A/в, F) называется факторалгеброй
частичной алгебры А по конгруэнции в.
Теорема 2.76. Ядро всякого (сильного) гомоморфизма
частичной алгебры является (сильной) конгруэнцией этой
алгебры. С другой стороны, всякая (сильная) конгруэнция
частичной алгебры представляет собой ядро подходящего
(сильного) гомоморфизма этой алгебры.
Доказательство. Рассмотрим случай сильного
гомоморфизма. Пусть А = (Л, F) и В = (В, F)—однотипные
частичные алгебры и <р: А -* В—сильный гомоморфизм. Если
/ G F—произвольная n-арная операция и (a., b.) G Кег <р,
1 < i < п, причем (а , а2, ..., ап) G рг^, то
И*,), <Р(Ь ), ..., <р(Ь)) = (<р(а ), <р(а ), ..., <р(а )) е рг /,
X	а»	г X	X	а»	г X	X
откуда (А , Ь2, ..., bj G рг^, а тогда
а2, ..., ап)) = f(<p(ax), <р(а2), ..., <р(ап)) =
= f^(b ),	), ...,	)) = 'Pifib , b2, ..., b )),
и, значит, (f(ax, a2, ..., an),f(bx, by ..., bn)) e Q.
Мы получили, что в—сильная конгруэнция.
С другой стороны, если в—сильная конгруэнция на А, то
естественное отображение
nat в: А -* A/в; а » в(а),
210
оказывается сильным гомоморфизмом. В самом деле, если
(©(я/, 0(я2),	#(яп)) £ рг/, где f—произвольная n-арная частич-
ная операция в А, то, по определению, существуют
Ь,, Ь„, ..., Ь такие, что (a., b.) G 0, 1 i < п, и (Ь,, Ь„, ...
1	2 п	' I I'	'12
..., Лп) G рг/ Так как	в—сильная	конгруэнция, то и
(йр а2, ..., яд) G рг/. При этом
(nat0)(/(flj, аг ..., aj) = 0(f(av а2.яд)) :=
:= f(0(a ), 0(a),	0(a )) = /((nat 0)(а ), (nat 0)(а ), ..., (nat 0)(а )),
1	fl	IX	п
и, следовательно, nat 0—сильный гомоморфизм. □
Каждой частичной алгебре А = (A, f , f2, ..., f ) можно сопо-
ставить некоторую однотипную алгебру со всюду определенными
операциями. Делается это таким образом. К множеству А
добавляется новый элемент 0 и на расширенном множестве А®
доопределяется каждая частичная операция /. :
/. °(я , я , ..., я ) :=
Ji ' Г 2 п.'
7(аг а2, ..., ап ), если (а{, а2, .... ап ) е рг/.,
i	i
О во всех остальных случаях.
Алгебра А° = (AQ, / °, /2 °, ..., f °) называется нулевым расши-
рением частичной алгебры А.
Т е о р е м а 2.77 (см. [36]). Если 0—сильная конгруэнция
частичной алгебры А = (A, F), то отношение 0° := О U
U {(0, 0)} является конгруэнцией нулевого расширения А°. Об-
ратно, если 0—конгруэнция нулевого расширения А° частичной
алгебры А такая, что 0(0) = {0}, то 0 — {(0, 0)} будет
сильной конгруэнцией на А.
Доказательство. Первое утверждение непосред-
ственно следует из определения операций в нулевом расшире-
нии А°.
Пусть 0 G Соп А0 и 0(0) = |0}. Положим
:= «1ЛХЛ = « - «»•»)>
Очевидно, что 0*—конгруэнция частичной алгебры А. Пусть
/ G F—произвольная n-арная операция, (а{, а2, ..., ап) G рг/,
(a., b.) G О*, 1 < i < п. Предположим, что (Ь^, Ь2, ...,	£
£ рг/. Тогда /°(а1, а2, ..., aj * о, но /0(Лр Ь2, ..., Ьп) = 0 в
А°. Так как (a., b.) G 0, 1 < i < п, и в—конгруэнция алгебры
А, получаем, что	а2, ..., я^),	Ъ2, ..., Ь^) G 0, что
211
невозможно, так как 0(0) = {0}. Из полученного противоречия
следует, что (Ь1, Ь2, ..., bn) G рг}/, и, значит, 0*—сильная конг-
руэнция на А. □
Частичные алгебры возникают в приложениях как относитель-
ные подалгебры алгебр со всюду определенными операциями.
Проектирование сложных систем обычно осуществляется по
блокам, и, занимаясь данным блоком системы, исследователь до
какого-то этапа не интересуется его «внешними» связями, оставляя
неопределенными те или иные значения в таблицах функцио-
нирования. Понятие нулевого расширения, как показывает теорема
2.77, может оказаться полезным для изучения некоторых свойств
частичных алгебр и описываемых ими систем, хотя при этом
могут потеряться некоторые важные специфические особенности.
Например, относительные и слабые подалгебры не интерп-
ретируемы на языке подалгебр нулевого расширения.
Если возникновение частичных алгебр связано с расширением
понятия операции, то структуризация носителя алгебры приводит
к алгебраическим конструкциям иного рода.
Пусть А^ А2, ..., А^—некоторые	непустые множества и
/р/2> •••>—отображения вида А. х А. х ... х А( -» А. , где
1	2	п	л+I
z,, L,	..., i ,,	е {1, 2,...,	к}.	Система А = (А,, А~,	..., А.;
1’ 2’	п+1	1	’	J	' Г 2’ к
называется к-основной алгеброй с носителями
А,, А-, .... А, (их также называют основными множествами или
г 2 к
файлами) и операциями f{,f2, ->fm-
П р и м е р 90. Пусть А—некоторая группа, действующая
на множестве S, т. е. представленная обратимыми преобразо-
ваниями этого множества. Для произвольных a G А и s G 5
вместо <Pa(s')> где <ра—преобразование, соответствующее элементу
а, пишут s ° а. Получается двуосновная алгебра (A, S; •, °,
е) с носителями А и S, бинарными операциями
(а, Ь) •—» ab для a, b G А и (s, а) s° а для s S 5, a G А,
унарной операцией а •—» а-1 и нульарной операцией е, заданными
в множестве А. При этом редукт (Л, •,	е)—это исходная
группа А и, кроме того, выполняются тождества: s ° е = s,
s ° (ab) = (s ° а) ° b, где s е 5 и a, b G А.
П р и м е р 91. Автомат А = (S, X, У, <5, Л) также можно
рассматривать как многоосновную алгебру. Действительно, функ-
ции переходов <5: 5 х X -» 5 и выходов Л: S х X -» У представ-
ляют собой операции, осуществляемые над переменными двух
разных сортов: состояниями и входными сигналами. При этом у
Л файл возможных значений У объединяет переменные еще одного
дополнительного сорта—выходные сигналы.
212
Полуавтомат А = (S, X, <5) можно считать двуосновной алгеб-
рой, но ранее было показано, что эта ситуация вполне
укладывается в рамки обычной универсальной алгебры.
Для многоосновных алгебр вводятся все аналоги конструкций,
рассмотренных в § 2.1, причем соответствующие свойства часто
получаются непосредственным перенесением. Заметим еще, что
многоосновные алгебры часто называют также многосортными.
Пусть А = (Лр А2, ..., Ак; F)—некоторая ^-основная алгебра
с множеством операций F. Система подмножеств В,, В_, ..., В,,
1 г к
где В.	С А.,	1	<	i <	к, называется	устойчивой	в А,	если для
любой	n-арной	операции /: А. X А	х	... х А. -* А(	из F и
1	2	п	п +;
любых	Ь. е	В. ,	Л-G	В. , ..., b. G	В.	элемент	f(b,,	Z>_, ..., Ь )
1	t ’	2	i ’ ’ i	i	Г	2’ ’ и'
I	2	п	п
принадлежит подмножеству В. .В этом случае, ограничивая
л + 1
операции алгебры А на системе подмножеств В{, В^, ..., В^,
получаем ^-основную алгебру В = (В , В^, ..., Вк; F), называе-
мую подалгеброй алгебры А.
Под пересечением подалгебр В = (В В-, ..., В ; F) и
1	*• к
С = (Сг С2, ..., Ск; F) многоосновной алгебры А = (Л , Л2, ...
..., Ак, F) естественно понимать алгебру В Cl С := (Bj Cl Ср
В2 Ci С2, ..., Вк П Ск; F), операциями которой являются опе-
рации алгебры Л, ограниченные на соответствующих множествах.
Легко получаем, что пересечение любого семейства подалгебр
многоосновной алгебры Л снова будет ее подалгеброй, и,
следовательно, совокупность Sub Л всех подалгебр этой алгебры
будет полной решеткой (наименьшим ее элементом при отсутствии
нульарных операций является подалгебра с пустыми файлами и
пустыми операциями).
Пример 92. На рис. 62 изображен диаграммой переходов
автомат Л = (S, X, Y, д, А), где S = {sp s2, s3, -$4), X =
213
= {хр х2}, Y = {0, 1} (на стрелках переходов указаны пары
«вход-выход»), и три его ненулевых подавтомата с множеством
состояний {s2, s3). Заметим, что, трактуя автомат как трехоснов-
ную алгебру, мы не фиксируем входной и выходной алфавиты,
т. е. выходим за рамки класса сравнимых автоматов. С этой
точки зрения автономные компоненты полуавтомата будут его
подавтоматами.
Пусть А = (А , Лэ, ..., A,; F) и В = (В , В ..., В,; F)—две
1 х к	1 х /с
однотипные ^-основные алгебры. Гомоморфизмом из Л в В
называется семейство отображений <р.: А. -* В, 1 < i < к,
согласованное со всеми операциями в том смысле, что
, а , ..., а. )) = /(р((а.), <р[а. ), ..., >р.(а. ))
12л	12	л
для любой n-арной операции f G F и любых (а. , а. , ..., а. ) из
S 12 1п
области ее определения А. X А. X ... X А. . Гомоморфизм <р
S ‘2	‘п
называют инъективным (или вложением), сюръективным (или
наложением), биективным (или изоморфизмом), если соответст-
вующим свойством обладает каждая его компонента у>.,
1 < i: < к.
П р и м е р 93. Пусть А = (S, X, Y, <5, Л) и А' = (S',
X', Y', д', Л')—два автомата. Рассматривая их как трехосновные
алгебры, получаем, что гомоморфизм из А в А' следует определить
как тройку отображений у>: 5 -* S', у.. X -* X', %: Y -* Y' со
свойствами:
p(d(s, х)) = <5'(p(s), У’(х)),
Х(Л(х, х)) = A'(p(s), У>(х)).
Требуя еще, чтобы <р,	% были взаимно однозначными
соответствиями, приходим к понятию изоморфизма для автома-
определением, данным во введении.
тов—в точном согласовании с
S4 ~ SV У- X, н-» X', Х2 ~
В качестве конкретной иллю-
страции рассмотрим автомат
А' = (S', А", У, д', Л'), где
S' = {s', s', s'}, X' = {х/, x'},
Y = {O', Г}, а функции д' и Л'
заданы диаграммой, изображен-
ной на рис. 63. Он представляет
собой гомоморфный образ автома-
та А (рис. 62): тройка отобра-
жений <р: S] >—♦ Sp $2,s3	* S2’
xj; Х: 0 •—» О', 1	» Г образует
гомоморфизм автомата А на автомат А'.
214
Если <р: А -» В и ф: В -* С—гомоморфизмы ^-основных
алгебр, то можно определить композицию (произведение) этих
гомоморфизмов, полагая
<р ° ф ; = о у | 1 < I < к}.
Все алгебраические свойства гомоморфизмов универсальных ал-
гебр, связанные с умножением, без труда переносятся на случай
многоосновных алгебр. Например, произведение гомоморфизмов
является гомоморфизмом, инъективным, сюръективным или биек-
тивным вместе с сомножителями. Совокупность всех эндо-
морфизмов, т. е. гомоморфизмов ^-основной алгебры А в себя,
образует моноид (End А, °, А), где под А понимается семейство
тождественных отображений {Д.1 1 < i < к} на основных мно-
жествах (файлах) Ар А2, ..., Ак алгебры А.
Еще одним важным объектом является группа автоморфизмов
Aut Л. Конгруэнцией ^-основной алгебры А = (Ар А2, ..., А^ F)
называется семейство в = [в. С А. х А. I 1 < i к} эквивален-
тностей на файлах алгебры А, обладающее следующим свойством
устойчивости относительно любой n-арной операции /: А. х
S
X А. х ... х А. -» А. :
<	i i
2	п	л +1
(a.,b.) G в. & (a ,b.) G в. &	(а. , b. ) S 6. =>
1	1	1	2	2	2	п
=> (f(a. , а , а.), f(b. , b. , ..., b. )) G в. .
12	л	12	л	л+1
Факторалгебра А/6 определяется теперь как ^-основная алгебра
И./о,. л2/в2,....Лк!е-, Е)
того же типа, что и А, операции в которой выражаются через
одноименные операции алгебры А по формуле
f(6. (а.), в (а.), ..., 6. (а )) := в (f(a. , а. , а. )).
II 22	п п	л+1	12	л
Легко получается
Т е о р е м а 2.78. Пусть <р = {у>,1 1 < i < к}—гомомор-
физм многоосновной алгебры А. Тогда его ядро Кег <р : =
:= {Kery>.l 1 < i < к} является конгруэнцией алгебры А. С
другой стороны, если 6 = {0.1 1 < i < к}—конгруэнция на А,
то семейство естественных отображений {nat 0.1 1 < i < к}
будет гомоморфизмом алгебры А на факторалгебру А/6. о
Пример 94. Ядром гомоморфизма (у>, ф, %) автомата А
на автомат А', рассмотренного в примере 93, является конгру-
энция 0, состоящая из разбиения {sj, {s2, s3), {s4) множества 5
215
и тождественных отношений Д^. и Ду (отображения V* и Z взаимно
однозначны). Факторавтомат Al в представлен на рис. 64. Он не
совпадает с гомоморфным образом (см. рис. 63), но изоморфен
ему: изоморфизм осуществляется соответствиями {Sj} •—» s',
{s2, s'3} >-> s'2, {s4} —» s3; Ц} —» x'2, {x2} —» Xp {0} —» O',
{1} •—» Г. Это служит частной иллюстрацией следующего общего
принципа.
Т е о р е м а 2.79 (теорема о гомоморфизмах). Если р:
Рис. 64
А -» В—сюръехтивный гомоморфизм многоосновных алгебр, то
факторалгебра Л/Ker р изоморфна алгебре В.
Доказательство этой теоремы получается непосредственным
переносом соответствующих рассуждений из § 2.1. □
Некоторых комментариев—с точки зрения приложений—тре-
бует конструкция прямого произведения многоосновных алгебр.
Пусть А = (Л , А-, ..., A,; F) и В = (В , В,..., В ; F)—две
1 X	АС	1 X	АС
однотипные ^-основные алгебры. Их прямым произведением
называется алгебра А X В := (Aj X В{, А2 X В2, ..., А^ X F),
где
/((а. , Ь.), (а. , Ь. ), ..., (а. , Ь. )) : =
112	2	п п
:= (f(a. , а. , ..., а. ), f(b. , Ь. , ..., Ь. ))
12	п	12	п
для любых (а. , а. ,	..., а. )	G А.	X А.	X ... X А. , (Ь. , Ь.	, ...
' 1 ’	1	। > i I	i'ii
12	п	12	л 1	2
..., b. ) G В. X В. х ... х В. . Прямому произведению автоматов,
1п	\	2	п
рассматриваемых как трехосновные алгебры, технически соответ-
ствует их параллельное соединение как простейших (один
вход—один выход) структурных автоматов. В то же время
параллельные декомпозиции автоматов осуществляются в рамках
другой алгебраической схемы и предполагают сравнимость всех
используемых автоматов, т. е. наличие у них общего входного (и
выходного в случае его участия) алфавита.
216
При рассмотрении глобальных межсистемных связей обычные
алгебраические средства оказываются недостаточными. Полезным
дополнением к ним во многих случаях могут служить конструкции
и методы теории категорий, привлекающей все большее внимание
в различных прикладных областях.
Категория состоит из объектов и морфизмов, связанных
следующими требованиями:
1)	Каждый морфизм <р приписан к некоторой единственной
для него упорядоченной паре объектов (А, В). При этом пишут
<р: А -* В или А -» В , объект А называют началом или
областью определения морфизма <р, а объект В—его концом или
областью изменения. Множество всех морфизмов, приписанных
к данной паре объектов (А, В), обозначается Нош (А, В).
2)	Для любых морфизмов у>: А -» В и хр: В С определено
их произведение <рхр, причем <рхр G Hom (А, С).
3)	Если <р: А -* В, хр: В -» С и. %: С -» D, то ф(хрх) =
— (Р^)Х> т- е- (частичное) умножение морфизмов ассоциативно.
4)	Для любого объекта А существует морфизм 1 G
G Нош (Л, А) такой, что 1А<р = <р и хр\^ = хр для любых
<р: А -» В и хр: С -» А. Морфизм называется тождест-
венным или единичным на А.
Из определения категории следует, что Нош (А, А) для любого
объекта А является моноидом.
Пример 95. Категория Rel имеет своими объектами
всевозможные множества, а морфизмами—отношения между
множествами, т. е. Нот (А, В) = Р(А х В) для любых двух
множеств А, В. Умножение отношений удовлетворяет требо-
ваниям, предъявляемым к частичному умножению в категориях.
При этом 1 = А для любого множества А.
А А
Пример 96. Категория Set имеет своими объектами
всевозможные множества, а морфизмами—всевозможные отобра-
жения. Таким образом, Нот {А, В) есть не что иное, как
совокупность всех функций, заданных на Л и принимающих
значения в множестве В. Тождественный морфизм 1 —это
тождественная функция Д^: а а, а произведение морфизмов
f: А В, g: В С совпадает с обычной суперпозицией функ-
ций f°g.
Пример 97. Категория Alg (т) всех алгебр данного типа
г и их гомоморфизмов. Если А и В—две алгебры типа т, то
Нот (Л, В)—это совокупность всех гомоморфизмов алгебры А в
алгебру В, а 1 —тождественный автоморфизм А алгебры Л.
А	А
Категория Ж* называется подкатегорией категории «#, если
каждый Jif’-объект является Jtf-объектом, каждый ЛГ*-морфизм
является Jf-морфизмом, тождественные —морфизмы тождест-
217
венны в Jtf и произведение ЛГ*-морфизмов то же, что и в <Ж.
Например, категория Set будет подкатегорией категории Rel, а
категория Boole-А булевых алгебр и их гомоморфизмов будет
подкатегорией категории Alg (2, 2, 1,0, 0).
П р и м е р 98. Категория Orgr ориентированных графов и
их гомоморфизмов. (Гомоморфизмом графа Gj = (V^, а J в граф
G2 = (У2, а2) называется отображение -» V2 такое, что
(и, у) е =» (<р(и), <р(у)) е а2
ДЛЯ любых U, V е Ур)
П р и м е р 99. Категория Aut, объектами которой являются
автоматы общего вида А = (S, X, У, <5, Л), а морфизмами—го-
моморфизмы автоматов, т. е. тройки / = (<р, ip, %), удовлетворя-
ющие условиям
?(£>($, х)) =	У(х)),
X(A(s, х)) = Л( <p(s), ip(x))
для любых s G S, х G X. Умножение гомоморфизмов произ-
водится покомпонентно, как у многоосновных алгебр, тождествен-
ными морфизмами являются тройки вида
ДА =	Ду)’
Пример 100. Категория SAut (X), объектами которой
являются полуавтоматы с фиксированным входным алфавитом X,
а морфизмами—гомоморфизмы сравнимых полуавтоматов.
В дальнейшем будут приведены примеры других категорий.
Одной из задач при изучении данной категории является
классификация ее морфизмов по тем или иным их свойствам.
Морфизм <р: А -» В категории Jtf называется мономорфизмом,
если для любых у», % G Hom (С, А) из равенства ip<p — ХР
следует, что — х- Стандартный пример мономорфизмов дает
Т е о р е м а 2.80. В категории Set мономорфизмами явля-
ются инъективные отображения, и только они.
Доказательство. Необходимость.
Пусть <р: А -* В—мономорфизм. Предположим, что у? не инъек-
тивно, т. е. что существуют различные а^, а2 G А, для которых
= <р(а2). Для произвольного непустого множества С поло-
жим ip: С •—» А, с •—♦ tip и х- С "* А, с •—> а2, для любого
с G С. Тогда ip # %, но
(^°у>)(с) = у>(^(с)) = <р(а^ = <р(а2) = <р(х(с)) = (z°p)(c),
откуда ip ° >р = х °Р> что невозможно, так как <р—мономорфизм.
218
Достаточность. Если у>: А -» В—инъективное
отображение, то р°р~1 = Д^. Следовательно, для 1р, % G
е Hom (С, Л) получаем:
Хр о р — о р => хр = Хр о Д
= Хр О ( pop 1) = (хр О p'j Op 1
= (z ° (?) ° (Р 1 = Z ° Лл = Z,
и, значит, р—мономорфизм, о
Т е о р е м а 2.81. Если в категории произведение мор-
физмов pip является мономорфизмом, то р—мономорфизм.
Доказательство. Пусть р: А -* В, ip: В -* Си
Xt, х2: D А. Предположим, что = %2у>. Тогда %1(П') =
= (z^)^ = (z2^)^ = Z2(y’V')> и, следовательно, = %2, посколь-
ку рр—мономорфизм. Таким образом, получили, что для любых
%г х2 е Нот (О, А) из Хх'Р = Z2P следует равенство = х2-
Значит, р—мономорфизм, о
Поскольку тождественные морфизмы категории являются
ее мономорфизмами и произведение мономорфизмов, как нетрудно
проверить, тоже будет мономорфизмом, то класс всех объектов
категории и класс всех ее мономорфизмов образуют подкате-
горию. Она обозначается обычно через Mono
Морфизм р: А -* В категории называется эпиморфизмом,
если для любых ip, х е Нот (В, С) из равенства р\р = рх
следует, что \р — х-
Т е о р е м а 2.82. В категории Set эпиморфизмами явля-
ются сюръективные отображения, и только они.
Доказательство. Необходимость.
Пусть р: А -* В—эпиморфизм. Предположим, что р не сюръ-
ективно, т. е. что существует элемент Z>0 G В — рг2у>. В качестве
С выберем двухэлементное множество {Ср с2} и положим
¥’(*) : =
с2’
если b bQ,
если b =
а также %(Z>) := для всех b е В. Тогда р
* Z, но
(p°V’)(*) = Ч'(ф(ЬУ) = Cj = x(fp(b)) = (p°x)(b),
откуда р ° ip = р °Xi что невозможно, так как р—эпиморфизм.
Достаточность. Пусть р: А -* В—сюръективное
отображение. Тогда р~1 ° р = Д£ и для любых ip, х е
G Нот (В, С) получаем:
219
р о Ip = ф ° % * V* =	° ‘P = I ° (f>) ° Ip = tp ' °	°	=
<P 1 °(У’°Х) = Дв°Х
= x.
и, следовательно, p—эпиморфизм. □
Легко получается аналог теоремы 2.81
Теорема 2.83. Если в категории JC произведение мор-
физмов <pip является эпиморфизмом, то ip—эпиморфизм. =
Класс всех объектов категории Ж и класс всех ее эпиморфиз-
мов образуют подкатегорию Epi Jif.
Морфизм <р: А -» В категории называется изоморфизмом,
ф 1g если существует морфизм ip-. В -* А
А в ** В такой, что <pip = 1^ и ipip = 1Д. Вместо
/	последних двух равенств говорят, что
v	коммутативна диаграмма, приведенная
/	на рис. 65. В этом случае говорят,
А	также, что объекты А и В изоморфны.
Рис 65	Так как тождественные морфизмы
являются одновременно мономорфизма-
ми и эпиморфизмами, то из теорем 2.81 и 2.83 получаем, что
каждый изоморфизм тоже будет и мономорфизмом и эпимор-
физмом. Следовательно, класс всех объектов категории Л и класс
всех ее изоморфизмов образует подкатегорию, которая обознача-
ется Iso .
Из теорем 2.80 и 2.82 следует, что морфизмами подкатегории
Iso Set будут в точности биективные отображения, т. е. взаимно
однозначные соответствия между множествами.
Заметим еще, что морфизм ip, участвующий в определении
изоморфизма, определяется однозначно, например, в силу моно-
морфности р. Его обычно обозначают символом р~\ что вполне
согласуется с обозначением в категории Set.
Т е о р е м а 2.84. Если объектами категории Ж являют-
ся множества, снабженные дополнительной структурой, а
морфизмами—некоторые специальные отображения, связанные
с этой структурой, то каждый инъективный морфизм категории
Л будет ее мономорфизмом, а каждый сюръективный морфизм
будет эпиморфизмом.
Доказательство следует из теорем 2.80 и 2.82. а
В общем случае теорема 2.84 не допускает обращения, т. е.
не во всякой категории структуризованных множеств моно-
морфизмы будут инъекциями (хотя привести пример такой
категории не просто), а эпиморфизмы—сюръекциями.
Пример 101. Рассмотрим категорию SGr полугрупп с их
гомоморфизмами. Пусть (N, •) и (Q+, )—мультипликативные
полугруппы соответственно натуральных чисел и положительных
рациональных чисел. Покажем, что тождественное вложение
220
An: N -» Q+, n •—» n, является эпиморфизмом категории SGr,
хотя оно и не сюръективно. Пусть А—произвольная полугруппа
и X- Q+ * Л—гомоморфизмы, причем = AN°X, т- е-
tp(n) = х(п) для любого натурального числа п. Тогда tp(l) =
= Х(1) = е будет идемпотентом в А, и, следовательно, V и X
оказываются групповыми гомоморфизмами группы (Q+, •) на
подполугруппу G в А, являющуюся группой с единицей е. Если
теперь р/q—произвольное положительное рациональное число, то
ч>{р/ч) = V(pq~l) = v(p)(v(q))~l = х(р)(х(ч))~1 = х(р<Г1) = x(p/<i)>
т. е. V = X- D
В доказательстве теоремы 2.87 потребуется следующий факт,
имеющий и самостоятельный интерес.
Теорема 2.85. Во всякой категории SAut (X) полуав-
томатов и их гомоморфизмов мономорфизмами являются
инъективные гомоморфизмы, а эпиморфизмами являются сюръ-
ективные гомоморфизмы.
Доказательство. Пусть <р: А -* В—произволь-
ный мономорфизм категории SAut (X), и он не инъективен. Тогда
в полуавтомате А = (S, X, д) существуют состояния и s2
такие, что s1 # s2, но y’(Sj) = <p(s2). Рассмотрим прямое
произведение (в смысле § 2.1) главных подавтоматов A(st) и
A(s2) полуавтомата А. В полуавтомате A(s() х A(s2) выделим
главный подавтомат С, порожденный состоянием (Sp s2). Очевид-
но, что С будет подпрямым произведением полуавтоматов A(st)
и A(s2). Проекции
л^ С -» Ар (s, /) •—» s, л2: С -» А2, (s, t) •—» t,
являются гомоморфизмами и притом различными, поскольку
^«Sp S2)) =	* S2 = Л2((5г S2)).
Понятно, что Лр л2 G Hom (С, А). Пусть (s, f)—произвольное
состояние полуавтомата С. Тогда существует слово р G X такое,
что (s, f) = 6((Sp s2), p), откуда получаем, учитывая, что
<р—гомоморфизм:
(л,’?)^, 0) = (л^ y>)(d((Sp s2), р)) = (л^ y>)((<5(Sp р), d(s2, р))) =
= ^((«Hsp р), 6(s2, р)))) = y>(<5(Sp р)) = d(^(Sj), р) =
= 6(^(s2), р) = ... = (л2 oy>)((s, 0).
221
Следовательно, л( ° <р = %2 ° <р. Так как # л2 и <р—моно-
морфизм, то полученное равенство невозможно. Поэтому предпо-
ложение об неинъективности мономорфизма у отклоняется.
Пусть теперь <р: А -* В—эпиморфизм категории SAut (X), и
он не сюръективен. Тогда в полуавтомате В = (Т, X, д)
существует состояние tQ, не принадлежащее В* = рг2у>. Поскольку
В* является подавтоматом в В, можно определить на В конгру-
энцию в := (В* х В*) U . В факторавтомате В/в состояние
В* образует одноэлементный подавтомат. Кроме него, в В/в есть
еще и другие состояния, например, 0(Q = {<0}. Отображения
nat 0: Т - Т/д и гр: Т - Т/9, t — В*,
будут гомоморфизмами полуавтомата В в полуавтомат В/в и
притом различными, так как (nat 0)((о) = {tQ}, a V’(?o) = в*-
Однако <р ° nat 9 = <р ° гр, что противоречит эпиморфности <р. =
Большой интерес при изучении заданной категории представ-
ляет выделение в ней некоторых специальных объектов.
Объект А категории называется начальным (или инициаль-
ным), если для каждого объекта В этой категории множество
Нот (А, В) состоит точно из одного морфизма.
Конечный (или терминальный) объект А определяется требо-
ванием одноэлементности множества Нот (В, А) для каждого
«Х-объекта В. В категории Set единственным начальным объектом
является пустое множество, так как Нот (0, А) состоит только
из пустого отображения, конечными объектами будут пустое
множество и любое одноэлементное множество.
Т е о р е м а 2.86. Если А, В—начальные (конечные) объ-
екты некоторой категории, то А и В изоморфны.
Доказательство. Если А и В—начальные объек-
ты, то существует четыре однозначно определенных морфизма:
<р: А -* A, ip: А -* В, В -» А, а>: В -» В.
В силу единственности, <р = 1^, ш = 1 и грх = 1^, хЧ' =
Следовательно, У’—изоморфизм. =
Таким образом, единственным с точностью до изоморфизма
начальным (и одновременно конечным) объектом категории Gr
групп и их гомоморфизмов является единичная группа {е}, а в
категории Ring колец—нулевое кольцо {0}.
Объект А категории X называется инъективным, если для
любого морфизма <р: В -» А и любого мономорфизма у>: В -» С
существует морфизм х- С -* А такой, что <р = У7, т. е. комму-
тативна диаграмма а) на рис. 66. Объект А, по определению,
проективен, если для любого морфизма <р: А -» С и любого
эпиморфизма гр: В -* С существует морфизм А -* В такой,
222
что <р = х</’> т- е- коммутативна диаграмма б) на рис. 66. В
качестве конкретной иллюстрации приведем следующий результат
[54].
Рис. 66
Т е о р е м а 2.87. Автономный полуавтомат инъективен
тогда и только тогда, когда его граф переходов состоит из
циклов, среди которых есть хотя бы один одноэлементный.
Неавтономный полуавтомат инъективен тогда и только тогда,
когда он имеет только одно состояние.
Доказательство. Необходимость.
Пусть полуавтомат А = (S, X, д) является инъективным объек-
том категории SAut (X). Сначала покажем, что А содержит
одноэлементный подавтомат. В самом деле, рассмотрим полуавто-
мат Aq = (SQ, X, б0), где 50 := 5 и {sQ},	5, а
dQ(s, х) :=
<5(s, х), если s G S, х G X,
sQ, если s = х G X.
Так как мы имеем вложение (мономорфизм) Д^: А -» Ао и
тождественный автоморфизм Д^: А -* А, то, поскольку полуав-
томат А инъективен, существует гомоморфизм %: AQ А такой,
что /I = Д . Очевидно, что %(s) образует одноэлементный
подавтомат в А.
Теперь установим, что ни одна из автономных компонент
полуавтомата А не имеет нециклических состояний. Пусть это не
так, и для некоторого xQ G X автономный полуавтомат
(5, {х0}, <5) содержит недостижимое состояние s*. Рассмотрим
полуавтомат = (SQ, X, dQ), где SQ : = S U {sQ},	£ S, и
<50(s, x) : =
<5(s, x),
*
5 ,
если s & S, x & X,
если s = Sq, x G X.
Так как имеется вложение (мономорфизм) Д^: А -* Ло и
тождественный автоморфизм Д^: А -» А, то, в силу инъективности
полуавтомата А, найдется гомоморфизм %: А() -» А такой, что
Zl5 = Ау Тогда
223
s* = As(s*) = x(s*) = X0O(SO’ *0)) = d(x(sQ), XQ),
т. e. состояние s* оказывается достижимым в автономном
полуавтомате (S, {xQ}, б) из состояния %(sQ), что приводит нас к
противоречию.
Таким образом, инъективный объект любой категории
SAut (X) представляет собой полуавтомат, автономные компоненты
которого состоят из циклов, один из которых обязательно
одноэлементен. Отсюда следует утверждение для случая автоном-
ных полуавтоматов.
Допустим, что входной алфавит X содержит не менее двух
символов, и что А—инъективный объект в категории SAut (X).
Предположим, что кроме состояния л'0> образующего одноэлемен-
тный подавтомат, А имеет еще состояние Sp Выделим в X входной
сигнал Xq и рассмотрим полуавтомат А® = (SQ, X, где
SQ := 5 U {s*}, s* £ S, и
d(s,	x),	если	s	6	S,	x 6	X,
<50(s, x) :=	so-	если	s	=	s*,	x =	xQ,
Sp	если	s	=	s ,	x	х^.
Те же рассуждения, что и в предыдущих частях доказательства,
дают гомоморфизм %: А® -* А, тождественный на состояниях
полуавтомата А. Имеем:
50 = Д5^о) =	= X(do(s*’xo)) = ^(X(s*),xo),
откуда %(s*) = sQ, так как в автономной компоненте
(S, {х0}, б) состояние s0 образует одноэлементный цикл. Тогда
при х1 # х0 получаем:
S1 = Д5^1) =	=%(do(s*' \)) = 6(x(s*), s,) = <5(s0, Xj) = s0,
что противоречит предположению s0 * Sp Таким образом,
инъективные объекты в категориях SAut (X), где 1X1 > 2,
являются полуавтоматами с одним состоянием.
Достаточность. Очевидно, что полуавтомат с
одним состоянием инъективен в любой категории SAut (X). Пусть
А = (S, {х}, б)—автономный полуавтомат, граф переходов кото-
рого состоит из циклов, причем хотя бы один из них
одноэлементен, пусть его образует состояние sQ. Пусть В =
= (Г, {х}, б) и С = (U, {х}, б)—автономные полуавтоматы,
<р: В -* А—гомоморфизм, у»: В -* С—мономорфизм. Согласно те-
ореме 2.85, V» является инъективным гомоморфизмом, т. е.
224
вложением автомата В в автомат С. Будем считать, что
В—подавтомат в С и что у» =	• Пусть t 6 Т—произвольное
состояние автомата В и у>(/) принадлежит в А циклу длины I.
Через tk обозначим первое циклическое состояние среди состояний
= d(f), t2 = 6(Zj), ... в полуавтомате В и, значит, в С. В
компоненте связности Uf графа переходов полуавтомата С,
содержащей состояние t, положим (и, у) 6 тогда и только
тогда, когда и и у находятся на одинаковом по модулю I расстоянии
от tk (здесь под расстоянием понимается наименьшее число
итераций входного сигнала х, необходимых для перехода в С из
состояния и в состояние у). Легко видеть, что в := U Qf является
t е т 1
конгруэнцией, продолжающей конгруэнцию Кет <р на подавтомат
С* полуавтомата С, состоящий из всех компонент связности этого
полуавтомата, имеющих непустое пересечение с множеством Т.
Через <р* обозначим гомоморфизм подавтомата С* на полуавтомат
А. Теперь определим отображение	S, полагая:
<f>*(u), если и 6 U *,
' sQ, если и U*.
Очевидно, что х е Hom (С, А) и что <р = рх- D
Пусть даны категории и Функтор F из категории
Х( в категорию Х2 определяется как отображение класса объектов
категории Xj в класс объектов категории Х2 и класса морфизмов
категории Xj в класс морфизмов категории Х2, удовлетворяющее
следующим условиям:
1)	если <р 6 Нот (Л, В), то F(<p) 6 Hom (F(A), F(B)),
2)	если <p 6 Hom (А, В) и E Hom (В, С), to F(<pp) =
= F(<p)F(y),
3)	F(1A) = l/pt) для люб°го объекта А из X.
Пример 102. Для любой категории X отображение
А •—» А, <р •—» <р определяет тождественный функтор этой
категории на себя.
Пример 103. Пусть X—произвольная категория, А—не-
который ее фиксированный объект. Каждому Х-объекту В
сопоставим множество f\b) = Hom (Л, В), а каждому морфизму
у: в -* С—отображение	F(B) -* F(C), <р •—» <рр. Легко
проверить, что F4 представляет собой функтор из категории X
в категорию множеств Set. Функторы вида F^ называются
основными функторами из X в Set.
8 А.М.Богомолов, В.Н.Салий	225
П р и м е р 104. Пусть Alg (т)—категория алгебр типа т и
их гомоморфизмов. Сопоставляя каждой т-алгебре А ее носитель
А и рассматривая каждый гомоморфизм т-алгебр как отображение
носителя в носитель, получаем пренебрегающий функтор из
категории Alg (т) в категорию множеств Set. Аналогично строится
пренебрегающий функтор из каждой категории SAut (X) полуав-
томатов в категорию Set.
Категории X] и «#2 называются изоморфными, если сущест-
вует функтор F:	-* являющийся взаимно однозначным
отображением категории на категорию
П р и м е р 105. Категория SAut (X) сравнимых полуавто-
матов с входным алфавитом X, где IXI = т, изоморфна
категории Alg0(r) конечных унарных алгебр типа т =
= (1, 1, ..., 1). Действительно, в § 2.1 было показано, что между
т
полуавтоматами и алгебрами указанного вида существует взаимно
однозначное соответствие, при котором гомоморфизмы остаются
гомоморфизмами.
Пример 106. Категория Boole-А булевых алгебр изомор-
фна категории Boole-R булевых колец. В самом деле, в § 2.4
было установлено взаимно однозначное соответствие между
объектами этих категорий, причем отображение одной булевой
алгебры в другую тогда и только тогда является гомоморфизмом,
когда оно представляет собой гомоморфизм соответствующих
булевых колец.
ГЛАВА 3
ГРАФЫ
§ 3.1. Основные алгебраические конструкции
Под ориентированным графом (или, для краткости, орграфом)
понимается пара G = (V, а), где V—конечное непустое множество
(вершины орграфа), а а С v х V— отношение на множестве V
(пара (u, v) G а называется дугой орграфа с началом и и концом
у). Отношение а называют отношением смежности, а соответ-
ствующую ему двоичную булеву матрицу—матрицей смежности
орграфа G.
Каждому орграфу можно сопоставить некоторое изображение—
диаграмму, на которой вершины орграфа представляются точками
(или кружками), а дуги—непрерывными кривыми (например,
прямолинейными отрезками), ориентированными стрелкой от
начальной вершины к конечной. Ясно, что один и тот же орграф
допускает много различных изображений.
Очень распространенным требованием является исключение из
числа дуг орграфа петель, т. е. дуг с совпадающими началом и
концом. Отсутствие петель в орграфе G = (V, а) означает
антирефлексивность его отношения смежности а. Напротив,
рефлексивность отношения а обеспечивает наличие петли в
каждой вершине орграфа (другое распространенное требование).
Следующее определение мотивируется тем, что во многих
прикладных задачах ориентация дуг не имеет значения (например,
в электрических схемах). Неориентированным графом (или, для
краткости, графом) называется пара G = (V, а), где а—
симметричное и антирефлексивное отношение на множестве
—>
вершин V. Из каждого орграфа G = (V, а) можно получить
неориентированный граф G = (V, (a U а-1) — А), называемый
—>
симметризацией орграфа G. Чтобы построить изображение
симметризации G, в изображении орграфа G убирают стрелки на
дугах и петли, а каждую пару встречных дуг (и, у), (у, и)
заменяют одной линией. Различные орграфы могут иметь
совпадающие симметризации (рис. 67). Дуги неориентированного
8*
227
графа обычно называют ребрами. Ребро, образованное вершинами
и, v, иногда обозначают через {и, у}.
Рис. 67
Важный класс орграфов выделяется при рассмотрении блочных
схем дискретных устройств без обратных связей между элемен-
тами. Орграф G = (V, а) называется направленным графом (или
диграфом *)), если отношение а антисимметрично, т. е.
а О а-1 С Д^ . В изображении направленного графа нет встреч-
ных дуг.
Пусть G = (V, а)—некоторый орграф, v 6 V—одна из его
вершин. Степенью исхода вершины v называется число d+(v) дуг
орграфа G, имеющих своим началом у, т. е. a(v) := la(v)l.
Степень захода вершины v—это количество d~(y) дуг, имеющих
у своим концом, т. е. d~(y) := la-1(v)l. Числа d+(y) и d~(y)
легко находятся по матрице смежности орграфа G: первое из них
равно количеству единиц в строке, соответствующей вершине у,
а второе—количеству единиц в столбце, отвечающем этой
вершине.	.
(d . d ) (rf , <)
Если V = {vp v2, ..., у^}, то строка (Vj 1 1 , v2 2 2 , ...
(d+, d~)	,	.
..., v " " ), где J := d (у.), d. := d (v.), называется специ-
фикацией орграфа G = (V, a).
В неориентированном графе d+(v) = d~(y) =: d(v). Число
d(v) называется степенью вершины v. При этом вершина
считается четной или нечетной в зависимости от соответствую-
щего свойства числа cZ(v). Набор чисел, являющихся степенями
вершин данного графа G, называют его степенным множеством,
а вектор, компонентами которого являются расположенные в
убывающем порядке степени всех вершин,—вектором степеней.
Если с/(у) = 0, вершина у называется изолированной.
П р и м е р 107. Орграф называется функциональным, если
d+(y) = 1 для любой его вершины v (т. е. если из каждой
вершины исходит точно одна дуга). Очевидно, что функциональ-
ные орграфы с данным множеством вершин V находятся во
Слово «диграф» иногда используется как синоним термина «орграф».
228
взаимно однозначном соответствии с преобразованиями множества
V (они являются графами этих преобразований). Спецификация
-»	d
функционального графа G = (V, а) приобретает вид (я1,
d" d~
v22,..., у^") и, следовательно, совпадает со спецификацией
преобразования а: V -* V в смысле § 2.2.
—>
Орграф G = (V, а), по определению, является контрафунк-
ционалъным, если орграф G-1 = (V, а-1) функционален. Таким
образом, контрафункциональный орграф характеризуется тем, что
в каждую его вершину входит точно одна дуга. Спецификация
контрафункционального графа G = (V, а) приобретает вид
(vt 1, v“i, ..., vnn) и совпадает со спецификацией преобразования
а-1: V - V.
П р и м е р 108. Графы, изображенные на рис. 68, имеют
одинаковый вектор степеней (2, 2, 2, 1, 1) и, следовательно,
одинаковое степенное множество {1, 2}.
Рис. 68
Граф G = (V, а) называется полным, если любые две его
"вершины соединены ребром, т. е. если а = (VxV) — Д. Полный
граф с п вершинами обозначается символом К„. Каждая его
вершина имеет степень п - 1. На рис. 69 изображены полные
графы с п = 2, 3, 4, 5, 6 вершинами.
Дополнением графа
граф G — (V, а — А).
G = (V, а) называется
Таким образом, допол-
нение G графа G имеет то_же множество вершин,
и две вершины смежны в G тогда и только тогда,
когда они не смежны в G. На рис. 70 изображены
граф и его дополнение.
Объединение графов G1 = (V , а{) и G2 =
— (V2' а2^ определяется как граф GjUG2:=
Рис. 70
229
:= (у (J у U«2). Чтобы изобразить объединение G1 U G2
при	Cl V2 — 0, нужно расположить рядом изображения
графов G( и G2. Объединение графа G с его дополнением G дает
полный граф с соответствующим множеством вершин.
Соединение двух графов G( = (У(, и G^ = (V2, а2), где
^1 О У2 = 0,—это граф G( + G2 := (V{ U V2, at U a2 U
U У x V2 U V2 x V{). Граф G( + G2 сохраняет все ребра,
имевшиеся в Gj и G2, и, кроме того, в нем каждая вершина
графа Gj оказывается смежной с каждой вершиной графа G2. На
рис. 71 приведено соединение двух графов: К2 +	= К5.
Рис. 71
Следующий результат [80] показывает, что любой конечный
набор натуральных чисел может быть реализован в виде типовых
вход-выходных характеристик элементов подходящей сети.
Теорема 3.1. Для любого множества натуральных
чисел А = {d,, d~, ..., d.}, k > 1, где d. < d-< ... < d,, cyuie-
ствует граф c d^ + 1 вершинами, для которого А является
степенным множеством.
Доказательство. Индукция по числу к. При
к = 1 графом со степенным множеством А = {<7} является полный
граф Kd+V
При к = 2 степенное множество А = {d^ d2) имеет со-
единение двух графов G =	+ X, +1.
i аг 1
Пусть к > 2 и А = {d,, d~, ..., d,, d,, .}, d< d< ...
J	1 1’ 2 к k+1	1	2
...<d^<d^+l. По предположению индукции, существует граф
Gq с (d^ — c/j) + 1 вершинами, степенным множеством которого
является множество {d2 - d{, d$ — dv .... d^ — б^}. Тогда граф
G = К. + (К,	. U G„) имеет d. ,, + 1 вершин и степен-
а v а —а О'	к+1
1	*+i	*
ное множество А. а
Рис. 72 показывает, что четырехвершинные графы взаимно
однозначно кодируются их векторами степеней. В общем случае
это не так (см. пример 108).
230
: :i :ni жиипкыи
0000 1100	2110	1111	2220 2211
3111' 2222	3221 3322” 3333*
Рис. 72
Очевидно, что не любой вектор с целыми неотрицательными
компонентами является вектором степеней некоторого графа.
Например, имеет место
Т е о р^е м а 3.2. Во всяком графе G = (V, а):
1)	d(y) = 2т, где т—число ребер',
vev
2)	количество нечетных вершин четно',
3)	при IVI = п > 2 степенное множество графа G со-
держит не более п - 1 элементов, т. е. в G существуют по
крайней мере две вершины с одинаковой степенью.
Доказательство. 1) Каждое ребро соединяет
точно две вершины и, значит, при сложении степеней вершин
учитывается дважды.
2) Сумма степеней всех вершин, согласно 1), четна. Четной
будет и сумма степеней всех четных вершин. Так как сумма
степеней нечетных вершин оказывается четной, их должно быть
четное число.
3) Пусть п > 2. Если в графе G есть изолированная вершина,
т. е. d(u) = 0, то в нем нет вершины v такой, что d(v) = п — 1.
Следовательно, среди возможных в принципе степеней вершин
0, 1, ..., п - 1 две взаимно исключают друг друга, так что
разных степеней вершин в графе G не более чем п - 1. о
Если известно, что вектор (d{, d^, ..., tZ(;) является вектором
степеней некоторого графа, то следующая процедура позволяет
найти один из таких графов (см. [38]).
Шаг 1. Берутся п точек, которым присваиваются метки
d,, d., ..., d . Полагается d : = d,.
г 2 и	1
Шаг 2. Начальная точка, имеющая метку d, соединяется
ребром с d точками в порядке убывания их меток.
Шаг 3. Начальная точка получает метку 0, у всех связанных
с ней точек метка уменьшается на 1. Если у всех точек
новые метки равны 0,—конец, граф построен. Иначе—переход к
шагу 4.
Шаг 4. Начальной объявляется одна из точек с максимальной
ненулевой меткой, d присваивается значение, равное метке
выбранной вершины. Переход к шагу 2.
На рис. 73 работа алгоритма продемонстрирована на примере
вектора (3, 3, 3, 2, 2, 1).
Произвол, допускаемый при исполнении шага 4, может
привести к получению других (т. е. неизоморфных) графов с тем
же вектором степеней.
231
Рис. 73
Напомним, что два орграфа = (V{, и G2 = (У2, а2)
называются изоморфными, если можно установить взаимно
однозначное соответствие <р: Vl -* V2, сохраняющее отношение
смежности:
(u, v) е а{ (<р(и), <p(v)) 6 а2
для любых и, v G V . Понятно, что два орграфа изоморфны тогда
и только тогда, когда они допускают одно и то же изображение.
Проверка изоморфности двух графов в общем случае пред-
ставляет собой весьма трудоемкую задачу. Различные приемы
позволяют сократить перебор. Одним из таких приемов является
матричный метод нахождения изоморфизмов.
Пусть G = (U, а) и Н = (V, р)—два орграфа, для которых
требуется установить, изоморфны они или нет. Положим
) U\ = IVI = п (если у графов разное число вершин, они не
могут быть изоморфными). Через А обозначим матрицу смежности
орграфа G, а через В—матрицу смежности орграфа Н. Обе они
являются двоичными булевыми п X п-матрицами.
Предположим, что графы G и Н изоморфны и <р: U -* V—
один из изоморфизмов. Отображение <р можно записать в виде
двоичной булевой п X n-матрицы Ф, строки которой нумерованы
элементами множества U, метками столбцов являются элементы
множества V и при этом
1, если <р(и.) = г.,
Ф.. := (	'	1
Ч 0 в противном случае.
Поскольку —взаимно однозначное соответствие, в каждой строке
и в каждом столбце матрицы Ф точно один элемент равен 1.
Т е о р е м а 3.3. Пусть А и В—матрицы смежности
п-вершинных орграфов соответственно G = (I/, а) и Н =
= (V, [i) . Взаимно однозначное соответствие <р: U * V тогда
232
и только тогда является изоморфизмом орграфов G и Н,
когда для представляющей его матрицы Ф выполняется
равенство ЛФ = ФВ.
Доказательство. Покажем, что взаимно одно-
значное соответствие <р: U -* V тогда и только тогда будет
—> --------------------------------------
изоморфизмом орграфа G = (V, а) на орграф Н = (V, р), когда
<р(а(и)) — /3(<р(иУ) для любой вершины и G U.
Пусть <р—изоморфизм. Предположим, что v G y>(a(u)). Тогда
(u, p-1(v)) 6 ос. Так как <р—изоморфизм, получаем, что
(<р(и), v) G /3, откуда v 6 /?(у>(и)). Значит, y>(a(u)) С /?(у>(ц)). С
другой стороны, если v 6 /?(у>(и)), то (<р(и), у) 6 /3, откуда
(и, у>-1(у)) 6 а, т. е. <р~1(у) 6 сс(и), и следовательно, у 6
6 ср(а(и)). Получаем включение /3(ср(иУ) С у>(а(и)), так что
<р(а(и.у) = /3(<р(иУ) для всех и 6 U.
Пусть теперь ср(а(и)) = /3(у>(и)) для всех и G U. Если
(и{, и2) е а, то и2 е a(Uj), откуда </>(и2) 6 ^(«(Uj)) =
= /3(ср(и{У), и, значит, (<р(и{), <р(и2)) £ [3. С другой стороны, если
е Z3’ то	е /М“1» = ^(«(“i))- откуда
и2 G a(U\), т. е. (i/р и2) G а. Таким образом, для любых
Up и2 €= U истинна эквивалентность (Up u2) £ а » (y>(Uj),
y>(u2)) G /3, и, следовательно, ср—изоморфизм.
Тождественное равенство ^(а(и)) = /3(у>(и)) равносильно ра-
венству а ° <р = ср ° Р для отношений а С и X U, /3 С V X V,
ср Q U X V, в матричной форме имеющему вид ЛФ = ФВ. =
Чтобы найти все изоморфизмы л-вершинного орграфа G =
= (U, а) на л-вершинный орграф Н = (V, /3), составляют
матричное уравнение ЛФ = ФВ, где Л и В—матрицы смежности
соответственно орграфов G и Н, а Ф—двоичная булева п X п-
матрица с неопределенными элементами, и, приравнивая соответ-
ствующие элементы матриц ЛФ и ФВ, получают систему л2
булевых уравнений, из которой и находят возможные значения
для элементов матрицы Ф (напомним, что в каждой ее строке и
в каждом столбце точно один элемент равен 1).
Поскольку при изоморфизме степень исхода и степень захода
каждой вершины сохраняется, с помощью спецификаций орграфов
G и Н часть элементов матрицы Ф можно сразу положить
равными нулю. Покажем, как ищутся изоморфизмы графов на
конкретных примерах.
П р и м е р 109. Изоморфны ли орграфы, имеющие матри-
цы смежности
233
Пусть вершинами первого орграфа будут и{, и2, иу и^, а
второго—Vp v2, Vy v4> По матрицам смежности находим специфи-
кации:	и(31,2\ и™) и (тХ1’*»,	V^2\
Матрица, соответствующая возможному изоморфизму <р, имеет
вид
	^11	Л2	0	0
ф =	^21 0	^22 0	0 ^33	0 ^34
	0	0	^43	^44
Здесь, например, />13 = 0, поскольку равенство y’(Uj) = v3
невозможно из-за несовпадения степени захода у вершин
и v3-
Находим произведение матриц:
	0	0 ^43 ^44		0	0 ^12
АФ =	0 0 У’ЗЗ ^34	, ФВ =	0	0 ?22 ^21
	0 0 ^33 ^34		0 0 ^34 ^33
	0	0 ^43 ^44		0	0 ^44 ^43
Если АФ = ФВ, то >р33 = (4Ф)33 = (ФВ)33 = р34, что не-
возможно, поскольку один из элементов <р33, у>34 равен 0, а
другой 1.
Рассматриваемые орграфы не изоморфны.
П р и м е р ПО. Изоморфны ли орграфы, имеющие матри-
цы смежности
234
С помощью спецификаций (и^1,0\ и^1,0\	и^1,23) и
(у(1,0\ ^1,0\^1,2\ Уд1,2)) определяем априорно нулевые элементы
матрицы Ф, которая, как видим, будет иметь такой же вид, как
и в примере 109. Далее,
	° ° ^43	*44		0	3 Л1 Л2	
АФ =	0 0 У’зз	^34	, ФВ =	0 Л	° ^21 *22	
	0 0 ^33	^34		0	3 ?33 ^34	
	°	° ^43	^44		0	3 ^43 ^44	
Из равенства АФ = ФВ вытекает, что				рзз	= *>21’ ^34 =	^22
^43 = ^11’ ^44 = ^12-		Следовательно,				
			^12	0	О		
	Ф =	^21 0	^22	0 0	^21	0 ^22		
		0	0 ^11	^12		
Полагая	= 1, получаем изоморфизм у>р и				1 •—> Ур и2	V2
и3 >—» v	•—» Vy Полагая у>[2 = 1, получаем еще один
изоморфизм у>2:	►—» v2, и2 •—» vp	—* vy	►—» v*.
г П р и м е р 111. Проверить, изоморфны ли орграфы G и
Н, изображенные на рис. 74 (см. [43]).
Находим матрицы смежности для первого и второго орграфов:
А
0 1	0	0	0	0	0
0 0	1	0	0	0	0
0 0	0	1	1	1	0
0 0	0	0	1	0	0
0 0	0	1	0	1	0
1 0	0	0	0	0	1
0 0	1	0	0	0	0
0 0 10 10 0
0 0 0 0 0 0 1
0 0 0 1 0 1 0
0 1 0 0 0 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 1
10 10 10 0
в
235
Суммированием элементов строки и элементов столбца, соответ-
ствующих каждой вершине, находим ее степень исхода <1+ и
степень захода d~, откуда получаются спецификации
Ц'-1’) и 41-1’. ”з2,2’
v4v5 '2)’ V61’1^’ Ц3’2))- Матрица Ф имеет вид
	0	Л2	0	Л4	0	Лб	0
	0	У’22	0	^24	0	Лб	0
	0	0	0	0	0	0	1
ф =	0	0	0	0	1	0	0
	Ли	0	Лз	0	0	0	0
	Ля	0	Лз	0	0	0	0
	0	Лг2	0	^74	0	Лб	0
Вычисляем матрицы-произведения:
	0 0 Ли +	У’22 0			0 0 з + Л>з	Л4 0 0		0 0 1	Лб 0 0		0 1 0
		Ля 0		Л							
АФ =	Л	1	0		Лз		)	0	0		0
	Ля		0		Лз		)	1	0		0
	0		Л2 +	Л2	0	Л4	^74	0	Лб + *	’76	0
	0		0		0		0	0	0		1
		0	Л4	0	0	0	0	Л2	+ Лб		
		0	Л4	0	0	0	0	Лг	+ Лб		
		1	0	1	0	1	0		0		
ФВ =		1	0	0	0	0	0		0		
		0	0	Ли	Лз	Ли	Лз		0		
		0	0	Ля	Лз	Ля	Лз		0		
		0	Л4	0	0	0	0	Л2	+ Лб		
Полагая ЛФ = ФВ, сразу получаем 0 = у>24 = у>26 = <Р12 =
= ^16 = Лз = Ля = Лг = ^74’ 1 = Лг Учитывая взаимную
однозначность и сюръективность отношения </>, расшифровываем
236
значения всех элементов матрицы Ф и получаем единственный
изоморфизм
(и. и- U и U' и, и.\
1	2	3	4	5	6	7
=
V4	V2	V7	V5	V1	V3	V6
/
При локальном изучении больших систем ограничиваются
рассмотрением лишь части элементов и связей между элементами.
Как и в случае частичных алгебр (§ 2.6), в теории графов переход
—>
к подсистеме интерпретируется неоднозначно. Пусть G = (V, а)—
некоторый орграф. Частью его называется орграф G =
= (V*, а*), где V* С V и а* С (у* х V*) П а. Таким
образом, часть орграфа имеет своими вершинами некоторые
вершины исходного орграфа, а дугами—некоторые из дуг исходного
графа, соединяющие попавшие в данную часть вершины. Подграф
—*	~* *	♦ *
орграфа G—это такая его часть G = (V , а ), которая содержит
все дуги орграфа G, соединяющие попавшие в данную часть
вершины, т. е. а* = (V* X V*) А а. Сопоставляя орграфу G
частичный группоид (пример 87 из § 2.6), можно увидеть, что
части графа соответствуют подгруппоидам этого частичного
группоида, а подграфы—его относительным подгруппоидам (и
сильным подгруппоидам,—в данном случае эти два вида подалгебр
—>
совпадают). На рис. 75 слева от орграфа G помещены две его
части, а справа—подграф, имеющие одно и то же множество
вершин *). Части и подграфы неориентированного графа, конечно,
предполагаются неориентированными графами.
Рис. 75
Пусть функциональная схема системы задана некоторым
орграфом. Можно ли восстановить (с точностью до изоморфизма,
конечно) эту схему, имея тот или иной набор ее подсхем?
Подграф орграфа G называется максимальным, если он
получается из G удалением одной вершины (и всех связанных с
нею дуг). Следующий пример показывает, что в общем случае
*) .
1о, что мы определили как часть графа, иногда называется подграфом, а
вместо принятого нами термина «подграф» используют словосочетания «порожден-
ный подграф» или «наследственный подграф».
237
орграф не восстанавливается по набору всех его максимальных
подграфов, заданных с точностью до изоморфизма.
П р и м е р 112. На рис. 76 изображены пары орграфов, не
изоморфных, но имеющих одинаковые списки максимальных
подграфов. В случаях а) и б) проверка этих свойств тривиальна.
—>	—>
Убедимся в неизоморфности орграфов G = (U, а) и Н —
—>
= (V, Р) (рис. 76<з). В орграфе G вершины и и2 имеют
степени исхода и захода, выражаемые соответственно парами
(3, 1) и (1, 3), а для остальных вершин d+ = d~ = 2. При
этом (Up u2) 6 а. В орграфе Н имеем (3, 1) для вершины v(
и (1, 3) для вершины v5, но (Vp v5) £ fl (для всех остальных
вершин d+ = d~ = 2). Так что G h Н.
В то же время списки максимальных подграфов у орграфов
G и Н совпадают. Если через G. и Н. обозначить максимальные
подграфы, полученные из G и Я удалением соответственно
вершин и. и v., то, как нетрудно проверить, орграфы G$ и Н{
будут оба изоморфны орграфу, изображенному на рис. 76б слева,
—>	—>
орграфы G5 и Н5 изоморфны орграфу на том же рисунке справа,
а все остальные максимальные подграфы Gp G2, G4, Я2, Ну
попарно изоморфны между собой. Мы вернемся к этому
примеру в § 3.4.
Для неориентированных графов с п > 3 аналогичных приме-
ров пока нет, и, более того, предполагается, что каждый такой
граф с точностью до изоморфизма определяется набором своих
максимальных подграфов.
238
Естественно, что, переходя к подграфам с меньшим числом
вершин, мы сохраняем все меньше информации о структуре самого
графа. Рис. 77 показывает, что в общем случае граф не
восстанавливается по набору всех своих подграфов, получаемых
удалением двух вершин (впрочем, уже для шестивершинных
графов подобная восстановимость имеет место).
Взаимно однозначное отображение Vl -» множества
вершин орграфа G{ = (Ур с^) в множество вершин орграфа
G2 = (У2, а2) называется вложением, если (u, v) е а( =>
=> (<р(й), <р(у)) 6 а2 для любых и, v 6 Рр и называется сильным
вложением, если для любых и, v 6 имеет место эквивалент-
ность (u, v) G Oj о (у>(и), V’(v)) G а2>
Таким образом, если орграф G( вкладывается в орграф G2,
он будет изоморфен некоторой части орграфа G2, а при сильном
вложении—некоторому его подграфу.
Из соответствующих определений непосредственно вытекает
Т е о р е м а 3.4. Орграф G* = (V*, а*) тогда и только
тогда будет частью (подграфом) орграфа G = (V, а), V С V,
когда тождественное отношение Д . является вложением
v
ф	—>
(сильным вложением) орграфа G в орграф G. =
Вложения орграфов связаны с задачей функционального
моделирования одной системы в другой, более богатой системе.
Пусть функциональная модель системы представляется в' виде
орграфа, вершины которого соответствуют элементам системы, а
дуги—связям между элементами. При этом каждому элементу
приписан некоторый тип (разные элементы могут быть однотип-
ными). Будем говорить, что система, представленная орграфом
G{, моделируется системой, представленной орграфом G2> если
Gl вкладывается в G2 и при этом вложении каждой вершине из
G1 соответствует вершина того же типа в G^. Например, система
с функциональной моделью G1 на рис. 78 двумя способами
моделируется в системе с функциональной моделью G2’. только
239
вложения и.	> V.,	и. —> у_,	и,	> vc	и и,	> vc,	и- >—> v,,
1	1	о	о о 1 о	о
«3 >—» v4 сохраняют тип соответствующих вершин.
В дальнейшем для простоты будем рассматривать системы,
представленные неориентированными графами с однотипными
вершинами. Отказ элемента системы S будем интерпретировать
как удаление соответствующей ему вершины из графа G(S),
представляющего собой функциональную модель системы S. Будем
говорить, что система S2 k-отказоустойчиво моделирует систему
Sp если граф 0(2^) вкладывается в граф, получаемый из G(S2)
удалением любых к вершин, Система называется оптимальной
к-отказоустойнивой реализацией системы S, если выполняются
следующиие условия: 1) 2^ ^-отказоустойчиво моделирует
систему 2) G(Sj имеет наименьшее возможное число вершин;
3) среди графов всех систем, удовлетворяющих условиям 1) и 2),
G(S^) имеет наименьшее число ребер.
_ Заметим, что если система 2 имеет п элементов, то система
S, графом которой является полный граф	удовлетворяет
условиям 1) и 2) при к < п — 1. Следовательно, любая
оптимальная ^-отказоустойчивая реализация «-элементной систе-
мы содержит точно п + к элементов.
Цепью называется граф G = (У, а), где V = {ур у2> ..., v },
а а = {(у., у.) | I/-/I = 1}, а циклом—граф G = (У, а), где
v = {‘'i- v2 а а = {(у., у.) | I/-/I = 1} (J {(yp y;j),
(у У])}. Интуитивно очевидной представляется
T е о р е м а 3.5. Оптимальной l-отказоустойчивой реа-
лизацией п-элементной цепи является (п + \)-элементный цикл.
Доказательство. Пусть система 2 такова, что
граф G(S) представляет собой «-элементную цепь. Очевидно, что
система Z1, для которой G(S*)—цикл с п + 1 элементами,
удовлетворяет условиям 1) и 2) в определении оптимальной
1-отказоустойчивой реализации для S. Пусть S1 обладает теми
240
~1
же свойствами. Покажем, что степень каждой вершины в G(S )
не меньше 2. Пусть это не так, и d(v) S 1 для некоторой
вершины v графа G(S*). Тогда при d(v) = 1 отказ элемента
системы S1, соответствующего вершине, смежной с у, приводит
к тому, что из G(S') получйтся «-вершинный граф с изолирован-
ной вершиной v. Ясно, что он не вмещает «-элементную цепь,
и, значит, 2 не будет 1-отказоустойчиво моделировать S,—
приходим к противоречию. Если же d(v) = 0, то аналогичные
рассуждения проводятся для отказа в системе S1, удаляющего из
G(S*) любую отличную от v вершину.
Поскольку G(S!) имеет п + 1 вершину и степень каждой
вершины не меньше 2, то G^1) имеет не меньше чем п + 1
ребер (по теореме 3.2, сумма степеней всех вершин графа равна
удвоенному числу его ребер). Цикл G(S) имеет точно п + 1
ребер, о
Аналогично доказывается и следующий, менее очевидный
результат [77].
Т е о р е м а 3.6. Графы, изображенные на рис. 79, пред-
ставляют собой оптимальные 1-отказоустойчивые реализации
п-элементного цикла соответственно при п четном (рис. 79а)
и п нечетном (рис. 796).
Доказательство. Пусть система X такова, что
граф G(X) является «-элементным циклом. Непосредственно
убеждаемся, что системы sj и 2^, графы которых представлены
на рис. 79а и 796 соответственно, будут удовлетворять условиям
1) и 2) в определении оптимальной [-отказоустойчивой реализации
для 2: первая при четном п, вторая—при нечетном.
Пусть S1 обладает теми же свойствами. Покажем, что степень
каждой вершины в G(S') не меньше 3. Пусть это не так, и
d(y) < 2 для некоторой вершины у графа G(S*). Тогда при
d(v) = 2 отказ элемента системы S1, соответствующего одной из
вершин, смежных с у, приведет к тому, что из G(S*) получится
«-вершинный граф, в котором степень вершины у будет равна 1.
Ясно, что этот граф не вмещает «-элементный цикл (у которого
241
все вершины имеют степень 2), и, значит, S1 не будет
1-отказоустойчиво моделировать Е,—приходим к противоречию.
Если же d(v) = 1 в G(E1), то аналогичные рассуждения проводятся
для отказа в системе Е1, удаляющего из G^S1) любую отличную
от v вершину.
Поскольку G(Er) имеет п + 1 вершину и степень каждой
вершины не меньше 3, то в С(Е^ будет не меньше, чем
3(n + 1) л
	ребер. При п четном эту оценку можно усилить: число
ребер (целое число!) не должно быть меньше, чем
3(п + 1)	1
2	+ 2’
В графе G(Ej), т. е. при четном п, имеем (рис. 79а) п - 2
«горизонтальных» ребер, у «вертикальных» и 4 ребра, которым
принадлежит вершина	Всего, таким образом, т =
_ , и , .	3(п + 1)	1	-	_
= п — 2 + ^ + 4 = —*—-—~ + 2* Ре°еР- Если п—нечетное число,
то в графе С(Е^) имеем (рис. 796)	~ 1 «вертикальных»
_	„	„	3(п +1)	-	„
ребер и п + 2 остальных. Всего т - ------— ребер. Следова-
тельно, системы Ej и Е^ удовлетворяют и условию 3) в
определении оптимальной 1-отказоустойчивой реализации в рас-
сматриваемом случае n-элементного цикла, о
Гомоморфизмом орграфа Gj = (Ур в орграф G2 =
= (У2, «2) называется отображение <р:	-* такое, что
(u, v) 6 «! => (у>(и), G а2 для любых и, v G Vy Если для
любых и, v G	имеет место эквивалентность (u, v) 6
G а[ о (<р(и), <р(у)) G а2, говорят, что <р—сильный гомомор-
физм. Общее понятие гомоморфизма, восходящее к одноименной
конструкции для частичных алгебр, в теории графов представля-
ется мало интересным. Например, имеет место
Т е о р е м а 3.7. Пусть <р—произвольное отображение
множества Vt вершин орграфа Gj = (Ур а^) в некоторое
непустое множество Vy Тогда существует орграф G^ =
= (У2, «2) такой, что: 1) <р будет гомоморфизмом орграфа
G[ в G^, и 2) G2 является частью любого орграфа G =
= (Vy а), в который <р гомоморфно отображает Gp
242
Доказательство. На множестве У2 зададим от-
ношение а2 следующим образом:
а2 := {( и, v) G V2 х : (3 и, v 6	= и &
& ^(v) = v & (и, v) 6	)}.
Если (u, v) G для произвольных и, v G Vp то, по
определению, (y>(u), y’(v)) G а2, и значит, <р—гомоморфизм.
Очевидно, что при добавлении новых дуг к а2 отображение <р
останется гомоморфизмом, но что при удалении из а2 хотя бы
одной дуги свойство гомоморфности для <р нарушится.
На рис. 80 показано построение
орграфа G2 по заданным G1 и р. о
Из теоремы 3.7 следует, что если
определить конгруэнцию орграфа как
ядро Кег <р некоторого его гомомор-
физма р, то конгруэнциями окажутся
все эквивалентности на множестве
вершин орграфа, так что изучение
конгруэнций и факторграфов в общем
случае теряет смысл. Эти понятия
приобретают содержание, если их рассматривать в более узких
классах орграфов, налагая дополнительные ограничения, напри-
мер, допуская в качестве конгруэнций лишь такие эквивалент-
ности, факторизация по которым не выводит из данного класса
(см. § 3.4).
Орграф G2 = (Е2, а2) называется гомоморфным образом
орграфа Gj = (Ер а^, если существует сюръективный гомо-
морфизм р: Vl -* V2 такой, что для любых и, v G V2 при
( и, v) G а2 найдутся и, v G	для которых (u, v) 6 а и
при этом р(и) = и, p(v) = v, т. е. если
а2 = {( и, v) G V2 х V21 (э и, v G ^(^(и) = и &
& ^(v) = v & (u, v) G «])}
(как в доказательстве теоремы 3.7). Отображение р можно назвать
гомоморфным наложением орграфа Gj на орграф G2>
Орграф называется вполне несвязным, если он не содержит
ребер, т. е. если все его вершины являются изолированными.
Множество вершин орграфа, порождающее в нем вполне несвязный
подграф, называют иногда независимым.
Пусть р—гомоморфное наложение графа G = (V, а) на граф
И. Поскольку в Н нет петель, каждый класс ядерной эквивален-
243
тности Кег <р будет независимым подмножеством в G. Пусть
в С V х V—эквивалентность, каждый класс которой представляет
собой независимое подмножество в G. Определим факторграф G/в,
взяв в качестве множества его вершин фактормножество V/в и
считая, что вершина в(и) смежна с вершиной в(у) тогда и только
тогда, когда (u, v) G а для некоторых и G в(и), v G 0(v).
Понятно, что естественное отображение nat в будет гомоморфным
наложением графа G на G/в и что Ker nat в = в.
П р и м е р 113. На рис. 81 показаны все факторграфы
четырехэлементной цепи G с множеством вершин V =
= {1, 2, 3, 4). На множестве V существуют четыре нетривиальных
разбиения, блоки которых являются независимыми подмножест-
вами в G, именно, 0^ {1, 3}, {2}, {4}; 02: {1, 4}, {2}, {3};
в^: {1}, {2, 4}, {3}; 6^. {1, 3}, {2, 4}. Факторграфы G/6^ и
G/в^ оказываются изоморфными.
1	2	{1,3} {2} {1,4}	{2}	{1}	{2,4}
о- —..д	о Q	О	О	гл 11
4	3	{4}	{3}	{3}
G G/e-i G/ez G/e3 g/6a
Рис. 81
Для сильных гомоморфизмов аналог теоремы 3.7 не имеет
места, но их ядерные эквивалентности (т. е. сильные конгруэнции
орграфов) характеризуются достаточно просто. Чтобы не вводить
новых понятий (аналоги соединения графов для случая орграфов),
приведем эту характеризацию для симметричного случая.
Теорема 3.8. Эквивалентность в на множестве вер-
шин графа G = (V, а) тогда и только тогда будет ядром
некоторого сильного гомоморфизма этого графа, когда каждый
в-класс образует в G вполне несвязный подграф, а любые два
различных в-класса порождают в G либо вполне несвязный
подграф, либо подграф, представляющий собой соединение этих
8-классов.
Доказательство. Необходимость.
Пусть —сильный гомоморфизм графа G = (V, а) в некоторый
граф Н. Поскольку граф Н не содержит петель, (и, v) а для
всех и, v G V таких, что (u, v) G Кег <р = 6. Следовательно,
0-классы являются независимыми подмножествами графа G. Если
0(н) * 0(v), то могут представиться два случая: 1) вершины
<р(и) и <р(у) несмежны в графе Н, 2) <р(и) и <р(у) соединены в Н
ребром. В первом случае (и, v) £ а для любых й G 0(н),
v G 0(v), и, значит, 0(н) U 0(v) образует вполне несвязный
подграф в G. Во втором случае (и, v) G а для любых и G
244
е в(и), v G 0(у), и, следовательно, подграф графа G, определяе-
мый множеством вершин 0(u) U 0(у), будет соединением вполне
несвязных подграфов в(и) и 0(у).
Достаточность. Пусть эквивалентность в С
С V х V обладает свойствами, указанными в условии теоремы.
Рассмотрим факторграф G/в. Пусть в(и) и 0(у) смежны в G/в
для некоторых и, v G V. По определению,, существуют и G
е в(и) и у G 0(у), для которых (й, v) 6 а, и, следовательно,
в(и) U 0(у) не является вполне несвязным подмножеством в G.
Но тогда, по условию, в(и) U в (у) образует в G подграф,
являющийся соединением подграфов в(и) и в(у). Отсюда
(u, v) 6 а. Мы получили, что <р = nat в будет сильным гомо-
морфизмом графа G на факторграф G/в. При этом Кег <р =
= Ker nat в = в. □
Пример 114. Как видно из рис. 81, ни одна из
конгруэнций четырехэлементной цепи не будет сильной. Если же
к графу G добавить ребро, соединяющее вершины 1 и 4, т. е.
превратить G в четырехэлементный цикл Gp то сильными
конгруэнциями окажутся эквивалентности 3 z {1, 3}, {2}, {4};
в2: {1}, {2, 4}, {3}; в^ {1, 3}, {2, 4}. При этом G^ =
= Gj/^2 s G/в^, Gjd^ = G/в^. Можно ли сильной фактори-
зацией четырехвершинного графа получить треугольник? Добавим
к графу G, изображенному на рис. 81, ребра, соединяющие
вершины 1 и 3, а также 2 и 4, и рассмотрим разбиение 0: {1, 4},
{2}, {3}. Очевидно, что факторграф полученного графа по его
сильной конгруэнции в изоморфен факторграфу G/в^.
Прямым произведением орграфов G1 = (Vp aJ и G2 =
= (у2, а2) называется орграф Gt х G2 := х V2, а), где
а = {((и, и), (у, у)) е (Vt х V2) х (Vj х VJ I (и, у) G ау &
& ( й, у ) G а2}.
—>	—♦
Другими словами, вершинами орграфа G^ х G2 являются пары
(у, у), где у G Vp у G V2, и при этом из вершины (и, и) в
вершину (у, у) проводится дуга в том и только в том случае,
когда в G^ вершина и соединена дугой с у, а в G2 вершина и
соединена дугой с вершиной у. Из определения следует, что если
один из орграфов Gp G2 вполне несвязен, то вполне несвязным
будет и прямое произведение G^ х G2-
Т е о р е м а 3.9. Если ни один из орграфов Gp G2 не
является вполне несвязным, то проекции Яр V1 х V2 -* Vp
245
ЛТ х V2 “* ^2 бУдУт гомоморфными наложениями прямого
произведения G{ х G? соответственно на G^ и на G^.
Доказательство. Обе проекции представляют
собой сюръективные отображения. Если ((и, й), (v, v)) G а, то,
по определению, (и, v) G и (й, v)Ga2. Но и = ^((м, и))
иг — л}((р, у)), так что Jtj—гомоморфизм. Аналогично и
л2—гомоморфизм. Пусть (и, v) G а{. Так как орграф G2 не
является вполне несвязным, найдутся и, у G V^, такие, что
(й, у)6а2. Тогда ((и, й), (у, у) 6 а и при этом лх((и, и)) =
= и, л^((у, у)) = у. Таким образом, л(—гомоморфное нало-
жение орграфа Gy х G2 на орграф G^ Аналогично для л:2. о
§ 3.2. Неориентированные графы
Как уже отмечалось, во многих прикладных задачах, связан-
ных с орграфами, ориентация дуг не имеет значения. В этом
параграфе затрагиваются некоторые основные понятия и идеи
теории неориентированных графов. Большинство из них без труда
переносятся на случай орграфов общего вида.
Пусть G = (V, а)—некоторый граф. Путем в этом графе
называется последовательность ребер, в которой каждые два
соседних ребра имеют общую вершину и никакое ребро не
встречается более одного раза. При этом считается, что оба конца
каждого ребра, кроме первого и последнего, являются концами
соседних с ним ребер пути. Говорят, что путь проходит через
вершины, соединенные его ребрами. Путь в графе удобно задавать
перечислением входящих в него вершин в порядке их прохож-
дения. Если начальная и конечная вершины пути совпадают, путь
называется циклическим. Путь, каждая вершина которого принад-
лежит не более чем двум его ребрам, по определению, является
простым. Простой циклический путь называется циклом. Если
простой путь не является циклом, в
____________д2________?3 нем существуют вершины, принадле-
/х.___________________жащие только одному ребру этого
'у / х. / пути. Очевидно, что таких вершин
точно две. Их называют концами
4 данного пути, а сам путь—цепью,
Рис. 82	соединяющей указанные вершины.
П р и м е р 115. Для иллюстра-
ции введенных видов путей рассмотрим граф, изображенный на
рис. 82.
Последовательность ребер
{vr v5}, {Vp V2}, {v2, V3}, {V3, V4}, fv2, v4}, {V2, v5}, {V4, V5}
246
является путем, проходящим через все вершины графа и
содержащим все его ребра. Более наглядна запись через вершины:
V5V1V2V3V4V2V5V4’ Этот путь не будет простым (вершины v?, и
у5 принадлежат более чем двум его ребрам каждая) и не будет
циклическим.
Циклическими путями, содержащими вершину у , являются
у.у.у^у,, у.у.у.у^у., у. v-v-v.vKv., у.у_у_у.у_усу.. Первые три из
125 1	1245 1	12345 1	1 2 3 4 2 5 1 r г
них—циклы. Циклы обычно рассматриваются с точностью до
выбора начальной вершины и направления обхода, так что,
например, последовательности у у у,у и у у_у у, обозначают один
и тот же цикл. В рассматриваемом графе много цепей. Так,
вершины у и у, можно соединить цепями у v v,, v^.v.v,,
1	О	1 2 <3	1 2 *т
V1V2V5V4V3’ с°ДеРжащими соответственно 2, 3 и 4 ребра.
Длиной пути в графе называется количество входящих в
состав этого пути ребер. В n-вершинном графе наибольшая из
длин цепей не превосходит п - 1, а наибольшая из длин циклов
не превышает п. Если граф имеет т ребер, то никакой его путь
не может иметь длину, большую т.
Вершины и и у графа G называются связанными, если в G
существует проходящий через них путь. Ясно, что две разные
вершины будут связанными тогда и только тогда, когда в графе
найдется соединяющая их цепь. Считается, что каждая вершина
связана с собой. Если вершины и и у связаны, то наименьшая
из длин цепей, соединяющих и и у, называется расстоянием
между этими вершинами.
Очевидно, что отношение связанности является эквивалентно-
стью на множестве вершин графа. Классы этого отношения
называются компонентами связности (или просто компонен-
тами) графа. Граф с универсальным отношением связанности
называется связным. Таким образом, граф связен тогда и только
тогда, когда любые две его различные вершины могут быть
соединены цепью. Каждая компонента связности графа представ-
ляет собой связный граф. Очевидна
Т е о р е м а 3.10. Каждый граф является объединением
своих компонент. =
Следующее простое наблюдение оказывается полезным в
приложениях.
Т е о р е и а 3.11. Если и и v являются единственными
нечетными вершинами графа G, то они связаны в G.
Доказательство. Предположим, что и и у не
связаны в G, и рассмотрим компоненту связности Н графа G,
содержащую и (и, следовательно, не содержащую у). Согласно
теореме 3.2 из § 3.1, в любом графе количество нечетных вершин
должно быть четным. Но так как степень каждой вершины графа
Н совпадает с ее степенью как вершины графа G, в Н будет
только одна нечетная вершина, что невозможно, о
247
Для графов с большим числом ребер вопрос о связности может
решить
Т е о р е м а 3.12. Если в п-вершинном графе количество
Л	гЛ	(П ~ 1)(я ~	.
ребер т > Сп1 =	----% то этот граф связен.
Доказательство. Предположим, что граф G,
удовлетворяющий условию теоремы, несвязен. Пусть —одна из
его компонент связности. Тогда G будет объединением графа
Яо и подграфа Яр образованного вершинами графа G, не
входящими в Яо. Если в попало к вершин, где 2 < к <
< и — 2, то максимальное возможное число ребер в Я() будет
С2, а в Я1 оно будет равно С2_^ (случай, когда Яо и Я1—полные
графы). Тогда в G получается
2	, Г2 _ (и - к)(п - к - 1) к(к - 1)
-к Ч -	2	2
п2 - (2к + 1)и + 2к2
2
Однако
2	и2 — Зи + 2 п2 — (2к + 1)п + 2к2
С , - т > ---------х---- - -------------------- =
= (к - 1)[и - (к + 1)] > О,
что невозможно, так как С2_1 < т по условию. Следовательно,
Яо не может содержать больше одной или меньше и - 1 вершины.
Но в обоих этих случаях максимальное возможное число ребер
в G получается равным С t (одна компонента связности
одноэлементна, а другая—полный граф Я(1), что также противо-
речит неравенству из условия теоремы, о
Вершина v в графе G называется точкой сочленения', если ее
удаление увеличивает число компонент связности. Связный граф,
по определению, неразделим (или двусвязен), если он не имеет
точек сочленения. Если некоторая система S имеет своей
функциональной схемой неразделимый граф, то при отказе любого
элемента между произвольными двумя другими элементами в S
сохранится схемная связь. Блок графа—это его максимальный
неразделимый подграф.
Теорема 3.13. Связный граф, содержащий не менее
трех вершин, тогда и только тогда неразделим, когда любые
две его вершины принадлежат некоторому циклу.
Доказательство. Достаточность условия теоре-
мы вполне очевидна. Докажем необходимость. Пусть и и v—две
248
произвольные вершины неразделимого графа G. Доказательство
ведется индукцией по расстоянию к от и до у. Пусть к = 1, т. е.
вершина у смежна с вершиной и. По условию, в G есть вершина
w, отличная от и и у. Так как граф G неразделим, в нем
существует цепь, соединяющая у и w и не проходящая через и
(иначе и была бы точкой сочленения). Возьмем на этой цепи
вершину у*, смежную с у. Существует цепь Р, соединяющая и и
у* и не проходящая через у. Тогда путь uw*Pu будет циклом
(через у Ри обозначен путь по элементам цепи Р от у* до и).
Предположим, что у удалена от и на к + 1. Тогда в G
существует цепь Р: и = v0> Ур v^, v^+1 = v. По предполо-
жению индукции, вершины и и у^ принадлежат некоторому циклу
С. Этот цикл образует две цепи, соединяющие и и у^, которые
мы обозначим через Р^ и Р^.
Так как у^ не является точкой сочленения, в G найдется цепь
Р*, соединяющая и и у и не проходящая через у^. Пусть у* будет
вершиной, ближайшей вдоль этой цепи к у и входящей в
подмножество Р U Р1 U Р^. Могут представиться следующие
случаи. 1) у* = и. Путь uPvP*u является циклом, содержащим
и, у. Пусть далее у* и. 2) у* G Р1 U Р^. Для определенности
допустим, что у* G Рр Тогда путь «Р1у*Р*уу^Р2« будет циклом,
содержащим и и у. 3) у* Р[ U Р^. Тогда у* G Р, и, значит,
у* = у. для некоторого 0 j < к. Пусть v. будет вершиной,
ближайшей вдоль Р к у. и входящей в Р U Р_. Если i = 0, то
/	12
путь uPv.P*vvlPxu будет циклом, содержащим и и у. Если же
i 0, то таким циклом является путь uP^v. Pv. P*wkP^u (при
У. G Р,). а
Изображение графа G называется плоским, если никакие два
ребра в этом изображении не пересекаются. Графы, имеющие
плоское изображение, называют планарными. Легко можно
представить себе практические ситуации, когда необходимо
выяснить, является ли данный граф планарным (например, чтобы
не было непредусмотренных контактов в печатных электрических
схемах).
Важным классом планарных графов являются деревья. Дере-
во—это связный граф, в котором нет циклов.
Теорема 3.14. Граф G тогда и только тогда является
деревом, когда в нем выполняется одно из следующих условий:
1)	любые две вершины графа G соединены единственной
цепью;
249
2)	G—связный граф и число вершин в нем на единицу больше
числа ребер', п = т + 1;
3)	G не содержит циклов и п = т + 1.
Доказательство. Пусть G—дерево. В силу связ-
ности, любые две вершины и, v графа G соединены цепью. Если
между и и v существует две разные цепи, то в G можно построить
цикл (не обязательно содержащий и или у), что противоречит
определению дерева. Свойство 1) доказано.
Соотношение п = т + 1 для числа вершин и ребер дерева
доказывается индукцией по п. Оно очевидно при п - 1 и п = 2.
Пусть доказываемое равенство справедливо для всех графов,
имеющих меньше чем п вершин. В «-вершинном дереве, в силу
1), удаление любого ребра нарушает связность. В каждой из двух
полученных компонент число ребер на единицу меньше числа
вершин: к - 1 и (п — к) - 1, если в одной из компонент
находится к вершин (а в другой п - к). Складывая эти числа и
добавляя единицу (удаленное ребро), получаем, что в G будет
т = п - 1 ребер. Тем самым доказана выполнимость условий 2)
и 3).
Пусть выполняется условие 1). Тогда граф G связен. Если он
не является деревом, в нем найдется хотя бы один цикл. Любые
две различные вершины цикла могут быть соединены как минимум
двумя цепями,—приходим к противоречию.
Допустим, что в связном графе G имеет место соотношение
п = т + 1 и что в нем есть циклы. Удалим из G все вершины
степени 1 (такие вершины называются концевыми или висячими).
Поскольку с каждой такой вершиной удаляется точно одно ребро,
в полученном связном графе G} для числа вершин и ребер
сохранится равенство = т^ + 1. Продолжая этот процесс, мы
придем в конце концов к графу G', в котором уже не будет
висячих вершин. В этом графе останутся все циклические вершины
графа G. Теперь получаем противоречие: с одной стороны,
п' = т' + 1, а с другой стороны, так как d(v) > 2 для каждой
п'
вершины графа G', то 2п' < d(y} = 2т’, т. е. п' 5 т'.
1=1
Таким образом, в связном графе G нет циклов, и, значит,
G—дерево.
Пусть теперь выполнено условие 3). Нужно показать, что
G—связный граф. Допустим, что это не так и что G =
= G, U G_ U ... (J G,, где G., 1 < г < к,—связные компонен-
12	к' i
ты графа G. Каждая из этих компонент является деревом, и,
следовательно, п. — т. + 1, 1 < i < к. Но тогда п =
к	к
= п. =	(т. + 1) = т + к > т + 1, так как к > 1,—
i= 1	<=1
приходим к противоречию, о
250
Дерево с одной вершиной называется тривиальным. Из
теоремы 3.14 следует, что в каждом нетривиальном дереве
существуют по крайней мере две висячие вершины. Действительно,
сумма степеней всех вершин n-вершинного дерева равна 2п - 2.
п
Если же в дереве нет висячих вершин, то d(y.) > 2л, а при
z=i
п
одной висячей вершине было бы d(v.) > 1 + 2(л — 1) =
/=1
= 2п - 1.
Плоское изображение произвольного дерева G можно получить
следующим образом. Произвольно выберем некоторую вершину
v() (корень дерева). Если к—расстояние от v() до наиболее
удаленных от корня вершин, проведем к + 1 горизонталей,
нумеруя их снизу вверх числами 0, 1, ..., к. На нулевой
горизонтали поместим вершину v(), а на горизонтали 1 расположим
произвольным образом вершины, смежные с v() (т. е. находящиеся
на расстоянии 1 от корня). Пусть это будут (слева направо)
вершины v. , v. , ..., v.. На горизонтали 2 разместим вершины,
1	2	s
удаленные на расстояние 2 от корня vQ, таким образом, что
сначала будут идти вершины, смежные с v. , за ними—вершины,
1
смежные с v. и т.д. Завершив в соответствии с этим правилом
2
размещение всех вершин на горизонталях, соединим каждую из
них прямолинейными отрезками со смежными с ней вершинами
следующего уровня (если таковые есть). На рис. 83 показаны
различные плоские изображения дерева, получающиеся при
разных выборах корня.
Рис. 83
251
Пусть планарный граф G задан плоским изображением.
Гранями в этом изображении называются области, ограниченные
ребрами графа. Одной из них является внешняя грань, представ-
ляюащая собой бесконечную по протяженности часть плоскости.
Т е о р е м а 3.15 (формула Эйлера). Для плоского изобра-
жения связного планарного графа G, имеющего п вершин и т
ребер, справедливо равенство п - т + г = 2, где г—количество
граней (включая внешнюю).
Доказательство. Пусть G—связный граф, за-
данный плоским изображением. Если G—дерево, то г = 1 и
п - т = 1, так что формула Эйлера справедлива. Предположим,
что G—не дерево. Тогда в G существует по крайней мере один
цикл. Удалим одно из ребер этого цикла. В полученном связном
графе Gi будет п^ = п, mi = т — 1 и г1 = г — 1, так как при
удалении ребра, входящего в состав цикла, две разделявшиеся им
грани сливаются. Так что п1 — т{ + г = п — т + г. Продолжаем
этот процесс до тех пор, пока не получится дерево G^. Тогда
п — т + г = пк — т^ +	= 2. о
Из формулы Эйлера можно извлечь несколько важных
соотношений между количеством вершин и ребер тех или иных
плоских (т. е. заданных плоскими изображениями) графов.
Следствие 3.1. Если в плоском графе каждая грань
,	к(п - 2)
является к-элементным циклом, то т = fc _ 2 ’
Доказательство. В рассматриваемом случае
каждая грань имеет к граничных ребер и каждое ребро разделяет
две грани. Следовательно, кг = 2т, откуда 2 = п — т + и
_ к(п - 2)
т ~ к-2 • °
Плоский граф называется триангуляцией, если все его
грани—треугольники.
Следствие 3.2. В любой триангуляции т =
= 3(л - 2). а
Отсюда получается необходимое условие планарности:
Следствие 3.3. В планарном графе, содержащем не
менее трех вершин, т < Зп — 6.
Доказательство. Среди всех плоских и-вер-
шинных графов при п 2 3 наибольшее число ребер имеют
максимально плоские графы, т. е. такие графы, которые при
добавлении любого ребра перестают быть плоскими. Очевидно,
что все такие графы являются триангуляциями, и можно сослаться
на следствие 3.2. »
Следствие 3.4. В каждой триангуляции существует
вершина, степень которой не превосходит 5.
252
Доказательство. В любой триангуляции г =
2	1	”
= 2 т- Так как т — 2	d(v)' то’ применяя формулу Эйлера,
1=1
получаем:
1 А I А
2 = п-т + г = п-^т =	1 “ 6 X =
1=1 1=1
1 "
= I X [6-</(v,.)l,
1=1
п
откуда [6 — d(y(.)] = 12. Так как сумма положительна, в ней
1=1
должны быть положительные слагаемые, т. е. существует вершина
v такая, что d(y) < 6. о
Через 3 будем обозначать соединение двух трехвершинных
вполне несвязных графов (см. рис. 84).
Графом типа I назовем граф, полученный из полного
пятивершинного графа К$ добавлением новых вершин на ребрах
графа К5 не в точках их пересечения (рис. 85а), а графом типа
II—граф, полученный аналогичным образом из графа (рис.
856).
Рис. 85
253
Критерием планарности графа является следующая теорема
Понтрягина—Куратовского.
Т е о р е м а 3.16. Граф планарен тогда и только тогда,
когда он не содержит частей, изоморфных графам типа I или
типа II.
Доказательство. Необходимость.
Покажем, что графы К$ и 3 не являются планарными. В графе
К$ имеем 5 вершин и 10 ребер. Необходимое условие планарности
(следствие 3.3) нарушается. Предположим, что граф 3
допускает плоское изображение. Так как п = 6, т = 9, то из
формулы Эйлера следует, что г = 5. В графе	нет
трехэлементных циклов, и каждое ребро входит в состав
четырехэлементного цикла. Отсюда m > 2г = 10, что невозмож-
но.
Достаточность доказывается очень сложно (см. [55]). =
Из теоремы Понтрягина—Куратовского следует, например, что
с точностью до изоморфизма существует единственный максималь-
но плоский граф с пятью вершинами: он получается из К$
удалением любого ребра.
Орграф G = (V, а) считается планарным, если планарна его
симметризация G = (V, (a U а-1) - Д).
П р и м е р 2. Пусть А = (S, X, Y, д, А)—некоторый ав-
томат. Ему сопоставляется орграф G(A) следующим образом.
Множеством вершин этого орграфа является множество 5
состояний автомата Л, и из вершины $. в вершину s^. проводится
дуга тогда и только тогда, когда существует входной сигнал
х G X, переводящий в s., т. е. такой, что <5 (У, х) = s. .
Автомат А называется планарным, если планарным является
орграф G(A). Используя графы К$ и 3> можно построить
непланарные автоматы всего с двумя входными сигналами (см.
рис. 86). Однако имеет место следующий результат [65].
Теорема 3.17. Для каждого автомата, число состо-
яний которого не превосходит 6, существует эквивалентный
ему планарный автомат, имеющий не более 12 состояний.
254
Доказательство. Рассмотрим графы, представ-
ленные на рис. 87. Предположим, что имеется автомат А с числом
состояний, не превосходящим 6. Тогда симметризация G(A) его
графа будет частью полного шестивершинного графа К6 (рис.
87а). Из этой симметризации путем расщепления ребер, ориента-
ции и помечивания получающихся дуг входными и выходными
сигналами без труда восстанавливается диаграмма переходов
данного автомата. Теперь в графе, изображенном на рис. 876,
над каждым ребром, соединяющим вершины с индексами i и /,
проделаем те же операции, что в графе G(A) проделывались над
ребром, соединяющим вершины i и j (предварительно удалим все
вершины, индексы которых соответствуют «лишним» вершинам в
К^. Получится диаграмма переходов некоторого автомата, кото-
рый обозначим через В. Нетрудно заметить, что состояние s.
автомата В будет эквивалентно состоянию t. этого автомата и
состоянию i автомата А. Следовательно, автоматы А и В
эквивалентны. При этом В—планарный автомат, о
Рис. 87
Автомат А называется сильно непланарным, если каждый
эквивалентный ему автомат непланарен. Такие автоматы сущест-
вуют, как показывает
Пример 116. Пусть 5 = {0, 1, 2, 3, 4, 5, 6}, X =
— {х,, х_, х_, х., х,, х.}, Y = S, д(1, х.) = i + j (mod 7),
*12	3	4	5	6	J
X(i, x.) = i + j (mod 7). В автомате A = (5, X, Y, д, А) любые два
состояния различимы, следовательно, он не может быть эквива-
лентным никакому автомату с меньшим числом состояний. Граф
G(A) представляет собой полный семивершинный граф и,
значит, он не планарен (граф К$ будет его подграфом).
Предположим, что некоторый автомат В эквивалентен автомату
А. Тогда каждая вершина в графе G(B) должна иметь 6 смежных
вершин, т. е. иметь степень 6. Если граф G(B) имеет п вершин,
то, согласно теореме 3.2 из § 3.1, у него должно быть Зп ребер.
255
В планарном же графе с п > 3 вершинами число ребер не
превосходит Зп - 6 (следствие 3.3 из теоремы 3.15). Таким
образом, любой автомат, эквивалентный автомату А, не является
планарным. По определению, А—сильно непланарный автомат.
На рис. 88 планарный граф представлен двумя плоскими
изображениями, в одном из которых все ребра являются отрезками
прямых. Изображения такого рода могут оказаться полезными в
вопросах топологии сложных систем, и следующая теорема Фари
дает способ их получения.
Рис. 88
Т еорема3.18. Каждый планарный граф допускает
плоское изображение, в котором любое ребро является отрезком
прямой.
Доказательство. Проведем индукцию по числу
вершин для максимально плоских графов, поскольку любой
плоский граф является частью некоторого максимально плоского
графа. При п = 3 (треугольник) утверждение теоремы очевидно.
Пусть теорема верна для максимально плоских графов с
к > 3 вершинами, и пусть максимально плоский граф G имеет
Л+1 вершин.
Возьмем некоторую вершину v, находящуюся на одном из
внутренних (т.е. не принадлежащих внешней грани) ребер. Пусть
Wp vv?, ..., —выписанные по часовой стрелке все ребра,
выходящие из v. Тогда ребра Vjv2, v2v3, ..., vjv1 образуют цикл,
внутри которого нет вершин, кроме v (так как G—максимально
плоский граф, он является триангуляцией). Могут представиться
два случая.
1) В графе G нет ребра, соединяющего с какой-либо из
вершин Vy ..., v j (рис. 89а). Удалим из G вершину v вместе со
всеми ребрами w^, vv2, ..., vvs и соединим вершину v1 с вершинами
Vy ..., vs l- Тогда получится максимально плоский граф с к
вершинами (рис. 896). По предположению индукции он допускает
требуемое изображение (рис. 89в). В этом изображении рассмотрим
цикл v|v2’”vsvr Удалим все отрезки v[v3, ...,	Внутри
многоугольника v2 • • • vs нет ни одн°й вершины. Заметим, что
ни одна из прямых v.v , 2 < i < s — 1, не проходит через
Vj (иначе ребра VjV и VjV имели бы общий отрезок). Далее,
256
по крайней мере в одном из вертикальных углов, образуемых
прямыми vlv2 и нет вершин, иначе уг и у$ оказались бы
внутри треугольника, получившегося после удаления из G
вершины у и триангуляции полученного графа. Тогда прямые
V1V2’ V2V3’ vsvi выДеляют в многоугольнике y1y2...yj область,
из каждой точки которой видны все его вершины (рис. 89г). В
одну из этих точек поместим вершину у и соединим ее с
Ур у2, ..., ys прямолинейными отрезками. Получилось требуемое
изображение графа G (рис. 893).
Рис. 89
2) В графе G есть ребро, соединяющее уг с одной из вершин
у3, ..., у (рис. 90а). Тогда после удаления из G вершины у и
ребер, которым она принадлежит, нельзя у1 соединять с
у3, ..., у , поскольку получится хотя бы одно кратное ребро. В
этом случае предлагается другая процедура.
9 А.М.Богомолов, В.Н.Салий
257
Рис. 90
Пусть в графе G вершина смежна с вершиной v{,
3 < i < s — 1. Тогда цикл	имеет три ребра и разделяет
вершины v2 и Рассмотрим два графа: Gp образованный ребрами
w, v.Vj и принадлежащими им вершинами, а также всеми
ребрами и вершинами графа G, лежащими вне цикла v1 w.Vj (рис.
90б); и G2, образованный вершинами и ребрами этого цикла и
всеми вершинами и ребрами графа G, лежащими внутри цикла
(рис. 90в). Оба эти графа, по предположению индукции, имеют
требуемое изображение. При этом в изображении графа G1
треугольник с вершинами v, v. не содержит внутри себя ни
одной вершины, а, с другой стороны, в графе G часть G2 лежит
внутри этого треугольника.
Помещая изображение графа G2 с прямолинейными ребрами
внутрь треугольника VjVv.Vj в изображении графа Gp получим
требуемое изображение графа G (рис. 90г).
Теорема доказана, о
Заметим, что не любой максимально плоский граф с п + 1
вершиной можно получить из подходящего л-вершинного макси-
мально плоского графа добавлением вершины
внутрь некоторой грани и соединением ее
Д ребрами с вершинами этой грани (что сильно
облегчило бы доказательство теоремы 3.18).
Так, на рис. 91 приведен максимально
плоский граф, у которого ни один макси-
мальный подграф не является максимально
плоским.
Как уже отмечалось, в т-реберном графе
длина любого пути не больше т. Путь длины
Рис. 91	т в графе q называется эйлеровым путем,
а граф, в котором существует циклический
эйлеров путь—эйлеровым графом. Эйлеров путь проходит по
каждому ребру графа точно один раз, но одна и та же вершина
может встретиться неоднократно. Очевидно, что граф, в котором
есть эйлеров путь, связен (мы исключаем изолированные верши-
ны).
Т е о р е м а 3.19. Связный граф тогда и только тогда
является эйлеровым, когда все его вершины четны.
Доказательство. Необходимость.
Пусть G—эйлеров граф, т. е. в нем существует циклический путь,
проходящий по каждому ребру (точно один раз). Начнем движение
по этому пути из вершины vQ. Входя в каждую промежуточную
258
вершину v по некоторому ребру, мы должны выйти из нее по
еще не пройденному ребру, так что все ребра, которым
принадлежит эта вершина, распределяются по парам «вход—вы-
ход». Завершая путь, возвращаемся в вершину vQ, и последнее
пройденное ребро образует, пару с первым ребром пути. Все
вершины графа четные.
Достаточность. Пусть в связном графе G все
вершины четные. Выберем произвольную вершину v и будем
двигаться по ребрам графа, окрашивая каждое пройденное ребро,
скажем, в красный цвет. Поскольку все вершины графа—четные,
входя в каждую из них, мы будем иметь возможность выйти по
еще не окрашенному ребру. Понятно, что это движение может
завершиться только в вершине v. Окрашенные ребра образуют
циклический путь Если Ci содержит все ребра графа, мы
получили циклический эйлеров путь.
Пусть в G имеется неокрашенное ребро. В силу связности
графа, можно допустить, что одна из вершин этого ребра
принадлежит Ср Обозначим ее через v и начнем движение из
этой вершины по не входящим в ребрам, которые после
прохождения будем окрашивать в синий цвет. Это движение
завершится в вершине v*, и ребра синего цвета образуют
циклический путь С? Тогда путь vCJv*C2v*C1v будет циклическим,
и он содержит по крайней мере на три ребра больше, чем Ср
Продолжая этот процесс, получим в конце концов циклический
путь, содержащий все ребра графа, о
Следствие 3.5. Для того чтобы в связном графе G
существовал эйлеров путь, соединяющий две разные вершины и
и v, необходимо и достаточно, чтобы и и v были единственными
нечетными вершинами в G.
Доказательство. Необходимость.
Пусть в графе G имеется эйлеров путь, соединяющий вершины
и и v. Двигаясь по этому пути из и в v, убеждаемся, что
количество ребер, которым принадлежит каждая промежуточная
вершина, четно. У вершины и число ребер выхода на единицу
больше числа ребер захода, а у вершины v—наоборот.
Достаточность. Пусть и и v—единственные не-
четные вершины связного графа G. Могут представиться два
случая.
9*
259
1) и ир смежны в G. Удалим ребро, соединяющее эти
вершины, не удаляя сами вершины. Пусть после этого получится
связный граф. Все вершины его будут четными, и, значит, в этом
графе имеется эйлеров циклический путь. Проделаем этот путь,
отправляясь из вершины и, и, закончив его в этой же вершине,
пройдем по возвращенному ребру uv. Вершины и и v соединены
в G эйлеровым путем.
Пусть после удаления ребра uv граф G распадается на два
(связных) графа и С2- В каждом из них все вершины четные.
По теореме 3.19, в и в G2 имеются циклические эйлеровы
пути С( и С2 соответственно. Путь uC^vC^ будет эйлеровым
путем в графе G, соединяющим и и v.
2) и и v несмежны в G. Соединим их ребром. В полученном
графе G' все вершины четны, и, значит, он эйлеров. Рассмотрим
эйлеров циклический путь в G', начинающийся из v и имеющий
первым ребром vu. Забывая этот первый шаг, получим эйлеров
путь между и и v в графе G. =
П р и м е р 117. Линия, которую можно начертить, не
отрывая карандаш от бумаги и не проходя никакого ее участка
более одного раза, называется уникурсальной. Изображение графа,
обладающего эйлеровым путем, является уникурсальной линией.
Будут ли уникурсальными линии, изображенные на рис. 92? Какие
из них можно нарисовать с возвратом в исходную точку?
Рис. 92
Простой путь в «-вершинном графе имеет длину, не
превосходящую п. Простой путь длины п (он будет циклом) в
графе G называется гамильтоновым циклом, а граф, в котором
существует гамильтонов цикл,—гамильтоновым. Гамильтонов
цикл проходит через каждую вершину графа точно один раз.
Очевидно, что гамильтонов граф связен.
В отличие от эйлеровых графов, гамильтоновы графы не имеют
пока пригодной для применений характеризации. Одним из
сильных достаточных условий (44] является
Т е о р е м а 3.20. Если в связном п-вершинном (п > 3)
графе для любых двух несмежных вершин и, v выполняется
неравенство d(u) + d(v) > п, то этот граф гамильтонов.
260
Доказательство. Пусть граф G удовлетворяет
условиям теоремы. Рассмотрим в нем некоторую наибольшую по
длине цепь Р. Пусть она последовательно проходит через вершины
v0> Vp ..., v^. В силу максимальности цепи Р, вершина vQ смежна
только с вершинами, входящими в эту цепь, и так же обстоит
дело с вершиной v^. Пусть eZ(vQ) = Р- Через v. , v. , ..., v.
•	*2 lp
обозначим вершины, смежные с вершиной vQ, считая, что
iy < i'2 < ... < i (очевидно, что тогда ij = 1). Вершин вида
у. — 1, 1 < s < р, в цепи Р имеется р штук, и, значит,
остальных вершин (к + 1) - р. При этом к - р из них в
принципе могут быть концами ребер, исходящих из (все, кроме
самой vk). По условию теоремы, d(vQ) + d(yk) > п. Следователь-
но,
> п - d(vQ) = п - р > (к + 1) - Р = (к - р) + 1.
Так как из вершины vk в вершины цепи Р ведут не менее
чем (к - р) + 1 ребер, по крайней мере одно из них имеет своим
концом вершину вида 1 < s < р, пусть это будет v-_p
Тогда подграф GQ графа G, порожденный вершинами цепи Р,
будет гамильтоновым: цикл С = vnPv. _. v.Pv. vn проходит через
U /	1 л /U
t	t
все вершины графа GQ.
Осталось показать, что GQ = G. Предположим противное.
Тогда в Gq существует вершина v, не входящая в цепь Р. В силу
связности графа G, можно допустить, что эта вершина смежна с
одной из вершин подграфа GQ, например, с v. . Тогда в G строится
цепь, имеющая длину к + 1: ее первым ребром является w., а
затем проходится цикл С без последнего по счету ребра. Однако,
по условию, наибольшая из длин цепей в G равна к. =
Следствие 3.6. Если в связном графе с п > 3
вершинами d(v) > п/2 для любой вершины v, то этот граф
гамильтонов, о
Условие теоремы 3.20 не является необходимым: цикл длины,
большей чем 4, является гамильтоновым графом, но не удовлет-
воряет этому условию, так как степень каждой вершины
равна 2.
Некоторые экстремальные задачи для графов естественно
рассматривать в более общих ситуациях. Сетью называется
связный граф, каждому ребру которого приписано некоторое
положительное число—вес. Под весом сети понимают сумму весов
всех ее ребер.
261
Покрывающее (или остовное) дерево графа G = (V, а)—это
дерево Т = (V, а*), где а* С а. Таким образом, всякое покры-
вающее дерево данного графа содержит все вершины этого графа
и некоторые его ребра. Покрывающее дерево сети, по определению,
минимально, если оно имеет наименьший вес среди всех
покрывающих деревьев этой сети.
Следующий алгоритм [42] строит одно из минимальных
покрывающих деревьев сети.
Шаг 1. Ребра сети располагаются для просмотра в список в
порядке возрастания их весов.
Шаг 2. Первое по списку ребро окрашивается в некоторый
цвет, и вершины, которые оно соединяет, запоминаются как
принадлежащие одной компоненте.
Шаг 3. Рассматривается следующее по списку ребро.
С л у ч а й А. Это ребро соединяет вершины, принадле-
жащие одной компоненте. Ребро не окрашивается, состав компо-
нент не изменяется.
С л у ч а й Б. Одна из вершин ребра принадлежит некото-
рой компоненте, а вторая не принадлежит никакой компоненте.
Ребро окрашивается, вторая его вершина присоединяется к
компоненте, содержащей первую вершину.
С л у ч а й В. Концы ребра принадлежат разным компонен-
там. Ребро окрашивается, упомянутые компоненты сливаются в
одну.
С л у ч а й Г. Концы
1
Рис. 93
ребра не принадлежат никаким ком-
понентам. Ребро окрашивается, его
концы образуют новую компоненту.
Шаг 4. Если все ребра просмот-
рены—конец: окрашенные ребра об-
разуют минимальное покрывающее
дерево. В противном случае—переход
к шагу 3.
Прежде чем доказывать теорему,
обосновывающую этот алгоритм, рас-
смотрим
Пример 118. Построить
минимальное покрывающее дерево сети, изображенной на рис. 93.
Приводимая таблица заполняется по ходу работы алгоритма.
Веса	Ребра	Окраска	Компоненты
1	V4	4-	{v,.v4}
2	V2V3	4-	v4}, {v2, v3}
2	VIV6	4-	{Vp v4, v6), {v2, v3)
4	V1V2	4-	{V|t v2, v3, v4, v6}
5	V2V6	-	{v_, V2, V3, V4, V6}
7	0 0	-	O'.’ V2- V V V6>
7	5 о	4-	{V , v2, v3, v4. v5, v6}
262
Заметим, что в практической реализации работа алгоритма
заканчивается, когда все вершины сети окажутся в одной
компоненте.
Теорема 3.21. Описанный алгоритм приводит к пос-
троению минимального покрывающего дерева сети.
Доказательство. Окрашенные ребра образуют
связный граф. Действительно, пусть и и v—произвольные вершины
исходной сети G. В силу связности, существует цепь, соединяющая
и и v. В процессе просмотра ребер каждое ребро цепи было
окрашено или не окрашено. В первом случае концы ребра
оказались в одной компоненте после его окраски, во втором случае
ребро не окрашивалось потому, что его концы находились в одной
компоненте. Таким образом, любые две смежные вершины в
данной цепи принадлежат одной компоненте. Значит, и вершины
и, v тоже лежат в одной компоненте.
Покажем, что окрашенные ребра не образуют циклов. Пусть
это не так, и в сети существует цикл С, составленный из
окрашенных ребер. Пусть uv—последнее в порядке прохождения
алгоритма ребро этого цикла. Остальные ребра цикла С образуют
окрашенную цепь, соединяющую и и v. Значит, и и v лежат в
одной компоненте. Но тогда ребро uv не должно окрашиваться
(случай А),—противоречие. Таким образом, окрашенные ребра
образуют покрывающее дерево TQ сети G.
Покажем, что TQ—минимальное покрывающее дерево.
Очевидно, что в любой сети существует минимальное покры-
вающее дерево: в силу конечности множества ребер сети, можно
перебрать все возможные покрывающие деревья, вычислить их
веса и выбрать минимальное.
Предположим, что TQ не минимально, и пусть 7^ обозначает
некоторое минимальное покрывающее дерево сети G. Так как
TQ и Т1—различные покрывающие деревья, то должно существо-
вать по крайней мере одно ребро, входящее в Т^, но не входящее
в Тр Пусть uv—первое такое ребро в порядке просмотра ребер
в ходе алгоритма. Так как —покрывающее дерево, вершины и
и v входят в его состав, и существует единственный путь (цепь)
Р, соединяющий и и v в Т^. Не все ребра пути Р входят в TQ,
иначе вместе с uv они образовали бы в TQ цикл, что невозможно.
Пусть u*v—ребро из Р, не входящее в Т . Построим граф 7\,
который отличается от 7^ тем, что в нем нет ребра u*v*, но есть
ребро uv.
263
Покажем, что —покрывающее дерево сети G. Очевидно, что
Т2 содержит все вершины этой сети и что —связный граф.
Допустим, что в Т2 есть цикл С. Если в состав этого цикла не
входят вершины и и v, то все ребра цикла С будут ребрами
дерева Т^, т. е. в получается цикл. Следовательно, Т2-цикл
С содержит вершины и и v. Но тогда С ж uPvu, что невозможно,
поскольку в Т2 путь Р разорван удалением ребра u*v*. Итак,
Т2—покрывающее дерево.
Убедимся, что дерево Т2 минимально. Обозначая вес дерева
Т через w(T), получаем, что w(Tx) < w(T2), в силу минималь-
ности Гр Так как Т2 получилось из исключением ребра
uv* и добавлением ребра uv, из этого неравенства вытекает
неравенство для весов ребер: w(«*v*) < w(uv).
Предположим, что в ходе алгоритма ребро u*v* было
просмотрено раньше, чем uv (в случае равенства весов имеется
произвол в перечислении ребер). Так как ребро u*v* не вошло в
TQ, т. е. не окрашивалось, это могло произойти только в том
случае, если бы u*v* замыкало некоторый цикл, все остальные
ребра которого были бы уже окрашены. Так как первым в порядке
просмотра ребром, которое входит в TQ и не входит в Т^, является
uv, то получаем, что ребро u*v* и все окрашенные ребра, с
которыми оно образует упомянутый цикл, были просмотрены
раньше, чем uv, и, значит, принадлежат дереву в котором,
таким образом, обнаруживается цикл. Следовательно, ребро uv
было просмотрено раньше, чем u*v*, и, значит, H'(wv) < w(u*v*).
Из равенства w(uv) = w(u*v*) вытекает равенство ^(7^) =
= w(T2), означающее, что и будет минимальным покрывающим
деревом. По сравнению с Т{, дерево Т2 имеет общих ребер с
деревом TQ на одно больше. Если = Т , мы получаем
минимальность дерева TQ, в противном случае у есть ребро,
не входящее в состав Т2, и тогда мы построим минимальное
покрывающее дерево Т^, имеющее с То общих ребер на одно
больше, чем 7’2. Продолжая этот процесс, в конце концов получим
минимальное покрывающее дерево сети G, совпадающее с TQ. =
264
§ 3.3. Специальные пути в ориентированных графах
В случае ориентированных графов общего вида некоторые
вопросы, рассмотренные в предыдущем параграфе, требуют особого
подхода, возникают дополнительные трудности и на пути их
преодоления—новые понятия и методы.
Пусть G = (V, а)—некоторый орграф. Маршрутом в этом
орграфе называется последовательность дуг (v0> Vj), (v^ v2), ...
..., (v , v^), в которой v.) G а для всех 1 S i < n.
Говорят, что маршрут проходит через вершины vQ, Vp ..., v^.
Вершина называется его начальной вершиной, a vn—конечной.
Циклический маршрут в орграфе—это маршрут, в котором
начальная и конечная вершины совпадают.
Маршрут, в котором никакая дуга не встречается более одного
раза, называется путем. Путь, каждая вершина которого принад-
лежит не более чем двум его дугам, по определению, является
простым. Простой циклический путь называют контуром, а
простой путь, не являющийся контуром,—бесконтурным путем
или (ориентированной) цепью. Очевидно, что всякий путь в
орграфе содержит простой путь с теми же началом и концом. В
частности, всякий циклический путь содержит контур с тем же
началом и концом.
Длиной маршрута называется количество составляющих его
дуг. Если в неориентированном графе длина цикла не может быть
меньше 3, то в орграфе всякая петля образует тривиальный контур
длины 1. Орграф, не имеющий нетривиальных контуров, называ-
ется бесконтурным графом.
Говорят, что вершина v достижима из вершины и, если в
орграфе существует путь из и в v. Расстояние от и до v—это
длина кратчайшего пути из вершины и в вершину v. По
определению, всякая вершина достижима из себя (даже если в
ней нет петли) и удалена от себя на расстояние 0. Если орграф
имеет п вершин, то наибольшая из длин его контуров не
превышает п, а длины бесконтурных путей все не больше п - 1.
В орграфе, имеющем т дуг, никакой путь не может иметь длину,
большую чем т.
Отношение достижимости <5 является квазипорядком в любом
орграфе. Порядком оно будет в данном орграфе G тогда и только
тогда, когда G—бесконтурный орграф (см. § 1.4).
Пусть G = (V, а)—орграф с п вершинами. Через М =
= М(а) обозначим его матрицу смежности. Это двоичная булева
п х n-матрица, в которой
265
V
1, если (у? v.) G а;
О в противном случае.
Теорема 3.22. Элемент матрицы отличен от
нуля тогда и только тогда, когда в G есть маршрут длины
к из вершины V. в вершину v. .
Доказательство. Проведем индукцию по к. При
к = 1 утверждение очевидно: т^ = 1 означает, что в G есть
дуга (у., v.) (путь длины 1). Далее
п
m^+l^ = 1 о V . = 1 о (э sn) (п№ = 1 & т = 1).
IJ	4j IS Sj	' О7 '	sy '
Последнее предложение означает, что в G существуют маршрут
длины к из V. в v (предложение индукции) и дуга (v , v.), т. е.
о	о '
маршрут длины к + 1 из v. в v. . =
Следствие 3.7. Вершина v. достижима в п-вершин-
ном графе с матрицей смежности М из вершины v(. тогда и
п-1
только тогда, когда в матрице D = М* + Е имеет место
k=l
равенство d.. = 1 (здесь Е—тождественная булева п х п-
матрица).
Доказательство. Равенство d.. = 1 означает,
что вершина v. достижима из вершины v. за к шагов, где
1 < к < п — 1, т. е. что в орграфе G существует маршрут длины
Л < п — 1 из V. в V. . Так как бесконтурные пути в G имеют
длину < п — 1, получаем, что равенство d„ = 1 равносильно
тому, что в G существует бесконтурный путь из v. в v. . .Матрица
Е прибавляется, чтобы охватить случай v. = v. . а
п-1
Таким образом, матрица D = М* + Е является матрицей
£=1 t
отношения достижимости <5 в орграфе G, имеющем матрицу
смежности М. Рекуррентная формула
М := М + Е, М .	:= М ,М ,
1	2	2	2
позволяет более экономно вычислить матрицу D: если
М^+| = М к, то £> = М^к. Матрица D называется матрицей
достижимости орграфа G.
266
Симметричная часть е = <5 П <5-1 отношения достижимости
называется отношением взаимной достижимости. Это отношение
эквивалентности на множестве вершин графа. Классы отношения
взаимной достижимости называют сильными компонентами (или
слоями) орграфа. Орграф, по определению, является сильно
связным, если отношение е универсально на нем, т. е. если
каждая его вершина достижима из любой другой.
Любой ли связный граф G можно ориентировать так, чтобы
полученный орграф G оказался сильно связным? Ответ на этот
вопрос дает
Т е о р е м а 3.23. Связный граф G тогда и только тогда
допускает ориентацию,приводящую к сильно связному орграфу
G, когда каждое ребро графа G входит по крайней мере в один
цикл.
Доказательство. Необходимость.
Пусть G—сильно связный орграф и ребро {«, v} в его симмет-
ризации G не входит ни в один цикл. Тогда uv является
единственным путем в G, соединяющим вершины и и v.
Следовательно, если (и, v)—дуга орграфа G, то вершина и не
достижима в нем из v, а если дугой в G будет (v, и), то v не
достижима в G из и. Получилось противоречие с сильной
связностью орграфа G. Значит, каждое ребро в G входит в состав
некоторого цикла.
Достаточность. Пусть в графе G каждое ребро
входит в некоторый подходящий цикл. Возьмем произвольный
цикл С: Vj v2 ... и ориентируем составляющие его ребра в
указанном порядке прохождения этого цикла. Если в С входят
все вершины графа G (т.е. если С—гамильтонов цикл), теорема
доказана: при любой ориентации остальных ребер полученный
орграф сильно связен. Допустим, что в G существует вершина v,
не входящая в С. Не нарушая общности, можно считать, что v
смежна с некоторой из вершин v. (здесь используется связность
графа G). Рассмотрим цикл С*, содержащий ребро {v(., v}.
Ориентируем ребра цикла С * в одном из двух направлений его
обхода, пропуская те ребра, которые получили ориентацию ранее
(т. е. те ребра, которые входят в состав цикла С). Полученный
орграф сильно связен и содержит не менее чем k + 1 вершину
графа G. Продолжаем этот процесс до тех пор, пока не будут
охвачены все вершины графа G, после чего придаем произвольную
ориентацию оставшимся ребрам, о
Пусть G = (V, а)—орграф и е С v х V—отношение взаимной
достижимости на нем. Конденсацией орграфа G называется
факторграф G/e. Очевидно, что конденсация всякого орграфа будет
бесконтурным графом.
267
Под связным орграфом понимают орграф G со связной
симметризацией G. Связность для орграфов играет меньшую роль,
чем сильная связность.
П р и м е р 119. Напомним, что полуавтомат А =
= (S, X, д) называется сильно связным, если для любых
Sp s2 G S найдется слово р G X* такое, что s2 = <5($р Р)-
Очевидно, что полуавтомат сильно связен тогда и только тогда,
когда сильно связным будет его орграф G(A). Менее очевидным
кажется соотношение между связностью полуавтомата А и
связностью орграфа G(A) (под связностью полуавтомата А
понимается отсутствие в нем непересекающихся устойчивых
подмножеств).
Т е о р е м а 3.24. Полуавтомат А связен тогда и только
тогда, когда связен его орграф G(A).
Доказательство. Пусть А—связный полуавто-
мат. Тогда в нем существует (и притом только один) сильно
связный подавтомат, множество состояний которого обозначим
через SQ. Если s , s2—произвольные состояния полуавтомата А и
s0—любое состояние из SQ, то найдутся слова pl, р2 6 X * такие,
что d(^1, р() = «о = <5(s2’ р2^' Тогда в графе G(A), двигаясь по
ребрам, соответствующим переходам под действием входных
сигналов, входящих в р(, а затем в р2, придем из вершины s{
в вершину s2. Граф G(A) связен, следовательно, связен и орграф
С(Л).
С другой стороны, пусть орграф G(A) полуавтомата А связен.
Допустим, что А не является связным полуавтоматом. Тогда в
решетке Sub А подавтоматов существуют по крайней мере два
различных атома, т. е. у А имеются два сильно связных
подавтомата, множества состояний которых—обозначим их через
Sj и S2—не пересекаются. Но тогда никакое входное слово не
может перевести состояние из в состояние из S2. Таким
образом, в графе G(A) множества вершин Sj и S2 содержатся в
разных компонентах связности. Граф G(A) несвязен, что противо-
речит связности орграфа G(A). о
Неодноэлементные сильные компоненты орграфа называют
также его максимальными сильно связными подграфами. Заметим,
что орграф в общем случае не является объединением своих
сильных компонент: в нем могут найтись дуги, концы которых
лежат в различных сильных компонентах (в отличие от ситуации
с неориентированными графами,—см. теорему 3.1 из § 3.2).
Вершина орграфа, не достижимая из других его вершин,
называется источником, а вершина, из которой не достижима
никакая другая вершина—стоком. Всякая одноэлементная компо-
268
нента связности орграфа является тривиальным источником и
стоком.
Под базой орграфа G = (V, а) понимается подмножество
Vo С у такое, что любая вершина орграфа G достижима хотя
бы из одной вершины, входящей в подмножество VQ, а различные
вершины из VQ взаимно не достижимы.
Т е о р е м а 3.25. Подмножество VQ С v тогда и только
тогда является базой орграфа G, когда оно образовано
вершинами, взятыми по одной из каждого источника фактор-
графа G/e.
Доказательство. Если е(р)—источник фактор-
графа G/e, то никакая его вершина не достижима извне, т. е.
из других е-классов. Следовательно, в состав базы должны входить
представители из каждого источника факторграфа G/e, и притом
по одному, поскольку все Е-классы являются сильно связными
подграфами в G. Теперь нужно доказать, что любая вершина v
орграфа G достижима из множества вершин указанного вида.
Пусть вершина s(v) не является источником в G/e. Тогда в нее
входит некоторая дуга из другой вершины е(р1) орграфа G/e. Если
и s(v1)—не источник, существует дуга, входящая в вершину
s(v1) из отличной от нее вершины е(у2) орграфа G/e и т. д. Так
как G/e—бесконтурный граф, в нем в конце концов найдется
источник е(р^), из которого по выбранным дугам будет достижима
вершина e(v). Очевидно, что тем самым в орграфе G доказано
существование пути из вершины, представляющей источник
е(р^), в вершину v. □
Выделение максимальных сильно связных подграфов в функ-
циональных схемах дискретных устройств является одной из
основных процедур при диагностировании этих устройств (см.
[46]). Рассмотрим способ построения таких подграфов, связанный
с анализом матрицы достижимости. В его основе лежит почти
очевидная
Теорема 3.26. Вершины v. и v. орграфа G взаимно
достижимы тогда и только тогда, когда в матрице достижи-
мости D строки, соответствующие этим вершинам, равны.
Доказательство. Если v. и Vj взаимно дости-
жимы, то каждая вершина v орграфа G одновременно достижима
из V. и Vj или не достижима ни из v., ни из v. . Следовательно,
i-я и j-я строки матрицы D равны (djk = 1 означает, что
достижима из v.). С другой стороны, если i-я и /-я строки матрицы
269
D равны, то поскольку d.. = 1,
должно быть d.. = 1, и, значит, v
‘J	J
достижима из v.; из d.. = 1 следует,
что dj. = 1, так что и v. достижима
из V. . о
1
Пример 120. Выделим
максимальные сильно связные подг-
рафы орграфа G, представленного на
рис. 94.
Прежде чем вычислять матрицу
некоторую предварительную обра-
достижимости D, произведем
ботку матрицы смежности
0 110 10 0 0
0	0	1	1	0	0	0	0
0	1	0	1	0	0	0	0
1	0	0	0	0	0	1	1
0	0	0	0	0	0	0	1
10 0 11110
0	0	0	0	0	0	0	1
0	0	0	0	0	0	0	1
данного орграфа. Заметим, что если в орграфе есть сток, то он
не может входить ни в один максимальный сильно связный
подграф, точно так же обстоит дело и с источниками. Поэтому
удаление всех источников и стоков вместе с дугами, которым они
принадлежат, не изменяет состав максимальных сильно связных
подграфов орграфа. Источник распознается в матрице М наличием
самое большее одной единицы в соответствующем столбце, причем
единица должна стоять на главной диагонали, а сток—аналогичной
ситуацией в строке, которая ему соответствует. Руководствуясь
этими соображениями, вычеркиваем из матрицы М шестую строку
и шестой столбец (вершина —источник), а также восьмую строку
и восьмой столбец (вершина v8—сток). В полученной матрице
строки, соответствующие вершинам v5 и v , оказываются нуле-
выми: после удаления вершин v, и vo вершины v. и v. стали
стоками. Вычеркнем связанные с вершинами v5 и v7 строки и
столбцы. Оставшаяся матрица М° размерности 4x4 уже не
поддается дальнейшей редукции, и дальше действуем с ней.
Удачным обстоятельством в данном примере является то, что
нумерация строк и столбцов в М° осталась согласованной с
номерами вершин исходного орграфа G; в общем случае этого,
конечно, не будет, и необходимо следить за нужным соот-
ветствием.
270
Последовательно вычисляя матрицы
к > 1 (при = Л/°), получаем:
Л/?	:= лЛм° + М°,
я+1	к	’
«? =
О 1
о о
О 1
1 о
1 о
1 1
О 1 ’
о о
и? =
0 111
1111
1111’
1111
1 1 1
1 1 1
1 1 1
1 1 1
+ Е = D°.
Единственным максимально связным подграфом орграфа G явля-
ется его подграф, порожденный вершинами Vp v2, v3> v4.
В бесконтурном графе приведенная процедура завершится
вычеркиванием всех строк и столбцов матрицы смежности.
Пусть орграф G(S) является функциональной моделью неко-
торой системы Е, допускающей одиночный отказ. Для обнаружения
отказа производится проверка элементов системы, имеющая для
каждого элемента два исхода: 0, если реакция элемента допустима,
1 в противном случае. Предположим, система 2 такова, что
реакция 1, отмеченная у некоторого элемента, наследуется всеми
достижимыми из него (в смысле орграфа G(E)) элементами. Под
проверяющим тестом понимается некоторая совокупность про-
верок элементов системы, позволяющая выяснить, имеется ли в
системе отказ (без его локализации). Проверяющим тестом будет,
например, тест, содержащий проверки всех элементов системы.
Естественно попытаться найти минимальные по количеству
проверок тесты.
Теорема 3.27. Проверяющий тест для системы Е
минимален тогда и только тогда, когда он состоит из проверок
элементов, которые соответствуют вершинам орграфа G(E),
взятым по одной из каждого стока факторграфа G(E)/e.
Доказательство. Пусть тест не содержит про-
верки ни одного представителя стока e(v) факторграфа G(E)/e.
Тогда отказ любого элемента, представленного вершиной, входя-
щей в класс e(v), не распознается данным тестом, и, значит, тест
не является проверяющим. Таким образом, любой проверяющий
тест содержит проверки представителей всех стоков в G(Z)/e.
Пусть в состав проверяющего теста входит проверка некоторой
вершины и орграфа G(E), не входящей ни в один сток факторграфа
G(E)/e. В случае отказа соответствующего элемента исходом
проверки будет 1. Но тогда значение 1 дает и проверка любого
271
представителя того стока в G(E)/e, который достижим из и (граф
(7(Е)/е не содержит контуров, и, значит, из каждой его вершины
имеется путь, приводящий к некоторому стоку). Таким образом,
проверка вершины и оказывается излишней.
Предположим, наконец, что в состав проверяющего теста
входят две вершины из одного стока: e(u) = e(v). Вершины и и
v взаимно достижимы в орграфе (7(E), и, следовательно, исходы
их проверок будут совпадать, так что одну из проверок можно
не проводить, а
Пример 121 (см. [17]). Построим минимальные прове-
ряющие тесты для системы, функциональная модель которой
представлена на рис. 95а.
Вычисляем матрицу достижимости:
MJ
0 10 0 11
0 0 0 0 0 0
10 110 0
0 0 10 10 ’
0 0 0 0 0 1
0 0 0 0 1 1
М2
0 10 0 11
0 0 0 0 0 0
111110
10 1111
0 0 0 0 1 1
0 0 0 0 1 1
М3
0 10 0 11
0 0 0 0 0 0
111111
111111
0 0 0 0 1 1
0 0 0 0 1 1
откуда
110 0 11
0 1 0 0 0 0
111111
111111
0 0 0 0 1 1
0 0 0 0 1 1
272
Факторграф G/e изображен на рис. 956. Его стоками являются
е-классы {v2J и {v5, v^}. Минимальные проверяющие тесты:
t, = {л_, я,} и (, = {я,, я } (здесь я обозначает проверку
вершины v. ).
Заметим, что—в отличие от процедуры отыскания максималь-
ных сильно связных подграфов—при построении минимальных
проверяющих тестов предварительная редукция матрицы смеж-
ности М не производится.
Как уже отмечалось в начале параграфа, в орграфе, имеющем
т дуг, длина любого пути не больше т. Путь длины т в орграфе
G называется эйлеровым путем, а орграф, в котором существует
циклический эйлеров путь—эйлеровым орграфом. Как видим, эти
определения дословно совпадают с соответствующими опреде-
лениями для неориентированных графов (§ 3.2), но только нужно
помнить, что в данном случае речь идет об ориентированных
путях (изолированные вершины без петель мы исключаем).
Очевидно, что эйлеров орграф является сильно связным, а наличие
эйлерова пути в орграфе обеспечивает лишь его связность.
Незначительной модификацией доказательств теоремы 3.19 из
§ 3.2 и ее следствия получается
Теорема 3.28. Связный орграф G тогда и только
тогда является эйлеровым орграфом, когда для любой его
вершины v выполняется равенство d+(v) = d (v). В связном
орграфе G существует эйлеров путь в том и только том
случае, когда в этом орграфе имеются такие две вершины и и
v, что d+(u) = d~(u) + 1 и d~(v) = d+(v) + 1, а для каждой
из остальных вершин степень исхода совпадает со степенью
захода. □
Пример 122. Пусть X = {хр х2, ..., хп}—некоторый ал-
фавит, х{ х. ...х. —слово над X. Циклическим подсловом длины
о li	Л—1
т этого слова называется последовательность вида х. х.
S $+ 1
...х/	, где 0 < s < к — 1 и все числа s + 1, s + 2, ...
s+m— 1
..., s + т - 1 рассматриваются по модулю к. Требуется найти
кратчайшее слово такое, в котором в качестве циклического
подслова по крайней мере один раз появилось бы каждое слово
длины т над алфавитом X. Так как в n-буквенном алфавите
существует точно пт различных m-буквенных слов, то искомое
слово не может иметь меньше чем пт букв (с каждой буквы
начинается новое m-буквенное слово). Оказывается, что при
т, п > 2 эта нижняя граница достигается. Чтобы показать это,
рассмотрим орграф Gnm, вершинами которого являются (т — 1)-
273
буквенные слова над X и при этом из вершины х. х. ... х.
О 1	т-2
проводятся дуги в вершины вида х. х. . ..х. х. , х. G X.
1	2	т-2 т-l т— 1
Для каждой вершины этого орграфа степень исхода и степень
захода равны п. Очевидно, что Gnm—(сильно) связный орграф.
Согласно теореме 3.28, он будет эйлеровым. Выписывая первые
буквы слов, обозначающих вершины вдоль эйлерова циклического
пути, получим слово длины пт, «упаковы-
вающее» все m-буквенные слова над X.
На рис. 96 изображен орграф Gn для
случая п = 2, т = 3. Последовательность
прохождения дуг указана номерами на них.
Выбранному эйлерову пути соответствует
слово 01011100 (первой в порядке прохож-
дения вершиной является 01).
При построении контрольных экс-
периментов с автоматами возникает необ-
ходимость рассмотрения так называемых обходов ориентированных
графов, сопоставляемых автоматам (см. [8]).
Маршрут в орграфе G называется обходом, если он содержит
все дуги орграфа. Обход, в котором никакая дуга не встречается
более одного раза, будет эйлеровым путем в G. Существенную
роль при отыскании обходов орграфа играют его сильные
компоненты (слои). Очевидно, что каждый сильно связный орграф
имеет обход, соединяющий любые две вершины.
Теорема 3.29. Для того чтобы связный орграф G
имел обход, необходимо и достаточно, чтобы для любого слоя
—>
в G существовало не более одной дуги с началом (концом) в
этом слое и с концом (началом) вне его.
Доказательство. Пусть П—некоторый обход ор-
графа G, и пусть для некоторого слоя e(v) существуют две
различные дуги (и^, и (и2, v2) такие, что и{, и2 G e(v), но
Vp v2 (£ e(v). Предположим, что при обходе П сначала встреча-
ется дуга (Wp v^, а потом (и2, v2), т. е. обход имеет следующую
структуру: П = П (и , v )П (и , v )П где П П П —соот-
1	1	1	£	£ О	1	£ Д
ветствующие отрезки обхода П. Рассмотрим вершину Vp Посколь-
ку e(v)—сильно связный граф, в нем существует путь из v в
и . Значит, вершина достижима из v. С другой стороны, v
достижима из и2 в e(v), а и2 достижима из (вдоль Пр, откуда
следует, что v достижима из Vp Таким образом, (v, G
G д П д 1 = E, ЧТО невозможно, поскольку Vj £ e(v).
274
С другой стороны, предположим, что связный орграф G =
= (V, а) удовлетворяет условию теоремы и имеет к слоев. В силу
связности, получаем, что существует единственный слой e(vJ), в
который извне не входит ни одна дуга, и существует единственный
слой е(р^), из которого вовне не выходит ни одна дуга. Все слои
получают теперь естественную нумерацию e(vJ), e(v2), •••> £(vic) по
критерию: единственная выходящая из слоя е(у.) дуга ведет в
слой e(v.+ 1), 1 < i < к — 1. Не нарушая общности, будем
считать, что вершины Vj, v2, ..., vk выбраны так, что
(v., v.+ 1) 6 а, 1 < i < к — 1. Через ГЕ обозначим обход сильно
связного графа e(v.), начинающийся и заканчивающийся в вершине
V., 1 < i < к. Тогда последовательность дуг П^Ур у2)П2(р2,
v3) ... ПА1(уА1, vk)YIk будет обходом орграфа G. о
В n-вершинном орграфе бесконтурный путь не может иметь
длину, большую чем п - 1, а длина любого контура не
превосходит п. Бесконтурный путь длины п - 1 в орграфе G
называется гамильтоновой цепью, а контур длины п—гамильто-
новым контуром. Орграф, в котором существует гамильтонов
контур, по определению, является гамильтоновым. Очевидно, что
гамильтонов орграф сильно связен.
Прежде чем описать процедуру отыскания гамильтоновых
путей в орграфе, введем некоторые необходимые для этого
понятия.	г
Пусть П—некоторый маршрут в орграфе G, соединяющий
вершину и с вершиной v (они могут совпадать). Пусть П записан
в виде последовательности вершин, регистрируемых в порядке их
прохождения: и = vn,v,,...,v ,,v = v. Если П—цепь, то
никакая из вершин не встретится в указанной последовательности
более одного раза. Допустим, что П не является цепью.
Зафиксируем вершину vQ и будем просматривать вершины
маршрута П в обратном порядке, начиная с v . Если окажется,
что vk = vQ, это означает, что подпоследовательность, заключен-
ная между vQ и vk, будет циклическим подмаршрутом в П. Удаляя
участок от vQ до j включительно, получим маршрут из
v0 ( = vk) в у в котором vQ уже не будет повторяться. Понятно,
что если vQ не повторялась в П, то = П. Переходя в к
вершине, следующей за вершиной vQ, повторяем указанную
процедуру поиска циклического участка и его удаления. Процесс
этот дает в конце концов однозначно определенную цепь П*,
соединяющую и с v (в случае если П—циклический маршрут,
275
П* вырождается в одноэлементную цепь длины 0). Переход от
П к П* назовем (стандартным) упрощением маршрута П.
Понятно, что при иных способах «вычеркивания» циклических
участков данного маршрута П могут получаться другие цепи из
и в у.	_»
Для маршрутов в произвольном орграфе G вводится частичная
операция композиции: если имеет своим концом вершину v,
а П2 имеет ее своим началом, то композицией этих маршрутов
называется маршрут П = П[П2, состоящий в последовательном
прохождении сначала маршрута Пр а затем маршрута П2.
Л е м м а 3.1. Для любых трех допустимых маршрутов
Пр П2, П3 орграфа G имеет место равенство ПД^Пд) =
Доказательство. Доказываемое равенство сле-
дует понимать в том смысле, что левая и правая части его
определены одновременно и совпадают. Ассоциативность ком-
позиции очевидным образом следует из того, что обе части
определены тогда и только тогда, когда конец маршрута П(
совпадает с началом маршрута П2, а конец маршрута П2—с
началом маршрута П3, причем в результате и слева и справа
получится маршрут из начала маршрута nt в конец маршрута
П3 последовательным прохождением Пр П2 и П3- =
Связкой маршрутов в орграфе G называется произвольное
множество В(и, v) маршрутов с началом в вершине и и концом
в вершине v. Для связок маршрутов введем две частичные
операции: теоретико-множественное объединение связок, отно-
сящихся к одной и той же упорядоченной паре вершин, и
ком позицию
В.(и, v)B.(y, w) := {n^j I G B.(u, v) & П2 G B.(y, w)}.
Под пустой связкой будем понимать связку, не содержащую
ни одного маршрута и не связанную ни с какой парой вершин.
Ее обозначим символом О. Положим В О = О-В = О для любой
связки В.
Т е о р е м а 3.30. В частичной алгебре (£B(G), U, •, О)
всех связок маршрутов орграфа G выполняются следующие
соотношения (t, и, v, w—произвольные вершины орграфа G):
1)	В (и, v) U (В (и, v) U В (и, v)) =
‘	J	*
= (Я.О, V) и в (и, v)) U В Au, v);
1	J	*
2)	В.(и, v) U В.(и, v) = В .(и, v) U В.(и, v);
276
3)	В.(и, v) U О = В.(и, v);
4)	B.(u, v)(B.(v, wyBJw, 0) = (B.(u, v)B.(v, w))Bk(w, t);
5)	B(u, v)(B(y, w) U B,(v, w)) =
1	J	*
= (£.(«, v)Bj(v, w)) U (B.(u, v)Bk(y, w)),
(B.(u, v) U B.(u, v))Bk(v, w) =
= (B.(u, v)Bk(v, w)) U (B.(u, V)Bk(V, w)).
Доказательство. Равенства 1) и 2) вытекают
из ассоциативности и коммутативности теоретико-множественного
объединения. Столь же очевидна истинность соотношения 3).
Ассоциативность композиции для связок обеспечивается леммой
3.1. Докажем левый дистрибутивный закон. Пусть П 6
6 В.(и, v)(B.(v, w) U Вк(у, w)). Тогда существуют маршруты
6 В.(и, v) и П2 е By(v, и*) U Вк(у, и») такие, что ^n2 = П.
При этом П2 е В.(у, и») или П2 G w)- Следовательно,
П е В.(и, v)B.(y, w) или П 6 В.(и, v)Bk(y, w), откуда получаем,
что П G (В.(и, v)B.(v, w)) U (В.(и, v)Bk(y, w)). Таким образом,
связка, стоящая в левой части равенства, включается в связку,
фигурирующую в его правой части. Столь же просто доказывается
обратное включение. □
Как видим, (^(G, U, •, О)) является частичным полуколь-
цом. Матрицы над этим частичным полукольцом умножаются по
обычным правилам, причем произведение двух таких матриц
считается определенным, если можно выполнить все необходимые
для его вычисления операции в &(G).
Пусть G = (V, а)—орграф с п вершинами v2, ..., v^.
Матрицей соединений этого орграфа называется п х n-матрица А
—>
над частичным полукольцом tB(G), где
v.v., если (у„ v.) 6 а,
а.. :=	' 1	' i
V О в противном случае.
Нетрудно заметить, что элемент матрицы-степени А*
представляет собой связку всевозможных маршрутов длины к из
вершины V. в вершину v. в орграфе G.
Следующий алгоритм [89, 46] позволяет найти все гамильто-
новы пути в орграфе G, имеющем п вершин.
Шаг 1. Положить А := А, к := 1.
Шаг 2. Построить матрицу Ак упрощением всех маршрутов,
входящих в состав элементов матрицы Ак, с последующим
277
удалением всех цепей длины, меньшей чем к. Если Ак = О,—
конец: гамильтоновых путей в орграфе G нет. Если Л* * О и
к = п - 1, то элемент этой матрицы дает все гамильтоновы
цепи из вершины v. в вершину v. .
Шаг 3. Построить матрицу Л^+1 = При к = п — 1
конец: если хотя бы один элемент главной диагонали равен О,
гамильтоновых контуров в G нет. В противном случае любой
элемент главной диагонали дает все гамильтоновы контуры. При
к < п — 1 положить к := Л+1 и перейти к шагу 2.
Заметим, что в практической реализации алгоритма при
построении матрицы Л* (шаг 2) из элементов матьрицы Л* просто
2^^-—вычеркиваются все маршруты, не явля-
6	/лХ\ ющиеся цепями, а при выполнении шага
л / \ / \\)	3 в случае к = п - 1 вычисляется только
рис 97	Пример 123. Найти гамильтоно-
вы пути в орграфе G, изображенном на
рис. 97. Для упрощения записей вершины
будем обозначать числами. В данном случае они однозначны, и
запись 1243 обозначает вполне определенный простой путь (цепь)
из вершины 1 в вершину 3.
Сначала строится матрица соединений:
А =		11 О 31 о 51	12 13 О		О О о 45 О	= лг		
			О О 32 О О 43 52 53	24 О О 54				
Далее получаем:								
А	1		О 12 О О 31 32 О о 51 52	13 О о 43 53	О 24 О О 54	О О О 45 О		
	131		132	О	124	О		
		О	О	243	О	245		
V1 =		о	312	313	324	О		Л2.
	[431 [451 531		[432 1452 [512 1532	453 513 543	454 524	О 545		
278
Матрица Л2 содержит все пути длины 2 в орграфе G. В
частности, на главной ее диагонали перечислены (с повторениями)
все контуры длины 2 (их два: 131 и 454). Для получения матрицы
Л2 нужно заменить нулями элементы главной диагонали в А^.
Следующий этап дает
^3	^2^1
О	О	1243	1324	1245
2431 2451	2432 2452	2453	2454	О
О	О	3243	3124	3245
4531	4312 4512 4532	4313 4513	4324 4524	О
5131 5431	5312 5132 5432	5313 5243	5124 5324	5245
С главной диагонали матрицы выписываем все контуры
длины 3 (это пригодится в § 3.4): 2432, 2452. Для получения
матрицы А^ вычеркиваем маршруты, в которых есть повторя-
ющиеся вершины: кроме ненулевых элементов главной диагонали
таковыми будут еще 2454 = а^, 4313 (в составе 5131 (в
</?)) и 5313 6 Умножая полученную матрицу А на А ,
находим
4
12431 12451	12432 12452	13243 12453	12454	13245
24531	24312 24512 24532	24313 24513	О	О
32451	32452	31243 32453	32454	31245
45131	45312 45132	45313	43124 45124 45324	О
52431	54312 52432	54313 51243 53243	53124 51324 54324	51245 53245
Выпишем контуры длины 4 в орграфе G: 12431, 12451, 24532.
Следующий шаг приводит к получению всех гамильтоновых цепей:
279
о	О	12453	О	13245
24531	О	24513	О	О
32451	О	О	О	31245
О	45312 45132	О	О	О
52431	54312	51243	53124 51324	О
Например, из вершины 4 в вершину 2 ведут две такие цепи:
45312 и 45132. Для получения гамильтоновых контуров вычисляем
элемент cfff = {124531, 132451}.
При решении многих прикладных задач возникает необ-
ходимость находить кратчайшие пути в заданных орграфах. При
этом под кратчайшим путем между вершинами понимается путь,
имеющий наименьшее число дуг. Очевидно, что всякий такой
путь будет бесконтурным путем, т. е. цепью. В приводимом ниже
алгоритме существенную роль играют два специальных разбиения
на множестве вершин орграфа [8].
Пусть G = (V, а)—некоторый орграф и и, v—две его различ-
ные вершины. Требуется найти кратчайший путь из вершины и
в вершину у. Через Ак(и) обозначим множество всех таких вершин
орграфа G, которые достижимы из и за к шагов (т. е. путями
длины Л) и не достижимы за меньшее число шагов. Положим
Aq := {д} и Аж := {и» е VI (и, w) £ <5} (множество Аж состоит
из вершин, которые не достижимы в G из вершины и). Ясно,
что классы вида образуют разбиение множества V (см.
§ 1.3). Через В^у) обозначим множество всех таких вершин
орграфа G, из которых вершина v достижима за к шагов и не
достижима за меньшее число шагов. Положим BQ := {у} и
^оо := {и» 6 VI (и», у) £ <5}.
Заметим, что В-разбиение множества вершин орграфа G =
= (У, а) совпадает с Л-разбиением орграфа G~l = (V, а-1),
—>
получаемого из G сменой ориентации всех дуг на противополож-
ную.
Общая идея алгоритма состоит в том, что для множества
А.(и) Л В.(у) проверяется выполнение условия Л.(д) Л В.(у) *
* 0. Если А(д) Л В.(у) = 0, то строится множество А.+ 1(и)
или #;+1(у) и указанное выше условие проверяется для
Л В.(у) или для А^и) Л В.+ 1(у). Если же А.(и) Л
Л В.(у)	0, то из этого множества выбирается элемент	и
строятся такие последовательности вершин и , ..., и и у , ..., у.,
что для всех 1 < £ < i вершина является элементом
280
множества A k(u) Г)	и для всех 1 < I < j вершина
у^ является элементом множества	Г) <3(Уу_1), причем
u0 = v0- Описанный метод можно назвать методом сращивания
деревьев. Следующий алгоритм, основанный на этом методе,
находит один из кратчайших путей из вершины и в вершину у
в орграфе G = (V, а) или обнаруживает недостижимость вершины
у из и.
Шаг 1. Aq := {u}, BQ := {у}, i := 0, / := 0.
Шаг 2. Если А Г) В. # 0, то переход к шагу 6, иначе
переход к шагу 3.
।
Шаг 3. Если 1Л.1 < IB.I, то Л.+ 1 := а(А) — U А и пере-
171	1	s=0 s
_j	j
ход к шагу 4. Иначе В := а (В.) — U В и переход к
шагу 5.
Шаг 4. Если А.,, #
i+i
иначе конец. Вершина у
Шаг 5. Если В. , #
/+1
иначе конец. Вершина у
Шаг 6. В А. Г) В.
‘ !
0, то i := i + 1 и переход к шагу
не достижима из и.
0, то j := j + 1 и переход к шагу
не достижима из и.
выбирается вершина uQ, к :=
2,
2,
1,
Шаг 7. Выбирается вершина и^ из множества « ’(«t-P л
Л А. ,, Р. := и.и. , ...ип.
i-k к к к—\	0
Шаг 8. Если к < z, то к := к + 1 и переход к шагу 7,
иначе—к шагу 9.
Шаг 9. Р := Р..
i
Шаг 10. Если j = 0, то конец: последовательность Р является
кратчайшим путем из и в у. Иначе I := 1, yQ := uQ и переход
к шагу 11.
Шаг 11. Выбирается вершина у^ из «(vz_i) Л В , Р1. : =

Шаг 12. Если I < j, то I := I + 1 и переход к шагу 11, иначе
конец: последовательность Р.1 является кратчайшим путем из
и в у.
Покажем, что если остановка работы алгоритма не произошла
при выполнении шага 4 или шага 5, то построенный путь P.J
является одним из кратчайших путей из и в у. Пусть
Р = uw1w2...w$_1у—некоторый кратчайший путь из и в у, а
281
путь Р,1 = ииj ... UqVj ... v._ j v, построенный в результате работы
алгоритма, не является кратчайшим. Тогда i + j > s. Однако для
всех 0 < к < 5 вершина wk входит одновременно в Ak(u) и в
В Ау) (мы считаем, что = и и w = v), т. е. А, Г) В . * 0
при 0 < к < 5. Последний факт противоречит тому, что путь
Р 1 построен в результате работы алгоритма (в силу условия,
проверяемого в шаге 2, А. Г) В^ = 0 при i + j < s).
Пример 124. Найти кратчайший путь из вершины Vj в
вершину v9 в орграфе G, изображенном на рис. 98а. В ходе
работы алгоритма последовательно строятся множества А1 =
= {v2, v4} (на рис. 98б оно показано вместе с дугами, идущими
в него из Aq = {Vj}), В^ = {yg} (дуга, идущая из В^ в
BQ = {v9} для наглядности нарисована на рис. 98в пунктиром),
В = {у,, у , у } (рис. 98г), А = {у , у,, у,} (рис. 98д). Дерево,
£	<Э О /	L	□ О О
исходящее из вершины у^ соединяется с деревом, входящим в
у„, в вершинах у, и v,. Кратчайшие пути у,у„у,уоу„, у,у,у,уоу„,
9	3 о	1238914389
V1V2V6V8V9 из веРшины vi в вершину У9 имеют длину 4.
Рис. 98
Менее экономным, но более наглядным является алгоритм
нахождения кратчайшего пути, который просто последовательно
строит множества А(и), проверяя принадлежность вершины у
очередному полученному множеству.
Рассмотрим теперь более общую задачу нахождения крат-
чайших путей в ориентированных сетях (т. е. в орграфах, дуги
которых помечены положительными числами). Будем считать, что
в сети G имеется вершина yQ, из которой достижима любая
другая вершина (такую вершину называют корнем, а сеть,
имеющую корень, корневой). Следующий алгоритм Дейкстры
определяет кратчайший путь из корня yQ в каждую вершину сети
G (т. е. путь, сумма весов дуг вдоль которого будет наименьшей).
282
Перед началом выполнения алгоритма все вершины и все дуги
сети считаются не окрашенными.
Шаг 1. Положить l(yQ) = 0 и Л(у) = » для всех вершин v,
отличных от yQ. Окрасить вершину yQ и положить U := {vQ}.
Шаг 2. Для каждой неокрашенной вершины у найти новое
значение Л(у) := min {Л(у), l(u) + w(u, у)}, где w(u, у) обозначает
и 6 и
вес дуги (и, у). Окрасить одну из вершин у, для которых величина
Л(у) является наименьшей, присоединить эту вершину к U.
Окрасить также одну из дуг, ведущих из множества окрашенных
вершин в выбранную вершину и дающих наименьшее значение
для Л(у).
Шаг 3. Если все вершины окрашены, т. е. U = V,—конец:
для любой вершины у кратчайший путь из yQ в у однозначно
определяется, состоит из окрашенных дуг и имеет длину Л(у).
Иначе перейти к шагу 2.
Прежде чем доказывать теорему, обосновывающую этот
алгоритм, рассмотрим
Пример 125 (см. [42]). Найту кратчайший путь из
вершины у1 в каждую вершину сети G, изображенной на рис.
99. Приводимая таблица заполняется по ходу работы алгоритма.
На первом этапе выставляются
начальные значения Л(у) для всех
вершин у, окрашивается вершина
yj (соответствующее ей значение
обведено), дуги не окрашиваются.
На втором этапе пересчитываются
значения Л(у), выбирается вершина
у., имеющая наименьшее значение
4
l(v4) = 3, она окрашивается (квад-
рат) и окрашивается дуга (у^ у4), дающая значение Л(у4) = 3.
На третьем этапе тоже все определяется однозначно. На четвертом
можно окрашивать или вершину у3, или вершину у5: для обеих
1 = 7. После выбора вершины у^ снова имеем произвол: значение
283
Л(у5) = 7 получается как на пути р(р2р5, так и на пути р^р^
т. е. можно окрашивать дугу (р2, р5) или дугу (р4> р5). Выбрана
дуга (р2, р5). Еще один выбор (дуги) предстоит сделать на этапе
5. На последнем этапе окрашивается вершина р6 и дуга
(р3, р6). Все вершины окрашены. В изображении графа окрашен-
ные дуги выделены. Однозначно определенный путь из вершины
Pj по окрашенным дугам в любую вершину р будет кратчайшим.
Выбирая на этапах 4 и 5 другие возможные вершины и (или)
дуги, мы получили бы иные кратчайшие пути в вершины
Р3, Р5 и Р6.
Т е о р е м а 3.31. Описанный алгоритм приводит к пос-
троению одной из систем кратчайших путей в корневой сети.
Доказательство. Нужно показать, что для лю-
бой вершины р путь в нее из pQ по окрашенным дугам является
одним из кратчайших и что его длина равна Л(р). Доказательство
ведем индукцией по расстоянию вершины р от pq. Для вершин,
ближайших к р0, это следует из описания алгоритма. Пусть это
верно для всех вершин, более близких к pQ, чем вершина р. К
моменту окраски вершины р она имеет метку Л(р) = А(й) +
+ и»((и, р)), где и—одна из ранее окрашенных вершин. Будем
считать, что это именно та вершина, которая соответствует
окрашиваемой вместе с р дуге (и, р). По предположению
индукции, Л(и)—расстояние (наименьшая из длин путей) от pq
до и, и оно реализуется вдоль некоторого пути vq?u п0
окрашенным дугам. Значит, 1(р) = l(u) + w((u, р))—это длина
пути vQPuv. Пусть vQP*u*v—один из кратчайших путей от pQ до
р. Можно считать, что дуги, составляющие путь vQP*u*, окрашены.
Кроме того, тоже по предположению индукции, длина пути
vQP*u* равна 1(и*). Тогда l(u*) + w((u*, р))—расстояние от pQ до
р. Поэтому имеем неравенство Л(и*) + w((u*, р)) < Х(й) +
+ и»((и, р)) = 1(р). С другой стороны, согласно предписанию
алгоритма (шаг 2), дуга (и, р) окрашена, потому что Л(р) =
= 1(ц) + и»((и, р)) < 1(и*) + и»((и*> v)) Для любой из окрашен-
ных вершин и*. Отсюда получаем, что Л(р) = Л(и*) + w((u*, р))—
расстояние от р0 до р, а оно реализуется и вдоль окрашенного
пути vQPuv. о
§ 3.4. Направленные графы
Напомним, что орграф D = (V, а) называется направленным
графом (или кратко диграфом), если отношение а антисим-
284
метрично, т. е. если а О а 1 С Д. Условие антисимметричности
означает, что в D нет встречных дуг или, что то же, нет контуров
длины 2. Важнейшими классами направленных графов являются
бесконтурные графы и среди них ориентированные деревья, а
также турниры. Но прежде чем перейти к изучению этих видов
направленных графов, рассмотрим один представляющий интерес
специальный случай.
Орграф G = (V, а) с п > 2 вершинами называется регуляр-
ным полигональным орграфом степени t S п — 1, если степень
исхода каждой вершины равна t (т. е. cZ+(y) = f) и существует
такая нумерация вершин yQ, у^ ..., у , что дуги из у. ведут в
вершины у.у.у.,., О < i < п — 1, где сложение в
г	1 + 1	1+2 i+t
индексах производится по модулю п. Если вершины орграфа G
расположить в этой нумерации на равных расстояниях вдоль
окружности, двигаясь по часовой стрелке, а дуги изобразить
прямолинейными отрезками, то полученный рисунок хорошо
объясняет название: в контуре, образующем правильный п-
угольник, из каждой вершины проведены диагонали в следующие
за ней по часовой стрелке t - 1 вершин (не считая ближайшей).
Понятно, что в каждую вершину входят t дуг (из ближайших
против часовой стрелки вершин), так что с/-(у) = t для любой
у 6 V. Нетрудно заметить, что G тогда и только тогда будет
направленным графом, когда t < nil. Регулярный полигональный
л-вершинный диграф степени t будем обозначать через D . При
этом понимается, что t < л/2. На рис. 100 показаны изображения
регулярных полигональных орграфов с пятью вершинами (встреч-
ные дуги заменены неориентированным ребром). Первые два будут
направленными графами D , и D , а последний—полным
1 &
графом К$.
Рис. 100
Диграфы вида f находят применение в технической
диагностике. В этой связи рассмотрим
Пример 126. Пусть некоторая система S состоит из л
элементов (блоков) и каждый элемент у. может проверять любой
другой элемент v. . Результат проверки л„ будем считать равным
285
О, если оба элемента исправны, равным 1, если элемент у(
исправен, а у неисправен, а в случае когда у( неисправен,
результат проверки может оказаться равным 0 или 1 (это одна
из возможных моделей [84, 46]). Задача состоит в построении
локализующего теста, т. е. такого набора проверок л.. , по
результатам которых можно было бы однозначно определить
отказавшие элементы. При этом считается, что количество
отказавших элементов не превосходит некоторого числа t.
Заметим, что при и < 2/ поставленная задача в общем виде
неразрешима. Действительно, допустим, что в системе S, где
п < 2/, откажут и/2 элементов при четном п или (и + 1)/2
элементов при нечетном п. Тогда однократное применение любого
теста может дать результаты проверок л^ = 0, когда элементы
у. и V. оба исправны или оба неисправны, и л.. = 1, когда один
неисправен. Такие
из элементов у., v. исправен, а другой
результаты тестирования дают возможность разве лишь разбить
элементы системы на две группы, в одной из которых все элементы
предположительно исправны, а в другой неисправны, но точно
определить, какая из этих групп состоит из отказавших элементов,
не удастся. Таким образом, будем считать, что t < п/2 или, что
равносильно, п > It + 1.
Необходимым требованием для локализующего теста является
то, чтобы каждый элемент системы проверялся в нем не менее
чем t элементами. В самом деле, допустим, что некоторый элемент
у проверяется в данном тесте элементами у^ у2, ..., у*, где
к < t, и что элементы у , у , ..., у^ в момент применения теста
оказались неисправными. Тогда исходами всех проверок, так или
иначе связанных с отказавшими элементами, может быть 1, а
исходами всех остальных проверок—0. Легко видеть, что в этом
случае нам не удастся определить состояние элемента у. Заметим,
что при выполнении обсуждаемого условия каждый неисправный
элемент будет проверяться хотя бы одним исправным элементом.
Каждому тесту (набору проверок) сопоставляется орграф,
вершинами которого являются элементы системы, и из вершины
у. в вершину у. проводится дуга тогда и только тогда, когда в
данный тест входит проверка л
Орграфы такого вида называ-
У ’
ются диагностическими графами для данной системы или графами
ее проверочных связей. Выставляя на каждой дуге диагностичес-
кого графа результат соответствующей проверки (0 или 1),
получаем ориентированную сеть, называемую синдромом, анализ
которой и проводится для выделения отказавших элементов.
Локализующий тест позволяет найти неисправные элементы по
любому связанному с ним синдрому.
286
Т е о р е м а 3.32. Диграф Dn t является диагностическим
графом локализующего теста для любой п-элементной системы
с не более чем t отказами.
Доказательство. Рассмотрим максимальный до-
пустимый случай п = 2/ + 1. Пусть система S имеет п элементов
и известно, что в ней одновременно могут отказать не более чем
t элементов, п = It + 1. Возьмем тест с диагностическим графом
Dn . Предположим, что в момент тестирования отказали k < t
элементов. Какие бы вершины диграфа D* t ни соответствовали
неисправным элементам, в Dn t существует контур, проходящий
через все остальные вершины, причем в каждую вершину,
соответствующую отказавшему элементу, будет идти дуга из
некоторой вершины этого контура. В любом синдроме, связанном
с диагностическим графом Dn , дуги контура будут иметь метку
О, а дуги, исходящие из него в неисправные вершины,—метку 1.
Так как число отказов не превосходит t, все элементы,
соответствующие вершинам контура, должны быть признаны
исправными, а тогда остальные элементы опознаются как
неисправные (разные синдромы будут отличаться друг от друга
лишь метками на дугах., исходящих из вершин, представляющих
неисправные элементы).
Пусть в момент тестирования в системе отказали t элементов.
Здесь возможны два случая.
1) Отказавшие элементы представлены последовательными
вершинами многоугольника в стандартном изображении диаграфа
Dnt' Vi’Vi+r Vi+f-i (сложение в индексах производится по
модулю л). Так как элементы (вершины) vj+t> vi+t+i’ —>
исправны, то в любом синдроме, связанном с D t, будет
л. =0 для i + t < j < i — 2 и л._1 . = 1. Результат
последней проверки может означать, что элемент у неисправен.
Но тогда равенство л(._2	=0 свидетельствует об отказе
элемента у._2, и т. д. В итоге отказавшими придется признать
t + 1
число
если
i /
элементов у. , у. ,, ..., v ,, что невозможно, так как
i+t i + t+l	t-г
отказов не превышает t.
элемент у t исправен.
< i + t — 1, всегда будут
Это противоречие
Тогда проверки
устраняется,
V1,/ ’ где
иметь результат 1, и элементы
у., v р ..., v(+f_! опознаются как неисправные.
2) При любом другом расположении вершин, соответствующих
t отказавшим блокам, в диграфе D t найдется контур, проходящий
через остальные вершины, причем в каждую вершину, представ-
287
ляющую неисправный элемент, будет идти дуга из некоторой
вершины контура. Этот случай был рассмотрен ранее, о
К числу направленных графов относятся все бесконтурные
графы—орграфы, не содержащие нетривиальных контуров (петли
в вершинах допускаются).
Пример 127. Бесконтурным антирефлексивным (т. е.
без петель) графом является ориентированная диаграмма любого
конечного упорядоченного множества (§ 1.4).
Пример 128. В корневой сети построим все кратчайшие
пути из корня в каждую вершину. Полученная сеть называется
сетью кратчайших путей для исходной сети. Она будет
бесконтурной сетью, не имеющей петель. На рис. 101 выделены
дуги, образующие граф кратчайших путей и сеть кратчайших
путей соответственно в орграфе и сети, рассматривавшихся в § 3.3
(рис. 98, 99).
Пусть G = (У, а)—орграф с корнем vQ и Gp—граф крат-
чайших путей для G. На множестве V введем отношение <,
полагая v. < v. тогда и только тогда, когда некоторый кратчайший
путь из v0 в V. проходит через v. . Тогда (У, <) является
упорядоченным множеством, ориентированная диаграмма которого
изоморфна орграфу G . Очевидно, что в (У, <) выполняется
условие Жордана—Дедекинда для цепей (см. § 1.4).
В § 3.3 отмечалось, что конденсация любого орграфа является
бесконтурным графом. Так как отношение взаимной достижимости
вершин на бесконтурном графе тождественно, то конденсация
любого бесконтурного графа совпадает с ним самим.
В § 1.4 было показано, что в бесконтурных графах, и только
в таких орграфах, отношение достижимости <5 будет отношением
порядка.
Пусть G = (У, а)—произвольный орграф. Говорят, что его
вершины правильно пронумерованы: Vp v?, ..., v , если из
(у.,	& а следует неравенство i
< j, т. е. если дуги ведут из
вершин с меньшими номерами в вершины с большими номерами.
288
Т е о р е м а 3.33. В орграфе G существует правильная
нумерация вершин тогда и только тогда, когда G—бесконтурный
граф.
Доказательство. Необходимость.
Пусть G = (V, а)—бесконтурный и-вершинный граф. Тогда
(У, <5)—упорядоченное множество. Согласно теореме Шпильрайна
(§ 1.4), существует вложение у этого упорядоченного множества
в начальный отрезок {1, 2, ..., и} естественно упорядоченного
натурального ряда, причем из (и, у) G <5 следует неравенство
<р(и) < >р(у) для любых двух различных вершин и, v G V. Считая
<р(у) номером вершины v, получаем правильную нумерацию
вершин орграфа G.
Достаточность. Пусть Ур у2, ..., у^—правильная
нумерация вершин орграфа G к v. V. ... v.v. —некоторый контур
,	I 2 lk *1
в G, k > 1. Тогда должно быть z^ < z’2 < ... <	что
невозможно в силу антисимметричности порядка. Следовательно,
G не содержат нетривиальных контуров. о
Следствие 3.8. Во всяком бесконтурном графе суще-
ствует по крайней мере один источник и по крайней мере один
сток.
Доказательство. Пусть Ур уэ, ..., у^—вершины
бесконтурного графа G в правильной нумерации. Тогда не
существует вершины и * Ур такой, что (zz, Vj) 6 а, иначе и
имела бы номер, меньший 1. Значит, Vj—источник. Аналогично,
не существует вершины у, отличной от у^, такой, что
(v , у) G а, и, значит, v —сток. о
к п '	п
Следствие 3.9. Каждый бесконтурный граф имеет
единственную базу.
Доказательство. Поскольку в конечном упоря-
доченном множестве каждый элемент содержит некоторый мини-
мальный элемент, из доказательства следствия 3.8 извлекаем, что
каждая вершина бесконтурного графа достижима из некоторого
источника. Поскольку никакой источник не достижим из другого
источника, совокупность всех источников и образует единственную
базу бесконтурного графа. =
Следствие 3.10. В любом графе можно ввести ори-
ентацию ребер так, что он станет бесконтурным графом.
Доказательство. Пусть Ур у2> ..., vn—произ-
вольная нумерация вершин графа G. Если z < j и в графе есть
ребро {у., г.}, ориентируем его от у. к у. . Проделав эту процедуру
над всеми ребрами графа, получим орграф G с правильной
Ю А.М.Богомолов, В.Н.Салий	289
нумерацией вершин. Согласно теореме 3.33, G будет бесконтуряым
графом, о
Следствие 3.11. В любом направленном графе мож-
но переориентировать некоторые дуги так, что получится
бесконтурный граф.
Доказательство. Если в орграфе G вершины
V., v. таковы, что z
i j
< j, сохраним ориентацию дуги (v., v.), а если
z > j—сменим ее на противоположную. Так как в G нет встречных
дуг, имеющаяся нумерация вершин в новой ориентации дуг будет
правильной, о
Рангом г(у) вершины v в бесконтурном графе G — (У, а)
называется наибольшая из длин простых путей, заканчивающихся
в вершине v.
Т е о р е м а 3.34. Если вершина v не является
источником в бесконтурном графе G = (V, а), то
г(у) = max r(u) + 1.
и 6 a~\v)
Доказательство. Пусть v{v2 ... v^v—некоторый
простой путь в G. Тогда в упорядоченном множестве (V, <5) имеем
убывающую цепь v >	> ... > v2 > ур и эта цепь неуплот-
няема (каждый элемент ее, начиная с является нижним соседом
предыдущего). С другой стороны, каждая неуплотняемая убыва-
ющая цепь в (V, д), которая начинается с v, будет простым путем
—>
в G от последнего ее элемента к v. Из этого соответствия между
—>
цепями в орграфе G и неуплотняемыми убывающими цепями в
упорядоченном множестве (V, д) можно заключить, что ранг
вершины у в G—это ее высота в упорядоченном множестве
(У, <5). Но высотой элемента как раз и является увеличенная на
единицу наибольшая из высот его нижних соседей. о
Рассмотрим правильную нумерацию вершин, диаграмму упо-
рядоченного множества (У, д) и ранжированное изображение
бесконтурного графа на рис. 102.
Рис. 102
290
Ранжированное изображение бесконтурного графа G =
= (У, а) получают из (неориентированной) диаграммы упорядо-
ченного множества (V, <5) ориентацией ее ребер и добавлением
дуг орграфа G, не представленных в этой диаграмме. Заметим,
что в практических действиях сначала строится диаграмма
упорядоченного множества (V, <5), а уже из нее получают
ранжированное изображение данного бесконтурного графа и
правильную нумерацию его вершин (двигаясь снизу вверх и на
каждом уровне слева направо).
Одним из наиболее используемых критериев бесконтурности
графа является
Теорема 3.35. Орграф G тогда и только тогда будет
бесконтурным графом, когда при некоторой нумерации его
вершин матрица смежности М оказывается верхней треугольной
матрицей (т. е. все ее элементы, стоящие ниже главной
диагонали, равны 0).
Доказательство. Пусть G = (V, а)—бескон-
турный граф. Согласно теореме 3.33, существует правильная
нумерация его вершин v^ v^, ..., v . Следовательно, для любых
номеров i, j имеем
m = 1 => (v„ v.) 6 a => i < /,
и, значит, все элементы матрицы
смежности М, равные 1,
расположены выше главной диагонали или на ней. Все остальные
элементы двоичной булевой матрицы М равны нулю.
С другой стороны, пусть при некоторой нумерации вершин
орграфа G матрица смежности М оказалась верхней треугольной
матрицей. Тогда для любых двух вершин v„ v. в этой нумерации
имеем:
(v., V.) Е а => т.. = 1 => i < j,
\ ;> у	у
—>
—нумерация правильная, и, в силу теоремы 3.33, орграф G
бесконтурный. □
Расконтуриванием орграфа G называется всякая совокупность
его дуг, удаление которых превращает G в бесконтурный граф.
Расконтуривание, по определению, является минимальным, если
никакое его собственное подмножество не является раскон-
туриванием. Оптимальное расконтуривание содержит наименьшее
возможное для расконтуриваний данного орграфа число дуг (в
ориентированных сетях под оптимальностью понимают наимень-
шую возможную сумму весов дуг, удаляемых для устранения всех
нетривиальных контуров). Прямой метод нахождения оптимальных
расконтуриваний опирается на теорему 3.35: перебираются все
нумерации вершин орграфа (сети) и для каждой подсчитывается
количество (или суммарный вес) дуг, соответствующих единицам
под главной диагональю матрицы смежности (см. [17]).
10*
291
Другая возможность связана с алгоритмом поиска гамильто-
новых путей в орграфе (§ 3.3). По ходу работы алгоритма можно
получить список всех контуров орграфа. Составляется матрица,
строки которой помечаются нетривиальными контурами орграфа
в порядке возрастания их длины, а столбцы—дугами, входящими
каждая хотя бы в один контур. В строке, соответствующей данному
контуру, проставляется символ 1 в тех столбцах, которые
обозначены дугами, образующими этот контур. Анализ полученной
матрицы позволяет выделить все расконтуривания нужного вида
(произвольные, или минимальные, или оптимальные) (см. [46]).
Пример 129. Орграф, рассмотренный в примере 123 из
§ 3.3, имеет 9 нетривиальных контуров, в которых задействовано
11 различных дуг (контур г. г. ...у. у. образован к дугами
I 2	* I
(v. > vi )> (vi > vi )> •••> (vj > vi ))• Составляем матрицу контуров и
дуг.
Контуры	Дуги										
	13	31	45	54	24	43	32	52	12	51	$3
131	1	1									
454			1	1							
2432					1	1	1				
2452			1		1			1			
12451			1		1				1	1	
12431		1			1	1			1		
24532			1		1		1				1
124531		1	1		1				1		1
132451	1		1		1		1			1	
Нетрудно заметить, что никакое расконтуривание не содержит
меньше трех дуг. Поэтому, например, {(1, 3), (5, 4), (2, 4)} или
{(1, 3), (4, 5), (4, 3)} будут оптимальными расконтуриваниями,
а {(1, 3), (5, 4), (3, 2), (5, 2), (1, 2)}—минимальным (ни одну
из дуг исключить нельзя), но не оптимальным.
Теорема 3.36. Минимальное расконтуривание связного
орграфа не нарушает связности.
Доказательство. Пусть а С. а—минимальное
расконтуривание связного орграфа G. Будем удалять дуги,
входящие в а по одной. Предположим, что (и, у)—первая по
порядку дуга из а*, удаление которой нарушает связность орграфа,
полученного из G исключением предыдущих а*-дуг. Но это
означает, что дуга (и, у) не входит ни в один из оставшихся
контуров, и, следовательно, она избыточна в а*, что противоречит
минимальности а*. □
Понятно, что теорема 3.36 справедлива также и для оптималь-
ных расконтуриваний связных орграфов и сетей.
292
Заметим, что теорема 3.35 может быть использована также
для нахождения таких переориентаций дуг направленного графа,
которые привели бы к бесконтурному графу: нужно изменить
ориентацию всех дуг, которым в матрице смежности соответствуют
единицы, расположенные ниже главной диагонали. При подходя-
щей нумерации вершин количество таких дуг будет наименьшим.
Алгоритм Дейкстры поиска кратчайших путей в корневой сети
(§ 3.3) в случае бесконтурных сетей приобретает более простой
вид. Согласно теореме 3.33, в такой сети существует правильная
нумерация вершин. При такой нумерации любой кратчайший путь
из корня Vj в вершину проходит через вершины с номерами,
меньшими чем к. Поэтому на втором шаге для фиксированной
вершины V. пересчет числа Л(ур производится с использованием
лишь тех вершин у, которые будут иметь меньшие чем j номера.
Итак, пусть G—произвольная бесконтурная сеть с корнем yt
и правильной нумерацией вершин. Следующий алгоритм находит
кратчайшие пути от корня У] до всех остальных вершин.
Шаг 1. Положить Л(У]) := 0 и Л(у.) := » для i > 2, а также
/ := 2.
Шаг 2. Для вершины v. найти новое значение Л(ур : =
:= min (А (у.), Л (у.) + w(y., у)), где w(v., у^.) обозначает вес
У. 6 «"'(У.)
дуги (у., у.). Окрашивается одна
Л(у.).
Шаг 3. Если / = п,—конец:
чайший путь из yt в у ведет
длину Л(у.). Иначе /:=/+! и
из дуг, дающих новое значение
для любой вершины v. крат-
по окрашенным дугам и имеет
переход к шагу 2.
Сеть, рассматривавшаяся в примере 125 из § 3.3, не имеет
контуров, и нумерация ее вершин правильная. Применяя к ней
приведенный выше алгоритм, получаем следующую последователь-
ность окраски дуг: 1) (у., у_), 2) (у, у,) или (у, у), ?)
1	£	1 J	Л/ О
(Vp v4), 4) (У2, У5) или (у4, У5), 5) (У3, у6).
Если к понятию конгруэнции орграфа подойти с точки зрения,
обсуждавшейся в § 3.1, то под конгруэнцией бесконтурного графа
G следует понимать такую эквивалентность в на множестве его
вершин, что факторграф G/в является бесконтурным графом.
Рассмотрим одну встречающуюся в приложениях конгруэнцию
бесконтурных графов.
Пусть G = (V', а)—бесконтурный граф. Согласно следствию
3.8 из теоремы 3.33, в нем есть стоки. Именно, стоками будут
максимальные элементы упорядоченного множества (V, <5), где
д—отношение достижимости на G. Поскольку в конечном
293
упорядоченном множестве всякий элемент содержится в подходя-
щем максимальном элементе (см. § 1.4), получаем, что любой
путь из фиксированной вершины v 6 V ведет в некоторый сток.
Множество всех стоков для вершины v обозначим через S(y).
Т е о р е м а 3.37. Отношение а := {(u, у) 6 V х
х V I S(u) = S(y)} является конгруэнцией бесконтурного графа
G = (V, а).
Доказательство. Очевидно, что а будет эквива-
лентностью на множестве вершин орграфа G. Покажем, что
факторграф G/a не имеет нетривиальных контуров. Пусть это не
так, и <7(Vj), <т(у2), •••, <r(v^), CT(vj)—последовательность вершин
факторграфа Gio, выписанная в порядке прохождения некоторого
контура.
Заметим, что при (и, у) 6 а всякий путь из вершины v в
какой-либо сток является частью пути из и в этот же сток, так
что S(u) □ S(y). Поскольку в факторграфе G/a имеется дуга из
вершины c^Vj) в вершину cr(v2), то в орграфе G найдутся вершины
и и и такие, что (и , у) 6 а, (и , v ) 6 а и (и , и ) 6 а.
Отсюда, согласно сделанному выше замечанию, S(U]) D S(zz2)
(равенство исключается, поскольку (zz^ «2) £ а). Следовательно,
S(Vj) = S(Uj) D S(u2) = S(v2). Продолжая аналогичные рассужде-
ния, получаем: S(vt) D S(v2) D ... D S(v^) D S(v1),—противоречие.
Таким образом, факторграф G/a не содержит контуров. □
Конгруэнция а находится по матрице достижимости D орграфа.
Сначала в ней выделяются стоки—им соответствуют те строчки
матрицы D, в которых лишь один (стоящий на главной диагонали)
элемент равен 1. Пусть стоками будут вершины у. , у. , ..., у..
S ‘г ‘к
Затем из матрицы D удаляются все столбцы, кроме столбцов с
номерами z , z'2, ..., z^. Получится матрица Dg размерности п х к
(считаем, что данный орграф имеет п вершин). Теперь очевидно,
что (и, у) 6 а тогда и только, когда в матрице Dg совпадают
строки, соответствующие вершинам и и у.
П р и м е р 130 (см. [46]). Пусть функциональная схема
устройства без обратных связей элементов представлена орграфом
G, изображенным на рис. 103а
Непосредственно из графического представления получаем, что
стоками (выходами схемы) будут у5, у8 и у10. Из вершин yt и
у5 достижим только сток у5, из у2 достижимы все три стока, из
у, и у„—только у„, из у. ведут пути лишь в у, и у , вершины
294
v6, v7> v9 и v10 имеют единственный достижимый сток—v1Q.
Факторграф G/a показан на рис. 1036 (стоки подчеркнуты).
Полный бесконтурный граф определяется как такой реф-
лексивный бесконтурный граф, в котором добавление любой новой
дуги приводит к появлению контура.
Т е о р е м а 3.38. Для каждого натурального числа п
существует единственный с точностью до изоморфизма полный
п-вершинный бесконтурный граф.
Доказательство. Пусть G = (V, а)—полный
бесконтурный граф, и пусть у]5 у2, ..., у—некоторая правильная
нумерация его вершин. В силу полноты для любых у., v. при
i: < j в G существует дуга (v., v/) 6 а. Предположим, что
Н = ([/, /3)—другой полный бесконтурный граф с вершинами
«р u2, ..., u(( в произвольной правильной их нумерации. Тогда
соответствие и. ** у, 1 < i < п, очевидно, будет изоморфизмом:
оно взаимно однозначно отображает U на V и при этом для
любых z, j получаем равносильности (и., и/) (=. /3 «ь i < j о
о (у;., у.) 6 а. о
На рис. 104 приведены полные бесконтурные графы для
п = 2, 3, 4, 5 (петли опущены).
Рис. 104
Матрица смежности М полного бесконтурного графа G =
= (V, а) является полной верхней треугольной матрицей: все
элементы, стоящие выше главной диагонали и на ней, равны 1.
Понятно, что все степени такой матрицы совпадают с ней самой,
и, следовательно, М = D, откуда а = <5, т. е. отношение
достижимости совпадает с отношением смежности. Из этого факта
вытекает транзитивность отношения а: для любых трех вершин
и, у, w полного бесконтурного графа из (и, у) 6 а & (у, ty) 6 а
295
следует, что (u, w) G а. Диаграмма упорядоченного множества
(V, а) (вместо д пишем а) представляет собой цепь, поскольку
а—линейный порядок (для любых и, v G V имеем (и, у) G а
или (у, и) G а). Каждая вершина получает индивидуальный ранг,
равный количеству входящих в нее дуг (не считая петли).
Среди бесконтурных графов выделяют важный класс ориенти-
рованных деревьев. Орграф Т называется выходящим деревом,
если в нем существует корень (т. е. вершина, из которой
достижима любая другая вершина) и если его симметризация Т
является деревом. Выходящие деревья называют также растущими
или корневыми деревьями. Входящее дерево определяют как такой
орграф Т, что обратный для него орграф Т~1 представляет собой
выходящее дерево. Из приведенных определений следует, что
ориентированные деревья обоих типов являются связными оргра-
фами и не содержат никаких контуров. Следующая теорема
характеризует выходящие деревья при помощи степеней захода
вершин.
Т е о р е м а 3.39. Связный орграф Т тогда и только
тогда будет выходящим деревом, когда в нем существует точно
одна вершина с нулевой степенью захода, а у всех остальных
вершин <1 (у) = 1.
Доказательство. Пусть Т — (V, а)—выходя-
щее дерево и yQ—его корень. Так как Т—дерево, в нем существует
единственный неориентированный путь из yQ в любую другую
вершину у. Отсюда следует, что в Т из у0 в любую другую
вершину ведет единственный ориентированный путь и, значит,
d (у) > 1 для всех у # у(). Очевидно, что d~\v^) = 0, иначе
получился бы некоторый контур, проходящий через вершину yQ.
Далее, если d (у) > 2, то найдутся у , у G У такие, что
(Ур у) G а и (у2, у) G а. Тогда существует по крайней мере
два разных пути из yQ в у в орграфе Т. Это противоречие
показывает, что d~(v) < 1 для всех у # у(). Итак, й?-(у0) = О
и t/ (y) = 1 при у * у0.
С другой стороны, пусть у()—единственная вершина в связном
—> __________________
графе Т, для которой d (у0) = 0, а для всех остальных вершин
d (у) = 1. Пусть у—произвольная отличная от у0 вершина. В
силу связности, в неориентированном графе Т существует цепь
Р, соединяющая v0 с у. Пусть vQ, v2, ..., у*, у—вершины,
входящие в эту цепь, в порядке движения от у0 к у. Так как в
орграфе Т имеем d (yQ) = 0, то (yQ, у^ G а. Поскольку
296
d (Vj) = 1, получаем, что (v , у2) G а. Продолжая этот процесс
выяснения ориентации ребер указанного пути, заключаем, что
(у^, у) G а, и, следовательно, в Т цепь Р имеет однозначно
определенную ориентацию, превращающую ее в путь от yQ к v
->	—1>
в орграфе Т. Отсюда вытекает, что yQ—корень орграфа Т.
Допустим, что в графе Г имеется другой путь Р* от yQ к v
(т. е. отличный от Р). Предположим, что v.—первая из вершин
цепи Р, не входящая в состав Р*, a v.—первая после нее вершина
цепи Р, принадлежащая Р*. Тогда (v.) > 2, что невозможно.
Следовательно, в графе Т из вершины yQ в любую другую
вершину v ведет единственный путь. т. е. любые две вершины в
Т соединены единственной цепью. Следовательно, Т—дерево, о
Входящие деревья выделяются из связных орграфов тем, что
в них ^+(v0) = 0 для единственной вершины (ее тоже иногда
называют корнем) и d+(v) = 1 для всех остальных вершин.
Отсюда получается
Следствие 3.12. Связный орграф G тогда и только
тогда будет функциональным, когда в нем имеется контур,
удаление любой дуги которого превращает G в входящее дерево.
Доказательство. В функциональном графе
й?+(у) = 1 для любой вершины. Связный функциональный граф
представляет собой контур с навешенными на него входящими
деревьями. При удалении из контура дуги (у., v.) в новом орграфе
Т получаем d+(y.) = 0 и d+(y) = 1 при v v.. Следовательно,
Т—входящее дерево с корнем—стоком v..
Пусть в связном орграфе G выполняется условие доказываемого
предложения. Удалим в контуре, о котором идет речь, некоторую
ДУГУ (Уг г.).
Полученное входящее дерево обозначим через Т.
Предположим, что v. не является корнем-стоком в Т. Тогда в
Т имеем d (v.) = 1. Возвращаясь в G (т. е. присоединяя к Т
Дугу (v., у.)), получаем для у. степень исхода 2. Удалим теперь
—> 1 1 1
из G дугу рассматриваемого контура, имеющую конец в вершине
V.. Согласно условию, новый орграф будет входящим деревом.
Однако в нем вершина у имеет степень исхода 2, что невозможно.
Полученное противоречие показывает, что в дереве Т будет
d (у.) = 0. Но тогда d (у) = 1 для всех остальных вершин Т.
297
ООО
о.
0.
010
.1 10
011
Рис. 105
о
1
1
0
Отсюда получаем, что в орграфе G степень исхода каждой
вершины равна 1, т. е. G—функциональный граф, о
Выходящее дерево называется двоичным, если d+(v) < 2 для
любой его вершины v (обычно предполагается при этом наличие
хотя бы одной вершины и с d+(u) = 2).
Пример 131. Префиксным кодом в алфавите {0, 1}
называется множество слов в этом алфавите таких, что никакое
из них не является начальным отрезком другого. Пусть Т—
двоичное дерево. Каждую дугу помечаем символом 0 или 1,
применяя разные метки для двух дуг, исходящих из одной
вершины. Тогда с каждой концевой (висячей) вершиной будет
связано некоторое двоичное слово, образованное последователь-
ными метками дуг вдоль (единственного) пути от корня к данной
вершине. Очевидно, что множество
слов, соответствующих всем конце-
вым вершинам, образует префиксный
\1 код (см. рис. 105).
1 До сих пор мы рассматривали
/О Xjj направленные графы, не содержащие
по 111 контуров. Другой весьма распростра-
ненный в прикладных задачах тип
направленных графов—турниры. Тур-
ниром называется полный направлен-
ный граф, т. е. такой направленный граф, в котором добавление
любой новой дуги приводит к появлению контура длины 2.
Согласно этому определению в каждой вершине турнира имеется
петля. Петли никогда не изображают на рисунках и часто
игнорируют при формулировке предложений о турнирах.
П р и м е р 132. Всякий полный бесконтурный граф явля-
ется турниром. Поскольку отношение смежности в таких турнирах
транзитивно, они и называются транзитивными. На рис. 104
изображены транзитивные турниры с л = 2, 3, 4, 5 вершинами.
Пример 133. Пусть проводится однокруговой турнир с
л участниками в некоторой игре без ничьих (например, волейбол
или теннис). Сопоставим итоговой таблице этого соревнования
ориентированный граф Т, вершинами которого являются участники
игр и из вершины и в вершину v проводится дуга, если игрок
(или команда) и одержал победу над v. Присоединяя петли во
всех вершинах, получаем полный направленный л-вершинный
граф—турнир. (Есть некоторое неудобство в том, что в наиболее
распространенных системах обозначений и деревьям и турнирам
отводится один и тот же символ Т (tree, tournament). Впрочем,
свойства этих направленных графов столь различны, что можно
не опасаться смешения).
П р и м е р 134. Если в полном л-вершинном графе К
произвольным образом ориентировать каждое ребро (и в вершинах
добавить петли), получится л-вершинный турнир. Очевидно, что
298
любой турнир с п вершинами может быть получен из К
подходящей ориентацией ребер.
Очевидно, что каждый подграф турнира сам будет турниром.
В примере 112 из § 3.1 рассматривались пары неизоморфных
орграфов с одинаковым набором максимальных подграфов. Не-
трудно заметить, что все шесть орграфов, изображенных на рис.
76 (§ 3.1) являются турнирами. Таким образом, вообще говоря,
турнир не восстанавливается по списку его максимальных
подтурниров. Однако до настоящего времени, кроме трех пар
турниров из § 3.1 и трех пар шестивершинных турниров,
показанных на рис. 106, других примеров невосстановимых
турниров не найдено (см. [62]).
Рис. 106
Под автоморфизмами орграфа понимаются его изоморфизмы
на себя. Автоморфизмы орграфа G = (V, а) образуют группу
Aut G относительно умножения (суперпозиции) автоморфизмов и
их обращения как взаимно однозначных преобразований множе-
ства вершин V. Нейтральным элементом (единицей) этой группы
будет тождественное преобразование А множества V.
Т е о р е м а 3.40. Группа автоморфизмов любого турнира
имеет нечетный порядок (т. е. нечетное число элементов).
Доказательство. Пусть группа автоморфизмов
—►	—►	—►
Aut Т турнира Т имеет четный порядок. Тогда Т имеет нечетное
число нетождественных автоморфизмов. Поскольку при <р * ч[>
299
будет <р 1 # у *, а А 1 = А, получаем, что найдется <р G
€Е Aut Т такой, что <р * А и <р = <р , откуда <р = А. Пусть
и—произвольная вершина турнира Т и v = <р(и) # и. Тогда
р(у) = <р(<р(и)) = Д(и) = и. Так как Т—полный направленный
граф, то (u, v) G а, либо (у, и) G а. Пусть (u, v) G а. Тогда
(р(и), p(v)) G а, т. е. (у, и) G а, и, значит, в Т имеем
встречные дуги (и, у) и (у, и), что невозможно. Допущение о
четности порядка группы Aut Т привело к противоречию. □
Один из широко используемых способов ранжирования вершин
турнира—по степеням их исхода (именно так располагаются
участники в итоговой таблице однокругового турнира игры без
ничьих: по числу одержанных побед,—см. пример 133).
Т е о р е м а 3.41. Пусть vQ—одна из вершин турнира,
имеющих наибольшую степень исхода. Тогда расстояние от
vQ до любой другой вершины равно 1 или 2.
t Доказательство. Предположим, что в турнире
Т = (V, а) вершина v0 имеет наибольшую степень исхода, а
вершина v G V удалена от v0 на расстояние, большее 2. Тогда
(v0, v) £ а. В силу полноты, (v, vQ) G а.
Пусть (v0, u) G а. Если (и, у) 6 а, то расстояние от vQ до
v равно 2, что противоречит предположению. Значит, (u, v)$ а,
откуда (у, и) G а. Так как вершина и выбиралась произвольно,
то d+(v0) < J+(v). За счет дуги (у, vQ) получаем строгое
неравенство d+(y^ < d+(y), невозможное, поскольку, согласно
условию, v0 имеет наибольшую степень исхода. Таким образом,
в турнире Т нет вершин, удаленных от vQ на расстояние, боль-
шее 2. □
В основе другого способа ранжирования вершин турнира лежит
Т е о р е м а 3.42. В каждом турнире имеется гамильто-
нов путь.
Доказательство. Индукция по числу вершин п.
При и = 2 утверждение очевидно. Пусть оно справедливо для
всех турниров с к вершинами. Возьмем произвольный турнир Т
с к + 1 вершинами. В максимальном подтурнире, полученном из
Т удалением некоторой вершины v0, по предположению, сущест-
вует гамильтонов путь Р, проходящий через вершины
Up u2, ..., и^. Очевидно, что Р будет путем из и{ в и^ и в Т.
Если (у , и ) G а в Т, то vи. и. ...и, будет гамильтоновым путем
в Т. Если (и*, v0) 6 а, то гамильтоновым путем в Т будет
300
и{и2 ... ukv0. Предположим, что ни одна из двух этих возможностей
не имеет места. Тогда в Р существует первая в порядке
прохождения этого пути вершина us такая, что (yQ, us) 6 а. При
этом (yQ, u j) £ а и, в силу полноты, (us l, у0) G а, так что
и в этом случае имеем в Т гамильтонов путь: и{и2...
...и ,vnu ...и,, о
s-l 0 s к
Пусть Р—некоторый гамильтонов путь в турнире Т. Вершинам
турнира можно присваивать ранги в порядке их прохождения по
данному пути. Ранжирование при помощи фиксированного гамиль-
тонова пути и ранжирование по количеству исходящих дуг (без
петель) существенно различны: например, в транзитивном турнире
они дают линейные порядки, антиизоморфные друг другу (но и
в игровых турнирах набравший наибольшее число очков занимает
место с наименьшим номером—первое).
Заметим, что в транзитивном турнире существует только один
гамильтонов путь: вершины проходятся в порядке единственной
правильной их нумерации.
Для турниров наличие гамильтонова контура оказывается
эквивалентом сильной связности. Этот результат получается как
следствие более общего предложения. Именно, имеет место
Т е о р е м а 3.43. Пусть Т—сильно связный турнир с
п > 3 вершинами. Каково бы ни было натуральное число к,
3 < к < и, для всякой вершины турнира Т найдется контур
длины к, проходящий через эту вершину.
Доказательство. Пусть у(—произвольная вер-
шина сильно связного турнира Т, имеющего не менее трех вершин.
Так как у[—не сток, найдется вершина у2, в которую направлена
дуга из v . Ввиду сильной связности турнира Т существует путь
у,у, ...у,у из вершины у в вершину у. Так как дуга (v, v_)
выходит из v , а дуга (у^, Vj) входит в эту вершину, для
некоторого 2 < i < к — 1 получим (у^ у) 6 а и (v-+1, vt) S «•
Тогда вершины у^ у, у образуют контур длины 3 («треу-
гольник»). Далее действуем индукцией. Предположим, что
С: у^.....—контур длины к < п в сильно связном турнире
Т. Рассмотрим два случая.
1) Существует вершина у, не лежащая на контуре С и такая,
что (у., у) 6 а и (у, у,.) €Е а для некоторых вершин v„ у^„
принадлежащих С. Не нарушая общности, можно считать, что
i < j. Пусть у$—первая при прохождении контура С вершина
между у. и V., для которой (у, v$) 6 а. Тогда (vsl, v) G а, и
получаем контур у .Су _ уу Су, у. длины к + 1.
1	5* 1	5* К 1
301
2) Для любой вершины у, не лежащей на контуре С,
(у, v) G а для всех 1 < i < к или (у, у) G а для всех
1 < i < к. Вершины первого типа объединим в подмножество
Ур а второго—в V?	Так	как Т—сильно	связный турнир, то	У(
и V2 оба не пусты.	При	этом существуют вершины и( 6	и
и2 G V2 такие, что	(Up	u2) G а. Тогда	в Т получаем контур
Uj^VjCv^ jUj длины	к +	1. о
Следствие 3.13. Турнир является гамильтоновым
тогда и только тогда, когда он сильно связен, о
В соответствии с общим принципом, сформулированным в
§ 3.1, под конгруэнцией турнира следует понимать' такую
эквивалентность на множестве его вершин, что факторграф по
ней является турниром. Турнир—это полный направленный граф.
Очевидно, что свойство полноты сохраняется при любой фак-
торизации турнира, так что единственным ограничением является
исключение в факторграфе встречных дуг. Итак, конгруэнция
турнира Т = (V, а)—это такая эквивалентность в С V х V, что
никакие два различных 0-класса не имеют встречных дуг:
(«0> vQ) £ в & (uQ, у0) 6 а =>
=> (v u G 0(uo))(v у 6 0(УО))((Ц, у) 6 а).
Совокупность всех конгруэнций турнира Т обозначим через
Con Т. Разбиение множества вершин турнира Т = (V, а) назовем
правильным, если оно соответствует некоторой конгруэнции на
Т. Для подмножеств А, В С у введем обозначение
А -» В .<» (у и 6 А, у G B)((u, v) €Е а).
Получаем, что разбиение л = {У(, V2, ..., V^J множества вершин
V турнира Т будет правильным тогда и только тогда, когда для
любых 1 < i < / < к либо V. -» V., либо V. -» V..
i J	J i
Т е о р е м а 3.44. Конгруэнции турнира, упорядоченные
теоретико-множественным включением, образуют решетку.
Доказательство. Пусть Т = (V, а)—произ-
вольный турнир. Очевидно, что универсальная эквивалентность
V х V является конгруэнцией турнира Т. Покажем, что если 0
и в2—конгруэнции на Т, то конгруэнцией будет и в =
= 0j Г1 &2- Допустим, что (uQ, vQ) £ в и (uQ, vQ) 6 а. Тогда
(%- v0) £ в-j или (%- Vq) £ 62. Пусть (u0, v0) £ 0Г Так как
конгруэнция, то в^и^ - 0^). Но 0(uQ) С в^и^ и
0(vQ) £ 0j(vo), откуда получаем, что 0(uQ) -» 0(vQ).
302
Согласно теореме 1.34 из § 1.4, упорядоченное множество
(Con Т, С)—решетка, о
Турнир Т = (V, а) называется простым, если решетка
Con Т двухэлементна, т. е. если Т не содержит собственных
нетождественных конгруэнций. Турнир с п вершинами будет
простым тогда и только тогда, когда он не имеет правильных
разбиений с числом блоков 2 < к < п—1. Это означает, что
каково бы ни было непустое подмножество U С V, найдется
вершина v G V — U такая, что (u, v) G а и (v, u*) G а для
некоторых и, и 6 U. Из двух турниров с тремя вершинами
простым будет «треугольник» (рис. 76а из § 3.1, левый турнир),
простых турниров с четырьмя вершинами нет. Из двух пятивер-
шинных турниров, представленных на рис. 76<з, турнир G будет
простым, а у турнира Н есть собственная нетождественная
конгруэнция, соответствующая разбиению {1}, {2, 3, 4}, {5} (что
еще раз подтверждает неизоморфность этих турниров).
В примере 45 из § 2.2 произвольному турниру Т = (V, а)
был сопоставлен группоид А(Т) = (V, •), где uv = и, если
(U, У) 6 а, и uv = у, если (у, и) 6 а. Очевидно, что этот
2
группоид идемпотентен и коммутативен, т.е. и = и и uv = vu
для любых и, v 6 V.
Т е о р е м а 3.45. Умножение в группоиде А(Т~) ассоциа-
тивно тогда и только тогда, когда Т—транзитивный турнир.
Доказательство. Необходимость.
Пусть .4(7”)—полугруппа, но Т не является транзитивным
турниром. Тогда в Т существует некоторый контур у(у2 ... v^Vj.
В группоиде А(Т) рассмотрим произведение элементов у,
1 < i < к, в порядке прохождения контура. Имеем v^^...
...V, ,У, = (у,У_...У, ,)у, = у, у, = у, и у, уп ... у, ,у. =
к-1 к 4 2	к-1' к 1 к к	12	к-1 к
= v1(v2 ... ^ [Уд) = У(У2 = у(,—противоречие. Значит, Т—бес-
контурный, т. е. транзитивный турнир.
Достаточность. Пусть Т—транзитивный турнир
и VjV2, ..., v(—правильная нумерация его вершин. Покажем, что
группоид А(Т) изоморфен полурешетке ({1, 2, ..., п}, min),
элементами которой являются первые п натуральных чисел, а
операция min выбирает из двух натуральных чисел меньшее.
Положим ^>(v.) = i для любого i = 1, ..., п. Это соответствие
взаимно однозначно и p(v.v.) =	= т>п (Л j) =
= min (р(у.), /’(гр) (т. е. р сохраняет бинарную операцию).
303
Отображение <р—изоморфизм, и следовательно, А (Т)—полурешетка
(коммутативная идемпотентная полугруппа). □
Теорема 3.45 позволяет свести изучение многих конструкций
для турниров к чисто алгебраическим понятиям. Например:
Т е о р е м а 3.46. Эквивалентность в С v х V тогда и
только тогда будет конгруэнцией турнира Т = (V, а), когда
она является конгруэнцией группоида А(Т).
Доказательство. Необходимость.
Пусть в G Con Т и (и, /), (v, w) G в, (и, v) £ в. Нужно пока-
зать, что (uv, tw) G в. Предположим, что 0(и) -* 0(v) (противо-
положный случай вполне аналогичен). Тогда (u, v) G а и
(Z, w) G а, откуда uv = и и tw = t, и, значит, (uv, tw) G а.
Следовательно, в G Con А (Т).
Достаточность. Пусть в G Con А(Т), (и, v) £ в,
t G 0(u), w G 0(v). Тогда (uv, tw) G а. Если (u, v) G а, то
uv = и. Произведение tw равно t или w, но так как tw G f?(u),
то tw =* t. Следовательно, 0(u) -» 0(v), и, значит, в G Con Т. □
В заключение главы, посвященной графам, рассмотрим один
полезный результат [81] о диагностировании дискретных систем.
Пусть S—некоторая система, снабженная структурой самодиаг-
ностирования. Как описано в примере 126, тесту (набору проверок)
сопоставляется диагностический орграф D, вершины которого
соответствуют элементам системы S, а дуги—проверкам, которым
одни элементы подвергаются со стороны других элементов. Если
элемент v. исправен, то результат проверки л , которой он
подвергает элемент v. в данном тесте, считается равным 0 или 1
в зависимости от того, исправен или неисправен элемент v.. В
случае, когда v. неисправен, в раезличных моделях диаг-
ностирования результаты проверок л
интерпретируются по-раз-
ному. В отличие от модели, с которой мы имели дело в примере
126, будем считать, что л.. = 1, если элемент v. исправен, и
л.. G {0, 1}, если V. неисправен.
Система 2 называется t-диагностируемой, если по любому
синдрому, связанному с тестом D, можно однозначно определить
состояние каждого ее элемента при условии, что число отказов
в Е не превосходит t. Пусть л обозначает некоторое включение
схемы самодиагностирования системы 2 в соответствии с тестом
D. Тогда каждая проверка, входящая в D, примет значение О
или 1 по указанным выше правилам и получится синдром D^.
Подмножество F С V (через V обозначается множество вершин
диагностического графа D и сети £>л, т. е. множество элементов
304
системы 2) называется л-допустимым множеством отказов, если
синдром не противоречит гипотезе о том, что неисправными
элментами системы £ являются в точности элементы, входящие
в F. Очевидно, что система 2 будет /-диагностируемой тогда и
только тогда, когда для любого возможного синдрома
существует не более одного л-допустимого множества отказов.
Пусть D = (V, а) будет симметризация диагностического
графа D данной системы 2.
Т е о р е м а 3.47. Система 2 тогда и только тогда
t-диагностируема, когда для любого непустого подмножества
U С V имеет место неравенство lce(tT) — С\ +	1^1 — t.
Доказательство. Необходимость.
Пусть 2—система со структурой самодиагностирования D, в
которой существует непустое подмножество U Q V такое, что
la(lf) — Cl + I Cl > t. Покажем, что 2 не является /-диаг-
ностируемой. Именно, установим, что для некоторого синдрома
существует не менее двух л-допустимых множеств отказов.
Разобьем С на два подмножества С^ и С^, различающиеся по
количеству элементов не более чем на единицу. Пусть I Cl I >
> IС^ I. Положим F. = CXJ (а(С) — U), i = 1, 2. Предпо-
ложим, что а(Г/) — С состоит только из неисправных элементов,
а V — (С U а(С))—только из исправных. Полоцким л.. = 0 во
всех случаях, кроме следующих: 1) один из элементов v., v.
входит в С{, а другой—в С^, 2) один из элементов у., v. входит
в а(С) — С, а другой—в дополнение этого подмножества (рис.
107). Заметим, что в D вершины, входящие в
вершинами из V — (С U a(t/)), так что в D
проверочные связи отсутствуют.
На рис. 107 приведена схема синдрома,
(заштриховано) распознается как допустимое множество отказов.
Нетрудно заметить, что F{ и F^ можно интерпретировать как
л-допустимые множества отказов при построенном синдроме D^.
Правда, еще нужно убедиться в том, что каждое из этих множеств
содержит не более чем / элементов (нам известно, что S допускает
не более / отказов).
U, не смежны с
соответствующие
при котором
Если I CI
IF.I = I U.\ +
i	I
11 А.М.Богомолов,
четно, то IС^ I = IС2 I = IС I, откуда
la(t/) - С! = |lC7l + la(t/) - С\ < / (по
В.Н.Салий	305
Рис. 107
условию). Если же 1[71 нечетно, то, так как 1«(Г7) — UI—целое
число, получаем, что 1а([/) — 1/1 + I U\ + < t. Далее,
I77J = |ll/l + откуда IFJ = | IUI + | + ।«(^0 “
— U\ < t. Тем более, IF2I < t.
Достаточность. Пусть выполнено условие теоре-
мы, но 2 не является Z-диагностируемой системой. Значит,
существуют два различных л-допустимых множества отказов F
и хотя бы при одном синдроме D^. При этом IFJ < t,
i = 1, 2. По условию, 1«(Г7) — UI + у I [71 > t для любого
непустого подмножества U С V. В частности, при U = V
получаем, что I> 2/, т. е. I VI > It + 1. Следовательно,
дополнение F U F^ не пусто. Положим U = (Fj U F2) -
- (Fj П F2). В диагностическом графе D не существует проверок
между элементами подмножеств U и F U F2, поскольку наличие
любой такой проверки давало бы в синдроме результат,
противоречащий либо л-допустимости F , либо л-допустимости
F2. Значит, a(lf) - U С FJ П F^ и \a(U) - [71 < IF{ Cl F2I.
Так как I [71 + 2IFj П F2I = IFJ + IF2I < 2t, то la([/) - U I +
+ I U I < I Fj П F2 I + I [71 < t, что невозможно. Получен-
ное противоречие показывает, что при любом синдроме
существует не более чем одно множество л-допустимых отказов.
Система 2 является г-диагностируемой. о
Заметим, что если система 2 имеет п элементов, то из условия
теоремы 3.47, как уже отмечалось в доказательстве, вытекает
необходимое условие г-диагностируемости п > 2t + 1,—неравен-
ство, которое другим путем было получено и для модели,
рассматривавшейся в примере 126.
ГЛАВА 4
АВТОМАТЫ
§ 4.1. Гомоморфизмы и конгруэнции
В предыдущих главах уже были введены основные конструкции
теории автоматов и исследованы различные их свойства. Здесь
мы подробнее рассмотрим некоторые отношения между состо-
яниями автоматов. В основном это будет касаться полуавтоматов,
так как внешние реакции автомата, описываемые функцией
выходов, налагают дополнительные ограничения и требуют
дальнейшего усложнения методов (см. § 4.2).
Пусть А = (S, X, <$л) и В = (Т, X, дв)—два полуавтомата
с одним и тем же входным алфавитом. Напомним, что
отображение <р: S -» Т называется гомоморфизмом полуавтомата
А в полуавтомат В, если p(<5^(s, х)) =	х) для любых
s 6 S и х 6 X. Взаимно однозначные сюръективные гомо-
морфизмы называются изоморфизмами. Полуавтомат В, явля-
ющийся гомоморфным образом полуавтомата А, представляет
собой как бы огрубленную модель этого последнего: сохраняя
основные особенности функционирования полуавтомата А (выра-
жаемые функцией переходов <5^), он теряет часть информации о
состояниях, не различая некоторые из них. Нахождение гомомор-
фных образов данного полуавтомата и, в частности, проверка
изоморфности двух полуавтоматов являются практически важными
и в то же время весьма сложными задачами.
Пусть А = (S, X, <5)—полуавтомат. Как уже делалось в § 2.4,
сопоставим ему булеву матрицу А, строки и столбцы которой
помечены элементами множества состояний S = {s,, s„, .... s },
1 г 2’	’ п1
и при этом := {х 6 X I d(s., х) = s^.}. Таким образом,
элементами матрицы А (будем называть ее матрицей переходов
полуавтомата А) будут подмножества множества X (т. е. элементы
булевой алгебры (Р(Х), U, П, “, 0, X)) и а состоит в точности
из таких входных сигналов, которые состояние s. переводят в
11*	307
состояние Sj. Для удобства обозначений вместо 0 будем писать
О, а вместо X использовать символ 1.
Пример 135. Пусть X = {хр х2} и полуавтоматы А и
В заданы следующими таблицами переходов:
	*1	X2	ЛВ	*1	X2
S1 S2 S3 *4	S3	S4	'1 'l	*4	f2 S4	S1	f3 S2	S1	f4	f2	f3 f3 f4	fl fl	f3
Булева алгебра Р(Х) состоит из четырех элементов, для
которых в целях удобства примем следующие обозначения:
О := 0, а := {Xj}, Д := {х2}, 1 := X. Тогда матрицы переходов
полуавтоматов А и В предстанут в виде
A =		0 0 a 0 a 0 0 0 0 0 0a 0 a 0 0		bo II		а 'Со'йь о о о O ft "Со О ft "Со о ft с о	
Пусть <р—гомоморфизм полуавтомата А в полуавтомат В. Если
А имеет т состояний, а В имеет п состояний, то <р можно
представить в виде т X «-матрицы Ф с элементами из двоичной
булевой алгебры, полагая f.. = 1, если y>(s.) = t., и <р.. = 0 в
противном случае. Поскольку двоичную булеву алгебру можно
вложить в любую булеву алгебру, можно считать, что Ф так же,
как и матрицы переходов А и В для полуавтоматов А и В,
является матрицей над булевой алгеброй Р(Х). Следующая теорема
лежит в основе матричного метода нахождения всех гомо-
морфизмов одного полуавтомата в другой, а также служит для
проверки изоморфности полуавтоматов (см. [50, 51]).
Т е о р е м а 4.1. Пусть А = (S, X, <$л) и В = (7, X, дв)—
два сравнимых полуавтомата. Отображение <р: S -* Т тогда и
только тогда будет гомоморфизмом, когда АФ = ФВ, где
А, В—матрицы переходов полуавтоматов А и В, а Ф—матрица,
представляющая отображение <р.
Доказательство. Необходимость.
Пусть <р: S -* Т—гомоморфизм полуавтомата А в полуавтомат В.
Тогда
(ЛФ)/Ч = U (a.. A <p.k) = U {a.. I <pjk = 1} = U {a.. I = rj =}
= {х S X I (Э	х) = Sj & <p(Sj) = tk)} =
308
= {х 6 X I <p(flA(s., x)) = tk} = {x 6 X I <5B(p(s.), x) = tk} =
= {x 6 X I (3/)(^(S.) = tf & dB(tr x) = tk)} =
- и {blt I = 9 - U v>lt I F(, - I) - и n у -
откуда АФ = ФВ.
Достаточность. Пусть АФ = ФВ, a s. 6 S,
tk 6 Т—произвольные состояния полуавтоматов А и В. Используя
предыдущие выкладки, получаем, что {х 6 Х\ <p(dA(s., х)) =
=	= {х G Х\ dB(<p(s.), х) = tk}, и, следовательно,
(V X 6 X)(v S. 6 S)(v tk 6 T)(<p(dA(s., x)) = tko
° дв(<Р(^), x) = rp,
t. e. <p(6A(s., x)) = <5B(p(s.), x) для любых s. 6 S, x 6 X. Это
и означает, что <р—гомоморфизм полуавтомата А в полуавтомат
В. =
Таким образом, чтобы найти все гомоморфизмы полуавтомата
А в полуавтомат В, нужно решить систему булевых уравнений,
возникающую при приравнивании соответствующих элементов
булевых матриц АФ и ФВ. При этом в каждой строке матрицы
неизвестных Ф один элемент равен единице булевой алгебры Р(.Х),
а все остальные—ее нулю. Если Ф представляет изоморфизм, то
и в каждом столбце этой матрицы точно один элемент равен 1
(а все остальные равны 0).
Возвращаясь к примеру 135, положим
и,	U.	и,	и.
1	2	3	4
V.	V	V	V
ф =	1	2	3	4
И>,	И>	W.	W.
1	2	3	4
Z1	z2	z3	z4
Для удобства будем объединение в булевой алгебре Р(Х)
обозначать знаком +, а пересечение—знаком • (как в двоичной
булевой алгебре). Тогда, приравнивая соответствующие элементы
первых строк матриц АФ и ФВ, получаем:
aw + flz =	+	flu. + au.,	aw. + flz.	=	au,,
aw + flz - flu	+	au. + flu.,	aw. + flz.	=	au..
ooi	Z'4	4'4	□
Условия, налагаемые на элементы матрицы Ф, получаются
приравниванием коэффициентов при одинаковых атомах булевой
алгебры Р(Х) в левой и правой части каждого уравнения. В
309
нашем случае имеем: и» = и., z, = и. + и,, и» = и,,
J	1	4	1	2	3	2	1
z_	= 0, w.	= и-,, Z,	= и,	+ и., w.	= и-, z.	= О.
2	3	2	3	1	4	4	3	4
Приравниваем соответствующие элементы вторых строк матриц
АФ и ФВ и получаем новые соотношения = Ир Zj =
= V2 + V3’ V1 = U2’ V2 = U3’ Z3 = V1 + V4> V3 = W4‘
Сравнивая третьи строки, имеем и2 = 0,	= 0.
Наконец, сравнение четвертых строк матриц АФ и ФВ новых
связей между элементами матрицы Ф не дает. После проделанных
вычислений матрица Ф приобретает следующий вид:
“1	0	“з	°
А	_	0	“з	0	“1
Ф	"	0	0	и3	•
“з	0	“1	О
Придавая параметрам и значения 1 и 0 (но так, чтобы
в каждой строчке матрицы Ф была точно одна единица), находим
два гомоморфизма полуавтомата А в полуавтомат В. Ими будут
Sj >—»/р s2 »(4, s3 •—» t2, s4 •—» t3 и <p2t Sj •—» ty «2 l—> *2’
s3 •—» ty s4 •—» /р Оба они—изоморфизмы.
В основе другого метода распознавания изоморфности полуав-
томатов лежит один способ проверки изоморфизма ориентирован-
ных (входящих) деревьев (см. [21, 37, 45]). Пусть А =
= (S, X, <5)—полуавтомат. Фиксируя входной сигнал х G X,
получим автономный полуавтомат А* = (3, д*), где д*. S -» 3,
s *—» <5($, х). Граф переходов автономного полуавтомата распада-
ется в общем случае на компоненты связности, каждая из которых
представляет собой контур с навешенными на него входящими
деревьями (контур может вырождаться в петлю).
Возьмем автономный полуавтомат А = (3, д), который имеет
только одно циклическое состояние sQ. Этот полуавтомат будет
связным и, согласно теореме 3.34 из § 3.3, граф переходов
G(A) тоже связен. Тогда G(A) представляет собой входящее дерево
с петлей в корне sQ. Пусть s G 3—произвольное состояние
полуавтомата А. Построим автономный полуавтомат А$ следующим
образом. Множество состояний в А$ образуют все те и только те
состояния полуавтомата А, из которых в А достижимо s (сюда
входит и само s). Функция переходов в А$ совпадает с д на всех
состояниях нового полуавтомата, кроме одного случая: считается,
что состояние s она переводит в себя. Ясно, что G(Ap представляет
собой поддерево дерева G(A), входящее в корень s, с петлей в s.
ЗЮ
Характеристикой
состояния
s G S в полуавтомате А ука-
занного вида назовем число
g(s) :=
l<5-1(s)l - 1
l<5-1(s)l
при
при
S = s0,
s # So.
Характеристика самого полуавтомата А = (5, <5) получает-
ся выписыванием характеристик всех состояний полуавтомата А
после некоторого специального линейного упорядочения множества
S. Характеристика %(А) определяется индуктивно по высоте Л
дерева G(A) (т, е. по наибольшему из расстояний от его вершин
до корня sQ). Для Л - 0 полагаем /(А) = gts^.
Предположим, что определена характеристика полуавтомата
указанного вида для случая Л = к. Пусть дерево G(A) имеет
высоту к + 1. Для каждого s G <5-1(s0), s # sQ, имеем харак-
теристику x(As)- Произведем лексикографическое упорядочение (по
убыванию) последовательностей %(А$), s 6 <5-1(s0) — {sQ} (если
какие-то из них совпадают, порядок между ними фиксируется
произвольно). Соответствующим образом расположим состояния
из <5-1(s0) - {sQ} в ряд s. , s. , ..., s. . Пусть 2 < I < к + 1.
1	2	п
Состояния, находящиеся в G(A) на расстоянии I от корня sQ,
упорядочим таким образом, чтобы сначала были выписаны
состояния, входящие в ), затем в ), и т. д. Внутри
группы состояний, входящих в одно из этих деревьев С(Л^),
сохраним тот порядок, который был
установлен между ними при получении
характеристики x(As)- Таким образом
множество 5 оказывается линейно упо-
рядоченным (первым элементом счита-
ем s0). Выписывая последовательно
характеристики всех его элементов,
получаем %(А).
П ример 136. Найдем харак-
теристику полуавтомата А, представ-
ленного графом переходов на рис. 108. Состояния полуавтомата
А распределяются по расстояниям от корня следующим образом:
S7 Sg S10 S3
Рис. 108
311
Я0 Ц1’	(S5’ S1J’ ^2	(S2’ S4’ s6’ S8’ S12^’ *3
= {s3, s7, s9, s10). Выпишем характеристики состояний:
x(s) 200021030030
Положим A. := As, 1 < i < 12. По определению, z(^3) =
i
= X(^7) = X(^9) = X(^10) — 0, поэтому состояния на уровне
I = 3 упорядочиваются произвольно. Далее, при I = 2 получаем,
Х(Л2) = 0,	х(Л4) = 0, Z(A6) = (1, 0), х(Л8) = (3, 0, 0, 0),
Х(Л12) = 0. В соответствии с лексикографическим порядком этих
характеристик получаем следующее расположение состояний
уровня 2: sa, s,, s~, s., s,~. В связи с этим Я = {s_, sn, s,„, s,}.
При I = 1 имеем: %(A5) = (2, 3, 0, 0, 0, 0) (это соответствует
порядку состояний s5, s8, s12, s7, s9, s10), хИи) = (3, 1, 0, 0, 0)
(в порядке s , s,, s9, s., sA. Отсюда H = {s , s }, в связи с
чем получаем следующее упорядочение множества состояний
полуавтомата: s,; s,,, s_; s., s_, s., so, s’ s,, s_, sn, s,„. Ha-
*	1	11	5	0 Z 4 6 1Z 3 7	9	10
конец, выписываем характеристику /(A) = (2, 3, 2, 1, 0, 0,
3, 0, 0, 0, 0, 0).
Пусть А—связный автономный полуавтомат с п циклическими
состояниями, п > 1. Некоторые из этих состояний являются
корнями входящих деревьев в орграфе G(A). Если s—такое
состояние, то через х(А$) обозначим характеристику автономного
полуавтомата, графом переходов которого является дерево, вхо-
дящее в s (в вершине s петля). Лексикографически упорядочим
характеристики х(А$), где s пробегает все циклические состояния
полуавтомата А. При этом множество всех циклических состояний
разобьется на классы по признаку равенства характеристик. Все
состояния s с минимальной характеристикой %(As) получают метку
1, состояния s со второй в лексикографическом порядке харак-
теристикой /(Ар—метку 2, и т. д. Выписав метки состояний в
некотором обходе контура, находим n-мерный вектор пометок.
Циклической перестановкой его компонент отыскиваем лексиког-
рафически минимальный вариант. Пусть ему соответствует
нумерация циклических состояний s , s2, ..., s)(. Характеристикой
связного автономного полуавтомата А назовем последователь-
ность %(А) := п, /(А ), х(.А ),..., %(А ). Если для связного
1	2	п
автономного полуавтомата В будет /(J3) = т, x(&t)y x(BtY---
), то будем считать, что /(А) < /(В), если п < т, или
m •
если п = т, ио последовательность /(А ), /(А ),...,/(А ) лек-
1	2	п
сикографически предшествует последовательности %(В(),
X(Btx(Bt ).
2	m
Характеристикой произвольного автономного полуавтомата
А называется упорядоченная указанным способом последователь-
ность /(А) характеристик всех его компонент связности.
Т е о р е м а 4.2. Два автономных полуавтомата изомор-
фны тогда и только тогда, когда совпадают их характеристики.
Доказательство. Необходимость очевидна, пос-
кальку если А а В, то изоморфны орграфы G(A) и G(B). Тогда
оии допускают одинаковое изображение, по которому и строится
характеристика.
Достаточность. Пусть для автономных полуав-
томатов А = (S, <$л) и В = (Т, дв) будет /(А) = /(В). При
построении характеристики множество состояний полуавтомата
линейно упорядочивается. Каждому состоянию s G S сопоставим
состояние <p(s) G Т, имеющее тот же иомер в смысле указанного
линейного порядка. Очевидно, что <р—взаимно одиозиачиое
соответствие. Покажем, что
Р(<5Л(*)) =
для любого s G S.
Из равенства /(А) = /(В) следует, что А и В имеют
одинаковое число компонент связности и, если t = <p(s), то s и
t входят в компоненты связности, имеющие одинаковое число
циклических элементов. Пусть s принадлежит компоненте связ-
ности, имеющей характеристику п, /(А ), /(А ),...,/(А ), a t
1	2	\
входит в компоненту связности полуавтомата В, имеющую
характеристику п, х(В , Bf , ..., В ). По определению отображения
1	2	п
<р, состояния s и t принадлежат полуавтоматам А$ п В
\ < i < п, причем /(АД = /(ВД
i	i
Если s = s и f = t., то s и t—циклические состояния в
соответствующих компонентах. Согласно определению харак-
теристики связного автономного полуавтомата, контурами в А и
В будут s. •—» s.,,	»s •—‘ s, •—»...•—‘ s., I.	...
J J l l+l	n 1	i I	i + 1
•••	zi ••• fi’ откуда р(<5л(*)) = р(<5л(«)) =
= Р(*/+1) = ti+l =	= ^(y>(s.)).
313
Пусть s—вершина дерева G(As), отличная от корня s.. Тогда
и t—вершина в	отличная от корня t.. Характеристики
i
полуавтоматов и Bf совпадают, и теперь достаточно показать,
что р(<5Л (s)) = дв	где p(s) = t. В деревьях G(A^) и
S.	'
G(Bf) вершины s и t находятся на одинаковом расстоянии I от
i
соответствующих корней. Пусть и., п. ,	п.—фрагмент харак-
*1	2	к
теристики Z(^s) = относящийся к уровню I - 1. Тогда в
I	i
следующем по порядку отрезке последовательности z(^s) сначала
выписываются характеристики вершин, из которых в С(А^) идут
дуги в вершину s. , затем характеристики вершин, относящихся
1
в этом смысле к s. , и т. д. Аналогично обстоит дело и с
распределением характеристик вершин уровня I в Пусть s
входит в группу, ассоциированную с вершиной s уровня I - 1.
Тогда дд
нарушится
т
= s. . Если окажется, что <5_ # Л , то
i	Bl
т	t т
i
одно из равенств d+(s.) = d+(t.),
S	i
, d+(s.) = d+(t.), что невозможно,
<P$A О)) = <P(<si ) =
s	mm
неизбежно
d+(s.) =
2
так как
к
Итак,
= дв &
= d+(t.)
2
=	Этим и заканчивается доказательство теоремы, о
t
i
Метод характеристик годится для проверки изоморфности не
только функциональных орграфов (именно они являются графами
переходов автономных полуавтоматов), но и контрафункциональ-
ных орграфов (ясно, что если (7	G^, то G[ н G2 ). В общем
случае проблема изоморфизма графов сводится к проблеме
изоморфизма полуавтоматов с двумя входными сигналами. Дела-
ется это так. Пусть G = (V, а)—произвольный орграф. Рас-
смотрим полуавтомат A(G) — (V U а, {0, 1}, <5), где
А/ nx Is, если s 6 У,
o(s, 0) := J	_
v	| и, если s = (и, v) 6 а;
314
n •— Is’ если s £ К
'S’	' у, если s = (и, v) 6 a.
Очевидно, что G^ st G2 тогда и только тогда, когда A(Gj) s
St A(G2). □
Решетка конгруэнций Con А полуавтомата A = (S, X, d),
является одним из основных его производных объектов. Напомним,
что эквивалентность 0 на множестве состояний S полуавтомата
А называется конгруэнцией, если она устойчива относительно
функции переходов д в том смысле, что
(Sj, s2) 6 в => (V х 6 X)((d(Sp х), d(s2, x)) 6 0)
ДЛЯ любых Sp S2 6 S.
В основе всех известных алгоритмов построения решетки
конгруэнций полуавтоматов лежит следующая
Л е м м а 4.1. Всякий разложимый элемент конечной ре-
шетки L может быть представлен в виде объединения двух
элементов одинаковой высоты.
Доказательство. Пусть в конечной решетке L
имеем а = а{ V а2> где at # а # а2, и h(at) * h(a2)- В
интервалах [ар а) и [а2, а) выберем по одному максимальному
элементу—соответственно и Ь2 (здесь мы ссылаемся на теорему
1.30 из § 1.4). Если A(3j) = Л(й2), то все в порядке, так как,
конечно, V Ь2 = а и st a st Ь^. Пусть h(b{) < h(b2). В
интервале [0, Ь2) возьмем любой элемент с такой, что Л(с) =
= Н(ЬХ). Тогда а = b{ V b2 > V с > Ь{. Так как а является
верхним соседом для b , то v с = а. □
Любая конгруэнция 0 полуавтомата А является объединением
(в решетке Con А) подходящего набора главных конгруэнций:
0 = V {0(sr s2) I (sr s2) 6 0},
где 0(Sp s2) обозначает наименьшую из конгруэнций, содержащих
пару (Sp s2).
Не все главные конгруэнции будут неразложимыми элементами
решетки Con А. Например, в шестиэлементном цикле
1>—‘ 2 * 3 >—»4>—» 5 » 6 >—» 1 имеем: 0(1, 2) = {1, 2, 3,
4, 5, 6}, 0(1, 3) = {1, 3, 5}, {2, 4, 6}, 0(1, 4) = {1, 4}, {2,
5}, {3, 6} (мы отождествляем конгруэнции и соответствующие им
разбиения). При этом получаем: 0(1, 2) = 0(1, 3) V 0(1, 4).
С другой стороны, всякая неразложимая конгруэнция, как
нетрудно заметить, будет главной. Полагая
315
e*(Sp S2) :=
'0(s , s2), если 0(Sp s2) неразложима,
Д в противном случае,
получаем, что для любой в 6 Con А имеет место представление
в = V {e*(s , s2) I (sp s2) G 0}. Оно и лежит в основе алгоритма
построения решетки конгруэнций полуавтомата [70, 51]].
Шаг 1. На уровень А = 0 записать элементы множества
М(0) = {А}.
Шаг 2. Найти множество 0(0) всех главных конгруэнций
полуавтомата А = (S, X, б).
Шаг 3. Положить А := 1.
Шаг 4. Построить множество
0, если M(h — 1) одноэлементно;
/(Л) = попарное объединение элементов из M(h — 1)
в противном случае.
Шаг 5. Построить множество 0(A) = (0(А — 1) —
- M(h - 1)) U /(А).
Шаг 6. Выделить в 0(A) множество М(А) минимальных
элементов.
Шаг 7. Если Л/(А) пусто, конец. Иначе записать элементы
множества M(h) на уровень А и перейти к шагу 4, полагая
А А + 1.
После выполнения алгоритма все конгруэнции полуавтомата
(их удобно представлять в виде разбиений) распределятся в
соответствии с их высотой в решетке (Con А, С). Двигаясь снизу
вверх, соединяем каждый элемент этой решетки с его нижними
соседями прямолинейным отрезком, завершая таким образом
построение ее диаграммы.
Пример 137 (см. [76]). Пусть полуавтомат А задан
таблицей переходов
<5
1
2
3
4
5
6
7
8
3	7
4	8
1	6
2	5
2	4
1	3
4	4
3	3
316
В алгоритме построения решетки Con А используется множе-
ство главных конгруэнций полуавтомата А. Всего мы имеем
= 28 пар различных состояний. Вычислим конгруэнцию
в1 2 = 0(1, 2). Так как (1, 2) G 2, то пары, получаемые из
(1, 2) действием входных сигналов, тоже входят в в1 2> Так что
(3, 4) = (5(1, X!), 5(2, X!)) е 012, (7,8) = (<5(l,x2),’d(2,x2))G
G в1 2. Далее, в 0} 2 получаем новые пары (5, 6) и (3, 4). Больше
отождествлений не будет, так что 0j 2 = {1> 2}, {3, 4}, {5, 6},
{7, 8}.
Вычисляем 0} 3< Сигнал х} множество {1, 3} переводит в себя,
а х2—в {6, 7}. Далее работаем с {6, 7}. Под действием Xj это
подмножество переходит в {1, 4}, а под действием х2—в {3, 4}.
Поскольку блоки конгруэнции не должны перекрываться, состо-
яния 1, 3 и 4 оказываются в одном блоке. Формируем
подмножество {1, 3, 4}, вычеркивая первоначальное {1, 3}. Те-
перь {1, 3, 4} перейдет под действием в {1, 2, 3}, а под
действием х2—в {5, 6, 7}. Формируем подмножества {1, 2, 3, 4}
и {5, 6, 7}, вычеркивая {1, 3, 4} и {6, 7}, и действуем входными
сигналами на новые подмножества. Из {1, 2, 3, 4} получится
{5, 6, 7, 8} (сигнал х2). Вычеркиваем {5, 6, 7} и видим, что
подмножество {5, 6, 7, 8} вместе с {1, 2, 3, 4} образует ус-
тойчивое разбиение: 3 построена. Все описанные этапы можно
проследить по следующей рабочей таблице:
Этапы	1	2	3	4	5	6	7	8	Вычеркнутые строки
1 2 3 4 5 6 7 8 9	X	X X X X	X X X X	XX XXX XXX X X X X X X X X	1, 3, 4 2 5, 6 7
Дальнейшие вычисления главных конгруэнций проводятся по
указанной схеме, причем чем дальше мы движемся, тем быстрее
строятся таблицы, поскольку можно использовать уже полученные
результаты. Приведем без комментариев таблицы, вычисляющие
015 = 0(1, 5) и 035 = 0(3, 5):
317
	1 2 3 4 5 6 7 8	
1 2 3 4 5 6 7 8 9	X	X X X X	X X	X X	X X	XXX X	X X	X X X	X	X хххххххх	1, 3, 4 2, 6. 7 5, 8
	1 2 3 4 5 6 7 8	
1 2 3 4 5 6	X	X X X X	X X X X X X X X X	1, 3, 4
В результате получаем, что полуавтомат А имеет шесть
различных главных конгруэнций, именно
= {1,2}, {3,4}, {5,6}, {7,8} (= 012 = 03>4 = 056 = 078),
в2 = {1, 2, 3, 4}, {5, 6, 7, 8}
(= 01,3 = 01,4 = ®2,3 = 02,4 = в5Л = ®5,8 = 06,7 ~ д6.8^’
63 = {1, 2, 3, 4, 5, 6, 7, 8} = 5x5
(=	,5 =	,6 = $1,7 = $1,8 ~ $2,5 = $2,6 = $2,7 = $2,8 = $3,7 ~
= $3,8 ~ $4,6 = $4,7 = $4,8^’
в4 = {1,2}, {3,4, 5, 6}, {7,8} (= 03 5),
в5 = {1}, {2}, {3,6}, {4}, {5}, {7}, {8}	(= 036),
= {1}, {2}, {3}, {4,5}, {6}, {7}, {8}	(= 045).
Элементы решетки Соп А распределяются по уровням в соот-
ветствии с алгоритмом.
При h = 0 имеем Л/(0) = Д, 0(0) = {0(, 02, 03, 04, 05, 06}.
При h = 1 находим /(1) = 0, 0(1) = 0(0) = {0р в^, в^,
в.,в,6Л, М(1) = {0,0,0,}. Элементы множества Л/(1) обра-
*т	О	1	О
зуют первый уровень.
При h = 2 будет /(2) = (в^, 0?}, где ®4 = v =
= 0, V 06, а 07 = 05 V 06 = {1}, {2}, {3, 6}, {4, 5}, {7}, {8}
(эта конгруэнция не является главной); ©2 = {02,03,04, 07},
М(2) = {02, 07}. Элементы множества М(2) составляют второй
уровень диаграммы решетки Соп А.
При h = 3 получаем /(3) = 03 = 02 V 0?, 0(3) = {03> 04},
М(3) = {04}.
318
При h = 4 множество /(4) оказывается пустым, 0(4) =
= {в3}, М(4) = {03}.
При h = 5 все множества /(5), 0(5), Л/(5) пусты—работа
алгоритма закончена. На рис. 109 приведена
диаграмма решетки Соп А. Эта решетка
немодулярна (элементы 0^ в6, 07, об-
разуют пятиугольник N5).
Применяя результаты о параллельных
декомпозициях полуавтомата (см. § 2.1),
видим, что конгруэнция в2 имеет в решетке
Соп А три дополнения: в5, и в , но так
как она не перестановочна ни с одной из
этих конгруэнций (пара (1, 6) входит в
в2 ° #5 и в в2 ° 0 , но не входит ни в
#5 ° в2, ни в 01°в2, и, далее, (1,5) G
6	но (1,5) g
Z О	\	/
£ ®б°^’ полУавтомат Л не допускает
полных параллельных декомпозиций. Зато у него много парал-
лельных декомпозиций, определяемых парами конгруэнций, име-
ющих тождественное пересечение. Минимальной по числу
используемых в компонентах состояний будет параллельная
декомпозиция полуавтомата А, порождаемая конгруэнциями в2 и
в7 (рис. ПО).
Рис. ПО
Рассмотрим теперь некоторые вопросы, связанные с мо-
делированием систем, представленных полуавтоматами. Будем
говорить, что полуавтомат А моделируется полуавтоматом В, если
А вкладывается в В, т. е. если А изоморфен некоторому
подавтомату в В. Представляет интерес характеризация полуав-
томатов, моделируюших все свои гомоморфные образы. В случае
автономных полуавтоматов получено полное описание [28J.
Т е о р е м а 4.3. Для автономного полуавтомата А сле-
дующие условия равносильны'.
1) каждый факторавтомат полуавтомата А изоморфен
подходящему подавтомату в А;
319
2) среди компонент связности графа переходов G(A) может
быть не более одной неодноэлементной, причем эта компонента
представляет собой петлю с входящими в нее цепями, из
которых не более чем одна имеет длину, большую 1 (рис. 111).
Рис. 111
Доказательство. 1) =» 2). Пусть каждый фак-
торавтомат автономного полуавтомата А = (S, д) изоморфен
подходящему подавтомату в А. Предположим, что одна из
—♦
компонент связности графа переходов G(A) содержит неодноэле-
ментный контур. Определим на полуавтомате А конгруэнцию в,
единственным неодноэлементным классом которой является этот
контур. В факторавтомате A/в контур будет представлен петлей.
Число компонент орграфа G(A/0), содержащих петли, будет на
единицу больше, чем в А, и, следовательно, полуавтомат A/в не
вложим в А (при любом вложении петли переходят в петли).
Таким образом, в орграфе G(A) нет неодноэлементных контуров.
Предположим, что одной из компонент связности в G(A)
является петля в вершине sQ с входящим в нее деревом, не
сводящимся к набору входящих в «0 цепей. Тогда найдутся
состояния Sp $2, $3 полуавтомата А такие, что <5(Sj) = $2 =
= <5(«3), Sj * $3. В орграфе G(A/0(sQ, s2)) степень захода
корневой вершины по крайней мере на единицу больше, чем
__ -♦
d ($0) в G(A). Понятно, что факторавтомат А/0($ц, s2) не вложим
в А. Следовательно, входящее в sQ дерево представляет собой
набор входящих в $0 цепей.
Предположим, далее, что в одной из компонент связности
—♦
орграфа G(A) в вершину s образующую одноэлементный цикл,
входят две цепи неединичной длины. Пусть <5^) = sQ = д(«2),
Sj * s2. В факторавтомате A/6(sl, s2) образом рассматриваемой
компоненты будет петля с входящим в нее деревом, не
распадающимся на входящие в корень цепи. Вложение факторав-
томата A/0(slt $2) в А невозможно, и, значит, каждая компонента
связности орграфа G(A) является входящим деревом, распада-
ющимся на входящие в корень цепи, длина разве лишь одной из
которых больше единицы.
320
Допустим, наконец, что в орграфе G(A) существуют по крайней
мере две компоненты связности, удовлетворяющие уже найденным
необходимым условиям. Пусть и «2—корни соответствующих
входящих деревьев, d-(Sj) и сГ(s2)—их степени захода в орграфе
G(A). Тогда в факторавтомате A/6(sl, s2) количество компонент
связности, в которых корневая вершина имеет степень захода
+ б/-(«2), на единицу больше количества аналогичных
компонент в G(A). Факторавтомат A/6(S\, «2) нельзя вложить в
А. Отсюда заключаем, что все компоненты орграфа кроме разве
лишь одной одноэлементны.
2) => 1). Пусть А—автономный полуавтомат, у которого граф
переходов G(A) удовлетворяет условию теоремы. Ясно, что для
различных главных конгруэнций полуавтомата А в орграфе
переходов соответствующего факторавтомата будем получать либо
уменьшение на единицу числа компонент, либо уменьшение на
единицу числа цепей, входящих в корневые вершины компонент,
либо уменьшение длины одной из таких цепей. Во всех случаях
факторавтомат вложим в А. □
Очевидно, что каждая конгруэнция полуавтомата А =
= (S, X, д) является конгруэнцией любой его автономной
компоненты А , х G X. Поэтому Con А = О Con А . Это пред-
*	хех х
ставление часто используется для отыскания в полуавтомате
конгруэнций специального вида.
Пример 138. Циклическим называется полуавтомат
А = (S, X, <5), в котором все входные сигналы действуют
одинаково и все состояния образуют при этом цикл. Каждый
полуавтомат имеет циклический гомоморфный образ—одноэлемен-
тный полуавтомат. Интерес представляют полуавтоматы с нетриви-
альными циклическими гомоморфными образами [72].
Пусть А = (S, д)—связный автономный полуавтомат. Если
/—длина контура в орграфе G(A), то длина контура во всяком
гомоморфном образе А/в не превосходит I. Вместе с тем, на А
существует конгруэнция вс такая, что G(A/6c) представляет собой
контур длины I (мы уже имели дело с этой конгруэнцией в § 2.6
при описании инъективных автономных автоматов). Зафиксируем
некоторое циклическое состояние «0 и положим (Sj, $2) G тогда
и только тогда, когда Sj и s2 находятся на одинаковом по модулю
I расстоянии от sQ. Это и будет искомая наибольшая циклическая
конгруэнция на А (образно факторизацию по можно представить
себе так: контур вращается и входящие деревья равномерно
«накручиваются» на него).
321
Предположим теперь, что А = (S, д)—произвольный автоном-
ный полуавтомат, компоненты связности которого имеют соответ-
ственно /р /2, ..., 1т циклических состояний. Через в.,
1 < i < т, обозначим конгруэнцию на А, тождественную всюду,
кроме г-й компоненты связности, которую она факторизует в цикл
т
длины Тогда в = V в. будет конгруэнцией полуавтомата А и
' <=1 1
при этом G(A/6) будет набором контуров с длинами /р 12, ...
...,/ . Пусть I = НОД(/.,	В каждой компоненте
факторавтомата А/0 зафиксируем одно из состояний:
.Sp 6'2» •••> s^n и положим (5., sp G $0 тогда и только тогда, когда
s. и S. находятся на одинаковом по mod I расстоянии от
выделенных в соответствующих компонентах состояний. Полуав-
томат (А/ву/в^ будет циклом длины I. Это максимальный (по
длине цикла) циклический гомоморфный образ полуавтомата А.
Явное описание наибольшей циклической конгруэнции 0?
автономного полуавтомата А выглядит, в свете сказанного,
следующим образом: (Sp s2) 6 0? тогда и только тогда, когда
.Sj и s2 находятся на одинаковом по модулю I расстоянии от
выделенных в соответствующих компонентах циклических состо-
яний, где I—наибольший общий делитель длин контуров компонент
связности полуавтомата А.
Переходя к произвольному случаю, для каждой автономной
компоненты А*, 1 < t' < т, полуавтомата А строим наибольшую
i
циклическую конгруэнцию в., а затем берем наибольшую из
т
конгруэнций полуавтомата А, содержащихся в пересечении О в..
1=1
Это и будет наибольшая циклическая конгруэнция 0с полуавтомата
А, а факторавтомат А10^—максимальным циклическим гомомор-
фным образом полуавтомата А.
Конгруэнции автономных циклических полуавтоматов описаны
в § 1.4.
Пусть А = (S, X, д)—произвольный полуавтомат, е С
С 5 х 5—некоторая эквивалентность на множестве его состояний.
Разбиение множества 5, индуцируемое отношением е, можно
интерпретировать как классификацию состояний автомата по
набору взаимно исключающих свойств: в один блок объединяются
все состояния, обладающие одним из указанных свойств. Конгру-
энции—это классификации состояний, совместимые с функцией
переходов <5 полуавтомата А. Однако в полуавтоматах, мо-
делирующих реальные системы, не всегда обнаруживаются есте-
322
ственные классификации состояний по их свойствам, описываемые
конгруэнциями. Одно и то же состояние может обладать, скажем,
несколькими из интересующих нас свойств. Алгебраическим
инструментом для изучения подобных ситуаций являются ус-
тойчивые толерантности на множестве состояний полуавтомата.
Напомним, что отношение т С S х S называется толерантно-
стью, если оно рефлексивно и симметрично. Толерантность т, по
определению, устойчива относительно функции переходов полу-
автомата А = (S, X, д), если
(Sj, s2) g Т =» (Ух е X)((5(sr X), d(s2, X)) g т)
для любых Sp s2 G S.
Транзитивные устойчивые толерантности—это конгруэнции
полуавтомата.
В § 1.3 рассматривались факторизации множества по базисам
заданной на этом множестве толерантности. В простых (т. е. не
имеющих собственных нетождественных конгруэнций) полуавто-
матах подобные факторизации могут играть полезную роль.
Пример 139 (см. [24]). Пусть полуавтомат А имеет 9
состояний, 2 входных сигнала и функцию переходов, заданную
таблицей
Х1 Х2
Покажем, что он имеет собственные нетождественные толе-
рантности, устойчивые относительно функции переходов (заметим,
что полуавтомат А—простой). Построим наименьшую устойчивую
толерантность, содержащую пару (Sp s2). Если (Sp s2) 6 т, то,
В СИЛУ УСТОЙЧИВОСТИ, (S2, $3) = (<5(Sp %2), <5(s2, х2^ е г> н0
тогда (Sp s5) = (<5(s2,	d(s3, Xj)) G т и (sp sp = (<5(s3,
x2), <3(s2, x2)) G г. Чтобы контролировать этот ветвящийся
процесс присоединения все новых пар, составим таблицу, которая
в конце концов дает двоичную булеву матрицу, задающую
323
искомую толерантность т^, s2). При получении очередной новой
пары (5., в составе конструируемой толерантности будем
рисовать на пересечении z-й строки и /-го столбца таблицы кружок
(в силу симметричности толерантностей, используем только
верхний треугольник таблицы, так что берем i < j ). Просмотр
полученных пар (для получения следующих) осуществляется в
порядке построчного просмотра таблицы. Использованная пара
(вернее, соответствующий ей кружок) вычеркивается. На рабочих
таблицах показаны три характерных этапа в построении матрицы
для t(si; s2) (в кружках стоят номера, фиксирующие порядок
просмотра получающихся пар). Первая таблица соответствует
ситуации после использования пары (s2, s4): появятся новые пары
(Sp s8) и (s3, $7), а пара («2, $9) была получена на пятом шаге.
Теперь на очереди пара (Sp s&). Вторая таблица характеризует
состав искомой толерантности после одиннадцатого шага (анализ
пары (s3, s4)). Третья таблица—финальная: двадцать пятый шаг
новых пар не дает, а все полученные ранее пары просмотрены.
1 234567 89
1Х©@ @	О®
2	Х©@® О
зхО
4	X
5	X
6	X
7	X
8	X
9	X
1 23456789
1 2' 3456789
1Х®@@О®®
2	X®®® ® (©
3	X® ОО
4	X
X о
6	X
7	X
8	X
9	X
1Х®@®®®®@©
2 X ® ®® ® ® @ ®
3 X ® ® ® ® ©
4 X ®
5	X ©@®
6	X
7	X ®
8	X
9	X
Теперь видно, что полученная устойчивая толерантность
t(Sj, s2) совпадает с толерантностью т, рассмотренной в примере
Рис. 112
15 из § 1.3. Диаграмма переходов факто-
равтомата А/т представлена на рис. 112,
где С{ = {Sp s2, sy s4, s6}, C2 = Ц, sy
sy s5, s2, sg}, C3 - Ц, sy sy s8}, C4 =
= {sp s2, s3}, Cs = {Sp s2}, C6 =
= {Sp s2, s5}.
Совокупность всех устойчивых толе-
рантностей на полуавтомате А =
= (S, X, д) обозначим через ST (Л). Так
как теоретико-множественное пересечение
устойчивых толерантностей снова является
устойчивой толерантностью на Л и
5x56 ST(X), то упорядоченное множе-
ство (ST(X), С) оказывается решеткой (здесь используется след-
ствие 1.11 из теоремы 1.34 § 1.4). Более того, как нетрудно
324
заметить, множество ST (Л) замкнуто и относительно теоретико-
множественного объединения, так что ST(A) будет подрешеткой
дистрибутивной решетки (Р(5 х S), U, П) всех отношений на
множестве S состояний полуавтомата А. Следовательно,
(ST(Л), U, П)—дистрибутивная решетка.
Алгоритм построения решетки ST(A) устойчивых толерантно-
стей полуавтомата А полностью совпадает с алгоритмом построения
решетки Соп А конгруэнций этого полуавтомата с той лишь
разницей, что на шаге 2, конечно, нужно искать множество всех
главных устойчивых толерантностей полуавтомата А. Заметим,
что, хотя Con А С ST(A) (всякая конгруэнция полуавтомата
является его устойчивой толерантностью), конгруэнции не обра-
зуют в ST(A) подрешетку: если д^, в2 G Соп А, то
U 6 ST(А), но в общем случае устойчивая толерантность
U в2 не совпадает с наименьшей конгруэнцией U в2,
содержащей и в2 (как правило, 0 U 62 не будет транзитивным
отношением).
§ 4.2. Некоторые оптимизационные задачи для автоматов
Задачи, о которых мы будем говорить, в общем виде можно
было бы сформулировать следующим образом: как, сохраняя те
или иные структурные свойства автомата, изменить другие его
характеристики в нужном направлении? Одна из таких задач
была решена в § 2.4: было показано, что для любого полуавтомата
А существует полуавтомат В с двоичным входным алфавитом
такой, что Sub В s Sub А. Другими словами, сохраняя структуру
подсистем данного полуавтомата, можно минимизировать воздей-
ствующие параметры внешней среды, ограничиваясь рассмот-
рением лишь двух различных входных сигналов.
Примером оптимизации в указанном смысле служит также
Теорема 4.4. Для любого полуавтомата А существу-
ет сильно связный полуавтомат В такой, что Соп В s Соп А.
Доказательство. Пусть А = (S, X, <5^)—дан-
ный полуавтомат и Соп А—его решетка конгруэнций. Рассмотрим
полуавтомат В = (5, Z, <5Д), где Z = X U S (считаем, что
X П 5 = 0), и для любого s 6 5 положим
z) :=
<5л(х’ z)’
z,
если z 6 X,
если z 6 S.
Полуавтомат В сильно связен,
поскольку для любых Sp
s2 6 5 имеем <5д(Хр s2) = s2' Поскольку в автономной компо-
ненте В$ = (S, {.?}, функция переходов является постоянной
функцией (со значением s), решетка Соп А$ изоморфна решетке
325
E(S) всех эквивалентностей на множестве 5. Отсюда получаем,
что
Con В = П СопЛ2 = П Con Л* П П E(S) =
zeZ	хе X	seS
= Con Л П E(S) = Con Л. □
Таким образом, в вопросах, связанных с изучением решеточ-
ных свойств конгруэнций полуавтоматов, можно ограничиться
рассмотрением полуавтоматов с минимально возможной решеткой
подавтоматов (сильно связный полуавтомат примитивен, т. е. не
содержит собственных ненулевых подавтоматов).
Следующий замечательный результат принадлежит Маккензи
(см. [51]).
Теорема 4.5. Для любого полуавтомата А существу-
ет полуавтомат В с четырьмя входными сигналами такой, что
Con В as Con А.
Доказательство. Пусть А = (S, X, д), 5 =
= {s ,	} , X = {х., х~, ..., х ), где т > 4. Построим
1.	*	rl	1	£	ГЦ
полуавтомат В = (Т, {zp z2, z3, zj, дв), полагая Т := sm+n+l
(декартова (m + п + 1)-я степень множества S) и для t =
= (s1, s2, ..., sw+”+1), определяя
:= (sr s2,...,sn, <5л(Д xt),.... d/s1, xm), s1),
dB(t, z2) := (s2, s2,	..., s"'+"+1),
dB(t, z3) := (s"'+n+1, s1, s2, ..., sm+n),
dB(t, z4) := (s2, s1, s3, s4, ..., s"'^1).
Пусть в G Con A—произвольная конгруэнция полуавтомата A.
В множестве Т введем отношение
ё := {(/, *t) G Тх Т I (s', *s') G в, 1 < i < m + n+ 1},
где *t = (‘s1, *s2, ..., *sw+n+1).
Из этого определения следует сразу, что если в, у G Con А,
то О С тр тогда и только тогда, когда в С В частности,
6 = tp в том и только том случае, когда в = 1р.
Докажем, что в является конгруэнцией полуавтомата В. Для
этого нужно проверить, что из (t, *t) G в следует соотношение
Zj), &BCt, zj)) e при ; == 1, 2, 3, 4. Если j = 2, 3, 4,
выполнимость доказываемого вполне очевидна. Рассмотрим случай
i = 1.
326
Пусть (t, *f) G в. Тогда (s', *s‘) G 0, 1 < i < m + n + 1. В
полуавтомате В имеем:
zl) = (SL’ S2' Sn'	Xm>'
<V‘Z’ Zl> = (Sl’ S2.....V dx(‘s1’	дл(‘®1’ Xm>' *sl)-
Так как в G Con Л, то («^(s1, x^, &A(*sl, x^)) G 0,
1 < j < m, откуда (<5Д(Г, z{), dB(*t, zj) G 0.
Таким образом, соответствие 0 >—* 0 отображает решетку
Con А в решетку Con В,
Покажем, что отображение 0 >—4 0 сюръективно. Для
Ф G Con В положим
:= {(s, *s) G S X S I ((s, s, ..., s),(*s, *s, ..., *s)) G Ф}.
Отношение 0^ будет конгруэнцией полуавтомата А. Действи-
тельно, если (s, *s) G 0^, то ((s, s, ..., s), (*s, *s, ..., *s)) G Ф.
Подавая на вход полуавтомата В сигнал zl и учитывая, что
Ф G Con В, получаем, что
«Sl’ S2....Sn' 6a(S'	....Хт)' S)’
(sr s2,...,sn, dAfs, Xj), ..., dx(‘s, xm), ‘s)) G Ф.
Используя входное слово z^z^...z^ длины m + 2, приходим к
соотношению
((s , <5 .(s, х.),..., d .(s, x ), s, s,, ..., s .),
'' n Л' i' ’ д'-	’ ne' г	’ n-v
(s , d.(*s, x,),..., d (*s, x ), *s, s , ..., s ,)) G Ф.
'	n Л' И’	’ Л'	’	m'’	1’	’
Наконец, входное слово z (z,z ) ... (z z_) длины 2n + 1 дает
((дл(«> *j)..dx(s> *j)), (дЛ(*5’ Xl>’ dA<*S’ Xl))) S
откуда (d^(s, Xj), &A(*S> *i)) e Аналогично доказывается, что
(dA(s, хк), &A(*s, хк)) е 0у для всех 2 < к < т.
Установим включение Ф С 0 Если (t, *t) G Ф, то, подавая
на вход полуавтомата В слово (z z )(z z ) ... (z,z ) длины
2(m + n), получаем, что
((s1, s1,..., s1), (‘s1, ‘s1, ...,‘s1)) G Ф,
327
откуда (s1, ‘s1) G ву Входная последовательность z^z^) ...
... (z z ) длины 2(т + п) + 1 приведет к обнаружению того, что
(s2, *s2) 6 0ф. И так для любого i < т + п + 1 можно подобрать
входную последовательность, приводящую В из состояния t в
состояние (s‘, sl, .... s') Е Т. Следовательно, (s', *sl) G 0ф для
всех г. Значит, (s, *s) G 0^.
Для доказательства включения С ф потребуется
Лемма 4.2. Пусть т, *т—два состояния полуавтомата
В, причем с/ = s', с/ = *s' для некоторого фиксированного I
и о1 = *о1 для всех j * i. Тогда из (Z, *f) G Ф вытекает,
что (т, *т) G Ф.
Действительно, рассмотрим сначала случай i = 1. Тогда
т = (s1, о2, ...,о"'+"+1) и *т = (‘s1, о2, ..., с/"+''+1). Так как
(/, */) G Ф, то отношение Ф будет содержать и пару
(<5В(Л zp, dBCt,Zl)) = ((Sj,..., sn, 6A(s',Xl), ..., <5/,xm), s1),
(s,,...^, d/s1,	..„d/s1, xm), ‘s1)).
Поскольку каждая из двух этих (т + п + 1)-систем содержит
все состояния полуавтомата А, с помощью входных сигналов
z2, Zy z4 из пары (<5Д(Л	z])) можно получить пару
(т, *т). При этом получающиеся на каждом шаге состояния
полуавтомата В будут Ф-конгруэнтными. Значит, (г, *т) G Ф.
Если i = 2, будем подавать на вход полуавтомата В сигнал
z3 до тех пор, пока из (/, *t) G Ф не получим, что
((s2, s3..s”!+,! + 1, s1), (*s2, *s3, ..., V'+"+1, *s’)) G Ф,
после чего повторим проведенные для i = 1 рассуждения. Лемма
доказана.
Пусть теперь (t, *f) G 0ф. Тогда (s', *s') G для любого i,
и, значит, ((s', ..., s'), (“s', ..., *s')) G Ф. Полагая i = 1 и пользу-
ясь леммой, получим, что ((s1, s2, ..., s"'+,l+1), (‘s1, s2, ...
..., s"'+"+1)) G Ф.
При i = 2 лемма дает соотношение
((’s1, s2, s3, ..., s"l+"+1), (*s‘, *s2, s3.s"'+"+1)) 6 Ф.
Вследствие транзитивности отношения Ф будет
328
((?, ?, ?,..., ?',+n+1), (*?, *?, sm+n+l)) 6 Ф.
Полагая i = 3 и применяя лемму, ставим во второй
(т + п + 1)-системе третью звездочку, и т. д. Следовательно,
(Z, *1) 6 Ф. Равенство = Ф доказано.
Таким образом, соответствие в >--» в является изоморфизмом
упорядоченных множеств (Con А, С) и (Con В, С). о
Неизвестно, можно ли в доказанной теореме ограничиться
двумя входными сигналами.
Важнейшей оптимизационной задачей для автоматов является
их минимизация. В § 1.3 рассматривалось отношение эквивален-
тности (неразличимости) автоматов. Пусть А = (S, X, Y, д, А)—
некоторый автомат. Среди автоматов, эквивалентных автомату А,
требуется найти автомат с наименьшим возможным числом
состояний. Он и называется минимальным автоматом в данном
классе эквивалентных автоматов. Очевидно, что автомат минима-
лен тогда и только тогда, когда любые два его состояния
различимы, т. е. когда отношение эквивалентности состояний е
тождественно на данном автомате.
Как отмечалось в § 1.3, в любом автомате цепочка эквива-
лентностей е( 2 е2 2 ... 2 е* 2 ... конечна и последний ее
элемент совпадает с е. Здесь
ек := {(s, Z) е 5 х 5 I (vp е Х*)(1р1 < к => А($, р) = A(Z, р))}.
(Заметим, что в определении эквивалентности неравенство
Ipl < к можно заменить равенством I pl = к: если состояния s
и Z не различимы входными последовательностями длины к, то
они не различимы и входными последовательностями меньшей
длины.)
Под конгруэнциями автомата А = (5, X, Y, д, Л) далее
понимаются конгруэнции его редукта (5, X, <5).
Т е о р е м а 4.6. Отношение эквивалентности (.неразли-
чимости) состояний е является наибольшей из конгруэнций
автомата А = (5, X, У, <5, А), содержащихся в отношении
gj := {(s, Z) 6 S x 5 I (v x 6 X)(A(s, x) = A(Z, x))}.
Доказательство. Пусть в 6 Con А и в С £
Покажем, что в С Е. Для этого достаточно установить, что
0-конгруэнтные состояния автомата А не различимы входными
словами никакой длины к. При к = 1 это следует из включения
в С е	Дальше действуем индукцией. Пусть в С и
(s, Z) 6 в. Тогда для любого х G X будет (<5(s, х), <5(Z, х)) £
6 в С е^. Беря произвольное слово р длины к и произвольный
входной сигнал х 6 X, получаем:
329
A(s, хр) = A(s, x)A(d(s, x), p) = A(t, x)A(d(t, x), p) = A(t, xp),
t. e. (s, t) G £jfc+1.
Итак, 0 C £. Тот факт, что само отношение е является
конгруэнцией автомата А, был установлен в § 1.4 (теоре-
ма 1.39). о
О конгруэнциях автомата, содержащихся в эквивалентности
Гр говорят также, что они согласованы с функцией выходов.
Поскольку теоретико-множественное пересечение двух конгру-
энций такого вида также будет согласовано с функцией выходов
Л, то в силу теоремы 4.6 и следствия из теоремы 1.34 § 1.4
получаем, что конгруэнции автомата А, согласованные с функцией
выходов, образуют подрешетку решетки Соп А всех его конгру-
энций.
Пусть А = (S, X, У, дА, АЛ) и В = (Т, X, У, &в, Ад)—
сравнимые автоматы. Отображение <р: S -» Т, по определению,
является гомоморфизмом, если для любых s 6 S, х G X
выполняются равенства
х)) = &B(<p(s), х), Ад(^(5), х) = Ал(л, х).
Т е о р е м а 4.7. Конгруэнция в автомата А = (S, X,
У, д, А) тогда и только тогда является ядром некоторого
гомоморфизма этого автомата, когда она согласована с
функцией выходов А.
Доказательство. Если <р—гомоморфизм автома-
та А и (Sp s2) 6 Кегу>, т. е. ^(.s^ = y>(s2), то для любого
х G X имеем:
А($Р х) = Aft^), х) = A(^(s2), х) = А(52, х),
откуда (Хр $2) е е.
С другой стороны, если в G Соп А и в С £ то для любых
0-конгруэнтных состояний Sp s2 6 S будет A(Sp х) = A(s2, х)
при всех х 6 X. Значит, в факторавтомате A/в имеем
A(0(s), х) = А(х, х) для любых s 6 S, х 6 X. Тогда естественное
отображение nat 6: S -» SlQ, s 0(s), оказывается гомоморфизмом
автомата А на факторавтомат А/в, причем Ker nat в = 0. =,
Следствие 4.1. Каждый автомат эквивалентен лю-
бому своему сравнимому гомоморфному образу.
Доказательство. Пусть <р—гомоморфизм авто-
мата А = (S, X, У, А ) на сравнимый с А автомат В =
= (Т, X, У, &в, Ав). Так как AB(<p(s), х) = Aa(s, х) при любых
s 6 S, х 6 X, то для продолженной функции выходов имеем
AB(<p(s), р) = A^(s, р), каковы бы ни были s G S и р £ X*.
330
Но это равенство означает, . что состояние s автомата А
эквивалентно состоянию <p(s) автомата В. В силу сюръективности
отображения >р, каждое состояние автомата В имеет вид <p(s),
s 6 S, и потому эквивалентно соответствующему состоянию s
автомата А. а
Если автомат А простой, т. е. не имеет собственных
нетождественных конгруэнций, то в нем е = Д, и он, следова-
тельно, будет минимальным. Как показывает пример 141,
рассматриваемый ниже, минимальный автомат не обязан быть
простым, в нем отсутствуют лишь нетождественные конгруэнции,
согласованные с функцией выходов.
Следующее интересное само по себе утверждение позволяет
установить максимальную возможную длину убывающей цепи
эквивалентностей е2 □ ... □ е.
Лемма 4.3. В решетке Е(п) разбиений п-элементного
множества высота элемента П может быть вычислена по
формуле й(П) = п — 1П1, где 1П1—число блоков разбие-
ния П.
Доказательство. Действуем индукцией по п.
Для п = 1, 2, 3 утверждение очевидно. Для проверки случая
п = 4 можно использовать диаграмму решетки (£'(4), С), приве-
денную в § 1.4 (рис. 27).
Пусть доказываемое утверждение справедливо при п = к, и
рассмотрим решетку Е(к + 1) разбиений множества {1, 2, ...
..., к, к + 1}. Каждое разбиение П 6 Е(к +1) получается из
некоторого однозначно определенного разбиения П* 6 Е(к) одним
из двух способов: 1) присоединением одноэлементного блока
{к + 1}, 2) добавлением в один из П*-блоков элемента к + 1. В
первом случае, очевидно, /г(П) = А(П*) (высоты вычисляются в
соответствующих решетках), а во втором й(П) = А(П*) + 1. В
обеих ситуациях А(П) = (к + 1) — 1П1. о
Длиной конечного упорядоченного множества называется
наибольшая из высот его элементов, т. е. наибольшая из длин
его цепей.
Следствие 4.2. Решетка Е(п) разбиений п-элемент-
ного множества имеет длину п - 1.
Доказательство. Наибольшим элементом ре-
шетки Е(п) является разбиение, соответствующее универсальной
эквивалентности. Оно имеет один блок и потому, согласно лемме
4.3, его высота равна п - 1. Это число и будет длиной решетки
Е(п). =
Утверждение следствия 4.3 известно в теории автоматов как
теорема Мура.
Следствие 4.3. Для автомата с п состояниями
331
Доказательство. Поскольку цепь 2
2 е2 2 ... составлена из эквивалентностей на п-элементном
множестве, длина ее, ввиду следствия 4.2, не может быть больше
чем п - 1. о
Таким образом, теорема Мура утверждает, что если в автомате
А с п состояниями состояния s и t не различимы входными
последовательностями длины, не превосходящей п - 1, то эти
состояния эквивалентны, т. е. не различимы никакими входными
п осл едовател ьностям и.
Существует много разработанных приемов минимизации авто-
матов. Все они, по существу, сводятся к построению отношения
эквивалентности состояний е в данном автомате А и последующей
факторизации автомата А по конгруэнции е. Разберем несколько
примеров, основываясь непосредственно на теореме 4.6. Дело в
том, что отношение легко определяется по таблице, задающей
автомат. Если решетка конгруэнций автомата А известна, то в
ней без труда выделяется наибольшая из конгруэнций, содер-
жащихся в е Это и будет е. Если же Con Л не известна, строим
главные конгруэнции автомата А, порожденные е^эквивалентными
парами, отбираем те из полученных конгруэнций, которые
содержатся в все их объединяем. В результате получится
конгруэнция е.
Пример 140. В автомате А из примера 4 во введении
(где на рис. 4 показана диаграмма переходов и графы автономных
компонент этого автомата) отношение имеет своими классами
подмножества х4) и {s2, х3) (в подтаблице выходов совпадают
строки 1 и 4, а также 2 и 3). Решетка конгруэнций автомата А
(пример 14 из § 1.4) содержит пять элементов. Наибольшей
конгруэнцией, включающейся в отношение будет 0р {sj,
{х2, х3), {х4}. Следовательно, е = 6 , и минимальный автомат,
эквивалентный данному автомату А, можно задать диаграммой
переходов, изображенной на рис. 113.
Рис. 114
Пример 141. Диаграмма автомата В, представленного на
рис. 114, отличается от диаграммы автомата А, рассмотренного в
332
предыдущем примере, лишь метками дуг, т. е. эти два автомата
имеют один и тот же полуавтоматный редукт и отличаются
функцией выходов. Очевидно, что Con В = Con А, но отношение
в автомате В иное: его классами будут {Sp s2). {s3, sj. Отсюда
заключаем, что в отношении е1 автомата В содержится лишь
тождественная конгруэнция Д. Автомат В не минимизируем, так
как он сам является минимальным. Этот пример показывает, что
минимальный автомат не обязан быть простым.
П р и м е р 142 (см. [53]). Пусть автомат А задан табли-
цей
А
1
2
3
4
5
6
7
8
2
5
4
7
1
5
3
7
8
3
6
1
8
2
6
4
____h
О о
О 1
о о
О 1
о о
1	1
о о
1	1
и диаграммой рис. 115. Непосредственно из таблицы находим
отношение Cj = {1, 3, 5, 7}, {2, 4}, {6, 8}. Для каждой пары,
входящей в Ер вычисляем соответ-
ствующую главную конгруэнцию.
При этом вычисление конгруэнции
прекращается, как только в составе
ее обнаруживается пара, не входя-
щая в отношение £р Первой на-
ходим в} з = 0(1, 3) = {1, 3},
{2, 4}, {5, 7}, {6, 8}. В 5 сразу
обнаруживается пара (1,2) £ Ер
Рис. 115
вычисление прекращается. В 0( 7 на
первом же шаге получаем (2, 3) £ £р Конгруэнция 5
содержит пару (1, 4) £ £р Так как (3, 4) <£ Ер нас не
интересует конгруэнция в . Далее, в = в в = в ,
0, _ = в, .. Таким образом, единственной главной конгруэнцией
автомата А, содержащейся в отношении 1-неразличимости состо-
яний е , будет в ,, откуда е = 0 Факторавтомат А/0. , (с
1	1,0	1,0	1,0
соответствующей функцией выходов) представляет собой мини-
мальный автомат, эквивалентный автомату А.
333
Автомат А является популярной иллюстрацией процесса
построения минимального автомата, эквивалентного данному.
Выписываем отношение е1 = {1, 3, 5, 7, 8}, {2, 4, 6, 9}.
Последовательно вычисляем главные конгруэнции автомата А,
порожденные г -эквивалентными парами (пишем только неодно-
элементные блоки): 3 = {1, 3};	5 = S х S; 0j 7 = 5 х 5;
в, 8	=	(1. з, 8), (2, 4), {5, 2}; в3 } 2	в, ,	- S X	S;	О, ,	2
э'е1	5	- SXS; в3 8	- (1,3.8), (2,4),	(5>)	= в,	6^	С
=	«S.S = «з.,' =	Sx^«,,s= «1.7	=	<4	=
«2. 4	=	«1,, = 5 * *	«2.9 = «1.7 = SxS'	«4.4	=	«2.9	=
= 5x5; 0, о □ в. fi = 5 х 5. Отсюда е = в, в = {1, 3, 8},
О, Ч 7,0	1,о
{2, 4}, {5, 7}. В таблице, задающей факторавтомат А/е, Sj :=
:= {1,3,8}, s2 := {2,4}, s3 := {5,7}, s* := {6},	:= {9}.
Следующее предложение означает, что в каждом классе
эквивалентных автоматов существует единственный—с точностью
до изоморфизма—минимальный автомат.
Теорема 4.8. Если два минимальных автомата эквива-
лентны, то они изоморфны.
Доказательство. Пусть А = (5, X, У, <5., Л )
А А'
и В = (Т, X, У, дв, Лд)—эквивалентные минимальные автома-
ты. Пусть s 6 5—произвольное состояние автомата А. Так как
А и В эквивалентны, в В найдется состояние t G Т такое, что
Ад($, р) = Ад(?, р) для любого входного слова р 6 X *. Очевидно,
что такое t единственно, поскольку иначе отношение эквивален-
тности состояний е в автомате В не было бы тождественным в
противоречие с минимальностью В. Аналогичные рассуждения
показывают, что для каждого состояния t G Т автомата В
334
существует единственное неразличимое с ним состояние s G 5
автомата А. Таким образом, отношение
Р := {(s, г) е 5 х т I (vp е Х*)(Лл($, р) = Ав(г, р))}
является взаимно однозначным соответствием между множест-
вами 5 и Т. Непосредственно из определения получаем, что
х) = Ал(«, х) для любых S 6 5, х 6 X. Покажем, что
<р согласовано с функциями переходов, т. е. что для любых
s 6 5, х G X выполняется равенство у>(дл(5, х)) = <5Д(^(5), х).
Пусть s 6 5, х 6 X, р 6 X*—произвольные элементы соответ-
ствующих множеств. Тогда
ЛЛ(Х, хр) = Ал(5, х)Лл(дл(5, х), р),
хр) = kB{p{s), x)kB{dB(.p(s), X), Р).
Так как, по определению отображения <р, имеют место
равенства Ал(х, хр) = kB(y>(s), хр) и Ал(х, х) = A^(y>(s), х), то
^л(^л($, *), р) = ^(^(^(s), *)> Р) (эти два выходных слова
получаются, если в равных словах Ал($, хр) и XB(<p(s), хр)
отбросить равные префиксы ^л($, х) и XB(<p(s), х). Следовательно,
состояния <5л(х, х) в автомате А и dB(<p(s), х) в автомате В
неразличимы, т. е.
^(<5л(х, х)) = dB(<p(s), х). ~
В практике приходится встречаться с частичными автома-
тами, т. е. с автоматами, которые имеют не всюду определенные
функции переходов и (или) выходов. Такие автоматы обычно
задают таблицами, в которых прочерками отмечают отсутствие
соответствующих данных. Например,
А	*1	X2	X3	\	X,	X2	X3	\
si S2 S3 \ S5	S2	“	S3	S2 S3	S5	S2	~ S3	S4	"	S5 "	*1	S2	~ - ~ "	0 0	10- 0	1-0 1 1
Может возникнуть вопрос о минимизации частичного автомата,
т. е. об уменьшении числа его состояний с сохранением выходных
реакций на все входные последовательности.
Понятно, что частичные функции ЗиЛ можно пытаться
доопределить тем или иным способом и затем минимизировать
335
полученный полный (т. е. не частичный) автомат уже рассмот-
ренными методами. Однако опыт показывает, что такой путь
малоэффективен: для каждого из многочисленных пополнений
нужно проводить процедуру минимизации, а затем из по-
лучившихся минимальных автоматов выбрать тот (или те),
который имеет наименьшее число состояний.
В основе обычно применяемой процедуры минимизации
частичных автоматов лежит построение некоторых устойчивых
толерантностей на них.
Состояния s и t частичного автомата А называются сов-
местимыми, если A(s, х) = А((, х) для всех х 6 X, для которых
обе части равенства определены. Отношение совместимости,
очевидно, рефлексивно и симметрично, т. е. является толерант-
ностью на множестве состояний 5 частичного автомата А.
Обозначим эту толерантность через rQ. Например, в частичном
автомате А, определенном ранее таблицей, в состав tq входят все
пары состояний, кроме пар (s2, s5) и (s5, $2), так как
A(s,, х,) = 0 * 1 = A (.s' х _). Толерантность т в случае полных
автоматов превращается в 1-эквивалентность состояний
Как в случае полных автоматов мы отыскивали главные
конгруэнции, содержащиеся в эквивалентности так для
частичного автомата строятся главные устойчивые толерантности,
включающиеся в отношение Каждая такая толерантность т
определит покрытие множества состояний 5, совпадающее с
базисом этой толерантности. Пусть {Ср С2, ..., С^}—упомянутый
базис. Входящие в него классы считаются состояниями нового
частичного автомата. При этом <5(С., х) := С. в том и только
том случае, когда существует s 6 С. такое, что <5(s, х) 6 С. .
В противном случае значение д(С., х) считается неопределенным
(в таблице ставится прочерк). Заметим, что, поскольку толеран-
тность т устойчива, то для t 6 С. такого, что <5((, х) определено,
обязательно d((, х) 6 С. . Может случиться так, что при всех
•s 6 С, для которых <5(s, х) определено, окажется, что
d(s, х) 6	, где Z т* /. В этом случае можно было бы положить
<5(С., х) := С{. В конкретных ситуациях этот произвол устраня-
ется принятием удобного в том или ином смысле варианта. В
допустимости такого произвола существенное отличие от проце-
дуры построения факторавтомата А/т по устойчивой толерантности
т (см. пример 139 в § 4.1), где не заботятся о минимальности
числа состояний получаемого автомата.
Частичная функция выходов определяется очевидным образом:
если s G С. и A(s, х) определено, то Л(С., х) := A(s, х). Пос-
336
кольку все состояния, входящие в один т-класс, совместимы,
указанное определение корректно.
Далее, минимальный по числу состояний частичный авто-
мат выбирается из всех частичных автоматов рассмотренной
конструкции, полученных по всевозможным устойчивым толеран-
тностям, содержащимся в rQ. Общего метода сокращения возника-
ющего перебора нет. Если для эквивалентностей из включения
е С следует, что количество ^-классов не превосходит количе-
ства е-классов, то для толерантностей аналогичное утверждение
о количестве классов в базисах неверно, так что наибольшая
устойчивая толерантность, содержащаяся в т0, в общем случае,
не приведет к минимизации (что резко контрастирует с ситуацией
для полных автоматов—см. теорему 4.6).
П р и м е р 144 (см. [5]). Проведем процедуру миними-
зации частичного автомата А, заданного выше таблицей (с. 336).
Как уже отмечалось, в данном случае = (S х S) —
- {(s2, s5), (s5, s2)}. Ниже представлены рабочие таблицы вычис-
ления всех девяти главных устойчивых толерантностей, порож-
денных т0-толерантными парами состояний (для удобства
состояния обозначены соответствующими индексами, таблица для
т2 5 включена из соображений полноты).
Из рассмотрения исключаются: т2 5 (так как пара (2, 5) не
входит в т ), т з (так как т , □ т J, т _ (так как
О	1)0	1)0	X) О	1)0
Т1.5 3 Т1, 3>’ Т2. 4 (ТаК КаК Т2,4 2 Т1>
Далее,
г имеет три класса: {1, 2}, {2, 3}, {4, 5} (базис),
имеет четыре класса: {1, 2}, {1, 4}, {2, 3}, {4, 5} (базис),
т3 имеет пять классов: {1, 2}, {1, 4}, {2, 3}, {3, 4}, {4, 5}
(базис),
т3 5 имеет четыре класса: {1}, {2}, {3, 5}, {4} (базис),
12 А.М.Богомолов, В.П.Салий	337
Т2, 3	Г1, 2	Г4, 5"
При этом т( 2 С Tj 4 С т3 4. Базис из четырех классов
наряду с т , U т, . имеет и объединение г. и т —это
1.» it О» Э	О* 4 и, э
{1, 2}, {1, 4}, {2, 3}, {3, 4, 5} (заметим, что содержащаяся в
этом объединении толерантность т3 4 обладает пятиэлементным
базисом). У объединения и т3 единственный базис вклю-
чает пять классов.
Таким образом, минимальный частичный автомат для исход-
ного частичного автомата А строится при помощи стабильной
толерантности т . Обозначая С := {s., s_}, С, := {s,, s,},
С3 := {«4, $5}, получим частичный автомат В, задаваемый
таблицей
Заметим, что позиции, занятые элементами, объединенными
фигурной скобкой, допускают альтернативные варианты: состояние
д(Сх, х4) можно считать равным С1 или С2, так же, как и
состояние <5(С2, х3). Следовательно, эта таблица на самом деле
задает четыре различные минимизации исходного частичного
автомата А.
Пример 145 (см. [14]). Пусть частичный автомат А
задан приводимой ниже таблицей. Из подтаблицы выходов
находим отношение совместимости т .
A *1 x2 x3 *4
S5
ss
s6
S3
-111
0
0	1
-	-	1 -
-001
0-01
338
В состав этой толерантности входят все пары, кроме s5),
(sr s6), (s4, s5), (s4, s6) и симметричных им пар. Обозначим
через т толерантность, получаемую из tq удалением пар
(Ч , Л' ) и (sr, sA. Эта толерантность имеет четырехэлементный
х 2 6х х 6 2х
базис: Cj = {sr sy sy s4), C2 =	$5}, C3 = {s3, sfi},
C4 = {$5, sfi}. Пользуясь подтаблицей переходов частичного
автомата А, без труда обнаруживаем, что т—устойчивая толеран-
тность (например, <5(С., х.) = С., <5(0., х_) = С,, <3(0 , х,) =
= С_, <5(0,, хл) = {хп} = С, П С_ и т. д.). Следовательно, т
является наибольшей устойчивой толерантностью, содержащейся
в Тд. Предположим, что толерантность т* устойчива и содержится
в TQ. Тогда т* С т. Каждый класс толерантности т* включается
в подходящий т-класс. Если т* имеет базис, состоящий менее чем
из четырех классов, то этот базис может получиться только
удалением из базиса толерантности т одного из классов С2, С3
или С4. Анализ таблицы переходов автомата В (приведен ниже
в таблице), построенного на т-классах как на состояниях,
показывает, что любая из этих редукций приводит к не-
устойчивости толерантности т*. Следовательно, именно В дает все
минимизации исходного частичного автомата А.
в
с,
С2
Сз
С4
1Сз
Iе,
1Сз
С
I 4
1С3
С
I 4
С
I
(с>
|С2
С,
[С>
С2
С
I
1е,
с,
х
i
О
о
о
о
1	1	1
О	О	1
1	0	1
О	0	1
2
Фигурными скобками отмечены альтернативные возможности
переходов. Среди 256 минимальных автоматов, получаемых из
схемы В, легко обнаруживаются неизоморфные и, следовательно
(теорема 4.8), неэквивалентные автоматы.
12*
339
§ 4.3. Алгебраические свойства автоматов общего вида
Успешное применение алгебраических методов для изучения
структурных свойств полуавтоматов основано на возможности
трактовки полуавтоматов как конечных унарных алгебр (§ 2.1).
Рассматривая автоматы общего вида как трехосновные алгебры
(§ 2.6), можно применить при решении тех или иных автоматных
задач технику теории многосортных алгебр.
Пусть А = (S, X, У, <5, А)—некоторый автомат. Автомат
А' = (S’, X', У, д', А') называется подавтоматом автомата А,
если S' С S, X' С X, У С у и d'(s, х) = <3(s, х), A'(s, х) =
= A(s, х) для любых s € S', х & X'. В дальнейшем будем
писать А' = (S', X', У, <5, А).
Очевидно, что подмножества S' Q S, X' Q X, Y' Q У тогда
и только тогда определяют подавтомат автомата А, когда для
любых s & S' и х G X' выполняются соотношения <5(s, х) G
G S' и A(s, х) G У, где <5 и А—функции переходов и выходов
автомата А.
Совокупность всех подавтоматов автомата А обозначим через
Sub А. Для подавтоматов Ар А^ G Sub А будем писать
А1 < А2, если множества состояний, входов и выходов подавто-
мата Aj содержатся в соответствующих множествах (файлах)
подавтомата А^. Упорядоченное множество (Sub А, <) имеет
наибольший элемент—сам автомат А. Для того чтобы ввести на
множестве Sub А структуру решетки, нам придется допустить,
что в определении автомата множества S, X, У (и функции <3 и
А в соответствующих случаях) могут быть пустыми. Тогда
наименьшим элементом в упорядоченном множестве (Sub А, <)
оказывается нулевой подавтомат 0, у которого все пять состав-
ляющих являются пустыми множествами. В рамках принятого
допущения для любых двух подавтоматов А1 и А2 автомата А
будет определено их пересечение А} л А2 := (Sj Г1 S2,
X, О АС, У, П У,, <3, А). Очевидно, что А л А, является
наибольшим подавтоматом, содержащимся в Aj и в А2> т. е.
точной нижней гранью для Aj и А^ в (Sub А, <). Согласно
следствию из теоремы 1.34 § 1.4, упорядоченное множество
(Sub А, <) будет решеткой. Это решетка подавтоматов авто-
мата А. Точная верхняя грань А{ V А2 вычисляется в ней как
пересечение всех подавтоматов автомата А, содержащих подавто-
маты А1 и А2.
Решетка подавтоматов любого полуавтомата дистрибутивна
(§ 2.4). Следующий пример показывает, что для автоматов общего
вида решетка Sub А не обязана быть даже модулярной.
340
цей
Пример 146. Покажем, что автомат А, заданный табли-
s,
2
S2
S2
S3
и диаграммой рис. 116, имеет немодулярную решетку подавтома-
тов. В самом деле, рассмотрим в нем три подавтомата Ар А2,
Аз' где Л1 = (ЦЬ ЦЬ W)’ Л2 =
= ({s2, $3}> {х2}, {1}) (СИМВОЛЫ (3 и
Л в этих записях опущены). Имеем
А^ < Ау А} л А3 = О, А{ V А^ = А.
Следовательно, подавтоматы О, Ар А2,
Ау А образуют в решетке Sub А
подрешетку, изоморфную пятиугольни-
ку N , и, значит, Sub А не моду-
({s2}, {х2}, {1}), Л3 =
Рис. 116
лярна.
Пусть SQ С S, XQ С X и Уо С у.
Подавтомат, порожден-
ный тройкой подмножеств
(SQ, XQ, Уо) в автомате А—это, по
определению, наименьший
подавтомат A' G Sub А такой, что
С S', Хо С X', Yq С У'. Он строится следующим образом.
А
О	1
О	1
О	1
Положим X' := Хп.	Далее, пусть S.	:= S„	, S.,.	:= S„	U
о	1 о z+l о
U {<3(s, х) I s G S & х G X’}, S' := U S. Наконец, У' : =
i
:= Уо U {A(s, х) I s G S' & х G X'}. Отметим одно очевидное,
но полезное наблюдение.
Лемма 4.4. Если А} = (Sp Ху Ур <5, Л)—подавтомат
автомата А и X. С X , У 2 У, 2 У., то А = (S , Х-,
XI	XI	X	1 X
У , д, Л) тоже будет подавтоматом, а
Атомами решетки Sub А являются подавтоматы автомата А,
у которых одно из трех множеств S, X, У одноэлементно, а два
другие пусты. С точки зрения приложений более интересны
простейшие подавтоматы другого типа. Это подавтоматы, порож-
денные одним состоянием и одним входным сигналом. Они
называются главными автономными подавтоматами данного
автомата и входят в состав множества неразложимых элементов
решетки Sub А. Минимальными подавтоматами с непустыми
файлами S, X, У являются циклы: главные автономные подавто-
маты, в которых каждое состояние циклическое.
341
В общем случае решетка подавтоматов Sub А устроена очень
сложно.
Пусть А. = (S , X., У, <5,, АА- = (S?, X,, У, <5„ АЛ
произвольные автоматы. Рассматривая их как многоосновные
алгебры (§ 2.6), мы должны определить гомоморфизм /:
At -* Л2 как тройку отображений ц>'. Sj -> 52, уч Х^ -» Х^,
X'. У] У2, удовлетворяющих соотношениям
р(<\(Л X)) = <32(у>(х), у>(х)),
Х(Л,О, х)) = A2(9p(s), у>(х))
для любых j 6 Sp хЕХ . Прямое произведение автоматов
А и Л,—это автомат А х А. := (S. X S X. х Х-, У х У,,
1	лг	IX	1	X	1	лг	1	лг
д, Л), где
<5((sp s2), (Xj, х2)) := (<\(Sp х(), d2(s2, х2)),
я(0'р s2), (хр х2)) := (Л](5р X]), A2(s2, х2))
для любых (s , s ) G S х S (х. , х ) G X х X .
Автоматы вместе с их гомоморфизмами образуют категорию.
В соответствии с категорной символикой, совокупность всех
гомоморфизмов автомата А{ в автомат А2 будем обозначать через
Нош (Ар Л2).
Теорема 4.9. Тройка отображений f = (у>, у», %) тог-
да и только тогда является гомоморфизмом автомата А1 в
автомат А2, когда f—подавтомат прямого произведения
А1 х А2'
Доказательство. Пусть f G Hom (Ар А2). Ес-
ли (Sp s2) G у> и (Хр х2) 6 у, то в прямом произведении
Aj х А2 получаем:
<3((Sp s2), (Хр х2)) = (<5](5р X]), <52(s2, х2)) =
=	*i)> <52^(51), V’(-^))) = (^О,, -«i),	*,))) G
Л(($Р s2), (Хр х2)) = (A((Sp xt), A2(s2, х2)) =
= (^^«Р •*,)> X(A,(Sp Xj))) G %.
Следовательно, подмножества y> C x S2, ip С X{ X X2, x —
С У, x У2 определяют в At x A2 подавтомат.
342
С другой стороны, пусть f = (у>, у, %) G Sub (т^ X Л2). Для
произвольных s 6 S(, х G X] получаем:
(*, у>0)) G. <р & (х, у(х)) G => (dj(s, х), <52(у>0), у(х))) =
= ‘ИС*, ?(*)), (х> ¥’(•«))) G <Р =* У’С'ИС*, •*)) = <52(y»(s), У(х)),
(*, у>(х)) е. ч> & (х, у(х)) G => (AjCs, х), А2(у>(х), у(х))) =
= ^((*, Н*)), (*, ¥<*))) G X =* Z(VS’ ХУ> =	V(x)),
откуда следует, что f—гомоморфизм автомата в автомат
АГ °
Переформулируем для автоматов общий результат о связи
между подалгебрами и гомоморфизмами.
Теорема 4.10. Пусть f: Л -* —гомоморфизм авто-
мата в автомат А^. Если Aj — (Sp Xj, У^, <3р	—
подавтомат в Лр то f(Aj) := (p(Sj), ip(Xj), x(^j)> $2’	—
подавтомат в А . Если А' = (S', X Y' д Л,)—подавтомат
в А2, то подавтоматом в будет f \л2) := (<р ^S^),
<‘(^2)’ %-1(У2)> д1’ Л1)‘
Доказательство. Пусть Aj е Sub уЦ и G
G <p(Sj), х^ G ¥’(^1)—произвольные элементы. Тогда найдутся
s G Sj и х( G Xj такие, что s2 = х2 = y’(Xj). Так как
d](Sp X]) G Sj и Л](Хр G Ур то, поскольку f е
G Нош (Лр Л2), имеем:
<32(s2, х2) =	^(Xj)) =	х)) G <p(Sj),
Л2(х2, x2) = ^(p^),	= x(Aj(Sp X])) G /(У/),
и, значит, /(ylj) G Sub A2-
Пусть теперь A2 G Sub A2. Если хотя бы одно из множеств
y?~1(S2), у>-1(Х2) пусто, то Г\а'^) G 5иЬЛр Допустим, что
p-1(S2) * 0 и у~1(Х2)	0. Тогда и x~\y2)	0. Возьмем
произвольные элементы & <р Х1	Используя
то, что А'2 G Sub А2, а /—гомоморфизм из уЦ в А2, получаем:
p(<\(Sp X])) = ^(Sj), ^(х^) G Sj,
%(Л1(5р X])) = A2(<p(s{), ^(Xj)) G Yj,
343
откуда djOj, x() G <p ’(Sp и -«p G z ’(УР> и> значит,
Л’(Лр G 5иЬЛг =
Подавтомат A{ автомата Л* называется насыщенным относи-
тельно гомоморфизма f: Л] -* А?, если имеет место равенство
(s;, х;, ур = (Ker/)(sp х;, ур :=
:= ((Кег^)(5р, (Кег^)(*р, (Кег х)(Ур),
где Кег /—ядро гомоморфизма /.
Т е о р е м а 4.11. Подавтоматы автомата Лр насыщен-
ные относительно гомоморфного наложения f: Л1 -* Л2, обра-
зуют решетку, изоморфную решетке Sub А^ подавтоматов
автомата А^.
Доказательство. Пусть е—отношение эквива-
лентности на непустом множестве А и В, С—некоторые е-насы-
щенные подмножества в А, т. е. е(В) = В и е(С) = С. Тогда В
и С представляют собой объединение е-классов, и, значит,
пересечение В Г) С будет объединением е-классов, содержащихся
одновременно в В и С. Отсюда е(В О С) = В О С, так что
пересечение е-насыщенных подмножеств е-насыщено. Отсюда и из
того, что пересечение двух подавтоматов имеет своими файлами
пересечение соответствующих файлов этих подавтоматов, получа-
ем замкнутость множества насыщенных относительно f подавто-
матов в А} по пересечению. Так как сам автомат А} насыщенный
относительно /, то согласно следствию из теоремы 1.34 § 1.4,
совокупность всех Кег /-насыщенных подавтоматов автомата
образует решетку. Конечно, эта решетка не обязательно будет
подрешеткой решетки Sub Л всех подавтоматов в Л1—могут не
совпадать операции объединения.
Пусть Л2 G 8иЬЛ2> Согласно теореме 4.10, А' = /-1(лр
будет подавтоматом автомата Лр Так как Кег/ = /°/-1, а
/-1°/ = А (тройка тождественных отображений на множествах
S2, Х2, У2), то
(Кег/)(Лр = (/о/-1)(Лр = /-1(/(Лр) = f-l(f(f-\A^ =
= /_1(^_1»/)(л')) = /-1(А(л')) =	= л;,
и, значит, Л^—насыщенный относительно / подавтомат автомата
Лр Ясно, что если А’2 * Л", то /-1(Лр * /-1(Лр. Наконец,
344
если А{—произвольный Кег/-насыщенный подавтомат автомата Л^
то л; = (Кег/)(Л1') = (/О/-1)(Л1')=/-1(/(Л1'))=/-1(лр, где
Л2 = /(Л^) является подавтоматом автомата (теорема 4.10).
Таким образом, сопоставляя каждому Л2 G Sub Л2 его /-про-
образ /-1(Лр, мы устанавливаем взаимно однозначное соот-
ветствие между решеткой Sub Л2 и решеткой всех насыщенных
относительно / подавтоматов автомата Лр Поскольку неравенство
/-1(Л') < /-1(Л") равносильно неравенству Л2 < Л", указанное
соответствие является порядковым изоморфизмом, о
Пусть Л = (S, X, Y, 6, Л)—произвольный автомат с непу-
стыми файлами S, X, Y. Тройка эквивалентностей в =
= (е, р, а), где е G E(S), р € Е(Х), а е E(Y), называется
согласованной с функциями (ЗиЛ переходов и выходов автомата
Л, если для любых $ 6 5 и х 6 X истинна импликация
s2) G е & (хр х2) G р =>
=> (d(sp X]), <3(s2, х2)) е е & (Л($г Xj), Л(х2, х2)) S а.
Из этого определения видно, что согласованные тройки
эквивалентностей на автомате—это в точности его конгруэнции
как трехосновной алгебры.
Очевидно, что на любом автомате А согласованными будут
тройки (А, А, А) и (S X S, X х X, Y х У). Далее, к числу
согласованных принадлежат все тройки вида (А, А, а), где
а G E(Y)—произвольная эквивалентность на У. Если тройка
(е, р, о) согласована, то согласованной будет и тройка
(е, А, а).
Тройка (е, А, А) согласована тогда и только тогда, когда
е—конгруэнция полуавтоматного редукта (S, X, 6), согласованная
с функцией выходов Л автомата А (см. § 4.2).
Непосредственно из определения получается
Теорема 4.12. Тройка эквивалентностей в = (е,
р, о) тогда и только тогда согласована в автомате Л, когда
она является подавтоматом прямого квадрата А х Л. о
Совокупность всех согласованных троек эквивалентностей на
автомате Л обозначим через С(Л).
Пусть в = (е, р, o') G С(Л). В соответствии с теорией
многоосновных алгебр (§ 4.2) определим факторавтомат авто-
мата Л по в, полагая
А/в := (S/e, Х/р, Y/a, д, Л),
где
(3(£(s), р(х)) := £(<3(s, х)),
Л(£(.$), р(х)) := a(A(s, х))
345
для любых s G S, х G X.
Обычная связь между гомоморфизмами и конгруэнциями
алгебр в данной конкретной ситуации приобретает следующую
формулировку.
Теорема 4.13. Если f ~ (<р, у, %)—гомоморфизм ав-
томата А, то Кег/ = (Кег <р, Кег^, Кег%) является согласо-
ванной тройкой эквивалентностей на А. С другой стороны, если
в = (е, р, a) G С(А)< то тройка отображений nat# : =
:= (nat е, natp, nat о) будет гомоморфизмом автомата А на
факторавтомат A/в и при этом Ker nat# = #. о
Пусть / = (<р, у, %)—гомоморфизм автомата А1 на автомат
А?. Согласно теореме 4.13, Кег / = (Кег <р, Кегу>, Кег %) G С(А).
Тогда, как уже отмечалось, будет согласованной и тройка
(Кег^>, А, Кег %). Положим А^ := ^/(Кег <р, А, Кег %), и через
g обозначим естественный гомоморфизм автомата А( на его
факторавтомат А{. Далее, если отождествить фактормножество
Х/А с самим X, то тройка (А, Кегу>, А), как нетрудно заметить,
окажется согласованной в автомате А{. Положим А" : =
:= А'/(Д, Кегу>, А), и через h обозначим естественный гомо-
морфизм автомата А^ на его факторавтомат А". Теперь мы видим,
что автомат А" изоморфен факторавтомату Aj/Ker/, причем
изоморфизмом является тождественная тройка А.
Покажем, что тройка (<р \ ip~l, %-1) является изоморфизмом
автомата А^ на факторавтомат А /Кег/. Очевидно, что отобра-
жения <р~х: S2 S{/Ker<p, Х2 -* XjKerip, %-1: У2 -*
-» Kj/Ker/ представляют собой взаимно однозначные соответствия
между указанными множествами. При этом для любых s2 G S2,
х2 е. Х2, если положить s2 =	х2 = ip(x{), где Sj G 5 ,
Xj G X , и через <5, Л обозначить функции переходов и выходов
факторавтомата А^Кег/, получаем:
<Р~'02^2’ х2^ =	=	\))) =
= Ker^d^Sj, хр) = <5(Кегр($р, Кегу>(хр) =
= ^-1(^2))'
Х-1(Л2(52>	=	V’(^P)) = X~l(x(*(sv х{))) =
=	хр) =Л(Кегу>($р, Ker^(xp) = A«‘(s2), ^“‘(хр),
346
откуда и следует, что тройка (р \ у» \ % ')—изоморфизм.
Если теперь определить i := ((nat Ker у>)-1 ° у>, (nat Ker У')-1 ° у,
(nat Ker /) 1 ° %), то проведенные рассуждения показывают, что
справедлива (см. [22])
Теорема 4.14. Пусть f—гомоморфизм автомата А на
автомат Ау Тогда существует, и
притом единственный, изоморфизм i
факторавтомата т^/Ker/ на авто-
мат Ау при котором коммутативна
диаграмма, представленная на рис.
117. о
Отдельно выделим часто применяе-
мое
Следствие 4.4. Если f—го-
моморфизм автомата на автомат
Ау то автомат А? изоморфен факторавтомату т^/Ker/. о
Пусть А, В—произвольные непустые множества, /: А -* В—
отображение и в G Е(В)—эквивалентность на множестве В.
Положим Кег^У := {(х, у) 6 А х А I (/(х), /(у)) 6 в}.
Легко проверяется, что Кег^/ является эквивалентностью на
множестве А. Она называется 9-ядром отображения /. В частности,
Ker f = Кег. /. Каждый класс эквивалентности Кег„/ представляет
А	и
собой объединение некоторого множества классов ядра Кег /
отображения /. Соотнося каждому 0-классу 9(b) его /-прообраз
/-1(0(5)), мы устанавливаем взаимно однозначное соответствие
между фактормножествами В/9 и Л/Кег^/.
Т е о р е м а 4.15. Пусть f = (р, ip, %)—гомоморфизм ав-
томата А на некоторый автомат А', и пусть 9' =
= (е1, р', ст')—согласованная тройка эквивалентностей в авто-
мате А'. Тогда тройка 9 = (е, р, а), где е = Кег^, <р,
р = Кег^, у>, о = Кег^,/, согласована в автомате А и фактор-
автоматы А/9 и А'19' изоморфны.
Доказательство. Пусть s,, s~ G S, x,, x_ G
•'121’2
G X—произвольные элементы. Тогда
($р s2) G e & (xr x2) G p => (5p s2) G Ker£,p & (xp x2) G
G Ker^y => (у(^), <p(s2)) G e' & (V’(Xj), ip(x2)) Gp' *
=*	V’Oj)),	V'(^2))) G e‘ &
347
&	Л'(^(х2), у>(х2))) G а' =>
=* Gp(<5(sp X])), y?(d(s2, х2))) G
G е' & (х(Л(5р X])), Х(^(«2> *2))) G <?' =>
=> (д(хг х^, d(s2> х2)) G Kerg, р = е & (A(s{, х^, Л(х2, х2)) G
G Кег , у = а,
откуда заключаем, что (с, р, a) G С(А).
Так как f G Hom (Л, А') и nat в' G Нот (Л', А'/в'), то
произведение /°nat0' этих гомоморфизмов будет гомоморфизмом
автомата Л на факторавтомат Л 70'. При этом, как нетрудно
заметить, Кег (/° nat 0') = Кег^,/ = 0. Согласно следствию 4.4
из теоремы 4.14, автоматы Л/0 и Л'/0' изоморфны, а
Пусть E(S), Е(Х), Е(У)—решетки эквивалентностей на фай-
лах автомата Л. Положим Е(А) := E(S) X Е(Х) х Е(У).
Теорема 4.16. Решетка С(А) согласованных троек
эквивалентностей в автомате А является подрешеткой решет-
ки Е(А).
Доказательство. В качестве вступительных за-
мечаний отметим, что £(Л) является решеткой как прямое
произведение решеток и что С(Л) представляет собой решетку
в силу следствия из теоремы 1.34 § 1.4: пересечение
0' л 0" := (е' П е", р' П р':, а' П а") двух согласованных тро-
ек согласовано и (5 х S, X х X, У х У) является наибольшей в
смысле покомпонентного включения из согласованных в автомате
Л троек.
Нужно показать, . что если 0', 0" G С(Л), то тройка
(е' У Е е", р' У р", o' VЕ а") также будет согласованной (здесь
У Е означает объединение в соответствующей решетке эквивален-
тностей). Пусть Sp s2 G 5, Хр х2 G X—произвольные элементы,
(s s-) е. е’ У е" и (х., хА £ р' У р". Согласно следствию
1.5 § 1.3, существуют элементы Г, (2, ..., G 5 такие, что
($., ?.) G е' & (J., (,) G е" & ...& (Л, G £",
11	£	At
и существуют элементы и^, и2, ..., uk G X, для которых
(Хр u() G р' & (Up u2) G р” & ...& (uA, х2) G р”
(в силу рефлексивности отношений £', е", р', р" длины обеих
выписанных последовательностей можно выровнять, добавляя
нужное число пар с одинаковыми элементами).
348
Так как тройки в' = (е', р', а') и 6" = (е”, р", о") согласо-
ваны в автомате Л, то
(<5(Sj, Xj), Ы])) G. e' & (Л(5р Xj), Л(<], «])) G a' &
& (d(^, a,), d(i2, u2)) G e" & (A(Zp uj, A(<2, a2)) G o" & ...
...& (6(tk, uk), d(s2, x2)) G e" & (A(tk, uk), A(s2, %2)) G ст",
откуда (<3(s x.), <3(5,, x,)) Ge' V e" и (A(s , x.), A(s,, x,)) G
g o' v E u".
Значит, (e' V£ e", p' V£ p", a' V£ ст") G С(Л). =,
Доказанная теорема означает, что операция объединения в
решетке С(Л) та же, что и в решетке £(Л), т. е. наименьшая
тройка эквивалентностей, содержащая две данные согласованные
тройки, уже будет согласованной.
Из определения порядка в прямом произведении решеток
(покомпонентное сравнение) следует, что
(е', р', ст’) < (е", р", ст") тогда и только
тогда, когда е' С е", р' С р" и ст' С ст".
Теорема 4.17. Если f G
G Hom , Л2) и 6 < Кег /, то сущест-
вует, и притом единственный, гомомор-
физм f G Hom (А /9, Л2), делающий
А./е
коммутативной диаграмму, представлен-
ную на рис. 118.
Доказательство. Пусть
А =	^1> Л’ ^1’	^2 = ^2’ ^2’ ^2’ ^2’ ^2^’
Рис. 118
/ = (?>. У'- /)>
6 = (е, р, ст), а <3, А обозначают соответственно функции
переходов и выходов в факторавтомате AJQ. Определим тройку
отображений / ' = (у7'полагая <р': Sjs -* S2 (e(s) >—> <p(s)),
4>’- Xjp - X2 (p(x) — V’W)> X'- YJ° -* Y2 (°V) ZW)’ где
s G Sj, x G X^, у G Yj—произвольные элементы. Тогда
p'(<3(£(s), p(x))) =	x))) = y>(<3j(s, x)) =
= 62(<p(s), У>(х)) = <32(^>'(e(5)), У>'(р(х))),
xW(s), P(x))) = x'(^i(s, X))) = x(At(s, X)) =
= A2(<p(s), y>(x)) = A2(p'(e(s)), y>'(p(x))),
откуда следует, что тройка /'= (<р', гр', /') является гомо-
морфизмом автомата А^в в автомат Л2. о
Следствие 4.5. Если в{, в2 G С(Л) а < в2, то
существует гомоморфизм автомата А/в^ на автомат А/в2.
349
Доказательство. Если в теореме 4.17 положить
А := А, Л2 := AlQ^, f := nat в2, в := 0р то получающийся
гомоморфизм f' и будет искомым. □
Приемы, использованные в предыдущих доказательствах,
позволяют без труда перенести на случай автоматов теорему 2.9
о соответствии. Именно, имеет место
Т е о р е м а 4.18. Если в—согласованная тройка в авто-
мате А, то решетка С(А/в) изоморфна интервалу 10, 1]
решетки С(А), где 1 := (S х S, X х X, Ух У), о
Автомат А = (5, X, У, д, А) называется простым, если
единственными согласованными тройками в нем являются обяза-
тельные тройки Д = (Д, Д, Д) и 1 = (5 X 5, X X X, Y X У).
Следующая теорема [67] дает полное описание простых автоматов.
Т е о р е м а 4.19. Автомат А с непустыми файлами S,
X, У будет простым автоматом тогда и только тогда, когда:
1) один из этих файлов имеет не более двух элементов, а два
других—одноэлементны, или 2) диаграмма автомата А пред-
ставляет собой цикл простой длины с одинаковыми метками
на дугах.
Доказательство. Необходимость.
Пусть А—простой автомат. Прежде всего заметим, что
IУ1 <2, иначе при yj * у2 тройка (Д$, Д^, Ду U {(ур у2),
(у2, У1))) будет согласованной и отличной от Д и 1.
Если IУ1 = 2, то ISI = 1X1 = 1, поскольку в противном
случае простоте автомата А будет противоречить согласованность
в нем тройки (Д , Д , Ух Y).
□ -А
Пусть IУ1 = 1. Тогда А^, х^ = А($2, х2) для любых
Sp s2 G S, Xp x2 G X, и, следовательно, любая конгруэнция
полуавтомата (S, X, <3) будет согласована с функцией выходов
автомата А, т. е. любая тройка вида (е, Д, Д), где е G Con А,
будет согласованной в А. Так как А—простой автомат, е = Д$
или е = S х S. Значит, полуавтомат (S, X, д) простой. Предпо-
ложим, что IXI >2. Тогда тройка (S х 5, Д^., Ду) будет
отличной от Д и 1 согласованной в А тройкой, что невозможно.
Итак, 1X1 = 1, откуда следует, что редукт (S, X, <5) является
простым автономным полуавтоматом. Согласно следствию 1.17
§ 1.4, граф переходов этого полуавтомата представляет собой цикл
простой длины. Диаграмма автомата А получается из упомянутого
графа разметкой дуг соответствующими элементами выходного
алфавита У. Так как I У1 = 1, все метки на дугах одинаковы.
Достаточность. Если выполнено условие 1), то
решетка Е(А) всевозможных троек эквивалентностей на файлах
автомата А содержит всего два элемента: Д и 1, так что автомат
А—простой. В случае 2) имеем 1X1 = IУ1 = 1, так что все
согласованные в А тройки имеют вид (е, Д, Д), где s—конгру-
350
энция полуавтоматного редукта (5, X, 6). В силу следствия 1.17
§ 1.4, е = Д$ или е = 5 х 5, и, значит, А не имеет согласованных
троек, кроме А и 1, т. е. является простым автоматом. □
Пусть (е, р, ст)—согласованная тройка эквивалентностей в
автомате А ж (5, X, У, <5, А). Тогда, как уже отмечалось,
согласованной в А будет и тройка (е, А, ст), откуда следует, что
е—конгруэнция полуавтоматного редукта (5, X, 6) автомата А.
Как в § 4.2, будем называть конгруэнциями автомата А
конгруэнции полуавтомата (5, X, <3).
Пусть е G Con А, т. е. е—конгруэнция автомата А. Положим
р(е) := {(хр х2) G X X X I (VSp s2 G 5)((Sp s2) G e =»
=» (<5(Sj, хр, <5(s2, x2)) G e)}. Так как e—конгруэнция, то
отношение р(е) будет рефлексивным. Его симметричность очевид-
на. Проверим транзитивность. Пусть (Хр х2) G р(е) и
(х2, х3) G р(е). Тогда для любых sp s2 G S из (Sp s2) G е
следует, что (<3(Sp х^, <3(s2, х2)) G е. Поскольку (s2, s2) G е,
то (<5(s2, х2), <5(s2, х3)) Ge. В силу транзитивности отноше
ния е получаем, что (<5(Sp Xj), <5(s2, х3)) G е. Значит,
(Хр х3) G р(е).
Итак, р(е) G Е(Х), и, значит, соответствие е 1—* р(е) отобра-
жает решетку Con А в решетку Е(Х).
Теорема 4.20. /э(е1 О е2) = р^) Cl р(е2) для любых
Ер е2 G Con Л.
Доказательство. Проверим включение р^) А
А р(е2) С р{ех П е2). Пусть (хр х2) G р^) А р(е2) и sp
s2 G S—произвольные состояния автомата А. Имеем:
(Sp s2) G £1 А е2 =» (Sp s2) G £j & (sp s2) G e2 =>
=* (<5(sp x^, d(s2, x2)) G £] & (<5(Sp X]), <3(s2, x2)) G e2 =»
=> (<5(Sp xf), <3(s2, x2)) G £j A e2,
откуда (Xp x2) 6 p(£j A e2).
Докажем обратное включение p(£j A e2) C p(£j) A p(e2).
Пусть (Xp x2) G p(el A e2). Тогда (<3(s, x(), <3(s, x2)) G
G £j A e2 для любого s G S. Отсюда получаем:
(Sp s2) G C1 => (<5(Sp X]), <5(s2, x^) G Ej &
& (<5(s2, Xj), <5(s2, x2)) G Ej A e2 C =>
=> (<5(Sp X]), <5(s2, x2)) G Ep
351
и, значит, (хр х2) 6 Р^)- Аналогично (Хр х2) G р(£2). Следо-
вательно, (Хр х2) G p(£j) Cl p(e2). □
Следствие 4.6. Соответствие е •—♦ р(г) является
изотонным отображением решетки Соп А конгруэнций авто-
мата А в решетку Е(Х) эквивалентностей на входном
алфавите X.
Доказательство. Пусть е С е Тогда е =
= £j П е2> Применяем теорему 4.20: р(ех) = р(ех П е2) =
= Cl р(е2), откуда р^) С р(е2). □
Из доказанного следствия вытекает, что р(ех V е2) 2
2 p(£j) V р(£2) для любых конгруэнций £р е2 автомата А.
Пусть теперь £—конгруэнция автомата А, а р—произвольная
эквивалентность на входном алфавите X. Положим
т(е, р) :=
:= A U {(у, у ) G У X У I (3 s , s G S)(3 х , х, G X)((s, s ) G e &
& (*!> *2> G P & ?1 = A<S1’ *1> & У2 = A(S2’
Из определения следует рефлексивность и симметричность
отношения т(е, р), так что оно является толерантностью на
множестве выходных сигналов У.
Наименьшее отношение эквивалентности, содержащее т(е, р),
обозначим через а(е, р). Согласно следствию 1.5 § 1.4,
(Ур у2) G <7(£, р) О (3Zp z2, ..., zk G У)((ур zp G r &
& (Zp z2) G т & (zk, y2) G T),
где т = т(е, p), а Ур y2 G У—произвольные элементы.
Теорема 4.21. ст(£1 V e2,pl V р2) = ст(£р pt) V а(е2, р?)
для любых £р £2 G Con А, рр р2 G Е(Х).
Доказательство. Проверим включение V
V £2, рх М р2) С <7(£р Р1) V ст(£2, р2). Пусть (Ур у2) G T(£j V £2,
Pj V р2). Тогда для некоторых s , s2 G S, Хр х2 G X таких,
ЧТО (Sp s2) G £j V £2 и (Xp x2) Gp( V p2, будет yj =
= A(Sp x^, y2 = Л(х2, x2). Согласно следствию 1.5 § 1.4, суще-
ствуют t , t7, ..., t, G S и и.,	..., и. G X, для которых
(Sp 9 G £j & (Zp t2) G £2 & (tk, s2) G £2,
(Xp Uj) G px & (Up u2) G p2 & (uk, x2) G p2
352
(длины цепочек можно считать одинаковыми в силу реф-
лексивности отношений бр е2, /Эр р2). Тогда
(Л(Хр Xj), A(Zp Mj)) G ст(ер Pj) & (Л(<р Uj), Л(<2> u2)) G
G CT(e2’ P^	(*(^> “*)’ A(s2’ x2^ G CT(e2> ^2>’
откуда (ур y2) = (A(Sp Xj), Л(«2, x2)) G o(ep P1) V a(e2, pj.
Итак, V e2, p} V p2) С a(ep Pj) V a(e2, p2), откуда и
следует доказываемое включение.
Докажем обратное включение сг(е , pj) V а(е2, р2) С
С v е2> р^ V р2), которое, впрочем, почти очевидно. Пусть
(Уг У2) G т(ер Pl). Тогда yj = Л(Хр Xj), у2 = Л(«2, х2) для
некоторых s , s G S, Хр х2 G X таких, что (^, s2) G и
(Хр х2) G /Эр Но так как £ fj V е2 и р{ С р^ м р?
то получаем, что (^, s2) G V e2, (xp x2) G px V p2, yJ =
= ЛЦ, x^, y2 = Л(х2, x2), откуда (yp y2) G V £2,p, V p2).
Следовательно, т(£р Pj) £ <7^ v e2, px V p2) и, значит,
o(£p Pj) £ o(£j V e2, р1 V p2). Аналогично ст(е2, p2) £
£ <7(£1 V £2, px M p2). □
Следствие 4.7. Соответствие (e, p) •—» a(£, p) яв-
ляется изотонным отображением решетки Con А х Е(Х) в
решетку Е(У).
Доказательство. Пусть (ег, рх) < (е2, р2), т. е.
£| £ £2 и pf £ р2 (порядок в прямом произведении решеток
устанавливается покомпонентным сравнением пар). Тогда
<е2’ Pl) = <е1’ ^1) V <е2’ ^2) = (е1 v е2’ Pl v Р2^- Применяем
теорему 4.21: ст(е2, р2) = а(е{ V е2, р{ V р2) = а(ег р{) V
v ст(е2> Р2У' откУДа CT(ei> Pi) - а(£2’ Рг)’ D
Из доказанного следствия вытекает, что П е2, р^ П р2) £
£ a(ev pj) (Т ст(е2, р2) для любых Ej, е2 G Соп А и р}, р2 G
g ад.
Следующая теорема [26] показывает, что если известна
решетка Соп А конгруэнций автомата А, то достаточно просто
могут быть получены все согласованные тройки этого автомата.
Т е о р е м а 4.22. Тройка эквивалентностей (е, р, <э) тог-
да и только тогда согласована в автомате А = (S, X, У, <5, Л),
когда е—конгруэнция полуавтоматного редукта (S, X, д) и
имеют место включения р £ р(е) и а 2 <т(£, р).
Доказательство. Необходимость.
Пусть (е, р, ст) G С(А). Тогда, как уже отмечалось, е G Соп Л.
353
Если (Хр Х2) 6 Р, ТО ДЛЯ любых Sp $2 6 S из того, что
(s,, s,) 6 е, следует, что (<5(s., х.), <3(s,, х,)) 6 е. По опреде-
лению отношения р(£), имеем (Хр х2) 6 р(е). Следовательно,
Р С Р(е)-
Предположим, что (у, у2) G т(е, р). Тогда существует
s , s, G S, х , х, G X такие, что (s., s,) 6 £, (х., х,) G р и
l(Sp х^ = Ур A(s2, х2) = у2- Так как тройка (е, р, а)—согла-
сованная, то (ур у2) = (A(Sp Xj), l(s2, х2)) G а. Значит,
т(е, р) С а. Отсюда сг(£, р) £ а.
Достаточность. Пусть £ 6 Con А, р С р(е) и
а 2 <т(£, р). Возьмем произвольные элементы Sp s2 G S,
Xp x2 G Хи предположим, что (Sp s2) G e, (Xp x2) G p. Так
как (Xp x2) G p(£), to (<5(Sj, Xj), <3(s2, x2)) G e. Кроме того, из
определения эквивалентности а(е, р) следует, что (l(Sp Xj),
l(s2, х2)) G cr(£, р) С а. Таким образом, если (Sp s2) G е и
(Хр х2) G р, то (<3(Sp хр, <3(s2, х2)) G £ и (A(Sp Xj),
l(s2, x2)) G cr, t. e. тройка (e, p, а) согласованная, о
П p и м e p 147. Проиллюстрируем процесс построения ре-
шетки согласованных троек автомата на простейшем примере.
Пусть автомат А задан таблицей
и диаграммой,
изображенной
s3	0	1
$з	0	1
s2	0	1
S]	0	1
на рис. 119.
(SxS, Ххх, YxY)
Рис. 120
354
Единственной собственной нетождественной конгруэнцией ав-
томата А является в = {х]5 s3), {s2, s4), так что решетка
Con А конгруэнций этого автомата является трехэлементной цепью
(рис. 120а).
В силу теоремы 4.22 ключевым моментом в поисках согласо-
ванных троек автомата А является построение эквивалентностей
р(е) е Е(Х) и а(е, р) е £(У), где е пробегает множество всех
конгруэнций автомата А. В следующей таблице определяются все
согласованные тройки рассматриваемого автомата А.
е	Р(£)	Р	а(г, р)	а	Согласованные тройки
д	Д	Д	Д	д	(Д, Д, )Д
				Ух Y	(Д, Д, У х У)
в	X х X	Д	Д	Д	(0, д, Д)
				Yx Y	(в, Д, У X У)
		X х X	УХУ	Ух Y	(б, X х X, У х У)
5 х 5	X х X	Д	Д	Д	(5 х 5, Д, Д)
				Уху	(5 х 5, Д, У х У)
		X х X	Y X У	Уху	(5 х 5, X х X, У х У)
В первом столбце перечисляются все конгруэнции автомата А.
Во втором для каждой конгруэнции е вычисляется эквивалентность
Р(£) с х х X. Третий столбец содержит варианты выбора эквива-
лентности р £ /э(е). В четвертом для каждого выбранного р
строится эквивалентность <?(£, р) С У х У. Пятый столбец пред-
лагает возможности для конкретных значений эквивалентности
о 2 о(е, р). Наконец, в последнем столбце выписываются согла-
сованные тройки—для данной конгруэнции е с заданными
эквивалентностями р С р(е) и а 2 сг(£, р).
Решетка всех согласованных троек автомата А показана на
рис. 1206 (напомним, что тройки сравниваются покомпонентно).
§ 4.4. Представление языков в автоматах
Одной из важнейших характеристик автомата является его
взаимодействие с внешней средой, в роли которой выступает
множество всех слов над входным алфавитом. В точной фор-
мулировке поведение автомата описывается следующим образом.
Пусть X—некоторый конечный алфавит, X —множество всех
(включая пустое) слов в этом алфавите. Говорят, что язык
L С X * представлен в автомате А = (S, X, У, <5, Л) начальным
состоянием sQ 6 S и заключительным подмножеством F Q S,
если
L = {Р е х*\d(sQ, р) е Л}.
355
Язык L С X * называется представимым, если он может быть
представлен в некотором автомате при подходящем выборе
начального состояния и заключительного подмножества. Пред-
ставимые языки называют также распознаваемыми.
Поскольку в приведенных определениях не участвуют ни
выходной алфавит Y, ни функция выходов А, речь, по существу,
идет о представлении языков в полуавтоматах. В дальнейшем мы
будем придерживаться именно такой точки зрения.
Теорема 4.23. Язык L С X* представим тогда и
только тогда, когда существует гомоморфизм >р моноида X* в
некоторый конечный моноид А*, для которого L = (Ker
Доказательство. Необходимость.
Пусть L представлен в полуавтомате А “ (S, X, д) начальным
состоянием s0 и заключительным подмножеством F С S.
Рассмотрим отображение р: X * F(S х S), р •—* др, где
<3 : S -* S, s ►—» <3(s, р). Используя свойства расширенной функ-
ции переходов, получаем
<P(P1P2)(S) = Spp® = <5(s> pip2> = d(d(s' р1>’ p2> =
=	=	° дР2)(х) =	°
откуда следует, что >р сохраняет умножение. Поскольку для
пустого слова е будет <р(е) = Д, то <р оказывается гомоморфизмом
моноида X * в конечный моноид всех преобразований F(S х S)
множества S.
Так как Д*,. С Ker <р, то L = Д(Ь) С (Ker <p)(L). С другой
стороны, если q G (Ker то существует слово р € L такое,
что (р, q) G Кег р, т. е. <р(р) = <p(q). В частности, (y>(p))(s0) =
= (Р(<7))(*о)> откуда <3(s0, q) =	= (<p(q))(sQ) = (<p(p))(sQ) =
= <3p(s0) = <3(s0, P) G и’ значит, q G L. Следовательно,
(Ker<p)(L) C L.
Достаточность. Пусть L = (Ker y>)(£) для неко-
торого гомоморфизма <p моноида X * в конечный моноид А.
Рассмотрим полуавтомат А = (X */Ker <р, X, <3), где
<5((Кег <р)(р), х) := (Кег у>)(рх) для любых х G X, р G X*. Опре-
деление функции переходов не зависит от выбора представителей
в Кег ^-классах, поскольку Кег <р—конгруэнция моноида X *.
Язык L представим в построенном полуавтомате А, если в
качестве начального состояния выбрать класс (Кег у?)(е), а в
качестве заключительного подмножества—совокупность L/Ker <р
классов конгруэнции Кег >р, содержащих элементы подмно-
356
жества L С X *. Действительно, для любого р G X * имеем
<3((Кег у>)(е), р) = (Кег р)(ер) = (Кег р)(р). Поэтому, если р G L,
то (Кег <р)(р) входит в заключительное подмножество. Если
же (Кег <р)(р) е £/Кег <р, то для некоторого q G L будет
(р, q) G Кег <р, а поскольку (Ker р)(£) = L, то q G L. □
Множество Р(Х *) всех языков в алфавите X является
полукольцом относительно операций теоретико-множественного
объединения и конкатенации (см. § 2.3). Матрицей над этим
полукольцом будет матрица М переходов полуавтомата А “
“ (S, X, <3), элементы которой определяются формулой
М.. := {х G XI <3(s., х) = Sj}.
Если элементы множества X, как это принято, считать
однобуквенными словами, то элементы матрицы М можно
рассматривать как некоторые языки над X. Положим = Е,
где
Е ,= (И ПРИ г = л
v 10 в противном случае.
При к > 0 матрица Мк (возведение матрицы в степень
производится над полукольцом (X*, U, •)) имеет своими элемен-
тами языки следующего вида:
(Мк).. = {р 6 Х*| 1р1 = к & 6(s., р) = S/}.
Пусть первая строка (и первый столбец) матрицы М
закреплены за начальным состоянием s0 полуавтомата А. Тогда
для языка L, представимого в полуавтомате А заключительным
подмножеством F С S, получаем следующее выражение:
00
L = U U (Мк)
s Ef к=0
i
00
Полагая М* := U Мк, находим, что L = U (М'). ..
к=0	sEF
i
К имеющимся операциям объединения и конкатенации языков
добавим еще итерацию L •—» L*, полагая
00
L* := U Lk.
к=0
Пусть б(Л)—орграф, сопоставляемый полуавтомату А =
= (S, X, б) (см. § 3.2). Дугу (s., пометим элементом М..
матрицы переходов этого полуавтомата. Полученную сеть будем
называть диаграммой полуавтомата А (в общем, это не противо-
речит понятию диаграммы автомата, определенному во введении:
357
просто все дуги, ведущие из s. в s^., заменяются одной дугой, на
которой выставляется объединенная метка).
Пример 148. Рассмотрим полуавтомат
л х( х2
с диаграммой, изображенной
на рис. 121, и матрицей перехода
М =
Ц}
0
0
{*2}
Ц}
0
0
{х2}
Пусть начальным состоянием будет а заключительным
подмножеством F =	s2}. Поскольку
~	„	(Л/*).. = х* а (М\, = х*х-,х* то язык
—1	/д'	7	1 V 7	12 1
пРеДставимый в полуавтомате А, имеет
/ 8г	вид L = х* U х*х^х* (мы опускаем фигур-
/^2	ные скобки у выражений типа {х^*).
5д/	Структуру языка L в рассмотренном
примере легко выяснить, обращаясь к диаг-
рамме полуавтомата А: находим всевозмож-
Рис. 121	ные переходы из начального состояния $
в заключительные состояния $j и s^, и
словами языка L будут в точности последовательности входных
сигналов, выписываемые при прохождении таких маршрутов.
В дальнейшем нам потребуется более общая схема. Диаграм-
мой над алфавитом X (или Х-диаграммой) будем называть
ориентированную сеть, дуги которой помечены подмножествами
множества X U {е}, где е—пустое слово. Очевидным примером
Х-диаграммы может служить диаграмма переходов любого полу-
автомата с входным алфавитом X. Такого рода диаграммы
называются автоматными. Автоматные диаграммы выделяются из
всех A-диаграмм двумя требованиями: 1) в них не используется
пустое слово е; 2) метки дуг, исходящих из произвольной
вершины, образуют разбиение множества X.
Пусть D = (V, а, р)—некоторая Х-диаграмма (здесь р:
а -» Р(Х U {е})—функция, сопоставляющая каждой дуге орграфа
(V, а) ее метку). Маршрутом, ведущим из вершины и в вершину
v, называется любая последовательность примыкающих дуг (т. е.
конец каждой дуги является началом следующей), первая дуга в
которой имеет начало и, а последняя—конец v. Каждому маршруту
П диаграммы D соответствует язык Л(П) £ X , представляющий
358
собой конкатенацию всех меток вдоль этого маршрута. Пусть
П(ц, v)—множество всех D-маршрутов из и в у. Будем говорить,
ф
что язык L С X представим в диаграмме D начальной
вершиной v0 и заключительным множеством вершин VQ С V,
если L = U (£(П) I П G П(у0, v) & v G Уф}. Языки, представи-
мые в диаграммах при подходящем выборе начальных вершин и
заключительных подмножеств, называются диаграммно пред-
ставимыми.
Теорема 4.24. Класс диаграммно представимых языков
совпадает с классом языков, представимых в автоматах.
Доказательство. Каждый язык, представимый в
некотором полуавтомате, представим в диаграмме этого полуав-
томата, так что смысл теоремы в том, чтобы для языка L,
представленного в некоторой Х-диаграмме D = = (V, а, р),
найти полуавтомат А » (S, X, <5), представляющий этот язык.
Пусть U С V, х € X. Через U* обозначим множество таких
вершин и G U, из которых исходит хотя бы одна дуга с меткой,
содержащей символ х. Подмножество U С V назовем замкнутым,
если a(t/e) £ U, т. е. если концы всех дуг, исходящих из U и
имеющих в своих метках символ е, лежат в U. Наименьшее
замкнутое подмножество, содержащее U С V, обозначим через
U. Очевидно, что U—пересечение всех замкнутых подмножеств,
включающих U. Заметим, что пустое подмножество 0 замкнуто.
Состояниями полуавтомата А, по определению, будут всевоз-
можные замкнутые подмножества диаграммы D (их конечное
число, так как V конечно). Далее, для произвольных D 6 S,
х G X положим <5 (и, х) := а((/р, т. е. входной сигнал х
переводит замкнутое подмножество U в наименьшее замкнутое
подмножество, содержащее концы всех таких исходящих из U
дуг, в состав меток которых входит х. В частности, если
U* = 0, то d(U, х) = 0.
Пусть язык L представлен в диаграмме D начальной вершиной
v0 и заключительным подмножеством Уо С V. Покажем, что L
представим в полуавтомате А начальным состоянием s0 := {v^}
и заключительным подмножеством F := {(/ С V I U =
= U 8г U Q Уф * 0} (т. е. F состоит из замкнутых подмно-
жеств, содержащих хотя бы одну заключительную вершину).
Если р*е и р 6 L, то в алфавите X U {е} найдется слово
р = ZjZ2 ... zn такое, что р получается из р исключением символа
е во всех его вхождениях и при этом в D имеется маршрут
v„v,у- ... у ,у , где у € Vn и z. G p(v. ,, v), 1 < i < n.
0 1 2 n-l n’	n 0 i i-Г P
359
Заметим, что при z. = е для некоторого i будет v. G {vf_ j}, так
что обе вершины v _], v. окажутся элементами одного состояния
полуавтомата А. Тогда слово р переведет начальное состояние
s0 = в заключительное состояние {vn_^.}, где i—длина
максимального конечного отрезка в слове р, состоящего только
из символов е (может случиться, что j = 0). Если же р = е, то
в D существует маршрут из в некоторую заключительную
вершину у €= VQ, все метки вдоль которого содержат символ е.
Но тогда у е {v0} и в полуавтомате А начальное состояние $0
будет одним из заключительных состояний, так что пустое слово
р == е представимо в А.
Теперь рассмотрим произвольное слово р = х. х. ... х. над X,
1 2 п
переводящее начальное состояние полуавтомата А в одно из
заключительных состояний s. €= F. Положим s. : =
‘п	‘к
:= <5($0, х. х. ...х.), 1 < к < п. Согласно определению множе-
1 2 к
ства состояний 5 и функции переходов <5 полуавтомата А, в
диаграмме D существует последовательность вершин v0 = у(°\
у<°), у(Ч У<Х\ у<"\ у<"\ где у?-1) €	=
х 1 х	1 х	х	1 х 1
*к
= a(v^-1)), х. G ^(у(2А-1),	1 - & - n- При этом из
к
вершины в вершину у^ ведет некоторый маршрут П^, каждая
дуга которого в своей метке содержит символ е (здесь
0 < к < л), a G VQ. Теперь конкатенация меток дуг вдоль
маршрута	дает язык, содержащий
слово р. Следовательно, р 6 L. □
Как и каждому полуавтомату, каждой Х-диаграмме D =
= (V, а, р) сопоставляется матрица переходов М. Ее строчки и
столбцы нумерованы вершинами диаграммы, и М.. :=
:= р(у, у.) С X U {е}. Если первая строка (и первый столбец)
матрицы М закреплены за начальной вершиной У] диаграммы
D, то язык L, представленный в этой диаграмме начальной
вершиной Vj и заключительным множеством вершин Уо С V,
можно записать в виде L = U (М *)j ..
подмножеств алфавита X путем применения конечного числа
объединений, конкатенаций и итераций.
Следующая теорема Клини дает характеризацию языков,
представимых в автоматах.
Т е о р е м а 4.25. Регулярные языки, и только они, пред-
ставимы в автоматах.
Доказательство. Сначала покажем, что любой
представимый язык регулярен. Для этого установим, что если
D—произвольная диаграмма над алфавитом X и М—матрица
переходов этой диаграммы, то все элементы матрицы М * являются
регулярными языками. Отсюда и будет следовать требуемое
утверждение.
Доказательство ведется индукцией по размерности п матрицы
М, т. е. по числу вершин диаграммы.
При п = 1 диаграмма состоит из одной вершины, которая
будет начальной и заключительной одновременно, и одной петли,
меткой которой является конечное подмножество L С X U {е}.
Язык, представимый в этой диаграмме есть не что иное, как
итерация L* языка L.
Пусть доказываемое утверждение справедливо при п = к, т. е.
для любой ^-вершинной Х-диаграммы все элементы матрицы
М * являются регулярными языками. В произвольной Х-диаграмме
D с к + 1 вершинами у2, ..., у^+] рассмотрим поддиаграмму
D^, получающуюся удалением начальной вершины у( и всех
связанных с нею дуг. Матрицу переходов этой поддиаграммы
обозначим через М, а матрицу переходов диаграммы D—через
М. Тогда М имеет вид, показанный ниже
Л/ц
^21
Мк+\, 1
М =
М\2 •••	М\,к+\
|---------------------
I
। м
।
Так как (М*)	= U {ЦП) I П G П(Ур Vj)}, то необходимо
описать все маршруты в диаграмме D, начинающиеся и заканчива-
ющиеся в начальной вершине Ур В принципе имеются два типа
таких маршрутов. Во-первых, это многократное прохождение петли
в вершине Ур
и во-вторых,
маршруты вида у( уП vv( ,
где
i, j > 2, а П G П(у;, у^.). Заметим, что П—это маршрут в
поддиаграмме D^. Из этих соображений получаем, что
361
/	/ к+1	__ n1
(M‘)n = м и и М ,(М‘) м .
к к i,y=2	J /I
Поскольку Л/ц, Л/j., Л/ при всех i, j > 2 будут конечными
подмножествами алфавита X U {е}, а элементы матрицы М *
согласно предположению индукции являются регулярными язы-
ками, то из указанного представления следует, что (Л/ *) —регу-
лярный язык над X.
Аналогичным образом классифицируя маршруты из вершины
Vj в вершину у, i > 2, имеющиеся в диаграмме D, находим
(A/‘)h. =	U (М‘)11М1.(М‘)11М1.)‘.
Так как (Л/*)п (по доказанному) и (М*).. (по предположению
индукции)—регулярные знаки, то регулярным будет и язык
(Л/*) при любом 2 < I < к + 1.
Для i > 2 имеем
(Л/*)п
(к+1 _
и	(М‘)
и’
и следовательно, (Af*)zl—регулярный язык при всех 2 < i
< к + 1. Наконец, при i, j > 2 получаем
(М*).. = (Л/у и М^Щ*,
что снова дает регулярный язык вследствие регулярности языка
(м‘)п.
Таким образом, все элементы матрицы М* оказываются
регулярными языками.
Теперь покажем, что каждый регулярный язык над произволь-
ным алфавитом X представим в некотором полуавтомате с входным
алфавитом X.
Прежде всего, нужно построить полуавтоматы, представляющие
конечные (включая пустое) подмножества множества X. Впрочем,
в силу теоремы 4.24, можно (что проще) конструировать
соответствующие диаграммы. Пустой язык 0 представляет диаг-
рамма с вершинами У] и у2, единственной дугой которой является
петля в Ур имеющая метку е,—если начальной вершиной считать
Ур а заключительной—у2> Для языка {х. , х. , ..., х.} С X строим
диаграмму с вершинами vQ (начальная), у, ..., у^ (множество
362
заключительных вершин), в которой дуга (v0, у^) помечена
символом х., 1 < j < к.
>
Пусть регулярные языки Ll и представлены в полуавтоматах
А и В соответственно, причем в А начальным состоянием является
$0> в В таковым будет tQ, а заключительными подмножествами—F
(в Л) и Ф (в В). Изобразим диаграммы полуавтоматов Л и В и
проведем дополнительную дугу ($0, Q, снабдив ее меткой е. Легко
видеть, что полученная диаграмма представляет язык Ll U
начальной вершиной $0 и заключительным подмножеством
F U Ф.
Чтобы представить конкатенацию упомянутых языков, к
диаграммам полуавтоматов Л и В присоединим множество дуг
F X {?0}, помечая каждую из них символом е. При этом начальной
вершиной построенной диаграммы будем считать $0, а за-
ключительным подмножеством—Ф.
Наконец, итерация Л* языка L, представленного в полуавто-
мате Л начальным состоянием $0 и заключительным подмноже-
ством F, представляется в диаграмме, получаемой из диаграммы
полуавтомата Л добавлением множества дуг F X {sQ} с меткой е
каждая. При этом начальным (и единственным) заключительным
состоянием объявляется
По определению, каждый регулярный язык над X получается
из конечных (включая пустое) подмножеств алфавита X при
помощи конечного числа объединений, конкатенаций и итераций.
Используя описанные конструкции и теорему 4.24, можем для
каждого регулярного языка построить представляющий его полу-
автомат. о
Поскольку в каждом конкретном полуавтомате может быть
представлено лишь конечное число языков над данным алфавитом
X, и поскольку имеется счетное число попарно неизоморфных
полуавтоматов, то множество регулярных (т. е. автоматно пред-
ставимых) языков над X счетно. Однако множество Р(Х *) всех
языков над X континуально. Поэтому должны существовать
нерегулярные языки.
Пример 149. Над однобуквенным алфавитом X = {1}
рассмотрим язык L := {р G Х*1(зк G N)(lpl = к2)}, состоя-
щий, таким образом, из слов, длинами которых являются квадраты
натуральных чисел. Предположим, что L представлен в некотором
автономном полуавтомате А начальным состоянием $0 и за-
ключительным подмножеством F. Не теряя общности, можно
считать А связным полуавтоматом. Тогда орграф D(A) представ-
363
ляет собой цикл с входящей в него цепью, начинающейся в $
Существуют ли в F циклические (т. е. принадлежащие циклу)
состояния? С одной стороны, ответ должен быть утвердительным,
ибо какой бы длинной ни была цепь, при достаточно большом к
мы войдем в цикл и останемся в нем. С другой стороны, если
входное слово длины Л2 привело полуавтомат в циклическое
состояние s £ f, то следующие 2к + 1 шагов (до завершения
входной последовательности длины (к + I)2) дадут состояния, не
входящие в F. Учитывая, что расстояние между соседними
квадратами может быть сколь угодно большим, приходим к
выводу, что в цикле не должно быть заключительных состояний.
Невозможность ответить на поставленный вопрос и доказывает
непредставимость, т. е. нерегулярность языка L.
СПИСОК ЛИТЕРАТУРЫ
1.	Агибалов Г.П. Дискретные автоматы на полурешетках.—Томск, 1993.
2.	Артамонов В.А., Салий В.И., Скорняков Л.А., Шеврин Л.Н., Шульгей-
фер Е.Г. Общая алгебра.—М.: Наука, 1991.—Т. 2.
3.	Бабак С.Ф., Ильясов Б.Г., Кабельное Ю.С. Об одном подходе к построению
структурной теоррии систем //Изв. РАН. Теория и ситстемы упр.—1995.—
№ 2.—С. 15—21.
4.	Биркгоф Г. Теория решеток.—М.: Наука, 1984.
5.	Биркгоф Г., Барти Т. Современная прикладная алгебра.—М.: Мир, 1976.
6.	Богомолов А.М. Частичные тесты //Кибернетика.—1973.—№ 2.—С. 10—22.
7.	Богомолов А.М., Барашко А.С., Грунский И.С. Эксперименты с автоматами.—
Киев: Наукова думка, 1973.
8.	Богомолов А.М., Грунский И.С., Сперанский Д.В. Контроль и преобразования
дискретных автоматов.—Киев: Наукова думка, 1975.
9.	Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля
и анализа дискретных устройств.—Саратов, 1986.
10.	Богомолов А.М., Сытник А.А. Универсальные конечные автоматы //Докл.
АН СССР —1987.—Т. 294, № 3.—С. 4—9.
11.	Богомолов А.М., Твердохлебов В.А. Применение тео- рии бинарных отно-
шений к контролю и поиску неисправностей сложных систем //Вычислитель-
ные методы и программирование для «Урал-2» и «Урал-4».—Саратов,
1966.—С. 103—127.
12.	Богомолов А.М., Твердохлебов В.А. Диагностика сложных систем.—Киев:
Наукова думка, 1974.
13.	Богомолов А.М., Твердохлебов В.А. Целенаправленное поведение автоматов.—
Киев: Наукова думка, 1975.
14.	Брауэр В. Введение в теорию конечных автоматов.—М.: Радио и связь, 1987.
15.	Бродский Г.М. Алгебраическая теория автоматов.—Ярославль, 1988.
16.	Вагнер В.В. Теория отношений и алгебра частичных отображений //Теория
полугрупп и ее приложения.—Саратов, 1965.—С. 3—178.
17.	Верзаков Г.Ф., Кишит И.В., Рабинович. В.И., Тимэнен Л.С. Введение в
техническую диагностику.—М.: Энергия, 1968.
18.	Гилл А. Введение в теорию конечных автоматов.—М.: Наука, 1966.
19.	Глушков В.М., Цейтлин Г.Е., Ющенко Е.А. Алгебра, языки, программи-
рование.—Киев: Наукова Думка, 1978.
20.	Горелов О.И. Поиск дефектов в сложных технических системах методами
анализа диагностических графов //Автоматика и телемеханика.—1989. № 9.—
С. 148—159.
21.	Гороховский С.С., Рысцов И.К. Об изоморфизме графов отображений //Кибер-
нетика.—1982,—№ 6,—С. 117—118.
22.	Дидидзе Ц.Е. О гомоморфизмах автоматов //Тр. Вычисл. центра АН
ГрузССР.—1973 —12, № 1,—С. 118—131.
23.	Житомирский Г.И. Основные понятия универсальной алгебры.—Саратов,
1981.
365
24.	Ильичева И.П. Гомоморфизмы и композиции конечных автоматов //Саратов,
гос. ун-т.—Саратов, 1986.—28с.; Деп. в ВИНИТИ 10.07.86, № 5018—В86.
25.	Ильичева И.П., Печенкин В.В. Контроль структурных автоматов по стабильным
отношениям //Методы и системы технической диагностики. Вып. 5.—Саратов,
1985.—С. 31—43.
26.	Кабанов М.А. Функциональные конгруэнции ориентированных графов //Упо-
рядоченные множества и решетки. Вып. 11.—Саратов, 1995.—С. 15—23.
27-	Кац М.М. Об упорядочиваемое™ автоматов //Упорядоченные множества и
решетки. Вып. 11.—Саратов, 1995.—С. 24—31.
28.	Киреева А.В. О некоторых соответствиях между решеткой подавтоматов и
решеткой конгруэнций автомата //Упорядоченные множества и решетки.
Вып. 10.—Саратов, 1991.—С. 51—56.
29.	Киреева А.В. Подграфы и факторизации функциональных графов //Успехи
мат. наук.—1993.—Т. 48, № 2.—С. 183—184.
30.	Киреева А.В. Отказоустойчивость в функциональных графах //Упорядоченные
множества и решетки. Вып. 11.—Саратов, 1995.—С. 32—38.
31.	Кострикин А.И. Введение в алгебру.—М.: Наука, 1977.
32.	Кофман А. Введение в теорию нечетких множеств.—М.: Радио и связь, 1982.
33.	Кривой С.Л. Алгоритмы вычисления конгруэнтных замыканий конечных
автоматов и некоторые их приложения //Кибернетика и системный анализ.—
1994.—№ 1,—С. 34—44.
34.	Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автома-
тов.—М.: Наука, 1985.
35.	Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инжене-
ра.—М.: Энергоатомиздат, 1988.
36.	Кулик В.Т. О наибольших сильных отношениях конгруэнтности частичных
универсальных алгебр //Исследования по алгебре. Вып. 2.—Саратов, 1970.—
С. 40—46.
37.	Лаврушин В.И. Об изоморфизмах автономных автоматов //Методы и системы
технической диагностики. Вып. 5.—Саратов, 1985.—С. 43—49.
38.	Лекции по теории графов /Емеличев В.А., Мельников О.И., Сарванов В.И.,
Тышкевич Р.И.—М.: Наука, 1990.
39.	Лидл Р., Пильц Г. Прикладная австрактная алгебра.—Екатеринбург, 1996.
40.	Логвинов Ю.Н., Фалькович М.А. Формализация задачи диагностирования в
теории систем //Техническая диагностика.—Ростов-на-Дону, 1982.—С. 65—71.
41.	Мальцев А.И. Итеративные алгебры Поста.—Новосибирск, 1976.
42.	Майника 3. Алгоритмы оптимизации на сетях и графах.—М.: Мир, 1981.
43.	Мелихов А.Н. Ориентированные графы и конечные автоматы.—М.: Наука,
1971.
44.	Оре О. Теория графов.—М.: Наука, 1968.
45.	Папшев С.В. Об изоморфизме конечных автоматов.—Саратов: Саратов, гос.
ун-т, 1989,—40 с.; Деп. в ВИНИТИ 31.05.89, № 4212—В89.
46.	Пархоменко П.П., Согомонян КС. Основы технической диагностики.—М.:
Энергоиздат, 1981.
47.	Печенкин В.В. Структурные свойства контролирующих автоматов //Методы и
системы технической диагностики. Вып. 6.—Саратов, 1987.—С. 46—53.
48.	Плоткин Б.И., Григлаз Л.Я., Гварамия А.А. Элементы алгебраической теории
автоматов.—М.: Высшая школа, 1994.
49.	Салий В.Н. Решетки с единственными дополнениями.—М.: Наука, 1984.
50.	Салий В.Н. О булевозначных автономных автоматах //Методы и системы
технической диагностики. Вып. 6.—Саратов, 1987.—С. 53—59.
51.	Салий В.Н. Универсальная алгебра и автоматы.—Саратов, 1988.
52.	Скорняков Л.А. Элементы алгебры.—М.: Наука, 1980.
53.	Спивак М.А. Введение в абстрактную теорию автоматов.—Саратов, 1970.
54.	Урастаев Д.Д. Инъективные автоматы //Теория полугрупп и ее приложения.
Вып. 9.—Саратов, 1988.—С. 83—86.
55.	Харари Ф. Теория графов.—М.: Мир, 1973.
366
56.	Хрусталев П.М. Контрольные отношения в дискретных устройствах.—Саратов:
Саратов, гос. ун-т, 1985 —68с.; Деп. в ВИНИТИ 25.12.85, № 8811—В85.
57.	Шахбазян КВ. Решетки процессов в графах со входами //Кибернетика и
системный анализ.—1995.—№ 1.—С. 23—29.
58.	Шрейдер Ю.А. Равенство, сходство, порядок.—М.: Наука, 1971.
59.	Яблонский С.В. Введение в дискретную математику.—М.: Наука, 1979.
60.	Babcsanyi /., Nagy A. Mealy-automata in which the output-equivalence is a
congruence //Acta cybem.—1994.—V. 11, № 3.—P. 121 — 126.
61.	Barsi F., Grandoni F., Maestrini P. A theory of diagnosability without repair
//IEEE Trans. Cotnput.—1976.—C. 25, № 6.—P. 585—593.
62.	Beineke J.W., Wilson R.J. A survey of recent results on tournaments //Recent
Adv. Graph Theory. Proc. Symp.—Prague: Academia, 1975.—P. 31—48.
63.	Birkhoff G., Lipson JD. Heterogeneous algebras Hi. Combin. Theory.—1970.—
V. 8, № 1.—P. 115—133.
64.	Birkhoff G., Lipson J.D. Universal algebra and automata //Proc. Tarski Symp'
(Proc. Symp. Pure Math., V. 25). V. 2.—Providence, R.I., 1974.— P. 41—51.
65.	Book R.V., Chandra A.K. Inherently nonplanar automata //Acta Inform. —1976.—
V. 6, № 1,—P. 89—94.
66.	Booth KS. Isomorphism testing for graphs, semigroups, and Pinite automata are
polinomially equivalente problems //SIAM J. Comput.—1978.—V. 7, № 3.—
P. 273—279.
67.	Casanescu V.E. Quelques proprietes algebriques des automates //Discrete Math.—
1972.—V. 2, № 2 —P. 97—109.
68.	Dicker R.M. The substitutive law //Proc. London Math. Soc.—1963.—V. 13.—
P. 493—510.
69.	Eilenberg S. Automata, languages, and machines. Vols. A.B.—N.Y.: Academic Press,
1974, 1976.
70.	Farr E.H. Lattice properties of sequential machines //J. Assoc. Comput.
Mach.—1963.—V. 10, № 3.—P. 365—385.
71.	Garding L, Tambour T. Algebra for computer science.—N.Y.: Springer, 1988.
72.	Gill A., Flexer R. Periodic decomposition of sequential machines //J. Assoc.
Comput. Mach —1967 —V. 15 —P. 666—676.
73.	Goguen J.A., Thatcher J.W., Wagner EG., Wright J.B. Factorization, congruences,
and the decomposition of automata and systems //Leet. Notes Comput.
Sci.—1975.—V. 28.—P. 33—45.
74.	Gratzer G. On the endomorphism semigroup of simple algebras //Math.
Ann.—1976.—V. 170, № 4.—P. 334—338.
75.	Grzymala-Busse J.W. On the representation of finite lattices in the class of finite
automata //MTA Szamitastechn. es autom. kut. intez. tanul.—1982.—№ 137.—
P. 199—204.
76.	Hartmais J., Steams R.E. Algebraic structure theory of sequential machines.—
Prentice Hall, 1966.
77.	Hayes J.P. A graph model for fault—tolerante computing systems //IEEE Trans.
Comput.—1976. —C. 25, № 9.—P. 875—884.
78.	Hayes J.P. Fault tolerance in computers and graphs //Proc. 1st Esy. Conf. Graphs
and Appl.—Tartu, 1993.—P. 77—89.
79.	Imreh B. On finite definite automata //Acta cybem.—1985.—V. 7, № 1.—P. 61 —
65.
76. Jonsson B. Topics in universal algebra.—Springer, N.Y., 1972.
80.	Kapoor S.F., Polimeni A.D., Wall C.E. Degree sets for graphs //Fund. Math.—
1977.—V. 95.—P. 189—194.
81.	Kreutzer S.E., Hakimi S.L. System-level diagnosis: analysis of two new models
//Inform. Sci.—1986,—V. 40, № 2,—P. 117—130.
82.	Lugowski H. Grundzuge der universellen Algebra.—Leipzig: Teubner, 1976.
83.	Menger K. The algebra of functions: past, present, future //Rend. Mat. et
applic.—1961— V. 20, № 3—4.—P. 409—430.
367
84.	Preparata F.P., Metze G., Chien R.T. On the connection assignment problem of
diagnosable systems //IEEE Trans. Electron. Comput.—1967.—EC-16, № 12.—
P. 848—854.
85.	Schmidt G., Stroleln Th. Relationen und Graphen.—N.Y.: Springer, 1989.
86.	Weeg G.P. The structure of an automaton and its operation—preserving
transformation group //J.Assoc. Comput. Mach.—1962.—V. 9.—P. 345—349.
87.	Wei Y.J., Caines P.E. Lattice structure and hierarhial COCOLOG for finite
machines //Proc. 33d IEEE Conf. Decis. and Contr. V. 3.—Pascataway, N.J.,
1994,—P. 3125—3130.
88.	Whitlock H.A. A composition algebra for multiplace functions //Math. Ann.—
1964.—V. 157, № 2—P. 167—178.
89.	Yau 5.5. Generation of all Hamiltonian circuits, paths and center of a graph, and
related topics //IEEE Trans. Circuit Theory.—1967.—CT-14, № 3.—P. 79—81.
90.	Yoely M. Subdirectiy irreducible unary algebras //Amer. Math. Monthly.—1967.—
V. 74, № 8,—P. 957—960.