Автор: Айвазян С.А. Фантаццини Д.
Теги: экономика народное хозяйство экономические науки экономическая статистика финансы эконометрика
ISBN: 978-5-9776-0333-1
Год: 2014
Текст
С. А. Айвазян, д. Фантаццини
Эконометрика-2
Продвинутый курс
с приложениями в финансах
магистр
м
г ~i--:-
московская,..........
мшэ
школа
экономики
МОСКОВСКАЯ ШКОЛА ЭКОНОМИКИ
МГУ имени М. В. ЛОМОНОСОВА
С.А.Айвазян
Д. Фантаццини
Эконометри ка-2:
продвинутый курс
с приложениями в финансах
Учебник
~Москва
магистр
ИНФРА-М
2014
УДК
[31:33)(075.8)
ББК 65.051я73-1
А36
А36
Айвазян С. А., Фантаццини Д.
Эконометрика-2: продвинутый курс с приложениями в финан-
сах
: учебник / С. А. Айвазян, Д. Фантаццини. фра-М, 2014. - 944 с. (www.znanium.com)
ISBN 978-5-9776-0333-1
ISBN 978-5-16-010136-1
Агентство CIP РГБ
Продвинутый
курс
М.
: Магистр : Ин
(в пер.)
эконометрики
охватывает
ряд
важнейших
разделов
дисциплины. В частности представлены методы и модели анализа многомерных
временных рядов, последние достижения в области финансовой эконометрики (ко
пула-функции, методы управления финансовыми рисками).
Для решения задач используется экономический инструментарий, включаю
щий относительно недавно разработанные современные методы анализа многомер
ных временных рядов, байесовский подход в сочетании с приемами имитационного
статистического
моделирования,
продвинутые
численные
методы
оптимизации.
Вычислительная реализация описываемых в учебнике примеров основана на ис
пользовании статистических и эконометрических пакетов R, Stata, Eviews, GAUSS.
Для студентов и аспирантов экономической и математической специализации,
интересующихся продвинутыми эконометрическими методами и их приложениями
в финансах, а также сотрудников аналитических служб банков и инвестиционных
компаний.
УДК [31:33)(075.8)
ББК 65.051я73-1
©Айвазян С. А, Фа1Па1Щини Д.,
ISBN 978-5-9776-0333-1
ISBN 978-5-16-010136-1
©
Издательство •Магистр•,
Подписано в печать 25.07.2014. Формат 70хl00 1 / 1 в.
Печать офсетная. Гарнитура •Ньютон•.
Усл. печ. л.
76,11.
Тираж
500
экз.
(1-100
экз.). Заказ
2014
2014
ОГЛАВЛЕНИЕ
Предисловие
Гл а в а
1.
............................................. 7
Выбор общего вида модели и нелинейная
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.1. О подходах к выбору общего вида модели .................... 11
1.2. Нелинейные модели регрессии и линеаризация ............... 16
1.3. Вычислительные вопросы нелинейного метода наименьших
квадратов ............................................................. 31
Выводы ............................................................ 54
Гл а в а 2. Построение интегральных измерителей для
синтетических латентных категорий ....................... 57
2.1. Концептуальные основы подхода к измерению
синтетических латентных категорий ................................. 58
2.2. Исходные данные ............................................. 60
2.3. Методология построения интегральных индикаторов регрессия
измерителей синтетических латентных категорий и методы
многокритериального рейтингования ................................. 68
2.4.
Примеры построения интегральных индикаторов
-
измерителей
качества анализируемых синтетических латентных категорий ....... 89
Выводы
.......................................................... 119
Гл а в а З. Байесовский подход в эконометрическом
анализе
3.1.
Философия и общая логическая схема байесовского
подхода
3.2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
.............................................................. 121
Априорные распределения, сопряженные с наблюдаемой гене-
ральной совокупностью (определение и условие существования)
3.3.
3.4.
Генезис априорных сопряженных
... 125
распределений ............ 131
Пересчет значений параметров при переходе от априорного
сопряженного распределения к апостериорному
3.5.
.................... 143
Примеры задач на точечное и интервальное байесовское
оценивание параметров модели ......................................
3.6.
148
Байесовский прогноз зависимой переменной, основанный на
нормальной классической линейной модели множественной
регрессии
............................................................ 157
Выводы .......................................................... 161
ОГЛАВЛЕНИЕ
6
Глава
4.1.
4.
Анализ многомерных временных рядов
........ 163
Многомерные временные ряды: определения и основные
понятия ..............................................................
163
4.2. Модели векторной авторегрессии (VАR-модели) ............ 166
4.3. Структурные VАR-модели (SVАR-модели) .................. 202
4.4. Системы одновременных уравнений (СОУ) ................. 223
4.5. Коинтеграция ................................................ 281
4.6. Регрессионные модели с распределенными лагами .......... 360
Выводы .......................................................... 375
Глава 5. Анализ и моделирование волатильности ....... 385
5.1. Одномерные модели авторегрессионной условной
гетероскедастичности (ARCH- и GАRСН-модели) .................. 385
5.2. Многомерные GАRСН-модели (MGARCH) .................. 433
5.3. Реализованная волатильность ............................... 468
Выводы .......................................................... 502
Гл а в а 6. Моделирование многомерных распределений
с использованием копула-функций . . . . . . . . . . . . . . . . . . . . . . . . 507
6.1. Копула-функции ............................................. 509
6.2. Эллиптические копула-функции ............................. 516
6.3. Архимедовы копула-функции ................................ 528
6.4. Парные копула-функции ..................................... 545
6.5. Меры зависимости ........................................... 557
6.6. Процедуры оценивания: параметрические методы .......... 567
6.7. Процедуры оценивания: полупараметрические и
непараметрические методы .......................................... 572
6.8. Выбор копула-функции ...................................... 583
6.9. Критерии согласия для копула-функций .................... 590
Выводы .......................................................... 618
Гл а в а 7. Анализ финансовых данных в задачах
управления риском . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 625
7.1. Введение: имеющийся опыт и некоторые общие понятия .... 625
7.2. Управление рыночным риском .............................. 632
7.3. Управление операционным риском .......................... 678
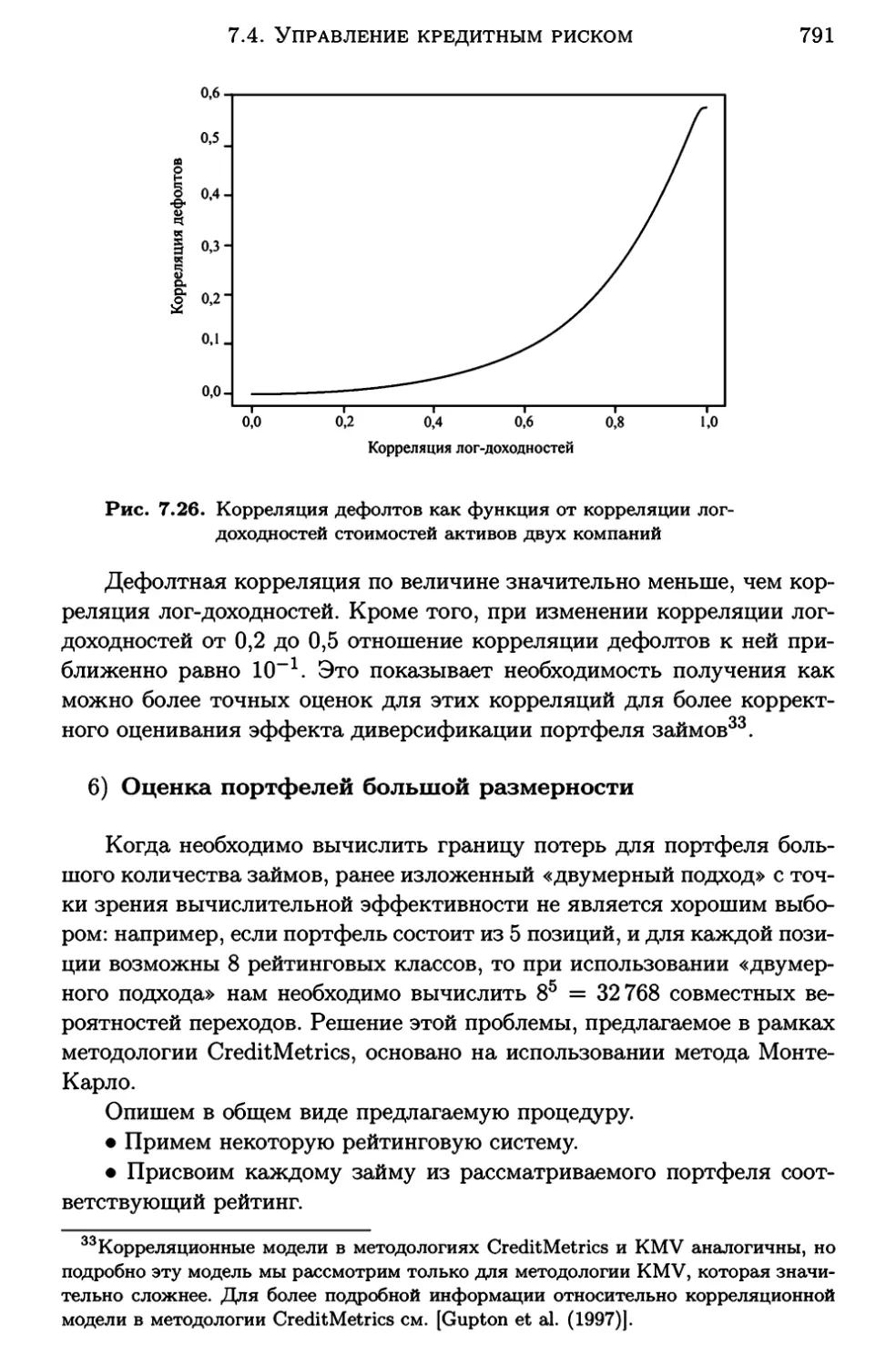
7.4. Управление кредитным риском .............................. 718
Выводы .......................................................... 855
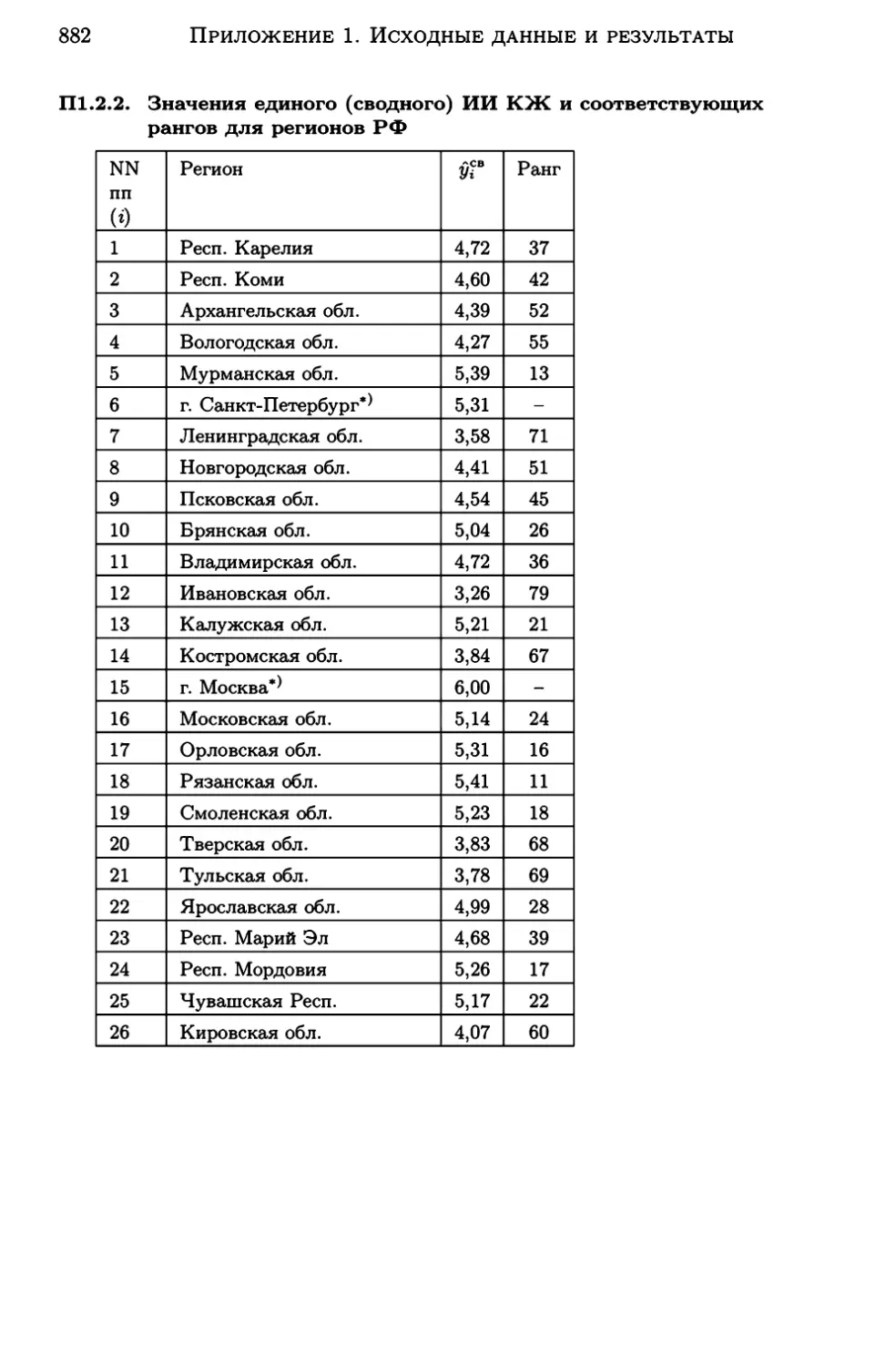
Приложение 1. Исходные данные и результаты межстранового и
межрегионального анализа КЖН . . • • • • . . • • • . . . • • • . . . • • . . . . . • • 865
Приложение 2. Некоторые сведения об одномерных и многомерных
законах распределения вероятностей, используемые в байесовском
подходе
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 885
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 891
Алфавитн~предметный указатель
....................... 935
Предисловие
Дорогой -читатель!
В предисловии к «Методам эконометрики» [Айвазян
я гово
(2010))
рил о том, что они «охватывают весьма полный спектр методов матема
тико-статистического инструментария эконометрики по ее традицион
ным разделам», включая:
(1)
классическую линейную модель регрес
сии и классический метод наименьших квадратов;
обобщенную ли
(2)
нейную модель регрессии и обобщенный метод наименьших квадратов;
(3)
линейные модели регрессии с переменной структурой;
(4)
модели
с дискретными и дискретно-непрерывными зависимыми переменными
(модель бинарного и множественного выбора, тобит-модели);
(5)
стати
стический анализ одномерных временных рядов. Но уже в той книге
я пытался преодолеть распространенный недостаток, заключающий
ся в том, что «важнейшие для эконометрического анализа прик.л.ад
нш метоUьt многомерной статистики (дискриминантный и кластер
анализы, метод главных компонент и др.) по непонятным причинам от
сутствуют в эконометрических курсах и классических университетских
учебниках Северной Америки и Западной Европы» ([Айвазян
(2010),
с.10)). Правда, в том же предисловии признавалось, что в «Методах
эконометрики»
2010 г.
«представлены далеко не все важнейшие разделы
современной эконометрики ... Нет, например, методов и моделей анали
за многомернъtХ временн'ЬtХ рядов ... не отражены последние достижения
в области финансовой эконометрики (копула-функции, методы управ
ления финансовыми рисками), не представлены байесовский подход к
эконометрическому анализу и методы измерения и анализа синтети
ческих латентн'ЬtХ категорий, комплексно характеризующих качество
или эффективность функционирования анализируемой системы» (с.
11).
И я пообещал тогда, что «вся эта проблематика будет представлена
в продвинутом курсе эконометрики (предназначенном для магистер
ского уровня образования)».
Но, должен признаться, было непросто решиться на создание такого
учебника. Причин тому несколько.
Во-перв'ЬtХ, он охватывает области знаний, с одной стороны, еще
фактически не представленные в отечественной учебной и монографи
ческой литературе (здесь я, в первую очередь, имею в виду эконометри
ческий анализ моделей волатильности, копула-функций, разного рода
задачи управления финансовыми рисками), а с другой
-
еще не устояв
шиеся, продолжающие бурно развиваться, а потому содержащие подчас
«сырые», полуэвристические подходы и рекомендации.
Во-вторЪtХ, представленные в данном учебнике содержательные по
становки задач (построение интегральных измерителей для так пазы-
ПРЕДИСЛОВИЕ
8
ваемых синтетических латентных категорий, проблемы спецификации
анализируемых зависимостей, разноаспектный анализ и моделирование
операционных, рыночных и кредитных финансовых рисков) требуют
при своем решении использования необбятного по диапазону эконо
метрического инструментария, включающего, в частности, относитель
но недавно разработанные современные методы анализа многомерных
временных рядов, байесовский подход в сочетании с приемами имитаци
онного статистического моделирования, продвинутые численные мето
ды оптимизации. Уместить весь этот инструментарий в рамках одной,
пусть даже такой как эта объемной книги, задача невыполнимая, а по
тому в некоторых местах учебника (в основном, относящихся к главе
7,
посвященной задачам управления финансовыми рисками) нам прихо
дилось переходить к обзорному стилю изложения, предлагая читателю
находить уточнение и углубление деталей описываемых методов в ра
ботах других авторов.
В-третьих, существенное осложнение процесса создания книги бы
ло связано с ~разноязычием~ авторов. Главы
5, 6, 7
и часть главы
4
были написаны моим коллегой по Московской школе экономики МГУ
им. М.В. Ломоносова Деаном Фантаццини на английском языке, они
требовали перевода, тщательного редактирования, унификации стиля
подачи материала. Большую помощь в переводе англоязычной части
книги оказал Александр Владимирович Кудров. В переводе участво
вал и я, мне же пришлось осуществить общее научное редактирование
текста учебника.
Что же подтолкнуло авторов к выполнению столь объемной работы
по созданию предлагаемого Вашему вниманию учебника?
В первую очередь, это твердое осознание того факта, что назрела
объективная необходимость в подобном учебно-научно-методологическом
издании. Дело в том, что мировые финансовые кризисы
1998 и
2008гг.,
продолжающиеся явления экономической рецессии продемонстрирова
ли общее неблагополучие в сфере управления финансовыми рисками.
По-видимому, в определенной мере этим можно объяснить и тот про
рыв в финансовой эконометрике и связанных с ней разделах мно
гомерного статистического анализа, который мы наблюдаем в послед
ние полтора-два десятилетия. И, конечно, требуются определенные уси
лия, направленные на оснащение обучающейся молодежи и сотрудни
ков аналитических служб банков, инвестиционных компаний последни
ми научно-методологическими достижениями в этой области. Можно
признать, что в плане освоения теоретической ООзы (методов и моде
лей финансовой математики) такие усилия в отечественной научно
образовательной практике уже предприняты (см. работы А.И. Ширяе
ва, например, [Ширяев
(2004)],
и его учеников). Наша книга, насколько
ПРЕДИСЛОВИЕ
9
мне известно, является «первой ласточкой» в области знаний, посвя
щенных «приземлению» этой теоретической базы на конкретные усло
вия и конкретн'Ьtе исходн.ые данные, что и составляет главное предна
значение методов эконометрики. Отмечу также, что в книгу включены
некоторые оригинальные научно-методологические разработки авторов
(это относится, в основном, к главам
2
и
7).
Итак, наша книга адресована студентам и аспирантам экономиче
ской и математической специализации, интересующимся продвинутыми
эконометрическими методами и их приложениями в финансах, а также
сотрудникам аналитических служб банков и инвестиционных компа
ний.
Представленные в книге методы и модели могут составить содер
жание одного или нескольких (в зависимости от отведенного в учебном
плане вуза времени) семестровых курсов магистерского или аспирант
ского уровня по схеме
- 2
часа лекций,
2
часа семинарских занятий.
Вычислительная реализация описываемых в учебнике примеров осно
вана на использовании статистических и эконометрических пакетов
Stata, Eviews, GAUSS.
В заключение - о признательности
R,
авторов учебника. Прежде все
го они благодарны коллективам и администрации Московской школы
экономики Московского государственного университета им. М.В. Ломо
носова и Центрального экономико-математического института Россий
ской академии наук, плодотворная профессиональная среда которых
существенно помогала в работе над учебником. Мы благодарны так
же профессору Эдуардо Росси
(Eduardo Rossi)
из Университета Павии,
(Италия) и профессору Станиславу Анатольеву (Российская экономи
ческая школа) за любезное представление материалов по одномерным
GАRСН-моделям, которые были использованы при написании главы,
посвященной анализу волатильности. Свое любезное согласие на ис
пользование материалов по структурным VАR-моделям мы получили
также от профессора Эрика Зив6
(Eric Zivot)
из Университета Вашинг
тона, США), за что мы ему также благодарны. Наконец, мы благодарны
Алле Павловне и Галине Юрьевне Грохотовым за их нелегкий, самоот
верженный и профессиональный труд по подготовке оригинал-макета
книги.
Я отдаю себе отчет в том, что объемность и пионерный характер
предлагаемого издания являются «питательной средой» для выявления
его слабых мест и недостатков. Всю ответственность за них, конечно,
несут авторы, которые будут признательны читателям, приславшим им
или в издательство свои отзывы и критические замечания.
С.А. Айвазян
Глава
1
Выбор общего вида модели
u
и нелинеиная регрессия
1.1.
О подходах к выбору общего вида модели
Как по отдельным, частным наблюдениям выявить и описать интересу
ющую нас зависимость некоторого результирующего признака Т/ от на
бора так называемых обiJясняющих перемен:н:ых {
= ({<1>, {(2), ... {(р))',
характеризующих (наряду с другими, не подцающимися учету факто
рами) условия функционирования анализируемой системы? 1 Эта про
блема бесспорно занимает центральное место во всем прикладном ма
тематическом (и, в частности, в эконометрическом) анализе!
Попробуем уточнить и формализовать сказанное, одновременно
определив место тематики в'Ыбора общего вида модели регрессии во
всей этой проблеме. Будем полагать, что в серии экспериментов (наблю
дений) за анализируемой системой есть возможность регистрации зна
чений У1, У2,
. . . . .. , Yn
количественного (случайного по своей природе)
(1) (2)
(р))' х
х
признака Т/ и соответствующих значений
=
( х 2(1) ,х 2(2) , ...
(р) )'
,х 2
, ... ,
х
n
объясняющих переменных { =
1
= (х 1
, х1
= (Xn(1) ,xn(2) , ... ,xn(р) )'
, ••• , х 1
,
2
=
количественных
({(I), {( 2), ... , {(р))' (последние могут
быть как случайными, так и не случайными переменными). Тогда об
щая задача статистического исследования зависимости, связывающей
признак Т/ с переменными {
= ({< 1>,{<2>, ... ,{(р))',
может быть сформу
лирована следующим образом:
по результатам наблюдений
{хР>' х~ 2>' ... 'xr>; Yi}i=l,2, ... ,n
1 Верхний
(1.1)
индекс сmтрих• у вектора или матрицы здесь и далее означает опера
цию транспонирования.
Гл.
12
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
исследуемых переменных, произведенных в ходе функциони
рования анализируемой системы, построить (оценить) такую функцию
(1.2)
которая позволи.л.а бы наи.л.уч.шим (в определенном смысле}
образом восстанавливать неизвестные значения результи
рующей переменной у по заданным значениям об"бясняющих
переменных Х = (х< 1 >, х< 2 >, ... , х(р>)'.
При широко распространенных в практике эконометрического ана
лиза критериях качества «подгонки~ наилучшее решение сформули
рованной выше проблемы получается при использовании в роли
J(X)
функции регрессии Т/ по ~, т. е. функции Е( 111~ = Х) (о других возмож
ных подходах к построению функции
и др.
f(X)
см., например, в [Айвазян
(1985)], п. 5.2 и 5.3). Поэтому речь идет обычно о выборе общего
вида именно функции регрессии Т/ по ~' причем в параметриче
ской постановке задачи, т. е. в предположении, что искомая функция
J(X)
ству
= E(ТJI~ = Х) принадлежит некоторому параметрическому семей
функций F = f (Х; 0). Так что задачей исследователя является
выбор того или иного параметрического семейства
F,
основанный на
анализе имеющихся в нашем распоряжении исходных статистических
данных
(1.1)
и на некоторых априорных сведениях о природе искомой
зависимости.
Тогда модель зависимости результирующего признака Т/ от объяс
няющих переменных ~ может быть представлена в форме:
Т/
где е
-
= Ф(~; е; 0),
(1.3)
некоторая остаточная случайная составляющая, аккумули
рующая в себе влияние на Т/ всех неучтенных в ~ факторов, а
0
=
= (81, 82, ... ... , 8т)' - вектор-столбец неизвестных (подлежащих оцениванию по наблюдениям
(1.1))
Соответственно, функция
параметров модели.
f(X)
из
(1.2)
определяется как функция
регрессии Т/ по~' т. е.
f(X; 0) =
Е(ТJ 1 ~
= Х) = Е(Ф(~; е; 0)
1~
= Х),
(1.4)
где операция усреднения (Е) производится по всем возможным значе
ниям случайной величины е.
Отметим, что как в нашем учебнике [Айвазян
(2010)], так и в боль
шинстве других отечественных и зарубежных учебников по экономет
рике выбор структуры функции Ф(~; е; 0), а вместе с ней и выбор об
f (Х; 0) был предопределен, а именно:
Ф(~; е; 0) = 80 + 81~< 1 > + · · · + 8р~(р) + е
щего вида функции
1.1. 0
ПОДХОДАХ К ВЫБОРУ ОБЩЕГО ВИДА МОДЕЛИ
13
и, соответственно:
f(X; 0) = 80 + 81х< 1 >
+ · · · + 8рх(Р)
(равенство нулю среднего значения остатка, т. е. тождество Ее
=
О,
обеспечивается соответствующим подбором значения свободного члена
80).
Таким образом, рассматривались только линейные (и относи
те.п:ьно об~ясняющих переменных, и относите.п:ьно оцениваемых пара
метров) модели.
Подчеркнем, что главная специфика модели, главные неудобства
исследователю доставляет
f(X; 0)
факт нелинейности функции регрессии
по оцениваемым пара.метрам
0.
Если же функция
f(X; 0)
линейна по параметрам, но нелинейна по объясняющим переменным,
то дополнительных принципиальных сложностей в оценке параметров
и в исследовании свойств получаемых оценок обычно не возникает.
В качестве примера подобной ситуации рассмотрим так называемую
полиномиальную регрессию.
Полиномиальная регрессия. Пусть функция регрессии
f (Х; 0)
имеет вид алгебраического полинома от объясняющих переменных х< 1 >,
х< 2 >, ... , х(р> степени т. Ограничимся в своем примере для определен
ности случаем одной объясняющей переменной, т.е. р
тичным порядком полинома, т. е. т
=
2
= 1,
и квадра
(переход к общему случаю
осуществляется без каких-либо принципиальных трудностей). Итак:
так что, располагая наблюдениями
{Xi, Yi} i=I,n, мы имеем уравнения
регрессии вида
где регрессионные остатки
e1,E:2, ••• ,E:n
полагаются одинаково (О;и 2 )
нормально распределенными и взаимнонезависимыми.
Представим функцию регрессии
f (х; 0) = 80 + 81х + 82х2
в системе
базисных функций
{<ро ( х); <р1 ( х); <р2 ( х)}, являющихся ортогональными
(на множестве наблюдений {xi}i=l,n) полиномами Чебышева (см.,
например, п. 7.1.4 в [Айвазян и др. (1985))), т. е. :
i
= 1,2, .. . ,n,
(1.5)
14
Гл.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
n
n
Ех~-хЕх~
=
( )
ср2 Xi
i=l
2
Xi -
i=l
n
Ex~-nx2
i=l
1 n
а
х= - LXi·
n.i=l
Ортогональность полиномов <ро( х), <р1 ( х) и <р2 (х) на множестве наблю
дений {х1,х2,
... ,xn}
означает, что
n
L cpj(Xi)<pk(xi) =О
при j =f. k.
(1.6)
i=l
Интерпретируя в уравнении
(1.5)
функции сро, <р1 и <р2 как объяс
няющие переменные в классической линейной модели множественной
регрессии (КЛММР) и воспользовавшись свойством
(1.6),
а также фор
мулами и свойствами МНК-оценок КЛММР (см., например, [Айвазян
(2010)),
гл.
4),
имеем:
k
2
=О;
1; 2;
А
у- LBk<pk(x) < t1 2P(n- 3) · u ·
k=O
(выполнение последнего неравенства гарантируется с доверительной ве
роятностью Р, а ta(v)
это 100а%-ная точка распределения Стьюдента
-
с v степенями свободы).
В этой главе мы выходим за пределы линейных (по оцениваемым
параметрам) моделей регрессии. Подразумевается, что мы решили
предварительно вопрос о подборе таких функций Ф (и, соответствен
но,
/),
которые наилучшим в определенном смысле образом соответ
ствовали бы имеющимся в нашем распоряжении данным
(1.1)
и апри
орным сведениям о природе искомой зависимости. Приходится кон
статировать, что этап исследования, посвященный выбору общего ви
да функции регрессии
(параметризация
модели), бесспорно, является
ПОДХОДАХ К ВЫБОРУ ОБЩЕГО ВИДА МОДЕЛИ
1.1. 0
15
ключевым: от того, насколько удачно он будет реализован, решающим
образом зависит точность восстановления значения результирующего
показателя у по значениям объясняющих переменных. В то же время
приходится признать, что этот этап находится, пожалуй, в самом невы
годном положении: к сожалению, не существует системы стандартных
рекомендаций и методов, которые образовывали бы строгую теорети
ческую базу для его наиболее эффективной реализации.
Остановимся на некоторых рекомендациях, связанных с реализаци
ей тех основных моментов, учет которых необходим при решении про
блемы выбора общего вида функции регрессии.
(i)
Максима.л:ьное испо.л:ьзование априорной информации о содер:нса
телъной сущности анализируемой зависимости (см. п.
[Айвазян
(ii)
(iii)
п. 6.1 в [Айвазян и др.
в
(1985)]).
Предварите.л:ьный анализ геометрической структуры мно
:жества
исходных
[Айвазян
(2010)],
статистических
данных
п. 6.2 в [Айвазян и др.
(см.
п.
2.5.2
в
(1985)]).
Испо.л:ьзование специал'ЬНЫХ математико-статистических кри
териев
об
согласия,
общем
[Айвазян
(iv)
(2010)],
2.5.1
виде
с помощ'Ью которых проверяются гипотезы
анализируемой
зависимости
(см.
п.
2.5.3
в
(2010)]).
Математико-статистический и графический анализ оценен
ных остатков €i
= Yi- J(Xi; е), -i = 1, 2, ... , n, которые долж:
ны «вести себя» определенн'ЫМ образом в случае прави.л:ьного вы
бора общего вида функции
J(Xi; 0)
(см., например, [Дрейнер,
Смит
(1986)], гл. 3, а так:нсе [Мостеллер, Тьюки (1982)],
1, стр. 189-192 и выпуск 2, гл. 16, с.144-182).
(v)
Поиск
модели,
наиболее
устойчивой
к
выпуск
варьированию
состава выборочных данных, на основании которых она оце
нивается (см. п. 6.3.2 в [Айвазян и др.
(vi)
(1985)]).
Поиск компромисса ме:нсду сло:нсностъю модели и mоч
ностъю ее оценивания (которая зависит от соотношения
числа
n
исполмуемых наблюдений и числа т оцениваемых па
раметров).
В распространенных компьютерных пакетах программ
SPSS, E-views
(STATA,
и др.) эта идея реализована с помощью подсче
та так называемых информационных статистик Акаике
(AIC)
и
16
Гл.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
Шварца
и
(Schwarz), определяемых
[Schwarz {1978))):
AIC
формулами {см.
[Akaike {1973))
= 2m +ln (~ te~);
n
n
Schwarz = m · lnn
n
i=l
+ ln (~ te~).
n
i=l
Выбирают ту модель, для которой значения этих статистик мень
ше.
С учетом того факта, что с ростом сложности модели
стом числа оцениваемых параметров
еме выборки
n
m)
(т. е.
с ро
при фиксированном объ
точность оценивания падает, в этих статистиках к
минимизируемому обычно критерию метода наименьших квадра-
n
тов ( Е €~) добавляется штраф за перепараметризацию модели {в
i=l
критерии Шварца он несколько выше). Это, в общем-то, некая эвристи'Ческа.я попытка реализации идеи поиска компромисса меж
ду
m
и
n.
Гораздо более тонкий подход к реализации этой идеи
предложен в работе [Вапник
{1979)).
Здесь мы ограничимся, в ос
новном, ссылками на работы, в которых все эти идеи развиваются,
с тем чтобы в дальнейшем сосредоточиться на анализе нелиней
ных моделей: способах их линеаризации (п.1.2), вычислительных
аспектах оценивания их параметров и свойствах получаемых при
этом оценок (п.1.3).
1.2.
Нелинейные модели регрессии
и линеаризация
Многие важные связи в экономике являются нелинейными. Примеры
такого рода регрессионных моделей доставляет нам изучение так на
зываемых производственных функций (зависимостей, существующих
между объемом произведенной продукции и основными факторами про
изводства
-
трудом, капиталом и т. п.), функций спрос.а (зависимостей,
существующих между спросом на какой-либо вид товаров или услуг, с
одной стороны, и доходом и ценами на этот и другие товары
-
с дру
гой), доходностей и рисков на фондовых рынках. Ниже мы подробнее
обсудим возможный общий вид этих и других моделей. Как уже было
отмечено выше, этап параметризации регрессионной модели, т. е. вы
бора параметрического семейства функций
{! (Х; 0)},
в рамках кото
рого производится дальнейший поиск неизвестной функции регрессии
1.2.
f(X) =
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
17
Е(у 1 Х), является одновременно наиболее важным и наименее
формализованным и теоретически обоснованным этапом регрессионно
го анализа. Если же в результате реализации этого этапа эконометрист
пришел к выводу, что функция
f (Х; 0)
нелинейна, то далее он обычно
действует следующим образом:
•
вначале он пытается подобрать такие преобразования к анализи
руемым переменным у, х< 1 >, ... , х<Р), которые позволили бы пред
ставить искомую зависимость в виде линейного соотношения меж
ду преобразованными переменными; другими словами, если
rpo,
<р1, ••• , <рр -
те самые искомые функции, которые определяют пе
преобразованным переменным, т. е. у = tpo(y), х< 1 > =
реход к
= <р1 (x(l>), ... , х(р) = <рр(х(р>), то связь между у и х = (х< 1 >' ... ,
х(р>) мож~т быть представлена в виде линейной функции регрес
сии у по Х, а именно:
i
= 1, 2, ... , n;
эту часть исследования обычно называют процедурой линеа
ризации модели;
•
в случае невозможности линеаризации модели приходится иссле
довать искомую регрессионную зависимость в терминах исходн:ых
переменных, а именно:
если спецификация регрессионных остатков
ei соответствует усло
виям классической модели, то для вычисления МНК-оценок емнк
векторного параметра 0 решается оптимизационная задача вида
. . . = argmш. L {Yi 0мнк
n
е
.
i=l
f(Xi; 0)) 2 .
Методам преодоления возникающих при этом вычислительных
трудностей посвящен п.
1.2.1.
1.3.
Некоторые виды нелинейных зависимостей,
подцающиеся непосредственной линеаризации
Итак, пусть у и Х
=
(х< 1 >,х< 2 >, ... ,х(р>)'
- исходные анализируемые
переменные (соответственно результирующая и объясняющие), а е
-
случайная остаточная компонента, участвующая в записи регрессион
ной зависимости, связывающей между собой у и Х.
18
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
В представлении исходн:ых наблюдений
(1.1)
нам будут удобны в
дальнейшем следующие обозначения:
Х=
1
1
(1)
Х1
(1)
Х2
(2)
х(р)
(2)
х(р)
Х1
Х2
1 Xn(1) Xn(2)
У = (У1У2 ... Yn)'
1
2
xw>
rv
(n
х (р
+ 1}} -
матрица
наблюденных значений
(1.la}
объясняющих переменных;
вектор-столбец наблюденных значений зависимой
rv
переменной.
За редким исключением вопросы линеаризации анализируемых связей
решаются на основе рассмотрения nарных зависимостей (и графиче-
ски представляющих их парных корреляционных полей} типа (х~Л, Yi)
(j) , xi(l)) , i. = 1, 2 , ... , n. поэтому ниже будут представлены и проанаи ( xi
лизированы именно парные регрессионные зависимости, поддающиеся
линеаризации.
Зависимости гиперболического типа
1}
Предположим, что анализируемые переменные и случайные регрес
сионные остатки соответственно х, у и е связаны между собой стати
стической зависимостью вида
(О< х
< оо).
/(z;e)
Во
------------------------81 <о
о
Рис. 1.1. График гиперболической зависимости вида /(х; 0) = 80
+~
1.2.
+
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
19
+
Соответствующая кривая регрессии f {х; 0) = f {х; 80, 81)
80
81/х (см. рис.1.1) характеризуется двумя асимптотами (т. е. прямы
ми, к которым график функции неограниченно приближается, не до
стигая их)
-
горизонтальной (у=
80)
и вертикальной (х =О). С помо
щью преобразования объясняющей переменной х
= 1/х
( т. е. при пере
ходе к новой объясняющей переменной х) эта зависимость приводится
к линейному виду у
= 80 + 81 х + €.
МНК-оценок параметров
80
и
81
Соответственно при вычислении
второй столбец матрицы Х должен
быть сформирован из чисел 1/х1, 1/х2,
.. ., 1/xn.
f(z; 8)
б)
f(z; 0)
а)
о
О
Рис.
1.2.
Во
- 81
График гиперболической зависимости вида /(х; 0)
а) случай
б} случай
2)
80
80
<О;
>О;
81 >О
81 < О
(для х
(для х
=
1/(8о
+ 81х):
> -80/81);
> -80/81)
Пусть переменные х, у и случайные регрессионные остатки €
связаны между собой статистической зависимостью вида
1
у=-----
80 + 81х + е
(см. рис.1.2). Очевидно, мы придем к линейной модели у=
+ €,
80 + 81х
+
если в качестве результирующего признака рассмотрим перемен
ную у
оценок
=
1/у. Следует не забыть только, что при вычислении МНК
80 и 81
надо использовать в качестве вектора наблюденных зна
чений зависимой переменной вектор У= (1/у1, 1/у2, .. ., 1/уп)'.
3) Если этап параметризации модели регрессии приводит нас
висимости вида
х
у=-----
8ох
+ 81 + хе
к за
Гл.
20
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
(см. рис.1.3), то линеаризацию исследуемой связи обеспечит переход к
новым переменным у= 1/у их= 1/х. Легко видеть, что эти перемен
ные будут связаны между собой зависимостью вида
/(z; 0)
/(z; 8)
а)
б)
1
80
81
80
Рис.
1.3.
о
График гиперболической зависимости вида /(х; 0) = Вож~в 1 :
а) случай 80 > О; 81 < О (для х > -81/80);
6)
случай
80 > О; 81 > О
(для х
> -81/80)
Очевидно, что матрицы Х и У, используемые в формулах метода
наименьших квадратов при вычислении оценок Во и
должны фор
мироваться не из наблюденных значений, соответственно Xi и Yi, а из
обратных к ним величин Xi = 1/xi и Yi = 1/Yi·
Заметим, что функции, изображенные на рис.1.1 (вариант 81 <О)
и 1.3 (вариант б)) используются в определенных ситуациях при постро
81,
ении так называемых кривых Энгеля, которые описывают зависимость
спроса на определенный вид товаров или услуг (у) от уровня доходов (х)
потребителей. При этом спрос определяется либо абсолютными, либо
относительными (по отношению к общим потребительским расходам)
расходами на данный вид товаров или услуг. Функции, изображенные
на рис.
1.1
(вариант
81
>О),
1.2. а)
и
1.3. а)
могут оказаться полезными
при изучении спроса на товар (у) в зависимости от его цены (х).
Зависимости показательного (экспоненциального) типа
4)
Достаточно широкий класс экономических показателей характери
зуется приблизите.л:ьно постоянн'ЬLМ. темпом относите.л:ьного приро
ста во времени. Этому соответствует следующая форма зависимости
этого показателя (у) от времени (х):
1.2.
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
21
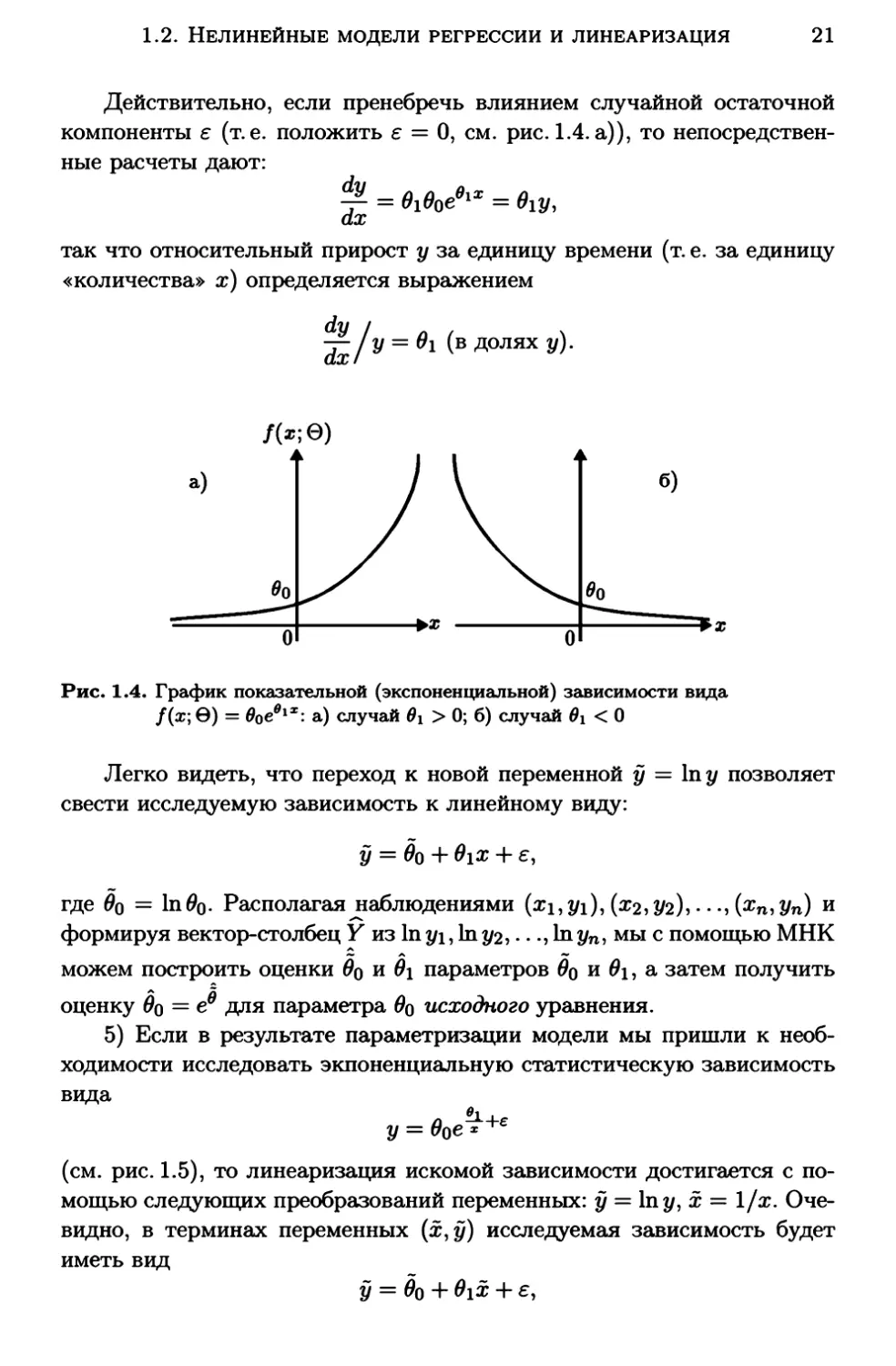
Действительно, если пренебречь влиянием случайной остаточной
компоненты е (т. е. положить е
= О,
см. рис.1.4. а)), то непосредствен-
ные расчеты дают:
dy 8 () 8 х 8
dx = 1 ое 1 = lY,
так что относительный прирост у за единицу времени
(т. е.
за единицу
~количества~ х) определяется выражением
dy/ у= 81 (в ДОЛЯХ у).
dx
/(z;0)
б)
а)
о
Рис.
1.4.
График показательной (экспоненциальной} зависимости вида
/(х; 0) = 8ое 81 ж: а) случай 81 >О; б} случай 81 <О
Легко видеть, что переход к новой переменной у
=
ln у
позволяет
свести исследуемую зависимость к линейному виду:
у=Во+81х+е,
где Во = ln 80. Располагая .......наблюдениями (х1, У1), (х2, У2), ... , (xn, Yn) и
формируя вектор-столбец у из ln Yl, ln у2, ... , ln Yn, мы с помощью МНК
можем построАить оценки Во и 81 параметров Во и 81, а затем получить
оценку Во
5)
=
её для параметра 80 исходного уравнения.
Если в результате параметризации модели мы пришли к необ
ходимости исследовать экпоненциальную статистическую зависимость
вида
.o.i.
у= 80 е ж +е
(см. рис.1.5), то линеаризация искомой зависимости достигается с по
мощью следующих преобразований переменных: у
= ln у, х = 1/х. Оче
видно, в терминах переменных (х, у) исследуемая зависимость будет
иметь вид
Гл.
22
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
f(z; 0)
f(z; 0)
а)
б)
Во ------------------
Во ------------------
0
Рис.
1.5.
z
0---------z
График показательной (экспоненциальной) зависимости вида
f(x; 0) = 8oe 81 f':z: а) случай 81 > О; 6) случай 81 < О
где Во = ln8o. Соответственно вектор-столбец У и матрица Х, участ
вующие в формулах МНК, определяются по исходным наблюдениям
{(xi, Yi)}i=l,2, ... ,n
следующим образом:
х
6)
-- (l/x1,
1
1
l/x2
...
1 )'
. . . 1/xn
Весьма гибкую форму параметризации искомой регрессионной
зависимости представляет один из частных случаев так называемой ло
гистической кривой (см. рис.1.6)
1
(-оо
у=------
80
+81е-х +е
< х < +оо).
/(z;0)
1
Во
Рис.
1.6.
График логистической кривой вида
случай
Кривая
у
=
81 >
f (х; 0)
f(x; 0) =
1/(8о
+ 81е-"'):
О
имеет две горизонтальные асимптоты у
l/80 и «точку перегиба~ (хо
=
In(81/80), Уо
=
=
О и
1/280). Линеариза
ция этой зависимости производится с помощью перехода к переменным
у
=
1/у их
=
е-х. Соответственно, вектор-столбец У и матрица Х,
1.2.
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
23
участвующие в формулах МНК, определяются по исходным наблюде
ниям {(xi, Yi)}i=l,2, ... ,n следующим образом:
1
Логистические кривые используются для описания поведения по
казателей, имеющих определенные «уровни насыщения~, например для
описания зависимости спроса на товар (у) от дохода (х).
Зависимости степенного типа
7)
Широко распространены в практике социально-экономических ис
следований так называемые стеnенн'Ьtе зависимости. Степенная мо
дель множественной регрессии имеет вид
Очевидно, при переходе к переменным fj
=
1, 2, .. . ,р)
=
ln у, х<Л
=
ln х<Л (j
=
можно представить эту зависимость в виде КЛММР, а
именно:
где iio
= ln Оо.
При оценке параметров iio, 81, ... , Ор участвующие в фор-
.....
.......
мулах МНК вектор-столбец У и матрица Х будут определяться по
исходным наблюдениям {х~ 1 ), х?>, . .. , х?'>; Yi}i=l,2, ... ,n следующим обра
зом: У = (lny1,lny2, ... ,lnyn)', а (j + 1)-й столбец матрицы Х есть
(j) '
.
.......
(lnx 1(j) , lnx2(j) , ... ,lnxn),
J = 1,2, ... ,р (первый столбец матрицы Х,
как обычно, составлен из одних единиц). Графики зависимостей данно
го типа для случая р
= 1
представлены на рис.1.7.
Важную роль играют зависимости степенного типа в задачах по
строения и анализа производственн:ы.х функций (у - объем произведен
ной продукции, х< 1 >, х< 2 >, ... - основные факторы производства: труд,
капитал и т. д.). Достаточно часто используются степенные зависимости
и при построении и анализе функций спроса (у - спрос на определен
ный вид товаров или услуг, х< 1 > - доход потребителя, х< 2 >, х< 3 >,
... -
цены на данный и другие виды товаров).
Гл.
24
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
/(z;0)
/(z;0)
б)
Рис. 1.7. График степенной зависимости вида /(х;0} = 8ох 81 : а) случай 81 >О;
б} случай
81 <
О
Отметим, что при анализе степенных регрессионных зависимостей
прозрачную содержательную интерпретацию получают коэффициенты
81, 82, .. ., 8р,
а именно: в соответствии с определением коэффициента
эластичности признака у по объясняющей переменной х<Л (см., на
приметр, п.2.9.4 в [Айвазян (2001)]) величина 8j = дlnf(X;0)/дlnxШ
есть не что иное, как коэффициент эластичности анализируемого ре
зультирующего показателя по j-й объясняющей переменной. Можно,
кстати, показать, что если эластичность у по каждой из объясняющих
переменных х<Л постоянна ( т. е. не зависит от того, при каких именно
значениях объясняющих переменных она вычисляется), то у и Х могут
быть связаны только зависимостью степенного типа.
Зависимости логарифмического типа
8)
На рис.1.8 представлены графики зависимостей логарифмического
типа:
(О <х
/(z;0)
Рис.
1.8.
/(z;0)
а)
График логарифмической зависимости вида
а) случай
81
>О; б} случай
Кривые на рис.
1.8
< оо).
81
f (х; 0) = 80 + 81 ln х:
<О
проходят через точку
(1; 80)
стве вертикальной асимптоты ось у (т. е. прямую х
и имеют в каче
=
О). Переход к
1.2.
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
25
линейному виду зависимости осуществляется с помощью логарифми
ческого преобразования объясняющей переменной: х
......
= lnx. Соответ-
ственно, второй столбец матрицы Х, участвующей в формулах МНК,
будет иметь вид:
(lnx1, lnx2, ... , lnxn)'.
Подбор линеаризующего преобразования
1.2.2.
(подход Бокса-Кокса)
В предыдущем пункте описан набор зависимостей, поддающихся лине
аризации с помощью подходящих преобразований анализируемых пере
менных. Но решение вопроса о том, к какому именно из перечисленных
линеаризуе.м:ых типов зависимостей следует отнести наш конкретный
случай, является задачей непростой. Можно, конечно, действовать ме
тодом «проб и ошибок~: последовательно построить по имеющимся у
нас исходным статистическим данным
(1.1)
каждую из альтернативно
го набора линеаризуемых моделей, а затем выбрать из них наилучшую
в смысле какого-то «критерия качества~
(например, по максимально
му значению подправленной на несмещенность оценки коэффициента
детерминации
....... 2
R* , см.
формулу
(3.35)
в [Айвазян
(2010)]).
Английские статистики Г. Бокс и Д. Кокс предложили более форма
лизованную процедуру подбора линеаризующего преобразования 2 • Их
метод основан на предположении, что искомое преобразование принад
лежит определенному однопараметрическому семейству преобразова
ний вида
Уi(Л)
,\
= Yi;
1
' х~j)(Л) =
(
(j)),\
xi л -
1
'
i
= 1, 2, ... , n.
(1.7)
Точнее их гипотезу можно сформулировать следующим образом:
существует такое вещественное
( по.яо:жите.л:ьное
или отрицатель
ное) число Л *, что один из двух ни:жеследующих вариантов представ
ления искомой регрессионной зависимости ме:жду наблюдаем'Ьl.Ми пе
ременнъши у и Х
(х< 1 >,х< 2 >,
,х<Р>):
=
...
или
- (л'*)
Yi
= (}о + (}1Xi(1) + ... + (}pXi(р) + Ei,
i = 1, 2, ... , n,
(1.8')
будет удовлетворять всем требованиям нормальной классической ли
нейной модели мно:жественной регрессии (см.
2 См.:
(4.1)
в [Айвазян
(2010)]).
Вох G.E.P. and Сох D.R. An Analysis of Тransformations / / Journ. of Royal
Statist. Soc. Series В. Vol. 26 (1964}. Р. 211-243.
Гл.
26
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
а меч ан и е
3
1.
Преобразования вида
(1.7)
применяются обычно
к переменным, принимающим только nоложительн:ы.е значения. По
этому если это не так, то вначале подбирают «сдвиговые~ констан
ты с< 0 >, с< 1 >,
с(Р), которые обеспечивают положительность значений
... ,
Yi + с< 0 > их?>+ c(j) (j = 1, 2, ... ,р), а затем к сдвинутым значениям
переменных применяют данное преобразование, т. е.:
( ·
(О))~ - 1
--(')=
Yi+c Л
Yi
л
а меч ан и е
3
2.
--(')=
' Xi
л
(
(j)
xi
(j))~ - 1
+сЛ
(·=12
) (17')
i
' ' ... ' n .
.
Семейство степенных преобразований вида
(1.7)
(или (1.7')) весьма широко и гибко. При Л = 1 модели (1.8) и (1.8')
являются линейными относительно Yi и х~ 1 ), х~ 2 ), ••• , х~р). При Л = О
мы имеем степенную зависимость между у и Х (см. п.1.2.1), поскольку
Yi(O) = lim(yf - 1)/Л = lnyi и х~Л(о) = lim[(x(j))~ - 1]/Л = lnx?>. При
~~о
~~о
других значениях Л уравнения
(1.8)
и
будут связывать между
(1.8')
собой какие-то степени исходных переменных.
Оценка неизвестного значения параметра Л. Таким образом,
если исходить из справедливости сформулированной выше гипотезы,
подбор линеаризующего преобразования анализируемых переменных
сводится к оценке параметра Л в формулах
(1.7)
или
(1.7')
по имею
щимся в нашем распоряжении исходным статистическим данным
(1.1 ).
Эта проблема решается с помощью метода максимального правдопо
добия. Будем исходить для определенности из справедливости нашего
допущения применительно к представлению искомой модели в форме
(1.81),
т. е. в матричной записи при неизвестном значении параметра Л
у(Л) и Х связаны между собой уравнением
У(Л) =Х0+е,
(1.8")
где У(Л) = (у1(Л), ii2(Л), ... , iin(Л))', Уi(Л) = (yf - 1)/ Л (мы предполага
ем, что все Yi положительны), Х- матрица размерности nx (p+l) ранга
р+ 1 из наблюденых значений объясняющих переменных (см. (1.la)), а
е = (е1, е2, ... , en)' - вектор-столбец (О, и2 )-нормально распределенных
и взаимнонезависимых регрессионных случайных остатков.
Для составления уравнений метода максимального правдоподобия
относительно неизвестных параметров Л, 0 и и 2 при заданных значе
ниях У и Х выпишем вначале функцию правдоподобия
iin
1
L(y1,ii2, ... ,
Х; Л, 0, и2 ) для преобразованных значений Уi(Л), а затем, вос
пользовавшись правилом вычисления закона распределения вероятно
стей случайных величин, являющихся заданными функциями от из
вестных случайных величин (см. п.
4.4,
формулу
(4.11)
из [Айвазян,
1.2.
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
27
Мхитарян
(2001)]), определим нужную нам функцию правдоподобия
L(y1, у2, ... , Yn 1 Х; Л, 0, и 2 ) для непосредственно наблюденн'ЫХ значе
ний Yi·
Таблица 1.1. Соответствия в обозначениях формулы (4.11)
из [Айвазян, Мхитарян (2001)] и п. 1.2.2 текста
№
п/п
Смысл понятия
Обозначения
или характеристи-
формулы
(4.11)
Обозначения, принятые в данном пункте
ки, используемой в
формуле
1
(4.11)
Размерность
р
п
анализируемых
случайных
величин
2
~ = (~(1)' ... '~(Р))
Случайная ве-
У(Л) = (У1 (Л), ... , Уп(Л))'
личина, распре-
деление которой
задано
3
1J = (ТJ(l)' ... '1/(Р))
Случайная ве-
У = {У1' · · · 'Уп)'
личина, распре-
деление которой
надо вычислить
4
У= g(У(Л)),
1J = g(~)
Преобразование,
где Yi = (Луi
связывающее ис-
+ 1) 1 1~
следуемые случайвые величины
5
~
Обратное пре-
= g-1(1/) =
(g!l(ТJ), ... , g;l(ТJ))
образование, свя-
6
У(Л) = g- 1(Y) =
(g!l{Y), ... ,g;l(Y)),
зывающее исследу-
где
емые величины
9i 1 (Y) = Yi = (yt - 1)/Л
J = ldet ( дg~1<~;>) 1,
Определитель
матрицы преобра-
i,l=l,2, ... ,p
зования (якобиан)
J(Л)
.
}il =
= ldet (jil)I,
Yi
с-1
о
при
при
где
i = l;
i =F l,
i,l = 1,2, ... ,n
Опираясь на результаты п.
4.2.2 и,
в частности, соотношения
(4.20)-
(4.23) из [Айвазян (2010)], и с учетом взаимной независимости и
(80 + 8 1 х?> + · · · + 8рх?'>, и 2 )-нормальной распределенности случайных
величин Yi (i = 1, 2, ... , n) имеем:
L(y1, й2, ... , Уп 1 Х; Л, 0, и 2 )
=
1
!!
(27Г)2(и
2
!!
)2
=
1 (У-Х0)'(У-Х0)
} .
х ехр { -22 и
(1.9)
28
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Воспользуемся далее формулой
(4.11)
из
[Айвазян,
Мхитарян
(2001)], позволяющей перейти от известного распределения (1.9) много
мерной случайной величины У= (у1, у2, ... , Yn)' к распределению слу
~айной величины У, являющейся некоторой (заданной) функцией от
У. Таблица
1.1, устанавливающая соответствие между обозначениями
формулы (4.11) [Айвазян, Мхитарян (2001)] и обозначениями, приня
тыми в данном пункте, облегчит читателю понимание этого перехода.
Итак, в соответствии с формулой
(4.11) из [Айвазян, Мхитарян
(2001)] имеем:
или (в терминах логарифмической функции правдоподобия
l(y1,Y2, ... ,ynlX;Л,0,u
2
)=const+lnJ(Л)-
1
.-..
n
2
1 .-..
Inи
2
l
= ln L)
-
..-..
(1.10)
- 2и 2 (У - Х0) (У - Х0),
n
где J(Л) = ( П Yi)~-l
>
О (так как все Yi
>
О), а const -
некоторая
i=l
постоянная величина, не зависящая от оцениваемых параметров Л,
0
и
и2.
Предположим, что значение параметра Л зафиксировано. Тогда
дифференцирование (1.10) по 0 и и 2 и приравнивание полученных част
ных производных к нулю (см.
е(Л)
(4.21)-(4.23) из [Айвазян (2010)]) дает:
= (Х'Х)- 1 Х'У(Л),
(1.11)
u2 (Л) = ~ (У(Л) - хе(Л)) 1 (У(Л) - хе(л)).
(1.12)
Для того чтобы подобрать теперь оптимальное значение парамет
ра Л, вернемся к соотношению
(1.10), подставив в него оптимальные
выражения (1.11) и (1.12) соответственно для 0(Л) и и 2 (Л). Обозначим
полученное при этом значение
lmax(Л)
= l(y1, .. ., Yn
l
с помощью lmax(Л). Итак:
.....
А2
1 Х; Л, 0, О" )
= const +
(Л - 1)
=
n
L lnyi i=l
;
lnu 2 (Л)
(1.13)
1.2.
НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
(при выводе
tl.13)
29
использован тот факт, что при оптимальных выра
жениях для 0(Л) и u 2 (Л) последний член в правой части (1.10) равен
п/2, т.е. не зависит от Л).
Далее анализируется функция lmax(Л) и отыскивается такое значе
ние Л *, при котором
lmax (Л*) =
шах lmax (Л). С этой целью определя.л
ется априорный диапазон (Лmin, Лmах) возможных значений Л (обычно
достаточно рассмотреть в качестве области возможных значений Л от
резок от
Amin
=
до Лmах
-1
= 2),
на этом диапазоне выбирается сетка
Ai = Amin + i(Лmax - Amin)/N, i = О, 1, ... , N и
для каждого такого значения Лi последовательно вычисляются е(Лi),
(«решето~) значений
u 2 (Лi) и lтах(Лi)· То значение Л*, при котором
lтах(Л*) =
шах
.Л=.Ло,.Л1 ,••. ,.Лн
lmax(Лi),
и будет определять искомое линеаризующее преобразование
( 1. 7). Оцен
ки Л *, В( Л *) и u2 ( Л *) являются оценками метода максима.л:ьного прав
доподобия, а процеi}уру 'l.IX поиска часто називают «решетчатой~.
3
вания
ам е ч ан и е
3.
Оценка параметра Л в случае, если преобразо
применяются одновременно к результирующей и к об'бяс
( 1. 7)
няющим переменным, производится тем же способом с единственным
видоизменением процедУры: в формулах
(1.8"), (1.9)-(1.13) матрицу Х
следУет заменить на матрицу Х(Л) наблюденных значений преобразо
ваннъ~х объясняющих переменных.
Пр им ер
1.1
(заимствован из [А. Зельнер, с.
182-184)).
Изложен
ный выше подход к подбору линеаризующего преобразования с исполь
зованием метода максимального правдоподобия был применен в при
ложении к анализу функции спроса на деньги. Результаты предвари
тельного анализа показали, что функция спроса на деньги может быть
записана в виде
у~ - 1
i
Л
= 80 + 81
где индекс
Yi -
i
(хР>).л - 1
i
Л
+ 82
(х~ 2 )).л - 1
i
Л
+ Ei,
i
= 1, 2, ... , п,
(1.14)
обозначает, что значение переменной относится к ГОдУ
i,
денежная наличность, включая текущие и срочные депозиты (де
флятированные индексом цен), х~ 1 ) - измеренный доход (дефлятиро
ванный индексом цен), х~ 2 ) - средняя норма процента по коммерче
ским бумагам и Ei -
остаточная случайная компонента, удовлетворяю
щая всем требованиям нормальной КЛММР (исходные статистические
данные (х~ 1 ), х~ 2 ), Yi) представляют собой годичные наблюдения по эко
1869 - 1963гг., причем i = 1соответствует1869 годУ,
95 соответствует 1963 годУ, а общее число наблюдений п = 95).
номике США за
i
=
30
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
При реализации «решетчатой» процедуры был определен диапазон
возможных значений Л от
д
Лj
Amin = -0,90 до Amax = 1,30 и
«шаг», равный
= (Лmах - Amin)/N = 2,20/22 = 0,1. Затем для каждого
= -0,90 + j · 0,1 (j =О, 1, ... 22) были подсчитаны:
где
- ('Лj ) =
Yi
~-
у/
-
значения
1
Лj
1
х~1 >(Лj)
х~2 >(Лj)
и
-(2)('·)-
xi
л3
-
1
( (2))~;
xi
Л·
'
3
а также значения е(Лj) и u 2 (Лj), соответственно, по формулам (1.11)
и (1.12) с заменой матрицы Х матрицей Х(Л); и, наконец, величина
-
n
lmax(Лj) = (Лj-1) Е lnyi-~ lnu 2 (Лj) по формуле (1.13) (с исключением
i=l
константы).
График функции lтах(Л) изображен на рис. 1.9. Он позволяет вы
числить Л* ~ 0,20, т. е. такое значение Л, при котором функция Zmax(Л)
достигает своего максимума. Стандартный регрессионный анализ ре
грессии у(О,2) по х< 1 >(О,2) и х< 2 >(О,2) дает:
Yi(o,2) = - 1,055 + 1,112 х~ 1 >(0,2) - о,097 х~ 2 >(0,2)
(0,239)
(0,016)
+ ei; ii: 2
= 0,12
(0,016)
(напомним, что в скобках под значениями оценок коэффициентов ре
грессии Оо,
01
и
02
указаны величины среднеквадратических ошибок
этих оценок).
Следовательно, отправляясь от
можно по
казать, что функция регрессии спроса на деньги (у) по доходу (х< 1 >) и
средней норме процента (х< 2 >) в исходн:ых переменных будет иметь вид:
(1.14)
(при Л
= 0,20),
Е(у 1 х< 1 >, х< 2 >) = (-о,226 + 1,112 W - 0,097 ~ 5 .
(1.15)
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
31
lma•(~)
-100
Рис.
1.9.
«Решето•
значений логарифмической функции правдоподобия
(без учета величины константы)
Заметим, что близость к нулю оптимального значения Л (Л*
= 0,2)
говорит о том, что и «логарифмический~ вариант функции спроса на
деньги (т. е. переход К переменным у= lny, X(l) = lnx(l) И х( 2 ) = lnx( 2 ))
находится в приближенном согласии с имеющимися выборочными дан
ными. Так что наряду с функцией
(1.15)
можно было бы рассчитать и
конкурирующую функцию регрессии вида
(1.16)
Вычислительные вопросы нелинейного
1.3.
метода наименьших квадратов 3
Итак, в ходе решения задачи выбора общего вида функции регрессии
f(X; 0)
(сле,цуя, например, рекомендациям п.
2.5 из [Айвазян (2010)]),
мы пришли к выво,цу о существенной нелинейности этой функции от
носительно оцениваемых параметров
ственной нелинейностью функции
торых описанные в п.
0 = (8 1 , 82, ... , Вт)' (под суще
f (Х; 0) понимаются ситуации, в ко
1.2 подходы к линеаризации анализируемого урав
нения регрессии не дают желаемого результата). Тогда, отправляясь от
модели
i = 1, 2, ... , n
и стремясь получить МНК-оценки неизвестных параметров
(1.17)
0,
имею
щих область допустимых значений Г, мы, при достаточно общих пред3В
данном параграфе использованы материалы В.В. Федорова и Е.З. Демиденко,
подготовленные ими для гл.
9
книги [Айвазян и др.
(1985)).
Гл.
32
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
положениях относительно вероятностной природы остатков
ei,
прихо
дим к необходимости решения оптимизационной задачи вида
(1.18)
а также
-
получения ответов на вопросы о свойствах оценок
.......
0
(их
существовании, единственности, состоятельности, несмещенности, эф
фективности). Именно этим вопросам и посвящен данный пункт гл.
1.
В целях упрощения записей там, где это не вызовет разночтений,
n
вместо f(Xi; 0) будет использоваться fi(0), а вместо Е wi(Yi- fi(0)) 2i=l
J(0),
так что оптимизационная зада
(1.18)
может быть представлена в
виде
0=
Задачу
(1.18)
argminJ(0).
(соответственно,
(1.18')
еег
можно рассматривать как
(1.18'))
одну из задач нелинейного программирования, алгоритмы и програм
мы для которых можно найти в современных пакетах программ, в том
числе статистических и эконометрических, таких как
SPSS
STATA, E-views,
и др.
Особенности использования общих алгоритмов оптимизации имен
но в статистических и эконометрических задачах давно и подр~
но обсуждается в литературе: например, в
[Chambers (1973)],
где со
держится обширная библиография по теме; см. также [Химмельблау
(1975)],
[Демиденко
(1981)] ,
[Успенский, Федоров
(1975)].
Вообще го
воря, практически любой из общих алгоритмов пригоден для решения
задач
( 1.18'),
однако имеются веские аргументы для развития сnеци
ал:ьных алгоритмов и программ решения оптимизационных задач, свя
занных именно с эконометрическим анализом.
Во-первых, учет специфики функции
J(0)
позволяет выбрать те
алгоритмы, которые будут работать наиболее эффективно именно при
решении задач типа
(1.18).
Во-вторых, решение оптимизационной задачи
(1.18)
составляет
приблизительно лишь половину от общего объема вычислительной ра
боты, необходимой для выполнения полноценного эконометрического
анализа модели (1.17). Действительно, помимо самих оценок
0 иссле
дователю необходимы оценки ковариационных матриц этих оценок, до
верительные интервалы для неизвестного значения
результирующего
=
показателя у при заданных значениях объясняющих переменных Х
(х< 1 >, ... , х<Р>)', ряд характеристик степени адекватности оцененной
=
модели
(1.17)
и т. п. (см. ниже, п.1.3.8). В вычислительном плане крайне
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
33
удобно, когда упомянутая числовая информация подсчитывается па
раллельно с отысканием самих оценок. Именно алгоритмам, облада
ющим такими свойствами, отдается предпочтение при создании про
грамм по эконометрике и анализу данных.
Отметим, что все описанные ниже методы поиска оценок имеют
итерационный характер.
1.3.1.
Алгоритмы квазиградиентного типа
Предположим, что область Г допустимых значений параметров совпа
дает со всем евклидовым пространством
Rm
(напомним, что т
неизвестных параметров, т. е. размерность вектора
-
число
0).
Наибольшее распространение в настоящее время получили алгорит
мы итерационного типа
{1.19)
где
s-
номер итерации; д8
жения на s-й итерации;
-
Ps -
вектор, определяющий направление дви
длина шага.
Идея, лежащая в основе этих алгоритмов, очень проста: на каждом
шаге двигаться в направлении минимума функции
J(0 ).
Различные ал
горитмы отличаются способом выбора этого направления и правилами
выбора длины шага.
В данной главе обсуждаются лишь алгоритмы, движение в кото
рых осуществляется в направлении под острым углом к антиградиенту
(-grad(J(0)))
функции
J(0)
{или некоторой ее аппроксимации). Такие
алгоритмы будут называться в дальнейшем алгоритмами квазигради
ентного типа. Напомним, что антиградиент
-
это направление, про
тивоположное градиенту, а градиент в точке перпендикулярен к линии
постоянного значения функции
J(0),
проходящей через эту точку (рис.
1.10).
Рис.
1.10.
Определение направления градиента
Гл.
34
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
Таким образом, градиент в каком-то смысле указывает направле
ние локального наискорейшего возрастания функции
J(0).
Компонен
ты градиента определяются формулой
V J(0)
д J(0) = ( д81
д J(0), ... ' д8m
д J(0) )'
= де
Легко проверить, что для функции
J(0 ),
соответствующей задаче
МНК,
VJ(0)
= -2~(0),
i=n
где R (0) = ~ Wi (Yi - fi (0)) д~~е).
i=l
По рисунку видно, что в некоторых точках направление, указываемое антиградиентом, существенно отличается от направления, указы
вающего на точку
0. По этой причине многие алгоритмы предусматри
вают движение, вообще говоря, отличное от антиградиента.
Таблица
1.2.
Характеристики наиболее распространенных
алгоритмов безусловной оптимизации
Пункт
№
п/п
Матрица
Алгоритм
книги,
Hs
где
описан
алго-
Тип
ти
скороеС:ХОДИМО-
сти
ритм
1
Градиент-
1.3.2
Im
ный
кая
спуск
2
Геометричеспрогрес-
сия
Ньютона
1.3.3
(~[Ms + Vs])-l
Сверхлинейна.я (ква,цра-
тична.я)
3
1.3.4
Ньютона-
Гаусса
(~Ms)- 1
{линеа-
Геометрическа.я
прогрес-
сия
ризации)
4
Вариант
1.3.4
(~[Ms +-ysAs])- 1 , As >0
Марквардта
5
Сопряженных
гра-
Геометрическа.я
прогрес-
сия
Но
(1m -
g.VJ'(eв-1)
VJ'(0в-1)HoVJ(8в-1)
Н
)
s-l
1.3.5
Сверхлинейна.я
диентов
Для алгоритмов квазиградиентного типа соотношение
нимает вид:
(1.19)
при-
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
35
Вектор VJs либо совпадает с градиентом V J(0 8 ), подсчитанным в
точке es, либо представляет собой его некоторую аппроксимацию.
l\_!атрица Н 8 - положительно полуопределенная матрица, т. е. VJ~ х
х Н 8 V J 8 ~ О, что и гарантирует движение под острым углом к анти
градиенту.
В табл.
1.2
представлены выражения для матрицы Н 8 , которые ис
пользуются в наиболее распространенных алгоритмах безусловной ми
нимизации.
Алгоритмы градиентного спуска
1.3.2.
Описание общей схемы алгоритма. При градиентном спуске дви
жение осуществляется непосредственно в направлении антиградиента,
т. е. Н 8
= Im
т х
Итерационная процедура, таким образом, принимает вид:
m).
(напомним, что
Im -
единичная матрица размерности
(1.20)
где ~s
= ~(08 ), а вектор-столбец Э10 определен выше.
Перечислим несколько возможных способов выбора величины шага
Ps·
Обозначим Ps
=
~Э18 направление минимизации. Существуют два
основных способа, приводящих к снижению значения
J( 0)
на каждом
шаге и к сходимости итерационного процесса.
1)
Зададимся некоторым О
<
е
< 1.
Дроблением шага добьемся
того, чтобы
~
~
J(0s+1) - J(0s)
/
~
~ еР8 V J(0s).
Поскольку р~ V J(es) < О, всегда J(0s+ 1) - J(es) < О.
2) Длина шага определяется из условия
Ps
= argminJ(0s
+ р · Ps)·
р~О
(1.21)
При таком выборе шага обычно говорят о «наискорейшем спуске~.
Оптимизационная задача
(1.21)
чаще всего решается с помощью квад
ратичной аппроксимации по р.
Решение задачи минимизации вторым способом может оказаться
чрезвычайно трудоемким. Дело может осложниться тем, что функция
J (0)
вдоль выбранного направления может быть му.л,ьтимода.л/ьной.
Поэтому первый способ нам кажется более предпочтительным. Опи
санные способы выбора шага могут применяться и в других методах
минимизации (см.
1.3.3-1.3.5).
36
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Сравнение эффективности различных способов выбора длины шага
применительно к задачам регрессии проведено в
Алгоритмы типа
(1.20)
[Bard {1970)].
[Бард (1979)], [Васильев
(см., например,
(1980)]) обеспечивают при определенных ограничениях на функцию
J(0) сходимость последовательности {ев} со скоростью геометрической прогрессии
В частности, такая скорость сходимости обеспечивается так назы
ваемой линейной сходимостъю, при которой
о< q
< 1,
где 110в+~ -011-длина вектора 0в-0; и q- константы, определяемые
видом J(0).
Например, если помимо некоторых не очень существенных ограни
чений градиент удовлетворяет условию Липшица:
llVJ(0)-VJ(e)ll ~ Lll0-011
при всех 0, е Е R!"', L = const >О, а функция J(0) сильно выпукла с
показателем µ, т. е.:
J(a0 + (1 - a)eJ ~ a:J(0)
+ (1 -
a)J(e)-
-- '
...... при всех 0,
- µ. a:(l - а:)(0 - 0) . (0 - 0)
е Е Rm
и
О ~ а ~ 1,
то величина q определяется соотношением q =
1 - µ/2L.
Замечание об зффехтивности алгоритма. Одним из основ
ных достоинств градиентного спуска является его простота. Однако ре
альная скорость его сходимости уменьшается при приближении ев к
точке е. Для функций овражного типа с сильно вытянутыми линия
ми уровня в окрестности е эффективность методов типа градиентного
спуска особенно низка, так как обычно для таких функций µ близко к
нулю.
При решении статистических задач с помощью градиентного спуска
приходится на заключительном этапе проводить дополнительные рас
четы по отысканию оценок ковариационных матриц и прочих величин,
описывающих статистические свойства оценок.
Обычно градиентный спуск целесообразно применять лишь на на
чальных этапах минимизации, используя найденные в результате срав
нительно небольшого числа итераций величины es в качестве началь
ного приближения для более сложных методов, обладающих большей
скоростью сходимости.
1.3.
1.3.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
37
Метод Ньютона
Описание общей схемы метода. Идея метода Ньютона (иногда
его называют методом Ньютона- Рафсона) заключается в квадратич
ной аппроксимации функции J(e) в окрестности точки 0s+l· Значения
8s+l находятся из условия минимума аппроксимирующего полинома
второй степени и определяются в случае положительной определенности матрицы
по формуле
{1.22)
Положительная определенность
Gs
является существенным огра
ничением использования метода Ньютона. Вместе с тем, чем ближе на
чальное приближение к минимуму, тем скорее можно ожидать выпол
нение этого условия. Ведь в точке минимума, весьма вероятно, матрица
G(e) положительно определена, а из непрерывности G(0) следует, что
в некоторой окрестности е гессиан также будет положительно опреде
лен. Поэтому наибольший эффект имеет применение этого метода в
достаточно близкой окрестности решения.
Иными словами, Ps
1, Н 8 G; 1 . Несложные
=
вают, что для
J(e)
вида
=
выкладки показы
{1.18)
Gs = 1/2{М 8 + V 8 ),
..,
Ms = "' Wifisfis;
n
где
i. - дfi(0)
L.,,,
Jis -
де
0=0s
i=l
i=n
Vs
= LWi(Yi - fi{e))Фis;
Фis=
i=l
При линейной параметризации
. . . +0m~m(Xi),
где
{rpk(X)}k=l,m......-
fi(0)
=
д2 fi(e)
---
деде'
81~1(х1)
e=es
+ 02rp2(Xi) + ...
некоторая система базисных функ-
ций, не зависящих от е, решение е получается на первом же шаге независимо от выбора 0о. На практике предпочитают использовать метод
Ньютона с регулировкой шаrа
{1.23)
где р выбирается, например, в соответствии со способом
или из условия
Ps
= argmin
J [es + р (Ms + Vs)- 1 Э1s] .
р>О
1
из п.
1.3.2
38
Гл.
1.
Процедура
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
{1.23)
оказывается более стабильной по сравнению с
{1.22),
которая особенно чувствительна к выбору начального приближения <Эо
и подвержена эффекту «раскачки» при его неудачном выборе.
Скорость сходимости процедуры. Если дополнительно к усло
виям, сформулированным в конце описания общей схемы алгоритма
градиентного спуска, потребовать, чтобы llG(0 - G(ЁЭ)ll ~ Kll0 - ЁЭll
при всех 0, е Е Rm, то при упомянутых последовательностях {Ps}
НеЗаВИСИМО ОТ выбора 0о ПОСЛеДОВатеJIЬНОСТЬ {08 ) СХОДИТСЯ К е С КВад
раТИЧНОЙ скоростью, т. е.
........
........
ll0s+l - 011
~
.......
..... 2
Cll0s - 011 '
где константа определяется видом функции
J(0)
и не зависит от
s.
При решении практических задач на данное утверждение (впро
чем, как и на аналогичное утверждение из п.1.3.2) не следует особенно
полагаться. Дело в том, что проверка условий, его сопровождающих,
за исключением тривиальных случаев, реально невозможна. К тому же
большинство из них для «экзотических» выборок (маловероятных вы
борок) заведомо не будут выполняться. Тем не менее подобные утвер
ждения все же имеют смысл, так как позволяют дать оценку той макси
мальной скорости сходимости, которую можно достигнуть с помощью
данного метода. Данное замечание имеет место для всех рассматрива
емых здесь методов.
Одним из наиболее существенных недоста:ков метода Ньютона яв
ляется необходимость подсчета производных
Для достаточно сложных функций
lis и Фis·
/i (0) это приводит к весьма гро
моздким вычислениям и заметно усложняет работу пользователя, так
как
приходится
составлять специальные дополнительные программы
по подсчету производных.
1.3.4.
Метод Ньютона -
Гаусса и его модификации
Общая сжема метода. Заметно более простым по сравнению с преды
дущим методом является метод Ньютона- Гаусса, в котором матрица
Н 8 = М; 1 . Тем не менее практика показывает, что именно для регрес
сионных задач вида
{1.18)
его эффективность оказывается не худшей,
чем в методе Ньютона.
К итерационной процедуре Ньютона- Гаусса
можно прийти из следующих соображений. Для достаточно гладких
функций /i(0) в окрестности точки ев можно полагаться на простей-
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
39
шую аппроксимацию
(1.24)
Полагая Yi
= Yi - fi(es) и е = е - es, приходим к необходимости
минимизации (см.
(1.19))
функции
i=l
А это значит, что задача сведена к реализации взвешенного МНК в
условиях линейной (по оцениваемым параметрам) функции регрессии.
Но в этом случае, как известно (см., например [Айвазян и др.
гл. 7), минимум достигается при е
= м; 1 !ls.
(1985)],
Отсюда следует, что
Для линейного случая решение достигается за один шаг. При нели
нейной параметризации процедура повторяется:
Именно эта процедура и носит название метода Ньютона- Гаусса.
Для рассматриваемой
экстремальной задачи
метод Ньютона
Гаусса близок методу Ньютона. При линейной параметризации они сов
падают. Их близость при малых вторых производных Фis очевидна.
Имеется и более глубокая причина их близости. Действительно, при
п
--+
оо и некоторых не слишком ограничительных предположениях в
силу закона больших чисел имеем следующую сходимость (с вероятно
стью единица)
n
n- 1
где
0u -
L:wi(Yi - fi(es))Фis--+
i=l
n
li~n- 1
:L:wi(/i(0u) - fi(es))Фis,
i=l
истинные значения искомых параметров.
Обсуждение скорости сходимости процедуры. Метод Нью
тона- Гаусса очень чувствителен к обусловленности матриц М 8 • При
плохо обусловленных матрицах М8 наблюдается «раскачка~ итераци
онного процесса, а если он и сходится, то его предельные точки меня
ются с изменением начального приближения
00.
Наиболее распростра
ненной причиной плохой обусловленности матриц
Ms
является неудач
ный выбор режимов наблюдений Х. Поэтому, сталкиваясь с плохо обу
словленными матрицами М 8 , экспериментатору следует попытаться в
первую очередь разобраться в своих опытных данных, и, может быть,
40
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
провести дополнительные наблюдения. Если же структура данных не
может быть улучшена, то приходится обращаться к методам, которые
менее чувствительны к виду матриц М8 • Одним из наиболее широко
применяемых является метод Марквардта:
(1.25)
который может трактоваться как некоторое усовершенствование метода
Ньютона- Гаусса.
В
'Ys =
(1.25) 'Ys
~ О,
As -
неотрицательно определенная матрица. При
О реализуется метод Ньютона-Гаусса, при
'Ys
4- оо и
правление движения приближается к антиградиенту.
большинстве модификаций
(1.25)
As = 1 на
Выбор Ps и 'Ys в
проводится из соображений монотон
ного убывания
J (0).
Матрица As в большинстве компьютерных реализаций (1.25)
выби
рается диагональной, причем ее элементы совпадают с диагональными
элементами матрицы М 8 •
Полезно иметь в виду следующий факт. Если опираться на линей
ную аппроксимацию
(1.24),
то при
Ps = 1
каждый шаг в методе Марк
вардта может быть истолкован как минимизация функции
n
Lwi (1ii -iise)
2
+'Yse'Ase.
i=l
Иными словами, в этом методе на каждом шаге проводится регуляри
зация исходной задачи.
Сходимость метода Ньютона- Гаусса и его модификаций изуча
лась, например, в [Поляк
(1971)], [Hartley (1961)], [Pereyra (1967)],
раз
личные комментарии и дополнительную библиографию можно найти в
[Химмульблау
(1975)],
[Бард
(1979)],
[Демиденко
(1981)].
Скорость сходимости в зависимости от условий, накладываемых на
функции /i(8), Лs, Фis, и способов выбора р8 , 'Ys, А 8 может быть:
линейной:
сверхлинейной
квадратичной
:
:
110s+1 - 011 :::; qll0s - 011;
110s+l - 011 :::; qsll0s - 011, qs 4- О или
....
........
........
........ 2
ll0s+l - 811 :::; Cll8s - 811 ·
Рекомендации по правилу остановки итерационной про
цедуры. Для регрессионной задачи (1.18) матрица D
=
м- 1 (0) мо
жет быть использована в качестве оценки ковариационной матрицы
МНК-оценок. Если lim 0s
s-+оо
= 0,
на- Гаусса наряду с оценками
0
то итерационная процедура Ньютопоставляет и матрицу D(D : : : : м;..1 ,
1.3.
где s* -
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
41
номер заключительной итерации). Этот факт позволяет также
сформулировать простое и естественное правило остановки. Расчеты
прекращаются, как только
где о
-
наперед заданная точность.
Данное правило более естественно, чем, например, правило, исполь
зуемое в общих программах минимизации - (es+l - 0s)'(0s+l - es) ~
~ о. Действительно, точность нахождения 0 целесообразно соизмерять
со статисти-ческой точностью (ее ковариационной матрицей) МНК
оценок.
1.3.5.
Методы, не использующие вычисления
производных
Основные noдxoiJ'bl к устранению необжодu.мости вычисления
nроuаводн,-ых. Как уже отмечалось, существенным недостатком мето
дов, изложенных выше, является необходимость подсчета производных
Лs, а в методе Ньютона - и вторых производных Фis, на каждой ите
рации. При сложных функциях
fi(0)
это, во-первых, оказывается уто
мительным с программистской точки зрения, а во-вторых, приводит к
громоздким вычислениям на каждой итерации.
Возможны несколько способов избавления от необходимости под
счета производных:
-использование методов прямого поиска (нулевого порядка), таких,
как симплекс-метод, метод случайного поиска и т. п. (см., например,
[Fletcher {1965)];
- аппроксимация производных конечно-разностными аналогами;
- специальные методы аппроксимации матриц Н 8 , V J8 , позволяющие реализовать итерационные процедуры, близкие по эффективности
к процедурам Ньютона и Ньютона- Гаусса, но с меньшим объемом вы
числений.
Прямые методы минимизации оказались малоэффективными для
задач регрессионного типа даже по сравнению с градиентными мето
дами ([Бард
{1979)]). К тому же после отыскания с их помощью экс
тремальных значений 0 требуется проведение объемистых вычислений
по нахождению статистических характеристик, описывающих качество
оценок.
Конечно-разностная аппроксимация хотя и избавляет потребителя
от утомительной работы по составлению дополнительных программ для
вычисления производных, но не решает проблемы сокращения объема
вычислений. Чаще всего она приводит к его заметному увеличению.
42
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Наиболее перспективными и удобными оказались методы третьей
группы. Они завоевали весьма прочное место во многих эконометриче
ских и статистических пакетах.
Разностные аналоги метода Ньютона
-
Гаусса. Основная
идея, на которую опираются методы третьей группы, заключается в ис
пользовании на
дущих
s
(s
+ 1)-й итерации информации, полученной на преды
итерациях, для построения разумных аппроксимаций элемен
тов матрицы
Hs
и компонент градиента
V J8 •
При решении регрессионных задач хорошо зарекомендовали себя
методы, являющиеся, по существу, аппроксимациями метода Ньюто
на- Гаусса. По-видимому, работа
[Peckham (1970)]
является в этом на
правлении пионерской. Упрощенный и непосредственно приспособлен
ный к задачам регрессии алгоритм предложен в
(1978)].
[Ralston, Jennrich
Достаточно подробный анализ алгоритмов подобного типа и их
дальнейшее развитие содержатся, например, в [Вересков и др.
(1981)).
Данную совокупность методов целесообразно назвать методами
Ньютона- Гаусса без подсчета производных. Как и обычный метод
Ньютона-Гаусса (см. п.
1.3.4), эти методы опираются
аппроксимацию функций fi(0) в окрестности точки 0 8 :
на линейную
В отличие от метода Ньютона- Гаусс~ коэффициенты в векторе
столбце 'Уis не совпадают с производными fis, а подсчитываются по зна
чениям функции
ципе величины
fi(0),
полученным по прошлым итерациям. В прин
'Yis могут быть подсчитаны самыми различными спосо
бами, но в программах по регрессионному анализу оказывается очень
удобным отыскивать их с помощью все того же метода наименьших
квадратов. Определим
'Yis
=
'Yis как решение следующей задачи МНК:
s+q
argmin LWst [!i(et) - fi(et) -'Y'(et 'У
0s)] 2 '
t=l
где Wst - веса, описывающие вклад того или иного значения fi(et)·
При этом s значений получены непосредственно из итерационной про
цедуры, а выбор остальных q значений параметров 0 будет объяснен
позднее. В частности, в алгоритме, предложенном в [Ralston, Jennrich
(1978)], Ws,s+q = Ws,s+q-1 = · · · = Ws,s+q-m = 1, а остальные веса пола
гаются нулевыми.
Хорошие результаты дает выбор весов вида Ws,l
убывающая функция, например
exp[-kJ(0)).
= cp(J(0l)), где <р -
Можно показать, что
(1.26)
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
43
-fi(es)·
Подставляя
(1.18) приближенное значение функции
/i(0) = fi(es)+f1s(e-es) (ер. с (1.24)), получим, что функция J(0) до
стигает своего минимума при e-es = м;ЧRs, где Ms = E~=l C.Vi'Yis'Y:s;
Rs
теперь
в
= E~=I C.Vi"'fis(Yi - fi(es)).
После несложных преобразований приходим к очень удобной в вы
числительном плане формуле
n
е - es = Qsm; 1
L Uis(Yi -
(1.27)
fi(es)),
i=l
n
где ms =
L C.ViUisUis·
i=l
Итерационная процедура Ньютона- Гаусса, опирающаяся на
(1.27),
принимает вид
n
0s+l
= es + PsQsm; 1 L
(1.28)
Uis(Yi - fi(0s)).
i=l
Выбор
Ps
осуществляется по одному из правил, принимаемых для
процедуры Ньютона- Гаусса с переменным шагом.
Остановимся на некоторых особенностях процедуры
(1.28).
Ее ос
новное достоинство состоит в том, что на каждом шаге достаточно всего
одного вычисления функции
fi (0)
(естественно, при всех i
= 1, n). Дан
ное свойство оказывается чрезвычайно полезным при сложных функци
ях
f(i; 0).
Например, в тех случаях, когда эта функция удовлетворяет
некоторому дифференциальному уравнению, допускающему лишь чис
ленное решение, для получения которого требуются специальные объ
емистые вычисления.
Процедура
(1.28)
содержит операцию обращения матрицы, от ко
торой можно было бы избавиться, заменив ее обращением с помощью
рекуррентных формул. Однако, как правило, трудоемкость этой опера
ции несущественна по сравнению с трудоемкостью подсчета значений
функций
fi( е).
В [Ralston, Jennrich (1978)) утверждается, что вместо непосредствен
ного обращения матрицы ms целесообразно использовать пошаговые
процедуры, применяемые при отборе существенных факторов (см., на
пример, [Айвазян
функциях
J(0)
(2010)),
п.
4.4 ).
Подобный прием особенно удобен при
~овражного» типа (матрица
m8
плохо обусловлена).
Гл.
44
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Для определения
мере в (m+l)-й точке
требуется подсчет функций
'Yil
/i (е)
по крайней
ei. На последующих итерациях достаточно прове
дения подсчета функций
/i(0)
хо обусловленных матрицах
лишь в одной точке
m8
08.
Однако при пло
рекомендуется использовать в
полнительные значения функций, подсчитанные в точках
s
Таким образом, упоминавшееся ранее q равно Е
точки рекомендуется располагать
направлению, определяемому
(1.26) до
0i 1 , ••• , eiks.
k1. Дополнительные
l=1
на направлениях,
ортогональных
к
(1.26).
При линейной параметризации метод Ньютона- Гаусса без подсче
та производных дает точное решение задачи МНК на первой итерации,
если р1=1.
На наш взгляд, выигрыш в объеме вычислений при переходе от
итерационной процедуры
(1.27)
к более сложным процедурам весьма
сомнителен ввид,у резкого увеличения сложности расчетов на каждой
итерации.
Некоторые аамечанuя о вwборе длины шага. Один из глав
ных недостатков изложенного метода состоит в следующем. Как пока
зано ранее, существенным свойством квазиградиентных методов явля
ется возможность отыскания такого (может быть, достаточно малого)
шага
Ps
(в выбранном направлении), который приводит к уменьшению
значения минимизируемой функции. Это имеет место всякий раз, когда
направление минимизации составляет острый угол с антиградиентом.
Выбор же направления в формуле
(1.28)
Ps > О мы будем
[Ralston, Jennrich (1978))
не гарантирует нам этого. По
этому даже при малых
не в состоянии уменьшить зна
чение
предлагается попеременно для
Ps
J(0).
В
пробовать как положительные, так и отрицательные значения. На
пример, если задаться коэффициентом редукции О
положить р
= (-{З)r, где r =О, 1, ... ; величина Ps
первому r, для которого J(es+1 < J(es)·
< f3 < 1, то
можно
тогда соответствует
Однако и эта процедура иногда может не привести к уменьшению
функции (например, в случае, когда направление минимизации орто
гонально градиенту). Тогда следующую точку можно искать методом
случайного поиска в окрестности es.
Разностные аналоги метода Ньютона. В предыдущем пунк
те отправной точкой при конструировании итерационных процедур слу
жила доступность информации лишь о функциях /i (es). Иногда в ре
грессионных
задачах,
оказывается,
сравнительно
просто
подсчитать
производные Лs· .Подчеркнем, что речь идет о непосредственном под
счете величины fis, а не их разностных аналогов, которые требуют, по
крайней мере, (m + 1)-го вычисления функций fi(e 8 ).
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
45
Обращение к разностным формулам для вычисления Лs делает
применение изложенной ниже группы методов бессмысленным. Каж
дый шаг, ими определяемый, будет по трудоемкости близок к несколь
ким шагам из итерационных процедур, рассмотренных в п.
1.3.4 и 1.3.5.
По-видимому, наиболее известным из рассматриваемой группы ме
тодов является метод Дэвидона-Флетчера-Пауэлла. Идея, лежащая
в основе данных методов, состоит в отыскании на каждом шаге направ
лений спуска, близких к направлению метода Ньютона, но без исполь
зования матрl!_ЦЫ вторых производных.
Матрица Н8 , аппроксимирующая матрицу Н8 из метода Ньютона,
может быть, например, определена как решение системы
........
........
V J(0t) - V J(0t-1) = Н
где Н
-
-1 ........
........
(0t - 0t-1);
t
~ S,
(1.29)
симметричная матрица.
Решение системы
(1.29)
при
s<
т неоднозначно, поэтому возмож
ны различные способы конструирования матрицы Н. Различные мето
ды рассматриваемой группы отличаются способами конструирования
ЭТОЙ матрицы И правилами выбора напуавлений Н; 1 VJ(0 8 ), если ОНИ
не определены однозначно. Матрица Н 8 должна удовлетворять одно
временно уравнениям
(1.29)
при всех
t
~
s.
Приведем способы конструирования матриц Н 8 для некоторых наи
более распространенных методов (см. [Поляк
нилин
(1969)), [Пшеничный, Да
(1975)], [Powell (1970], [Huang (1970)]):
)
а мето
~А...
•
д соnряженн:ых c.J:'U'Vu.eнmoв.
Н-
_ НHogsVJ'(0s)Hs
s+1 o-VJ'(es)HoVJ(es) ·
где g8 = VJ(es) - VJ(es-1), матрицу Но часто выбирают единичной
или диагональной с элементами fJi.o/(д~i J(0))e=e0 , i = 1, 2, ... , т;
б) метод Дэвидона
-
Флетчера
-
Пауэ.л.л.а:
Hs-19s9~Hs-1.
g~Hs-19s
в) измененный вариант метода Дэвидона
-
Флетчера
-
'
Пауэ.л.л.а:
Hs-1us(es - es-1Y
(es - es-1)'gs
При квадратичной функции
J(0)
(в нашем случае
-
линейной па
раметризации) после т шагов матрица Н, подсчитываемая любым из
методов а)
п.
-
в), в точности совпадает с матрицей Н 8 , определенной в
1.3.3. Иными словами,
при р8
= 1 в этом случае точное решение исход
ной экстремальной задачи будет заведомо получено за т шагов. Если
46
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Ps = 1 выбирается из условия наискорейшего спуска в направлении :Й;- 1 '\!J(0 8 ), ТО при выполнении не СЛИШКОМ ограничительных условий
последовательность {es} сходится при s --+ 00 к е со сверхлинейной
скоростью независимо от выбора 0о.
1.3.6.
Способы нахождения начального приближения
В задаче минимизации функции
J( 0)
первостепенное значение имеет
удачный выбор начального приближения 0о. Разумеется, невозможно
придумать общего правила, которое было бы удовлетворительно для
всех случаев, т. е. для всех возможных нелинейных функций
{fi}·
Каж
дый раз приходится искать свое решение. Ниже предлагается набор
некоторых способов нахождения грубого начального приближения, ко
торое на практике может служить отправной точкой поиска удовлетво
рительных приближений в конкретной задаче.
Поиск на сетке. Особенно эффективен этот метод при неболь
шом числе собственно нелинейных пара.метров. Часто функции
fi
устроены так, что при фиксации значений одних параметров (которые
и называем собственно нелинейными) остальная часть параметров ста
новится линейной.
Задаваясь тогда нижней и верхней границей для нелинейных па
раметров, с некоторым шагом можно устроить перебор вариантов на
полученной сетке значений этих собственно нелинейных параметров и
выявить ту линейную регрессию, которая приводит к минимальной сум
ме квадратов.
В качестве примера рассмотрим функцию
f (Xi; 0)
= 81+82xi(1) + 83 ев4 xi< >•
2
Здесь собственно нелинейным параметром будет
{1.30)
84.
Допустим, известно, что~ ~ 84 ~ 04. Пусть h - шаг для параметра
84. Вычислим К= (04 - ~)/h линейных регрессий
-
fk (Xi; 0) = 81
+ 82xi(1) + 8зzik,
где Zik = ехр [(~ + hk) х~ 2 >] , k = 1, К, и найдем для каждой из них
минимальную сумму квадратов. Наименьшей из них соответствует оп
тимальное начальное приближение. В принципе шаг
h,
от которого за
висит «густота~ сетки, может варьироваться, так что за счет умень
шения величины
h
значения параметров могут быть найдены с любой
точностью.
Преобразование модели. Иногда некоторым преобразованием
модель можно свести к линейной (см. п.1.2) или же уменьшить число
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
47
собственно нелинейных параметров. Покажем, как этого можно добить
ся, на примере логистической кривой
f (xi;B)
=
В1
1 + В2 ехр (Взхi)
.
Производя над соответствующими уравнениями регрессии обратное
преобразование, получим
_.!.. ~ _!:_
Yi
В1
Обозначая Zi
= l/yi,l/B1
+ В2 е8зжi •
В1
=В~, В2/В1 =В~, приходим к новой функ
ции, число линейных параметров которой увеличилось с одного (В1) до
двух (В~ и В~). Оценка для параметра Вз в новой модели может быть
найдена, например, по предыдУщему методУ.
Здесь уместно сделать следующее замечание о преобразованиях ре
грессионных моделей. СледУет иметь в ВИдУ, что ошибка е, входившая
аддитивно в исходное уравнение, после преобразования, вообще говоря,
уже не будет аддитивна.
Пользуясь разложением в ряд Тейлора и обозначая преобразование
fi(8) через q(fi), получим, пренебрегая слагаемыми порядка ef:
Zi
1
2
= q(yi) = q(fi + ei) = q(fi) + q(fi)Ei + 2q(fi)ei ·
Отсюда следУет, что Ezi
= Eq(yi) + !q(fi)u2.
Последнее равенство можно взять за основу для анализа задачи с
преобразованной моделью.
Разбиение выборки на подвыборки. Для нахождения началь
ного приближения можно разбить всю выборку на т подвыборок
(с приблизительно равными объемами), где т -
число неизвестных
параметров. Для каждой подвыборки найдем средние по у и по Х, ко
торые обозначим соответственно (у3, Х3),
j
= 1,
т.
Решим систему нелинейных уравнений относительно
В1,
{
У1
Ут
... , Вт :
= f(X 1; 81,"., Вт)
= J(Хт;
81," ·,Вт)·
Решение этой системы и будет являться начальным приближением
параметров. Очевидно, для того чтобы данный метод «работал~, необ
ходимо, чтобы эта система нелинейных уравнений решалась довольно
легко (в лучшем случае аналитически).
48
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Разло:нсенuе в ряд Тейлора
no
независимым переменным.
Основой итерационной минимизации суммы квадратов является разло
жение функции регрессии в ряд Тейлора до линейных членов по па
раметрам. Для нахождения грубого начального приближения иногда
бывает полезна процедура аппроксимации регрессии путем разложения
ее в ряд Тейлора по независимым переменным
считать
Xi
одномерным. Пусть х
-
Xi.
Будем для простоты
среднее значение, тогда приближен
но
f (xi; 0) ~ f (х; 0) + (xi - х) f~ 1 > (х; 0) + ... + -
1
1 (xi
т.
- x)m f~m> (х; 0).
Обозначим (xi - x)k = Zik, f~k) (х; 0) = Фk, таким образом прихо
дим к линейной
модели j (Zi; Ф) = Фо + Ф1Zi1 + ... + Фm1Zim·
.......
Пусть Фk - МНК-оценки параметров этой линейной регрессии. В
качестве начальных приближений примем решение нелинейной систе
мы уравнений относительно
f(x; 0)
81, ... ,8m:
= Фо, ... , f~т>(х; 0) = Фm.
Очевидно, этот метод приемлем в том случае, когда последняя си
стема
относительно
первоначальных
параметров
решается
довольно
просто (аналитически).
Продемонстрируем использование этого приема на примере нели
нейной регрессии (1.30). Для простоты будем считать х< 2 >
е84 х~ 2 ) ~ 1 + (х?> - х< 2 >)84 + ~(х~ 2 > - х< 2 >) 2 8~.
Подставляя это разложение в
(1.30),
= О.
Тогда
получим
Обозначив Фо = 81 + 03, Ф1 = 82, Ф3 = 8384, Ф4 = 8~/2, х~ 1 > = Zil,
х~ 2 ) = Zi2, (х~ 2 )) 2 = Zi3, приходим к линейной по Ф модели j (Zi; Ф) =
+ Ф3Zi3·
= Фо + Ф1Zi1 + +Ф2Zi2
.......
Тогда если Фi
-
МНК-оценки линейной регрессии, то легко прове-
рить, что начальным приближением для параметров
0
будут
В реальности возможна комбинация предложенных способов. Прак
тика показывает, что таким образом можно получить достаточно хоро
шее начальное приближение для широкого круга нелинейных регресси
онных задач.
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
49
Вопросы существования и единственности
1.3.7.
МНК-оценки
Существование. Запись
(1.18},
строго говоря, не совсем корректна,
так как МНК-оценка может отсутствовать, если априорное множество
допустимых значений параметров Г не является компактом (по предпо
ложению
fi
считаем непрерывными на Г). Отсутствие решения в задаче
МНК практически приведет к тому, что итерационный процесс мини
мизации
/(0)
будет расходиться и
ll0sll -+ оо при s-+ оо.
Естественно, перед тем как решать задачу минимизации, желатель
но удостовериться, что она корректна. Изложим один подход к реше
нию этой проблемы {более подробно см. [Демиденко
ниж:ней границей функции
J(0)
J=
{1981))).
Назовем
на бесконечности число
lim
inf J(0).
r~oo ll0lll~r
Можно показать, что если существует такое начальное приближе
ние 0о, что J(0o)
S(0o)
= {0
Е
< J,
то МНК-оценка существует, а множество
R!7" : J(0)
~
L{0o)} компактно. Компактность его
гарантирует существование хотя бы одной предельной точки последо
вательности значений параметров, вырабатываемой одним из методов
минимизации.
Нелинейная регрессия имеет бесконечные хвосты, если при
-+ оо 1fi (0) 1 -+ оо для любого i
= 1,
11011 -+
п. Наоборот, регрессия имеет ко
нечный хвост, если существует такая последовательность параметров
ll0kll -+ оо, k -+ оо, что l/i(0)1 ~ М
<
оо для всех i
=
1, п. Можно
показать, что J = +оо тогда и только тогда, когда регрессия имеет бес
конечные хвосты. В случае J = оо МНК-оценка всегда существует. На
f(Xi; 0) = ехр(0' Xi),
векторы Х1, ... , Xn Е Rm
пример, в случае логлинейной модели, т. е. когда
регрессия имеет бесконечные хвосты, если
'JХLЗНОнаправлены (для любого о:' Е
торого
Yi
> О,
ot.'X;
R!7"
существует вектор Х;, для ко
<О). В то же время можно показать, что если наблюдения
то в логлинейной модели МНК-оценка всегда существует.
Оценки снизу для величины
J в каждом конкретном случае находят
аналитически до начала процесса минимизации.
Едuнсmвенносmь. Сумма квадратов
J(0)
(см.
{1.18}}
может быть
мультимода.л:ьной. Более того, можно доказать, что вероятность муль
тимодальности
J(0)
отлична от нуля для любой нелинейной регрессии,
не сводящейся к линейной преобразованием в пространстве параметров.
Дело усугубляется тем, что все методы минимизации в лучшем случае
приводят к локальному минимуму функции. Проверка того, является
ли этот минимум глобальным, является следующей, возможно, не ме
нее трудоемкой операцией. На практике часто поступают следующим
Гл.
50
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
образом. Процесс итераций начинают из другого начального прибли
жения. Тогда, если он сойдется к точке, полученной в первой попытке,
можно быть более уверенным в том, что нелинейный минимум является
глобальным.
Существуют аналитические методы проверки на достижимость гло
бального минимума суммы квадратов. Все они предполагают анали
тическое исследование поверхности отклика. Иногда при исследова
нии этой проблемы бывает полезен следующий результат. Пусть най
дено выпуклое множество значений параметров
ан
на котором гесси
S,
д2 J /
(д0д0') положительно определен. Пусть да.лее найдена оценка
снизу, такая, что J(0) ~ М для всех 0 Е S. Тогда, если найденной точ
ке в процессе итераций е Е S соответствует локальный минимум со зна
чением J(e) < М, то J(е)-глоба.льный минимум функции. Например
(см. [Демиденко (1981)]), для логлинейной модели f(Xi; 0) = ехр(0' Xi)
с положительными наблюдениями Yi множеством S будет
S = {0 Е Rm: 0'Xi > ln(yi) - ln(2),
i
= 1, Ь},
а в качестве простейшей оценки снизу можно взять М
=
1min(yl).
Подобные оценки, как и в случае исследования на существование МНК
оценки, необходимо проводить аналитическими методами.
1.3.8.
Основные свойства МНК-оценок
В данном пункте исследуются основные свойства МНК-оценок парамет
ров и связанные с ними вопросы точности построенной модели регрес
сии, в которой наблюденные значения
и
xi =
(х?>' х~ 2 >'
Yi
результирующего показателя ТJ
... 'xf>) объясняющих переменных ~ = (~(l)' ~< 2>' ... '
~(р)) связаны соотношениями (1.17).
При этом постулируется выполнение следующих допущений:
(i) выбранный исследователем класс допустимых решений F содер
жит в себе искомую функцию регрессии f(X; 0) = Е(ТJ 1 ~ = Х), т.е.
f(X; 0)
(ii)
регрессионные остатки€
Е
F;
(1.31)
= (е1,е2, ... ,en)'
несмещены относи
тельно нуля, взаимно некоррелированы и одинаково (О; и 2 )-норма.льно
распределены, т. е.
(iii)
ее N (о, и 2 • ln);
(1.32)
f (Х; 0)
нелинейно зависит от под
искомая функция регрессии
лежащих статистическому оцениванию параметров
0
= (81, ... , 8m)',
1.3.
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
51
однако характер этой зависимости достато-чно гладкий (например, су
ществуют всевозможные вторые производные от
f (Х; 0) по параметрам
8k,8j; k,j = 1, ... ,m).
Напомним, что главным
( nринциnиалън'ЬtМ)
пунктом сидеализа
ции~ анализируемой схемы является первый, т. е. допущение
(1.31). Два
других носят, скорее, полутехнический характер.
Относительная сложность решения различных вопросов, относя
щихся К СВОЙСТВам ОЦеНОК е И К ТОЧНОСТИ реГреССИОННОГО анализа (ПО
сравнению с линейным вариантом), состоит в том, что в данном слу
чае МНК-оценки е неизвестных параметров 0 определяются не в виде
явных аналитических выражений, а лишь в ходе итерационных алго
ритмических процедур (см. п.1.3.1-1.3.5), что существенно затрудняет
исследование их свойств. В основе обычно используемых в данной схеме
подходов
- разложение в ряд Тейлора (по параметрам 0 в окрестно
сти наилучшей оценки е) оптимизируемого критерия мнк и искомой
функции регрессии /(Х;0).
ях
Поскольку МНК-оценки е параметра 0 модели (1.17) в услови
(1.31)-(1.32) совпадают с оценками максимального правдоподобия,
то мы можем воспользоваться общими результатами о свойствах последних. Из них, в частности, следует, что МНК-оценки
ных коэффициентов
0
модели
(1.17)
-.
0
регрессион-
являются (при условии соблюде
ния упомянутых условий) состоятелън'ЬtМи, асимптоти-чески-несме
щенными,
асимnтоти-чески-эффективн'ЬtМи и асимnтоти-чески-нор
малъными (асимптотика по
n -+
оо).
Для того чтобы перейти непосредственно к решению задач анализа
точности нелинейной регрессионной модели, нам необходимо получить
предварительно выражение для ковариационной матрицы Ее МНК-
оценок е.
С этой целью воспользуемся разложением функции регрессии
0) в ряд Тейлора в окрестности точки 0
параметра
1.3.5),
0,
= е, (где е
-
f(Xi;
МНК-оценка
полученная с помощью процедур, описанных в п.1.3.1-
ограничиваясь линейными членами разложения:
или, в более удобных обозначениях,
,,,,,,,....,
/i(0) ~ /i(0)
+ (0 -
,,,,,,,....,
/
.
0) fi,
где /i(0) = f(Xi; 0) и Л = (дfi/д81, ... , дfi/д8т)'.
Выражение (1.33) для произвольного значения Х
1(x;0)-J(x;e) ~ (0- e)'i.
(1.33)
дает:
(1.34)
52
Гл.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
1.
Введение обозначений
фk(Х)= дf(Х; 8 )
д8k
е=в
в= 0- е; f(x;e)
Ф(Х)
=
, k=l,2, ... ,m;
i(x;0 + е)
- J(x;e);
= j = ({J1(X), ... ,фm(Х)) 1
позволяет записать выражение
( 1.34)
в виде
f(X; е) ~ е'Ф(Х)
(1.34')
и свести, таким образом, нелинейную модель
(1.17)
к ее аппроксимации
линейной схемой.
Решение задач анализа точности регрессионной модели основано на
исследовании точности оценок е и отклонений J(X; 0) - J(X; е).
Примем во внимание приближенные соотношения (1.34) и (1.34'),
равенство ковариационных матриц оценок е и е т. е. Ев = Ев) и воз
(
можность использования обычного приближенного приема вычисления
вторых моментов статистических оценок, когда в полученные выраже
ния для этих моментов, зависящие от неизвестных значений оценивае
мых параметров, вставляются их оценки.
Тогда можно (см., например, [Бард
(1979)], § 7.5) получить следу
ющие выражения для ковариационной матрицы Ев оценок е и для ее
......
оценки Ев:
(1.35)
и, соответственно,
где
А2
и
1
= n-m
Ln Wi(Yi -
.. '
f(X;; 0))
2
n
Ме= L:Me(X),
i=l
i=l
а
дf(Xi;0) д/(Хi;0)
д81
д8m
д/(Хi;0) д/(Хi;0)
д82
д8m
д/(Хi;0) д/(Хi;0)
д8m
д81
причем
производные,
Me(Xi),
д/(Хi;0) д/(Хi;0)
д8m
д82
участвующие в выражении элементов
берутся в точке
0
= 0*, т. е.
матрицы
ВЫЧИСЛИТЕЛЬНЫЕ ВОПРОСЫ НЕЛИНЕЙНОГО МЕТОДА
1.3.
дf(Xi;
53
8) дf(Xi; 8)
дfJk
д83
k,j = 1, ... ,т;
Подчеркнем два главных отличия данного случая от линейного.
Во-первых, используемые для построения доверительных интерва
лов свойства состоятельных МНК-оценок
8 -
несмещенность, опти
мальность, нормальность, а также свойства б), в) и г) из п.
вазян и др.
11.1.1 [Ай
(1985)) справедливы лишь в асимптотическом (поп~ оо)
смысле.
Во-вторых, следует учитывать приближенн:ый характер базовых
соотношений
(1.34)
и соответственно
(1.35).
Следует признать, что воз
можны различные уточнения описываемого здесь приближенного под
хода (см., например,
[Beale (1974))).
Однако вряд ли они существенно усовершенствуют предлагаемые в
данном пункте практические рекомендации: ведь даже так называемые
точные критерии и доверительные интервалы на практике оказъtвают
с.я всего лишь приближеннъtМи (они точны лишь в той мере, в какой
соблюдаются в реальной ситуации те идеализированные допущения, на
которых строятся соответствующие статистические выводы). Поэтому,
говоря о том, что интересующая нас погрешность не превзойдет опре
деленной величины с доверительной вероятностью, например, равной
0,95,
мы должны всегда отдавать себе отчет в приближенном характе
ре подобных заключений.
В заключение отметим, что приведенные выше результаты дают
основание
использовать в
построении
интервальных
зультирующего показателя у и функции регрессии
f
оценок для
ре
(при заданных
значениях объясняющих переменных Х) рекомендации п. 6.3 из [Ай
вазян
(2010)), полученные для линейной модели регрессии, в которых,
однако, следует заменить:
• матрицу хтЕ 0 1 Х на матрицу Мв;
•
вектор-столбец Xn+l на вектор-столбец
.т.(Хn+l ) -_
~
f·(xn+l ) -_
(дf(Xn+1i е)
А
д81
,
•••
,
дf(Xn+1i е))'
........
дет
54
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
Выводы
1.
Этап nараметризации регрессионной модели, т. е. выбора па
раметрического семейства функций (класса допустимых решений), в
рамках которого производится дальнейший поиск неизвестной функ
ции регрессии, является одновременно наиболее ва:жн'ЫМ и наименее
теоретически обоснованн'Ьl.М этапом регрессионного анализа.
2.
Прежде всего, исследователь должен сосредоточить свои усилия
на анализе содержательной сущности искомой статистической зави
симости, чтобы максимально использовать имеющиеся априорные све
дения о «физическом)) механизме изучаемой связи при выборе общего
вида функции регрессии, (см. п.
из [Айвазян и др.
3.
2.5.1
в [Айвазян
а также п.
(2010)],
6.1
(1985)] .
Важную роль в правильном выборе параметрического класса
допустимых решений играет предварительный анализ геометрической
структуры совокупности исходных данных, и в первую очередь ана
лиз геометрии парных корреляционных полей, включающий в себя, в
частности, учет и формализацию «гладких)) свойств искомой функции
регрессии (см. п.
(1989)]),
2.5.2
из [Айвазян
(2010)],
а также п.
6.2
[Айвазян и др.
использование вспомогательных линеаризующих преобразова
ний (см. п.1.2 книги).
4.
Сформулированные с помощью содержательного
(эконометри
ческого) и геометрического анализа рабочие гипотезы об общем виде
искомой функции регрессии могут быть проверены с привлечением со
ответствующих математико-статистических критериев.
Среди фундаментальных идей, на которых базируются эти стати
стические критерии, следУет выделить:
а)
идею компромисса между сложностью регрессионной модели
(«емкостью)) класса допустимых решений) и точностью ее оценивания;
б)
идею поиска модели, наиболее устойчивой к варьированию со
става выборочных данных, на основании которых она оценивается;
в) идею проверки гипотез об общем виде функции регрессии на базе
сравнения выборочных критериев адекватности и исследования стати
стических свойств получаемых при этом оценок размерности модели
(п. 6.3 из [Айвазян и др.
5.
(1985)],
а также п.
2.5.3
из [Айвазян
(2010)]).
При исследовании параметрических моделей регрессии весьма
распространенным типом оптимизируемого (с целью нахождения оце
нок неизвестных значений параметров регрессии) критерия адекват
ности модели является взвешенний (или обобщенний) критерий наи
меньших квадратов (см.
(1.18)).
СледУет стремиться к построению та
ких вычислительных алгоритмов решения оптимизационных задач, ко
торые нарядУ с решениями этих задач - значениями оценок е неиз-
Выводы
вестных параметров е,
-
55
давали бы необходимые характеристики их
точности (оценки элементов ковариационных матриц, доверительные
области и т. п.).
6.
Наибольшее распространение среди методов поиска оценок наи
меньших квадратов получили алгоритмы итерационного типа, позволя
ющие на каждой следующей
......
((s + 1)-й)
итерации получать приближен-
ные значения
0 8 +1 искомых оценок параметров, лежащие «ближе~ к
истинному решению е соответствующей оптимизационной задачи, чем
значения е предыдущей итерации, т. е. 0s+1 = ев + Ps · fJ8 , где s - но
мер итерации, fJ8 - вектор, определяющий направление движения на
s-й итерации, Ps - длина шага.
Если движение осуществляется в направлении под острым углом
к антиградиенту оптимизируемой функции, то алгоритм относится к
классу алгоритмов квазиградиентного типа (см. п.
7.
1.3.1).
Если движение в итерационной процедуре уточнения значений
оценок параметров осуществляется непосредственно в направлении ан
тиградиента, то процедуру относят к алгоритмам градиентного спус
ка. Подобные алгоритмы обеспечивают (при определенных ограничени
ях на минимизируемую функцию) сходимость последовательности
es
со скоростью геометрической прогрессии (линейная сходимость). Из-за
того,
что реальная скорость сходимости таких алгоритмов резко сни
жается при приближении
08 к предельному значению е, градиентный
спуск целесообразно применять лишь на начальных этапах минимиза
ции, используя найденные в результате сравнительно небольшого числа
.......
итераций величины 0 8 в качестве начальных приближений для более
сложных методов, обладающих более высокой скоростью сходимости
(см. п.
1.3.2).
8. В методе Ньютона значения неизвестных параметров на каж
дой следующей итерации 0s+I находятся из условия минимума квадра
тичного
полинома,
аппроксимирующего
функцию в окрестности точки
0
8•
исходную
критериальную
При этом соответствующая проце
дура будет менее чувствительна к выбору начального приближения
(в частности, будет менее подвержена эффекту «раскачки~ при его
неудачном выборе), если использовать ее вариант с регулировкой шага.
При определенных условиях метод Ньютона обеспечивает квадратич
es
ную скорость сходимости последовательности
к е (см. п. 1.3.3).
9. Используя линейную (по параметрам) ~ппроксимацию исследуе
мой функции регрессии в окрестности точки 0 8 , можно прийти к моди
фикации метода Ньютона - методу Ньютона - Гаусса. Он существен
но проще в вычислительном плане, однако бывает слишком чувстви
тельным к эффекту слабой обусловленности используемых в нем мат
риц М 8 • Скорость сходимости этого метода в зависимости от условий,
56
Гл.
1.
ВЫБОР ОБЩЕГО ВИДА МОДЕЛИ И НЕЛИНЕЙНАЯ РЕГРЕССИЯ
накладываемых на регрессионную функцию и свободные параметры ал
горитма, может быть линейной, сверхлинейной или квадратичной (см.
п.
1.3.4).
10. Существенн'Ьl.М
недостатком методов квазиградиентного ти
па, в том числе метода Ньютона, метода Ньютона- Гаусса и других,
является необходимость подсчета производных от искомых регресси
онных функций на каждой итерации.
Основная идея, на которую опираются методы, позволяющие об
ходиться без подсчета производных, заключается в использовании на
(s
+ 1)-й
итерации информации, полученной на предыдущих
s итера
циях, для построения разумных аппроксимаций для элементов матриц,
определяющих выбор направления и шаг движения к решению е (см.
п. 1.3.5).
11. Первостепенное значение для скорости сходимости используе
мых итерационных процедур решения оптимизационной задачи метода
наименьших квадратов имеет удачный выбор начального приближения
00. Для реализации этого выбора используется ряд приемов: «поиск
на сетке~ вспомогательного преобразования (линеаризующего) модели,
разбиение имеющейся выборки на подвыборки, разложение регрессион
ной функции в ряд Тейлора (см. п.
12.
1.3.6).
При вычислительной реализации метода наименьших квадра
тов в нелинейном (по оцениваемым параметрам е) случае приходит
ся исследовать вопросы существования и единственности решения (см.
п.1.3.7). Необходимо помнить, что используемые (в том числе все опи
санные выше) методы оптимизации приводят в лучшем случае лишь к
локальному минимуму критериальной функции. Проверка того, явля
ется ли этот минимум глобальным, является следующей, зачастую не
менее трудоемкой, вычислительной операцией.
Глава
2
Построение интегральных
u
измерителеи для
синтетических латентных
u
категории
И в профессиональной деятельности, и в своей повседневной жизни
человек постоянно сталкивается с ситуациями, когда ему приходится
сравнивать между собой и упорядочивать по некоторому (не подда
ющемуся непосредственному измерению) свойству ряд объектов. Речь
может идти, в частности, о сравнении стран по тем или иным аспектам
качества жизни, предприятий отрасли по эффективности их деятельно
сти, сложных изделий по обобщенной характеристике их качества, спе
циалистов по эффективности их участия в выполнении поставленной
задачи, участников игровых видов спорта по уровню проявленного ими
мастерства и т. д. Формализации подобных ситуаций и вытекающим из
нее
рекомендациям
по
построению некоторого условного
измерителя
упомянутого свойства и посвящена глава.
В частности, рассматривается задача измерения так называемых
синтетических латентных категорий, т. е. категорий, которые яв
ляются одновременно синтетическими, т. е. объединяющими в себе ши
рокий спектр свойств анализируемого качества, и латентн'ЫМи, т. е. не
поддающимися непосредственному измерению. К подобным синтетиче
ским латентным категориям
(СЛК)
относятся, например, такие поня
тия, как качество жизни населения определенной территории
(стра
ны, региона), уровень социальной напряженности в обществе, уровень
взяточничества и коррупции, уровень материального благосостояния,
индекс здоровья определенного конгломерата населения, качество эко-
Гл.
58
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
логической ниши для данной территории, инновационный уровень на
циональной экономики и т.п. Каждой такой синтетической латентной
категории можно сопоставить (конечно, не единственным способом) на
бор статистических показателей х< 1 >, х< 2 >, ... , х<Р), достаточно полно и
разноаспектно ее характеризующих. Эти статистические показатели
естественно интерпретировать как частные критерии анализируемой
синтетической категории. Тогда измеритель у (интегральный индика
тор) или измерители у< 1 >,
,y(k), k < р (интегральные индикаторы)
...
такой синтетической категории строится (строятся) в виде некоторой
свертки (функции) этих показателей, т.е. у
f(x< 1>,x< 2 >, ... ,х<Р>)
=
(в случае несколысих интегральных индикаторов: у< 1 >
. . . 'х<Р>), ... 'y(k) = fk(x(l>' х<2)' ... 'х<Р>) ).
= fi(x< 1>, х<2 >, ...
Тогда, очевидно, сформулированную задачу можно охарактеризо
вать как некоторую проблему редукции многокритериальных
схем. Этой проблеме посвящена обширная литература (см., например,
[Хованов
(1996)),
[Фишберн
[Каплинский и др.
(1978)), [Тангян (1980)), [Полищук (1989)),
(1991)), [Steuer (1986)). Однако описанные ниже ме
тоды ее решения отличаются тем, что, во-первых, они являются эконо
метрическими по своей природе (т. е. они, являясь математико-статис
тическими, основаны на сочетании использования результатов некото
рых измерений и соответствующих теоретических положений той об
ласти науки, к которой эти измерения и сама задача относятся), а во
вторых, предложенные методы формирования упомянутых выше свер
ток f(x< 1>, ... , х<Р>) лишены тех существенных недостатков, которые
свойственны другим (к сожалению, широко распространенным) мето
дам (подробнее об этом см. ниже).
3
а м е ч а н и е. Сле,цует
подчеркнуть
возможность
объективно
оправданного отсутствия удовлетворительного решения проблемы пе
рехода от многокритериальной схемы (с частными критериями х< 1 >, х< 2 >,
... ,х<Р>) к однокритериальной (у). В этом случае возникает задача
определения числа и вида нескольких критериев у< 1 >, ... , y(k), позво
ляющих существенно ре,цуцировать размерность р исходной многокри
териальной схемы (т. е.
2.1.
k
<
р ).
Концептуальные основы подхода
к измерению синтетических латентных
категорий
Итак, пусть обобщенная сводная характеристика
f
анализируемого
свойства объекта определяется набором частных критериев, задавае
мых подцающимися учету и измерению переменными х< 1 >, ... , х(р),
2.1.
КОНЦЕПТУАЛЬНЫЕ ОСНОВЫ ПОДХОДА
59
однако сама эта характеристика является латентной, т. е. не поддается
непосредственному количественному измерению (для нее не существу
ет объективно обусловленной шкалы). Естественно предположить, что
интуитивную количественную экспертную (профессиональную) оценку
этой характеристики (обозначим ее Уз) можно представить как несколь
ко искаженное значение f(x< 1>, ... , х<Р>), причем это искажение о носит
случайный характер и обусловлено как разрешающей способностью та
кого «измерительного прибора», каковым в данной схеме является экс
перт, так и существованием ряда относительно слабо влияющих на Уз,
но не входящих в состав Х = (х< 1 >, ... ,х(р>)', частных критериев. Тогда
модель, связывающая меж.цу собой интуитивное представление о свод
ном показателе качества (Уз) с самим сводным показателем
f(X)
(как
функцией от Х) и случайной погрешностью о(Х), может быть опреде
лена в виде
Уз
= f (Х) + о(Х).
(2.1)
Если принять естественные, практически не ограничивающие общ
ности данной схемы допущения относительно первых двух моментов
остаточной случайной компоненты о(Х):
Ео(Х) =О,
Do(X)
= и2 (Х) < оо,
то в случае, когда мы располагаем наблюдениями
. . . , n, ка f(X)
(Xi; Узi), -i = 1, 2, ...
очевидно, обобщенная сводн.ая ( интег·ра.л:ьная) характеристи
может интерпретироваться как регрессия Уз по Х.
Замечание о целевых функциях. Весьма распространенной в
области социально-экономических исследований является интерпрета
ция обобщенной сводной (интегральной) характеристики качества
f(X)
как целевой функции. При этом под целевой функцией анализируемо
f
го выходного качества у понимается любое преобразование
частных
1
2
критериев Х = (х< >, х< >, ... , х(р>)', сохраняющее заданное соотношение
порядка меж.цу n рассматриваемыми объектами по у, т. е. обладающее
тем свойством, что из
с необходимостью следует выполнение неравенств
где
f(Xi)
и
Yi
-значения, соответственно, целевой функции и истинно
го (ненаблюдаемого) сводного показателя качества, характеризующие
60
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
i-й объект. Очевидно, данное здесь определение целевой функции неод
нозначно. Действительно, если
f (Х)
есть целевая функция и <р (!)
-
любая монотонно возрастающая функция, то всякая функция вида
f(X) =ер (f(X))
также будет целевой функцией. Это означает, что наше допущение о
наличии определенной шкалы в измерении у в ряде случаев играет чи
сто вспомогательную роль и не нацеливает нас на поиск, связанный с ее
выявлением. Ведь в соответствии с этим определением само значение
целевой функции не отражает никакой реальной, физически содержа
тельной количественной закономерности. Реальные закономерности от
ражаются только соотношениями «больше» или «меньше» между зна
чениями этой функции для различных наборов величин входных пара
метров Х
= (х< 1 >, х<2 >, ... , х(р>)'. Тем самым эти соотношения отражают
предпочтение (с точки зрения анализируемого выходного качества) од
них значений Х перед другими. Поэтому в задачах, в которых возможно
регулирование значений Х (в некоторой допустимой области), наиболее
рациональным (оптимальным) управлением естественно признать то,
которое максимизирует (при заданных ограничениях на Х) значения
целевой функции.
Вопросы построения разного рода целевых функций широко пред
ставлены в литературе (см. [Хованов
(1996)],
[Полищук
манский и др.
[Айвазян
(1989)], [До
в гл. 4 книги
(2006)]). Они обсуждаются, в частности,
(2012)] в связи с проблемой статистической оценки
целевой
функции потребительских предпочтений по данным выборочных бюд
жетных обследований домашних хозяйств (см. п.
4.1.2
этой работы).
Резюмируя сказанное, мы приходим к следующей общей логической
схеме редукции многокритериальных схем (см. рис.
2.1).
Комментарии к реализации этой общей логической схемы и, в част
ности, формулировка связанных с этим задач даются ниже (см. п.
2.2.
2.3.1 ).
Исходные данные
Исходные данные, необходимые в эконометрическом подходе для реше
ния задачи редукции многокритериальных схем, состоят, в зависимости
от объективных условий, либо из двух массивов
-
статистического
и экспертного (обучающего), либо только из одного
-
статистиче
ского.
Статистический массив объединяет в себе данные вида
(1)
(2)
(р)
(xi 'xi ' ... 'xi ),
i = 1, 2, ... , n,
(2.2)
2.2.
где x~j)
-
ИСХОДНЫЕ ДАННЫЕ
61
значение j-го частного критерия (статистического показате
ля), зарегистрированное на i-м объекте, а n -
общее число статистиче
ски обследованных объектов (объем выборки).
Сmпетическая латентная
каrеrq>ия (СЛК)
•1\
~
lf
Априорный набор частных криrериев
(стаmС'IИческих показателей) i'>, х< 2>, .•. , iP >,
харакrеризующих дmmую СЛК
Апостериорный набор частных
криrериев СЛК ;ю, ;ш, ... ,хир' >
(р'< р)
Инrегральные Ш1ДИкаторы
промежуточного уровня
у<'>' ... 'у<*>
где
y<I> =J(}il>, ... ,xuP·».
измериrели СЛК
(1 :1;; k :1;; р')
Сводный
интегральный
индикатор
у
Рис.
2.1.
Общая логическая схема редукции миогокритериальных схем
Экспертный (обучающий) массив (или просто «обучение~)
содержит некоторую информацию о сравнении статистически обследо
ванных (представленных в
(2.2))
объектов по анализируемой синтети
ческой латентной категории.
Эту информацию о сравнении объектов получают, как правило, с
помощью специально организованного опроса экспертов и соответству
ющей статистической обработки экспертных оценок. Она обычно пред
ставляется в одной из сле,цующих форм.
62
2.
Гл.
Форма
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
наиболее информативный (а потому наиболее трудный
(i) -
для экспертов) вариант. Она предусматривает получение экспертн:ых
бал.л:ьн:ых оценок выходного качества
Yllэ'
1/21э'
· · ·'
Ynlэ
У12э'
У22э'
···'
Уn2э
(2.За)
где Yiiэ
- оценка выходного качества объекта Oi, полученная от j-го
эксперта (здесь п - число оцениваемых объектов, т - число участву
ющих в оценке экспертов).
Форма
средний по информативности (и по степени трудно
(ii) -
сти для экспертов) вариант. Она предусматривает получение лишь экс
пертн:ых упорядочении обследованных объектов по степени проявления
в них анализируемого свойства, т. е. ранжировок вида
... '
... '
где R;,;э
-
(2.Зб)
ранг (место), присвоенный объекту
oi
j-м экспертом вря
ду из п обследованных объектов, упорядоченных этим экспертом по
степени проявления анализируемого свойства (от лучшего к худшему).
Форма
наименее информативный (и наименее трудный для
(iii) -
экспертов) вариант. Информация от каждого (j-го) эксперта поступает
в форме (п х п)
-
булевой матриц-ы парн-ых сравнений
i, l = 1, п,
где 'Yil.jэ -
ok'
(2.Зв)
j = 1, 2, ... 'т,
результат парного сравнения j-м экспертом объектов
oi
и
который определяется по следующему правилу:
'Yil.jэ
=
1,
если, по мнению
j
-го эксперта,
Oi
лучше
-1,
если, по мнению
j
-го эксперта,
Oi
хуже
О
в случае, если
j
(iv) -
Oi;
-й эксперт не может определить
предпочтений между
Форма
Oi,
oi и
о,.
пожалуй, наименее трудный для экспертов вариант.
Потому она является и наиболее распространенной формой эксперт
ного обучения. Речь идет о разбиении статистически обследованных
об'6ектов на небольшое число групп, упорядоченных по анализируемой
2.2.
ИСХОДНЫЕ ДАННЫЕ
63
синтетической категории, но не предусматривающее никаких предпо
чтений между об~ектами, принадлежащими одной какой-то группе
(например, разбиение всех анализируемых объектов на три группы: ли
деров, середняков и аутсайдеров). В этом случае мы имеем информа
цию вида
(уп, Yi2,
где Yil -
Е
... , Yim),
i
= 1, 2, ... , n,
(2.Зг)
номер класса, к которому l-й эксперт отнес i-й объект, Yil Е
{1, 2, ... , ko}
(для определенности будем считать, что чем выше номер
класса, тем выше качество анализируемой СЛК).
Строго говоря, эта форма экспертного обучения укладывается как
в рамки формы
(ii)
(если допустить существование так называемых
связнъ~х, т. е. неразличимых, рангов), так и в рамки формы
(iii).
Вычислительные трудности, связанные с реализацией алгоритмов
построения интегральных индикаторов (ИИ) в форме свертки
f(X),
естественно, возрастают по мере перехода от более информативных ва
риантов
(в п.
экспертного
2.3.4)
обучения
к
менее
информативным.
Ниже
мы рассмотрим эти алгоритмы для каждой из приведенных
выше форм обучения.
Некоторые общие требования к формированию исходного
(априорного) набора частных критериев. При формировании ис
ходного (априорного) набора статистических показателей (частных
критериев) х< 1 >, х< 2 >, ... , х<Р), характеризующих определенную синтети
ческую
латентную
категорию,
эксперты
должны
руководствоваться
следующими общими требованиями:
(А) представительности (релевантности), в соответствии с которым
в данном перечне должны быть представлены (при экзогенной
заданности всех прочих аспектов СЛК) все основные показате
ли рассматриваемой синтетической категории; так, например, для
синтетической категории «Качество жизни населения определен
ной территории)) в этом перечне должны присутствовать наиболее
существенные характеристики качества населения, материально
го благосостояния, качества социальной сферы и качества эколо
гической ниши (см., например, [Айвазян
(2012)];
(В) информационной доступности, в соответствии с которым привле
каемые к дальнейшему анализу показатели и частные критерии
должны быть, по меньшей мере, доступны для их статистической
регистрации и, более того, они должны входить в номенклатуру
периодически регистрируемых официальных статистических по
казателей (или могут быть вычислены по значениям последних);
64
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
(В) информацион:ной достоверности, в соответствии с которым ис
пользуемые статистические данные и частные критерии должны
адекватно отражать состояние анализируемого аспекта СЛК; так,
именно по причине нарушения этого требования нам в ряде иссле
дований пришлось отказаться от использования такого, казалось
бы, существенного для синтетической категории «Качество жиз
ни~ показателя, как «среднее число зарегистрированных тяжких
преступлений за год, приходящееся на
100
ООО жителей~: дело в
том, что малые значения этого показателя часто сигнализируют
не о благополучном состоянии дел в данной области, а о слабой
работе статистических и правоохранительных органов.
Формирование редуцированного (апостериорного) набора
частных критериев. При формировании исходного (априорного) на
бора статистических показателей для анализируемой латентной синте
тической категории экспертам предлагается опираться на определен
ную структуризацию частных критериев и интегральных свойств этой
СЛК (см., например, ниже, рис.
2.2)
и учитывать при этом сформули
рованные выше общие требования (А), (В) и (В).
Базовая идея, на которой строится методика формирования ре
дуцированных (апостериорных) наборов частных критериев
по каждой из анализируемых синтетических латентных кате
горий, заключается в сле,цующем.
Из состава сформированного (из теоретических, содержательных
соображений, на экспертном уровне) априорного набора частных кри
териев заданного интегрального свойства требуется выделить (оста
вить для дальнейшего анализа) сравнительно небольшое число пока
зателей таким образом, чтобы, во-первых, они являлись бы наиболее
существенно влияющим.и на анализируемую СЛК
(т. е.
были бы де
терминантами последней), а во-вторых, чтобы в оставшемся наборе
частных критериев (который мы будем называть апостериорным) бы
ло бы исключено явление мулътикоминеарности, при котором наблю
дается дублирование информации относительно анализируемой СЛК,
доставляемой тесно коррелированными частными критериями (заме
тим, что при описанном ниже способе устранения мультиколлинеарно
сти значения исключенных из априорного набора частных критериев
обычно поддаются достаточно точному восстановлению по значениям
переменных, вошедших в апостериорный набор).
Метод реализации этой общей идеи зависит от наличия (или отсут
ствия) «обучения~ в постановке задачи измерения латентной синтети
ческой категории.
2.2.
а)
ИСХОДНЫЕ ДАННЫЕ
65
Отбор наиболее существенных частных критериев в
условиях наличия обучения. Будем предполагать, что модель
параметризуется в классе
х< 1 >,
х<Р) и при этом мы
... ,
линейн-ых функций
частных
(2.1)
критериев
располагаем обучением в форме (i) в виде
единого варианта экспертных балльных оценок У1э, YZ3,
... , Упэ,
анали
зируемой синтетической категории для всех рассматриваемых объектов
(регионов, стран). В этом случае мы можем рассмотреть линейную ре
грессионную модель вида
(2.1')
Тогда отбор наиболее существенных частных критериев можно про
изводить, например, с помощью сочетания методов пошаговой регрес
сии (или «метода всех возможных регрессий») «С присоединением» и
«С исключением». Напомним общую схему этих процедур (см. п.
[Айвазян
4.4.2
в
(2010)]).
Пошаговая процедура последовательного присоединения
предназначена для отбора (в рамках линейной модели множественной
регрессии
(2.1')) наиболее информативного набора из р' объясняющих
переменных, отобранных из исходного (априорного) множества объяс
няющих переменных х< 1 >,
... , х(р)
(очевидно, р' < р).
На первом шаге этой процедуры (р' = 1) из исходного набора объ
ясняющих переменных Х = (х< 1 >, ... , х(р))' выбирается та переменная
xU1 >, которая имеет максимальное значение квадрата коэффициента
парной корреляции с зависимой переменной у, т. е.
На
(v + 1)-м
шаге этой процедур-ы (1~v~р-2) мы уже располагаем
отобранными до этого шага наиболее информативными переменными
xU1 >, ... , x<J"). Следующая (v + 1)-я информативная переменная xU"+ 1 )
отбирается таким образом, чтобы
R2 (у;
(x(ji)' ...
'x(j")' xUv+i)))
=
шах
ц;;;~р
R2 (у; (xU 1 >, ... , x<J"), х<Л)) ,
j~jl .;2 •... ,;"
где R 2 (y; (x(li), ... , х(lн))) - подправленный ("adjusting'') коэффициент
детерминации между у, с одной стороны, и набором (x(li), ... , х(lн)) С дРУГОЙ.
Обычно процедуру заканчивают на таком шаге, при котором пере
ход к следующему шагу не дает статистически значимого приращения
величине R 2 .
66
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Пошаговая процедура последовательного исключения пред
назначена для удаления из исходного (априорного) набора объясняю
щих переменных х< 1 >,
х(р) тех переменных, которые практически не
... ,
увеличивают прогностическую силу модели
(2.1').
На первом шаге этой процед-уры из исходного набора объясняю
щих переменных удаляется та переменная x<ii), исключение которой из
модели
приводит к минимальному уменьшению величины коэф
фициента детерминации R2 , т. е.
(2.1')
R 2 (у; X(i1)) = m~ R 2 (у; X(i)),
l~i~p
где
X(l) обозначает исходный набор
торого удалена переменная x<l).
объясняющих переменных, из ко
Перед реализацией (v+1)-го шага этой процед-уры
исходного набора останется
их x<v>
(1
~
v
~ р-2) из
p-v объясняющих переменных. Обозначим
= (xUi>, ... , x<jp-v>)'.
Тогда на (v
+ 1)-м шаге из этого набора
будет исключена та переменная x(ivн), удаление которой приводит к
минимальному уменьшению величины R2 (у ; (x(ji >, ... , x(jp-v >) ) , т. е.
R 2 (у; x<v>(iv+1)) = . _m~
R 2 (у; x<v>(i)),
i=31, ... ,Jp-v
где x<v>(l) обозначает набор объясняющих переменных x<v>' из кото
рого исключена переменная х< 1 >.
Обычно процедуру последовательного исключения проводят до то
го шага, после которого очередное удаление переменной приводит к
статистически значимому уменьшению величины коэффициента детер
минации R2 .
Возможно обобщение описанной процедуры на случаи, когда обуче
ние представлено в форме
(ii), (iii)
подходов, описанных в [Айвазян,
или
(iv) (например, с использованием
2012, п. 2.3.5)).
б) Отбор наиболее существенных частных критериев при
отсутствии обучения. Методологическая схема, по которой реализу
ется в данном случае общая базовая идея, состоит в следующем.
1)
Анализ мул:ьтико.л.яинеарности частних критериев априорного
набора показателей. С этой целью для переменных каждого из апри
орных наборов рассчитываются:
• матрица значений nарних коэффициентов корреляции, r(x<l),
х<"'>) (l, v = 1, 2, ... ,р), характеризующих степень тесноты попар
ных статистических связей меЖдУ частными критериями анали
зируемого свойства;
ИСХОДНЫЕ ДАННЫЕ
2.2.
67
• коэффициенты детерминации R2 ка:ждого из частных критериев
x<l) анализируемого априорного набора по всем остальнъш показа
телям этого набора.
Анализ полученных числовых характеристик позволяет провести
предварительную стадию выявления тесно связанных меж.цу собой пар,
троек и т.п. групп переменных и поставить вопрос об отборе от каж
дой такой группы по одному представителю. О необходимости редукции
каждого из априорных наборов частных критериев свидетельствует и
близость к единице значений подавляющего большинства упомянутых
выше коэффициентов детерминации R 2 (см. примеры результатов вы
числений по данной схеме в Приложении
2)
3
к работе [Айвазян
(2012)]).
Отбор наиболее информативных частных критериев среди по
казателей априорного набора каждого интегрального свойства. Пусть
задан количественный состав (р') редуцированного набора показателей
определенного интегрального свойства (р'
< р).
Назовем набор частных
критериев
x<l~}' x<lg)' ... 'x(l~)
наиболее информативным, если
где R 2 (y; (х< 1 >, ... , x<s>)) -
подправленный ("adjusting") коэффициент
детерминации зависимой переменной у по объясняющим переменным
х< 1 >, ... , x<s>. Очевидно, при подобном выборе апостериорных редуци
рованных ограниченных наборов частных критериев максимизирует
ся прогностическая сила регрессионных моделей, с помощью которых
можно восстановить значения всего априорного набора показателей
анализируемого интегрального свойства по значениям только тех част
ных критериев, которые попали в этот ограниченный набор.
Выбор количественного состава (р') ограниченного набора частных
показателей осуществляется в каждом конкретном случае на базе со
четания теоретических (содержательных) соображений и требований к
минимально допустимым значениям R~0 коэффициентов детермина-
ции R2 (x<l>; (x<l~}, ... , x(l~))).
3
а м е ч а н и е. Отбор наиболее существенных частных критериев
и в условиях наличия обучения, и без него основан на решении соот
ветствующих оптимизационных задач. Для того чтобы оставить воз
можность учета содержательных
(а не только формальных) сообра
жений, предлагается наряду с оптимальным составом апостериорного
68
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
набора переменных выводить и так называемые околооптималыtые со
ставы, т. е. такие наборы заданного числа переменных, значение
оптимизируемого критерия для которых мало (статистически
незначимо) отличаются от оптимального. И тогда окончательный
выбор состава апостериорного набора частных критериев (из вариан
тов, предоставляемых оптимальным и околооптимальными наборами)
производить, руководствуясь содержательными соображениями. Я бы
рекомендовал это замечание распространить на общий случай, включив
его в описание соответствующих процедур, содержащихся в статисти
ческих и эконометрических пакетах
(SPSS, E-views, STATA
и др.).
Методология построения интегральных
2.3.
индикаторов
-
измерителей синтетических
латентных категорий и методы
многокритериального рейтингования
Формулировка основных задач
2.3.1.
Итак, мы должны предложить и обосновать методологию построения
интегральных индикаторов (ИИ) для различных синтетических латент
ных категорий, основанную на специального вида свертках ряда част
ных (статистически регистрируемых) критериев соответствующей
синтетической категории, продемонстрировать работоспособность этой
методологии (например, при сравнительном макроэконометрическом
анализе и рейтинговании стран или регионов), а также предложить
подход к многокритериальному рейтингованию объектов по анализи
руемой СЛК в ситуациях, когда задача построения единственного ска
лярного ИИ не имеет удовлетворительного решения. Для достижения
поставленной цели мы должны уметь решать следующие задачи.
Задача
1 ( преданализ).
Определение исходного (априорного) пе
речня статистических показателей х< 1 >, х< 2 >, ... , х(р>, достаточно пол
но (разноаспектно) характеризующих анализируемую синтетическую
категорию. Учитывая смысловую нагрузку, приданную этим показа
телям,
мы
называем их также частными критери.я.ми рассматривае
мой синтетической категории. Решение этой задачи находится исклю
чительно в компетенции специалистов-экспертов той области, к которой
относится анализируемая СЛК.
Задача
2
(преданализ). Разработка определенной методики от
бора из априорного перечня частных критериев х< 1 >, х< 2 >, ... , х<Р>, полу
ченных в результате решения задачи 1, относительно небольшого числа
р' (р'
<
р) частных критериев, играющих главную роль в фор миро-
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
69
вании значений анализируемого интегрального и~щикатора. Другими
словами, речь идет о методике формирования апостериорного набора
частных критериев xU 1 >, xU2 >, ... , x(jrl >, отбираемых из априорного пе-
речня показателей х< 1 >, х< 2 >, ... , х<Р>. Подходы к решению этой задачи
были описаны в п.
Задача
3
2.2,
посвященном исходным данным.
(преданализ). Унификация измерите.л:ьных шкал всех
анализируемых переменных, т. е. переход к [О; N]
-
балльным шкалам в
измерении рассматриваемых частных и интегральных критериев СЛК
таким образом, чтобы значение «нуль» соответствовало самому низ
кому уровню качества СЛК, а значение
мерность шкалы
N
самому высокому (раз
выбирается исследователем). Решение этой задачи
представлено ниже, см. п.
Задача
N -
2.3.2.
(центральная). Разработка методики построения ин
4
тегрального индикатора
-
измерителя анализируемой синтетической
латентной категории (ИИ СЛК) в виде некоторой функции от xU 1 >,
xU2 >, ... , x<j~) в каждой из двух возможных постановок задач:
•
вариант с обу'Ч.ением: построение ИИ по значениям частных кри
териев xU 1 >, xU2 >, ... , xUr1 > апостериорного набора и по некоторой
(обучающей) экспертной информации о сравнении рассматривае
мых объектов по анализируемой синтетической латентной катего
рии (описание решения этого варианта центральной задачи см. в
п.
•
2.3.3);
вариант без обvчения: построение ИИ толъко по значениям част
ных критериев xU 1 >, xU2 >, ... , x(jP' >апостериорного набора (описа
ние решения этого варианта центральной задачи см. в п. 2.3.4).
Задача
5
(постанализ при наличии обучения). Оценка согла
сованности двух ранжировок рассматриваемых объектов по анализиру
емой СЛК, одна из которых основана на имеющемся экспертном обуче
нии, а другая
задачи
4
-
на значениях ИИ, построенного в результате решения
(в любом из двух возможных вариантов).
Задача
6
(постанализ). Построение и анализ показателей авто
и межобъектной динамики ИИ, позволяющих сравнивать во времени
анализируемое свойство объекта относительно себя самого
( « автодина
мика») и относительно других объектов
Подходы к решению задач
2.3.2.
5
и
( «межоббектная динамика»).
6 обсуждаются в п. 2.3.5.
Унификация шкал в измерениях частных
и интегральных критериев (задача
3)
Перед тем, как переходить непосредственно к проце.цуре свертки част
ных критериев, необходимо привести все эти частные критерии х к «об-
Гл.
70
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
щему знаменателю~, т. е. применить к каждому из них такое преобра
зование, в результате которого все они будут измеряться в N-балльной
шкале. При этом нулевое значение преобразованного показателя долж
но соответствовать самому низкому качеству анализируемой СЛК, а
максимальное
(N) -
самому высокому.
Конкретн:ый в'Ыбор унифицирующего преобразования зависит от
того, к какому из трех типов принадле:нсит анализируем'Ый показа
тель.
1)
Если исходный показатель (частный критерий) х связан с анали
зируемым интегральным свойством монотонно-возрастающей зависи
мостью (т. е. чем больше значение х, тем в'Ыше качество), то значение
соответствующей унифицированной переменной х подсчитывается по
формуле
Х=
Х
- Xmin
(2.4)
·N,
Xmax -Xmin
где Xmin и Xmax -
соответственно,
-
наименьшее (самое худшее) и наи
большее (самое лучшее) значения исходного показателя.
Если исходный показатель (частный критерий) х связан с ана
2)
лизируемым интегральным свойством монотонно-уб'Ывающей зависи
мостью (т. е. чем больше значение х, тем ни:ж:е качество}, то значение
соответствующей унифицированной переменной х подсчитывается по
формуле
Xmax
-х
x=-----·N.
(2.5)
Xmax - Xmin
3)
Если исходный показатель (частный критерий) х связан с анали
зируемым интегральным свойством немонотонной зависимостью (т. е.
между
Xmin
и
Xmax
существует некоторое оптимальное значение Хопт,
при котором достигается наивысшее качество), то значение соответству
ющей унифицированной переменной х подсчитывается по формуле
Х=
(1-
lx - Хопт.1
max{(Xmax - Хопт.), (Хопт. - Xmin)}
)
.
N.
(2.6)
Для реализации этих преобразований необходимо уметь определять
для каждого анализируемого частного критериях значения
Xmin, Xmax
и Хопт· Поскольку теоретико-нормативн'Ый подход в определении этих
значений в большинстве случаев сопряжен с большими трудностями
(и в частности, с необходимостью согласования различных точек зре
ния), то в данной работе предлагается использовать для этих целей
эмпирический подход. В частности, за Xmin и Xmax предлагается при
нимать, соответственно, минимальное и максимальное значения среди
всех наблюденных (по различным статистически обследованным объ
ектам или за различные такты времени) значений этой переменной.
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
71
Вопрос с определением значений Хопт решается в каждом конкретном
случае с учетом специфики ситуации.
Так, например, если мы располагаем обучением в форме эксперт
ных балльных оценок или ранжирования рассматриваемых территорий
по анализируемой синтетической категории, то в качестве Хопт можно
рекомендовать использовать результат усреднения этого показателя по
трем или пяти объектам, отнесен:ным экспертами к лидирующим по
анализируемой синтетической категории.
3
а м е ч а н и я.
1)
Легко видеть, что первые две формулы, с по
мощью которых производится унификация измерительных шкал ана
лизируемых показателей, являются частными случаями третьей, соот
=
=
ветственно, при Хопт
Xmax и Хопт
Xmin· 2) Выбор диапазона шкалы
(N) находится в компетенции исследователя.
2.3.3.
Построение ИИ СЛК при наличии обучения
(экспертн~статистический
1)
метод)
Построение ИИ СЛК при балльной форме обучения (см.
выше, форма
(i),
данные (2.За) 1 . В этом случае задача построения
ИИ СЛК сводится к статистическому оцениванию функции регрессии
(«свертки»)
f(X)
в модели
(2.1)
по исходным данным вида
(2.7)
т. е. к стандартной задаче регрессионного анализа. Так что, если мы
ограничиваем свой поиск свертки рамками параметрического семейства
{(f(X; 0)},
то
n
~
•
m
~~
2
2
f(X; 0) = arg пмn L.,, L.,, cij (Yiiэ - f(Xi; 0)) ,
(2.8)
i=l j=l
где «взвешивающие» коэффициенты
Cf;
определяются двумя фактора
ми:
•
сравнительной компетентностью экспертов (зависимость от
j);
•
сравнительной значимостью рассматриваемых об~ектов
или
сравнительной воспроизводимостью (точностью) экспертных
оценок по каж:дому из об~ектов (зависимость от
1В
i).
целях упрощения обозначений здесь и в дальнейшем будем обозначать с по
мощью р (а не р') общее число часrных критериев в апостериорном наборе.
72
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Один из возможных приемов определения коэффициентов
Cfj -
это
факторизация их значений с помощью произведения
1
1
~-=-·"'3
и? u2.'
·3
i·
где
"' (Yijэ - Yi.)- ,
= т1"'~
m
2
Ui·
2
3=1
и
и-i
= -LYiiэ;
т.
3=1
= -1"'"'
-
n
2
1 m
Yi.
L...J (Yiiэ - Yi.) 2 ·
n.i= 1
Очевидно величина и~ характеризует «размытость» в точности экс
пертной оценки i-го объекта, а значение и~ - меру уклонения в оценках
j-го эксперта от общего группового мнения.
В случае наличия единого (группового) варианта экспертного оце
нивания, т. е. при данных вида
i=l,2, ... ,n
искомый ИИ СЛК
f (Х; 0)
(2.7')
будет определяться как решение задачи
(2.8')
где при отсутствии информации о сравнительной значимости рассмат
риваемых объектов полагают
Cf = 1.
Программную реализацию решения задач
(2.8)
и
(2.8'),
осуществ
ляемого с помощью обычного или обобщенного (взвешенного) метода
наименьших квадратов, читатель может найти в любом из интегриро
ванных статистических (эконометрических) пакетов программ
Statistica, E-views
(SPSS,
и т.п.).
З ам е ч ан и е
о
в ы бо ре
бор параметрического семейства
о б ще го
{f(X; 0)},
в ида
ИИ СЛК. Вы
как правило, не удается
подкрепить строгим теоретическим обоснованием. Ведь скал.я,рнал ха
рактеристика анализируемого качества может и не существовать (см.
выше, замечание в конце введения к гл.
2),
так что в этом случае мы
имеем дело с некоторой аппроксимацией, имеющей условный смысл в
течение ограниченного промежутка времени и при определенных усло
виях. Поэтому, эксплуатируя идею разложения любой функции в ряд
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
73
Тейлора, обычно ограничиваются линейной или квадратичной аппрок
симацией искомой свертки, т. е.
р
f(X; 0)
(х(О)
= L8kX(k)
= 1)
k=O
или
р
f(X; 0)
р
= L8kx(k) +
k=O
L
8kl · x<k>x<l).
k,l=l
Заметим, что при конкретизации постановки задачи коэффициенты 8k
и 8kl часто удается наполнить реальным социально-экономическим
смыслом (см., например, [Слуцкий
2)
{1963))).
Построение ИИ СЛК при наличии экспертных ранжиро
вок объектов по анализируемой синтетической категории (см.
выше, форма
(ii),
данные (2.Зб)}. В этом случае мы располагаем
данными вида
i=l,2, ... ,n,
где /l;,jэ /JУ из
ранг (место), присвоенный i-му объекту j-м экспертном вря
n обследованных объектов, упорядоченных им по анализируемой
синтетической латентной категории (в порядке от лучшего к худшим).
Если бы мы уже располагали ИИ СЛК в форме
ли бы значение векторного параметра
0),
f(X; 0)
{т. е. зна
то подставляя в
f(X; 0)
(i = 1, 2, ... , n) и вычисляя соответствующие значения
fi = f(Xi; 0), мы могли бы получить упорядочение рассматриваемых
объектов по значениям fi, т. е. ранги R;,(0) (i = 1, 2, ... , n), которые,
конечно, буµут зависеть от значения параметров 0.
значения Xi
Но тогда мы можем вычислить согласованность этого упорядочения
с упорядочением каждого (j-го) из экспертов с помощью, например,
коэффициента ранговой корреляции Сnирмена
r·{0)
= 1- n3
3
6
n
_ n
2
~
L...,,, {R;,·Jэ -R;,(0)) .
i=l
При наличии так называемых связных рангов слеµует воспользоваться
соответствующей модификацией этой формулы, см., например, [Айва
зян
{2010)),
п.
3.3.4.
Естественно было бы ~настроить» значение параметров
0
на име
ющееся экспертное обучение, максимизировав согласованность ранжи
ровки, основанной на ИИ СЛК
f(X; 0),
с ранжировками экспертов.
74
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Это можно сделать, например, решая одну из двух задач:
m
е = arg ш:х LCjTj (0)
(2.9)
j=l
или
е
где с1, с2,
... , Crn -
= arg
шах
(2.9')
r(0),
е
неотрицательные веса,
пропорциональные степени
компетентности привлеченных экспертов (в частном случае с1 = с2 =
= · · · = ern = 1), а r (0)
на между
- коэффициент ранговой корреляции С пир ме
ранжировкой объектов, основанной на ИИ СЛК f (Х; 0), и
единым (групповым) вариантом экспертного упорядочения тех же
объектов.
3
амеч ание
о
весовых
коэфф ициентах
Ck·
В ка
честве одного из возможных способов определения весовых коэффи
циентов
Ck (k
=
1, 2, ... , m)
можно рекомендовать метод, основанный
на условной сравнительной оценке компетентности k-го эксперта с по
мощью значений коэффициентов конкордации (см., например, [Айвазян
(2010)),
п.
3.3.7)
W(m)
=
12
m 2 (n3 -
~ (~ ~n)
L,,,
L,,,
i=l
j=l
Jэ
_ m(n+1))
2
2
и
2
12
Wk(m - 1)
=
n
(m - 1)2(n3 - n)
m
(
~ ~ ~jэ -
(m - l)(n + 1) )
2
(;#)
Полагая, что чем больше возрастает коэффициент согласованности
в ранжировках экспертов
тов эксперта с номером
W
при исключении из общей группы экспер
k (т. е.
чем больше разность
тем менее компетентен этот эксперт, значения
ck
Wk( m - 1) - W (m)),
можно вычислить, на
пример, по следующей формуле:
Ck
= 1-
Wk(m-1)-W
-m--------
k
= 1, 2, ... , m.
~ (Wj(m-1)-W)
j=l
Замечание
э кс п ерт но го
об
оценке
группового
у п о р я д о ч е н и я.
Групповое
варианта
упорядочение
2.3.
R(гр)
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
75
(R~гр), .Щгр), ... , ffl:'P)) определяется как решение оптимизаци
=
онной задачи
R~гр)
= arg
IЩn
m
L 114;э - ~1,
i
= 1,2, ... ,n.
~ j=l
Как известно, решение этой задачи дается медианными значениями ря
да (J41 3 , J42э, · · · '14mэ)·
К сожалению, в плане вычислительной реализации задачи
и
(2.9')
(2.9)
весьма сложны и не имеют стандартного программного обес
печения. Избежать эти осложнения помогает некоторый специальный
прием, с помощью которого обучение
обучению
(iv)
(ii)
в форме (2.3б) сводится к
в форме (2.3г), после чего задача решается стандартны
ми программно-алгоритмическими средствами модели множественно
го уnор.ядо'Ченного вЪt,бО'JЮ (см. ниже, замечание к п. 4).
3)
Построение ИИ СЛК при наличии экспертных парных
сравнений объектов по анализируемой синтетической катего
рии (см. выше, форма
(iii), данные (2.Зв)). В этом случае обучение
предоставлено нам матрицами Гэ(j) (j = 1, 2, ... , m) парных сравнений
объектов, и задача, при заданном общем виде функции свертки f (Х; 8),
сводится к определению векторного параметра е из условия
т
е = arg nмn
L с; llГ(8) - Гэ(j)
(2.10)
11 2 ,
j=l
где Г( 8)
-
матрица парных сравнений анализируемых объектов, полу
ченных с помощью сравнения значений функций
f(Xi; 8)
и
J(X;; 8) (i,
j = 1, 2, ... , n), весовые коэффициенты с; имеют тот же смысл, что и
в задаче (2.9), а с помощью
llAll 2
определена евклидова норма матри
цы А. Существует разные подходы к решению задачи
(2.10),
см., на
пример, ~метод голосования~, предложенный Ю.М. Журавлевым (см.
(Айвазян и др.
(1974)), § 3 из гл. 5), или метод, основанный на линейном
(1980))). К сожалению, решение и этой за
как и задачи (2.9)) не имеет стандартного программно
программировании ([Киселев
дачи (так же,
алгоритмического обеспечения в общедоступных пакетах программ. По
этому и в этом случае целесообразно воспользоваться приемом сведения
формы
(iii)
обучения к форме
(iv),
см. ниже, замечание к следующему
пункту.
4)
Построение ИИ СЛК при наличии экспертного разбие
ния множества анализируемых объектов на определенное (как
правило, небольшое) число
ko однородных и упорядоченных по
СЛК групп (см. выше, форма
(iv),
данные (2.Зг)). В этом случае
2.
Гл.
76
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
в качестве исходных статистических данных мы располагаем данными
вида
{
где
Yi -
)(1)
(xi
(р) -
(2)
}
'xi ' ... 'xi ; Yi) '
i
= 1, 2, ... , n.
(2.11)
номер класса, к которому отнесен i-й объект в едином (груп
повом) экспертном разбиении объектов на классы 2 , т. е.
нимать одно из значений
{1, 2, ... , ko}.
Yi
может при
Будем предполагать для опреде
ленности, что чем выше номер класса, тем выше качество входящих в
него объектов по анализируемой синтетической категории. Тогда про
цедура многокритериальной упорядоченной классификации объектов
может быть получена как решение стандартной задачи множественно
го выбора при порядковой зависимой переменной в виде, например, со
ответствующей логит-модели. В ходе соответствующей процедуры (см.,
например, [Вербик (2008)), п.
функции от х< 1 >, х< 2 >,
х<Р>
... ,
7.2)
-
оценивается
-
в форме линейной
латентная переменная, которая и иг
рает в нашем случае роль ИИ СЛК.
Напомним вкратце общую схему реализации этой процедуры. Итак,
пусть случайная переменная
fj
может принимать значения
1, 2, ... ,
k{) (по числу анализируемых упорядоченных групп) и пусть чем вы
ше номер группы, к которой принадлежит регион
i,
тем выше каче
ство анализируемой синтетической категории этого региона. Поскольку
это качество определяется, в основном, значениями частных критериев
х?>, х~ 2 ), ... , х?>, то естественно предположить, что существует латент
ная переменная Yi в форме линейной комбинации
(2.12)
и пороговые значения со, с1,
... , Ck,
такие, что
P;(Xi) = P{fj = jlX = Xi} = Р{с;-1 < Yi <с;}=
= Р{с;-1 -x;w < €i <с; - x;w}.
Параметры линейной формы
роговые значения со, с1,
по имеющимся данным
... , Ck,
(2.11).
W
= (w1, w2, ... , wp)' так же, как и по
подлежат статистическому оцениванию
Постулируя нормальный или логистический вид функции распреде
ления
F(u)
остатков€ в соотношении
этих остатков €i (при E€i
20
= О и D€i
(2.12) и взаимную независимость
= 1, что не ограничивает общности
различных способах построения единого (группового) экспертного разбиения
см., например, (Миркин
(1976)).
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
77
модели), получаем следующее выражение для функции правдоподобия:
L(w1, ... , Wpi со, с1,
=
... , ck)
k
(2.13)
= П П (F(c; -x:w)-F(c;_ 1 -x;w))
j=l iii=j
(обычно, без ограничения общности, полагают: со
= -оо и Ck = +оо).
Максимизируя правую часть
лучаем оценки
W
(2.13) по w1, ... , wp; со, с1, ... , Ck, по
и ео, с1, ... , Ck для неизвестных параметров. Соот
ветствующие вычислительные процедуры реализованы в стандартных
пакетах программ
в
(SPSS, E-views и др.)
и подробно описаны, например,
[Greene (2000)).
3
а м е ч а н и е. Как упомянуто выше, случаи
сведены к случаю
(iv),
(ii)
и
(iii)
могут быть
что существенно облегчает задачу построения
ИИ СЛК при ранжировках и парных сравнениях объектов, полученных
от экспертов в качестве обучения. Поясним эту возможность подробнее.
И при обучении в форме
(ii),
и при обучении в форме
(iii)
каждый
i-й объект может быть оснащен характеристикой степени его пред
пuчтительности: в форме
(ii)
это средний ранг, полученный i-м объ
m
ектом от экспертов (т. е. Й,;, = ~ Е ~lэ), а в форме (iii) это среднее
l=1
число случаев, в которых i-й объект оказался предпочтительнее при
его парных сравнениях со всеми остальными
m n
(n - 1)
объектами
(т. е.
"Yi = m(~-l) Е Е 'Yil.;э). Переход к варианту (iv) разбиения объектов
j=1 l=1
на сравнительно небольшое число
ko
классов производится простым
агрегированием объектов с относительно близкими значениями
"Yi,
т. е.
с помощью решения простой одномерной задачи 'К.11.астер-ана.л.иза.
2.3.4.
Построение ИИ СЛК в условиях отсутствия
обучения
В данной постановке задачи мы располагаем то.л.ысо унифицированны
ми значениями частных критериев апостериорного набора
( -(1) -(2)
-(р))
xi 'xi ' ... 'xi
'
i
= 1, 2, ... , n,
(2.2')
т. е. не имеем никакой информации о сравнении рассматриваемых объ
ектов (территорий) по анализируемой синтетической категории
(зна-
чения х?> получены из исходных данных (2.2) с помощью операций
унификации шкал, описанных в п. 2.3.2).
Гл.
78
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Возникает вопрос: правомерно ли в такой ситуации ставить
задачу измерения анализируемой латентной синтетической ка
тегории с помощью некоторой свертки частных критериев?
Условно nоло:нсителъный ответ на этот вопрос основан на сле,цую
щей логике:
(а) Анализируемая синтетическая категория достаточно полно харак
теризуется унифицированными значениями частных критериев
x(l), х( 2 ), ... , Х(р) апостериорного набора.
(б} Если мы хотим ограничиться только одним (т.е. скалярным) аг
регированным показателем (интегральным индикатором) дан
ной синтетической категории, то естественно искать такой пока
затель
fj,
который среди всех других интегральных показателей
обладал бы сле,цующим свойством: среди всех скалярных пе
ременных,
характеризующих анализируемую
латентную
синтетическую категорию, именно по значениям этого по
казателя
fj можно наиболее точно (в определенном смыс
ле) восстановить значения всех частных критериев апо
стериорного набора, используя для этого соответствующие мо
дели парной регрессии.
А ведь если ограничить вид искомой свертки классом линейных
функций (т. е. строить ИИ СЛК в форме Е WjxU>), то именно тaj=l
ким свойством (б}, как известно (см., например, [Айвазян, Мхитарян
(2001}],
п.
13.2.5),
обладает первая главная компонента, построен
ная по частным критериям
(2.2'}
апостериорного набора!
Но возникает другой вопрос: всегда ли достаточно одной наи
лучшей, в смысле свойства (б), свертки частных критериев
для решения задачи восстановления значений всех частных
критериев апостериорного набора по значениям этой свертки
с удовлетворительной точностью, и если ~нет•, то какова ми
нимальная размерность соответствующей мультикритериаль
ной схемы? То есть если одной свертки мало, то сколько таких
сверток и каким образом мы должны построить?
Ведь возможны ситуации, когда не существует сколько-нибудь удо
влетворительного решения задачи построения скалярного индикатора
анализируемой СЛК. Подобные ситуации возникают, в частности, когда
в составе рассматриваемого набора частных критериев имеется опреде
ленное количество взаимно слабо коррелированных переменных, хотя
каждая из них вносит существенный вклад в описание и интерпрета
цию анализируемой синтетической категории. Тогда задача аппрокси-
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
79
мации (с приемлемой точностью) значений всех частных критериев по
значению единственного скалярного индикатора может в принципе не
иметь удовлетворительного решения, хотя скалярный индикатор в ви
де первой главной компоненты и является сравнительно наилучшим
предиктором в данной аппроксимационной схеме.
И тогда возникает вопрос определения минимальной размерности
k
<р
многокритериального пространства, в рамках которого возмож
но удовлетворительное решение задач рейтингования и типологизации
объектов по анализируемой синтетической категории.
В данном пункте учебника предлагается подход к решению постав
ленных выше вопросов.
3
а м е ч а н и е. Перед описанием предлагаемого подхода необхо
димо остановиться на двух достаточно общих недостатках, свойствен
ных абсолютному большинству известных (и широко практикуемых в
мире) методов построения интегральных измерителей синтетических
латентных категорий.
(1)
При построении линейной аппроксимации у =
f
w;х<Л искомо-
j=1
го интегра.л.ьного индикатора ана.л:изируемой синтетической ла-
тентной категории (ИИ СЛК), а именно линейной моделью огра
ничиваются в подавляющем бо.л:ьшинстве случаев, весов'Ьtе ко
эффициенты
w;
определяются методом прямой экспертной
оценки. Другими словами, эксперты в ходе той или иной про
цедуры согласования до.л;ж;ны численно оценить относительную
значимость каждого из частных критериев х<Л в формировании
значения ИИ (многочисленные примеръt такого рода из мировой
практики приведены, например, в [Айвазян
{2012)], гл.1). Меж
ду тем большое число экспериментальных исследований в эко
номике, социологии, психологии, педагогике подтверждает тот
факт, что эксперты гораздо устойчивее и согласованнее уме
ют давать интегральную оценку об"бекmу, чем раскладъtвать
эту интегральную оценку по значимости составляющих ее ком
понентов (пример именно такой ситуации приведен ниже, см.
п.
(11)
2.4.3).
Практически во всех известных нам работах по данной тема
тике возможность об"бекmивно оправданного отсутствия удо
влетворительного решения проблемы перехода от многокритери
альной схемы (с частными критериями х< 1 ), х< 2 >,
х<Р)) к од
... ,
нокрuтерuальной (у) либо игнорируется вовсе, либо не ста
вите.я задача определения числа и вида нескольких крите-
80
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
риев у(1), .•. , y(k), позволяющих существенно редуцировать раз
мерность р исходной много'К'ритериа.льной схемы
( т.
е.
k «:
р).
Предлагаемый ниж;е метод построения НИ СЛК лишен обоих
этих недостатков.
Общая логическая схема предлагаемого подхода предусмат
ривает -ч.етъtре основных этапа исследования. На первом этапе решает
ся вопрос определения минимальной размерности
k
пространства ин
тегральных индикаторов, достаточной для восстановления (по значе
ниям этих ИИ) с приемлемой точностью унифицированных значений
всех частных критериев апостериорного набора. Используемый для ре
шения этого вопроса критерий информативности основан на идеоло
гии факторного анализа, в частности, на известных свойствах главных
компонент. На втором этапе (который оказывается необходимым толь
ко в случае
> 1)
k
с помощью специальных методов анализа струк
туры корреляционных связей между частными критериями апостери
орного набора этот набор разбивается на
k
поднаборов (блоков) таким
образом, чтобы каждый из полученных поднаборов частных критериев
служил информационной базой для построения одного из
k искомых
интегральных критериев. На третьем этапе частные критерии каждого
из выявленных на предыдущем этапе поднаборов линейно сворачи
ваются таким образом, чтобы по полученной линейной свертке можно
было наилучшим образом предсказать (в рамках линейной модели пар
ной регрессии) значение каждого из частных критериев этого подна
бора. Наконец, четвертый этап (который, так же как и второй,
оказывается необходимым только в случае
k
> 1)
посвящен постро
ению единого (сводного) интегрального индикатора в форме некото
рой нелинейной свертки
k
индикаторов, построенных на предыдущем
этапе.
Теперь опишем каждый из этапов подробнее.
Эт ап
1.
Определение числа интегральных индикаторов,
необходимого для характеризации анализируемой синтетиче
ской категории. Во-первых, уточним в каком именно смысле мы по
нимаем точность восстановления унифицированных значений частных
критериев х< 1 >' х< 2 >'
'х(р) заданного апостериорного набора по зна
...
чениям k
у< 1 >, у< 2 >,
(1
~
k
... , y(k).
<
р) вспомогательных (интегральных) показателей
С этой целью рассмотрим линейные регрессии вида
j
= 1, 2, ... ,р,
где У= (1,y< 1>,y< 2 >, ... ,y<k>)', Ьj(У) = (Ьj.o(Y),Ьj.1(Y), ... ,Ьj.k(Y)) коэффициенты регрессии x<j) по У, а e<j) (У) - регрессионные остатки,
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
2.3.
81
удовлетворяющие требованиям классических линейных моделей регрес
сии.
Мы говорим, что k интегральных индикаторов У
= (1; у< 1 >, ... ,y(k))'
обеспечивают наилучшую точность восстановления значений р пере
менных х< 1 >' х< 2 >' ... 'х(р) (k
< р), если
р
р
LЕ(х<Л
-
Ьj(У). У) 2 = m~n LЕ(х<Л -ЬJ(У). У) 2 •
j=l
(2.14)
j=l
Так вот, известно (см., например, [Айвазян, Мхитарян
(2001)],
п.13.2.5), что именно этим свойством обладают первые k главных ком
понент, построенных по переменным х< 1 >' х< 2 >'
'х(р) (т. е. переменные
...
у< 1 >, у< 2 >, ... , y(k) - это и есть первые k главных компонент), причем пра
вая
часть
(Е
Aj/
j=k+l
(2.14)
может
быть
выражена
в
терминах
отношения
Е Aj), где А1, А2, ... , Ар - собственные числа ковариаци
j=l
онной матрицы Е х вектора Х = (х< 1 >, х< 2 >, .. . , х(р))', расположенные в
порядке убывания (невозрастания).
Именно на этих фактах основан наш критерий определения мини
мального числа
k
интегральных индикаторов, необходимых для харак
теризации анализируемой синтетической категории. В частности, пред
лагается определить
k=
где Qo -
k
min
из условия:
l~m~p-1
(2.15)
{m:
некоторое число (66льшее
0,5), конкретное значение
го зависит от требуемой точности восстановления значений Х
которо
=
(х< 1 >,
х( 2 ), ... , х(Р))' ПО значениям y(l), у( 2 ), ... , y(k) И ОТ вида КОррелЯЦИОННОЙ
матрицы вектора Х. Эмпирическая реализация правила (2.15) требует:
• оценки Ех матрицы Еяnо наблюдениям (2.2'), т. е.
•
вычисления собственных чисел А1, А2,
........
... , Ар матрицы Ех, т. е.
решения уравнения IEx -Alpl =О, где Ip - единичная матрица
размерности р.
82
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Заметим, что экспериментально установленный нами диапазон при
емлемых значений критической константы Qo колебался от
Если в результате реализации правила
(2.15)
0,55 до 0,60.
оказалось, что
k = 1,
то приемлема схема редукции к единственному интегральному инди
катору
и тогда сразу переходят к завершающему (в этой ситуа
ции) этапу 3. если же k > 1, то переходят к этапу 2.
jj< 1>,
Э т ап
териев на
2.
Разбиение анализируемого набора частных кри
k
непересекаюIЦИхся блоков. Как упоминалось выше,
именно наличие в составе апостериорного набора слабо коррелирован
ных между собой, но значимых для анализируемой синтетической ла
тентной категории частных критериев, является причиной недостаточ
ной информативности единственного интегрального индикатора, по
строенного на идеологии метода главных компонент. Напротив, пер
вая главная компонента будет обладать высокой прогностической силой
(в смысле
(2.14)),
если она строится по тесно взаимнокоррелирован
ным частным критериям. Отсюда мы имеем следующее правило фор
мирования блоков, на которые требуется разбить апостериорный набор
частных критериев в случае слабой работоспособности единственного
ИИ (т. е. при k
> 1):
принадле:жность частн-ых критериев к одному
блоку дол:жно определяться двумя требованиями: они должны харак
теризовать какой-то один аспект
анализируемой синтетической кате
гории (например, реальные доходы и расходы в синтетической катего
рии «Благосостояние населения», или социальную патологию в синте
тической категории «Качество социальной сферы» и т. п., см., напри
мер структуризацию анализируемых синтетических категорий качества
жизни населения, приведенную в [Айвазян
{2012)],
гл.
2)
и, одновремен
но, иметь относительно высокий уровень взаимной коррелированности
(как правило, но не всегда, последнее свойство является следствием
первого требования).
Разбиение апостериорного набора частных критериев на такие
группы (блоки) можно производить чисто экспертно, т. е. руковод
ствуясь вышеупомянутыми содержательными соображениями. Однако
полезной поддержкой в решении этой задачи может быть использова
ние некоторого специального алгоритма, а именно
-
процед-уры экс
тремальной группировки признаков (см. [Айвазян, Мхитарян
(2001)],
п.13.4.2). Эта процедура предназначена для такого разбиения рассмат
риваемой совокупности из р признаков на заданное число
непересекающихся блоков
k (k
<
р)
81, 82, .... 8k, при котором признаки, принад
лежащие одному блоку, были бы относительно сильно коррелированны,
в то время как переменные, принадлежащие разным блокам, коррели
рованны относительно слабо. Это требование формализуется в форме
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
задачи максимизации по
F
=
L
8 1, S2, . . . . 8 k
и
L
r2(x(i)' 1<1>) +
x(i)ES1
1(1) , 1(2) , ... , l(k)
L
критерия
r2(x(i)' 1<2>)+
x(i)ES2
+ ... +
83
(2.16}
r2(x(i)' 1<k>),
x(i)ESk
в котором под
r{{, 71)
понимается обычный парный коэффициент кор
реляции меж.цу случайными величинами {и 71, а l(l) -
так называе
мый общий фактор для признаков l-го блока, т. е. такая переменная,
которая максимизирует (при заданном составе l-го блока) величину
Е
r2(x(i)' 1(l>).
x<i>es,
Можно показать, что
1(l)
это, с точностью до линейного преоб
-
разования, 1-я главная компонента Pl показателей l-го блока. А именно
для заданного состава блока
81 (l
= 1, 2, ... , k):
Е а~'> х< i)
l(l)
= --;===ж=<·=">Е=S='======,
Е
(2.17}
a~ 1 >a}1 >r(x(i),x<Л)
x<i>xШes1
где
a<l) = ( a~l), a~I), ... , аШ
)' -
собственный вектор корреляционной
показателей блока 8l, соответствующий максимальному
матрицы R(l)
собственному значению этой матрицы, т. е. компоненты вектора a<l) это решение системы из
Pl
уравнений
(pl - число показателей, входящих в блок 81; очевидно Р1 +р2+ ... +Pk
=
=р).
С другой стороны, при заданных факторах
нетрудно построить разбиение
ционал
{2.16},
81, 82, ....8k,
1< 1>, 1<2>, ... , l(k)
максимизирующее функ
а именно:
Соотношения
{2.17}
максимума функционала
и
j.
(2.18}
являются необходимыми условиями
Поэтому для одновременного определения
оптимального состава блоков
81, 82, ....8k и оптимального набора фак
2
1
торов 1< >, 1< >, ... , l(k) используется следующий итерационный алго
ритм:
Гл.
84
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
пусть на v-м шаге итерации построено разбиение признаков х< 1 >,
, х (р) на блоки s<v>
k . 11огда для каждого блока при1 , s<v>
2 , ... , s<v>
2
х ( ) , ...
знаков sl(v) строят факторы f~l) по формуле (2.17} и новое разбиение
s~v+l)' ... 's~v+l) в соответствии с правилом (2.18}, т. е. показатель x(i)
относится к блоку sfv+l)' если
r 2 (x(i), f~1 >) ~ r 2 (x(i), f~q))
для всех
q
= 1, 2, ... , k.
Очевидно, на каждом шаге итерации функционал
F
не убывает,
поэтому данный алгоритм будет сходиться к максимуму (правда, мак
симум может оказаться .л.окал:ьн'ЫМ, поэтому желательна многократная
прогонка алгоритма при разных начальных условиях}.
Э т ап
3.
Построение блочных ИИ отдельно по частным
критериям, входяIЦИм в каждый из блоков, определенных на
предыдущем этапе. Итак, мы добились того, что частные критерии,
входяIЦИе в один блок, во-первых, характеризуют какой-то один аспект
анализируемой синтетической латентной категории и, во-вторых, доста
точно тесно взаимнокоррелированны. Теперь мы можем сформировать
состав k-мерного критерия анализируемой синтетической латентной ка
тегории (в частном случае
= 1 критерий
k
оказывается одномерным,
т. е. скалярным). Пусть
-·( .) _ (-(1)( .) -(2)( .)
-(Р;)( ·))'
х
i J xi J , xi J , ... , xi
J
(2.19}
(j = 1,2, ...
объект (i = 1, 2, ... , n).
(j = 1, 2, ... , k) в фор
значения унифицированных частных критериев jго блока
. . . , k),
характеризуюIЦИх i-й анализируемый
Будем строить j-й интегральный индикатор
ме унифицированной (или модифицированной, см. ниже) первой глав
ной компоненты переменных
(2.19}.
Для этого необходимо реализовать
следующие вычислительные процедуры (последовательно для каждого
j
= 1,2, ... ,k):
1) Вычислим оценки Е х (j) ковариационных матриц Е х (j) пере
менных (2.19}
n
Е.х(Л = ~ ~ (хi(Л -х(л) (хi(Л -х(л)',
i=l
где
;:;:.
n
1~-
X(j) = - L-Xi(j).
n.i= 1
2) Определим собственные значения Л1(j)
матрицы E_x(j), т. е. решим уравнения вида
IE_x(j) - Лlp;I =о.
~ Л2(j) ~
···
~ Лр;(j)
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
3) Вычислим собственный вектор C1(j)
85
= (сн(j), cl2(j), ... , C1p;(j))',
соответствующий наибольшему собственному значению Л1(j), т.е. ре
шим систему из Р; уравнений вида
(Ея(Л - Л1(ЛIР;) С1(Л =о.
4) Построим первую главную компоненту
a;(l)(j), a;(2)(j), ... , a;(p;)(j) j-го блока:
частных критериев
n
~
y(j)
= I:c1s(j). (x<s>(j)-x<s>(j)), где
= ~ I:x~ 8 )(j).
x<s>(j)
s=1
п.
i=l
5) В целях унификации измерительных
2.3.1) построим ИИ переменных j-го блока в
Р;
шкал (см. задачу
3
в
форме:
Р;
Yi (J.) = '°'-C1s ·
-(s)(J.) ,
Xi
L...,,,
где
C1s
= C1s /'°' '
(2.20а)
L...,,, с 18
s=1
s=1
если все коэффициент'Ы
c1 8(s
= 1, 2, ... ,р;)
одного знака, или
Р;
Yi(j)
=L
c?is. x~s\j),
i
= 1, 2, ... 'п,
(2.206)
s=1
если знаки коэффициентов с1 8
3
различаются.
а м е ч а н и е. Напомним что, по построению, все частные крите
рии a;<s>(j)
[О,
(s = 1, 2, ... , Р;)
N) -
унифицирован'Ы,
т. е.
измерены
в
одной
и
той
же
шкале, в которой О соответствует наихудшему качеству, а
наилучшему. Отсюда и из простого анализа формул (2.20а) и
N -
(2.20б), в частности, следует:
а) ИИ в форме (2.20а) так:же измерен в
[O;N) -
шкале, причем,
он отличается от 1-й главной компонент'Ы только прост'ЫМ линей
ным преобразованием. А значит, он не теряет свойства наивысшей
прогностической сил'Ы в отношении всех частн'ЫХ критериев x< 1>(j),
x< 2>(j), ... ,x(p;)(j) (см. в'Ыше формулу (2.14)).
6)
Использование ИИ в форме (2.20а) в случае, когда коэффици
ент'Ы с1 8 оказ'Ываются
«разнознаковымИ>> (хотя это б'Ывает весьма
редко при положительно взаимнокоррелированн'ЫХ частных критери
ях
(2.19)),
противоречило б'Ы естественному требованию монотон
но неотрицательной зависимости ИИ от частн'ЫХ критериев. Этим
об'бясняется переход к форме
(2.206),
которая, кроме того, обеспечивает
Р;
унифицированность шкалы измерения Yi(j) (т.к. Е
q8 = 1 в соответ-
s=l
ствии со свойствами компонент собственного вектора в методе главных
86
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
компонент). Правда, строго говоря, при этом теряется свойство наи
въtсшей прогностической силы ИИ в смысле
Однако наши ис
(2.14).
следования (основанные на вычислительном эксперименте) показали,
что прогностическая точность ИИ сн:и.:нсается при этом не более чем
на
10,...., 12%.
Интегральный индикатор в форме (2.20а) и (2.20б) будем называть,
соответственно, унифицированной и модифицированной первой главной
компонентой частных критериев.
Итак, «на выходе• этапа
3 мы
располагаем набором значений блоч
ных интегральных индикаторов (или мультикритерием)
i
(Yi(l), Yi(2), ... , Yi(k)),
= 1, 2, ... , n,
(2.21)
компоненты которого определяются по формулам (2.20а) или (2.20б).
Еще раз отметим, что в случае
дится к скалярному
Этап
4.
(т. е.
=
k
1
этот мультикритерий сво
к однокритериальной схеме).
Построение единственного (сводного) ИИ, харак
теризующего анализируемую синтетическую латентную кате
горию. Этот этап необходим только в случае
k
> 1.
По существу, речь
идет о переходе на один, более высокий, уровень иерархии в общей
схеме интегральных индикаторов (см. выше, рис.
2.1),
когда для анали
зируемой синтетической категории, характеризуемой набором ИИ вида
(2.21),
требуется построить единый (сводный) измеритель.
Решение задачи основано на следующей идее. Будем использовать
геометрический образ положения i-го анализируемого объекта в ви
де точки с координатами
в k-мерном пространстве интеграль
(2.21)
ных индикаторов. С учетом того, что все интегральные индикаторы
y(j) (j
= 1, 2, ... , k) измеряются в N-балльной шкале по принципу «чем
больше значение
y(j), тем выше качество•, естественно оценить инте
гральный уровень i-го объекта
(Oi)
по анализируемой синтетической
категории расстоянием от точки с координата.ми
лона• (Э), который задается координатами
изображена эта схема для случая
(2.21) до «эта
(N,N, ... ,N). На рис. 2.2
k = 2.
Остается ответить на два вопроса:
•
как именно измерять расстояние в k-мерном пространстве ин
тегральных индикаторов
•
как по расстоянию
Pi
Yi(1), Yi(2), ... , Yi(k)?
= p(Oi;
Э) определить сводный ИИ
-
ска
лярный измеритель анализируемой синтетической латентной
категории?
2.3.
МЕТОДОЛОГИЯ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
87
у(2)
N _ _ _ _ _ _ _'J:={N;N)
о
Рис.
2.2.
y(l)
Y;(l)
Расположение объекта
Oi
относительно эталона Э
Для измерения расстояний в пространстве
(y(l}, у(2}, ... , y(k))
предлагается использовать взвешенную евклидову метрику, в которой
веса, продолжая следовать идеологии метода главных компонент (в со
ответствии с которой и'Нформатив'Н.Ость показателя тем выше, чем
выше его вариабельность), мы определяем пропорционально разбросу
данных (дисперсии s 2 (j)) по каждой из осей y(j) и числу частных кри
териев
kj, входящих в состав j-го блока (j
= 1, 2, ... , k).
Итак:
k
р~
= L q(j). (Yi(j) - N} 2 ,
(2.22}
j=l
где q(j)
=
:гs
2(j)
Е P1·s 2 (l)
,s (j) =
2
~
n
L: (Yi(j) -
y(j)) 2 , а y(j)
n
= ~ L Yi(j).
i=l
i=l
1=1
Теперь мы можем определить значение
Yi
единого (сводного)
интегрального индикатора анализируемой синтетической ка
тегории для объекта (территории)
Yi = N
Oi:
(2.23}
- Pi·
Очевидно, определенный таким образом сводный ИИ
fJ
уже не яв
ляется линейной сверткой частных критериев и будет измеряться в
той же [О;
N] -
унифицированной шкале, что и все другие частные
критерии и интегральные индикаторы.
Отметим, что использование в задаче построения сводного ИИ по
блочным ИИ той :ж;е техники метода главн'ЫХ компонент, которая
была применена при построении каждого блочного ИИ, как правило,
не приносит успеха в силу «разнонаправленности• действия (а следо
вательно, слабой взаимной коррелированности) блочных интегральных
индикаторов.
Гл.
88
2.3.5.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
2.
Анализ дееспособности и динамики интегральных
индикаторов
Анализ дееспособности ИИ
-
это вопрос, в первую очередь, вы
полнения тех критериев качества, которые обычно предъявляются к
интегральным индикаторам при их построении. Десять таких критери
ев были обсуждены, например, в п.
1.3.4
книги [Айвазян
же мы располагаем какой-либо формой обучения (см.
(2012)]. Если
выше, п. 2.2), то
дееспособность построенных ИИ может быть дополнительно оценена
(при условии качественности, добротности этого обучения) сравнением
экспертных оценок и оценок, основанных на ИИ. При этом, в зависимо
сти от формы обучения, можно использовать коэффициенты обычной
парной или ранговой корреляции, процент ошибочно (по отношению к
экспертному варианту) расклассифицированных объектов и т. д.
Анализ динамики интегральных индикаторов существенно ис
пользуется, например, при оценке эффективности проводимой социаль
но-экономической политики и выявлении ее «проблемных зон». Он тре
бует введения и вычисления специальных характеристик, которые поз
воляли бы отслеживать улучшение или ухудшение рассматриваемого
аспекта качества жизни территории как по отношению к себе самой в
предыдущий такт времени (мы будем называть это автодинамикой),
так и по отношению к своему положению среди других территориаль
ных единиц (межобъектная, или в данном случае
-
межтерритори
альная динамика).
Говоря об автодинамике, отметим, что простое приращение во вре
мени даже всех частных критериев
xU>
апостериорного набора может
в действительности не означать улучшения СЛК на данном объекте.
Что, кстати, и подтвердит соответствующее значение ИИ, поскольку в
свертке ИИ участвуют унифицированн'Ые значения х<Л частных крите
риев, а они в силу одновременной динамики эталонных объектов
(т. е.
значений Xmin и Xmax) могут даже уменьшаться при увеличении х<Л 3 .
Так что, поскольку ИИ, как функция от унифицированных значений
частных критериев, учитывает этот эффект, то его значения могут ис
пользоваться для отслеживания автодинамики.
При измерении межоб'6екmной динамики каждого конкретного
(i-го)
объекта естественно ориентироваться на динамику его положе-
3 Действительно,
пусть значение частного критерия х<;) увеличилось за год на д,
а значения x~ln и x~lx за тот же год увеличилось на 2д. Тогда ун:ифиv,ирован:н.ое
-(1·)
-(1·)
· +2д)
N
значение х
за этот же год изменится до величины х
= (ж<Л+д)-(ж
.
~!'
•
=
(ж~l,. +2д)-(жДn +2д)
жШ-д-ж<;J
=
(;)
<;'fш
Жmах -жmin
жШ-ж(jJ
• N < Жmах
(;) -жmin
1'JY • N.
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
89
ния (ранга) в ряду других рассматриваемых объектов, т. е. на величину
где
R(yi(t)) -
ранг i-го объекта в рейтинге объектов, построенном в со
ответствии со значениями У1 (t ), У2 (t),
... , Yn (t).
Очевидно, положитель
ные значения бi (t) будут свидетельствовать о положительной межобъ
ектной динамике объекта
i.
Примеры построения интегральных
2.4.
индикаторов
-
измерителей качества
анализируемых синтетических латентных
категорий
Первые два из представленных ниже примеров относятся к проблема
тике измерения различных СЛК качества жизни населения (КЖН).
Они заимствованы из [Айвазян
стических данных по странам
Федерации (в п.
2.4.2)
{2012)]. В частности, в них на стати
(в п. 2.4.1) и по субъектам Российской
представлены конкретные иллюстрации решения
основных задач методологии измерения синтетических категорий каче
ства жизни населения (см. выше, п.
•
2.3.1),
задачи отбора из априорного
х< 1 >, х< 2 >, ... , х(р>реi}уцированного
а именно:
перечня
частн-ых
критериев
(апостериорного) набора пока
зателей х<; 1 >, х<;2 ), ••• , xU,1 >, где р' < р (задача 2 преданализа);
•
задачи унификации измерительн-ых шкал всех анализируемых пе
ременн'Ых, т. е. такого перехода к N-ба.л.л,ьн'ЫМ шкалам, при ко
тором значение
нуль свидетельствовало б'Ы о наихудшем каче
стве по анализируемой переменной, а значение
(задача
3
N -
о наилучшем
преданализа);
• задачи перехода от р' частн-ых критериев х<; 1 >, х<;2 ), ••• , xUJI > к
одному (у) или сравнительно небольшому числу (у< 1 >, ... , y(k})
интегральн'Ых индикаторов (k << р'), в которой последние стро
.ятс.я в форме некотор'ЫХ функций (сверток) от р1 частн'ЫХ кри
териев апостериорного набора (задача
4-
центральная зада
ча методики);
•
наконец, задач постанализа, в котор'ЫХ анализируете.я работо
способность построенн'ЫХ ИИ КЖ и их динамика (задачи
и
6).
5
90
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Что касается содержательных целей представленных в п.
2.4.2 эмпирических исследований
2.4.1
и
КЖН, то они ограничены рейтинго
ванием рассматриваемых территорий (стран, субъектов РФ) но ана
лизируемой синтетической категории КЖ.
Наконец, в п.
2.4.3
описан один из самых первых опытов эмпириче
ского анализа СЛК. Этот пример датируется 1973-м
(!)
годом и не отно
сится прямо к социально-экономической тематике. В нем речь идет об
оценке уровня мастерства спортсмена командного вида спорта, про
явленного им в отдельном матче или в серии матчей в рамках опре
деленных соревнований. Да и с точки зрения методологии построения
ИИ читатель не обнаружит здесь ничего нового (обучение в данном
примере имеет форму балльных экспертных оценок). Однако этот при
мер выделяется чистотой эксперимента (высокой квалификацией и
независимостью экспертов) и очевидной прикладной дееспособностъю.
Именно поэтому мы посчитали целесообразным включить его в учеб
ник. Так же, как и предыдущие два примера, этот пример относится к
личному опыту прикладной деятельности одного из авторов учебника
и заимствован из [Айвазян
2.4.1.
(1974)].
Межстрановой эмпирический анализ
синтетической категории «Качество жизни
населения» по данным
Цель данного исследования
2009 г.
рейтингование ряда статистически
-
обследованных стран по синтетической категории «Качество жизни на
селения» наивысшего уровня общности (см. «интегралъную характе
ристику высшего уровня» на рис.
2.3).
При этом рейтингование будет
основано на значениях ИИ, построенных в форме линейных сверток
частных критериев параллельно в двух вариантах: с обучением и без
него.
Информационная база исследования. Исходные статистиче
ские данные заимствованы из ежегодника
[WCY (2009)].
Эти ежегод
ники включают в себя макроэкономические данные по ряду стран мира
(общее число статистически обследованных стран, так же как количе
ство и состав показателей, претерпевают некоторые изменения во вре
мени), структурированные по блокам и разделам, и содержат значения
порядка
300
показателей, в том числе более
100
показателей, оценен
ных экспертно (см. краткое описание структуры и содержания инфор
мации, включаемой в ежегодники
(2012)]).
WCY в
Приложении П2.1 к [Айвазян
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
КнrтвоЖИЮI
/QR
насеииtя
ВЫШ!ОО
~/
~
L!J
l/Ьlf!
1
L!!!J
I<iN:cпlO
Б1вrооос1оппе
tв:е11Ю11
наа:nежя
КаЧflСПIО
~--------~
C(QllUВiН(ii
~
Ка~а:пю
J\:1чщо-
~
IOllDlllmea<Je
НИU1
~
сфр.а
•
Чоатые
(инпr:г
•
.L
.L
.L
V.l. НаJи~ие
L1. СIКЙ:Пlа
0.1.~
IП.1. YCDIНI
IV. l. Сос1а8ае
llJC~-
JUIQl'8I
1JJYJ8
.,,__::..
ван
рапьные)
91
.
и
.....
И CXIUВIЫICЙ
рк:хn
ro:vqxв.я.
__
<U
~
Сьр.с8Ь1t
381111Ы.
рс:с)рООВ.
кpnr!
v2. К1вм1rи-
JUIU
L2 Ур111121Ь
ll2 ОО:аечен-
Ш.2 сtюжеаа
IV.2 Сос1а8ае
расчi!11Кr
Щв:Datui
t11С'1Ъ ЖltММ
и~
l8QilO"O
ана111m
и JСУ'Ь'!)р.1.
и
бс:пв.юсп..
~--
~
L3. Урсаю.
~-
0.3. aieae:u"
Ш.3. Харакrqк-
IIY.3. Сос1а8ае
VJ.Часппа
t11С'1Ъ
1И1СН COJll.1Ыlii
11О'В.
фqх>-
№IIOC'DNI
1В131D11И.
-
··-
чсаое
ческие
CtmnlJCf/IJЧII04le
покшапе
ли 3-ю
ИD!q)lldll.
~
ypotl/R
~
апуацtК
обцс11в.
Ш.4. Харакrqк1И1СН COJll.1Wlli
lV.4.
-
HПWИJqll-
....oi~
-.
111С1И наа:11:111Я.
Ш.5. Санп.1о1О11ПJ1ЧеС1СDе
3lqx&e
обцс11в.
l
l
l
IV.5. Сос1а8ае
..
Эl«IC!al:М.
l
l
1
~~J'DJalЗll11ЯlбlrDuo)'IXВll:
абсоruн.еи~
Рис.
2.3.
Иерархическая система статистических показателей, частных
критериев и интегральных индикаторов качества жизни
населения страны (региона)
Априорный набор частных критериев качества жизни на
селения страны формировался с учетом требований {А)-(Б)-(В) и п. а)
параграфа
2.2
на базе источника
[WCY {2009)]
и содержал статисти
ческие показатели, характеризующие все четыре базисные синтетиче
ские категории: ~качество населения• (ожидаемая при рождении
продолжительность жизни - переменная х< 7> или 4.4.05 в кодиров
ке
[WCY {2009)]; доля неграмотных среди населения старше 15 лет х< 4 > или 4.5.14; младенческая смертность - х< 8 > или 4.4.07); ~Уровень
благосостояния• ( ВВП на душу в долларах США с учетом парите
та покупательной способности (ППС) - переменная х< 1 > или 1.1.22 в
кодировке [WCY {2009)]; расходъt на личное потребление на душу в
92
2.
Гл.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
долларах США с учетом ППС - х< 3 > или 1.1.23; индекс потребите.л:ь
ских цен в% - х< 6 > или 1.5.01; производите.л:ьностъ труда в долларах
США - х< 2 > или 3.1.04); «Качество социальной сферы)) (20%-н'ый
коэффициент фондов, т. е. отношение суммарных доходов
шего населения страны к суммарным доходам
х< 5 >
ления - переменная
20%
богатей
беднейшего насе
20%
или отношение переменной 2.5.07 к перемен
ной
2.5.06 в кодировке [WCY {2009)]; общие расходы на НИОКР в% к
ВВП - х< 10 > или 4.3.02) и «Качество экологической ниши)) (сум
марн'Ые в'ЫброС'Ы в атмосферу СО2 в метрических тоннах, приходящие
ся на один миллион долларов ВВП - переменная х< 9 > или 4.4.17 в коди
ровке
[WCY {2009)]).
Перечень и индексация частных критериев апри
орного набора приведены в табл.
Ограничение априорного набора
2.1.
частных критериев всего дес.ятъю показател.ями продиктовано сообра
жениями оптимальности соотношения числа
n
статистически обследо
ванных объектов (стран) и числа р переменных, участвующих в моде
ли ИИ, оцениваемой либо {в условиях наличия обучения) с помощью
линейной регрессии экспертной оценки КЖ Уiэпо какому-то
(j)
1
подмножеству частных критериев (xi
,
(j)
2
xi
(j)
, ••• ,
xi Р'
),
либо в форме
модифицированной 1-й главной компоненты всех десяти упомянутых
частных критериев х< 1 >, х< 2 >, ... , х< 10 > (в варианте построения ИИ без
обучени.я).
Таблица
2.1.
Априорный набор частных критериев синтетической
категории ~качество жизни» в межстрановом анализе
(по данным [WCY {2009)])*>
NN
Переменная (частный критерий): на-
Обозна-
Код
пп.
именование и единицы измерения
чение
[WCY
(2009)]
по
Формула
унифицирующего
преобразования
2
1
1
3
ВВП на душу с учетом паритета по-
4
5
х<1>
1.1.22
(2.4)
х<2>
3.1.04
(2.4)
Х(З)
1.1.23
(2.4)
х<4)
4.5.14
(2.5)
х(5)
2.5.07
2.5.06
(2.6)
купателъной способности (доллары
США)
2
Производительность труда (доллары
США)
3
Расходы на личное потребление на
душу (доллары США)
4
Доля неграмотных среди населения
старше
5
15
лет
20%-ный
(в разах)**)
(%)
коэффициент
фондов
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
Таблица
1
2
Индекс потребительских цен
7
Ожидаемая (при рождении) продол-
(%)
(окончание)
4
3
6
2.1
93
5
х<&>
1.5.01
(2.5)
х<1>
4.4.05
(2.4)
x(S)
4.4.07
(2.5)
х(9)
4.4.17
(2.5)
X(lO)
4.3.02
(2.6)
жительность жизни (лет)
Младенческая
8
смертность:
среднее
число умерших в возрасте до
приходящееся на
Выбросы
9
1
1000
года,
родившихся
(метрич.
СО2
1
тонны
млн долл. ВВП)
Общие расходы на НИОКР (в
10
на
%
к
ВВП)
(на
•) По некоторым показателям в [WCY (2009)] приведены лишь лагированн'Ьlе
1"'2 года) значения.
•• > 20%-ный коэффициент фондов вычисляется как отношение суммарных до
ходов
20% богатейшего населения
к суммарным доходам
20% беднейшего населения.
Отметим, что в соответствии с рекомендациями п.
2.3.2 была прове
дена унификация измерительных шкал анализируемых перемен
ных. Она была осуществлена по формулам
{2.4)""{2.6)
при
N
= 10, т. е.
все переменные оказываются измеренными в десятибалльной шка
ле
таким образом, что нулевое значение унифицированного показа
теля свидетельствует о наихудшем качестве, а оценка в
10
баллов
-
о наилучшем. Параметры, необходимые для унификации, приведены в
табл.
а исходные и унифицированные значения анализируемых пе
2.2,
ременных
-
в Приложении Пl.
Таблица
2.2.
Данные, используемые при унификации измерительных
шкал
NN
Частный
пп
критерий
(j)
х<;) (код)
х<;)
max
х<;~
m1n
х<;)
х<;)
max min
ш·>
Хоnт
Формула
унифицирующего
преобразования
1
2
4
3
5
7
6
1
х< 1 > (1.1.22)
3400,00
56000
52600,0
56000,0
(2.2)
2
х< 2 > (3.1.04)
4,09
59,45
55,36
59,45
(2.2)
3
Х(З)
928,0
37219,0
36291,0
37219,0
(2.2)
4
х< 4 > (4.5.14)
1,00
12,0
11,0
1,0
(2.3)
5
х(5)
3,37
18,50
15,13
5,00
(2.4)
1,40
19,0
17,6
1,4
(2.3)
60,00
83,0
23,0
83,0
(2.2)
(1.1.23)
6
(2.5.07)
2.5.06
х< 6 > (1.5.01)
7
х< 1 > (4.4.05)
Гл.
94
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Таблица
1
2
3
4
5
2.2
(окончание)
7
6
8
х< 8 > {4.4.07)
2,00
37,0
35,0
2,0
{2.3)
9
х< 9 > {4.4.17)
109,30
2300,0
2190,7
109,3
{2.3)
10
X(lO)
0,10
4,68
4,58
2,3
{2.4)
*)
(4.3.02)
В случае немонотонной зависимости КЖ от x<j) величина х~Jт определяется
как среднее значение этого показателя по трем лучшим по КЖ (по экспертной
десятибалльной оценке) странам.
Построение ИИ КЖ в условиях наличия обучения. В этом
Yi
случае ИИ КЖН
страны
i
строится (см. выше, п.
2.3.3,
пп.1)) по
исходным данным вида
( xi(J1) 'xi(J2) ' ... 'xiU"1 >;
Уiэ
)
i
'
= 1, ... '56,
в форме оценки Yi линейной регрессии Уiэ по (х? 1 >, ... ,x~J"i )) в уравне
нии
Уiэ
п + и1Хi
п (ii) + ... + 17р'
п
= 170
U"i)
• Xi
+ €i,
i
. = 1, 2, ... , 56 ,
где
А
Yi
Уiэ -
А
(j1)
А
= ОоА + 01xi
+ ... + Ор1
U"1)
· xi ,
экспертная оценка (в десятибалльной шкале) КЖН i-й страны,
(j )
х~ 1 >, ... ,xi Р' - значения р объясняющих переменных (частных критериев) апостериорного набора для той же i-й страны (р'
< р),
€i -
слу
чайные регрессионные остатки модели регрессии, а Во, 81, ... , Вр1 -оцен
ки коэффициентов регрессии, соответственно, Оо, 81, ... , Ор1. Метод оце
нивания коэффициентов Oj зависит от природы регрессионных остатков
€i· В нашем случае классические допущения о вероятностной приро
де остатков €1, €2, ... , €55 (их взаимная статистическая независимость,
гомоскедастичность и нормальный характер распределения) не были
опровергнуты в результате статистической проверки соответствующих
гипотез, а потому для оценки параметров
Oj
(j
=О,
1, ... ,р')
исполь
зовался обычный метод наименьших квадратов.
Апостериорный набор частных критериев КЖ и исходные
статистические данные. Формирование редуцированного (апостери
орного) набора частных критериев по синтетической категории высше
го уровня общности «Качество жизни~ было нацелено на устранение
присутствующей в объясняющих переменных (частных критериях) х< 1 >'
х( 2 ), ••. , x(lO) высокой степени муд:ьтико.л.линелрности (см. характери
стики мультиколлинеарности в табл.
2.3
и
2.4).
2.4.
Таблица
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
2.3.
95
Корреляционная матрица унифицированных частных
критериев*
х<1>
х<1>
х<2>
Х(З)
х<4>
X(S)
х<б>
х<1>
x<s>
х<9>
X(lO)
1
0,93
1
0,83
0,89
1
0,45
0,56
0,57
1
0,39
0,46
0,32
0,62
1
0,52
0,61
0,60
0,35
0,21
1
0,76
0,77
0,74
0,47
0,31
0,73
1
0,72
0,74
0,64
0,70
0,48
0,61
0,80
1
0,58
0,63
0,61
0,18
0,05
0,69
0,74
0,54
1
0,63
0,66
0,62
0,46
0,37
0,52
0,52
0,54
0,32
1
х<2>
Х(З)
х<4>
X(S)
х<б>
х<1>
x<s>
х<9>
X(lO)
•>На пересечении строки
x(i)
и столбца хШ приведено значение коэффициента
корреляции между x(i) и х<Л.
С этой целью была применена методика отбора наиболее суще
ственн'ЬtХ частных rритериев «в условиях наличия обучения», опи
санная в п.
2.2,
пп. а). В частности, по извлеченным из
исходным данным (обозначения табл.
[WCY (2009)]
2.1)
i
= 1, ... '56, 4
были реализованы пошаговые процедуры отбора наиболее информатив
ных объясняющих переменных в линейной модели регрессии, а именно
процедуры «nоследователъного присоединения» и
«последователъного
удаления». Ход процедуры «последовательного присоединения» отра
жен в табл.
2.5.
Добавим к этому, что процедура «последовательного
удаления», примененная К тому же набору предикторов х(З)
rv
x(lO),
дала точно такой же результат.
Почему из априорного набора частных критериев были исключены
переменные х< 1 > (ВВП на душу) и х< 2 > (производительность труда)? Это
было сделано по двум причинам.
4 0бъектом
годник
анализа являются 56 стран из 60 стран и регионов, включенных в еже
WCY (2009)
(см. Приложение П2.3). Ряд стран и регионов не были включены
в наше исследование либо из-за пропусков в исходных данных, либо из-за того, что
они не представляли страну в целом.
96
2.
Гл.
Таблица
2.4.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Характеристики мультиколлинеарности переменных
х< 1 > rv х< 10 > (значения RJ)**)
NN
Обозначение
пп
критерия
Название (смысл)
частного
частного
R'l:J
кри-
тер и я
(j)
1
х<Л
в
х<1>
IWCY (2009)1
1.1.22
кодах
ппс
0,897
труда
0,927
Расходы на личное потребление
0,855
ввп
на
113шу
с
учетом
(долл.)
х<2>
2
Производительность
3.1.04
(долл.)
Х(З)
3
1.1.23
на lJ3ШY (долл.)
х<4>
4
4.5.14
Доля
неграмотного
0,748
населения
(%)
х<5>
5
(2.5.07)
2.5.06
20о/о-ный
Индекс потребительских цен
6
х<&>
1.5.01
7
х<1>
4.4.05
коэффициент
фондов
0,504
(разы)
Ожидаемая
(%)
0,660
продолжительность
0,823
(ер.
0,825
жизни (лет)
x<s>
8
Младенческая
4.4.07
смертность
число случаев)
9
х<9>
4.4.17
Выбросы СО2 (метрич. тонны)
10
X(lO)
4.3.02
Общие расходы на НИОКР
0,694
(%
0,526
кВВП)
**)
R~ - это значение подправленного коэффициента детерминации между х<Л
и всеми остальными девятью частными критериями.
Таблица
2.5.
Ход пошаговой процедуры «последовательного присо
единения~ предикторов, примененной к переменным
x(l)
rv
N
Число
шага
бранных
(k)
предикторов
ото-
x(IO) при априорных исключенных x(l)
Состав
ных
отобран-
Коэффициент
предикторов
детерминации
x(j•>, х<;2>, ... , x(jk>
-- R24 dj(Y .
э,
rv
х( 2 )
R~
(k)
1
1
f(З)
0,569
2
2
х< 3 > и х< 1 >
0,629
3
3
-(3)
х
4
4
Дальнейшее увеличение числа предикторов по-
'
х<1> и х<10>
0,675
вышало R~ на каждом шаге менее, чем на 0,01,
8
8
а в конечном счете (т.е. при
k=8)
=
x(j•> , ... , x<;k»
всего до
0,708
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
97
Причина первая. Эти переменные высоко коррелированны меж
1 х< 2 >) = О, 93, см. табл. 2.3),
собой (коэффициент корреляции
/lУ
r(x< >,
и каждая из них тесно коррелированна с переменной х< 3 > - расходами
на личное потребление (r(x< 1>, х< 3 >) =О, 83; r(x< 2>, х< 3 >) =О, 89). Поэто
му одновременное включение всех трех переменных (или даже только
двух из них) в качестве предикторов в анализируемую модель регрес
сии приводило к плохо интерпретируемым результатам, давая при этом
минимальный выигрыш в значении коэффициента детерминации зави
симой переменной Уэ по всему набору частных критериев (прираще
ние R 2 составляло величину порядка 0,045, которая не может быть
квалифицирована как статистически значима.я при числе наблюдений
п
= 56 и числе оцениваемых параметров,
равном р
+ 1 = 11).
Причина вторая. Зададимся вопросом: так ли бесспорно важен
валовый внутренний доход страны как характеристика качества жиз
ни ее населения? В ряде исследований (см., например, [Сен
вазян
{2008)])
{2004)],
[Ай
приводятся убедительные примеры ситуаций, в которых
ВВП не мог квалифицироваться как детерминанта качества населения.
В этой связи, я l1J'MaIO, уместно привести здесь некоторые фрагмен
ты из доклада авторитетнейшей международной «Комиссии по оценке
экономических результатов и социального прогресса», возглавляемой
лауреатами Нобелевских премий Джозе,фом Стиглицем и Амартией
Сеном (см. [Доклад
1)
(Из
{2010-2011)]):
«Введения• к гл. 1) «... Он
(ВВП) представляет собой
механизм для измерения прежде всего совокупного предложения, а не
уровня жизни граждан. Хотя величина ВВП взаимосвязана со многи
ми показателями уровня жизни, корреляция не носит всеобъемлюще
го характера и значительно ослабевает, когда речь идет об отдельных
секторах экономики. Например, изменение реального дохода домашних
хозяйств (меры дохода, наиболее тесно связанной с уровнем жизни) в
ряде стран ОЭСР весьма отличалось от роста ВВП. Слишком большой
упор на ВВП как эталонную меру может привести к ложным представ
лениям о благосостоянии людей и повысить риск принятия ошибочных
политических решений».
2)
(Из п.
4
гл.
1)
«Большая часть общественных дискуссий об
уровне жизни сосредоточена на показателях экономики в целом, и чаще
всего на ВВП. Но конечной целью дискуссий об уровне жизни являются
индивидуумы, чье экономическое положение нужно оценивать. Взгляд
на эволюцию реального дохода домашних хозяйств и изменение объема
ВВП подтверждает, что, в общем, эти показатели плохо заменяют друг
друга. Несмотря на то что в некоторых странах реальный располагае
мый доход домашних хозяйств хорошо коррелирует с ростом объемов
ВВП, есть много стран, где ситуация иная. Италия, Япония, Корея,
98
2.
Гл.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Польша, Словакия, Германия
-
вот только некоторые из них~.
Итак, при построении ИИ КЖ населения страны в ситуации, ко
гда мы можем использовать экспертные оценки Уiэ КЖ для каждой
из анализируемых стран в качестве обучения, мы приходим к задаче
оценивания линейной регрессии Уiэ по:
'fХJСХОда.м на личное потребление на душу ( Х(З));
• о:жидаемой (при ро:ждении) продо.л.:жителъности :жизни (х< 7 >);
• общим 'fХJСХода.м на НИОКР (х< 10 >).
8
Результаты оценивания этой модели регрессии: значение оценок ко
эффициентов регрессии Во, 81, 82 и Вз, стандартных ошибок sв., в оценивании этих коэффициентов, значения t-статистик (t;, -j = О, 1, 2, 3, 4),
вероятности Р; статистической незначимости j-го предиктора, подправ
ленного
Дарбина
-
коэффициента
детерминации
Уотсона
приведены в табл.
(DW), -
(R~)
и
статистики
2.6.
Таким образом, значение ИИ КЖН страны
i (уi(об)), построенное
и вычисленное с использованием обучения, имеет вид:
Yi (об) = 2, 418 + о, 228х~ 3) + о, 308х~ 7) + о, 216хр 0>.
В Приложении Пlв приведены значения Уi(об) для всех анализиру
емых стран (т. е. для
i
=
1, 2, ... , 56), соответствующие рейтинги этих
стран, определенные по значениям Уi(об), и мера согласованности (ко
эффициент ранговой корреляции Спирмена р(у(об); Уэ)) рейтингования
стран по
Yi (об)
и по Уiэ. Отметим, что значение последней характери
= 0,855)
стики (р(у(об);уэ)
свидетельствует о хорошей согласованно
сти ранжировки стран по значениям
Yi (об)
с экспертной ранжировкой,
а следовательно, о высокой информативности выбранных трех част
ных критериев (х(З), х( 7) И X(lO)) В задаче формализации критериаль
НЫХ установок экспертов при ранжировании стран по КЖ!
Таблица
2.6.
Результаты статистического оценивания регрессии Уiэ
по (х< 3 > х< 1 > ' х< 10 >)
'
(част-
№№
Предиктор
п.п.
ный критерий)
(j)
Оценка
R2
,_.J.:.
Стандарт-
= о,, 675· DW = 2 14
"
t-
Значение
Р;
коэфф и-
ная ошиб-
статистика
циента
ка оценки
t;
регрессии
s·fJ;
8;
о
Свободный член
2,418
0,584
4,142
0,00013
1
Личное потребление
0,228
0,084
2,720
0,00886
жизни
0,308
0,105
2,925
0,00510
Расходы на НИОКР
0,216
0,074
2,911
0,00529
(х(З»
2
Продолжит.
(х(т»
3
(x(lO»
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
99
Построение ИИ КЖ в условиях отсутствия обучения
Получение от экспертов, в том или ином виде, оценок анализируемых
синтетических латентных категорий для каждого из рассматриваемых
объектов (стран, регионов, конгломерата населения)
дело затрат
-
ное и не всегда практически реализуемое. Это обусловливает актуаль
ность задачи построения ИИ КЖ только по имеющимся значениям
ряда частных критериев КЖ, т. е. в условиях отсутствия обуче
ния. Ниже описан пример решения такой задачи на тех же данных,
которые приведены в Приложении
1,
но только без информации о зна
чениях Уlэ, У2э, ... , У56э. При этом мы руководствуемся методикой и ре
комендациями, изложенными в п.
2.3.4.
Учитывая то обстоятельство, что априорный набор частных кри
териев сам по себе невелик (он содержит всего
10
показателей, о при
чинах сказано выше), мы не ста.ли его редуцировать, переходя к апо
стериорному набору (что было сделано при построении
f)
(об) в рамках
соответствующей модели регрессии в целях устранения мультиколли
неарности).
Результаты анализа главных компонент априорного набора
частных критериев КЖ приведены в табл.
2. 7 и 2.8.
Результаты, представленные в табл. 2.7, свидетельствуют: в зада
че межстранового анализа КЖ по данным [WCY {2009)) при построе
нии ИИ КЖ в условиях отсутствия обучения можно ограничиться
одним интегральным индикатором (см. правило
(2.15)
в п.
2.3.4
при
пороговом значении Qo =О, 55).
Таблица
2. 7.
Собственные значения ковариационной матрицы
унифицированных показателей X(l) ,..., X(lO) и процент
их общей вариации, объясненной первыми
j
главными
компонентами
Накопленный
%
Номер глав-
Собственные
%
ной
значения (Л;)
объясненной
объясненной ва-
j-й
риации
ком по-
ненты
(J)
вариации,
главной
компонентой
1
43,38
61,7
61,70
2
10,09
14,4
76,06
3
4
4,61
6,6
82,62
3,58
5,1
87,71
5
3,42
4,9
92,58
6
2,33
3,3
95,90
7
1,20
1,7
8
0,80
1,1
97,60
98,74
9
10
0,55
0,33
0,8
0,5
99,53
100,00
Гл.
100
Таблица
2.8.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Первый собственный вектор ковариационной матрицы
унифицированных показателей x(l)
коэффициенты w3
Номер
rv
x(IO) И весовые
= 1, 2, ... , 10) для ИИ
(j
Частные критерии (х<;))
Компоненты
соб-
КЖ
Нормированные
частного
1-го
критерия
ственного
1-го
(з)
вектора (с;)
ного
компоненты
собственвектора
(w;)
1
ВВП на душу (х< 1 >)
2
3
4
0,356
0,114
Производительность (х< 2 >)
0,373
0,120
(х< 3 >)
0,400
0,128
0,315
0,101
0,240
0,077
Личное потребление
Доля неграмотных
(х< 4 >)
(х< 5 >)
5
Коэффициент фондов
6
Индекс потребительских цен (х< 6 >)
0,257
0,083
7
Продолжительность жизни (х< 7>)
0,284
0,092
8
Младенческая смертность (х< 8 >)
0,361
0,116
9
Выбросы СО2
0,232
0,074
0,293
0,095
10
(х<9»
Расходы на НИОКР
(х< 10 >)
Поскольку все компоненты 1-го собственного вектора оказались од
ного знака, нормировка коэффициентов с3 произведена по формуле
(2.20а), имея в виду, что в данном случае мы не разбиваем наш набор
частных критериев на блоки.
Таким образом, значение ИИ КЖН страны i (Уi(б.о)), построенное
и вычисленное в условиях отсутствия обучения, имеет вид так назы
ваемой унифицированной первой главной компоненты, а именно:
10
А (б ) ~
-(j)
Yi .о = L...,, WjXi '
j=l
где значения коэффициентов w1, w2, ... , w10 представлены в последнем
столбце табл.
2.8.
В Приложении Пlв приведены значения Уi(б.о) для всех анализи
руемых стран (т. е. для
i = 1, 2, ... , 56),
соответствующие рейтинги этих
стран, определенные по значениям Уi(б.о), и мера согласованности (ко
эффициент ранговой корреляции Спирмена р (Уi(б.о); Уэ)) рейтинго
вания стран по Уi(б.о) и по Уiз· Отметим, что значение последней ха
рактеристики (р (у (б.о); Уэ) =О, 852) свидетельствует: интегральный
индикатор Уi(б.о), построенный без обучения по десяти частным крите
риям КЖ, дает практически столь же хорошее согласие с экспертной
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
101
ранжировкой стран, что и интегральный индикатор у (об), построен
ный при наличии обучения по наиболее информативным трем частным
критериям КЖ.
Так что анализ дееспособности построенных ИИ КЖ (с обу
чением и без него) базируется на сравнении и оценке согласованности
ранжирований стран, полученных на основании экспертных оценок Уiэ
качества жизни, с одной стороны, и на основании значений ИИ КЖ,
-
с другой.
2.4.2.
Межрегиональный сравнительный анализ
латентных синтетических категорий КЖ
населения субъектов РФ по данным
2003 г.
В данном примере целью эмпирического исследования является
сравнительный анализ
78 субъектов Российской Федерации по четырем
базисным синтетическим категориям - «Качеству населения (КН)»,
«Уровню благосостояния (УБ}», «Качеству социальной сферы (КСС)»
и «Качеству экологической ниши {КЭН)», - а также по синтетической
категории наивысшего уровня общности - «Качеству жизни» на базе
официальных статистических данных 2003 г. Для достижения этой цели
используется техника построения ИИ КЖ в условиях отсутствия
обучения, описанная в п.
2.3.4.
Информационная база исследования формировалась из источ
ников, перечень которых приведен в «Списке литературы» (см. соот
ветствующие источники в разделе «Информационные материал.ъt» )5 .
Принятый в ней такт времени
-
один год. Описанному ниже экономет
рическому анализу подверглись данные, датированные
2003 г.
Априорный набор частных критериев по каждой из четы
рех базисных латентных синтетических категорий КЖ формировался
с учетом требований (А)-(Б)-(В) (см. п.
2.2)
на базе упомянутых вы
ше источников. Перечень и индексация частных критериев априорного
набора приведены в Приложении П2.6 к монографии [Айвазян
(2012)].
Апостериорные наборы частных критериев и исходные ста
тистические данные. Для формирования редуцированного
(апосте
риорного) набора частных критериев по каждой из анализируемых син
тетических категорий КЖ (по КН, УБ, КСС и КЭН) была приме
нена методика отбора наиболее существенных показателей в услови
ях отсутствия
обучения, описанная в п.
2.2.
Отобранные в соответ
ствии с этой методикой переменные проиндексированы и приведены в
5 Соответствующая
база данных создана и подцерживается (начиная с 1997 г. по
настоящее время) сотрудниками Лаборатории вероятностно-статистических методов
и моделей в экономике Центрального экономико-математического института РАН.
102
Гл.
табл.
2.10.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Таким образом, из
40
частных критериев априорного набора
синтетической категории «Качество населения» в апостериорный на
бор было отобрано
14, из 15 частных критериев «УБ» в апостериорном
наборе осталось 10, из 33 частных критериев «КСС» в апостериорный
набор попало 23 и, наконец, из 27 частных критериев «КЭН» в апосте
риорный набор вошло только 9.
Исходные статистические данные по всем частным критериям (по
состоянию на
2003 г.)
для
78
П2.7 к монографии [Айвазян
субъектов РФ приведены в Приложении
{2012)].
Унификация измерительных шкал анализируемых пере
менных проводится по формулам
{2.4)""{2.6)
при
N
=
10,
т. е. осу
ществляется переход к десятибалльным шкалам измерений, в которых
нулевое значение унифицированного показателя свидетельствует о наи
худшем качестве, а десятибалльное
-
о наилучшем. Поскольку в дан
ном случае мы не располагаем обучением (а это, к сожалению, типичная
ситуация для задач межрегионального анализа), то возникают пробле-
мы с определением оптимальных значений (xiidт) тех показателей, ко
торые связаны с качеством :жизни немонотонной зависимостью (а
эти оптимальные значения нам необходимы для реализации унифици
рующего преобразования
{2.6)).
Однако, принимая во внимание совре
менную российскую специфику, а именно тот факт, что диапазон ре.аль
ных значений таких показателей весьма далек от соответствующих оп
тимальных значений, формула
{2.6) без ущерба для дела может быть за
менена подходящим вариантом «монотонной формулы» (т. е. либо фор
мулой {2.4), либо формулой {2.5)). В частности, именно эти соображе
ния были приняты во внимание при унификации измерительных шкал
переменных: коэффициент естественного прироста, миграция, безрабо
тица, общий размер социальных выплат, площадь особо охраняемых
природных территорий. В то же время анализ международного опыта
позволил определить оптимальную (на данный момент для России) ве
личину коэффициента фондов, равную
9,0.
Номер формулы унифици
рующего преобразования, примененного к каждой из переменных апо
стериорного набора, указан в последнем {6-м) столбце таблицы Прило
жения П2.6 к монографии [Айвазян
{2012)].
Результаты анализа главных компонент апостериорного на
бора частных критериев каждой из четырех анализируемых синтети
ческих категорий {КН, УБ, КСС и КЭН). Как было описано в п.
(см. этап
1.
1),
этот анализ нацелен на получение ответов на два вопроса:
Каково число
k(l)
интегральн-wх индикаторов, необходимое для
характеризации анализируемой
2.
2.3.4
( l-й)
синтетической категории?
Если мо:жно ограничиться одним интегральным индикатором
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
2.4.
( т.
е. если
103
то какова процедура его измерения на базе зна
k( l) = 1),
чений частнъ~х критериев апостериорного набора l-й синтетической
категории.
Ответ на первый вопрос основан на правиле
(2.15).
В частности,
если обозначить
Im(l) = Л1(l)
+ ... + Лm(l)
Л1(l) + · · · + Лp(t)(l)
накопленную долю (в
%)
. 100
общей вариации частных критериев апосте
риорного набора l-й синтетической категории, объясненную первыми т
главными компонентами этих частных критериев
(m = 1, 2, ... ,p(l)),
то предлагаемое формализованное правило определения необходимого
числа интегральных индикаторов
=
k(l)
где
p(l) -
min
l(m(p(l)-1
k( l)
основано на требовании
{m: Im(l) ~ qo(l)}, (l
= 1, 11, 111, IV),
(2.15')
общее число частных критериев в апостериорном наборе
l-й синтетической категории, а пороговое значение
диапазона значений
(0,5; 0,9)
q0 (l)
выбирается из
с учетом вида корреляционной матрицы
частных критериев апостериорного набора и требуемой точности вос
становления значений этих частных критериев по значениям искомых
иикж.
В нашем случае для всех синтетических категорий было выбрано
q(l) = 55% (l
Таблица
= 1, 11, 111, IV).
2.9.
Накопленная доля
Im(l) (в%) суммарной дисперсии
частных критериев апостериорного набора l-й
синтетической категории, объясненная первыми т
главными компонентами
Номер
Синтетическая категория
синте-
кж
Число главных компонент
(m)
Необходимое
чис-
k(l)
тиче-
ло
СКОЙ
ните-
кате-
граль-
гории
ных
( l)
индикаторов
1
11
1
2
3
4
Качество населения (КН)
31,0
53,4
63,85
Уровень
благосостояния
38,8
57,5
социальной
18,5
35,9
48,9
56,6
4
экологической
32,3
51,0
53,2
55,8
4
3
2
(УБ)
111
Качество
сферы (КСС)
IV
Качество
ниши (КЭН)
104
2.
Гл.
В табл.
2.9
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
представлены результаты расчетов значений
Im(l).
Из
них, в частности, следует, что для характеризации «Качества насе
ления» необходимо построить три ИИ КЖ, «Уровня благосостоя
ния»
-
два, «Качества социа..п:ьной сферы»
чества экологической ниши»
блочные ИИ
-
ставлена на рис.
четыре и, наконец, «Ка
четыре (соответствующая иерархиче
-
ская схема «Сводный ИИ КЖН
рий КЖ
-
ИИ основных синтетических катего
-
базовые статистические показатели» пред
-
2.4).
Ответ на второй вопрос при
в которых, соответственно,
P;(l)
k(l)
= p(l)
= 1 дается
формулами
{2.20},
- общему числу частных кри
териев анализируемой (L-й) синтетической категории. Однако в нашем
случае все
k(l)
> 1, так что необходимо переходить к разбиению ка:ждо
го апостериорного набора частных критериев на блоки и к построению
блочных ИИ КЖ (см. этапы
2
и
3
методики, описанной в п.
2.3.4).
Разбиение апостериорных наборов частных критериев на
блоки и построение блочных ИИ КЖ. Задавшись числом блоков
k(l)пo каждой {l-й) синтетической категории и используя результаты
проце(}уры экстре.ма.л:ьной группировки признаков (см.
п.
2.3.4}
{2.16)-(2.18}
в
как главную «подсказку» при выборе окончательного вариан
та разбиения частных критериев апостериорного набора на блоки, мы
приходим к результатам, представленным в табл. 2.10а"'2.10г.
СВОJUfЫЙ ИИ ЮКН
ии
СИIПе11!чес:хИХ
кareropиii
Сrаmсmчес
кие показаrели
(ЧасПIЫе
кршерии)
Рис.
Качесrво
БпаrоСОСТО11-
Качество
Качество
иасепеиЮ1
иие иаселеии11
СОШ18JIЬИОЙ
эколоrической
у<•>
у<П>
сферы
y<"I)
ниши
y<IV)
х 111 (1).К .х1Р 1111 (1)
х111 (11).К ,х 1 Р 161 (11)
х1 1 1(111),К ,xlPllll)(lll)
xl11(1V).K .x1PllVll(IV)
p(I) = 14
р(П)=
р(П1)=23
p(IV)=IO
2.4.
10
Иерархическая схема построения интегральных индикаторов КЖН
в межрегиональном анализе
Таблица 2.10. Блочные частные критерии (x< 1>(j),x< 2>(j), ... ,x<Pj)(j)) и их
весовые коэффициенты w1 (j), w2 (j),
КЖ синтетических категорий
Таблица
2.lOa.
(j -
... , Wpj (j)
в блочных ИИ
t.:)
номер блока)
~
По синтетической категории «Качество населения~
Переменные блока (в скобках
Номер
-
соответствующие весовые коэф-ты
.,,:::1
:s:
.,,::::
Ws(j))
tz:I
блока
о::
(;)
1
2
х<1> (J)
х<2> (J)
Х(З)(j)
х<4> (j)
Продолжи-
Младен чес-
Смертность
тельность
кая
от
жизни
ность
w1{1}=0,178
'WJ{l}=0,130
смерт-
Смертность
ный прирост
от
W1 {2}=0,262
гических
он коло-
tz:I
W7{1}=0,056
заболеваний
:s:
~
:s:
W'J{l}=0,133
~
и
ин-
фекционных
Смертность
от
ний
заболева-
от
болезней
нес част-
дыхания
пищеварения
ных случаев
W4{1}=0,155
ws{l}=0,150
Wб{l}=0,198
но-сосудне-
'WJ{2}=0,238
той системы
образов а-
дежи
ние
ни ем
среди
занятых
моло-
ВРП на одно-
обуче-
го занятого•>
о
:i::
:i::
tz:I
Инвалидность
"":!
W4{2)=0,211
~
сердеч-
заболеваний
Охват
Высшее
.,,
Врожденные
болезней
W'J(2}=0,289
3
о
(")
~
аномалии
леза
Естествен-
x<1>(J)
Смертность
от
Смертность
х<б>(J)
от
туберку-
Смертность
x<5>(J)
::i
W"J{3}=0,401
'WJ{3}=0,162
W1 {3}= 0,437
~
t:7'
:i::
!Z:
><
:s:
~
::i:::
~
.,,
о
о
ti:i
•) Характеризует так называемую приведенную производительность труда в регионе, т. е. вычисленную в единой {для всех реги
онов) стандартизованной структуре занятости.
......
о
ел
Таблица
2.106.
......
По синтетической категории «Уровень благосостояния»
Переменные блока (в скобках
Номер
-
о
Q')
соответствующие весовые коэф-ты щ,(j))
блока
{J)
1
ж<1> (j)
ж'2'{J)
ж<з> (j)
ж<4> (j)
ж<s> (j)
ж<в> (j)
"'"::1
ВРПна.цушу
Покупатель-
Доля бедных
Коэффициент
Обеспечен-
Товарооборот
t-.:)
W1 {1)=0,093
ная
Wз{l)=
фондов
ность
wв{1)=135
W4{1)=0,074
мобилями
ность
способ-
0,360
.цуше-
W5{1)=0,112
вых доходов
:::::1
о
(')
~
WJ{l)=0,226
2
авто-
~
Обеспечен-
Ввод жилья
Плотность
Ветхое
ность
WJ{2)= 0,370
автомобиль-
и
аварий-
жильем
ных дорог
ное жилье
W1 {2)=0,394
Wз{2)=
W4{2)= 0,108
0,128
о
[!]
:i::
:s::
[!]
:s::
:i::
~
"":!
~
~
cr
:i::
е::
><
:s::
"":::
.,,
[!]
:s::
>-:Э
~
:s:c
[!]
Таблица 2.lОв.
По синтетической категории сКачество социальной сферы~
Переменные блока и соответствующие весовые коэффициенты Ws (j)
Номер
t.:)
блока
~
(J)
1
ж<1> (j)
ж< 2 >ш
Изнаси-
Разбои,
Растраты,
Алкого-
Само-
вред
лования
грабежи,
хищения
лизм
убийства
кражи
wв(l}
W9(l}
=
= 0,040
W1o(l} =
=0,145
::i
Вредные
Производ-
Убийства
и опасные
ственный
и
болезни
условия
травма-
шения
ровью
и
труда
тизм
W4(l}
=
=О, 112
W5(l}
=
= 0,084
шения
w2(l}
=
wз(l}
=О,
=
по ку-
здо-
113
поку-
wв(l}
Глубина
Безрабо-
Нагрузка
Длитель-
бедности
тица
беэработ-
ная
w2(2}
wз(2}
ных
работица
по
W5(2}
=
= 0,225
плате
=
= 0,233
на
вакансию
W4(2}
=
=0,146
Покупа-
Социаль-
тельная
способность
пенсий
Социаль-
Обслу-
ные
ное обслу-
живание
выплаты
живание
в
w2(3}
=
=О, 113
на
социаль-
tw1(3} =
= 0,819
дому
wз(3}
=
центрах
но го
обеспе-
= 0,004
чения
W4(3}
=
=0,064
Коэфф и-
Наркома-
ВИЧ-
циент
ния
инфекции
фондов
токси-
wз(4)
ко мания
= 0,502
w1(4}
=
= 0,064
и
=
без-
=О,
зар-
121
=0,064
=
x(lO) (j)
tz:I
о::
о
(")
.,,
о
женность
wв(l}
w7(l}
=
= 1, 155
з:(9)(j)
ж<з>(;)
,.;з
За,цол-
Миграция
=
=
=0,069
w1(2}
=
=0,055
=О,220
4
Тяжкий
.,,:::1
:s:
.,,::::
ж< 5 >сл
Социально
=О,143
3
з:(7)(j)
Ж(4)(j)
значимые
w1(l}
=
=0,075
2
ж<в>ш
ж< 3 >сл
=
tz:I
:i::
:s:
~
:s:
:i::
,.;з
tz:I
"":!
~
~
t:7'
:i::
!Z:
><
:s:
~
::i:::
~
.,,
о
о
ti:i
w2(4}
=
=0,434
......
о
-.J
Гл.
108
Таблица
2.
2.10 г.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
По синтетической категории
«Качество экологической ниши~
Номер
Переменные блока и соответствующие весовые коэф-ты
Ws(j)
блока
(j)
ж<1>(j)
Объем
1
ж<з>(j)
ж<2>(j)
загряз-
ненных
вод на
сточных
1
кв. км
Общие
вы-
ж<4> (j)
ТОП, образо-
Токсичные
бросы от ста-
отходы
ционарных
изводства
про-
вавшиеся
год
территории
источников
(ТОП), захо-
wi(l)=0,147
загрязнения
роненные
атмосферы
год (на lкв.
W2(1)=0,136
км
за
том
за
за
выче-
исполь-
зованных
ша(l)=О,315
терр и-
тории)
wз(l)=0,402
2
Посеянный и по-
Молодняк
саженный лес
категории
Wi (2)=0,570
ценных
Сгоревший в
пожарах лес
по-
wз(2)=0,327
род леса
W2(2)=0,103
Особо
3
мая
охраняеприродная
территория
W1 (3)
= 1, ООО
Рекультивиро-
4
ванные
и
нару-
шенные земли
Wi(4)=1,000
Напомним (см. (2.20а) и
Yi(j)
(2.206)),
что значение блочного ИИ КЖ
для каждой (i-й) территории (и каждой синтетической категории)
вычисляется по формуле (2.20а) или
(2.206):
Р;
Yi(j)
= L Ws(j). X~8)(j),
s=l
где x~s) (j) - унифицированное значение s-го частного критерия f го
блока для i-й территории, а весовые коэффициенты w8 (j) определяют
ся по компонентам c1 8 (j) первого собственного вектора C1(j) = (сн(j),
с12 (j), ... , Ctp; (j)) ковариационной матрицы
E(j) апостериорного набо
ра унифицированных ЧаСТНЫХ критериев (x(l)(j), x( 2)(j), ... , x(P;)(j)) ПО
формуле:
Р;
( .)
Ws J
=
{
c1s(j)/ :Е c1"(j), если все с1 11 одного знака v
11=1
~ 8 (j)
в противном случае.
= 1, 2, ... ,pj;
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
Подсчитанные по этой формуле значения блочн:ых ИИ КЖ для
109
78 субъ
ектов РФ по каждой из четырех анализируемых синтетических катего
рий (по данным 2003г.) приведены в Приложении П2.1.
Построение сводного интегрального индикатора для анали
зируемой синтетической категории КЖ. Теперь, следуя методике,
описанной в п.
k(l) блочн'Ы.Х
ИИ КЖ данной (l-й) синтетической категории y(l>1, y(l)(2), ... , y(l)(k(l))
к одному сводному интегральному индикатору - скалярному измерите
лю этой синтетической категории y(l) (l = 1, 11, 111, IV). Из (2.22)-(2.23)
2.3.4
(см. «Этап
4» ),
мы должны перейти от
следует, что
(2.23а)
Подсчитанные таким образом по данным
2003
г. значения сводн'Ы.Х
интегральных индикаторов y~l) для 78 субъектов РФ (i = 1, 2, ... , 78) по
каждой из четырех анализируемых синтетических категорий КЖ
= 1, ... IV)
(l
=
приведены в Приложении П2.1.
Построение единого сводного интегрального индикатора
для синтетической категории КЖ высшего уровня общности
-уев. по сводным ИИ КЖ, характеризующим
«Качество населения»
(у< 1 >), «Уровень благосостояния» (у<щ), «Качество социальной сферы»
(y(III)) и «Качество экологической ниши» (y(IV)), осуществляется по той
же методике, что и построение y(l) по блочным ИИ КЖ, а именно:
ив.= N - [ Liit. (y~l) IV
N)2
]
!
2'
l=l
где
Qt
=
k(l)
р(l>.з1
IV
Е p<'>·s~
'
l
р<'> = Ер(>,
. 1 3
3=
l=l
n
-2 -
81 -
1 " ( A(l)
A(l))2
n L..,, Yi - У
i=l
n
A(l)
и У
=
-1 "L..,, YiA(l) ·
n i=l
(2.23б)
Гл.
110
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Вычисленные по этим формулам значения единого (сводного) ИИ
КЖ, так же как и значения соответствующих рангов регионов (по дан
ным
2003
г.), приведены в Приложении П2.2.
Итак, Приложения П2.1 и П2.2 содержат данные, необходимые для
сравнительного анализа и ранжирования субъектов РФ как по каж
дой из четырех рассмотренных синтетических категорий КЖ («КН»,
«УБ», «КСС» и «КЭН» ), так и по латентной синтетической категории
КЖ высшего уровня общности. Это
задача описательного характера,
-
представляющая определенный самостоятельный интерес. Однако, как
показано в [Айвазян
{2012)],
гл.
3,
подобные данные, рассмотрен:н:ые в
динамике, могут быть использованы для решения задач выявления про
блемных областей в социально-экономическом развитии региона, кор
ректировки проводимой социально-экономической политики и оценки
эффективности деятельности региональных администраций.
2.4.3.
Построение интегрального измерителя уровня
мастерства спортсмена (на примере хоккея)
Постановка. задачи, цель исследования. Исследование проводи
лось силами рабочей группы Центрального экономико-математического
института Академии наук СССР (ЦЭМИ АН СССР) по заказу Отде
ла хоккея Государственного комитета по физической культуре и спорту
Совета Министров СССР в рамках создания автоматизированной ин
формационной системы «АИС-Хоккей», предназначенной для инфор
мационного
обслуживания
чемпионата
мира
по
хоккею
(Москва,
1973г.). Практически на всех этапах работа проводилась при система
тических контактах и консультациях с представителями «Заказчика» 6 .
В качестве анализируемой синтетической латентной категории рассмат
ривался уровень мастерства хоккеиста, проявленного 1LМ в данном
матче или серии матчей.
Цель исследования
-
нию показателей ( частн-ых
выявление набора подцающихся измере
критериев) х< 1 >, х< 2 >,
х(р), характеризу
... ,
ющих уровень мастерства хоккеиста, и построение такой функции
у(х< 1 >, х< 2 >,
х<Р>) от этих показателей, которая может служить чис
... ,
ленной оценкой анализируемого уровня мастерства (в дальнейшем мы
будем называть ее целевой). Прикладное назначение этой функции:
6 Рабочую
группу ЦЭМИ АН СССР возглавили С. Айвазян и С. Шаталин. В
различных частях информационного и математического обеспечения этой большой
комплексной работы участвовали М. Ильменский, С. Забаринская, В. Когутовский,
Ю. Брыкни, В. Орлов. Со стороны сЗаказчика• непосредственное участие в рабо
те принимали Б. Майоров (в то время
-
начальник Отдела хоккея упомянутого
Комитета Госкомспорта) и Ю. Королев (зав. кафедрой футбола и хоккея Государ
ственного института физкультуры и спорта).
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
2.4.
111
(а) формализованная оценка уровня мастерства каждого (i-го) хокке
иста, проявленного им в данном матче или в серии матчей, по значе
ниям показателей х?>, х~ 2 ), ... , х~р), характеризующих его действия в
этом матче (или в серии матчей}; (б} построение (на основе мониторин-
га значений целевой функции у(х~ 1 >' х?>' ... 'xr>)) для каждого (i-го)
хоккеиста индивидуализированного
плана тренировочного
процесса с
акцентом на совершенствование тех компонентов игры, за счет которых
можно добиться наибольшего приращения в значениях целевой функ
ции у(х< 1 >, х< 2 >,
х<Р>).
... ,
Формирование априорного набора частных критериев. Как
было сказано выше, решение этой задачи находится целиком в ком
петенции экспертов той области, к которой относится анализируемая
СЛК. В данном случае
-
это хоккейные тренеры высокой квалифика
ции. Поэтому, отправляясь от согласованного с представителями «За
казчика» предварител:ьного списка показателей индивидуа.л:ьного ма
стерства хоккеистов, была составлена и размножена среди экспертов
«Анкета .No 1» следующего содержания 7 :
«Оцените, пожалуйста, исход.я из 100-ба.л.л:ьной системы оценок,
сравнительную значимость каждого из нижеприведенн'ЫХ факторов
(показателей качества игр'Ы хоккеиста), так или иначе учит'Ываем'ЫХ
при сравнительной характеристике степени мастерства, про.явлен
ного игроками в данном соревновании.
Если Вы считаете, что в указанном ниже перечне факторов не
учтены какие-либо из существенн'Ых, на Ваш взгл.яд, числов'ЫХ показа
телей качества игры хоккеиста, дополните его, пожалуйста, точным
описанием см'ЫСЛа этих неучтенн'ЫХ величин».
Пример заполнения такой анкеты одним из экспертов-специалистов
хоккея приведен в табл.
2.11.
Здесь следует подчеркнуть, что при предварительной обработке по
лученных
15
анкет обнаружилось полное отсутствие согласованно
сти в мнениях экспертов, относящихся к сравнительной оцен
ке значимости факторов (частных критериев) в формирова
нии интегральной оценки уровня мастерства хоккеиста (см.
последние три столбца табл.
7 Среди
2.11).
откликнувшихся на вопросы анкеты были такие признанные авторит~
ты отечественного и мирового хоккея, как А. Чернышев, А. Тарасов, В. Кулагин,
Ю. Морозов, В. Карпов, В. Егоров, В. Майоров, В. Старmинов, Ю. Ваулин, И. Ро
мишевский, Ю. Королев и др.
2.
Гл.
112
Таблица
2.11.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
Пример заполнения экспертом анкеты, нацеленной на
выявление основных частных критериев уровня
мастерства хоккеиста
NN
кри-
Содержательный смысл частного критерия
те-
Значимость фактора
при сравнении игры
риев
по.
напа-
защит-
всех
дающих
инков
участ-
ни ков
соревнован и я
1
100
45
80
80
40
65
выигранных силовых едино-
80
80
80
4
Общее число отборов шайбы у противника
40
100
65
5
Разность шайб, забитых и пропущенных ко-
60
60
60
40
20
40
70
40
30
парированных
20
65
30
Суммарное время участия хоккеиста в игре
60
60
60
75
20
55
20
10
15
Количество очков, начисляемых по системе
•полуторная сумма забитых голов
результативных передач• (х< 1 >)
+
число
Общее число эффективных (т. е. окончивших-
2
ся голом или парированием) бросков по воротам противника (х< 2 >)
Общее число
3
борств (х< 3 >)
(х<4>)
мандой в течение времени пребывания данно-
го игрока на площадке (х< 5 >)
Общее число точных передач (х< 6 >)
6
7
Общее число удачно
выполненных
•длин-
ных• (т. е. адресованных из одной зоны в другую) первых передач (х< 7 >)
Число
8
бросков
противника,
данным игроком (х<8>)
9
в
численном
меньшинстве
и
в
численном
большинстве (х< 9 >)
10
Общее число удачно выполненных обводок
11
Отношение числа обводок к числу передач,
-
в средней зоне и в зоне нападения (х< 10 >)
выполненных в средней зоне и в зоне вападе-
ния
(x<ll))
12
Сумма штрафного времени, сзаработавного•
игроком (х< 12 >)
30
40
35
13*
Процент
(х(lЗ>)
шайбы
30
-
15
14*
Действия на спятачке• противника (сумма
добиваний шайбы и помех вратарю)"' (х< 14 >)
40
-
20
*
выигранных
вбрасываний
Пункт дополнен экспертом, заполнявшим данную анкету.
Окончательное формирование апостериорного набо'fХL частных кри
териев осуществлялось в соответствии с рекомендациями п.
2.2,
отно-
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
113
сящимся к случаю ~с обучением». Получение данных
(2.24)
необходимых для реализации этих рекомендаций, потребовало перио
да экспериментальной апроооции методики. Этот период включал в
себя отрезок времени до чемпионата мира (а именно февраль 1973г.),
в течение которого в ходе трех контрольных матчей календаря пер
венства СССР (ЦСКА- Химки, Крьmья Советов -Динамо и ЦСКА
Спартак) была организована регистрация по каждому (i-му) участни
ку матча значений всех
14
упомянутых в табл.
2.11
частных критери
ев хР>, х~ 2 ), ... , хР 4 > и одновременно экспертная интегральная оценка
(в 100-балльной системе) уровня мастерства
Получение
экспертной
Yi хоккеиста.
(«обучающей•)
части
исходных
данных. Обучение было получено в процессе упомянутого периода
экспериментальной апробации, в ходе которого была организована (по
каждому i-му участнику каждого из трех матчей) регистрация зна-
хР 4 ) {это, по нашей терминологии,
исходн:ых данн'ЫХ), а также - экспертные ин
чений частных критериев хР>
статистическая часть
тегральные оценки
rv
Yi уровня мастерства, проявленного этим же (i-м)
участником в ходе данного матча. Для получения последней оценки
экспертам-специалистам отечественного и мирового хоккея (поименно
они упоминались выше) раздавались ~Анкеты
.No 2»
следующего со
держания.
«Оцените, пожалуйста, исходя из 100-ба.л.л.ьной системы оценок,
сравнительную
степень
мастерства,
проявленного
у-частниками
сегодняшнего соревнования. При этом Вы можете не оценивать дей
ствия всех у-частников сегодняшней встре-чи. Однако желательно,
-чтобы Вы включили в число оцениваем'ЫХ не менее
12 лу-чших,
на Ваш
взгляд, хоккеистов данного матча».
Отметим, что экспертные оценки
Yi
уровня мастерства хоккеиста,
участвующего в матче, производились на двух стадиях: на стадии экс
периментальной апроооции методики (см. выше), когда эти оценки ис
пользуются для уточнения состава частных критериев и для построения
искомых целевых функций (отдельно для форвардов и для защитников)
Yi = Оо + 81хР> + ... + Opxf>; и на стадии рабочей эксплуатации моде
лей (т. е. в ходе всех 30 матчей чемпионата мира 1973 г.), в ходе которой
одновременно тестируется прикладная дееспособность моделей и уточ
няются их параметры. Заметим, что на стадии рабочей эксплуатации
методики к упомянутым выше экспертам бьmи подключены главные
тренеры всех национальных сборных команд
-
участников чемпиона-
Гл.
114
та. В табл.
2.12
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
представлен пример заполнения «Анкеты № 2» по ре
зультатам матча второго круга «СССР - Чехословакия»
Таблица
2.12.
Пример заполнения анкеты, связанной с интегральной
оценкой уровня мастерства хоккеиста- участника
матча
Номер игрока
1
Команда
1
Оценка в баллах
Место
17
СССР
88
2
13
СССР
90
1
16
СССР
85
3"" 5
2
СССР
85
3"" 5
6
СССР
3
СССР
85
75
3"" 5
6"" 10
22
СССР
70
11"" 14
20
ЧССР
70
11"" 14
8
ЧССР
70
11"" 14
7
ЧССР
75
6"" 10
14
ЧССР
75
3
ЧССР
70
6"" 10
11"" 14
9
4
СССР
76
6"" 10
ЧССР
75
6"" 10
Следует особо подчеркнуть, что степень согласованности мнений
всех
12
rv
15
экспертов, отвечавших на вопросы «Анкеты № 2», оказы
валась, как правило, весьма высокой: парные коэффициенты ранговой
корреляции Спирмена в упорядочении участников матча по степени
проявленного ими мастерства (см. последний столбец в табл.
ли на уровне О,
экспертам)
-
7 rv
2.12}
бы
О, 9, а коэффициент коннордации Кендалла (по всем
порядка О,
5 rv
О,
7.
Эти коэффициенты всегда «С запасом»
выдерживали статистическую проверку на значимое отличие от нуля.
Совсем другую картину, напомним, мы наблюдали с согласованностью
оценок экспертов относительной значимости каждого из частных кри
териев!
Некоторые результаты построения и рабочей эксплуатации
ИИ уровня спортивного мастерства хоккеиста. В апостериорном
наборе частных критериев после проведения рекомендованных в п.
процедур осталось лишь
веденных в табд.
затели х< 11 >, х< 13 )
11
частных критериев: из
14 показателей,
2.2
при
в состав апостериорного набора не вышли пока
14
х< ).
2.11,
и
Описанный в п.
2.3.3
экспертно-статистический метод построения
линейной целевой функции, примененный к данным вида
(2.24),
при-
2.4.
ПРИМЕРЫ ПОСТРОЕНИЯ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
115
чем отдельно к данным по защитникам, нападающим и к общему (объ
единенному) массиву, дал следующие три варианта для вычисления ин
тегрального индикатора уровня спортивного мастерства хоккеиста:
вариант целевой функции, оценивающей индивидуальное мастер
ство защитника,
Уэащ(х< 1 >, х< 2 >, ... , х< 11 >)
= 10 + 4х< 1 > + х< 2 > + 4х(З) + х< 4>+
+ х< 5 > + О, 2х< 6 > + зх< 8 > + х< 9 > + х< 10 >;
(2.25а)
вариант целевой функции, оценивающей индивидуальное мастер
ство нападающего,
Унап(х< 1 >, х< 2 >, ... , х< 11 >)
= 8х< 1 > + х<2 > + х< 3 > +О, 5х< 4 >+
+ х< 5 > + О, 2х< 6 > + х< 8 > + х< 9 > + зх< 10 >;
(2.25б)
вариант целевой функции, оценивающей универсальное мастерство
хоккеиста, т. е. позволяющей сравнивать между собой защитников и
нападающих,
у(х< 1 >, х< 2 >, ... , х< 11 >) =
15 + бх< 1 > + х< 2 > + 2х< 3 > + х<4 >+
+ О, 5х< 5 > + О, 2х< 6 > + х< 8 > + 2х< 9 > + х< 10 >.
(2.25в)
Отметим, что последовательный пересчет весовых коэффициентов
по накапливающимся итогам матчей чемпионата мира выявил факт от
носительной стабилизации значений весовых коэффициентов, что дает
основание надеяться на содержательность и объективность полученно
го с помощью этих целевых функций формализованного метода оцени
вания мастерства хоккеистов.
3
а меч ан и я.
1)
Оценки коэффициентов (Jj в соотношениях
(2.25)
получались в результате усреднения и округления соответствующих
МНК-оценок, пмучаемЬtХ последовательно по массивам данн'Ьtх, нарас
тающим по мере добавления очереднЬtХ матчей чемпионата мира.
2)
Из с.амого способа построения НИ уровня спортивного мастер
ства хоккеиста сл.едует, что коэффициент'Ьt при xU> в моде.лях (2.25)
отражают неформализованн'Ьtе (в значительной мере интуитивные)
критерийные установки привлеченнЬtХ экспертов по поводу относи
тельной ва:нсности различнЬtХ характеристик игры хоккеиста в фор
мировании интег'fХJ,Льной оценки уровня про.явленного им мастерства.
Очевидно, со временем эти установки могут трансформироваться
в соответствии с меняющимися тенденциями в развитии хоккея.
Так, сегодня признанн'Ьtе в начале 70-х годов проWJЮго столетия несу
щественн'ЬtМи факторы х< 13 > (% в'ЬtuграннЬtХ вбрас'Ьtваний шайбы) и
Гл.
116
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИЗМЕРИТЕЛЕЙ
х< 14 > (действия на «пятачке» противника), скорее всего, оказались б'Ьt
достаточно в'Ьtсоко значим'ЫМи. Поэтому, говор.я о практическом ис
пользовании моделей вида
(2.25),
например в планировании трениро
вочного процесса, необходимо хот.я б'Ы один раз в пять лет произво
дить их переоценку по последним (по времени) исходн'ЬtМ данным.
Анализ прикладной дееспособности построенных ИИ уров
ня мастерства хоккеиста. Тридцатикратное (т. е. по
30
матчам чем
пионата) сопоставление экспертной и формализованной (т. е. произве
денной с помощью целевых функций) оценок мастерства хоккеистов на
матчах чемпионата мира, так же как и тщательный профессиональ
ный анализ накопленного итога, показал устойчивую обоснованность и
профессиональную состоятельность выводов, полученных с помощью
целевых функций
В табл.
2.13
(2.25).
приведен накопленный итог чемпионата по показате
лям индивидуальных действий
12 лучших защитников
и
20 лучших на
падающих, определенных с помощью целевых функций, соответственно
Уэащ(Х) и Унап(Х), выписанных выше.
Заметим, что выявленные с помощью построенных ИИ (см. (2.25а)
и (2.25б)) кандидатуры лучшего защитника, лучшего нападающего, так
же как и состав символической сборной мира, практически совпали с
мнением специального жюри чемпионата и прессы. В частности, по ито
гам чемпионата по значениям ИИ, определенным с помощью соотноше
ний (2.25а) и (2.25б), были выявлены следующие лучшие игроки:
лучший З81ЦИТНИК
Васильев
№6
СССР
лучший нападающий
Петров
№16
СССР
вратарь
Холечек
№2
ЧССР
правый защитник
Васильев
№6
СССР
левый защитник
Гусев
№2
СССР
правый нападающий
Михайлов
№13
СССР
центральный нападающий
Петров
№16
СССР
левый нападающий
Харламов
№17
СССР
Символическая
сборная
мира:
Единственное отличие этой символической сборной от той, которая
была определена в результате специального опроса спортивных журна
листов, заключается в том, что вместо Валерия Васильева в нее вошел
Сальминг (Швеция). При этом, правда, Директоратом Международной
организации хоккея В. Васильев был провозглашен лучшим защитни
ком чемпионата!
Таблица
2.13.
Накопленный итог чемпионата мира по хоккею (Москва,
197Зг.) по показателям индивидУальных действий хоккеистов
t.:)
Nt
Но-
Асс и с-
Броски
Выиг-
Прочие
Разност~,
Точ-
Прием
Время
Удач-
Штраф
пп.
мер
Страна
тирова-
ПО
равные
отборы
эаби-
ные
шай-
игры
ные
ное
Фамилии
иг-
ние
ротам
сило-
шайбы
тых
пере-
бы на
в
об-
время
игроков
ро-
голов
дачи
себя
равно-
вод-
в
числен-
ки
нутах
Голы
ка
во-
не-
вые
и
пущен-
бор-
ных
ных
о::
ства
шайб
соста-
::i
в
вах
про-
4
5
6
7
8
9
10
,.;з
о
tz:I
:i::
11
12
13
14
15
:s:
~
:s:
6
10
tz:I
По защитни-
:i::
кам
1
2
3
4
5
6
7
8
Васильев
Сальминг
Гусев
Поспешил
Махач
Лутченко
Цыган ков
Коскела
,.;з
6
5
2
7
4
3
7
6
СССР
о
Швеция
СССР
4
7
1
3
1
СССР
о
о
Фин-
о
1
Польша
о
о
Швеция
1
ЧССР
о
Швеция
2
3
1
3
СССР
ЧССР
ЧССР
7
6
7
6
1
о
39
42
46
17
56
25
33
22
53
41
10
28
16
33
24
13
179
185
164
149
163
105
149
159
43
17
46
8
8
14
20
-4
222
241
228
226
196
151
182
234
6
30
8
25
32
20
21
20
143
135
127
135
-20
10
9
12
136
156
177
142
6
9
3
8
7
6
1
48,5
54,3
37,9
58,5
57,0
33,3
32,1
60,9
34
34
30
18
10
21
15
17
6
3
2
2
26,5
31,9
28,7
35,3
6
о
о
4
11
12
6
8
ляндия
9
10
Чаховский
11
Вохралик
12
Юханссон
Шеберг
tz:I
.,,
игрока
3
ми-
о
(")
матче
2
.,,:::1
:s:
.,,::::
едино-
микро-
1
~
2
7
19
9
"":!
~
~
t:7'
:i::
!Z:
><
:s:
~
::i:::
~
.,,
о
17
14
17
8
2
2
10
о
ti:i
......
......
-.J
Таблица
1
2
2.13.
(окончание)
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13
17
20
14
15
15
19
10
14
16
16
22
23
11
СССР
18
16
9
4
6
1
9
6
7
2
7
3
6
7
2
15
13
14
10
2
2
6
2
7
1
8
1
6
6
5
49
44
39
40
66
27
33
44
41
49
38
24
31
28
25
24
19
9
23
10
42
18
14
9
23
25
15
10
14
21
101
83
136
120
75
137
85
112
117
114
77
71
80
86
89
43
42
47
11
12
-19
14
13
10
-10
12
9
17
13
4
258
193
205
212
186
167
197
190
140
191
146
122
142
160
166
о
52,6
50
26,5
50,1
27,7
50,5
25,4
22,7
43,2
34,7
17,9
12,5
27,3
52,7
45
38
54
53
48
46
31
35
36
32
23
20
20
2
17
12
4
35
23
2
12
2
2
12
14
6
2
4
7
2
2
3
2
3
4
3
2
5
4
7
19
32
30
28
18
15
15
20
21
11
89
95
94
66
60
8
10
7
7
14
119
162
151
149
161
47,7
29,8
21
35,2
17,5
33
10
13
22
9
2
......
......
00
По нападающим
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Петров
Михайлов
Харламов
Хопик
Недомански
Шлодер
Якушев
Хаммарстрем
Мальцев
Кюнхакль
Ольберг
Папечек
Анисии
Седерстрем
Леппя
СССР
СССР
ЧССР
ЧССР
ФРГ
СССР
Швеция
СССР
ФРГ
Швеция
ЧССР
ссен
Швеция
Финлян-
1
о
3
о
3
4
1
1
о
о
7
о
о
2
11,О
дня
16
17
18
19
20
Кохта
Лундстрем
Хедберг
Викберг
Шадрин
8
11
20
10
19
ЧССР
Швеция
Швеция
Швеция
СССР
1
1
о
о
о
о
о
о
4
1-j
~
t-.:)
:::::1
о
(')
~
о
[!]
:i::
:s::
[!]
:s::
:i::
~
'":1
t
cr
:i::
е::
><
:s::
"":::
[!]
":s::
>-:Э
~
[!]
:s::c
Гл.
2.
ПОСТРОЕНИЕ ИНТЕГРАЛЬНЫХ ИНДИКАТОРОВ
119
Выводы
1.
(ИИ
Интегральный индикатор синтетической латентной категории
СЛК)
строится
в
форме
определенной
свертки
(функции)
у= f(x< 1>, х< 2 >, ... , х(р)) от некоторых измери.м'ЬtХ частных свойств этой
категории, где в роли частных свойств х< 1 >, х< 2 >, ... , х<Р) в об'бективист
ском подходе выступают характеризующие эту категорию статистиче
ские показатели (см. п.
2.
щих в
2.2).
Главным недостатком подавляющего большинства существую
1 х< 2 >,
мире способов оценки этих сверток у
х(р>) яв
= f(x< >,
... ,
ляется прямое экспертное оценивание параметров, от которых за
висит конкретный вид функции/(·). Так, если задача решается в классе
линейн'ЬtХ сверток f(x< 1>, х< 2 >, ... ,х<Р>) =
t
WjX(j),
то неизвестные ве-
j=1
са Wj определяются непосредственно экспертами в результате той или
иной формализованной процедуры получения и обработки экспертных
мнений (см. п.
2.3.4).
3. Подбор значений параметров функции-свертки
f (х< 1 >, х< 2 >, ... ,
х(р>) при наличии обучения (т. е. при наличии априорной экспертной
информации о сравнении рассматриваемых объектов по анализируе
мой синтетической латентной категории) производится таким образом,
чтобы результат сравнения этих объектов, основанный на значениях
f (·),
наименее (в определенном смысле) отличался бы от априорного
экспертного (см. п.
2.3.3).
4. Подбор значений параметров функции-свертки
f (х< 1 >, х<2 >, ... ,
х(р>) в условиях отсутствия обучения основан на следующем требова
нии: среди всех скалярных переменных, характеризующих анализиру
емую синтетическую латентную категорию, именно по значениям у
=
= f(x< 1>, х<2>, ... ,х<Р>)
можно наиболее точно (в определенном смысле)
восстановить
значения
всех
частных
свойств
х< 1 >, х< 2 >,
... , х(р), используя для этого соответствующие модели парной регрес
сии х<Л по у (j = 1, 2, ... ,р) (см. п. 2.3.4).
5.
При формировании исходного (априорного) набора частных
свойств, характеризующих анализируемую синтетическую латентную
категорию, необходимо руководствоваться требованиями к их реле
вантности, информационной доступности и информационной досто
верности (см. п.
2.2).
Перед включением частных свойств в состав аргументов функ
ции-свертки
х< 2 >,
х(р)) необходимо их, во-первых, подверг
6.
f(x< 1>,
... ,
нуть процедуре ред-уцировани.я, т. е. отобрать по определенной методи
ке из исходного (априорного) набора более узкий по составу апостери
орный набор (в целях исключения эффекта мультиколлинеарности), и,
120
Выводы
во-вторых, с помощью соответствующих преобразований (см.
(2.6))
(2.4)-
произвести унификацию их измерительных шкал так, чтобы все
они измерялись в N-балльной шкале (выбор значения
N -
в компетен
ции исследователя), в которой нуль соответствует наихудшей ситуации,
а
N -
наилучшей (см. п.
2.3.2).
Глава
3
Байесовский подход
в эконометрическом анализе
Данная глава посвящена так называемому бо:йесовскому подходу в эко
нометрическом анализе, основанному на субъективно-вероятностном
способе операционализации принципа максимального использования
(наряду с исходными статистическими данными) априорной информа
ции об иссле,цуемом процессе.
Байесовские методы широко распространены в теории и практи
ке эконометрического анализа и являются обязательной составной ча
стью современных учебных программ магистерского уровня по эко
нометрике в ве,цущих университетах мира. Особенно заметные пре
имущества (по сравнению с классическими методами) с точки зрения
точности
получаемых
статистических
выводов
они
имеют
в
услови
ях о т н о с и т е л ь н о м ал ы х выборок, что весьма характерно для
эконометрического моделирования.
3.1.
Философия и общая логическая схема
байесовского подхода
Пусть в описании рассматриваемой эконометрической модели
(зако
на распределения анализируемой случайной величины, функции ре
грессии, временного ряда, системы одновременных уравнений и т. п.)
участвует s-мерный параметр е
= (81, 82, ... '8s)'
и нашей задачей
является ПОС_!I>Оение наилучшей, в определенном смысле, статистиче
ской оценки е этого параметра по имеющимся k-мерным наблюдениям
( xi(1) , xi(2) , ... , xi(k) )' , i.
Xi
1, 2, ... , n. Как и ранее, верхний индекс
=
=
~штрих» здесь и в дальнейшем означает операцию транспонирования
Гл.
122
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
вектора или матрицы, прописн'Ьl.Ми буквами будут обозначаться век
торн'Ьlе величины, а стрО'ЧН'Ые буквы будут использоваться для обо
значения одномерн'Ых (возможных или наблюденных) значений анали
зируемых случайных величин.
Байесовский подход является одним из возможных способов фор
мализации и операционализации тезиса, в справедливости которого нет
видимых причин сомневаться: степень нашей разумной уверенности
в некотором утверждении (касающемся, например, оценки неизвест
ного 'Численного зна'Чения интересующего нас параметра) возрастает
и корректируется по мере пополнения имеющейся у нас информации
относительно исслед-уемого явления. Могут быть различные формы
интерпретации и подтверждения этого тезиса, в том числе не имеющие
отношения к байесовскому подходу. Одна из них выражена, например,
в свойстве состоятельности оценки
больше объем выборки
en,
n,
.......
0n
неизвестного параметра
0:
чем
на основании которой мы строим свою оцен
ку
тем большей информацией об этом параметре мы располагаем
и тем ближе (в смысле сходимости en к е по вероятности) к истине
наше заключение.
Специфика именно байесовского способа операционализации этого
тезиса основана на двух положениях.
1)
Во-первых, «степень нашей разумной уверенности» в справед
ливости некоторого утверждения 'Численно в'Ыражается в виде веро
ятности. Это означает, что вероятность в байесовском подходе выхо
дит за рамки ее интерпретации в терминах условий статистического ан
самбля (см. п. В.2.1 в [Айвазян, Мхитарян
(2001))),
но относится к од
ной из категорий суб'6ективной школы теории вероятностей.
2)
Во-вторых, статистик при принятии решения использует в ка
честве исходной информации одновременно информацию двух типов:
априорную и содержащуюся в исходных статисти'Ческих данных (см.
п. В.3.2 в [Айвазян, Мхитарян
(2001))).
При этом априорная информа
ция предоставлена ему в виде некоторого априорного распределения ве
роятностей анализируемого неизвестного параметра, которое описы
вает степень его уверенности в том, что этот параметр примет то или
иное значение, еще до на'ЧаЛа сбора исходных статисти'Ческих данных.
По мере же поступления исходных статистических данных статистик
или эконометрист уточняет (пересчитывает) это распределение, пере
ходя от априорного распределения к апостериорному, используя для
этого известную формулу Байеса
P{AilB}
= NP{Ai} · P{BIAi}
Е
j=l
P{BIA;}. Р{А;}
(3.1)
3.1.
ФИЛОСОФИЯ И ЛОГИЧЕСКАЯ СХЕМА БАЙЕСОВСКОГО ПОДХОДА
123
которая определяет правило вычисления условной вероятности события
Ai
(при условии, что событие В уже имело место) по безусловной веро
ятности события
Ai
и условным вероятностям
При этом предполагается, что А1, А2,
событий, а событие В
-
... , AN
P{BIAj}, j
= 1, 2, ... , N.
образуют полную систему
ненулевой вероятности (т.е. Р{В} >О).
Общая логическая схема байесовского метода оценивания
значений параметров представлена на рис.
Априорные
сведения
о параметрее:
априорное
---
3.1.
Исходные
Вычисление
статиС"IИЧеские
функции
правдоподобия
данные
х.,х2····•хп
цх.
,...,хп 10)
распределение
р(Е>)
Вычисление
Закmочение
апостериорного
о значении
распределения
параме~ра е
параме~ра е
точечная или
р(01Х1, ... ,Хп)
:
икrервальная
оценка
Рис.
3.1.
Общая логическая схема байесовского подхода в статистическом
оценивании
Рассмотрим реализацию схемы байесовского оценивания неизвест
ного параметра.
Априорные сведения о параметре
0
основаны на предыстории
функционирования анализируемого процесса (если таковая имеется) и
на профессиональных теоретических соображениях о его сущности, спе
цифике, особенностях и т. п. В конечном итоге эти априорные сведения
должны быть представлены в виде функции р( е)' задающей априорное
распределение параметра и интерпретируемой как вероятность того,
что параметр примет значение, равное
0,
если параметр дискретен, и
как функция плотности распределения в точке
0,
если параметр непре
рывен по своей природе.
Исходные статистические данные Х1, Х2,
в соответствии с законом распределения
... , Xn порождаются
вероятностей /(Xl0), где под
Гл.
124
f(Xl0)
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
понимается значение функции плотности наблюдаемой случай
ной величины~ = (~(1), ~( 2 ), ... , ~(k))' в точке Х, если ~ непрерывна, или
вероятность Р{~ = Xl0}, если~ дискретна (при условии, что значение
неизвестного параметра равно
0).
По умолчанию предполагается, что
наблюдения
(3.2)
при фиксированном
являются статистически взаимонезависимыми,
0
т. е. образуют слу'Чайную выборку из анализируемой генеральной со
вокупности. Так что, получая исходные статистические данные
(3.2),
мы к имеющейся априорной информации о параметре (в виде функции
р( 0)) присоединяем соответствующую выборочную (эмnири'Ческую) ин
формацию.
Соответственно
функция
(условная, при данном
правдоподобия
имеющихся наблюдений
0)
L(X1, ... ,Xnl0)
(3.2) определится
(с учетом их взаимонезависимости) соотношением
Вычисление апостериорного распределения
осуществляется с помощью формулы Байеса
(3.1)
p(8IX1, ... , Хп)
(или ее непрерывно
го аналога), в которой роль события
Ai играет событие, заключающееся
в том, что значение оцениваемого параметра равно 0, а роль условия
В - событие, заключающееся в том, что значения n наблюдений, произ
веденных в анализируемой генеральной совокупности, зафиксированы
на уровнях Х1, Х2,
... , Xn.
-(el
Р
Соответственно имеем:
)
Xi, ... ,Xn
=
p(8)L(X1, ... , Xnl0)
f L(X1, ... ,Xnl8) ·p(0)de·
Построение байесовских точечных и
(3.4)
интервальных оце
нок основано на использовании знания апостериорного распределения
p(8IX1, ... , Xn), задаваемого соотношением (3.4). В частности, в каче
стве байесовских точечных оценок 0<6 > используют среднее или модаль
ное значение этого распределения, т. е.:
.-(б) -е(ср)
.-(б)
емод
E(8IX1, ... , Хп) - / 0p(8IX1,
... , Хп)d0,
-
-
(3.5)
- argmaxp(8IX1, ... ,Хп)·
е
Отметим, что для определения общего вида апостериорной плот
ности
p(8IX1, ... , Xn) нам достаточно знать только числитель правой
части (3.4), так как знаменатель этого выражения играет роль нор
мирующего множителя и от 0 не зависит (это существенно упрощает
процесс практического построения оценок е~~ и е~Jд)·
3.2.
125
АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
Отметим также ОДНО важное оптимальное свойство оценки е~~.
Пусть е(Х1, ... ,Хп) - любая оценка параметра 0. Оказывается, если
качество любой оценки е(Х1, ... , Хп) измерять так называемым апо
стериорным ба:йесовским риском
R<6>(X1, ... , Хп) = Е{(е(Х1, ... , Хп) - 0) 2 IX1, ... , Хп} =
=
! (е(Х1,
или его средним (усреднение
-
... 'Xn) - 0) 2.P(0IX1, ... 'Xn)de
по всем возможным выборкам
(3.2))
значением Щ~, то байесовская оценка (3.5) является наилучшей и в
том и в другом смысле.
Для
построения
параметра
0
p(0IX1, ... Хп)
байесовского
необходимо
доверите.л:ьного
вычислить
по
формуле
интервала
(3.4)
для
функцию
апостериорного закона распределения параметра
а
1
100 "";Ро
0,
затем по заданной доверительной вероятности Ро определить
и 100 1 -2Р0 %-ные точки этого закона, которые и дают соответственно
левый и правый концы искомой интервальной оценки.
Заметим, что байесовский способ оценивания может давать весьма
ощутимый выигрыш в точности при
ограниченнuх объемах выборок.
В процессе же неограниченного роста объема выборки п оба подхода
будут давать, в силу их состоятельности, все более похожие результаты.
«'Узкие места~ или три главных вопроса, возникающих при
практической реализации байесовского подхода:
i)
как выбрать общий вид (т. е. параметрическое семейство {р (0;
D)})
ii)
априорного распределения оцениваемого параметра?
как подобрать численные значения
Do
параметров
D,
определя
ющие конкретный вид априорного распределения при уже сде
ланном выборе общего вида р (0;
iii)
D)?
как преодолеваются трудности реализации формулы
вычислении апостериорного распределения
3.2.
(3.4)
р (0IX1, ... , Xn)?
при
Априорные распределения, сопряженные
с наблюдаемой генеральной совокупностью
(определение и условие существования)
В решении сформулированных выше трех главных вопросов практиче
ской реализации байесовского подхода существенную роль играют рас
пределения, сопряженные с наблюдаемой генеральной совокупностью
Гл.
126
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
(или, что то же, распределения, сопряженные с функцией правдоподо
бия
L(X1, ... Xnl8)).
Определение
3.1.
Семейство априорн:ых распределений
G =
{р(8; D)} назwваетс.я соnря:нсен.н.ым по отношению к наблюда
емой генерал:ьной совокупности
/(Xl0) (или по отношению к функ
ции правдоподобия L(X1, ... Xnl0)), если и апостериорное распределе
ние p(8IX1, ... , Хп), вwчисленное по формуле (3.4), снова принадле
жит этому же семейству G.
Другими
словами,
L(X1, ... Xnl0),
семейство
распределений
G
сопряжено
если оно замкнуто относительно операции
(3.4)
с
пере
счета априорного распределения в апостериорное.
Таким образом, использование в качестве априорных законов рас
пределения вероятностей (з.р.в.) сопряженных по отношению к
ностей ~расшивает~ узкое место
(iii):
L
плот
поскольку общий вид апостериор
ного з. р.в. в этом случае известен, остается лишь уметь пересчитывать
значения его параметров
D
при переходе от априорного распределения
к апостериорному.
Как мы увидим позже (см. ниже, п.
3.3),
использование сопряжен
ных з.р.в. в качестве априорных оказывается в широком классе случаев
вполне естественным и оправданным, что позволяет получить ответ и
на вопрос
(i).
Но всегда ли существует сопрЮ1Сенное по отношению к заданной
функции
L(X1, Х2, ... Xnl0) распределение,
и если оно существует, то
как его найти?
Условие существования сопряженного семейства априор
ных распределений: если функция правдоподобия
L(X1, ... Xnl0)
представима в форме
L(X1, ... Xnl0) = v(T1 (Х1, ... Хп), ... , Tm(X1, ... Хп); 0) х
х ф(Х1, ... Хп),
где
Tj(X1, ... Хп)
(3.6)
(j = 1, 2, ... , m) и ф(Х1, ... Хп) - некоторые функ
... , Хп, не зависящие от параметров 0, то суще
ции от наблюдений Х1,
G = {р(0; D)}
ное с L(X1, ... , Xnl0) 1 .
ствует семейство
1 Функции
априорных распределений, сопряжен
Т;(Х1, ... ,Xn), участвующие в представлении (3.6) (если таковое суще
ствует), называются досmаточн~u cmamucmuкaмu в задаче статистического оценива
0 = (81, 82, ... , 8в )'. Размерность m векторной достаточной статистики
= (T1(X1, ... ,Xn), ... ,Trn(X1, ... ,Xn)) конечна при n-+ оо и зависит от
ния параметров
T(X1, ... ,Xn)
специфики функции
L
и размерности
s
оцениваемого параметра
0.
Достаточные статисти
ки играют важную роль в теории и приложениях математической статистики. В частности,
они используются в задаче построения наилучших несмещенных оценок в следующей схеме:
3.2.
127
АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
Проверка условия существования сопряженного априорного рас
пределения на ряде примеров.
Пр им ер
3.1.
Анализируемая (наблюдаемая) генеральная сово
купность нормальна с неизвестным значением среднего Е~
= 8
и
из
вестной дисперсией D~ = и~ (будем обозначать в дальнейшем подоб
ный факт в форме ~ Е Nq(8; и~), где ~ - наблюдаемая случайная
величина, а нижний индекс при q определяет ее размерность; так что,
если~= (~(l), ... , ~(k))' - вектор, то~ Е Nk(0; Е~) означает, что много
мерная случайная величина размерности k распределена нормально с
вектором средних значений
0 = (81, 82, ... , 8k)'
и ковариационной мат
рицей Е~). В данном примере
(3.7)
Мы видим, что роль функции
сти
v(T(x1 ... Xn); 8)
из правой ча
играет первый сомножитель из правой части (3.7), причем
n
т = 1, Т(х1, ... , Xn) = х = ~ Е Xi (достаточная статистика), а следуi=l
ющие за v(x; 8) сомножители правой части (3.7) от 8 не зависят. Сле-
(3.6)
довательно, семейство априорных, сопря:ж:енных с
L
распределений су
ществует.
Пр им ер 3.2. ~ Е N1 (81; J-2 ) , где и среднее значение 81 = Е~, и
82 - параметр точности ( 82 = J~) являются неизвестными (т. е. 0 =
(81, 82)). Воспользовавшись тем же представлением (3.7) для
функции правдоподобия L, убеждаемся, что Т1(х1, ... ,xn) =
х,
n
Т2(х1, ... ,xn) = s 2 = ~ E(xi-x) 2 (достаточные статистики), так что в
данном случае т
шению к
L)
= 2
i=l
и семейство априорных, сопряженных (по отно-
распределений существует.
П р и ме р
3.3.
Анализируется биномиально распределенная слу
чайная величина ~в(М)
Бернулли, где
пусть
0-
8 -
-
число «успехов~ в серии из М испытаний
неизвестная вероятность «успеха~ в одном таком
некоторая несмещенная оценка параметров 0 и tr Ее< оо; тогда 01 = Е(01Т)
0, причем tr Ев 1 ~ tr Ев (под Ев понимаr-
будет снова несмещенной оценкой параметров
ется ковариационная матрица вектора
0, а под trE -
след матрицы Е).
Гл.
128
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
испытании, а М
-
общее число (известное) испытаний Бернулли в рас
сматриваемой серии, так что
х =о,
где
1, 2, ...
число сочетаний из М элементов по х.
Cf.t -
Наблюдаются
n
таких серий. Тогда
i=l
где Xi -
'м,
i=l
число ~успехов» в i-й серии.
Поэтому в рамках общего представления (3.6) в данном случае имеn
ем: т = 1, Т(х1, ... , Xn) = Е Xi - достаточная статистика, что под
i=l
тверждает существование априорного, сопряженного с
параметра
L
распределения
8.
П р и м ер
3.4. Анализируется отрицательно биномиа.л.ьно распре
деленная случайная величина {( 8; К) - число испытаний в схеме Бер
нулли до К-го появления интересующего нас события, где 8 - неиз
вестная вероятность появления этого события при одном испытании, а
К
некоторое заданное целое положительное число. Тогда
-
х =к, к+
1, ... '
так что
L( X1, ... ,Xn 18) -_
n
n
n
:Е Xi-Kn
п cK-18K(1-8)xi-K
. п сК-1
Xi-1
-_ 8Kn(1-8)i=l
Xi-1"
i=l
i=l
Поэтому в рамках общего представления (3.б) в данном случае имеем:
n
т =
1,
Т(х1,
... ,xn) =
Е Xi -
достаточная статистика, что подтвер
i=l
ждает существование априорного, соnр.яж;енного с
раметра
3.5.
В данном примере речь идет об оценивании пара
8 пуассоновского
з.р.в., т. е.
8Х
f(xl8)
так что
распределения па-
8.
П р и м ер
метра
L
= Р{{ = xl8} = - 1е- 8 ,
х.
х =о,
1,2, ... '
Сравнивая с общим представлением
т
= 1,
Т(х1,
=
... ,xn)
(3.6),
в данном случае имеем:
n
Е Xi -
достаточная статистика, что подтвер
i=l
ждает существование априорного, сопря:ж:енного с
раметра
129
АПРИОРНЫЕ РАСПРЕДЕЛЕНИЯ
3.2.
L
распределения па-
8.
Пр им ер
Анализируется экспоненциально распределенная
3.6.
(без сдвига) случайная величина с неизвестным значением параметра
масштаба
8,
т. е.
при
х~О
при
х <о.
Соответственно:
L( х1, ... , Xn 1 8) =
-(t Xi)·8
{8ne
0
i=l
В рамках общего представления
при
при
Xi ~
Xi
0
< 0.
в данном случае имеем:
(3.6)
m= 1,
n
Т(х1,
... , Xn)= Е
достаточная статистика, что подтверждает cyщe
Xi -
i=l
ствование априорного, сопря:ж:енного с
Пр им ер
3.7.
L
распределения параметра
8.
Анализируется случайная величина, распределен
ная равномерно на отрезке [О; 8] при неизвестном значении параметра
8, т. е.
f(xl8) =
Н
при
О~х~8
при
х
(j.
[О; 8].
Соответственно:
Следовательно,
т
=
1;
Т(х1,
в
... , Xn)
рамках
=
общего
Xma.x(n) -
представления
имеем:
достаточная статистика, что под
тверждает существование априорного, сопряженного с
параметра
(3.6)
L
распределения
8.
П р и мер
3.8.
Анализируется модель распределения Парето с
неизвестным значением параметра формы
8х8
f (xl8) =
{
~в.fi
8,
т. е.
при
х ~хо
при
х <хо,
где пороговое значение хо считается заданным.
Гл.
130
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
Соответственно:
1
где
х1, х2,
(.ft xi) п - среднее геометрическое значение наблюдений
=
9n
i=l
анализируемой случайной величины. Следовательно, об-
... , Xn
ращаясь к
{3.6),
имеем т =
1,
Т(х1 ... Xn) = 9n -
достаточная стати
стика, что подтверждает существование априорного, соnря:нсенного с
распределения параметра
П р и м ер
3.9.
L
(}.
Рассмотрим классическую линейную модель мно
жественной регрессии (КЛММР, см., например, [Айвазян
{2010)), п. 4.1,
4.2) с нормальными, в среднем нулевыми, взаимонезависимыми и гомос
кедастичными остатками е1, е2, ... , E'n :
У=Х0+е,
{3.8)
где
1
-
(1)
Xn
(k)
Xn
наблюденные значения, соответственно, зависимой (у) и объясняю-
(х -- {1 ,х (1) , ... ,х (k))') переменных, е -- ( e1,e2, ... ,en )' - случайные регрессионные остатки, а 0 = (Оо, 01, ... , Ok)' и h = (Dei)- 1 щих
неизвестные значения параметров модели. Напомним, что значения Х
в соответствии с требованиями КЛММР являются неслучайными и что
упомянутые выше свойства регрессионных остатков формулируются в
форме условий
е Е Nn (О; ~ In) ,
где
In -
{3.9)
единичная матрица размерности
остатков Ее
=
i
In, а параметр h =
n, ковариационная матрица
(Dei)- 1 обычно называют пара
метром точности.
С учетом
{3.8)"-'{3.9)
функция правдоподобия наблюдений (Х, У)
может быть представлена в форме:
n
L(X Yl0· h)
'
'
=
h2
{27r)~
е-~(У-Х0)'(У-Х0)_
{3.10)
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
РАСПРЕДЕЛЕНИЙ
131
Но (У-Х0)'(У-Х0) = (У-Хе+хе-хе)'(У-Хе+хе-хе) =
= [(У-Хе)+Х(е-0)]'[(У-Хе)+Х(е-0)], где е = (Х'Х)- 1 Х'У оценка метода наименьших квадратов параметров регрессии 0.
Поэтому
(У-Х0)'(У-Х0) = (У-Хе)'(У-Хе)+(е-0)'Х'Х(е-0), (3.11)
так как (У - Хе)'Х(е - 0) = [Х(е - 0)]'(У - Хе) = (У'Х
-е'Х'Х)(е - 0) = [У'Х - ((Х'х)- 1 Х'У)' . (Х'Х)](е - 0) = [У'Х-У'Х(Х'х)-1(Х'Х)](е - 0) =о.
Возвращаясь к (3.10) и выражая в (3.11) сумму квадратов МНК
оцененных остатков (У - хе)'(У - хе) через оценку остаточной дис
персии О- 2 =
(У - хе)'(У - хе), имеем:
n-k-1
(3.12)
Отметим, что и 2 и е в конечном счете определяются по У'У,
Х'У и Х'Х, так что и в данном случае функция правдоподобия L пред
ставима в форме (3.6), в которой набор достаточных статистик Т(Х; У)
конечен (при n --+ оо) и определяется статистиками У'У и Х'У. Сле
довательно, существует априорное распределение параметров 0 и h,
сопряженное с L.
3.3.
Генезис априорных сопряженных
распределений
Оказывается, для широкого класса наблюдаемых генеральных сово
купностей, функции правдоподобия которых допускают представление
(3.6) (т.е. эти генеральные совокупности располагают сопряженным с
L априорным распределением своих параметров), справедливо следую
щее
утверждение о генезисе сопряженных априорных распре
делений:
если в байесовском подходе стартовать с априорного 'fЮСпределе
ния, не несущего никакой дополнительной по отношению к име
ющимся статистическим данн'ЫМ полезной информации об ои,е
ниваем-wх параметрах (такие fХLСпределения мы будем называть
«'fЮСпределениями, отра:нсающими скудость априорн-wх знаний»,
см. ни:нсе п.
(3.4)
3.3.1),
то первый ::нее переход от нее по формуле
к апостериорному 'fЮСпределению приведет нас к семейству
Гл.
132
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
распределений, сопряж;ен.н.ому с н.аблюдаемой генеральной сово
купн.остью2.
Именно этот прием поиска априорного распределения, сопряженно
го с анализируемой функцией правдоподобия, представимой в формуле
и предлагается использовать в байесовском подходе.
(3.6),
Априорные распределения, отражающие
3.3.1.
~скудость априорных знаний»
( САЗ-априорные
распределения)
Для математической формализации ситуаций, в которых исследователь
не располагает никакой полезной априорной информацией о значе
ниях оцениваемого параметра, Джеффрис (см.
[Jeffreys (1957)]) пред
ложил следующие два правила выбора соответствующего априорного
распределения:
(а) если
оцениваемый
(теоретически)
скалярный
принимать
параметр
значения
на
может
8
конечном
интерва
ле
[8min, 8max]
или н.а бесконечном интервале от -оо до +оо,
то
априорную
функцию
плотности
р( 8)
следует
считать
постоянной на соответствующем интервале;
(б) если же из смысла оцениваемого параметра вытекает, что он.
может принимать любые положительные значения, то следу
ет считать постоянной на всей числовой прямой
( -оо;
+оо)
функцию плотности распределения логарифма от значения па
раметра, т. е.
p(ln 8)
= const при 8 Е
(О; +оо).
Будем называть такие априорные распределения «распределени
ями, отражающими скудость априорных зн.ан.ий», или коротко
-
«САЗ-априорными распределениями». Соответственно их одно
мерные функции плотности будем обозначать РСАз(8), а многомер
ные
- РСАз(0).
Тот факт, что для определенных таким образом на бесконечной
прямой (полупрямой) априорных распределений нарушается извест
ное правило нормировки функции плотности вероятности (поскольку
при этом
JРСАэ(8)
2 Строгое
d8 =1 1, но
JРСАэ(8)
d8
=
оо, где интегрирование
доказательство этого утверждения дпя однопараметрическоrо экспо
ненциального семейства наблюдаемых генеральных совокупностей см. в
{2006),
п.
5.1.5).
[Ghosh et all
Однако справедпивость этого утверждения подтверждается (непо
средственной проверкой) и дпя весьма широкого класса набJIЮдаемых генеральных
совокупностей, не принадлежащих экспоненциальному семейству.
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
проводится по всем возможным значениям
РАСПРЕДЕЛЕНИЙ
8),
133
не доставляет «техниче
ских неудобств»: во-первых, пересчет такой «несобственной» априор
ной функции плотности РСАз(8) в апостериорную по формуле
(3.4) дает
уже обычную (собственную) функцию плотности .РсАз(8IХ1, ... , Xn), а
во-вторых, при любых сколь угодно больших значениях С п.л.отность
РСАЗ
(8) = { 2~
при 8 Е [-С; +С),
О
при
8 f/.
[-С; +С)
с
= J р( 8) ln р( 8)d8
минимизирует энтропийную меру Н
ин.форма-
-с
ции, содержащейся в плотности р( 8) относите.л.ьно парамет'JХL
(см., например, [Зельнер
(1980),
с.
59)).
8
Последнее обстоятельство под
тверждает обоснованность использования равномерных распределений
РСАз(8)
= const или PcAз(In8) = const в качестве априорных рас
пределений, отражающих скудость априорных знаний (или - САЗ
априорных 'JХLСпреде.л.ений).
3 а м е ч а н и е 1. Общий вид апостериорного распределения
p(8IX1, ... , Xn), вычисляемого по формуле (3.4), определяется с точно
стью до нормирующей константы лишь числителем правой части этой
формулы.
Поэтому в дальнейшем при анализе 'JХLвенств, Сп'JХLвед.л.и
вых с точностью до нормирующей константы, мы будем использо
вать знак
rv.
Следуя этому правилу, сама формула
(3.4)
может быть
представлена в виде:
(3.4')
-
3 а м е ч а н и е 2. При анализе многомерн'ЫХ параметров 0 =
(81, ... , 88 )' априорные, в том числе САЗ-априорные, распределе
ния обычно предполагают статистическую независимость компонент
81, ... 88 ,
т. е.
р(0)
= р(81) · р(82) · ... · p(8s)·
(3.13)
И, наконец, в заключение этого пункта определим вид априорной плот
ности р(8) для случая
p(ln8)
= const, т. е.
в ситуации, когда параметр
8
может принимать любые, но только положительные значения.
Пусть
Fe (у)
= Р{8 <
у}
-
функция распределения параметра
Тогда
Fe(y) =
Р{8 <у}=
P{ln8 < lny} = F1ne(lny).
Соответственно, функция плотности распределения
1 (
J8
У
)
= дFе(у) = дF1ne(Iny). д(Iny) = /.
ду
д(In у)
ду
Jln8
8 будет
(ln ) . _!_
У
У
rv
_!_
У,
8.
Гл.
134
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
так как по условию /1nв(lny)
= p(ln8) = const.
Так что в сокращенной
записи имеем для положительнозначных параметров
8
1
РСАз(8) "' В'
а для параметров
(3.14а)
8 с возможными значениями, заполняющими всю чис
ловую прямую,
РсАз(8)
3.3.2.
= const.
(3.14б)
Общий подход к выводУ семейства априорных
распределений, сопряженных с наблюдаемой
генеральной совокупностью
Общий подход к выводу семейства априорных распределений, сопря
женных с наблюдаемой генеральной совокупностью, основан на утвер
ждении об их генезисе, сформулированном в начале п.
3.3.
Из этого
утверждения вытекает, в частности, следующая общая схема определе
ния такого семейства.
Шаг
1:
проверка условия
(3.6)
существования семейства априорных
распределений, сопряженных с функцией правдоподобия
L
для наблю
даемой генеральной совокупности.
Шаг
(3.6)
2:
если функция правдоподобия
L
допускает представление
(т. е. если существует семейство сопряженных априорных распре
делений р(0;
D)),
то осуществляется вывод САЗ-апостериорного рас
пределения .РсАз(0IХ1, ... , Xn) по формуле
РСАз(01Х1, ... , Xn)
(3.4'), т. е.
,..., РсАз(0) · L(X1, ... , Xnl0).
Правая часть соотношения
(3.15)
(3.15)
и будет определять общий вид
семейства априорных распределений, сопряженных с наблюдаемой ге
неральной совокупностью, характеризуемой функцией правдоподобия
L(X1, Х2, ... , Xnl0).
Продемонстрируем реализацию этой общей схемы на рассмотрен
ных выше примерах
шаг
3.1,...,3.9.
Очевидно нам остается реализовать лишь
2 из этой схемы, так как шаг 1 уже был реализован выше (см.
п.3.2).
Пр им ер 3.1 (продолжение). { Е Ni(8; иЮ, где 8 = Е{ - оценива
емый (неизвестный) параметр, а и~ = D{ - известное (заданное) зна
чение дисперсии наблюдаемой случайной величины. Ранее было уста
новлено (см. выше, пример
3.1,
формулу
(3.7)),
что в этом случае суще
ствует семейство сопряженных априорных распределений параметра
(}.
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
Определим РСАз(8)
,....,
е
-&<х-8) 2
2 0'о
=
const
РАСПРЕДЕЛЕНИЙ
и с учетом того, что
(см. выше, формулу
135
L(x1, ... , xnl8) ,....,
имеем:
(3.7)),
Но правая часть этого соотношения представляет собой (с точно
стью до нормирующего множителя, не зависящего от
8)
плотность нор
мального распределения со средним значением х и дисперсией и~/п.
Следовательно,
семейство
сопряженных
неизвестного среднего значения
априорных
8 нормально
распределений
распределенной генераль
ной совокупности (при известной дисперсии и~
=
D~) само принадле
жит классу норма.л.ьн-ых законов распределения.
Пр им ер 3.2 (продолжение). ~ Е Ni (8; k), где и среднее значе
ние 8 и параметр точности h = 1/D~ являются неизвестными (т. е.
0 = (8, h)). Ранее было установлено (см. выше, пример 3.2), что в
этом случае существует семейство двумерных сопряженных априор
ных распределений параметра е
РсАз(h) ,....,
= (8' h).
k и с учетом (3.13) и того, что
Определим РСАЗ (8)
= const и
(3.16)
имеем:
РсАз(8, hlx1, ... , Xn)
,....,
,...., РСАз(8) · РсАз(h) · L(x1, ... , xnl8, h) ,....,
!
_nh(e--)2
(пh) 2 е 2
х
Но правая часть
•h
(3.17)
n-1-1
2
е
-(! .Ё (xi-x)
2)
1=1
h
(3.17)
•
представляет собой (с точностью до норми
рующего множителя, не зависящего от
8 и h) n.л.отностъ двумерного
гамма-нормального распределения (см. Приложение П2.2а)
(3.18)
с параметрами Ло = п, 8° = х, а
0
= (8, h),
где
и
n
! Е (xi -
х) 2 .
i=l
Следовательно, семейство сопряженных априорных распределений
двумерного параметра
= п2 1
/3 =
8 и h, соответственно, среднее
значение и параметр точности наблюдаемой нормальной генеральной
136
Гл.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
совокупности, принадлежит классу двумерных гамма-нормальных рас
пределений
(3.18).
Пр им ер
(продолжение). Наблюдаемая случайная величина
3.3
~в(М) подчиняется биномиальному з.р.в. с неизвестным значением ве
роятности «успеха»
8
и заданным числом М испытаний Бернулли.
Ранее было установлено (см. выше, пример
что существует
3.3),
семейство сопряженных априорных распределений параметра
Определим РСАз(8)
n
Ежi
L(x1, ... , Xnl8) ,...., 8i=l
=
1
· (1 - 8)
для
Е
8
(О;
1)
и с учетом того, что
n
nM-E Жi
i=l
, имеем:
n
Е Жi
,...., 8i=l
Но правая часть соотношения
8.
(3.19)
(3.19)
n
. (1 - 8)
nM-E Жi
i=l
.
представляет собой (с точностью
до нормирующего множителя, не зависящего от
плотность бета
8)
распределения
Р
с параметрами а
правой части
n
Е Xi
=
(3.20)
(8 ) = Г(а + Ь) 8а-1(1- 8 )ь-1
Г(а) · Г(Ь)
+1
и Ь
= nM -
n
Е Xi
(3.20)
+1
(участвующая в
i=l
i=l
в выражении нормирующего множителя функция
Г(z) это известная гамма-функция Эйлера, т. е. Г(z)
00
= J xz-l
е-жdх).
о
Следовательно, семейство сопряженных априорных распределений
параметра
8
(вероятности «успеха») наблюдаемой биномиально рас
пределенной генеральной совокупности принадлежит классу бета
rюспределений
Пр им ер
пример
3.4),
(3.20).
3.4
(продолжение). Ранее было установлено (см. выше,
что отрицательно биномиально распределенная случай
ная величина ~(8; К) имеет сопряженное априорное распределение па
раметра
8-
вероятности «успеха» в одном испытании Бернулли. Как
и в предыдущем примере, определяем РсАз(8)
= 1 (для 8 Е
(О;
1)).
То-
п
гда с учетом того, что
пример
3.4),
Eжi-Kn
L(x1, ... , Xnl8) ,...., 8Kn(1 - 8)i=l
(см. выше,
имеем:
.Рслз(8lх1, ... , Xn)
,...., Рслз(8) · L(x1, ... , xnl8) ,....,
(3.21)
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
Правая часть
РАСПРЕДЕЛЕНИЙ
137
представляет собой (с точностью до нормирующего
(3.21)
множителя, не зависящего от
с параметрами а = К n
8)
+1 и Ь =
плотность бета-распределения
n
Е Xi - К n
(3.20)
+ 1.
i=l
Так что семейство сопряженных априорных распределений пара-
метра
8
(вероятности «успеха») наблюдаемой отрицательно биномиаль
но распределенной случайной величины ~ (8; К) принадле:жит классу
бета-распределений
Пр им ер
пример
3.5),
(3.20).
(продолжение). Ранее было установлено (см. выше,
3.5
что параметр
пуассоновского з.р.в. имеет сопряженное
8
априорное распределение. Из смысла параметра
8
следует, что он мо
жет принимать только положительные значения, поэтому определяем
n
РсАз(8),....,
LЖi
j. Тогда с учетом того, что L(x1, ... , Xnl8),...., 8i=l
выше, пример
•
e-nB (см.
имеем:
3.5),
(3.22)
Правая часть
(3.22)
представляет собой (с точностью до нормирующего
множителя, не зависящего от
р( 8 ) =
=
с параметрами о
8)
плотность гамма-распределения
f30l • 80t-1 е-138
Г(о)
n
Е Xi и
{3
'
8>0
(3.23)
= n.
i=l
Следовательно, семейство сопряженных априорных распределений
параметра
8
наблюдаемой генеральной совокупности принадле:жит
классу гамма-распределений
Пр им ер
пример
3.6),
3.6
(3.23).
(продолжение). Ранее было установлено (см. выше,
что параметр масштаба
8
экспоненциального распределе
8 > О,
Тогда с учетом того, что L(x1, ... ,xnl8) =
ния имеет сопряженное априорное распределение. Поскольку
определяем РсАз(8) ,....,
= 8n · е
-(Ё Жi)(J
i=l
j.
(см. выше, пример
_
РСАз(8lх1, ... 'Xn)
Правая часть
имеем:
n-l
,...., РСАз(8). L(x1, ... 'Xnl8) ,...., 8
(3.24)
= n
и
.е
-
(
n
.L
Жi )
t=l
8
•
(3.24)
определяет (с точностью до нормирующего
множителя, не зависящего от
с параметрами о
3.6),
{3
8) плотность гамма-распределения (3.23)
=
n
Е Xi· Так что семейство сопряженных
i=l
Гл.
138
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
априорных распределений параметра масштаба
8 экспоненциально рас
пределенной генеральной совокупности принадлежит классу гамма
распределений
(3.23).
П ри мер
3. 7),
3. 7
(продолжение). Как мы видели (см. выше, пример
и при равномерно распределенной на отрезке [О; 8] случайной ве
личине неизвестный параметр
имеет сопряженное априорное рас
8
пределение. Поскольку параметр
8
может принимать любые положи
тельные значения, определяем РсАз(8) ,...., j. Тогда с учетом того, что
L(x1, ... ,xnl8) = (j}n (и Хтах(п) = Ш!1Х {xi} < 8), имеем
l~i~n
.Рслз(8lх1,
... , Xn) "' {
РСАз(8) · L(x1, ... ,xnl8)"' (j}n+l
при
О
8 ~ Xmax(n),
8 < Xmax(n).
при
Но правая часть соотношения
(3.25)
(3.25)
представляет собой (с точно
стью до нормирующего множителя, не зависящего от
8)
плотность
распределения Парето вида
Ot~-
p( 8) =
с параметром формы а
~
Xmax (n).
{ ;o'!/. f
1
при
8~
при
8
8min
(3.26)
< 8min
= n и некоторым параметром сдвига
8min ~
Следовательно, семейство сопряженных априорных распре
делений параметра
8
равномерно (на [О; 8]) распределенной случайной
величины принадлежит классу распределений Парето вида
Пр им ер
3.8
(3.26).
(продолжение). В данном примере речь идет о на
блюдаемой генеральной совокупности, подчиняющейся распределению
Парето с неизвестным значением параметра формы
8
и некоторым за
данным значением параметра сдвига хо (см. выше, пример
L(x1, ... , xnl8)
где
= 8n ( 9n
хо )
-n8
n
n · g~ ,...., 8 · е
3.8),
[nln ( .flD. )] .()
жо
так что
,
1
9n =
(.ft xi) п. Но тогда САЗ-апостериорная функция плотно
~=l
сти распределения параметра
Рслз(0)"'
8
будет иметь вид (с учетом того, что
j)
.Рслз(8lх1, ... , Xn) "'Рслз(8) · L(x1,
... , xnl8) "'
,...., 8n-1. е -[n1n(~)]·8.
(3.27)
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
Мы видим, что правая часть соотношения
РАСПРЕДЕЛЕНИЙ
(3.27)
139
определяет (с точ
ностью до нормирующего множителя, не зависящего от параметра
плотность гамма-распределения
(3.23)
с параметром о=
n
8)
и парамет-
ром /3 = n ln ( ~), так что сопряженные априорные распределения па
раметра формы
8 наблюдаемой Парето-распределенной генеральной со
вокупности принадлежат семейству гамма-распределений.
Пр им ер
3.9
(продолжение). Выше при рассмотрении нормаль
ной классической линейной модели множественной регрессии с неиз
вестными значениями коэффициентов регрессии
параметра точности h = ~ (где
параметров
80, 81, ... , 8k, h
и2
0
=
(80, 81, ... , 8k)' и
= Dc-i) мы убедились в том, что у
существуют сопряженные априорные рас
пределения. Определим теперь общий вид сопряженного априорного
распределения р(0;
h)
параметров е и
h.
С учетом «Замечания
выше) и положительных значений параметра
Используя полученное ранее выражение
доподобия
L(X; Yl0; h),
2 )h
-(n-lc-la
2
хе
х e-(n-~-1п2)h х
(см.
имеем:
(3.12)
для функции прав
имеем:
Рсаз(0; hlX; У),...., Рсаз(0;
хе
h
2»
h) · L(X; Yl0; h),....,
-А(0-0)'(Х'Х)(0-0)
2
1
n
h · h2 х
= hn-lc-l_l
2
х
(3.28)
h 1ci1 х е-~(0-0)'(Х'Х)(0-0).
Но правая часть соотношения
(3.28)
определяет (с точностью до
нормирующего множителя, не зависящего от
0 и h) так называемое
многомерное гамма-нормальное распределение с параметром сдвига е,
матрицей точности (Х'Х) и параметрами о= n-~- 1 и f3 = n-~- 1 u 2 (по
дробнее о многомерном гамма-нормальном распределении и его свой
ствах см. в Приложении П2.26). Напомним, что е = (Х'Х)- 1 Х'У это МНК-оценка параметров регрессии 0, а u2 = n-~-l (У - Хе)'х
х (У - хе) - оценка остаточной дисперсии и2 .
Таким образом, сопряженные априорные распределения парамет
ров
(0; h)
нормальной классической линейной множественной регрес
сии имеют общий вид
(3.29)
в котором конкретное задание векторного параметра сдвига
+1)
х
(k
+ 1) -
00, (k+
матрицы точности Ло и скалярных параметров о и
/3
Гл.
140
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
однозначно определяет априорный закон распределения параметров е
и
h (напомним, что k + 1 - это общее число объясняющих переменных,
включая свободный член, в анализируемой модели регрессии).
Очевидно, семейство многомерных гамма-нормальных распреде
лений
{3.29)
является многомерным обобщением двумерного гамма
нормального распределения
3.3.3.
(3.18).
Рекомендации по подбору конкретных значений
параметров в сопряженных априорных
распределениях
Использование, в качестве априорных, законов распределения вероят
ностей
(з. р.в.),
соnряж:енных с наблюдаемой генеральной совокупно
стью (в ситуациях, когда они существуют), позволяет нам определить
их общий вид, т. е. задает целое семейство априорных распределений
{р{0;
D)}.
Однако при реализации байесовского подхода мы должны
оперировать конкретн'Ы.М априорным распределением, что требует зна
ния числовых значений
Do
параметров
D,
от которых наш априорный
з.р.в. зависит. Как :же подбирать эти значения
Do
в ка:ждом конкрет
ном с.л,учае? Ниже описывается один из возможных подходов к реше
нию данной задачи.
В широком классе ситуаций можно исходить из того, что нам из
вестны априорные средние значения оцениваемого параметра
00
=
= Е0 = {Е81,Е82, ... ,Е88 )' и их среднеквадратические ошибки д1 =
= y'D81, д2 = y'D82, ... , Лs = ~- Тогда параметры априорного
распределения, как правило, могут быть определены методом момен
тов (в случае многомерного параметра
0 -
с учетом «Замечания
статистической независимости компонент вектора
пределении, см.
0
2»
о
в априорном рас
(3.13)).
Продемонстрируем реализацию этого подхода на рассмотренных
выше примерах.
1)
Определение параметров априорного гамма-распределе
ния (см. формулу
{3.23)
и примеры
например, [Айвазян, Мхитарян
и дисперсия
а и
f3
(D8)
3.5, 3.6, 3.8). Как
{2001)], п. 3.2.4) среднее
известно (см.,
значение (ЕВ)
гамма-распределения выражаются через параметры
этого распределения по формулам:
Е8=
а
-·
f3'
Подставляя в эти соотношения вместо Е8 и
заданные значения 80 и
д2 ,
D8,
соответственно,
получаем в качестве решений системы из
3.3.
ГЕНЕЗИС АПРИОРНЫХ СОПРЯЖЕННЫХ
двух уравнений (относительно а и
РАСПРЕДЕЛЕНИЙ
{3):
,.,_ 8о2 {3- 80
2)
Определение
ления (см. формулу
-
Д2'
u; -
(3.30)
д2·
параметров
(3.20)
141
априорного
и примеры
3.3 и 3.4).
бета-распреде
Используя выражения
для среднего и дисперсии бета-рапсределения (см., например, [Айвазян,
Мхитарян
(2001)),
п.
3.2.5)
и решая систему из двух уравнений
{ Е8 =
а:ь = 80
D 8 = (а+Ь) 2fа+ь+1) = Л 2
относительно а и Ь, получаем:
- 8~(1 - 80)
а-
д2
-
8
о
ь = ( 8~ (1 - 80) - 8 ) 1 - 80
Д2
3)
о
80
.
Определение параметров априорного распределения Па
рето (см. формулу
(3.26)
и пример
формы а и параметр сдвига
ям 80 = Е8 и
Мхитарян
д2
8min
В данном случае параметр
3.7).
определяются по заданным значени
= D8 из системы уравнений
(2001)),
п.
(см., например, [Айвазян,
3.1.9)
= ~ =80 '
{ Е8
a8~jn
D8
а-1
=
(a-l)(a-2)
Решение этой системы относительно а и
Д2
=
8min
(3.32)
·
дает:
a=l+~,
8min
4)
(3.32')
1
= -80 ·(а - 1).
а
Определение параметров двумерного гамма-нормаль
ного распределения (см. формулу
в примере
(3.18)
3.2).
Из свойств
двумерного гамма-нормального распределения следует (см. Приложе
ние П2.2а), что частное априорное распределение параметра
гамма-распределение с параметрами а и
{3.
заданными значениями ho
= Dh,
= Eh
двух уравнений относительно а и
и д~
{3:
Eh= -f3 =ho
а
2
есть
Поэтому, воспользовавшись
а
{
h
Dh = f32 = дh.
составляем систему из
Гл.
142
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
Получаем решение:
ho
{3= д2·
и
(3.33)
h
Для определения параметра Ло и параметра сдвига 8° восполь
зуемся
8
тем,
что
частное
априорное
распределение
параметра
сдвига
есть обобщенное распределение Стьюдента с 2а степенями свобо
ды, параметром сдвига
дения о
t ( 2al8o;
8 и параметром точности, равным Ло~ (св~
Ло~ )-распределении см. в Приложении П2.1а). Из
свойств этого распределения следует, что
Dt ( 2al8o;
и д~
Et ( 2al8o;
Ло~) =
80
и
Ло~) =>.:а· 2~~ 2 , так что при заданных значениях 80 = Е8
= D8 имеем:
• зна-чение парамет'JХL сдвига 8° в 'JХLсnределении (3.18) 'JХLвно 80 ;
Д~
•
=
>.:а · a~l' откуда Ло = Р · a~l
(напомним, что а и
5)
(3.34)
(J
{3
уже определены соотношениями
(3.33)).
Определение параметров многомерного гамма-нормаль
ного распределения (см. формулу
(3.29)
в примере
3.9).
Воспользу
емся свойствами многомерного гамма-нормлаьного распределения (см.
Приложение П2.2б). В соответствии с ними:
(i)
-частное 'JХLСпределение -числового сомножителя
h матрици то-ч
ности
hAo нормад:ьной части распределения (3.29) является
гамма-'JХLсnределением с параметрами а и {3;
(ii)
-частное распределение параметра е есть обобщенное (k+1)-мер
ное 'JХLсnределение Стьюдента с 2а -числом степеней свободи, па
раметром сдвига
-чаем его
00 и матрицей точности В
как t(2al0o; В)-распределение).
= ~ Ло
Свойство (i) позволяет (при заданных значениях ho
(ми обозна
= Eh и д~ =
= Dh) определить значения параметров а и {3 по той же формуле (3.33).
Свойство
(ii),
дополненное «Замечанием 2~ и правилами вычис
ления вектора средних значений и ковариационной матрицы
мерной случайной величины
t ( 2al0o;
00
и элементы матрицы Ло. Действительно:
Е0 =
Et ( 2al0o;
+ 1)-
~Ло) (см. Приложение П2.1б),
позволяет определить остальные параметры распределения
раметр сдвига
(k
~Ло) =
00
(задано!)
(3.29) -
па
3.4.
ПЕРЕСЧЕТ ЗНАЧЕНИЙ ПАРАМЕТРОВ
Ев= Et(2al0o;:0 лo) = 2 а2~ 2 ( ~Ло
д~
143
)-1
о
(3.35)
д~
д2
о
k
где ЛJ - заданные значения априорных дисперсий компонент вектора
j=0,1, ... ,k.
8=(80,81, ... ,8k),
Таким образом, векторный параметр сдвига в распределении
(3.29)
определяется заданным вектором априорных средних значений
80, а
диагональные элементы л~> (j =О, 1, ... , k) матрицы Ло определяются
из уравнений
по формулам:
(3.35)
(j) -
1
{3
Ло - д~. а-1'
(3.36)
3
где значения а и
3.4.
{3
определены соотношениями
(3.33).
Пересчет значений параметров при
переходе от априорного сопряженного
распределения к апостериорному
Поскольку по определению семейство сопряженных априорных распре
делений {р(0;
D)}
замкнуто относительно операции
(3.4)
пересчета
априорного распределения в апостериорное, то общий вид апостериор
ного распределения
p(0IX1, ... , Xn)
при использовании соnр.яжен:н:ых
априорных распределений нам известен, и нам лишь надо уметь пере
считывать параметры D(X1 , ••• , Xn) этого апостериорного распределе
ния по заданным параметрам Do априорного распределения и имею
щимся наблюдениям Х1, Х2, ... , Xn.
Обща.я схема такого пересчета следующая. Пусть {р(0; D)} - се
мейство априорных распределений, сопряженных с функцией прав
доподобия
L(x1, ... , xnl0) имеющихся у нас наблюдений (D
= (dl, ... , dq) - вектор параметров, от которых зависит сопряженное
априорное распределение р(0; D)), и пусть Do - заданные (известные)
значения параметров D в анализируемом случае. Тогда с помощью ряда
тождественных преобразований правая часть соотношения
p(0IX1, ... , Хп)
rv
р(0;
Do) · L(X1, ... , Xnl0)
(3.37)
Гл.
144
3.
приводится
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
с
точностью
до
множителей,
не
зависящих
от
0,
к
D(X1, ... , Xn)), где последняя функция принадлежит се
мейству {р(0; D)}, а каждая из компонент d;(X1, ... , Xn) (j
= 1, 2, ... , q) вектора параметров D(X1, ... , Xn) является функцией от
вид,у р(0;
Do и
{X1,X2, ... ,Xn}·
Продемонстрируем реализацию этой общей схемы на наших приме
рах (с разной степенью подробности).
Пр им ер
(продолжение).
3.1
-;&-(ж-8)2
L(x1, Х2, ... , Xnl8)
е 2 сто
(т. е. di = 80, d2 = ЛЮ, так что
f'V
В
данном
(см. (3.7)), р(8; D)
=
примере
~до е
- (8-8~>2
2 до
где
(3.38)
и
Необходимые промежуточные выкладки нацелены на выделение
полного квадрата разности (8-d1) 2 из выражения
х) 2
J
2
1 (8(8-d 1 ) 2 +~
1n
и0
и не представляют принципиальных трудностей.
Мы видим, что среднее (d1) и дисперсия (d2) апостериорного нор
мального распределения являются определенным образом средневзве
шенными значениями априорных и выборочных, соответственно, сред
них и дисперсий.
Пр им ер
счета
(продолжение). При реализации общей схемы пере
3.2
априорных
параметров
в
апостериорные
в данном
д,ует учесть представление функции правдоподобия
(см. выше, пример
3.2),
вид
(3.18)
L
случае
в форме
сле
(3.16)
априорной плотности двумерно
го гамма-нормального распределения (в котором вектор параметров
Do
= (Ло;8о;а;,8)), а также справедливость тождества
n(8 -
х)2 + Ло(8 -
80)2 =
(Ло + n) (8 - Л~о + nx)2 + Л Лоn
o+n
o+n
(80 -
х)2.
3.4.
ПЕРЕСЧЕТ ЗНАЧЕНИЙ ПАРАМЕТРОВ
Тогда вычисление р(8;
h)
по схеме
145
приводит нас снова к дву
(3.37)
мерному гамма-нормальному распределению вида
(3.18),
но с парамет-
рам и
Ло = Ло
+n;
8 _ nx + Ло8о.
о-
n+Ло'
-
n
2'
1~
(3.39)
а=а+-·
-
_
(х - 80) 2
2
/3 = /3 + 2 ~ (xi - х) + 2(1
n
i=l
Пр им ер
ношения
(3.37)
3.3
...!..) .
+ .Ло
(продолжение). Непосредственная реализация соот
в данном случае дает:
п
=8
Но правая часть
(3.40)
i=l
(3.40)
п
а+ Е Xi-1
(1 - 8)
Ь+nМ-Е Xi-1
i=l
•
определяет (с точностью до нормирующего мно
жителя) снова бета-распределение с параметрами:
n
а=а+ LXii
i=l
(3.41)
n
b=b+nM-I:xi.
i=l
Пр им ер
шения
3.4
(продолжение). Подставляя в правую часть соотно
(3.37)
р(8; Do)
= р(8;
а, Ь) ,...., 8°- 1 (1 - 8)ь- 1 ,
имеем:
п
p(8lx1, ... 'Xn),...., 8a+Kn-1(1- 8)
ь+Е
i=l
Xi-Kn-1
•
Мы видим, что апостериорное распределение параметра (вероятно
сти «успеха~) отрицательно-биномиального закона, так же как и апри
орное, является бета-распределением и что его параметры
D=
(а, Ь)
определяются соотношениями:
a=a+Kn,
n
Ь=Ь+ LXi-Kn.
i=l
(3.42)
Гл.
146
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
Пр им ер
3.5
(продолжение). Как мы видели ранее, функция
правдоподобия наблюдений пуассоновской генеральной совокупности
имеет вид
п
LXi
L(x1, ... ,xnl8),..., 8i=l e-nfJ.
Так что, используя в качестве априорного распределения р( 8;
= р(8; а, /3)
Тем
параметра
самым
8 гамма-распределение (3.23),
подтверждается
сопряженность
D) =
имеем:
априорного гамма
распределения, причем, апостериорное гамма-распределение определя
ется параметрами
fJ = (а, Р),
где
n
а=а+ L:xi;
(3.43)
i=l
/3 = /3 +n.
Пр им ер
3.6
(продолжение). Функция правдоподобия экспонен
циально распределенных наблюдений (с параметром масштаба
8)
имеет
вид
L(x1, ... 'Xnl8) = 8ne
-( f: Xi)(J
i=l
•
Так что при априорном гамма-распределении параметра
8 имеем:
Мы видим, что апостериорное распределение параметра
подчиняется закону гамма-распределения
(3.23),
8
снова
но с параметрами
a=a+n;
n
р = /3+
LXi·
(3.44)
i=l
Пр им ер
3.7
(продолжение). Подставляя в правую часть соотно
шения
(3.37) функцию правдоподобия 'JЮВНомерно распределенных (на
отрезке [О; 8)) наблюдений и функцию плотности распределения Паре
то (3.26) в качестве априорного распределения р(8; D) = р(8; а; 8min),
имеем:
-( 8IХ1' ... 'Xn ) ,..., a8::iin
1
8а+1 . 8n
р
3.4.
ПЕРЕСЧЕТ ЗНАЧЕНИЙ ПАРАМЕТРОВ
147
Отсюда следует, что апостериорное распределение параметра
сывается, так же как и априорное, законом Парето
(3.26),
8 опи
но с парамет
рами:
a=a+n
Bmin = max{8min;X1,x2, ... ,xn},
Пр им ер
3.8
(3.45)
(продолжение). Как мы видели (см. выше, пример
3.8), функция правдоподобия Парето-распределенных наблюдений име
ет вид
n
L(x1, ... , Xnl8) ,...., 8 · е
-[n ln( 1l!l
)] ·8
жо
.
Подставляя ее в правую часть соотношения
в
качестве
априорного
распределения
(3.23),
распределения р(8;
Do),
(3.37),
а также,
плотность
гамма
имеем:
-(81 х1, ... , Xn ) ,...., 8а-1 е -/38 · 8n е -[n ln(~о )]в_
- 8a+n-1 е -(P+n ln(~о ))в ,
р
что определяет гамма-распределение с параметрами
a=a+n,
Р = {3 + n ln (;:),
где 9n
а хо
1
=
-
(.ft xi) п
-
(3.46)
среднее геометрическое наблюдений х1, ... ,xn,
i=l
параметр сдвига в анализируемом распределении Парето (его
значение считается заданным).
Пр им ер
3.9
(продолжение). Байесовское оценивание коэффици
ентов регрессии е = (80, 81, ... '8k)' и параметра
h в нормальной клас
сической модели множественной регрессии (3.8),....,(3.9) предполагает ис
пользование апостериорного распределения р(0; hlX, У) этих парамет
ров, определяемого по схеме (3.37). Подставляя в правую часть соот
ношения (3.37) в качестве априорного многомерное гамма-нормальное
распределение (3.29), а также функцию правдоподобия L(X, Yl0, h)
(см. (3.12)), преобразованную к ви.цу
L(X, Yl0; h) ,...., h п-~-1 е-(п-~-10-2)h. h ki1 е-~(0-е)'(Х'Х)(е-е)'
получаем после ряда тождественных преобразований (см., [Де Грот
(1974)])
апостериорную плотность р(0; hlX, У) в форме многомерного
Гл.
148
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
гамма-нормального распределения
(3.29),
ляются по параметрам 0о, Ло, а и
{3
параметры которого опреде
априорного распределения и на
блюдениям (Х, У) сле,цующими соотношениями:
= (Ло + Х'Х)- 1 (Ло0о + Х'У) - параметр сдвига;
Ло = Ло + Х'Х - матрица точности;
00
А
а=а+
n
2;
параметры частного
1
{3 = {3 + "2[(У - Х0о)'У +
(3.47)
апостериорного гаммараспределения параметра
+ (0о - 80)' Ло0о]+
точности
h.
Примеры задач на точечное и интервальное
3.5.
байесовское оценивание параметров модели
Задача
1.
Анализ закона 'JЮСпределения домашних хозяйств опреде
ленной социа.л:ьно-экономической страты в заданном регионе страны
по величине среднедушевого дохода
17.
Мы располагаем сле,цующей информацией об анализируемой гене
ральной совокупности:
(а) логарифм (натуральный) от величины средне,цушевого дохода
(т. е. {
=
ln 77)
домашних хозяйств рассматриваемой страты данного
региона распределен нормально с неизвестным средним значением
известной дисперсией и~
(6)
и
()
= 0,28;
имеются результаты обследования п
=
10
случайно отобран
ных от анализируемой страты домашних хозяйств по среднедушевому
дохо,цу Yi (в нижеследующей таблице даны значения Xi
i
Xi
1
0,54
2
1,20
3
0,36
4
0,80
5
0,42
6
2,10
7
0,70
= lnyi):
8
0,25
9
0,90
10
0,48
(в) из предыстории и опыта обследования домашних хозяйств той
же страты
в других регионах страны
среднего Е()
получены
априорные значения
= 80 = 0,60 и дисперсии D() = д~ = 0,03.
Треб у е т с я:
используя
сопряженное
априорное
распределение
параметра
(),
получить байесовские точечную и интервальную (с уровнем доверия
Ро
= 0,95) оценки средней величины логарифма среднедушевого дохода и
сравнить их с соответствующими оценками метода максимального
правдоподобия.
3.5.
ПРИМЕРЫ ЗАДАЧ
149
Решение. Мы уже знаем (см. выше, пример
3.1),
что сопряжен
ное априорное распределение в данном случае существует и является
нормальным, причем параметры этого распределения непосредственно
за.даны (Е8
= 80 = 0,60
и D8 =и~= 0,03). В соответствии с выведен
ными выше формулами пересчета (см. п.
Во
= E(8lx1, ... , Xn) =
3.4,
формулы
*·Ж+~·8о
<ro/ni
др
<r2/n +Д2'
о
о
(3.38))
имеем:
= 0,691
Л~ = D(8lx1, ... ,xn) = c,~1/n + ~)
-1
= 0,015.
Соответственно:
В(Б)
= ЬЕ(8lх1, ... , Xn) = 0,691
и с вероятностью Ро = 0,95 можем утверждать, что 8<Б)
-
ио,025 · Ло
<
< 8 < 8<Б> + ио,025 · Л.
С учетом того, что 2,5%-ная точка стандартного нормального рас-
пределения ио,025 = 1,96 и Ло = ~ = 0,120, имеем:
8Е
[О,451;
0,931]
с вероятностью Ро
= 0,95.
Решение этих же за.дач, основанное на методе максимального п'JЮвдо
подоби.я, дает:
Вмп
= х = О, 775
и 8 Е [О, 447; 1, 103] с вероятностью Ро
= 0,95
(концы последнего доверительного интервала вычислены по формулам
Вмп ± ио,025 · 7п).
Мы видим, что использование априорной информации о неизвест
ном значении параметра
8
=
E(ln Т/)
и применение, соответственно,
байесовского подхода в данной за.даче позволили уточнить оценку и, в
частности, сузить интервальную оценку по сравнению с классическим
подходом почти в полтора раза.
Задача
2.
Оценка интенсивности вЪ1.Зовов,
поступающих на
пункт «Скорой помощи» в час.
Число вызовов ~ поступающих на пункт ~скорой помощи~ в час,
описывается распределением Пуассона с неизвестным значением пара
метра
8 =
Е~ (см. выше, пример
3.5).
Результаты регистрации числа
вызовов Xi (в час), зафиксированные в течение одной смены (длящейся
8
часов), приведены в следующей таблице:
Из опыта работы аналогичных пунктов определено априорное сред
= Е8 = 3,6, причем случайный разброс значений этого
параметра характеризуется дисперсией д~ = D8 = 0,09.
нее значение
80
Гл.
150
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
Треб у е т с я:
испо.л:ьзуя сопряженное априорное распределение параметра
8,
полу
читъ байесовские точечную и интервалъную (с уровнем доверия Ро
= 0,95)
оценки средней интенсивности(}
=
=
Е{ в'ЫЗовов, поступаю
щих на пункт «Окорой помощи», и сравнитъ их с соответствующими
оценками метода максималъного правдоподобия.
Решение. Как было установлено выше (см. пример
ное априорное распределение параметра
(}
в этом случае существует и
описывается гамма-законом, параметры а и
(в соответствии с рекомендациями п.
{
Отсюда а
ЕО -
:"'
DfJ -
/3 2
3.3.3)
/3
которого определяются
из системы уравнений:
3,60,
-
0,09.
= 144 и /3 = 40.
В соответствии с выведенными выше (см. п.
счета
(3.43)
3.5), сопряжен
3.4)
формулами пере
параметров апостериорного гамма-распределения имеем:
8
&
= а + Е Xi = 144 + 24 = 168,
-
i=l
/3 = /3 + n = 40 + 8 = 48.
Таким образом:
iJ(Б)
= E(8lx1, ... , Xn) =
~
= 3,5,
и можно утверждать, что с вероятностью Ро
=
0,95
справедливы
неравенства
'Уо,915(&, ,8) < 8 < 'Уо,025(&, ,8),
где 'Yq(&, ,8) - 100qо/о-ная точка гамма-распределения с параметрами & и
,8. Воспользовавшись известными формулами (см. приложение П2.2а):
'Yq(&; ,8)
и при
m
= ~х~(2&)
2/3
> 100:
X~(m) ~ m
+ иq · ../2ffl,,
где x~(m) и иq - 100qо/о-ные точки хи-квадрат и стандартного нормаль
ного распределения соответственно, имеем:
(} Е [2,97; 4,03)с вероятностью Ро
= 0,95.
ПРИМЕРЫ ЗАДАЧ
3.5.
151
Решение этих же задач, основанное на методе максимального правдо
подобия, дает:
Вмп
= Х = 3,0;
(} Е
[1,80; 4,20; ]с вероятностью Ро = 0,953 .
Мы видим, что в данном случае использование априорной инфор
мации о параметре
(}
в рамках байесовского подхода позволило сузить
размах интервальной оценки более чем в два раза!
Задача
3.
Оценка необходимой доли брака
(}
в проi}укции, произво
димой автоматической линией.
Предприятие приобрело новую автоматическую линию (АЛ). Для
оценки так называемой необходимой доли брака
(}, -
вероятности то
го, что произведенное этой АЛ в режиме стационарного функциониро
вания изделие окажется некондиционным,
п
-
было проконтролировано
= 5 партий по М = 80 изделий в каждой партии. Число дефект
ных изделий
{,
обнаруженных в партии изделий объема М, адекватно
описывается биномиальным з. р.в. с параметрами
контроля представлены в таблице
(}
и М. Результаты
(xi - это число дефектных изделий,
обнаруженных в i-й проконтролированной партии):
Кроме того, проведенный анализ работы аналогичных АЛ, уста
новленных на других предприятиях, показал, что «необходимая доля
брака~ в среднем равна
0,01
и имеет разброс, характеризуемый средне
квадратическим отклонением
0,003.
Требуется:
используя сопряженное априорное распределение параметра
(},
полу
чить байесовские точечную и интервальную (с уровнем доверия Ро
= 0,90)
=
оценки «необходимой доли брака» (}и сравнить их с соответ
ствующими оценками метода максимального правдоподобия.
Решение. Выше (см. п.
3.3)
было установлено, что сопряженное
априорное распределение параметра
(}
в данном случае существует и
описывается бета-распределением, параметры а и Ь которого определя
ются из системы (см. п.
3.3):
а
{
--ь
а+
= 0,01
аЬ
2
(а+ Ь)2(а + Ь + 1) = (0,003) .
3
Данная интервальная оценка основана на асимптотической ( 8; Л) - нормаль
ности оценки максимального правдоподобия Вмп·
ГЛ.
152
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
Решение этой системы дает а=
и Ь
10
=
990.
Воспользовавшись
формулами пересчета (3.41}, получаем значения параметров а и Ь апо
стериорного распределения
(}:
5
а = а+
L
= 10 + 8 = 18;
Xi
i=l
5
L
ь = ь + 5 . 80 -
Xi
= 1382.
i=l
Таким образом:
(}(Б) = Е( 8lx1, ... , Xn) = _0 Ь = 0,01286,
а+
и можно утверждать, что с вероятностью Ро
-
0,90
справедливы
неравенства
.Во,9s(а, Ь) < (} < .ВО,оs(а, Ь},
~де ,Вq(а, Ь) - 1ооq%-ная точка бета-распределения с параметрами а и
Ь. Воспользовавшись известными равенствами
а (а· Ь) = _ а Fq(2a; 2Ь) _
ь +а Fq(2a; 2ь)'
/Jq '
и таблицами 100q-процентных точек
лами степеней свободы числителя
v1
Fq(v1, v2)
распределения
и знаменателя
Z12,
F
с чис
имеем:
= 0,90.
(} Е [0,0083; 0,0182] с вероятностьюРо
Решение этих же задач, основанное на методе максимального прав
доподобия4, дает:
А
8мп =
n
nit L
Xi
= 0,02;
i=l
(} Е [О,0085; 0,0315] с вероятностью Ро
Размах этой интервальной оценки в
= 0,90.
2,3
раза превосходит ширину
бо:йесовской интервальной оценки!
Задача
4.
Оценка интервала движения автобуоо
Приходящий в случайные моменты времени на остановку пассажир
в течение пяти своих поездок фиксировал время ожидания автобуса
(в минутах): х1 =
3,2; xs = 2,9. Известно,
что автобус ходит строго по расписанию с интервалом в (} минут, так что
1,2;
х2 =
2,5;
хз =
0,5;
Х4 =
время ожидания автобуса пассажиром можно считать случайной вели-
4 См.,
например: Айвазян С.А., Мхuтар.ян В.С. Прикладная статистика в задачах
и упражнениях. М.: Юнити,
2001.
Задача
1.18.
3.5.
чиной~' подчиненной [О;
3. 7).
ПРИМЕРЫ ЗАДАЧ
8] -
153
равномерному з.р.в. (см. выше, пример
Пытаясь оценить интервал движения автобуса, пассажир сумел по
лучить дополнительную информацию о параметре
8:
из анализа опыта
работы различных автобусных маршрутов города, функционирующих
в едином регламентном режиме, следовало, что среднее значение этого
параметра равно
мин, а случайный разброс в его значениях харак
5,38
теризуется средним квадратическим отклонением, равным
1,39
мин.
Треб у е т с я:
испо.л:ьзу.я сопряженное априорное распределение пара.метра
8,
полу
чить ба:йесовские точечную и интервальную (с уровнем доверия Ро
=
0,95)
=
оценки для неизвестного интервала двUЭ1Сени.я автобуса и
сравнить их с соответствующими оценками, основанн'ЬIМи на методе
максимального правдоподобия.
Решение. В п.
3.3
(см. пример
3. 7)
было установлено, что сопря
женное априорное рапсределение параметра
8
в данном случае суще
ствует и описывается распределением Парето с параметром формы а и
параметром сдвига
(3.32},
Bmin,
т. е. по формулам
- /
которые определяются из системы уравнений
(3.32'}.
В нашем случае имеем:
5 3g2
()2
= 1 + у 1 + ~ = 1 + 1 + 1:392 = 5,00
Bmin = ~Во· (а - 1} = ! ·5,38 · 4 = 4,30 (мин).
а
Параметры апостериорного распределения Парето определяются
формулами пересчета
б
(3.45):
= а + n = 5 + 5 = 10
Bmin = max{Bmin; х1, ... ,xs) = 4,3 (мин).
Соответственно:
8А(В)
= Е ( 8Iх1, ... ,xs } = б_· Bmin
1 = 4,78 (мин)
а-
и 8 Е [80,975(&; Bmin); 80,02s(б; Bmin)] с вероятностью Ро = 0,95, где
8q(б; Bmin) - это 100q%-ная точка распределения Парето с параметра
ми (б; Bmin). Поскольку функция распределения Парето определяется
соотношением
F(ll) = P{{(ii; 8mm) < 11} = 1-
e~m)",
ГЛ.
154
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
то значения 80,975(&; ёmin) и 80,025(&; ёmin) определяется из уравнений,
соответственно:
(
Bmin )
80,975(&; 8min)
&
= 0,975,
(
Bmin )
80,025(&; 8min)
&
= 0,025.
Решение э:их уравнений относительно 80,975(&; Bmin) и 80,025(&; ёmin)
при & = 10 и 8min = 4,3 дает:
80,975(&; ёmin) = 4,31 И 80,025(&; ёmin) = 6,22,
так что
8 Е (4,31; 6,22) с вероятностью Ро
= 0,95.
Решение тех же задач, основанное на методе макси.малъного правдопо
добия, дает:
Омп
= 3,84
(мин);
8 Е [3,22; 6,69) с вероятностью Ро
= 0,95
(здесь дается оценка максимального правдоподобия Омп, подправленная
на несмещенностъ). И в данном случае байесовский подход позволил
сузить ширину доверительного интервала почти в
2 раза
(точнее в
1,82
раза).
Задача
5.
Оценка параметров модели зависимости душев'Ьtх до
ходов от об'бема автономн'ЫХ инвестиций.
В нижеследующей таблице приведены макроэкономические данные
по США, характеризующие среднедушевой доход Yt и автономные ин
вестиции Xt (в долларах, в дефлированных с помощью индекса стоимо
сти жизни ценах) за
1922-1941
гг. Инвестиции определены приближен
но как разность между среднедушевым доходом и душевым расходом
на личное потребление (данные заимствованы из работы Haavelтo Т.
Methods of Measuring the Marginal Propensity to Consume / / JASA. Vol.
42 (1947). Р. 105-122).
t
Xt
Yt
t
Xt
Yt
1
2
(1922)
39
60
433
483
11
12
(1922)
22
17
372
381
3
4
5
6
7
8
9
10
42
479
52
486
47
494
51
498
45
511
60
534
39
478
41
440
13
14
15
16
17
18
19
27
419
33
449
48
511
51
520
33
477
46
517
54
548
20
(1941)
100
629
3.5.
ПРИМЕРЫ ЗАДАЧ
155
Анализируется нормальная классическая линейная модель парной
регрессии (см. пример
3.9
в п.
3.2
при
= 1):
k
t
= 1, 2, ... ' 20.
{3.48)
Анализ предыстории и экспертных оценок модели позволил по
лучить следующую априорную информацию о значениях параметров
Во, В1 и h
= {D€t)- 1 :
В8
= ЕВо = 330;
д~ = DBo = 225;
В~
= ЕВ1 = 2,85;
ho = Eh = 0,002;
д~V = DB1 = 0,01; д~ = Dh = 25 · 10-8 .
Требуется:
используя
соnряж:енное
априорное
распределение
параметров
(Во; В1; h), полу'Читъ байесовские то'Ч.е'Ч.ные и интервальные (с уровнем
доверия Ро
= 0,90)
оценки этих параметров и сравнить их с соответ
ствующими оценками метода максимального правдоподобия.
Решение. Проведенный в п.
3.2
и
анализ примера
3.3
3.9
показал,
что в данном случае существует сопряженное с наблюдаемой генераль
ной совокупностью распределение параметров (Во; В1;
h) и что оно опи
сывается трехмерным гамма-нормальным распределением
{3.29)
с па
раметрами е 0
= (В8; В~)', Ао, а и /3, определяемыми в соответствии с
рекомендациями {3.33) и {3.36), т. е. : е 0 = {330; 2, 85)'; а = ~ = 16;
h
/3 = ~h = 8000;
Ао = ( 2 '~7 533~3,3) .
Параметры апостериорного гамма-нормального распределения вы
числяются в соответствии с формулами пересчета
0- 0 = (
349,0)
2 ,9 ,а= 26, /3
= 14578,
-
Ао
=
(
{3.47):
22,37
907 )
907 100176 ·
То'Ч.е'Ч.ные байесовские оценки параметров (Во; В1; h) определяют
ся
средними
значениями
распределений.
соответствующих
С учетом свойств
(i)
и
нормального распределения (см. выше, п.
§(В)= Е(01Х, У)=
00 =
5
частных
(ii)
разд.
апостериорных
многомерного гамма
3.3.3)
имеем:
{349,0; 2,90)';
f,,(Б) = E{hlX, У)=~= 0,00178.
/3
При выводе интервалън'ЫХ байесовских оценок также используют
ся свойства
(i)
и
(ii)
многомерного гамма-нормального распределения, а
ГЛ.
156
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
также факт t{2а)-распределенности случайных величин (Ь~Б) -Bj)y'Cj,
где параметр то_:ности ёj вычисляется по блочным компонентам мат
рицы точности В частного апостериорного обобщенного многомерного
t{2al0< 5 >; В)-распределения по формуле
ё3· = Ь33·· - в·3·
.:8<1·) . в ·
{3.49)
·3
(см. Приложение П3.1~). Участвующие в этом с~ношении число bjj,
1 х (k - 1)-матрица Bj., (k - 1) х 1-матрица B.j и (k - 1) х (k -1 )-матр~а B(j) определяются сле,цующим блочным представлением
матрицы В:
-
в=
( _}3
Ь··
-
О или
1,
В·3. )
{3.50)
•
B.j B(j)
В нашем случае
k = 2, j =
матрица
в
ал(о, 040;
1, 618 )
=-::; о= 1 618· 178 665 .
f3
'
'
'
так что ёо
0,040 - {1,618) 2/178,665 = 0,0254 и ёl = 178,665-(1,618)2 /0,040 = 113,217. Следовательно, с вероятностью Ро = 0,90
мы можем утверждать, что IЬ~Б) - Bol · у'О, 0254 < to,05(52) и IВ~Б) _
-B1I·у'113,217 < to,05(52), так что {с учетом того, что to,05(52) = 1,676)
имеем:
Во Е
[338,5; 359,5]
с вероятностью Ро
= 0,90;
В1 Е
[2,743; 3,057]
с вероятностью Ро
= 0,90.
Поскольку
параметр
h
под~иняется
распределению с параметрами а и
{3,
апостериорному
гамма
то:
h Е ['Уо,95{а;,В);'Уо,05{а;,В)] с вероятностью Ро = 0,90. Используя
соотношение 'Yq(a; ,В) = ~Х~{2а), имеем (с учетом х~, 95 (52) ~ 36,4 и
х~. 05 (52) ~ 69,8):
h Е [О,00125; 0,00239] с вероятностью Ро = 0,90.
Оценивание модели
{3.48)
с помощью метода максима.л:ьного прав
доподобия (дающего в данном случае те же результаты, что и метод
наименьших квад-ратов) приводит к следующим точечным и интерваль
ным оценкам:
0мп = 0мнк = {Х'Х)- 1 Х'У = {344,7; 3,05)'.
А
hмп
1
.. '
. . ]-1 = 0,0015;
= IВ(У -Х0мп) {У - Х0мп)
[
316,1 <
Во
< 373,3; 2,45 <
В1
< 3,64 с
вероятностью Ро
= 0,90;
3.6.
h
БАЙЕСОВСКИЙ ПРОГНОЗ ЗАВИСИМОЙ ПЕРЕМЕННОЙ
Е [О,00093; 0,00285] с вероятностью Ро
157
= 0,90.
Мы видим, что байесовский подход позволяет сузить доверитель
ный интервал для Оо в
2,6
раза, для
01
-
в
3, 7
раза и для
h -
в
1,4
раза по сравнению с подходом, основанным на методе максимального
правдоподобия.
3.6.
Вайесовский прогноз зависимой
переменной, основанный на нормальной
классической линейной модели
множественной регрессии
Мы продолжаем рассматривать нормальную КЛММР
t = 1, 2, ... , n,
или, в матричной записи, модель
ки
Ei = c(Xi)
(3.8)-(3.9) (см. выше), в которой остат
нормальны, гомоскедастичны и взаимнонекоррелированы
при любом (а не тол:ько наблюденном) наборе значений объясняющих
переменных.
У
Введем в рассмотрение, наряду с наблюденными значениями Х и
анализируемых переменных Х
{1; х< 1 >, х< 2 >,
x(k))' и у, их про
... ,
=
гнозные (на
q тактов времени вперед) значения:
(1)
Х=
1 Xn~1
(1
1 Xn+2
(1)
1 Xn+q
(2)
xn~1
(2
Xn+2
(2)
Xn+q
а также соответствующие остатки
Тогда в соответствии с
(k)
xn~1
Уп+1
(k
Xn+2
(k)
Xn+q
€ = (En+1,
и
У=
Уп+2
Уп+q
En+2, • · • ,En+q)'.
(3.8),..,,(3.9):
{3.8а)
{3.9а)
Для того чтобы строит~ точечные и интервальные оценки для У
по заданным значениям Х, Х и У, очевидно, надо располагать плотно
стью условного распределения p(YIX; Х; У), которую обычно называют
~прогнозной функцией плотности вероятности». Но поскольку из
ГЛ.
158
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
(3.8а}-(3.9а} сле,цует, что распределение вектора У зависит также от па
раметров е и
h,
а они в байесовском подходе интерпретируются как
случайные величины, имеющие соответствующее апостериорное рас
пределение, то реализуется сле,цующая схема определения прогнозной
функции плотности p(YIX; Х; У):
p(YIX; Х; У) =
! ! р(У;
е
=
0; hlX; Х; Y)d0dh =
h
{3.51}
j j p(Yl0;h;X;X;Y) · p(0;hlX;X;Y) d0dh.
е
Правая часть
h
{3.51}
получена с использованием формулы произве
дения вероятностей
P(ABIC) = P(AIB, С) · P(BIC). С учетом то
го, что p(Yl0;h;X;X;Y} = p(Yl0;h;X) ,...., h~. е-~<'У-хеу('У-хе>, а
p(0;hlX;X;Y}_ =_p(0;hl~;Y) - гамма-нормальное распределение с
параметрами 0о,Ао,а и
/3
/3,
определяемыми по параметрам 00,Ао,а и
априорного гамма-нормального распределения р(0,
(3.47),
интегрирование в правой части
v(YIX; Х; У) ~ [1+ ~(У -
(3.51}
h) по формулам
дает:
Хёо)'В(У - Хёо)]
_v+q
2
(3.52}
,
где
v=n-k-1
и В=~
[1q-X(Ao+X'X+X'x)- 1 x']
(3.53}
(подробное доказательство этого факта читатель найдет, например, в
[Зельнер
{1980}]).
Таким обр~м, мы пришли к тому, что условно._е рас
пределение q-мерного вектора У при заданных значениях Х, У и Х опи
сывается обобщенным многомерным t-распределением с п -
k - _!.
степе-
нями свободы, параметром сдвига Х0о и матрицей точности В, опЕе
деленной соотношением (3.53) (т. е. (YIX; Х; У) = t(п - k - 1IX00 ; В},
см. Приложение П3.1б}.
Используя известные свойства обобщенного t-распределения Стью
дента {см. :О:риложение П3.1б}, получаем сле,цующие байесовские про
гнозы для У:
• точечный байесовский прогноз для компонент вектора У
определяется соотношением
Уn+m(прогнозное) = (е(Б))' · Xn+m,
m = 1, 2, ... , q;
(3.54)
3.6.
•
БАЙЕСОВСКИЙ ПРОГНОЗ ЗАВИСИМОЙ ПЕРЕМЕННОЙ
159
интервальный байесовский прогноз для компонент векто
ра У с вероятностъю Ро определяется соотношением
Yn+m
Е [!in+m - ti- Po (n 2
k -1) ·
+t•-,Po(n-k-1)·
где
~; !in+m+
~]·
{3.55)
m=1,2, ... ,q,
100с:%-ная точка стандартного t(v)-распределения Стыо
te(v) -
дента, а величины ~ вычисляются п~ схеме (3.49)"'{3.50) с заменой
(k х k )-матрицы В на (q х q )-матрицу В, определенную соотношением
(3.53);
• байесовская прогнозная доверительная область дУ для
вектора У= (Уп+1, ... , Yn+q)' состоит, с заданной вероятностью Ро, из
всех тех У= (Уп+1, ... , Yn+q)', которые удовлетворяют неравенству
~(У - хе<Б))':Е~ 1 (У - хе<Б>) < F1-Po(q; п q
k - 1),
{3.56)
где Fe(vi,v2) -100с:%-ная точка F(щ,v2)-распределения, е(Б) -байе--1
совская точечная оценка параметров регрессии 0, а Е-у = :=~=~ В
ковариационная матрица вектора У. Можно показать, что для модели
{3.8а)-{3.9а) эта область имеет форму q-мерного эллипсоида.
Рассмотрим реализацию описанной выше схемы построения точеч
ных и интервальных байесовских прогнозов значений зависимой пере
менной в нормальной КЛММР на нашем примере, проанализированном
в задаче
5.
Задача
5
(продолжение). В условиях примера, рассмотренного
выше, т р е б у е т с я:
по
заданн'Ьl,М
х21
=
120
и х22
(планируемым)
=
140
значениям
автономных
инвестиций
построить точечные и интерва.л.ьные байесов
ские прогнозы для среднеi}ушевых доходов населения У21 и У22, а также
прогнозную доверительную область дУ для этих значений с уровнем
доверия Ро = О, 90; сравнитъ полученные решения с решениями, осно
ванными на методе максима.л.ъного п'fХJвдоподобия.
Решение. Итак, в нашем случае:
-
х=
(
1 120)
1 140 ;
В соответствии с (3.52) плотность условного распределения вектора У при заданных Х, Х и У описывается обобщенным многомерным
ГЛ.
160
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
3.
t-распределением с числом степеней свободы
v = 20- 1- 1=18,
пара-
метром сдвига(~ ~~~) · (3~~9°) и матрицей точности :В, определенной соотношением
(3.53).
Произведя необходимые вычисления по формулам
(3.53)-(3.56)
и используя известные свойства обобщенного многомерного t-распре
деления (см. Приложение П3.16), имеем:
1/21(прогн.)
= 349 + 2, 9 · 120 = 697,4;
1/22(прогн.)
= 349 + 2, 9 · 140 = 755,5;
В = ( 0,00159 -0,00022) .
-0,00022 0,00152 '
Е _ = (721,8 106,8) .
у
106,8 757,4 '
У21 Е
[653,6; 741,2]
с вероятностью Ро
= 0,90;
У22 Е
[710,7; 800,3)
с вероятностью Ро
= 0,90;
Д-
у
= {
(У21)
У22
: ! (У21 - 697,4)' ( о, 00159 -0,00022)
2 У22 - 755,5
-0, 00022 0,00152 х
У21 - 697,4) 2 62}
х У22 - 755,5 < '
.
(
Сравним эти результаты с соответствующими прогнозами, основан-
ными на оценках метода макси.мального правдоподобия:
•
точечный прогноз
344,7 + 3,05 · 120 = 710,7;
у~Г (прогнозное)=
y~f (прогнозное)
•
= 344,7 + 3,05 · 140 = 771,7;
интервальный прогноз строится на основе
2)-распределен
t(n -
ности случайных величин
лмп
( прогн. )
Yn+m
Uмп.
1
-
Yn+m
+ ~ + <;п+т-х)2'
Е
m
= 1,2;
(xi-x) 2
i=l
в нашем случае
-- 666 ' 67·' Uмп
n = 20,
= 120, Xn+2 = 140,
2 - 5572·6 - О 976·
- 25 ' 82·' (хпн-х)
20
5711 - '
'
Xn+1
Е
(xi-x) 2
i=l
= 1,569
и
to,05(18) = 1,734,
так что:
У21 Е
[647,1; 774,3)
с вероятностью Ро
У22 Е
[699,2; 844,2] с вероятностью Ро = 0,90.
= 0,90;
Мы видим, что и в прогнозе байесовский подход позволяет сузить
ширину прогнозной интервальной оценки для У22 в
У22
-
в
1,62
раза!
1,45
раза, а для
Выводы
161
Выводы
1.
При принятии решения, основанного на байесовском подходе,
эконометрист использует в качестве исходной информации одновремен
но информацию двух типов: априорную и содержащуюся в исходн:ы,х
статистических дан:н:ых. При этом априорная информация предостав
лена ему в виде некоторого априорного распределения вероятностей
анализируемого неизвестного параметра, которое описывает степень его
уверенности в том, что этот параметр примет то или иное значение, еще
до нача.л.а сбора исходн:ы.х статистических данных. По мере же поступ
ления исходных статистических данных эконометрист уточняет (пере
считывает) это распределение, переходя от априорного распределения к
апостериорному, используя для этого известную формулу Байеса {см.
п.
3.1).
2. Априорные
сведения об оцениваемом параметре
0
основаны на
предыстории функционирования анализируемого процесса (если тако
вая имеется) и на профессиональных теоретических соображениях о
его сущности, специфике, особенностях и т. п. В конечном итоге эти
априорные СВедеНИЯ ДОЛЖНЫ быть Представлены В Виде функции р( 0),
задающей априорное распределение параметра и интерпретируемой как
вероятность того, что параметр примет значение, равное
0,
если пара
метр дискретен, и как функция плотности распределения в точке е,
если параметр непрерывен по своей природе.
З. При практической реализации байесовского подхода важное зна
чение имеет выбор семейства {р{0; D)} априорных распределений оце
ниваемого параметра. При этом существенную роль играют распреде
ления, сопряженн'Ьl,е по отношению к наблюдаемой генералъной сово
купности, т. е. такие априорные распределения, которые при пересчете
в апостериорн'Ьl,е не выходят за пределы семейства, к которому они
принадлежат (см. п.
4.
3.2).
В ситуациях, в которых исследователь не располагает никакой
полезной априорной информацией о значениях оцениваемого парамет
ра, обычно используются следующие два правила выбора соответству
ющего априорного распределения {см. п. 3.3.1):
(а) если оцениваем'Ьt,й ска.л.ярн'Ьl,й параметр (J может ( теоретиче-
ски) приниматъ значения на конечном интерва.л.е
[8min, 8max]
или на
бесконечном интервале от -оо до +оо, то априорную функцию плот
ности р( 8) след-ует считатъ постоянной на соответствующем ин
терва.л.е;
{б) если же из СМ'Ьt,сла оцениваемого параметра в'Ьl,текает, что
он может приниматъ любые положителъные значения, то следует
считатъ постоянной на всей числовой прямой (-оо; +оо) функцию
Гл.
162
3.
БАЙЕСОВСКИЙ ПОДХОД В ЭКОНОМЕТРИЧЕСКОМ АНАЛИЗЕ
плотности распределения логарифма от значения параметра, т. е.
p(ln 8)
= const при (J Е
(О; +оо). Такие априорные распределения обыч
но называют «распределения.ми, отражающими скудость априорных
знаний», или коротко
«САЗ-априорными распределениями».
-
5. Использование, в качестве априорных, законов распределения ве
роятностей (з.р.в.), сопр.яж;енных с наблюдаемой генеральной совокуп
ностью (в ситуациях, когда они существуют), позволяет нам определить
их общий вид, т. е. задает целое семейство априорных распределений
{р(8;
D)}.
Однако при реализации байесовского подхода мы должны
оперировать конкретн'ЬtМ априорным распределением, что требует зна
ния числовых значений
Do
параметров
D,
от которых наш априорный
з.р.в. зависит. Как же подбирать эти значения
ном случае? (см. п.
Do
в каждом конкрет
3.3.3).
В широком классе ситуаций можно исходить из того, что нам из
вестны априорные средние значения оцениваемого параметра
00
=
= Е8 = (Е81, Е82, ... , Е88 )' и их среднеквадратические ошибки д1 =
= .J]')81, д2 = v'D82, ... , Лs = JDВs. Тогда параметры априорного
распределения, как правило, могут быть определены методом момен
тов (в случае многомерного параметра
независимости компонент вектора
6.
8
0 -
с учетом статистической
в априорном распределении).
Поскольку по определению семейство сопряженных априорных
распределений {р(0;
D)}
замкнуто относительно операции пересчета
априорного распределения в апостериорное, то общий вид апостериор
ного распределения
p(8IX1, ... , Xn)
при использовании сопр.яж;енных
априорных распределений нам известен, и нам лишь надо уметь пере
считывать параметры D(X1, ... , Xn) этого апостериорного распределе
ния по заданным параметрам Do априорного распределения и имею
щимся наблюдениям Х1, Х2, ... , Xn.
Обща.я схема такого пересчета следующая (см. п. 3.4). Пусть
{р(8; D)} - семейство априорных распределений, сопряженных с функ
цией правдоподобия L(x1, ... , xnl0) имеющихся у нас наблюдений
х1, ... , Xn, и пусть Do - заданные (известные) значения параметров
lf/., ... , ~
в анализируемом случае. Тогда с помощью ряда тождествен-
ных преобразований правая часть соотношения, определяемого форму
лой Байеса,
p(8IX1, ... , Xn)
приводится,
виду р(0;
с
~ р(0;
Do) · L(X1, ... , Xnl0)
точностью до множителей,
не зависящих от
8,
к
D(X1, ... , Xn)), где последняя функция принадлежит се
мейству {p(0;D)}, а каждая из компонент dj(X1, ... ,Xn) (j
= 1, 2, ... , q) вектора параметров D(X1, ... , Xn) является функцией от
Do и {Х1, Х2, ... , Xn}·
Глава
4
Анализ многомерных
временных рядов
Весьма редко встречаются ситуации, когда изучаемые в динамике слож
ные явления {как, например, те, которые обычно изучаются в экономи
ке и финансах) могут быть описаны с использованием единственного
временного ряда. Напротив, более распространенным является описа
ние подобных явлений при помощи двух и более переменных, рассмат
риваемых в динамике. Однако всегда следует учитывать, что многие
временные ряды, например в финансах, изменяются синхронно в опре
деленной взаимозависимости.
В этой главе мы обратимся к вопросу совместного моделирования
двух или более временных рядов и обобщим некоторые подходы, ис
пользуемые для одномерных временных рядов, на многомерный слу
чай1.
4.1.
Многомерные временные ряды:
определения и основные понятия
В этом разделе мы обобщим основные инструменты, используемые при
анализе одномерных временных рядов, на многомерный случай.
Определение
4.1
(многомерная автоковариация).
Определим
j-ую компоненту многомерной автоковариационной функции много
мерного временного ряда
1 Анализу
(2010)].
{Yt }t=l,2,...
Е
Rm, представляющего собой
одномерных временных рядов посвящена гл. 10 учебника (Айвазян
164
Гл.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
т-мерный вектор-столбец с компонентами Y1,t,
... , Ym,t,
в форме (тх
х т )-матрицы:
Cov[Yi, Yi-j]
= Гt,t-j = E[(Yi - E[Yi])(Yt-i - E[Yi-j])'] =
Cov[Y1,t, Y2,t-;]
_ [Cov[Y1,;, Y1,t-;]
Cov[Y1,t;, Ym,t-;]]
Cov[Ym,t, Y1,t-j]
=
Cov[Ym,t, Ym,t-j] mxm
['Ylt,l~t-j)
'Y1t,2(t-j)
· ; · 'Ylt,m;(t-;)]]
'Ymt,l(t-j)
Определение
4.2
···
(4.1)
'Ymt,m(t-j) mxm
(ковариационная (слабая) стационарность).
Многомерный временной ряд
Yi
Е Rm с компонентами
(Y1,t, ... , Ym,tY
называется ковариационно стационарным. или слабо стационарнъш,
если
µt = E[Yi]
Cov[Yi, Yi-i] гдеµ Е
Vt;
µ,
Гt,t-j
= Гj, Vt,
Rm и Гj Е Rmxm.
В предположении ковариационной стационарности многомерная,
автоковариационная функция
(4.1)
принимает следующий вид:
'Y12,j
Cov[yt, Yi-j]
= Гj =
'Ylm,j]
'Ym~,j
mxm
Отметим, что эта матрица необязательно симметрична, поскольку
в общем случае 'Yiq.j
=/: 'Yqi.j.
Важно отметить, что несмотря на то, что в
случае скалярного процесса 'Yj
= 'Y-j, для векторного процесса в общем
случае мы имеем:
Гj
=/: Г -j·
Это неравенство выполняется в силу того, что, например, элемент
(1,2)
матрицы Гj
рицы Г -j
-
ковариация между
ковариация между
-
Y1,t
У1 может отличаться от отклика
Yi
и
Y1,t и Y2,t-j, элемент (1,2) мат
Y2,t+j, а отклик У2 на изменения
на изменения У2.
Заметим, что, заменив в автокорреляционной функции
t
мы получим
Гj
= E[(Yi+i -
µ)(Yi+i-i - µ) 1]
= E[(Yi+i -
µ)(yt - µ)'],
на
t + j,
165
МНОГОМЕРНЫЕ ВРЕМЕННЫЕ РЯДЫ
4.1.
а транспонировав эту матрицу, получим, что
Гj
= E[(Yi - µ)(Yi+j - µ)') = Г -j·
Соответственно ковариационная матрица многомерного временного
ряда
Yi
Е
IR.m
равна:
E[(Yi - E[yt))(yt - E[Yi))')
'У12,О
'Ylm,O]
'Ym~,O
Определение
4.3
=
mxm
(многомерная автокорреляция). Автокорреля
ция j-го порядка для ковариационно стационарного многомерного про
цесса yt Е
IR.m
с компонентами (Уц,
... , Ym,tY
определяете.я следую
щим образом:
Pll,j
Corr[Yi, Yi-j] = Rj
[
P12,j
:
Pml,j
Plm,j]
.
'
Pmm,j mxm
где
Cov[Yi,tYq,t-j)
[
]
Piq,j = Corr Yi,t, Yq,t-j = (DY. )112 . (DY, _ -)1/2 ·
i,t
q,t 3
3 а м е ч а н и е.
Математическое ожидание
µt
= E[Yi], автоковари
ационную и автокорреляционную функцию для стационарного много
мерного процесса yt с компонентами (Ун,
оценивать при
... , Уmt )'
помощи следующих статистик,
можно состоятельно
определяемых как эм
пирическое среднее и эмпирическая ковариационная функция
соответственно:
1 т
тL:Yi,
t=l
гj -
1
т
т
L: (Yi t=j+l
P.HYi-j - µ)',
Гл.
166
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Таким образом, автокорреляционная функция компоненты
Yi,t
со
стоятельно оценивается при помощи следующей статистики
А
А
Pii,j
'Yii,j
=-А-,
'Yii,O
а корреляционная функция Piq,j состоятельно оценивается при помощи:
Piq,j
:Yiq,j
= • • ,
А2
А2
'Yii,O'Yqq,0
где через :Yiq,j обозначается {i, q)-й элемент матрицы f'j.
Определение 4.4 (многомерный слабый белый шум).
ный процесс
Е
ct
IRm
с компонентами
c1,t, ... , cm,t
Многомер
называется с.л.аб'ЬtМ
бе.л.ЪtМ шумом, если выпол:н.яются с.л.ед-ующие свойства:
µ
= E[ct] = О Е IRm,
Гj =О Е
IRmxm Vj =f. 0.
Отметим, что многомерный белый шум имеет ковариационную мат
рицу Го, отличную от диагональной матрицы, так как компоненты мно
гомерного белого шума могут быть коррелированными. Если матрица
Го
= (}
обратима, то исходный белый шум может быть преобразован
к редуцированной форме (нулевое среднее и диагональная ко вариаци
онная матрица для компонент белого шума) при помощи перехода к
€t
= p- 1ct,
n=
где Р - квадратный корень из
РР', а Р
-
n
(разложение Холецкого),
нижнетреугольная матрица. Обратите внимание, что
при вычислении разложения Холецкого в пакете
ется как
n=
Р'Р, где Р
-
GAUSS
оно определя
верхнетреугол:ьна.я матрица.
Модели векторной авторегрессии
4.2.
{VАR-модели)
Векторные авторегрессии
(VAR)
впервые были использованы как ин
струмент эмпирического исследования в экономике Симсом (см. работу
[Sims {1980)),
ким
и
который показал, что VАR-модели могут послужить гиб
интерпретируемым
инструментом
анализа
экономических вре
менных рядов. Принятая ниже структуризация материала по VАR-мо
делям во многом следует схеме, описанной в
Определение
4.5.
[Gourieroux, Jasiak {2002)).
Многомерный процесс
yt
= {Y1,t, Y2,t, ... , Ym,t)'
называется VАR(р)-процессом, если он представим в виде
yt
=с+ Ф1Уi-1
+ Ф2Уi-2 + ... + ФрУi-р + Cf.
(4.2)
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
4.2.
167
Здесь с обозначает m-мерный векто~:rстолбец констант, а Фj при
j = 1, 2, ... ,р, - (т х m)-матрицы авторегрессионных коэффициентов.
Вектор остатков
et,
размерность которого
(m
х
1), -
многомерный бе
лый шум:
- {n,
о,
где
n-
сти
(m
для
t = s;
иначе,
симметричная положительно определенная матрица размерно
х
m).
Первое уравнение в системе
(4.2)
имеет вид:
Y1,t = с1 + Ф~~)У1,t-1 + Ф~~У2,t-1 + · · · + Ф~~Ут,t-1 +
(2)у,
(2)у;
(2) У.
+ Ф11
l,t-2 + Ф12 2,t-2 + ... + Ф1т m,t-2 +
+ · · · + Фri>Y1,t-p + Ф<ri.Y2,t-p + · · · + Ф~'% Ym,t-p + e1t,
где ф~~) - (i,j)-й элемент матрицы Фk. Таким образом, в этом случае
значение каждой компоненты вектора Yi в момент времени t зависит не
только от ее р прошлых значений, но и от р прошлых значений всех дру
гих компонент этого вектора. При помощи оператора сдвига
один такт времени система
(4.2)
L
назад на
может быть переписана в сле,цующем
виде:
Введя обозначение для полинома лагирования, получим:
Ф(L)yt =с+ et·
(4.3)
Предполагая, что Ф(L)- 1 существует, имеем:
Yi = Ф(L)- 1 с + Ф(L)- 1 et·
Следовательно,
µ = E[Yi] = Ф(L)- 1 с.
Таким образом, центрируя систему
Ф(L)yt
-
(4.2),
получим:
= -Ф(L)µ +с+ et
µ] = -Ф(L)Ф(L)- 1 с +с+ et
µ] = et
Ф(L)µ
Ф(L)[yt Ф(L)[Yi -
+ Ф2(Уi-2 · · · + Фр(Уi-р - µ) + et·
(Yi - µ) = Ф1(Уi-1 - µ)
µ)
+ ...
Гл.
168
4.2.1.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Модели
VAR{l)
Стационарный процесс
Yi с компонентами (Y1,t, ... , Уm,t }', описываемый
векторной авторегрессией первого порядка
VAR( 1),
удовлетворяет сле
дующему соотношению:
где
(4.4)
-
матрица коэффициентов авторегрессии размерности т х т, собствен
ные значения которой по модулю меньше единицы, а
et -
m-мерный
слабый белый шум. Представление в форме скользящего среднего бес
конечного порядка имеет вид:
(4.5)
=
Yi
-
ФУi-1 + et
Ф 2 Уi-2 + et
.
Ф1Yi-j
+ Феt-1 =
. 1
+ et + Феt-1 + ... + Ф3 -
et-j+l
= ... =
00
-
L:фiet-j·
(4.6)
j=O
Моменты первого и второго порядков для VAR(l)-пpoцecca равны:
E[Yi] =
Е [f:
фi
et-j] = f: фiE[et-j] = О
j=O
j=O
и
00
Го= Eyt = L:Фjnфi',
j=O
где
n=
EEt•
Учитывая, что
онная матрица Г j
et, ... ,et-j+l не коррелированы
при j = О, 1, ... равна:
.
Cov(yt, Yi-j) = Гj = Cov[Ф1Yi-j
с
Yi-j,
ковариаци
+ et + Феt-1 + ... + Ф1·-1 et-j+1, Yi-j] =
= фiv[Yt-j] = фiro.
4.2.
4.2.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
Модели
169
VAR(p)
Подобно одномерному случаю m-мерный VАR{р)-процесс может быть
представлен в виде mр-мерного VAR{l)-пpoцecca. Для простоты мы
предположим, что процесс центрирован. Определим
~t
F=
yt-µ
Yt-1 - µ
=
Yt-p+l -
µ
mpxl
Ф1
Ф2
Фз
Фр-1
Фр
lm
о
о
о
о
о
lm
о
о
о
о
о
о
lm
о
mpxmp
ft
о
Vt =
о
Систему
~t
E[vtv~]
а Ф;
(j
-
VAR(p)
F~t-1
{Q,
о,
мы можем переписать в виде:
+ Vt,
для
t = s;
Q=
где
иначе,
= 1, 2, ... , р) - (m
при значениях
mpxl
Yt-; -
n
о
о
о
о
о
о
о
о
mpxmp
х m )-матрица коэффициентов авторегрессии
µ (j = 1, 2, ... ,р).
Аналогично одномерному случаю для многомерного случая мож
но получить условие слабой стационарности. Если для процесса
ществует ковариационная матрица
n,
yt су
а автоковариационная функция
сходится к нулевой матрице с экспоненциальной скоростью, то эти же
свойства переносятся и на ~t· Это обеспечивается тем, что mp собствен
ных значений матрицы
F
лежат внутри единичного круга. Характери
стическое уравнение имеет вид:
Гл.
170
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Следовательно, условие стационарности VАR(р)-процесса состоит в сле
дующем.
Условие стационарности VАR(р)-процесса.
VAR(p)
является ста
ционарным процессом, если все собственные значения матрицы
F (опре
делена выше), определяемые из характеристического уравнения
лежат внутри единичного круга.
Таким образом,
VAR(p )-процесс
является ковариационно стацио
нарным, если для всех Л, удовлетворяющих
венство: IЛI
(4. 7),
выполняется нера
< 1.
Или, что эквивалентно,
VAR(p )-процесс
стационарным, если все значения
z,
является ковариационно
удовлетворяющие уравнению
лежат вне единичного круга. Более детальная информация приведена,
например, в
[Hamilton (1994}].
Когда р = 1 и корни уравнения IIm - Ф1zl
ного круга, т. е. lzl > 1, собственные значения
=О лежат вне единич
матрицы Ф1 находятся
внутри единичного круга. Отметим, что сопряженные значения корней
уравнения IФ1
-
Лlml =О являются корнями уравнения
llm -
Ф1zl =О
и наоборот.
Пусть процесс ковариационно стационарный. Возьмем математиче
ское ожидание от обеих частей
с+ Ф1µ+
-
... +Фрµ
[Im - Ф1 ... - Фр)- 1 с
-
Ф(1}- 1 с.
µ
µ
Если
VAR(p) -
(4.2}:
стационарный процесс, тогда для него справедливо
следующее представление в виде векторного процесса ско.л:ьзящего сред
него бесконечного порядка
Yi
т. е.
Yi-; -
=О,
1, ... ,
= µ + Et + Ф1Еt-1 + Ф2Еt-2 + ... = µ + Ф(L)et,
линейная функция от элементов
Yi+1
Yt+11t
Et-;, Et-;-1, ... ,
при
j -
каждый из которых не коррелирован с ен1- Следовательно,
ен1 не коррелирован с
прогноз
(Vector Moving Average process) VMA(oo}:
по
Yi-; для любых j
yt, Yi-1, ...
= µ + Ф1(Уi -
~ О. Таким образом, линейный
определяется соотношением:
µ) + Ф2(Уi-1 - µ) + ... + Фp(Yi-p+l - µ).
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
171
Так что сн1 можно интерпретировать как фундаментальный оста
ток
Yt+1,
т. е. как ошибку прогноза
линейную функцию от
Матрицы Ф j в
Yt+1,
который представляет собой
Yt, Yt-1, ....
VMA( оо )-представлении
вычисляются следующим
образом:
Ф(L) = [Ф(L)]- 1
Ф(L)Ф(L)
= lm
[Im + Ф1L + Ф2L 2 + ...][Im - Ф1L- Ф2L 2 + ... - Фр.LР]
Приравнивая коэффициент при
L
= Im.
к нулевой матрице, получим:
Ф1 -Ф1 =О.
Приравнивая коэффициент при L 2 к нулевой матрице, получаем:
В общем случае, приравнивая коэффициент при
L8
к нулевой мат
рице, мы получим:
Фо
= Im,
Фs
= О при s < О.
Существует альтернативное представление в виде скользящего
среднего, основанное на VWN-пpoцeccax2 , отличных от C't. Пусть Н -
несингулярная матрица размерности
(N
х
N),
тогда
Ut
= Hct
rv
VW N
и справедливо следующее представление:
Yt
+ н- 1 нсt + Ф1н- 1 Нft-1 + ... =
µ + JoUt + JlUt-1 + J2Ut-2 + · · ·
µ
Js
= Фsн-1.
В качестве Н можно взять любую матрицу, которая диагонализи
рует О:
НОН'=
при этом случайные величины
нарный процесс
VAR(p)
Ut
D,
взаимно не корелированы. Стацио
всегда можно представить в виде скользяще
го среднего многомерного белого шума, элементы которого взаимно не
коррелированы.
2 Так
в англоязычной литературе обозначают свекторн11&е nроцесС'Ы белого шума"»
(Vector White Noise processes,
т. е VWN-процессы).
Гл.
172
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Автоковариационная функция VАR-процессов
4.2.3.
В этом разделе мы вычислим автоковариационную функцию стацио
нарного m-мерного VАR(р)-процесса. Для достижения этой цели мы
будем использовать указанное выше m'Jrмepнoe
~t
VAR(l )-представление:
= F~t-1 + Vt
Yt-µ
Yt-1 - µ
Е
[(Yt -
µ)' · · · (Yt-p+l - µ)']
Yt-p+l - µ
Го
Г1
Гр-1
г~
Го
Гр-2
г~-1 г~-2
E[~t~;]
Го
(mpxmp)
E[(F~t-1 + Vt)(F~t-1 + Vt)'] =
-
FE(~t-1~;_ 1 )F' + E(vtv;),
где воспользовались тем, что FE(~t-1V~) =О. Следовательно, мы имеем:
E=FEF'+Q.
Решение этого уравнения может быть получено при помощи опера
тора
vec,
который определяется следующим образом.
Определение
ности
q
4.6
(оператор
vec).
Пусть А
х т. Тогда вектор-столбец размерности
-
матрица размер
(qm
х
1),
получен
ный вертикальным выстраиванием столбцов матрицы А, обознача
ется как
vec(A). Воспользуемся известным фактом, а именно: пусть
А, В и С - матрицы, размерности котор'ЫХ таковы, что АБС суще
ствует. Тогда: vec(ABC) =(С'® A)vec(B), где С® А - это кроне
керово произведение матриц С и А (см., например, [Айвазян (2010)],
п. П2.8). Применяя это к нашему случаю, имеем:
vec(E) = vec(FEF') + vec(Q)
vec(E) = vec(FEF') + vec(Q)
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
173
(F ® F)vec(E) + vec(Q) =
[I(mp)2 - (F ® F)]- 1vec(Q).
vec(E)
-
Собственные значения матрицы
(F ® F) имеют вид ЛjЛj, где Ai
и Aj - собственные значения матрицы F. Если IЛ.il < 1, Vi, то все
собственные значения матрицы (F ® F) находятся внутри единичного
круга II(mp)2 - (F ® F)I =/:-О.
Автоковариация j-го порядка для {t равна:
E[{t{;_j] = FE[{t-1{;_j] + E[vt{;_j]
Ej = FEj-1
Ej = FjE j = 1,2, ....
4.2.4.
Оценивание VАR-модели
Рассмотрим гауссовски:й m-мерны:й VАR(р)-процесс
yt,
определяемый
соотношением:
yt
ct
Е
=с+ Ф1Уt-1
Nm(O; Л)
+ р)
Пусть мы имеем (Т
+ ... +
ФрУi-р
+
(4.8)
Ct
и не коррелированы по
t.
наблюдений за этим процессом. Функция
условного правдоподобия имеет вид:
fУт,Ут-1 •.. "У1IУо, ... ,У1 -р(Ут, · · ·, Y1IYo, · · ·, У1-р; 8)
8 = (с', vec( Ф1)', vec( Ф2)', ... , vec( Фn)', vес(Л)')'.
Предполагая, что
YilYi-1, ... , У-р+1
Е
N(c +
Ф1Уi-1
+ ... +
Фр'Уt-р; Л),
и используя следующие обозначения:
1
Xt=
Yt-1
Yi-p
П'
=[с
(mp+l)xl
Ф1 Ф2 . . . Ф-.....~...1
" ' ] (mx (mp+ l))
E(YilYi-1, ... , У-1+р) = П'Хt,
,
Гл.
174
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
выразим функцию условного правдоподобия для
fYtlYi-1, ... ,Y1-p(YilYi-1, · · ·, У1-р; 8)
= (2")- ':' 1n- 11! ехр ( -~ (Yi -
yt:
=
п'x,)'n- 1(Y; - п'х,)).
Совместная плотность, при условии имеющихся наблюдений Уо,
. . . , У1-р,
...
определяется соотношением:
fYt, ... ,Y1IYo, ... ,Y1-p(Yi, · · · 'Y1IY0, · · · 'У1-р; 8) = fYtlYo, ... ,Y1-p(8) Х
х fYt-1, ... ,Y1IYo, ... ,Y1-p (8).
Соответственно функция правдоподобия для полной выборки, при
заданном условии на значения Уо,
... , У1-р,
равна:
т
fYт, ... ,Y1IYo, ... ,Y1-p = п fYtlYo, ... ,Y1-p·
t=l
Соответствующая логарифмическая условная функция правдопо
добия равна:
.С(8) =
-
т;" log(21Г)+ ~ log 10- 1 1-~
т
L [(Yi -П'Xt)'n- 1 (Yi - П'Хt)].
t=l
Можно показать, что оценки параметров П, получаемые методом
максимума правдоподобия, имеют вид (выполните в качестве упражне
ния):
j-я строка матрицы
fi' равна:
Заметим, что эта оценка метода максимального правдоподобия
(ММП-оценка) совпадает с МНК-оценкой регрессии
Xt. Таким
образом, ММП-оценки находятся как МНК-оценки регрессии }'jt на кон
YJt
на
станту и р лагов всех переменных из системы. ММП-оценка матрицы
О равна:
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
. . . . = Yit
........
........
где €it
Пи
n-
-
Х'
175
...
t1Гi,T·
оценки соответствующих параметров, полученные методом
максимума правдоподобия, будут состоятельными, даже если фактиче
ские остатки Et не будут иметь гауссовское распределение.
Предполагая, что
Ф(L)Yt
Et,
е1,с2, ... ,ст
l'V
iid(O,S1) 3 ,
E[eitEjtEltEqt)
<
оо
'Vi,j, l, q,
получаем:
1~
р Q
Т
L..J XtXt1 ...:.+
= Е ( XtXt') ,
t
1Гт ~ 1Г,
где 1Гт
= vec(llт),
fi~n
v'Т'(1Гт -1Г) ~ N(O, (n ® q- 1)),
v'Т'(1Гi,Т -1Г) ~ N(O, (u~Q- 1 )),
--2
иi
=
1~ 2 р 2
Т L..J fit ...:.+ иi'
где
2
иi
2
= E(cit)·
t
Формулы для
системы
VAR,
t-
и F-статистик коэффициентов любого уравнения
полученные с использованием МНК, асимптотически
справедливы. Если нам необходимо протестировать ограничения на па
раметры, имеющие следующий вид R1Г = с, мы можем использовать
основанный на МНК х2 -тест в обобщенной форме Вальда:
v'Т'(R1Гт - с)~ N (O,R (n ® q- 1) R')'
Т(R1Гт - с)' [R (fi ® Qт 1 ) R']- 1 (R1Гт - с)=
{2(q)
(R1Гт - с)' [R (n ® (ТQт)- 1 ) R']- 1 (R1Гт - с)=
(Rifт - с)' [ R ( fi ~х,х:)- 1 ) R']- (Rifт -c) ~
1
® (
l'V
x2(q),
3 Аббревиатура
«iid~ здесь и далее используется для обозначения одинаковой
распределенности и взаимной независимости случайных величин
identically distributed). «iid
(independent and
(О; О)~ означает, что каждая из взаимнонезависимых
многомерных случайных величин Е1, .•. , Ет имеет вектор средних значений О и ко
вариационную матрицу О.
ГЛ.
176
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
где т
см.
- число столбцов матрицы R (для более детальной
[ Haya.shi (2000)] или [Liitkepohl (2005)]).
4.2.5.
информации
Функция импульсного отклика
Yi -
Предположим, что
ковариационно-стационарный
VAR(p )-процесс
(4.9)
или, что то же:
(4.10)
Этот процесс имеет, в предположении обратимости лагового опера
тора Фр(L), следующее представление в виде
Yi -
VMA(oo):
Фр(L)- 1 с + Фp(L)- 1 et
=
(4.11)
а значит:
Аналогично одномерному случаю нам интересно исследовать, как
шоки влияют на нашу систему уравнений с течением времени. Шоки в
момент времени
t
задаются вектором остатков E:'t.
Функция импульсного отклика
= О, 1, 2, ... , которая задается
это матричная функция от
-
h =
следующим образом:
дYi,t+h
дem,t
дУ.~н•
)
дУ.
i,t+h
.
до;,t ]
= [
mxm .
дem,t
Таким образом,
(i, j)-элемент
этой матричной функции отражает
реакцию переменной Yi на шок в переменной }j. А именно д~~~+h
- это
3,t
реакция значения i-й переменной в момент времени t + h на единичное
изменение шока j-й переменной в момент времени t.
Функция импульсного отклика переменной
у;. 3
дYi,t
это последовательность де.
3,t
Пр им ер
4.1
де.
3,t
, ... ,
Yi
д'Yi,t+h
де.
3,t
на шок переменной
. ...
(двумерная VАR(l)-модель без ограничений).
Предположим, что
VAR(l )-процесс:
,
дУi,tн
(Yi) -
центрированный стационарный двумерный
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
177
Для того чтобы вычислить функцию импульсного отклика, зададимся
нулевым начальным значением
Yi-1·
Кроме того, мы предположим, что
ф 1 = ( 0,5 0,3)
о
о
'
2
Без ограничения общности положим, что
Yi
.
центрирована.
А. Рассмотрим эффект единичного шока сн на Y1,t в момент време
ни
t,
предполагая нулевыми значения шоков во все последующие
моменты времени (чтобы выделить изучаемые шоковые влияния),
т.е.:
~)
C°t+l = ct+2 = · · · = (
·
Таким образом:
Yt+1 =
Ф1Уt =
Yt+2 =
Ф1Уtн =
(
0о5
~:~ ) ( ~ )
( 005
~:~ )
(
= (
~,5
~' 5 )
) = (
~,25
) .
В. Аналогично рассмотрим эффект единичного шока E2t на Y2,t в
момент времени
t
ен1 = ен2 =." = ( ~ )
·
Мы получим:
Yt+1 =
Ф1У, =
(
Ун2 = Ф 1 Ун 1 =
0о5
~:~ ) ( ~ )
= (
0 ~:~) ( ~:~ )
( 05
~:~ )
= (
~:~ )
.
Следовательно, функция импульсного отклика задается последо
вательностью
0,3 ) ( 0,25 0,21 )
( 0,5
о
02 '
о
004 , ....
'
'
ГЛ.
178
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Проблема вышеописанной проце.цуры состоит в том, что она не
учитывает возможные единовременные корреляции меж.цу компонента
ми вектора
E[ete~]
et,
= f!.
означающие недиагональность ковариационной матрицы
Несмотря на то что эта проце.цура математически коррект
на, она не позволяет получить ответ на вопрос о том, в какой мере еди
ничный шок на
}j
в момент времени
элементы
et
в момент времени
t влияет на значение переменной Yi
t + h. Эта проблема возникает в силу того, что, когда
коррелированны, мы не можем рассуждать о рассматрива
емых шоках как об изолированных, поскольку в силу корреляции мы
будем иметь мгновенное воздействие на все другие элементы вектора.
В результате, с учетом этих единовременных эффектов, было предло
жено понятие ортогонализированной функции импульсного отклика.
Ортогонализированная функция импульсного отклика
Идея ортогонализации состоит в том, чтобы исходные ошибки преоб
разовать к ортогональным, т. е. к ошибкам, ковариационная матрица
которых диагональна. Ниже представлены два подхода получения та
ких преобразований.
А. Рекурсивная ортогонализация
Любая симметричная положительно определенная матрица
f!,
со
ставленная из действительных чисел (обычно это ковариационная
матрица ошибок), может быть представлена в виде:
f! = ADA',
где
D -
диагональная матрица, на главной диагонали которой
стоят положительные числа:
dн
о
D=
о
а А
-
нижнетреугольная матрица с единицами на главной диаго-
пали:
о
1
А=
а21
1
аз1
аз2
1
1
ат1
ат2
1
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
179
Тогда ортогонализированные ошибки иt определяются как:
иt
-А-1
=
€t.
Ковариационная матрица иt равна:
Откуда мы видим, что иt ортогонализированы (не коррелирова
ны), поскольку все ко вариации (кроме диагональных) оказались
нулевыми. Теперь рассмотрим
Aut = ct,
которое в явном виде
выписывается как:
Aut
= Ct
1
о
о
о
а21
1
о
о
аз1
аз2
1
о
ат1
ат2
...
1
Откуда получаем, что
ин
= сн,
и2t
= c2t -
изt
иjt
ut
= сзt = Cjt -
итt
€mt
вычисляются по следующей схеме:
а21 ин,
аз1 ин
- аз2и2t,
ajl ин -
aj2и2t
-
... -
ajj-1 иj-Н·
Так как:
Cjt
иjt и ин,
. .. ,
= аjlин + aj2и2t + ... + ajj-1иj-H + иjt =
= E[cjtlин, ... , иj-н] + иjt,
иj-Н некоррелированны с иjt, то иjt можно интерпре
тировать как ошибку прогнозирования €jt через ин, .. . , иj-Н· Для
того чтобы получить представление с ортогональными ошибками,
мы можем следующим образом переписать
ние
(4.11)
VMA{ оо )-представле
в терминах вектора щ:
00
00
Yt = с+ LФict-i =с+ LФiAA- 1 ct-i =
i=O
i=O
00
с+ LHiиt-i,
i=O
(4.12)
ГЛ.
180
Пр им ер
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.2
(случай т =
Ф11
Hi = ФiА = Ф21
[
Ф~1
3).
Фi2 Ф!з ]
Ф~2 Ф2з
Ф~2 Ф~з
[
~1
о
1
аз1
аз2
~] =
[ Ф1 1 + "21 Ф1 2 + аз1 Ф1з Фi2 + аз2Фiз Фiз ]
Ф21 + а21 Ф22 + аз1 Ф2з Ф~ 2 + аз2Ф~ 3 Ф~з
.
Ф~ 1 + а21 Ф~ 2 + аз1 Ф~ 3 Ф~ 2 + аз2Ф~ 3 ФЗз
Рассмотрим влияние единичного шока ин на переменную У1, ко
гда с
= О:
Полагая
Таким образом, имеется один шок, действующий на
времени
t,
Yi
в момент
и отсутствуют любые прошлые и будущие шоки.
Поскольку с
= О, то (4.12) может быть записано в виде:
Поскольку все вектора иt-j(j
= 1, 2, ... ) нулевые,
~][~]
то
= [:::]
Мы видим, что шок ин оказывает мгновенное воздействие на все
компоненты вектора
Yt.
В частности,
Y2t
меняется на а21, а Узt
меняется на аз1. Отметим, что параметры (Фi) не играют никакой
роли. Это происходит потому, что корреляционная структура
полностью описывается корреляционной структурой
et,
в свою очередь, полностью определяется матрицей А.
Yi
которая,
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
В момент времени
t + 1 мы
181
имеем следующий эффект:
~] [~]
=
Влияние на значение переменной, запаздывающей на один лаг,
зависит не только от А, но и от Ф 1 · Следовательно, имеются два
источника, через которые шок на У1 в момент времени
на состояние системы в момент времени
t + 1:
t
влияет
первый источник
-
единовременная зависимость, определяемая ковариационной мат
рицей Л (представляемая через элементы матрицы А); второй
источник
-
динамическая зависимость в векторе
Yt (представля
емая матрицей авторегрессионных коэффициентов Ф 1).
Теперь рассмотрим влияние единичного шока и2t на переменную
У2:
Тогда
Yt
=
Ноиt = [ а~1
аз1
о
1
аз2
Следовательно, шок на переменную У2 имеет мгновенное воздей
ствие на переменную Уз, но не на переменную У1. Это является
следствием рекурсивной ортогона.лизации: и2 ортогона.лизирова
но относительно и1, а значит, У2 не имеет мгновенного влияния на
У1.
ГЛ.
182
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Наконец, рассмотрим влияние единичного шока Uзt на перемен
ную Уз:
Тогда
Yt =
Ноиt = [ а~1
аз1
о
1
~] [~] [~]
Мы видим, что шок на переменную Уз не оказывает мгновенного
воздействия на другие переменные, поскольку была произведе
на ортогонализация ошибки изt относительно У1 и У2. Для того
чтобы завершить этот пример, рассмотрим эффект воздействия
единичного шока изt через один период.
Влияние единичного шока изt в момент
Yt+1 = Ноин1
=
t + 1:
+ Н1 Ut + Н2иt-1 + ... =
Ф1Аиt
Очевидно, что влияние единичного шока Uзt в момент
исходит из-за структуры динамики изменения
t +1
про
yt.
Этот пример показывает тот факт, что даже при ортогонализа
ции вектора ошибок их порядок играет важное значение. Как мы
только что видели в нашем примере, если переименовать У1 на Уз,
а Уз на У1, то мы будем иметь различные функции импульсного
отклика.
Для того чтобы получить осмысленное упорядочивание перемен
ных, оно должно быть осуществлено относительно скорости ре
акции на шоки, т. е. относительно потенциальной реакции пере
менных на шоки. Переменная, отвечающая наиболее медленной
реакции, должна быть первой, второй
реакции и так далее.
-
следующая по скорости
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
183
В. Ортогонал:изация при помощи разложения Холецкого
Альтернативная схема ортогонализации осуществляется с исполь
зованием разложения Холецкого, которое для матрицы А имеет
вид:
Л
ADA'=
AD1/2n1/2 А' =
-
РР'
где Р
= AD 112 и
1/2
Dl/2
dн
...
:.
.. .
...
(
=
о
-
'
~)
матрица, составленная из стандартных отклонений иt, которые
расположены на главной диагонали. Определим
( «ортогонализи
рованную») новую ошибку Vt:
p-l€'t
Vt
=
D -112л-1 €'t.
Тогда среднее и дисперсия Vt определяются следующим образом:
E[vt]
On-1
=
n-1/2 А -1E(ete~)A -1'n-1/2 =
n-112 А -1лл -1'n-112 =
n-112 А -1 лn-112n-112 А' А -1'n-112 =
D[vt] = Е(Vt • v~) -
Im.
В этом случае ортогонализация E"t влечет то, что ковариационная
матрица «новых» ошибок будет единичной. Используя это преоб
разование и VМА(оо)-представление (см.
(4.11)),
00
Yt
=
µ+ LФiE"t-i =
i=O
00
µ+ Lфipp- 1 et-i =
i=O
00
µ+
LHiVt-i,
i=O
получим:
ГЛ.
184
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
V t --р-1.,.
<;;.t -
-_ n-1/2A-1 et·
Поскольку ut
= A- 1et,
то мы получим:
Vt
= D-l/ 2 ut =
....!!.1.L -
v'd11 -3!2.L
./d22
Последнее равенство позволяет нам увидеть, в чем разница описан
ных подходов ортогонализации. Единичный шок
vt можно интерпрети
ровать как шок величины, равной стандартному отклонению соответ
ствующего элемента исходной переменной
yt.
В противоположность этому единичный шок Ut означает, что соот
ветствующий элемент
yt
изменился на единицу независимо от ее шкалы
измерения. Следовательно, ортогонализация с использованием разло
жения Холецкого более удобна, чем рекурсивное разложение.
4.2.6.
Причинность по Гранжеру
Классической областью приложения VАR-моделей является анализ
причинно-следственных связей. Как правило, при помощи эмпириче
ского анализа весьма сложно установить те или иные эффекты воздей
ствий. Даже если имеется сильная корреляционная зависимость между
переменными Х и У, в отсутствие дополнительной информации отно
сительно эффектов nри:чинного воздействия этих переменных друг на
друга мы сказать ничего не сможем. Корреляция не всегда позволяет
определить степень влияния тех или иных переменных. В эконометрике
имеется огромное количество примеров, в которых корреляция оказы
вается либо мнимой, либо незначимой. В качестве таких примеров отме
тим следующие: положительная корреляция между зарплатами учите
лей и потреблением алкоголя; положительная корреляция между коэф
фициентом смертности в Великобритании и долей браков, заключенных
с венчальной церемонией в англиканской церкви. Экономисты продол
жают спорить относительно значимых корреляций между объективно
несвязанными переменными.
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
185
Иногда в вопросе выделения объективно связанных переменных мо
жет помочь эконометрическая теория. Но, к сожалению, теория не все
гда дает недвусмысленный ответ: в таких случаях используется опреде
ление причинно-следственной связи, которое дает возможность иденти
фицировать влияние тех или иных переменных, основываясь только на
статистических результатах. Это определение строится на следующем
принципе: при-чина всегда предшествует следствию. Другими слова
ми, если переменная Х влияет на переменную У, то это означает, что
У меняется либо мгновенно, либо через короткое время после измене
ния Х. То есть сначала происходит изменение Х, и только после этого
мы наблюдаем его эффект, т. е. изменение У. И наоборот, если Х не яв
ляется причиной изменения У, то изменения Х не влияют на будущие
значения У.
Более формально мы можем определить «при-чинно-следственную
связъ по Гранжеру» следующим образом.
Определение
Пустъ
4.7
(причинно-следственная связь по Гранжеру).
E*(Yt+slYt, Yt-1, .. .) -
наи.л.у-ч.ший {в смъtс.ле среднего квадрата
ошибки) линейнъtй прогноз для
Yt+s, построеннъtй толъко по прошлъш
зна-ч.ениям переменнъtх У, а E*(Yt+slYt, Yt-1, ... , Xt, Xt-1, .. .) - наи
лу-ч.ший (в том же смъtс.ле) линейнъtй прогноз для Yt+s, построеннъtй
по nрошл'ЬIМ зна-ч.ениям переменной У и Х. Мъt говорим, -что Х не
влияет на У (по Гранжеру), ее.ли
E[(Yt+s - E*(Yt+slYt, Yt-1, .. .)) 2 ] =
= E[(Yi+s - E*(Yi+slYi, Yi-1, ... ,Xt, Xt-1, ... , )) 2 ].
Ее.ли Х не влияет на У по Гранжеру, то мъt будем писатъ:
а ее.ли Х влияет на У по Гранжеру, то будем nисатъ:
х--+ У.
Причинность в двумерных VАR-системах
Рассмотрим двумерный VAR(l)-пpoцecc:
+ Ф1,1У1,t-1 + Ф1,2У2,t-1 + €'1,t,
с2 + Ф2,1У1,t-1 + Ф2,2У2,t-1 + e2,t,
С1
(4.13)
ГЛ.
186
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
где ковариационная матрица слабого белого шума (e1,t,€2,t) 1 определя
ется следующим образом:
Л=
(
ан а12 ) .
а21
а22
Более того, рассмотрим регрессии каждой из переменных времен
ных рядов
(}j,t), j = 1, 2,
на его прошлые значения:
+ Ф1,1У1,t-1 + €1,t,
с2 + Ф2,1У2,t-1 + €2,t·
с1
Yit
'
(4.14)
Рассмотрим также следующие регрессии:
- + 'Ф2,0У1,t + 'Ф2,1У1,t-1 + 'Ф2,2У2,t-1 + €2,t·
-
с2
Y2,t -
(4.15)
Мы будем говорить, что:
(i) У2 «не влияет на
Yi.
по Гранжеру» тогда и только тогда, когда
наилучший линейный прогноз
зависит от
Y2,t-l·
Y1,t
при заданном значении
Y1,t-1
не
Для VAR(l)-пpoцecca эта гипотеза эквивалент
на гипотезе о равенстве нулю коэффициента Ф1,2 в соотношении
(4.13):
Но
:
У2-.'+ У1 # Ф1,2 =О#
D[ei,t]
=
D[e1,t]
против
Н1
(ii)
:
нулевая гипотеза неверна;
соответственно, «У1 не влияет на У2 по Гранжеру» тогда и толь
ко тогда, когда наилучший линейный прогноз для
ном
Y2,t-1
не зависит от
Y1,t-1·
Y2,t
при задан
Для VAR(l)-пpoцecca эта гипотеза
эквивалентна гипотезе о равенстве нулю коэффициента Ф2,1 в со
отношении
(4.13):
Но
:
У1
-.'+ У2 #
Ф2,1 =О#
D[e2,t]
=
D[e2,t]
против
Н1
:
нулевая гипотеза неверна;
(iii) «переменна.я У1 не оказъtвает мгновенного влияния на У2» тогда
и только тогда, когда наилучший линейный прогноз для
Y2,t
при
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
заданных У1
t, У1 t-1, У2 t-1
'
'
Но
'
У1
:
не зависит от У1
t·
'
Это означает, что:
#
and 'Ф1,о = О #
D[Й2,t] = D[e2,t] и D[Йi,t] = D[ei,t]
#
и12
#
det E(ei,t) =
+.t-+
187
У2 :# 'Ф2,о = О
#
= и21 = О #
e2,t
De1 t · De2 t
'
'
против
Н1 :
(iv)
нулевая гипотеза неверна;
«отсутствие линейной связи между переменной У1 и У2~ опре
деляется выполнением всех трех упомянутых выше нулевых ги
потез, а именно:
Но
:
У1 ~ У2 :# {У1 -т+ У2}
#
detE(11,t) =
n {У2
-т+ У1}
n {У1
+.t-+
У2} #
D€1,t · D€2,t
i2,t
против
Н1 :
нулевая гипотеза неверна.
Тест отношения правдоподобия при проверке наличия
причинности по Гранжеру
При тестировании справедливости гипотезы о параметрических ограни
чениях для одного или нескольких уравнений можно использовать тест
отношения
правдоподобия
(ОП-тест).
При
проверке
причинно
следственной связи по Гранжеру требуется тестирование нулевых огра
ничений определенных параметров VАR(р)-процесса. Для этого мы мо
жем воспользоваться ОП-тестом. Как мы увидим ниже, ОП-тест имеет
весьма привлекательную интерпретацию в терминах дисперсий ошибок
прогнозирования модели с ограничениями и без них. Для того чтобы по
казать это, нам необходимо вначале описать построение функции прав
доподобия для модели с ограничением, которую мы будем использовать
при вычислении ОП-статистик.
Рассмотрим стандартную модель линейной регрессии с нормальны
ми ошибками
yt = XtfЗ + et,
(t = 1, ... Т),
""d
где et iE N(O, и 2 ). Логарифмическая функция правдоподобия для соответствующих нормально-распределенных
yt
определяется следующим
ГЛ.
188
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
выражением:
т
ln L(,8, и 2 )
L ln f(YtlXt, ,8, и2 ) =
-
t=l
-
~ ln{21Г) - ~ lnu2 - 2 ~ 2 (У - Х,В)'(У - Х,8).
Условие первого порядка для экстремума функции ln L(,8, и 2 ) принима
ет вид:
дL(р,а-2)
д,8
-
дL(р,а-2)
1
'
~ х (У
О'
т
- 20- 2
ди2
А = о,
- х ,8)
+ 20-14 (У -
А
Х,8) (У
'
-
А
Х,8) =О.
Решая второе уравнение относительно &2 , получаем:
О-2 = т(Р) =~(У - ХР)'(У - ХР).
Таким образом, оценка максимума правдоподобия (МП-оценка) для
и 2 может быть представлена как функция от МП-оценки для
,8. Заме
няя в логарифмической функции правдоподобия lnL{P,& 2 ) величину
О- 2 на т{Р), получим:
т
--ln
2
т
(1
-(У
т
-
'
Х,8) (У -Х,8)
т
- 2 ln{21Г) - '2 -
т
) - -т - т
2
-ln{21Г)
2
=
А
2 1n{т(,8)).
Таким образом, в условиях нормальности, заменив в логарифмиче
ской функции правдоподобия ln L(P, О- 2 ) величину &2 на т{Р), мы можем
выразить функцию правдоподобия как функцию, зависящую только от
оценки дисперсии ошибки прогнозирования.
Теперь рассмотрим задачу максимизации правдоподобия с
ограничениями, в которой мы хотим оценить
,8
методом максимума
правдоподобия, учитывая при этом q нелинейных ограничений,
= О.
Более формально: ищем оценки для
,8
h(,8) =
и и 2 из условия
max ln L(,8, и 2 ) при ограничениях h(,8) = О,
fJ,
где
q2
h(,8) = (h1(,8), h2(,8), ... , hq(,8))' -
мерности
q.
векторнозначная функция раз
Функция Лагранжа этой задачи имеет вид:
.С= ln L(,8, и 2 ) - Л'h(,8),
4.2.
где Л.'
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
= (Л.1, Л.2, ... , Лq) -
189
вектор множителей Лагранжа.
Условие первого порядка упомянутой выше задачи максимизации с
ограничениями принимает следующий вид:
ainL(PR,uh) _ ah(PR)' _х
а.с
а13
а13
а13
au2
а.с
ал
(4.16)
2
А
а.с
=0
ainL(/3R,uR) =о
au2
(4.17)
h(PR) =о.
(4.18)
Решая уравнение а.с/аи 2 =О относительно uh, мы снова получим
оценку дисперсии ошибок прогнозирования в терминах оценки
/3,
но те
перь уже при максимизации функции правдоподобия с ограничениями:
2
uR =
А
т(f3R)
=
1
Т(У
А
- Xf3R)
'
(У
А
- Xf3R)·
Подставляя т(РR) в функцию правдоподобия для модели с ограни
чениями, имеем:
InLcR -
InL(PR,т(f3R))
=
л2
- - 2Т In(21Г) - 2т - 2т inuR.
Рассмотрим задачу получения оценок методом максимума правдо
подобия в общем случае, для k-мерного векторного параметра(). Стати
стика теста отношения правдоподобия при проверке нулевой гипотезы
h(())
=
О против альтернативы, что нулевая гипотеза неверна, имеет
вид:
LR = 2(ln L(Bu) - ln L(BR)) ~ х~,
(асимптотически по числу наблюдений), где q -
число ограничений,
q ~ k (k - размерность вектора 8u).
Рассмотрим стандартную регрессионную модель с ограничениями
на векторный параметр
/3.
Используя указанные выше результаты, по
лучаем, что статистика отношения правдоподобия принимает вид:
LR
ГЛ.
190
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Если оценки дисперсии ошибок прогнозирования для модели с огра
ничениями и без них близки друг к другу, тогда статистика отношения
правдоподобия принимает значения близкие к нулю, и мы не откло
няем нулевую гипотезу. Отметим, что тест отношения правдоподобия,
примененный к выявлению причинно-следственных связей по Гранже
ру, сравнивает оценки дисперсий ошибок двух линейних прогнозов, в
одном из которых предполагается отсутствие влияния по Гранжеру (мо
дель с ограничением), а в другом
-
влияние по Гранжеру учитывается
(модель без ограничений}.
Тестирование влияния по Гранжеру
Гипотезы о наличии влияния по Гранжеру может быть легко провере
на при помощи статистики отношения правдоподобия, построенной на
основании соответствующих регрессий
•
(4.13)-(4.15}:
тестирование влияния У2 на У1 по Гранжеру, где нулевая гипотеза
состоит в том, что У2 ~ У1:
t]
D€1 ' ;
С2-н1 = log [ - D
e1,t
•
тестирование влияния У1 на У2 по Гранжеру, где нулевая гипотеза
состоит в том, что У1 ~ У2:
•
тестирование мгновенного взаимовлияния У1 и У2, где нулевая ги
потеза состоит в том, что У1
+;<+
У2:
Используя введенные выше меры, получаем следующую формулу раз
ложения:
Заменяя теоретические дисперсии ошибок соответствующими оценками, т. е.
- e1,t
D
62-н1, 61-н2,
""'т eА21,t
= т-1 L.,,t=l
61-2
и
и т. д., мы получим оценки мер влияния
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
191
При нулевой гипотезе, состоящей в том, что У1 +..+ }2, статистики ТС2 ...... 1,
ТС1 ...... 2, ТС1-2 асимптотически независимы, а их предельные распреде
ления, при Т
--+
оо, совпадают с распределением х 2 {1). Таким обра
зом, распределение тестовой статистики ТС1Ф2 асимптотически, при
т--+ оо, совпадает с распределением х 2 {3).
4.2.7.
Выбор порядка VАR-модели
Перед тем как использовать VАR(р)-модель, нам необходимо оценить
структурный параметр модели, т. е. выбрать порядок этой модели р.
Этот выбор может быть основан на многомерных аналогах информа
ционных критериев, указанных ниже.
• Информационн:ый критериий Акаике (AIC):
А
2pm2
AIC(k) = ln{det(f!)) + ---т-·
• Вайесовский информационнь~й критерий (BIC) или информаци
онный критерий Шварца
(SIC):
А
BIC(k) = ln{det{f!)) +
pm2 InT
Т
.
• Информационнъ~й критерий Хэннана - Квина {HQ):
HQ(k) = ln(det(n)) + 2pm2 ~{lnT),
где
n = 1/т 2:Х=· 1 €t€~ -
оценка ковариационной матрицы вектора
остатков, построенной по остаткам оцененной VАR-модели р-го
порядка, т
-
размерность наблюдений, Т
Кроме того, мы предполагаем, что Et Е
- число
N{O, f!).
наблюдений.
Если основной целью является качество прогнозирования, то имеет
смысл выбирать этот порядок р таким, чтобы мера погрешности про
гнозов была минимальной. В качестве такой меры может быть исполь
зован СКО (средний квадрат ошибки). В результате мы приходим к
так называемому критерию ошибки прогнозирования
criterion -
(prediction error
РЕС), определяемого следующим образом:
• критерий ошибки прогнозирования {РЕС):
РЕС(т) = det [Т+тр+ 1 .
Т
Т
Т-тр-1
= [T+mp+l]m det(n).
Т-тр-1
. n]
ГЛ.
192
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Если порядок р увеличивать, то det(n) будет уменьшаться, а мно
житель (Т+тр+ 1)/(Т-тр-1) увеличиваться. Оценка порядка VАR
модели выбирается таким образом, чтобы значения двух составляющих
критерий множителей были оптимально сбалансированы.
Когда стоит задача выбора корректной оценки VАR-модели, имеет
смысл использовать ту оценку, которая обладает в некотором смыс
ле «наилучшими» выборочными свойствами. Для нас в этом разделе
основной интерес представляют статистические свойства таких оценок
параметра р, как, например, р( РЕС) и
p(AIC).
Необходимо, чтобы вы
бираемая оценка обладала, как минимум, свойством состоятельности.
Напомним, что оценка р параметра р VАR-модели называется состо.я
те.л:ьной, если
lim Р{р=р} = 1.
Т~оо
Оценку р называют сильно состоятельной, если
Р{
lim р=р}
Т~оо
= 1.
Мы будем называть критерий выбора состоятельным или сильно
состоятельным, если оценка порядка VАR-модели, получаемая с ис
пользованием этого
критерия,
состоятельна или сильно состоятельна
соответственно. К сожалению, можно показать, что оценки р(РЕС) и
p(AIC)
несостоятельны. Однако критерий
ятельным, а критерий
SIC
HQ
все же является состо
является сильно состоятельным. Если раз
мерность т наблюдений превышает единицу, то критерии
SIC
и
HQ
являются сильно состоятельными (доказательство см., например, в ра
боте
[Liitkepol (2005))).
Несмотря на то что в общем случае достаточно трудно оценивать
свойства оценок, построенных по малым выборкам, для упомянутых
выше критериев некоторые свойства все-таки можно получить. А имен
но:
p(SIC)
p(SIC)
p(HQ)
~
~
~
p(AIC),
p(HQ),
p(AIC),
если Т ~
8,
для всех Т,
если Т ~
16.
Важно отметить, что этот результат не требует стационарности
yt.
Более того, еще раз подчеркнем, что этот результат справедлив для
малых выборок (см.
[Liitkepol (2005))).
В качестве альтернативного подхода для выбора корректного зна
чения порядка VАR-модели можно использовать тест отношения прав
доподобия. Пусть
Yt
yt - ковариационно-стационарный VАR(М)-процесс
=
с+ Ф1Уt-1
+ ... + ФмУt-м + et,
4.2.
где М
-
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
193
верхняя граница для порядка VАR-модели. Следующую по
следовательность нулевых и альтернативных гипотез можно протести
ровать при помощи теста отношения правдоподобия:
н1
о
Фм=О
против
Hj:
н2
о
Фм-1 =О
против
н~: Фм-1
н&
Фм-н1 =о
против
нf: Фм-н1 "!- ОIФм = ...
... = Фм-н2 =О
Ф1
против
нf: Ф1
... = Ф2
=0
Фм #-О
"!- ОIФм =о
"!- ОIФм =
...
=О.
{4.19)
В этой схеме каждая нулевая гипотеза тестируется при условии, что
предыдущая нулевая гипотеза верна. Процедура прерывается на k-м
шаге, если отвергается соответствующая этому шагу нулевая гипотеза,
т. е., если отвергается Н~. В этом случае оценка порядка VАR-процесса
берется равной р
=
М
- i
+ 1.
Статистика отношения правдоподобия
для тестирования i-й нулевой гипотезы равна:
LR(i) = T[ln lsl{M - i)l - ln lsl{M - i
Асимптотически
эта
статистика
при
+ 1)1].
{4.20)
справедливости
нулевой
гипотезы имеет Х~ 2 -распределение. Кроме того, можно использовать
статистику LR(i)/m2 , которая при справедливости нулевой гипотезы
асимптотически имеет F{m2 , Т- т(М - i + 1) - 1)-распределение.
Выбор адекватных уровней значимости при схеме тестирования
{4.19)
является весьма трудной задачей, поскольку необходимо учиты
вать различия между общим и индивидуальным уровнями значимо
сти. Следует отметить, что если последовательность тестируемых ги
потез достаточно велика, то фактическая вероятность отклонить спра
ведливую нулевую гипотезу тоже достаточно велика. Более того, Х~ 2 распределение годится только как асимптотическое распределение. Та
ким образом, выбранные уровни значимости будут аппроксимировать
лишь вероятности ошибок первого рода. Кроме того, процедура по
следовательного
тестирования
не
позволяет
получить
состоятельную
оценку порядка VАR-модели, если последовательность индивидуаль
ных уровней значимости состоит из постоянных значений. Для того
чтобы показать это, необходимо заметить, что для М
>р
и фиксиро
:
Фм
=
ванного уровня значимости а нулевая гипотеза Но
О отвер
гается с вероятностью а. Следовательно, указанная процедура после-
194
ГЛ.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
довательного тестирования дает некорректную оценку порядка VАR
модели, равную Мс вероятностью а. А это означает, что существует
положительная вероятность выбора слишком большого значения для
порядка VАR-процесса. Эту проблему можно преодолеть, полагая, что
уровень значимости стремите.я к нулю при Т ~ оо.
После ряда исследований на примерах смоделированных данных
мы все еще не можем получить ясного ответа на вопрос относительно
того, какой критерий следует использовать в условиях малых выбо
рок (см., например,
[Liitkepol (2005))). Один из выводов, который мож
но сделать из этих исследований, состоит в том, что в условиях очень
малых выборок небольшая недооценка фактического значения поряд
ка VАR-процесса не столь опасна для точности прогнозов. Более того,
х 2 -аппроксимация для LR-статистики в условиях малых выборок не
слишком хороша. Следовательно, наилучшей стратегией представляет
ся сравнительный анализ оценок порядка р VАR-процесса, полученных
с использованием различных критериев и, возможно, прогнозного ана
лиза, основанного на различных значениях порядка VАR-процесса.
4.2.8.
Анализ остатков VАR-моделей
В предыдущем разделе мы рассматривали критерии выбора оптималь
ного порядка VАR-модели. В этом разделе мы сосредоточимся на про
цедурах проверки предположения о белом шуме для остатков рассмат
риваемой модели. Такая проверка необходима, например, в случае, ес
ли порядок модели выбран на основании экономической теории. Но,
поскольку разные методы отражают различные особенности генери
рующего данные процесса и каждый из них позволяет исследователю
получить полезную информацию, то, как правило, рекомендуется при
оценке модели полагаться не на одну процедуру, а на совокупность раз
личных статистических инструментов.
Тесты Портмант6
(Portmanteau Tests)
Эти тесты представляют собой многомерные аналоги одномерных те
стов Бокса- Пирса/ Льюнга- Бокса. Нулевая гипотеза здесь состоит в
том, что автокорреляция до h-го порядка рассматриваемого временного
ряда (остатков) равна нулю.
Пусть через
€t
обозначены оцененные остатки VАR(р)-процесса, то
гда автоковариационная матрица для
зом:
€t
оценивается следующим обра-
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
195
Соответственно, оценка автокорреляционной матрицы для
€t дается
4.2.
формулой:
~ ==
где
D-
:0- 1 ci:0- 1 ,
i = о, 1, ... , h,
диагональная матрица размерности (п х п), в которой диаго
нальные элементы равны квадратным корням соответствующих диаго
нальных элементов матрицы Со.
Портмант6-тест используется для проверки гипотезы:
против альтернативы
Н1: нулевая гипотеза не выполняется,
а тестовая статистика вычисляется по формуле:
Модифицированная версия этого теста
га- Бокса, предложенный в работе
- многомерный тест Льюн
[Hosking (1980)), который является
многомерной версией одномерного теста Льюнга- Бокса. Статистика
для теста Льюнга- Бокса определяется сле,цующим образом:
При справедливости нулевой гипотезы, состоящей в том, что серий
ная корреляция до h-го порядка включительно равна нулю, обе стати
стики асимптотически имеют х 2 -распределение с количеством степеней
свободы, равным m 2 ( h - р), где р - порядок VАR-модели, а
прежде,
-
m, как и
размерность анализируемого временного ряда.
Результаты исследования показали, что многомерный тест Льюн
га- Бокса оказывается более качественным в условиях малых выбо
рок. Как тест Портмант6, так и тест Льюнга-Бокса реализованы в
стандартных классических статистических пакетах. Для практических
целей важно помнить, что х2 -аппроксимация функции распределения
тестовой статистики может оказаться неприемлемой при малых зна
чениях Т. Для более подробной информации см., например, работы
[Davies,
Тriggs,
[Ahn (1988)].
Newbold (1977)), (Ljung,
Вох
(1978)), [Hosking (1980))
и
ГЛ.
196
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Тесты множителей Лагранжа
Другой способ тестирования автокорреляции остатков основан на пред
положении о том, что вектор ошибок описывается при помощи VАR
модели, т. е. et
=
Г1еt-1
+ ... + Гhet-h + Vt,
где Vt -
белый шум. По
следовательность et сама является белым шумом, если Г1
=
= Г2 = ... =
Гh =О. Таким образом, нулевая гипотеза и ее альтернатива опреде
ляются следующим образом:
Но
Г1
= ... = Гh = О,
Н1
Гj
=1 О
для хотя бы одного значения
j Е {1, ... , h}.
В этом случае для построения теста удобно использовать принцип
максимального правдоподобия (МП). Тестовая статистика для порядка
h VАR-модели
вычисляется при помощи вспомогательной регрессии ос
татков на исходные регрессоры и лагированные до h-го порядка остат
ки:
Формулу для МП-статистики см. в
[Liitkepol, (2005)]
с.
[Johansen (1995)],
с.
22, или
171-172. При справедливости нулевой гипотезы,
которая состоит в отсутствии серийной корреляции, МП-статистика
асимптотически имеет х 2 -распределение с hm2 степенями свободы.
Тесты на нормальность
Процедуры тестирования на нормальность обычно строятся с исполь
зованием оцененных остатков, а не исходных наблюдений
yt.
Это про
исходит потому, что в противном случае эти тесты могут быть менее
мощными.
.....
Пусть Р и Р
-
матрицы факторизации размерности т х т кова-
риационной и выборочной ковариационной матриц остатков, соответ
ственно такие, что РР' =
n и Р стремится (по вероятности) к Р при
росте числа наблюдений. Определим
А
(Ь11,
А
... , Ьт1)
'
с
i= 1, ... ,т,
i= 1, ... ,т.
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
Тогда можно показать, что (см., например,
[Liitkepol (2005)],
197
п.
4.5.2):
(4.21)
(сходимость по распределению).
Откуда следует, что
(4.22)
(4.23)
~sk
л
Лs
л
d
2
+ Лk --+ X2m ·
(4.24)
Все три приведенные выше тестовые статистики могут быть исполь
зованы для
..... тестирования нормальности. Отметим, что матрица факто-
ризации Р неединственна, а следовательно, тесты в некоторой степени
.....
будут зависеть от их выбора. На практике, если найдено какое-то Р,
для которого нулевая гипотеза отвергается, то это указывает на то, что
процесс не является нормально-распределенным.
4.2.9.
Эмпирические приложения с использованием
пакета
Eviews
Если мы откроем рабочий файл под названием
Tutorial_VAR. vf1,
то в
нем обнаружим наблюдения за следующими переменными (кварталь
ные данные).
Переменная
Описание
Inv
Inc
Cs
Данные по объему инвестиций в США за период
у1
dlog(inv) 1960:q2-1982q4
dlog(inc) 1960:q2-1982q4
dlog(cs) 1960:q2-1982q4
Данные о доходах в США
Данные по потреблению в
у2
уз
1960:ql-1982q4
за период 1960:ql-1982q4
США за период 1960:ql-1982q4
Наша цель состоит в написании программы в среде пакета
Eviews,
которая позволила бы решить следующие задачи:
1.
Оценить VАR-модель 2-го порядка для вектор-наблюдений, со
ставленных из переменных У1, У2, Уз, взятых за период с
по
2.
1960:1
1978:4.
Оценить результаты использования описанных выше критериев
выбора порядка VАR-модели
(LR, AIC, SC, HQ).
ГЛ.
198
3.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Оценить VАR-модель 3-го порядка и представить результаты те
ста Вальда лаговых исключений для оцененной VАR-модели.
Требуемый для этого код представлен ниже:
' estimate VAR
smpl 1960:1 1978:4
var var1.ls 1 2 у1
у2 уЗ ~ с
' lag length criteria
freeze(tab45) var1.laglen(4,vname=vlag,mname=mlag)
shov tab45
'Lag exclusion tests
var var1.ls 1 З у1 у2 уЗ ~ с
freeze(taЫ) var1.testlags(name=lags)
shov tаЫ
Ограничиваясь целями нашей задачи, мы представим только ре
зультаты использования критериев выбора длины лага.
Информационные критерии, представленные в табл.
4.1,
построены
с использованием значения функции правдоподобия и без учета кон
станты в VАR-модели. Однако после включения константы значения
AIC, HQ, and SC
Таблица
Lag
о
1
2
3
4
4.1.
в таблице
4.1
будут иными.
Информационные критерии
VAR Lag Order Selection Criteria
Endogenous variaЫes: Yl У2 УЗ
Exogenous variaЬles: С
Date: 04/22/03 Time: 00:22
Sample: 1960:1 1978:4
lncluded oЬservations: 71
LogL
LR
FPE
AIC
HQ
sc
564.7842
NA
2.69Е-11
-15.82491
-15.7293*
-15.78689*
2.50Е-11
-15.89884
-15.51641
-15.74676
576.4087
21.93905
22.44588*
2.27Е-11*
588.8591
-15.9960*
-15.32679
-15.72989
591.2373
4.086484
2.75Е-11
-15.80950
-14.85344
-15.42931
2.91Е-11
598.4565
11.79471
-15.75934
-14.51646
-15.26508
* indicates lag order selected Ьу the criterion
LR: sequential modified LR test statistic (each test at 5% level)
FPE: Final prediction error
AIC: Akaike information criterion
SC: Schwarz information criterion
HQ: Hannan-Quinn information criterion
Теперь мы хотим написать программу в
Eviews,
которая бы произ
водила диагностику остатков VАR-модели. Для коррелограммы (авто
корреляции) остатков следует помнить, что
EViews
позволяет сделать
выводы, справедливые лишь в асимптотическом смысле.
Для диагностики модели ставятся следующие задачи:
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
1.
Оценить VАR-модель 2-го порядка.
2.
Оценить коррелограмму остатков.
3.
Применить тест Портмант6.
4.
Применить тест на нормальность.
' estimate VAR of order 2
smpl 1960:1 1978:4
var var1.ls 1 2 у1 у2 уЗ ~
199
с
' residual correlograms (Fig 4.2, р.149)
freeze(fig42) var1.correl(12,graph)
shov fig42
' portmanteau test (р.152)
freeze(tab_p152) var1.qstats(12,name=qstat)
shov tab_p152
' normality test (р.158)
freeze(tab_p158) var1.jbera(factor=chol,name=jbera)
shov tab_p158
Наконец, мы напишем программу, которая позволяет решать сле
дующие задачи:
1.
Оценить VАR-модель.
2.
Построить прогноз по оцененной VАR-модели. Для этого нам необ
ходимо изменить объем текущей выборки с учетом выделенно
го периода прогнозирования, т. е. с учетом периода
1980: 1,
smpl 1979 : 1
после чего, пользуясь оцененной моделью по суженной
выборке, получить динамические прогнозы.
3.
Изобразить фактические значения и их прогнозы. Объединить все
графы в один.
Требуемый код приведен ниже:
' estimate VAR
smpl 1960:1 1978:4
var var1.ls 1 2 у1
у2 уЗ ~ с
' replicates р.72, (З.2.22) t (З.2.24)
' note that the variaЬles are ordered differently
freeze(out1) var1.output
shov out1
' make model out of estimated VAR
var1.makemodel(mod1)
' change sample to f orecast period
smpl 1979:1 1980:1
200
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
' solve model to obtain dynamic forecasts
mod1.solve
' plot actual and forecasts
smpl 1975:1 1980:1
for !i=1 to var1.Фneqn
group gtmp y!i y!i_O
freeze(gra!i) gtmp.line
Y.gname = Y.gname + "gra"+ str(!i)
next
Таблица
4.2.
Тесты Портмант6
VAR Residual Portmanteau Tests for Autocorrelations
НО: no residual autocorrelations up to lag h
Date: 04/21/03 Time: 23:39
Sample: 1960:1 1978:4
lncluded observations: 73
Lags
Q-Stat
Prob.
Adj Q-Stat
NA*
0.933556
1
0.920768
NA*
2
2.044941
2.089396
9.328680
0.4075
9.685295
3
4
21.03897
0.2775
22.07444
26.38946
0.4971
5
27.81836
30.77054
0.7154
32.59177
6
0.8416
37.90683
35.57594
7
44.83454
0.8085
48.30495
8
48.27351
0.9147
52.22752
9
10
56.81194
0.9051
62.12126
11
66.09500
0.8846
73.05132
73.51723
0.8966
81.93365
12
*The test is valid only for lags larger than the VAR lag order.
df is degrees of freedom for (approximate) chi-square distribution
Таблица
4.3.
Prob.
NA*
NA*
0.3766
0.2287
0.4204
0.6315
0.7642
0.6928
0.8315
0.7904
0.7235
0.7157
Тесты на нормальность
VAR Residual Normality Tests
Orthogonalization: Cholesky (Lutkepohl)
НО: residuals are multivariate normal
Chi-sq
Component
Skewness
1
0.119351
0.173310
2
-0.383159
1.786194
-0.312723
1.189845
3
Joint
3.149350
df
1
1
1
3
Prob.
0.6772
0.1814
0.2754
0.3692
Component
1
2
3
Joint
Kurtosis
3.933079
3.739590
2.648386
Chi-sq
2.648186
1.663770
0.376049
4.688005
df
1
1
1
3
Prob.
0.1037
0.1971
0.5397
0.1961
Component
1
2
3
Joint
Jarque-Bera
2.821496
3.449965
1.565894
7.837355
df
2
2
2
6
Prob.
0.2440
0.1782
0.4571
0.2503
df
NA*
NA*
9
18
27
36
45
54
63
72
81
90
4.2.
МОДЕЛИ ВЕКТОРНОЙ АВТОРЕГРЕССИИ (VАR-МОДЕЛИ)
201
Autocorrelations with 2 Std.Err. Bounds
Col(Yl.Yl!·i))
·1
·1
.,
_,
. ·--.-.--..-.-.-..-..-
"
1
:!
)
"
'
6
7
......................
8
Col(YI. Y3(-i))
Col(YI. Y2(·il)
9
10 11
-1
_,
_ ..... ..... .......... ..................... " _
_, ....., .-
1
1:!
2
.а
'
Col(Y2.Yl(·i))
s
ь
..-
1
а
•
10 11
12
1
_,.....,.....,......-............-.....................
2
J
"
s
6
7
•
9
10 11
12
Col(Y2. УЭ(-i))
Col(Y2. Y2(-i))
.!
•.1
·•
"
. ·--.-.--..--r-r-т-т--т--т--r--т-'
1 :! J .а 5 6 1 а • 10 11 12
_
"
" _,..........,......-............-.....................
1
2
·'
"
Col(Y3.Yl(-i))
s
6
7
•
9
10 11
. · - - ............,.-.-.......-т-..--т--r--т-'
12
1
2
J
"
Col(Y3.Y2(-i))
s • '
•
9
10
11
12
Col(Y3. Y3(-i))
·1
.,
_
"
. ·--.-.--..-.-r-т-т--т--т--r--т-'
1
:!
J
"
5
6
'
1
9
10 11
1:!
Рис.
" _,.....,.....,
......-............-.....................
J • s
" _ _,..........,......-..-..-+-..--т--r--т-'
1 2 J .а
s 6 1 а • 10 11 12
4.1.
1
2
6
'
Графики автокорреляций
.10
.08
.116
.см
.сп
.оо
-.сп
-.СМ
197S
1975
1--- YI
-
1976
1--- У2
YI (8a•ellle)I
1977
-
.см..-----------------.
.03
.02
'
ii'
ЛI
.00
•'
"•'
·······-···············································~·····
t
197S
1976
1--- УЗ
1977
-
1978
1979
Y318a•einell
Рис.
4.2.
Прогнозы VАR-модели
1978
У2 (8a•eine)I
1979
•
•
10 11
12
Гл.
202
Таблица
4.4.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Результаты оценивания VАR-модели
Vector Autoregression Estimates
Sample(adjusted): 1960:4 1978:4
Included observations: 73 after adjusting endpoints
Standard errors in ( ) & t-statistics in [ ]
Yl
У2
Yl(-1)
-0.319631
0.043931
(0.12546)
(0.03186)
(-2.54774]
[ 1.37891]
УЗ
-0.002423
(0.02568)
(-0.09435]
Yl(-2)
-0.160551
(0.12491)
(-1.28537]
0.050031
(0.03172)
[ 1.57728]
0.033880
(0.02556)
[ 1.32533]
У2(-1)
0.145989
(0.54567)
[ 0.26754]
-0.152732
(0.13857)
(-1.10220]
0.224813
(0.11168)
[ 2.01305]
У2(-2)
0.114605
(0.53457)
[ 0.21439)
0.019166
(0.13575)
[ 0.14118)
0.354912
(0.10941)
[ 3.24398)
У3(-1)
0.961219
(0.66431)
[ 1.44694]
0.934394
(0.66510)
[ 1.40490]
0.288502
(0.16870)
[ 1.71015]
-0.010205
(0.16890)
(-0.06042]
-0.263968
(0.13596)
(-1.94151]
-0.022230
(0.13612)
(-0.16331]
-0.016722
(0.01723)
(-0.97072)
R-squared
0.128562
Adj. R-squared
0.049340
Sum sq. resids
0.140556
S.E. equation
0.046148
F-statistic
1.622807
Log likelihood
124.6378
-3.222954
Akaike AIC
Schwarz SC
-3.003321
Mean dependent
0.018229
S.D. dependent
0.047330
Determinant Residual Covariance
Log Likelihood (d.f. adjusted)
Akaike Information Criteria
Schwarz Criteria
0.015767
(0.00437)
[ 3.60427]
0.114194
0.033666
0.009064
0.011719
1.418070
224.6938
-5.964214
-5.744581
0.020283
0.011922
0.012926
(0.00353)
[ 3.66629)
0.251282
0.183217
0.005887
0.009445
3.691778
240.4444
-6.395737
-6.176104
0.019802
0.010451
УЗ(-2)
с
4.3.
1.66Е-11
595.2689
-15.73339
-15.07449
Структурные VАR-модели (SVАR-модели)
В последние годы модели структурной векторной авторегрессии
(SVAR)
стали весьма популярным инструментом анализа механизмов монетар
ного перехода и источников флуктуаций бизнес-циклов. Методология
4.3.
SVAR
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
203
на сегодняшний момент реализована в широком списке стан
дартных эконометрических программных пакетов (например, в паке
тах
EViews
или
RATS),
что делает возможным достаточно простое ее
использование4 .
Следует отметить, что тематика
SVAR-
и VАR-моделей тесно свя
зана с тематикой моделей, представляемых в форме систем линейн:ых
одновременнъ~х уравнений (так называемых СОУ-моделей). Последним
посвящен п.
4.4
нашего учебника. Действительно, как будет видно поз
же, структурная и приведенная формы СОУ-модели отличается, соот
ветственно, от
деленного
SVAR-
количества
гированными
и VАR-модели лишь присутствием в СОУ опре
экзогенных
эндогенными
переменных,
переменными
у
которые
составляют
мые предопределенные переменнъ~е (см. ниже, п.
4.4).
вместе
так
с
ла
называе
Так что формаль
но всякую СОУ-модель можно представить в соответствующих терми
нах
SVAR-
(структурная форма СОУ) и
СОУ) модели (см., например,
VAR- (приведенная форма
[Diebolt (1998)]). Однако специфика СОУ
моделей обусловливает правомерность выделения этого класса моделей
для специального (автономного) описания.
В изложении п.
4.3.1-4.3.4 с любезного согласия автора использу
ются результаты Эрика Зиво (Eric Zivot), см. http://faculty.washington.
edu/ezivot/econ584/notes/svarslides.pdf, а также
http://faculty.washington.edu/ezivot/econ584/notes/svarslides2.pdf
4.3.1.
Представление в структурной и приведенной
формах
Рассмотрим структурную
Ун
Y2t
-
VAR
(SVАR)-модель вида:
+ 1'11Y1t-1 + ')'12Y2t-1 + t:н,
Ь21Ун + 1'21Y1t-1 + ')'22Y2t-1 + t:2t,
1'10 - Ь12У2t
')'20 -
(4.25)
(4.26)
где
€it и €2t называют структурными остатками и cov(y2t, cit) =F О,
cov(ylt, t:2t) =F О. Следовательно, все переменные являются эндогенны
ми и метод наименьших квадратов не является подходящей техникой
оценивания.
4 0бзор
работ, в которых для описания механизма монетарных переходов исполь
зуются SVАR-модели, см. в
основополагающую работу
[Christiano et al. {1999)]. Кроме того, следует отметить
[Blanchard and Quah {1989)], популяризирующую исполь
зование SVАR-моделей для анализа источников флуктуаций бизнес-циклов.
Гл.
204
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
В матричной форме эта модель имеет вид:
[
~1 Ь~2 ] [ ~: ] =
[ :: ]
+ [ ~:
'Уо
Byt -
E(EtE~)
~: ] [
:=: ]
+ [ :~: ] ,
+ Г1Уt-1 + et,
(4.27)
1 :~ ).
D = (
Если мы используем лаговый оператор, то SVАR-модель записыва
ется в виде:
B(L)Yt
B(L)
Выражая
Yt
через
Yt-1
и
et,
получаем приведенную форму:
Yt = в- 1 'Уо + в- 1 r1Yt-1
+ в- 1 еt =
= ао + A1Yt-1 + ut
(4.27')
ао = в- 1 ')'0, А1 = в- 1 г1, Ut = в- 1 еt.
Отметим, что
-Ь12)
в-1
1
Записывая
(4.27')
'
более компактно, получим приведенную форму
остатков:
{4.28)
{4.29)
A{L)Yt A{L)
Приведенная форма остатков
комбинацию структурных
Ut представляет собой линейную
остатков et. Ковариационная матрица Ut
равна:
Отметим, что параметры SVАR-модели в приведенной форме могут
быть оценены методом наименьших квадратов, поскольку лагированнъ~е
значения переменных у не коррелированы с остатками
Ut.
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
205
Представление в форме модели скользящего
4.3.2.
среднего (представление Волда)
Если мы умножим обе части уравнения приведенной формы
(4.28)-
(4.29) на A{L)- 1 = (12 -A 1 L)- 1, то получим:
Yt
+ Ф(L)ut,
µ
(4.30)
00
Ф(L)
{12 -A1L)- 1 =
L
ФkLk,
Фо = 12,
Фk =А~,
k=O
µ
-
E[utu~)
A{l)- 1 ao,
n.
Представление
в
( ССС-nредставление)
форме
для
Yt
структурного-скользящего
среднего
основано на модели скользящего средне
го бесконечного порядка. Учитывая в представлении Волда, что Ut
= в- 1 еt,
=
получим:
00
8(L)
L 8kLk = Ф(L)в- 1 = в- 1 + Ф 1 в- 1 L + ....
k=O
То есть
80 8k
П р и ме р
4.3
в- 1 =/: 12,
Фkв- 1 = А~в- 1 , k =о, 1, ....
(структурное СС-представление для двумерной си
стемы).
Отметим, что:
• 80 = в- 1 =/: 12. 80 отражает начальное влияние структурных шо
ков и определяет одномоментную корреляцию между Ун и Y2t;
• Элементы матрицы 8k, е~>, определяют множители, отвечающие
за динамику, или импульсные отклики Ун и Y2t на изменения в
структурных остатках ен и e2t.
Гл.
206
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Функции импульсного отклика
Рассмотрим структурное СС-представление в момент времени
[ Yit+s ]
Y2t+s
t
+ s:
=
Множители, отве-чающие за структурную динамику, удовлетво
ряют следующим соотношениям:
дун+s
ден
8(s)
-
11'
дy2t+s
8(s)
21 '
ден
Функции структурного
дун+s - 8(s)
-
де2t
12'
дy2t+s - 8(s)
-
д
e2t
импул'Ьсного
22.
отклика
(СИО-функции)
определяются как совокупность пар (s, 8~j>) для i,j = 1, 2. Эти функ
ции позволяют оценить, насколько единичные импульсы на структур
ные шоки в момент времени
t
+ s,
t
влияют на значение у в момент времени
s принимает различные значения.
Из стационарности Yt следует, что lim 8~3~) = О, i, j = 1, 2.
где
s-+oo
Долгосро-чное кумулятивное влияние структурных шоков определяется следующим образом:
00
Е 8<s>
8(1} = [ 811{1} 812{1} ] 821(1) 822(1)
f
s=O
00
e(L} = [ 811(L) 812 (L)
821 (L) 822(L)
4.3.З.
]
11
s=O
Е
8<s>
21
8(s) LS
11
f
f
s=O
s=O
00
Е
8<s>
12
8<s>
22
8(s) LS
12
s=O
s=O
Е 8(s) Ls Е 8(s) L 8
21
22
s=O
s=O
Вопросы идентификации: введение
Без некоторых определенных ограничений параметры SVАR-модели яв
ляются неидентифицируемыми. Это означает, что по заданным значе
ниям параметров приведенной формы SVАR-модели ао, А1 и
n невоз
можно однозначно восстановить структурные параметры В, 'Уо, Г1 и
D.
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
Например, когда мы имеем
10
207
структурных параметров и
9
пара
метров редуцированной формы, требуется как минимум одно ограни
чение на параметры SVАR-модели. Типичными идентифицирующими
ограничениями являются:
•
нулевые (исключающие) ограничения на элементы матрицы В;
например, Ь12 =О;
•
линейные ограничения на элементы матрицы В; например, Ь12+
+Ь21=1.
В некоторых приложениях идентификация параметров SVАR-мо
дели достигается при помощи ограничений на параметры структурного
СС-представления:
• идентификация при помощи единовременнъtХ ограни11,ений. Пред
положим, что E:2t не имеет единовременного влияния на
Y1t·
Тогда
8~~)=0 и
Поскольку 80
= в- 1 ,
8(О)
0 ]
[
8м)
8(О)
21
22
тогда
1 (
=д
1
-Ь21
-Ь12 )
1
===}
Ь12
= О.
Таким образом, предположение 8~~) =0 в структурном СС-пред
ставлении эквивалентно предположению, что Ь12
= О в SVАR
представлении;
• идентификация при помощи долгосро'Чнъ~х ограни11,ений. Предпо
ложим, что
E:2t
не имеет долгосрочного кумулятивного влияния на
Y1t· Тогда
00
812(1) -
L: 8~~ =о.
s=O
0(1)
=
Этот тип долгосрочных ограничений дает нелинейные ограниче
ния на коэффициенты SVАR-модели, поскольку
Гл.
208
4.3.4.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Идентификация с использованием
рекурсивно-причинного упорядочивания
Рассмотрим двумерную SVАR-модель. Для идентификации нам необ
ходимо как минимум одно ограничение на параметры. Предположим,
что Ь12
= О, а значит, матрица В нижнетреугольна. То есть
в
1
[ Ь21
=
о]
1
===> В
-1
[
= 80 =
1
о]
-Ь21 1 .
В этом случае SVАR-модель становится рекурсивной моделью:
+ 'Y11Y1t-1 + 'Y12Y2t-1 + сн,
1'20 - Ь21У2t + 'Y21Y1t-1 + 1'22Y2t-1 + C2t·
(4.31)
1'10
Yit
Y2t
(4.32)
Рекурсивная модель налагает следующие ограничения: значение Y2t
не имеет единовременный эффект на Ylt; поскольку априори Ь21
=F
О,
мы допускаем возможность, что Ун имеет единовременный эффект на
Y2t·
в этом случае приведенная форма VАR-остатков
Ut
= в- 1 сt
имеет
вид:
Ut
-
[ Uit ]
U2t
-
[
1
-Ь21
0] [
1
cit ]
E:2t
-
Теперь мы покажем, что ограничения Ь12
[ cit
]
E:2t - Ь21 Clt
.
= О достаточно для иден
тификации ~1, а следовательно, для идентификации матрицы В. Для
этого нам необходимо установить, можно ли единственным образом
идентифицировать Ь21 из элементов ковариационной матрицы
n
при
веденной формы. Заметим, что
Тогда мы можем выразить Ь2 1 следующим образом:
где р
= w12/w1w2
при условии р
-
=F О.
корреляция между и1 и и2. Отметим, что Ь21 =/:- О
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
4.3.
209
Оценка с использованием рекурсивно-причинного
упорядочивания
Учитывая описанные выше результаты, процесс оценки может быть
разделен на три шага:
•
оценить каждое уравнение приведенной формы VАR-модели при
помощи метода наименьших квадратов:
Yt
8о + A1Yt-l + Ut
А
l'""AA
Т L...J UtUti
11fi
т
-
t=l
• оценить Ь21 и В из
sl:
А
в=
•
[
1 о
Ь21 1
]
;
оценить параметры структурного СС-представления из оценок ао,
А1 и В:
Yt -
µ, -
Р, + 8(L)€t
80(12 - А.1)- 1
k -1
А1 В
,k=0,1, ...
А
-
А
А
А
А/
вnв.
Для того чтобы найти структурную функцию импульсного отклика,
необходимо оценить параметры структурного СС-представления. По
скольку
8(L) -
Ф(L)в- 1 ,
Ф(L)
A(L)- 1 = (12 - A1L)- 1,
процедуру оценки параметров для
8(L)
часто можно разбить на сле
дующие шаги:
•
А1 оценивается из приведенной формы
VAR.
• При заданном значении А1 матрицы в Ф(L) могут быть оценены
при помощи Фk = At .
•
В оценивается из идентифицируемой SVАR-модели.
• При заданных В и Фk оценки
ны как
ek
= Фkв- 1 .
ek, k = О, 1, ... могут быть получе
Гл.
210
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Восстановление структурного СС-представления
с использованием разложения Холецкого
SVАR-представление, основанное на рекурсивно-причинном упорядочи
вании, может быть вычислено с использованием разложения Холецкого
ковариационной матрицы{} приведенной формы. Разложение Холец
кого положительно-полуопределенной матрицы{} определяется как:
{} = РР',
где
Р
-
[
Рн
О
Р21
Р22
]
Из разложения Холецкого можно получить так называемое тре
угольное разложение:
А= [ Л1 О
{}=ТАТ',
О
Л2
]
'
Лi ~
O,i
= 1,2.
Рассмотрим приведенную форму VАR-модели:
ао
Yt =
+ AlYt-1 + Ut,
{} = E(utUt] =ТАТ'.
Умножая на т- 1 , построим псевдо SVАR-модель:
т- 1 Уt
===}
Byt
-
+ т- 1 AlYt-1 + т- 1 ut,
'Уо + Г1Уt-1 + et,
т- 1 ао
===}
где
Псевдоструктурные остатки
et
имеют диагональную ковариацион
ную матрицу А:
E[ete~] = т- 1 E[utu~]т- 1 ' = т- 1 nт- 1 ' = т- 1 тАт'т- 1 ' =А.
В псевдо SVАR-модели:
в=
[ 1
Ь21
о ] = т-1 =
1
[
Идентификация SVАR-модели с использованием треугольной фак
торизации зависит от упорядочивания компонент вектора
денном выше анализе предполагается,
что компоненты
Yt·
В приве
вектора
= (ун, Y2tY упорядочены так, что Y1t - первая компонента, Y2t -
Yt =
вто
рая. Когда осуществляется треугольная факторизация и оценивается
псевдо SVАR-модель, то в этом случае структурная матрица В равна:
В= т- 1 =
[ 1
Ь21
О1 ]
===}
Ь12 =О.
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
Если переменные упорядочены в обратном порядке, то
211
Yt
{Y2t,
ун)', тогда рекурсивно-причинное упорядочивание SVАR-модели пред
ставлено в обратном порядке и структурная матрица В становится рав
ной:
Упорядочивание переменных в
Yt
определяет рекурсивно-причин
ную структуру SVАR-модели. К сожалению, эти идентификационные
предположения не являются проверяемыми. Поэтому для определения
того,
как структурный
анализ, основанный на изучении поведения
СИО-функций, определяется предполагаемым причинным упорядочи
ванием, часто проводят «анализ 'Чувствите.л:ьности-».
Этот анализ чувствительности основан на оценке SVАR-модели для
различных вариантов упорядочиваний переменных. Если для различ
ных вариантов упорядочиваний переменных в
Yt
СИО-функции зна
чительно отличаются друг от друга, тогда очевидно,
что рекурсивно
причинная структура влияет на структурные выводы.
Один из способов определить, влияет ли предполагаемое причин
- взглянуть на ковариа
для оцененной VАR-модели в приведен
ное упорядочивание на структурные выводы
n
ционную матрицу остатков
ной форме. Если эта ковариационная матрица близка к диагональной,
тогда оцененная матрица В будет близка к диагональной матрице и
упорядочивание переменных не будет влиять на структурные выводы.
Замечание относительно обозначений
В некоторых работах вы можете найти модель в приведенной форме,
представленную в следующем виде:
A(L)Yt
= E:t,
E:t
Е
N{O, '1),
тогда как структурная моде.л:ь представлена как:
А
A(L )Yt
Ac:t
Ac:t
Bet,
et
Е
N{O, 12).
Остатки в приведенной форме E:t соответствуют Ut, тогда как струк
турнъtе остатки
et
ствует матрице В, а
соответствуют E:t. Более того, матрица А соответ
матрица В соответствует матрице D 112 (= Л 1 1 2 ).
ГЛ.
212
4.3.5.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Идентификация с использованием долгосрочных
ограничений
Рассмотрим два наблюдаемых временных ряда Ylt и Y2t таких, что
Ylt rv 1(1), а Y2t rv /(0) 5 . Это возможно, в частности, в случае примера,
представленного в работе
У1
У2
[Blanchard, Quah (1989)]:
логарифм реального ВВП,
доля безработных.
-
Определим
Yt
= (дун, Y2t)'
Предположим, что для
Yt
==> Yt
rv
1(0).
справедливо следующее структурное
представление:
Byt Yt 8(L)
E[ete~]
')'о
+ Г1Уt-1 + et
µ + 8(L)et
Ф(L)в- 1
D
(диагональна).
Приведенная форма этого представления имеет вид:
Yt -
в- 1 "0 + в- 1 г1Уt-1 + в- 1 еt =а.о+ AlYt-1 + ut =
µ+
Ф(L)
-
E[ut~]
Ф(L)ut,
(12 - AlL)- 1,
в- 1 Е[еtе~]в- 1 ' = в- 1 nв- 1 ' = л.
Отметим, что в работе
[Blanchard, Quah (1989)]
ен интерпретирует
ся как постоянный шок в уравнении «предложен», поскольку последний
является остатком в модели реального объема производства
Yt, E:2t
ин
терпретируется как временный шок в уравнении спроса, поскольку это
остатки в модели для доли безработных.
Структурная СИО-функция определяется соотношениями:
ддун+s
дt:н
ддун+s _ 8(s)
дt:2t
- 12 '
()(s)
дy2t+s _ ()(s)
дt:2t 22 .
н '
дy2t+s
дt:н
8(s)
-
21 '
5 Напомним,
что нестационарный временной ряд (процесс) Yt называется инте
грируемым порядка d (обозначается Yt "' 1 (d)), если он впервые становится ста
ционарным после d-кратного применения к нему операции взятия первой разности,
т. е. ряд (1-L)d-IYt является рядом нестационарным, в то время как ряд (1-L)dYt
стационарен. При этом под
Yt "'1(0)
подразумевается факт стационарности ряда Yt·
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
213
Поскольку ряд Ун (выпуск) имеет первый порядок интегрируемо
сти, долгосрочное кумулятивное влияние токов е1
и е2 на уровен:ь У1
равно:
00
. дун+s
1lffi
---
-
s-+oo ден
811(1)
=
L: 8~~>,
s=O
00
. дун+s
1lffi
---
812(1)
s-+oo де2t
=
L: 8~~>.
s=O
Поскольку Y2t (безработица) является стационарным временным
рядом, долгосрочное кумулятивное влияние токов е1
и е2
на уровень
у2 равно:
. дy2t+s
11
m---
.
1lffi
s-+oo ден
s-+oo
п(s)
172·
3
=
О
.
Для у2 долгосрочные кумулятивные влияния соответствующих токов
равны:
00
821 (1) =
L: 8~~>,
s=O
00
822(1)
= L:8~~
s=O
соответственно.
В работе
[Blanchard, Quah (1989))
идентификация SVАR/SМА-мо
дели достигается на основании следующих предположений:
•
временные (спрос) токи (токи в е2) не имеют долгосрочного вли
яния на уровень выпуска производства или безработицы;
•
постоянные (выпуск) токи (токи в е1) имеют долгосрочное вли
яние на уровень выпуска производства, но не на уровень безрабо
тицы.
Ограничение, состоящее в том, что токи в е2 не имеют долгосроч
ного влияния на уровень У1, формализуется в рассматриваемой модели
следующим образом:
00
012(1)
= L: о~~ =о.
s=O
Ограничение, состоящее в том, что токи в е1 и е2 не имеют долго
срочного воздействия на уровень У2, формализуется следующим обра
зом:
. дy2t+s
11
m---
s-+oo дejt
.
1lffi
s-+oo
п(s)
172·
3
=
О
,
ГЛ.
214
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
что следУет из того, что У2
l'V
1(0).
В предположениях, допускаемых в работе
матрица долгосрочного кумулятивного
[Blanchard, Quah {1989)],
влияния 8(1) является нижне
треугольной:
e(l)
= [
:::ш 822~1) ] .
Нижнетреугольная матрица
8(1)
может быть использована для
идентификации матрицы В. Для того чтобы увидеть это, рассмотрим
ковариационную
Волда
матрицу
для
Yt,
определяемую
из
представления
(4.30):
А= Ф{l)ПФ{l)' = {12 - Al)- 1 n{{l2 -А1)- 1 )'.
Эту матрицу называют «долгосрО"t'НОй'll
eiong-run covariance matric').
Так как
n -
в- 1 nв- 1 '
Ф(1)в- 1
0(1)
= (12 -
А1)- 1 в- 1 ,
то матрица А может быть представлена как:
А= (12 - Al)- 1 в- 1 n(в- 1 )'{{l2 - Al)- 1 )' = 8{1)D8{1)'.
Для того чтобы идентифицировать матрицу В, в работе
Quah {1989)]
[Blanchard,
делается дополнительное предположение:
D=l2,
т. е. предполагается, что структурные шоки ен и
€2t
имеют единичные
дисперсии. Тогда
А=
Поскольку матрица
8(1)
8(1)8(1)'.
нижнетреугольная, то матрица А един
ственна, и она может быть получена при помощи разложения Холецко
го; т. е.
8(1)
может быть вычислена как нижнетреугольная матрица в
разложении Холецкого для А. Разложение Холецкого для А имеет вид:
А
===> 8(1) При условии, что матрица
РР' = 8(1)8(1)',
Р.
8(1) =
Р может быть вычислена при
заданной матрице А, матрица В может быть вычислена следУющим
образом:
Р
===>В
-
8(1) = Ф{l)В- 1 = (12 - А1)- 1 в- 1 ,
[(12 - Al)P]- 1 .
В результате SVАR-модель полностью определена.
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
215
Оценка SVАR-модели при наличии долгосрочных
ограничений
Оценка матриц В и
8 (L)
с использованием идентификационной схе
мы, представленной в работе
[Blanchard, Quah (1989)],
может быть осу
ществлена сле,цующим образом:
•
Оценить приведенную форму VАR-модели при помощи метода
наименьших квадратов, примененного к каждому уравнению:
io + A1Yt-l + Ut
Yt
т
1
Т
'"""
",
L...J UtUt·
t=l
•
Вычислить параметрическую оценку долгосрочной ковариацион
ной матрицы остатков модели
(1.30):
• Вычислить разложение Холецкого для матрицы .Л.:
А
А
А
/
Л=РР.
•
Оценить
8(1)
как нижнетреугольную матрицу в разложении Хо
лецкого матрицы .Л.,
8(1) = Р.
•
Оценить В по формуле:
•
Оценить
8k
по формуле:
8" k -_
~.У.. в" -1 _А" kв" -1
"rk
Используя полученную оценку
-
ek,
1
.
можно вычислить матрицы
структурных функций импульсного отклика. Кроме того, оценки струк
турных токов .€н и .€2t могут быть получены по формуле: .€t
= Bii.t.
ГЛ.
216
4.3.6.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Эмпирические приложения с использованием
Eviews
Модель Бланчада -
Куаха
Представленный ниже программный код позволит обработать модель
с долгосрочными ограничениями из работы
[Blanchard, Quah {1989))
(обрабатываемые здесь данные отличны от тех, что рассматривались
в
[Blanchard, Quah {1989)),
поэтому результаты совпадать не будут).
Временные ряды дУ {выпуск) и И {безработица) центрированы при
помощи процедуры, представленной в работе
Пример включен в состав
[Blanchard, Quah {1989)).
E-views, 6.
Следующий код позволит оценить матрицу факторизации двумя
способами, которые приводят к одному результату.
' Модель Блаича,ца-Куаха с долrосроЧВЬIМИ
' оrрави"lевиями (11/5/99).
' Получение матрицы факторизации 1113укя методами
' изменить путь к проrракке
Y.path = Фrunpath
cd Y.path
' создать рабочий файл
vfcreate Ыanquah q 1948:1 1987:4
' извлечь даввые (уже децевтрироваввые даввые) из
fetch(d=data_svar) dy u
' оценить VАR-модель (без константы)
var var1.ls 1 8 dy u Ф
базы
'---------------------------------'
метод
1:
'----------------------------------
var1.cleartext(svar) var1.append(svar) Фlr1(Фu1)=0
freeze(taЫ) var1.svar(rtype=text,conv=1e-4)
shov tаЫ
' сохраяить оценки матриц А и В, получеввые
' с использоваяием метода 1
matrix mata1 = var1.Фsvaramat
' Матрица А допжиа быть единичной
matrix matЫ = var1. Фsvarbmat
'---------------------------------'
'
метод
2:
•рекомендуется использовать дпя проверки•
'----------------------------------
' получить единичное долrосрочное кумулятивное влияние
var1.impulse(imp=u)
matrix clr = var1.Фlrrsp
var1.cleartext(svar)
var1.append(svar) Фе1 = с(1)•Фu1 + с(2)•Фu2
var1.append(svar) Фе2 = -clr(1,1)•c(1)/clr(1,2)•Фu1 +
+
с(4)•Фu2
freeze(tab2) var1.svar(rtype=text,conv=1e-5)
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
4.3.
shov tab2
' сохравить оцеяв:и матриц А и В, получеявые
' с использованием метода 2
matrix mata2 = var1.~svaramat
' А должна быть е.цивичиой матрицей
matrix matb2 = var1.~svarbmat
Должны получиться следующие результаты.
Таблица
4.5.
Результаты оценки модели с долгосрочными
ограничениями по методу
1
Structural VAR Estimates
Sample (adjusted}: 1950Q2 1987Q4
Convergence achieved after 9 iterations
Structural VAR is just-identified
Model: Ае = Bu where E[uu')=I
Restriction Туре: long-run text form
Long-run response pattern:
о
С(2}
C(l}
С(3}
Coefficient
4.043213
С(2}
0.005186
С(3}
0.008335
Log likelihood
495.5765
Estimated А matrix:
1.000000
0.000000
0.000000
1.000000
Estimated В matrix:
0.000746
0.009296
-0.208221
0.219819
C(l}
Таблица
4.6.
Std. Error
0.232661
0.000298
0.329032
z-Statistic
17.37815
17.37815
0.025333
Prob.
0.0000
0.0000
0.9798
Результаты оценки модели с долгосрочными
эффектами по методу
2
Structural VAR Estimates
1
Sample (adjusted}: 1950Q2 1987Q4
1
Included oЬservations: 151 after adjustments
Convergence achieved after 8 iterations
Structural VAR is just-identified
1
Model: Ае = Bu where E[uu')=I
Restriction Туре: short-run text form
@El = C(l}*@Ul + C(2}*@U2
@Е2 = -CLR(l,l}*C(l}/CLR(l,2}*@Ul
where
1
@el represents DY residuals
@е2 represents U residuals
1
1
+ C(4}*@U2
1
217
218
ГЛ.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Таблица
Coefficient
0.009296
С(2)
0.000746
С(4)
0.219819
Log likelihood
495.5765
Estimated А matrix:
1.000000
0.000000
0.000000
1.000000
Estimated В matrix:
0.009296
0.000746
-0.208221
0.219819
C(l)
Std. Error
0.000535
0.000758
0.021145
Response of DY 10 DY
1.1..------------.
1.0
(продолжение)
4.6.
z-Statistic
17.37815
0.984581
10.39558
Prob.
0.0000
0.3248
0.0000
Response ofDY 10 U
1.1..------------.
1.0
::: \
0.4
0.8
0.6
о.•
\
0.2
\""""""""""
0.0+-----------'--''-=-""'"'-------·=-.--t
""" ... "" ...
.0.2-~~~~~~~~-f
1
0.2
0.О+-----------1
.0.2-~~~~~~~~-f
345678910
1
Response ofU 10 U
Response ofU to DY
10..------------.
3.&S678910
10..------------.
о
----------- -
-10
·20
-30
12345678910
Рис.
4.3.
12:t-IS678910
Графики влияния нефакторизованной одноэлементной инновации
Сле,цующая программа позволяет графически изобразить функции
импульсного отклика. Временные ряды дУ (выпуск) и
U
(безработи
ца) децентрированны с использованием проце,цуры, представленной в
работе
[Blanchard, Quah (1989)).
Для того чтобы изобразить как кумулятивное влияние, так и уро
вень отклика на одном рисунке, нам необходимо сохранять значения
функции импульсного отклика в отдельных матрицах. После этого из
влекать эти данные, вставлять их в соответствующие столбцы третьей
матрицы и использовать графические функции изображения элементов
матрицы.
'
'
rрафическое изображение функции инпульсвоrо оТКJIИКа
от долrосрочвых оrравичевий (см.
Quah (1989)]
[Blanchard,
4.3. СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
219
' изменить путь к проrрамме
%path = arunpath
cd %path
' создать рабочий файп
vfcreate Ыanquah q 1948:1 1987:4
' извлечь даивые (уже децеятрироваивые) из базы
fetch(d=data_svar) dy u
' преобразовать в проценты
dy = 100•dy
' оценить VАR-модепь (без константы)
var var1.ls 1 8 dy u а
' формирование допrосрочвых оrравичениi
' au1 = аrреrировавный шок (спрос)
' au2 = аrреrировавный шок (предпожевие)
var1.cleartext(svar)
var1.append(svar) alr1(Фu1)=0
' факторизация
freeze(taЫ) var1.svar(rtype=text,conv=1e-5)
' фиксация rоризовта влияние
!hrz = 40
' изображение рисунков 3-4
freeze(fig3) var1.impulse(!hrz,imp=struct,se=a,a,matbys=rsp_acc) dy а 1
freeze(fig4) var1.impulse(!hrz,imp=struct,se=a,a) dy а 2
freeze(fig34) fig3 fig4
shov fig34
' изображение рисунков 5-6
freeze(fig5) var1.impulse(!hrz,imp=struct,se=a,matbys=rsp_lvl) u а 1
freeze(figб) var1.impulse(!hrz,imp=struct,se=a) u а 2
freeze(fig56) fig5 figб
shov fig56
' изобразить рисунок 1
matrix(!hrz,2) mtmp
' получить кумулятивное впиявие объема выпуска продукции
vector v = acolumnextract(rsp_acc,1)
colplace(mtmp,v,1)
' получить уровень впиявия безработицы
v = Фcolumnextract(rsp_lvl,2)
colplace(mtmp,v,2)
freeze(fig1) mtmp.line
fig1.drav(line,left) О
fig1.elem(1) legend(Output response to demand)
fig1.elem(2) legend(Unemployment response to demand)
shov fig1
' получить кумулятивное впиявие объема выпуска продукции
vector v = acolumnextract(rsp_acc,3)
colplace(mtmp,v,1)
' получить уровень впиявия безработицы
v = Фcolumnextract(rsp_lvl,4)
colplace(mtmp,v,2)
freeze(fig2) mtmp.line
fig2.drav(line,left) О
ГЛ.
220
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
fig2.elem(1) legend(Output response to supply)
fig2.elem(2) legend(Unemployment response to supply)
shov fig2
1.6..---------------.
1.0..---------------.
1 -----------.~",
0.8
::
0.6
0.4
' .... .........
0.2
10
IS
20
2S
ЗО
3S
40
10
-··· Ou1pu1 rcsponsc 1О demand
-
Unemploymenl responr.e
1О demand
-
1.•----------•'·
" ••
: \
',
0.6
\
0.2
5upply
.О+----~-'-'-='--:..::.--:..::.-:=·-=--~-~---1
//---
-.3 \
.,_
•.4
0.0+-------"-=-=-----~--=--=-=--~---1
10
IS
20
2S
ЗО
3S
40
-.s
/
\
/
\ f
\,/
10
IS
20
2S
ЗО
3S
40
Response orU IOSllUCIUral
kcumublC'd Respon•c orDYtoSllUcNral
One S.D. Shock2
One S.O. Shoek:!
1.0-----------
0.2
ю
/,/
"\.
:: /
40
-.2
О.•
0.8
3S
.1..-----------~
·.1
\"
0.8
ЗО
2S
Response orU 1О Sьuc1ural
Onc S.D. Shockl
One S.D. Sbotkl
1.0,
20
Unempbymen1 n:sponse
kcumubced Respon!lic orDYюSuucwr.:111
1.2
IS
•••· Ou1put rc'ponsc 1О 'uppty
.3..-----------~
,r",
::
' ....... " ...
------------------------
/
о.о·..:
10
Рис.
4.4.
IS
20
2S
ЗО
3S
40
•.2 .........................~............................-
.............,...........-4
IOIS202SЗ03S40
Графики влияния дохода и безработицы на спрос и предложение
Разложение Холецкого как структурная: факторизация
Сле,цующая программа иллюстрирует две формы формализации крат
косрочных идентифицирующих ограничений в структурном разложе
нии. В целях проверки корректности формализации ограничений мы
будем использовать разложение Холецкого. Легко увидеть, что получа
емые с использованием каждого из трех методов результаты совпадают.
' Пользуясь SVАR-представлев:ием,
' примеиить разложеиие Холецкоrо
' измев:ить путь к проrрамме
7.path = Фrunpath
cd 7.path
4.3.
СТРУКТУРНЫЕ VАR-МОДЕЛИ (SVАR-МОДЕЛИ)
' создать рабочий файл
vfcreate cholsvar q 1948:1 1979:3
' извлечь даввые из базы
fetch(d=data_svar) rgnp rinv m1
' Применить лоrарифиическое преобразоваиие
' к каждому из рассматриваемых времевиых рядов
series lgnp = log(rgnp)
series linv = log(rinv)
series lm1 = log(m1)
' оценить VАR-модель без оrраиичевий
var var1.ls 1 4 lgnp linv lm1 <О с
'---------------------------------'
метод
1:
краткосрочные оrраиичевия в текстовой форме
'----------------------------------
var1.cleartext(svar)
var1.append(svar) <Ое1
c(1)*<0u1
var1.append(svar) <Ое2 = -с(2)*<0е1 + c(3)*<0u2
var1.append(svar) <Ое3 = -с(4)*<0е1 - с(5)*<0е2 + c(6)*<0u3
freeze(taЫ) var1.svar(rtype=text,conv=1e-5)
shov tаЫ
' сохранить оценки матриц А и В,
' получаемые с использоваиием метода 1
matrix mata1 = var1.<0svaramat
matrix matЫ = var1.<0svarЬmat
' вычислить матрицу факторизации
matrix fact1 = <Oinverse(mata1)*matЫ
'---------------------------------'
2:
'---------------------------------метод
краткосрочные оrраиичевия в матрице-образце
' создать и заполвитъ матрицу-образец
matrix(3,3) pata
pata.fill(by=r) 1,0,0, na,1,0, na,na,1
matrix(3,3) patb
patb.fill(by=r) na,0,0, 0,na,0, 0,0,na
freeze(tab2) var1.svar(rtype=patsr,conv=1e-5,namea=pata,
nameb=patb)
shov tab2
' сохранить оценки матриц А и В,
' получаемые с использоваиием метода 2
matrix mata2 = var1.<0svaramat
matrix matb2 = var1.<0svarЬmat
' вычислить матрицу факторизации
matrix fact2 = <Oinverse(mata2)*matb2
'---------------------------------' метод 3: встроеввое разложевие Холецкоrо
'---------------------------------'
коrо
Оценить импульсное влияние с задаввым разложевием Холец-
пор.ядк:ом
var1.impulse(10)
' сохранить матрицу в разложевии
matrix fact3 = var1.<0impfact
Холецкоrо
221
ГЛ.
222
Таблица
4. 7.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Результаты оценки модели по методу
1
Ае = Bu where Eluu'l=I
Restriction Туре: short-run text form
@El = C(l)*@Ul
@Е2 = -C(2)'"@El + C(3)'"@U2
@Е3 = -C(4)*@El - С(5)*@Е2 + C(6)*@U3
@el represents LGNP residuals
@е2 represents LINV residuals
@е3 represents LMl residuals
Coefficient
Std. Error
z-Statistic
-1.267693
0.174224
-7.276223
vt2)
-0.163608
0.052334
-3.126221
C(4J
С(5)
0.024427
0.022646
1.078662
C(l)
0.010597
0.000676
15.68439
0.020475
0.001305
15.68439
С(3)
С(6)
0.005142
0.000328
15.68439
Estimated А matrix:
1.000000
0.000000
0.000000
-1.267693
1.000000
0.000000
0.024427
-0.163608
1.000000
Estimated В matrix:
0.010597
0.000000
0.000000
0.000000
0.020475
0.000000
0.000000
0.000000
О.005142
Model:
Таблица
Model:
4.8.
Ае
Результаты оценки модели по методу
= Bu where Eluu'l=I Restriction
Туре:
where
Prob.
0.0000
0.0018
0.2807
0.0000
0.0000
0.0000
2
short-run pattern matrix
А=
1
C(l)
vt2)
о
о
1
vt3)
о
C(4J
о
о
о
С(5)
о
о
о
С(6)
Coefficient
-1.267693
-0.163608
0.024427
Std. Error
0.174224
0.052334
0.022646
1
В-
C(l)
С(2)
С(З)
С(4)
О.010597
О.000676
С(5}
0.020475
0.001305
0.000328
С(6)
О.005142
1.000000
-1.267693
-0.163608
О.010597
Estimated А matrix:
0.000000
1.000000
0.024427
Estimated В matrix:
0.000000
О.020475
0.000000
0.000000
0.000000
При использовании метода
матрицы
FACTl, FACT2
FACT
=
и
z-Statistic
-7.276223
-3.126221
1.078662
15.68439
15.68439
15.68439
Prob.
0.0000
0.0018
0.2807
0.0000
0.0000
0.0000
0.000000
0.000000
1.000000
0.000000
0.000000
0.005142
3 {встроенного
FACT3 все равны:
разложения Холецкого)
0,010597 0,000000 0,000000)
( О, 013433 0,020475 0,000000 .
0,001406 -0,000500 0,005142
Вид соответствующих функций импульсного отклика представлен
на рис.4.5.
4.4.
СИСТЕМЫ
ОДНОВРЕМЕННЫХ
УРАВНЕНИЙ (СОУ)
223
Response 10 Cholesky One S.D. Jnnova1ions
Responsc ofLGNP
ао
LGNP
Responsc of LGNP
1О
UNV
Responsc of LGNP
""
01~
""
.010
010
010
""'
00$
.ООО
ООО
""' ~
mo
..,.,
·00$
.
-.010
' ' •
1
s
• , •
..,.,
.
-010
9
10
1
' ' •
Response or UNV 10 WNP
s
•
7
•
-010
9
10
Response of UNV to UNV
1
"'
.112
.02
.о>
'"
.01
01
00
""
00
2
1
' •
s
• , •
·.01
9
10
1
Re"ponse of 1.МI 10 l..ONP
""°
·""'
1
' ' •
s
• , •
s
•
7
•
-01
9
10
1
2
9
.012
....
....
·""'
Рис.
4.5.
• , •
s
10
9
10
LМI
• , •
or 1.МI
9
ю 1.МI
.OOI
ООО
10
' •
Re~poni.e
.01~
...
-
""' .......
' •
s
Response of UNV to
Re11opon11oe of 1.МI to UNV
.012
-
2
' ' •
".
.о.•
-.01
10 LМI
ООО
"----1
' ' •
s
•
7
•
9
10
·""'
1
2
' •
s
• , • •
10
Функции импульсного отклика
Системы одновременных уравнений (СОУ)
4.4.
В данном пункте четвертой главы мы продолжаем описание экономет
рических моделей, представим'Ь/,Х в форме системъt уравнений. При
этом мы получаем в определенном смысле развитие проблематики
и SWАR-моделей, которой были посвящены п.4.2 и
4.3.
VAR-
Выделим две
отличительные особенности СОУ-моделей:
(а) в о
-пе
р в ы х, среди уравнений СОУ могут присутствовать так
называемые балансовые тождества, т. е. детерминированн'Ь/,е
(вытекающие из экономической теории) соотношения между ана
лизируемыми показателями, не содержащие подлежащих стати
стическому оцениванию параметров;
{б) в о- вторых, в правые части описывающих SVАR-модели сто
хастических уравнений
ные
переменные
хt
(4.27)
= (xt
(1)
могут быть включены экзоген(2)
(k) )'
, xt , ... , xt
,
измеренные одно-
временно с эндогенными переменными yt = (у~ 1 ), у~ 2 ), . .. , у~т))',
ГЛ.
224
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
участвующими в модели
времени
(т. е.
измеренными в текущий момент
t).
Строго говоря, как мы уже отмечали в начале п.
4.3,
при некото
ром расширении понятий и обозначений, связанных со SVАR-моделями,
СОУ-модели можно было бы описать, не выходя за рамки расширенного
таким образом класса SVАR-моделей. Однако специфика СОУ-моделей
и решение некоторых вопросов их прикладных возможностей оправды
вают отде.л/ьное рассмотрение этого класса моделей.
4.4.1.
СОУ-модели: определения, основные понятия,
пример
Определение
Система взаимосвязанн'ЬtХ регрессионных урав
4.8.
нений и балансов'Ь~х тождеств, в котор'ЬtХ одни и те же переменные
могут одновременно играть роль (в разн'Ь~х регрессионн'ЬtХ уравнениях)
и результирующих показателей и об-~ясняющих переменн'Ьtх, наз'Ьtва
ется системой одновременн'ЬtХ уравнений (СО .У) .
Участвующие в СОУ-модели переменные подразделяются на:
•
экзогенные, т. е. задаваемые как бы «извне~ системы, автоном
но, причем некоторые из этих переменных могут быть управляе
мыми (хотя бы
•
-
в определенной мере), планируемыми;
эндогенные, т. е. такие переменные, значения которых форми
руются в процессе и внутри функционирования анализируемой
системы в существенной мере под воздействием экзогенных пере
менных и, конечно, во взаимодействии друг с другом и со своими
же прошлыми во времени
(т. е.
лаговыми) значениями; в модели
они как раз и являются предметом объяснения;
•
предопределенные, т. е. выступающие в системе в роли факто
ров-аргументов, или об~ясняющих переменных.
Из данных определений и из обычно принимаемого допущения о
взаимной некоррелированности экзогенных и лагированных эндоген
ных переменных с текущими остатками уравнений системы следует, что
множество предопределенных переменных формируется из всех экзо
генных переменных (значения которых могут быть зарегистрированы
в текущий
(t),
прошлые или будущие моменты времени) и так назы
ваемых лаговых эндогенных переменных, т. е. таких эндогенных пере
менных, значения которых входят в уравнения анализируемой системы
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
225
измеренными в прошлые (по отношению к текущему) моменты вре
мени, а следовательно, являются (к текущему моменту времени) уже
известными, заданными.
При построении и анализе СОУ-модели следует различать (так же,
как и при анализе SVАR-моделей) ее структурную и приведенную фор
мы. Для пояснения этих понятий условимся в дальнейшем обозначать
прописной латинской буквой Х = (х< 1 ), х< 2 ), ... , x(k))' все предопре
деленные переменные, т. е. все экзогенные переменные, включа.я сво
боднъtй 'ЧJ/,ен, и все участвующие в системе лагированные эндогенные пе
ременные. Пусть общее число эндогенных переменных равно
m,
а общее
число предопределенных переменных, включая свободный член,
равно
k.
Примем (пока без объяснения), что общее число уравнений и
тождеств в СОУ равно числу участвующих в ней эндогенных перемен
ных, т. е. равно
имеем
и
v
i
и
m1
тождеств
( (1) (2)
m2
t =
Yt
у;< 2 )
=
m.
И пусть из общего числа
m
соотношений модели мы
уравнений, включающих случайные остаточные компоненты,
, Yt
(m1 +m2 = m).
(m))'
, ... , Yt
Разобьем вектор эндогенных переменных
v(l)
( (1) (2)
(m1))'
на два подвектора i
t
=
Yt
, Yt
, ... , Yt
(y~mi+l), ... , y~mi+m 2 ))', при этом порядок, в котором перену
мерованы эндогенные переменные, не имеет значения.
Тогда общий вид линейной СОУ может быть представлен в форме
(4.33)
где В1 = (fЗij)i,j=l,mi - матрица размерности (m1 xm1) из коэффициен-
тов при ур), ... ,y~mi) в m1 первых уравнениях; В2 = (fЗij)
i=I;m"l
j-m1 +1,m1 +m2
матрица размерности (m1 х m2) из коэффициентов при y~mi+l), ...
(m1 +m2)
... , Yt
в
m1
первых уравнениях
б. Х
,
_ ( xt(1) , xt(2) , ... , xt(k))' -
t -
тор-столбец предопределенных переменных, в котором хР>
= (Cij) i=1,m 1 -
С1
матрица размерности
(m1
век-
-
1;
х k) из коэффициентов при
j=l,k
предопределенных переменных в первых
эффициенты
Вз
=
cil
играют
(f3ij)i-m 1 н,m 1 +m 2 ;=1,m1
уравнениях (очевидно, ко-
свободных
матрица размерности
циентов при ур>, .. .,y~mi)
= (fЗij) i-mi +1,m 1+m2 -
роль
m1
членов
уравнений);
(m2 х m1) из коэффи-
в m2 тождествах системы; В4
матрица размерности
(m2 х m2) из априори за
;-m1 +l,m1 +m2
данных коэффициентов при y~mi+l}, ... , y~mi+m2 ) в m2 тождествах си6С
помощью символов i = n 1 , n 2 кратко обозначается тот факт, что индекс i мо
жет принимать все целые значения от
n1
до
n2,
т.е.
i = n1,n1+1, ... ,n2.
ГЛ.
226
стемы; С2
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
= (Cij) i=mi н,m 1 +m2
матрица размерности
-
(m2 х k) из коэф-
;=1,k
фициентов при предопределенных переменных в
m2
тождествах систе-
мы; Лt = (бр>, 8?>, .. .,б~mi))' - вектор-столбец размерности m1 слу
чайных остаточных составляющих m 1 первых уравнений системы и
Om2 =(О, О, ... , О)' - вектор-столбец размерности m2, состоящий из ну
лей.
Заметим, что исходн:ы.ми статистическими дан:н:ы.ми, необходимы
ми для проведения статистического анализа системы
(4.33)
(а именно,
для оценки неизвестных коэффициентов /Зij и Cij, проверки статисти
ческих гипотез, например, о линейном характере исследуемых зависи
мостей и т. п.), являются матрицы
У=(~)
(4.34)
соответственно размерностей (п х
m)
и (п х
k),
а все элементы матриц
Вз, В4 и С2 являются известн'Ьtми (их числовые значения определяют
ся содержательным смыслом соответствующих тождеств системы).
Система
(4.33)
может быть записана также в виде
Byt + CXt =
Лt,
t = 1, 2, ... , n,
(4.33')
или в виде
У · В'
+ Х · С' = д,
(4.33")
где
(:J.
а матрицы У и Х определены в
Определение
4.9.
(4.34).
Система уравнений и тождеств вида
(или эквивалентн'ЬtХ ей записей
(4.33)
(4.33') или (4.33")) наз'Ьtвается струк
турной формой линейной СОУ. При этом предполагается, что коэф
фициент при i-й эндогенной переменной в i-м структурном стохасти
ческом уравнении
(i = 1, 2, ... , m)
равен единице (правило нормировки
систем'Ьt), а матриц'Ьt В 4 и В нев-ьtрожден'Ьt (допускаются и другие
способ'Ьt нормировки систем'Ьt).
3 а м е ч а н и е. Пользуясь тем, что эндогенные переменные Yi( 2)
из (4.33) могут быть явно выражены через "Vi(l) и Xt, их можно ис
ключить из общей системы и рассматривать систему, содержащую в
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
качестве эндогенных переменных только переменные
}f;(l},
227
а именно:
t = 1,2, .. .,п,
(4.33а)
где В* = В1 - В2В4 1 Вз и С* = С1В2В4 1 С2. Поэтому в дальнейшем,
говоря о статисти-ческом анализе системы соотношений, описываю
щих линейную СОУ-модель, можно рассматривать системы, содержа
щие только т1 регрессионных стохастических уравнений и не содер
жащие тождеств. Правда, этот переход может приводить к определен
ной «перепараметризации~ модели, т. е. к утрате автономности первона
чально введенных параметров (см. ниже реализацию данного перехода
в примере
4.4).
Поскольку при реализации одной из конечных прикладных целей
эконометрического моделирования (а именно, при прогнозе значений
эндогенных переменных и при различных имитационных расчетах)
главный интерес представляют соотношения, позволяющие явно вы
разить все эндогенные переменные
yt
через предопределенные
Xt,
то
одновременно со структурной формой имеет смысл рассмотреть так на
зываемую приведенную (редуцированную) форму линейной СОУ7 . Тре
буемый результат мы получим, домножив слева обе части соотношений
(4.33') на матрицу в- 1 и уединив затем yt:
(4.35)
Аналогично можно поступить и со структурной формой, записан
ной в виде (4.33а):
}f;(l} =
-(В*)- 1 С* Xt
+ (В*)- 1 Лt, t =
1, 2, ... , n.
(4.36)
В дальнейшем, говоря о приведенной (редуцированной) форме
СОУ-модели, мы будем иметь в виду запись
yt = П · Xt
+ C:t, t =
1, 2, ... , п
(4.35')
= П*Хt
+ C:t'* t =
1, 2, ... , п,
(4.36')
или
v(l}
.l
где
(т
х
k)
t
матрица П, ( т1 х
k)
матрица П* и векторы остаточных
случайных составляющих C:t и с:; определяются соотношениями
(4.37)
7 Более
распространенный в русскоязычной литературе термин «приведенная
форма• в действительности менее точно передает в переводе с английского смысл
«reduced form model•,
так как основное отличие последней
-
в меньшем (редуциро
ванном) числе содержащихся в ней параметров по сравнению со структурной фор
мой (более подробно об этом см. ниже, в п.
4.4.2).
228
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
П*
= -(В*)- 1 С*,
et
(4.38)
1-
=в- Лt,
(4.39)
е; = (В*)- 1 Лt.
Определение
(4.40)
4.10. Система соотношений (4.35') ( или (4.36')),
в которой все эндогенн'Ьtе переменн'Ьtе эконометри'Ческой моде.ли яв
но линейно в'Ьtражен'Ьt 'Через предопреде.ленн'Ьtе переменн'Ьtе и слу'Чайн'Ьtе
остато'Чн'Ьtе компонент'Ьt, наз'Ьtвается приведенной формой линей
ной СОУ-моде.ли.
Определение
4.11.
Параметр'Ьt СОУ, определяющие общее 'Чис
ло т уравнений и тождеств моде.ли (и одновременно
-
общее 'Число
у'Частвующих в ней эндогенн'ЬtХ переменн'Ь~х), 'Число т1 у'Частвующих
в моде.ли эндогенн'ЬtХ переменн'Ьtх, 'Число т2 входящих в моде.лъ балан
сов'ЬtХ тождеств и 'Число
k
у'Частвующих в модели предопределенн'ЬtХ
переменн'Ьtх, наз'Ьtваются структурными параметрами модели.
Проиллюстрируем введенные понятия на примере.
П ри м ер
4.4
(упрощенный вариант динамической модели нацио
нальной экономики Клейна). Рассмотрим СОУ вида
Yi 1>= eto + et1 (yi 3>- хР>) + oi 1>'
Yi 2> = f31Y~:>1 + f32 · х~ 2 ) + oi2>,
(4.42)
Yi 3 ) = ур> + Yi 2) + х~з),
(4.43)
(4.41)
где априорные ограничения выражены неравенствами
О
< et1 < 1; f31 > О; f32 < О.
Эти три соотношения вместе с ограничениями образуют модель. В ней
ур> обозначает потребление, у?> - инвестиции, yi 3 ) - национальный
доход, хР> - подоходный налог, х?> - норму процента как инструмент
государственного регулирования, х~ 3 ) - государственные закупки това
ров и услуг, измеренн'Ьtе в «момент времени» t.
Присутствие в уравнениях (4.41) и (4.42) «остаточных» случайных
составляющих oi 1> и о?> обусловлено необходимостью учесть влияние
соответственно на ур> и yi 2>ряда неучтенных факторов. Действитель
но, нереалистично ожидать, что величина потребления ур> будет од
нозна'Чно определяться уровнями национального дохода (yi 3>) и подо
ходного налога (хр>); аналогично величина инвестиций yi 2> зависит,
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
229
очевидно, не только от достигнутого в предыдущий год уровня нацио
нального дохода (у~~1 ) и от величины нормы процента (х~ 2 >), но и от
ряда не учтенных в уравнении
факторов.
(4.42)
Полученная модель содержит два уравнения, объясняющие поведе
ние потребителей и инвесторов, и одно тождество. Мы сформулировали
ее для дискретных периодов времени и выбрали запаздывание (лаг) в
один период для отражения воздействия национального дохода на ин
вестиции.
В этом примере число эндогенных переменных, так же как и общее
число всех соотношений модели, равно трем
Среди этих соот
(m = 3).
ношений мы имеем одно тождество (следовательно, m1
Общее число предопределеных переменных
k = 4,
=
2,
m2
=
1).
в том числе три эк
зогенные переменные (хр>, х~ 2 ), х~ 3 )) и одна лаговая эндогенная пере
менная (у~~1 ), которую мы в соответствии с принятой договоренностью
кодируем как
(4) (
xt
т.
е.
(3) (4))
Yt-l = xt .
Структурная форма модели в данном примере задается соотноше
ниями
ных в
(4.41)-(4.43). В общих
формуле (4.33), имеем:
в1 =
(1;О;
о). в 2 =
1 '
Вз
матричных обозначениях, использован
(-01) с
О
В4
= (-1; -1);
и
д
1
(-оо;
=
О;
= (1);
_ ( .r(l)
t -
Ut
О;
-/32;
С2 =(О; О; О;
О;
О )
О; -/31 ;
-1; О)
.r(2) )т
'Ut
•
Если же структурная форма записана в виде
(4.33'), то в данном
примере участвующие в этой записи матрицы конкретизируются в виде
В= ( -1~
о
1
-1
-а1)
о
;
(щ
С=
1
~
-01
о
о
о
-/32
о
о
о
-1
+)
(4.44)
и
д
t
=
(fJ(l)
t
8(2) О) т .
' t '
Отметим, что, во-первых, выполнено условие нормировки (y~i) вхо
дит в
i-e
уравнение системы,
i = 1, 2,
с коэффициентом единица); во
вторых, значения элементов матриц Вз, В4 и С2 известны, они опре
деляются содержательным смыслом тождества; в-третьих, требование
невырожденности матриц В4 и В соблюдено; и, наконец, в-четвертых,
матриц'Ы В1, В2 и С1 относительно «слабо заполненъt» неизвестнъши
(подлежащими статисти'Ческому оцениванию) коэффициентами: их
230
ГЛ.
всего четыре
-
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
ао, а 1 ,/3 1 и /32. Последняя особенность рассматриваемой
эконометрической модели является, к счастью, достаточно общей отли
чительной чертой СОУ. Если бы это было не так, т. е. если бы мы были
вынуждены иметь дело с системами, «сильно заполненными~ неизвест
ными коэффициентами, то задача статистического анализа таких си
стем оказывалась бы принципиа.л:ьно неразрешимой: имеющихся в на
шем распоряжении исходных статистических данных просто нехватало
бы для корректного проведения такого анализа. Ведь при построении и
анализе систем эконометрических уравнений, описывающих макроэко
номические модели, исследователю зачастую приходится иметь дело с
десятками и сотнями эндогенных и экзогенных переменных!
Рассмотрим далее структурную форму в записи (4.33а), при кото
рой исключается часть эндогенных переменных у;< 2 > посредством их вы
ражения через у;< 1 > из тождеств системы. В нашем примере эта струк
турная форма имеет вид:
{
(1 - a:1)Y~l}
у~2}
/32х~2)
-
-
а:1у~ 2 )
/31х~4}
-
ао + а1х~ 1 > - а:1х~ 3 ) = д?>
= д?>'
т. е. матрицы В* и С*, участвующие в общей записи (4.33а), в данном
примере конкретизируются в форме
В* = (1 -
о
0:1
С* = (-а:о
-0:1)
1
о
'
0:1
о
И, наконец, приведенная форма модели
-~J·
О
-/32
(4.36'),
в которой все эн-
догенные переменные выражаются через предопределенные, в данном
примере имеет вид
У~ 1 ) = 1 ~ а 1 (ао - а1х~ 1 > + а1/32х?> + а:1х~ 3) + а:1/31х~4))
+
(б(l}
t
у~2} = /32Х~2}
+
0:1
8(2))
1 - 0:1 t
+ /31Х~4} + 8~2}'
т. е. матрица П* и вектор случайных остаточных составляющих е;,
участвующие в общей записи приведенной формы
(4.36'),
мере конкретизируются в виде:
П*=
о
*-
ct -
(.r(l}
Ut
о
+ 1 0:1
-0:1
.r(2} _r(2}) т
Ut
' Ut
•
в данном при
4.4.
4.4.2.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
231
Основные проблемы СО-У-моделирования
Для пояснения сущности именно эконометрической модели и описания
основных возникающих при ее построении и анализе проблем нам бу
дет удобно разбить весь процесс моделирования на шесть основных
этапов.
1-й этап ( постановочнъtй)
-
определение конечных целей модели
рования, набора участвующих в модели факторов и показателей, их
роли;
2-й этап ( априорнъ~й)
-
предмодельный анализ экономической сущ
ности изучаемого явления, формирование и формализация априорной
информации, в частности, относящейся к природе и генезису исходных
статистических данных и случайных остаточных составляющих;
3-й этап
( параметризация) -
собственно моделирование, т. е. вы
бор общего вида модели, в том числе состава и формы входящих в нее
связей;
4-й этап
( информационнъ~й) -
сбор необходимой статистической
информации, т. е. регистрация значений участвующих в модели фак
торов и показателей на различных временных или пространственных
тактах функционирования изучаемого явления;
5-й этап (идентификация модели)
-
статистический анализ моде
ли и в первую очередь статистическое оценивание неизвестных пара
метров модели;
б-й этап (верификация модели)
-
сопоставление реальных и мо
дельных данных, проверка адекватности модели, оценка точности мо
дельных данных.
Последние три этапа (4-й, 5-й и 6-й) сопровождаются крайне трудо
емкой процедурой калибровки модели. Дело в том, что при постро
ении СОУ-модели исследователь, как правило, находится в ситуации,
когда, с одной стороны, действует большое число «нормативных» (т. е.
определенных содержательным смыслом анализируемых связей) огра
ничений на коэффициенты матриц В и С, а с другой стороны, ему при
ходится действовать в условиях определенной нечеткости (или непол
ноты) исходной статистической информации
(4.34).
Процедура калиб
ровки модели заключается в переборе большого числа различных вари
антов «нормативные ограничения
-
значения отдельных переменных»
(что связано с многократными «вычислительными прогонами» модели)
в целях получения совместной, непротиворечивой и идентифицируемой
модели.
Математическая модель, в том числе математическая модель эко
номического явления или процесса, может быть сформулирована на
общем (качественном) уровне, без настройки на конкретные статисти-
ГЛ.
232
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
ческие данные, т. е. она может иметь смысл и без 4-го и 5-го этапов.
Тогда она не является эконометрической. Суть именно экономет
рической модели заключается в том, что она, будучи представленной в
виде набора математических соотношений, описывает функционирова
ние конкретной экономической системы, а не системы вообще (именно
экономики России или процесса «спрос
-
предложение~ в данном кон
кретном месте и в данное время). Поэтому она обязательно «настраива
ется~ на конкретных статистических данных, а значит предусматривает
обязательную реализацию 4-го и 5-го этапов моделирования.
Обратимся теперь непосредственно к описанию основных проблем,
которые приходится решать в процессе СОУ-моделирования.
Проблема спецификации модели. Эта проблема по существу
решается на первых трех этапах моделирования и включает в себя 8 :
(а) определение конечных целей моделирования (прогноз, имитация
различных сценариев социально-экономического развития анали
зируемой системы, управление);
(б)
определение списка экзогенных и эндогенных переменных;
(в) определение состава анализируемой системы уравнений и тож
деств, их структуры и соответственно списка предопределенных
переменных;
(г) формулировка исходных предпосылок и априорных ограничений
относительно:
•
стохастической природы остатков Лt (в классических вариантах
моделей постулируются их взаимная
статистическая
независи
мость или некоррелированность, нулевые значения их средних ве
личин и иногда сохранение постоянными в процессе наблюдения
значений их дисперсий
•
-
гомоскедастичностъ);
числовых значений отдельных элементов матриц В и С в струк
турной форме модели
(4.33')
Итак, спецификация модели
-
или
(4.33").
это первый и, быть может, важней
ший шаг эконометрического исследования. От того, насколько удачно
8 Ниже
описывается содержание проблемы спецификации СОУ-модели в nредnо
.л.ожен.ии ее .л.ин.ейн.ости, т. е. при условии, что в результате проведения 3-го этапа
(этапа nараметризации и.л.и выбора общего вида модели) эконометрист пришел к
выводу о непротиворечивости гипотезы линейности анализируемых связей имею
щимся в его распоряжении исходным статистическим данным. Тому, как поступать
в противном случае, посвящена гл.
1 учебника.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
233
решена проблема спецификации и, в частности, насколько реалистичны
наши решения и предположения относительно состава эндогенных, эк
зогенных и предопределенных переменных, структуры самой системы
уравнений и тождеств, стохастической природы случайных остатков и
конкретных числовых значений части элементов матриц В и С, реша
ющим образом зависит успех всего эконометрического исследования.
Спецификация опирается на имеющиеся экономические теории, спе
циальные знания или на интуитивные представления исследователя об
анализируемой экономической системе. Эти априорные сведения опре
деляют, в частности, природу матриц В и С. Например, информация
(или предположение) о том, что определенные переменные непосред
ственно не участвуют в том или ином уравнении,
означает равенство
нулю соответствующих элементов в строках матриц В и С. Дополни
тельные сведения о системе могут иметь вид ограничений на комбина
ции элементов матриц В и С.
Проиллюстрируем сказанное на нашем примере из
4.4.
Мы видим,
что непосредственно из состава и смысла уравнений системы
(4.41 )-
(т. е. из решения части вопросов проблемы спецификации модели)
(4.43)
непосредственно следует специальный вид матриц В и С (см.
(4.44))
и, в
частности, их слабая заполненность априори неизвестными элементами
(из
24
элементов этих матриц нам предстоит статистически оценить
лишь четыре: ао, ai, .81 и
.82).
Априорные сведения о системе находят свое отражение при спе
цификации модели не только в определении конфигурации матриц В и
С, но и в выборе предположений относительно стохастической природы
участвующих в уравнении переменных, в первую очередь относительно
случайных остатков д~). Обычно принимаются допущения о том, что
все случайные остатки д~j) (j = 1, 2, ... , m1):
• имеют нулевые средние значения, т. е. Ед~j)
=О, t = 1, ... ,
n;
• не коррелируют друг с другом, т. е. Е(д~) · д~ 1 )) =О, (j :/: l);
• не имеют автокорреляций, т. е. Е(д~1) · д~~)) =О, ti :/: t2;
•
не коррелируют ни с одной из предопределенных переменных.
Как правило, подобные допущения в процессе спецификации моде
ли оказываются достаточно реалистичными.
Проблема идентифицируемости. При анализе эконометриче
ской
модели,
представленной
системой
уравнений
вида
(4.33)
ГЛ.
234
(или
(4.33')),
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
исследователя в коне-чном с-чете интересует прежде все
го поведение эндогенн'Ых переменн·ых
денной формы модели
(4.35)
yt.
Из соответствующей приве
видно, что эндогенные переменные yt яв
ляются по своей природе случайными величинами, поведение которых
определяется внутренней структурой модели, а именно элементами
матриц В и С и природой случайных остатков Лt. Возникает вопрос:
а возможно ли, следуя в «обратном направлении», восстановить струк
турную форму
(4.33') (т. е.
все элементы матриц В и С), располагая
знанием приведенной формы
(4.35') (т. е.
знанием числовых значений
всех элементов матрицы Пи природы случайных остатков
et)?
Имен
но этот вопрос и отражает сущность проблемы идентифицируемости
эконометрической модели (не смешивать с проблемой идентификации
модели, заключающейся в выборе и реализации методов статистическо
го оценивания ее неизвестных параметров, см. ниже).
Ответ на поставленный вопрос в общем случае, очевидно, отрица
тельный: без дополнительных ограничений на внутреннюю структуру
модели (т. е. без соблюдения некоторых условий идентифицируемости)
по т1 х
(k
+ 1)
элементам матрицы П невозможно восстановить го
раздо большее число элементов матриц В и С (нетрудно подсчитать,
что общее число коэффициентов /3ij и Ciq в структурной форме равно
+
+
т1 х (m1
m2 k), хотя, конечно, общее число коэффициентов, подле
жащих статисти-ческому оцениванию, оказывается меньшим).
В эконометрической теории приняты следующие определения, свя
занные с проблемой идентифицируем ости (в узком СМ'Ьtсле).
Определение
4.12.
Уравнение структурной форм'Ы экономет
ри-ческой модели назъtвается точно идентифицируемым (в узком
смысле), если все участвующие в нем неизвестн'Ьtе
( т.
е. априори не
заданн'Ые) коэффициент'Ы однозна-чно восстанавливаются по коэффи
циентам приведенной форм'Ы без каких-либо ограни-чений на зна-чения
последних.
Определение
4.13.
СОУ-модель наз'Ьtвается точно идентифи
цируемой (в узком СМ'ЫСЛе), если все уравнения ее структурной форм'Ы
являются точно идентифицируемыми.
Определение
4.14.
Уравнение структурной форм'Ы наз'Ьtвается
сверхидентифицируемым (в узком смысле), если все участву
ющие в нем неизвестн'Ые коэффициент'Ы восстанавливаются по коэф
фициентам приведенной форм'Ы, при-чем некотор'Ьlе из его коэффициен
тов могут принимать одновременно несколько (более одного) числов'Ых
значений, соответствующих одной и той же приведенной форме.
Определение
4.15.
Уравнение структурной форм'Ы наз'Ьtвает
ся неидентифицируемым (в узком смысле), если хотя б'Ьt один из
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
235
участвующих в нем неизвестных коэффициентов не может бъ~ть вос
становлен по коэффициентам приведенной формъt. Соответственно
модель называете.я неидентифицируемой, если хот.я бъt одно из урав
нений ее структурной формъt .являете.я неидентифицируемъш.
Говоря о проблеме идентифицируемости модели, мы начали с того,
что исследователя в конечном счете интересует поведение эндогенных
переменных, и с этой точки зрения может показаться несущественной,
более того, надуманной проблема «однозначного возврата~ от приве
денной формы к структурной. Однако в действительности проблема
идентифицируемости крайне важна, в первую очередь с позиций вы
работки предложений по решению следующей проблемы
-
проблемы
идентификации СОУ-модели, т. е. проблемы выбора и реализации ме
тодов статистического оценивания участвующих в ней неизвестных па
раметров.
Более подробное рассмотрение проблемы идентифицируемости эко
нометрической модели, включающее в себя, в частности, формулиров
ки необходимых условий идентифицируемости отдельного параметра,
целого уравнения и всей системъt уравнений структурной формъ~, при
ведено в слудующем пункте.
Проблема идентификации. Решение этой проблемы предусмат
ривает «настройку~ записанной в общей структурной форме
модели на реальные статистические даннъtе
(4.34).
(4.331)
Другими словами,
речь идет о выборе и реализации методов статистического оценивания
неизвестных параметров модели
(4.33)
(т. е. той части элементов мат
риц В и С, значения которых не являются априори известными) по
исходным статистическим данным
(4.34).
Описание необходимых мето
дов статистического оценивания параметров в подобных моделях и в
их отдельных фрагментах приводится в п.
4.4.4.
Проблема верификации модели. Эта проблема, так же как и
проблема идентификации, является специфичной, связанной с постро
ением именно эконометри-ческой модели. Собственно построение эко
нометрической модели завершается ее идентификацией, т. е. статисти
ческим оцениванием участвующих в ней неизвестных коэффициентов
(параметров) Ьij и Ctq· После этого, однако, возникают вопросы: (а) на
сколько удачно удалось решить проблемы спецификации, идентифи
цируемости и идентификации модели, т. е. можно ли рассчитывать на
то, что использование построенной модели в целях прогноза эндоген
ных переменных и имитационных расчетов,
определяющих варианты
социально-экономического развития анализируемой системы, даст ре
зультаты, достаточно адекватные реальной действительности? (б) како
ва точность (абсолютная, относительная) прогнозных и имитационных
236
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
расчетов, основанных на построенной модели? Полу'Чение ответов на
эти вопросъt с помощью тех или инъtх математико-статисти'Ческих
методов и составляет содержание проблемъt верификации экономет
ри'Ческой модели.
Некоторые подходы к верификации модели описаны в п.
4.4.6.
Здесь
же отметим лишь, что эти методы основаны на процедурах статистиче
ской проверки гипотез (при ответе на вопрос (а)) и на статистическом
анализе характеристик точности различных приемов статистического
оценивания параметров (при ответе на вопрос (б)). Отметим также, что
наиболее распространенным и эффективным подходом к верификации
эконометрической модели можно признать принцип так называемых
ретроспективнъ~х рас'Четов. Конкретная схема построения таких рас
четов зависит от конечных прикладных целей моделирования, однако,
их общая сущность заключается в следующем.
Предположим, мы строим эконометрическую модель в целях про
гноза эндогенных переменных или
имитационных расчетов
на т
меннъ~х тактов вперед. Тогда исходные статистические данные
вре
(4.34)
делятся на две части:
обу'Чающую въtборку
(4.34а)
экзаменующую въtборку
(4.34б)
Далее все ранее принятые решения по проблемам спецификации,
идентифицируемости и идентификации модели применяются только к
наблюдениям обучающей выборки (4.34а). Из полученной таким обра
зом модели подстановкой в ее приведенную форму значений экзогенных
переменных Хn-т+ 1, Хn-т+2, ... , Xn получают моделънъtе (ретроспек
тивно прогнознъtе) значения соответственно У n-т+1, У n-т+2, ... , У n·
Сравнение этих модельных значений с соответствующими реальными
значениями экзаменующей выборки Уп-т+1, Уn-т+2 1
••• ,
Yn позволяет
проанализировать и адекватность модельных выводов реальной дей
ствительности, и их точность. Реализация этого принципа описана, на
пример, в связи с построением и анализом моделей регрессии в п.
учебника [Айвазян
(2010)).
6.4
Применительно к СОУ некоторые рекомен
дации на этот счет будут представлены в п.
4.4.6.
4.4.
4.4.3.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
237
Условия идентифицируемости отдельных уравне
ний и системы в целом
Как было отмечено в предыдУщем пункте, эта проблема логически
предшествует
статистическому
оцениванию
параметров
системы,
по
скольку от ее решения зависит и выбор методов оценивания. Отсутствие
идентифицируемости СОУ означает либо принципиальную невозмож
ность состоятельного оценивания параметров структурной формы СОУ
по имеющимся в нашем распоряжении наблюдениям (неидентифици
руемость в широком смысле), либо существование бесконечного
множества моделей, не противоречащих имеющимся в нашем распоря
жении наблюдениям. В результате анализа проблемы идентифициру
емости конкретного параметра структурной формы системы мы при
ходим к одной из трех принципиально возмоЖН'Ы,Х ситуаций:
1)
этот
параметр может быть однозначно выражен через коэффициенты при
веденной системы;
2)
параметр допускает несколько разных вариантов
определения по значениям параметров приведенной формы;
3)
пара
метр не может быть выражен через параметры приведенной формы.
Очевидно, идентифицируемость или неидентифицируемость системы,
ее уравнений и параметров зависят только от внутренней структур'Ьl,
модели (числа уравнений, соотношения количеств эндогенных и пред
определенных переменных
в
системе
и в
каждом уравнении,
мульти
коллинеарности анализируемых переменных, некоторых свойств мат
риц структурных коэффициентов), но никак не связаны со статистиче
скими свойствами исходных наблюдений.
СледУя, в основном, обозначениям, введенным в п.
4.4.1, 4.4.2,
мы
будем полагать, что балансовые тождества уже исключены из анали
зируемой системы, так что ее структурная форма имеет вид (4.ЗЗа),
т.е. 9
t
где В= (/Зij)-матрицаразмерности
= 1, 2, ... 'п,
(mxm)
(т.е.
(4.45)
i,j = 1,2, ... ,m) ко-
эффициентов при m эндогенных переменных yt = (у~ 1 ), у~ 2 ), ... , у~т))';
С = (Чj) - матрица размерности (m х k) (т. е. i = 1, 2, ... , m; j =
= 1, 2, ... , k) коэффициентов при k предопределенных переменных Xt =
(1)
(2)
(k) '
= (xt , xt , ... , xt ) , в состав которых, если необходимо, включен и
свободный член; а вектор-столбец случайных остатков Лt
= ( оР>' о?>'
."
9 В целях упрощения обозначений в соотношении (4.ЗЗа) мы далее не будем снаб
жать верхним индексом• матрицы В и С и верхним индексом <1 > вектор-столбец
эндогенных переменных У, а также будем полагать, что общее число эндогенных
переменных (так же, как общее число регрессионных уравнений в системе после
исключения из нее балансовых тождеств) равно
m.
ГЛ.
238
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
... , о~т))' удовлетворяет в общем случае следующим условиям: ЕЛt
=Om;
=
ковариационная матрица остатков Ед = Е(ЛtЛ[) положительно
t; векторы Лt 1 и Лt 2 взаимно не коррелированы при ti =/:- t2, а б~i) не коррелированы со всеми предопределенными
.t"(i)( xt(j) - Е xt(j))] -- О при i. -- 1 , 2 , ... , т,
переменными системы, т. е. E[ ut
j = 1, 2, ... , k. Коэффициенты /3ij пронормированы с помощью условия
определена и не зависит от
/3ii
= 1.
Таким образом, рассматривается система из
щая т эндогенных и
k
m уравнений, содержа
предопределенных (т. е. экзогенных и лаговых
эндогенных) переменных.
Прежде всего сформулируем условия идентифицируемости систе
мы в целом в широком смысле, т. е. условия, обеспечивающие в
принципе
возможность
состоятельного
оценивания
всех
параметров
структурной формы СОУ. Во-первых, для того чтобы мы могли уеди
нить эндогенные переменные
переменные
Xt
Yt,
выразив их через предопределенные
(т. е. осуществить переход к приведенной форме и уста
новить соотношения, связывающие коэффициенты структурной и при
веденной форм), необходимо потребовать, чтобы матрица В была квад
ратной и обратимой (т. е. невырожденной). Так мы приходим к фор
мулировке 1-го (необходимого) условия идентифицируемости системы
в целом (в широком смысле).
1-е условие (необходимое) идентифицируемости системы в
целом (в широком смысле): 'Число уравнений систем'Ы (m) должно
бъtтъ равно 'Числу анализируем'ЫХ эндогенн'Ых переменн'Ых (т), а мат
рица В должна б'Ьlтъ нев'Ырожденной.
Тогда приведенная форма анализируемой системы будет иметь вид:
t
= 1, 2, ... 'п,
(4.46)
где
(4.47)
матрица размерности (т х k) коэффициентов приведенной формы, а
et -- ( et(1) , et(2) , ... , et(m))' -- в-1д t - вектор-столб ец остатков.
Очевидно, необходимым условием возможности оценить все коэф
фициенты '1Гij матрицы П параметров приведенной формы
ляется требование, чтобы предопределенные переменные
Xt
(4.46)
яв
не были
мультиколлинеарны. Итак,
2-е условие (необходимое) идентифицируемости системы в
целом (в широком смысле): матрица наблюдений предопределен-
Н'ЫХ переменн'Ых Х
= (хр>), t = 1, 2, ... , n; j = 1, 2, ... , k, размерности
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
239
(n х k) должна иметь полн'Ый ранг k (очевидно, при этом число наблю
дений
n
должно существенно превышать общее число анализируемых
переменных т
+ k).
На интуитивном уровне достаточно очевидна «перегруженносты
модели
(4.45) неизвестными значениями параметров /3ij и Ciq (i = 1, 2, ...
... ,т; q = 1,2, ... ,k). Более того, можно доказать (см., например,
[Джонстон (1980)], с. 357), что если не дополнить модель (4.45) никаки
ми априорнъ~ми ограничениями относительно числовых значений этих
параметров, то ни одно из уравнений не может б'Ыть идентифици
руемо. При этом априорные ограничения носят чаще всего исключаю
щий характер, т. е. они определяют в каждом (i-м) уравнении «адреса~
(i,j)
и
(i,q)
тех коэффициентов, которые априори считаются нулевыми
(априорные ограничения могут быть сформулированы и в виде опреде
ленных линейных связей, априори существующих между оцениваемы
ми коэффициентами). Поставим в соответствие каждому (i-му) уравне
(4.45) (m + k)-мерный булевский (т.е. состоящий только
(1)
(m)
(m+l)
(m+k+l))
единиц) вектор "'Yi = ("'Yi , ••• , "'Yi
; "'Yi
, ••• , "'Yi
, за-
нию системы
из нулей и
дающий исключающие априорные ограничения для параметров этого
уравнения по следующему правилу: нулевые значения компонент "'Y;q)
определяют «адреса~ отсутствующих в уравнении переменных, или, что
то же, априори равных нулю параметров i-го уравнения структурной
формы.
3-е условие (необходимое) идентифицируемости системы в
целом (в широком смысле): среди исключающих априорн'Ых ограни"
( "'Y(1)
чении "'Yi =
i , ••• , "'Y(m+k))
i
, i. = 1, 2, ... , т, не должно б'Ыть о ди наков'Ых, структурная форма систем'Ы не должна содержать уравнений,
одинаков'Ых по составу входящих в него переменн'Ых.
Чтобы пояснить, к чему может приводить нарушение 3-го условия
идентифицируемости системы, рассмотрим пример.
П р и мер
(простейшая модель «спрос - предложение~). Пусть
- -(l) , Yt 2>) , t = 1, 2, ... , n, характен аблюдениями (Xt, Yt
4.5
мы располагаем
-<
ризующими динамику среднедушевого дохода (xt), предложения некоторого товара fj~l), спроса на него (jj~ 3 )) и цены на этот товар (jj~ 2 >).
Нам будет удобнее в дальнейшем оперировать не с самими наблюда
емыми переменными (х, у< 1 >, у< 2 >), у< 3 >), а с их отклонениями от своих
средних уровней, т. е., соответственно, с наблюдениями Xt = Xt - х,
ур> = ур> y(l), у~ 2 ) = у~ 2 ) - у(2) и у~ 3 ) = fj~з) - у< 3 > (черта сверху озна
_
чает усреднение соответствующей переменной по всем ее наблюденным
значениям). Для центрированн'Ых таким образом переменных извест-
ГЛ.
240
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
ные линейн:ые уравнения спроса, предложения и равновесия запишутся
в виде
ур> = Ь 1 у~ 2 ) +др>
у~з) = Ь 2 у~ 2 )
-
уравнение предложения,
+ CXt + д~2 )
(4.48)
уравнение спроса,
-
(4.49)
ур> = у~з) - уравнение равновесия,
(4.50)
t = 1,2, ... ,п,
где Ь1, Ь2 и с
-
некоторые неизвестные коэффициенты, а каждая из
последовательностей {др>} и {д~ 2 )} (t = 1, 2, ... , п) представляет со
бой ряд взаимно не коррелированных случайных величин, имеющих
нулевые средние значения и дисперсии, соответственно, и~ и и~, не за
t. Кроме того, предполагается, что регрессионные остатки
др> и д?> не коррелированы между собой, а также не коррелированы с
висящие от
переменной Xt.
Заметим, что в системе (4.48)-(4.50) значения цены (у< 2 >), спро
са (у< 3 >) и предложения (у< 1 >) формируются как бы «внутрu"J> нее, в
процессе взаимодействия связей, описываемых этой моделью. В то же
время значения среднедушевого дохода х поступают в систему как ха
рактеристики внешней среды, в которой взаимодействуют эти анали
зируемые связи. Поэтому в данной модели спрос, предложение и цена
отнесены к эндогенным переменным, а доход
-
к экзогенным.
Желая несколько упростить модель, положим, что спрос у~з) так
же, как и предложение у~ 1 ), зависит только от цены товара у~ 2 ) (т. е.
не зависит от дохода). Тем самым мы воспользовались двум.я одина
ков·ыми
исклю'Чающими
априорн'Ы.Ми
ограни'Чениями
-
и в
первом,
и
во втором уравнениях системы «обнулили'J>коэффициент при доходе х.
В результате получаем систему
(2)
+ Ut.t"(l) '
у~З) = Ь2 у~2)
+ д~2),
(1) -
Yt
-
Yt(l)
_
-
ь
1Yt
у(З)
t
.
На плоскости, где по оси ординат откладываются значения предло
жения и спроса, а на оси абсцисс
-
значения цены, равновесие пред
ставляется как пересечение линий предложения (А) и спроса (Б), см.
рис.
4.6.
Поскольку мы собираем
( Yt(2) , Yt(1) , Yt(3)) , t
= 1, 2, ... , n,
исходные статистические данные
в условиях равновесия, то различие в на-
блюдаемых значениях обусловлено только случайными остатками д~ 1 )
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
241
и 8~ 2 ), что, кстати, подтверждается и приведенной формой этой модели
(1) -
Yt
-
(2) -
Yt
-
Ь
Ь
1
1 -
1
1 -
Ь
Ь
(Ь
2
1
8(2)
t
Ь
-
2
(8(2) - 8(1))
2
t
t
8(1))
t
,
,
так как правые части уравнений выражаются только в терминах слу
чайных остатков модели. Очевидно, располагая только разбросанными
около точки равновесия значениями случайных остатков еР) и е~ 2 ) (см.
(4.40)),
мы ничего не можем сказать о самих функциях предложения
(А) и спроса (Б). А это и значит, что мы не можем оценить параметры Ь1
и Ь2 в уравнениях
(4.48)
и
(4.49),
т. е. оба анализируемых регрессионных
уравнения неидентифицируемы.
ур>
,. . , ур>
(предложение,...., спрос)
А
у~ 2 ) (цена)
Рис.
4.6.
Линии предложения (А}, спроса (В) и наблюдения (крестики},
произведенные в условиях равновесия
Заметим, что к точно такому же результату мы пришли бы, если
бы пошли по линии некоторого усложнения (а не упрощения) модели
(4.48)-(4.50),
введя в 1-е уравнение системы доход х. Это снова означа
ло бы использование идентичных векторов априорных ограничений и
снова привело бы нас к неидентифицируемости системы.
Далее формулируются и доказываются два условия идентифи
цируемости отдельного уравнения системы
•
условие порядка (необходимое);
•
условие ранга (необходимое и достаточное).
(4.45):
ГЛ.
242
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Пусть нас интересует идентифицируемость некоторого отдельного
уравнения системы
(4.45).
Без ограничения общности мы можем так пе
ренумеровать уравнения системы и анализируемые в ней переменные,
что
наше уравнение
окажется
перв'Ым,
входящие в
переменные будут иметь номера с 1-го по m1-й
него эндогенные
(m1 -
число эндоген
ных переменных, участвующих в этом уравнении), а входящие в него
предопределенные переменные будут иметь номера с 1-го по kl-й
(k1 -
число предопределенных переменных, участвующих в анализируемом
уравнении, включая свободный член, если он присутствует в этом урав
нении).
Тогда анализируемое уравнение может быть записано в виде
(1/312 · · · f3 lm1 о · · · о)( Yt(1) Yt{2) · · · Yt(m1) Yt(m1 +1)
+ (с11 с12 ... C1k1 о ... о ) (Xt(1) Xt(2)
(m))'
· · · Yt
(k1) (k1 +1)
... Xt
Xt
+
(k) )' - 1'(i)
... Xt
- Ut '
или, что то же,
f3'(1)yt(1)
+ c'(l)Xt(l) = б~ 1 ),
(4.51)
где
(4.52)
(первая компонента вектора
/3(1)
равна единице по условию нормиров
ки),
_ ( {1) {2)
(m1))'
yt ( 1) - Yt ' Yt ' ... ' Yt
и
( ) _ ( (1)
Xt 1 -
Xt
(2)
' Xt
(k1))
' ... ' Xt
.
(4.53)
Нас будут интересовать соотношения, связывающие между собой
коэффициенты структурной и приведенной форм именно анализиру
емого (1-го) уравнения системы
(4.45)
с точки зрения возможности
однозначно въtразить коэффициент'Ы структурной форм'Ы
{3(1)
и
c(l)
по известнъш значениям коэффициентов приведенной форм'Ы (т. е. по
элементам матрицы П из
(4.46)).
Для этого мы, конечно, используем в
качестве отправного пункта базовое соотношение
(4.4 7),
а точнее, экви
валентное ему соотношение
ВП=-С.
(4.47')
Для того чтобы извлечь отсюда интересующие нас соотношения,
связывающие первые строки матриц, стоящих в левой и правой частях
(4.47'), нам придется разбить матрицу П на четыре блока двумя вооб
ражаемыми линиями: одна (горизонтальная) отделяет первые m1 строк
от т-т1 последующих, а вторая (вертикальная) - первые kl столбцов
4.4.
от
k - k1
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
243
последующих:
П{l)
п
mxk+1
Пху{l)
(т
- m1) х (k - kl)
(под матрицами указаны их размерности).
Тогда мы можем записать приведенную форму
анализируе
(4.46)
мой СОУ в виде
{1))
.
)
(
(~:Ш) = (-~~1·)·. ~. -~~~1·)· (~:Ш) + ";~) ,
Пу{l)
:
Пху{l)
et
где Yt{l) и Xt{l) определены в {4.53), а Yt{l)
-Xt (1) = (Xt(k1+l) ' ... 'Xt(k))' .
Теперь выпишем вытекающее из
(4.54)
= (y~mi+l), ... , у~т))' и
(4.4 7') равенство первых m1 строк
матриц ВП и -С:
(!.в~2J (-~~~) .. ~. -~~~1·)·) -(~~~,)'
{4.55)
=
Пу{l)
{векторы
,8(1)
и
c{l)
Пху{l)
:
определены в
(4.52)).
Произведя перемножение матриц в левой части
{
,8'{1) П{l)
{4.55),
получаем
= -d{l),
,8'{1) Пх{l)
(4.56)
{4.57)
= ok-ki.
Мы получили систему уравнений, связывающих коэффициенты
1-й строки структурной формы СОУ с параметрами приведенной фор
мы. Эта система, как мы видим, распалась на две подсистемы:
(4.56)
и
(4.57). По-видимому, сначала надо попытаться решить подсистему
{4.57) относительно коэффициентов ,8(1), а затем, подставив найден
ные решения в (4.56), решить эту подсистему относительно параметров
c{l).
Поэтому определим, в первую очередь, условия, при которых под
система
(4.57)
имеет хотя бы одно решение. Соотношения
ставляют собой систему из
k- k1
уравнений относительно
(4.57) пред
,812, ... , .В1m 1
ГЛ.
244
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
с т1 -
неизвестными. Для того чтобы параметры
ме
можно было бы выразить через элементы матрицы Пх{l),
1
{4.57)
необходимо, чтобы число уравнений в
(4.57)
,8(1)
в подсисте
было бы не меньше числа
неизвестных, т. е.
Таким образом, мы пришли к следующему необходимому усло
вию идентифицируемости отдельного уравнения системы.
Условие порядка (необходимое): чис.л.о исключеннъ~х (при спе
цификации моде.ли) из i-го уравнения системъt предопреде.леннъ~х пе
ременных (т. е. чис.л.о
(k - ki))
должно бъ~ть не меньше чис.л.а вклю
ченных в него эндогеннъ~х переменных, уменьшенного на единицу. За
метим, что выполнение условия
=
k - ki
mi -
1
является необходи
мым условием точной идентифицируемости i-го уравнения, в то время
как при
k - ki
> mi -1
уравнение будет сверхидентифицируемъ~м. Из
анализа подсистемы уравнений
(4.57)
можно извлечь также необхо
димое и достаточное условие идентифицируемости 1-го уравнения
СОУ. Известно, в частности, что для разрешимости системы
носительно
,8(1)
(4.57)
от
необходимо и достаточно, чтобы матрица Пх{l) имела
бы ранг, равный числу неизвестных (т. е. т1 -1). Таким образом получа
ем следующее необходимое и достаточное условие идентифицируемости
отдельного {i-го) уравнения.
Условие ранга (необходимое и достаточное): ранг матрицы
Пх(i)
= mi - 1.
Следует отметить, что в отличие от правила порядка, которое может
проверяться на стадии спецификации системы, соблюдение рангового
условия мы можем проверить в общем случае только после вычисления
матрицы Пх (i), т. е. после применения обычного МНК к приведенной
форме
{4.54)
анализируемой системы. Правда, в отдельных простых
случаях это можно сделать и до применения МНК, просто анализируя
элементы матрицы Пх (i), выраженные через параметры структурной
формы /3ij и Ckl (что мы и продемонстрируем сейчас на примере).
Пр им ер
4.5
(продолжение). Исключая из модели
{4.48)-(4.50)
балансовое тождество и решая полученную систему относительно у~ 1 )
и У?), получаем приведенную форму модели в виде:
У?) = 7r1xt + с-Р),
У?) = 11'2Xt + €~ 2 ),
где
t
= 1, 2, ... , n,
{4.58)
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
245
{4.58")
В рамках сделанных выше предположений о постоянстве дисперсий
D8p> и D8~ 2 ) и о некоррелированности др> и 8~ 2 ) меж,цу собой и с экзо
генной переменной Xt из (4.5811 ) сле,цует, что с.лучайн:ы,е остатки с:Р> и
с:~ 2 ) приведенной формы также имеют не зависящие от t дисперсии,
не корре.лированъ~ между собой и с экзогенной переменной Xt в урав
нениях
{4.58).
Сле,цуя определениям
4.12-4.13,
попробуем ответить на
вопрос об идентифицируемости параметров Ь1, Ь2 и с структурной фор
мы, т. е.
о возможности их однозначного выражения через параметры
7r1 и 7r2 приведенной формы. Поделив первое из уравнений
(4.58')
на
второе, получаем
1l'1
Ь1 = - .
(4.59)
1l'2
Однако соотношений
(4.58')
оказывается недостаточно для того, чтобы
определить из них значения коэффициентов ~ и с второго уравнения
структурной формы. Это значит, что первое уравнение структурной
формы анализируемой СОУ идентифицируемо, а второе и вся систе
ма
-
неидентифицируемы.
Чтобы пояснить ситуацию со сверхидентифицируемостью пара
метра структурной формы, несколько видоизменим рассматриваемую
модель {4.48)-(4.50). Полагая, что и ставка процентах?> может влиять
на спрос, мы решили дополнить наши наблюдения за средне,цушевым
доходом (xt), предложением некоторого товара (ур>) и ценой на него
(у~ 2 )) регистрацией во времени этой величины. Тогда, как и прежде,
переходя от значений самих анализируемых величин к их отклонени
ям от средних (соответственно Xt, у~ 1 ), у~ 2 ) их?>) и вводя в модель еще
одну экзогенную переменную (х~ 2 )) в виде аргумента функции спроса
(т. е. в уравнение
{4.49)),
мы получаем после исключения балансового
тождества структурную форму СОУ в виде:
у~ 1 ) = Ь 1 у?>
+ 8~ 1 )
- уравнение предложения;
ур> = Ь2у~ 2 ) + с1хР> + с2х~ 2 > + 8i2> - уравнение спроса,
{4.48а)
{4.49а)
t = 1, 2, ... , n,
в которой для удобства доход (в отклонениях от среднего) и коэффици
ент при нем мы теперь обозначаем, соответственно, хР> и с1. Структур
нъ~е параметръ~ этой системъ~: число уравнений равно общему числу
эндогенных переменных и равно т
переменных
k
= 2; общее число предопределенных
= 2; число эндогенных и предопределенных переменных,
ГЛ.
246
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
включенных в 1-е уравнение, соответственно, m1
=
2, kl
=
О; число
эндогенных и предопределенных переменных, включенных во 2-е урав
нение, соответственно, m2
= 2, k2 = 2; матрица В коэффициентов при
эндогенных переменных (при канонической записи системы)
1
-Ь1)
в -_ ( _.!.
1
Ь2
.
Таким образом, 1-е условие идентифицируемости будет выполнен
ным, если потребовать
det В
=/=О, т. е. Ь2
=/=
Ь1 (и Ь2 =/=О).
Для проверки 2-го условия надо убедиться в том, что наблюдения
хР> и х~ 2 ) (t = 1, 2, ... , п) не связаны пропорциональной зависимостью,
(2) _J_
{1)
т. е. что xt 1 Лхt .
Очевидно и выполнение 3-го общего условия идентифицируемости
системы, т. е. векторы исключающих ограничений первого
рого (1'2) уравнений системы различны, а именно: ')'1
(1'1) и вто
= (1, 1, О, О); ')'2 =
= (1, 1, 1, 1).
Теперь сосредоточимся на проверке идентифицируемости отде.л:ь
ного (например, 1-го) уравнения системы. П]Ювило порядка (4-е усло
вие) выполняется со строгим знаком неравенства, т. е. число исклю
ченных в 1-м уравнении предопределенных переменных равно двум
(k - k1 = 2 -
О), а число включенных в него эндогенных переменных,
уменьшенное на единицу, равно единице (m1 -
1 = 2 - 1).
Это означает,
что 1-е уравнение системы является сверхидентифицируем'ЬLМ, т. е. его
структурные параметры (в данном случае это один параметр Ь1) допус
кают неоднозначное выражение через параметры приведенной формы.
Этот факт в анализируемом примере легко проверить непосредствен
но. Действительно, решение системы (4.48 а)-(4.49а) относительно у~ 1 )
и у?> дает нам приведенную форму
ур> = 11'11хР> + 7r12x~ 2 > + е:Р>,
У~ 2 > = 7r21xP> + 7r22x~ 2 > + е~ 2 >,
где
11'21
=
ь1 - ь2
'
11'22
=
ь1 - ь2
'
а еР> и е~ 2 ) такие же, как в (4.58"). Мы видим, что структурный коэф
фициент Ь1 может быть определен по параметрам приведенной формы
4.4.
247
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
двумя различными способами, которые дают, вообще говоря, два разных результата.
1-й вариант:
Ь1 = 7ГН;
2-й вариант:
Ь1 = 7Г12.
7Г21
7Г22
Для полноты картины проверим выполнение необходимого и достато'Чного условия идентифицируемости 1-го уравнения так называемого
рангового условия, хотя мы уже знаем, что 1-е уравнение сверхиденти
фицируемо.
В нашем случае матрица Пх{l), имеющая размерность m1 х
-k1) = 2
х
(k-
совпадает со всей матрицей П, т. е.
2,
Очевидно, что строки этой матрицы связаны пропорциональной за
висимостью {2-я строка получается из 1-й делением на Ь1), так что ранг
матрицы Пх{l) равен единице, что и требуется в ранговом условии (т. е.
в нашем случае m1
= 2 и,
следовательно, ранг Пх{l)
=
т1 -
1 = 1).
Методы статистического оценивания неизвестных
4.4.4.
значений параметров СОУ
В данном пункте речь идет только о той части проблемы идентифи
кации СОУ, которая связана с методами статистического оценивания
неизвестных значений параметров /Зij и Ciq
т;
(i = 1, 2, ... , т; j = 1, 2, ... ,
q = 1, 2, ... , k) в уравнениях {4.45) по имеющимся в нашем распоря
жении наблюдениям
(1)
(1)
(m)
У1
У1
У2
У2
У2
(1)
У=
(2)
(2)
У1
.. .... . ........
(1)
(2)
. .. Yn(m)
Уп
Уп
Х1
Х1
Х2
Х2
Х2
(1)
(m)
Х=
(k)
(2)
(2)
Х1
(k)
..............
(1)
Xn
(2)
Xn
Мы будем предполагать, что число наблюдений
n
...
(k)
Xn
«много больше~,
чем
m+k (n ~ m+k), матрица В в (4.45) невырождена и что предопре
деленные переменные х~ 1 ), ... , x~k) не мультиколлинеарны, т. е. матрица
Х имеет полный ранг
k.
Среди столбцов матрицы Х может присутство
вать столбец, состоящий из одних единиц (если в правую часть модели
{4.45)
включен свободный член). Другие структурные предположения о
модели
(4.45)
и, в частности, допущения о природе случайных остатков
ГЛ.
248
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Лt, будут формулироваться в ходе изложения того или иного метода
статистического оценивания.
Мы уже убедились в том, что независимо от того, хотим ли мы
оценить только одно из уравнений системы
или же намерены
(4.45)
оценить все уравнения этой системы, в общем случае мы оказываем
ся
в
ситуации,
когда известные
нам
методы
регрессионного
анализа
(МНК, различные версии ОМНК) не обеспечивают удовлетворитель
ную процедуру оценивания. Причина подобной ситуации заключается
в том, что при отсутствии специальных предположений о структуре
СОУ (например, о ее рекурсивном хшрактере, см. ниже) в анализируе
мом уравнении среди объясняющих переменных присутствует одна или
несколько эндогенных переменных,
которые коррелируют с регресси
онн'ЬtМи остатками. Правда, существует достаточно простой, так на
зываемый косвеннъ~й метод наименьших квадратов, когда с помощью
обычного МНК, примененного к каждому отдельному уравнению при
веденной формы
(4.46),
сначала оцениваются элементы 1Гij матрицы П,
а затем, используя соотношение
{4.47) {в которое вместо матрицы П
подставляется ее оценка fi), определяются значения оценок -Дij и C;,q
параметров структурной формы. Но этот метод применим лишь к
точно идентифицируем'ЬtМ уравнениям.
Переходя к описанию специальных методов оценивания структур
ных параметров модели
{4.45),
разделим их на два класса: методы, поз
воляющие оценивать каждое отдельное уравнение системы
(4.45)
по
очередно, и методы, предназначенные для оценивания всех уравнений
сразу. Правда, существует специальный тип СОУ
-
так называемые
рекурсивнъ~е системъ~, для которых при определенном выборе порядка
и взаимосвязей оцениваемых отдельных уравнений системы процеду
ра МНК приводит к состоятельному оцениванию всех ее уравнений.
С точки зрения задач статистического оценивания этот тип СОУ явля
ется простейшим, поэтому мы с него и начнем.
Идентификация рекурсивных систем
Во многом потому, что рекурсивнъ~е СОУ относительно просты для
решения задачи статистического оценивания параметров структурной
формы, в большом числе прикладных работ (может быть, в большей их
части!) при спецификации модели стараются построить ее так, чтобы
она удовлетворяла свойству рекурсивности. Для этого действуют сле
дующим образом 10 . В качестве 1-го уравнения системы специфицируют
10 Следует,
правда, признать, что в ряде публикаций ведущих эконометристов
(в том числе, например, в работах Х. Волда) делаются серьезные попытки дать
содержате.11:ьное (исходящее из сущности реа.11:ьн'ЫХ экономических систем) обос
нование правомерности использования именно рекурсивных СОУ. Главные доводы
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
249
соотношение, в котором присутствует то.л:ько одна эндогенная перемен
ная у<1) (соответственно и индексируют ее первым номером). Так что 1-е
уравнение системы содержит m1 = 1 эндогенных переменных и какое-то
количество
ki
предопределенных переменных. Второе уравнение систе
мы может содержать не более двух эндогенных переменных; это, если
необходимо, эндогенная переменная y(l) («участница» 1-го уравнения)
и, кроме нее, еще толъко одна эндогенная переменная (обозначим ее
у< 2 )). При комплектации состава и числа k2 предопределенных пере
менных руководствуются содержательными соображениями и «прави
лом порядка»(см. «условие порядка» в предыдУщем пункте). В третье
уравнение, кроме уже участвовавших во 2-м уравнении эндогенных пе
ременных y(l) и у( 2 ), можно включить еще оп.ятъ толъко одну эндо
генную переменную у( 3 ) и т. д. В результате мы получим модель вида
(4.45),
в которой матрица В является нижней треугольной матри
цей, т. е. /Зij
= О при j
> i
условия нормировки /Зii =
для всех
1).
i = 1, 2, ... , т
(при сохранении
Оказывается, если для систем такого вида
дополнительно потребовать взаимную некоррелированность случайных
остатков д~ii) и д~i 2 ) при всех t и для всех ii
=/:-
i2 {i1, i2 = 1, 2, ... , т),
то оценки структурнъ~х пара.метров в каждом отделъном уравнении
системъt с помощью прямого метода наименьших квадратов будут со
стоятелънЪt.ми, а при нормалъности д~i)
-
и аси.мптоти-чески эффек
тивнъши. Под прямым МНК понимается следУющая процедУра, по
следовательно примененная к i-му уравнению системы
{i
= 1, 2, ... , m):
с помощью обычного МНК строятся оценки коэффициентов регрессии
у?) по всем включенным в это уравнение эндогенным и предопределен
ным переменным.
Достаточно естественно выглядит приведенная выше схема специ
фикации модели в виде СОУ при описании процесса формирования рав
новесных цен и количеств предлагаемых на рынке товаров. Рассмотрим
пример.
П р и м е р 4.6. Пусть у?) - цена некоторого товара в момент вре
мени t, а у~ 2 ) - объем продаж этого товара в тот же момент времени.
Естественно предположить, что объем продаж у~ 2 ) зависит от цены у?)
и от объема продаж в предыдущий момент времени у~~1 • В свою оче
редь, цена товара у?) зависит от объема его продаж в предыдущий
момент времени (т. е. от у~~1 ). В данной схеме цена У?) и объем продаж
их аргументации основаны на тезисе, что большинство реальных механизмов фор
мирования рассматриваемых в модели экономических показателей функционирует
в рекурсивном (а не одновременном) режиме. Так, например, трудно представить
себе рыночные механизмы, одновременно формирующие цены и количества предла.
гаемых товаров (см. ниже, пример
4.6).
ГЛ.
250
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
у?) играют роль эндогенных переменных, а лаговой переменной у~~1
естественно отвести роль единственной предопределенной переменной
Xt
(т. е.
Xt
= у~~1 ).
В результате анализируемая модель будет описана системой
{4.60)
t = 1, 2, ... , n.
Первое уравнение системы без дополнительных ограничений яв
ляется идентифицируемым, так как приведенная форма модели
{4.60)
имеет вид
{4.60а)
где св = -7Г11, а .В21с11 - с21 = 7Г21·
Однако если дополнительно потребовать некоррелированность ос-
татков ьР) и д~ 2 ), т. е. диагональности ковариационной матрицы остатков
Е-
д -
д(l))
t't
( cov(д(l)
( ~(2) ~(1))
COV Ut
, Ut
cov(fJ(l) r,( 2) ))
t't
( ~(2) ~(2))
COV Ut
то коэффициенты .821 и с21 2-го уравнения
'
, Ut
(4.60)
могут быть состоя
тельно оценены с помощью обычного МНК, примененного к уравнению
регрессии у~ 2 ) по ур) и
(4.60)
Xt.
Действительно, перепишем 2-е уравнение
в виде
t
= 1, 2, ... , n.
Поскольку объясняющая переменная ур) = -c11 xt + ьР) в правой
части этого уравнения не коррелирована с ь?) (так как ни Xt' ни ьР) не
коррелированы по условию с д~ 2 )), то в соответствии с общей теорией
КЛММР (см. гл.
7
в [Айвазян
{2010)])
МНК-оценки параметров .821 и
с21 будут состоятельными.
З а м е ч а н и е. Очень важным моментом в правильной специфи
кации модели, рассмотренной в примере
4.6,
является выбор продол
жите.л:ьности такта времени. Действительно, продавец устанавли
вает цены, а покупатель на них реагирует. При этом торговые запа
сы будут либо накапливаться, либо рассасываться. Продавец среаги
рует на эту динамику и т. д. Если выбрать в качестве такта времени
один денъ, то сделанные нами в модели примера
4.6
допущения выгля
дят естественными, поскольку последовательность причинных связей
4.4.
у~:>1
-t
ур)
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
-t
251
у~ 2 ) является линейной цепью (т. е. не содержит ника
ких петель обратной связи). Это позволяет нам, в частности, предпо
ложить возмущения, влияющие на спрос (д~ 2 )) и предложение (др)),
независимыми. Однако если бы публиковались, скажем, только недель
ные данные о средней недельной цене (ур)) и среднем объеме дневных
продаж (у~ 2 )), то вынужденное агрегирование соответствующих воз
мущений JP) и J~ 2 ) в системе (4.60) делает эти возмущения взаимно
коррелированными, а саму модель - неидентифицированной. Введение
же в модель дополнительных переменных в целях достижения иденти
фицируемости модели (если бы такие переменные существовали), как
правило, превращает рекурсивную модель в обычную СОУ со всеми
вытекающими отсюда проблемами ее оценивания.
Перейдем
к
описанию
процедуры
статистического
оценивания
структурных параметров структурной формы общей рекурсивной моде
ли СОУ. Пусть анализируется система из т стохастических уравнений
с т эндогенными переменными yt = (у~ 1 ), у~ 2 ), ••• , y~m))' и k предопре
деленными переменными Xt = (хР), х~ 2 ), ... , x~k))'
= 1,2, ... ,п,
t
(4.61)
где В
- (m х m)-матрица коэффициентов fЗij при эндогенных перемен
ных (i,j = 1, 2, ... , т; fЗii = 1 - условие нормировки), С - (m х k)матрица коэффициентов Cij при предопределенных переменных (i =
= 1, 2, ... , т; J· = 1, 2, ... , k) ,
а вектор
Д
=
t
(.r(l) .r(2)
иt
, иt
.r(m))T
, •.• , иt
-
вектор-столбец возмущений (или случайных остатков), не корре.л,иро
ваннъ~х с предопределеннъ~ми переменнЪtми.
Определение
Система одновременнъ~х уравнений
4.16.
(4.61)
на
зъ~ваетс.я чисто рекурсивной, если:
(i)
матрица В .являете.я н?Ю1Сней треугольной, т. е.
fЗij =О
при
j
>i
для всех
i = 1, 2, ... , т - 1;
(ii) ковариационна.я матрица Ед случайнъ~х остатков Лt диагональ
на и не зависит от
t,
т. е.
Ед Е(д,дi}
=
=
?..~~-2 ~
•• •• ·.·: •
О
О
О
...
~ ~
••• •• )
О
•
Umm
Иногда при спецификации модели удобнее ориентироваться на
эквивалентное
(ii)
условие:
ГЛ.
252
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
(iia) случайн:ые возмущения др>, 8~ 2 ), .•. , б~m) обладают тем свойст
вом, что б(q) не коррелирует со всеми «nредшествующими'$)эндо
генн'Ы.Ми nеременнъtми, т. е. с y(l), у( 2 ), ••• , y(q-l) (q = 2, 3, ... , m).
Если выполняется только условие
(i),
то система называется фор
малъно рекурсивной, или просто рекурсивной.
Выпишем теперь явный вид МНК-оценок структурных коэффици
ентов i-го уравнения системы
q1
< q2 < ... qki
-
(4.61). Пусть ji
<
j2
< ... <
jmi-1 и
номера, соответственно, эндогенных (кроме пере
менной y(i)) и предопределенных переменных, участвующих в i-м урав
нении системы (в силу ее рекурсивности, очевидно,
mi
~
i).
Тогда
i-e
уравнение можно записать в виде
Q .. Y(j1) _
Yt(i) -__ fJ'tJ
1 t
Q ..
Y(j2) _
fJ'tJ2 t
_
(qki)
(k1)
- Ciq1 Xt
•••
-
••• -
Ciqk · Xt
•
Q..
fJ'tJmi -1
y(jmi-1)
(4.62)
.t"(i)
+ Ut
'
t = 1, 2, ... 'п.
Обозначим y(l) и x<s), соответственно, l-й столбец матрицы У и s-й
(.t"(i)
.t"(i)
.t"(i))' , 0(
х . пусть д(i') стол б ец
матрицы
и 1 , u 2 , ••• , иn
- i')
-
=
-(fЗij 1 , ... , fЗijm·-l; Ciq1, ... , Ciqk·) т - вектор-столбец, составленный из
•
•
(4.62), а
коэффициентов правой части
Z(i) = (Y(j1) ... y(jmi-1) x<q1) ... x<qki)) _
матрица размерности п х
(mi - 1 + ki),
составленная из столбцов, ото
бранных из матриц У и Х. Тогда уравнение
(4.62)
может быть пред-
ставлено в виде
y(i)
= Z(i)0(i) + д(i),
(4.62')
а МНК-оценки коэффициентов
том
0(i) в соответствии с общим результа
(4.22) из [Айвазян (2010)) можно вычислить по формуле
e(i)
= (zT(i)Z(i))-lzT(i)Y(i).
При этом, конечно, необходимо, чтобы матрица
ранг (т. е. ранг
Z(i)
(4.63)
имела бы полный
Z(i) = mi - 1 + ki) или, что то же, матрица Z'(i)Z(i)
должна быть невырожденной.
4.4.5.
Оценивание уравнений структурной формы СОУ
Косвенный
метод
наименьших
квадратов.
Косвенный
МНК
(КМНК) предназначен для оценивания параметров отде.лъного урав
нения структурной формы системы и может дать результат (без со
четания с другими методами, например, с двухшаговым методом наи
меньших квадратов) только в применении к точно идентифицируемо
му уравнению.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
Итак, рассмотрим систему
которой (см.
(4.45)
253
и ее приведенную форму
(4.46),
в
(4.4 7))
матрица коэффициентов 1Гij предопределенных переменных
... , т; j = 1, 2, ... , k),
перемен:н:ые
Xt
(i - 1, 2,
не .мул:ьтико.ллинеарнъt, а
t=1,2, ...
,п,
-
(4.64)
вектор-столбец случайных остатков, не коррелированных с предопреде
ленными переменн'ЬtМи Xt = (хр>, х~ 2 ), .•. , х~р))' по условию (так как
все компоненты вектора Лt не коррелированы с
Наша цель
-
Xt)·
оценить параметры i-го уравнения системы
Для анализа i-го уравнения воспользуемся общей схемой
(4.45).
(4.51)-(4.55),
которая была рассмотрена при выводе условий идентифицируемости
отдельного уравнения системы.
Процедуру статистического оценивания параметров i-го уравнения
системы
(4.45)
разобъем на два этапа.
На 1-м этапе оцениваем с помощью обычного МНК все пара
метры 1Гij
(i = 1, 2, ... , т; j = 1, 2, ... ,р)
приведенной формы
(4.46),
последовательно (и автономно) решая эту задачу для каждого отдель
ного уравнения системы
оценок
(4.46).
Хорошие свойства получаемых МНК-
(их состоятельность, а в случае нормальности б~k) - и их
эффективность) обеспечиваются тем, что в модели (4.46)-(4.47)-(4.64)
1fij
выполняются все условия классической линейной модели множествен
ной регрессии.
На 2-м этапе используются соотношения
вающие структурные параметры i-го уравнения
(4.56)-(4.57), связы
системы (4.61) с па
раметрами 1Гij приведенной формы. В случае точной (или сверх-) иден
тифицируемости i-го уравнения структурной формы (т.е. при выпол
нении условий порядка и ранга или только условия порядка со зна
ком строгого неравенства) его параметры /З(i) и
неоднозначно) определяются из системы
c(i) однозначно (или
(4.56)-(4.57) по значениям 1Гij·
Подставив в эти соотношения вместо 1Гij их оценки 1fij и решив систему
уравнений
(4.56)-( 4.57) относительно /3( i) и с( i), мы получим состоя
тельные оценки P(i) и c(i) параметров i-го уравнения системы (4.45).
В случае неидентифицируемости анализируемого уравнения струк
турной формы (т. е. при невыполнении условия порядка идентифициру
емости) число взаимно независимых связей между /З(i),
жащихся в системе
(4.56)-(4.57),
c(i)
и 1Гij, содер
будет .менъше общего числатi+ki-1
неизвестных. Поэтому без дополнительной информации мы не сможем
из
(4.56)-(4.57)
определить значения структурных коэффициентов /З(i)
ГЛ.
254
и
c(i).
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
Один из самых распространенных способов получения необходи
мой дополнительной информации в данном случае, который позволяет
получать оценки параметров неидентифицируемого уравнения струк
турной формы,
это двухшаговый метод наименьших квадратов. Од
-
нако прежде чем переходить к его рассмотрению, проанализируем про
цесс оценивания параметров структурной формы на нашем примере
4.5.
Пр им ер
4.5
(продолжение).
Попробуем сначала формально воспользоваться обычным методом
наименьших
уравнений
квадратов,
(4.48)
и
примененным
(4.49)
в
отдельности
к
каждому
из
(при исключенном балансовом тождестве
(4.50)), и проанализируем состоятельность полученных оценок.
1) Несостоятельность объt-чн·ых МНК-оценок параметров уравне
ний структурной формъt. Начнем с уравнения (4.48) и воспользуемся
формулой для вычисления МНК-оценки в простейшем варианте модели
регрессии с единственной объясняющей переменной (в уравнении
(4.48)
ее роль выполняет цена товара у< 2 )):
А
Ь1 мнк
~ (1) (2)
L...J Yt Yt
t=l_ __
= _n
(4.65)
Е (у~2))2
t=1
Как обычно это делается при исследовании свойств несмещенно
сти и состоятельности оценки, подставим в правую часть
(4.65)
вместо
переменной У?) ее модельное выражение из (4.48):
~ (Ь
L...J
ЬА 1 мнк = t=1
(2)
1Yt
+ Ut.t"(l)) Yt(2)
f:
(у~2))2
t=1
1 ~
-- ь 1
+
.t"(l) (2)
n L...J Ut Yt
t=1
--n----.
~ Е (у~2))2
(4.66)
t=1
Исследуем поведение (при п ~ оо) 2-го слагаемого в правой ча
сти
(4.66), поскольку от него зависят свойства асимптотической несме
щенности и состоятельности оценки Ь1 мнк. Если принять естественное
допущение о существовании пределов (при п ~ оо) числителя и знаме
нателя этого отношения, то в силу закона больших чисел будем иметь:
( i: oi'>yi >)
~ ~
2
lim
n-+oo
=
E(Oi 1>yi2»= COV <oi'>,yi2>),
[.!_n ~
(у~2))2]
L....i
t=1
=
Е (у~2))2 = Dy~2)
(4.67)
(4.68)
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
255
(в этих соотношениях учтено, что по построению Ебр> = Еу~ 2 ) = О
при всех t, а сходимость пределов понимается ~по вероятности~). Оста
ется выразить значения соv(бр>, у?>) и Dy~ 2 ) в терминах параметров
модели. Для этого воспользуемся выражением у?> из второго соотно
шения приведенной формы
и
(4.58)
анализируемой СОУ (с учетом
(4.58')
(4.58")):
cov
(Oi'>, Yi 1J = Е [011> ( 1Г2Хt + 01:: ~'))]
=
2
=
(4.69)
С
ь1 - ь 2
COV
(1°(1)
)
Ut , Xt
+
( 1°(1) 1"(2)) - D1°(1)
COV Ut 1 Ut
Ot
Ь
Ь
1- 2
Dy~2) = Е (CXt + (8?) - 8?))) 2
Ь1
-
Ь2
1
2
(Ь 1 _ Ь2 ) 2 (с Dxt
(4.70)
(1)
(2)
+ Dбt + Dбt
).
Теперь мы можем вычислить предельное выражение (при п --t оо)
для Ь1мнк, вернувшись к (4.66) и учтя (4.67)-(4.70):
2
. ЬА
11m
1 мнк
n-+oo
=
ь
_ __!1_
1
+ с2 n
Ь1 -Ь2
2
2
Xt+0'1 +0"2
(Ь1 -Ь2) 2
=
ь
1-
(Ь
1-
ь
)
2 2D
С
2
О' 1
Xt
+ 0'12 + 0'22 ·
Мы видим, что обычная МНК-оценка Ь1 мнк параметра Ь1 имеет в
общем случае (т. е. при Ь1
=/; Ь2 и и~ =/; О) асимптотически неустрани
мое смещение, а следовательно, она не является ни несмещенной, ни
(что более важно) состоятел:ьной. Поскольку результат отрицатель
ный, оценивание 2-го уравнения системы с помощью обычного МНК,
очевидно, не имеет смысла.
2)
Использование косвенного метода наименьших квадратов. При
переходе к приведенной форме
что регрессионные остатки в
(4.58)-(4.58')-(4.58") было подмечено,
уравнениях (4.58) удовлетворяют услови
ям классической модели регрессии. Следовательно, оценки параметров
?r1 и ?r2 могут быть получены с помощью обычного метода наименьших
квадратов, и при этом они будут несмещенными и состоятельными. Но
в случае идентифицируемости параметров структурной формы они по
определению могут быть выражены через параметры приведенной фор
мы. Поэтому если в эти выражения мы вместо параметров 1t'j подставим
их МНК-оценки 1Гj, то получим (в соответствии с теоремой Слуцкого)
состоятельные оценки для соответствующих идентифицируемых пара
метров структурной формы. Такой способ оценивания идентифицируе
мых параметров структурной формы выше назван косвенн·ым методом
ГЛ.
256
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
наимен:ьших квадратов. В нашем примере идентифицируемым являет
ся только 1-е уравнение. В соответствии с
(4.59)
получаем состоятель
ную оценку косвенного метода наименьших квадратов для параметра
Ь1:
......
л
7Гlмнк
Ь1мнк = ......
7Г2мнк
где 1Гj мнк -
(4.71)
,
обычнъtе МНК-оценки параметров 7Гj в уравнениях
(4.58)
приведенной формы анализируемой СОУ.
3)
Испо.л:ьзование метода инструмента.л:ьных переменных. Причи
на непригодности обычного метода наименьших квадратов в оценива
нии параметров 1-го уравнения структурной формы, как мы знаем (см.
п.
7.2 в [Айвазян (2010)]), - в коррелированности объясняющей пере
менной (в нашем случае - у~ 2 )) с регрессионными остатками (в на
шем случае - с бр>). В соответствии с рекомендациями п. 7.2 из [Айва
зян (2010)] в уравнении (4.48) в качестве инструментальной переменной
естественно использовать доход х, поскольку:
•
Xt
не коррелирован по условию с бр>;
•
Xt
по построению достаточно си.л,-ьно коррелирован с у~ 2 ) (что,
в частности, подтверждается осмысленностью рассмотрения 2-го
уравнения приведенной формы
(4.58)).
Тогда в соответствии с (7.11') из [Айвазян (2010)] оценка Ь1х пара
метра Ь1 по методу инструментальных переменных будет
(4.72)
Если принять во внимание, что МНК-оценки 1Гj параметров 7Гj урав
нений приведенной формы
(4.58)
имеют вид
......
7Г2
f:: y~2)Xt
t=l
= --n--
E х~
t=1
то сравнение оценки
(4.71),
полученной с помощью косвенного метода
наименьших квадратов, с оценкой
(4.72),
полученной с помощью мето
да инструментальных переменных, приводит к выводу, что в данном
случае эти оценки совпадают.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
257
Оценивание неидентифицируемых уравнений структурной
формы СОУ: двухшаговый метод наименьших квадратов
(2МНК)
Пусть, как и прежде,
(4.62),
i-e уравнение системы (4.45)
представлено в форме
и пусть
матрица размерности (n х (mi -
1)),
составленная из соответствующих
mi - 1 столбцов матрицы У,
(4.35)
матрица размерности
ki), составленная из соответствующих ki
столбцов матрицы Х, а Хост(i) - матрица размерности (nx (k-ki)), со
(n
х
ставленная из тех столбцов матрицы Х, которые остались после отбора
из нее столбцов для матрицы Х( i). Тогда анализируемое
системы
(4.62)
(i-e)
уравнение
можно представить в виде
y(i)
= Y(i) b_(i) + X(i) c_(i) + Л(i),
(4.73)
1-й шаг 2МНК. С помощью обычного МНК строится регрессия
выступающих в роли предикторов в уравнении
(4. 73)
эндогенн,-ых пере
менных У (i) по всем предопределенным переменным Х. В результате
получаем регрессионную аппроксимацию У (i) эндогенных переменных
У (i) в виде линейной комбинации всех предопределенных переменных
в форме
(4.74)
где §Yi/x = (X'X)- 1X'Y(i), а Х = (X(i): Хост(i)) - матрица размерно
сти (n х k) наблюденных значений всех предопределенных переменных,
составленная из матриц X(i) и Хост(i).
2-й шаг
2 МНК. С помощью обычного МНК строится регрессия
эндогенной переменной y(i) по Y(i) и X(i). Другими словами, в уравне
нии (4.73) объясняющие переменные Y(i) заменяются на их аппрокси
мации Y(i), выраженные формулой (4.74). Реализация МНК в данном
случае, проведенная в соответствии с общей теорией классической ли
нейной модели множественной регрессии (см. п. 4.2 в [Айвазян
(2010)],
приводит к следующей системе нормальных уравнений относительно
ГЛ.
258
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
оценок Ь_ (i) и с_ (i) неизвестных параметров, соответственно, Ь_ (i) и
c_(i):
ь_(i))
(C,_(i)
_ (Y'(i). y<i>)
- X'(i) · y(i) .
(4.75)
Заметим, что квадратная матрица А, являющаяся первым сомно
жителем в левой части соотношения
(4.75)
(она составлена из мат
риц Y'(i)Y(i), Y'(i)X(i), X'(i)Y(i) и X'(i)X(i)), имеет размерность
(mi - 1 + ki) х (mi - 1 + ki) и может оказаться въtрожденной в силу
мулътикоj/,j/,инеарности, возникающей (по построению) между объяс
няющими переменными Y(i) и X(i) в случае X(i) = Х. В этих случаях
явные выражения оценок b_(i) и c_(i) из (4.75) получить невозможно.
Однако объединение соотношений (4.75) и системы (4.56)-(4.57) даст
нам систему линейных уравнений относительно ь_ i) и С,_ ( i) (т. е. отно
(
сительно неизвестных параметров i-го уравнения структурной формы),
которая позволит вычислить значения всех этих параметров. В осталь
ных же случаях матрица А обратима и, следовательно, мы имеем воз
можность получить явные выражения оценок, а именно:
( b-(i)) _
C,_(i) где
(mi - 1 + ki)
х
А
(mi - 1 + ki) -
_ 1 (Y'(i)Y<i>)
X'(i)Y(i} '
(4.76)
матрица А имеет вид
(4.77)
или, что то же,
А= (~'~i~~~~:~~~ 1~'~(~) ~:(~)-~~i~)
•. :••
X'(i)Y(i)
Заметим, что первые
mi -1
.
(4.77')
: X'(i)X(i)
компонент вектора-столбца, являющегося
вторым сомножителем в правой части
(4.76), могут быть также пред
ставлены в терминах исходнъtх наблюдений, а именно:
Y'(i) y<i>
= Y'(i) x(x'x)- 1x 1y<i>.
(4.78)
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
259
В задачах анализа точности 2МНК-оценок отдельного уравнения
СОУ важную роль играет ковариационная матрица Е этих оценок.
Можно показать {см., например, [Джонстон
большом числе наблюдений
(т. е.
{1980)],
асимптотически по
с.
383), что при
n -+ оо) матри
ца Е может быть оценена (в случае невырожденности матрицы А) с
ПОМОЩЬЮ матрицы
{4.79)
где матрица А определяется соотношениями
82
=
l
n-mi-1-pi
(Y(i) -
(4.77)
или
(4.77'),
Y(i)b-{i) - X(i) c_(i))' х
а
{4.80)
х (Y(i) - Y{i)b_(i) - X{i) c_(i)).
Пр им ер
4.5
(продолжение).
Снова вернемся к рассмотренному выше примеру, в котором анали
зировалась модель спроса и предложения. Чтобы обойти главное пре
пятствие в применении обычного МНК к отде.л/ьному неидентифициру
емому уравнению (в данном примере это было уравнение, описывающее
зависимость спроса у! 1 ) от цены у! 2 ) и дохода Xt: у! 1 ) = ~у! 2 ) + cxt+
+б! 2 )) - коррелированность играющей роль предиктора эндогенной пе
ременной у! 2 ) со случайными остатками б! 2 ), - н а 1 - м ш а г е стро
ится регрессия эндогенной переменной-предиктора У?) по предопреде
ленной переменной Xt· В результате получаем оцененное регрессионное
уравнение у! 2 ) = 8y<2>;xXt + et. На 2 - м шаге в правую часть анализируемого уравнения вместо эндогенной переменной у! 2 ) вставляется ее
регрессионное выражение через Xt, в результате чего получаем уравне
ние
После этого к данному уравнению применяется обычный МНК в
целях состоятельного оценивания коэффициента (}у<•> /ж = Ь28у<2> /х
+с
(очевидно, вести речь об отдельном оценивании коэффициентов Ь2 и с
в уравнении ур) = Ь2х~ 2 ) + CXt + (б! 2 ) + Ь2еt), в котором х~ 2 ) = 8y<2>;xxt,
не имеет смысла, так как переменные
Xt и Xt связаны чистой муль
тиколлинеарностью по построению). Получив оценку еу<•> /х параметра
(}y<•>jx = Ь28у<2>;х +с, мы к имеющимся уже двум соотношениям, свя
зывающим параметры структурной и приведенной форм (вытекающим
из общей формулы {4.47)), добавляем еще одно: ey(l>/x = Ь28у<2>;х +с.
260
ГЛ.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
После этого, решая систему
А
7Г1
А
7Г2
Ь1с
= --Ь2
=
-
Ь1
с
Ь2
-
Ь1
Ь28у<2> /х + с = 8у<1> /х
относительно коэффициентов Ь1, Ь2 и с, мы получаем оценки всех пара
метров структурной формы анализируемой системы.
Использование метода главных компонент в 2МНК. В двух
шаговом методе наименьших квадратов, как мы видим, на 1-м шаге
вычисляется регрессия
Y(i)
ным, т. е. в каждом из mi дится оценивать
k
по всем(!)
1
k
предопределенным перемен
регрессион:н:ых уравнений
(4.74)
прихо
параметров. В моделях небольшой размерности,
т. е. при относительно малых значениях
k,
это не создает трудностей,
но в средних и больших моделях общее число предопределенных пере
менных может быть одного порядка с общим числом наблюдений
(n),
и
тогда статистическая надежность выводов становится неудовлетвори
тельной (бывают случаи, когда
k
>
n; однако при этом состоятельное
оценивание параметров модели становится в принципе невозможным).
В подобных ситуациях возникает необходимость снизить общее число
предопределенных переменных, через которые выражается У (i)
число
k
участвующих в правой части выражения
(4.74)
(т. е.
предопреде
ленных переменных Х). Клоек и Меннес предложили с этой целью ис
пользовать в качестве аргументов аппроксимирующей функции У (i)
не все предопределенн·ые переменные Х( i) и Хост( i) (что предусмотрено
в (4.74)), а лишь те, которые участвуют в i-м уравнении (т. е. X(i)),
плюс небольшое количество главных компонент, построенных по про
чим предопределенным переменным Хост 11 • Что касается переменных
X(i),
то, с одной стороны, их не следует трогать, так как они вклю
чались в
i-e
уравнение и по содержательному смыслу, и с учетом вы
полнения условия порядка идентифицируемости (см. выше), а с другой
стороны,
ими
нельзя ограничиваться
при построении
аппроксимации
У (i) для У (i), так как в этом случае мы столкнулись бы со строгой
мультиколлинеарностью.
Поэтому предлагается следующая процедура.
Матрица Хост(i) размерности n х (k-ki), состоящая из наблюде
ний предопределенных переменных, не вошедших в анализируемое (i-e)
1)
уравнение, стандартизируется, т. е. из каждого наблюдения перемен
ной вычитается ее выборочное среднее значение и результат делится на
11 См.:
Kloek Т., Mennes L.B.M. Simultaneous Equation Estimation Based on
Principal Components VariaЫes // Econometrica. Vol. 28 {1960). Р. 45--61.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
261
ее выборочное среднеквадратическое отклонение. В результате получа
ем матрицу Х0ст(i).
2) По наблюдениям стандартизированной матрицы Хост( i) строятся
(l) -- ( и (l) , и (l) , •.• , Un
(l))' , l -- 1 , 2, .•. , k - k·i (см.,
главные компоненты U
1
2
например, п. 3.4 в [Айвазян (2010))).
3) Из k - ki построенных главных компонент u<l) отбирается срав
нительно небольшое число q (q :s:;; 4) наиболее информативных с точки
зрения точности аппроксимации значений y(i) в виде функции от X(i) и
U(lk).
В качестве критерия информативности можно ис
пользовать, например, величину коэффициента детерминации R 2 , опре
деляющего степень тесноты связи между y(i), с одной стороны, и на
бором X(i), u(li), ... , U(lq) - с другой.
u(li), U(l2 ),
••• ,
Иначе говоря, главные компоненты u(lY>, ... , u<Ф отбираются из
общего числа k - ki в соответствии с условием 12
~)
И i ,И
4)
u(lY>'
~)
2 , ••• ,
И
~)
q
2
~ l1,l2,
max Ry(i).<x<·> u(li) u(Lq)>·
... ,lq
••
,... ,
В качестве 1-го шага 2МНК строится регрессия
Y(i) по X(i),
u(lg)' ... 'и<Ф (а не по X(i), Хост(i), как это рекомендовано в
обычном 2МНК).
3
а м е ч а н и е. Иногда строят главные компоненты по всей мат
рице Х, и тогда аппроксимация У (i) осуществляется только по
ным компонентам этой матрицы, причем
k
k глав
должно подбираться с уче
том условия порядка идентифицируемости уравнения. Тем самым об
ходится неудобство этого метода, возникающее при необходимости оце
нивания сразу нескольких (а тем более
-
всех) уравнений системы. В
вышеизложенном варианте тогда придется строить главные компонен
ты для каждого уравнения в отдельности. Однако существуют работы,
демонстрирующие преимущества (в точности) именно изложенного вы
ше метода по сравнению с подходом, в котором главные компоненты
строятся по всей матрице Х для всех уравнений системы.
В заключение отметим, что эконометрическая теория и практи
ка свидетельствуют о том, что
2 МНК,
наряду с методом инструмен
тальных переменных, является, пожалуй, наиболее важным и широко
применяемым методом оценивания параметров отделъного уравнения
структурной формы СОУ.
12 В
эконометрической литературе и практике предлагались и использовались и
другие критерии отбора главных компонент: критерий минимизации мультиколли
неарности меж.цу X(i) и и(!~) 1 ••• 1 u<Lq)i критерий максимальной дисперсии, когда
отбираются главные компоненты, соответствующие максимальным характеристиче
ским числам (см., например, [Джонстон Дж.
(1980)], с. 393-395).
ный нами критерий представляется более предпочтительным.
Однако предложен
ГЛ.
262
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Трехшаговый метод наименьших квадратов одновременной
оценки всех параметров системы (ЗМНК)
Трехшаговый метод наименьших квадратов был предложен впервые
Зельнером и Тейлом 13 в качестве метода статистического оценивания
одновременно всех уравнений модели
(4.61)
с у'Четом возможной вза
имной коррелированности регрессионн·ых остатков разли'ЧН'ЫХ уравне
ний этой систем'Ьt. Этот метод оказывается более эффективным, чем
2МНК, если случайные остатки 8~ 1 ), 8~ 2 ), ... , 8~m) различных уравнений
системы (4.61) взаимно коррелированы, т. е. если их ковариационная
матрица Ед= (E(8~i)8~l))i,l=l,2,".,m) отлична от диагональной. Хотя от
метим, что и в этой ситуации 2МНК-оценки структурных параметров
системы остаются состоятельными.
В трехшаговом методе наименьших квадратов (3МНК) сохранены
первые два шага 2МНК. Однако полученные в результате этих двух
шагов, автономно для каждого отдельного
(i-го)
уравнения, оценки
структурных параметров fi2мнк(i) = -b-(i) и с2мнк(i) = -c-(i), i =
= 1, 2, ... , т (b_(i) и c_(i) определены соотношениями (4.76)), не яв
ляются окончательными, а перес'Читываютс.я на 3-м шаге следующим
образом: оценки
......
/32 мнк
и с2 мнк используются для подсчета
выбороч......
ной ковариационной матрицы случайных остатков Ед, а последняя,
в свою очередь, используется для одновременного вычисления оценок
всех структурных параметров В и С системы
(4.61)
с помощью обоб
щенного метода наименьших квадратов в рамках соответствующим
образом построенной обобщенной линейной модели множественной ре
грессии (см., например, п.
5.2
в [Айвазян
(2010)]).
Рассмотрим подробнее, как реализуется описанная выше общая схе
ма 3МНК. Можно было бы начать сразу с 3-го шага, так как первые
два, как было отмечено, совпадают с соответствующими шагами 2МНК.
Однако мы вернемся вначале к 2МНК, чтобы описать прием, эквива
лентный двум шагам этого метода, поскольку он приводит к тем же
самым оценкам
(4.76),
что и 2МНК.
Замечание о 2МНК-оценках. Итак, снова рассмотрим отдель
ное
(i-e)
уравнение
(4.73)
анализируемой СОУ
(4.61).
Так же, как и при
анализе рекурсивных систем, введем матрицу
Z(i)
составленную из матриц
13 См.:
= (Y(i)
Y(i)
и
X(i),
(4.81)
и вектор-столбец неизвестных
Zellner А., Theil Н. Three-stage Least-squares: Simultaneous Estimation of
Simultaneous Equations // Econometrica. Vol. 30 (1962). Р. 54-78.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
263
параметров
(4.82)
составленный из векторов Ь_ (i) и с_ (i). Тогда мы можем записать урав
нение
(4.73)
в виде
y(i) = Z(i) 0(i) + д(i).
(4.73')
В 2МНК мы обходили неприятности, связанные с взаимной кор
релированностью объясняющих переменных
Y(i)
и остатков д(i), под
становкой в уравнение
(4.73) вместо Y(i) их регрессионного выражения
через Х (см. формулу (4.74)). Оказывается, можно добиться того же и
прийти к 2МНК-оценкам (4.76), действуя формально несколько иным
способом. А именно, домножим все члены уравнения (4. 73') слева на
матрицу Х':
x'y(i) = (X'Z(i)) 0(i) + Х' д(i),
(4.82)
y<i> = Z(i) e(i) + д(i),
(4.82')
y<i> = x'y(i),
(4.83)
Z(i) = X'Z(i),
(4.84)
д(i)
(4.85)
или, что то же,
где
= Х' д(i).
Можно показать, что в уравнении
(4.82')
объясняющие переменные
Z( i) не коррелиЕ_ованы с остатками Л( i) и что ковариационная матрица
Ед(i) остатков д(i) имеет вид
Ед(i) = Е{д(i)д'(i)) = O"ii(X'X),
где
O"ii
(4.86)
= D8~i).
Соотношение
(4.82')
(и эквивалентное ему
(4.82))
можно рассмат
ривать как обобщенную линейную моде.л:ь множественной регрессии,
в которой у( i) играет роль вектора наблюдений зависимой перемен
ной, Z(i) - матрица наблюдений объясняющих переменных, 0(i) вектор-столбец оцениваемых параметров, а Л(i) - вектор-столбец ре
грессионных остатков с заданной (с точностью до постоянного множи
теля O"ii) ковариационной матрицей 14 . Тогда в соответствии с формулой
14 Если
в состав предопределенных переменных Х входят помимо нес.t1.у'Чй.йных эк
зогенн'Ых переменных лаговые эндогенн'Ые переменные (которые по своей природе
являются стохастическими), то, как известно (см. [Айвазян
(2010)J,
п. 7.1), обоб
щенный метод наименьших квад1>атов будет продолжать давать тем не менее состоя
тельные оценки параметров, если эти стохастические предикторы не коррелированы
с регрессионными остатками (что и имеет место в нашем случае).
ГЛ.
264
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
ОМНК-оценок получаем:
0омнк(i)
= [Z'(i)(X'x)- 1Z(i)]- 1Z'(i)(X'x)- 1y(i)
= [Z'(i)X(X'x)- 1X'Z(i)]- 1Z'(i)X(X'x)- 1x'y(i).
Сравнение правых частей формул
ний
(4.82) приводит
оценок (4.87).
(4.77'), (4.81)
2МНК-оценок и
и
(4.87)
и
(4. 76)
(4.87)
с учетом соотноше
к заключению об эквивалентности
3-й шаг ЗМНК. От отде.л:ьн:ых уравнений
СОУ
(4.61).
С этой целью, составив уравнения
(4.82) вернемся ко всей
(4.82) для i = 1, 2, ... , т,
объединим их в одной обобщенной линейной модели множественной
регрессии вида
х'у<1>
Х 1 У< 2 >
X'Y(m)
(~,~~~). ~:~(.2~ .~. ": ·.....~...)
О
О
О
X'Z(m)
.•.
0(1)
0(2)
+
0(m)
(4.88)
Х' д(l)
+
Х'д(2)
Х'д(m)
Матрица ковариаций Ед вектора случайных остатков Л
= (Л.1 (1),
д. 1 (2), ... , Л 1 (т))' = (д'(l)Х:д'(2)Х: ... :д'(m)Х)' будет иметь вид
инХ'Х
и12Х'Х
Ед = ( .и~~~,.~ . .~2~~:~
. ·.·.· . ~2~~'~.
u1mX'X)
= Ед®Х'Х,
(4.89)
um1X'X um2X'X . . . O'mmX'X
где через O'ij обозначена ковариация случайных остатков i-го и j-го
уравнений структурной формы (она по условию не зависит от
и··
i3
=
cov(д(i)
t ' д<Л)
t
=
Е(б(i)б(j)))
t t
' Ед
=
t,
т. е.
(а")·
·-12
i3 i,3, ,.",m, а символ ®
означает кронекерово перемножение матриц (см. п. П2.8 в Приложении 2).
Чтобы воспользоваться обобщенным методом наименьших квадра
тов в одновременном оценивании параметров
0(1), 0(2), ... , 0(m) обоб
щенной линейной модели множественной регрессии (4.88), необходимо
знать ковариационную матрицу остатков Ед. Из (4.89) видно, что для
этого нам необходимо знать матрицу Ед ковариаций слу'Чайных воз
мущений анализируемой структурной формъt
(4.61).
Сущность 3-го
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
шага трехшагового
метода
наименьших
квадратов
......
как
раз
265
и
заклю-
чается в том, что для построения оценки Ед неизвестной матрицы Ед
используются 2МНК-оценки 02мнк(i) параметров <Э(i), а именно: (i,j)-й
элемент Uij этой матрицы оценивается по формуле
Uij
=
.!_
n
(Y(i) -
Z(i)82мнк(i))'(у<Л -
Z(j)82
мнк(j)),
(4.90)
где Z(l) и 82мнк(l) определены соотношениями, соответственно, (4.81)
и (4.76) (или (4.87)), а y(l) = (y~l), y~l), .•. , у~))', l = 1, 2, ... , т.
После этого мы можем воспользоваться формулой обобщенного ме
тода наименьших квадратов, примененного к модели
0змнк =
где
(Z'E= 1z)- 1Z'E= 1Y,
д
д
......
0=
Х'У( 2 )
У=
......
x'y(m)
0(m)
(&11Х'Х &12Х'Х
...
(4.91)
Х'У( 1 )
0(1)
......
0(2)
......
(4.88):
Ед= .&~~~,.~ . . ~2~~:~
. ·. .· . ~2~~'~. ,
&1mX'X)
&m1X'X &m2X'X ... &mmX'X
Uij определены формулой
Z=
(напомним, что
(4.90),
а
X'Z(l)
о
о
о
о
X'Z(2)
О
о
о
о
О
Z(i) и 0(i), i = 1, 2, ... , т,
соответственно, (4.81) и (4.82)).
. • . X'Z(m)
определены соотношениями,
Как уже было упомянуто, процедура ЗМНК обеспечивает лучшую
по сравнению с двухшаговым методом эффективность оценок лишь в
случае, когда матрица Ед не является диагональной, т. е. когда случай
ные остатки бii), входящие в различные структурные уравнения, кор
релируют друг с другом. Если матрица ковариаций Ед для структур
ных остатков может быть приведена (соответствующим упорядочением
уравнений системы) к блочно-диагональному виду, то всю процедуру
трехшагового оценивания лучше применять отдельно к каждой группе
уравнений, соответствующих одному блоку. Тем самым существенно
снижается трудоемкость вычислительной реализации ЗМНК.
266
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Другие методы оценивания СОУ и некоторые общие
рекомендации
Помимо методов статистического оценивания СОУ, описанных выше,
в эконометрической литературе и практике существуют и другие про
цедуры. Так, если дополнительно постулировать нормальность струк
турных возмущений д~i), то для оценки отдельного уравнения наряду
с 2МНК может быть использован метод максимального правдоподоби.я
с ограни-ченной информацией, или, что то же, метод наименьшего дис
персионного отношени.я15 . Для одновременной оценки всех параметров
системы в рамках тех же условий нормальности д~i) разработан также
метод максимального правдоподоби.я с полной информацией 16 • В рас
ширении класса методов оценивания СОУ можно идти также по линии
введения целых параметри-ческих семейств методов, когда при кон
кретном выборе значения свободного параметра этого семейства мы
приходим к тому или
иному уже известному методу как к
частному
случаю 17 .
Мы оставили эти методы за рамками учебника, поскольку трудо
емкость их вычислительной реализации, по меньшей мере, не уступает
описанным выше косвенному, двухшаговому и трехшаговому методам
наименьших квадратов. В то же время они требуют дополнительных
модельных ограничивающих предположений. Поэтому они реже дру
гих методов применяются в эконометрической практике.
В заключение приведем несколько общих рекомендаций по постро
ению и статистическому анализу СОУ.
1)
Прежде всего следует провести процедуру исключения из СОУ
всех уравнений, являющихся тождествами.
2)
В ходе этапа «спецификация модели~ надо стремиться к обеспе
чению выполнения условий идентифицируемости отдельных уравнений
и системы в целом. Если среди конечных прикладных целей моделиро
вания ставится задача интервального прогноза значений эндогенных
переменных (см. ниже, п.
4.4.6),
то следует стремиться к обеспечению
нормальности и взаимной независимости (по
~(i)
Ut
t)
случайных возмущений
•
3)
Приступая к статистическому оцениванию СОУ, следует приме-
15 Метод
впервые предложен в работе: Anderson Т. W., RuЬin Н. Estimation of the
Parameters of а Singl Equation in а Complete System of Stochastic Equations / / Ann.
Math. Statistics. Vol. 20 (1949). Р. 46-63
16 См.: Hood W. С., Koopmans Т. С. (eds). Studies in Econometric Method. New York,
1953.
17 См.:
Тейп. Г. Экономические прогнозы и принятие решений. (Пер. с англ.). М.:
Статистика,
1971.
С.
281-282.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
267
нить, в первую очередь, 2МНК последовательно ко всем уравнениям
системы и использовать полученные оценки структурных параметров
для оценки ковариационной матрицы :Ед структурных остатков (см.
формулу
(4.90)).
4) По полученной оценке Ед ковариационной матрицы :Ед прове
рить гипотезу о ее диагональной (или блочно-диагональной) структу
ре. Если гипотеза о диагональности :Ед не отвергается, то использо
вать полученные ранее 2МНК-оценки структурных параметров В и С
для вычисления оценок fi параметров приведенной формы по формуле
fi = -:В- 1 6 и далее - для прогноза и имитационных расчетов.
5) Если гипотеза о диагональности матрицы
:Ед отвергается, то еле.......
дует использовать полученную ранее оценку :Ед для реализации процедуры ЗМНК.
6) Если в процессе статистического анализа оценки Ед выяснит
ся, что блочно-диагональная структура матрицы :Ед не противоречит
имеющимся наблюдениям, то процедуру ЗМНК следует применить от
дельно к каждой группе уравнений СОУ, соответствующих тому или
иному блоку матрицы :Ед.
4.4.6.
Точечный и интервальный прогноз значений
эндогенных переменных
Можно выделить два основных типа конечных прикладных целей, пре
следуемых при построении эконометрических моделей в виде СОУ.
Один из них связан с получением сведений о структурных параметрах
модели и (или) коэффициентах приведенной формы. Это бывает обыч
но в ситуациях, когда интересующие исследователя параметры модели
имеют четкую экономическую интерпретацию (они могут играть роль
различных эластичностей, мультипликаторов, характеристик ~склон
ности к сбережениям» и т. п.). Другой тип конечных прикладных целей
заключается в стремлении осуществить с помощью анализируемой СОУ
условный прогноз эндогенных пере.м.еннъtХ (при определенных услови
ях, накладываемых на значения предопределенных переменных), про
извести многовариантные (в соответствии с различными вариантами
условий) сценарные расчеты, показывающие, как себя будут вести эн
догенные переменные при различных условиях, касающихся значений
предопределенных переменных.
Если интерес сосредоточен на структурнъtх параметрах В и С,
то следует воспользоваться состоятельными методами их оценивания
(2МНК, ЗМНК) и по той же исходной информации оценить точность
примененных процедур (либо с помощью аналитических методов, т. е.
выводя и статистически оценивания ковариационную матрицу исполь-
268
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
зуемых оценок параметров, см., например,
(4.79)-(4.80),
либо с по
мощью разного рода компъютерно-имитационнъ~х методов, о послед
них см. ниже).
Если же нас могут удовлетворить коэффициенты П приведенной
формы (сами по себе или как средство получения точечного прогно......
......
за эндогенных переменных по формуле Уn+т
ПХn+т, где Хn+т заданные для момента времени п
ременных, а т
-
+т
=
значения предопределенных пе
~глубина~ прогноза), то анализ точности получен
ных оценок и (или) прогноза можно проводить одним из двух способов.
В первом из них {?оле~ сложном) отправным пунктом служат состо
ятельные оценки В и С (структурных параметров В и С) и их кова......
риационные матрицы Ев и Е5, а точнее, - состоятельные оценки Ев
и Еа этих матриц. По ним строят оценки fi: = -:В-ЧS (см. (4.47))
и стараются вывести общий вид состоятельной оценки Еп ковариаци
онной матрицы Еп. Решение последней задачи составляет аналити
ческую базу для решения задачи построения интервалъного прогноза
для эндогенных переменных У и интервалъных оценок для параметров
приведенной формы П. Этот путь анализа точности точечного прогноза
......
......
Уn+т и точечных оценок П считается более предпочтительным в ситуациях, когда есть основания полагать, что спецификация модели в ее
структурной форме осуществлена правильно 18 . Однако сопутствующие
этому пункту громоздкость вывода вида ковариационной матрицы Еп
и связанные с этим аналитико-вычислительные сложности побудили
нас не включать подробное описание данного подхода в учебник (ин
тересующийся читатель может обратиться непосредственно к работам:
1) Goldberger А. S., Nagar А. L., Odeh Н. S. The Covariance Matrices of
Reduced-Form Coefficients and of Forecasts for а Structural Econometric
Model // Econometrica. Vol. 29 (1961). Р. 556-573; 2) Нитапs S. Н. Simultaneous Confidence Intervals in Econometric Forecasting / / Econometrica.
Vol. 36 (1968). Р.18-30).
Мы же остановимся здесь подробнее на относительно более простом
пути построения интервальных прогнозов для эндогенных переменных
и для отдельных параметров приведенной формы. Этот путь основан на
непосредственном вычислении оценок
fi
коэффициентов приведенной
формы П с помощъю обыкновенного метода наименъших квадратов,
примененного к каждому уравнению системы
(4.46).
Состоятельность
и несмещенность этих оценок обеспечиваются стандартными модельны
ми допущениями, относящимися к системе
(4.45),
а их ковариационная
матрица выводится на базе фундаментальных соотношений классиче18 См.
Klein L. R. The Efficiency of Estimation in Econometric Models / / Cowles
Foundation Paper. № 157. Yale University, 1960.
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
269
ского мнк.
Итак, по исходным статистическим данным анализируется приве
денная форма СОУ вида
Yt=ПXt+et,
,,,. _ ( (1)
где L
t-
Yt , Yt(2) , ... , Yt(m))'
и
блюденных в момент времени
t=1,2, ... ,n,
(4.92)
t -_ (xt(1) , xt(2) , ... , xt(k))' -
Х
t
векторы на-
значений, соответственно, эндогенных
и предопределенных переменных, П = ( 1щ) i~1,2, ... ,m; -
матрица коэф-
з=1,2, ... ,k.
фициентов приведенной формы, а случайные остатки et = (ер>, е~ 2 ),
... ,e~m))' имеют нулевые средние значения, постоянные (не зависящие
от времени) дисперсии и не коррелированы с предопределенными пере
менными
Xt.
Заметим, что модель
(4.92)
состоит из т обобщенных линейных
моделей множественной регрессии вида
y(i) =XП(i)+e(i),
i= 1,2, ... ,m,
(4.92')
Y (i) = ( у 1(i) ,у2(i) , •.• ,yn(i))' , П( i.) = (1ri1,7ri2, .•. ,1rik )' - i-· й стол бец
матрицы П', e(i) = (e~i), e~i), ... , е~>)', а Х- матрица наблюдений пред
где
определенных переменных.
Даже при взаимной коррелированности остатков e~i), e~i), ... , е~>
(а они могут быть таковыми в нашем случае, если не потребовать некор-
релированности структурных возмущений дi:> и дg> разных уравнений
для разных моментов времени) обычные оценки наименьших квадратов
7?мнк(i) параметров
7r(i) в уравнении (4.92') являются состоятельными
(см. п. 5.2 в [Айвазян (2010))). Применяя известную формулу для вы
числения МНК-оценок, получаем
fiмнк(i) = (X'X)- 1x'y(i),
i = 1, 2, ... , т.
(4.93)
Матрицу, составленную из столбцов llмнк(l), llмнк(2), ... , llмнк(m), оче
видно, можно записать в виде
1
....
·: Пмнк(2)
....
·: . . . ·: Пмнк(m)
....
( Пмнк(l)
:·) -- (хтх)- хту ' (4 ·94)
где матрица У составлена из столбцов y(l), у( 2 ), ... , y(m), т. е. является
матрицей наблюденных значений эндогенн·ых переменных. Но матрица,
стоящая в левой части
(4.94), есть не что иное, как
П', следовательно, вместо (4.94) мы можем записать
fi'
мнк
= (Х'Х)- 1 Х'У '
МНК-оценка для
(4.94')
ГЛ.
270
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
или, транспонируя обе части этого соотношения {воспользовавшись
правилом транспонирования произведения матриц, см. Приложение
2),
получаем:
fiмнк
= У'Х(Х'Х)- 1 .
{4.95)
,...
Точечный прогноз эндогенных переменных Уn+т на т тактов времени вперед, т. е. точечная оценка значений Уn+т по заданным
значениям предопределенных переменных Хn+т, опирающийся на на
блюденные значения этих переменных до момента времени t =
n
(т. е.
на исходные данные), строится с помощью формулы
,...
,...
Уn+т
,...
= ПмнкХn+т,
(4.96)
где матрица МНК-оценок Пмнк коэффициентов приведенной формы
модели
{4.45)
определена соотношением
(4.95).
Заметим, что истин:н:ые
значения эндогенных переменных в прогнозируемый период будут рав
ны в соответствии с
(4.92)
Уn+т = ПХn+т
Следовательно, ошибка €(т) прогноза
+ Е:n+т·
(4.96)
может быть выражена в
виде
€(т) = Уn+т - Уn+т = {llмнк - П)Хn+т - Е:n+т·
{4.97)
А поскольку Еfiмнк = П (в силу свойства несмещенности МНК-оценок
в обобщенной линейной модели множественной регрессии) и Ееn+т =
= Om, то, применяя к {4.97) операцию усреднения Е, убеждаемся в
несмещен:н.ости прогноза
(4.96),
т. е. в том, что Е€{т)
= Om.
Интервальный прогноз эндогенных переменных
yt
или по
строение совместнъ~х доверительных интервалов для различных соче
таний компонент этого вектора на т тактов времени вперед возможны,
если мы будем знать (сможем оценить) ковариационную матрицу оши
бок прогноза €(т) = Уn+т - Уn+т, т. е. матрицу
Ее(т) = Е{€{т)€'{т)) = Е[(Уп+т - Уn+т)(Уп+т - Уn+т)'].
{4.98)
В условиях соблюдения стандартных модельных допущений, сфор
мулированных, в частности, при описании модели
(4.45), удается полу
чить несмещенную оценку f:€(т) для ковариационной матрицы Ее(т) в
виде
(4.99)
,...
где матрица ЕЕ является несмещенной оценкой ковариационной мат-
рицы остатков приведенной формы ЕЕ
= E(eteJ) =
{sij)i,j=l,2,".,m
и
задается формулой
,...
ЕЕ=
-1n-p
(У
,... '
'
,... '
- хпмнк)
(У - хпмнк)
(4.100)
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
(вывод соотношения
(4. 99)
271
дается ниже).
Теперь, если дополнителъно предnоложитъ нор.малънъtй характер
распределения слу-чайнъ~х возмущений структурной (б~i)), а зна-чит, и
приведенной (e~i)) форм анализируемой .модели, мы располагаем всем
необходимым для построения интервальных (как сов.местных
новременно по набору эндогенных переменных,
нъ~х
-
-
од
так и покоординат
для каждой эндогенной переменной в отделъности) прогнозов.
-.
_ ( л(l} л(2}
л(m) )'
о тклонения значени й У.
n+т Уn+т' Уn+т' ... , Уn+т
эндогенных пе-
-
ременных, спрогнозированнъ~х на т тактов времени вперед, от их истин
нъ~х будущих значений Уn+т с заданной доверительной вероятностью
Р
= 1-
а должны концентрироваться внутри эллипсоида рассеяния,
определяемого уравнением
(Уn+т - Уn+т )'Е;- 1 (Уn+т - Уn+т) ~ [1 + Х~+т(Х'Х)- 1 Хn+т] Х
х
(п - р)т
Fa(m;n-p-m+1),
п-р-т+1
(4.101)
где Хn+т = (х~12т, х~22т, ... , х~2тУ - заданные (на прогнозный период)
значения предопределенных переменных, а
Fa(m; п-k-т+1) -
100а%
ная точка F-распределения с числами степеней свободы числителя и
знаменателя, равными т и п - k - т 119.
+
С практической точки зрения бывает удобнее знать гарантирован
ные (одновременно для всех эндогенных переменнъ~х) пределы варьиро-
вания каждой из компонент у~~т (i
= 1, 2, ... , п), обозначенные на своей
координатной оси Oy(i). Геометрически эти покоординатные интервалы
определяются проекциями эллипсоида (4.101) на каждую из коорди
натных осей Oy(i). Хьюманс показал, 20 что эти проекции могут быть
заданы соотношениями вида (одновременно выполняющимися для всех
у~~т с вероятностью Р = 1 - а):
л(i}
{ Уn+т
-
г::-:;- ~
~ л(i}
(i}
V.CaSii -..: Уn+т
-..:
i=l,2, ... ,m,
Уn+т
+ Уг::-:;
CaSii,
(4.101')
где
Са= [1
+ Х~+т(Х'Х)- 1Хn+т]
(пп-
k
k)m
Fa(m; n - k - т + 1),
-m+l
19 Этот
вывод опирается на результат Хупера и Зельнера, которые показали, что
статистика "(n':_-k~! 1 (Уnн - Уn+т )'Ei<~J(Ynн - У) подчиняется F(m; n- k- т + 1)распределению.
м.: Hooper J. W" Zel ner А. The Error of Forecast for Multivariate
Regression Models // Econometrica. Vol. 29 (1961). Р. 544-555.
20 См.: Humans S. Н. Simultaneous Confidence Intervals in Econometric Forecasting
// Econometrica. Vol. 36 {1968). Р. 18-30.
ГЛ.
272
а
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
.......
Sii -
нием
i-й диагональный элемент матрицы Ее, определенной соотноше-
{4.100).
Соотношения
{4.101)
и
{4.101')
задают совместн:ы,е доверительные
области (интервалы) для всех анализируемых эндогенных переменных
одновременно. Если же нас интересует интервальн:ы,й прогноз одной
отдельно взятой эндогенной переменной y(i), выполняющийся с задан
ной вероятностью Р = 1 - а, то он определяется неравенствами
(4.102)
J
где t~ (n-k) =
Fa(1; п - k) - 100~%-ная точка распределения Стью
дента с п - k степенями свободы. Из общих соображений следует ожи
дать (и это можно доказать строго математически), что ширина интер
вального прогноза
(4.102)
для одной отдельно взятой эндогенной пе
ременной всегда существенно меньше, чем ширина интервального про
гноза для той же самой переменной, получающаяся в рамках задачи
построения совместнъtх доверительнъ~х интервалов
Вывод формулы
(4.99)
(4.101').
для несмещенной оценки ковари
ационной матрицы ошибок прогноза. Вернемся к задаче вычис
ления ковариационной матрицы ошибок прогноза Ее(т) (см.
{4.98))
и
построения ее несмещенной оценки Ее(т)·
1) Подставим в правую часть (4.98) вместо ошибки прогноза Уn+т
-Уn+т ее выражение из {4.97):
Ее(т) = Е {[(Пмнк - П)Хn+т - сn+т][(Пмнк - П)Хn+т - сn+т]
.......
.......
.......
1
.......
= Е [ {Пмнк - П)Хn+тХn+т{Пмнк - П)
']
'}
=
+ Е{сn+тсn+т)1
.......
1
- Е [ сn+тХn+т(П
мнк - П) '] -
- Е [{fi мнк - П)Хn+тс~+т].
{4.61')
Два последних члена в правой части этого выражения равны ну
лю. Действительно, рассмотрим, например, произведение сn+т · [Х~+тх
х {fiмнк - П)']. Его первый сомножитель {сn+т) не коррелирован со вто
рым, так как сn+т не коррелированы и с предопределенными перемен
ными Х~+т (по условию), и с (fi - П)', так как последнее выражение
+ т)
= 1, 2,"., m; t =
зависит только от прошлъ~х (по отношению к моменту времени п
наблюденных значений хР> и y~l) (j
=
1, 2,"., k; l
= 1, 2, ... ,п), см. формулу {4.95). А по условию случайные возмущения
приведенной формы не коррелированы ни с предопределенными, ни с
лагированными (т. е. измеренными в прошлом) значениями эндогенных
переменных. В точности те же доводы относятся и к последнему члену
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
правой части соотношения
-..
(4.98').
Таким образом, получаем:
1
Ее(т) = Е [ {П мнк
273
-..
1
- П)Хn+тХn+т(П мнк - П)] +ЕЕ,
{4.103)
где ЕЕ = E(ctc~) = Е(сn+тс~+т)
- ковариационная матрица остатков
приведенной формы (она по условию не зависит от t); Sij = cov(c~i) х
Xc~j)) = E(c~i)g~j)) - {i,j)-й элемент этой матрицы.
2) Займемся теперь приведением первого слагаемого правой ча
сти (4.103) к ~работоспособному» виду, т. е. постараемся выразить его
в терминах имеющихся у нас наблюдений. С этой целью вернемся к
оценке fiмнк и подставим в правую часть соотношения (4.95) матрицу
У, выраженную в терминах приведенной формы анализируемой моде
ли, т. е. У = ХП'
+ е,
где матрица е составлена из столбцов
c{i) -
)
= (с (1i) ,€2(i) , ... ,En(i) )' (i. = 1, 2 , ... ,m:
fiмнк = У'Х(Х'Х)- 1 = {ХП' + е)'Х(Х'Х)- 1 =
= ПХ'Х(Х'Х)- 1
+ е'Х(Х'Х)- 1
= П + е'Х(Х'Х)- 1 ,
откуда
-..
Пмнк
-
1
1
П = е Х(Х Х)
-1
.
Подставим это выражение в первое слагаемое правой части
(4.104)
(4.103) и
попробуем упростить получившееся выражение с учетом представления
= (c{l):c{2): ... :c(m)):
-..
1
-..
']
Е [ (Пмнк - П)Хn+тХп+АП мнк - П) =
= Е[е'Х(Х'Х)- 1 Хn+тХ~+т(Х'Х)- 1 Х'е] =
матрицы ев виде е
=
c'{l)M'Mc{l)
Е ( c'{2)M'Mc{l)
c'{l)M'Mc{2)
с'{2)М'Мс{2)
.......................................
c1{m)M'Mc{l) c'(m)M'Mc{2)
где М
...
c'{l)M'Mc(m)) (4.105)
c'{2)M'Mc(m) ,
=
Х~+т(Х'Х)- 1 Х'
. . . c1{m)M'Mc(m)
- строка длины п (т. е. матрица размерно
сти
{1 х п)). Заметим, что все блоки матрицы, стоящей в правой части
(4.105), являются -чис.л.ами, или, формально, матрицами размерности
1 х 1. А такие матрицы равны своему следу. Мы воспользуемся этим
при вычислении блоков правой части (4.105), а также известным свой
ством коммутативности при вычислении следа произведения квадрат
ных матриц (т. е.
tr (АВ)
= tr (ВА),
см. Приложение П2.2):
E{c'{i)M'Mc(j)) = E[tr {c'(i)M'Mc(j))] =
= E[tr (Mc(j)c'(i)M')] = tr {M[E(c(j)c'(i))]M'} =
= tr {Mcov (c(i), g<Л)InM') = cov (c(i), gU>) tr (ММ') =
= SijX~+AX'X)- 1 Хn+т·
(4.106)
Гл.
274
При выводе
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
(4.106)
мы воспользовались также следующими факта-
ми:
{i)
значения М неслучайны, так как выражаются только через на
блюденные в прошлом и заданные на прогнозируемый момент зна
чения предикторных переменных;
(ii) ММ' =
[Х~+АХ'Х)- 1 Х'][Х(Х'Х)- 1 Хn+т]
Х'n+т (Х'х)- 1 х
xXn+тi
. . . c~j)c~)
...
где
In -
,,.(j) ,,.(i)
"2 .-п
единичная матрица (п х п) {в данных выкладках исполь
зовались модельные допущения о равенстве нулю ковариаций ви
да cov(c~~), с~~)) при tl ::/; t2, а также независимость ковариаций
cov(c~i), c~j)) от времени t).
3) Теперь вернемся к матрице {4.103), подставим в нее правую часть
(4.105) (с учетом (4.106)) и получим окончательный вид для матрицы
Е€(т)· Действительно, после подстановки в правую часть (4.105) эле
ментов этой матрицы, выраженных соотношениями (4.106), имеем:
где матрица Ее составлена из элементов
{4.107)
в правую часть
{4.103),
Е€(т) = [1
Sij
= cov(c(i), с<Л). Подставляя
получаем:
+ Х~+7 {Х'Х)- 1 Хn+т] Ее.
{4.108)
4) Несмещенная оценка Е€(т) матрицы Е€(т) получается подстанов
кой в правую часть (4.108) вместо теоретической ковариационной мат
рицы Ее ее несмещенной оценки (4.100). Вывод формулы {4.99) закон
чен.
4.4.
4.4. 7.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
275
Некоторые общие подходы к анализу точности
оценивания и к сравнению методов и моделей
Подавляющее большинство методов и моделей эконометрики базирует
ся, как мы видели, на математическом аппарате .м:ногомерного стати
сти-ческого анализа. Соответственно, «болевые точки», «узкие места»,
словом, главные трудности этого аппарата как бы ретранслируются на
эконометрический инструментарий. Среди этих главных трудностей в
первую очередь следует упомянуть о проблемах, вынесенных в заглавие
данного пункта учебника. Действительно, мы неоднократно видели, как
непросто достаются результаты, связанные с аналити-ческим выводом
характеристик точности статистически построенных методов
лей, их прогностической силы (вывод формулы
дущего пункта
-
{4.99)
и моде
в конце преды
последнее тому доказательство). Более того, даже
тогда, когда нам удается аналитический способ исследования качества
методов статистического оценивания неизвестных значений парамет
ров
модели и
построенных на их основе прогнозов,
следует помнить,
что, как правило, полученные результаты имеют асимптоти-ческий (по
п -t оо) характер (свойство состоятельности оценок, например, или
асимптотический вид ковариационных матриц и т. п.). В эконометри
ческой же практике работают с коне-чнъ~ми выборками (т. е. при суще
ственно ограниченных п), и поэтому важно уметь проана.лизироватъ
свойства разли-чнъ~х способов оценивания и разли-чнъ~х методов про
гнозирования в условиях относительно малъ~х выборок. К сожалению,
как правило, это не удается сделать с помощью аналитических методов
и приходится прибегать к разного рода имитационно-компьютернъtм
экспериментам.
Ниже мы кратко остановимся на описании трех наиболее распро
страненных в эконометрической практике подходах такого типа.
Метод Монте-Карло статистических испытаний.
Сущность
метода статистических испытаний заключается в следующем. В ком
пьютер закладываются все параметры анализируемой стохастической
модели, после чего компьютер с помощью специальных датчиков слу
чайных чисел генерирует требуемое -число въ~борок заданного об~ема,
которые, соответственно, интерпретируются как наблюдения, произве
денные над данной моделью. Затем эти выборки используются в той
статистической процедуре (в статистическом оценивании параметров
анализируемой модели, в построении различного рода прогнозов и т. п.),
качество которой мы хотим исследовать. Наличие большого числа сге
нерированных компьютером выборок заданного объема п позволяет ис
следовать поведение интересующих нас выходных характеристик ана
лизируемой процедуры (оценок е( п) или прогнозов Уп) и, в первую оче-
ГЛ.
276
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
редь, оценить их смещение и среднеквадратическую ошибку. Конечно,
результаты такого исследования как бы «условно-локальны~, т. е. зави
сят от тех численных значений параметров модели, которые мы зало
жили в компьютер и которые, соответственно, определяют специфику
сгенерированных «наблюдений~. Однако подобные эксперименты, про
веденные в большом объеме и в широком диапазоне значений заклады
ваемых в компьютер параметров, способны доставить исследователю
ценную информацию.
Конкретизируем описанную процедуру применительно к анализу
методов оценивания параметров СОУ и точности построенных на осно
вании этой модели прогнозов. Итак, зададимся:
1)
структурными параметрами СОУ, т. е. числом уравнений эндоген
ных переменных
ных
2)
m,
а также числом предопределенных перемен
k;
конкретными значениями параметров В и С структурной формы;
3) вероятностными распределениями возмущений б?), б~ 2 ), ••• , б~т)
структурной формы;
4)
требуемым объемом генерируемых выборок
5)
конкретными
«наблюденными~
(1) (2)
(k)
переменных xt
6)
, xt , ... , xt
,
n;
значениями предопределенных
t = 1, 2, ... , п;
значениями предопределенных переменных в прогнозный период
времени (при анализе качества прогноза).
После этого:
7)
с помощью компьютерного датчика случайных чисел моделиру~(1)
ются случайные остатки иt
8)
в
соответствии
с
~(2)
соотношениями
= -в- 1 CXt + в- 1 Лt
~(m)
, иt , ... , иt
,
t = 1, 2, ... , п;
приведенной
вычисляются значения
формы
yt
yt, t = 1, 2, ... , п.
В результате п.1)-8) сгенерирована 1-я выборка объема
n: {X{l),
Y{l)}.
Затем п.
лучаем еще
7)-8) повторяются еще N - 1 раз, в результате чего по
N - 1 выборок того же самого объема из той же самой
генеральной совокупности (т. е. для той же самой модели).
Таким образом, в нашем распоряжении оказываются
N
объема п, сгенерированных в рамках одной и той же модели:
{X{l), Y{l) }, {Х{2), У{2) }, ... , {X(N), Y(N) }.
выборок
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
277
По «наблюдениям» каждой (j-й) выборки строим интересующие
нас выходные характеристики анализируемой процед,уры (оценки па
раметров B(j), C(j), прогнозы Yn+т(j) и т. п.). Сравниваем полученные
оценки B(j), C(j) и прогнозы Yn+т(j) с имеющимися у нас истинн:ы.
ми значениями, соответственно, В, С и Уn+т: оцениваем среднюю (по
всем выборкам) величину смещения, среднеквадратическую ошибку и
другие интересующие нас характеристики качества анализируемой про
цед,уры.
Проиллюстрируем применение метода Монте-Карло на примере.
Пр им ер
4.7 (заимствован из: Simister L. Т. Monte Carlo Stadies of
Simultaneous Equations System. Ph. D Thesis, University of Manchester,
1969). Автор этой работы исследовал с помощью метода Монте-Карло
влияние различных способов спецификации структурных остатков б~i)
системы из двух уравнений
(i
= 1, 2) на точность прогноза, осуществля
емого разными методами. Из методов, описанных выше в данной главе,
сравнивались три процед,уры:
•
МНК, непосредственно примененный для оценивания параметров
f3
и с каждого из двух структурных уравнений; затем на основании
соотношения
определялись оценки параметров приведенной
формы и строился прогноз для y(l) и у< 2 > по формуле (4.96);
•
(4.46)
МНК без ограничений (МНК ВО) применялся непосредственно
для оценивания параметров 1Г приведенной формы, после чего
строился прогноз для y(l) и у< 2 > по формуле (4.96);
•
2МНК, с помощью которого оценивались параметры структурной
формы, по ним (с помощью
(4.46)) -
параметры приведенной фор
мы, а затем строился прогноз по формуле
и
(4.96).
В качестве возможных спецификаций структурных возмущений бр>
рассматривались четыре варианта:
б~ 2 )
(i) бр> и б~ 2 ) (t = 1, 2, ... n) образуют белый шум;
(ii) бр> связаны автокорреляцией 1-го порядка с параметром Р1 = r(l) = 0,9, а б~ 2 ) связаны автокорреляцией 1-го порядка с пара
метром р2 = r(l) = 0,225;
(iii)
на стандартные возмущения
(i)
накладываются ошибки в изме
рении переменных модели (вариации ошибок составляли
более от вариаций соответствующих переменных);
10%
и
278
ГЛ.
{iv)
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
на случайные возмущения марковского типа
ошибки
В табл.
{iii)
4.9
{ii)
накладываются
в измерении анализируемых переменных.
приведены результаты оценки с помощью метода Монте
Карло среднеквадратических ошибок прогнозов значений переменных
y(l) и у( 2 ) для различных сочетаний «метод оценивания - вариант спе
цификации структурных возмущений модели». Величина среднеквад
ратической ошибки прогноза, получаемой при оценивании параметров
модели с помощью 2МНК при спецификации остатков типа
(i),
принята
за эталонную единицу в сравнении различных методов.
Таблица 4.9. Среднеквадратические ошибки прогнозов у~~т и у~~т
при различных методах оценивания параметров модели
При прогнозе у< 1 >
Метод
При прогнозе у< 2 >
Вариант спецификации
возмущений др>
оценивания
Вариант спецификации
возмущений 6~ 2 )
(i)
(ii)
(iii)
(iv)
(i)
(ii)
(iii)
(iv)
2МНК
д
1,47д
1,83д
2,25д
д'
1,86д'
3,lд'
2,98д'
мнк
3,59д
1,36д
2,39д
2,74д
12,32д'
1,64д'
8,4д'
8,12д'
МНКБО
1,13д
2,98д
3,86д
2,36д
1,17 д'
2,44д'
5,53д'
3,Обд'
Из анализа табл.
4.9
следует, что 2МНК оказался самым точным во
всех ситуациях, кроме случая автокоррелированных возмущений о~ 1 )
и 8~ 2 ). В последнем случае несколько неожиданно лучше других про
явил себя обыкновенный метод наименьших квадратов, примененный в
отдельности к каждому из двух уравнений структурной формы.
Бутстреп-метод тиражирования наблюдений. Этот метод по
лучил весьма широкое распространение в последние три десятилетия в
задачах статистического анализа, основанного на относительно малых
выборках. Заложенная в его основание идея внешне выглядит несколь
ко странной: метод предлагает тиражировать уже имеющиеся в нашем
распоряжении наблюдения, генерируя их, как и в методе Монте-Карло,
с помощью специальных компьютерных датчиков случайных чисел. Од
нако в методе Монте-Карло эти датчики «настраиваются» на экзоген
но заданные параметры модели (там мы «на старте» не имели ника
ких наблюдений), в то время как в бутстреп-процедурах «настройка»
датчиков определ.яется структурой и спецификой уже имеющейся в
нашем распоряжении въtборки. Грубо говоря, схема действия бутстреп
процедуры заключается в следующем: по имеющейся выборке строит
ся некоторая оценка (параметрическая или непараметрическая) закона
распределения анализируемой генеральной совокупности, а затем ге
нерируются (в необходимом количестве) наблюдения, подчиняющиеся
4.4.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ (СОУ)
279
этому закону распределения вероятностей. Как обрабатываются полу
ченные таким образом «наблюдения~ и какие с их помощью решаются
задачи оценки качества модели или прогноза
-
это предмет для специ
ального обсуждения, и мы оставляем его за рамками данного учебни
ка21.
Перекрестный анализ дееспособности модели (или ПАД-про
цедура)22. Идеи этого подхода были сформулированы достаточно дав
но, однако высокую прикладную значимость и популярность различные
версии ПАД-процедур обрели лишь с появлением современных вычис
лительных мощностей. Их сущность заключается в следующем.
Пусть мы решаем проблему подбора модели по имеющимся в
нашем распоряжении исходным статистическим данным, но не уверенъt
в ее общем виде, в ее структуре. Так, если речь идет о подборе регрес
сионной модели, то мы не знаем, является ли она линейной, степенной
или еще какой-нибудь, нужно ли проводить линеаризующие преобразо
вания переменных, каким выбрать значение «гребневого~ параметра в
методе ридж-регрессии и т. д. Если речь идет о модели временных ря
дов, то мы обычно испытываем затруднения в выборе структурных па
раметров p,q и
k АРПСС-моделей (см. п.10.5.3 в [Айвазян (2010)]), па
раметров адаптации (сглаживания) Л1, Л2, Лз в различных процедурах
экспоненциального сглаживания (см. п.
10.6.2
в [Айвазян
(2010)])
или
параметров дисконтирования Л или 'У в моделях распределенных лагов
с геометрической структурой (см. п.
4.6
в данном учебнике). Аналогич
ные вопросы, связанные с подбором значений некоторых свободных (или
структурных) параметров модели, возникают при построении и иссле
довании моделей дискриминантного или факторного анализа, систем
одновременных уравнений и т. д. При этом под свободнъши (структур
нъtми) параметрами модели А= (Л1, Л2,
21 Интересующемуся
... , Лm)
мы в общем случае бу-
этой проблематикой читателю мы можем порекомендовать,
например, книгу: В. Эфрон. Нетрадиционные методы многомерного статистического
анализа. Пер. с англ. М.: Финансы и статистика, 1988.
22 Здесь предложен вариант перевода английского названия
вые достаточно полно описанного как
« Cross-validatioп
этого подхода, впер
тethod•, по-видимому, в
англо-язычной специальной литературе (см., например: Stoпe С. Cross-validatory
choice and assesment of statistical predictions // Journ. Roy. Stat. Soc. Ser. В. Vol. 36
{1974). Р. 111-147). К сожалению, нет единой точки зрения на состав методов, объ
единяемых этим названием. Некоторые специалисты включают в рамки этого подхо
да и бутстреп-метод, и различные варианты метода «скользящего экзамена•, кото
рый упоминается в п. 6.4 учебника (см.: Hiпkliey D. V. Jackknife, bootstrap and other
cross-validation methods. London; New York : Chapman and Hall, 1983). Нам пред
ставляется, что из методических соображений удобнее несколько сузить столь ши
рокое толкование
«Cross-validation•,
акцентируя внимание на многократн-ых вычис
.11.ите.яьн-ых «прогонах. уже оцененных моде.11.ей при раэ.11.ичных вариантах значений
их свободн:ых (т. е. не поддающихся статистичеС1Сому оцениванию) параметров.
280
ГЛ.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
дем понимать параметры, от которых зависит общий вид (структура)
модели, но для которъtх не существует математически корректнъ~х
процедур статистического оценивания. И пусть существует некоторый
экзогенно заданный критерий качества модели
К(А; 8; Хэкз),
(4.109)
значение которого зависит от значений использованных в модели сво
бодных параметров Л, статистических оценок неизвестных параметров
модели
8 И состава
«Экзаменующей выборки» Х экз, Т. е. ОТ состава тех
экспериментальных {наблюдаемых) данных, на которых была проведе
на верификация построенной модели. В моделях регрессии и временных
рядов в качестве критерия К чаще других используется среднеквадра
тическая ошибка прогноза, в моделях дискриминантного и кластерного
анализов
-
доля неправильно расклассифицированных наблюдений из
состава Хэкэ и т. п.
Тогда общую схему процедуръt перекрестного анализа дееспособно
сти модели можно описать в виде реализации следующих двух этапов.
1-й э т а п.
Все имеющиеся в нашем распоряжении наблюдения Х
(исходные статистические данные, результаты эксперимента) случай
ным образом разбиваются на две части Х 00 и Хэкэ· Первая из них (Хоб)
используется для подбора («настройки») модели. Этот подбор обяза
тельно включает в себя определение значений свободных параметров Л
и, если необходимо, статистическое оценивание параметров
0.
Поэтому
эту часть исходных статистических данных называют обычно
«обуча
ющей въ~боркой»(хотя, строго говоря, это может не совпадать с клас
сическим понятием обучающей выборки, принятым в математической
статистике). Данная стадия процедуры, в частности, включает в себя
выдвижение и предварительную проверку рабочих гипотез о структу
ре модели, перебор различных вариантов моделей в целях «нащупы
вания» относительно устойчивых результатов и т. п. При этом перебор
различных вариантов модели обычно включает в себя задание некото
рой сетки возможных значений структурных параметров Л1, Л2,
... , Лт
и проведение полного цикла всех необходимых вычислений по иденти
фикации модели для каждого фиксированного сочетания этих значений
(т. е.
оценку параметров е и т. п.).
2-й э т а п.
На этой стадии каждый из вычисленных на предыду
щем этапе вариантов модели верифицируется (с помощью критерия
{4.109)
на даннъtх «экзаменующей въtборки» Хэкэ)· Поскольку модели
«настраивалисЬ»на данных Х00 , очевидно, значения критерия качества
на данных Хэкэ будут существенно менее оптимистичными, чем на дан
ных Хоб· Из всех возможных значений структурного параметра Л вы-
4.5.
КОИНТЕГРАЦИЯ
281
бирается такое (Ло), при котором значение критерия К(Ао; 0; Хэкз) оп
тимально. Заметим, что в современных процедурах метода ПАД при де
лении массива исходных данных Х на Х00 и Хэкз действуют так же, как
и в методах скользящего экзамена (и в частности, в методе «складного
ножа»
- «jackknife»,
см. п.
6.4
в [Айвазян
(2010)]):
в составе Хэкэ остав
ляют единствеН'Н/Ый элемент, по остальным данным подбирают модель
и вычисляют значение критерия К в этой единственной точке; затем
в качестве Хэкз берут другой элемент из Х и т. д. до тех пор, пока
роль единственной «экзаменующей»точки не исполнят поочередно все
элементы из массива исходных статистических данных Х. «Настрой
ка» модели на обучающих данных Хоб и последующая перекрестная
«перепроверка» (верификация) модели на других (экзаменующих) дан
ных Хэкз с непременным многовариантным перебором значений струк
турных параметров на 1-й стадии процедуры
-
в этом и состоит сущ
ность метода перекрестного анализа дееспособности модели (кстати, в
некоторых переведенных с английского на русский язык работах, от
носящихся к данной тематике, метод
«Cross-validation» переведен
как
«перепроверка», см., например, упомянутую выше книгу В. Эфрона).
К о интеграция
4.5.
Анализ связей, существующих между нестационарными временными
рядами,
может
приводить
к
так
называемым
ложн'ым
регрессиям.
В целях «остационаривания»таких рядов обычно используются следу
ющие подходы:
• исклю-ч.ение неслу-ч.айной составляющей ( «детрендирование»);
главным недостатком этого подхода является его неприменимость
по отношению к временным рядам, природа нестационарности ко
торых заключается не только в наличии неслучайной составляю
щей;
• переход к последовател'ЬН'ЫМ разностям анализируемого времен
ного ряда;
к основным недостаткам этого подхода можно отнести:
-
чувствительность к компонентам краткосрочного шума;
тот факт, что это может приводить к смещенным оценкам в
случае, если временные ряды имеют так называемое долго
сро-ч.ное равновесие.
Идея коинтеграции была впервые сформулирована в работе
ger (1981)],
а более подробное описание представлено в работе
[Gran[Engle,
Гл.
282
Granger (1987)].
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Идея коинтеграции состоит в том, что две или более
переменных могут изменяться синхронно так, что их разность (или, в
более общем случае, некоторая линейная функция) является стацио
нарным процессом (см. рис.
4.7, 4.8).
В этом случае временные ряды
называют коинтегрированн'Ы,Мu.
Рис.
4. 7.
Коинтегрированные временные ряды
2500
2000
1500
1000
500
О;..-.,,......,....................---.-.......-.........-.-...,.......,,......,............,.......--.-.......-..........-.-........
60
Рис.
4.8.
62
64
66
68
70
72
74
76
78
80
82
Потребление, инвестиции, доходы в США
Коинтеграция может быть интерпретирована как статистическое
выражение для природы равновесного соотношения: например, Ун и Y2t
могут быть связаны некоторым долгосрочным соотношением, от кото
рого эти временные ряды могут отклоняться в краткосрочный перспек
тиве, но к которому должны возвращаться в долгосрочной перспективе.
Если переменные безгранично расходятся (т. е. имеют нестационарные
остатки), то говорят, что отсутствует равновесное соотношение. Приме
рами возможной коинтеграции являются:
•
потребление, доходы и благосостояние;
4.5.
283
КОИНТЕГРАЦИЯ
•
цены акций и дивиденды;
•
обменные курсы и уровни внутренних, внешних цен;
•
долгосрочные и краткосрочные процентные ставки;
•
деньги, уровень цен и доход;
Более формальное определение коинтеграции представлено ниже:
Определение
4.17
(коинтеграция по Энглу- Гранжеру). Компо
ненты многомерн·ых временных рядов
1 являются
коинтегрированнъши порядка (d, Ь) (это обозна-чается yt ,...., С1 (d, Ь), Ь
и
d -
yt
размерности т х
некоторъtе неотрицате.л,-ьнъtе це.л.ъtе -числа), ее.ли
i)
все компоненты
yt являются рядами интегрируемости порядка
d, т. е. }jt ,...., l(d), j = 1, 2, ... , т;
ii)
существует вектор 'У (коинтегрирующий вектор) размерности
т х
1,
для которого линейная комбинация
Zt
т. е. ряд
Zt
= 'Y'Yt ,. . , 1 (d -
Ь),
О
< Ь ~ d,
имеет интегрируемость порядка
d-
Ь.
(определение понятия порядка интегрируемости одномерного неста
ционарного ряда см. в сноске
5
в п.
4.3.5).
В качестве типичного примера коинтегрированных временных ря
дов можно привести ряды
где иlt и и2t
-
ylt
= ,8Y2t + иlt,
Y2t
= Y2,t-l + и2t'
некоррелированные процессы, каждый из которых явля
ется белым шумом. Линейная комбинация этих двух интегрированных
переменных может быть стационарным процессом. Очевидно
Y2t,...., /(1),
тогда иlt
= Ylt -
.ВУ2t,...., /(О), так что
Yit
и
Y2t
Ylt ,...., 1(1),
оказываются
коинтегрированнъши.
Типичным примером подбора вектора 'У при
Ylt,...., /(1)
и
Y2t,...., /(1)
является:
'У= (1, -,В)'=> 'Y1Yt = Ylt - ,8Y2t = иlt ,...., белый шум.
Альтернативным и более гибким для работы определением является
определение, данное в работе
[Liitkepohl (1993)]:
Определение 4.17а (коинтеграция по Люткеполю).
Векторнъtй
Гл.
284
процесс
d,
Yt
rv
Yt
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
размерности т х
1
назъtвается интегрированнъ~м порядка
I(d), ее.ли его разность d-го порядка, дdYt, является стацио
нарн'Ьt.ми процессом, а разность d-1-го порядка, дd-IYt, нестационар
Н'Ьt.м.
1 (d)-процесс Yt
называют коинтегрированн'Ьt.м, если существует
линейная комбинация Zt =
-y'Yt,
которая является интегрированнъ~м
процессом с порядком, меньшим, -чем
d.
Заметим, что второе определение не требует, чтобы все элементы
являлись интегрированными порядка
нент является
1 (d),
d,
Yt
но если лишь одна из компо
а все другие являются интегрированными процесса
ми порядка, не превосходящего d (например, /(О)), тогда многомерный
процесс будет
4.5.1.
I(d).
Представление коинтегрированных систем
В этом разделе мы предположим, что процесс
Yt
размерности т х
1
является коинтегрированным. Рассмотрим различные эквивалентные
представления для такой системы. Эти представления позволят нам
более глубоко взглянуть на динамику системы.
Многомерное разложение Бевериджа- Нельсона
Далее мы рассмотрим случай, когда векторный процесс
сти т х
1 является 1 ( 1)
Yt
размерно
и сгенерирован при помощи векторной модели
скользящего среднего бесконечного порядка (в англоязычной версии
-
Vector Moviпg Average Model (оо), или VМА(оо)-модель) для первых
разностей д}'f,
д}'f = б
+ иt = б + Ф(L)t:t,
где иt имеет нулевое среднее и является
1(0),
(4.110)
а б = Е(дУt)
-
вектор
констант. Кроме того, отметим, что линейный процесс иt с нулевым
средним является УМА( оо )-процессом
если выполняются следующие два условия:
матрица
Ф(l) = Фо
+ Ф1 + Ф2 + Фз + ... =F Omxm
(4.111)
(но не обязательно полного ранга) и
матрицы
Фj
= { 'Фj,kl}
суммируемы первого порядка,
что означает: L:~o j l'Фj,kl 1 < оо для всех k, l
= 1, ... т.
чения последнего предположения мы увидим позже.
Причину вклю
КОИНТЕГРАЦИЯ
4.5.
Запишем модель для
Yi
285
в виде:
t
Yi
=
Уо + бt +
L иs.
(4.112)
s=O
Пользуясь соотношением: Ф(L)
=
+ да(L), где
Ф(l)
00
a(L) = l:ajLj,
j=O
O.j
= -(Фj+l
+ Фj+2 + ".)
для j =О,
1, ... ,
мы можем записать:
иt = Ф(L)C:t = Ф(l)C:t
где
1Jt = a(L )c:t -
+ 'Г/t + 'Г/t-1,
(4.113)
это 1(0)-процесс с нулевым средним, а
но суммируемо. Если мы заменим иt в
(4.112)
на
a(L) абсолют
(4.113), то получим
многомерное разложение Бевериджа- Нельсона.
Определение
сона). Пустъ
Yi
4.18
(многомерное разложение Бевериджа- Нель
опис-ываетс.я
(4.110),
тогда
Yi
может бъ~тъ представ
лено в виде:
б·t
Yi=
~
детерминированнъ1:й тренд
+
стожастический тренд
'Г/О
'Г/t
+ Уо
~
'-У--'
стационарн'Ый nроцесс
началън'Ые условшr.
где:
(4.114)
00
Ф(l)
= LФj,
j=O
00
1Jt
= a(L)c:t = L O.jC:t-j,
j=O
O.j = -(Фj+l
+ Фj+2 + Фj+З + ... )
00
а существование O.j обеспе'Чиваетс.я неравенством Е
справедлив'ЫМ при всех
ряда
жа
-
Yi
в виде
(4.114)
k, l = 1, ...
j ·
IФ j·kll
<
оо,
j=O
, т. Представление многомерного
назъ~вается многомернъш разложением Беверид
Нелъсона.
Таким образом, если Ф(l) =О, тогда в уравнении
стохастический тренд и процесс
Yi
не будет
1 ( 1).
(4.114)
исчезает
Гл.
286
Если (т х
мощью
h
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
1)-мерный
процесс
yt является коинтегрированным с по
коинтегрирующих соотношений, определенных в форме
(mx
xh) матрицы Г, тогда (h х 1)-мерный процесс Г'уt является тренд
стационарнъш, т. е. стационарным с точностью до наличия неслучай
ной составляющей. Для того чтобы увидеть это, умножим слева обе
части
(4.114)
на Г', получим:
Г'уt = Г'б · t
+ Г'Ф(l)(е1 + е2 + ... + E:t) + Г'ТJt + Г'(Уо -
Из полученного выражения для Г'уt следует, что Г'уt
ТJо).
- h
х
1-
мерный процесс. Более того, мы можем получить необходимое условие
для коинтегрируемости:
Г'Ф(l) =О,
(4.115)
которое обеспечивает исчезновение стохастического тренда. К сожале
нию, при отсутствии стохастического тренда процесс не всегда является
стационарным, поскольку начальное условие Г'(Уо-ТJо) может быть кор
релированно с Г'ТJt· Процесс будет тренд-стационарным только в слу
чае, если Г'(Уо -ТJо) =О. Далее мы будем предполагать, что начальное
значение Уо может быть выбрано таким образом, что либо выполняет
ся равенство Г'(Уо
-
ТJо) =О, либо не возникает проблема корреляции.
Для стационарности необходимо предположить, что Г' выбрано таким
образом, что выполняется следующее условие:
Г'б =О.
(4.116)
Отметим, что ненулевые элементы матрицы Г коинтегрирующих
векторов Г определяют то, какие элементы
грирующего соотношения. Если
yt
yt
являются частью коинте
коинтегрирован, то может существо
вать несколько линейно независимых коинтегрирующих векторов. Их
число h называют коинтеграционн'ЬIМ рангом. Пространство, натянутое
на коинтегрирующие вектора (множество точек в
Rm,
принадлежащих
линейному подпространству, составленному из линейных комбинаций
коинтегрирующих векторов), называют коинтеграционнъш простран
ством.
Более того, отметим, что из уравнения
(4.115)
следует, что
h
строк
матрицы Ф ( 1) линейно зависимы. Поэтому детерминант Ф ( L) равен
нулю при
L
= 1, т. е.
det(Ф(l)) =О,
а ранг Ф(l) равен т
- h,
rank[Ф(l)] = т
- h.
(4.117)
287
КОИНТЕГРАЦИЯ
4.5.
Это означает, что коинтеграционный ранг может быть вычислен
как
m -
rank[Ф(l)).
Важным следствием условия
(4.117)
является то, что Ф (L) необра
тим: таким образом, коинтегрированная система
Yi
никогда не может
быть представлена процессом векторной авторегрессии конечного по
рядка, VАR(р)-процессом. Поэтому, если нам дан вектор интегрирован
ных временных рядов
yt,
о которых мы знаем, что они коинтегриро
ванны, то специфицирование первых разностей дуt в качестве VАR(р)
процесса является некорректным.
Кроме того, из условий
(4.115)
и
(4.116)
следует, чтоб должно быть
линейной комбинацией столбцов матрицы Ф(l). Это означает, что ранг
матрицы, составленной изб и Ф(l), равен
rank
[б:Ф(l)]
т. е. коинтеграционный ранг равен
m - h,
= m - h,
h.
Следующее следствие состоит в том, что коинтеграционный ранг
никогда не может быть равным
m,
так как иначе rank[Ф(l)) =О и в
этом случае Ф(l) =О, что противоречит условию
(4.111).
Наконец, рассмотрим ковариационную матрицу для дуt, которая
может быть найдена с использованием уравнения:
дуt
= б + Ф(L)t:t
и выражения для Ф(l). Таким образом, ковариационная матрица для
дуt определяется выражением:
Едуt = Ф(L)S1Ф'(L) = Ф(l)S1Ф'(l),
где
S1 -
ковариационная матрица
Если
Yi
t:t.
является коинтегрируемым векторным процессом, то де
терминант матрицы Ф(l) равен нулю (см.
(4.117)),
поэтому детерми
нант матрицы ЕдУi также равен нулю. Это означает, что ковариацион
ная матрица дуt является сингулярной. Отсюда следует: коинтеграция
и ковариационная матрица VМА(оо)-процесса дуt .являете.я положи
те.л:ьно определенной тогда и только тогда, когда
Yi
не .являете.я ко
интегрируем'Ым векторнъш процессом.
Перед тем как продолжить изложение, рассмотрим пример, иллю
стрирующий некоторые из описанных выше результатов.
Пр им ер
имствован из
4.8 (коинтеграция для двумерного процесса) пример за
[Hayashi (2000)). Рассмотрим следующий двумерный
VМА(l)-процесс:
(Ult)
U2t = (€1,t)
€2,t + (-10
'У)
0
(€1,t-1)
€2,t-1 .
Гл.
288
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
В этом случае мы имеем:
Ф(L) = (~ ~) + ( ~l ~) L =
...............
(1 /
--yL)
L .
~
Фо
Ф1
Легко показать 1-суммируемость Ф j и равенство:
Ф(l) = (~
Анализируемый вектор Ut -
i) =J О.
линейная 1(0)-система с нулевым сред
ним; Ui,t является 1(0)-процессом, если "У =F О, иначе и1,t -
1(1)-процесс;
и2t является 1(0)-процессом. Линейной 1(0)-системой является любая
сумма
8 + Ut.
Следовательно, векторный 1(1)-процесс
Yt
определяется
соотношением
или в терминах компонент вектора
=
(Ylt)
Y2t
Поскольку
(У1,о) + (81) t + (e1,t - е1,о) + ("У~~:~ e2,s) .
У2,О
82
о
Es=l e2,s
a:(L) =
-Ф1,
'1t =
и
Yt:
(°'·' ~'YE2,t)
Ф(l)(е 1 + ... + et) = (О "У) (Er=l e1,s)
о
1
Es=1 e2,s
=
("У ~~=1 e2,s) ,
Es=1 e2,s
многомерное представление Бевериджа- Нельсона имеет вид:
Yt
=
(81) t + ("У ~~=1 e2,s) + (€'1,t - --ye2,t) +
82
Es=l e2,s
о
+ (У1,о) _ (е1,о - 1е2,о) .
У2,О
(4.118)
0
Таким образом, если Ф(l) = О, то стохастический тренд исчезает из
уравнения
(4.118),
и процесс
Yt
не будет 1(1)-процессом.
Более того, матрица
(о
Ф(l)) = (~~ ~
i)
4.5.
289
КОИНТЕГРАЦИЯ
имеет ранг, равный единице. Поэтому коинтеграционный ранг равен
1(=2-1).
Все коинтегрирующие вектора могут быть записаны в виде:
[с, -с-у'] =F О, где с =F О. Кроме того, предположение о том, что коин
тегрующий вектор исключает детерминированный тренд, может быть
записано как: с81
с-у82 = О.
-
Треугольное представление Филлипса
Кроме описанного выше
ные представления.
VMA( оо )-представления, имеются другие удоб
Одно из них предложено в работе [Phillips (1_991)].
Идея этого представления состоит в построении нового базиса Г, ли
нейная оболочка которого совпадает с Г и который представим в форме
составной матрицы
г = [ ~h.
]
-Aт-h,h
где Ih -
'
mxh
единичная матрица размерности
h
х
h,
а Am-h,h -
матрица
коэффициентов, соответствующих переупорядочиванию строк матрицы
Г. Тогда
это, соответственно:
-
[~1~
yt =
Y2t
где Ун и
Y2t
имеют размерности
(h
х
]'
mxh
1)
и
((m - h)
х
соответственно.
1),
Более подробное описание переупорядочивания и процедуры разделе
ния матрицы см. в работе
Умножая
(4.114) на
f',
[Hamilton (1994)].
многомерное
представление
Бевериджа- Нельсона
получаем:
Yit
= A'Y2t + µ1 + z;
(первая часть),
z;
(4.119)
где µ1 = f''(Yo - rJo),
= f''11t и f' 18 = О. Кроме того, f''Ф(l) = О.
Поскольку 1Jt - стационарный временной ряд, то и ряд
тоже будет
стационарным. Система (4.119) содержит h коинтегрирующих регрес
z;
сий и позволяет получить первую часть треугольного представления
Филлипса. Вторая часть определяется последними т
(возможно переупорядоченными) в уравнении
- h
(4.110),
строками
yt
которое имеет
вид:
дУ2t
где Ф2(L)
= 82t + Ф2(L)c:t,
-
(т
- h х 1)
(вторая часть),
это лаговый полином размерности
ность C:t равна (т х
1).
((m - h)
(4.120)
х т); размер
Гл.
290
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Если указанная выше система имеет в точности
щих соотношений, тогда вектор
1(1)
Y2t
размерности
h коинтегрирую
((m- h) х 1) является
и не имеет коинтегрирующих соотношений. Это представление ока
зывается весьма полезным при оценивании.
Пр им ер
4.8
(продолжение) коинтегрирация для двумерного про
цесса. В нашей двумерной системе коинтеграционный ранг равен
интегрирующий вектор равен
(1, -'У)'.
z; = (1, -'Y)ТJt = cl,t -
Таким образом,
1.
Ко
z; иµ равны
'Yc2,t
µ = (1, -'У)(Уо - ТJо) = (У1,о - 'УУ2,о) - (t:1,o - 'Ус2,о).
Следовательно, треугольное представление имеет вид:
Y1,t
дУ2 t
'
= µ + 'YY2,t + (ci,t - 'Yc2,t)
= 82 + с2 't·
Представление общего тренда Стока- Ватсона
Применяя многомерное разложение Бевериджа-Нельсона
(4.114)
второй части треугольного представления Филлипса
получим:
Y2t
(4.120),
= 82 · t + Ф2,(l)(с1 + с2 + ... + ct) + ТJ2t + (У2,о -
ко
Т/2,о),
где
00
Ф2(l) =
L Ф2,j,
j=O
00
ТJ2,t = a:2(L)ct =
L 0:2,jC't-j,
j=O
0:2,j
= -(Ф2,j+1 + Ф2,j+2 + Ф2,j+з + ... )
и
00
L
1a2j1 < оо.
j=O
Поскольку
ct -
белый шум, то Ф2(l)ct также является белым шумом.
А следовательно,
-
случайное блуждание. Таким образом, справедливо следующее пред
ставление:
(4.121)
4.5.
291
КОИНТЕГРАЦИЯ
где µ2 = У2,о -1J2,0· Подставляя уравнение (4.121) в первую часть тре
угольного представления Филлипса (4.119), получим:
(4.122)
где д1 = µi +А' µ2 и
Уравнения
fi1t =
(4.121)
и
z; + A'112t·
(4.122)
определяют представление общего трен
да, впервые полученное в работе
=
[Stock, Watson (1988)].
Система
yt
=
[~:] включает стационарную компоненту:
[~~] + [~:] '
линейные комбинации
общих детерминированн/ЫХ трендов о2 · t с количеством слагаемых, не
превышающим (т
- h),
а также линейные комбинации
A'(6,t)
общих стохасти-ческих трендов
вышающим
6t
с количеством слагаемых, не пре
(m-h).
Пр им ер
4.8 (продолжение) коинтеграция для двумерного про
цесса. Двумерный стохастический тренд определяется суммой E~=l e2,s
(см. уравнение (4.118)).
Представление в виде векторной авторегрессии
Выше мы рассмотрели случай, когда система
ставлением
в виде
yt,
определяемая пред
векторной авторегрессии бесконечного порядка
(VMA(oo)),
дуt =о+ Ф(L)et.
(4.123)
является коинтегрированной. При этом в случае коинтегрированной си
стемы не существует VАR(р)-представления (где~ некоторое нату
ральное число) для ее первых разностей дуt. Однако предположим,
что существует коинтегрированная m-мерная VАR(р)-система для
h
yt
с
коинтегрирующими соотношениями, которая имеет вид:
Yt
=а+ Ф1Уi-1
Фp(L)Yt =а+
+ Ф2Уi-2 + ... + ФрУi-р + et,
et.
(4.124)
Гл.
292
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Умножая VМА(оо)-представление
(1 -
(4.123)
L)Фp(L)yt = Фр(l)о
Подставляя VАR(р)-представление
на Фр(L), получим:
+ Фp(L)Ф(L)et.
в это уравнение, получим:
(4.124)
(4.125)
при этом следует учитывать, что
уравнение
(4.125)
(1 - L )ск. =
дек. = О. Таким образом,
должно выполняться для всех C:-t. Откуда следует, что
Фр(l)о =О
и
(1 - L)Im =
Фр(L)Ф(L).
(4.126)
Решая эти уравнения относительно Ф(L), получим:
Таким образом, вопрос состоит в том, чтобы определить условия
на Фр(L), при которых Ф(L) является 1-суммируемым и имеет ранг,
равный т -
= т-
h). Заметим, что эти условия обеспечи
вают наличие коинтеграции (с h коинтегрирующими соотношениями)
для
h ( rank[ Ф ( 1)]
VMA( оо )-представления.
Необходимое условие, получаемое из уравнения
жении
L = 1,
(4.126)
в предполо
имеет вид:
Фр(l)Ф(l) =О.
(4.127)
Поскольку из условий для VМА(оо)-представления Ф(l) имеет ранг
(т
- h),
то ранг Фр(l) не превосходит
h.
VАR-представление. Необходимым и достаточным условием для
того, чтобы VАR(р)-процесс размерности т был коинтегрированной
системой
1(1)
с коинтегрирующим рангом
h,
является разложимость
Фр(L) в форме:
Фр(L)
где
U(L)
и
V(L)-
= U(L)M(L)V(L),
матричные лаговые операторы размерности
корни которых находятся вне единичного круга, а М (L)
(mxm),
-
матричный
(1 - L),
а остальные
лаговый оператор размерности т х т следующего вида:
M(L) =
где первые (т -
h
h)
[(1 Ohxm-h
- L)Im-h
Om-hxh] ,
lh
диагональных элементов равны
диагональных элементов равны
1.
4.5.
293
КОИНТЕГРАЦИЯ
Используя это утверждение, можно показать, что ранг Фр(l) равен
в точности
h.
Учитывая, что
Фр(l)
а
= U(l)M(l)V(l),
V (1) - невырождены (так как все корни матричных много
членов U(L) и V(L) находятся вне единичного круга), ранг Фр(l) равен
рангу M(l), который, в свою очередь, равен h,
U (1)
и
rank[Фp(l)] =
h.
Тогда мы можем выразить так называемое ус.л,овие редуцированного
'[Юнга в форме:
Фр(l) = ВГ',
где В и Г
-
матрицы размерности
(m
х
(4.128)
h),
ранги которых равны
h.
Поскольку ранг матрицы В равен количеству ее столбцов, то, учитывая
(4.127),
получим:
Г'Ф(l) =О
и
Г'б =О,
что означает Г
коинтегрирующая матрица.
-
Представление в форме векторных моделей коррекции
остатками
- ВМКО (в англо.язычной
Correction Model, или VЕС-модели)
версии:
Vector Error
Аналогично одномерному АR(р)-процессу, VАR(р)-система
(4.124)
мо
жет быть записана как:
где
и
(j =
-(Фj+l
Вычитая
+
Фj+2
+ ... +Фр),
for
j = 1,2, ... ,р-1.
(4.129)
Yt-1 из обеих частей уравнения, получим VЕС-представле-
ние:
ЛУt
= a+(oYt-1 +(1ЛУt-1 +(2ЛУt-2 + ... +(р-1ЛУi-(р-1) +et, (4.130)
Гл.
294
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
где
{4.131)
В предположении наличия в точности
h
коинтегрирующих соот
ношений мы можем воспользоваться условием редуцированного ранга
В результате получим:
{4.128).
(о= -Фр{l)
так что уравнение
где Г'Уi
-
{4.130)
= -ВГ',
примет вид:
тренд-стационарный временной ряд.
Обозначив
Zt = Г'Уi,
мы приходим к так называемому представлению в форме VЕС-модели:
Заметим, что если
BZt-1
было бы равным нулю, то для разно
стей первого порядка дуt мы получили бы VАR-процесс. Но равенство
BZt-1
нулю невозможно, так как
Yi -
коинтегрированный вектор. В
-
матрица коэффициентов нагрузки или коррекции, поскольку она опре
деляет, каким образом флуктуации (ошибки, отклонения от среднего
или отклонения от долгосрочного соотношения равновесия) стационар
Zt корректируют изменения в переменных yt, т. е. дуt.
Напомним, что Zt - стационарный вектор, выражающий h коинтегри
рующих соотношений между элементами yt.
ного процесса
Название «коррекция остатками» (см.
ражает наличие слагаемого
[Davidson et al. {1978)]) от
-BZt-1· Zt-1 =f. О - отклонение от долго
срочного равновесия. В отсутствие этого слагаемого такая коррекция
отсутствует и система перестает быть коинтегрированной.
Отметим, что матрицы В и Г не определены однозначно, поскольку
для любой невырожденной матрицы
F
(размерности
(h
х
h))
справед
BFF- 1 Г'.
ливо равенство: ВГ' =
Следовательно, для процедуры оце
2
нивания необходимы h идентификационных ограничений. Например,
если
h
=
1, то Г'
= (')'1, ')'2)
нормировки мы получим
П ри м ер
4.8
должна быть нормирована. В результате
{1, -Ь), где Ь
= -')'2/'Yl·
(окончание): коинтеграция для двумерного процес
са. Выше, пользуясь векторной моделью скользящего среднего (VМА
модель), мы получили представление общего тренда и треугольное
4.5.
КОИНТЕГРАЦИЯ
295
представление. Теперь мы получим представление в форме VАR-модели
и VЕС-модели.
Для
VАR-представления
Ф(L)Ф(L) =
{1 - L)Im
воспользуемся
тем,
что
равенство
выполняется при
где
Ф1 = (~
i).
Таким образом, VМА-модель может быть представлена в виде VАR
модели конечного порядка. Для такого VАR-представления мы имеем
Представление в форме VЕС-модели можно получить, записывая VАR
модель с
в=
(1, о]',
г
= (1, -')']
(например).
В результате получим:
где
Zt = Г'Уi =
У1
t-
'
"llY2 t·
/
'
Детерминированный тренд исчезает в случае, если
81 =
')'82, т. е. если
коинтегрирующий вектор исключает этот детерминированный тренд.
Указанные выше различные представления для коинтегрирован
ных процессов могут быть объединены в следующей теореме.
Теорема о представлении Гранжера. Рассмотрим
н.-ый процесс
Yi
нерированъ~
VMA (оо )-процессом
где
et -
размерности т х
1,
I ( 1)
вектор
первъ~е разности дуt которого сге
многомерный белый шум с положителъно определенной ко
вариационной матрицей О; элементъ~ {Фj} лагового полинома Ф(L)
1-суммируемъ~, т. е. {jФj}~ 0 абсолютно суммируемъ~. Более того, мы
требуем, 'Чтобы зна'Чение лагового полинома в «единице» не бъt.л.о равно
нулю, т. е.
Гл.
296
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Предположим, 'Что существует в то'Чности
отношений среди элементов
ца Г размерности
'Что вектор
Zt
=
(m
х
h)
Yi.
h
коинтегрирующих со
Это зна'Чит, 'Что существует матри
с линейно независимъши столбцами, такая,
Г'Уi размерности
(h
х
1)
является стационарнъш,
при'Чем
Г'Ф(l) =О.
В этом слу'Чае VМА{оо)-процесс может бъtть записан в форме тре
угольного разложения Филлипса и в форме разложения общего трен.да
Стока
Ватсона.
-
Более того, если процесс может быть представлен в виде
V AR(p)-
процесса коне'Чного порядка (условия такого представления см. выше, в
«VАR-nредсmавлении»), то существует матрица В размерности
(m
х
для которой выполняется условие редуцированного ранга
h) ,
Фр(l)
= ВГ'
и, кроме того, существуют матрицъt
торых
(m
4.5.2.
х
m),
(i, (2, ... , (р-1,
размерность ко
такие, 'Что справедливо VЕС-представление
Процедуры оценивания моделей коинтеграции
Все предложенные подходы оценивания моделей коинтеграции могут
быть разделены на два семейства.
1.
Подходъt одного уравнения:
•
2-шаговый
подход
Энгла-Гранжера
([Engle,
Grander
(1987)]);
• 3-шаговый подход Энгла-Гранжера-Йю ([Engle, Уоо
(1991)]);
• подход динамического МНК (ДМНК) Стока- Ватсона
([Stock, Watson (1993)]);
•
подход авторегрессионно распределенных лагов (АРЛ) Песа
рана- Шина
2.
([Pesaran, Shin, Smith (1998)]).
Многомерные VАR-модели (более чем одно коинтеграционное со
отношение):
• VЕСМ-методология
(1988)]).
Йохансена,
МL-подход
([Johansen
4.5.
КОИНТЕГРАЦИЯ
297
В этом разделе мы коротко рассмотрим вопрос о том, как оценивать
коинтеграционную систему, имеющую VЕС-представление:
где (о
=
-ВГ' удовлетворяет условию редуцированного ранга. Выпи
шем логарифмическую функцию правдоподобия для гауссовского
мерного
m-
VAR(p )-процесса
для которого
Et(t = 1, 2, ... ) -
независимые, одинаково распределенные
случайные величины, подчиняющиеся (О; 0)-нормальному распределе
нию. Эта функция имеет вид:
lnL(П, О)=
тТ
- 2 1n(27Г)
+ 2Т in(det(n- 1 ))-
т
- ~ L {(Yt - п' Xt)'n-
1 (Yi
-
п' Xt) },
(4.132)
t=l
где
1
Yt-1
Xt = Yt-2 ,
Yt-p
а
Фр]
-
параметры.
Поскольку уравнения
соответствие между
(4.129) и (4.131) задают взаимнооднозначное
(Ф1, Ф2, ... , Фр) и ((о, (1, ... , (р-1), то логарифми
ческая функция правдоподобия для VЕС-системы принимает такой же
вид, как
(4.132),
в котором
1
Yt-1
ЛУt-1
ЛУt-2
ЛУt-р+1
и
П' =[а
(о
(2
(р-1].
Гл.
298
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Оценка методом максимума правдоподобия параметров VЕС-пред
ставления коинтеграции (а, (о,
... , (р-1)
максимизирует целевую функ
цию при выполнении условия редуцированного ранга, т. е. -(о = ВГ'
для некоторых матриц полного ранга Г и В, размерность которых
(т
х
h).
Это ограничение обеспечивает наличие
соотношений в
h
коинтегрирующих
1( 1)-системе.
Алгоритм Йохансена
В этом разделе мы опишем основные шаги для вычисления оценок мак
симума правдоподобия при помощи алгоритма Йохансена. Для более
детального ознакомления см.
гл.
[Hamilton (1994)],
20.
Алгоритм Йохансена можно разделить на три этапа.
1.
На первом этапе сначала при помощи метода наименьших квадра
тов (МНК) мы оцениваем следующую m-мерную VАR(р-1)-систе
му:
и вычисляем вектор МЯК-остатков
Ut,
размерность которого
(mx
х 1). Затем с помощью МНК оцениваем модель:
и снова вычисляем вектор МЯК-остатков
гот х
2.
Vt,
размерность которо
1.
На втором этапе сначала вычисляем выборочные ковариационные
матрицы остатков
Ut
и
Vt:
(4.134)
......
т
1 ~А А/
Т L.J UtVt
А'
= Evu·
(4.135)
Далее мы находим собственные значения А1
> А2 > ... > Ат из
Euv =
t=l
характеристического уравнения
(4.136)
4.5.
299
КОИНТЕГРАЦИЯ
и связанные с ними собственные вектора
формируется матрица
f
91, ... , 9h,
из которых
= (91, ... ,9h)·
Оказывается, что максимальное значение логарифмической функ
ции правдоподобия при ограничении, состоящем в том, что суще
ствуют
h
коинтегрирующих соотношений, равно:
lnLc{(o) =
тТ
--ln{21Г)
2
т
тТ
- -2
h
А
т"'
- 2 ln{det(Euu)) - 2
А
L.,, ln{l - Лi)·
(4.137)
t=l
3.
Наконец, мы находим необходимые оценки максимального прав
доподобия для {а, (о,
(р-1 1 П).
...
Мы знаем, что задание базиса для коинтегрированной системы
не единственно. Йохансен предложил нормализовать i'i таким об
разом, чтобы i'~Evvi'i = 1. Заметим, что это может быть сделано
при помощи стандартных статистических программ, взяв, напри
мер, i'i = JA'~i А
'УiЕvv'Уi
. Тогда оценки метода максимума правдоподо-
бия равны:
,..
,..
,.. ,.. /
(о= ЕиvГГ,
(i = fii - (оВ, for
А
i
= 1, 2, ... ,р- 1,
А
& =?Го - (о{о,
т
n= ~ L ((иt - (avtHйt -
(avt)'),
t=l
Детерминированные тренды
До сих пор мы не накладывали никаких ограничений на а и, в общем
случае, на детерминированную составляющую. Наличие детерминиро
ванных компонент в VЕС-моделях является во многом определяющим,
поскольку их учет заставляет менять процедуры статистического те
стирования, для которых используются другие критические значения.
Рассмотрим следующую общую модель, учитывающую детермини
рованную компоненту:
р-1
дУi = ВГ'Уi-1
+ L (jЛYi-j + TDt + €t,
j=l
Гл.
300
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
р-1
то есть:
дУt = ВГ'Уt-1
+ L (3ЛУt-3 + ао + alt + et.
j=l
Пусть матрица В .L, размерность которой
(т
х
(т - h)),
являет
ся ортогональным дополнением линейного подпространства столбцов
матрицы В, т. е.
B'B.L
=О и
rank(B.L) =
т
- h.
После некоторых мат
ричных преобразований получим следующий результат:
В(В'В)- 1 В' + B.L(B~B.L)- 1 B~
= Im.
Как следствие, детерминированная компонента может быть запи
сана в виде:
а**
о
а*
о
а**
1
а*1
и мы можем идентифицировать пять возможных случаев в соответ
ствии с различными типами ограничений на параметры.
•
Случай
1:
ао
= al
=О. Отсутствие детерминированных компо
нент в данных, и все свободные члены в коинтеграционных соот
ношениях равны нулю. Этот случай встречается редко, свободные
члены в коинтеграционных соотношениях необходимы для учета
единиц измерения:
р-1
дуt
= ВГ'Уt-1 + L
(3дуt_3 + et.
j=l
•
Случай 2: al = О и В~ ао = О. Отсутствует тренд в данных
и отсутствует тренд в коинтеграционном соотношении (а1 =0), но
свободный член в коинтеграционных соотношениях быть может,
поскольку В' ао
=f;
О. А значит,
р-1
дУt = В(Г'Уt-1 +а(;)+
L (3дУt-3 + et.
j=l
4.5.
•
Случай
3:
КОИНТЕГРАЦИЯ
301
а 1 =О и компоненты вектора ао не связаны за
данными условиями. Это означает, что может быть линейный
тренд в уровнях
yt (т. е. константа в первых разностях), но в коин
теграционных соотношениях тренд отсутствует. Однако, в коин
теграционных соотношениях может быть свободный член. Таким
образом,
р-1
дуt = В(Г'Уt-1) + ао +
L (jдyt_j + et,
j=l
р-1
дуt = В(Г'Уt-1 +а;))+ B.Lao*
+ L(jЛYt-j + et.
j=l
•
Случай
4:
компоненты вектора ао не связаны заданными
условиями, а В~ а1 = О. Поскольку В~ а1 = О, то в модели име
ются ограничения, исключающие квадратические тренды в уров
нях yt. Однако если В'а 1
=F
О, то коинтеграционные соотношения
могут иметь линейные тренды, так же как и свободные члены. Из
того, что В~ ао
yt.
=F
О, следует наличие линейных трендов в уровнях
Таким образом,
р-1
дуt = В(Г'Уt-1
+ ait) + ао + L
(jдyt_j
+ et =
j=l
р-1
= В{Г'Уt-1 +а;)+ ait) + B.Lao* + L(jЛYt-j + et.
j=l
•
Случай
5:
а 0 и а 1 не связаны заданными условиями. Тогда
модель содержит линейный тренд в разностях дуt, и квадратиче
ский тренд в уровнях
yt (это весьма нереалистичный случай).
р-1
дуt = В(Г'Уt-1) + ао + a1t +
L (jЛYt-j + et =
j=l
р-1
= В(Г'Уt-1 + ао * +ait) + B.La0* + B.Lai*t + L (jЛYt-j + et.
j=l
4.5.3.
Спецификация модели и тестирование
В случае, когда все временные ряды
ytj, j
=
1, "., m,
стационарны,
можно специфицировать для yt модель из класса VАR{р)-моделей, рас
смотренных в разделе
4.2.
В случае, когда все временные ряды
ytj,
Гл.
302
j = 1, ... , т
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
являются интегрированными порядка
d,
нам необходимо
выяснить, являются ли они коинтегрированными или нет. Это мож
но
сделать
при
помощи
тестов
же. Если оказывается, что
yt
на
коинтеграцию,
рассмотренных
ни
не является коинтегрированным вектор
процессом, то можно специфицировать VАR(р)-модель для его разно
стей d-го порядка. Если же вектор-процесс оказался коинтегрирован
ным, то для него используется одно из представлений для коинтегри
рованных систем, описанных выше.
Тест Энгла- Гранжера для остатков
Предположим, что вектор-процесс
является
Yi
1(1).
yt,
размерность которого
(m
х
1),
Основной целью является выяснение того, является ли
коинтегрированным вектор-процессом с
h
соотношениями или это не так, что означало
~
1 коинтегрирующими
бы h =О. Тест Энгла
Гранжера для остатков состоит из двух шагов.
1.
На первом шаге осуществляется регрессия
Yi1
на константу
- 1 компонент yt, для удобства обозначенных
ром у-,?>, размерность которого ((m -1) х 1):
остальные т
Yi1 = µ + a'yt( 2) + Zt,
µ
и
векто
(4.138)
где интересующая нулевая и альтернативная гипотезы состоят в
следующем:
Но
Регрессия
а
Yi1
:h=
О
против
Н1
:h
~
1.
(4.138) будет коинтегрирующей регрессией, если h ~ 1,
будет частью коинтегрирующего соотношения. В этом случае
временной ряд остатков
Zt
будет стационарным. Оценки
µи
&
парамаетров µи а, полученные при помощи метода наименьших
квадратов, будут состоятельными. Кроме того, мы имеем:
В случае
h
= О,
т. е. если между компонентами вектора
Yi
ствуют коинтегрирующие соотношения, МНК-оценки µи
ляются состоятельными, а
Zt
&
отсут
не яв
является интегрированным времен
ным рядом и имеет стохастический тренд. Этот феномен впервые
был отмечен в работе
[Granger, Newbold (1974)) и назван ложной
регрессией: даже если Yi1 не связано с yt( 2), t- и F- статистики для
оценок
µи
&
становятся бесконечно большими при увеличении
4.5.
КОИНТЕГРАЦИЯ
303
размера выборок Т. Таким образом, параметры Р, и
&
оказывают
ся всегда значимо отличными от нуля (при условии, что выборка
достаточно большая). В случае коинтеграции Yt1 и
Yi( 2)
отличие
тестовых статистик от соответствующих пороговых значений ста
новится еще более значимым. Причиной этого является то, что в
случае, когда h =О, Zt имеет стохастический тренд, тогда как в
случае
h
~
1 это
не так. В частности, можно показать, что оценка
дисперсии ошибок отвечает следующему вероятностному закону
(доказательство см. в
~
где
[Hamilton {1994)]):
i;z; ~ (
>.2 [
W(r) 2 dr)
·Т,
стандартное броуновское движение, а Л
W(r) -
{4.139)
-
параметр,
зависящий от автоковариации для Zt и Zt-1·
Основная идея доказательства последнего свойства состоит в том,
что числитель F-статистики зависит от квадратов компонент 2),
Yi(
и он увеличивается со скоростью О(Т2 ), а ее знаменатель равен
~
Ef= 1 Zl. Поскольку при h = О сумма ~ Ef= 1 Zl растет как О(Т)
(в то время как при
h
~
сумма стационарна), то соответству
1-
ющая F-статистика растет со скоростью О(Т), когда
скоростью
О(Т2 ),
h
=О, и со
когда h ~ 1. Как следствие, коэффициент де
терминации R 2 коинтегрирующей регрессии Yt1 по Yi(2 ) сходится
к 1 при h ~ 1, тогда как при h = О R 2 принимает умеренные
значения.
Кроме того, из
(4.139)
следует, что при
h
=О параметрыµ и а не
могут быть состоятельно оценены при использовании МНК, по
скольку процедура минимизации расходится, тогда как при
~
1
МНК-оценки
Ji,
h
~
и а будут состоятельными, поскольку проце
дура минимизации сходится.
2.
На втором этапе применяется тест на наличие единичного корня
для МНК-остатков
Z t --
'V
i
А
t1 - µ -
A/v(2)
а i
t
.
В результате мы выясним, действительно ли Zt является интегри
рованным рядом или нет. Для этого можно применить для
Zt рас
ширенный тест Дики- Фуллера или тест Филлипса- Перрона: к
сожалению, критические значения данного текста отличаются от
критических значений расширенного теста Дики - Фуллера, по
скольку Zt -
это остатки, зависящие от случайных величин Р, и
Гл.
304
&.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
А следовательно, от размерности т вектора
чае, когда известен коинтегрирующий вектор
необходимости оценивать
µ
yt.
Только в слу
{1, -"(')',
нам нет
и о, и тогда могут быть использованы
критические значения стандартного теста.
Критические значения для расширенного теста Дики - Фуллера и теста
Филлипса- Перрона, примененные к остаткам, могут быть найдены из
табл.
4.10,
представленной ниже. При этом мы должны учитывать раз
мерность ур>, т. е. учитывать число регрессоров в уравнении (4.138).
Кроме того, необходимо различать следующие три случая.
• Отсутствуют сдвиги. В случае, когда Е[дУi1] = О и Е[дуt< 2 >] =
=О, отсутствует сдвиг в каждой из компонент вектора
yt.
В этом
случае нам необходимо брать критические значения из столбцов
таблицы (а), учитывая при этом, что число регрессоров (констан
ту не включая) равно
(m - 1).
• Имеется сдвиг в yt< 2>. В случае, когда отсутствуют ограничения
на Е[дУi1], а Е[дуt( 2 )] =/:-О, сдвиг может иметь любая из компонент
yt, а компонента yt< 2 > должна иметь сдвиг всегда. В этом случае
нам необходимо брать критические значения из столбцов табли
цы (в), учитывая при этом, что число регрессоров (константу не
включая) равно (т -
1).
• Имеется сдвиг в yt 1 , но отсутствует в yt< 2>. В случае, когда
Е[дУi1] =/:- О, а Е[дуt< 2 >] = О, то имеется сдвиг только в Yi1, но не
в yt< 2>. В этом случае нам необходимо брать критические значе
ния из столбцов таблицы (в), учитывая, что размерность системы
равна
m.
Альтернативная гипотеза приведенного выше теста состоит в том,
что
Yi1
может
не является частью коинтегрирующего соотношения, которое
существовать между переменными, формирующими yt< 2 Сле
>.
довательно, результаты теста зависят от того, какая переменная берет
ся в качестве
Yi1.
Более того, приведенный выше подход не позволяет
определить число коинтегрирующих соотношений
левая гипотеза, состоящая в том, что
h =
hв
случае, когда ну
О, отвергается. Кроме того,
отсутствуют какие-либо статистические тесты для коинтеграционных
векторов (долгосрочная модель), поскольку стандартные ошибки недо
стоверны, а оценки долгосрочной модели имеют смещение в условиях
малых выборок.
4.5.
Таблица
4.10.
КОИНТЕГРАЦИЯ
305
Критические значения t-статистик расширенного
теста Дики - Фуллера, рассчитанные для остатков
коинтеграционного соотношения
Оцениваема.я регрессия: Ун =
µ
+ a'Y2t
Число регрессоров,
исключая константу
(m - 1)
1%
2.50%
5%
10%
-3.37
-3.77
-4.11
-4.45
-4.71
-3.07
-3.45
-3.83
-4.16
-4.43
(а) регрессоры без сдвига
1
2
3
4
5
-3.96
-4.31
-4.73
-5.07
-5.28
-3.64
-4.02
-4.37
-4.71
-4.98
(Ь) некоторые регрессоры имеют сдвиг
1
2
3
4
5
-3.96
-4.36
-4.65
-5.04
-5.36
-3.67
-4.07
-4.39
-4.77
-5.02
-3.41
-3.8
-4.16
-4.49
-4.74
-3.13
-3.52
-3.84
-4.2
-4.46
И ст о ч н и к : Phillips Р., Ouliaris S. (1990). Assymptotic Properties of Residual
Based Tests for Cointegration // Econometrica. Vol. 58. Р. 165-193; Fuller W. (1996).
Introduction to Statistical Time Series (2ed. ed) New York, Wiley.
В работе
[Banerjee et al. (1998))
предложена альтернативная про
цедура, которая позволяет получить более надежный, чем указанный
выше, тест на коинтеграцию и одновременно иметь менее смещенные
оценки для долгосрочного соотношения между переменными. Общий
коинтеграционный
тест
строится
на
модели
коррекции
остатками
(МКО) следующего вида:
ЛУt1 = б(L)ЛУt-1.1 + w(L)дyt< 2 > + 'YZt-1 + t:н.
Модель может быть оценена при помощи метода наименьших квадра
тов. Мы тестируем нулевую гипотезу о том, что 'У
< О,
используя стан
дартную t-статистику, для которой были рассчитаны специальные таб
лицы в условиях различных предположений. Указанная выше модель
может быть оценена при помощи нелинейного МНК, уменьшающего
смещение регрессоров:
ЛУt1 = б(L)ЛУt-1.1 + w(L)дyt< 2 > + 'Y1Yt-1.1 - 'У1µ - 'У1а~~~ + с:н.
Тем не менее упомянутые выше подходы и другие тесты типа
Энгла- Гранжера обладают некоторыми существенными недостатка
ми. А именно:
Гл.
306
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
• все компоненты вектора yt<2> предполагаются экзогенными;
•
отсутствуют статистические тесты для коинтеграционных векто
ров (долгосрочная модель), поскольку стандартные ошибки недо
стоверны;
•
оценки долгосрочной модели оказываются смещенными в услови
ях малых выборок;
•
эти
модели
не учитывают
наличия
коинтеграционных
векторов
между более чем двумя переменными;
•
пошаговая процедура тестирования приводит к увеличению оши
бок;
•
одномерные коинтеграционные тесты могут накладывать некор
ректные ограничения на краткосрочный характер изменения пе
ременных.
Далее описывается тест, который позволяет решить большинство из
этих проблем - тест Йохансена на на.л.и-чие коинтеграции.
Тест Йохансена
Рассмотрим m-мерное VЕС-представление коинтеграционной системы,
которое имеет вид:
ЛУt =а +(oYt-1
+ (1ЛУt-1 + (2ЛУt-2 + ... +(р-1Л1t-(р-1) +et· (4.140)
Многое зависит от ранга матрицы (о. В связи с этим условия на
матрицу (о могут приводить к разным возможностям:
• ранг h = m: все переменные в
Yt
являются
1(0)
(неинтересный
случай);
•
ранг
h
=О: отсутствуют линейные комбинации компонент
торые были бы
1(0),
Yt,
ко
отсутствует коинтеграция, и (о составлена из
нулей;
• 1
~ ранг
h
~
(т - 1):
существует не более (т -
онных соотношений Г'Уt-1, т. е. имеется
комбинаций компонент вектора
1(0).
Yt,
1(1)
коинтеграци
h линейно независимых
каждая из которых является
Или, что эквивалентно, существует
векторов, формирующих
1)
{m- h)
нестационарных
стохастические тренды.
КОИНТЕГРАЦИЯ
4.5.
Например, рассмотрим вектор [q
1{1).
нег
цен
-
доходов- процентных
р
307
у
i],
ставок»,
составленный из «де
которые
предполагаются
Экономическая теория предлагает следующее долгосрочное урав
нение спроса на деньги:
q-
р
= с + а:у -
/i.
Таким образом, если мы рассмотрим регрессионное уравнение для
q,
то
получим:
q-
р
а:у
-
+ /i =С+€ rv 1(0).
Но мы можем также получить его в терминах у:
у
- (1/a:)q + (1/а:)р - (1/a:)i
=-с/а:
-
е/а:
rv
1(0).
Подобная процедура может быть реализована для р и
тыре переменных (m =
Однако че
имеют единственный линейно независимый
4)
коинтеграционный вектор
i.
(h
= 1 < 4).
Отметим, что, в общем случае,
переменные могут быть объяснены при помощи дополнительных пере
менных (например, у и фискальная политика,
i и монетарная политика,
и т.д.).
Оценка коинтеграционного ранга
h
производится при помощи те
ста отношения правдоподобия. Поскольку
h
равняется числу ненуле-
вых собственных чисел для матрицы (о= -Ф(l), то тест строится на
оценках этих собственных чисел, полученных как решение уравнения
(4.136).
1.
Существует две версии теста.
Тест наибольшего собственного значения, который проверя
ет для любого выбранного натурального значения
Но
: h :::;; ho
против
Н1
ho
гипотезу
: h = ho + 1
и строится на базе оценки
(ho
+ 1)-го
наибольшего собственного
значения матрицы (о.
2.
Тест следа. Этот тест проверяет для любого выбранного нату
рального значения
Но
: h :::;; ho
ho
против
гипотезу
Н1
:h
и строится на базе суммы
> ho
(m - ho)
оцененных наименьших соб
ственных значений матрицы (о.
Тесты реализуются последовательно для
ho
=
О,
1, ... , m - 1.
При
справедливости Но обе статистики описываются при помощи винеров
ского процесса, и их критические значения могут быть затабулированы.
Из уравнения
(4.137)
можно увидеть, что максимальное значение лога
рифмической функции правдоподобия при ограничении, состоящем в
Гл.
308
4.
том, что имеется
h
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
коинтеграционных соотношений, т. е. при справед
ливости нулевой гипотезы, равно:
тТ
тТ
lnLo,c((o) = -21n(27Г)- 2
Т
h
Т~
л
л
- 2ln(det(~uu)) - 2 L...Jln(l - Лi)·
i=l
Максимальное значение логарифмической функции правдоподобия при
справедливости альтернативной гипотезы Н1, состоящей в том, что име
ется т коинтегрирующих соотношений, равно:
тТ
тТ
lnL1,c((o) = - 2 ln(21Г) - 2
Т
л
Т~
л
- 2 ln(det(~uu)) - 2 L...Jln(l - Лi)·
i=l
В последнем случае любая линейная комбинация компонент вектора
будет стационарным временным рядом, а
нение
h=
(4.140)
Yt-1
yt
будет входить в урав
без каких-либо ограничений на (о. Отметим, что случай
т отвечает стационарной системе в уровнях
yt.
Статистика теста отношения правдоподобия для проверки гипотезы
Но против Н1 , т.е. так называемого теста следа, определяется выра
жением:
m
L
LRh = 2 · (lnL1,c - Lo,c) = -Т
ln(l - ~i)·
i=h+1
Следовательно, мы можем проверить наличие или отсутствие ко
интеграционных соотношений и в случае их наличия протестировать
гипотезу о числе таких соотношений с использованием последователь
ности тестов следа в соответствии со схемой, указанной в табл.
Таблица
4.11.
4.11.
Схема последовательности тестов следа для проверки
существования коинтеграции
Число
Статистика теста следа
Нулевая гипотеза
коинтеграцион-
ных
соотно-
шений
при Но
-Т Е~ 1 ln(l - Лi)
Но
: Л1 = ... =
LRtr(hlm) = -TL:~h+ 1 ln(l - ~i)
Но
: Лh+1 = ... =
LRtr(m - 2lm) =
= -Т E~mn-1 ln(l - ~i)
LRtr(m - llm) = -Tln(l - ~m)
Но
: Лm-1 =
LRtr(Olm) =
Но: Лm
=0
Лm-1
= Лm =О
Лm-1
Лm =О
= Лm = О
о
h
m-2
m-1
4.5.
КОИНТЕГРАЦИЯ
309
Первое отклонение нулевой гипотезы показывает, что число коинте
грирующих соотношений равно числу, указанному в предыдущей стро
ке. Ниже (см. табл.
4.12)
приводятся результаты реализации этого те
ста, осуществленной на данных примера, заимствованного из пакета
E-views.
Таблица 4.12 Пример в Eviews-тecт следа (Йохансен)
Диапазон времени регистрации данных:
Общее число наблюдений:
1959:06 1989:12
367
Допущение о линейности детерминированного тренда
Используемые лаги: от
Значение
ся
Собственное
Критическая
5%-ное
1%-ное
значение
статистика
крити-
крити-
h
(проверяет-
1 до 4
гипотеза
Но:
h = ho
теста следа
при
ческое
ческое
значение
значение
29,68
15,41
3,76
35,65
20,04
6,65
альтернативе
Н1:
h > ho
о**
не более
не более
**
равном
1
2
0,102191
0,03444
0,00373
53,7974
14,2355
1,3724
означает отклонение гипотезы Но при уровне значимости критерия,
0,05 (5%).
Результаты теста указывают на наличие одного коинтегрированно
го соотношения при уровнях значимости критерия, равных и
Рассмотрим два крайних случая. Первый из них, когда
5%, и 1%.
h = О, т. е.
отсутствуют коинтегрирующие соотношения между компонентами век
тора
yt
yt, а система yt является коинтегрированной.
является скалярным процессом, т. е. т
=
1,
и
Второй случай, когда
h
=т-
1
=
О. Тогда
мы можем использовать тест Йохансена в качестве теста на наличие
единичных корней.
Наконец, рассмотрим случай, когда мы тестируем гипотезу Но о на
личии
h коинтегрирующих соотношений
против гипотезы Н1 о наличии
(h+l)
коинтегрирующих соотношений. Для проверки Но против Н1 ис
пользуется тест отношения правдоподобия, он же тест наибольших
собственных значений, статистика которого определяется следую
щим выражением:
LRh = -Tln(l - ~h+1).
Очевидно, оба указанных выше теста могут быть последовательно при
менены для тестирования числа коинтегрирующих соотношений
h.
Ос
новное отличие заключается в том, что тест следа тестирует гипотезу
(h + 1) - е и все последующие наименьшие из т собствен
ных чисел ~i, i = h + 1, ... , т, равны нулю, тогда как тест наибольших
о том, что
Гл.
310
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
собственных чисел рассматривает наибол:ьшие собственные числа. Од
нако статистика теста следа является более устойчивой к отклонениям
от предположения о нормальности, см., например,
[Cheung, Lai {1993)).
Критические значения статистик этих двух тестов являются нестан
дартными и оцениваются при помощи симуляционного моделирования,
но они обычно имеются в большинстве стандартных статистических па
кетов.
Тестирование ограничений на коинтегрирующие вектора
После того как мы обнаружили, что система из
ризуется
h
m
переменных характе
коинтегрирующими соотношениями, мы хотим протестиро
вать некоторые ограничения на коинтегрирующие вектора (например,
что только
q
h =/:- q =/:- m).
переменных входят в коинтегрирующие соотношения, где
Отметим, что если
= h,
q
тогда все
быть стационарными в уровнях, а если
= m,
q
q переменных должны
то нулевая гипотеза не
накладывает никаких ограничений на коинтегрирующие соотношения.
Рассмотрим матрицу
включают только
слагаемое в
D'yt.
{4.140)
D' такую, что коинтегрирующие соотношения
Следовательно, скорректированное ошибками
примет вид:
= -ВГ' D'Yt-1,
(oYt-1
где В, как и прежде, матрица размерности
(m
х
h).
Процедура оцени
вания методом максимума правдоподобия подобна той, которая пред
ставлена в предыдущем разделе, где Vt из
регрессии
D'Yt-1
на константу и дУt-1,
(4.133)
заменяется остаками
... , дYf-(p-l)'
оцененную при
помощи МНК. Это эквивалентно замене Е 1111 в {4.134) и Euv в {4.135) на
Evv = D'EvvD и Euv = EuvD соответственно.
Пусть .Лi - i-e по величине собственное значение матрицы
1
Е;11 E 11uE~~ Euv· Тогда максимальное значение для логарифмического
функции правдоподобия с ограничением равно:
lnLo,c((o)
mT
mT
= -2 ln{27Г) - 2
т
А
h
т~
- 2 ln{det(Euu)) - 2 LJln{l -
А
Лi)·
t=l
Мы можем построить тест отношения правдоподобия для проверки
нулевой гипотезы, состоящей в том, что
h
коинтегрирующих соотноше
ний: включают только элементы
D'yt,
зы, заключающейся в том, что
коинтегрирующих соотношений могут
h
включать любые компоненты вектора
против альтернативной гипоте
yt:
h
LRq = -Т
L ln{l i=l
h
.Лi) + Т
L ln{l i=l
Ai)·
4.5.
КОИНТЕГРАЦИЯ
311
Следовательно, нулевая гипотеза предполагает включение только
скорректированные ошибками слагаемые
Г'Уi. В работе
Zt =
[Johansen
(1988, 1991)] показано, что статистика отношения правдоподобия асимп
тотически имеет х2 -распределение с
h·(m-q) степенями свободы. Одна
ко имеются некоторые случаи, когда распределение тестовой статисти
ки асимптотически не совпадает с х 2 -распределением, см., например,
[Toda, Phillips (1994)], [Mosconi, Giannini (1992)].
Основные выводы по процедуре Йохансена
Основные шаги процедуры Йохансена состоят в следующем.
•
Тестирование переменных на нестационарность (используется, на
пример, расширенный тест Дики - Фуллера и др.). Отметим, что
стандартный метод Йохансена позволяет использовать только
лишь
/(1)
и /(О) переменные, тогда как для
/(2)
переменных тре
буются иные методы (для более детальной информации см.
[Johan-
sen (1995)]).
•
Если переменные нестационарны, осуществляется проверка того,
что они коинтегрированы.
(i)
Выбор VЕС-модели:
* вопрос о числе лагов в VАR-модели решается с исполь
зованием критерия лаговой длины (например, с исполь
зованием
* вопрос
и иных критериев);
AIC, SIC
о включении констант или трендов в
VAR
ре
шается из содержательных соображений или, если от
сутствуют
априорные
знания,
при
помощи
теста отно
шения правдоподобия. В последнем случае нет ясности
относительно выбора детерминированной части, несмот
ря на то, что имеются многочисленные работы, в кото
рых
предлагаются
[Liitkepol (2005)];
различные
подходы,
см.,
например,
простой подход от общего к частно
му начинается с наиболее общего случая (случай
п.
4.5.2),
5,
см.
а затем для выявления оптимальной детермини
рованной компоненты (и оценки коинтеграционнго ран
га) последовательно реализуются тесты отношения прав
доподобия.
(ii)
Использование статистики следа или статистики наибольших
собственных значений для тестирования гипотезы о числе ко
интеграционных соотношений (ранг
h).
312
Гл.
•
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Переоценивается VЕС-модель с заданным значением коинтегра
ционных уравнений
h
и накладываются необходимые ограниче
ния. Имеется два типа ограничений:
•
идентификационные ограничения;
связывающие ограничения.
Производится VАR/VЕС-анализ: прогнозирование, функция им
пульсного отклика, тесты причинности.
Динамический метод наименьших квадратов
Несмотря на то что методология Йохансена является наиболее часто
используемым подходом для тестирования коинтеграции и оценки ко
интегрированных систем, она обладает некоторыми недостатками: этот
метод весьма чувствителен к выбору переменных и их лагов. Кроме
того, этот метод не дает хороших результатов в условиях малых выбо
рок. Альтернативным подходом, который не обладает этими недостат
ками, является подход, предложенный в работах
и
[Stock, Watson {1993)]
[Saikonnen {1991)].
Этот альтернативный
подход,
названный
динами'Ческим МНК,
представляет собой качественное улучшение подхода Энгла- Гранжера.
В нем учитывается возможная эндогенность регрессоров. Этот подход
состоит из двух шагов.
1.
Методом наименьших квадратов оценивается следующая регрессия:
т
т
Yt1 = /30 + L /3iYti + L
i=2
р
L
')'i,jЛYt-j.i + E:t,
i=2 j=-p
где через -р и р обозначено число ~будущих» и ~прошлых» лагов
соответственно. Величина р обычно выбирается при помощи кри
териев
AIC/SIC/HQ
и др. МНК-оценки коэффициентов
/3
явля
ются суперсостоятельными, а серийная корреляция остатков оце
нивается при помощи процедуры Нью-Веста, учитывающей гете
роскедастичность и автокоррелированность стандартных ошибок.
2.
Тестирование на коинтеграцию осуществляется так же, как в про
цедуре Энгла- Гранжера, с использованием одномерного теста на
единичные корни для остатков или VЕС-теста на коинтеграцию.
В работе
[Stock, Watson {1993)]
сделан сравнительный анализ мно
жества оценок в условиях малых выборок и в качестве вывода указыва
ется, что метод динамического МНК дает обычно наименьшую средне
квадратическую ошибку по сравнению со статическим МНК-подходом
КОИНТЕГРАЦИЯ
4.5.
313
и подходом Йохансена. Эти выводы совпадают с выводами, сделанными
в работе
[Maddala, Kim (1998)],
раздел
5.7.
В некоторых исследованиях
для тестирования на коинтеграцию вначале используется подход Йо
хансена, а затем для уточнения оценок коэффициентов коинтеграции и
тестирования применяется динамический МНК.
4.5.4.
Эмпирические приложения в статистическом
пакете
Eviews:
коинтеграция
Рассмотрим ежемесячные наблюдения за следующими индексами и про
центными ставками. Возьмем период с января
(этот период включает
372
1965
г. по декабрь
месяца, данные заимствованы
1995 г.
из [Mills
(2008)]:
• FTA All Share index (FTAprice),
• FTA Dividend index (FTAdiv),
• Yield on 20 year UK Gilts (R20),
• 91 day
Тreasury Ьills
(RS),
графики которых представлены на рис.
4.9.
Все тесты на единичные корни указывают на то, что все четыре рас
сматриваемые переменные являются
1(1)
(более формальные результа
ты мы не приводим).
Для фондового рынка основной идеей в теоретическом смысле яв
ляется следующая дивидендная дисконтная модель:
которая может быть записана в виде модели роста Гордона:
Pt = Dt+1
Tt - Yt
или, если рассматривать эту модель в логарифмах,
Pt
где
= dt+1
- log(rt - Yt) ~ dt+1
+ ао -
a1rt,
Pt = log (цена актива), dt = log (дивидендов), Tt = доходность за
один период.
Гл.
314
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
LPRICE
lDIV
8.0
4.4
7.S
4.0
7.0
3.6
6.S
3.2
6.0
2.8
s.s
s.o
2.4
2.0
4.S
1970
197S
1980
198S
1990
19\IS
1970
197S
R20
1980
1985
1990
199S
198S
1990
199S
RS
18
18
16
16
14
14
12
12
10
10
8
6
1970
197S
1980
Рис.
198S
1990
4.9.
199S
1970
197S
1980
Временные ряды в уровнях
Реализация подхода Энгла- Гранжера для коинтеграции
(Э-Г шаг
1)
дает результаты, представленные в табл.
Таблица
4.13.
4.13.
Подход Энгла- Гранжера для коинтеграции (шаг
Dependent VariaЫe: LPRICE
Method: Least Squares
Sample: 1965МО1 1995М12
Included observations: 372
VariaЬle
Coefficient
с
3.472363
LDIV
1.065223
R20
-0.04961
-0.01039
RS
R-squared
0.970405
Adjusted R-squared
0.970164
S.E. of regression
0.167567
Sum squared resid
10.3329
Log likelihood
138.6972
Durbln-Watson stat
0.120788
Std. Error
0.04899
0.010775
0.005175
0.004478
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
t-Statistic
70.87869
98.85835
-9.58788
-2.32007
1)
Prob.
о
о
о
0.0209
5.936924
0.970096
-0.724178
-0.68204
4022.17
о
t-статистики, полученные после использования метода наименьших
квадратов, не являются надежными оценками в условиях
1(1)
регрес
соров, а значит, они использоваться не могут. Мы сохраним остатки,
полученные из долгосрочной модели, и протестируем их на стационар
ность (шаг
2
в процедуре Энгла-Гранжера).
4.5.
КОИНТЕГРАЦИЯ
315
Для рассматриваемых остатков не могут быть использованы кри
тические значения расширенного теста Дики - Фуллера, так как эти
остатки ненаблюдаемы, а получены в результате оценивания. Поэто
му следует использовать критические значения из табл.
но столбец (а) из этой таблицы с т
4.14).
- 1 = 3
4.10,
а имен
регрессорами (см. табл.
Результаты проверки показывают, что остатки нестационарны на
10%-м уровне значимости, а значит, отсутствует подтверждение того,
что коинтеграционное соотношение существует.
Таблица
4.14.
Подход Энгла-Гранжера для коинтеграции (шаг
2)
Null Hypothesis: ЕСМ has а unit root
Exogenous: None
Lag Length: О (Automatic based on SIC,
MAXLAG=lб)
Augmented Dickey-Fuller test statistic
Test critical values:
1% level
5% level
10% level
t-Statistic
-3.54413
-2.57121
-1.94168
-1.61613
Prob.*
0.0004
Однако если мы будем следовать подходу, предложенному в работе
[Banerjee et al. {1998)],
то реализуем тест на коинтеграцию, оценивая
при этом модель для краткосрочной динамики с механизмом коррек
ции ошибками. Мы рассмотрим стратегию моделирования от общего к
частному,
удаляя все незначимые лаговые переменные и накладывая
ограничения везде, где возможно {см. табл.
Таблица
4.15.
4.15).
Тест на коинтеграцию: подход, представленный в
[Banerjee et al. {1998)]
и основанный на модели
коррекции ошибками
Dependent VariaЬle: DLPRICE
Method: Least Squares
Sample: 1965МО5 1995М12
lncluded observations: 368
VariaЬle
Coefficient
с
0.010044
D(DLPRICE(-1))
0.147663
DLPRICE(-3)
0.135877
DLDIV(-3)
-0.42393
DR20(-1)
-0.03008
DRS(-1)
0.012719
ЕСМ(-1)
-0.06516
R-squared
0.107784
Adjusted R-squared
0.092955
0.058457
S.E. of regression
Sum squared resid
1.233617
Log likelihood
526.287
2.001159
Durbln-Watson stat
Std. Error
0.003399
0.038114
0.051167
0.214837
0.009418
0.006347
0.01857
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
t-Statistic
2.95473
3.874195
2.655553
-1.97328
-3.19347
2.003798
-3.5091
Prob.
0.0033
0.0001
0.0083
0.0492
0.0015
0.0458
0.0005
0.007884
0.061379
-2.822212
-2.747874
7.26841
0.00000
Гл.
316
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
В этом случае ЕСМ(-1) значим и отрицателен. Таким образом,
коинтеграционное соотношение существует. Более того, другое подтвер
ждение этому можно получить
при помощи динамического
МНК
Стока- Ватсона для оценки коинтеграционного уравнения и реализа
ции коинтеграционного теста для остатков (результаты здесь не пред
ставлены, предлагается читателю в качестве упражнения).
Теперь мы рассмотрим тест Йохансена на коинтеграцию. Для рас
сматриваемых переменных возможными коинтеграционными уравнени
ями могут быть:
•
дивидендная дисконтная модель, включающая
•
временная структура процентных ставок,
R20
Pt,
и
dн1 и
rt;
RS.
Следуя результатам критериев лаговой длины, число лагов в VАR
модели для уровней полагается равным
Таблица
Lag
4.16.
(см. табл.
4.16).
Критерий лаговой длины для уровневых VАR-моделей
1
2
3
LogL
-1892.19
1128.801
1187.997
1201.042
LR
NA
5958.073
115.4306*
25.1493
12
1281.702
14.18673
о
2
sc
HQ
1.99Е-08
AIC
10.53441
-6.16001
-6.399981*
-6.38357
10.57759
-5.94411
-6.011370*
-5.82224
10.55158
-6.07416
-6.245462*
-6.16037
2.84Е-08
-6.03168
-3.91591
-5.19041
FPE
0.44171
2.48Е-08
1.95е-08*
Как следствие число лагов в векторной модели коррекции ошибка
ми будет равным
1.
Исходя из теоретических и логических соображе
ний, мы решили предположить, что в коинтеграционном уравнении от
сутствует тренд, но имеется свободный член, тогда как свободный член
отсутствует в VАR-модели: ранее использованные экономические моде
ли включают константу в линейную аппроксимацию, тогда как ни для
одной из наблюдаемых и рассматриваемых переменных не наблюдает
ся детерминированный тренд. Кроме того, для таких ненаблюдаемых
переменных, как премия за риск, также тренд не наблюдается.
После выбора векторной модели коррекции ошибками мы тестиру
ем число коинтеграционных соотношений (ранг
h).
Для этого мы вос
пользуемся статистикой теста следа или статистикой теста наибольших
собственных значений (результаты представлены в табл.
4.17).
Ранговый тест показывает, что число коинтеграционных соотноше
ний равно
1.
Тест следа и тест наибольших собственных значений под
тверждают это. Таким образом, мы продолжим тем, что оценим век
торную модель коррекции ошибками для 1-го коинтеграционного соот
ношения и 1-лагадля разностей переменных в авторегрессионной части,
4.5.
без
каких-либо
табл.
4.18).
КОИНТЕГРАЦИЯ
ограничений
317
(результаты
представлены
в
Оценки векторной модели коррекции остатками при дру
гих предположениях относительно числа коинтеграционных уравнений
и наличия/отсутствия ограничений представлены в табл.
4.19
и
4.20.
Таблица 4.17. Тест Йохансена на коинтеграцию
Sample (adjusted): 1965МО3 1995М12
Included observations: 370 after adjustments
Тrend assumption: No deterministic trend (restricted constant)
Series: LPIOCE LDIV R20 RS
Lags interval (in first differences): 1 to 1
Unrestricted Cointegration R.ank Test (Тrасе)
Hypothesized
Тrасе
5.ООЕ-02
Eigenvalue
Prob.**
No. of CE(s)
Statistic Critical Value
None *
111.1825
0.186256
5.41Е+01
о
At most 1
0.044154
34.9219
3.52Е+01
0.0534
At most 2
0.029391
18.2134
0.0934
2.03Е+01
At most 3
0.019207
7.175812
9.164546
0.1174
Тrасе test indicates 1 cointegrating eqn(s) at the 0.05 level
* denotes rejection of the hypothesis at the 0.05 level
**MacKinnon-Haug-Michelis (1999) p-values
Unrestricted Cointegration R.ank Test (Maximum Eigenvalue)
Hypothesized
Max-Eigen
0.05
No. of CE(s)
Eigenvalue
Statistic Critical Value
Prob. **
None *
0.186256
76.26057
28.58808
О
At most 1
0.044154
16. 7085
22.29962
0.2508
At most 2
0.029391
11.03759
15.8921
0.249
At most 3
0.019207
7.175812
9.164546
0.1174
Max-eigenvalue test indicates 1 cointegrating eqn(s) at the 0.05 level
* denotes rejection of the hypothesis at the 0.05 level
**MacKinnon-Haug-Michelis (1999) p-values
Переменные
циент при
LDIV
R20
и
RS
оказались незначимыми, тогда как коэффи
не отличается значимо от
1.
Эти ограничения могут
быть учтены в векторной модели коррекции ошибками: ограничения
В(1, 1)= 1,В(1,2)= -1,В(1,3)= О, В(1,4)= О отклоняются; ограничения
В(1,1)=1,В(1,2)=-1, В(1,4)=0 и В(1,1)=1, В(1,2)=-1, В(1,3)=0 не
отклоняются (результаты представлены в табл.
4.16
и
4.17).
Однако по
следние ограничения приводят к тому, что значение коэффициента при
RS
оказывается неадекватным с точки зрения экономистов-теоретиков.
В любом случае, учитывая, что финансовый рынок в данный пери
од проходит через ~смутное время-», характеризующееся, в частности,
тем, что, по утверждению главы Федеральной резервной системы США,
Гл.
318
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
мы являемся свидетелями существенных недостатков в идеологии сво
бодного рынка23 , следует быть очень осторожным в суждениях о том,
что является правдоподобным, а что нет.
Таблица
4.18.
Оценки векторной модели коррекции ошибками (без
ограничений) в предположении существования лишь
одного коинтеграционного уравнения
Vector Error Correction Estimates
Sample (adjusted): 1965МО3 1995М12
Included observations: 370 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:
CointEql
LPRJCE(-1)
1
LDIV(-1)
-0.96576
-0.14746
[-6.54912]
0.098373
R20(-1)
-0.07042
[ 1.39695]
0.113301
RS(-1)
-0.06132
[ 1.84766]
с
-4.08668
-0.66663
[-6.13039]
Error Correction: D(LPRJCE) D(LDIV)
CointEql
0.005394
0.006072
-0.00294
-0.00068
[ 1.83561] [ 8.90517]
D(R20)
-0.01472
-0.01726
[-0.85257]
D(RS)
-0.03171
-0.02584
[-1.22693]
В обоих случаях член, отвечающий коррекции остатками, значим
и имеет положительный знак в уравнении для (разностей) логарифмов
дивидендов, как и ожидалось, и слабо значим и положителен коэф
фициент для (разностей) логарифмов цен, которые не соответствуют
стандартной экономической теории. Однако, нулевое ограничение на
этот коэффициент отклоняется на 5%-м уровне значимости.
Наконец, можно продолжить анализ, изучая качество прогнозиро
вания, функции импульсного отклика, результаты тестов причинности
идр.
23 Алан
Гринспан
(Alan
Greenspan),
23
октября
http://www.iht.com/articles/2008/10/23/business/gspan.php).
2008
г.
(см.:
4.5.
Таблица
4.19.
КОИНТЕГРАЦИЯ
319
Оценки векторной модели коррекции ошибками
в предположении наличия одного коинтеграционного
уравнения и ограничений В ( 1, 1) =
1, В ( 1 , 2) = -1,
В(1,3)=0
Vector Error Correction Estimates
Sample (adjusted): 1965МО3 1995М12
Included observations: 370 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegration Restrictions:
B(l,1)=1,B(l,2)=-1 ,B(l,3)=0
Convergence achieved after 221 iterations.
Restrictions identify all cointegrating vectors
LR test for Ьinding restrictions (rank = 1):
Chi-square(2)
1.344701
Probabllity
0.510507
Cointegrating Eq:
CointEql
LPRICE(-1)
1
LDIV(-1)
-1
R20(-1)
о
RS(-1)
0.269681
-0.06697
[ 4.02662)
с
-3.64417
-0.64023
[-5.69199)
Error Correction: D(LPRICE) D(LDIV)
CointEql
0.003388
0.003589
-0.00176
-0.00041
[ 1.91999) [ 8.73233)
Таблица
4.20.
D(R20)
-0.00687
-0.01037
[-0.66233]
D(RS)
-0.02206
-0.01551
[-1.42171]
Оценки векторной модели коррекции ошибками
в предположении наличия одного коинтеграционного
уравнения и ограничений В(1,
В(1,4)= О
Vector Error Correction Estimates
Sample (adjusted): 1965МО3 1995М12
Included observations: 370 after adjustments
Standard errors in ( ) & t-statistics in [ J
Cointegration Restrictions:
B(l,1)=1,B(l,2)=-1 ,B(l,4)=0
Convergence achieved after 98 iterations.
Restrictions identify all cointegrating vectors
LR test for Ьinding restrictions (rank = 1):
1)= 1, В(1,2)= -1,
320
Гл.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Таблица
Chi-square(2)
Probabllity
Cointegrating Eq:
LPRICE(-1)
LDIV(-1)
R20(-1)
4.20.
(продолжение)
4.153492
0.125337
CointEql
1
-1
0.177477
-0.04289
[ 4.13803]
RS(-1)
о
с
-3.89083
-0.45587
[-8.53496]
Error Correction:
CointEql
D(LPRICE)
D(LDIV)
D(R20)
D(RS)
0.006394
-0.00335
[ 1.90871]
0.006823
-0.00078
[ 8.74625]
-0.01529
-0.01969
[-0.77672]
-0.0182
-0.02952
[-0.61646]
Обзор нелинейных моделей коинтеграции
4.5.5.
В нескольких относительно недавних работах показано (см., например,
[Michael et al. (1997)], [Sarantis (1999)]), что пороговые нелинейные мо
дели позволяют объяснить характер изменения обменных валютных
курсов. Кроме того, показано, как с использованием пороговых авто
регрессионных моделей (ПАР-моделей) можно показать характерные
пороговые нелинейности в узких панелях европейских индексов потре
бительских цен и обменных валютных курсов (см.
В работе
[Obstfeld, Taylor (1997)]
[O'Connell (1998)]).
показано, что линейность для большо
го числа временных рядов внутристрановых детализированных цен на
рушается, так же как и для временных рядов агрегированных межстра
новых обменных курсов. В работах
(1996)]
[O'Connell, Wei (1997)], [Parsley, Wei
продемонстрировано, что нелинейности существуют и в детали
зированных данных по ценам в США; в работе
[Lo and Zivot (2001)]
про
демонстрировано наличие пороговой коинтеграции для цен пар ~торгу
емых~ товаров. Принятая ниже структуризация материала во многом
опирается на работу
[Ihle, von Cramon-Taubadel (2008)].
Все эти работы в большей или меньшей степени мотивированы иде
ей, которая заключается в том, что арбитраж
-
это сила, которая ис
ключает паритет покупательной способности или закон единой цены:
т. е. если разница между ценами на один и тот же товар в двух странах
больше, чем величина трансакционных издержек в торговле между эти
ми странами, тогда арбитраж приводит к тому, что разница цен на этот
4.5.
321
КОИНТЕГРАЦИЯ
товар уменьшается до нуля, и этот механизм ~нащупывания» равнове
сия отражен в наблюдаемом соотношении рассматриваемых цен. Одна
ко, если разница между этими ценами меньше, чем величина транзак
ционных издержек в торговле, арбитраж не возникает и в простейшем
случае цены будут меняться независимо друг от друга. Закон единой
цены изучается эмпирически, главным образом, двумя способами: абсо
лютн:ые разности (разности цен Рн
- P2t) или фиксированные транс
портные расходы (см. [O'Connell, Wei (1997)], [Park et al. (2007)]) и отно
сителънъtе отклонения (разности логарифмов цен = ln Рн - ln P2t) или
пропорциональные транспортные расходы (см. [O'Connell, Wei (1997)],
[Lo, Zivot (2001)]).
По большей части в эмпирических работах для описания характера
данных используются нелинейные модели и не производится никаких
спецификационных тестов для того, чтобы убедиться в том, что эти
модели адекватны в действительности. Кроме того, транзакционные
издержки накладывают ограничения симметричности порогов и сим
метричности скорректированных параметров. Эти ограничения обычно
не тестируются. Лишь совсем недавно, благодаря теоретическим изыс
каниям, отраженным в работах
[Balke, Fomby (1997)], [Tsay (1998)],
[Hansen (1999)], [Lo, Zivot (2001)], [Hansen, Seo (2002)], [Gonzalo, Pitarakis (2006)] и [Seo (2006)], процедуры тестирования начали использо
ваться практиками, см., например, [Sепа, Goodwin (2003)] и [Park et al.
(2007)].
Многие классы нелинейных моделей временных рядов возникли в
70-80-хх гг. прошлого века. По-видимому, именно в работе
[Tong (1978)]
впервые введен класс так называемых nороговъtх моделей. Достаточ
но общая формулировка нелинейных моделей предложена в работах
[Priestley (1980)]
и [TjgФstheim
(1986)].
В работе
[Tong (1990)]
содержит
ся общая классификация нелинейных моделей временных рядов.
Класс nороговъtх авторегрессионных
ressive models:
моделей
(thershold autoreg-
ПАР- или, в англоязычной литературе, ТАR-модели), по
всей видимости, один из наиболее интересных классов, которому уде
ляется большое внимание как со стороны практиков, так и со стороны
теоретиков. Этот класс моделей подразделяется на три группы: группу
кусо-чно-nолиномиалънъtх моделей, группу кусо-чно-линейнъ~х моделей
и группу гладких авторегрессионнъtх моделей. Принадлежность к той
или иной группе определяется функциональной зависимостью значе
ния временного ряда
{Xp}p<t·
Xt
в момент времени
t
от исторических значений
Общий вид линейной пороговой модели может быть записан
как:
(4.141)
Гл.
322
где
Xt
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
(Xt,Xt-1, ... ,Xt-k+1)',
а через
личина, которая при фиксированном
{1, 2, ... , l}.
Другими словами,
Jt -
t
Jt
обозначена случайная ве
принимает одно из значений
индикаторная переменная, сигна
лизирующая о состоянии/режиме, в котором находится временной ряд
{Xt}
в момент времени
t.
При фиксированном состоянии
Jt = j
неслу
чайные матрицы А (j) и нИ> размерности (k х k) содержат авторегресси
онные коэффициенты и коэффициенты, которые отвечают за гетероске
дастичность соответственно. Вектор с<Л, размерность которого (k х 1),
включает константы, а через €t обозначена последовательность незави
симых одинаково распределенных k-мерных случайных векторов, име
ющих нулевые средние значения и некоторую ковариационную матри
цу. Таким образом, для каждого фиксированного состояния
Jt = j
соот
ношение является .л.окал:ьно линейным с некоторыми фиксированными
коэффициентами и константами: в рамках этой модели .л.ока.л.ъностъ
относиться не к близости к конкретной точке во времени, а к опреде
ленной области пространства состояний временного ряда. В этом смыс
ле, линейность относится к постоянству параметров в такой области.
Таким образом, локальная линейность является ключевым свойством
ПАР-моделей. Это свойство состоит в том, что параметры этой моде
ли могут быть непостоянными, но они обязаны быть постоянными при
фиксированном состоянии/режиме временного ряда. Такие параметры
модели называют зависимьши от состояния или зависимы.ми от ре
жима.
Индикаторная переменная
Jt
в
(4.141)
является определяющим эле
ментом нелинейного характера уравнения. Реализации
моменты времени
t
Jt
в различные
формируют временной ряд состояний (режимов)
{Jt}, который называют процессом,
генерирующим режим'Ьt (ПГР) вре
менного ряда. Состояния пороговой модели могут быть сгенерированы
при помощи одного из следующих базовых механизмов:
Jt Jt Jt
f (Xt-p), t > р, t > q
f (Yi-p), t > р, t > q
f (Xt-p, Yi-q), t > р, t > q
(смысл целочисленности неотрицательного параметра q см. ниже).
Первый случай отвечает эндогенной детерминации режимов для
временного ряда
(1990)]
{Xt}
по его историческим данным. В работе
[Tong
этот класс моделей называется самовозбуждаемой пороговой ав
торегрессией
(self-exciting TAR models: СВПАР- или SЕТАR-модели),
поскольку режимы временного ряда {Xt} полностью генерируются по
значениям самого временного ряда. В работе [Tong (1990)] такие моде
ли обозначены как СВПАР(l; ki, k2, ... , kl), где через l обозначено число
режимов, а
(в работе
l -
kj, j
= 1, 2, ... , l
[Hansen (1999)]
323
КОИНТЕГРАЦИЯ
4.5.
-
лаговая длина модели при j-м состоянии
такие модели обозначены как СВПАР(l), где
число режимов модели).
Второй случай отвечает экзоген:ной детерминации лагированны
ми на q периодов значениями некоторых других временных рядов
В этом случае состояния пороговой модели не зависят от
руются
при
помощи
В работе
[Tong (1990)]
другого
наблюдаемого
{Xt}
{Yt}.
и генери
временного
ряда.
такая детерминация режимов называется неза
мкнутой пороговой авторегрессионной системой
(open-loop threshold
autoregressive system: НПАРС или TARSO). Если {Yt} представляет со
бой реализацию пороговой модели, а ее режимы экзогенно детермини
рованы временным рядом
{Xt},
то в этом случае пороговую модель
называют замкнутой пороговой авторегрессионной системой (ЗПАРС
или
TARSC),
т. е. в этом случае состояния каждого из двух временных
рядов определяется состояниями другого. Другой возможностью, сре
ди прочих, является детерминация состояния множеством неизвестных
(экзогенных) переменных, которые по тем или иным причинам немо
гут быть идентифицированы или измерены, поэтому описание процесса
состояний возможно только при помощи условных вероятностей. Таким
образом, состояния временного ряда
{Xt}
могут быть сгененрированы
при помощи марковской цепи, и тогда результирующая модель называ
ется авторегрессией с марковскими переключениями
autoregressive:
АРсМП или
MSAR),
(Markov-switching
которую можно легко преобразо
вать в моде.л/ь коррекции остатками с марковскими переклю'Чениями
(МКОсМП или
MSVECM).
Третий случай детерминации режимов можно понимать как смесь
двух упомянутых выше случаев, в котором состояния временного ряда
{Xt}
определяются комбинацией лагированных значений временного
ряда
{Xt}
и некоторых экзогенных временных рядов
{Yt}.
Если зави
симые переменные такой системы выражены не в уровнях, а в разно
стях, то результирующая кусочно-линейная ПАР-модель со смешанной
детерминацией режимов называется пороговой векторной моделью кор
рекции остатками (ПВМКО или
TVECM).
Таким образом, ПВМКО и
МКОсМП принадлежат классу кусочно-линейных ПАР-моделей.
4.5.6.
Пороговая векторная модель коррекции остатками
(ПВМКО)
Общее определение ПВМКО. Несмотря на то что статистическая
модель, основанная на идее введения порогов, была впервые предло
жена в работе
[Whittle (1954)],
класс пороговых моделей был впервые
математически формализован в работе
[Tong (1978)],
автор которой и
Гл.
324
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
далее совместно с другими исследователями, последовательно развива
ли это направление исследований (см.
[Tong {2007)]
и ссылки в этой ра
боте). Как следует из вышеизложенного, коинтеграционная теория ста
ла развиваться во второй половине 80-хх гг., что дало дополнительный
толчок исследованиям, посвященным анализу нестационарных времен
ных рядов.
Пороговая коинтеграци.я впервые была
[Balke, Fomby {1997)].
представлена
в работе
Авторы этой работы заметили, что коррекция от
клонений от долгосрочного состояния равновесия, т. е. коррекция остат
ками равновесия, может иметь пороговый характер. С тех пор порого
вые векторные модели коррекции остатками привлекли внимание ис
следователей занятых как в области финансов, так и в области эко
номики (см., например,
[Serra, Goodwin {2003, 2004)], [Balcombe et al.
{2007)], [Ben-Kaabla, Gil {2006)], [Frey, Manera {2007)], [Park et al. {2007)]
и ссылки в этих работах).
Возможность существования нелинейных ценовых переходов была
впервые высказана в качестве гипотезы в работе
[Heckscher {1916)],
ко
торая опиралась на закон единой цены, сформулированный в работе
[Marshall {1890),
с.
325].
В контексте международной торговли Хекшер
предложил так называемый интервал бездействия, который определя
ется тем, что малые отклонения от равновесной цены не корректируют
ся. Это происходит в силу того, что транзакционные издержки выше,
чем потенциальная прибыль от разницы в ценах на один и тот же то
вар. Важно отметить, что эти транзакционные издержки включают не
только транспортные расходы, но и, например, стоимость поиска пред
ложений, стоимость организации переговоров, страхование, премию за
риск. Следовательно, переход ценовых сигналов между рынками за
висит от того, входит ли отклонение от равновесной цены в интервал
бездействия. Таким образом, ценовой переход зависит от величины це
нового спреда pf -pf между рынком В и рынком А, что демонстрирует
характер, определяемый режимом/состоянием. Если спред больше, чем
определенное значение т, то торговый сдвиг предложения от рынка А
к рынку В вызовет увеличение цены
pf
и снижение цены
pf.
Этот ме
ханизм будет снижать разность между этими ценами до тех пор, пока
она не станет меньше порогового значения т. Таким образом, уравне
ние
pf -
являются
pt 1 ( 1),
т = О является соотношением равновесия. Если
pf
и
pf
то мы получаем коинтеграционное соотношение с ошиб
кой равновесия равной
pf - pf -
т, которая корректируется процессом
торговли до тех пор, пока оно не станет отрицательным. Однако отрица
тельные значения ошибки ограничены снизу вторым порогом, который
измеряет транзакционные издержки торговли в обратном направлении
(этот второй порог не обязательно совпадает по абсолютной величине с
4.5.
325
КОИНТЕГРАЦИЯ
первым порогом). В этом смысле пороговые модели являются адекват
ными как с теоретической точки зрения, так и с позиции интуитивного
понимания. Более того, зависимые переменные обычно выражаются в
первых разностях, т. е. в терминах дрf
= pf - Pf-1,
дрf
= pf - Pf-1,
так что режимы каждого из ценовых рядов определяются в соответ
ствующей модели коррекции остатками членом, который сам являет
ся функцией от обоих этих ценовых рядов. Таким образом, пороговая
авторегрессионная модель с третьим типом детерминации режимов в
форме пороговой векторной модели коррекции остатками (т. е. ЗПАРС
в форме ПВМКО) является подходящей моделью.
Работа
[Obstfeld, Taylor (1997)]
является первой публикацией, в ко
торой дана ссылка на так называемую гипотезу Хекшер. В работах
[O'Connel, Wei (1997)]
и [Тrenkler,
Wolf (2003)]
эта идея извлечена из эко
номической теории. Несколько теоретических моделей в области ана
лиза обменных валютных курсов позволили получить результаты, сов
падающие с гипотезой Хекшер (см., например,
[Dumas (1992)], [Uppal
(1993)], [Sercu et al. (1995)], [Coleman (1995, 2004)]).
В общем виде ПВМКО может быть представлена в форме:
р-1
дрt =
a(Jt) -
в(Jt)Г'Pt-1
+L
,yt) ЛPt-j +
j=l
если
e<r-l) < Г'Pt-d ~
Et,
(4.142)
(J(r),
где Pt = (pf ,pf)' - вектор цен на рынках А и В, а r = 1, 2, ... , l, l + 1
- индекс для режимов. Через a(Jt) обозначено среднее, зависящее от
режима, где верхний индекс Jt = r сигнализирует о зависимости па
раметра от режима. B(Jt) - вектор нагрузки, который состоит из па
раметров, зависящих от режима и характеризующих, в какой степени
изменения цены Лрt реагируют на отклонения от долгосрочного рав
новесия, лагированные на
<
d
периодов.
Значения (J(r) упорядочены таким образом, что (J(O) < (J(l) < ... <
(J(l) < (J(l+l), где (J(O) = -оо, (J(l+l) = оо, называемые порогов'Ьtми па
раметрами, или, если коротко, порогами. Важно отметить, что число
эффективных порогов, (J(l)
< ... < (J(l)
равно l. Мы предполагаем, что
пороги не зависят от времени, поскольку именно такая спецификация
используется в прикладной литературе. Лишь недавно начали появ
ляться некоторые модели, которые ослабляют это предположение (см.,
например,
модель от
[Van Campenhout (2007)], где для порогов строится линейная
времени, или [Park et al. (2007)], где предложена динамиче
ская модель изменения ежедневных порогов).
Переменная, определяющая соответствующий режим в момент вре
мени
t,
называется пороговой переменной, а в случае ПВМКО это все-
326
Гл.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
гда отклонение от долгосрочного равновесия. Предполагается, что она
образует стационарную случайную последовательность, которая имеет
непрерывную функцию распределения, тогда как d Е
N+
называют
параметром запаздъtвания.
Очевидно, что нелинейная ПВМКО является обобщением вектор
ной модели коррекции остатками и каждый порог (J(r) значим (в ве
роятностном смысле) только в случае, если О < P[(J(r-l) < Г'Pt-d :::;;
:::;; (J(r-l)] :::;; 1. Другими словами, если реализации пороговой перемен
ной возникают с вероятностью, большей нуля, то они наблюдаемы в
каждом режиме.
Путем введения фиктивных переменных для каждого режима мо
дель может быть сформулирована в более компактной форме в терми
нах многомерной регрессионной модели подобно тому, как это сделано
в работе
[Hansen, Seo (2002)):
дрt = А (l)'Xt-1 dp>
+ ... + А (l)'Xt-1 d~l) + Et =
l
= LA(r)'Xt-ld~r)
+ Et =
A(Jt)'Xt-1
(4.143)
+ Et,
r=l
где A(Jt) - матрица коэффициентов, а Xt-1 = (lГ'Pt-1ЛPt-1 ... дх
XPt-p+1Y вектор регрессоров модели (4.143). Далее, d~r) = l(e<r-lkГ'Pt-d::;;;e<r)) обозначает фиктивную переменную, сигнализи
рующую об r-м режиме временного ряда в момент времени
t,
а
1(·) -
индикаторная функция. Выражая режимы ценовых временных рядов
в терминах индикаторной переменной
модели
Jt,
мы получим частный случай
(4.141).
Отметим, что в большинстве приложений коинтегрирующий век
= (1, -1) 1 (поскольку из
pf - pf должна быть 1(0)),
тор предполагается известным и равным Г
закона единой цены следует, что разность
поэтому пороговая переменная равна остатку из коинтегрирующего со
отношения Г'Рt-1 =
pf -pf, а остатки в каждом режиме имеют общую
ковариационнуюматрицу:Е.
Частные случаи модели. В работах
Zivot (2001)]
[Balke, Fomby (1997)]
и
[Lo,
введены определенные ограничения на модель, которые
могут быть весьма приемлемыми для прикладного анализа. Следуя
идее Хекшера, пара ценовых временных рядов может не быть коин
тегрированной парой в случае, если цены попадают в так называемый
интервал бездействия, определяемый транзакционными издержками.
В этом случае разность дрt ведет себя как случайное блуждание около
=
нуля. Следовательно, в режиме j
2, когда цены попадают в «интер
вал бездействия~, в< 2 > =О, и зависимое от режима среднее равняется
нулю а( 2 )
= О.
4.5.
КОИНТЕГРАЦИЯ
327
В зависимости от центра притяжения механизма коррекции остат
ками (который определяется режимом) мы будем различать следую
щие частные случаи. Если остатки осуществляют коррекцию так, что
бы временной ряд попадал в некоторый интервал вокруг долгосрочного
равновесия, которое равно зависящему от режима среднему (равному
а< 1 > - для режима j = 1; нулю - для режима j = 2; а< 3 > - для режима
j = 3),
то модель называется интервалъной ПВМКО (И-ПВМКО или
BAND-TVECМ) и принимает следующий вид:
Лрt=
а:<1> -
в< 1 >Г'Рt-1
р-1
+ Е (';1>ЛPt-j + Et,
если fJ(O) < Г'Pt-d ~ fJ(l)
j=l
р-1
+ Е (';2 >ЛPt-j + Et, если fJ(l) < Г'Pt-d ~ е< 2 >
j=l
р-1
+ Е (';з) ЛPt-j + Et, если е< 2 > < Г'Pt-d ~ е< 3 >.
j=l
Если же остатки корректируют так, чтобы временной ряд «при
тягивался» к долгосрочному равновесию, тогда аР> = а< 3 ) = О, и в
этом случае модель называется ]ХLвновесной-ПВМКО (Р-ПВМКО или
EQ-TVECM)
и принимает вид:
-в< 1 >Г'Рt-1
р-1
+Е
j=l
р-1
+Е
Лрt=
j=l
-в< 3 >г'Рt-1
р-1
+Е
j=l
'j
'j
'j
(1)
(2)
(3)
ЛPt-j
+ Et,
if fJ(O) < Г'Pt-d ~ fJ(l)
ЛPt-j
+ Et,
if fJ(l) < Г'Pt-d ~ е< 2 >
ЛPt-j
+ Et,
if 8( 2 ) < Г'Pt-d ~ 8( 3) ·
Если оба порога равны по величине, т. е. если
-8< 1> = 8(2), то в этом
случае мы имеем дело с так называемой симметричной ПВМКО
(С-ПВМКО или
S-TVECM).
Равенство порогов отражает идентичность
транзакционных издержек в обоих направлениях торговли.
Процедура оценивания. Существуют различные техники оцени
вания пороговых моделей в целом и ПВМКО в частности. Эти подходы
могут быть разделены на два класса.
•
Класс моделей, в которых критерий выбора порогов состоит в ми
нимизации суммы квадратов остатков модели (см., например,
[Balke, Fomby {1997)], [Hansen {1999)], [Goodwin, Piggott {2001)],
[Lo, Zivot {2001)], [Park et al. {2007)]).
Гл.
328
•
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Класс моделей, в которых пороги выбираются при помощи макси
мизации функции n]ХLвдоnодобия (см., например,
[Obstfeld, Taylor
{1997)], [Hansen, Seo {2002)], [Serra, Goodwin {2003)]).
Эти два критерия отнюдь не эквивалентны, поскольку последний из
них не учитывает корреляцию между уравнениями, тогда как первый
из них учитывает это в явном виде. Однако результаты симуляционного
моделирования Монте-Карло, представленные в работе
{2002)],
[Serra, Goodwin
показывают, что учет корреляции между уравнениями не уве
личивает точность оценок параметров в условиях малых выборок, и оба
упомянутых метода дают похожие результаты оценивания.
Опишем указанные выше методологии при помощи компактной за
писи, представленной уравнением
мя режимами и (р
- 1)
{4.143) для двумерной ПВМКО с дву
лагами:
{4.144)
d< 2>
1 1
{-oo=8< 0 kГ'Pt-d~e< 1 >} и
t
{8< ><Г'Pt-d~e< 2 >=+00}' а
I{ci <У~С2} = 1 при выполнении указанного неравенства и I{ci <у~с2 } =О
в противном случае (lo - так называемая индикаторная функция многде
d t(l)
=
1
=
жества {}).В прикладных работах необходимо ограничивать порог е< 1 >
таким образом, чтобы каждый режим включал бы минимальное чис
ло наблюдений. Если обозначить через Тт число наблюдений в режиме
r,
а через Т
- общее число наблюдений, то, как предлагается в ра
боте [Hansen {1999)), ограничения порогов должны быть такими, что
при Т --+ оо, Тт/Т ~ т для некоторого т Е {О, 1). Хансен предлагает
полагать травным О, 1. Модель (4.144) можно оценивать при помощи
nоследователъного многомерного метода наuменъшuх квад
ратов, реализуемого в два этапа:
1) при заданных 8( 1) и d параметры (А< 1 > 1 , А( 2 )') могут быть оценены
при помощи многомерного метода наименьших квадратов. При
этом сумма квадратов остатков равна:
SLs(8< 1>, d) = trace[E(8< 1>, d)],
где Е(8(1), d) обозначает оценку Е
(4.145)
многомерным мето
дом наименьших квадратов при заданных (8( 1), d).
2)
= var(et)
на втором шаге методом наименьших квадратов вычисляются
оценки (8( 1), d):
(8< 1>, d) = arg min SLs(8< 1>, d);
8( 1 ),d
4.5.
329
КОИНТЕГРАЦИЯ
требование Tr ~ тТ ограничивает процедуру поиска 8( 1) значе
ниями Г'Pt-d, которые должны лежать между Т-м и (1 - Т)-м
квантилями. Итоговые оценки A(Jt) даются .Д.(Jt) = .Д.(Jt)(0( 1 ),J),
а оценка ковариационной матрицы остатков определяется матри-
цей :Е(8( 1 ), J).
В работе
[Tsay (1998)] показано, что при достаточно слабых услови
ях регулярности оценки, полученные последовательным условным мно
гомерным методом наименьших квадратов (А (l), А (2), O(l), d), являются
сильно состоятельными, а МНК-оценки А (l), А (2) еще и асимптотиче
ски нормально распределены и не зависят от 8( 1), d. Кроме того, оценки
O(l) и d сходятся со скоростью Т.
Если мы рассмотрим общий вид ПВМКО с тремя режимами,
(4.146)
то при заданных (8( 1),8( 2 ),d) мы можем оценить параметры (А( 1 ),А( 2 ),
А( 3 )) при помощи многомерного метода наименьших квадратов. Полу
чив сумму квадратов остатков Sз(8( 1 ), 8( 2), d), оценки для (8( 1), 8( 2)) и d
могут быть найдены путем минимизации Sз(8( 1 ), 8( 2 ), d) с использова
нием трехмерного поиска по сетке. Однако этот метод является весьма
затратным с вычислительной точки зрения, поскольку если для каж
дой пары 8(l) и 8( 2) оцениваются N точек, то поиск по сетке значений
(8( 1), 8( 2 ), d), реализуемый на втором шаге, включает d х N 2 регрессий.
Если
N
достаточно велико, то эта процедура достаточно трудоемка.
В работе
[Hansen (1999)] предлагается использовать способ вычисли
тельной экономии при помощи последовательного оценивания множе
ственных контрольных точек, описанного в работе
[Bai (1997)].
На пер
вом шаге мы оцениваем методом наименьших квадратов (неправильно
специфицированную) двухрежимную модель (4.144) и получаем значе
ния 1 ,
Результаты работы [Bai (1997)] показывают, что будет со
(0 d).
d
стоятельной оценкой для d, тогда как 01 будет состоятельной для одной
из компонент пороговой пары (8( 1), 8( 2)). Далее, методом наименьших
квадратов для (4.146) мы оцениваем (8( 1), 8( 2)) при d = d и при усло
вии, что одна из компонент вектора (8( 1); 8( 2 )) равна 01 • Полученная
оценка 02 будет состоятельной оценкой для другой компоненты пары
(8(1)' 8(2)).
Для других классов моделей пороги выбираются с использованием
метода максимума n'JIО,вдоnодобия. Этот и описанный выше ме
тоды оценки могут показаться на первый взгляд очень непохожими.
Но они значительно более близки, чем может показаться: предыдущий
метод минимизирует след матрицы Е, т. е. trace[E(8( 1 ), d)), тогда как
Гл.
330
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
второй метод минимизирует логарифм детерминанта ковариационной
матрицы остатков, т. е. ln IE(lJ(l), d)I.
Отметим, что в первом классе моделей коинтеграционный вектор
Г
= {1, -7) 1 предполагается известным (7 = 1), а d должно быть оцене
но, тогда как во втором классе
d
фиксировано и равно
1,
а
7
необходи
мо оценить: таким образом, мы имеем два параметра, которые должны
быть оценены в обоих случаях.
С учетом этих замечаний алгоритм, основанный на методе макси
мума правдоподобия, состоит из следующих шагов.
•
С использованием подхода, представленного в
из линейной ВМКО получим оценку
=
Zt-1 (
1') =
1'·
[Johansen (1988)],
При заданном Zt-1
=
Г1 Pt-l1 формируем равномерную сетку на [(JL; еи) и
на [7L; 1Р].
• Для всех попарных комбинаций (7, е< 1 >) соответствующей сетки
при помощи МНК оцениваем (А <1>1 , А <2>1) и :Е.
• Определим оценки {i', 8< 1>) как значения (7, е< 1 >), при которых
максимизируется функция максимального правдоподобия:
lnLc(7, 8(1))
=
= L [А.< 1 > 1 (7,е< 1 >),А.< 2 > 1 (7,8< 1 >),Е(7,8(1)),7,8< 1 >] =
(4.147)
= - nT - т In(IE{7,e(I>)I).
2
2
• Возьмем А.< 1 > 1 =A_(l)l{i',8< 1 >), А.< 2 > 1 =А.< 2 > 1 (..у,8< 1 >) и :Е
Из
(4.146)
= E{i', 8< 1>).
следует, что оценки максимума правдоподобия миними
зируют логарифм детерминанта ковариационной матрицы:
{i', 8< 1>) = argmin SмL(7, е< 1 >) = argmin ln IE{7, е(1>)1.
",8(1)
Сравнивая
(4.145)
{4.148)
",8(1)
и
(4.148),
легко заметить, что оценка максимума
правдоподобия учитывает корреляцию между уравнениями, тогда как
первый подход, основанный на последовательных наименьших квадра
тах, ее не учитывает. Следовательно, вполне возможно, что два раз
личных подхода могут дать различные ответы в терминах пороговых
эффектов. Однако, как указывалось выше, в работе
{2002))
[Serra, Goodwin
показано, что оба критерия дают одни и те же результаты оце
нивания. Наконец, в работе
[Hansen, Seo {2002)] отмечается, что нельзя
с уверенностью заявлять, что точка (..у,8< 1 >), в которой достигается ми
нимум, будет единственна, поскольку логарифмическая функция прав
доподобия невыпукла.
4.5.
4.5.7.
КОИНТЕГРАЦИЯ
331
Тестирование пороговой коинтеграции
Обзор результатов. В работе
[Balke, Fomby (1997)]
были впервые рас
смотрены некоторые проблемы, связанные с тестированием пороговой
коинтеграции. В ней отмечается, что тестирование нулевой гипотезы,
предполагающей отсутствие коинтеграции, против альтернативной ги
потезы, предполагающей наличие пороговой коинтеграции, осложняет
ся тем, что необходимо сочетать использование асимптотической стати
стики для тестирования на единичный корень и наличие параметров,
которые присутствуют только в модели, отвечающей альтернативной
гипотезе. В качестве решения в работе
[Balke, Fomby (1997)]
предлага
ется двухшаговая стратегия: на первом шаге тестируется нулевая ги
потеза, которая предполагает, что модель линейная без коинтеграции,
против альтернативы, что модель линейная с наличием коинтеграции;
если нулевая гипотеза отвергается, то тестируется нулевая гипотеза о
наличии линейной коинтеграции против альтернативы о наличии поро
говой коинтеграции.
В работе
[Lo, Zivot (2001)]
используется подход, похожий на двух
шаговый подход Белке- Фомби, но применительно к процедурам мно
гомерного оценивания и тестирования. Их идея заключается в том, что,
если двумерная ПВМКО является подходящей моделью, тогда мно
гомерные процедуры, которые учитывают структуру модели, должны
иметь большую мощность, чем одномерные процедуры, в которых не
учитываются ограничения, возникающие из многомерной структуры.
Они анализируют мощность многомерного теста гипотезы об отсут
ствии коинтеграции на первом шаге, а затем рассматривают мощность
многомерных тестов линейности на втором шаге. В работе впервые
сформулировано утверждение, состоящее в том, что пороговая приро
да альтернативной гипотезы может значительно уменьшить мощность
стандартного теста, реализуемого на первом шаге. Соответственно в
работе рассматриваются тесты на единичные корни, предложенные в
работах
[Enders, Granger (1998)], [Berben, van Dijk (1999)], которые стро
ятся таким образом, что обладают достаточной мощностью против по
роговых альтернатив. Более того, Ло и Зивот предложили еще и третий
шаг, включающий спецификационный анализ формы пороговой моде
ли, основанный на тестах вложенных гипотез в рамках пороговой мо
дели достаточно общего вида без ограничений.
В работе
[Hansen, Seo (2002)]
развивается теория оценивания и те
стирования, основанная на методе максимума правдоподобия. Авторы
в своем исследовании исходили из представления коинтегрированных
систем в форме модели коррекции остатками с потенциальными поро
говыми эффектами. Они рассмотрели ВМКО, включающую известный
332
Гл.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
единственный коинтегрирующий вектор, в которой пороговый эффект
отвечает слагаемому коррекции остатком. В частности, на первом шаге
авторы применили расширенный тест Дикки- Фуллера, а затем вос
пользовались Suр-LМ-тестом, разработанным ими для двухрежимной
пвмко.
Однако, этот подход может оказаться недееспособным, поскольку
при альтернативной пороговой коинтеграции стандартные коинтегра
ционные тесты могут приводить к существенной потере мощности (см.
работы
[Pippenger, Goering {2000)], [Taylor {2001)], [Lo, Zivot {2001)] и
[Seo {2006)]). В связи с этим в работе [Seo {2006)] был предложен тест на
коинтеграцию для ПВМКО с заданным коинтегрирующим вектором, в
котором проверяется нулевая гипотеза об отсутствии коинтеграции в
линейной модели. В частности, в работе
[Seo {2006)]
предложена suр
Wаld-статистика для тестирования нулевой гипотезы об отсутствии ко
интеграции против альтернативной ПВМКО и показана ее состоятель
ность. Кроме того, в этой статье для аппроксимации функции распре
деления этой статистики предлагается бутстреп-процедура, основанная
на остатках. Этот тест демонстрирует значительно большую эмпири
ческую мощность при пороговой коинтеграционной альтернативе, чем
другие стандартные тесты. При этом разница в мощностях становится
больше при увеличении объема выборки.
В работе
[Gonzalo, Pitarakis {2006)]
представлены дальнейшие ре
зультаты анализа пороговых эффектов и предложен тест вальдовского
типа для проверки нулевой гипотезы о линейности против пороговой
нелинейности в долгосрочном равновесии ВМКО. Предлагаемый тест
строится без каких-либо предположений относительно коинтеграцион
ных свойств системы и применим безотносительно к тому, является
ли система коинтегрированной или нет. Более того, в работе
Pitarakis {2006)]
[Gonzalo,
изучается использование внешней пороговой перемен
ной, которая может иметь экономический или финансовый характер,
но которая должна быть стационарной и эргодической. Таким образом,
предлагается процедура вне стандартного случая, в которой величина
слагаемого, корректирующего остатки, вызывает пороговые эффекты.
Наконец, отметим, что в пороговых коинтеграционных моделях воз
можны четыре гипотезы: линейность без коинтеграции, наличие поро
гов без коинтеграции, линейность с коинтеграцией и пороговая коинте
грация. Однако ранее рассмотренный двухшаговый подход не включа
ет гипотезу о пороговой модели без коинтеграции. Важно подчеркнуть,
что тестирование на адекватность пороговой модели без коинтеграции
(нулевая гипотеза) требует совершенно иных функций распределения,
отличных от тех, которые используются при тестировании нулевой ги
потезы о линейности без коинтеграции, а значит, невозможно предло-
4.5.
333
КОИНТЕГРАЦИЯ
жить единый тест, при помощи которого одновременно проверялись бы
все нулевые гипотезы.
Тестирование отсутствия коинтеграции против линейной
коинтеграции. Когда коинтеграционное соотношение меж,цу
pf
и
pf
предполагается линейным, мы можем использовать стандартный ана
лиз для линейной коинтеграции. Следует отметить, что некоторые
асимптотические результаты, справедливые для линейной коинтегра
ции, остаются таковыми и для случая пороговой коинтеграции. Одной
из причин этого является то, что пороговая нелинейность Zt не влия
ет на порядок интеграции
Zt
pf, pf
и
Zt.
Если отклонение от равновесия
удовлетворяет так называемому условию а-перемешивания, описан
ному, например, в работе
[Phillips (1987)],
единичные корни для
и
ские результаты
pf
pf
то для статистик тестов на
выполняются некоторые асимптотиче
[Phillips (1987)];
кроме того, выполняется суперсосто
ятельность оценок наименьших квадратов коинтегрирующего вектора
(1, -у),
боты
см., например,
[Stock (1987)]. Эти свойства побудили
[Balke, Fomby ( 1997)] предложить для тестирован.и.я
авторов ра
нулевой ги
потез·ы об отсутствии коинтеграции использовать стандартнъtе од
номернъtе тесты на едини-чнъtе корни для коинтеграционных остатков
Zt
= Г'Рt-1·
В работе
[Balke, Fomby (1997)]
показано, что тест Филлипса-Пер
рона (ФП-тест) имеет большую мощность, чем расширенный тест Ди
ки-Фуллера (РДФ-тест). Это возможно, как указывается в работе, в
силу непараметрической природы ФП-теста, который оказывается бо
лее мощным против пороговой коинтеграции, чем РДФ-тест. В работе
[Balke, Fomby (1997)]
показано, что оценка коинтегрирующего вектора
приводит к потере мощности как РДФ-теста, так и ФП-теста на единич
ные корни, но потеря мощности для пороговых моделей по величине
незначительно отличается по сравнению с линейными авторегрессия
ми. Однако результаты работ
(1997)]
[Pippenger, Goering (1993)], [Balke, Fomby
показывают, что стандартные тесты на единичные корни могут
иметь меньшую мощность для пороговых моделей, если авторегресси
онные коэффициенты во внешних режимах близки к
1и
(или) ширина
интервалов (er-l, ()(r)] в модели с индикаторной переменной переклю
чения: 4-Jt = f(Xt-p), t > р, t > q"> (см. (4.141)), велика относительно
дисперсии ошибок.
В работе
[Horvath, Watson (1995)]
предложен многомернъtй НW
тест на проверку отсутствия коинтеграции, который строится при
условии, что коинтегрирующий вектор задан. Линейная ВМКО для
без пороговых эффектов дается соотношением:
Pt
Гл.
334
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
р-1
Лрt =а: - ВГ'Рt-1
+L
'jЛPt-j
+ Et
(4.149)
j=l
и проверяется нулевая гипотеза В
= О об отсутствии коинтеграции.
Статистики Ховэса и Ватсона для тестирования условия В
= О прини
мают вид стандартной регрессионной статистики Вальда, используемой
при анализе «видимо не связанных~ уравнений регрессии:
HW
= B'var(в)- 1 :8,
где В обозначает МНК-оценку (для каждого уравнения в отдельно
сти) параметра В, а var(B) - МНК-оценка ковариационной матрицы
В. При справедливости нулевой гипотезы об отсутствии коинтеграции
предельной функцией распределения статистики
HW
ция от двумерного броуновского движения, и в работе
(1995)]
является функ
[Horvath, Watson
представлена таблица с соответствующими критическим значе
ниями. Кроме того, в этой работе показано, что предлагаемый тест мо
жет быть более мощным против коинтегрированных альтернатив, чем
одномерный РДФ-тест на единичные корни, в особенности, когда кор
реляция между компонентами остатков Et велика. Более того, в работе
[Zivot (2000)]
показано, что, когда динамика данных не соответсвует
ограничениям, накладываемым РДФ-тестом, тестовая НW-статистика,
как правило, имеет большую мощность, чем РДФ-тест. В работе
Zivot (2001)]
[Lo,
показано, что НW-тестовая статистика имеет вдвое боль
шую мощность по сравнению с одномерными РДФ-тестами в широком
классе случаев.
Одновременно, правда, показано, что тесты, которые учитывают
пороговую природу альтернативных гипотез, имеют еще большую мощ
ность, чем НW-тест.
Тестирование отсутствия коинтеграции против пороговой
коинтеграции. Как отмечалось выше, стандартные тесты на коинте
грацию могут оказаться маломощными, когда в качестве альтернати
вы выступает пороговая коинтеграция. В работах
[Gonzales, Gonzalo
(1997)], [Caner, Hansen (1998)], [Enders, Granger (1998)] и [Berben, van
Dijk (1999)] рассматривается проблема тестирования наличия единич
ных корней в одномерной авторегрессионной модели против альтерна
тивной стационарной пороговой авторегрессионной модели. В резуль
тате было установлено, что тесты на единичные корни могут иметь
большую мощность при учете специфической природы пороговой аль
тернативы.
Как оказалось, методы, используемые в работах
[Gonzales, Gonzalo
(1997)], [Caner, Hansen (1998)], [Enders, Granger (1998)] и [Berben, van
4.5.
Dijk {1999)),
335
КОИНТЕГРАЦИЯ
могут быть применены к коинтеграционным остаткам Zt
=
= Г'Рt-1· Но при этом необходимо проявить осторожность, поскольку
некоторые из этих тестов требуют выполнения определенных предпо
ложений относительно природы переменной перехода
Zt-1,
которые не
выполняются в случае ПВМКО. Правда, тесты, предложенные в рабо
тах
[Enders, Granger {1998)), [Berben, van Dijk {1999)), не требуют,
чтобы
при справедливости нулевой гипотезы переменная перехода была ста
ционарной, а потому их использование в данном контексте является
корректным. В частности, в работе
[Enders, Granger {1998))
рассматри
вается тестирование на единичные корни для следующей двухрежим
ной пороговой авторегрессионной модели:
Лzt = {
ф( 2 )(zt-1
ф
(l)
-
с)+ et,
если
Zt-1
+ et,
если
Zt-1 =::;; с.
(zt-1 - с)
> с,
(4.150)
Пороговое значение с оценивается как выборочное среднее Zt- 1 , а те
стирование нулевой гипотезы, состоящей в том, что ф( 1 )
=
ф( 2 )
=
О,
производится с использованием стандартной F-статистики следующей
регрессии:
Лzt = ф(l)(Zt-1
-
c)I(Zt-1~c) + ф( 2 )(Zt-1
-
c)I(Zt-1>c)+
р-1
{4.151)
+ ~ (jЛZt-j + et,
j=l
где с
-
выборочное среднее для Zt-1, а
lo -
индикаторная функция
{}, т. е. Io = 1, если множество в фигурных скобках вы
полняются, и lo =О во всех остальных случаях. При справедливости
множества
нулевой гипотезы о наличии единичного корня функция распределения
F-статистики представляет собой функцию от броуновского движения.
В работе
[Enders, Granger {1998))
даны соответствующие критические
значения при различных гипотезах, касающихся детерминированной
компоненты. При этом в
[Enders, Granger {1998))
показано, что F-тест
имеет меньшую мощность, чем РДФ-тест, в котором игнорируется по
роговая природа двухрежимной альтернативы. Но F-тест может иметь
большую мощность, чем РДФ-тест в трехрежимных моделях с асим
метричными порогами и динамиками. Следовательно, это может быть
полезно при использовании пороговых векторных моделей коррекции
остатками.
В работе
[Berben, van Dijk {1999))
указывается, что меньшая мощ
ность теста Эндерса- Гранжера относительно РДФ-теста возникает, ве
роятно, в результате того, что первый из них строится с использованием
Гл.
336
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
смещенной: оценки порогового параметра в условиях, когда справедли
ва альтернативная гипотеза. В работе
[Berben, van Dijk (1999)]
пред
ложен более мощный тест, который: при справедливости альтернатив
ной: гипотезы использует состоятельную оценку порога. В частности, их
тест нулевой гипотезъt ф( 1 ) = ф( 2 ) =О в (4.151) основан на испол:ьзо
вании стандартной F-статистики, где с оценивается из
(4.150)
при
помощи последователъного условного метода наименъших квадратов.
В работе
[Berben, van Dijk (1999)]
показано, что предлагаемая ее авто
рами F-статистика может иметь значительно большую мощность, чем
F-статистика для двухрежимной: модели
(4.150),
ся сильно асимметричной:. Кроме того, в работе
если динамика являет
[Lo, Zivot (2001)]
пока
зано, что мощность тестов Эндерса- Гранжера и Ван Дий:ка- Вербена
значительно больше, чем мощности теста Хорваса- Ватсона (который:
не учитывает пороговую приро,цу альтернативы). В частности, тест Ван
Дий:ка-Бербена (см.
[Berben, Van Dijk (1999)])
имеет хорошую мощ
ность в условиях выборок среднего размера.
В работе [Вес
Granger (1998)],
et al. (2004)],
сле,цуя идее, представленной: в
[Enders,
описан тест для нулевой: гипотезы на наличие еди
ничных корней против порогового (симметричного) процесса. Одна
ко вместо F-теста для произвольного порогового значения, использу
емого Эндерсом и Гранжером, авторы предложили sир- Wald-тecт при
неизвестном пороговом зншчении. Им удалось получить асимптотиче
ское распределение в аналитическом виде, которое представляет собой
функцию сложного вида от броуновского движения, и показать, что оно
не зависит от «мешающего» параметра. Отметим, что в
(1998)]
[Enders, Granger
показано, что процесс, отвечающий: трехрежимной: так называе
мой самовозбуждаемой: пороговой авторегрессионной: модели порядка р
(SETAR(p))
и общего вида (с произвольным порядком авторегрессии),
может быть стационарным процессом, для которого выполняется усло
вие перемешивания, даже при наличии единичного корня или корня, по
мо,цулю большего единицы в среднем режиме. Упомянутая трехрежим
ная
SETAR(p )-модель может быть представлена в сле,цующем виде:
а
( )
1
р-1
+ Л1zt-1 + Е
j=l
если
Лрt
=
а
( )
2
р-1
+ Л2zt-1 + j=l
Е
если
а
( )
3
р-1
+ Лзzt-1 + Е
j=l
если
'j
'j
'j
(1)
ЛPt-j
Zt-1
(2)
~ -8(1);
ЛPt-j
- 8( 1)
(3)
+ Et,
< Zt-1
ЛPt-j
8(1)
+ Et,
+ Et,
< Zt-1·
(4.152)
~ 8< 1>;
КОИНТЕГРАЦИЯ
4.5.
337
Цены описываются 1(1)-процессом, задаваемым уравнением
ли гипотеза Но: Л1
{2004)]
=
Л2
=
Лз =О не отклоняется. В
для тестирования Но
: Л1 =
Л2
(4.152), ес
работе [Вес et al.
Лз =О предложен тест, осно
=
ванный на статистике, равной супремуму отношения правдоподобия, а
именно:
Sup LR =
Sup LR( fJ),
e(l)e[eL,eu1
где LR(fJ) = Tln{0- 2 /0- 2 ), а О- 2 и О- 2 -
{4.153)
суммы квадратов остатков в
предположении справедливости Но и при ее отклонении соответствен
но. Авторы этой работы решили обратиться к suр-тестам, имея в виду,
что (J{l) на практике неизвестно и при справедливости нулевой гипоте
зы неидентифицируемо. А значит, не может быть оценено состоятельно.
Возникновение класса таких тестов было инициировано работой
[Davies
{1987)], где был предложен suр-тест для проверки наличия структурных
сдвигов. Для того чтобы гарантировать независимость распределений
suр-тестов от неизвестных параметров, в работе [Вес
et al. {2004)]
было
предложено выбирать интервал [fJL, fJИ] следующим образом:
1. Абсолютные значения (zt)f= 1 выстраиваются в порядке возраста
ния, lzl(1)
< ... < lzl(T)·
2. Берем (JL = lzl{[o,iТ]) and fJИ = lzl{[o,9Т])' для которых по мень
шей мере 20% наблюдений лежат во внешних режимах, что обес
печивает оценивание SЕТАR-модели по достаточному количеству
выбросов.
Поскольку при справедливости нулевой гипотезы статистики suр-тестов
имеют асимптотические распределения, которые представимы в анали
тическом виде, в работе [Вес
et al. {2004)]
вычислены необходимые кри
тические значения. Оценка критических значений возможна и при по
мощи параметрической бутстреп-процедуры, см., например,
{2008)],
[Wu, Chen
где изучается сходимость паритета покупательной способности
с обменными курсами, привязанными к немецкой марке, при помощи
пороговой векторной модели коррекции остатками. Отметим, что в ра
боте [Вес
et al. {2004)]
рассматриваются как
sup-Wald,
так и
sup-LM
тестовые статистики, но основное внимание в этой работе уделяется
supLR-тecтaм, поскольку LR-тест известен как более надежный, чем
LM-
и Wаld-тесты (см.
[Dufour {1997)]).
Более того, они показали, что
мощность этих тестов значительно больше, чем РДФ-тест против ши
рокого класса стационарных пороговых альтернатив.
В работе
[Seo {2006)]
представлен тест, при помощи которого прове
ряется нулевая гипотеза об отсутствии коинтеграции Но
: Л1 =
Л2 =О
Гл.
338
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
в следующей модели:
р-1
+
Е 'jЛPt-j
j=l
+ Et,
если
+ Et,
если
+ Е 'jЛPt-j + Et,
если
р-1
Лрt=
+
Е 'jЛPt-j
j=l
р-1
fJ( 2 )
< Zt-11
j=l
которая в компактной форме представлена как (см. уравнение
(4.143)):
(4.154)
В отличие от результатов работы [Вес
et al. (2004)),
в
[Seo (2006))
предлагается использовать suр-Wаld-статистику. Авторы этой работы
аргументируют такой выбор тем, что тест Вальда является типичным
для линейных ВМКО при проверке нулевой гипотезы об отсутствии ко
интеграции, когда имеется лишь одно коинтегрирующее соотношение,
известное при справедливости альтернативной гипотезы. Кроме того,
в условиях нормальности остатков
ct
suр-Wаld-статистика асимптоти
чески эквивалентна LR-статистике (для более подробной информации
см.
[Watson (1994))). В работе [Seo (2006)) показано, что предельное
распределение sup-Wald тестовой статистики не зависит от неизвест
ных параметров. Кроме того, для распределения suр-Wаld-статистики
предложена бутстреп-аппроксимация, основанная на остатках, и пока
зано, что бутстреп дает состоятельную оценку. Указанная бутстреп
процедура состоит в следующем.
1.
При помощи последовательного метода максимального правдо
подобия, описанного выше, вычислим
(B(l), 2))'. Так что:
8<
iJ =
iJ =
2.
argmin IE(B)I и (j =
'j(iJ),j =
1, ... ,р - 1.
Тогда бутстреп-выборка генерируется из модели:
р-1
др; = :Е 'jлp;_j + е;,
j=l
где е;
-
случайная величина, распределение которой совпадает
с эмпирической функцией распределения для
чальных значений этого ряда в работе
Et.
В качестве на
[Seo (2006))
предлагается
использовать соответствующие выборочные значения.
4.5.
3.
КОИНТЕГРАЦИЯ
339
По бутстреп-выборке переоцениваются параметры и вычисляется
suр-Wаld-статистика:
Sup Wald*
= Supvec(A(Jt)*(8))'x
вее
{4.155)
х Var[vec(A (Jt)*(8))Г 1 vec(A (Jt)*(8)).
4.
Повторяются шаги
1-3
большое число раз. В работе
число повторений бутстреп-процедуры равняется
В работе
(Seo {2006))
200.
[Seo {2006)] предлагается зависимый от данных способ кон
струирования параметрического пространства е' в котором использу
lzt-11· В частности, предлагается
[-8, 8], где 8 - некоторый квантиль для lzt-11· В результате
ются квантили пороговой переменной
брать 8 =
suр-Wаld-статистика вычисляется по множеству:
{ O{l), 0< 2>
Е 8 при условии
O(l) ,;;;
0(2),
'Lт: n(zt-1~8< 1 » ~ т, 'Lт: n
»~ т } .
(zt-1>8< 2
t=2
В работе
[Seo {2006))
t=2
не изучается вопрос оптимального выбора
квантиля, а попросту берется максимум последовательности
лее того, в ней берется т
lzt-11· Бо
= 10 для того, чтобы получить осмыслен
ную оценку для зависящего от режима параметра Лi, i
=
1, 2.
При
помощи большого числа симуляций методом Монте-Карло показано,
что мощность suр-Wаld-статистики превосходит мощности
ADF-
и НW
тестовых статистик, тогда как в случае справедливости альтенативной
гипотезы о наличии коинтеграции мощность
ADF-
или НW-тестов боль
ше, чем мощность sup-Wald-тecтa. Это вполне естественно, поскольку
ADF-
или НW-тесты построены для линейн:ых альтернатив. На прак
тике может иметь смысл использование как тестов,
построенных для
линейных альтернатив, так и тестов, предлагаемых для пороговой аль
тернативы. Отклонение нулевой гипотезы одним из тестов можно ин
терпретировать как признак наличия коинтеграции (либо линейной, ли
бо пороговой).
Тестирование
линейной
коинтеграции против
коинтеграции. Если удалось определить, что
Pt
пороговой
коинтегрировано с
коинтегрирующим вектором Г, тогда следующий шаг в эмпирическом
анализе
-
это определение того, является ли динамика в коинтегриру
ющем соотношении линейной или демонстрирует пороговую нелиней-
Гл.
340
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
ность. Далее будут описаны несколько одномерных и многомерных те
стов линейности при альтернативах против пороговой нелинейности.
Первой попыткой решить эту задачу явилась работа
(1997)],
[Balke, Fomby
в которой тестировалась линейность одномерного коинтегриру
ющего остатка Zt
= ГРt-1 путем тестирования структурных сдвигов
авторегрессий для Zt, которые упорядочивают данные в соответствии
со значением пороговой переменной (в случае, если берется Zt-1) вместо
упорядочивания по времени. Переупорядочивание данных не наруша
ет динамической связи между Zt и ее лагами, но позволяет обнаружи
вать пороговую нелинейность. Это происходит в силу того, что наличие
порога в упорядоченных по времени данных переходит в структурный
сдвиг переупорядоченных данных. Используя переупорядоченные авто
регрессии для Zt, Балке и Фомби анализируют непараметрический тест
на структурные сдвиги для рекурсивных остатков, представленный в
работе
[Tsay (1989)],
и процедуры типа sup-Wald-тeтcтoв для одного
или двух структурных сдвигов. Тест, описанный в работе
[Tsay (1989)],
имеет весьма привлекательное преимущество, состоящее в том, что он
не зависит от формы пороговой нелинейности, а предельное распределе
ние, используемое в этом тесте, не зависит от неизвестных параметров.
Однако в тестах
sup-Wald
типа используется нестандартная оценка по
роговых значений, которые неидентифицируемы при справедливости
нулевой гипотезы о линейности, и поэтому оцениваются при помощи
бутстрепа. Беря в качестве нулевой гипотезы предположение о линей
ной авторегресии, можно попросту повторно смоделировать выборку
остатков этой модели для того, чтобы создать бутстреп-выборку, из
которой можно вычислить suр-Wаld-статистику. Это переупорядочива
ние повторяется несколько раз. В результате мы получаем распределе
ние suр-Wаld-статистики при справедливости нулевой гипотезы о ли
нейной авторегрессионности модели. Моделирования методом Монте
Карло, реализованные в работе
[Balke, Fomby (1997)],
обнаруживают,
что тест Тсея и sup-Wald-тecт для одного структурного сдвига имеет
примерно одну и ту же мощность против асимметричной трехрежим
ной интервальной пороговой авторегрессии и равновесной пороговой
авторегрессии
(EQ-TAR).
А sup-Wald-тecт для двух струткурных сдви
гов имеет наибольшую мощность, несмотря на то, что результаты этого
теста зависят от размера выборки.
В работах /Напsеп {1997, 1999}] опис·ывается метод тестирова
ния нулевой гипотезы линейной ПАР-модели (или ПАР(1)) против
альтернативной ПАР(т)-моде.л.и (где т обозначает -число режимов).
Он основан на вложенном тестировании гипотез. В рамках рассмат
риваемых нами проблем мы можем применить эту процедуру, рассмат
ривая ПАР(m)-модель для
Zt
=
Г'Рt· Например, если мы рассмат-
4.5.
КОИНТЕГРАЦИЯ
341
риваем общую ВМКО-модель, определяемую соотношением
(4.149) с
р = О, то легко показать, что коинтеграционное слагаемое Г'Рt имеет
следующее специфицированное некоторым образом
AP(l)-
или ПАР-
представление:
где
n(Jt) _ Г' ..,(Jt)
•tt
-
,_t
.
Линейная пороговая авторегрессионная модель, или ПАР(l)-модель,
получается при ограничениях: tS(Jt) = б и p(Jt) = р, \;/ Jt. Тест Хансена
на линейность позволяет проверить нулевую гипотезу об адекватности
ПАР(l)-модели против альтернативы об адекватности ПАР(m)-модели
m > 1. Тестирование осуществляется с использованием
теста suр-F-типа (sup-Wald), статистика которого принимает вид:
при некотором
(4.156)
где через
81
и
Sm
обозначены суммы квадратов остатков, полученных в
результате оценивания ПАР(l)- и ПАР(m)-моделей соответственно. Эта
тестовая статистика совпадает со статистикой отношения правдоподо
бия в условиях, когда ошибки независимы и нормально распределены,
а также эквивалентна статистике F-теста (или теста Вальда) и ста
тистике множителей Лагранжа. Асимптотические распределения этих
suр-F-тестов зависят от неидентифицируемых (при справедливости ну
левой гипотезы о линейности) пороговых параметров. А это означает,
что для оценки этих распределений должна быть использована техни
ка имитационного моделирования. Хансен показал, что в различных
линейных тестах для вычисления р-значений может быть использова
на простая бутстреп-процедура. При справедливости нулевой гипотезы
доля смоделированных значений, превышающих наблюдаемое значение
F1m-статистики, дает асимптотическое р-значение sup-F-тecтa. В рабо
те
[Hansen (1999)]
также предлагается бутстреп-процедура для случая
гетероскедастичных остатков, которая строится на основании вспомога
тельной регрессии МЯК-остатков на квадраты лагированных значений
регрессоров. Адаптируя подход Хансена к нашему случаю, мы получим:
ul_
Таким образом, мы получим оценку
1 = zl_ 1 ~, а значит, масшта
бированные остатки равны f/t = f/t/Ut-1· При заданных начальных зна
чениях [z0, z~ 1 ] положим и;:. 1 = max(z;:. 1 ~, О). Кроме того, пусть {11;}независимые реализации случайных величин из эмпирической функции
ГЛ.
342
распределения
4.
{ -
1Jt } .
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
l'f"I
.1.огда положим:
А*
1Jt
=
*
*
ut-l 1Jt и
Zt* =
А
~
и
* + 1Jt .
+ pzt-l
А
А*
Эта рекурсия позволяет создать смоделированный временной ряд
{z;}
с заданными значениями условного среднего и условной дисперсии. Ис
пользуя эту выборку, мы можем вычислить тестовую статистику
Fim.
Кроме того, повторяя эту процедуру большое число раз, можно найти
бутстреп-распределение.
В работе
[Lo, Zivot {2001)) отме'Ч.ается, 'Что метод Хансена для
тестирования линейности в одномернъtх ПАР-моделях, основаннъtй
на тестах вложенн'Ьtх гипотез, может б'Ьtтъ легко обобщен на слу
'Чай тестирования линейности в многомернъtХ ПВМКО. Тестирова
ние линейности предполагает проверку нулевой гипотезы о линейно
сти ВМКО- против альтернативной ПВМКО(m)-модели для некоторо
гот>
1.
Наиболее удобная тестовая статистика для этого
-
suр-LR
статистика, которая эквивалентна suр-Wаld-статистике:
LR1m =
Т [1n(IEI) - ln{IE(O(l), 0< 2), d)I)] ,
(4.157)
где Е и Е{ O(l), О( 2 ), d) обозначают оценки ковариационных матриц для
остатков линейной ВМКО и m-режимной ПВМКО соответственно, а
O(l), 2 ) - оцененные пороговые значения,
оценка параметра за
d-
8<
паздывания. В соответствии с результатами работы
[Hansen {1997)]
рас
пределение suр-LR-статистики принимает нестандартный вид, поэтому
часто р-значения различных линейных тестов, основанных на
LR1m-
статистиках, рассчитываются при помощи бутстреп-процедур (в част
ности, в работе
[Lo, Zivot {2001))
используется бутстреп-процедура Хан
сена).
В работе
[Lo, Zivot {2001)]
на примерах смоделированных данных
представлен сравнительный анализ различных тестов на линейность,
из которого следует, что эти тесты имеют большую мощность для спе
цификации в виде равновесной ПВМКО-модели (Р-ПВМКО), чем для
спецификации интервальной ПВМКО. Кроме того, для последней спе
цификации все тесты имеют меньшую (в сравнении с Р-ПВМКО) мощ
ность в условиях малых выборок, и эта мощность убывает вместе с
величиной порогов. Несколько удивительным результатом этой работы
является то, что одномерные тесты, в основном, имеют большую мощ
ность, чем многомерные тесты даже в условиях больших выборок. Воз
можно, такой эффект может быть объяснен природой генерирующего
данные процесса, рассмотренного в работе. Отметим также, что одно
мерная F1m-статистика имеет немного большую мощность, чем одно
мерная статистика Тсея, тогда как многомерная LR1m-статистика име
ет большую мощность, чем многомерная статистика Тсея, предложен
ная в
[Tsay {1998)].
4.5.
В работе [Напsеп,
КОИНТЕГРАЦИЯ
Seo {2002)]
343
представлен Sир-LМ-тест приме
нительно к двумерной ПВМКО с известнъtм коинтегрирующим век
тором и единствеНН'Ьl,М порогом, в которой пороговые эффекты снова
определяются
корректирующим
остатки
слагаемым
вида
Г'Pt-d·
В частности, в этой работе авторы на первом шаге применили рас
ширенный тест Дики- Фуллера, а затем использовали Suр-LМ-тесты,
полученные авторами для двухрежимной ПВМКО. Предложенным в
этой работе Suр-LМ-тестам на линейную коинтеграцию против порого
вой коинтеграции отвечают две гетероскедастичные состоятельные LМ
тестовые статистки (основанные на оценках Эйкера- Уайта для кова
риационных матриц). Первая из двух упомянутых тестовых статистик
должна быть использована в ситуации, когда коинтегрирующий вектор
известен априори. Обозначим эту статистику через:
SupLM0 =
LM {Го, О) ,
Sup
{4.158)
()L~()~()U
где Го
-
известный коинтегрирующий вектор. Вторая тестовая стати
стика может быть использована в ситуации, когда коинтегрирующий
вектор неизвестен. Обозначим эту тестовую статистику как
Sup LM =
Sup
LM
()L~()~()U
где Г
-
(r,o)'
оценка Г в предположении справедливости нулевой гипотезы
о наличии линейной коинтеграции (при альтернативе пороговой коин
теграции). В обоих тестах
такую, что (}L -
[OL, Ou]
это ?Го-квантиль
представляет собой область поиска,
- это {1 - 1Го)-квантиль.
В работе [Andrews {1993)] брались ?Го между 0,05 и 0,15. Для вычис
Zt-1,
а Ои
ления асимптотических критических значений и р-значений распреде
ления
Sup-LM* -статистик
использовались бутстреп-процедуры с
3000
смоделированных выборок: для каждой смоделированной выборки вы
числяется
Sup-LM* -статистика,
после чего строится бутстреп-оценка
функции распределения этой статистики.
Наконец, в работе
[Goпzalo, Pitarakis {2006)]
для тестирования
линейности против пороговой нелинейности в долгосро-чной матрице
вли.яни.я ВМКО предлагаете.я исполъзоватъ тест sир- Wаld-типа. Этот
анализ не предполагает каких-либо специфических коинтеграционных
свойств системы и справедлив безотносительно тому, является ли систе
ма коинтегрированной или не является. Более того, вместо того, чтобы
брать слагаемое, корректирующее остатки в качестве значения, опре
деляющего пороговые эффекты, авторы предложили брать внешнюю
пороговую переменную, которая может быть как экономической, так и
финансовой переменной. Такая переменная должна быть стационарной
Гл.
344
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
и эргодической (например, этой переменной может быть скорость роста
ВВП). Авторы работы
временные ряды
рекции
Pt,
остатками,
[Gonzalo, Pitarakis (2006)]
рассмотрели k-мерные
генерируемые при помощи следующей модели кор
которая
позволяет
учитывать
наличие
пороговых
эффектов в долгосрочной матрице влияния:
р-1
Лрt =
Q
+ П1Pt-1I(qt-d :::;; 81) + П2Pt-1I(qt-d > 81) + Е ';ЛPt-j + Et.
j=l
Эта спецификация совпадает со спецификацией, рассмотренной в
[Seo (2006)], за исключением того, что в спецификации [Gonzalo, Pitrakis
(2006)] не делается никаких предположений относительно ранговой
структуры П1 или П2, а пороговая переменная необязательно явля
ется qt
= Г'Рt· При отсутствии пороговых эффектов, определяемых
qt, мы получим стандартную линейную ВМКО с
пороговой переменной
П1
=
П2, и это ограничение может быть протестировано против аль
: П1 =/: П2 при помощи тестовой статистики Wаld-типа.
[Gonzalo, Pitarakis (2006)] показано, что sup-Wald тестовая ста
тернативы Н1
В работе
тистика имеет предельное распределение, которое эквивалентно распре
делению нормированного квадрата броуновского моста, совпадающего
с тестовой статистикой на наличие структурных сдвигов из
[Andrews
Авторы отмечают, что при известном 8 эта тестовая статистика
имеет предельное х 2 -распределение с k 2 степенями свободы. Следует
(1993)].
отметить, что предельное распределение этой статистики не зависит
от
неизвестных параметров
и
полностью
определяется
числом
тести
руемых параметров. Это предельное распределение затабулировано в
работе [Andrews (1993)]. Более широкое множество р-значений соответ
ствующих предельных распределений см. в работе [Hansen (1997)].
4.5.8.
Спецификация модели
Если нулевая гипотеза об отсутствии коинтеграции и линейности от
клоняется, то следующий шаг состоит в том, чтобы подобрать к дан
ным наиболее подходящую пороговую модель. Первый предложенный
для этого подход был представлен в работах
Krolzig (1998)]
и
[Tsay (1998)].
[Tong (1990)], [Clements,
Основная идея этого подхода состоит
в том, что для определения наилучшей спецификации модели данных
следует использовать такие критерии въtбора модели, как, например,
информационный критерий Акаике
(AIC).
Второй подход был предложен в работах
[Hansen (1999)], [Lo, Zivot
(2001)], где использовалась последовате.л:ьная процедура тестирования,
основанная на так наз'Ьtваем'Ьtх вложенн'Ьtх моделях. Например, сим-
4.5.
КОИНТЕГРАЦИЯ
345
метричные интервальные ПАР-модели для Zt вложены в ПАР{З)-моде
ли без ограничений, а симметричные интервальные ПВМКО для
Pt
вложены в ПВМКО{З) без ограничений. Следуя этому подходу, вна
чале необходимо определить число режимов. При условии, что пред
положение о линейности коинтеграционного соотношения отклоняется
в пользу пороговой нелинейности, мы можем определить, является ли
ПАР{З)-модель адекватной для Zt при помощи тестирования нулевой
гипотезы об адекватности данным ПАР{2)-модели против альтернатив
ной ПАР{З)-модели, в котором используется следующая F-статистика,
где через В2 и Вз обозначены суммы квадратов остатков, полученных
в результате оценки ПАР{2)-модели без ограничений и ПАР{З)-модели
без ограничений соответственно. В общем случае мы можем тестиро
вать нулевую гипотезу об ПАР{m
-
j)-модели против альтернативной
ПАР(m)-модели с использованием следующей F-статистики:
z;r
.
=
.гт3 ,т
Т (Вт-jВт- Вт) , 1 ~ j
~
m - 1.
Аналогично для определения того, является ли ПВМКО{З) адекватной
моделью
для
Pt,
можно
протестировать
нулевую
гипотезу
о
ПВМКО{2) против альтернативной ПВМКО{З), пользуясь LR-статистикой
где Е2 и Ез обозначают оценки ковариационных матриц, полученных
из ПВМК0{2) и ПВМКО{З) соответсвенно. В более общем случае мы
будем использовать следующую статистику:
Как мы видели в случае ранее описанных тестов на линейность, асимп
тотические распределения статистик Fт-j,т и LRm-j,т являются не
стандартными, поэтому для вычисления р-значений могут использо
ваться бутстреп-методы.
Что касается статистических выводов относительно оценок пара
метров модели, в работе
[Chan {1993)]
показано, что оценки порогов
для (устойчивых) ПАР-моделей без ограничений являются суперсосто
ятельными (т. е. сходятся к своим фактическим значениям со скоростью
т- 1 ), а оценки всех остальных параметров являются независимыми от
Гл.
346
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
оценок порогов и асимптотически нормальными со стандартными фор
мулами для ковариационных матриц. В работе
[Tsay {1998)]
даются
аналогичные результаты для параметров устойчивых или коинтегри
рованных пороговых векторных авторегрессионных моделей. Таким об
разом, суперсостоятельность оценок порогов позволяет рассматривать
эти оценки в качестве фактических значений при статистических вы
водах относительно остальных параметров. Следовательно, статисти
ка теста Ба.льда на ограничения параметров, исключая пороги, мо
гут быть вычислены обычным образом, а полученная статистика будет
иметь асимптотическое хи-квадрат распределение. LR-тестовые стати
стики могут быть тоже вычислены, но для этого потребуется оценка
пороговых моделей с ограничениями. Получение статистических выво
дов относительно порогов весьма проблематично, поскольку предельное
распределение порогов для модели без ограничений является нестан
дартным и в общем случае зависит от неизвестных параметров и ис
ходных данных, см., например,
В недавней работе
[Seo {2009)]
[Hansen {1997)], [Hansen, Seo {2002)].
показана состоятельность МНК-оценки
для коинтеграционного вектора нелинейной ВМКО, имеющей завися
щую от режима краткосрочную динамику. Кроме того, представле
ны некоторые асимптотические результаты для пороговых коинтегра
ций, которые устанавливают скорости сходимости и асимптотические
распределения МНК- и сглаженных МНК-оценок параметров модели.
В частности, в этой работе показано, что скорость сходимости для
МНК-оценки коинтеграционного параметра 'У равна п- 3 / 2 и п- 1 для
порогового параметра O(l). Помимо этого в работе на смоделированных
данных показано, что точность статистических выводов относительно
порогового параметра может быть улучшена при использовании 2МНК
оценки. Несмотря на то что авторы работы рассматривали лишь модели
с двумя режимами, эти результаты могут быть обобщены на случай мо
делей с большим числом режимов при условии, что выполнены пред
положения относительно стационарности и принципа инвариантности
(см. предположение 1 в работе
[Seo {2009)]).
Векторные модели коррекции остатками
4.5.9.
с марковскими переключениями в коэффициентах
Использование моделей с марковскими переключениями направлено на
описание неоднородных данных и
работе
[Goldfeld, Quandt {1973)]
структурных сдвигов:
например,
в
предложена регрессионная модель с
переключениями в коэффициентах, которые описываются марковской
цепью; в
[Hamilton {1989)]
предложен более общий подход к анализу
временных рядов. Нелинейные ВМКО, отклонения от равновесного со-
4.5.
КОИНТЕГРАЦИЯ
347
стояния которых описываются марковским процессом, были впервые
предложены в работе
[Jackman (1995)]
для моделирования детерми
нант, характеризующих результаты президентских выборов в США.
В работе
[Krolzig (1996, 1997)]
ВМКО с марковскими переключения
ми получена как частный случай более общей векторной авторегрес
сионной модели с марковскими переключениями; в
[Hall et al. (1997)]
ВМКО с марковскими переключениями используется для анализа цен
на недвижимость в Соединенном Королевстве. Модели, подобные упо
мянутым выше, главным образом используются при исследовании биз
нес-циклов, в финансовых исследованиях: здесь в качестве примеров
следует выделить
В работе
[Krolzig, Toro (2001)], [Psaradakis et al. (2004)].
[Krolzig et al. (2002)] анализируется британский рынок труда.
С другой стороны, при анализе ценовых трансмиссий ВМКО с марков
скими переключениями применяется значительно реже, чем обычная
ВМКО, см., например,
[Briimmer et al. (2006)],
где ВМКО использует
ся при анализе вертикальных ценовых трансмиссий между стоимостью
муки и мяса на рынке Украины.
ВМКО с марковскими переключениями может быть представлена
в виде ПАР-модели с экзогенными состояниями, т. е. режимы не явля
ются функцией от анализируемого ценового ряда, а являются экзоген
ными и ненаблюдаемыми. Режимы могут определяться общими движу
щими силами торговли, ценами, иными экономическими переменными.
Например, временная неуверенность трейдеров относительно будущего
может быть вызвана предстоящими выборами или политическими по
трясениями в нестабильных странах; или, напротив, уверенность трей
деров в ближайшем будущем может быть вызвана исключительно по
зитивными или негативными ожиданиями, основанными, например, на
прогнозах цен. Таким образом, трейдеры могут столкнуться с весьма
различными условиями, как отвечающими увеличению неопределенно
сти, так и условиями, не сопоставимыми с торговлей, что, как след
ствие, сказывается на характере изменения цен.
В общем виде ВМКО с марковскими переключениями может быть
представлена аналогично представлению ПВМКО
(4.149)
как:
р-1
Лрt
= Q(Jt) - B(Jt)Г'Pt-1 +
L ,yt) ЛPt-j +
Et,
(4.159)
j=l
где число режимов обозначено через М, а номера режимов
Е
Jt = j
Е
{1,2,"., М}.
Аналогично
(4.143)
модель
(4.159)
может быть представлена в со-
кращенном виде:
(4.160)
Гл.
348
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
где A{Jt) - матрица коэффициентов, а регрессоры из (4.159) представ
лены в матричном виде: Xt-1 = (1 Г'Рt-1 ЛРt-1 · .. ЛРt-р+1)'. Каждая
переменная, зависящая от режима, принимает значения в зависимости
от значения в момент времени
t индикаторной переменной Jt. Напри
мер,
если
если
М режимов ВМКО с марковскими переключениями
(4.159)
представля
ют собой вероятностный процесс с М состояниями, которые являются
реализацией латентной дискретной марковской цепи с М состояниями.
Зависящие от режима значения параметров являются постоянными при
заданном режиме, но могут не совпадать для разных режимов. Таким
образом, именно марковская цепь отвечает за переключение режимов.
Ключевым элементом модели является (М х М)-матрица переходов
П, которая состоит из вероятностей 1Гhj переходов из состояния
состояние
h
в
j:
1Г1М
1Г2М
П=
1ГМ1
где 1Гhj
=
P(lt+l
=
jlJt
=
1ГМ2
1ГММ
h). Марковская цепь предполагается од
нородной, т. е. вероятности переходов предполагаются не зависящими
от времени. Однако можно предположить, что вероятности переходов
являются динамически меняющимися во времени. В качестве примера
см., например,
[Hall et al. (1997)],
где переходные вероятности представ
ляют собой функции отклонения от траектории равновесноя. Кроме то
го, следует упомянуть, например,
(2002)], [Camacho (2005)],
[Diebold et al. (1994)], [Hamilton, Raj
где представлены иные модели для динами
чески меняющихся вероятностей переходов. В настоящем разделе мы
рассмотрим наиболее простую и наиболее часто используемую ВМКО
с марковскими переключениями. Поскольку из состояния
h
возможно
переключение только в одно из М состояний, сумма элементов в лю
бой из строк матрицы П равна
1, т.е. Пlм = lм, где lм = (1, 1, ... ,
1)' - вектор-столбец размерности (М х 1), что эквивалентно: Е~ 1 1Гhj =
= 1, h = 1, ... , М. Большая вероятность на главной диагонали матрицы
П отвечает более устойчивому характеру соответствующего состояния,
что также означает в среднем наличие меньшего числа переходов из
этого состояния в другие.
4.5.
КОИНТЕГРАЦИЯ
349
Для того чтобы гарантировать некоторые желательные свойства
временных рядов и режимов, необходимо сделать несколько предпо
ложений относительно свойств марковской цепи. А именно положить,
что:
это свойство еще называют марковским свойством первого порядка. Со
держательно это свойство означает, что вероятность перехода в момент
времени
(t + 1)
в новое состояние зависит только от состояния в преды
дущий момент времени
t.
Ни более ранние состояния, ни любые другие
переменные, такие как наблюдаемые цены до момента времени
t,
не со
держат дополнительную информацию относительно переключающихся
режимов. Это предположение не является ограничительным, поскольку
любая более сложная модель может быть перепараметризирована в мо
дель первого порядка, см., например,
[MacDonald, Zucchini {1997,
глава
[Hamilton {1994, глава 22.4)] или
1.3)]. Более того, необходимо предпо
ложить, что марковская цепь является эргодической и неприводимой 24 :
первое условие необходимо для того, чтобы гарантировать стационар
ность безусловной функции распределения режимов, тогда как второе
условие необходимо для стационарности временного ряда. Необходимо,
чтобы эргодические вероятности всех состояний были больше нуля. Из
последнего предположения следует, что каждое состояние марковской
цепи может быть достигнуто из любого другого состояния, т. е. это озна
чает отсутствие поглощающего состояния.
Процедура
оценивания.
В отличие от оценки ПВМКО для
ВМКО с марковскими переключениями используется главным обра
зом лишь один метод оценивания параметров. Так же как и в случае
ПВМКО, мы имеем дело с неопределенностью на двух уровнях: первый
уровень - процесс состояний {Jt} определяет A(j) в (4.160) и должен
быть оценен, поскольку не является изначально заданным; второй уро
вень - параметры модели А (j).
Используемая ЕМ-процедура оценивания включает два шага: шаг
"Expectation"
и шаг
"Maximization".
Эти шаги итеративно повторяют
ся до тех пор, пока не будет выполнен некоторый критерий сходимо
сти. ЕМ-процедура была впервые представлена в работе
al. {1977)).
В работе
[Krolzig {1997, §5-8)]
[Dempster et
дан подробный анализ мето
да с указанием его основных преимуществ (вычислительная простота и
скорость сходимости), кроме того, рассматриваются различные обобще
ния. Ниже мы коротко опишем основные шаги этого алгоритма, что же
24 0жидаемые
безусловные вероятности нахождения в любом из М состояний в
произвольный момент времени называют эргодическими вероятностями марковской
цепи.
Гл.
350
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
касается более детального описания, мы отсылаем читателя к работе
[Krolzig (1997)].
Приступая к шагу
"Expectation"
(«Математическое ожидание») ал
горитма, необходимо инициализировать начальные значения парамет
ров модели, переходной матрицы и вероятности режимов в момент вре
мени
t = 1. На шаге «Математического ожидания» осуществляется
статистическая оценка ненаблюдаемых режимов. Сначала наблюдения
фильтруются при помощи так называемой фильтрации Баума- Линдг
рена- Гамильтона- Кима (более детальное описание см. в
(1997)], §5).
[Krolzig
В результате мы получаем филътрован:н:ы,е вероятности,
т. е. условные вероятности того, что наблюдение в момент времени
t
сгенерировано под влиянием одного из М режимов при условии нали
чия наблюдений до момента времени
t,
а также при заданных значе
ниях параметров модели, которые на первой итерации принимают ини
циализированные значения. После этого на основании фильтрованных
вероятностей и с использованием обратной рекурсии рассчитываются
сглаженн'Ьl.е вероятности по полной выборке. Они представляют со
бой условную вероятность того, что в момент времени
t мы имеем один
из М режимов при условии наличия полной выборки. Или, что эк
вивалентно, они могут интерпретироваться как вероятности того,
наблюдение в момент времени
t
генерируется в режиме
j
что
при условии
наличии полной выборки.
На шаге
"Maximization"
вычисляются оценки максимального прав
доподобия для всех параметров модели, что включает переходные ве
t = 1
роятности, вероятности режимов в момент времени
и парамет
ры соответствующих векторных моделей коррекции остатками. Оцен
ки переходных вероятностей 1Гhj равны отношению суммы вероятно
стей переходов из режима
режима
h
h
в режим
j
и вероятности возникновения
за весь временной период, охватываемый рассматриваемой
выборкой. И числитель, и знаменатель последнего отношения рассчи
тывается с использованием сглаженных вероятностей, рассчитываемых
на шаге
"Expectation".
Зависящие от режима параметры векторной мо
дели коррекции остатками А (j) оцениваются при помощи обобщенного
метода наименьших квадратов, в котором наблюдения взвешиваются
по значениям их сглаженных вероятностей. На шаге
"Maximization"
об
новляются вероятности нахождения в каждом из М режимов в момент
времени
момент
t = 1,
которые рассчитываются как сглаженные вероятности в
t = 1. На этом первая итерация завершается.
Вторая итерация начинается с использования для реализации ша
га
"Expectation"
обновленных параметров, полученных на предыдущем
шаге. Далее, на М-шаге снова обновляются оценки параметров. Далее
шаг за шагом переходим к следующей итерации до тех пор, пока не
4.5.
КОИНТЕГРАЦИЯ
351
будет выполнен критерий сходимости.
Этот алгоритм применим для оценки более общих моделей с мар
ковскими переключениями. В частности, для ВМКОсМП в работе
zig (1996)]
[Krol-
рекомендуется двухшаговая процедура оценки, где сначала
находятся коинтеграционный вектор и остатки равновесия Zt-1 · Остат
ки равновесия используются в качестве экзогенного регрессора, в ре
зультате чего мы получаем ВАРсМП-модель. Далее, для получения оце
нок параметров модели применяется описанный выше ЕМ-алгоритм.
ВМКОсМП можно оценить с использованием пакета процедур для
ВАРсМП-модели (см.
[Krolzig (2004)]), написанных на языке програм
мирования Ох (см. [Doornik (2002)]) и которые могут быть загружены с
http: / /wТN. krolzig. со . uk/, где, кроме того, можно найти множество
данных и примеров.
Дальнейшие комментарии. В случае ВМКОсМП описание ре
жимов имеет вероятностную природу и исследователь не может одно
значно заключить, какой режим возникает в некоторый момент вре
мени
t.
Несмотря на то что в работе
[Hamilton, Raj (2002)]
отмечает
ся растущий консенсус среди экономистов относительно большей це
лесообразности моделирования изменений режимов при помощи таких
вероятностных процессов, как марковский процесс, тем не менее, ин
терпретация режимов далеко не очевидна априори,
и она значитель
но менее тривиальна, чем в случае ПВМКО. И задачей исследовате
ля является придание смысла идентифицированным режимам. Режи
мы должны быть тщательно проанализированы и сопоставлены. Более
того, перед проведением эконометрического анализа иногда представ
ляется необходимым гипотетическое введение числа режимов, времени
пребывания в них или иных потенциальных детерминант. Тщательно
анализируя события политической и экономической среды во времен
ной период, охватываемый выборкой, можно дать некоторую оценку
причин изменения динамики рынков. Однако, как отмечается в работе
[Jackman (1995)],
следует учитывать опасность, связанную с так назы
ваемой экспост маркировкой состояний.
Подобно ВМКО, ВМКОсМП позволяет использовать не только ре
жимы, характеризуемые разными скоростями коррекции остатками, но
и допускает отсутствие корректирующих остатков, см., например, рабо
ту
[Psaradakis et al. (2004)]:
в отличие от ПВМКО в ВМКОсМП режимы
не ограничены в том смысле, что режимы с преобладанием значительно
отстоящих друг от друга некоинтегрированных ценовых временных ря
дов не являются более продолжительными или допускают отклонения
от равновесной траектории. Такого рода характер модели приводит к
большим отклонениям от равновесия в отсутствие коррекции. Режим,
отвечающий большим отклонениям, может быть вызван, например, по-
352
Гл.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
литическими событиями, запретительными мерами.
Суммируя вышесказанное, ПВМКО характеризуется эндогенным
переключением
режимов,
полностью
определенным
рассматриваемы
ми переменными. Определение механизма переключения при помощи
формальной процедуры облегчает интерпретацию модели. Такое огра
ничение имеет следующие последствия: во-первых, если экзогенная ин
формация, включенная в определяющее соотношение для порогов, кор
ректна, модель позволит получить более надежные и эффективные ре
зультаты, чем те, которые можно получить с помощью общих моделей.
Однако если информация неточна, тогда результаты будут значительно
отличаться от истинных результатов более общих моделей.
ВМКОсМП является более общей моделью по сравнению с моделя
ми с упомянутым выше механизмом переключений, поскольку позво
ляет рассматривать переключения независимо от анализируемого вре
менного ряда. Более того, детерминанты, вызывающие переключения,
могут даже оставаться полностью неспецифицированными. Это явля
ется ключевым свойством моделирования режимов при помощи ла
тентных марковских последовательностей. Однако большая гибкость
модели возникает за счет менее явной интерпретируемости, и прида
ние смысла идентифицируемым режимам требует значительно больших
усилий, чем в случае предыдущей модели.
Таким образом, если анализируемые данные о ценах преимуще
ственно не подпадают под действие таких внешних воздействий, как
изменение политических, экономических или природных условий, то
можно считать, что рынки и торговые процессы были основными сила
ми, генерирующими данные. ПВМКО будет более подходящей моделью
в этом случае, поскольку она явно опирается на информацию, содер
жащуюся в ценах и других экономических переменных. Тем не менее
ПВМКО требует наличия не менее двух режимов. Однако если торгов
ля происходит в условиях доминирующего внешнего вмешательства, то
МП-ВПКО может оказаться более подходящей. Чаще всего реальность
будет лежать между этими двумя крайними случаями. В таком случае
выбор наиболее подходящей модели зависит от наличия доминирующе
го влияния.
4.5.10.
Эмпирические приложения в пакете
R:
СВПАР-модель, ПВАР-модель
и ПВМКО-модели
Процедура оценивания. Мы начнем наше рассмотрение с одномер
ной самовозбуждаемой векторной пороговой авторегрессионной модели
(СВПАР-модели) на примере данных по канадским рысям. Эти данные
4.5.
353
КОИНТЕГРАЦИЯ
включают ежегодные отчеты о численности канадских рысей, пойман
ных в районе реки Маккензи в северо-западной Канаде за период с
1821
по
1934
называемые
г. Эти временные ряды (см. рис.
lynx,
4.10},
далее сокращенно
доступны в базовой комплектации пакета
R,
а бо
лее подробная информация относительно этих временных рядов может
быть получена при помощи следующих команд:
#LYNX DATASET
str(lynx)
summary(lynx)
plot(lynx)
Мы можем использовать СВПАР(2} с порогом, заданным как в ста-
тье
[Tong (1990}],
оценивая ее при помощи пакета
tsDyn
в
R:
#SETAR
mod.setar <- setar(log10(lynx), m=2, thDelay=1, th=3.25)
mod.setar
summary(mod.setar)
1820
1840
1В.
1880
1800
1820
Time
Рис.
4.10.
Численность канадских рысей, пойманных в районе реки Маккензи в
северо-западной Канаде за период с 1821по1934 г.
последняя команда дает следующие выходные данные:
Non linear autoregressive model
SETAR model (2 regimes)
Coefficients:
Lov regime:
phi1 . о phi1 . 1 phi 1. 2
0.5908673 1.2538064 -0.4184042
High regime:
phi2.0 phi2.1 phi2.2
2.232671 1.526853 -1.238662
Тhreshold
VariaЫe: Z(t) = + (О) X(t) + (1) X(t-1)
Value: 3.25 (fixed)
Proportion of points in lov regime: 671.
Residuals:
Min 1Q Median 3Q Мах
Гл.
354
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
-0.5769141 -0.1198456 0.0034299 0.1191886 0.5173509
Fit:
residuals variance = 0.04053, AIC = -353, МАРЕ= 5.76
Coefficient(s):
Estimate Std. Error t value Pr(>ltl)
phi1.0 0.590867 0.152011 3.8870 0.0001755 ***
phi1.1 1.253806 0.071265 17.5936 < 2.2е-16 ***
phi1.2 -0.418404 0.087630 -4.7746 5.690е-06 ***
phi2.0 2.232671 0.801695 2.7849 0.0063238 **
phi2.1 1.526853 0.103082 14.8121 < 2.2е-16 ***
phi2.2 -1.238662 0.255539 -4.8473 4.219е-06 ***
Signif. codes:
О'***'
0.001 '**' 0.01 '*' 0.05 '·' 0.1 ' ' 1
Результаты оценки, записанные в виде уравнения:
Xt __ { +0.591+1.254Xt-1 - 0.418Xt-2 Zt ~ +3.250
+2.233 + 1.527Xt-1 - 1.239Xt-2 Zt > +3.250,
где
zt = Хt-1·
В качестве команды, позволяющей выбирать автоматически пара
метры SЕТАR-моделей (или СВПАР-моделей), следует использовать
selectSETAR, который выполняет перебор по всем возможным комби
нациям значений специфицированных параметров. Возможные крите
рии выбора модели: критерий Акаике (AIC). Например, если мы хотим
найти SЕТАR(2)-модель (СВПАР(2)-модель), которая минимизирует
АIС-критерий, мы должны набрать:
llynx <- log10(lynx)
selectSETAR(llynx, m=2)
thDelay th mL mН pooled.AIC
1 1 3.397996 2 2 -27.34785
2 1 3.196735 2 2 -26.62503
3 1 2.886993 2 2 -25.07846
4 о 2.556463 2 2 -23.45258
5 1 3.397996 2 1 -23.43047
6 1 2.720070 2 2 -21.25830
7 1 2.350992 1 2 -19.62207
8 1 2.350992 2 2 -19.20628
9 1 2.556463 2 2 -18.11027
10 1 2.556463 1 2 -17.51734
Если
мы
хотим
оценить
многомерную пороговую
ВАР-моде.л:ь
(ПВАР-модель) для пар процентных ставок, используемых в работе
[Hansen, Seo (2002)] (см. исходные данные
на рис. 4.11), мы должны набрать:
и результаты моделирования
#ТVAR
data(zeroyld)
dat<-zeroyld
tvar<-ТVAR(dat,
summary(tvar)
lag=2, nthresh=2, thDelay=1, trim=0.1,
plot=ТRUE)
4.5.
КОИНТЕГРАЦИЯ
355
Ниже мы показываем лишь часть выдаваемых командой результатов:
Model ТVAR vith 2 thresholds
Full sample size: 482 End sample size: 480
Nwnber of variaЬles: 2 Nwnber of estimated parameters: 30 + 2
AIC -2155.439 BIC -2021.878 SSR 164.1456
[ [1]]
Equation
Equation
Equation
Equation
Intercept
short.run -1
long.run -1
short.run 0.0150(0.0491) 1.0061(0.0990)••• 0.0386(0.0595)
long.run -0.0347(0.0836) 0.3622(0.1685)• 1.0209(0.1014)•••
short.run -2
long.run -2
short.run -0.0074(0.0969) -0.0346(0.0589)
long.run -0.2872(0.1650). -0.0920(0.1003)
[ [2]]
Equation
Equation
Equation
Equation
Intercept
short.run -1
long.run -1
short.run -0.2169(0.4479) 0.8306(0.1566)••• 0.0127(0.1005)
long.run -0.1387(0.7625) -0.0214(0.2666) 0.8490(0.1711)•••
short.run -2
long.run -2
short.run 0.1351(0.1459) 0.0494(0.1013)
long.run 0.0209(0.2483) 0.1693(0.1724)
[ [3]]
Equation
Equation
Equation
Equation
Intercept
short.run -1
long.run -1
short.run 1.5619(0.5115)•• 1.1781(0.1349)••• -0.0308(0.0657)
long.run 2.0372(0.8707)• 0.7989(0.2297)••• 0.8182(0.1118)•••
short.run -2
long.run -2
short.run -0.3468(0.1249)•• 0.0699(0.0640)
long.run -0.8563(0.2127)••• 0.0577(0.1089)
Signif. codes: О'***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Тhreshold value: 8.129 10.698
Percentage of Observations in each regime: 71.51. 16.51. 12.11.
Предыдущая оценка показывает, что для первого порога (два режи
ма) модель дает значение
вания
чение
10,698
и значение
1 для
параметра запазды
D. Учитывая это, поиск второго порога (три режима) дает зна
8,129. Начиная вычисления с этих значений, расширенный поиск
по сетке значений позволяет получить те же значения.
Используя следующую команду, реализованную в пакете
tsDyn,
toLatex( summa.ry( tvar), digits=2),
мы можем выразить предыдущие результаты в компактной матричной
форме (в скобках указаны стандартные ошибки):
Гл.
356
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
( 0.01(0.05) )
-0.03(0.08)
(Xf_ 1) +
Xl_ 1
+ -7.4е-03(0.10) -0.03(0.06)) (Xi-2)
+
1.01(0.10)
0.36(0.17)
0.04(0.06))
1.02(0.10)
-0.29(0.16)
( -0.22(0.45))
-0.14(0. 76)
( 1.56(0.51))
2.04(0.87)
+
+
о.83(0.16)
0.01(0.10))
0.85(0.17)
-0.02(0.27)
0.14(0.15)
0.02(0.25)
+
1.18(0.13)
0.80(0.23)
+
-0.35(0.12)
-0.86(0.21)
-0.09(0.10)
Xt-2
(xi-1) +
Xt-i
Xt1-2
0.05(0.10)
0.17(0.17)
Xl-2
Xf-1 +
Xl-1
Xf-2
Xl-2
-0.03(0.07)
0.82(0.11)
0.07(0.06)
0.06(0.11)
if Xf_ 1 < 8.129
{ if 8.129 < Xf_ 1 < 10.698
if Xt1_ 1 > 10.698
1hl88hold V8rl8Ьle U88CI
100
200
400
300
1lme
Ord- lllN811old verleЫe
·~ j ~-~11:гl
1
о
- :=:==:
1
100
200
"\
1
300
1
1
400
Reaull8of1118 grld .......
-----....... ... "•\.·...
--...,
Рис.
4.11.
-v-
8
1
10
'
112
ПВАР-модель, примененная к месячным котировкам 1-годичных
и 10-годичных бонов
(1952-1991)
Наконец, если мы хотим оценить ПВМКО, необходимо набрать:
#ТVЕСМ
tvecm<-ТVECM(dat, nthresh=2,lag=1, bn=20, ngridG=20, plot=FALSE,
trim=0.05, model="All")
summary(tvecm)
4.5.
КОИНТЕГРАЦИЯ
357
toLatex(tvecm)
options(shov.signif.stars=FALSE)
toLatex(summary(tvecm))
где
lag -
bn ngridG -
число лагов, включаемых в каждый из режимов,
элементов для поиска коинтегрирующих соотношений,
элементов для поиска пороговых значений,
nthresh -
число
число
число порогов.
Модель может быть оценена либо с пороговыми эффектами на все пе
ременные
("All"), либо с пороговыми эффектами на корректирующие
слагаемые "only_ECT". Для более подробной информации см. руковод
ство к пакету tsDyn. Результаты процедУры оценки в матричной форме
принимают вид:
( 0.2226(0.0970))
1.0936(0.1583)
ЕСТ_ + (0.5699(0.2001)) +
1
1.9832(0.3267)
-О.1362(0.0936)) (дхf-1)
дХl_ 1
0.2244(0.1742)
=
( дхf)
ЛХl
+ ( 0.8186(0.2845)
( -0.0018(0.0381)) ЕСТ_ + (
1
0.0218(0.0622)
+
-0.0024(0.1529)
0.0087(0.0195) )
-0.0047(0.0319)
( 0.1113(0.1092)
0.3392(0.1782)
( -0.0365(0.0589))
0.0984(0.0962)
ЕСТ_ + (
1
0.0657(0.0561))
0.2332(0.0916)
0.0455(0.0709) )
-0.0704(0.1158)
+ (-0.1077(0.1031)
0.0932(0.1682)
if ЕСТ-1 < -1.414
{ if - 1.414 < ЕСТ-1
if ЕСТ-1 > 0.643
< 0.643
=> (where
+
(ЛХt1_ 1 )
дХl_ 1
+
0.0426(0.0719) )
-0.0316(0.1173)
ЕСТ-1
[Hansen (1999)],
дХl_ 1
corresponds to our Zt-1).
Тестирование. Если необходимо реализовать F-тест
ложенный в работе
(дХf_ 1 )
(4.156),
пред
в которой для тестирования линей
ности против пороговой линейности использовалось бутстреп-распреде
ление, то мы снова можем использовать tsDyn-пaкeт. Как и в работе
[Hansen (1999)],
мы рассмотрим годовые средние размеры солнечных
пятен за период времени
1700-1988 гг. Эти данные хорошо известны
3 из [Tong (1990)]. В работе [Hansen
(1999)], следУя [Ghaddar, Tong (1981)], делается следУющее преобразо
вание данных: Nt = 2( ..jl + Nt* - 1), где Nt* обозначает исходное наблю
и представлены в Приложении
дение в t-ый год. Код для реализации используемого преобразования
представлен ниже:
#HANSEN F-TEST (1999) FOR LINEARIТY AGAINST
sun<-(sqrt(sunspot.year+1)-1)•2
#Sunsport test
#Test 1vs2 and 1vs3
ТНRESHOLD LINEARIТY
Гл.
358
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Han1<-setarTest(sun, m=11, thDelay=0:1, nboot=2, trim=0.1, test="1vs")
print (Han1)
summary(Han1)
plot(Han1)
#Test 2vs3
Han2<-setarTest(sun, m=11, thDelay=0:1, nboot=10, trim=0.1,
test="2vs3")
print(Han2)
summary(Han2)
plot(Han2)
Часть результатов представлены ниже:
Test of linearity against setar(2) and setar(3)
Test
Pval
1vs2 69.70779
О
1vs3 132.37276
О
Critical values:
0.9
0.95
0.975
0.99
1vs2 27. 40061 27. 69683 27.84494
27.9338
1vs3 52. 49458 52 . 79585 52 . 94648 53 . 03686
SSR of original series:
SSR
AR 1134.982
SETAR(2) 907.4427
SETAR(3) 768.8739
Тhreshold of original series:
th2
th1
SETAR(2) 7.423375
NA
SETAR(3) 5.321202 8.03992
Number of bootstrap replications: 2 Asymptotic bound: 5608.298
Результаты представлены на рис.
Teet
llnмr
4.12.
AR V81 thl'88hold
SEТAR
=Chl2
~~----~~--~~---~
~:·_·
..:
! ........~~-~-~--------.--=·-~·-=---...--~··-~-·~---.-·-~---=-·~-.:.. . . .
Teat llnear AR V8 2 threaholcl8
-
1
SEТAR
~:·_- ==~12
:
!--r====r====r'-'="'""Т""=-=-·-=--~--=--=---=--~--=--=--=--~--=·--=--~-:
80
о
100
120
Ftest13
Рис.
4.12.
F-тест Хансена для тестирования линейной АП-модели против
СВПАР-(SЕТАR)-модели. Солнечные пятна, 1700-1988гг.
4.5.
КОИНТЕГРАЦИЯ
359
Кроме того, мы также можем вычислить многомерные обобщения
теста Хансена, представленные в работе
ется использовать статистику
[Lo, Zivot (2001)], где предлага
Sup-LR-тecтa (4.157), вычисленную при
помощи оценки остаточной ковариационной матрицы линейной ВМКО
и М-режимной ПВМКО,
#LR test Ьу Lo and Zivot (2001)
data(zeroyld)
data<-zeroyld
test<-ТVAR_LRtest(data, lag=2,
plot=TRUE, trim=0.1, test= 11 1vs 11 )
print(test)
mТh=1,thDelay=1:2,
nboot=199,
summary(test),
где
thDelay -
время запаздывания для пороговой переменной в много
мерном случае, а mTh
-
комбинация переменных с одним и тем же лагом
для формирования переходной переменной. Последнее может опреде
лять как одно значение, так и комбинацию переменных:
#Results:
Test of linear AR against TAR(1) and TAR(2)
1vs3
1vs2
LR test:
Test 30.27935 42.97058
P-Val
о
о
Bootstrap critical values for test 1 vs 2 regimes
901.
951.
97. 501.
991.
23.7491 24.12506 24.31304 24.42583
Bootstrap critical values for test 1 vs 3 regime
901.
951.
97. 501.
991.
40. 01341 40. 07361 40 .10371 40 .12177
Мы можем протестировать процесс на наличие единичных корней
против стационарной трехрежимной СВПАР-модели при помощи
LR-тecтa
(4.153),
предложенного [Вес
Sup-
et al. (2004)]:
#ВЕС et al. (2004) ТЕSТ: ve perform the test vith the previous Lynx
dataset ...
BBCTest(lynx, m=3, test= 11 LRgrid= 11 minPerc 11 )
# ... and then vith а random valk:
RW<-cumsum(rnorm(100))
BBCTest(RW, m=3, test= 11 Wald 11 )
BBCTest(RW, m=3, test= 11 LR 11 )
BBCTest(RW, m=3, test= 11 LM 11 )
#Results:
Test of unit root against stationary setar
Test statistic:
maxLR 42.80371
Гл.
360
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
0.9
0.95
0.99
15. 772 17 .898 22.232
#Results for the random valk:
Test statistic: maxWald 7.650939
0.9 0.95
0.99
Critical values:
16.181 18.4 23. 01
Test statistic: maxLR 7.361348
Critical values:
Регрессионные модели с распределенными
4.6.
лагами
Данный параграф посвящен специальному классу линейных моделей,
связывающих между собой значения двух временных рядов. В частно-
сти,
в качестве исходных статистических данных мы располагаем на
блюдениями двух времен:н:ых рядов
х(1), х(2),
... , x(N),
y(l), у(2), ... , y(N).
(4.161)
Нашей целью является построение линейной регрессионной моде
ли, позволяющей с наименьшими (в определенном смысле) ошибка
ми восстанавливать и прогнозировать значения
Т) для
x(t - 1), ... , x(t что Т
< N).
t
~ Т
y(t)
по значениям
+ 1 (при этом предполагается,
x(t),
конечно,
Иначе говоря, мы будем рассматривать модели вида
т
y(t) =со+
2: ekx(t -
k) + б(t),
t = т + 1, т + 2, ... '
(4.162)
k=O
где б(t),
t = 1, 2, ... , N,
как и прежде, последовательность гомоске
дастичных и взаимно не коррелированных (и не коррелированных с
x(t), x(t - 1), ... , x(t - Т)) регрессионных остатков, а со, ео, (}1, ... , ет и
и3 = Dб(t) - неизвестные параметры модели. При этом, для «очень
длинных~ (теоретически-бесконе-чнъш) временных рядов
лизируемой модели
ние в правой части
(4.162)
(4.162)
(4.161)
в ана
допускается случай Т = оо, т. е. суммирова
ведется по
k от О до оо.
Подобные модели оказываются естественными (и, соответственно,
правильно специфицированными) в ситуациях, когда две переменные х
и у связаны так, что воздействие единовременного изменения одной из
них (х) на другую (у) сказывается в течение достаточно продолжитель
ного периода времени (Т), т. е. наблюдается 'JЮ.Сnределеннъtй во времени
эrИJект воздействия. В частности, такие связи возникают, в первую
очередь,
между
регистрируемыми
во
времени
входными
и
выходны
ми характеристиками процессов накопления и распределения ресурсов
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
361
(например, процессов преобразования доходов населения в его расходы)
или процессов трансформации затрат в результаты (например, процес
сов воспроизводства основных доходов). Рассмотрим эти примеры.
Пр им ер
4.9.
Зависимость общих расходов населения
его наблюдаемъtх доходов
(x(t)).
(y(t))
от
При такой интерпретации участвую
щих в модели
(4.162) переменных x(t) и y(t) коэффициенты регрессии
8k имеют прозрачный содержательный смысл, а именно: 8k - это, грубо
говоря, доля дохода, которая тратится через k лет после его приобрете
ния. Можно было бы обойтись без «грубо говоря», если бы в качестве
х( t) мы располагали бы величиной истинного (а не наблюдаемого) до
хода, полученного в году
в
среднем
несколько
В действительности же наблюдаемый доход
меньше
т
го соотношения Е
t.
8k
=1
истинного,
(при О ~
8k
поэтому вместо естественно-
< 1)
мы будем иметь обычно
k=O
Ek=o 8k > 1. Обращаем внимание читателя на тот факт, что вытекаю
щие из содержательного смысла коэффициентов
8k
ограничения на их
значения задают некоторую их априорную структуру.
П р и ме р
(y(t))
4.10.
Зависимость об3емов введеннъ~х основных фондов
от капитальных вложений
эффициентов регрессии
(x(t)).
80, 81, ... , 8т
В данном случае значения ко
показывают, какими долями ре
ализуются капитальные вложения х( т), соответственно, в году т, т
1, ... , т+Т.
+
В силу существования определенной доли «нефондообразу
ющих» капитальных вложений (которая идет на постройки временного
типа, содержание управленческого аппарата, обучение персонала в пе
риод строительства и т. п.) в данном случае мы будем иметь
т
rз =
I: 8k < 1,
k=O
где
f3
мы можем интерпретировать как долю фондообразующих капи
тальных вложений.
Прежде чем перейти к систематическому анализу подобных моде
лей, зададимся двумя вопросами.
1)
Почему модель типа
(4.162)
требует специального рассмотре
ния, а не может быть проанализирована и идентифицирована в рамках
классической линейной модели множественной регрессии (см. гл. 4 в
(Айвазян
(2010)) или модели со стохастическими предикторами, не кор
релированными с регрессионными остатками (см. п. 7.1, там же), в ко
торой роль Т + 1 объясняющих переменных играют члены временного
ряда x(t), x(t - 1), ... , x(t - Т)?
2) В чем заключается общая специфика того подкласса КЛММР,
362
ГЛ.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
который принято называть моделями с распределен:н:ыми лага.ми и ко
торому посвящен данный пункт учебника?
Формально при сделанных предположениях о природе регрессион
ных остатков д(t) в
-1), ... ,x(t -
Т)
(4.162) и о некоррелированности д(t) и x(t), x(tмодель (4.162), действительно, может быть отнесена
к КЛММР (при неслучайном характере временного ряда
x(t)) или к
линейным регрессионным моделям со стохастическим предикторами,
не коррелированными с регрессионными остатками. И в том, и в дру
гом случае статистический анализ этой модели может быть произведен
с помощью обычного метода наименьших квадратов (МНК). Однако
при практи-ческой реализации этого метода в данном случае возника
ют принципиальные трудности. Так, величина Т, определяющая число
включенных в модель объясняющих переменных, как правило, отно
сится к неизвестнъtм параметрам модели. Чтобы определить значение
Т, приходится, выбрав вначале его достаточно большим, исследовать
статистическую значимость получающихся при этом оценок коэффици
ентов регрессии
8k
для различных значений
k.
Но здесь нас подстерега
ют две серьезные (взаимосвязанные) ~неприятности»: высокая корре
ляция между объясняющими переменными (и, следовательно, высокая
степень мультиколлинеарности) и слабая статистическая достоверность
наших выводов, недостаточная их точность (из-за низких значений от
ношения числа имеющихся в нашем распоряжении наблюдений к числу
оцениваемых параметров модели). Именно эти обстоятельства стимули
руют поиск некоторых специальных подходов к анализу моделей типа
(4.162).
Что касается второго вопроса, то ответ на него как раз и подска
зывает направление этого поиска. Общая специфика моделей
(4.162)
заключается в том, что из их содержательной сущности, как прави
ло, вытекают определенные априорные сведения о значениях и взаимо
связях, существующих между весовыми коэффициентами
80, 81, ... , 8т,
или, иначе говоря, об их структуре. Так, в некоторых ситуациях коэф
фициенты 8k экспоненциально убывают по мере роста k, т. е. 8k = с8~,
где О<
80 < 1,
а это значит, что вместо Т
нам придется оценивать всего два: с и
+ 1 неизвестных параметров
80 !
Таким образом, главная идея, на которой базируется общий
подход к анализу и построению моделей вида
(4.162), может быть
сформулирована следующим образом:
•
отправляясь от содержательной сущности моделируемwх зави
симостей и смwсла весовwх коэффициентов
8k (k
=
О,
1, 2, ... ),
определить их структурнwе связи с помощью введения неболь
шого -числа пара.метров а1,
... , ат (т
<< Т),
по зна-чениям кото-
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
363
р·ых можно восстановить значения всех неизвестнъtх коэффици
ентов регрессии
8k ( т.
е. речь идет об экономичной параметри-
зации последовательности
дится к оценке
Модели
(4.162),
80, 81, 82, .. .); после
параметров а1, а2, ... , От.
этого задача сво-
рассматриваемые в рамках этого общего подхода,
называются, как мы уже упоминали, регрессионными моделями с
распределенными лагами или просто моделями с распределенными
лагами. Поясним это название.
Если переменная (эндогенная или экзогенная) участвует в записи
анализируемой модели, будучи измеренной в один из прошлuх (по отно
шению к текущему моменту времени
t)
временн:Ь1х тактов
t- k (k
>О),
то эту переменную называют лаговой или запаздъtвающей, а число еди
ниц времени запаздывания
эти лаги
k
в модели
ным с весами
8k,
(k) - лагом (запаздывание.м). А поскольку
(4.162) распределен'Ьt по объясняющим перемен
то естественно называть такие модели моделями с
распределеннuми лагами (ниже мы увидим, что при некоторых спо
собах параметризации весов
8k
их пронормированные значения могут
интепретироваться как эле.ментu закона распределения вероятностей,
что снова подтверждает правомерность использования слова «распре
деленнъtе» в названии соответствующих моделей). Последовательность
весовых коэффициентов
80, 81, ...
называют структурой лага (конеч
ной или бесконечной в зависимости от конечности или бесконечности
их числа Т). Если все
8j ~ О (j
=
О,
коэффициентов wo, w1, w2, .. ., где Wj
1, 2, ... ),
=
то последовательность
т
8j/ Е 8j, называют нормиро
j=О
т
ванной структурой лага модели
(4.162) (очевидно, Е Wj = 1).
j=O
Нормированная структура лага как распределение вероятностей. Можно воспользоваться формальным сходством нормирован
ной структуры лага и закона распределения вероятностей дискретной
случайной величины. Для этого введем случайную величину т («время
задержки») с законом распределения вероятностей
k=0,1,2, ... ,T,
(4.163)
где Т может принимать и бесконечные значения.
Подобная интерпретация нормированной структуры лага открыва
ет широкие возможности в построении экономичной параметризации
последовательности весов
Wk
с помощью различных широко известных
моделей законов распределения для дискретных случайных величин
(см., например, п.
3.1.1-3.1.3 в [Айвазян, Мхитарян (2001)]). Кстати, ин
терпретация весов Wk как вероятностей в ряде ситуаций оказывается
ГЛ.
364
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
вполне оправданной. Так, в примере
4.9
случайная величина тв
(4.163)
интерпретируется как число тактов времени, прошедших с момента по
лучения дохода до момента расходования одной случайно выбранной
из него единицы. Тогда вероятность Р{т
= k} = Wk
определится, оче
видно, отношением
такте времени,
Yt,k/Xt, где Xt - истинн-ьtй доход, полученный в t-м
а Yt,k - та его часть, которая израсходована в (t + k )-м
такте времени. Точно так же вероятностная интепретация механизма
зависимости
(4.162) в примере 4.10 может быть сформулирована сле
дующим образом: некоторая случайным образом выбранная единица
фондообразующих капитальных вложений будет освоена на объекте в
том же году с вероятностью
wo,
в следующем году
-
с вероятностью
т
w1,
через два года
- с вероятностью
w2 и т.д. (здесь
Wk
= 8k/ Е 8k)·
k=1
При такой интерпретации вполне определенный смысл приобретают и
основные характеристики вероятностных распределений. Так, среднее
значение Ет в примере
4.10 будет задавать
средний срок реализуемости
фондообразующих капитальных вложений, дисперсия Dт будет харак
теризовать точность в определении среднего срока с помощью Ет и т. д.
Итак, из описанного выше следует, что одна типовая модель рас
пределенных лагов отличается от другой способом параметризации ве
совых коэффициентов
80, 81, .. .,
т. е. способом параметризации своей
лаговой структуръt. Опишем несколько наиболее распространенных в
практике эконометрического моделирования способов параметризации
лаговых структур.
Полиномиальная лаrовая структура Ширли Алмон (см.
Аlтоп
S. The Distributed Lag between Capital Appropriations and Expenditures // Econometrica. Vol. 30 (1965). Р.178-196). Мы рассмотрим здесь
простейший вариант этой модели.
Подход основан на полиномиальной форме параметризации коне-ч
ной лаговой структуры
80, 81, ... , 8т.
А именно, опираясь на теорему
Вейерштрасса (которая утверждает, что непрерывная на замкнутом ин
тервале функция может быть приближена на всем отрезке многочленом
подходящей степени от ее аргумента, отличающимся от этой функции
в любой точке меньше, чем на любое заданное число) и рассматривая
весовые коэффициенты
8k
как функции
k,
их в виде полиномов невысокой степени m
автор предложила выразить
(m
k=
где аю, а1,
... , ат -
~
3)
о,
от
k,
т. е.
1, 2, ... ' т,
(4.164)
некоторые неизвестные параметры, которые опре
деляются из условия наиболее точной (в определенном смысле) подгон
ки модели
(4.162).
Подставляя последовательно в
(4.164) k =О, 1, 2, ... , Т, получаем:
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
365
Во= оо,
В1
оо
В2
=
=
оо
+ 01 + ... + От,
+ 201+ ... +2тот,
Вт
=
оо
+
То1
+ ... +
(4.164')
ттот.
Возвращаемся к анализируемой модели
(4.162), заменяя
эффициенты Bk их выражениями по формулам (4.164'):
в ней ко
т
y(t) =со+
:L: вkx(t -
k) + 8(t) =со
k=O
+ oox(t)
(4.165)
+ oox(t - 1) + 01x(t - 1) + ... + отх(t - 1)
+ oox(t - 2) + 201x(t - 2) + ... + 2тотх(t - 2)
+ oox(t -Т) +
То1х(tт)
+ ... +
ттотх(t -Т)
Суммируя со и остальные слагаемые правой части
+ 8(t).
(4.165)
по столбцам,
получаем:
y(t) =со+ оо [x(t) + x(t - 1) + ... + x(t - Т)]
+ 01 [x(t - 1) + 2x(t - 2) + ... + Tx(t - Т)]
(4.165')
+От [x(t - 1) + 2тх(t - 2) + ... + тmx(t -Т)]
+ 8(t).
Обозначая первую квадратную скобку в правой части (4.165') как
X(l)(t'), вторую- как x( 2)(t'), ... , (m+l)-ю- как X(т+l)(t'), где «НОВОе~
время t' «привязано~ к моменту времени t-T (т. е. t' = t-T), получаем:
y(t' + Т) =со+ oox< 1>(t1) + 01x< 2>(t') + ... + отх<т+ 1 >(t 1 ) + 8(t' + Т),
(4.165")
Т.
t' = 1, 2, ... , N -
В результате мы свели задачу оценивания Т
вых коэффициентов со, Во, В1,
... , Вт
+2
неизвестных весо
к статистическому анализу стан
дартной линейной модели множественной регрессии всего с т
(т ~
3)
+1
неизвестнъши параметрами (при этом предполагается, конеч
но, что длина исходных временных рядов
Так что оценки Со и
O-j
N
параметров со и Oj
много больше, чем Т + т).
(j = 1, 2, ... , т)
получаются
ГЛ.
366
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
с помощью обычного МНК, после чего по формулам
ются оценки
(k =О, 1, ... , Т).
Bk
(4.164') вычисля
Заметим, что мы полагали в данной схеме максимальную величи
ну лага Т известной. В действительности она, как правило, опреде
ляется статистически. Обычно проводят описанные выше расчеты для
нескольких предположительных значений Т и окончательный выбор
между ними производят на основании диагностики полученных моде
лей, т. е. путем сравнения различных характеристик их точности.
Геометрическая лаговая структура Койка (см.:
Koyck L.M.
Distributed Lags and Investment Analysis. North - Holland PuЫishing
Company, Amsterdam, 1954). В данном подходе рассматривается бес
коне'Чная лаговая структура (т. е. в (4.162) полагается Т = оо), поэтому
он применим лишь к достаточно длинным временным рядам (4.161).
Общим (и естественным!) допущением при анализе бесконечных лаго-
вых структур является требование сходимости ряда
т
:Е
lim
~00~
влияние
8k = f3 <
x(t)
оо и, следовательно,
y(t + k)
на
lim 8k
~00
=
f3 =
оо
:Е
8k,
т. е.
k=O
О. Это означает, что
уменьшается до нуля по мере неограниченного
увеличения временного интервала
k,
что естественно, так как текущее
значение у практически не должно зависеть от поведения х в бесконеч
но да.леком прошлом. Койк в своем подходе конкретизировал и усилил
это допущение. В частности, он постулировал, что все нормированные
00
веса
Wk = 8k/
:Е
j=O
8j,
являясь положительными, убывают с ростом
k по
геометрической прогрессии, т. е.
0<Л<1
(множитель
(4.166)
(1- Л) в соотношении (4.166) нужен для того, чтобы обес
оо
печить условие нормировки :Е
Wk = 1).
k=1
Как мы сейчас увидим, это допущение приводит к огромным упро-
щениям модели
(4.162), так как вместо оценивания бесконе'Чного ряда
весовых коэффициентов 80, 81, 82, ... нам придется оценить лишь два(!)
параметра: Л и
f3 =
00
:Е
k=O
8k.
Действительно, возвращаясь к
(4.162),
имеем:
00
y(t) =со+
L
00
8kx(t - k) + д(t) =со+ f3
k=O
х x(t -
k)
+ O(t) =со+ /3(1- >.)
L(1 - Л)Лkх
k=O
(~ лk F".) x(t) + O(t),
(4.167)
4.6.
где
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
оператор сдвига назад на единицу, т. е.
F_ -
367
F_x(t) = x(t - 1).
Произведя формальные операции с операторами сдвига, получаем
y(t) = ео + ,8(1 - Л)[l + ЛF_ + Л 2 F~ + .. .]x(t) + 8(t)
x(t)
= с0 + ,8( 1 - Л) l _ ЛF_ + 8(t),
или, что то же,
ЛF_)y(t)
(1 -
= (1 -
ЛF_) ео
+ ,8(1 -
Л)х(t)
+ (1 -
ЛF_)8(t).
Применяя в соответствии с этим соотношением оператор сдвига
к ео,
y(t)
и
8(t),
F_
получаем
y(t) = (1 - Л) ео + ,8(1- Л)х(t) + Лу(t -1) + (8(t) - Лб(t- 1)). (4.167')
В результате мы получили уравнение регрессии
щим переменным
x(t)
и
y(t)
по объясняю
всего с двумя неизвестными коэффи
y(t - 1)
циентами
,8 и Л (не считая свободного члена со и дисперсии остатков
и~ = D8(t)). Однако поскольку в правой части уравнения остаточная
случайная компонента c:(t) = 8(t) - Л8(t - 1) зависит от оцениваемо
го параметра Л и, вообще говоря, коррелирована, по крайней мере, с
объясняющей переменной у( t -
1),
метод оценивания параметров
,8
и
Л нестандартен и зависит от дополнительных предположений относи
тельно природы остатков
8(t)
и (или)
c:(t).
Процедуры состоятельного оценивания параметров модели
(4.167')
при нескольких вариантах специфицирующих условий, касающихся
природы случайных остатков
8(t)
и
c:(t),
описаны, например, в [Джон
стон
(1980)], с. 303-320.
Замечание 1. Фина.11:ьньtй вид (4.167') модели Койка может
быть получен и без помощи операций с оператором сдвига F _. Для этого
выпишем исходный вид модели для двух текущих моментов времени
и
t
t-1:
00
y(t) =со+ ,8(1 - Л)
L лkx(t -
k) + 8(t),
k=O
00
y(t - 1) =со+ ,8(1 - Л)
L лkx(t -
1 - k) + 8(t - 1).
k=O
Умножив второе уравнение на Л и вычтя полученный результат из пер
вого уравнения, приходим к
(4.167').
Рассмотрим две хорошо известные динамические модели экономи
ческих процессов, сводящиеся к модели Койка, хотя их базовые апри
орные допущения прямо не формулируются в виде
(4.166).
ГЛ.
368
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Модель частичного приспособления (или- «частичной кор
ректировки» )25 • Предположим, что желаемое (или оптима.л:ьное, це
левое) значение у* (t) некоторого экономического показателя определяется уравнением
y*(t) = ёо + ёix(t)
+ 8(t),
(4.168)
где регрессионные остатки б(t) гомоскедастичны и сериально некорре
лированы, а
x(t) -
переменная, выполняющая роль объясняющей, не
коррелирована с б(t). Однако желаемое значение исследуемой результи
рующей переменной не всегда является наблюдаемьtм. Экономический
объект, характеризуемый этой переменной, может не иметь возможно
сти сразу (т. е. в то-ч.ности к моменту времени
емое значение
y*(t).
t)
«выходиты на жела
Так -что факти-ч.еское (наблюдаемое) зна-ч.ение
этого показателя будет со временем как бы «подтягиваться»
y(t)
к же
лаемому у* (t) в соответствии с правилом, формализуемым с помощью
соотношения
y(t) = y(t - 1) + -y(y*(t) - y(t - 1)) + o(t),
о~ 'У~
где остатки
(4.169)
o(t)
(4.169)
1,
гомоскедастичны и сериально некоррелированы. Из
следует, что на каждом следующем временном такте наблюдае
мое значение
y(t)
будет «подправляться» в направлении целевого зна
чения у* (t) на величину, пропорциональную разнице между оптималь
ным и текущим уровнями результирующего показателя. Соотношение
(4.162)
может быть переписано в виде
y(t) = -yy*(t) + (1 - -y)y(t - 1) + o(t),
(4.169')
откуда следует, что наблюдаемое значение исследуемой результирую
щей переменной есть (с точностью до регрессионного остатка о
(t)) взве
шенное среднее желаемого уровня (на данный момент времени) и фак
тического значения в предыдущем такте времени. Подставляя модель
ное оптимальное значение
y(t) = -уёо + -уё1х(t)
(4.168)
+ (1 -
в
(4.169'),
имеем
-y)y(t - 1) + (o(t)
Сравнивая это соотношение с
(4.167'),
+ -уб(t)).
(4.169")
мы видим, что исследуемая
зависимость относится по своему типу к геометрической структуре Кой
ка. В этом можно еще раз убедиться, «разматывая»
25 Впервые
(4.169")
в обратную
подобная схема модели была описана в работах:
1) Nerlove М. Estimates of the elasticities of supply of selected agricultural commodities
11 Journ farm econ. Vol. 38 (1956). Р. 496-509;
2) Nerlove М. The dyna.mics of supply: estimation of farmers response to price. The
Johns Hopkins Press. Baltimore, 1958.
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
369
сторону по сравнению с тем, как мы это делали при выводе финально
го соотношения структуры Койка. Действительно, выразим у( t -
руководствуясь соотношением
y(t - 1) = 'Уёо + 'Уё1х(t -1)
Подставив это выражение
1),
(4.169"):
+ (1-"f)y(t - 2) + (o(t- 1) + 'Уб(t -1)).
y(t - 1)
в
(4.169"),
получим
где
ё(t)
= [o(t) + (1 - 'Y)o(t - 1)] + 'У[б(t) + (1 -
'У)б(t - 1)].
Неограниченно продолжая подобную подстановку, т. е. последова
тельно выражая
y(t-2), y(t-3)
и т. д. по формуле
их в соответствующее выражение для
y(t),
(4.169")
и подставляя
получим в конечном счете
= ё0 +80 [x(t) + (1-"()x(t-1) + (1-"() 2x(t- 2) + ... ] +e(t),
y(t)
(4.170)
где свободный член получен в результате бесконечного суммирования
величин 'Уёо+ (1-'У)'Уёо+ (1-"() 2 'Уёо+ ... , коэффициент 80 = 'Уё1, а слу
чайные остатки е( t) получаются как бесконечные скользящие средние
исходных остатков o(t) и б(t), а именно:
00
e(t) =
L {(1 - 'Y)k [o(t -
k)
+ 'Уб(t -
k)]}.
k=O
Сравнив
(4.170)
со средним выражением в соотношении
(4.167),
убеждаемся в том, что модель частичного приспособления действитель
но относится к классу геометрических структур Койка (с точностью до
условий, специфицирующих случайные остатки).
Схема «частичного приспособления»
имеет довольно широкий
спектр экономических приложений. Упомянем о некоторых из них.
Пусть
x(t)
в соотношении
торого товара, а у* (t)
-
(4.168)
определяет уровень продаж неко
соответствующая оптимальная (с позиций рав
новесия) реакция со стороны производства (т. е. оптимальный объем
предложения этого товара). Если принимать в расчет затраты двух ти
пов
-
потери, связанные с нарушением равновесия, и затраты, связан
ные с изменениями состояния производителя,
-
оба типа потерь, составляющие суммарные потери
и если полагать, что
L,
квадратам соответствующих отклонений, т. е.
L(y(t))
= с1 (y(t) -y*(t)) 2 + c2(y(t) - y(t - 1)) 2 ,
пропорциональны
ГЛ.
370
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
то задача состоит в выборе (при задан:н:ых величинах
значения
y(t),
минимизирующего потери
L(y(t)).
y(t - 1)
и
y*(t))
Приравняем к нулю
производную
Отсюда определяем
y(t) = y(t - 1) +
С1
ci
+ С2
(y*(t) - y(t - 1)),
что в точности соответствует основному принципу
(4.169)
частичного
приспособления.
По совершенно аналогичной схеме может быть рассмотрена модель,
связывающая между собой доход
т. е. наблюдаемой
(y(t)),
x(t)
с оптимальной
(y*(t))
и реальной,
величинами потребительских расходов. Ведь
потребитель не располагает всей необходимой информацией о своем
«Пространстве потребностей», так что не может мгновенно оптима.л:ьно
среагировать в своих расходах на изменение (в б6льшую или меньшую
сторону) своего дохода. Этой мгновенной реакции препятствуют также
определенная инерционность потребительского процесса, наличие опре
деленных (пусть неформальных) обязательств, связанных с прежним
уровнем его дохода.
Наконец, модель частичного приспособления используется при кор
ректировке (в динамике) доли прибыли, выплачиваемой компанией в
виде доходов своим акционерам. При росте прибыли
x(t)
выплачивае
мые дивиденды
же пропорции
y(t) также увеличиваются, но, как правило, не в той
(}, которая определена компанией в качестве целевой
долгосрочной доли выплат. Это объясняется рядом причин, в том чис
ле осторожностью руководства компании: возрастание прибыли может
оказаться временным, поэтому если при этом сохранить долю
(},
то в
случае последующего понижения прибыли дивиденды придется сокра
щать, а это
-
серьезный удар по репутации фирмы. Как следствие,
динамика выплаты дивидендов у( t) в зависимости от текущей прибыли
x(t)
и Э1Селаемого (в долгосрочной перспективе) объема выплат диви
дендов
y*(t)
= 8x(t)
регулируется во многих случаях соотношением
(4.169).
«Узкое место»
модели частичного приспособления состоит в том,
что иногда предположение о зависимости оптимального значения у* (t)
толысо от текущего значения х( t) оказывается не адекватным дей
ствительности. Другими словами, часто решающим мотивом для при
нятия ответственных решений не может служить единственное зна
чение объясняющей переменной. Один из способов преодоления этой
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
371
ограниченности отражен в описываемой ниже модели адаптивных ожи
даний.
Модель адаптивных ожиданий. Моделирование закономерно
стей с у'Четом ожидаемъ~х ситуаций
-
одна из важнейших проблем
прикладной экономики. Это, в первую очередь, верно для макроуров
ня, на котором инвестиции, сбережения и спрос на активы оказываются
особенно чувствительными к ожиданиям относительно будущего. Если
в модели частичного приспособления в роли корректируемой величины
выступала зависимая переменная (результирующий показатель) у( t),
то в модели адаптивных ожиданий корректируется об'lJясняющая пере
менная х* (t
+ 1),
которая определяет ожидаемое на момент
экспертно формируемое в момент
t)
t
+1
(но
значение аргумента в исследуемой
зависимости вида
y(t) =Во+ B1x*(t + 1) + б(t),
(4.171)
где возмущающие воздействия б (t) гомоскедастичны и сериально некор
релированы, а также не коррелированы с наблюдаемым значением ар
гумента х( t). В соответствии с основным допущением модели механизм
формирования ожидаемого значения х* (t
+ 1)
описывается соотноше-
ни ем
x*(t + 1) = x*(t)
+ 1(x(t) -
о~ 'У~
x*(t)),
(4.172)
1,
или, что то же,
x*(t + 1) = 1x(t) + (1 - 1)x*(t).
(4.172')
Это означает, что значение объясняющей переменной, ожидаемое в
момент времени
t
+ 1,
формируется в момент времени
t
как взвешен
ное среднее ее реального и ожидаемого значений в текущий момент
времени. От значения 'У зависит скорость адаптации ожидаемых зна
чений к реальности. Мы видим, что в отличие от процесса частичного
приспособления, который базируется на инерции и прошлой динамике
показателей, процесс адаптивных ожиданий направлен в будущее. Дру
гими словами, мы формируем зна'Чение резул:ьтирующего показателя
на текущий момент времени с у'Четом будущего зна'Чени.я об'lJясн.яю
щей переменной.
Покажем, что и процесс адаптивных ожиданий вкладывается в об
щую схему моделей с распределенными лагами, имеющих геометриче
скую структуру Койка. Для этого перепишем
x*(t + 1) - (1 - 1)x*(t)
(4.172')
= 1x(t),
в виде
ГЛ.
372
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
или, что то же,
[1 - (1 - -y)F-]x*(t + 1)
где с помощью
F _,
= -yx(t),
как и прежде, обозначен оператор сдвига функции
времени на один временной такт назад. Выражая отсюда х* (t
подставляя это выражение в
(4.171),
+ 1)
и
получаем
-yx(t)
y(t) = 80 + 81 1 _ (l _ -y)F_
+ д(t).
После домножения всех членов этого выражения на
(4.173)
1 - (1 - -y)F_
и применения этого оператора к y(t), ёо и д(t) получаем
y(t) = -уёо + (1 - -y)y(t - 1) + -уё1х(t) + (д(t) - (1 - -у)д(t - 1)). (4.173')
Сравнение модели
(4.173') с финальной формой (4.167') модели
Койка свидетельствует об их эквивалентности.
Модель гиперинфляции Кагана и модель потребления Фридмана
(основанная на «гипотезе о перманентном доходе~) представляют со
бой наиболее известные примеры эконометрических приложений мо
дели адаптивных ожиданий 26 . В модели гиперинфляции исследуется
соотношение между спросом на денежные остатки и ожидаемъш из
менением уровня инфляции. В несколько упрощенном (по сравнению
с первоисточником) варианте модель может быть описана следующим
образом. Изменение спроса на денежные остатки в момент времени
t
определяется показателем
M(t)]
y(t) = ln [ P(t) ,
где
индекс изменения объема денег в обращении, а
M(t) -
P(t) -
ин
декс цен. Зависимость изменения спроса на денежные остатки в момент
t
от ожидаемого в момент
t + 1 уровня инфляции х* (t + 1)
определяется
уравнением
y(t) = -80 - 81x*(t + 1) + д(t),
80 > о, 81 > о.
Адаптивные ожидания уровня инфляции определялись формулой
(4.172).
Модель рассчитывалась по месячным данным, характеризую
щим семь инфляционных периодов в США в промежутке
26 См.:
1921-1956
гг.
Cagan Р. The Monatary Dynamics of Hyperinflation // Studies in the Quantity
Theory of Money. Chicago: University of Chicago Press, 1956;
FНedman М. А Theory of the Consumption Function. Princeton, N.J.: Princeton
University Press, 1957.
4.6.
РЕГРЕССИОННЫЕ МОДЕЛИ С РАСПРЕДЕЛЕННЫМИ ЛАГАМИ
373
(как отдельно для каждого периода, так и агрегированно по совокуп
ности всех семи периодов).
Моде.л:ь потребления Фридмана основана на двух постулатах. Один
из них выделяет эту модель среди других многочисленных моделей,
исследующих зависимость объема потребления (у) от дохода
(эта
задача также рассматривалась в п.
свя
7.2 учебника [Айвазян
(х)
(2010)) в
зи с методом инструментальных переменных, используемым в проблеме
построения регрессионной модели со стохастическими предикторами).
В соответствии с этим постулатом фактический объем потребления у( t)
и фактический уровень дохода
x(t)
складываются из перманентной (по
стоянной) и временной (случайной) составляющих, т. е.
y(t) = y*(t) + Ув(t),
x(t) = x*(t) + X 8 (t).
Предполагается, что временная составляющая потребления
y(t)
и
временная составляющая дохода х (t) являются случайными перемен
ными со средними значениями, равными нулю, и постоянными значе
ниями дисперсий и что распределены они независимо от постоянного
дохода, постоянного потребления и друг от друга.
Второй постулат не отличается от базовых допущений большинства
других аналогичных моделей и состоит в допущении, что х* (t) и у* (t)
связаны между собой классической линейной регрессионной моделью,
т.е.
y*(t) =
Оо
+ 01x*(t) + д(t).
Однако величина постоянного дохода
величина у* ( t)) в модели
(4.174)
x*(t)
(4.174)
(впрочем, так же, как и
ненаблюдаема. Эта проблема обходит
ся с помощью предположения, что изменение постоянного дохода х* (t)
подчиняется закону адаптивных ожиданий
(4.172).
Другими словами,
домашние хозяйства (индивиды) корректируют свое представление об
ожидаемом постоянном доходе по мере роста (убывания) фактическо
го дохода, но не на полное значение прироста (убывания), сознавая,
что изменения фактического дохода частично объясняются вариацией
временной его составляющей.
Возвращаясь к
(4.174) и подставляя вместо y*(t) разность y(t)-y(t), а вместо x*(t) его выражение, полученное из соотношения (4.172),
имеем
y(t)
= Оо +01 1 _
7x(t)
(l -f')F_
Сравнивая это выражение с
(4.173)
+ (д(t) +y(t)).
(4.175)
и учитывая эквивалентность
(4.173), (4.173') и (4.167'), мы видим, что модель потребления Фрид-
ГЛ.
374
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
мана также может быть отнесена к моделям распределенных лагов с
геометрической структурой.
З ам е ч ан и е
2.
И в моделях частичной корректировки, и в моде
лях адаптивных ожиданий мы сталкиваемся с проблемой оценки вели
чины 'У· Один из распространенных подходов к решению данной зада
чи
-
это использование эвристического по своей природе общего метода
перекрестного ана.л:иза дееспособности модели (в англоязычной литера
туре он известен как
« cross
validatioп тethod"»
.
Применительно к дан
ной проблеме это означает следующую последовательность действий.
Все имеющиеся в нашем распоряжении исходные статистические дан
ные
M(l, N) = {x(t), y(t); t = 1, 2, ... , N} разбиваются на две части:
«обучающую"» M(l, Ni) = {x(t), y(t);
t = 1, 2, ... , Ni (N1 < N)} и
«экзаменующую"» M(N1 +1, N) = {x(t), y(t);
t = Ni +1, Ni +2, ... , N}.
Задаются сеткой значений параметра 'У на интервале [О; 1]. Для каждого
значения 'У из этой сетки по «обучающим» данным M(l, Ni) строится
модель (4.175). Затем по «Экзаменующим» данным М (Ni + 1, N) вычис
ляется значение критерия качества полученной модели (роль такого
критерия в данной задаче обычно играет соответствующий коэффици
ент детерминации R 2 . Выбирают то значение 'У, при котором значение
критерия качества модели максимально.
Лаговые структуры, основанные на вероятностной пара
метризации Мы уже упоминали, что одним из способов экономичной
параметризации лаговых структур является их интерпретация в терми
нах вероятностных распределений (см.
(4.163)). Приведем в заключение
два примера такой параметризации: один - для бесконечной лаговой
структуры (структура Паскаля), другой - для конечной лаговой струк
туры.
Лаговая структура Ласка.ля была предложена в 1960 г. Р. Солоу 27 .
Она основана на так называемом отрицательном биномиальном рас
пределении (см. п. 3.1.1 в [Айвазян, Мхитарян
(2001)]),
т. е. элементы Wk
нормированной бесконечной лаговой структуры Паскаля
определяются в соответствии с
(4.156)
(k
=О,
1, 2, ... )
с помощью соотношений
k =о, 1,2, ... '
где р (О
<
р
< 1)
и М (М
- любое целое положительное число)
два параметра, определяющие (наряду с
f3
00
= Е (Jk) конкретную лаго
k=О
вую структуру в данном параметрическом семействе. Отметим, что из
свойств отрицательного биномиального распределения следует:
27 См.:
Р.
Solow R. М. On а family of lag distributions // Econometrica. Vol. 28 (1960).
393-406.
Выводы
375
элементы Wk нормированной лаговой структуры при М
(i)
возрастают (при
k
(ii)
> (рМ - 1)/(1 -
k <
(рМ
- 1)/(1 -
> 1 сначала
р)), а затем убывают (при
р));
среднее значение лага (Ет) и его дисперсия (Dт) являются воз
растающими функциями как М, так и р, а именно:
рМ
Ет=--;
1-р
рМ
Dт = (l -p)2·
Лаговая структура, основанная на биномиальном законе распреде
ления вероятностей, является естественным аналогом структуры Пас
каля в классе коне-чнъtх моделей с распределенными лагами. Ее норми
рованные элементы Wk задаются с помощью соотношений
k = 0,1, ... ,т.
(4.176)
Мы видим, что данный класс конечных лаговых структур описывает
ся однопараметрическим семейством (параметр р
между О и
1).
-
некоторое число
Из свойств биномиального распределения следует, что
последовательность
(4.176)
образует так же, как и в структуре Паска
ля, унимодальнъ~й ряд, причем Ет = рТ и Dт = р(1
- р)Т.
Описанные вероятностные лаговые структуры применимы в ситу
ациях, когда из содержательного смысла анализируемых зависимостей
вида
(4.162) следует, что весовые коэффициенты
(}k (а значит, и wk)
начинают монотонно убывать не сразу, а только после некоторого
ko.
С подобными ситуациями исследователь имеет дело, например, при ана
лизе зависимостей, связывающих между собой входнъtе и въ~ходнъtе ха
рактеристики процессов накопления и распределения ресурсов (см. вы
ше, примеры
4.9
и
4.10).
Выводы
1.
В гл.
4 представлен обзор VАR-моделей,
которые играют важ
ную роль в современном экономическом и финансовом анализе. Особое
внимание уделяется аспектам, связанным с выбором модели и оценкой
ее параметров; также представлены некоторые эмпирические приложе
ния.
Ниже в данном пункте «Выводов» приведены ключевые результа
ты, относящиеся к тематике VАR-моделей.
Гл.
376
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
• m-мерный VАR(р)-процесс Yt = (Y1,t, Y2,t, ... , Ym,t)' задается фор
мулой
Yt
=с+ Ф1Уt-1
где через с обозначен
(m
+ Ф2Уt-2 + ... + Фр'Уt-р + Et,
х 1)-вектор констант, а Фj
матрица авторегрессионных коэффициентов для
Et -
-
=
j
(т х
m)1, 2, ... ,р,
(т х 1)-вектор, отвечающий многомерному белому шуму.
• VAR(p )-процесс
является ковариационно-стационарным, если все
собственные значения, определяемые как решения детерминант
ного уравнения:
лежат внутри единичного круга. Таким образом, VАR(р)-процесс
является ковариационно-стационарным в случае, если l.ЛI
всех Л, удовлетворяющих
< 1 для
(*).
Это равносильно утверждению: VАR(р)-процесс является кова
риационно-стационарным, если все значения
z,
удовлетворяющие
следующему уравнению:
лежат вне единичного круга.
• VMA(oo)
представление для VАR(р)-модели дается выражением:
а функция импульсного отклика для
h
=О,
1, 2, ...
определяется
-
[дYi,t+h]
следующим образом:
д~
t+h де' t
(
дУц+h
дУц+h
де1,t
дem,t
.:
дYn,t+h
дej,t
mxm.
де1,t
•
Единичный шок при использовании разложения Холецкого ин
терпретируется как шок величиной, равной одному стандартному
отклонению соответствующего элемента исходной
yt. Однако еди
ничный шок в случае рекурсивной ортогонализации имеет прямой
смысл, который отвечает тому, что соответствующий элемент
Yt
изменен на одну единицу (в каких бы единицах он не измерялся).
377
Выводы
• Пусть E*(Yt+slYt, Yt-1, .. . ) линейный предиктор для Yt+s, который
использует только историческую информацию для У;
E*(Yt+slYt,
Yt-1, ... , Xt, Xt-1, .. . ) - линейный предиктор для Yt+s, использу
ющий историческую информацию для У и Х. Мы будем говорить,
что Х не является причиной по Гранжеру для У, если (см. п.
4.2.6):
E[(Yt+s - E*(Yt+slYt, Yt-1, · · .)) 2 ] =
= E[(Yt+s - E*(Yt+slYt, Yt-1, ... , Xt, Xt-1, ... , )) 2].
•
Оптимальное число лагов для VАR(р)-модели может быть выбра
но при помощи информационного критерия Акаике, информаци
онного критерия Шварца, информационного критерия Ханнана
Куинна, критерия итоговой ошибки прогнозирования, тестов от
ношения правдоподобия. Следует помнить, что в условиях очень
малых выборок небольшая недооценка фактического числа лагов
не обязательно оказывает пагубное влияние на точность прогно
зов.
•
Следует помнить о необходимости проверять свойства остатков
модели с использованием тестов Портманто, тестов множителей
Лагранжа и тестов на нормальность (см. п.
2.
4.2.8).
В главе рассмотрен также класс структурных
VAR
(SVАR)
моделей, при помощи которых можно анализировать механизмы мо
нетарных переходов и источники флуктуаций бизнес-циклов (п.
4.3).
Поясним некоторые важные моменты анализа таких моделей на при
мере двумерного случая.
•
В матричном виде двумерная SVАR-модель имеет вид:
[
1
Ь21
Ь12 ] [ Ун
1
]
[ /'10 ]
Y2t
+[
1'20
Byt
E[eti.]
-
/'О
/'11
/'21
/'12 ] [
/'22
Yit-1 ]
Y2t-1
+[
e1t ]
e2t
+ Г1Уt-1 + et
D= (
1 ~~ ).
Все переменные являются эндогенными и поэтому МНК не яв
ляется подходящим методом оценки параметров модели. Пред
ставление средствами структурных скользящих средних (SМА
представление) такой модели имеет вид:
Гл.
378
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
+ [ о~~> о~~> ] [ е-н-1 ] + ... ,
о~~> о~~>
e2t-1
где 80=в- 1 =F12. 80 отвечает начальным воздействиям струк
турных шоков и определяет одномоментную корреляцию между
Ун и Y2t, тогда как элементы матриц 8k, о~;>, определяют динами
ческие множители или импульсные отклики
Ylt
и
Y2t
на изменения
в структурных ошибках ен и t:2t·
•
Типичные идентификационные ограничения включают: нулевые
ограничения на элементы В (например, Ь12 =О); линейные огра
ничения на элементы В (например, Ь12
+ ~1
= 1); долгосрочные
ограничения на кумулятивное влияние.
•
Идентификация такой SVАR/SМА-модели достигается в предпо
ложении о том, что временные шоки (шоки е2) не имеют долго
срочного влияния на
Ylt
или
Y2t,
в то же время допускается нали
чие постоянных шоков (шоки е1), имеющих долгосрочное влияние
на Ун, но не на
3.
Y2t·
Эконометрическая модель, выраженная системой одновремен
Н'ЬtХ уравнений (СОУ), служит для объяснения поведения эндогенных
(т. е.
формирующихся в процессе и внутри функционирования описы
ваемой социально-экономической системы) переменных в зависимости
от значений экзогенных (задаваемых извне) и лаговых эндогенных пе
ременных. СОУ широко используются в проведении многовариантных
сценарных расчетов,
касающихся социально-экономического развития
анализируемой системы, а также в задачах прогноза экономических и
социально-экономических показателей (п.
4.
4.4).
Обща.я проблема идентификации СОУ является, наряду со спе
цификацией модели, центральной в построении и анализе модели. Она
включает в себя проверку соблюдения условий идентифицируемости
каждого отдельного уравнения и всей системы в целом (см. п.
4.4.3),
а также реализацию процедур статистического оценивания неизвест
Н'ЬtХ значений параметров системы (см. п.
5.
4.4.4).
Проверка и соблюдение условий идентифицируемости произво
дится как на стадии составления уравнений системы ( 1-е, 3-е и 4-е усло
вия) и формирования массива исходных статистических данных (2-е
379
Выводы
условие), так и на стадии анализа результатов статистического оценива
ния неизвестных параметров системы ( 1-е условие в части, касающейся
обратимости матрицы В, а также 5-е условие).
6.
Методы статистического оценивания параметров СОУ подразде
ляются на два класса:
1)
методы, предназначенные для оценки пара
метров одного отдельно взятого уравнения системы (МНК, косвенный
МНК, 2МНК, метод максимального правдоподобия с ограниченной: ин
формацией:, «оценки класса
k'j> ); 2)
методы, предназначенные для одно
временного оценивания параметров всех уравнений системы с учетом
их взаимосвязей: (ЗМНК, метод максимального правдоподобия с полной:
информацией:).
7.
Если уравнения структурной: формы модели могут быть располо
жены в таком порядке, что
i-e
уравнение
(i = 1, 2, ... , m)
может содер
жать в качестве объясняющих эндогенных переменных только перемен
ные у< 1 >, у< 2 >, ... , y(i-l} (или часть из них), а случайное возмущение б~i)
этого уравнения не коррелирует со всеми этими эндогенными перемен
ными, то такая система называется рекурсивной, и последовательное
применение к каждому уравнению такой: системы обычного МНК дает
состоятельные оценки ее структурных параметров (см. п.
4.4.4).
Класс
рекурсивных систем является простейшим с точки зрения решения за
дачи оценивания структурных параметров СОУ.
8.
Если исследователя интересуют только параметры приведенной:
формы и задача прогноза эндогенных переменных, то он может ограни
читься применением обычного метода наименьших квадратов к каждо
му отдельному уравнению приведенной формы (с последующей: оцен
кой, если это необходимо, идентифицируемъ~х параметров структур
ной: формы). Такой: образ действий: называют косвеннъш методом наи
меньших квадратов, или методом наименьших квадратов без ог])(),ни
-чений, а оценки, полученные с его помощью, будут состоятельными (см.
п.
4.4.5).
9. В
ситуациях, когда среди уравнений: системы имеются неиден
тифицируемые, так же как и в случаях, когда оценивание и анализ
параметров структурной формы представляют для исследователя са
мостоятельный интерес, рекомендуется применять двухшаговъ~й метод
наименьших квадратов (2МНК). Этот метод предназначен для оцени
вания параметров отдельного у])(J,внения структурной: формы, а его по
следовательное применение к каждому из уравнений: структурной фор
мы СОУ позволяет получить состоятельные оценки всех параметров
анализируемого уравнения (хотя 2МНК и не учитывает возможные вза
имосвязи между уравнениями системы).
Гл.
380
10.
4.
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Сущность двух шагов 2МНК заключается в следующем. На 1-м
шаге для каждой эндогенной переменной, играющей роль объясняющей
в анализируемом уравнении структурной формы, с помощью обычно
го МНК строится регрессия на все предопределенные переменные Х.
На 2-м шаге эта эндогенная переменная заменяется в рассматривае
мом уравнении ее регрессионным выражением через Х, после чего в
правой части этого уравнения остаются только предопределенные пе
ременные и к нему применяется обычный МНК. В моделях с большим
числом предопределенных переменных в целях снижения размерности
рекомендуется на 1-м шаге строить регрессию предикторной эндоген
ной переменной не на все предопределенные переменные, а лишь на
небольшое число их главных компонент.
11. Если структурные случайные возмущения б~ i) различных урав
нений системы взаимно коррелированы, то для оценивания парамет
ров структурной формы рекомендуется применять трехшаговъtй ме
тод наименьших квадратов (ЗМНК). Этот метод предназначен для
одновременного оценивания структурных параметров всех уравнений
системы и дает их состоятельные оценки, по эффективности превосхо
дящие в данном случае оценки (тоже состоятельные) 2МНК.
12.
ЗМНК использует полученные на первых двух шагах 2МНК
оценки параметров каждого из уравнений для вычисления оценки ко
вариационной матрицы возмущений различных уравнений структурной
формы. Затем на 3-м шаге оценки структурных параметров системы пе
ресчитываются с помощью обобщенного МНК в рамках соответству
ющей схемы обобщенной линейной модели множественной регрессии,
в которой в качестве ковариационной матрицы остатков используется
полученная ранее оценка ковариационной матрицы возмущений.
13.
В ряде ситуаций могут оказаться полезными и другие методы
статистического оценивания параметров СОУ. Для оценивания пара
метров одного отдельно взятого уравнения
-
это метод максимально
го правдоподобия с ограниченной информацией (требующий, правда,
дополнительного априорного предположения о нормальном характере
распределения структурных возмущений модели), «оценки класса
k'I>;
для одновременной оценки всех параметров структурной формы систе
мы
-
это метод максимального правдоподобия с полной информацией.
Однако эти методы из-за их относительно сложной вычислительной ре
ализации и дополнительных априорных допущений существенно реже
используются в эконометрических приложениях.
14. Одна из главных конечных прикладных целей построения и ана
лиза эконометрических моделей в виде СОУ - это точечный и интер
вальный прогноз эндогеннъ~х переменнъtх по заданным значениям пред
определенных переменных и связанная с этим задача проведения мно-
Выводы
381
говариантн:ых сценарнъtх расчетов, показывающих, как бу,цут «себя ве
сти~эндогенные переменные при различных сочетаниях значений пред
определенных переменных.
« Точечное решение~
этих задач основано на
подсчете значений эндогенных переменных с помощью статистически
оцененной приведенной формы СОУ. Для получения «интервальных~
вариантов решения необходимо уметь оценивать ковариационную мат
рицу ошибок точечного прогноза, что является задачей аналитически
достаточно сложной (см. п. 4.4.6).
15.
Важные средства анализа качества построенных моделей, точ
ности получаемых с их помощью прогнозов, наконец, решения задачи
выбора наилучшей модели предоставляют исследователю разного ро
да имитационно-компъютерные системы экспериментирования. Сре
ди них сле,цует выделить метод Монте
Карло, бутстреп-метод, а
-
также схему перекрестного анализа дееспособности модели (или мето
да
Cross-validation),
16. Бывает так,
см. п.
4.4.7.
что две или более нестационарных переменных ме
няются во времени синхронно так, что их линейная (или нелинейная)
комбинация представляет собой стационарный процесс. Эта важное на
блюдение является основой понятия коинтеграции (см. п.
4.5).
В главе
представлен обзор основных свойств коинтеграционных систем, а также
обзор подходов к их спецификации и тестированию. Ниже приведены
некоторые ключевые результаты по теме коинтеграции.
•
Определение коинтеграции по Энглу- Гранжеру:
(т х 1)-вектора
Yt
коинтегрированы с порядком
чается обычно через
ты
Yt являются l(d)
Yt
rv
компоненты
(d, Ь)
(что обозна
Cl(d, Ь), с Ь, d Е N+), если все компонен
и существует (п х 1)-вектор 'У (коинтегрирую
Zt = 'Y'Yt rv l(d-b)
with Ь > О является интегрированной порядка (d - Ь). Типичный
пример: 'У= (1, -(3)' => 'Y'Yt =Ун - f3Y2t =ин rv WN.
щий вектор), такой, что линейная комбинация:
•
Многомерное разложение Бевериджа-Нельсона (п.
смотрим случай, когда
(m
х 1)-вектор
Yt
является
4.5.1): рас
1(1) и описы
вается VМА(оо)-процессом в первых разностях д}t, д}t = о+
+иt
а о
= о+ Ф(L)t:t, где иt имеет нулевое среднее и является 1(0),
=
Е(дУt)
+Ф2+Фз+ ...
Тогда
Yt
-
#
вектор констант. Более того, Ф(l)
Omxm and L:~0 jl'l/Jj,kll
= lm +
< оо для всех k, l
может быть записан как:
Yt=
детерминированный тренд
+
стохастический тренд
~
'f/t
'f/O + Уо
...._.,......,
стационарный процесс
начальные условия
Ф1 +
= 1, ... т.
Гл.
382
где Ф(l)
4.
=
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
00
00
Е Фj, 'f/t
= a(L)et =
j=O
Е OjEt-j Oj
=
-(Фj+l + Фj+2+
j=O
00
+Фj+З + ... )и Е lajl
< оо.
j=O
•
Если
(m х
ванным с
тогда
•
1)-мерный процесс
h
Yt,...., CI(1, 1) является коинтегриро
коинтеграционными соотношениями, задаваемыми Г,
(h х 1)-мерный процесс Г'Уt является тренд-стационарным.
VАR-представление: если система
Yt
является коинтегрирован
ной, конечного VАR(р)-представления в первых разностях ЛУt
не существует. Однако предположим, что коинтегрированная
мерная
VAR(p )-система Yt
с
m-
h коинтегрирующими соотношениями
существует и задается как:
Q
+ Ф1Уt-1 + Ф2Уt-2 + ... + Фр°Уt-р +
Et
a+et.
Необходимым условием является так называемое условие реду
цированного ранга Фр(l)
матрицами полного
•
= ВГ', где В и Г являются (m х h)столбцового ранга h.
VЕС-представление: если мы вычтем
Yt-1
из обеих частей пред
ставленной выше VАR(р)-системы, то, с использованием редуди
рованного ранга, получим:
где
Zt = Г'Уt - тренд стационарно, а В - матрица нагрузок или
корректирующие факторы, поскольку она определяет то, каким
образом прежние флуктуации (ошибки или отклонения от сред
него, или отклонения от долгосрочного соотношения равновесия)
стационарного процесса
Zt
корректируют изменения процесса
т. е. дУt. Следует помнить, что
жающий
•
h
Zt -
Yt,
стационарный вектор, выра
коинтеграционных соотношений среди
Yt.
Наличие детерминированных компонент в VЕС-моделях является
важным, поскольку они меняют процедуру тестирования и про
верку гипотез (в частности, должны использоваться другие кри
тические значения). Может быть идентифицировано пять возмож
ных случаев, соответствующих различным ограничениям на пара
метры.
Выводы
•
Тест Энгла
383
Гранжера, основаннъtй на использовании остат
-
ков. На первом шаге строится регрессия
ных элементов
вектор
Yi,
для
Y2t; µ - вектор
Yi.t
на
(m - 1) осталь
удобства обозначенная как ((m - 1) х 1)констант: Ун = µ + a'Y2t + Zt. На втором
шаге производится тест на единичные корни для МНК-остатков
Zt =
Ун
-
ляется ли
Р,
Zt
- aY2t·
Это делается для того, чтобы выяснить, яв
интегрированным или нет. Критические значения
отличны от тех,
которые используются для расширенного теста
Дики- Фуллера.
• Тест Йохансена. Выводы относительно ранга коинтеграции h про
изводятся с использованием теста отношения правдоподобия. По
скольку
h
равно числу ненулевых собственных значений матрицы
(о = -Ф(l), тест использует эти собственные значения. В тесте
следа рассматривается гипотеза Но
:h
~
ho
против Н1
: h > ho.
Он основан на сумме (m-ho) наименьших собственных значений.
Мы можем проверять наличие и число коинтеграционных соот
ношений с использованием последовательности тестов следа, где
принятие нулевой гипотезы в первый раз отвечает числу коинте
грационных соотношений.
17.
Проанализированы важные нелинейные модели, рассматривае
мые в экономической и финансовой литературе (п.
4.5.5).
В частности,
рассмотрены модели для анализа паритета покупательной способности
(ППС) или закона единственной цены. Отметим, что лишь недавно по
явились несколько теоретических работ, в которых представлены со
ответствующие процедуры тестирования и оценивания. В этой связи в
главе представлен обзор недавних результатов для тестирования поро
говой коинтеграции и для спецификации этой модели. Ниже приве
дены некоторые ключевые результаты по этой тематике.
•
В общем виде пороговая векторная модель коррекции остатками
(TVECM)
имеет следующий вид (см. п.
4.5.6):
р-1
Лрt = a(Jt)
-
B{Jt)Г'Pt-1
+L
('}Jt) ЛPt-j
+ Et,
j=l
если
где Pt
e<r-l)
< Г'Pt-d
~
e<r),
вектор цен на рынках А и В, а r = 1, 2, ... , l,
l + 1 - индексы, отвечающие различным режимам. Через a{Jt)
обозначены зависящие от режима средние, где Jt = r сигнали
зирует об r-м режиме. B{Jt) включает параметры, зависящие от
= (pfpf1)' -
Гл.
384
АНАЛИЗ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
4.
режима, характеризующие степень реагирования изменений цен
д Pt на отклонения от долгосрочного равновесия с лагами на
d
периодов. Значения (J(r) упорядочены таким образом, что (J(O)
<
<
(J(1)
< ... <
(J(l)
<
(J(l+l), где (J(O)
=
-оо, (J(l+l)
=
оо; их называ-
ют пороговъши параметрами, или, если коротко, порогами.
•
Оценивание ТVЕСМ-модели: один способ оценивания состоит в
минимизации суммы квадратов ошибок; другой способ состоит в
максимизации функции правдоподобия.
•
Тестирование пороговой коинтеграции (п. 4.5.7): в работах [Balke,
предложена двухшаговая про
Fomby (1997)], [Lo, Zivot (2001)]
цедура, в которой на первом шаге тестируется нулевая гипотеза
об отсутствии линейной коинтеграции против альтернативы о ее
наличии;
на
втором
шаге,
если
нулевая
гипотеза отклонена,
то
тестируется нулевая гипотеза о наличии линейной коинтеграции
против альтернативы о наличии пороговой коинтеграции. Однако
пороговая природа альтернативной гипотезы может значительно
снижать мощность стандартных тестов на первом шаге. В рабо
те
[Seo (2006)]
впервые представлена suр-Wаld-статистика для те
стирования нулевой гипотезы об отсутствии коинтеграции против
альтернативы об адекватности ТVЕСМ-модели. Наконец, отме
тим, что возможны всего четыре гипотезы: отсутствие линейной
коинтеграции, отсутствие пороговой коинтеграции, наличие ли
нейной коинтеграции и пороговая коинтеграция. Однако упомя
нутая выше двухшаговая процедура не предполагает гипотезу об
отсутствии пороговой коинтеграции.
•
В ситуациях, когда нестационарные однородные временные ряды
{x(t)}
и
{y(t)}, t = 1, 2, ... , N,
являются исходными данными для
построения регрессии у по х, причем воздействие единовременного
изменения одной из них (х) на другую (у) растянуто (распределе
но) во времени, большой прикладной интерес представляют так
называемые модели с распределеннъши лагами. В рамках этого
специального класса моделей проводится, в частности, интерес
ный эконометрический анализ таких важных экономических яв
лений, как «процесс 'Часmи'Чного приспособления», «модели адап
тивнъtх ожиданий»
и др. (см. п.
4.6).
Глава
5
Анализ и моделирование
волатильности
Одномерные модели авторегрессионной
5.1.
условной гетероскедастичности (АRСН
и GАRСН-модели) 1
5.1.1.
Введение
Изучение волатильности доходности активов внесло важный вклад в
понимание современных финансовых рынков. Волатильность считает
ся мерой риска, а рисковость любого финансового актива
-
решающая
характеристика, определяющая его равновесную цену. Модели авторе
грессионной условной гетероскедасmи'Чности
(ARCH)
были разрабо
таны для учета эмпирических закономерностей в финансовых данных.
Многим финансовым временным рядам свойственны следующие стили
зованные факты:
•
Цены активов, вообще говоря, нестационарны. Доходности обычно
стационарны. Некоторые финансовые временные ряды являются
дробно интегрированными.
•
Автокорреляция в рядах доходностей обычно слаба или отсут
ствует.
1 Этот
раздел главы представляет собой сокращенный вариант русскоязычной
версии работы Э. Росси (Е.
тиль• (№ 8,
2010}
Rossi},
опубликованной в электронном журнале «Кван
в переводе Б. Гершмана. Любезные согласия на включение этого
материала в наш учебник мы получили от автора Эдуардо Росси и главного редак
тора электронного журнала «Квантилы Станислава Анатольева.
Гл.
386
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Серийная независимость между квадратами значений ряда часто
•
отвергается в пользу наличия нелинейной зависимости между по
следовательными наблюдениями.
•
Волатильность рядов доходностей кластеризована.
•
Нормальность отвергается в пользу некоторого распределения с
тяжелыми хвостами.
В некоторых рядах присутствует так называемый эффект р'Ы'Чага,
•
т. е. изменения цен акций отрицательно коррелируют с изменени
ями волатильности. Когда рыночная стоимость фирмы падает, со
отношение заемного и собственного капиталов обычно растет. Это
повышает волатильность акционерного капитала, если доходность
постоянна. Однако Блэк утверждает (см.
[Black (1976))),
что реак
ция волатильности на направление изменения доходности слиш
ком велика, чтобы полностью объясняться эффектом рычага.
•
Волатильности динамических характеристик различных ценных
бумаг очень часто движутся вместе.
Модель
ARCH
и ее обобщения применяются для моделирования во
латильности доходностей большого числа финансовых активов, таких
как ценные бумаги с фиксированным доходом, обменные курсы, ин
дивидуальные акции и фондовые индексы. В классе АRСН-моделей с
дискретным временем ожидания формулируются в терминах напрямую
наблюдаемых величин, в то время как модели стохастической волатиль
ности
в дискретном
или
непрерывном
времени
включают латентные
переменные состояния. Предложено, оценено и изучено огромное число
моделей. Продолжают появляться новые модификации. Однако Энгл
GARCH, пред
ложенную Боллерслевом [Bollerslev (1986)), и модель EGARCH Нель
сона [N elson ( 1991)]. Имеется множество обзоров разрастающейся ли
тературы об АRСН-моделях, например [Andersen & Bollerslev (1998)),
[Andersen et al. (2006)), [Bauwens et al. (2006)), [Bera & Higgins (1993)),
[Bollerslev et al. (1992)), [Bollerslev et al. (1994)), [Degiannakis & Xekalaki
(2004)), [Diebold (2004)), [Diebold & Lopez (1995)), [Engle (2001, 2004)),
[Engle & Patton (2001)), [Pagan (1996)), [Palm (1996)), [Shephard (1996))
и [Terasvirta (2009)].
[Engle (2002))
выделяет как наиболее влиятельные модель
Эти обзоры и главы в учебниках содержат все увеличивающийся
список акронимов и аббревиатур, используемых для обозначения все
го изобилия предложенных моделей и методов. Например,
(2009))
[Bollerslev
в качестве приложения к традиционным обзорам приводит спра
вочник с длинным списком связанных с АRСН-моделями сокращений.
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
387
Первые исследования в области эконометрического моделирования
волатильности были исключительно параметрическими, но в послед
ние годы происходит сдвиг в сторону менее параметрических и даже
полностью непараметрических методов. Непараметрические подходы к
моделированию волатильности, которые, как правило, не делают пред
положений о функциональных формах, позволяют получать гибкие и
в то же время состоятельные (по мере увеличения частоты выборки
для ряда доходностей) оценки реализованной волатильности, см. обзор
в
[Andersen et al. (2009)).
5.1.2.
Для чего нужны АRСН-модели?
Теорема Волда о разложении устанавливает, что любой ковариационно
стационарный ряд
{Yt}
можно записать в виде суммы линейно детер
минированной компоненты и линейно стохастической, представимой в
виде квадратично суммируемого одностороннего скользящего среднего.
Таким образом,
Yt
где
dt -
= dt +иt,
линейно детерминированная компонента, а
Ut -
линейно регу
лярный ковариационно стационарный случайный процесс:
00
в (L)
00
= 'L:,ЬiLi, L:,ь~ < оо, Ьо = 1,
i=O
где
L -
i=O
лаговый оператор, т. е.
Xt-1
= Lxt,
и
о,
{
(]'~
< оо, t = т,
о,
иначе.
Некоррелированная последовательность остатков gt необязатель
но гауссова, а следовательно, необязательно независимая. Зависимые
остатки свойственны нелинейным временным рядам вообще и условно
гетероскедастичным временным рядам в частности.
Предположим, что
процесс с
iid
Yt -
линейный ковариационно стационарный
остатками, а не просто белый шум. Безусловные среднее
и дисперсия равны
-
о,
00
u~ L:,ь~,
i=O
Гл.
388
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
и оба неизменны во времени. Условное среднее меняется во времени и
имеет вид
00
Е [Yt l9"t-1] = Lbiet-i,
i=l
где
информационное множество, состоящее
9"t-1 = {et-1, et-2, ... } -
из прошлых значений процесса и другой информации, доступной в мо
мент времени
t - 1.
Эта модель не способна уловить динамику условной
дисперсии. Действительно, условная дисперсия
Yt
постоянна:
Это ограничение проявляется в свойствах условной дисперсии ошиб
ки прогноза на
k
шагов вперед. Условный прогноз на
k
шагов вперед
имеет вид
00
Е [Yt+k l9"t] = Lbk+iet-i,
i=O
а соответствующая ошибка прогноза равна
k-1
Yt+k -
Е [Yt+k l9"t] = Lbit:t+k-i
i=O
с условной дисперсией
Е [(Yt+k - Е [Yt+k
k-1
l9"t]) 2
l9°t]
=и~ Lь~.
i=O
При
k--+-
оо условная дисперсия ошибки прогноза сходится к без
оо
условной дисперсии и: Е ь1. для любого k условная дисперсия ошибки
i=O
прогноза зависит только от
модель с
iid
остатками не способна учесть важную информацию, до
ступную в момент времени
5.1.З.
k, но не от 9"t. Таким образом, простая
t.
АRСН-модели (определения, свойства)
Обозначим
{et (8)}
случайный процесс в дискретном времени с услов
ными средним и дисперсией, параметризованными конечномерным век
тором
8
Е
0
С
9-tm,
где
80 -
Предположим для начала, что
Обозначим
истинное значение вектора параметров.
et (80)
является скалярным.
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
389
Аналогично определяется условная дисперсия:
Dt-1 [·]
Определение
ет
модели
= D [· l9"t-1].
5.1 [Bollerslev et al. (1994)].
авторегрессион'Н.Ой
условной
Процесс
{et
(Во)} следу
гетероскедасти'Чности
(ARCH), если
Et-1 [et (Во)] =О,
(5.1)
t = 1,2, ... '
и условная дисперсия
at (Во)= Dt-1 [et (Во)] = Et-1
[е~ (Во)] ,
t
= 1,2, ... ,
(5.2)
нетривиально зависит от а-пол.я, порожденного прошл:ьши наблюде
ниями
{et-1(Bo), C:t-2(Bo), ... }.
Пусть
{Yt
(Во)}
-
исследуемый случайный процесс с условным сред-
ним
t
= 1,2, ....
al
Как µt (Во), так и
(Во) измеримы относительно информационного
множества на момент времени t - 12 . Обозначим {et (Во)} процесс
C:t (Во) = Yt - µt (Во).
Из уравнений
(5.1)
и
(5.2)
следует, что стандартизированный про-
цесс
Zt (Во) = C:t (Во) at (Во)- 112 ,
t = 1, 2, ... '
имеет нулевое условное среднее
мени единичную условную
(Et-1 [zt (Во)] =О) и неизменную во вре
дисперсию. Можно считать, что C:t (Во) по
рождается процессом
C:t (Во) = Zt (Во) af (Во) 112 ,
al
где е~ (Во) - несмещенная оценка
(Во). Предположим, что Zt (Во)
,...., nid (О, 1) и не зависит от
(Во). Тогда
al
Et-1 [е~]
2 [Andersen
,....,
= Et-1 [at] Et-1 [zt] = Et-1 [at] ,
(1996)J различает детерминированный, условно гетероскедастичный,
условно стохастический и современно стохастический процессы для волатильности.
Процесс волатильности является детерминирован:н.ым, если информационное мно
жество (и-поле), обозначаемое как§, совпадает с и-полем всех случайных векторов
в системе до момента
t=
О включительно; ус.л.овно гетероскедастичным, если §
держит информацию, доступную и наблюдаемую в момент времени
стохастическим, если §
t - 1;
со
ус.л.овно
содержит все случайные вектора до момента t-1; и совре
менно стохастическим, если информационное множество §
векторы вплоть до момента времени
t.
содержит случайные
Гл.
390
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
zl
поскольку
l9"t-1
х 2 (1). Медиана х 2 (1) равна 0,455, так что
Р [ < !иl] >
Прокси
создает потенциально значительную ошиб
ку при анализе малых выборок
t = 1, 2, ... , Т, хотя ошибка умень
el
!.
f'V
el
ul,
шается по мере роста Т.
Если условное распределение Zt неизменно во времени и имеет ко
нечный четвертый момент, то
Е [etJ
Е [zi] Е [иi] ~ Е [zi] {Е [иl]) 2
=
т.е. Е [ef] ~ Е
Е [zi] {Е [е~]) 2 ,
=
[zt] {Е [el]) 2 , согласно неравенству Йенсена3 • Строгое
равенство имеет место только в случае постоянной условной диспер
сии. Если
Zt
f'V
распределение
nid(O, 1), то Е
et
[zt] =
3, а следовательно, безусловное
имеет положительный эксцесс:
Более того, эксцесс можно выразить как функцию от изменчивости
условной дисперсии. Если et
х [el]) 2 и
Е [etJ
=
l9"t-1
f'V
N (о, ul), то Et-1 [ef]
=
З(Еt-1 х
ЗЕ [{Et-1 [е~]) 2 ] ~ 3 {Е [Et-1 [e~JJ) 2 = З(Е [е~]) 2 •
Далее
Е [4] = 3 {Е [е~]) 2 + ЗЕ [{Et-1 [е~]) 2 ]
-
3 {Е [Et-1 [e~JJ) 2
и
Другое важное свойство АRСН-процесса состоит в отсутствии услов
ной серийной корреляции. Учитывая, что
Et-1 [et] =
О, по закону по
вторных математических ожиданий, имеем
Et-h [et] = Et-h [ЬЕt-1 (et)] = Et-h [О] =О.
Из этого свойства ортогональности следует, что процесс
{et}
услов
но некоррелирован:
covt-h [et, енk] -
3 Неравенство
Тогда
если
Et-h [eteнk] - Et-h [et] Et-h [енk]
=
Et-h [etet+k] = Et-h [Et+k-1 [eteнk]] =
Е [etEt+k-1 [енk]] = О.
Йенсена. Пусть Х и g(X) - интегрируемые случайные величины.
E[g(X)] ~ g(E[X]},
g (·) выпуклая.
если
g(·) -
вогнутая функция, и
E[g(X)] ;;;:: g(E[X]},
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
Модель
ARCH(q),
предложенная в
[Engle {1982)),
391
представляет
условную дисперсию как линейную функцию квадратов прошлых воз
мущений:
q
ul = w + Laie~-i·
{5.З)
i=l
В этой модели для обеспечения положительности условной диспер
сии параметры должны удовлетворять следующим условиям:
ai
~ О, а2 ~ О,
w
>
О,
~ О. Определив
... , aq
ul = е~ -Vt,
где
Et-1[vt]
=
О, можно записать модель {5.З) в виде АR(q)-процесса
для е~:
е~ = w +а (L) е~ + Vt,
где а (L) = aiL+a2L2+ .. . +aqLq. Этот процесс является слабо стацио
q
парным тогда и только тогда, когда
L:ai < 1; в этом случае безусловная
i=l
дисперсия равна
Е[е~] =
w/ {1 -
ai - ... - aq).
Процесс характеризуется положительным эксцессом. Например, в слу
чае модели ARCH{l) с
Et
l§t-1 Е N (О, ul), эксцесс равен
Е [ef] / (Е [е~] )2 = з (1 - аП / (1 - зап '
если За~< 1, а при За~= 1
Е [ef] / (Е [е~]) 2 = оо.
В обоих случаях эксцесс превышает значение
3,
характерное для
нормального распределения, для которого коэффициент эксцесса, как
известно, равен нулю.
Важнейшее свойство АRСН-модели состоит в том, что cov[e~, е~_;]
=/:
=F О, хотя cov [et, f:t-;] =О для j =F О. Рассмотрим связь АRСН-модели с
билинейной моделью. Временной ряд {et} следует билинейной модели,
если
r
р
f:t
s
= LФiE:t-i + LLЬjkCt-jиt-k + иt,
i=l
j=lk=l
где иt - последовательность iid(O, и~) величин. Первые два условных
момента имеют вид
р
r
s
LФiE:t-i + LLЬ;kf:t-jиt-k + иt,
i=l
2
Uu·
j=lk=l
Гл.
392
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
В отличие от АRСН-модели, в которой условная дисперсия меняется
во времени, в билинейной модели условная дисперсия постоянна. Тем
не менее безусловные моменты в обеих моделях могут быть похожи.
Например, билинейной модели
автокоррелированной для квадратов наблюдений, свойственна класте
ризация больших и малых отклонений, как и АRСН-процессу.
GARCH(p, q)-модели
5.1.4.
,ЦЛя
лаконичного
моделирования
условной
гетероскедастичности
[Bollerslev (1986)) и независимо от него [Taylor (1986)) предложили обоб
щенную АRСН-модель
- GARCH(p, q):
ul = w + а (L) е~ + {З (L) ul,
где а
(L) = a1L+ ... +aqLq, {З (L) = f31L+ ... +{ЗрLР.
наиболее популярна в прикладных
(5.4)
Модель
GARCH(l, 1)
исследованиях4 :
(5.5)
,ЦЛя
корректного
GARCH (р, q)
определения
условной
дисперсии
в
модели
все коэффициенты в соответствующей линейной АRСН
модели бесконечного порядка должны быть положительными. Записы
вая
GARCH(p, q)-модель
как
ARCH(oo),
получаем:
(5.6)
Таким образом, иl ~ О, если w* ~ О и все Фk ~ О. Неотрицательность
w* и Фk является также и необходимым условием неотрицательности иl.
Чтобы w* и {Фk}~ 0 были корректно определены, предположим, что:
1. Корни уравнения {З(х)=1 лежат вне единичного круга, и w~O. Это
условие гарантирует, что величина
11. Полиномы а (х) и
4 Модель
1-
w*
конечна и положительна.
{З (х) не имеют общих корней.
GARCH принадлежит к классу моделей детерминированной условной
гетероскедастичности, в которых условная дисперсия является функцией от пере
менных, находящихся в информационном множестве на момент времени
t.
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
393
Эти условия не гарантируют ни то, что al ~ оо, ни строгую стаци
онарность ряда {о}} :,_ 00 • В простой GARCH{l, 1)-модели для положительности
условиями
al
почти наверное требуется [Nelson & Сао {1992)], наряду с
(i)
и
{ii),
чтобы
w~O,
/31
~о,
01 ~о.
В моделях
Например, в
GARCH{l, q) и GARCH{2, q) эти условия можно ослабить.
модели GARCH{l, 2) необходимыми и достаточными уело-
виями являются:
w~O,
1>
/31
~о,
(5.7)
/3101+02 ~о,
01 ~о.
Для модели
GARCH{2, 1)
условия имеют вид:
w
~о,
01 ~о,
/31
~ о,
+ /32
< 1,
+ 4/32
~ о.
/31
(3~
(5.8)
Эти условия не такие строгие, как предложенные в
[Bollerslev {1986)]:
w ~о,
Модель
/Зi ~ о,
i = 1, ... 'р,
Oj ~
j
0,
{5.9)
= 1, ... ,q.
GARCH{2, 2) изучена в [Не & Terasvirta {1999)]. Эти резуль
таты нельзя перенести на многомерный случай, в котором условие по
ложительности { al} означает положительную определенность услов
ной ковариационной матрицы. Для идентификации GАRСН-модели, в
которой по крайней мере один из коэффициентов
/3; >
О, необходи
мо также потребовать, чтобы как минимум один из коэффициентов
о;
Et
>
О. Если 01
равны, и
= ... =
/31, ... , /Зр -
aq
=
О, условная и безусловная дисперсии
неидентифицируемые мешающие параметры.
С точки зрения оценивания модели
GARCH (р, q)
методом максималь
ного правдоподобия необходимо рекурсивно подсчитать { al} :,0 , начи
ная с момента О и применяя
(5.4),
предполагая произвольные значе
ния { а: 1 , ... , а:Р, е: 1 , ... , e:q} для периодов, предшествующих выбор
ке. Условия (5.9) гарантируют, что ряд { al} :,0 неотрицательный при
Гл.
394
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
любых неотрицательных значениях { а: 1 ,
... , а:Р' е: 1 , ... , e:q}.
гой стороны, условия, гарантирующие, что w* ;;;:: О и Фk
для модели
и
GARCH(l, 2)
(5.8)
для модели
;;;::
GARCH(2, 1)),
С дру
О (см.
(5. 7)
этого обеспе
чить не могут. Проблему можно решить, выбрав начальные значения,
al} :
которые гарантируют неотрицательность {
0 с вероятностью 1 при
неотрицательных w* и {Фk}~ 0 . [Nelson & Сао (1992)] предлагают слу
чайно выбрать е 2 ;;;:: О и положить е~ = е 2 для t от -1 до -оо и
= а2
al
для
1-
р ~
t
~ О, где
00
= w* + e2LФk·
k=O
Таким образом, получаем последовательность {
t ;;;::
О с вероятностью
1,
al} ; ;:
О для всех
поскольку
t-1
00
al = w* + LФke~-k-1 + LФke 2 .
k=O
р
Предполагая, что
'Ef3i
+
k=t
q
'Е aj
< 1,
можно положить а 2 и е 2 paв-
i=l
j=l
ными их общему безусловному среднему:
а2 =е2 =(1 -t/3i - taj)-l w.
i=l
В стационарной GАRСН-модели в
j=l
[Engle & Mezrich (1996)] предло
жено таргетирование дисперсии, а именно замена константы w в
на (1 - 'Ej aj -
'Ei /3i)a 2. Оценка а 2 , т. е.
0:2
(5.4)
т
~ 'Е €t, подставляется
=
t=l
вместо а 2 перед оцениванием других параметров. Модель содержит на
один параметр меньше, чем стандартная модель
GARCH (р, q).
Уравнения Юла-Уолкера для процесса квадратов
Процесс { е~} можно представить в виде ARMA(m,p):
где т
=
max(p,q), Et-1 [vt] =О,
Vt
Е
[-al,oo).
Таким образом, приме
нимы классические результаты для АRМА-моделей. В частности, рас-
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
смотрим автоковариационную функцию, см.
[Bollerslev (1988)],
395
т. е.
'У2 (k) = cov [е~, e~-k] ,
'У2 (k) = cov [w +
t
(aj
+ fjj)
e~-j + (v• -t/J;Vt-•), e~-k] ,
i=l
3=1
m
'У2 (k) =
(5.10)
L (aj + fjj) cov [e~-j' e~-k] +
j=l
+ cov [vt - t/J;vн, e~-k]
i=l
.
Когда
k достаточно велико, последний член в правой части вы
ражения (5.10) равен нулю. Последовательность автоковариаций удо
влетворяет линейному разностному уравнению порядка max (р, q) для
k ~ р+ 1:
m
'У2 (k)
= L:: (aj + fjj) 'У2 (k -
л.
j=l
Эту систему можно использовать для идентификации лаговых по
рядков т и р, т. е. р и q, если q ~ р, и р при q
< р.
Автокорреляционная
функция е~, если таковая существует, убывает медленно, хотя и экспо-
ненциально. В АRСН-модели скорость убывания слишком высокая по
сравнению с той, которая обычно наблюдается в финансовых времен
ных рядах, если только максимальный лаг
q
невелик.
Стационарность
Процесс
{et},
следующий модели
GARCH(p, q),
является последователь
ностью мартингальных приращений. Для доказательства ковариацион
ной стационарности достаточно показать, что дисперсия
D [et) = D [Et-1 [et]) + Е (Dt-1 [et]) = Е
[o'l)
асимптотически постоянна во времени.
Утверждение. Процесс
{et}, следующий модели GARCH(p, q)
ложительными коэффициентами
i = 1, ... ,р,
w
~ О, Oi ~ О,
i = 1, ... , q, fii
с по-
~ О,
является ковариационно стационарным тогда и только то
гда, когда
Q
(1)
+ /j(l) < 1.
Это условие является достаточным, но не необходимым для стро-
гой стационарности. Каждый слабо стационарный GАRСН-процесс яв
ляется также строго стационарным. Поскольку АRСН-процессы имеют
Гл.
396
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
тяжелые хвосты, условия ковариационной стационарности часто более
жесткие, чем условия строгой стационарности. Если а
(1)
+ ,8(1) <
1,
слабо стационарное решение единственно и совпадает с единственным
стационарным решением.
Для поиска строго стационарного решения рассмотрим е~ =
Модель
GARCH{l, 1)
zlal.
можно записать в виде
(5.11)
Рекурсивная подстановка приводит к записи
ul ="'
(i + ~п
(/11
GARCH{l, 1)-модели в виде
+а,zц).
Обозначая
получаем, что yt = al+ 1 является решением стохастического рекуррент
ного уравнения yt = AtYt-1 + Bt, где {At, Bt} - IID. Каждое строго
стационарное решение {al} уравнения {5.11) можно выразить в виде
функции процесса {Zt}, так что из стационарности {al} следует ста
ционарность {al,zt}, а значит, и {et,at}· Таким образом, существова
ние строго стационарных решений для
GARCH{l, 1)-процесса сводится к
изучению строго стационарных решений уравнения
см.
[Lindner
рекуррентного уравнения (с iid
{2009Ь)]. Решение
{Yt} стохастического
коэффициентами) - это последовательность
(5.11),
случайных величин. Каж
дое решение удовлетворяет
AtYt-1 + Bt =
AtAt-1Yt-2 + AtBt-1
yt
-
(
+ Bt =
(i-1 )
Ц At-j Yi-k-1 + ~ Ц At-j Bt-i
k
з=О
)
k
i=O
з=О
для всех k Е N U {О}, где Пj2 0 At-j = 1 для произведения по пустому
множеству индексов. Для существования стационарного решения необ
ходимо, чтобы
lim
k~oo
(П At-j) Yi-k-1 = О почти наверное (п.н.)
. 0
з=
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
5.1.
397
и сумма Е:=о (П~::t At-j) Bt-i сходилась почти наверное (п.н.) при
k
~ оо. В случаях
GARCH{l, 1)
и;+ 1 = Yt =
(
и
ARCH{l)
Ц At-i и;_k + w ~
k
)
k
i=O
(i-1 )
Ц At-j
.
3=0
i=O
Поскольку это сумма неотрицательных компонент, ряд Е~о п~::t At-j
СХОДИТСЯ почти наверное для каждого t, и, следовательно, п:=О At-i
сходится почти наверное к О при k ~ оо. Если процесс {иl+ 1 } строго
стационарный, то ( п:=О At-i) u;_k СХОДИТСЯ к о по распределению и по
вероятности при
~ оо. Следовательно, существует не более одного
k
строго стационарного решения
ul =
yt = w ~
00
Yt-1:
(iд-1 )
At-j
.
Таким образом, из существования строго стационарного процесса
GARCH{l, 1) или ARCH{l) следует сходимость к О почти наверное произ
ведения п:=о At-i при k ~ оо. Но верно также и обратное утверждение,
а значит, строго стационарное решение GARCH{l, 1)/АRСН{l)-процесса
существует тогда и только тогда, когда п:=О At-i СХОДИТСЯ п.н. к о при
k~oo.
В (Nelson {1990Ь)) показано, что при w > О иl < оо (почти на
верное), и {et, ul} строго стационарны тогда и только тогда, когда
Е [ln (/31
+ a1zl)]
~ О. Учитывая, что
Е [ln (/31
+ a1z;)]
~ ln (Е [/31
+ a1z;]) = ln {а1 + /31),
= 1 модель строго стационарна. Поэтому Е [ln (/31 + a1zl)] ~
+ /31 < 1. Для модели
ARCH{l) при а1 = 1, /31 =О и zt rv iid (О, 1)
при а1 +/31
~О является более мягким требованием, чем а1
Е [ln (z;)] ~ ln (Е
[zl])
= ln (1).
Таким образом, интегрированная АRСН{l)-модель является строго ста
ционарной, но не ковариационно стационарной.
Для анализа условий существования строго стационарных решений
модели
GARCH (р, q)
необходимо расширить стохастическое рекуррент
ное уравнение на многомерный случай, см.
[Bougerol & Picard
{1992а)].
Строгая стационарность многомерных стохастических рекуррентных
Гл.
398
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
уравнений исследуется в терминах максимальной экспоненты Ляпуно
ва.
[Bougerol & Picard {1992Ь)] показали, что неприводимые рекуррент
ные
уравнения
E[ln+ llAoll]
с
коэффициентами
iid
{At, Bt},
такими,
что
< оо и E[ln+ llBoll] < оо, допускают неупреждающее строго
стационарное решение тогда и только тогда, когда максимальная экс
понента Ляпунова, связанная с
показали, что
{ At}, строго отрицательна. Они также
GARCH{p, q)-процесс
допускает строго стационарное ре
шение тогда и только тогда, когда максимальная экспонента Ляпунова
для последовательности
{At} строго отрицательна. Это решение един
ственно.
Прогнозирование волатильности
Модель
GARCH{p,q) можно представить в виде АRМА-процесса,
вая, что е~ = al + Vt, где Et-1 [vt] =О, Vt Е [-al, оо):
Таким образом, е~
учиты
ARMA{m, р), где т = тах(р, q). Прогнозиро
вание для GARCH{p, q)-модели рассмотрено в [Engle & Bollerslev {1986)].
l"V
Запишем
ai+k = w +
где п =
n
т
i=l
i=k
L (aчe;+k-i + f3iai+k-i) + L (aie;+k-i + f3iai+k-i) ,
и по определению суммы от
min{m,k-1}
1
до О и от
k
>
т
до т обе равны нулю.
Тогда
n
Et [ai+k]
=w +L
т
((ai
+ f3i) Et
[ai+k-i])
+L
(aie;+k-i
при
> 2 имеем
+ f3iai+k-i)
i=k
i=l
В частности, для
GARCH{l, 1)-модели
k
k-2
Et [ai+k]
-
L (а1 + f31)i w + (а1 + f31)k-l ai+1 =
i=O
( 1 - (а1
+ f31)k-l)
f3 )k-1 2
(
{1 - (а1 + f31)) + а1 + 1
at+1
-
w
-
а2
(
а2
+ (а1 + f31)k-l
1-
(а1 + f31)k-l) + (а1 + f31)k-l al+1
(ai+ 1 - а 2 ).
=
=
·
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
399
Когда процесс является ковариационно стационарным, Et [al+k]
СХОДИТСЯ к а 2 при k ---t 00.
Модель
IGARCH(p,q)
Определение
5.2. GARCH(p, q)-процесс,
имеющий первъtе два ус
ловнъtХ момента вида
= О,
Et-1 [et)
al
где
w~
О, Cti ~ О и .Вi ~ О для всех
d >
р
i=l
i=l
=Et-1 [е~] = w + Laie~-i + L.Вial-i,
1-
имеет
q
а (х)
i,
-
О едини'Чных корней, а
и для которого уравнение
,В(х) =О
max {р, q} - d
корней лежат вне
едини'Чного круга, называют:
i} интегрированным относите.л:ьно дисперсии порядка d,
w =О;
если
ii} интегрированным относительно дисперсии порядка d с трен.дом,
если w >О.
Интегрированные
GARCH(p, q)-модели {IGARCH)
как с трен
дом, так и без него являются, таким образом, частью более широкого
класса моделей со свойством «устойчивой дисперсии», когда текущая
информация остается важной для прогнозирования условных диспер
сий при любом горизонте планирования.
Интегрированная
GARCH{p, q)-модель
имеет место, если выполня
ется необходимое условие
Q
(1)
+ ,8(1) = 1.
Для примера рассмотрим модель
IGARCH{l, 1),
в которой et1
+ ,81
= 1.
Процесс можно записать в виде
(5.12)
Для этой конкретной модели прогноз условной дисперсии на
вперед имеет вид
k
шагов
Гл.
400
[Nelson (1991))
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
показал, что при инициализации процесса
IGARCH
в
некоторый конечный момент времени его поведение зависит от пара
метра
w > О, то безусловная дисперсия et
Если w = О, реализации процесса почти
Если
w.
временем.
к нулю. Параметр
/31
линейно растет со
наверное сходятся
влияет на скорость этой сходимости. Важно от
метить, что безусловная дисперсия
дисперсия следует модели
IGARCH.
et
не существует, когда условная
В случае
GARCH(l, 1)-модели
можное объяснение того факта, что оценка а1
+ /31
воз
близка к единице,
состоит в том, что во время периода оценивания GАRСН-модели проис
ходит смена константы
[Diebold (1986)), [Lamoureux & Lastrapes (1990)).
Это означает, что порождающий данные GАRСН-процесс нестационар
ный.
Модель
IGARCH(l, 1) в (5.12) также можно
ARIMA(O, 1, 1):
(1 - L)e~ = w + Vt - /31Vt-1,
где
Vt =
записать в форме
el - al является мартингальным приращением относительно
2
at.
Являются ли шоки у { al} устойчивыми или нет, напрямую зависит
от используемого определения. Условный момент может расходиться
для одного значения
77,
но сходиться к конкретному пределу, не завися
щему от начальных условий, для другого значения 77, даже если { al}
стационарна и эргодична.
Для
GARCH(l, 1)-модели
t-s-1
Es [al] = w
L
(а1
+ /31)k + al-s (а1 + /31)t-s.
k=O
Е 8 [al] сходится к безусловной дисперсии
тогда и только тогда, когда а1
и а1
+ /31
w/ (1 -
а1 - /31) при
t --+ оо
+ /31 < 1. В модели IGARCH(l, 1) с w >О
= 1 величина Е 8 [ al]
--+ оо п.н. при t --+ оо. Тем не менее
IGАRСН-модели строго стационарны и эргодичны.
зал, что в IGARCH(l, 1)-модели
Е 8 [а:11 )
[Nelson (1990)) пока
сходится к конечному пределу,
не зависящему от информации на момент времени
s
при
t --+
оо, если
77 < 1. Если носитель Zt неограничен, из этого следует, что в каждой
стационарной и эргодичной GARCH(l, 1)-модели Е 8 [а: 11 ) расходится для
всех достаточно больших значений 77 и сходится для всех достаточно
малых значений 77.
5.1.5.
Асимметричные модели
Для повышения гибкости исходная GАRСН-модель была обобщена и
расширена в разных направлениях.
Первоначальная спецификация
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
401
GАRСН-модели предполагает, что реакция на шок не зависит от зна
ка шока, а является функцией только от его размера. Тем не менее
один из стилизованных фактов о финансовой волатильности состоит
в том, что плохие новости (отрицательные шоки) обычно оказывают
большее влияние на волатильность, чем хорошие новости (положитель
ные шоки). То есть волатильность стремится быть выше на падающем
рынке, чем на растущем.
[Black (1976))
объясняет этот эффект тем, что
плохие новости обычно снижают цену акций, увеличивая коэффициент
рычага (т. е. отношение заемного и собственного капитала) и приводя
к большей волатильности капитала. На основании этого предположе
ния асимметричное воздействие новостей на волатильность обычно на
зывают эффектом рычага. Альтернативные параметризации пытаются
учесть асимметрию поведения волатильности. В этой главе представ
лены наиболее популярные в литературе асимметричные модели.
Модель
EGARCH(p,q)
Простая структура (5.4) накладывает
GАRСН-модели (Nelson, 1991).
•
важные
ограничения
на
Существует отрицательная корреляция между доходностью капи
тала и
изменениями
волатильности доходов,
т. е.
волатильность
обычно растет в ответ на «плохие новости» (избыточная доход
ность меньше ожидаемой) и падает в ответ на «хорошие новости»
(избыточная доходность выше ожидаемой). GАRСН-модели, тем
не менее, предполагают, что только величина, но не положитель
ность или отрицательность неожиданной избыточной доходности
определяет иl. Если распределение
Zt
симметрично, изменение
дисперсии завтра условно не коррелирует с избыточной доходно
стью сегодня (Nelson (1991)). Если записать иl как функцию лагов
2
ut
и
2
Zt ,
где
2_ 22
et - Zt ut,
т. е.
становится очевидным, что условная дисперсия не зависит от из
менений знака
•
z:. Более того, инновации zl-;иl-; не являются iid.
Другое ограничение
GАRСН-моделей возникает из-за условий
неотрицательности на w* и Фk в
(5.6),
ul
которые накладываются для
обеспечения неотрицательности
для всех t с вероятностью 1. Из
этих ограничений следует, что рост
в любом периоде увеличи
вает иl+m для всех т ~ 1, исключая случайное осциллирование
процесса иl.
zl
ГЛ.
402
•
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
GАRСН-модели неспособны объяснить наблюдаемую ковариацию
междr е~ и et-j· Это возможно, только если условная дисперсия
является асимметричной функцией от
•
В модели
ме
и
et-j.
GARCH(l, 1) шоки могут быть устойчивыми в одной нор
затухающими
в
другой,
так
что
условные
GARCH(l, 1)-модели могут взрываться, даже
моменты
когда процесс строго
стационарный и эргодичный.
•
GАRСН-модели, по сути, специфицируют поведение квадратов
данных. Поэтому несколько больших наблюдений могут домини
ровать в выборке.
Асимметричные модели дают объяснение так называемому эффек
ту р·ычага,
когда
неожиданное
падение
цены
увеличивает
волатиль
ность больше, чем аналогичное неожиданное повышение цены. В экс
поненциальной
GARCH(p, q)-модели (EGARCH(p, q)),
ной в [Nelson (1991)],
предложен
ul впервые зависит как от размера, так и от знака
лагированных шоков. Модель определяется следrющим образом:
q
р
ln (иl) = w+ Lai (Фzt-i + Ф (lzt-il - Е [lzt-il]))+ L.Вi ln (ul-i), (5.13)
i=l
i=l
=
где ai
1, Е [lztl] = (2/1Г) 1 / 2 , если Zt "'iidn(O, 1), и где на параметры
w, .Вi, ai не накладывается ограничение неотрицательности. Положим
g (zt)
По построению,
левым средним.
=
Фzt
+ Ф (lztl -
Е [lztl]).
iid случайная последовательность с ну
Компонентами g (zt) являются Фzt и ф (lztl - Е [lztl]),
{g (zt)}:,_ 00
-
и каждая имеет нулевое среднее. Если распределение
Zt
симметрично,
компоненты ортогональны, хотя не являются независимыми. На мно
< Zt < оо функция g (zt) линейна по Zt с углом наклона ф + ф,
множестве -оо < Zt ~ О g (zt) линейна с углом наклона ф - ф.
жестве О
а на
Таким образом, g (zt) позволяет процессу для условной дисперсии { иl}
асимметрично реагировать на увеличение и падение цены акций. Член
ф
(lztl -
Е
[lztl])
представляет собой эффект величины. Если ф
>
О и
ф =О, инновация в ln (иl+i) положительна (отрицательна), когда вели
чина
Zt
больше (меньше), чем ее математическое ожидание. Если ф =О
и ф <О, инновация в ln(иl+i) положительна (отрицательна), когда ин
новации доходностей отрицательны (положительны). Отрицательный
шок доходностей, увеличивающий отношение заемного и собственного
капитала и, следовательно, неопределенность будrщих доходов, можно
учесть при
ai > О
и ф
< О.
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
403
Как и в случае стандартной GАRСН-модели, модель первого поряд
ка на практике является самой популярной в семействе
Многие авторы, например
[Nelson (1991)],
EGARCH.
обнаружили, что рас
пределение стандартизированных остатков оцененных GАRСН-моделей
имеет положительный коэффициент эксцесса, см. также
В
zalez-Rivera (1991)].
[Nelson (1991)]
[Engle & Gon-
предполагается, что Zt имеет так
называемое GЕD-распределение (также называемое семейством экспо
ненциа.л:ьно-степен:н:ых
распределений).
Плотность
нормированной
(с нулевым средним и единичной дисперсией) GЕD-распределенной слу
чайной величины имеет вид
f (z; v)
где Г
=
vexp [- П) lz/Лlv]
л2<1+1fv>г (1/v) '
-оо < z < оо,
О< v ~ оо,
гамма-функция, а
( ·) -
Л = (2<- 2/v)r (1/v) /Г (3/v)) 112 .
Параметр
z
v
отвечает за толщину хвостов распределения. Если
имеет стандартное нормальное распределение. При
ление
z
v = 1z
v < 2
v = 2,
распреде
имеет более толстые хвосты, чем нормальное (например, при
имеет двойное экспоненциальное распределение), а при
распределение
v >2
имеет более тонкие хвосты, чем нормальное (напри
оо z равномерно распределена на отрезке [-3 112 , 3112 ]).
z
мер, при v =
Для такой функции плотности Е [lztl]
=
Л2 1 fvг (2/v) /Г (1/v) [Hamilton
(1994)].
Для анализа стационарности перепишем модель
EGARCH(p, q)
в ви-
де
~ ,В;L') ln (U:) ="' + t,a;L'(фz, + 'Ф (lz,I - Е [lztl])),
( 1-
ln
(иl)
( 1-
t,.в.)- 1 "' + ( 1- p,L')-l (t,a,L') g (zt),
00
ln (иl)
-
w*
+ L1Pi9 (zt-i).
i=l
В EGARCH(p, q)-модели ln (иl)
онарность
(ковариационную
-
линейный процесс, поэтому его стаци
или строгую) и эргодичность легко уста
новить. В этом важная разница по сравнению с GАRСН-моделями, для
ГЛ.
404
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
которых сложно оценить устойчивость шоков дисперсии. Если ф
=/=
О
или ф =/=О, процессы {exp(-w*)cтl} и {exp(-w*/2)et} строго стацио
нарны и эргодичны, а процесс {ln (ul) - w*} ковариационно стационаоо
рен тогда и только тогда, когда L,q;~ <О см. [Nelson (1991)]. Поскольку
i=l
процесс ln (стl) записан в форме ARMA(p, q), если полиномы 1- Ef3ixi
i=l
и
q
.
L, aixi
не имеют общих корней, то условия строгой стационарности
i=l
ln (иl)
эквивалентны требованию, чтобы все корни
1-
Е f3ixi лежали
i=l
вне единичного круга.
Из строгой стационарности {ехр (-w*) стl} и {ехр (-w* /2) E:t} необя
зательно следует ковариационная стационарность ul, так как
{ехр (-w*) иl} и {ехр (-w* /2) E:t} могут не иметь конечные безусловные
среднее и дисперсию. Для некоторых распределений
{zt}
(например,
для t-распределения Стьюдента с конечным числом степеней свободы),
конечные безусловные моменты { ехр (-w*) стl} и {ехр (-w* /2) E:t} не су
ществуют. Если Zt имеет GЕD-распределение с более тонкими хвостами,
чем у двойного экспоненциального распределения, и если
00
L, q;~ <
оо,
i=l
то { ul} и {E:t} не только строго стационарны и эргодичны, но и имеют
произвольные конечные моменты, из чего следует их ковариационная
стационарность.
В [Не
et al. (2002)]
замечено, что убывание автокорреляций квадра
тов наблюдений в модели
EGARCH
первого порядка быстрее экспонен
циального в начале, а затем замедляется, достигая экспоненциального
падения. Более того,
метричная
[Malmsten & Terasvirta (2004)] показали, что сим
EGARCH(l, 1)-модель с нормальными остатками недостаточ
но гибка для характеризации рядов как с большим эксцессом, так и с
медленно убывающими автокорреляциями. В этом случае выбор рас
пределения стандартизированных остатков особенно важен. Предполо
жение о нормальных остатках означает, что автокорреляция квадратов
наблюдений первого порядка растет достаточно быстро как функция от
эксцесса для любого фиксированного значения
ние замедляется.
[Nelson (1991)]
f31,
прежде чем увеличе
предложил использовать для остатков
GЕD-распределение, в то время как выбор t-распределения может озна
чать бесконечную безусловную дисперсию
GARCH(l, 1),
{et}·
Как и в случае модели
выбор распределения остатков с более толстыми, чем у
нормального распределения, хвостами увеличивает эксцесс и в то же
время уменьшает автокорреляцию квадратов или абсолютных значе
ний наблюдений.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
5.1.
405
Другие асимметричные модели
Нелинейная
GARCH(p, q)-модель [Engle & Bollerslev (1986)]:
q
иl
= w
р
+ L:ai let-i - kl + L.Вiиl-i,
6
i=l
где k =/= О и инновации в
ul
i=l
зависят как от размера, так и от знака
лагированных остатков, улавливая таким образом эффект рычага в во
латильности доходности капитала.
Модель
предложенная в
GJR-GARCH,
[Glosten et al. (1993)]:
q
р
ul = w + L.Вiul-i + L (aie~-1 + 'Yis;_ie~-i) ,
i=l
i=l
где
s; =
{ 1,
О,
et <о,
et ~О,
относится к так называемым пороговым.
Асимметричная
ная в
GARCH(p, q)-модель (AGARCH),
предложен
[Engle (1990)]:
q
р
ul = w + L:ai (et-i + 'У) 2 + L.Вiul-i·
i=l
i=l
Отрицательные значения 'У означают, что положительные шоки ве
дут к меньшим увеличениям будущей волатильности, чем отрицатель
ные шоки той же абсолютной величины.
Нелинейная
(1993)]
AGARCH(l, 1)-модель {NAGARCH)
[Engle & Ng
имеет вид:
Так называемая квадратичная
(1995)]
из
QGARCH(p, q)-модель
из
[Sentana
определяется соотношением:
р
O"t2 =О" 2
/ АXt-q + '°'!3
2
+ Ф' Xt-q + Xt-q
L- iO"t-i1
i=l
где
Xt-q
= (et-1, ... , E:t-q) 1•
Линейный член (Ф'xt-q) допускает асим
метрию. Внедиагональные элементы симметричной матрицы парамет
ров А учитывают эффекты взаимодействия лагированных значений Xt
на условную дисперсию. Условная дисперсия
ul
положительна тогда
Гл.
406
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
и только тогда, когда А в квадратичной форме положительно опреде
лена. Модель
QGARCH
включает как частные случаи несколько асим
метричных моделей. Обобщенная расширенная АRСН-модель
являющаяся обобщением ААRСН-модели из
{AARCH),
[Bera et al. {1992)), предпо
лагает, что Ф =О. Модель
ARCH(q)
Ф =О, fЗi =О,
и А диагональна. Асимметричная GАRСН
i = 1, ... ,q,
соответствует случаю, в котором
модель предполагает диагональную А. Модель линейного стандартно
го отклонения соответствует значениям fЗi = О, и 2 = р2 , Ф = 2рф и
А= фф':
Кривая воздействия новостей
Новости оказывают асимметричное воздействие на волатильность. В
модели с асимметричной волатильностью хорошие и плохие новости
имеют разную предсказательную силу для будущей волатильности.
Кривая воздействия новостей (КВН),
предложенная в
[Pagan &
Schwert {1990)) и получившая свое название в [Engle & Ng ( 1993)], ха
рактеризует воздействие прошлых шоков доходности на волатильность
доходности, неявное в модели волатильности. Фиксируя информацию
на момент
t- 2 и раньше, можно исследовать подразумеваемую взаимо
связь между C-t-1 и иl. Все лагированные условные дисперсии оценива
ются на уровне безусловной дисперсии доходности акций. КВН связы
вает прошлые шоки доходности (новости) с текущей волатильностью.
Эта кривая указывает на то, как новая информация включается в оцен
ки волатильности.
В GАRСН-модели КВН центрирована в
ct-1
= О. В случае ЕGАRСН
модели кривая достигает наименьшего значения в
C-t-1
=О и экспонен
циально возрастает в обоих направлениях, но с разными параметрами.
GARCH{l, 1):
иl = w + ас-~-1
Если иl_ 1
+ fЗиl-1 ·
= и2 , КВН имеет следующий вид:
EGARCH{l, 1):
ln (иl)
где Zt
= w + fЗ ln (иl-1) + Фzt-1 + 'Ф (lzt-1 I - Е [lzt-1 I]) ,
= ct/Ut. Кривая воздействия новостей имеет вид
2 -(
O"t -
Аехр ~ф; 'Ф €t-1J, при C-t-1 >О,
Аехр
ф- 'Ф
О"
C-t-1
,
при ct-1 <О,
5.1.
407
=и2Р ехр ( w - Ф#), ф < О, ф + ф > О.
где А
•
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
Модель
позволяет хорошим и плохим новостям иметь
EGARCH
различный эффект на волатильность, в отличие от стандартной
GАRСН-модели.
•
Модель
EGARCH
позволяет важным новостям иметь большее воз
действие на волатильность по сравнению с обычной GАRСН
моделью. В ЕGАRСН-модели дисперсия в обоих направлениях вы
ше,
поскольку экспонента в конечном счете доминирует квадра
тичную функцию.
Для асимметричной
GARCH{l, 1)-модели [Engle {1990)]
иl = w +а (c:t-1 + 'У) 2 + /3иl-1
КВН, имеющая вид
иl = A+a(C:t-1 +'У) 2 ,
где А= w + {3и 2 , w >О, О~ /3
центрирована в
E't-1
< 1,
и > О, О~ а< 1, асимметрична и
=-'У·
Для GJR-GARCH-мoдeли
ul = w +ас:~+ f3ul_ 1 + 'Y8t- 1 c:~-1
КВН имеет вид
2 _ {
O"t -
где А
=w +
А+ ас:~_ 1 ,
C:t-1 ~ О,
А + (а+ 'У ) c:t-1,
2
C:t-1 < О,
{3и 2 , w > О, О ~ /3
центрирована в
C:t-1 =
< 1,
и > О, О ~ а
< 1,
а+ /3
< 1,
и
-'У.
Эти различия между кривыми воздействия новостей имеют боль
шие последствия для выбора портфеля и ценообразования активов. По
скольку предсказуемая волатильность рынка связана с рыночной пре
мией, две модели ведут к очень разным рыночным рисковым преми
ям, а следовательно, разным рисковым премиям для индивидуальных
акций в условной версии модели САРМ 5 . Различия в предсказуемой
волатильности после выхода некоторой важной новости ведут к суще
ственным различиям текущей цены опционов и разным динамическим
стратегиям хеджирования.
5 САРМ
- Capital Asset Pricing Model (модель ценообразования на основной ка
(2005)), с. 31.
питал), см., например, [Берндт
ГЛ.
408
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.1.6.
Нелинейные и порговые GАRСН-модели
GARCH
с плавным переходом
Реакция условной дисперсии на шоки может быть нелинейной, как,
например, в модели
GARCH
GJR-GARCH.
Нелинейная версия модели
GJR-
получается, если сделать переход меж.цу режимами плавным.
Модель
GARCH с плавным переходом STGARCH [Gonzalez-Rivera
(1998)], и [Anderson et al. (1999)] позволяет эффекту квадратов про
шлых инноваций зависеть как от знака, так и от величины €t-i через
функцию плавного перехода:
где функция перехода имеет вид
G(-y,
с; Et-i) =
( 1+
ехр {-'У П (Et-i -
(подробнее см., например, в [Росси
Пороговая
ck)}
)-!
(2010)]).
GARCH (TGARCH)
В пороговой GАRСН-модели, предложенной в
[Zakolan (1994)],
условное
стандартное отклонение определяется соотношением:
q
at =
р
w + L(aici-i
- aici"-i) + L f3iat-i,
i=l
где ci-i
i=l
= max (ct-i, О), ct-i = min (ct-i, О), и at, а;, i = 1, ... , q, -
пара
метры. ТGАRСН-модель линейна по параметрам, поскольку пороговый
параметр полагается равным нулю. АRСН-модель с двойным порогом
(DTARCH),
условного
предложенная в
среднего
и
[Li & Li (1996)],
дисперсии
меняться
в
позволяет параметрам
зависимости
от
режима.
Условное среднее определяется следующим образом:
(5.14)
а условная дисперсия имеет вид
(5.15)
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
409
где Ь и
d - параметры запаздывания, Ь, d ~ 1. Число режимов в (5.14) и
(5.15),
К и
L,
соответственно, не должно совпадать, как и две порого
вые переменные. Можно использовать другие пороговые переменные,
помимо лагов
GARCH
Yt.
с марковскими переключениями
Модель с марковскими переключениями
(MS)
имеет нелинейную спе
цификацию, в которой различные состояния среды воздействуют на
динамику временного ряда. Динамические свойства зависят от теку
щего режима, а сами режимы являются реализациями скрытой мар
ковской цепи с конечным пространством состояний. Модели с марков
скими переключениями были введены в мейнстрим эконометрики в
[Hamilton (1989, 1990)]. [Hamilton & Susmel (1994)]
заметили, что по
следствия очень больших шоков, таких как биржевой крах в октябре
1987г., для последующей волатильности могут настолько отличаться от
последствий малых шоков, что стандартная
ARCH
или GАRСН-модель
неспособны это уловить надлежащим образом. Более того, они разли
чают режимы с низкой, средней и высокой волатильностью в данных о
недельных доходностях акций, причем режимы высокой волатильности
связаны с рецессиями, в то время как
[Maheu & McCurdy (2000)] выде
ляют «рынки медведей и быков~ и обнаруживают, что волатильность
намного выше на медвежьих рынках.
Модель
ARCH с переключением режимов (SWARCH), независимо
предложенная в [Cai (1994)] и [Hamilton & Susmel (1994)], расширяет
стандартную линейную АRСН(q)-модель, позволяя константе, Ws(t)' или
величине квадратов инноваций, входящих в уравнение условной диспер
сии, зависеть от некоторой латентной переменной
s(t),
причем переход
между разными состояниями происходит в соответствии с марковской
цепью. Модель из
[Hamilton & Susmel (1994)] выглядит следующим об
разом:
q
и~= w(st) +
L ai(st)e~-i'
(5.16)
i=l
где St -
дискретная ненаблюдаемая эргодичная марковская цепь, за
данная на множестве § = { 1,
... , S}
индикаторов режимов с переход
ными вероятностями
Pij
где по определению
= P{st = jlst = i},
E;es Pij
реключениями переменная
i,j
= 1, ... , S,
= 1, \:/i Е §. В моделях с марковскими пе
переключения
St
экзогенна в том смысле,
что она не подвержена обратному воздействию со стороны наблюда
емого процесса. При q
= 1
D[etlst
=
i, et-1)
=
w(i)
+ a1(i)c:~_ 1 .
Эта
ГЛ.
410
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
модель позволяет
al меняться между режимами высокой и низкой во
латильности, что измеряется значениями параметров
рассматривает частный случай
константа
w(st)
и
S
=
2.
(5.16),
ARCH. Cai (1994)
в котором переключается только
Обобщение моделей с марковскими переклю
чениями на случай GАRСН-моделей было предложено в
и
[Dueker (1997)] и позже модифицировано в
GARCH(l, 1) с марковскими переключениями
[Gray (1996)]
[Klaassen (2002)]. Модель
имеет вид
Условия стационарности, существование моментов, автокорреляци
онные функции и эргодичность были изучены в
[Francq et al. (2001)]
и
[Francq & Zakolan (2005)].
Подробнее о моделях с марковскими переключениями и о так на
зываемых обобщающих моделях см., например, в [Росси
5.1. 7.
Модели
GARCH
в среднем
(2010)].
(GARCH-M)
GАRСН-модели часто используют для прогнозирования риска портфе
ля в определенный момент времени.
[Engle et al. (1987)]
рассматривают
экономику, в которой не склонные к риску агенты выбирают из двух
видов финансовых вложений, чтобы максимизировать свою ожидае
мую полезность. Первая возможность представлена рисковым активом
с нормально распределенной доходностью, для которого риск измеря
ется дисперсией доходности, а компенсация
-
ростом ожидаемой до
ходности. Второй тип инвестиций представлен безрисковым активом.
Максимизация агентами своей функции полезности при условиях ба
ланса на рынках приводит к стандартной связи между математическим
ожиданием и дисперсией доходности рискового актива. Авторы иссле
дуют эту взаимосвязь в случае, когда дисперсия доходности рискового
актива меняется во
времени,
а следовательно,
меняется
и
цена рис
кового актива. Приведенные предположения определяют взаимосвязь
между средним и дисперсией доходности актива, которая по-прежнему
положительна, но не постоянна. Из этого следует, что модель условной
дисперсии наподобие
GARCH
может быть полезным представлением ме
няющейся во времени рисковой премии при объяснении избыточной до
ходности. Избыточная доходность в таком случае является комбинаци
ей непредсказуемой разности
et между ожидаемой и реализованной нор
мами доходности и функции условной дисперсии портфеля
[Terasvirta
(2009)). Таким образом, если Yt - избыточная доходность на момент t,
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
модель
GARCH
в среднем
(1987)],
представляет собой систему
(GARCH-M),
предложенная в
411
[Engle et al.
Yt ="У+ g (иl) - E[g (и;)]+ et,
и; = w +
q
р
i=l
i=l
L aie~-i + L /3iи;_i.
(5.17)
Эта модель одновременно характеризует динамику среднего и дис
персии временного ряда.
[Engle et al. {1987)] использовали функцию g (и;) = o/U[, но аль
тернативные варианты g (и;) = ln (и;) и g (и;) = иt также предлага
лись в литературе. Процесс GARCH-M обладает интересной структурой
моментов. Предположим, что E[zl] = О и E[ef] < оо. Из уравнения
(5.17) следует, что
Е [(Yt - E[yt])(Yt-k - E[yt])] = E[et-k9(ul)] + cov[g(ul), g(и;_k)].
Это означает, что в
Yt
присутствует прогнозируемая компонента.
Более того,
E[(Yt-E[yt]) 3 ] = 3Е [ul (g(ul) - E[g(ul)])]+E [ (g(ul) - E[g(ul)]) 3 ] ~О.
Отсюда следует, что модель
GARCH-M
подразумевает скошенное
частное распределение Yt, если только g(ut) не константа. При (g(ul)
= OUt и о < О это частное распределение отрицательно скошено.
5.1.8.
На
=
GАRСН-модели с долгой памятью
практике
часто
случается,
что
оценка
суммы
параметров
GARCH(l, 1)-модели, а1 + Р1, близка к единице. Другими словами, ока
зывается, что модель IGARCH(l, 1) является разумным приближени
ем процесса, порождающего данные. Однако применение IGARCH(l, 1)
означает предположение о том, что безусловная дисперсия моделируе
мого процесса не существует. Более того, в модели
IGARCH
воздействие
шока на оптимальный прогноз будущей условной дисперсии приводит
к тому,
что соответствующие накопленные веса импульсного отклика
сходятся к ненулевой константе, так что прогнозы линейно возраста
ют по мере расширения горизонта прогнозирования. Это означает, что
ценообразование рисковых ценных бумаг, включая долгосрочные опци
оны и фьючерсы, может крайне сильно зависеть от начальных условий
или текущего состояния экономики. Но такая сильная зависимость не
соответствует наблюдаемому поведению цен.
[Taylor (1986)], [Dacorogna
et al. (1993)], [Ding et al. (1993)] указывают на явные признаки долгой
ГЛ.
412
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
памяти в рядах эмпирических автокорреляций для абсолютных зна
чений и квадратов доходностей различных финансовых активов. Эти
исследования четко свидетельствуют в пользу моделей с автокореляци
ями, медленно убывающими по лагу как функция
о< 'У<
k-'Y,
для некоторого
1.
Хотя эмпирический анализ свидетельствует о том, что долгая па
мять
-
это свойство квадратов или абсолютных значений доходностей,
нет согласия по поводу возможных причин этого стилизованного фак
та.
[Granger & Ding (1996)) показали, что текущее агрегирование ста
бильных GARCH(l, !)-процессов дает агрегированный процесс с гипер
болически убывающими автокорреляциями. Хотя это свойство вроде
бы согласуется с долгой памятью,
[Zaffaroni (2007))
показал, что ав
токорреляционная функция этого процесса суммируема, что не позво
ляет классифицировать его как процесс с долгой памятью.
& Bollerslev (1997))
[Andersen
показывают, что текущее агрегирование потоковых
процессов со слабо зависимой информацией может привести к долгой
памяти в рядах волатильности. Еще одно обоснование приводят
et al. (1997)),
[Miiller
предполагая, что долгая память в рядах волатильности
может возникать из-за реакции краткосрочных дилеров на динамику
прокси-переменной для тренда ожидаемой волатильности (грубой во
латильности), что ведет к устойчивости процессов волатильности для
более высоких частот (очищенной волатильности).
Если приведенные выше статьи исследовали причины долгой памя
ти в рядах волатильности, то другие, в сущности, ставили под сомнение
само наличие долгой памяти. В частности, один из аргументов состоит
в том, что структурные сдвиги различных типов способны объяснить
крайнюю устойчивость волатильности, а также могут порождать ряд,
который выглядит как ряд с долгой памятью.
и
[Granger & Hyung (2004))
[Mikosch & Starica (1998))
приводят теорию и симуляции в подтвер
ждение того, что ложные свидетельства долгой памяти можно обна
ружить во временном ряде со сдвигами. Более того, хотя
Hyung (2004)) показали для
декса S&P500, что модель с
[Granger &
ряда абсолютных значений доходности ин
нерегулярными сдвигами обладает худшей
предсказательной силой, чем модель с долгой памятью; для того же
ряда
[Starica & Granger (2005))
получили, что нестационарная модель,
позволяющая сдвиги в безусловной дисперсии, превосходит модель с
долгой памятью при прогнозировании, но не на коротком горизонте.
[Diebold & Inoue (2001))
также показали, как процессы с марковскими
переключениями могут порождать долгую память в условном среднем,
а
[Granger & Terasvirta (1999))
показали, что процесс с переключениями
знака обладает признаками процесса с долгой памятью. Возможное на
личие структурных сдвигов в условной дисперсии как причину крайней
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
устойчивости в форме
Lastrapes (1990)]
и
IGARCH изначально
[Diebold (1986)].
предложили
413
[Lamoureux &
Долгосрочная зависимость, или долгая память (иногда также на
зываемые строгой зависимостью или устойчивостью), означает устой
чивое поведение временных рядов. Концепция долгой памяти впервые
была разработана в
[Hurst (1951)].
Долгую память можно определить
в терминах скорости убывания автокорреляций для больших лагов.
В частности, стационарный процесс обладает долгой памятью (или дол
госрочной зависимостью), если существует вещественное число
станта ер
> О,
такие, что
.
p(k)
11m
k-+oo
где
p(k) -
d и кон
Ср
k2d-l
автокорреляция для лага
k,
= 1,
а
d-
параметр долгой памяти.
Автокорреляции процесса с долгой памятью несуммируемы. Альтерна
тивное, хотя и не эквивалентное определение долгосрочной зависимости
можно дать, используя спектральную плотность
f(Л)
lim
Л-+О+ CJIЛl- 2 d
Спектральная плотность
дет себя как константа
Cf,
=
1,
f (Л)
процесса:
О< Cf < оо.
f (Л) имеет полюс и в начале координат ве
помноженная на л- 2 d. Автокорреляции ста
ционарного и обратимого АRМА-процесса геометрически ограничены,
т. е. lp(k)I ~ ст-k, где О
<
т
< 1,
и, следовательно, это процесс с ко
роткой памятью. Популярный подход к моделированию долгой памяти
состоит в использовании класса моделей
ARFIMA (the AutoRegressive,
Fractionally Integrated, Moving А verage models), предложенного в
[Granger & Joyeux (1980)] и [Hosking (1981)]. Он обобщает АRIМА
модели, позволяя дробную степень интегрированности. В классе
l (d)
дробно интегрированных дискретных процессов с долгой памятью в
дискретном времени распространение шоков среднего происходит с мед
ленной гиперболической скоростью убывания, по сравнению с крайни
ми случаями: классом стационарных и обратимых
1(0) процессов ARMA
с экспоненциальным убыванием и классом 1(1)-процессов с бесконечной
устойчивостью.
Класс моделей
ARFIMA(k, d, l)
для дискретного процесса
щественными значениями имеет вид (см.
{yt} с ве
[Granger & Joyeux (1980)] и
[Hosking (1981))):
a(L)(1 - L)dYt = Ь(L)et,
где
a(L) и Ь(L) - полиномы от L порядков k и l, соответственно,
а {et}- сериально некоррелированный процесс с нулевым средним. Все
Гл.
414
корни
a(L)
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
и Ь(L) лежат вне единичного круга. Процесс определяется
как I(d). Оператор дробной разности, (1-L)d, имеет биномиальное раз
ложение. Используя разложение Тейлора-Маклорена в точке z = О,
получаем
(d)j -
= 1-dL+ d( d21- 1) L 2 + ... = ~
L...J (d)
. (-1)3.z3,.
(1-z) d
.
з=
о
J
d!
{d-j)!j!"
Коэффициенты при /) убывают медленно и асимптотически про
порциональны j-(l+d). Учитывая, что Г(j + 1) = j! = jГ(j), где Г(j) =
= 000 xj-l ехр (-x)dx, j > О, - гамма-функция, можно записать
J
d!
Г(j - d)
( d)
j - (d- j)!j! - Г(-d)Г(j + 1).
Тогда получаем
~
d
(d)
··
~
d)
Г(j -
.
(1-L) = ~ . (-1)3z3=~Г(-d)Г(.+1)L3 =
з=О J
з=О
J
00
= LФjLj = F(-d,1,1;L),
j=O
где
F(-d, 1, 1; L) -
F(m,n,s;x)
гипергеометрическая функция, определяемая как
=
00
=
Г(s)Г(т)- 1 Г(п)- 1
LГ(т + j)Г(п + j)Г(s + л- 1 г(j
+ 1)- 1xi.
j=O
Если
V[et] < оо и -1/2 < d < 1/2, процесс {Yt} является сла
бо стационарным и обратимым и единственным образом представим
в виде скользящего среднего и авторегрессии бесконечных порядков.
При
d
<1
процесс возвращается к среднему. При
является ковариационно стационарным,
Модель
ARFIMA
1/2 < d < 1, Yt
не
но возвращается к среднему.
разделяет краткосрочную и долгосрочную динамику,
улавливая краткосрочное поведение с помощью обыкновенных лаговых
полиномов
ARMA, a(L)
интегрированности
Модель
и Ь(L), а долгосрочное
-
параметром дробной
d.
(Fractionally Integrated Generalized
Autoregressive Conditional Heteroskedasticity Models). Процесс
FIGARCH, предложенный в [Baillie et al. {1996)], объединяет многие
FIGARCH
свойства дробно интегрированных процессов для среднего с обыкно
венным GАRСН-процессом для условной дисперсии. Модели
FIGARCH
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
415
свойственна медленная гиперболическая скорость убывания лагирован
ных квадратов инноваций в условной дисперсии, хотя накопленные ве
са импульсных откликов, связанных с воздействием шока волатильно
сти на оптимальные прогнозы будущей условной дисперсии, сходят
ся к нулю. Это свойство модель разделяет со слабо стационарными
GАRСН-процессами. Модель
FIGARCH
предлагает альтернативу подхо
ду, рассматривающему изменения параметров GАRСН-модели как глав
ную причину медленного убывания автокорреляций. Тем не менее свой
ство долгой памяти (и даже существование стационарного режима) для
модели
FIGARCH не доказано (см. [Giraitis et al. (2000)], GARCH(p,q)пpoцecc как ARMA(m,p) для€~, где т = max(p,q),
(1 - a(L) - {З(L))е~ = w + (1 - {З(L))vt,
Vt = €t - и;,
является последовательностью мартингальных приращений. В ковари
ационно стационарной GАRСН-модели эффект квадратов прошлых
остатков на текущую условную дисперсию экспоненциально убывает по
величине лага. Если авторегрессионный полином 1- а(х) -{З(х) содер
жит единичный корень, получаем модель
IGARCH(p, q),
определяемую
как
ф(L)(1 - L)e~
= w + (1 -
{З(L))vt,
где ф(L)
= (1-a(L)-{З(L))(1-L)- 1 имеет порядок т-1, т = max(p, q).
Модель
FIGARCH
получается простой заменой оператора
ратором дробной разности. Аналогично
среднего,
FIGARCH(p, d, q)
для
{et}
(1 - L)
опе
ARFIMA(k, d, l)-процессу
для
естественно определяется как
ф(L)(1 - L)de~ = w + (1 - {З(L))vt,
где О< d
(1- fЗ(L)) лежат вне единичного кру
га. Это означает, что процесс для {с~} является ARFIMA(m - 1,d,p).
< 1,
и все корни ф(L) и
Учитывая, что Vt = €~ - и;, альтернативное представление модели
FIGARCH(p, d, q) имеет вид
(1 - {З(L))иt = w + (1- {З(L) - ф(L)(1 - L)d)e~,
и;= (1 - f3(1))- 1w + Л(L)е~,
(5.18)
где
= 1 - (1 - {З(L))- 1 ф(L)(1 - L)d
Л1L + Л2L 2 + ЛзL3 + .. " FIGARCH(p, d, q)-модель
Л(L)
и Л(L) но определена, и иl
>
О п.н. для любого
t,
коррект
если все коэффициенты
бесконечного АRСН-представления неотрицательны, т. е. Лk
k =
О,
1, 2, ....
При О
< d < 1 F(-d, 1, 1; L = 1) =
>
О для
О, так что Л(l) =
1.
ГЛ.
416
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Следовательно, второй момент безусловного распределения
et
бесконе
чен, и FIGARCH-пpoцecc не является слабо стационарным. Это свой
ство он делит с классом IGАRСН-процессов.
[Baillie et al. (1996)]
утвер
ждают, что, поскольку лаги высоких порядков в бесконечном АRСН
представлении любой FIGАRСН-модели могут доминироваться в смыс
ле абсолютных значений соответствующими IGАRСН-коэффициентами,
класс
FIGARCH(p, d, q)
Однако
строго стационарен и эргодичен для О~
доказательство
существования
стационарного
d
~
1.
решения
(5.18), приведенное в [Baillie et al. (1996)], по всей видимости, неверно
(см. [Giraitis et al. (2007)]). Вопрос существования стационарного реше
ния уравнения FIGARCH («проблема FIGARCH~) остается открытым и
весьма сложным. [Giraitis et al. (2000)], [Mikosch & Starica (2000, 2003)]
обсуждают споры вокруг FIGАRСН-модели.
Модель FIGARCH(p, d, q) включает ковариационно стационарную
GARCH(p, q)-модель при d = О и IGARCH(p, q)-модель при d = 1. Ес
ли позволить параметру d принимать значения в интервале от нуля до
единицы, модель получает дополнительную гибкость, что важно при
моделировании долговременной зависимости в условной дисперсии.
Следует проявлять осторожность при интерпретации устойчивости
в нелинейных моделях. В случае, когда условная дисперсия являет
ся линейной функцией прошлых е~, устойчивость просто характеризо
вать в терминах коэффициентов импульсного отклика для оптималь
ного прогноза будущей условной дисперсии как функции от инновации
в момент времени
t,
щ:
_ дEt[e~+k]
'Yk
=
д
Vt
-
дEt[e~+k-i]
д
Vt
.
В более общих моделях условной дисперсии параметры
информационного множества на момент
t.
В моделях
фициенты импульсного отклика не зависят от
по коэффициентам лагового полинома
(1-L)e~
=
t.
'Yi зависят от
FIGARCH коэф
Их можно определить
-y(L):
(1-L) 1 -dф(L)- 1 w+(1-L) 1 -dф(L)- 1 (1-,8(L))vt
= (+-y(L)vt
Долгосрочное воздействие прошлых шоков на процесс волатильности
теперь можно оценить в терминах предела накопленных весов импульс
ного отклика. Действительно,
а
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
417
Тогда
k
f'(l) = lim
2: 'Yi =
k~oo i=O
lim Лk = F(d - 1, 1, 1; l)ф(l)- 1 (1 - ,8(1)).
k~oo
В ковариационно стационарной
< d < 1 шоки
модели с О
GARCH(p, q)-модели и FIGARCH(p, d, q)-
в условной дисперсии в конечном счете исче
зают с точки зрения прогнозирования. В то время как шоки в GАRСН
процессах
(d
=О) убывают с быстрой экспоненциальной скоростью, в
FIGАRСН-модели Лk доминируется гиперболической скоростью убыва
ния. Таким образом, несмотря на то, что кумулятивная функция им
пульсного отклика сходится к нулю при О ~
d
< 1,
параметр дробной
разности несет важную информацию относительно того, как и с какой
скоростью распространяются шоки волатильности. С другой стороны,
при
d = 1 F (d - 1, 1, 1; 1) = 1,
и накопленные веса импульсных откликов
сходятся к не равной нулю константе f'(l) = ф(l)- 1 (1-,8(1)). Поэтому с
точки зрения прогнозирования шоки a'f в модели IGARCH сохраняются
навсегда. При d > 1F(d-1,1, 1; 1) = оо, что ведет к не наблюдаемому в
данных взрывному процессу для условной дисперсии, и
f'(l)
становится
не определена.
Рассмотрим в качестве примера модель
а; = w + а1е~_ 1
в форме
где Ф1
GARCH(l, 1)
+ ,Ваl-1
ARMA:
=
а1
(1 - Ф1L )е~
= w + (1 - ,81L )vt,
+ ,81. Веса импульсных откликов для этой модели являются
коэффициентами полинома
т.е.
')'О
1,
1'1
l'k
Ф1
- ,81 - 1,
(Ф1 -,81)(Ф1 - l)Ф~- 2 , k > 2.
Накопленные веса импульсных откликов равны
Лk
и в пределе
f'(l) = О,
= (Ф1 - .В1)Ф~- 1 , k > 1,
если О < Ф1 < 1. Следовательно,
эффект шока
на прогноз будущей условной дисперсии сходится к нулю с быстрой
экспоненциальной скоростью. В модели
IGARCH(l, 1), т. е. при Ф1
(1 - L)e~ = w + (1 - ,81L)vt,
= 1,
Гл.
418
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
коэффициенты Л(L) имеют вид
лk
= (1 - /31),
Vk
> 1,
и накопленные веса импульсных откликов равны ненулевой константе
1'(1)
= 1-/31.
Модель
FIGARCH(l,d,O)
имеет вид
(1 - Ф1L)de~ = w + (1 - f31L)vt.
Можно показать, что накопленные коэффициенты отклика в АRСН
представлении бесконечного порядка для
FIGARCH(l, d, 0)-модели
равны
при
k
> 1 и Ло = 1. Поэтому, если w > О, условие О
~
/31 < d ~ 1 являет
ся необходимым и достаточным для гарантии, что условная дисперсия
в
FIGARCH(l, d, 0)-модели
положительна п.н. для всех
формулы Стирлинга следует, что для больших лагов
В отличие от ковариационно стационарной
модели
IGARCH(l, 1), в которых
t.
Более того, из
k
GARCH(l, 1)-модели или
воздействие шоков условной дисперсии
либо экспоненциально убывает, либо сохраняется бесконечно, в модели
FIGARCH(l, d, О)
реакция условной дисперсии на прошлые шоки убыва
ет медленно, гиперболически.
Модели
FIEGARCH
Поскольку оценки стандартной
GARCH(p, q)-модели
часто указывают
на близкий к единичному корень в авторегрессионном полиноме, при
оценивании модели
EGARCH(p, q), имеющей вид (5.13), наибольший ко
рень оцененного полинома 1 - fi(x) очень близок к единице. Тем не
менее, как заметил [Nelson (1991)), модель EGARCH(p, q) также можно
расширить, позволив дробный порядок интегрированности. В работе
[Bollerslev & Mikkelsen (1996)) предложено разложение на множители
авторегрессионного полинома (1 - fЗ(L)) = ф(L)(1 - L)d, где все кор
ни ф(х) = О лежат вне единичного круга. Тогда модель может быть
записана в виде
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
419
где o(L) = 01L+o2L 2 + . .. +oqLq. Очевидно, модель FIEGARCH(p,d,q)
включает в себя обычную ЕGАRСН-модель при d = О и интегрирован
ную ЕGАRСН-модель при d = 1. По аналогии с классом ARFIMA моделей
условного среднего, {ln (af)} является ковариационно стационарным и
обратимым при
-1/2 до 1/2. Шоки на оптимальные
прогнозы будущих значений ln (af) исчезают при всех d < 1. Более то
го, в отличие от формулировки FIGARCH, параметры FIEGARCH необя
d
в интервале от
зательно должны удовлетворять каким-либо ограничениям неотрица
тельности, чтобы модель была корректно поставлена.
5.1.9.
Процедуры оценивания параметров моделей
По сравнению с другими моделями волатильности (например, стандарт
ной моделью стохастической волатильности) GАRСН-модели легче оце
нивать, что сильно способствовало их популярности. Поскольку вола
тильность является функцией прошлых наблюдений, функция прав
доподобия имеет явный вид и с ней просто работать, см.
Zakoi'an (2009)).
[Francq &
Оценивание АRСН-моделей методом наименьших квад
ратов и максимального квазиправдоподобия рассмотрено в пионерской
статье Энгла
[Engle (1982)).
Асимптотические свойства оценки мето
дом максимального квазиправдоподобия (ММКП) получили широкий
интерес за последние
20 лет. Первые статьи ограничивались моделя
ми ARCH (см. [Weiss (1986))) или GARCH(l, 1) [Lee & Hansen (1994)),
[Lumsdaine (1996)). ММКП-оценивание общей GARCH(p, q)-модели изу
чено в [Berkes & Horvath (2003), (2004)], [Berkes, Horvath & Kokosza
(2003)), [Francq & Zakoi'an (2004)) и [Hall & Уао (2003)). [Straumann
(2005)] является обширной монографией об оценивании GАRСН-мо
делей. Подробнее о реализации обсуждаемых в этих работах подходах к
оцениванию и о свойствах получаемых при этом оценок см., например,
в [Росси
5.1.10.
(2010)].
Процедуры статистической проверки гипотез
Тестирование на АRСН-эффекты
Тесты на наличие АRСН-эффектов подробно рассмотрены в литературе.
Простой и часто применяемый тест нулевой гипотезы
Но
против альтернативы
: 01 =
02 = ... =
oq =
О
Гл.
420
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
хотя бы с одним строгим неравенством
Лагранжа (LМ-тест), предложенный в
- это тест м:ножите.лей
[Engle (1982)]. Тест основан на
так называемой скор-функции и информационной матрице при нуле
вой гипотезе, в предположении, что стандартизированные инновации
нормально распределены. Рассмотрим АRСН-модель в (5.3): иl = (to.
Пусть (t = (1,q_ 1 , ... , q_q), о= (00,01, ... ,oq)', где = Yt - µt(B) остатки. При справедливости нулевой гипотезы
постоянна, т. е.
= и~. Скор-функция гауссовского логарифмического правдоподобия
Zt
et
ul
ul
(см. [Росси
(2010)]) при справедливости нулевой гипотезы имеет вид
где J0 = [( ~ -
1) , ... , ( ~ - 1)]
1
,
и
Z'
= ((~, ... , (~) - (q + 1) х Т
матрица. Матрица вторых производных имеет вид
Отсюда находим информационную матрицу при нулевой гипотезе,
равную среднему по всем
t
ожидаемым значениям условного матема
тического ожидания:
LМ-статистика равна
CLM
~
)'
= _!_ (дLт
-1 (дLт
Т до О Ааа,0 до О
)
•
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
421
LМ-статистику можно состоятельно оценить:
{Lм =
=
/
О'
1 1 2т
/ ]-1 1
[
Z
-2 Z 1
2 -2 -2 (2) LE [(t(t]
1
ио
ио
t=l
2
1 о
ио
=
~1°' z (z'z)- 1 z 1°.
1
Если предположить нормальность, то р lim ( 1°' 1° /Т)
= 2.
Таким
образом, асимптотически эквивалентная статистика имеет вид
{5.19)
где
и
R2
-
квадрат коэффициента множественной корреляции между
1°
Поскольку добавление константы и умножение на число не меняют
R 2 регрессии, это также R 2 регрессии на константу и q лагированных
Z.
q
q.
значений
Статистика имеет асимптотическое хн-квадрат распреде
ление с q степенями свободы, если нулевая гипотеза верна. Тест состоит
в регрессировании квадратов остатков на константу и q лагов и срав
нением Т R 2 с х 2 ( q). Это асимптотически локально наиболее мощный
тест.
Однако LМ-тест
{5.19)
может отвергать нулевую гипотезу при
неверной спецификации уравнения для условного среднего
(5.10).
Мож
но показать, что ошибки спецификации приводят к серийной корреля
ции остатков
ft,
а следовательно, и их квадратов,
q.
Следовательно,
нужно быть аккуратным при спецификации уравнения условного сред
него
в
(5.10) прежде, чем тестировать на АRСН-эффекты.
В [Lee & Hansen {1993)] обсуждается локально наиболее мощный
среднем скор-тест на наличие ARCH и GАRСН-эффектов. Тест осно
ван на сумме скор-функций при нулевой гипотезе, когда мешающие
параметры заменяются ММП-оценками. В отсутствие мешающих па
раметров этот тест локально наиболее мощный в среднем. Затем сум
ма скор-функций стандартизируется путем деления на асимптотиче
скую стандартную ошибку. Полученный тест имеет асимптотическое
N{O, !)-распределение.
Тест-статистики, применяемые для тестирова
ния против АRСН(q)-процесса, можно также использовать для тестиро
вания против
GARCH{p, q)-процесса.
В малых выборках этот тест более
мощный, чем LМ-тест, и его асимптотические критические значения по
меньшей мере так же точны.
Критерии Вальда и отношения правдоподобия
(LR)
также можно
применять для тестирования гипотезы об условной гомоскедастично
сти, например, против
GARCH{l, 1)
в качестве альтернативы.
Гл.
422
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Статистика для тестирования Но: а1
=О против Н1
= f31
:
а1 ~О
или f31 ~ О с хотя бы одним строгим неравенством не следует х 2 распределению с двумя степенями свободы, поскольку стандартное
предположение о том, что истинный параметр при Но не лежит на гра
нице пространства параметров, нарушается.
IGARCH(l,1}
Если
против
необходимо
GARCH(l,1}
тестировать
GARCH{l, 1), можно
(LR), скор-тест (LM)
наличие
использовать
единичного
корня
в
тест отношения правдоподобия
или тест Вальда. Хорошо известно, что при ну
левой гипотезе все три статистики асимптоти-чески распределены как
х 2 (1). Однако их свойства в коне-чнъtх выборках различаются. Предпо
ложим, что истинная модель имеет вид
+ eot, eot l9"t-1 rv N (О, и~t),
2
R
2
""'о + aoeot-1 + tJOO"ot-1,
Yt = µ
2
D"ot =
Определим нулевую гипотезу:
Но
: ао
+ f3o = 1,
или
Но
: g (80) = ао + f3o - 1 =О,
против альтернативы
Н1: ао
+ f3o < 1.
Теперь предположим, что оцениваемая модель верно специфицирована
для условного среднего и дисперсии:
иf =
t.V
+ ac:~-l + {Зиf-1,
т
Lт (8) =
L lt (8),
8 = (µ,""''а, {3)''
А = -Е [д2 lt (80)]
о
t=l
д8д8'
.
Оцененная матрица Гессе имеет вид
д 2 lt (8)
1
Ат (8 ) = -Т L д8д8'
t
'
а в случае GАRСН-моделей
1[12 ~ (
Ат (8) = Т
2)-2
~ иt
диf диt
88 88 ,
~ ( 2)-1 деt дс:t]
+ ~ иt
88 88 ,
·
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
423
Информационная матрица
В = _!_Е [дLт (80) дLт (80)]
о
т
д8
д8'
оценивается с помощью
т
Вт (8 ) =
1 ~ дlt дlt
Т L.-t 88 881 •
t=l
Здесь Ат(О) и Вт(8) - состоятельные оценки А и В, где 8 - ММП
оценка
80.
Если условное распределение ео нормально, то А
= В.
Более
того,
DV'i'(8 -
80) ~ N (О, Ik)
D равна А 112 в случае условного нормального распределения и в- 1 1 2 А
в общем случае.
В
[Lumsdaine (1996))
исследованы свойства в конечных выборках
......
в предположении, что истинное распределение нормально. Пусть 8п и
8u -
ММП-оценки моделей с ограничением и без ограничения соот
ветственно. При нулевой гипотезе следующие статистики имеют х 2 (1)распределение:
{LR
= -2 ( Lт(8п) - Lт(Ои)) ,
~NR = _!_Т (дLт(8n))'
л=1(8R ) (8Lт(8n))
88
"~
88
'
"'LM
{а,н = Tg(liu)' [ ( дg;и)) ЛТ'(liи) ( дg~н)) Г g(liu).
Робастные версии
(5.20)
и
(5.21)
~R = Т_!_ [(дLт(8n))'
А-1(8
) (8g(8n))]
88
Т R
88
Х
[( - )
дg(8п)
88,
1 --
(5.21)
имеют вид
f.,,LM
х
(5.20)
--
1 --
Ат (8п)Вт(8п)Ат (8п)
Х
]-1
х
А-1(8
) (дLт(8n))]
[( дg(8n))
д(}'
Т R
д8
'
{li- = Tg(liu)' [ ( д~:~)) ЛТ'(liи)Вт(liи)ЛТ'(liи) ( дg~н)) ]-' g(liu).
424
ГЛ.
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Статистики Ба.льда (~fi и ~(t,R) равны квадратам (робастной и не
робастной соответственно) t-статистик для
сравнивает робастную и неробастную
g (8) =О. [Lumsdaine (1995)]
версии LM и вальдовской ста
тистик методом Монте-Карло и обнаруживает, что робастные версии
обладают более желательными свойствами размера теста и частоты от
вержения нулевой гипотезы. LМ-тесты склонны к значительному пре
вышению размера при нулевой гипотезе.
Тест на асимметричные эффекты
В каждой модели волатильности неявно присутствует определенная
кривая воздействия новостей. В стандартной GАRСН-модели кривая
воздействия новостей симметрична и центрирована в et-1 =О. То есть
положительные и отрицательные шоки доходности одного размера при
водят к одинаковой волатильности. Кроме того, большие шоки доходно
сти предсказывают большую волатильность, пропорционально квадра
ту размера шока доходности. Если отрицательный шок доходности ве
дет к большей волатильности, чем положительный шок того же разме
ра, прогноз GАRСН-модели занижает объем волатильности вследствие
плохих новостей и завышает его для хороших новостей. Далее, если
большие шоки доходности ве,цут к большей волатильности, чем допус
кает квадратичная функция, прогноз стандартной GАRСН-модели зани
жает волатильность вследствие большого шока доходности и завышает
ее для малого шока доходности.
[Engle & Ng (1993)]
предложили три диагностических теста для
моделей волатильности: тест на смещение для шоков разного знака,
тест на смещение для размера отрицателънъtх шоков и тест на сме
щение для размера положителънъ~х шоков. Эти тесты проверяют, мож
но ли прогнозировать квадрат нормализованных остатков некоторыми
переменными, наблюденными в прошлом, которые не включены в ис
пользуемую модель волатильности. Если эти переменные могут прогно
зировать квадрат нормализованного остатка, то модель для дисперсии
неверно специфицирована. Тест на смещение для шоков разного зна
ка рассматривает воздействие положительных и отрицательных шоков
доходности на волатильность, не прогнозируемое рассматриваемой мо
делью. Тест на смещение для размера отрицательных шоков рассматри
вает разные эффекты, оказываемые большими и малыми отрицатель
ными шоками доходности на волатильность, которые не предсказыва
ются моделью для волатильности. Тест на смещение для размера поло
жительных шоков рассматривает разные эффекты, которые большие и
малые положительные шоки доходности оказывают на волатильность,
не предсказываемые моделью для волатильности.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
5.1.
Для получения оптимальной формы этих тестов в
425
[Engle & Ng
предполагается, что модель волатильности при верной нулевой
(1993)]
гипотезе является частным случаем более общей модели следующего
вида:
(5.22)
где абt (б0 z0t) -
модель волатильности при верной нулевой гипотезе,
бо
- (k х 1) вектор параметров при верной нулевой гипотезе, zot (k х 1) вектор объясняющих переменных при верной нулевой гипотезе,
ба - (т х 1) - вектор дополнительных параметров, Zat - (т х 1) вектор пропущенных объясняющих переменных. Эта форма включа
ет как
GARCH,
так и
EGARCH
модели. Например,
GARCH(l, 1)-модель
соответствует случаю
a~t (б0 zot) = б0 zot, zot = [1,а;_ 1 ,е;_ 1 ]',
бо = [c.v, ,8, а]', ба = [,В*, ф*, 'Ф*]',
Zat
=
(let-11
O't-1
O't-1
2 ) ,et-1
[ log ( O't-l
-,
-
умт=)]'
2/1Г
Обобщающая модель имеет вид
log (а;)
= log (c.v + ,ва;_ 1+ ае;_ 1) + ,8* log (а;_ 1) +
+ ф* et-1 + -ф* ( let-1 I _ .;;ц;)
O't-1
и при а=
,8
=О это модель
,
O't-1
EGARCH(l, 1),
а при ,В*= ф*
=
-ф* =О это
GARCH(l, 1)-модель.
Нулевая гипотеза имеет вид ба= О. Пусть
остаток, соответствующий наблюдению
соответствующей нулевой гипотезе, т.е.
для Но
:
ба
О в
(5.22) -
Vt -
нормализованный
t при модели волатильности,
Vt
= et/Ut.
это тест на ба
=
LМ-тест статистика
О во вспомогательной
регрессии
Vt2
где
*' r + ZatUa
*' r + Ut,
= Z0tUO
* _ -2 (даl) * _ -2 (даl) К даl
z0t = a0t дбо , Zat = a0t дда . ак дбо,
(5.23)
даl
так и дба оценива-
ются в ба= О и до (ММП-оценка до при верной Но). Если ограничения
на параметры соблюдены, переменные в правой части
(5.23)
не должны
иметь объясняющей силы. Поэтому тест часто подсчитывается как
{Lм = TR2,
Гл.
426
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
где R2 - квадрат коэффициента множественной корреляции в {5.23),
а Т - число наблюдений в выборке6 . LМ-статистика имеет асимптоти
ческое распределение хн-квадрат с т степенями свободы при верной
нулевой гипотезе, где т
щающей модели (5.22)
- число ограничений на параметры. Для обобди2
дб: равна7 u~tZat при верной нулевой гипотезе,
vl
а следовательно, z;t = Zat·
Переменные в Zat - это Bt-1,
регрессируется на константу z 0t и Zat·
S-;_ 1ct-1 и St_ 1ct-1· Оптимальная форма
теста на смещение для шоков разного знака следующая:
где
s-t-1 -{
-
1,
о
'
ct-1
< 0,
иначе.
Регрессия для теста на смещение для размера отрицательных шо
ков имеет вид
vt2 =а+ ь2 s-t-1ct-1 +'У'Zot* +
et,
а для теста на смещение для размера отрицательных шоков
s+t-1 -- {
1,
о
'
ct-1
> 0,
иначе.
t-статистики для Ь1, Ь2 и Ьз являются статистиками для тестов на сме
щение знака отрицательное смещение знака и положительное смещение
знака соответственно. Совместный тест
трех переменных в уравнение дисперсии
- это LМ-тест на добавление
(5.22) при предполагаемой спе
цификации:
Тестовая статистика - это Т R 2 . Если модель волатильности верна,
то Ь1
=
Ь2
=
Ьз
=
О, 'У
=
О и et является
iid.
Если Zot не включать,
то тест будет консервативен; размер (уровень значимости) теста будет
меньше либо равен номинальному, а мощность, вероятно, снижена.
6 Для сильно нелинейных моделей алгоритмы численной оптимизации обычно не
гарантируют точную ортогональность
и Zot· В [Engle & Ng (1993)] предлагается
регрессировать
только на Zot, а затем использовать полученные остатки (которые
ортогональны zot) вместо
в (5.23).
7 Действительно,
= q~t (б0 zot) ехр (б~zat), диl/дба = q~tZat ехр (o~Zat) при нуле
вой гипотезе, Оа =О, диl/дба = U~tZat·
vl
Yl
ul
vl
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
5.1.
427
Эмпирические приложения в статистическом
5.1.11.
пакете
и
Eviews: одномерные ARCH
GARCH модели
Цены на нефть, добытую на западе Техаса
На сайте Федеральной резервной службы Сент-Луиса в свободном дсг
ступе размещаются данные для экономических и финансовых времен
ных рядов (база этих данных называется
мость топлива
-
FRED 11).
Поскольку стои
это одна из основных статей расходов, которые при
ходится нести компании, мы проанализируем спотовые цены на нефть,
добытые на западе Техаса. Месячные данные для этих цен могут быть
загружены из вышеупомянутого сайта.
Мы рассмотрим выборку за период с января
1981
г. по апрель
2005
г., поскольку более ранние данные отвечают совершенно иной структуре
рынка и нескольким структурным сдвигам, произошедшим в результате
некоторых шоков. Анализ будет включать в себя использование фик
тивных переменных как в уравнении для условного среднего, так и в
уравнении для условной дисперсии, так же как и использование рас
пределений, отличных от нормального.
Графики логарифмов цен, первых разностей логарифмов цен и их
коррелограммы представлены на рис.
44
5.1
и
5.2.
4
.3
40
2
.1
36
.о
•1
32
.2
.3
28
-4
-.5
24
1985
Рис.
5.1.
1990
1995
2000
2005
1985
1990
1995
2000
2005
Графики логарифмов цен и разностей логарифмов цен
Из графиков, приведенных выше, можно предположить, что лег
гарифмы цен интегрированные порядка
1.
Чтобы проверить это, мы
проведем три теста на единичные корни {из тех, что мы рассматривали
выше). Эти тесты могут быть проведены при помощи следующих ксr
манд в
Eviews
(описание самих тестов см. в гл.
4):
ГЛ.
428
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
log_price.uroot(adf ,const)
log_price.uroot(pp,const)
log_price.uroot(kpss,const)
Autocorrelation
Partial Correlation
АС
РАС
Q.Stat Prob
1 о.953 о.953 268.10
2 о.890 .о.205 502.62
3 о.833 о.оп 70!.87
4 o.7m .о.о;ю 890.34
5 о.736 0.1&1 1052.4
6 о.694 .о.039 1196.8
1 о.654 0.019 1325.5
0 о.620 о.034 1441.5
9 о.583 .о.059 1544.6
10 о.546 .o.oos 1635.4
11 о.507 .o.os1 1114.О
12 ОАБЗ .о.054 1779.8
13 о.425 о.032 1835.3
14 о.394 о.040 1883.3
15 о.367 0.001 1925.1
16 о.348 о.058 1962.9
11 о.338 0.076 1998.6
10 о.зз1 .о.004 2032.9
19 o.m 0.011 211i5.7
20 о.314 .о.008 2096. 1
Рис.
5.2.
Коррелограммы для
Autocorrelation
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
1 о.255
2 .о.047
3 .о.050
4 .0.101
5 .о.mб
6 .0.002
1 .о.озо
0 о.048
9 o.m1
10 0.059
11 0.050
12 .Q.026
13 .Q.112
14 .Q.014
15 .0.158
16 .0.137
11 .0.010
10 0.011
19 0.1&
20 0.131
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
log(price)
и
РАС
Q.Stat Prob
о.255
19.213
19.875
20.626
24.013
25.295
27.299
21.572
20.273
29.399
30.467
31 .234
31.437
35.281
35.337
43.1m
-0.120
-0.001
.0.104
.0.015
.о.004
о.ооз
о.034
о.029
0.029
0.031
·0.041
·0.1117
0.055
.0.193
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
о.аю
0.001
0.001
0.001
0.002
0.001
0.001
о.аю
.о.046 48.эm о.аю
.о.008 48.939
-0.011 48.977
0.010 50.356
о.099 55.813
о.аю
о.аю
о.аю
о.аю
dlog(price)
АDF-статистикаравна-2,42 ер-значением, равным
равна
АС
Partial Correlation
0,13.
РР-статистика
равна
-1,84 с р-значением, равным 0,36. Наконец, КРSS-статистика
0,350, что больше, чем 10%-ное критическое значение, равное
0,347:
все три теста подтверждают тот факт, что логарифмы цен на
нефть представляют собой 1(1)-процесс. Более того, если мы взглянем
на график и коррелограмму квадратов логарифмов цен (см. рис.
5.3),
мы заключим, что условная дисперсия меняется со временем. Для учета
временных эффектов мы можем использовать АRСН-модель. Начнем с
АRIМА{2,1,О)-модели с АRСН{l)-моделью для условной дисперсии. Ре
зультаты оценивания параметров этой модели представлены в табл.
Autocorrelation
АС
Partial Correlation
1
2
3
4
5
6
7
1 1
1
1 1
1 1
1
1 1
1985
1990
1995
2000
8
9
10
11
12
0.292
0.075
0.123
0.097
0.142
0.202
.Q.022
.Q.030
.Q.073
.Q.028
.Q.Olll
.0.045
РАС
0.292
.0.011
0.114
0.034
0.112
0.136
.Q.143
.0.012
.Q.119
0.013
.0.028
.0.037
5.1.
Q.Stat Prob
25.102
26. 769
31.254
34.073
40.094
52.396
52.542
52.817
54.453
54.694
54.714
55.332
2005
Рис. 5.З. График для (dlog(price) )2 и коррелограмма для (dlog(price) )2
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
О.ООО
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
Таблица
429
Оценки для АRIМА{2,1,О)-АRСН{1)-модели
5.1
Dependent VariaЬle: DLOG(PRICE)
Method: ML - ARCH (Marquardt)
Sample: 1981:01 2005:04
Included observations: 292 after adjusting endpoints
Convergence achieved after 13 iterations
VariaЫe
Coefficient Std. Error z-Statistic
с
0.003775
0.003710
1.017407
DLOG(PRICE{-1))
0.221628
0.049148
4.509390
DLOG{PRICE{-2))
-0.100077
0.054719
-1.828923
Variance Equation
с
0.003110
0.000361
8.607234
ARCH{l)
0.091644
5.964438
0.546603
R-squared
0.073894
Mean dependent var
Adjusted R-squared
0.060986 S.D. dependent var
S.E. of regression
0.076464 Akaike info criterion
Sum squared resid
1.678009 Schwarz criterion
Log likelihood
358.3380 F-statistic
1.868037 Prob{F-statistic)
Durbln-Watson stat
Prob.
0.3090
0.0000
0.0674
0.0000
0.0000
0.001233
0.078908
-2.420123
-2.357165
5.724908
0.000191
Эта модель дает неплохие результаты, но коррелограммы стандар
тизированных
(см. рис.
Aulocorrelation
5.4)
остатков
Partial Correlation
1
1
1
1
1
1
1
1
1
1
1
1•
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
•••
•••
•1•
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1•
••
••
1
1
1
1
1
1
1
1
•1 •
1
1
1
••
Рис.
1
1 ••
5.4.
квадратов
стандартизированных
остатков
указывают на наличие некоторой остаточной корреляции.
1
••
и
At;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
PAJ:; Q.S\81 Prob
0.002 0.002 0.0013
.Q.ООБ .Q.ООБ 0.0136
0.030 0.030 0.2861
.Q.102 .Q.102 3.3997
.0.028 .Q.027 3.6346
0.005 0.003 3.6429
.Q.020 .Q.014 3.7604
0.036 0.027 4.1443
0.053 0.047 4.9830
0.053 0.055 5.8281
0.050 0.046 6.5872
.Q.014 .Q.011 6.6491
.Q.142 .Q.135 12.818
0.026 0.036 13.021
.Q.168 .Q.163 21.788
.Q.110 .Q.107 25.525
0.013 .Q.025 25.574
.Q.040 .Q.042 26.077
0.007 .Q.026 26.090
0.105 0.073 29.577
0.971
0.993
0.963
0.493
0.603
0.725
O.II07
0.1144
0.836
0.829
0.831
0.880
0.462
0.525
0.113
0.061
0.083
0.098
0.128
0.077
Aulocorrelation
Partial Correlation
•1 •
•1 •
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
•1 •
••
••••
•••
•1 •
1
1
1
1
1
•1 •
•1 •
•1 •
1
1
1
1
•1 •
1
1
1
1
1
1
1
1
1
•••
1
1
1
1
1
1
1
1
•1 •
•1 •
1
1
1
1
At;
1 .Q.073
2 0.024
3 0.120
4 0.020
5 0.108
6 0.127
7 .Q.040
8 0.114
9 .Q.048
10 .Q.004
11 .0.018
12 .Q.052
13 0.040
14 .Q.048
15 0.036
16 .0.030
17 0.004
18 0.031
19 .Q.069
20 0.054
PAJ:; Q.Stat Prob
.Q.073
0.018
0.123
0.038
0.108
0.132
.Q.030
0.081
.Q.070
.Q.031
.Q.071
.Q.068
0.026
.Q.048
0.074
.Q.022
0.047
0.038
.Q.061
0.057
1.5794
1.7434
6.0037
6.1216
9.5978
14.403
14.877
18.787
19.491
19.495
19.589
20.418
20.901
21.612
22.018
22.306
22.311
22.615
24.099
25.021
0.209
0.418
0.111
0.190
0.087
0.025
0.038
0.016
0.021
0.034
0.051
0.060
0.075
0.087
0.107
0.134
0.173
0.206
0.192
0.201
Коррелограммы для стандартизированных остатков и квадратов
стандартизированных остатков
arch1.correl(20)
arch1.correlsq(20)
ГЛ.
430
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Аналогичные результаты получены с использованием LМ-АRСН
теста порядка
6
arch1.archtest(б),
который отвергает нулевую гипотезу об отсутствии гетероскедастично
сти на 5%-ном уровне. Более того, тест
Jarque-Bera
на 1%-ном уровне
отвергает нулевую гипотезу о наличии нормальности
arch1 . hist.
Основываясь на вышеприведенных графиках, включим 15-ый лаг
в авторегрессионную компоненту, описывающую уравнение для услов
ного среднего, и вторую АRСН-компоненту в уравнение для условной
дисперсии, см. таблицу
5.2.
Теперь все диагностические тесты не сиг
нализируют о наличии остаточной корреляции, и нулевая гипотеза о
нормальности также не отвергается на
10%
уровне. Более того, крите
рии Акаике и Шварца достигают своих наименьших значений. Значи
мость 15-го лага можно легко интерпретировать тем, что все крупные
нефтяные корпорации и производители стремятся сохранить запасы и
резервы для того, чтобы иметь возможность сгладить дисбалансы в
поставках нефти и ее потреблении.
Таблица
5.2 Результаты для АRIМА{2,1,О)-АRСН{1)-модели
Dependent VariaЫe: DLOG(PRICE)
Method: Method: ML - ARCH {Marquardt)
Sample: 1981:01 2005:04
Included observations: 292 after adjusting endpoints
Convergence achieved after 12 iterations
Prob.
VariaЬle
Coefficient Std. Error z-Statistic
0.6122
с
0.001734
0.003421
0.506993
0.0016
DLOG(PRICE{-1))
0.205768
0.065161
3.157871
0.0036
DLOG(PRICE{-2))
-0.171889
0.059001
-2.913333
0.0001
DLOG{PRICE{-15))
-0.182143
0.047582
-3.827992
Variance Equation
0.0000
с
0.002219
0.000343
6.468073
0.0001
ARCH{l)
0.434721
0.107615
4.039610
0.0146
ARCH{2)
0.260177
0.106528
2.442334
0.001233
R-squared
0.100088
Mean dependent var
Adjusted R-squared
0.078908
0.081142 S.D. dependent var
S.E. of regression
Akaike info criterion
-2.485958
0.075639
Sum squared resid
1.630548 Schwarz criterion
-2.397816
Log likelihood
5.282912
369.9498 F-statistic
0.000035
Durbln-Watson stat
1.844087 Prob{F-statistic)
Наконец, мы представим результаты прогнозирования на один шаг
времени вперед на интервале от
2000:05
до
2005:04
(см. рис.
5.5).
5.1.
АВТОРЕГРЕССИОННАЯ УСЛОВНАЯ ГЕТЕРОСКЕДАСТИЧНОСТЬ
431
smpl 1980:1 2000:4
equation eq80_final.arch(2,0) DLOG(PRICE) С DLOG(PRICE(-1))
DLOG(PRICE(-2)) DLOG(PRICE(-15))
smpl 2000:05 2005:4
eq80_final.fit(g,e,f=na) price_f price_se price_Var
ForecвS1:
Acluвl:
60
PRICEF
PRICE
ForecвS1 sвmple:
.
50
30 . · j
20 f
.·)Vi
./\ .,/: . .
40
'\r .
·" ·.. \.:../ \/.
2000:05 2005:04
lncluded observllllons: 60
Root
Мевn Squвred
Error
Мевn AЬsolute Error
Мевn АЬs. Percent Error
Thell lnequвllly Codlclent
Bl•s Proportlon
Vвrlвnce Proportlon
Covвrtвnce Proporllon
·.J . l'\r1
2.746802
2.207788
6.668527
0.041291
0.025074
0.010603
0.964323
10.w..-~-~-~~~~-~--"
2000
2001
2002
2003
2004
1-PRICEFI
.020-------------~
.016
=~\ \~J]\]J
.ooo.w..-~-~-~~~~-~--"
2000
2001
2002
2003
1 - Forec•S1
Рис.
мы
orvвrtвnce
5.5.
2004
I
Одношаговый прогноз
Поскольку фактическая волатильность является ненаблюдаемой,
будем использовать квадраты доходностей (DLOG(PRICE)) 2 в ка
честве оценки реализованной волатильности (см. ниже, п.
5.3).
График
реализованной волатильности против спрогнозированной волатильно
сти указывает на способность модели следовать изменениям рыночной
волатильности (см. рис.
5.6).
бОт----------------,
50
оз
40
30
20
10 ......2000
v·· ~ ..
J\~·
.......~......- -.....~-..,..,~~.......
2001
2002
2003
2004
1- PRICE
Рис.
5.6.
Цена
-
•
PRICE_F
1
02
01
00 ............. , + d _......, . . , . . _...........~.................."'"'"
2001
2000
2002
2003
2004
1- DLOG2
•
PRICE_VAR
1
спрогнозированная цена, реализованная волатильность
спрогнозированная условная дисперсия
-
Гл.
432
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
АR-GАRСН-модель дл.я российского фондового индекса
RTS
Рассмотрим дневные цены закрытия для российского фондового индек
са
между
RTS
стей (см. рис.
22/10/2003
5.7).
и
22/10/2007,
так же как квадраты доходно
.012
2400
.010
2000
.008
1600
.006
1200
.004
800
.002
400
100 200 300 400
1 - CLOSE •
Рис.
5. 7.
soo
.ООО " "
•
.lllllJlt.11..oW••
100 200 300 400 soo 600
600 700 800 900
1- Squared retums 1
RТS index (22110/2003·22110/2007)1
Индекс
RTS:
(2003-2007)
700 800 900
дневные цены закрытия и квадраты доходностей
Мы хотим найти наилучшую модель в классе АR-GАRСН-моделей
для первых разностей логарифмов индекса
рим на:
i)
дуt. Если мы посмот
информационный критерий Шварца (см. табл.
ства остатков
iii)
RTS,
{ACF & PACF, Ljung-Box
5.3); ii)
статистики, см. табл.
свой
5.4)
и
значимость оценок параметров вместе с результатами тестов множи
телей
Лагранжа
(LМ-тестов),
то
выясним,
что
AR{l)-Threshold-
GARCH{l,1)-мoдeль со стандартизированными остатками, имеющими
распределение Стьюдента, адекватно описывает эмпирические свойства
индекса
RTS.
Таблица 5.3
Результаты оценивания AR{l)-TGARCH{l,1)-мoдeли
со стандартизированными остатками, подчиняющимися
распределению Стьюдента
Dependent VariaЫe: DLOG(CLOSE)
Method: ML - ARCH (Marquardt} - Student's t distribution
Sample (adjusted): 3 996
lncluded observations: 994 after adjustments
Convergence achieved after 17 iterations
Coefficient
Std. Error
0.002329
0.000439
с
0.063278
0.032911
DLOG(CLOSE(-1))
Variance Equation
2.0lE-05
5.66Е-06
с
RESID(-l}Л2
0.032684
0.039363
RESID(-l}Л2*(RESID(-1}<0}
0.047118
0.134842
GARCH(-1}
0.037875
0.813445
4.994905
T-DIST. DOF
0.875731
R-squared
0.001184 Mean dependent var
S.D. dependent var
Adjusted R-squared
-0.00489
S.E. of regression
0.01774 Akaike info criterion
Schwarz criterion
Sum squared resid
0.310627
Log likelihood
F-statistic
2749.92
Prob(F-statistic}
1.967154
Durbln-Watson stat
z-Statistic Prob.
5.307604 0.0000
1.922667 0.0545
3.552492 0.0004
1.204348 0.2285
2.861799 0.0042
21.47732 0.0000
5. 703696 0.0000
0.001288
0.017697
-5.51895
-5.48444
0.195019
0.978255
Таблица
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
5.4
Ljung-Box-тecты для стандартизированных остатков
(MGARCH)
433
(левая часть таблицы) и квадратов
стандартизированных
остатков (правая часть таблицы)
5.2.
5.2.1.
Standardized Residuals
Lag Q-Stat P-value
1 0.9523
0.329
2 1.7626
0.414
0.415
3 2.8505
4 3.5951
0.464
4.177
0.524
5
0.292
6 7.3259
7 7.4971
0.379
0.422
8 8.1215
0.285
9 10.862
10 10.983
0.359
11
17.089
0.105
12 17.133
0.145
19.05
0.122
13
0.150
14 19.405
15 19.469
0.193
0.242
16 19.525
17 20.612
0.244
18 21.298
0.265
19 21.306
0.320
0.262
20 23.572
Standardized Residuals Squared
Lag Q-Stat
P-value
1 1.0782
0.299
2 2.7034
0.259
0.260
3 4.0098
4 4.0109
0.405
0.536
5 4.0921
0.567
6 4.8179
7
4.826
0.681
8 5.9319
0.655
0.746
9 5.9356
10 6.3304
0.787
11
6.3308
0.850
12 6.6783
0.878
0.832
13 8.1772
0.872
14 8.3205
15 9.1009
0.872
16 9.1656
0.906
17 10.245
0.893
18 11.048
0.892
0.776
19 14.134
20 14.156
0.823
200
200
168.77
0.947
153.11
Многомерные GАRСН-модели
0.994
(MGARCH)
Введение
Обобщение одномерных GАRСН-моделей на п-мерный случай требу
ет некоторых предположений относительно зависимости условной ко
вариационной матрицы п-мерных случайных величин
et
с нулевым и
средними значениями от элементов информационного множества §t .
Основными областями приложения многомерных GАRСН-моделей
{МGАRСН-моделей) являются управление портфелън/ьtми инвестици
ями и риском, хеджирование, анализ внешних воздействий на вола
тильность отдельно взятого рынка, условные САРМ-модели и ценооб
разование опционов. Для того чтобы более четко продемонстрировать
необходимость развития этих моделей, рассмотрим следующий пример.
Пр им ер
5.1
(граница потерь для портфеля активов).
Предположим, что имеется инвестор, который заинтересован в оценке
границы потерь (ГП) своего портфеля, составленного из
n
акций. ГП
Гл.
434
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
широко используется в качестве числовой меры риска. Более детальное
рассмотрение этой меры будет представлено в гл.
7.
Обозначим n х 1-вектор доходностей для n акций через r. А доход
ность портфеля, составленного из этих акций с весами
через
rp
µр
= E[rp] -
w'r
w' µ,
E[r]
а~= Drp =
где Е
обозначим
Тогда мы имеем следующие соотношения:
rp.
гдеµ=
w,
-
w'Ew,
это ковариационная матрица вектора
Пусть
W -
r.
суммарный объем денежных средств, инвестиорован
ных в портфель. ГП уровня а для портфеля определяется как ми
нимальный объем средств, который может быть утрачен с вероятно
стью, меньшей или равной а. ГП уровня а (в англоязычной литературе
VaR(a)) -
это а-квантиль распределения убытков и прибылей порт
феля. В нашем примере:
VaR(a) = Wgp(a),
где 9р(а)
< gp(a)]
-
это квантиль случайной величины
rp
уровня а, т. е.
P[rp <
=а. Поскольку ГП определяется в денежных средствах, то
W
входит в формулу для ГП мультипликативно. В предположении нор
мальности rp (т. е. rp Е N(µp, а:)) мы имеем:
VaR(a) = (µр + Zaap)W = (w' µ + ZaVw'Ew)W,
где
Za -
а-квантиль стандартного нормального распределения.
В приведенном выше примере предположение о постоянстве во вре
мени параметровµ и Е является весьма ограничительным. Одной из
возможностей обойти такое ограничение
GАRСН-модель для условной дисперсии
-
это оценить одномерную
a:.t случайной величины rp
(при условии известной информации до момента
t).
Но ограничитель
ной особенностью такого подхода является необходимость переоценки
модели для каждого набора весов
w. Если мы используем МGАRСН
модель, то нам нет необходимости переоценивать модель при каждом
новом наборе весов
на
w'Ew.
w,
поскольку дисперсия доходности портфеля рав
Более того, значительно проще оценить чувствительность ГП
портфеля относительно изменений весов портфеля.
5.2.
а
(MGARCH)
435
Общая структура многомерной модели
5.2.2.
Пусть
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
Yt -
векторный стохастический процесс размерности
(п
х
1),
конечный вектор параметров:
() -
с
где E(t)(()) - положительно определенная матрица размерности п х п,
iid
Zt -
случайные вектора размерности (п х
1),
для которых:
• E[zt) =О
• Ezt =
In,
а
9"t -
информационное множество, накопленное до момента времени
t
(т. е. состоящее из значений
Yt, Yt-1, Yt-2, ... ).
Учитывая заданную спецификацию ошибки, мы можем вычислить
ковариационную матрицу
где для простоты
мы
Yt,
а именно:
использовали сокращенное обозначение для
~<t-1)
условной ковариационной матрицы """'Yt
Параметризация E(t) в виде многомерной GАRСН-модели позво
ляет выражать каждый элемент матрицы E(t) через q лагированных
значений квадратов и попарных произведений
et,
так же, как с ис
пользованием р лагированных значений элементов матрицы E(t). Та
ким образом, элементы ковариационой матрицы отвечают векторному
АRМА-процессу для квадратов и попарных произведений остатков.
Хотя МGАRСН-модели представляют собой прямое обобщение од
номерных GАRСН-моделей, они обладают рядом недостатков:
•
необходимы условия на
(),
обеспечивающие положительную опре
деленность E(t) для всех t;
•
параметров должно быть немного, чтобы оценка модели была воз
можной;
•
необходимы условия, обеспечивающие стационарность остатков
et.
Для решения указанных выше проблем были предложены различ
ные спецификации,
группы:
которые
могут быть
категоризированы
в две
Гл.
436
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
• модели для условной ковариационной матрицы E(t);
•
модели для условной корреляционной матрицы
Rt,
получаемой
из разложения E(t) = DtRtDt, где Dt - диагональная матрица с
частными дисперсиями на главной диагонали.
5.2.3.
VЕС-модели
VEC{p, q)-модель была впервые предложена в работе [Bollerslev et al.
(1988)]. При построении этой модели используется так называемый
''vесh"-оператор, который позволяет представить нижнетреугольную
матрицу размерности пхп вектором размерности (n(~+l} xl). VEC(p, q)модель определяется следующим соотношением:
q
иt =с+
р
:2: Aтt-i + :2: GjO't-j,
i=l
(5.24)
j=l
где
vechE(t)
Т/t = vech(ete~),
vechE(t),
O't
-
(и11t, u21t, u22t, 0'31t, ... O'nnt)',
Ai и Gj - квадратные матрицы параметров размерности ( (n~l}n х
х (n~l}n), а с - вектор-параметр размерности ((n~l}n х 1). Количество
параметров в модели равно [1 + (р + q)[n(n + 1)/2] 2], что соответству
ет порядку п4 . Даже при малых размерностях п и малых значениях р
и
количество параметров довольно велико: для п
q,
«неурезанная~ версия модели
(5.24)
включает в себя
= 5 и р = q = 1,
465 параметров.
Для того чтобы проиллюстировать действие "vесh"-оператора и
дать
общее
представление
относительно
VЕС-моделью, мы рассмотрим двумерную
Пр им ер
иш
5.2
динамики,
VEC(l,
описываемой
1)-модель:
(двумерная VЕС(l,1)-модель).
[ 0'21:t ] = [
0'22,t
~С2 ]
С3
+
[
а11
а21
а31
[ 911
+ 921
931
а12
а22
а32
а1з]
а23
e1,t-1
e1,t 221e2,t-1
e2,t-1
[
а33
]
+
912
913 ] [ U11t-l ]
и21:t-1 .
922 923
0'22,t-1
932 933
В этом случае уравнение для условной ковариации имеет вид:
и2н
=
с2
2
2
+ a21e1,t-1 + a22e1,t-1e2,t-1 + a23e2,t-1 +
+ 922u21,t-1 + 923u22,t-l ·
921и11,t-1 +
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
437
В соответствии с определением VЕС-модели каждый элемент ее ко
вариационной матрицы в момент времени
t
является функцией не толь
ко своих лаговых значений и соответствующих квадратов остатков, но
также и лаговых значений других компонент ковариационной матри
цы и лаговых значений квадратов других компонент вектора остатков.
Это позволяет рассматривать довольно гибкую спецификацию, в кото
рой можно изучать влияние волатильности одного актива (или рыноч
ного индекса) на волатильность других активов (рыночных индексов),
которое известно в литературе как «эффект распространения волатилъ
ности~. В целом волатильность отдельного актива зависит не только от
своих прошлых значений, но также от прошлых значений волатильно
стей других активов. Однако учет этого свойства в рамках VЕС-модели
связан с использованием большого числа параметров.
Естественным шагом, позволяющим сократить количество пара
метров, является использование диагонального представления, в кото
ром каждый элемент ковариационной матрицы зависит только от сво
их прошлых значений и прошлых значений для
модели
Ai
и
Gj -
ejtekt· В диагональной
диагональные матрицы. Для n = 2 и р = q = 1
диагональная модель записывается следующим образом:
иш
[ u21:t ]
0'22,t
=
[ q
с2 ]
+ [ан
О
С3
0
+
[ 911
о
а22
о
о
о
922
о
о
а~]
l]
[
e1,t-1
2
e1,t-1e2,t-1
2
e2t-1
'
[
ин,t-1
0'21,t-1
0'22,t-1
]+
]
,
где
O'ij,t = Ci
+ aiifi,t-lfj,t-1 + 9iiO'ij,t-1·
Таким образом, (i, j)-й элемент матрицы E(t) зависит от соответ
ствующих {i,j)-x элементов матриц et-1e~-l и E(t-l}. Это ограничение
позволяет снизить количество параметров до
[n (п + 1) /2] {1 + р + q).
Однако такая модель не позволяет обнаруживать эффекты причинно
сти в дисперсии, персистентности и асимметрии.
Следующее упрощение VЕС-модели
торой
Ai = aiU, Gj = gjU,
где
-
скалярная VЕС-модель, в ко
ai и gj - скалярные величины, а U -
матрица, составленная из единиц.
Условия стационарности для VЕС{l,1)-модели могут быть полу
чены при помощи представления в виде
Ut = с+ A11t-1
VARMA{l,1)
+ Gиt-1 + G11t-1 -
G11t-1
системы:
+ Т/t -
Т/t
Гл.
438
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
или, что то же:
Т/t
с+ (А+ G)ТJt-1
-
с+ (А+ G)ТJt-1
Процесс Wt
= Т/t -
+ (ТJt - иt) - G(ТJt-1 - Ut-1)
+ Wt - Gwt-1·
O't является мартинга.лом-разностью, поскольку
В результате условия стационарности могут быть получены как
условия для стационарности АRМА-модели. Таким образом, VЕС(l,1)
модель слабостационарна, если собственные значения матрицы (А+ G)
по модулю меньше единицы. В этом случае безусловное среднее для O't
равно:
Е[иt]
где п*
=
n(n + 1)/2.
= E[vechE(t)] = (In* -
А - G)- 1c,
Из представленного выше следует, что необходи
мым и достаточным условием стационарности для диагональной VЕС
модели является условие: aii
+ 9ii < 1 для всех i.
Другой недостаток этой модели (помимо большого числа парамет
ров)
это ограничения на параметры, которые необходимы для обес
-
печения того, чтобы E(t) была положительно определена (см. [Bauwens
et al. (2006)]).
ВЕКК-модели
5.2.4.
В работе
[Engle, Kroner (1995)]
предложена параметризация, которая
обеспечивает положительную определенность матрицы ковариаций.
ВЕКК(р,
q, К)-модель
к
E(t) = С*'С* +
определяется следующим образом:
q
Ajk
и
р
L L AjA:et-je~-jAJk + L L GjA:E(t-j)Gjk,
k=lj=l
где С*,
к
Gjk -
(5.25)
k=lj=l
матрицы размерности
(n
х
n),
а С*
- верхне
треугольная матрица. Число К определяет уровень общности модели,
которая при больших К аппроксимирует VЕС-модель. Количество па
раметров ВЕКК(l,1,1)-модели равно n(S~+l), что значительно меньше,
чем количество параметров в VЕС(l,1)-модели. Одно из главных пре
имуществ ВЕКК-моделей состоит в том, что такие модели гарантируют
положительную определенность ковариационных матриц.
Пр им ер
При р
=q=К
5.3 (ВЕКК(l,1,1)-модель).
= 1 мы имеем:
E(t)
= С*'С* + Aiiet-1et-11Ai 1 + GiiEt-1Gi1,
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
для двумерного случая (т. е. при
[""'
0'21t
+ [ а!1
а21
*
а12
и2н
]'[
*
921
с! 1
С21
0'22t
а22
+ [ 9!1
] = [
n
€'1,t-l
2
€'2,t-1€'1,t-1
= 2)
~
С22
(MGARCH)
439
мы имеем:
][ ci1
Q
~1] +
С22
E1,12102,t-l ] [
€'2,t-1
а!1
а12
а21
а22
*
*
/
9!2 ] [
<711,t- l
<721,1-1 ] [
9!1
9!2 ] .
922
0'21,t-1
0'22,t-1
921
922
]+
Записывая уравнения для элементов ковариационной матрицы, по
лучим:
анt
-
•2 + ан
•2 €'1,t-1
2
+
сн
•2
+9н ан,t-1 +
а2н
2ан
* а21
* €'1,t-1€'2,t-1 +
•2 2
а21 €'2,t-1
+
29229210'21,t-1
* •2
•2
+ 9210'22,t-li
** + ана12€'1,t-1
**2
* * + а21а12
* * ) €'1,t-1€'2,t-1 +
СнС21
+ (ана22
*
•2
* *
* *
+
+а21 а22 €'2,t-1 + 9н912ан,t-1 + 9219220"22,t-1
a22t
+(9i1922 + 9219i2)a21,t-1i
* * + a12€'1,t-1
•2 2
+ 2a12a22€'1,t-1€'2,t-1
* *
+ a22€'2,t-1
•2 2
+
сн С22
•2
+
+ 9120'H,t-l
29129220"21,t-l
* •2
+ •2
9220"22,t-l·
Теперь мы видим, что ВЕКК(l,1,1)-модель можно интерпретиро
вать как VЕС(l,1)-модель с ограничениями. В частности, в терминах
обозначений описанных выше VЕС-моделей, мы имеем следующие огра
ничения на параметры:
а21
а22
Jаназ1,
-
Jаназз + Ja13a31.
Сравнивая VЕС-модель, в которой количество параметров поряд
ка n 4 , отметим, что в ВЕКК-модели имеется параметров порядка n 2 .
Однако по сравнению с VЕС-моделями интерпретация параметров в
ВЕКК-моделях довольно затруднительна.
Соотношение между ВЕКК- и VЕС-моделями. Рассмотрим
соотношения между ВЕКК- и vесh-параметризациями. Соотношения
между параметрами двух моделей может быть найдено при помощи
векторизации уравнения
(5.25),
где для простоты мы предположим
K=l:
q
vec(E(t))
р
= vec(C*'C*) + :L:vec(Aj'et-iE:'~-iAj) + :L:vec(Gj'E(t-i)Gj),
j=l
j=l
Гл.
440
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
где
vec(A) - оператор, примененный к (n х п)-матрице А и дающий
вектор vec(A) размерности {n 2 х 1). Для оператора vec ( ·) выполняется
сле,цующее свойство:
vec(ABC)
= (С'® A)vec(B).
Для симметричной
(n х п)-матрицы А вектор vech(A) содержит в
точности n(n2+l) элементов матрицы А, расположенные ниже главной
диагонали (включая элементы самой главной диагонали). Существует
единственное линейное преобразование, которому отвечает матрица Dn
размерности n 2 х n(~+l), на основании которого vech(A) переходит в
vec(A).
Эта матрица называется матрицей дублирования:
vec(A)
= Dnvech(A).
Тогда
q
vec(E(t)) = vec(C*'C*)
+ L(Aj ® Aj)'vec(ct-1c~_ 1 )+
j=1
р
+L
vec(Gj ® Gj)'vec(E(t-l)).
j=1
Из этого следует:
q
Dnvech(E(t))
= Dnvech(C*'C*) + L(Aj ® Aj)'Dnvech(ct-1€~_ 1 )+
j=1
р
+ L(Gj ® Gj)'Dnvech(E(t-l)).
j=1
Если матрица
DN
полного ранга, то мы можем определить обоб
щенное обращение матрицы
Dt
D N:
= {DNDN)- 1 DN,
nt есть матрица размерности n(~+l) х n
в результате, умножая на nt, получим:
т. е.
vech(E(t)) = vech(C*'C*)
+ Dt
2'
причем
®
(f)Gj Gj)')
®
3=1
IN.
(t(Aj Aj)') Dnvech(ct-1c~_ 1 )+
3=1
+ Dt
ntnN =
Dnvech(E<t- 1>).
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
441
Одним из следствий этого результата является тот факт, что vесh
модель для ВЕКК-модели является единственной. Переход от vесh
модели к ВЕКК-модели не определен единственным образом, посколь
ку для заданного
Ai выбор Ai не единственен. Это можно подтвердить
тем, что (Ai ® Ai) = (-Ai ® -Ai). При этом Ai = Dt (Ai ® Ai)'DN
единственно, а выбор Ai не единственен. Можно также показать, что
все положительно-определенные диагональные vесh-модели могут быть
записаны в виде ВЕКК-модели.
Условия
стационарности
для
ВЕКК(l,1,1)-модели.
Для
ВЕКК{l,1,1)-модели имеем: :E(t) = !1 + A*'ft-1€~_ 1 A* + G*'E(t-l)G*.
Соответственно ВЕКК{l,1,1)-модель может быть записана в виде VЕС
модели следующим образом:
vec(:E(t))
= vech(C* 1 C*)+(A*®A*)'vec(c:t-1C:~_ 1 )+(G*®G*)'vec(E<t-l)).
Таким
образом,
ВЕКК-модель
будет
слабостационарной,
если
собственные значения матрицы (А* ®А*)+ ( G *®G *) по модулю меньше
единицы.
Если
это
условие
выполнено,
безусловное
среднее
для
vec(:E(t)) дается выражением:
E[vec(E<t>)] = (In2 - (А*® А*)' - (G* ® G*)')- 1 vech(C*'C*).
Наконец, для диагональной ВЕКК-модели необходимое и достаточ
ное условие для слабой стационарности имеет вид: a~i
5.2.5.
+ g~ < 1.
Факторная GАRСН-модель
Факторную GАRСН-модель, введенную в работе
[Engle et al. {1990)],
можно рассматривать в качестве альтернативы для ВЕКК-модели.
Предположим, что процесс
yt,
размерность которого (п х
торную структуру с К факторами
ft
1), имеет фак
и с не зависящей от времени мат
рицей нагрузок В размерности (п х К):
Yt = Bft + C:t·
Предположим, что ошибки
C:t имеют условную (при заданном 9"t-1)
ковариационную матрицу Ф, которая постоянна во времени и поло
жительно полуопределена, а общие факторы характеризуются следу
ющим:
E{ft 19"t-1) =О,
E{ft-kf: 19"t-1)
= At,
где At = diag(лp>, ... , Л~к» и положительно определена. Информаци
онное множество
9"t-1 определится в данном случае значениями {Yt-1,
Гл.
442
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
ft-1, ... , У1, f1}. Также предположим, что E{fte~) =О. Условная ковари
ационная матрица для
yt
равна:
к
E(YiYf 1 §t-1) = E(t) = Ф + BAtB' = Ф + L,Вk,В~Л~k),
k=1
где .Вk обозначает k-й столбец матрицы В. Таким образом, прогноз дис
персий
и
ковариаций
портфеля
активов
основан
на
прогнозах
К-статистик.
Введем веса Фk
=
(Фk1Фk2
... Фkп)', k = 1, 2, ... , К, -
удовлетворяю
щие условиям
ф'k ,вj
=
{
1 при
о
k
n
= j,
LФki = 1.
в противном случае;
i=l
Тогда существует факторное представление портфелей вида
= Ф' · yt,
rt
где (К х п )-матрица Ф составлена из столбцов Ф1,
а компонен
тами вектора-столбца
1, 2, ... , К).
rt являются числа rkt = фk
Условная дисперсия
Tkt
равна:
ФkE(ytYf 1 §t-1)Фk = ФkEtФk =
D(rkt 1 §t-1)
-
Фk {Ф
'Фk
где 'Фk
... , ф к,
· Yi (k =
+ BAtB') Фk =
+ Лkt,
= фk ФФk· Для того чтобы оценить эту модель,
необходимо па
раметризовать зависимость Л~k) от исторической информации. С этой
целью введем параметры Okt:
В результате мы получим:
к
к
к
k=1
k=1
k=1
L,Вk,В~Okt = L.Вk.В~'Фk + L.Вk,В~Л~k);
к
L,Вk,В~Л~k)
k=1
=
к
к
k=1
k=1
L,Вk,В~Okt - L,Вk,8~1/;k;
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
к
к
Ф + L,Вk,ВkЛ~k)
k=1
E(t)
(MGARCH)
=
443
к
Ф + L,8k,8k8kt - L.Вk.Вk'Фk
k=1
k=1
=
к
-
Ф*
+ L.Вk,Вk(Jkt,
k=1
где Ф* = (Ф - Е .Вk.Вk 'Фk) . Сделаем наиболее простое предположение,
k=1
состоящее в том, что существует множество фактор-портфелей, имею-
щих одномерное GАRСН{l,1)-представление. Условная дисперсия
отвечает
(Jkt
G ARCH( 1, 1)-процессу:
Wk + ak (Ф~еt-1) 2 + 'YkE(r~.t-1 l 9"t-2) =
Wk + аkф~ (et-1E:~-1) Фk + 'YkE [(Ф~Уi-1)(Ф~Уi-1) 1 9"t-2] =
wk + аkф~ (et-1E:~-1) Фk + 'Yk [Ф~Е(Уi-1У/_1) l 9"t-2)Фk] =
8kt -
Wk + аkф~ (et-1E:~-1) Фk + 'Yk [Ф~E(t-l)Фk] .
Тогда условная ковариационная матрица для
yt
может быть запи
сана в виде:
к
E(t) =
Ф*
+ L,8k,8k8kt =
k=1
к
= Ф* + L.Вk.Вk { wk + ak [Ф~ (et-1E:~-1) Фk] + 'Yk [Ф~E(t-l)Фk]} =
k=1
= (
ф* + t.f3kPk"'k) + t.f3kPk {"k [ф~ (Et-iE~-1) Фk] +
+ 'Yk [Ф~Е<t- 1 >Фk]}.
Таким образом, мы получим:
E(t) =
к
к
k=1
k=1
Г + L:ak [.ВkФ~ (et-1E:~-1) Фk.Вk] + L 'Yk [.ВkФ~E(t-l)Фk.Вk] ·
к
где Г
=
Ф*
+ L: ,Вk,Вkwk.
k=1
Следовательно, факторная GАRСН-модель
может рассматриваться как частный случай ВЕКК-параметризации.
Оценка факторной GАRСН-модели осуществляется методом макси
мального правдоподобия.
Часто удобно предполагать, что фактор
портфели известны априори.
Гл.
444
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Ортогональные модели
5.2.6.
Ортогональные модели представляют собой частный случай фактор
ных моделей. Они основаны на предположении, состоящем в том, что
исходные наблюдения являются реализациями случайных векторов,
представимых в виде линейной комбинации набора независимых ком
понент. Компоненты линейной комбинации
главные компоненты век
-
тор-наблюдений. В ортогональной GАRСН-модели, предложенной в ра
ботах
(Alexander, Chibumba {1997)]
времени ковариационная матрица
и
(Alexander {2001)], меняющаяся во
Et размерности (п х п) сгенерирова
на т одномерными GАRСН-моделями, где т (т ~ п) определяется
с использованием метода главных компонент (см., например, [Айвазян
{2010),
п. ПЗ.4)).
Возьмем диагональную матрицу
V,
которая составлена из эмпири
yt,
ческих оценок дисперсий для компонент
V
т. е.
= diag{s~, ... , s~}.
Будем полагать в дальнейшем, что
yt уже центрированы, т. е. Eyt =
=О. Тогда стандартизированные доходности Ut равны:
E[ut] =О,
Ортогональная GАRСН-модель
E[utu~] = R.
(OGARCH
(р; q;
m)).
В этой
модели выборочная корреляционная матрица может быть представлена
в следующем виде:
R=РЛР',
где Р
-
ортонормированная матрица, строками которой являются соб
ственные вектора матрицы
R,
А
-
диагональная матрица, составлен
ная из собственных значений этой матрицы, отранжированных по убы
ванию:
А= diag{Л1,
... , Лп},
при этом Р удовлетворяет следующим условиям:
Р'
Следовательно,
R
= р-1,
Р'Р
= In,
РР'
= In.
может быть представлена как:
R = РЛ 1 l 2 л 1 / 2 р' = LL',
Вектор главных компонент для Ut равен
где
L = РЛ 1 1 2 .
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
445
Безусловная ковариационная матрица равна единичной матрице, раз
мерность которой
(n
х
n):
L - 1 E[utu~]L - 11 = L - 1RL - 11 =L-lpА 1 1 2 А - 112P 1L - 11 =
L- 1LL1L1- 1 = In.
E[ftf:J
Будем предполагать, что условная ковариационная матрица для
является диагональной
мент
Qii,t
Et-1[ftf:J = Qt,
ft
где каждый диагональный эле
отвечает одномерной модели GАRСН-типа (см. п. 5.1). При
этом:
Et-1[utu~) = Et-1[Lftf:L1) = LQtL1.
Таким образом, мы имеем:
Et-1[YtYf] = Et-1[v 1 l 2 utu~v 1 l 2 ] = v 1l 2LQtL1v 112.
Мы можем работать с ограниченным числом т
<n
главных ком
понент (собственных значений), которые объясняют наибольшую долю
суммарной дисперсии исходных данных. В этом случае матрица
заменяется на матрицу размерности (т х
L-1
т
где Рт
-
матрица размерности
n),
L -l
равную:
--л-1/2р т,
(n х т),
состоящая из собственных век
торов матрицы Р, отвечающих т наибольшим собственным значениям.
Суммируя все вышеизложенное,
OGARCH(p, q, m)-модель
опреде-
ляется следующим образом:
y-1/2yt = Ut = Lmft,
Et-1[ft] =О,
Et-1[ftf:J = Qt = diag(aJ1,t, ... , a]m,t),
a]i,t =
(1 -t
l=1
O!it -
t /Зit) + t ailfi~t-t+
l=1
l=1
р
+ °Lf3ita]1,t-1,
i = 1, ... ,т.
l=1
Обобщенная ортогональная GАRСН-модель
model).
В работе
[Van der Weide (2002)]
(GOGARCH-
указано, что условие ортого
нальности, предполагаемое в ОGАRСН-модели, является весьма огра
ничительным и возникает вопрос: если существует связь с множеством
некоррелированных экономических характеристик,
то почему ассоци
ированная матрица является ортогональной? Таким образом, если мы
предположим, что
Гл.
446
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
причем наблюдаемый экономический процесс
Yt
представим в виде ли
нейной комбинации независимых экономических компонент
где
ft -
взаимно некоррелированные компоненты, а
IZI =F
{ft},
т. е.
О. Ненаблю
даемые компоненты нормированы:
E[ftf:J
= ln
V = E[YtY/) = ZZ'
а от матрицы
Z
требуется лишь невырожденность (т. е.
требуется ортогональности, как это было с матрицей
IZI =F
Lm
О), но не
в ОGАRСН
модели.
Vt = Et-1[YtY/) = ZEt-1[ftf:JZ' = ZHtZ',
Ht = diag{h1,t, ... , hn,t},
hi,t = {1 - ai - /Зi)
V
+ aiYl.t-i + /Зihi,t-1
Н - диагональная матрица.
= E[Vt) = ZHZ',
Определенная
таким
i = 1, ... , n,
образом
модель
называется
обобщенной
ОGАRСН-моделью. Возьмем следующее разложение безусловной кова
риационной матрицы
V:
V
где Р
с
Z
-
= РЛР',
некоторая ортогональная матрица. Тогда она будет совпадать
только в том случае, когда диагональные элементы матрицы Н
различны. Предположим, что Н
= 1, тогда мы имеем:
V = E[Vt) = ZIZ' = ZZ'.
Матрица
Z
ниями матрицы
теперь не определена однозначно собственными значе
V,
поскольку для каждой ортогональной матрицы
Q
мы имеем:
(ZQ)(ZQ)'
Матрица
= 1.
Z однозначно определена только в том случае, если учиты
вается информационное условие. С использованием сингулярного разложения мы получим:
Pл 1 J 2 uo
= z.
Матрицы Р и А определяются n(n2- 1> и n параметрами соответ
ственно. Таким образом, для матрицы Z мы имеем n 2 параметров. Мат
рицы Р и А могут быть оценены с использованием безусловной инфор
мации, как если бы они были получены из выборочной ковариационной
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
447
(MGARCH)
матрицы V, которая имеет n(n2+1> параметров. Условная информация
необходима для оценки Uo, для которой мы имеем n(n2- 1> параметров.
ОGАRСН-модель (когда т = п) отвечает случаю, когда U = In.
В целях параметризации матрицы
Uо
воспользуемся сле,цующим
фактом из линейной алгебры. Каждая п-мерная ортогональная матри
ца U с det(U) = 1 может быть представлена в виде произведения
n{n2- 1>
матриц поворота:
U
= П Gij(Oij),
i<j
где
Gij (Oij) представляет поворот плоскости, натянутой на i-й и j-й
вектора канонического базиса Rn, на угол Oij. В компактной записи,
при п = 3, мы имеем: U = Gi2G1зG23. Параметры О измеряют степень
некоррелированности компонент, отображаемых в одном направлении.
Для О
= О отображение необратимое, что соответствует зависимости
меж,цу наблюдаемыми переменными, тогда как при О=~'
Z
= 1,
что
соответствует тому, что наблюдаемые переменные некоррелированы.
Тогда ортогональная матрица
помощи (п х п)-матриц
U о может быть параметризована при
поворота. Gij(Oij), i,j = 1, 2, ... , п:
9ii
= {9ij}
= 9ss = cos(Oij)
= 1 i = 1, ... , п i =! r, s
9sr
= - sin(Oij)
9rs
= sin(Oij),
Gij(Oij)
9rr
а все другие параметры предполагаются нулевыми. Например, в трех
мерном случае п
= 3,
~]
а G2з является блочной с соs(О2з) и sin(02з) функциями в правом ниж
нем углу.
n(n - 1)/2
углов поворота являются параметрами, которые
необходимо оценить.
Условная корреляционная матрица может быть представлена в сле
,цующем виде:
Rt = Dt" 1VtDt" 1 ,
Dt
= (Vt ® Im) 112 .
Гл.
448
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Например, для п
= 2
мы имеем:
условная корреляционная матрица равна:
и
hн cos (8)
Pt
ylVart-1 (Ун) ylVart-1 (Y2t)
cos (8)
Jcos2 (8)
где
Zt
=
+ ~ sin2 (8)
Vhltvhн cos2 (8)
Vl +
+ h2t sin2 (8)
1
Zt
tan2 (8)'
!ш..
h2t
Обозначим через (а', (З', 8')' вектор-параметры, которые необходимо
оценить с использованием условной информации. Тогда
-
(0.1, · · ·, O.n),
((31 , · · · , fЗn) ,
8 -
(81, ... , Вт),
а
(З
m=
n(n - 1)
2
.
Логарифмическая функция правдоподобия для t-го наблюдения
имеет вид:
lt
-
-21 (nlog(27r) + log IVtl + x~Vt- 1xt) =
1
- -2 (nlog(27r) + log IZHtZI + x~(ZHtZ')- 1 xt)
=
-21 (nlog(27r) + log IZZ'I + log IHtl + x~(ZHtZ') - 1xt),
так что логарифмическая функция правдоподобия для всей обучающей
выборки равна
два шага:
log Lт
= Et lt.
Оценка этой модели осуществляется в
5.2.
1.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
449
Оценим Р и А из выборочной ковариационной матрицы. Мы получим:
........
........
...............
,
V=РЛР,
2 . о ценим
log Lт(·).
z = РЛ 1 ! 2 u.
'""' {3', 8')'
("'',
вектор-параметры
путем
максимизации
Ортогональные модели вкладываются в факторную GАRСН-модель,
а значит, и в ВЕКК-модель. Как следствие, результаты, связанные со
стационарностью, безусловными моментами и др. для ВЕКК-модели,
могут быть применены к факторным моделям. В частности, очевидно
также, что GОGАRСН-модель является ковариационно-стационарной
в случае, если m-образующих одномерных GАRСН-процессов одновре
менно являются стационарными.
5.2.7.
Модели для условной корреляционной матрицы
В МGАRСН-моделях, рассматриваемых до сих пор, спецификация
условной ковариационной матрицы производилась в дополнение к спе
цификации условных дисперсий. Это можно интерпретировать как
МGАRСН-модели «первого уровня». Ниже мы рассмотрим модели,
представляющие собой МGАRСН-модели «второго уровня». Такие мо
дели допускают большую гибкость в спецификации дисперсий, посколь
ку они допускают использование разных спецификаций для каждой из
одномерных условных дисперсий: например,
GARCH(l,1)
спецификацией для одной одномерной условной дисперсии,
может быть
EGARCH -
для другой и т.д. Однако спецификация корреляций менее гибка, при
этом накладываются условия положительной определенности для
Et,
что должно быть учтено в процедуре оценки.
МGАRСН-модели «второго уровня» основаны на использовании
следующего разложения:
Et
Dt
= DtRtDt
. ( 1/2
1/2 )
= diag
0"11,t · · · O"nn,t
Rt = (Pij,t),
Pii,t = 1,
где
Rt -
матрица условных корреляций, размерность которой
(5.26)
(n
х
n),
а элементы Dt, O"ii,t - одномерные условные дисперсии, для ali,t будет
выбрана GАRСН-спецификация. Таким образом, ковариация равна:
O"ij,t
= Pij,tJaii,tO"jj,t
i =/; j.
Гл.
450
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Положительная определенность
ленности
Rt
следУет из положительной опреде
Et
и положительности каждой Uii,t для
i = 1, ... , п.
Модель с постоянной условной корреляцией ( ССС-модель).
ССС-модель, представленная в работе
[Bollerslev {1990)],
определяется
следУющим образом:
Et = DtRDt =
где
Rt = R =
(Pij) и Pii
= 1.
(PijJuiitUjjt),
Таким образом, условная корреляционная
матрица постоянна. Следовательно,
Uij,t
=
PijJUii,tUjj,t
i =F j,
а значит, динамики ковариаций зависят только от динамик условных
дисперсий. Число параметров корреляционной матрицы, которые долж
ны быть оценены в дополнение к параметрам GАRСН-моделей, равно
n(n -1)/2.
Каждый элемент последовательности условных ковариационных
матриц
всех
{Et} является положительно определенным почти наверное для
t при условии, что диагональные элементы матрицы Dt также по
ложительны, а условная корреляционная матрица
R
является положи
тельно-определенной.
Модель
с
динамической
условной
корреляцией
модель ). DСС-модель впервые предложена в работе
(DСС
[Tse, Tsui {2002)],
которую иногда называют DССт(М)-моделью. Она определяется в со
ответствии с
{5.26),
где Uii,t специфицируется при помощи одномерной
GАRСН-модели, а
Rt
1/lij,t-1
-
Ui,t
где Ui,t -
определяется следУющим образом:
=
(E~=l и~,t-т и1t-т)
ei,t /
..;;r:;,
стандартизированные (одномерные) остатки, полученные в
предположении справедливости одномерной GАRСН-модели для услов
ной дисперсии. Таким образом, условная корреляционная матрица име
ет в некотором смысле АRМА-структуру. Кроме того, отметим, что Ut
не совпадают с
Zt.
Параметры модели должны удовлетворять следУющим ограничени
ям:
81, 82
>О,
81 +82 < 1, R- постоянна. Таким образом, Rt представля
ет собой взвешенное среднее долгосрочной (безусловной) корреляции,
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
451
условной корреляции для последнего периода и шока, также рассчитан
ного для последнего периода. Сумма весов
(1 - 81 - 82), 82
и
81
равна
единице.
Поскольку 'Фt-1 -
это выборочная корреляционная матрица, то
условие ее положительной определенности требует, чтобы число наблю
дений превышало число активов (размерность системы), что означает
T>n.
Более того, по построению мы имеем, что Фii,t-1
печивает равенство корреляции единице при
Положительная определенность
условиями:
81, 82 >
что обес
= j.
обеспечивается следующими
О при условии, что матрицы 'Фt-1 и Rt-1 также
положительно-определены для всех
что м
Rt
i
= 1, 't/i,
t. Для 'Фt-1
это обеспечивается тем,
> п.
Недостатки DСС-модели в сравнении с
VEC-
и ВЕКК-моделями
возникают оттого, что в DСС-модели только два параметра
отвечающих за динамику всех п( п
- 1) /2
81
и
82,
корреляционных последова
тельностей. ССС-модель можно рассматривать как DСС-модель с огра
ничениями, когда
81
= 82 = О.
Тест отношения правдоподобия для те
стирования статистической значимости ограничений. Значит, для те
стирования нулевой гипотезы о неизменности во времени условной кор
реляционной матрицы против альтернативы о наличии меняющихся во
времени условных корреляций может быть использован тест отношения
правдоподобия.
В качестве альтернативы в работе
[Engle (2002)] предлагается дРУ
гая DСС-модель, которую обычно называют DCCE(S, L )-моделью. Эта
модель определяется в соответствии с (5.26), где Rt определено в сле
дующим образом,
(5.27)
При этом симметрическая положительно-определенная матрица
Qt,
размерность которой (п х п), имеет вид:
где Uit = eit/ ~ как и прежде, Q - это безусловная ковариационная
матрица для Ut, размерность которой (п х п),
81,l (;;:: О) и 82,s (;;:: О) скалярные параметры, удовлетворяющие: Ef= 1 81,l + E:=l 82,s < 1, при
условии Qt >О и Rt >О. Если 81,l = 82,s =О, 't/l, s и Qii = 1, то мы полу
чим ССС-модель. Таким образом, Qt - ковариационная матрица для
Гл.
452
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Ut (по построению Qii,t не равны единице). При помощи преобразования
мы получим корреляционную матрицу.
(5.27)
Отличие
DCCE(S, L)-модели
от DСС-модели из [Тsе,
в том, что в первой из них мы сначала моделируем
Qt,
Tsui (2002)]
которая не
является корреляционной матрицей, а затем строим корреляционную
матрицу
Rt.
Для того чтобы показать более явно разницу между двумя моделя
ми DССт и
DCCE,
запишем формулу для коэффициентов корреляции
в двумерном случае. Для DССт(М)-модели мы имеем:
P12,t
= (1 -
для модели
Е~-1 U1 t-mU2 t-m
'
~
'
у (Em=l и~,t-m) (Eh=l и~,t-m)
() 1 - () 2)Р12 + () 2P12,t-1 + () 1 _/
м
DCCE(1, 1)-модели:
=
(1- 01- 02)Q12 + 01ut,t-1U2,t-l + 02q12,t-l
=-;::======================================================
P12,t
((1 - 01 - 02)q11 +01u~.t-l + 02q11,t-1) (1 - 01 - 02)q22 + 01u~.t-l + 02q22,t-1)
Корреляция в DССт( М)-модели специфицирована как взвешенная
сумма корреляций. В
DCCE(1, 1)-модели
напрямую это не делается, а
вместо этого корреляция конструируется с использованием
Qt
Ut:
матрица
моделируется аналогично GАRСН-модели, а затем осуществляется
преобразование к корреляционной матрице.
5.2.8.
Оценивание МGАRСН-моделей
Оценивание МGАRСН-модели обычно производится при помощи мето
да максимального правдоподобия. Это требует задания плотности нор
мированных остатков Zt в уравнении МGАRСН-модели
Обозначим эту плотность через
который
должен
быть
где
g(zt; 17),
оценен
вместе
с
17 -
векторный параметр,
другими
параметрами
()
МGАRСН-модели. Логарифмическая функция правдоподобия имеет
вид:
т
InL((),17)
=
Llnf(ytl(),17,9't-1),
t=l
где
f (yt
1 (),
17, 9't-1) -
плотность распределения процесса
что для того, чтобы получить плотность
yt.
Отметим,
yt, зная плотность Zt, нам необ
ходимо воспользоваться правилом преобразования функции плотности
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
5.2.
(MGARCH)
453
при преобразовании случайных величин (см., например, формулу
в [Айвазян, Мхитарян
(4.11)
(2001)]).
В нашем случае мы имеем плотность для
Zt, обозначенную через
g(zt; 1J). Функция yt = µt + (E(t)(B))~ · Zt имеет обратную Zt = (E(t) х
1
x(B))-2(yt - µt)· Якобиан этой обратной функции равен J(zt, Yt) =
= det((E(t)(B))-~). Применяя правило преобразования функции плот
ности при преобразовании случайных величин, получим:
где I:(t) = I:(t)(B) и µt = µt(B), т. е. условное среднее и условная кова
риационная матрица являются функциями от вектор-параметра В.
Гауссовское
Zt
Е
N(O,In),
дений У1, У2,
правдоподобие.
Если
предположить,
что
тогда функция логарифмического правдоподобия наблю
... , Ут
имеет вид:
(5.28)
Максимизируя
ln L( В), мы получим оценку квазимаксимального
правдоподобия, если µt и Et правильно специфицированы, даже если
фактическая плотность для Zt не является (О, In)-нормальной.
Оценка квазимаксимального правдоподобия. Предположение
об условной нормальности может быть несколько ограничительным.
Кроме того, симметричность, свойственную нормальному распределе
нию, весьма трудно оправдать. Более того, хвосты фактических услов
ных распределений часто оказываются «тяжелее~ по сравнению с хво
стами нормального распределения.
Пусть
{ (yt, Xt) : t
= 1, 2, ... }
-
последовательность наблюдений
случайных векторов, где yt имеет размерность (п х
мерность
Xt
(L
х
1).
Вектор
yt
1),
а
Xt
имеет раз
включает в себя эндогенные переменные, а
состоит из экзогенных переменных. Пусть
Условные среднее и ковариационная матрица параметризованы при
помощи конечномерного вектора В:
Гл.
454
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
{:E(t)(Wt,B),B Е 0},
где 0 с RP, а µt и :E(t) - детерминированные и известные функции от
Wt
и В. Процедуры оценивания в большинстве случаев дают корректный
результат в предположении справедливости нулевой гипотезы, состоя
щей в том, что первые два условных момента правильно специфициро
ваны, т. е. при некотором Во Е
Е (Yi
1
0
справедливо следующее:
Wt) = µt (wt, Во),
V (Yi 1 Wt) = :E(t) (wt, Во)
t = 1, 2, ....
Достаточно часто для оценки Во используется процедура, основан
ная на максимизации функции правдоподобия, которая построена в
предположении условной многомерной нормальности случайных век
торов
(Yilwt)·
Подход, изложенный ниже, аналогичен, но не основан на предполо
жении о том, что условное распределение для
Yi
является нормальным
распределением.
Для наблюдения в момент времени
t
квазиусловное логарифмиче
ское правдоподобие определяется выражением:
lt (В; yt, Wt) =
-
~ ln (21Г) - ~ ln l:E(t) (wt, B)I -
-~ (Yi- µt (wt,B))' (E(t)(wt,B))- 1 (Yi- µt (wt,B)).
Обозначим через
времени
t.
et (Yi, Wt, Во) = Yi - µt (wt, В)
остаток в момент
Тогда логарифмическая функция правдоподобия равна:
т
InLт (В)= ~)t (В),
t=l
где
lt (В)=
N
1
1
-2
log (21Г) - 2 1og IEt (B)I - 2 е~ (В) (E(t)(B))- 1et (В).
(5.29)
Если µt (wt,B) и :E(t)(B) = :E(t) (wt,B) дифференцируемы по В и если
:E(t) (В) является почти наверное невырожденной матрицей для всех В Е
Е
0,
тогда, дифференцируя
St (В)' =
(5.29)
по В, получим:
\lelt (В)' - \leµt (О)' (E(t)(B))- 1et (В)+
+~\le (E~t) (В))' [(E(t)(B))- 1 ® (E(t)(B))- 1] х
х vec [et (B)et (В)' - E(t) (В)],
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
455
где
V eµt (8) -
матрица размерности
(п
х Р)
,
а
V eE(t) (8) - матрица размерности (п 2 х Р)
.
Если первые два условных момента правильно специфицированы,
то вектор ошибок равен е~
= e"t (80) = yt -
µt (Wt, 80), так что
Е (е~ lwt) =О,
Е (e~e~' lwt) = E(t) (wt,80).
При правильной спецификации первых двух условных моментов
для
yt,
при заданном
Wt,
мы имеем:
Следовательно, значение
метра
8
при фактическом значении пара
St (8)
представляет собой вектор мартингал-разности относитель
но а-алгебры {а
(yt, Wt) : t = 1, 2, ... }.
Этот результат может быть ис
пользован для того, чтобы установить с.лабую состоятелъностъ оценки
квазимаксималъного правдоподобия
нам также необходимо выражение
(QMLE). Для надежности в'Ьl.водов
для гессиана ht (8) для lt (8). Опре
делим следующую Р х Р-матрицу:
at (80) = -Е [Vest (80) lwt] = Е [-ht (80) lwt];
at (80) -
Veµt (80)' (E(t)(8))- 1Veµt (80) +
+~VeE(t) (8)' [(E(t)(8))-1 ® (E(t)(8))-1] VeE(t) (8).
В предположении нормальности матрица
мационная матрица. Однако, если
yt
at (80 )
-
условная инфор
не подчиняется условному нор
мальному распределению, то ковариационная матрица вектора-строки
St(8) (V[st(8)lwt])
не равна
at(8o).
QМL-оценка имеет следующие свойства:
где
456
Гл.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
и
т
в~= v [т- 1 !2 sт (Во)] = ~2.:Е [st (Во)' St (Во)].
t=l
В дополнение:
....
о
р
Ат -Ат..::.+ О
....
Вт
о
р
Вт..::.+ О.
-
Матрица Ат 1 ВтАт 1 представляет собой состоятельную оценку
асимптотической ковариационной матрицы вектора ,,/Т (Вт - Во). При
этом асимптотически по Т --t оо
В условиях нормальности
Yt
оценка ковариационной матрицы для
8т может быть приближенно вычислена как Ат 1 /Т (форма гессиана)
или как Вт 1 /Т (внешнее произведение градиентных форм).
Вычисление статистки, отвечающей тесту Ва.л:ьда, довольно тру
доемко. Пусть нулевая гипотеза
Но:
где r : 0 --t
mQ
r(Bo)
=О,
является непрерывно-дифференцируемой на int (0)
(внутренней части области
0)
и
Q < Р.
R(B) =
градиент функции
r(·)
на
int (0).
Пусть
\lвr (В)
(Q
х Р)-матрица
-
Если Во Е
int (0)
и
rank (R (Во))= Q,
тогда статистика Вальда имеет вид:
Таким образом, при большом числе наблюдений и при справедли
вости нулевой гипотезы распределение статистики Вальда стремится к
х2 ( Q)-распределению.
Двухшаговая оценка ССС- и
DCC-
моделей. Если мы учтем
соотношение
Et = DtRtDt в гауссовской логарифмической функции
правдоподобия (5.28) и проигнорируем константную часть, которая не
влияет на оценки параметров, то получим:
т
lnL(B)
rv
-~ L(log IDtRtDtl + и~Ri- 1 иt),
t=l
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
457
где Ut = Dt" 1 (Yi-µt), так что u~Rt" 1 ut = (Yi-µt)'Dt" 1 Ri- 1 Dt" 1 (yt-µi).
Таким образом,
т
InL(8)
rv
-~ ~::)loglDtRtDtl +и~Rt" 1 ut) =
t=l
1 т
-2 L 2 log IDtl + и~ut t=l
lnL(Bi)
т
-~ L(log IRtl + и~Ri- 1 ut - и~иt),
t=l
lnL(8218i)
где
8i -
параметры условных дисперсий
корреляций
Rt.
Dt, а 82 -
параметры условных
В результате логарифмическую функцию правдоподо
бия можно разложить следующим образом:
Это разложение позволяет использовать двухшаговую процедуру
для оценки DСС-модели, поскольку вначале мы можем оценить моде
ли для условных дисперсий, а затем, используя полученные для них
оценки, максимизировать вторую часть функции лог-правдоподобия,
которая включает параметры, необходимые для спецификации услов
ных корреляций.
Опишем более формально упомянутую выше двухшаговую про
цедуру:
Шаг
1.
Оценим
8i
как:
8i
= argmax
ln L(8i).
На этом шаге мы оцениваем одномерные GАRСН-модели для каж
дой условной дисперсии в отдельности.
Шаг
2.
Оценим
82
как:
82
= argmax
ln L( 8218i).
На этом шаге используются оценки, полученные на первом шаге.
Эти оценки являются состоятельными, но не являются асимптоти
8i теряется
матрица оценки 82 долж
чески эффективными, поскольку некоторая информация об
на первом шаге. Более того, ковариационная
на быть скорректирована с учетом процедуры оценки на первом шаге
(см.
[Newey, McFadden (1994)] и [Engle (2002)]).
Гл.
458
5.2.9.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Эмпирические приложения в статистических
пакетах
1)
Eviews
и
R
Диагональная VЕС{l,1)-модель.
Мы рассмотрим дневные цены закрытия для акций четырех рос
сийских компаний (Газпром, Лукойл, РБК, Сбербанк) за
(рис.
2003-2007
гг.
5.8):
CLOSE_WKOП.
CLOSE_GAZPROM
160
:!JOO
140
:!400
120
2000
100
1600
80
1200
60
800
40
400
100 200 300 400 500 600 700 800 900
100 200 300 400 500 600 700 800 900
CLOSE_RBK
CLOSE_SBERBANK
350
120
300
100
250
80
200
60
150
40
100
20
50
100 200 300 400 500 600 700 800 900
Рис.
5.8.
Газпром, Лукойл, РБК, Сбербанк
100 200 300 400 500 600 700 800 900
-
дневные цены закрытия
(2003-2007)
Сначала мы рассмотрим диагональную VЕС-модель, описанную ни
же с использованием Е Views
шестой версии
Таблица
5.5.
System Representation
Eviews (рис. 5.9, табл. 5.5 и 5.6).
и реализованную в
Спецификация диагональной VЕС(l,1)-модели
-
многомерное распределение Стьюдента
Variance-Covariance Representation:
GARCH =
GARCHl =
GARCH2 =
GARCH3 =
GARCH4 =
COV1_2 =
COV1_3 =
COVl_ 4 =
COV2_3 =
COV2_ 4 =
COV3_ 4 =
М
+ Al.*RESID(-l)*RESID(-1)' + Bl.*GARCH(-1)
Variance and Covariance Equations:
+ Al(l,l)*RESID1(-l)Л2 + Bl(l,l)*GARCHl(-1)
М(2,2) + A1(2,2)*RESID2(-l)Л2 + B1(2,2)*GARCH2(-1)
М(3,3) + A1(3,3)*RESID3(-l)Л2 + B1(3,3)*GARCH3(-1)
М(4,4) + A1(4,4)*RESID4(-l)Л2 + B1(4,4)*GARCH4(-1)
M(l,2) + Al(l,2)*RESID1(-l)*RESID2(-1) + Bl(l,2)*COV1_2(-1)
M(l,3) + Al(l,3)*RESID1(-l)*RESID3(-1) + Bl(l,3)*COV1_3(-1)
M(l,4) + Al(l,4)*RESID1(-l)*RESID4(-1) + Bl(l,4)*COV1_ 4(-1)
М(2,3) + A1(2,3)*RESID2(-l)*RESID3(-1) + B1(2,3)*COV2_3(-1)
М(2,4) + A1(2,4)*RESID2(-l)*RESID4(-1) + B1(2,4)*COV2_ 4(-1)
М(3,4) + A1(3,4)*RESID3(-l)*RESID4(-1) + B1(3,4)*COV3_ 4(-1)
M(l,1)
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
459
Результаты оценивания параметров представлены ниже:
Таблица
5.6.
Диагональная VЕС{l,1)-модель: оценки параметров
Covariance specification: Diagonal VECH
GARCH = М + Al.*RESID(-l)*RESID(-1)' + Bl.*GARCH(-1)
Prob.
Coefficient Std. Error z-Statistic
4.012423
0.0001
M(l,1)
1.92Е-05
4.79Е-06
M(l,2)
1.50Е-05
3.50Е-06
4.293874
0.0000
1.lOE-05
3.20Е-06
0.0006
M(l,3)
3.434227
M(l,4)
1.59Е-05
3.76Е-06
4.222375
0.0000
М(2,2)
2.67Е-05
6.73Е-06
3.965723
0.0001
М(2,3)
1.96Е-05
8.20Е-06
2.390615
0.0168
М(2,4)
2.45Е-05
5.87Е-06
4.183931
0.0000
6.75Е-05
1.25Е-05
5.392105
0.0000
М(3,3)
М(3,4)
2.08Е-05
8.63Е-06
2.406971
0.0161
М(4,4)
5.67Е-05
1.26Е-05
4.513535
0.0000
Al(l,1)
0.062662
0.012209
5.132319
0.0000
0.042805
4.013512
0.0001
0.010665
Al(l,2)
Al(l,3)
0.011144
0.016048
0.694419
0.4874
Al(l,4)
0.038029
0.011746
3.237696
0.0012
А1(2,2)
0.065807
0.013848
4.751968
0.0000
А1(2,3)
0.045811
0.022035
2.079006
0.0376
0.060513
0.013821
4.378413
0.0000
А1(2,4)
А1(3,3)
0.208071
0.03877
5.366783
0.0000
А1(3,4)
0.053145
0.025392
2.092989
0.0364
А1(4,4)
0.108757
0.021529
5.051679
0.0000
0.899386
0.015475
58.12053
0.0000
Bl(l,1)
Bl(l,2)
0.904834
0.015346
58.96254
0.0000
Bl(l,3)
0.862866
0.032105
26.87638
0.0000
Bl(l,4)
0.888205
0.019318
45.97851
0.0000
В1(2,2)
0.881425
0.021476
41.04203
0.0000
0.790895
0.073417
10.7726
0.0000
В1(2,3)
В1(2,4)
0.851076
0.027217
31.26962
0.0000
В1(3,3)
0.589838
0.053945
10.93414
0.0000
В1(3,4)
0.748108
0.084375
8.866447
0.0000
В1(4,4)
0.784261
0.03496
22.43306
0.0000
С(39)
t-Distribution (Degree of Freedom)
4.753774
0.412660
11.51983
0.0000
Мы можем оценить свойства остатков с использованием многомер-
ных версий тестов на наличие автокорреляций (так называемых портманто-тестов, см. п.
4.2.8).
Мы напомним, что при справедливости ну-
левой гипотезы статистики этих тестов имеют распределения, близкие
к х 2 -распределению, для более детальной информации см. раздел об
оценке VАR-моделей, см. также работу
ки в ней.
[Liitkepol {2005), §16.5)
и ссыл-
Гл.
460
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Conditiona 1Corre1а tion
Col(DLOG(GдZPROМ).DLOGCWKOR.))
Col(DLOGcGAZPROMJ.DLOGcRBKJJ
Col(DLOGcWKOILJ.DLOGIRBKJJ
Col(DLOG(GAZPROМ).DLOG(SBERBANKJ)
Col(DLOG(LUКOR.).DLOG(SBERBANJ())
Рис.
5.9.
Col(DLOG(RBKiDLOG(SBERBANK))
Диагональная VЕС{l,1)-модель: условные корреляции
Результаты тестов портманто на наличие автокорреляций в стан
дартизированных остатках
Zt
и их квадратах приведены в табл.
5. 7
5.8.
Таблица
5.7.
Диагональная VЕС(l,1)-модель: портманто-тесты на
наличие автокорреляций в стандартизированных
остатках
Zt
System Residual Portmanteau Tests for Autocorrelations
Null Hypothesis: no residual autocorrelations up to lag h
Orthogonalization: Cholesky (Lutkepohl)
Sample: 3 994
Included oЬservations: 993
Lags
Q-Stat
Prob. Adj Q-Stat
Prob.
1
23.25884
0.107
23.28231 0.1064
2
42.44774 0.1025
42.50998 0.1014
df
16
32
11
202.9479 0.0802
176
204.2023 0.0715
12
217.0118 0.1041
218.4384 0.0925
192
*The test is valid only for lags larger than the System lag order.
df is degrees of freedom for (approximate) chi-square distribution
и
5.2.
Таблица
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
5.8.
(MGARCH)
461
Диагональная VЕС{l,1)-модель: портманто-тесты
на наличие автокорреляций в квадратах
стандартизированных остатков
LM TESTS on zl
Sample: 1 994
Included observations: 992
z'f
PORTMANTEAU TESTS on
Sa.mple: 1 994
Included observations: 992
zl
LM-Stat
Prob
Lags
Q-Stat
Prob.
Adj Q-Stat
Prob.
df
11.72963
0.7624
1
11.75901
0.7604
11.77088
0.7596
16
2
12.69721
0.6948
2
24.48956
0.8262
24.52715
0.8247
32
11
8.813674
0.9209
11
171.7978
0.5754
172.8443
0.5531
176
12
20.09204
0.2161
12
191.7841
0.4908
193.0753
0.4646
192
Lags
2)
Диагональная ВЕКК(l,1,1)-модель.
Теперь мы рассмотрим диагональную ВЕКК{l,1,1)-модель, предпо
лагая при этом снова многомерное распределение Стьюдента. Специфи
кация модели представлена в табл.
5.9
с использованием
Representation.
Оценки параметров представлены в
Таблица
Диагональная ВЕКК{l,1,1)-модель
5.9.
EViews System
табл. 5.10.
-
многомерное
распределение Стьдента
Variance-Covariance Representation:
GARCH =
М
+ Al*RESID(-l)*RESID(-l)'*Al + Bl*GARCH(-l)*Bl
Variance and Covariance Equations:
COV1_2 = M(l,2) +
+ Al(l,l)*Al(2,2)*RESID1(-l)*RESID2(-l)*RESID1(-l)*RESID2(-l)*RESID1(-l)*RESID2(-l) +
Bl(l,l)*Bl(2,2)*COV1_2(-l)*COVl _ 2(-l)*COVl _ 2(-1)
COV1_3 = M(l,3) +
+ Al (1,1)* Al (3,3)*RESID1 (-l)*RESID3(-l)*RESID1 (-1 )*RESID3(-l)
+ Bl(l,l)*Bl(3,3)*COV1_3(-l)*COV1_3(-l)
COVl_ 4 = M(l,4) + Al(l,l)*Al(4,4)*RESID1(-l)*RESID4(-l) + Bl(l,l)*Bl(4,4)*COV1_ 4(-1)
COV2_3 = M(2,3)*RESID2(-l)*RESID3(-1) +
+ Al (2,2)* A1(3,3)*RESID2(-l)*RESID3(-l)*RESID2(-l)*RESID3(-l)*COV2 _ 3(-1)+
+ Bl(2,2)*Bl(3,3)*COV2 _ 3(-l)*COV2 _ 3(-l)
COV2_ 4 = M(2,4)*RESID2(-l)*RESID4(-1) + Al(2,2)*Al(4,4)*RESID2(-l)*RESID4(-l)*COV2_ 4(-1) +
+ Bl(2,2)*Bl(4,4)*COV2_ 4(-1)
COV3_ 4 = M(3,4)*RESID3(-l)*RESID4(-l)*RESID3(-l)*RESID4(-l) +
+A1(3,3)*Al(4,4)*RESID3(-l)*RESID4(-l)*COV3_ 4(-l)*COV3_ 4(-1) +
+ Bl(3,3)*Bl(4,4)*COV3 4(-1)
Гл.
462
Таблица
5.
5.10.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Диагональная ВЕКК(l,1,1)-модель: оценки
параметров
Covariance speciflcation: ВЕКК
GARCH = М + Al*RESID{-l)*RESID{-l)'*Al
М is an indefinite matrix
Al is diagonal matrix
Bl is diagonal matrix
Тranformed Variance Coefficients
Coefficient Std. Error z-Statistic
+ Bl*GARCH{-l)*Bl
Prob.
M{l,1)
1.41Е-05
3.0lE-06
4.685195
0.0000
M{l,2)
1.09Е-05
2.46Е-06
4.419519
0.0000
M{l,3)
1.40Е-05
4.12Е-06
3.392721
0.0007
M{l,4)
1.54Е-05
3.59Е-06
4.282469
0.0000
М{2,2)
2.04Е-05
5.17Е-06
3.945453
0.0001
М{2,3)
1.85Е-05
4.76Е-06
3.874584
0.0001
М{2,4)
1.93Е-05
4.31Е-06
4.484269
0.0000
М{3,3)
6.67Е-05
1.32Е-05
5.038907
0.0000
М(3,4)
1.76Е-05
4.57Е-06
3.844844
0.0001
М(4,4)
4.69Е-05
1.06Е-05
4.438965
Al{l,1)
0.173441
0.017345
9.999267
0.0000
0.0000
А1{2,2)
0.223354
0.022188
10.06634
0.0000
А1{3,3)
0.370344
0.039327
9.417132
0.0000
А1{4,4)
0.286524
0.026814
10.6858
0.0000
Bl{l,1)
0.969862
0.004159
233.2025
0.0000
В1{2,2)
0.955668
0.007782
122.809
0.0000
В1{3,3)
0.813025
0.031718
25.63285
0.0000
В1{4,4)
0.912848
0.014869
61.39391
0.0000
С целью
остатков
проверки
автокоррелированности
и их квадратов
стандартизированных
мы также осуществим многомерную версию
тестов портманто. Результаты этих тестов для Zt иzl представлены в
табл.
5.11
и
5.12
соответственно. Наконец, условные корреляции, полу
ченные в предположении диагональной ВЕКК(l,1,1)-модели, представ
лены на рис.
5.10.
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
463
Condiliona 1Corre lalion
Cor1Dl.OG(GAZPROМ),Dl.OG(LUKOR.JJ
10.-------~
0.9
2!0
!00
7!0
Cor1Dl..OG(LUKOR.J.Dl..OG(R8КJJ
Cor1Dl..OG(GAZPROMJ.Dl.OG(R8KJJ
.а..-----------.
:м~,r\~~~~~~
о~~-.---~~
2!О
!00
2$0
1$0
CorjDl..OG(GAZPROМ).Dl..OG(SBERBANK))
1.0
!00
7!0
Cor(Dl..OG(LUКOR.).Dl..OG(SBERBANКJ)
1.0
0.2·~~-.---~~
2!О
Рис.
5.10.
Таблица
!00
7!0
Corфl..OG(RBK).Dl..OG(SBERBANK))
.8 . . . . - - - - - - - - - - - - .
"2~~-.---~~
2!0
!00
1!0
Диагональная ВЕКК(l,1,1)-модель: условные корреляции
5.11.
Диагональная ВЕКК(l,1)-модель: тесты портманто
на наличие автокорреляций в стандартизированных
остатках
Zt
System Residual Portmanteau Tests for Autocorrelations
Null Hypothesis: no residual autocorrelations up to lag h
Orthogonalization: Cholesky (Lutkepohl)
Sample: 3 994
Included observations: 993
Lags
Q-Stat Prob. Adj Q-Stat Prob.
1
23.42153 0.1029
23.39794 0.1035
46.54835 0.0465
46.61866 0.0459
2
df
16
32
205.9609 0.0606
207.2165 0.0537
176
12
219.2309 0.0865
220.6488 0.0766
192
*The test is valid only for lags larger than the System lag order.
df is degrees of freedom for (approximate) chi-square distribution
11
Гл.
464
Таблица
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Диагональная ВЕКК(l,1)-модель: тесты портманто
5.12.
на наличие автокорреляций в квадратах
стандартизированных остатков
LM TESTS on zl
Sample: 1 994
Included oЬservations: 992
Lags
LM-Stat
Prob
1 29.04697
0.0236
2 23.34343
0.1049
11
12
3)
9.995047
33.22188
0.8669
0.0069
ССС- и
DCC-
z'f
PORTMANTEAU TESTS on
Sample: 1 994
Included observations: 992
Q-Stat
Prob.
Adj Q-Stat
Lags
1 28.93447
0.0244
28.96364
2
52.2799 0.0133
52.35618
11
12
207.3001
240.185
0.0533
0.0104
208.4106
241.6977
zl
Prob.
0.0242
0.0130
df
16
32
0.0478
0.0087
176
192
модели.
В этом разделе мы займемся оценкой
мoдeли с использованием процедуры
модели
мы
оставим
в
качестве
GARCH(l,1)-DCC(l,1,1)ccgarch в пакете R. Оценку ССС
упражнения,
решение
которого
пред
ставляет собой небольшую модификацию программы, представленной
ниже. Учитывая программные возможности статистического пакета
R,
мы вычислим:
•
статистику портманто-теста для проверки гипотезы об отсутствии
серийной корреляции до порядка
h
включительно, которая опре
деляется следующим образом:
h
Qh
где
Ci =
= тL:tr(6j60 1 6j60 1 ),
j=l
~ E[=i+l Ut"U~-i' а (n х 1)-векторы остатков Ut стандар
тизированы при помощи условной: дисперсии (первый: шаг проце
дуры оценки). Распределение тестовой статистики при большом
числе наблюдений: и справедливости нулевой гипотезы об отсут
ствии серийной: корреляции до порядка включительно
x2 (n 2 (h -
h
близка к
h
скоррек
р))-распределению.
Для малих въ~борок и (или) при небольших значениях
тированная тестовая статистика может быть вычислена следую
щим образом:
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
5.2.
•
(MGARCH)
465
Вреуш-Годфри LМ-статистику, которая строится с использовани
ем следующих вспомогательных регрессий:
Нулевая гипотеза Но
:
В1
= . . . = Bh =
альтернативная гипотеза Н1
: 3 Bi =/;
О
О, а соответствующая
for i = 1, 2, ... , h.
Тестовая
статистка определяется следующим образом:
где
-
ER
-
и Ее
-
ковариационные матрицы остатков для модели с
ограничениями и без ограничений: соответственно. Тестовая ста
тистика LMh имеет асимптотическое х 2 (hп 2 )-распределение.
В работе
[Edgerton, Shukur (1999))
предложена модификация ста
тистики на слу'Чай ма.л,ой вьtборки. Эта модифицированная ста
тистика имеет вид:
1 - (1 - Щ.)l/r Nr - q
LMFh
= (1-Щ)l/r
Кт '
= 1 - IЁel/IЁRI, r = ((n2m 2 - 4)/(п2 + m 2 - 5)) 112 , q = n;i - 1
и N = Т - п* - т - 1/2(n - т + 1), где п* - число регрессоров
в исходной системе, а т = nh. Модифицированная тестовая ста
с IR~
тистика имеет распределение
F(hn 2 ,int(Nr- q)), где f(Z) - это
целочисленная часть от числа
•
Z.
Статистику многомерного АRСН-LМ-теста, который основан
на использовании следующей регрессии:
где Vt -
сферические ошибки,
vech -
оператор, преобразующий:
симметрическую матрицу в вектор-столбец (см. выше более по
дробное определение). Размерность f3o равна !n( n + 1), а размер
ность матриц-коэффициентов Bi с i = 1, ... , q, равна !n(n + 1) х
x!n(n + 1). Нулевая гипотеза состоит в том, что Но: В1 = В2 =
= ... = Bq = Q, а альтернатива - Н1 : В1 =/;О или В2 =/;О или
... Bq =/;
О. Тестовая статистика для проверки нулевой гипотезы
Но против альтернативы Н1 имеет вид:
VARCHLм(q) =
2
R:n = 1 -
1
2 тп(п + 1)R~,
2
...
"-1
n(n + l) tr(!1!10
),
где
Гл.
466
а
n-
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
ковариационная матрица для остатков указанной выше ре
грессии. Эта тестовая статистика имеет ассимптотическое х 2 ( qn 2 х
х (n + 1) 2 /4)-распределение.
Основное тело кода представлено ниже, тогда как дополнительные
скрипты
tests. R,
включающие все вспомогательные процедуры для
вычисления статистик многомерных тестов, доступны на веб-сайте.
library(urca) library(zoo) library(sandvich) library(vars)
library(fArma) library(ccgarch)
# Load the functions for Multivariate testing
setvd("C:/DEAN/LEZIONI/Econometric_softvare/cccgarch")
source ( "tests. R11 )
#Read the data
dat <- read. tаЫе ("С: /DEAN/Lezioni/russian_stocks. txt 11 , header =
ТRUE)
#Generate the returns in
y1=100•diff(log(dat[,1]))
y2=100•diff(log(dat[,2]))
y3=100•diff(log(dat[,3]))
y4=100•diff(log(dat[,4]))
#I estimate an (eventual) АRМА model vith constant
fit1 = armaFit( ar(O), data = у1)
fit2 = armaFit( ar(O), data = у2)
fit3 = armaFit( ar(O), data = у3)
fit4 = armaFit( ar(O), data = у4)
#I extract the residuals ...
res1=residuals(fit1)
res2=residuals(fit2)
res3=residuals(fit3)
res4=residuals(fit4)
# ... and collect them in а matrix
data_res=cbind(res1,res2,res3,res4)
#I set the starting values for the DCC model
а = с(О.0003, 0.0005, 0.0004, 0.0004)
А= diag(c(0.06,0.11,0.22,0.14))
В= diag(c(0.87, 0.80, 0.56,0.78))
dcc.para = с(О.003, 0.95)
#I estimate the DCC model ...
dcc.data.est=dcc.estimation(a,
model="diagonal 11 )
А, В,
dcc.para, data_res,
# ... and compute the standardized residuals of the first step estimation
std.res=data_res/ sqrt(dcc.data.est$h)
#I extract the conditional correlations ...
DCC_corr_all=dcc.data.est$DCC
# ... at time 10 ...
Rt.10 <- matrix(DCC_corr_al1[10,], nrov=length(a))
Rt.10
#I initialize the matrix that vill contain the residuals standardized
5.2.
МНОГОМЕРНЫЕ GАRСН-МОДЕЛИ
(MGARCH)
467
using
# the inverse of the lover triangular Cholesky factor of the residual
conditional
# correlation matrix (second step)
std.res.all=NULL
for (i in 1:nrov(std.res))
Rt.i <- matrix(DCC_corr_all[i,], nrov=length(a))
inv.chol.i=solve( chol(Rt.i) )
std.res.i = inv.chol.i%•%as.vector(std.res[i,])
std.res.all = rbind(std.res.all, t(std.res.i) )
Ьу
#Tests f or а single lag
#portmanteau.multi(std.res.all,ncol(dcc.data.est$out) , 20)
#BG.multi(std.res.all, О, ncol(dcc.data.est$out), 10)
#arch.multi(std.res.all, 10)
#We compute the multivariate tests recursively for а series of lags
recursive.portmanteau.multi(std.res.all, ncol(dcc.data.est$out), 20)
recursive.BG.multi(std.res.all, О, ncol(dcc.data.est$out), 20)
recursive.arch.multi(std.res.all, 20)
Значения тестовых статистик и р-значения для них представлены
в табл.
5.13.
Таблица
5.13. GARCH{l,1)-DCC{l,1)
модель: многомерные
портманто-тесты, Бреуша-Годфри LМ-статистика и
многомерный АRСН-тест
Portmanteau TEST
Lag Statistic P-value
1
27.59
О.ООО
2
О.ООО
48.18
О.ООО
72.24
3
4
85.09
0.001
102.62
0.003
5
113.61
0.012
6
7
124.58
0.036
140.31
0.048
8
155.84
0.061
9
10
178.88
0.033
11
206.28
0.011
12
218.13
0.022
13
236.46
0.020
258.09
0.013
14
272.89
15
0.018
16
286.87
0.025
17
298.56
0.042
18
306.51
0.086
323.58
0.085
19
20
330.86
0.157
Multivariate Breusch-Godfrey LM
Lag Statistic
P-value
27.62
0.035
1
2
47.10
0.042
71.21
0.016
3
4
83.64
0.050
102.50
0.046
5
112.98
0.114
6
123.14
0.222
7
140.92
0.205
8
155.53
0.242
9
10
176.13
0.181
11
203.92
0.073
12
214.92
0.123
13
231.09
0.130
250.74
0.106
14
262.33
15
0.154
16
277.62
0.169
17
290.93
0.206
299.68
18
0.306
321.63
0.233
19
20
332.19
0.308
Multivariate ARCH test
Lag Statistic P-value
1
136.77
0.009
2
224.63
0.112
398.13
О.ООО
3
4
492.31
0.001
596.61
0.002
5
667.01
0.030
6
766.15
0.042
7
890.09
0.014
8
1011.18
9
0.006
10
1078.88
0.041
11
1159.44
0.104
12
1255.13
0.131
13
1370.44
0.085
1460.03
0.129
14
1576.77
0.082
15
16
1753.89
0.004
17
1850.62
0.006
18
1919.72
0.025
2024.15
0.024
19
20
2125.28
0.026
Гл.
468
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Реализованная волатильность
5.3.
5.3.1.
Введение
Волатильность финансового рынка является ключевым элементом в
теории управления риском, ценообразования активов и формирования
портфелей.
В большинстве исследований волатильность рассматривается как
ненаблюдаемая переменная, и для ее оценки используются специфици
рованные модели для условного среднего и дисперсии.
Ненаблюдаемая волатильность Ut на следующий день обычно опре
деляется как
информация,
y'D(YtlFt-1), где Yt - дневная доходность, а
доступная к моменту (t - 1).
Ut =
Моделирование и прогнозирование
ul
Ft-1 -
может быть осуществлено
при помощи параметрических моделей для дневных данных (таких как
ARCH-
или GАRСН-моделей, рассмотренных выше) или с использова
нием так называемой подразумеваемой волатильности, получаемой из
формулы Блэка-Шоулза (см. ниже, гл.
7).
Однако стандартные мо
дели для ненаблюдаемой волатильности не способны адекватно описы
вать малые, но медленно убывающие автокорреляции квадратов доход
ностей. Правильное описание динамики доходностей очень важно для
того, чтобы получать точные прогнозы будущей волатильности, кото
рая, в свою очередь, является важной в анализе рисков и управлении.
Идея использования высокочастотных данных для оценки вола
тильности возникла в 70-х-80-х гг. прошлого столетия:
•
в работе
[Officer (1973))
вычисляются годовые волатильности из
месячных доходностей, что позволило не терять промежуточную
информацию о траектории цены;
•
в работе
[Merton (1980))
используются дневные доходности для
измерения месячных волатильностей.
Однако идея использования высокочастотных внутридневных дан
ных для оценки дневных волатильностей возникла относительно недав
но: в работе
тогда как в
[Schwert (1998)) обрабатывались 15-минутные доходности,
работах [Taylor, Xu (1997)) и [Andersen, Bollerslev (1998))
для оценки дневной волатильности обменных курсов использовались
5-минутные доходности.
В работе
[Andersen, Bollerslev (1998))
вычислялась оценка волатиль
ности, получаемая из агрегированных высокочастотных доходностей.
Эта оценка оказалась достаточно точной, и для нее был введен спе
циальный термин реализованная волати.л:ьностъ (РВ). Реализованные
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
469
волатильности, бу,цучи наблюдаемыми аппроксимациями для ненаблю
даемой волатильности Ut, дают новые возможности для прогнозирова
ния бу,цущих волатильностей.
Как только волатильность становится «наблюдаемой~, она может
моделироваться непосредственно. В работах
[Barndorff-Nielsen, Shephard
(2002)], [Andersen et al. (2003)], [Meddahi (2002)] и др. представлены
теоретические результаты, описывающие свойства реализованной во
латильности, полученной из высокочастотных данных. Однако, как мы
увидим позже, микроструктурные эффекты вносят значимое смеще
ние в оценки дневных волатильностей. В работах [Ait-Sahalia et al.
(2005)], [Bandi, Russell (2005а, 2006Ь)], [Zhang et al. (2005)], [Hansen,
Lunde (2006а,Ь)] рассмотрены различные решения проблемы несостоя
тельности.
5.3.2.
Теоретические основы
Для того чтобы понять то, как устроена РВ, нам необходимо ввести
понятие интегрированной волатил:ьности. Предположим, что модель
для приращения логарифма цены представляет собой диффузионный
процесс:
dp(t)* = µ(t)dt
где
p(t)* -
процесс, а
+ u(t)dW(t),
логарифм цены в момент времени
u(t) -
t, dW(t) -
(5.30)
винеровский
стохастический процесс, не зависящий от
dW(t).
Для этого диффузионного процесса интегрированная волатиль
ность (ГVi+1) в день t определяется соотношением:
ГVi+1 =
В работе
[Merton (1980)]
1
t+1
t
u 2 (s)ds.
показано, что определенная таким образом ин
тегрированная волатильность броуновского движения может быть ап
проксимирована с любой степенью точности при помощи суммы квад
ратов внутридневных логарифмических доходностей.
Однако в качестве меры волатильности Ut квадраты дневных лога
рифмических доходностей являются плохими оценками, поскольку они
переоценивают эти волатильности. В то же время интегрированная во
латильность, являясь хорошей мерой волатильности, может быть ис
пользована как образец сравнения для других оценок волатильности.
В работах
[Andersen et al. (2001а,Ь, 2003)] и [Barndorff-Nielsen,
Shephard (2002)] представлены обобщенные результаты для оценки ин
тегрированной волатильности в классе специальных (с конечным сред
ним) семи-мартингалов с использованием теории квадратической вари-
Гл.
470
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
ации: этот класс включает в себя процессы, используемые в приложе
ниях, связанных с ценообразованием активов. Среди таких процессов
следует выделить диффузионные процессы Ито, процессы со скачками
и смешанные диффузии со скачками.
При определенных условиях регулярности сумма квадратов внут
ридневных лог-доходностей сходится к интегрированной волатильности
цен, что позволяет нам построить достаточно точную оценку факти
ческой волатильности на временном интервале фиксированной длины.
Эта непараметрическая оценка называется реализованной волатилъно
стъю. Если определить Yt,o = p(t)-p(t-a), а Yt = Yt-1,1, то в [BarndorffNielsen, Shephard (2002)) показано, что квадрати-ческая вариация семи
мартингала, определенная как:
t;<t
[Yt] = plim L(Yt; -Yt;_J 2 ,
j=l
эквивалентна интегрированной волатильности в условиях, когда доход
ности изменяются в соответствии с
а элемент сноса
(5.30),
µ(t)
является
непрерывной функцией. Сумма квадратов последовательных высоко
частотных лог-доходностей сходится к квадратической вариации цены,
(см.
[Meddahi (2002)]
и
[Andersen et al.
(2001а)]). Реализованная вола
тильность является состоятельной оценкой интегрированной волатиль
ности при неограниченно возрастающей частоте выборки.
Рассмотрим дискретную выборку д-периодичной доходности, ко
торая в момент времени
Yt+1 = Yt+1,1·
1/ д
t
равна Уt,д
=
p(t) - p(t -
д). Обозначим
Дневная реализованная волатильность R'\1t;~~ равна сумме
высокочастотных внутридневных квадратов доходностей:
1/д
nt
- ~ 2
- ~ 2
R v:;(d)
t+l - L..J Уt+jд,д - L..J Yt,i,
j=l
где nt -
(5.31)
i=l
количество тактов времени длины д в одном дне. При опре
деленных условиях
регулярности реализованная
волатильность явля
ется несмещенной оценкой волатильности. Более того, с увеличением
частоты выборки из диффузионного процесса (т.е. при д
--+
О) реа
лизованная волатильность представляет собой состоятельную оценку
интегрированной волатильности за фиксированный интервал времени
(см.
[Andersen et al.
(2001а,Ь)),
plimд-+O
[Andersen et al. (2003, 2007)]):
1
t+1
RVt+1 =
t
a 2 (s)ds.
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
471
Реализованную волатильность можно рассматривать для различ
ных временных горизонтов, превышающих один день: многопериодные
волатильности представляют собой нормированные суммы однопери
одных волатильностей, т. е. это простые средние дневных RV(d) [Corsi
(2009)].
Например, недельная реализованная волатильность
мент времени
t
в мо
Rv;_(w)
равна:
яv.;<w>
= !5 (яv.;<d>
+ яv.;<d>
+ ... + яv.;<d>)
t
t-1
t-2
t-s
(5.31')
'
где недельный временной интервал равен пяти рабочим дням.
Поскольку
в
дальнейшем
мы
будем
дневную волатильность, то верхний индекс
рассматривать
d
только
в ее определении
(5.31)
будет опускаться.
Различные схемы формирования выборки для
высокочастотных данных
Выше мы привели анализ в условиях непрерывного времени. Но на
практике цены наблюдаются в дискретные и нерегулярно отстоящие
друг от друга моменты времени. Существует множество схем форми
рования выборки внутредневных данных.
(i)
Наиболее широко используемая схема - формирование в'Ьtборки по
календарному времени, в которой рассматриваемые моменты вре
мени являются равноотстоящими друг от друга. Предположим,
что в заданный день t мы делим интервал [О,
1]
на
nt
подинтерва
лов. Пусть сетка моментов времени, в которые фиксируются на
блюдения, определяется значениями: О= то< т1
< ... < Tni = 1.
Длина i-го подинтервала равна дi
= Ti,ni = Ti -Ti-1 · В случае фор
мирования выборки по календарному времени мы имеем д = 1/nt
для всех i. Например, может извлекаться выборка пяти- или 30минутных цен. Поскольку внутредневные данные обычно наблю
даются в нерегулярные моменты времени, формирование выбор
ки
по
календарному
времени должно
осуществляться в
некото
ром смысле искусственно (более подробно см.
(1997)], [Dacorogna et al. (2001)]).
В работе
[Andersen, Bollerslev
[Hansen, Lunde (2006Ь)]
показано, что так называемый метод предъtдущего тика является
приемлемым способом формирования выборки цен в календар
ном времени. Например, в течение пятиминутного интервала, мы
можем наблюдать несколько цен. Согласно методу предыдущего
тика в качестве цены для этого пятиминутного интервала следует
брать первое наблюдение.
Гл.
472
{ii)
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Во втором варианте способа формирования выборки ширина вре
менного интервала определяется заданнъt.м. числом транзакций,
которое этот интервал должен содержать. В каждом таком ин
тервале определяются цены, равные ценам m-й транзакции.
{iii)
Третья схема формирования выборки оперирует понятием «биз
нес времени», т.е. производится деление дня на
nt
интервалов та
ким образом, чтобы интегрированная волатильность на каждом
интервале была одной и той же.
(iv)
Еще одной схемой является формирование выборки в «mшсовом»
времени; в ней цены фиксируются при каждом изменении цены.
Важное различие между приведенными выше схемами состоит в
том, что моменты времени, в которые осуществляются наблюдения,
в схеме
(iii)
являются ненаблюдаемыми, тогда как в схемах
{i), {ii) и
[Andersen,
{iv) моменты времени являются наблюдаемыми. В работах
Bollerslev {1997)) и [Curci, Corsi {2004)) показано, что схема {iii) мо
жет быть аппроксимирована схемой {iv). К тому же мы не коснемся в
дальнейшем схемы
только
{iv)
и
{ii).
Таким образом, далее мы будем рассматривать
{i).
Распределение реализованной волатильности
Используя результаты работ
Shephard {2002)),
[Jacod, Protter {1998)), [Barndorff-Nielsen,
при выполнении некоторых условий регулярности мы
имеем следующее:
Гпi
1
d
(Rvt+1 - lvt+1)--+ N(O, 1),
2
J lQн1
где
IQн1 =
1
(5.32)
t+1
t
u 4 (s)dw(s).
Величину IQн1 будем называть интегрированной квартисивно
стью.
Более того, в работах
[Barndorff-Nielsen, Shephard {2002))
показано,
что в предположении отсутствия микроструктурного шума интегриро
ванная квартисивность состоятельно оценивается при помощи реализо
ванной квартисивности, которая определяется следующим образом:
3 '°'
nt
4
RQн1 = nt L.J Yt,i
i=O
(5.32')
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
473
и
./nt.
1
d
JiRQн1
(Rvt+1 - Ivt+1)---+ N(O, 1).
Однако в работах
(2002)],
[Gon~alves,
но, что
(5.32)
[Barndorff-Nielsen, Shephard (2005Ь)], [Meddahi
Meddahi (2005)], [Nielsen, Frederiksen (2006)] показа
плохо соответствует действительности в условиях малых
выборок.
В качестве альтернативного приближения для распределения инте
грированной квартисивности можно использовать:
1
d
.jnt,--;::===;::;::::::::::::==(ln(Rvt+1) - ln(Ivt+1)]---+ N(O, 1).
2
RQн1
3 (Rvtн)2
В работах [Gon~alves,
Meddahi (2005, 2008)]
показано как бутстреп
процедура и разложения Эджворта могут улучшить приведенные выше
асимптотические результаты.
Ошибки измерения и микроструктурный шум
Эмпирические высокочастотные данные во многом отличаются от дан
ных из безарбитражного непрерывного процесса, что делает RV-оценку
(5.31)
сильно смещенной в условиях выборок из малых интервалов.
В силу наличия микроструктурных эффектов на фондовом рынке,
предположение о том, что логарифмы цен активов описываются диф
фузионным процессом, становится все менее адекватным по мере того,
как уменьшается масштаб времени. Как следствие, реализованная во
латильность, рассчитанная для очень коротких интервалов времени, не
является несмещенной и состоятельной оценкой дневной интегрирован
ной волатильности.
Ключом к пониманию недостатков RV-оценки является проблема
ошибок при измерении переменных. В идеальном случае RV-оценка
должна
вычисляться
на
основании
высокочастотных
внутредневных
лог-доходностей, рассчитанных на основании процесса фактических цен
р*. Однако на практике RV-оценка вычисляется на основании наблюда
емых котировок, которые загрязнены микроструктурным шумом. Это
означает, что цена р* ненаблюдаема. Ошибки измерения формируют ав
токорреляцию внутридневных доходностей, а это, в свою очередь, дела
ет реализованную волатильность смещенной и несостоятельной оценкой
интегрированной волатильности
[Hansen, Lunde (2004, 2006а)].
Например, в работах [Harris (1990)], [Zhou (1996)], [Corsi et al. (2001)]
показано, что для интервалов времени, меньших, чем несколько часов,
RV-оценка подвержена значимому влиянию систематической ошибки,
Гл.
474
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
которая влечет за собой увеличение смещенности оценки с увеличением
частоты выборки. В этих работах обнаружено: для рынков Форекс сме
щение RV-оценки положительно, т. е. математическое ожидание днев
ной реализованной волатильности, вычисленной по лог-доходностям с
частотой, превышающей один час, систематически больше, чем стан
дартное отклонение дневных лог-доходностей. Таким образом, мы сто
им перед выбором между:
большим числом наблюдений, что позволило бы сократить стоха
•
стическую ошибку измерения;
•
рыночным микроструктурным шумом, который вносит смещен
ность, растущую с увеличением частоты выборки.
Предположим, что наблюдаемые цены:
Pt 'i
где Pt~i
-
= P.t*•~t
,... 'i
= 1, 2, ... , nt,
i
эффективная цена, а ~t,i -
микроструктурный шум. Таким
образом, если мы рассмотрим логарифмы цен, то получим:
Pt,i - Pt,i-1
* - Pt,i-1
* + et,i - et,i-1,
= Pt,i
~~~
Ut,i
Yt,i
где р*
= ln(P*),
р
= ln(P),
а е
=
ln(~). Если мы предположим, что
процесс для эффективной лог-цены р*
непрерывный локальный мар
-
тингал, тогда состоятельной оценкой для интегрированной дисперсии
является реализованная волатильность для процесса эффективной лог
цены:
nt
Rvt~1 = LY;,~.
i=l
Однако
y;,i -
ненаблюдаемая величина, а реализованная волатильность
вычисляется на основании наблюдаемой
Yt,i:
nt
Rvt+1 = LYl.i,
i=l
которая является смещенной оценкой интегрированной волатильности
при
nt ---+
оо в силу наличия микроструктурного шума
et,i.
Величина
смещения представима в виде:
nt
Rvt+1
nt
nt
nt
= L Yl.i = L Y;,~ + L и~,i + 2 L Y;,iut,i ·
i=l
i=l
i=l
i=l
~~~
RVi+1
R\1t;_1
2пс;+е1
(5.33)
5.3.
Соотношение
475
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
показывает, что смещение состоит из двух ком
{5.33}
понент: реализованной волатильности шума
RVi+ 1 и реализованной ко
вариации яс;,:1 между эффективной ценой и шумом. Смещение обычно
является положительной величиной при nt --t оо в силу отрицательной
автокорреляции шума, формируемого за счет различия между ценой
спроса и ценой предложения (обзор результатов, описывающих рыноч
ную микроструктуру, см. в работах
{2007))).
[Bias et al. ( 2005})
и
[Hasbrouck
Мы будем предполагать, что шум и эффективная цена некор
релированы, т.е. яс:.:1 =о.
К настоящему времени предложено множество статистических оце
нок интегрированной волатильности, построенных в предположении
различных
структур
формирования
шума
и
эффективной
цены.
Несмотря на то что в определенных предположениях относительно шу
ма некоторые из этих оценок являются состоятельными, эмпирические
результаты от их использования указывают на то,
что они
не всегда
являются приемлемыми. Поэтому среди эконометристов нет однознач
ного выбора в пользу той или иной эмпирической оценки реализованной
волатильности {см.
[Hansen, Lunde
{2006а,Ь}),
[McAleer, Medeiros {2008})
и ссылки в них).
Одним из решений проблемы микроструктурного смещения, кото
рое часто используется на практике, является снижение частоты выбор
ки, что обеспечивает уменьшение смещения реализованной волатильно
сти как оценки интегрированной волатильности. Эта процедура назы
вается прореживанием въtборки: например, в работах
{2000,
2001а,
2003))
было предложено формировать выборку цен не из
каждого тика, а каждые
волатильности оценки.
где
(sparse)
nt
-
[Andersen et al.
5-15 минут.
Еели
Однако это приводит к увеличению
(sparse)
мы определим новую сетку с
число равноотстоящих н
аб
nt
< nt,
людений, оставшихся после
прореживания, тогда мы имеем
(sparse)
nt
_
R тт(sparse)
vн 1
-
"'""'
L....J
j=l
2
Ун
.
з
(sparse) '
nt
1
(sparse)
nt
В работах
[Barndorff-Nielsen, Shephard {2002)), [Mykland, Zhang
{2006)), [Zhang et al. {2005)), [Zhang {2006)), [AYt-Sahalia et al. {2006}) пo(sparse)
казано: несмотря то что при nt
< nt смещение уменьшается, дисперсия оценки увеличивается. Выбирая частоту выборки на основании
построенной по конечной выборке среднеквадратической ошибки оцен
ки интегрированной волатильности, мы получим, что реализованная
волатильность будет в определенном смысле оптимальной оценкой ин
тегрированной волатильности. Однако следует отметить, что существу
ют альтернативные оценки для интегрированной волатильности (мы их
Гл.
476
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
рассмотрим ниже), которые являются более точными по сравнению с
реализованной волатильностью.
В
работах
Lunde
(2006Ъ)],
[Barndorff-Nielsen,
Shepard
(2002)],
[Hansen,
[Zhang et al. (2005)], [Zhou (1996)], [Hansen, Lunde (2004)]
основное внимание уделяется разработке в условиях наличия микро
структурного шума менее смещенных и более эффективных оценок ин
тегрированной волатильности, чем RV-оценка. В результате было пред
ложено два типа оценок: ядерн:ые оценки (см.
[Hansen, Lunde (2004,
2006а, 2006в)] и [Zhou (1996)]) и оценки на подвъtборках (см. [Zhang et
al. (2005)]). В работе [Barndorff-Nielsen et al. (2005)] показано, что оцен
ки на подвыборках могут интерпретироваться как модифицированные
ядерные оценки.
5.3.3.
Ядерные оценки
Если нам необходимо получить состоятельную оценку интегрирован
ной волатильности в условиях наличия микроструктурного шума, то
мы можем прибегнуть к хорошо известным автокорреляционным по
правкам, которые используются, например, для оценки долгосрочной
дисперсии и ковариации стационарных стохастических процессов (см.,
например,
[Andrews (1991)], [Newey, West (1987)].
работах [Hansen, Lunde (2004), (2006а,Ъ)] применяется
В
аналогич
ная техника коррекции RV-оценки для уменьшения смещенности оцен
ки в условиях микроструктурного шума. В работе
[Hansen, Lunde (2004)]
делаются следующие предположения относительно микроструктурного
шума:
1)
шум является процессом с ограниченным числом ненулевых авто
кореляций;
2)
шум коррелирован с приращениями ненаблюдаемой (эффектив
ной) цены р*.
Подход, использованный в работах
[Hansen, Lunde (2004,
2006а,Ъ)],
состоит в том, чтобы скорректировать оценку реализованной волатиль
ности в предположении наличия только
(где
q
q
ненулевых автокорреляций
растет с увеличением частоты наблюдений, т. е. с увеличением
объема выборки
nt).
Мотивация использования такого подхода состоит
в том, что автокорреляция внутридневных доходностей практически
бывает ненулевой лишь до некоторого конечного порядка: например,
если «ошибки ценообразования~ исчезают через две минуты, то нам
следует выбирать порядок q таким, что он покрывал, по крайней мере,
двухминутное временное окно.
5.3.
477
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
При выполнении условий, упомянутых выше, а также при неко
торых добавочных слабых условиях в работах
[Hansen, Lunde (2004,
2006а, Ь)] предлагается скорректированная реализованная волатиль
ность,
которая
вычисляется
на основании
эмпирических
автоковари
аций. Она является несмещенной оценкой и имеет вид:
nt
RVAc
=L
q
Yl.i
+2L
i=l
nt ~ h
h=l
nt-h
L
(5.34)
Yt,jYt,j+h·
j=l
Недостатком RVАс-оценки является то, что она может принимать
отрицательные значения, тогда как волатильность всегда положитель
на. Это происходит в силу того, что ковариационные слагаемые масшта
бируются множителем n~_:h. В работах
[Hansen, Lunde (2004,
2006а,Ь))
на примере эмпирических данных показано, что эта проблема возникает
на практике, когда берутся внутридневные доходности очень высокой
частотности. Однако когда берутся данные умеренной частотности, то
такой проблемы не возникает. В этих работах предложена формула для
вычисления подходящего порядка
чтобы
где
qi:
предлагается выбирать
q
таким,
q/nt было бы постоянным при любом nt. А именно:
w-
рассматриваемая длина лагового окна,
ceil(x) обозначает наи
меньшее целое число, превосходящее или равное х, а (Ь
-
а)
-
длина
периода, охватываемого выборкой и измеренного в единицах времени
(при этом, (Ь-
a)/nt - период внутридневной доходности). Например,
если w = 15 минут, а Ь - а= 390 минут, тогда q = ceil(nt/26).
Для того чтобы полностью исключить возможность получения от
рицательных значений оценки волатильности, Лунде и Хансен предло
жили использовать разные методы уменьшения несмещенности, кото
рые предполагают использование различных ядер. Например, для яд
ра Бартлетта, описание которого представлено в работе
(1987)]
[Newey, West
на примере оценки ковариации, скорректированная оценка реа
лизованной волатильности имеет вид:
nt
RVAcNw
=L
i=l
q
Yl.i
+ 2L
h=l
h )
(
1-
+i
q
nt
п~ h
nt-h
L
Yt,JYt,J+h,
(5.35)
j=1
где q = [(~) 2 1 9 ]. Однако обе оценки (5.34) и (5.35) являются несостоя
тельными.
Гл.
478
В работе
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
[Barndorff-Nielsen et al.
(2006а)] предложена следующая
ядерная оценка интегрированной волаильности:
RVвнLs =
nt
q
(h- 1)
LYl,i
+ Lk - - (ih +i-h),
i=l
q
h=l
где
л
'Yh
ni-h
=
nt ""' Yt,jYt,j+h,
nt - h L.J
. 1
J=
а
k(x) для х Е [О, 1) k(O) = 1 и k(l) =О.
нестохастическая весовая функция такая, что
Они доказали, что утверждение о том, что все скорректированные
с использованием ядер оценки интегрированной волатильности несо
стоятельны, является несправедливым. Предложено несколько состо
ятельных оценок, основанных на ядрах. Кроме того, построены ядра,
которые имеют меньшую дисперсию, чем ~оценки множественного шка
лирования», которые рассмотрены ниже.
5.3.4.
Оценки по подвыборкам
В работе
[Zhang et al. (2005)]
обычная RV-оценка категоризирована как
одна из лучших оценок реализованной волатильности (пятая по каче
ству из рассмотренных в статье). Но если при этом несколько снизить
частотность данных, то RV(sparse) становится более точной оценкой ин
тегрированной волатильности.
Рассмотрим
более
подробно
идею
построения
улучшенных
RV-оценок на подвыборках. Когда мы выбираем меньшую частотность,
мы используем только долю имеющихся данных. Например, если мы
имеем минутные котировки цен, а используем пятиминутные доходно
сти, тогда для вычисления реализованной волатильности использует
ся лишь каждое пятое наблюдение, т. е. наблюдения в моменты време
ни:
1, 6, 11, 16, ...
Но следует учесть, что существуют и другие схемы
формирования подвыборки, например:
2, 7, 12, 17, ...
или
3, 8, 13, 18, ....
Обозначим множество моментов времени, отвечающих наблюдениям,
через Л. Пусть число элементов в множестве Л равно
nt.
Разобьем Л на
К непересекающихся подмножеств Л(k), k = 1, ... , К размера n(k), так
что:
к
л
=
Uл
k=1
(k),
л (k)
n л <Л = Ф
для
k
:f: j.
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
479
RV-оценка, отвечающая множеству моментов времени Л(k), определяется как:
L
*RVi~~ =
Yli·
iEЛ(k)
Еще одна достаточно качественная RV-оценка (вторая по точности
среди рассмотренных в статье
[Zhang et al. (2005)])
дается формулой:
к
R ттAvg
1 ""R'т(k)
vt+1 =к L....J vн1·
k=1
Однако оценка
(5.36)
(5.36)
является смещенной для высоких частотно
стей, но при этом она более сглаженная. Лучшая оценка RVi~ISE ре
ализованной волатильности, известная как оценка в двух временнъtх
шкалах (Тwо Time Scales Estimator), использует RVi~~g и оценку реализованной волатильности RVi~~l,sparse)(k) , вычисленную для макси
мально возможной частоты:
RV.TTSE - RV.Avg - n(k) RV.(all,sparse)(k)
t+I
t+I
nt
t+I
'
(5.37)
где k - номер подмножества Л (k) максимальной частоты.
В работе
[AYt-Sahalia et al. (2006)]
представлена модифицированная
оценка для RViTTSE:
_
RттТТSЕ,аdj
Vt+1
-
(i _
n(k))-l R'тТТSЕ
Vt+1
•
nt
Свойства обеих оценок, задаваемых формулами
(5.37)
(5.38)
и
(5.38),
получе
ныв предположении н.о.р.с.в. (независимости и одинаковой распреде
ленности случайных величин), отвечающих микроструктурному шуму.
В случае зависимых с.в. (случайных величин), отвечающих шуму, в
работах
[Zhang
(2006а)] и
[AYt-Sahalia et al. (2006)]
предложена альтер
нативная оценка. Для того чтобы представить эту оценку, нам необхо
дима так называемая реализованная волати.л:ьностъ усредненного лага
J (average lag}, RVi<:"1~j, которая определяется следующим образом:
AL
1n~
2
RVi+1,J = J L....J (Yt,i+J - Yt,i) ·
i=O
Альтернативная оценка для случая зависимых с.в., отвечающих
шуму, представляет собой обобщение ТSSЕ-оценки и впервые была по
лучена в работе
[Zhang et al. (2005)].
Она имеет вид:
-(К)
nt
ттАL
R тт(GТТSЕ) _ ттАL
vt+1
- Rvн1,к - -(J) Rvt+1,J'
nt
Гл.
480
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
где 1 ~ J ~ К ~ nt, К
= o(nt),
n~K)
=
(nt-:+l)
и n~J)
=
(nt-;+l).
Отметим, что последняя оценка совпадает с ТТSЕ-оценкой из работы
[Zhang et al. (2005)] при J
=
1 и К --+ оо при nt --+ оо. Следrющая
=
-(К))-1
(l _ !1__
модификация имеет вид:
RV..(GTTSE,adj)
t+l
-(J)
nt
RV..(GТТSE)
t+l
.
(5.38')
Следrет выразить некоторое предостережение в случае, когда вы
числяются оценки по подвыборкам: если, например, в сетку разбиения
временной оси не попадает момент открытия
тия
или момент закры
9:30
16:00, то будет пропущено большое количество совершенных сделок,
так как обычно наблюдается большая торговая активность вначале и в
конце торгового дня. В результате мы получим заниженную оценку ин
тегрированной волатильности. Следовательно, рекомендrется форми
ровать временные подинтервалы таким образом, чтобы моменты вре
мени, отвечающие сделкам при открытии и закрытии торгов, попадали
в узлы разбиения, см.
5.3.5.
[Payseur
(2007а)].
Оптимальные частоты для формирования
выборки
В предположении н.о.р.с.в., отвечающих шуму, в работах
{2006а)] и
[Zhang et al. (2005)]
[Bandi, Russell
предложено выбирать оптимальную ча
стоту, основываясь на минимизации среднеквадратической ошибки
(MSE):
MSE ( n~sparse))
= 2. n~sparse)E(e~,i) + 4n~sparse)E(et,i)+
+ [8 . RV..(sparse)E(e2
·) _
t+l
t,i
2V(e2 ·)]
t,i
+
2
(sparse)
nt
. IQ(sparse).
t+l
Приближенное решение этой задачи дается формулой:
*,......, {
nt ,. . . ,
IQн1
4[Е(е2 .))2
1/3
}
t,i
'
где определение
IQt см. в формуле (5.32).
В работе [Bandi, Russell (2006а)] рассматриваются равноотстоящие
узлы разбиения временной оси, тогда как в работе [Zhang et al. {2005)]
представлена более общая формула для неравноотстоящих узлов разби
ения временной оси. В работе
[Bandi, Russell
(2005а)] рассматривается
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
481
проблема выбора оптимальной частоты в случае зависимых с.в., отве
чающих шуму, для реализованной волатильности, скорректированной
на смещение.
В работах
[Bandi, Russell
что:
(2006а)] и
[Zhang et al. (2005))
показано,
1
(all) Р
( 2 )
-2 RVi+1 --=--+ Е €t i ,
nt
'
где RVi~~l) - реализованная волатильность с использованием всех до
ступных данных.
Кроме того, в работах
[Bandi, Russell
(2006а)] и
[Zhang et al. (2005))
используется реализованная квартисивность
интегрированной квартисивности. Однако
(5.32') в качестве оценки
(5.32') будет достаточно точ
ной оценкой интегрированной квартисивности только в случае, если
микроструктурный шум отсутствует. В работе
предлагается брать частоту выборки, равную
новании
смоделированных данных
показано,
[Bandi, Russell (2006а)]
15 минутам. В ней на ос
что
такая
прореженная
выборка не приводит к негативному эффекту при выборе оптимальной
частоты. В работе
[Zhang et al. (2005))
представлено альтернативное ре
шение для оценки интегрированной квартисивности
что оценка
RQ
ная частота
5.3.6.
(RQ).
Учитывая,
может быть сильно изменчивой, получаемая оптималь
nt может быть также сильно изменчивой.
Скачки
В относительно недавних исследованиях представлены аргументы в
пользу использования моделей со ска-чка.ми, или разрывами, в зада
че оценки стохастической волатильности, ценообразовании опционов и
дРУГИХ производных финансовых инструментов (см., например,
[Andersen et al. (2002)), [Chan, Maheu (2002)), [Chernov et al. (2003)), [Eraker
et al. (2003)), [Maheu, McCurdy (2004)), [Khalaf et al. (2003)), [Huang,
Tauchen (2005))).
Эмпирические исследования указывают на то, что условная дис
персия большинства активов представима в виде комбинации гладкой и
медленно меняющейся компоненты, являющейся непрерывным процес
сом, возвращающимся к среднему, и менее устойчивой компоненты, от
вечающей за скачки, см.
, например, [Andersen et al. (2007))
и
[Bollerslev
et al. (2009)).
Для того чтобы лучше понять этот феномен, мы коротко пред
ставим основы теории би-степенной вариации, см.
[Barndorff-Nielsen,
Shephard (2004, 2006)).
Если мы обозначим логарифм цены актива в момент времени
t
че
рез р( t )*, диффузионный процесс, традиционно используемый в цено-
Гл.
482
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
образовании активов, имеет следующий вид:
dp(t)* = µ(t)dt + u(t)dW(t)
где
µ( t) -
+ k(t)dq(t),
непрерывный процесс, имеющий локально-ограниченную ва
риацию; стохастическая волатильность u(t) является строго положи
тельной и caglad8 функцией; W (t) - стандартное броуновское движе
ние;
q(t) -
дискретный процесс, который при
кам в момент времени
t,
а при
dq(t)
=
О
dq(t)
= 1,
отвечает скач
- отсутствию скачков; k(t)
соответствует величине скачков. Квадратическая вариация кумулятив
y(t) = p(t) - р(О), имеет вид
Shephard {2004, 2006)], [Andersen et al. {2007)]):
ной доходности
[у, Y]t =
rt u2 (s)ds +
Jo
L
(см.
[Barndorff-Nielsen,
k 2 (s).
O<s~t
(5.39)
Второе слагаемое в правой части аннулируется, когда отсутствуют
скачки. И в этом случае квадратическая вариация равна интегрирован
ной волатильности.
В работе
[Andersen et al. {2007)]
представлен новый непараметри
ческий подход для идентификации двух компонент в уравнении
В этой более общей ситуации RV-оценка
(5.31)
{5.39).
при стремлении частоты
выборки к бесконечности равномерно сходится по вероятности к при
ращению квадратической вариации, определенной выше, т. е.:
plim R\/t+1(д) =
д--+0
1
t+1
u2 (s)ds +
t
L
{5.40)
k2 (s).
t<s~t+1
Таким образом, в отсутствие скачков реализованная вариация явля
ется
состоятельной
оценкой
для
интегрированной
волатильности.
В общем случае реализованная волатильность наследует динамики как
непрерывной составляющей, так и скачкообразной составляющей.
Используя
недавние
асимптотические
[Barndorff-Nielsen, Shephard {2004, 2006)],
результаты
из
работы
можно идентифицировать
(непараметрическими методами) две компоненты квадратической ва
риации. Определим стандартизированную меру реализован:н,ой бисте
nенной вариации (или ВV-волатильность) следующим образом:
1/д
В\/t+1(д) = µ1 2
L
j=2
8 То
nt
IYt+jд,лllYt+(j-1)д,дl = µ1 2
L IYt,illYt,i-11,
(5.40')
i=2
есть непрерывной справа функцией, у которой существует предел слева. Это
предположение позволяет допустить наличие дискретных скачков стохастической
волатильности.
5.3.
где µ1 =
.j2fi
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
483
= E(IZI) обозначает математическое ожидание аб
солютного значения стандартной нормальной случайной величины
В работах
Z.
[Barndorff-Nielsen, Shephard {2004, 2006)] показано, что:
1
BVi+1(д) = t
plim
д--+0
Следовательно, комбинируя результаты
t+1
u 2 (s)ds.
{5.40)
и
{5.41)
{5.41),
можно оценить
вклад в квадратическую вариацию компоненты, отвечающей скачкам:
plim
д--+0
RVi+1(д) - BVi+1(д)
L
=
{5.42)
k 2 (s).
t<s~t+1
Поскольку правая часть
{5.42) может быть отрицательной, в работе
[Barndorff-Nielsen, Shephard {2004)) предлагается ввести корректировку
эмпирической меры для скачков, обеспечивающую неотрицательность:
Jt+1(д)
= max[RVi+1(д) -
BVi+1(д), О].
{5.43)
Стягивающие оценки для скачков. Теоретические свойства
непараметрической оценки для скачков, определенной выше в виде раз
ниць1 между реализованной волатильностью и бистепенной вариацией,
получены в предположении, что частота выборки д
---+
О. Однако на
практике мы имеем дело с данными в дискретном времени д
>
О, в
которых присутсвуют ошибки измерения. Кроме того, корректировка
(5.43),
обеспечивающая неотрицательность, представляет собой лишь
частичное решение проблемы.
В работе
[Huang, Tauchen {2005))
на смоделированных данных по
казано, что более робастая мера вклада скачков в вариацию цены дается
статистикой относите.11/ЬН'ЬtХ ска-ч.ков, RJt+1
или соответствующим
= (RVi+1-BVi+1)/ RVi+1,
Jt+1 =
индекса SP 500,
логарифмическим отношением,
= ln RVi+1 - ln BVi+ 1 · Эмпирические исследования для
представленные в работе
т. е.
[Huang, Tauchen {2005)], показывают, что от
носительный вклад скачков в вариацию цены, измеряемый при помощи
RJt+1,
равен приблизительно
7%.
Используя теорию асимптотических распределений, авторы рабо
ты
[Barndorff-Nielsen, Shephard {2004а)) показали, что можно урезать
Jt+1 и рассматривать только те скачки, которые превышают опреде
ленный порог. Этот подход адаптирован к расчетам в работе [Andersen
et al. {2007)), где используется достаточно большое критическое значе
ние для идентификации только наиболее значимых скачков, которые
затем используются в модели прогнозирования
RVi+1 ·
В этой работе
предлагается интерпретировать небольшие скачки как ошибки измере
ния и рассматривать их как непрерывную часть траектории вариации.
Гл.
484
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
И только достаточно большие значения
RVt+ 1 ( д) - BVt+ 1 ( д)
ассоции
руются с компонентой, отвечающей скачкам. Такой подход основан на
результатах из работы
[Barndorff-Nielsen, Shephard
(2004а)], где показа
но, что при отсутствие скачков и при д -t О:
(5.44)
Определим стандартизированную меру реализованной тристепен
ной квартисивности соотношением
1/д
TQt+1(д) = д- 1 µ4/~
L
1Yt+jд,лl 413 1Yt+(j-l)д,дl 413 1Yн(j-2)д,дl 413 ,
j=З
(5.45)
где µ4/3
=
22/ 3 · Г(7 /6) · Г(l/2)- 1
= E(IZl 413 ).
Эта мера используется
как оценка для интегрированной квартисивности
[Barndorff-Nielsen, Shephard (2004)]
ТQн1(д)
plim
д--+0
Учитывая
(5.44)-(5.46),
показано, что:
=
1
t+l
J и 4 ( s )ds. В работе
t
t+1
t
(5.46)
u 4 (s)ds.
мы получим следующую тестовую статистику:
(5.47)
Большое значение этой стандартизированной разности между реа
лизованной волатильностью и бистепенной вариацией (см.
(5.40')) ин
терпретируется как указатель на то, что имеется «значимый~ скачок
на промежутке времени
[t, t + 1].
Однако результаты на смоделированных данных, представленные
в
[Huang, Tauchen (2005)], показывают, что статистика, определяемая
(5.47), тяготеет к слишком частому отклонению нулевой гипотезы об
отсутствии значительных скачков. В этой работе, следуя [BarndorffNielsen, Shephard (2005Ь)], представлена модификация (5.47):
Zнl(д) =
_;og(R~~+1(д)) - log(BVt+1(д))
[д(µ1
+ 2µ1
- 5)ТQн1 (д)BVt+1 (д)- 2 )11 2
-t N(O,
l).
(5.48)
Статистика Zн1 ( д) лучше аппроксимируется нормальным распреде
лением на хвостах. Еще одна альтернативная версия вспомогательной
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
485
статистики для идентификации скачков, дающая очень похожие резуль
таты:
z
(д) _
t+l
-
[RVi+1(д) - BVi+1(д)]/ RVi+1(д)
[д(µ1 4 + 2µ1 2 - 5) max{l, ТQн1(д)ВVi+1(д)- 2 }]1/2 --+
--+ N(O; 1).
(5.48')
В работе
ются как
[Andersen et al. (2007)) значимые скачки идентифициру
превышение статистик (5.48) критического значения, Ф0t:
Jн1,0t(д) = l{zн 1 (д)>Фа.} · [RVi+1(д) - BVi+1(д)],
где Iн
-
(5.49)
индикаторная функция. Непрерывная составляющая вариации
оценивается как:
Сн1,0t(д)
= l{zн 1 (д)~Фа.} · RVi+1(д) + l{Zt+i(д)>Фa.} · BVi+1(д).
Если учесть, что Ф0t
>
О и
(5.49), (5.50),
то автоматически полу
чаем положительность Jн1,0t и Сн1,0t· Интересно отметить, что
отвечает случаю, когда а
[Andersen et al. (2007))
= 0.5,
или
Jt =
(5.50)
(5.43)
Jt,0.5· Более того, в работе
отмечается, что эта оценка может быть интер
претирована как стягивающая оценка для скачков.
Меры бистепенной вариации и коррекция микроструктур
ного шума. Как мы уже отмечали, наблюдаемая цена «загрязнена~
рыночным микроструктурным шумом. А наблюдаемый процесс лога
рифма цены в непрерывном времени предполагается семимартингалом;
а при высокой частотности выборки зашумленность приводит к поло
жительной смещенности оценки
скольку E(IY;,il)
<
(5.40') для бистепенной вариации, по
E(IY;,i + Ut,il). Серийная автокорреляция для Ut,i
является дополнительным источником смещения ВРУ-оценки. Анало
гичное справедливо для оценки тристепенной квартисивности
Как указано в работе
[Huang, Tauchen (2005)],
(5.45).
это, в свою очередь,
влечет то, что описанные выше тестовые статистики для скачков будут
иметь положительное смещение. Числовые расчеты и эксперименты,
представленные в этой работе, подтверждают, что для высокочастот
ных выборок (т. е. при малых д), тестовые статистики имеют положи
тельное смещение вместе с величиной дисперсии микроструктурного
шума.
Ложная серийная корреляция наблюдаемых доходностей может
быть ликвидирована при помощи «пошатывания~ доходностей или
«пропуском одной~ доходности. Если мы заменим сумму абсолютных
значений последовательных доходностей в (5.40') соответствующими
Гл.
486
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
«пошатанными» абсолютными доходностями, мы можем получить мо
дифицированную реализованную бистепенную вариацию:
1/д
BV1,t+1(д) =
µ1
2 (1-
2д)- 1
L
IYt+jл,лllYt+(j-2)д,лl =
j=З
nt
= µ1
2 (1-
2д)- 1
L IYt,illYt,i-21,
i=З
где нормирующий множитель перед суммой отражает потери в резуль
тате «пошатывания» доходностей.
Аналогичным образом мы можем действовать с серийной зависимо
стью более высокого порядка, попросту увеличивая длину лага. Анало
гично интегрированная квартисивность может быть оценена при помо
щи «пошатывания» реализованной тристепенной квартисивности:
ТQ1,н1(д)
= д- 1 µ41~(1- 4д)- 1 х
1/д
х
L
1Yt+jд,лl 413 1Yt+(j-2)д,лl 413 1Yн(j-4)д,дl 413 .
j=5
В работе
сутствие
[Barndorff-Nielsen, Shephard
шума
эти
«пошатанные»
(2004а)] показано, что в от
реализованные
вариации
остаются
состоятельными оценками для соответствующих интегрированных ва
риаций. Таким образом, асимптотическое распределение тестовой ста
тистики, полученное путем замены BVi+1(д) и TQt+1(д) в (5.48) и
(5.48') «пошатанными» аналогами, будет также стандартным нормаль
ным распределением. Важно отметить, что процедура «пошатывания»
ослабит смешанное влияние рыночного микроструктурного шума, что
обеспечит более точную аппроксимацию в условиях малых выборок,
как подтверждается экспериментами, проведенными в работе
[Huang,
Tauchen (2005)].
Альтернативные пороговые оценки. В работе
[Mancini (2009)]
предложен альтернативный метод идентификации непрерывной компо
ненты реализованной волатильности, который основан на использова
нии следующей статистики:
nt
TRVi+1
=
LYli. I{IYt,il<O]}'
i=l
где
() -
пороговая функция. В этой статистике исключаются больше
доходностей в периоды высокой волатильности, чем в периоды низкой
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
волатильности. В статье
[Mancini, Reno (2006)]
487
рассматривается меня
ющаяся во времени пороговая функция:
где
условная дисперсия, для которой предполагается GАRСН-мо
ht -
дель. Параметр се предполагается равным
тистику Т R"Vt+1 не входят наблюдения
3. Это означает, что в ста
Yt,i, которые по абсолютному
значению превышают три условных стандартных отклонения. Исполь
зование динамической пороговой функции позволяет получить более
точную процедУРУ обнаружения скачков в условиях, когда дисперсия
диффузии большая
(т. е.
когда более вероятно, что значительные дви
жения образованы за счет диффузионной компоненты, а не скачками).
В работе
санной в
[Corsi et al. (2008Ь)] представлено решение проблемы, опи
[Andersen, Bollerslev, Diebold (2007)] и состоящей в том, что
скачки в результате смещения, обеспеченного ошибкой измерения, не
имеют предсказательной силы при прогнозировании будУщей волатиль
ности. А именно, предположим
Yt,i
включает в себя скачок. В случае
бистепенной вариации оно будет умножаться на две соседние доходно
сти,
и
Yt,i-1
Yt,i+1 · Асимптотически
обе эти доходности будУт стремить
ся к нулю, а бистепенная вариация будет сходиться к интегрированной
непрерывной компоненте волатильности. Но когда nt конечно, эти до
ходности будУт отличаться от нуля, что обеспечивает положительное
смещение, которое будет тем больше, чем большее значение принима
ет
Yt,i·
Это указывает на то, что смещение бистепенной вариации бу
дет чрезвычайно большим в случае последовательных скачков. Таким
образом, в случае, когда используется бистепенная вариация для уче
та непрерывной компоненты волатильности, возникает положительное
смещение.
В работе
[Corsi et al.
(2008Ь)] представлена альтернативная оценка
непрерывной компоненты волатильности, названная оценкой скоррек
тированной пороговой бистепенной вариации ( СТВV-оценкой), имеющая вид:
CTB"Vt+1
=;
nt
LZ1(Yt,i,Oi)Z1(Yt,i-1,0i-1),
i=2
где Z1(Yt,i, 8i)-функция, равная IYt,il, когдаУt,i
когда
Yt,i
~
(Ji,
при этом,
(Ji -
< 8, и равная 1.094./0i,
порог, вычисляемый итеративно:
Гл.
488
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Даже если CTBYt+1 и
д > О мы имеем:
CTBvt+1
TRYt+1
TRYt+1
сходятся к
BV
---+ RV
---+
Ivt+1
при
се--+ оо
при
С{)--+ оо.
при д
--+
О, для
Компонента, отвечающая скачкам, вычисляется как разность меж
/lУ реализованной RV-оценкой и СТВV-оценкой:
В работе
[Corsi et al. {2008Ь)) используется «более очищенная» те
стовая статистика, чем {5.48'). Более детальную информацию см. в этой
статье.
5.3. 7.
Модели для прогнозирования реализованной
волатильности
Во многих эмпирических исследованиях указывается на наличие зави
симости с длинной памятью для волатильности финансового рынка.
Для моделирования этого феномена предлагается несколько методо
логий. Вот лишь некоторые из них: см. [RoЬinson
{1991)), [Ding et al.
{1993)), [Baillie, Bollerslev, Mikkelsen {1996)), [Andersen, Bollerslev {1997)),
[Breidt et al. {1998)), [Dacorogna et al. {2001)). Однако до сих пор основ
ное внимание исследователей уделяется двум основным классам моде
лей.
•
Авторегрессионн:ы.е фракталъно-интегрированн'Ьtе модели сколъ
з.ящего среднего
(ARFIMA)
с длинной памятью для реализован
ных волатильностей, которые рассмотрены, например, в работах
[Areal, Taylor {2002)), [Andersen et al. {2003)), [Shackleton, Taylor,
Xu {2004)), [Deo et al. {2006)), [Koopman, Jungbacker, Hol {2005)).
•
Модели
гетерогенной
авторегрессионной
реализованной
волатилъности
(HAR-RV), которые рассмотрены в работах [Corsi
{2009)), [Andersen et al. {2007)), [Corsi et al. {2008а)], [Bollerslev
et al. {2009)). НАR-RV-модели основаны на так называемой ге
тероскедастичной АRСН-модели {HARCH). Этот класс моделей
анализируется в работе [Miiller et al. {1997)]. В моделях из это
го класса условная дисперсия доходностей, взятых в дискретные
моменты времени, парамеризована как линейная функция от ла
гированных квадратов доходностей за длинные и {или) короткие
5.3.
489
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
временные горизонты. Хотя формально НАR-структура не обла
дает длинной памятью, перемешивание сравнительно небольшо
го числа компонент-волатильностей позволяет воспроизвести эф
фект медленного убывания автокорреляции волатильности, кото
рое имеет скорость убывания, почти неотличимую от гиперболи
ческого, что соответствует длинной памяти.
АRFIМА-модели
для
реализованной
волатильности.
Как мы указывали выше, имеются существенные эмпирические основа
ния, представленные в работах многих исследователей, которые указы
вают на то, что реализованная волатильность является фрактально ин
тегрированной, т. е. эффект влияния шока медленно (с гиперболической
скоростью) убывает. Этот факт указывает на неприемлемость АRМА
модели для реализованной волатильности {которой отвечает экспонен
циальное убывание авто корреляции).
Для того чтобы учесть эффект длинной памяти, в работе
et al. {2003)]
предлагается использовать
[Andersen
ARFIMA{p, d, q)-модель для ре
ализованной волатильности:
Ф(L){l - L)d(Rvt+1 - µ) = 0(L)иt,
где
(5.51)
{1- L)d определяется при помощи следующего разложения:
d
~
Г(j-d)
.
{l - L) ={:о Г(-d)Г(j + 1) LJ.
Если
ldl Е
сутствует
{О,
1/2), то процесс является стационарным и в данных при
эффект длинной памяти. Если d Е {-1/2,0), то процесс бу
дет антиустойчивым с короткой памятью. Процедура оценки состоит
из двух шагов:
• На первом шаге оценивается параметр d с использованием оценки
из работы [Geweke, Porter-Hudak {1984)], в которой предлагается
семипараметрическая оценка параметра d. Пусть через J(wj) обо
значена выборочная периодограмма j-й Фурье-частотности, Wj
=
= 21Гj/Т, где Т- число наблюдений в выборке. Оценка параметра
d
получается из регрессионного уравнения:
где
j
= 1, ... , т, и т таковы, что
1
т
-+--+О
т
т
Гл.
490
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
при Т, стремящемся к бесконечности. Результаты симуляционного
моделирования из работы [Hurvich et al. (1998)] указывают на то,
что можно брать m
Т4 1 5 в качестве ширины окна.
=
На втором шаге вычисляются остатки, которые получаются при
•
помощи фильтрации исходных данных (с использованием оценен
ного фильтра фрактальной интеграции), а затем с использовани
ем МНК оценивается модель
В модель
(5.51)
(5.51).
могут быть включены дополнительные экономические
и финансовые объясняющие переменные. Отметим при этом следующее
важное обстоятельство: если мы рассматриваем модели для дневных во
латильностей, то механика включенных дополнительных объясняющих
переменных более сложна.
Класс
(2009)]
моделей
волатильности
HAR-RV.
В работе
[Corsi
предложен класс моделей волатильности, которые позволяют
весьма просто достигнуть цель моделирования длинной памяти вола
тильности.
Для того чтобы описать
HAR-RV модель,
нам необходимо использо
вать многопериодные реализованные волатильности, определяемые как
нормированная сумма однопериодных волатильностей (см.
RVt,t+h = h- 1[RVt+1
(5.31')):
+ RVt+2 + ... + RVt+h]·
В работе
меры
[Andersen et al. (2007)] рассматриваются нормированные
волатильностей для h = 5 и h = 22, интерпретируемые как
недельные и месячные волатильности соответственно. Более того, по
определению дневных волатильностей: RVt,н1
Дневная
= RVt+1·
HAR-RV модель в работе [Corsi (2009)] имеет вид: as
RVt,н1
= fЗо + fЗvRVt + fЗwRVt-s,t + fЗмRVt-22,t + ft+l·
В модели в качестве объясняющих переменных могут использовать
ся реализованные волатильности для других временных горизонтов, но
дневные, недельные и месячные реализованные волатильности имеют
весьма естественную экономическую интерпретацию (см.
[Andersen et
al. (2007)], [Corsi (2009)]).
Эта модель прогнозирования может быть обобщена на более дли
тельные временные горизонты и может учитывать скачки, которые мо
гут быть включены в модель в качестве дополнительной объясняющей
переменной. В результате в качестве возможного обобщения мы полу
чим так называемую НАR-RV-J-модель (т.е.
HAR-RV
модель с оцен
ками скачков, используемыми в качестве объясняющих переменных):
RVt,t+h = fЗо + fЗvRVt + fЗwRVt-s,t + fЗмRVt-22,t + fЗJJt + ft,t+h·
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
491
Важно отметить, что, имея однопериодные наблюдения и более
длинные горизонты прогнозирования, т. е.
h
> 1,
ошибка будет серий
но коррелирована до порядка
h - 1 в силу использования одинаковых
данных. В работе [Andersen et al. (2007)] эта проблема исправлена при
помощи использования состоятельной оценки ковариационной матрицы
Бартлетта/Ньи-Веста, учитывающей гетероскедастичность (с
лагами для дневных
(h=l),
для недельных
(h=5)
5, 10 и 44
и месячных
(h=22)
оценок).
Следует отметить три весьма интересных результата, представлен
ных в работе
1.
[Andersen et al. (2007)].
Статистическая значимость оценок
f3v, f3w
и f3м указывает на
существование устойчивой зависимости волатильностей.
2.
Компонента, отвечающая дневной волатильности, является срав
нительно более важной для дневных прогнозов, тогда как компо
нента, отвечающая месячным волатильностям, является сравни
тельно более важной для долгосрочных месячных пронозов.
3.
Коэффициент при компоненте, отвечающей скачкам,
f3J,
отрица
тельный во всех моделях и на всех рынках. Это означает, что для
дней, в которые часть реализованной волатильности формируется
за счет компоненты, отвечающей скачкам, последняя не привно
сит никакой прогнозной мощности реализованной волатильности
на следующей день.
В работе
[Andersen et al. (2007)]
аналогичная модель также исполь
зуется для прогнозирования стандартных отклонений:
(R'Vt,нh) 1 1 2 =
+ f3v(RVt) 1l 2 + f3w(RVt-s,t) 112 + f3м(RVt-22,t) 1 12 +
+f3JJt1/2 + ft,t+h·
f3o
Процедура оценки параметров аналогична той, что используется
в модели для дисперсии. Но более робастые стандартные отклонения
приводят к большим значениям R 2 , чем для модели дисперсий.
НАR-RV-J-модель также используется для моделирования лога
рифмов реализованных волатильностей (поскольку в работах
et al. (2007)]
и
[Andersen et al. (2003)]
[Andersen
показано, что распределение ло
гарифмов дневных реализованных волатильностей аппроксимируются
нормальным распределением):
ln(R'Vt,нh)
= f3o + f3v ln(RVt) + f3w ln(RVt-s,t) + fЗмlog(RVt-22,t) +
+f3J ln(Jt + 1) + ft,t+h·
Гл.
492
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
Результаты, полученные на основании последней модели, весьма
схожи с теми, что были представлены в предыдущих моделях. Исхо
дя
из
эмпирических
результатов,
мы
снова
получаем
то,
что
скачки
обычно ассоциируются с очень «короткоживущими» вспышками вола
тильности.
В работе
[Andersen et al. (2007)]
модель
HAR-RV-J
модифицирована
с использованием разложения реализованных волатильностей на непре
рывную составляющую и скачки (см. формулы
(5.49)
определим нормированные многопериодные скачки
ные составляющие
Ct,t+h
и
(5.50)).
Jt,t+h
Если мы
и непрерыв
соотношениями:
h- 1 [Jн1
+ Jн2 + · · · + Jнh],
h- 1 [Сн1 + Сн2 + ... + Снh],
то обобщенная, так называемая НАR-RV-СJ-модель представится в
форме:
/30 + /3cvCt + /3cwCt-5,t + /3cмCt-22,t +
+/3JvJt + /3JwJt-5,t + /3JмJt-22,t + ft,t+h·
Rvt,t+h
Аналогичные модели могут быть использованы для моделирования
стандартных отклонений и логарифмических реализованных волатиль
ностей. В работе
•
[Andersen et al. (2007)]
показано, что:
большинство оценок коэффициентов при компоненте, отвечающей
скачкам, являются незначимыми; это означает, что прогноз
RV-
оценки определяется непрерывной составляющей;
• НАR-RV-СJ-модели дают увеличение R 2 на О, 01, или на 2-3% от
носительно R 2 для НАR-RV-J-модели;
•
НАR-RV-СJ-модели позволяют учесть сильную серийную корре
ляцию
RVi,t+h,
но все еще остаются статистические значимые ав
то корреляции, отвечающие более высоким лагам.
Совместное моделирование реализованной волатильности,
бистепенной вариации и скачков. В работе
[Bollerslev et al. (2009)]
представлена модель дневной стохастической волатильности, в которой
для ценовых движений различаются скачки и непрерывная компонен
та (с использованием реализованной волатильности и бистепенной ва
риации). Такая модель позволяет описывать структурную зависимость
между шоками и рыночныыми доходностями; зависимость между дву
мя различными компонентами волатильности (непрерывная часть и
скачки). Кроме того, в работе
[Bollerslev et al. (2009)]
показано, что
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
493
левередж-эффект формируется, главным образом, через непрерывную
составляющую волатильности.
В работах
[Corsi et al.
(2008а)],
[Bollerslev et al. (2009))
предложе
на НАR-GАRСН-ВV-модель, которая представляет собой обобщение
НАR-RV-модели и которая учитывает структурную зависимость между
шоками и доходностями, а также между двумя компонентами волатиль
ности. В отличие от НАR-RV-моделей, рассмотренных выше, которые
оцениваются при помощи МНК, в работе
[Bollerslev et al. (2009))
исполь
зуется метод максимального правдоподобия, учитывающий условную
гетероскедастичность остатков.
Для того чтобы определить модель из
[Bollerslev et al. (2009)),
вве
дем логарифмическую мультипериодную бистепенную вариацию:
(ln BV)н1-k:t
1 k
= k L ln(BVi-j),
j=l
где
k
=5
и
=
k
отвечает неделе или месяцу соответственно. НАR
22
GАRСН-ВV-модель для непрерывной компоненты реализованной вола
тильности (т. е. для Вvt-волатильности) имеет вид:
ln Bvt = ао
+ ad ln BVi-1 + aw(ln BV)t-Б:t-1 +
+ ат ( ln BV ) t-22:t-1 + 81
IYt-11
vRVi-1
+ 82I{Yt-t <О}+
/L
IYt-11
+ 8з JRVt-l l{Yt-t <0} + у htUt,
(5.52)
q
ht = c.v + L:aj(InBVi-1 - х~v.Ввv) 2 +
j=l
р
8
+ L:.Вjht-j + LAjBVi-j,
j=l
где
ht -
j=l
условная дисперсия в момент времени
t,
которая описыва
ется GАRСН-моделью; хвv включает все регрессоры из
(5.52).
Модель
также включает компоненту I{Yt-i <О}, которая определяет скачкообраз
ные изменения в свободном члене и коэффициенте при IYt-11 (подобный
механизм часто называют «левередж-эффектом~). Для моделирования
отклонений от нормальности ошибки
Ut
предполагаются распределен
ными в соответствии со смешанным нормальным распределением:
iid {
щ~
Nl(O, 1)
с вероятностью (1 - Pu)
N2(Jhu,
с вероятностью
2
ии.)
Pu
.
(5.53)
Гл.
494
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
Что касается скачков
Jt = lnRvt - lnB\/t,
для них в работе
[Bollerslev et al. (2009)) специфицируется следующая
авторегрессионная модель:
ln
(Rvt)
IYt-11
Bvt = 6о + " v'Rtlt-1
+
1,
'f'l
IYt-11
+ 'l/J2l{Yt-i <О} + '1/Jз JRv;
l{Yt-i
t-1
(Rvt-j)
<О} + L...t Oj ln BVI . +
~
j=1
(5.54)
llt.
t-3
В качестве распределения, предложенного для остатков в уравне
нии для скачков
(5.54),
берется смесь обратного гауссовского распре
деления с нулевым средним, сосредоточенного на всей действительной
оси
(NIG),
и обратного гауссовского распределения, сосредоточенного
на положительной полуоси
llt
IG,
а именно:
i2 { NIG(aюG, f3юG, ОюG) с вероятностью
IG(Л1G,µ1G)
В работе
(1 -
с вероятностью
[Bollerslev et al. (2009))
р,.,
р,.,) . (5.55 )
аргументируется этот выбор тем,
что смесь распределений обеспечивает приемлемую интерпретацию, по
скольку NIG-распределение можно рассматривать как модель для мо
делирования небольших дневных флуктуаций для логарифмической ре
ализованной волатильности вокруг логарифмической бистепенной ва
риации, тогда как обратное гауссовское распределение, сосредоточен
ное на положительной полуоси, рассматривается как модель для боль
ших отклонений. Плотность обратного гауссовского распределения имеет вид:
f(х,µ,Л) =
- µ)
1
J2n3>..
ехр [ 21х (х
---µ>:
2
]
.
Наконец, модель для дневных доходностей, использующая
Rvt
в
качестве меры изменчивости цены, и имеющая вид
d
Yt
= "Уо +
L
l'jYt-j
+ VRYtet,
(5.56)
j=1
допускает наличие серийной корреляции до d-го порядка включитель
но, а остатки предполагаются гауссовскими, ft
rv
N(O, 1).
Предполагая ошибки в разных уравнениях независимыми, в рабо
те
[Bollerslev et al. (2009))
используется рекурсивная структура систе
мы указанных выше трех уравнений, для оценки параметров каждого
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
495
из которых в отдельности используется стандартный метод максимума
правдоподобия. Интересно отметить, что с использованием этой моде
ли обнаружен значимый негативный левередж-эффект в уравнении для
непрерывной компоненты волатильности (т. е.
параметров
1/J2
и 'Фз в
Bvt),
тогда как оценки
оказались незначимыми. Это указывает
(5.54)
на то, что скачки не подвержены ассиметричному влиянию лагирован
ных доходностей-шоков, а это подтверждает справедливость использо
вания большинства параметрических диффузионных моделей со скач
ками, рассмотренных в работах
[Bates {2000)), [Eraker et al. {2003))
и
[Pan {2002)).
Однако оценка системы указанных выше уравнений не учитыва
ет возможность наличия нелинейных зависимостей остатков. В работе
[Bollerslev et al. {2009))
предлагается моделировать нелинейную зависи
мость с использованием следующей системы:
d
Yt = 'Уо + L 'YjYt-j + JRYtEt;
j=l
lnBvt = аю + adlnBVt-1 + aw(lnBV)t-Б:t-1+
+ат (ln BV )t-22:t-l
+ 82l[Yt-1
<О]+ 8з
+ 81 IYt-11 +
JR\l't-1
IYt-ll l[Yt-1
JRVt-1
<О]+ Vht(иt + g(Et));
q
ht = w + l::aj{lnBvt-1 - хБv.Ввv) 2 +
j=l
р
8
+ L/Зjht-j + LЛjB\lt-j;
j=l
Rvt)
ln ( Bvt
j=l
IYt-11
IYt-11
= 80 + 1/J1 J Rvt-l + 1/J2/[yt-1 < О) + 1/Jз J Rvt-l l[Yt-1 < О] +
+
t
j=l
8j ln
(;~=~) + (vt + т(иt) + k(Et)),
t J
где ошибки распределены в соответствии с
(5.53), (5.55)
и
(5.56).
Эта
система явным образом допускает наличие ошибок в непрерывной со
ставляющей волатильности, а уравнение для скачков нелинейно зави
сят от ошибок из уравнения для доходностей через функции общего
вида
g( Et)
и
k( Et)
соответственно. Аналогично ошибки в модели для
скачков предполагаются зависимыми от шоков непрерывной составля
ющей доходности через функцию т(иt)· Эти нелинейные зависимости
Гл.
496
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
моделируются с использованием полиномов второй степени:
+ 92€~,
g(Et) = 91ft
+ k2f~,
т(иt) = т1иt + т2и~,
k(Et) = kift
где в целях идентификации в работе
свободные
[Bollerslev et al. {2009))
члены трех используемых полиномов второй степени берутся равными
нулю. Плотность для (t = {ln BVt, ln ( ~~) , Yt) равна:
(Yt - х~/Зу
vmv; lfJ€ )
1
fy((tlXt-1i fJ) = Vh;,VRJ1; Х f€
х f и (ln BVt - х'вvfЗвv
Vht
_ 9 [ Yt
] lfJu)
exp{2 lnRVt}
х f v ( ln ( ~~) - х'вv.Ввv В работе
~ х~/Зт
Х
[Bollerslev et al. {2009))
m( ut) - k(<,)
х
10.).
получены аналогичные результаты
для системы уравнений, но в основном имеются меньшие стандартные
ошибки для оцененных параметров. Интересное обобщение в этом на
правлении относительно длинной памяти и хвостовой зависимости для
торговых объемов и волатильностей представлены в работе
[Rossi et al.
{2008)).
Эмпирический анализ с использованием
5.3.8.
статистического пакета
R:
RV-оценки.
В этом разделе с использованием пакета процедур
realized
в
R
мы
представим вычислительную процедуру для стандартных и модифици
рованных RV-оценок. Мы следуем описанию пакета процедур
представленному
[Payseur
realized,
{2007Ь)).
В этом пакете процедур имеется возможность использования вы
сокочастотных данных за период в
(MSFT)
и
General Electric (GE).
11
дней для компании
Microsoft
Эти данные мы можем загрузить при
помощи следующих команд:
library(realized)
data(msft.real.cts)
data(msft.real.tts)
data(ge.real.cts).
Первые
пании
10 высокочастотных доходностей за 5/1/1997 CTS для ком
MSFT можно загрузить при помощи следующей команды:
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
497
msft.real.cts[[1]][1:10].
Для указания дат, отвечающих данным из рассматриваемого при
мера, необходимо использовать:
data(dates.example)
dates. example.
Положительное смещение традиционной оценки реализованной во
латильности в условиях высокочастотных данных отмечается в работах
[Andersen et al.
{2000Ь)] и
[Fang, {1996)].
На рис.
5.4
изображено выбо
рочное среднее значение реализованной волатильности за п дней, т. е.
RV
=
ция
rSignature
1/п L:~=l RV(д), как функции от частоты выборки д. Функ
используется для изображения графика так называе
мой сигнатуры волатильности.
Однако усреднение по большому числу дней может стабилизиро
вать волатильный характер реализованной волатильности для малых
частот. Например, в литературе по реализованной волатильности ча
сто предлагаются альтернативные мнения относительно того, выборки
какой частоты следует использовать
{5-, 10-, 15-
или 20-минутные ко
тировки).
В работе
[Payseur
{2007а)] изучается график сигнатуры волатильно
сти, на котором представлены значения реализованной волатильности
за один день в зависимости от частоты выборки. Этот график демон
стрирует, насколько волатильными являются оценки в зависимости от
небольшого изменения частоты выборки. Функция
rSignature
исполь
зует следующие входные данные:
• range -
действительнозначный вектор, который специфицирует
входные параметры для вычисления реализованной волатильно
сти;
•
х
- real izedOb j ect
•
у
- real izedOb j ect для второго
для первого актива;
актива (в случае ковариации или
корреляции);
• makeReturns;
если мы имеем цены, то эти опции позволяют транс
формировать их в лог-доходности;
• type -
тип используемой оценки; если
y=NULL,
тогда тип будет
отвечать реализованной волатильности; если у не
NULL,
тогда тип
будет отвечать реализованной ковариации или корреляции;
•
если
cor равно TRUE
и у не равен
NULL,
то будет выведен на экран
график сигнатуры реализованной волатильности;
Гл.
498
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
определяет масштаб оси х (например, если мы имеем се
• xscale
кундные доходности и хотим ось х масштабировать в минутах,
тогда
xscale=1/60).
График сигнатуры для
MSFT за Мау 1, 1997,
при исходной частоте
выборки, равной одной секунде, на котором по оси х откладываются ча
стоты от одной секунды до
20
минут, может быть получен при помощи
команд:
test.sig <- rSignature(1:1200, msft.real.cts[[1]], xscale=1/60)
names(test.sig)
plot (test. sig, ylab= 11 Realized Variance 11 , xlab= 11 Sampling Frequency
(Minutes) 11 , main= 11 MSFТ 11 , sub=dates. example [ [1]])
# See Figure 5.4 (left plot)
Для того чтобы показать вариабельность реализованных волатиль
ностей, рекомендуется удалить на графике значения для очень больших
частот (см. рис. 5.ll(б)):
plot(x=test.sig$x[-(1:20)], y=test.sig$y[-(1:20)], ylab= 11 Realized
Variance 11 , xlab= 11 Sampling Frequency (Minutes) 11 ,
sub=dates.example[[1]])
# See Figure 5.11 (right plot).
main= 11 MSFТ 11 ,
MSFТ
MSFТ
,
~
о
§
~
" ~
~
·с
о
1
~
а:
о
~
о
о
§
"
~
]
о
·i::
о
8
о
о
\
................
о
5
10
15
20
i
8
•
=i
а:
i
о
Sampling Frequency (Minules)
15
20
(б)
(а)
5.11.
10
511/1997
511/1997
Рис.
5
Sampling Frequency (Minutes)
График сигнатуры волатильности по данным за один день для
MSFT, 5/1/1997
На рис.
ности
5.11 видно,
что если используется частота выборки в окрест
5 минут, тогда оценка принимает значения между 0,0003 и 0,0006.
Этот разброс значений представляется достаточно значимым, поэтому
выбор частоты выборки для вычисления реализованной волатильности
не представляется простым (см. более подробно
[Payseur
(2007а)]).
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
499
Ядерные оценки. Смещение реализованной волатильности, о ко
тором мы упоминали выше, возникает в результате разницы между це
ной спроса и ценой предложения, которое, в свою очередь, формирует
отрицательную автокорреляцию в микроструктурном шуме. Это можно
увидеть из графика автокорреляции доходностей для цен, наблюдаемых
с большой частотностью:
acf(msft.real.cts[[1]]$data, main="ACF:
MSFТ").
В работах [Hansen, Lunde (2006, 2004)], [Zhou (1996)], [BarndorffNielsen et al. (2004)] для того, чтобы исключить смещение, вызванное
автокорреляцией микроструктурного шума, предлагается использовать
ядерные оценки. При помощи следующих команд мы сможем вычис
лить ядерную оценку интегрированной волатильности (с использова
нием высокочастотных данных), построить для нее график сигнатуры
волатильности и наложить этот график на аналогичный для стандарт
ной RV-оценки (см. рис.
5.11).
plot(x=test.sig$x[-(1:20)],y=test.sig$y[-(1:20)],ylab="Realized Variance",
xlab=" Sampling Frequency (Minutes) 11 , main= "MSFT" , sub=dates. example [[1] ] )
test.rect <- rSignature(1:400, msft.real.cts[[1]], xscale=1/20,
type="kernel", args=list(type="rectangular"))
lines(test.rect, со1=2, lvd=2)
axis(З, с(О, (1 :5)•4), c("Lags: 11 ,as. character((1: 5)•80)))
legend(15,.0008,c("Rectangular"), lvd=c(2), col=c(2))
# See Figure 5.12 (right plot).
Можно видеть, что разброс значений ядерной оценки реализован
ной волатильности слабо зависит от количества лагов, используемых
при ее вычислении.
В пакете функций
realized
можно найти разные ядерные оценки,
которые обычно дают значительно лучшие результаты (см.
Nielsen et al. (2004)]
и
[Payseur
[Barndorff-
(2007а,Ь)]):
rKernel.availaЬle()
[1] "Rectangular" "Bartlett" "Second" "Epanechnikov" "Cubic" "Fifth"
[7] "Sixth" "Seventh" "Eighth" "Parzen" "ТukeyHanning" "ModifiedТukeyHanning"
Если мы выберем модифицированные ядра Тукея- Ханнинга и Барт-
летта, то итоговые оценки окажутся значительно лучше (см. рис.
par(mfrov=c(1,1))
plot(x=test.sig$x[-(1:20)],y=test.sig$y[-(1:20)],ylab="Realized
Variance", xlab="Minutes", main="MSFT",sub=dates.example[[1]])
test.mth <- rSignature(1:400, msft.real.cts[[1]], xscale=1/20,
type="kernel 11 , args=list(type="mth"))
test.bart <- rSignature(1:400, msft.real.cts[[1]], xscale=1/20,
type="kernel", args=list(type="bartlett"))
lines(test.mth, col=З,lvd=2)
lines(test.bart, со1=4, lvd=2)
5.12).
Гл.
500
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
с (О, (1: 5) *4), с ("Lags:" ,as. character( (1: 5) *80)))
legend(15,.0008,c("Mod Т-Н", "Bartlett"), lvd=c(2,2), соl=с(З,4))
# See Figure 5.12 (left plot).
axis(З,
.._,
ACF:MSFТ
u.
~
~
i
~
~
--
240
320
.1 i
~
400
>
1i
~
i
""
о
<'!
о
о
о
---
-,гr
---------------- -
<'!
q
о
20
10
30
40
1
i
о
5.12.
15
20
Sampllng Frequency (MlnU188)
51111897
Автокорреляционная функция для
1997
10
5
Lag
Рис.
MSFТ
180
80
MSFT,
по данным от Мау
1,
и ядерная оценка реализованной волатильности
как функция от частоты выборки
Оценки по подвыборкам. В работах
Sahalia et al. {2005)]
[Zhang et al. {2005)]
и
[Ait-
предложены RV-оценки, основанные на идее про
реживания выборок. Как мы указывали ранее, если, например, исполь
зовать минутные цены для актива, а д
= 5 минут, тогда для вы
числения реализованной волатильности будет использоваться ка,)КДое
пятое наблюдение. Это могут быть наблюдения в моменты времени:
1, 6, 11, 16, ....
Однако, помимо этого, могут быть подвыборки, наблю
даемые в моменты времени:
В пакет процедур
2, 7, 12, 17, ... и 3, 8, 13, 18, ... , и т.д.
realized входит функция, позволяющая вычис
лять оценку реализованной волатильности в двух временных шкалах,
см.
(5.37),
оценку реализованной волатильности в двух временных шка
ла с поправками, см.
(5.38), а также
[Ait-Sahalia et al. {2005)], см. {5.38').
другие оценки, предложенные в
Необходимые для вычислений команды представлены ниже:
test.sig.min <- rSignature(1:120, msft.real.cts[[1]], xscale=1/2,
args=list(align.period=ЗO))
plot(test.sig.min, ylab="Realized Variance", xlab="Minutes",
main="MSFT'' ,
sub=dates.example[[1]])
test.tt <- rSignature(1:20, msft.real.cts[[1]], xscale=З,
type="timescale",
args=list(adj.type="classic", align.period=60))
test.tt.adj <- rSignature(1:20, msft.real.cts[[1]], xscale=З,
type="timescale", args=list(adj.type="adj", align.period=60))
test.tt.aa <- rSignature(1:20, msft.real.cts[[1]], xscale=З,
type="timescale", args=list(adj.type="aa", align.period=60))
5.3.
РЕАЛИЗОВАННАЯ ВОЛАТИЛЬНОСТЬ
501
lines(test.tt, соl=З, lwd=2)
lines(test.tt.adj, со1=4, lwd=2)
lines(test.tt.aa, со1=5, lwd=2)
axis(З, с(О, (1:5)*12), c("Subgrids: ",as.character((1:5)*4)))
legend(45, .0006,c("Classic'', "Adj", "АА"), lwd=c(2,2,2) ,соl=с(З,4,5)).
На рис.
5.13
представлены графики упомянутых выше RV-оценок в за
висимости от частоты выборки.
MSFТ
i
.1
~
i
]
1 i
i
i
i
~
Рис.
5.13.
160
80
Lags:
240
1
1
1
1
320
400
1=::::1
1:
11
о
5
10
Minuleo
511/1997
15
20
Ядерные оценки и оценки в двух временных шкалах для
реализованной волатильности
RV-оценки. В предыдущем разделе представлены различные оцен
ки реализованной волатильности с использованием графиков сигнатур.
Но анализ показывает, что следует весьма осторожно подходить к выбо
ру типа используемой оценки, так же как к выбору параметров, необхо
димых для вычисления оценок. Для вычисления стандартных и моди
фицированных RV-оценок используется функция
Входные параметры для нее такие же, как и для
rRealizedVariance.
функции rSignature.
Некоторые примеры представлены ниже:
Traditional Estimate at highest frequency
rRealizedVariance(x=msft .real.cts[[1]], type="naive", period=1)
[1] о. 004642229
# Traditional Estimate at one minute frequency
rRealizedVariance(x=msft.real.cts[[1]], type="naive", period=1,
args=list(align.period=60))
[1] 0.0004884795
# Traditional Estimate at 10 minute frequency
rRealizedVariance(x=msft.real.cts[[1]], type="naive", period=10,
args=list(align.period=60))
[1] 0.0005299257
# Bartlett Kernel Estimate with minute aligned data at 20 lags
rRealizedVariance(x=msft.real.cts[[1]], type="kernel", lags=20,
args=list(align.period=60, type="Bartlett"))
[1] 0.0003815077
# Cubic Kernel Estimate with second aligned data at 400 lags
#
Гл.
502
5.
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
rRealizedVariance(x=msft.real.cts[[1]], type="kernel", lags=400,
args=list(type="CuЬic"))
[1] 0.0003986213
Two-Timescale Estimate with minute aligned data at 10 subgrids
rRealizedVariance(x=msft.real.cts[[1]], type="timescale", period=10,
args=list(align.period=60))
[1] 0.0003724935
# Subsample Average Estimate with second aligned data at 600 subgrids
rRealizedVariance(x=msft .real. cts [[1]], type="avg", period=600)
[1] 0.0004016684.
#
Выводы
1. Моделирование волатильности является одним из ключевых раз
делов в финансовой эконометрике, поскольку оно используется в мо
дели САРМ, при анализе карты среднего-дисперсии, ценообразовании
опционов, при управлении портфелем, управлении риском и во многих
других финансовых приложениях.
В этой главе представлен обзор теоретических результатов для ча
сто используемых одномерных и многомерных моделей волатильности.
В частности, рассмотрен GАRСН-класс моделей для условной вола
тильности, а также модели реализованной волатильности. Кроме
того, представлены некоторые приложения рассмотренных моделей.
2.
В данном пункте «Выводов~ приведены ключевые результаты по
классу GАRСН-моделей (обощенных авторегрессионных моделей услов
ной гетероскедастичности).
• Процесс иl называется GАRСН{1,1}-процессом, если иl = w+
+ а1е~_ 1 + /31 иl_ 1 . Достаточным условием, гарантирующим поло
жительность ul, является: w >О, а1 ~О и /31 ~О (см. п. 5.1.4).
• EGARCH{p, q)-моделъ
(экспоненциальная
определяется формулой (см. п.
= w + LfЗi ln (ul-i) + Lai [Фzt-i + Ф (lzt-il - Е lzt-il)],
i=l
где а1
5.1.5):
q
р
ln (ul)
GARCH(p, q)-модель)
= 1, Е lztl =
либо ограничения
i=l
(2/7r) 1 1 2 при условии, что Zt Е NID(O, 1); какие
значений параметров w, /Зi, ai отсутствуют.
• TGARCH{p, q)-модель (пороговая GARCH(p, q)-модель)
формулой (см. п. 5.1.6):
q
р
иl = w + L(aie~-i + /'iC:~-il{et-i<O}) + L /Зiul-i,
i=l
i=l
задается
Выводы
где
индикаторная функция множества. В этой модели хоро
1{.} -
шие новости имеют влияние
ai
•
503
ai,
а плохие новости имеют влияние
+ 'Yi·
Класс моделей
ARFIMA(k, d, l)
(авторегрессионных фрактальных
интегрированных скользящего среднего) для дискретного процес
са
и
{Yi} определяется формулой: a(L)(1 - L)dyt = b(L)et, где a(L)
Ь(L) - полиномы порядка k от L в качестве аргумента (см.
п.
5.1.8).
При этом:
00
(1 - L)d
=
F(-d; 1, 1; L)
=L
Г(k - d)Г(k + 1)- 1 Г(-d)- 1 Lk.
k=O
• FIGARCH (р, d, q)-модель
(фрактальная
GАRСН-модель) имеет вид (см. п.
интегрированная
5.1.8):
[1 - ,В(L)]al = UJ + [1 - ,В(L) - ф(L)(1 - L)d]e~
al = UJ[l - ,В(l)]- 1
где Л(L)
•
=1 -
~
+ Л(L)е~,
[1 - ,В(L)]- 1 ф(L)(1 - L)d и Л(L)
= Л1L + Л2L2 + ...
Оценивание пара.метров GАRСН-моделей с произвольной плот
ностью (см. п.
5.1.9 и
f (1Jt (8); 17) - плотность рас
величины 1Jt (8) = E:t (8) /at (8), среднее ко
п.
пределения случайной
5.2.8).
Пусть
торой равно нулю, а дисперсия равна единице. Пусть (у1,
-
выборка из АRСН-модели, а ф
-
... , Ут)
вектор параметров, которые
входят в условное среднее, условную дисперсию и функцию плот
ности и которые необходимо оценить. Логарифмическая функция
правдоподобия для t-го наблюдения имеет вид:
lt (Yti 'Ф)
1
= ln {/ [1Jt (8)]} - 2 ln [al (8)]
t = 1, 2, ...
Переход от стандартизированных остатков
1Jt (8) к наблюдениям
Yt соответствует следующему соотношению: f (Yt; ф) = f (1Jt (8)) 1JI,
д1]t
1
где J = дуt = O"t (8) ·
• VEC(p, q)-модель имеет вид (см. п. 5.2.3): Ut = с+ Ei=l Ai1Jt-i+
+ E~=l GjO"t-j, где O"t = vech(Et), 1Jt = vech(ete~), vech:Et =
= (a11t, ... , O"nnt)', Ai и Gj - квадратные матрицы порядка (n+
+l)n/2, а с - вектор с размерностью (n + l)n/2 х 1. Число пара
метров в этой модели имеет порядок n 4 .
Гл.
504
•
ВЕКК(р,
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
q, К)-модель
имеет вид (см. п.
к
С*'С* +
Et =
5.2.4):
к
q
L L Aj~ct-jf:~-jAjk + L L Gj~Et-jGjk,
k=1j=1
где С*,
р
Ajk и Gjk -
k=1j=1
(п х n)-матрицы, С*
- верхнетреугольная
матрица. Число параметров в этой модели имеет порядок n 2 .
• Моде.л,ъ с постоянной условной корреляцией (ССС-моделъ) опре
деляется следующей формулой (см. п.
(Pijy'O'iitO'jjt), где Rt
=
= diag(u~{~ ... O'~~~t), а
=
R
5.2.7): Et = DtRDt =
(Pij) и Pii = 1, Dt =
=
O'ii,t описываются одномерными GАRСН
моделями. Таким образом, условные корреляции предполагаются
постоянными во времени.
•
Моделъ
с
динамической
условной
корреляцией
(DСС-моделъ)
предложена в работе [Тsе,
образом (см.
Tsui (2002)) и определяется следующим
п. 5.2.7): Et = DtRtDt, где Dt и O'ii,t определяются
так же, как в ССС-модели. При этом:
Фij,t-1
где
Ui,t -
L:~=l Ui,t-mиj,t-m
одномерные стандартизированные
остатки,
получен
ные путем GАRСН-фильтрации.
•
DСС-модель, представленная в работе
значается как DCCв(S,
L).
[Engle (2002)],
обычно обо
В ней имеются некоторые отличитель
ные особенности в спецификации условной корреляционной мат
рицы,
=
модель для
которой
определенная матрица
где иit
= Eit/ ~'
Qt
(см.
п.
5.2. 7):
Rt
определяется соотношением:
а Q - безусловная ковариационная матрица
Ut, размерность которой
3.
имеет вид
(diagQt)- 112 х Qt( diagQt)- 1!2 , где симметричная положительно
(п
х п).
В главе представлены модели реализованной волатильно
сти, в которых используются высокочастотные внутридневные данные
Выводы
505
и при помощи которых строится оценка дневных волатильностей. Идея,
на которой основано использование реализованной волатильности, со
стоит в том, что если мы наблюдаем ценовой процесс в непрерывном
времени, то можно по наблюдениям измерить волатильность. Очевид
но, что на практике мы никогда не имеем наблюдения в непрерывном
времени,
но
при
использовании
высокочастотных данных
можно
по
строить оценку волатильности, которая будет достаточно близка к сво
ему фактическому значению. Ниже приводятся ключевые результаты
по теме «реализованная волатильность~.
•
Реализованная волати.л:ьностъ
(RV).
Для определения
RV
рас
смотрим выборку д-периодной доходности, которая вычисляется
как
Yt = p(t) -p(t- д),
где длительность рабочего дня предпола
гается равной единице, в течение которого мы будем иметь nt
=
= [1/ д] доходностей. Дневная реализованная волатилъностъ вы
числяется как сумма квадратов соответствующих высокочастот-
1/д
nt
ных Л-доходностей, т. е. Rvt+1 = Е Yl+jд д = Е Yl i· При некоj=l
'
i=l
'
торых дополнительных предположениях реализованная волатиль-
ность является состоятельной оценкой так называемой интегриро
ванной волатильности за соответствующий временной интервал,
а именно: plimд-+O
•
Rvt+1 = ftt+ 1 u 2 (s)ds (см. п. 5.3.2).
При использовании высокочастотных данных существует пробле
ма «баланса~: с одной стороны, статистическая теория указывает
на необходимость использования большого числа наблюдений (вы
борка доходностей) для снижения погрешностей статистических
выводов; с другой стороны, при использовании высокочастотных
наблюдений свой вклад вносит так называемый рыночный микро
структурный шум, что сказывается на величине смещения оценки,
которая растет вместе с частотой выборки (см. п.
•
5.3.2).
Одно из возможных решений проблемы микроструктурного сме
щения, адаптированное к практическим расчетам, состоит в сни
жении частоты выборки. Предлагается использовать выборки до
ходностей, сформированных по наблюдениям цен с частотой
или
15
5
минут, вместо того чтобы использовать тиковые наблю
дения. Эта процедура называется прореживанием выборки (см.
п. 5.3.2). Другим более эффективным решением (с теоретической
точки зрения) является использование ядерн·ых оценок и подвы
борочных оценок (см. пп.
•
5.3.3
и
5.3.4).
Предположим, что p(t)* -логарифм цены актива в момент време
ни
t.
Диффузионный процесс в непрерывном времени со скачка-
Гл.
506
АНАЛИЗ И МОДЕЛИРОВАНИЕ ВОЛАТИЛЬНОСТИ
5.
ми традиционно используется при моделировании ценообразова
ния активов (см. п.
5.3.6).
Он задается следующим стохастическим
дифференциальным уравнением:
+ k(t)dq(t),
где
µ(t) -
dp(t)* = µ(t)dt
+ u(t)dW(t) +
непрерывная функция с локально-огра
ниченной вариацией, стохастическая волатильность
положительна,
W (t) -
стандартное броуновское движение,
дискретный процесс, для которого
мент времени
t,
а
dq(t)
строго
u(t)
=О
dq( t)
q( t) -
= 1 отвечает скачку в мо
- отсутствию скачка; k(t) отвечает ве
личине соответствующего скачка. Тогда имеем: plimд--+O
х (д) = ftt+ 1u 2(s)ds Lt<s:::;;;t+l k 2 (s).
RVi+1 х
+
•
Стандартизированная реализованная бистепенная вариация В V
2 nt
определяется как (см. п. 5.3.7): BVi+1(д) =
µ1 L
IYt,illYt,i-11, где
i=2
µ1 =
= E(IZI)- математическое ожидание абсолютного зна
чения случайной величины Z, имеющей стандартное нормальное
распределение. Более того, plimд--+O В\1t+1(д) = ftt+ 1u 2 (s)ds.
./2fff
Эмпирический измеритель величины скачков определяется фор
мулой Jн1(д) = max[Rvt+1(д)
•
Если предполагается, что
-
Bvt+1(д),O].
ARFIMA(p, d, q)-модель
описывает вре
менной ряд реализованных волатильностей, тогда: Ф(L)(l х (RVi+1 - µ) = 0(L)ut (см. п. 5.3.7).
•
L)dx
Мультипериодные реализованные волатильности определяются
как нормированные суммы однопериодных волатильностей (см.
п. 5.3.7). А именно: RVi,t+h
обычно
= h- 1[RVi+1 +RVi+2 + ... +RVi+h], где
h = 5 и h = 22 для недельных и
соответственно. Следует отметить, что
НАR-RV-модель из работы
Rvt,н1
месячных волатильностей
RVi,t+1 = RVi+1 ·
[Corsi (2009)]
имеет вид:
= /30 + /3nRvt + /3wRVi-s,t + /3мRVi-22,t + ен1·
Глава
6
Моделирование многомерных
u
распределении
с использованием
ко пула-функций
Доказательства того, что не все совместные распределения экономи
ческих характеристик могут быть описаны при помощи многомерного
нормального закона, широко представлены в различных работах, на
чиная с
[Mills (1927)].
Наиболее распространенными статистиками, поз
воляющими охарактеризовать степень отклонения от нормального рас
пределения, являются коэффициенты эксцесса и асимметрии. Послед
ние исследования показывают, что для финансовых данных также на
блюдается отклонение их совместного распределения от многомерного
нормального закона а именно отклонение в форме зависимостей компо
нент анализируемого многомерного признака. Один из таких примеров
-
асимметрия зависимостей доходностей рыночных активов, которая
больше в периоды спада на рынке, чем в периоды рыночного роста,
см.
[Erb et al. (1994)), [Longin, Solnik (2001)), [Ang, Chen (2002)], [Patton
(2004, 2006а, б)] и др.
Основной вывод этих статей заключается в том, что многомерное
нормальное распределение не является хорошей моделью для описания
совместного распределения многих экономических и финансовых пере
менных. Это приводит к проблеме поиска более адекватных многомер
ных моделей. Теория копула-функций
ее решения.
-
один из возможных способов
Гл.
508
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Начало теории копула-функций было положено работами
ding {1940)]
и
[Sklar {1959)],
[Hoeff-
но статистическое моделирование с ис
пользованием копула-функций в приложениях появилось относительно
недавно и относится к концу 1990-х гг. Количество статистических ис
следований на тему копула-функций увеличивается достаточно быстро,
см.
[Wang {1998)], [Frees, Valdez {1998)], [Embrechts et al. {1999)].
Сего
дня копула-функции успешно применяются в финансах и страховании,
биостатистике (например,
[Lambert, Vandenhende {2002)]), гидрологии
(например, [Zhang, Singh {2006)]) и климатологии (например, [Salvadori,
De Michele {2007)]). Среди учебников по теории копула-функций следу
ет отметить [Joe {1997)] и [Nelsen {1999)], где представлено введение
в теорию, тогда как в [Cherublni et al. {2004)] и [Malevergne, Sornette
{2006)] излагается использование техники копула-функций в финансо
вых приложениях.
Копула-функция является функцией, агрегирующей всю информа
цию
относительно структуры
зависимости
между
компонентами
слу
чайного вектора. Когда в качестве компонент копула-функции берутся
частные функции распределения, которые необязательно принадлежат
одному и тому же семейству распределений, получаем многомерную
функцию распределения. Как следствие, эта теория позволяет доста
точно гибко моделировать структуру зависимости между различными
переменными, которые могут иметь разные частные распределения.
Несмотря на то что теория копула-моделей исследована относитель
но полно, проблема оценивания и статистические выводы для копула
моделей, в определенном контексте, все еще требуют дальнейших ис
следований, см.
[Genest, Favre {2007)].
За последние годы предложены
различные методы оценивания параметров копула-функций, начиная с
параметрических
[Jondeau, Rockinger {2003)], [Patton {2004, 2006а,б)],
[Fantazzini {2009б)], полупараметрических [Genest et al. {1995)], [Breymann et al. {2003)], [Fantazzini {2010)] и заканчивая непараметрически
ми методами [Fermanian, Scaillet {2003)]. Более того, недавние исследо
вания направлены на исследование ~смеси~ указанных выше методов,
которые позволили бы сэкономить время на вычислениях
[Bouye et al.
{2000)], [Marshal, Zeevi {2002)], [Cherublni et al. {2004)].
В данной главе будет представлен некоторый обзор теории копула
функций, основные методы оценивания, а также сделана попытка отве
тить на, вероятно, самый важный вопрос теории копула-функций: как
следует подбирать копула-функцию под конкретные {имеющиеся в на
шем распоряжении) исходные статистические данные?
6.1.
КОПУЛА-ФУНКЦИИ
509
Копула-функции
6.1.
Определения и основные свойства
6.1.1.
С помощью копула-функций описываются законы многомерного рас
пределения вероятностей. Они определяются частными одномерными
распределениями
анализируемого многомерного закона и характером
зависимостей, существующих между компонентами рассматриваемой
многомерной случайной величины.
Определение
6.1.
Функция С(и1,и2,
определенная на едини'Чном гиперкубе
... ,иn)
1n =
[О,
от
n
пере.меннъ~х,
(т. е. щ Е [О,
l]n
1],
i = 1, 2, ... , n), называется копула-функцией, если она обладает сле
дующими свойствами:
1)
область зна'Чений функции
2)
если иi =
С(и1, и2,
С(и1, и2,
едини'Чный интервал [О,
О по крайней мере для одного
1];
i Е {1, 2, ... , n}, то
... , иn) =О;
3) C{l, ... , 1, иi, 1, ... , 1) =
4)
-
... , иn)
щ для любых иi Е [О,
является n-возрастающей
смысле, 'Что для всех (а1,
1];
функцией
в
том
... , an), (Ь1, ... , Ьn) Е [О, l]n с ai ~ qbi
справедливо неравенство:
2
2
i1=l
iп=l
L ···L {-l)ii+··+inC{ин 1 , · · ·, иnin) ~О,
где иj1
=щ
и иj2
= Ьj
Например, если
n
для всех j Е
=
вид: для всех (а1, а2), (Ь1,
2
L
{1, ... , n}.
четвертое свойство принимает следующий
Ь2) Е [О, 1] 2 с ai ~ qbi мы имеем
2,
2
L::{-l)i 1 +i 2 C(ин 1 ,и2i 2 ) ~О
2
#
L
#
(-1) 2 С(и11, и21)
[{-l)i 1 + 1 с(ин 1 ,и21)
~О
+ (-1) 3 С(и11, и22) + (-1) 3 С(и12, и21)+
+ (-1) 4 С(и12, и22)
#
+ {-l)i 1 + 2 с(ин1'и22)
~О
С(и11, и21) - С(и11, и22) - С(и12, и21)
+ С(и12, и22)
~О,
Гл.
510
где иj1
=
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
и иj2
aj
=
Ьj при
j Е {1, 2}. Таким образом, свойство 4
равносильно тому, что
Следовательно,
(6.1)
можно интерпретировать как:
Р(О ~ qи1 ~
qa1, О~ qи2 ~ qa2) - Р(О ~ qи1 ~ qa1, О ~ qи2 ~ qb2)- Р(О ~ qи1 ~ qb1, О ~ qи2 ~ qa2)+
+ Р(О ~ qи1
~
qb1, О~ qи2 ~ qb2) ~ О.
Теперь сформулируем теорему Шкляра, которая показывает роль
копула-функций в описании многомерных распределений вероятностей.
Теорема
6.1
(теорема Шкляра).
распределения
с
-частн'Ы.Ми
Пусть Н(·)
-
распределениями
п-мерная функция
Тогда
F1, ... , Fn.
существует п-мерна.я копула-функция С(·) такая, -что для всех дей
ствительнъtх х1,
... , Xn :
(6.2)
Если все -частные функции распределения непрерывны, то копула
функция определена единственным образом; в противном слу-чае С(·)
определена
RanF1
единственн'ЫМ
х RaпF2 х
образом
лишь
... х RaпFn, где Rап -
на
области
определения
область зна-чений -част
ных функций распределения. Обратно, если С(·)
-
копула-функци.я, а
F1, ... , Fn - некоторые одномернъtе функции распределения, то функ
ция Н ( ·), определяемая выршжением (6.2), .являете.я совместной функ
цией распределения с -частными распределениями F1, ... , Fn.
До к аз ат ель ст в о. См. (Sklar (1959, 1996), [Joe (1997), [Nelsen
(1999)].
Последнее утверждение теоремы представляет большой интерес в
задаче моделирования многомерных функций распределения, посколь
ку из него следует, что можно связывать вместе любые
n (n
~
2)
од
номерных функций распределения разного типа (не обязательно из од
ного семейства), используя любую копула-функцию, для того чтобы
получить двумерные или многомерные функции распределения 1 .
Следствие.
Пусть Ff- 1>(·), ... , F~-l)(·) - обратные (в обоб
щенном смысле) функции -частных распределений. Тогда для каждого
1
0 4:Не замеченной~ разрабатывающими теорию копул авторами фундамен
тальной роли в развитии этой теории классической теоремы А.И. Колмогоро
ва, формулирующей условия, которым должна удовлетворять n-мерная функция
Н(х1, х2,
ский
... , Xn),
{2012)].
чтобы быть функцией распределения, см. в работе [Благовещен
6.1.
(и1,
.. ., un)
КОПУЛА-ФУНКЦИИ
511
из едини'Чного п-мерного куба существует единственная
копула-функция С: [О,
1)
х
... х [О, 1) -t [О, 1) такая, 'Что
(6.3)
До к аз ат ель ст в о. См. теорему
Таким образом, копула-функция
-
2.10.9 в [Nelsen (1999)).
это такая функция, которая, с
использованием знания об одномерных частных распределениях, позво
ляет получить многомерную функцию распределения, поскольку функ
ция распределения случайного вектора полностью описывает его веро
ятностную структуру, куда, в частности, входит структура зависимости
его компонент. Копула-функции дают возможность разделить описание
распределения случайного вектора на две части: частные распределе
ния компонент и структура их зависимостей.
Перечислим кратко варианты использования результатов теоремы
Шкляра и рассмотренного следствия:
•
извлечение копула-функций из хорошо известных многомерных
распределений, например, из многомерного нормального распре
деления, из многомерного распределения Стьюдента и т.д.;
•
конструирование новых многомерных распределений, связывая
произвольные одномерные распределения при помощи некоторой
копула-функции;
•
в то время как соотношение
(6.2)
обычно служит отправной точ
кой в задаче моделирования, соотношение
(6.3)
является теорети
ческим инструментом для получения копула-функции из много
мерной функции распределения.
Следует отметить, что для дискретных распределений копула
функции имеют не столь простую форму, как в случае непрерывных
распределений. Покажем это на следующем примере.
П р и ме р
6.1.
Рассмотрим две одинаковые кости, на которых вы
падают два числа Х1 и Х2 из множества
{1, 2, ... 6}.
Предположим, что
мы знаем значение Х1 и можем делать ставки на значения Х2, которые
выпадают на второй кости. Важным вопросом является следующий: су
ществует ли взаимосвязь или зависимость между этими двумя случай
ными величинами, т. е. возможно ли получить некоторую информацию
относительно значений Х2, зная Х1. Мы знаем, что каждая случай
ная величина полностью описывается своей функцией распределения
Fi(x) = P(Xi :s:;; qx).
В нашем случае мы имеем
F1(·) = F2(·) = F(·).
Гл.
512
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Однако в общем случае одномерная функция распределения не да
ет нам никакой информации относительно совместного распределения
двумерной случайной величины (Х1, Х2). Правда, в нашем случае пред
полагается независимость
(Х1, Х2),
поэтому совместное распределение
(Х1, Х2) имеет вид:
Для того чтобы получить полное описание (Х1, Х2), мы использо
вали два элемента: частные распределения и тип взаимосвязи (в нашем
случае
-
независимость). Возможность разделения между частными
распределениями
и
зависимостью
-
это
именно
то,
что
утверждает
теорема Шкляра. Поскольку мы рассматриваем дискретные частные
распределения, то копула-функция будет определена единственным об
разом только на
Ran F1
х
Ran F2.
В случае независимости имеем:
i,j
= 1, ... ,6.
Любая копула-функция, удовлетворяющая этому ограничению, яв
ляется подходящей: например, С(и, v) =и·
v
будет естественным выбо
ром.
Важное свойство, которым обладают все копула-функции
-
это ин
вариантность относительно строго возрастающих преобразований слу
чайных величин (см. приведенную ниже теорему
Теорема
6.2.
Рассмотрим
n
6.2).
случайн/ы,х величин Х1, ... , Xn, зави
симость между которъши определяется коnула-функцией С(·). Если
преобразования
Ti: R
~
R, i = 1, ... , п,
растающими функциями (т. е. дхТi
сти случайнъtх величин Т1(Х1),
>
определяются строго воз
О), то структура зависимо
... , Tn(Xn)
определяется той же са
мой копула-функцией С(·).
До к аз ат ель ст в о. См.
двумерного случая
[Schweizer, Wolff {1976, 1981)],
- [Malevergne, Sornette {2006)].
для
Последнее утверждение означает, что строго возрастающие пре
образования не меняют структуру зависимости. Это значит, что при
заданных частных распределениях сохраняется структура зависимости,
которая определяется копула-функцией.
Более того, можно показать, что любая копула-функция ограниче
на так называемыми границами Фреше
-
Хёффдинга:
6.1.
КОПУЛА-ФУНКЦИИ
513
где
W(u1, ... ,un) = max(u1 + ... + Un - n
М(и1, ... , Un) = min(u1, ... , un)·
+ 1,0),
В качестве примера рассмотрим две равномерно распределенные на
[О,
1]
случайные величины И1 и И2. Если И1 = И2, то эти две случайные
величины имеют копула-функции вида
и называются абсолютно зависимыми.
Ту же самую копула-функцию можно получить, если взять Х2
=
Т(Х1), где Т(·)
-
-
монотонно возрастающее преобразование. Такие
случайные величины Х1 и Х2 называются комонотонн:ыми. Прямо про
тивоположным
понятию
комонотонности
является
противомонотон
ностъ случайных величин. В качестве примера возьмем равномерные
случайные величины (И1, И2), для которых И2
= 1-
И1. Копула-функ
ция случайного вектора (И1, И2) равна
С(и1, и2)
= Р(И1 ~ и1, 1 = Р(И1~и1,1 -
И1 ~
u2)
и2 ~ И1)
=
= и1 + u2 -
В противном случае она равна нулю (рис.
Lower Frechet-Hoeffding bound
W(u,v)=max(u+v-1,0)
1 при и1
+ и2 > 1.
6.1).
Upper Frechet-Hoeffding bound
M(u1v)=min(u,v)
u
u
Product copula
P=u'v
u
Рис.
6.1.
Графики нижней
(W)
и верхней (М) границ Фреше-Хёффдинга
копула-функции, а также копула-функции Р, соответствующей
независимым случайным величинам
Гл.
514
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
В двумерном случае границы Фреше - Хёффдинга являются ко
пула-функциями, но для случаев большей размерности нижняя граница
Фреше-Хёффдинга
в Определении
W уже не является n-возрастающей (см. свойство 4
6.1). Однако неравенство в левой части нельзя улуч
шить, поскольку для любого фиксированного и из единичного n-куба
существует С(·) такая, что
2.10.12
в
W(u)
=
С(и), см. доказательство теоремы
[Nelsen (1999)].
Копула-функции равномерно непрерывны и (почти всюду) диффе
ренцируемы по каждому из аргументов
[Nelsen (1999)].
см. теоремы
2.2.4
и
2.2. 7
в
Более детальная информация относительно этих и дру
гих свойств приведена в
6.1.2.
-
[Joe (1997)], [Nelsen (1999, 2006)].
Плотности копула-функций
Для копула-функций, аналогично функциям распределения, можно
определить понятие плотности. В частности, плотность с(и1, и2,
ассоциированная с копула-функцией С(и1, и2,
отношением
_
(
cu1,u2,
... ,un ) -
дС(и1, и2,
д
... , иn),
... , Un)
U1, . •. ,
д
иn
... , un),
определяется со-
·
Плотность может быть использована для того, чтобы определить
так называемые абсолютно непрер'Ывную Ас и сингулярную
Sc
компо
ненты копула-функции С(·):
Копула-функция, для которой С(·) =Ас(·) на 1п, называется аб
солютно непрер'Ывноu. В противном случае
(т. е.
при С =
Sc
на 1п)
копула-функция называется сингулярной.
Существуют копула-функции, которые имеют как абсолютно непре
рывную, так и сингулярную компоненты. Например, копула-функция
Р
= и~ и2из
является абсолютно непрерывной, поскольку
дС(s1, s2, sз)
дs1, дs2, дsз
и для любого (и1, и2, из) Е 13 имеем:
=1
6.1.
515
КОПУЛА-ФУНКЦИИ
Более того, применяя следствие теоремы Шкляра и рассматривая
непрерывные случайные величины, можно видеть, что плотность ко
пула-функции
c(F1(x1), ... , Fn(xn))
ассоциирована с плотностью сов
местной функции распределения Н ( ·), обозначенной как
f н ( ·), следую
щим образом (канони-ческое представление):
[C(F1(x1), ... ,Fn(xn))) . пn ~-( ·) _
f Н (Х1, · · · , Xn ) -_ ап дF
( )
дг ( )
J i Xi 1 Х1
,···,
.Гn
Xn
·
i= 1
n
= c(F1(x1), ... , Fn(xn)) · П fi(Xi),
i=l
где
с
... ,xn)
(F1 (х1 ) ' ... ' Fn (Xn )) = f(x1,
n
.
П fi(Xi)
(6.4)
i=l
6.1.3.
Эмпирические приложения в статистическом
пакете
R:
двумерные границы Фреше -
Хёффдинга и копула-функция,
отвечающая случаю независимости
Если необходимо изобразить линии уровня двумерных границ Фреше Хёффдинга и копула-функции, соответствующей случаю независимо
сти, то для этого можно использовать следующий код пакета
зультаты представлены на рис.
6.2):
library( fCopulae)
# Generate Grid:
N = 50; uv = grid2d(x = (O:N)/N); u = uvx; v = uvy
# Compute Frechet and Product Copulae:
W = matrix(apply(cblnd(u+v-1, О), 1, max), ncol = N+l)
Pi = matrix(u*v, ncol = N+l)
М = matrix(apply(cblnd(u, v), 1, min), ncol = N+l)
# Create Perspective Plots:
persp(z = W, theta = -40, phi = 30, main = 11 Lower Frechet 11 ,
сех = 0.5, ticktype = ''detailed 11 , col = 11 steelЫue 11 )
persp(z = Pi, theta = -40, phi = 30, main = 11 Pi Copula 11 ,
сех = 0.5, ticktype = 11 detailed 11 , col = 11 steelЬlue 11 )
persp(z = М, theta = -40, phi = 30, main = 11 Upper Frechet 11 ,
сех = 0.5, ticktype = 11 detailed 11 , col = 11 steelЫue 11 )
# Create Contour Plots:
contour(W, xlab = 11 u 11 , ylab = 11 v 11 , main = 11 Lower Frechet 11 )
contour(Pi, xlab = 11 u 11 , ylab = 11 v 11 , main = 11 Pi Copula 11 )
contour(M, xlab
=
11
u 11 , ylab
=
11
v 11 , main
=
11
Upper Frechet 11 )
R
(ре
Гл.
516
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Upper Fnм:hel
a.-Fnм:hel
:
~
~~
:
·~
:
>
~
'~
:;i
:
PICopulв
""
~
"
••
:;
~
>
0.2
о.о
0.4
0.8
0.8
1.0
u
Рис.
6.2.
о
:
>
~
ОА
о
••
о·
"
о
01
::
::
:
.
о.о
0.2
о.е
0.4
0.8
::
о.о
1.0
0.2
0.4
0.8
0.8
10
u
u
Линии уровня двумерных границ Фреше - Хёффдинга и
копула-функции, отвечающей случаю независимости
Эллиптические копула-функции
6.2.
6.2.1.
Обзор
Класс эллиптических распределений включает главным образом класс
симметричных распределений, который весьма популярен в актуарной
математике, страховании и финансах. Этот класс включает интересные
примеры многомерных распределений, и многие из них имеют некото
рые общие свойства с многомерным нормальным распределением. Они
позволяют моделировать многомерные экстремальные события, форми
руя зависимость, не совпадающую с зависимостью многомерного нор
мального распределения, и использовать распределение с большим экс
цессом, чем эксцесс нормального распределения. Кроме того, с их по
мощью можно моделировать феномен «тяжелых хвостов», который ча
сто наблюдается для финансовых данных, см.
[Embrechts et al. {1999)],
[Schmidt {2002)].
Эллиптические копула-функции
-
это попросту копула-функции
многомерных распределений эллиптического типа. Если следовать ра
боте
[Fang et al. {1987)],
то эллиптические распределения определяются
следующим образом.
Определение
6.2
(эллиптические распределения).
естъ п-мерный случайнъtй вектор и Е Е
Rnxn -
Пустъ Х
симметричная и
неотрицателъно определенная матрица. Если существуют
µ
Е
Rn
и
функция ф:
вектора
R --+ R+ такие, что характеристическая функция Фх-µ(t)
Х - µ имеет вид
Фх-µ(t) = exp(it'µ)ф (-~t':Et)
для любого
t
Е
Rn,
то Х называют случайным вектором, имеющим
распределение эллиптического типа с параметрами
µ,
Е.
6.2.
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
517
Копула-функция С(·) называется э.л.л.ипти-ческой, если она отвечает
распределению эллиптического типа. Функция плотности распределе
ния эллиптического типа, если она существует, имеет вид
f(x) = ~g ((х- µ)'Е- 1 (х- µ)),
IEI
х Е Rn
для некоторой функции
g: R---+ R+, которая удовлетворяет условию:
J0 g(x)dx < оо. Функцию g(·) называют оператором плотности распре
деления эллиптического типа или генерирующей функцией, см. [Fang
et al. (1987)]. Нормирующая константа 'У может быть определена яв
00
ным образом с использованием перехода к полярным координатам, см.
[Landsman, Valdez (2003)].
В результате получим:
"/ = ( 21'
l )-!
g(z)dz
В качестве примеров распределений эллиптического типа следует
привести нормальное распределение, распределение Коши, распределе
ние Стьюдента, логистическое распределение, распределение Лапласа,
распределение Котца и экспоненциальное распределение, см. табл.
Таблица
6.1.
Список генерирующих функций
g(t)
6.1.
и нормирующих
констант 'У для некоторых копула-функций
эллиптического типа
Распределение
Генератор
Константа
Нормальное
e-t/2
(21Г)-1
Коши
(1 + 2t)- 312
_"_2
~)--Г
(21Г)-1
Стьдента
(1 +
Логистическое
еt(1
Лапласа
К отца
е-..Л
e-rt/2
r(21Г)- 1
Экспоненциальное
e-r(t/2)"
sr 1 1 8 (21ГГ(1/ s)- 1
+ e-t)-2
21Г)-1
1Г-1
(21Г)-1
Отметим, что в некоторых работах используются иные определения
генерирующих функций
g(·),
где
t/2 заменено t,
что влияет на значение
нормирующих констант 'У.
П р и м е р
Х
= (Х,У)'
и
6.2.
Рассмотрим
двумерный
случай.
Предположим
Гл.
518
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Тогда Х имеет функцию плотности распределения
fp(x,y) =
J1 'У- p2g (х
2рху + у2 )
2 -
1-
р2
'
(х,у) Е R 2 •
Следовательно, в соответствии с теоремой Шкляра двумерная ко
пула-функция эллиптического типа имеет вид:
{6.5)
-оо
-оо
Далее более детально рассмотрим две наиболее распространенные
копула-функции эллиптического типа, а именно нормального распреде
ления и распределения Стьюдента.
6.2.2.
Нормальная копула-функция
Копула-функция двумерного нормального распределения с коэффици
ентом корреляции р может быть вычислена из уравнения
(6.5)
при
g = e-t/2 и 'У= 1/{27Г):
-00
-00
что может быть представлено в виде:
где Ф 2 ( ·) обозначает функцию двумерного нормального распределения
с единичными дисперсиями компонент, корреляцией р и нулевыми сред
ними значениями, а Ф- 1 (·) - обратная функция для одномерного стан
дартного нормального распределения.
В общем случае многомерная нормальная копула-функция опреде
ляется следующим образом:
где Фn{·,
... , ·; Е) -
это п-мерная нормальная функция распределения
с нулевыми средними значениями и ковариационной матрицей Е.
6.2.
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
519
Плотность нормальной копула-функции может быть получена из
уравнения
С
(6.4)
с использованием канонического представления:
(ф( Х1 ) , ... , ф( Xn )) -_
JGaussian(xi, .•• ,xn) _
n
П Jfaussian {Xi)
i=l
{27r)-n/2 IEl1/2 ехр (-!x'E-lx)
n
П {27r)- 1/ 2 ехр (-!х~)
i=l
1
(
= IEll/2 ехр
1 '( -1
-2(
Е - 1) ( ) '
где ( = {Ф- 1 (и1), ... , Ф- 1 (ип))' - вектор, компонентами которого явля
ются значения обратной функции для стандартного одномерного гаус
совского распределения в точках щ = Ф(хi),
i = 1, ... , n; 1 -
единичная
матрица.
Представим основные шаги алгоритма моделирования нормальной
копула-функции {более детальное описание моделирования копула
функции см. в
•
[Cherublni et al. {2004), [McNeil et al. {2005)]):
найти матрицу разложения Холецкого А для корреляционной
матрицыЕ;
•
смоделировать из стандартного нормального распределения
зависимых случайных величин
z
n
не
= (z1, ... , Zn)';
= Az;
•
взять х
•
вычислить компоненты Ui = <р( Xi),
i = 1, ... , n, где <р( ·) - одно
мерное стандартное нормальное распределение.
В результате получим вектор (и1, ... , un)', являющийся реализаци
ей случайного вектора из n-мерной гауссовской копула-функции.
6.2.3.
Т копула-функция (копула Стьюдента)
Копула-функция для двумерного распределения Стьюдента с корреля
цией р может быть получена из формулы
g
2t
-v-2
= {1 +-)-2-,
v
{6.5)
при
1
'У= 27Г.
Для Т копула-функции справедливо соотношение:
Гл.
520
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
где Т 2 (.' ·; р, v) - функция распределения двумерного распределения
Стьюдента с корреляцией р и v степенями свободы; t; 1 (·) - обратная
функция одномерного распределения Стьюдента. При v -t оо копула
функция Стьюдента сходится к нормальной копула-функции, а при
v -t 1 сходится
к копула-функции распределения Коши.
В общем случае многомерная Т копула-функция определяется сле
дующим образом:
а плотность Т копула-функции может быть получена из уравнения
(6.4)
и канонического представления:
где ( = (t;;- 1(u1), ... , t;;- 1(un))' - вектор, компонентами которого явля
ются значения обратной функции распределения Стьюдента в точках
Ui = tv(xi)·
Приведем алгоритм моделирования наблюдений, подчиняющихся
распределению с Т копула-функцией:
•
найти матрицу разложения Холецкого А матрицы :Е;
•
смоделировать п независимых случайных величин из стандартно
го нормального распределения,
•
= (z1, ... , zп)';
смоделировать случайную величину
висящую ОТ
•
z
s
из Хv-распределения, не за
i
= 1, ... , n, где tv(·) -
Zj
определить вектор у
= Az;
• положить х = ~у;
•
определить компоненты щ
= tv(xi),
мерное стандартное распределение Стьюдента с
v
одно
степенями сво
боды.
Вектор (и1,
... , un)'
смоделирован из п-мерной Т копула-функции.
Нормальная и Т копула-функции весьма популярны при анализе
финансовых данных, поскольку они позволяют моделировать портфели
6.2.
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
521
высокой размерности, являясь при этом относительно легко оценивае
мыми. Кроме того, они позволяют генерировать наблюдения при помо
щи относительно простых алгоритмов. На рис.
6.3 представлены графи
ки плотностей некоторых эллиптических копула-функций, построенных
с использованием функции
Нормальное: р
Логистическое: р
Рис.
6.3.
fcopulae
из пакета
= 0,5
=
R.
Стьюдента: р
= 0,5; 11= 4
Экспоненциальное: р
0,5
= 0,5; s = 1
Плотности эллиптических копула-функций: нормальное распределение,
распределение Стьюдента, логистическое и экспоненциальное
распределения. Параметры указаны над соответствующими им
графиками
Обобщение: сгруппированные Т копула-функции. Сгруппи
рованные Т копула-функции впервые были предложены в работах
et al. (2003)]
и
[Demarta, McNeil (2005)].
[Daul
Калибровка таких копула
функций не сложнее, чем калибровка Т копула-функций, но для пер
вых имеется возможность определять различные структуры зависимо
сти для подгрупп компонент вектора из Т копула-функции.
Пусть
(n
х
n)
Z
Е
Nn(O, R),
где
R -
ковариационная матрица размерности
с единичными диагональными элементами. Далее рассмотрим
случайную величину
U, равномерно распределенную на отрезке [О, 1]
и не зависящую от Z. Пусть через G 11 (·) обозначена функция распре
деления случайной величины
где х~ - случайная величина,
J'V!X!,
Гл.
522
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
имеющая хи-квадрат распределение с
v степенями свободы. Кроме то
го, задано разбиение множества 1, ... , n на т подмножеств с размерами
s1, . .. ,sm (т.е. s1, ... ,sm ~ 1, s1 + ... + Sm = n) и для каждого k =
= 1, 2, ... , т задано число степеней свободы vk. Возьмем Wk = G-;;k1(U),
k = 1, ... ,т, и У= (W1Z1, ... ,W1ZspW2Zs 1 +1, ... ,W2Zs1 +s2 , ••• ,
W mZn). Случайная величина У имеет так называемое сгруппирован
ное t-распределение. Наконец, определим
Случайный вектор
U
имеет распределение на [О,
ненты имеют равномерное распределение на [О,
пределение вектора
U
Отметим, что (У1,
1].
l]n,
а его компо
Будем называть рас
сгруппированной Т копула-функцией.
... , Ys 1 )
имеет многомерное Т-распределение с
v1 степенями свободы, и для k = 1, ... ,т - 1 вектор (Ys 1 +... +sk+1, ... ,
Ys 1 + ... +sk+J имеет многомерное Т-распределение с Vk+1 степенями сво
боды. Соответствующее распределение подвектора вектора U представ
ляет собой Т копула-функцию с Vk+1 степенями свободы, для k =О, ... ,
т - 1. Для сгруппированной Т копула-функции нет простого выраже
ния для плотности. Однако существует весьма полезная аппроксимация
для автокорреляции (в предположении ее постоянства), полученная в
работе
где
i
и
[Daul et al. (2003)]:
j
принадлежат различным группам, а Tij -
парный коэффи
циент ранговой корреляции Кендалла. Эта аппроксимация позволяет
производить оценку параметров методом максимального правдоподо
бия независимо для каждой подгруппы. В работе
представлено обобщение модели из
[Fantazzini (2009а)]
[Daul et al. (2003)], в котором рас
сматривается динамическая структура корреляционной матрицы
6.2.4.
ftt.
Численные примеры: оценивание эллиптических
ко пула-функций
Нормальная копула-функция. Выше было показано, как, применяя
теорему Шкляра и используя соотношение между функцией распреде
ления и ее плотностью, можно получить плотность нормальной (гаус
совской) копула-функции:
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
6.2.
где (
523
= (Ф- 1 (и1), ... ,Ф- 1 (иn))', а щ = Ф(хi); логарифмическая функция
правдоподобия имеет вид:
т
zGaussian((J) = -
~ ln IEI - ~ L <НЕ-1 -
I)(t.
t=l
Если логарифмическая функция правдоподобия дифференцируема
по параметрам
(J,
а решение уравнений де
ного максимума функции
l((J),
l((J)
=О дает точку глобаль
можно получить оценку максимально
го правдоподобия для ковариационной матрицы 8м L = Е гауссовской
копула-функции:
~ -l
дЕ
zGaussian((J) =
ТЕ_!~ /" 1"' =О
2
2 L....J':.t':.t
t=l
'
а следовательно,
-..
т
Е= ~Е
t=l
<t<:,
т. е. получаем классическую оценку для ковариационной матрицы. Сле
довательно, в качестве приближенной оценки корреляционной матрицы
можно использовать матрицу:
R. = (diag t)- 112 t
(diag :Е)- 1 1 2 .
Т копула-функция. Плотность Т копула-функции равна:
а логарифмическая функция правдоподобия имеет вид
(6.6)
Гл.
524
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
В случае Т копула-функции невозможно получить аналитическое
выражение для оценки максимального правдоподобия, поэтому необхо
димо использовать численные алгоритмы максимизации функции прав
доподобия. Однако в случае большой размерности Т копула-функции
такие алгоритмы являются слишком затратными по времени. В связи
с этим предлагаются альтернативные алгоритмы, многошаговые пара
метрические или полупараметрические подходы. Рассмотрим три наи
более часто применяемых метода: первый из них предложен в работе
[Bouye et al. (2000)]
и основан на процедуре рекурсивной оптимизации
для корреляционной матрицы; второй представлен в работе
Zeevi (2002)]
[Marshal,
и базируется на использовании оценки ранговой корреля
ции Кендалла; третий является смешанным параметрическим методом
и основан на методах моментов и максимального правдоподобия
[Chen
et al. (2004)].
Метод
1.
1 [Bouye et al. (2000)].
Используя эмпирические функции одномерных частных распре
делений, преобразуем (хн, X2t, ... Xnt),
равномерно распределенным (йн, й2t,
2.
t = 1, ... , Т, к приблизительно
... , Unt ).
Дм каждого зна-ч.ения степени свободьt
v
из рассматриваемого
интервала значений оцениваем корреляционную матрицу
а) для каждого фиксированного
= 1, ... , Т)
t (t
R 11 :
положим:
б) пусть Е
корреляционная матрица для гауссовской копулафункции, оцениваемая по формуле (6.6), положим Е 11 ,1 = Е;
в) пусть Ev,k+1 удовлетворяет следующей рекурсивной схеме:
г) перемасштабируем элементы матрицы следующим образом:
( Ev,k+1) iJ =
(Ev,k+1) . .
---.r=======i=,з===,
( E11,k+1) .. (t11,k+1) ..
J,J
i,i
в результате получим, в частности, единичные диагональные элементы;
А
Ev
д) Аповторяем шаги в)-г) до тех пор, пока Evk+l
= Ev,k·
'
= E11 k и положим
)
6.2.
3.
Оценим
v
525
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
путем максимизации логарифмической функции прав
доподобия плотности Т копула-функции:
т
vА
= argmax L lncStudent (
11
Метод
А
А ti ~
t, ... , Un
~11, v .
и1
)
'
t=l
'
2 [Marshall, Zeevi (2002)).
Предыдущая процедура является вычислительно трудоемкой в слу
чае большой обучающей выборки. Более того, она может давать не
устойчивые результаты в ситуациях, когда существует
k (k ~ 1), для
которого матрица E11,k близка к вырожденной. Для преодоления этой
проблемы в работе [Marshall, Zeevi (2002)] предлагается следующий ал
горитм.
1.
Используя эмпирические функции одномерных частных распре
делений, преобразуем (хн, X2t,
t = 1, ... , Т,
... Xnt),
к приблизительно
равномерно распределенным (йн, й2t,
го
... , Unt)·
2. Оценим Е с использованием непараметрической оценки рангово
коэффициента Кендалла [Lindskog et al. (2003)]:
~
~ij
=
о
sш
(1Г А
2 тij
)
'
i,j=1, ... ,n.
Как указано в работах
имеется два временных
[Lindskog (2000)], [Genest et al. (1995)], если
ряда Xt и yt, t = 1, ... , Т, то состоятельной
оценкой коэффициента Кендалла будет:
fi,j
i
J
где sign(x)
3.
=:
= т('f-l) ~<. sign[(Xi - Xj)(Yi - }j)],
Оценим
v
= {
-~',
i,j
= 1, ... , n,
~ ~.
путем максимизации логарифмической функции прав
доподобия плотности Т копула-функции:
'°'
т
vА_
-
А
~.
argmax ~ 1ncStudent(Aин, ... ,Unt,
~,v.
•
)
t=l
Метод
3 [Chen et al. (2004)].
1. Используя эмпирические или параметрически оцененные функ
ции одномерных частных распределений, преобразуем (хн, X2t,
t = 1, ... , Т,
. . . ,йnt)·
к приблизительно равномерно распределенным
... Xnt),
(йн, й2t, ...
Гл.
526
R-
2. Пусть
функции,
корреляционная матрица для гауссовской копула
оцененной
Eaaussian =
3.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
с
использованием уравнения
(6.6).
Положим
R.
Оценим
v
путем максимизации логарифмической функции прав
доподобия плотности Т копула-функции:
= arg max "°'
L....J l
т
А
V
Student ( А
А
..f,
)
U 1t, · · · , Unt; LJGaussian; V •
D С:-
t=l
4. Пусть (11t = (t; 1 (uн), ... , t; 1 (йпt))'. Наконец, используя уравне
ние (6.6), вычислим:
Здесь также могла быть применена итеративная процедура, но ав
торы работы
[Chen et al. (2004)]
не делали этого. Однако после первого
шага разница между фактической ковариационной матрицей и ее оцен
кой весьма мала.
6.2.5.
Эмпирические приложения в статистическом
пакете
R:
эллиптические копула-функции
В модуль «fCopulae~ входит множество интересных функций, позво
ляющих исследовать эллиптические функции. Приведем некоторые ко
манды:
fсориlае
Описание
функция
ellipticalList
список
доступных
эллиптических
копула
функций
ellipticalParam
ellipticalRange
установка параметров по умолчанию
диапазон допустимых значений коэффициента
корреляции
ellipticalCheck
проверка принадлежности коэффициента кор
реляции допустимому диапазону
Для функции распределения и плотностей имеются следующие
команды:
6.2.
ЭЛЛИПТИЧЕСКИЕ КОПУЛА-ФУНКЦИИ
fсориlае
527
Описание
функция
relliptical Copula
моделирование наблюдений из эллиптической
копула-функции
pellipticalCopula
вычисление
значения
эллиптической
копула
функции
delli ptical Copula
вычисление значения плотности эллиптической
копула-функции
rellipticalSlider
график случайных величин, смоделированных
из эллиптической копула-функции
pellipticalSlider
dellipticalSlider
график функции распределения
график функции плотности
Если необходимо изобразить график функции плотности и линий
уровня нормальной копула-функции, нужно использовать следующие
команды (результат см. на рис.
6.4):
# Generate the 2D Grid:
N
= 50; х = (O:N)/N; uv = grid2d(x); и= uv$x; v = uv$y
# Compute the Normal Copula Density:
c.uv = dellipticalCopula(u, v, rho = 3/4, type = "norm",
output = "list")
# Create а Perspective Plot:
persp(c.uv, theta = -40, phi = 30, ticktype = "detailed",
col = "steelЫue", main = "Normal Copula Density 11 , сех = 0.5)
# Create а Contour Plot:
contour(c.uv, nlevels = 20, main = "Normal Copula Density",
сех = 0.5)
Плотность: р
= 0,5
Линии уровня
~
"!
о
~
:
"
о
~
~~
~
.
~
~)]
~-
о.о
Рис.
6.4.
0.2
0.4
0.6
0.8
1.0
График плотности нормальной копула--функции и ее линий уровня
Для представления о графике эллиптической копула-функции и ее
плотности при различном выборе параметров рекомендуем воспользо
ваться «слайдером» функций:
Гл.
528
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
# Start Slider for Perspective Distribution Plots:
pellipticalSlider(}
llcm! isn't in document
# Start Slider for Perspective Density Plots:
dellipticalSlider()
В случае, если необходимо оценить эллиптические копула-функции
и сгенерировать соответствующие им наблюдения, можно использовать
следующий код:
# Estimation of 100 Samples:
est = NULL
for (i in 1:100)
R = ellipticalCopulaSim(n = 100, rho = 0.6, param = 4, type = 11 t 11 )
ans = ellipticalCopulaFit(R, type = 11 t 11 )
ans=ans$par
est = rblnd(est, ans)
# Print the Result:
for (i in 1:2) print(c( mean = mean(est[, i]), sd = sd(est[, i]) ) )
# Make а kernel density of the 100 estimates
densl=density(est[,1]) plot(densl,main=''kernel density of estimated Rho")
dens2=density(est[,2]) plot(dens2,main="kernel density of estimated NU 11 )
Архимедовы копула-функции
6.3.
6.3.1.
Основные понятия и определения
Архимедовы копула-функции обеспечивают аналитическую гибкость и
широкий спектр различных мер зависимости. По следующим причинам
эти копула-функции могут быть использованы в широком диапазоне
приложений:
•
архимедов'Ь~ копула-функции могут бытъ представлены в .явном
аналитическом виде, в отличие от семейства эллиптических ко
пула-функций, которые определяются в неявной форме;
•
архимедовъ~ копула-функции допускают относителъно простое
построение, включая вычислителъную реализацию (см. табл.
•
6.2);
многие параметрические семейства копула-функций принадле
жат этому классу;
•
архимедовы копула-функции не ограничены об.язателъным нали
чием радиалъной симметрии, что свойственно случаю нормаль
ной копула-функции или общему случаю эллиптических копула
функций. Это является преимуществом, так как во многих фи
нансовых и страховых приложениях наблюдается более сильная
6.3.
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
529
зависимость между большими убытками, чем между большими
доходами.
Двумерные архимедовы копула-функции могут быть определены
следующим образом.
Определение
6.3.
Рассмотрим непреръ~вную, строго убъ~вающую
и въ~пуклую функцию ф( и) с неотрицателън'Ьt.Ми значениями, опре
и удовлетворяющую ус.ловию ф(1) = О (см.
Определим псевдообратную функцию фl- 1 1(t) соотношением:
деленную при и Е [О,
рис. 6.5).
1]
для
для
где ф- 1 (t)
О~ t < ф(О);
t ~ ф(О),
- объ~чная обратная функция к функции ф(и).
Тогда функцию С: [О, 1] 2 --+ [О,
1], определенную как:
С(и1, и2) = ф[-l][ф(и1)
+ ф(и2)],
(6.7)
называют архимедовой копула-функцией с генератором ф( ·). Более то
го, если ф(О) = оо, то псевдообращение дает обычную обратную функ
цию, т. е. фl- 1 1(·) = ф- 1 (·)), а Ф(·) и С(·) в этом случае называют строгим
генератором и строгой архимедовой копула-функцией, соответственно
(в противном случае они называются нестрогими), см. рис.
6.5.
Нестро11111
(/)(О)
Обратная
Обратная
(/)(0)
Рис.
В работе
6.5.
Строгие и нестроmе генераторы и их обращения
[Nelsen (1999)]
представлен список из
22
однопараметри
ческих двумерных архимедовых копула-функций. Этот список вместе
с генерирующими функциями ф( ·) и соответствующими диапазонами
параметра а воспроизведен в табл.
6.2.
530
Гл.
Таблица
6.2.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Список архимедовых копула-функций
Са(и,
Номер
v)
Генератор
Диапазон
Фа(t)
параметра
а
1
mах([и-°' +
v-°' - 1]- 11°, О)
2
3
max(l - [(1- и)°'+ (1- v)°'] 11°', О)
(Г°'
- 1)/а
(1 - t)°'
1n 1-ar(l-t)
t
uv
[-1,оо)\{О}
[1,оо)
[-1, 1)
5
1-ar(l-u)(l-v)
exp(-[(-lnu)°' + (-lnv)°'] 11°')
-.!. ln
+ (e-""'-l)(e-av_l))
6
1- [(1-и)°' + (1-v)°' -(1-u)°'(l-v)°'] 11°
- ln[l - (1- t)°']
[1,оо)
7
max(auv + (1 -
-ln[at+(l-a)]
1-t
l+(ar-l)t
ln(l - а ln t)
(О,
4
(1
0<
е
"'-1
а)(и + v - 1), О)
ar 2 uv-(1-u)(l-v) о)
ar2-(ar-1)2(1-u)(l-v)'
uv ехр(-а ln и ln v)
max (
8
9
v°')Г 1 /°'
uv[1 + (1 - u°')(l -
11
max([u°'v°' - 2(1 - u)°'(l - v)°'] 11°', О)
(1+[(и-1_1)°' + (v-1 _ l)°']lfar)-1
exp(l - [(1 - ln и)°' + (1 - ln v)°' - 1] 11°')
13
(1+[(u-1/ar_1)°' + (v-1/ar_ -l)°'jl/ar)-°'
max ( {1 - [(1 - и 1 1°')°'+
14
15
[1, оо)
ln(2Г°'
10
12
(-lnt)°'
1 e-at_l
- n е- 0 -1
- 1)
(-00 1 00)\{О}
1]
[1,оо)
(О,
1]
(О, 1]
ln(2 - t°')
(О,~]
(Г 1 - 1)°'
[1,оо)
(1 - lnt)°' - 1
(Гl/ar - 1)°'
(1 _ tlfar)°'
(О,оо)
(аГ 1 +1)(1-t)
[О,оо)
-ln (l+t)-"'-1
(-00 1 00)\{О}
e°'/(u-1)
[2,оо)
[1,оо)
[1,оо)
+(1 _ vl/ar)°'jl/ar}°', О)
16
~(S+Js2+4a),
17
18
-a(u-1 + v- 1 - 1)
_
( 1 + [(l+u)-"'-l][(l+v)-"'-1))-l/ar
2-<>-1
1
max ( 1 +а/ ln[e°'/(u-l)+ +e°'/(v- 1>], О)
19
a/ln(e°'/u + e°'/v - е°')
20
[ln(exp(u-°') + exp(v-°') - e)]-l/ar
ехр(Г°')- е
(О,оо)
21
1 - (1 - { max([l - (1 - и)°'] 1 1°'+
+[1 - (1 - v)°'jl/ar - 1, O)}°')l/ar
1- [1-
[1,оо)
22
S=u+v-1-
[О,оо)
max ([ 1 - (1 - u°')J1 - (1 - (1-v°')Jl - (1-v 0
2- 0 -1
)
2]
и0 )2-
-(1 - t)°'jl/ar
arcsin(l - t°')
(О,
1]
11°' ,о)
Копула-функции с номерами
3-6, 9, 10, 12-14, 17, 19, 20, 22
явля
ются строгими копула-функциями, тогда как копула-функции с номе
рами
1
и
из табл.
16 6.2 не
функций
строгие только для а> О. Остальные копула-функции
являются строгими. Некоторые из архимедовых копула
имеют
специальные
функцию под номером
номером
4 -
1
названия.
Например,
копула
называют копула-функцией Клейтона, под
копула-функцией Гумбе.л.я, а под номером
5 -
копула
функцией Ф'fXLttKa. Учитывая, что последние три копула-функции до
вольно популярны, они будут рассмотрены ниже более подробно.
6.3.
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
531
Плотность архимедовых копула-функций может быть вычислена по
формуле:
- д2 С(и1,и2)
)
(
с и1,и2 д д
U1 U2
или, если генератор ф( ·) дважды непрерывно дифференцируем,
Это означает, что, зная генератор ф( ·), его обратную функцию
ф(-l](·), ее первую и вторую производные, можно получить архимедову
копула-функцию и ее плотность. Однако, за исключением некоторых
простых случаев, плотности копула-функций оцениваются с использо
ванием таких программ, как
Maple
или
Mathematica.
Некоторые однопараметрические двумерные
6.3.2.
архимедовы копула-функции
Копула-функция Клейтона. Семейство копула-функций Клейтона
было впервые предложено в работе
[Clayton (1978)).
Рассмотрим гене
ратор ф(t) = (t-a - 1)/а с а Е [-1, оо)\{0}. Тогда ф- 1 (t) = (1
Используя
(6.7),
+ t)-lfa.
получим:
cClayton(u1,u2;a) = max [(и1а +и2а -1)-1/а,0].
Если а
>
О, то ф(О) =
оо, и вышеприведенное выражение для
копула-функции примет вид:
с( и1,и2 )
= (и1-а +и2-а -
l)-1/a
'
а плотность копула-функции Клейтона будет равна:
Отметим, что в отличие от случая а
>
О, при
-1
~ а
<О
копула
функция Клейтона не является строгой, поскольку ф(О) = 1/а. При
а
--+
О получим копула-фунцию, отвечающую случаю независимости,
а при а
При а
--+
=
оо
-1
-
копула-функцию, соответствующую комонотонности.
получим нижнюю границу Фреше-Хёффдинга. Таким
образом, копула-функция позволяет интерполировать промежуточные
структуры
зависимости
стью и независимостью.
между
противомонотонностью,
комонотонно
Гл.
532
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Копула-функция Гумбеля. Семейство копула-функций Гумбе
ля было впервые представлено в работе
[Gumbel (1960)],
но поскольку
подробный анализ этого семейства был приведен в работе
(1986)],
[Hougaard
то его иногда называют семейством Гумбеля-Хоугарда. Гене
ратор этого семейства имеет вид: ф(t) = (- ln t)'\ где а ;;::: 1. Обратная
функция генератора равна ф- 1 (t) = exp(-t 1fa). Таким образом, копула
функции из этого семейства имеют вид:
с функцией плотности:
с(и1, и2; а) = С(и1, и2) · и1 1 и2 1 [(- ln и1)а + (-ln и2)аг 2 +t/а х
х [ln и1 ln u2]0t-l · {[(- ln u1)0t + (- ln u2)0t]-l/a +а - 1}.
При а
= 1 получаем
копула-функцию, соответствующую случаю
независимости; а при а ---t оо копула-функция Гумбеля С(и1,и2;а)
стремится к копула-функции, отвечающей комонотонности. Таким об
разом, копула-функция Гумбеля интерполирует структуру зависимо
сти, промежуточную между независимостью и абсолютной положитель
ной зависимостью.
Копула-функция Франка. Впервые копула-функция Франка бы
ла представлена в работе
проведен в работе
[Frank (1979)], а более подробный ее анализ
[Genest (1987)]. Эта копула-функция имеет генера-
тор:
ф(t) = ln
:-at-=_ 1)
1 .
-Ot
(
Обратная функция этого генератора равна:
ф- 1 ( t)
= -
.!, ln (1 + et (е-а -
1)) ,
а
а сама копула-функция и ее плотность имеют вид:
для а=/: О.
При а
=
О копула-функция Франка имеет вид копула-функции,
отвечающей случаю независимости; а при а ---t -оо и а ---t +оо копула
функция Франка принимает вид, соответственно, нижней и верхней
границ Фреше.
6.3.
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
Для того чтобы
533
продемонстрировать различия
функциями Клейтона, Гумбеля и Франка, на рис.
меж.цу
копула
они представ
6.6
лены графически. Видно, что изображенные копула-функции имеют
различный характер поведения в окрестностях точек (О, О) и
пример, копула-функция Гумбеля в окрестности
(1, 1)
(1, 1).
На
демонстрирует
резкий рост, тогда как рост в окрестности точки (О, О) менее резок.
Как будет показано далее, хорошим измерителем характера хвостов
этих копула-функций является коэффициент «хвостовой зависимости».
Копула-функция Гумбеля имеет «верхнюю хвостовую зависимость»,
копула-функция Клейтона
«нижнюю хвостовую зависимость», а ко
-
пула-функция Франка не имеет хвостовой зависимости.
Архимедова: Гумбеля-Хоугарда
Архимедова: Клейтона
(а=2;
t=0,5; р=О,582)
Рис.
6.3.3.
6.6.
(а=2; т=О,5; р=О,682)
Архимедова: Франка
(а=5;
t=0,451; р=О,634)
Плотности копула-функций Клейтона, Гумбеля и Франка
Многомерные перестановочные архимедовы
копула-функции
В работе
[Nelsen (2006)]
показано, что п-мерную копула-функцию для
случая независимости можно записать в следующем виде:
Р( и1, и2, . " , Un)
= и1 · и2 · "
. · Un
= ехр( -[ (- ln и1) + (- ln и2) + ...
. . . + (-lnun)]).
Это наблюдение подсказывает возможность обобщения
(6. 7)
на п
мерный случай:
(6.7а)
Функции С(·) в (6.7а) называют серийно-итеративн:ыми функци
ями
[Schweizer, Sklar (1983)],
копула-функции с
основанными на двумерной архимедовой
генератором
= ф[-ll[ф(и 1 ) + ф(и2 )],
Ф(·).
Если
положить
С(и1,и2)
то для п;;;::: 3 получим следующее обобщение:
С(и1, и2, ... , Un) = С(С(и1, и2, ... , Un-1), Un)·
-
Гл.
534
6.
Двумерные
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
архимедовы
копула-функции
симметричности и ассоциативности (см. теорему
обладают
свойствами
4.1.5 в [Nelsen (2006)]),
а именно:
С(и, v) =
C(v, и) 't/u, v Е [О, 1] (симметричность),
С (С(и, v), w) =С (и, C(v, w)) 't/и, v, w Е [О, 1] (ассоциативность).
Копула-функции вида (6.7а) также известны как перестановочн:ые
архимедовы копула-функции: случайные величины Х и У называются
перестановочнъши, если векторы (Х, У) и (У, Х) являются одинаково
распределенными. В нашем случае перестановочность копула-функции
эквивалентна ее симметричности (см. теорему
2.7.4 в [Nelsen (2006)]).
Для того чтобы С(·) была копула-функцией при n ~ 3, требуются
некоторые дополнительные свойства функций Ф(·) и ф[- 1 1(·). Для этого
понадобится следующее определение.
Определение
Неотрицательная функция
6.4.
абсолютно монотонной на интервале
J,
g(t)
назъtвается
ес.л.и она непреръtвна на этом
интервале и имеет производные любого порядка, причем
t Е J и k = 1, 2, ....
Например, функция g(t) = e-t, t Е R, является абсолютно моно
тонной, так как g'(t) = -e-t, g"(t) = e-t, ... ,g(k)(t) = (-1)ke-t, .. "
Следует отметить, что если g(t) абсолютно монотонна на [О, оо) и
g(c) = О для некоторого с > О, то g(·) = О на [О, оо). Более того, ес
для всех внутренних точек
ли псевдообратная функция ф[-l](·) генератора архимедовой копула
функции ф( ·) абсолютно монотонна, то на интервале [О, оо) функция
ф[-l](·) положительна, функция Ф(·) абсолютно монотонна и ф[-l](·) =
= ф-1(·).
Ниже приведем необходимое и достаточное условие, налагаемое на
строгий генератор Ф(·) для того, чтобы функция (6.7а) была n-мерной
копула-функцией при
Теорема
6.3.
n
~
Пусть ф
2 [Kimberling (1974)].
: [О, 1] --+ [О, оо] непреръtвна.я и строго убъt
вающая функция, така.я, что ф(О)
=
на.я функция для Ф(·), С
[О,
:
[О,
l]n --+
оо и ф(1)
1]
=
0,ф- 1 (·)- обрат
определяется соотношением
(6.7а). Тогда необходим'ЫМ и достаточнъш ус.л.овием для того, чтобы
С(·)n-мерной копула-функцией для всех
n
~
2,
является требование
абсолютной монотонности функции ф- 1 (·)[0, оо).
До к аз ат ель ст в о. См.
(1983)], [Alsina et al. (2005)].
[Kimberling (1974)], [Schweizer, Sklar
6.3.
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
535
Однако требование абсолютной монотонности в вышеприведенном
условии является весьма жестким, что приводит к ограничениям струк
туры зависимости. В работах
[Miiller, Scarsini (2005)]
[Genest, Rivest (1993)], [Nelsen (2005)],
было предложено заменить это условие более
слабым, в котором для функции ф( ·) требуется существование произ
водных лишь до некоторого конечного порядка. В
(2009)]
[McNeil, Neslehova
представлено необходимое и достаточное условие для того, что
бы функция Ф(·) обладала свойством n-монотонности (d-монотонности
в терминах этой работы). Это условие показывает, что существуют
n-
мерные архимедовы копула-функции, не имеющие плотностей. Кроме
того, из результатов работы следует существование точных ниж;них
границ для множества всех n-мерных архимедовых копула-функций от
носительно так называемого конкордационного упорядочивания (более
детальную информацию см. в
[McNeil, Neslehova (2009))).
Представленное выше многомерное обобщение архимедовых копу
ла-функций является весьма ограничительным, поскольку в своей спе
цификации оно использует лишь один генератор, не зависящий от рас
сматриваемой размерности. Как следствие, все k-мерные частные рас
пределения
(k
< n)
имеют идентичный вид. Для того чтобы обеспечить
большую гибкость, было предложено множество подходов, некоторые
из которых мы рассмотрим ниже.
6.3.4.
Вложенные архимедовы копула-функции
Построение
полностью
вложенных
архимедовых
копула
функций. Описание и исследование одного из обобщений для функций
(6.7а) имеется в работах
[Joe (1997)], [Embrechts et al. (2003)], [Whelan
(2004)], [Savu, Тrede (2009)], [McNeil (2008)]. Структура такого обобще
ния для четырехмерного случая показана на рис. 6. 7.
Рис.
6. 7.
Построение полностью вложенных архимедовых копула-функций
Гл.
536
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Узлы иl и и2 связываются при помощи копула-функции С1(·), узел
из связывается с С1 ( и1, и2) при помощи копула-функции С2 (·) и, на
конец, узел и4 связывается с С2(из, С1(и1, и2)) при помощи копула
функции Сз(·). Таким образом, четырехмерный случай требует трех
двумерных копула-функций С1(·), С2(·) и Сз(·), генераторы которых
равны Ф1 (·), Ф2 (·) и Фз ( ·) соответственно. Несмотря на то что структура
«связывания»
довольно проста,
ее выражение в виде
аналитического
уравнения является весьма непростой задачей:
С(и1,и2,из,и4)
= Сз(и4,С2(из,С1(и1,и2))) =
= ФЗ 1 {Фз(и4) + Фз(Ф2 1 {Ф2(из) + Ф2(Ф1 1 {Ф1(и1) + Ф1(и2)})} )}.
Другими словами, пары (и1, из) и (и2, из) имеют одну и ту же копу
ла-функцию С2(·) с параметром зависимости а2, тогда как пары (и1, и4),
(и2, и4) и (из, и4) имеют копула-функцию Сз(·) с параметром зависимо
сти аз. В общем п-мерном случае:
С(и1, ... ,иn) = Ф-;;~1 (Фn-1 о Ф-;;~2[· .. (Ф2 о Ф1 1 [Ф1(и1) + Ф1(и2)]+ (6 .8)
+ Ф2(из)) + · · · + Ф2(иn-1)] + Фn-1(иn)).
Эта копула-функция называется полностью вложенной архимедо
вой копула-функцией, поскольку получается путем пошагового увели
чения размерности на единицу. Такая структура построения копула
функций является более общей, чем (6.7а). Кроме того, она обладает
лишь частичной перестановочностью. Полностью вложенная архиме
дова копула-функция имеет
распределений, но только
n( n - 1) /2 различных двумерных частных
(n - 1) несовпадающих двумерных копула
функций со свободной спецификацией, остальные двумерные функции
неявным образом определяются из структуры построения.
Выражение
(6.8)
будет n-мерной копула-функцией только тогда, ко
гда, в дополнение к свойству абсолютной монотонности для обратных
функций генераторов, «композитная» функция Фн1 о Фi 1 будет иметь
абсолютно монотонные первые производные для вложений всех уров
ней
i.
Как оказывается, если все генераторы однотипны, степень зави
симости, выражаемая параметром копула-функции, должна убывать с
увеличением уровня вложения, т. е. al ~ а2 ~
... an-1·
Если же генера
торы принадлежат разным семействам, то ограничения на параметры
бу,цут еще более жесткими, а список генераторов, которые могут быть
связаны, не столь велик (более детальную информацию см., например,
в
[Whelan (2004)], [Savu,
Построение
функций.
Тrede
частично
Построение
(2009)), [McNeil (2008))).
вложенных
частично
архимедовых
вложенных архимедовых
копула
копула-
6.3.
функций
-
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
537
альтернативный способ обобщения многомерных копула
функций вида (6.7а). Эта структура связывания изначально была пред
ложена в работе
ставлен в
[Joe (1997)], а дальнейший подробный анализ пред
[Whelan (2004)], [McNeil et al. (2005)], [McNeil (2008)]. Струк
тура этого метода связывания представляет собой смесь структур, ис
пользуемых при построении перестановочной и полностью вложенной
копула-функций, и носит название частично вложенной структур'Ьt.
Наименьшая размерность, для которой частично вложенная структура
связывания дает копула-функции, равна четырем. Для нее:
С(и1, и2, из, и4) = Сз(С1(и1, и2), С2(из, и4)) =
=
Ф3 1 { Фз(Ф1 1 { Ф1(и1) + Ф1(и2)}) + Фз(Ф2 1 { Ф2(из) + Ф2(и4)} )}.
(6.9)
Как и в предыдущих случаях, имеем громоздкие аналитические
выражения, но весьма ясное описание: на первом шаге связываем пары
(и1, и2) и (из, и4) копула-функциями С1(·) и С2(·), генераторы которых
равны Ф1 и Ф2 соответственно. Эти две копула-функции связываются
при помощи третьей копула-функции Сз (·). Случайные величины и~ и
и2 являются перестановочными, так же как из и и4, но все другие пары
перестановочными не являются. Однако пары (и1, из), (и1, и4), (и2, из)
и (и2, и4) имеют копула-функцию Сз(·) (см. рис.
6.8).
Для того чтобы
получить п-мерную копула-функцию с использованием такого способа
связывания, требуются ограничения, похожие на рассмотренные выше
при построении полностью вложенных архимедовых копула-функций.
Сз
Рис.
Общий
6.8.
Частично вложенные архимедовы копула-функции
случай:
иерархически
вложенные
архимедовы
копула-функции. Этот класс копула-функций впервые был предло
жен в работе
[Joe (1997)],
а в дальнейшем подробно изучался в
[Whelan
Гл.
538
(2004)].
6.
В работе
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
[Savu,
Тrede
(2009)]
представлена первая попытка раз
работки иерархически вложенных архимедовых копула-функций в об
щем виде. Такая структура связывания является расширением струк
туры частичного вложения в том смысле, что участвующие в процедуре
связывания копула-функции не обязательно двумерные.
Основная идея структуры связывания, предложенная в
Тrede
(2009)],
заключается в использовании иерархического вложения.
При этом предполагается, что имеется
ектов на каждом уровне
l
n1
L
уровней, по n1 различных объ
(объектом может быть либо копула-функция,
либо переменная). На уровне
ся на
[Savu,
l
=1
переменные и1, ... , Un разбивают
групп, в каждой из которых переменные связываются при
помощи перестановочной архимедовой копула-функции. В свою оче
редь, на уровне
l = 2
эти копула-функции связываются при помощи
n2 копула-функций и т.д. Более формально, на уровне l = 1 величи
ны и1, ... , Un связываются при помощи n1 многомерных архимедовых
копула-функций C1,j(·), j = 1, ... , n1, имеющих вид:
где Ф1,;(·) -
генератор копула-функции С1,;(·);
u1,; (j = 1,"., n1) -
подмножество элементов и1, ... , Un, связываемых при помощи С1,; ( ·).
Копула-функции С1,1 ( ·), ... , C1,n 1 ( ·) могут принадлежать разным се
мействам архимедовых копула-функций, таким как семейство Франка
или Гумбеля. Копула-функции уровня
l = 1,
ются при помощи копула-функций уровня
l
в свою очередь, агрегиру
= 2.
В результате получа
ем n2 обобщенных архимедовых копула-функций С2,;(·),
j
= 1, ... ,n2,
структура зависимости которых является частично перестановочной.
Их компоненты
-
копула-функции предыдущего уровня. Более фор-
мально:
где j
1, ... , n2;
Ф2,; ( ·)
-
генератор ко пула-функции С2,; ( ·);
множество всех копула-функций уровня
l = 1,
C2,j -
агрегируемых копула
функцией С2,; ( ·). Далее продолжаем шаг за шагом до тех пор, пока не
достигнем уровня
L, на котором получим единственную иерархическую
архимедову копула-функцию CL,1(·).
В работе
[Savu,
Тrede
(2009)]
используются несколько отличные
от используемых нами, но эквивалентные обозначения: поскольку j-ая
копула-функция l-го
(l = 1, ... , L) уровня C1,j(·) имеет в качестве аргу-
6.3.
ментов
ul,j,
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
т. е. подмножество из и1,
... , Un,
539
элементы которого в каче
стве аргументов входят явным или неявным образом в
Cl,j (·),
или (что
эквивалентно) аргументы
Cl,j ( ·) (т. е. множество всех копула-функций
уровня (l-1), участвующих в Cl,j(·)), то cl,j(Cl,j) и Cl,j(Ul,j) суть ОДНО
и то же.
Для того чтобы иметь хорошо определенную иерархию, число ис
пользуемых на каждом уровне копула-функци:й должно убывать с уве
личением уровня, т. е.
nl < nl-1
для всех
l
= 2, ... , L,
а на самом верх
нем уровне должен использоваться лишь один агрегирующи:й объект
CL,1(·),
т.е.
nL = 1.
Кроме того, размерность используемых копула
функций на каждом следующем уровне должна увеличиваться. На са
мом верхнем уровне размерность
данных
n,
CL,1 (·)
равна размерности исходных
nL,1 = n.
т. е.
П р и м е р
6.3.
Четырехмерные частично вложенные архимедовы
копула-функции, описанные в
C2,1(u) =
(6.9)
С2,1(и1,и2,из,и4)
(см. рис.
6.8),
имеют вид:
= С2,1(С1,1(и1,и2),С1,2(из,и4)) =
= Ф2,~ (Ф2,1 о Ф1J[Ф1,1(и1) + Ф1,1(и2)]+
+
П р и ме р
рис.
6.9.
С(и1,
6.4.
Ф2,1 (Ф1,~[Ф1,2(из) + Ф1,2(и4)J) ).
Рассмотрим 9-мерную структуру, определенную на
Копула-функция для нее имеет вид:
... ,ug) =
= С4,1 (Сз,1(С2,1 (С1,1(и1, и2), из, u4), u5, иб), С2,2(и1, С1,2(ив, ug))).
Рис.
6.9.
Иерархически вложенная архимедова конструкция
Гл.
540
В работе
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
[Savu,
Тrede
(2009)]
указаны некоторые условия для того,
чтобы иерархическое вложение давало многомерную функцию распре
деления. Во-первых, требуется, чтобы все обратные функции генерато
ров Ф~} (·) были абсолютно монотонными. Во-вторых, для l
= 1, ... , L и
j = 1, ... , nl, i = 1, ... , nl+1, сложные функции Фl+1,i (Ф~}(·)) должны
иметь абсолютно монотоннъtе производнъtе при всех l = 1, 2, ... , L и
j = 1, ... , щ. В работе [Embrechts et al. (2003)] показано, что в случае
полного вложения копула-функций либо из семейства Гумбеля, либо из
семейства Клейтона степень зависимости, выраженная параметром а,
должна убывать с увеличением уровня иерархических вложений. В при
мере
это означает, что а1,1 ;;;::: а2,1 ;;;::: аз,1 ;;;::: а4,1 и а1,2 ;;;::: а2,2 ;;;::: а4,1.
6.4
Если же агрегируемые копула-функции принадлежат разным се
мействам архимедовых копула-функций, то, как показано в
(2008)],
[McN eil
две архимедовы копула-функции из двух различных семейств
а и Ь могут быть иерархически вложены только в том случае, если
производная «композитной~ функции Фа офЬ 1 является абсолютно мо
нотонной. Вопрос о том, какие семейства копула-функций могут быть
агрегированы, в некоторой степени рассмотрен в работе
[Joe (1997)].
В силу достаточно сложной структуры иерархических копула
функций их плотности задаются весьма непростыми выражениями.
В
[Savu,
Тrede
(2009)]
используется рекурсивный подход для диффе
ренцирования п-мерной копула-функции CL,1 ( ·) верхнего уровня по ар
гументам UL,1 · А именно, в силу того, что
CL,1(uL,1) = CL,1(CL,1) = CL,1(CL-1,1, · · ·, CL-1,nL_i) =
= CL,1(CL-1,1(CL-1,1), · · ·, CL-1,nL-l (CL-1,nL-1)) =
= CL,1(CL-1,1(UL-1,1), · · ·, CL-1,nL-l (uL-1,nL_ 1 )),
плотность для CL,1(uL, 1) может быть вычислена следующим образом:
сL1 (u L1 ) -'
ancL,1(UL,1) д
'
Х nпL-l
д
U1". Un
~
-
Е
ди1
L...J
k
L-1,1
дlи1ICL-1,r(UL,1)
r=l и={ u1,".,ur}
х
an-icL,1(UL,1)
дCkl
".дС nL-1
L-1,nL-l
дlиrlCL-1,r(UL,1)
(6.10)
дur
где внешняя сумма берется по всем kl, ... ,knL-l Е
maxj
k j ":::::::: nL-1,j
~nL-1
и L...Jj=l
kj =
·
п - i для
всех
N U {О} таким, что
·i = 0, ... , п - nL-1·
Вторая часть формулы включает в себя производные копула-
функций уровня
(L - 1)
с аргументами UL-1,j,
мирование во второй части производится по
r
j
Е
=
1, ... ,nL-1· Сум{О, 1, ... , nL-1} раз-
личным подмножествам {и1, ... ,ur} множества UL-1,r, а произведение
берется по всем порядковым номерам копула-функций уровня (L - 1).
6.3.
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
541
Алгоритм нахождения плотности п-мерной копула-функции
CL,1 ( ·)
является рекурсивным: плотность для
CL, 1 (·) определяется через част
ные производные копула-функций CL-1,1(·), ... , CL-1,nL-i {·), которые
в свою очередь могут быть вычислены с использованием
{6.10)
для
копула-функций, используемых на более низких уровнях. Рекурсивная
проце,цура завершается на самом низком уровне, когда требуется найти
частные производные (различных порядков) лишь стандартных архи
медовых копула-функций.
В силу рекурсивной природы алгоритма нахождения плотности для
CL,1(·) количество вычислительных операций растет вместе с усложне
нием копула-функции. На практике для вычисления плотности иерар
хической п-мерной копула-функции приходится прибегать к компью
терным алгебраическим системам, таким как
ция
D).
Mathematica
или
R (функ
Нет необходимости упоминать о том, что время, необходимое
для вычисления оценок максимального правдоподобия, растет вместе с
ростом размерности п (более детально см.
Пр им ер
четырехмерной
6.5.
Используя формулу
иерархической
представленной рис.
6.3.5.
6.9,
[Aas et al. {2009))).
{6.10),
получим, что плотность
архимедовой
копула-функции,
определяется соотношением:
Моделирование наблюдений из архимедовых
копула-функций
Прямое применение традиционных методов генерирования многомер
ных наблюдений, подчиняющихся заданному закону распределения, в
принципе возможно и к распределениям, описанным с помощью копула
функций, см.
[Frees, Valdez {1998)], [McNeil {2008)].
К сожалению, эти
методы оказываются чрезмерно трудоемкими в случае вложенных ар
химедовых копула-функций и многомерных перестановочных архиме
довых копула-функций. Для последних моделирование наблюдений це-
Гл.
542
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
лесообразно проводить с использованием метода ус.л,овной инверсии,
который также можно использовать для любой копула-функции.
Если имеется копула-функция С
=
С(и1,
... , иn) (не обязательно
архимедова) и необходимо сгенерировать наблюдения (и1, ... , Un) п
мерного распределения случайного вектора (U1, ... , Иn), копула-функ
ция которого равна С ( ·), а частные распределения являются равномер
ными на отрезке [О,
1),
то можно воспользоваться методом ус.ловно-
го распределения. Пусть Сk(и1,и2, ... ,иk)
=
С(и1,и2, ... ,иk,1, ... ,1),
k = 1, ... , n; при этом С1(и1) = и1 и Сn(и1, и2, ... , иn) = С(и1, ... , иn)·
Условное распределение Uk, k = 2, ... ,п, при заданных И1, ... ,Иk-1
равно:
Ck(иklи1, и2,
... , иk-1) = P(Uk ~ иklИ1 = и1, ... , Иk-1 = иk-1) =
= Сk(и1, и2, ... , иk)/Ck-1 (и1, и2, ... , иk-1).
Для реализации алгоритма моделирования необходимо:
•
смоделировать
п независимых равномерно распределенных слу
чайных величин
V1, ... , Vn;
= V1 j
8
ПОЛОЖИТЬ и1
•
аналитически или с использованием численных методов найти об
ратные функции условных распределений Сk(и1, и2,
... , иk)
при
k=2, ... ,n.
Результатом этого алгоритма является вектор наблюдений
. . . , иn), смоделированный в соответствии с распределением
(и1, ...
С ( ·). Не
смотря на то что моделирование с использованием условных распреде
лений весьма элегантно, сама процедура может быть весьма трудоемкой
с вычислительной точки зрения.
в случае архимедовых копула-функций условное распределение
при заданных значениях И1,
Теорема 6.4.
... , Иk-1
определяется теоремой
Пусть С(и1, и2,"., иn) = ф- 1 (ф(и1)
6.4.
+ ф(и2) + ". +
+Ф(ип))
Тогда
uk
- п-мерна.я архимедова копула-функци.я с генератором Ф(·).
для k = 2, ... , п
До к аз ат ель ст в о. См.
[Cherublni et al. (2004),
с.
183).
АРХИМЕДОВЫ КОПУЛА-ФУНКЦИИ
6.3.
В работе
[Marshall, Olkin (1988)]
543
предложен метод построения ар
химедовых копула-функций с использованием преобразования Лапла
са и обратной к нему функции. Этот метод особенно полезен, учиты
вая то, что каждое абсолютно монотонное отображение [О, оо] в [О,
1]
можно представить в терминах преобразования Лапласа и обратной к
нему функции. Пусть G(·) - функция распределения на R+ такая, что
G(O)
=О, а ее преобразование Лапласа-Стилтьеса определяется соот-
ношением
00
e-tжdG(x),
G(t) = /
t ;?;:
О.
о
Можно показать, что G: [О, оо]--+ [О, 1] является непрерывной, абсо
лютно
монотонной
и
строго
убывающей
функцией.
Поэтому
G( ·) - хороший выбор для обратной функции генератора архимедовой
ко пулы.
Как показано в работах
(2004)], [McNeil et al. (2005)],
[Frees, Valdez (1998)], [Cherublni et al.
с использованием преобразования Лапла
са- Стилтьеса можно предложить алгоритм моделирования наблюде
ний из распределения, описанного многомерной архимедовой копула
функцией. Его реализация состоит из следующей последовательности
действий:
•
смоделировать случайную величину
V
из распределения
G (·)
та
кого, что G(·) (преобразование Лапласа функции G(·)) является
обратной функцией генератора ф( ·) копула-функции, из которой
моделируются наблюдения; например:
-
для копула-функции Клейтона
V
имеет гамма-распределение
Ga(1/a., 1), а. > О, а G(t) = (1 + t)-lfo:; отметим, что д- 1 =
= (t-o: - 1) отличается от генератора под номером 1 из табл.
6.2 лишь на константу;
-
для копула-функции Гумбеля
деление St(1/a., 1, -у, О) с 'У
= exp(-t1fo:);
-
для копула-функции Франка
ление P(V
•
= k) =
V имеет дискретное распреде
(1 - e-o:)k /(ka.) при k = 1, 2, ... и а. > О;
сгенерировать независимые одинаково распределенные случайные
величины Х1,
•
=
V имеет устойчивое распре
соsо:(тга./2), а. > 1 и G(t) =
ВЗЯТЬ Ui. --
... , Xn;
GA ( -
!!!.Ь)
V
,
.- 1
i -
, ... ,
n.
Гл.
544
Вектор
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
(и1, ... , ип)'
смоделирован
из
п-мерной
архимедовой
копула-функции. Отметим, что для рассмотренных выше случаев алго
ритм предполагает необходимость моделирования случайных величин
из гамма-распределения, устойчивого распределения или дискретного
распределения. Более подробную информацию см. в
[Cherublni et al.
{2004)], [Schoutens {2003)], [McNeil et al. {2005)], [McNeil {2008)].
Эмпирические приложения в статистическом
6.3.6.
пакете
R:
архимедовы копула-функции
Для того чтобы вычислить значения функции распределения двумер
ной архимедовой копула-функции и ее плотности, необходимо восполь
зоваться некоторыми процедурами из модуля
fCopulae
в пакете
R:
fсориlае-функция
Описание
rarchmCopula
моделирование случайных величин из архиме
довой копула-функции
parchmCopula
вычисление
значения
архимедовой
копула
функции
darchmCopula
вычисление значения плотности архимедовой
ко пула-функции
parchmSlider
график наблюдений, смоделированных из архи
медовой копула-функции
parchmSlider
darchmSlider
archmCopulaFit
график функции распределения
график функции ПЛОТНОСТИ
оценка
параметров
архимедовой
копула-
функции
Например, для того чтобы смоделировать наблюдения из двумер
ной копула-функции Гумбеля, а затем по ним оценить параметры той
же копула-функции, необходимо использовать код:
# Random Variates:
R
= archmCopulaSim(n = 1000, alpha = 1, type = "4")
# Fit:
fit
fit
= archmCopulaFit(u = R[, 1], v = R[, 2], type = "4")
Если же рассматривать многомерную перестановочную архимедову
копула-функцию, то необходимо прибегнуть к использованию модуля
copula.
Ниже представлен пример кода для трехмерной перестановоч
ной архимедовой копула-функции (для более детальной информации
рекомендуем обратиться к руководству статистическим пакетом
результаты моделирования изображены на рис.
6.10.
R),
а
6.4.
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
545
library(copula)
#Some graphical examples
v <- rcopula(claytonCopula(2, dim = 3), 1000)
scatterplot3d( v)
frank.cop <- frankCopula(3)
persp(frank.cop, dcopula)
gumbel.cop <- archmCopula( 11 gumbel 11 , 5)
contour(gumbel.cop, dcopula)
# А 5-dim Frank copula
frank.cop <- frankCopula(3, dim = 5)
1.0
0.2
Рис.
0.4
0.8
0.8
График смоделированных наблюдений из трехмерной копула-функции
6.10.
Клейтона
Для моделирования и оценки -ч.етъ~рехмерной полности вложен
ной архимедовой копулъt можно было бы обратиться к МОдУЛЮ
GOF»
«copula
(недавно разработанному Дэниелем Бергом). Однако к момен
ту написания данной работы этот МОдУЛЬ находился в состоянии «/З
версии» и не был общедоступным, т. е. он еще не был загружен в средУ
пакета
6.4.
6.4.1.
R.
Парные копула-функции
Введение
Детальное изучение парных копула-функций было начато в работе
[Joe
(1997)], а позднее продолжено в [Bedford, Cooke (2001, 2002)], [Kurowicka,
Cooke (2006)] (моделирование) и [Aas et al. (2009)] (статистические вы
воды). Их использование дает возможность получить значительно более
гибкую структуру зависимости, чем структура перестановочных или
иерархически вложенных архимедовых копула-функций. При помощи
парных копула-функций можно разложить многомерную плотность на
Гл.
546
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
произведение
являются
n(n-1)/2 двумерных копула-функций, из которых (п-1)
безусловными, а остальные - условными. Важно отметить,
что используемые двумерные копула-функции не обязаны принадле
жать одному классу.
Рассмотрим п случайных величин (Х 1 , ... ,
цией распределения Н(х1,
i
=
1, ... , п,
с совместной функ
частными распределениями
... , Xn),
совместной плотностью
ных распределений
Xn)
f(x1, ... , Хп)
fi(Xi), i = 1, ... , п.
Fi(Xi),
и плотностями част
Тогда для точек, в которых все
плотности непрерывны и положительны 2 :
n
= П f (xtlx1,"., Xt-1) · fi (х1).
{6.11)
t=2
Из теоремы Шкляра известно, что для абсолютно непрерывного
п-мерного распределения Н(·), имеющего строго возрастающие непре
рывные частные распределения
где с1,".,п(·,
F1(·), ... , Fn(·),
имеем:
... , ·)- п-мерная плотность копула-функции, описывающей
... , Хп), а F1 (х1), ... , Fп(хп) - зна
анализируемое распределение Н(х1,
чения частных функций распределения рассматриваемых случайных
величин в точках х1,
... , Xn
соответственно.
В двумерном случае
откуда легко следует, что:
Для трех случайных величин Х1, Х2 и Хз имеем:
где с 12 1 3 ( ·) - копула-функция для условных функций распределений
((Х1!Хз), (Х2!Хз)). Кроме того,
f(x1lx2, хз) = с1з12 (F(x1lx2), F(xзlx2)) f(x1lx2).
2В
правой части формулы {6.11) и некоторых других местах далее для того,
чтобы избежать усложнения обозначений, функции условной плотности и условного
распределения случайной величины
Xi
при условиях на переменные с номерами
ji,j2, ... ,jk не будут помечаться соответствующими индексами ilj1,j2, ... ,jk.
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
6.4.
547
Последнее соотношение может быть обобщено на п-мерный случай:
(6.12)
где
щ
-
v -
вектор значений компонент, на которые наложены условия,
произвольно выбранная компонента вектора
значен вектор
v,
v,
а через
v -j
обо
из которого исключена j-я компонента.
Теперь, если воспользоваться
щее представление для
(6.12), то
f(xtlx1, ... , Xt-1):
из
получим следую
(6.11)
(6.13)
где для различающихся индексов
< ... < ik,
i,j,i1, ... ,ik,
таких, что
i <j
и
il <
можно выразить двумерную условную копула-функцию при
значениях аргументов, равных соответствующим условным функциям
распределения, а именно:
~.Лi1,".,ik = Ci,jli1,".,ik (F(xilXi11 ... ,Xik), (F(xjlXi1, ... ,Xik)).
Используя
(6.13),
можно записать
(6.11)
в виде:
n t-1
f(x1, · · ·, Xn)
= f(x1) · П П ct-k,ф,".,t-k-1 · f(xt) =
n
=
=
где
j =
t - k,
j
t=2 k=l
n
t-1
П f (xr) · П П ct-k,ф,".,t-k-1
r=l
n
П
r=l
t=2 k=l
n-1 n-j
f (xr) ·
=
(6.14)
П П Cj,j+lll,".,j-l 1
j=l i=l
+ i = t.
Представление
(6.14)
называют разложением парных копула-фун
кций. Для многомерных распределений существует много возможно
стей разложения на парные копула-функции. В
2002)]
[Bedford, Cooke {2001,
представлена графическая модель, называемая модел:ью регуляр
ной ветвизации. Основной идеей этого метода является представление
разложения на парные копула-функции типа
(6.14)
в виде последова
тельности вложенных деревьев с неориентированными ребрами, назван
ными ветвями. В п-мерном случае ветвизация представлена (п
ревом так, что
j-e дерево имеет (п + 1- j)
узлов и (п -
j)
-1)
де
ребер. Каждое
ребро отвечает плотности некоторой парной копула-функции, а ребра
j-го дерева становятся узлами
(j
+ 1)-го
дерева. Два узла
(j
+ 1)-го
дерева связаны ребром в том случае, если соответствующие ребра
j-
го дерева имеют общий узел. Разложение на парные копула-функции
Гл.
548
6.
определяется
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
ребрами, а также плотностями частных рас
n( n - 1) /2
пределений.
Сосредоточим внимание на двух примерах регулярной ветвизации,
которые на сегодняшний день привлекли большое внимание исследова
телей. Речь пойдет о канонической ветвизации и D-ветвизации. Для
более детальной информации относительно общей теории регулярной
ветвизации и ее графического представления рекомендуется работа
[Kurowicka, Cooke {2006)].
Рассмотрение упомянутых выше примеров регулярной ветвизации
начнем с двумерных условных распределений, которые являются клю
чевыми элементами этой процедуры.
Условные распределения для наиболее часто используемых
двумерных копула-функций. В работе
F{xlv)
=
[Joe {1997)]
8Cx,v;lv-; (F(xlv-j), F(щlv-j))
дF{щlv-j)
показано, что:
для любого j,
{6.15)
где Cx,v;lv-; -условная двумерная копула-функция {формальное опре
деление см. выше). Если v имеет размерность 1 (т. е. v = v), то {6.15)
принимает вид:
F(
Пусть
F1(x) =
1 )
xv
= 8Cx,v (F1(x),F2(v))
8F(v)
Р(Х ~ х) = х и
F2(v) = P(V
.
~
v) = v
(т. е.
f(x) =
= f(v) = 1). Введем обозначение:
h(x, v; 0) = F(xlv) =
где через
0
8Cx,v~: v; 0)'
{6.16)
обозначены параметры копула-функции совместного рас
пределения Р(Х ~ х, V ~ v). Согласно терминологии работы [Aas
et al. {2009)] функцию h(x, v; 0) назовем h-функцией, а h- 1(u, v; 0) обратной h-функцией относительно первого аргумента и.
Для двумерной нормальной копула-функции h-функция имеет вид:
h(и1,и2,Р12
. ) -_
Ф (Ф- 1 (и1)_ - Р12Ф- 1 (и2))
11
v
2
,
-Р12
а обратная h-функция относительно первого аргумента равна:
h- 1(u,,uo;p12) =
где Ф(z)
-
Ф ( Ф- 1 (щ)..j1 - ~2 + Р12Ф- 1 (uо)),
значение функции распределения стандартного нормального
закона в точке
z,
а р12
-
коэффициент корреляции между анализиру
емыми случайными величинами.
6.4.
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
Для двумерной копула-фун:кции Стъюдента с
549
1112
числом степеней
свободы h-функция равна:
а обратная h-функция относительно первого аргумента равна
h- 1 (и1,
и2; Р12, 1112) = tv12 ( t~1~+l (
(1112+(t;;1;(и2)) 2 )(1-р~2 ))+
1112 + 1
"2)}
+ P12t;;-.~ (
В приведенных формулах используются следующие обозначения:
tv(z) -
значение функции распределения Стьюдента с
боды в точке
а t; 1 (u)
z,
-
значение обратной к
tv(z)
v
степенями сво
функции распре
деления в точке и.
Для двумерной копула-функции Клейтона h-функция имеет вид:
а обратная h-функция относительно первого аргумента равна:
Для двумерной копула-функции Гумбел.я, h-функция принимает вид:
h(u1, и2; а12)
= С12(и1, и2) · _!._ · (-ln и2)°' 12 - 1 .
и2
. {(-lnu1)a12 + (-lnu2)a12}l/a12-1,
где С12(и1, и2)
-
двумерное распределение Гумбеля. К сожалению, в
случае копула-функции Гумбеля обратная h-функция может быть вы
числена лишь с использованием численных методов. В условиях боль
шой размерности целесообразнее использовать копула-функцию Клей
тона, см.
[Joe (1997)]
или
[Cherublni et al. (2004)].
Гл.
550
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Каноническая ветвизация
6.4.2.
Регулярную ветвизацию, при которой каждое дерево имеет единствен
ный узел, называют канон.и-ческой ветвизацией. Разложение n-мерной
плотности, отвечающее канонической ветвизации, представлено в фор
муле
(6.14),
т. е.
n
f(x1,x2, ... ,xn)
n-1n-j
= П f(xk) П П Cj,j+ill,".,j-1
(6.17)
k=1
j=l i=l
{F(xjlx1, ... , Xj-1), F(xj+ilx1, ... , Xj-1)}.
На рис.
6.11
показаны канонические ветвизации в 5-мерном случае:
0
т.
2511
Тз
~~
~~
Рис.
6.11.
Примеры канонических ветвизаций в пятимерном случае
Представления вида
(6.17)
обладают преимуществом в ситуациях,
когда можно выделить одну ключевую переменную, влияющую на дру
гие переменные. Такая переменная может быть использована в качестве
корня канонической ветвизации (переменная
1 на
рис.
6.11).
Генерирование многомерных наблюдений. В работе
(2009)]
показано, что алгоритм генерирования
величин
является
общим
как
для
n
[Aas et al.
зависимых случайных
канонической,
так
и
для
D-ветвизации:
•
смоделируем независимые равномерно распределенные на [О,
случайные величины
w1, ... , wn;
1]
6.4.
• возьмем х1
. . . ; Xn
=
551
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
х2 = p- 1(w2lx1); хз
p- 1(wnlx1, ... ,Xn-1).
= w1;
= p- 1 (wзlx1,x2); ...
Для того чтобы при любом
j определить распределение случай
ной величины (XjlX1, Х2, ... , Xj-1), в работе [Aas et al. (2009)] предла
гается использовать h-функцию, заданную соотношением
отношение
(6.15).
(6.16),
и со
Отметим, что отличие канонической ветвизации от
D-ветвизации состоит в выборе переменной щ для
(6.15).
Кроме того,
F(xjlx1, ... ,Xj-1) =
- acj,j-111,".,j-2 {F(xjlX1, ... ,Xj-2), F(Xj-1lx1, ... 'Xj-2)}
-
8F(Xj-1lx1, ... , Xj-2)
На основании этих результатов в работе
[Aas et al. (2009)]
предложе
на следующая процедура генерирования наблюдений, имеющих плот
ность в форме канонической ветвизации:
Sample w1, ... , Wn independent uniform on
Set х1 = V1,1 = w1
for i +- 2, ... , п
Vi,l
[О,
1]
= Wi
for k +- i - 1, i - 2, ... , 1
vц = h- 1(vi,1,vk,k;ek,i-k)
end for
Xi
= Vi,l
if i == п then
Stop
end if
for j +- 1, ... , i - 1
vi,j+1
= h(vi,;,v;,;;0;,i-;)
end for
end for
Внешний цикл указанной выше процедуры работает по порядко
вым номерам компонент моделируемых многомерных наблюдений. Он
включает в себя два подцикла: первый из них позволяет вычислить смо
делированное значение i-й компоненты наблюдения, второй
лить
условные
(i + 1)-й
распределения,
необходимые
для
-
вычис
вычисления
компоненты. Для вычисления этих условных распределений
в работе
[Aas et al. (2009)] используется h-функция, определенная соот
ношением (6.16), для которой в качестве аргументов берутся рассчитан
ные Vi,j = F(xilx1, ... ,Xj-1). Параметры ej,i для h-функции - это па
раметры плотности соответствующей копула-функции Cj,j+ф,".,j-l(·I·).
Оценивание параметров. Копула-функции с канонической вет
визацией могут быть оценены с помощью метода максимального прав
доподобия. Для простоты положим, как и в
[Aas et al. (2009)],
что
Гл.
552
Xi
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
= (xi,1, ... ,хi,т),
i
=
1, ... ,п
независимы во времени. Такое пред
положение не является ограничительным,
поскольку при наличии за
висимости можно на первом этапе оценить одномерные модели времен
ных рядов,
а затем для стандартизированных остатков использовать
копула-функцию с канонической ветвизацией. Такой подход к оценива
нию можно считать расширением метода максимального псевдоправ
доподоби.я. Для копула-функций он впервые был предложен в работе
[Oakes (1994)], а позднее в работах [Genest et al. (1995)], [Shih, Louis
(1995)] были представлены такие асимптотические свойства получа
емых оценок,
В
как
состоятельность
[Kim et al. (2007)]
и
асимптотическая
нормальность.
при помощи методов симуляционного моделирова
ния показано, что в условиях, когда частные распределения неизвест
ны (это довольно распространенная ситуация в прикладных задачах),
метод максимального псевдоправдоподобия дает более точные оцен
ки, чем метод максимального правдоподобия. Кроме того, в
al. (2008)]
[Kim et
показано, что в случае многомерных моделей с гетероске
дастичностью этот метод дает оценки, являющиеся состоятельными и
асимптотически нормальными.
Однако в случае, когда вместо многомерной копула-функции ис
пользуется разложение на парные копула-функции, методология оцени
вания будет отличаться от представленной выше (см.
[Aas et al. (2009)]).
Для копула-функции с канонической ветвизацией логарифмическая
функция правдоподобия имеет следующий вид:
n-1 n-j
Т
LLL
ln [cj,j+ф,".,j-1F(xj,tlx1,t, ... , Xj-1,t),
j=l i=l t=l
(6.18)
F(xj+i,tlx1,t, ... , Xj-1,t)].
В работе
[Aas et al. (2009)]
предложен следующий алгоритм вычис-
ления логарифмической функции правдоподобия
log-likelihood =
for i f-- 1, ... , п
VQ,i
=
(6.18):
О.
Xi
end for
for j f-- 1, ... , n - 1
for i f-- 1, . " , n - j
log-likelihood = log-likelihood
end for
if j == n - 1 then
Stop
end if
for i f-- 1, ... , n - j
+
L{vj-1,1, Vj-1,i+li ej,i)
6.4.
553
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
Vj,i = h(Vj-1,i+l, Vj-1,1; 03,i)
end for
end for
Здесь
L(x, v; 0) -
логарифмическая функция правдоподобия вы
бираемой двумерной копула-функции, параметры которой определены
вектором
0,
а наблюдениях и
v
заданы. Кроме того, в упомянутой ра
боте представлена процедура нахождения начальных значений оценок
параметров, вычисляемых при помощи численной максимизации лога
рифмического правдоподобия. Эмпирический анализ показывает, что
начальные значения оценок,
[Aas et al. (2009)],
вычисленных при помощи процедуры из
и итоговые значения оценок, полученных при одно
временном оценивании всех параметров, весьма близки, в то время как
значение функции правдоподобия увеличивается незначительно. Это
может означать, что процедура вычисления начальных значений оце
нок параметров дает состоятельную оценку всех параметров, что зна
чительно облегчает вычислительную процедуру. Однако этот вопрос
требует более детального исследования.
6.4.3.
D-ветвизация
Регулярная ветвизация, при которой у любого дерева
Tj
не существует
узла, соединенного с более чем двумя ребрами, называется D-ветвиза
цией. Многомерная (п-мерная) плотность, отвечающая D-ветвизации,
имеет вид:
n
n-1 n-j
П f (xk) П П
k=1
ci,i+jli+l,".,i+j-1 х
j=l i=l
х {F(xilxн1, ... , Xi+j-1), F(xнjlxн1, ... , Xi+j-1)}.
На рис.
6.12
показана 5-мерная D-ветвизация.
®-------@
151234
Рис.
6.12.
D-ветвизация для пяти переменных
Гл.
554
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Генерирование многомерных наблюдений. В работе
(2009)]
[Aas et al.
предложена следующая процедура моделирования наблюдений,
закон распределения которых представлен с помощью D-ветвизации:
Sample w 1 , ... , Wn independent uniform on
1]
= v1,1 = w1
= V2,1 = h- 1(w2, v1,1; 01,1)
Set х1
Set х2
v2,2
[О,
= h{v1,1, v2,1; 01,1)
for i t- 3, ... , п
Vi,1
= Wi
for k t- i - 1, i - 2, ... , 2
Vi,1
=
h- 1 {Vi,1, Vi-1,2k-2i 0k,i-k)
end for
Vi,1
Xi
= h- 1 (Vi,1, Vi-1,li 01,i-1)
= Vi,1
if i = п then
Stop
end if
Vi,2
=
Vi,3
= h(vi,1, Vi-1,li 01,i-1)
h{Vi-1,1, Vi,lj 01,i-1)
for i > 3 then
for j t- 2, ... , i - 2
Vi,2j
=
h{Vi-1,2j-2, Vi,2j-li 0j,i-j)
Vi,2j+l = h{vi,2j-1' Vi-1,2j-2i 0j,i-j)
end for
end if
Vi,2i-2 = h{Vi-1,2i-4'
Vi,2i-Зi 0i-1,1)
end for
Как и в случае канонической ветвизации, процедура моделирова
ния D-ветвизации состоит из одного внешнего цикла, включающего
один подцикл для моделирования переменных, а также один подцикл
для вычисления необходимых условных распределений. Тем не менее
с вычислительной точки зрения этот алгоритм является менее эффек
тивным, чем алгоритм моделирования канонической ветвизации, по
скольку число условных распределений, которые необходимо вычис
лить, для D-ветвизации равно (n - 2) 2 , а для канонической ветвиза
ции
ры
- (n - 2)(n - 1)/2.
0j,i в h-функции -
Отметим, что в случае D-ветвизации парамет
это множество параметров соответствующей
копула-функции ci,i+jli+l,".,i+j-1(·1·).
6.4.
ПАРНЫЕ КОПУЛА-ФУНКЦИИ
555
Оценивание параметров. В случае D-ветвизации логарифмиче
ская функция правдоподобия имеет следующий вид:
n-1 n-j
Т
LLL
ln [<;,нлн1,".,i+j-1Ьig(F(xi,tlxнi,t, ... , Xi+j-1,t),
j=l i=l t=l
F(xнj,tlxн1,t, ... , Xi+j-1,t))].
В работе
[Aas et al. (2009)]
предлагается следующий алгоритм вы-
числения логарифмической функции правдоподобия:
log-likelihood =О.
for i = 1, ... ,п
Vo,i
= Xi
end for
for i = 1, ... , п - 1
log-likelihood = log-likelihood
end for
v1,1
+
l{vo,i, vо,н1; 01,i)
= h(vo,1, vo,2; 0ц)
for k = 1, ... , п - 3
v1,2k = h(vo,k+2, vo,kн; 81,kн)
v1,2k+i
= h{vo,kн, vo,k+2; 01,kн)
end for
V1,2n-4 = h{vo,ni Vo,n-1; 81,n-1)
for j
2, ... , п - 1
=
for i = 1, ... , п - j
log-likelihood = log-likelihood
end for
if j = n - 1 then
Stop
end if
+
l{Vj-1,2i-1' Vj-1,2i; 0j,i)
Vj,1 = h{Vj-1,1, Vj-1,2; 0j,1)
if n > 4 then
for i = 1, ... , п - j - 2
Vj,2i
= h{Vj-1,2i+2, Vj-1,2i+l; 0j,i+l)
Vj,2i+l = h{Vj-1,2i+l, Vj-1,2i+2j 0j,i+l)
end for
end if
Vj,2n-2j-2
= h{Vj-1,2n-2j, Vj-1,2n-2j-lj 0j,n-j)
end for
Здесь
l(x, v; 0) -
логарифмическая функция правдоподобия для
выбираемой копула-функции, параметры которой определяются век
тором
0,
а векторы наблюдений х и
v
заданы. Отметим, что
параметры плотности копула-функции ci,i+jli+l,".,i+j-1(·1·).
0j,i -
Гл.
556
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Эмпирические приложения в статистическом
6.4.4.
пакете
R:
построение парных копула-функций
Если нужно смоделировать и оценить копула-функцию, используя ее
разложение на парные копула-функции, необходимо воспользоваться
модулем процедур
«copulaGOF»
из пакета
R,
разработанного Даниэлем
Бергом. Так, например, D-ветвизация в четырехмерном случае может
быть смоделирована и оценена следующим образом:
х
= SimulateCopulae(n=1000,d=4,construction =list(type = 11 dpcc 11 ,copula
=с( 11 clayton 11 , 11 gumbel 11 , 11 frank 11 , 11 gumbel 11 , 11 clayton 11 , 11 gumbel 11 )),
param = list(c{2,3,6,1.3,1,1.4),
rep{0,6)))
pairs(x)
dpcc. par = EstimateCopulaParameter{x,construction=list (type=
11 dpcc 11 ,copula =
c( 11 clayton 11 , 11 gumbel 11 , 11 frank 11 , 11 gumbel 11 , 11 clayton 11 ,
"gumbel 11 )))
dpcc.par
$t [1) 1.951387 2.991580 6.052075 1.343258 0.949556 1.410108
$nu [1) О
$loglik [1) 1899.111
Биплоты (диаграммы рассеяния пар компонент) для наблюдений
из четырехмерной копула-функции с D-ветвизацией представлены на
рис.
6.13.
о.о
0.4
о.о
0.8
0.4
0.8
в•••~
:•в••
о
•~в•:
~--~
.,
о
о о
0
•
о
ci
о.о
Рис.
6.13.
0.4
0.8
о.о
0.4
EJar4
0.8
Диаграмма рассеяния пар компонент для наблюдений из
четырехмерной копула-функции с D-ветвизацией
6.5.
МЕРЫ ЗАВИСИМОСТИ
557
Меры зависимости
6.5.
Меры зависимости являются весьма полезными инструментами для
описания структуры двумерной зависимости. В этой главе рассмотрим
три возможные меры: коэффициент корреляции, коэффициент ранговой
корреляции и коэффициент хвостовой зависимости.
Достаточно хорошей мерой зависимости в классе эллиптических
распределений является коэффициент корреляции. Этот класс вклю
чает в себя, например, нормальное распределение, смеси нормальных
распределений. Однако коэффициент корреляции как мера зависимо
сти для многомерных распределений вне класса эллиптических распре
делений: обладает рядом недостатков. В качестве альтернативы пред
лагаются две другие меры зависимости, которые в некоторых случаях
оказываются более приемлемыми.
6.5.1.
Коэффициент корреляции
Коэффициент корреляции между случайными величинами Х и У, как
известно, определяется следующим образом (см., например, [Айвазян
(2010), п. 3.2.2)):
Р
где
Cov(X, У) -
(Х
У) _
'
Cov(X, У)
- vfVar(X)Var(Y)'
ковариация между Х и У,
Var(X)
и
Var(Y) -
дис
персии Х и У соответственно. Ниже представлены основные свойства
коэффициента корреляции.
1. lp(X, Y)I ::;;; 1.
2.
Если Х и У независимы, то р(Х, У)= О.
3. lp(X, У) 1 = 1 тогда
и только тогда, когда Р(Х
= а+ ЬУ) = 1 для
некоторых а и Ь ~ О.
4.
5.
р(аХ
+ (З, -уУ + 8) = sign(a-y)p(X, У).
Пусть (Х, У) имеет совместное двумерное нормальное распреде
ление с частными стандартными нормальными распределениями.
Тогда коэффициент корреляции р между Х и У однозначно опре
деляет совместное распределение (Х, У).
Обобщение коэффициента корреляции на многомерный случай
можно найти во многих учебниках по статистике, например
et al. (1997)].
[Mardia
Гл.
558
Пусть р
6.
-
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
выборочный коэффициент корреляции. Хорошо извест
но, что для проверки гипотезы Но
р
=1 О может быть
:
р =О против альтернативы Н1
использована сле,цующая тестовая статистика:
А
t
=
руп
2
----;:=::::::;
J1-µ2'
которая при справедливости нулевой гипотезы имеет tn-2-распределе
ние
-
см., например, [Айвазян
(2010),
с.78].
Если воспользоваться z-преобразованием Фишера, то получим:
1
(1-р)
z= 2
1og Щ
, ( = 21 1og (1-р)
1+р
,
Jn - З(z - ()~N(O, 1),
где знаком
d
---+
обозначена асимптотическая сходимость по распределе-
нию при бесконечно растущем объеме выборки п (п --t оо). Более того,
хорошо известно, что если р
=1 О,
то
Если Х и У имеют распределения (не обязательно нормальные), для
которых конечен четвертый момент и р(Х, У)
=1 О,
то
vn(fJ - р) ~ N (о, 1'2 )
при некотором " 2 (см. [Fang et al. (1987)], [Rodgers, Nicewander (1988)],
[Embrechts et al. (2002)]
и ссылки в этих работах).
К сожалению, для многомерных распределений неэллиптического
типа коэффициент корреляции обладает рядом недостатков.
1.
Равенство коэффициента корреляции нулю эквивалентно незави
симости в случае многомерного нормального распределения. Од
нако уже для многомерного распределения Стьюдента это не так.
2.
Коэффициент корреляции инвариантен относительно линейных
преобразований, но, как правило, не инвариантен относительно
более общих преобразований Т( ·):
р(Т(Х), Т(У))
# р(Х, У).
Например, две случайные величины, имеющие логнормальное рас
пределение, имеют коэффициент корреляции, отличный от коэффици
ента корреляции меж,цу их лог-преобразованиями.
6.5.
1.
МЕРЫ ЗАВИСИМОСТИ
559
Частные распределения и корреляционная матрица однозначно
определяют
лишь
только
совместное
распределение
эллиптиче
ского типа, но это неверно в общем случае.
2.
Дисперсии случайных величин Х и У должны быть конечными,
иначе корреляция не определена. Это свойство указывает на то,
что коэффициент корреляции
-
далеко не идеальная мера зави
симости, которая может быть неопределенной для распределений
с «тяжелыми хвостами~.
Рассмотрим пример, иллюстрирующий один из вышеупомянутых
случаев. Пусть Х1, Х2
-
чины с нулевым средним
нормально распределенные случайные вели
и дисперсией и 2
О, а коэффициент корреля
>
ции между ними равен р. Тогда коэффициент корреляции случайных
величин
Yi = exp(Xi), i = 1, 2,
имеющих логнормальное распределение,
равен
Corr(Y1, У2) =
При р
е/Ю
еи
2
2
-
1
- 1
•
= 1 всегда получим, что Corr(Y1, У2) = 1, но наименьшее воз
можное (при
Corr(Y1, У2) всегда будет больше -1.
Например, если и= 1, то Corr(Y1, У2) Е [-0,368, 1]. Кроме того, интер
вал достижимых значений Corr(Y1, У2) будет тем меньше, чем больше и.
-1:::;;
р:::;;
1)
значение
В качестве другого примера, иллюстрирующего недостатки коэф
фициента корреляции, рассмотрим величину Х1 со стандартным нор
мальным распределением N(O, 1) и Х2
= Xf.
Тогда
Таким образом, с одной стороны, имеем функциональную зависимость
между Х1 и Х2, а с дРугой стороны, нулевую корреляцию между ними.
6.5.2.
Коэффициенты ранговой корреляции: р-Спирмена
и т-Кендалла
Для того чтобы преодолеть указанные выше недостатки, необходимо
обратиться к идее, возникшей в теории непараметрических статистик,
которая предлагает сосредоточить внимание не на самих данных, а на
их рангах. В результате были предложены две важные меры зависимо
сти: р-Спирмена и т-Кендалла (определение и основные свойства этих
мер парной зависимости см., например, в [Айвазян
(2010),
с.
96-107]).
Перед тем, как приступить к обсуждению этих мер зависимости, корот
ко представим понятия согласованности и рассогласованности.
Гл.
560
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Определение
Наблюдения
(xi, Yi)(Xj, Yj) назъtвают согла
Yj, или если Xi > XjYi > Yj· Анало
6.5.
сованнъши, если Xi < XjYi <
ги-ч.но, (xi, Yi)(xj, Yj) называют рассогласованнъши наблюдениями, ес
ли
Xi
< XjYi > Yj
или если
Xi
> XjYi < Yj.
Это эквивалентно то
му, -что
(xi, Yi)(Xj, Yj) являются согласованнъши наблюдениями, если
(xi - Xj)(Yi -yj) >О, и рассогласованнъши, если (xi - Xj)(Yi -yj) <О.
Другими словами, согласованность наблюдений возникает в случае,
если большие значения одного наблюдения соответствуют большим зна
чениям другого наблюдения, а малые значения также соответствуют
малым значениям. Если это не так, то наблюдения называют рассогла
сованными.
Коэффициент ранговой
корреляции
мена). Коэффициент р-Спирмена
-
Спирмена
(р-Спир
мера согласованности междУ дву
мя случайными величинами, основанная на использовании понятий со
гласованности и рассогласованности.
Определение
6.6.
Для двух непрерывных слу-ч.айных вели-чин Х
и У, совместное распределение которых имеет копула-функцию С ( ·),
р-Спирмена определяется как
ps(X, У)= 3Q(C,P)
= 12
jj иvdC(и,v)-3 = 12 jj C(и,v)dиdv-3,
(6.19)
где и =
Fx(x), v = Fy(y),
а
Q(·) -
разность между вероятностями
согласованности и рассогласованности {для более детальной информа
ции см. [Nelseп
(2006)]).
Эквивалентное выражение для р-Спирмена может быть дано в
форме
Ps(X, У)
где корреляция
функции
(Corr)
частных
= Corr (F(X), G(Y)),
понимается в классическом смысле, а
распределений
случайных
величин
У. Этот результат вытекает из того факта, что ранги и и
ся наблюдениями из равномерно распределенных на (О;
величин И
1)
v
F
и
G -
Х
и
являют
случайных
= F(X) и V = G(Y), совместное распределение которых
определяется копула-функцией С.
Поскольку И и
для
ps(X, У)
в
V
(6.19)
р8 (Х, У) = 12
!"f
имеют среднее
1/2
и дисперсию
1/12,
выражение
может быть представлено в следУющем виде:
} uvdC(и, v) - 3 = 12E(UV) - 3 =
E(UV) - E(U)E(V)
JVar(U)Var(V)
E(UV) -1/4
l/l 2
=
6.5.
МЕРЫ ЗАВИСИМОСТИ
561
Таким образом, р-Спирмена для пары непрерывных случайных ве
личин Х и У равно корреляции между рангами Х и У.
В многомерном случае р-Спирмена (матрица) определяется как
где
корреляционная матрица; компоненты матрицы
Corr(·) -
ps(X)
определяются как
Перечислим основные свойства коэффициента р-Спирмена.
1. Ps
2.
симметричен.
IPsl
~
- строго возраста
ющая функция, ps(X, У)= 1; а для У= Т(Х), где Т(·) - строго
убывающая функция, ps(X, У)= -1.
1.
В частности, для У= Т(Х), где Т(·)
3. ps(Tx(X), Ту(У)) = ps(X, У)
отображений Тх ( ·) и Ту (·).
для любых строго возрастающих
4.
Если Х и У независимы, то
ps(X, У)
=О.
5.
Если (Х, У) имеет нормальное распределение с коэффициентом
корреляции р и стандартными нормальными частными распреде
лениями, то
Последний результат справедлив также в случае, когда совместное
распределение случайных величин Х и У имеет нормальную копула
функцию, а частные распределения непрерывны. К сожалению, соот
ношение между коэффициентом р-Спирмена и коэффициентом корре
ляции не выполняется для всех распределений из эллиптического се
мейства
-
см., например,
[Hult, Lindskog {2002)), [Nelsen {2006)).
Можно показать, что непараметрическая оценка для Ps, построен
ная по наблюдениям (Xi, Yi), i = 1, ... , Т, имеет вид
Ps =
Т(Т- l~(T- 2)
L
3 · sign(Xi - Xj) · sign(Yi - Yk)
1~i<j<k~T
и является несмещенной.
Если Xi и
Yi
независимы, i
асимптотически сходится к
=
N{O, 1).
1, ... , Т, то распределение
Vf'fJs
Более детальную информацию см.
Гл.
562
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
в
[Hollander, Wolfe (1973)], [Conover (1999)], [van de Wiel, Bucchianico
(2001)].
Коэффициент ранговой корреляции Кендалла ( т-Кен
далла). Коэффициент т-Кендалла - это также мера связи между дву
мя случайными величинами, основанная на использовании понятий со
гласованности и рассогласованности и определяемая сле,цующим обра
зом.
Определение 6.7 (заимствовано из [Kruskal (195§)]1· Пустъ (Х,
У) - слу-чай:н:ый вектор с распределением Н(х, у), а (Х, У) - слу-чай
Н'Ый вектор, такой, -ч~о Х и У независи.м.'Ы, распределение Х совпада
ет с распределением Х, распределение У совпадает с распределением
У. Коэффициент т-Кендама для вектора (Х, У), компонентъt которо
го есть непрер'Ывн'Ьlе слу-чайнъ~е вели-чин'Ы, определяется как разность
между вероятностью согласованности и вероятностью рассогласо
ванности, т. е.
т(Х, У)
=
Р { (Х - Х)(У - У) > О}
- Р { (Х -
Х)(У - У) < О}
=
= E[sigп(X - X)sigп(Y - У] =
=Р{Х>Х, У>У}+Р{Х<Х, У<У}
-
р { х < х, у> У-}- р { х > х, у< У-}.
Тогда для п-мерного случайного вектора Х и случайного вектора
Х, компоненты которого независимы, а их частные распределения рав
ны частным распределениям соответствующих компонент вектора Х,
матрица т-Кендалла Рт(Х) определяется сле,цующим образом:
Рт(Х)
= Cov [sign(X -
Х)] ,
где (i,j)-й элемент этой матрицы определяется формулой Pт(X)ij
-
= Cov[sign(Xi - Xi), sign(Xj - Xj)].
В частности, в двумерном случае
(n = 2)
матрицей т-Кендалла
будет
Рт(Х)
=(
1
т(Х; У)
т(Х, У) )
1
.
Сле,цует отметить, что существуют некоторые другие п-мерные
обобщения т-Кендалла. Более детальную информацию можно найти,
например, в
[Clemen, Jouini (1996)]
и
[Barbe et al. (1996)].
Основные
свойства этой меры зависимости, а также соответствующие доказатель
ства представлены в работах
[Embrechts et al. (2002)]
и
[Nelsen (2006)].
6.5.
МЕРЫ ЗАВИСИМОСТИ
563
Как правило, если т-Кендалла положителен, то с большой вероят
ностью мы имеем положительную зависимость. Если этот коэффициент
отрицателен, то следует ожидать отрицательную зависимость. Кроме
того, т-Кендалла может быть представлен в терминах копула-функции,
что облегчает вычислительную работу.
Теорема
6.5.
Коэффициент т-Кендама для двумерной слу-чайной ве
ли-чин·ы, характеризующейся копулой (и, v), определяется формулой
т(Х, У)= 4
1
1
JJC(и,v)dC(и,v)
о
-1.
о
До к аз ат ель ст в о. См. в
[Nelsen {1999),
р.
127-129).
Основные свойства коэффициента т-Кендалла:
1. т(Х, У) симметричен.
2. -1
3.
~ т (Х, У) ~
1.
Если Х и У независимы, то т(Х, У) = О.
4. т(Тх(Х), Ту(У)) = т(Х, У) для любых строго возрастающих отоб
ражений Тх(·) и Ту(·).
Оценка коэффициента т-Кендалла требует вычисления двойного
интеграла, что для распределений эллиптического типа представляет
собой довольно непростую задачу. Однако можно показать (см.
kog et al. {2003)]),
[Linds-
что т-Кендама для эмипти-ческих распределений
определяется следующим образом:
т(Х, У)=
где р -
2 arcsinp,
7Г
обычный парный коэффициент корреляции.
Для архимедовых копула-функций ситуация значительно проще,
так как т(Х, У) может быть оценен с использованием генератора копу
ла-функции. А именно, в работе
[Genest,
МасКау
{1986)] показано, что
т-Кендама для архимедов'ЬtХ копула-функций определяется соотношени ем
!
1
т(Х, У)
= 1+4
<p(t)
<p'(t) dt,
о
где <р( ·)
-
генератор копула-функции. Например, можно показать, что
для копула-функций Клейтона или Гумбеля мы имеем следующие ре
зультаты:
Гл.
564
•
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
для копула-функции Клейтона: т(Х, У)= а~ 2 ;
• для копула-функции Гумбеля: т(Х, У)
где а
-
=1-
~'
параметр копула-функции.
Можно показать, что непараметрическая оценка длят-Кендалла,
построенная по наблюдениям
f =
Т(Т2- l)
(Xi, Yi),
L
i = 1, ... , Т, и имеющая вид
sign(Xi - Xj) sign(Yi - }j),
1~i<j~T
является несмещенной.
Xi и Yi независимы, то распределение случайной величины
-Jf'f сходится к N(O, 4/9). Более подробная информация содержится,
например, в [Ferguson et al. (2000)].
Если
6.5.3.
Хвостовая зависимость
Определим понятия верхней и нижней хвостовой зависимости
[J ое
(1997)]:
Определение
6.8.
Пусть (Х, У)
-
слу-чайн'Ьtй вектор, компо
нент'Ьt которого естъ непрер'ЬtвН'Ьtе слу-чайн'Ьtе вели-чин'Ьt с -частн'Ьtми
распределениями Fx и Fy. Тогда коэффициент ли верхней хвостовой
зависимости Х и У определяется соотношением:
>.У= lim Р[У > F.y 1 (и)IX > FХ: 1 (и)] =
u-+1
= lim Р[Х
и-+1
> FX: 1 (и)IY > F.у 1 (и)]
=
= lim 1- 2и + С(и,и)
и-+1
1- U
при условии, -что предел'Ьt существуют, где С(и,
v) -
двумерная копу
ла-функция слу-чайного вектора (Х, У).
При этом случайные величины Х и У называют асимптотически
зависимыми на верхнем хвосте, если >.U Е (О, 1], Х и У называют асимп
тотически независимыми, если >Р =О.
Другими словами, верхняя хвостовая зависимость существует то
гда, когда имеется положительная вероятность одновременного возник
новения положительные выбросов. Л. и широко используется в теории
экстремальных значений и представляет собой вероятность того, что
одна переменная примет экстремальные значения при условии, что дру
гая переменная также принимает экстремальные значения. Коэффици
ент Ли можно рассматривать как меру зависимости квантилей - см.,
например,
[Coles et al. (1999)].
6.5.
МЕРЫ ЗАВИСИМОСТИ
565
Аналогично можно определить нижнюю хвостовую зависимость.
Определение
6.9.
Пустъ (Х, У) -дву.мерн:ый слу-чайн.ъ~й вектор,
компонента.ми которого являются н.епреръ~вн.ъ~е слу-чайн.ъ~е вели-чин.ъ~,
-частные распределения которъtх равны
и
Fx
Тогда коэффициент
Fy.
Л L нижней хвостовой зависимости .между Х и У равен.:
лL
= lim Р[У ~ F.y 1 (и)IX ~ F_x 1(u)) =
и-+0
=
lim
и-+0
Р[Х ~ F_x 1 (u)IY ~ F.y 1 (u)] =
lim
и-+0
С(и, и)
U
при условии, -что предел существует.
Случайные величины Х и У называются асимптотически зависи
мыми на нижнем хвосте, если ЛL Е (О, 1), и асимптотически независи
мыми на нижнем хвосте, если лL =О.
Таким образом, нижняя хвостовая зависимость существует тогда,
когда существует
положительная вероятность возникающих одновре
менно отрицательных выбросов.
Поскольку эллиптические распределения являются радиально сим
метричными, для них коэффициенты верхней и нижней хвостовой зави
симости будут равны между собой. Например, для н.ор.малън.ой копула
функции коэффициенты верхней и нижней хвостовой зависимости
определяются соотношением
ЛL =Ли = 2 х-+оо
lim (Р(У > xlX = х)) = 2 lim
х-+оо
Ф (х ~)]
=О.
1+р
[1 -
Таким образом, вне зависимости от величины парного коэффици
ента корреляции р (р
=f:. 1),
если рассматривать экстремально большие
положительные значения Х и У на правом хвосте, то для них полу
чим асимптотическую независимость. Этот факт хорошо известен
см., например,
-
[Sibuya (1961)], [Resnick (1987)].
Для копула-фун.кции Стъюден.та коэффициенты верхней и нижней
хвостовой зависимости также совпадают и равны
ЛL =Ли = 2 х-+оо
lim (Р(У > xlX = х)) = 2 -
2t11+1
Очевидно, они возрастают пор и убывают по
через
·
(JV+Т ~)
1+р
·
v. В этой формуле
t 11+1, как и ранее, обозначена одномерная функция распределения
Стьюдента с
(v
+ 1)
степенями свободы. Если число степеней свободы
устремить к бесконечности, то Ли будет стремиться к О при р < 1.
Рассмотрим коэффициенты лL, ли для архимедовых копула-функ
ций. Так, для копула-функции Гу.мбеля лишь верхняя хвостовая за
висимость положительна: ли = 2 - 21/0t, а лL = О; тогда как для
Гл.
566
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
копула-функции Клейтона положительна лишь нижняя хвостовая за
висимость: )+.И = 0, )+.L = 2-l/0t.
Следует отметить, что хвостовая зависимость для архимедовых ко
пула-функций может быть представлена в терминах генераторов, об
ратных к ним функций и первых производных, см.
(2006)].
В работах
[Joe (1997), (Nelsen
[Coles et al. (1999)], [Poon et al. (2004)) представле
ны робастные непараметрические оценки для коэффициентов хвосто
вой зависимости.
6.5.4.
Эмпирические приложения в статистическом
пакете
В пакете
R
R:
меры зависимости
использование модулей
«Copula»
и
«fcopulae»
дает возмож
ность вычислять упомянутые выше меры зависимости для множества
типов копула-функций. Ниже представлены некоторые примеры (заин
тересованным читателям рекомендуется ознакомиться с руководством
к пакету
R).
# EXAMPLES WITH ARCHIMEDEAN COPULAS AND
ТНЕ
copula 11 PACKAGE
gumbel.cop <- gumbe1Copula(3)
kendallsTau(gumbel.cop)
[1] 0.6666667
spearmansRho(gumbel.cop)
[1] 0.848167
taillndex(gumbel.cop)
lower upper
0.000000 0.740079
# let us compute the sample versions
х <- rcopula(gumbel.cop, 200)
cor(x, method = 11 kendall 11 )
11
[,1] [,2]
[1,] 1.0000000 0.6592965
[2,] 0.6592965 1.0000000
cor(x, method = 11 spearman 11 )
[,1] [,2]
[1,] 1.0000000 0.8483507
[2,] 0.8483507 1.0000000
# compare with the true parameter value 3
calibKendallsTau(gumbel.cop, cor(x, method= 11 kendall 11 ) [1,2])
[1] 2.935103
calibSpearmansRho(gumbel.cop, cor(x, method= 11 spearman 11 )[1,2])
[1] 3.001893
calibSpearmansRho(gumbel.cop, cor(x, method= 11 spearman 11 )[1,2])
[1] 3.001893
# EXAMPLES WITH ARCHIMEDEAN COPULAS AND ТНЕ
11 fcopulae 11 PACKAGE
# ellipticalTau Computes Kendall's tau for elliptical copulae
6.6.
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ: ПАРАМЕТРИЧЕСКИЕ
МЕТОДЫ
567
# ellipticalRho computes Spearman's rho for elliptical copulae
ellipticalTau(rho = -0.5)
Tau
-0.3333333 attr(, 11 control 11 )
rho
-0.5
ellipticalRho(rho
= 0.75, type = 11 t 11 , subdivisions = 100)
Rho
0.71
attr(, 11 control11)
rho type tau
11 t 11
11 0.5399 11
11 0.75 11
# ellipticalTailCoeff
# Student-t Tail Coefficient:
ellipticalTailCoeff(rho = 0.25, param
lambda
0.1962612
attr(, 11 control11)
= 3, type = 11 t 11 )
rho type param.nu
11 0.25 11
11 t 11
11 3 11
Процедуры оценивания: параметрические
6.6.
методы
Пусть хн,
... , Xnt, t
= 1, ... , Т, -
многомерные наблюдения, где
мерность наблюдаемой случайной величины, а Т
-
n- раз
число имеющихся
наблюдений.
Метод максимального правдоподобия (ММП или
6.6.1.
одношаговый метод)
Пусть
f (·) -
(Х1,Х2,
плотность совместного распределения случайного вектора
... ,Xn)·
f(x1., ... , Xn.i
а1,
... , an, '"У)= c(F1(i1.; а1), ...
n
... ,F1(in.iOn)i'"Y) · п fi(Xi.iai),
i=l
где fi - плотность одномерного частного распределения Xi, i1, i2, ... ,
Xn - некоторые заданные (текущие) значения случайных величин Х1,
Х2, ... , Xn соответственно, а с(·) - плотность копула-функции, опреде
ляемая следующим соотношением:
(
с и1,
. )- anc(u1,u2, ... ,Un;'"Y)
... , Un, '"У -
д
и1
д
и2...
ди
n
·
Гл.
568
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Пусть
8 = (0:1, ... , a:n; -у) - вектор
i = 1, ... , n, - параметры частных
O:i,
оцениваемых параметров, где
распределений
F;,,
'У
-
вектор
параметров копула-функции. Логарифмическая функция правдоподо
бия имеет следующий вид:
Т
l(8) =
Т
L
ln{c(F1(xi,t;0:1),"., Fn(Xn,ti й:п); -у))+
t=l
n
LL
ln fi(Xi,ti O:i,t)·
t=l i=l
Оценка максимального правдоподобия {J м L для параметров опре
деляется как
ОмL
= argmaxl{8).
(J
Ниже приводится результат, описывающий асимптотические свой
ства оценки максимального правдоподобия.
Теорема
6.6
(состоятельность и асимптотическое распределе
ние ММП-оценок). Пусть ОмL - ММП-оцен:ка. Тогда при въtполне
нии некоторъtх стандартных условий регулярности, с.м. [ White {1994)],
А
р
справедливо следующее: 8мL ~ 80 , где 80
=
(0:1, ... ,a:n,')')'. Кроме
того,
./Т'(ОмL - 80) --+ N (о, 1- 1(80)) '
где
1 (80) -
информационная матрица Фишера.
До к аз ат ель ст в о. См.
6.6.2.
[White (1994)].
Двухшаговый метод максимального
правдоподобия 3
В соответствии с этим методом параметры частных распределений оце
ниваются независимо от параметров копула-функции. Другими слова
ми, процедура оценивания разделена на следующие два шага.
Шаг
1:
Используя ММП, оцениваются параметръt й:i,
'Частнъtх одномернъtх распределений
i = 1 ... , n,
Fi (·) :
т
&i = argmaxli(a:)
= arg max ~ lnfi(xi,t;a:),
Q
Q
L.,,,
t=l
где
zi -
логарифми'Ческая функция правдоподобия для 'Частного рас
пределения
3В
Fi (·).
англоязычном оригинале этот метод назван The Inference Functions for Margins
method (IFM-method).
6.6.
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ: ПАРАМЕТРИЧЕСКИЕ
Шаг
МЕТОДЫ
569
Оцениваются параметръt 'У копула-функции при заданных
2:
зна'Чениях оценок, полу'Ченнъ~х на шаге
1:
т
i' = arg max lc('Y) = arg max
'У
где
lc -
"°' ln(c(F1(x1 'ti &1),"., Fn(Xn'ti &n)i 'У)),
'YL.....J
t=l
логарифми"Ческая функция правдоподобия для копула-функции.
Ниже (см. теоремы
6.7-6.9)
описаны асимптотические свойства оце
нок, получаемых IFМ-методом. Эти результаты представляют собой
простые обобщения результатов, полученных для ММП-проце,цуры, см.
[Newey, McFadden (1994)], [White (1994)], [Patton
(2006а, Ь)].
Представленные ниже результаты получены в предположении не
которых стандартных условий регулярности, которые мы не будем кон
кретизировать, заинтересованный читатель может ознакомиться с ни
ми в работе
[White (1994)].
Из соображений простоты рассматривается
двумерный случай. Отметим, что обобщения на многомерный случай
получаются достаточно просто.
Теорема 6.7 (состоятельность &1 и &2). Если п---+ оо, то &1 ~ а1
А
и а2
р
.....:....+
а2.
До к аз ат ель ст в о. См.
Теорема
6.8
[White (1994),
теорема
(состоятельность параметра 'У).
3.13].
Пусть функция
т
п- 1
L lnc(F1(xi,t; &1), F2(x2,ti &2); 'У)
t=l
имеет единственный максимум в то"Чке 'Уо Е iпt (Г). Тогда i'~'Yo
при п ---+ оо , где Г - область допустимъ~х зна"Чений параметра 'У,
а iпt (Г) - внутренность этого множества.
До к аз ат ель ст в о. См.
[White (1994), теорема 3.10].
Перед формулировкой теоремы 6.9 введем ряд обозначений.
делим штрафы для оценки B1FM = (&1, &2, i')':
д
S2t
sзt
=
= да2 lnf2(x2,ti а2),
д
д-у lnc(F1(x1,ti а1), F2(x2,ti а2); -у).
Матрица Гесса (гессиан)
Hess (8)
для штрафов равна:
Опре
Гл.
570
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
о
о
о
Последний столбец матрицы
о
Hess(8)
Матрица
т
т -1 "'""'
'
L.J SH · Sн
т
т -1 "'""'
L.J
t=l
т -1
т
"'""'
'
L.J S2t · S2t
т -1
t=l
т
sзt
"'""'
'
L.J SЗt 'S2t
t=l
ниже обозначается как
'
sн 'S3t
т
"'""'
'
L.J S2t 'S3t
t=l
т
'
т -1
· sн
t=l
6.9
т -1 "'""'
L.J
t=l
т
т -1
t=l
Теорема
'
'S2t
t=l
"'""'
'
L.J S2t · Sн
т -1 "'""'
L.J
т
sн
т -1
т
"'""'
L.J sзt
t=l
'
· sзt
OPG( 8)-матрица.
(асимптотика оценок, получаемых IFМ-методом).
Для IFМ-оценок въtnо.л,-н,яется свойство асимптотической нормалъно
сти, а именно
../Т(В1рм - Во)...!!+ N (О, Н0 1 Во (Н0 1 )'),
где Но= Е
[Hess(Bo)], Во=
Е
[OPG(Bo)],
т. е. Но и Во
-
средние зна
чения для гессиана штрафов и матрицъt OPG. Матрица Н0 1 В0 (Н0 1 )'
известна в теории копула-функций как информационная матрица Го
дамби
[Joe,
Хи
Из теорем
{1996)], [Joe {1997)].
6.7-6.9
вытекает сле,цующий весьма интересный факт.
Равная эффективность IFМ-метода и ММП. Пусть хн и X2t
независимы (т. е. совместное распределение (хн, X2t) имеет копула
функцию С(и1, и2; -у) = и1 · и2, плотность которой
с(и1, и2; -у) =
1),
и для плотностей частных распределений выполнено информационное
равенство. Тогда IFМ-метод и ММП дают оценки, имеющие одинаковые
асимптотические распределения.
6.6.
6.6.3.
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ: ПАРАМЕТРИЧЕСКИЕ
МЕТОДЫ
571
Эмпирические приложения в статистическом
пакете
R:
процедуры параметрического
оценивания
Модуль ~copula» в статистическом пакете
R
позволяет получать как
ММП, так и IFМ-оценки. Ниже представлен пример, взятый из работы
[Yan (2007)]. Вначале генерируется выборка из двумерного распределе
ния, частные распределения которого гамма-распределения с пара
метрами О-у = {(2; 1), (3; 2)}, а копула-функция - нормальная с пара
метром а = 0.5; затем по сгенерированной выборке строятся ММП- и
IFМ-оценки параметров.
# One step EML example from [Yan (2007)]
myMvd <- mvdc(copula=ellipCopula(family="normal", param=0.5),
margins=c("gamma", "gamma"),
paramMargins=list(list(shape=2, scale= 1),
list(shape=3, scale=2)))
n <- 200
dat <- rmvdc(myMvd, n)
loglikMvdc(c(2,1,3,2,0.5), dat, myMvd)
[1] -778.3114
mm <- apply(dat, 2, mean)
vv <- apply(dat, 2, var)
Ы.0 <- c(mm[l]Л2 / vv[l], vv[l] / mm[l])
Ь2.О <- c(mm[2]Л2 / vv[2], vv[2] / mm[2])
а.О <- sin(cor(dat[,1], dat[,2], method = "kendall") * pi / 2)
start <- с(Ы.О, Ь2.О, а.О)
fit.eml <- fitMvdc(dat, myMvd, start=start, optim.control=list
(trace=TRUE, maxit=2000))
fit.eml
The Maximum Likelihood estimation is based on 200 observations.
Margin 1:
Estimate Std. Error
ml.shape 2.1279360 0.19842701
ml.scale 0.9246803 0.09716286
Margin 2:
Estimate Std. Error
m2.shape 3.213331 0.3061706
m2.scale 1.778994 0.1835066
Copula:
Estimate Std. Error
rho.1 0.4671964 0.0552821
The maximized loglikelihood is -777.1381
The convergence code is О see ?optim.
# IFM method
Гл.
572
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
loglik.marg <- function(b, х) sum(dgamma(x, shape=b[l], scale=b[2],
log=TRUE))
ctrl <- list(fnscale = -1)
Ыhat <- optim(Ы.O, fn=loglik.marg, x=dat[,1], control=ctrl)$par
b2hat <- optim(b2.0, fn=loglik.marg, x=dat[,2], control=ctrl)$par
udat <- cblnd(pgamma(dat[,1], shape=Ьlhat[l], scale=Ьlhat[2]),
pgamma(dat[,2], shape=b2hat[l], scale=b2hat[2]))
fit.ifm <- fitCopula(myMvd, udat, method="ml" ,start=a.O)
c(Ыhat, b2hat, fit.ifl@estimate) fit.ifl
[1] 2.3494821 0.9395788 3.1645483 2.0540858 0.4782428
fit.ifm
The estimation method is Maximum Likelihood based on 200 observations.
Estimate Std. Error z value Pr(>lzl)
rho.1 0.4782428 0.04920972 9.718461 О
The maximized loglikelihood is 25.95508
The convergence code is О
Процедуры оценивания:
6.7.
полупараметрические и непараметрические
методы
6. 7.1.
Канонический метод максимального
правдоподобия (КММП) 4
КММП отличается от описанных выше методов тем, что в нем не де
лается никаких предположений относительно параметрической формы
частных распределений. Процесс оценивания в КММП состоит из сле
дующих двух шагов.
1.
Преобразуем наблюдения
(x1t, X2t, .•. , Xnt),
t
= 1, ... , Т, следую
щим образом:
т
где Fi,т(·) = т~ 1 Е l{xit~·}1 i = 1, ... , n, а 1{·} - индикаторная
t=l
функция множества{·}. Другими словами, .Fi,т(x)
-
это непара-
метрическая оценка частной функции распределения переменной
xi.
4В
англоязычном оригинале -
The Canonical Махiтит Likelihood (CML).
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ
6.7.
2.
573
Оценим параметры копула-функции, максимизируя логарифми
ческую функцию правдоподобия 5 :
т
icмL
= argmax
'У ~
L-
lnc (F1 ,т(хн), ... , Fnт(Xnt)il')·
,
t=l
Для простоты при описании асимптотических свойств КММП
оценки снова будем рассматривать только двумерный случай. Пусть
l(u1, и2, "У) = lnc(u1, и2; ')').
Далее индексами
частные производные функции
l (и1, и2, ')')
1, 2, ')'
будем обозначать
относительно и1, и2, ')' соот
ветственно. В частности, обозначим первую и вторую производную
функции
l
по
')':
1 т
Вт= Т
L
l-y (F1,т(хн), F2,т(x2t)i "У),
t=1
1 т
Нт = Т
L l-y-y (F1,т(хн), F2,т(x2t)i "У).
t=1
Поскольку iсм L является решением следующего дифференциаль
ного уравнения:
то, используя члены первого порядка разложения функции Вт в ряд
Тейлора, получим:
1 т
О= Т
L
l-y (F1,т(хн), F2,т(x2t)i "У)
t=1
~Вт+ Нт(iсмL - ')'),
'У=.:УсмL
и, следовательно,
./Т(iсмL -1') ~ ./Т -Нт
Вт ·
Из работ
(2000)]
[Ruymgaart et al. (1972)], [Genest et al. (1995)], [Ruud
отметим, в частности, следующие результаты, справедливые при
соблюдении некоторых условий регулярности:
а) icмL -t ')'о (п.н.) при Т -t оо;
б) ./Т(iсмL - ')'о) ~ N (О, u 2h- 2), где
и 2 = Var [l-y (F1(хн), F2(x2t)i "У)+ W1(хн) + W2(x2t)],
5В
дальнейшем предполагается, что анализируемое семейство копул зависит от
единственного параметра 'У.
Гл.
574
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
h = Е [l-y-y (F1(хн), F2(X2t)i 1')]; выражение для и 2 дано здесь для дву
мерного случая (n = 2), а Wi(xit) определяются соотношениями (i =
= 1,2):
в) полупараметрическая оценка i'c м L менее эффективна, чем оцен
ка, полученная с помощью одношагового метода максимального прав
доподобия i'мL (за исключением случая, когда хн и
X2t
статистически
независимы).
Трехшаговый канонический метод максимального
6. 7.2.
правдоподобия (КМЕ-СМL-метод) 6
Начиная с момента выхода работы
[Genest et al. (1995)]
использование
полупараметрических методов для копула-функций эллиптического ти
па стало обычной практикой, см., например, [CheruЬini
[McNeil et al. (2005)].
et al. (2004)],
В частности, для копула-функций Стьюдента, по
сле того, как на первом шаге получены непараметрические оценки част
ных функций распределения, можно получить оценку корреляционной
матрицы,
вычисленную
с
использованием
метода моментов
и
оценок
ранговых коэффициентов корреляции т-Кендалла. При этом степени
свободы оцениваются с использованием метода максимального правдо
подобия. Отметим, что оценка частных распределений на первом шаге
не является необходимым условием для оценки корреляционной матри
цы, поскольку оценка т-Кендалла основана на количестве согласован
ных наблюдений, которое не зависит от монотонных преобразований.
Однако оценивание частных распределений является необходимым при
оценке числа степеней свободы.
Ниже дается описание трехшагового КМЕ-СМL-метода (см. также
[Bouye et al. (2000)], [McNeil et al. (2005)], [Fantazzini (2010)]).
Трехшаrовый
КМЕ-СМL-метод
оценивания
параметров
копула-функций
1. Преобразуем
(хн,
X2t, ... , Xnt)
к
нормированным
рангам
(F1т(хн), F2т(x2t), ... , Fпт(Хпt)), испол:ьзу.я эмпирическую функцию
распределения для каждой компоненты вектора наблюдений ( здесъ и
далее п
-
размерностъ анализируемой случайной величинъt, Т
-
общее
число ее наблюдений).
6В
англоязычном оригинале метод называется Kendall-т Moment-Estimator of
Canonical
Махiтит
Likelihood
Мethod.
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ
6.7.
2.
Для всех пар
(j, k)
575
компонент вектора наблюдений оценим
т-Кендама:
Rjk = т [Fjт(Xj), Fkт(Xk)] = (Cf )- 1
L
sign ((xit - X1s)(X2t - X2s)).
1~t<s~T
Возьмем оценку корреляции для
(j, k)
компонент вектора наблюде
ний 'Ejk = sin(~Rjk). Поскольку покомпонентное преобразование, осу
ществленное на первом шаге, не гарантирует положительной опреде-
ленности матрицы 'Е = ( 'Ejk), то для ее обеспечения обычно вносятся
некоторъtе поправки [Roиsseeиw, Moleпberghs
3.
Находим
оценку
степеней
(1993)].
свободы
РсмL
копула-функций
Стьюдента с использованием метода максимального правдоподобия:
т
РсмL = axgm~ L lncт-copula (F1т(xit), ... , Fnт(Xnt); Е, v).
t=l
Второй шаг описанной процедУры реализует метод моментов, ос
нованный на оценках q
=
п(п
- 1)/2
моментов и такого же количе
ства коэффициентов т-Кендалла, оцененных с использованием эмпи
рических распределений (эта оценка известна как моментная оценка
т-Кендалла). СледУет еще раз отметить, что нет необходимости исполь
зовать оценку т-Кендалла, полученную с использованием именно эмпи
рических распределений, так как т-Кендалла сохраняет одно и то же
значение при всех монотонных преобразованиях. Таким образом, можно
взять q моментов от некоторой векторнозначной функции
от корреляций Во = (р1, ... , pq )1 , а именно:
1/J, зависящей
Тогда теоретические моментные тождества могут быть представле
ныв виде
,,P(F1, ... , Fn; Во) = (О, О, ... , О)',
(6.20)
где Во
- истинное значение оцениваемого векторного параметра. Со
ответственно оценка fJ определится из (6.20) с заменой теоретических
моментов их выборочными аналогами.
Для оценки, полученной с помощью метода
KME-CML,
справедли
вы следУющие теоремы (все доказательства представлены в приложе
нии А работы
[Fantazzini (2010)]).
Гл.
576
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Теорема 6.10 (состоятельность В). Предположим, 'Что (хн, ...
. . . , Xnt )- независимьtе {по t) наблюдения п-мерной слу'Чайной вели'Чи
нь~ (Х1, ... , Хп) со структурой зависимости, заданной плотностъю
копула-функции с(и1,t, ... , ип,t; Ео, vo). Предположим, 'Что:
а) пространство параметров
ством
0
является компактным подмноже
Rq;
б) q-мернь~й вектор моментов ф
(F1 (Х1), ... , Fn(Xп); 80) непреры
вен относителъно
80 для любых Xj;
в) 'Фi (F1(X1), ... , Fn(Xn); 8) измеримы относителъно Xj для всех
8 Е 0;
г) ф
(F1(X1), ... , Fп(Хп); 8) =/:-О для всех 8 =/:- 80, 8 Е 0;
д) SUPeee llФ (F1(X1), ... , Fn(Xn)i 8) 11 < оо, где llAll обозна'Чает ев
клидову норму матрицы А.
Тогда
А
8
р
~
80
при Т-+ оо.
При условиях теоремы
6.10, дополненных некоторыми условиями
регулярности [Genest et al. (1995)], доказана и состоятельность оценки
i/cмL (т. е. vcмL -14 vo при Т--+ оо).
Асимптотическая
KME-CML,
нормальность
оценок,
полученных
методом
неочевидна, так как используется трехшаговая процедура,
при которой на втором и третьем шагах используются разные мето
ды оценивания. Возможным решением является представление оценки
на третьем шаге КММП как оценки специального вида, полученной
методом моментов. Отметим, что КММП-оценка определяется путем
приравнивания к нулю производной (относительно параметра
v)
лога
рифма функции правдоподобия:
т
дl(·;
v) = """
(
А А)
дv
L.,,, lv F1т(хн), . .. , Fnт(Xnt); Е , v = О.
t=l
Разделив обе части на
, получим
определение оценки по методу момен
тов:
1 т
ТL
lv ( F1т(хн), ... , Fпт(Хпt);
А
Е, v) =
t=l
1 т
=тL
А
Фv(F1т(хн), ... 'Fnт(Xnt)i Е, v) =о.
t=l
Таким образом, КММП-оценка может быть представлена как оцен
ка, получаемая методом моментов (ММ).
Оценка методом моментов
-
это то значение
8,
которое обеспечи
вает равенство между выборочными моментами (выборочные средние)
6.7.
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ
577
и их теоретическими аналогами. Поскольку число параметров равно
q,
то требуются q моментных уравнений с неизвестными 8 (более подроб
но см. [Greene (2002)]). Таким образом, можно использовать известные
асимптотические результаты, справедливые для метода моментов.
Определим выборочные моменты вектора ФкмЕ-СМL, зависящего
от параметров§= (р1, ... , pq, il)':
Ф KME-CML ( F1т(хн), ... , Fnт(Xnt)i В)
=
т
~ Е Ф1 (F1т(xi1), F2т(xi2); Р1)
t=l
........................................
т
~ Е
(6.21)
=0.
1/Jq (Fcn-1),т(X(n-1)t), Fnт(Xnt)i Pq)
t=l
~ Е Фv (F1т(xit), ... 'Fnт(Xnt)i t, v)
t=l
В работе [Genest et al. (1995), § 4) получено асимптотическое распре
деление полученных из (6.21) оценок§ векторного параметра В (при
этом используются непараметрические оценки частных распределений
Fi)·
С учетом вышеизложенного справедлива следующая теорема.
Теорема
оценок).
(асимптотическое
6.11
распределение
КМЕ-СМL
Пусть въtпол:н.ен:ы предположения предъ~дущей теоремы и
некоторые дополнительные условия [Geпest
et al. (1995)]. Кроме того,
предположим, что матрица дФ км вg;:f, м L ( ·;Е} имеет ограниченные (по
Т) элементы и является отрицательно определенной.
Тогда при Т ---t оо
:
v'т(В-Во) ~ N{o, Е[дФк~~~СМLГI
То ( Е [дФ ю~~~СМL Г1 )' }·
где матрица То
-
до=
ковариационная матрица вектора
1/Jq (Fn-1(Xn-1), Fn(Xn)i Pq)
Фv
(F1(X1), ... , Fn(Xn)i
Ео,
vo) +
n
Е
j=l
Wj,v(Xj)
(6.22)
Гл.
578
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
а
Отметим, что последнее асимптотическое свойство выполняется и
для многомерных моделей с гетероскедастичностъю. Для таких моде
лей на первом этапе получают состоятельные оценки параметров одно
мерных частных распределений, а затем рассчитывают соответствую
щие оценки остатков (так называемые невязки), которые используются
для оценки совместного распределения многомерного вектора остатков
при помощи копула-функций. Этот результат является прямым след
ствием теорем
[Kim et al. (2008)], которая, в свою
очередь, использует работы [Koul, Ling (2006)], [Koul (2002)]. Отметим,
что похожие результаты представлены также и в [Chen, Fan (2006)], но
1
и
2
из работы
без доказательств. Соответствующий результат формулируется в тео
реме
6.12.
Теорема
6.12
(асимптотика КМЕ-СМL-оценок для многомер
ных моделей с гетероскедастичностью).
полненъ~ условия а)-д) теоремъ~
(2008)].
6.10,
Предположим, что въ~
а также А.1-А.9 из [Кiт
et al.
Тогда для КМЕ-СМL-оценки имеет место аси.мптотическа.я
сходимость
(6.22).
Условия (А.1)-(А.4) справедливы для моделей достаточно обще
го вида. В частности, условия (А.1)-(А.2) требуют, чтобы плотность
копула-функций имела непрерывные частные производные до третьего
порядка включительно. Кроме того, они должны быть конечными вме
сте с их вторым моментом. Условие (А.3)
-
это техническое условие на
частные производные, а условие (А.4) требует, чтобы было выполнено
условие А.1 из
[Genest et al. (1995)].
ются техническими и взяты из работ
Условия (А.5)-(А.8) также явля
[Koul (2002)]
и
[Koul, Ling (2006)].
Условие (А.9) не является слишком ограничительным. Например, ес
ли условное среднее является функцией исторических значений строго
стационарных и эргодических временных рядов, то каждое слагаемое
суммы является строго стационарным и эргодическим процессом с ну
левым средним, а значит, условие (А.9) выполняется (см.
Kakizawa (2000),
теоремы
1.3.3-1.3.5],
а также
[Taniguchi,
[Kim et al. (2008)]).
Свойства и вычислительные аспекты в условиях малых
выборок
Поскольку основные свойства предлагаемого полупараметрическо
го метода являются асимптотическими, то на примерах смоделирован
ных выборок в работе
[Fantazzini (2010)]
было проведено исследова-
6.7.
579
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ
ние, показавшее, что в условиях малых выборок и больших значений
v
численная максимизация логарифмической функции правдоподобия
не сходилась значительно чаще при использовании КМЕ-СМL-оценок,
чем при использовании ММП оценок. В то время как ММП-оценка па
раметра попадала в 95%-ный доверительный интервал примерно для
95%
случаев, КМЕ-СМL-оценка попадала в соответствующий довери
тельный интервал лишь в
30%
случаев. Однако такое снижение до
ли случаев со сходимостью более значительно для двумерных копула
функций Стьюдента по сравнению с копула-функциями Стьюдента
большей размерности, которые типичны для финансовых портфелей.
Кроме того, как ММП, так и КМЕ-СМL-метод показали весьма суще
ственные значения средних и медиан смещений для оцененных корре
ляций, когда фактические значения последних принимают значения,
близкие к нулю.
Наконец, в работе
[Fantazzini {2010)] показано, что метод собствен
[Rousseeuw, Molenberghs {1993)], дол
ных значений, представленный в
жен быть использован для получения положительно определенной кор
реляционной матрицы не только в условиях малых выборок (Т
но и в условиях,
< 100),
когда описываемому процессу отвечает наименьшее
собственное значение, близкое к нулю. Эта поправка влечет положи
тельное смещение оценки
параметра
v,
но ее влияние на сходимость
при максимизации для получения параметра
v
весьма ограничено.
Таким образом, предыдущие результаты показывают, что КМЕ
СМL-метод может быть использован в случае малых выборок и при от
носительно небольших значениях числа степеней свободы, однако ММП
является более привлекательной альтернативой. Возможной стратегией
при оценке параметров является следующее: на первом этапе исполь
зовать КМЕ-СМL-метод; если оценка числа степеней свободы больше
20, то следует
использовать ММП-оценку, если последняя обеспечивает
сходимость при максимизации соответствующей функции правдоподо
бия. Иначе, в качестве альтернативного решения следует использовать
нормальную копула-функцию, к которой стремится копула-функция
Стьюдента при
v -t
оо (нормальная и стьюдентовская копула-функции
достаточно близки уже при
6. 7.3.
v > 20).
Методы непараметрического оценивания
В работе
[Fermanian, Scaillet {2003)]
предлагается непараметрическая
оценка для копула-функций многомерных стационарных процессов,
удовлетворяющих условиям сильного перемешивания.
Перед тем как обратиться к асимптотическим свойствам этой оцен
ки, определим понятие ядерной функции.
Гл.
580
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Определение
Ядерная функция
6.10.
это действите.л:ьнознач
-
ная функция К(и), -оо <и< +оо, которая удовлетворяет следующим
условиям:
1)
2)
симметричность: К(и)
= К(-и);
в точке и= О достигается максимум;
+оо
3)
J К(и)dи = 1;
-00
4)
неотрицательность: К(и)
5)
К (и) ограничена;
;;::
О;
00
6)
J и2 К(и)dи < оо.
-оо
Свойства
5и6
необходимы для вывода
асимптотических свойств
оценок, получаемых на основе ядерных функций. Возьмем n-мерное
ядро и его кумулятивную функцию:
n
n
k(x) = п kj(Xj),
К(Х) = П
j=l
!
х·
n
3
kj(x)dx =
j=l-00
П Kj(Xj),
j=l
где для простоты взяты произведения одномерных ядерных функций.
Кроме того, возьмем
k(x; h) =
fI
3=1
kj
(h ~~)) ,
K{X;h) =
3
fI
Kj
3=1
(h~~)),
3
hj(T), j = 1, ... , п на
главной диагонали и детерминантом lh{T)I. При этом hj(T) положи
тельна и hj ~О при Т ~ оо. h{T) обычно называют «шириной окна»
где
h{T) -
диагональная матрица с элементами
ядерной функции.
Определение 6.11. Ядерная оценка fj(·) плотности fj(·) распре
деления случайной величины }'jt Yj определяется как
а ядерная оценка плотности случайного вектора
Yt
... , Уп)' равна
А
/(у)=
1
Tlh(T)I
т
~ k (у -
Yt; h{T)).
в точке у = (у1,
ПРОЦЕДУРЫ ОЦЕНИВАНИЯ
6.7.
581
Аналогичным образом, ядерная оценка кумулятивной функции рас
пределения случайной величины
}jt
в точке
Yj
равна
Yj
Fj(Yj) =
j
fj(x)dx,
-оо
а ядерная оценка кумулятивной функции распределения случайного
вектора
Yt
в точке у
равна:
J... J
Yt
F(y) =
Yn
f(x)dx.
-оо
-оо
Например, для гауссовской ядерной функции
kj(x) =
<р(х) получа
ются следующие ядерные оценки функций распределения:
т
F·( ·)
з Уз
=Т
_!_""
ф (Yj -h· }jt) '
L.i=l
F(y)
= _!_
3
т
t ll Ф
i=1 j=l
(Yj -.}jt)'
h3
где через ер(·) и Ф( ·) обозначены соответственно плотность и функция
распределения стандартного нормального распределения.
Определение
6.12
(ядерная
В силу следствия из теорем'Ьt Шкл.яра
=
оценка
копула-функции).
C(u) =
С(и1,
... ,иn) =
Н (Ff- 1 >(и1), ... , F~- 1 >(иn)), где Н(·) - многомерна.я функция рас-
пределения. Тогда .ядерная оценка C(u) копула-функции C(u) определя
ете.я следующим образом:
где
(j = iпfyeR {у : Fj (у) ~ Uj} соответствует .ядерной оценке кван
Uj для функции распределения слу-чайной вели-чин'Ьt }jt.
работах [Fermanian, Scaillet (2003)], [van der Vaart, Wellner (1996)]
тил.я уровня
В
доказывается состоятельность и асимптотическая нормальность ядер
ных оценок C(u).
6. 7.4.
Эмпирические приложения в статистическом
пакете
R:
процедуры полупараметрического
оценивания
Продолжим рассмотрение примера, начатое в п.
таццини,
(2011)]).
6.6.3
(см. также [Фан
Можно оценить параметр зависимости а при помощи
582
Гл.
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
канонического метода максимума правдоподобия (КММП) без специ
фикации частных распределений.
# CML method
eu <- cblnd((rank(dat[,1]) - 0.5)/n, (rank(dat[,2]) - 0.5)/n)
fit.cml <- fitCopula(myMvd, eu, method="mpl", start=a.O)
fit.cml
The estimation method is Maximum Pseudo-Likelihood based on 200
observations.
Estimate Std. Error z value Pr(>lzl)
rho.1 0.4806303 0.05066396 9.48663 О
The maximized loglikelihood is 26.02639
The convergence code is О
Ниже представлены другие примеры, взятые из
copula
пакета.
# Example: Gumbel copula
gumbel.cop <- gumbelCopula(3, dim=2)
n <- 200 х <- rcopula(gumbel.cop, n) ## true observations
u <- apply(x, 2, rank) / (n + 1) ## pseudo-observations
## inverting Kendall's tau
fit.tau <- fitCopula(gumbel.cop, u, method="itau")
fit.tau
## inverting Spearman's rho
fit.rho <- fitCopula(gumbel.cop, u, method="irho")
fit.rho
## maximum pseudo-likelihood
fit.mpl <- fitCopula(gumbel.cop, u, method="mpl")
fit.mpl
## maximum likelihood
fit.ml <- fitCopula(gumbel.cop, х, method="ml")
fit.ml
## А multiparameter example
normal.cop <- normalCopula(c(0.6,0.36, 0.6),dim=3,dispstr="un")
х <- rcopula(normal.cop, n) ## true observations
u <- apply(x, 2, rank) / (n + 1) ## pseudo-observations
## inverting Kendall's tau
fit.tau <- fitCopula(normal.cop, u, method="itau")
fit.tau
## inverting Spearman's rho
fit.rho <- fitCopula(normal.cop, u, method="irho")
fit.rho
## maximum pseudo-likelihood
fit.mpl <- fitCopula(normal.cop, u, method="mpl")
fit.mpl
## maximum likelihood
fit.ml <- fitCopula(normal.cop, х, method="ml")
fit.ml
6.8.
6.8.
ВЫБОР КОПУЛА-ФУНКЦИИ
583
Выбор копула-функции
Из нескольких моделей копула-функций следует выбрать ту, которая
наилучшим образом описывает рассматриваемые данные. В разделах
6.8.1-6.8.3
описываются различные критерии, руководствуясь которы
ми исследователи обычно осуществляют такой выбор.
Информационный критерий Акаике
6.8.1.
(AIC)
Этот метод выбора копула-функций является достаточно простым, см.,
например,
[Breymann et al. (2003)], [Dias, Embrechts (2004)].
AIC (Akaike lnformation Criterion) - это критерий, позволяющий
выбрать копула-функцию, которая отвечает наименьшему значению из
следующих:
т
AIC(Ck,&k)
= -2 L
logck( ин, ... , Unt; &k)
+ 2qk,
t=l
(6.23)
k= 1, ... ,к,
где ck -
k-я модель копула-функции, Ck(·) -
плотность для Ck;
&k - вектор параметров копула-функции ck' qk - число параметров,
от которых зависит функция Ck. Функция AIC(Ck,&k) в определенном
смысле штрафует модели с большим числом параметров.
AIC
предполагает, что наиболее адекватная модель находится сре
ди рассматриваемых моделей. Если сравнивать «невложенные~ модели,
то слагаемое
2qk
является не вполне корректным штрафом, и указанная
выше формула становится неприменимой. Для того чтобы разрешить
эту проблему, Такеучи предложил в
критерий
TIC.
Однако
TIC
[Takeuchi (1976)]
информационный
редко используется на практике, посколь
ку для него требуется наличие весьма больших (по размеру) выборок
наблюдений.
В применении
AIC
некоторые вопросы остаются открытыми. На
пример, до сих пор неизвестно, что происходит с
AIC
в случае, если в
качестве частных одномерных распределений использовать эмпириче
скую функцию распределения. Использование эмпирической функции
распределения как оценки соответствующей частной функции распре
деления на практике является стандартной процедурой, но последствия
такого использования для
6.8.2.
В работе
AIC
до сих пор не изучены.
Тесты отношения псевдоправдоподобия
[Chen, Fan (2006)]
предлагаются так называемые тесты отно
шения псевдоправдоподобия, которые учитывают случайность, возни-
Гл.
584
кающую в
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
при использовании нормированных рангов. Эти тесты
AIC
позволяют удостовериться в том, что среди рассматриваемых моделей
нет такой, которая была бы значительно лучше выбранной (проверя
емой) модели. При этом не требуется, чтобы рассматриваемый класс
моделей содержал истинную модель. Таким образом можно сравнивать
невложенные модели.
Основной идеей тестов является сравнение каждой из рассматри
ваемых моделей-кандидатов с остальными моделями с точки зрения
меры их правдоподобия, по результатам сравнения выбирается та мо
дель, которая оказывается наиболее правдоподобной. А именно, пусть
С1(и1,
... , Uni а1) -
выбранная из числа рассматриваемых модел:ь-обра
=
зец копула-функции, Ci(u1, ... , Uni ai), i
2, ... , М - остальные моде
C 0 (u 1 , ... , ип) - истинная (и ненаблюдаемая) копула
ли-кандидаты,
функция, в действительности описывающая зависимости между компо
нентами многомерных наблюдений. В работе
[Chen, Fan (2006))
предла
гается, используя расстояние Каллбэка-Лейблера, тестировать гипо
тезу о том, является ли модель-образец наиболее правдоподобной среди
всех рассматриваемых моделей. Таким образом, нулевой гипотезой яв
ляется гипотеза
а;)]
ном... шах Ео [ln Ci (Ffо (eit), · · ·, F~(ent)i
о
С1 (F1 (eit), ... , Fn (C:nt)i ai)
i=2, ... ,M
где а;,
= 1, ... , М,
i
-
,.,
0
~'
параметры рассматриваемых моделей копула
функций; FJ( ·) - истинные (неизвестные) частные распределения для
C:jt, j
= 1, ... , n 1 . Указанная
нулевая гипотеза означает, что среди всех
рассматриваемых моделей модель-образец оказывается в определенном
смысле ближе к истинной модели, чем все остальные из рассматривае
мых. Альтернативная гипотеза
н1м:
.шах
i=2, ... ,M
Ео
[l Ci (Ff(eit), · · ·, F~(ent)i а;)] 0
n
о
о
>
с1 (F1 (eit), ... , Fn (ent)i ai)
означает, что среди рассматриваемых моделей существует модель-кан
дидат, которая ближе к истинной модели, чем модель-образец. Тест из
работы
[Chen, Fan (2006)) основан на следующей статистике отношения
псевдоправдоподобия (i = 2, ... , М):
D(F
г . -. - ) L .L"n
1т, · · ·, L'nT, O'i, а1 7 Верхний
]:
~ [ Ci(F1(eit),
... ,Fnт(ent)i&i)]
L...J 1n
(
( )
( ) _ ) ,
Т t=l
С1 F1т
C:it , ... , Fпт C:nt ; а1
индекс 0 здесь и в дальнейшем означает, что соответствующая харак
теристика вычислена в условиях гипотезы нr.
6.8.
где Fjт,
j
=
ВЫБОР КОПУЛА-ФУНКЦИИ
1, ... , п, -
585
нормированные ранги; знак
над буквой
fV
означает, что соответствующий параметр о оценен при помощи ква
зи метода максимального правдоподобия (КММП). Введем матрицу
n = (uik)t1=2' где
. _С ovО [ln
O"ik -
Ci(Uit, ... ,Unt;aj)
c1(Uн, ... ,Unt;ai)
+~
{Q·~,з·(И·3t,. oi*) - Q1,3·(И·3t1. 01*)} '
~
3=1
... ,Unt;ak)
1n ck(Uн,
c1(Uн 1 ,Unt;ai)
•••
{Q k,3·(И·3t,. ok*) - Q1,3·(И·3t,. 0 *)}]
+~
~
1
3=1
=
при Иjt = Fj0 (ejt) и Qi,j(Иjt; oi)
E 0 {lij(Иs; oi)[l{ujt~Иjs} - Иjs]IИjt}
для i = 1, ... , М,
j = 1, ... , d; добавочные слагаемые Qi,j(·) введе
ны в связи с необходимостью оценивать частные распределения Fj0 ( ·),
j = 1, ... , п, а l{x<xo}' как и прежде, индикаторная функция множе
ства {х
<
хо}. Более подробно см.
[Chen, Fan (2006)]. Отметим, что
если частные распределения известны, то эти слагаемые исчезают. Как
показано в работе
[Chen, Fan (2006)],
при некоторых условиях регуляр
ности:
п
1/2
{L D(F
.it.n
1т,
1:'1
• - • )
... , .гnт,
Oi, 01,
_
Ео
[l
n
oi)]}
Ci(Ult, · · ·, Иnti
(И
U . *)
С1
lt1 • · · ' nt, 01
i=2, ... ,M
~ (Z2, ... , Zм)',
где вектор
(Z2, ... , Zм )'
имеет нормальное распределение
N(O, !1), так
что
(6.24)
В
[Chen, Fan (2006)] показано, что при так называемой наименее
благоприятной конфигурации
fТIM
_
.Lт -
. max
i=2, ... ,M
(п 1/2LD(F
.it.n
1т,
1:'1
• - • d . max
... '.гnт,
Oi, о1, ()-)) ---+
i=2, ... ,M
z.i,
(6.25)
так как второе слагаемое в (6.24) обнуляется: Е 0 [·] = О. Поскольку
асимптотическая ковариационная матрица
от
oi, ... , ом,
распределение m~
Zi
n для
Z2, ... , Z м
зависит
неизвестно. Но, несмотря на это,
можно использовать р-значения, получаемые либо методом Монте-Кар
ло, либо бутстрэп методом, см.
[White (2000)], [Chen, Fan (2006)].
Гл.
586
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Состоятельная оценка для f!
= (aik):,1= 2 определяется формулой:
Ck(Ftтi ak) 1 ~ 1
------L...Jn
с1 (Ftтi б1)
+
где
QiJ -
t, (
Т s=l
Ck(Fsтi ak) +
с1 (Fsтi б1)
Qk,;(Fj,;&k) -Q1,;(F;,;&1))}
состоятельная оценка Qi,j, которая вычисляется следующим
образом:
Qi,j(Ujsi&i) =
т
~
L
lij(Ut;&i)
(1{Иjs~Иjt} -
Ujt) .8
t=1,t:Fs
Затем можно вычислить разложение Холецкого
,..
мировать Zь
=
А
(Zь,2,
А
... , Zь,м)
'
=
А
С11ь, где 'f/ь Е
n = 66
1
N(O, Iм-1),
и сфор-
т. е. име-
ет
( М - 1)-мерное стандартное нормальное распределение. После че
го найдем наибольшую порядковую статистику (ь,м-1 = шах Zь,k, а
k=2, ... ,M
для того, чтобы вычислить р-значение методом Монте-Карло, повторим
эти итерации много раз (например, порядка В=
100000), см. [Chen, Fan
(2006)]:
Баiiесовский выбор копула-функций
6.8.3.
В
[Huard et al. (2006)]
предлагается байесовская процедура выбора наи
более вероятного двумерного семейства копула-функций среди задан
ного множества копула-функций. В этом подходе параметры копула
функций интерпретируются как случайные величины. Кроме того, в
указанной работе
параметризация
плотности
копула-функции осу
ществляется в терминах т-Кендалла (см. выше, п. 6.5.2), так что апри
орные
распределения
параметров
заменены
априорными
распределе
ниями т-Кендалла, которое концептуально является более удобным.
8 3десь,
как и прежде,
10 означает индикаторную функцию множества{·}.
6.8.
587
ВЫБОР КОПУЛА-ФУНКЦИИ
Априорное распределение т-Кендалла берется одним и тем же для всех
тестируемых копула-функций и используется как базис для сравнения.
Пусть Ctf -
множество всех копула-функций. Возьмем из Ctf конечное
подмножество CtfQ С Ctf копула-функций, которые необходимо включить
в предложенный метод. Каждая копула-функция из CtfQ обозначается
Cl, l = 1, ... , Q. Метод, предложенный в работе [Huard et al. (2006)], на
первом шаге состоит в проверке следующих
Hl :
Q
гипотез:
данные извлечены из копула-функции
Cl,
l
= 1, ... , Q.
Для этого вычисляются
Hl
при заданных
P(HllD) - вероятности реализации гипотезы
наблюдениях D, которые представляют собой Т неза
висимых пар (Ut, Vt),
нентами (в работе
t = 1, ... , Т с равномерно распределенными компо
[Huard et al. (2006)]
называемые квантилями). Если
используются нормированные ранги, то условие независимости может
нарушаться, и предложенный метод следует рассматривать как аппрок
симацию и применять с некоторой осторожностью. Используя теорему
Байеса, получим:
Р(Н
ID
l
где
P(DIHl, 1) -
= P(DIHl, l)P(Hlll)
1)
'
P(Dll)
функция правдоподобия,
пределение для копула-функции,
1
P(Dll) -
(6.26)
'
P(Hlll) -
априорное рас
нормирующая константа;
соответствует дополнительной информации. ~Правильной~ копула
функцией, в терминах работы
[Huard et al. (2006)],
называют копула
функцию, отвечающую наибольшему значению апостериорной вероят
ности P(HllD, 1).
В [Huard et al.
(2006)]
плотность копула-функции перепараметри
зируется в терминах параметра т-Кендалла (т
= g1(a)),
который ста
новится общим параметром для всех копула-функций из CtfQ.
Таблица
6.3.
Выражения параметра т-Кендалла для некоторых
копула-функций
Область изменения
Копула-функция
т
Клейтон
1- 2(2 + а)- 1
Гумбель
l-a- 1
Франк
Гаусс
1 - 4а- 1 ( 1 - а- 1
J; s / (е
27r"- 1 arcsinp
8
-
1) ds)
[О; 1]\{О}
[О; 1]
[-1; 1]\{О}
[-1; 1]
Гл.
588
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Следовательно, т-Кендалла может использоваться в
(6.26) как слу
чайная величина
+1
P(HllD, 1) =
!
!
P(Hl, тlD, l)dт =
-1
+1
=
(6.27)
P(DIHl, т, l)P(Hllт, l)P(тll)dт
P(Dll)
'
-1
где P(Hllт, 1)
априорная вероятность гипотезы
-
ции; P(тll)
- априорная плотность для
P(DIHl, т, 1), которое теперь зависит от т,
Hl
для копула-функ
т-Кендалла; правдоподобие
может быть вычислено сле
дующим образом:
т
т
P(DIHl, т, 1) = П P(ut, Vtlт, l, 1) = П cl (иt, Vt1Bi 1 (т)),
t=1
(6.28)
t=1
где cl(ut, Vtlвi 1 (т)) - плотность l-й копула-функции, параметризован
ной в терминах т-Кендалла.
Для того
чтобы
выбрать
априорные
распределения,
в
работе
[Huard et al. (2006)] указываются некоторые требования и правила:
(11) т-Кендалла принадлежит множеству Л и каждая реализация
т Е Л равновероятна;
(12)
для заданного т все копула-функции, для которых т Е f!l, рав
новероятны, здесь
гипотезы
nl -
область значений т в условиях справедливости
Hl.
Область Л необходима для того, чтобы включать дополнительную
информацию относительно зависимости между переменными. Напри
мер, если известно, что т положительно, то можно предположить, что
Л = [О;
1];
если априорная информация относительно значений т отсут
ствует, то Л
= [-1; 1). Следовательно, учитывая (/1), априорное распре
деление т есть:
P(тlI1) =
{
~('л)
при
иначе,
где Л(·) обозначает меру Лебега, т. е. Л(А)
ме того, условие
(12)
т ЕЛ;
-
(6.29)
длина интервала Л. Кро
определяет априорное распределение для копула
функции:
(6.30)
6.8.
589
ВЫБОР КОПУЛА-ФУНКЦИИ
где предполагается, что все копула-функции равновероятны относи
тельно т. В случае, если известно, что т концентрируется вокруг опреде
ленного значения, то в работе
зовать бета-распределение на
[Huard et al. (2006)] предлагается исполь
интервале [-1; 1] с параметрами, обеспе
чивающими такую форму распределения, которая соответствует апри
орной информации.
Если подставить
P(HllD, 1) =
(6.28), (6.30)
P(~II)
+1
т
j IJ
cl
и
(6.29)
в
(6.27),
то получим:
(иt, Vtl91 1 (т)) х
-1 t-1
х
1{т
е nl n л}
Л(Л)
1
dт = P(DII)Л(A)
j
Пт
_ cl
(6.31)
-1
(иt,Vtl9l (т)) dт,
nnл t-l
где нормирующая константа
P(DII) в (6.31) вычисляется при помощи
так называемого правила суммы, более подробно об этом см.
[Jaynes,
Bretthorst (2003)]:
Q
P(DII)
=L
P(DIHl, I)P(Hlll).
l=1
Важно отметить, что правило суммы справедливо только тогда, ко
гда гипотезы
Hl
являются взаимоисключающими и исчерпывающими
(в совокупности). К сожалению, эти условия обычно не выполняются
по двум причинам. Во-первых, если данные сгенерированы из копула
функции, не входящей в
CCQ
(что является довольно распространенной
ситуацией), то гипотезы
Hl в совокупности не являются исчерпываю
щими. Во-вторых, если множество гипотез Hl содержит две или более
похожих копула-функций, то в этом случае гипотезы Hl не являются
взаимно исключающими. В работе
[Huard et al. (2006)]
весьма кратко
рассматриваются возможные решения, которые бы обеспечили полноту,
но более детальное изучение этого вопроса оставлено для дальнейшего
исследования.
Этот метод представляется весьма интересным, поскольку не тре
бует предварительного оценивания параметров копула-функций. Более
того, отметим, что рассматриваемые копула-функции не обязаны быть
вложенными.
6.8.4.
Эмпирические приложения: пример выбора
копула-функций
Критерий
AIC
не вычисляется напрямую в пакете
R,
но несложно на
писать небольшую функцию, которая бы вычисляла значение
AIC
при
Гл.
590
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
заданных значении максимума логарифмической функции правдоподо
бия и числе параметров. Эта задача остается в качестве упражнения.
В пакете
MATLAB
реализован код для байесовского выбора копу
ла-функции из работы
который доступен на сайте
[Huard et al. (2006)],
http://code.google.com/ р / copula/.
6.9.
Критерии согласия для копула-функций
После того как, согласно указанным выше процедурам, выбрана «наи
более подходящая~ копула-функция, следующим шагом является про
верка того, насколько хорошо она согласуется с имеющимися данными.
Одним из вариантов такой проверки является неформальна.я графи
'Ческая диагностика, в соответствии с которой сравниваются нормиро
ванные ранги со случайными выборками, сгенерированными в соответ
ствии с используемой копула-функцией. А именно, графически сравни
вается эмпирическая оценка копула-функции с параметрической моде
лью. Однако эту процедуру можно рассматривать в качестве предва
рительного и приблизительного анализа.
С недавнего времени начали появляться работы, в которых изуча
ются статистические тесты, используемые в критериях согласия. Вот
лишь некоторые из них:
[Genest, Rivest {1993)], [Shih (1998)], [Breymann
et al. (2003)], [Malevergne, Sornette (2003)], [Scaillet (2005)], [Fermanian
(2005)], [Panchenko (2005)], [Genest et al. (2006а)], [Berg, Bakken (2007)],
[Dobric, Schmid (2007)], [Quessy et al. (2007)], [Genest et al. (2009)],
[Genest, Remillard (2008)], [Berg (2009)].
Пусть С(·) - некоторая п-мерная копула-функция. Необходимо
протестировать следующую гипотезу для рассматриваемой выборки:
Но
где Со. (·)
-
:
СЕ
W
={Са; а Е
0}
против Н1
параметрическая копула-функция,
0 -
:
С ф
W,
пространство пара
метров.
В случае, когда выбирается наиболее приемлемая одномерная мо
дель, обычно используются такие критерии согласия, как критерий
Колмогорова- Смирнова или критерий Андерсона- Дарлинга.
Возможным вариантом построения критерия согласия для копула
функций, используемых для описания многомерных распределений, яв
ляются подходы, основанные на многомерном группировании, см., на
пример,
[Dobric, Schmid (2005)].
К сожалению, при этом, как и во всех
подходах, основанных на группировании, используется дискретизация
вероятностного пространства, которая практически нереализуема в слу
чае задач большой размерности. Более того, группирование данных
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
591
в некотором смысле произвольно и весьма нетривиально. Аналогич
но, подходы, основанные на использовании многомерных ядерных оце
нок копула-функций, представленные, например, в работах
(2005)], [Scaillet (2005)],
[Fermanian
являются в случае большой размерности (ха
рактерной для задач из области финансов и страхования) чрезмерно
затратными с вычислительной точки зрения. Поэтому далее, характе
ризуя многомерный случай, будут рассматриваться некоторые другие
подходы.
Перед тем как приступить к анализу различных тестов, коротко
определим, что представляет собой преобразование Розенблатта. Изна
чально оно было предложено в работе [RosenЫatt
(1952)]
и стало извест
ным как условно-вероятностное интегральное преобразование
tional
ProbaЬility
Integral
Тransform,
CPIT).
(Condi-
Оно позволяет преобразо
вать набор зависимых случайных величин, описываемых некоторым
многомерным распределением, в набор независимых равномерно рас
пределенных на [О;
1)
случайных величин. Таким образом, если для
многомерных случайных величин имеется тест на независимость и рав
номерность, то, используя преобразование Розенблатта, можно проте
стировать адекватность любой модели.
Если взять случайную величину
v = F(X), где F(·) - функция
распределения случайной величины Х, то v будет иметь равномерное
распределение на [О; 1). Если в качестве F(·) взять иную функцию рас
пределения, скажем, G(·), то v = G(X) уже не будет равномерно рас
пределенной. Это простое свойство лежит в основе большинства работ,
в которых изучаются вопросы, связанные с тестированием распределе
ний и копула-функций.
Дадим формальное определение преобразования Розенблатта.
Определение
6.13
(преобразование Розенблатта). Пустъ Х
(Х1, ... , Xn) случайный вектор с функцией распределения
Fx(x1, х2, ... , Xn); Fxi = P(Xi ~ Xi) - функция распределения случайной величиН'Ьt xi, i = 1, ... 'п. Рассмотрим следующее вероятностно
интегралъное
Vi
преобразование,
определяющее п
случайных
= T(Xi):
Т(х1) = Р(Х1 ~ х1) = Fx1 (х1);
Т(х2)
= Р(Х2
T(xn)
= P(Xn ~ XnlX1 = х1, ... 'Xn-1 = Xn-1) =
~ x2IX1
= х1) = Fx2 1x1(x2lx1);
= FxnlX1,".,Xn-1 (xnlx1, · · · 'Xn-1).
величин
Гл.
592
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Тогда случайные величины
Vi = T(Xi) (i = 1, 2, ... , п)
равномерно распределенными на отрезке [О;
ми, а сами преобразования
T(Xi)
1)
являются
и взаимно независимы
называются преобразованиями Розен
блатта или условно-вероятностными интегральными преобразованиями
(CPIT).
Предположим, что многомерная функция распределения
Fx(·)
име
ет копула-функцию С(·), т. е.
Обозначим через
Ci(u1, ... , щ) совместное i-мерное распределение,
такое, что:
Ci(u1, ... , щ) = С(и1, ... , Ui, 1, ... , 1),
i = 1, 2, ... , п - 1.
При этом С1(и1) = и1 и Cn(u1, ... ,un) = С(и1, ... ,иn). Пусть слу
чайный вектор
(U1, ... , Ui) имеет распределение Ci(u1, ... , un)· Тогда
ui в точке Ui при заданных зна
и1, и2, ... , Ui-1 случайных величин И1, ... , Иi-1 соответственно
плотность условного распределения
чениях
равна:
при
i
= 1, ... , п. Теперь с использованием условных распределений Ci ( ·)
можно определить случайные величины
Как указано в работе
Vi
[Berg {2009)],
при
i = 2, ... , n:
преобразование Розенблатта
дает значительные преимущества при тестировании критериев согла
сия. В
[Hong, Li {2005)]
представлены результаты многомерных тестов с
использованием имитационного моделирования и преобразованных ис
ходных случайных величин, которые оказались лучше, чем результа
ты с использованием не преобразованн'ЫХ случайных величин. В работе
[Chen et al. {2004)]
высказывается предположение, что аналогичный вы
вод справедлив и для критериев согласия для копула-функций.
В качестве недостатка тестов, основанных на преобразовании Ро
зенблатта, следует отметить отсутствие инвариантности относительно
принятого порядка нумерации рассматриваемых случайных величин.
Общее число возможных преобразований случайных величин тогда бу
дет равно
n!.
В
[Berg {2009)]
показано, что для некоторых подходов,
основанных на преобразовании Розенблатта, оценки р-значений кри
тической статистики зависят от того, какой порядок преобразований
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
593
выбран для рассматриваемых случайных величин. Однако в этой рабо
те также указывается, что по мере роста числа наблюдений различия
в р-значениях уменьшаются,
причем,
эти р-значения
асимптотически
сходятся к некоторым общим критическим уровням. Таким образом, в
работе
[Berg {2009)]
высказывается предположение, что выбор порядка
преобразований лишь незначительным образом влияет на результаты
теста.
Следуя схеме, представленной в
[Berg {2009)],
критерии согласия
для копула-функций могут быть классифицированы в девять семейств:
.w''i : Тест-ьt,
жены в работе
основан:н.ые на преоб'/J{},зовании Розенблатта. П редло
[Berg, Bekken (2007)].
Этот подход в качестве частных
случаев включает в себя подходы, предложенные в работах
[Malevergne,
Sornette {2003)], [Breymann et al. {2003)], [Chen et al. {2004)].
J/12 :
Тестъt, основаннъtе на эмпирических оценках копула-функций.
Предложены в работах
J/13 :
[Kole et al. {2007)], [Genest, Remillard {2008)].
Тестъt, основанные на подходе о'2 и преоб'/J{},зовании Розен
блатта. Предложены в
J/14 :
[Genest et al. {2009)].
Тесты, основанные на эмпирических оценках копула-функций
и их функций '/J{},Спределени.я. Предложены в работах
{1993)], [Wang, Wells {2000)], [Savu,
J/15 :
Тrede
[Genest, Rivest
{2008)], [Genest et al. {2006а)].
Тестъt, основанные на функциях спирменовской меръt зависи
мости. Предложены в
[Quessy et al. {2007)].
J/16 : Тестъt, основанmtе на критерии Шиха [Shih {1998)] для дву
мерной модели Клейтона. Обобщены на случай произвольной размер
ности в работе
J/17 :
[Berg {2009)].
Тестъt, основанные на внутреннем произведении векторов,
как мере '/J{},Сстояни.я между ними. Предложены в работе
[Panchenko
{2005)].
J/18 :
Тесты, основанные на подходе
блатта. Предложены в
J/19 :
J/17
и преоб'/J{},зовании Розен
[Berg {2009)].
Тесты, основанные на об'6единении указанных выше подходов.
Предложены в
Подходы
статистики
ка подхода
[Berg {2009)].
oli - ds
этих
J/16
основаны на снижении размерности, поскольку
тестов
являются
одномерными,
тогда
как
статисти
строится с использованием моментов; критерии
J/17, Jt/g
представляют собой многомерные подходы. В следующих разделах
6.9.1-6.9.4 будем придерживаться структуры,
[Berg {2009)], [Berg, Bekken {2007)].
предложенной в работах
Гл.
594
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Тесты, основанные на преобразовании Розенблатта
6.9.1.
Подход
d1 ( СРIТ-подход)
Подход d1 основан на преобразовании Розенблатта, примененного
к нормированным рангам fi.1 = (u11, ... , Un1), ... , U.т = (u1т, ... , йпт),
где компоненты Uit вектора Ut вычисляются в предположении справед
ливости нулевой гипотезы о копула-функции Са. по следующей формуле
(см. выше, п.
6.7.1):
(6.32)
i=l,2, ... ,n.
В соотношении
(6.32)
правая часть определяет непараметрическую
оценку частной функции распределения переменной
справедливости нулевой гипотезы выборка
Xi
в точке Xit. При
V = ( v1, ... , vт)
представ
ляет собой выборку из копула-функции Р, отвечающей случаю неза
висимости (также обозначаемой как С.1.). К сожалению, эмпирический
аналог преобразования Розенблатта предполагает использование ран
гов, что индуцирует зависимость эмпирических значений
Таким образом,
2, ... , n.
Vi,
i
=
1, ... , n
Vi,
i
= 1,
не являются независимыми
одинаково распределенными случайными величинами. Тем не менее,
как показано в работе
[Genest et al.
(2006а)], можно получать достаточ
но надежные оценки р-значений тестовых статистик при помощи пара
метрической бутстреп-процедуры. Теоретические свойства этих оценок
представлены в работе [Genest, Remillard (2008)] 9 .
Общий вид тестовой статистики критериев согласия для подхода
J2(i следующий:
n
Wн
=L
Г { Vit},
t = 1, ... , Т,
(6.33)
i=l
где Г { ·}
ции из
-
весовая функция, используемая для взвешивания информа
(v1, ... , vт).
В качестве весовой функции может быть исполь
зована, например, Г{vit}
=
(Ф- 1 (vit)) 2 , что соответствует подходу из
[Breymann et al. (2003)].
Более того, если нулевая гипотеза соответ
ствует гауссовской копула-функции, тогда имеем подход, предложен
ный в работе
[Malevergne, Sornette (2003)].
В двух последних упомяну
тых работах используется статистика Андерсона- Дарлинга
9 Асимптотические
[Anderson,
свойства этой бутстреп-проце.цуры до сих пор были получе
ны лишь для подходов Р'2 и ~. Однако результаты, полученные в работах
Bekken (2007)], [Dobric, Schmid (2007)], [Berg (2009)],
[Berg,
указывают на справедливость
упомянутых асимптотических свойств и для других подходов.
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
595
В работе
[Berg, Bekken {2007)] показано, что статисти
ка Андерсона-Дарлинга с Г{vit} = IVit - 0.51 дает достаточно хорошие
Darling {1954)].
результаты при тестировании нулевой гипотезы, соответствующей гаус
совской копула-функции. Следовательно, для двух упомянутых выше
вариантов выбора весовой функции имеем два подхода:
.rdi~a) =
n
L
(Ф- 1 (Vit)) 2
и
.rdi~Ь)
n
=
L lvit - 0.51 .
i=l
i=l
Можно показать, что для подхода .rdi~a) функция распределения
F 1 (·) статистики Wн для любых t представляет собой х~-распределение.
Однако, как говорилось выше, если использовать нормированные ран
ги, распределение Wн неизвестно. Но для аппроксимации функции рас
пределения
F1 ( ·) при справедливости нулевой гипотезы необходимо об
ратиться к бутстреп-процедуре.
Так называемый «тестовый датчик»
di
( test observator)
81 подхода
определяется как функция распределения для F1(Wн), см.
[Berg
{2009)]:
8н(w) = Р (F1(Wн):::; w),
w Е [О; 1].
При справедливости нулевой гипотезы имеем 8н(w)
= w при всех t.
Эмпирическая версия тестового датчика может быть вычислена в виде:
т
1
w= Т+1''"'Т+1·
{6.34)
Для всех подходов, которые предполагают снижение размерности, в
работе
[Berg {2009)]
рассматривается статистика Крамера-фон Мизе
са, но следует иметь в виду, что могут быть использованы и другие ста
тистики (например, Андерсона- Дарлинга, Колмогорова- Смирнова,
см.
[Berg, Bekken {2007)], [Marsaglia, Marsaglia {2004)]).
Если использо
вать статистику Крамера- фон Мизеса, то тестовая статистика имеет
вид:
А
т
т
т А
Т1 = 3 + Т + 1 L
t=l
81
(
t
Т+ 1
) 2
-
т
т
А
t )
(Т + 1)2~{2t+1)81 Т + 1
{6.35)
2
(
(см. доказательство в
Некоторое
ken {2007)]
[Berg {2009)]).
расширение: CPIT-2
подход. В работе
[Berg, Bek-
показано, что описанный выше подход, в котором исполь
зуется весовая функция (Ф- 1 (·)) 2 , не всегда является адекватным, по-
Гл.
596
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
скольку данным, расположенным на границе n-мерного единичного ги
перкуба, присваиваются большие веса: при небольших выборках такой
способ взвешивания делает подход менее устойчивым и менее мощным,
поскольку будут присутствовать несколько наблюдений в граничных
областях. Более того, в
может давать
плохие
[Berg, Bekken (2007)] показано, что СРIТ-подход
результаты
в
случаях,
когда
рассматриваемые
данные расположены радиально асимметрично.
Учитывая указанные недостатки, в
ложен новый подход, названный
вать любую весовую функцию в
[Berg, Bekken (2007)] был пред
CPIT-2, который позволяет использо
(6.33) и при помощи дополнительного
интегрального условно-вероятностного преобразования, построенного с
использованием порядковых статистик, идентифицировать радиальную
асимметрию. По существу, в работе
на
первом
шаге
применить
[Berg, Bekken (2007)]
условное
предлагается
интегрально-вероятностное
образование к нормированным рангам
U,
пре
а на втором шаге применить
условное интегрально-вероятностное преобразование к
V,
полученному
на первом шаге.
Пусть
V =
(V1, ... , Vn), где V1, ... , Vn -
распределенные на [О;
V
Е
U(O; l)n).
1)
Вектор
случайные величины (будем обозначать это
V
получен путем применения интегрального
условно-вероятностного преобразования к
(2007)]
независимые равномерно
U.
В работе [Berg, Bekken
соответствующие порядковые статистики обозначаются как
Если V( 1), ... , V(п) -
порядковые статистики выборки независимых
одинаково распределенных из
U(O; 1)
случайных величин, тогда V(i)
имеет бета-распределение с параметрами
Stephens (1986),
гл.
8).
(i, n-(i-1)),
см.
[D'Agostino,
Для того чтобы вычислить интегральное ус
ловно-вероятностное преобразование для порядковых статистик, Берг
и Беккен используют результаты теоремы
2.7 из [David (1981)]. С ис
пользованием результатов теоремы 1 из [Deheuvels (1984)) и того факта,
что в условиях справедливости нулевой гипотезы V Е U(O; l)n, в работе
[Berg, Bekken (2007)) получено следующее выражение для интегрально
го условно-вероятностного преобразования порядковой статистики V:
1 - V(i) ) n-(i-1)
Н1 = Fv.(i)(v(i)IV(i-1) = V(i-1)) = 1- ( 1
'
- V(i-1)
i = 1, ... , п;
V(o) =О.
Слишком большое или слишком малое значение
ошибочность нулевой гипотезы, см.
(6.36)
Hi может означать
[Glen et al. (2001)]. Позднее в работе
597
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
6.9.
[Berg, Bekken (2007)) получена
ном использовании V и Н:
статистика, основанная на одновремен
n
L Гv(V(i,t)) · Гн(Нit),
=
W2t
t
= 1,"., Т,
(6.37)
i=l
где Гv(·) и Гн(·)
информации из
- весовые функции, используемые для взвешивания
V
и Н соответственно. Выбор весовых функций за
висит от того, какой области определения копула-функции уделяется
наибольшее внимание. Например, если Гv
(Ф- 1 (·)) 2 и Гн
1, то
=
=
получим исходный СРIТ-подход
В работе
(6.33) из [Breymann et al. (2003)).
[Berg, Bekken (2007)) указывается на то, что во многих
тестах могут быть получены достаточно хорошие результаты при ис
пользовании следующей комбинации двух весовых функций:
а) Гv(Х) =
IX -
0.51, Гн(Х) = 1,
б) Гv(Х) = (Х - 0.5) 2 , Гн(Х) = 1.
Наконец, важно отметить, что в целом распределение
W2t
неизвест
но, и для его оценки необходимо использовать бутстреп-приближение.
Если вычислить
W2t
с использованием некоторых весовых функций Гv
и Г н, то можно смоделировать
n
ных U(O; 1) случайных величин
независимых одинаково распределен
V, вычислить W2t,
мые весовые функции, что и для
W2t·
используя те же са
Повторяя эту процедуру большое
число раз в предположении справедливости нулевой гипотезы, можно
аппроксимировать функцию распределения
F2t
для
W2t·
Реализация тестов
Далее представлено подробное описание тестовых процедур, вклю
чая вычисление оценок соответствующих р-значений в предположении
справедливости нулевой гипотезы о параметрическом виде
функции. Среди описанных процедур
Процедура
1.
6.9.1.
2.
и
CPIT-2
Реализация теста в подходе
Получить псевдонаблюдения
выборочных данных (х1,
нием
- CPIT
... , хт)
(fi.1, ... , ilт)
копула
подходы.
Jt/i.
путем преобразования
в нормированные ранги с использова
(6.32).
Оценить параметры копула-функции а с использованием состоя
& = argmaxl(fi.1, ... , U.т; а), где l - логарифми
правдоподобия наблюдений fi.1, ... , ilт, т. е. полупара-
тельной ММП-оценки
а
ческая функция
метрического метода.
3.
Вычислить
(v1, ... , vт),
полученные путем применения интег
рального условно-вероятностного преобразования к
(fi.1, ... , ilт)
в пред
положении справедливости нулевой гипотезы о том, что копула-функ
ция равна Са:.
Гл.
598
4.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Вычислить
CPIT-2
выборку
(h1, ... , hт),
условно-вероятностное преобразование
5.
W2t
(6.36)
к
применяя интегральное
(v1, ... , vт).
Используя весовые функции Гv и Гн (если Гн
совпадают), вычислить Wн или
W2t
по формулам
=
1, то Wн и
(6.33) или (6.37)
соответственно.
Если при справедливости нулевой гипотезы для Wн или
6.
функция распределения известна, вычислить
F1(W1)
или
F2(W2)
W2t
и пе
рейти к шагу
F1(W1)
или
8. Если распределение неизвестно, аппроксимировать
F2(W2) следующим образом: для некоторого достаточно
большого целого Nь итеративно повторять нижеприведенную процеду
ру для каждого
l
Е
{1, ... , Nь}:
а) сгенерировать случайную выборку
vi =
ненты которой представляет собой компоненты
v: l),
(vi l' ... ,
' 1)n
U(O;
компо-
'
случайного
вектора;
б) применяя интегральное условно-вероятностное преобразование
(6.36) к (vi,l' ... , v:,l), вычислить hi = (hip ... , h~,l);
в) в соответствии с (6.33) или (6.37), используя те же весовые функ
ции, что и на шаге 5, и беря (vi,l, ... , v:,l) и (hi,l, ... , h~,l), вычислить
Wi l
'
или
w;'l соответственно.
7. Вычислить F1(W1)
= Nь1+ 1 'Е~1 l{w;,,>Wi}·
F2(W2) вычисляется
аналогичным образом.
8. В соответствии с (6.34) и (6.35) вычислить Т1 (относительно ста
тистики Андерсона-Дарлинга см. [Berg, Bekken (2007)]). Т2 вычисля
ется аналогично.
9.
Для некоторого достаточно большого целого К повторить следу
ющие шаги для каждого
k = 1, ... , К:
а) получить псевдонаблюдения (il~,k' ... , il.},k) путем преобразова
ния выборочных данных (x~,k' ... ,x!J.,k) в нормированные ранги с ис
пользованием
(6.32);
б) по полученным таким образом псевдонаблюдениям оценить па
раметры копула-функции а. 0 с использованием состоятельной ММП
оценки &~ = arg max l ( u~ k' •.. ' u~ k; а)' т. е. полупараметрического меQ
тода;
'
'
в) вычислить (v~,k' ... , v~,k), полученные путем применения инте
грального условно-вероятностного преобразования к (il~,k' ... , il.},k) в
предположении справедливости нулевой гипотезы о том, что копула
функция равна С&О;
k
г) вычислить CPIT-2 выборку (h~,k' ... , ~,k) путем применения интегрального условно-вероятностного преобразования (6.36) к (v~,k' ...
. . . ,v~k);
'
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
599
д) используя такие же весовые функции, как на шаге
5, приме
ненные к (v~ k' ... 'v~ k) и (h~ k' ... '14 k), вычислить wp k или w~ k по
'
'
'
'
'
'
формулам (6.33) или (6.37) соответственно;
е) если при справедливости нулевой гипотезы для wp k или W~ k
'
'
функция распределения известна, вычислить F1(Wf k) или F2(W~k) и
'
'
перейти к шагу 3; если распределение неизвестно, аппроксимировать
F1 (·) или F2 (·), итеративно повторяя (для некоторого достаточно боль
шого целого Nь) нижеприведенную процедуру для каждого
l
Е
{1, ...
... ,Nь}:
• сгенерировать случайную выборку v?,A: -
U(O; 1)n
•
применяя
интегральное условно-вероятностное
(6.36) к (v~~,k' ... , v~:l,k), вычислить
•
(v~~,k' ... , v~:l,k) из
случайного вектора;
преобразование
h?* = (h~j,k, ... , h~:l,k);
в соответствии с
(6.33) или (6.37), используя те же весовые функ
ции, что и на шаге 5, и беря (v~~,k' ... , v~:l,k) и (h~j,k, ... , h~7l,k),
вычислить wf,i,k или w~i,k соответственно;
ж) вычислить F1(wr,k) = Nь1+ 1 Er;:1l{wf.i.k>wf,k}· F2(W~k) вычис
ляется аналогичным образом;
з) в соответствии с (6.34) и (6.35) вычислить трk (относительно
статистики Андерсона-Дарлинга см. [Berg, Bekken (2007))); T~k вы'
числяется аналогично.
10. Для оценки р-значения для подхода di
воспользоваться форму-
лой:
6.9.2.
Тесты, основанные на использовании
эмпирических копула-функци:й
Подход~
Подход ~' описанный в
женном в работе
[Berg (2009)),
[Genest, Remillard (2008)).
основан на тесте, предло
А именно, этот подход ос
нован на использовании эмпирической копула-функции, впервые пред
ставленной в
[Deheuvels (1979)):
(6.38)
Гл.
600
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
где u = ( и1, ... , un) Е [О;
1]n.
Идея, лежащая в основе этого теста, состо
ит в сравнении С(·) с параметри'Ческой оценкой копула-функции С&(·).
Это
-
классический подход в статистике, который состоит в построе
нии одномерного критерия согласия, основанного на расстоянии между
эмпирической функцией распределения и распределением, предполага
емым при нулевой гипотезе. С использованием статистики Крамера
фон Мизеса в работе
[Genest et al. (2009)]
получена следующая тестовая
статистика:
i'2 = т f.
110,11
т
d (
2
C(u) - C&(fi)) dC(u) =
L: (C(fit) -
C&(fit)) 2 •
(6.39)
t=l
Далее более подробно представлено описание параметрической бут
стреп-процедуры вычисления оценок р-значений при тестировании па
раметрической нулевой гипотезы для копула-функции.
Процедура
1.
6.9.2.
Реализация теста в подходе
Получить псевдонаблюдения
выборочных данных (х1,
нием
2.
... ,хт)
(i11, ... , fiт)
J.?12
путем преобразования
в нормированные ранги с использова
(6.32).
Оценить параметры а копула-функции с использованием состо
ятельной ММП-оценки
& = argmaxl(i11, ... , fiт; а), т. е. полупарамет
а
рического метода.
3. В соответствии с формулой (6.38) вычислить C(u).
4. Если имеется аналитическое выражение для Са ( ·), то, подставляя
C(u) и C&(fi) в (6.39), вычислить оценку Т2 и перейти к шагу 5.
Если аналитического выражения для Са(·) нет, то выбрать доста
точно большое натуральное Nь ~ Т и реализовать следующие шаги:
а) согласно предположению о справедливости нулевой гипотезы сге
нерировать случайную выборку
(xi, ... ,хЛть)
лить ассоциированную с ней псевдовыборку
и, согласно
(6.32),
вычис
(fii, ... , i1Лть);
б) вычислить аппроксимацию С& при помощи
l
C&(u) = N.
ь
в) по формуле
ра-фон Мизеса:
Nь
+ 1 L l{u;~u}i
u
Е [О; l]n;
l=1
(6.39) вычислить приближение
л
т ( л
Т2 = Е C(fit) - C&(fit)
.
)2
t=l
статистики Краме-
5. При некотором достаточно большом натуральном
= 1, ... , К последовательно повторить следующие шаги:
К для
k =
а) согласно предположению о справедливости нулевой гипотезы сге
нерировать случайную выборку (х~ k' ... ,4k) и, используя (6.32), вы'
'
числить ассоциированную с ней псевдовыборку (u~ k' ... , u~ k);
'
'
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
601
б) по полученным таким образом псевдонаблюдениям оценить па
раметры а 0 копула-функции с использованием состоятельной ММПАо
l ("'о
. . о а о) , т. е. с использованием полупаоценки ak = arg m~
u 1.k, . .. , UТ.ki
а
раметрического метода;
А
А
т
в) определить СZ(и) по формуле CZ(u) = T~l Е l{ft~k ~ u},
t=l
u Е [О; l]n ;
'
г) если определено аналитическое выражение для Са(·), то положить:
т
t~k = L (6Z(u.~,k) - c&2 (u.~,k) ) 2
t=l
и перейти к шагу
6;
если аналитическое выражение для Са(·) не опре
делено, то выбрать достаточно большое натуральное Nь ~ Т и реали
зовать следующие шаги:
•
согласно предположению о справедливости нулевой гипотезы сге
нерировать случайную выборку (x~*k, ... , xf}J k) и, используя
'
ь.
(6.32), вычислить ассоциированную с ней псевдовыборку (ft~*k, ... ,
'
ftO* )·
Nь,k'
•
вычислить аппроксимацию С&о при помощи:
•
по формуле
k
(6.39)
вычислить приближение статистики Крамера
фон Мизеса:
т
* =~
(сАо(
. . о ) сО•
))2 ·
т.А2,k
~
k Ut,k &2 ("'о
Ut,k
t=l
6.
Для оценки р-значения в подходе
J/t2
Некоторое расширение. В работе
воспользоваться формулой
[Kole et al. (2007)]
предложен
тест, который можно рассматривать в качестве расширения подхода
J/t2
на случаи, когда аналитическое выражение (гауссовское, стьюден
товское и т.п.) для копула-функции отсутствует.
Гл.
602
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
В основе этого теста лежит та же идея, что и в
[Genest et al. {2009)],
состоящая в вычислении расстояния меЖдУ эмпирической и парамет
рической копула-функциями. Однако формальное представление функ
ции распределения эллиптического типа, как правило, невозможно, и
вычисление их значений с вычислительной точки зрения очень тру
доемко в условиях большой размерности. В работе
[Kole et al. {2007)]
используется свойство постоянства функции плотности эллиптических
распределений на эллипсоидах. Каждой случайной величине, имеющей
эллиптическое распределение, отвечает одномерная случайная величи
на со специфическим распределением, которое соответствует радиаль
ным эллипсоидам, для которых плотность постоянна (см.
[Fang et al.
{1990)]). Вместо того чтобы рассматривать исходные наблюдения, в ра
[Kole et al. {2007)] рассматриваются квадраты радиусов эллипсои
боте
да, отвечающего постоянной плотности. Как следствие, авторы послед
ней упомянутой работы сравнивают эмпирические распределения квад
ратов радиусов с их теоретическими распределениями,
которые пред
ставляют собой некоторые стандартные распределения в случае гаус
совской и стьюдентовской копула-функции.
Пусть имеется случайный вектор И= (ин,
частными равномерными на [О;
1]
... , ипt)', t = 1, ... , Т,
с
распределениями, зависимости меж
ду компонентами которого определяются гауссовской копула-функv,ией
с корреляционной матрицей Е. В работе
[Kole et al. {2007)]
строится
квадрат радиуса следующим образом:
{6.40)
где ( = (Ф- 1 (ин),
... , Ф- 1 (иnt))1 - вектор значений обратной функции
гауссовского одномерного распределения в точках ин,
... , иnt.
Легко по
казать, что случайная величина ZФ имеет х~-распределение.
Пусть V = ( vi, ... , vп)' - случайный вектор, в котором Vi имеет рав
номерное распределение на [О;
1],
а зависимости между компонентами
совместного распределения определяются копула-функцией Стьюдента
с корреляционной матрицей Е и числом степеней свободы
al. {2007)]
v.
В
[Kole et
квадрат радиуса строится следующим образом:
{6.41)
где ( 11
= (t; 1(v1), ... , t; 1 (vп)) 1
-
вектор значений обратной функции
одномерного распределения Стьюдента с числом степеней свободы
Случайная величина
так как
Z 11
имеет F-распределение с параметрами
n
и
v.
v,
( 11 имеет распределение Стьюдента и может быть представлено
как ( 11 = W //Sfii,, где W - п-мерная нормальная случайная величина
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
с ковариационной матрицей Е, а
S -
603
одномерная случайная величина
с х~-распределением. Как следствие для Zv из (6.41) имеем:
W':E- 1W/n
Zv =
S/v
.
Это представление показывает, что Zv есть отношение двух неза
висимых х 2 -распределенных случайных величин, каждая из которых
делится на соответствующее ей количество степеней свободы. А это зна
чит, что
Zv
имеет Fп,v-распределение.
Практическая реализация этого расширения подхода
гична реализации самого
1.
d2
.912
анало
и состоит из четырех шагов.
При помощи IFМ-метода (см. п.
оценить параметры а
6.6.2)
копула-функции следующим образом:
а) для моделирования частных распределений воспользоваться по
лупараметрическим методом из работы
[Danielsson, de Vries (2000)),
ко
торый состоит в том, чтобы моделировать центральную часть функции
распределения при помощи эмпирического распределения, а хвосты
-
при помощи одномерных распределений из теории экстремальных зна
чений; в частности, для моделирования хвостов можно использовать
распределение Парето; соответственно, хвосты определяются левым эм
пирическим 0,01-квантилем и правым эмпирическим 0,99-квантилем;
б) при помощи метода максимума правдоподобия оценить парамет
ры а копула-функции.
2.
Оценить качество выбранной параметрической копула-функции,
вычисляя ее расстояние до эмпирической копула-функции; если копула
функция принадлежит эллиптическому семейству (например, гауссов
ская или стьюдентовская), то с использованием
(6.41)
вос
пользоваться одним из стандартных критериев согласия. В работе
[Kole
et. al. (2007))
(6.40)
или
используются следующие меры расстояния:
Dкs = max l~E
t
D'f<s =
-
Fнl,
! l~E - FнldFн,
х
D m - max
t
AD -
va
AD
где ~Е -
= {
Jx
l~в-Fнl
----;=::::::;::::==::::::;:::
JFн(1- Fн)'
l~в-Fнl dF
../Fн(1 - Fн) н,
эмпирическая функция распределения, а Fн
ское распределение. Первая мера расстояния
ва- Смирнова, второе расстояние
-
-
-
гипотетиче
расстояние Колмогоро
среднее абсолютное отклонение,
Гл.
604
третья мера
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
-
расстояние Андерсона- Дарлинга, четвертое
-
ана
лог расстояния Андерсона- Дарлинга с усреднением. Для того чтобы
уменьшить влияние выбросов при использовании расстояний Андерсо
на - Дарлинга, в работе
[Kote et al. (2007)),
следуя
[Malevergne, Sornette
(2003)), исходное IFв - Fнl заменено на (Fв - Fн) 2 .
3. Если форма меры расстояния известна, а параметры
копула
функции оценены, для вычисления распределения случайных величин,
отвечающих указанным выше четырем расстояниям, в работе
al. (2007))
[Kole et
используется параметрическая бутстреп-процедура с Ките
рациями, это отвечает в точности шагу
5в
реализации подхода
Jf12.
От
метим, что двухшаговый IFМ-метод также должен быть использован в
упомянутой бутстреп-процедуре.
4.
Подобно шагу
6
в реализации подхода
Jd2 для оценки р-значений
использовать полученное на предыдущем шаге распределение для мер
расстояний, т. е. подсчитать, сколько раз значения меры расстояния,
вычисленные с использованием бутстреп-выборок, превышают значе
ние, отвечающее исходной выборке, и поделить это число на (К+
1).
Подход dз
В работе
подход
Jf12
[Genest et al. (2009)]
предложено применить предыдущий
к случайным величинам, подвергнутым преобразованию Ро
зенблатта, т. е. к
V = ( v1, ... , vт). Следующий шаг состоит в сравнении
C(v) с копула-функцией C.l(v), отвечающей независимости, с исполь
зованием статистики Крамера-фон Мизеса, см. [Genest et al. (2009)):
Тз= т
l.
т
d
(c(v)-C.l(v)) dC(v)
(0,1]
Процедура
1.
2
2.
(c(vt)-C.l(vt)) 2 . (6.42)
t=l
6.9.3.
Реллизация теста в подходе Jtfз.
Получить псевдонаблюдения
выборочных данных (х1,
нием
=L
... , хт)
(U.1, ... , ftт)
путем преобразования
в нормированные ранги с использова
(6.32).
Оценить параметры а копула-функции с использованием состоя
тельной ММП-оценки
& = argmaxl(U.1, ... , ftт; а), т. е. с использовани
а
ем полупараметрического метода.
3.
В предположении справедливости нулевой гипотезы относитель
но копула-функции С& вычислить интегральное условно-вероятностное
преобразование
(CPIT) выборочных данных (v1, ... , vт) путем приме
нения CPIT к (U.1, ... , ftт ).
4. Согласно формуле (6.38) вычислить C(v).
5. Согласно формуле (6.42) вычислить Тз.
6. При некотором достаточно большом натуральном Кдля k = 1,
2, ... , К последовательно повторить следующие шаги:
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
605
а) отправляясь от справедливости нулевой гипотезы, сгенерировать
случайную выборку (х~ k' ... ,
4 k) и, используя (6.32), вычислить
ассоциированную с ней 'псевдов~:rборку (u~,k' ... , Щ.,k);
б) по сгенерированной таким образом псевдовыборке оценить пара
метры а. 0 копула-функции с использованием состоятельной ММП
оценки &~ = arg max l ( fi.~ k, ••• , fi.~ k; а. 0 ), т. е. С использованием ПОао
'
'
лупараметрического метода;
в) в предположении справедливости нулевой гипотезы о параметри
ческом виде ко пула-функции Со.о вычислить интегральное услов
k
но-вероятностное преобразование выборочных данных (v~ k' ... ,
v~,k), применяя CPIT к (ii~,k' ... , Щ.,k);
г) определить
АО
=
Ck(u)
1
т
т+~ Е
о
l{vt k ~ u},
t=l
АО
д) вычислить T3,k
7.
'
u Е [О; l]n;
'
т (А о о
о )2
= t~
Ck(vt,k) - Cl.(vt,k) .
Вычислить оценку р-значения следующим образом:
к
1
Р = К+ 1 L 1 {fз,k>Тз}'
k=1
Подход
Jti4
В работах [Genest, Rivest (1993)], [Wang, Wells (2000)], [Savu, Тrede
(2008)], [Genest et al. (2006а)] для построения критериев согласия для
копула-функций предлагается использовать так называемую функцию
зависимости Кендалла K(w)
датчик
84
для подхода
Jfi4
= Р ( C(U) ~ w) (см. п. 6.5.2). Тестовый
определяется в форме этой функции, т. е.
84(w) = Р (c(U) ~ w),
w Е [О; 1],
где U - псевдовектор, каждая компонента которого составлена из соот
ветствующих нормированных рангов. При справедливости нулевой ги
потезы
84 (w) = 84,0. (w),
где 84 ,о. (w)
функция зависимости Кендалла,
-
рассчитанная в условиях нулевой гипотезы Но и зависящая от парамет
ров соответствующей копула-функции. Непараметрическая оценка для
тестового датчика
84
равна:
А
84(w) =
1
Т+1
т
L I{C(iit)~w}'
t=l
(6.43)
Гл.
606
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Статистика Крамера-фон Мизеса вычисляется следУющим образом:
{6.44)
Процедура
1.
6.9.4.
Реализация теста в подходе
Получить псевдонаблюдения
выборочных данных (х1,
нием
... , хт)
(U.1, ... , U.т)
Jt'4,
путем преобразования
в нормированные ранги с использова
{6.32).
2.
Оценить параметры а копула-функции с использованием состоя
тельной ММП-оценки а=
argmaxl(U.1, ... , U.т; а),
т. е. полупараметри
а
ческого метода.
3. В соответствии с формулой {6.38) вычислить C(u).
4. Если для 84 а можно получить аналитическую выражение, то в
соответствии с {6.43) и {6.44) вычислить статистику Т4, а затем перейти
к шагу 5. Если аналитическое выражение для 84 10 получить невозмож
но, то выбрать Nь ~ Т и реализовать следУющие шаги:
а) согласно предположению о справедливости нулевой гипотезы сге
нерировать случайную выборку
(xi, ... , хЛrь)
и, используя
вычислить ассоциированную с ней псевдовыборку
б) вычислить аппроксимацию 84,& при помощи
(6.32),
{fti, ... , U.Лrь);
84 {w)
=
Nь1+ 1 х
Nь
х l~ I{C*{iii)~w}' где
А*
С (u)
в) по
формуле
=
{6.44)
1
Nь+l
Nь
L:
l=1
l{u.;~u}
вычислить
приближение
для
статистики
Крамера-фон Мизеса:
5. При некотором достаточно большом натуральном
= 1, ... , К последовательно повторить следУющие шаги:
К для
k -
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
607
а) согласно предположению нулевой гипотезы сгенерировать случай
ную выборку (х~ k' ... ,x~k) и, используя (6.32), вычислить ассо'
1
циированную с ней псевдовыборку (ii~,k' ... , ~.k);
б) оценить параметры а. 0 копула-функции с использованием состо
ятельной ММП-оценки
&2
= argmaxl(ii~k, ... ,~k; а. 0 ), т.е. с
аО
1
1
использованием полупараметрического метода;
т
1
Т+1 Е х
t=l
г) если для 84,а можно получить аналитическое выражение, то с
А
-::::()
использованием 8 4 ,k и 84 ,&~ в формуле (6.44) вычислить T2,k и
перейти к шагу
6;
если аналитическое выражение для 84,а полу
чить невозможно, тогда выбрать достаточно большое натуральное
Nь ~ Т и реализовать следующие шаги:
•
в условиях справедливости нулевой гипотезы сгенерировать
случайную выборку (x~~k' ... , x'lJь,k) и в соответствии с (6.32)
вычислить ассоциированную с ней псевдовыборку ( ii~~k, ...
)
'"'о*
... ,uNь,k;
• вычислить аппроксимацию 8 4 &оk по формуле:
1
_
-
1
N +1
ь
u Е [О;
•
Nь
х l=1
Е
l]n;
по формуле
I{C,O*(uO• ):!(w}'
k
(6.44)
l,k ""'
где
А О•
ck
(u) -
1
N +1
ь
B2ic(w) =
1
Nь
Е l{u.0l,k• ~U}'
l=1
вычислить приближение для статистики
Крамера-фон Мизеса:
Nь
т ~
(8Ао4,k (сАо*('"'о*))
ТАо4,k = Nь
L...,,,
k ul,k
м. (сА0*('"'0*)))2
k ul,k
·
- ~4,k
l=1
6.
Вычислить оценку р-значения с использованием формулы:
Подход
ds
В работе
[Quessy et al. (2007)] предлагается критерий согласия для
двумерных копула-функций, который основан на функции зависи
мости Спирмена L2(w)
= P(U1U2
~ w). При этом P(U1U2 ~ w)
=
Гл.
608
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
= P(C1-(U1U2) ~ w). Этот подход обобщается на случай произвольной
размерности п, при этом Ln(w)
85
Р ( Cl.(U) ~ w) и тестовый датчик
=
подхода~ определяется соотношением:
85(w) = Р ( Cl.(U) ~ w),
w Е [О; 1),
где U - псевдовектор, каждая компонента которого составлена из со
ответствующих нормированных рангов. При справедливости нулевой
гипотезы (Но),
S5(w) = 85,&(w),
где
85,&(w) -
функция зависимости
Кендалла, рассчитанная при справедливости Но и зависящая от па
раметров соответствующей копула-функции. Возьмем непараметриче
скую оценку для
85:
А
1
85(w) = Т + 1
т
L l{c.L(fit)~w}·
(6.45)
t=l
Статистика Крамера-фон Мизеса вычисляется следующим образом:
1
Т5 = Т
J
(s5(w) - 85,&(w)) 2 dS5(w) =
о
(6.46)
т
= L (s5
(т~1) - 85,& (т~1) )2 •
t=l
Процедура
1.
6.9.5.
Реллизация теста в подходе~
Получить псевдонаблюдения
выборочных данных (х1,
нием
... , хт)
(U.1, ... , iiт)
путем преобразования
в нормированные ранги с использова
(6.32).
Оценить параметры а копула-функции с использованием состо
2.
ятельной ММП-оценки
&
= argmaxl(ii1, ... , iiт;
а), т. е. полупарамет
а
рического метода.
3.
Если для 85,а существует аналити:._еское выражение, то, исполь
зуя формулы (6.45) и (6.46), вычислить
T3,k
и перейти к шагу 4. Если
аналитическое выражение для 85,а получить невозможно, тогда вы
брать достаточно большое натуральное Nь ~ Т и реализовать следую
щие шаги:
а) согласно предположению о справедливости нулевой гипотезы сге
нерировать случайную выборку
(xi, ... ,хЛrь)
и, используя
вычислить ассоциированную с ней псевдовыборку
(6.32),
(fti, ... , iiЛrь);
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
6.9.
б) вычислить аппроксимацию 85,& при помощи:
609
85 (w)
1
Nь+1 Х
Nь
х Е l{c.L(iii )~w};
l=1
в) по
формуле
вычислить
{6.46)
приближение для
статистики
Крамера-фон Мизеса:
Т5 = ~
Nь
L (85 (С
.L ( ui))
ь l=1
=
-
85 (с.L ( ui))) 2
4. При некотором достаточно большом натуральном
1, ... , К последовательно повторить следующие шаги:
К для
k -
а) в условиях справедливости нулевой гипотезы сгенерировать слу
чайную выборку (x~,k' ... , x~,k) и, используя {6.32), вычислить ас
социированную с ней псевдовыборку (u~ k' ... ' ~ k);
'
'
б) оценить параметры а. 0 копула-функции с использованием состоя
тельной ММП-оценки
= argmaxl{u~k''"'~k;a. 0 ), т.е. полу-
&2
ао
параметрического метода;
в) определить
г) если для
А
8g'k(w) =
85 а
'
т
Т~1 Е
t=l
I{c.L(iio
t,k
'
)~w};
существует аналитическое выражение, то с исполь
зованием 8g,k и 85,&~ по формуле {6.46) вычислить тg,k и перейти к
шагу
5;
если аналитическое выражение для 85,а получить невоз
можно, то выбрать достаточно большое натуральное Nь ~ Т и
реализовать следующие шаги:
•
в условиях справедливости нулевой гипотезы сгенерировать
случайную выборку (x~~k' ... , x'lJь,k) и, используя (6.32), вы
числить ассоциированную с ней псевдовыборку ( u~~k, ...
... о. )
··· ,uNь,k;
•
вычислить
8g~(w)
•
аппроксимацию
= Nь1+1
по формуле
85 00
'
Nь
при
помощи
формулы
k
Е I{c.L(ii?'k>~w};
•
l=1
{6.46)
вычислить приближение для статистики
Крамера-фон Мизеса
Nь
tg,k = ~ь :L: (8g,k (с.L ( u?,ic)) - 8g~ (с.L ( u?,ic))) 2 •
l=1
Гл.
610
5.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
6.
Вычислить оценку р-значения по формуле
к
1
Р = К + 1 L l{i'~,k>Ts}.
k=1
Другие подходы к построению критериев согласия
6.9.3.
Подход шб
В работе
[Shih (1998)] предложен основанный на моментных тожде
ствах критерий согласия для двумерных моделей, задаваемых копула
функцией Клейтона. В ней рассматривается невзвешенные и взвешен
ные оценки параметра зависимости а с использованием т-Кендалла и
взвешенной ранговой оценки, а именно:
л
2f
(6.47)
От=-1
л
-т
где f
=
-1
а Wi3· = Ltт-l
-
дij/T(T - 1), дij =
+ 4 Li<j
l{UAlt<::::Ш
_,, ax(UAli1. UA13·) 1 V2t<::::Ш
rAr _,, ax(UA2i1. UA23·)}.
являются несмещенными
оценками для
ливости нулевой гипотезы (С
=
а, в
l{(Uн-U1 ;)(U2 i-U2;)>0}'
Учитывая, что &т и &w
предположении справед-
Са для а ~ О) в
[Shih (1998)]
была
предложена следующая тестовая статистика:
i'shih = Vr(&т -
&w).
Там же показано, что при справедливости нулевой гипотезы приве
денная выше статистика имеет асимптотически нормальное распреде
ление. Однако позднее в
ставленная в
[Genest et al. (2006б)] было указано, что пред
[Shih (1998)] формула для дисперсии этого асимптоти
ческого нормального распределения неверна, и предложен исправлен
ный вариант этой формулы. В работе
[Berg (2009)]
предлагается расши
рить этот подход на случай произвольной размерности п путем срав
нения &т и
&w
для каждой пары случайных величин. Как следствие,
результирующий вектор, составленный из
иметь асимптотическое
n(n -
n( n - 1) /2
статистик, будет
1)/2-мерное нормальное распределение с
невырожденной ковариационной матрицей, формула для которой пока
не выведена. Если умножить вектор статистик на матрицу, обратную
к квадратному корню ковариационной матрицы, то результирующий
нормированный вектор имеет асимптотическое стандартное нормаль
ное распределение, а сумма квадратов нормированных статистик будет
иметь х 2 -распределение с n(n - 1)/2 степенями свободы.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
6.9.
611
Не имея формулы ковариационной матрицы, Берг вычисляет не
нормированные суммы квадратов и использует параметрическую бут
стреп-процедуру для оценки р-значения. Тестовая статистика для под
хода .о'6 равна:
n-1
Тб =
n
L L
(&т,ij -&w,ij) 2
(6.48)
·
i=l j=i+l
Отметим, что
&w и в целом подход .о'6 может быть использован только
для тестирования копула-функции Клейтона.
Процедура
1.
Реализация теста в подходе .о'6
6.9.6.
Получить псевдонаблюдения
выборочных данных (х1,
нием
... , хт)
(U.1 1 • • • , U.т)
путем преобразования
в нормированные ранги с использова
(6.32).
2.
Оценить параметры а копула-функции с использованием состоя
тельной ММП-оценки
& = argmaxl(U.1, ... , U.т; а),
т. е. полупараметри
а
ческого метода.
=
3. В соответствии с (6.47) вычислить параметры &т и &w.
4. В соответствии с (6.48) вычислить Тб.
5. При некотором достаточно большом натуральном К для k 1, ... ,К последовательно повторить следующие шаги:
а) в условиях справедливости нулевой гипотезы сгенерировать слу
чайную выборку (х~ k' ... , x~k) и, используя (6.32), вычислить ас'
'
социированную с ней псевдовыборку (u~ k' ... , Щ k);
'
'
б) в соответствии с (6.47) вычислить&~ k и &~k;
'
'
в) в соответствии с
лQ
шаге ат,k и
6.
лQ
aw,k'
(6.48)
и используя полученные на предыдущем
вычислить
т.лО
б,k·
Вычислить оценку р-значения, используя формулу
Подход
В
JZl1
работе [Panchenko (2005)]
предложен тест, основанный на так на-
зываемом внутреннем произведении
........
........
U -Ua
на
........
........
U -Ua,
где
........
U -
псевдо-
вектор, каждая компонента которого равна соответствующему норми-
-.
U&
тезе (при этом
состоятельная оценка параметра копула-функции).
&-
-
аналог вектора
-.
рованному рангу, а
U,
отвечающий нулевой гипо-
Идея этого теста состоит в использовании внутреннего произведения в
Гл.
612
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
качестве меры расстояния между двумя векторами. Определим квадрат
расстояния Q между двумя векторами
Q=
где
Kn -
fJ
И
fJое формулой
f f kn(дu, ди)f2 (ди)d(ди)d(ди),
10
положительно определенное симметричное ядро; в частности,
в качестве Kn может быть взято гауссовское ядро:
Кn(ди, Ли) = exp{-llдиll 2 /2nh 2 },
11·11 обозначает евклидову норму в Rn; h > О - ширина «окна», а
ди - одно из возможных значений дU. Очевидно, что Q будет равно
.......
.......
нулю тогда и только тогда, когда U = U&.
Если имеются случайные выборки (il1, ... , ilт) из U, то следующим
шагом является генерация случайных выборок (ili, ... , UТ) вектора U& ,
где
отвечающего нулевой гипотезе. Тестовая статистика подхода
.Pl1
имеет
вид:
(6.49)
Процедура
1.
6.9.7.
Реализация теста в подходе .Р11
Получить псевдонаблюдения
выборочных данных (х1,
нием
... , хт)
(il1, ... , ilт)
путем преобразования
в нормированные ранги с использова
(6.32).
2.
Оценить параметры а: копула-функции с использованием состоя
тельной ММП-оценки
& = argmaxl(il1, ... , ilт; а:),
т. е. полупараметри-
ое
ческого метода.
3.
В условиях справедливости нулевой гипотезы сгенерировать слу
чайную выборку
(xi, ... ,4)
и, используя
(6.32),
вычислить ассоцииро
ванную с ней псевдовыборку
(ili, ... , UТ).
(6.49), используя (u1, ... , ilт)
4. В соответствии с
и (ili, ... , fiТ),
вычислить 1'1.
5. При некотором достаточно большом натуральном К для k =
= 1, ... , К последовательно повторить следующие шаги:
а) в условиях справедливости нулевой гипотезы сгенерировать слу
4
чайную выборку (х~ k' ... ,
k) и, используя (6.32), вычислить ас'
'
социированную с ней псевдовыборку (u~,k' ... , ~.k);
10 Определение
и подРобности см. в [Panchenko (2005)].
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
6.9.
613
б) оценить параметры о. 0 копула-функции с использованием состоя
0 ), т.е. полутельной ММП-оценки
= argmaxl(б.~k,
, ... ,б.~k;o.
,
&2
аr
параметрического метода;
в) используя копула-функцию СаР, отвечающую нулевой гипотезе,
k
сгенерировать случайную выборку (x~~k' ... , 4:k) и, используя
(6.32), вычислить ассоциированную с ней псевдовыборку (б.~*k,
, ...
... ,~\);
,
г) в соответствии с (6.49) и с использованием (б.~,k' ... , б.~,k) и
АО•
( U1
,k' ...
6.
АО• )
'UТk
,
вычислить
7 ,k•
Вычислить оценку р-значения по формуле
Подход
ds
В работе
[Berg (2009))
предложено расширение подхода
состоит в применении подхода
разованию Розенблатта, т. е. к
ки
т.Ао
.fll., к величинам,
V = (v1, ... , vт).
которое
подвергнутым преоб
Если имеются выбор
извлеченные из копула-функции, отвечающей случаю
(vi, ... , vf),
независимости, статистика подхода
1
А
.Pl7,
т
2
т
LL
Тв= т2
.Pls
Kn(Vi,
Vj) - т2
i=l j=l
1
+ т2
т
равна:
т
т
LL
Kn(Vi,
vj)+
i=l j=l
(6.50)
т
LL
Kn(v;,vj).
i=l j=l
В работе
[Berg (2009))
отмечается, что может показаться странным
желание строить выводы относительно отклонения от проверяемой (ну
левой) гипотезы на основании единственной выборки, отвечающей ну
левой гипотезе. Тем не менее этот подход изначально рассматривался
в работе
[Panchenko (2005)],
и Берг предпочел рассматривать этот тест
именно в таком виде. Более того, подход
dg
направлен на то, чтобы
проверить эффект преобразования Розенблатта в случае использова
ния подхода
.Pl7.
Процедура
1.
6.9.8.
Реализация теста в подходе
Получить псевдонаблюдения
выборочных данных (х1,
нием
(6.32).
... ,хт)
(U.1, ... , б.т)
ds
путем преобразования
в нормированные ранги с использова
Гл.
614
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Оценить параметры а: копула-функции с использованием состоя
2.
тельной ММП-оценки
& = argmaxl(U.1, ... , U.т; а:), т. е. полупараметри
а
ческого метода.
В предположении справедливости нулевой гипотезы относитель
3.
но копула-функции Са: вычислить интегральное условно-вероятностное
преобразование
(CPIT) выборочных данных (v1, ... , vт) путем приме
нения CPIT к (U.1, ... , U.т).
4. Сгенерировать выборку (vi, ... , vт) из копула-функции, отвеча
ющей независимости.
5. В соответствии с (6.50) и с использованием (v1, ... , vт)
. . . , vт) вычислить тв.
6. При некотором достаточно большом натуральном К
= 1, ... , К последовательно повторить следующие шаги:
и
(vi, ...
для
k =
а) в условиях справедливости нулевой гипотезы сгенерировать слу
чайную выборку (х? k' ... ,4k) и, используя (6.32), вычислить ас'
'
социированную с ней псевдовыборку (u? k' ... , ~k);
'
'
б) оценить параметры а: 0 копула-функции с использованием состоя
тельной ММП-оценки &~ = argmaxl(u?k, ... ,~k;a: 0 ), т.е. полуа
параметрического метода;
'
'
в) в предположении справедливости нулевой гипотезы относитель
но копула-функции С0:0 вычислить интегральное условно-вероят
k
постное преобразование (CPIT) выборочных данных (v? k' ...
'
0
... 'vт k) путем применения CPIT к (u? k' ... 'u~ k);
'
'
'
г) используя копула-функцию, отвечающую независимости, сгенери
ровать случайную выборку (v?~k' ... , v~7k).
7. В соответствии с (6.50), используя (v?,k, ... , v~,k) и (v?~k' ...
о
АО
... , vт7k), вычислить T8 ,k.
8. Вычислить оценку р-значения по формуле
1
к
Р = К + 1 L I{т~,k>Ts}.
k=1
6.9.4.
Тесты, основанные на усреднении критических
статистик
Выше были рассмотрены некоторые критерии согласия для копула
функций. Справедливо задаться вопросом, а может ли усреднение этих
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
615
тестов (с разными способами измерения отклонений от нулевой гипоте
зы) дать более устойчивые результаты? Ответ на этот вопрос дается в
работе
[Berg (2009)], где подход с усреднением обозначен как dg.
Понятно, что усреднение должно осуществляться по стандартизи
рованным переменным. Более того, следует использовать оптимальные
веса для расчета взвешенного среднего. Тем не менее в силу некоторых
вычислительных аспектов в работе
[Berg (2009)] представлены только
два варианта усреднения:
•
первый вариант состоит в усреднении всех девяти указанных вы
ше подходов; ему отвечает статистика:
А (а) -- g1 { ТА (а)
А (Ь) ~ А
1 +Т 1 + L...J Т3
Т9
•
}
(6.51)
•
,
j=2
•
второй вариант состоит в усреднении лишь тех подходов, кото
рые основаны на использовании эмпирической копула-функции, а
-04;
именно подходов ~, dз и
статистика для такого усреднения
равна:
А (Ь)
Т9
Процедура
6.9.9.
А
Т2 +Тз
+ Т4А
)
(6.52)
.
Реализация теста в подходе
Получить псевдонаблюдения
1.
выборочных данных (х1,
нием
1( А
=3
... , хт)
(fi.1, ... , fi.т)
olg
путем преобразования
в нормированные ранги с использова
(6.32).
Оценить параметры а копула-функции с использованием состоя
2.
тельной ММП-оценки
& = argmaxl(U.1, ... , fi.т;a), т.е. с использовани
а
ем полупараметрического метода.
Используя
(fi.1, ... , fi.т) и&, реализовать необходимые шаги для
вычисления тестовых статистик процедур 6.9.1-6.9.8 и вычислить tfa),
3.
А (Ь)
Т1
А
А
, Т2-Тв.
4. В соответствии с (6.51)-(6.52) вычислить 'f'Ja) И fJЬ) соответствен-
но.
5. При некотором достаточно большом натуральном
= 1, ... ,К последовательно повторить следующие шаги:
К для
k
=
а) в условиях справедливости нулевой гипотезы сгенерировать слу
чайную выборку (х~ k' ... , x~k) и, используя (6.32), вычислить ас'
,
социированную с ней псевдовыборку (fi.~ k' ... , Щ, k);
'
,
Гл.
616
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
б) оценить параметры о. 0 копула-функции с использованием состоя
тельной ММП-оценки
&2
=
0 ), т.е. с исargmaxl(u~k,
... ,u~k;o.
,
,
ао
пользованием полупараметрического метода;
в) используя (u~,k' ... , u~,k) и
&2, реализовать необходимые шаги для
вычисления тестовых статистик из процедур
~.(а)
АО,(Ь)
АО
АО
6.9.1-6.9.8
и вычис-
.
лить ·11,k , т1,k , т2,k - тв,k'
г) в соответствии с
,
АО (а)
вычислить т.
9,k
6.
АО,(а)
(6.51)-(6.52), используя T 1,k
,
АО,(Ь)
T 1,k
,
АО
T 2,k
-
АО
T8 ,k,
, .
АО (Ь)
и т.
9,k
Вычислить оценку р-значений по формулам:
Сравнение подходов с помощью имитационного моделирова
ния. В работе
[Berg (2009))
проведено объемное имитационное моде
лирование в целях сравнения описанных выше подходов к построению
критериев согласия для копула-функций. И хотя показано, что не су
ществует критерия, превосходящего по мощности любой другой из рас
сматриваемых подходов, подходы
.0'2,
~и dg дают очень хорошие ре
зультаты, причем последний из них можно признать лучшим.
Интересно, что при тестировании гипотезы гауссовости (при аль
тернативе распределения с «тяжелыми хвостами») слабый в других си
туациях подход
di
дает очень хорошие результаты для высоких раз
мерностей и больших объемов выборок. Следовательно, его целесооб
разно использовать в качестве предварительного теста проверки эллип
соидальности распределения с тем, чтобы решить, какой из подходов
выбрать для дальнейшего исследования, см.
6.9.5.
[Huffera, Park (2007)).
Эмпирические приложения с пакетом
реализации подхода
Модули пакета
R
R:
пример
Jd2
дают возможность численно реализовать критерии
согласия, основанные на сравнении эмпири'Ческой копула-функции с ее
параметри'Ческой оценкой (в предположении справедливости проверяе
мой гипотезы), т. е. практически осуществить подход
.912.
Тестовая ста
тистика строится с использованием расстояния Крамера-фон Мизе
са. Приближения для р-значений тестовой статистики вычисляются с
использованием параметрических бутстреп-процедур, предложенных в
6.9.
КРИТЕРИИ СОГЛАСИЯ ДЛЯ КОПУЛА-ФУНКЦИЙ
617
[Genest, Remillard {2008)], [Genest et.al. {2009)], или с помощью подхо
да, изложенного в [Kojadinovic et al. {2011)], [Kojadinovic, Yan {2011)].
Ниже приведен код проце,цуры в соответствующем мо,цуле пакета
R.
library(copula}
х <- rcopula(claytonCopula(3}, 200}
## Does the Gumbel family seem to Ье а good choice?
gofCopula(gumbelCopula(l}, х)
## What about the Clayton family?
gofCopula(claytonCopula(l} , х)
## The same with а different estimation method
gofCopula(gumbelCopula(l}, х, method= 11 itau 11 )
gofCopula(claytonCopula( 1), х, method= 11 itau 11 )
##А three-dimensional example
х <- rcopula(tCopula(c(0.5, 0.6, 0.7), dim = 3, dispstr = 11 un 11 },200}
## Does the Clayton family seem to Ье а good choice?
gofCopula(gumbelCopula(l, dim =3}, х)
## What about the t copula?
t.copula <- tCopula(rep(O, 3), dim = 3, dispstr = 11 un 11 , df.fixed=TRUE)
gofCopula(t.copula, х)
# # The same with а different estimation method
gofCopula(gumbelCopula(l, dim =3}, х, method= 11 itau 11 )
gofCopula( t.copula, х, method= 11 itau 11 )
## The same using the multiplier approach
gofCopula(gumbelCopula(l, dim =3}, х, simulation= 11 mult 11 )
gofCopula( t.copula, х, simulation= 11 mult 11 )
For sake of space, we report only the output relative to the first two goodness-of-fit
tests:
>gofCopula(gumbelCopula(l}, х)
Progress will Ье displayed every 100 iterations.
lteration 100
Iteration 1000
$statistic [1] 0.2648942
$pvalue [1] 0.0004995005
$parameters [1] 1.980118
>gofCopula(claytonCopula( 1), х}
Progress will Ье displayed every 100 iterations.
Iteration 100
Iteration 1000
$statistic [1] 0.01489807
$pvalue [1] 0.54995
$parameters [1] 3.317709
Отметим, что в пакете, созданном Даниэлем Бергом, рассмотрен
более широкий диапазон критериев согласия для копула-функций. Од
нако к моменту написания данной главы книги (июль
вала только предварительная версия этого пакета.
2011 г.)
существо
Гл.
618
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Выводы
1.
Очевидные недостатки универсального использования много
мерного нормального
распределения для
моделирования совместного
распределения многих экономических и финансовых временных рядов
явились мотивирующими факторами для развития теории копула
функций. Учитывая растущую значимость этой теории в многомерном
статистическом анализе, мы представили в этой главе как обзор основ
ных результатов теории копула-функций, так и некоторое обсуждение
наиболее часто используемых копула-функций, среди которых копула
функции эллиптического типа, архимедовы копула-функции, копула
функции, формируемые при помощи парных копула-функций.
2.
Копула-функция. п-мерная копула-функция представляет со
бой многомерную функцию распределения с частными распределения
ми, имеющими равномерное распределение на отрезке [О;
важным результатом является теорема Шкмра (см. п.
1]. Особенно
6.1.1): пусть
Н(·)
- п-мерная функция распределения с частными распределениями
F1 . .. Fn . Тогда существует п-мерная копула-функция С(·) такая, что
для всех действительных чисел (х1, ... , Xn), мы имеем: Н(х1, ... , Xn) =
= C(F1(x1), ... ,Fn(Xn)). Если все частные распределения непрерыв
ны, тогда копула-функция единственна; иначе С(·) определена един
ственным образом на
RanF1
х
RanF2 ... RanFn,
где
Ran
область зна
чений соответствующего частного распределения. Обратно, если С(·)
-
копула-функция, а
F1 ( ·), ... Fn (·) -
одномерные функции распреде
ления, тогда функция Н(·), определенная выше, является совместной
функцией распределения с частными распределения
F1 ( ·), ... Fn (·).
3. Эллиптические распределения и копула-функции (см. п.
6.2.1). Пусть Z - п-мерный случайный вектор, а Е Е IRnxn - симметрич
ная положительно-полуопределенная матрица. Если (Х - µ)при неко
тором µ Е IRn, имеет характеристическую функцию вида Фх-µ(t) =
= exp(itT µ) х ф (-~tTEt), тогда Х называют случайной величиной,
подчиняющейся распределению эллиптического типа с параметрами µ,
Х и ф. Ко пула-функцию С ( ·) называют эллипmи'Ческой, если она пред
ставляет собой копула-функцию многомерного распределения эллипти
ческого типа.
Нормальная двумерная копула-функция с линейной кор
реляцией р определяется формулой cNormal(u1, u2; р) = Ф 2 (ф- 1 (и1),
4.
ф- 1 (и2); р), где Ф 2 (·) обозначает совместную функцию распределения
двумерного
стандартного
нормального
распределения
с
единичными
дисперсиями компонент, корреляцией р и нулевыми средними значени
ями, а ф- 1 (·) - обратная функция для одномерного стандартного нор
мального распределения.
Выводы
5.
с
619
Копула-функция двумерного распределения Стьюдента
линейной
корреляцией
р
определяется
следующей
формулой:
ct-copula(u1, и2; р, 11) = T 2(t;; 1(u1), t;; 1(u2); р, 11), где Т 2 (·) - двумерная
функция распределения Стьюдента, 11 - степени свободы, а t;; 1(·) обратная функция для одномерного распределения Стьюдента (см. п.
6.2.2).
6.
Архимедовы копула-функции (см. п.
6.3).
Для их описания
используются аналитические выражения, они легко строятся, и в это се
мейство входит множество параметрических подсемейств. Более того,
это семейство не ограничено копула-функциями, имеющими радиаль
ную симметрию, как это в случае нормальных копула-функций или, в
более общем случае, эллиптических копула-функций.
Если мы рассмотрим функцию <р : [О,
рывна, строго убывает <р1 (и)
<
О, выпукла
<р(О)
= оо и ip{l) = О, тогда мы можем
<р(-1) : [О, оо] ---+ [О, 1], для которого:
1Р
[-ll(t) = {
1] ---+
[О,
1],
ip" (и) >
которая непре
О и для которой
определить псевдообращение
для О~ t ~ <р(О) } .
О для <р{О) ~ t ~ оо
<p- 1 (t)
Если <р выпукла, тогда функция С : [О, 1] 2 ---+ [О, 1], определяемая как
С(и1, и2) = ip- 1[ip(u1) +ip(u2)], является архимедовой копула-функцией
(см. п. 6.3.1). Функцию <р( ·) называют ~генератором» копула-функции.
7.
(см. п.
Конструкции, составленные из парных копула-функций
6.4).
Из теоремы Шкляра известно, что для плотности fн(·)
некоторого абсолютно непрерывного совместного распределения Н ( ·)
со строго возрастающими, непрерывными частными функциями рас
пределения
F1{·), ... , Fn(·),
плотности которых
fi(·), ... , fn(·),
мы име
ем:
f(x1, ... , Xn) = c1, ... ,n(F1 (х1), ... , Fn(Xn)) · fi(x1) · ... · fn(Xn)·
В двумерном случае вышеприведенное утверждение имеет вид:
f(x1, х2) = c12(F1 (х1), F2(x2)) · fi (х1) · f2(x2).
В этом случае, с12{-, ·)
плотность парной копула-функции, откуда следует, что f(x1lx2)
-
=
= c12(F1(x1), F2(x2)) · fi(x1). Для случая совместного распределения
трех случайных величин Х1,Х2 и Хз мы имеем, что f(x1lx2,xз)
=
= С121з[F(х1lхз), F(x2lxз)]f(x1lxз), где, как видно, плотность парной
копула-функции с 12 1з(·) применяется к F(x1lxз) и F(x2lxз), которые
используются в качестве аргументов. Однако можно предложить нес
колько
=
альтернативных
разложений.
Например:
f(x1lx2,xз)
-
c1з12[F(x1lx2), F(xзlx2)]f(x1lx2). В п-мерном случае возможны ана
логичные разложения:
Гл.
620
где щ
-
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
это произвольно выбранная компонента вектора
v;
через
v -j
обозначен v-вектор, в котором исключена компонента щ. Теперь, если
мы рассмотрим следующее разложение:
n
(**)
= П f (xtlx1, ... , Xt-1) · fi (х1)
t=2
и воспользуемся
(*),
то получим
Для различных индексов
i,j, il, ... , ik
с
i
<
j
и
il
< ... <
ik
мы
будем использовать следующие обозначения для двумерных условных
плотностей копула-функций:
Рекурсивно используя замену, мы можем переписать
n
(**)
в виде:
n-1 n-j
fн(х1, ... , Xn) = П f(xr) · П П Cj,j+lll, ... ,j-1
r=l
с
j=li=l
(j = t - k,j + i = t).
Последнее представление имеет вид разложения в виде произведе
ния парных копула-функций. Существует множество возможных раз
ложений в виде произведения парных копула-функций.
8.
Для функций распределений случайных векторов вы
сокой размерности существует множество возможных разложений в
виде произведения парных копула-функций. В работе
{2001, 2002)]
[Bedford, Cooke
впервые введена графическая модель, называемая регу
лярной ветвизацией, которая используется для того, чтобы помочь ор
ганизовать произведения парных копула-функций. Регулярную ветви
зацию, для которой каждое дерево имеет единственный корень, назы
вают канони-ческой ветвизацией (см. п.
для которой у любого дерева
Tj,
6.4.2).
Регулярная ветвизация,
соединенного с более чем одним узлом,
отсутствуют листья называют D-ветвизацией (см. п.
9.
6.4.3).
В главе рассмотрены альтернативные меры статистиче
ской зависимости между случайными величинами, полезные для
того, чтобы описывать структуру зависимости анализируемого случай
ного вектора (см. п.
6.5).
Среди них меры хвостовой зависимости,
621
Выводы
которые позволяют учесть асимметричность функций распределения,
обычно свойственную временным рядам доходностей финансовых дан
ных.
Ниже приведены основные результаты по этой тематике.
•
Недостатки линеii:ной корреляции (см. п.
6.5.1).
Равенство нулю
линейной корреляции отвечает независимости в случае многомер
ного нормального распределения; линейная корреляция инвари
антна относительно линейных преобразований, но это не так в
случае преобразований более общего вида. Частные распределе
ния и корреляционные матрицы однозначно определяют совмест
ное распределение только в условиях эллиптических семейств, но
в общем случае это неверно. Дисперсии двух случайных величин
Х и У должны быть конечными, иначе линейная корреляция не
определена.
•
р-Сnирмена (см. п.
Для двух непрерывных случайных ве
6.5.2).
личин Х и У, копула-функция которых С(·), р-Спирмена дается
формулой
ps(X, У)
= 12 J f12 С(и, v)dиdv-3, где и= Fx(x), v = Fy(y). Кроме
того, р-Спирмена может быть выражено как корреляция рангов
Ps(X, У) = Corr (Fx(X), Fy(Y)). Перечислим основные свойства
р-Спирмена: ps симметрично; IPsl ~ 1. В частности, ps(X, У) = 1,
если У
=
ps(X, У)
функция;
Т(Х), где Т(·)
=
-1, если У
-
=
ps(Tx(X), Ту(У))
строго возрастающая функция; или
Т(Х), где Т(·)
-
строго убывающая
= ps(X, У) для любых строго возрас
тающих Тх(·) и Ту(·); если Х и У независимы, то
•
т-Кендалла (см. п.
6.5.2).
Ps(X, У)=
О.
Пусть (Х1, У1) - случайный вектор, сов
местное распределение которого Н(х, у), (Х2, У2)
-
случайный век
тор, компоненты которого независимы, а их функции распреде
ления совпадают с функциями распределения Х1 и У1, соответ
ственно ((Х2, У2) называют независимой копией (Х1, У1)). Тогда
т-Кендалла для случайного вектора (Х, У), компоненты которого
являются непрерывными случайными величинами, определяется
как вероятность согласованности минус вероятность рассогла
сованности:
т(Х, У)
= Р {(Х1 -
Х2)(У1
-
У2) >О}
-
- Р {(Х1 - Х2)(У1 - У2) < О} =
= E[sign(X1 - X2)sign(Y1 - У2)].
Для п-мерной случайной величины Х и ее независимой копии Х
Гл.
622
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
мы определим т-Кендалла как Рт(Х) = Cov [sign(X - Х)]. Пе
речислим основные свойства т-Кендалла: т(Х, У) симметрична;
-1
~ Рт(Х, У) ~
+1;
если Х1 и У1 независимы, тогда т(Х, У)= О;
т(Тх(Х), Ту(У)) = т(Х, У) для любых строго возрастающих Тх(·)
и Ту(·).
• Верхняя хвостовая зависимость ').,.И (см. п. 6.5.3). Она существует
тогда, когда имеется положительная вероятность положительных
выбросов, возникающих одновременно. Мера >.и широко исполь
зуется в теории экстремальных значений: она представляет собой
вероятность того, что одна случайная величина принимает экс
тремальные значения при условии,
что другая также принимает
экстремальные значения. Х и У называют асимптоти-чески за
висим'Ыми на верхнем хвосте, если ли Е (О,
тоти-чески независим'Ыми, если >.и = О.
1], и называют
асимп
• Нижняя хвостовая зависимость >.L. Она существует тогда, когда
имеется положительная вероятность негативных выбросов, возни
кающих одновременно. Х и У называют асимптотически зависи
мыми на нижнем хвосте, если >.L Е (О, 1], и называют асимптоти
чески независимыми, если >.L = О.
Параметрические, полупараметрические и непарамет
10.
рические
методы
(см. п.
В частности, описаны вычислительные преимущества, ко
6.6).
статистической
оценки
копула-функций
торые становятся возможными при использовании копула-функций, ко
торые позволяют разделить проблему анализа многомерного распреде
ления на функцию, описывающую зависимость (копула-функцию), и
частных распределений. Представлены следующие методы.
•
Метод максима.л:ьного правдоподобия (ММП). Оценка параметров
ВмL, получаемая этим методом, находится путем максимизации
логарифмической функции правдоподобия, в которой имеется как
компонента, отвечающая копула-функции, так и компонента, от
вечающая частным распределениям.
•
Двухшагов'Ьtй метод максимального правдоподобия. На первом
шаге, с использованием метода максимального правдоподобия
оцениваются параметры
Fi.
ai, i = 1, ... , п
частных распределений
Затем при заданных частных распределениях, оценки пара
метров которых получены на первом шаге, с использованием ме
тода максимума логарифмического правдоподобия оцениваются
параметры копула-функции 'У·
623
Выводы
• Канонический метод максимума правдоподобия (КММП}. На
первом шаге ряд (хн, X2t ... Xnt), t = 1 ... Т, преобразуется в ряд
(uн, й2t, ... , Unt) с использованием эмпирической функции распре
т
деления Fiт(·) таким образом, что: Uit = Fiт(xit) = т~ 1 Е х
xl{xiт<xit} i =
1 ... п,
т=1
где l{x:;;;;•} -
индикаторная функция. Затем
оцениваются параметры копула-функции путем максимизации ло
гарифмической функции правдоподобия для копула-функции.
•
Трехшаговъtй канонический метод максимального правдоподобия
для многомерного распределения,
которому отвечает копула
функция Стъюдента. На первом шаге из (хн,
X2t, ... , Xnt), путем
соответствующего преобразования нормированных рангов (с ис
пользованием эмпирической функции распределения), приводит
ся к (F1т(хн), F2т(x2t),
... , Fnт(Xnt)). На втором шаге для всех
пар вычисляются оценки коэффициента Кендалла. В результате
получим матрицу эмпирических оценок коэффициента Кендал
ла ftт, (j, k)-й элемент которой равен Rjk = т[Fjт(Xj), Fkт(Xk)].
Затем строится оценка корреляционной матрицы, которая основа
на на следующем соотношении 'Ej,k
уникальных параметров равно q
=
sin(~Rj,k), где количество
n· (n-1)/2. Поскольку нет ни
=
каких оснований гарантировать положительную определенность
матрицы Е, то используются соответсвующие поправки (см., на
пример, процедуру, основанную на методе собственных значений,
из работы
[Rousseeuw, Molenberghs (1993))).
На третьем шаге, пу
тем максимизации функции лог-правдоподобия копула-функции
Стьюдента, находится оценка параметра, отвечающего за количе
ство степеней свободы,
11.
v CML·
Методы выбора копула-функций (см. п.
6.8)
позволяют
идентифицировать ту модель для копула-функции, которая обеспечи
вает наилучшее приближение имеющихся данных, так же как в дета
лях рассмотрены вопросы,
связанные
с критериями
согласия
для
копула-функций. Основываясь на ранее проведенных исследовани
ях, представлены некоторые рекомендации относительно того, какой
подход следует использовать на практике. В частности,
•
выбор копула-функций: можно выбирать из нескольких альтерна
тивных моделей для копула-функци:й ту, которая отвечает наи
меньшему значению информационного критерия Акаике, или ос
новываясь на более сложных методах, таких, как тесты отношения
псевдоправдоподобия, см.
см.
[Chen, Fan (2006)],
[Huard et al. (2006)] (см. п. 6.8.1- 6.8.3).
байесовские методы,
Гл.
624
•
6.
МОДЕЛИРОВАНИЕ МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
критерии согласия для копула-функций могут быть разделены на
девять семейств (см. п.
Jt/i:
Jf12:
6.9):
тесты, основанные на преобразовании Розенблатта,
тесты, основанные на эмпирических оценках копула-функ
ций,
Jtfз: тесты, основанные на подходе
Jt12
и преобразовании Розен
блатта,
~: тесты, основанные на эмпирических оценках копула-функций
(другой принцип),
Jtfs:
тесты, основанные на спирменовской функции зависимости,
dв: тест, основанный на тесте Шиха (см.
[Shih {1998)))
для дву
мерной модели Клейтона,
Р/.т: тест, основанный на внутреннем произведении векторов как
на мере расстояния между ними,
Jtlg:
тест, основанный на подходе
Jlf.,
и преобразовании Розенблат
та,
Jt/g:
•
тест, основанный на объединении указанных выше подходов;
в работе
[Berg {2009))
представлены результаты сравнения крите
риев согласия для копула-функций на смоделированных данных.
Показано, что не существует подхода, который бы всегда превос
ходил по мощности любой другой из рассматриваемых подходов.
Глава
7
Анализ финансовых данных
в задачах управления риском
7.1.
Введение: имеющийся опыт и некоторые
общие понятия
7.1.1.
Исторические примеры
За последние десятилетия объемы торговли на мировых финансовых
рынках значительно выросли. В
1970 г.
средний ежедневный объем тор
говли на Нью-Йоркской фондовой бирже составлял 3,5 миллиона акций.
В
2002 г.
он уже составил
1,4
миллиарда акций. В последние несколь
ко лет мы наблюдаем существенное увеличение объемов торгов и на
рынках производных ценных бумаг.
На финансовых рынках имеется огромное число игроков, которые
занимают рискованные позиции, и для должной оценки своих позиций
им необходимы количественные инструменты.
Недавние события показали ряд примеров, когда большие потери
на финансовом рынке происходят, главным образом, из-за отсутствия
надлежащего управления рисками.
Джерри Корриган, бывший президент Нью-Йорского отделения Фе
деральной резервной системы США, в ходе ежегодной встречи Ассо
циации банкиров штата Нью-Йорк, имевшей место в январе 1992 г.,
сказал: ~вы все можете побиться об заклад, что нужно обратить
очень серьезное внимание на забалансовую деятельность. Рост об'{jе
мов и сложность /этой/ деятельности и характер расчетного риска
непогашени.я кредита, которъtй они влекут за собой, должны стать
дл.я всех нас поводом для беспокойства .... Я надеюсь, что это звучит
как предупреждение, потому что так оно и есть. Забалансова.я де.я-
626
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
те.л:ьность очень нужна, но она должна тщательно управляться и
контролироваться, и она должна бъtть понятна как въ~сшему испол
нительному руководству, так и трейдерам и аналитикам». К сожа
лению, Джерри Корриган стал настоящей современной «Кассандрой».
•Округ Ориндж
(1994). 6
декабря
1994
г. округ Ориндж, пре
успевающий район в Калифорнии, объявил о банкротстве после то
го, как понес потери приблизительно в
1,6
млрд долл. из-за ошибоч
ной сделки с процентными ставками, совершенной одним из крупней
ших инвестиционных фондов этого округа. Роберт Сайтрон, казначей
округа Ориндж и управляющий фондом, размер которого составлял
7,5
млрд долл., инвестировал средства в портфель (это были в основ
ном процентные ценные бумаги), включавший в себя рискованные акти
вы, приобретенные за счет заемных средств. Его стратегия зависела от
краткосрочных процентных ставок, остававшихся на относительно низ
ком уровне по сравнению со среднесрочными процентными ставками.
Но с февраля
1994 г.
Федеральный резервный банк США начал повы
шать процентные ставки, что вызвало падение цен многих активов в
инвестиционном пуле фонда округа Ориндж. В течение почти всего
1994 г.
Сайтрон игнорировал изменение процентных ставок и увели
чивающиеся номинальные убытки в своем портфеле. Однако к кон
цу
1994 г.
требования на миллиарды долларов по поручительствам от
контрагентов Сайтрона с Уолл-стрит, а также угроза массового снятия
денег с депозитов напуганными инвесторами местного правительства
создали ловушку ликвидности, которую он не смог преодолеть.
•
Банк
Barings (1995).
Банк
Barings имел долгую историю успеш
ной работы и был весьма уважаемым коммерческим банком, уже дли
тельное время проработавшим в Великобритании. Но в феврале
этот высоконадежный банк с капиталом в
ротство из-за
1 млрд долл.
900 млн долл.
1995 г.
потерпел банк
торговых убытков по несанкционированным
операциям. Как же такое могло произойти? Трейдер Ник Лисон должен
был использовать возможности низко-рисковых арбитражных опера
ций, которые усилили бы различия в ценах сходных производных цен
ных бумаг на Сингапурской валютной бирже
(Simex)
и бирже в Осаке.
Фактически же он занимал намного более рискованные позиции, поку
пая и продавая контракты разного типа на различные суммы на двух
этих биржах. Из-за халатности со стороны высшего руководства Лисон
получил контроль над функциями как торгового подразделения, так и
бэк-офиса. Когда потери Лисона увеличивались, он повышал ставки.
Однако после того как произошло землетрясение в Японии и индекс
Nikkei резко снизился, его потери быстро выросли и составили более
1 млрд долл. Это были слишком большие убытки для банка, с кото
рыми он не сумел справиться; в марте 1995 г. банк Barings был куплен
ВВЕДЕНИЕ
7 .1.
голландским банком
•Банк
627
всего за один английский фунт стерлингов.
ING
Daiwa {1995).
Трейдер Тосихиде Игучи из банка
Daiwa
в Нью-Йорке подцелывал подтверждения на продажу ценных бумаг,
принадлежавших его клиентам. Сокрытие информации этим недобро
совестным трейдером о потерях за более чем
чиной убытков в
1,1
11
лет послужило при
млрд долл., что привело к банкротству банка в
1995г.
•Банк
Sumimoto {1996).
Неучтенные убытки за три года, допу
щенные трейдером Ясуо Хаманакой, занимавшимся торговлей медью,
привели к убыткам величиной более чем
2,6
млрд долл. к концу июня
1996г.
ем
• LTCM {1998). В 1994г. был
Long-Term Capital Management, в
основан хедж-фонд под названи
нем собралась команда успешных
трейдеров и ученых. Инвесторы и инвестиционные банки вложили око
ло
1,3
млрд долл. в этот фонд, и спустя два года ежегодная доходность
на капитал составила почти
мость активов достигла
4
40%.
В начале
1998 г.
номинальная стои
млрд долл., но в конце года фонд потерял
существенную долю акционерного капитала, и фонд находился на гра
ни дефолта. Федеральная резервная система США сумела предпринять
пакет спасательных мер, расходовав
3,5
млрд долл., чтобы избежать
угрозы системного кризиса в мировой финансовой системе.
• Allied Irish Bank ( «Элайд Айриш Бзик», «Объединенный
Банк Ирландии») {2002). Трейдер Джон Раснак накопил убытки на
спотовом и форвардном
$/Yen
рынках, скрывая их путем регистрации
подцельных опционов, возмещающих сумму его обязательств (он вы
писывал опционы, которые «глубоко в деньгах»
К февралю
•
2002 г.
потери составили более чем
Национальный Банк Австралии
маскировали свои убытки с октября
2003 г.
, не регистрируя
750 млн долл.
(2004).
Четыре трейдера
на позициях по австралий
скому доллару на рынке
убытки составили
Forex с помощью фиктивных сделок.
более чем 277 млн долл.
• Societe Generale
24
января
2008 г.
(банк
их).
«Сосьете
Конечные
Женераль»)
банк объявил, что один трейдер
{2008).
( Jerome Kerviel,
Же
ром Кервель), торговавший фьючерсами, мошенническим путем нанес
банку ущерб в размере
4,9 млрд евро
(это эквивалентно
7,2 млрд долл.),
что стало наибольшим убытком в истории жульничеств подобного ти
па. Руководители банка сообщали, что трейдер действовал в одиночку
и что он, возможно, не извлек прямую выгоду из своих мошеннических
сделок. Помощник президента Франции Раймон Суби
(Raymond Souble)
заявил, что Кервель имел отношение к сделкам по фьючерсам общей
стоимостью
73,3
млрд долл. (что больше, чем рыночная капитализа
ция банка, составлявшая
52,6
млрд долл.). Расследование, проводимое
628
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
органами правопорядка, все еще продолжается, и детали пока неизвест
ны, но предполагаемые масштабы мошенничества намного больше, чем
сделки Ника Лисона, который разорил Банк
7.1.2.
Barings.
Регуляторный капитал и Базельский комитет по
банковскому надзору
Чтобы быть в состоянии покрыть большую часть финансовых убытков,
многие банки и финансовые учреждения откладывают необходимый ка
питал, также называемый регуляторн:ы.м капиталом. Величина необ
ходимого капитала, конечно, связана с величиной риска, взятой на себя
банком или финансовым учреждением, т. е. с распределением доходов
и убытков. Эта величина регламентируется законом, а национальные
надзорные органы следят за тем, чтобы банки и финансовые учрежде
ния следовали этим правилам. Одновременно с этим прилагаются уси
лия по разработке международных стандартов и методик для расчета
регуляторного капитала. Это основная задача так называемого Базелъ
ского комитета по банковскому надзору
Sиpervisioп
(BCBS)).
(Basel
Coттittee оп Baпkiпg
Базельский комитет, основанный в 1974г., не об
ладает формальными наднациональными надзорными полномочиями,
и его заключения не имеют юридической силы.
BCBS
состоит из председателей национальных банков стран
G-10
плюс Люксембург, Швейцария и является подкомитетом содействия
при Банке международных расчетов
(BIS)).
(Bank for International Settlements
Он формулирует (юридически ни к чему не обязывающие) стан
дарты банковского надзора для:
•
содействия безопасности и прочности глобальной финансовой си
стемы;
•
создания равных условий для всех международных финансовых
организаций;
•
установки минимальных требований для основных финансовых
институтов;
•
расчета минимального достаточного капитала для банков, дей
ствующих на международном уровне.
BCBS
формулирует стандарты, основополагающие принципы над
зора и дает основанные на передовом опыте рекомендации по осуществ
лению деятельности в банках и других финансовых организациях. Та
ким образом, базельский комитет имеет сильное влияние на националь
ные надзорные органы. Кратко об истории базельских соглашений.
•Базель
1 (1988).
Первое базельское соглашение по банковскому
надзору стало важным шагом к созданию международных стандартов
по расчету достаточности капитала. Основное внимание в соглашении
7 .1.
629
ВВЕДЕНИЕ
сосредоточено на определении структуры капитальной базы на основе
уровня риска для активов с кредитным риском.
•
Поправка к Первому базельскому соглашению
(1996}
пред
писывает так называемую стандартизированную модель для рыночного
риска с возможностью выбора для больших банков использовать внут
ренние модели так называемых границ потерь уровня а 1 • Кроме того,
предписываемая модель учитывала риски по
Forex
и риски торговых
портфелей.
Базель
•
11 (2001-2012}.
В
2001 г.
были начаты консультации
по новому базельскому соглашению, основными темами которых бы
ло обсуждение передового опыта описания кредитного риска, а также
обсуждение подходов к расчету достаточности капитала для операци
онного риска. Последние изменения в документации были сделаны в
ноябре
2007 г.
Регуляторы большинства юрисдикций мира планируют
разработать и внедрить новое соглашение, где будет учтена разница в
часовых поясах и определены более формальные методологии. Евро
пейский союз уже внедрил подобное соглашение, оно называется Ди
рективой ЕС достаточности капитала. Многие европейские банки уже
сообщили о своих коэффициентах достаточности капитала согласно но
вой директиве. К
BCBS
2008 г.
все кредитные учреждения из стран - членов
полностью перешли к работе в соответствии с вышеупомянутой
директивой. Подробное обсуждение основ моделей оценки рисков, за
ложенных в соглашении Базель
др.
(2010)].
Рекомендации
11, можно найти в книге [Алексеров и
Базель 11 нашли свое отражение в таких до
кументах Банка России, как письмо 192-Т от
29
щенное первому из трех компонентов Базель
рисков) и письмо
96- Т
от
29
июня
2011 г.
декабря 2012г. (посвя
11
об оценке кредитных
(раскрывающее принципы
оценки экономического капитала в рамках второй компоненты Базель
11).
•Базель
2007-2009 гг.
111 (2011-2013}. В ответ на мировой финансовый кризис
эксперты BCBS подготовили свод предложений по повы
шению финансовой устойчивости кредитных учреждений. Все рекомен
дации были разделены на два блока: касающиеся требований к капита
лу (соответствующий документ был опубликован в июне
2011 г.)
и каса
ющиеся ограничения риска ликвидности (последние обновления были
опубликованы в январе
2013 г.).
Предложения по структуре капитала
включают следующие: отказ от капитала третьего уровня, введенного
в Базель
11
для краткосрочного субординированного долга; выделение
в капитале первого уровня базового капитала и переопределение мини1В
англоязычной версии этот показатель называется Value at Risk уровня а
(VaRa)·
Гл.
630
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
мальных порогов для уровней капитала
{4,5%
и вместо
2%
и
4%
соот
ветственно); введение трех надбавок к минимальному требованию до
статочности капитала
{8%)
для обеспечения рисков системнозначимых
финансовых организаций (до
3,5%),
для ограничения проциклических
эффектов в виде контрциклического буфера (до
полнительного обеспечения в виде
2,5%), для создания до
консервирующего буфера (до 2,5%).
В части требований по ликвидности были предложены общемировые
показатели краткосрочной (до одного месяца) и долгосрочной (до од
ного года) ликвидности
и
StaЫe
Net
- показатели Liquidity Coverage Ratio (LCR)
Funding Ratio (NSFR). Дополнительно эксперты BCBS
обязали системно значимые банки разработать планы самооздоровле
ния, чтобы с минимальными потерями такие организации могли пройти
очередной кризис, и планы ликвидации, чтобы в случае банкротства
минимизировать негативные последствия на уровне всей финансовой
системы. Рекомендации Базель
111
уже внедрены Банком России по
средствам публикации положения 395-П от
2012 г. о новых
требованиях к капиталу, определяющих новые нормативы Hl.1 и Hl.2
в дополнение к существовавшему Hl (теперь Hl.O) и письма 193-Т от
29 декабря 2012 г.
7.1.3.
28
декабря
Типы рисков
Риск для организации в общих словах можно определить как любое со
бытие или действие, которое может неблагоприятно повлиять на эту
организацию в достижении обязательств и следовании ее стратегии.
В финансовом риск-менеджменте мы можем разделить большинство
рисков на пять категорий.
•
Рыночный риск. Рыночный риск
-
это риск того, что измене
ния цен и ставок (курсы акций, обменные курсы, процентные ставки,
цены на сырьевые товары) на финансовом рынке ослабят позиции бан
ка. Рыночный риск капитала часто измеряется относительно эталонно
го индекса или портфеля ценных бумаг. В этом случае его называют
«риском относительно отслеживания ошибки~.
•
Кредитный риск. Кредитный риск
-
это риск того, что на
дежность контрагента отразится на положении банка (кредитный риск
контрагента). Способность контрагента отвечать по долговым обяза
тельствам определяет надежность контрагента, которая определяется
вероятностью невыполнения обязательств и ожидаемой нормой восста
новления. Невыполнение обязательств происходит тогда, когда контр
агент не желает или неспособен выполнить свои обязательства по кон
тракту. Это экстремальная ситуация.
7 .1.
Кредитный
контрагента
риск
являются
ВВЕДЕНИЕ
631
возникает только тогда,
активом,
т. е.
они
имеют
когда обязательства
положительную
вос
становительную стоимость. Если контрагент отказывается выполнять
обязательства, убыток может составить общую рыночную стоимость
этих обязательств или некоторый процент от этой величины
(называ
емый убытком из-за невыполнения обязательств). Процент от общей
рыночной стоимости, который должен быть возмещен, называется нор
мой восстановления.
•
Риск потери ликвидности. Мы различаем два связанных друг
с другом типа риска потери ликвидности: риск финансовой ликвидно
сти и риск торговой ликвидности. Риск финансовой ликвидности свя
зан со способностью финансовых организаций находить необходимые
средства в достаточном объеме для рефинансирования долгов, удовле
творения потребности в наличных средствах, в марже, дополнитель
ных требований контрагентов, а также для осуществления выплаты при
изъятии капитала. Другими словами, риск потери ликвидности
-
это
риск недостаточности наличных средств для подцержания нормальной
хозяйственной деятельности.
Риск торговой ликвидности - риск того, что организация не сможет
осуществлять торговые операции на рынке с преобладающей рыночной
ценой, потому как отсутствует интерес к заключению сделок с этой
организацией со стороны участников рынка {неликвидный рынок).
•
Операционный риск
-
риск потерь в результате неадекватной
работы внутренних процессов, ошибочных действий персонала и систем
или внешнего воздействия. В него входят -челове-ческие риски, такие как
некомпетентность и мошенничество; процесснъtе риски, такие как риск
контроля сделок и риск операционного контроля; а также технологи-че
ский риск сбоя систем, ошибок программирования и т.д. Операционный
риск может повлечь за собой рыночный и кредитный риски.
•
Юридический риск. Юридический риск
-
это риск, являю
щийся результатом неопределенности из-за судебных исков или неопре
деленности, связанной с применимостью или трактовкой контрактов,
законов и инструкций. Источники юридического риска включают в се
бя: проблемы кредитоспособности и обеспечения исполнения, так же
как проблемы законности финансовых инструментов и их подвержен
ность непредвиденным изменениям законов и инструкций. Юридиче
ский риск связан с кредитным риском, поскольку контрагенты могут
найти юридические основания для того, чтобы лишить сделку законной
силы.
Как мы видим из данных выше определений, описанные катего
рии риска не вписываются в четкие, отделенные друг от друга классы.
Операционный риск может создать рыночный и кредитный риск, и на-
632
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
оборот. Вот почему важно рассматривать финансовые риски с точки
зрения компании в целом. Управление совокупным риском обеспечива
ет общую и последовательную картину риска в деятельности компании.
Для этого требуется измерять риск во всех подразделениях компании и
по всем факторам риска, с использованием согласованных методик, си
стем и данных. Учитывая значимость всего этого для финансовых учре
ждений, мы сосредоточим внимание на управлении рыночным, кредит
ным и операционным рисками. Для получения более подробной инфор
мации о рисках ликвидности,
юридических рисках,
а также управле
нии совокупным риском мы обращаем ваше внимание на работу
[Jorion
(2007)].
Управление рыночным риском
7.2.
Меры риска: определения и свойства
7.2.1.
Мера риска необходима:
•
для определения рискового капитала, т. е. определения капитала,
необходимого финансовому учреждению для покрытия неожиданных
убытков;
•
как инструмент управления
-
это означает, что мера риска ис
пользуется менеджментом для того, чтобы оценивать и контролировать
уровень риска, свойственный тем или иным подразделением компании.
Задача определения подходящей меры риска Ф всегда была особен
но важной как с теоретической точки зрения, так и с практической. Су
ществуют подходы к ее определению, предложенные в статье
[Artzner,
Heath (1999)] (далее мы будем ссылаться на эту работу,
используя сокращение [ADEH (1999)]), которые в настоящее время при
Delbaen, Eber
и
няты ученым сообществом, но еще не всеми специалистами в области
финансов.
Для простоты и финансовой целесообразности, мы будем иметь де
ло с изменением цены некоторого финансового актива за один шаг
ЛРt =
Pt - Pt-1
(мы предпочитаем использовать ЛРt, а не
Pt,
посколь
ку понятие риска Ф интуитивно ассоциируется с доходами и убытка
ми). Мы могли бы использовать нетто-доходности (определяемые как
ЛРt/ Pt-1), но обычно удобнее использовать меру риска, которая из
меряет убытки в денежных единицах. Впрочем, мы также рассмотрим
примеры с использованием нетто-доходностей и лог-доходностей.
Сформулируем и обсудим свойства, которыми должны обладать ме
ры риска Ф как функции от д.Рt.
Если мы определяем Ф(ЛРt) как меру риска ЛРt, то в статье
ADEH
утверждается, что величина Ф(ЛРt) должна обладать следующими
свойствами.
7.2.
•
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
633
Трансляционная инвариантность. Пусть даны случайная ве
личина ЛРt, безрисковая процентная ставка
константа
Br
Е
R,
r (r
Е [О;
1))
и некоторая
тогда
(7.1)
•
Субадцитивность. Пусть даны изменения цен (или доходностей)
двух финансовых активов ЛРt,1, ЛРt,2, тогда имеет место неравенство
Ф(ЛРt,1
+ ЛРt,2)
~ Ф(ЛРt,1)
+ Ф(дРt,2).
(7.2)
•Положительная однородность. Пусть дана случайная вели
чина ЛРt и неотрицательная константа .Л, тогда
Ф(.ЛЛРt)
= .ЛФ(дРt).
(7.3)
Монотонность. Пусть даны изменения цен (или доходностей)
•
двух финансовых активов ЛРt,1, ЛРt,2, такие что ЛРt,1 ~ ЛРt,2, тогда
Ф(ЛРt,2) ~ Ф(ЛРt,1).
(7.4)
Первое свойство говорит о том, что, если мы прибавим детерми
нированную компоненту (безрисковый актив) к случайной величине,
то мера риска уменьшится на величину, инвестируемую в безрисковый
актив.
Второе свойство требует, чтобы мера риска портфеля, состоящего
из двух активов, (Ф(ЛРt,1
+ ЛРt,2)),
была не больше, чем сумма мер
риска каждого из составляющих портфель активов. Субадцитивность
гарантирует, что объединение позиций уменьшит общий риск.
Третье свойство говорит о том, что если мы увеличим сумму, ко
торая инвестирована в актив
Pt,
то мера риска также должна увели
читься. В частности, эта гипотеза требует, чтобы риск увеличивался
пропорционально увеличению инвестируемой суммы.
Отметим, что если выполнены свойства трансляционной инвари
антности и положительной однородности, то для любого действитель
ного
()
и заданной безрисковой ставке
r
имеем:
Кроме того, если мы воспользуемся свойством положительной однород
ности, взяв Л
= 2, то получим следующее равенство:
Ф(дРt
+ ЛРt) = Ф(ЛРt) + Ф(дРt),
которое показывает, что инвестирование равной суммы в другой, пол
ностью коррелированный с первым актив удваивает риск портфеля. Из
Гл.
634
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
последнего равенства следует, что в данном случае свойство субадди
тивности выполнено со знаком равенства.
Наконец, последнее свойство выражается в том, что если актив А
дает всегда более высокий: доход, чем актив В, то мера риска должна
показать нам, что инвестирование средств в актив А выгоднее, чем в В.
Другими словами, убытки, которым мы можем подвергнуться, инвести
руя средства в актив А, должны быть меньше, чем убытки, которым мы
можем подвергнуться, инвестируя средства в В. Конечно, если А все
гда выгоднее, чем В, мы имеем так называемый: арбитраж, и хорошая
мера риска должна указать на это.
Мера, которая удовлетворяет всем четырем перечисленным выше
свойствам, называется
согласованной мерой риска (а
coherent risk
measиre). Любую меру, для которой: не выполняется хотя бы одно из
этих свойств, нельзя рассматривать как согласованную меру риска.
1)
Ни дисперсия, ни стандартное отклонение не являются
согласованными мерами риска
Теперь мы хотим выяснить, является ли дисперсия Ф( ЛРt)
=
= Var(ЛPt), а также стандартное отклонение Ф(д.Рt) = .jVar(ЛPt),
согласованными мерами риска. Для этого мы должны проверить, удо
влетворяют ли эти функции свойствам
•
(7.3.2.)-(7.10).
Трансляционная инвариантность. Мы должны вычислить
и
Поскольку величина
Brr
детерминированна, немедленно получаем, что
справедливы равенства:
Var(ЛPt
+ Brr) =
Var(ЛPt)
и
из
которых
(7.3.2.)
следует,
что
свойство
трансляционной:
инвариантности
для дисперсии и стандартного отклонения не выполняется. Хо
тя на этом мы могли бы завершить наш анализ, но ради интереса мы
проверим оставшиеся три свойства.
•
Субаддитивность. Дисперсия суммы изменений: цен (илидоход
носте:й) двух активов может быть представлена как
Var(ЛPt,i
+ ЛРt,2) =
Var(ЛPt,i)
+ Var(ЛPt,2) + 2Cov(ЛPt,i, ЛРt,2),
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
635
а ковариация равна
Cov(ЛPt,1, ЛРt,2) =
где р -
Jv ar(ЛPt,1) · Jv ar(ЛPt,2) · р,
коэффициент корреляции. Так как коэффициент корреляции
по модулю меньше или равен единице, то верно неравенство
Cov(ЛPt,i, ЛРt,2) ~
Jv ar(ЛPt,1) · Jv ar(ЛPt,2),
воспользовавшись которым, получаем
+ Var(дl't,2)+
+2y'Var(дl't,1) · y'Var(ЛPt,2) => Var(ЛPt,i + дl't,2)
~ ( y'Var(ЛPt,i) + y'Var(ЛPt,2)) 2 .
Var(ЛPt,i
+ ЛРt,2)
~ Var(ЛPt,i)
~
Последнее неравенство эквивалентно неравенству
y'Var(ЛPt,i
+ ЛРt,2)
~
y'Var(ЛPt,i)
Таким образом, стандартное отклонение
-
+ y'Var(ЛPt,2).
это субадцитивная функция.
Дисперсия, тем не менее, не является субадцитивной функцией, так
как для нее свойство субадцитивности выполняется тогда и только то
гда, когда р ~ О, что неверно в общем случае.
•
Положительная
однородность.
Доказательство того,
что
стандартное отклонение удовлетворяет этому свойству, тривиально:
y'Var(ЛЛPt) = y'Л 2 Var(ЛPt) = Лy'Var(ЛPt)·
Следовательно, стандартное отклонение обладает свойством положи
тельной однородности.
Однако для дисперсии это свойство не выполняется. Докажем это,
предположив противное: пусть даны ЛРt и неотрицательная константа
Л, тогда в соответствии со свойством
(7.3)
Var(ЛЛPt) = ЛVar(ЛPt)·
Но в силу свойств дисперсии
Var(ЛЛPt) = Л 2 Var(ЛPt),
поэтому
Var(ЛЛPt) = ЛVar(ЛPt) = Л 2 Var(дJ't).
Откуда следует, что, с учетом Var(ЛPt) >О, величина Л должна удо
влетворять квадратному уравнению
Гл.
636
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
решениями которого являются Л1
= О, Л2 = 1. Но это противоречит
предположению о том, что Л может быть любым неотрицательным чис
лом. Таким образом, мы видим, что дисперсия не обладает свойством
положительной однородности.
•
Монотонность. Рассмотрим случайный доход ЛРt и строго по
ложительную константу е. Определим случайную величину дРj следу
ющим образом:
Заметим, что всегда дРj
>
ЛРt. Если дисперсия удовлетворяет свой
ству монотонности, то дисперсия случайной величины дРj должна
быть больше, чем дисперсия случайной величины ЛРt. Вместо этого
мы имеем:
Var(дPj) = Var(ЛPt +е) = Var(ЛPt),
а значит, свойство монотонности в этом случае не выполняется.
Мы можем рассмотреть более общий случай, когда е является слу
чайной
величиной,
принимающей только положительные значения.
В этом случае, поскольку справедливо следующее равенство:
Var(дPj)
= Var(ЛPt + е) = Var(ЛPt) + Var(e) + 2Cov(дl't,e),
величина Var(дPj) меньше, чем Var(ЛPt) тогда и только тогда, когда
Var(e)
=>
+ 2Cov(ЛPt, е) < О
Cov(ЛPt, е)
<
-~ Var(e).
Однако, так как свойство монотонности должно выполняться для про
извольных положительных случайных величин е, мы заключаем, что
дисперсия не удовлетворяет этому свойству. А значит, и стандартное
отклонение также не обладает свойством монотонности.
Таким образом, мы убедились, что: ни дисперсия, ни стандарт
ное отклонение не являются согласованными мерами риска!
Если дисперсия (и стандартное отклонение) не является согласован
ной мерой риска, то чем она (оно) является? Ответ прост: это, в соот
ветствии с ее определением, мера случайного рассеяния относительно
среднего. Желание того, чтобы наши доходы от портфельных инвести
ций были несильно рассеяны вокруг среднего, оправданно, однако мы
не можем утверждать, что инвестор, минимизирующий дисперсию (или
стандартное отклонение), в то же самое время минимизирует и риск!
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
637
Теорема о представлении
2)
Так как дисперсия не является согласованной мерой риска, мы мо
жем задаться вопросом: имеют ли согласованные меры некоторую спе
цифическую форму? Ответ на этот вопрос дает следующая теорема (см.
[ADEH (1999))):
Теорема
7.1.
Ф(ЛРt) является согласованной мерой риска тогда и
то.л:ько тогда, когда существует семейство вероятностнъ~х законов
Р, таких, что2
Ф(ЛРt) =
- inf {ЕР
[~J:.] 'р ЕР}.
Доказательство этой теоремы читатель найдет в
[ADEH (1999)].
Отметим некоторые важные аспекты:
•во-первых, усредняется прибыль (или убыток) рискового актива
с учетом безрисковой процентной ставки;
•
во-вторых, возможность выбирать вероятностный закон из семей
ства Р позволяет создавать бесконечно много согласованных мер риска.
Этот результат имеет как положительный аспект, так как можно вы
бирать наиболее подходящую меру риска, так и отрицательный аспект,
поскольку выбор меры риска становится субъективным выбором риск
менеджера;
•
в-третьих, результат теоремы получен для случая одного периода.
В работе
[Riedel (2004)]
он обобщен на многопериодный случай с уче
том всех возможных потоков наличности б(s), которые могут возник
нуть между моментами времени
t
и Т. Рассматривая капитализацию в
дискретном времени, он получает следующий, более общий, результат:
т. е. мы вычисляем ожидаемое значение всех потоков наличности, дис
контированных в соответствии с безрисковой ставкой процента
r.
Отметим очень простое, но весьма любопытное следствие предыду
щей теоремы.
Теорема
мер
7.2. Любая въ~пук.л,ая линейная комбинация
риска снова согласованная мeJXL риска.
2 Под
согласованнъ~х
ЕР~ понимается среднее значение случайной величины~' подчиняющейся
закону распределения вероятностей Р.
Гл.
638
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Пусть мы имеем п мер риска Фj(ЛРt) (где
j
Е
{1, 2, ... , п} ).
Возь
мем п положительных констант Cj, сумма которых равна единице. Тогда
результирующая мера
n
Ф(ЛРt) = :LcjФj(ЛPt)
j=l
будет согласованной мерой риска.
Средние ожидаемые потери уровня а (СОПа) как
3)
согласованная мера риска3
Вводимая в данном разделе характеристика
-
~средние ожидае
мые потери уровня а» (СОПа) измеряет среднее значение потерь доли
а худших результатов, которые мы можем получить от инвестиций.
Очевидно, при ЛРt =
Pt - Pt-1
эта величина должна принимать от
рицательные значения. Однако при определении и интерпретации ме
ры риска как монотонно неубывающей функции потерь нам удобнее
оперировать с потерями как с положительными величинами. Читатель
должен принять во внимание это замечание при усвоении последующе
го материала. Перед тем как мы дадим формальное определение СО Па,
рассмотрим следующие характеристики.
Предположим, что случайная величина ЛРt = ЛРt/(1 + r) имеет
функцию плотности f (ЛРt), которая непрерывна на всей действитель
ной оси. Для простоты и без ограничения общности мы рассмотрим
случай, когда r =О, так что ЛРt = ЛРt. Тогда кумулятивная функция
распределения случайной величины дf>t в точке х имеет вид
х
F(x) = /
f(y)dy.
-оо
Заметим, что, в силу существования плотности f(ЛPt), функция рас
пределения F(ЛPt) непрерывна.
Рассмотрим уравнение
F(x)
где а
-
=а,
константа, принадлежащая интервалу (О;
ности функции
F
для любого а Е (О;
1)
1).
В силу непрерыв
будет существовать хотя бы
одно решение этого уравнения.
3В
англоязычной литературе этот показатель называется ''Тhе Expected Shortfall"
и обозначается через
ESa.
7.2.
Если функция
639
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
F
строго возрастает, то она обратима (причем, обрат
ная функция будет также непрерывной), а значит, решение уравнения
единственно и дается формулой
'У= р-1(0).
Если же функция
F
не является строго возрастающей, мы можем
воспользоваться понятием обобщенного обращения (или обобщенного
квантиля), в соответствии с которым
р- 1 (о)
= sup{xlF(x)
~о},
так что величина
'У=
sup{xlF{x)
~о}
будет решением уравнения.
На рис.
7.1
изображен пример функции плотности, кумулятивная
функция распределения, построенная по этой плотности, и функция,
обратная к кумулятивной функции распределения.
f(x)
а
х
F(x)
1 -------------------
р-1 а)
Рис.
7.1.
О
х
Функция плотности, кумулятивная функция распределения и
обратная функция
Теперь может быть определена величина СОПа для о Е {О;
Определение
7 .1.
Средние о:жидаем'Ь/,е потери уровня о для слу
'Ч.айной ве.1~и'Ч.инъt ЛРt с функцией распределения
СОПа(ЛРt))
-
1).
F ( обозна'Ч.аются
это cpeдttee зна'Ч.ение доли о худших потеръ, взятое
со знаком минус:
!
Q
СОПа(ЛРt) = - ~
о
p- 1 (z)dz.
(7.5)
Гл.
640
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Для СОПа выполнены свойства трансляционной инвариантности,
положительной однородности и монотонности, что легко следrет из
свойств квантилей. Выполняется и свойство субадцитивности, одна
ко его доказательство значительно более сложно (см.
(2002)]).
Таким образом, СОП 0 (.)
Если в выражении
[Acerbl, Tasche
согласованная мера риска!
-
устремить а к нулю, то, используя правило
(7.5)
Лопиталя, мы получим:
а
lim СОП 0 (ЛРt)
а-+О
=
-/а J p- 1 (z)dz
lim _ _
о .......
8- - -
а-+0
да а
= - lim р- 1 (а) = -F- 1(0) = СОПо(ЛРt),
а-+0
т. е. СОПо(ЛРt)
-
наибольший убыток, который можно получить для
случайной величины ЛРt. Если функция плотности
f
непрерывна и
положительна на всей отрицательной действительной полуоси, как это
представлено на рис. 7.1, то СОПо(.)
= +оо.
Отметим еще один важный
факт, касающийся СОПа (ЛРt):
!
1
СОП1(ЛРt) = -
p- 1 (z)dz
= -Е[ЛРt]·
о
Последнее равенство мы получили, воспользовавшись заменой пе
ременных
у= p- 1 (z)
=Ф-
F(y) = z
=Ф-
f(y)dy = dz,
в интеграле
+оо
F- 1 (1)
СОП1(ЛРt) = -
f
f
yf(y)dy = -
F-l(o)
yf(y)dy
-оо
=
-Е[д.Рt].
В случае, когда а Е (О; 1), воспользовавшись этой заменой, получим
а
r1 ~
О
F-l(O)
СОП 0 (ЛРt) = -~ f p- 1(z)dz = -~ f
yf(y)dy
=-
Ft~>
~
f
yf(y)dy.
-оо
Таким образом, мы определили меру риска СОП 0 (.) для любого а Е
Е [О; 1).
Пр им ер
7.1. СОП 0 (ЛРt) для случайной величины ЛРt, равно
мерно распределенной на интервале (а; Ь).
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
641
Функция плотности случайной величины ЛРt, распределенной рав
номерно на интервале (а; Ь), как известно, задается соотношением:
ь~а,
/(у)= { о
у Е (а; Ь);
в остальных случаях.
Соответствующая ей кумулятивная функция распределения равна
=
F(x)
l
x
f(y)dy
=
{
-оо
х ~ Ь;
1,
ь=:,
о
F
< Ь;
иначе,
'
и обратная функция для функции
а< х
равна
р- 1 (а) =а+ а(Ь - а),
где а Е [О;
1].
Тогда для а Е (О;
СОПа(ЛРt)
1]
= --11а p- 1 (x)dx =
а
о
11а (а+
= -а
х(Ь-
a))dx
=-а
0
1
- -а(Ь2
а).
Если а = О, то СОПа(ЛРt) = -а (СОПо(ЛРt) положительны, ес
ли а отрицательно). Кроме того, СОП1(ЛРt)
= _аtь,
т.е. СОП1(ЛРt)
равно среднему значению ЛРt, взятому с обратным знаком.
4)
Спектральные меры риска
В предыдущем разделе СОПа(.) было определено как среднее зна
чение потерь доли а худших результатов, которые мы можем получить
от инвестиций. Однако вместо того, чтобы вычислять среднее значе
ние, мы можем рассмотреть взвешенное среднее значение, тем самым
обобщая СОПа(.).
Обозначив весовую функцию через
отрезке [О;
1]),
<p(z)
(которая определена на
введем понятие спектральной меры.
Определение
7.2.
Мера риска Mip(ЛPt) назь~вается спектра.л:ь-
ной, если
Mip(ЛPt) = - lof 1 <p(z)FДA dz,
t
где FД}t (z), как и прежде, функция, обратная к функции распределения
случайной величины ЛРt.
Величину
ятия риска
rp( z)
( ''the
еще называют спектром риска или функцией непри
risk-aversioп fипсtiоп'~.
Гл.
642
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Легко видеть, что СОП 0 (.) при о Е (О;
ка, спектр риска которой <p(z) -
1] -
спектральная мера рис
разрывная функция, принимающая
значение О для прибылей или небольших убытков и постоянное неот
рицательное значение для больших убытков. Если более формально,
то для спектра риска меры СОП 0 (.) мы определяем <p(z) с помощью
индикаторной функции множества:
где
1
1, z < Q
- { О, иначе.
{z<a} -
Возникает вопрос: всегда ли спектральная мера является согласо
ванной мерой риска? Ответ на этот вопрос дает следующая теорема
(см. [AcerЬi
Теорема
(2002)]).
7.3.
Спектра.л:ьна.я мера согласованна тогда и только тогда,
когда
• <p(z) неотрицательна;
• <p(z) невозрастающая;
• f01 <p(z)dz = 1.
Следовательно, если мы хотим доказать, что СОП 0 (.) для о Е (О;
1]
является согласованной мерой риска, то нам необходимо проверить три
условия из теоремы
7.3.
Вместо того чтобы проверять эти условия ал
гебраически, мы предпочитаем дать более наглядный ответ, используя
графическое представление спектра СОП 0 (.), приведенного на рис.
7.2:
1
a-i------
о
Рис.
7.2.
а
z
Графическое представление спектра СОП(.)
Можно заметить, что спектр СОП 0 (.) нигде не принимает отрица
тельных значений, нигде не возрастает и его интеграл по отрезку [О;
графически определяемый как площадь под графиком, равен
1.
1),
7.2.
Отметим,
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
что первые два условия
643
из теоремы
отражают
7.3
несклонность к риску. В соответствии с этими условиями, весовые ко
эффициенты, отвечающие большим убыткам, должны быть не меньше,
чем весовые коэффициенты, отвечающие меньшим убыткам.
Из рисунка
7.2
видно, что инвестор, использующий СОП 0 (.), при
писывает одинаковые веса всем убыткам, большим, чем определенный
порог, в то время как меньшим потерям и прибылям он приписывает
нулевые веса. Однако эта мера не является «идеальной» спектраль
ной мерой, потому что она несовместима с теорией неприятия риска.
Если мы имеем «идеальную» функцию неприятия риска, то веса, соот
ветствующие этой функции, должны убывать гладко, и скорость этого
убывания связана со степенью неприятия риска следующим образом:
чем больше инвестор не расположен к риску, тем быстрее будут убы
z.
вать веса с ростом аргумента
Таким образом, чтобы получить спектральную меру риска, инве
стор должен выбрать подходящую для себя функцию неприятия риска.
Этот выбор субъективен, но в нем можно руководствоваться исследо
ваниями по теории функций полезности. Обращаем ваше внимание на
статью
[Acerbl (2004)]
и на имеющиеся в ней ссылки для более подроб
ной информации о теории полезности.
5) Граница потерь уровня а (ГП 0 ) 4
ГП 0 определяется следующим образом:
Определение
Граница потерь уровня а (ГП0 )
7.3.
-
это мини
мальнъtе потери в доле а всех худших результатов.
Пусть ЛРt
случайная величина, описывающая доходы/убытки,
-
с функцией распределения
что
F
F.
При заданном уровне а и при условии,
строго возрастающая и обратимая функция, ГП 0
-
это величина
потери 'У, равная
'У= -F- 1 (a).
Другими словами, ГП 0
-
это квантиль функции распределения убыт
ков/доходов, взятый со знаком «минус» (объяснение появления знака
«минус» в этом определении было дано выше). Если функция
F
не
является обратимой, то мы воспользуемся понятием обобщенного обра
щения (или обобщенного квантиля):
р- 1 (х) = sup{xlF(x) ~а},
таким образом,
'У=
4 Как
-sup{xlF(x)
~а}.
уже было отмечено, в англоязычной литературе этот показатель называется
"The Value at Risk"
и обозначается
VaRa.
Гл.
644
ГПа
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
это не величина убытка, который мы можем получить, а
-
это уровень убытков, который будет превышен с определенной вероят
ностью, установленной априорно. Подобно СОПа, ГПа
-
спектральная
мера с функцией неприятия риска <р( z), имеющей вид невырожденной
дельта-функции Дирака, которая придает убытку 'У (см. рис.
7.3)
конечный вес, а всем другим возможным убыткам/доходам
нулевой
-
бес
вес. Напомним, что дельта-функция Дирака определяется как функ
ция, равная нулю на всей действительной оси, кроме О, где она равна
бесконечности, при этом ее интеграл равен
1.
Если мы положим
rp(z)
= Dirac(z -
а),
то получим:
ГЦ,= В выражении
[
(7.6)
Dirac(z - o)F- 1 (z)dz = -F- 1 (o).
(7.6)
мы воспользовались функцией Дирака, которая
аккумулирует всю плотность в точке а (функция не равна нулю только
при
z
=а). Спектр ГПа представлен на рис.
7.3.
<p(z)=Dirac (z-a)
о
Рис.
7.3.
z
а
Графическое представление спектра меры ГПа
Воспользовавшись теоремой
7.3,
получаем, что ГПа не является со
гласованной мерой риска, так как, хотя спектр меры неотрицателен и
его интеграл по отрезку [О;
1)
равен единице (в соответствии с определе
нием функции Дирака), ее спектр не является невозрастающей функ
цией: формально он сначала возрастает, а затем убывает.
Можно спросить: какое именно условие в определении согласован
ной меры риска не выполняется? Ответ: для ГПа не въtполняется свой
ство субаддитивности. Таким образом, можно составить два портфеля
так, что
Пр им ер
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
Несубадцитивность ГПа.
645
Предположим, имеется объединенный портфель, составленный из
портфеля трейдера А и портфеля трейдера В. Портфель трейдера А
состоит из проданного опциона
PUT (без денег), а портфель трейдера В
состоит из проданного опциона CALL (без денег), причем до истечения
срока их действия остается один день5.
Обработка данных предыстории подобных опционов позволила оце
нить вероятность исполнения
величиной
«В деньгах»
каждого из этих опционов
4%.
Таким образом, каждый из трейдеров А и В имеет портфель, кото
рый имеет 96%-ный шанс вообще не потерять деньги. Например,
ГПо.05
= О для каждого из них.
Однако объединенный портфель имеет
лишь 92%-ный шанс не потерять деньги, так что для него ГПо.05
Подходы к оценке риска с использованием ГПа
> О.
подвергаются
серьезной критике на том основании, что эта мера не является согла
сованной (из-за того, что ГПа не обладает свойством субадцитивности,
см.
[Artzner
и др.
(1999)], [Acerbl (2004)]).
Если не выполняется свойство субадцитивности, то это может при
вести к странным и нежелательным последствиям: например, при ис
пользовании ГПа для установки размера гарантийного депозита на
фьючерсных рынках не учитываются возможные убытки, превыша
ющие ГПа, что может подвергнуть оценщиков значительному риску
очень больших потерь, превышающих ГПа. Одно из важных послед
ствий использования такой несубадцитивной меры риска, как ГПа, для
установки размера гарантийного депозита состоит в том, что инвесторы
могут разбить свои счета на несколько так, чтобы уменьшить суммар
ный размер гарантийного депозита и тем самым подвергнуть органи
заторов биржи скрытому остаточному риску, против которого они не
будут иметь никакого эффективного обеспечения со стороны ее инве
сторов. Кроме того, банк, открывающий эти счета, мог бъt оставать
ся в неведении относите.л.ьно взятого на себя риска: подобный метод
вкупе с фальшивыми хедж-позициями использовал французский трей
дер Жером Кервьель, чтобы скрыть свои огромные позиции на рынке
Eurex, что впоследствии
в Societe Generale.
5 Опционы
вызвало более чем пятимиллиардные убытки
PUT и CALL дают право их владельцам соответственно продать и
PUT оговоренная
купить определенный товар по определенной цене. Если в опционе
цена продажи ниже рыночной, то он называется на настоящий момент опционом
«без денег». Соответственно, если в опционе
CALL оговоренная
цена покупки выше
рыночной, то он называется на текущий момент опционом «без денег». Владелец
опциона реализует свое право покупки (продажи) у продавшего ему опцион трейдера
в «безденежной» ситуации. В этом случае трейдер несет убытки.
Гл.
646
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Несмотря на вышеизложенные критические замечания, Второе ба
зельское соглашение сосредоточено в значительной степени на исполь
зовании ГП 0 . Как так могло получиться? Основное препятствие для
перехода к согласованной мере риска (например, к СОП 0 )
-
тести
рование на исторических данных: тестирование ГП 0 на исторических
данных довольно просто, и это мы увидим в следУющем разделе, тогда
как тестирование СОП 0 (или в общем случае любой спектральной меры
риска) на исторических данных
-
более сложная задача, предлагаемые
решения которой оцениваются неоднозначно. Поэтому везде далее мы
сосредоточимся главным образом на использовании ГП 0 , даже если ис
пользование другой меры риска кажется более целесообразным.
П р и м е р
7.3.
ГП 0 для случайной величины, имеющей нормаль
ное распределение.
Пусть случайная величина подчинена(µ, и2 )-нормальному распре
делению (т. е. ЛРt,..., N(µ, и 2 )). Тогда
р (др, ,,,; -'У) = р { др~1
= V27Г
27ГО'
где Ф( х)
-
µ ,,,;
-'У"- µ }
1-"( -~
-оо
е
2и
=
dy = Ф
(-"'(- µ)
О'
,
стандартное нормальное распределение, квантиль уровня о
которого обозначим через Ф- 1 (о). Тогда
Последнее равенство справедливо в силу симметричности стандарт
ного нормального распределения относительно нуля.
На рис.
7.4
графически представлен квантиль уровня о
стандартного нормального распределения (Ф- 1 (0,05)
ветственно ГПо,оs
Пр им ер
ке
=
= 0,05
-1,645, соот
= 1,645).
7.4.
Нефтяные теплоэнергетические фьючерсы на рын
NYMEX.
Ниже изображен график функции плотности распределения сто
имости портфеля фьючерсов с трехдневным сроком, построенный по
историческим данным.
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
647
0,40
0,3S
0.30
o.2s
0,20
O,IS
0,10
o.os
0-4
-3
о
-1
-2
4
Квантиль
Рис.
7 .4.
Квантиль уровня
0,05
для случайной величины, имеющей стандартное
нормальное распределение (соответственно ГПо,оs
= 1,645)
Значение позиции (в тыс. долл)
Рис.
7 .5.
График функции плотности распределения стоимости портфеля фью
черсов с трехдневным сроком, построенный по историческим данным
На графике (рис.
7.5)
отмечены величина «сегодняшней» стоимо-
сти портфеля («текущее значение позиции») и 5%-ный уровень границы
потерь ГП = ГПо,оs(t,
3). Разница между текущим значением позиции и
ГПо,оs(t, 3) составляет 5 млн долл. Таким образом, когда мы говорим,
что позиция имеет трехдневный ГПо,оs в 5 млн долл., подразумевается,
что мы на 95% уверены, что значение позиции не уменьшиться боль
ше, чем на 5 млн долл. за следующие три дня. Однако есть 5%-ная
вероятность того, что потери могут превысить уровень в 5 млн долл.,
а в экстремальных случаях они могут составить значительно большую
сумму.
6)
Расчет границы потерь по нетто-доходностям
И ЛОГ-ДОХОДНОСТЯМ
Пока что мы вычислили ГПа для изменения цены некоторого фи
нансового актива за один шаг дРt,
= Pt -
Pt-1·
Однако во многих фи
нансовых приложениях вместо предположений относительно распреде-
Гл.
648
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ления изменений цены за
l
шагов, ЛРt
=
делаются неко
Pt - Pt-l,
торые предположения относительно распределения l-периодных нетто
или лог-доходностей.
Вычислим ГП 0 ( t, l) для ЛРt
= Pt - Pt-l, если задано распределе
ние l-периодной нетто-доходности rt(l) = (Pt - Pt-l)/ Pt-l=
•
где rt(l) -
l-периодная нетто-доходность, а
Fz- 1 (a)
- квантиль (или
обобщенная обратная функция) функции распределения
доходности
rt(l).
.Fl (х)
нетто
Отсюда следует
(7.7)
•
Вычислим ГП 0 ( t,
l)
для ЛРt
ление l-периодной лог-доходности
Q
= Pt - Pt-l , если
ft(l) = ln(Pt/ Pt-l):
=P{R-R
(tl)}=P{
Pt
t
t-l -.:::::-ГП
.;;:
Q
!
D
=
=
р {in
(Ji.) ~ ln (- ГПа(t,
задано распреде
:::::_ГПa(t,l)+Pt-l}=
-..;;:
D
.Гt-l
.Гt-l
l) + Pt-l) } =
Pt-l
Pt-l
Р {r,(l).;; Jn (- Щ,(t~~~ Рн)} = Р {r1(I).;; F,- 1 (a)},
.Fz-
1 (a) - квантиль (или обоб
где ft(l) - l-периодная лог-доходность, а
щенная обратная функция) функции распределения
х) лог-доходнос
ти ft(l). Отсюда немедленно получаем, что
ГП 0 (t, l) =
Fl (
- 1
-Pt-l · (exp(Fz(а)) - 1).
(7.7а)
Обычно в литературе по финансам используются лог-доходности.
Одно из преимуществ лог-доходностей состоит в том, что можно легко
вычислить лог-доходность за К дней, которая равна сумме ежеднев
ных лог-доходностей за каждый из этих К дней. Однако в рыночной
практике обычно используется формула ГП 0 для нетто-доходностей, в
которую вместо нетто-доходностей подставляют лог-доходности: необ
ходимо помнить, что это лишь приближение, справедливое для ма
Л'ЫХ значений лог-доходностей. Для более подробной информации см.
[Christoffersen (2003),
гл.
3
и приложение
3.10].
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
Пр им ер
7.5.
Предположим,
что
649
ежедневные
лог-доходности
портфеля имеют нормальное распределение со средним
µr
и диспер
сией и~.
•Пусть а=
Ur
1%, l = 10 дней, Pt-l = 10млн долл., µr =О, 1% и
= 1,5%.
Среднее и стандартное отклонение 10-дневной доходности равны
10 · µr = 0,01,
y'iO · Ur = y'iO · 0,0015
= 0,0474,
соответственно.
1%-ный
квантиль стандартного нормального распределения равен
Ф- 1 (0, 01)
= -2, 3263.
Следовательно, граница потерь уровня
1% для
10-дневного периода по
лог-доходностям равна
ГП0,01(t, 10)
= -10
Ur
= -Pt-l ( e<Ф-1(0,01)v'Wиr+loµr) - 1) =
млн долл.· (О, 9044
-1)
=О,
956
млн долл.
• Пусть а = 1%, l = 30 дней, Pt-l = 500 млн долл., µr = 0,05% и
= 1,3%, тогда
ГПо,01(t,30) = -500 ( е<- 2 · 3263 ·v'ЗО·О,ОlЗ+ЗО·О,ОООS} - 1) = 69,9220848.
Следовательно, ГП0,01(t, 30)
Ur
= 69,922 млн долл.
или
13,98%.
• Пусть а = 1%, l = 30 дней, Pt-l = 500 млн долл., µr = 0,05% и
= 1,4%, тогда
ГПо,01(t,30) = -500 ( е<-2,з26З·v'ЗО·о,014+зо-о,оооs) - 1) = 75,3672319.
Следовательно, ГП0,01(t, 30)
= 75,367 млн долл.
или
15,07%.
Заметим, что, если изменить ежедневную волатильность лишь на
0,1%
(это соответствует изменению годовой волатильности на
идет пересчет на год с
250
1,58%, где
операционными днями), абсолютная разница
меж.цу рассчитанными границами потерь уровня
ода в каждом из этих двух случаев составит
тельная разница
1,09%.
0,01 30-дневного пери
5,445 млн долл., а относи
Этот пример показывает, что даже небольшие
ошибки в расчетах существенно влияют на величину границы потерь.
Гл.
650
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
7) Условная граница потерь уровн.я а: (УГП 0 )
6
Для того чтобы преодолеть недостатки меры ГПа, была предложе
на другая мера риска: условная ГП 0 , УГПа. Основная проблема меры
ГП 0 состоит в том, что она не учитывает убытки, большие определенно
го уровня, поэтому было предложено решать эту проблему, беря среднее
значение по всем ГПq от
q =О
до необходимого уровня (например, до
уровня а:):
УГПа
= -11а ГПqdq.
Q
о
Пусть случайная величина ЛРt имеет функцию распределения
торая непрерывна. Тогда, вспоминая определение ГПq(ЛРt)
F,
ко
(7.6),
по-
лучим:
11а p- 1 (q)dq,
УГПа(ЛРt) = - Q
о
т. е. УГПа(ЛРt) совпадает с СОПа(ЛРt)· Если распределение
F не яв
ляется непрерывным, то УГП 0 (ЛРt) и СОПа(ЛРt) уже не совпадают
(см. [Rockafellar, Uryasev {2002)]). Перед тем как продолжить описание
свойств УГПа, введем некоторые обозначения. Пусть:
случайный вектор у описывает неопределенность. Это может
•
быть, например, вектор доходностей или вектор курсов акций (послед
нее соответствует вектору, i-я компонента которого ЛРi, где i = 1,
... ,N);
• вектор
х
вектор весов портфеля, независимый от у (условие
-
независимости весьма важно при описании свойства выпуклости);
• z
= f(x, у)
-
доход/убыток портфеля с вектором весов х; далее
мы будем рассматривать в качестве «дохода/убытков'> разность дРt =
= Pt-1 - Pt,
так что убыточные значения
z
будут положительными, а
ГП 0 будет квантилем функции распределения случайной величины
z
при значениях а:, близких к единице;
• Ф(х, ·) - функция распределения дохода/убытка z;
(0 (х)
•
-
ГПа дохода/убытка портфеля с вектором весов х.
Теперь опишем предложенный в статье
[Rockafellar, Uryasev {2002)]
подход к определению УГП 0 в общем случае, когда функция распре
деления
F
произвольна (необязательно непрерывна). Прежде введем
четыре определения:
1.
УГПt)
Верхняя
условная
граница потерь уровня
а:
(обозначается
- это среднее значение худших потерь строго больших ГПа
(в использованных ранее терминах, это СОПа):
УГПt
6В
= E[f(x, y)lf(x, у) > (а(х)];
англоязычной литературе этот показатель называется ''Тhе Conditional Value
at Risk"
и обозначается
CV aRo..
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
651
Нижняя условная граница потерь уровня а
2.
УГП~)
(обозначается
это среднее значение худших потерь, не меньших ГПа, т. е.
-
потерь, которые больше или равны ГПа:
УГП~ =
~ (а(х)];
E[f(x,y)lf(x,y)
УГП~ также называют «хвостовой границей потерь уровня а».
3.
«а-хвостовое распределение» {обозначается Фа{х,()), соответ
ствующее функции распределения Ф{х,() случайной величины
= f(x,
z
=
у), определяется следующим образом:
О, ( < (а(х);
{
Фа(х, () = [Ф{х, () - а]/[1 -
а], ( ~ (а(х).
4. Условная граница потерь уровня а {обозначается УГПа), отвеча
ющая случайной величине z = f (х, у), - это среднее случайной величи
ны, имеющей а- «хвостовое» распределение, соответствующее функции
распределения Ф{х,
случайной величины
()
z
= f(x, у).
Согласно следующей теореме УГПа равна взвешенному среднему
ГПа и УГПt.
Теорема
7.4.
Пусть Ла(х)
-
зна-ч.ение а-хвостового распределения в
то-ч.ке (а ( х), а именно
Ла(х) = [Ф{х, (а(х))
Если Ф(х, (а(х))
- а]/[1 - а],
О~ Ла ~
1.
<
1 (т. е. существует ненулевая вероятность того,
-ч.то потери будут не больше (а (х)), тогда
О~ Ла(х)
<1
и
УГПа
= Ла(х)(а(х) + [1- Ла(х)]УГЩ = Ла(х)ГПа + [1- Ла(х)]УГЩ.
Если же Ф (х, (а (х))
=
1 ( т. е. (а (х) - это наибольшая возможная
потеря), тогда
УГПа
= (а(х).
Результаты теоремы не должны удивлять, поскольку они относят
ся к произвольным функциям распределения, которые могут быть и
дискретными.
Более того, в статье
[Rockafellar,Uryasev {2002)]
доказывается, что
УГПа является согласованной мерой риска и выпукла. Последнее имеет
значение для линейного программирования и оптимизации портфеля
(см. рис.
7.6).
Гл.
652
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Риск
х
Рис. 7.6. УГП 0 выпукла, но ГП 0 , УГП;, УГП;t могут быть невыпуклыми!
Пр им ер
7.6.
ГПа и УГПа для случайной величины, подчиняю
щейся нормальному распределению.
Пусть случайная величина ~ имеет нормальное распределение со
среднимµ и стандартным отклонением и. Тогда получим:
ГПа{~) =(а{~)=µ+
ki{0,05) = -1,65
УГПа(~) = Е[ ~ 1 ~~(а(~)]=µ+ k2(a)u, k2{0,05) = -2,06.
Пр им ер
чай
7.7.
ki{a)u,
ГПа и УГПа для дискретного распределения {слу
1).
Предположим, что дискретная случайная величина~ может прини
1· Возьмем
мать шесть равновероятных значений: р1 = р2 = ... = Рб =
а= =
тогда:
i g,
Ла
= {Ф{(а) - а)/{1 - а) = {4/6 - 4/6)/{1 - 4/12) =О,
УГПа =О· ГПа + 1 · УГП~ = УГП~ = ~/s + ~fб·
Следовательно, мы получаем: ГПа :::;; УГП~ :::;; УГПа = УГП~ (см.
рис.
7.7).
CVaR
Вероятность
1
1
1
1
6
6
6
6
о
12
о
9
-о
fi
Потери
fз
1
6
/!4 1
VaR
.......
CVaR"
l
1
6
л
fffi)
:ii::
fs
~
16
1
CVaR+
Рис. 7. 7. ГПа, УГП;, УГП;t, УГПа для дискретной случайной величины ~
П ри мер
чай
653
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.8.
ГПа и УГПа для дискретного распределения (слу
2).
Предположим, что дискретная случайная величина ~ может прини
1· Возьмем
мать шесть равновероятных значений: р1 = р2 = ... = Рб =
а = 152 , тогда:
Ла =(а
- Ф{(а))/а = {5/12 - 4/12)/(5/12) = 1/5
УГПа = 1/5 · ГПа + 4/5 · УГП~ = ~fi + if2.
Следовательно, мы получаем: ГПа ~ УГП~ ~ УГПа ~ УГП~ (см.
рис.
7.8).
CVaR
Вероятность
1
1
1
1
_!_
l!
1
-O~----<Q-~----1Q-~-~--+6
__~/~12_л_4l-6--~-~-6--/,
!,
1з
fs
\ 1,
1fs + 1f: =
/1. /
Потери
VaR
CVaR-
CVaR+
Рис. 7 .8. ГПа, УГП;;, УГПt, УГПа для дискретной случайной величины ~
7.2.2.
Обзор стандартных методов управления
рыночными рисками
До сих пор мы определили основные понятия и инструменты, исполь
зуемые в управлении финансовым риском. Далее мы проанализируем
стандартные методологии управления рыночными рисками.
Стандартные методики, связанные с управлением рыночными рис
ками, можно разделить на две группы.
•
Ана.л.ити-ческие методъt: текущая стоимость портфеля вычисля
ется в зависимости от текущих значений факторов риска на основании
некоторой параметрической модели, в которой обусловливается воздей
ствие изменений факторов риска на стоимость портфеля.
Стандартная техника этого семейства методов реализована, напри
мер, в дисперсионно-ковариационном методе (ДКМ) и в методе дельта
гамма; оба эти метода дают подходы к управлению риском.
•
Имитационн:ые методъt: для каждого сценария из некоторого
диапазона сценариев изменений факторов риска оценивается стоимость
портфеля. В результате получим ряд из стоимостей портфеля, по ко
торому построим эмпирическую функцию распределения. ГПа этого
Гл.
654
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
портфеля будем оценивать соответствующим квантилем построенной
эмпирической функции распределения.
В зависимости от условий факторами рыночного риска могут быть
курсы акций, индексы, процентные ставки, обменные курсы, цены на
драгоценные металлы, цены на сырьевые товары и т.д.
Важные примеры методов этой группы
-
историческое моделиро
вание (ИМ), моделирование методом Монте-Карло (МММК) и полная
оценка (ПО) для управления опционным риском.
Если мы используем аналитические методы, тогда нам необходи
мо выбрать некоторую функцию распределения, которую мы считаем
адекватной нашим данным. После чего оцениваем параметры выбран
ного
распределения,
например,
в
случае
нормального
распределения
мы оцениваем среднюю величину и стандартное отклонение. Однако
часто бывает, что, выбирая какую-нибудь хорошо известную функцию
распределения, мы неадекватно описываем распределение анализируе
мых данных. Но мы можем воспользоваться методами имитационного
моделирования, с помощью которых иногда можно получить более точ
ное приближение для функции распределения.
1)
Дисперсионно-ковариационный метод (ДКМ)
Идея, лежащая в основе этого метода, состоит в том, чтобы оце
нивать распределение доходностей (или изменений цен), линеаризируя
доходность портфеля и предполагая, что факторы риска имеют нор
мальное распределение.
Пусть
{ri,t, i
= 1, ... , n}
-
совокупность лог-доходностей на день t
(факторы риска). Положим, rp,t -
и пусть
rp,t
лог-доходность портфеля на день
t
= Е~ 1 WiTi,t = w'rt. Поскольку rt Е N(µ, Е), мы получим,
что
rp,t Е
Вектор средних
µ
1
1
N(w µ, w Ew).
и ковариационная матрица Е оцениваются по
наблюдениям Тt-т, • .. , Tt, и в результате функция распределения лог
доходностей портфеля оценивается нормальным распределением со
средним Р, и дисперсией
1 ...
w Ew,
где
fL
Е соответственно.
Тогда ГПа оценивается величиной
...
и Е
-
оценки параметров
µ
и
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
2)
655
Дельта-гамма аппроксимации для нелинейных
портфелей
Если в наш портфель включены нелинейные инструменты, такие
как опционы, то предыдущий метод использовать уже нельзя. Один из
первых подходов к решению такой задачи состоял в том, что необходимо
измерять влияние локального изменения факторов риска на стоимость
портфеля с помощью среднего для производных (стоимости портфеля
по факторам риска), т. е. использовать приближения к нелинейным це
нам опциона. Если использовать приближение первого порядка, то мы
имеем дельта-подход, а если использовать приближение второго поряд
ка, тогда мы имеем гамма-подход.
Для более детального описания этого подхода рассмотрим совокуп
ность факторов риска
{xi,i = 1, ... ,n} и предположим, что стоимость
такт времени t может быть записана в виде:
нашего портфеля в
Xp,t = f(Xi,t, ... , Xn,t),
где
Xi,t -
значение фактора риска
функция, отображающая
Rn
в
R.
в такт времени
Xi
или опцион С на базисный актив
f(S).
а
f -
некоторая
Например, это может быть линейный
портфель, составленный из акций, для которого
обращения т, где С=
t,
Xp,t
=
Е~ 1 WiXi,t;
с ценой исполнения К и сроком
S
Функцию
можно получить, например, из
f
формулы Блэка-Шоулса (см., например, [Ширяев
{2004), с. 911-912)).
Предположим, что факторы риска изменяются за один такт време
ни на дi, i
+ дi.
= 1, ... , n, т. е. Xi,t+l = Xi,t
непрерывно дифференцируема по всем
Xi, i
Тогда, если
f (х1, ... , Xn)
= 1, ... , n, мы можем полу
чить аппроксимацию первого порядка для изменения стоимости порт
феля:
д
= J(X1,t + д1, ... , Xn,t + дп) - f (Xi,t, ... , Хп,t) ~
n д1_
~ Е дх· (X1,t, · · · ,Xn,t)Лi.
i=l
Отметим, что если
i
Xi д·i
это цена, т. е.
xi
= Si,t и дi = Si,t+l - si,t, тогда
S·н1- S·t
= S·t
i, s
i, = S·t'D·t+1·
i,
i, .&"i,
i,t
Значение первой частной производной для
{Xi,t, ... , Xn,t) обозначим через Oi (oi
=
J(x1, ... , Xn) по Xi в точке
3!;(X1,t, ... , Xn,t)). Из того, что
n
л~ ~oiдi,
i=l
Гл.
656
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
мы получим приближение для условного математического ожидания и
условной дисперсии изменения стоимости портфеля в следующий такт
времени
(t + 1),
при условии информации на сегодняшний день t:
n
µ(д) ~
L OiEдi,
i=l
L
и 2 (д) ~
OiOjCov(дi, дj)
l~i,j~n
или, если
Xi,t = Si,t:
n
µ(д) ~
L OiSi,tERi,t+1,
i=l
l~i,j~n
Гауссовское приближение для ГПа(д) дается следующим выражением
+ Ф- 1 (а)и(д).
ГПа(д) = µ(д)
Если
Xi,
i
f(x1, ... , Xn)
= 1, ... , п,
дважды непрерывно дифференцируема по всем
мы можем получить аппроксимацию второго порядка
для изменения стоимости портфеля:
f(X1,t + д1, ... , Xn,t + дn) - f(Xi,t, ... , Хп,t)
д =
n
дf
~ Е ах;(Х1, · · ·, Xn)дi
i=l
i
+ 21
Е
l~i,j~n
~
д2/
дх;Х;(Х1, · · ·, Xn)дiдj
i
3
Следовательно,
n
д ~ "'""'~.д.
L- и" i
i=l
1
+ -2 "'""'
L-
г"д.д.
i3 i J'
l~i,j~n
где Гij = ~(X1,t, ... ,Xn,t)·
Для вычисления ГПа (или УГПа) можно воспользоваться так назы
ваемым приближением
Cornish - Fisher вместе с гамма-аппроксимацией
или обратиться к гамма-аппроксимации на основе имитационного моде
лирования: при наличии предварительно заданной модели, описываю
щей многомерное распределение доходностей активов (обычно берется
многомерное нормальное распределение), вектор доходностей модели
руется
N
раз из этого распределения. Эти смоделированные значения
затем используются для расчета функции распределения изменения
стоимости портфеля, после чего мы можем на основании этого распре
деления вычислять необходимые нам меры риска (для более подробной
информации см.
[Christoffersen (2003))).
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
7.2.
3)
657
Историческое моделирование
Идея, лежащая в основе этого метода, состоит в том, что распре
деление доходностей (или изменений цены) портфеля необходимо оце
нивать с помощью эмпирической функции распределения без исполь
зования каких-либо параметрических моделей. Если доходности пред
ставляют собой независимые одинаково распределенные случайные ве
личины или, в более общем случае, стационарны, то сходимость эмпи
рической функции распределения к истинному распределению следует
из закона больших чисел.
Пусть {ri,t, i
день
t
=
1, ... , n} - это совокупность риск-доходностей на
(факторы риска). Обозначим через r p,t лог-доходность портфеля
на день t и предположим, что rp,t = f(ri,t, ... , Tn,t), например, rp,t =
= E~=l WiTi,t, как в случае предположений метода вариации-ковариа
ции. Далее, рассмотрим исторические наблюдения за доходностями
портфеля, т. е.
Тр,t-т
= f(r1,t-т, · · ·, Tn,t-т ),
Упорядочим rp,t-т, т
= 1, ... , т
Т
= 1, · · ·, т
по возрастанию
Тр,t-т1 ~ Тр,t-Т2 ~ · · · ~ Тр,t-т,.,.·
Тогда оценка границы потерь уровня а для
r p,t равняется
ГП~,t = Tt-тk*'
где
k* =
4)
. {k
mш
k-1 < а
= 1, ... , т : ---;;;:---
k}
~ т
·
Моделирование методом Монте-Карло
Идея, лежащая в основе моделирования методом Монте-Карло, со
стоит в том, что распределение доходностей (или изменений цен) порт
феля необходимо оценивать по некоторой явной параметрической моде
ли. В отличие от метода вариации-ковариации нам нет необходимости
представлять задачу в аналитически удобном виде, например, линеари
зируя портфельную доходность rp,t и делая предположение о том, что
вектор, составленный из факторов риска, имеет многомерное нормаль
ное распределение. Вместо этого мы делаем выводы относительно rp,t,
используя Монте-Карло-моделирование.
Пусть
{Ti,t, i
=
1, ... , п} - это совокупность риск-доходностей на
день t (факторы риска), rp,t -
это лог-доходность портфеля на тот
Гл.
658
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
же день. Как и раньше, предположим, что
rp,t = f(r1,t, ... , rп,t). Те
перь вместо того, чтобы строить модель на основе прошлых наблю
дений, примем некоторое допущение относительно закона распределе
ния доходностей (факторов риска). Пусть это будет многомерное
t-
распределение 7, т. е.
rt
= Zt,
где
Zt Е t(O, Е, v).
Здесь О определяет вектор нулевых средних, Е
матрицу, а
-
ковариационную
число степеней свободы.
v -
Затем в соответствии с этим допущением смоделируем доходности,
в результате чего получим прогнозы модели для доходностей на день
t.
Например, для того чтобы подсчитать гипотетические доходности
(факторы риска) на день
смоделируем
t,
N
раз случайный вектор
Zt,
подчиняющийся t-распределению (см. выше):
-k
rt =
Имея
{r~, k
множество
= 1, ... , N},
k = 1' ... ' N .
-k
Zt '
смоделированных
прогнозов
факторов
риска
можно получить для каждого такого прогноза до
ходность портфеля, которая равна
-k
!( r1,t1
k
k )
rp,t
=
· · · 'rn,t
'
k
= 1, ... ,N.
Упорядочим их по возрастанию
-(1) ~
rp,t
...
~
~ -N
~
Оценка границы потерь уровня а для
rp,t·
rp,t
равна
ГПР (1 t) = f(k*)
а
'
t
'
где
k*
5)
. { k = 1, ... , N
= mш
k- 1<
:~
а
:::;; Nk } .
Метод полной оценки
Линейные и квадратичные приближения к нелинейности, возника
ющей в результате включения в портфель таких инструментов, как оп
ционы, дают в некоторых случаях весьма плохие оценки ГП. Это обыч
но происходит в случаях, когда портфель содержит опционы с различ
ными ценами исполнения.
7 Многомерное
t(a; Е; 11)-распределение является обобщением стандартного одно
мерного распределения Стьюдента. Оно определяется параметрами трех видов: век
тором сдвига (средних значений
свободы 11. Подробнее см. в гл.
) а, ковариационной матрицей Е
3 и в приложении к этой главе.
и числом степеней
7.2.
659
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
В таких сложных портфелях единственно возможный метод, кото
рый мы можем использовать для вычисления необходимой меры рис
ка,
-
это так называемый метод полной оценки (МПО). Метод полной
оценки состоит в том, что много раз моделируется будущая (гипоте
тическая) цена базового актива и, используя модели ценообразования
опционов, для каждой смоделированной цены базового актива рассчи
тывается цена опционов.
Вновь рассмотрим
= 1, ... ,n}
набор значений факторов риска
f -
-
в день t и предположим, что стоимость портфеля равна
Xp,t
где
{Xi,t, i
= f(Xi,t, ... , Xn,t),
некоторая функция, переводящая
Rn
в
R.
В качестве примера
можно привести портфель, состоящий из опциона С на базисный актив
S
с ценой исполнения К и сроком обращения т, где С=
f
можно получить, например, из формулы Блэка- Шоулса.
f(S).
Функцию
При использовании метода полной оценки делаются предположе
ния относительно вида функции распределения доходностей базовых
активов, т. е. относительно функции распределения факторов риска Xi
и, применяя для моделирования будущих (гипотетических) доходностей
базовых активов на К дней вперед метод Монте-Карло, получим
Xf.t+Ki ... ,X::,t+Ki
h = 1, ... , N.
На основании этих смоделированных сценариев для доходностей
базовых активов на К дней вперед мы определяем стоимости нашего
нелинейного портфеля для каждого такого сценария, используя, на
пример, формулы Блэка-Шоулса, после чего по ряду стоимостей (для
каждого сценария доходностей) нашего портфеля можно вычислять
необходимые нам меры риска.
Метод полной оценки имеет преимущество в том, что он концепту
ально очень прост и не использует аппроксимаций. Однако он требует
намного б6льших вычислительных усилий, поскольку должны быть вы
числены будущие (гипотетические) цены каждого опционного контрак
та для каждого смоделированного сценария будущих цен на базисный
актив. Поэтому критерии скорости вычислений могут диктовать выбор
между более точным, но медленным методом полной оценки и методами
приближений, которые работают намного быстрее.
7.2.3.
Использование одномерной GАRСН-модели
в анализе границы потерь
До сих пор мы рассматривали модели, с помощью которых изучали
рыночные доходности с точки зрения безусловной перспективы. Одна-
Гл.
660
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ко хорошо известно, что для финансовых рынков характерны меняю
щиеся во времени моменты, и, если мы пренебрегаем этим аспектом,
мы
можем недооценить
или переоценить нужную меру
риска,
напри
мер ГПа. Кроме того, с помощью условных моделей с меняющимися во
времени характеристиками можно проще (чем с помощью безусловных
моделей) учитывать безусловную ненормальность данных. Вот поче
му использование моделей GARCH8 для управления рыночным риском
стало обычной практикой среди специалистов в области финансов.
Предположим, что в момент
t
мы инвестировали сумму
торый актив, и нам необходимо вычислить ГПа в момент
Pt в неко
(t + 1). То
гда, если мы используем условную АRМА-GАRСН-модель для нетто
доходностей или лог-доходностей этого актива, то мы получим:
•для нетто-доходностей ГПа на момент времени
•
для лог-доходностей ГПа на момент времени
(t + 1)
(t + 1)
равно
равно
ГП"(t,l = 1) = Р,. [rн1 + F,; 1 • ~]'
где мы воспользовались соотношением
(7.7а)
для
лог-доходностей.
Если
же
(7.7)
для нетто-доходностей и
стандартизованные
ошибки
GАRСН-модели 'Г/ имеют стандартное нормальное распределение, то
Если же стандартизованные ошибки GАRСН-модели 'Г/ имеют стан
дартное t-распределение, т. е.
условное
t,
Jv/(11 -
2)'f/,...., tv, где tv - это одномерное
тогда
Пр им ер
7.9.
Рассмотрим временной ряд, состоящий из
9190 еже
дневных лог-доходностей ((rt)~!,1° ). Для того чтобы рассчитать
однодневную ГП в момент времени
10
t = 9190
по длинной позиции в
млн долл., воспользуемся АR-GАRСН-моделью.
Пусть Zt имеет стандартное нормальное распределение и подобран
ная модель для (rt)~!,1° такова:
= 0,00066 - 0,0247rt-2 + C:t,
C:t = Z t P .
иl = 0,00000389 + О,0799с:~_ 1 + О,9073иl_ 1 .
Tt
8 Сведения
об ARCH- и GАRСН-моделях см. в гл. 4 и 5 данной книги.
7.2.
Поскольку r91s9
=
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
-0,00201, r9190
=
соответствии с подобранной моделью
-О,0128а~ 190
661
0,00033455, то в
AR(2)-GARCH(l,1) одношаговый
=
прогноз таков:
= E(r9191lrl9190] = 0,00066 -
f919o(l)
А2
а9190 (1)
= 0,00071
0,0247 · (-0,00201)
= Var(e9191 lrl9190] = 0,00000389+
А
+ 0,0799. (-0,0128 - 0,00066 + 0,0247. (-0,00201)) 2 +
+ 0,9073. 0,00033455 = 0,0003211.
Однодневная граница потерь на уровне
ГПо,05(t,1) =
-10
5%
ООО ООО [ехр (r919o(l) -
равна
1,6449.
Jиг190(1))
- 1] =
= -10 ООО ООО [ехр (0,00071 - 1,6449 · у'О,0003211) - 1] =
= 283, 556 долл.
С вероятностью
95%
возможные потери на следующий день по та
кой позиции составят сумму, не большую, чем
Если мы расчитываем границу потерь на
283,556 долл.
уровне 1%, получим
ГПо,01(t,1) = -10 ООО ООО [ехр (0,00071- 2,3262 · у'О,0003211) - 1]
= 401,457 долл.,
т. е. в этом случае граница потерь позиции равна
401,457
=
долл.
Методы оценки ГПа, использующие
7.2.4.
МGАRСН-модели9
Предположим, что портфель составлен из
активов. Пусть в началь
N
ный момент в i-й актив инвестируется сумма Wi
сумма инвестиций в портфель, Wi Пусть
стей,
w-
доля актива
i
-
- общая
в портфеле.
вектор долей активов в портфеле, У
вектор ожидаемых доходностей и Е
µ-
= Wi W, где W
-
вектор доходно
ковариацонная матрица
доходностей. Тогда доходности портфеля
Rp = w'Y будет иметь сред
нее значение E[Rp] = w'µ и дисперсию Var[Rp] =а~= w'Ew. Граница
потерь уровня о для портфеля стоимостью
мени
-
- wхq
qp(a)
90
в начальный момент вре
это минимальная потеря в доле о всех худших результатов:
гп<Р>
а
где
W
Р
(а) '
определяется условием
многомерных GАRСН-моделях (MGARCH) см. в п. 5.2 данной книги.
662
Гл.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Например, если Rp Е N(w'µ,u~),
гп~> = (w' µ
где Za -
+ ZaO'p)W =
это а%-квантиль
N(O, 1)
(w' µ
+ Za Vw'Ew)W,
распределения.
Предположение о том, что вектор средних
µ
и коварационная мат
рица Е не меняются со временем, весьма ограничительно. Одна из
возможностей обойти это ограничение
-
оценивать одномерную мо
дель GARCH для и~,t· Но у такого подхода есть недостаток, заклю
чающийся в том, что каждый раз, как мы меняем структуру портфеля
w,
нам необходимо переоценивать модель. Однако если мы подгоня
ем МGАRСН-модель к нашим данным
(µt
и
Et
вместоµ и Е), тогда
многомерное распределение доходностей может быть использовано для
расчета функции распределения и границ потерь в момент
t для лю
бого портфеля, и в этом случае нет необходимости каждый раз при
изменении структуры портфеля переоценивать модель. Следователь
но, мы можем легко определять чувствительность границы потерь (ГП)
по отношению к изменениям в структуре портфеля. А значит, можно
выбрать вектор весов
w
таким образом, что прогнозируемое значение
границы потерь для следующего периода будет равно некоторому пред
определенному значению.
Следует отметить важность учета ковариаций для вычисления гра
ницы потерь (ГП). Когда корреляция между доходностями отдельных
активов меньше, чем
1,
тогда очевидно, что ГП портфеля меньше, чем
сумма ГП активов, составляющих этот портфель.
Пр им ер
тивов
мы
7.10.
В данном примере для расчета ГП портфеля ак
используем
модель
ми (т. е. ССС-модель) (см. п.
с
постоянными
5.2.7).
условными
корреляция
Ковариационная матрица
Et
может
быть записана как
Et = DtRtDt,
1/2 )
. ( 1/2
D t = d iag
O'llt · · · O'NNt '
Rt = (Pi;t), Piit = 1.
Rt -
это матрица условных корреляций размера
(N
х
N),
и O'iit опре
деляется как одномерная GАRСН-модель. Следовательно,
Положительная определенность матрицы
тельной определенности матрицы
Rt
Et
и положительности всех O'iit· По
стоянство корреляций означает, что
Rt
следует из положи
= R = (Pi;),
Pii
= 1,
7.2.
663
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
т. е. все условные корреляции являются постоянными (не зависят от
t!).
Следовательно,
O'ij,t
= PijVO'ii,tO'jj,t
\;;/i =/:- j.
Таким образом, динамика ковариации определяется только динамикой
двух условных дисперсий. Общее число параметров в
R
равно
N(N-
-1)/2.
7.2.5.
Эмпирические приложения с использованием
пакета
1)
Eviews
Одномерная ГП
Предположим, мы имеем массив данных, составленный из 1250 на
блюдений за немецким фондовым индексом DAX, и мы хотим использо
вать первые 1000 наблюдений для построения модели AR(l)GARCH(l,1) со стандартизованными ошибками, имеющими распреде
ление Стьюдента, тогда как оставшиеся 250 наблюдений использовать
для тестирования
(backtesting)
ГП. В таком случае нам необходимо на
брать сле,цующие команды:
smpl @all
'series d_dax=dlog(dax) 'IF WE USE LOGRETURNS
series d_dax=@pch(dax) 'IF WE USE NET-RETURNS
matrix(250,5) v _a_risk
for !i=lOOO to 1249
smpl 1 !i
equation tarcl.arch(l,1, thrsh=l,tdist,m=lOO) d_dax с d_dax(-1)
smpl !i+l !i+l
'FORECAST CONDITIONAL MEAN AND VARIANCE
tgarcl.fit(f=na) yhat y _se y _garch
'COLLECT ТНЕ TRUE REALIZED RETURNS
v _a_risk(!i-999,1) = @elem(d_dax,@otod(!i+l))
!gradi = tgarcl.@coefs(б)
'COMPUTE ТНЕ VAR АТ DIFFERENT PROBABILITY LEVELS
v _a_risk(!i-999,2) = @elem(yhat, @otod(!i+l)) +
@sqrt((!gradi-2)/!gradi)*@qtdist(0.01, !gradi)*sqr( @elem(y _garch, @otod(!i+l)))
v _a_risk(!i-999,3) = @elem(yhat, @otod(!i+l)) +
@sqrt((!gradi-2)/!gradi)*@qtdist(0.05, !gradi)*sqr( @elem(y _garch, @otod(!i+l)))
v _a_risk(!i-999,4) = @elem(yhat, @otod(!i+l)) +
@sqrt((!gradi-2)/!gradi)*@qtdist(0.95, !gradi)*sqr( @elem(y _garch, @otod(!i+l)))
v _a_risk(!i-999,5) = @elem(yhat, @otod(!i+l)) +
@sqrt((!gradi-2)/!gradi)*@qtdist(0.99, !gradi)*sqr( @elem(y _garch, @otod(!i+l)))
next
v а risk.line
Гл.
664
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Результаты представлены на рис.
7.9.
0,99
0,95
0,05
0,01
25
Рис.
7.9.
2)
ГП на уровне
50
75
100 125 150 175 200 225 250
1%, 5%, 95%
и
99% -
индекс
DAX
Многомерная ГП для ССС-модели
Рассмотрим равновзвешенный портфель из трех фондовых индек
сов (японского, европейского и американского), с ежедневными данны
ми. Тогда программа для расчета ГП на один шаг вперед в
Eviews будет
выглядеть так:
'SET ТНЕ ESTIMATION SAMPLE
smpl 01/01/1990 05/28/2001
series yl = rseusa
series у2 = rsejap
series уЗ = reuro
'CREATE ТНЕ VECTOR OF WEIGHTS
vector(З) omega = 1/3
'ESTIMATE ТНЕ THREE UNIVARIATE GARCH(l,1) MODEL
equation eql.arch(m=lOO, c=le-5) yl с yl(-1)
equation eq2.arch(m=100, c=le-5) у2 с у2(-1)
equation eqЗ.arch(m=lOO, c=le-5) уЗ с уЗ(-1)
'SET ТНЕ FORECASTING SAMPLE
smpl 05/29/2001 05/29/2001
'FORECAST ТНЕ UNIVARIATE CONDITIONAL MEANS AND VARIANCES
eql.forecast ylhat ylse cvarl
eq2.forecast y2hat y2se cvar2
eqЗ.forecast yЗhat уЗsе cvarЗ
' INITIALIZE А VECTOR ТНАТ WILL CONTAIN ТНЕ FORECASTED MEANS
mu
'EXTRACT ТНЕ FORECASTED MEANS
mu(l)=ylhat(@dtoo("05/29/2001 "))
mu(2)=y2hat(@dtoo("05/29/2001 11 ))
mu(З)=y3hat(@dtoo("05/29/2001 "))
соеf(З)
7.2.
665
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
'INITIALIZE А MATRIX ТНАТ WILL CONTAIN ТНЕ FORECASTED
STANDARD DEVIATIONS
matrix(3,3) dm=O
'EXTRACT ТНЕ FORECASTED VARIANCES
dm(l,l)=@sqrt(cvarl(@dtoo(''05/29/2001 ")))
dm(2,2)=@sqrt(cvar2(@dtoo("05/29/2001 ")))
dm(3,3)=@sqrt(cvar3(@dtoo("05/29/2001 ")))
'SET ТНЕ ESTIMATION SAMPLE
smpl 01/01/1990 05/28/2001
'COMPUTE ТНЕ STANDARDIZED RESIDUALS
eql.makeresids(s) stdresl
eq2.makeresids(s) stdres2
eq3.makeresids(s) stdres3
'INITIALIZE ТНЕ CORRELATION MATRIX
matrix(3,3) rm=l
'INSERT ТНЕ ESTIMATED CORRELATIONS AMONG RESIDUALS
IN ТНЕ CORRELATION MATRIX
rm(l,2)=@cor(stdresl,stdres2)
rm(l,3)=@cor(stdresl,stdres3)
rm(2,3)=@cor(stdres2,stdres3)
rm(2,l)=rm(l,2)
rm(3,l)=rm(l,3)
rm(3,2)=rm(2,3)
'GENERATE ТНЕ CONDITIONAL COVARIANCES
genr ccov12=rm(l,2)*@sqrt(cvarl*cvar2)
genr ccov13=rm(l,3)*@sqrt( cvarl *cvar3)
genr ccov23=rm(2,3)*@sqrt( cvar2*cvar3)
'CREATE ТНЕ CONDITIONAL VARIANCE/COVARIANCE MATRIX
matrix hm=dm*rm*dm
'COMPUTE ТНЕ CONDITIONAL FORECASTED VARIANCE OF ТНЕ
TRIVARIATE 'PORTFOLIO
matrix cvarpf=@transpose(omega)*hm*omega
'COMPUTE ТНЕ CONDITIONAL FORECASTED MEAN OF ТНЕ
TRIVARIATE PORTFOLIO
matrix cmeanpf=@transpose( omega) *mu
'COMPUTE ТНЕ VAR АТ ТНЕ 5% LEVEL
matrix Var_port = cmeanpf + @qnorm(0.05)*@sqrt(cvarpf)
3)
Многомерная ГП с использованием диагональной
ВЕКК-модели
Сейчас мы рассмотрим иной подход к моделированию меняющийся
во времени условной ковариационной матрицы
Et,
а именно рассмот
рим многомерную диагональную ВЕКК-модель, впервые предложенную
в статье
[Engle, Kroner (1995)]:
Yt = E[YtlFt-1] + E~ 12 c:t, et Е N(O, In)
Е~/ 2 = nn' + Aet-1e~_ 1 А' + BEt-1B
1
,
666
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
где
E[YtlFt-1] - спецификация условного среднего для векторной
АR(l)-модели, Е:/ 2 - разложение Холецкого для Et, в котором А и
В - диагональные матрицы: требование того, чтобы А и В были диа
гональными, позволяет снизить число оцениваемых параметров.
Отметим, что, хотя в
Eviews 6
можно оценивать D-ВЕКК-модель,
на данный момент в этом пакете не предусмотрена процедура, которая
позволила бы рассчитывать прогноз условной ковариационной матри
цы Е. Однако в личной беседе представители группы поддержки
Eviews
заверили, что в ближайшее время эта процедура будет включена в па
кет. Следовательно, для простоты мы будем рассматривать
бы это был прогноз на один шаг вперед к моменту
Et как если
времени (t + 1).
Рассмотрим портфель из акций четырех российских эмитентов:
Газпрома, Лукойла, РБК, Сбербанка. Процедура расчета ГП портфеля
на один шаг вперед в
Eviews
выглядит следующим образом:
!n=4
matrix(!n) omega=l/!n
matrix(250,5) Var _port _ final
for !i=751 to 950 'THIS CYCLE WILL ВЕ REPEATED FOR 250 TIMES
'ESTIMATE ТНЕ MODEL
smpl 1 !i
system sysOl
sysOl.append @pch(gazprom)=c(l)+c(lO)*@pch(gazprom(-1))
sysOl.append @pch(lukoil)=c(2)+c(ll)*@pch(lukoil(-1))
sysOl.append @pch(rbk)=c(3)+c(12)*@pch(rbk(-1))
sysOl.append @pch(sberbank)=c(4)+c(13)*@pch(sberbank(-1))
'sysOl.arch @diagvech c(fullra.nk) arch(l,diag) garch(l,diag)
sys01.arch(m=70) @diagbekk c(indef) arch(l,diag) garch(l,diag)
'DO ТНЕ FORECASTING АТ TIME T+l FOR ТНЕ VECTOR OF RETURNS
AND SIGMA
smpl !i+l !i+l
series forel = c(l)+c(lO)*@pch(gazprom(-1))
series fore2 = c(2)+c(ll)*@pch(lukoil(-1))
series foreЗ = c(3)+c(12)*@pch(rbk(-1))
series fore4 = c(4)+c(13)*@pch(sberbank(-1))
true return=
(@pch(gazprom)+@pch(lukoil)+@pch(rbk)+
series
+@pch(sberbank)) /!n
vector4) mu
mu(l)= @elem(forel, @otod(!i+l))
mu(2)= @elem(fore2, @otod(!i+l))
mu(З)= @elem(foreЗ, @otod(!i+l))
mu(4)= @elem(fore4, @otod(!i+l))
vector( 1) true _ ret=true _ return
'WE CONSIDER ТНЕ LAST CONDITIONAL SIGMA AS ТНЕ FORECASTED
ONE АТ TIME t+l.
sysOl.makegarch(mat, cov, date=!i, name=cov _mat)
matrix cvarpf=@transpose(omega)*cov _ mat*omega
matrix cmeanpf=@transpose(omega)*mu
'INSERT ТНЕ TRUE REALIZED RETURN
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
667
matplace(Var_port_final, true_ret, !i-700,1)
'COMPUTE ТНЕ LONG-POSITION VALUE АТ RISK (1% AND 5 %)
matrix Var_port = cmeanpf + @qnorm(O.Ol)*@sqrt(cvarpf)
matplace(Var _port _ final, Var _port, !i-700,2)
matrix Var_port = cmeanpf + @qnorm(0.05)*@sqrt(cvarpf)
matplace(Var _port _ final, Var _port, !i-700,3)
"COMPUTE ТНЕ SHORT-POSITION VALUE АТ RISK (95% AND 99 %)
matrix Var_port = cmeanpf + @qnorm(0.95)*@sqrt(cvarpf)
matplace(Var_port_final, Var_port, !i-700,4)
matrix Var_port = cmeanpf + @qnorm(0.99)*@sqrt(cvarpf)
matplace(Var _port _ final, Var _port, !i-700,5)
'SAVE ТНЕ WORKFILE
wfsave azioni russe sol
next
Результаты частично отражены на рис.
7.10.
0,99
0,95
0,05
0.01
25
Рис.
7.10.
ГП на уровне
50
75
100
1%, 5%, 95%
125
и
99%
150
175
200
225
250
(нормальная диагональная
ВЕКК(l,1,1)-модель, равновзвешенный портфель: Газпром,
Лукойл, РБК, Сбербанк)
7.2.6.
Продвинутые методы управления рыночным
риском: Сорulа-GАRСН-модели 10
Несмотря на то что оценка одномерной ГП достаточно хорошо изуче
на, многомерным случаем занимались только в небольшом количестве
недавних работ о прогнозе корреляций между активами. Эмпириче
ские результаты, посвященные этой проблеме, см., например, в работах
[Engle,Sheppard (2001)], [Giot,Laurent (2003)], [Bauwens,Laurent (2005)] и
[Rosenberg,Schuermann (2006)]. Когда мы используем параметрические
методы, оценивание ГП для портфеля активов может оказаться очень
10 Информацию
о копула-моделях см. в гл. 6.
Гл.
668
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
затрудненным из-за сложности совместного многомерного моделирова
ния.
Кроме того, с ростом количества активов в портфеле возникают вы
числительные трудности 11 . По-видимому, вследствие этой сложности на
данный момент практики и исследователи уделили большое внимание
двум моделям:
•~постоянная условная корреляция» (ПУК-модель), впервые пред
ложенная в
[Bollerslev (1990)];
~динамическая условная корреляция» (ДУК-модель), впервые
предложенная в [Engle (2002)] 12 .
•
Можно показать, что модели ПУК и ДУК могут быть представле
ны как частные случаи более общей копула-структуры (см., например,
[Patton(2006a)], [Patton(2006b)], [Fantazzini(2008)]
и
[Fantazzini(2009c)].
В частности, функция правдоподобия многомерного нормального
распределения может быть представлена как произведение нормальной
копула с корреляционной матрицей Е
= Rt
и маргинальных нормаль
ных распределений:
! Normal(
Х1,
... ,Xn
) -_
n
= cNormal(F{'ormal(x 1), ... , p:ormal(xп); Rt) х П Jformal(xi),
i=l
где
Jformal - плотность частного нормального распределения. Если
мы рассматриваем общую модель для условных средних значений и
дисперсий, две модели могут быть переформулированы следующим об
разом:
Xt = E[XtlFt-1] + Dt11t
11t rv Н(171, ... ,11п) cNormal(F{'ormal(111), ... ,F:ormal(11п);Rt),
=
где Dt = diag(h~e ... h1,/n~t), hii,t определяется как одномерная GАRСН
модель.
Кроме того, двухшаговая процедура оценки ДУК-модели, описан
ная в
[Engle,Sheppard (2001)], соответствует методу Inferencefor Margins
(IFМ), впервые предложенному в статье [Joe,Xu (1996)] для оценки
копула-функции. Согласно методу IFM на первом шаге оцениваются
параметры маргинальных (частных) распределений, в то время как на
втором шаге оцениваются отдельно параметры копула-функции. Как и
11 Для
более подробной информации смотри обзор многомерных GАRСН-моделей,
данный в гл. 5.
12 В англоязычной
литературе эти модели называют, соответственно, "CCC-model"
("Constant Conditional Correlation model")
Correlation model"), см. гл. 5, п. 5.2.7.
и
"DCC-model" ("Dynamic Conditional
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
669
оценки метода максимального правдоподобия, оценки, полученные по
методу
IFM, обладают свойствами
[Joe,Xu (1996)] и [Joe (1997)]):
асимптотической нормальности (см.
V'i'(B1Fм - 80) Е N(O, V(8o))
где
80 -
(асимптотически),
вектор параметров маргинальной функции распределения и
копула-функции,
V(80 ) = n- 1 м(n- 1 )т - это так называемая инфор
мационная матрица Godambe, где D = Е[дg( 8) т / 88], М = E[g( 8)g( 8) т]
и g( 8) - некоторая так называемая sсоrе-функция.
Свойство асимптотической нормальности выполняется и для двух
шаговой ДУК-оценки (см.
[Engle,Sheppard (2001)]).
Поэтому, если мы рассматриваем модель ПУК, это подразумева
ет оценку
n
одномерных GАRСН-моделей любого типа с нормальным
распределением на первой стадии. Нормальные функции распределе
ния нормированных остатков Ui,t = Ф(77i,t) используются как аргумен
ты нормальной копула-плотности с постоянной матрицей корреляции
R. Однако так как 11t = (Ф- 1 (и~,t), ... , Ф- 1 (иn,t))', оцениваемая
Rt =
постоянная матрица корреляции равна оцениваемой матрице корреля
ции стандартизированных остатков в ПУК-модели.
Аналогичным образом, если мы рассмотрим ДУК-модель, нормаль
ная кумулятивная функция распределения и ее обратная функция ней
трализуют друг друга, и логарифмическое правдоподобие копула-плот
ности максимизируется в предположении, что справедлива следующая
динамическая структура для корреляционной матрицы
Rt:
где симметричная положительно определенная матрица
сти
(n
х
n)
Qt
размерно
равна:
(7.8)
Здесь
Q-
безусловная ковариационная матрица случайной величины
7Jt, al (~О) и
/38
(~ ~
-
скалярные параметры удовлетворяющие нера
венству Ef= 1 al+ 'Es=l f3s < 1. Эти условия необходимы для того, чтобы
Qt >
О и
Rt > О.
11t , так как по по
строению Qii,t не равно 1. Значит, выражением (7.8) Qt преобразуется в
корреляционную матрицу. Если 81 = 82 =О и Qii = 1, то получим ПУК
Qt -
ковариационная матрица для
модель. Для более подробной информации об ДУК-моделировании см.
[Engle (2002)].
Гл.
670
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Некоторые обобщения: маргинальные (частные) функции
1)
распределения, имеющие асимметричные
t-распределения, и динамические копула-функции
Итак, мы видим, что подход с помощью копула-функций позволяет
нам рассмотреть намного более общие случаи, чем нормальные ПУК
И ДУК-модели.
Два хорошо известных отклонения от нормального распределе
ния
~тяжелые хвосты~ и асимметрия. Например, t-распределение
-
Стьюдента имеет эксцесс больший, чем у стандартного нормального
распределения, и это распределение было обобщено так, чтобы полу
чившееся обобщенное распределение имело асимметрию, отличную от
асимметрии нормального распределения (см.
[Hansen (1994)]).
Хотя бы
ли предложены и другие обобщения, мы выбрали именно это в связи
с его простотой и возможностью использовать в моделировании эко
номических переменных (см.
[Patton
(2006а)] и
[Patton
[Jondeau,Rockinger(2003)], [Patton (2004)],
(2006Ь)]).
Следовательно, многомерная модель, позволяющая маргинальным
функциям распределения иметь асимметрию и эксцесс, отличные от
асимметрии и эксцесса стандартного нормального распределения, а так
же иметь нормальную зависимость, может быть выражена следующим
образом:
Xt
= E{XtlFt-1} + Dt1Jt
11t Е H(1Jl, ... , 1Jn)
= cNm-mal (Ffkewed-t(1Jl), ... , p;kewed-t(1Jn); Rt),
где FiSkewed-t - функция распределения асимметричного t-распределе
ния, а матрица
Rt
может быть как константой, так и меняющейся во
времени, так же как в ПУК- и ДУК-моделях.
Если финансовые активы демонстрируют симметричную хвосто
вую зависимость, то мы можем использовать копула-функцию Стыо
дента
Xt =
E{XtlFt-1} + Dt11t
= cstudent'st(pSkewed-t(n)
1
·11 , ... , pSkewed-t(n
n
·1n )· D. v) '
'1'1 )
·1t Е H(n
·11, ... ,.1n
-
'1'1
где
,.Lч,
v - число степеней свободы копула-функции Стьюдента. Если же
финансовые активы могут быть распределены по т различным груп
пам, то мы можем использовать сгруппированную t-копула-функцию:
Xt
= E{XtlFt-1} + Dt1Jt,
= cGrouped t(pSkewed-t(n
1
·11 ) , ...
71 )
·1t Е H(n
·1l,•••,•1n
-
n
Skewed-t ( ) . R
)
· · ·' Fn
11n , t, 1.11, · · ·, Vm ·
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
671
Наконец, если же финансовые активы демонстрируют только «ниж
нюю хвостовую зависимосты, мы можем использовать копула-функцию
Клейтона,
= E{XtlFt-1} + Dt77t
Xt
7Jt Е H(7Ji, ... , 7Jп)
где а
=cclayton (Ffkewed-t(7Ji), ... ,
F,!kewed-t(7Jп); at),
параметр зависимости Клейтона, который может, вообще гово
-
ря, меняться во времени.
Подобные подходы предложены в
ger (2006))
и
[Granger и др. (2006)).
[Patton (2004)), [Jondeau, Rockin-
Однако в этих работах авторы сосре
доточиваются только на двумерных приложениях и не рассчитывают
гп.
2)
Оценка границы потерь с помощью
Сорulа-GАRСН-моделей
Общий алгоритм для оценки границы потерь уровней
1%, 5%, 95%, 99%, 99,5% and 99,75%
0,25%, 0,5%,
на один день вперед для портфеля
Р, составленного из п активов с инвестиционными позициями, равными
Mi, i
= 1, ... , п,
строится следующим образом.
а) Пусть дано множество значений оцененных параметров для мо
мента времени
(t - 1),
смоделируем
доходностей каждого актива,
N = 100 ООО сценариев для лог
{Y1,t, ... , Yn,t} за период времени [t - 1, t],
используя общее метараспределение с помощью следующей процедуры:
al)
сначала сгенерируем наблюдение n-размерной случайной ве
личины (иi,t,
... : .. , Un,t)
копула-функции
Ct,
из спрогнозированной в момент времени t
которая может быть нормальной копула-функцией,
t-копула-функцией, копула-функцией Клейтона и др.;
а2) на втором шаге, получим вектор
тизированных лог-доходностей
Qt размерности (п х 1) стандар
активов 7Ji,t, используя обратные функ
ции спрогнозированных в момент времени
t маргинальных функций
распределения, которые могут быть нормальными распределениями,
асимметричными t-распределениями и др.:
аЗ) на третьем шаге изменяем масштаб стандартизированных лог
доходностей активов, используя прогнозы для средних и дисперсий,
оцененных с помощью АR-GАRСН-моделей:
{Y1,t, · · • , Yn,t} =
(!i1,t + '71,t • ~, · • · , /in, + 'ln,t · ~ ;
ГЛ.
672
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
а4) наконец, повторяем эту процедуру
б) Используя эти
100 ООО
N = 100 ООО раз.
сценариев, в момент времени
t
портфель
Р переоценивают, т. е.:
.
(j)
Р/ = M1,t-1 · exp(y1,t)
(j)
+ ... + Мп,t-1 · ехр(Уп,t),
в) Для каждого сценария
LOSSj
= Р/
j
нарий, где
ГП уровня
рассчитывается убыток портфеля:
- Pt-1,
г) Граница потерь уровня а
j = 1, ... '100 ООО.
(1- а)· 100 ООО порядковый сце
а= {0,25%, 0,5%, 1%, 95%, 5%, 1%, 0,5%, 0,25%}. Например,
0,25% равна 99 750-му порядковому сценарию.
-
это
Эмпирические приложения с использованием
7.2.7.
статистического пакета
1)
j = 1 ... 100 ООО.
R
Оценка Сорulа-GАRСН-модели для доходностей
Мы
SP500
и
рассмотрим
DAX
ежедневные
за период с
1994
показатели доходностей
индексов
по 2000г. (данные файла
Процедура оценки Сорulа-GАRСН-модели в
sp_dax.txt).
статистическом пакете R:
# Read the data
dat <- read.taЫe{''C:/sp_dax.txt", header = TRUE)
# Generate the returns in %
yl=lOO*diff{log{dat[,1]))
y2=100*diff{log(dat[,2]))
# Estimate the GARCH models with а Student's t distribution
fitl = garchFit{ garch{l, 1), cond.dist = "dstd", data=yl)
fit2 = garchFit{ garch{l, 1), cond.dist = "dstd", data=y2)
#Have а look at what there is inside the output of the GARCH estimation
#{which is an S4 object, see р.9 of the manual Ьу Grant Farnsworth
fitl@fit
#Get the standardized residuals
sp _res=fitl@fit$series$z
dax res=fit2@fit$series$z
#Get the Cumulative Distribution F\inctions:
#Remember that the standardized residuals are {0,1), while when computing
#the cdf of а central standard Student's t, the variance is nu/{nu-2).
cdf_ sp= pt(sqrt(fitl@fit$coef[5]/ (fitl@fit$coef[5]-2) )*sp _ res,fitl@fit$coef[5])
cdf_dax=pt(sqrt(fit2@fit$coef[5]/{fit2@fit$coef[5]-2))*dax_res, fit2@fit$coef[5])
#Estimate а Ьivariate Т copula
ellipticalCopulaFit{cdf_sp,cdf_dax, type = "t")
#Estimate а Ьivariate Gumbel
archmCopulaFit(cdf_ sp,cdf_ dax,type="4")
Для
t-copula
функции Стьюдента должно получиться
$par [1] 0.2781346 10.2533838
:
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
673
$objective [1\ -0.06653569
... ,
а для сорulа-функции Гумбеля
-
такие результаты:
$par [1) 1.200167
$objective [1] -0.05549976
Вы можете попробовать использовать другие двумерные копула
функции, включенные в пакет
«fcopulae»,
начиная с эллиптических
копула-функций и кончая копула-функциями экстремальных значений.
2)
Оценка границы потерь с помощью
Сорulа-GАRСН-модели
Рассмотрим те же данные, что и в предыдущем пункте, и рассчи
таем границу потерь уровня
1% для
равновзвешенного портфеля. Для
описания совместного распределения доходностей мы воспользуемся Т
копула-функцией с маргинальными (частными) функциями распреде
ления, имеющими t-распределение. Программа в
R
выглядит следую
щим образом:
#1 load the packages needed for my following work
library{fGarch)
library( fCopulae)
#Read the data dat <read. taЫe( "C: /Lezioni/Moscow _ master _ 2 _ anno/COPULA/sp _ dax.txt",
header = TRUE)
#Generate the returns in % REMARК: If you don 't multiply for 100, the resulting
#cdfs are not precisely estimated and the elliptical copula cannot Ье estimated
yl_all=lOO*diff{log{dat[,1\))
y2_all=100*diff{log{dat[,2\))
#lnizialize the vectors which will contain the realized returns
# and the VaRs estimates
var final=
true ret=
for {i in 1000:1249)
yl=yl _ all[l:i\
y2=y2_all[l:i\
#Estimate the GARCH models
fitl = garchFit{ garch{l, 1), cond.dist = ''dstd", data=yl, trace=FALSE)
fit2 = garchFit{ garch{l, 1), cond.dist = "dstd", data=y2, trace=FALSE)
#1-step ahead Forecast
fore_l=predict(fitl, n.ahead = 1)
fore_2=predict(fit2, n.ahead = 1)
#Example mean forecast {DAX return)
fore_2[,1\
#Example variance forecast (DAX variance)
fore_2[,3\
674
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
#Have а look at what there is inside the output of the GARCH estimation
#{which is an S4 object, see р. 9 of the manual Ьу Grant Farnsworth fitl@fit
#Get the standardized residuals
sp _ res=fitl@fitseriesz
dax res=fit2@fitseriesz
#Get the Cumulative Distribution Functions:
#Remember that the standardized residuals are {0,1}, while when computing the
cdf
#of а central standard Student's t, the variance is nu/(nu-2).
#REMARК: IF you add ARMA terms, then coef[5) is no more correct!
cdf_ sp= pt(sqrt{fitlfit$coef[5)/(fitlfit$coef[5)-2} )*sp _ res, fitlfit$coef[5]}
cdf_dax=pt{sqrt{fit2fit$coef[5)/{fit2fit$coef[5)-2}}*dax_res, fit2fit$coef[5]}
#Estimate а Ьivariate Т copula
t_est=ellipticalCopulaFit{cdf_sp,cdf_dax, type = "t") t_est
#Estimate а Ьivariate Gumbel
a_est=archmCopulaFit{cdf_sp,cdf_dax, type = "4"} a_est
#Simulate the estimated elliptical copula
e_sim=ellipticalCopulaSim{lOOOO, rho = t_estpar[1),param = t_estpar[2), type =
c(''t"))
#REMARK: we use only 10000 simulations for the elliptical and 1000 for the
archimedean
# since the R procedures are very slow compared to Gauss and Matlab. However,
# remember that to have а good approximation of the quantile you need at 100.000
#МС simulations!
#Simulate the estimated archimedean copula
#a_sim=archmCopulaSim{lOOO, alpha = a_est$par[l], type = "4"}
#Simulate the standardized residuals [F _1-l{u_l},F _2-l{u_2})
sim _ stdl=sqrt( {fitlfit$coef[5)-2} /fitlfit$coef[5)) *qt( е _ sim[,1) ,fitlfit$coef[5))
sim _ std2=sqrt( {fit2fit$coef[5)-2} /fit2fit$coef[5))*qt( е _ sim[,2) ,fit2fit$coef[5))
#Simulated returns
sim _ retl=fore _ l[,l)+sqrt(fore _ l[,З)}*sim _ stdl
sim _ ret2=fore _ 2[,l)+sqrt{fore _ 2[,3)}*sim _ std2
#Portfolio simulated returns
sim _port=sim _ retl +sim _ ret2
#Sort the simulated returns
sort _ sim=sort( sim _port)
#Value at Risk at 1% quantile = (O.Ol*(ROWS OF ТНЕ VECTOR)) sorted
#returns
var=sort_sim[O.Ol*NROW(sort_sim})
#1 save the estimated VaR and the realized return
var _ final=rЬind{ var _ final, var)
ret=yl_all[i+l)+y2_all[i+l)
true _ ret=rЬind{ true _ ret,ret)
#Create the hit series for the Var at 1% level and compute the sum
#for the basel test
hitOl=l *(true _ret<var _final}
basel _ test=sum{hitOl)
#plot the true returns and the VaR
plot(true_ret,type="l",col=2,xlab="Date",ylab="Тrue realized return and VaR at
1% level",main="VaR at 1% level of а Ьivariate portfolio - Т marg./Norm с.")
lines( var _ final,col=З}
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
Результаты отражены на рис.
675
7.11.
Уровень
ДОХОДJIОСТИ
о
50
150
100
200
250
Дни
Рис.
7.11.
ГП на уровне
1%
(Сорulа-GАRСН-модель, равновзвешенный портфель:
Газпром, Лукойл, РБК, Сбербанк)
7.2.8.
Тестирование ГП на исторических данных
Определим последовательность «успехов»
Iн1=1,
lн1 =О,
если
если
(It):
Yt+1 < -Гa(t; 1)
Yt+1 ~ -ГПа(t; 1).
Если мы используем идеальную модель для получения оценки гра
ницы потерь ГП, то превышения -ГПа(t;
1)
следует ожидать в доле
а) случаев ежедневно. При справедливости нулевой гипотезы о
(1 -
правильной спецификации последовательность «успехов»
-
последо
вательность независимых одинаково распределенных бернуллиевских
случайных величин с вероятностью «успеха» а.
Но: Iн1
f(It, а)
1)
,...., Bernoulli(a)
(1 _
a)1-Itнalнi.
Тестирование на безусловный охват
Пусть мы хотим протестировать, отличается ли доля наблюдений
1Г, меньших -ГПа некоторой модели риска, статистически значимо от
а. Функция правдоподобия для последовательности Бернулли равна:
L(1Г)
= П (1_1Г)l-lн11Гlн1 = (1_1Г)То1ГТ1,
t
Гл.
676
где То и Т1
-
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
число нулей и единиц в нашей выборке (а Т = То
+ Т1 ).
Тогда оценка максимального правдоподобия для 1Г равна
Т1
"
1Г----
То+т1·
-
Интересующая нас гипотеза о том, что истинная доля потерь, б6ль
ших границы потерь, равна о, может быть проверена {в предположении
независимости
11, 12, ... )с
помощью статистики отношения правдоподо
бия
LRuc = -2ln[L(o)/lnL(*)] =
= -2 ln [{1 - о)Т0 от1 / { {1 - Т1/Т)То (Т1/Т)Т1 }]
В соответствии с теорией статистика
,....,
х 2 {1).
LRuc должна подчиняться х 2 {1)
распределению при больших выборках. При малых Т распределение
критических значений статистики
LRuc
могут быть получены с помо
щью статистического моделирования.
2)
Тест на независимость
Возможны ситуации, когда модель проходит тест на безусловный
охват, но при этом все наблюдения
t,
для которых
lt
=
1,
сконцен
трированы в малой окрестности некоторого момента времени. В этом
случае, возможно, нарушена независимость наблюдений, и необходим
тест, с помощью которого можно было бы проверить нашу гипотезу и
при наличии таких сгущений
t.
С этой целью предположим, что после
довательность попаданий зависима по времени и что она может быть
описана как так называемая марковская
последовательность
первого
порядка с матрицей вероятностей переходов
П1
где 1Го1
-
= ( 1 - 1ГОl 1 1ГО1 ) '
1 - 1Г11, 1Г11
вероятность того, что завтра lн1=1, при условии, что сего
дня lн1
= О. Вероятность {lt = О, lt+1 = О} равна {1 - 1Го1), а вероят
ность события {lt = О, lн 1 = 1} равна (1 - 1Г11).
Для выборки Т наблюдений из марковского процесса первого по
рядка функция правдоподобия равна
L(П1) = {1 - 1Го1)Тоо1Гбf1 {1 - 1Г11)Т101Гf{1,
где Tij -
число наблюдений, для которых
lt
=i
и lн1
= j. Беря первую
производную по 1Го1,1Г11 и приравнивая эти производные к нулю, полу
чим оценки максимального правдоподобия
*_
01 -
*н
То1
То?г+То1
'
= т10~~11 ·
:
7.2.
УПРАВЛЕНИЕ РЫНОЧНЫМ РИСКОМ
677
Используя тот факт, что вероятности должны давать в сумме единицу,
мы получим
1Гоо
1Г10
= 1 -1Го1,
= 1 -1Г11.
Допущение о зависимости «последовательности попаданий» соот
ветствует допущению, что 1ГО1 должно отличаться от 1Г11: в нашем слу
чае типичной будет ситуация, при которой 1Г11
> 1ГО1 ·
Если, с другой стороны, попадания независимы, тогда мы имеем
1Го 1 =1Г 11 =1Г. При условии независимости оцененная матрица перехода
равна
,. = (
п
1
1 - ?Г,
,.. 1Г,.. ) .
-
1Г, 1Г
Мы можем тестировать независимость, используя тест отношения
правдоподобия:
В случае, если оказалось, что Т11
=
О, функция правдоподобия при-
мет вид
3)
Тестирование на условный охват
Наконец, если нам необходимо протестировать одновременно гипо
тезу о том, что
11, 12 , •••
образует последовательность независимых слу
чайных величин и что доля нулей этой последовательности согласуется
с предположением нашей модели (т. е. равна 1 - а), то мы можем вос
пользоваться тестом «на условный охват»:
который соответствует тестированию гипотезы 1ГО1
=
1Г11 =а. Необхо
димо помнить, что
4)
Базельский тест для моделей ГП
Этот тест основан на числе потерь, больших, чем оценка одноднев
ной границы потерь
на
250
1%-ного уровня. Длина периода тестирования рав
дням.
Масштабн:ый множителъ, на который должна быть умножена
оценка ГПо,01 (t,
деляется
1) при расчете требуемого банку объема капитала, опре
нормативно в зависимости от результатов теста (см. табл. 7.1).
Гл.
678
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Отметим, что это односторонний тест, направленный на то, чтобы опре
делять уровни очень малого риска.
Таблица
7 .1.
Определение масштабного множителя
Зоны
Число наблюдений,
меньших ГПо,01 (t,
Зеленая зона
Желтая зона
Желтая зона
Желтая зона
Желтая зона
Желтая зона
Красная зона
ГП0,01(t,
1)
за
60
t,
множитель
0-4
5
6
7
8
9
10
~
3
3,4
3,5
3,65
3,75
3,85
4
Уровень рыночного рискового капитала
жен иметь в момент
Масштабный
1)
(MRC),
который банк дол
равен максимуму из ГП0,01(t
- 1, 1)
и среднего
последних периодов, умноженного на так называемый
масштабный параметр
SF,
а именно:
1
М RC =Мах ( ГПо,01(1, t - 1), SF · 60 ·
L ГПо,01(1, t 60
1 - i)
)
.
t=l
7.3.
Управление операционным риском
Количественный анализ операционного риска
-
это относительно не
давняя область изучения, возникшая в рамках количественного управ
ления рисками (см.
[King (2001)]
и
[Cruz (2002)]).
Проблема изучения
операционного риска возникла в момент, когда было обнаружено, что
ни управление рыночным риском, ни управление кредитным риском не
позволяет хеджировать все возможные события, влияющие на эконо
мические и финансовые результаты работы финансовых организаций.
Развитие этой области напрямую связано с новой концепцией доста
точности капитала, также называемой Базель 11-соглашением. В этом
разделе будут представлены и рассмотрены основные методологии рас
чета достаточности капитала, требуемого в рамках управления опера
ционным риском.
Во Втором базельском соглашении операционный риск определя
ется как «риск убъtтков в результате неадекватной или ошибочной
работъt процессов, персонала, систем или в результате внешних воз
действий». Для того чтобы классифицировать все возможные опера
ционные риски, во Втором базельском соглашении (см.
[BCBS(2003) ])
выделены семь типов событий (ТС) и восемь бизнес-направлений (БН),
см. табл.
7.2.
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
679
Однако в Базель 11-соглашении не представлено четких моделей
для анализа и агрегирования рисков по всем те и БН. Оно лишь опи
сывает некоторые основные правила, которым должно следовать каж
дое финансовое учреждение: уровень доверия, временной горизонт и
анализ некоторых зависимостей. В частности, в Базель 11-соглашении
для анализа операционных рисков требуется одногодичный временной
горизонт и уровень доверия, равный
99,9%.
Что касается анализа за
висимостей, он еще не вполне развит, поэтому каждый банк должен
следовать более консервативным моделям агрегирования: те, как пред
полагается, должны быть комонотонны 13 , а при агрегировании исполь
зуется простая сумма «границ потерь» (ГП 0 ) для каждого сочетания
те и БН.
Таблица
7.2.
Типы событий и бизнес-направлений, составленные
в соответствии со Вторым базельским соглашением
Thn'Ы собъ~тий (ТС)
Внутренние махинации
Внешние махинации
Служебная практика и безопасность рабочего места
Клиенты, продукты и деловая практика
Ущерб, причиненный физическими активами
Перерывы в хозяйственной деятельности, отказы системы и исполнение
Доставка и система управления процессами
Бизн.ес-н.аnравлен:ия (БН)
Корпоративные финансы
Торговля и продажи
Банковская розница
Банковская коммерция
Платежи и урегулирование
Агентские услуги
Управление активами
Розничные брокерские услуги
В этом разделе при помощи различных подходов мы вычислим ве
личину достаточного рискового капитала: мы начнем с базовых подхо
дов и завершим недавно предложенными моделями канонической агре
гации, основанной на понятии копула-функций (см.
[Di elemente, Romano (2004)), [Fantazzini et al. (2007)) и [Fantazzini et al. (2008Ь))), пуас
соновской моделью шоков (см. [Embrechts, Puccetti (2007)), [Rachedi,
Fantazzini (2008)), а также байесовскими методами (см. [Dalla Valle,
Giudici (2008а)], [Dalla Valle (2008))).
13 Случайные
величины Х1 , ••• , Xd называются комонотонными, если найдутся та.
кие возрастающие функции
v1, ... , Vd и случайная величина Z, что функция рас
... , Xd) совпадает с функцией распределения
(v1 (Z), ... , Vd ( Z)).
пределения случайного вектора (Х1,
случайного вектора
Гл.
680
7.3.1.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Регулирование операционного риска по Второму
базельскому соглашению
В Базель 11-соглашении введено понятие операционного риска как но
вого класса риска, под который финансовые учреждения обязаны от
ложить регулирующий капитал. Базель
11
определяет операционный
риск, как это представлено в последней редакции документа, следую
щим образом:
« Опера'Цион·н/ый
риск определяете.я как риск убытков в
результате неадекватной или ошибо'Чной работъt про'Цессов, персона
ла, систем или в результате внешних воздействий. Это определение
вклю'Чает юриди'Ческий риск, но исклю'Чает стратеги'Ческий и репута
'Ционн'Ьtй риск"».
Следуя
[BCBS (2005)],
банки имеют возможность выбирать между
тремя различными подходами.
•
•
•
Подход базовых индикаторов (ПБИ).
Стандартный подход (СП).
Подход, основанный на усовершенствованных моделях измерения
риска (УМИР-подход).
Банкам рекомендуется работать в этом спектре методов до того мо
мента, пока они не достигнут уровня, когда смогут разработать более
совершенные модели. Если банком выбран подход базов'Ьtх индикато
ров, он обязан удержать определенную процентную долю от положи
тельного валового дохода за каждый год из последних трех лет. Ес
ли выбран стандартн'Ьtй подход, деятельность банков делится на ряд
бизнес-направлений, и процентная доля удержания применяется к сред
нему валовому доходу за три года для каждого бизнес-направления.
Если же выбран подход, основанн'Ьtй на УМИР, банкам разрешается
развивать более сложные внутренние модели, в которых учитывается
взаимодействие между различными ТС и БН и которые направлены на
создание более «мягких"» рисковых стратегий. Однако для этого банку
необходимо сделать значительные инвестиции в управление операцион
ными рисками. В частности, в контроле за операционным риском долж
ны принимать активное участие совет директоров и топ-менеджмент
банка, система управления операционным риском должна быть кон
цептуально обоснованной, целостной и должна выделять достаточные
ресурсы для использования усовершенствованных подходов на основ
ных бизнес-направлениях, так же как для контроля и аудита. Перед
окончательным внедрением таких систем банки должны продемонстри
ровать их надежность и соответствие надлежащей оценке неожиданных
потерь, основанной на комплексном использовании внутренних и соот
ветствующих внешних данных, сценарном анализе и анализе факторов,
определяющих особенности деятельности и внутреннего контроля. Во-
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
681
лее того, банк должен иметь независимую функцию управления опе
рационными рисками, которая отвечает за разработку и функциони
рование структуры управления операционными рисками. Внутренняя
банковская система управления операционным риском должна быть
тесно интегрирована
в
систему
повседневного управления
рисками
с
топ-менеджментом и советом директоров. Банковская система управ
ления операционными рисками должна быть хорошо документирована
и должна регулярно
проверяться
как
внутренними,
так
и
внешними
аудиторами.
Что касается количественных требований, относящихся к подходу
УМИР, Базельский комитет указывает, что
«... у-читъ~вая
продол:жаю
щееся развитие аналити-ческих подходов к анализу операционного рис
ка, комитет не оговаривает какой-либо определеннъ~й подход или пред
поло:жения относите.л:ьно распределения, которое, в целях регулирова
ния, следует использовать для генерации меръ~ операционного риска.
Тем не менее банк дол:жен бъ~ть в состоянии показать, -что используе
мый им подход у-читъ~вает потенциально возмо:жнъ~е собъ~тия, влеку
щие за собой большие убъ~тки. Какой бъ~ подход ни исполъзовался, банк
дол:жен продемонстрировать, -что исполъзуемая им мера операцион
ного риска соответствует разумнъ~м стандартам, исполъзуемъ~м в
подходах к построению внутренних рейтингов для кредитного риска
(то есть сопоставима с 99,9-процентнъ~м доверительнъ~м интерва
лом, рассчитаннъ~м для одногодичного периода) ... Комитет призна
ет, -что УМИР
-
это достато-чно гибкий стандарт, дающий банкам
возмо:жность развивать как систему измерения операционного риска,
так и систему управления. Вместе с тем в развитии этих систем
банки дол:жнъ~ придер:живаться строгих процедур как при разработке
моделей операционного риска, так и при реализации утвер:жденной мо
дели. Пре:жде -чем на-чать внедрение того или иного подхода, Комитет
предполагает провести обзор передового опъ~та в данной области от
носительно достоверности и устой-чивости оценок возмо:жнъ~х опера
ционнъ~х убытков. Комитет так:же рассмотрит накопленнъ~е даннъ~е
и уровень достато-чности капитала, определенного в соответствии с
УМИР-подходом измерения, и в случае необходимости мо:жет внести
некоторъ~е поправки.,,.
В том же документе Базельский комитет заявляет, что
у-чета банковских рисков дол:жна
... у-читъ~вать
« ... система
все основнъ~е факто
ръ~ операционного риска, влияющие на форму хвоста оценок потерь.,,.
Это означает, что любая модель, предлагаемая в рамках УМИР-подхода
должна учитывать возможность экстремальных событий. Кроме то
го, в этом же документе говорится, что
« ... для
рас-чета минимального
достато-чного регулирующего капитала дол:жнъ~ у-читъ~ваться разнъ~е
Гл.
682
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
оценки меръt операционного риска. Однако банку может бытъ разреше
но исполъзование внутренне определенных корреляций убытков меж
ду отделъными оценками операционного риска, если, к удовлетворе
нию националъных надзорных органов, системы, определяющие корре
ляции, надежны, хорошо интегрированы и у-читывают неопределен
ностъ каждой из оценок корреляций (особенно в 'К'J)UЗисные периоды}.
Он должен подтвердитъ свои предположения относителъно корре
ляции
с
исполъзованием
соответствующих коли-чественных
и
ка-че
ственных методов». Этот комментарий подчеркивает возможность ди
версификации операционных рисков. Тем не менее установлено, что в
кризисные периоды, т. е. в периоды, когда почти все функционирует
некорректно, это может быть невозможным.
Далее в документе представленном Базельским комитетом, рас
сматриваются требования к данным, необходимым для системы контро
ля внутренних рисков. Данные по внутренним убыткам имеют важное
значение для надежного моделирования профиля операционного риска
организации. Излишне упоминать о том, что создание базы историче
ских данных об убытках крайне необходимо при переходе к УМИР
подходу для управления операционными рисками. База данных по бан
ковским
внутренним
стандартам,
потерям
установленными
должна соответствовать
Комитетом:
определенным
« ... банковские данные по
внутренним убыткам должны бытъ достато-чно подробными,
по
сколъку должны отражатъ как всю банковскую деятелъностъ, так
и воздействие на нее всех соответствующих подсистем и географи
-ческого местоположения. Банк должен уметъ обосновыватъ, -что ис
клю-чение любой деятелъности или воздействия, как отделъно взятой
(взятого), так и в со-четании, не будут иметъ существенного влия
ния на оценку совокупного риска. Для собранных данных о внутренних
убытках банк должен иметъ соответствующий порог минималъного
валового убытка, например
1О
ООО евро. Вели-чина этого порога может
варъироватъся как от банка к банку, так и внутри банка, в зависимо
сти от банковских бизнес-направлений и (или) типов событий. Тем
не менее вели'Ч.ины отделъных порогов должны бытъ в целом согласо
ваны с соответствующими порогами,
исполъзуемыми в равноценных
банках».
Понятие порога становится особенно важным, когда данные из раз
личных банков объединяются в единую базу или когда внешние данные
объединяются с внутренними данными банка, и это должно быть сде
лано в строго систематизированной форме для того, чтобы избежать
потери информации о существенных операционных убытках.
683
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
7.3.
Подход базовых индикаторов (ПБИ)
7.3.2.
Банкам, использующим подход базовых индикаторов, необходимо отло
жить резервный капитал, равный фиксированной доле (обозначенной
через
q)
от положительного годового валового дохода (ВД). Если же
годовой валовой доход отрицателен или равен нулю, то он должен быть
исключен из рассмотрения при вычислении среднего. Таким образом,
резервный капитал под операционный риск в год
t
дается выражени
ем14:
t
RСв1
=
z
3
1 '""
L.Jqmax(GIt-i ,О),
t i=l
где Zt = E~=l I{GJt-i>O} и c1t-i обозначает валовой ДОХОД за (t - i)-й
год. Отметим, что резервный капитал под операционный риск рассчи
тывается ежегодно. БИ-подход дает довольно простую, основанную на
размере капитала процедуру расчета резервных средств.
Базельский комитет по-прежнему занимается сбором данных в це
лях определения фиксированной доли
q, которая
вычисляется как сред
нее из долей операционных резервных капиталов
12%
банков, характе
ризуемых минимальными операционными резервными капиталами. Це
левой уровень в
12% соответствует данным, полученным в рамках
«Изу
чения количественного воздействия» (ИКВ), проведенного Базельским
комитетом. В этом исследовании рассматривалась выборка из
41
банка.
В частности, оказалось, что среднее отношений операционного капита
ла к экономическому капиталу 15 по каждому из рассматриваемых бан
ков равно
14,9%. Как это описано Базельским комитетом, цифра в 12%
была выбрана для того, чтобы «калибровать капитал при помощи, в
некоторой степени, менее жесткого по сравнению с интервальнъtм
экономическим капиталом, но разумного стандарта». После установ
ления 12%-ного целевого уровня был произведен анализ зависимости
между целевым операционным резервным капиталом и валовым дохо
дом на основе выборки, включающей данные по
140 банкам из 24 стран.
После проведения этих и иных ИКВ Базельский комитет предложил
q = 15%.
Схема БИ-подхода иллюстрирует классический подход «сверху
вниз», который калибрует капитал так, чтобы задавать общее требова
ние к резервному капиталу. Этот подход отличается от так называемо
го подхода «снизу-вверх», в соответствии с которым размер резервного
14 Предполагается,
что описанная процедура приемлема только для тех банков,
которые не имели трехлетних периодов функционирования с отрицательным или
нулевым ВД.
15 Экономический
капитал - это капитал, необходимый для адекватного покрытия
всех рисков, принимаемых конкретным банком.
Гл.
684
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
капитала определяется на основании истории фактических убытков и
которому в настоящее время Базельский комитет отдает предпочтение.
7.3.З.
Стандартизированный подход (СП)
Подход БИ предназначен для реализации в крупных банках. Переход
же к стандартизированному подходу требует от банка учета валово
го дохода по каждому из бизнес-направлений отдельно. Модель разде
ляет восемь бизнес-направлений: корпоративные финансы, торговля и
продажи, банковская розница, банковская коммерция, платежи и уре
гулирование,
агентские и депозитарные услуги, управление активами
и брокерские услуги. Для каждого бизнес-направления рассчитывает
ся резервный капитал, величина которого равна валовому доходу по
рассматриваемому бизнес-направлению, умноженному на множитель,
обозначенный через
f3
(для каждого из бизнес-направлений свой). Сум
марный резервный капитал RCkA в t-й год рассчитывается как трехго
дичное среднее неотрицательных валовых доходов, а именно:
t
RCsA =
1
3
[ 8
3 ~max
~fЗ;Gl; ,О]
Заметим, что в формуле
t-i
(7.9)
(7.9)
.
в любой фиксированный год
(t - i)
отрицательное значение резервного капитала по некоторому бизнес-на
правлению
j (отрицательное значение возникает из-за отрицательно
сти валового дохода по этому направлению) может быть компенсиро
вано за счет положительных резервных капиталов по другим бизнес
направлениям. Взаимозачеты такого рода должны побудить банки к
переходу от подхода БИ к СП. В табл.
для каждого из бизнес-направлений.
7.3 представлены бета-множители
В работе [Moscadelli (2004)] пред
ставлен критический анализ этих бета-множителей, основанный на ин
формационной базе по более чем
ИКВ лета
47 ООО операционным убыткам
2002 г.).
Стандартизированный подход
деленным
(второе
f3
-
это обобщение подхода БИ с опре
для каждого из бизнес-направлений. В рамках этих двух
подходов Комитет планирует дальнейшую разработку основополагаю
щих принципов. Кроме того, по усмотрению национальных надзорных
органов в вышеизложенные правила могут вноситься незначительные
изменения (часто более консервативные).
7.3.
Таблица
7.3.
Бета-множители для стандартизированного подхода
Бизнес-направления
Бета-множители,
Корпоративные финансы
%
18
18
12
15
18
15
12
12
Торговля и продажи
Банковская розница
Банковская коммерция
Платежи и урегулирование
Агентские и депозитарные услуги
Управление активами
Брокерские услуги
7.3.4.
685
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
Введение в подход, основанный на
усовершенствованных моделях измерения риска
(УМИР-подход)
Наиболее совершенный из трех подходов регулирующего операционного
рискового капитала
-
это УМИР-подход. Этот подход позволяет бан
кам использовать собственную внутреннюю систему управления опе
рационным риском для расчета минимального уровня регулирующего
капитала с учетом
количественных и качественных стандартов, уста
новленных регуляторами. Однако как в случае рыночного и кредитно
го риска, внедрение УМИР возможно только при условии одобрения и
непрерывного контроля качества со стороны национальных надзорных
органов. В соответствии с предъявляемыми требованиями банк дол
жен отразить убытки по каждому бизнес-направлению и типу события.
В частности, банки, как ожидается, объединяют внутренние регуляр
ные, высокочастотные убытки, так же как и соответствующие внеш
ние нерегулярные низкочастотные убытки. Более того, банки должны
дополнить свои отчеты описанием кризисных ситуаций как на уровне
серьезности ущерба, так и на уровне зависимости между разными ви
дами убытков. При отсутствии детализированных совместных моделей
для различных видов убытков мера риска совокупного убытка долж
на рассчитываться как сумма соответствующих мер риска убытков по
каждой категории.
В Базельском соглашении от
2001 г.
в рамках УМИР-подхода Ко
митет описывает три метода.
•
Подход внутренних изменений (ВИ-подход). В соответствии
с этим методом резервный капитал по операционным рискам зависит от
суммы ожидаемых и непредвиденных убытков: ожидаемые убытки рас
считываются с использованием исторических данных банка, а непред
виденные убытки находятся путем умножения ожидаемых убытков на
Гл.
686
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
соответствующий множитель 'У, полученный на основании анализа сек
торов.
•
Подход распределения убытков (РУ-подход). Используя
внутренние
данные,
можно
рассчитать
для
каждой
комбинации
БН/ТС вероятностное распределение частоты возникновения убытков,
так же как и его влияние (степень влияния) на определенном промежут
ке времени. Сворачивая функцию распределения частоты с функцией
распределения величины убытка, аналитически или численно, можно
получить вероятностное распределение суммарного убытка. Итоговая
величина резервного капитала будет равна процентной точке этого рас
пределения.
•Оценочная карточка (ОК). Эксперты должны структуриро
вать процесс идентификации факторов, определяющих те или иные ка
тегории рисков, а затем на основании этого сформулировать вопросы,
которые могут быть помещены в оценочную карточку. Некоторые из
этих вопросов спрашивают о численной информации (например, ско
рость текучести кадров), другие спрашивают об экспертной оценке (на
пример, скорость изменения в различных сферах бизнеса), а третьи
-
просто да/нет вопросы (как, например, вопросы о соблюдении опреде
ленных принципов, о следовании определенной политике). Эти вопро
сы отобраны так, чтобы охватить факторы, определяющие как веро
ятность операционных событий, так и характер и силу их влияния на
риски, а также чтобы определить действия банка для смягчения это
го влияния. Параллельно с внедрением оценочных карточек и учетом
их результатов рассчитывается банковский суммарный резервный ка
питал под операционные риски, который затем распределяется между
категориями риска.
В последней версии Второго базельского соглашения эти модели
не упоминаются с тем, чтобы обеспечить б6льшую гибкость в выборе
методов внутреннего измерения рисков.
Учитывая все возрастающее значение и возможность применения
эконометрических методов (см., например,
(Cruz (2002)]), мы сосредо
точим наше внимание только на РУ-подходе.
7.3.5.
Стандартный РУ-подход с комонотонными
убытками
РУ-подход использует два типа распределений: один тип распределе
ний описывает частоту возникновения рисковых ситуаций, а другой
описывает функцию распределения величины убытка, возникающего
для каждой рассматриваемой рисковой ситуации. Определим частоту
операционных убытков как число случаев возникновения этих убыт-
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
687
ков за некоторый промежуток времени, а степень убытка k-го слу
чая определим как величину соответствующего убытка. Формально для
каждого типа риска
i (т. е.
типа, отвечающего некоторому пересечению
БН/ТС) операционные убытки, накопленные за t-й период времени, где
t = 1, ... , М, М - число периодов времени, могут быть определены как
сумма Sit случайного числа nit убытков (Xij(t)), j = 1, ... , nit:
Отметим, что для каждого пересечения БН/ТС суммарный убыток,
накопленный за t-й период, может быть представлен в следующем виде:
где
nit -
частота операционных убытков, а
Sit -
средний убыток i-го
пересечения за t-й период времени.
РУ-подход предполагает, что для каждого t-го периода времени:
•индивидуальные убытки
{Xij(t)},
где t= 1, ... , М;
j = 1, ... , пit,
независимые и одинаково распределенные случайные величины;
• случайная величина nit не зависит от случайных величин Xij, где
t=l, ... ,M; j=1, ... ,nit;
• Sit, где t = 1, ... ,М, - независимые и одинаково распределенные
случайные величины.
Для заданного (i-го) пересечения БН/ТС мы строим дискретную
функцию распределения числа убытков
nit
за t-й период и
непрерывных вероятностных плотностей величин убытков
nit -
nit штук
Xij(t) (где
наблюдаемое значение частоты убытков i-го пересечения за t-й
период; обозначим через
Xij(t)
наблюдаемый j-й убыток i-го пересе
чения за t-й период). Для каждого пересечения
добия наблюдений
i функция правдопоil.i = (nil, ... , niм ), Xi = (xil(l), Xi2(l), ... , Xinil (1),
xil(M), xi2(M), ... , Xini 2 (M), ... , xil(M), xi2(M), ... , Xiniм(M))
имеет
вид:
(7.10)
где
p(nitl8i) -
вероятность возникновения
чения в t-й период времени, а через
8i
nit
убытков для i-го пересе
обозначен вектор-параметр этой
вероятности;
в точке
f(Xij(t)l1Ji) - плотность величины убытка i-го пересечения
Xij(t), а Т/i обозначает вектор-параметр этой плотности.
В РУ-подходе частота возникновения убытков за некоторый вре
менной период может быть смоделирована при помощи пуассоновско
го или отрицательного биномиального распределения. Отрицательное
биномиальное распределение может быть получено из пуассоновского
Гл.
688
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
распределения, если предположить, что параметр последнего не детер
минированная величина, а случайная, имеющая гамма-распределение.
Другими словами, отрицательное биномиальное распределение может
быть представлено как смесь пуассоновского и гамма-распределений.
Для моделирования величины убытка можно использовать экспонен
циальное распределение, Парето-распределение, гамма-распределение
или обобщенное Парето-распределение (ОПР) (см. ниже). Функция рас
пределения
Fit
суммарных операционных убытков
Sit
для i-го пересе
чения между бизнес-направлениями и типами событий за t-й период
может быть получена сверткой распределения частоты и распределе
ний величин убытка. Однако следует отметить, что представление в
аналитическом
виде
этого
распределения
-
весьма сложная
задача.
По этой причине стало обычной практикой аппроксимировать это рас
пределение методом Монте-Карло, а именно: из некоторых теоретиче
ских распределений много раз (например, 106 раз) генерируется число
убытков и соответствующие величины убытков; после чего в каждом
из смоделированных случаев рассчитывается суммарный убыток и по
совокупности смоделированных суммарных убытков строится эмпири
ческая функция распределения, которая и аппроксимирует функцию
распределения суммарных операционных убытков i-го пересечения за
t-й период.
Если у нас есть функция распределения суммарного операцион
ного убытка для i-го пересечения, по ней можно оценить такие меры
риска, как граница nотеръ (ГП}, среднее ожидаемъ~х nотеръ (СОП},
и на основании этих оценок определить величину резервного капитала
для i-го пересечения на следующий период. После того как оценены ГП
для каждого пересечения БН/ТС, рассчитывается граница потерь для
всей совокупности операционных рисков (совокупная граница потерь),
которая обычно вычисляется как сумма ГП всех пересечений БН/ТС,
а тем самым предполагается, что суммарные убытки
sit
комонотонны.
Излишне говорить о том, что такое предположение нереалистично. Из
теоремы Шкляра (см.
[Sklar (1959)))
в силу комонотонности суммарных
убытков следует, что:
Hs1t, ... ,SRt(x1, ... , хп)
= min (Fs1t(x1), ... , FsRt(xn)),
где
Hsit, ... ,SRt(·) - совместное распределение вектора суммарных убыт
ков Sit, i = 1, ... , R, а Fsit(·) - кумулятивная функция распределения
суммарного убытка Sit.
1)
Модель для частоты возникновения убытков
Анализ убытков по операционным рискам подразделяется на по
строение модели частоты возникновения убытков и построение модели
7.3.
689
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
величины среднего убытка. Учитывая тот факт, что убытки возникают
в нерегулярные моменты времени, мы будем использовать дискретные
распределения для описания частоты возникновения убытков. В стан
дартном РУ-подходе в качестве моделей для частоты возникновения
убытков используется либо однородное пуассоновское распределение,
либо отрицательное биномиальное распределение.
Пуассоновское распределение дает вероятность реализации опре
деленного числа событий за фиксированный интервал времени при
условии, что эти события происходят с известной интенсивностью и
вероятность реализации следующего события не зависит от времени,
прошедшего с момента реализации предыдущего.
Если ожидаемое число реализованных событий за определенный
период времени равно Л, тогда вероятность того, что число реализован
ных событий nit в точности равно
целое,
k
=О,
1, 2, ... )
k (k -
некоторое неотрицательное
задается формулой
Обозначим пуассоновское распределение с параметром Л через
PO'isson (Л). Для этого распределения Е (nit)
= D (nit) = Л. Таким обра
зом, число реализованных событий флуктуирует около своего среднего
Л со стандартным отклонением
Unit
=
Д. Эти флуктуации обычно
называют пуассоновским шумом.
Альтернативным распределением для моделирования частоты ~t
является отрицательное биномиальное распределение. Это рас
пределение имеет два действительнозначных параметра р и
< р < 1 и r > О.
negBin(r, р)
Р {~t
где
где О
<
Обозначим отрицательное биномиальное распределе
ние с параметрами р и
для
r,
r
через
negBin(r,p).
Распределение вероятностей
имеет следующий вид:
= klЛ} = p(k; r,p) = ( k+r-1)
k
pr (1 -
( k+r-1)
k
-
число сочетаний из
р)
k
(k + r -1)
для
k =о, 1, ... '
элементов по
k,
т. е.
Г(k + r)
( k + r -1 ) =
k
Г(k + l)Г(r)'
где Г
(k)
= (k -
1)!.
Следует отметить, что отрицательное биномиальное распределение
с параметрами
r
и
r / (Л
+ r)
при
r
~ оо сходится к пуассоновскому
Гл.
690
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
распределению с параметром Л:
Poisson(Л)
= lim negBin(r,r/(Л+r)).
r-+oo
При такой параметризации
отвечает за отклонение от пуассонов
r
ского распределения. Поэтому отрицательное биномиальное распреде
ление
-
весьма
приемлемая
и
содержательная
альтернатива
пуассо
новскому распределению. Это распределение сходится к пуассоновско
му распределению при бесконечно больших
r,
но при малых
r
имеет
большую дисперсию, чем пуассоновское распределение.
Параметры этих распределений могут быть оценены по эмпириче
ским данным при помощи метода моментов или метода максимально
го nравдоnодоби.я. Что касается оценки параметра пуассоновского рас
пределения для i-го пересечения, если мы воспользуемся методом мо
ментов, то получим следующую оценку этого параметра:
Если же пользуемся методом максимального правдоподобия, то нам
необходима функция правдоподобия, которая принимает следующий
вид:
м
l: iiit
L
(ftilЛi) = е-м~i л~=1
П пit!
t=l
Логарифмическая функции правдоподобия дается выражением
а производная по Л логарифмической функции правдоподобия равна
дlnL(~IЛi) _ -М
дЛ·
i
-
2_ ~А.
+ Л· Lti
nit·
t=l
Приравнивая эту производную к нулю
i
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
691
и решая это уравнение относительно Лi, получим оценку максимального
правдоподобия, которая равна
Таким образом, в этом случае, используя оба метода, мы получим
одинаковые результаты.
Что касается отрицательного биномиального распределения, в усло
виях относительно малых выборок метод моментов обычно предпочти
тельнее метода максимума правдоподобия в силу проблемы сходимости.
Учитывая, что
D (nit) = ri 1 - Pi ( 1 + 1 - Pi)
Pi
Pi
,
мы имеем
µ2
где
µi -
= ri 1-pi
первый момент, а
Pi
µ2 -
( 1 + 1-pi)
Pi
+ ( r1-pi)
i--
2
Pi
второй момент. Применяя метод мо
ментов, мы получим следующие оценки параметров
Ti
и
Pi=
где оценки для Р,1 и Р,2 вычисляются следующим образом:
и
Вместе с тем мы подчеркиваем, что методы стохастического моде
лирования (см.
[Fantazzini et al.
(2008в))) показывают, что пуассоновское
распределение дает устойчивые оценки даже в условиях малых выбо
рок, в то время как результаты, показываемые отрицательным биноми
альным распределением, значительно отличаются. При М
=
72
симу
ляциях отрицательное биномиальное распределение дает некорректные
оценки в
40%
случаев, а средний квадрат ошибки и коэффициент вари
ации имеют большие значения. Более того, даже при М
ri
вариации по-прежнему много больше 0,1.
лированных наблюдениях оценки для
= 2000 смоде
неустойчивы, а коэффициент
Не публикуемые здесь резуль
таты моделирования показывают, что оценки стабилизируются вокруг
действительных значений только при более чем
наблюдениях.
5000
смоделированных
Гл.
692
2)
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Моделирование величины убытка
Закон распределения величины
Xij(t)
j-го убытка
(j
= 1, 2, ... , nit),
наблюдаемого в период t в условиях i-го пересечения БН/ТС, может
быть описан при помощи широкого спектра непрерывных распределе
ний, начиная от экспоненциального распределения и кончая обощенным
Парето-распределением (ОПР).
Обозначим через
за t-й период, где
Xij(t) наблюдаемый j-й
t = 1, ... , М; j = 1, ... , nit·
убыток i-го пересечения
Одной из возможных моделей, с помощью которых можно попы
таться описать распределение случайной величины
Xij(t),
является
двухпараметрическое гамма-распределение, функция плотности кото
рого имеет вид:
(х >О),
где параметры
ai
и /Зi удовлетворяют условиям
ai > 1,
/Зi
> О,
а Г( ·)
-
гамма-функция Эйлера, т. е.
J
00
Г(аi) =
zai- 1 e-zdz.
о
Взяв эту функцию плотности и применив метод моментов, получим
следующие оценки ее параметров
7.3.
693
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
Другим приемлемым распределением для моделирования величины
убытка i-го пересечения за период
t
является экспоненциальное распре
деление. Плотность этого распределения может быть получена из плот
ности гамма-распределения, если в последнем взять ai
= 1, (}i = Лi, т. е.
плотность экспоненциального распределения равна
r.p ( х 1лi )
=
1 -...!..х
лi е ~i '
Лi >О.
Оценка методом моментов параметра Лi равна:
м
Enit
,Xi = __t_=_l_ __
м nit
ЕЕ
Xij(t)
t=lj=l
Кроме того, величину убытка
Xij(t)
можно моделировать при по
мощи Пареm~распределения, плотность которого равна:
Заметив, что
и применив метод моментов, мы получим следующие оценки парамет
ров:
Mnit
Е
Е Xij(t)
( t=lj=l
)2
2
Учитывая экстремальный характер операционных убытков, хвост
распределения величины убытка может быть смоделирован при помощи
распределений, рассматриваемых в теории экстремалънъ~х значений
(ТЭЗ). В ТЭЗ анализируются редкие события. В финансы и страхова
ние эта теория пришла из гидрологии как для прогнозирования редких
событий, так и для построения более устойчивых моделей непредвиден
ных экстремальных событий.
Гл.
694
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ТЭЗ позволяет нам отказаться от парадигмы гауссовского распре
деления для операционного риска, сосредоточив особое внимание на
хвосте этого распределения. Это становится особенно важным, когда
рассчитываются такие меры риска, как ГП или СОП при больших до
верительных
уровнях,
например
в
случае
операционных
рисков
при
99,9%-ном доверительном уровне.
ТЭЗ утверждает, что распределение убытков, превышающих неко
торый высокий порог и, асимптотически (по и) стремящихся к мак
симально допустимым значениям, которые, в частности, могут быть
и +оо, сходится к обобщенному распределению Парето, кумулятив
ная функция распределения которого обычно выражается в следующем
виде:
GPD~,p(y)
)
(
= { 1- 1 + ~J
1-
-1/~
ехр (-~)
В нашем случае мы полагаем у
=
х
-
,
' ~#О;
~=О.
и, при этом у ~ О, если
~ ~ О, и О ~ у ~ -{З / ~, если ~ ~ О; у называют остатком, а х называют
превышением. Условную функцию распределения остатка от аргумента
у можно определить как функцию от х:
Fи(У)=Р(Х-и~ уlХ>и)=
F(x)-F(u)
l-F(u) .
Параметр~ в обобщенном Парето-распределении играет определяющую роль:
•
при ~ = О ОПР совпадает с экспоненциальным распределением;
•при~< О ОПР совпадает с распределением Парето
•при~> О ОПР совпадает с распределением Парето
11 типа;
1 типа.
Более того, этот параметр напрямую связан с существованием ко
нечных моментов распределений убытков. При этом
Е (xk) = оо, если k ~ 1/~.
Следовательно, в случае, если ОПР совпадает с распределением
Парето
1 типа и~~ 1, мы имеем бесконечное среднее (см. [Neslehova,
Embrechts et al. (2006))).
Следуя работам [Di Clemente, Romano (2004)) и [Fantazzini et al.
(2008в)], мы предлагаем моделировать величину j-го убытка i-го пере
сечения за период
t,
обозначенную через Xij ( t), на правом хвосте при
помощи ОПР, а для остальных значений
-
при помощи логнормального
695
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
7.3.
распределения. А именно, при помощи следующего распределения:
ф (lnx-щ)
Fi(X) =
где Ф
Ui
{
О< Х <и··
'
(
''
~;i 1 + ~ (х - Ui)
1-
)-1/f.i
,
функция стандартного нормального распределения,
-
Nu,i - чис
ло убытков, превышающих уровень Ui, Ni-число наблюдаемых убыт
ков i-го типа, а /Зi и ~i -
параметры ОПР.
Например, графический анализ третьего ТС (см. табл.
ставленный на рисунках
(2008)]),
и
7.12
7.2), пред
[Rachedi, Fantazzini
(из работы
7.13
явно свидетельствует о том, что операционные убытки харак
теризуются высокой частотой малых убытков и низкой частотой боль
ших убытков. Следовательно, операционные убытки имеют двойствен
ный характер: один процесс лежит в основе малых и частых убытков,
а другой
в основе больших и редких убытков. Разделение модели на
-
две части позволяет нам разумным образом оценивать влияние экстре
мальных убытков.
Важный вопрос, который следует рассмотреть, это оценка парамет
ров предложенной выше функции распределения
Fi (х).
В то время как
для случая логнормального распределения оценка при помощи мето
да максимального правдоподобия достаточно проста, для случая ОПР
крайне важно поразмыслить над тем, какой из методов (например, ме
тод максимального правдоподобия или метод взвешенных моментов)
лучше улавливает динамику изучаемых величин убытков.
~
---- mean
•
---- 90%
---- 95%
~- ---- 99%
-
~
!2
•
~_!- -----------------------------------------------~---------•--------~--• •
• •
•
•
_ --i---- -- - " ___•- - -- - --· -- -- · · - - - - ---• - - ~J
-----~---------~-~-~--:.:~~-_.~_:
~
".
'
а
~
~
·:
:а c;r!\О~
.......
...-
'iv.
•
----~- - • - - - ---
____________ _.__. _ :_________
•
i-
••
:~~-----
··. . . .
. ....".... _. .. . ...... .. -. .. .....
......••
" •"
••"" ,_, •.,. •• -- • ,.
V>
i:a
-!!.
•
!'., __ - • - --- - -- - - -
•
•
•
• - •
•
•••• ".
•
•
~
•• '
•• "
••
•
-~--·-:··~----~"~---;;·:~~---~-:~-,:-,~;:-~~-=--~~;."::···:-•
•
•• •• • •
:
... "а\••
" . ~ ••• •
•
·-·
• •
••'•
#
••
• •••
"
•
•
."
•
•••
•
•
-.•.
~···
·~~~
• -••• , z•
•• -а •.".,,. ••• ~....
1..-. • ••• - •". ~• - ·~· ••
.
100
о
.
200
.
300
.
400
Индекс
Рис.
7.12.
Диаграмма рассеяния убытков третьего ТС
Гл.
696
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ШIШU,_ _
50000
100000
150000
200000
250000
300000
350000
Убыток
Рис.
7.13.
Гистограмма убытков третьего ТС
Рассмотрим метод максимального правдоподобия для ОПР. Лога
рифмическая функция правдоподобия наблюдений
Xij(t),
которые пре
вышают соответствующий уровень щ, равна
где l{xi;(t)>ui} -
индикаторная функция события
{Xij(t) > щ}.
Обозначим через ~i,/зi, оценки параметров ~i, /Зi, даваемые методом
максимального правдоподобия.
Этот метод хорошо работает, если ~i
> -1/2.
В этом случае можно
показать, что
где
у-1 =
{1 + {;) ( 1 +1{; -;1 ) .
Рассмотрим метод взвешеннъ~х по вероятности моментов ( ВВМ).
В отличие от стандартного метода моментов, в котором приравнивают
ся эмпирические и соответствующие теоретические моменты анализи
руемой случайной величины, в ВВМ приравниваются моменты некото
рым специальным образом взвешенной (преобразованной) анализиру-
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
697
емой случайной величины. При этом взвешивание подбирается преж
де всего из соображений обеспечения существования используемых мо
ментных тождеств. Метод ВВМ зачастую дает лучшие оценки, чем
стандартный метод моментов (ММ).
Предположим, что случайная величина
(Xij(t)- Ui)l{xij(t)>ui} име
ет распределение GPD~i ..Вi(x). Тогда соотношения, на которых основан
метод ВВМ, имеют вид:
Wr
=
Е [ (Xij(t) -
Ui) l{xi;(t)>ui} Х
х(GP D~i •.Вi ( (Xij(t) где
r
=О,
l{xi;(t)>щ})) r] = (r + l)(:~ 1 _ ~i)'
1, ... ; GPD~i •.Вi(x) = 1 - GPD~i ..вi(x). Из выражений для тео
ретических взвешенных по
порядков
Ui)
(wo
вероятности моментов нулевого и первого
и W1 соответственно) мы можем выразить /Зi и ~i:
и
~i=2-
wo
---wo -2w1
Если в этих выражениях мы заменим теоретические взвешенные по
вероятности моменты соответствующими эмпирическими моментами:
r =О, 1,
м пit
где Nui,i = Е Е I{жi;(t)>ui}' а Н(х)
-
эмпирическая функция pacпpe
t=lj=l
деления ненулевых превышений (Xij(t)-Ui)I{жi;(t)>ui} (t =
1, ... , M;j =
= 1, ... , nit), получим ВВМ-оценки для параметров /Зi и ~i·
В статье [Hosking, Wallis (1987)] показано, что при ~ ~ О ВВМ
оценка является ни в чем не уступающей оценке, полученной методом
максимального правдоподобия.
В статье
[Rachedi, Fantazzini (2008)]
параметр ОПР ~наряду с уже
упомянутыми подходами оценивается также при помощи оценки Хил
ла (более детальную информацию об этой непараметрической оценке
см.
[Cruz (2002)]).
Чтобы выделить наилучшую процедуру оценивания
параметра ~, гарантирующую устойчивость оценок этого параметра,
мы вычислили оценки~ для разных пороговых уровней. Как видно из
рис.
7.14,
эмпирический анализ для оценки~ указывает на преимуще
ство ВВМ-метода над методом максимального правдоподобия и оцен
кой Хилла. Отметим устойчивость ВВМ-оценки для различных поро
говых значений
Ui·
Гл.
698
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
L1J
1
'
'
=
00
"'
=
'--~~-т-~~~~....-~~~........~~~~~
100
50
Рис.
7.14.
150
200
U;
Сравнительный анализ оценок, полученных методом максимального
правдоподобия, ВВМ-методом и методом Хилла
3)
Смешивание при помощи метода Монте-Карло
После того как построена модель частоты возникновения убытков
и модель величины среднего убытка, необходимо их эмпирически сме
шать при помощи метода Монте-Карло для того, чтобы смоделировать
новую серию агрегированных убытков. А при большом количестве дан
ных мы сможем вычислить такие меры риска, как ГП и СОП.
Разумно предположить, что случайные величины Хн(t),
(Xij(t) -
j-й убыток i-го пересечения в период
делены. Обозначим
Fx,t (х) = Pr (Xij(t) :s:;
Sit =
Хн(t)
+ Xi2(t)+
равна:
00
Fsit(x)
одинаково распре
х).
Функция распределения случайной суммы
+ ... + Xinit(t)
t)
... , Xin(t)
= P(Sit :s:; х) =
L PnitP(Sit :s:; х
00
1
nit)
=
L PnitFJc~ft(x),
nit=O
где
FJcnit (·) - свертка функций распределений случайных величин
Хн(t), ... , Xinit(t), а Pnit - вероятность того, что число убытков i-го
пересечения в течение периода
t
окажется равным ~t·
Следовательно, функция распределения смеси частот и величин
убытков равна сумме сверток функций распределений величин убыт
ков. Отсюда получаем, что плотность с.в.
00
fsit(x) =
Sit
равна:
L PnitfJc~ft(x).
nit=O
7.3.
699
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
Однако получение аналитического представления для распределе
ния
Fsit -
вычислительно весьма сложная (иногда неразрешимая) за
дача. В силу этого приближают это распределение при помощи метода
Монте-Карло.
В предположении независимости операционных убытков приведем
описание процедуры моделирования ГП и СОП суммарных операцион
ных убытков с использованием метода Монте-Карло.
Оценим частную функцию распределения убытка
1.
каждого типа рискового события
i, i = 1, ... , R,
Fsit (х) для
следующим образом:
(а) в соответствии с функцией распределения частоты убытков i-го
типа риска (пуассоновское или отрицательное биномиальное распреде
ление) сгенерируем случайную величину nit (обозначим сгенерирован
ное значение через
nit)i
(Ь) из функции распределения среднего убытка i-го типа риска (экс
поненциальное распределение, Парето-распределение, гамма-распреде
ление, ОРП-распределение) сгенерируем случайную величину
значим сгенерированное значение через
(с) умножив
ток типа
(d)
Sit (обо
sit)i
sit на nit, получим смоделированный суммарный убы
i;
повторим шаги (а)-(с)
(е) сортируя по
N = 100 ООО раз;
возрастанию 100 ООО значений
суммарных убытков,
полученных на предыдущем шаге, генерируем функцию распределения
суммарного убытка i-го типа
2.
Fsit(x).
Для каждого типа рискового события
i,
используя сгенерирован
ную функцию распределения суммарного убытка i-го рискового собы
тия
Fsit(x),
вычисляем ГП и СОП необходимого доверительного уров
ня.
3.
Наконец, вычисляем совокупную ГП (СОП) как сумму всех ГП
(СОП) для каждого типа рискового события
7.3.6.
i.
Каноническая агрегация при помощи
копула-функций
Для финансовых организаций, не способных оценить зависимости меж
ду ТС (или БН), Базель
11
требует реализацию весьма консерватив
ного подхода. Вместе с тем связь между суммарными операционными
убытками различных БН отнюдь не описывается комонотонной зависи
мостью. Это обстоятельство предоставляет нам широкие возможности
диверсификации и получения меньшего по величине и более эффектив
ного резервного капитала.
В этом разделе мы рассмотрим, как может быть использована копу
ла-функция для описания структуры зависимости между суммарными
Гл.
700
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
убытками (Sit)~ 1 • Отметим, что ее использование приводит к уменьше
нию величины полной ГП (см.
[Di Clemente, Romano (2004)], [Fantazzini
et al. (2007)], [Fantazzini (2008а)]).
Теорема Шкляра [Sklar (1959)]
утверждает, что совместное распре
деление Н вектора суммарных убытков
Sit, i = 1 ... R, t = 1, ... , М,
может быть представлена как ко пула-функция от маргинальных (част
ных) функций распределения компонент вектора:
где
функция распределения случайной величины
Fsit(·) -
Sit,
С(·)
-
копула-функция.
Каноническая агрегация при помощи копула-функций предполага
ет агрегацию убытков за какой-то временной период, после чего оце
нивается зависимость этих суммарных убытков
Sit, i
=
1, ... , R,
при
помощи копула-функции. Таким образом, мы можем изучать недель
ные, месячные или годовые суммарные убытки в зависимости от ин
формации, представленной в базе данных по операционным убыткам,
и поставленных задач.
Для описания зависимости суммарных убытков обычно используют
либо нормальную копула-функцию, либо Т копула-функцию, плотности
которых представлены ниже. Так, для нормальной копула-функции
с
где
ления,
Е
-
(х1,
( =
Normal( и1, ... ,un ) -_
... ,xn)';
Ф- 1 (·) -
1
( 11"'(~-1
IEl112 ехр -2~ LJ
щ = Ф(х1), Ф(·)
-
-
/)/")
~
'
гауссовская функция распреде
обобщенное обращение 16 гауссовского распределения,
корреляционная матрица;
I -
единичная матрица размера
n.
Для Т копула-функции мы имеем:
) - IEl-1/2 Г (v+n)
-2-
и
CStudent't(u
1, ... '
Г (~)
n -
v±n
('Е-1()- 2
[ Г (v)
1+
2 ] n -'----v----'--(
Г (v!l)
.ТТ (1 + ~)-~ '
i=l
где
( = (х1, ... , Xn)'; щ Е tv(Xi), tv(·) - t-распределение с v степенями
свободы, t;;- 1 (·) - обобщенное обращение t распределения с v степенями
свободы, а Е
Обе
эти
-
корреляционная матрица.
копула-функции
копула-функций (см. п.
6.2
принадлежат
классу
эллиптических
книги). Альтернативным классу эллипти
ческих копула-функций является класс архимедовых копула-функций.
16 Если
нам дана некоторая функция F(·), то ее обобщенным обращением будет
функция р- 1 (11.) = inf{y :
обобщенное обращение
F(y) ~ u}. Далее везде через р- 1 0 будем обозначать
функции F(·).
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
7.3.
701
Однако использование представителей этого класса имеет существенное
ограничение, состоящее в том, что такие копула-функции моделируют
только положительную зависимость (или только частную отрицатель
ную зависимость), в то время как их многомерные обощения имеют
ограничения на параметры двумерной зависимости. Вот почему архи
медовы копула-функции не используются при описании операционного
риска.
Аналитическое представление многомерной функции всех суммар
ных убытков Sit с помощью копула-функции невозможно, поэтому необ
ходимо приближенное решение, которое можно получить, например,
методом Монте-Карло.
После того как оценены параметры копула-функции С и марги
нальных функций распределения
Fsit, i = 1, ... , R, мы моделируем
R, имеющий функцию распре
многомерный случайный вектор длиной
деления, представимую как копула-функция С от равномерных на от
резке [О;
1]
распределений. Далее, значение i-й компоненты,
i = 1 ... R,
полученного вектора заменяем значением функции, обратной к марги
нальной функции распределения
нальная функция
F Sit, от этой компоненты. Если марги
распределения Fsit, i = 1, ... , R, оценена при помощи
метода Монте-Карло, то эта функция-оценка разрывна (имеет скачки),
и мы должны использовать понятие обобщенного обращения функции.
После чего просуммируем все компоненты преобразованного вектора и
получим смоделированный суммарный по всем БН и ТС убыток. Нако
нец, повторим последние три шага большое количество раз и вычислим
значения требуемых мер риска (например, ГП, СОП).
Опишем более подробно процедуру расчета резервного капи
тала.
1.
Оценим маргинальную (частную) функцию распределения Fsit
суммарных убытков i-го типа за период
t для каждого i = 1, ... , R
следующим образом:
(а) подберем функцию распределения частоты убытков (пуассонов
ское или отрицательное биномиальное распределение) и функцию рас
пределения среднего убытка (экспоненциальное распределение, Парето
распределение, гамма-распределение, О ПР-распределение);
(Ь) в соответствии с функцией распределения частоты убытков i-го
типа сгенерируем случайную величину nit (обозначим сгенерированное
значение через
nit)i
(с) из функции распределения среднего убытка i-го типа сгенериру
ем случайную величину Sit (обозначим сгенерированное значение через
sit)i
(d)
умножив
ток типа
i;
Sit
на ~t, получим смоделированный суммарный убы
ГЛ.
702
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
(е) повторим шаги
сортируя по
(f)
(b)-(d) N = 100 ООО раз;
возрастанию 100 ООО значений
суммарных убытков,
полученных на предыдущем шаге, генерируем функцию распределения
суммарного убытка i-го типа
F Sit ( х).
2. Смоделируем многомерный
i = 1, ... , R, имеющий некоторую
вектор суммарных убытков
Sit,
многомерную функцию распреде
ления, и оценим кумулятивную функцию распределения совокупного
убытка следующим образом:
(а) подберем для кумулятивных функций распределения суммар
ных убытков
Fsit
копула-функцию С;
(Ь) сгенерируем случайный многомерный вектор (и1,
... ,ия), функ
ция распределения которого представима в виде копула-функции С от
равномерных на отрезке [О;
1]
распределений;
(с) взяв F~~ (щ), получим сгенерированный суммарный убыток для
i-го пересечения (т. е. i-го типа риска), i = 1, ... , R;
(d)
просуммировав смоделированные суммарные убытки
пересечениям
i, i = 1, ... , R ,
по всем
Sit
получим совокупный по всем БН и ТС
убыток;
(е) повторим шаги
(f)
сортируя по
(b)-(d) N = 100 ООО раз;
возрастанию 100 ООО значений
смоделированных
совокупных убытков, полученных на предыдущем шаге, генерируем
функцию распределения совокупного по всем БН и ТС убытка.
3.
Вычислим ГП (или СОП):
(а) ГП 99%-ного доверительного уровня равна 1000-му элементу
упорядоченной по возрастанию последовательности
совокупных убытков (см. шаг
100 ООО
значений
2(f));
(Ь) СОП 99%-ного доверительного уровня равна среднему первых
1000 элементов упорядоченной по возрастанию последовательности
100 ООО значений совокупных убытков (см. шаг 2(f)).
7.3.7.
Пуассоновская модель шоков
В этом пункте мы представим модель агрегации, предложенную в рабо
тах
[Lindskog, McNeil (2003)], [Embrechts, Puccetti (2007)] и [Fantazzini
et al. (2008в)]. При этом зависимость моделируется как между суммар
ными убытками, так и между частотами убытков разного типа (при
помощи пуассоновского процесса).
Предположим, что мы имеем
Обозначим через
ni,
е
=
m
1, ... , m,
разных типов шоков или событий.
пуассоновский процесс с интенсив
ностью Л е, описывающий количество реализованных событий типа е
на промежутке времени (О,
t].
Далее, предположим, что эти процессы
независимы. Рассмотрим убытки
R
различных типов, и пусть
nit,
при
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
7.3.
i
= 1, ... , R,
мени {О,
703
обозначает частоту убытков i-го типа на промежутке вре
t].
Для r-й реализации события типа е определим бернуллиевскую слу
чайную величину
ток типа
i,
и ноль
I[ r,
-
'
которая равна единице, если мы наблюдаем убы-
в противном случае. Векторы
е
е )'
Irе = {11,r,
· · · 'In,r '
предполагаются
независимыми
и
-1 , ... ,nt,
е
Т-
одинаково распределенными,
имею
щими многомерное распределение Бернулли 17 . Другими словами, каж
дое новое событие представляет новую независимую возможность воз
никновения убытков, но фиксированному событию отвечают бернул
лиевские случайные величины, характеризующие реализацию убытков
того или иного типа, которые могут быть зависимыми. Форма зависи
мости определяется спецификацией многомерного распределения Бер
нулли, а независимость этих случайных величин
-
частный случай этой
спецификации.
В соответствии с пуассоновской моделью шоков частота убытков
i-го типа
nit, i
= 1, ... , R,
имеет пуассоновское распределение, посколь
ку она образуется в результате суперпозиции т независимых пуассонов
ских процессов, порожденных т типами определяющих событий. Рас
пределение вектора (пн,
... , nRt)
будем называть многомерным пуас
соновским распределением. Тем не менее суммарное число убытков не
является пуассоновским
процессом,
но
является
сложным
пуассонов
ским процессом:
т
nt
п:
R
= LLLli.r
e=lr=li=l
i, i = 1, ... , R, токи вызывают опре
деленное число убытков величиной {Xfr), r = 1, ... , п~, где {Xfr) - неза
В каждом пересечении ТС/БН
висимые одинаково распределенные случайные величины с функцией
распределения
Fit
и независимые от п~.
Как можно понять из предыдущих рассуждений, ключевым момен
том этого подхода является идентификация т определяющих пуассо
новских процессов (к сожалению, это весьма недавно возникшая об
ласть исследования, и она требует более детального изучения). Про
стым подходом к идентификации т определяющих процессов с
R
ти
пами рисков (ТС /БН пересечения) является подход, аналогичный стан
дартному РУ-подходу. Хотя положительная/отрицательная зависи17 Распределение
случайного вектора (I 1, ••• , I N), i-я компонента которого - это
случайная величина, принимающая либо значение О, либо
называть многомерным распределением Бернулли.
1, i = 1, ... , N,
будем
Гл.
704
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
мость 18 как меЖдУ шоками (nit), так и меЖдУ величинами суммарных
убытков
(Sit)
допускается, число шоков и величины убытков предпола
гаются независимыми:
Hnit, ... ,nнt (х1, · · · 'XR) Hsit, ... ,Sнt (х1, · · ·, XR)
Hnit, ... ,nнt .l Hsн,".,Sнt'
где
Hnн,".,nнt(·)
(nн, ... , nRt),
nit1 а с!
(.) -
функция
Fnit (·) -
с! (Fnн (х1), ... 'FnRt (xR)),
C8 (Fsн(x1), ... ,Fsнt(xR)),
распределения
случайного
вектора
функция распределения случайной величины
копула-функция многомерной функции распределения
Hnн, ... ,nнt(·); Hsн, ... ,Sнt(·) - функция распределения случайного векто
ра (Sн, ... , SRt), Fsit(·) -функция распределения случайной величины
sit' а С 8 (.) - ко пула-функция многомерной функции распределения
Hsн, ... ,sнt (·).
Если же вместо суммарного убытка за период мы используем сред
ний убыток за период (т. е. вместо Sit используем
Hn1t, ... ,nнt (х1, ... 'XR) Hsн, ... ,sнt (х1, ... 'XR)
Hnit, ... ,nнt .l Hsн,.",SRt'
где
C 8 (Fsн(x1),
... 'FSRt(xR)),
- функция распределения
(s1j, ... ,SRj), F 8 it(·) - функция распределения
-
тогда:
с! (Fпн(х1), ... 'FnRt (xR)),
Hsн, ... ,sнt(·)
Sit, а С 8 ( ·)
Sit),
случайного
вектора
случайной величины
ко пула-функция многомерной функции распределения
Hsн, ... ,Sнt ·
Приведем процедуру реализации этого подхода
1.
Для каждого пересечения БН/ТС подберем функцию распреде
ления частоты убытков, функцию распределения среднего убытка, как
это делалось в стандартном РУ-подходе.
2.
Подберем для функции распределения вектора частот убытков
(nн, ... , nRt) копула-функцию Qf (см. ниже ~Дополнение~ к этому раз
делу).
3.
Оценим маргинальные функции распределения
убытков i-го типа за период
Fsit
суммарных
t, i
= 1, ... , R, следующим образом:
(а) сгенерируем случайный вектор uf = (и{t, ... , u-k,t), функция рас
пределения которого представима в виде копула-функции с! от равно
мерных на отрезке (О;
18 Случайные
Р(Х1
1]
распределений;
величины Х 1 , Х2 называются положительно зависимыми, если
> х1, Х2 > х2]
~ Р(Х1
> х1)Р(Х2 > х2].
Соответственно отрицательно зависимыми, если
Р(Х1
> х1, Х2 > х2) < Р(Х1 > х1)Р(Х2 > х2).
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
705
(Ь) взяв F~~(u{i), получим сгенерированный: вектор частот убытков
(nн, ... , nnt), описывающий: число наблюдаемых убытков каждого из R
типов риска (обозначим этот вектор через (nн, ... ,nnt));
(с) для каждого типа риска i, i = 1, ... , R, из функции распределе
ния среднего убытка сгенерируем случайную величину sit (обозначим
сгенерированное значение через Sit)i
(d) умножив sit на nit, получим смоделированный: суммарный: убы
ток типа i;
(е) повторим шаги (a)-(d) N = 100 ООО раз;
(f) для каждого типа риска i, i = 1, ... , R, сортируя по возрастанию
100 ООО значений: суммарных убытков, полученных на предьщущем ша
ге, генерируем функцию распределения суммарного убытка
Fsit(x).
4. Подберем для функций: распределения вектора суммарных убыт
ков (81;, ... , Sn;) копула-функцию С 8 .
5. Сгенерируем случайный: вектор u 8 = (uf, ... , и~), функция рас
пределения которого представима в виде копула-функции С 8 от равно
мерных на отрезке [О;
1] распределений:.
6. Взяв вектор (FS.~(uf), ... , Fs~t (и~)), получим сгенерированный
вектор суммарных убытков.
7.
Повторим предыдущие шаги
N
= 100 ООО раз.
Таким образом можно смоделировать новые вектора суммарных
убытков, которые затем могут быть использованы для вычисления мер
риска совокупного убытка (например, ГП и СОП).
Дополнение: оценка копула-функций многомерых
функций распределения с дискретными маргинальными
функциями распределения
Согласно результатам, представленным в работе
[Sklar (1959)],
в
случае, если некоторые маргинальные функции многомерной: функции
распределения дискретны (как в нашем случае, см. выше), то копула
функция для такого распределения определена не единственным об
разом. Для преодоления этой проблемы было предложено два метода.
Первый метод был предложен в работе
[Cameron,
Тrivedi
et al. (2004)]
и
был основан на конечно-разностной: аппроксимации производных копу
ла-функции
Fxi(·) -функция распределения случайной: величины Xi, i = 1, ... ,
n; С(·) - копула-функция; дk, k = 1, ... , n, обозначает k-ю компоненту
где
Гл.
706
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
разностного оператора первого порядка, которая определяется следую
щим образом:
дkC[Fx 1 (х1),
... , Fxk (xk), ... Fxn (хп)] =
= C[Fx1(х1), ... , Fxk(xk), ... Fxn(xn)]-C[Fx1 (х1), ... , Fxk (xk - 1), ... Fxn (xn)].
Второй метод
- это метод ~онепрерывнивания~, предложенный в
[Stevens (1950)), [Denuit, Lambert (2005)). Этот метод основан
работах
на генерации искусственных случайных величин
Xi, ... , Х~,
получаю
щихся путем прибавления независимых случайных величин и1,
... ,
(каждая из которых имеет равномерное распределеное на отрезке
к дискретным случайным величинам Х1,
... , Xn.
Un
[0,1))
Отметим, что такой
метод не меняет значение меры согласованности между переменными 19 .
Эмпирические исследования показывают, что максимизация функ
ции правдоподобия с маргинальными дискретными распределениями
часто
приводит к
случае
вычислительным
следствием
отсутствия
трудностям,
сходимости
являющимся
алгоритма
в этом
максимизации.
В таких случаях может оказаться полезным описанный выше прием
перехода к величинам
Xi, ... , Х~,
а затем использовать модель, осно
ванную на копулах для непрерывных случайных величин. Вот почему
мы рекомендуем полагаться на второй метод.
7.3.8.
Байесовские подходы: байесовские маргинальные
функции и копула-функции в задачах управления
операционным риском
Существенным ограничением усовершенствованных моделей измерения
риска (УМИР-подход) является наличие неточных данных или (и) их
малое количество. Это в основном можно объяснить относительно
недавним
возникновением
понятия
операционного
риска
и
понятия
управления операционным риском. Поскольку финансовые учрежде
ния приступили к сбору данных по операционным убыткам всего лишь
несколько
лет
назад,
это делает задачу
исследования
операционных
рисков еще более сложной. В этом контексте использование байесовских
методов
и
методов
стохастического
моделирования
является
вполне
естественным решением указанной проблемы. В самом деле, эти мето
дь1 позволяют нам сочетать количественную информацию (данные по
19 Мерой
функции
согласованности
распределения
F1
Р ( (Х1 - Х1)((Х2 - Х2)) >о)
случайных
-
и
F2
величин
соответственно,
Х1 ,
имеющих
величину
Р ( (Х1 - Х1)((Х2 - Х2)) <о), где Х1, Х2 -
независимые случайные величины с функциями распределения
ственно.
Х2,
называют
F1
и
F2,
соответ
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
707
операционным убыткам, накопленные банком) и качественные данные
(мнения экспертов), учитывая форму априорной информации. Кроме
того, методы стохастического моделирования являются широко исполь
зуемым статистическим инструментом, который позволяет преодолеть
некоторые вычислительные проблемы. Сочетание описанных методоло
гий приводит к использованипю Монте-Карло моделирования для це
пей Маркова, которое позволяет синтезировать основные преимущества
как байесовских методов, так и методов стохастического моделирова
ния.
В следующих разделах мы рассмотрим байесовский подход для
маргинальных функций распределения убытка, предложенный в рабо
те
[Dalla Valle, Giudici (2008)), и байесовские копула-функции, предло
[Dalla Valle (2008)). В конечном итоге для того, что
женные в работе
бы представить подход полного байесовского мета-распределения для
управления операционным риском, мы объединим эти две методологии.
1)
Вайесовские маргинальные функции
Идея, лежащая в основе подхода, предложенного в работе
Valle, Giudici (2008)),
[Dalla
состоит в том, чтобы оценивать параметры мар
гинальных распределений убытков не только при помощи классическо
го подхода, но и при помощи байесовского подхода с использованием
метода Монте-Карло для цепей Маркова. Как и ранее, конечной целью
является получение при помощи моделирования функции распределе
ния совокупного убытка, что в конечном счете позволяет вычислить
меру риска совокупного убытка.
Мы рассмотрим подробно байсовский подход на двух примерах.
В первом примере частота убытков моделируется при помощи пуассо
новского распределения, величины убытков моделируются при помощи
экспоненциального распределения; во втором примере частота убытков
моделируется пуассоновским распределением, а величины убытков мо
делируется гамма-распределением.
Пусть для i-го пересечения БН/ТС частота убытков имеет пуассо
новское распределение с параметром
Ai, величины убытков имеют экс
поненциальное распределение с параметром Л~s). Тогда функция прав
доподобия L (см. (7.11)) примет вид:
L(xi, ftilЛ~s), Лi)
м
[nit
1
--jsyxi;(t)]
= П П (S)e >-/
t=1
Если мы обозначим через
j=l
(Ji
лi
л'!-ite-.Xi
i А. 1
(7.11)
n;,t.
= 1/Л~s), то получим такое же выра
жение для функции правдоподобия, как в работе
[Dalla Valle, Giudici
Гл.
708
(2008)].
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Мы предположим, что параметры,
Ai
и 8i-случайные вели
чины. Выберем для каждой из них сопр.яж;ен:н,ую априорную функ
цию распределения, т. е. функцию распределения, апостериорная функ
ция которой принадлежит тому же классу, что и априорная функция
распределения. В частности, мы можем выбрать двухпараметрическое
гамма-распределение (см. выше, п.
7.3.5, 2)):
Лi Е Г(а, Ь),
8i
Е Г(с,d),
где знак Е определяет, что соответствующая случайная величина под
чиняется указанному справа закону распределения вероятностей, а а, Ь,
с,
d -
параметры априорного распределения.
Если у нас нет априорной информации относительно некоторого
параметра модели, то это может быть отражено в априорной функ
ции распределения, предполагая его дисперсию достаточно большой.
В этом случае можно, например, предложить использование плоских
априорн·ых распределений, которые придают равные вероятности всем
возможным значениям параметра. Однако этот подход имеет ряд недо
статков. Например, для плоских априорных распределений в некото
рых случаях, не выполняется условие нормировки 20 , и они инвариант
ны относительно репараметризации модели (см.
[Brooks (1997)]).
Если
условие нормировки для априорных распределений не выполнено, то
это может привести к тому, что апостериорные распределения не будут
иметь среднего (см.
[Gamerman (1997)]).
Одним из решений этой про
блемы является использование слабых априорн·ых '[ХLСnределений: для
них выполняется условие нормировки, но они имеют достаточно боль
шую дисперсию.
Следуя этому подходу, мы можем вычислить так называемые гипер
оценки параметра априорного распределения, приравняв математиче
ское ожидание параметра,
имеющего заданное априорное распределе
ние, к его оценке, полученной методом максимума правдоподобия (при
использовании которого параметры предполагаются константами), и
положив дисперсию этого параметра равной очень большому числу
(например, полагаем равной
1000).
Вычислим, например, гипероцен
ки параметров а и Ь функции априорного распределения параметра
20 Под
условием нормировки для дискретной случайной величины подРазумевает
ся предписываемое теорией вероятностей условие, когда сумма вероятностей всевоз
можных исходов этой случайной величины равна единице; под условием нормировки
для непрерывной случайной величины, функция распределения которой имеет плот
ность, подРазумевается равенство единице интеграла по множеству всевозможных
исходов этой случайной величины от ее плотности. Более подРобная информация о
байесовском подходе и априорных распределениях, отражающих 4:скудность апри
орных знаний•, содержится в гл.
3.
7.3.
Ai,
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
709
рассматривая данные по операционным убыткам 1-го пересечения,
представленные в работе
правдоподобия для
[Dalla Valle, Giudici (2008)]. Оценка максимума
параметра Ai равна 1,4028. Приравнивая это значе
ние к математическому ожиданию этого параметра, в предположении,
что он имеет априорное распределение Г(а, Ь), а дисперсию этого па
раметра к
1000 (Е(Лi) = 1,4028,V(Лi) = 1000),
оценки параметров а и Ь: а = 0,0019, Ь = 0,0014.
получаем следrющие
В дальнейшем при анализе равенств, справедливых с точностью до
нормирующей константы, мы будем использовать знак «l"V~.
В соответствии с теоремой Байеса условное апостериорное распре
деление параметра
Ai
с точностью до нормирующей константы равно
априорному распределению, умноженному на функцию правдоподобия.
Откуда получаем, что апостериорное распределение снова равно гамма
распределению, но уже с функцией плотности
7Г_xi(·lxi, fi.i, 8i) l"V г (Ё
nit +а; м + ь) '
t=l
а апостериорное распределение для параметра
8
снова совпадает с
гамма-распределением, но с плотностью
Пусть для i-го пересечения БН/ТС частота убытков имеет, как и ра
нее, пуассоновское распределение с параметром
Ai,
ков
параметрами
теперь
имеют
гамма-распределение
x(Г(ai,{)i)). Тогда функция правдоподобия
Обозначая через
f3i
= 1/{)i,
с
(7.10)
но величины убыт
ai, {) i х
примет вид:
мы выберем независимые сопряженные
априорные функции для параметров
Ai
и
f3i·
Возьмем
Лi Е Г(а, Ь),
f3i
Е Г(с, d).
Аналогично случаю, рассмотренному ранее (случай, когда частота
имеет пуассоновское распределение, а величины убытков
-
экспонен
циальное распределение), мы можем снова выбрать с.л.абъtе априорнъtе
распределения, для которых выполняется условие нормировки и кото
рые имеют достаточно большую дисперсию. Следrя этому подходr, вы
числим гипероценки параметров априорного распределения, приравняв
Гл.
710
математическое
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
ожидание
параметра,
в
предположении,
что
он
име
ет заданное априорное распределение, к его оценке, полученной мето
дом максимума правдоподобия (при использовании которого парамет
ры предполагаются константами), и положив дисперсию этого парамет
ра, равной очень большому числу (например, полагаем равной
Воспользовавшись
теоремой
Байеса,
вычислим
1000).
апостериорную
плотность параметра Л. Она будет равна:
Аналогично вычислим апостериорную плотность параметра
(3.
Она
имеет вид:
Если в качестве априорного распределения параметра ai взять
гамма-распределение
ai
с параметрами е,
Е Г(е,
f)
f, то апостериорная плотность параметра а будет рав
на:
Заметим, что в отличие от апостериорных плотностей параметров
f3i' лi
апостериорная плотность параметра Cti не принимает ни одну из
стандартных форм. По этой причине для моделирования функции рас
пределения с плотностью
7rOii ( • lxi ,~; f3i, Лi)
воспользуемся одним из ал
горитмов типа Монте-Карло моделирования цепей Маркова, а именно
алгоритмом Метрополиса- Хестинга.
Обозначим через
отрезке
q(·lz)
[z - 0.25; z + 0.25].
плотность равномерного распределения на
Опишем алгоритм Метрополиса -
Хестинга для нашего слу-
чая.
1. Возьмем некоторое начальное значение в0 из области определе
ния 7rQ(·lxi,fti; f3i, Лi)·
2. Смоделируем случайную величину, равномерно распределенную
на отрезке [Во - 0.25; Во+ 0.25] (обозначим ее через ф).
7.3.
3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
711
Вычислим величину
м
= min
(1, ll ll (xij(t))<P - ео [г(~~г(оо;_1] t~1
<р
t=l j=l
о
n.it
х
х [toГI exp[-J<<P-ll°J1).
(а) Если а(8°, rj;) ~ 1, тогда полагаем 81 = ф.
(Ъ) Если а( е 0 , rj;) < 1, тогда с вероятностью а( е 0 , rj;) полагаем 81 =
= rj;, а с вероятностью 1 - а( е 0 , ф) полагаем (} 1 = е 0 •
4. Повторим N раз шаги 1-3, беря вместо е 0 смоделированные
()1, ()2, ... , ()N.
При некоторых условиях регулярности эмпирическая функция рас
пределения последовательности
{8t}
будет сходиться по вероятности
к функции распределения, имеющей плотность 1Гаi ( • l~,:fii; .Вi, Лi) (см.
[Gelman (2003).]).
Реализация этого алгоритма требует вычисления значения функ
ции (а((}, <р) в точках <р и
et
и моделирования случайных величин с
равномерным распределением.
Нормирующая константа для апостериорной плотности не требу
ется, так как в алгоритме используются только отношения значений
плотности в соответствующих точках.
Мы не будем здесь рассматривать случай, когда частоты имеют от
рицательное биномиальное распределение, а величины убытков имеют
Парето-распределение, поскольку, как показано в работе
al.
[Fantazzini et
{2008в)], в ситуации, когда выборка достаточно мала, мы сталкива
емся с проблемой точности оценок. Кроме того, использование байесов
ского подхода для этих распределений может привести к нереалистич
ным значениям оценок мер ГП/СОП, а также к численным ошибкам
(см. таблицы
12-14
в работе
[Dalla Valle, Giudici (2008)],
из которых
видно, что оценки для СОП больше е+ 27 ).
2)
Байесовские копула-функции
В работе
[Dalla Valle (2008)]
представлен РУ-подход с использова
нием байесовских копул. В байесовском подходе нам необходимо вы
числять апостериорное распределение, которое равно, с точностью до
нормирующего множителя, произведению априорной функции распре
деления на функцию правдоподобия.
712
ГЛ.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Используя плотность нормал'Ьной копула-функции, мы можем вы
числить функцию правдоподобия, которая имеет следующий вид:
где St = (Sн, ... , SRt), а Sit - суммарный убыток i-го типа за период
t, = (S1, ... ,Sм).
s
Здесь нам необходимо оценить корреляционную матрицу Е и в ра
боте
[Dalla Valle (2008)) для этого в качестве априорного сопряженно
го распределения этого параметра выбрано обратное распределение
Уишарта:
Е
rv
InverseWishart(a, В).
Распределение Уишарта является обобщением одномерного х 2 распределения на случай большей размерности. Как правило, оно ис
пользуется для описания функции распределения симметричных поло
жительно-полуопределенных матриц (обычно, ковариационных матриц,
диагональные элементы которых - случайные величины, имеющие х 2 распределение, см.
[Ripley (1987))).
Если случайная матрица имеет рас
пределение Уишарта с параметрами в- 1 и а, то обратная к ней случай
ная матрица имеет обратное распределение Уишарта с параметрами В
и а (см.
[Kotz, Balakrishnan et al. (2000))).
Если априорной информации у нас нет, то рекомендуется исполь
зовать слабъtе априорн-ьtе распределения.
В работе
[Dalla Valle (2008)] степени свободы а взяты равными R+l,
т. е. числу типов риска (число пересечений БН/ТС) плюс один. Более
того, в этой работе в качестве матрицы точности В взята диагональная
матрица, для которой:
В=
diag(!'i), l'i
Е Г(О.001;
0.001),
i = 1, ... , R.
Таким образом, математическое ожидание случайной величины
l'i
равно
1, а дисперсия очень велика по сравнению с математическим ожи
данием и равна 1000. Для l'i мы имеем слабое распределение. Апосте
риорное распределение случайной величины Е вычисляется согласно
теореме Байеса:
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
713
Таким образом, апостериорное распределение случайной матрицы
Е
это снова обратное распределение Уишарта:
-
..
м
7Г:r;{·IS),..., InverseWishart ( 2 +а; В+
м
) .
2 LXtSt
1
...... ,
t=l
Для моделирования функции апостериорного распределения пара
метра Е мы можем воспользоваться алгоритмом Метрополиса- Хес
тинга для многомерных величин, взяв в качестве начального значения
в этом алгоритме оценку максимума правдоподобия корреляционной
матрицы (как это делалось в работе
100 ООО
[Brooks {1997)]).
Смоделировав
(или больше) матриц из этого апостериорного распределения,
мы их используем для вычисления мер риска ГП/СОП.
Мы не будем здесь рассматривать байесовскую Т копула-функцию,
поскольку при больших значениях степеней свободы (часто возникаю
щих для данных по операционным убыткам) она дает нереалистичные
оценки мер риска. Для более подробной информации об этих проблемах
см. табл.
3)
12
в работе
[Dalla Valle {2008)].
Подход полного бай:есовского метараспределения
Изложенные ранее подходы могут быть объединены для получения
полного байесовского подхода. Подробное описание этой процедуры
вычисления величины резервного капитала выглядит следующим
образом.
Для каждого пересечения БН/ТС подберем функцию распре
1.
деления частоты убытков (пуассоновское или отрицательное биноми
альное распределение), функцию распределения среднего убытка, как
это делалось в стандартном РУ-подходе, и оценим маргинальные функ
ции распределения
Fsit(x) суммарных убытков i-го типа за период t,
i = 1, ... , R. Для функций распределения вектора суммарных убытков
(S1j, ... , Sнj) с маргинальными функциями Fsit(x) подберем копулафункцию С8 . Оценки параметров маргинальных функций распределе
ния и копула-функции методом максимума правдоподобия далее будут
использованы как отправные точки цепей, строящихся на следующих
шагах.
2.
Для каждого типа риска из апостериорного распределения па
раметров функции распределения частоm'Ьt смоделируем
Ni
= 100 ООО
значений.
3.
Для каждого типа риска из апостериорного распределения па
раметров функции распределения среднего убъtтка смоделируем
= 100
ООО значений.
Ni
=
714
Гл.
Смоделируем
4.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Ni = 100
ООО значений параметров копула-функ
ции, имеющих заданные апостериорные распределения.
5.
Генерируем апостериорное распределение Нв совокупного убыт
i, i = 1, ... , R. Для этого:
типа риска i, i =, ... , R, смоделируем
ка по всем типам риска
(а) для каждого
ные распределения
Fft
апостериор
суммарных убытков:
i) сгенерируем значение Bit из функции распределения частоты
2);
ii) из апостериорного распределения, описывающего величину
убытка (с параметрами, рассчитанными на шаге 3), сгенерируем nsit
убытков i-го типа (с параметрами, рассчитанными на шаге
значений;
просуммировав nit, смоделированных на предыдущем шаге зна
iii)
чений, вычислим смоделированный суммарный убыток типа
повторим шаги
iv)
(i)-(iii) N2 = 100 ООО раз
i;
(для тех же параметров
маргинальных распределений);
v)
отсортировав
N2 = 100 ООО сгенерированных суммарных убытков
по возрастанию, сгенерируем апостериорные распределения
Fft;
(Ь) сгенерируем случайный вектор и1, ... , ин, функция распределе
ния которого представима в виде копула-функции С (параметры кото
рой сгенерированны на шаге
4)
с равномерными на отрезке [О;
1)
рас
пределениями;
(с) взяв вектор ((F/it)- 1 (uf), ... , (Ffяt)- 1 (u~)), получим сгенери
рованный вектор суммарных убытков;
сложив смоделированные суммарные убытки Sit по всем пересе
(d)
чениям
i, i = 1, ... , R,
получим сгенерированный совокупный по всем
БН и ТС убыток;
(a)-(d) Ni = 100 ООО раз;
по возрастанию Ni = 100 ООО
(е) повторим шаги
(f)
отсортировав
значений совокупно
го убытка, генерируем апостериорную функцию распределения НВ·
6.
Как это делалось ранее, вычислим ГП и (или) СОП.
Излишне говорить о том, что точность оценки апостериорного рас
пределения совокупного убытка Нв увеличивается с ростом числа гене
раций
и
Ni
N2.
Однако требуемая для этого вычислительная мощность
может расти экспоненциально, что может привести к проблеме пере
полнения.
Если априорная информация отсутствует и мы пользуемся слабыми
априорными распределениями, то используется несколько измененный
алгоритм. Он дает менее точные оценки ГП и (или) СОП, чем первый
алгоритм, но в нем моделируется только
Ni
х
N2,
Ni
случайных величин, вместо
что позволяет значительно сократить время работы.
7.3.
7.3.9.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
Эмпирические приложения в пакете
715
Gauss:
случай
комонотонных убытков и канонической агрегации
с помощью копула-функций
Чтобы продемонстрировать некоторые из изложенных выше подходов,
мы вычислим ГП и СОП для разных уровней доверия, используя смоде
лированные
данные,
подобные
тем,
что
используются
в
работе
(2008в)). Исходная база данных представляет собой ин
[Fantazzini et al.
формацию по операционным убыткам некоторого банка (название ко
торого не раскрывается) с января
из более чем
72
1999 по декабрь
2004г., составленная
наблюдений. Общее число убытков за рассматриваемый
период составляет
407.
Рассматриваемые операционные убытки берутся
из двух бизнес-направлений и четырех типов событий:. Таким образом,
мы имеем восемь возможных типов рисков (или пересечений). В целях
соблюдения конфиденциальных сведений банк присвоил случайный: ин
декс каждому из рассматриваемых бизнес-направлений и типов собы
тий; однако связь между этими присвоенными индексами и реальными
была сохранена.
Для описания каждого типа риска мы используем пуассоновское и
гамма-распределения, параметры которых представлены в табл.
[Fantazzini et al.
7-8
из
(2008в)].
Мы получим маргинальные распределения суммарных убытков
Sit
для каждого пересечения БН/ТС с помощью свертки распределений
частот убытков и величин убытков, которую будем аппроксимировать
при помощи метода Монте-Карло. Затем мы вычислим ГП и СОП для
95%
и
99%
доверительных уровней:, а их сумма по всем пересечениям
i
даст нам совокупную ГП и СОП для случая комонотонных убытков.
Кроме того, мы вычислим совокупную ГП при помощи нормальной:
копула-функции, которая более реалистично моделирует зависимость
между маргинальными суммарными убытками
sit,
чем предположение
о комонотонности убытков.
new;cls;
//Загрузка данных по операционным убыткам
(8
пересечений БН/ТС)
perdite=0.00000000 123287.00 ...
//В целлх экономии места полн.ал таблица имеющихсл дан.н.'ЫХ здесь н.е представ
лен.а,
н.о их можно получить по запросу у авторов
9876.000 1957.0000 0.00000000 ;
//Число сценариев
scenarios= 100000;
//Загрузка параметров пуассоновского и гамма распределений
parameters=l.4027778 0.15180904 64847.807,
2.1944444 0.19869481 109320.57,
0.083333333 0.20179152 759717.47,
716
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
0.45833333 0.11280330 1827627.2,
0.097222222 0.19542678 495700.99,
0.62500000 0.3849401119734.007,
0.68055556 0.059798776 211098.10,
0.11111111 0.26302912 135643.25;
//Инициализация матрицы, в которой будут представлены значения ГП, СОП, а
также совокупный убыток.
var95= zeros( rows(parameters), 1);
var99= zeros(rows(parameters),1);
es95= zeros(rows(parameters), 1);
es99= zeros( rows(parameters), 1);
losstot= zeros(scenarios,rows(parameters));
//Оценка маргинальных распределений суммарных убытков
Fsit
для каждого типа
риска
i, i = 1, ... , R;
for j(l,rows(parameters),1);
frequencyl=zeros(scenarios, 1);
lossl=zeros(scenarios,1);
for i(l,scenarios,1);
/ /Морделируем пуассоновскую случайную
frequencyl[i,l]=rndp(l,l,parameters[j,1]);
aa=frequencyl[i,1];
if аа ==О;
lossl[i,1]=0;
else;
величину
//Моделируем случайную величину из гамма-распределения
severity=rndgam(aa,1,parametersU,2])*parametersU,3];
lossl[i,l]=sumc(severity);
endif;
endfor;
//Сортируя по возрастанию 100000 сгенерированных суммарных
руем распределение Fsit
rankindex = rankindx(Lossl,1);
matrixrank=Lossl rankindex;
finalsortl = sortc(matrixrank,2);
losstot[.J]=finalsortl[.,1];
var95[j,l)=finalsortl[0.95*scenarios,1];
es95U,l]=meanc(finalsortl[0.95*scenarios:rows(finalsortl),1]);
var99U,l]=finalsortl[0.99*scenarios,1];
es99[j,l)=meanc(finalsortl[0.99*scenarios:rows(finalsortl),1]);
endfor;
убытков, генери
//Вывод таблицы для значений мер риска по каждому типу риска
i (пересечения
БН/ТС)
print 11 VaR 95 % VaR 99 % ES 95 % ES 99 % для
var95:var99:es95:es99;
каждого типа риска
i
11 ;
//Вычисление мер риска в предположении комонотонности суммарных убытков:
простая сумма ГП по всем типам риска
i
var95 _ dip _perf=sumc( var95);
var99 _ dip _perf=sumc( var99);
es95 _ dip _perf=sumc( es95);
es99 _ dip _perf=sumc(es99);
print 11 VaR 95 % VaR 99 % ES 95 % ES 99 % (Perfect Dependence)";
7.3.
УПРАВЛЕНИЕ ОПЕРАЦИОННЫМ РИСКОМ
717
var95 _ dip _perf:var99 _ dip _perf:es95 _ dip _perf:es99 _ dip _perf;
//Генерация функции распределения суммарного убытка по каждому типа риска
i
cdf= zeros( rows(perdite) ,cols{perdite));
for j{l,cols{perdite},1};
for i{l,rows{perdite},1};
n=l; do while perdite[i,j] .>losstot[n,j];
if n <scenarios;
cdf[iJ]= n/scenarios;
else;
cdf[iJ]=l;
break;
endif;
n = n+l; endo;
endfor;
endfor;
//Оценка корреляционной матрицы нормальной копула-функции при помощи ме
тода максимума правдоподобия
invcdf=cdfni{ cdf};
corr _ matrix=corrx(invcdf};
//Моделирование 100000 случайных векторов
matrixR =corr _ matrix;
randomunif=rndn{ rows(parameters) ,scenarios);
хх = chol{matrixr}*randomunif;
uu = cdfn(xx)';
из нормальной копула-функции
//Обращая. при помощи функции F~~(·) вектор {и~, ... , UR}, составленный из смо
делированных случайных величин, имеющих равномерное распределение, и зависи
мость которых описывается нормальной копула-функцией, моделируем суммарные
убытки i-го типа;
invtot= zeros( scenarios,rows(parameters));
for j ( 1,rows(parameters}, 1);
for i{l,scenarios,1};
аа= uu[i,j]*scenarios;
aa=ceil{ аа);
invtot[i,j] = losstot[aa,j];
endfor;
endfor;
//Суммируя Sit по всем типам риска i, моделируем совокупный убыток;
portsim=sumc(invtot ');
//Сортируя по возрастанию 100000 смоделированных совокупных убытков,
генери
руем функцию распределения совокупного убытка;
rankindex = rankindx{portsim, 1);
matrixrank=portsim rankindex;
portcop = sortc(matrixrank,2};
//Вычисляем ГП и СОП
var95=portcop[0.95*scenarios,1];
es95=meanc(portcop[0.95*scenarios:rows(portcop) ,1 ]} ;
var99=portcop[0.99*scenarios,1];
es99=meanc(portcop[0.99*scenarios:rows(portcop) ,1 ]} ;
print 11 VaR 95 % VaR 99 % ES 95 % ES 99 % (Нормальная
var95:var99:es95:es99;
копула-функция}";
Гл.
718
В табл.
7.4
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
представлены значения ГП и СОП, полученные с по
мощью описанного выше моделирования данных.
Таблица
7.4.
Результаты оценок ГП и СОП
Тип риска
i
1
2
3
4
5
6
7
8
Совокупный риск в случае
VaR95 %
74528.044
209042.19
3938.9093
522287.94
7973.9140
26839.249
42613.419
9223.3096
896446.98
VaR 99 %
158972.50
372002.60
375488.17
2147631.5
303487.86
55567.369
208104.22
112151.18
3733405.4
ES 95 %
127410.69
311679.27
247692.28
1564485.9
191622.96
44637.456
148306.02
74077.702
2709912.3
ES 99 %
215643.86
480297.24
867696.32
3539469.7
625686.14
73431.526
360775.84
206885.85
6369886.5
812585.45
2388738.8
1809044.9
3713432.1
комонотонности
Совокупный риск в случае
использования нормальной
ко пула-функции
Во-первых, следует заметить, что гипотеза о комонотонности убыт
ков
нереалистична,
поскольку
все
корреляции
близки
к
нулю.
Во-вторых, следует отметить, что использование копула-функций поз
воляет значительно сократить количество средств, выделяемых в ка
честве резервного капитала под операционные риски. Если мы срав
ним величину резервного капитала, полученную в предположении ко
монотонности убытков, и величину резервного капитала, полученную
с использованием копула-функций, мы увидим, что в последнем слу
чае резервный капитал всегда меньше где-то на
10-50% по сравнению
с первым случаем.
Управление кредитным риском
7.4.
7.4.1.
Введение в управление кредитным риском
Что представляет собой кредитный риск, т. е. риск нарушения обяза
тельств по платежам? В
[Crosble, Bohn (2001)]
этому понятию дается
следующее определение: Риск нарушения обязательств по плате
жам
-
это неопределен:н,остъ, связанная со способностъю компании
обслуживатъ свои долги и отве-чатъ по взятым на себя финансовъш
об.я.зателъствам. При этом заранее невозможно идентифицироватъ
те компании, которъtе въtпо.л,н.я.т свои финансовъtе обязателъства, и
те, которъ~е не въ~по.л,н.я.т. В .л,у-чшем слу-чае мъt .л,ишъ сможем датъ
вероятностную оценку кредитного риска. Как резу.л,ътат, компании,
подверженнъtе кредитному риску, объt-ч.но платят за по.л,ъзование за
емнъши средствами по процентной ставке, равной безрисковой про-
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
719
центной ставке, умноженной на коэффициент, пропорциона.л/ьнъtй ве
роятности нарушения обязательств по платежам, с помощью ко
торого регулируете.я размер возмещения кредиторам за неопределен
ность, связанную с этими кредитнъши обязательствами.
Если компания (заемщик) не в состоянии выполнить свои обяза
тельства перед кредитором или один из
контрагентов не в состоянии
следовать условиям финансового соглашения, тогда мы говорим, что
компания или контрагент находится в состоянии дефолта. Кредитный
риск также включает риск, связанный с событиями, отличными от де
фолта, а именно с движением кредитного рейтинга вверх или вниз.
Кредитный риск возникает в результате неопределенности, связан
ной со способностью контрагента или с его желанием выполнять свои
контрактные обязательства. Этот риск характерен для банковской ком
мерции. Отсутствие диверсификации кредитного риска в банках (в ре
зультате концентрации в географических и индустриальных секторах)
в ряде случаев приводило к банкротству. Кроме того, с введением в
использование свопов и фьючерсных контрактов, а также в результате
стремительного роста объемов внебиржевых рынков кредитный риск
стал иметь ключевое значение при управлении инвестициями.
Компоненты кредитного риска определяются следующим образом.
•
(2)
Вероятность дефолта (ВД), которая может быть рассмотрена:
как с позиции двух простых событий:
(1)
платежеспособность и
неплатежеспособность заемщика; вероятность дефолта в этом слу
чае иногда называют -чистъtм риском дефолта;
-
так и с позиции ухудшения кредитного рейтинга, которое указы
вает на увеличение вероятности дефолта; вероятность дефолта в этом
случае иногда называют риском миграции, а риск дефолта является
последним «поглощающим~ состоянием.
•
Доля невозвращенных при дефолте по кредиту средств
(ДНС(Д))
В случае возникновения дефолта, при условии наличия залогового
обеспечения или каких-либо гарантий, теряется не вся сумма кредита.
Таким образом, мы приходим к понятию так называемой нормы вос
становления (НВ) заемщика, которая определяется как доля всех кре
дитных обязательств заемщика, которая может быть покрыта в случае
дефолта. При этом:
ДНС(Д)
•
= 1-
НВ.
Величина номинальных потерь при дефолте (ВНП(Д))
Эта величина представляет собой сумму всех кредитных обяза
тельств заемщика в случае его банкротства в результате реализации
некоторого кредитного события (дефолта или миграции). Очевидно,
Гл.
720
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
что, если мы хотим определить ВНП(Д), мы должны рассмотреть все
позиции, подверженные кредитному риску:
кредитъt: обеспеченные кредиты (например, ипотека) и необес
-
печенные кредиты (например, кредитные карты, беззалоговое кредито
вание домохозяйств, потребительское кредитование, коммерческое кре
дитование);
облигации: долговые ценные бумаги, выпускаемые компанией
-
или государством на фиксированный период обращения и дающие ин
вестору право на возврат номинала таких ценных бумаг, а также на
получение дополнительного процента от номинала (выплаты по этому
проценту от номинала называют купонами);
гарантии, въtnущеннъtе для клиентов;
-
внебиржев-ьtе производнъtе ценнъtе бумаги; эти внебиржевые про-
изводные ценные бумаги (например, свопы) несут в себе риск того, что
с контрагентом может произойти дефолт, и он не сможет осуществить
выплату по контракту;
кредитнъtе деривативъt; внебиржевые производные ценные бу
-
маги были введены специально для того, чтобы перераспределять кре
дитный риск от одного контрагента к другому; кредитные деривативы
могут принимать разнообразные формы.
•
Дефолтная зависимость и (или) миграционная зависи
мость
Измерение такой зависимости является весьма сложной задачей:
исторических данных немного, но даже, если нам было бы доступ
но большее количество данных, одновременные дефолты в нескольких
компаниях были бы редки. В связи с этим эта область все еще требует
тщательного изучения.
Среди всех кредитнъtх деривативов дефолтный своп (ДС) являет
ся наиболее известным и наиболее торгуемым: покупатель дефолтного
свопа периодически платит комиссию (купон) в обмен на обязатель
ство продавца кредитного дериватива произвести оговоренные выпла
ты по определенному активу в случае реализации кредитного события
для этого актива. Таким образом, покупатель дефолтного свопа может
управлять/хеджировать кредитным риском своего актива, не продавая
его; в свою очередь, продавец дефолтного свопа берет на себя забалан
совый кредитный риск в спекулятивных целях.
Что касается корзинъt/nортфе.ля кредитн'ЬtХ деривативов, то су
ществуют долговые ценные бумаги, покрывающие потенциальный риск
дефолта нескольких заемщиков: портфель из
k
дефолтных свопов, обес
печенные кредитные облигации (ОКО) и др. Для ОКО активы с кре
дитным риском (обычно это облигации или кредиты) объединяются
в пул обеспечения, после чего риск пула обеспечения делится между
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
721
траншами выпускаемых облигаций с разными степенями риска. В этом
случае инвесторы несут кредитный риск залоговых активов. ОКО ис
пользуются для осуществления регулируемых арбитражных операций,
поскольку они позволяют с помощью специального целевого механизма
(СЦМ) 21 , перепаковывающего риск, удалять из баланса активы. ОКО
часто используются хедж-фондами в спекулятивных целях.
С лета
2007 г.
финансовые рынки и мировая экономика находились
в условиях резкого ограничения размеров кредитования, которое объяс
няется кризисом в США, связанным с субстандартн·ыми ипоте'Чн'Ы.Ми
кредитами. Субстандартными ипотечными кредитами называют кре
диты, предоставленные заемщикам с более низким кредитным рейтин
гом, чем у первоклассных заемщиков. Многие из заемщиков субстан
дартных ипотечных кредитов с увеличением учетной ставки потерпе
ли дефолт по своим выплатам, в то же время упали цены на жилье,
что также сыграло на снижение стоимости залога. Во многих случа
ях субстандартные кредитные портфели были переупакованы в кре
дитные деривативы (например, в ОКО) и проданы инвесторам, таким
как хедж-фонды, стремящиеся получить большую доходность на капи
тал. Эти хедж-фонды в результате дефолта многочисленных субстан
дартных ипотечных кредитов оказались в весьма сложном положении.
Вследствие наличия в обороте банков безнадежных кредитов они стали
неохотно выдавать кредиты. Рынок межбанковских кредитов, который
является ключевым элементом финансовой системы, иссяк и заимство
вания на нем в этой ситуации весьма дороги. Это вызвало проблемы
с ликвидностью в таких крупных банках, как
JP-Morgan, Northern Rock
(этот банк
Citigroup, Credit Suisse,
разорился), UBS и др.
Задача банка состоит в том, чтобы управл.ятъ рисками своих кре
дитнъ~х портфелей. Управление включает в себя серию мероприятий,
в том числе удержание определенной величины резервного капитала
на случай кризисных ситуаций, диктуемой надзорными за банковской
деятельностью органами (для более подробной информации см.
(2005)]).
[BCBS
Существуют следующие основные виды деятельности, на
правленные на управление рисками:
•оценка риска кредитного портфеля;
•
•
•
расчет величины регулирующего капитала и его удержание;
определение экономического капитала для внутренних целей;
обеспечение диверсификации портфеля и выявления очагов или
концентраций рисков;
21 СЦМ
также называют специальным целевым объектом (СЦО). СЦМ-это ком
пания или юридическое лицо, созданное для достижения некоторых узкоопределен
ных или временных целей.
ГЛ.
722
•
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
уменьшение концентраций риска путем использования хеджиро
вания кредитными деривативами;
•решение о приобретении новых кредитных рисков или ~разгруз
ка» старых;
•
сопоставление скорректированных риском эффективностей раз
личных секторов портфеля;
•
уменьшение величины резервного капитала путем перемещения
определенных кредитных рисков вне баланса банка с помощью струк
турированных финансовых продуктов, таких как ОКО.
7.4.2.
Оценка кредитного риска: ожидаемые,
неожидаемые убытки и экономический капитал
В процессе оценки кредитного риска важно различать ожидаемъtе и
неожидаемъtе убытки.
•
Ожидаемые убытки (ОУ): убытки такого рода не представляют
никаких проблем для банка, поскольку если фактические убытки
L
в
точности равнялись бы ожидаемым убыткам ОУ, то для этого банка не
было бы никаких негативных последствий. Если бы банк отложил ре
зервный капитал, размер которого равен этой величине, то каких-либо
неожиданных изменений величины прибыли в этом случае не произо
шло бы. Кроме того, банк эффективно покрывает ожидаемые убытки,
взимая их со своих заемщиков в форме премии за риск. Это явным
образом происходит, например, при ценообразовании кредитов, когда
заемщик платит премии, зависящие от его уровня кредитоспособности.
В случае облигаций купонные платежи являются неявными рисковыми
премиями.
•
Неожидаемые убытки (НУ): риск-менеджеры в большей сте
пени беспокоятся об убытках
L,
которые превышают ОУ, т. е. о неожи
даемых убытках
НУ= I{L-OY>O} х
Фактические убытки
L
(L -
ОУ).
являются слу-чайной вели-чиной, в то время
как ОУ оцениваются обычно ее средним значением
EL.
Соответственно
НУ измеряются с помощью о-квантиля функции распределения
случайной величины
L
FL(x)
(при некотором заданном, достаточно малом
положительном значении о), т. е. с помощью границы потерь уровня
о (ГПа). Следовательно, для того чтобы измерить полный потенциал
возможных убытков, нам необходимо рассмотреть распределение убыт
ков
L
и на основании него вычислить все требуемые меры риска. Про
анализируем это распределение для случая простой модели, в которой
рассматриваются только убытки, возникающие в результате дефолта
заемщиков.
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
723
С этой целью рассмотрим фиксированный период времени [О, Т] и
обозначим через 'Гi случайную величину, отвечающую моменту дефолта
i-го заемщика. Индикатор возникновения дефолта
Yi -
это бернулли
евская случайная величина, определенная как
если
'Гi ~ Т,
если
'Гi
> Т,
и для нее справедливы следующие соотношения:
P(Yi = 1) = 1- P(Yi
где Fтi ( ·)
-
=О)= Р(тi ~ Т)
= Fтi(T)
= ВД,
функция распределения случайной величины 'Гi·
Соответственно имеем
m
Убыток в портфеле= L =
L ДНС(Д)i · Yi · ВНП(Д)i.
i=l
Предполагая все ДНС(Д)i и ВНП(Д)i детерминированными и усредняя
правую часть этого выражения, мы получим
m
E(L) = z:=днс(д). вдi. ВНП(Д)i.
i=l
Тогда для функции
P(L
~ х)
= FL(x)
граница потерь уровня о опре
делится как
ГПа = Qa(FL) = Fi 1 (a),
где мы используем обозначение
Qa(FL) или Qa(L) для квантилей уровня
о функции распределения убытка L, а Fi 1 (·) определяет обобщенное
обращение FL (·).
Перед тем как перейти к нормативным и эконометрическим аспек
там управления кредитным риском, следует ввести понятие экономи-че
ского капитала. Экономический капитал
-
это капитал, требуемый
банку для того, чтобы снизить вероятность банкротства до данного до
верительного уровня на заданный промежуток времени. Несмотря на
то что расчет величины регулирующего капитала основан главным об
разом на внешних правилах (правила, устанавливаемые надзорными в
банковской сфере органами), которые направлены на обеспечение неко
торого уровня сигрового поля», экономический капитал используется в
задаче оценки риска с точки зрения экономических реалий. Модели эко
номического капитала оказываются более реалистичными, чем модели
регулирующего капитала. Во многих крупных банках имеются проекты
Гл.
724
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
разработки таких моделей. В целом экономический капитал предлага
ет расширенный язык для обсуждения ценовой оценки риска, а также
оценки доходности на рисковый капитал. Банк, имеющий хорошую мо
дель экономического капитала, может более эффективно использовать
свой капитал.
Следующая мера риска наиболее часто используется в моделях эко
номического капитала для кредитного риска:
ЭКа = ГПа
- E(L).
Иногда сама эта мера называется экономическим капиталом. Это обос
новано следующими соображениями: поскольку ожидаемые потери уже
включены в цену кредита, эта мера дает хороший показатель величины
рискового капитала, необходимого для обеспечения платежеспособно
сти банка с данной вероятностью в течение заданного периода времени.
Например, для компании, желающей придерживаться
дарта в течение одного года, установлен уровень
поскольку компании с рейтингом Аа
фолта в течение одного года, равную
Moody's
0,03%.
Moody's Аа стан
вероятности 99,97%,
имеют вероятность де
Подводя итог, можно сказать, что хотя при управлении кредитным
риском возникают задачи, аналогичные тем, что возникают при управ
лении рыночным риском, существует ряд специфических для управле
ния кредитным риском задач, в частности:
•
даннъtе: недостаток публичной информации, касающейся кредит
ного качества заемщиков; рейтинговые агентства играют важную роль,
но не все кредитные риски рейтингуются;
•
•
более длинный временной горизонт (обычно не менее одного года);
функции распределени.я убытков обы-ч,но сильно скошенны, имеют
«длинный правый хвост~, что указывает на частые малые убытки и
редкие большие убытки;
•
моделирование зависимости в кредитном портфеле более важ
но, -ч,ем при управлении рыно-ч,ным риском, поскольку на хвост функции
распределения убытка сильно влияет спецификация зависимости меж
ду дефолтами.
7.4.З.
Регулирование кредитных рисков: исторический
процесс и соглашение Базель
В соглашении Базель
1 предприняты
11
первые шаги к созданию между
народных стандартов расчета минимального регулирующего капитала.
Однако подход, предложенный в нем, был достаточно грубым и недо
статочно дифференцированным: основное внимание в этом подходе уде
лялось различению кредитного риска государственных, банковских и
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
725
ипотечных облигаций (имеющих низкий риск) небанковского частного
сектора или коммерческих кредитных обязательств (имеющих высокий
риск). В этом соглашении очень мало или вообще ничего не говорилось
относительно дифференциации кредитного риска в рамках классифи
кации коммерческих кредитов. Для всех коммерческих кредитов неяв
но требовался 8%-ный совокупный резервный капитал вне зависимости
от кредитоспособности заемщиков, их внешнего кредитного рейтинга,
предложенных гарантий уплаты займа, срока кредита и др. Поскольку
для высокорискованных кредитов был установлен слишком низкий уро
вень резервного капитала, а для низкорискованных кредитов
-
слиш
ком высокий, эта ошибочная оценка уровня резервного капитала созда
ла у банков стимул к переходу к портфелям, составленным из кредитов
с недооценненным уровнем регулирующего рискового капитала, т. е. к
портфелям с повышенным риском. Кроме того, в этом соглашении ни
чего не сказано о политике снижения рисков.
Цель соглашения Базель
11 заключалась
в том, чтобы скорректиро
вать процедуру оценки уровня резервного капитала, принятую в согла
шении Базель
1,
и сделать ее более гибкой и чувствительной к риску.
Для оценки кредитных рисков банки могут использовать стандарти
зированнъ~й подход, введенный в соглашении Базель
1,
а в крупных бан
ках оставлялась возможность выбора в пользу использования подхода
внутренних рейтингов (ПВР).
1)
Стандартизированный подход
При использовании этого подхода риск актива вычисляется путем
умножения величины номинальных потерь при дефолте (ВНП(Д)) на
соответсвующий вес риска. Веса риска определяются внешними рейтин
гами заемщиков (табл.
Таблица
7.5. Вес
7.5).
риска (в%) при различных кредитных рейтингах
Активы
Государство
Банк Вариант
Банк Вариант
1
2
Корпорации
Розничный портфель
Кредиты с залогом
Коммерческие кредиты
Просроченные ссуды с залогом
Другие просроченные ссуды
От
От
От
От
Ниже Без
ААА
А+
BBB-J
вв+
ВВ-
ДО
ДО
ДО
ДО
тин-
АА-
А-
ВВВ-
ВВ-
га
о
20
50
50
50
50
100
50
20
20
20
100
100
100
100
75
35
100
100
150
150
150
150
150
рей-
100
100
100
100
Гл.
726
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Например, корпоративные облигации с рейтингами от ААА до АА
имеют вес
20%,
а корпоративные облигации С рейтингами ОТ ВВ+ ДО
ВВ- имеют вес
карты) имеют
100%. Розничные продrкты (овердрафты и кредитные
вес 75%, а кредиты с залоговой собственностью - 35%.
После того как риск каждого из составляющих портфель активов
вычислен, можно вычислить риск всего кредитного портфеля, который
равен сумме рисков активов, его составляющих. Регулирующий капи
тал тогда определяется путем умножения риска портфеля на величину,
известную как норма покръtтия Куки, или норма покръtтия МакДона
фа, которая приблизительно равна
2)
0,08.
Подход внутренних рейтингов (ПВР)
Существует две разновидности этого подхода
( базовъtй
ПВР и усо
вершенствованнъtй ПВР), но в разных странах они реализуются по раз
ным схемам.
Основная идея этого подхода заключается в том, что банки само
стоятельно оценивают вероятность дефолта (ВД) заемщиков. Также в
некоторых случаях (например, в случае усовершенствованного ПВР)
банки могут самостоятельно оценивать долю невозвращенных при де
фолте по кредиту средств (ДНС(Д)). Эти оценки должны быть осно
ваны на количественных моделях, которые с точки зрения регулятора
являются приемлемыми.
В соглашении Базель П величина капитала на покрытие кредит
ных рисков определяется формулами, в которых в качестве исходных
данных используются оцененные ВД, ДНС(Д) и ВНП(Д) (для более
подробной информации см.
[BCBS (2005)]).
Вкратце, в любом ПВР существует пять основных элементов:
а) внутренняя рейтинговая модель;
б) компоненты риска;
в) весовая функция рисков;
г) перечень минимальных требований для применения ПВР;
д) обзор случаев соблюдения минимальных требований, предостав
ленный надзорными органами.
Среди рисковых компонентов ПВР выделим следrющие.
•
Вероятность дефолта (ВД): она может быть рассчитана на ос
новании исторического опыта или на основании скоринговых моделей
оценки кредитоспособности.
•
Вели'Чина номинальнъtх потерь при дефолте (ВНП(Д)) для ба
лансовых сделок равна номинальной сумме (балансовой стоимости) не
выплаченной задолженности. Следrя принципам базового ПВР (см.
раздел
Pillar
П в
[BCBS (2005)] ),
в качестве факторов, смягчающих
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
727
последствия невыплат кредитов и корректирующих величину ВНП{Д)
(рекомендации относительно величины корректировки см.
Pillar 11
из
[BCBS {2005)]),
разделе
следует выделить за.логи, кредитные де
ривативы или гарантии, балансовые взаимозачеты. ВНП(Д) для за
ба.лансовой деятельности рассчитывается на основании подхода Банка
международных расчетов
(BIS-1)
к переводу результатов внеба.лансо
вой деятельности в эквивалент результатов балансовой деятельности с
использованием соответствующих коэффициентов перехода (для более
подробной информации см. гл.
20
из
[Saunders {1997)]).
•Доля невозвращенн:ых при дефолте по кредиту средств (ДНС{Д)}
при использовании базового ПВР для необеспеченных преимуществен
ных требований устанавливается равной
ных требований- равной
75%.
45%,
а для субординирован
При расчете ДНС{Д) для обеспеченных
требований следует использовать комплексный подход в рамках стан
дартизированной модели, а именно:
ДНС(Д)* = ДНС(Д) х (ВНП(Д)* /ВНП{Д)),
где ДНС(Д)
-
доля невозвращенных при дефолте средств для необеспе
ченных преимущественных требований
{45%);
ВНП(Д)
-
текущее зна
чение величины номинальных потерь при дефолте; ВНП{Д)*
-
значе
ние величины номинальных потерь при дефолте после снижения риска
(для более подробной информации см.
•
[BCBS {2005)]).
ДНС(Д) при исполъзовании усовершенствованного ПВР равна
оценке фактического ДНС(Д), полученной банком.
•
Эффективньtй срок долгового обязательства (ЭСДО): для базо
вого ПВР эффективный срок долгового обязательства равен
2,5
годам;
для усовершенствованного ПВР эффективный срок долгового обяза
тельства равен максимуму из одного года и величины, полученной с
помощью весовой функции, определяемой денежными потоками:
где дпt
мени
t.
-
денежный поток, поступающий по договору в момент вре
Во всех случаях, ЭСДО будет не более пяти лет.
Веса рисков корпоративных, государственных и банковских обяза
тельств зависят от оценок ВД, ВНП{Д), ДНС{Д), а в некоторых случа
ях и от ЭСДО. Описание весов риска активов выходит за рамки этой
книги, и для получения более полной информации мы рекомендуем ис
пользовать материалы
[BCBS {2005)].
Гл.
728
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Обзор одномерных моделей кредитного риска
7.4.4.
Перечислим задачи, о которых будет рассказано в этом пункте.
•
•
Как вычислять вероятность дефолта?
Как вычислять долю невозвращенных при дефолте по кредиту
средств (или норму восстановления)?
•Как вычислять величину номинальных потерь при дефолте?
Далее представлены основные подходы и модели, используемые при
решении этих задач.
•
Экспертный подход
Решение о том, выдавать или не выдавать кредит, выносится ло
кальным
или
отраслевым
инспектором
по
кредитам,
локальным
или
отраслевым менеджером по связям с клиентами. Он может учитывать
разные факторы риска, но обычно концентрирует внимание на следу
ющих пяти.
-
Характер. Рассматривается мера репутации компании, ее готов
ности возвратить долг и истории погашения обязательств. Как правило,
большой срок существования компании является составляющей репу
тации надежного заемщика.
-
Капитал. Капиталовложения владельцев и отношение этих ка
питаловложений к величине кредита (плечо). Эти показатели являются
хорошими предикторами вероятности банкротства.
-
Способность погашать задо.л,;ж;енность отражает неустойчи
вость доходов заемщика. Если погашение задолженности по контракту
представляет собой постоянный во времени поток, а доходы неустой
чивы (имеют большое стандартное отклонение), то могут возникать
периоды, когда способность компании погашать задолженность будет
ограничена.
-
Обеспе-ч,ение. В случае дефолта по кредиту, финансовые органи
зации (кредиторы) требуют от заемщика предоставленное им залоговое
имущество. Большее преимущество требований и большая рыночная
стоимость залогового имущества по кредиту влекут его меньшую рис
кованность.
-
Экономи-ч,еские условия (циклъt). Состояние бизнес-цикла
-
важ
ный элемент при определении кредитного риска, в особенности для цик
лично функционирующих отраслей.
Рассмотренный (экспертный) подход относится к достаточно ста
рым, мало востребованным в современной практике. Поэтому мы не
будем его рассматривать в деталях (для получения более подробной
информации об этом подходе см. работы
et al. {1987)],
[Тrеасу,
Carey {2000)]).
[Libby {1975)], [Libby,
Тrotman
7.4.
•
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
729
Подход, основанный на системе кредитного скоринга
Основной принцип функционирования этой системы заключается
в идентификации ключевых факторов, определяющих вероятность де
фолта, и в получении путем их комбинированного взвешивания коли
чественной оценки действия совокупности этих факторов. Эта количе
ственная оценка может быть использована в системе классификации.
В некоторых случаях полученная количественная оценка может быть
буквально истолкована как вероятность дефолта.
Существуют четыре методологические формы моделей кредитного
скоринга:
(i) линейная модель
(ii) логит-модель;
(iii) пробит-модель;
(iv)
вероятности;
модели, полученные на основе дискриминантного анализа
(описание теоретических аспектов всех этих моделей можно найти в
[Айвазян
В
(2010)]).
работе [Mester (1997)]
представлен достаточно широкий обзор
примеров использования моделей кредитного скоринга:
97%
процентов
банков используют кредитный скоринг при рассмотрении заявлений на
выдачу кредитных карт, тогда как лишь
70% -
при рассмотрении заяв
лений на получение кредитов предприятиями малого бизнеса. Однако,
используя модели кредитного скоринга, банки проявляют ряд заблуж
дений: во-первых, они часто используют линейные модели, тогда как
более адекватными моделями для описания банкротства могут быть
нелинейные модели. Во-вторых, такие модели главным образом основа
ны на бухгалтерских коэффициентах. В большинстве стран данные бух
галтерского учета фиксируются в дискретные моменты времени и пред
ставлены в форме, соответствующей принципам бухгалтерского учета.
Поэтому сомнительно, что такие модели в состоянии распознать компа
нии, чье состояние может стремительно ухудшиться. В-третьих, расту
щая сложность и взаимодействие мировых экономик может ухудшить
качество
прогнозирования
простыми
моделями
кредитного
скоринга.
Как сообщается в работе
банков оказалось, что в
[Mester ( 1997)], при анализе деятельности 33
56% из них системы кредитного скоринга, ис
пользуемые при рассмотрении заявлений на выдачу кредитных карт,
не распознали низкокачественные кредиты. Если модели кредитного
скоринга дают неточные результаты оценки относительно одн.ородн:ых
кредитов (кредитных карт), то как с помощью таких модей можно оце
нивать денежноемкое и сложное по структуре бизнес-кредитование?!
В заключение хотелось бы отметить, что специфическая природа
этих моделей и их слабая взаимосвязь с существующей теорией фи
нансов
-
те особенности, которые, вероятно, в наибольшей степени
Гл.
730
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
беспокоят экономистов. Тем не менее эти модели по-прежнему широ
ко используются в финансовом секторе, см.
[Altman, Sabato (2007)]
и
ссылки в этой работе. Более подробно различные модели, используемые
при решении вышеупомянутых «дефолтных» задач, в том числе модели
кредитного скоринга, будут рассмотрены ниже (см. пп.
•
7.4.6-7.4.8).
Модели панельных данных
Панельные данные сочетают в себе данные как пространственного
типа, так и данные типа временных рядов. Исследования по исполь
зованию моделей панельных данных в финансах имеют непродолжи
тельную историю. В работах, представленных в рамках этих исследо
ваний, для оценки вероятности дефолта по кредитам, выданным малым
и средним предприятиям, предлагаются как модели панельных данных
со случайным эффектом, так и модели с фиксированным эффектом.
Учет наличия таких качественных особенностей, как, например, харак
теристики бизнес-сектора, качество управления, позволяет объяснить,
почему среди компаний А и В, имеющих одинаковое финансовое по
ложение и структуру долга, одна оказывается в состоянии дефолта, а
другая продолжает выполнять свои долговые обязательства. Вопрос,
способствует ли учет неоднородности компаний или бизнес-секторов
построению моделей с более качественными оценками вероятности де
фолта, весьма актуален для финансовых организаций и рейтинговых
агентств, большинство из которых главным образом заинтересованы
в ответе на вопрос «когда возникнет дефолт ?» нежели
«nо'Чему
воз
никнет дефолт?». Более того, использование байесовского подхода для
этих моделей позволяет учитывать априорные знания (например, реко
мендации аналитиков). Этим моделям посвящен п.
•
7.4.6.
Внешние и внутренние рейтинговые системы
Построение кредитных рейтингов является традиционным подхо
дом к оценке кредитного риска. Системы построения кредитных рей
тингов основаны, как правило, на качественных и количественных оцен
ках. Вычисление итогового рейтинга основано не на каких-либо мате
матических моделях, а зависит от общих соображений и опыта. Рей
тинг представляет собой категорию, которая описывает правдоподоб
ность дефолта, но при его использовании всегда надо иметь в виду, что
может быть выбран другой критерий присвоения того или иного рей
тинга. Рейтинговые системы нельзя рассматривать как системы точной
оценки кредитного качества; кроме того, кредитный рейтинг во многом
зависит от мнения специалиста по оценке рейтинга.
В целом кредитные рейтинги основываются в большей или меньшей
степени на оценке следующих элементов:
а) возможность выплаты
полнять
-
способность и готовность заемщика вы
свои обязательства в
соответствии с тем,
что указано в
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
731
кредитном договоре;
б) характер и обеспечение кредитного обязательства;
и) защита, предусмотренная обязательствами в случае банкротства,
реорганизации или в других случаях, упомянутых в законе о банкрот
стве и других законах, касающихся прав кредиторов.
Рейтинг выражается в терминах риска дефолта. Как правило, рей
тингуются преимущественные облигации. Однако в некоторых случаях
рейтинг присваивается и облигациям более низкого уровня (непреиму
щественным облигациям), которые в основном имеют рейтинг меньший,
чем рейтинг преимущественных облигаций, что отражает более низ
кий приоритет исполнения обязательств в случае банкротства. Соответ
ственно в случае низкого приоритета исполнения обязательств присва
иваемый этим обязательствам рейтинг может не соответствовать фор
мальному определению категории этого рейтинга.
В качестве примера системы категорий рейтинга коротко опишем
систему кредитных рейтингов, используемую агентством
"Standard and
Poor's".
ААА. Это самый высокий рейтинг, присваиваемый агентством
S&P.
Заемщик обладает исключительно высокой способностью своевре
менно и полностью выполнять свои долговые обязательства.
АА. Этот рейтинг лишь в небольшой степени отличается от самого
высокого рейтинга, присваиваемого агентством
S&P.
Заемщик обладает
очень высокой способностью своевременно и полностью выполнять свои
долговые обязательства.
А. Обязательства, которым присваивается рейтинг ~А», более чув
ствительны к воздействию неблагоприятных перемен в коммерческих,
финансовых и экономических условиях, чем обязательства, имеющий
более высокий рейтинг. Заемщик имеет умеренно высокую способность
своевременно и полностью выполнять свои долговые обязательства.
ВВВ. Заемщик с таким рейтингом имеет достаточную способность
своевременно и полностью выполнять свои долговые обязательства. Од
нако такой заемщик имеет более высокую чувствительность к воздей
ствию неблагоприятных перемен в коммерческих, финансовых и эконо
мических условиях, чем более высокие рейтинги ~ААА», ~АА» и ~А».
ВВ. По сравнению с другими спекулятивными обязательствами 22 ,
имеющими более низкие рейтинги (чем ~ААА», ~АА», ~А» и ~вВВ» ),
обязательства с этим рейтингом наименее подвержены неплатежам. Од
нако заемщик с таким рейтингом имеет более высокую чувствитель
ность к воздействию неблагоприятных перемен в коммерческих, фи22 К
классу спекулятивных относят обязательства, которым присваиваются рей
тинги «ВВ», «В», «ССС», «СС» и «С».
ГЛ.
732
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
нансовых и экономических условиях, которые могут отрицательно по
влиять на способность заемщика своевременно и полностью выполнять
свои долговые обязательства, чем заемщик, имеющий более высокий
рейтинг.
В. Обязательства с рейтингом «В» в большей степени подвержены
неплатежам, чем обязательства с рейтингом «ВВ», но в текущий мо
мент заемщик с рейтингом «В» способен исполнить свои обязательства
в срок и в полном объеме. Однако у таких обязательств имеется более
высокая уязвимость при наличии неблагоприятных коммерческих, фи
нансовых и экономических условий, чем у обязательств с более высоким
рейтингом.
ССС. На данный момент существует потенциальная возможность
невыполнения эмитентом своих долговых обязательств; своевременное
выполнение долговых обязательств в значительной степени зависит от
благоприятных коммерческих, финансовых и экономических условий.
В случае неблагоприятных перемен в коммерческих, финансовых и эко
номических условиях весьма маловероятно,
что заемщик сможет вы
полнить свои обязательства в срок и в полном объеме.
СС. Заемщик с таким рейтингом в настоящее время имеет высокую
вероятность невыполнения своих долговых обязательств.
С. Для субординированного кредита или иных обязательств с рей
тингом «С» существует очень большая вероятность их неисполнения.
Рейтинг «С» может быть присвоен заемщику, в отношении которо
го возбуждена процедура банкротства или предпринято аналогичное
банкротству действие, но платежи или выполнение долговых обяза
тельств продолжаются. Рейтинг «С» может быть также присвоен вы
пускам привелегированных акций в случае возникновения в будущем
долгов
по
выплате дивидендов
или
недостатка средств для
исполне
ния иных обязательств, предусмотренных привелегированными акция
ми, хотя в текущий момент заемщик выполняет все свои обязательства
в срок и в полном объеме.
D.
Дефолт по долговым обязательствам. Рейтинг
«D»
присваива
ется заемщику в том случае, если выплаты по обязательствам не про
изводятся, и аналитики агентства
S&P полагают,
будут сделаны даже в льготный период. Рейтинг
что такие выплаты не
«D»
присваивается:
а) заемщику, на которого подана петиция о банкротстве;
б) заемщику, который признан банкротом или в отношении которо
го предприняты действия, аналогичные банкротству, в случае, если он
отказывается от выплат по своим обязательствам.
Далее мы не будем рассматривать рейтинговые системы, поскольку
их детальный анализ выходит за рамки нашей книги. Однако для по
лучения более полной информации относительно рейтинговых систем
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
мы рекомендУем обратиться к работам [Тrеасу,
733
Carey (2000)], [BCBS
(2000)], [Griep, De Stefano (2001)], а также к технической документа
ции рейтинговых агентств "Standard and Poor's", "Moody's" и "Fitch",
которую легко можно найти в Интернете.
•
Структурные модели
Иногда ценные бумаги, выпущенные той или иной компанией, оце
ниваются с помощью моделей мертоновского типа (или структурных
моделей), основанных на структурных переменных компании (т. е. на
значениях, отражающих состояние активов и пассивов компании). Пер
вые работы, в которых впервые были изложены модели этого типа, по
явились в начале 1970-х гг. (см.
[Merton (1970)], [Merton (1977)], [Bielecki,
Rutkowski (2002)] и [Bharath, Shumway (2006)]). Как в работе [Black,
Scholes (1973)], так и в работе [Merton (1974)] отмечается, что корпо
ративные облигации могут быть оценены так же, как простые ваниль
ные
опционы.
Излишне
говорить,
что
использование
формулы
Блэка- Шоулса для ценообразования ванильных опционов требует
некоторых основополагающих предположений относительно поведения
базового актива, безарбитражности и возможности хеджирования в лю
бой момент времени. Кроме того, недавние разбирательства по дефол
там таких транснациональных корпораций, как «Энрон», «Пармалат»
и «Вордлком», четко показали, насколько бухгалтерские данные могут
быть искажены и далеки от подлинного финансового положения компа
нии. Когда имеют место финансовые мошенничества, модели, которые
используют бухгалтерские данные для прогнозирования вероятности
дефолта (например, модели мертоновского типа), не могут быть при
менены, поскольку их прогнозы абсолютно ненадежны. Во избежание
подобных проблем был предложен иной подход, в котором используют
ся только курсовые стоимости акций, а также возникает возможность
при моделировании динамики курсовой стоимости акций использовать
не только нормальное распределение. Более подробно эти модели пред
ставлены в пп.
7.4.5.
7.4.7.
и
7.4.8.
Оценка качества моделей: оперативная кривая,
площадь под ней и функции потерь
Для того чтобы сравнить различные модели, в эмпирической литерату
ре, как правило, используются критерии, основанные на статистических
тестах (см.
[Burnham, Anderson (1998)]), на функциях информационно
го типа (см. [Akaike, (1974)], [Schwarz, (1978)], [Bernardo, Smith (1994)]
и [Vapnik (1998)]), на функциях потерь (см., например, [Kohavi, Provost
(1998)]), а также на вычислительных критериях (см., например, [Efron
(1979)], [Hastie, Tibshirani et al. (2001)]). Обзор подходов к сравнитель-
734
Гл.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
ному анализу моделей смотри, например, в [Giudici (2003)] 23 .
Повсеместное распространение вычислительных методов привело
к интенсификации развития критериев выбора модели. Эти критерии
обычно основаны на разбиении имеющейся выборки на две подвыбор
ки: «обучающую» и «экзаменующую». По первой выборке оцениваются
параметры, а вторая используется для оценки ее дееспособности. При
этом возможно сравнение моделей разной структуры.
Сосредоточимся на результатах, полученных из таблицы классифи
кации подходов к прогнозированию, которую назовем таблицей «факт
прогноз» (см.
[Kohavi, Provost (1998)]).
дает тем преимуществом,
Как правило, эта таблица обла
что с ее помощью можно легко сравнивать
различные модели, но, с другой стороны, для такого сравнения необхо
дима аккуратная формализация и математическая строгость.
Таблица содержит информацию о фактических и прогнозируемых
классах, полученных в результате классификации. Эффективность мо
дели обычно оценивается на основании данных, представленных в таб
лице. В табл.
7.6
представлена схема «факт-прогноз» для двух клас
сов24.
Таблица
7 .6. Теоретическая
схема «факт-прогноз»
Прогноз
Факт
Неплатежноспособные
Платежноспособные
компании
компании
Неплатежоспособные
а
ь
с
d
компании
Платежноспособные
компании
В контексте предмета нашего исследования, элементы таблицы име
ют следующий смысл:
а
-
количество правильных прогнозов того,
что компания непла
тежеспособна;
Ь
-
количество неправильных прогнозов, утверждающих, что ком
пания платежеспособна;
с
-
количество неправильных прогнозов, утверждающих, что ком
пания неплатежеспособна;
d-
количество правильных прогнозов того, что компания плате
жеспособна.
23 Некоторым
аспектам этой темы посвящена также гл. 1 данной книги.
проводятся в контексте схемы проверки двух простых гипотез:
24 Рассуждения
Но
-
компания в состоянии дефолта (основная гипотеза) и Н1
-
компания плате
жеспособна (конкурирующая гипотеза). Поэтому понятия «позитив» и «негатив»
означают, соответственно, принятие или отклонение основной гипотезы Но.
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
735
Важным инструментом оценки эффективности модели прогнози
рования вероятностей является кривая соотношений правильной
и ложной классификации объектов, так называемая оператив
ная кривая) 25 (ОК), рассмотренная, в частности, в работах [Metz,
Kronman (1980)], [Goin (1982)]
и
[Hanley, McNeil (1982)].
При условии,
что нам задана таблица «факт-прогноз» и пороговое значение (для от
несения к тому или иному классу), оперативная кривая строится на ос
нове совместных частот правильных прогнозов и фактических событий,
совместных частот неправильных прогнозов и фактических событий.
Более точно эта кривая строится на основании следующих условных
вероятностей:
•
чувствите.л:ьность: а/ (а+ Ь)
-
доля случаев, в которых спрогно
зирована неплатежеспособность компании, при условии, что в действи
тельности компания была неплатежеспособной;
•
специфичность:
d/(d +с) -
доля случаев, в которых спрогнози
рована платежеспособность компании, при условии, что в действитель
ности она и была платежеспособной;
•
ложна.я позитивность (или !-специфичность): с/(с
+ d)
доля
-
случаев, в которых спрогнозирована неплатежеспособность компании,
при условии, что компания была платежеспособной (ошибка
•ложна.я негативность (или !-чувствительность): Ь/(а
11
рода);
+ Ь) -
до
ля случаев, в которых спрогнозирована платежеспособность компании,
при условии, что компания была неплатежеспособной (ошибка
1 рода).
Оперативная кривая строится следующим образом: для каждого
фиксированного порогового значения ставиться в соответствие точка
на декартовой плоскости, на которой ось х отвечает значениям ложной
позитивности (или !-специфичности), также называемая нормой лож
ной тревоги, а ось у отвечает значениям чувствительности, также назы
ваемая нормой попадания (рис.
7.15).
Следовательно, каждая точка на
этой кривой будет отвечать некоторому фиксированному пороговому
значению. А значит, ОК может быть использована для выбора поро
гового значения, балансирующего чувствительность и специфичность.
В терминах сравнения моделей наилучшей из двух кривых признаем ту,
которая расположена левее (в идеальном случае эта кривая совпадает
с осью у).
Одна из особенностей хорошей модели состоит в том, что она имеет:
•
большую (насколько это возможно) норму попадания (правиль
на.я классификация заемщика в качестве потенциального банкрота);
25 В
англоязычной литературе кривая соотношений правильной и ложной клас
сификации объектов называется
curve".
"Receiver Operating Characteristic curve"
или
"ROC
Гл.
736
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
малую (насколько это возможно} норму ложной тревоги ( непра
вильная классификация кредитоспособного заемщика как потенциаль
ного банкрота).
Для того чтобы проанализировать мощность дискриминации рей
тинговой системы независимо от выбранного порогового значения, нор
ма ложной тревоги и норма попадания рассчитываются для всех воз
можных пороговых значений. Точки, определенные таким образом, об
разуют ОК.
Чем круче изменяется кривая, тем более точна рейтинговая систе
ма. ОК идеальной рейтинговой системы будет расположена на траек
тории, соединяющей точки (О; О), (О;
100)
и
(100; 100).
А в случае чисто
случайной рейтинговой системы, ОК будет расположена вдоль прямой,
соединяющей точки (О; О) и
(100; 100).
Идеальная модель
попок
QIL-~~~~~~~~~--'-----
Hopмa ложной тревоги
Рис.
7.15.
1ОООА.
Оперативная крива.я (ОК) и площадь области под ней (ПОпОК)
Однако несмотря на то что ОК не зависит от типа распределения
по классам или потерь, связанных с ошибочной классификацией (см.
[Provost, Fawcett et al. (1998)]),
они зависят от пороговых значений, от
деляющих платежеспособные компании от неплатежеспособных. Опуб
ликованы работы (см., например,
[Buckland et al. (1997)]),
в которых
предлагается определять область под ОК как меру эффективности про
гнозирования с помощью бутстреп-доверительных интервалов. Область
под ОК всегда заключена в квадрате с вершинами (О; О), (О;
100), (100; О)
и
(100; 100). Площадь области под ОК всегда заключена между нулем
и 104 . Чем ближе значение этой площади к 104 , тем более точна рей
тинговая система.
Было показано, что площадь под эмпирической ОК, рассчитанная
методом трапеций, совпадает с U-статистикой Манна-Уитни, исполь
зуемой для сравнения распределений двух выборок (см.
[Bamber, 1975)).
7.4.
В работе
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
[Hanley, McNeil (1983)]
737
используются некоторые свойства этой
непараметрической статистики для сравнения двух мер области под
ОК, соответствующих двум разным методам, примененным к одной и
той же совокупности данных. Аналогичный подход предложен в работе
[DeLong, Clarke-Pearson et al. (1988)].
Кроме того, в работе [Fielding, Bell (1997)]
представлены разнооб
разные критерии эффективности, зависящие от порогов. Следуя
этим критериям, оптимальное значение порога определяется на основа
нии:
•
см. в
•
максимизации каппа (Р-каппа), более подробную информацию
[Fielding, Bell (1997)];
минимизации разности между чувствительностью и специфично
стью (в работе [Schrцder,
•
Richter (1999)]
эта разность называется
P-fair);
максимизации нормы правильной классификации или,
торая вычисляется на основании оперативной кривой (см.
bell (1993)])
P-opt, ко
[Zweig, Camp-
и учитывает значения как ложно позитивных прогнозов,
так и ложно негативных прогнозов;
•
фиксированного порогового значения Р
= 50%
(или Р
= 0,5
в
долях), которое является эталонным в финансовой литературе.
Более того, как отмечает Базельской комитет по банковскому над
зору, величина и число правильных прогнозов являются вопросами, ко
торыми должны заниматься надзорные за банковской деятельностью
органы. Эти вопросы могут изучаться с помощью так называемой
функции потерь. Следовательно, в этом контексте, учитывая как таб
лицу «факт-прогноз», так и функцию потерь, мы хотим выбирать наи
лучшую модель прогнозирования. В частности, согласно структурной
схеме, предложенной в
[Granger, Pesaran (2000)],
платежная матрица,
суммирующая результаты принятия решений, имеет вид, представлен
ный в табл.
Таблица
7.7.
7. 7. Платежная
матрица
Фактическое состояние
Прогноз
=1
Yit
1
(Pi,t > Порог)
о
Yit =О
()9i, t
Yit =о
(Pi,t ~ Порог)
()~i, t
о
Yit
=
В таблице
дит компании
8?,t i,
издержки банка в ситуации, когда он не выдает кре
которая в действительности не находится в состоянии
дефолта, а величина
8f t
1
(обязательства перед банком, умноженные на
Гл.
738
норму восстановления)
i
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
-
убыток в ситуации, когда кредит компании
предоставляется, но она оказывается в состоянии банкротства. По
тери банка при правильном прогнозе равны нулю. Это позволяет вы
писать следующее выражение для функции финансового убытка (см.
[Fantazzini, Figini
{2009а)],
[Fantazzini, Degiuli et al. {2008)]):
Loss = EE8f,tYi,t(1-1{.Pi,t >порог}) +8?,t(1-yi,t)1{.Pi,t >порог},
i
t
которая представляет собой сумму взвешенных элементов четырех ти
пов из таблицы ~факт-прогноз». Что касается нормы восстановления,
то, например, при использовании базового подхода внутренних рейтин
гов для необеспеченных кредитов с первоочередным правом требования
она равна
7.4.6.
55%
(НВ=100%-ДНС(Д), где ДНС(Д)=45%).
Применение классических и байесовских моделей
панельных данных для прогнозирования дефолта
по кредиту
1)
Классические модели панельных данных
Первые работы, в которых модели панельных данных использу
ются для прогнозирования дефолта по кредиту для малых и средних
предприятий, появились относительно недавно. К ним относится работа
[Dietsch, Petey {2007)],
в которой для оценки корреляции между стои
мостями активов малых и средних компаний во Франции использует
ся пробит-модель для панельных данных, в которой сектор занятости,
местоположение и еще некоторые характеристики рассматривались в
качестве специфических эффектов (но в этой работе не были представ
лены результаты прогнозирования). Точно так же в работе
Hainz et al. {2007)]
[Fidrmuc,
для описания рынка кредитования малых и средних
предприятий в Словакии используется пробит-модель для панельных
данных. В работе
[Fantazzini, Figini
{2009а)] для прогнозирования веро
ятностей дефолта малых и средних предприятий предлагаются и срав
ниваются модели панельных данных из достаточно широкого спектра,
в частности, рассматриваются такие классические модели, как модели
со случайными эффектами, модели со случайными коэффициентами,
учитывающими ненаблюдаемые неоднородности.
Большинство рейтинговых агентств обычно анализируют отдельно
каждую компанию и оценивают риск дефолта с помощью критериев,
основанных на годовых финансовых данных. Однако, как указывается
в рекомендациях Международного валютного фонда относительно мо
делирования странового дефолта, ~использование пробит-модели для
7.4.
панельных данных
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
в
ситуации,
739
когда постулируются
временная
ста
бильность и межстрановая однородность, может быть весьма пробле
матичным~ (см.
[Oka, 2003),
с. 33). Те же рекомендации могут быть
распространены на случай моделирования кредитного риска любого за
емщика, в частности, кредитного риска средних и малых предприятий.
Предположим, что задана стандартная несбалансированная база
панельных данных по кредитам. В моделях панельных данных мы бу
дем использовать следующие обозначения: заемщики идентифициру
= 1, ... , n), время -
ются при помощи индекса
i (i
t (t = 1, ... , Т),
при помощи индекса
сектора
чим также через
Yitj
-
при помощи индекса
j (j = 1, ... , J). Обозна
переменную, отвечающую за платежеспособность
(она может принимать либо значение О в случае платежеспособности,
либо значение
1
в противном случае), а через Xitj обозначим вектор
предикторов (объясняющих переменных) платежеспособности, размер
ность которого (р х
1).
Необходимо представить математическое ожидание случайной ве
личины, отвечающей за платежеспособность, как некоторую функцию
от ее предикторов (объясняющих переменных). Математическое ожи
дание бинарной случайной величины (случайная величина принимает
либо значение О, либо значение
нимает значение
1)
равно вероятности того, что она при
1:
Можно моделировать это математическое ожидание как линейную
функцию регрессоров (31 Хщ. Для бинарной случайной величины ис
пользование этого подхода может быть проблематичным, поскольку ве
роятность принимает значения из отрезка [О;
1],
а регрессионная пря
мая с бесконечным ростом значений регрессоров либо бесконечно воз
растает, либо бесконечно убывает. Поэтому математическое ожидание
будем моделировать с помощью функций, специфицированных следу
ющим образом:
или
g{ P(Yitj = 1 IХщ)} = (3
1
Хщ.
Эти две спецификации эквивалентны, если функция
ратной к функции связи
h( ·)
является об
g( ·).
Мы ввели две компоненты анализируемой модели: линейный пре
диктор
(3' Хщ и функцию связи (h или g) линейного предиктора и веро
ятности P(Yitj = llXщ). Третьей компонентой является условное рас
пределение случайной величины Yitj, отвечающей за платежеспособ-
Гл.
740
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ность при заданных значениях предикторов
P(Yitj = llXitj)·
Для би
нарной случайной величины всегда берется распределение Бернулли.
Типичным выбором для функции связи является логит- или пробит
функция. Логит-функция связи более привлекательна, поскольку при
1 { P(Y.·t ·-llX·) } (
ее выборе линейная модель строится для
см. [DoЬson
n
l-P(;{t~=llXi)
подробнее
(2002)]).
Отметим, что здесь используются классические обозначения для
моделей такого типа, см.
[Rabe-Hesketh, Skrondal (2004, 2005)]
и ссыл
ки в этой работе. Однако логистическую регрессионную модель можно
рассматривать как модель латентного отклика, в которой предполага
ется, что рассматриваемой бинарной величине
соответствует неко
Yitj
торая латентная непрерывная случайная величина
Yi:j:
переменная больше нуля, наблюдаемый отклик равен
например, [Айвазян
(2010),
п.
9.1)).
если латентная
1,
иначе О (см.,
Модель линейной регрессии специ
фицируется для этой латентной величины, и ошибка в такой регресси
онной модели имеет нормальное или логит-распределение. Итак:
Yu;= {
где Yi;j
Yi:j > О;
1,
если
О,
иначе,
= /3 Xitj + eitj .
1
Для того чтобы ослабить предположение об условной независимо
сти между компаниями/заемщиками при заданных значениях предик
торов, в линейную регрессионную модель в качестве предиктора вклю
чают индивидуальные нормальные слу-чаii:н:ы.е эффектъt ~i:
В частности, в работе
[Fantazzini, Fegini
(2009а)] предлагаются сле
дующие модели (с пробит- и логит-функциями связи):
g{P(Yitj = llXitj)} = /3 1 Xitj
Е N(O, и~, 1 )
+ ~1,i
(7.12)
g{P(Yitj = llXitj)} = /3 1 Xitj
'j Е N(O, и~, 2 )
+ ~2,j
(7.13)
'i
g{ P(Yitj = 1IXitj)} = /3 1 Xitj
~i Е N(O, и~,1),
'j Е N(O, и~, 2 ),
+ ~1,i + ~2,j,
(7.14)
i (i = 1, ... , п,) - это индекс, идентифицирующий компании,
j (j = 1, ... , J) - индекс, идентифицирующий бизнес сектора.
где
а
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
741
Можно получить еще более гибкую модель, если в моделях
(7.14)
{7.12)-
предположить, что некоторые или все коэффициентъ~ слу-чайнъ~.
Например, в приложениях, связанных с оценкой кредитного риска, мы
хотим протестировать, является ли эффект между бизнес-секторами,
вносимый отдельной финансовой характеристикой, случайным. Это
можно сделать, если положить коэффициент при соответствующей ха
рактеристике случайным.
Пусть случайная величина t;2,j отвечает за случайный эффект меж
ду бизнес-секторами 2-й характеристики, и она равна отклонению от
среднего этого случайного эффекта. Тогда модель может быть специ
фицирована следующим образом:
g{ P(Yitj = 1IXitj)} = {3 1 Xitj
где x~:J
+ t;l,i + t;2,j • x~:J,
- рассматриваемый предиктор (в нашем случае некоторая фи
нансовая характеристика) 26 и
[
t;l,~ ] Е N2 ( [ О ] , [ и~,1 и~,12 ] )
о
t;2,J
О'<,12
О'<,2
.
Предиктор x~:J подбирается на основании содержательных сообра
жений.
Для иллюстрации различий между моделью с фиксированными
эффектами и моделью со случайными коэффициентами обратимся к
рис.
7.16,
на котором представлен пример с единственным регрессором
Xij. Для более детального ознакомления с этими примерами см. работы
[Rabe-Hesketh and Skrondal {2004, 2005)].
б)
а)
о.о
o.s
1.0
l.S
X1j
Рис.
7.16.
2.0
о.о
o.s
1.0
l.S
2.0
X1j
Модель со случайным эффектом (а) и модель со случайными
коэффициентами
26 0тметим,
(6)
что в этой модели через и~. 2 обозначена дисперсия случайного коэф
фициента ~2,j, который, вообще говоря, может быть отличен от дисперсии случай
ного эффекта бизнес-сектора.
ГЛ.
742
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Заметим, что совместное распределение случайных величин
(см.
(7.11))
(3' Xitj
в этих моделях при условии наблюдаемых регрессоров не
может быть представлено в функциональной форме и оценивается с
помощью приближенных методов, например с помощью квадратурных
формул Гаусса- Эрмита. Однако если их плотность островершинна, то
обычные квадратуры могут давать весьма плохие приближения (см.
[Rabe-Hesketh et al. (2002, 2005)]).
Такая ситуация может возникнуть
тогда, когда имеются достаточно большие кластеры, что типично для
баз данных по кредитам. В этом случае рекомендуется использовать
альтернативный метод, известный как метод адаптивных квадратур,
поскольку с его помощью можно получить более точные приближения,
что, в свою очередь, возможно благодаря масштабированию квадра
туры и ее весов, а также преобразованию подынтегральной функции.
Но все же качество приближения, обусловленное этим методом, зави
сит от параметров модели. Подробное описание алгоритма применения
метода адаптивных квадратур можно найти в работах
[Rabe-Hesketh
et al. (2002, 2005)], [Rabe-Hesketh, Skrondal (2004, 2005)]. Для оценки
рассматриваемых моделей Рейб-Хескес, Скрондал и Пиклес написали в
статистическом пакете
на сайте
STATA
www .gllamm.org.
процедуру
GLLAMM,
которая доступна
Наконец отметим, что мы не рассматривали логит-модели с фикси
рованным эффектом для панельных данных, поскольку такие модели
оцениваются только по реализациям, отличным от «нулевых~ (т.е. толь
ко по данным о тех заемщиках, которые подверглись дефолту). Слабая
информативность других данных в задаче оценивания модели приводит
к существенному снижению эффективности оценивания (см.
Тrivedi
2)
[Cameron,
(2005)]).
Применение байесовских моделей панельных данных
к кредитному риску
В работе
[Fantazzini, Fegini
(2009а)] предлагается объединить раз
личные типы информации. Цель этого состоит в том, чтобы соединить
результаты «экспериментирования~, которые мы получаем в виде ба
лансовых данных, и априорные знания. Как правило, априорные знания
представлены в виде неструктурированных данных (качественная ин
формация), например, в виде комментариев аналитиков, текстовой ин
формации и т. д. Для того чтобы показать, как достичь эту цель на при
мере данных по средним и малым предприятиям, в работе
Fegini
[Fantazzini,
(2009а)] рассмотрен набор байесовских моделей для панельных
данных, использующих моделирование цепей Маркова.
Качественная информация, которой обладали авторы этой рабо
ты, включала в себя описания аналитиков рассматриваемых средних
7.4.
743
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
и малых предприятий. В этих описаниях были изложены вероятные
перспективы развития предприятий, без каких-либо четких указаний
относительно того, стоит ли выдавать кредит или нет. В личной бесе
де с ответственными лицами, предоставившими эту информацию, по
следние отметили, что подобное описание с общими рекомендациями
было обусловлено тем, что не только аналитик участвует в принятии
окончательного решения. Последнее слово всегда за финансовым ди
ректором: указания последнего могут вызвать проблемы в некоторых
спорных случаях. Кроме того, следует отметить, что для многих рас
сматриваемых малых и средних предприятий априорная информация
не была указана. Более того, упомянутые ответственные лица отмечали
невозможность определить четкие закономерности относительно изме
нения баланса этих предприятий, так как доходные предприятия с по
ложительными денежными потоками могут иметь {во многом случай
ные) негативные перспективы и наоборот. Принимая во внимание имею
щуюся качественную информацию, исследователи решили выбрать так
называемые неинформативнь~е функции априорнь~х распределений для
параметров, определяющих фиксированный эффект, тогда как для па
раметров, отвечающих за случайный эффект, было выбрано [О;
равномерное распределение
U(O, 100),
100] -
отражающее неоднородность ре
комендаций аналитиков (о неинформативных априорных распределе
ниях, используемых в байесовском подходе, см. также гл.
3 книги).
Хо
тя такая ситуация часто встречается при работе с данными по малым и
средним предприятиям, мы хотим подчеркнуть, что для получения бо
лее надежной априорной информации и более реалистичных априорных
распределений необходимо больше данных, отражающих качественную
информацию, и больше исследований в этой области.
В работе
[Fantazzini , Fegini
{2009а)] предложена методология, ос
нованная на байесовским подходе для моделей панельных данных по
малым и средним предприятиям, имеющих следующую структуру:
и~.2ЕU{O;100).
При оценивании параметров авторы следовали стандартной схеме
анализа байесовских моделей со случайными эффектами, предложен
ной в работах
{2004)]
и
[Crowder {1978)], [Breslow, Clayton {1993)], [Gelman et al.
[Gamerman {1997а,Ь)]. Описание реализации байесовского под-
744
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
хода на примерах многих моделей общедоступно по адресу в Интернете:
http:/ /www.mrc-bsu.cam.ac.uk/bugs/.
Возможны и другие подходы (для более подробной информации
см.
[Cai, Dunson (2006)] и ссылки в этой работе). В статье [Fantazzini,
Figini (2009а)] предложена модель с использованием цепей Маркова.
В частности, при прогнозировании использовался формализованный
алгоритм моделирования Гиббса (для более подробной информации от
носительно этого алгоритма см.
водство к программному
[Fantazzini, Figini
[Gamerman (1997а,Ь)], а также руко
обеспечению Winbugs). В упомянутой работе
(2009а)] рассматривается байесовский подход и моде
ли со случайными коэффициентами:
g{P(J:'itj = llXitj)} = {3 1 Xitj
где x~:J
+ ~1,j + ~2,j • x~:J,
- это некоторый финансовый показатель, а
и~.1 Е
и~.2 Е
U(O, 100),
U(O, 100).
Отметим, что в моделях со случайными эффектами имеются неко
торые проблемы идентификации. Несколько достаточно общих резуль
татов относительно идентификации, неподходящих функций априор
ных распределений и моделирования при помощи алгоритма Гиббса
рассмотрено в работах
7.4. 7.
[Gelfand, Sahu (1999)], [Chen, Fan et al. (2006)].
Модель Мертона
Модель Мертона была предложена в 1974г. (см.
[Merton (1974)])
и яв
ляется прототипом всех моделей стоимости компании. Эта модель яв
ляется эталонной и по сей день.
Модель Мертона является основной представительницей класса так
называемых моделей стоимости активов. Она объясняет дефолт ком
пании падением стоимостей активов компании. В модели Мертона пред
полагается, что стоимость активов
Vi
хорошо описывается процессом
броуновского движения, а компания финансируется из своего собствен
ного капитала
S
и своих долговых обязательств номиналом В со сроком
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
745
погашения в момент времени Т, которые могут быть в форме, напри
мер, облигаций или банковских кредитов.
Кредит, выданный какой-либо компании, создает для кредитора
кредитный риск, а именно риск того, что стоимость активов компании
в момент времени Т упадет ниже уровня В, т. е. Vт ~ В. В этом слу
чае мы говорим, что фирма находится в состоянии дефолта. Для того
чтобы компенсировать кредитный риск владельца облигации компании,
доходность по ней
ставка
r в должна быть выше, чем безрисковая процентная
r. Разность (r в - r) называют дефолтн:ым спрэдом. В модели
предполагается, что:
•рынок непрерывен и «не имеет трения» (рынок эффективен) или
транзакционных издержек;
•
агенты рынка (покупатели или продавцы) не имеют влияния на
формирование цен;
•
•
нет ограничений на объем коротких продаж;
процентные ставки при заимствовании и кредитовании одинаковы
и равны
r.
Основной целью модели является определение цены облигации
О~
t
Bt,
~ Т, некоторой компании в предположении, что динамика стои
мости ее активов описывается процессом броуновского движения сле
дующего типа:
dvt = µ Vidt + и VidWt,
Vi (µ = Evt),
ZVdt и Z Е N{O; 1).
гдеµ ожидаемая доходность для
процесс, т. е. dWt
=
а
dWt -
это винеровский
Если цена активов х подчинена уравнению
dx =
а(х, t)dt
+ Ь(х, t)dW,
то можно показать, что дифференциал функции
G(x, t),
являющейся
функцией указанной цены активов и времени, равен
дG
дG 1 д 2 G 2)
дG
(
dG = дх а + дt + '2 · дх 2 Ь dt + дх ЬdW.
Это знаменитая лемма Ито, и за более подробной информацией мы
отсылаем читателя к работе
[Hull {2005)].
В условиях справедливости
принятых допущений получим:
Далее предположим, что
Положим
Gt
= ln Vi
Vi
имеет логнормальное распределение.
и, применив лемму Ито, придем к соотношениям:
Гл.
746
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
дGt = О д 2 Gt =
1
vt ' дt
' дV,,2
- vt2 '
дGt _ 1
дvt
dG, = (
=
~ µ V. + О + ~ · ( - ~2 ) и2 V,2 ) dt + ~иV.dWt =
(µ - ~и2 ) dt + udW
1.
Наконец, сделав замену
Gt = ln Vt,
ln Vт - ln Vo =
получим
(µ - ~и2 )т + и./ТZт
или, что эквивалентно,
Следовательно, вероятность дефолта компании легко вычислить по сле
дующей формуле:
Р(Vт <В)= P{ln Vт < lnB) = Ф [
где Ф( ·)
-
2 )T]
ln lI - (µ - lu
2
Vo
иVТ
,
(7.15)
функция распределения стандартного нормального закона.
На рис.
7.17
графически представлен пример моделирования сто
имости активов компании. В соответствии с экономической интуици
ей вероятность дефолта возрастает с ростом В, и и убывает с ростом
Vo,
µ.
~
&.
~ ю
=
~
~ lil
"=
с
::Е
2 :!!
i
ID
=
-
!;; о
""
t
о
::Е
="
б
о
о
Время, дни
Рис.
7.17.
Смоделированная стоимость активов компании (процесс броуновского
движения)
7.4.
1)
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
747
Структура капитала и ценообразование активов
и долговых обязательств
Структура
(табл.
капитала
в
мертоновской
модели
весьма
проста
7.8)
Таблица
7.8. Структура
капитала компании в момент времени
Обязательства/Собственный капитал
Актив
Рискованные активы:
Vi
Долг:
Bt
Собственный капитал:
Итого:
Vi
Итого:
Предположим,
t
St
Vi
что выполнены условия теоремы Модиглиани -
Миллера (см.
В не влияет
[Miller, Modigliani (1958), (1961)]). Тогда выбор величины
на стоимость активов компании V, а выплата по долгу Вт
и величина остаточного после выплаты долга собственного капитала Sт
в момент времени Т будут равны:
Вт =
min(B, Vт) =В - max(B - Vт, О),
Sт = max(Vт - В, О).
Итак, Вт равно номиналу безрисковой облигации минус стоимость
опциона
PUT на базисный
актив
vt
с ценой исполнения В, истекающего
в момент времени Т, а Sт равна стоимости опциона
актив
vt
CALL
на базисный
с ценой исполнения В, истекающего в момент времени Т (объ
яснение смысла опционов
PUT
и
CALL
см. в сноске
5,
п.
7.2.1).
Таким
образом, получаем
Bt =В exp(-r(T- t)) - P(vt, В, и, r, Т - t),
St = C(vt, В, и, r, Т - t).
Используя формулу ценообразования опционов Блэка- Шоулса,
можно определить С(·) и Р( ·) (для более ПОдРобной информации см.
[Hull (2005)]):
C(vt, В, и, r, Т - t) = vtФ(dн) - В exp(-r(T- t))Ф(d2t),
P(vt, В, и, r, Т - t) = -Ф(-dн)Vt +В exp(-r(T- t))Ф(-d2t),
где Ф(·)
-
функция стандартного нормального распределения, а
d
1t
d2t
_ ln(vt/ В)+ (r + !и 2 )(Т - t)
uJT t
'
= dн -
иvт
t.
748
Гл.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Более того, учитывая, что в момент времени
t
выплата по долгу
равна разности между стоимостью в момент времени
t безрисковой об
лигации с номиналом В, сроком погашения Т и стоимостью опциона
PUT
на базисный актив
vt
с ценой исполнения В, истекающего в мо
мент времени Т, получим, что стоимость долга в момент времени
t
равна
Bt = Bexp(-r(T- t))Ф{d2t) + vtФ(-dн).
(7.16)
В связи с тем что увеличение волатильности и повышает как цену
опциона
PUT,
так и цену опциона
CALL,
держатели долговых обяза
тельств и акционеры имеют несколько конфликтующие предпочтения:
первые
предпочитают
низкую
чае маловероятно, что опцион
волатильность,
PUT
поскольку
в
этом
слу
будет реализован в момент истече
ния; акционеры же, наоборот, предпочитают высокую волатильность,
поскольку в этом случае прибыль, ассоциированная с длинной позици
ей по опциону
2)
CALL,
будет выше.
Вычисление вероятности дефолта: некоторые замечания
Сделаем некоторые пояснения относительно вычисления вероятно
сти дефолта. В зависимости от целей проводимого анализа, эта вероят
ность может быть вычислена двумя способами:
•
если целью является описание ценообразования, например рис
кованных облигаций, тогда риск-нейтральная вероятность дефолта
(РНВД), получаемая в предположениях модели Блэка- Шоулса, рав
на
РНВД
= Р(Vт
=Ф (
< В) = P{ln Vт < ln В) =
ln ~ - (r - ~и 2 )Т)
0
и-VТ
= Ф{-d2.о);
(7.17)
в модели Мертона для описания ценообразования облигаций и акций
используется формула Блэка- Шоулса;
•
если же цель состоит в том, чтобы вычислить актуальную ве
роятность дефолта (также называемую ожидаемой -частотой дефол
та
-
ОЧД), что является достаточно распространенной ситуацией при
управлении рисками, тогда мы должны использовать формулу
(7.15),
т.е.:
ОЧД
= Р(Vт <В)= P{ln Vт < lnB) =
=Ф (
ln ll.. - (µ Vo
и-VТ
lu2 )T) =
2
Ф{-d2),
(7.18)
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
749
где
d* _ ln(Vo/ В)+(µ - !а 2 )Т _ d + (µ - r)T
2 аv!Т
- 2·0
аv!Т '
а
ожидаемая доходность активов
µ -
Сравнивая
(7.17)
с
Vt
компании.
получаем
(7.18),
РНВД = Ф(-dо.о) = Ф [Ф- 1 (0ЧД) +µи r
v'f].
(7.19)
В модели ценообразования основного капитала (ЦОК-модель )27
используется представление µ - r = /31Г, где f3 - бета-коэффициент,
рассчитанный для модели ценообразования капитальных активов, а 7Г рыночная премия за риск:
/3 -_
7Г
Здесь р -
=
и _
Рим µм
cov(R,Rм)
var(Rм) '
-r.
корреляция между рыночными (Rм) и фондовой
ностями, а µми ам
-
(R)
доход
ожидаемая рыночная доходность и ее дисперсия
соответственно. Используя ранее упомянутые определения, можно вы
писать следующие соотношения:
µ- r
/31Г
-- = а
где
(} -
чим
а
а
7Г
7Г
= р- . - = р- = р(},
ам
а
ам
µм-r
(} =
рыночное отношение Шарпа. Подставляя
РНВД = Ф(-d2.о)
=
(7.20)
(7.20)
'
ам
в
(7.19),
полу-
Ф [Ф- 1 (0ЧД) + р8\!'Т].
Калибровка моделей реальными данными
3)
Если мы хотим вычислить вероятность дефолта, предполагая вы
полненными условия модели Мертона и модели Блэка- Шоулса, нам
необходимы оценки для
Vt
и а. К сожалению, ни один из этих двух
параметров в явном виде не наблюдается. Тем не менее для торгуе
мых собственных активов мы можем использовать величину стоимости
акции в момент времени
t,
т. е.
St,
в задаче решения системы из двух
уравнений относительно двух неизвестных параметров:
первое уравнение получается из условия, что стоимость собствен
•
ного капитала равна стоимости опциона
St = C(Vt, В, а, r, Т - t) =
27 В
VtФ(dн)
-
CALL,
а именно:
В exp(-r(T
-
t))Ф(d2t); (7.21а)
англоязычной литературе модель ценообразования основного капитала назы
вается
"Capital Asset Pricing Model" или "САРМ model". Подробную информацию
[Cochrane (2005)) или [Берндт (2005)).
относительно этой модели см. в
Гл.
750
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
•второе уравнение получается, если воспользоваться леммой Ито:
иsSt = g~uVi = Ф(dн)и\/i.
(7.21б)
Наконец, мы должны решить эту систему нелинейных уравнений
относительно
Vi
и и.
Уравнение {7.21б) справедливо выписывать только для текущего
момента, поскольку на практике отношение
Vi/ St
изменяется слишком
стремительно. Более того, модель систематически дает неверные оцен
ки вероятности дефолта. Например, если отношение
Vi/ St
быстро убы
вает, тогда модель будет систематически переоценивать волатильность
актива, а значит вероятность дефолта будет завышена. Обратно, если
отношение
Vi/ St
быстро возрастает, тогда модель будет систематически
недооценивать волатильность актива, а значит, вероятность дефолта
будет недооценена.
4)
Кредитные спреды
Кредитные спреды измеряют разность между доходностью нулевой
безрисковой безкупонной облигации (с непрерывно начисляемой про
центной ставкой) и рисковой безкупонной облигации.
Если параметры и и
Vi
вычислены, спред может быть определен
явным образом. Если для описания ценообразования рискованных об
лигаций мы используем формулу
(7.16)
Bt = Bexp(-r(T- t))Ф{d2t) + ViФ(-dн),
а также учитывая, что доходность рискованных облигаций определяет
ся следующим соотношением:
1
rв = (Т- t) ln(B/Bt),
после некоторых преобразований мы получим:
Vi
rв - r = - (Т 1_ t) ln [ Ф{d2t) +В exp(-r(Tt)) Ф{-dн) ] .
Кредитный спред, полученный в предположениях модели Мертона,
обладает следующими свойствами:
•
он растет с увеличением величины
Vi/ В exp(-r(T - t)),
которая
является мерой задолженности компании и отражает финансовый риск;
•
он растет при увеличении и, которая отражает бизнес-риск;
7.4.
•
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
751
он не имеет определенной тенденции в своем поведении при уве
личении
(T-t).
Если мы рассматриваем компанию, имеющую малень
кую вероятность дефолта, то график кривой спреда имеет положитель
ную крутизну. Если мы имеем дело с очень рискованной компанией с
большой вероятностью дефолта, кривая спреда имеет отрицательную
крутизну: если компания не подверглась дефолту в течение первого го
да, вероятность дефолта в последующие годы, как правило, снижается
(а кредитный рейтинг увеличивается).
7.4.8.
Прогнозирование вероятности дефолта без учета
данных из бухгалтерских отчетов: вероятность
нулевой: цены (ВНЦ)
Модель Мертона, а также некоторые другие структурные и статисти
ческие подходы к прогнозированию предполагают, что данные из бух
галтерских отчетов отражают реальную финансовую ситуацию, скла
дывающуюся в компании. Что касается модели Мертона, то в ней ис
пользуются бухгалтерские данные, отражающие величину суммарных
долговых обязательств компании. Обычной практикой является вычис
ление суммарных долговых финансовых обязательств как суммы всех
краткосрочных займов и половины долгосрочных. Эта практика впер
вые была предложена корпорацией
KMV
рейтинговому агентству
для североамериканских компаний,
Moody's)
(которая сейчас принадлежит
и использование такой практики гарантирует, что величина долговых
обязательств компании не завышена (см.
(2006)]).
Хотя в работе
[Vassalou, Xing (2004)], [Нао
[Vassalou, Xing (2004)] указывается, что исполь
зование различных процентных ставок для долгосрочных финансовых
долговых обязательств не обнаруживает значительного изменения ка
чественных результатов, такой подход может быть неустойчивым к ме
рам по «декорированию баланса», проводимым для улучшения финан
совых показателей компании, или, в наихудшем случае, к финансовым
мошенничествам.
Анализ дефолта пищевого гиганта компании «Пармалат» в
2003 г.
ясно показал, как информация относительно долговых финансовых
обязательств, представленная в подтвержденном (аудитором) балансо
вом отчете, может отражать только часть реальных долгов.
Коротко об этой истории. В феврале
2003 г.
финансовый директор
Фаусто Тонна объявил о новом выпуске облигаций на сумму
500
млн
евро. Это стало неожиданностью как для инвесторов, так и для ге
нерального директора Калисто Танци. Танци настоял на увольнении
Тонна и назначил финансовым директором Альберто Феррариса. Со
гласно интервью, которое Феррарис в
2004 г.
дал журналу «Тайм», он
ГЛ.
752
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
с удивлением обнаружил, что, будучи финансовым директором, тем не
менее, не имеет доступа к некоторым корпоративным бухгалтерским
книгам, которые находятся в ведении главного бухгалтера компании
Лучиано Дель Солдато: «Феррарис обратился к двум доверенным ли
цам из своего штата с просьбой провести тайное расследование. По
сле прояснения ситуации вокруг операций, осуществленных компанией
«Пармалат» по всему миру, они поделились шокирующими новостями:
суммарные долговые финансовые обязательства компании составили
14
млрд евро, т. е. величину более, чем в два раза, превышающую сум
му долговых обязательств, указанных в балансовом отчете». О кри
зисе в компании стало общеизвестно в ноябре
2003 г.,
когда возникли
вопросы относительно сделок с взаимным фондом «Эпикурум», ком
панией, расположенной на Каймановых островах и связанной с ком
панией «Пармалат» 28 . Впоследствии это сотрудничество сыграло ро
ковую роль для компании «Пармалат». Феррарис подал в отставку и
на посту финансового директора его заменил Дель Солдато. В декабре
Дель Солдато также подал в отставку, после того как вывел наличные
средства из фонда «Эпикурум», необходимые для выплат по долговым
обязательствам. После того как в балансе возникла брешь размером в
7
млрд евро, Танци сложил с себя полномочия члена совета директо
ров и генерального директора компании. Позднее «Бэнк оф Америка»,
через который компания «Пармалат» осуществляла финансовые опера
ции, выпустил документ, показывающий, что свидетельство о наличии
млрд евро на счету компании «Бонлат» является фальсификаци
3,95
ей. Через несколько часов после того, как компания официально была
объявлена неплатежеспособной и были предъявлены обвинения в фи
нансовых мошенничествах и отмывании денег, Калисто Танци был аре
стован.
Среди сомнительной практики ведения бухгалтерского учета, ис
пользованной в компании «Пармалат», есть и такая ситуация: продажа
собственных облигаций, привязанных к кредитному риску этой ком
пании, когда фактически делалась ставка на собственную кредитоспо
собность и «ИЗ воздуха раздувался баланс». Для более подробной ин
формации см. статьи, опубликованные в нескольких номерах за
журнала «Тайм», а также работу
2004 г.
[Castri, Benedetto {2006)].
Приведенное описание скандала вокруг компании «Пармалат» яс
но показывает, что использование данных из бухгалтерских отчетов для
вычисления вероятности дефолта компании может вести по неправиль
ному пути, в результате чего будет получена очень неточная оценка ве28 В
1999 г. компания «Пармалат• учредила на Каймановых островах дочернюю
компанию «Бонлат•.
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
753
роятности дефолта. Для того чтобы избежать таких проблем, рекомен
дУется использовать новый подход, предложенный в работах
et al.
(2008а)],
[Fantazzini, Figini
[Fantazzini
(2009а)], в котором нулевая цена ис
пользуется как дефолтная граница для отделения функционирующих
компаний от компаний, находящихся в состоянии дефолта, а вероят
ность дефолта оценивается без использования данных из публичных
бухгалтерских отчетов. Авторы оправдывают адекватность предлага
емого подхода тем, что, как показано во многих работах, котировки
акций в основном обусловлены конфиденциальными сведениями, а сле
довательно, должны быть ближе к оценке реальной ситуации, чем све
дения, полученные из официальных бухгалтерских отчетов.
О важности конфиденциальных сведений в определении справед
ливой цены было впервые упомянуто в работе
[French, Roll (1986)],
посвященной теоретическому исследованию волатильности доходности
акций в торговые дни и неторговые дни, а также за первые часы после
открытия рабочей сессии биржи и за несколько часов до ее закрытия.
В работе показано, что во многих случаях большая волатильность до
ходностей активов была вызвана действиями информированных трей
деров, чьи конфиденциальные сведения начинали работать в момент
открытия рабочей сессии на бирже. Все большая доступность высо
кочастотных данных с недавнего времени позволила проводить более
точные тесты на качество микроструктурных моделей. Вот лишь неко
торые работы
([Hasbrouck (1988)], [Madhavan, Smith (1991)], [Hasbrouk,
Sofianos (1993)], [Madhavan, Sofianos (1997)]), в которых показана важ
ность асимметрии конфиденциальной информации относительно дина
мики цен акций и фьючерсов (в работах
(2007)]
[Biais et al. (2005)], [Hasbrouck
представлены обзоры недавних исследований микроструктуры
рынка).
Рассмотрим два следУющих тождества, основанных на реальных
бухгалтерских данных в момент времени Т:
{
Ет =Ат-Вт
Е~
= Ат = (Ат -
Вт)
+ Вт = Ет + Вт.
'
Финансовый смысл величин Ет и Ет зависит от ситуаций, с кото-
рыми сталкивается фирма (табл.
В табл.
7.9
показано,
что
7.9)
величина Ет
о т р и ц ат ел ь н а,
когда компания находится в состоянии дефолта, поскольку в этом слу
чае она представляет собой убытки держателей долговых обязательств
в условиях дефолта компании, и Ет
п о л о ж и т е л ь н а, когда ком
пания является функционирующей, представляя собой величину соб
ственного капитала компании, принадлежащего акционерам. Отрица-
Гл.
754
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
тельность значения Ет является прямым следствием ограниченной от
ветственности,
свойственной
всем
современным
западным
законо
дательствам. Кроме того, убытки могут быть теоретически бесконечны
ми так же, как и доходы: убытки авиакомпаний вследствие воздушной
атаки
11
сентября
2001 г.
или убытки вследствие эпидемии коровьего
бешенства среди животных или птичьего гриппа. Следовательно, для
описания доходности компании мы можем использовать плотности ве
роятности, принимающие положительные значения для отрицательных
значений аргумента.
Таблица
7.9.
Et
Финансовый смысл и знаки Ет, Е~
= Ат-Вt
Еfг
= At
Фун:кционирующая компания
Собственный капитал компании
Стоимость активов
(+)
(+)
Компания в состоянии дефолта
Убытки держателей долговых обя-
Активы,
зательств при дефолте
рам(+)
(- )
принадлежащие
кредито-
Основное следствие предыдущего рассуждения состоит в том, что
мы можем оценить склонность к дефолту, просто используя величину
Ет вместо величины
d2,
как в модели Мертона, а вероятность дефолта
оценивать как Р[Ет ~ О], поскольку компания подвергается дефол
ту в случае, если
Ет
S -
=S
Et
х Рт, где Рт
неположительно. Более того, при условии, что
-
котировка цены акции в момент времени Т, а
число акций, вероятность дефолта компании может быть вычис
лена как Р[Рт ~О], те. как вероятность нулевой цены (ВНЦ). Несмот
ря на то что котировка цены Рт
-
это усеченная величина, которая
не может принимать отрицательных значений, величина Ет не имеет
нижней границы, поскольку она имеет различное финансовое значение
для функционирующих компаний и компаний, находящихся в состоя
нии дефолта: в первом случае на финансовом рынке Ет вычисляется
(в электронном виде) ежедневно, тогда как в последнем случае убытки
в условиях дефолта вычисляются согласно предписанной в суде про
цедуре.
Цены акций, как правило, представляют собой нестационарные вре
менные ряды первого порядка интегрируемости
(1(1)),
и обычной прак
тикой является моделирование их динамики при помощи лог-доходнос
тей таким образом, чтобы цены были положительными. Однако нам
необходимо найти Р[Рт ~ О], поскольку, как было показано ранее, ну
левая цена может быть использована как дефолтный барьер. Простым
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
755
способом для вычисления упомянутой вероятности является использо
вание условной модели для разностей в уровнях цен,
Xt = Pt - Pt-1,
вместо разностей в уровнях логарифмов цен.
Аналитическое выражение для Р[Рт ~ О] можно выписать для
нескольких частных и не встречающихся на практике случаев, напри
мер для случая нормально распределенных цен с неменяющимися
времени
дисперсиями.
Когда
выписать
аналитическое
во
выражение
невозможно, необходимо пользоваться методами стохастического мо
делирования. Если в текущий момент времени
роятность дефолта в момент времени
(t
+ Т),
t
мы хотим оценить ве
то для этого мы можем
воспользоваться следующим достаточно общим алгоритмом.
Алгоритм оценки ВНЦ
Шаг
нях цен
условии,
1. Рассмотрим общую условную модель для разностей в уров
Xt = Pt - Pt-1, без логарифмического преобразования, при
что мы располагаем всей информацией Ft об анализируемом
процессе до момента времени
t:
Xt = E[XtlFt] + et,
et = Ht1121Jt, 1Jt rv н.о.р.с.в.(О, 1),
где
1Jt
rv
н.о.р.с.в.(0,
1)
означает, что
(1Jt) -
(7.22)
последовательность незави
симых одинаково распределенных случайных величин с нулевым сред
ним и единичной дисперсией, а
Ht
= D(etlFt) -
Шаг
2. Смоделируем большое число N
времени (t + Т), используя оцененную на
рядов (7.22).
дисперсия
et.
траекторий цен до момента
шаге
1 модель временных
Шаг З. Оценка вероятности дефолта равна отношению
n-
количество смоделированных траекторий из
N,
n/N,
где
которые касаются
или пересекают барьер нулевой цены.
Этот метод позволяет получить ряд важных преимуществ:
•
нам необходимы только курсовые стоимости акций;
•нам не нужны ни значение волатильности О"А компании, ни вели
чина номинала задолженности, как в моделях типа мертоновской мо
дели;
•
мы можем использовать более реалистичные, чем логнормальное,
распределения;
•
мы можем оценить вероятность дефолта для любого временного
горизонта
•
(t + Т);
мы можем рассчитывать ежедневные или даже внутридневные
вероятности дефолта. Следовательно, ВНЦ может быть использована
как инструмент управления рисками;
Гл.
756
•
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
ВНЦ может быть использована в качестве системы раннего предУ
преждения о финансовых дефолтах, поскольку она может быть оценена
для любых финансовых временных рядов.
7.4.9.
Бутстреп-полосы доверия
Впервые бутстреп-методология (ее описание можно найти в работе
[Efron, Tibshirani, 1993])
была использована для изучения воспроизво
димости некоторых признаков филогенетических деревьев (см. работу
[Felsenstein {1985)].
Позднее в работе
[Efron, Tibshirani {1998)]
эта ме
тодология была рассмотрена с более общих позиций и была названа
«проблемой областей». В этой работе эта мера доверия представлена в
связи с так называемыми р-значениями
{p-value)
эмпирической функ
ции распределения и байесовскими апостериорными вероятностями.
С появлением бутстреп-техники значительно расширились возмож
ности статистики в ситуациях, когда классические статистические про
цедУрЫ неприменимы. Бутстреп-оценки стандартных ошибок парамет
ров моделей оказываются весьма полезными в ситуации, когда вычисле
ние стандартных ошибок (асимптотических или неасимптотических) в
явном виде невозможно
{1993)]).
(см.,
например, работу
[Efron, Tibshirani
Кроме того, стандартные ошибки, рассчитанные с помощью
бутстреп-техники, могут лучше отражать свойства оценок в условиях
малых выборок.
На сегодняшний день весьма мало сделано для количественной
оценки неопределенности оценок вероятностей дефолта, поскольку ос
новной интерес исследований до сих пор был смещен к области по
строения точечн-ьtх оценок. Подобная ситуация складывается в дру
гих областях исследования, например в биостатистических исследова
ниях, когда в задаче вычисления вероятности корректной идентифи
кации отдельных генов
и
их
ческая бутсреп-техника (см.
[Karlis, Kostaki {2002)]
распределения используется
параметри
[Van der Laan, Bryan {2001)]).
В работе
для оценки коэффициентов смертности различ
ных групп населения используется техника, подобная той, что в ра
боте
[Van der Laan, Bryan {2001)]. В работе [Zwane, Van der Heijden
{2003)] представлен алгоритм для параметрической бутстреп-техники,
который может использоваться в логлинейных моделях с непрерывны
ми независимыми переменными. В работе
[Zwane et al. (2004)]
парамет
рический бутстреп-подход используется при построении доверительных
интервалов для оценок систем множественных записей, когда регистра
ционные записи делаются для разных, но пересекающихся популяций.
Некоторые авторы
использовали
непараметрическую бутстреп
технику при логлинейном моделировании (см., например,
[Huggins
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
757
(1989)], [Tilling, Sterne (1999)], [Tilling et al. (2001)]). Но, как отмечается
в работе [Norris, Pollock (1996)], при использовании непараметрическо
го бутстреп-метода для оценки дисперсии значение оценки часто мень
ше, чем реальное значение дисперсии. Это соответствует результатам
моделирования, представленным в работе
[Tilling, Sterne (1999)],
из ко
торых мы можем сделать вывод, что оценка, полученная непараметри
ческим бутстреп-методом, имеет устойчиво меньшее значение, чем ре
альное. Аналогичные выводы сделаны в работе
[Zwane, Van der Heijden
(2003)]. Кроме того, параметрический бутстреп-метод дает асимптоти
чески правильные результаты при достаточно слабых условиях по срав
нению с условиями, требуемыми в непараметрическом бутстреп-методе
(см.
[Gine, Zinn (1990)].
В общем-то, для того чтобы оценка, даваемая параметрическим
бутстреп-методом, асимптотически совпадала с действительным зна
чением, требуется корректность выбранной параметрической модели.
Однако в работе
[Van der Laan, Bryan (2001)]
показано, что в случае
усеченного многомерного нормального распределения, в параметриче
ской модели которой нет никаких ограничений на параметры, парамет
рический бутстреп-метод будет состоятельно оценивать вырожденное
предельное распределение, даже если модель некорректна. Принимая
во внимание вышеизложенные результаты, мы обратимся к параметри
ческим бутстреп-методам.
Процедура построения доверительных границ для оценки
вероятности дефолта
Шаг
1.
ных ошибок
Смоделируем вектор размера (Т х
rJt,
1)
стандартизирован
имеющих заданную маргинальную плотность (напри
мер, плотность распределения Стьюдента).
Шаг
2. Заменяя все параметры значениями их оценок и подставляя
значения стандартизированных ошибок 'Г/t, полученных на предыдущем
шаге, создадим искусственно сгенерированную историю для случайной
величины
Xt.
Шаг З. Используя данные из искусственно сгенерированной исто
рии, оценим параметры модели
Шаг
4.
AR(l)-TGARCH(l,l).
Используя предыдущие оценки, полученные на основе ис
кусственно сгенерированной истории, вычислим бутстреп-оценку для
ВНЦ;
Шаг
ВНЦ,
5. Для того чтобы получить численную оценку распределения
повторим шаги 1-4 большое количество раз (пв).
Это распределение формирует основу для вычисления бутстреп
доверительных интервалов для вероятностей дефолта.
В работе
[Fantazzini et al.
(2008а)] проанализирован американский
и европейский рынки, а в работе
[Fantazzini
(2009а)]
-
российский ры-
Гл.
758
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
нок. В целях экономии места мы здесь рассмотрим только четыре из
вестные компании, оказавшиеся в состоянии дефолта, чьи финансовые
отчеты позднее были юридически признаны неправдоподобными, а сле
довательно, для них нельзя использовать стандартные подходы (см.
[Fantazzini et al. {2008а)]). Это следующие четыре компании:
• «Чирио». 24.09.1999-24.07.2003. Второй по величине крупный де
фолт в пищевом секторе Европы (первый по величине - дефолт ком
пании «Пармалат», см. выше п. 7.4.8);
• «Энрон». 20.01.1998-10.01.2002. Второй по величине крупный де
фолт в американской истории;
•
«Пармалат».
22.02.2000-22.12.2003.
Крупнейший дефолт в евро
пейской истории;
•
«Ворлдком».
16.07.1998-12.07.2002.
Крупнейший дефолт в амери
канской истории.
В статье
[Fantazzini et al.
{2008а)] сначала представлены результаты
тестирования на наличие единичных корней для рассматриваемых фи
нансовых временных рядов при помощи теста Дикки - Фуллера с «дет
рендированием» обобщенным методом наименьших квадратов, полу
ченные с помощью метода, предложенного в работе
а также с помощью теста, предложенного в
{1992)].
[Elliott et al. {1996)],
работе [Кwiatkowski et al.
Нулевая гипотеза в первом методе (ДФ-ОМНК) состоит в нали
чии единичного корня (т.е. в нестационарности анализируемого времен
ного ряда), в то время как в методе Квятковского и др. {КРSS-методе)
нулевая гипотеза состоит в ковариационной стационарности ряда (про
тив альтернативы о его интегрируемости первого порядка). Тщатель
ный анализ уровней и разностей первого порядка ценовых временных
рядов за рассматриваемый период наблюдений показывает, что основ
ной их особенностью является их нестационарность {табл.
Таблица
7.10. Тест
7.10).
на наличие единичных корней для данных
по четырем компаниям
Компания
ДФ-ОМНК
Уровни
KPSS
Разности
пер-
Уровни
вого порядка
«Чирио»
«Пармалат»
«Энрон»
«Ворлдком»
(*)
-2,083
-1,372
-2,620
-1,359
-20,583
-12,395
-38, 785
-34,876
(**)
(**)
(**)
(**)
Разности
пер-
вого порядка
0,256
0,768
0,353
0,833
(**)
(**)
(**)
(**)
статистическая значимость на 5%-ном уровне.
(**)статистическая значимость на 1%-ном уровне.
0,065
0,045
0,022
0,057
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
Далее в этой работе рассматривается модель
для разностей уровней цен
Xt
759
AR{l)-TGARCH{l, 1)
= Pt-Pt-1, стандартизированные ошибки
которой имеют распределение Стьюдента (для более подробной инфор
мации относительно этой модели см. работу
[Biais, Glosten et al. 1993)):
Xt = µ + <p1Xt-1 + et,
et = 'Г/tvnt, 'Г/t rv н.о.р.с.в.{О, 1),
ht = w + ае~_ 1 + "'fe~_ 1 Dt-1 + fЗht-1,
где Dt-1 =
если Et-1
1,
<
О. Авторы работы
[Fantazzini et al.
{2008а)]
объясняют выбор такой спецификации тем, что она позволяла получить
хорошие результаты при моделировании финансовых данных (см.
[Tsay (2002)],
а также
[Hansen, Lunde {2005)]
§3
и ссылки в этих работах).
Что касается выбора числа смоделированных ценовых траекторий
для оценки ВНЦ, в работе
N
[Fantazzini et al.
в
N
{2008а)] оно взято равным
= 5000.
Наконец, в работе
ты тестирования
[Fantazzini et al. {2008а)] представлены результа
качества AR{l)-TGARCH{l, 1) моделей, использован
ных для описания условных маргинальных распределений. Тестирова
ние качества осуществлялось при помощи теста Льюнга- Бокса для
стандартизированных остатков в уровнях
i/t и их квадратов iJl, нулевая
гипотеза которого состоит в отсутствии автокорреляции. Использова
лись также тесты спецификации, рассмотренные в работе
[Granger et al.
{2006)]. Для проверки корректности спецификации плотности использо
вался тест Колмогорова- Смирнова, а для того, чтобы протестировать
совместно адекватность динамики и спецификации плотности марги
нального распределения модели, использовался
«тест на охват», ну
левая гипотеза которого состоит в том, что модель для плотности хоро
шо специфицирована. В последнем тесте носитель функции плотности
делится на пять областей. После этого техника интервального прогно
зирования применяется к каждой из этих областей в отдельности, а
затем ко всем областям совместно (для более подробной информации
см.
[Granger et al. {2006))).
В целях экономии места в табл.
7.11
пред
ставлены только р-значения каждого из рассматриваемых тестов.
Таблица
7.11.
Компания
р-значения спецификационных тестов
Тест Льюнга-Бокса
f/t
«Чирио»
«Энрон»
«Пармалат»
«Ворлдком»
0,112
0,953
0,906
0,167
Тест Колмогорова-
Тест на
~2
"lt
Смирнова
охват
0,182
0,096
0,971
0,758
0,018
0,380
0,091
0,435
0,017
0,837
0,530
0,058
(25)
Гл.
760
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Во всех упомянутых в табл.
7.11
тестах для каждой из рассмотрен
ных маргинальных моделей принимается нулевая гипотеза (по край
ней мере, на 1%-ном уровне значимости), что указывает на коррект
ную спецификацию моделей. В целом, представленные результаты ука
зывают на то, что выбранная
AR{l)-TGARCH{l, 1)-модель,
в которой
стандартизированные ошибки имеют распределение Стьюдента, адек
ватна рассматриваемым финансовым временным рядам. Последнее об
стоятельство очень важно, поскольку оно позволяет нам использовать
параметрические бутстреп-процедуры для построения доверительных
интервалов оценок вероятностей дефолта.
На рис.
7.18
и
7.19
показаны котировки цен акций рассматривае
мых четырех компаний за
1000 дней до дефолта,
а также вычисленные
оценки вероятностей дефолта и 90%-ные доверительные полосы (по оси
х отложено количество дней).
а)
Оценми вд компании "Чирио"
Цены на &ICllllИ компании "Чирно·
38 1000 дней до дефоnта
'
:
381000диеilдодефоmа
!
8!
1
1
8.d
ае ~г
:::il
о
i;••
......
.."".,/.:,"''":'"
:i::
"'а
d
t
"d
JI
N
d
;;
~
00
100
6)
-
- --
300 400
500
700
24/08/1198 - 24/07/2003
1-
Цены на &IQlllИ комnании ·энрои·
38 1000 ДИ8Й до дефоmа
!
Оценми вд комnании "Энрои"
1
8
./i!
li!
is
ае
:::i
•:
8
ijiX
t
JI
2
о
о
о
100
JI
2
- - - -300
500
700
о
7.18.
- - - --
.. !
о
1-
20/01/1118 - 10/01/2002
Рис.
1-
38 1000 дней до дефоmа
!
1
8
--
о
100
300
500
700
1-
20/01/1118 - 10/01/2002
Цены на акции и оценки ВД с 90%-ми бутстреп-доверительными
полосами (верхняя граница
-
пунктирная линия, нижняя
штриховая) для компании «Чирио• (а) и «Энрон•
(6)
-
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
761
а)
Цены на акции компании "Пармалат"
38 1000 днеii до дефоnта
Оценки ВД компании "Пармалат"
за 1000 днеii до дефоnта
!
'
""
8
8
8.:
"~~
:t 8
~
.,. li/
ia
""
%
t
SI
:!:
~
:!
"
о,
100
б)
200
300 400 500 800 100
22/02/2000 - 22/12/2003
-
о
1ОО
1000
Цены на акции компании "ВорJWСОм"
38 1000 днеii до дефоnта
!
!
8
8
8
8
. li/
.,_ 2
ia
~8
1а
:! t
CD
8
t
51
51
2
2
- -
о
о
о
Рис.
Оценки ВД компании "ВорJWСОм"
эа 1000днеiiдодефоnта
100
7.19.
200
300
500 800 100
111/07/1998 - 12/07/2002
о
1ОО
1000
о
о
100
200
300 400 500 800 100
16/07/1998 - 12/07/2002
-
1ОО
1000
Цены на акции и оценки ВД с 90%-ми бутстреп-доверительными
полосами (верхняя граница
-
пунктирная линия, нижняя
штриховая) для компании «Пармалат» (а) и «Ворлдком»
(6)
Обратим особое внимание на тот факт, что доверительные интерва
лы в определенной степени асимметричны. Кроме того, мы наблюдаем
сильное различие меж.цу американскими и итальянскими компаниями.
Вычисленное значение оценки вероятности дефолта за один год
до
дефолта для компании «Энрон~ и компании «Ворлдком~ составляет
более чем
50%
от значения оценки вероятности дефолта за два месяца
до дефолта. Что касается итальянских компаний, интересно отметить,
что уже за
2/3 года до
50%. Эти
та превышает
дефолта величина оценки вероятности дефол
результаты соответствуют развитию ситуации,
связанному с предварительным расследованием. Оно показало, что фи
нансовые трудности в двух компаниях были известны менеджменту уже
в 1990-хгг. Кроме того, хотя достаточно широкие полосы доверия ука
зывают нам на то, что мы должны рассматривать корректность оцен
ки вероятностей дефолта только с некоторой степенью уверенности (в
частности, для компании «Пармалат~), мы можем интерпретировать
это как знак, указывающий на рыночную неопределенность относитель
но бу.цущего компании.
В целом предыдущие результаты указывают на разную степень эф
фективности итальянского и американского рынков в случае финансо-
ГЛ.
762
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
вых махинаций. Некоторые эпизоды вокруг дефолтов компаний «Эн
рон» и «Пармалат» могут помочь прояснить причины такого различия.
Жена генерального директора компании «Энрон» Лиза Лей бы
ла обвинена в продаже
мой в
1,2
млн долл.
28
500 ООО
ноября
акций компании «Энрон» общей сум
2001 г.
Отчеты показывают, что миссис
Лей размещала предложение на продажу в промежутке времени меж
ду
10:00
и
10:20.
Новости относительно проблем в компании «Энрон»,
включая информацию о миллионных (в долларах) убытках, которые
были скрыты, стали общеизвестны около
10:30,
и вскоре после этого
сообщения котировки цен акций упали до одного доллара. Кроме того,
бывшей работнице компании «Энрон» Пауле Райекер было предъяв
лено уголовное обвинение в использовании инсайдерской информации.
Райекер получила
18 380
акций компании «Энрон» по цене
за каждую акцию, а продала эти акции по цене
июле
49,77
15,51
долл.
долл. за акцию в
2001 г., за неделю до того, как стала общеизвестна информация об
102 млн долл., которая была ей известна на момент продажи
убытках в
ее акций.
Что касается компании «Пармалат», то финансовая полиция обна
ружила, что сумма приблизительно в
1-2
млрд евро была выведена с
банковских счетов компании «Пармалат» на счета туристических об
ществ, а также других компаний, принадлежащих семье Танци (до тех
пор не имевших отношений с пищевым гигантом), между
1993
и
2003 г.
Следовательно, дефолты этих двух компаний разного типа: хотя
информация относительно серьезных проблем в компании «Энрон» бы
ла известна работникам этой компании еще за год до того, как она стала
общеизвестной, продажи в последние минуты, по-видимому, свидетель
ствуют о том, что продавцы акций «покидали тонущий корабль». Слу
чай с компанией «Пармалат» несколько отличен от предыдущего слу
чая: по-видимому, менеджмент организовал незаконную систему выво
да денег из компании.
7.4.10.
Модели для нормы восстановления (ИВ)
и величин номинальных потерь
при дефолте (ВНП(Д))
Как мы упоминали в п.
7.4.3,
существует две разновидности подхода,
основанного на внутренних рейтингах (ПВР): базовwй подход и усовер
шенствован:н:ый подход. Они имеют принципиальные различия в том,
как рассчитывать параметры ВД, ДНС(Д)(= 1-НВ), ВНП(Д), ЭСДО.
Например, при использовании базового подхода только ВД может быть
рассчитана на основе внутренних моделей, используемых в банке, тогда
как для усовершенствованного подхода на основе внутренних моделей
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
763
рассчитываются все четыре параметра и, разумеется, подлежат инспек
ции надзорных органов в банковской сфере.
Гибкость существующих моделей для вычисления НВ портфеля
кредитных активов, вероятно, будет мотивацией перехода банков от ис
пользования базового подхода к использованию усовершенствованного
подхода. То, как воспользуется банк имеющейся гибкостью, зависит,
конечно, от того, насколько хорошо банк представляет общий и диф
ференцированный характер НВ имеющихся кредитных активов.
В связи с этим перечислим наиболее характерные особенности
и основные факторы, определяющие НВ.
•
Норма восстановления как процент от величины номинальных
потерь при дефолте либо высока
(70-80%),
либо низка
(20-30%).
Ха
рактерной особенностью распределения, описывающего норму восста
новления, является бимодальность: следовательно, не совсем корректно
рассматривать среднюю норму восстановления.
•
Одним из основных определяющих факторов является наличие
и.л.и отсутствие секъюритизации дефолтного кредитного обязатель
ства, а также место этого дефолтного обязательства в структуре
капитала заемщика (степень субординированности требования). Таким
образом, банковские кредиты, будучи на вершине структуры капитала,
как правило, имеют большую норму восстановления, чем, например,
долговые расписки.
•
Наличие какого-либо залога и степень его ликвидности являются
еще одним определяющим фактором.
•
Тип процедуръt банкротства, определяемый существующим за
конодательством, влияет на срок восстановления всей величины номи
нальных потерь или ее части; в частности, в развитых странах суще
ствует множество правил, защищающих интересы служащих, а также
семей с низкими совокупными доходами.
•
Бизнес-циклъt и политика определения процентнъ~х ставок так
же являются определяющими факторами; нормы восстановления си
стематически меньше в периоды рецессии, и разница может достигать
значительных величин (до
35%).
Другими словами, убытки больше в
периоды рецессии и меньше в противоположной ситуации.
•
Характер бизнеса заемщика: фондоемкие отрасли промышленно
сти, в особенности муниципальные, коммунальные предприятия, имеют
более высокие нормы восстановления, чем компании из сектора сферы
услуг (с некоторыми исключениями, такими как, например, телекому
никационные и наукоемкие компании).
•
•
Географическое положение также имеет значение.
Величина номинальных потерь, как представляется, не имеет
сильного влияния на реальные потери.
Гл.
764
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Для более подробной информации см. работы
[Altman et al. {2001)],
[Altman et al. {2005)], [Varma, Cantor {2005)], [Acharya et al. {2007)] и
ссылки в этих работах.
Решения, предложенные для оценки НВ, могут быть разделены на
четыре категории.
•
Суб'Dективна.я оценка основана на историческом опыте и сегмен
тации кредитного портфеля.
•
Стандартная .мера рассчитывается как фиксированная процент
ная ставка на основе имеющихся собственных данных.
•
Подразу.мевае.ма.я р·ыночная норма восстановления рассчитывает
ся на основе цен рискованных (но не дефолтных) облигаций, с исполь
зованием теоретических моделей ценообразования активов. В эту кате
горию мы также можем включить оценки НВ, рассчитанные на основе
рыночных цен облигаций, оказавшихся в дефолте, или цен ликвидных
займов вскоре после фактического дефолта. Эта процедура является
классической для английских и американских банков, в то же время
она менее распространена в континентальной Европе.
•
Финансовъtй подход к оценке НВ. В этом подходе рассматривает
ся множество оценок движения наличных средств и затрат, полученных
на основе опыта работы с просроченной задолженностью и {или) с иной
собранной информацией и надлежащим образом дисконтированных, а
также оценки номинальных потерь. Этот подход достаточно распро
странен в континентальной Европе.
Если мы рассмотрим последнюю методологию, то в соответствии с
ней НВ вычисляется на основе ожидаемого восстановления (ОВ), т. е.
НВ, которую банк ожидает получить от заемщика рассматриваемого
типа, учитывая его залог, величину ад.министративнъ~х расходов (АР),
связанных с процедурой ликвидации, а также оценку необходимого для
восстановления времени
(t)
и .маргинальную стоимость фондирования
(МСФ), в качестве которой может быть взята процентная ставка по
межбанковским операциям или своп-ставка. Сохраняя ранее введенные
обозначения, НВ вычисляется следующим образом:
ОВ-АР
НВ = {1 + МСФ)t
или
ОВ-АР
ДНС(Д) = l - {1 + МСФ)t·
Важно отметить, что процедура вычисления НВ сильно зависит от
определения неплатежеспособности, которого мы придерживаемся при
анализе: если определение очень строгое, оценка НВ будет, как прави
ло, достаточно низкой и, соответственно, дефолтные заемщики будут
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
765
в крайне жестких условиях. Если определение не является строгим, то
оценка НВ возрастет и заемщики, классифицированные как неплатеже
способные, будут в более хороших условиях, чем заемщики, классифи
цируемые как дефолтные в соответствии с более строгим определением.
Кроме того, существование различных законов о банкротстве неизбеж
но сказывается на оценках НВ (см., например, табл.
ническая Документация
7.4.11.
CreditMetrics
в работе
G.1 из главы Тех
[Gupton et al. (1997))).
Эмпирические свидетельства для значений норм
восстановления
Существует множество исследований, отраженных в финансовой лите
ратуре, касающихся изучения восстановления облигаций или займов.
В большинстве из опубликованных исследований изучается восстанов
ление облигаций, а не восстановление займов. Это объясняется тем, что
по облигациям имеется достаточное количество данных. Однако хоте
лось бы, чтобы займы были столь же хорошо исследованы, как и обли
гации. Банковские займы обычно имеют большой приоритет в струк
туре капитала и банкам следует более активно следить за меняющимся
финансовым здоровьем заемщиков.
ПриоР1пе1нwе oGec:ntt1eннwc
~
oOl'J81'e.11iCJ81
...... ..,,,.... . - ......" ....
обnа ~
....
~иориnm1wссубордин11роВ1нные -~
i [ ~1111ровu111wекроmпы
Влаоельцы
об.1иrаuнn
Банки
]
Пр11ппеrнроu11нwе акцJ111
Обwкноееннwс 11щин
Рис.
В работе
7.20.
Степень приоритета
[Hu, Perraudin (2002)]
показано, что НВ должника зави
сит от промышленного сектора, в котором занят должник. А в работе
[Altman, Kishore (1996))
показано, что должники из ряда отраслей, та
ких как, например, коммунальный сектор, имеют большую НВ, чем
другие.
Как показано в работе
[Altman, Kishore (1996)),
наиболее устой
чиво повторяющимся результатом является результат, состоящий том,
Гл.
766
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
что приоритет обязательств в структуре капитала должника и наличие
обеспечения (обеспеченные обязательства против необеспеченных)
-
это наиболее важные составляющие НВ долговых обязательств. В этой
связи структура капитала компании может быть разделена следующим
образом (рис.
7.20).
В США и многих других странах законы о банкротстве имеют важ
ную особенность, называемую «правилом абсолютного приоритета'$>
(ПАП). Коротко говоря, это правило гласит, что стоимость компании,
оказавшейся в состоянии банкротства, должна быть распределена меж
ду поставщиками капитала таким образом, чтобы сначала долг был по
гашен перед кредиторами, обязательства перед которыми имеют наи
больший приоритет, затем долг должен быть погашен перед кредитора
ми, обязательства перед которыми имеют меньший приоритет, а затем
оставшаяся
стоимость
компании распределяется
между
акционерами
компании.
Однако на практике ПАП систематически нарушается. В действи
тельности, некоторыми исследователями обнаружено, что в
65-80%
банкротствах акционеры получают какие-то средства до того, как долги
будут полностью погашены перед кредиторами (см., например, работу
[Eberhart, Weiss (1998)] и ссылки в этой работе). Основной причиной
этого является скорость погашения долгов (кредиторы согласны с на
рушениями ПАП ради того, что побыстрее получить причитающиеся
средства).
Если мы рассмотрим значения НВ, представленные в некоторых
недавних исследовательских работах, то мы можем рассчитать средние
значения НВ для каждого класса и получить более надежные значения
(табл.
7.12).
Таблица
7.12. Средние
значения НВ
Авторы
(%)
Банков-
Приори-
Приори-
Приори-
Субор-
ские
тетные
тетные
тетные
диниро-
креди-
обеспе-
необес-
субор-
ванные
ты
ченные
печен-
дини-
креди-
обяза-
ные
рован-
ты
тельст-
обяза-
ные
ва
тель-
креди-
ства
ты
57
66
52
46
49
44
37
35
34
26
32
65
57
53
52
57,57
48
48
50
35
45,71
40
34
387
39
35,67
30
31
33
31
31,00
(Carty, Lieberman (1996))
(Van de Castle, Keisman (2000))
(Hamilton, Cantor, Ou (2002))
(Emery, Cantor, Avner (2004))
(Fons (1994))
(Altman, Кishore (1996)]
[Hu, Perraudin (2002))
(Altman, Fanjul (2004))
71
84
67
67
Средние значения
72,25
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
767
Тем не менее эти значения должны рассматриваться с некоторой
степенью предосторожности, поскольку количество изучаемых данных
обычно не очень велико. При расчете значений НВ главным образом
рассматривается рынок облигаций и не рассматриваются банковские
кредиты. Следовательно, гораздо лучше, если банк сосредоточивает
свой бизнес в основном на локальном рынке, поскольку это позволя
ет полагаться как на данные, собранные самим этим банком, так и на
информацию, получаемую с подобных рынков.
7.4.12.
Распределение нормы восстановления
Распределение норм восстановления, как правило, имеет две верши
ны (моды). Последнее означает, что НВ либо очень маленькая, либо
очень большая. Кроме того, маленькое значение НВ является более рас
пространенным явлением. Как указывалось ранее, существует вполне
четкая взаимосвязь между уровнем приоритета долгового обязатель
ства и НВ. Последнее можно обнаружить, если, например, рассмотреть
данные из базы по дефолтным рискам рейтингового агентства
(Moody's Default Risk Service Database),
см. рис.
Moody's
7.21.
По мере того, как мы двигаемся вниз в капитальной структуре к
позициям с меньшим приоритетом, масса смещается влево, т. е. нормы
восстановления становятся меньше. Интересно отметить, что для функ
ции распределения приоритетных несекьюритизированных инструмен
тов сохраняется бимодальность, тогда как для субординированных и
приоритетных субординированных кредитов большинство вероятност
ной массы сосредоточено при малых значениях НВ (около 15%) 29 . Од
нако
приоритетные
плоское
секьритизированные
распределение,
указывающее
инструменты
на то,
что
ния относительно равномерно распределены от
что нормы восстановления могут превосходить
имеют
нормы
почти
восстановле
30% до 80%. Отметим,
100% ввиду различий в
период восстановления между купонными ставками и преобладающи
ми процентными
ставками, т. е.
в случаях,
когда купоны превышают
величину преобладающей процентной ставки.
Если бы мы ничего не знали относительно норм восстановления и
предполагали бы, что все возможные нормы восстановления равноверо
ятны, то мы моделировали бы их с помощью равномерного распределе
ния И(О;
(см.
100). Однако такой выбор редко описывает реальную ситуацию
рис. 7.21).
29 Субординированные
кредиты с низким уровнем приоритета включены в катего
рию субординированных кредитов, поскольку выборка по ним мала.
Гл.
768
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
2.4%
2.2%
~ Прнор1rтстныс о6сс11счсннwс
-tr
Пр11ор111СТ11wс нсобсс
псчснныс обlvrельстеа
-
С)'борд1111нро•1111wе
о6111rепьсnа
2.0%
Пpнop1m:n1we суборлн11нрова1111ые
-
ICpCДIПU
1.8"/о
крсдlПЫ
.а
u
'""
о
=
!;
i::
t::
1.2%
1.0%
О
10
20
30
SO
40
60
70
80
Норма восстановления,
Рис.
7.21.
90
100
110
120
IIO
%
Плотности функций распределения НВ для кредитов с разным
уровнем приоритета
(Moody's, 1970-2003).
Источник:
[Shimko (2004)]
Другой альтернативой является выбор бета-распределения, которое
позволяет моделировать вероятностную массу вокруг моды и толщину
хвостов. Плотность этого распределения равна30
где О ~ х ~
1,
а> О, Ь
> О,
В(а, Ь)
бета-функция, т. е.:
-
Jха- (1
1
В(а, Ь) =
1
-
х)Ь- 1 dх.
о
Если а
= Ь = 1, то бета-распределение сводится к равномерному
распределению на отрезке [О,
среднегоµ, и дисперсии
fт 2
1].
При заданных оценках выборочного
оценки параметров бета-распределения, по
лученные методом моментов, равны соответственно:
А
ьµ
а= р,-1·
Анализируя данные рейтингового агенства
Moody's за 1970-2003 гг.
с целью оценить бета-распределения для каждой категории приоритета,
получаем следующие результаты (табл. 7.13) 31 .
30 Информацию
31 Следуя
о бета-распределении см. также в Приложении 2 к гл. 3 книги.
принятым в данной области правилам, все линейные характеристики
бета-распределений случайной величины даются в процентах (т.е. шкала ее возмож
ных значений умножается на
100%).
7.4.
Таблица
7.13.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
769
Оценки параметров бета-распределения,
описывающего НВ для каждой категории приоритета
Параметры
Среднее
Уровень приоритета
Стандартное
Приоритетные обеспеченные
бета-
N
отклонение
распределения
а
ь
54,26
25,82
433
1,48
1,25
38,71
27,80
971
0,80
1,27
28,51
23,41
260
0,78
1,94
34,65
14,39
22,23
8,99
347
12
1,24
2,05
2,34
12,19
обязательства
Приоритетные необеспеченные
обязательства
Приоритетные
субординированные кредиты
Субординированные кредиты
Неприоритетные
субординированные кредиты
Графики плотности бета-распределений для всех категорий прио
ритета изображены на рис.
7.22
(при этом с помощью соответствую
щего масштабного множителя шкала возможных значений [О;
1] бета
распределений случайной величины преобразована в шкалу [0%; 100%)).
Однако плотности, представленные на рис. 7.22, лишь частично на
поминают эмпирические плотности, представленные на рис. 7.21.
Нспрноритетныс субордн11нрова11ныс кредиты
/
j ~"
0,010
10
20
30
40
so
60
Норма восстановления,
Рис.
7.22.
7.4.13.
70
80
90
100
%
Функции бета-плотности для всех классов
(Moody's, 1970-2003)
Связь между ВД и НВ
Как отмечалось ранее, вероятность дефолта или доля дефолтов
(т. е.
доля дефолтных компаний в экономике) и среднее значение для норм
восстановления отрицательно коррелированны (см., например,
[Altman,
Resti et al. (2001)], [Altman, Brady et al. (2005)] и [Acharya, Bharath et
al. (2007)]), что отражено, в частности, на рис. 7.23.
Гл.
770
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
65
'$.
Di'
:s:
:с
С1)
:а
о
:с
~
()
о
111
«1
::Е
С1.
о
::с
60
у= -2.617х + 50.9
у= О.5609х 2- 8.7564х + 60.61
R2= 0.4498
R2= 0.6091
55
у =-11.181 Ln(x)+52.332
•1992
50
у=52.739.т""· 1»~
R2= 0.5815
R2= 0.6004
45
40
• 1991
35
30
25
20
о
2
4
6
Доля дефолтов,
Рис.
7.23.
Норма восстановления
-
10
8
12
%
доля дефолтов: взяты данные по облигациям
за период 1982-2000гг. Источник:
[Altman et al. (2001}]
Этот результат подтверждается результатами, полученными в рабо
те
[Hu, Perraudin (2002)],
в которой установлено, что корреляция меж
ду нормами восстановления и агрегированными долями дефолта для
США равна в среднем
-0, 2
и около
-0, 3,
если рассматривать только
достаточно большие или достаточно малые значения агрегированной
доли дефолта и соответствующие им средние значения норм восстанов
ления.
В работе
[Altman et al. (2001)]
сделана попытка рассчитать, на
сколько сильно увеличивается 99%-ная граница потерь, если учесть
отрицательную
корреляцию
между
нормами
восстановления
и доля
ми дефолта. На основе статической модели авторы утверждают, что
99%-ная граница потерь для репрезентативного портфеля может ме
няться от значения, равного приблизительно 3,8%-ной доли убытков,
до значения, равного 4,9%-ной доли убытков при переходе от модели,
в которой нормы восстановления постоянны, к модели, в которой учи
тывается отрицательная зависимость между нормами восстановления
и долями дефолта.
Представляется, что ИВ и ВД движимы одним и тем же общим
фактором, который достаточно устойчив во времени и связан с бизнес
циклами: в периоды рецессии или спада в промышленности вероятно
сти дефолтов велики, а нормы восстановления малы. Можно продемон
стрировать этот результат снова, воспользовавшись данными по дефол
там, собранными рейтинговым агентством
Moody's,
отдельно анализи
руя нормы восстановления в периоды спадов и в периоды подъемов аме
риканской экономики с
ставлены в табл.
7.14.
1970
г. Сводные выборочные статистики пред
7.4.
Таблица
7.14.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
771
Нормы восстановления для разных периодов
бизнес-цикла
(Moody's, 1970-2003)
НВ при вероятности дефолта
Период
Среднее
Стан-
бизнес-
дартное
цикла
откло-
25%
50%
75%
N
нение
Рецессии
Рост
По всей
32,07
41,39
39,91
26,86
26,98
27,17
10
19,5
18
25
36
34,5
48,5
62,5
61,37
322
1703
2025
выборке
В периоды рецессии нормы восстановления меньше, чем в периоды
роста. Кроме того, в периоды роста экономики нормы восстановления
распределены более равномерно. В работе
[Altman et al. (2005)]
приведе
на регрессия среднего норм восстановления на агрегированные вероят
ности дефолта и макроэкономические переменные, анализируя которую
можно увидеть, что нормы восстановления и агрегированные вероятно
сти дефолта тесно взаимосвязаны, а макроэкономические переменные
становятся незначимыми
как только
агрегированные вероятности де
фолта включаютя в регрессию в качестве объясняющих переменных.
Авторы предполагают, что это происходит в силу неэластичности спро
са на дефолтные ценные бумаги. Гипотеза авторов заключается в том,
что типичные инвесторы, вкладывающие средства в дефолтные ценные
бумаги, имеют ограниченные возможности, и, как результат, когда про
исходит много дефолтов, цена дефолтных ценных бумаг быстро падает.
В работе
ный в
[Acharya et al. (2007)] принимается аргумент, предложен
[Shleifer, Vishny (1992)], который используется в качестве отправ
ной: точки: предположим, некоторый: сектор промышленности находит
ся в бедственном положении, и некоторые компании, занятые в этом
секторе, оказались в состоянии дефолта. Если активы компаний, ока
завшихся в дефолте, состоят из промышленных активов, то для эффек
тивного управления компаниям лучше всего реализовать эти активы,
но в период управления покупателями этих активов проблемы могут
усугубиться, а следовательно, может возникнуть ситуация, когда эти
активы невозможно будет выкупить. А это может привести к низким
ценам этих активов, а следовательно, к низким значениям нормы вос
становления. По смыслу этот аргумент аналогичен аргументу, предло
женному в работе
[Altman et al. (2005)],
за исключением того, что в
первом аргументе цена перепродажи реальных активов снижается, то
гда как в случае аргумента из
[Altman et al. (2005)]
цена перепродажи
финансовых активов (дефолтные облигации) повышается.
Гл.
772
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Однако, как следует из работы
[Altman, Kishore {1996)],
корпора
тивные облигации компаний некоторых отраслей экономики (например,
коммунальные службы) надежнее. Их исследование охватывает доста
точно длинный период
результаты в табл.
Таблица
7.15.
{1971-1995),
7.15.
и мы воспроизведем некоторые их
Средняя норма восстановления для разных отраслей
экономики и секторов промышленности
Среди.
Отрасль экономики
Сектор промышленности
нв
Коммунальные службы
Сфера услуг
Пищевая
Среди.
нв
70%
46%
45%
Телекоммуникации
Недвижимость
37%
36%
35%
44%
Магазины со смешанным
33%
Финансовые компании
промышленность
Торговля
ассортиментом
Производство
42%
Текстильная
32%
промышленность
Строительство
39%
Бумажная
30%
промышленность
Транспорт
Исmо'Чник:
38%
Сдача помещений в арендУ
26%
[Altman and Kishore {1996)].
Эти общие выводы подтверждаются на более поздних данных (см.
[Grossman et al. {2001)]) по рейтингуемым агентством Fitch облигациям
и займам за период 1997-2000 гг. В соответствии с работой [Grossman et
al. {2001)] различия в ставках восстановления займов и облигаций для
одних и тех же секторов экономики достаточно значительны. Напри
мер, облигации компаний сферы услуг имеют удивительно низкие нор
мы восстановления (около
займов (около
42%).
3%)
сравнительно с нормой восстановления
Конечно, мы не обладаем информацией относи
тельно уровня приоритетности долговых обязательств, поэтому следу
ет принимать эти результаты с некоторой степенью предосторожности.
Более того, поскольку это средние значения, бимодальность распреде
ления нормы восстановления не учитывается.
7.4.14.
Величина номинальных потерь при дефолте
Величина номинальных потерь при дефолте для срочных кредитов, как
правило, определяется однозначно. Эта ситуация несвойственна таким
схемам кредитования, как, например, кредитная линия, когда заемщик
теоретически может отклониться от первоначально установленной схе
мы возвращения долга. Более того, в случае ухудшения финансово
го положения заемщики, как правило, отклоняются от первоначально
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
773
установленной схемы кредитной линии настолько, насколько это воз
можно в сложившихся условиях для того, чтобы избежать дефолта.
В базовом ПВР вычисление величины номинальных потерь при дефол
те
в
случае,
когда процедура измерения
не
вполне
четкая,
основано
на контрольных значениях. Например, ВНП(Д) для безотзывных неис
пользованных обязательств равна
75%.
Однако для усовершенствован
ного ПВР величина номинальных потерь при дефолте может быть опре
делена на основе модели, используемой в банке.
Анализ кредитных линий и соответствующих им величин номи
нальных потерь, значения которых неизвестны в начальный момент
времени, требует тщательной оценки следующих элементов:
•
ве.л.ичин·ы кредита, т. е. максимальной суммы, которая может быть
использована заемщиком;
•
извлеченной сумм'Ы, т. е. использованной заемщиком части кре
дита;
•
неизвлеченной суммъ~, т. е. неиспользованной заемщиком части
кредита.
В качестве примера рассмотрим статистический бюллетень Банка
Италии, в котором отражено осуществляемое банками финансирование
заемщиков с помощью кредитных линий или похожими схемами с сен
тября 2004г. {табл.
Таблица
7.16).
7.16. Величины
кредитов и извлеченные суммы
(Банк Италии, сентябрь 2004г.)
Среднее извлеченных сумм
Сумма выде-
Число
ленного
щиков
кре-
дита,евро
заем-
Среднее
величин
евро
%
кредитов,
евро
От
75000 до
125000
От 125000 до
250000
От 250000 до
500000
От 500000 до
2500000
2500000
От
ДО 5000000
От
5000000
до 25000000
778918
83375
74681
89,59
417587
84479
69508
82,28
146492
71478
50727
70,97
134 747
206749
139555
67,50
18271
93498
63034
67,42
13339
196898
130275
66,16
Более
2438
522694
350201
67,00
25000000
Гл.
774
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Очевидно, что чем меньше величина кредита, тем больше процент
извлеченных заемщиками сумм.
С учетом вышеупомянутых элементов ВНП(Д) может быть разло
жена на два компонента:
•
рисковую составляющую, которую обычно называют скорректи
рованной ВНП(Д) или фактором эквивалентности займа
= Извлеченная сумма +(Величина кредита -
ФЭЗ
где ДИС(Д)
-
( ФЭЗ):
Извлеченная сумма) ХДИС(Д),
оценка доли использованных средств компанией, ока
завшейся в состоянии дефолта;
•
безрисковую составляющую, которая определяется следующим
образом:
(Величина кредита - Извлеченная сумма) Х
(1 -
ДИС(Д)).
При нормальных условиях ДИС(Д) достаточно стабильно во вре
мени. Однако если у заемщика возникают некоторые финансовые про
блемы, то он берет больше денег и его ДИС(Д) увеличивается. С фи
нансовой точки зрения ДИС(Д) можно рассматривать как опцион, ко
торый заемщик может исполнить в случае финансовой необходимости.
В качестве компенсации банк берет комиссию, равную фиксированному
проценту от неиспользованной суммы.
Как оценить ДИС(Д) и ФЭЗ? Эти величины зависят от кредитного
качества, типа кредитной схемы и географического положения. Одна
ко довольно мало эмпирических исследований на эту тему. В одной из
немногих работ, в которых рассматривается эта тема, а именно в работе
[Asarnow, Marker (1995)],
анализируется характер больших корпоратив
ных заемных обязательств перед Ситибанком за период с
1988 по 1993 г.
и показана важность кредитных рейтингов, в особенности на спекуля
тивном уровне (табл.
Таблица
7.17).
7.17. Извлеченные суммы в%,
(Ситибанк, 1988-1993)
Рейтинг
Извлеченная
ДИС(Д) и ФЭЗ
ДИС(Д),
%
ФЭЗ,%
сумма,%
(А)
ААА
АА
А
ввв
вв
в
ссс
0,10%
1,60%
4,60%
20,00%
46,80%
63,70%
75,00%
(В)
69,00%
73,00%
71,00%
65,00%
52,00%
48,00%
44,00%
(A)+[lOO-(A)]·
69,03%
73,43%
72,33%
72,00%
74,46%
81,12%
86,00%
(В)
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
*
*
775
*
В предыдущих пунктах параграфа 7.4, посвященного теме кредит
ного риска, были представлены одномерные модели кредитного рис
ка. Пункты
7.4.15-7.4.19
посвящены анализу многомерных моделей,
позволяющих оценивать неожиданные убытки, дефолтную и миграци
онную зависимость, вероятности дефолтов и другие рисковые характе
ристики «портфеля заемщиков~.
Вообще говоря, существуют четыре основных метода для построе
ния моделей кредитных портфелей. Предлагаем их читателю.
Модели кредитной миграции. Подход
женный
J.P. Morgan
CreditMetrics,
предло
в 1997г., основан на анализе кредитной миграции,
т. е. вероятности перемещения из одного рейтингового класса в дру
гой (включая дефолт, являющийся поглощающим состоянием) за за
данный период времени, который обычно берется равным одному году.
В подходе
CreditMetrics
оценивается функция распределения на один
год вперед для стоимости кредитного портфеля, которая меняется в ре
зультате кредитной миграции. Этот подход предполагает, что матрица
переход, оцененная по историческим данным нескольких тысяч рейтин
гуемых облигаций, достаточно точно описывает вероятность миграции
из одного рейтингового класса в другой.
Структурные модели. «Прародителем~ большинства из этих мо
делей является моде.л:ь Мертона, которая постулирует механизм дефол
та с точки зрения его связи со стоимостью активов компании и ее обя
зательств (см. п.
7.4.7).
Корпорация
MV
(которая сейчас принадлежит
рейтинговому агентству) развила методологию кредитного риска и со
здала большую базу данных для расчета вероятностей дефолта и вы
числения функции распределения убытков с учетом рисков дефолта и
рисков миграции. КМV-модель отличается от CreditMetrics-мoдeли, по
скольку она строится на основе так называемой ожидаемой частотъt
дефолтов для каждого эмитента, а не на основе средних частот перехо
дов, построенных по историческим данным, как это делается в модели
CreditMetrics.
Актуарные
Credit Suisse
модели.
в конце
1997 г.
CreditRisk+
это
подход,
предложенный
и основанный на результатах акутарной
науки. В этом подходе уделяется основное внимание описанию веро
ятности дефолта, а не кредитной миграции. Кроме того, в отличие от
KMV-
и CreditMetrics-пoдxoдoв, в
ны дефолта. Однако этот подход
CreditRisk+ игонорируются причи
- единственный, который позволя
ет получить решения в аналитическом виде, а не с помощью методов
стохастического моделирования, что позволяет значительно уменьшить
количество необходимых вычислительных ресурсов.
Гл.
776
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Макроэкономические модели. В работах
предложена модель, названная
[Wilson {1997а, 1997Ь)]
CreditPortfolioView и направленная на
то, чтобы улучшить подход кредитной миграции путем допущения того,
что вероятности миграций могут меняться в зависимости от кредитных
циклов. В этом подходе вероятности дефолтов являются функциями
макропеременн-ь~х, таких как безработица, уровень процентных ставок
и др., которые предполагаются факторами, определяющими кредитные
циклы.
В CreditMetrics-мoдeли и в модели
KMV,
предложенной
Moody's,
используются похожие предположения, основанные на модели Мерто
на и факторном анализе. Хотя эти две модели концептуально анало
гичны, вторая из них более сложная, чем первая, и для ее построения
требуется больше данных. Вот почему КМV-модель на данный момент
наиболее популярна и обследование рынка в
из
50
2004 г.
показало, что
40
крупнейших финансовых организаций используют именно этот
подход. Мы начнем наш анализ с CreditMetrics-мoдeли, которая в свое
время была серьезным прорывом в этой области и открыла путь для
развития моделей кредитных портфелей.
7.4.15.
Модель
Модель
CreditMetrics
CreditMetrics ([Gupton et al. {1997)])
представляет собой ме
тодологию расчета границы потерь (ГП) для финансовых инструмен
тов, которые не котируются на финансовых рынках (например, бан
ковские ссуды и корпоративные займы). Модель
CreditMetrics
принад
лежит классу моделей с корректировкой по рынку, в которых учиты
вается, что убыток по кредиту возможен не только в результате де
фолта, но и в случае понижения рейтинга. В частности, уровни рей
тинга определяются в соответствии с рейтинговыми классами одного
из основных рейтинговых агентств, таких как
Poor's:
следовательно, в модели
Moody's или Standard &
CreditMetrics используется дискретная
классификация возможных рейтинговых уровней. Кроме того, модель
CreditMetrics является безусловной моделью:
оценки, даваемые этой мо
делью, основаны на исторической информации, которая в свою очередь
не корректируется в зависимости от текущей экономической ситуации.
Информационное множество в этой модели состоит из сле,цующих
элементов:
•
Вероятностей миграции кредитнъ~х рейтингов, т. е. вероятностей
изменения кредитного качества некоторого рейтингуемого обязатель
ства во всех возможных условиях за фиксированный промежуток вре
мени. Эти вероятности представлены в матрице кредитных переходов,
публикуемой рейтинговыми агентствами;
7.4.
•
•
•
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
777
норм восстановления в случае дефолта;
форварднъtХ ставок;
матрицы корреляций между займами (когда рассматривается
два и более займов).
Матрица переходов (матрица вероятностей миграции кредитных
рейтингов)
-
это таблица, в которой представлены вероятности того,
что текущий рейтинг заемщика через определенный промежуток време
ни (например, через год) будет повышен, понижен или заемщик окажет
ся неплатежеспособным. Эти вероятности обычно рассчитываются как
среднее значение частот миграций заемщиков из одного рейтингового
класса в другой через заданный промежуток времени. Помимо матриц
перехода, рейтинговые агентства также публикуют нормы восстановле
ния, тогда как корреляционная матрица между займами рассчитыва
ется только компанией
J.P. Morgan.
Что касается форвардных ставок,
они находятся из кривых доходностей для займов, и их расчет также
осуществляется компанией
J.P. Morgan.
При условии, что задано ука
занное выше информационное множество, мы можем вычислить мате
матическое ожидание, дисперсию и границу потерь {некоторого уровня
доверия) стоимости кредитного портфеля.
1)
Оценка кредитного портфеля, составленного из одного
долгового обязательства
Основная идея процедуры оценки состоит в том, что состояние кре
дитного качества любого долгового обязательства, имеющего рейтинг,
может измениться с вероятностями, определяемыми матрицей перехо
да. Таким образом, стоимость долгового обязательства равна взвешен
ной сумме стоимостей этого долгового обязательства при всех возмож
ных рейтингах, где взвешивание осуществляется с учетом вероятностей
перехода из текущего состояния в состояние, соответствующее рассмат
риваемой сумме долгового обязательства. Следовательно, для того что
бы оценить долговое обязательство, необходимо следовать следующей
процедуре:
•
определить кредитный рейтинг рассматриваемого заемщика и со
ответствующую ему переходную матрицу;
•
зафиксировать временной период. Довольно часто он берется рав
ным одному году;
•
оценить стоимость долгового обязательства при всех возможных
кредитных рейтингах; в случае, если мы пользуемся данными рейтин
гового агентства
S&P,
рейтинговая система этого агентства состоит из
семи классов и дефолтной позиции;
Гл.
778
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
оценить математическое ожидание стоимости долгового обяза
тельства в конце следУющего периода; в качестве оценки берется взве
шенное среднее стоимостей долговых обязательств для всех рейтингов,
с весами, равными соответствующим вероятностям из матрицы перехо
да;
•
наконец, для стоимости долгового обязательства вычислить гра
ницу потерь необходимого уровня.
Наиболее сложным шагом в этой процедУре, конечно, является
оценка стоимости долгового обязательства при всех возможных кре
дитных рейтингах. ПроцедУра оценки может быть разделена на два
случая: один случай
-
дефолт, другой
-
увеличение или пониже
ние кредитного рейтинга: если заемщик оказывается в состоянии
дефолта, основной целью является выяснение того, какая доля требова
ний по кредиту или кредитам может быть возмещена через процедУры
банкротства заемщика. В исходной CreditMetrics-мoдeли предполагает
ся,
что возмещения
кредиторам осуществляются
в соответствии с
их
классом приоритета. Однако в относительно недавних исследованиях
предлагается отказаться от этого предположения и упростить анализ
норм восстановления, используя для их описания во всех случаях бета
распределение со средним, равным
50%,
и дисперсией, равной
20%.
Для того чтобы вычислить границу потерь на конец следУющего
периода, необходимо рассчитать текущую стоимость долгового обяза
тельства. В случае долговых обязательств используемые дисконтные
процентные ставки берутся равными соответствующим значениям на
кривой доходности. Долговые обязательства с разными кредитными
рейтингами дисконтируются с процентными ставками, взятыми из раз
личных кривых доходностей, в зависимости от их рейтингового класса.
При условии, что ставки определены, общая формула для приве
денной стоимости долгового обязательства со сроком погашения через
один год принимает следУющий вид:
с
V =
где С
-
с
с
в+с
С+ 1 + fi + (1 + !2) 2 + (1 + fз) 3 + · · · + (1 + f n)n'
величина купона, В
тельства, а
/i -
-
(7.23)
номинальная стоимость долгового обяза
дисконтные процентные ставки, определенные из кри
вой доходности.
2)
Пример оценки кредитного портфеля, составленного из
одного долгового обязательства
Предположим, что компания, имеющая рейтинг ВВВ, выпускает
долговые обязательства номинальной стоимостью в
100
млн евро со
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
сроком погашения через
составляющими
6%
779
лет и ежегодными купонными платежами,
5
от номинальной стоимости. Кроме того, предполо
жим, что вероятности миграции кредитного рейтинга для компании,
имеющей рейтинг ВВВ, равны значениям, указанным в табл.
Таблица
7.18.
7.18.
Вероятности миграции кредитного рейтинга для
компаний, имеющих текущий рейтинг ВВВ
Рейтинг в конце года
Вероятность,%
ААА
0,02
АА
0,33
А
5,95
ввв
86,93
вв
5,30
в
1,17
ссс
0,12
Дефолт
0,18
Для этой компании вероятность остаться в том же рейтинговом
классе равна
86,93%, вероятность улучшить кредитное качество до наи
высшего рейтинга ААА равна 0,02%, а вероятность банкротства этой
компании в течение одного года равна 0,18%. Матрица перехода для
всех рейтинговых классов представлена в табл. 7.19.
Таблица
7.19.
Матрица перехода: вероятности миграций кредитного
рейтинга из одного класса в другой в течение
одного года
Рейтинг в конце года (в%)
Текущий
рейтинг
ААА
АА
А
ввв
вв
в
ссс
Дефолт
ААА
0,22
о
0,12
0,06
0,74
5,3
80,53
6,48
2,38
0,14
0,26
1,17
8,84
83,46
11,24
0,02
0,01
1,12
1
4,07
64,86
о
ссс
0,06
0,64
5,52
86,93
7,73
0,43
1,3
о
о
0,68
7,79
91,05
5,95
0,67
0,24
0,22
о
в
8,33
90,65
2,27
0,33
0,14
0,11
о
вв
90,81
0,7
0,09
0,02
0,03
АА
А
ввв
Источник:
0,06
0,18
1,06
5,2
19,79
[Gupton et al. (1997)).
После того как зафиксирован временной горизонт кредитного рис
ка, который часто берется равным одному году, необходимо специфици-
Гл.
780
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
ровать форвардную модель ценообразования. Оценка кредитного порт
феля, составленного из одного долгового обязательства, строится на ос
новании кривой доходности, соответствующей рейтингу его эммитента.
Спотовая кривая бескупонного обязательства используется для опре
деления текущей спотовой стоимости этого долгового обязательства.
Тогда как форвадная цена долгового обязательства через один год вы
числяется на основании форвардной: кривой для бескупонного долго
вого обязательства, процентные ставки которой затем применяются к
остаточным денежным потокам за период с конца первого года от мо
мента выпуска долгового обязательства до срока его погашения.
В нашем примере мы взяли одногодичные значения доходностей:,
полученных из форвардной: кривой для бескупонного долгового обяза
тельства, из документации CreditMetrics-мoдeли (соответствующие до
ходности представлены ниже, в табл.
Таблица
7.20.
7.20).
Значения доходностей: из форвардной кривой через
1 год для
бескупонных долговых обязательств
из всех рейтинговых классов,%
Рейтинговый класс
ААА
АА
А
ввв
вв
в
ссс
Исmо'Чник:
Год
1
3,60
3,65
3,72
4,10
5,55
6,05
15,05
Год2
Год3
Год4
4,17
4,22
4,32
4,67
6,02
7,02
15,05
4,73
4,78
4,93
5,25
6,78
8,03
14,03
5,12
5,17
5,32
5,63
7,27
8,52
13,52
[Gupton et al. {1997)].
Отметим, что, если эмитент оказывается в состоянии дефолта в
конце года, это не означает, что не удастся возместить хотя бы часть
суммы долга, так как инвестор может восстановить определенный: про
цент выданных в долг средств, который зависит от степени приори
тетности долга. Эти нормы восстановления оцениваются рейтинговыми
агентствами по историческим данным. В качестве примера в табл.
7.21
представлены средние и стандартные отклонения норм восстановления
для долговых обязательств из разных классов приоритетности, оценки
которых получены компанией
Moody's
в
1996 г.
Предполагается, что рассматриваемый: займ принадлежит к классу
приоритетных необеспеченных обязательств, поэтому в случае дефол
та его норма восстановления в среднем равна
стоимости.
51,13%
от номинальной:
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
781
С этой точки зрения, если предположить, что компания сохранит
уровень рейтинга ВВВ через один год, форвардная цена рассматривае
мого ее долгового обязательства через один год составит:
Vввв
Таблица
6
6
6
6
= + 1 + О,0410 + (1+0,0467) 2 + (1+0,0525) 3 +
100+6
+ (1 + 0,0563)4 = 107,55.
7.21.
Средние и стандартные отклонения норм
восстановления в зависимости от степени
приоритета (в
% от
номинальной стоимости)
Среднее
Стандартное
отклонение
отклонение
Приоритетные обеспеченные обязательства
53,80
26,86
Приоритетные необеспеченные обязательства
51,13
25,45
Приоритетные субординированные кредиты
23,81
Субординированные кредиты
38,52
32,74
20,18
Неприоритетные субординированные кредиты
17,09
10,90
Класс приоритетности
Источник:
[Carty, Lieberman (1996)), [Gupton et al. (1997)).
Если осуществить аналогичные вычисления в предположении, что
через год компания изменит свой кредитный рейтинг, получим следу
ющую таблицу стоимостей рассматриваемого займа (см. табл.
Таблица
7.22.
7.22).
Форвардная цена долгового обязательства с текущим
рейтингом ВВВ через один год, вероятности
различных состояний и изменения стоимости этого
обязательства
Рейтинговый
Стоимость, долл.
класс к концу
первого года
ААА
АА
А
ввв
вв
в
ссс
Дефолт
Источник:
109,37
109,19
108,66
107,55
102,02
98,10
83,64
51,13
[Gupton et al. (1997)).
Вероятность
Изменение
измененения
стоимости
рейтинга,%
дV, долл.
0,02
0,33
5,95
86,93
5,30
1,17
0,12
0,18
1,82
1,64
1,11
о
-5,53
-9,45
-23,91
-56,42
ГЛ.
782
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Используя распределение изменений стоимости рассматриваемого
займа, задаваемое двумя последними столбцами табл.
7.22,
можно вы
числить математическое ожидание и стандартное отклонение д V.
В результате получим значения, равные
Граница потерь
-23,91,
1%-ного
-0,46
и
2,99,
соответственно.
доверительного уровня для этого займа равна
что соответствует значительно большим потерям, чем граница
потерь, вычисленная в предположении нормальности функции распре
деления дV (которая равна
-0,46 - 2,33 · 2,99 = -7,43,
где
-2,33
это
квантиль стандартного нормального распределения).
0,01
3)
Оценка кредитного портфеля, составленного из двух
долговых обязательств
Основная цель модели
CreditMetrics
состоит не в оценке стоимо
сти одного-единственного кредитного инструмента, а в оценке портфе
ля таких инструментов. В сущности, модель
CreditMetrics
строится на
следующих трех основных предположениях.
•
В рамках одного кредитного класса все эмитенты долговых обя
зательств с точки зрения кредитного качества однородны. А следова
тельно, они характеризуются одной и той же матрицей вероятностей
переходов.
•
Матрица вероятностей переходов, отвечающая некоторой компа
нии, зависит только от рейтинговой категории, к которой принадлежит
эта компания в момент оценки ее долговых обязательств.
•
Переходные вероятности стационарны, т. е. не зависят от времени.
Рассмотрим следующую задачу: как, зная характер каждого от
дельного кредитного инструмента, описать характер портфеля этих ин
струментов. Если бы мы предположили, что изменения стоимостей раз
личных инструментов, составляющих рассматриваемый портфель, вза
имно независимы, то совместная вероятность события, состоящего в
изменении стоимостей рассматриваемых активов, была бы равна про
изведению соответствующих маргинальных вероятностей для каждо
го отдельного актива, вычисляемых на основании элементов матрицы
переходов этого актива. Однако, к сожалению, такое предположение
нереалистично. К примеру, общеизвестно, что среди компаний, работа
ющих в одном индустриальном секторе или (и) геополитическом реги
оне, корреляции выше или что корреляции значительно изменяются в
зависимости от состояния экономики.
Если корреляции среди заемщиков отличны от нуля, то в этом слу
чае необходимо вычислить совместную миграционную вероятность, при
этом учитывая следующее:
•
кредитное качество заемщиков может как улучшаться, так и ухуд
шаться;
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
•
783
существуют корреляции междУ рейтинговыми миграциями.
В методологии
CreditMetrics
указанные выше особенности учиты
ваются следующим образом:
•
в модели
CreditMetrics оценка кредитного рейтинга связывается с
изменениями стоимостей/ доходностей активов, что весьма схоже с ме
тодологией, основанной на модели Мертона; в частности,
CreditMetrics
обобщает последнюю модель на случай п «этапов к дефолту» (ЭД), где
п
-
количество рейтинговых классов;
•в отличие от так называемой КМV-модели (см. ниже), в модели
CreditMetrics для
оценки стоимости компании, которая ненаблюдаема,
используется цена акций этой компании.
В целом процедУра оценки портфеля кредитных обязательств на
основании модели
Шаг
CreditMetrics
состоит из четырех шагов.
На основании вероятностей миграций для двух рассмат
1.
риваемых заемщиков вычисляются пороговые уровни
(Z),
отвечающие
каждому рейтинговому классу. Эталонной моделью здесь является мо
дель, предложенная Мертоном: динамика стоимости активов компании
Vt
описывается стандартным геометрическим броуновским движением,
т.е.
(7.24)
гдеµ
-
ожидаемая стоимость для
Случайная величина
Vt
vt,
волатильность для
-
yt.
имеет логномальное распределение с ма
тематическим ожиданием, равным
CreditMetrics
а и
E(vt)
= Vo exp(µt).
Методология
обобщает модель Мертона путем «нарезания» функции
распределения стандартизированной лог-доходности на полосы так, что
они в точности воспроизводят миграционные частоты, представленные
в матрице переходов.
ZАМ
Zccc
Finn defaults
А
Рис.
7.24.
Обобщение модели Мертона с учетом изменений рейтинга:
функция плотности распределения нормированных лог-доходностей
для стоимости активов компании с рейтингом ВВВ
784
Гл.
На рис.
7.24
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
в дополнение к порогу, соответствующему дефолту,
изображены также пороги, отвечающие всем другим рейтинговым клас
сам. Значение лог-доходности стоимости активов компании за некото
рый период, лежащее между двумя ближайшими порогами, определяет
рейтинг этой компании в конце рассматриваемого периода.
В обобщенной модели Мертона предполагается, что стандартизи
рованные для всех заемщиков лог-доходности за некоторый фиксиро
ванный промежуток времени имеют стандартное нормальное распреде
ление
N(O; 1),
и нормировка, определяющая стандартизацию, для всех
заемщиков из одного рейтингового класса одна и та же. Обозначим че
рез
P(DEF)
вероятность дефолта для некоторого заемщика из рей
тингового класса ВВВ. Тогда критический уровень
VvEF
стоимости
активов заемщика, отвечающий дефолту, определяется соотношением:
P(DEF)
= P[Vt :::;; VvEF]·
Зная вероятность дефолта, мы можем найти
для стандартизированной лог-доходности порог
Zccc,
соответствую
щий дефолту, поскольку площадь под графиком плотности стандарти
зированной лог-доходности на интервале (-оо;
Используя выражение
Zt.
P(DEF) =
-
t
в терминах стандартизированных лог
2)
в п.
7.4.7):
р [ln(VDEF/Vo) - (µ- и 2 /2)t ~ Zt]
[z ~ t
P(DEF).
перепишем вероятность возникновения
Получим (по аналогии с пп.
- р
равна
(7.24),
дефолта в момент времени
доходностей
Zccc]
=
uVf,
ln(Vo/VDEF)
+ (µ - и2 /2)t]
uVi
""'=
-- Ф(-d*2t ) '
где стандартизированная лог-доходность Zt = [ln(Yt/Vo) - (µ - и 2 /2)t]/
/(uVt) имеет стандартное нормальное распределение N(O; 1). Zccc это квантиль стандартного нормального распределения, отвечающий
кумулятивной вероятности
тивов заемщика
VvEF,
дующего соотношения:
PvEF,
а критический уровень стоимости ак
соответствующий дефолту, определяется из сле
Zccc = -d2t·
Следует отметить, что совмест
ные вероятности миграций необходимы только для определения поро
гов
Z,
для вычисления которых не нужно знать величину стоимости
активов, оценивать математическое ожидание или дисперсию. Порого
вые значения рассчитываются с использованием обращения стандарт
ной нормальной функции распределения и определяются кумулятивны
ми вероятностями. Например,
Zв -
пороговый уровень, соответствую
щий кумулятивной вероятности нахождения рейтинга либо на уровне
ССС, либо в состоянии дефолта.
Шаг
2.
После того как определены пороговые уровни, при помощи
двумерного нормального распределения вычисляются совместные веро-
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
785
ятности миграций, где в качестве входных параметров используются по
роговые уровни и коэффициенты корреляции между лог-доходностями
стоимостей активов.
Шаг
+ 1)
х (n
3.
Теперь переходная матрица строится с учетом
(n
+ 1) х
возможных состояний. Это означает, что стоимость портфе
ля, составленного из двух долговых обязательств, может принимать
(n 1) 2 значений, где каждое значение рассчитывается согласно ранее
+
изложенной проце,цуре для оценки единственной позиции.
Шаг
4.
Наконец, используя распределение (дискретное) возмож
ных стоимостей портфеля, можно оценить математическое ожидание,
стандартное отклонение, а также когерентные меры риска его стоимо
сти.
4)
Пример оценки портфеля, составленного из двух
долговых обязательств
Предположим, что наш портфель состоит из двух долговых обяза
тельств: первое
-
долговое обязательство компании, имеющей рейтинг
ВВВ, номинальной стоимостью в
через
5
100
млн евро со сроком погашения
лет и ежегодными купонными платежами, составляющими
от номинальной стоимости, второе
-
долговое обязательство компании,
имеющей рейтинг А, номинальной стоимостью
погашения через
ляющими
5%
3
6%
100
млн евро со сроком
года и ежегодными купонными платежами, состав
от номинальной стоимости. Используя ранее описанную
методологию для оценки портфеля из единственной кредитной позиции
и данные, представленные в табл.
7.20
и
7.21,
мы получим сле,цующие
результаты для второго долгового обязательства {табл.
Таблица
7.23.
7.23).
Форвардная стоимость долгового обязательства с
рейтингом А на конец первого года, вероятности
различных состояний и изменения его стоимости
Рейтинговый
Стоимость в конце
Вероятность
класс
первого года, долл.
стояния,%
мости д
ААА
106,59
106,49
106,30
105,64
103,15
101,39
88,71
51,13
2,27
91,05
5,52
0,74
0,6
0,01
0,06
0,29
0,19
0,00
-0,66
-3,15
-4,91
-17,59
-55,17
АА
А
ввв
вв
в
ссс
Дефолт
Источник:
[Gupton et al. {1997)].
со-
Изменение
сто и-
v' долл.
Гл.
786
В рамках модели
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
CreditMetrics
утверждается, что компания ока
зывается неплатежеспособной в случае, если стандартизированная лог
доходность стоимости ее активов меньше, чем пороговое значение
Zccc.
Компания будет иметь рейтинг ССС, если значение ее стандартизиро
ванной
лог-доходности
стоимости
будет
принадлежать
интервалу
(Zccc; Z в], и т. д. Используя пороговые уровни (получены на основании
табл.
7.24),
Таблица
можно преобразовать табл.
7.24.
7.18
к виду табл.
7.25.
Вероятности миграции кредитного рейтинга
для компании с рейтингом ВВВ и
соответствующие вероятности в рамках обобщенной
модели Мертона
Рейтинг
в
конце
первого года
Вероятности
матрицы
перехода,
%
ААА
А
ввв
вв
в
ссс
Default
Таблица
7.25.
Вероятности,
соответ-
ствующие модели стоимости активов
1- Ф(ZААА)
0,02
0,33
5,95
86,93
5,30
1,17
0,12
0,18
АА
из
Ф(ZААА) - Ф(ZАА)
Ф(ZАА) - Ф(ZА)
Ф(ZА) - Ф(Zввв)
Ф(Zввв) - Ф(Zвв)
Ф(Zвв) - Ф(Zв)
Ф(Zв) - Ф(Zссс)
Ф(Zссс)
Переходные вероятности и пороги кредитного качества
для заемщиков с текущими рейтингами ВВВ и А
Рейтинг
Компания
через
ГОМ ВВВ
ГОМ А
Вероятность, Пороги
Вероятность, Пороги
с
рейтин-
Компания
с
рейтин-
Один год
ААА
АА
А
ввв
вв
в
ссс
Дефолт
%
(Z)
%
(Z)
0,02
0,33
5,95
86,93
5,3
1,17
0,12
0,18
3,54
2,78
1,53
-1,49
-2,18
-2,75
-2,91
0,09
2,27
91,05
5,52
0,74
0,26
0,01
0,06
3,12
1,98
-1,51
-2,3
-2 72
'
-3,19
-3,24
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
787
Что касается расчета пороговых уровней, то, например, для компа
нии с текущим рейтингом ВВВ пороговый уровень
Zccc
определяется
следующим выражением:
Zccc = Ф- 1 (0,0018) = -2,91,
а пороговый уровень
Zв
Z в:
= Ф- 1 (0,0018 + 0,0012) = -2,75.
Подобным образом как для заемщиков с рейтингом ВВВ, так и за
емщиков с рейтингом А получим таблицу определяемых порогами по
лос,
каждая
{табл.
из
которых
соответствует
определенному
рейтингу
7.25).
Если портфель состоит из двух и более займов, то при вычислении
мер риска необходимо учитывать дополнительные элементы: корреля
цию между различными займами. Методология
CreditMetrics предпола
гает, что стандартизированные лог-доходности стоимости активов двух
компаний имеют двумерное нормальное распределение с корреляцион
ной матрицей :Е 32 • В нашем примере мы предположим, что корреляция
рассматриваемых лог-доходностей равна
:Е = (
1
0,3
0,3:
0,3 ) .
1
Следовательно, когда мы хотим вычислить вероятность того, что
оба заемщика сохранят свой текущий рейтинг
ственно), мы должны, согласно методологии
(т. е. ВВВ и А соответ
CreditMetrics, использо
вать двумерное нормальное распределение. Таким образом:
Р(Zввв
=
< Rввв < ZA, ZA < RA < ZAA) =
J/Аf(rввв,rл;Е)drвввdrл
Zввв
где f(rввв,rА;:Е)
= 79,69%,
(7.25)
ZA
211"~ехр{
-
2 ( 1 .:Р2)[rЪвв - 2рrввв
· rA+
+r~]} - плотность двумерного нормального распределения случайного
вектора (Rввв, RA) в точке (rввв, r A)i Rввв, RA
- стандартизирован
ные лог-доходности стоимостей активов рассматриваемых компаний;
р- коэффициент корреляции между Rввв и
32 Следует
RA.
отметить, что, если каждая из двух рассматриваемых случайных вели
чин имеет стандартное нормальное распределение, ковариационная матрица совпа
дает с корреляционной.
Гл.
788
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Выполняя эту процедуру для оставшихся
табл.
63
комбинаций, получим
7.26.
Таблица
7.26.
Совместные вероятности сохранения или изменения
рейтингов для двух компаний с текущими рейтингами
ВВВ и А (при коэффициенте корреляции, равном
Рейтинг второй компании (А)
Рейтинг первой
компании (ВВВ)
ААА
АА
А
ввв
вв
в
ссс
Дефолт
91,05
0.02
0,29
5,44
79,69
4,47
0,92
0,09
0,13
5,52
0,74
0,26
0,01
0,06
о
о
о
о
о
о
о
о
о
о
0,08
4,55
0,64
0,18
0,02
0,04
0,01
0,57
0,11
0,04
о
о
о
0,19
0,04
0,02
0,01
о
0,04
0,01
о
о
о
о
о
о
0,01
о
о
о
0,09
2,27
о
о
О,33
о
0,02
0,07
о
0,04
0,39
1,81
0,02
о
о
ссс
5,95
86,93
5,3
1,17
0,12
о
о
Дефолт
О,18
о
о
ААА
0,02
АА
А
ввв
вв
в
0,3)
Переходная матрица содержит
торых отвечает одному их
64
8 х 8 = 64 элементов,
каждый из ко
состояний для стоимости портфеля. Стои
мость портфеля в каждом отдельном состоянии вычисляется точно так
же, как в случае одной кредитной позиции. Таким образом, приходим
к табл.
7.27.
Используя результаты, отраженные в табл.
7.26
и
7.27,
мы можем
вычислить, например, ожидаемую стоимость портфеля и ее стандарт
ное отклонение, которые равны
ляем вычисление границы
213,63 и 3,35 соответственно. Мы остав
потерь 1%-ного уровня в качестве упражне
ния.
Таблица
7.27.
Стоимости портфеля из двух заемщиков с текущими
рейтингами ВВВ и А соответственно
Рейтинг первой
компании (ВВВ}
ААА
АА
А
ввв
вв
в
ссс
Дефолт
109,37
109,19
108,66
107,55
102,02
98,1
83,64
51,13
Рейтинг второй компании (А}
iAAA IAA
А
106,59 106,49 106,3
~15,96 ~15,86 215,67
~15,78 ~15,68 215,49
~15,25 ~15,15 214,96
~14,14 ~14,04 213,85
~08,61 ~08,51 208,33
~04,69 ~04,59 204,4
190,23 190,13 189,28
157,72 157,62 157,43
ввв
105,64
215,01
214,83
214,3
213,19
tвв
103,15
212,52
212,34
211,81
210,7
~07,66 205,17
~03,74 201,25
189,28 186,79
156,77 154,28
в
КJСС
Дефолт
101,39
210,76
210,58
210,05
208,94
203,41
199,49
185,03
152,52
88,71
198,08
197,9
197,37
196,26
190,73
186,81
172,35
139,84
51,13
160,5
160,32
159,79
158,68
153,15
149,23
134,77
102,26
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
789
Отметим, что если лог-доходности стоимостей активов двух рас
сматриваемых компаний были бы независимыми, то совместная веро
ятность сохранения этими компаниями текущего рейтинга (т. е. ВВВ и
А соответственно) равнялась бы
86,93% х 91,05%
= 79,15%, что меньше,
чем значение, полученное на основании методологии
формулу
5)
(7.25))
и равное
CreditMetrics
(см.
79,69%.
Корреляция дефолтов и корреляция активов
Интуитивно ясно, что корреляция между дефолтами должна быть
малой. Действительно, рассмотрим две компании,
01
и
02
и предполо
жим, что стоимости активов этих компаний описываются моделью Мер
тона. При таком предположении корреляция дефолтов будет опреде
ляться вероятностью того, что за некоторый промежуток времени (на
пример, за один год) стоимости обеих компаний окажутся меньше соот
ветствующих пороговых уровней, отвечающих дефолту (см. рис.
Markct Valuc of
Asscts - Finn 02
7.25).
High Probabllity
Low Probabllity
Market Value of
Assets - Finn 01
...~
о
]
"
~8
::4-
100(\-LGD) - -
1.1. 11
Face value ofDebt
-------------1
100
Finn 01 's Debt Payoff
Рис.
7.25.
Совместная вероятность дефолтов двух компаний
Определим случайные величины
~j
={
6
и
6:
1, если j-я компания оказалась в состоянии дефолта;
О, в противном случае.
Гл.
790
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Тогда коэффициент корреляции меж.цу
ношением
6
и
6
определяется соот
[Lucas (1995)]:
р( 6 , 6 ) =
Р(6 = 1,6 = 1) - Р(~1=1) · Р(6 = 1)
.jP(~1 = 1) · (1 - Р(6 = 1)) · .jP(6 = 1) · (1 - Р(6 = 1))
Поскольку стандартизированные лог-доходности активов имеют
совместное стандартное нормальное распределение с корреляционной
матрицей Е, мы имеем:
-d~ -d~
P(DEF1, DEF2)
=
!!
f(r1, r2; E)dr1dr2,
-00-00
где-~=
Zbcc' i = 1, 2 -
пороги, соответствующие дефолту первой и
второй компаний.
Предположим, что, как и в рассматриваемом выше примере, два
заемщика имеют рейтинги ВВВ и А. Зададимся совместным распреде
лением лог-доходностей заемщиков ВВВ и А, соответствующим данным
табл.
~1
7.26,
дополненными предположением, что р(~ввв, ~А)
= 0,3,
где
= ~ввв и 6 = ~А. Тогда:
Р(~ввв =
Р( ~А
1) = 0,0018;
= 1) = 0,0006;
-dfBB -d:
Р(~ввв = 1, ~А = 1) =
J J
-оо
f(rввв, r А; E)drвввdrА =
-оо
-2,91-3.24
- J J
-оо
р(~ввв ~A)d
'
(с
Р ~ввв
f(rввв, r А; E)drвввdrА= 0,0000156;
-оо
_
Р(~ввв.~А)-Р(~ввв=1)-Р(~А=1)
.
- у°Р(~ввв=1)·(1-Р(~ввв=1))·у°Р(~А=1)·(1-Р(~А=1))'
= 1 с = l) =
o,00001s6-o,001s.o,0006
= 0 014
'~А
Jo,001s(1-o,001в)·Jo,0006(1-o,0006)
'
·
Если графически изобразить, как меняется корреляция дефолтов
для двух взятых компаний в зависимости от изменения корреляции
меж.цу лог-доходностями стоимостей их активов от О до
рис.
7.26.
1,
то получим
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
791
0,6
0,5
1111
~
а
-&
0,4
~
1111
а
1111
0,3
~
0,2
5
i:i..
0,1
о.о
о.о
0,2
0,4
0,6
1,0
0,8
Корреляция лог-доходностей
Рис.
7.26.
Корреляция дефолтов как функция от корреляции лог
доходностей стоимостей активов Щ3ух компаний
Дефолтная корреляция по величине значительно меньше, чем кор
реляция лог-доходностей. Кроме того, при изменении корреляции лог
доходностей от
0,2 до 0,5 отношение корреляции дефолтов к ней при
ближенно равно 10- 1 . Это показывает необходимость получения как
можно более точных оценок для этих корреляций для более коррект
ного оценивания эффекта диверсификации портфеля займов 33 .
6)
Оценка портфелей большой размерности
Когда необходимо вычислить границу потерь для портфеля боль
шого количества займов, ранее изложенный «двумерный подход~ с точ
ки зрения вычислительной эффективности не является хорошим выбо
ром: например, если портфель состоит из
ции возможны
8
5 позиций, и для каждой пози
рейтинговых классов, то при использовании «двумер
ного подхода~ нам необходимо вычислить 85
= 32 768
совместных ве
роятностей переходов. Решение этой проблемы, предлагаемое в рамках
методологии
CreditMetrics,
основано на использовании метода Монте
Карло.
Опишем в общем виде предлагаемую процедуру.
•Примем некоторую рейтинговую систему.
•
Присвоим каждому займу из рассматриваемого портфеля соот
ветствующий рейтинг.
33 Корреляционные
модели в методологиях CreditMetrics и KMV аналогичны, но
подробно эту модель мы рассмотрим только для методологии
KMV,
которая значи
тельно сложнее. Для более подробной информации относительно корреляционной
модели в методологии
CreditMetrics
см.
[Gupton et al. (1997)).
ГЛ.
792
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Вычислим (или используем) матрицу переходов, в которой указа
ны вероятности миграции из одного рейтингового класса в другой.
•
С использованием вероятностей миграций вычислим пороговые
уровни
Zi, отвечающие кредитным рейтингам.
Отметим, что эти уровни
зависят от текущего рейтинга заемщика.
•
Вычислим корреляционную матрицу Е стандартизированных
лог-доходностей стоимостей активов рассматриваемых компаний с ис
пользованием факторной модели (т.е. корреляционной КМV-модели,
см. следующий раздел, а также работу
•Смоделируем вектор
(N
х
1)
[Gupton et al. (1997))).
лог-доходностей стоимостей активов
из совместного N-мерного нормального распределения
N(O, Е).
При
моделировании вектора лог-доходностей можно воспользоваться стан
дартной техникой генерирования коррелированных нормальных слу
чайных величин, основанной на разложении Холецкого (напомним, что
оно позволяет представить корреляционную (ковариационную) матри
цу в виде произведения нижнетреугольной матрицы А и матрицы А1 ,
полученной ее транспонированием). В случае простого двумерного слу
чая мы получим:
ана11 +О· О=
1 --+-ан = 1
а21а11 + а22 ·О= р--+- а21 = р
ана21 +О· а22 = р--+- а21 = р
а21а21 + а22 · а22 = 1--+- а22 = J1 - р2 .
О
A=(Pl
J1-p2
)
А для того чтобы получить две нормально распределенные случай
ные величины с корреляцией р, нам необходимо вычислить
У=Ахе--+'
(уI - е1
У2 = ре1
+ e2Jl -
р2
)
'
где е = (е1, е2)' - вектор, составленный из независимых стандартных
нормальных случайных величин.
•
С использованием пороговых уровней
Zi,
полученных на шаге
4
для соответствующих текущих рейтингов взятых заемщиков, опреде
лим по каждому смоделированному вектору стандартизированных лог
доходностей (У1, ... , YN )1 рейтинговый класс каждой из рассматривае
мых компаний.
•
Оценим стоимость каждой позиции в соответствии с форвардной
кривой, при этом учитывая рейтинговый класс, соответсвующий концу
рассматриваемого периода.
7.4.
•
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
793
Если к концу рассматриваемого периода заемщик оказывается
в состоянии дефолта, тогда моделируем из бета-распределения норму
восстановления, и рассматриваем стоимость этого займа как стоимость
дефолтного обязательства.
•
Повторим предыдУщие шаги большое количество раз и получим
смоделированную функцию распределения стоимости портфеля.
•
Наконец, вычислим необходимую нам меру риска (границу по
терь, среднее ожидаемых потерь и т. д.).
7)
Эмпирические приложения в статистическом пакете
методология
R:
CreditMetrics
Предположим, мы имеем портфель, составленный из
N
= 3
кре
дитных позиций компаний, а матрица корреляций лог-доходностей сто
имостей активов этих компаний равна
1 0,4 0,4)
( 0,4 1 0,5
.
0,6 0,5 1
Кроме того, мы положим, что риск-нейтральная процентная став
ка равна
r = 0,03,
величины номинальных потерь при дефолте
{ead)
для этих трех компаний равны
невозвращенных средств
{4000000, 1000000, 10000000), а доли
при дефолте по кредиту {ldg) равны 45% (что
соответствует доле невозвращенных средств при дефолте по кредиту
для необеспеченных преимущественных требований в рамках подхода
«внутренних рейтингов~). Три рассматриваемые компании имеют рей
тинги (ВВВ, АА, В) соответственно. Задача состоит в вычислении гра
ницы потерь 99%-ного доверительного уровня для временного горизон
та в ОДИН год.
Прежде чем приступить к решению этой задачи, следУет сказать,
что мы будем использовать набор процедур
ском пакете
R.
CreditMetrics в
статистиче
Перед разъяснением кода программы необходимо сде
лать несколько замечаний относительно этого набора процедур.
•
В этом наборе для ценообразования займов не используются фор
вардные кривые. Вместо этого используется риск-нейтральная ставка с
добавленным кредитным спредом
(CSt),
который вычисляется следУЮ
щим образом:
CSt = _ ln{l - ВНГ (Д) · Вдt)'
t
где
t
берется равным
1,
а вдt
-
маргинальная вероятность дефолта,
которая меняется в зависимости от рейтингового класса {для более по
дробной информации см. руководство к набору процедур
CreditMetrics).
Гл.
794
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Доля невозвращенных средств при дефолте по кредиту одна и та
же для всех компаний.
•
Несмотря на то что убыткам по портфелю, рассчитываемым с
помощью команды
cm.gain,
отвечают отрицательные числа, ГПа, вы
числяемая с помощью команды
cm.CVaR, положительна.
ли вычислить
Например, ес
1%-ный квантиль построенной функции распределения
(с помощью команды cm.gain) и получить -100, то результатом исполь
зования команды cm.CVaR будет +100.
# Удалим все объекты активизированной среды
rm(list = ls(all = TRUE))
# Загрузим набор процедур CreditMetrics
library(CreditMetrics)
# Зададим входные параметры
N <- 3
n <- 50000
r <- 0.03
ead <- с(4000000, 1000000, 10000000)
rc <- с("ААА", "АА", "А", "ВВВ", "ВВ", "В", "ССС", "D")
lgd <- 0.45
rating <- с("ВВВ", "АА", "В")
firmna.mes <- c("firm 1 ", "firm 2", "firm 3")
alpha <- 0.99
# Корреляционная матрица
rho <- matrix(c( 1, 0.4, 0.6,
0.4, 1, 0.5,
0.6, 0.5, 1), 3, 3, dimna.mes = list(firmna.mes, firmna.mes),
byrow = TRUE)
# эмпирическая матрица миграций за один год,
# взятая с вебсайта рейтингового агентства standard&poors
rc <- с("ААА", "АА", "А", "ВВВ", "ВВ", "В", "ССС", "D'')
М <- matrix(c(90.81, 8.33, 0.68, 0.06, 0.08, 0.02, 0.01, 0.01,
0.70, 90.65, 7.79, 0.64, 0.06, 0.13, 0.02, 0.01,
0.09, 2.27, 91.05, 5.52, 0.74, 0.26, 0.01, 0.06,
0.02, 0.33, 5.95, 85.93, 5.30, 1.17, 1.12, 0.18,
0.03, 0.14, 0.67, 7.73, 80.53, 8.84, 1.00, 1.06,
0.01, 0.11, 0.24, 0.43, 6.48, 83.46, 4.07, 5.20,
0.21, о, 0.22, 1.30, 2.38, 11.24, 64.86, 19.79,
о, о, о, о, 0,0,0, 100
)/100, 8, 8, dimnames = list(rc, rc), byrow = TRUE)
# С помощью команды cm.CVaR вычислим границу потерь
cm.CVaR(M, lgd, ead, N, n, r, rho, alpha, rating)
# С помощью команды cm.gain вычислим
# смоделированные доходы и убытки
cm.gain(M, lgd, ead, N, n, r, rho, rating)
# С помощью команды cm. val разобьем смоделированные
#лог-доходности по рейтинговым классам
cm.val(M, lgd, ead, N, n, r, rho, rating)
#С помощью команды cm.portfolio вычислим
# смоделированную стоимость портфеля займов
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
795
cm.portfolio(M, lgd, ead, N, n, r, rho, rating)
#
Изобразим гистограмму для смоделированных доходов/убытков
cm.hist(M, lgd, ead, N, n, r, rho, rating,
col = 11 stee1Ыue4 1 ', main = 11 Profit / Loss Distribution",
xlab = "loss / profit", ylab = "frequency 11 )
Поскольку мы использовали метод Монте-Карло, то полученный
результат оценки границы потерь должен быть близок к
4015891.
А гистограмма смоделированных доходов/убытков должна напоминать
гистограмму на рис.
7.27.
-5с+О6 -4с+О6
-3с+О6 -2с+06
доходы
Рис.
7.27.
Модель
-Jc+06
Ое+ОО
убытки
Гистограмма смоделированных доходов/убытков
Модель
7.4.16.
/
KMV,
KMV
широко используемая при оценке кредитных рисков,
строится на основе модели Мертона. Модель
KMV
еще известна как
модель Васичека-Килхофера (ВК-модель). Буква «М~ в аббревиатуре
«KMV ~
отвечает первой букве в фамилии
нователей компании
Moody's.
KMV,
McQuown,
одного из трех ос
которую впоследствии выкупило агентство
Инновация модели
KMV
заложена не столько в теоретиче
ской части, сколько в практической реализации модели. Моделируют
ся несколько классов долговых обязательств: краткосрочные долговые
обязательства, долгосрочные долговые обязательства, конвертируемые
долговые обязательства и др. Кроме того, явным образом моделируют
ся выплаты наличных денежных средств, такие как,
например, диви
денды. Общие принципы реализации этой модели будут описаны ниже.
В КМV-модели вводится два ранее не встречавшихся понятия:
«расстояние до дефолта~
(РД)
и
«ожидаемая частота дефолтов~
(ОЧД). ОЧД- это просто вероятность дефолта в течение ближайшего
года (ряда лет). Для того чтобы вычислить ОЧД, необходимо пошагово
выполнить следующую процедуру:
Гл.
796
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
•решая систему из двух уравнений {см. уравнения {7.21а) и {7.21б)),
оценим стоимость активов и ее волатильность;
•
используя стоимость активов, ее волатильность и балансовые зна
чения долговых обязательств, вычислим РД {способ вычисления РД см.
ниже);
•
в соответствии с оценкой РД вычислим вероятность дефолта.
Как отмечалось ранее, из-за некоторой численной неустойчивости
коэффициентов уравнения (7.21б) можно получить некорректные ре
зультаты. В частности, такое возможно при работе с «зашумленны
ми~ данными, см. работы
[Crosble, Bohn {2001)), [Нао {2006)), [Bharath,
Shumway {2008)] и [Fantazzini et al. {2008а)].
Чтобы преодолеть эту проблему модели KMV, необходимо исполь
зовать итеративный подход. Для этого следует:
•получить исторические данные по стоимостям акций,
{Bt-n, ... ,
St};
•
получить
начальную
оценку
волатильности
стоимости
активов
u<0 > на
основании волатильности курсовых стоимостей акций иs;
•используя u<0 > и {Bt-n, ... , St}, вычислить соответствующие сто-
имости активов, {\/i~~, ... , vt<0 >};
•
вычислить доходности стоимостей активов:
R~O}
i
= ln v;(O) i
ln v;< 01>
i-
'
и их среднее значение:
t
R,(O}
=
.!_ ~ R~O};
n L..J
i=t-n
i
•
вычислить следующую оценку волатильности стоимости активов
•
повторять первые пять шагов, пока не будет достигнута сходимость
волатильностей стоимостей акций, т. е. пока не будет выполняться нера
венство
где е
-
некоторый заданный «порог чувствительности'>.
После того как будет достигнута сходимость в вышеописанном ал
горитме, мы получим оценку для стоимости активов и ее волатильно
сти в момент времени
t,
т. е. определим
Vt.
Поскольку нам необходимо
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
797
оценить вероятность того, что в момент Т стоимости активов не бy
llJ'T
превосходить величину долговых обязательств, т. е. Р(Vт ~В), мы
должны воспользоваться формулой
ОЧД = Р(Vт
< В)
(7.18),
= Ф (
т. е.
la )T)
ln ~ - (µVo
2
2
аVТ
•
Однако разработчики КМV-модели признают, что используемая
модель Мертона является слишком простой для описания динамики
финансовых рынков. В частности, в ней:
•
предполагается логнормальность распределения для доходностей
стоимостей активов;
•
предполагается чрезмерно упрощенная структура капитала ком
пании;
•
рассматривается состояние компании в момент времени Т, но де
фолт может наступить в любой момент времени
•
t
< Т;
cлellJ'eT также отметить, что дефолт нельзя рассматривать как
поглощающее состояние, поскольку он не влечет автоматическое банк
ротство. Особенно в развитых странах законодательство коммерческой
деятельности устроено таким образом, что законы направлены на со
хранение любой возможности для компании продолжить свою работу
(после соответствующей реструктуризации), и это делается в целях со
хранения рабочих мест.
Поэтому в модели
KMV
предложены определенные модификации.
В частности, вводится понятие «расстояния до дефолта~, которое опре
деляется слеllJ'ющим образом:
РД= vt-B,
vta
где В
-
ве.л.и'Чина краткосро'Чtt'ЬtХ обязате.л.ьств
+ 50% ве.л.и'ЧU'Н.'Ьt дол
госро'Чtt'ЬtХ обязате.л.ьств, которая определяется на основании данных,
представленных в балансовом отчете компании. Если
µv
и
av
малы, а
ln(vt/ В) ~ (vt - В) /vt, тогда РД аппроксимируется величиной d2 (см.
(7.18)), которую часто называют числом стандартных отклонений от
дефолта.
В модели
KMV
предполагается, что компании с одним и тем же РД
имеют равные вероятности дефолта. Для того чтобы построить выра
жение, связывающее РД и наблюдаемые частоты дефолтов, в
KMV
ис
пользуется база исторических данных по дефолтам. Эта модель позво
ляет вычислять долю компаний с РД из малого интервала, которые ока
жутся в состоянии дефолта за некоторый фиксированный промежуток
времени. Это эмпирическая пpoцellJ'pa оценки опубликована агентством
Гл.
798
Moody's KMV.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Услуги, предлагаемые компанией
в рамках мони
KMV
торинга кредитного риска: оценки ОЧД (начиная с 1993г.) с использо
ванием базы данных по
100 ООО американским компаниям, включая 2000
случаев неплатежеспособности компаний. Таким образом, несмотря на
то что КМV-модель весьма похожа на модель Мертона, результаты их
практической реализации могут существенно различаться.
1)
Модель
KMV
и рейтинги
В КМV-модели матрица переходов строится не на основании рей
тинговых классов, а на основании вероятностей дефолтов. Во-первых,
в методологии
KMV
классификация компаний на группы основана на
непересекающихся интервалах принадлежности вероятностей дефолта,
которые являются типичными для рейтинговых классов. Например, все
компании с ОЧД, меньшей чем
2 базовых
пункта (или
0,02%),
относят
ся к классу компаний с рейтингом ААА, тогда как те компании, кото
рые имеют ОЧД, заключенное между
3
и
6
базовыми пунктами, при
надлежат к классу компаний с рейтингом АА, а компании, чьи ОЧД
заключены между
7
и
15
базовыми пунктами, принадлежат к классу
компаний с рейтингом А, и т. д. Во-вторых, в модели
перехода, показанная в табл.
KMV
матрица
оценивается с использованием ин
7.28,
формации относительно истории изменений ОЧД. Эта матрица весьма
схожа по структуре с ее аналогами, рассчитываемыми такими рейтин
говыми агентствами, как, например,
Standard and Poors
(см. табл.
Различия в соответствующих вероятностях из табл.
7.28
и
7.29).
7.29 по
разительны: в соответствии с КМV-моделью, кроме рейтинга ААА, ве
роятность сохранения рейтинга составляет от одной трети до одной
второй от исторических вероятностей перехода, предоставленных рей
тинговым агентством. Вероятности дефолта в модели
KMV
меньше, в
особенности для низких рейтингов. Миграционные вероятности, напро
тив, значительно больше в модели
KMV
для всех рейтингов, не совпа
дающих с текущим рейтингом. Эти различия можно легко объяснить.
Во-первых, поскольку рейтинговые агентства не спешат менять при
писываемые рейтинги, исторические частоты сохранения рейтинга, как
правило, переоценивают фактическую вероятность сохранения кредит
ного качества. Во-вторых, средняя историческая вероятность дефолта
переоценивает фактическую вероятность дефолта для компаний из од
ного рейтингового класса. Это происходит в силу того, что каждый рей
тинговый класс включает группу компаний, которые имеют значитель
но большие вероятности дефолта, и, соответственно, их рейтинг дол
жен был быть понижен, но такого понижения рейтинга не происходило.
В-третьих, если вероятность сохранения в текущем рейтинговом классе
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
799
и вероятность дефолта очень велики, то отсюда следует, что вероятно
сти перехода должны быть малы.
Нет необходимости упоминать, что эти различия могут оказать зна
чительное влияние на значение границы потерь или других мер риска.
Таблица
7 .28.
Матрица перехода за год в модели
KMV,
построенная по непересекающимся интервалам
ранжирования ОЧД
Рейтинг через год,
Текущий
%
рейтинг
ААА
АА
А
ввв
вв
в
ссс
ААА
АА
А
ввв
вв
в
ссс
Дефолт
66,26
21,66
2,76
0,3
0,08
0,01
0,00
22,22
43,04
20,34
2,8
0,24
0,05
0,01
7,37
25,83
44,19
22,63
3,69
0,39
0,09
2,45
6,56
22,94
42,54
22,93
3,48
0,26
0,86
1,99
7,42
23,52
44,41
20,47
1,79
0,67
0,68
1,97
6,95
24,53
53
17,77
0,14
0,2
0,28
1
3,41
20,58
69,94
0,02
0,04
0,1
0,26
0,71
2,01
10,13
Исто-чник: Корпорация
Таблица
7.29.
KMV.
Матрица перехода за год, построенная по
фактическим изменениям рейтингов
Рейтинг через год,
Текущий
%
рейтинг
ААА
АА
А
ввв
вв
в
ссс
Дефолт
0,22
о
0,12
0,06
0,74
5,3
80,53
6,48
2,38
0,14
0,26
1,17
8,84
83,46
11,24
0,02
0,01
1,12
1
4,07
64,86
о
ссс
0,06
0,64
5,52
86,93
7,73
0,43
1,3
о
о
0,68
7,79
91,05
5,95
0,67
0,24
0,22
о
в
8,33
90,65
2,27
0,33
0,14
0,11
о
вв
90,81
0,7
0,09
0,02
0,03
ААА
АА
А
ввв
Исто-чник:
Standard & Poor's CreditWeek (15
0,06
0,18
1,06
5,2
19,79
апреля 1996г.).
Оценка долгового обязательства или займа с учетом риска
2)
дефолта
В
то
время
как
при
оценке
обязательств
в
рамках
модели
CreditMetrics
используются кривые форвардных ставок, ценообразова
ние в модели
KMV
строится иным образом и основано на модели риск
нейтрального ценообразования. В этом подходе цены рассчитываются
Гл.
800
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
как дисконтированная ожидаемая стоимость будущих платежей, а ма
тематическое ожидание вычисляется с использованием так называемых
риск-нейтральных, а не фактических вероятностей. Первые могут быть
получены из исторических данных или ОЧД, для более подробной ин
формации см., например,
[Jarrow,
Тurnbull
(1999),
гл.
5
и
6).
Оценка рисковых выплат осуществляется в два шага: на первом ша
ге оценивается безрисковая компонента, на втором шаге
-
компоненты,
подверженные кредитному риску. Например, рассмотрим ценообразо
вание бескупонного долгового обязательства с обязательным платежом
М в конце года Т
ной
(1 -
= 1,
с нормой восстановления в случае дефолта, рав
ДНС(Д)), где ДНС(Д)
-
доля невозвращенных при дефолте
средств. Тогда получим:
•
безрисковую компоненту М(1
ние которой
(PVRF)
-
ДНС(Д)), приведенное значе
оценивается с использованием кривой безрискового
дисконта
_ М(l -ДНС(Д))
RF(l+r)
'
PVi
где через
•
r
обозначена годовая безрисковая ставка процента.
рисковъ~е вътлатъ~, которые оцениваются с использованием риск
нейтрального подхода
PVQ = EQ (дисконтные рисковые платежи) =
М · ДНС(Д)(l
- Q)
l+r
где
математическое
ожидание
нейтральной вероятности
+О
·Q
вычисляется
с
использованием
риск
Q.
Текущая стоимость рискового бескупонного долгового обязатель
ства
(PV)
вычисляется как сумма текущих стоимостей безрисковой и
рисковой компонент:
Кредитный спред (КС) рассматриваемого долгового обязательства
мы находим, решая следующее уравнение:
М
· (1-ОЧД)
(l+r)
~~~~~~+
М
· ОЧД(l-Q)
М
=
.
(l+r)
l+r+KC
Откуда получаем:
КС= OЧД·Q·(l+r).
1-ОЧД·Q
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
801
Описанная выше методология оценки может быть обобщена на слу
чай серии рисковых выплат следующим образом:
или, если мы рассматриваем непрерывное время,
PV = (1 - ОЧД)
где через
Qi
риод времени
n
n
i=l
i=l
L ci exp(-fiti) + очд L(l - Qi)Ci exp(-fiti),
обозначена кумулятивная риск-нейтральная ОЧД за пе
ti, fi
= ln(l + ri),
а
Ci -
величина купона в i-м периоде
времени.
3)
Оценка портфеля долговых обязательств: аналитическое
решение на основании методологии
На основании методологии
KMV
KMV не моделируется вся функция рас
пределения стоимости портфеля через время Н. Вместо этого мы, делая
некоторые упрощающие предположения, получаем асимптотику функ
ции распределения убытков в любой момент времени за некоторый пе
риод Н. Среди них предположение о том, что сроки всех займов исте
кают в момент времени Н, а их номиналы равны одному доллару. Кро
ме того, предполагается, что все компании, из долговых обязательств
которых составлен наш портфель, оказываются в состоянии дефолта
с одинаковой вероятностью, т.е.
P({i = 1) = P({j = 1) = р, \/i,j, а
лог-доходности стоимостей активов одинаково коррелированы с корре
ляцией, равной р.
Обозначим через Vн,RF дисконтированную стоимость портфеля в
момент времени Н в предположении, что компания не оказалась в со
стоянии дефолта, а через
Vн -
стоимость портфеля в момент време
ни Н, которая определяется в соответствии с формулой
(7.24).
Тогда
убыток по портфелю в момент времени Н определяется как разность
между рисковой стоимостью портфеля и его рыночной стоимостью в
этот момент времени, т. е.
L
= Vн,RF -
Vн.
Предполагая, что портфель займов диверсифицирован, а число зай
мов
N,
его составляющих, стремится к бесконечности, получим, что
в рамках КМV-модели предельной функцией распределения убытков
портфеля будет обратное гауссовское распределение (см.
(1994)]).
[Johnson et al.
Таким образом, как граница потерь, так и другие меры риска
для портфеля с большим количеством кредитных позиций могут быть
Гл.
802
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
оценены относительно легко и без обращения к процедурам стохастиче
ского моделирования. Однако следует отметить, что все детали методо
логии
KMV не
раскрываются и неизвестно, как эта модель калибруется
по реальным данным.
4)
Корреляции в модели
KMV
Когда мы имеем дело с портфелем, составленным из большого коли
чества (например, тысячи) облигаций и займов, расчет корреляционной
матрицы с вычислительной точки зрения сопряжен с некоторыми труд
ностями оценивания. Для того чтобы их преодолеть, в методологиях
CreditMetrics
и
KMV
[Айвазян, Мхитарян
используется факторный анализ (см., например,
(2001),
п.13.3)). В частности, предполагается, что
доходности стоимостей активов компании формируются под влияни
ем следующих факторов: множества общих факторов (или факторов
систематического риска) и множества специфи-ческих факторов
(спе
цифических для компании факторов риска). Специфические факторы
могут быть свойственны отдельной компании, стране или отрасли, но
корреляция между лог-доходностями стоимостей активов от них не за
висит, поскольку специфические факторы не коррелируют как друг с
другом, так и с общими факторами. Корреляции лог-доходностей сто
имостей активов двух компаний объясняются только общими фактора
ми, воздействующими на эти компании.
Методологии
CreditMetrics
и
KMV довольно
схожи, и далее мы об
судим это более подробно. Однако они имеют два ключевых отличия:
•
модель для корреляции в методологии
KMV
использует стоимо
сти активов, тогда как факторная модель в методологии
CreditMetrics
использует курсовые стоимости акций;
•
в методологии
CreditMetrics
используются сочетания некоторых
отраслей и отдельных стран, тогда как в методологии
KMV
отрасли и
страны рассматриваются раздельно.
Как же в рамках методологии
KMV реализу~ся
го анализа? Лог-доходности стоимости активов
N
Ri
модель факторно
компаний
i
= 1, ... ,
за некоторый временной промежуток (обычно за один год) представ
ляются в виде:
(7.26)
или, если записать в матричной форме:
R= ,ВF'+z,
F =(F1, ... ,FN), Z =(Z1, ... ,ZN), F.LZ,
1
1
(7.26а)
803
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
-(
где ii- (N х 1) вектор лог-доходностей стоимостей активов, Р N х N)
диагональная матрица, F - (N х 1) вектор, содержащий составные об
щие факторы, а Z - (N х 1) вектор, содержащий специфические факто
ры. Построение о~щих факторов - крайне сложная задача, поскольку
каждый эл~мент
!;, представляет собой взвешенную сумму К основных
факторов, Ф 1 ... Ф к. Отметим, что модель
невой иерархической модели (рис.
KMV основана на трехуров
7.28):
• первъtй уровен'Ь: представляет факторы как систематического, так
и специфического риска для каждой компании;
• второй уровен'Ь: подразделяет факторы систематического риска
на отраслевые и страновые;
• третий уровен'Ь: отражает глобальную, региональную и сектори
альную специфику в представлении общих (систематических) факто
ров.
Риск компании
~
Систематический риск
Первый уровень:
~
Секториальный риск
Второй уровень:
Специфический риск
компании
Страновой риск
секториальный риск
Третий уровень:
Рис.
7.28.
Глобальный, реmональный и секториальный риск
Трехуровневая факторная структура корреляционной модели в
методологии
Поскольку
-
Fi
и
-
Zi
KMV
некоррелированы, то в предположении, что оба
этих случайных фактора имеют гауссовское распределение, они явля
ются независимыми. Лог-доходности~ коррелированы. Степень этой
коррелированности определя~тся составными общими факторами. По
следнее объясняет, почему
-часть~' тогда как
Fi
рассматривают как системати-ческую
zi можно рассматривать как случайный эффект,
свойственный компании
i.
Это разложение на систематическую и специ
фическую части соответствует первому уровню в трехуровневой фак
торной модели методологии
KMV.
Второму уровню соответствует разложение вектора составных об
щих факторов
F
на отраслевые и страновые факторы, характеризую-
Гл.
804
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
щие средУ, в которой функционируют компании:
Ко
К
Fi = LWi,kфk
k=1
+
L
Wi,kФk,
k=Ko+1
i = 1, ... ,N,
(7.27)
где параметры wi,k и Фk считаются заданными. При этом Ф1, ... , Фк0 это так называемые отраслевъtе индексъt, которые для компании i суммируются с весами Wi,1, ... , Wi,Ko; а Ф к0 +1, ... , Ф к - страновые индексы, которые для компании i суммируются с весами Wi,Ko+1, ... , wi,K.
Веса предполагаются неотрицательными для всех i, k и нормированны
ми в следУющем смысле:
Ко
К
LWi,k = L
Wi,k = 1.
k=1
k=Ko+1
(Ф1, ... , Ф к)', и подставляя (7.27) в (7.26а), мы
Обозначая Ф
получим следУющее:
- -- - {3WФ
- - + Z,-
R = {3F + Z =
где W
= (Wi,k)i=1, ... ,N;
(7.28)
k=1, ... ,к - матрица отраслевых и страновых весов
для компаний из рассматриваемого портфеля.
Наконец, третьему уровню соответствует представление отраслево
го и странового факторов в виде линейной комбинации независимъtх
общих факторов
f'1, f'2, ... , f' m:
м
Фk =
:L:: ьk,тгт + бk,
k=1,.",к.
(7.29)
m=l
Последний шаг осуществляется при помощи метода главнъ~х ком
понент
( МГК), примененного к отраслевым и страновым индексам.
Это делается скорее с точки зрения вычислительного удобства (найти
экономическую интерпретацию этим общим факторам обычно бывает
трудно). В векторных обозначениях мы получим:
(7.30)
где В = (Ьk,т)k:,1 •... ,к..i m=l, ... 1..M эффициентов, Г
факторов, а
(7.28),
_,
6 =
=
(Г 1, ... , Гм)
(81, ... , дк) -
матрица отраслевых и страновых ко
-
вектор главных компонент
-
вектор остатков. Подставляя
общих
(7.30)
в
мы получим
ii = ,8W(Bf' + 6) + Z.
(7.31)
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
805
После того как мы получили составной фактор, при п_омощи
{7.26)
можно легко вычислить коэффициент чувствительности !Зi для компа
нии
i,
а значит, может быть вычислена корреляция между лог-доход
ностями стоимостей активов. Рассмотрим стандартизированную вер
сию модели
(7.26):
где иl = D(~), Fi = Fi - µi, а zi = zi - µi. Корреляция между лог
доходностями стоимостей компаний i, j определяется соотношением
поскольку
Zi
предполагаются некоррелированными и независимыми от
общих факторов. Используя коэффициент детерминации
грессии
(7.26),
R 2 парной ре
который равен
{7.32)
мы можем упростить выражение для
и представить его в виде
p(Ri, R;)
(7.33)
поскольку D[.fii] = D[Fi]· Используя оценки коэффициентов уравне
ния {7.31), мы можем вычислить по формуле (7.33) оценку корреляции
лог-доходностей стоимостей активов. Если произвести стандартизацию
переменных уравнения
(7.31),
R
мы получим
= ~W(ВГ +б) + Z,
где~
- (N х N) матрица, полученная шкалированием
нального элемента в (3 множителем 1/ui, а
Е[Г] =О,
E[Z]
=О,
Е[б] =О,
Г .lб,
каждого диаго
Г .lZ.
Гл.
806
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Теперь, вычислив матрицу E[FF1 ], которая равна:
E[FF = [w(ВГ + б) (W(ВГ + 6))
1
]
1
]
=
=
w [(вг + б) ((ВГ + б))'] w' =
=
w
(вЕ[ГГ']в' + ВЕ[Гб1 ] + '-----v---""'
Е[б(ВГ)'] +
~
=0
(7.34)
=0
+ Е[66']) w' =
= w ( ВЕ[ГГ 1 ]В 1
+ Е[бб 1 ]) w''
мы можем, пользуясь формулой
(7.33),
вычислить корреляции лог
доходностей стоимостей активов.
Отметим, что в уравнении (7.34) матрица Е[ГГ 1 ] диагональна, по
скольку общие факторы ортогональны, с диагональными элементами
D[Г m]
(m = 1, ... , М), а Е[бб'] - диагональная матрица с диаго
нальными элементами D[бk] (k = 1, ... , К). Следовательно, вычис
ление корреляций лог-доходностей стоимостей акций в соответствии с
(7.34)
может быть существенно в случае, если известна матрица отрас
левых и страновых весов, дисперсии общих факторов (вычисленные для
стандартизированных случайных величин), дисперсии для отраслевых
и страновых стандартизированных остатков, коэффициенты отрасле
вых и страновых индексов относительно общих факторов. Пользовате
ли услугами компании
KMV
имеют доступ к такой информации, а зна
чит, можно использовать уравнение
(7.34)
для вычисления корреляции
лог-доходностей стоимостей активов, которое обеспечено инструмента
рием
KMV
под названием
полезно знать,
поскольку
GCorr.
Тем не менее формулы
(7.33)-(7.34)
они позволяют вычислять корреляции лог
доходностей стоимостей активов компаний, даже если информация об
этих компаниях не содержится в базе данных
5)
KMV.
Корреляционная КМV-модель: процедура оценивания
Факторы, используемые в модели
KMV,
наблюдаемы, поэтому упо
мянутые выше модели могут быть оценены по историческим данным
для каждого фактора и с использованием стандартной регрессионной
техники 34 . А именно, вся процедура состоит из следующих шагов.
•Чтобы извлечь отраслевые и страновые факторы, оценим коэф
фициенты регрессии для данных пространственного типа: зависимая
34 Это,
в частности, означает, что модель
(7.26} должна быть представлена для
7.4.
807
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
- лог-доходности стоимостей активов, независимые пере
менные - 45 страновых и 61 отраслевая фиктивные переменные.
•Отраслевые веса Wi,k в (7.27) вычисляются путем усреднения ак
переменная
тивов и продаж по каждому бизнес-направлению (БН), в котором осу
ществляет деятельность рассматриваемая компания
смотрим итальянскую компанию,
в двух бизнес-направлениях (табл.
Таблица
7.30.
i.
Например, рас
которая осуществляет деятельность
7.30).
Активы и продажи для разных БН
Бизнес-направление
Спортивные машины
Спортивные мотоциклы
Общее число
Активы,%
Продажи,%
40
60
100
30
70
100
Веса Wi,k вычисляются как среднее весов (измеряемых в
%)
для
каждого БН по активам и продажам. Таким образом, в этом примере
35% = (40+30)/2, а вес для спортив
65% = (60+70)/2. Страновые веса вычисляются
вес для спортивных машин равен
ных мотоциклов равен
похожим образом. После того как определены веса, можно построить
факторы
•
Fi.
_
Применим метод главных компонент к факторам
Fi
и вычис
лим 14 главных компонент Г m· Интерпертация полученных главных
компонент позволила разбить их на два глобальных фактора, пять
региональных факторов и семь отраслевых факторов. Этот шаг дела
ется главным образом для обеспечения вычислительного удобства реа
лизации моделирования методом Монте-Карло.
•Отраслевые и страновые коэффициенты Ьk,m в уравнении
(7.29)
вычисляются с использованием стандартной техники оценивания коэф
фициентов линейной регрессии.
• Составные факторы
Fi строятся с использованием ортогональных
факторов и весов Wi, k.
•После того как найдены составные факторы, оценим в линейном
регрессионном уравнении
коэффициент чувствительности
(7.26)
f3i·
Имея оценки всех параметров модели, можно оценить функцию
распределения убытков портфеля, а затем получить численную оценку
влияния различных факторов, представляющих систематический риск,
набора исторических данных в форме
R;t =
где
t -
PiЙt
+ zit, t =
1, ... , т,
номер такта времени, к которому «привязаны» наблюдаемые значения
(Ёi;t, Йt)· Это и позволяет нам оценивать коэффициент чувствительности
ках указанной выше модели парной регрессии k;t по Fit.
Pi в рам
Гл.
808
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
на убыток портфеля. Кроме того, можно использовать оцененную мо
дель
(7.26)
в различных сценарных расчетах (в так называемом стресс
тестировании).
6)
Корреляционная КМV-модель: имитационное
моделирование функции распределения убытков
портфеля
Функция распределения убытков портфеля вычисляется с исполь
зованием Монте-Карло-моделирования. Далее мы будем символом
«*»
сопровождать смоделированные случайные величины. Процедура мо
делирования состоит из следующих шагов:
• смоделируем ортогональные глобальные фак:оры f'1, ... ,Гм; в
результате получим М смоделированных значений Гi,
... , Гм;
•смоделируем ошибки в (7.29); получим б~, ... , бк; чтобы получить
страновые и секторальны~ индексы Фi,
ванные ошибки и Гi,
в
• чтобы
(7.27);
... , Гм
... , Ф:К,
в это уравнение;
смоделировать составной фактор
_
Fi,
•используя оценки параметров уравнения
подставим смоделиро
подставим Фi,
(7.27),
... , Фк
сгенерируем слу
чайный вектор лог-доходностей стоимостей активов; для этого из
N-
мерного нормального распределения со средним {ЗF и ковариационной
матрицей Е, элементы
Uij
которой определяются по формулам
(7.33), смоделируем N-мерный случайный вектор;
• повторим предыдущие шаги большое количество
(7.32)-
раз.
По смоделированным доходностям можно вычислить РД и ОЧД,
зная которые, можно оценить среднюю норму потерь портфеля. Од
нако ранее предложенный анализ для оценки функции распределения
убытков портфеля можно провести и с использованием рыночных сто
имостей портфеля.
7)
Эмпирические приложения с использованием
статистического пакета
GAUSS:
модель
KMV
с одним фактором
После того как была рассмотрена теория для общего случая, приве
дем простой прикладной пример модели
KMV
с одним фактором. Од
нофакторная модель широко используется на практике и дает вполне
адекватные результаты для многих портфелей. Она представима в ви
де:
~ = fЗiF + J1 - fЗlZi,
cov(Zi, Zj) = О, i =J j, cov(F, Zi)
F Е N(O, 1), Zi Е N(O, 1) 'v'i,
=О, 'v'i
7.4.
809
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
где
Ri - стандартизированные доходности стоимостей активов компа
нии i, f3i - коэффициент чувствительности, а F - систематический
фактор. В подходе стоимостей активов стандартный способ получения
функции распределения портфеля имеет следующую структуру.
•Смоделируем стандартизированные лог-доходности
Ri
для каж
дого заемщика в нашем портфеле (по построению они подчиняются
стандартному нормальному распределению).
•
Для каждого заемщика проверим, оказался ли он в состоянии
дефолта или нет, т. е. оказалась ли стоимость активов меньше некото
рого порога
di,
отвечающего заданной
Bi.
Если мы предположим для
простоты, что стоимости активов имеют стандартное нормальное рас
пределение, то di
=
Ф- 1 (Вi), где Ф- 1 обозначает обращение стандарт
ного нормального распределения. Если активы окажутся в состоянии
дефолта, определим значение ДНС(Д)i х ВНП(Д)i.
•
Сложим убытки всех индивидуальных заемщиков, входящих в
портфель.
•
Повторим описанные выше шаги достаточно большое количество
раз и получим функцию распределения убытков кредитного портфеля.
new;cls; et=hsec;
//Классы ВД
pd=seqa(0.01,0.01,5);
//Число моделирований
scenarios= 100000;
//Число заемщиков
number _ ob=lOOO;
//Матрица вероятностей переходов для всех заемщиков
//во всех моделированиях
pd _ all=pd. * .ones( number _ оЬ, 1);
//Инициализируем матрицу,
//составленную из убытков по портфелю
//для каждого моделирования
port _ all=zeros(scenarios, 1);
//Создадим цикл для вычисления смоделированного много
//раз убытка по портфелю (представленого в переменной
/ /'' scenarios")
for i(l,scenarios,1);
//Фиксированная ДНС(Д)
lgd _ all=0.45;
//Случайная ДНС(Д)
//LGD _all=rndbeta(l, 1,0.2,0.6);
/ /Невозвращенные при дефолте средства
//зафиксируем их на уровне 1000 $,
(для простоты
//но она может меняться случайным образом)
ead_all=lOOO*ones(rows(pd_all), 1);
//Коэффициент чувствительности beta _ i
//Фиксированный
beta_i=0.4;
Гл.
810
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
//Случайный (предположим, что он был оценен для каждой
//компании методом наименьших квадратов)
//beta_i=rndu(rows(pd_all), 1);
//Порог дефолта: для простоты будем использовать
//обращение нормального распределения для ВД
dt _ all=cdfni(pd). * .ones(number _ оЬ,1);
//Моделируем фактор
zz=rndn(l,1);
//Генерируем лог-доходности стоимостей активов
//для всех компаний
a_i_all = beta_i.*zz
+ sqrt(l-beta_iл 2 ).*rndn(rows(pd_all),
1);
//Убыток на займ
loss_i=lgd_all.*ead_all.*(a_i_all.<dt_all};
//Убыток портфеля
port _ loss=sumc(loss _ i);
port _ all[i, 1] =port _ loss;
endfor;
//Покажем эмпирическую функцию распределения портфеля
library pgraph; _pdate=O; xlabel("PORTFOLIO LOSSES'');
histp(port _ all, 100);
"Time requested to simulated the portfolio loss distribution
(in seconds)";
ht=hsec-et;ht/100;
"VaR 99 %"; quantile(port_all,0.99);
Величина смоделированной границы потерь 99%-ного доверитель
ного уровня должна быть близка к числу
327150 долл.,
а смоделирован
ная гистограмма убытков портфеля должна быть похожа на функцию
распределения, представленную на рис.
0.1
Рис.
7.4.17.
7.29.
0.3
0.4 o.s 0.6 0.7 0.8
Убытки по портфелю
0.9
х 1о"
Гистограмма убытков портфеля для однофакторной модели
Модель
CreditRisk+
0.2
7.29.
(далее
CreditRisk+
- CR+) -
это модель оценки и управления кредит
ным риском, разработанная в 1997г. банком
Credit Suisse [Credit Suisse
7.4.
(1997)].
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
811
Она может быть рассмотрена как актуарная модель, поскольку
при ее реализации используются некоторые методы управления риска
ми, а также алгоритмы, заимствованные из страхования. На основа
нии этой модели можно оценить функцию распределения убытков по
кредитному портфелю как для одногодичного, так и для многогодич
ного временного горизонта. В двух этих случаях доли дефолтов могут
рассматриваться либо в качестве детерминированных, либо в качестве
случайных величин.
1)
Информационное множество модели
Основная особенность этой модели состоит в том, что для нее требу
ется ограниченное и легко доступное информационное множество. Оно
состоит из следующих компонентов:
•
•
•
•
величины номинальных потерь при дефолте;
вероятности дефолта;
стандартных отклонений вероятностей дефолта;
норм восстановления.
Модель может управлять финансовыми инструментами различных
типов. Например, облигациями, займами, аккредитивами с гарантией
оплаты, деривативами. Каждый из этих инструментов имеет свою нор
му восстановления, что учитывается при оценке функции распределе
ния убытков по портфелю. Кроме того, если мы рассматриваем убыт
ки за несколько лет, то важно учитывать, что уровень ВНП(Д) может
меняться с течением времени. Более того, вероятности дефолта меня
ются от года к году, а финансовые организации могут использовать
свои собственные оценки, построенные на основании внутренних моде
лей прогнозов. Стандартные отклонения вероятностей дефолта могут
быть легко вычислены на основании временных рядов, характеризую
щих платежеспособность компании. Следует отметить, что более длин
ные временные ряды позволяют получить более надежные оценки стан
дартных отклонений, поскольку в этом случае учитываются эффекты
экономических циклов. Нормы восстановления могут быть получены
либо от специализированных рейтинговых агентств, либо вычислены с
использованием внутренних ресурсов финансовой организации.
2)
Основная модель с фиксированной долей дефолтов
В модели
•
CR+
делаются следующие предположения:
для займов вероятность дефолта за заданный период
за один год
-
-
скажем,
зависит только от длины периода и не зависит от
момента отсчета этого периода;
812
Гл.
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
для большого количества заемщиков вероятность дефолта хотя
бы одного из них мала, а число дефолтов, возникших за заданный
период, не зависит от числа дефолтов, возникших в любой другой
период.
В модели
CR+
не делается никаких предположений относительно
причин неплатежеспособности: заемщик А становится неплатежеспо
собным с вероятностью РА и остается платежеспособным с вероятно
стью
(1 -
РА). Таким образом, отправной точкой является бернуллиев
ская случайная величина с функцией плотности
f(x) = рА_(1- РА) 1 -х.
Учитывая эти предположения, можно показать, что число дефолтов
в портфеле имеет пуассоновское распределение (доказательство см. в
разделе §А2.1 методологии
[Credit Suisse (1997)]).
CR+ состоит в определении рекурсивного соот
Назначение модели
ношения, которое позволило бы легко оценить функцию распределения
убытков по портфелю. Для этого в
CR+
на первом шаге определяется
функция распределения количества дефолтов в портфеле. После это
го можно выписать рекурсивную формулу для функции распределения
убытков, связанных с дефолтами.
Чтобы получить функцию распределения убытков и уменьшить вы
числительную сложность, убытки (которые представляют собой чистый
убыток, полученный после корректировки с учетом нормы восстанов
ления) делятся на т групп, в каждой из которых уровень кредитного
риска характеризуется единственным числом.
Обозначения, используемые для каждой из этих групп, представ
лены ниже:
Указатель
Символ
Заемщик
А
ВНП(Д)
LA
Вероятность дефолта
РА
Ожидаемая ВНП(Д)
ЛА = LA х РА
Прежде чем представить вычисления, условимся считать, что в
некоторой базовой валюте выбрана единица измерения ВНП(Д), кото
рую обозначим через
vА
L.
Для каждого заемщика А определим числа Е:А
такие, что
Следовательно,
v А и Е: А -
это соответственно величина невозвра
щенных при дефолте средств и ожидаемый убыток, выраженные в еди
ницах
L.
7.4.
Пр им ер
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.11.
Предположим, банк имеет портфель, составлен
ный из займов и облигаций
няющимися от
813
50 ООО
различных заемщиков с ВНП(Д), ме
500
долл. до
1
млн долл. Пусть для первых шести
заемщиков ВНП (Д) составит следующие значения (табл.
Таблица
7.31.
ВНП(Д) для первых шести заемщиков
ВНП(Д)
Заем-
(в долл.)
щикА
Нормир. ВНП(Д)
(в
LA
100000 долл.)
Округленная нормир.
Группа
ВНП(Д)
j
Vj
(в
1
150000
460000
435000
370000
190000
480000
2
3
4
5
6
Единица
среднем равна
В модели
ВНП(Д)
В каждой группе
llj
или
100000 долл.)
1,5
4,6
4,35
3,7
1,9
4,8
измерения
= 100 ООО долл.
7.31).
j, j
100 ООО долл.
х
2
2
5
5
4
5
5
4
2
2
5
5
предполагается
= 1, ... , т,
llj
равной
где т
= 10,
L
=
ВНП(Д) в
j.
CR+ займы и облигации одной группы j
рассматриваются
как независимый портфель.
Введем следующие обозначения:
Символ
Указатель
Средняя ВНП(Д) в группе j, измеряемая в единицах
Ожидаемый убыток в группе
измеренный в единицах
j,
Ожидаемое число дефолтов в группе
j
= llj. µj,
е·
µj = ...1..
llj
Кроме того, ожидаемый (за год) убыток €j в группе
единицах
11J·
L
€j
µj
Тогда
€j
L
(7.35)
j, измеренный в
L, равен сумме ожидаемых убытков €А по каждому заемщику,
принадлежащему группе
j:
€j
2:
=
€А·
A:llA=llj
Пусть
µ - ожидаемое (среднее) суммарное число дефолтов в порт
феле за один год. Поскольку µ равна сумме ожидаемого числа дефолтов
в каждой из групп, то:
т
т
µ=l:µj=l:;.
j=l
j=l
J
(7.36)
Гл.
814
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Для анализа распределения числа дефолтов по всем рассмат
риваемым заемщикам в модели
водящей функции
F(z),
CR+
воспользуемся понятием произ
определяемой для любого действительного
z
выражением:
00
F(z) =
L znР(возникло п дефолтов).
n=O
Предполагая, что факт возникновения дефолта может быть опи
сан бинарной случайной величиной, имеющей распределение Бернулли,
можно показать справедливость следующего соотношения:
(7.37)
гдеµ= ЕРА·
А
Зная генерирующую вероятность функцию, можно найти вероят-
ность возникновения п дефолтов р( п), которая оказывается равной:
п - _!_ dnF(z) 1
- e-µµn
р( ) - п! dzn z=O - п!
Поскольку портфель разделен на т независимых групп, генериру
ющая вероятность функция для портфеля, составленного из всех рас
сматриваемых заемщиков, равна произведению генерирующих вероят
ность функций для каждой группы:
m
F(z) = П Fj(z) = е-Е~1щ+Е~1щz_
j=l
В качестве упражнения мы предлагаем показать, что сумма неза
висимых пуассоновских случайных величин также является пуассонов
ской случайной величиной, имеющей параметр, равный сумме парамет
ров пуассоновских распределений слагаемых.
По
аналогии
с
числом
дефолтов
убытков при дефолте в методологии
функция
CR+
распределения
описывается с помощью
производящей функции, которая в данном случае равна
00
G(z) =
L zn Р (агрегированные убытки = п х L).
n=O
Следовательно, получаем:
Gj(z) -
e-µ;+µzv;,
m
G(z)
п Gj(z)
j=l
'°'m
'°'m
v·
= e-L.....;=1Щ+L.....;=1µ;z
з.
(7.38)
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
815
Поскольку в разных группах ВНП(Д) различны, одни дефолты вле
кут большие убытки, чем другие. А значит, анализ убытка при дефолте
включает изучение двух компонентов случайности. Обозначив
(7.39)
получим:
G(z) =
eµ(P(z)-l) =
F(P(z)).
(7.40)
Последнее выражение позволяет выразить распределение агрегиро
ванного убытка с учетом двух источников случайности: пуассоновского
потока возникновения дефолтов и величины ВНП(Д).
Если известна производящая функция
разложением функции
G(z)
(7.38),
то, воспользовавшись
в ряд Тейлора, можно получить функцию
распределения убытка,
Р (убыток равен п х
1
L) = -11 d!"G(z)
d
= An.
n.
zn z=O
С помощью формулы Лейбница можно показать, что выполняется
следующее рекуррентное соотношение (доказательство см. в разделе
§А4.1 в
[Credit Suisse (1997))):
µ ·v · An-v; = """'
е · An-v;,
L..,, -1......1.
L..,, ...1.
An = """'
. /
п
. / п
3:v;.,,,,n
3: v;.,,,,n
(7.41)
где
m
Ао
3)
-L,µ;
= G(O) = F(P(O)) = е-µ = е ;= 1
m
е·
-L,~
= е ;= 1
3
Расширения базовой модели: неоднородность
односекторной доли дефолтов
Если мы предположим, что число дефолтов
-
случайная величина,
имеющая распределение Пуассона с параметром
µj, тогда ее стандарт
ное отклонение равно
VJii·
Однако анализ эмпирических данных пока
зывает, что пуассоновское распределение недооценивает эмпирическое
стандартное отклонение (см., например, работу
[Crouhy et al. (2000))
и ссылки в ней). Как отмечается в технических руководствах мето
дологии
CR+,
наблюдаемые вероятности дефолта весьма неустойчивы
с течением времени, даже в случае заемщиков, обладающих сравни
тельно высоким кредитным качеством. Эта неустойчивость может быть
Гл.
816
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
следствием изменчивости такого внешнего фактора, как состояние эко
номики, которое влияет на платежеспособность заемщиков. Например,
ухудшение состояния экономики может привести к неплатежеспособно
сти большинства заемщиков. Следовательно, пуассоновское распреде
ление не так сильно рассеяно, чтобы быть распределением, описываю
щим число дефолтов.
Одним из способов моделирования ситуаций, когда дефолты воз
никают в результате влияния неких общих факторов
это использова
-
ние смесей распределений. Оценка величины агрегированных убытков
по кредитному портфелю может быть вычислена при помощи следую
щей двухшаговой процедуры: на первом шаге из некоторого распределе
ния (в методологии
CreditRisk+
это гамма-распределение) моделирует
ся управляющий дефолтами внешний параметр. На втором шаге число
дефолтов моделируется с помощью условного распределения, при усло
вии того, что управляющий внешний параметр равен значению, смоде
лированному на предыдущем шаге (в методологии
CreditRisk+
это рас
пределение Пуассона с параметром, равным значению, полученному на
первом шаге).
В частности, следует отметить, что в методологии
CR+
управляю
щие внешние параметры измеряются для группы заемщиков из каждо
го сектора. Группа заемщиков из одного сектора подвержена влиянию
общих внешних факторов, определяющих число дефолтов. Например,
можно разделить всех заемщиков по страновой принадлежности. Для
удобства описания результатов при разделении заемщиков по секторам
в
CR+
вводятся новые обозначения: каждому сектору
Sk, 1 :::;; k:::;; n,
ставится в соответствие случайная величина Xk, равная числу дефолтов
в этом секторе, математическое ожидание которой обозначается через
µk, а стандартное отклонение
-
через Uk· Необходимые в дальнейшем
обозначения, с учетом разделения по секторам, приведены в табл.
Таблица
7.32.
7.32.
Необходимые обозначения, с учетом разделения по
секторам
Внутрисекторные характеристики
Базовая единица измерения ВНП(Д)
ВНП(Д) в единицах
L
Ожидаемая ВНП(Д) в каждой группе,
измеренная в единицах
L
Старое
Новое
обозначение
обозначение
L
L; = Lv;
1 ~j ~m
>.; = LE;
1 ~j ~m
1~
L
L}k> = Lv/k>
k ~ n; 1 ~ j ~ m(k)
>. ~k) = LE~k)
J
J
1 ~ k ~ n; 1 ~ j ~ m(k)
Математическое ожидание µk числа убытков в секторе
k
может
быть выражено через математические ожидания числа убытков в груп-
7.4.
пах
заемщиков,
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
входящих
в
этот
сектор,
или,
что
817
эквивалентно,
µk
представимо в виде суммы вероятностей дефолта по всем заемщикам
из рассматриваемого сектора, т. е.
mL:(k) g(k)
J
•
{7.42)
(k)'
j=l vj
LeA,
А VA
где ц
11А
= РА,
а РА -
(7.43)
вероятность дефолта заемщика А за рассматрива-
емый период.
Выражения
дологии
CR+
{7.42)-(7.43)
являются аналогами
(7.35)-(7.36).
В мето
фактическая вероятность дефолта заемщика А из рас
сматриваемого сектора моделируется как случайная величина, пропор
циональная Xk, математическое ожидание которой равно РА· Для то
го чтобы выразить эту зависимость, в методологии
CR+
определяется
случайная вероятность дефолта х А заемщика А:
еА
Xk
VA
µk
{7.44)
ХА=-·-,
где математическое ожидание ХА равно РА =
eA/VA.
Тогда стандартное отклонение случайной вероятности дефолта сре
ди заемщиков из сектора
k
равно сумме стандартных отклонений слу
чайных вероятностей дефолтов по всем заемщикам из этого сектора:
L иА = L еА
L еА
. Uk = Uk_.!._
= Uk·
А VА µk
µk А VА
А
Представив отношение Uk к µk как отношение суммы стандартных
отклонений случайных вероятностей дефолтов для каждого заемщика
из сектора
k
к сумме математических ожиданий этих вероятностей,
взвешенных с учетом их вклада в вероятность дефолта всех заемщиков
в этом секторе, получим:
-
~РА (~)
ЕРА
А
откуда следует:
Uk
=
µk · Wk,
где
Wk
=
~РА(~)
Е
РА
.
А
Распределение де.фолтов со случайными вероятностями дефолтов
рассчитывается по той же схеме, как и в случае фиксированных веро
ятностей дефолтов. Налагая условие
Xk =
х и используя соотношение
Гл.
818
(7.37),
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
можно выписать приближенное выражение для производящей
функции распределения числа дефолтов 35 :
(7.45)
Если мы предположим, что Xk имеет плотность
грировав
fk(x),
то, проинте
х), мы сможем найти безусловную производящую
Fk(zlxk =
функцию для распределения числа дефолтов:
J
00
Fk(z)
=
ex(z-l) fk(x)dx.
(7.46)
о
В модели
Г(аk,
f3k)
CR+
предполагается, что Xk имеет гамма-распределение
со средним
и стандартным отклонением
µk
ющую систему уравнений относительно
ak
и
Uk·
Решая следу
f3k
µk= ~
{
~
uk2 = 73'[
'
получаем требуемые параметры гамма-распределения
µ~
21
ak
f3k
(7.47)
uk
-
и2
_}f
(7.48)
µk
Подставляя аналитическое выражение плотности гамма-распреде
ления в
(7.46),
получим:
-!
00
Fk(z) -
е
x(z-1) е
1
_ _L
fJk xOtk-
fЗ:kг(ak) dx
о
(7.49)
- f3:k(1
где
Pk = f3k/(1
+
1
f3i; 1 -
( 1 - Pk )0tk
z)0tk 1 - PkZ
'
+ f3k)·
Разложив функцию
Fk(z)
в ряд Тейлора, найдем выражение для
вероятности р( п) возникновения п дефолтов в секторе
р
35 В
() (1 ) (n + 1)
n =
-pk Otk
ak п
k:
n
Pk·
данном приближенном представлении производящей функции Fk(zlXk = х)
подразумеваются взаимная статистическая независимость дефолтов заемщиков од
ного сектора и малость величины РА.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
819
Последнее распределение представляет собой отрицательное бино
миальное распределение.
Наконец, функция распределения числа убытков по всему портфе
лю определяется с помощью следующей производящей функции:
n
n ( 1~р: )ak
F(z) = П Fk(z) = П
k=1
1
k=1
Pk
Функция распределения числа дефолтов по всему портфелю в об
щем случае не является отрицательным биномиальным распределени
ем, а представляет собой смесь отрицательных биномиальных распре
делений по всем секторам.
Закон распределения убъtтков банка в резул:ьтате дефолтов заем
щиков со случайными вероятностями индивидуальных дефолтов опре
деляется
с
использованием
производящей
функции
распределения
убытков по портфелю, а именно функции:
00
G(z) =
L Р (агрегированные убытки= n х L)zn,
n=O
которая в силу предположения о независимости может быть также вы
ражена как произведение производящих функций по каждому из
n
сек
торов,
n
G(z) = П Gk(z).
k=1
Аналогично выражению
m(k) (
Pk(Z) =
(7.39)
ik>)
Е -1щ
j=l
,,,j
введем следующее обозначение:
(k)
z,,,j
---(-(-k)_)_
j~l :~k)
1 ~
= - L...J
µk j=1
(k) (
(k))
ej
(k)
z
,,,~k>
:J
•
(7.50)
llj
Тогда можно показать, что производящая функция распределения
убытков от заемщиков из k-го сектора является аналогом уравнения
(7.40):
(7.51)
Подобно тому, как это делалось в
(7.45),
можно выписать условную
производящую функцию распределения убытков, где каждый заемщик
А оказывается в состоянии дефолта с вероятностью ХА:
е
- ExA+ExAz"A
А
А
exk(Pk(z)-1).
=
ExA(z"A-1)
еА
=
~ Е ;л(z"А-1)
е k А
А
(7.52)
820
Гл.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Здесь мы воспользовались выражением
представлением
(7.50),
п
и альтернативным
выраженным в виде суммы по всем заемщикам,
принадлежащим сектору
k:
L: !дzVA
.Гk
(7.44)
( ) -
z -
А VA
"
L.J
А
-
!А
-
VA
-
1 ""'С:А VA
µk
(7.53)
L....J - z .
А
ZIA
Аналогично тому, как это делалось в случае функции распределе
ния числа убытков, воспользовавшись
(7.52),
можно найти безусловную
производящую функцию распределения убытков от заемщиков в сек
торе
k:
Наконец, если мы воспользуемся
(7.49),
(7.50)
и
(7.51),
подставив их в
и возьмем произведение полученных выражений по всем сек
торам, то получим:
n
n
G(z) = П Gk(z) = П
k=1
k=1
В руководстве к методологии
Suisse (1997)])
(7.54)
CR+
(см. приложение§
на основании выражения
(7.54)
AlO
в
[Credit
получено рекуррентное
соотношение для вычисления распределения убытков по портфелю, ко
торое мы коротко рассмотрим ниже.
Производящую функцию можно представить в виде многочлена
00
G(z) = LAnzn.
n=O
Продифференцировав обе части этого равенства, получим:
d(logG(z))
dz
1 dG(z)
G(z)
dz
A(z)
ао + a1z 1 + ... + arzr
- B(z) - Ьо + Ь1z 1 + ... + Ьrzr ·
Рекуррентное соотношение для коэффициентов многочлена
G(z)
имеет вид:
An+1 = Ь (
l
оп+
(min(r,n)
l)
L
aiAn-i ·о
i=
min(s-1,n-1)
L
·о
з=
)
Ьj+1(n - j)An-j .
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
821
Используя ранее полученные соотношения, выражение для произ
водящей функции, определенной в
енты
A(z)
и
B(z)
(7.54),
можно вычислить коэффици
с учетом того, что
A(z) B(z)
m(k) (k)
(k) -1
~ Е €- zv;
ILk
. l 3
3=
~~~~~~~~
m(k) E~k)
1-
&.µ
k
Е
.
3=
(k)
+,zv;
1 v.
3
Наконец, получаем распределение убытков. Заинтересованным чи
тателям мы рекомендуем ознакомиться с работой
[Melchiori (2004)],
в
которой подробно описан пример использования вышеуказанного ре
куррентного соотношения.
4)
Расширение базовой модели: несколько секторов
и распределение числа дефолтов зависит от случайных
внешних факторов
В наиболее общей версии модели
CR+ уже предполагается
наличие
нескольких факторов, объясняющих систематическую волатильность
распределения числа дефолтов в портфеле. Это предположение учиты
вается путем замены понятия «сектор» на понятие «систематический
фактор».
Рассмотрим
(7.52),
производящую
функцию
условного
распределения
которая представляет собой экспоненту в некоторой степени.
В схеме с несколькими секторами эта степень может быть представ
лена в виде:
где
бA,k --{О1 А~К
А Е К.
В расширенной версии модели
CR+
делается допущение о том, что
каждый заемщик подвержен влиянию более одного фактора. Чтобы
учесть этот факт, заменим дельта-функцию бA,k, задающую принад
лежность заемщика определенному сектору, весовой функцией:
n
lJA,k :
2::
k=1
lJA,k
= 1.
Гл.
822
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Веса () A,k определяют степень зависимости вероятности дефолта за
емщика А от воздействия фактора сектора
Таким образом, выражение
k,
к которому он относится.
преобразуется к виду:
(7.55)
где вклад заемщика А равен
(7.56)
В силу того что математическое ожидание ~ равно единице, мате
матическое ожидание х А равно РА = е А/ vА. Следовательно, выражение
(7.53)
заменяется на следующее:
Pk(z)
= _.!._ L
А
µk
()Ak
еА zvA,
VA
()
где µk = Е Ak ~, а математическое ожидание и стандартное отклоА
нение числа убытков по всем секторам равны сумме соответствующих
вкладов каждым из заемщиков в портфеле, взвешенных с помощью
функции
() A,k:
µk
-
L
()A,kµA,
А
O'k
L()A,kO'A·
А
5)
Методология
Creditrisk+
и быстрое преобразование
Фурье
Одним из недавно примененных подходов к оценке функции рас
пределения убытков является быстрое преобразование Фурье (БПФ),
в котором вместо производящей функции используется хшрактеристи
ческая. Основным преимуществом такой техники является ее вычисли
тельная эффективность в условиях больших портфелей заемщиков из
нескольких секторов. Более того, алгоритм, построенный по этой техни
ке, функционирует более быстро и устойчиво по сравнению со стандарт
ными алгоритмами, которые основаны на рекуррентных соотношениях,
или такими алгоритмами, как алгоритм Панжера для рекурсий (для
получения более подробной информации см. работу
ссылки в ней).
[Melchiori (2004))
и
823
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
Перед тем как перейти к более подробному изложению техники ис
пользования быстрого преобразования Фурье, опишем некоторые вспо
могательные функции, ассоциированные с распределением
f(x)
для
случайной величины Х, а именно: а) производящая функция; б) про
изводящая функция моментов; в) характеристическая функция.
В методологии
CreditRisk+
используется производящая функция,
но в этом параграфе мы применим инструмент характеристических
функций.
Пусть Х
-
неотрицательная дискретная или непрерывная случай
ная величина (или случайная величина смешанного типа). Пусть
f (х) -
плотность распределения случайной величины Х, т. е.:
f(x) = { Р(Х = х), если Х - дискретная случайная величина;
fxFx(x),
если Х - непрерывная случайная величина.
Как известно,
t-e
моменты случайной величины Х определяются
соотношениями:
Px(t) = E[xt] = {
если Х - дискретная с. в.;
L: xt fx(x),
J xtfx(x)dx,
если Х
- непрерывная с. в.
Производящая функция моментов и характеристическая функция
случайной величины Х определяются следующим образом:
• Производящая функция моментов Mx(t) случайной величины Х:
•
Характеристическая функция
<px(t)
также называемая преобра
зованием Фурье для случайной величины Х:
<px(t) = E[eitx] = Mx(it),
где i =
J=I -
мнимая единица.
Отметим, что функция плотности
f(x)
может быть восстановлена
по характеристической функции <р х (t) при помощи обратного преобра
зования Фурье (для более подробной информации см., например, рабо
ту
[Abramowitz, Stegun (1972)]).
Характеристическая функция отображает непрерывную плотность
функции распределения в пространство комплекснозначных непрерыв
ных функций. Преобразование Фурье, примененное к дискретной слу
чайной величине, будем называть б'Ьtстр'Ьt.М преобразованием Фурье
Гл.
824
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
(БП Ф). Оно отображает вектор, составленный из п действительных
чисел, в вектор, составленный из п комплексных чисел, т. е. являет
ся алгоритмом дискретного преобразования, что значительно снижает
вычислительную сложность.
Поскольку в стандартной методологии
CreditRisk+ мы имеем дело с
производящей функцией для дискретного распределения, то для полу
чения характеристической функции убытков целесообразно применить
технику быстрого преобразования Фурье.
Отметим
одно
Предположим, что
важное
N
и К
свойство
-
характеристической
функции.
независимые неотрицательные дискрет
ные случайные величины. Тогда характеристическая функция суммы
независимых случайных величин равна произведению характеристиче
ских функций случайных величин
В методологии
CreditRisk+
N
и К соответственно:
связанный с дефолтом суммарный убы
ток
Z равен сумме случайного числа N индивидуальных убытков (Х1,
Х2, ... , XN ). Характеристическая функция этого суммарного убытка
имеет вид:
<pz(t)
= E(eit(Z)) = EN(E(eit(X1+X2+ ... +XN)IN]) =
= EN(<px(t)N).
Благодаря удобному виду характеристической функции для сум
марного убытка БПФ может быть использовано для вычисления свер
ток: БПФ для суммы двух (или большего числа) независимых дискрет
ных случайных величин равно произведению БПФ этих случайных ве
личин.
Как мы видели ранее,
CreditRisk+
моделирует число дефолтов в
кредитном портфеле как сумму случайных величин, имеющих отри
цательное биномиальное распределение. Однако при расчете функции
распределения убытков по этому портфелю такой способ моделирова
ния не подходит, поскольку никак не учитывается зависимость между
величинами убытков.
В качестве отправной точки рассмотрим производящую функцию
моментов гамма-распределения Г( о, {З):
(7.57)
Теперь рассмотрим п дискретных случайных величин
Ni, N2, ... ,
Nn. Предположим, что существует такая случайная величина Xk с неко
торой плотностью f(x) и производящей функцией моментов Mxk, что
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
для любого фиксированного значения
ны
Njlx
Xk (Xk =
825
х), случайные величи
независимы и
(NjlXk
= х)
Е
Poisson (xµj),
j
= 1, 2, ... , п.
Тогда совместная условна.я производящая функция равна:
PN1,N2, ... ,Nn (t1, t2, ... 'tnlXk = х) =
= E[t{'\ ... , t~nlXk = х] = ex[µ1(t-1)+ ... +µn(t-1)J.
Однако случайные величины
Ni, N2, ... , Nn
коррелированны, по
скольку они зависят от общего случайного параметра
безусловна.я производящая функция для
Xk. Совместная
Ni, N2, ... , Nn равна
00
=/
ex[µi(t-l)+ ... +µn(t-l))
f(x)dx
= Mxk (µ1 (t - 1) + ... + µn(t - 1)),
о
где
Mxk (·) -
производящая функция моментов.
Учитывая, что
Xk
Е Г{а, {3), и используя выражение для ее произ
водящей функции
щую функцию
(7.57), получим совместную
для Ni, N2, ... , Nn:
PN1,N2,... ,Nn {t1, t2, · · ·, tn)
безусловную производя
- 1) + ... + µn(t - 1)) =
= [1 - f3µ1(t -1) + ... f3µn(t - 1)]-а. {7.58)
= Mxk (µ1(t
Перед тем как приступить к изложению алгоритма вычисления
функции распределения убытков по портфелю заемщиков из несколь
ких секторов, сделаем некоторое замечание относительно условной ве
роятности ХА дефолта заемщика А, которая возникала в
В работах
{7.44)
и
(7.56).
[Gordy {2000)), [Melchiori {2004)) эта условная вероятность
определяется следующим образом:
n
ХА= РА
2: 8A,kXk,
(7.59)
k=1
где случайная величина Xk имеет гамма-распределение со средним, рав
ным единице, и стандартным отклонением O"k. Сравнивая
легко
видеть,
Xk/ µk
в
(7.56)
что
эти
представления
эквивалентны,
с
(7.59),
поскольку
имеет гамма-распределение со средним, равным единице.
Однако представление
константа
два
(7.56)
1/µk,
(7.59)
более удобно, поскольку в нем отсутствует
нормирующая
Xk,
а значит, нет необходимости ее оце
нивать. Далее мы будем придерживаться именно этого представления.
826
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Анализ распределения убытков в модели
CR+
с помощью
ВПФ (случай одного сектора)
(7.47)-(7.48), при k = 1,
гамма-распределения Г(аk, f3k):
1.
Используя
вычислим оценки параметров
а2
/3k-- -k.
1
2.
Построим вектор размерности т (т
-
число групп заемщиков,
образованных при их разбиении по величине номинальных потерь, см.
пример
7.11),
на j-м месте которого стоит доля дефолтов в j-й группе
от общего числа дефолтов в кредитном портфеле:
3.
Вычислим БПФ для вектора, полученного на предыдущем шаге:
j
4.
= БПФ (f).
Применив формулу для производящей функции частот
(7.58),
получим вектор распределения числа дефолтов во всем портфеле:
5.
Применим БПФ для восстановления функции распределения ве
личины суммарного убытка по портфелю:
fz
= БПФ (f).
Если в нашем кредитном портфеле имеются заемщики из
симых секторов, тогда портфель необходимо разделить на
n
n
незави
подпорт
фелей для того, чтобы разбить заемщиков по категориям так, чтобы
учесть как систематический, так и специфический риски. В соответ
ствии с методологией
CR+ специфический риск влияет на число дефол
тов в отдельно взятом секторе, не связанных с воздействием системати
ческих рисков этого сектора, и он может быть диверсифицирован. По
скольку каждый сектор рассматривается как независимый портфель,
описанный выше алгоритм может быть применен к каждому такому
подпортфелю.
7.4.
827
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
Анализ распределения убытков в модели
CR+
с помощью
ВПФ (случай нескольких секторов)
1.
2.
Повторим шаги
1-4 предыдущего
алгоритма для всех п секторов.
Вычислим поэлементное произведение (умножение комплексных
чисел) п векторов, полученных на предьщущем шаге:
-
-
-
h = fz,1 · · · · · fz,n+1·
_ 3. Д.l!я того чтобы восс:ановить вектор вероятностей как
fz,1, ... , fz,n+1, применим к h обратную функцию для БПФ.
свертку
Так как при БПФ мы имеем дело с комплексными числами, конеч
ная характеристическая функция также будет иметь комплексные ко
эффициенты. А значит, для получения искомого вектора вероятностей
необходимо брать действительную часть. О сравнительном анализе раз
личных подходов в методологии
в работе
6)
CreditRisk+
читатель может прочитать
[Melchiori (2004)].
Эмпирические приложения в пакете
GAUSS: CreditRisk+
для трех секторов
Продемонстрируем технику БПФ на примере данных, взятых из
работы
[Crouhy et al. {2000)] (они представлены в табл. 7.33).
Таблица
7.33.
Информация о заемщиках
Группа
1
2
3
4
5
6
7
8
9
10
j
Число заемщиков
Ej
µj
30
40
50
70
100
60
50
40
40
20
1.5
8
6
25.2
35
14.4
38.5
19.2
25.2
4
1.5
4
2
6.3
7
2.4
5.5
2.4
2.8
0.4
/ / CreditRisk+ - торговая марка финасовых продуктов
//Credit Suisse.
/ / Данные брались из работы "А comparative analysis of
// current credit risk models",
828
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
/ / Michel Crouhy, Dan Galai, Robert Mark,
// Journal of Banking and Finance 24, (2000),
// sigma_k=0.5 как для сектора А, так и для
new;cls;
сектора В
//Определим размер вектора вероятностей
r=lO· n=2лr· x=seqa(O 1 n)·
'
'
' ' j'
//Установим число групп
m=lO; //j=l:m;
//Установим число секторов
sectors=З;
//Ожидаемое число дефолтов для каждой группы
j
mu=l.5,4,2,6.3,7,2.4,5.5,2.4,2.8,0.40;
//Интересующие уровни вероятностей для функции
/ / распределения убытков
percentiles=0.5,0. 75,О.95,О.975,О.99,О.995,0.9975,О.999;
percentiles=percentiles zeros(8,1);
//Установим стандартное отклонение для гамма-распределения
u=ones(sectors,1); sigma _ k=0.000001 I0.510.5;
//Секторные проценты
sector _percentage=zeros( m,sectors);
sector_percentage[.,1)=0.5*ones(m,1);
sector _percentage[l:m/2,2)=0.25*ones(m/2,1);
sector _percentage[m/2+ l:m,2)=0.5*ones(m/2,1);
sector_percentage[l:m/2,3)=0.25*ones(m/2,1);
//Инициализируем вектор для произведения БПФ
conv _fft=ones(n,1);
for k(l,sectors,1);
//Вычисление вектора числа вероятностей числа дефолтов
/ / в портфеле
severity=zeros(n,1);
severity[l)=O;
severity[2:m+ l)=mu. *sector _percentage[.,k)/
sumc( mu. *sector _percentage[. ,k));
//Вычисление БПФ
tt=zeros( n, 1);
tt=ffti(severity);
//Вычисление параметров гамма-распределения
alfa=u[k,l)л2./sigma_k[k,l)л2;
beta=sigma_k[k,l).л2./u[k,1);
//Применим безусловную производящую функцию
//частоты и перемножим полученные комплексные числа
conv _ fft=conv _ fft. *( ( 1-sumc(mu. *sector _percentage[ .,k). *beta) *(tt-1)).
л-alfa);
endfor;
//Вычислим БПФ
cr=real(fft(conv _fft)); mean=sumc(x.*cr); 11 Mean 11 mean;
sd=sqrt(sumc(((x-mean).л2).*cr)); 11 SD 11 sd; cr_acum=cumsumc(cr);
//Вычислим квантили функции распределения убытков
for i(l,rows(percentiles),1);
j=l;
do until cr_acumUJ .>= percentiles[i,1);
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
829
j=j+l;
endo;
percentiles[i,2]= j;
endfor;
''Квантили:" уровни вероятностей;
//Изобразим функцию распределения убытков
library pgraph; _pdate=O; xlabel("PORTFOLIO LOSSES");
ylabel("Frequency"); xtics(0,1000,100,1);
ytics(-0.002,0.0l,0.002,1); xy(x,cr);
Среднее, стандартное отклонение и квантили функции распределения убытков должны быть равны:
Mean: 176.98605 SD: 48.761539
Quantiles:
0.50000000 173.00000
0.75000000 207.00000
0.95000000 266.00000
0.97500000 288.00000
0.99000000 315.00000
0.99500000 335.00000
0.99750000 354.00000
0.99900000 378.00000
График искомой функции распределения убытков приведен на рис.
7.30.
Частота
с
~r---т----т~....---.----..---.---.-~...--т----.
~,___.___._~...___.___...___.__._~.....___.___,
q О 100 200 300 400 500 600 700 800 900 1ООО
Убытки по портфелю
Рис.
7.30.
Функция распределения убытков по портфелю, полученная на
основании методологии
7 .4.18.
Модель
на в
Методология
CreditRisk+
с использованием БПФ
CreditPortfolioView
CreditPortfolioView (далее - CPV) впервые была представле
работах [Wilson (1997а, 1997Ъ)]. CPV представляет собой доволь-
Гл.
830
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
но гибкую многофакторную эконометрическую модель, используемую
в качестве достаточно точного инструмента измерения и контроля кре
дитного риска. Основная идея этой модели заключается в следующем:
моделируются совместные распределения числа дефолтов и миграцион
ных вероятностей в различных рейтинговых классах, странах, промыш
ленных секторах в зависимости от основных макроэкономических ин
дикаторов. Моделирование такого рода базируется на предположении
о том, что состояние экономики значительно влияет как на вероятно
сти дефолтов, так и на миграционные вероятности переходов из одного
рейтингового класса в другой. Существует множество подтверждений
тому, что спад в экономике обычно приводит к увеличению числа слу
чаев снижения рейтингов и банкротств (см., например, работу
et al. (2000)]
1)
[Crouhy
и ссылки в ней).
Базовая модель методологии
CreditPortfolioView:
CreditPortfolioView Macro
Целью этого раздела является описание того, как с помощью моде
ли
CPV Macro
определять вероятность дефолта заемщиков из разных
промышленных секторов. В начальной версии модели
CPV вероятность
дефолта заемщика из j-го сектора в момент времени
t определялась с
использованием логит-функций:
1
Pj,t = 1 + e-Y;,t'
где
(7.60)
условная вероятность дефолта заемщика в момент времени
Pj,t -
t, принадлежащего j-му промышленному сектору (j = 1, 2, ... , К), а
}j,t - значение макроэкономического индикатора j-го сектора в момент
времени t, который строится как взвешенная сумма прошлых и текущих
значений основных макроэкономических факторов:
(7.61)
Здесь (Xj,1,t, Xj,2,t, ... , Xj,M,t) сектора
j
ванном
j),
в момент времени
t,
вектор значений регрессоров для
а
Vj,t - случайная величина, имеющая
нормальное распределение с нулевым средним и дисперсией иJ. Пред
полагается, что случайные величины Vjt независимы по t (при фиксиро
а ковариационная матрица
не зависит от
t,
Ev вектора Vt
= (vн, V2t, ... , Vкt)'
так что
Vt Е N(O; Ev)·
36 3начения
весов fJ;,o, fJ;,1, ... , fJ;,м предполагаются заданными.
7.4.
В работе
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
[Wilson
{1997а)] предполагается, что каждый макроэконо
мический фактор описывается одномерной моделью
ХJ,i,
· ·t
где е j,i,t
-
831
= "'·о
,,,,, +
AR{2):
"'·
· · t - 1 + "'·
· · t - 2 + еJ,i,
· ·t'
,,,,, 1ХJ,i,
,,,,, 2ХJ,i,
(7.62)
случайная величина, имеющая нормальное распределение с
нулевым средним и дисперсией и;, для i = 1, ... 'м.
Поскольку ej,i,t,
i = 1, ... , М, предполагаются независимыми (по t),
получаем следующее:
где et -
вектор-столбец размерности
матрица размерности
(М
{1
х М), а ЕЕ
-
ковариационная
х М). Таким образом, суммируя все предпо
ложения, получаем следующую систему уравнений:
где
P;,t
-
Xj,i,t
-
1
1 + e-Y;,t'
f3j,O + f3j,1Xj,1,t + f3j,2Xj,2,t + · · · + fЗj,MXj,M,t + Vj,t,
1'i,O + 'l'i,IXj,i,t-1+1'i,2Xj,i,t-2 + ej,i,t,
i = 1,2, ... ,м, aj = 1,2, ... ,к.
Определим
Et
как случайный вектор-столбец размерности
+М), компоненты которого Et. =
где Е
-
вектора
[:.]
v
и
1х
(К+
et:
Е N(O; I:),
матрица размерности (К+ М) х (К+ М), определяемая сле
дующим образом:
а
Ev,E, EE,v -
соответствующие межковариационные матрицы.
При условии, что оценки всех параметров рассматриваемой модели
известны, мы можем использовать представление матрицы Ев форме
разложения Холецкого,
Е = АА',
на основании которого смоделируем распределение вероятности дефол
тов Pj,t. Используя нижнетреугольную матрицу А и смоделированный
из многомерного стандартного нормального распределения случайный
вектор,
Zt
Е
N{O; 1),
получим смоделированное значение вектора
По смоделированным значениям вектора
Et
Et.
получим смоделирован
ные вектора ошибок Vj;t и ej,i,t, которые могут быть использованы для
Гл.
832
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
получения вектора смоделированных значений: вероятностей: дефолтов
Pt = (p1,t,P2,t, ... ,рк,t)· При использовании так называемого алгорит
ма сдвига этот смоделированный: вектор вместе с переходными без
условными вероятностями, отвечающими моменту времени
t,
позволя
ют смоделировать условную переходную матрицу.
Перед тем как приступить к описанию этого алгоритма, коротко
рассмотрим модификацию СРV-модели, предложенную через несколь
ко лет после появления базовой: СРV-модели.
2)
Модифицированная модель:
CreditPortfolioView Direct
Модель
CreditPortfolioView Direct является модификацией: базовой:
модели CreditPortfolioView Macro. Она была предложена в 2001 г. кол
лективом специалистов компании McKinsey37 . Ее основной: целью яв
лялось получение более простой: калибровки модели по сравнению с
калибровкой:
CPV Macro.
модели CPV Direct
В
вектор вероятностей: дефолтов Pt = (P1,t,
P2,t, ... ,Рк,t) может быть напрямую получен из многомерного гамма
распределения.
Параметры гамма распределения определяются для каждого секто
ра
j
(см.
методом моментов подобно тому, как это делалось в модели
(7.47)-(7.48)).
CR+
Неизвестно, как оценивается корреляционная матри
ца многомерного гамма-распределения в этой: методологии, но, скорее
всего, это делать проще, чем оценивать модель
CPV Macro.
Отметим,
что поскольку вероятности гамма-распределения принимают ненулевые
значения только для положительных действительных аргументов, тео
ретически может случиться, что смоделированное значение
ся больше
1,
Pj,t
окажет
а это значение, очевидно, не может интерпретироваться
как вероятность. В некоторой: степени это должно напомнить нам об
аналогичной: проблеме нескольких дефолтов одного заемщика в рамках
методологии
CreditRisk+.
Однако на практике такие сценарии малове
роятны и обычно они отбрасываются.
Наконец, после того как смоделирован вектор вероятностей: дефол
тов, при помощи алгоритма сдвига мы можем вычислить матрицу ве
роятностей: условных переходов38 .
37 Интересно,
что исходная документация, в которой описывалась эта модель, в
Интернете более на является общедоступной.
38 Под условным переходом понимается вероятность
перехода заемщика из одной
категории в другую при условии, что заемщик принадлежит определенному сектору
j.
7.4.
3)
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
833
Алгоритм сдвига
В методологии
CPV
для каждого сектора
j
на основании матрицы
вероятностей: безусловных переходов (полученной: от специализирован
ных агентств,
-
например, от агентства
S&P's
или
Moody's)
и с ис
пользованием одного из двух описанных выше методов моделируется
матрица вероятностей: условных переходов в момент времени
t
и веро
ятность дефолта заемщика.
Обозначим через
Mt = (msh)
переходов в момент времени
t,
матрицу вероятностей: безусловных
где
s, h
могут меняться от
1
до
8,
по
скольку число рейтинговых классов равно восьми: ААА, АА, А, ВВВ,
ВВ, В, ССС и дефолт. Так как состояние дефолта является поглощаю
щим, мы положим mвj =О, при
При заданном векторе
j = 1, ... , 7,
и mвв
Pt = (P1,t,P1,t, ... ,рв,t)
= 1.
алгоритм сдвига со
стоит из двух шагов.
1.
На первом шаге вычисляется так называемый индекс риска Tj,t:
Tj,t
Pj,t
= -=--'
Pj
т
где Pj - ~ Е Pj,t - безусловная вероятность дефолта заемщика
t=l
из j-го сектора. Если индекс риска больше единицы, т. е. экономика находится в состоянии рецессии, тогда матрица вероятностей:
условных переходов поправляется таким образом, чтобы увели
чить вероятности возникновения дефолтов и вероятности пони
жения рейтингов и при этом уменьшить вероятности повышения
рейтингов. В случае экономического подъема поступаем проти
воположным образом. Поправка должна быть больше для заем
щиков из нижних рейтинговых классов, поскольку считается, что
их чувствительность к экономической цикличности больше, чем у
заемщиков из верхних рейтинговых классов.
2.
На втором шаге вычисляется матрица вероятностей: условных пе
реходов для каждого сектора в момент времени t, м~Л
где
j = 1, 2, ... , К. Общий: вид элементов
тора j определяется следующим образом:
этой: матрицы для сек
s,h=l,2, ... ,8,
где а?~
= (m~~),
(7.63)
- коэффициентъ~ сдвига, которые должны калибровать
ся пользователем методологии
CPV.
Вычислив сумму элементов
Гл.
834
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
произвольной строки матрицы мр>' получим:
8
8
"""
(j) -L....J msh
8
(j)
- 1) """
L....J a.sh
( rз,t
.
h=1
+ """
L....J ffish·
h=1
h=1
Следовательно, учитывая, что сумма элементов в каждом рядУ
матрицы мр> должна быть равна единице и Е~= 1 тsh = 1, имеем:
8
L:a.~~ =о.
h=1
3.
Если правая часть выражения
(7.63)
оказывается отрицательным
числом, то алгоритм корректирует это значение, присваивая соот
ветствующей миграционной вероятности нулевое значение. Кроме
того, предполагается, что коэффициенты сдвига должны удовле
творять следУющим условиям:
a.sh ;;;:: О
4.
ДЛЯ
S
<h
И
a. 8 h ~ О
ДЛЯ
S
> h.
Таким образом, мы получим К матриц вероятностей условных пе
реходов в момент времени
t
(по одной матрице в каждом секторе).
Более того, мы можем следовать той же процедУре при вычисле
= (р1,t+1,Р2,н1, ... ,рк,t+1) и получить К обусловленных
матриц М~ 1 на момент времени (t + 1). Если умножить мр> на
М~~ 1 , получим матрицу вероятностей миграции из одного рейтин
нии Pt+l
гового класса в другой для фиксированного сектора
времени
Подход
j
на момент
(t + 1).
макромоделирования,
описанный
только одно смоделированное значение для
Pt,
выше,
рассматривает
получаемое при един
ственной симуляции шоков Vj,t и с j,i,t. Этот процесс должен моделиро
ваться большое количество раз (например,
сгенерировать
100 ООО
оценок
Pt
и
100 ООО
100 ООО
раз, что позволит
возможных матриц вероятно
стей условных переходов). Тогда эти смоделированные матрицы перехо
дов мр> можно использовать вместо матриц вероятностей безусловных
переходов, построенных по историческим данным. Например, при фик
сированном текущем рейтинге отдельно взятого займа (скажем, ВВ)
функция распределения стоимости этого займа, построенная по макро
скорректированным переходным вероятностям из матрицы мр>, может
быть использована для рассчета ГП на один год вперед. Обобщения на
случай больших портфелей займов осуществляются подобно тому, как
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
835
это делалось в методологии
рассматривать как подход,
CreditMetrics. В этом смысле CPV можно
дополняющий CreditMetrics, с помощью ко
торого удается преодолеть некоторые смещения в результате предполо
жения о статичности или стационарности переходных вероятностей 39 .
4)
Эмпирические приложения с использованием пакетов
GAUSS
и
STATA: CreditPortfolioView
Финансовые компании могут столкнуться с двумя типами возмож
ных ситуаций:
•
компания обладает достаточно полной информацией относитель
но каждого сектора
j, кредитованием которого она занимается. На ос
новании этой информации можно вычислить вероятности дефолтов за
емщиков в зависимости от сектора, к которому они принадлежат;
•
компания обладает ограниченной информацией, на основании ко
торой невозможно вычислить вероятности дефолтов заемщиков из каж
дого рассматриваемого сектора. Такая ситуация весьма распространена
в малых финансовых организациях, которые занимаются кредитовани
ем небольшого числа заемщиков.
В первом случае, предполагая, что Vt и
стема уравнений
(7.60)-(7.62)
et
некоррелированны, си
может быть оценена методом наименьших
квадратов с использованием логит-преобразования
Yj,t = 1n
Таким образом, уравнение
ров. Если же Vt и
et
(
Pj,t )
·
1- Pj,t
(7.61)
линейно зависит от своих парамет
коррелированны, для оценки параметров следует
воспользоваться либо методом максимума правдоподобия, либо иными
методами (например, обобщенным методом моментов).
Во втором случае невозможно осуществить анализ по секторам, по
этому модель
(7.60)-(7.61)
следует использовать без деления заемщи
ков по принципу секторальной принадлежности. Следовательно, эта
модель может интерпретироваться как логит-модель. Однако следует
отметить, что совместное моделирование
(7.60)-(7.62)
нетривиально и
труднее обрабатывается. Этим можно объяснить ограниченное исполь
зование моделирования такого типа.
Ниже мы рассмотрим обе эти ситуации: в первой ситуации пара
метры уравнений
(7.60)-(7.62)
оцениваются для каждого сектора
j;
во
второй ситуации мы имеем дело с панелью малых и средних предпри
ятий (МСП).
39 Отметим,
компании
что полная информация об этом подходе является собственностью
McKinsey
и не распространяется свободно в сети
Internet.
Гл.
836
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
new;cls;
//Мы предположим, что ошибки процессов авторегрессии
//коррелированы, но независимы от ошибок логит процесса. Мы сделали
//такой выбор в пользу упрощения, поскольку оно позволяет нам исполь
/ /зовать для оценки параметров модели метод наименьших квадратов.
/ / Напомним читателю, что это становится невозможным, если ошибки
/ / логит-модели коррелированы с ошибками процессов авторегрессии:
//в этом случае следует использовать иные методы оценки параметров
//модели. Например, метод максимума правдоподобия.
//Для того чтобы измерить величину отклонений оценок параметров
//от их фактических значений, мы предлагаем читателю произвести
//небольшое количество симуляций методом Монте-Карло для коррели
/ /рованных ошибок.
/ / ======Моделирование данных из
scenarios=lOOO; //Число сценариев Т
генер. процесса=========
//Фактическая ковариационная матрица
vcov=0.11 0.07 0.00,
0.07 0.09 0.00,
0.00 0.00 1.14;
//Вычислим разложение Холецкого
c_ chol=chol(vcov)';
//Вычислив ошибки для всех сценариев,
//мы получим составленную из них матрицу размером
err _ term
3
на Т
=с_ chol*rndn( cols( vcov) ,scenarios);
//Транспонируем эту матрицу ошибок
err _ term=err _ term ';
//Инициализация временных рядов
n
х_
l=zeros(scenarios, 1);
х _ 2=zeros(scenarios,1);
logit_p=ones(scenarios,1)*-5;
//Сгенерируем временные ряды для макрофакторов
x_l and
AR(2)
for i(3,scenarios,1);
x_l[i)= 0.1 + 0.4*x_l[i-1) - 0.2*x_l[i-2) + err_term[i,1);
x_2[i)= 0.1 + 0.5*x_2[i-1) - 0.3*x_2[i-2) + err_term[i,2);
logit_p[i) = -3 - 0.9*x_l[i) + 0.3*x_2[i) + err_term[i,3);
endfor;
х_2
//из процесса
//С использованием логит-функции вычислим вероятности
/ / дефолтов и изобразим их графически
pd=l/(l+exp(-logit_p)); library pgraph;_pdate=O;
ylabel(''Probabllity of Default"); ху( seqa(l,1,rows(pd)) ,pd);
//================Процесс оценивания================
//Мы оценим три маргинальные модели с использование МНК.
//Еще раз подчеркнем, что это возможно только в предположении, что
//ошибки логит процесса не зависят от других ошибок.
//Создадим лагированные переменных для макрофакторов.
//
Создадим пропущенные наблюдения. Можно поставить
//на месте пропущенных значений нули, либо "выбросить"
//эти пропуски.
reg_xl=lagn(x_l,1) lagn(x_l,2);
reg_x2=lagn(x_2,1) lagn(x_2,2);
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
837
//Оценим параметры модели методом наименьших квадратов
{naml,ml,Ы,stЫ,vcl,stdl,sigl,cxl,rsql,residl,dbwl}=
= ols(O,x_l,reg_xl);
{nam2,m2,b2,stb2,vc2,std2,sig2,cx2,rsq2,resid2,dbw2}=
=ols(O,x _ 2,reg_ x2);
{nam _p,m _p, b _p,stb _p, vc _p,std _p,sig_p,cx _p,rsq_p,resid _p,dbw _р }=
= ols(O,logit_p,x_l х_2);
На рис.
7.31
дано графическое представление смоделированных ве
роятностей дефолта для сектора
j,
а в табл.
таты трех вариантов оценивания модели
7.34 представлены
(7.60)-(7.62).
резуль
Вероятность дефолта
d..--~~~~~~~~~~~
"'
.:)
100 200 300 400 500 600 700 800 900 1ООО
Время
Рис.
7.31.
Таблица
Смоделированные вероятности дефолтов для сектора
7.34.
Результаты трех вариантов оценивания
модели
VariaЫe
Estimate
(7.60)-(7.62)
Prob
Х2
0.086
0.354
-0.169
Standard
Error
0.012
0.031
0.031
t-value
7.432
11.315
-5.418
...
.. .
.. .
...
.. .
...
.. .
.. .
.. .
.. .
.. .
.. .
VariaЫe
Estimate
Standard
Error
0.010
0.030
0.030
t-value
8.505
16.411
-9.649
.. .
...
.. .
.. .
.. .
...
CONSTANТ
Xl
CONSTANТ
Xl
Х2
...
...
. ..
j
0.089
0.498
-0.293
...
. ..
...
>ltl
О.ООО
О.ООО
Standardized
Estimate
-
Cor. With
Dep. Var.
-
О.ООО
0.354
-0.169
0.302
-0.062
.. .
.. .
. ..
. ..
. ..
. ..
...
. ..
. ..
Prob
Standardized
Estimate
Cor. With
Dep. Var.
-
-
О.ООО
0.498
-0.293
0.385
-0.101
...
. ..
. ..
...
.. .
...
. ..
...
. ..
>ltl
О.ООО
О.ООО
Гл.
838
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Таблица
VariaЫe
tIONSTAm
Xl
Х2
Estimate
-3.005
-0.916
0.260
Standard
Error
0.036
0.130
0.136
Prob
t-value
-83.239
-7.052
1.906
>ltl
0.057
(окончание)
Standardized
Estimate
О.ООО
О.ООО
7 .34
Cor. With
Dep. Var.
-
-
-0.300
0.081
-0.244
-0.127
Во второй ситуации мы рассмотрим временной ряд, составленный
из
1000
наблюдений по
318
МСП за период с
1996 г.
по
2004
г. Исполь
зуем два финансовых коэффициента и два макрофактора (ВВП и
месячную процентную ставку). Переменная
Solvency
12-
информирует ана
литика относительно того, оказалась ли та или иная компания в состо
янии дефолта или нет. В целях безопасности информация относительно
названий МСП и финансовых коэффициентов не раскрывается.
Перед тем как использовать возможности пакета
STATA,
удосто
верьтесь, что в нем установлена GLLАММ-библиотека. Инсталлировать
этот пакет можно при помощи следующей команды:
net install gllamm, replace
Для получения более подробной: информации см. вебсайт
w-w. gllamm. org.
*Задание пространственных переменных и временных рядов
tsset id years
*Оценка логит-функции при помощи команд библиотеки GLLAMM.
gllamm solvency finratiol finratio2 macrol macro2, i(id) l(logit) f(Ьinom)
number of level 1 units = 999
number of level 2 units = 318
Condition Number = 6209.3743
gllamm model
log likelihood = -247.17223
solvency
finratiol
finratio2
macrol
macro2
- cons
Coef.
-2.592
1.029
0.150
-0.364
-15.986
Std.Err
1.473
1.822
0.067
0.231
7.424
z
P>lzl
-1.760
0.570
2.220
-1.570
-2.150
0.078
0.572
0.026
0.116
0.031
Variances and covariances of random effects
***level 2 (id)
var(l): 2.995е-18
(9.672е-10)
(95% Conf.
-5.479
-2.541
0.018
-0.817
-30.536
Interval)
0.295
4.600
0.281
0.090
-1.435
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
Если мы хотим смоделировать случайный
нашем случае
Solvency), то для
мандой gllasim:
gllasim solvency_simul
839
(random)
отклик (т. е. в
этого мы можем воспользоваться ко
Смоделированные отклики будут сохранены в
solvency_ siтиl.
Пе
реоценив модель с учетом смоделированных откликов, мы получим:
gllamm solvency finratiol finratio2 macrol macro2, i(id) I(logit)
number of level 1 units = 999 number of level 2 units = 318
Condition Number = 6253.9837
gllamm model
log likelihood = -265.1514
solvency
finratiol
finratio2
macrol
macro2
- cons
Coef.
-3.086
1.560
0.168
-0.464
-17.554
Std.Err
1.587
1.928
0.063
0.219
7.046
z
P>lzl
-1.940
0.810
2.640
-2.120
-2.490
0.052
0.418
0.008
0.034
0.013
f(Ьinom)
[95% Conf.
-6.197
-2.219
0.043
-0.893
-31.363
Interval]
0.026
5.338
0.292
-0.036
-3.745
Variances and covariances of random effects
***level 2 (id)
var(l): 2.366е-24
7.4.19.
(9.461е-13)
Сравнительный анализ многомерных моделей
кредитного риска
В пунктах
7.4.15-7.4.18 были
представлены основные особенности неко
торых наиболее известных многомерных моделей кредитного риска. На
первый взгляд эти модели представляются весьма разными, что, как
кажется, приводит к несовпадению сгенерированных убытков и оценок
границ потерь (ГП). Однако аналитически и эмпирически эти модели
не столь различны, как это кажется вначале. Подтверждения струк
турного сходства даны в работах
(1998)], [Crouhy et al. (2000)].
В табл. 7.35 представлены
[Gordy (2000)], [Koyluoglu, Hickman
семь характеристик, по которым осу
ществлено сравнение описанных ранее многомерных моделей кредитно
го риска. В первой части этого пункта мы сравним четыре рассмотрен
ные выше модели по этим семи характеристикам, выделив их ключевые
отличия и сходства. Вторая часть посвящена сравнительному анали
зу качества моделей с точки зрения точности оцен.иван.ия различных
характеристик кредитного риска, основанного на этих моделях.
Гл.
840
Таблица
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
Сравнительный анализ различных многомерных
7 .35.
моделей кредитного риска
Сравниваемые
CreditMetrics
(J. Р. Morgan)
CreditPortfolioView
Корреляция
Многомерное
кредитных
событий
характеристи-
CreditRisk+
(CSFP)
KMV
(Moody's)
Факторный
Предположе-
Многомерное
нормальное
анализ
корре-
ние о независи-
нормальное
распределе-
ляции остаточ-
МОСТИ или учет
распределе-
ного риска
корреляции
ние
(McКinsey)
ки
ние
для
цен
с
ожидаемой
активов
цен
ДЛЯ
активов
вероятностью
дефолта
Кредитные со-
Кредитная ми-
Кредитная
Случайная ве-
Расстояние
бытия
грация
миграция,
роятность
ДО
обусловленная
фолта
де-
дефолта:
структурная
и
макроэконо-
эмпирическая
мическими
задолженность
факторами
Необходимые
Историческая
Матрица пере-
Вероятности
данные
матрица
ходов,
дефолтов
ходов,
пере-
кредит-
макро-
Цены активов,
и
кредитные
экономические
волатиль-
спреды,
реляции,
ные
спреды
переменные,
ность,
и
кривые
макро-
кор-
кредитные
факторы,
фактическая
доходности,
спреды,
НВП(Д),
задолженность
НВП(Д),
НВП(Д),
фактическая
корреляции,
фактическая
задолженность
фактическая
задолженность
задолженность
Численные ме-
Моделирование
тоды
или
Моделирование
Аналитическое
Аналитическое
решение
решение
Случайные
Постоянные
Постоянные
Макроэкономи-
Ожидаемые
Стоимость
вероятности
тивов
аналити-
ческий подход
Нормы восста-
Случайные
или случайные
новления
Определяющие
Стоимость
риск факторы
тивов
Волатильность
Постоянная
ак-
ческие
факто-
ры
дефолтов
Цикличная
Переменная
ак-
Переменная
кредитных
событий
1)
Сравнение моделей по их ключевым структурным
свойствам
(а) Корреляция кредитных событий. Структура корреляции
во всех четырех моделях может быть соотнесена с систематическими
связями кредитов и ключевых факторов-детерминант. Сходства детер
минант корреляции кредитного риска будут рассмотрены ниже (см.
п. (е)).
(б) Кредитные события. Если наблюдаются какие-либо измене
ния, связанные с кредитоспособностью, отвечающей некоторому дол
говому обязательству, то говорят, что произошло кредитное событие.
В методологиях
CreditMetrics и CreditPortfolio View кредитное событие
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
841
возникает в случае рейтинговой миграции. Тогда как в методологии
KMV (Moody's)
кредитное событие отвечает изменению расстояния до
состояния дефолта, что влечет изменение вероятности дефолта. Хоро
шо известно, что изменения рейтингов отстают от изменений вероят
ности дефолта (см., например,
[Crouhy et al. (2000)]
и ссылки в этой
работе). Таким образом, кредитные события возникают чаще, чем в
CreditMetrics и CreditPortfolioView. Аналогичные проблемы характери
зуют CreditRiskPlus, в которой кредитные события эквивалентны со
стоянию дефолта. Однако изменения распределения частоты дефолтов
можно рассматривать как ухудшение кредитного качества.
(в) Необходимые данные. Рассмотренные четыре модели отли
чаются в том, какие данные в каждой из них используются для оценки
мер кредитного риска. Переходные матрицы, оцененные по историче
ским
данным,
являются
основным
входным
параметром
для
CreditMetrics и CreditPortfolioView. В отличие от этих моделей в мето
дологии CreditRiskPlus оценка долей дефолтов строится на основе дан
ных о дефолтах. В результате последнюю методологию можно исполь
зовать для оценки кредитных рисков розничных портфелей. В методо
логии
Moody's KMV
требуется временной ряд цен следующих ценных
бумаг: безрисковой облигации, облигации актива и котировка акции
актива. Нет необходимости говорить о том, что эта информация может
быть доступна не для всех активов. Все модели используют величи
ну номинальных потерь при дефолте. Наконец, в
требуется корреляция цен активов, в
CreditMetrics и KMV
CreditPortfolioView оценивается
корреляция стоимостей активов с использованием некоторых общих
макроэкономических факторов риска, а в методологии
CreditRiskPlus
корреляции вычисляются с использованием вероятностей дефолта при
заданных макроэкономических факторах.
(г) Численные методы. Величина оценки границы потерь или
иных мер риска может различаться в зависимости от используемой мо
дели. Например, при использовании методологии
CreditMetrics
ГП мо
жет быть вычислена аналитически как для отдельного кредитного зай
ма, так и для портфелей кредитных займов. Однако этот подход пере
стает быть привлекательным по мере того, как число займов в портфе
ле растет. Как результат, для аппроксимации функции распределения
убытков по большим портфелям займов используется техника симуля
ционного моделирования, после чего вычисляется граница потерь. Ана
логично, в методологии
CreditPortfolioView
используются техника си
муляционного моделирования для генерации макроэкономических шо
ков и аппроксимации функции распределения убытков по портфелю
кредитных займов при заданной переходной матрице для кредитных
рейтингов. В методологии
CreditRisk+
делаются предположения, поз-
Гл.
842
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
воляющие получить аналитическое выражение для плотности функции
распределения убытков. В КМV-модели также можно получить анали
тическое решение для плотности функции распределения убытков.
(д) Нормы восстановления. Функция распределения убытков и
граница потерь зависят не только от вероятности дефолта, но также
от ВНП(Д) и НВ. Эмпирические данные свидетельствует о том, что
ВНП(Д) и НВ весьма волатильны во времени, а это увеличивает гра
ницу потерь или другие меры риска.
CreditMetrics,
в контексте вычис
ления границы потерь, допускает возможность изменения во времени
норм восстановления. В частности, предполагается, что нормы восста
новления имеют бета-распределение, а граница потерь портфеля вы
числяется при помощи симуляционного моделирования. В КМV-модели
нормы восстановления предполагаются постоянными во времени. Одна
ко в недавних модификациях этой модели нормы восстановления также
полагаются случайными величинами, имеющими бета-распределение.
В методологии
CreditPortfolioView
нормы восстановления моделиру
ются из бета-распределения. Однако в методологии
CreditRisk+
нор
мы восстановления в подпортфелях предполагаются постоянными во
времени.
(е) Определяющие риск факторы (драйверы
CreditMetrics и KMV основаны на модели мертоновского типа,
марные
активы
компании
и
их
волатильность
драйверами риска дефолта. В методологии
являются
риска).
где сум
ключевыми
CreditPortfolioView
драйве
рами риска являются такие макроэкономические факторы, как инфля
ция, ВВП, кредитные спреды и т.д.). В
ры риска
-
CreditRisk+,
напротив, драйве
средний уровень риска дефолта и его волатильность. Если
все рассмотренные четыре модели выразить в терминах многофактор
ных моделей, то мы увидим некоторое сходство (см.
ссылки в ней). В частности, изменчивость стоимости
Metrics
и
KMV
[Gordy (2000)] и
активов в Credit-
моделируется как величина, напрямую связанная с ка
питализацией. Корреляции между доходностями, построенными по це
нам активов, капитализация отдельных компаний подвержена влиянию
совокупности факторов систематического риска (секторальные факто
ры, страновые факторы и др.) и факторов несистематического риска.
Систематические факторы риска вместе с их корреляциями определяют
доходности активов компаний и дефолтную корреляцию между компа
ниями. Драйверы риска в
с тем, что мы имеем
CreditPortfolioView имеют похожие основания
для CreditMetrics и KMV. В частности, совокуп
ность систематических макроэкономических факторов и несистемати
ческих (или идиосинкратических) макроэкономических шоков управля
ет риском дефолта и корреляцией между рисками дефолтов заемщиков,
принадлежащих однородной рыночной среде. Ключевой драйвер риска
7.4.
в
CreditRisk+ -
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
843
изменчивая средняя доля дефолтов в экономике. Эта
средняя доля дефолтов может быть ассоциирована с состоянием эконо
мики,
поскольку, когда состояние экономики ухудшается, средняя до
ля дефолтов обычно увеличивается, растет и величина убытков. Улуч
шение экономических условий имеет противоположный эффект. Таким
образом, драйверы риска во всех четырех рассмотренных моделях кор
релируют в определенной степени с макроэкономическими факторами,
описывающими меняющиеся экономические условия.
(ж) Волатильность кредитных событий. В рассмотренных ме
тодологиях оценки кредитного риска моделируется вероятность дефол
та в течение ближайшего года. В
CreditMetrics
вероятность дефолта
(увеличение/уменьшение кредитного рейтинга) оценивается по исто
рическим данным. В КМV-методологии ожидаемая частота дефолтов
связана с волатильностью рыночной капитализации компании. В ме
тодологии
CreditPortfolioView
вероятность дефолта
-
логистическая
функция от макроэкономических факторов и шоков, имеющих нор
мальное распределение. По мере изменения макроэкономического по
ложения вероятность дефолта и переходные матрицы будут меняться.
В
CreditRisk+
вероятность дефолта каждого отдельного займа предпо
лагается изменчивой; число дефолтов за фиксированный интервал вре
мени описывается пуассоновским распределением со случайным сред
ним, имеющим гамма-распределение. В зависимости от параметров
гамма-распределения можно обеспечить возможность того, что функ
ция распределения убытков может иметь хвосты, тяжелее хвостов рас
пределения, полученного в соответствии с методологиями
или
CreditMetrics
CreditPortfolioView.
Общий взгляд на сравнение структурных свойств моделей.
Международная ассоциация по свопам и деривативам
народный институт финансов
(IIF)
опубликовали в
(ISDA) и Между
2000 г. результаты
совместного проекта, направленного на тестирование моделей измере
ния кредитного риска в
25
коммерческих банках из
10
стран. Банки
различались по своему размеру и специализации. В этом совместном
исследовании четыре модели
Risk+
и
(CreditMetrics, CreditPortfolio View, Credit
KMV's Portfolio Manager) сравнивались с внутренними моделя
ми, примененными к стандартизированным портфелям, сформирован
ным так, чтобы охватить четыре рынка: р'Ынок корnоративнь~х облига
ций и займов, р'Ынок займов компаний среднего размера, р'Ынок иnоmе'Ч
нь~х об.язателъств и рынок розни'Чных кредитов. Ниже представлены
наиболее важные выводы этого исследования40 .
40 Полный
ке
текст совместного IIF /ISDА-исследова.ния можно приобрести по ссыл
http://www.isda.org,
основные результаты представлены и рассмотрены в работе
844
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
Модели дают весьма близкие результаты, когда используются од
•
ни и те же входные данные.
Имеющиеся расхождения возникают в результате различия во
•
входных параметрах, технике обработки, оценки, ошибок исполь
зования моделей в процессе тестирования, а также неадекватности
моделей при использовании стандартизированных параметров.
Наиболее существенные отличия могут быть объяснены различи
•
ями в методах оценки и процедурами вычисления корреляции.
Наиболее значимыми драйверами риска являются кредитное ка
•
чество, корреляция активов и величина номинальных потерь при
дефолте.
Внутренние модели основаны на использовании скоринговых ме
•
тодологий, при которых агрегируются меры дефолта (но не от
дельные вероятности дефолта и (или) кредитные миграции).
В
работе
[Crouhy et al. (2000)) сравнивается методология
CreditMetrics и CreditRisk+ с KMV и внутренней моделью CIBC's
(Canadian lmperial Bank of Commerce), которую называют Credit VARl.
Изучая диверсифицированный портфель, составленный из более чем
1800
облигаций, номинированных в
13
различных валютах, с широким
спектром кредитного качества и сроков до погашения, авторы обнару
жили, что неожиданные убытки оказываются в довольно узкой полосе
возможных значений.
В работе
[Gordy (2000))
показано, что все рассмотренные модели
кредитного риска структурно похожи,
но различия между этими мо
делями состоят в предположениях относительно функций распределе
ния и функциональных форм. Например, в методологии
CreditMetrics
вероятности дефолта предполагаются обусловленными ~уровнями от
сечки~, отвечающими переходным матрицам, оцененным по историче
ским данным, и макроэкономическими факторами. Аналогично в ме
тодологии
CreditRisk+
вероятность дефолта обусловлена исторически
ми данными по макроэкономическим факторам. Однако невозможно
игнорировать влияние предположений относительно функций распре
делений и оценок параметров на результаты модели. В методологии
CreditMetrics
предполагается, что макроэкономические факторы име
ют нормальное распределение, тогда как в
CreditRisk+ средняя частота
возникновения дефолтов за фиксированный интервал времени описы
вается гамма-распределением. В связи с этим в
но, что ограниченная форма методологии
[Allen et al. (2003)).
[Gordy (2000)) показа
CreditMetrics дает значения
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
845
неожиданных убытков приблизительно равное значению, полученному
в соответствии с методологией
CreditRisk+,
а волатильность O'k для
средней доли дефолтов за заданный интервал равна соответствующей
исторической волатильности. Однако для экстремально больших зна
чений волатильности средней доли дефолтов неожиданные убытки для
этих двух моделей существенно различаются.
В работе
[Koyluoglu, Hickman (1998)]
впервые упоминается про важ
ность свойств оценок параметров модели при оценивании кредитного
риска. Показано, что в случае, когда оценки параметров несостоятель
ны, модели дают значимо разные результаты. В работе
(2002)]
[Koyluoglu et al.
показано, что значимые различия в оценках границ потерь воз
никают, главным образом, в результате использования несостятельных
оценок параметров и неправильной спецификации модели. В частности,
потенциальными источниками несостоятельности являются дефекты в
калибровке ожидаемой доли дефолтов, норм восстановления, ВНП(Д)
и корреляций активов. Например, используя одни и те же данные, в
методологиях
тивов, чем в
CreditMetrics и KMV получаем большие корреляции ак
CreditRisk+, что обеспечивает большую величину грани
цы потерь. Эти различия возникают как результат возникновения в
CreditRisk+
тенденции переоценивать фактическую волатильность де
фолтов. В работе
[Koyluoglu et al. (2002)]
дается рекомендация сегмен
тировать портфель и переоценивать модели кредитного риска незави
симо для каждого подпортфеля. В этом случае, как показали авторы, в
оценках границы потерь имеются меньшие различия меж.цу моделями,
чем в случае, когда рассматривается весъ портфель.
Авторы
[Diaz, Gemmill (2001)] опираются на работу [Koyluoglu,
Hickman (1998)] и несколько расширяют ее результаты. Они показали,
что для портфелей с низким кредитным качеством миграционный риск
играет несущественную роль, поскольку для экстремальных значений
на хвостах важна только информация относительно дефолтов. Следо
вательно, в этом случае проблема выбора модели менее актуальна. Но
следУет отметить, что
CreditRisk+
оказывается значительно быстрее
при решении задачи вычисления резервного капитала. С другой сторо
ны, если целью является оценка резервного капитала для внутренних
целей, тогда модели, основанные на кредитных миграциях (например,
CreditMetrics),
обеспечивают значительно большую информацию отно
сительно источников убытков.
Замечание по поводу определения кредитного риска. В раз
ных моделях используются различные входные параметры и, соответ
ственно, различные способы оценки кредитного риска. В так называ
емых МТМ-моде.л.ях (к которым относится
CreditMetrics)
допускается
возможность ухудшения или улучшения кредитного рейтинга (отдельно
Гл.
846
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
выделен рейтинговый класс, отвечающий состоянию дефолта), на осно
вании которого определяются убытки/доходы по выданным займам и
рассчитываются резервы. В DМ-.моделях, к которым относятся
Risk+
и
KMV,
Credit
допускается только два состояния: дефолт и недефолт.
Ключевым отличием МТМ-моделей от DМ-моделей является включе
ние риска кредитной миграции, или риска изменения спреда. Однако
риск спреда также включает в себя риск изменения кредитных спредов
для заданной рейтинговой категории. Таким образом, изменение в стои
мости кредитного портфеля может быть результатом:
(i) возникновения
дефолтов в портфеле;
(ii) изменений кредитного качества
миграции); (iii) изменений кредитных спредов,
(например,
рейтинговой
которые не
вызваны изменением кредитного качества.
МТМ-модели учитывают первые два из вышеперечисленных ком
понентов, влияющие на стоимость портфеля долговых обязательств,
тогда как третий компонент отвечает уже рыночному риску (модель
CreditPortfolioView
может быть реализована и как МТМ-, и как DМ
модель).
2)
Сравнительный анализ качества многомерных моделей,
бэктестирование
Теперь попытаемся дать ответ на вопрос, насколько точные оценки
дают эти модели. Например, в работе
[Nickell et al. (2001)]
впервые пред
ставлен сравнительный анализ точности оценок кредитного риска для
портфелей, составленных из большого количества еврооблигаций, но
минированных в долларах, с использованием методологий
и
KMV.
CreditMetrics
В этой работе показано, что обе эти методологии значимо недо
оценивают кредитный риск портфеля еврооблигаций.
Задача бэктестирования является особенно важной для оценки ка
чества моделей кредитного риска. Поскольку обычно кредитные риски
оцениваются на один год вперед, то это сильно ограничивает количество
наблюдений для тестирования модели. Например, если мы рассмотрим
стандартизированный подход из Базельского соглашения, то нам необ
ходимо будет дожидаться
250
лет для того, чтобы получить столь же
много наблюдений, как в стандартных процедурах бэктестирования для
моделей рыночного риска. Однако существует способ выхода из этого
затруднительного положения. Если мы не будем ограничиваться только
экстремальными событиями, а рассмотрим прогнозируемую функцию
распределения убытков в целом, то мы сможем изучить качество моде
ли оценки кредитного риска с использованием наблюдений за период в
пять или десять лет.
а) Тест Берковица. Среди многих процедур, предложенных для
тестирования качества оценки функции распределения, рассмотрим
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
847
тест Верковица, который является достаточно мощным инструментом
тестирования как для моделей оценки кредитного риска, так и для мо
делей рыночного риска (см.
[Berkowitz (2001)]
и
[Frerichs, Loffier (2003)],
где представлены некоторые свойства этого теста). Основное внимание
в этом тесте уделяется
качеству аппроксимации всего распределения
убытков. В этом тесте дважды преобразовываются наблюдаемые убыт
ки:
1.
Заменим
Lt
(фактические убытки в момент времени
t)
значением
прогнозируемой функции распределения убытков в точке
Lt,
а
именно:
Lt
Pt =
Jf(и)dи
= F(Lt)·
-оо
Если мы используем корректную модель оценки кредитных рис
ков в терминах функции распределения убытков, то временной
ряд наблюдаемых вероятностей
Pt
должен отвечать реализации
н.о.р.с.в., имеющих И(О, !)-распределение. Это преобразование
впервые было представлено в работе [RosenЫatt
(1952)].
Более то
го, это свойство справедливо вне зависимости от функции рас
пределения убытков портфеля долговых обязательств, и даже в
условиях, когда эта функция распределения меняется во времени.
2.
К сожалению, тестирование гипотезы о независимости и одина
ковой распределенности случайных величин, имеющих равномер
ное распределение, представляется довольно громоздким в силу
ограниченности области определения равномерного распределе
ния. Используя обращение гауссовской функции распределения,
преобразуем
Pt
в
Zt
следующим образом:
Это простая модификация преобразования Розенблатта, и она
позволяет нам использовать тесты на гауссовость.
В работе
[Berkowitz (2001)]
предлагается тестировать гипотезы о ну
левом среднем и единичной дисперсии для
можно тестировать нормальность
(zt),
Zt.
Дополнительно к этому
но известные нам тесты на нор
мальность не очень мощны в условиях, когда имеется малая выборка
наблюдений.
Удобным и достаточно мощным тестом проверки сложной гипоте
зы о нулевом среднем и единичной дисперсии является тест отношения
правдоподобия. Можно показать, что для некоторых классов моделей
Гл.
848
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
тест отношения правдоподобия является равномерно наиболее мощным:
т. е. тест отношения правдоподобия имеет большую мощность, чем лю
бой другой тест. Кроме того, даже когда этот тест нельзя считать рав
номерно наиболее мощным, он часто имеет желаемые статистические
свойства даже в условиях малых выборок (более детальное описание
см.
[Hogg, Craig (1965),
р.
253-265)).
В общем виде тест имеет следующий вид. Предположим, существу
ет переменная
которая может помочь спрогнозировать
Xt-1,
Zt.
Тогда
мы можем записать:
Zt = /Зо + /З~Хt-1
+ U{t,
{t
rv
i.i.d. N(O, 1).
Логарифмическая функция правдоподобия для выборки, состав
ленной из Т наблюдений, может быть записана в виде:
lnL(,8o,,81,u2 ) = -
~ In(21r)- ~ Jn(u2 ) -
t
((zt -
/Зо ~ ~i'Xt- 1 ) 2 ).
и
t=2
Для получения оценок вышеуказанной линейной регрессии мы можем
использовать метод наименьших квадратов:
fio, fil, 0-2. Статистика теста
логарифма отношения правдоподобия имеет вид:
LR = -2 ln L(O, О, 1) (
А
А
ln(/Зo, /31, а
2))
rv
2
Хк+2,
где степени свободы для х 2 -распределения зависят от числа компонент
вектора
/31
равного К. Если относительно выбора
Xt-1
нет определен
ности, тогда приемлемым может быть выбор лаговых значений
качестве предиктора
Zt.
В работе
[Berkowitz (2001)]
Zt
в
показано, что если
это допускает размер выборки, то в качестве предикторов можно также
включать лаговые значения
zl и (или) Zt в степенях больших, чем 2.
Этот тест можно использовать как для измерения качества оценки
рыночного риска для портфеля фондовых активов, так и для оцен
ки качества кредитного риска для портфеля долговых обязательств.
В последнем случае, при ограниченном числе наблюдений Т, наилуч
шей практикой является тестирование гипотезы о {30 = О и и 2 = 1 без
использования
Xt.
В этом случае LR-статистика будет иметь асимпто
тически хн-квадрат-распределение с двумя степенями свободы.
6)
Тест Берковица в условиях малых выборок. Однако мы
не можем полагаться на вышеупомянутые асимптотические свойства
в условиях малых выборок. Один из способов разрешения этой про
блемы
-
моделирование критических значений в предположении, что
модель прогнозирования корректна. Если мы повторим этот процесс
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
849
большое количество раз, то мы получим смоделированное распределе
ние тестовой статистики, которое можно использовать при проверке
гипотез по актуальным данным.
Таким образом, в нашем случае мы можем смоделировать
Pt
из рав
номерного распределения, взять от них обратную функцию для гауссов
ского распределения. Далее, вычислим статистику отношения правдо
подобия. Для удобства поместим в табл.
7.36 критические значения для
различных Т и вероятностных уровней а, полученных по функции рас
пределения LR-статистики, построенной по смоделированным
100 ООО
симуляциям (см. также пример эмпирического анализа в пункте г)).
Таблица
7.36.
Критические значения для теста Берковица
в условиях малых выборок
а
5
лет
6
лет
7
лет
8
лет
9
лет
10
лет
15
лет
20
лет
Асимптотические
значения
0,1
0,05
0,01
5,68
7,39
11,26
5,44
7,11
10,85
5,31
6,91
10,53
5,19
6,77
10,39
5,12
6,68
10,26
5,08
6,63
10,20
4,90
6,39
9,77
4,83
6,27
9,70
4,61
5,99
9,21
Однако следует высказать некоторые слова предостережения. При
симуляции критических значений в соответствии с представленной вы
ше процедурой мы предполагаем, что фактическая функция распреде
ления убытков и прогнозируемая плотность, используемые для преоб
разования непрерывны. Хотя это предположение, как правило, адекват
но в случаях крупных банковских портфелей, составленных из тысяч
кредитных займов, но оно не вполне корректно в случае небольших
портфелей. В последнем случае модель при нулевой гипотезе должна
отвечать предположению о дискретном распределении убытков: напри
мер, можно смоделировать
(Lt)
из структурной КМV-модели с задан
ной вероятностью дефолта и корреляцией активов. Затем воспользо
ваться эмпирической функцией распределения для того, чтобы вычис
лить
Pt
(первый шаг в преобразовании Берковица).
Учет кросс-секционной информации с использованием под
портфелей. Выше был представлен тест Берковица применительно к
распределению убытков по всему портфелю долговых обязательств, что
дает возможность проверить корректность некоторых предположений
в среднем. Однако, модель для всего портфеля может давать агрегиро
ванный прогноз, который согласуется с фактическими данными даже
в условиях, когда предположения не соответствуют какой-то отдельной
части долговых обязательств в портфеле. Для одних заемщиков корре
ляции активов могут быть довольно большими, тогда как для других
заемщиков корреляции могут быть малыми. Если эти ошибки усредня
ются по всему портфелю в целом, то тест вряд ли даст свидетельства
о неправильной спецификации. С другой стороны, тест для некоторых
Гл.
850
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
подпортфелей обнаруживает неправильную спецификацию модели, по
скольку она влечет неадекватную оценку убытков по этому подпортфе
лю: например, мы можем сгруппировать заемщиков в две группы оди
накового размера, где подпортфель
1 включает заемщиков
а подпортфель 2 включает заемщиков
с большей
корреляцией активов,
с меньшей
корреляцией активов. Затем мы вычисляем прогноз функции распреде
ления убытков по каждому из этих подпортфелей и преобразовываем
наблюдаемые убытки по подпортфелям так, как мы это делали выше.
Очевидно, что не существует универсального правила формирова
ния подпортфелей. Хорошая стратегия формирования подпортфелей
такова, что разница между спрогнозированными рисками для каждого
из подпортфелей максимальна. Во многих ситуациях это легко разре
шаемая задача для специалистов-практиков. Для наглядности, мы рас
смотрим двумерный случай, но такая процедура может быть обобщена
на N-мерный случай.
После того как мы вычислили две последовательности преобразо
ванных убытков по каждому из подпортфелей,
(zt,1)
и
(zt,2), мы должны
учесть тот факт, что убытки вероятнее всего коррелированны. Предпо
ложим, что совместное распределение (zц,
Zt,2) - двумерное нормаль
ное распределение. Тогда:
lnL
= -Tln27Г -Tlnu1 -Tlnu2 -
Х
t
t=l
[(Zt,1-/301)
2
_
0"1
+(
т
2
1
- ln(l - р 12 ) 2 х
2
2(1 - Р12)
2р 12 (Zt,1-/301)
0"1
(Zt,2 -/302)
0"2
+ ( 7 .б4 )
zt,2 ~/02) 2]'
где Р12 - корреляция между Zt,1 и Zt,2; /Зоi и иl обозначают математи
ческое ожидание и дисперсию для
Zt,i
соответственно
(i = 1, 2).
Оцен
ки максимального правдоподобия для математических ожиданий, стан
дартных отклонений и коэффициента корреляции представлены ниже:
1 т
т
L:zt,i
i = 1,2
t=l
1~
А 2
Т L..J(zt,i - /Зоi)
t=l
т
А
i
= 1,2
А
1 t~ (zt,1 - /301)(zt,2 - /302)
/J12
-
т
д-1д-2
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
7.4.
851
В качестве нулевой гипотезы рассматриваются следующие условия:
f301
=
f302
=
=
О, 0-1
=
0-2
1.
Таким образом, мы можем вычислить
оценку максимального правдоподобия для коэффициента корреляции
=
Р12· В предположении f301
f302
=
О, 0-1
=
0-2
=
1 правая часть (7.64)
принимает вид:
lnL = -
Tln27Г
- 2 (1 ~
т
- - ln(l 2
2
Р 1 2)-
т
2 )
L
Р12 t=l
(zl, 1 - 2p12Zt,1Zt,2
+ zl,2) .
Учитывая малость выборки, приемлемым является поиск значения
Р12, при котором достигается максимум
на отрезке
lnL
на решетке, построенной
[-1; + 1]. Метод Ньютона или другие стандартные числен
ные методы в этом случае могут не сойтись из-за наличия локальнъtх
максимумов.
Поскольку при разбиении на подпортфели мы оцениваем больше
параметров, чем в случае рассмотрения всего портфеля (без разбие
ния на подпортфели), то асимптотическое распределение будет менее
точным приближением. Тем не менее, таким образом, мы снова можем
построить распределение тестовой статистики. Однако мы не можем
просто
смоделировать
независимые
равномерно
чайные величины для первых преобразований
распределенные
слу
Ptl и Pt2, поскольку это
предполагало бы наличие нулевой корреляции. Вместо этого нам необ
ходимо учесть структуру корреляции между подпортфелями. Одним из
способов разрешения этой проблемы является моделирование случай
ных величин
из
двумерного
нормального
распределения
средними, единичными дисперсиями и корреляцией
ства в табл.
7.37
с
Р12 41 .
нулевыми
Для удоб
представлены смоделированные на основании
100 ООО
симуляций критические значения для различных Т и различных уров
ней корреляции (при
1%-ном
вероятностном уровне, см. также ниже
эмпирический пример в п. г)).
Можно обобщить двумерный случай
так, что мы будем иметь
N
(7.64)
на N-мерный случай
подпортфелей вместо двух. Однако суще
ствуют некоторые ограничения на число подпортфелей, которые можно
рассматривать, поскольку число параметров в функции правдоподобия
(N(N-1)/2+2N)
(N
растет быстрее, чем число используемых наблюдений
х Т).
41 Это
соответствует моделированию двумерной нормальной копула-функции с
корреляцией р12 и применению к компонентам смоделированных векторов обрат
ных функций к стандартным нормальным распределениям. Это представляет собой
простое обобщение двухшаговой процедуры в тесте Берковица.
Гл.
852
Таблица
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
7.
7 .37. Критические
значения для теста Берковица в
условиях малых выборок при
1%-ном
уровне значимости, различных уровнях корреляции
и временных горизонтов Т
Р12
5
лет
6
лет
7
лет
8
лет
9
лет
10
лет
15
лет
20
лет
Асимптотические
эна~1ения
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
19,08
18,98
19,19
19,20
19,26
19,11
19,02
19,36
19,38
19,57
17,71
17,60
17,64
17,56
17,70
17,62
17,59
17,88
17,76
17,91
16,74
16,52
16,47
16,55
16,64
16,98
16,77
16,99
16,94
17,06
16,08
16,08
16,12
16,14
16,07
16,00
16,37
16,34
16,36
16,41
15,63
15,55
15,57
15,74
15,76
15,90
15,92
15,84
15,77
15,89
15,31
15,32
15,50
15,31
15,32
15,31
15,54
15,52
15,67
15,71
14,45
14,52
14,58
14,55
14,49
14,58
14,70
14,72
14,81
14,75
14,09
14,14
14,18
14,16
14,23
14,20
14,34
14,37
14,29
14,32
13,28
13,28
13,28
13,28
13,28
13,28
13,28
13,28
13,28
13,28
в) Оценка мощности теста Берковица. Мощностью теста назы
вают вероятность того, что тест отклонит нулевую гипотезу при усло
вии, что она ложная. Поскольку существует много неопределенности
относительно того,
какая практика управления кредитными рисками
является правильной, проверка того, отклоняет ли тест Берковица
неправильную модель, является важной задачей.
Если в банке используется модель М1, но рассматриваются несколь
ко дРугих моделей в качестве возможных альтернатив, то можно ис
пользовать симуляционное моделирование для оценки вероятности то
го, что модель М1 отклоняется, если одна из альтернативных моделей
оказывается наиболее адекватной. Процедура вычисления мощности те
ста состоит из следующих шагов:
•
сгенерируем случайный вектор смоделированных убытков из аль
тернативной модели М2;
•
используя данные из шага
1,
вычислим статистику отношения
правдоподобия изначально используемой модели М1;
•
повторим шаги
1и2
большое количество раз;
•
вычислим мощность как относительную частоту того, что стати
стика отношения правдоподобия оказалась значимой при задан
ном уровне значимости.
Отметим, что мощность увеличится, если мы будем использовать
менее строгие уровни значимости (скажем,
5%
вместо
1%).
Тест Берковица обеспечивает весьма гибкий инструмент и представ
ляет собой обычно достаточно мощный тест (как это показано в работе
[Frerichs, Loffi.er (2003))).
Тем не менее этот тест можно критиковать по
7.4.
УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ
853
причине того, что он основан на точности приближения функции рас
пределения для всех значений из области определения42 . В этой связи
следует отметить, что значимые отличия в хвостах функций распре
деления часто сопровождаются значимыми отличиями средней части
функции распределения. Кроме того, даже в ситуациях, когда некор
ректная модель отличается от корректной главным образом на экстре
мальных квантилях, это не является проблемой, вызванной тестом Бер
ковица. Этот тест может быть ценным инструментом для специалистов.
На сегодняшний момент не существует идеального теста и, вероятней
всего, никогда не будет существовать.
г)
Эмпирические приложения в статистическом пакете:
критические значения для теста Берковица в условиях малых
выборок. Ниже показано, как моделировать критические значения в
тесте Берковица в условиях малых выборок, когда асимптотические
значения весьма неточны. Сначала мы разберем случай целого порт
феля.
new;cls;
/ /N umber of replications
replications= 100000;
/ /Time dimension
tt=seqa(S,1,16);
/ /Inizialize vector that will contain the simulated LR statistics
lr _ all=zeros( replications,rows( tt));
for cc(l,rows(tt),1);
for rr(l,replications,1);
/ /Simulate random uniform numbers
uu=rndu(tt[cc],1);
/ /Тrasform uniform into standard normal
std _ norm=cdfni( uu);
/ /Compute sigmaл2 Ьу ML
sig2=( sqrt((tt[cc]-1)/tt[cc])*stdc(std_norm) )л2;
//Compute the unrestricted Log lik
ll_unres=-tt[cc]/2*In( sig2) - sumc( (std_norm-meanc(std_norm))л2 )/
/(2*sig2);
//Compute the restricted Log lik
II _ res=-sumc( (std _ normл2) /2);
//Compute the LR statistics
lr_stat=-2*(II_res - II_unres);
/ /1 collect the computed LR
42 Использование
теста Берковица в случае, когда рассматриваются только экстре
мальные хвосты, возможно только в условиях наличия достаточно большого числа
наблюдений (сотни или даже тысячи наблюдений). Хотя это отвечает данным, ис
пользуемым для оценки рыночного риска, это не отвечает данным, используемым
для оценки кредитного риска. Более подробно об этом см. в работах:
(2001)]
и
[Christoffersen (2003)].
[Berkowitz
Гл.
854
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
lr _ all[rr ,се] =lr _ stat;
endfor;
endfor;
// Quantile levels at different confidence levels (1-alpha)
= 0.90, 0.95, 0.99 ;
/ /Compute the quantile levels and show them
qq = quantile(lr_all,e); qq;
е
Смоделированные критические значения должны быть довольно
близки к значениям, представленным в табл.
рем случай
2 подпортфелей
7.37).
7.36.
Теперь мы разбе
при различных значениях Р12 (сравните со
значениями из табл.
new;cls;
/ /Number of replications
replications= 100000;
/ /Time dimension
tt={5,6,7,8,9,10,15,20};
/ / All possiЬle rho levels
rho_all=seqa(0,0.1,10);
/ /Inizialize vector that will contain the simulated LR statistics
qq_ all=zeros(rows(rho _ all),rows(tt) );
for qqf(l,rows(rho _ all),1);
/ /Тrue correlation matrix
vcov= 1-rho _ all[qqf] 1
rho_all[qqf],...,1;
/ /1 compute the Cholesky decomposition
c_ chol=chol(vcov)';
/ /lnizialize vector that will contain the simulated LR statistics
lr _ all=zeros(replications,rows(tt));
for cc(l,rows(tt),1);
for rr(l,replications,1);
/ /1 compute the stacked vector of error terms, one for every
/ / scenarios so that we have а 2 Х Т vector
zz =c_chol*rndn(cols(vcov),tt!cc]);
/ /1 put them in time series format: Т Х 2
zz=zz';
//Compute sigmaл2_i Ьу unrestricted ML
sig2i=( sqrt((ttjcc]-1)/ttlcc])*stdc(zz) )л2;
//Compute the means Ьу unrestricted ML
betaOi=meanc( zz);
/ /Compute the correlation Ьу unrestricted ML
/ / 11 corrx 11 gives me the full correlation matrix. 1 extract
rho12=corrx(zz);rho12=rho12l2,1];
/ /Compute the unrestricted Log lik
11_ unres=-ttlccJ*ln(sig2ф]лo.5)-ttlccJ*ln(sig2il2]лo.5) -
р12
Выводы
855
- (tt[cc]/2)*In(l-rho12л2)-1/ (2*(1-rho12л2) )*
*sumc( ((zz[.,1]-beta0i[l])/sig2i[l]лo.s)л2 - 2*rho12*((zz[.,1J-beta0i[l])/sig2i[l]л0.5).*
.*((zz[.,2]-beta0i[2])/sig2i[2]л0.5) +
+ ((zz[.,2J-beta0i[2J)/sig2i[2Jл0.5)л2 );
/ /Compute the correlation Ьу restricted ML and the corresponding
//Iog-lik. See the procedure 11 rho_linesearch 11 below.
II_res, rho12_res= rho _linesearch(tt[cc],zz[.,1],zz[.,2]);
//Compute the LR statistics
lr_stat=-2*(II_res - ll_unres);
/ /1 collect the computed LR
lr _all[rr,cc]=lr _ stat;
endfor;
/ /Compute the quantile and show it
qq = quantile(Ir _ all,0.99);
/ /1 collect the computed quantile
qq_all[qqf,.J=qq;save qq_all;
endfor;
endfor;
/ /Show quantiles for small samples;
qq_all;
-------------pn,ocEDURES-----------------// ------------~
------------------
//Procedure to perform а line search for rho12 Ьу using the restricted
/ /Ьivariate normal likelihood
proc(2)=rho _ linesearch(t,zl,z2);
local rho _ s,lnl,rho _ max,ll _ max;
/ /1 compute а column vector of possiЬle rho values between -0.9999 and 0.9996
rho_s=seqa(-0.9999,0.0005,4000);
/ /1 compute the log-lik for each rho
lnl= -(t/2)*In(l - rho_sл2) - (1/(2*(1 - rho_sл2))).*( sumc(zlл2)- 2*rho_s.*sumc(zl.*z2) +sumc( z2л2) );
/ /1 extract the rho which delivers the maximized log-lik and the
corresponding log-lik
rho _ max=rho _ s[maxindc(lnl) J;
ll_max=lnl[maxindc(lnl)J;
retp(ll _ max,rho _ max);
endp;
Выводы
1.
У правление рисками представляет собой одну из ключевых
сфер деятельности финансовых организаций и один из центральных
разделов финансовой эконометрики.
Гл.
856
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
В этой главе мы представили определение когерентных мер рис
ка и их свойства, показав, что граница потерь (ГП или
VaR)
и диспер
сия не являются адекватными мерами риска в случае, когда доходности
имеют распределение неэллиптического типа.
Для простоты и финансовой целесообразности мы ограничились
анализом изменения цены некоторого финансового актива за один шаг
ЛРt
= Pt - Pt-1
(мы предпочитаем использовать ЛРt, а не
Pt,
поскольку
понятие риска интуитивно ассоциируется с доходами и убытками).
Согласованная (когерентная) мера риска Ф(д.Рt) опреде
2.
ляется как мера, имеющая следующие свойства.
Трансл.яционная инвариантность: пусть даны случайная величи
•
на ЛРt, безрисковая процентная ставка дG и некоторая константа
Ва Е
•
JR,
тогда Ф(ЛРt
+
ВадG)
= Ф(ЛРt) -
Ва.
Субаддитивность: пусть даны изменения цен двух финансовых
активов ЛРt,1 и ЛРt,2, тогда имеет место неравенство: Ф(ЛРt,1 +
+ЛРt,2) ~ Ф(ЛРt,1)
•
+ Ф(ЛРt,2).
Положительная однородность: при заданном неотрицательном Л
справедливо следующее: Ф(ЛЛРt)
•
= ЛФ(д.Рt).
Монотонность: для заданных двух изменений цен (или доходно
стей) ЛРt,1 и д.Рt,2 таких, что ЛРt,1 ~ ЛРt,2, будет выполняться
неравенство Ф(ЛРt,1) ~ Ф(ЛРt,2).
•
Дисперсия не является согласованной (когерентной) мерой риска.
3.
Среднее ожидаемых потерь уровня а
(ESa)
представляет
собой математическое ожидание всех потерь доли а худших резуль
татов для доходностей, которые мы можем получить от инвестиций.
Q
А именно: ESa = -~
J p- 1 (д.Pt)dЛPt.
о
4.
Граница потерь уровня а (ГПа или
VaRa) -
это минималь-
ные потери в доле а всех худших результатов для доходностей. А имен
но: VaRa = - f01 Dirac(ЛPt - a)F- 1 (ЛPt)dЛPt = -F- 1(a).
5. Стандартные методологии для оценки рыночного
рис
ка могут быть разделены на два семейства: семейство аналити-ческих
методов и семейство имитационнъtх методов (см. п.
6.
7.2.2).
Аналитические методы позволяют вычислять текущую сто
имость портфеля в зависимости от текущих значений факторов риска
на основании некоторой параметрической модели, в которой обусловли
вается воздействие изменений факторов риска на стоимость портфеля.
Стандартные техники, входящие в это семейство:
Выводы
857
• дисперсионно-ковариацион:н:ый метод (ДКМ): идея, лежащая в ос
нове этого метода, состоит в том, чтобы оценивать распределение
доходностей (или изменений цен), линеаризируя доходность порт
феля и предполагая, что факторы риска имеют нормальное рас
пределение;
•
де.л:ьта-гамма-аппроксимации для не.л.инейних портфе.л.ей: если в
наш портфель включены нелинейные инструменты, такие как оп
ционы, то предыдущий метод использовать уже нельзя. Один из
возможных подходов к решению такой задачи состоит в том, что
бы измерять влияние локального изменения факторов риска на
стоимость портфеля с помощью среднего производных, т. е. ис
пользовать приближения к нелинейным ценам опциона. Если ис
пользовать приближение первого порядка, то мы имеем де.л.ьта
подход, а если использовать приближение второго порядка, тогда
мы имеем гамма-подход.
7.
Имитационные методы: используются при оценивании стои
мости портфеля для каждого сценария из некоторого диапазона сцена
риев изменений факторов риска. В зависимости от условий факторами
рыночного риска могут быть курсы акций, индексы, процентные став
ки, обменные курсы, цены на драгоценные металлы, цены на сырьевые
товары и т.д. В результате получим ряд из стоимостей портфеля, по
которому построим эмпирическую функцию распределения, используя
которую можно оценивать меры риска. Среди имитационных методов
выделим:
•
историческое моде.л.ирование: идея, лежащая в основе этого мето
да, состоит в том, что распределение доходностей (или изменений
цены) портфеля необходимо оценивать с помощью эмпирической
функции распределения без использования каких-либо парамет
рических моделей;
•
моде.л.ирование методом Монте-Карло: идея, лежащая в основе
моделирования методом Монте-Карло, состоит в том, что распре
деление доходностей (или изменений цен) портфеля необходимо
оценивать по некоторой явной параметрической модели. В отли
чие от метода вариации-ковариации в данном подходе нет необхо
димости представлять задачу в аналитически удобном виде;
•
моде.ли полной оценки: много раз моделируются будущие
(гипо
тетические) цены базового актива и, используя модели ценообра
зования опционов, для каждой смоделированной цены базового
актива рассчитываются цены опционов.
Гл.
858
8.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
t мы инвестировали сумму Pt в неко
вычислить VaRa на момент (t + 1). То
Предположим, что в момент
торый актив и нам необходимо
гда, если мы используем условную АRМА-GАRСН-модель для нетто
доходностей и лог-доходностей этого актива, мы получим соответствен
но:
VaRa(t, l = 1)
Р, [r•н + F,; 1 • ~]
VaR,,(t,l = 1) =
(см. п.
7.2.3).
Если стандартизованные остатки GАRСН-модели имеют
нормальное распределение, то
F;; 1
= Ф- 1 (а); если стандартизован
ные остатки GАRСН-модели ТJ имеют стандартное t-распределение, т. е.
Jv/(v 9.
l'V
2)ТJ
l'V
t тогда F;; 1 = Rt; 1 (a).
11 ,
Если доходности
Rp
линейного портфеля такие, что
N(w'µt;и~,t), тогда Va~ = (w'µt
где
W -
величина
+ ZaO'p)W =
инвестированных
а-квантиль N(О,1)-распределения.
Et
в
(w'µt
Rp
l'V
+ zav'w'Etw)W,
портфель
средств,
Za -
может быть оценено с использо
ванием многомернъtх GАRСН-моде.л,ей (см. п.
7.2.4).
Сорulа-GАRСН-модели. Их использование позволяет рас
10.
сматривать более общие случаи, выходящие за рамки многомерного
нормального распределения или многомерного распределения Стью
дента. Например, многомерная модель, допускающая наличие своего
эксцесса и асимметрии для каждого отдельного частного распределе
ния, отвечающего соответствующей компоненте случайного вектора,
имеет вид (см. п.
Xt
')')t
•1
7.2.6):
-
E{Xtlб't-1}
l'V
Н('П
.,1, ...
где piSkewed-t матрица
Rt
+ DtТJt
')') ) -= cNormal(pSkewed-t('Y)
)
pSkewed-t('Y)
)· R)
,.,n
1
·11 , ••• , n
·1n'
t'
частное скошенное t-распределение; корреляционная
может предполагаться постоянной или меняющейся во вре
мени (например, как предполагается в стандартной ССС-модели или
DСС-модели), а Dt
= diag(h~e, ... , h1,!n~t)
(h;,i,t
определяется как одно
мерная GАRСН-модель). Следует отметить, что могут использоваться
более гибкие копула-функции (например, архимедовы копула-функции,
копула-функции, полученные при помощи канонической ветвизации
или D-ветвизации).
11.
цедуры
В главе также представлены базовые и модифицированные про
управления
кредитным
риском
в
контексте
рекомендаций
соглашения Базель-11, в том числе одномерные модели кредитного рис-
Выводы
859
ка, используемые для оценки вероятности дефолта заемщика, а также
многомерные модели измерения риска кредитного портфеля.
Ключевыми компонентами кредитного риска являются веро
12.
ятность дефолта
(ВД),
до.ля невозвращеннъ~х при дефолте по креди
ту средств (ДНС(Д)), вели-чина номинальнъ~х потерь при дефолте
(ВНП(Д)), которая представляет собой сумму всех кредитных обяза
тельств заемщика в случае его банкротства в результате реализации
некоторого кредитного события (дефолта или миграции), дефолтная
зависимость и (и.ли) миграционная зависимость (см. п.
13.
7.4.1).
Специфические для управления кредитным риском задачи: дан
нъ~е, недостаток публичной информации, касающейся кредитного каче
ства заемщиков; более длиннъ~е временнъ~е горизонтъ~ прогнозирования
(обычно не менее одного года). Функции распределения убъ~тков объ~-ч
но сильно скошены, имеют «длинный правый хвост~, что указывает на
частые малые убытки и редкие большие убытки. Моделирование за
висимости в кредитном портфеле более важно, -чем при управлении
ръто-чнъtм риском, поскольку на хвост функции распределения убытка
сильно влияет спецификация зависимости между дефолтами.
14.
•
Одномерные модели кредитного риска (см. п.
7.4.4):
экспертный подход. Решение о том, выдавать или не выдавать
кредит,
выносится
локальным
или
отраслевым
инспектором
по
кредитам, локальным или отраслевым менеджером по связям с
клиентами. Он может учитывать разные факторы риска, но обыч
но концентрирует внимание на следующих пяти: характер, капи
тал, способность погашать задолженность, обеспечение, экономи
ческие условия (циклы);
•
системъ~ кредитного скоринга. Основной принцип функциониро
вания этой системы заключается в идентификации ключевых
факторов, определяющих вероятность дефолта, и путем их комби
нированного взвешивания получение количественной оценки дей
ствия совокупности этих факторов. Эта количественная оценка
может быть использована в системе классификации. В некоторых
случаях полученная количественная оценка может быть букваль
но истолкована как вероятность дефолта. Существуют четыре ме
тодологические формы многомерных моделей кредитного скорин
га:
(1) линейная модель вероятности, (2) логит-модель, (3) пробит
модель и (4) модели, полученные на основе дискриминантного
анализа;
•
моде.ли пане.льнъ~х даннъ~х, которые сочетают в себе данные как
пространственного типа, так и данные типа временных рядов;
Гл.
860
•
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
внешние и внутренние рейтинговъtе системъt, где системы по
строения кредитных рейтингов основаны, как правило, на каче
ственных и количественных оценках. Рейтинг представляет собой
категорию, которая описывает правдоподобность дефолта, но при
его использовании всегда надо иметь в ВИдУ, что может быть вы
бран другой критерий присвоения того или иного рейтинга;
•
одномернъtе структурнъtе модели. При помощи моделей мерто
новского типа (или структурных моделей) оцениваются ценные
бумаги, выпущенные той или иной компанией. Эти модели осно
ваны на использовании структурных переменных компании
(т. е.
на значениях, отражающих состояние активов и пассивов компа
нии).
Сравнительно недавно предложен алгоритм оценки вероятности
нулевой цены (ВНЦ), который представляет собой подход, исполь
зующий только цены активов. ВНЦ-алгоритм допускает возмож
ность моделирования распределения доходностей цены при помо
щи распределения, отличного от нормального. В нем не использу
ются данные из балансовых отчетов, которые могут дать непра
вильные ориентиры и которые могут не отвечать фактическому
финансовому положению компании.
15.
Важными инструментами оценки эффективности модели про
гнозирования вероятностей являются таблица «факт-прогноз~ и кри
вая соотношений правильной и ложной классификации объектов (так
называемая оперативная кривая (ОК)), см. п.
7.4.5.
При условии, что
нам задана таблица «факт-прогноз~ и пороговое значение (для отнесе
ния к тому или иному классу), оперативная кривая строится на осно
ве совместных частот правильных прогнозов и фактических событий,
совместных частот неправильных прогнозов и фактических событий, а
именно:
•
-чувствительность: а/(а
+ Ь) доля случаев, в которых спрогнози
рована неплатежеспособность компании, при условии, что в дей
ствительности компания была неплатежеспособной;
•
специфи-чность:
d/(d
+с) доля случаев, в которых спрогнозиро
вана платежеспособность компании, при условии, что в действи
тельности она и была платежеспособной;
•
ложная позитивность: с/ (с+ d) или 1-специфи-чность, доля слу
чаев, в которых спрогнозирована неплатежеспособность компа
нии, при условии, что компания была платежеспособной (ошибка
11
рода);
•
Выводы
861
+ Ь)
или 1-чувствителъностъ, доля
ложна.я негативность: Ь/(а
случаев, в которых спрогнозирована платежеспособность компа
нии, при условии, что компания была неплатежеспособной (ошиб
ка
1 рода).
ОК строится следующим образом: каждому фиксированному поро
говому значению ставится в соответствие точка на декартовой плоско
сти, на которой ось х отвечает значениям ложной позитивности (или
1-специфичности), также называемой нормой ложной тревоги, а ось у
отвечает значениям чувствительности, также называемой нормой по
падания. Следовательно, каждая точка на этой кривой будет отвечать
некоторому фиксированному пороговому значению. А значит, ОК мо
жет быть использована для выбора порогового значения, балансиру
ющего чувствительность и специфичность. В терминах сравнения мо
делей, наилучшей из двух кривых признаем ту, которая расположена
левее (в идеальном случае эта кривая совпадает с осью у).
16.
В .модели Мертона (см. п.
Vt
активов
7.4.7)
предполагается, что стоимость
хорошо описывается броуновским движением, а компания
финансируется из своего собственного капитала
S
и своих долговых
обязательств номиналом В со сроком погашения в момент времени Т
(могут быть в форме, например, облигаций или банковских кредитов).
Кредит, выданный какой-либо компании, создает для кредитора кре
дитный риск, а именно риск того, что стоимость активов компании в
момент времени Т упадет ниже уровня В, т. е. Vт ~ В. В этом случае
мы говорим, что фирма находится в состоянии дефолта.
17.
Алгоритм оценивания ВНЦ (см. п.
7.4.8)
позволяет вычислить
вероятность дефолта и состоит из следующих шагов:
1)
ется условная модель для разностей в уровнях цен
= Pt -
Xt
рассмотрива
Pt-1,
(без
логарифмического преобразования), при условии, что мы располагаем
всей информацией
число
Ft
до момента времени
t; 2)
траекторий цен до момента времени
N
моделируется большое
+ Т)
(t
с использовани
ем оцененной на первом шаге модели временных рядов;
вероятность дефолта как отношение
рованных траекторий из
N,
n/N,
где п
-
3)
оценивается
количество смодели
которые касаются или пересекают барьер
нулевой цены.
18.
Существуют четыре основных типа многомерных моделей
кредитных портфелей:
•
.модели кредитной .миграции: подход
ный
CreditMetrics,
предложен
J .Р. Morgan в 1997 г., основан на анализе кредитной миграции,
т. е. вероятности перемещения из одного рейтингового класса в
другой (включая дефолт, являющийся поглощающим состоянием)
862
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
за заданный период времени, который обычно берется равным од
ному году. В подходе
CreditMetrics
оценивается функция распре
деления на один год вперед для стоимости кредитного портфеля,
которая меняется в результате кредитной миграции. Этот подход
предполагает, что матрица переходов, оцененная по историческим
данным нескольких тысяч рейтингуемых облигаций, достаточно
точно описывает вероятность миграции из одного рейтингового
класса в другой (см. п.
•
7.4.15);
структурнъ~е моде.ли (см. п.
7.4.16).
Прародителем большинства
из этих моделей является модель Мертона, которая постулирует
механизм дефолта с точки зрения его связи со стоимостью акти
вов компании и ее обязательств. Наиболее известная в этом классе
КМV-модель, которая строится на основе так называемой ожи
даемой частоты дефолтов для каждого эмитента, а не на основе
средних частот переходов, построенных по историческим данным,
как это делается в модели
•
CreditMetrics;
актуарнъ~е моде.ли. CreditRisk+-мoдeль основана на результатах
актуарной науки (см. п.
7.4.17).
В этом подходе уделяется основное
внимание описанию вероятности дефолта, а не кредитной мигра
ции. Кроме того, в отличие от
CreditRisk+
KMV-
и CreditMetrics-пoдxoдoв в
игонорируются причины дефолта. Однако это един
ственный подход, в котором можно получить решения в аналити
ческом виде, а не с помощью методов стохастического моделиро
вания, что позволяет значительно уменьшить объем необходимых
вычислительных ресурсов;
•
макроэкономи'Ческие моде.ли.
CreditPortfolioView
(см.
п.
7.4.18)
представляет собой улучшенный подход кредитной миграции пу
тем допущения того, что вероятности миграций могут меняться
в зависимости от кредитных циклов. В этом подходе вероятно
сти дефолтов являются функциями макропеременных, таких как
безработица, уровень процентных ставок и др., которые предпо
лагаются факторами, определяющими кредитные циклы.
19.
Тест Берюовuца (см. п.
7.4.19)
представляет собой мощный
инструмент тестирования как моделей кредитного риска, так и моде
лей рыночного риска. Он дает надежные результаты и в условиях ма
лых выборок и состоит из трех шагов:
мени
t
убытки, сумма которых равна
1) наблюдаемые в
Lt, заменяется на
момент вре
вероятность
наблюдения этих или меньших убытков; для расчета этой вероятности
используется прогнозируемая на момент времени
t
плотность распре
деления суммарных убытков на этот момент времени, т. е. оценивается
863
Выводы
кумулятивная функция распределения в точке суммарного убытка на
момент времени t, а именно: Pt = F(Lt)· Если используется корректная
модель риска для прогнозирования распределения суммарного убытка,
то временной ряд наблюдаемых
Pt
должен представлять реализацию
н.о.р.с.в, имеющих равномерное распределение на отрезке [О;
менной ряд Pt преобразуется в ряд Zt =
Ф- 1 (Pt)i
1]; 2)
вре
3) с помощью теста
отношения правдоподобия тестируются ограничения, состоящие в том,
Zt имеет условное нулевое среднее и единичную дисперсию.
20. В главе представлена также методология количественного ана
лиза операционного риска (п. 7.3), который является относитель
что
но недавней областью изучения, возникшей в рамках количественного
управления рисками. Проблема изучения операционного риска возник
ла в момент, когда было обнаружено, что ни управление рыночным
риском,
ни
управление кредитным риском
не позволяет хеджировать
все возможные события, влияющие на экономические и финансовые
результаты работы финансовых организаций. Изложение в главе начи
нается с базовых подходов, используемых для оценки операционного
риска и резервного капитала под этот риск в банках и финансовых
организациях с небольшой капитализацией, а завершается описанием
сравнительно недавно предложенных моделей канонической агрегации,
основанных на понятии копула-функций и байесовских методах, ис
пользуемых в финансовых организациях с большой капитализацией,
где операционным риском,
как правило, занимается специально отве
денное подразделение.
21.
В Базель 11-соглашении введено понятие операционного риска
как нового класса риска, под который финансовые учреждения обяза
ны отложить резервный капитал. Базель
11
определяет операционный
риск следующим образом: ~ Операционнъ~й риск определяется как риск
убытков в резул:ьтате неадекватной или ошибочной работъ~ процес
сов, персонала, систем или в результате внешних воздействий. Это
определение включает юридический риск, но исключает стратегиче
ский и репутационнъ~й риск». В Базель 11-соглашении для классифика
ции всех возможных источников операционного риска было определено
восемь бизнес-направлений (БН) и семь типов событий (ТС).
22.
пользуя
Подход распределения убытков (см. п.
внутренние
данные,
рассчитать
для
7.3.5)
позволяет, ис
каждой
комбинации
БН/ТС вероятностное распределение частоты возникновения убытков,
так же как и ее влияние (степень влияния) на определенном промежут
ке времени. Сворачивая функцию распределения частоты с функцией
распределения величины убытка, аналитически или численно можно
получить вероятностное распределение суммарного убытка. Итоговая
величина резервного капитала будет равна процентной точке этого рас-
864
Гл.
7.
АНАЛИЗ ФИНАНСОВЫХ ДАННЫХ
пределения. Данный подход использует два типа распределений: один
тип распределений описывает частоту возникновения рисковъtх ситу
аций, а другой описывает функцию распределения величинъt убъtтка,
возникающего для каждой рассматриваемой рисковой ситуации. Ча
стота возникновения убытков за некоторый временной период модели
руется при помощи пуассоновского или отрицательного биномиального
распределения. Для моделирования величины убытка можно использо
вать экспоненциальное распределение, Парето-распределение, гамма
распределение или обобщенное Парето-распределение, полученное из
теории экстремальных значений. Если у нас есть функция распределе
ния суммарного операционного убытка для любого пересечения меж.цу
бизнес-направлениями (БН) и типами событий (ТС), то по ней можно
оценить такие меры риска, как граница потерь (ГП), среднее ожида
емых потерь (СОП), и на основании этих оценок определить величи
ну резервного капитала для этого пересечения на следующий период.
После того как оценены ГП для каждого пересечения БН/ТС, рассчи
тывается граница потерь для всей совокупности операционных рисков
(совокупная граница потерь), которая обычно вычисляется как сумма
ГП всех пересечений БН/ТС, а тем самым предполагается, что суммар
ные убытки
sit комонотонны.
23. Каноническая агрегация при помощи копула-функций
(п. 7.3.6). В этом подходе для описания структуры зависимости меж
ду суммарными убытками Si используются копула-функции. Отметим,
что их использование приводит к объективно оправданному уменьше
нию величины полной ГП. Каноническая агрегация при помощи копула
функций предполагает агрегацию убытков за какой-то временной пери
од, после чего оценивается зависимость этих суммарных убытков.
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
МЕЖСТРАНОВОГО
И МЕЖРЕГИОНАЛЬНОГО АНАЛИЗА
кжн
Пl.1.
Исходные данные и результаты межстранового
анализа
№
Частные критерии
Страна
пп
x(l)
х(2)
х(З)
х(4)
х(5)
х(б)
х(7)
x(S)
х(9)
x(lO)
1
Австралия
34935
17,36 25063
1
7,00
4,4
82
6
521,6
2,09
2
Австрия
37913
39,24 26229
1
4,40
3,2
80
4
225,5
2,56
3
Аргентина
13775
44,71 4662
2,4
17,87 8,1
75
17
698,6
0,51
4
Бельгия
35183
48,08 25260
1
4,87
4,5
79
5
293
1,87
5
Болгария
11923
12,06 4423
1,7
4,40
12,3
73
12
1501,8
0,48
6
Бразилия
10041
11,01 4983
9,5
21,82 5,6
72
20
305,1
1,1
Великобри-
35347
39,08 28011
1
7,21
3,7
79
6
220,4
1,76
6,1
73
7
498,9
0,97
7
тания
8
Венгрия
18868
25,31 10066
1,1
3,84
9
Венесуэла
12197
14,40 7142
7
15,79 30,6
74
21
808,6
0,23
10
Германия
34907
41,26 25009
1
4,34
80
5
282,8
2,53
11
Гон-Конг
43040
36,13 18702
1,7
14,72 4,3
82,3
2
220,7
0,81
12
Греция
29280
39,93 22580
2,9
6,19
4,2
80
4
351,4
0,57
13
Дания
35677
39,51 30495
1
4,31
3,4
79
4
201,4
2,55
14
Израиль
26642
35,78 15613
2,9
7,88
4,6
81
5
435,6
4,68
2,6
15
Индонезия
3888
4,09
1362
8,6
5,15
10,3
68
34
923,3
0,35
16
Иордания
5088
11,65 2777
6,9
6,91
14,9
71
25
1233,2
0,75
17
Ирландия
42993
49,63 30262
1
5,68
4,2
80
4
201,9
1,31
18
Испания
31053
38,62 19865
2,6
6,00
4,1
81
4
265,8
1,2
19
Италия
30057
41,47 22776
1,1
6,46
3,3
81
4
240,4
1,13
20
Казахстан
11000
10,96 3575
1
4,67
17
64
29
2244,7
0,28
21
Канада
35669
37,33 25161
1
5,54
2,4
81
6
421,4
1,89
15,1
22
Катар
54779
33,86 12206
9,8
7,16
77
11
698,8
0,31
23
КНР
5825
4,70
928
8,4
12,07 5,9
73
24
2109,4
1,49
24
Колумбия
8716
9,59
3440
6,4
25,08 7
74
21
365,3
0,16
25
Литва
18266
21,91 9300
1
6,35
11,1
71
9
454,4
0,82
26
Люксембург
79379
59,45 36014
1
4,63
3,4
80
4
263,3
1,63
27
Малайзия
13538
16,51 3613
8,1
12,34 5,4
72
12
984,8
0,57
28
Мексика
13986
14,37 6613
7,6
12,81 5,2
74
35
437,3
0,46
29
Нидерланды
39215
45,74 24429
1
5,09
2,5
80
5
263,2
1,7
Новая
26985
29,50 16922
1
6,84
4
80
6
348,5
1,18
1
3,88
3,8
80
4
109,3
1,57
9,5
15,32 7,3
73
25
302,6
0,15
30
Зе-
ландия
31
Норвегия
53481
57,23 36689
32
Перу
8374
7,36
2834
866
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.1 (окончание)
33
Польшая
16747
21,39 8348
1
5,63
4,2
75
7
895,8
0,56
34
Португалия
22781
25,84 15273
5,1
7,91
2,6
79
4
288,7
1,18
35
Россия
15524
17,95 5780
1
8,65
14,1
66
13
1604,2
1,12
36
Румыния
13271
15,90 6100
2,4
4,84
7,9
73
16
771,7
0,53
37
Сингапур
47646
36,36 15416
5,6
9,80
6,5
80
3
309,9
2,27
38
Словакия
21302
25,57 9917
1
3,95
4,6
74
8
670,1
0,46
39
Словения
27941
31,39 13879
1
4,14
5,7
78
4
405,8
1,53
40
США
45017
47,78 32564
1
8,48
3,8
78
8
432,3
2,67
41
Таиланд
8013
6,76
5,9
7,78
5,4
72
8
1049,7
0,2
42
Тайвань
30254
29,70 10462
2,4
6,03
3,5
77,9
7
740
2,62
43
Турция
13526
21,06 7161
11,3
7,28
10,4
73
26
452,3
0,58
44
Украина
7075
8,69
2353
1
4,08
25,3
67
24
2879,6
0,85
45
Филиппины
3400
4,22
1287
6,6
11,00 9,3
68
32
565,7
0,1
46
Финляндия
34750
43,12 26437
1
3,82
3,8
79
3
318,8
3,47
47
Франция
33693
50,14 25738
1
5,58
3,3
81
5
166,5
2,08
48
Хорватия
16760
20,90 9433
1,3
4,77
6,1
76
6
422
0,81
49
Чехия
24688
27,44 10179
1
3,49
6,3
77
4
850
1,54
50
Чили
14176
16,26 5992
3,5
15,79 8,7
78
9
410,3
0,68
2251
51
Швейцария
41068
36,59 37219
1
5,43
2,5
82
5
113,5
2,9
52
Швеция
36180
40,48 24068
1
4,02
3,4
81
4
122,8
3,64
53
Эстония
19638
21,82 9482
1
5,53
10,4
73
6
920,5
1,14
54
Южная
9887
17,32 3443
12
17,77 10,6
51
69
1326,1
0,92
25268
25,33 10142
2
4,75
4,7
79
5
500,6
3,01
33403
37,28 21747
1
3,37
1,4
83
4
278,2
3,4
Африка
55
Южная
Корея
56
Япония
Пl.2. Унифицированные исходные статистические данные
NN
Страны
Унифицированные значения частных критериев
Уiэ
пп
(i)
x(l)
х(2)
х(З)
х(4)
х(5)
х(6)
х(7)
x(S)
х(9)
x(lO
1
Австралия
6,00
6,35
6,65
10,00 8,52
8,30
9,57
8,86
8,12
9,12
9,28
2
Австрия
6,56
7,34
6,97
10,00 9,55
8,98
8,70
9,43
9,47
8,91
9,64
3
Аргентина
1,97
2,40
8,97
8,73
0,47
6,19
6,52
5,71
7,31
2,48
4,58
4
Бельгия
6,04
7,95
6,70
10,00 9,90
8,24
8,26
9,14
9,16
8,19
8,71
5
Болгария
1,62
1,44
0,96
9,36
9,56
3,81
5,65
7,14
3,64
2,35
3,53
6
Бразилия
1,26
1,25
1,12
2,27
0,30
7,61
5,22
4,86
9,11
4,96
4,79
Великобри-
6,07
6,32
7,46
10,00 8,36
8,69
8,26
8,86
9,49
7,73
7,16
7
тания
8
Венгрия
2,94
3,83
2,52
9,91
9,14
7,33
5,65
8,57
8,22
4,41
5,25
9
Венесуэла
1,67
1,86
1,71
4,55
2,01
0,00
6,09
4,57
6,81
1,30
2,44
10
Германия
5,99
6,71
6,64
10,00 9,51
9,32
8,70
9,14
9,21
9,03
8,89
ПРИЛОЖЕНИЕ
1.
867
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2 (продолжение)
11
Гон-Конг
7,54
5,79
4,90
7,27
2,80
8,35
9,70
10,00 9,49
3,74
6,59
12
Греция
4,92
6,47
5,97
8,27
9,12
8,41
8,70
9,43
8,89
2,73
6,18
13
Дания
6,14
6,40
8,15
10,00 9,49
8,86
8,26
9,43
9,58
8,95
8,98
14
Израиль
4,42
5,72
4,05
7,87
8,18
8,51
0,00
Индонезия
0,09
0,00
0,12
9,89
4,94
9,13
3,48
9,14
15
8,27
3,09
0,86
6,28
1,81
6,91
4,26
16
Иордания
0,32
1,37
0,51
4,64
8,58
2,33
4,78
3,43
4,87
3,49
5,66
17
Ирландия
7,53
8,23
8,08
10,00 9,50
8,41
8,70
9,43
9,58
5,84
8,39
18
Испания
5,26
6,24
5,22
8,55
9,26
8,47
9,13
9,43
9,29
5,38
7,71
19
20
Италия
5,07
6,75
6,02
9,91
8,92
8,92
9,13
9,43
9,40
5,08
6,86
Казахстан
1,44
1,24
0,73
10,00 9,76
1,14
1,74
2,29
0,25
1,51
4,45
21
Канада
6,13
6,00
6,68
10,00 9,60
9,43
9,13
8,86
8,58
8,28
9,27
22
Катар
9,77
5,38
3,11
2,00
2,22
7,39
7,43
7,31
1,64 8,13
23
КНР
0,46
0,11
0,00
3,27
4,76
7,44
5,65
3,71
0,87
6,60
4,72
24
Колумбия
1,01
0,99
0,69
5,09
0,00
6,82
6,09
4,57
8,83
1,01
4,82
25
Литва
2,83
3,22
2,31
10,00 9,00
4,49
4,78
8,00
8,42
3,78
5,22
26
Люксембург
10,00 10,00 9,67
10,00 9,73
8,86
8,70
9,43
9,30
7,18
9,21
27
Малайзия
1,93
2,24
0,74
3,55
4,56
7,73
5,22
7,14
6,00
2,73
7,43
28
Мексика
2,01
1,86
1,57
4,00
4,21
7,84
6,09
0,57
8,50
2,27
4,63
29
Нидерланды
6,81
7,52
10,00 9,93
9,38
8,70
9,14
9,30
7,48
8,91
4,48
4,59
6,48
4,41
10,00 8,63
8,52
8,70
8,86
8,91
5,29
8,91
30
Новая
Зе-
8,40
ландия
31
Норвегия
9,52
9,60
9,85
10,00 9,17
8,64
8,70
9,43
10,00 6,93
9,16
32
Перу
0,95
0,59
0,53
2,27
2,35
6,65
5,65
3,43
9,12
0,97
4,33
33
Польшая
2,54
3,13
2,04
10,00 9,54
8,41
6,52
8,57
6,41
2,69
4,26
34
Португалия
Россия
3,93
2,50
3,95
1,34
10,00 7,30
9,32
2,78
8,26
2,61
9,43
6,86
9,18
3,18
5,29
5,04
6,12
35
3,68
2,30
6,27
36
Румыния
1,88
2,13
1,43
8,73
9,88
6,31
5,65
6,00
6,98
2,56
2,68
37
Сингапур
8,41
5,83
3,99
5,82
6,44
7,10
8,70
9,71
38
3,40
3,88
2,48
10,00 9,23
8,18
6,09
8,29
9,08
7,44
9,87 8,89
Словакия
2,27
6,30
39
Словения
4,67
4,93
3,57
10,00 9,37
7,56
7,83
9,43
8,65
6,76
6,81
40
США
7,91
7,89
8,72
10,00 7,42
8,64
8,29
8,53
8,45
8,53
41
Таиланд
0,88
0,48
0,36
5,55
7,94
7,73
7,83
5,22
8,29
5,71
1,18
5,93
42
Тайвань
5,11
4,63
2,63
8,73
9,24
8,81
7,78
8,57
7,12
8,66
5,84
43
Турция
1,93
3,07
1,72
0,64
8,31
4,89
5,65
3,14
8,43
2,77
5,00
44
Украина
0,83
0,02
0,39
0,10
10,00 9,32
4,91 5,56
1,14
3,71
3,91
2,73
7,84
2,89
45
Филиппины
0,70
0,00
5,51
3,04
3,48
1,43
0,00
7,92
0,76
4,81
46
Финляндия
5,96
7,05
7,03
10,00 9,13
8,64
8,26
9,71
9,04
5,08
8,12
47
Франция
5,76
8,32
6,84
10,00 9,57
8,92
9,13
9,14
9,74
9,08
8,17
48
Хорватия
2,54
3,04
2,34
9,73
7,33
6,96
8,86
8,57
3,74
5,58
9,83
49
Чехия
4,05
4,22
2,55
10,00 8,88
7,22
7,39
9,43
6,62
6,81
7,59
50
Чили
2,05
2,20
1,40
7,73
2,01
5,85
7,83
8,00
8,63
3,19
6,68
51
Швейцария
7,16
5,87
10,00 10,00 9,68
9,38
9,57
9,14
9,98
7,48
9,71
ПРИЛОЖЕНИЕ
868
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
1.
Пl.2 (окончание)
52
Швеция
6,23
6,57
6,38
10,00 9,28
8,86
9,13
9,43
9,94
4,37
9,08
53
Эстония
3,09
3,20
2,36
10,00 9,60
4,89
5,65
8,86
6,30
5,13
6,20
54
Южная
Африка
1,23
2,39
0,69
0,00
0,54
4,77
0,00
0,00
4,45
4,20
5,08
55
Южная
4,16
3,84
2,54
9,09
9,81
8,13
8,26
9,14
8,21
7,02
6,18
5,70
6,00
5,74
10,00 8,79
10,00 10,00 9,43
9,23
5,38
6,90
Корея
56
Япония
Пl.3.
Результаты построения ИИ КЖН и ранжирования
стран по данным
NN
Страна
[WCY (2009)]
Значения ИИ КЖ
Ранги стран по КЖ
пп
(i)
Уi(б.о)
Уiэ
Уi(об)
по
по
по
Уi(б.о)
Уiэ
Уi(об)
1
Австралия
8,023
9,28
9,29
13
3
3
2
Австрия
8,451
9,64
8,88
6
2
8
3
Аргентина
5,134
4,58
6,13
37
47
27
4
Бельгия
8,234
8,71
8,28
11
13
12
5
Болгария
4,320
3,53
2,48
40
52
45
6
Бразилия
3,507
4,79
3,27
45
44
38
7
Великобритания
8,006
7,16
8,41
14
22
11
8
Венгрия
5,973
5,25
3,85
30
38
35
9
Венесуэла
2,967
2,44
2,61
51
56
44
10
Германия
8,252
8,89
8,80
10
11
9
11
Гон-Конг
6,934
6,59
6,68
24
28
21
12
Греция
7,151
6,18
6,19
21
31
26
13
Дания
8,399
8,98
9,13
7
8
5
14
Израиль
6,362
6,91
4,65
29
23
30
15
Индонезия
2,567
4,26
0,79
54
50
53
16
Иордания
3,117
5,66
2,26
49
36
47
17
Ирландия
8,479
8,39
8,18
5
15
13
18
Испания
7,427
7,71
7,11
19
19
20
19
Италия
7,700
6,86
7,32
18
25
17
20
Казахстан
2,852
4,45
0,00
53
48
56
21
Канада
8,094
9,27
8,76
12
4
10
22
Катар
5,432
8,13
3,97
36
17
34
23
КНР
3,015
4,72
3,68
50
45
36
24
Колумбия
3,243
4,82
2,10
47
42
48
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
869
Пl.З (окончание)
25
Литва
5,433
5,22
3,07
35
39
40
26
Люксембург
9,339
9,21
9,30
1
5
2
27
Малайзия
3,945
7,43
2,30
43
21
46
28
Мексика
3,503
4,63
2,91
46
46
42
29
Нидерланды
8,320
8,91
8,16
9
9
14
30
Новая Зеландия
6,998
8,91
6,53
23
9
23
31
Норвегия
9,227
9,16
9,28
2
6
4
32
Перу
2,893
4,33
1,79
52
49
50
33
Польшая
5,692
4,26
3,49
34
50
37
34
Португалия
6,443
6,12
6,12
28
33
28
35
Россия
4,287
2,89
2,01
41
53
49
36
Румыния
4,795
2,68
2,74
38
55
43
37
Сингапур
7,377
8,89
8,07
20
11
15
38
Словакия
5,859
6,3
3,27
32
29
39
39
Словения
7,034
6,81
6,29
22
26
24
40
США
8,378
8,53
8,94
8
14
7
41
Таиланд
3,993
5,93
1,57
42
34
51
42
Тайвань
6,853
5,84
6,60
25
35
22
43
Турция
3,690
5
2,93
44
41
41
44
Украина
3,132
2,73
1,45
48
54
52
45
Филиппины
2,542
4,81
0,39
55
43
54
46
Финляндия
7,896
8,12
7,25
15
18
18
47
Франция
8,499
8,17
9,12
4
16
6
48
Хорватия
5,960
5,58
4,22
31
37
31
49
Чехия
6,494
7,59
5,67
27
20
29
50
Чили
4,686
6,68
4,11
39
27
32
51
Швейцария
8,726
9,71
10,00
3
1
1
52
Швеция
7,862
9,08
7,19
16
7
19
53
Эстония
5,694
6,2
4,05
33
30
33
54
Южная Африка
1,680
5,08
0,06
56
40
55
55
Южная Корея
6,700
6,18
6,21
26
31
25
56
Япония
7,828
6,9
7,78
17
24
16
ВЕКТОР (Оо,О1,О2,Оз) коэффициентов модели
Коэффициенты ранговой корре-
множественной регрессии
ляции: соответственно, между
2,4177
0,228339
0,308022
0,216314
ранжировками по Уз и по у( об)
и между ранжировками по Уз и
по у(б.о).
0,8545
0,8517
ПРИЛОЖЕНИЕ
870
Пl.2.
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Результаты межрегионального анализа СЛК КЖН
Пl.2.1. Блочные и сводный ИИ по каждой из четырех
синтетических категорий КЖН
Пl.2.la. Качество населения
NN
Регион
Блочный ИИ (его вес)
(1)
Рассто-
Yi
Ранг
пп
яние
сводный
регио-
(i)
до эта-
ИИ «Ка-
на
лона
чества
кн
населеНИЯ»
y~l)(l)
(0,409)
ур>(2)
(0,407}
ур>(3)
(0,184}
1
Респ. Карелия
3,41
2,66
2,56
7,063
2,94
70
2
Респ. Коми
3,65
7,33
1,48
5,725
4,28
46
Архангельская
4,04
4,70
2,12
6,112
3,89
51
3,41
2,31
2,07
7,304
2,70
71
6,67
7,96
2,68
4,013
5,99
19
7,83
1,75
9,71
5,443
4,56
40
3,12
1,27
1,86
7,912
2,09
75
2,06
0,61
3,61
8,314
1,69
77
3
обл.
4
Вологодская
обл.
5
Мурманская
обл.
6
г.СанктПетербург
7
Ленинградская
обл.
8
Новгородская
обл.
9
Псковская обл.
2,03
0,89
2,22
8,420
1,58
78
10
Брянская обл.
5,35
2,48
4,18
6,168
3,83
53
Владимирская
4,96
1,53
6,22
6,497
3,50
59
11
обл.
12
Ивановская обл.
3,28
1,76
5,66
7,040
2,96
69
13
Калужская обл.
5,36
2,25
4,45
6,235
3,77
56
Костромская
3,71
1,76
1,46
7,566
2,43
73
14
обл.
15
г. Москва
8,78
2,49
10,00
4,854
5,15
29
16
Московская обл.
5,90
2,51
8,46
5,486
4,51
41
17
Орловская обл.
5,71
2,46
8,09
5,596
4,40
43
18
Рязанская обл.
4,47
1,19
6,57
6,801
3,20
65
19
Смоленская обл.
3,48
1,60
3,67
7,312
2,69
72
20
Тверская обл.
2,14
1,45
2,94
8,009
1,99
76
по
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
871
Пl.2.la (продолжение)
21
Тульская обл.
3,42
1,06
2,11
7,854
2,15
74
22
Ярославская обл.
2,01
4,71
6,813
3,19
66
23
Респ. Марий Эл
3,89
4,48
5,77
6,84
4,645
5,35
27
24
Респ. Мордовия
7,62
3,23
8,18
4,642
5,36
26
25
Чувашская Респ.
5,40
7,14
15
Кировская обл.
4,06
3,50
3,766
6,138
6,23
26
6,56
4,28
3,86
52
27
Нижегородская
4,67
1,50
6,23
6,607
3,39
61
5,22
4,516
5,48
25
8,75
4,187
5,81
22
обл.
28
Белгородская обл.
8,97
29
Воронежская обл.
8,00
3,77
3,81
30
Курская обл.
6,15
2,51
7,38
5,491
4,51
42
31
Липецкая обл.
7,30
2,94
3,36
5,600
4,40
44
32
Тамбовская обл.
5,52
1,35
3,73
6,772
3,23
63
33
Респ. Калмыкия
6,58
8,57
6,99
2,702
7,30
2
34
Респ. Татарстан
8,11
6,65
6,70
2,834
7,17
5
Астраханская
6,35
6,55
5,09
3,837
6,16
17
6,21
3,74
5,65
5,029
4,97
33
35
обл.
36
Волгоградская
обл.
37
Пензенская обл.
5,90
4,03
6,01
4,929
5,07
31
38
Самарская обл.
6,97
5,57
8,44
3,492
6,51
10
39
Саратовская обл.
6,60
4,87
7,77
4,044
5,96
20
40
Ульяновская обл.
6,08
3,42
5,06
5,328
4,67
38
41
42
Респ. Адыгея
7,51
5,03
6,58
3,841
18
Респ. Дагестан
8,30
8,86
1,70
3,793
6,16
6,21
16
43
Кабардино-Бал-
7,55
8,81
4,98
2,769
7,23
3
7,91
6,98
5,02
3,170
6,83
6
7,69
7,30
6,58
2,701
7,30
1
7,57
5,07
3,57
4,461
5,54
24
7,94
5,28
6,03
3,700
7,30
13
7,22
3,85
7,78
4,412
5,59
23
карская Респ.
44
Карачаево-
Черкесская Респ.
45
Респ.
Сев.Осетия А лани я
46
Краснодарский
край
47
Ставропольский
край
48
Ростовская обл.
ПРИЛОЖЕНИЕ
872
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.la (окончание)
Башкорто-
7,51
7,61
3,74
3,473
6,53
8
50
Удмуртская Респ.
3,69
7,19
5,29
4,854
5,15
30
51
Курганская обл.
3,52
5,28
1,79
6,215
3,88
55
Оренбургская
5,63
4,82
3,67
5,113
4,89
36
Пермская обл.
2,44
4,54
2,02
6,876
3,12
68
Свердловская
4,13
4,36
4,98
5,627
4,37
45
49
Респ.
стан
52
обл.
53
54
обл.
55
Челябинская обл.
4,72
5,02
6,71
4,848
5,15
28
56
Респ. Алтай
1,93
6,74
5,64
5,873
4,13
48
57
Алтайский край
6,02
4,80
3,79
4,958
5,04
32
58
Кемеровская обл.
2,32
4,77
3,22
6,611
3,39
62
Новосибирская
6,20
5,65
8,81
3,722
6,28
14
59
обл.
60
Омская обл.
6,32
5,44
5,76
4,159
5,84
21
61
Томская обл.
5,46
7,01
9,44
3,483
6,52
9
62
Тюменская обл.
7,83
9,17
4,39
2,830
7,17
4
63
Респ. Бурятия
2,42
7,34
3,15
5,916
4,08
49
64
Респ. Тыва
0,55
8,23
3,09
6,825
3,17
67
65
Респ. Хакасия
1,34
5,50
5,32
6,556
3,44
60
66
Красноярский
3,26
6,59
6,66
5,040
4,96
34
край
67
Иркутская обл.
1,40
6,44
6,90
6,102
3,90
50
68
Читинская обл.
1,43
6,72
2,06
6,788
3,21
64
69
Респ. Саха (Яку-
6,37
9,35
4,76
3,258
6,74
7
тия)
70
Еврейская АО
2,75
6,25
1,31
6,412
3,59
58
71
Чукотский АО
3,15
9,39
3,30
5,259
4,74
37
72
Приморский край
3,52
6,32
6,10
5,050
4,95
35
73
Хабаровский край
2,52
5,99
9,08
5,440
4,56
39
74
Амурская обл.
2,42
6,74
4,29
5,820
4,18
47
75
Камчатская обл.
5,27
8,53
5,95
3,613
6,39
11
76
Магаданская обл.
5,23
8,15
5,96
3,700
6,30
12
77
Сахалинская обл.
2,94
6,15
1,52
6,298
3,70
57
Калининградская
2,30
5,31
4,66
6,202
3,80
54
78
обл.
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
873
Пl.2.16. Уровень благосостояния
NN
Регион
Блочный ИИ
(его вес)
пп
(i)
Yi
яние
сводный
реги-
ИИ «Уров
она
ня благосо-
по
СТОЯНИЯ»
УБ
до
эталона
y}l)(l)
(0,595)
y}l) (2)
(0,405)
(11)
Рассто-
Ранг
1
Респ. Карелия
7,38
3,09
4,840
5,16
36
2
Респ. Коми
8,67
2,23
5,053
4,95
39
3
Архангельская обл.
6,35
1,57
6,062
3,94
58
4
Вологодская обл.
7,15
4,30
4,239
5,76
20
5
Мурманская обл.
7,51
3,32
4,665
5,33
30
6
г. Санкт-Петербург
8,05
9,29
1,572
8,43
2
7
Ленинградская обл.
3,09
6,15
5,864
4,14
53
8
Новгородская обл.
6,00
5,27
4,310
5,69
21
9
Псковская обл.
4,84
5,76
4,812
5,19
35
10
Брянская обл.
4,47
6,98
4,676
5,33
31
11
Владимирская обл.
3,39
6,61
5,532
4,47
50
12
Ивановская обл.
1,08
5,49
7,451
2,55
74
13
Калужская обл.
4,24
5,49
5,288
4,71
45
14
Костромская обл.
3,30
4,19
6,354
3,65
63
15
г. Москва
9,09
9,27
0,842
9,16
1
16
Московская обл.
6,68
9,45
2,585
7,41
7
17
Орловская обл.
5,85
6,86
3,775
6,22
15
18
Рязанская обл.
5,13
6,61
4,330
5,67
22
19
Смоленская обл.
6,22
7,48
3,324
6,68
9
20
Тверская обл.
3,07
6,10
5,891
4,11
54
21
Тульская обл.
5,98
4,88
4,500
5,50
25
22
Ярославская обл.
7,23
4,93
3,869
6,13
16
23
Респ. Марий Эл
1,45
6,12
7,040
2,96
68
24
Респ. Мордовия
2,52
6,50
6,184
3,82
61
25
Чувашская Респ.
3,35
8,35
5,231
4,77
43
26
Кировская обл.
3,07
3,22
6,865
3,13
66
27
Нижегородская обл.
6,98
6,12
3,392
6,61
10
28
Белгородская обл.
6,66
8,73
2,699
7,30
8
29
Воронежская обл.
5,03
8,33
3,980
6,02
17
ПРИЛОЖЕНИЕ
874
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.16 (продолжение)
30
Курская обл.
3,85
8,36
4,859
5,14
37
31
Липецкая обл.
7,83
8,70
1,871
8,13
4
32
Тамбовская обл.
6,55
6,02
3,677
6,32
13
33
Респ. Калмыкия
1,91
4,90
7,037
2,96
67
34
Респ. Татарстан
8,49
7,85
1,800
8,20
3
35
Астраханская обл.
6,73
4,02
4,566
5,43
26
36
Волгоградская обл.
7,11
4,63
4,083
5,92
19
37
Пензенская обл.
3,03
5,97
5,956
4,04
57
38
Самарская обл.
8,71
6,84
2,243
7,76
6
39
Саратовская обл.
4,97
4,60
5,186
4,83
42
40
Ульяновска.я обл.
3,91
5,72
5,431
4,57
48
41
Респ. Адыгея
2,71
7,11
5,917
4,08
55
42
Респ. Дагестан
1,07
3,94
7,892
2,11
76
43
Кабардино-Балкарская
3,51
6,54
5,466
4,53
49
2,14
5,96
6,586
3,41
64
4,74
7,60
4,337
5,66
23
Респ.
44
Карачаево-Черкесска.я
Респ.
45
Респ. Сев. ОсетияАлан и я
46
Краснодарский край
6,35
6,91
3,433
6,57
11
47
Ставропольский край
4,44
6,57
4,810
5,19
34
48
Ростовская обл.
6,68
5,66
3,768
6,23
14
49
Респ. Башкортостан
8,48
7,44
2,008
8,99
5
50
Удмуртская Респ.
4,41
5,58
5,152
4,85
41
51
Курганская обл.
1,83
2,77
7,800
2,20
75
52
Оренбургская обл.
4,85
4,90
5,130
4,87
40
53
Пермская обл.
7,83
3,23
4,622
5,38
29
54
Свердловская обл.
8,47
4,88
3,467
6,53
12
55
Челябинская обл.
5,10
5,94
4,575
5,42
27
56
Респ. Алтай
1,85
2,12
8,040
2,96
77
57
Алтайский край
3,95
4,47
5,843
4,16
52
58
Кемеровская обл.
7,22
3,29
4,782
5,22
32
59
Новосибирская обл.
4,94
4,47
5,256
4,74
44
60
Омская обл.
6,94
4,85
4,040
5,96
18
61
Томская обл.
6,31
2,91
5,335
4,66
46
62
Тюменская обл.
9,35
3,00
4,484
5,52
24
63
Респ. Бурятия
2,82
2,38
7,363
2,64
73
64
Респ. Тыва
1,07
0,94
8,984
1,02
78
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
875
Пl.2.16 (окончание)
65
Респ. Хакасия
4,42
3,23
6,093
3,91
60
66
Красноярский край
7,26
3,22
4,808
5,19
33
67
Иркутская обл.
5,49
1,82
6,258
3,74
62
68
Читинская обл.
3,13
2,43
7,164
2,84
70
69
Респ. Са.ха (Якутия)
7,85
2,53
5,038
4,96
38
70
Еврейская АО
4,03
1,29
7,207
2,79
71
71
Чукотский АО
3,65
5,21
5,768
4,23
51
72
Приморский край
2,81
3,09
7,076
2,93
69
73
Хабаровский край
6,41
2,74
5,391
4,61
47
74
Амурская обл.
3,13
2,02
7,342
2,66
72
75
Камчатская обл.
4,83
1,50
6,725
3,23
65
76
Магаданская обл.
7,45
1,22
5,926
4,07
56
77
Сахалинская обл.
6,68
1,35
6,076
3,92
59
78
Калининградская обл.
4,58
6,90
4,622
5,38
28
Пl.2.lв. Качество социальной сферы
NN
Блочный ИИ
Регион
(его вес)
пп
{i)
Рас-
(III)
Yi
Ранг
сто-
сводню
ре-
яние
ии
ги-
ДО
«Ка-
она
эта-
чества
по
лона
соци-
ксс
аль ной
сферы»
1
y}l) {1)
(0,260)
У?>(2)
y}l) {3)
(0,156)
у}1){4)
(0,452)
6,05
2,93
7,59
6,93
5,36
4,64
44
Респ. Коми
2,73
1,76
4,77
7,70
7,02
2,97
70
Архангель-
4,76
4,27
8,49
6,57
4,88
5,12
32
7,78
3,37
6,40
7,45
4,90
5,10
33
3,24
5,49
3,68
6,57
5,37
4,63
45
8,86
7,73
2,37
8,15
3,49
6,51
6
7,67
4,27
4,24
4,37
5,05
4,95
38
7,41
4,28
4,34
4,98
4,98
5,02
36
Респ. Каре-
(0,132)
лия
2
3
екая обл.
4
Вологодская
обл.
5
Мурманская
обл.
6
г.СанктПетербург
7
Ленинградекая обл.
8
Новгородекая обл.
ПРИЛОЖЕНИЕ
876
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.lв (продолжение)
9
Псковская обл.
5,53
5,21
8,05
6,18
4,24
5,74
16
10
Брянская обл.
4,56
6,42
7,40
4,82
4,24
5,75
17
11
Владимирская
5,00
5,41
7,78
5,93
4,35
5,65
19
6,11
4,10
6,17
3,20
5,29
4,71
41
7,40
6,51
6,51
3,99
3,72
6,23
10
5,91
4,53
6,18
5,66
4,75
5,25
30
г. Москва
9,36
8,52
1,91
8,21
3,42
6,58
4
Московская
8,89
6,59
3,94
8,01
3,43
6,57
5
обл.
12
Ивановская
обл.
13
Калужская
обл.
14
Костромская
обл.
15
16
обл.
17
Орловская обл.
5,54
6,79
5,88
5,00
3,96
6,03
11
18
Рязанская обл.
6,29
7,48
6,90
4,06
3,54
6,46
7
Смоленская
4,53
5,43
5,76
5,73
4,73
5,27
29
19
обл.
20
Тверская обл.
6,58
4,29
5,90
4,56
4,92
5,08
34
21
Тульская обл.
7,56
6,10
5,30
6,96
3,61
6,38
8
Ярославская
8,26
4,13
5,84
9,05
4,37
5,62
22
2,82
4,10
6,18
2,42
6,24
3,76
58
4,19
6,36
7,74
5,42
4,27
5,72
18
5,27
5,92
7,79
3,50
4,42
5,57
23
Кировская обл.
5,89
4,80
9,29
4,62
4,52
5,48
26
Нижегородская
8,25
6,16
5,35
7,63
3,39
6,60
3
7,28
8,16
8,14
6,70
2,32
7,67
1
4,62
7,72
5,16
5,27
4,05
5,94
13
22
обл.
23
Респ. Марий
Эл
24
Респ.
Мордовия
25
Чувашская
Респ.
26
27
обл.
28
Белгородская
обл.
29
Воронежская
обл.
30
Курская обл.
5,11
6,47
8,15
3,79
4,17
5,83
14
31
Липецкая обл.
7,70
6,68
6,90
5,59
3,21
6,78
2
32
Тамбовская
2,90
8,10
5,62
5,02
4,57
5,42
28
0,76
5,18
5,66
3,88
6,37
3,63
62
7,33
6,94
2,81
6,21
3,99
6,00
12
обл.
33
Респ.
Калмыкия
34
Респ.
Татарстан
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
877
Пl.2.lв (продолжение)
35
Астраханская
3,88
5,01
4,30
5,83
5,32
5,68
42
5,93
5,35
5,09
5,71
4,49
5,50
25
обл.
36
Волгоградская
обл.
37
Пензенская обл.
4,44
7,89
6,18
3,51
4,22
5,78
15
38
Самарская обл.
7,65
5,86
0,31
7,87
4,93
5,06
35
Саратовская
4,88
6,51
3,83
5,50
4,57
5,43
27
4,11
5,45
2,15
5,36
5,54
4,45
48
39
обл.
40
Ульяновская
обл.
41
Респ. Адыгея
2,70
7,83
5,81
1,75
5,25
4,74
40
42
Респ. Дагестан
1,00
9,51
6,53
0,72
5,85
4,14
53
43
Кабардино-Бал-
1,20
9,31
7,08
2,83
5,33
4,66
43
1,26
7,50
5,69
1,25
5,97
4,03
55
2,53
8,65
5,07
4,28
4,84
5,16
31
6,23
8,12
2,20
4,32
4,36
5,64
20
5,76
7,76
6,55
3,76
3,72
6,27
9
Ростовская обл.
5,71
7,14
3,12
5,06
4,36
5,64
21
Респ. Башкорто-
6,24
6,32
4,04
4,03
4,47
5,43
24
5,94
3,18
7,17
3,92
5,59
4,40
49
Курганская обл.
3,24
3,49
2,47
2,48
6,87
3,12
67
Оренбургская
4,55
4,64
4,09
4,98
5,42
4,57
47
Пермская обл.
5,54
1,53
1,92
5,60
7,09
2,91
72
Свердловская
7,13
2,61
1,73
5,31
6,35
3,65
61
6,47
3,14
2,63
5,20
6,00
4,00
56
карская Респ.
44
Карачаево-Черкесская Респ.
45
Респ. Сев. Осетия-Алания
46
Краснодарский
край
47
Ставропольский
край
48
49
стан
50
Удмуртская
Респ.
51
52
обл.
53
54
обл.
55
Челябинская
обл.
56
Респ. Алтай
2,60
1,96
6,24
1,89
7,36
2,73
75
57
Алтайский край
2,46
3,59
2,50
2,85
6,98
3,01
69
Кемеровская
4,93
2,56
1,50
8,07
6,59
3,41
63
3,62
3,95
3,49
3,48
6,26
3,73
60
4,31
4,69
3,67
6,47
5,38
4,61
46
58
обл.
59
Новосибирская
обл.
60
Омская обл.
ПРИЛОЖЕНИЕ
878
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.lв (окончание)
61
Томская обл.
3,57
3,95
2,40
5,26
6,26
3,74
59
62
Тюменская
6,84
3,62
0,52
8,69
5,93
4,07
54
обл.
63
64
Респ. Бурятия
2,73
1,71
4,19
4,76
7,32
2,67
74
Респ. Тыва
0,81
1,42
5,39
4,58
7,90
2,10
77
65
Респ. Хакасия
3,68
2,44
2,90
6,74
3,26
65
Красноярский
3,04
3,71
5,85
1,61
5,09
6,67
3,32
64
66
край
67
Иркутская обл.
2,93
2,09
0,49
2,99
7,86
2,14
76
68
Читинская обл.
0,92
1,43
4,93
1,47
8,25
1,75
78
69
Респ.Саха
4,21
2,68
5,86
6,22
6,12
3,88
57
(Якутия)
70
Еврейская АО
4,81
1,44
7,27
1,16
7,17
2,83
73
71
Чукотский АО
3,19
5,16
4,84
Приморский
2,67
6,78
2,83
7,25
72
6,56
4,17
2,05
7,03
2,97
39
71
5,29
1,39
3,08
6,29
6,96
3,04
68
край
73
Хабаровский
край
74
Амурская обл.
2,58
2,94
5,61
3,03
6,79
3,20
66
75
Камчатская
2,35
4,24
5,99
7,08
5,81
4,18
51
3,39
3,76
5,00
7,63
5,79
4,20
50
5,31
2,82
4,58
7,87
5,84
4,15
52
6,30
4,98
4,15
3,74
5,03
4,96
37
обл.
76
Магаданская
обл.
77
Сахалинская
обл.
78
Калининградекая обл.
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
879
Пl.2.lг. Качество экологической ниши
NN
Регион
Блочный ИИ
(его вес)
Рас-
(III)
Yi
Ранг
пп
стоя-
СВОДНЫЙ
ре-
(i)
ние
ИИ «Ка-
ги-
до
чества
она
эта-
экологи-
по
лона
ческой
кэн
ниши~
1
y~l) (1)
y}l) (2)
y}l) (3)
(0,392)
(0,276)
(0,185)
у}1>(4)
(0,147)
5,61
6,60
7,26
8,02
3,55
6,44
3
Респ. Коми
4,99
3,98
9,10
9,57
4,46
5,54
12
Архангель-
5,86
5,24
3,88
0,97
5,64
4,35
40
2,12
4,97
5,48
8,48
5,94
4,06
49
5,84
2,25
6,61
0,94
6,12
3,88
59
2,02
7,08
3,45
9,62
5,93
4,06
48
4,15
5,37
7,85
8,94
4,50
5,50
13
6,71
4,19
5,47
4,47
4,67
5,33
14
7,01
6,65
2,94
3,28
4,73
5,26
17
4,13
7,40
8,35
6,45
4,20
5,80
10
4,65
7,20
0,00
2,23
6,38
3,61
65
6,45
5,19
8,20
6,11
3,75
6,24
6
8,04
6,92
0,00
8,36
4,80
5,19
18
0,84
3,71
2,57
1,65
8,01
1,99
75
4,06
2,52
7,75
5,00
5,81
4,19
44
5,79
6,53
8,28
6,86
3,49
6,50
2
Респ. Карелия
2
3
екая обл.
4
Вологодская
обл.
5
Мурманская
обл.
6
г. Санкт-Пе-
тербург*>
7
Ленинградекая обл.
8
Новгородекая обл.
9
Псковская
обл.
10
Брянская
обл.
11
Владимирекая обл.
12
Ивановская
обл.
13
Калужская
обл.
14
Костромская
обл.
15
16
г. Москва*>
Московская
обл.
17
Орловская
обл.
18
Рязанская
обл.
880
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.lг (продолжение)
19
Смоленская обл.
6,28
3,95
7,33
1,50
5,23
4,76
31
20
Тверская обл.
5,88
3,41
2,59
6,16
5,56
4,44
38
21
Тульская обл.
1,14
3,39
0,00
4,23
8,13
1,86
76
Ярославская
4,05
5,46
6,02
3,88
5,28
4,71
32
22
обл.
23
Респ. Марий Эл
6,70
7,29
6,83
8,17
2,93
7,06
1
24
Респ. Мордовия
6,43
6,97
6,94
4,82
3,63
6,37
5
25
Чувашская
2,42
8,82
5,98
8,99
5,09
4,92
24
Кировская обл.
5,85
6,94
1,49
7,47
4,86
5,13
20
Нижегородская
3,09
5,72
3,93
3,63
6,04
4,95
55
3,60
4,69
1,71
6,20
6,21
3,78
62
3,88
6,42
3,43
2,80
5,81
4,19
45
Респ.
26
27
обл.
28
Белгородская
обл.
29
Воронежская
обл.
30
Курска.я обл.
4,84
5,76
1,91
5,32
5,54
4,46
37
31
Липецка.я обл.
1,51
6,79
2,28
2,42
7,10
2,89
71
32
Тамбовская обл.
4,03
5,60
2,68
5,39
5,68
4,32
42
33
Респ. Калмыкия
9,22
7,37
5,48
2,12
3,88
6,12
8
34
Респ. Татарстан
4,00
9,43
3,11
7,90
4,86
5,14
19
Астраханская
5,91
7,07
6,11
4,42
4,03
5,96
9
5,32
7,28
0,00
3,17
6,00
3,00
53
35
обл.
36
Волгоградская
обл.
37
Пензенская обл.
5,27
6,98
3,37
5,74
4,69
5,30
16
38
Самарская обл.
2,24
6,29
7,33
6,96
5,47
4,53
35
Саратовская
2,91
8,87
2,25
2,21
6,33
3,67
63
5,59
7,80
1,65
4,55
5,12
4,87
26
39
обл.
40
Ульяновская
обл.
41
Респ. Адыгея
7,68
5,54
9,54
3,88
3,62
6,38
4
42
Респ. Дагестан
8,14
9,20
3,07
2,77
4,26
5,74
11
Кабардино-Бал-
3,11
3,31
9,61
2,92
6,19
3,81
61
3,00
3,60
9,21
3,57
6,05
3,95
57
2,77
3,87
9,48
5,32
5,83
4,17
46
2,93
4,42
8,79
7,50
5,41
4,59
34
43
карская Респ.
44
Карачаево-
Черкесска.я Респ.
45
Респ. Сев. Осетия-Алания
46
Краснодарский
край
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
881
Пl.2.lг (продолжение)
47
Ставропольский
5,97
8,15
0,00
6,74
5,23
4,76
30
край
48
Ростовская обл.
3,25
7,25
1,65
5,26
6,01
3,99
54
49
Респ. Башкортостан
1,39
8,22
7,01
3,37
6,16
3,84
60
50
Удмуртская Респ.
3,84
8,33
3,50
7,75
4,91
5,08
21
51
Курганская обл.
7,40
4,27
0,00
4,77
5,85
4,14
47
52
Оренбургская обл.
1,39
5,78
2,00
5,78
6,95
3,05
70
53
Пермская обл.
3,90
6,39
5,66
8,84
4,67
5,33
15
54
Свердловская обл.
1,65
6,23
4,31
8,56
6,12
3,88
58
55
Челябинская обл.
0,28
4,89
6,58
6,58
6,92
3,07
69
56
Респ. Алтай
9,10
2,25
9,50
1,92
5,14
4,85
27
57
Алтайский край
4,08
6,71
2,19
2,64
5,99
4,00
52
58
Кемеровская обл.
0,76
4,90
9,35
8,87
6,38
3,61
64
59
Новосибирска.я обл.
5,14
3,24
0,00
3,64
6,80
3,19
68
60
Омска.я обл.
2,66
3,76
0,00
6,77
7,20
2,80
73
61
Томская обл.
5,08
2,08
0,00
1,04
7,55
2,44
74
62
Тюменская обл.
4,30
2,97
5,52
0,40
6,60
3,39
66
63
Респ. Бурятия
8,74
1,22
9,09
1,66
5,67
4,32
41
64
Респ. Тыва
8,97
1,54
7,97
1,84
5,54
4,46
36
65
Респ. Хакасия
5,91
4,05
8,51
1,55
5,21
4,79
29
66
Красноярский край
3,27
2,34
8,35
7,27
5,95
4,05
50
67
Иркутская обл.
4,83
3,29
6,38
5,64
5,29
4,70
33
68
Читинская обл.
4,67
1,87
4,58
7,55
5,96
4,03
51
69
Респ.
9,02
1,56
4,21
7,96
5,17
4,82
28
Са.ха
(Яку-
тия)
70
Еврейская АО
6,44
4,60
6,83
9,44
3,85
6,14
7
71
Чукотский АО
8,84
0,27
0,00
3,88
7,11
2,88
72
72
Приморский край
2,21
2,07
8,37
6,08
6,61
3,38
67
73
Хабаровский край
5,74
3,29
6,37
1,14
5,78
4,21
43
74
Амурская обл.
8,89
1,48
5,00
9,43
5,01
4,99
22
75
Камчатская обл.
7,95
1,10
7,49
0,98
6,04
3,95
56
76
Магаданская обл.
6,21
0,90
6,07
9,68
5,59
4,41
39
77
Сахалинская обл.
5,17
3,98
4,03
8,90
5,08
4,91
23
Калининградская
5,73
7,01
3,27
2,57
5,11
4,89
25
78
обл.
*) Специфика мегаполисов Москвы и Санкт-Петербурга обусловила их исклю
чение из числа регионов, для которых рассчитывались блочные и сводный ИИ «Ка
чества экологической ниши».
882
ПРИЛОЖЕНИЕ
Пl.2.2.
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Значения единого (сводного) ИИ КЖ и соответствующих
рангов для регионов РФ
Регион
Yi
~св
Ранг
1
Респ. Карелия
4,72
37
2
Респ. Коми
4,60
42
3
Архангельская обл.
4,39
52
4
Вологодская обл.
4,27
55
5
Мурманская обл.
5,39
13
6
г. Санкт-Петербург*>
5,31
-
7
Ленинградская обл.
3,58
71
8
Новгородская обл.
4,41
51
9
Псковская обл.
4,54
45
10
Брянская обл.
5,04
26
11
Владимирская обл.
4,72
36
12
Ивановская обл.
3,26
79
13
Калужская обл.
5,21
21
14
Костромская обл.
3,84
67
15
г. Москва*>
6,00
-
16
Московская обл.
5,14
24
17
Орловская обл.
5,31
16
18
Рязанская обл.
5,41
11
19
Смоленская обл.
5,23
18
20
Тверская обл.
3,83
68
21
Тульская обл.
3,78
69
22
Ярославская обл.
4,99
28
23
Респ. Марий Эл
4,68
39
24
Респ. Мордовия
5,26
17
25
Чувашская Респ.
5,17
22
26
Кировская обл.
4,07
60
NN
пп
( i)
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
883
Пl.2.2 (продолжение)
27
Нижегородская обл.
5,10
25
28
Белгородская обл.
5,88
4
29
Воронежская обл.
5,45
10
30
Курская обл.
4,81
34
31
Липецкая обл.
5,53
8
32
Тамбовская обл.
4,73
35
33
Респ. Калмыкия
5,22
19
34
Респ. Татарстан
6,66
1
35
Астраханская обл.
5,69
5
36
Волгоградская обл.
5,01
27
37
Пензенская обл.
4,83
32
38
Самарская обл.
6,05
2
39
Саратовская обл.
4,81
33
40
Ульяновская обл.
4,54
44
41
Респ. Адыгея
5.52
9
42
Респ. Дагестан
4,51
46
43
Кабардино-Балкарская Респ.
5,15
23
44
Карачаево-Черкесская Респ.
4,59
43
45
Респ. Сев. Осетия - Алания
5,63
7
46
Краснодарский край
5,63
6
47
Ставропольский край
5,36
14
48
Ростовская обл.
5,22
20
49
Респ. Баmкортостан
6,00
3
50
Удмуртская Респ.
4,69
38
51
Курганская обл.
3,19
74
52
Оренбургская обл.
4,11
59
53
Пермская обл.
4,26
56
54
Свердловская обл.
4,61
41
884
ПРИЛОЖЕНИЕ
1.
ИСХОДНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ
Пl.2.2 (окончание)
55
Челябинская обл.
4,33
54
56
Респ. Алтай
3,92
63
57
Алтайский край
3,99
62
58
Кемеровская обл.
3,90
65
59
Новосибирская обл.
4,50
47
60
Омская обл.
4,67
40
61
Томская обл.
4,48
48
62
Тюменская обл.
5,34
15
63
Респ. Бурятия
4,00
61
64
Респ. Тыва
3,17
75
65
Респ. Хакасия
4,17
57
66
Красноярский край
4,45
49
67
Иркутская обл.
3,73
70
68
Читинская обл.
3,03
76
69
Респ. Са.ха (Якутия)
5,40
12
70
Еврейская АО
3,85
66
71
Чукотский АО
4,36
53
72
Приморский край
3,54
72
73
Хабаровский край
4,41
50
74
Амурская обл.
3,91
64
75
Камчатская обл.
4,95
29
76
Магаданская обл.
4,92
30
77
Сахалинская обл.
4,13
58
78
Калининградская обл.
4,84
31
* > Специфика мегаполисов Москвы и Санкт-Петербурга обусловила их исклю
чение из числа регионов, сравниваемых по единому (сводному) ИИ КЖН.
ПРИЛОЖЕНИЕ
2.
НЕКОТОРЫЕ СВЕДЕНИЯ ОБ
ОДНОМЕРНЫХ И МНОГОМЕРНЫХ
ЗАКОНАХ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ, ИСПОЛЬЗУЕМЫЕ
В ВАЙЕСОВСКОМ ПОДХОДЕ
П2.1а. Обобщенное одномерное распределение Стьюдента с
v
степенями свободы, параметром сдвига Во
и параметром точности
c(t(vlBo;
с)- распределение)
Как известно (см., например, [Айвазян, Мхитарян
стандартн:ый з. р.в. Стьюдента с
v
(2001)],
п.
3.2.2),
степенями свободы (ст. св.) описы
вает распределение случайной величины
{~
t(v) = ----;::::::==
(П2.1)
где {о,{!, ... , {v - статистически взаимонезависимые (О; и 2 ) - нормаль
но распределенные случайные величины. Значение соответствующей
функция плотности вероятности ft(v)(x) в точке х задается соотношени ем
Г (v!l)
ft(v)(x) - y'iii.
х2
Г (~)
(
-"!1
1+-;;) ,
(П2.2)
00
где Г(z)
= J хz- 1 е-ж
о
dx, а среднее значение и дисперсия случайной
D(v) = v~ 2 (v > 2).
Введем в рассмотрение случайную величину t(vlBo; с), являющуюся
линейной функцией от t(v), а именно:
величины
t(v)
равны соответственно:
Et(v)
=О и
1
t(vlBo; с) = Vct(v) +Во.
(П2.З)
Легко показать, что функция плотности вероятности ft(vlfJo; с)(х) слу
чайной величины
t(vlBo;
с) в точке х имеет вид:
1
Vc · Г ( ~) (
с( х - Во )2 ) ft(vlfJo; с)(х) = у'V1Г. Г (~)
1+
v
причем Et(vlBO; с) =Во и Dt(vlBo; с) =
tl.!
2
'
(П2.4)
*·v~ 2 (v > 2).
Распределение, задаваемое плотностью (П2.4), называют обобщен
н·ым распределением Стъюдента (или
t(vlBo;
с)-распреде.л.ением) с па
раметром сдвига Во и параметром точности с. Отметим, что в данном
886
ПРИЛОЖЕНИЕ
2.
СВЕДЕНИЯ О РАСПРЕДЕЛЕНИИ ВЕРОЯТНОСТЕЙ
случае параметр точности с не есть величина, обратная к дисперсии
случайной величины
ll
~
с): дисперсия может и не существовать (при
t(vl8o;
2).
П2.1б. Обобщенное k-мерное
Стьюдента с
v
(k
~
2)
распределение
степенями свободы, параметром сдвига
0о = (8?, 8g, ... , 82)' и (k х k) - матрицей точности В (или
так называемое
f(vl0o;
В)-распределение)
Стандартн:ый k-мерный з.р.в. Стьюдента с
v
ст. св. описывает рас
пределение k-мерной случайной величины
(П2.5)
где каждая из компонент
стандартная стьюдентовская случай
tj(v) -
ная величина (П2.1), и все компоненты
нонекоррелированы. Функция плотности
tj(v) (j = 1, 2, ... , k) взаим
вероятности ft(v)(X) в точке
Х = (х< 1 >, х< 2 >, ... , x(k))' задается соотношением
ff(v)(X)
причем Et(v)
=
Г (v+k)
2
/с
(1Гll) 2 . г (~)
(
·
1
)-~
1 + -Х' · Х
,
= Ok и ковариационная матрица Ef(v) = v~ 2 ·lk где Ok обо
значает k-мерный вектор-столбец из нулей, а
размерности
Ik -
единичная матрица
k.
Обобщенное
f(vl0o;
(П2.6)
ll
k-мерное
В)-расnреде.л.ение) с
распределение
Стьюдента
(или
v ст. св., параметром сдвига 0о и мат
рицей то-чности В описывает распределение случайной величины
f(vl0o;
где С -
В) =С·
t(v)
+ 0о,
(П2.7)
(СС')- 1 ,
некоторая невырожденная (k х k)-матрица, В
00 = (8?, 82°, ... , 82), а t(v) - стандартная стьюдентовская k-мерная
случайная величина (П2.5), подчиняющаяся з.р.в. с плотностью (П2.6).
Значение функции плотности вероятности ft(vl0o;B) (Х) случайной вели
чины f(vl0o; В) в точке Х = (х< 1 >, х< 2 >,
"_
Jt(vl0o;
В)
(Х) -
Г
(v+k)
-2
х
(1Гv)~Г (~)
1 (
х 1в12
причем
хВ.
... , x(k))' задается соотношением
1
1 + ~(Х - 0 0 )'В(Х - 0 0 )
Ef(vl0o; В)= 0о и ковариационная матрица
)-v1k
(П2.8)
,
Et(vl0o;B)
= v~ 2 х
ПРИЛОЖЕНИЕ
2.
СВЕДЕНИЯ О РАСПРЕДЕЛЕНИИ ВЕРОЯТНОСТЕЙ
887
Именно этим з.р.в. описывается сопряженное априорное (а сле
довательно, и апостериорное) частное распределение вектора
0
=
= (Во, 81, ... , 8k)' коэффициентов регрессии в нормальной КЛММР, а
также условное (при фиксированных Х, У и Х) апостериорное распре
деление вектора У= (Уп+1, Yn+2 1 • • • , Yn+q)' прогнозных значений зави
симой переменной в этой модели (см. пример 3.9 и задачу 5 в п. 3.5).
При построении байесовских интервальных оценок и доверитель
ных областей для параметров
так же как и при построении бай
0,
есовских интервальных оценок и доверительных областей для про
гнозных значений У, используются следующие свойства t(vl0о;В)-рас
пределения.
Свойство {А). Пусть анализируемая k-мерная случайная вели
чина t(vl0o; В) разбита на два подвектора f(l)(vl0o; В) и
соответственно размерностей kl и k2 ( k1 + k2 = k), т. е.
f< 2)(vl0o; В)
.
_ (f(l)(vl0o; В))
t(vl0o, В) - f(2)(vl0o; В) .
Соответственно этому разобьются на блоки вектор средних значе
ний
00
и матрица точности В:
Тогда 'Частное (маржинальное) распределение вектора f< 1)(vl0o; В)
.являете.я
k1-мерн·ым
обобщеннъ~м
распределением
t(vl0o(l);B(l)) с параметром сдвига0о(1)
то'Чности B(l) = Вн - В12В221 В21.
Стьюдента
= (8~, ... ,82)' и матрицей
При построении интервальных оценок нас интересует частное рас
пределение отдельной (j-й) компоненты t<Л(vl0o; В) анализируемой kмерной обобщенной стьюдентовской случайной величины
t(vl0o; В).
Соответственно, при этом используется частный случай данного свой
ства, когда в роли
f< 1)(vl0o; В)
выступает компонента t(j)(vl0o; В). То-
гда:
k1
= 1;
00(1)
= BJ;
В(1)
= Ьjj -
Bj. · B(j) · B.j,
(П2.9)
- j-й диагональный элемент матрицы точности В, Bj. = (Ьj1, ...
. . . , Ьj·j-1, Ьj-j+1, ... , Ьjk) - (k - 1)-мерная строка, B.j = (Ь1j, ... , Ьj-1-j,
bj+1-j, ... , Ьkj)' - (k - 1)-мерный столбец, а B(j) - это (k - 1) х (kгде Ьjj
-1)-матрица, получающаяся из матрицы В вычеркиванием из нее j-й
строки и j-го столбца.
Заметим, что в данном случае
B(l) -
это 'Числовой параметр то'Ч
ности в частном обобщенном одномерном стьюдентовском распределе
нии компоненты t<Л(vl0o; В).
ПРИЛОЖЕНИЕ
888
2.
СВЕДЕНИЯ О РАСПРЕДЕЛЕНИИ ВЕРОЯТНОСТЕЙ
Свойство (В) используется при построении доверите.л:ьн:ых обла
стей для неизвестных значений параметров КЛММР или одновременно
для нескольких прогнозных значений зависимой переменной и заклю
-чается в том, -что статистика
'У= ~(t(vl0o; В) асимптоти-чески (по
0o)'B(t(vl0o; В) -
0о)
v -t оо) под-чиняется F(k; v)-распределению.
Поэтому, определяя из таблиц по заданной доверительной вероят
ности Ро значение 100(1-Ро)%-ной точки F1-P0 (k;
v) соответствующего
F-распределения, мы можем с помощью неравенства
~(t(vl0o;B)- 0o)'B(t(vl0o;B)- 0о) < F1-P (k;v)
0
(П2.10)
определить k-мерную область, в которую попадает 100Р% наблюдений
случайной величины
t(vl0o; В).
П2.2а. Двумерное гамма-нормальное распределение и его
свойства
Совместное двумерное распределение слу-чайной вели-чинъt
на
(8; h)
зывается гамма-нормальным, если его функция плотности вероят
ности р(8;
h)
задается (с то-чностью до нормирующего множителя)
соотношением
(П2.11)
где Ло,
80, а
и fЗ
-
некоторые числовые значения параметров этого се
мейства распределений.
Свойства двумерного гамма-нормального распределения
(1)
Частное распределение параметра
8
есть одномерное обобщен
ное распределение Стьюдента (П2.4) с 2а ст. св., параметром сдвига
80
и параметром точности с= Ло ·а/ {З, т. е.
Отсюда, в частности, следует, что случайная величина ~(0-Оо)
подчиняется стандартному распределению Стьюдента с 2а ст. св.
(11)
(3.23) с
Частное распределение параметра
h
есть гамма-распределение
параметрами (а, {З) и, следовательно,
Eh =
~, Dh = ~ и
h
Е
ПРИЛОЖЕНИЕ
СВЕДЕНИЯ О РАСПРЕДЕЛЕНИИ ВЕРОЯТНОСТЕЙ
2.
889
Е ['У1-е(а; {3); 'Уе(а; {3)] с вероятностью Ро = 1 - 2с:, где 'Yq(a, {3)
100q%-ная точка гамма-распределения с параметрами а и {3.
Отметим, что при а, кратном
0,5,
-
это
справедлива формула:
1
2
(П2.12)
'Yq(a, {3) = 2f3xq(2a),
где х~(т) - это 100q%-ная точка «ХИ квадрат~-распределения ст ст.
св.
Условное распределение параметра 8 (при условии заданности
(111)
значения параметра
ется
(80;
1/Лоhо)
-
h,
т. е. при
h
= ho,
где
ho -
заданное число) явля
нормальным распределением (вытекает из (П2.11)
при подстановке в правую часть этого соотношения заданного значения
h = ho).
П2.26. Многомерное
((k + 1)-мерное, k > 1)
гамма-нормальное
распределение и его свойства.
Совместное
. . . , 8k)'
и
h
(k+ 1)-мерное распределение параметров 0 = (81, 82, ...
называется многомерным гамма-нормальным, если его
функция плотности вероятности р( 0; h) задается (с точностью до нор
мирующего множителя) соотношением:
(П2.13)
где
заданные
численные
значения
векторного
параметра
сдвига
00 = (8~,8g, ... ,82)', элементов (k х k)-матрицы точности Ао, а так
же - параметров а и f3 однозначно определяют з.р.в. параметров е и
h.
Свойства многомерного гамма-нормального распределения
(1) Частное распределение векторного параметра 0 = (81, 82, ...
. . . , 8k)' есть многомерное обобщенное распределение Стьюдента (П3.8)
с 2а ст. св.' параметром сдвига е = (8~' 8g' ... ' 82)' и матрицей точности
В=~ ·Ло.
(11)
Частное распределение скалярного параметра
распределение
(111)
(3.23)
с параметрами а и
h
есть гамма
{3.
Условное распределение векторного параметра е (при условии
h, т. е. при h = ho, где ho - заданное
значение) является k-мерным (80; (hоЛо)- 1 ) - нормальным распреде
заданности значения параметра
лением.
ПРИЛОЖЕНИЕ
890
2. СВЕДЕНИЯ О РАСПРЕДЕЛЕНИИ ВЕРОЯТНОСТЕЙ
П2.3. Некоторые сведения об априорных з.р.в., сопряженных по
отношению к наблюдаемым генеральным совокупностям,
зависящим от единственного неизвестного параметра
NtNt
З.р.в. наблюдаемой гене-
Сопряженный
пп
ральной совокупности
з.р.в. р(д), выражения для
Ед и D8
1
(д; и~)-нормальный,
(до; и0 )-нормальный; Ед=
f(xlд)
Ж;е- ~
2а
=
(значение
~
априорный
= до;Dд =и~
(до и и~ - за.даны)
(д0 ; 0-0)-нормальный,
8 _
-
ж+180
l+"Y
где
и
а 'У= и 2 /пи~
Экспоненциальный
р(д) = Ra>дa-le-.88
Гамма-распределение с па-
f(xlд)
(д
раметрами
=
_ {де- 8 "'
-
о
х;;;::: о
ление;
при
х<О
Ед= а//3; Dд = 0://32
р(д)
f(xl8) =
{~
гамма-распреде-
-
при
[О; д)-равномерный:
=
О),
>
(а и
3
выраже-
ния для его параметров
о
известны)
2
з.р.в.
... , Xn),
и~ = и 2 /n(l +-у),
0'2
дисперсии
Апостериорный
р(дlх1, х2,
для
~
=
о~ х ~ 8;
х ~ [О;д)
для
/3 - за.даны)
=
{ а8°
при
о
при
&=a+n;
n
р = /3 + L: Xi
i=l
Распределение Парето с па-
д;;;::: до;
д
< дО;
(д >О),
раметрами_
& = a+n,80 =
=
mах{до;х1,х2,
... ,xn}
распределение Парето:
Ед= а8о.
Dд-
а-1'
а83
(а-1)2<а-2)
(а и до
4
Распределение Пуассона:
Р{~ = х}~~ е- 8
х =О,
р(8)
--
1,2, ....
Биномиальное
распреде-
ление: Р{~
=
х}
=
= С~д"'(1-д)N-ж (значение параметра N известно)
Отрицательное
альное
бином и-
распределение
Р{~=х}=
c;:f дk(1 -
=
чение
д)Ж-k (зна-
целочисл.
парамет-
ра
х
7
'
~а)
D8-
k известно)
= k,k + 1, ...
Бета-распределение с пара-
/3 - за.даны)
_ 1·1aHJ 8а-1 Х
- Г(а)Г(Ь)
x(l - д)Ь-l (О~ д ~ 1), -
бета-распределение;
Ед-~·
D8-
а+Ь'
=
о
при
;;;:::
х <хо
(значение параметра хо
известно),
хо~ х
< +оо
хо
-
n
a=a+L:xi
i=l
n
Ь = Ь + nN -
р(д)
Бета-распределение с пара-
бета-распределение;
a=a+kn
n
Ь = Ь + L: Xi - kn
i=l
- па+оJ да-1 х
- Г(а)Г(Ь)
x(l - 8)Ь-l(0 ~ 8 ~ 1), -
Ед=~·
а+Ь'
аЬ
(а+Ь)2(а+Ь+1)
(а и Ь - за.даны)
D8-
хе-.8 8 (д > О),
х
метрами
аЬ
(а+Ь)2(а+Ь+1)
(а и Ь - за.даны)
р(д) = ~д 0 - 1 х
при
n
L: Xi
(а и
f(xl8) =
8ж 1
Т+r
Q =а+
р(д)
а
-fj'Z
Распределение Парето
{
=
раметрами
i=l
P=/3+n
а.
--л·
6
Гамма-распределение с па-
.во 8а-1е-.В8 (8 > О) -
гамма-распределение; Ед
-
5
за.даны)
-
=
распределение;
Ед- а. Dд-Л•
-
(а и
а
- fj'Z
/3 -
за.даны)
L: Xi
i=l
метрами
Гамма-распределение с па-
-
гамма-
раметрами
&=a+n;
P=/3+nln(~),
где 9n =
(.fJi=l
Xi) -fi
Литература
Айвазян С.А.
Анализ качества и образа жизни населения (эко
(2012).
нометрический подход). М.: Наука.
Айвазян С.А.
Об опыте применения экспертно-статистического
(1974).
метода построения неизвестной целевой функции
//
Многомерный
статистический анализ в социально-экономических исследованиях.
М.: Наука.
Айвазян С.А.
(2008).
туционального
Роль социально-экономической политики и инсти
развития
в
повышении
качества жизни:
межстранового эконометрического анализа
//
результаты
Россия в глобализиру
ющемся мире. М.: Наука.
Айвазян С.А.
(2010).
Методы эконометрики. М.: Магистр.
Айвазян С.А., Бежаева З.И., Староверов О.В.
(1974).
Классификация
многомерных наблюдений. М.: Статистика.
Айвазян С.А., Енюков И.С., Меша.л:кин Л.Д.
(1985).
Прикладная ста
тистика: исследование зависимостей. М.: Финансы и статистика.
Айвазян С.А., Мхитарян В. С.
эконометрики. Том
1:
(2001). Прикладная статистика и основы
Теория вероятностей и прикладная статистика.
М.:ЮНИТИ.
Бард Й. (1979). Нелинейное оценивание параметров/ Пер. с англ. М:
Статистика.
Берндт Э.
(2005).
Практика эконометрики: классика и современность
/Пер. с англ. М.: ЮНИТИ.
Благовещенский Ю.Н.
кладная
(2012). Основные элементы теории копул //При
эконометрика. No 2 (26). С. 113-130.
Ваnник В.Н.
(1979).
Восстановление зависимостей по эмпирическим
данным. М.: Наука.
Вересков А.И., Левин В.Е., Федоров В.В.
м.н.к. без производных
//
(1981).
Линейная и нелинейная параметризация в
задачах планирования экспериментов. М. С.
Васuлъев Ф.П.
(1980).
Регуляризированный
20-27.
Численные методы решения экстремальных за
дач. М.: Наука.
Де Гроот М.
(1974).
англ. М.: Мир.
Оптимальные статистические решения
/
Пер. с
892
ЛИТЕРАТУРА
Демиденко Е.3.
(1981).
Линейная и нелинейная регрессии. М.: Финансы
и статистика.
Доклад Комиссии по оценке экономических результатов и социального
прогресса
//
Вопросы статистики.
2010.
№
№
11-12; 2011.
(Пол
2-3.
ные англоязычная и франкоязычная версии доклада размещены на
сайте:
www .stiglitz-sen-fitoussi.fr.)
Доманскиu В.К., Крепе В.Л., Калягина Л.В.
Построение целе
(2006).
вой функции для оценки экономических событий на основе эксперт
ного ранжирования// Вестник КрасГАУ. №
Дpeunep П., Смит Г.
с англ. Книга
Зелънер А.
1.
(1980).
(1986).
11.
Прикладной регрессионный анализ/ Пер.
М.: Финансы и статистика.
Байесовские методы в эконометрике
/
Пер. с англ.
(1991).
Моделирова
М.: Статистика.
Каnлинскиu А.И., Руссман И.В., Умъ~вакин В.М.
ние и алгоритмизация слабоформализованных задач выбора наилуч
ших вариантов систем. Воронеж: Изд-во Воронежского университета.
Киселев Н.И.
(1980).
Экспертно-статистический метод определения
функции предпочтения по результатам парных сравнений объектов
//
Алгоритмическое и программное обеспечение прикладного стати
стического анализа. М.: Наука.
Миркин Б.Г.
(1976).
Анализ качественных признаков. М.: Статистика.
Мостеллер Ф., Тъюки Дж.
с англ. Вып.
Полищук Л.И.
1 и 2.
(1982).
Анализ данных и регрессия
/
Пер.
М.: Финансы и статистика.
(1989).
Анализ многокритериальных экономико-матема
тических моделей. Новосибирск: Наука.
Пол.як В. Т.
//
(1967).
Методы минимизации функций многих переменных
Экономика и математические методы. Т.
Пол.як В. Т.
тремум
//
Пол.як В. Т.
(1969).
3.
№
6.
881-902.
Метод сопряженных градиентов в задачах на экс
Журн. вычисл. матем. и матем. физ. Т.
(1971).
С.
9.
№
4.
С.
807-821.
Сходимость методов возможных направлений в экс
тремальных задачах// Журн. вычисл. матем. и матем. физ. Т.
№
4.
с.
11.
855-869.
Пшени-ч,нъ~u Б.Н., Данилин Ю.М.
(1975).
Численные методы в экстре
мальных задачах. М.: Наука.
Росси Э.
(2010).
Одномерные GАRСН-модели: обзор
журнал ~квантиль». №
8.
С.
1-67.
/
Электронный
ЛИТЕРАТУРА
Сен А.
{2004).
Слуцкий Е.Е.
ля
//
893
Развитие как свобода. М.: Новое издательство.
{1963).
К теории сбалансированного бюджета потребите
Народнохозяйственные модели. Теоретические вопросы потреб
ления. М.: Изд-во АН СССР.
Тангян А. С.
( 1980).
Практическое построение адцитивной целевой
функции. М.: ЦЭМИ АН СССР.
Успенский А.В., Федоров В.В.
{1975).
Вычислительные аспекты метода
наименьших квадратов при анализе и планировании регрессионных
экспериментов. М.: МГУ.
Фишберн П.
{1978).
Теория полезности для принятия решений. М.: На
ука.
Химмелъблау Д.
{1975).
Прикладное нелинейное программирование/
Пер. с англ. М.: Мир.
Хованов Н.В.
{1996).
Анализ и синтез показателей при информацион
ном дефиците. СПб.: Изд-во С.-Петербургского университета.
Ширяев А.Н.
Т.
2.
{2004).
Основы стохастической и финансовой математики.
М.: Фазис.
Aas К., Czado С., F'rigessi А. and Bakken Н. {2009). Pair-copula Constructions of Multiple Dependence, Insиrance: Mathematics and Economics,
44(2), 182-198.
Abramowitz М. and Stegиn /. {1972). Handbook of Mathematical Functions
with Formиlas, Graphs, and Mathematical ТаЫеs, Dover PuЬlications,
New York.
AcerЬi С.
{2002). Spectral Measures of Risk: а Coherent Representation of
Subjective Risk Aversion, Journal of Banking and Finance, 26, 1505-1518.
AcerЬi С.
{2004). Coherent Representations of Subjective Risk-Aversion, in
G. Szego {Ed), Risk Measures for the 21st Century, Wiley, New York, рр.
147-207.
AcerЬi С.
and Tasche D. {2002). On the Coherence of Expected Shortfall,
Journal of Banking and Finance, 26(7), 1487-1503.
Acharya V., Bharath S. and Srinivasan А. {2007). Does Industry-wide
Distress Affect Defaulted Firms? - Evidence from Creditor Recoveries,
Journal of Financial Economics, 85(3), 787-821.
ADEH {1999). Artzner Р., Delbaen F., Eber J.M. and Heath D. {1999).
Coherent Measures of Risk, Mathematical Finance, 9, 203-228.
894
ЛИТЕРАТУРА
Аhп
S.K. {1988). Distribution for Residual Autocovariances in Multivariate
Autoregressive Models with Structured Parameterization, Biometrika, 75,
590-593.
Ait-Sahalia У., Myklaпd Р.А. апd Zhaпg L. {2005). How Often to Sample а
Continuous Time Process in the Presence of Market Microstructure Noise,
Review of Fiпaпcial Studies, 18, 351-416.
Ait-Sahalia У., Myklaпd Р.А. апd Zhaпg L. {2006). Ultra High Frequency
Volatility Estimation with Dependent Microstructure Noise. Working
Paper, w11380, NBER.
Akaike Н. {1974). Information Theory and an Extension of the Maximum
Likelihood Principle, Secoпd Iпteraпtioпal Symposium оп Iпformatioп
Theory, 267-281.
Alexaпder С.
{2001).
Centre, Mimeo.
А
Primer
оп
the
Orthogoпal
GARCH Model, ISMA
Alexaпder С.О. апd
Chibumba А.М. {1997). Multivariate Orthogonal Factor
GARCH, University of Sussex Discussion Papers in Mathematics
Alleп,
L., Deloпg, G. апd Sauпders, А. {2003). Issues in the Credit Risk
Modeling of Retail Markets, NYU Stern School of Business Working Paper
No. FIN-03-007.
Alsiпa М., Praпk
Functions,
J.
апd
Aequatioпes
Schweizer В. {2005). ProЫems on Associative
Mathematicae, 66, 128-140.
Altmaп Е./.
{1968). Financial Ratios, Discriminant Analysis and Prediction
of Corporate Bankruptcy, Joumal of Fiпапсе, 23(4), 589-609.
Altmaп Е./. апd
Kishore V.M. {1996). Almost Everything You Wanted to
Know About Recoveries on Defaulted Bonds, Fiпaпcial Aпalysts Joumal,
57Ц64.
Altmaп Е./., Faпjul
G. {2004). Defaults and Returns in High Yield Bond
Market: Analysis through 2003, NY Stern School of Business, Salomon
Center Working Paper, January 2004.
Altmaп Е. апd
Sabato G. {2007). Modeling Credit Risk for SMEs: Evidence
from the U.S. Market, ABACUS, 43(3), 332-357.
Altmaп
E.I., Resti А. апd Siroпi А. {2001). Analyzing and Explaining
Default Recovery Rates. Report submitted to ISDA, London.
Altmaп Е./.,
Brady В., Resti А. апd Siroпi А. {2005). The Link Between
Default and Recovery Rates: Theory, Empirical Evidence, and Implications, Joumal of Busiпess, 78(6), 2203-2227.
895
ЛИТЕРАТУРА
Andersen T.G. and Bollerslev Т. {1998). ARCH and GARCH Models. Гла
ва в Encyclopedia of Statistical Sciences {ed. S. Kotz, С. Read & D.
Banks), 2. John Wiley and Sons.
Andersen T.G., Т. Bollerslev, Р. Christoffersen and Diebold F.X. {2006).
Volatility and Correlation Forecasting. Глава в Handbook of Economic
Forecasting {ed. C.W.J. Granger, G.Elliott & А. Timmermann), 777-878,
North-Holland.
Andersen T.G. and Bollerslev Т. {1997). Heterogeneous Information Arrivals and Return Volatility Dynamics: Uncovering the Long-Run in High
Frequency Returns. Joumal of Finance 52, 975-1005.
Andersen T.G., Т. Bollerslev and Diebold F.X. {2009). Parametric and
Nonparametric Volatility Measurement. Глава в Handbook of Financial
Econometrics (под редакцией У. Ait-Sahalia & L. Hansen). North-Holland.
Anderson Н.,
К.
Nam and Vahid F. {1999). Asymmetric Nonlinear Smooth
Тransition GARCH Models. Глава в Nonlinear Time Series Analysis of
Economic and Financial Data (под редакцией Р. Rothman), 191-207.
Kluwer.
Andersen T.G., Bollerslev Т. {1997). Intraday Periodicity and Volatility
Persistence in Financial Markets, Joumal of Empirical Finance, 4, 115158.
Andersen T.G. and Bollerslev Т. {1998). Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts, Intemational Economic Review, 39, 885-905.
Andersen T.G., Bollerslev Т. and Diebold F.X. {2007). Roughing It Up:
Including Jump Components in the Measurement, Modeling and Forecasting of Return Volatility, Review of Economics and Statistics, 89, 701-720.
Andersen T.G., Bollerslev Т., Diebold F.X., Labys Р. {2000а). Exchange
Rate Returns Standardized Ьу Realized Volatility Are {Nearly) Gaussian,
Multinational Finance Joumal, 4, 159-179.
Andersen Т., Bollerslev Т., Diebold F.X. and Labys
Realizations, Risk, 13, 105-108.
Р. {2000Ь).
Great
Andersen T.G., Bollerslev Т., Diebold F.X. and Ebens Н. {2001а). The
Distribution of Realized Stock Return Volatility, Joumal of Financial
Economics, 61{1), 43-76.
Andersen T.G., Bollerslev Т., Diebold F.X., Labys Р. {2001Ь). The Distribution of Exchange Rate Volatility, Joumal of the American Statistical
Association, 96, 42-55.
896
ЛИТЕРАТУРА
Andersen T.G., L. Benzoni and Lund J. (2002). Estimating Jump-Diffusions for Equity Returns, Joumal of Finance, 57, 1239-1284.
Andersen T.G., Bollerslev Т., Diebold F.X., Labys Р. (2003). Modeling and
Forecasting Realized Volatility, Econometrica, 71, 529-626.
Anderson Т. W. and Darling D.A. (1954). А Test of Goodness ofFit, Joumal
of the American Statistical Association, 49, 765-769.
Andrews D. W.K. (1991). Heteroskedasticity and Autocorrelation Consistent
Covariance Matrix Estimation, Econometrica, 59, 817-858.
Andrews D. W.K. (1993). Tests for Parameter Stabllity and Structural Change with Unknown Change Point, Econometrica, 61, 821-856.
Ang А. and Chen J. (2002). Asymmetric Correlations of Equity Portfolios,
Joumal of Financial Economics, 63(3), 443-494.
Areal N.M.P.C. and Taylor S.J. (2002). The Realized Volatility of FTSE100 Futures Prices, Joumal of Futures Markets, 22, 627-648.
Asamow Е. and Marker J. (1995). Historical Performance of the U.S. Corporate Loan Market: 1988-1993, Commercial Lending Review, Spring,
13-32.
Bai J. (1997). Estimating Multiple Breaks One at
Theory, 13, 315-352.
а
Time, Econometric
Baillie R. Т., Bollerslev Т. and Mikkelsen Н.О. (1996). Fractionally Integrated Generalized Autoregressive Conditional Heteroskedasticity, Joumal of
Econometrics, 74, 3-30.
Balke N.S. and Fomby
627-645.
Balcombe
Т.В.
(1997). Intemational Economic Review, 38,
К., А.
Bailey and Brooks J. (2007). Threshold Effects in Price
Тransmission: The Case of Brazilian Wheat, Maize, and Soya Prices,
American Journal of Agricultural Economics, 89(2), 308-323.
Bamber D. (1975). The Area Above the Ordinal Dominance Graph and
the Area Below the Receiver Operating Characteristic Graph, Joumal of
Mathematical Psychology, 12, 387-415.
Bandi F.M., Russell J.R. (2005а). Microstructure Noise, Realized Volatility,
and Optimal Sampling. UnpuЬlished Paper. Graduate School of Business,
University of Chicago.
Bandi F.M., Russell J.R. (2006а). Volatility. In: Birge, J. R., Linetsky V.,
eds. Handbook of Financial Engineering, Elsevier.
897
ЛИТЕРАТУРА
Bandi F.M., Russell J.R. {2006Ь). Separating Market Microstructure Noise
from Volatility. Joumal of Financial Economics 79, 655-692.
Banerjee А., J. Dolado and Mestre R. {1998). Error Correction Mechanism
Tests For Cointegration In А Single Equation Framework, Joumal of
Time Series Analysis, 3(9), 267-83.
Barbe Р., Genest С., Ghoudi К., Remillard В. {1996). On Kendall's Process,
Joumal of Multivariate Analysis, 58, 197-229.
Bard У. {1970). Comparison of Gradient Methods for the Solution of Nonlinear Parametric Estimation ProЫems. - SIAM J. N umerical Analysis,
vol. 7, 157-186.
Bamdorff-Nielsen О.Е. and Shephard N. {2002). Econometric Analysis of
Realised Volatility and its Use in Estimating Stochastic Volatility Models,
Joumal of the Royal Statistical Society В, 64, 253-280.
Bamdorff-Nielsen 0.Е. and Shephard N. {2004а). Power and Bipower Variation with Stochastic Volatility and Jumps, Joumal of Financial Econometrics, 2(1), 1-37.
Bamdorff-Nielsen 0.Е. and Shephard N. {2005Ь). How Accurate is the
Asymptotic Approximation to the Distribution of Realised Volatility?
In: Andrews, D. W. К., Stock, J. Н., (eds), Identification and Inference
for Econometric Models. А Festschrift for Тот Rothenberg. Cambridge
University Press, 306-331.
Bamdorff-Nielsen 0.Е. and Shephard N. {2006). Econometrics of Testing
for Jumps in Financial Economics Using Bipower Variation, Joumal of
Financial Econometrics, 4(1), 1-30.
Bates D.S. {2000). Post-'87 Crash Fears in the S&P 500 Futures Option
Market, Joumal of Econometrics, 94, 181-238.
Bauwens L., Laurent S., Rombouts J. {2006). Multivariate GARCH Models:
а Survey, Joumal of Applied Econometrics, 21{1), 79-109.
Bauwens L., Laurent S. {2005). А New Class of Multivariate Skew Densities,
with Application to GARCH Models. - Journal of Business and Economic
Statistics, N 23(3), 346-354.
BCBS {1998). Basel Committee on Banking Supervision.
the Capital Accord to /ncorporate Market Risks,BASEL.
А
Mendment to
BCBS {2003а). Range of Practice in BanksT Intemal Ratings Systems.
Basel Committee on Banking Supervision, Document No 66.
898
ЛИТЕРАТУРА
BCBS (2003Ь). The 2002 Loss Data Collection Exercise for Operational
Risk : Summary of the Data Collected, Bank for International Settlement
document.
BCBS (2005). Basel Il: International Convergence of Capital Measurement
and Capital Standards: а Revised Framework, Bank for International Settlement document.
Beale E.M.L. (1974). The Scope of Jordan Estimation in Statistical Computing. - Journ. Inst. Math. Appl., vol. 10, 138-140.
Вес
F., Salem М.В., Carrasco М. (2004). Tests for Unit-Root Versus Threshold Specification with an Application to the Purchasing Power Parity
Relationship, Journal of Business and Economic Statistics, 22, 382-395.
Bedford Т. and Cooke R.M. (2001). Probability Density Decomposition for
Conditionally Dependent Random VariaЫes Modeled Ьу Vines, Annals
of Mathematics and Artificial lntelligence, 32, 245-268.
Bedford Т. and Cooke R.M. (2002) Vines - а New Graphical Model for
Dependent Random VariaЫes, Annals of Statistics, 30, 1031-1068.
Ben-Kaabia М. and Gil J.M. (2006). Asymmetric Price Тransmission in
the Spanish Lamb Sector, European Review of Agricultural Economics,
34, 53-80
Bera А. and Higgins М. (1993). ARCH Models: Properties, Estimation and
Testing. Journal of Economic Surveys 7, 305-362.
Berben R.P. and D. van Dijk (1999). Unit Root Tests and Asymmetric
Adjustment: А Reassessment, Working paper, Tinbergen Institute, Erasmus University of Rotterdam
Berg D., Bakken Н. (2007). Copula Goodness-of-Fit Testing: an Overview
and Power Comparison. Technical Report, University of Oslo, Statistical
Research Report no. 10.
Berg D. (2009). Copula Goodness-of-Fit Testing: An Overview and Power
Comparison, The European Joumal of Finance, forthcoming.
Berkes !. and Horv ath L. (2003). The Rate of Consistency of the QuasiMaximum Likelihood Estimator. Statistics and Probability Letters 61,
133-143.
Berkes l. and Horv ath L. (2004). The Efliciency of the Estimators of the
Parameters in GARCH Processes. Annals of Statistics 32, 633-655.
Berkes !., L. Horv ath and Kokoszka Р.(2003). GARCH Processes: Structure
and Estimation. Bernoulli 9, 201-227.
ЛИТЕРАТУРА
899
Berkowitz, J. (2001). Testing Density Forecasts with Applications to Risk
Management, Joumal of Business and Economic Statistics, 19, 465-474.
Bemardo J.M. and Smith A.F.M. (1994). Bayesian Theory, Wiley.
Biais В., Glosten L., Spatt С. (2005). Market Microstructure: А Survey of
Microfoundations, Empirical Results, and Policy lmplications, Joumal of
Financial Markets, 8, 217-264.
Bharath S. and Shumway Т. (2008). Forecasting Default with the Merton
Distance to Default Model, Review of Financial Studies, 21(3), 1339-1369.
Biais В., Glosten L. and Spatt С. (2005). Market Microstructure: а Survey
of Microfoundations, Empirical Results and Policy lmplications, Joumal
of Financial Markets, 8(2), 217-264.
Bielecki Т. and Rutkowski М. (2002). Credit Risk: Modeling, Valuation and
Hedging, Springer-Verlag.
Black F. (1976). Studies in Stock Price Volatility Changes. Глава в Proceedings of the 1976 Business Meeting of the Business and Economics Statistics Section, American Statistical Association, 177-181.
Black F. and Scholes М. (1973). The Pricing of Options and Corporate
LiaЬilities, Joumal of Political Есопоту, 81(3), 637-654.
Blanchard О. and Quah D. (1989). The Dynamic Effects of Aggregate
Demand and Aggregate Supply Disturbances, American Economic Review,
79, 655-673.
Bollerslev Т. (2009). Glossary to ARCH (GARCH). Глава в Volatility and
Time Series Econometrics: Essays in Honour of Robert F. Engle (под
редакцией Т. Bollerslev, J.R. Russell & М. Watson). Oxford University
Press.
Bollerslev Т., Chou R. and Kroner К. (1992). ARCH Modeling in Finance:
а Selective Review of the Theory and Empirical Evidence. Joumal of
Econometrics 52, 5-59.
Bollerslev Т., Engle R.F. and Nelson D.B. (1994). ARCH Models. Глава в
Handbook of Econometrics (под редакцией R. Engle & D. McFadden),
oii 4. Elsevier Science.
Bollerslev Т. (1986). Generalized Autoregressive Conditional Heteroskedasticity, Joumal of Econometrics, 31, 307-327.
Bollerslev Т. (1988). On the Correlation Structure for the Generalized
Autoregressive Conditional Heteroskedastic Process, Joumal of Time
Series Analysis, 9, 121-131.
900
ЛИТЕРАТУРА
Bollerslev Т. {1990). Modelling the Coherence in Short-run Nominal
Exchange Rates: А Multivariate Generalized ARCH Model, The Review
of Economics and Statistics, 72(3), 498-505.
Bollerslev Т. and Mikkelsen Н.О. {1996). Modeling and Pricing LongMemory in Stock Market Volatility, Joumal of Econometrics, 73, 151184.
Bollerslev Т., Engle R. and Wooldridge J. {1988). А Capital Asset Pricing
Model with Time Varying Covariances, Joumal of Political Есопоту, 96,
116-131.
Bollerslev Т., Uta Kretschmer U., Pigorsch С. and Tauchen G. {2009). А
Discrete-Time Model for Daily S&P500 Returns and Realized Variations:
Jumps and Leverage Effects Joumal of Econometrics, 150(2), 151-166.
Bougerol Р. and Picard N. {1992а). Stationarity of GARCH Processes and
of Some Nonnegative Time Series. Joumal of Econometrics 52, 115-127.
Bougerol Р. and Picard N. {1992Ь). Strict Stationarity of Generalized Autoregressive Process. The Annals of ProbaЬility 20, 1714-1730.
Воиуе Е.,
Durrleman V., Nikeghbali А., Riboulet G. and Roncalli Т. {2000).
Copulas for Finance а Reading Guide and Some Applications, Groupe de
Recherche Operationnelle, Credit Lyonnais, Working Paper.
Brandt М. and Diebold F. {2006) А No-Arbltrage Approach to Range-Based
Estimation of Return Covariances and Correlations, Joumal of Business,
79, 61-74.
Brandt М. and Jones {2006). Volatility Forecasting With Range-Based
EGARCH Models, Joumal of Business and Economic Statistics, 24, 470486.
Breidt F., Crato N. and de Lima Р. {1998). The Detection and Estimation
of Long Memory in Stochastic Volatility, Joumal of Econometrics, 83,
325-348.
Breslow N.E. and Clayton D. G. {1993). Approximate Inference in Generalized Linear Mixed Models, Joumal of the American Statistical Association,
88, 9-25.
Breymann W., Dias А. and Embrechts Р. {2003). Dependence Structures
for Multivariate High-Frequency Data in Finance, Quantitative Finance,
3, 1-14.
Brooks S.P. {1997). Markov Chain Monte Carlo Method and Its Application,
The Statistician, 47{1), 69-100.
ЛИТЕРАТУРА
Brummer
901
В.,
von Cmmon-Taubadel S. and Zorya S. (2006). Vertical Price
Тransmission Between Wheat and Flour in Ukraine: А Markov-Switching
Vector Error Correction Approach, 2006 Annual Meeting, August 12-18,
2006, Queensland, Australia, lnternational Association of Agricultural
Economists.
Buckland S. Т., Bumham К.Р. and Augustin N.Н. (1997). Model Selection:
ап Integral Part of Inference, Biometrics, 53, 603-618.
Bumham К.Р. and Anderson D.R. (1998). Model Selection and Inference:
а Practical Information-Theoretic Approach, Springer-Verlag, New York.
Cai J. (1994). А Markov Model of Switching-Regime ARCH. Joumal of
Business & Economic Statistics 12, 309-316.
Cai В. and Dunson D.B. (2006). Bayesian Covariance Selection in Generalized Linear Mixed Models, Biometrics, 62(2), 446-457.
Camacho М. (2005). Markov-Switching Stochastic Тrends and Economic
Fluctuations, Journal of Economic Dynamics and Control, 29, 135-158.
Cameron С., Li Т., 'Гrivedi Р. and Zimmer D. (2004). Modelling the Differences in Counted Outcomes Using Bivariate Copula Models with Application to Mismesured Counts, Econometrics Joumal, 7, 566-584.
Cameron С., Li Т., 'Гrivedi Р. (2005). Microeconometrics: Methods and
Applications. - New York, Cambride University Press.
Campbell J., Lo А. and MacKinlay С. (1997). The Econometrics of Financial Markets, Princeton University Press: New Jersey.
Caner М. and Hansen В.Е. (1998). Threshold Autoregressions with
Root, Working paper, University of Wisconsin, Madison.
а
Unit
Castri S. and Benedetto F. (2006). There is Something about Parmalat (On
Directors and Gatekeepers), Discussion paper, Bocconi University, Milan.
Carty L. and Lieberman D. (1996). Defaulted Bank Loan Recoveries.
Moody's Special Report, November 1996.
Chambers J. (1973). Fitting Nonlinear Models: Numerical Techniques. Biometrika, vol. 60, 1-13.
Chan K.S. (1993). Consistency and Limiting Distribution of the Least Squares Estimator of а Threshold Autoregressive Model, Annals of Statistics,
21, 520-533
Chan W.H. and Maheu J.M. (2002). Conditional Jump Dynamics in Stock
Market Returns, Joumal of Business and Economic Statistics, 20, 377389.
902
ЛИТЕРАТУРА
Chen Х. and Fan У. (2006). Estimation and Model Selection of Semiparametric Copula-Based Multivariate Dynamic Models Under Copula Misspecification, Joumal of Econometrics, 135, 125-154.
Chen Х., Fan У. and Patton А. (2004). Simple Tests for Models of Dependence Between Multiple Financial Time Series, with Applications to U.S.
Equity Returns and Exchange Rates, London Economics Financial Markets Group Working paper n. 483.
Chen К., Fan J. and Jin Z. (2006). Design-Adaptive Minimax Local Linear
Regression for Longitudinal/Clustered Data. to appear in Statistica Sinica.
Chemov М., Gallant A.R., Ghysels Е. and Tauchen G. (2003). Alternative
Models for Stock Price Dynamics, Joumal of Econometrics, 116, 225-257.
CherиЬini
U., Vecchiato W. and Luciano
Finance, Wiley.
Е.
(2004). Copula Methods in
Cheung У. W. and Lai K.S. (1993). Finite-sample Sizes of Johansen's Likelihood Ratio Tests for Cointegration, Oxford Bulletin of Economics and
Statistics, 55, 313-328.
Choi /. (2001). Unit Root Tests for Panel Data, Joumal of Intemational
Money and Finance, 20, 249-272.
Christiano L.J., Eichenbaum М., Evans C.L. (1999). Monetary Policy
Shocks: What Have We Learned and to What End?, Chapter 2 in J. В.
Taylor and М. Woodford, (eds.), Handbook of Macroeconomics, Volume
1А, Amsterdam: Elsevier Science PuЬlishers.
Christoffersen
mic Press.
Р.
(2003). Elements Of Financial Risk Management, Acede-
Clayton D.G. (1978). А Model for Association in Bivariate Life ТаЫеs
and its Application in Epidemiological Studies of Familial Tendency in
Chronic Disease Incidence, Biometrika, 65, 141-151.
Clemen M.N. and Jouini R. Т. (1996). Copula Models for Aggregating Expert Opinions, Operations Research, 44, 444-457.
Clements М.Р. and Krolzig Н.М. (1998) Acomparison of the Forecast Performance of Markov-Switching and Threshold Autoregressive Models of
US GNP, Econometrics Joumal, 1, 47-75.
Cochrane J. (2005). Asset Pricing, Princeton University Press.
Cohen К. J., Hawanini G.A., Maier S.F., Schwartz R.A., Whitcomb D.K.
(1983) Friction in the Тrading Process and the Estimation of Systematic
Risk, Joumal of Financial Economics, 12, 263-278.
ЛИТЕРАТУРА
903
Coleman A.M.G. (1995). Arbltrage, Storage and the 'Law of One Price':
New Theory for the Time Series Analysis of an Old ProЫem. Working
paper, Princeton University, USA.
Coleman A.M.G. (2004). Storage, Slow Тransport, and the Law of One
Price: Evidence from the Nineteenth Century U.S. Corn Market. Discussion Paper No. 502, University of Michigan, USA.
Coles 8., Heffeman J. and Tawn J. (1999). Dependence Measures for Extreme Value Analyses, Extremes, 2(4), 339-365.
Conover W.J. (1999). Practical Nonparametric Statistics, 3rd ed. Wiley.
Corsi F. (2009). А Simple Approximate Long-Memory Model of Realized
Volatility, Joumal of Financial Econometrics, 7(2), 174-196.
Corsi F., Zumbach G., Muller U. and Dacorogna М. (2001). Consistent
High-Precision Volatility from High Frequency Data, Economic Notes,
30, 183-204.
Corsi F., Mittnik 8., Pigorsch С., Pigorsch U. (2008а). The Volatility of
Realized Volatility, Econometric Reviews, 27, 46-78.
Corsi F., Pirino D. and Reno' R. (2008Ь) Volatility Forecasting: the Jumps
do Matter, Discussion paper, Quaderni del Dipartimento Di Economia
Politica, Universita' Degli Studi Di Siena.
Credit Suisse Financial Products (1997). CreditRisk+:
gement
Framework, Technical document.
Christoffersen
mic Press.
Р.
А
Credit Risk Mana-
(2003). Elements of Financial Risk Management. Akade-
Crouhy М., Galai D. and Mark R. (2000). А Comparative Analysis of
Current Credit Risk Models, Joumal of Banking and Finance, 24(1-2),
59-117.
CrosЬie Р.
and Bohn J. (2001-2003). Modeling Default Risk. Moody's KMV,
Technical document.
Crowder M.J. (1978). Beta-Binomial Anova for Proportions, Applied Statistics, 27, 34-37.
Gruz M.G. (2002). Modelling, Measuring and Hedging Operational Risk.New York, Wiley.
Curci G. and Corsi F. (2004). Discrete Sine Тransform Approach for Realized Volatility Measurement. Working Paper, University of Southern Switzerland.
904
ЛИТЕРАТУРА
Dacorogna М.М., М uller U.A., Nagler R.J., Olsen R.B. and Pictet О. V.
(1993). Geographical Model for the Daily and Weekly Sea.sonal Volatility
in the Foreign Exchange Market. Joumal of Intemational Мопеу and
Finance 12, 413-438.
Dacorogna М., Gencay R., Miiller U., Olsen R.B., Pictet О. V. (2001).
Introduction to Нigh-Frequency Finance. Academic Press: London.
Ап
D'Agostino R.B. and Stephens М.А. (1986). Goodness-of-Fit Techniques,
Marcel Dekker Inc.: New York.
Dalla Valle L. and Giudici Р. (2008). А Bayesian Approach to Estimate the
Marginal Loss Distributions in Operational Risk Management, Computational Statistics and Data Analysis, 52, 3107-3127.
Dalla Valle L. (2008). Bayesian Copulae Distributions, with Application to
Operational Risk Management, Methodology and Computing in Applied
ProbaЬility, forthcoming.
Danielsson J. and de Vries С. G. (2000). Value-at-Risk and Extreme Returns,
Annales d'Economie et de Statistique, 60, 239-270.
Daul S., De Giorgi Е., Lindskog F. and McNeil А. (2003). The Grouped
t-Copula with an Application to Credit Risk, Risk, 1, 73-76.
David
Н.А.
(1981) Order Statistics, 2 ed., Wiley.
Davidson J.Е.Н., Hendry D.F., Srba F. and Уео S. (1978). Econometric
Modelling of the Aggregate Time-Series Relationship Between Consumer's
Expenditure and Income in the United Kingdom, Economic Joumal, 88,
661-692
Davies R.B. (1987). Hypothesis Testing when а Nuisance Parameter is
Present Only under the Alternative. Biometrika 75, 33-43.
Davies N., Тriggs С.М. and Newbold Р. (1977). Significance Levels of the
Box-Pierce Portmanteau Statistic in Finite Samples, Biometrika, 64, 517522.
Degiannakis S. and Xekalaki Е. (2004). Autoregressive Conditional Heterosceda.sticity (ARCH) Models: а Review. Quality Technology and Quantitative Management 1, 271-324.
Deheuvels Р. (1979). La Fonction de Dependance Empirique et ses Proprietes: Un Test Non Parametrique d'lndependence, Bulletin de l'Academie
Royale de Belgique, Classe des Sciences, 5е serie, 65, 274-292.
Deheuvels Р. (1984). The characterization of distributions Ьу order statistics
and record values - а unified approach. Journal of Applied Probabllity,
21, 326-334.
ЛИТЕРАТУРА
905
DeLong E.R., DeLong D. М. and Clarke-Pearson D.L. (1988). Comparing
the Areas under Тwо or More Correlated Receiver Operating Characteristic Curves: А Non-parametric Approach, Biometrics, 44(3), 837-845.
Demarta S. and McNeil А. (2005). The t Copula and Related Copulas,
Intemational Statistical Review, 73, 111-129.
Dempster А.Р., N.M. Laird and RuЬin D.B. (1977). Maximum Likelihood
from Incomplete Data via the ЕМ Algorithm, Joumal of the Royal
Statistical Society, В, 39, 1-38.
Denker М. and Keller G. (1983). On U-Statistics and V. Mises' Statistics for
Weakly Dependent Processes, Zeitschrift fuer Wahrscheinlichkeitstheorie
und Verwandte GeЬiete, 64, 505-522.
Denuit М. and Lambert Р. (2005). Constraints on Concordance Measures
in Bivariate Discrete Data, Joumal of Multivariate Analysis, 93 , 40-57.
Deo R., Hurvich С. and Lu У. (2006), Forecasting Realized Volatility Using
а Long-Memory Stochastic Volatility Model: Estimation, Prediction and
Seasonal Adjustment, Joumal of Econometrics, 131(1-2), 29-58.
Dias А. and Embrechts Р. (2004). Change-Point Analysis for Dependence
Structures in Finance and Insurance. In: Risk Measures for the 21st Century, ed. Ьу Giorgio Szegoe, 321-335, Wiley Finance Series.
Diaz D. and Gemmill G. (2001). А Comparison of Тwo Credit-Risk Models,
Presented at the Australasian Finance Conference 2001.
Di Clemente А. and Romano С. (2004). А Copula-Extreme Value Theory
Approach for Modelling Operational Risk. In: M.G. Cruz (ed.), Operational Risk Modelling and Analysis: Theory and Practice, Risk Books, London.
Diebold F. (1986). Modeling the Persistence of Conditional Variances:
Comment. Econometric Reviews 5, 51-56.
а
Diebold F. (2004). The Nobel Memorial Prize for Robert F. Engle. Scandinavian Joumal of Economics 106, 165-185.
Diebold F. and Inoue А. (2001). Long Memory and Regime Switching.
Joumal of Econometrics 105, 131-159.
Diebold F. and Lopez J. (1995). Modeling Volatility Dynamics. Глава в
Macroeconometrics: Developments, Tensions and Prospects (под редак
цией К. Hoover), 427-472. Kluwer Academic Press.
Diebold F.X., Lee JH. and Weinbach G. (1994) Regime Switching with
Time-Varying Тransition Probabllities, in С.Р. Hargreaves (ed), Nonstationary time series analysis and cointegration, chapter 10, Oxford University Press: Oxford, UK.
906
ЛИТЕРАТУРА
Dietsch М. and Petey J. (2007). The lmpact of Size, Sector and Location on
Credit Risk in SME Loans Portfolios, Working Paper, Universite Robert
Schuman de Strasbourg
Ding Z., Granger С. W.J. and Engle R.F. (1993). А Long Memory Property
of Stock Market Returns and а New Model, Joumal of Empirical Finance,
1, 83-106.
Dobric J. and Schmid F. (2007). Testing Goodness-of-Fit for Parametric
Families of Copulas with an Application to Financial Data, Communications in Statistics: Simulation and Computation, 34(4), 1053-1068.
Dobric J. and Schmid F. (2007). А Goodness of Fit Test for Copulas
Based on RosenЫatt 's Тransformation, Computational Statistics and Data
Analysis, 51(9), 4633-4642.
Dobson A.J. (2002). Introduction to Generalized Linear Model. - Chapman
and Hall.
Doomik J.A. (2002) Object-Oriented Matrix Programming Using Ох, Timberlake Consultants Press: London, and http: / /wvv. doornik. com/index.
html, Oxford, UK.
Dueker J. (1997). Markov Switching in GARCH Processes and Mean-Reverting Stock Market Volatility. Joumal of Business & Economic Statistics
15, 26-34.
Dufour J.M. (1997). Some lmpossibllity Theorems in Econometrics with
Applications to Structural and Dynamic Models, Econometrica, 65(6),
1365-1388.
Dumas В. (1992). Dynamics Equilibrium and the Real Exchange Rate in
Spatially Separated World, Review of Financial Studies, 5, 153-180.
а
Eberhart А.С. and Weiss L.A. (1998). The lmportance of Deviations from
the Absolute Priority Rule in Chapter 11 Bankruptcy Proceedings, Financial Management, 27(4), 106-110.
Edgerton D. and Shukur G. (1999). Testing Autocorrelation in
Perspective, Econometric Reviews, 18, 343-386.
Efron
а
System
В.
(1979) Computer and the Theory of Statistics: Thinking the
UnthincaЫe. - SIAM Review.
Efron В. and Tibshirani R. (1993).
man & Hall, London.
Ап
Introduction to the Bootstrap, Chap-
Efron В. and Tibshirani R. (1998). The
Statistics, 26, 1687-1718.
ProЫem
of Regions, Annals of
ЛИТЕРАТУРА
907
Elliott G., Rothenberg Т., Stock J. (1996). Efficient Tests for an Autoregressive Unit Root, Econometrica, 64, 813-836.
Embrechts Р., McNeil А. and Straumann D. Correlation and Dependence
in Risk Management: Properties and Pitfalls. ln М.А.Н. Dempster (ed.),
Risk Management: Value at Risk and Beyond, Cambridge University
Press: Cambridge.
Embrechts Р. and Puccetti G. (2007). Aggregating Risk Across Matrix
Structures Loss Data: the Case of Operational Risk. Working Paper, ЕТН
Zurich. 2007.
Emery К., Cantor R. and Avner R. (2004). Recovery Rates on North
American Syndicated Bank Loans 1989-2003, Moody's lnvestors Service,
March 2004.
Enders W. and Granger С. W.J. (1998). Unit-Root Tests and Asymmetric
Adjustment with an Example Using the Term Structure of Interest Rates,
Journal о/ Business and Economic Statistics, 16, 304-311.
Engle R.F. (1982). Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation, Econometrica, 50,
987-1007.
Engle R.F. (1990). Discussion: Stock Market Volatility and the Crash of 87.
Review о/ Financial Studies 3, 103-106.
Engle R.F. (2001). GARCH 101: The use of ARCH/GARCH Models in
Applied Econometrics. Journal о/ Economic Perspectives 15, 157-168.
Engle R.F. (2004). Nobel Lecture. Risk and Volatility: Econometric Models
and Financial Practice. American Economic Review 94, 405-420.
Engle R.F. and Gonzalez-Rivera G. (1991). Semiparametric ARCH Models.
Journal о/ Business & Economic Statistics 19, 3-29.
Engle R.F. and Patton A.J. (2001). What Good is
Quantitative Finance 1, 237-245.
а
Volatility Model?
Engle R.F. (2002а). Dynamic Conditional Correlation - А Simple Class of
Multivariate GARCH Models, Journal о/ Business and Economic Statistics, 20, 339-350.
Engle R.F. (2002Ь). New Frontiers for Arch Models, Journal
Econometrics, 17, 425-446.
о/
Applied
Engle R.F. and Bollerslev Т. (1986). Modelling the Persistence of Conditional Variances, Econometric Reviews, 5, 1-50.
908
ЛИТЕРАТУРА
Engle R. F. and Granger С. W.J. (1987). Co-integration and Error Correction: Representation, Estimation, and Testing, Econometrica, 55, 251276.
Engle R.F. and Уоо С. W.J. (1991). Cointegrated Economic Time Series:
An Overview with New Results, in R.F. Engle and C.W.J. Granger (eds.),
Long-run Economic Relationships: Readings in Cointegration, Oxford
University Press, New York.
Engle R.F. and Ng V.K. (1993). Measuring and Testing the lmpact of News
on Volatility, Joumal of Finance, 48, 1749-1778.
Engle R. and Kroner F. (1995). Multivariate Simultaneous Generalized
ARCH, Econometric Theory, 11, 122-150.
Engle R.F., Sheppard К. (2001). Theoretical and Empirical properties of
Dynamic Conditional Correlation Multivariate GARCH, NBER Working
Papers, n. 8554.
Engle R.F., Lilien D.M. and RobЬins R.P. (1987) Estimating Time Varying
Risk Premia in the Term Structure: The ARCH-M Model, Econometrica,
55, 391-407.
Engle R.F., Ng V.K. and Rothschild М. (1990). Asset Pricing with а FactorARCH Covariance Structure: Empirical Estimates for Тreasury Bills,
Joumal of Econometrics, 45, 213-238.
Eraker В., Johannes M.S. and Polson N.G. (2003). The lmpact of Jumps
in Volatility, Joumal of Finance, 58, 1269-1300.
Erb С., Harvey С. and Viskanta Т. (1994). Forecasting International Equity
Correlations, Financial Analysts Joumal, 50, 32-45.
Fang. У. (1996). Volatility Modeling and Estimation of High-Frequency
Data with Gaussian Noise, UnpuЬlished doctoral thesis, MIT, Sloan
School of Management.
Fang К., Kotz S. and Hg К. (1987). Symmetric Multivariate and Related
Distributions, Chapman Hall: London.
Fantazzini D. (2008). Dynamic Copula Modelling for Value at Risk, Frontiers in Finance and Economics, 5(2), 1-36.
Fantazzini D. (2009а). Forecasting Default Probabllity without Accounting
Data: Evidence from Russia, ln: G. Gregoriou (ed.), Stock Market Volatility, 527-548, Chapman Hall-CRC/Taylor and Francis: London.
Fantazzini D. {2009Ь). The Effects of Misspecified Marginals and Copulas
on Computing the Value at Risk: А Monte Carlo Study, Computational
Statistics and Data Analysis, 53(6), 2168-2188.
ЛИТЕРАТУРА
909
Fantazzini D. (2009с). А Dynamic Grouped-T Copula Approach For Market
Risk Management, ln: G. Gregoriou (Ed.), А VaR lmplementation
Handbook, 253-282, McGraw-Hill: New York.
Fantazzini D. (2010). Three-Stage Semi-parametric Estimation of T-Copulas: Asymptotics, Finite-Sample Properties and Computational Aspects
Computational Statistics and Data Analysis, forthcoming.
Fantazzini D. and Figini S. (2009а). Random Survival Forest Models for
SME Credit Risk Measurement, Methodology and Computing in Applied
ProbaЬility, 11(1), 29-45.
Fantazzini D. and Figini S. (2009Ь). Default Forecasting for Small-Medium
Enterprises: Does Heterogeneity Matter? Intemational Joumal of Risk
Assessment and Management, 11(1/2), 138-163.
Fantazzini D., Dalla Valle L. and Giudici Р. (2007). Empirical Studies
with Operational Loss Data: DallaValle, Fantazzini and Giudici Study.
In: Operational Risk: А Guide to Basel П Capital Requirements, Models,
and Analysis, рр. 274-277. Wiley, New Jersey.
Fantazzini D., Degiuli Е. and Maggi М. (2008а). А new Approach for Firm
Value and Default Probabllity Estimation beyond the Merton Models
Computational Economics, Computational Economics, 31(2), 161-180.
Fantazzini D., Dalla Valle L. and Giudici Р. (2008Ь). Copulae and Operational Risks, Intemational Joumal of Risk Assessment and Management,
9(3), 238-257.
Felsenstein J. (1985). Confidence Limits on Phylogenies: an Approach Using
the Bootstrap, Evolution, 39, 783-791.
Ferguson S. Т., Genest С. and Hallin М. (2000). Kendall's Tau for Serial
Dependence, Canadian Journal of Statistics, 28, 587-604.
Fermanian J. and Scaillet О. (2003). Nonparametric Estimation of Copulas
for Time Series, Joumal of Risk, 5, (2003), 25-54.
Fermanian J. (2005). Goodness of Fit Tests for Copulas, Joumal of Multivariate Analysis, 95, 119-152.
Fidrmuc J., Hainz С., Malesich А. (2007). Default Rates in the Loan
Market for SMEs: Evidence from Slovakia. - William Davidson Institute
- University of Michigan (Working Paper).
Fielding А.Н. and Bell J.F. (1997). А Review of Methods for the Assessment
of Prediction Errors in Conservation Presence/ Absence Models, Environmental Conservation 24, 38-49.
910
ЛИТЕРАТУРА
Fletcher R. (1965). Function Minimization without Evaluating Derivatives.
- а Review, Comput. J., vol. 8, 33-41.
Fons J.S. (1994). Using Default Rates to Model the Term Structure of
Credit Risk, Financial Analysts Joumal, September-October, 25-32.
Francq С., Roussignol М. and Zako ian J. (2001). Conditional Heteroskedasticity Driven Ьу Hidden Markov Chains. Joumal о/ Time Series Analysis 22, 197-220.
Francq С. and Zako ian J. (2005). The 12-Structures of Standard and
Switching-Regime GARCH Models. Stochastic Processes and their Applications 115, 1557-1582.
Francq С. and Zako ian J. (2009). А Tour in the Asymptotic Theory of
GARCH Estimation. Глава в Handbook о/ Financial Time Series (под ре
дакцией Т. Andersen, R.A. Davis, J.-P. Kreiss and Т. Mikosch). Springer.
Frank M.J. (1979). On the Simultaneous Associativity of F(x, у) and
- F(x, у), Aequationes Mathematicae, 19, 194-226.
х +у
Frees Е. W. and Valdez Е. (1998). Understanding Relationship Using Copulas, North American Actuarial Joumal, 2, 1-25.
French K.R. and Roll R. (1986). Stock Return Variances: The Arrival of
Information and the Reaction of Тraders, Joumal о/ Financial Economics,
17{1), 5-26.
Frerichs Н. and Lбffter G. (2003). Evaluating Credit Risk Models Using
Loss Density Forecasts, Joumal о/ Risk, 5, 1-23.
Frey G. and Manera М. (2007). Econometric Models Of Asymmetric Price
Тransmission, Journal of Economic Surveys, Blackwell PuЫishing, vol.
21(2), pages 349-415, 04.
Fuertes А.М. and Kalotychou Е. (2006). Early Warning Systems for Sovereign DeЬt Crises: The Role of Heterogeneity, Computational Statistics
and Data Analysis 51, 1420-1441.
Gamerman D. (1997а). Sampling from the Posterior Distribution in Generalized Linear Mixed Models, Statistics and Computing, 7, 57-68.
Gamerman D. (1997Ь). Markov Chain Monte Carlo: Stochastic Simulation
f or Bayesian Inference, Chapman and Hall, London.
Gelfand А.Е. and Sahu 8. (1999). Gibbs Sampling, ldentifiabllity and Improper Priors in Generalized Linear Mixed Models, Joumal American
Statistical Association, 94, 247-253.
ЛИТЕРАТУРА
911
Gelman А., Carlin J.C., Stern Н., RuЬin D.B. (1995). Bayesian DataAnalysis. - New York, Chapman and Hall.
Gelman А., Carlin J. С., Stem Н. and RuЬin D.B. (2004). Bayesian Data
Analysis. Second edition. Chapman and Hall, New York.
Genest С. (1987). Frank's Family of Bivariate Distributions, Biometrika,
74, 549-555.
Genest С. and МасКау J. (1986). The Joy of Copulas: Bivariate Distributions with Uniform Marginals, American Statistics, 40, 280-285.
Genest С. and Rivest L. (1993). Statistical Inference Procedures for Bivariate Archimedean Copulas, Joumal of the American Statistical Association,
88, 1034-1043.
Genest С. and Favre А.С. (2007). Everything you Always Wanted to Know
About Copula Modeling but were Afraid to Ask, Joumal of Hydrologic
Engineering, 12, 347-368.
Genest С. and Remillard В. (2008) Validity of the Parametric Bootstrap for
Goodness-of-Fit Testing in Semiparametric Models, Annales de l'lnstitut
Henri Poincare, ProbaЬilites et Statistiques, 44(6), 1096-1127.
Genest С., Ghoudi К. and Rivest L. (1995). А Semiparametric Estimation
Procedure of Dependence Parameters in Multivariate Families of Distributions, Biometrika, 82, 543-552.
Genest С., Quessy J.F. and Remillard В. (2006а) Goodness-of-Fit Procedures for Copula Models Based on the ProbaЬility Integral Тransform, Scandinavian Joumal of Statistics, 33, 337-366.
Genest С., Quessy J.F. and Remillard В. (2006Ь). On the Joint Asymptotic
Behavior of Тwо Rank-Based Estimators of the Association Parameter in
the Gamma Frailty Model, Statistics and ProbaЬility Letters, 76, 10-18.
Genest С., Remillard В. and Beaudoin D. (2009) Omnibus Goodness-of-Fit
Tests for Copulas: А Review and а Power Study, Insurance: Mathematics
and Economics, 44(2), 199-213.
Geweke J. and Porter-Hudak S. (1984). The Estimation and Application of
Long Memory Time Series Models, Joumal of Тiте Series Analysis, 4,
221-238.
Ghaddar D.K. and Tong Н. (1981). Data Тransformation and Self-Exciting
Threshold Autoregression, Joumal of the Royal Statistical Society, С, 30,
238-248.
Gine Е. and Zinn J. (1990). Bootstrapping General Empirical Measures,
The Annals of ProbaЬility, 18(2), 851-869.
912
ЛИТЕРАТУРА
Giot Р., Laurent S. {2003). Value-at-Risk for Long and Short Positions,
Journal of Applied Econometrics, 18, 641-664.
Giraitis L., Kokoszka Р. and Leipus R. {2000). Stationary ARCH Models:
Dependence Structure and Central Limit Theorem. Econometric Theory
16, 3-22.
Giraitis L., Leipus R. and Surgailis D. {2007). Recent Advances in ARCH
Modelling. Глава в Long Мemory in Economics (под редакцией G.
Teyssiere and А.Р. Kirman). Springer.
Giudici Р. {2003). Applied Data Mining, Statistical Methods for Business
and Industry, Wiley.
Glen A.G., Leemis L.M., and Barr D.R. {2001). Order Statistics in Goodness-of-Fit Testing, IEEE Тransactions оп ReliaЬility, 50{2), 209-213.
Glosten L.R., Jaganathan R. and Runkle D. {1993). On the Relation Between the Expected Value and the Volatility of the Normal Excess Return
on Stocks, Joumal of Finance, 48, 1779-1801.
Goin J.E. {1982). ROC Curve Estimation and Hypothesis Testing: Applications to Breast Cancer Detection, The Journal of the Pattern Recognition
Society, 15, 263-269.
Goldfeld S.M. and Quandt R.E. {1973). А Markov Model for Switching
Regressions, Joumal of Econometrics, 1, 3-16.
Gonfalves S. and Meddahi N. {2005). Boostraping Realized Volatility.
Working Paper, Universite de Montreal.
Gonfalves S. and Meddahi {2008). Edgeworth Corrections for Realized Volatility, Econometric Reviews, 27, 139-162
Gonzalez М. and Gonzalo J. {1997). Threshold Unit Root Models,
Working paper n. 97-50, Universidad Carlos 111 de Madrid.
Gonzalez-Rivera G. {1998). Smooth Тransition GARCH Models. Studies in
Nonlinear Dynamics and Econometrics 3, 61-78.
Gonzalo J. and Pitarakis J. У. {2006). Threshold Effects in Multivariate
Error Correction Models, Palgrave Handbook of Econometrics, Vol. 1,
Chapter 15.
Goodwin В.К. and Piggott N. {2001) Spatial Market lntegration in the
Presence of Threshold Effects, American Journal of Agricultural Economics, 83, 302-317.
Gordy М. {2000). А Comparative Anatomy of Credit risk Models, Journal
of Banking and Finance, 24(1-2), 119-149.
ЛИТЕРАТУРА
913
Gourieroux С. and Monfort А. {1995). Statistics and Econometric Models,
Cambridge University Press: Cambridge.
Gourieroux С., Jasiak J. {2001). Financial Econometrics: ProЫems, Models,
and Methods. Princeton University Press.
Granger С. {1981). Some Properties of Time Series Data and Their Use in
Econometric Model Specification, Joumal of Econometrics, 16, 121-130.
Granger С. and Ding Z. {1996). Modeling Volatility Persistence of Speculative Returns. Joumal of Econometrics 73, 185-215.
Granger С. and Hyung N. {2004). Occasional structural breaks and long
memory with an application to the S&P500 absolute returns. Joumal of
Empirical Finance 11, 399-421.
Granger С. and Ter asvirta Т. {1999). А Simple Nonlinear Time Series
Model with Misleading Linear Properties. Economics Letters 62, 161-165.
Granger С. and Joyeux R. {1980). An lntroduction to Long-Memory Time
Series Models and Fractional Differencing. Joumal of Time Series Analysis 4, 221-238.
Granger С. {1981). Some Properties of Time Series Data and Their Use in
Econometric Model Specification, Joumal of Econometrics, 16, 121-130.
Granger С. and Pesaran М. {2000). Economic and Statistical Measures of
Forecast Accuracy, Joumal of Forecasting 19, 537-560.
Granger С., Patton А., Terasvirta Т. {2006). Common Factors in Conditional Distributions for Bivariate Time Series, Joumal of Econometrics,
132, 43-57.
Gray S. {1996). Modeling the Conditional Distribution of Interest Rates as
а Regime-switching Process. Joumal of Financial Economics 42, 27-62.
Greene W. {2002). Econometric Analysis, Prentice Hall.
Griep С. and De Stefano М. {2001). Standard & Poor's Official Response to
the Basel Committee's Proposal, Joumal of Banking and Finance, 25{1),
149-170.
Grossman R., O'Shea S. and Bonelli S. {2001). Bank Loan and Bond Recovery Study: 1997-2000, Fitch Loan Products Special Report, March 2001.
Gumbel E.J. {1960). Bivariate Exponential Distributions, Joumal of the
American Statistal Association, 55, 698-707.
Gupton G.M., Finger С. С. and Bhatia
document, J .Р. Morgan and Со.
М.
{1997). CreditMetrics. Technical
914
ЛИТЕРАТУРА
Hall S., Psaradakis Z. and Sola М. (1997). Switching Error-Correction
Models of House Prices in the United Kingdom, Economic Modelling,
14, 517-527.
Hall Р. and Уао Q. (2003). Inference in ARCH and GARCH Models with
Heavy-tailed Errors. Econometrica 71, 285-317.
Hamilton J.D. (1989). А New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle, Econometrica, 57, 357384.
Hamilton J. (1990). Analysis of Time Series Subject to Changes in Regime.
Journal of Econometrics 45, 39-70.
Hamilton J. and Susmel R. (1994). Autoregressive Conditional Heteroskedasticity and Changes in Regime. Journal of Econometrics 64, 307-333.
Hamilton J.D. (1994). Time Series Analysis, Princeton University Press.
Hamilton J.D. and Raj В. (2002). Advances in Markov-Switching Models.
Applications in Business Cycle Research and Finance, Physica-Verlag:
Heidelberg, Germany.
Hamilton D., Cantor R. and Ои S. (2002). Default and Recovery Rates of
Corporate Bond Issuers, Moody's Investors Services, February 2002.
and McNeil В. (1983). А Method of Comparing the Area under
Тwо ROC Curves Derived from the Same Cases, Diagnostic Radiology,
148, 839-843.
Hanley
А.
Hansen В. (1994). Autoregressive Conditional Density Estimation, International Economic Review, 35(3), 705-730.
Hansen В.(1997). lnference in TAR Models, Studies in Nonlinear Dynamics
and Econometrics, 2, 1-14.
Hansen
576.
В.
(1999). Testing Linearity, Journal of Economic Surveys, 13, 551-
Hansen В.Е. and Seo В. (2002). Testing for Тwo-Regime Threshold Cointegration in Vector Error-Correction Models, Journal of Econometrics, 110,
293-318.
Hansen P.R. and Lunde А. (2004). An Unblased Measure of Realized
Variance. UnpuЬlished Manuscript, Stanford University.
Hansen P.R. and Lunde А. (2005). А Forecast Comparison of Volatility
Models: Does Anything Beat а GARCH (1;1)? - Journ. Appl. Econom.,
no 20, рр. 873-889.
ЛИТЕРАТУРА
915
Hansen P.R. and Lunde А. (2006а). Consistent Ranking of Volatility Models, Journal of Econometrics, 131, 97-121.
Hansen P.R. and Lunde А. (2006Ъ). Realized Variance and Market Microstructure Noise (with discussion), Joumal of Business and Economic
Statistics, 24, 127-218.
Harris L. (1990). Estimation of Stock Variance and Serial Covariance from
Discrete OЬservations, Journal of Financial and Quantitative Analysis,
25, 291-306.
Нао Н.
(2006). Is the Structural Approach More Accurate than the Statistical Approach in Bankruptcy Prediction?. Queen's School of Business
Working Paper, Мау - 2006.
Hartley Н.О. (1961). Modified Gauss-Newton Method for the Fitting of
Nonlinear Regression Function. Technometrics, vol. 3, 269-275.
Hasbrouck J. (1988). Тrades, Quotes, lnventories and Information, Journal
of Financial Economics, 22, 229-252.
Hasbrouck J. and Sofianos G. (1993). The Тrades of Market Makers: An
Empirical Analysis of NYSE Specialists, Journal of Finance, 48(5), 15651593.
Hasbrouck J. (2007). Empirical Market Microstructure, Oxford University
Press.
Hastie Т., Tibshirani R. and Friedman J.H. (2001). The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Springer.
Hayashi F. (2000). Econometrics, Princeton University Press.
Не С.
and Terasvirta Т. (1999). Properties of Moments of
GARCH Processes. Joumal of Econometrics 92, 173-192.
а
Family of
Не С.,
Terasvirta Т. and Malmsten Н. (2002). Moment structure of а family
of first-order exponential GARCH models. Econometric Theory 18, 868885.
Нeckscher
E.F. (1916). Vaxelkursens Grundval vid Pappersmyntfot, Ekonomisk Tidskrift, 18, 309-312.
Hiiffding D. (1940). Masstablnvariante Korrelationstheorie, Schriften des
Mathematischen Seminars und des /nstituts fuur Angewandte Mathematik
der Universitat, 5, 181-233.
Hogg R. V. and Craig
А. Т.
(1965). Mathematical Statistics, Macmillan.
Hollander М. and Wolfe D.A. (1973). Nonparametric Statistical /nference.
Wiley: New York.
916
ЛИТЕРАТУРА
Hong У. and Li Н. (2005). Nonparametric Specification Testing for Continuous-Time Models with Application to Spot Interest Rates, Review of
Financial Studies, 18, 37-84.
Horvath М. Т.К. and Watson М. W. (1995). Testing for Cointegration when
Some of the Cointegrating Vectors Are Prespecified, Econometric Theory,
11, 984-1014.
Hosking J.R.M. (1980). The Multivariate Portmanteau Statistic, Joumal of
the American Statistical Association, 75, 602-608.
Hosking J. (1981). Fractional Differencing. Biometrika 68, 165-176.
Hosking J.R.M. and Wallis J.R. (2007). Parameter and Quantile Estimation
for the Generalized Pareto Distribution, Technometrics, 29, 339-349.
Hougaard Р. (1986). А Class of Multivariate Failure Time Distributions,
Biometrika, 73, 671-678.
Ни У.
and Perraudin W. (2002). The Dependence of Recovery Rates and
Defaults, Mimeo, Birbeck College.
Huang N. У. (1970). Unified Approach to Quadratically Convergent Algorithms for Function: Minimization. - Journ. Optim. Theory Applic., vol.
5,6, 405-423.
Huang Х. and Tauchen G. (2005). The Relative Contribution of Jumps to
Total Price Variance, Journal of Financial Econometrics, 3(4), 456-499.
Huard D., Ivin G. and Favre А.С. (2006). Bayesian Copula Selection, Computational Statistics and Data Analysis, 51(2), 809-822.
Huffera F. W. and Park С. (2007). А Test for Elliptical Symmetry, Journal
of Multivariate Analysis, 98(2), 256-281.
Huggins R. (1989). On the Statistical Analysis of Capture Experiments,
Biometrika, 76, 133-140.
Hull J. С. (2005). Options, Futurs and Other Derivatives. Prentice Hall.
Hult Н. and Lindskog F. (2002). Multivariate Extremes, Aggregation and
Dependence in Elliptical Distributions, Advances in Applied Probability,
34, 587-608.
Hurst Н. (1951). Long Term Storage Capacity of Reservoirs.
of the American Society of Civil Engineers 116, 770-799.
Тransactions
Hurvich С.М., Deo R. and Brodsky J. (1998). The Mean Squared Error of
Geweke and Porter Hudak's Estimator of the Memory Parameter of а
Long Memory Time Series, Journal of Time Series Analysis, 19, 19-46.
ЛИТЕРАТУРА
917
/hle., Von Cramon-Taubadel S. (1998). А Comparison of Threshold Cointegration and Markov-Switching Vector Error Correction Models in Price
Тransmission Analysis. NCCC-134 Conference of Applied Commodity
Price Analysis, Forecasting, and Market Risk Management, St. Louis,
Missouri.
Jacod J. and Protter Р. (1998). Asymptotic Error Distributions for the Euler
Method for Stochastic Differential Equations, А nnals of ProbaЬility, 26,
267-307.
Jackman S. Re-Thinking Equilibrium Presidential Approval - MarkovSwitching Error Correction. Paper presented at the 12th Annual Political
Methodology Summer Conference, lndiana University, Bloomington, USA,
1995.
Jarrow R., Тumbull S. (1999). Deriative Securities: The Complete Investor's
Quide. - South-Western PuЬlications.
Jaynes Е. Т., Bretthors G.L. (2003). Probabllity Theory: The Logic of Science. - Cambridge University Press.
Joe Н., Хи J. (1996). The Estimation Method of Inference Functions for
Margins for Multivariate Models, Department of Statistics, University of
British Columbla, Technical Report n. 166.
Joe Н. (1997). Multivariate Models and Dependence Concepts, London:
Chapman Hall.
Johansen S. (1995). Likelihood-based lnference in Cointegrated Vector Autoregressive Models, Oxford: Oxford University Press.
Johansen S. (1988). Statistical Analysis of Cointegration Vectors, Joumal
of Economic Dynamics and Control, 12, 231-254.
Johansen S. (1991). Estimation and Hypothesis Testing of Cointegration
Vectors in Gaussian Vector Autoregressive Models, Econometrica, 59,
1551-1580.
Johnson N., Kotz S., Balakrishan N. (1994). Continuous Univariate Distributions. Vol. 1. - Wiley series in probabllity and statistics.
Jondeau Е. and Rockinger (2006). The Copula-GARCH Model of Conditional Dependencies: An International Stock-Market Application. Journal of
International Money and Finance, N 25, р. 827-853.
Jondeau Е. and Rockinger М. (2003). Conditional Volatility, Skewness, and
Kurtosis: Existence, Persistence, and Comovements, Joumal of Economic
Dynamics and Control, 27, 1699-1737.
918
Jorion
ЛИТЕРАТУРА
Р.
(2007). Financial Risk Manager Handbook, 4th edition, Wiley.
Karlis D. and Kostaki А. (2002). Bootstrap Techniques for Mortality Models, Biometrical Joumal, 44(7), 850-866.
Khalaf L., Saphores J.D. and Bilodeau J.F. (2003). Simulation-Based Exact
Jump Tests in Models with Conditional Heteroskedasticity, Joumal of
Economic Dynamics and Control, 28, 531-553.
Kim G., Silvapulle M.J. and Silvapulle Р. (2007). Comparison of Semiparametric and Parametric Methods for Estimating Copulas, Computational
Statistics and Data Analysis, 51(6), 2836-2850.
Kim G. Silvapulle M.J. and Silvapulle Р. (2008). Estimating the Error
Distribution in Multivariate Heteroscedastic Time Series Models, Joumal
of Statistical Planning and Inference, 138(5), 1442-1458.
Kimberling С.Н. (1974). А Probabllistic Interpretation of Complete Monotonicity, Aequationes Mathematicae, 10, 152-164.
King J.L. (2001). Operational Risk: Measurement and Modelling. Wiley,
New York.
Kohavi R., Provost F. (1998). Glossary of Terms. Editorial for the Special
Issue on Applications of Machine Learning and the Knowledge Discovery
Process. - Machine Learning, N 30 (2/3), р. 271-274.
Kojadinovic 1., J. Уап Holmes (2011а). Fast Large-Sample Goodness-of-Fit
Tests for Copulas, Submitted.
Kojadinovic 1. and Уап J. (2011Ь). А Goodness-of-Fit Test for Multivariate
Multiparameter Copulas Based on Multiplier Central Limit Theorems,
Submitted. Statistics and Computing, 21 (1), 17-30.
Kole Е., Koedijk К. and Verbeek М. (2007). Selecting Copulas for Risk
Management, Journal of Banking and Finance, 31, 2405-2423.
Коортап
S.J., Jungbacker В. and Hol Е. (2005). Forecasting Daily Variabllity of the S&PlOO Stock lndex Using Historical, Realised and lmplied
Volatility Measures, Joumal of Empirical Finance, 12(3), 445-475
Koul H.L. (2002). Weighted Empirical Processes in Dynamic Nonlinear
Models, Lecture Notes in Statistics, Vol 166. Springer Verlag.
Koul H.L. and Ling S. (2006). Fitting an Error Distribution in Some Heteroscedastic Time Series Model, Annals of Statistics, 34, 994-1012.
Kotz S., Balakrishnan N. and Johnson N.L. (2000). Continuous Multivariate
Distributions, volume 1, 2nd ed., Models and Applications, Wiley, New
York.
ЛИТЕРАТУРА
Koyluoglu Н. and
11(10), 56-62.
Нickman А.
Koyluoglu Н. Bangia А., Garside
13(3), 26-30.
(1998).
Т.
ReconcilaЫe
919
Differences, RISK,
(2002). Devil in the Parameters, RISK,
Krolzig Н.М. (1996). Statistical Analysis of Cointegrated VAR Processes
with Markovian Regime Shifts, SFB 373 Discussion Paper 25/1996, Humboldt-Universitat zu Berlin, Berlin, Germany.
Krolzig Н.М. (1997). Markov-Switching Vector Autoregressions. Modelling,
Statistical Inference, and Applications to Business Cycle Analysis. Springer: Berlin, Germany.
Krolzig Н.М. and Toro J. (2001). А New Approach to the Analysis of
Business Cycle Тransitions in а Model of Output and Employment, Department of economics discussion paper series No. 59, University of Oxford, Oxford.
Krolzig Н.М., Marcellino М. and Mizon G. (2002). А Markov-Switching
Vector Equilibrium Correction Model of the UK Labor Market, Empirical
Economics, 27, 233-254.
Krolzig Н.М. (2004). MSVAR- an Ох Package Designed for the Econometric
Modelling of Univariate and Multiple Time Series Subject to Shifts in
Regime.
Kruskal W. (1958). Ordinal measures of Association, Journal of the American Statistical Association, 53, 814-861.
Kurowicka D. and Cooke R.M. (2006). Uncertainty Analysis with
Dimensional Dependence Modelling, Wiley: New York.
Нigh
Kwiatkowski D., Phillips Р. and Schmidt Р. and Shin У. (1992). Testing
the Null Hypothesis of Stationary against the Alternative of а Unit Root,
Journal of Econometrics, 54, 159-178.
Lambert Р. and Vandenhende F. (2002). А Copula-Based Model for Multivariate Non-normal Longitudinal Lata: Analysis of а Dose Titration Safety
Study on а New Antidepressant, Statistics in Medicine, 21, 3197-3217.
Lamoureux С. and Lastrapes W. (1990). Persistence in Variance, Structural
Change and the GARCH Model. Journal of Business & Economic Statistics 8, 225-234.
Lee S. W. and Hansen В.Е. (1994). Asymptotic Properties of the Maximum
Likelihood Estimator and Test of the Stabllity of Parameters of the
GARCH and IGARCH Models, Econometric Theory, 10, 29-52.
920
ЛИТЕРАТУРА
Li С. and Li W. (1996). On а DouЫe Threshold Autoregressive Heteroskedasticity Time Series Model. Journal of Applied Econometrics 11, 253274.
Libby R. (1975). Ratios and the Prediction of Failure: Some Behavioral
Evidence, Joumal of Accounting Research, (Spring 1975), 150-161.
Libby R., Тrotman К. Т. and Zimmer,I. (1987). Member Variation, Recognition of Expertise, and Group Performance. Joumal of Applied Psychology,
(February 1987), 81-87.
Lindner А. (2009). Stationarity, Mixing, Distributional Properties and Moments of GARCH(p; q)-Processes. Глава в Handbook of Financial Time
Series (под редакцией Т. Andersen, R. Davis, J.-P. Kreiss & Т. Mikosch).
Springer.
Lindskog F., McNeil А., Schmock U. (2003). Kendall's Tau for Elliptical
Distributions. - ln: G. Bol, Nakhacizaden, S. Rachev, Т. Ridder, К.-Н.
Vollmer (eds.), Credit Risk Measurement, Evaluation and Management.
Physica-Verlag, А Springer-Verlag Company, Heidelberg, р. 149-156.
Lindskog F. and McNeil А. (2003). Common Poisson Shock Models: Applications to Insurance and Credit Risk Modelling, ASTIN Bulletin, 33(2) ,
209-238.
Lindskog F. (2000). Linear Correlation Estimation, Research Report,
RiskLab Switzerland, August,
http://vvv.risklab.ch/Papers.html#LCELindskog.
Ljung G.M. and Вох G.E.P. (1978). On а Measure of Lack of Fit in Time
Series Models, Biometrika, 65, 297-303.
Lo М.С. and Zivot Е. (2001). Threshold Cointegration and Nonlinear
Adjustment to the Law of One Price, Macroeconomic Dynamics, 5, 533576.
Longin F. and Solnik В. (2001). Extreme Correlation of International Equity
Markets, Joumal of Finance, 56(2), 649-676.
Lutkepohl Н. (1993). Introduction to Multiple Time Series Analysis, 2nd
edition, New York: Springer-Verlag.
Lutkepohl Н. (2005). New Introduction to Multiple Time Series Analysis,
New York: Springer-Verlag.
Lucas D. (1995). Default Correlation and Credit Analysis. - Journ. of Fixed
Income, N 11, рр. 76-87.
ЛИТЕРАТУРА
921
Lumsdaine R.L. {1996). Asymptotic Properties of the Quasi Maximum
Likelihood Estimator in GARCH{l,1) and IGARCH{l,1) Models, Econometrica, 64, 575-559.
MacDonald /.L. and Zucchini W. {1997). Hidden Markov and Other Models
for Discrete-valued Time Series. Chapman and Hall: London, UK.
Maddala G.S. and Kim /.М. {1998). Unit Roots, Cointegration, and Structural Change, Cambridge University Press, Cambridge.
Madhavan А. and Smidt S. {1991). А Bayesian Model of Intraday Specialist
Pricing, Joumal of Financial Economics, 30, 99-134.
Madhavan А. and Sofianos G. {1997). An Empirical Analysis of the NYSE
Specialist Тrading, Joumal of Financial Economics, 48, 189-210.
Maheu J. and McCurdy Т. {2000). ldentifying Bear and Bull Markets in
Stock Markets. Joumal of Business & Economic Statistics 18, 100-112.
Maheu J.M. and McCurdy Т.Н. {2004). News Arrival, Jump Dynamics and
Volatility Components for Individual Stock Returns, Joumal of Finance,
59, 755-793.
Malevergne У. and Somette D. {2003). Testing the Gaussian Copula Hypothesis for Financial Assets Dependence, Quantitative Finance, 3, 231-250.
Malevergne У. and Somette D. {2006). Extreme Financial Risks {F'rom
Dependence to Risk Management}, Springer: Heidelberg.
Мalmsten Н.
and Ter asvirta Т. (2004). Stylized Facts on Financial Time
Series and Three Popular Models of Volatility. SSE/EFI Working Paper
Series in Economics and Finance 563. Stockholm School of Economics.
Mancini С. {2009). Non-parametric Threshold Estimation for Models with
Stochastic Diffusion Coefficient and Jumps, Scandinavian Joumal of Statistics, 36{2), 270-296.
Mardia К. V., Kent J. and Bibby J.M. {1997). Multivariate Analysis, Academic Press: San Diego.
Marsaglia G. and Marsaglia J. {2004). Evaluating the Anderson-Darling
Distribution, Joumal of Statistical Software, 9(2), 1-5.
Marshall А. {1890). Principles of Economics, Macmillan Company, 8th ed.,
New York, USA.
Marshall А. and Olkin /. {1988). Families of Multivariate Distributions,
Journal of the American Statistal Association, 83, 834-841.
Marshall R. and Zeevi А. {2002). Beyond Correlation: Extreme Co-movements Between Financial Assets, Columbla University, Working Paper.
922
ЛИТЕРАТУРА
McAleer М. and Medeiros М.С. (2008). Realized Volatility:
nometric Reviews, 27(1Ц3), 10-45.
А
Review, Eco-
McNeil А. (2008). Sampling Nested Archimedean Copulas, Journal of Statistical Computation and Simulation, 78(6), 567-581.
McNeil А. and Neslehova J. (2009). Multivariate Archimedean Copulas,
d-monotone Functions and Ll-norm Symmetric Distributions, Annals of
Statistics, 37(5), 3059-3097.
McNeil А. Frey R. and Embrechts Р. (2005). Quantitative Risk Management: Concepts, Techniques and Tools, Princeton Series in Finance: New
Jersey.
Meddahi N. (2002). А Theoretical Comparison Between Integrated and
Realized Volatility, Joumal of Applied Econometrics, 17, 479-508.
Melchiori М. (2004). CreditRisk+
July 2004.
Ьу
Fast Fourier
Тransform,
YieldCurve,
Merton R. (1970). Analytical Optimal Control Theory as Applied to Stochastic and Non-Stochastic Economics, Ph.D. diss., Massachusetts Institute
of Technology.
Merton R. (1974). On the Pricing of Corporate DeЬt: The Risk Structure
of Interest Rates, The Joumal of Finance, 29, 449-470.
Мerton
R. (1977). On the Pricing of Contingent Claims and the ModiglianiMiller Theorem, Journal of Financial Economics, 5(2), 241-249.
Merton R. (1980). On Estimating the Expected Return on the Market: An
Exploratory lnvestigation, Journal of Financial Economics, 8, 323-361.
Mester L. (1997). WhatTs the Point of Credit Scoring?, Federal Reserve
Bank of Philadelphia, Business Review, (September/October 1997), 316.
Metz С.Е. and Kronman Н.В. (1980). Statistical Significance Tests for
Binormal ROC Curves, Journal of Mathematical Psychology, 22, 218243.
Michael Р., Nobay R.A. and Peel D.A. (1997). Тransactions Costs and
Nonlinear Adjustment in Real Exchange Rates: An Empirical Investigation, Joumal of Political Есопоту, 105, 862-879.
Mikosch Т. and Starica С. (1998). Change of Structure in Financial Time
Series, Long Range Dependence and the GARCH Model. Technical Report, University of Groningen.
ЛИТЕРАТУРА
923
Mikosch Т. and Starica С. (2000). Is it Really Long Memory We See in
Financial Returns? Глава в Extremes and Integrated Risk Мanagement
(под редакцией Р. Embrechts). Risk Books.
Mikosch Т. and Starica С. (2003). Long-range Dependence Effects and
ARCH Modeling. Глава в Theory and Applications of Long-Range Dependence (под редакцией Р. Doukhan, G. Oppenheim & M.S. Taqqu).
Birkh auser.
Miller М.Н. and Modigliani F. (1958). The Cost of Capital, Corporation
Finance and the Theory of lnvestment. American Economic Review, 48,
261-297.
Miller М.Н. and Modigliani F. (1961). Dividend Policy, Growth, and the
Valuation of Shares. Joumal of Business, 34, 411-433.
Mills F.C. (1927). The Behaviour of Prices, National Bureau of Economic
Research, New York.
Moscadelli М. (2004). The Modelling of Operational Risk: Experience with
the Analysis of the Data Collected Ьу the Basel Commitee. - Banca
d'ltalia, N 17.
М
uller И.А., Dacorogna М.М., Dave R.D., Olsen R.B., Pictet О. V. and
von Weizs acker J.E. (1997). Volatilities of Different Time Resolutions
- Analyzing the Dynamics of Market Components. Joumal of Empirical
Finance 4, 213-239.
Muller А. and Scarsini М. (2005). Archimedean Copulae and Positive Dependence, Jourпal of Multivariate Analysis, 93, 434-445.
Mykland Р.А. and Zhang L. (2006). ANOVA for Diffusions and Ito Processes, Annals of Statistics, 34(4), 1931-1963.
Mosconi R. and Giannini С. (1992). Non-causality in Cointegrated Systems:
Representation Estimation and Testing, Oxford Bulletin of Economics
and Statistics, 54(3), 399-417.
Nelson D. (1990). Stationarity and Persistence in the GARCH(l,1) Model.
Econometric Theory 6, 318-334.
Nelson D. and Сао С. (1992). lnequality Constraints in the Univariate
GARCH Model. Joumal of Business & Economic Statistics 10, 229-235.
Nelsen R.B. (1999). Ап Introduction to Copulas, Lecture Notes in Statistics,
Springer-Verlag: New York.
Nelsen R.B. (2005). Some Properties of Schur-constant Survival Models
and Their Copulas, Brazilian Journal of ProbaЬility and Statistics, 19,
179-190.
924
ЛИТЕРАТУРА
Nelsen R.B. (2006). Ап Introduction to Copulas, Lecture Notes in Statistics,
2nd Edition, Springer-Verlag: New York.
Nelson D. (1991). Conditional Heteroskedasticity in Asset Returns:
Approach, Econometrica, 59, 347-370.
А
New
Neslehova J., Embrechts Р., Chavez-Demoulin V. (2006). Infinite Mean
Models and the LDA for Operational Risk, Journal of Operational Risk,
1 '3-25.
Newey W.K. and West K.D. (1987). А Simple Positive Semi-definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix, Econometrica, 55, 703-708.
Newey W.K. and McFadden D. (1994). Large Sample Estimation and Hypothesis Testing, Handbook of Econometrics, volume 4, 2111-2245, Elsevier
Science B.V.: Amsterdam.
Nickell Р., Perraudin W., Varotto S. (2006). Ratings Versus Equity-based
Credit Risk Modelling: An Empirical Analysis, Bank of England Quarterly
Bulletin, 41, 215-255.
Nielsen М.О. and Frederiksen Р.Н. (2006). Finite Sample Accuracy and
Choice of Sampling Frequency in Integrated Volatility Estimation. Working Paper, Cornell University.
Norris J. and Pollock К. (1996). Including Model Uncertainty in Estimating
Variances in Multiple Capture Studies. Environmental and Ecological Statistics, 3, 235-244.
Oakes D. (1994). Multivariate Survival Distributions, Journal of Nonparametric Statistics, 3, 343-354.
Obstfeld М. and Taylor А.М. (1997). Nonlinear Aspects of Goods-market
Arbltrage and Adjustment: Heckscher's Commodity Points Revisited,
Journal of the Japanese and International Economies, 11, 441-479.
O'Connell P.G.J. (1998а). Market Frictions and Real Exchange Rates,
Journal of International Мопеу and Finance, 17, 71-95.
O'Connell G.J. (1998Ь). The Overvaluation of Purchasing Power Parity,
Journal of International Economics, 44(1), 1-19.
O'Connell P.G.J. and Wei S.J. (1997). The Bigger They Are, the Harder
They Fall: How Price Differences Across U.S. Cities Are Arbltraged,
Working paper n. 6089, National Bureau of Economic Research.
Officer R.R. (1973). The Variabllity of the Market Factor of the NYSE,
Journal of Business, 46, 434-453.
ЛИТЕРАТУРА
925
Oka (2003). Anticipating Arrears to the IMF: Early Earnings Systems, IMF
Working Paper, 18.
Pagan А. (1996). The Econometrics of Financial Markets. Journal
pirical Finance 3, 15-102.
о/
Em-
Pagan А. and Schwert G. (1990). Alternative Models for Conditional Volatility. Journal о/ Econometrics 45, 267-290.
Рап
J. (2002). The Jump-Risk Premia lmplicit in Options: Evidence from
an Integrated Time-Series Study, Journal о/ Financial Economics, 63,
3-50.
Panchenko V. (2005). Goodness-of-Fit Test for Copulas, Physica
176-182.
А,
355(1),
Park Н., Mjelde J. W. and Bessler D.A. (2007). Time-Varying Threshold
Cointegration and the Law of One Price, Applied Economics, 39, 10911105.
Parsley D. С. and Wei S.J. (1996). Convergence to the Law of One Price
Without Тrade Barriers or Currency Fluctuations, Quarterly Journal о/
Economics, 111, 1211-1236.
Patton А. (2004). On the Out-of-Sample lmportance of Skewness and Asymmetric Dependence for Asset Allocation, Journal о/ Financial Econometrics, 2(1), 130-168.
Patton А. (2006а). Estimation of Copula Models for Time Series of PossiЬly
Different Lengths, Joumal о/ Applied Econometrics, 21, 147-173.
Patton А. (2006Ь). Modelling Asymmetric Exchange Rate Dependence,
International Economic Review, 47(2), 527-556.
Payseur S. (2007а). А One Day Comparison of Realized Variance and
Covariance Estimators, Working Paper, Мау 2007, University ofWashington.
Payseur S.
(2007Ь).
"Realized Software Package" version 0.8 Manual,
http://students.vashington.edu/spayseur/realized/users.manual.08.pdf.
Peckham G. (1970). А New Method for Minimizating а Sum of Squares
Without Calculating Gradients. - Computer J., vol. 13, 418-420.
Pereyra V. (1967). Iterative Methods for Solving Nonlinear Least Squares
ProЫems, - SIAM J. Numerical Analysis, vol. 4, N 1, 27-36.
Pesaran М.Н., Shin У. and Smith R.P. (1999). Pooled Mean Group Estimation of Dynamic Heterogeneous Panels, Journal о/ the American Statistical Association, 94, 621-624.
926
ЛИТЕРАТУРА
Phillips Р. С. (1991). Optimal Inference in Cointegrated Systems, Econometrica, 59, 283-306.
Pippenger М. and Goering G. (1993). А Note on the Empirical Power of
Unit Root Tests under Threshold Processes, Oxford Bulletin of Economics
and Statistics, 55, 473-481.
Pippenger М. and Goering G. (2000). Additional Results on the Power of
Unit Root and Cointegration Tests Under Threshold Processes, Applied
Economic Letters, 7, 641-644.
Рооп
S., Rockinger М. and Tawn J. (2004). Extreme Value Dependence
in Financial Markets: Diagnostics, Models, and Financial lmplications,
Review of Financial Studies, 17, 581-610.
Powell M.l.D. (1970). А Survey of Numerical Methods for Unconstrained
Optimization. - SIAM Rev., vol. 12, N 1, 79-97.
Priestley М.В. (1980). State-Dependent Models: А General Approach to
Non-linear Time Series Analysis, Joumal of Time Series Analysis, 1, 5771.
Provost F., Fawcett Т. and Kohavi R. (1998). The Case Against Accuracy
Estimation for Comparing Classifiers. In Proceedings of the Fifteenth /ntemational Conference оп Machine Leaming, (ICML-98).
Psamdakis Z., Sola М. and Spangolo F. (2004). On Markov-Switching Models, with an Application to Stock Prices and Dividends, Joumal of
Applied Econometrics, 19, 69-88.
Rabe-Hesketh S. and Skrondal
deling, Chapman and Hall.
А.
(2004). Genemlized Latent
VariaЫe
Mo-
Rabe-Hesketh S. and Skrondal А. (2005). Multilevel and Longitudinal Modeling using Stata, STATA press.
Rabe-Hesketh S., Skrondal А. and Pickles А. (2002). ReliaЫe Estimation
of Generalized Linear Mixed Models Using Adaptive Quadrature, Stata
Joumal, 2(1}, 1-21.
Rabe-Hesketh S., Skrondal А. and Pickles А. (2005). Maximum Likelihood
Estimation of Limited and Discrete Dependent VariaЫe Models with
Nested Random Effects, Joumal of Econometrics, 128(2}, 301-323.
Rachedi О. and Fantazzini D. (2008). Multivariate Models for Operational
Risk : А Copula Approach using Extreme Value Theory and Poisson
Shock Models, In: G. Gregoriou (ed.), Opemtional Risk towards Basel
///: Best Practices and /ssues in Modelling, Management and Regulation,
Wiley, December.
ЛИТЕРАТУРА
927
Ralston M.L., Jennrich R.l. {1978). Dud, а Derivative-free Algorithm for
Non-linear Estimation. - Technometrics, vol. 20, 7-14.
Resnick S./. {1987). Extreme Values, Regular Variation and Point Processes
Springer: New York.
Riedel F. {2004). Dynamic Coherent Risk Measures. - Stochastic Processes
and their Applications, 112(2), 185-200.
Ripley B.D. (1987). Stochastic Simulation, Wiley, London.
RoЬinson Р.М.
{1991). Testing for Strong Serial Correlation and Dynamic
Conditional Heteroskedasticity in Multiple Regression, Joumal of Econometrics, 47, 67-84.
Rockafellar Т. and Uryasev S. {2002). Conditional Value-at-Risk for General
Loss Distributions. - Journal of Banking and Finance, 26(7), 1443-1471
Rodgers J.L. and Nicewander W.A. (1988). Thirteen Ways to Look at the
Correlation Coefficient, The American Statistician, 42, 59-66.
Rodriguez Р. and Rodriguez А. {2006). Understanding and Predicting Sovereign Debt Rescheduling: А Comparison of the Areas under Receiver
Operating Characteristic Curves, Joumal of Forecasting, 25, 459-479.
Rosenberg J. V. and Schuermann Т. (2006). А General Approach to Integrated Risk Management with Skewed, Fat-tailed Risks, Joumal of Financial
Economics, 79, 569-614.
RosenЫatt М.
{1952). Remarks on а Multivariate
nals of Mathematical Statistics, 23, 470-472.
Тransformation,
The An-
Rossi B.D., Santucci P.D.M. and Fantazzini D. (2008). Long Memory and
Tail dependence in Тrading Volume and Volatility, Working paper n.
209/12-08, University of Pavia, Italy.
Rousseuw P.J. and Molenberghs G. (1993). Тransformation of Non Positive
Semide@nite Correlation Matrices. Commun. Statist.-Theory Meth. 22,
965-984.
Ruud Р. (2000). Ап Introduction to Classical Econometric Theory, Oxford
University Press.
Ruymgaart F.H., Shorack G.R. and Van Zwet W.R. (1972). Asymptotic
Normality of Nonparametric Tests for lndependence, The Annales of
Statistics, 43, 1972, 1122-1135.
Saikkonen Р. {1991). Asymptotically Efficient Estimation of Cointegration
Regressions, Econometric Theory, 7, 1-21.
928
ЛИТЕРАТУРА
Salvadori G. and De Michele С. (2007). On the Use of Copulas in Hydrology:
Theory and Practice, Joumal of Hydrologic Engineering, 12(4), 369-380.
Sarantis N. (1999). Modeling Non-linearities in Real Effective Exchange
Rates, Joumal of Intemational Мопеу and Finance, 18, 27-45.
Saunders А. (1997). Financial Institutions Management:
spective, Second Ed. lrwin, Illinois.
А
Modem Per-
Savu С. and Тrede М. (2008). Goodness-of-Fit Tests for Parametric Families
of Archimedean Copulas, Quantitative Finance, 8(2), 109-116.
Savu С. and Тrede М. (2009). Hierarchies of Archimedean Copulas, Quantitative Finance, forthcoming.
Scaillet О. (2005). Kernel Based Goodness-of-Fit Tests for Copulas with
Fixed Smoothing Parameters. FAME Research Paper Series n. 145, International Center for Financial Asset Management and Engineering.
AvailaЫe at http://ideas.repec.org/p/fam/rpseri/ rp145.html.
Schmidt R. (2002). Tail Dependence for Elliptically Contoured Distributions, Mathematical Methods of Operations Research, 55(2), 301-327.
Schoutens W. (2003). Levy Processes in Finance: Pricing Financial Derivatives, Wiley.
Schroder В. and Richter О. (1999-2000). Are HaЬitat Models ТransferaЫe
in Space and Time? Joumal of Nature Conservation, 8, 195-205.
Schwert G. W. (1998). Stock Market Volatility: Ten Years After the Crash.
Brookings- Wharton Papers on Financial Services, 1, 65-114.
Schwarz G. (1978). Estimating the Dimension of
Statistics, 6, 461-464.
а
Schweizer В. and Sklar
Science: New York.
Metric Spaces, Elsevier
А.
(1983).
ProbaЬilistic
Model. The Annals of
Schweizer В. and Wolff Е. (1976). Sur Une Mesure de Dependance Pour
Les VariaЫes Aleatoires, C.R. Acad. Sci. Paris, 283, 659-661.
Schweizer В. and Wolff Е. (1981). On Non-parametric Measures of Dependence for Random VariaЫes, Annals of Statistics, 9, 879-885.
Sentana Е. (1995). Quadratic ARCH Models. Review of Economic Studies
62, 639-661.
Seo М. (2006). Bootstrap Testing for the Null of no Cointegration in а
Threshold Vector Error Correction Model, Joumal of Econometrics, 134,
129-150
929
ЛИТЕРАТУРА
Seo М. (2009). Estimation of Nonlinear Error Correction Models, Working
Paper, London School of Economics.
Sercu Р., Uppal R. and Van Hulle С. (1995). The Exchange Rate in the
Presence of Тransaction Costs: lmplications for Tests of Purchasing Power
Parity, Joumal о/ Finance, 10, 1309-1319.
Serra Т. and Goodwin В.К. (2002). Specification Selection Issues In Multivariate Threshold And Switching Models, 2002 Annual meeting, July 2831, Long Beach, СА 19843, American Agricultural Economics Association
(New Name 2008: Agricultural and Applied Economics Association).
Serra Т. and Goodwin В.К. (2003). Price Тransmission and Asymmetric
Adjustment in the Spanish Dairy Sector, Applied Economics, 35, 18891899.
Serra Т. and Goodwin В.К. (2004). Regional Integration of Nineteenth
Century U.S. Egg Markets, Joumal о/ Agricultural Economics, 55, 5974.
Shackleton М.В. Shiuyan Р., Taylor S. and Хи Х. (2004). Forecasting
Currency Volatility: А Comparison of lmplied Volatilities and AR(FI)MA
Models, Joumal о/ Banking and Finance, 28(10), 2541-2563.
Shephard N. (1996). Statistical Aspects of ARCH and Stochastic Volatility
Models. Глава в Time Series Models in Econometrics, Finance and Other
Fields (под редакцией D. Сох, D. Hinkley & О. Barndorff-Nielsen), 1-67.
Chapman & Hall.
Shih J.H. (1998). А Goodness-of-Fit Test for Association in
Survival Model, Biometrika, 85, 189-200.
а
Bivariate
Shih J.H. and Louis Т.А. (1995). Inferences on the Association Parameter
in Copula Models for Bivariate Survival Data, Biometrics, 51, 1384-1399.
Shimko D. (2004). Credit Risk: Models and Management, Second Edition,
Risk Books.
Shleifer А. and Vishny R. W. (1992). Liquidation Values and DeЬt Capacity:
А Market Equilibrium Approach, Journal о/ Finance, 47(4), 1343-1366.
Sibuya М. (1961). Bivariate Extreme Statistics, Annals
Statistics, 11, 195-210.
Sims
С.
Sklar
А.
РиЫ.
о/
Mathematical
(1980). Macroeconomics and Reality, Econometrica, 48, 1-48.
(1959). Fonctions de Repartition а n Dimensions et leurs Marges,
Inst. Statis. Univ. Paris, 8, 229-231.
930
ЛИТЕРАТУРА
Sklar А. (1996). Random VariaЫes, Distribution Functions, and Copula:
Personal Look Backward and Forward. - Lecture Notes. Monograph
Series, 28, 1-14.
Starica С. and Granger С. (2005). Non-stationarities in Stock Returns.
Review of Economics and Statistics 87, 503-522.
Steuer R.E. (1986). Multiple Criteria Optimization: Theory, Computation
and Application. - N.-Y.: Wiley.
Stevens W.L. (1950). Fiducial Limits of the Parameter of а Discontinuous
Distribution, Biometrika, 37, 117-129.
Stock J.H. (1987). Asymptotic Properties of Least Squares Estimators of
Cointegrating Vectors, Econometrica, 55 1035-1056.
Stock J.Н. and Watson М. W. (1993). А Simple Estimator of Cointegrating
Vectors in Higher Order Integrated Systems, Econometrica, 61, 783-820.
Straumann D. (2005). Estimation in Conditionally Heteroscedastic Time
Series Models. Lecture Notes in Statistics. Springer.
Takeuchi К. (1976). Distribution of information statistics and criteria for
adequacy of models, Mathematical Sciences, 153, 12-18.
Taniguchi М. and Kakizawa У. (2000). Asymptotic Theory of Statistical
Inference for Time Series, Springer: New York.
Taylor S. (1986). Modeling Financial
Тiте
Series, Wiley: New York.
Taylor А.М. (2001). Potential Pitfalls for the Purchasing Power Parity
Puzzle-sampling and Specification Biases in Mean-reversion Tests of the
Law of One Price, Econometrica, 69, 473-498.
Taylor S.J. and Хи Х. (1997). The lncremental Volatility lnformation in
One Million Foreign Exchange Quotations, Joumal of Empirical Finance,
4, 317-340.
Terasvirta Т. (2009). An introduction to Univariate GARCH Models. Глава
в Handbook of Financial Тiте Series (под редакцией Т. Andersen, R.
Davis, J.-P. Kreiss & Т. Mikosch). Springer.
Tilling К. and Steme J. (1999). Capture-recapture Models Including Covariate Effects, American Joumal of Epidemiology, 149, 392-400.
Tilling К., Steme J. and Wolfe С. (2001). Estimation of Incidence of Stroke
Using а Capture-recapture Model Including Covariates, Intemational
Joumal of Epidemiology, 30, 1351-1359.
Tj/Jstheim D. (1986) Some DouЬly Stochastic Time Series Models, Journal
of Time Series Analysis, 7, 225-273.
ЛИТЕРАТУРА
931
Toda Н. and Phillips Р. (1994). Vector Autoregression and Causality: а
Theoretical Overview and Simulation Study, Econometric Reviews, 13(2),
259-284.
Tong Н. (1978). On а Threshold Model, in С.И. Chen (ed), Pattem recognition and Signal Processing, Sijthoff and Noordhoff, Amsterdam, The
Netherlands.
Tong Н. (1990). Non-linear Time Series.
Clarendon Press, Oxford, UK.
А
Dynamical System Approach.
Tong Н. (2007). Birth of the Threshold Time Series Model, Statistica Sinica,
17, 8-14.
1'reacy W.F. and Carey М. (2000). Credit Risk Rating Systems at Large
U.S. Banks, Joumal of Banking and Finance, 24(1-2), 167-201.
1'renkler С. and Wolf N. (2003). Economic Integration in Interwar Poland А Threshold Cointegration Analysis of the Law of One Price for Poland
(1924-1937), European University Institute Working Paper ЕСО, No.
2003/5, San Domenico, Italy.
Tsay R.S. (1989). Testing and Modeling Threshold Autoregressive Processes, Joumal of the American Statistical Association, 84, 231-240.
Tsay R.S. (1998). Testing and Modeling Multivariate Threshold Models,
Joumal of the American Statistical Association, 93, 1188-1202.
Tsay R.S. (2002). Analysis of Financial Time Series. Wiley.
Tse У.К. (1998). The Conditional Heteroscedasticity of the Yen-Dollar
Exchange Rate, Joumal of Applied Econometrics, 193, 49-55
Tse У. and Tsui А. (2002). А Multivariate GARCH Model with TimeVarying Correlations, Joumal of Business and Economic Statistics, 20,
351-362.
Uppal R. (1993). А General Equilibrium Model of International Portfolio
Choice, Joumal of Finance, 48, 529-553.
Van Campenhout В. (2007). Modelling Тrends in Food Market Integration:
Method and an Application to Tanzanian Maize Markets, Food Policy,
32, 112-127.
Van de Castle, Karen and David Keisman (2000). Suddenly Structure Mattered: Insights into Recoveries of Defaulted, Standard and Poor's Corporate Ratings, Мау 24.
Van Der Laan М. and Bryan J. (2001). Gene Expression Analysis with the
Parametric Bootstrap, Biostatistics, 2(4), 445-461.
932
ЛИТЕРАТУРА
Van der Vaart А. and Wellner J. (1996). Weak Convergence and Empirical
Processes, Springer-Verlag: New York.
Van der Weide R. (2002). GO-GARCH: А Multivariate Generalized Orthogonal GARCH Model, Joumal of Applied Econometrics, 17, 549-564.
Van De Wiel М.А. and Bucchianico А. (2001). Fast Computation of the
Exact Null Distribution of Spearman's rho and Page's L Statistic for
Samples with and Without Ties, Joumal of Statistical Planning and Inference, 92, 133-145.
Vapnik V. (1998). Statistical Leaming Theory, Wiley.
Varma Р. and Cantor R. (2005). Determinants ofRecovery Rates on Defaulted Bonds and Loans for North American Corporate Issuers: 1983-2003,
Joumal of Fixed Income, 14(4), 29-44.
Vassalou М. and Xing У. (2004). Default Risk in Equity Returns, Joumal
of Finance, 59(2), 831-68.
Zaffaroni Р. (2007). Contemporaneous Aggregation of GARCH Processes.
Joumal of Time Series Analysis 28, 521-544.
Zako ап J.-M. (1994). Threshold Heteroskedastic Models. Joumal of Economic Dynamics and Control 18, 931-955.
Zhang L., Mykland Р.А., Aяt-Sahalia У. (2005). А Tale of Тwo Time Scales:
Determining Integrated Volatility with Noisy High Frequency Data, Journal of the American Statistical Association 100, 1394-1411.
Zhang L. and Singh V. (2006). Bivariate Flood Frequency Analysis Using
the Copula Method, Joumal of Hydrologic Engineering, 11(2), 150-164.
Zhang L. (2006). Efficient Estimation of Stochastic Volatility Using Noisy
Observations: А Multi-scale Approach, Bemoulli, 12, 1019-1043.
Zhou В. (1996). High Frequency Data and Volatility in Foreign-exchange
Rates, Joumal of Business and Economic Statistics, 14, 45-52.
Zivot Е. (2000). The Power of Single Equation Tests for Cointegration when
the Cointegrating Vector is Pre-specified, Econometric Theory, 16, 407440.
Zwane Е., Van der Heijden Р. (2003). lmplementing the Parametric Bootstrap in Capture-recapture Models with Continuous Covariates, Statistics
and ProbaЬility Letters, 65, 121-125.
Zwane Е., Van der Pal-de Bruin, Van der Heijden Р. (2004). The Multiplerecord Systems Estimator when Registrations Refer to Different but Overlapping Populations, Statistics in Medicine, 23, 2267-2281.
ЛИТЕРАТУРА
933
Zweig and Campbell (1993). Receiver-Operating Characteristic (ROC)
Plots: а Fundamental Evaluation Tool in Clinical Medicine, Clinical chemistry 39, 561-577.
Wang S.(1998) Aggregation of Correlated Risk Portfolios: Model and Algorithms, Proceedings of the Casualty Actuarial Society, LXV, 848-893.
Wang W. and Wells М. Т. (2000). Model Selection and Semiparametric
lnference for Bivariate Failure-time Data, Journal of the American Statistical Association, 95, 62-72.
Watson М. W. (1994). Vector Autoregressions and Cointegration. In: Engle
R.F., McFadden D.L. (Eds.), Handbook of Econometrics, vol. 4., NorthHolland, Amsterdam, 2843-2915.
WCY. The World Competitiveness Yearbook. Edition IMD lnternational,
Lausanne, Switzerland. 1997-2011.
Weiss А.А. (1986). Asymptotic Theory for ARCH Models: Estimation and
Testing, Econometric Theory, 2, 107-131.
Whelan N. (2004). Sampling from Archimedean copulas, Quantitative Finance, 4(3), 339-352.
White Н. (1994). Estimation, Inference and Specification Analysis, Cambridge University Press.
White Н. (2000).
1097-1126.
А
Reality Check for Data Snooping, Econometrica, 68,
Whittle Р. (1954). The Statistical Analysis of
Marine Research, 13, 76-100.
а
Seiche Record, Journal of
Wilson Т. (1997а). Measuring and Managing Credit Portfolio Risk: Part 1:
Modelling Systematic Default Risk, The Journal of Lending and Credit
Risk Management, July, 61-72.
Wilson Т. (1997Ь). Measuring and Managing Credit Portfolio Risk: Part 11:
Portfolio Loss Distributions, The Journal of Lending and d Credit Risk
Management, August , 67-78.
Wu J.L and Chen P.F. (2008). А Revisit on Dissecting the РРР Puzzle:
Evidence from а Nonlinear Approach, Economic Modelling, 25, 684-695.
Уап
J. (2007). Enjoy the Joy of Copulas: With
of Statistical Software, 21(4), 1-21.
а
Package Copula, Journal
Алфавитно-предметный
указатель
А
Байеса формула
Абсолютная монотонность
функции
534
Автодинамика интегральных
индикаторов
88
Авто корреляция (многомерная)
165
Авторегрессионная дробно
(фрактально )-интегрированная
скользящего среднего модель
{ARFIMA) 413, 488-489
Авторегрессионной условной
122
Байесовский выбор
копула-функций
586
Байесовский подход к оценке
функции распределения
совокупного операционного
убытка
707
Байесовский подход в
эконометрическом анализе
Балльные оценки (экспертные)
62
БЕКК-модели (ВЕКК-модели)
438
гетероскедастичности модель
Белый шум (многомерный,
(АRСН-модель)
слабый)
385, 389
122
166, 171
Авторегрессионной условной
Бокса- Кокса преобразование
гетероскедастичности модель с
Бевериджа- Нельсона разложение
переключением режимов
{временного ряда)
{SWАRСН-модель)
Бистепенная вариация
409
284-285
Акаике информационный
(ВV-волатильность)
критерий
Бутстреп
15, 1915, 583
Апостериорное распределение
параметра
122
Априорное распределение
параметра
122
25
482, 485
756
Быстрое преобразование Фурье
(БПФ)
822
Бэк-тестирование
846
Асимметричная обобщенная
модель условной
в
гетероскедастичности
(АGАRСН-модель)
405
Валовой внутренний продукт
{ВВП)
Б
Базельский Комитет по
банковскому надзору
(BCBS) 628
91-92, 95-97
ВАР- (VAR-) модели (процессы)
166, 168, 169
ВЕК- (VEK-) модель 436
Векторная авторегрессия 166
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
936
д
Векторная модель коррекции
остатками {ВМКО- или
VЕС-модель)
-
-
-
-
D-ветвизация
293
Двухпороговая авторегрессионная
с марковскими
модель условной
переключениями в
коэффициентах (ВМКОсМП)
346
Векторный процесс белого шума
(VWN-) 171
- - скользящего
(VMA-) 170
553
(DТАRСН-модель)
408
Двухшаговый метод
максимального правдоподобия
среднего
при дефолте (ВНП(Д))
762, 772
748
Вероятность нулевой цены (ВНЦ)
751
квадратов {2МНК)
257
Дельта-гамма аппроксимации для
нелинейных портфелей
655
Динамическая условная
корреляция
(DCC) 450, 668
Динамический метод наименьших
Вертикальное выстраивание
квадратов (ДМНК)
столбцов матрицы {А)
Дисперсионно-ковариационный
{vec{{A)))
172
312
метод управления рыночным
Волатильность
385-387
риском
654
Волатильность интегрированная
Доля использованных средств
488
компанией, оказавшейся в
Волда представление
состоянии дефолта (ДИС(Д))
Выбор
Доля невозвращенных при
205
копула-функции 583
Выбор порядка VАR-модели
191
774
дефолте средств (ДНС(Д))
Достаточные статистики
800
127
Дробно-интегрированная
обобщенная модель условной
г
гетероскедастичности
Генезис сопряженных априорных
распределений
131
Генерирование многомерных
наблюдений
550, 554
Главная компонента первая
-
568
Двухшаговый метод наименьших
Величина номинальных потерь
Вероятность дефолта
гетероскедастичности
-
-
78
модифицированная 86
Главных компонент метод в
оценивании СОУ
261
(FIGАRСН-модель)
-
-
414
экспоненциальная
обобщенная модель условной
гетероскедастичности
(FIЕGАRСН-модель)
418
з
Гранжера теорема о
Зависимость гиперболического
представлении
типа
295
Граница потерь уровня а (ГПа:
или
VaRa:) 643
18
степенного типа
-
23
логарифмического типа
24
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
-
-
множественного
упорядоченного выбора
75-76
Задача нелинейного
программирования
-
937
тест (на число
конинтегрирующих соотношений)
306
32
статистического исследования
зависимости
к
11-12
Калибровка моделей
и
749
Канонический метод максимума
правдоподобия
572
Идентифицируемости условия
Качество жизни населения
(в узком смысле) отдельного
Квартисимность интегрирования
уравнения СОУ
472
234
90, 101
Идентифицируемость
Ко интеграция (временных рядов)
SVАR-модели
281
- пороговая 324
208
СОУ в узком смысле
234
- в широком смысле 238
Индикаторная переменная 322
-
Коинтегрированность временных
рядов
282-283
Интегральный индикатор
Комонотонность случайных
(измеритель)
величин
-
-
-
58, 71, 77
блочный 84, 103-108
СВОДНЫЙ 86, 109-110
-
-
-
уровня мастерства
спортсмена
Интегрированная обобщенная
модель условной
гетероскедастичности
399
Интегрируемость временных
рядов порядка
d 212, 283-284
Интервальная пороговая
векторная модель коррекции
остатками (И-ПВМКО- или
ВАND-ТVЕСМ-модель)
Компромисс между сложностью
модели и точностью ее
оценивания
15-16
Копула GАRСН-модель
110-118
(IGАRСН-модель)
513
327
й
671
Копула-функции
509
архимедовы 528
- вложенные 535
Гумбеля 532
Клейтона 531, 533
Котца 517
Коши 517
Лапласа 517
логистические 517
нормальные 517, 518
парные 545
Стьюдента 517, 519
Франка 532, 533
эллиптического типа
516
Йохансена алгоритм вычисления
Косвенный метод наименьших
оценок максимального
квадратов (КМНК)
правдоподобия
Коэффициент корреляции
298
252
557
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
938
-
Спирмена
-
-
-
560
Кендала
Ньютона- Гаусса
-
ранговой корреляции
полной оценки мер риска
(МПО)
562
658-659
сопряженных градиентов
Кредитного риска компоненты
-
719
Методология
Кредитные события
-
спреды
38
34, 45
Credit Portfolio View
829
840
Многомерные временные ряды
750
Критерии согласия для
163
копула-функций
Многомерные GАRН-модели
590
(МGАRСН-модели)
433
Модель адаптивных ожиданий
371
л
Модель Бланчада-Куаха
17, 25 -
Линеаризация зависимостей
216
гетерогенной
авторегрессионной реализованной
волатильности (НАR-RV-модель)
488
- -
м
Макроэкономические модели
кредитного риска
776
Матрица парных сравнений
-
62
авторегрессионных
коэффициентов
предикторов (НАR-RV-J-модель)
490
---------с
кредитной миграции
Мертона
775
744
372
со скачками (разрывами) 481
частичного приспособления 368
Метод взвешенных по
вероятности моментов
ценообразования на основной
696
капитал
407
Credit Risk+ 810
Credit Metrics 776
KMV 795
35
Метод максимального
правдоподобия с ограниченной
информацией
372
потребления (Фридмана)
632
Метод градиентного спуска
492
гиперинфляции (Кагана)
88-89
557
(ВВМ-метод)
со скачками,
используемыми в качестве
Меры зависимости случайных
Меры риска
-
(НАR-RV-СJ-модель)
Межобъектная динамика
величин
-
учетом серийной корреляции
169
интегральных индикаторов
-
266
- - - с полной информацией
266
- Марквардта 40
- Монте-Карло статистических
испытаний 275, 657
- Ньютона 37
н
Нелинейная обобщенная модель
условной гетероскедастичности
(NАGАRСН-модель)
405
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
939
Нелинейный метод наименьших
квазимаксимального
квадратов
правдоподобия
31-33
Нелинейные модели коинтеграции
320
Нелинейные модели регрессии
16
Непараметрическое оценивание
580
Норма восстановления (НВ)
(QMLE) 453
Оценка состоятельная 192
- сильно состоятельная 192
- ядерная 4 76
Оценки по подвыборкам 4 78
- стягивающие (для скачков) 483
762-763
п
о
Панельные данные
Подход базовых индикаторов
Обобщенная модель
(ПБИ) к управлению
авторегрессионной условной
операционным риском
гетероскедастичности
(GАRСН-модель)
-
-
-
-
-
-
-
-
(ПВР) к управлению кредитным
в среднем
-
риском
410
с долгой памятью
411
61
взаимная независимость
(iid) 175
Ожидаемая частота дефолтов
(ОЧД)
13
Пороговая авторегрессионная
Пороговая векторная модель
445
Одинаковая распределенность и
случайных величин
Полиномы Чебышева
321
GАRСН-модель
Обучающий массив данных
726
модель (ПАР- или ТАR-модель)
Обобщенная ортогональная
(GОGАRСН-модель)
683
Подход внутренних рейтингов
392
(GАRСН-М-модель)
-
738
коррекции остатками (ПВМКО
или ТУЕС-модель)
323
Пороговая обобщенная модель
условной гетероскедастичности
(ТGАRСН-модель)
408
Последовательный многомерный
795
Оперативная кривая
733-735
метод наименьших квадратов
328
L сдвига (по времени
назад) 167
Оператор vech 436
Опционы PUT и CALL 645
Постоянная условная корреляция
Ортогональная GАRСН-модель
Приведенная форма СОУ
444
Причинно-следственная связь (по
Остаточная случайная
Гранжеру)
составляющая
Прогнозирование волатильности
Оператор
12
(ССС)
450, 668
Предопределенные переменные
224
227
185
Отношения правдоподобия тест
398
(ОП-тест или LR-тест)
Правило абсолютного приоритета
Оценка метода
187
(ПАП)
766
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
940
р
Синтетическая латентная
категория
Равновесная пороговая векторная
342
Распределения, сопряженные с
наблюдаемой генеральной
-
-
-
риском
158
795
Расширенный тест
Дики- Фуллера (РДВ- или
339
Реализованная волатильность
468-469, 471
Регрессионные модели с
распределенными лагами
360
Регрессия полиномиальная 13
Регуляторный капитал 628
Редукция многокритериальных
схем
58
Рейтинговые системы
730
Риск кредитный 630, 718
операционный 631, 678
потери ЛИКВИДНОСТИ 631
рыночный 630, 632
юридический 631
- 725
684
кредитным
Стационарность временного ряда
ковариационная (слабая)
164
Стока- Ватсона представление
общего тренда
Структура
-
-
290
лагов 363
геометрическая (Койка)
(вероятностная)
-
-
с
363
полиномиальная (Ширли
Алмон)
364
Структурная форма СОУ
226
Структурно-скользящее среднее
(SМА-представление)
205
Структурные VАR-модели
(SVАR-модели)
202
модели кредитного риска
-
параметры СОУ
228
Теорема Шкляра (о
Самовозбуждаемая пороговая
копула-функциях)
авторегрессия (СВПАР- или
Тест
SЕТАR-модели)
Тест множителей Лагранжа
322
366
нормированная
т
510
Берковица 846-847
Свертка (функция) нескольких
(LМ-тест)
показателей
-
58
251
Средние ожидаемые потери
операционным риском
обобщенное многомерное
АDF-тест)
чисто рекурсивные
(СП) к управлению
139
Расстояние до дефолта (РД)
-
Стандартизированный подход
многомерное
Стьюдента
-
ESa) 638
Спектральные меры риска 641
Спецификация модели 232, 344
125-126
САЗ-априорное 132
бета 136
гамма 137
-
-
223
уровня а (СОПа или
совокупностью
гамма-нормальное
Системы одновременных
уравнений ( СОУ)
модель коррекции остатками
(Р-ПВМКО-модель)
58
196
на нормальность
196
775
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Портмандо
941
Филлипса треугольное
194
Энгла- Гранжера (на
представление временного ряда
коинтегрируемость
289
вектор-процесса)
Функция автокорреляционная
302
Тренд детерминированный
299
Трехшаговый канонический метод
максимального правдоподобия
(КМЕ-СМL-метод)
-
574
метод наименьших квадратов
(3МНК)
262
у
(многомерного временного ряда)
163-164
- импульсного отклика 176
- правдоподобия имеющихся
наблюдений 26-27, 124
- регрессии 12
- структурного импульсного
отклика (СИО-функция) 206
- целевая 59
Убытки неожидаемые (НУ)
Убытки ожидаемые (ОУ)
722
722
х
Унификация измерительных
шкал наблюдаемых переменных
Хвостовая зависимость
69
Холецкого разложение
564
210, 220
Упорядочения (ранжировки)
Хэннана- Квина
экспертные
информационный критерий
62
Управление рыночным риском
632
- операционным риском 678
- кредитным риском 718
Условие порядка
(идентифицируемости отдельного
уравнения СОУ)
-
ранга
-
-
241-244
- - 241-244
(НQ-тест)
191
III
Шварца информационный
критерий
15-16, 191
Условная граница потерь уровня
а (УГПа или
CVa.Ra) 650
Усовершенствованные модели
измерения риска (УМИР-модели)
680
э
Экзогенные переменные
Экономический капитал
224
722, 723
Экспоненциальная обобщенная
ф
модель условной
гетероскедастичности
Факторная GАRСН-модель
441
(ЕGАRСН-модель)
401
Фактор эквивалентности займа
Экстремальной группировки
774
признаков процедура
82
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
942
Энгеля кривая
20
Эндогенные переменные
224
ю
Юла-Уолкера уравнения
394-395
я
Ядерная функция
-
оценка
580
581
Якобиан (определитель матрицы
преобразования)
27
Учебное издание
Айвазян Сергей Артемьевич
Фантаццини Деан
ЭКОНОМЕТРИКА-2:
продвинутый курс
с приложениями в финансах
Учебник
Издательство ~магистр~.
101000
Москва, Колпачный пер., 9А.
Тел.:
(495) 621-62-95.
e-mail: magistr-book@mail.ru