Г государственный университет
Высшая школа экономики
1роект TACIS
Преподавание
бизнес-
С.А. Айвазян
В.С. Мхитарян
средних
классических
ПРИКЛАДНАЯ
СТАТИСТИКА
И ОСНОВЫ
ЭКОНОМЕТРИКИ
Допущено Министерством общего
и профессионального образования Российской
Федерации в качестве учебника для студентов
экономических специальностей высших учебных
заведений
Москва
Издал сльскос объединенис “ К)Н ИТИ ”
1998
ОГЛАВЛЕНИЕ
Предисловие.	19
Введение. Вероятностно-статистические методы в моделировании
социально-экономических процессов и анализе данных	23
В. 1. Математико-статистический инструментарии экономических
исследований	24
В. 1.1. Назначение и составные части учебника	24
В. 1.2. Прикладная статистика	2б
В. 1.3. Теория вероятностей и математическая статистика	28
В.2.	Теоретико-вероятностнвш способ рассуждения в прикладной статистике
и эконометрике	29
В.2.1.	Гранпцв! применимости теоретико-вероятностного способа
рассуждения	29
В.2.2.	Что дает объединение теоретико-вероятностного и
статистического способов рассуждения ?	35
В.3.	Вероятностно-статистическая (эконометрическая) модели как частный
случай математической модели	40
В. 3.1. Математическая модели	40
В.3.2.	Основные этапы вероятностно-статистического моделирования 43
В. 3.3. Моделирование механизма явления вместо формалвной
статистической фотографии	45
Раздел I . Основы теории вероятностей	51
Г лава 1.	Правила действий со случайными событиями и вероятностями их
осуществления	52
1.1.	Дискретное вероятностное пространство	52
1.1.1.	Процесс регистрации наблюдения на обиекте исследуемой
совокупности (случайный эксперимент)	52
1.1.2.	Случайные события н правила действий с ними	5 3
1.1.3.	Вероятностное пространство. Вероятности н правила действий с
ними	58
1.2.	Непрерывное вероятностное пространство (аксиоматика А, Н.
Колмогорова)	69
1.2.1.	Специфика общего (непрерывного) случая вероятностного
пространства	69
1.2.2.	Случайные события, нх вероятности н правила действий с ними
(аксиоматический подход А.Н, Колмогорова)	71
Въ1водъ1	75
Глава 2. Случайные величины (исследуемые признаки)	77
2.1.	Определение и прнмеръ! случайных величин	77
2.2.	Возможные и наблюденные значения случайной величины	79
2.3.	Типы случайных величин	8О
2.4.	Одномерные н многомерные (совместные) законы распределения
вероятностен случайных величин	83
2.5.	Способы задания закона распределения: функция распределения,
функция плотности	89
2.5.1.	Функция распределения вероятностей одномерной случайной
величины	89
2.5.2.	Функция плотности вероятности одномерной случайной
величины	92
2.5.3.	Многомерные функции распределения н плотности.
Статистическая независимости случайных величин	94
2.6.	Основные числовые характеристики случайных величин	98
2.6.1.	Понятие о математических ожиданиях н моментах	99
2.6.2.	Характеристики центра группирования значений случайной
величины	102
2.6.3.	Характеристики степени рассеяния значений случайной
величины	104
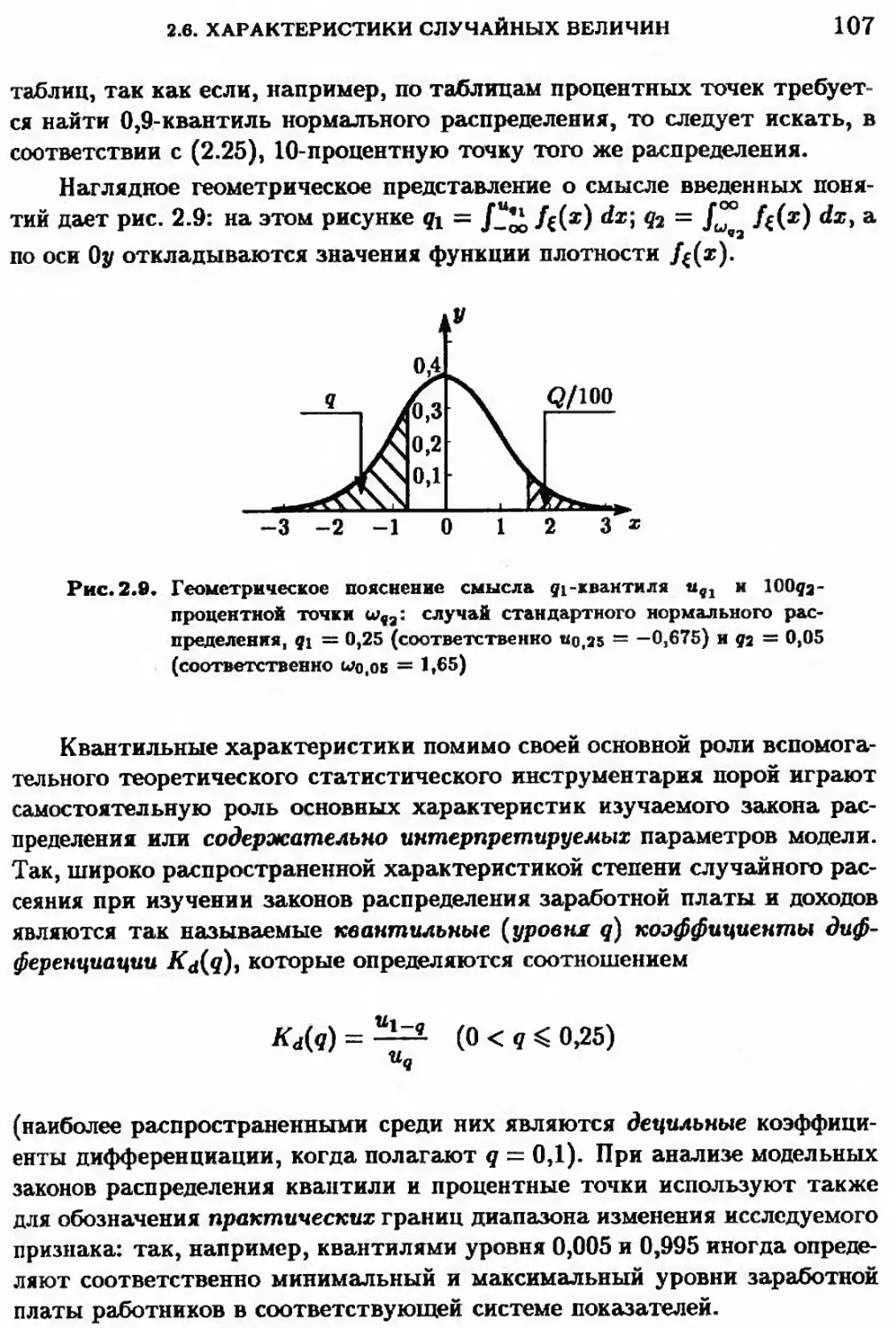
2.6.4.	Квантили и процентные точки распределения	106
2.6.5.	Асимметрия н эксцесс .	108
2.6.6.	Основные характеристики многомерных распределений
(ковариации, корреляции, обобщенная дисперсия н др.)	109
Выводы	112
Глава 3. Модели законов распределения вероятностей, наиболее
распространенные в практике статистических исследований	114
3.1.	Законы распределения, используемые для описания механизмов
генерации реальных социально-экономических данных	115
3.1.1.	Распределения, возникающие при анализе последовательности
испытаний Бернулли: биномиальное и отрицательное
биномиальное	115
3.1.2.	Гнпергеометрнческое распределение	119
3.1.3.	Распределение Пуассона	121
3.1.4.	Полиномиальное (мультиномиальное) распределение	123
3.1.5.	Нормальное (гауссовское) распределение	125
3.1.6.	Логарпфмнческн-нормальное распределение	129
3.1.7.	Равномерное (прямоугольное) распределение	132
3.1.8.	Распределения Вейбулла и экспоненциальное (показательное) 134
3.1.9.	Распределение Парето	13 9
3.1.10.	Распределение Кошн	140
3.2.	Законы распределения вероятностей, используемые при реализации
техники статистических вычислений	141
"Хи-квадрат" - распределение с m степенями свободы (
-распределение)	141
3.2.2.	Распределение Ствюдента с m степенями свободв!
(1(т)-распределение)	143
3.2.3.	Распределение дисперсионного отношения с числом степеней
свободв! числителя ml и числом степеней свободвх знаменателя
m2 (Р(т1дп2)-распределенне)	144
3.2.4.	Гамма-распределенне (Г-распределенне)	146
3.2.5.	Бета-распределенне (р-распределенне)	148
Ввшодв!	150
Глава 4. Основные результаты теории вероятностей	152
4.1.	Неравенство Чебвшева	152
4.2.	Закон болвшнх чисел н его следствия	154
4.2.1.	Закон болвшнх чисел	154
4.2.2.	Теорема Я, Бернулли	155
4.3.	Особая ролв нормалвного распределения: централвнвх пределвная
теорема	156
4.3.1.	Централвная пределвная теорема	157
4.3.2.	Многомерная централвная пределвная теорема	158
4.3.3.	Комментарии к централвной пределвной теореме	158
4.4.	Закрыв! распределения вероятностей случайных признаков, являющихся
функциями от пзвестнв1х случайных величин	150
Ввгеодв!	155
Глава 5. Цепи Маркова	157
5.1.	Последователвностн случайных экспериментов н случайных величин в
дискретном вероятностном пространстве	157
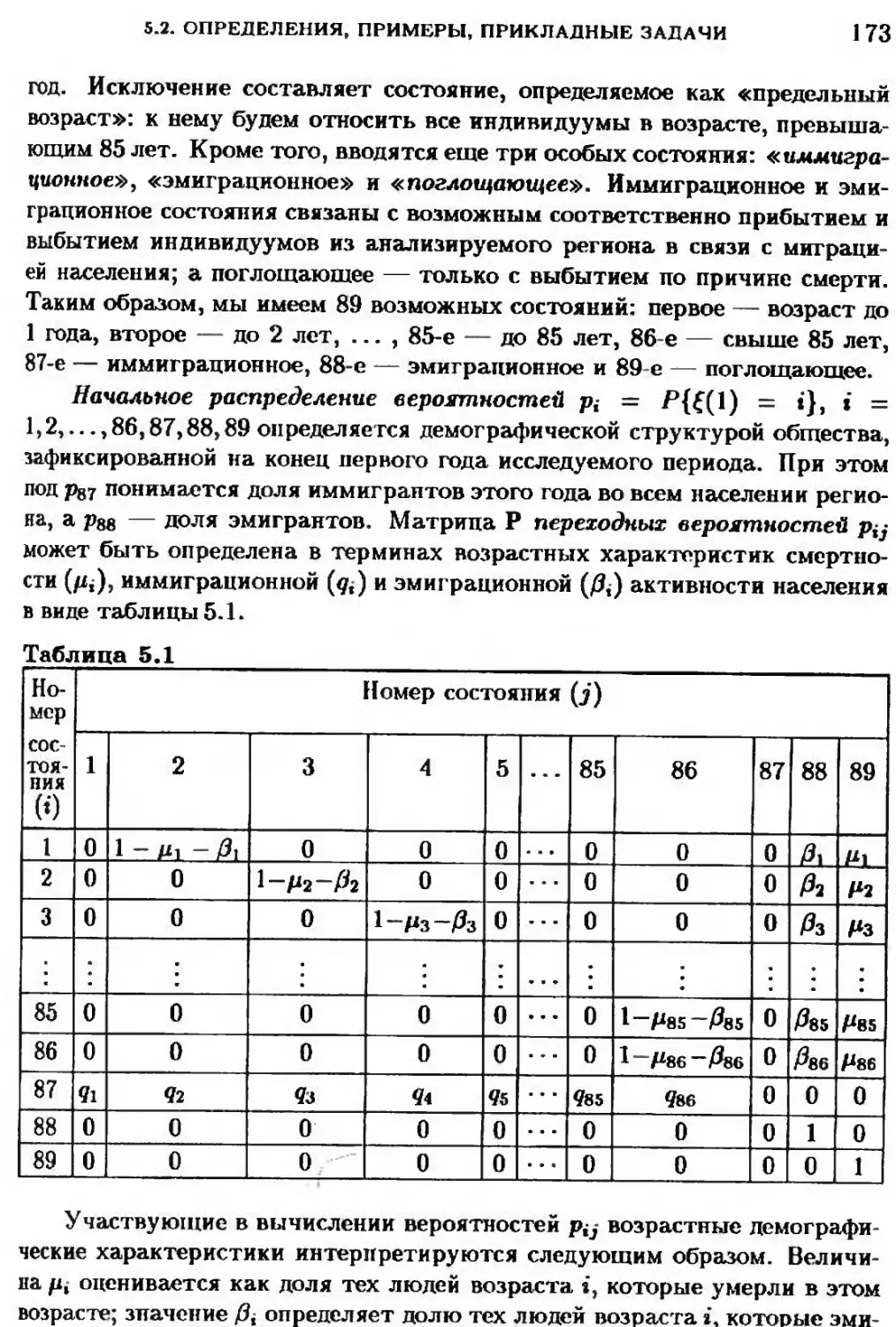
5.2.	Последователвностн, образующие цепв Маркова (определения,	примеры,
прикладные задачи)	169
5.3.	QcHOBHBie характеристики н свойства цепей Маркова	176
5.3.1.	QcHOBHBie характеристики	176
5.3.2.	Классификация состояний	н цепей	178
5.3.3.	Свойства цепей Маркова	181
5.4.	Анализ некоторвгк задач н примеров	184
Ввгеодв!	189
Раздел II. Основы математической статистики	193
Глава 6. Основы статистического описании и статистика нормального
закона	194
6.1.	Генералвная совокупноств, вв!борка из нее и основные способв!
организации вв!боркн	194
6.2.	QcHOBHBie вв!борочнв1е характеристики н	нх свойства	200
6.2.1.	Выборочные (эмпирические) функции распределения,
относительные частоты и функции плотности	201
6.2.2.	Выборочные аналоги начальных и центральных моментов
случайной величины	207
6.2.3.	Эмпирические аналоги центра группирования генеральной
совокупности	208
6.2.4.	Эмпирические аналоги показателей вариации рассеивания
случайной величины	209
6.2.5.	Выборочные коэффициенты асимметрии н эксцесса	210
6.2.6.	Статистическая устойчивость выборочных характеристик	214
6.2.7.	Аспмптотнческн-нормальный характер случайного
варьирования основных выборочных характеристик	216
6.2.8.	Поведение выборочных характеристик в нормальной
генеральной совокупности (статистика нормального закона)	219
6.3.	Вариационный ряд н порядковые статистики	224
6.3.1.	Закон распределения вероятностей i-ro члена вариационного
ряда	225
6.3.2.	Совместные (многомерные) распределения членов
вариационного ряда	227
6.3.3.	Порядковые статистики как эмпирические (выборочные)
аналоги квантилей н процентных точек распределения	229
Выводы	229
Глава?. Статистическое оцепивапие параметров	231
7.1.	Начальные сведения о задаче статистического оценивания	параметров 232
7.1.1.	Постановка задачи	232
7.1.2.	Статистики, статистические оценки, нх основные свойства	233
7.1.3.	Состоятельность	234
7.1.4.	Несмещенность	236
7.1.5.	Эффективность	23 8
7.2.	Функция правдоподобия. Количество информации, содержащееся в л
независимых наблюдениях относительно неизвестного значения
параметра	241
7.3.	Неравенство Рао - Крамера - Фреше и измерение эффективности оценок 244
7.4.	Понятие об интервальном оценивании н доверительных областях
(постановка задач)	248
7.5.	Методы статистического оценивания неизвестных параметров	249
7.5.1.	Метод максимального (наибольшего) правдоподобия	249
7.5.2.	Метод моментов	258
7.5.3.	Оценивание с помощью <взвешенных> статистик;
цензурирование, урезание выборок н порядковые статистики как
частный случай взвешивания	261
7.5.4.	Построение интервальных оценок (доверительных областей)	263
7.6.	Байесовский подход к статистическому оцениванию	269
7.6.1.	<Философия> байесовского подхода	269
7.6.2.	Общая логическая схема и базовые формы байесовского метода
оценивания параметров	270
7.6.3.	Примеры байесовского оценивания	273
Выводы	279
Глава 8. Статистическая проверка гипотез (статистические критерии)	282
8.1.	Основные типы гипотез, проверяемых в ходе статистического анализа и
моделирования	283
8.1.1.	Гипотезы о типе закона распределения исследуемой случайной
величины	283
8.1.2.	Гипотезы об однородности двух или нескольких
обрабатываемых выборок пли некоторых характеристик
анализируемых совокупностей	284
8.1.3.	Гипотезы о числовых значениях параметров исследуемой
генеральной совокупности	284
8.1.4.	Гипотезы об общем виде модели описывающей, статистическую
зависимость между признаками	285
8.2.	Общая логическая схема статистического критерия	286
8.3.	Построение статистического критерия; принцип отношения
правдоподобия	289
8.3.1.	Сущность принципа отношения правдоподобия	289
8.3.2.	Критерий логарифма отношения правдоподобия для проверки
простой гипотезы	291
8.3.3.	Критерий отношения правдоподобия для проверки сложной
гипотезы	292
8.4.	Характеристики качества статистического критерия	293
8.5.	Последовательная схема принятия решения (последовательные
критерии)	296
8.5.1.	Последовательная схема наблюдений	296
8.5.2.	Последовательный критерий отношения правдоподобия
(критерий Вальда) и его свойства	298
8.6.	Методы проверки статистических гипотез: примеры	статистических
критериев	299
8.6.1.	Критерии согласия	299
8.6.2.	Критерии однородности	304
8.6.3.	Проверка гипотез о числовых значениях параметра	312
Выводы	319
Раздел III.	Методы прикладной статистики	321
Глава 9.	Введение в прикладной статистический анализ	323
9.1.	Назначение и содержание прикладной статистики	323
9.1.1.	Два подхода к интерпретации и анализу исходных
статистических данных	323
9.1.2.	Три центральные проблемы прикладной статистики	326
9.1.3.	Новые постановки задач и ослабление ограничительных условий
в канонических математико-статистических и эконометрических
моделях	333
9.2.	Основные этапы прикладного	статистического анализа	334
Выводы	341
Глава 10. Статистическое исследование зависимостей (основные понятия и
постановки задач)	344
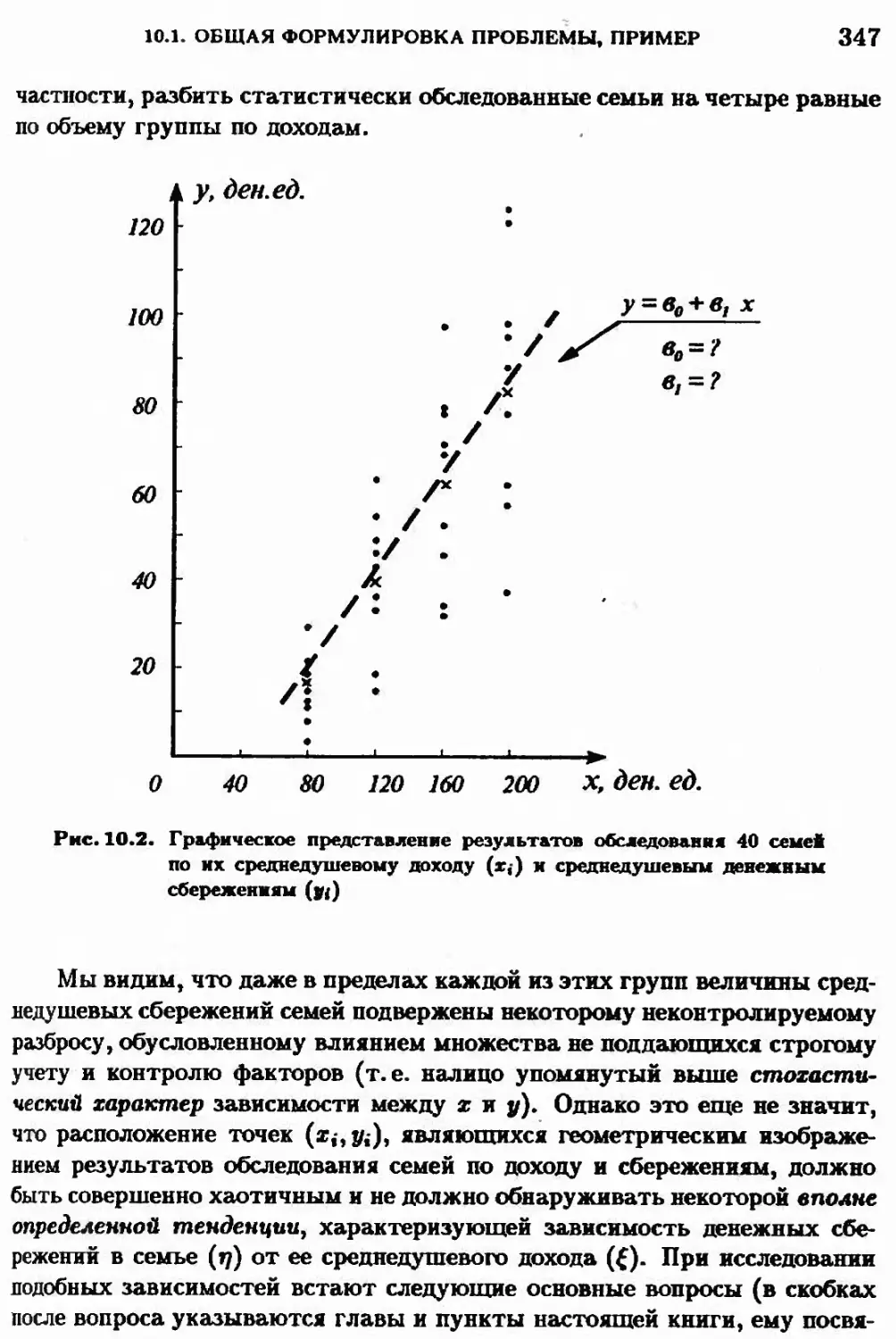
10.1.	Общая формулировка проблемы, пример	344
10.2.	Какова конечная прикладная	цель статистического исследования
зависимостей	354
10.3.	Математический инструментарий	357
10.4.	Некоторые типовые задачи практики эконометрического моделирования	359
10.5.	Основные типы зависимостей между количественными переменными	365
10.6.	Основные этапы статистического исследования зависимостей	370
10.7.	Выбор общего вида функции регрессии	377
10.7.1.	Использование априорной информации о содержательной
сущности анализируемой зависимости	378
10.7.2.	Предварительный анализ геометрической структуры исходных
данных	380
10.7.3.	Статистические критерии проверки гипотез об общем виде
функции	регрессии	381
10.7.4.	Некоторые	общие	рекомендации	385
Выводы	387
Глава 11. Корреляционный анализ многомерной генеральной совокупности 391
11.1.	Назначение и место корреляционного анализа в статистическом
исследовании	391
11.2.	Корреляционный анализ количественных признаков	393
11.2.1.	Коэффициент детерминации как универсальная характеристика
степени тесноты статистической связи	394
11.2.2.	Исследование линейной зависимости у от единственной
объясняющей переменной ю: парный коэффициент корреляции 399
11.2.3.	Исследование парных нелинейных связей: корреляционное
отношение	407
11.2.4.	Исследование линейной зависимости у от нескольких
объясняющих переменных множественный п частные
коэффициенты корреляции	412
11.3.	Корреляционный анализ порядковых (ординальных) переменных:
ранговая корреляция	423
11.3.1.	Исходные статистические данные (таблица плп матрица рангов
типа «объект-свопством)	424
11.3.2.	Понятие ранговой корреляции	425
11.3.3.	Основные задачи статистического анализа связей между
ранжировками	426
11.3.4.	Ранговый коэффициент корреляции Сппрмэна	427
11.3.5.	Ранговый коэффициент корреляции Кендалла	429
11.3.6.	Обобщенная формула для парного коэффициента корреляции п
связь между коэффициентами Сппрмэна п Кендалла	433
11.3.7.	Статистические свойства выборочных характеристик парной
ранговой связи	434
11.3.8.	Коэффициент конкордацпп (согласованности) как измеритель
статистической связи между несколькими порядковыми
переменными	437
11.3.9.	Проверка статистической значимости выборочного значения
коэффициента конкордацпп	439
11.4.	Корреляционный анализ категоризованных переменных: таблицы
сопряженности	442
11.4.1.	Исходные статистические данные (таблицы сопряженности)	442
11.4.2.	Основные измерители степени тесноты статистической связи
между двумя категоризованными переменными	443
Выводы	448
Глава 12. Распознавание образов и типологизация объектов в
социально-экономических исследованиях (методы классификации) 452
12.1.	Сущность, типологизация п прикладная направленность задач
классификации объектов	452
12.2.	Классификация при наличии обучающих выборок (дискриминантный
анализ)	466
12.2.1.	Класс как генеральная совокупность п базовая идея
вероятностно-статистических методов классификации	466
12.2.2.	Функции потерь п вероятности неправильной классификации 467
12.2.3.	Принципиальное решение общей задачи построения
оптимальных (байесовских) процедур классификации	468
12.2.4.	Параметрический дискриминантный анализ в случае
нормальных классов	471
12.3.	Классификация без обучения (параметрический случай): расщепление
смесей	вероятностных распределений	474
12.3.1.	Понятие смеси вероятностных распределений	475
12.3.2.	Задача расщепления смесей распределений	481
12.3.3.	Общая схема решения задачи автоматической классификации в
рамках модели смеси распределений (сведение к схеме
дискриминантного анализа)	482
12.4.	Классификация без обучения (непараметрический случай):
кластер-анализ	483
12.4.1.	Общая постановка задачи автоматической классификации	483
12.4.2.	Расстояния между отдельными объектами и меры близости
объектов друг к другу	486
12.4.3.	Расстояния между классами объектов	490
12.4.4.	Функционалы качества разбиения на классы и экстремальная
постановка задачи кластер-анализа	493
12.4.5.	Формулировка экстремальных задач разбиения исходного
множества объектов на классы при неизвестном числе классов 498
12.4.6.	Основные типы задач кластер-аналнза и основные типы
кластер-процедур	498
12.4.7.	Иерархические процедуры	500
12.4.8.	Параллельные кластер-процедуры	502
12.4.9.	Последовательные кластер-процедуры	507
Выводы	511
Глава 13. Снижение размерности исследуемого многомерного признака и
отбор наиболее информационных показателей	515
13.1.	Метод главных компонент	515
13.2.	Сущность, тппологпзацпя и прикладная направленность задач снижения
размерности	521
13.2.1.	Основные понятия и определения	521
13.2.2.	Вычисление главных компонент	524
13.2.3.	Основные числовые характеристики главных	компонент	526
13.2.4.	Геометрнческая интерпретация главных компонент	533
13.2.5.	Оптимальные свойства главных компонент	536
13.2.6.	Статпстпчеспке свойства выборочных главных компонент;
статистическая проверка некоторых гипотез.	639
13.2.7	Прпменпе свойств выборочных характеристик главных
компонент.	642
13.3	Факторный анализ.	546
13.3.1.	Сущность модели факторного анализа	546
13.3.2.	Общий вид линейной модели, ее связь с главными
компонентами	547
13.3.3.	Основные задачи факторного анализа	551
13.3.4.	Вопросы идентификации модели факторного	анализа	553
13.3.5.	Статистическое исследование модели факторного анализа	554
13.4.	Некоторые эвристические методы снижения размерности	565
13.4.1.	Природа эвристических методов	565
13.4.2.	Метод экспериментальной группировки признаков	566
13.4.3.	Метод корреляционнв1х плеяд	572
13.5.	Построение сводного (интегралвного) латентного показателя качества
(или эффективности функционирования) сложной системы	575
13.5.1.	Общая постановка задачи	575
13.5.2.	Сводный показателв (евыходное качеством) и его целевая
функция	576
13.5.3.	Исходные данные	578
13.5.4.	Алгоритмические н вычислительные вопросы построения
неизвестной целевой функции	580
13.5.5.	Примеры построения интегрального показателя с помощью
экспертно-статистического метода	584
13.6.	Многомерное шкалирование	587
13.6.1.	Постановка задачи метрического многомерного шкалирования
13.6.2.	Решение задачи метрического многомерного шкалирования	588
13.6.3.	Понятие о неметрическом многомерном шкалировании (Mill) 590
Выводы (МП!)	590
Раздел IV. Основы эконометрики	595
Глава 14. Эконометрика и эконометрическое моделирование: основные
понятия и определения	597
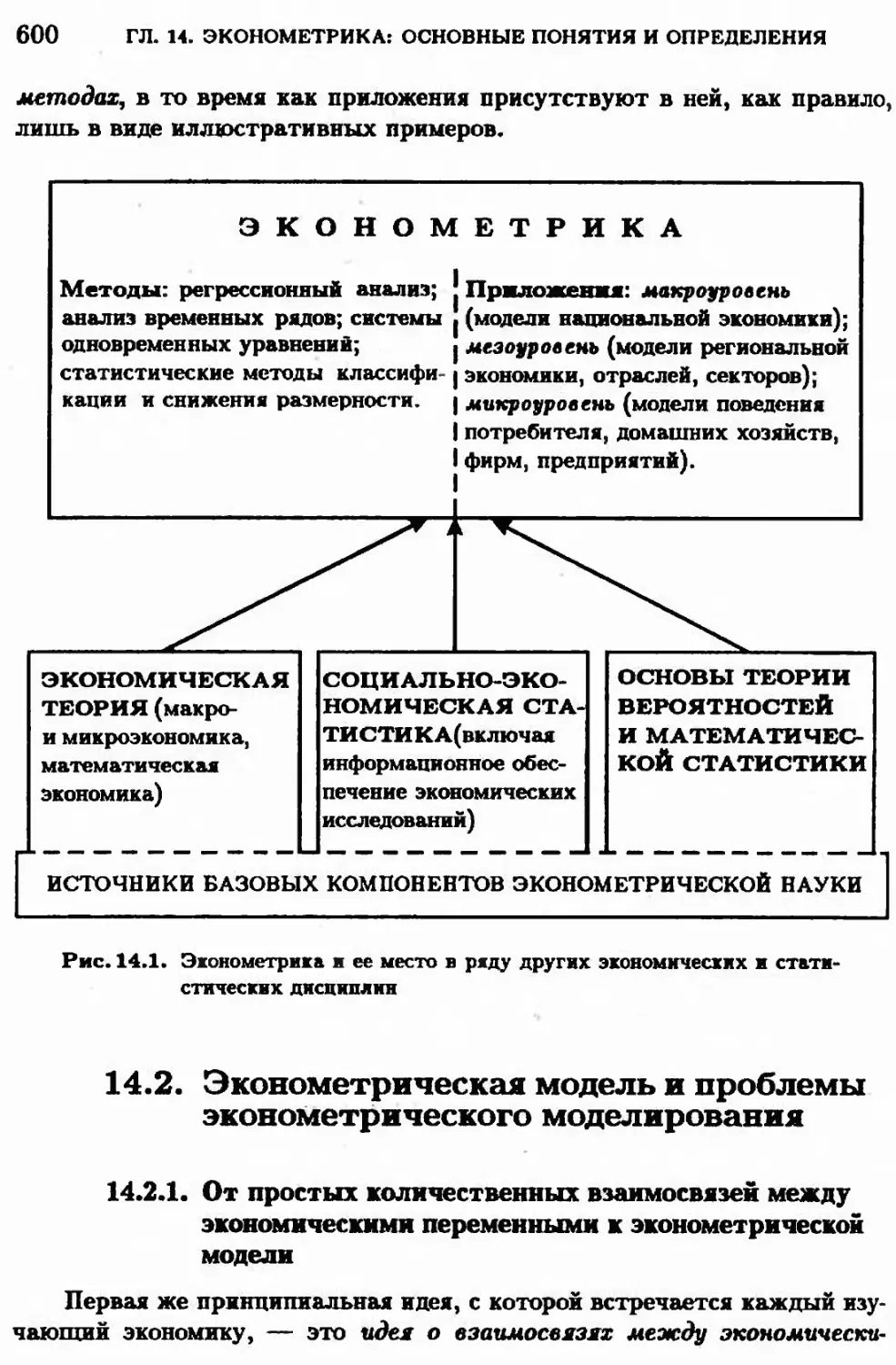
14.1.	Эконометрика и ее место в ряду математнко-статнстнческнх н
экономических дисциплин	597
14.2.	Эконометрическая модель н проблемы эконометрического
моделирования	600
14.2.1.	От простых количественных взаимосвязей между
экономическими переменными к эконометрической модели	600
14.2.2.	Основные понятия эконометрического моделирования	605
14.2.3.	Основные проблемы эконометрического моделирования	611
14.3.	Математнко-статнстнческнй инструментарий эконометрики	617
14.3.1.	Традиционный состав математнко-статнстнческнх методов
эконометрики	617
14.3.2.	Некоторые задачи социально-экономической теории н практики,
решение которых требует методов прикладной статистики,
выходящих за рамкн традиционного эконометрического
инструментария	617
Выводы	618
Глава 15. Модели и методы регрессионного анализа	621
15.1.	Введение в регрессионный анализ (основные понятия н определения) 621
15.1.1.	Результирующая (зависимая, эндогенная) переменная у	622
15.1.2.	Объясняющие (предпкторные, экзогенные) переменные X 622
15.1.3.	Функция регрессии у по X	622
15.1.4.	Уравнения регрессионной связи между у и X	624
15.1.5.	Измерители степени тесноты статистической связи между у и X 625
15.1.6. Исходные статистические данные	626
15.1.7.	Основные задачи прикладного регрессионного анализа	627
15.2.	Классическая линейная модель множественной регрессии (КЛММР) 628
15.3. Оценивание неизвестных параметров КЛММР: метод наименьших
квадратов и метод максимального правдоподобия	632
15.3.1	.	Метод наименьших квадратов (МИК)	633
15.3.2	.	Метод максимального правдоподобия	(ММП)	636
15.3.3	. Анализ вариации результирующего показателя у и выборочный
коэффициент детерминации	638
15.3.4	.	Статистические свойства оценок параметров КЛММР	641
15.4.	Мультпколлпнеарность и отбор наиболее существенных объясняющих
переменных в КЛММР	653
15.4.1.	Признаки и причины мультпколлпнеарностп	653
15.4.2.	Методы устранения мультпколлпнеарностп	656
15.5.	Ошибки спецификации модели	668
15.6.	Обобщенная линейная модель множественной регрессии (ОЛММР) и
обобщенный метод наименьших квадратов (ОМНЕ)	672
15.6.1.	Обобщенная линейная модель множественной регрессии
(ОЛМР)	672
15.6.2.	Обобщенный метод наименьших квадратов (ОМНЕ)	676
15.7.	ОЛММР с гетероскедастнчнымн остатками	681
15.7.1.	Сравнение ОМНЕ- и МНК-оценок в моделях регрессии с
гетероскедастнчнымн остатками	684
15.7.2.	Некоторые практические рекомендации по анализу модели
регрессии с гетероскедастнчнымн остатками	686
15.8.	ОЛММР с автокоррелпрованнымн остатками	690
15.8.1.	Искажение характеристик точности МНК-оценок,
обусловленное игнорированием автокоррелпрован ноет и
остатков	693
15.8.2.	Проверка гипотезы о налпчнн/отсутствнн
автокоррелпрованностн регрессионных остатков	696
15.8.3.	Некоторые практические рекомендации по анализу модели
регрессии с автокоррелпрованнымн остатками	698
15.9.	Практические рекомендации по построению, анализу и интерпретации
регрессионной модели	699
15.9.1.	Построение и анализ обобщенной ЛММР при неизвестной
ковариационной матрице регрессионных остатков (практически
реализуемый ОМНЕ)	699
15.9.2.	Точечный и интервальный прогноз, основанный на моделях
линейной регрессии	702
15.9.3.	Исследование точности	регрессионной модели в реалистической
ситуации	712
15.9.4.	Анализ эластичностей с	использованием моделей	регрессии	715
15.10.	Линейные регрессионные модели со стохастическими объясняющими
переменными	717
15.10.1.	Случайные остатки не зависят от предикторов X и оцениваемых
коэффициентов регрессии	719
15.10.2.	Общий случай: стохастические предикторы X коррелпрованы с
регрессионными остатками е. Метод инструментальных
переменных	723
15.10.3.	Случайные ошибки в измерении объясняющих переменных 729
15.11.	Линейные регрессионные модели с переменной структурой (построение
линейной модели по неоднородным регрессионным данным)	735
15.11.1.	Проблема неоднородных (в регрессионном смысле) данных 735
15.11.2. Введение <манекенов> (фиктивных переменных) в линейную
модель регрессии	738
15.11.3.	Проверка регрессионной однородности двух групп наблюдений
(критерий Г, Чоу)	746
15.11.4.	Построение КЛММР по неоднородным данным в условиях,
когда значения сопутствующих переменных	неизвестны	749
15.12.	Нелинейные модели регрессии и линеаризация	751
15.12.1.	Некоторые виды нелинейных зависимостей, поддающиеся
непосредственной линеаризации	752
15.12.2.	Подбор линеаризующего преобразования (подход Бокса - Кокса) 759
15.13.	Дихотомические (бинарные) результирующие показатели и связанные с
ними логит- и пробпт-моделп	766
Выводы	772
Глава 16. Анализ временных рядов (модели и прогнозирование)	778
16.1.	Временной ряд (определения, примеры, формулировки основных задач) 780
16.2.	Стационарные временные ряды и их основные характеристики	787
16.3.	Неслучайная составляющая временного ряда и методы его сглаживания 796
16.3.1.	Проверка гипотезы о неизменности среднего значения
временного ряда	797
16.3.2.	Методы сглаживания временного ряда (выделение неслучайной
составляющей)	803
16.3.3.	Подбор порядка аппроксимирующего полинома с помощью
метода последовательных	разностей	816
16.4.	Модели стационарных временных	рядов и их идентификация	820
16.4.1.	Модели авторегрессии порядка р (АР(р)-моделп)	822
16.4.2.	Модели скользящего среднего порядка q (СС(д)-моделп)	837
16.4.3.	Авторегрессионные модели со скользящими средними в
остатках (АРСС(р, д)-модели)	846
16.4.4.	Простая и обобщенная модели авторегрессионных условно
гетероскедастичных остатков	860
16.5.	Модели нестационарных временных рядов и их идентификация	863
16.5.1.	Модель авторегрессии - проинтегрированного скользящего
среднего (АРПСС(р, q, п)-модель)	863
16.5.2.	Модели рядов, содержащих сезонную компоненту	867
16.5.3.	Регрессионные модели с распределенными лагами	872
16.6.	Прогнозирование экономических показателен, основанное на
использовании моделей временных рядов	888
16.6.1.	Прогнозирование на базе АРПСС-моделеп	889
16.6.2.	Адаптивные методы прогнозирования	896
Выводы	903
Глава 17. Системы линейных одновременных уравнений	907
17.1.	Модель спроса-предложення как пример системы одновременных
уравнении	908
17.2.	Условия идентифицируемости уравнении системы	915
17.3.	Идентификация систем одновременных уравнении (статистическое
оценивание неизвестных значении параметров системы)	924
17.3.1.	Идентификация рекурсивных систем	925
17.3.2.	Косвенный метод наименьших квадратов	929
17.3.3.	Двухшаговын МНК оценивания структурных параметров
отдельного уравнения	931
17.3.4.	Трехшаговын МНК одновременного оценивания всех
параметров системы	936
17.3.5.	Другие методы оценивания СОУ и некоторые общие
рекомендации	940
17.4.	Точечный н интервальный прогноз значении эндогенных переменных 942
17.5. Некоторые общие подходы к анализу точности оценивания н к
сравнению методов н моделей	950
Выводы	957
Литература	960
Приложение 1.	Таблицы математической статистики	963
Приложение 2.	Необходимые сведения нз матричной алгебры	983
Алфавитно-предметный указатель	1006
ПРЕДИСЛОВИЕ
Эконометрика — одна из базовых (наряду с микро- и макроэконо-
микой) дисциплин экономического образования во всем мире. К сожале-
нию, до начала 90-х годов эконометрика по существу не была признана в
СССР и России, не включалась в учебные планы подготовки специалистов
(студентов, аспирантов) экономического профиля. Объяснение этому най-
ти нетрудно: из трех основных составляющих эконометрики — экономи-
ческой теории, экономической статистики и математико-статистического
инструментария две первые были представлены в нашей стране явно не-
удовлетворительно. Не было доброкачественной экономической теории,
не было системы национальных счетов и необходимого информационного
обеспечения эконометрического моделирования.
Теперь ситуация изменилась. Авторам предлагаемого вниманию чи-
тателя учебника довелось принять непосредственное участие в процессе
«восстановления в своих законных правах» эконометрики: в формиро-
вании базовых положений концепции современного экономического обра-
зования в российской высшей школе, в составлении первых программ и
чтении первых курсов лекций по этой дисциплине на экономическом фа-
культете Московского государственного университета им. М. В. Ломоно-
сова (МГУ), начиная с 1992 г., и в Московском государственном универ-
ситете экономики, статистики и информатики (МЭСИ), — с 1993 г. В
формировании своей позиции по данной проблеме авторы опирались на
многолетний опыт исследовательской и педагогической работы в обла-
сти разработки и практического использования методов эконометрическо-
го моделирования: один из них (С. А. Айвазян), работая с 1969 года в
Центральном экономико-математическом институте Российской академии
наук, занимается эконометрическим моделированием распределительных
отношений в обществе, одновременно являясь автором учебных программ
и постоянным лектором по всему спектру дисциплин эконометрического
профиля — теории вероятностей, математической статистике, мно-
гомерному статистическому анализу (МГУ им. М. В. Ломоносова, МЭ-
СИ, Российская экономическая школа — РЭШ), методам прогнозирова-
ния в бизнесе (Московское отделение Калифорнийского государственного
университета, г. Хэйвард); другой (В. С. Мхитарян) использует эконо-
20
ПРЕДИСЛОВИЕ
метрические методы в социально-экономических исследованиях и задачах
статистического контроля качества изделий, а также много лет читает
курсы лекций вероятностно-статистического профиля в МЭСИ.
Что побудило авторов написать этот учебник? Ведь богатые тра-
диции европейских и северо-американских университетов в области эконо-
метрической науки и ее преподавания в системе экономического образова-
ния всех уровней (undergraduate, graduate, post-graduate) отражены в раз-
нообразной и интересной монографической и учебно-методической литера-
туре по данному предмету. Достаточно назвать широко распространен-
ные учебники Дж. Джонстона, Э. Маленво, A. Goldberger, R. S. Pindyck-
D.L. Rubinfeld, W. Greene, C. Dougherty, E. R. Berndt (см. список литера-
туры в конце книги). Почему бы не повторить переводы двадцатилетней
давности первых двух учебников и не перевести с английского языка неко-
торые из других, здесь упомянутых? Мы полагаем, что в условиях острого
дефицита на отечественном рынке эконометрической учебной литературы
эта деятельность была бы крайне желательной, более того — необходи-
мой. Однако издание нашей книги имеет свой замысел, свою специфику,
и вот в чем они заключаются.
Во-первых, в предлагаемом учебнике отражено понимание содержа-
ния математико-статистического инструментария эконометрики, несколь-
ко отличающееся от общепринятого. По нашему мнению, современные
достижения математико-статистической науки (особенно в многомерном
статистическом анализе), с одной стороны, и существенное расширение
круга экономических задач, требующих эконометрических методов ре-
шения, — с другой, обусловили необходимость более широкого взгляда
на математико-статистический инструментарий эконометрики и, в
частности, включения в него, помимо традиционных разделов по регрес-
сионным моделям, анализу временных рядов и системам одновременных
уравнений, таких разделов многомерного статистического анализа, как
марковские цепи, классификация многомерных наблюдений и снижение
размерности анализируемого факторного пространства. Говоря о ши-
роком спектре экономических задач, требующих выходящих за тради-
ционные рамки эконометрических методов решения, мы имели в виду,
в частности, статистическое исследование динамики структурных изме-
нений (в демографии, в стратификационной структуре общества и т.п.),
выявление скрытых (латентных) факторов, определяющих течение того
или иного социально-экономического процесса, построение интегральных
индикаторов качества или эффективности функционирования социально-
экономической системы, типологизацию социально-экономических объек-
тов и др.
ПРЕДИСЛОВИЕ
21
Во-вторых, в ходе многолетнего опыта преподавания различных дис-
циплин вероятностно-статистического профиля в экономических вузах и
на экономических факультетах университетов мы пришли к убеждению,
что необходимо строить учебный процесс таким образом, чтобы доби-
ваться цельного, системного восприятия всего блока этих дисциплин.
Речь идет, в частности, о курсах по элементарным методам статистиче-
ской обработки данных (или дескриптивной статистике), теории вероят-
ностей, математической статистике, многомерному статистическому ана-
лизу (или многомерным статистическим методам), анализу временных ря-
дов и, наконец, эконометрике. Очевидно, реализации этой цели должен
способствовать и учебник, одновременно содержащий взаимосвязанное
изложение всех этих курсов.
Другими словами, мы попытались написать такую книгу, которую
нам бы хотелось иметь под рукой в процессе нашей преподавательской де-
ятельности. К сожалению, среди многих прекрасных зарубежных книг по
эконометрике книги, обладающей двумя вышеуказанными особенностями,
не оказалось.
Заметим, что несмотря на наличие ряда иллюстративных примеров
и упражнений, предлагаемый учебник не решает проблемы задачника по
эконометрике. Поэтому для проведения полноценного учебного процесса
он должен быть дополнен набором эконометрических задач и упражнений
(например, в духе книги [Berndt, Е. R.]).
Материал учебника и ответственность распределены между автора-
ми следующим образом. В. С. Мхитарян принимал участие в написании*
глав 6, 7, 8 и 13, а также предложил большую часть задач, которыми
снабжены главы учебника. Остальной материал (включая упомянутые
главы) написаны С. А. Айвазяном. Им же выполнено общее научное ре-
дактирование учебника.
В заключение мы хотим выразить свою признательность. Мы бла-
годарны, во-первых, руководителям образовательного проекта EU-TACIS
«Преподавание экономических и бизнес дисциплин в средних школах, тех-
нических и классических университетах» профессору Соломону Кохену
(S. Cohen, SEOR и Эразмус Университет, Роттердам, Голландия) и рек-
тору Государственного университета-Высшей школы экономики — про-
фессору Ярославу Ивановичу Кузьминову: финансовая поддержка этого
проекта сыграла решающую роль в том, чтобы авторы смогли определить
для себя приоритетной задачей написание данного учебника. Мы выра-
жаем также свою признательность нашим коллегам: профессору экономе-
трики Тилбургского университета и Высшей экономической школы Лон-
дона Яну Магнусу и профессору Государственного университета-Высшей
22
ПРЕДИСЛОВИЕ
школы экономики — Эмилю Борисовичу Бршову. Их внимание к учеб-
нику было постоянным (в процессе его написания), взыскательным и од-
новременно доброжелательным. Высказанные ими замечания и советы,
бесспорно, способствовали улучшению качества рукописи. Существенное
влияние на замысел и содержание книги оказал опыт исследовательской
и педагогической работы авторов, их постоянные контакты с коллегами
по ЦЭМИ РАН, по научному семинару «Многомерный статистический
анализ и вероятностное моделирование реальных процессов». Без них и
без наших главных критиков и генераторов вопросов — многих поколении
студентов МГУ им. М. В. Ломоносова, МЭСИ, РЭШ, — эта книга вряд ли
появилась бы на свет. Мы благодарны Алле Павловне и Галине Юрьев-
не Грохотовым за самоотверженный труд по подготовке оригинал-макета
рукописи книги, а также Николаю Владимировичу Третьякову и Елене
Владимировне Герасимовой за очень полезную и профессиональную кон-
сультационную поддержку Грохотовых в этом объемном и непростом про-
изводственном процессе. Что касается слабых мест и недостатков учеб-
ника, то за них всю ответственность несут, естественно, только авторы.
Мы будем признательны читателям за их отзывы о книге и критические
замечания, направленные в издательство или непосредственно нам.
Москва-Роттердам-
деревня «Плужково»	С. А. Айвазян
Московской области.	В. С. Мхитарян
1996-1998 гг.
Введение
ВВЕДЕНИЕ. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ
МЕТОДЫ В МОДЕЛИРОВАНИИ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ПРОЦЕССОВ И АНАЛИЗЕ ДАННЫХ
В.1. Математико-статистический
инструментарий экономических
исследовании
В.1.1. Назначение и составные части учебника
Если экономист строит рассуждения и выводы, опираясь в своих мо-
дельных построениях на результаты конкретных измерений интересую-
щих его экономических, социально-экономических и (или) демографиче-
ских показателей, то тем самым определяется эконометрическим под-
ход к проблеме, а инструментарий, которым он при этом пользуется,
обязательно содержит те или иные методы и модели прикладной ма-
тематической статистики. Ведь назначение эконометрики — прида-
вать конкретное количественное выражение общим (качественным) зако-
номерностям экономической теории на базе экономической статистики и
с использованием средств математической статистики (подробнее опреде-
ление эконометрики см. в п. 14.1).
Так вот, предлагаемый вниманию читателя учебник как раз и по-
священ описанию математико-статистического инструментария эко-
номических исследований. Почему же тогда не назвать этот учебник про-
сто «Методы эконометрики»? По-существу можно было бы считать такое
название этой книги вполне оправданным. Однако от такого решения ав-
торов удержали два обстоятельства.
Первое обстоятельство связано с установившимся традиционным
пониманием методов эконометрики, при котором они ограничивались
В.1. ИНСТРУМЕНТАРИЙ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ
25
линейным регрессионным анализом (включающим классический и
обобщенный методы наименьших квадратов, случаи гетероскедастичных
и автокор рели рованных регрессионных остатков, стохастических объяс-
няющих переменных, а также использование фиктивных и инструмен-
тальных переменных), методами и моделями анализа временных
рядов (так называемые AR-, МА-, ARMA- и ARIMA-модели, а в послед-
ние годы и модели коинтеграции, ARCH- и GARCH-модели) и, наконец,
системами одновременных уравнений. Этот набор традиционных
эконометрических методов описан в разделе IV данного учебника.
Второе обстоятельство связано с первым и заключается в том, что
по своему назначению, по своим инструментальным возможностям при-
кладная статистика самостоятельная научная дисциплина, обслуживаю-
щая значительно более широкий класс реальных задач статистического
анализа данных, чем тот, который традиционно непосредственно связыва-
ется с эконометрикой. К таким задачам в сфере социально-экономической
теории и практики относятся, в частности:
•	исследование динамики структуры состояний объектов (демографи-
ческой или социальной структуры общества, структуры типологии потре-
бительского поведения домашних хозяйств и т.п.);
•	типологизация социально-экономических объектов (семей, фирм,
предприятий, регионов, стран и т. п.);
•	построение интегральных индикаторов качества или эффектив-
ности функционирования социально-экономической системы (уровня или
качества жизни, качества населения, эффективности функционирования
предприятия и т. п.);
•	выявление скрытых (латентных) факторов, определяющих течение
того или иного социально-экономического процесса;
•	исследование и моделирование генезиса анализируемых статистиче-
ских данных.
К традиционным экономическим задачам применения эконометриче-
ских методов принято относить (эта точка зрения представлена, напри-
мер, в [Джонстон Дж., с. 16]) макромоделирование функционирования на-
циональной экономики (агрегированное, не агрегированное, детализиро-
ванное) или ее секторов. Традиционные приложения эконометрических
методов на лшкро-уровне сводятся обычно к моделированию поведения по-
требителя, производителя и продавца, а также к моделированию некото-
рых процессов, происходящих на финансовых рынках.
Современные университетские учебные планы подготовки экономи-
стов и экономистов-статистиков построены таким образом, чтобы обес-
печивать непрерывность и преемственность обучения по блокам дисци-
26
В. ВВЕДЕНИЕ
плин:
•	гуманитарному;
•	экономическому;
•	предметной статистики;
•	математико-статистического инструментария;
•	информационных технологий.
В качестве обязательных компонентов в блоке математико-ста-
тистического инструментария представлены курсы по элементарным
методам статистического анализа данных (или дескриптивной стати-
стике), теории вероятностей^ математической статистике) приклад-
ной статистике (или многомерным статистическим методам), экономе-
трике. Данный учебник посвящен взаимосвязному изложению всех упо-
мянутых дисциплин блока математико-статистического инструментария.
ВЛ.2. Прикладная статистика
Нужно ли использовать этот термин или можно ограничиться более
привычным понятием «математическая статистика»? Как соотносится
прикладная статистика с другими статистическими дисциплинами, таки-
ми, как «математическая статистика», «анализ данных», «методы эконо-
метрики»? Для обоснования правомерности и целесообразности рассмо-
трения прикладной статистики как самостоятельной научной дисциплины
следует упомянуть, как минимум, о двух моментах.
Во-первых, до сих пор развитие теории, методологии и практики ста-
тистической обработки анализируемых данных шло по существу в двух
параллельных направлениях. Одно из них представлено методами, пре-
дусматривающими возможность вероятностной интерпретации обра-
батываемых данных и полученных в результате обработки статистиче-
ских выводов. Именно эти методы и составляют содержание подавляю-
щего большинства монографий и руководств по математической статисти-
ке. Другими словами, под методами математической статистики принято
понимать лишь те методы статистической обработки исходных данных,
разработка и использование которых апеллируют к Вероятностной приро-
де этих данных.1 При этом развиваемый в рамках второго направления
1 Такова ситуация, сложившаяся лишь de facto. Формально же, de jure, если исходить
из определения Большого энциклопедического словаря (М., Большая Российская эн-
циклопедия, 1997, с. 701), математическая статистика понимается более широко, а
именно как «наука о математических методах систематизации и использования ста-
тистических данных для научных и практических выводов. Во многих своих разде-
лах математическая статистика опирается на теорию вероятностей, позволяющую
В.1. ИНСТРУМЕНТАРИЙ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ
27
весьма широкий и актуальный класс методов статистической переработ-
ки исходной информации, а именно вся совокупность тех методов, которые
априори не опираются на вероятностную природу обрабатываемых дан-
ных (представителями методов такого типа являются, например, разно-
образные методы кластер-анализа, многомерного шкалирования, теории
измерений и др.), остается за общепринятыми рамками научной дисци-
плины «математическая статистика».
Во-вторых, специалисты, занимающиеся разработкой и конкретными
применениями методов статистической обработки исходной информации,
ае могут игнорировать ту внушительную дистанцию, которая разделяет
момент успешного завершения разработки собственно математического
метода и момент получения результата от использования этого метода в
решении конкретной практической задачи. В процессе прохождения этой
грудной дистанции математику-прикладнику приходится, в частности:
•	глубоко вникать в содержательную сущность задачи, адекватно «при-
лаживать» исходные модельные допущения (на которых строится лю-
бой математический метод) к выяснению сущности реальной задачи;
•	решать задачу преобразования имеющейся исходной информации к
стандартной (унифицированной) форме записи обрабатываемых ста-
тистических данных;
•	разрабатывать практически реализуемые вычислительные алгорит-
мы и программное обеспечение с учетом специфики обрабатываемой
статистической информации и возможностей имеющейся вычисли-
тельной техники.
Понятийный аппарат, методы и результаты, позволяющие проходить
эту дистанцию, вместе с этапом «прилаживания» и доработки необхо-
димого математического инструментария и составляют главное содер-
жание прикладной статистики.
Таким образом, мы приходим к определению прикладной статисти-
ки как самостоятельной научной дисциплины, разрабатывающей и си-
стематизирующей понятия, приемы, математические методы и моде-
ли, предназначенные для организации сбора , стандартной записи, си-
оценнть надежность и точность выводов, делаемых на основании ограниченного ста-
тистического материала».
1 Говоря об «организации сбора» статистических данных, мы имеем в виду лишь опре-
деление способа отбора подлежащих статистическому обследованию единиц (семей,
предприятий, стран, пациентов и т.п.) из всей исследуемой совокупности (см. п.6.1,
а также в п. 9.1 описание типа 2). Мы не включаем сюда разработку методологии
измерителей анализируемых свойств отображаемого объекта: эта работа предпо-
лагает профессиональное (экономическое, техническое, медицинское и т. п.) изуче-
28
В. ВВЕДЕНИЕ
стематизации и обработки статистических данных с целью их удобно-
го представления, интерпретации и получения научных и практических
выводов.
Для определения той же самой системы понятий, приемов, матема-
тических методов и моделей некоторые специалисты используют термин
«анализ данных», понимаемый в расширительном толковании. Описанию
методов прикладной статистики, выходящих за традиционные рамки ме-
тодов эконометрики и одновременно наиболее актуальных для экономиче-
ских и социально-экономических приложений, посвящен раздел III данного
учебника.
ВЛ.3. Теория вероятностен и математическая статистика
Эти две дисциплины основные «поставщики» математического ин-
струментария для прикладной статистики и эконометрики.
« Теория вероятностей — наука, позволяющая по вероятностям од-
них случайных событий находить вероятности других случайных собы-
тий, связанных каким-либо образом с первыми ... Можно также ска-
зать, что теория вероятностей есть математическая наука, выясня-
ющая закономерности, которые возникают при взаимодействии боль-
шого числа случайных факторов» (Математическая энциклопедия, М.,
Советская энциклопедия, 1976, т. 1, с. 655-656). Подчеркнем, что упомяну-
тые в определении закономерности формулируются в терминах модельных
соотношений.
Идеальной средой применимости теоретико-вероятностного способа
рассуждения (и соответствующего математического аппарата) является
ситуация, когда мы находимся в условиях стационарного (т. е. не изменя-
ющегося во времени) действия некоторого реального комплекса условий,
включающего в себя неизбежность «мешающего» влияния большого чи-
сла случайных (не поддающихся строгому учету и контролю) факторов,
которые в свою очередь не позволяют делать полностью достоверные вы-
воды о том, произойдет или не произойдет интересующее нас событие.
При этом предполагается, что мы имеем принципиальную возможность
(хотя бы мысленно реально осуществимую) многократного повторения наг
шего эксперимента или наблюдения в рамках того же самого реального
комплекса условий. Именно такую ситуацию принято называть условия-
ми действия статистического ансамбля или условиями соблюдения стат
мне сущности задач, для решения которых требуется статистическая информация,
а потому она относится к компетенции предметной статистики соответствующей
области.
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ
29
тистической однородности исследуемой совокупности (подробнее об этом
см. п. В.2).
Необходимый для нормального понимания методов прикладной ста-
тистики и эконометрики минимум сведений из теории вероятностей при-
водится в разделе I данного учебника.
Одно из возможных определений математической статистики при-
ведено в п. В. 1.2 (см. сноску на с. 26). Добавим к этому, что матема-
тическая статистика, являясь по отношению к прикладной статистике и
эконометрике разработчиком и поставщиком существенной части исполь-
зуемого в них математического аппарата, полностью отстранена от таких
функций этих прикладных дисциплин, как:
•	«прилаживание» и доработка необходимого математического инстру-
ментария в соответствии со спецификой анализируемого класса ре-
альных социально-экономических задач;
•	разработка невероятностных (логико-алгебраических, оптимизацион-
ных и др.) методов анализа и моделирования реальных исходных
данных, т. е. методов, не опирающихся на модельные допущения о
вероятностной природе этих данных;
•	преобразование разнообразных форм исходных социально-экономи-
ческих данных с целью их удобного представления для дальнейшего
анализа и моделирования;
•	разработка практически реализуемых вычислительных алгоритмов и
удобного программного обеспечения для используемых в ходе эконо-
метрического анализа методов и моделей.
Раздел II учебника посвящен изложению основных результатов мате-
матической статистики, включая элементарные методы статистического
анализа данных (методы дескриптивной статистики).
В.2.	Теоретико-вероятностный способ
рассуждения в прикладной статистике
и эконометрике
В.2.1.	Границы применимости теоретико-вероятностного
способа рассуждения
В п. В.1.2 упоминалось о двух подходах к статистическому анализу
данных: математико-статистическом, основанном на вероятностном спо-
собе рассуждения, и логико-алгебраическом. Ко второму подходу исследо-
ватель вынужден обращаться лишь тогда, когда условия сбора (регистра-
30
В. ВВЕДЕНИЕ
ции) исходных данных не укладываются в рамки так называемого стати-
стического ансамбля, т. е. в ситуациях, когда не имеется практиче-
ской или хотя бы принципиально мысленно представимой возможности
многократного тождественного воспроизведения основного комплекса
условий, при которых производились измерения анализируемых данных.
В условиях же статистического ансамбля исследователь имеет воз-
можность воспользоваться классическими математико-статистическими
методами обработки данных, когда для обоснования наилучшего выбора
методов статистической переработки, итогового представления и интер-
претации анализируемых данных он использует те или иные априорные
сведения об их случайной (стохастической) природе. При этом мы ис-
ходим из того, что даже постулируемая нами тождественность воспро-
изведения основного комплекса условий эксперимента или наблюдения в
большинстве реальных ситуаций (с учетом их сложности, множественно-
сти и частичной неизученности формирующих их факторов) не избавляет
нас от неконтролируемого (случайного) разброса в самих результатах
наблюдения. Так, даже практически идеально отлаженный станок ав-
томатической линии не в состоянии производить абсолютно идентичные
между собой (и заданному номиналу) изделия. В аналогичных условиях
статистического ансамбля и соответствующего неконтролируемого раз-
броса изучаемых показателей или событий мы окажемся, например, при
изучении числа дефектных изделий в партиях заданного объема, отби-
раемых от массовой продукции и производимых в стационарном режиме
производства, или при регистрации среднедушевого дохода семей, случай-
но отбираемых из некоторой однородной (в социальном, географическом и
экономическом смысле) совокупности, и т. д.
Именно разнообразные математические модели таких скрытых зако-
номерностей вместе с теоретическим и эмпирическим анализом их свойств
и взаимоотношений и предоставляют исследователю теория вероятно-
стей и математическая статистика.
Наиболее простые и убедительные примеры реальных ситуаций, под-
чиняющихся требованию статистической устойчивости (или укладываю-
щихся в рамки статистического ансамбля), предоставляет нам область
азартных игр.1 Действительно, подбрасывая монету, бросая игральную
1 Исторически именно эта область существенно стимулировала зарождение и развитие
элементов теоретико-вероятностной научной дисциплины. Первые достаточно инте-
ресные результаты теории вероятностей принято связывать с работами Л. Пачоли
(«Сумма арифметики, геометрии, учения о пропорциях и отношениях», 1494 г.),
Д. Кардано («Книга об игре в хости», 1526 г.) и Н. Тартальн («Общий трактат
о числе и мере» 1556-1560 гг.). См. [Майстров Л. Е., с. 6, 25-37].
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ
31
кость или вытягивая наугад карту из колоды и интересуясь при этом ве-
роятностью осуществления события» заключающегося соответственно в
появлении «герба», «шестерки» или «дамы пик», мы имеем все основа-
ния полагать, что
а)	можно многократно повторить тот же самый эксперимент в тех же
самых условиях;
б)	наличие большого числа случайных факторов, характеризующих
условия проведения каждого такого эксперимента, не позволяет делать
полностью определенного (детерминированного) заключения о том, про-
изойдет в результате данного эксперимента интересующее нас событие
или не произойдет;
в)	чем большее число однотипных экспериментов мы произведем, тем
ближе будут подсчитанные по результатам экспериментов относительные
частоты появления интересующих нас событий к некоторым постоянным
величинам, называемым вероятностными для этих событий, а именно:
относительная частота появления «герба» будет приближаться к 1/2, вы-
падения «шестерки» — к 1/6, а извлечения «дамы пик» (из колоды, со-
держащей 52 карты) — к 1 /52.
Очевидно, требования статистического ансамбля применительно к
указанным выше трем типам экспериментов означают необходимость ис-
пользования одной и той же (или совершенно идентичных) симметрич-
ной монеты, симметричной кости, а в последнем случае — необходимость
возвращения извлеченной в предыдущем эксперименте карты в колоду и
тщательного случайного перемешивания последней.
Соблюдение условий статистического ансамбля в более серьезных и
сложных сферах человеческой деятельности — в экономике, в социаль-
ных процессах, в технике и промышленности, в медицине, в различных
отраслях науки — это вопрос, требующий специального рассмотрения в
каждом конкретном случае.
Оценивая специфику задач в различных областях человеческого зна-
ния с позиции соблюдения в них свойств а)-в) статистической устой-
чивости и принимая во внимание накопившийся опыт вероятностно-
статистических приложений, можно условно разбить все возможные при-
ложения на три категории.
К первой категории возможных областей применения — категории
высокой работоспособности вероятностно-статистических мето-
дов — отнесем те ситуации, в которых свойства а)-в) статистической
устойчивости исследуемой совокупности бесспорно имеют место либо на-
рушаются столь незначительно, что это практически не влияет на точ-
ность статистических выводов, полученных с использованием теоретико-
32
В. ВВЕДЕНИЕ
вероятностных моделей. Сюда (помимо упоминавшейся «игровой» обла-
сти) могут быть отнесены отдельные разделы экономики и социологии и
в первую очередь задачи, связанные с исследованием поведения объекта
(индивидуума, семьи или другой социально-экономической или производ-
ственной единицы) как представителя большой однородной совокупности
подобных же объектов. Традиционной областью эффективного использо-
вания вероятностно-статистического аппарата давно стала демография.
Теоретико-вероятностные понятия являются основным языком в таких ин-
женерных областях, как теория надежности систем, состоящих из очень
большого числа элементов, и теория выборочного контроля качества
продукции. В медицине вероятностно-статистический подход позволил
ввести понятие факторов риска развития основных хронических заболе-
ваний и провести количественное изучение их влияния, способствуя тем
самым большей индивидуализации, а значит, и эффективности профилак-
тики и лечения. Результаты специальных вероятностно-статистических
исследований выявили, что вероятность дожить до определенного возра-
ста подвержена не слишком значительным колебаниям (в зависимости от
условий жизни). Эти результаты и послужили основой составления так
называемых таблиц выживаемости, в определенной мере и в определен-
ном смысле (а именно, в среднестатистическом, но не в индивидуальном,
конечно!) поколебавшим известное древнее изречение «никто не знает
часа своей смерти». Вероятностно-статистический способ рассуждения
играет видную роль в исследованиях, проводимых в современной физике
(в первую очередь в статистической физике) и в классической механике
(в статистической теории газов).
Отметим одну важную общую черту, характеризующую подавляю-
щее большинство задач перечисленных выше областей человеческой дея-
тельности, в которых оказывается правомерным и эффективным приме-
нение вероятностно-статистических методов. Речь идет о существенной
многомерности обрабатываемой информации, характеризующей исследу-
емые явления или объекты, т.е. о ситуациях, когда состояние или пове-
дение каждого из этих объектов в любой фиксированный момент времени
описывается набором соответствующих показателей. Среди этих показа-
телей могут быть как количественные (среднедушевой доход в семье, раз-
мер семьи, объем валовой продукции предприятия и т. д.), так и не количе-
ственные, т. е. ранговые (классификация специалиста, сравнительная ха-
рактеристика жилищных условий) и классификационные, или номиналь-
ные (профессия, национальность, пол, причины миграции и т. п.). Все эти
показатели находятся в сложной взаимосвязи друг с другом. Именно в та-
ких ситуациях принято говорить о многомерности исследуемой схемы, а
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ
33
исследователю приходится обращаться к методам многомерного стати-
стического анализа.
Ко второй категории возможных областей применения — категории
допустимых вероятностно-статистических приложений — отне-
сем ситуации, характеризующиеся весьма значительными нарушениями
требования сохранения неизменными условий эксперимента (вторая поло-
вина требования а)) и вытекающими отсюда отклонениями от требования
в). Характерной формой такого рода отклонений от условий статистиче-
ского ансамбля является объединение в одном ряду наблюдений (подлежат
щих обработке) различных порций исходных данных, зарегистрирован-
ных в разных условиях (в разное время или в разных совокупностях). К
этой же категории приложений можно отнести определенный класс за-
дач, связанных с анализом коротких временных рядов, зарегистрирован-
ных в условиях, практически исключающих возможность статистической
фиксации сразу нескольких эмпирических реализаций исследуемого вре-
менного ряда на одном и том же временном интервале. Использование
вероятностно-статистических методов обработки в этом случае допусти-
мо, но должно сопровождаться пояснениями о несовершенстве и прибли-
женном характере получаемых при этом выводов (например, не следует
слишком доверять в подобных ситуациях различным числовым характе-
ристикам степени достоверности этих выводов, т. е. доверительным ве-
роятностям, уровням значимости критерия и т. п.) и по возможности
должно дополняться другими методами научного анализа.
И наконец, к третьей категории задач статистической обработ-
ки исходных данных — категории недопустимых вероятностно-
статистических приложений — следует отнести ситуации, характери-
зующиеся либо принципиальным неприятием главной идеи понятия стати-
стического ансамбля — массовости исследуемой совокупности (т. е. кон-
кретной бессодержательностью идеи многократного повторения одного и
того же эксперимента в неизменных условиях, сформулированной в тре-
бовании а)), либо полной детерминированностью изучаемого явления,
т.е. — отсутствием «мешающего» влияния множества случайных фак-
торов (нарушение требования б)). В подобных ситуациях исследователь
должен пользоваться методами анализа данных (см. [ДидеЭ. и др.]) и не
должен претендовать на вероятностную интерпретацию обрабатываемых
данных и получаемых в результате их обработки выводов.
Строгих математических методов, позволяющих точно определять,
находимся ли мы в условиях статистического ансамбля, не существует:
любая вероятностная модель, так же как и любая математическая модель
вообще, есть лишь некоторая аппроксимация исследуемой реальной дей-
34
В. ВВЕДЕНИЕ
ствительности. Можно говорить лишь о ситуациях, очевидно укладыва-
ющихся в рамки статистического ансамбля (бросание монеты, игральной
кости; контроль продукции массового производства, работающего в от-
лаженном стационарном режиме, и т. п.), укладывающихся в эти рамки
лишь приблизительно, с оговорками, и явно не соответствующих условиям
статистического ансамбля. Однако даже с последней категорией ситуаций
(названных у нас категорией недопустимых вероятностно-статистических
приложений) нет полной ясности. Так, например, с позиций статистиче-
ского ансамбля события типа «в 2050 г. начнется война между странами
А и В» явно не относятся к сфере возможных применений вероятностно-
статистических методов — налицо нарушение требования а)!
Однако существует концепция так называемых субъективных веро-
ятностей, в рамках которой оказывается правомерным говорить и о веро-
ятности таких событий. Для этого следует прибегнуть к помощи экспер-
тов и вместо действительной многократной реализации интересующего
нас эксперимента в одних и тех же условиях ограничиться воображае-
мой прогонкой исследуемой ситуации «через сознание» многих экспертов.
При этом, очевидно, эксперт интерпретируется как некий измеритель-
ный прибор, работающий со случайной ошибкой. Точность работы этого
«измерительного прибора», т. е. точность «прочтения» (в сознании экс-
перта) исхода интересующего нас события в будущем, очевидно, зависит
как от степени объективного влияния «мешающих» случайных факто-
ров (т. е. от степени временндй отдаленности интересующего нас момента
времени, обшей сложности ситуации и т. п.), так и от степени осведомлен-
ности, компетентности и других субъективных качеств самого эксперта.
Мы не собираемся здесь вмешиваться в спор между субъективистской и
классической вероятностными концепциями. Останемся на той точке зре-
ния, что единственным объективным судьей в подобных вопросах может
быть лишь критерий практики. В этой связи уместно напомнить читате-
лю следующие слова Ф. Энгельса из «Анти-Дюринга»: «... Математика,
вообще столь строго нравственная, совершила грехопадение: она вкуси-
ла от яблока познания, и это открыло ей путь к гигантским успехам, но
вместе с тем и к заблуждениям. Девственное состояние абсолютной зна-
чимости, неопровержимой доказанности всего математического навсегда
ушло в прошлое; наступила эра разногласий, и мы дошли до того, что
большинство людей дифференцирует и интегрирует не потому, что люди
понимают, что они делают, а просто потому, что верят в это, так как до
сих пор результат всегда получался правильным»1
1 Маркс К., Энгельс Ф. Соч., т. 20, с. 89.
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ
35
Резюмируя содержащееся в данном пункте обсуждение сущности, на-
значения и границ применимости теории вероятностей, мы можем через
полтора века после замечательного французского ученого Лапласа повто-
рить, более обоснованно и убедительно, что «замечательно, что наука,
которая начала с изучения игр, возвысилась до наиболее важных предме-
тов человеческого знания» .2
В.2.2.	Что дает объединение теоретико-вероятностного и
статистического способов рассуждения?
Теперь попытаемся на простом примере показать преимущества
вероятностно-статистического (или математико-статистического) спосо-
ба принятия решения, его отличие как от чисто статистического, так и
от чисто теоретико-вероятностного.
Статистический способ принятия решения. Пусть читатель
представит себя наблюдающим за игрой двух лиц в кости, происходя-
щей по следующим правилам. Производится 4 последовательных бросания
игральной кости. Игрок А получает одну денежную единицу от игрока В,
если в результате этих четырех бросаний хотя бы один раз выпало шесть
очков (назовем этот исход «шесть»), и платит одну денежную единицу
игроку В в противном случае (назовем этот исход «не шесть»). После
ста туров читатель должен сменить одного из игроков, причем он имеет
право выбрать ситуацию, на которую он будет ставить свою денежную
единицу в следующей серии туров: за появление хотя бы одной «шестер-
ки» или против. Как правильно осуществить этот выбор?
Статистический способ решения этой задачи диктуется обычным
здравым смыслом и заключается в следующем. Пронаблюдав сто туров
игры предыдущих партнеров и подсчитав относительные частоты их вы-
игрыша, казалось бы, естественно поставить на ту ситуацию, которая ча-
ще возникала в процессе игры. Например, было зафиксировано, что в 52
партиях из 100 выиграл игрок В, т. е. в 52 турах из 100 «шестерка» не вы-
падала ни разу при четырехкратном выбрасывании кости (соответственно
в остальных 48 партиях из ста осуществлялся исход «шесть»). Следо-
вательно, делает вывод читатель, применивший статистический способ
рассуждения, выгоднее ставить на исход «не шесть», т.е. на тот исход,
относительная частота появления которого (р) равна 0,52 (больше поло-
вины). 3
3 См.: Oeuvres completes de Laplace. T. 7: cTheorie anal у tique des probability». Paris,
Gauthier-Villara, 1886, p/ CLI1.
36
В. ВВЕДЕНИЕ
Теоретико-вероятностный способ решения. Этот способ осно-
ван на определенной математической модели изучаемого явления: по-
лагая кость правильной (т. е. симметричной), а следовательно, принимая
шансы выпадения любой грани кости при одном бросании равными между
собой (другими словами, относительная частота, или вероятность, выпа-
дения «единицы» равна относительной частоте выпадения «двойки» и
т. д... равна относительной частоте выпадения «шестерки» и равна 1/6),
можно подсчитать вероятность Р {«не шесть»} осуществления ситуации
«не шесть», т.е. вероятность события, заключающегося в том, что при
четырех последовательных бросаниях игральной кости ни разу не появит-
ся «шестерка». Этот расчет основан на следующих фактах, вытекающих
из принятой нами математической модели. Вероятность не выбросить
шестерку при одном бросании кости складывается из шансов появиться в
результате одного бросания «единице», «двойке», «тройке», «четверке»
и «пятерке» и, следовательно, составляет (в соответствии с определением
вероятности любого события, см. п. 1.1) 5/6. Затем используем теорему
умножения вероятностей (см. п. 1.1.3), в соответствии с которой вероят-
ность наступления нескольких независимых событий равна произведению
вероятностей этих событий. В нашем случае мы рассматриваем факт
наступления четырех независимых событий, каждое из которых заключа-
ется в невыпадении «шестерки» при одном бросании и имеет вероятность
осуществления, равную 5/6. Поэтому
г	,55
р = Р {<не шесть»} = - • -
о о
5 5
6 'б
625
1296
= 0,482.
Как йидно, вероятность ситуации «не шесть» оказалась меньше по-
ловины, следовательно, шансы ситуации «шесть» предпочтительнее (со-
ответствующая вероятность равна: 1 — 0,482 = 0,518). А значит, чи-
татель, использовавший теоретико-вероятностный способ рассуждения,
придет к диаметрально противоположному по сравнению с читателем со
статистическим образом мышления решению и будет ставить в игре на
ситуацию «шесть».
Вероятностно-статистический (или математико-статисти-
ческий) способ принятия решения. Этот способ как бы синтезирует
инструментарий двух предыдущих, так как при выработке с его помо-
щью окончательного вывода используются и накопленные в результате
наблюдения за игрой исходные статистические данные (в виде относи-
тельных частот появления ситуаций «шесть» и «не шесть», которые,
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ
37
как мы помним, были равны соответственно 0,48 и 0,52), и теоретико-
вероятностные модельные соображения. Однако модель, принимаемая в
данном случае, менее жестка, менее ограниченна, она как бы настраива-
ется на реальную действительность^ используя для этого накопленную
статистическую информацию. В частности, эта модель уже не посту-
лирует правильность используемых костей, допуская, что центр тяжести
игральной кости может быть и смещен некоторым специальным образом.
Характер этого смещения (если оно есть) должен как-то проявиться в тех
исходных статистических данных, которыми мы располагаем. Однако
читатель, владеющий вероятностно-статистическим образом мышления,
должен отдавать себе отчет в том, что полученные из этих данных вели-
чины относительных частот исходов «шесть» и «не шесть» дают лишь
некоторые приближенные оценки истинных (теоретических) шансов той и
другой ситуации: ведь подбрасывая, скажем, 10 раз даже идеально симме-
тричную монету, мы можем случайно получить семь выпадений «гербов»;
соответственно относительная частота выпадения «герба», подсчитанная
по этим результатам испытаний, будет равна 0,7; но это еще не значит,
что истинные (теоретические) шансы (вероятности) появления «герба»
и другой стороны монеты оцениваются величинами соответственно 0,7 и
0,3 — эти вероятности, как мы знаем, равны 0,5. Точно так же наблю-
денная нами в серии из ста игровых туров относительная частота исхода
«не шесть» (равная 0,52) может отличаться от истинной (теоретической)
вероятности того же события и, значит, может не быть достаточным осно-
ванием для выбора этой ситуации в игре! Весь вопрос в том, насколько
сильно может отличаться наблюденная (в результате осуществления п
испытаний) относительная частота рп интересующего нас события от ис-
тинной вероятности р появления этого события и как это отличие, т.е.
погрешность рп — р, зависит от числа п имеющихся в нашем распоряже-
нии наблюдений? (интуитивно ясно, что чем дольше мы наблюдали за
игрой, т. е. чем больше общее число п использованных нами наблюдений,
тем больше доверия заслуживают вычисленные нами эмпирические отно-
сительные частоты рЛ, т.е. тем меньше их отличие от неизвестных нам
истинных значений вероятностей р.) Ответ на этот вопрос можно полу-
чить в нашем случае, если воспользоваться рядом модельных соображе-
ний: а) интерпретировать реализацию любого числа игровых партий как
последовательность так называемых испытаний Бернулли, что означает,
что результат каждого тура никак не зависит от результатов предыду-
щих туров, а неизвестная нам вероятность р осуществления ситуации «не
шесть» остается одной и той же на протяжении всех туров игры; б) ис-
пользовать тот факт, что поведение случайно меняющейся (при повторе-
38
В. ВВЕДЕНИЕ
ниях эксперимента) погрешности Дп = рп — р приближенно описывается
законом нормального распределения вероятностей со средним значением,
равным нулю, и дисперсией, равной р(1 — р)/п (см. п. 3.1.5).
Эти соображения, в частности, позволяют оценить абсолютную ве-
личину погрешности |ДП|, которую мы можем допустить, заменяя неиз-
вестную величину р вероятности интересующего нас события (в нашем
случае — исхода «не шесть») относительной частотой рп этого события,
зафиксированной в серии из п испытаний (в нашем случае п = 100, а
Рюо = 0,25). Если же мы смогли численно оценить абсолютную величину
возможной погрешности Дп, то естественно применить следующее прави-
ло принятия решения: если относительная частота рп появления исхода
«не шесть» больше половины и продолжает превосходить 0,5 после вы-
читания из нее возможной погрешности |ДП|, то выгоднее ставить на «не
шесть»; если относительная частота рп меньше половины и продолжает
быть меньше 0,5 после прибавления к ней возможной погрешности |ДП|,
то выгоднее ставить на «шесть»; в других случаях у наблюдателя нет
оснований для статистического вывода о преимуществах того или ино-
го выбора ставки в игре (т. е. надо либо продолжить наблюдения, либо
участвовать в игре с произвольным выбором ставки, ожидая, что это не
может привести к сколь-нибудь ощутимому выигрышу или проигрышу).
Приближенный подсчет максимально возможной величины этой по-
грешности, опирающийся на модельное соображение б) (т.е. теорему
Муавра-Лапласа, см. п. 4.3), дает в рассматриваемом примере, что с прак-
тической достоверностью, а именно с вероятностью 0,95, справедливо не-
равенство
|р„ - р| С 2^^.	(В.1)
Возведение (В.1) в квадрат и решение получившегося квадратного
неравенства относительно неизвестного параметра р дает
или, с точностью до величин порядка малости выше, чем \/у/п‘.
Рп - 2	(В.2)
V 71	V 71
В.2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ	39
В данном случае (при рп = 0,52 и п = 100) получаем
|Д„| и 2>/р„(1 - М/у/п = гт/О.бг-С! -0,52)/УП)0 и 0,10.
Следовательно,
0,52 - 0,10 р < 0,52 4- 0,10.
Таким образом, имеющиеся в нашем распоряжении наблюдения за ис-
ходами ста партий дают нам основания лишь заключить, что интересую-
щая нас неизвестная величина вероятности исхода «не шесть» на самом
деле может быть любым числом из отрезка [0,42; 0,62], т.е. может быть
как величиной, меньшей 0,5 (и тогда надо ставить в игре на ситуацию
«шесть»), так и величиной, большей 0,5 (и тогда надо ставить в игре на
ситуацию «не шесть» ).
Иначе говоря, читатель, воспользовавшийся вероятностно-статисти-
ческим способом решения задачи, вынужден будет прийти в данном слу-
чае к более осторожному выводу: ста партий в качестве исходного стати-
стического материала оказалось недостаточно для вынесения надежного
заключения о том, какой из исходов игры является более вероятным. От-
сюда решение: либо продолжить роль «зрителя» до тех пор, пока область
возможных значений для вероятности р, полученная из оценок вида (В.2),
не окажется целиком лежащей левее или правее 0,5, либо вступить в игру,
оценивая ее как близкую к «безобидной», т. е. к такой, в которой в длинной
серии туров практически останешься «при своих».
Приведенный пример иллюстрирует роль и назначение теоретико-
вероятностных и математико-статистических методов, их взаимоотноше-
ния. Если теория вероятностей предоставляет исследователю набор
математических моделей, предназначенных для описания закономерно-
стей в поведении реальных явлений или систем, функционирование кото-
рых происходит под влиянием большого числа взаимодействующих слу-
чайных факторов, то средства математической статистики позволя-
ют подбирать среди множества возможных теоретико-вероятностных
моделей ту, которая в определенном смысле наилучшим образом со-
ответствует имеющимся в распоряжении исследователя статистиче-
ским данным, характеризующим реальное поведение конкретной исследу-
емой системы.
40
В. ВВЕДЕНИЕ
В.З.	Вероятностно-статистическая
(эконометрическая) модель как частный
случаи математической модели
В.3.1.	Математическая модель
Математическая модель — это абстракция реального мира, в кото-
рой интересующие исследователя отношения между реальными элемента-
ми заменены подходящими отношениями между математическими кате-
гориями. Эти отношения, как правило, представлены в форме уравнений
и (или) неравенств между показателями (переменными), характеризую-
щими функционирование моделируемой реальной системы. Искусство по-
строения математической модели состоит в том, чтобы совместить как
можно большую лаконичность в ее математическом описании с достаточ-
ной точностью модельного воспроизводства именно тех сторон анализиру-
емой реальности, которые интересуют исследователя.
Выше, анализируя в п. В.2.2 взаимоотношения чисто статистиче-
ского, чисто теоретико-вероятностного и смешанного — вероятностно-
статистического способа рассуждения, мы уже пользовались простейши-
ми моделями, а именно:
•	статистической частотной моделью интересующего нас случай-
ного события, заключающегося в том, что в результате четырех после-
довательных бросаний игральной кости ни разу не выпадет «шестерка»;
оценив по предыстории относительную частоту р = 0,52 этого события
и приняв ее за вероятность появления этого события в будущем
ряду испытаний, мы, тем самым, используем модель случайного экспе-
римента с известной вероятностью его исхода;
•	теоретико-вероятностной моделью последовательности испыта-
ний Бернулли (см. п. 3.1.1), которая никак не связана с использованием
результатов наблюдений (т.е. со статистикой); для подсчета вероятности
интересующего нас события достаточно принятия гипотетического допу-
щения о том, что используемая игральная кость идеально симметрична;
тогда в соответствии с моделью серии независимых испытаний и справед-
ливой, в рамках этой модели, теоремой умножения вероятностей подсчи-
тывается интересующая нас вероятность по формуле (В.1);
•	вероятностно-статистической моделью, интерпретирующей оце-
ненную в чисто статистическом подходе относительную частоту р как
некую случайную величину (см. п.2.1), поведение которой подчиняется
правилам, определяемым так называемой теоремой Муавра-Лапласа; при
юстроении этой модели были использованы как теоретико-вероятностные
В.З. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ
41
понятия и правила, так и статистические приемы, основанные на резуль-
татах наблюдений.
Обобщая этот пример, можно сказать, что:
•	вероятностная модель — это математическая модель, имитирую-
щая механизм функционирования гипотетического (не конкретного)
реального явления (или системы) стохастической природы; в нашем
примере гипотетичность относилась к свойствам игральной кости:
она должна была быть идеально симметричной;
•	вероятностно-статистическая модель — это вероятностная мо-
дель, значения отдельных характеристик (параметров) которой оце-
ниваются по результатам наблюдений (исходным статистическим
данным), характеризующим функционирование моделируемого кон-
кретного (а не гипотетического) явления (или системы).
Вероятностно-статистическая модель, описывающая механизм функ-
ционирования экономической или социально-экономической системы, на-
зывается эконометрической. Бели же речь идет о любой математи-
ческой модели, описывающей механизм функционирования некой гипоте-
тической экономической или социально-экономической системы, то такую
модель принято называть экономико-математической или просто эко-
номической.
В качестве примера экономической модели рассмотрим простейший
(идеализированный) вариант так называемой «паутинной модели», ко-
торая описывает процесс формирования спроса и предложения определен-
ного товара или вида услуг на конкурентном рынке. Речь идет о форма-
лизации экономического закона спроса и предложения, гласящего: коли-
чество товара, которое можно продать на рынке (т. е. спрос) изменя-
ется в направлении, противоположном изменению его цены, количество
товара, которое продавцы доставляют на рынок (т.е. предложение)
изменяется в том же направлении, что и цена; при этом реальная ры-
ночная цена складывается на уровне, при котором спрос и предложение
равны друг другу (т. е. находятся в равновесии).1
Займемся математической формализацией этих положений. Пусть xt
(ден. ед.) — цена товара в «момент времени» t. И пусть и — ко-
личество товара, соответственно предложенного и купленного («спрошен-
ного») на рынке в тот же момент времени t. Тогда, с учетом одного такта
времени, необходимого производителям-продавцам на то, чтобы «среаги-
ровать» на цену х, можно математически сформулировать приведенные
1 Первым, кто попытался математически сформулировать этот закон, был А. Курно
(Cournot A., Recherches sur les principes mathematiques de la thdorie des richesses, Paris,
1838).
42
В. ВВЕДЕНИЕ
выше общие закономерности в виде:
3/tn) = /(«t-i);
!/tC) =
lim	= Um g(xt);
Um xt = xgi
t—*oo	*
где f(x) — некоторая монотонно возрастающая, a g(x) — монотонно убы-
вающая функции от аргумента х (т. е. от цены).
Математические соотношения, отражающие закон спроса-предложе-
ния, могут быть проиллюстрированы рисунком ВЛ
Рис. В.1. График процесса формирования слроса-предложения («паутин-
ная» модель)
Из рисунка видно, что процесс формирования равновесной цены на-
чался с назначения в 1-й (начальный) момент времени цены на уровне
«1. Производитель-продавец отреагировал на это в следующий (2-й) мо-
мент времени величиной предложения, равной — /(ж1)> в то время
как спрос на этот товар сформировался всего на уровне у1 = д(х\). За-
метное превышение предложения над спросом привело к понижению цены
в следующий (2-й) момент времени до уровня х2. Это сразу отразилось
на предложении в следующий (3-й) момент времени: оно снизилось до
В.З. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ
43
у^ = /(г2). Зато спрос резко подскочил и составил во 2-й момент вре-
мени величину з/2 = у(ж2), и т.д., и т.п. Продолжение этого процесса
обозначено траекторией ( она индексирована стрелками), которая сходит-
ся паутинообразно к точке равновесия — к точке пересечения кривых
$(z) и f(x).
Реалистическая модель закона спроса-предложения, конечно, сложнее.
В частности, и у^ зависят не только от цены х, поскольку связь
между у^ и у^с\ с одной стороны, и ценой х — с другой, носит не
детерминированный, а стохастический характер (о подобных зависимо-
стях см. гл. 11 и 15).
Наконец, для того, чтобы эта модель превратилась из экономиче-
ской в эконометрическую, следует говорить не вообще о законе спроса-
предложения, а о конкретном его действии в данном месте, данное
время и применительно к данному конкретному товару (или ви-
ду услуг). Соответственно конкретизация вида функций f(x) и д(х)
должна производиться на базе исходных статистических данных о зна-
чениях xt, у^ и за ряд тактов времени (т. е. для t = 1,2,..., п).
В.3.2.	Основные этапы вероятностно-статистического
моделирования
Построение и экспериментальная проверка (верификация) вероятностно-
статистической модели обычно основаны на одновременном использовании
информации двух типов:
(а)	априорной информации о природе и содержательной сущности ана-
лизируемого явления, представленной, как правило, в виде тех или иных
теоретических закономерностей, ограничений, гипотез;
(6)	исходных статистических данных, характеризующих процесс и
результаты функционирования анализируемого явления или системы.
Можно выделить следующие основные этапы вероятностно-статисти-
ческого моделирования.
1-й этап (постановочный) включает в себя определение: конечных
прикладных целей моделирования; набора факторов и показателей (пере-
менных), описание взаимосвязей между которыми нас интересует; нако-
нец, роли этих факторов и показателей — какие из них, в рамках поста-
вленной конкретной задачи, можно считать входными (т. е. полностью или
частично регулируемыми или хотя бы легко поддающимися регистрации
и прогнозу; подобные факторы несут смысловую нагрузку объясняющих
в модели), а какие —выходными (эти факторы обычно трудно поддаются
непосредственному прогнозу; их значения формируются как бы в процессе
44
В. ВВЕДЕНИЕ
функционирования моделируемой системы, а сами факторы несут смысло-
вую нагрузку объясняемых).
2-й этап (априорный, предмоделъный) состоит в предмодельном ана-
лизе содержательной сущности моделируемого явления, формировании и
формализации имеющейся априорной информации об этом явлении в виде
ряда гипотез и исходных допущений (последние должны быть подкрепле-
ны теоретическими рассуждениями о механизме изучаемого явления или,
если возможно, экспериментальной проверкой).
3-й этап (информационно-статистический) посвящен сбору необхо-
димой статистической информации, т.е. регистрации значений участвую-
щих в описании модели факторов и показателей на различных временных
и (или) пространственных тактах функционирования моделируемой си-
стемы.
4-й этап (спецификация модели) включает в себя непосредственный
вывод (опирающийся на принятые на 2-м этапе гипотезы и исходные допу-
щения) общего вида модельных соотношений, связывающих между собой
интересующие нас входные и выходные переменные. Говоря об общем
виде модельных соотношений, мы имеем в виду то обстоятельство, что
на данном этапе будет определена лишь структура модели, ее символи-
ческая аналитическая запись, в которой наряду с известными числовыми
значениями (представленными в основном исходными статистическими
данными) будут присутствовать величины, содержательный смысл кото-
рых определен, а числовые значения — нет (их обычно называют параме-
трами модели, неизвестные значения которых подлежат статистическому
оцениванию).
5-й этап (идентифицируемость и идентификация модели) предна-
значен для проведения статистического анализа модели с целью «настрой-
ки» значений ее неизвестных параметров на те исходные статистические
данные, которыми мы располагаем. При реализации этого этапа «мо-
дельер» должен сначала ответить на вопрос, возможно ли в принципе
однозначно восстановить значения неизвестных параметров модели по
имеющимся исходным статистическим данным при принятой на 4-м этапе
структуре (способе спецификации) модели. Это составляет так называе-
мую проблему идентифицируемости модели. А затем, после положитель-
ного ответа на этот вопрос, необходимо решить уже проблему идентифи-
кации модели, т. е. предложить и реализовать математически корректную
процедуру оценивания неизвестных значений параметров модели по име-
ющимся исходным статистическим данным. Если проблема идентифици-
руемости решается отрицательно, то возвращаются к 4-му этапу и вносят
необходимые коррективы в решение задачи спецификации модели.
В.З. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ
45
6-й этап (верификация модели) заключается в использовании различ-
ных процедур сопоставления модельных заключений, оценок, следствий и
выводов с реально наблюдаемой действительностью. Этот этап называ-
ют также этапом статистического анализа точности и адекватности моде-
ли. При пессимистическом характере результатов этого этапа необходимо
возвратиться к этапу 4, а иногда и к этапу 1.
Построение и анализ модели могут быть основаны только на априор-
ной информации (а) и не предусматривать проведения этапов 3 и 5. Тогда
модель не является вероятностно-статистической (эконометрической
при моделировании экономических закономерностей). Более подробно о
сущности и специфике именно эконометрического моделирования речь бу-
дет идти в гл. 14-17.
В.3.3.	Моделирование механизма явления вместо
формальной статистической фотографии
Обращаем внимание читателя на ключевую роль успешного проведе-
ния 2-го этапа в общей оценке степени реалистичности и работоспособно-
сти построенной модели.
Другими словами, адекватность и соответственно эффективность мо-
дели будут решающим образом зависеть от того, насколько глубоко и про-
фессионально был проведен анализ реальной сущности изучаемого явле-
ния при формировании априорной информации (т. е. в рамках второго эта-
па). Поясним этот тезис. При вероятностно-статистическом моделиро-
вании и, в частности, на этапе формирования априорной информации о
физической природе реального механизма преобразования входных пока-
зателей в выходные (результирующие) какая-то часть этого механизма
остается скрытой от исследователя (именно об этой части принято в
соответствии с обиходной кибернетической терминологией говорить как
о «черном ящике»). Чем большее профессиональное знание механизма
исследуемого явления продемонстрирует исследователь, тем меньше бу-
дет доля «черного ящика» в общей логической схеме моделирования и
тем работоспособнее и точнее будет построенная модель. Вероятностно-
статистическое моделирование, полностью основанное на логике «черно-
го ящика», позволяет получить исследователю лишь как бы мгновенную
статистическую фотографию анализируемого явления, в общем случае
непригодную, например, для целей прогнозирования. Напротив, модели-
рование, опирающееся на глубокий профессиональный анализ природы
изучаемого явления, позволяет в значительной мере теоретически обосно-
вать общий вид конструируемой модели, что дает основание к ее широко-
46
В. ВВЕДЕНИЕ
му и правомерному использованию в прогнозных расчетах. Поясним это
на примере из п. 8.6.1.
Пусть целью нашего исследования является лаконичное {параметри-
зованное с помощью модели) описание функции плотности анализируемой
случайной величины (заработной платы наугад выбранного из общей гене-
ральной совокупности работника) по исходным данным, представленным
случайной выборкой работников £1,22,...,^750 объема п = 750. Игнори-
руя экономические закономерности формирования искомого закона распре-
деления, т.е. руководствуясь формальным подходом наилучшей мгновен-
ной статистической фотографии, мы должны были бы запастись доста-
точно богатым классом модельных плотностей (например, классом кри-
вых Пирсона [Кендалл М. Дж., Стьюарт А., 1966] и, перебирая эти модели
(с одновременной статистической оценкой участвующих в их записи пара-
метров методами, описанными в гл. 7), найти такую функцию плотности,
которая наилучшим в определенном смысле образом (например, в смысле
критерия «хи-квадрат» Пирсона, см. п. 8.1.1, аппроксимирует поведение
имеющейся у нас эмпирической плотности (см. изображение соответству-
ющей гистограммы на рис. 8.1). На этом пути в результате расширения
запаса гипотетичных модельных плотностей можно добиться очень высо-
кой точности аппроксимации, вплоть до повторения модельной функцией
неожиданных провалов гистограммы, подобных тем, которые мы имеем
на 14-м и 15-м интервалах группирования на рис. 8.1. Однако, поступая
таким образом, мы добиваемся лишь кажущегося хорошего результата, в
чем легко можно убедиться, попробовав применить выявленный модель-
ный закон к описанию эмпирической плотности, построенной по другой
выборке, извлеченной из той же самой совокупности. В подавляющем
большинстве случаев выявленная ранее модельная плотность оказывается
непригодной для описания распределительных закономерностей, наблю-
даемых в другой выборке. Следовательно, для этой выборки нужно стро-
ить другую модель, а значит, и само моделирование практически теряет
смысл, так как главное назначение модели — распространение закономер-
ностей, подмеченных в выборке, на всю генеральную совокупность (что и
является основой решения задач планирования, прогноза, диагностики).
В качестве альтернативного рассмотрим подход, предусматриваю-
щий тщательный предмодельный профессиональный анализ локальных
закономерностей, в соответствии с которыми формируется закон распре-
деления заработной платы. Эти закономерности (мультипликативный ха-
рактер редукции труда, принцип оплаты по труду, постоянство относи-
тельного варьирования заработной платы при переходе от работников од-
ной категории сложности труда к другой и т.п., см. [Айвазян С. А., 1980]
В.З. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ
47
позволяют уже на следующем, третьем этапе моделирования теоретиче-
ски (т. е. без апелляции к имеющейся у нас эмпирической функции плот-
ности) обосновать выбор класса моделей, в пределах которого мы должны
оставаться при подборе искомой модельной плотности. В рассмотренном
примере таким классом был класс логарифмически-нормальных распре-
делений (см. п. 3.1.6). После этого мы переходим к статистическому оце-
ниванию параметров, участвующих в записи законов этого класса, т. е.
переходим к четвертому этапу.
Модель, полученная таким образом, как правило, несколько хуже (по
формальным критериям), чем предыдущая, аппроксимирует эмпириче-
скую плотность, построенную по данной конкретной выборке. Однако в
отличие от модели, полученной в результате формальной статистической
подгонки экспериментальных данных под одну из теоретических кривых,
она останется устойчивой, инвариантной по отношению к смене выбо-
рок, т.е. она одинаково хорошо может описывать характер распределе-
ния, наблюдаемого в различных выборках из одной и той же генеральной
совокупности. А если все-таки моделирование, идущее от более или ме-
нее бесспорных (быть может, частично подтвержденных экспериментом)
исходных предпосылок о физической природе изучаемого явления, дает
результаты, плохо согласующиеся с реальной действительностью? При-
чина этого (при условии аккуратного проведения третьего и четвертого
этапов) одна: плохое соблюдение на практике всех (или части) принятых
при моделировании в качестве априорных допущений исходных предпо-
сылок. Оценка же этого явления может быть двоякой: если заложенные в
основание модели исходные допущения признаются специалистами объек-
тивными закономерностями, в соответствии с которыми должен функцио-
нировать механизм исследуемого явления, то следует искать и устранять
причины, приведшие к нарушению этих закономерностей, в самой моде-
лируемой реальности; если же принятые допущения были результатом
вынужденного упрощения на самом деле плохо различимого механизма,
то следует усовершенствовать эти допущения, что приведет, естественно,
и к изменению модели.
В рассмотренном примере интерпретация временного рассогласова-
ния модели и действительности относилась как раз к первому типу. Про-
веденные сопоставления модельных и экспериментальных данных по рас-
пределению заработной платы работников за ряд лет (1956-1972 гг., см.
[Айвазян С. А., 1980]) четко обозначили период их резкого рассогласования
(1960-1966 гг.). Однако по мере удаления этого периода в прошлое просле-
живается явная тенденция к сближению модельных и реальных данных.
Более внимательный анализ показал, что момент резкого рассогласования
48
В. ВВЕДЕНИЕ
следовал непосредственно за весьма существенным директивным вмеша-
тельством в существующие тарифные условия, вмешательством, которое,
как показал дальнейший ход развития, плохо согласовывалось с целым
рядом объективных экономических закономерностей. И факт, что в даль-
нейшем мы наблюдаем сближение модельных и реальных данных, говорит
лишь о том, что эти объективные экономические закономерности посте-
пенно все более сказывались на характере распределения, все более «вы-
ступали на поверхность», отвоевывая себе те или иные правовые формы.
ВЫВОДЫ
1.	Предлагаемый учебник посвящен описанию математико-статисти-
ческого инструментария экономических исследований, который охватыва-
ет как традиционные методы эконометрики (регрессионный анализ, ана-
лиз временных рядов и системы одновременных уравнений), так и ряд
наиболее актуальных, в смысле социально-экономических приложений,
разделов прикладной статистики (кластер-анализ и расщепление смесей
распределений, дискриминантный анализ, методы снижения размерности,
построение интегральных индикаторов и др.).
2.	Изложение в учебнике строится в соответствии с современ-
ными университетскими учебными планами подготовки экономистов и
экономистов-статистиков и охватывает весь блок математико-статисти-
ческого инструментария, в который входят следующие дисциплины: де-
скриптивная статистика, теория вероятностей, математическая статисти-
ка, многомерный статистический анализ, эконометрика.
3.	Теория вероятностей — математическая наука, предназначенная
для разработки (и исследования свойств) математических моделей, ими-
тирующих механизмы функционирования реальных явлений или систем,
условия «жизни» которых включают в себя неизбежность «мешающего»
влияния большого числа случайных (т. е. не поддающихся строгому учету
и контролю) факторов.
4.	Математическая статистика — система основанных на теорети-
ко-вероятностных моделях понятий, приемов и математических методов,
предназначенных для сбора, систематизации, интерпретации и обработ-
ки статистических данных с целью получения научных и практических
выводов. Одно из главных назначений методов математической стати-
стики — обоснованный выбор среди множества возможных теоретико-
вероятностных моделей той модели, которая наилучшим образом соответ-
ствует имеющимся в распоряжении исследователя статистическим дан-
ным, характеризующим реальное поведение конкретной исследуемой си-
выводы
49
стены.
Б. Прикладная статистика — научная дисциплина, разрабатываю-
щая и систематизирующая понятия, приемы, математические методы и
модели, предназначенные для организации сбора, стандартной записи, си-
стематизации и обработки статистических данных с целью их удобного
представления, интерпретации и получения научных и практических вы-
водов.
в. Эконометрика — экономико-математическая научная дисципли-.
на, разрабатывающая и использующая методы, модели, приемы, позво-
ляющие придавать конкретное количественное выражение общим (каче-
ственным) закономерностям экономической теории на базе экономической
статистики и с использованием математико-статистического инструмен-
тария.
7.	Теория вероятностей и математическая статистика являются по
отношению к прикладной статистике и эконометрике разработчиками и
поставщиками существенной части используемого в них математического
аппарата. Однако доводка и развитие этого аппарата, подчиненные тре-
бованиям и запросам различного типа приложений, производятся уже в
рамках дисциплин «прикладная статистика» и «эконометрика».
8.	Границы применимости вероятностно-статистических методов
определяются, строго говоря, требованием соблюдения (хотя бы прибли-
зительно) в исследуемой реальной действительности условий статистиче-
ского ансамбля, а именно: а) возможностью (хотя бы мысленно реально
представимой) многократного повторения наших экспериментов или на-
блюдений в одних и тех же условиях; б) наличием большого числа случай-
ных факторов, характеризующих условия проведения наших эксперимен-
тов (наблюдений) и не позволяющих делать полностью предопределенного
(детерминированного) заключения о том, произойдет или не произойдет в
результате этих экспериментов интересующее нас событие.
9.	Строгих математических методов, позволяющих точно опреде-
лять, находимся ли мы в условиях статистического ансамбля, не су-
ществует: любая вероятностная модель, так же как и любая матема-
тическая модель вообще, есть лишь некоторое приближение к исследуе-
мой реальной действительности. Можно лишь условно разделять иссле-
дуемые реальные ситуации на: 1) относящиеся к области высокой рабо-
тоспособности вероятностно-статистических методов; 2) лишь с натяж-
кой укладывающиеся в рамки статистического ансамбля (категория до-
пустимых вероятностно-статистических приложений); 3) недопустимые
для вероятностно-статистических приложений. Однако и применительно
к последней категории ситуаций в ряде случаев помимо методов анали-
50
В. ВВЕДЕНИЕ
за данных используют статистические методы, основанные на концепции
субъективных вероятностей.
10.	Всякая математическая модель является упрощенным представле-
нием действительности, и искусство ее построения состоит в том, чтобы
совместить как можно большую лаконичность параметризации модели с
достаточной адекватностью описания изучаемой действительности или,
другими словами, чтобы достигнуть максимальной концентрации реаль-
ности в простой математической форме.
11.	Вероятностная модель — это математическая модель, имити-
рующая механизм функционирования гипотетического (не конкретного)
реального явления или системы стохастической природы; вероятностно-
статистическая модель — это вероятностная модель, значения отдель-
ных характеристик (параметров) которой оцениваются по результатам
наблюдений, характеризующим функционирование моделируемого кон-
кретного (а не гипотетического) явления или системы; вероятностно-
статистическая модель, описывающая механизм функционирования эко-
номической или социально-экономической системы, называется экономе-
трической.
12.	Важнейшим условием достижения высокой «работоспособности»
модели является успешная реализация второго этапа моделирования, т. е.
проведение тщательного предмодельного анализа физической сущности
изучаемого явления с целью формирования добротной априорной инфор-
мации и ее использования при выводе (или выборе) общего вида искомой
модели. Вынужденная (но нежелательная) альтернатива к такому под-
ходу это логика «черного ящика», т. е. чисто формальная аппроксимация
реальных данных.
Раздел I
И Jii'i;’
ИГ'ГРЯйГ	алЛПВШ
-г /
>1
ероятнб
Глава 1
- । *
П равила действииюо
случаиньми сооцтаШ
, вероятностями их '| |
ветвления i
К
а^НЫС;ВеЛ№ЖНЫ
(исследуемые признаки)
Модели законов рйспфедё1ени|
г вероятностей, наиболее^
1яяНгак	£ • **! ||У<4!гЙЙ!1 *	~1Ч
^пространенные в практике *
г.»ттп/м/тхiir>n тт/аттлч'г>Г1 truii
« ' ” Wife,'".........'"Ж:
Глава 4. ОсноЬйке результаты
вероятное^!;.. 'г'1
Глава 5. Цепи Маркова
Т Аравия
В ’
ЯМИ и
nr
ОС
ЛЯВЙ
IM
1 • -
S1
J?
л;
статистических исследований i
i теории
' If
. .ijr'ii ii|
ГЛАВА 1. ПРАВИЛА ДЕЙСТВИЙ
СО СЛУЧАЙНЫМИ СОБЫТИЯМИ
И ВЕРОЯТНОСТЯМИ ИХ
ОСУЩЕСТВЛЕНИЯ
1.1. Дискретное вероятностное
пространство
1.1.1. Процесс регистрации наблюдении на объекте
исследуемой совокупности (случайный эксперимент)
При построении любой математической теории прежде всего следует
договориться об определениях некоторых понятий и о принятии в качест-
ве исходных фактов, не требующих доказательства, некоторых допущений
(аксиолс). Отправным понятием теории вероятностей является понятие
случайного эксперимента, который определяется как процесс регистра-
ции наблюдения на единице обследуемой совокупности, произведенный
в условиях статистического ансамбля. В зависимости от конкретного
содержания этого понятия и применяется соответствующий математиче-
ский аппарат к решению той или иной конкретной задачи. Одна и та же
реальная задача допускает в зависимости от конечных целей исследо-
вания несколько вариантов конкретизации понятия «случайный экспе-
римент». Так, при контроле изделия по альтернативному признаку (т. е.
когда в результате контроля одного изделия оно признается либо годным,
либо дефектным) пользуются в зависимости от конечных целей исследо-
вания по меньшей мере тремя вариантами интерпретации этого понятия:
а) контроль одного изделия; б) контроль партии (выборки), состоящей из
N изделий; в) контроль двух партий (выборок), состоящих соответственно
из Ni и JVj изделий (схема повторной выборки). Очевидно, в первом ва-
рианте могут быть только два различных исхода («годное - дефектное»),
во втором, если нас интересует только общее количество обнаруженных в
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
53
партии дефектных изделий и не интересует порядок, в котором они были
обнаружены, — (JV + 1) возможных исходов (в партии обнаружено нуль,
или одно, или два, ..., или N дефектных изделий), а в третьем — при
том же подходе — (Ni +1 )(JV2 + 1) возможных исходов (результат каждого
случайного эксперимента задается в этом случае парой чисел (£,»}), где £
и — числа дефектных изделий, обнаруженных соответственно в первой
и во второй партиях).
Точно так же при анализе результатов выбрасывания игральных ко-
стей можно понимать под случайным экспериментом одно бросание (со-
ответственно будем иметь шесть возможных исходов), а можно — после-
довательность из заданного числа бросаний, как мы и должны были бы
поступить при строгой формализации примера игры с четырехкратным
бросанием игральной кости, рассмотренного в п. В.2 (нетрудно подсчи-
тать, что общее число возможных исходов в этом примере выразится чи-
слом б4 = 1296).
Число возможных исходов случайного эксперимента не всегда можно
пересчитать. Всякий случайный эксперимент, связанный с необходимо-
стью фиксации величины какого-либо параметра обследуемого объекта,
измеряемого в физических единицах непрерывной природы (температура,
давление, время, вес, размеры и т. п.), имеет, как принято говорить, кон-
тинуальное множество возможных исходов1. Однако о том, как был
осуществлен перенос построения строгой вероятностной теории на этот
общий случай, речь будет идти в следующем п.
1.1.2. Случайные события и правила действий с ними
Как уже упоминалось, с каждым случайным экспериментом связа-
но понятие совокупности всех возможных его исходов. Каждый из этих
возможных исходов будем называть элементарным (неразложимым) со-
бытием (или элементарным исходом), а совокупность всех таких возмож-
ных исходов — пространством элементарных событий (исходов). Таким
образом, в результате анализируемого случайного эксперимента обяза-
тельно происходит одно из элементарных событий, причем одновременно
с ним не может произойти ни одно из остальных элементарных событий (о
событиях, обладающих последним свойством, говорят, что они являются
1 Как известно, множество элементов, составляющих какую-либо совокупность, может
быть конечным (если число элементов в нем конечно), счетным (если его элементы
можно занумеровать числами 1,2,...	множество целых чисел, множество
рациональных чисел и т.п.) и континуальным (множество всех точек числовой
прямой, плоскости и т.п.).
54
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
несовместными, см. ниже).
Рассмотрим пока лишь дискретный случай, т. е. только те ситуации,
когда все элементарные события можно занумеровать числами 1,2,..., п,
... Иначе говоря, рассматриваемое пространство элементарных событий
состоит лишь из конечного или счетного множества элементарных собы-
тий (обозначим их tvi ,о>2,... ,ып,...), а сам факт «пространство П состоит
из элементарных событий Wj, о>2,... ,о/п,...» кратко обозначим
П= {wi,w2,...,wn,...},
или
(1-1)
Й = {“<}> «' = 1,2,...
Рассмотрим несколько примеров случайных экспериментов и соответ-
ствующих им пространств элементарных событий.
Пример 1.1. Подбрасывание монеты:
Q = {ц?! = аверс (лицевая сторона монеты);
о>2 = реверс (обратная сторона монеты)} .
Пример 1.2. Выбрасывание одной игральной кости:
Q = {wj — 1; ц>2 — 2; о>з = 3;	= 4; w5 =5;	= 6}.
Пример 1.3. Четырехкратное бросание игральной кости:
Q =	= (1,1,1,1); w2 = (1,1,1,2); ...; u>i296 = (6,6, 6,6)}.
Пример 1.4. Проверка (по альтернативному признаку) одного из-
делия, случайно отобранного из продукции массового производства:
П =	= годно; uj2 = дефектно}.
Пример 1.5. Проверка (по альтернативному признаку) N изде-
лий, случайно отобранных из продукции массового производства:
П = {wj = 0; о>2 = 1; ...; wjv+i = N],
где и — число обнаруженных дефектных изделий.
Пр и м е р 1.6. Проверка (по альтернативному признаку) двух выбо-
рок, состоящих соответственно из JVX и изделий, случайно отобранных
из продукции массового производства:
Q = {wj = (0,0); w2 = (0,1); ...;	+i)(N3+i) = (^1,^2)}-
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
55
Пример 1.7. Определение ш — числа сбоев станков автоматиче-
ской линии за наугад выбранную смену:
О = {wi = 0; w2 = 1;	= n- 1; wn+1 = n;...}.
Кроме элементарных событий исследователю приходится иметь дело
с так называемыми составными (или разложимыми) событиями.
Событие С называется составным (разложимым), если можно ука-
зать по меньшей мере два таких элементарных события и w,-2, что из
осуществления каждого из них в отдельности следует факт осуществле-
ния события С. Этот факт коротко формулируют — «событие С состоит
из элементарных событий и — и записывают символически в
виде С =
Пользуясь такой терминологией, случайным событием А называют
любое подмножество {wtl, ш,а,..., wgJk,...} пространства элементарных
событий (1.1), т.е.
А = j ,	> * * • »	»
что следует понимать так: осуществление любого из элементарных со-
бытий	«входящих в Л», влечет за собой осуществление
события А.
Поясним эту терминологию на некоторых из примеров 1.1-1.7.
В примере 1.2 события Aj = {выпадет четное число очков} и А2 =
{выпавшее число очков не превзойдет 3} запишутся соответственно Aj =
{cJ2,W4,We} И Л2 = {w15W2,W3}.
В примере 1.3 интересовавшее нас в п.В.2 событие А = {хотя бы
один раз при четырехкратном бросании кости появится шестерка} будет
состоять из всех тех четырехмерных векторов w,, в которых хотя бы одна
из компонент равна шести (можно подсчитать, что число таких векторов
равно 671).
В примере 1.5 событие А — {число обнаруженных дефектных изделий
не более 4}, очевидно, может быть записано А = {wi,u>2, w3,W4,cjs}.
В примере 1.7 событие А = {число зафиксированных за смену сбоев
станков автоматической линии меньше 3} можно представить в виде А =
{o>i,w2,w3}.
Из определения теории вероятностей (см. п. В.2) следует, что в пер-
вую очередь надо запастись определенной структурой всех возможных свя-
зей между случайными событиями или, другими словами, определенными
правилами действий с событиями и соответствующей терминологией.
Сумма (объединение) событии Aj, Л2,..., А* — это такое собы-
тие А (А = Ai 4- Л2 4- • • • + Afc), которое заключается в наступлении хотя
бы одного из событий Ai,A2...,A*. На языке элементарных событий,
56
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
следовательно, сумма событий Aj, А2 ..., А* определяется как событие А,
состоящее из всех различных элементарных событий, составляющих со-
бытия Ai, А2,..., А*. Таким образом, если нас интересует, например,
сумма А событий А! = {число обнаруженных дефектных изделий не более
4}={и>ьы2,...,w5} (см. пример 1.5) и А2 = {число обнаруженных дефект-
ных изделий заключено между 2 и 6 включительно}={w3,w4,w5,w6,w7},
то, очевидно, А = Ai + А2 = {wi,w2,...,Ws,We,W7}, так как о том, что
событие А произошло, будет сигнализировать реализация любого из эле-
ментарных событий Wj ,... , W7.
Произведение (пересечение) событий А1,А2,...,Аь — это такое
событие А (А = Ai • А2 •...• А*), которое заключается в обязательном
наступлении всех событий Aj, А2,..., А*. На языке элементарных со-
бытий, следовательно, произведение событий А}, А2,..., Ад определяется
как событие А, состоящее лишь из тех элементарных событий, которые
одновременно входят во все рассматриваемые события А],Аз,...,Ад .
Так что произведением упомянутых выше событий Ai = {a>i,w2,... ,w5}
и А2 = {t^3,w4,... ,<^7} (см- пример 1.5) будет, очевидно, событие А =
Ai • А2 = {о>з,w4,cus}, так как реализация каждого из элементарных собы-
тий о?з, оц и W5 в отдельности означает, как легко видеть, одновременное
наступление событий Ai и А2.
Разность событии Ai и А2 — это такое событие А, которое за-
ключается в одновременном осуществлении двух фактов: событие Aj про-
изошло, а событие А2 не произошло. На языке элементарных событий,
следовательно, разность А = А4 — А2 определяется как событие, состоя-
щее из всех тех элементарных событий, которые вводят в А1э но не входят
в А2. Так что разностью рассмотренных выше в схеме примера 1.5 собы-
тий Ai = {wi, о^,...,0,5} и А2 = {уз,«4,«* •,^7} будет, очевидно, событие
А = Ai — А2 = {wijWj}, т. е. событие, заключающееся в том, что число
обнаруженных в партии дефектных изделий окажется не превосходящим
единицы.
Противоположное (дополнительное) событие (к событию А) —
это такое событие А, которое состоит в ненаступлении события А. На
языке элементарных событий, следовательно, А определяется как собы-
тие, состоящее из всех возможных элементарных событий, не входящих
в А. Поэтому, используя понятие разности событий, можно записать
А = (1 - А. Так, например, событием, противоположным событию
Ai = {u>i,a>2,...,o>s} из примера 1.5, очевидно, будет событие, заключа-
ющееся в том, что число обнаруженных в партии объема N дефектных
изделий окажется большим 4, т. е. Ai = {w6,u>7,... ,wN}.
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
57
Достоверное событие определяется как событие, состоящее из всех
возможных элементарных событий, т.е. это событие П —	« =
1,2,... (см. (1.1)). Название этого события оправдано тем обстоятель-
ством, что пространство элементарных событий состоит из всех возмож-
ных исходов, т. е. в результате анализируемого случайного эксперимента
обязательно произойдет одно из элементарных событий Wj, а следователь-
но, тот факт, что событие 12 произойдет, достоверен.
Невозможное (пустое) событие 0 — это событие, противополож-
ное достоверному, т. е. 0 = 12 — 12 — 12. Из определения непосредственно
следует объяснение названия этого события: оно не содержит ни одного
элементарного события Wi и, следовательно, при реализации исследуемо-
го случайного эксперимента его осуществление невозможно.
Несовместными называются события , 42,..., Л*, если в резуль-
тате исследуемого случайного эксперимента никакие два из них не могут
произойти одновременно. На языке элементарных событий это означает,
что среди событий 4],42,...,4* нельзя найти такую пару событий 4, и
4j, в которой обнаружилось бы хотя бы по одному общему элементарно-
му событию. Используя понятия произведения событий и невозможного
события, можно определить несовместные события как такую последовав
тельность событий 41,42,..., 4*, для любой пары которой 4, и 4у спра-
ведливо соотношение 4; • Aj = 0. Очевидно, любые пары (4,4) противо-
положных событий являются несовместными. Таковыми же являются (по
определению) и все элементарные события.
Полная система событий — это такой набор несовместных собы-
тий 4j,42,...,4^, который в сумме исчерпывает все пространство эле-
ментарных событий, т. е.
41 + 4г + • —Ь 4fc = 12;
Ai' Aj = 0
для всех itj = 1,2,... ,k и : / j.
Очевидно, набор всех элементарных событий можно рассматривать
как частный случай полной системы событий. И вообще любое разбиение
множества элементарных событий О на непересекающиеся классы дает
полную систему событий, в которой каждое из событий задается соответ-
ствующим классом разбиения. Так, обратившись вновь к примеру 1.5,
положив в нем для определенности N = 100 и обозначив буквой d число
дефектных изделий, обнаруженных в партии, состоящей из 100 наугад из-
влеченных изделий, отобранных от стационарно действующего массового
58
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
производства, определим систему событии следующим образом:
Aj = {d = 0} = {wi}
—	партия отличного качества;
А2 = {1 d 5} = {w2,W3,u;4,Wfi,we}
—	брак в пределах допустимой нормы (партия принимается);
Аз = {6 d < 10} = {й>7,(*>8, • • • ,^11}
—	брак выше допустимой нормы (партия принимается по сниженным рас-
ценкам);
А4 = {d > 11} = {^12 > W13 • • • ,^Ю1}
—	партия целиком возвращается.
Очевидно, события Aj, A2t А3, А4 образуют полную систему событий.
1.1.3. Вероятностное пространство. Вероятности и правила
действий с ними
Для полного описания механизма исследуемого случайного экспери-
мента недостаточно задать лишь пространство элементарных событий.
Очевидно, наряду с перечислением всех возможных исходов исследуемого
случайного эксперимента мы должны также знать, как часто в длинной се-
рии таких экспериментов могут происходить те или другие элементарные
события. Действительно, возвращаясь, скажем, к примерам 1.1-1.7, легко
представить себе, что в рамках каждого из описанных в них пространств
элементарных событий можно рассмотреть бесчисленное множество слу-
чайных экспериментов, существенно различающихся по своему механиз-
му. Так, в примерах 1.1-1.3 мы будем иметь существенно различающиеся
относительные частоты появления одних и тех же элементарных исходов,
если будем пользоваться различными монетами и игральными костями
(симметричными, со слегка смещенным центром тяжести, с сильно сме-
щенным центром тяжести и т. п.). В примерах 1.4-1.7 частота появле-
ния дефектных изделий, характер засоренности дефектными изделиями
проконтролированных партий и частоты появления определенного числа
сбоев станков автоматической линии будут зависеть от уровня техноло-
гической оснащенности изучаемого производства: при одном и том же
пространстве элементарных событии частота появления «хороших» эле-
ментарных исходов будет выше в производстве с более высоким уровнем
технологии.
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
59
Для построения (в дискретном случае) полной и законченной ма-
тематической теории случайного эксперимента — теории вероятно-
стей — помимо уже введенных исходных понятий случайного эксперимен-
та, элементарного исхода и случайного события необходимо запастись
еще одним исходным допущением (аксиомой), постулирующим существо-
вание вероятностей элементарных событий (удовлетворяющих определен-
ной нормировке), и определением вероятности любого случайного собы-
тия.
Аксиома. Каждому элементу w, пространства элементарных собы-
тий Q соответствует некоторая неотрицательная числовая характеристи-
ка р, шансов его появления, называемая вероятностью события причем
Р1+Рг + - -+Рп + *•= 52 p<==1	(L2)
к
(отсюда, в частности, следует, что 0 р, 1 для всех i).
Определение вероятности события. Вероятность любого собы-
тия А определяется как сумма вероятностей всех элементарных событий,
составляющих событие А, т.е. если использовать символику Р{Л} для
обозначения «вероятности события Л», то
Р{Л} = 52 р{^} = £ й.	(1.3)
ил, G А	»: ы, GA
Отсюда и из (1.2) непосредственно следует, что всегда 0 Р{Л} 1,
причем вероятность достоверного события равна единице, а вероятность
невозможного события равна нулю. Все остальные понятия и правила
действий с вероятностями и событиями будут уже производными от вве-
денных выше четырех исходных определений (случайного эксперимента,
элементарного исхода, случайного события н его вероятности) и одной
аксиомы.
Таким образом, для исчерпывающего описания механизма исследуе-
мого случайного эксперимента (в дискретном случае) необходимо задать
конечное или счетное множество всех возможных элементарных исходов
Q и каждому элементарному исходу и, поставить в соответствие некото-
рую неотрицательную (не превосходящую единицы) числовую характери-
стику р,, интерпретируемую как вероятность появления исхода w, (будем
обозначать эту вероятность символами P{w,}), причем установленное со-
ответствие типа bJi pi должно удовлетворять требованию нормировки
(1.2).
Вероятностное пространство как раз и является понятием, форма-
лизующим такое описание механизма случайного эксперимента. Задать
60
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
вероятностное пространство — это значит задать пространство элемен-
тарных событий Я и определить в нем вышеуказанное соответствие типа
Pi =	(14)
Очевидно, соответствие типа (1.4) может быть задано различными
способами: с помощью таблиц, графиков, аналитических формул, наконец,
алгоритмически.
Как же построить вероятностное пространство, соответствующее ис-
следуемому реальному комплексу условий? С наполнением конкретным
содержанием понятий случайного эксперимента, элементарного события,
пространства элементарных событий, а в дискретном случае — и любого
разложимого случайного события затруднений, как правило, не бывает.
А вот определить из конкретных условий решаемой задачи вероятности
P{w,} отдельных элементарных событий не так-то просто! С этой целью
используется один из следующих трех подходов.
Априорный подход к вычислению вероятностей Р{^} заключается в
теоретическом, умозрительном анализе специфических условий данного
конкретного случайного эксперимента (до проведения самого эксперимен-
та). В ряде ситуаций этот предопытный анализ позволяет теоретически
обосновать способ определения искомых вероятностей. Например, возмо-
жен случай, когда пространство всех возможных элементарных исходов
состоит из конечного числа N элементов, причем условия производства
исследуемого случайного эксперимента таковы, что вероятности осуще-
ствления каждого из этих N элементарных исходов нам представляют-
ся равными (именно в такой ситуации мы находимся при подбрасывании
симметричной монеты, бросании правильной игральной кости, случайном
извлечении игральной карты из хорошо перемешанной колоды и т. п.). В
силу аксиомы (1.2) вероятность каждого элементарного события равна в
этом случае 1/N. Это позволяет получить простой рецепт и для подсчета
вероятности любого события: если событие А содержит N& элементарных
событий, то в соответствия с определением (1.3)
Р{Л} =	(1.3')
Смысл формулы (1.3*) состоит в том, что вероятность события в данном
классе ситуаций может быть определена как отношение числа благопри-
ятных исходов (т. е. элементарных исходов, входящих в это событие) к
числу всех возможных исходов (так называемое классическое определение
вероятности). В современной трактовке формула (1.3*) не является опре-
делением вероятности: она применима лишь в том частном случае, когда
все элементарные исходы равновероятны.
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
61
Апостериорно-частотный подход к вычислению вероятностей }
отталкивается, по существу, от определения вероятности, принятого так
называемой частотной концепцией вероятности. В соответствии с этой
концепцией вероятность Р{^} определяется как предел относительной
частоты появления исхода в процессе неограниченного увеличения об-
щего числа случайных экспериментов п, т.е.
пг , тп(шЛ	.
Pi = P{w,} = hm ------- ,	(1.5)
n-»oo n
где mn(w,) — число случайных экспериментов (из общего числа п про-
изведенных случайных экспериментов), в которых зарегистрировано по-
явление элементарного события cjj. Соответственно для практическогр
(приближенного) определения вероятностей р, предлагается брать отно-
сительные частоты появления события в достаточно длинном ряду слу-
чайных экспериментов1. Подобный способ вычисления вероятностей pt
не противоречит современной (аксиоматической) концепции теории веро-
ятностей, поскольку последняя построена таким образом, что эмпириче-
ским (или выборочным) аналогом объективно существующей вероятности
Р{Л} любого события А является относительная частота осуществления
этого события в ряду из п независимых испытаний. Разными в этих двух
концепциях оказываются определения вероятностей: в соответствии с ча-
стотной концепцией вероятность не является объективным, существую-
щим до опыта, свойством изучаемого явления, а появляется только в
связи с проведением опыта или наблюдения; это приводит к смешению
теоретических (истинных, обусловленных реальным комплексом условий
«существования» исследуемого явления) вероятностных характеристик и
их эмпирических (выборочных) аналогов.
Как пишет Г. Крамер, «указанное определение вероятности можно
сравнить, например, с определением геометрической точки как предела пя-
тен мела неограниченно убывающих размеров, но подобного определения
современная аксиоматическая геометрия не вводит» ([Крамер Г., с. 172]).
1 Немецкий математик Р. Мизес, с именем которого связывают развитие частотной
концепции вероятности, считал, что каждой вероятностной задаче обязательно со-
ответствует некоторый реальный процесс (удовлетворяющий введенным им услови-
ям «статистического коллектива»), а потому полагал теорию вероятностей дисци-
плиной естественно-научной («наукой о явлениях реального мира»), но не матема-
тической. Сущность понятия мизесского «коллектива» — в требовании реальной
массовости изучаемого явления (и соответствующего эксперимента), существования
пределов вида (1.5) и независимости этих пределов от того, по какой подпоследова-
тельности произведенных случайных экспериментов, отобранной из всей такой по-
следовательности, мы этот предел будем вычислять.
62
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Мы не будем здесь останавливаться на математических изъянах частот-
ной концепции вероятности. Отметим лишь принципиальные сложности
реализации вычислительного приема получения приближенных значений
р, с помощью относительных частот mn(w,)/n. Во-первых^ сохранение
неизменными условий случайного эксперимента (т. е. сохранение условий
статистического ансамбля), при котором оказывается справедливым до-
пущение о тенденции относительных частот группироваться вокруг по-
стоянного значения, не может поддерживаться неограниченно долго и с
высокой точностью. Поэтому для оценки вероятностей р, с помощью от-
носительных частот mn(oji)/n не имеет смысла брать слишком длинные
ряды (т.е. слишком большие п) и потому же, кстати, точный переход к
пределу (1.5) не может иметь реального смысла. Во-вторых, в ситуаци-
ях, когда мы имеем достаточно большое число возможных элементарных
исходов (а они могут образовывать и бесконечное, и даже, как это было
уже отмечено в п. 1.1.1, континуальное множество), даже в сколь угодно
длинном ряду случайных экспериментов, мы будем иметь возможные ис-
ходы i*?i, ни разу не осуществившиеся в ходе нашего эксперимента; да и
по другим редко реализующимся возможным исходам полученные с помо-
щью относительных частот приближенные значения вероятностей будут
в этих условиях крайне мало надежными.
Апостериорно-модельный подход к заданию вероятностей Р{щ}, от-
вечающему конкретно исследуемому реальному комплексу условий, явля-
ется в настоящее время, пожалуй, наиболее распространенным и наиболее
практически удобным. Логика этого подхода следующая. С одной сторо-
ны, в рамках априорного подхода, т. е. в рамках теоретического, умозри-
тельного анализа возможных вариантов специфики гипотетичных реаль-
ных комплексов условий разработан и исследован набор модельных веро-
ятностных пространств (биномиальное, пуассоновское, нормальное, пока-
зательное и т. п., см. гл. 3). С другой стороны, исследователь располагает
результатами ограниченного ряда случайных экспериментов. Далее с
помощью специальных математико-статистических приемов (основанных
на методах статистического оценивания неизвестных параметров и ста-
тистической проверки гипотез, см. гл. 6-8) исследователь как бы прила-
живает гипотетичные модели вероятностных пространств к имеющимся у
него результатам наблюдения (отражающим специфику изучаемой реаль-
ной действительности) и оставляет для дальнейшего использования лишь
ту модель или те модели, которые не противоречат этим результатам и в
некотором смысле наилучшим образом им соответствуют.
Опишем теперь основные правила действий с вероятностями событий,
являющиеся следствиями принятых выше определений и аксиомы.
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
63
Вероятность суммы событий (теорема сложения вероятно-
стей). Сформулируем и докажем правило вычисления вероятности сум-
мы двух событий Л1 и А2. Для этого разобьем каждое из множеств эле-
ментарных событий, составляющих события Aj и Л2, на две части:
= А? + Ап;
А2 = А2 + А12,
где А* объединяет все элементарные события w,, входящие в А к, но не
входящие в Ат(кут =1,2; к / т), а А12 состоит из всех тех элементар-
ных событий, которые одновременно входят и в А1} и в А2. Пользуясь
определением (1.3) и определением произведения событий А] и А2, имеем:
Р{А,} =	£ Pi=	£	Pi+	£	р, = Р{А?) + P{At • А2); (1.6)
t:	»:	*:<^i€Aia
P{A1}=	£ p,=	£	Pi+	£	P, = P{A?} + P{A142}. (1.7)
«: w,€A2	fciUtCAj	i: w«€Ai2
В то же время в соответствии с определением суммы событий А = Ai + А2
ис (1.3) имеем
р{а1ч-а2}= 52	52	52 pi' (L8)
Из (1.6), (1.7) и (1.8) получаем формулу сложения вероятностей (для
двух событий):
Р{Аг + А2] = Р{Аг} 4- Р{А2} - Р{А2 А2}.	(1.9)
Формула (1.9) сложения вероятностей может быть обобщена на слу-
чай произвольного числа слагаемых:
к
Р{А, + А2 +  •  + А*} = £ P{AJ - А, + Д2 - • • • + (-I)*’1 Д*_1, (1.9')
«=1
где «добавки» Дт(т = 1,2,..., к - 1) вычисляются в форме суммы веро-
ятностей вида
к к	к
д>» = ££••• Е w»*,-
«1 = 1 «3=1 «т + 1=1
причем суммирование в правой части производится, очевидно, при усло-
вии, что все ii,i2,
*m+i различны и ij < »2 < ••• < iTO+i. В частном
64
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
случае, когда интересующая нас система А1э А2,..., А* состоит лишь из
несовместных событий, все произведения вида А^ • А,а- ... *А,т+1 (m > 1)
будут пустыми (или невозможными) событиями и соответственно форму-
ла (1.9*) дает
Р{А. + А2 4- •  • + Ак} = Р{А1} + Р{А2} + • • • + Р{Ак}. (1.9м)
Вероятность произведения событий (теорема умножения ве-
роятностей). Условная вероятность. Рассмотрим ситуации, когда
заранее поставленное условие или фиксация некоторого уже осуществив-
шегося события исключают из числа возможных часть элементарных со-
бытий анализируемого вероятностного пространства. Так, анализируя
совокупность из N изделий массового производства, содержащую Ni из-
делий первого, N2 — второго, Na — третьего и N4 — четвертого сорта
(Ni + N2 + N3 + N4 = N), мы рассматриваем вероятностное простран-
ство с элементарными исходами u>i,w2,W3 и и их вероятностями —
соответственно pi = Nj/N, р2 = N2/N, рз = N3/N и р4 = N4/N (здесь
и, означает событие, заключающееся в том, что наугад извлеченное из
совокупности изделие оказалось t-ro сорта). Предположим, условия сор-
тировки изделий таковы, что на каком-то этапе изделия первого сорта от-
деляются от общей совокупности и все вероятностные выводы (и, в част-
ности, подсчет вероятностей различных событий) нам предстоит строить
применительно к урезанной совокупности, состоящей только из изделий
второго, третьего и четвертого сорта. В таких случаях принято гово-
рить об условных вероятностях, т.е. о вероятностях, вычисленных при
условии уже осуществленного некоторого события. В данном случае таг
ким осуществленным событием является событие В =	т.е.
событие, заключающееся в том, что любое наугад извлеченное изделие
является либо второго, либо третьего, либо четвертого сорта. Поэтому,
если нас интересует подсчет условной вероятности события А (при усло-
вии, что событие В уже имеет место), заключающегося, например, в том,
что наугад извлеченное изделие окажется второго или третьего сорта, то,
очевидно, эта условная вероятность (обозначим ее Р{А | В}) может быть
определена следующим соотношением:
Р1А I В\ =	+	= N2+N3 /N2 + N3 + N4 = Р{АВ}
1	1 1 N2 + N3 + N4 N / N	P{B] ’
Как легко понять из этого примера, подсчет условных вероятно-
стей — это, по существу, переход в другое, урезанное заданным условием
В пространство элементарных событий, когда соотношение вероятно-
стей элементарных событий в урезанном пространстве остается тем же.
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
65
что и в исходном (более широком), но все они нормируются (делятся на
Р{В]|) для того, чтобы и в новом вероятностном пространстве выпол-
нялось требование нормировки (1.2). Конечно, можно было бы не вво-
дить терминологии с условными вероятностями, а просто использовать
аппарат обычных («безусловных») вероятностей в новом пространстве.
Запись в терминах вероятностей «старого» пространства бывает полез-
ной в тех случаях, когда по условиям конкретной задачи мы должны все
время помнить о существовании исходного, более широкого пространства
элементарных событий.
Получим формулу условной вероятности в общем случае. Пусть В —
событие (непустое), считающееся уже состоявшимся («условие»), а А —
событие, условную вероятность которого Р{А | В требует вычислить.
Новое (урезанное) пространство элементарных событий Я состоит только
из элементарных событий, входящих в В, и, следовательно, их вероятно-
сти (с условием нормировки (1.2)) определяются соотношениями1:
Г Рп{ьл,} _ Pi
=	{ Pn{B} Pn{B}’
I о,
если € B;
если bjt B.
(110)
По определению вероятность P{A | В} — это вероятность события
А в «урезанном» вероятностном пространстве {П,р}, и, следовательно, в
соответствии с (1.3) и (1.10)
Ра{А | В] = РЙ{Л} = <£ Рй{ш.} =
w* €А
Е Pi
т. е.
Ра{А 1 в)=
или, что то же,
Ра{АВ) = Ра{А | В} - РП{В}.
(1-П)
(111')
1 Нижний индекс у буквы Р, означающей «вероятность» (Р — первая буква латинской
транскрипции этого слова), поясняет, в каком именно вероятностном пространстве
иля пространстве элементарных событий производится вычисление вероятности со-
ответствующего события.
66
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Эквивалентные формулы (1.11) и (1.11*) принято называть соответ-
ственно формулой условной вероятности и правилом умножения веро-
ятностей.
Еще раз подчеркнем, что рассмотрение условных вероятностей раз-
личных событий при одном и том же условии В равносильно рассмо-
трению обычных вероятностей в другом (урезанном) пространстве эле-
ментарных событий О = В с пересчетом соответствующих вероятностей
элементарных событий по формуле (1.10). Поэтому все общие теоремы и
правила действий с вероятностями остаются в силе и для условных ве-
роятностей, если эти условные вероятности берутся при одном и том
же условии.
Независимость событии. Два события А и В называют независи-
мыми, если
Р{АВ} = Р{А} • Р{В}.	(1.12)
Для пояснения естественности такого определения вернемся к теореме
умножения вероятностей (1.11 ) и посмотрим, в каких ситуациях из нее
следует (1.12). Очевидно, это может быть тогда, когда условная вероят-
ность Р{А | В] равна соответствующей безусловной вероятности Р{4},
т.е., грубо говоря, тогда, когда знание того, что произошло событие В,
никак не влияет на оценку шансов появления события А.
Распространение определения независимости на систему более чем
двух событий выглядит следующим образом. События Ai, А2,..., А* на-
зываются взаимно (или совместно) независимыми, если для любых пар,
троек, четверок и т. д. событий, отобранных от этого набора событий,
справедливы следующие правила умножения:
P{AjlAia} = P{A,1}P{A.a};
P{AhAhA}3} = P{AhP{At,}P{Ah}-,
P{Ai • A3 • • • A*} = P{A, }P{A,} •  • P{A*}.
Очевидно, в первой строке подразумевается
2	к(к - 1)
Ск = ~П2~
(число сочетаний из к по два) уравнений, во второй — С* уравнений и
т. д. Всего, следовательно, (1.13^ объединяет С% 4- С* 4- • - - 4- С* = 2* —
к — 1 условий. В то же время Ct условий первой строки достаточно для
обеспечения попарной независимости этих событий. И хотя попарная и
1.1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
67
взаимная независимость системы событий, строго говоря, не одно и то
же, их различие представляет скорее теоретический, чем практический
интерес.
Свойство независимости событий сильно облегчает анализ различных
вероятностей, связанных с исследуемой системой событий. Достаточно
сказать, что если в общем случае для описания вероятностей всевозмож-
ных комбинаций событий системы Ai,Ла,...,А* нужно задать 2к веро-
ятностей, то в случае взаимной независимости этих событий достаточно
лишь к вероятностей P{Aj}, P{Aj},..., Р{А*}.
Независимые события весьма часто встречаются в изучаемой реаль-
ной действительности: они осуществляются в экспериментах (наблюдени-
ях), проводимых независимо друг от друга в обычном физическом смысле.
Именно свойство независимости исходов четырех последовательных
бросаний игральной кости позволило (с помощью (1.13)) легко подсчитать
вероятность невыпадения (ни при одном из этих бросаний) шестерки в
задаче из п. В.2. Действительно, обозначив А; событие, заключающееся
в невыпадении шестерки в i-м бросании (t = 1,2,3,4), и учитывая, что
Р{А,} = 5/6 для всех t = 1,2,3,4, получаем
Р{А,А2А3А4} = /’{А1}Р{А2}Р{А3}Р{А4}
= (5/6)4 = 625/1296.
Формула полной вероятности. При решении многих практических
задач зачастую сталкиваются с ситуацией, когда прямое вычисление ве-
роятности интересующего нас события А трудно или невозможно, в то
время как вполне доступно вычисление (или задание) условных вероятно-
стей того же события (при различных условиях). В случае, когда условия
при которых известны (или легко вычисляемы) условные
вероятности события А, образуют полную систему событий (см. п. 1.1.2),
для подсчета вероятности Р{А} можно использовать соотношение
Р{4} = Р{А | В,}Р{В1}
+ Р{А | В2)Р{В2) + • • • + Р{А |	(1М)
которое принято называть формулой полной вероятности.
Для доказательства формулы (1.14) заметим, что элементарные со-
бытия, составляющие событие А, можно разбить на к непересекающихся
групп, каждая из которых является общей частью (пересечением) события
А с одним из событий В, (эта возможность непосредственно вытекает из
того, что события Bi, В2,.. -, Bk исчерпывают в сумме все пространство
68	ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
элементарных событий и попарно не пересекаются), т. е.
А = ABj + АВ% • 4* ABff.
Далее, воспользовавшись теоремой сложения вероятностей (1.9й)
(применительно к несовместным событиям, каковыми являются события
ABi, ЛВ2,..., ЛВ*.) и вычислив вероятность каждого из произведений
ABi по формуле произведения вероятностей (1.1 Г), мы и получаем (1.14).
Формула Байеса. Обратимся вначале к следующей задаче. На скла-
де имеются приборы, изготовленные тремя заводами: 20% приборов на
складе изготовлены заводом N* 1, 50% — заводом № 2 и 30% — заводом
N1 3. Вероятности того, что в течение гарантийного срока прибору потре-
буется ремонт, для продукции каждого из заводов равны соответственно
0,2; 0,1; 0,3. Взятый со склада прибор не имел заводской маркировки и
потребовал ремонта (в течение гарантийного срока). Каким заводом ве-
роятнее всего был изготовлен прибор? Какова эта вероятность? Если
обозначить А, событие, заключающееся в том, что случайно взятый со
склада прибор оказался изготовленным на t-м заводе (» = 1,2,3), а В —
событие, заключающееся в том, что наугад отобранный от продукции всех
трех заводов прибор оказался дефектным (потребовал ремонта), то сфор-
мулированная выше задача, очевидно, сводится к вычислению условных
вероятностей Р{Л,- | В) по заданным вероятностям Р{Л1} = 0,2; Р{Л2} =
0,5; Р{Л3} = ОД Р{В I ЛО = 0,2; Р{В | Л2} = 0,1 и Р{В | Л3} = 0,3.
Поскольку события Л1,Л2,Л3 образуют полную систему, воспользуемся
для выражения искомых вероятностей Р{Л, | В} известными нам основ-
ными правилами действий с вероятностями. По формуле условной веро-
ятности (1.11)
р{л< 1 в} = (115)
Числитель этой дроби по теореме умножения вероятностей (1.11*) мо-
жет быть представлен в виде
Р{4,В} = Р{В4,} = Р{В | А,}Р{А<},	(1.16)
а знаменатель Р{ В) выражается с помощью формулы полной вероятности
(1-14):
Р{В} = Р{В | 4,}Р{А,} + Р{В | А2}Г{А2}4- Р{В | А3}Р{А3}. (1.17)
Подставляя (1.16) и (1.17) в (1.15), получаем
1.2. НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
69
,(А I л).	(1
Е л(в I л, 1 '(л,)
7=1
Воспользовавшись этой формулой, нетрудно подсчитать искомые ве-
роятности:
Pf А I /?1 =_________0*2 '	_ 0,04 _
111 1	0,2  0,2 + 0,1  0,5 + 0,3  0,3	0,18	’ ’
р{а3 | в} =	= ^ = °>278;
U,1O	U,lo
в{А, | В} =	= о>мо-
и,10
Следовательно, вероятнее всего некондиционный прибор был изгото-
влен на заводе К* 3.
Доказательство формулы (1.18) в случае полной системы событий,
состоящей из произвольного числа к событий, в точности повторяет дока-
зательство формулы (1.18). В таком общем виде формулу
в{ Л I В} =
Р{Л,}Р{В | Aj]
Е Р{В | А,}Р{ЛД
j=i
(119)
принято называть формулой Байеса.
1.2.	Непрерывное вероятностное
пространство (аксиоматика
А. Н. Колмогорова)
1.2.1.	Специфика общего (непрерывного) случая
вероятностного пространства
Ранее упоминалось о ситуациях, в которых множество всех возмож-
ных элементарных исходов (пространство элементарных событий П) мо-
жет оказаться более чем счетным. Так, например, именно с контину-
альным пространством элементарных событий придется иметь дело, если
70
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
каждому элементарному исходу w, исследуемого случайного эксперимен-
та (наблюдения) может быть поставлена в соответствие регистрация од-
ной или нескольких числовых характеристик обследуемого объекта ана-
лизируемой совокупности, измеренных в физических единицах непрерыв-
ной природы (в единицах времени, длины, веса, температуры, давления и
т. п.). Можно, правда, возразить, что, поскольку все измерения делаются с
ограниченной точностью, реальное множество элементарных исходов все
равно окажется не более чем счетным. Однако, с одной стороны, возмож-
ности точности измерений со временем совершенствуются и вместе с этим
должна соответственно трансформироваться и структура рассматривае-
мого дискретного вероятностного пространства. С другой стороны, рас-
смотрение непрерывных моделей, отвечая физической сущности анализи-
руемого явления, одновременно расширяет аналитические возможности
теории, предоставляет исследователю более мощный математический ап-
парат: достаточно сопоставить возможности простого суммирования и
интегрирования, аппарата разностных и дифференциальных уравнений и
т. д.
Как же осуществляется переход от дискретного к непрерывному слу-
чаю в построении строгой математической теории вероятностей? Авто-
матический перенос всей схемы построения дискретного вероятностного
пространства (см. п. 1.1) на непрерывный случай невозможен. Одно из
принципиальных отличий непрерывного случая от дискретного заключа-
ется в том, что в общем случае мы не можем объявить, подобно тому
как это делалось в дискретном вероятностном пространстве, любое под-
множество множества элементарных исходов Q случайным событием,
т.е. событием, характеризующимся принципиальной возможностью его
наблюдения в результате исследуемого случайного эксперимента. Други-
ми словами, в общем вероятностном пространстве среди всех возможных
подмножеств пространства элементарных событий П часть подмножеств
характеризуется такой возможностью (и их принято называть случайны-
ми событиями или измеримыми подмножествами П), а другая часть —
нет (подмножества Q этого типа принято называть неизмеримыми).
Отмеченная особенность общего (непрерывного) случая, по-видимому,
требует введения дополнительных определений и аксиом, относящихся
к определению случайных событий и к правилам действий с ними и
их вероятностями. Это и делается при аксиоматическом (теоретико-
множественном 1 построении сов семенной теории вероятностей, первое
1.2. НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
71
строгое и полное изложение которой принадлежит А. Н. Колмогорову
[Колмогоров]1.
1.2.2.	Случайные события, их вероятности и правила
действий с ними (аксиоматический подход
А. Н. Колмогорова)
Определим ту часть подмножеств пространства элементарных собы-
тий Q, которая содержит подмножества-события. Схема определения
случайного события А в общем случае подобна той, которая была при-
нята в дискретном случае. Но если в той ситуации нам достаточно бы-
ло определить в качестве исходных понятий элементарные события wj,
wj,...	. (и любое подмножество пространства элементарных собы-
тий объявлялось событием), то в общем случае мы в каждой конкретной
реальной ситуации должны (из физических, содержательных соображе-
ний) определить дополнительно к П категорию подмножеств Q, которые,
очевидно, являются событиями. А затем любое случайное событие А опре-
деляется как некоторое производное от «очевидно событийных» подмно-
жеств введенной категории.
Определение случайного события. Рассмотрим систему (конеч-
ную или счетную) подмножеств Ai,A2}... пространства элементарных
событий Q, каждое из которых является событием. Определим, что
множество П, состоящее из всех элементарных событий, все дополне-
ния А, = О — А,-, пустое множество 0 = О — П и всевозможные суммы
А =	+ А1а + • • • + А,и + • • • также являются событиями. Отсюда
непосредственно следует, что и произведения П = Atl А^ • • • А^в • • • так-
же являются событиями, так как их дополнения П = А<, 4- А,а + ••• в
соответствии с данным определением являются событиями.
Будем обозначать в дальнейшем систему тех подмножеств простран-
ства элементарных исходов П, которые являются событиями, буквой С.
Аксиома. Каждому подмножеству-событию А из системы С соответ-
ствует неотрицательное и не превосходящее единицы число р(А) = Р{А},
называемое вероятностью события А, причем задающая это соответствие
числовая функция множеств р(А) обладает следующими свойствами:
1 Впервые интерпретация случайного события как множества с одновременной трак-
товкой его вероятности как меры этого множества была дана, по-виднмому, в
работе польского математика А. Ломницкого (Lomnicki A. Nouveau fondements du
calcul des probability — Fundam. Math., 1923, 4). Однако теория вероятностей хак
точная математическая теория в надлежащем объеме впервые была построена
А. Н. Колмогоровым.
72
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
а)	р(П) = Р{П} = 1;
б)	если события Ai, А2,..., Ап,... несовместны, то
P{4i 4- Л2 4- ••• + Ап + •••} = Р{Л1} 4- Р{А2} 4- .•• + Р{Ап} 4- •••.
Из этой аксиомы непосредственно следует, в частности, связь между
вероятностями прямого (А) и противоположного (А) событий:
Р{А} = 1 - Р{А}.
Аксиоматическое свойство б) вероятностей формулировалось и дока-
зывалось в дискретном случае в виде теоремы сложения вероятностей.
Точно так же то, что называлось теоремой умножения вероятно-
стей (и выводилось из определения и аксиомы в дискретном случае), в
общем случае принимается по определению.
Определение условной вероятности. Условная вероятность
Р{А | В} события А при условии, что уже имеет место событие В, опре-
деляется с помощью формулы
Р{АВ} = Р{А | В}Р{В}.
Правила действий с событиями и их вероятностями и, в част-
ности, формула полной вероятности (1.14), формула Байеса (1.19), опре-
деление независимости для системы событий (1.12), (1.13) и другие, дока-
занные в дискретном случае, имеют место (и могут быть доказаны) и в
случае общего вероятностного пространства.
Итак, для исчерпывающего описания механизма исследуемого слу-
чайного эксперимента в общем случае, т.е. для задания в этом случае
вероятностного пространства, необходимо: 1) описать пространство эле-
ментарных событий Я; 2) описать систему С измеримых подмножеств
этого пространства или таких подмножеств, которые должны быть прин-
ципиально наблюдаемыми (т.е. являются событиями); 3) каждому такому
событию А из системы С поставить в соответствие неотрицательное чи-
сло Р{А}, называемое вероятностью события А, причем это соответствие
должно удовлетворять требованиям а) и 6) аксиомы (очевидно, такое со-
ответствие Р есть числовая функция множества, определенная на под-
множествах системы С; функции такого типа принято называть вероят-
ностными мерами, определенными на системе подмножеств С). Поэтому
если в дискретном случае для краткого символического описания вероят-
ностного пространства достаточно было пары символов {Я,р}, то в общем
случае для этой же цели требуется уже «тройка» {Я,С,Р}.
Следует, однако, помнить, что всякая модель, всякая теория, и в том
числе современная аксиоматическая концепция теории вероятностей, есть
1.2. НЕПРЕРЫВНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
73
лишь форма приближенного представления реальной действительности,
форма, не свободная от недостатков. Чтобы предостеречь читателя от
переоценки возможностей аксиоматической теоретико-вероятностной мо-
дели, рассмотрим несложный пример.
Практика долгосрочного социально-экономического и научно-техни-
ческого прогнозирования широко использует различные формы эксперт-
ных опросов. Одной из таких форм является подход, при котором каждо-
го из опрашиваемых экспертов просят субъективно оценить вероятность
осуществления интересующего нас события в будущем1. Подходя к мо-
делированию этого процесса с позиций субъективистской школы вероят-
ностей и соответственно интерпретируя каждого из опрашиваемых экс-
пертов в качестве своеобразного «измерительного прибора», мы можем
определить понятие случайного эксперимента как результат ответа экс-
перта на поставленный ему вопрос. В этом случае пространство элемен-
тарных исходов Q, очевидно, должно состоять из всех точек отрезка [0, 1].
При конструировании системы С «наблюдаемых» подмножеств простран-
ства П естественно было бы априори потребовать, чтобы любой отрезок
Д = [ci,c2], лежащий внутри отрезка [0, 1] (т.е. О Cj < с2 < 1), при-
надлежал бы к категории событий (т.е. для любого отрезка Д = [ci,c2]
должна быть определена вероятность Р{ Д) = Р{[с!, с2]} того, что числен-
ный ответ наугад выбранного эксперта будет принадлежать этому отрез-
ку). Но тогда в соответствии с определением случайного события в общем
случае событиями будут не только отрезки, но и все, что можно получить
из них применением к ним (взятым в счетном числе) суммирования и пере-
множения, а также взятием дополнения (т. е. противоположного события).
Поэтому, выбирая произвольную точку с на отрезке [0, 1] и рассматривая
последовательность отрезков Дп вида Дп = [с — 1/п, с 4- 1/п], мы обна-
руживаем, что точка должна быть событием, так как она является, как
легко видеть, счетным произведением отрезков Дп. Итак, любая точка
отрезка [0, 1] — событие. Множество рациональных точек, как известно,
складывается из счетного числа точек. Следовательно, это множество —
тоже событие. Но множество иррациональных точек есть дополнение к
множеству рациональных точек. Значит, и множество иррациональных
точек — событие. Но вряд ли естественно, с физической точки зрения,
считать наблюдаемыми (и, следовательно, физически различимыми) со-
бытиями факты принадлежности точки к множеству рациональных и к
множеству иррациональных чисел.
1 Подобная форма экспертиз используется, например, при построении сценариев буду-
щего социально-экономического и промышленного развития стран.
74	ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
Как видно из этого примера, и использование общепринятой сейчас
аксиоматической концепции теории вероятностей может приводить к
плохо физически интерпретируемым выводам. В данном примере мы не
провели до конца построение вероятностного пространства, так как не
определили (аксиоматически) способ вычисления вероятностей на отрез-
ках, т.е. величин Р{Д} = P{[ci,с2]}. Физически естественное аксиомати-
ческое задание этих вероятностей также обусловлено спецификой реаль-
ного комплекса условий, характеризующих наш случайный эксперимент.
Так, если представить, что мы находимся в самой ^неблагоприят-
ной» для прогноза ситуации (интересующее нас событие настолько уда-
лено во времени и неопределено или опрашиваемые эксперты настолько
некомпетентны, что ответы экспертов оказываются приблизительно рав-
номерно «разбросанными» по всей длине отрезка [0, 1]), то естественно
предположить, что вероятности Р{Д} будут зависеть только от длины
отрезка Д и не будут зависеть от того, в каком именно месте отрезок
располагается, и определить их соответственно с помощью соотношений1
f{[ei,C2]} = C2-Cl.	(1-20)
Легко проверить, что заданные этим соотношением вероятности удо-
влетворяют свойствам а) и б) аксиомы.
Подчеркнем, кстати, на этом примере одно из существенных отличий
широкого класса непрерывных вероятностных пространств от дискрет-
ных: вероятность осуществления любого элементарного события (т. е. лю-
бого возможного исхода) и в данном примере равна нулю; однако для
сколь угодно малого отрезка Д вероятность Р{Д} всегда будет положи-
тельной (это непосредственно следует из (1.20)). Таким образом, в этом
примере мы впервые встретились с казалось бы парадоксальной ситуаци-
ей, когда события хотя и являются возможными, но обладают ну-
левой вероятностью. Соответственно события й = Q — w, являющиеся
дополнением к событиям нулевой вероятности хотя и не могут быть
названы достоверными, но имеют вероятность осуществления, равную
единице. О событиях типа ы часто говорят как о событиях, происходящих
«почти всегда». При более глубоком рассмотрении можно понять, что
подобные ситуации в непрерывном вероятностном пространстве на самом
деле не являются парадоксальными. Для пояснения этой мысли можно
привести аналогию с физическим телом, имеющим определенную массу,
1 О трех возможных подходах (априорном, апостериорно-частотном и апостериорно-
модельном) к выработке и обоснованию подобных предположений о природе аксио-
матически определяемых вероятностей см. п. 1.1.3.
выводы
75
в то время как ни одна из точек, составляющих это тело, сама массой не
обладает. Очевидно, тело в этой аналогии играет роль события, точка —
роль элементарного исхода, а масса — роль вероятности.
ВЫВОДЫ
1.	Основаниями теоретике-вероятностного математического аппара-
та являются: понятия случайного эксперимента, его возможного исхода и
пространства элементарных событий: аксиома о существовании и норми-
ровке вероятностей элементарных событий; определение случайного со-
бытия и способа вычисления его вероятности.
2.	Способ построения современной строгой вероятностной теории ак-
сиоматический, причем для построения дискретного вероятностного про-
странства, т. е. для модельного математического описания механизма слу-
чайного эксперимента, имеющего лишь конечное или счетное множество
возможных элементарных исходов, достаточно постулировать одну акси-
ому (о существовании и нормировке вероятностей элементарных исходов)
и одно определение (о способе вычисления вероятности любого события).
3.	Термины «механизм случайного экспериментам, «реальный ком-
плекс условий, индуцирующий исследуемый статистический ансамбль*
и «вероятностное пространством являются синонимами и могут быть
математически заданы в дискретном случае с помощью описания всех воз-
можных элементарных исходов и сопоставления с каждым из них вероят-
ности своего появления (с помощью аналитического задания, таблично,
графически, алгоритмически).
4.	Главная сложность построения вероятностного пространства, со-
ответствующего исследуемому реальному комплексу условий, — в кон-
кретном задании вероятностей элементарных событий в дискретном слу-
чае или вероятностной меры — в непрерывном. Из трех возможных под-
ходов к решению этой задачи — априорного, апостериорно-частотного
и апостериорно-модельного — последний является наиболее легко прак-
тически реализуемым и наиболее эффективным.
Б. Основные правила действий в дискретном вероятностном про-
странстве задаются теоремами сложения и умножения вероятностей,
формулами полной вероятности и Байеса.
6.	В общем (непрерывном) вероятностном пространстве в отличие от
дискретного среди подмножеств пространства элементарных событий П
могут быть такие, для которых не существует принципиальной возмож-
ности их наблюдения в результате исследуемого случайного эксперимента
(«ненаблюдаемые» или «неизмеримые» подмножества). Такие подмноже-
76
ГЛ. 1. ПРАВИЛА ДЕЙСТВИЙ С ВЕРОЯТНОСТЯМИ
ства не могут быть названы событиями, так как если А — событие, то
мы должны иметь возможность сказать, наступило оно или не наступи-
ло в результате эксперимента (в этом смысле оно «наблюдаемо»); только
тогда можно говорить об относительной частоте его наступления в серии
экспериментов, а следовательно, и о вероятности Р{А}.
7.	Отмеченная в предыдущем пункте особенность общего вероят-
ностного пространства требует введения дополнительных определений
и аксиом, относящихся к определению случайных событий и к пра-
вилам действий с их вероятностями. Современная аксиоматическая
концепция теории вероятностей (впервые полно и строго изложенная
А. Н. Колмогоровым в 1933 г.) строит общее вероятностное простран-
ство, отправляясь от определения случайного события (с помощью пере-
числения допустимых теоретико-множественных комбинаций над подмно-
жествами, априори являющимися событиями) и аксиомы о вероятностях
как о неотрицательных и ограниченных единицей числовых функциях,
аргументами которых являются подмножества-события. Эта концепция
не противоречит рассмотренному ранее способу построения дискретного
вероятностного пространства (она включает в себя этот способ в каче-
стве частного случая и соответственно сохраняет все правила действий
с вероятностями и событиями) и обусловливает возможность физической
интерпретации вероятности события как относительной частоты его по-
явления в достаточно длинной серии экспериментов.
8.	Использование аксиоматической концепции теории вероятностей
может в некоторых случаях, как и всякая другая модель, приводить к
плохо физически интерпретируемым выводам.
9.	В общем (непрерывном) вероятностном пространстве в отличие от
дискретного могут существовать возможные события, обладающие ну-
левой вероятностью появления. Соответственно противоположные к ним
события (их дополнения) хотя и не могут быть названы достоверными, но
имеют вероятность осуществления, равную единице.
ГЛАВА 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1.	Определение и примеры случайных
величин
Рассматривая приведенные выше примеры случайных экспериментов
(см. п. 1.1.2, примеры 1.1-1.7), мы видим, что в большинстве случаев ре-
зультат случайного эксперимента может быть описан одним или несколь-
кими числами. Так, в примерах 1.2, 1.5 и 1.7 эти результаты означают
соответственно число очков, выпавших при бросании игральной кости;
число дефектных изделий, обнаруженных при качественном контроле N
случайно отобранных из массовой продукции изделий; число сбоев автома-
тической линии за наугад выбранную рабочую смену. В примере 1.3 (че-
тырехкратное бросание игральной кости) результат каждого случайного
эксперимента может быть записан четверкой чисел, или четырехмерным
вектором, а в примере 1.6 (проверка основной и дополнительной выборок
изделий объема соответственно и N2, случайно отобранных из продук-
ции массового производства) — парой чисел, или двумерным вектором.
Даже в примерах 1.1 и 1.4, на первый взгляд не связанных с регистрацией
числовых характеристик, можно для удобства закодировать соответству-
ющие случайные исходы, приписывая, например, исходам «аверс» (при-
мер 1.1) и «изделие годно» (пример 1.4) числовую метку «нуль», а исходам
«реверс» и «изделие дефектно» — числовую метку «единица». Продол-
жая наши примеры и рассматривая в рамках теоретико-вероятностной
схемы регистрацию одного или одновременно нескольких интересующих
нас свойств (выраженных реальными или условно закодированными чи-
слами) у каждого из анализируемых объектов, мы приходим к общей схе-
ме, в которой понятие случайного эксперимента реализуется в регистра-
ции на каждом из таких случайно отобранных объектов набора числовых
характеристик
{<”>), р>1.	(2.1)
78
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Какие именно числовые значения £ мы будем иметь в результате дан-
ного конкретного эксперимента, зависит от множества не поддающихся
учету случайных факторов и однозначно определяется в конечном счете
осуществившимся в результате данного случайного эксперимента элемен-
тарным исходом и (а это означает, что £ является числовой (в случае
р = 1) или векторной (в случае р 2) функцией аргумента и). Таким
образом, мы приходим к следующему определению случайной величины
(иногда пользуются равнозначным термином «случайный признак» или
просто «признак»).
Таблица 2.1
Анализируемые свойства (характеристики) объектов	Анализируемые объекты			(семьи)
	1	2	• • •	я
Социально-демографические и экономические характеристики семьи				
Д1) С — социальная принадлежность			• • •	х(1)
Д2)	. С — профессия главы семьи		ж(2) ж2	• • •	®(2) *п
ДЗ) С — качество жилищных условии	4”	х(3)	♦ • •	а:<3)
— размер (число членов) семьи	44)	х2	• • •	XW
— количество детей		аг(б) г2	• • •	х(5) Ьп
Дб) С — среднедушевой доход		®2	* • •	?в) •*-п
Характеристики «поведения» семьи (структура потребления)				
С ' — расходы на питание		Х1	• • •	х(7) •сп
f^8^ — расходы на промышленные товары текущего пользования		х(в) Х2	 « •	г(8)
Д9) 4 1 — расходы на предметы роскоши и длительного пользования	г<9)	х(9) Х2	• • •	а;(9)
>(ю) £ * — расходы на услуги	,(Ю)	,(10) х2	• • •	,(1°)
е(11) С — прочие расходы, включая 1 сбережения	J”)	J11) Х2	• • ♦	
Случайной величиной называется поддающаяся измерению скаляр-
ная (р = 1) или векторная (р 2) величина определенного физического
2.2. ВОЗМОЖНЫЕ И НАБЛЮДЕННЫЕ ЗНАЧЕНИЯ
79
смысла, значения (компоненты) которой подвержены некоторому не-
контролируемому разбросу при повторениях исследуемого эксперимента
(наблюдения, процесса). Можно сказать, что случайная величина ( —
это функция, определенная на множестве элементарных событий, т. е.
е=ем-
Пример 2.1. В табл. 2.1 приведен еще один пример векторной
(или многомерной) случайной величины вместе с соответствующей ей об-
шей формой регистрации серии наблюдений (результатов случайных экс-
периментов).
Обозначения случайной величины (которая по существу определяет
лишь перечень анализируемых характеристик и по сложившейся в специ-
альной литературе традиции чаще всего обозначается с помощью одной из
букв греческого алфавита —	и т. д.) отличаются от обозначений
ее наблюденных значений.
В табл. 2.1 и в дальнейшем эти наблюденные значения в целях общ-
ности обозначаются с помощью строчных букв латинского алфавита (в
таблице — с помощью буквы х) с верхним индексом, указывающим номер
зафиксированной характеристики, и с нижним индексом, определяющим
номер эксперимента или объекта, в котором эта характеристика зареги-
стрирована; но в любом случае нужно помнить, что за этими символами
«скрываются» реальные числовые значения соответствующих характери-
стик или их условные числовые метки. Так, очевидно, в табл. 2.1 первые
три строки будут состоять из условных числовых меток, а последующие
восемь — из числовых значений, измеренных в определенной шкале и име-
ющих четкий физический смысл.
2.2.	Возможные и наблюденные значения
случайной величины
Поскольку в соответствии с одним из определений случайная вели-
чина — это функция, определенная на множестве элементарных исходов,
то ее возможные значения и их общее число определяются структурой
соответствующего пространства Q элементарных событий: каждому эле-
ментарному событию w соответствует свое возможное значение При
этом, правда, может быть, что нескольким элементарным исходам соот-
ветствует одно и то же возможное значение анализируемой случайной
величины, так что, вообще говоря, в конечном дискретном вероятност-
ном пространстве число возможных значений случайной величины все-
гда меньше или равно числу различных элементарных исходов. Так, в
приведенных выше примерах из п. 1.1.2 мы имеем: в примерах 1.1 и 1.4
80
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
всего по два возможных «значения», соответствующих элементарным ис-
ходам, — «аверс» и «реверс» (в примере 1.1) и «изделие годно» и «из-
делие дефектно» (в примере 1.4); в примере 1.2 — шесть первых поло-
жительных натуральных чисел задают одновременно и все элементарные
исходы, и все возможные значения анализируемой случайной величины;
в примере 1.7 возможными значениями числа сбоев автоматической ли-
нии за смену являются все неотрицательные целые числа. Что касается
примеров 1.3, 1.5 и 1.6, то в них мы как раз оказываемся в ситуации,
при которой число возможных значений анализируемой случайной вели-
чины будет меньше общего числа элементарных событий. Поясним это
на примере 1.3 (примеры 1.5 и 1.6 могут быть проанализированы по ана-
логичной схеме). Пусть в примере 1.3 нас интересует число появившихся
«шестерок» в серии из четырех бросаний игральной кости (независимо от
порядка, в котором они будут появляться). Элементарный исход в этом
примере может быть описан последовательностью из четырех символов,
в которой на t-м месте записывают 1, если в результате i-ro бросания
игральной кости выпала «шестерка», и 0 — в противном случае. Тогда с
точки зрения классификации элементарных событий последовательности
(0,1, 0, 0) и (0, 0, 0,1) дают разные элементарные исходы, в то время как
с точки зрения анализируемой случайной величины оба эти элементар-
ных события дают неразличимый результат: и в том, и в другом случае
наблюденное значение анализируемой случайной величины равно единице
(«шестерка» появилась ровно один раз). Конечно, нам не удастся «пере-
считать» все возможные значения случайной величины, определенной на
множестве элементарных исходов непрерывного пространства элементар-
ных событий П: их общее число образует континуум. Именно такого рода
величины представлены компонентами £	4- £ многомерной (вектор-
ной) случайной величины £, рассмотренной в примере 2.1.
Следует отличать теоретически возможные значения случайной ве-
личины (обозначим их ж?, ж®,..., ж?,... в дискретном случае и просто х —
в непрерывном) от практически осуществившихся в экспериментах^ т.е.
от наблюденных ее значений (последние обозначим х^,Х2,... ,®п)1*
2.3.	Типы случайных величин
Общая классификация возможных типов случайных величин может
1 Если интересующая нас случайная величина многомерная (или векторная, см. (2.1)),
то обозначения сохраняются с заменой строчных латинских букв ж®, ж, Х{ соответ-
ствующими прописными Х°,Х, Х{.
2.3. ТИПЫ СЛУЧАЙНЫХ ВЕЛИЧИН
81
быть представлена с помощью схемы рис. 2.1.
Если мы в качестве результата эксперимента (наблюдения) регистри-
руем одно число (примеры 1.1, 1.2, 1.4, 1.5 и 1.7 из п. 1.1.2; см. также
случай р = 1 в записи (2.1)), то соответствующую случайную величи-
ну принято называть одномерной или скалярной. Если же результатом
каждого эксперимента (наблюдения) является регистрация целого набора
интересующих нас характеристик (примеры 1.3, 1.6 и 2.1, а также случай
р > 2 в общей записи (2.1)), то соответствующую случайную величину
называют многомерной или векторной.
Рис. 2.1. Общая схема классификации основных типов случайных величин
Одномерную случайную величину называют дискретной или непре-
рывной в зависимости от того, в каком пространстве элементарных собы-
тий она определена — в дискретном или в непрерывном. Очевидно, во
всех рассмотренных выше примерах 1.1 - 1.7, так же как и в первых пяти
компонентах из примера 2.1 (табл. 2.1), мы имеем дело с дискретными
случайными величинами. Как уже сказано выше, некоторые исследовате-
ли, отправляясь от ограниченности наших практических возможностей
точности измерений, предлагают вообще обходиться только дискретны-
ми вероятностными пространствами и соответственно только дискретны-
82
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ми случайными величинами. Действительно, даже при измерении непре-
рывных по своей природе величин (длины, веса, температуры, давления
и т. д.) всегда существует обусловленная разрешающей способностью ис-
пользуемого «измерительного прибора» максимально различимая едини-
ца измерения, своеобразный неразложимый квант, в целом числе которых
и будет представлено в конечном счете наше измерение. Однако аналити-
ческие возможности непрерывных математических моделей, практика их
непосредственного использования говорят за то, что они являются эффек-
тивным прикладным аппаратом применительно не только к непрерыв-
ным по своей физической природе случайным величинам, но и к таким
дискретным, множество возможных значений которых достаточно велико
(несколько десятков и более).
В зависимости от своей природы, своего назначения одномерные дис-
кретные случайные величины подразделяются на количественные, орди-
нальные (или порядковые) и номинальные (или классификационные).
Количественная случайная величина позволяет измерять сте-
пень проявления анализируемого свойства обследуемого объекта в опре-
деленной шкале (см. примеры 1.2, 1.3, 1.5, 1.6, 1.7, а также компоненты
в примере 2.1).
Ординальная (порядковая) случайная величина позволяет упо-
рядочивать обследуемые в ходе случайных экспериментов (наблюдений)
объекты по степени проявления в них анализируемого свойства. Иссле-
дователь обращается к ординальным случайным величинам в ситуациях,
когда шкала, в которой можно было бы количественно измерить степень
проявления анализируемого свойства, объективно не существует или ему
не известна. В табл. 2.1 случайная величина — качество жилищных
условий — предусматривает четыре возможные градации (категории ка-
чества): «плохое», «удовлетворительное», «хорошее» и «очень хорошее».
Приписав каждой из обследованных семей (в соответствии с принятыми
нормативными правилами) одну из градаций, мы тем самым получаем
возможность упорядочить обследованные семьи по этому свойству. Об-
щее число градаций ординального признака может быть меньше, равно и
даже больше числа обследованных объектов (случайных экспериментов).
Номинальная (классификационная) случайная величина по-
зволяет разбивать обследуемые в ходе случайных экспериментов (наблю-
дений) объекты на не поддающиеся упорядочению однородные по анализи-
руемому свойству классы. Если исследователю наряду с анализируемым
свойством известны все возможные его градации (не поддающиеся упоря-
дочению), вместе с правилом отнесения обследованного в ходе случайного
эксперимента (наблюдения) объекта к одной из этих градаций, то соответ-
2.4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
83
ствующую номинальную величину принято называть категоризованной.
Именно к таким признакам относятся случайные величины — соци-
альная принадлежность семьи и ' — профессия главы семьи из табл. 2.1.
Если условия эксперимента таковы, что его элементарным исходом явля-
ется так называемое парное сравнение задающее меру сходства (или
различия) по анализируемому свойству объектов с номерами i и j из обсле-
дуемой совокупности, то такую номинальную случайную величину будем
называть некатегоризов анной, а ее наблюденные значения представляют-
ся соответственно так называемой матрицей смежности :
д = (М> J = К»-
Примером некатегоризованного номинального признака может слу-
жить случайная величина, индуцированная случайным экспериментом на
различных парах семей, результатом которого является отнесение или не-
отнесение каждой пары к общему классу с точки зрения однородности
(сходства) их потребительского поведения.
2.4.	Одномерные и многомерные
(совместные^ законы распределения
вероятностей случайных величин
Мы уже знаем (см. п. 1.1.3), что для полного описания вероятностного
пространства или, что то же, для исчерпывающего задания интересую-
щей нас случайной величины недостаточно задать лишь пространство
элементарных событий П (и тем самым описать множество теорети-
чески возможных значений анализируемой случайной величины). К этому
необходимо добавить также: в дискретном случае — правило сопоставле-
ния с каждым возможным значением Хр случайной величины £ вероят-
ности его появления р, = Р{£ = X?}; в непрерывном случае — правило
сопоставления с каждой измеримой2 областью АХ возможных значений
случайной величины £ вероятности р(ДХ) = Р{£ € АХ} события, за-
ключающегося в том, что в случайном эксперименте реализуется одно из
1 В наиболее распространенном частном случае элементы 6,у могут принимать лишь
два значения: 1, если объекты t и j отнесены в результате случайного эксперимента
(наблюдения) к одной градации (или к одному классу), и 0 — в противном случае.
7 Область возможных значений АХ называется изжерижо£1, если элементарные исхо-
ды ш, соответствующие значениям, вошедшим в эту область, образуют измеримое
подмножество или событие, т.е. подмножество, принадлежащее системе С всех
возможных событий (см. п. 1.2.1 и 1.2 2).
84
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
возможных значений, принадлежащих заданной области ДХ. Это прави-
ло, позволяющее устанавливать соответствия вида
х? - Pi = Р{( = X?};
ДХ - р(ДХ) = Р{£ 6 ДХ},
(2-2)
принято называть законом распределения вероятностей исследуемой
случайной величины Прозрачное пояснение такой терминологии мы
получаем в рамках дискретного вероятностного пространства, поскольку
в этом случае речь идет о правиле распределения суммарной единичной
вероятности (т.е. вероятности достоверного события) между отдельны-
ми возможными значениями Х°(х = 1,2,...).
Очевидно, задание закона распределения вероятностей, т. е. соответ-
ствий типа (2.2), может осуществляться с помощью таблиц (только в дис-
кретном случае), графиков, а также с помощью функций и алгоритмиче-
ски (об основных формах задания законов распределения и примерах их
модельной, т. е. аналитической, записи см. гл. 3).
Приведем примеры табличного и графического задания законов рас-
пределения вероятностей.
Тщательный статистический анализ засоренности партий дефектны-
ми изделиями (пример 1.5) позволил построить следующее распределение
вероятностей для случайной величины £, выражающей число дефектных
изделий, обнаруженных при контроле партии, состоящей из N = 30 из-
делий, случайно отобранных из продукции массового производства (та-
бл. 2.2):
Таблица 2.2
i	1	2	3	4	5	6	7	8	9	10	11	12	• • •	31
0	0	1	2	3	4	5	6	7	8	9	10	11	• • •	30
1000• Pi	42	141	228	236	177	102	47	18	6	1	0	0	« • •	0
Значения вероятностей, приведенные в табл. 2.2, даны с точностью до
третьего десятичного знака, поэтому то, что суммирование представлен-
ных в таблице вероятностей дает 0,998 (вместо единицы), легко объясни-
мо: недостающие 0,002 как-то «размазаны» между возможными значени-
ями 10,11,..., 30, но на каждое отдельное возможное значение приходится
вероятность, меньшая 0,0005.
Тот же закон распределения может быть представлен графически
(рис. 2.2).
2.4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
85
О О О О 0 0 оооооо
®2 *3 ®4	х8 х9 ®Ю *11 *12- • ’
Рис. 2.2. Графическое задание закона распределения вероятностей для чи-
сла дефектных изделий, обнаруженных в наугад извлеченной пар-
тии, состоящей из 30 изделий массового производства
Геометрическое изображение закона распределения вероятностей дис-
кретной случайной величины часто называют полигоном распределения
или полигоном вероятностей.
В качестве другого примера рассмотрим фрагмент табл. 2.1, выбрав
из одиннадцати представленных в ней компонент только две: качество
жилищных условий £ и среднедушевой доход Еще более упростим
рассматриваемую схему, перейдя от по существу непрерывной случайной
величины ^ к ее дискретному аналогу £ , т. е. отказываясь от точного
знания среднедушевого дохода каждой семьи и ограничиваясь лишь тре-
мя возможными градациями: семья имеет низкий доход (градация я^),
средний доход (градация и высокий доход (градация Я36)). С учетом
четырех градации качества жилищных условии: а* ' — качество низкое;
(з)	(3)	(з)
— качество удовлетворительное; х3 ' — качество хорошее и х4 —
качество очень хорошее — и проведенного вероятностно-статистического
анализа получаем следующий закон распределения вероятностей двумер-
ной случайной величины (?в\(^):
Соответствующий двумерный полигон распределения представлен на
рис. 2.3.
86
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Рис. 2.3. Полигон двумерного распределения семей по качеству жилищных
условий (£<3>) и уровню дохода p,-j = Р{^6^ =	=
Ч”’}
Закон распределения вероятностей многомерной случайной величи-
ны называют многомерным или совместным. Если каждая из компо-
нент = 1,2,..., р; см. (2.1)) анализируемого многомерного признака
( дискретна и имеет конечное число т* всех возможных значении, то,
очевидно, общее число возможных «значений» случайного вектора ( бу-
дет т = mi • т2 ... тр. В этом случае вместо общей индексации всех
возможных многомерных значений Х/° (/ = 1,2,...,т) удобнее пользо-
ваться р-мерной индексацией вида ij_q, где первый индекс t опреде-
ляет номер возможного значения по первой компоненте, второй индекс
j — по второй компоненте и т. д. Тогда будет означать возмож-
ное значение £, полученное сочетанием t-ro возможного значения компо-
ненты , j-ro возможного значения компоненты и т. д. до g-го воз-
можного значения компоненты а вероятности	удобно
обозначать р,у 9. Таким образом, в табл. 2.3 представлены вероятности
РУ=Р{^=Ф°'Р>=ХФ'},
2.4. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
87
Таблица 2.3
i	г-	1	2	3	4	Pi
	J					
	«<в>°	J3)0	_(3)0 х2	J3)0 х3	х<3>°	
1		0,06	0,03	0,01	0,00	0,10
2	*2	0,05	0,25	0,35	0,05	0,70
3	f(6)° х3	0,01	0,02	0,07	0,10	0,20
р-з		0,12	0,30	0,43	0,15	1,00
При анализе многомерных (совместных) распределений часто бы-
вает достаточно знать закон распределения лишь для какой-то ча-
сти компонент анализируемого векторного признака. Так, много-
мерная случайная величина рассмотренная в табл. 2.1, естествен-
но разбивается на два подвектора: ft = (^1\...,4^), описывающий
социально-демографические и экономическую характеристики семьи, и
(2 = (^7\-)» описывающий структуру семейного потребления.
Поэтому, если нас интересует лишь социально-демографо-экономическая
структура исследуемой совокупности семей, то предметом нашего ана-
лиза будет закон распределения вероятностей только по компонентам
• 1	подвектора &.
Частный (маржинальный) закон распределения подвектора &
анализируемой многомерной случайной величины £ = ((ь&) описывает
распределение вероятностей признака в ситуации, когда на значения
другой части компонент £2 не накладывается никаких условий. В дискрет-
ном случае соответствующие вероятности определяются по формулам:
Pi. = /’{fl =	} = Е Р{Ь =	6 =	};	(2.3)
р, = Р{€, = хГ’°} = £р{6 =	(23')
t
где Хр) и Aj2) — *-е и у-е возможные значения векторных признаков
соответственно и &, а суммирование производится по всем возможным
значениям Xj в формуле (2.3) и по всем возможным значениям Xi в фор-
муле (2.3*).
Формулы (2.3) и (2.3Z) получаются как непосредственные следствия
88
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
теоремы сложения вероятностей (1.9W), если принять во внимание следу-
ющие очевидные связи между интересующими нас событиями:
В рассматриваемом примере (см. табл. 2.3) частные распределения
Pi. =	} и p.j =	= х^ } подсчитаны по формулам (2.3)
и (2.3*) и задают соответственно распределение семей отдельно по уровню
дохода и по качеству жилищных условий (они приведены соответственно
в последнем столбце и в последней строке табл. 2.3).
Условный закон распределения подвектора £1 анализируемой
многомерной случайной величины £ = (£1,£з) ПРИ условии, что значе-
(2)°
ние другого подвектора £2 зафиксировано на уровне X) ' , вычисляется
по формуле
л.(хГ)0) = Р{6 = хГ|& = хГ}
_ р{6 =	6 =	} = к <2-4)
Р{Ь = ХР°} P-i'
Аналогично
р.,<) = р{6 = л)!),|(.=^}
= Р{б=Х.Р)°;6=Хр>°} _	(2-4')
F{6 = Xp’’}	л-’
Формулы (2.4) и (2.41) получаются как простые следствия теоремы
умножения вероятностей (1.11).
Так, например, если нас интересует условное распределение группы
семей с высоким доходом по качеству жилищных условий, т. е. распреде-
ление p.j(a	= х^ | {	= я }, то вычисления по (2.4) на
2.Б. СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
89
основе данных табл. 2.3 дают:
М46)°) =
0,01
0,20
0,02
0,20
0,07
0,20
0,10
0,20
= 0,05;
= 0,10;
= 0,35;
= 0,50,
О
М*Г) =
что означает, в частности, что из всем совокупности высокодоходных се-
мей в плохих жилищных условиях проживает 5%, в удовлетворитель-
ных — 10%, в хороших — 35% и в очень хороших — 50% (то, что речь идет
только о высокодоходных семьях, определяется условием = £ > }).
2.5.	Способы задания закона распределения:
функция распределения и функция
плотности вероятности
2.5.1.	Функция распределения вероятностен одномерной
случайном величины
Как установлено выше (см. п. 2.4), всякая генеральная совокупность
(случайная величина) определяется своим законом распределения вероят-
ностей р(ДХ). Поскольку интересующие нас области ДХ могут быть в
общем случае подмножествами общей природы, то возникает вопрос: ка-
ковы те способы задания числовых функций р, определенных на подмноже-
ствах ДХ, которые были бы достаточно удобны в плане конструктивном,
практическом?
Оказывается, для описания распределений одномерных случайных ве-
личин f достаточно задать способ вычисления вероятностей р(ДХ) =
Р{£ € ДХ) лишь для подмножеств ДХ некоторого специального ви-
да, а именно лишь для полузамкнутых слева интервалов вида
ДХ = [zmjn,z),
где zmjn — минимально возможное значение исследуемой случайной ве-
личины £ (оно может быть равно и — оо), а х — любое «текущее» (т. е.
задаваемое нами) возможное значение Вероятность же p([arrojn, ®)) =
90
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
7 {£ < а:} однозначно определяется заданием правого конца интервала,
т.е. числа х, а потому может интерпретироваться как обычная функция
от одного числового аргумента х.
Функцией распределения вероятностей (накопленной частотой)
F^(x) случайной величины £ называют функцию, ставящую в соответ-
ствие любому заданному значению х величину вероятности события
{f <«}, т.е.
*ё(«) = Р{« < «}•	(2.5)
В дальнейшем, если это не будет вызывать недоразумений, будем
опускать нижний индекс £ у функции F и называть ее просто «функцией
распределения*.
Рассмотрим поведение функции распределения. Во-первых, отметим,
что в дискретном случае событие А(х) =	< х} состоит из всех эле-
ментарных событий = {£ = х°}, таких, что х° < х. Поэтому в со-
ответствии с определением вероятности составного события (см. п. 1.1.3)
имеем
F(г) = Р{« < г} = £ P{f = ®?}= £ Pi (2.5')
«: r°<;r	t: <x
(суммирование в правых частях (2.5*) проводится по всем тем «, для ко-
о . ч
торых Xi < х).
Из (2.5Z) видно, что значения функции F(x) изменяются при увели-
чении аргумента х скачками, а именно при «переползании» величины х
через очередное возможное значение х? функция F(x) скачком увеличива-
ет свое значение на величину р,- = Р{£ = х?}.
Несколько иную картину мы будем наблюдать, анализируя поведение
функции распределения F^(x) в случае непрерывного исследуемого при-
знака Большинство представляющих практический интерес непрерыв-
ных случайных величин обладает тем свойством, что для любого отрезка
Ах вероятности Р{£ 6 Да:} стремятся к нулю по мере стремления к нулю
длины этого отрезка, и, следовательно, вероятности отдельных возмож-
ных значений х равны нулю (конкретный пример такого рода приведен
в п. 1.2.2 в задаче с экспертным оцениванием вероятности интересующе-
го нас события). Нетрудно понять, что для таких случайных величин
их функции распределения оказываются непрерывными. На рис. 2.4, а-г
представлены графики функций распределения случайных величин, рас-
смотренных соответственно в примерах 1.1, 1.2, 1.5 (с учетом табл. 2.2)
и в примере с экспертным оцениванием вероятности интересующего нас
события (п. 1.2.2).
2.5. СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
91
Рмс. 2.4. Графики функций распределения для: а — оцифрованного резуль-
тата подбрасывания монеты (нуль соответствует аверсу, едини-
ца — реверсу); б — числа очков, выпадающих при бросании пра-
вильной игральной кости; в — числа дефектных изделий, обна-
руженных в наугад выбранной партии, состоящей из 30 изделий
(см. табл. 2.2); г — экспертной оценки вероятности интересую-
щего нас события (при полной некомпетентности экспертов), см.
пример из п. 1.2.2. Стрёлжи на графиках означают, что точки, в
которые они направлены, не включаются в состав обозначенных
ими интервалов группирования
Из определения функции распределения непосредственно вытекают
следующие ее основные свойства:
a)	Ffa) — неубывающая функция аргумента х;
б)	Ff(ar) = 0 для всех х < zmin;
в)	Ff(a?) = 1 для всех х > а:т1П (жт|п и zmax — соответственно ми-
нимальное и максимальное возможные значения исследуемой случайной
величины £);
92
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
г)	Р{а < b] = Fffl) — F{(a) для любых заданных значений а и Ь
(для доказательства последнего свойства следует воспользоваться теоре-
мой сложения вероятностей (см. п. 1.1.3), а также тем обстоятельством,
что события А = {£ < а}, В = {£ < 6} и С — {а < £ < 6} связаны между
собой соотношением В = А + С).
2.5.2.	Функция плотности вероятности одномерной
случайной величины
В классе таких непрерывных случайных величин, функции распреде-
лений которых всюду непрерывны и дифференцируемы (а, как уже отме-
чалось, этот класс охватывает большинство представляющих практиче-
ский интерес непрерывных случайных величин), другой удобной формой
задания генеральной совокупности (исследуемой случайной величины ()
является функция плотности вероятности Д(«), определяемая как пре-
дел
Цх) = Птп	€[»>* + &}
7 д->о Д
F((x + А) - F^x)
11111	ж	}
или, что то же,
/«(*) = ffc),
(2.6)
(2.6')
т. е. /^(z) — это производная функции распределения F^(x) в точке х. Из
эквивалентных соотношений (2.6) и (2.6*), определяющих функцию плот-
ности f^(x)t вытекают непосредственно следующие ее свойства:
a)	/^ («)	0, так как функция F^(x) неубывающая;
б)	Р{£ € [ж, х 4- Д)} « Д(я) • А для малых отрезков Д (следует из
сравнения первых двух членов тождества (2.6));
в)	Р{£ € [«min,*)} = Ffa) = / f(u) du для любых х\
®min
®о+Д
г)	Р{£ 6 [«о, то + А)} = *i(s0 + А) - F^(x0) = J f(u) du для любых
*0
«о И Д;
хтвя
Д) € l^mim ®тах]} = J dx = 1.
®mln
Прокомментируем некоторые из этих свойств функции плотности.
Свойство б) позволяет пояснить вероятностный смысл функции плот-
ности. Так, предположив для определенности область возможных значе-
ний [«min,«max] исследуемой случайной величины £ конечной и разбив ее
2.5. СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
93
на, одинаковые и достаточно мелкие интервалы группирования А с цен-
трами
° .До о , А о о , А
= ®min + у, ar2 = я?1 4- А, х3 = х2 + А
и т. д., мы можем поставить в соответствие каждому t-му интервалу ве-
роятность осуществления события
приближенно равную в соответствии со свойством б) величине Д(ж?) * А.
Таким образом, по своему смыслу значения функции Д(ж) пропорциональ-
ны вероятности того, что исследуемая случайная величина примет зна-
чение б непосредственной близости от точки х. Этот факт, в частно-
сти, может служить основанием к тому, что дискретным аналогом функ-
ции плотности в случае дискретной случайной величины является по-
лигон частот, т. е. последовательность точек с координатами (х®,р,).
Отсюда же следует, что наиболее вероятным (модальным) значением ис-
следуемой непрерывной случайной величины является такое ее возможное
значение armod, в котором функция плотности достигает своего максимума,
т.е. Д(а:то<1) = maxjtfx).
X
хо zo4-A
Рис. 2.5. Функции: (а) распределения F( иормС»;®;®’3) и (б) плотности
ft норм (*;«; ff3) нормального закона
94
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Геометрическая интерпретация свойства г) состоит в том, что веро-
ятность события {£ € [яо> + Д)} оказывается (при любых заданных
z0 и Д) равной площади «столбика» под кривой плотности у = Д(х) с
основанием [г0, ж0 + А).
На рис. 2.5 показаны функции распределения ^норм(г; а; а2) и плотно-
сти Диоры(ж;а;ff2) одного из распространенных законов распределения —
нормального (подробнее см. и. 3.1 и 4.3). Заштрихованная площадь на
рис. 2.5, б дает геометрически наглядное представление о величине веро-
ятности Р{£ € [«о, «о + Д)}-
2.5.3.	Многомерные функции распределения и плотности.
Статистическая независимость случайных величин
Из вышеизложенного ясно, что вопрос об удобных способах задания
закона распределения случайной величины особенно актуален в непрерыв-
ном случае: для описания «поведения» дискретной случайной величины
£ универсальной и одновременно конструктивной формой (при «не слиш-
ком большом» числе возможных значений исследуемой случайной вели-
чины) является полигон вероятностей, т.е. форма, при которой каждому
о
возможному значению ставится в соответствие вероятность его осуще-
ствления Pi = Р{£ —	}. Поэтому сосредоточим теперь свое внимание
на непрерывном случае. Специфика многомерных схем в этом случае за-
ключается в том, что е отличие от одномерного случая многомерная
функция распределения


,f(p) <
(2-7)
перестает быть исчерпывающей (по информативности) формой задания
изучаемого закона распределения.
Многомерными аналогами конечных и полубесконечных отрезков (ко-
торые можно получить суммированием и пересечением полубесконечных
отрезков вида [—оо,ж)) являются конечные и полубесконечные гиперпа-
раллелепипеды. Именно для многомерных областей такого типа и опре-
деляет функция распределения (2.7) правило вычисления вероятностей.
Однако, если в одномерном случае этого было достаточно для «работы»
в соответствующем вероятностном пространстве, то в многомерном слу-
чае нас это уже не удовлетворяет. В частности, знание одной лишь фор-
мы (2.7) оказывается недостаточным для конструктивного решения такой
важной для статистических приложений задачи, какой является задача
описания закона распределения интересующих нас преобразований от ис-
ходных случайных величин	(общий подход к решению
2.5. СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
95
этой проблемы описан в п. 4.4).
Поэтому для описания закона распределения многомерной величины
С =	) в непрерывном случае используют функцию плот-
ности вероятности f^(x^\x^2\.. .,ж^), которую определим как такую
функцию f(x^ ,...,х^) от р переменных, что для любого (измеримого)
подмножества А возможных значении £ вероятность события G Л} мо-
жет быть вычислена с помощью соотношения
Р{£ € Л} = [	di(1) ...dxM,
А
(2.8)
где интегрирование ведется по данной области Л в соответствующем
р-мерном пространстве возможных значений £ (т. е. знак интеграла в (2.8)
определяет операцию р-кратного интегрирования).
Из данного определения функции плотности вероятности (фпв) не-
посредственно следует, что фпв и функция распределения (2.7) связаны
между собой соотношениями1:
ж(1) х(2)	*(₽)
= /
du^du^ ... dv№,
и
Л(*(1)
—оо —оо	— со
(Р) _
дх™дх™...дхМ'
(2.9)
Вероятностный смысл функции плотности тот же, что и в одно-
мерном случае: вероятность осуществления значения случайной величи-
ны £, лежащего в некоторой малой окрестности ДХ =	<
г<*> + Дг(1>, х<2> $	< х™ + Дг<2’,...,^> <	< хМ + Д»'”’}
точки X = (а/^а/2),.. .,а/р)), пропорциональна значению Д(Х) функции
плотности в этой точке и приблизительно равна, в частности, «элементу
1 Так же, как и в одномерном случае, наше описание относится лишь к таким непре-
рывным случайным величинам, функция распределения (2.7) которых непрерывна
по всем переменным внутри области возможных значений и имеет в этой области по
всем своим переменным непрерывную частную производную. Как отмечалось, такие
случайные величины составляют большинство в классе ситуаций, представляющих
практический интерес.
96
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
вероятности» Д(Х)ДХ, т.е.
/>{/» < £(1) < х(,) +	. ,zM <	< хМ + Дх<’>}
(2Л0)
Функции, определяемые соотношениями (2.7), или (2.7*), а также
(2.9), называют соответственно совместной функцией распределения и
совместной плотностью вероятности многомерного случайного признака
Для описания частного закона распределения вероятностей некото-
рой части компонент = (^1\^2\.. .,(^)» л < р, вектора £ (см.
п. 2.4.1) используются частная (маржинальная) функция распреде-
ления /(Дз/1),... ,а/я)) и частная (маржинальная) плотность веро-
ятности, задаваемые соотношениями:
где под понимается интегрирование по всему множеству возможных
значений случайной величины (ср. с (2.3) и (2-3*)).
Условная плотность вероятности f^(x^\x^2\... tx^ | & = С)
случайного вектора & = (f^l\/2\... ,£^) при условии, что значения
другого подвектора fa =	... ,^р^) зафиксированы на уров-
не С = (с(*+1),с(в+2),...,с<р)) (т.е. при условии = с^>+1\...,=
с(р)), определяется аналогично условным вероятностям р$. и p.j (см. (2.4) и
(2.4*)) с помощью теоремы умножения вероятностей (см. п. 1.1.3, формулу
(1.1/)):
/€1 (х(1),...,Ж(в) | £(в+1) = с(в+1),... ,?р) = с(р>)
_	(2.13)
Аа(с(э+1)^(в+2>,---»с(р))
2.5. СПОСОБЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ
97
Аналогично
л3(/’+1)>...,ж(₽)|{(1) = с<1»,...,{<•> = «<’>)
" —/е,(с<‘>........J’b •
В знаменателях правых частей (2.13) и (2.13*) стоят частные (маржи-
нальные) плотности подвекторов — соответственно & — (^*+1\.. .,^р^)
и = (^1\...,^в^), вычисленные в соответствии с (2.12).
Обратим внимание на существенное отличие частной (маржиналь-
ной) плотности fa(x^y.. .уХ^) от условной f^(x^,.. .уХ^ |	=
с(в+1),...	= с(р)), хотя обе они описывают распределение одного и то-
го же набора признаков С »• • •	' первая плотность не зависит от того,
какие значения имеют остальные компоненты анализируемой многомер-
ной случайной величины, в то время как условная плотность существенно
(в+1)	(р)	.
зависит от того, на каких именно уровнях <г	с' ' зафиксированы
Дл+i) Ар)
значения остальных компонент £'	,...,	'.
и
Рис. 2.6. Поверхность двумерной плотности вероятности (нормальный за-
кон с «отсеченными> краями)
На рис. 2.6 изображен график функции плотности двумерного закона
распределения вероятностей — двумерного нормального закона (его опи-
сание см. в п. 3.1). Там же изображены сечения поверхности двумерной
плотности плоскостями а/1) = с, т. е. плоскостями, перпендикулярными
98
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
оси Оа^. В сечении получаются с точностью до нормирующего множите-
ля одномерные законы (один из них указан стрелкой), характеризующие
условное распределение компоненты при условии = с. Прямая О А
прослеживает характер изменения наиболее вероятного значения случай-
ной величины в условном распределении этого признака (при условии
= с) в зависимости от зафиксированного значения с.
Статистическая независимость случайных величин
•••»€* (гДе признаки могут быть дискретными и непрерывными, ска-
лярными и векторными) вводится на базе понятия независимости системы
событий (см. (1.12) и (1.13)). Случайные величины &, , •• •, €к называют
статистически независимыми, если для любых (измеримых) областей их
возможных значений, соответственно А], А2,..., А*, имеют место соот-
ношения
Р{6 G Ai,6 G А2,...,& 6 AfcJ = Р{6 € А!} ... Р{£к € Afc}. (2.14)
В терминах вероятностей р^{3...1Л (для дискретных случайных вели-
чин) и плотностей	(для непрерывных случайных
величин) условие (2.14) может быть записано в виде:
2.6.	Основные числовые характеристики
случайных величин
Итак, исчерпывающие сведения об интересующем нас законе распре-
деления вероятностей можно задать и в виде полигона вероятностей (в
дискретном случае), и в виде функции плотности вероятностей (в общем
случае). Однако при практическом (статистическом) изучении поведения
случайных величин зачастую оказывается достаточной гораздо более
скромная информация в виде нескольких числовых характеристик распре-
деления, позволяющих оценить такие его свойства, как центр группирова-
ния значений исследуемой случайной величины, мера их случайного рас-
сеивания, степень взаимозависимости различных компонент изучаемого
многомерного признака. Так, например, при изучении закона распределе-
ния заработной платы работников интересуются в первую очередь средней
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
99
заработной платой и одной из мер ее случайного рассеивания — коэффи-
циентом дифференциации или дисперсией. К тому же подавляющее боль-
шинство используемых в статистических приложениях модельных зако-
нов распределения (биномиальный, пуассоновский, Парето, нормальный,
логар ифмически-нормальный, экспоненциальный и др., см. гл. 3) может
быть однозначно восстановлено по одной-двум своим числовым характе-
ристикам, например по среднему значению и дисперсии.
2.6.1.	Понятие о математических ожиданиях и моментах
Будем рассматривать различные функции р(£) от исследуемой слу-
чайной величины £ = f(w) (в эту схему, очевидно, может быть включен и
частный случай р(£) = £). Очевидно, и функция <z(f(w)) будет случайной
величиной, так как она является в конечном счете функцией, определенной
на множестве элементарных событий Результат операции «осредне-
ния» случайной величины <;(£), произведенной с учетом «взвешивания»,
отвечающего заданному распределению вероятностей случайной величи-
ны £, носит название математического ожидания д(£) и обозначается
Итак: если £ — непрерывная (может быть, и многомерная) слу-
чайная величина с плотностью (совместной) вероятности Д(Х), то
= У dX
(2.15)
(интегрирование производится по области всех возможных значений при-
знака £); если £ — дискретная случайная величина с возможными значе-
ниями и вероятностями их осуществления pi (i = 1,2,...), то
Ejr(e) = 53ff(x,°)-p..
(2.15')
Важную роль в теории и практике статистических исследований игра-
ют функции д(£) некоторого специального вида: дь(£) = £к и <?°(£) =
1 Если $(£) — векторная функция, т.е. д(() =	/’ЧО» • • •»1X5 Речь
идет о покомпонентном взвешенном осреднении. Общепринятая символика с ис-
пользованием буквы Е объясняется тем, что с этой буквы начинается латинское
написание слова «ожидание».
100
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(£ — Е£ (к = 1,2,...)? Математические ожидания функции дь(£) и ffk(£)
носят названия соответственно начальных и центральных моментов к-го
порядка случайной величины £.
Рассмотрим вначале начальные и центральные моменты одномерной
случайной величины £.
Итак, если для некоторого целого положительного числа к функция
xk интегрируема с весами Д(г) (суммируема с весами р,) на области воз-
можных значений £, то величина
mjk = Е£* =
’ xf((.x) dx>
если £ непрерывна;
если £ дискретна
(2.16)
называется начальным моментом А-го порядка или просто к-м моментом
этого распределения или соответствующей ему случайной величины £, и
мы говорим, что момент конечен или существует.1 2
Очевидно, что если существует момент ш*, то существует и цен-
тральный момент
т(0) _	_ Ш1 )* _ J /(х “mi )*/(х) dx> если £ непрерывна;
I “ mi) Pi» если £ дискретна.
Раскрывая (z — mi)* под знаком интеграла (или суммы), легко уста-
новить связи, существующие между центральными и начальными момен-
тами:
т<°> = 0;
1 Если случайная величина ( многомерна, т.е. ( = (^1\^2\ ... ,^₽^), то под ыо =
и $$(£) = (£ — Е£) мы будем понимать векторные случайные величины, компо-
ненты которых имеют вид соответственно
_ Е£(й))*1 .	_ Еб’а))*2-.-- • «(’лг) -
где »/ = 1,2,. ,.,р и к\ + къ + ... + kN = к. Так, например, при к — 2 в качестве
компонент функции <72 (О = £ могут рассматриваться всевозможные произведения
£<*) . (W), t,j = 1,2, ...,р, в том числе, конечно, квадраты (б^1^)3,^3^)3,..., (^F^)3,
а в качестве компонент функции 0°(£) — всевозможные попарные произведения вида
(£<*> - Е£<0)(£<Л _ Ее<')).
2 Ниже (см. пп. 3.1.9, 3.1.10, 3.2.2, 3.2.3) будут приведены примеры ситуаций, когда мо-
менты определенных порядков анализируемой случайной величины не существуют,
т.е. операции интегрирования (суммирования) вида (2.16) приводят к «бесконечно
большим» величинам.
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
(О)	2
mJ — тп2 — ту;
(О)	о । п з
mJ 1 — m3 — Зтгт2 4- 2т1;
mff = тп4 — 4т! т3 4- 6т?тг — Зт}
101
(2-18)
(ограничиваемся здесь первыми четырьмя моментами).
Наконец, при исследовании поведения многомерных случайных вели-
чин f =	... ,€^) важную роль играют р2-мерные векторные
функции д(£) =	••	\f)), компонентами которых являются
всевозможные попарные произведения центрированных компонент векто-
ра £, т. е. элементы матрицы

где
Ча = (f(<) - m(I°)(eW - m«>).
Математические ожидания элементов принято называть смешан-
ными вторыми центральными моментами или ковариациями многомер-
ного признака (, а матрицу

составленную из ковариаций
cov (С<ж),€<J)) = Е«и = Е{«(,) -	- mV’)} = °ij,
(2.19)
(2.20)
ковариационной матрицей признака По определению, все ковариацион-
ные матрицы являются симметричными (т. е. всегда = <7у); нетрудно
показать, что они являются и неотрицательно-определенными, Действи-
тельно, по определению (см. приложение 2) квадратная (р х р)-матрица
А называется неотрицательно-определенной, если для любого вектора с
действительными компонентами Л = (Л^\А^2\...,А^)т произведение
Хт • А - А будет неотрицательным. Беря последовательность любых дей-
ствительных чисел А^,А<2>,...,А^ и используя тождества
р р
<rtj = Ат • S • А,
(2.21)
получаем доказательство неотрицательной определенности ковариацион-
ной матрицы S = т. к. левая часть соотношения (2.21), очевидно, не
может выражаться отрицательным числом.
102
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.2.	Характеристики центра группирования значении
случайной величины
В качестве характеристик центра группирования значений исследу-
емого признака в статистической практике используют несколько видов
средних значений, моду и медиану. Опишем эти числовые характеристи-
ки.
Теоретическое среднее Е£ исследуемой случайной величины £ опре-
деляется как ее первый начальный момент, или, что то же, как ее мате-
матическое ожидание (см. (2.15) и (2.16)):
« • Д(ж) dxy
если £ непрерывна;
если £ дискретна.
(2.22)
Среднее значение Е£ является, пожалуй, основной и наиболее упо-
требительной характеристикой центра группирования значений случай-
ной величины.
Непосредственно из определения среднего значения легко получить
следующие его основные свойства:
а)	Ес = с, где с — любая неслучайная величина;
б)	E(cf) = cEf;
в)	Е({1 + fa + • • • + fw) = Efi + Efj + • • • + Efw;
г)	E(f  !?) = Ef • Ei?, если случайные величины f и tj статистически
взаимно независимы (см. п. 2>5.3).
Среднее геометрическое (теоретическое) значение €?(£) случайной
величины £ определяется (для признаков с положительными возможными
значениями) с помощью формулы
G(f) = eE<lB£)>
где е « 2,71828... — основание, а In — обозначение натурального логаг
рифма.
Можно показать, что геометрическое среднее значение G(f) всегда
меньше теоретического среднего Е£.
Геометрическое среднее находит применение при расчетах темпов из-
менения величин и, в частности, в тех случаях, когда имеют дело с ве-
личиной, изменения которой происходят приблизительно в прямо пропор-
циональной зависимости с достигнутым к этому моменту уровнем самой
величины (например, численность населения), или же когда имеют дело
со средней из отношений, например, при расчетах «индексов цен».
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
103
Среднее гармоническое значение случайной величины £ зада-
ется (лишь для признаков с положительными возможными значениями)
соотношением
Гармоническое среднее значение ряда чисел всегда меньше геометри-
ческого среднего значения тех же чисел, а тем более — их среднего ариф-
метического. Область его применения весьма ограничена. В экономике, в
частности, пользуются иногда гармоническим средним при анализе сред-
них норм времени, а также в некоторых видах индексных расчетов.
Модальное значение (или просто мода) zmod случайной величины
определяется как такое возможное значение исследуемого признака, при
котором значение плотности Д(я) (в непрерывном случае) или вероятно-
сти р{£ = ж} (в дискретном случае) достигает своего максимума. Таким
образом, мода представляет собой как бы наиболее часто осуществля-
ющееся (в экспериментах или наблюдениях), наиболее типичное значе-
ние случайной величины, т.е. значение, которое действительно является
«модным»1.
д Медиана a?me(j исследуемого признака определяется как его средневе-
роятяое значение, т. е. такое значение, которое обладает следующим свой-
ством: вероятность того, что анализируемая случайная величина окажет-
ся больше жте<1, равна вероятности того, что она окажется меньше zmed-
Для обладающих непрерывной плотностью непрерывных случайных ве-
личин, очевидно,
P{f > *m.d} = Р{( < *med) = 0,5
и медиану можно определить как такое значение armed на оси возможных
значений (оси абсцисс), при котором прямая, параллельная оси ординат
и проходящая через точку aimed» делит площадь под кривой плотности на
две равные части (рис. 2.7). В некоторых случаях дискретных распреде-
лений может не существовать величины, точно удовлетворяющей сформу-
лированному требованию. Поэтому для дискретных случайных величин
1 Мода является естественной характеристикой центра группирования значений слу-
чайной величины лишь в случаях так называемых одновершинных (одномодальных)
распределений. Многовершинные (многомодальные) распределения свидетельству-
ют о существенной неоднородности исследуемой совокупности. Их изучение пред-
ставляет интерес в первую очередь с точки зрения задач классификации объектов и
наблюдений (см. гл. 12).
104
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
медиану можно определить как любое число a:med, лежащее между двумя
о о
соседними возможными значениями zt0 и z,o+1, такими, что
Ге(4) < 0,5,
) > 0,5.
Рис. 2.7. Характер расположения моды zmod * медианы zmed и среднего зна-
чения Е( для некоторой асимметричной плотности распределения
/(х)
ЧО *i(4>+l
В случае симметричной плотности (или полигона распределения)
среднее Е£, мода ято<] и медиана zmed совпадают между собой. Для асим-
метричных распределений это не так (см. рис. 2.7).
2.6.3.	Характеристики степени рассеяния значений
случайной величины
Каждая из описанных ниже характеристик степени рассеяния — дис-
персия, среднеквадратическое отклонение и коэффициент вариации — да-
ет представление о том, как сильно могут отклоняться от своего центра
группирования значения исследуемой случайной величины. Если говорить
о форме кривой плотности, то эти характеристики описывают степень ее
«размазанности» по всему диапазону изменения чем больше величи-
на каждой из этих характеристик, тем более «размазанным» выглядит
соответствующее распределение (рис. 2.8).
Дисперсия Df случайной величины £ определяется как ее второй
центральный момент, т. е.
Df = m<0) =

если 4 непрерывна;
если £ дискретна.
(2.23)
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
105
Рис. 2.8. График плотностей (нормальных законов распределения) с раз-
личными значениями дисперсии и с одинаковым (нулевым) сред-
ним значением
Из определения дисперсии (и из свойств математического ожидания)
можно вывести следующие ее свойства:
a)	De = 0 (с — некоторая неслучайная величина);
б)	D(cf) = ?£>«;
в)	D(a + 6£) = 62 -Df (а и 6 — некоторые неслучайные величины);
г)	D(f 4- г}) = Df 4- Dr; — в случае, когда £ и rj являются взаимно
независимыми.
Часто для обозначения дисперсии используют греческую букву «сиг-
ма» (в квадрате), т. е. записывают = Df.
Среднеквадратическое отклонение сг% получается из дисперсии
извлечением квадратного корня сг^ = \/Т5£. Оно используется наряду с
дисперсией для характеристики степени рассеивания случайной величи-
ны и оказывается в ряде случаев более удобным и естественным, в первую
очередь, из-за своей однородности (в смысле единиц измерения) с различ-
ными характеристиками центра группирования.
Коэффициент вариации V( используется в тех случаях, когда сте-
пень рассеивания естественнее описывать некоторой относительной ха-
рактеристикой в сопоставлении со средним. В частности,
= Т? •100% = й • 100%>
т. е. коэффициент вариации — это отношение (в процентах) среднеквадра-
тического отклонения к соответствующему математическому ожиданию.
Из определения ясно, что Vf — величина безразмерная.
106
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.4.	Квантили и процентные точки распределения
При использовании различных методов математической статистики,
особенно разнообразных статистических критериев (см. гл. 8) и методов
построения интервальных оценок неизвестных параметров (см. гл. 7), ши-
роко используются понятия g-квантилей ug(F) и lOOg-процентных точек
wq(F) распределения F(x).
Квантилем уровня q (или q-квантилем) непрерывной случайной ве-
личины £, обладающей непрерывной функцией распределения F(x)y на-
зывается такое возможное значение uq(F) этой случайной величины, для
которого вероятность события £ < uq(F) равна заданной величине q, т.е.
F(ug) = Р{£ < ug} = q.	(2.24)
Очевидно, чем больше заданное значение q (0 < q < 1), тем больше
будет и соответствующая величина квантиля ид. Частным случаем кван-
тиля — 0,5-квантилем является характеристика центра группирования —
медиана.
Для всякой дискретной случайной величины функция распределения
F^(x) с увеличением аргумента х меняется, как мы видели, скачками,
и, следовательно, существуют такие значения уровней qy для каждого из
которых не найдется возможного значения uqy точно удовлетворяющего
уравнению (2.24). Поэтому в дискретном случае g-квантиль определяется
как любое число ug(F), лежащее между двумя возможными соседними
значениями х?(д) и z?(g)+i, такое, что Г(х?(д)) < q, но F(x^+1) q.
Часто вместо понятия квантиля используют тесно связанное с ним
понятие процентной точки. Под 100д%-ной точкой случайной величины
£ понимается такое ее возможное значение wg, для которого вероятность
события £ cjq равна д, т. е.
1 ~	= Р{£	= <?.
Для дискретных случайных величин это определение корректируется
аналогично тому, как это делалось при определении квантилей.
Из определения квантилей и процентных точек вытекает простое со-
отношение, их связывающее:
«« =	(2-25)
Для ряда наиболее часто встречающихся в статистической практике зако-
нов распределения (см. гл. 3) составлены специальные таблицы квантилей
и процентных точек. Очевидно, достаточно иметь только одну из таких
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
107
таблиц, так как если, например, по таблицам процентных точек требует-
ся найти 0,9-квантиль нормального распределения, то следует искать, в
соответствии с (2.25), 10-процентную точку того же распределения.
Наглядное геометрическое представление о смысле введенных поня-
тий дает рис. 2.9: на этом рисунке	Л(ж) 92 = Мх) а
по оси Оу откладываются значения функции плотности Д(ж).
Рис. 2.9. Геометрическое пояснение смысла gi-квантиля «91 и ЮОдо-
процентной точки случай стандартного нормального рас-
пределения, gi = 0,25 (соответственно «0,25 = —0,675) и 52 = 0,05
(соответственно wo.os = 1»65)
Квантильные характеристики помимо своей основной роли вспомога-
тельного теоретического статистического инструментария порой играют
самостоятельную роль основных характеристик изучаемого закона рас-
пределения или содержательно интерпретируемых параметров модели.
Так, широко распространенной характеристикой степени случайного рас-
сеяния при изучении законов распределения заработной платы и доходов
являются так называемые квантильные (уровня q) коэффициенты диф-
ференциации Kd(q)t которые определяются соотношением
Kd(q)=^- (0 < ? 0,25)
(наиболее распространенными среди них являются децильные коэффици-
енты дифференциации, когда полагают q = 0,1). При анализе модельных
законов распределения квантили и процентные точки используют также
для обозначения практических границ диапазона изменения исследуемого
признака: так, например, квантилями уровня 0,005 и 0,995 иногда опреде-
ляют соответственно минимальный и максимальный уровни заработной
платы работников в соответствующей системе показателей.
108
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.6.5.	Асимметрия и эксцесс
Обращаясь к формуле (2.17), определяющей центральные моменты
распределения, легко понять, что если плотность Д(х) (или последова-
тельность вероятностей = х?}) симметрична относительно среднего
значения = Е£ (т. е. /(n»i — ж) = /(пи +ж)), то все нечетные централь-
ные моменты (если они существуют) j равны нулю. Поэтому любой
нечетный, не равный нулю, момент можно рассматривать как характе-
ристику асимметрии соответствующего распределения. Простейшая из
(о)
этих характеристик и взята за основу вычисления так называемо-
го коэффициента асимметрии fa — количественной характеристики
степени скошенности распределения
Eg-m,)3
(4°’)* [Etf-tn,)2]*'
(2.26)
Нормировка с помощью деления т^ на (т^)^ введена для того,
чтобы эта характеристика не зависела от выбора физических единиц из-
мерения исследуемой случайной величины: формула (2.26) определяет без-
размерную характеристику степени скошенности распределения, инвари-
антную относительно физических единиц измерения f.
Таким образом, все симметричные распределения будут иметь нуле-
вой коэффициент асимметрии (см. рис. 2.5, 2.8, 2.9), в то время как рас-
пределения вероятностей с «длинной частью» кривой плотности, располо-
женной справа от ее вершины, характеризуются положительной асимме-
трией (см. рис. 2.7), а распределения с «длинной частью» кривой плот-
ности, расположенной слева от ее вершины, обладают отрицательной
асимметрией.
Поведение плотности (полигона) распределения в районе его модаль-
ного значения обуславливает геометрическую форму соответствующей
кривой в окрестности точки ее максимума, ее островершинность. Коли-
чественная характеристика островершинности — эксцесс (или коэффи-
циент эксцесса) fa оказывается полезной характеристикой при решении
ряда задач, например при определении общего вида исследуемого распре-
деления или при его аппроксимации с помощью некоторых специальных
разложений. Эта характеристика задается с помощью соотношения
в m«0) Т E(f-mi)4
(40’)2-	[E(f-mi)2]2’X
Ниже мы увидим, что своеобразным началом отсчета в измерении сте-
пени островершинности служит нормальное (гауссовское) распределение,
(2.27)
2.6. ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
109
ДЛЯ которого /?2 — 0-
Рис. 2.10. Примеры плотностей для положительной, отрицательной и нуле-
вой характеристик островершинности (эксцесса)
Как правило, распределения с более высокой и более острой вершиной
кривой плотности (полигона) имеют положительный эксцесс, а с менее
острой — отрицательный (рис. 2.10)1.
2.6.6.	Основные характеристики многомерных
распределений (ковариации, корреляции, обобщенная
дисперсия и др.)
Если при описании поведения одномерных и в какой-то мере двумер-
ных случайных величин исследователь еще имеет практически реализуе-
мые возможности использования подходящих модельных законов распре-
деления (см. гл. 3), то при исследовании признаков £ = (£<,	...»£^)Т
размерности большей, чем два (р > 2), как правило, приходится ограни-
чиваться лишь той информацией, которую ему доставляет знание первых
двух моментов: вектором средних значений
(2.28)
1 Правда, можно построить примеры, свидетельствующие о нарушении этой общей
закономерности.
110
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
и матрицей ковариаций
(^п	^1р\
<721 <722 ... <72р ,	(2.29)
^р2	• • • &рр'
(0	л(»)
где средние значения т\ компонент £ определяются в соответствии с
формулой (2.22) с использованием одномерных частных плотностей (по-
лигонов) распределения случайных величин а ковариации =
“ т 1*^)1 подсчитываются с использованием соответ-
ствующих двумерных частных плотностей (полигонов) распределения па-
ры случайных величин (^J\f^)-
Как и в одномерном случае, вектор средних значений является основ-
ной характеристикой центра группирования наблюдений исследуемого
многомерного признака £ (в соответствующем р~мерном пространстве ее
возможных значений).
Матрица ковариаций Е характеризует следующие свойства исследу-
емого многомерного признака.
1. Степень случайного разброса отдельно по каждой компоненте и
в целом по многомерному признаку. Легко видеть, что диагональные эле-
менты оц матрицы Е определяют частные дисперсии компонент ( , т. е.
степень случайного разброса значений одномерной случайной величины
Итак,
<7« = E(t(,) - mV’)2 = Df(i).
Многомерным аналогом дисперсии является величина определителя
ковариационной матрицы, называемая обобщенной дисперсией многомер-
ного случайного признака £1:
Do6f = det (Е).	(2.30)
Часто используется и другая характеристика степени случайного рас-
сеяния значений многомерной случайной величины — так называемый
след ковариационной матрицы Е, т.е. сумма ее диагональных элементов:
/Г (Е) = (Гц 4- С?22 + • • • + «Трр.	(2.31)
1 Мы придерживаемся распространенных матричных обозначений: det (А) или 1| —
определитель или детерминант (determinant, англ.) матрицы А; 1г(А) —след (trace,
англ.) матрицы А.
2.6.	ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
111
Из неотрицательной определенности матрицы Е (см. п. 2.6.1) и смы-
сла диагональных элементов о,* следует, что величины, определенные со-
отношениями (2.30) и (2.31), всегда неотрицательны.
Поясним геометрический смысл обобщенной дисперсии. Можно ска-
зать, что если, например, исследуемый многомерный признак подчинен
нормальному закону распределения (см. гл. 3), то для любого заданного
уровня вероятности Ро объем области (окружающей центр группирования
Mi), вероятность попадания в которую значении анализируемой случай-
[ой величины £ равна Pq, пропорционален \Д)<>б£ (этот объем пропорци-
онален также некоторому множителю, зависящему от размерности р, и
пропорционален, кроме того, некоторому числу, определяемому в зависи-
мости от заданного уровня вероятности Ро).
Характер и структура статистических взаимосвязей, суще-
ствующих между компонентами анализируемого многомерного признака,
также могут быть описаны с помощью ковариационной матрицы. Однако
в этом случае удобнее перейти к определенным образом нормированной
ковариационной матрице, называемой корреляционной, а именно к матри-
це
где элементы получаются из элементов с помощью нормировки

(2.33)
Характеристики называются коэффициентами корреляции меж-
ду случайными величинами и являются измерителями степени
тесноты линейной статистической связи между этими признаками и
обладают следующими свойствами:
а)	— 1 < ry* С 1, что следует непосредственно из неравенств
- т<л
б)	максимальная степень тесноты связи соответствует значениям ко-
эффициента корреляции, равным +1 или —1, и достигается либо при изме-
рении связи признака с самим собой (тогда, очевидно, т3] = 1), либо при
наличии линейной функциональной связи между  и т.е. в случае
112
ГЛ. 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
+ гДе &о и 61 — некоторые постоянные величины (при этом
если 61 > 0, то связь называется положительной, а если 61 < 0, то связь
называется отрицательной);
\	-	М М
в)	если случайные компоненты ' и ' статистически независимы,
то Tjk = 0 (следует непосредственно из того факта, что для независимых
случайных величин и E(^J^ • ^) = (Е£^)(Е£^)). Обратное
утверждение (из rj* = 0 следует независимость и £'*)) верно лишь для
некоторых частных случаев (например, для нормально распределенных
пар (^\^к^)) и неверно в общем случае.
ВЫВОДЫ
1.	Случайная величина (случайный признак) определяет перечень по-
казателей — количественных, ординальных (порядковых) или номиналь-
ных (классификационных), которые подлежат статистическому исследо-
ванию в ходе проводимых случайных экспериментов (наблюдений).
2.	«Возможные значения» случайной величины определяются при-
родой и составом пространства элементарных событий П: каждому эле-
ментарному исходу и соответствует «возможное значение» х(ы) исследу-
емой случайной величиной величины £, поэтому последнюю можно опре-
делить как функцию £ = £(w), заданную на множестве элементарных со-
бытий.
3.	Закон распределения вероятностей исследуемой случайной вели-
чины позволяет сопоставлять с любой измеримой областью ДХ возмож-
ных значений вероятность р(ДХ) события, заключающегося в том, что ре-
ализовавшееся в результате случайного эксперимента (наблюдения) зна-
чение данной случайной величины окажется принадлежащим этой обла-
сти, т. е.
Р(ДХ) = Р{< е ДХ}.
4.	Для описания закона распределения вероятностей многомерного
признака £ = (^1\...,(^) могут, как и в одномерном случае, использо-
ваться функция распределения F$(z<l\..., х^) =	<
а/р)} и функция плотности f^(x^ ...х^) = dpF^(x^, ...,х^)/дх^\
1 Помимо числовой (скалярной) формы эти «возможные значения» могут быть пред-
ставлены и в векторной, к в матричной форме н, более того, могут быть определены
в пространстве самой общей природы (в зависимости от сущности и целей исследу-
емого случайного эксперимента).
выводы
113
. ..,да/р\ Однако в отличие от одномерного случая исчерпывающей фор-
мой задания многомерного закона распределения является только со-
вместная функция плотности вероятности.
5.	Зная совместный закон распределения многомерной случайной ве-
личины £ =	можно получить частный (маржиналь-
ный) закон распределения любого подвектора	1
р, 1 к < р, а также условный закон распределения, описывающий
распределение любого подвектора , когда все или какая-то часть осталь-
ных компонент исходного векторного признака фиксируются на заданных
уровнях (см. (2.12) и (2.13)).
в. Если компоненты	анализируемого случайного при-
знака ( =	статистически независимы, то многомерный
закон распределения f^(x^\ ... ,я^р^) может быть описан р частными од-
номерными законами, так как в этом случае по определению
f((x™,XW,...,XM) =
7. При практическом изучении поведения исследуемого случайного
признака £ зачастую оказывается достаточным знания ограниченного на-
бора его числовых характеристик: среднего значения Е£, дисперсии Df,
коэффициентов асимметрии и эксцесса (/3j и fa), а в многомерном слу-
чае — еще элементов Ojk ковариационной матрицы Е.
ГЛАВА 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ
РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ
СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
Говоря о распространенности той или иной модели распределения в
практике статистических исследований, следует иметь в виду две возмож-
ные роли, которые эта модель может играть. Первая из них заключается
в адекватном описании механизма исследуемого реального процесса, гене-
рирующего подлежащие статистическому анализу исходные статистиче-
ские данные. В этом случае выбранная по тем или иным соображениям
(или выведенная теоретически) модель описывает закон распределения
вероятностей непосредственно анализируемой и имеющей четкую фи-
зическую интерпретацию случайной величины (заработной платы работ-
ника, дохода семьи, числа сбоев автоматической линии в единицу времени,
числа дефектных изделий, обнаруженных в проконтролированной партии
заданного объема, и т. д.). Подходы к построению таких моделей, методы
их анализа и обоснования относятся к области «реалистического» (или
содержательного) моделирования.
Другая роль широко распространенных в статистических исследо-
ваниях моделей — использование их в качестве вспомогательного тех-
нического средства при реализации методов статистической обработки
данных. С помощью моделей этого типа описываются распределения ве-
роятностей некоторых вспомогательных функций от исследуемых случай-
ных величин. Эти функции используются при построении разного рода
статистических оценок и статистических критериев (о способах постро-
ения оценок и критериев см. главы 6-8). К распределениям этого типа
относятся в первую очередь распределения «хи-квадрат», Стьюдента (t-
распределение) и F-распределение.
Этой условной классификации распределений мы и будем придержи-
ваться при изложении содержания данной главы.
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
115
3.1. Законы распределения, используемые
для описания механизмов генерации
реальных социально-экономических
данных
3.1.1. Распределения, возникающие при анализе
последовательности испытании Бернулли:
биномиальное и отрицательное биномиальное
Широкий класс случайных величин, которые приходится изучать в
практике статистических исследований, индуцируется последовательно-
стью независимых случайных экспериментов следующего типа: в резуль-
тате реализации каждого случайного эксперимента (наблюдения) некото-
рое интересующее нас событие А может произойти (с некоторой вероятно-
стью р) или не произойти (соответственно с вероятностью q = 1 — р); при
многократном (т-кратном) повторении этого эксперимента вероятность
р осуществления события А остается одной и той же, а наблюдения,
составляющие эту последовательность экспериментов, являются вза-
имно независимыми. Серию экспериментов подобного типа принято на-
зывать последовательностью испытаний Бернулли. Можно описать эту
последовательность в терминах случайных величин, сопоставляя с i-м по
счету экспериментом данной последовательности случайную величину
. _ ( 1, если событие А произошло;	. .
0, если событие А не произошло.	' ' '
Тогда «бернуллиевость» последовательности	означает, что
^{6 = 1} = ?{& = !} = ••’ = Р{£т = 1} = р, причем случайные величи-
ны •••»&» статистически независимы (определение статистической
независимости случайных величин дано в п.2.5.3).
При определенных (как правило, приблизительно соблюдающихся на
практике) условиях в схему испытаний Бернулли хорошо укладывают-
ся такие случайные эксперименты, как бросание монеты или игральной
кости, проверка (по альтернативному признаку) изделий массовой про-
дукции, обращение к «обслуживающему устройству» (с исходами «сво-
боден — занят»), попытка выполнения некоторого задания (с исходами
«выполнено — не выполнено»), стрельба по цели (с исходами «попада-
ние — промах») и т. п.
«Единичное» испытание Бернулли можно интерпретировать и как
извлечение объекта из воображаемой бесконечной совокупности, в которой
поля d объектов обладает некоторым интересующим нас свойством. Тогда
116 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
интересующее нас событие А заключается в том, что при этом извлечении
мы «вытащим» один из объектов, обладающих упомянутым свойством.
Биномиальный закон описывает распределение случайной величи-
ны ир(тп) = & 4-^2 4- - • • 4- т.е. числа появления интересующего нас
события в последовательности из т независимых испытаний, когда веро-
ятность появления этого события в одном испытании равна р.
Из определения биномиальной случайной величины следует, что ее
возможными значениями являются все целые неотрицательные числа от
нуля до пг. Для вывода вероятностей Р{ир(т) = ж} (ж = 0,2,...,ш) рас
смотрим внимательнее пространство элементарных событий, порожден-
ное последовательностью испытаний Бернулли. Очевидно, каждому эле-
ментарному событию w соответствует последовательность из нулей и еди-
ниц длины т

(3-2)
Разобьем эти последовательности на классы, включая в один (ж-й) класс
все последовательности типа (3.2), содержащие одинаковое число х еди
ниц:
х — 0:	(0,0, ...,0,0) = w(0)
1(l,0,...,0,0)=w1(l)
(0,1,...,0,0)=а>2(1)
(0,0,...,0,l) = wm(l)
Ik
(1,1,1,..., 1,0... ,0,0) = w1(fc)
(0,1,...,0,...,0,0) = и2(Л)
(0,0,... ,0,..., 1,1) = ^щху(к)
k = m: (1,1,...,1) = w(m).
Имея в виду, что число N(x) элементарных событий в классе с номе-
ром х равно числу сочетаний из тп элементов по х (поскольку х единиц
можно разместить на m местах именно таким числом различных спосо-
бов), а также тот факт, что вероятность осуществления любого элемен-
тарного исхода, входящего в класс с номером ж, равна, как нетрудно под-
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
117
_____	\Ш-Г	1
считать, величине р (1 — р) , получаем
= х} =	4- w2(x) + • • • 4- wc« (z)}
С*
=	(1 - рГ~* = cjpx(i - P)m’^
i
(3.3)
Это и есть формула (аналитическая запись, модель) биномиального
Рис. 3.1. Полигон вероятностей биномиального распределения для различ-
ных значений р и т = 10: а) р = 0,2; т = 10; р = 0,5; т = 10
закона1 * 3 распределения (см. рис. 3.1). Подсчет его основных числовых ха-
рактеристик (который в данном случае легче реализовать, не используя
прямые формулы типа (2.17)-(2.18), а опираясь на соотношение ир(т) =
6 + • • • + &п > взаимную независимость & и простоту вычисления их мо-
ментов) дает:
среднее:
мода хмод:
дисперсия:
асимметрия:
эксцесс:
Ei/p(m) = тр\
р(т 4-1) - 1 хмод С р(т 4-1);
Di/p(m) = mp(l-p);
0 --?~2р •
1	\/тр(1 -р)’
_ 1-6р(1-р)
2	тр(1-р)
1 Далее используется одно из широко используемых обозначений для числа сочетаний
из т элементов по z, а именно С^.
3 «Биномиальным» этот закон называется потому, что правая часть (3.3) представля-
ет собой z-й член биномиального разложения (р+(1 — р))т. Этот же факт позволяет
легко проверить соблюдение аксиомы о нормировке вероятностей, т.е. справедли-
вость тождества	“ Р)т~х = !•
118 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Биномиальное распределение широко используется в теории и практ
ке статистического контроля качества продукции, при описании функци
пирования систем массового обслуживания, в теории стрельбы и в друп
областях практической деятельности.
Отрицательный биномиальный закон описывает распределение сл
чайной величины и~(Л), определяемой испытаниями Бернулли G, G?--
(см. (3.1)) следующим образом:
£ (i = k — l, £& = *•
i=l	i=l
Другими словами Vp (к) — это число испытаний в схеме Бернулли (св
роятностью р появления интересующего нас события в результате пров
дения одного испытания) до к-го появления интересующего нас событ-
(включая последнее испытание). Нетрудно вывести аналитический bi
распределения случайной величины Ур(к). Зафиксируем любое ее вс
можное значение х. Из того, что при числе испытаний и~(к) = х enepei
осуществилось заданное число к появлений интересующего нас событи
следует, что на предыдущем шаге, т. е. при числе испытаний, равном х —
мы имели к — 1 появлений того же события. Следовательно, опирая
на теорему умножения вероятностей, мы можем выразить вероятное'
Р{&р (А) = ж} в терминах вероятностей, связанных с поведением бином
альных случайных величин рр(х — 1) и рр(1), а именно:
Г{^(к) = г} = %(г - 1) = к - 1} • Р{^(1) = 1}
=	(3.
= C*Z}p*(lх = к, к + 1,...
Рис. 3.2. Полигон вероятностей отрицательного биномиального закона рас-
пределения для различных значений к при р = 0,5
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
119
Название данного закона объясняется тем, что правые части (3.4}
являются последовательными членами разложения некоторого бинома с
отрицательным показателем. Соответствующий (3.4) полигон вероят-
ностей изображен на рис. 3.2.
Основные числовые характеристики закона:
среднее:
дисперсия:
асимметрия:
эксцесс:
е«<(*) = р
D^-(fc) =	_ ;
р
А =
1 + 4(1-р)+(1-р)2
fc(l-p)
Модель отрицательного биномиального распределения применяется в
статистике несчастных случаев и заболеваний, в задачах, связанных с
анализом количеств индивидуумов данного вида в выборках из биологи-
ческих совокупностей, в задачах оптимального резервирования элементов,
в теории стрельбы.
3.1.2.	Гипергеометрическое распределение
В одном из вариантов интерпретации биномиальной случайной ве-
личины Мр(тп) мы рассматривали некоторую воображаемую бесконечную
совокупность, доля р объектов которой обладает интересующим нас свой-
ством. Тогда i/p(m) означает число объектов, обладающих этим свой-
ством среди т объектов, случайно извлеченных из данной совокупности.
Гипергеометрическую случайную величину vM можно считать мо-
дификацией биномиальной случайной величины //р(т), приспособленной
к случаю конечной совокупности, состоящей из N объектов, среди кото-
рых имеются М объектов с интересующим нас свойством. Иначе говоря,
— это число объектов, обладающих заданным свойством среди
т объектов, случайно извлеченных (без возвращения) из совокупности N
объектов, М из которых обладают этим свойством. Очевидно, возмож-
ными значениями случайной величины i/M N(rn) будут все целые неотри-
цательные числа от max{0, т — (N - М)} до т'т{т,М}. Для вывода
аналитического вида ее закона распределения подсчитаем вероятность со-
бытия {i/д^ дгС771) = как отношение числа всевозможных выборок объема
т, приводящих к осуществлению этого события (числа «благоприятных»
120 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
исходов), к общему числу способов, которыми можно выбрать т объектов
из N (к числу всех возможных исходов). Очевидно, каждому набору из
х объектов с заданным свойством соответствует способов, кото-
рыми можно отобрать остальные т — х объектов из числа объектов, не
обладающих этим свойством. А поскольку такие наборы из х объектов
с заданным свойством можно сформировать различными способами,
то общее число «благоприятных» (для события N(m) = я}) исходов
будет	Учитывая, что число всех возможных исходов, т.е. всех
возможных способов, которыми можно извлечь т объектов из N предло-
Ст
N, получаем
= «} =
^т-х
' UN-M
(3.5)
Этот закон широко используется в практике статистического приемоч-
ного контроля качества промышленной продукции, а также в различных
задачах, связанных с организацией выборочных обследований.
Его основные числовые характеристики:
m у;
, „ м
среднее:
дисперсия:
асимметрия:
эксцесс:
а . 0-2^)
у/т% (1 - %) (N ~ 2WN ~ т ’
m~N I ~ 7 7
где
Ц 1 (N - 2)(N - 3)(N - т)'
(N - 1)№
с3(АГ) = 3
(JV - 2)(W - 3)QV - m) ’
(N - 1)№
(JV - 2)(N - 3)(N - m)
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
121
г глп =	18(7? - 1)___________6(7У - 1)
41 '	(N-2)(N-3) (N - 2)(АГ - 3)т% (1 - #)
3(N - l)Nm
(АГ — 2)(7V — 3)(АГ — m)’
При TV —> оо правая часть (3.5) стремится, как и следовало ожидать, к вы-
ражению для биномиального закона распределения (3.3), и соответственно
среднее значение, дисперсия, асимметрия и эксцесс гипергеометрического
распределения сходятся к аналогичным числовым характеристикам бино-
миально распределенной случайной величины (что легко устанавливается
с помощью соответствующего предельного перехода).
3.1.3.	Распределение Пуассона
Если нас интересует число наступлений определенного случайного со-
бытия за единицу времени, когда факт наступления этого события в дан-
ном эксперименте не зависит от того, сколько раз и в какие моменты вре-
мени оно осуществлялось в прошлом, и не влияет на будущее, а испыта-
ния производятся в стационарных условиях, то для описания распределе-
ния такой случайной величины обычно используют закон Пуассона (дан-
ное распределение впервые предложено и опубликовано этим ученым в
1837 г.). Этот закон можно также описывать как предельный случай би-
номиального распределения, когда вероятность р осуществления интере-
сующего нас события в единичном эксперименте очень мала, но число
экспериментов т, производимых в единицу времени, достаточно велико,
а именно такое, что в процессе р —» 0 и т —* оо произведение тр стре-
мится к некоторой положительной постоянной величине А (т.е. тр —> А).
Поэтому закон Пуассона часто называют также законом редких событий.
Обозначим пуассоновскую случайную величину Pq(oo) или просто 1/0 (имея
в виду предельный переход от биномиальной случайной величины ир(т)
по р —> 0 и т —* оо) и выведем ее закон распределения:
P{i/0 =	= ^lim^ Р{ир(т) = г} = limC® р®(1 - р)т
122 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Как видим, закон распределения Пуассона зависит от единственного
параметра Л, содержательно интерпретируемого как среднее число осу-
ществления интересующего нас события в единицу времени (см. рис. 3.3).
Рис. 3.3. Полигон вероятностей пуассоновского закона распределения для
различных значений А
С помощью «прямого счета» по формулам (2Л7)-(2.18) могут быть
подсчитаны основные числовые характеристики пуассоновской случайной
величины:
среднее:
дисперсия:
асимметрия:
эксцесс:
ЕЦ) — ^5
Оц) = А;
Пуассоновская случайная величина используется для описания числа
сбоев автоматической линии или числа отказов сложной системы (рабо-
тающих в «нормальном» режиме) в единицу времени; числа «требований
на обслуживание», поступивших в единицу времени в систему массово-
го обслуживания; статистических закономерностей несчастных случаев и
редких заболеваний.
Привлекательные прикладные свойства этого закона не исчерпыва-
ются вычислительными удобствами и лаконичностью формулы (3.6) (мо-
дель зависит всего от одного числового параметра А!). Оказывается, эта
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
123
модель остается работоспособной и в ситуациях, отклоняющихся от выше-
описанной схемы ее формирования. Например, можно допустить, что раз-
ные бернуллиевские испытания имеют разные вероятности осуществления
интересующего нас события рьрз, • • ->Рт- В этом случае биномиальный
закон применительно к такой серии испытаний уже не может быть при-
менен, в то время как выражение (3.6) остается приблизительно справед-
ливым и дает достаточно точное описание распределения интересующей
нас случайной величины, если только в него вместо А = тр доставить ве-
личину А = тр, где р = (pj Н-|-рт)/т. Сказанное означает, что можно
предположить, что анализируемая совокупность состоит из смеси множе-
ства разнородных подсовокупностей, таких, что при переходе из одной
подсовокупности в другую меняется доля р содержащихся в них объектов
с заданным свойством, а следовательно, меняется и среднее число А осу-
ществления интересующего нас события в единицу времени. Можно далее
показать, что если вместо использования среднего значения этих р (или А)
(при котором мы остаемся в рамках модели (3.6)) ввести в рассмотрение
закон распределения меняющегося параметра А, интерпретируемого как
случайная величина, то мы придем к другому, но в определенном смысле
близкому к пуассоновскому закону распределения. Так, например, если
предположить, что функция плотности распределения случайного пара-
метра А имеет вид
со k 1 х
yuh F(fc) = / х е' Xdx — гамма-функция Эйлера, положительные числа
о
к и р — параметры закона, а х > 0 — возможные значения А, число
осуществления (в единицу времени) интересующего нас события будет
подчинено известному нам отрицательному биномиальному закону (3.4)
(подробнее о распределении f\(x) см. в п. 3.2.5).
3.1.4.	Полиномиальное (мультиномиальное) распределение
Полезным обобщением биномиального распределения на случай бо-
лее чем двух возможных исходов является полиномиальный (мультиноми-
альный) закон распределения. Можно интерпретировать анализируемую
в этом случае ситуацию таким образом, что мы имеем дело с некото-
рой бесконечной совокупностью, содержащей объекты I различных типов
(/ > 2), представленных соответственно в долях РьРг,(в биноми-
альной генеральной совокупности мы имели I = 2, pi = р и рг = 1 — р).
Таким образом, в результате одного случайного эксперимента (случай-
124 ГЛ 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
ного извлечения объекта из этой бесконечной совокупности) объект ти-
па j появляется с вероятностью pj. Нас будет интересовать распределе-
ние многомерной случайной величины (i/J^m),^2^™),...	по“
рожденной m-кратным случайным экспериментом (т.е. извлечением тп
объектов), где v^\m) — число объектов j-ro типа, оказавшихся в этой
выборке, а р = (pi,p2,... , Pz) (очевидно £ pj = 1 и £	= т).
j=i	j=i
Соответствующее многомерное дискретное распределение описывает-
ся выражением (доказывается прямым вероятностным рассуждением)
Р{1/^(т) =	..., i^(m) =	}
_ ml x(i) х<о	(3.7)
_ Z<o7p’ ’
где а/г\а/2\...	— любые (заданные) целые неотрицательные числа,
подчиненные условию J3 = ш, а выражение (3.7) определяет вероят-
j=i
ность того, что среди т извлеченных объектов оказалось ровно а/1) объ-
(2)
ектов 1-го типа, х объектов 2-го типа и т. д. Можно также связывать
полиномиальную случайную величину с тп-кратным случайным экспери-
ментом, каждый из которых может закончиться одним из / возможных
исходов Ai, Ла,..., Л/, причем вероятность исхода Aj в единичном экспе-
рименте равна pj.
Название распределения объясняется тем, что выражение (3.7) явля-
ется общим членом разложения многочлена (полинома) (pi 4----
Вектор средних значений (Е|/^(т),..., Ez/{/\m)) и ковариации Ojk =
E{(i/pJ\m) — Ei/^(m))(i4*\m) — Ei/J*\m))} компонент исследуемой мно-
гомерной случайной величины определяются соотношениями:
средние:	Ez/^ (т) = mpj-t j = 1,2,...,/;
дисперсии:	Di/Jj)(m) = <тя = тр,(1 - pj), j = 1,2,... ,/;
ковариации:	ojk = -mpjpk\ = 1,2,...,/, j/E
Полиномиальное распределение применяется главным образом при
статистической обработке выборок из больших совокупностей, элементы
которых разделяются более чем на две категории (например, в различ-
ных социологических, экономило-социологических, медицинских и других
выборочных обследованиях).
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
125
3.1.5.	Нормальное (гауссовское) распределение
Это распределение занимает центральное место в теории и практике
вероятностно-статистических исследований. В качестве непрерывной ап-
проксимации к биномиальному распределению оно впервые рассматрива-
лось А. Муавром еще в 1733 г. (см. ниже теорему Муавра-Лапласа, п. 4.3).
Некоторое время спустя нормальное распределение было снова открыто и
изучено независимо друг от друга К. Гауссом (1809 г.) и П. Лапласом
(1812 г.). Оба ученых пришли к нормальному закону в связи со своей
работой по теории ошибок наблюдений. Идея их объяснения механизма
формирования нормально распределенных случайных величин заключает-
ся в следующем. Постулируется, что значения исследуемой непрерывной
случайной величины формируются под воздействием очень большого чи-
сла независимых случайных факторов, причем сила воздействия каждого
отдельного фактора мала и не может превалировать среди остальных,
а характер воздействия — аддитивный (т. е. при воздействиях случай-
ного фактора F на величину а получается величина а + Д(Г), где случай-
ная «добавка» Д(^) мала и равновероятна по знаку1. Можно показать,
что функция плотности распределения случайных величин подобного типа
имеет вид
у?(ж; а, о2) =	—е-<	,	(3.8)
V2?r • о
2
где а я а — параметры закона, интерпретируемые соответственно как
среднее значение и дисперсия данной случайной величины (в виду осо-
бой роли нормального распределения мы будем использовать специальную
символику для обозначения его функции плотности и функции распреде-
ления).
Соответствующая функция распределения нормальной случайной ве-
личины £(а,а2) обозначается Ф (х; а, а2) и задается соотношением
Ф(ж; а,о2) = Р{((а,о2) < х} =
е dt .
(3-8')
Условимся называть нормальный закон с параметрами а = 0 и
а2 = 1 стандартным, а его функции плотности и распределения обозна-
чать соответственно у>(х) = <р(х; 0,1) и Ф(я) = Ф(х; 0,1). Соответственно
1 Строгая теоретическая формализация этих условий содержится, например, в цен-
тральной предельной теореме, см. п. 4.3.
126 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
**	2
нормальный з.р.в. с произвольными значениями параметров а и а будем
называть (а,<т ) нормальным.
Во многих случайных величинах, изучаемых в экономике, технике,
медицине, биологии и в других областях, естественно видеть суммарный
аддитивный эффект большого числа независимых причин. Но централь-
ное место нормального закона не следует объяснять его универсальной
приложимостью, как это было принято долгое время (по-видимому, под
влиянием выдающихся работ К. Гаусса и П. Лапласса).
В этом смысле нормальный закон — это один из многих типов распре-
деления, имеющихся в природе, правда, с относительно большим удель-
ным весом практической приложимости. И потому нам понятна ирония,
звучащая в известном высказывании Липмана (цитируемом А. Пуанкаре в
своем труде «Исчисление вероятностей», Париж, 1912 г ): «Каждый уве-
рен в справедливости нормального закона: экспериментаторы — потому,
что они думают, что это математическая теорема; математики — потому,
что они думают, что это экспериментальный факт».
Однако не следует упускать из виду, что полнота теоретических ис-
следований, относящихся к нормальному закону, а также сравнительно
простые математические свойства делают его наиболее привлекательным
и удобным в применении. Даже в случае отклонения исследуемых экс-
периментальных данных от нормального закона существуют по крайней
мере два пути его целесообразной эксплуатации: а) использовать его в ка-
честве первого приближения; при этом нередко оказывается, что подобное
допущение дает достаточно точные с точки зрения конкретных целей ис-
следования результаты; б) подобрать такое преобразование исследуемой
случайной величины £, которое видоизменяет исходный «ненормальный»
закон распределения, превращая его в нормальный. Удобным для ста-
тистических приложений является и свойство «самовоспроизводимости»
нормального закона, заключающееся в том, что сумма любого числа нор-
мально распределенных случайных величин тоже подчиняется нормаль-
ному закону распределения. Кроме того, закон нормального распределе-
ния имеет большое теоретическое значение: с его помощью выведен целый
ряд других важных распределений, построены различные статистические
критерии и т.п. (х -э Г и F-распределения и опирающиеся на них крите-
рии, см.п. 3.2.1-3.2.3, а также гл. 8).
Графики нормальных плотностей приведены на рис. 2.5, 2.6, 2.8 и 2.9.
Основные числовые характеристики нормального закона:
среднее, мода, медиана:	Ef = ®mod = ®med = а;
дисперсия:	D£ = а2;
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
127
асимметрия:
эксцесс:
центральные
моменты
порядка к > з:
01 =0;
02 = 0;
{0	при к = 2т — 1,
1 • 3 •... (2m — 1 Jo-2”* при к = 2т
т = 3,4,- • ••
Двумерный нормальный закон описывает совместное распределе-
ние двумерной случайной величины £ =	с непрерывными ком-
понентами и механизм формирования значений которых тот же,
что и в одномерном случае, причем множества случайных факторов, под
воздействием которых формируются значения с и С > вообще говоря,
пересекаются (отсюда возможная зависимость и
Введем в рассмотрение основные числовые характеристики двумер-
ной случайной величины £ =
вектор средних:
т(1)
т
(2)
тп
, где = Е^’);
М =
ковариационная матрица:
где = Е{(£0) - m0)) (£{k} -
<7j2
коэфф ициент корреляции:	r=-------
Совместная двумерная плотность <р(х^\х^\ М, S) нормального за-
кона может быть записана в виде
<f{xw,xw-, M,S)=--------------------j-
2ir(<zna22(l - r’)l
1	Г(х(1> - m(1))
2(1 - r’) [
(xW - m<2’)2'
х ехр
^11
(1)\2
—-------2т
х<'> - т<‘>
х<2> - mW
1/2	(3-9)
°22
°22
или в виде
^,xW; М, £) = ?(%; М,Е) =
2ir|E|1/2
(39<)
128 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
где X = (^(2)), верхний индекс Т означает транспонирование матрицы или
вектора, |Е| = det (Е) — определитель ковариационной матрицы, Е”1 —
матрица, обратная к ковариационной, а ехр{с} = ес. Изображение поверх-
ности плотности двумерного нормального закона приведено на рис. 2.6.
Частные плотности	,<тц) и ^(2)(з/2\п/2\(Тц) могут
быть получены из совместной по формуле (2.12):

1
—=6 a*n
у2эгац
/ (2)	(2) х 1	-^-^h2
Эти формулы означают, что частные законы распределения ком-
понент двумерного нормального закона сами являются одномерными
нормальными законами с параметрами соответственно (т^^ац) и
(m(3),cr22).
Условные плотности	|	= а/2)) и ^(а)(а/2) |	= z^)
получаются с использованием общих формул (2.13) и (2.13'):
Отсюда следует, в частности, что условное распределение компонен-
ты при фиксированном значении другой компоненты = х^) снова
описывается нормальным законом, параметр среднего значения которого,
как и следовало ожидать, зависит от фиксированного значения х^:
1/2
Е(^’> |	= z^) =	- rr№),
и дисперсия которого не зависит от х^ и равна
D(f(0 | *0) =	= а..(1 _ г»).
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
129
Многомерный нормальный закон описывает совместное распре-
деление р-мерной случайной величины £ =	с непре-
рывными компонентами механизм формирования значений каждой из
которых тот же, что и в одномерном случае, причем множества случай-
ных факторов, под воздействием которых формируются значения
вообще говоря, пересекаются (отсюда их возможная взаимоза-
висимость). Задавшись р-мерным вектор-столбцом М средних значений
компонент и (р х р)-матрицей ковариаций S (см. п. 2.6.6), можно выписать
р-мерную совместную плотность многомерного нормального закона:
v(xW,xW,...,xM; М,Е)
_	1	-|(Х-М)ТЕ“1(Х-М) •	(3.10)
" е
Здесь, как и прежде, X =	.. .,х^)Т — вектор-столбец те-
кущих переменных, a |S| = det(E) — определитель ковариационной ма-
трицы.
Вырожденность матрицы Е (т.е. равенство нулю определителя 1=1)
делает соответствующее многомерное распределение вырожденным (или
несобственным); это означает, в частности, что разброс значений иссле-
дуемого многомерного признака сосредоточен в подпространстве меньшей,
чем р, размерности. За исключением некоторых специальных случаев мы
всегда будем полагать, что нами уже осуществлен переход в это подпро-
странство меньшей размерности, так что в наших рассуждениях предпо-
лагается |Е| > 0.
3.1.6.	Логарифмически-нормальное распределение
Случайная величина т] называется логарифмически-нормально рас-
пределенной, если ее логарифм (Inq) подчинен нормальному закону рас-
пределения. Это означает, в частности, что значения логарифмически-
нормальной случайной величины формируются под воздействием очень
большого числа взаимно независимых факторов, причем воздействие ка-
ждого отдельного фактора «равномерно незначительно» и равновероятно
по знаку. При этом в отличие от схемы формирования механизма нормаль-
ного закона последовательный характер воздействия случайных факторов
таков, что случайный прирост, вызываемый действием каждого следую-
щего фактора, пропорционален уже достигнутому к этому моменту значе-
нию исследуемой величины (в этом случае говорят о мультипликативном
характере воздействия фактора). Математически сказанное может быть
5 Прикладная статистика и оспины эконометрики
130 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
формализовано следующим образом. Если ffo = а — неслучайная компо-
нента исследуемого признака Т] (т. е. как бы «истинное» значение 1} в идеа-
лизированной схеме, когда устранено влияние всех случайных факторов),
а ^1,^2, ...,^дг — численное выражение эффектов воздействия упомяну-
тых выше случайных факторов, то последовательно трансформированные
действием этих факторов значения исследуемого признака будут:
Ш = По + 6 ' %;
% = п\ + 6 • т;

Отсюда легко получить
= €1 + + • • • +
(3.11)
где Атц = T]i+i — гц, Но правая часть (3.11) есть результат аддитивно-
го действия множества случайных факторов, что при сделанных выше
предположениях должно приводить, как мы .знаем, к нормальному рас-
пределению этой суммы. В то же время, учитывая достаточную много-
численность числа случайных слагаемых (т.е. полагая N —* оо) и отно-
сительную незначительность воздействия каждого из них (т.е. полагая
Атц —> 0), можно от суммы в левой части (3.11) перейти к интегралу
/ — = In Т] — In rfy = In if — In a.
П
4o
Это и означает в конечном счете, что логарифм интересующей нас
величины (уменьшенный на постоянную величину In а) подчиняется нор-
мальному закону с нулевым средним значением, т. е.
F4(x) = P{q < х} = Р{1п 7) < 1ns}
In X
Г
0
dt,
откуда дифференцированием по x левой и правой частей этого соотноше-
ния получаем
/»(«) =
1	-(In «-In а)3
--------С
2% • ох
(3.12)
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
131
(правомерность использованного при вычислении Д(ж) тождества
Р{т} < ж} = Р{1пт/ < In ж} вытекает из строгой монотонности преобра-
зования In Т]).
Описанная схема формирования значении логарифмически-нормаль-
ной случайной величины оказывается характерной для многих конкрет-
ных физических и социально-экономических ситуаций (размеры и вес ча-
стиц, образующихся при дроблении; заработная плата работника; доход
семьи; размеры космических образований; долговечность изделия, работа-
ющего в режиме износа и старения, и др). Примеры графиков плотности
логарифмически-нормального распределения представлены на рис. 3.4
Рмс.3.4. График функции плотности логарифмически-нормального рас-
пределения для различных <г при а = 1
Ниже приводятся результаты вычисления основных числовых харак-
теристик логарифмически-нормального распределения (в терминах пара-
метров закона а и а ):
среднее:
мода:
медиана:
дисперсия:
асимметрия:
эксцесс:
Ет} = ае^а ;
-а\
®mod —	j
®med =
Di? = (ЕЧ)2(е°'Э - 1) = «’/(/ - 1);
2	13
Д = (е"	+2);
Дг = (е’3 - 1)(е3"3 + Зе2"’ + бе"’ + 6).
Из этих выражений видно, что асимметрия и эксцесс логарифми-
132 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
чески-нормального распределения всегда положительны (и тем ближе к
нулю, чем ближе к нулю ст ), а мода, медиана и среднее выстраиваются как
раз в том порядке, который мы видим на рис. 2.7, причем они будут стре-
миться к слиянию (а кривая плотности — к симметрии) по мере стрем-
ления к нулю величины а2. При этом, хотя значения логарифмически-
нормальной случайной величины образуются как «случайные искажения»
некоторого «истинного значения» а, последнее в конечном счете выступа-
ет не в роли среднего значения, а в роли медианы,
3.1.7.	Равномерное (прямоугольное) распределение
Случайная величина £ называется равномерно распределенной на от-
резке [а, 6], если ее плотность вероятности Д(х) постоянна на этом отрезке
и равна нулю вне его, т. е.
{1
Ь-а
О
при а х Ь\
при а < а и х > Ь.
(3.13)
Так как график функции изображается в виде прямоугольника
(см. рис. 3.5), то такое распределение также называют прямоугольным.
Рмс.З.Б. Функция плотности равномерной случайной величины (/;(х)) и
суммы двух (/q3(z)) и трех (Дз(х)) независимых равномерно рас-
пределенных на [0,1] случайных величин
Соответственно функция распределения F^(x) равномерного закона
задается соотношениями:
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
133
(О при х а;
7—- при а < х Ь;	(3.13*)
о — а
1 при х > Ь,
Примерами реальных ситуаций, связанных с необходимостью рас-
смотрения равномерно распределенных случайных величин, могут слу-
жить: анализ ошибок округления при проведении числовых расче-
тов (такая ошибка, как правило, оказывается равномерно распределен-
ной на интервале от —5 до +5 единиц округляемого десятичного зна-
ка); время ожидания «обслуживания» при точно периодическом, че-
рез каждые Т единиц времени, включении (прибытии) «обслуживаю-
щего устройства» и при случайном поступлении (прибытии) заявки на
обслуживание в этом интервале (например, время ожидания пассажи-
ром прибытия поезда метро при условии точных двухминутных интер-
валов движения и случайного момента появления пассажира на плат-
форме будет распределено приблизительно равномерно на интервале
[О мин, 2 мин]).
Отметим еще две важные ситуации, в которых используется равно-
мерный закон. Во-первых, в теории и практике статистического анализа
данных широко используется вспомогательный переход от исследуемой
случайной величины £ с функцией распределения F(x) к случайной вели-
чине rj = F(£), которая оказывается равномерно распределенной на отрез-
ке [0,1] (см. п. 4.4). Этот прием является полезным при статистическом
моделировании наблюдений, подчиненных заданному закону распределе-
ния вероятностей, при построении доверительных границ для исследуе-
мой функции распределения и в ряде других задач математической ста-
тистики. Во-вторых, равномерное распределение иногда используется в
качестве «нулевого приближения» в описании априорного распределения
анализируемых параметров в так называемом байесовском подходе в усло-
виях полного отсутствия априорной информации об этом распределении
(см. п. 7.6.).
Числовые характеристики равномерного закона:
среднее, медиана:
дисперсия:
асимметрия:
эксцесс:
"С — ®med —
Df=^;
s 12 ’
0i =0;
134 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Отметим в заключение одно важное свойство суммы п независимых
равномерно распределенных случайных величин: распределение этой сум-
мы очень быстро (по мере роста числа слагаемых) приближается к нор-
мальному закону. В частности, если — равномерно распределенные на
отрезке [0,1] и независимые случайные величины, то можно показать, что
плотность Дж(я?) случайной величины qn = fi 4 F имеет вид
n-l
при
n—1
при
при
n—1
n—1
(область возможных значений случайной величины Т]п, очевидно, задает-
ся отрезком [0,п]). Геометрическое изображение последовательного из-
менения вида плотности Д.(я) по мере роста числа слагаемых п (для
п = 1,2,3) дано на рис. 3.5. Это свойство используется, в частности, при
статистическом моделировании нормально распределенных наблюдений.
3.1.8.	Распределения Вейбулла и экспоненциальное
(показательное)
Рассмотрим один общий механизм формирования распределений, от-
носящийся, в частности, к случайным величинам, характеризующим дли-
тельность жизни элемента, сложной системы или индивидуума (задачи
теории надежности, анализ коэффициентов смертности в демографии и
т. п.). Пусть £ — время жизни анализируемого объекта (системы, инди-
видуума) и F(t) = Р{£ < t] — его функция распределения, которую мы
полагаем непрерывной и дифференцируемой. В задачах данного профиля
важной характеристикой является интенсивность отказа (коэффициент
смертности) X(t) исследуемых элементов возраста t, определяемая соот-
ношением
А(г) = -ГгШ’	<3-14’
Разрешая уравнение (3.14) относительно функции распределения
F^(f), получаем
- f X(t)dt
F^(x) = 1 - е о	(3.15)
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
135
Таким образом, конкретизация вида функции распределения F^(x)
полностью определяется видом функции интенсивности отказов (времен-
ной зависимостью коэффициентов смертности) A(t).
Многочисленные экспериментальные данные (и в области демогра-
фии, и в области анализа надежности технических элементов и систем)
показывают, что в широком классе случаев функция A(t) имеет характер-
ный вид кривой, изображенной на рис. 3.6. Из этого графика видно, что
весь интервал времени можно разбить на три периода.
1	.1 I I I I I 1! I I 1 1 1 1 I—
1 .4 9 14 19 24 29 34 3&44 49 54 59 64 69 74
,	-----I	I
; Прира*! Нормальная ; Старение и износ
^ботка * эксплуатация v
Рис. З.в. Типичное поведение кривой смертности (интенсивности отказов):
кривая описывает изменение коэффициента смертности мужского
населения Франции по данным 1955 г.1
На первом из них функция A(t) имеет высокие значения и явную тен-
денцию к убыванию. На техническом языке это можно объяснить нали-
чием в исследуемой совокупности элементов с явными и скрытыми де-
фектами (сборки, некондиционности отдельных свойств и т. п.), которые
приводят к относительно быстрому выходу из строя этих элементов. Этот
период принято называть периодом «приработки» (или «обкатки»).
Затем наступает период нормальной эксплуатации, характеризующийся
приблизительно постоянным и сравнительно низким уровнем «смертно-
сти» элементов. Природа смертей (или «отказов») в этот период носит
внезапный характер (аварии, несчастные случаи и т.п.) и не зависит от
возраста объекта. И наконец, последний период жизни (или эксплуата-
ции) элемента — период старения и износа. Природа «отказов» в этот
период — в необратимых физиологических или физико-химических явле-
136 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
ниях, приводящих к ухудшению качества элемента, к его «старению». В
соответствии с этой кривой смертности периоду «приработки» соответ-
ствует возраст от 0 до 9 лет, периоду «нормальной эксплуатации» — от
9 до 39 лет, а периоду «старения» — возраст после 39 лет.
Каждому периоду соответствует свой вид функции А($), а следова-
тельно, и свой закон распределения времени жизни
Рассмотрим класс степенных зависимостей, описывающих поведение
A(t), а именно
>(() = Аоа‘а-1,	(3.16)
где Ао > 0 и о > 0 — некоторые числовые параметры. Очевидно, зна-
чения а<1,а=1иа>1 отвечают поведению функции интенсивности
отказов соответственно в период приработки, нормальной эксплуатации
и старения.
Подставляя (3.16) в (3.15), получаем вид функции распределения Frft)
времени жизни £ элемента:
F£(0=l-e“Ao‘*,
ОО.
(3.17)
Соответственно плотность вероятности
/е(0 = Лоа<“_1е_Ло‘",
ОО.
(3-17')
Это и есть распределение Вейбулла. Поведение графиков функции
плотности распределения Вейбулла представлено на рис. 3.7. К тому
же самому типу распределения можно прийти, отправляясь от широкого
класса различных вероятностных законов и интересуясь распределением
крайних членов их вариационных рядов.
Рис. S.7. Графики функций плотности^ распределения Вейбулла для раз-
личных значений а
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
137
Основные числовые характеристики распределения Вейбулла:
среднее:
мода:
дисперсия:
момент к—го порядка:
(здесь Г(г) — так называемая гамма-функция Эйлера, т.е. Г(г) =
J zx-1e-xdx).
о
Экспоненциальное (показательное) распределение хотя и является
частным случаем распределения Вейбулла (когда а = 1, см. соответ-
ствующую кривую плотности на рис. 3.7), но представляет большой са-
мостоятельный интерес. Из вышесказанного следует, что оно адекватно
описывает распределение длительности жизни элемента, работающего в
режиме нормальной эксплуатации. Экспоненциальный закон (и только
он) обладает, в частности, тем важным свойством, что вероятность бе-
зотказной работы элемента на данном временном интервале (t, t 4- Д) не
зависит от времени предшествующей работы t, а зависит только от дли-
ны интервала Д. Экспоненциально распределенную случайную величину
можно интерпретировать так же, как промежуток времени между двумя
последовательными наступлениями «пуассоновского» события. Приклад-
ная популярность экспоненциального закона объясняется не только разно-
образными возможностями его естественной физической интерпретации,
по и исключительной простотой и удобством его модельных свойств. Ни-
же приводятся его функция распределения и плотность вероятности, а
также его основные числовые характеристики:
Г€(х) = 1 - е-4*, х > 0;
Л(*) = Аое-Л°х, х>0;
среднее:
мода:
медиана:
®mod — 0,
1	1 г»
®med — » • 1П 2,
АО
138 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
дисперсия:
асимметрия:
эксцесс:
d^=72;
/?2=6.
Двустороннее экспоненциальное распределение (распределе-
ние Лапласа). Симметричная унимодальная функция плотности этого
закона с «острым» максимумом в точке х = 0 часто используется для
описания распределения остаточных случайных компонент («ошибок») £
в моделях регрессионного типа (см. гл. 11.). График этой функции плот-
нос1и представляет собой как бы результат «склеивания» графика пока-
зательного распределения со своим зеркальным — относительно верти-
кальной оси — отражением (с учетом необходимой нормировки), так что
уравнение функции плотности имеет вид
/(*) = 1а .
(-оо < X < оо).
Рис. S.8. График функции плотности распределения Лапла сж
Нетрудно подсчитать основные числовые характеристики этого зако-
на распределения:
среднее:
мода:
медиана:
дисперсия:
асимметрия:
эксцесс:
Е< = 0;
®mod ~ О'
•^med = 0;
Df = 2/А2;
Л = 0;
& = 3.
3.1. МОДЕЛИ З.Р.В. В ОПИСАНИИ ГЕНЕЗИСА ДАННЫХ
139
3.1.9.	Распределение Парето
В различных задачах прикладной статистики довольно часто встре-
чаются так называемые «усеченные» распределения. Такие распределе-
ния описывают вероятностные закономерности в неполных («усеченных»)
генеральных совокупностях, т. е. в таких совокупностях, из которых зара-
нее изъяты все элементы с количественным признаком, превышающим не-
который заданный уровень с0 (или, наоборот, меньшим, чем со). Скажем,
налоговые органы обычно интересуются распределением годовых доходов
тех лиц, годовой доход которых превосходит некоторый порог Со, уста-
новленный законами о налогообложении. Эти и некоторые аналогичные
распределения иногда оказываются приближенно совпадающими с распре-
делением Парето, задаваемым функциями:
В этих формулах а > 0, а х > с0, т. е. область мыслимых значений данной
случайной величины £ есть полупрямая (со. + оо). Функция плотности
имеет вид монотонно убывающей кривой, выходящей из точки (со,а/со).
Рис. 3.9. График функции плотности распределения Парето для различных
значений а
140 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Основные числовые характеристики этого распределения существуют
не всегда, а лишь при соблюдении определенных требований к величине
параметра а:
среднее:
(существует при а > 1);
мода:
медиана:
®mod —
•^med — 2" • CqJ
дисперсия:
F е* _ Q А
Ь? — --------- Cq
(существует при а > 2);
момент к—го порядка:
(существует при а > к).
3.1.10.	Распределение Коши
Этот закон весьма специфичен, поскольку ни один из его моментов
положительного порядка (в том числе даже среднее значение) не суще-
ствует. Распределение Коши унимодально, симметрично относительно
своего модального значения (которое, следовательно, одновременно явля-
ется медианой) и задается функцией плотности вероятности
/(Z) = i
с
2 . / Г2 » —00 < Х < 00 ’
с + (z — а)
где с > 0 — параметр масштаба ио — параметр центра группирования,
определяющий одновременно значение моды и медианы.
0,4
Рис. 3.10. График функции плотности распределения Коши
3.2. З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
141
Соответственно функция распределения задается соотношением
F(x) = i 4- — arcth -—
v }	2 я-	с
Отметим два важных свойства («сожовоспроизво<^л<ости») распре-
деления Коши.
1. Если случайная величина £ имеет распределение Коши с параме-
трами с и а, то любая линейная функция	имеет распределение того
же типа с параметрами с =	| • с и а = 61  а 4- 60;
2. Если случайные величины	... ,£п независимы и имеют одно и
то же распределение Коши, то среднее арифметическое £ = (fi 4-1-£п)/я
имеет то же самое распределение, что и каждое &.
3.2.	Законы распределения вероятностей,
используемые при реализации техники
статистических вычислений
Ниже описываются пять законов, основное назначение которых —
предоставление исследователю необходимого аппарата для построения
разного £>ода статистических критериев и интервальных оценок параме-
тров: х -распределение («хи-квадрат»-распределение); t-распределение
(Стьюдента); распределение (распределение дисперсионного отноше-
ния); ©-распределение (бета-распределение) и Г-распределение (гамма-
распределение). Объяснение механизма их действия можно связывать со
«статистикой нормального закона», т. е. с изучением распределений неко-
торых функций от набора независимых и одинаково стандартно нормаль-
но распределенных случайных величин.
3.2.1.	«Хи-квадрат»-распределение с т степенями свободы
(№ (т)-распределение)
В связи с гауссовской теорией ошибок астроном Ф. Хельмерт исследо-
вал суммы квадратов т независимых стандартно нормально распределен-
ных случайных величин, придя таким образом к функции распределения
Fxa(m)(z), которую позднее К. Пирсон назвал функцией распределения «хи
квадрат»1. Для отрицательных х функция Fx2(my(x) = 0, а для неотри-
1 Н е 1 m е г t F. R. Uber die Wahrscheinlichkeit von Potenzsummen der Beobachtungs*
fehler etc. Z. F. Math, und Phys., 21 (1876); Pearson K. On the criterion that
a given system of deviation from the probable in the case of correlated system of
142 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
дательных х
Fxa(m)(z) = р{х* 2(т) < *}

(3.18)
где параметр закона т — целое положительное число, которое принято
называть числом степеней свободы, а Г(у) — значение гамма-функции
„	з
Эйлера в точке у.
Соответствующая плотность вероятности задается функцией
ф-1
х3 * е s,
х > 0.
(3.18')
При in 2 функция плотности постоянно убывает (для х > 0), а при
in > 2 имеет единственный максимум в точке zmod = т — 2.
Рис. 3.11. График функции плотности Х*т) -распределения для различных
значении тп
variables..., «Phil Mag.», V. 50 (1900), 157.
2 Значение Гамма-функции Эйлера в точке у определяется интегралом: Г(у) =
ОО
f dt. Из определения непосредственно следует, например, что при целых по-
о
ложвтельных значениях у: Г(у) = (у-1)! и Г(у+ |) = 2“вУ*-1-3-5- -• (2у-1) (более
подробные сведения о гамма-функции см. в книге [Большей Л. Н., Смирнов Н. В.]).
3.2. З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
143
_	2
Распределение х появилось впервые при исследовании распределения
последовательности независимых и одинаково стандартно нормально рас-
пределенных сл^чайных^величин^1,^2»Выяснилось, что случай-
ная величина % (тп) = fi 4-Ь подчиняется закону % -распределения
с т степенями свободы.
Основные числовые характеристики х2(т)'РаспРеделения:
среднее:
мода:
дисперсия:
асимметрия:
эксцесс:
Ех’(тп) = тп;
ramod = тп - 2
(тп > 2);
Dx2(*n) = 2m;
23/2
3.2.2.	Распределение Стыодента с т степенями свободы
(<(тп)-распределение)
Английский статистик В. Госсет (писавший под псевдонимом «Стью-
дент») получил в 1908г.1 следующий результат. Пусть	— не-
зависимые (0, ст2)-нормально распределенные случайные величины. Тогда
плотность распределения случайной величины
описывается функцией
(—оо < х < 4-оо).
(3.19)
Распределение (3.19) получило название распределения Стьюдента
с т степенями свободы (или f(m)-распределения). Из выражения (3.19)
Student. The probable error of a mean. — Biometrika, B, 6 (1908), 1.
144 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
следует, что функция плотности ft(z) не зависит от дисперсии <т2 слу-
чайных величин & и, кроме того, является унимодальной и симметричной
относительно точки х = 0, (см. рис. 3.12).
Рис. 3.12. Графики функции плотности <(т)-распределею<я при т = 4 и
стандартного нормального распределения е(х; 0,1)
Основные числовые характеристики 1(т)-распределения:
среднее, мода, медиана:
дисперсия:
асимметрия:
эксцесс:
Et(rn) — ^mod — ®med —
z x m
Di(m) = ——5
m — z
(существует только при m > 2);
Д=0;
т — 4
(существует только при т > 4).
3.2.3.	Распределение дисперсионного отношения с числом
степеней свободы числителя тА и числом степеней
свободы знаменателя т2 (Г(тп1, тп2 ^распределение)
Рассмотрим mi + т2 независимых и (0, tr2)-нормально распределен-
ных величин fi,...,	щ,..., i?ma и положим
3.2. З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
145
r(mi, т2) =---
Очевидно (см. п. 3.2.1), та же самая случайная величина может быть
пределена и как отношение двух независимых и соответствующим обра-
)м нормированных х -распределенных величин х (mi) и X (”»2), т.е.
F(rai,ra2) — 1	2/	\
X ("»з)
Английский статистик Р. Фишер в 1924 году показал , что плотность
ероятности случайной величины F(m1,m2) задается функцией
/р(т!,тэ)(ж
(V)-r(T)
х3
т ।
(mix 4- т2) 4
(О О < оо),
(3.20)
не, как обычно, Г(у) — значение гамма-функпии Эйлера в точке у, а сам
1кон называется F-распределеиием с числами степеней свободы числите-
я и знаменателя, равными соответственно иц и т2.
Основные числовые характеристики F(rai, газораспределения:
среднее:
мода:
дисперсия:
асимметрия:
эксцесс:
EF(mi,m2) = —1712	(существует при т2 > 2);
т2 — 2
(rai - 2) • т2
Xmo,I_ тДтг + 2) (для те1 > О.
ВГ(тьт2) =	+ ”*2—(при щ2 > 4);
1	21	m,(m3-2)2(m2-4)	”
(2raj + т2 - 2) у/8(т2 - 4)
Рл = --------7====== (при т2 >6);
(га2 - 6) у/{тх 4- тг - 2)т1
3("12 - 6) (2 + 1)3?)
$2 =---------------- - 3 (при т2 > 8).
т2 — о
Fisher R. On a distribution yielding the error functions of several well-known
statistics. — Proc. Intern. Math. Congr. Toronto, 1924, 805.
146 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Рис. 3.13. График функции плотности F(mi, m2 ^распределения для раз-
личных значений m2 при mi = 10
Отсюда непосредственно следует, что при mi,m2 > 2 F-распреде-
ление всегда имеет модальное значение, меньшее единицы, и среднее зна
чение, большее единицы. Это означает, в частности, что данное распре-
деление имеет асимметрию, подобную той, что изображена на рис. 2.6 (в
этих случаях говорят, что распределение имеет положительную асимме-
трию независимо от того, существует ли коэффициент асимметрии fa).
Р. Фишером данный тип распределений выводился не для случайной
величины	а для ее натурального логарифма (поделенного по-
полам), т.е. для случайной величины С = | lnF(mi,m2). Распределение
этой случайной величины часто называют z- распределением Фишера. Од-
нако в современной статистической практике предпочитают использовать
F-распределение, обладающее более простыми свойствами.
3.2.4.	Гамма-распределение (Г-распределение)
Описанные ниже два типа распределения представляют весьма ши-
рокие и гибкие двухпараметрические семейства законов, которые включа-
ют в себя в качестве частных случаев различные комбинации уже из-
вестных нам случайных величин. Основное прикладное значение Г- и В-
распределений — в их богатых вычислительных возможностях: функции
распределения %2,t, F и ряд других могут быть вычислены (после подхо-
дящего преобразования переменных) в терминах Г- или В-распределений.
3.2. З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
147
(роме того, Г-распределение иногда используется и при реалистическом
юделировании: с его помощью описывается, например, распределение до-
:одов и сбережений населения в определенных специальных ситуациях.
Рис. 3.14. График функции плотности гамма-распределения для различных
значений а к b
Двухпараметрический закон Г-распределения случайной величины
(в, Ъ) описывается функцией плотности:
А(а,Ь)(ж) —
при 0 х < оо;
при х < О
(3.21)
де Г(в) — Г-функция Эйлера, а > 0 — параметр «формы» и 6 > 0 — па-
аметр масштаба. Легко понять, что Г-распределенная случайная величи-
а с параметрами а и b (будем обозначать ее у(а, 6)) связана со случайной
еличиной 7(0,1) простым соотношением:
6т(в,6) = 7(а,1).
Отметим несколько полезных свойств Г-распределения.
1.	Из вида функции плотности х2(т)-распределения (см. (3.18)) непо-
редственно следует, что оно является частным случаем Г-распределения:
остаточно положить в (3.21) а = т/2 и Ь = 1/2.
2.	Сумма любого числа независимых Г-распределенных случайных
сличив (с одинаковым параметром масштаба Ь) 7i(«i,6) 4- 7г(а2> 6) +
•• + 7п(ап, Ь) также подчиняется Г-распределению, но с параметрами
•а? + • • • 4-ап и Ь.
148 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
Основные числовые характеристики случайной величины 7(0,6):
среднее*.
мода:
дисперсия:
асимметрия:
эксцесс:
Ет(в, 6) =
а — 1	.	.
Smod = —(при а 1);
D7(a,6) = 4;
О
3.2.5.	Бета-распределение (В-распределение)
Как отмечалось выше, двухпараметрический закон В-распределения
обладает весьма высокой гибкостью и общностью: в частности, через
функцию В-распределения могут быть вычислены такие часто используе-
мые распределения, как t , F, биномиальное, отрицательное биномиальное
и др. В-распределение используется и для описания некоторых реальных
распределений, сосредоточенных на отрезке [0,1] (например, для описания
распределения величин субъективных вероятностей, полученных в ходе
экспертного опроса, см.п.2.1.3). Случайная величина ^(ajjOj), подчиня-
ющаяся закону В-распределения с параметрами «ц и а2 (0 < ai < 00,
0 < aj < 00), имеет плотность вероятности
/д(аъ aa)(s) —
[ Г(а\г(^\ ’	- ж)Оа~’ ПР” 0 < г < 1;	(3.22)
I 0	для остальных значений х.
Отметим несколько полезных свойств В-распределения.
1.	Если 7(«],6) и 7(а2,6) — две независимые Г-распределенные слу-
чайные величины, то отношение 0(ai,a2) = 7(а1»6)/(7(а1,6) + 7(a2,6))
подчиняется закону В-распределения с параметрами <Xj и a2.
2.	Случайная величина 0(1,1) распределена равномерно на отрезке
[0,1] (см. п. 3.1.7).
3.	Функция распределения квадрата стьюдентовской величины t2(m)
(см. п. 3.2.2) связана с функцией распределения случайной величины 0 со-
3.2. З.Р.В. В ТЕХНИКЕ СТАТИСТИЧЕСКИХ ВЫЧИСЛЕНИЙ
149
/ ж2
^(т)(«) = *Jj( I 2
43 3 * \ т + х
4.	Функция распределения случайной величины F(mi,m2) (см.
.3.2.3) связана с функцией распределения случайной величины 0 соот-
+lmjx j 
5.	Между функцией распределения случайной величины /9 и распре-
ниями биномиального типа (см. п. 3.1.1) существуют соотношения:
Гр(т,п-т+1) (з) — 52 ^пХ (1 ~	*»
к=т
со
^(„,о.)(1 - *) = £ С”^_1гт(1 - х)\
к=п
6.	Непосредственный анализ плотности (3.22) обнаруживает симме-
ричность плотностей /j(abaa)W И /р(а^,аг)(х) ОТНОСИТвЛЬНО ПрЯМОЙ X =
,5 (рис. 3.15), что в терминах соответствующих функций распределения
Рис. 3.16. Графики функций плотности ^-распределения при различных
значениях параметров ai н аз: 1) 01 = 2, аз — 4; 2) ах =4, аз =
2; 3) ai = 1/2, а2 = 1/2
ожет быть записано в виде
^(ai.aajC®) — 1	Х)
150 ГЛ. 3. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (З.Р.В.)
(поэтому, в частности, при составлении таблиц В-распределения обычно
ограничиваются случаем 0 <	а2).
Основные числовые характеристики В-распределенной (с параметра-
ми и а2) случайной величины Д(в1,а2):
среднее:
мода:
дисперсия:
асимметрия:
эксцесс:
/?2 =
Е/5(а1}а2) — —;
«1 + а2
Xmod =	----о (ПРИ «I > 1 « «2 > 1);
D/?(a1>O2) = --------
(в] 4- а2) (ai + «2 + 1)
а — ^(а2 ~~ °1 )у^д1 ~Ь fl2 ~Ь 1,
(<Zj + а2 4- 2)^/aia2
-3.
ВЫВОДЫ
1.	Модельный (т.е. аналитический) способ задания закона распреде-
ления вероятностей (з.р.в.) является наиболее удобной формой его опи-
сания. При этом способ вычисления вероятности того, что исследуемая
дискретная случайная величина £ примет заданное значение х (т.е. способ
вычисления значения Р{£ = я}), так же как и способ вычисления значения
функции плотности распределения вероятностей ж(ж) в заданной точке х
для непрерывной случайной величины, определяется явным аналитиче-
ским заданием подходящей функции (см. формулы (З.З)-(З.Ю), (3.12),
(3.13), (3.17 )). Иногда этот способ называют параметрической формой
задания з.р.в.
2.	Следует выделить два направления использования моделей з.р.в.
в теории и практике вероятностно-статистических и эконометрических
исследований. Первое направление связано с так называемым реали-
стическим моделированием поведения конкретных анализируемых при-
знаков — среднедушевого семейного.дохода, тех или иных поведенческих
или производственных характеристик хозяйственных субъектов, параме-
тров финансового рынка или демографической ситуации и т. п. В этом
случае модель з.р.в. призвана описать и объяснить механизм генериро-
вания (генезис) анализируемых исходных данных. Другая роль широко
распространенных моделей з.р.в. — их использование в качестве вспомо-
гательного технического средства при реализации различных методов
выводы
151
статистического анализа данных — при построении разного рода ста-
тистических оценок и статистических критериев (см. гл. 6-8).
3.	К наиболее распространенным в практике вероятностно-статисти-
ческих исследований моделям з.р.в., описывающим поведение дискрет-
ных случайных величин, следует отнести биномиальный, гипергеометри-
ческий, пуассоновский, полиномиальный и отрицательный биномиальный
законы.
4.	При описании поведения непрерывных случайных величин в
области социально-экономических исследований наиболее распространен-
ными являются модели нормального (гауссовского), логарифмически-
нормального, паретовского, вейбулловского, экспоненциального, лапласов-
ского, равномерного, Коши, гамма- и бета-распределений.
5.	При подборе модели «под анализируемые реальные данные» сле-
дует представлять себе общую схему (или механизм) формиро-
вания значений той или иной «модельной» случайной величины.
Так, например, условия генерирования и специфика пуассоновской слу-
чайной величины определяют ее как число наступления интересующего
нас события за единицу времени, когда факт наступления такого собы-
тия в случайном эксперименте (испытании, наблюдении) не зависит от
того, сколько раз и в какие моменты времени оно наступило в прошлом,
и не влияет на будущее, а испытания проводятся в стационарном ре-
жиме. Аналогично могут быть описаны и условия генерирования других
модельных случайных величин.
6.	Грамотная реализация основных процедур математико-статисти-
аеского анализа данных, в частности, построение точечных и интерваль-
ных оценок для неизвестных значений параметров анализируемой модели
см. гл. 7), статистическая проверка гипотез, связанных со структурой и
1араметрами рассматриваемой модели (см. гл. 8), невозможна без знания
моделей «хи-квадрат», стьюдентовского и фишеровского F-распределений
[ умения пользоваться их таблицами.
7.	Прикладные возможности моделей многомерных з.р.в. значитель-
но скромнее. Наибольшее распространение здесь получили многомерный
юрмальный закон (для непрерывной многомерной случайной величины,
м. (3.10)) и полиномиальный з.р.в. (для дискретной многомерной слу-
сайной величины, см. (3.7)).
ГЛАВА 4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
В гл. 2 и 3 изложены основные понятия теории вероятностей, включая
набор моделей законов распределения, наиболее распространенных в тео-
рии и практике статистической обработки данных. Настоящая глава по-
священа описанию некоторых связей, существующих между этими поня-
тиями и моделями, а также отдельных их свойств, полезных для понима-
ния сущности излагаемых далее методов экономического моделирования и
статистического анализа данных.
4.1.	Неравенство Чебышева
В п. 2.6.3 мы познакомились с основной характеристикой степени
случайного разброса значений случайной величины — с ее дисперсией
<72 = Df. Из смысла этой характеристики следует, что вероятность зафик-
сировать при наблюдении случайной величины ( значение, отклоняющее
от ее среднего а = Е£ не менее чем на заданную величину Д, должна
расти с ростом о2. Чем больше величина дисперсии и2, тем более вероят-
ны значительные отклонения значений исследуемой случайной величины
от своего центра группирования а = Е£. Конечно, зная плотность (или
полигон) распределения вероятностей Д(х), можно точно вычислить ве-
роятность событий вида {|£ — а| Д}, а именно
Р{|£ - а| > А) =
яп |г—а|>Д
Е р.,
если £ непрерывна;
если £ дискретна.
(4-1)
Так, например, если ( подчиняется (а, о2)-нормальному закону рас-
пределения, то вероятность событий вида |£ - а| > Д зависит только от
того, сколько раз в заданной величине отклонения Д «уложится» средне-
квадратическое отклонение а — x/DJ•
4.1. НЕРАВЕНСТВО ЧЕБЫШЕВА
153
Однако хотелось бы уметь оценивать вероятности таких событий,
пираясь только на знание величины дисперсии о2 — Df, не обращаясь к
точному знанию закона распределения анализируемого признака Имен-
о эта задача и решается с помощью неравенства, выведенного русским
атематиком П. Л. Чебышевым1:
2
F{|f - а| > А) <	(4.2)
ie а = Ef и <? = Df = Е({ - а)2.
Доказательство этого неравенства несложно:
2
л.. I*— U|^U	ж-.	S
СО
X Д(«) dx < J(x- a?f((x) dx =
—bo
i случае дискретного признака доказательство проводится аналогично с
иеной «элементов вероятностей» Д(ж) dx вероятностями Pi = Р£ =
}, а интегралов — соответствующими суммами).
Из хода доказательства видно, что если распределение исследуемо-
► признака £ симметрично (относительно а = Е£), то имеют место и
посторонние аналоги неравенства:
2
P{f - а > А} = Р{а - ( > А} С	(4.2')
Как и всякий общий результат, не использующий сведения о кон-
фетном виде распределения случайной величины £, неравенство Чебы-
эва дает лишь грубые оценки сверху для вероятностей событий вида
J - а| А}. Так, например, если оценивать вероятность события
' - а| > За} для нормального признака £, не зная, что он подчиняется
уссовскому закону (т. е. используя неравенство Чебышева), то получим
(Ja j	5»
См.: Чебышев П.Л. О средних величинах. — Математический сборник, 1867,
II. В том же 1867 г. во французском журнале «Journ. math, puree et appl», XII, была
опубликована работа Бьенэмэк также содержащая как идею доказательства этого
неравенства, так и само неравенство. Поэтому неравенство (4.2) часто называют
также неравенством Бьенэме-Чебышева.
154
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Интересно сравнить эту величину с точным значением этой же ве-
роятности, которое получается с помощью таблиц нормального распре-
деления и равно 0,0027: мы видим, что точное значение вероятности в
40 (!) раз меньше ее грубой оценки, полученной на основании неравенства
Чебышева.
4.2.	Закон больших чисел и его следствия
Давно было замечено, что результаты отдельных наблюдений (будь
то экономические, демографические, физические, метеорологические или
иные наблюдения), хотя и произведенных в относительно однородных
условиях, колеблются сильно, в то время как средние из большого числа
наблюдений обнаруживают замечательную устойчивость.
Математическим основанием этого факта служат различные формы
так называемого закона больших чисел. Формулировку первого частно-
го варианта этого закона связывают с именем французского математи-
ка С. Д. Пуассона (Poisson S. D. Recherches sur la probability de jugements
en matiere criminelle et en matiere civile..., Paris, Gauthier-Villars, 1837).
В формулировке, приведенной ниже, этот закон был впервые доказан
А.Я.Хинчиным (см. Hintchin A. Sur la loi des grands nombres. Comptes
rendus de Г Academie des Sciences, 189 (1929), 477-479).
4.2.1.	Закон больших чисел
Пусть G	— последовательность независимых и одинаково
распределенных случайных величин. Если среднее значение а = Е& суще-
ствует, то среднее арифметическое случайных величин	по мере
неограниченного роста числа слагаемых (т.е. при п —* оо) сходится по
вероятности к этому теоретическому среднему значению а, т. е. для лю-
бых сколь угодно малых положительных величин е и У наступает такой
«момент* По, начиная с которого (т. е. при всех п «о) будет справедливо
неравенство
Доказательство этого утверждения не вызывает затруднений, если
дополнительно потребовать существования конечной дисперсии случай-
ных слагаемых т.е. существования D& = о2 < оо. Действитель-
но, в этом случае для доказательства (4.3) достаточно воспользовать-
ся неравенством Чебышева (4.2) применительно к случайной величине
4.2. ЗАКОН БОЛЬШИХ ЧИСЕЛ И ЕГО СЛЕДСТВИЯ
155
(п) = (6 н---Ь^п)/П- Легко подсчитываются Е£(п) = а и Df(n) = ст2/п,
г, следовательно, в соответствии с (4.2)
Р{1««)-«!>*} <
D{(n) _ <72
Выбрав п0 > мы обеспечим выполнение (4.3) при любых сколь
годно малых заданных значениях е и б.
В качестве следствия закона больших чисел рассмотрим следующим
ажный результат, объясняющий эффект устойчивости относительных
астот .
4.2.2.	Теорема Бернулли
Пусть производится п независимых случайных экспериментов (или
аблюдений случайной величины £), в результате каждого из которых
ожет осуществиться или не осуществиться некоторое интересующее нас
эбытие А (например, событие, заключающееся в том, что £ 6 ДХ, где
X — заданная измеримая область возможных значений случайной вели-
ины £). Тогда при неограниченном увеличении числа экспериментов п
гносительная частота р^п\Л) появления события А сходится по вероят-
ости к вероятности этого события р(А), т. е. для любых наперед задан-
ых и сколь угодно малых положительных величин е и б наступит такой
момент» (в проведении эксперимента) По, что для всех п > п0 будет
траведливо неравенство
Р{|р*п)(А)-р(4)|<£}>1-й.
(4.3')
Доказательство этого утверждения получается из (4.3), если в каче-
гве участвующих там случайных величин рассмотреть признаки
если в результате t-ro эксперимента
осуществилось событие А;
(4-4)
О — в противном случае.
Из определения следует, что все эти случайные величины
Теорема Бернулли исторически появилась как первая самостоятельная версия закона
больших чисел намного раньше более сильной теоремы (4.3) — в 1713 г. Однако в
современном изложении ее, естественно, удобнее подавать как простое следствие
результата (4.3).
156
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
независимы и имеют один и тот же закон распределения, в частности:
Ef, = 1 -р(4) + О • (1 - р(4)) = р(4);
Df,= (1-р(4))2-р(4)+(0-р(4))2(1-р(А))	(4.5)
= р(4)(1-р(4)).
Очевидно, в этом случае £(п) = (& + ... + £л)/п есть не что иное, как
относительная частота	появления события А в п произведенных
случайных экспериментах, причем
Ef(n) = Ер<п,(4) = р(4);
Dew = 0^(4) =
(4-6)
Применяя к случайным величинам (4.4) закон больших чисел (4.3),
мы и получаем, с учетом (4.5) и (4.6), доказательство теоремы Бернулли
(4.3').
4.3.	Особая роль нормального
распределения: центральная предельная
теорема (ЦПТ)
Смысл результатов п. 4.2 заключается, грубо говоря, в том, что при
осреднении большого числа (п) случайных слагаемых все менее ощуща-
ется характерный для случайных величин неконтролируемый разброс в
их значениях, так что в пределе по п —* оо этот разброс исчезает вовсе
или, как принято говорить, случайная величина вырождается в неслучай-
ную. Однако при любом конечном числе слагаемых п случайный разброс у
среднего арифметического этих слагаемых остается. Поэтому возникает
вопрос исследования (опять-таки асимптотического по п —> оо) характера
этого разброса. Фундаментальный результат в этом направлении (извест-
ный как «центральная предельная теорема») был впервые сформулирован
в упомянутом выше труде Лапласа (1812 г.) и заключается он в том, что
для широкого класса независимых случайных величин	предель-
ный (по п —> оо) закон распределения их нормированной суммы вне за-
висимости от типа распределения слагаемых стремится к нормальному
закону распределения. Однако эта формулировка нуждается в уточне-
ниях: что значит «нормированная» сумма случайных величии и б каком
именно смысле закон распределения одной случайной величины стремится
к закону распределения другой? Существует несколько вариантов точных
4.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЦПТ
157
формулировок центральной предельной теоремы, отличающихся друг от
друга степенью общности и видом постулируемых ограничительных усло-
вии. Мы приведем здесь формулировку Линдеберга и Леви1.
4.3.1.	Центральная предельная теорема
Если	— независимые случайные, величины, имеющие
один и тот же закон распределения со средним значением Е& = а и с
дисперсией D& = а2, то по мере неограниченного увеличения п функция
распределения случайной величины
Г(«) =
стремится к функции распределения стандартного нормального закона
при любом заданном значении их аргументов, т. е.
*?(•.)(«)
при п —» оо
для любого значения х. где Ф(ж) = -fx е dt.
' '	v2k •»—оо
Таким образом, центральная предельная теорема дает математически
строгое описание условий, индуцирующих механизм нормального закона
распределения (см. неформальное обсуждение этих условий в п. 3.1.5).
Она оправдывает, в частности, закономерность той центральной роли,
которую играет нормальное распределение в теории и практике стати-
стических исследований. Содержание центральной предельной теоремы
можно считать дальнейшим (после закона больших чисел) уточнением
стохастического поведения среднего арифметического из ряда случайных
величин.
Центральная предельная теорема может быть распространена в раз-
личных направлениях: когда случайные слагаемые не являются одинаково
распределенными (формулировка А. М. Ляпунова); когда компоненты & не
являются независимыми; наконец, когда случайные величины & являются
многомерными.
1 L ё v у Р. Calcul des probability. Paris, 1925; Lindeberg J. W. Eine nene Herleitung des
Exponentialgesetzes in der Wahrscheinlichkeitsrechung. — Math. Zeitschr., 15 (1922),
211.
158
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
4.3.2.	Многомерная центральная предельная теорема
Пусть •••ifn — независимые и одинаково распределенные
р-мерные случайные величины с вектором средних значений М = Е£ =
(Е^1\ Е^2\.. -, Е^-Р^)Т и ковариационной матрицей S = Е{(& - М) х (& -
М) }. Тогда при п —» оо совместная функция распределения случайного
вектора £*(n) =	(& — М)]/^/п сходится (для любого значения век-
торного аргумента X) к совместной функции распределения р-мерной нор-
мальной случайной величины, имеющей вектор средних 0 = (0,0,...,0)' и
ковариационную матрицу Е.
4.3.3.	Комментарии к центральной предельной теореме
Замечание 1. Необходима известная осторожность при исполь-
зовании центральной предельной теоремы в практике статистических ис-
следований.
Во-первых, если предельный вид распределения суммы случайных
слагаемых при определенных условиях всегда нормален и не зависит от
вида распределения самих слагаемых, то скорость сходимости распреде-
ления суммы к нормальному закону существенно зависит от типа распре-
деления исходных компонент. Так, например, при суммировании равно-
мерно распределенных случайных величин уже при 6-10 слагаемых можно
добиться достаточной близости к нормальному закону, в то время как для
достижения той же близости при суммировании £2-распределенных сла-
гаемых понадобится более 100 слагаемых.
Во-вторых, центральной предельной теоремой вообще не рекоменду-
ется пользоваться для аппроксимации вероятностей на «хвостах» распре-
деления, т.е. при оценке вероятностей событий вида {£ (n) < smjn} и
{£ (я) zm&x}, где zmin и zmax — возможные значения, близкие соот-
ветственно к левой и правой границам диапазона изменения исследуемого
признака £ (п). Поскольку в этом случае числовые значения вероятностей
(^) < 3>min} —	И (п) > ^max} = 1 -^*(n)(®max) МИЛЫ,
то из малости разностей Fr(n)(smIn) - Ф(хт|п) и F^(n)(zmax) - Ф(хт№)
(которая вытекает из центральной предельной теоремы) вовсе не следует
малость относительных ошибок аппроксимации
^£*(п)(жпип)	1 ^f*(n)(’Cniax)
Ф(^тт) И 1 ~ Ф(*тдх)
которые, как правило, оказываются чрезмерно большими. Так, напри-
мер, пусть £ (п) — нормированный среднедушевой доход в семье (соответ-
4.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЦПТ
159
ственно	• — заработная плата работающих членов семьи и другие
составляющие семейного дохода) и пусть нас интересует доля q семей с
очень высоким доходом, а именно с доходом, не меньшим некоторого до-
статочно высокого уровня zmax (руб.) Исследования показали, что точное
значение этой доли q = 1 — р£-{п)(хтлк) = 0,03, в то время как соответству-
ющая нормальная аппроксимация дала результат q = 1 — Ф(жтах) = 0,003.
Разность q—q сама по себе мала (как и следует из центральной предельной
теоремы), однако относительная погрешность нормальной аппроксимации
в данном случае составляет десятикратную величину, т. е. 1000%! Особен-
но важным это предостережение оказывается при попытках использования
нормальных аппроксимаций в задачах расчета зависимостей типа «пре-
дельная прочность (или пропускная способность) системы — вероятность
разрушения (отказа в обслуживании)».
Замечание 2. Центральная предельная теорема позволяет про-
следить асимптотические связи, существующие между различными мо-
дельными законами распределения (см. гл. 3), с одной стороны, и нормаль-
ным законом — с другой. Опираясь на центральную предельную теорему,
можно объяснить, в частности, следующие полезные для статистической
практики факты:
1.	Распределение (р, п) биномиальной случайной величины £(р,п)
асимптотически (по п —> оо) нормально* с параметрами Е£(р, п) = пр
и D£(p,n) = пр(1 — р). Данный результат известен как теорема Муавра-
Лапла с а (доказана впервые Муавром в 1733 г., когда еще не была из-
вестна центральная предельная теорема) и является прямым следствием
центральной предельной теоремы, примененной к случайным величинам
(4.4) с учетом (4.5).
2.	Распределение А пуассоновской случайной величины £(А) асимпто-
тически (но А —> оо) нормально с параметрами Е£(А) = А и D£(A) = А.
3.	Распределение (jV, М, п) гипергеометрической случайной величины
((JV,Af, п) асимптотически (по N —► оо,М —* оо, $ —> р > 0 и п —> оо)
нормально с параметрами Е£(А\ ЛГ,п) = пр и Df(A,Af, п) = пр(1 — р).
4.	Функция распределения нормированной fc-мерной (pi,pa, • .. ,Рк] п)
1 Случайная величина 6(п), зависящая от параметра п, называется асиииптотически
(по п) нормальной, если существуют такие нормирующие не случайные переменные
А(п) и В(л), что функция распределения случайной величины т;(п) = А(п) • Цп) +
В(в) стремится при п —* со к функции распределения стандартного нормального
закона при любом заданном значении их аргумента г.
160
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
полиномиальной случайной величины
при п —* оо стремится к функции распределения несобственного (выро-
жденного) Аг-мерного нормального закона с вектором нулевых средних зна-
чений и с ковариационной матрицей
имеющий ранг, равный к — I1.
5.	Распределение случайной величины у2(тп) асимптотически (по
т —> оо) нормально с параметрами Еу2(т) = т и D%2(m) = 2т.
6.	Распределение случайной величины 1(т) асимптотически (по т -»
оо) нормально с параметрами Ei(m) = 0и Ш(т) = 1.
4.4. Законы распределения вероятностей
случайных признаков, являющихся
функциями от известных случайных
величин
В теории и практике статистических исследований очень важно уметь
вычислять закон распределения вероятностей для функций от случайных
величин, распределение которых известно. Именно на этом, главный
образом, основана теория статистического оценивания и проверки ста-
тистических гипотез (см. гл. 7 и 8), так как и статистическая оценка,
и критическая статистика, используемые соответственно при оценива-
нии неизвестных значений параметров и при построении критериев ста-
тистической проверки гипотез, суть не что иное, как функции от резуль-
татов наблюдения исследуемой случайной величины £. Для того чтобы
ими осмысленно пользоваться и знать их статистические свойства, мы
должны уметь восстанавливать их закон распределения по распределе-
нию изучаемой случайном величины £ (а значит, и ее наблюдений). Ниже
1 Здесь и далее символ I* означает единичную матрицу размерности к.
4.4. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
161
описываются основные правила, руководствуясь которыми можно решать
эту задачу.
1.	Пусть случайная величина у является монотонно возрастающей
непрерывной функцией от заданной непрерывной случайной величины
имеющей всюду дифференцируемую функцию распределения 7^(г), т.е.
у = у(£). Каждому возможному значению х случайной величины £ будет
соответствовать возможное значение у = д(х) случайной величины г].
В силу монотонности и непрерывности преобразования д по заданно-
му значению т/ можно однозначно восстановить соответствующее £ с помо-
щью преобразования, обратного к д (обозначим его д~ ), т. е. £ = д~ (»/).
Аналогичное соотношение связывает и возможные значения этих случай-
ных величин, т. е. х = д ’(у). Заметим, что функция у-1(у), так же как и
функция д(х), является монотонно возрастающей непрерывной функцией.
Попробуем выразить функцию распределения F^(y в терминах за-
данных нам функций Frfx'), д и д
Г,(у) = Р{г) < У} =	'(ч) <<*(»)}	,47>
=	< <*(?)} = ^«’(у))-
Дифференцирование обеих частей (4.7) по у дает
Ш =	0-8)
Точно такие же рассуждения в случае монотонно убывающей функ-
ции д(х) приведут нас к некоторому видоизменению формулы (4.8):
/,(у) = /{(?”(»)) • ( -	-	(4-8')
\	z
Можно объединить формулы (4.8) и (4.8*) в одной, справедливой для
любого взаимно-однозначного преобразования д:
Пример 4.1. Вычислить функцию плотности случайной величины
у = е^, если известно, что £ подчиняется (а,а2) — нормальному закону.
В данном примере д(х) = ex,g^~l\y) = In у, следовательно,
dy -1}(у) d(ln у) _ _1
dy dy у'
бИрИШЦМ ЧЛ1ИЧИВ.Л II №||<>НЫ эконометрики
162
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Подставляя это в (4.8"), получаем
Му) =
е а*я
1
У
т.е. плотность логарифмически-нормального закона (см. п.3.1.6).
Пример 4.2. Вычислить функцию плотности случайной величины
т] = а+6£, если известна плотность Д(ж) случайной величины £. В данной
случае д(х) = а + Ьх, У^Чу) = (у - «)Л и (dg^~1\y)/dy) = 1/Ь. В
соответствии с (4.7) и (4.8 ) имеем:

/,(») =
(4.9)
>
Это правило пересчета функций распределения и плотности позво-
ляет, в частности, использовать таблицы стандартного (т.е. (0; 1)-)
нормального закона для определения значений функции распределения к
функции плотности нормальной случайной величины £(а, а2) с произволь-
ными параметрами а — Е£(а,«т2) и о2 = Df(a,a2). При этом, как легко
видеть, роль f играет стандартная нормальная величина £ (0,1), а роль
1? — произвольная нормальная величина £(а,а2), т.е.
f(a,<r2) = а + <г • {(0,1).	(4.10)
Соответственно имеем:
/ж — а л \	/х — а\
) = Ф (----;0,1 ) = Ф (---) ;
\ а )	\ о )	.
/ ч 1
= - ^(o.l)
2.	Если интересующее нас преобразование 17 = д(() не является
взаимно-однозначными, то сколько-нибудь общие формулы получать не
удается. Вместо этого приходится каждый раз решать определенный
тип задач, прилаживаясь к их специфике. Рассмотрим, например, слу-
чаи rj = £ :
FM = P{4<y} = P{\(l<Vy} = P{-Vy<i< V5}
= F((Vy)-Pd-Vy)-
4.4. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
163
Следовательно, после дифференцирования левой и правой частей по
у имеем:
/ч(у) - /if(Vs) •	+ /{( “ Vs) 
= 2^(^Vs)+/f(-^))-
Применение данной формулы к случаю, когда £ является стандартной
нормальной величиной, дает
w	2
что является функцией плотности х распределения с одной степенью сво-
боды и одновременно — частным случаем гамма-распределения с параме-
трами а = b = 1/2 (см. п. 3.2.5).
3.	Обобщим формулу (4.8W) на многомерный случай. Пусть С =
‘	мерная случайная величина с известной функци-
ей распределения F^fX) и плотностью вероятности Д(Х) и пусть другая
р-мерная случайная величина т] =	определяется как задан-
ная непрерывная векторная функция от компонент £, т.е.
„О) _ „ (М М\.
У - 9l >•••>< )?
4(rt = 9p(f(,),-.,€(p)).
Предполагается, что соответствие 7] — р(£) является взаимно-
однозначным, т. е. существуем обратное преобразование (?-1, позволяющее
по заданному «значению» 17 однозначно восстанавливать соответствую-
щее «значение» £:
4(1) = si~1(’/,),--->’/F));
f(F) = s;’(^),...,f(p)).
Соответственно между многомерными возможными «значениями»
X =	и У =	случайных величин £ и rj име-
ют место векторные соотношения
Y = g(X) и Х = 0-‘(П
164
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Тогда совместная плотность вероятности случайных величин т) =
(i/1), ..., т/р^) равна
А(»(1)....,»(₽)) = л(?г,(у),А2_1(П--,р;1(у))-и(у)1.	(4.Н)
где определи! ель преобразования (якобиан)
	8g;'(Y) Syt1) (У)	8g;\(Y) ву(2> 8gi'(Y)	Эд?г(У) 8V(Fi <(И
J(Y) =	8УЫ		•  •	’ 8уЫ
	8S,~'(V)	8g^(Y)	8g-\(Y)
	ду'Т	dy(^)	Эу(р)
так же, как и в формуле (4.8”), берется по абсолютной величипе.
4.	Выведем распределение суммы двух независимых случайных слага-
емых (формулу композиции). Пусть независимые случайные величины &
и имеют плотности вероятности соответственно f^(x) и Д2(у). Требу-
ется произвести композицию этих плотностей, т.е. найти плотность рас-
пределения случайной величины т} = fi 4- По существу, мы должны
рассмотреть совместное двумерное распределение f(£lt&)(xyy) и для опре-
деления функции распределения случайной величины т] найти в плоско-
сти хОу область возможных значений (&, G), соответствующих событию
{?? < z}. На рис. 4.1 эта область заштрихована и обозначена Az. Получаем
ад = Р{*1 < *} = P{G + ь < г] = />{(«„е2) € Аг}
А,
—оо —оо
— оо
dx. (4.12)
Здесь мы воспользовались тождеством	у) = /^(х) • Да(у)
(справедливым в силу независимости ft и (2)> а при интегрировании по
области А2 пределы интегрирования по оси Oz брали от —оо до -f-oo, а по
оси Оу — от —оо до прямой у = z — х.
выводы
165
Рис. 4.1. Попадание в область Л, на плоскости хОу соответствует событию
R1 + < *}
Дифференцирование по z левой и правой частей соотношения (4.12)
дает
А(г) = / Л1(г)/&(-г-а')Лг-
(4.13)
Формулу (4.13) называют формулой композиции двух распределений
или формулой свертки. Для обозначения композиции (свертки) законов
распределения часто применяют символическую запись
Воспользовавшись формулой (4.13), можно вывести упомянутое в
п. 3.1.5 и 3.1.10 свойство «самовоспроизводимости» законов Гаусса и Коши
(сумма нормальных случайных величин сама распределена по нормально-
му закону; сумма одинаково по Коши распределенных случайных величин
сама подчиняется закону распределения Кдши), а также получить форму-
лы для плотности распределения сумм равномерно распределенных вели-
чин, приведенные в п. 3.1.7.
ВЫВОДЫ
1.	Следует выделить три типа основных результатов теории вероят-
ностей:
доасимптотические, позволяющие анализировать основные законо-
мерности в поведении случайной величины по ее главным числовым ха-
рактеристикам — среднему значению, дисперсии и т. п. — без апелляции
к знанию общего вида закона ее распределения;
166
ГЛ. 4. РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
асимптотические, позволяющие анализировать основные закономер-
ности в поведении сумм большого числа случайных слагаемых (а именно
устанавливать их асимптотическую устойчивость, т.е. их сходимость к
некоторым постоянным значениям по мере роста числа слагаемых, или
описывать асимптотический вид закона распределения этих сумм) без точ-
ного знания законов распределения отдельных слагаемых;
относящиеся к теории преобразований случайных величин, позволяю-
щие находить закон распределения интересующих нас функций от набора
случайных величин, совместное распределение которых нам известно.
2.	Первый тип результатов представлен в данном учебнике неравен-
ством Чебышева, позволяющим оценивать вероятность зафиксировать
при наблюдении случайной величины £ значение, отклоняющееся от ее
среднего значения а = Е£ не менее чем на заданную величину А, без зна-
ния закона распределения исследуемой случайной величины £ (см. (4.2)).
3.	Закон больших чисел и его следствия относятся к первому (менее
глубокому) уровню асимптотических результатов и позволяют устанавли-
вать сходимость (по вероятности) нормированных сумм большого числа
случайных слагаемых к некоторым постоянным значениям — по мере ро-
ста числа слагаемых — практически независимо от вида распределения
самих слагаемых.
4.	Центральная предельная теорема относится к следующему (бо-
лее глубокому) уровню асимптотических результатов. Она утверждает,
в частности, что закон распределения нормированной суммы большого
числа случайных слагаемых практически вне зависимости от типа рас-
пределения самих слагаемых стремится (по мере роста числа слагаемых)
к нормальному (гауссовскому) закону распределения (см. п. 4.3.1).
Однако необходима известная осторожность при практическом ис-
пользовании центральной предельной теоремы: во-первых, часто можно
подобрать весьма простые (и более точные, чем нормальные!) аппрокси-
мации для распределения суммы небольшого конечного числа случайных
слагаемых; во-вторых, центральная предельная теорема плохо работа-
ет на «хвостах» распределений, т.е. при оценке вероятностей больших
уклонений анализируемой суммы случайных величин от своего среднего
значения.
5.	Основным результатом теории преобразования случайных величин
является правило (4.8W) (или (4.11) в многомерном случае), позволяющее
вычислять закон распределения (функцию плотности или полигон частот)
случайной величины, являющейся заданной функцией от набора исходных
случайных величин, совместный закон распределения которых нам изве-
стен.
ГЛАВА 5. ЦЕПИ МАРКОВА
5.1.	Последовательности случайных
экспериментов и случайных величин
в дискретном вероятностном
пространстве
Рассмотрим дискретное вероятностное пространство с конечным чи-
слом элементарных исходов	. ,wN и вероятностями их появле-
ния (в результате реализации случайного эксперимента), соответственно
Р1 = P{wi}> Рз =	• • • ,PN = P{wN}. Пусть нас интересует ве-
роятность появления заданной последовательности элементарных исходов
..,и,-м в результате реализации п последовательных случайных
экспериментов. Если случайные эксперименты производятся в рамках од-
ного и того же вероятностного пространства и независимы друг от друга,
то мы имеем дело с последовательностью независимых случайных
экспериментов, и интересующая нас вероятность определится по фор-
муле вероятности независимых событий (1.13), что в нашем случае дает
‘	1 = 14^1} • Пч2} • • • • *	= PiiPi2 -• Pi.- (5.1)
Из независимости рассматриваемых событий следует также, что если
бы нас интересовал только результат, полученный на одном каком то
«шаге» этой последовательности (например, на шаге t), то вероятность
P{w,t} определяется единственно величиной рч и никак не зависит от
предыстории, т. е. от того, какие именно результаты мы имели на преды-
дущих шагах этой последовательности. Очевидно, в рамки подобной схе-
мы укладываются ранее рассмотренные примеры 1.1 (последовательность
подбрасываний одной и той же монеты), 1.3 (четырехкратное бросание
игральной кости), 1.5 (проверка по альтернативному признаку п изделий,
случайно отобранных из продукции стационарно функционирующего про-
изводства).
168
ГЛ. 5. ЦЕПИ МАРКОВА
Однако нетрудно представить себе реальные ситуации, в которых ре-
зультат случайного эксперимента на определенном шаге последователь-
ности в определенном смысле зависит от того, какие именно результаты
наблюдались на предыдущих шагах этой последовательности. Очевидно,
в подобных ситуациях речь следует вести о последовательности зави-
симых случайных экспериментов.
В дальнейшем несколько видоизменим терминологию с целью ее бо-
лее естественного приспособления к реальным задачам. А именно будем
интерпретировать каждый из элементарных исходов ы; как «возможное
состояние» анализируемого объекта (индивидуума, работника, семьи, до-
машнего хозяйства и т. п.). Введем в рассмотрение дискретное время t и
случайную величину £t(tj), значения которой (1,2, ...,7V) определяют, в
каком именно состоянии находился анализируемый объект в момент вре-
мени t (t = 1,2, ...,п), т.е. &(w,) — i. В каждый следующий момент
времени t -f- 1 объект из состояния и», в котором он находился, может
перейти в любое другое состояние u>j или остаться в том же самом со-
стоянии Таким образом, от рассмотрения последовательностей слу-
чайных экспериментов мы переходим к рассмотрению последовательно-
сти случайных величин f](g>),£2(^)5,£n(w), вообще говоря, взаимно-
зависимых. А чтобы «задать поведение» многомерной случайной вели-
чины £ = (£, (w)>&(w),..., £п(^))> необходимо, как мы знаем (см. выше,
п. 2.5.3), задать соответствующий совместный п-мерный закон распреде-
ления вероятностей, который в данном случае (с учетом того, что каждая
из компонент £ может принимать одно из N возможных значений) описы-
вается с помощью Nn конкретных чисел (вероятностей).
Правда, в случае последовательности независимых случайных экспе-
риментов мы имеем соответствующую последовательность независи-
мых случайных величин, так что в соответствии с (2.14 ) и (5.1)
^{€1 = h, & = «2, • • ,	= «п} = Pix • Pi3 • • • • • Р».	(5.2)
и распределение п-мерной случайной величины £ = (£1,, £п) задается
всего лишь N числами: Pi, Р2,...,PN-
Можно ожидать, что и при некоторых специальных типах зависимо-
стей, существующих между элементами последовательности fi, £2» • • • >
способ задания ее поведения окажется более простым и экономичным, чем
в самом общем случае. Именно к рассмотрению одного из таких специ-
альных типов зависимостей мы и переходим.
5.2. ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ
169
5.2.	Последовательности, образующие
цепь Маркова (определения, примеры,
прикладные задачи)
Продолжая рассмотрение системы «объект — его состояние в за-
данный момент времени 1», предположим, что эта система характери-
зуется «ограниченной памятью», а именно вероятность того, что объект
в момент времени t окажется в заданном состоянии «у», зависит не от
всей предыстории, а только от того, в каком состоянии он находился в
предыдущий момент времени t — 1, т. е.
PR. = 3 I £1 = «1, (2 = «2,- • R.-1 = •} = PR. = 3 I f.-l = «•}.	(5.3)
О таких зависимостях последовательности случайных величин	- - - > &
говорят как о зависимостях марковского типа, а соответствующие по-
следовательности называют цепями Маркова. Если дополнительно пред-
положить, что вероятности pjp = P{£t = j |	= 1} остаются одними
и теми же при всех t (т.е. не зависят от А), то соответствующая марков-
ская цепь называется однородной. Именно однородным цепям Маркова и
посвящена данная глава.
Чтобы дать строгое определение однородной цепи Маркова, необходи-
мо задать способ вычисления совместного распределения вероятностей для
многомерных случайных величин (£ьпри любых t = 1,2,... .
Определение. Последовательность случайных величин СрСз»
..., каждая из которых может принимать конечное число значении
• называется однородной цепью Маркова, если вероятности
событий вида
U1 =*?!> 6 =	•••,& = *£()
определяются формулой
(5.*)
(5-4)

через начальное распределение вероятностей
Pi = PRi = *?}, Р2 = PR. = £}, ..., PN = PR, = 4}	(5.5)
1 Требование конечности числа возможных состояний не обязательно при определе-
нии цепи Маркова. На самом деле допускается и счетное число состояний. Однако
В рамках наших целей можно обойтись и конечным числом состояний.
170
ГЛ. 5. ЦЕПИ МАРКОВА
и матрицу переходных вероятностей1
(Р11	Р12	P1JV \
Р21	Р22	 P2N I >	(5 6)
?Nl ?N2	’ ’ ’ ?NN'
где
Pij = p{£t = 3 I G-i = о для всех t=l,2,... .	(5.7)
Выше в качестве возможных значении rr1, х2,..., xN случайных вели-
чин £t (t = 1,2,...) мы рассматривали лишь номера «состояний» анали-
зируемых объектов (т.е. полагали х° = j). Однако иногда возможным
значениям анализируемых случайных величин удобнее придавать более
общий смысл.
Проверим корректность приведенного определения и его непротиворе-
чивость с «марковским свойством» (5.3). Для этого, во-первых, требуется
убедиться, что определенные с помощью соотношений (5.4)-(5.6) вероят-
ности действительно образуют закон распределения вероятностей, т.е.
53 53' * ' 53^й *	* ’ • • * Ptj-it, — 1	(5.8)
»1	»2	*<
(суммирование в каждой сумме ведется по всем возможным значениям
оо о ч
% 1 > ®2 > • •  1
А во-вторых, показать, что из этого определения следует соотношение
(5.3).
Справедливость (5.8) вытекает из следующих фактов:
а)	очевидно, для любого к = 1,2,	— 1
Р«*1+Р»*2 + ••• + Pijt№ 1,	(5.9)
т. к. левая часть (5.9) определяет вероятность достоверного события, ка-
ковым является событие, заключающееся в том, что анализируемый объ-
ект на следующем «шаге» перейдет из состояния в одно из всех воз-
можных состояний;
б)	учитывая (5.9) и последовательно проводя суммирование в правой
части (5.8), начиная от суммы переходя к сумме £ и т.д., имеем:
»«	«t-i
1 Матрицы переходных вероятностей, по определению, обладают следующим свой-
ством; все их элементы р,} неотрицательны, и суммы элементов любой стро-
ки равны единице. Матрицы, обладающие этим свойством, принято называть
стохастическими.
6.2. ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ
171
* Ptpa * • • • ’
»«
= Р»1 *Рй»2 ’ ••	+ Pit-12 + * * * 4“ Pit—j/v)
= P»iPijta ’ • •  * Pii-a^-i j
5 v P*i ’ P*j»2 ’ • • • ’ Pit-3*1-2 ' Pi»—ait-i
«1-1
Pit * P»i<2 • • • * Pit—3*1—2 ’ (P*t —al 4" P»t—a2 "1“ ‘ * * 4" Pif—aTv)
= PtiPiiG ’-----‘ Pi.-gij-a
53 Рп = pi + P2 + - - •+pn = i
«1
(последнее тождество следует из определения вероятностей pj).
Соотношение (5.3) непосредственно следует из теоремы умножения
вероятностей (1.11), если принять обозначения
— {ft — J}; В — {fi — ’iJ fa = *2» • • • ,ft-i = «}>
а для подсчета вероятностей Р{Д/7} и Р{В} воспользоваться формулой
(5.4).
Заметим, что последовательность независимых случайных величин
fi,f2»---tfn» определенных в одном и том же дискретном вероятностном
- о о о
пространстве с конечным числом возможных значении xt, х2} -.., xN и со-
ответствующими вероятностями р,- = P{£t = ж,} (» = 1,2,	t =
1,2,...,п), можно рассматривать как частный случай цепи Маркова, в
которой начальное распределение вероятностей (5.5) задается вектором
Р = (РьРа, • • • >Руу)> а матрица переходных вероятностей (5.6) имеет вид
Pi Р2 **• PN
Pi Р2 • ’' PN
Pl Р2 ’ * ‘ PN
Впервые понятие зависимости типа (5.4)-(5.6) было введено в 1911 году заме-
чательным русским математиком Андреем Андреевичем Марковым. Он предложил
простейшее обобщение серии испытаний Бернулли (см. п. 3.1.1), в котором вероятно-
сти двух возможных исходов Р{б« = 1} и Р{6 — 0), в отличие от схемы независимых
испытаний, уже зависели от того, каков был предыдущий исход, т.е. от того, какое
именно значение приняла случайная величина б-i. Итак, в предложенной схеме
= 1 I 6-1 = °} = Г01 и Р{6 = 1 | 6-1 — 1} = рн
172
ГЛ. 5. ЦЕПИ МАРКОВА
(очевидно, при этом poo = 1 — poi и Pio = 1 —’Рп)- А. А. Марков показал, как, распо-
лагая, помимо значений вероятностей pot и рц, еще величиной вероятности появления
события {£ = 1} в первом испытании, можно вычислить вероятность любого события
вида (5.*). Он назвал эту схему простейшей цепью. В дальнейшем он обобщил
эту схему на случай произвольного конечного или даже счетного числа возможных
значений случайной величины. Это обобщение и получило название цепи Маркова.
Пример 5.1. Динамика типологии семейного потребления.
В данном примере исследуемыми объектами являются семьи, точнее, до-
машние хозяйства. Возможные «состояния» объекта — типы потреби-
тельского поведения. Единица измерения (такт) времени — один год.
Соответственно, элемент р, начального распределения вероятностей ин-
терпретируется как доля домашних хозяйств, относящихся к «-му типу
потребительского поведения в начальный (первый) «момент времени», а
переходная вероятность p,j — как доля семей «-го типа потребительского
поведения, переходящих за 1 год в «состояние» j.
Пример 5.2. Игра двух лиц до разорения. Исследуемый объ-
ект — один из двух участников игры, которая происходит по следую-
щим правилам. Суммарный капитал двух игроков фиксирован и равен
7V денежным единицам. Выигрыш одного кона составляет одну денеж-
ную единицу. Анализируемый игрок начинает игру, имея п единиц, и
выигрывает кон с вероятностью р. После проигрыша последней единицы
t-м игроком («* =1,2) игра заканчивается его разорением. Очевидно, «со-
стояние» объекта в этой схеме следует понимать в буквальном смысле:
оно определяется имеющейся у него в наличии суммой денежных единиц
в соответствующий «момент времени», а последний интерпретируется
как очередной кон игры. Итак, мы имеем N + 1 возможных состояний, а
именно: 0; 1; 2;...;Л.
Начальное распределение вероятностей в данном случае определяет-
ся формулой
1 при г = п]
0 для всех « п.
В соответствии с правилами игры переходные вероятности р^ опре-
деляются соотношениями
А = />{£(!) = «} = {
Р
1 -р
1
при j — « = 1
при i — j = 1
при i = j = 0
и »* > 1;
и t > 1;
и при « = j = N.
Пример 5.3. Демографическая модель передвижки возрас-
тов. В качестве объекта рассматривается элемент населения страны
или региона (индивидуум), а его «состояние» определяется его возрас-
том. Смежные «состояния-возрасты» отличаются друг от друга на один
5.2. ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ
173
год. Исключение составляет состояние, определяемое как «предельный
возраст»: к нему будем относить все индивидуумы в возрасте, превыша-
ющим 85 лет. Кроме того, вводятся еще три особых состояния: «иммигра-
ционное^, «эмиграционное» и «поглощающее». Иммиграционное и эми-
грационное состояния связаны с возможным соответственно прибытием и
выбытием индивидуумов из анализируемого региона в связи с миграци-
ей населения; а поглощающее — только с выбытием по причине смерти.
Таким образом, мы имеем 89 возможных состояний: первое — возраст до
1 года, второе — до 2 лет, ... , 85-е — до 85 лет, 86-е — свыше 85 лет,
87-е — иммиграционное, 88-е — эмиграционное и 89-е — поглощающее.
Начальное распределение вероятностей pi = Р{£(1) = t}, i =
1,2,.. .,86,87,88,89 определяется демографической структурой общества,
зафиксированной на конец первого года исследуемого периода. При этом
под pg? понимается доля иммигрантов этого года во всем населении регио-
на, а Рее — доля эмигрантов. Матрица Р переходных вероятностей Pij
может быть определена в терминах возрастных характеристик смертно-
сти (р,), иммиграционной (</t) и эмиграционной (ft) активности населения
в виде таблицы 5.1.
Таблица 5.1
Но- мер сос- тоя- ния (0	Номер состояния (j)										
	1	2	3	4	5	• • а	85	86	87	88	89
1	0	1 - Д1 — ft	0	0	0	• * •	0	0	0		Ml
2	0	0	1—/*2~ft	0	0	. . .	0	0	0	л	7*2
3	0	0	0	1 ~7*з —ft	0	...	0	0	0	ft	7*з
	•				• •		• *	• • •	-	• а	• •
85	0	0	0	0	0	• • •	0	1~7*85 ~fts	0	fts	7*85
86	0	0	0	0	0	• а а	0	1~7*86“ft©	0	fte	7*86
87	91	<72	9з	9<	95	. • .	985	986	0	0	0
88	0	0	0	0	0	. • .	0	0	0	1	0
89	0	0	0	0	0	• а '	0	0	0	0	1
Участвующие в вычислении вероятностей возрастные демографи-
ческие характеристики интерпретируются следующим образом. Величи-
на р, оценивается как доля тех людей возраста i, которые умерли в этом
возрасте; значение Hi определяет долю тех людей возраста i. которые эми-
174
ГЛ. 5. ЦЕПИ МАРКОВА
грировали из анализируемого региона (страны) в данном возрасте; нако-
нец, qi выражает удельный вес людей t-ro возраста среди всех иммигран-
тов данного региона, т. е. среди всех людей, прибывающих в анализируе-
мый регион на постоянное поселение.
Пример 5.4. Модель пребывания студента в вузе. В каче-
стве объекта рассматривается студент вуза с пятилетним сроком обу-
чения. Его i-e состояние соответствует его обучению на t-м кур-
се (t = 1,2,..., 5); 6-е состояние — специалист, окончивший дан-
ный вуз; 7-е — лицо, обучавшееся в данном вузе, но по каким-
то причинам не окончившее его. Чтобы не увеличивать числа воз-
можных состояний примем допущение, что по правилам данного ву-
за зачисление в него переводом студентов из других вузов невоз-
можно. Из смысла состояний следует, что ненулевыми элемента-
ми матрицы Р переходных вероятностей могут быть только вели-
чины Pll,P12,Pi7JP22>P23}P27,JP33>P34»P37iP44iP45iP47>P551P5eJP57i В Также
Рбб = Р77 = 1-
Пример 5.5. Игровые возможности двух шахматистов.
Объектом в данном примере является соревнующийся шахматист, а со-
стоянием — результат сыгранной им партии (1-е состояние — выигрыш,
2-е состояние — ничья, 3-е состояние — поражение). Анализируется тур-
нирное поведение двух шахматистов А и В. Игрок А каждую партию
турнира независимо от исходов предыдущих партий выигрывает с веро-
ятностью «в», делает ничью с вероятностью «н» и проигрывает с веро-
ятностью «п» = 1 — в — н. Игрок В менее уравновешен: он выигрывает
партию с вероятностями в+е, в и в-е (0 < е < тш(в, 1-в,н, 1—н) соот-
ветственно, если предыдущая партия была им выиграна, сыграна вничью
или проиграна. Аналогично ведет себя вероятность его проигрыша: она
равна в этих трех случаях соответственно п — £, п и п 4- е. Очевидно,
закономерности появления того или иного результата в зависимости от
результата предыдущей партии у каждого из игроков могут быть описа-
ны с помощью соответствующим образом подобранной однородной цепи
Маркова с тремя возможными состояниями и с матрицами переходных
вероятностей Р(А) (у игрока А) и 'Р(В) (у игрока В):
(в н п
внп
внп
Р(й) =
H П - £
Н П
Н П 4- £
Заметим, что матрица Р(А) в действительности описывает последо-
вательность независимых испытаний (которая, как мы видели, является
частным случаем цепи Маркова), а матрица Р(В) иллюстрирует реаль-
5.2. ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ПРИКЛАДНЫЕ ЗАДАЧИ
175
ную ситуацию, подтверждающую базовую идею А. А. Маркова в постро-
енной им простейшей цепи, в соответствии с которой вероятность опреде-
ленного исхода случайного эксперимента в серии таких испытаний может
зависеть от результата предыдущего исхода.
Очевидно, аналогично могут быть построены примеры марковских
цепей, описывающих динамику межотраслевой структуры трудовых ре-
сурсов («объект» — работник, «состояние» — отрасль экономики, в кото-
рой он занят в данный «момент времени»), динамику социальной страти-
фикационной структуры общества («объект» — индивидуум, «состоя-
ние» — социальная страта, к которой он принадлежит в данный «момент
времени») и т. д.
Как и всякое другое моделирование, построение моделей цепей Мар-
кова не является самоцелью, а лишь инструментом для решения опреде-
ленного класса прикладных задач. Сформулируем кратко те основные
прикладные задачи, которые решает исследователь при анализе цепей
Маркова.
Задача 1. Прогноз распределения объектов по возможным состоя-
ниям /срез Т тактов времени. Другими словами, это означает, что иссле-
дователь хотел бы подсчитать по исходным данным р и Р вероятности то-
го, что анализируемый объект через заданное число тактов времени Т бу-
дет находиться в заданном «состоянии» j (j = 1,2,..., N). В примере 1 —
это прог.^з распределения домашних хозяйств по различным типам по-
требительского поведения, в примере 2 — это прогноз платежеспособности
игроков через заданное число сыгранных конов, в примере 3 — это прогноз
демографической структуры общества.
Задача 2. Расчет среднего времени перехода объекта из состояния
i в заданное состояние j.
Задача 3. Расчет вероятностей перехода из состояния i в состо-
яние j за заданное число тактов времени т.
Задача 4. Расчет среднего времени пребывания объекта в задан-
ном состоянии i.
Задача 5. Решение проблемы существования и вычисления стацио-
нарного распределения объектов по возможным состояниям. Речь идет
о ситуациях, когда меняющееся во времени распределение объектов по со-
стояниям со временем стабилизируется и, начиная с некоторого «момента
времени», остается практически неизменным.
176
ГЛ. 5. ЦЕПИ МАРКОВА
5.3.	Основные характеристики и свойства
цепей Маркова
5.3.1.	Основные характеристики
Исходными характеристиками однородной марковской цепи, как это
следует из определения (5.4)—(5.6), являются:
•	вектор вероятностей начального распределения р = (pi,Pa> • •
и
•	матрица Р переходных вероятностей pij (i,j = 1,2,.. .tN).
Однако в процессе анализа цепи Маркова приходится сталкиваться с
рядом ее производных характеристик^ которые тем или иным способом
вычисляются по исходным.
Вероятность перехода из состояния t в состояние j за t тактов
(О	К	Л.
времени p\j может быть подсчитана по формуле
=	(510)
9=1
которая является непосредственным следствием формулы полной вероят-
ности (1.14), если в качестве участвующих в ней событий Ли Вч рассмо-
треть
А = {ft = j | 6 = «} и В, = {f,_i = q | f, = »}.
Если по аналогии с матрицей Р вероятностей перехода за один шаг
ввести в рассмотрение матрицы Р вероятностей перехода за q шагов
(q = 2,3,...), то, как легко убедиться, формула (5.10) может быть пред-
ставлена в следующем матричном виде:
р(0 _ р(|-1). Р	(5.10')
Последовательно применяя эту формулу к случаям t = 2, t = 3 и т.д.,
получаем:
р(2) _р(1) .р = р.р = pj>
р(3) _ р(2) . р _ р2 . р _ рЗ
т. е. для того, чтобы получить матрицу вероятностей перехода Р^ за t
шагов, надо просто возвести в степень t исходную матрицу вероятностей
перехода Р.
5.3. ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА	177
Безусловная вероятность р\^ того, что объект в момент t на-
ходятся в состоянии t, подсчитывается также с использованием фор-
мулы полной вероятности:
(512)
t=l
В формуле (5.12) вероятности	» = 1,2,..., N, образуют j-й столбец
матрицы вычисляемой по формуле (5.11).
Вероятности первого возвращения объекта в заданное состо-
яние. Введем в рассмотрение вероятность первого возвращения в
состояние j через t шагов, т. е.
4? = р{&+1 = 3\ it ± J; 6-1 / 3\ •••;&# j I 6 = Л-
Опираясь на формулу полной вероятности, можно получить следую-
щие рекуррентные соотношения для вычисления вероятностей
fjj* = Pjh
(5.13)
М = „(*) _ ЯП _0-1) _ г(2) (*-2)’2___/-1)
hi Pji Pjj	Pjj	Jjj Pir
Умение вычислять вероятности позволяет определять и значения
некоторых других характеристик, которые могут оказаться полезными
при анализе марковской цепи. К таким характеристикам можно отнести,
например:
•	вероятность fa тогоу чтоу выйдя из состояния j в момент времени
t = 1, объект когда-нибудь вернется в это же состояние:
оо
t=i
•	среднее время jijj первого возвращения в состояние j (при условии
fii = О:
ОО
мл=Е<
t=l
Вероятности первого достижения состояния j при выхо-
де из состояния i ровно через t тактов времени являются естественным
178
ГЛ. 5. ЦЕПИ МАРКОВА
обобщением вероятностей первого возвращения fj9. Соотношения, по-
зволяющие их рассчитать, также являются следствием формулы полной
вероятности. Они имеют вид:
(2)
Pjj»
Л*> = „(*) _ f(D J*-i)
rij Jij Pjj
(2) (t-2) _
По этим вероятностям, в частности, могут быть подсчитаны:
•	вероятность fa того, что выйдя из состояния i в момент времени
I = 1, объект когда-нибудь попадет в состояние j:
•	среднее время первого достижения состояния j при выходе из
состояния i:
со
3=1
5.3.2.	Классификация состояний и цепей
Свойства цепи Маркова и соответственно способы решения связан-
ных с ее анализом задач (см., например, формулировку задач 1-5 в п. 5.2)
существенно зависят от того, из каких именно состояний она состоит.
Поэтому приведем здесь принятую классификацию состояний конечной це-
пи Маркова и обусловленную ею классификацию самих марковских цепей.
Состояние j называется достижимым из состояния з, если су-
ществует такое to > 1, что > 0, т.е. если имеется положительная
вероятность попасть из состояния з в состояние j (включая случай i = j).
В терминах вероятностей первого достижения достижимость j из » мо-
жет быть определена условиями fa > 0 и fa > 0 (для i / j). Возвращаясь
к нашим примерам, можно без труда убедиться в том, что в примере 5.2
все состояния достижимы из состояний 1,2,...,N — 1, а в примере 5.3
состояние j является достижимым из любого состояния », кроме з = 87,
только при условии j > i; состояние 87 — особое: из него достижимы все
состояния цепи, кроме 88-го и 89-го.
Состояние з называется поглощающим, если никакое другое состо-
яние цепи не может быть из него достигнуто, т. е. если pile = 0 для всех
5.3. ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА	179
к / i (отсюда следует, что рц = 1). Мы уже имели дело с поглощающими
состояниями в примерах 5.2 (состояния i = б и t = TV), 5.3 (состояния 88
и 89) и 5.4 (состояния 6 и 7).
Свойство поглощения может быть «коллективным», а именно: мно-
жество С состояний называется поглощающим (или замкнутым),
если никакое состояние вне С не может быть достигнуто ни из какого со-
стояния, входящего в С. В терминах переходных вероятностей это озна-
чает, что pjk = 0 для всех j и к таких, что j входит в С, а к не вхо-
дит. Отсюда, в частности, следует, что всякое входягцее в цепь замкну-
тое множество состояний может быть изучено как самостоятельная
(автономная) цепь Маркова независимо от прочих состояний исходной
цепи. Так, если в нашем примере 5.1 допустить существование некого
«элитного» подмножества типов потребительского поведения, за пределы
которого принадлежащие этому подмножеству семьи в процессе своих пе-
реходов из одного состояния в другое никогда не выходят, то мы и будем
иметь пример замкнутого (поглощающего) множества состояний, кото-
рое одновременно можно рассматривать как самостоятельную «подцепь»
Маркова.
Возвратные состояния. Состояние i называется возвратным, если,
отправляясь от него, объект с вероятностью единица когда-нибудь в него
вернется, т.е. fa = I1. Соответственно состояние j называется невоз-
вратным, если fjj < 1; можно показать, что для этого необходимо и
достаточно, чтобы > t р-- < оо.
t=i
Периодические состояния. Состояние i называется периодиче-
ским с периодом г > 1, если pj-p = 0 для любого t, не кратного т, и
т — наименьшее целое число, обладающее этим свойством (т. е. объект не
может вернуться в состояние i за время, отличное от т, 2т, Зт,...).
Состояние принято называть эргодическим, если оно возврат- ,
ное и непериодическое.
Определив различные типы состояний марковской цепи, мы перехо-
дим к классификации самих цепей Маркова.
Цепь называется неприводимой тогда, когда в ней нет никаких
замкнутых множеств, кроме множества всех состояний. Применитель-
но к конечной марковской цепи (которая и является предметом нашего
1 В марковских цепях со с четны.*» числом возможных состояний допускаются ситуа-
ции, когда, несмотря на возвратность состояния (и соответственно выполнение соот-
ношения /ц = 1), среднее время возвращения цц оказывается бесконечно большим.
В этом случае состояние i называется возвратным нулевым. Однако в конечны#
цепях Маркова все возвратные состояния ненулевые.
180
ГЛ. 5. ЦЕПИ МАРКОВА
анализа в данной главе) это означает, что неприводимая цепь Марком
должна состоять только из возвратных состояний, каждое из кото-
рых достижимо из любого другого состояния цепи. В терминах матри-
цы переходных вероятностей Р это означает, что существует такое t©» что
все элементы матрицы Р*° являются положительными. Таким образом,
из определения замкнутого (поглощающего) множества состояний следу-
ет, что любое такое множество может рассматриваться как неприводимая
конечная цепь Маркова.
Следует отличать определенное выше поглощающее (замкнутое) мно-
жество состояний от множества поглощающих состояний. Действитель-
но, цепь Маркова может содержать одно или несколько (целое множество)
поглощающих состояний. Очевидно, в этом случае она уже не может быть
неприводимой хотя бы потому, что не все состояния взаимодостижимы (из
поглощающего состояния ни одно другое состояние не является достижи-
мым по определению). Ясно также, что такая цепь должна содержать
невозвратные состояния, поскольку если поглощающее состояние являет-
ся достижимым для какого-либо состояния j, то объект уже не может
вернуться в состояние j с вероятностью единица (а значит, состояние j
невозвратное). Правда, в состав сложной цепи могут входить и замкнутые
множества состояний, но их, как было отмечено, можно отдельно анали-
зировать каждое как неприводимую цепь Маркова. Поэтому представляет
интерес рассмотреть класс марковских цепей, которые состоят только из
поглощающих и невозвратных состояний.
Конечные марковские цепи с поглощением (или поглощаю-
щие цепи Маркова) и определяются как цепи, состоящие только из
поглощающих и невозвратных состояний. Объекты, описываемые такой
цепью Маркова, постепенно переходят из невозвратных состояний в погло-
щающие, находясь в невозвратных состояниях некоторое случайное вре-
мя. Очевидно, если такая цепь содержит всего N состояний, из которых
т-поглощающих, то при соответствующей нумерации состояний ее ма-
трица переходных вероятностей Р может быть представлена в виде
где — единичная матрица порядка т х т\ О — матрица порядка
т х (N — ш), состоящая из нулей; Рнп — матрица порядка (N - тп) х т,
задающая вероятности перехода из невозвратных состояний в поглощаю-
щие» Рни — матрица порядка (JV— m)x(N—m), состоящая из вероятностей
перехода между невозвратными состояниями.
5.3. ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА
181
Очевидно, модели зависимостей, описанные в наших примерах 5.2-
5.4, относятся как раз к этому типу цепей Маркова.
Определим, наконец, для полноты картины еще один тип цепей Мар-
кова, который, однако, в дальнейшем нам не понадобится.
Периодическая цепь — это неприводимая цепь Маркова, все воз-
вратные состояния которой имеют один и тот же период т. Строго говоря,
в определении периодической цепи достаточно было бы потребовать пери-
одичности любого из возвратных неприводимой цепи, т. к. по известной
♦теореме солидарности» (см., например, [Боровков А. А., стр. 199]) в не-
приводимой цепи Маркова все состояния принадлежат одному типу, и,
в частности, если хоть одно из них периодично с периодом т, то и все
остальные состояния этой цепи будут иметь тот же самый период.
5.3.3.	Свойства цепей Маркова
Опишем теперь ряд свойств марковских цепей, знание которых со-
ставит необходимую базу при решении прикладных задач, связанных
с их анализом. Доказательства сформулированных ниже утверждений
опускаются (их можно найти, например, в [КемениДж., Снелл Дж.] и
в [Феллер В.]).
Эргодическое свойство. Пусть N — общее число состояний цепи
Маркова. Для того, чтобы при любом j существовал не зависящий от
i предел
lim р^} = р^оо), i,j = 1,2,...,АГ,
необходимо и достаточно, чтобы цепь была неприводимой и неперио-
дической, т. е. представляла бы собой одно замкнутое множество воз-
вратных и взаимодостижимых состояний. При зтом числа р^°°^ явля-
ются единственным решением системы уравнений
N
•=1
(5.21)
J=1
Кроме того, существует такое h (0 < h < 1), что
\р^-р^\<^-
Напомним, что / ' — это безусловные вероятности того, что объект
182
ГЛ. 6. ЦЕПИ МАРКОВА
в момент t находится в состоянии j (см. выше (5.12)). Так что есть,
по-существу, вероятности попадания объекта в состояние j через боль-
шой интервал времени. При этом оказывается, что объект «забывает»,
откуда он начал движение, т.к. эти вероятности не зависят от началь-
ного состояния объекта. Распределение (p^^pj00^,... ,р^°^) называют
стационарным, или финальным. Устойчивый режим, в который вхо-
дит конечная неприводимая непериодическая цепь Маркова при t —> оо,
характеризуется к тому же следующими свойствами:
(а)	среднее время возвращения в состояние j
1
“ п(оо) ’
(б)	при больших t среднее время пребывания в состоянии j приблизи-
телъно равно t • р) .
Заметим, что перенесение эргодических свойств цепи на периодиче-
ский случай не представляет принципиальных трудностей, хотя и приво-
дит к заметному усложнению формулировок.
Свойства поглощающих цепей Маркова. Эти цепи были опре-
делены в п. 5.3.2 как состоящие только из невозвратных и поглощающих
состояний конечные цепи Маркова, матрица переходных вероятностей ко-
торых представима в виде (5.20). Итак, пусть из общего числа N состоя-
ний такой цепи первые т состояний отнесены к поглощающим. И пусть
нас интересуют величины:
•	otij = 'Etij — среднее значение времени пребывания в невоз-
вратном состоянии j объекта, вышедшего из невозвратного состояния i
(ij=m+l, т + 2,...,Л);
N
•	Qi. = Е( tij) — общее время, включая время пребывания в ис-
ходном невозвратном состоянии t, которое объект проводит во всех невоз-
вратных состояниях до попадания в какое-либо поглощающее состояние;
•	7,-j — вероятность попадания в поглощающее состояние j (j =
l,2,...,m) объекта, вышедшего из невозвратного состояния i (t = m +
1, m + 2,...,2V).
Для поглощающих цепей Маркова, задаваемых матрицами переход-
ных вероятностей вида (5.20), имеют место следующие утверждения:
Утверждение 1. Значения ощ определяются как элементы
матрицы
А = (Iw_m - Pm.)’1.	(5-22)
5.3. ХАРАКТЕРИСТИКИ И СВОЙСТВА ЦЕПЕЙ МАРКОВА
183
где — единичная матрица порядка (N — т) к (N - т), а Рнн — ма-
трица вероятностей перехода между невозвратными состояниями по-
рядка (N - т) x(N — т) (см. (5.20));
Утверждение 2. Значения определяются как компоненты век-
тора
(«1. \
: I = А • 1,	(5.23)
aN-m. /
где 1 — вектор-столбец порядка (N — т) х 1 с компонентами, равными
единице, а А — матрица, определенная соотношением (5.22);
Утверждение 3. Значения вероятностей jij определяются как
(i,j)-e элементы матрицы
Г = А.РЯП,	(5.24)
где А — матрица, определенная соотношением (5.22), а Рнп — матрица
порядка (N — m) х т, задающая вероятности перехода из невозвратных
состояний в поглощающие (см. (5.20)).
Свойства цепи, содержащей множество невозвратных состо-
яний J и замкнутое (поглощающее) множество возвратных со-
стояний С. При анализе подобных цепей нас могут интересовать ответы
на следующие вопросы:
-	какова вероятность того, что объект, отправляясь из невозвратного
состояния, все время будет находиться в множестве невозвратных состо-
яний J?
-	как подсчитать вероятность fj.c того, что объект, выходя из невоз-
вратного состояния j, когда-нибудь достигнет поглощающего множества
возвратных состояний С?
Ответы на эти вопросы дает, например, следствие теоремы 1 из
[Феллер В., с. 393]:
1) В конечной цепи Маркова вероятность того, что объект все
время будет находиться в множестве невозвратных состояний, равна
нулю.
2) Вероятности fj.c того, что исходя из невозвратного состояния
j объект достигнет когда-нибудь поглощающего множества С, опреде-
ляются как единственное решение системы линейных уравнений
fi-C - 52 РЛ • Ас = /у-с, 3 € J.	(5.25)
184
ГЛ. 5. ЦЕПИ МАРКОВА
В этой системе суммирование производится по всем невозвратным состо-
яниям цепи, a — это вероятность перейти из j в любое из состояний
множества С за один шаг.
5.4. Анализ некоторых задач и примеров
Теперь, когда мы проанализировали возможные типы состояний и
основные свойства марковской цепи, мы можем приступить к прикладно-
му анализу некоторых описанных в п. 5.2 примеров. Прикладной анализ
предусматривает решение ряда конкретных задач, в том числе тех, кото-
рые были сформулированы в п. 5.2 (см. задачи 1-5).
Пример 5.1. Динамика типологии семейного потребления.
Здесь нас в первую очередь будет интересовать тип и структура цени
(классификация состояний, наличие среди них замкнутых множеств воз-
вратных состояний, невозвратные и поглощающие состояния и т. п.), а
также прогноз распределения домашних хозяйств по типам потребитель-
ского поведения па заданное число тактов времени вперед (задача 1) и на
отдаленное будущее (задача 5). Подавляющее большинство состояний це-
пи представлено реально существующими типами потребительского пове-
дения (методика их статистического выявления описана в п. 12.4). Однако
среди состояний может быть небольшое число гипотетических (перспек-
тивных) типов, которые в начальный (наблюдаемый) момент времени
имеют «нулевое реальное представительство» (очевидно, соответствую-
щие элементы начального распределения	будут равны нулю).
Что касается типов состояний, то из смысла задачи следует, что данная
цепь, скорее всего, будет состоять из невозвратных состояний и какого-то
числа поглощающих множеств и состояний. Все определится конкрет-
ными значениями переходных вероятностей (методика статистической
оценки последних описана, например, в [Митоян А. А.]). Что касается ре-
шений задач 1 и 5, то они получаются с помощью формул — соответствен-
но (5.11)-(5.12) и, в случае существования стационарного распределения,
(5.21). Может представить практический интерес и вопрос о среднем вре-
мени пребывания домашнего хозяйства я-го типа в заданном или даже
во всех невозвратных состояниях до момента его поглощения замкнутым
множеством или поглощающим состоянием. Ответ на этот вопрос может
быть получен с помощью соотношений (5.22) и (5.23).
Пример 5.2. Игра двух лиц до разорения. Очевидно, перед
тем, как соглашаться на тот или иной регламент игры, наш участник
хотел бы подсчитать вероятность своего разорения (при игре до разо-
рения), а также свои наиболее вероятные состояния на 2-м, 3-м, 4-м и
5.4. АНАЛИЗ ЗАДАЧ И ПРИМЕРОВ
185
последующих конах.
Займемся решением первой задачи. На языке цепи Маркова разорение
нашего участника означает его «поглощение» состоянием / = 0 (оно соот-
ветствует его нулевому наличному капиталу, т. е. разорению). Несложный
анализ состояний цепи показывает, что она состоит из N — 1 невозврат-
ных состояний (состояния 1,2,	— 1)и двух поглощающих состояний
(состояния 0 и N). Поглощающий тип состояний 0 и N очевиден, а невоз-
вратность остальных состояний следует из того, что из каждого из них
с положительной вероятностью достигается одно из поглощающих состо-
яний (в этом легко убедиться, подсчитав для любого начального капита-
ла п вероятность n-кратных последовательных проигрышей или (7V — п)-
кратных последовательных выигрышей). Итак, наша схема относится к
категории марковских цепей, содержащих множество невозвратных со-
стояний и замкнутое (поглощающее) множество возвратных состоя-
ний С. В нашем случае мы имеем два таких вырожденных замкнутых
множества, каждое из которых состоит из единственного поглощающего
состояния. Нас интересует состояние 0. Для определения вероятности
разорения нашего участника /я.о составим и решим систему уравнений
(5.25). Очевидно, в нашем случае
/1°о =1 - р; До = 0 для всех > > L’
так что система (5.25) имеет вид:
/1.0 - Р/2.0 = 1 - Р
fj.o — (1 - р) ~ P/j+i.o = о
Jn-1.0 ~ (1 ~P)Jn-2.0 = 0
для j = 2,3,
N-2
Решение этой системы (с учетом очевидных граничных условий
/о.о = 1 и fN,0 = 0) лает:
, 1
при р /
1
при р = -
(подробное решение можно найти в [Феллер В., с. 338-339]).
Пример 5.3. Демографическая модель передвижки возрас-
тов. Рассуждения, аналогичные тем, которые мы использовали при ана-
лизе предыдущего примера, приводят нас к выводу, что данная цепь Мар-
кова (ее матрица переходных вероятностей приведена в п. 5.2) содержит
186
ГЛ. 5. ЦЕПИ МАРКОВА
невозвратные состояния 1-87 и два поглощающих (88-е и 89-е). Следова-
тельно, при анализе данной модели мы можем воспользоваться описании*
ми в п. 5.3.3 свойствами поглощающих цепей Маркова (5.22)—(5.24). Это
позволит нам, в частности, при подходящей интерпретации состояния
«предельный возраст» вычислить ряд важных демографических харак-
теристик. Так, если удалить «предельный возраст» достаточно далеко
(например, понимать под ним возраст свыше 150 лет; при этом, конеч-
но, возрастет общее число возможных состояний), то соответствующая
этому состоянию компонента вектора а, определяемого с помощью соот-
ношения (5.23), есть не что иное, как средняя (ожидаемая) продолжитель-
ность жизни населения данной страны или региона. Если же понимать
под «предельным возрастом» возраст выхода на пенсию, то аналогично
можно определить среднее число лет, которое человек пребывает в пенси-
онном возрасте (т. е. получает пенсию), и т. д.
Пример 5.4. Модель пребывания студента в вузе. По типу
цепь Маркова, описывающая эту модель, не отличается от предыдущей.
Разница состоит только в том, что из каждого невозвратного состояли
можно не только перейти в соседнее или в одно из двух поглощающих,
но и остаться в том же самом состоянии. Рассмотрим данный пример
подробнее.
Во-первых, приведем анализируемую матрицу Р переходных вероят-
ностей к виду (5.20). Для этого перенумеруем возможные состояния объ-
екта следующим образом:
1-е состояние:	«отчислен из института»;
2-е состояние:	«окончил институт»;
3-е состояние:	«обучение на 5-м курсе»;
4-е состояние:	«обучение на 4-м курсе»;
5-е состояние:	«обучение на 3-м курсе»;
6-е состояние:	«обучение на 2-м курсе»;
7-е состояние:	«обучение на 1-м курсе».
Зададимся для	определенности численными значениями переходных
вероятностей (данные заимствованы из [Кемени Дж., Снелл Дж.]) и
6.4. АНАЛИЗ ЗАДАЧ И ПРИМЕРОВ
187
выпишем приведенную форму матрицы Р:
нп х ин
1	0	0	0	0	0	0
0	1	0	0	0	0	0
0,2	0,7	0,1	0	0	0	0
0,2	0	0,7	0.1	0	0	0
0,2	0	0	0,7	0,1	0	0
0,2	0	0	0	0,7	0,1	0
0,2	0	0	0	0	0,7	0,1
О
Нас будут интересовать вероятности окончить институт для сту-
дента 1-го, 2-го и т. д. курсов (на языке модели марковской цепи — это
вероятности поглощения 7^-, см. п. 5.3.3, формулу (5.24)), а также средние
времена пребывания студента i-го курса в институте (на языке модели
марковской цепи — это компоненты вектора а, см. п. 5.3.3, соотношения
(5.22)-(5.23)).
Вычисления по формулам (5.22)-(5.24) дают:
	/ 0,9 -0,7	0 0,9	0 0	0 0	° \ 0
А ~	Р-н) “	0	-0,7	0,9	0	0
	0	0	-0,7	0,9	0
	\ 0	0	0	-0,7	0,9/
	/1,11	0	0	0	0 \
	0,86	1,11	0	0	0
	0,67	0,86	1,11	0	0
	0,52	0,67	0,86	1,111	0
	к 0,41	0,52	0,67	0,86	1,11/
Соответственно:
/1,П\
1,98
2,65
3,17
\3,58/
188
ГЛ. 5. ЦЕПИ МАРКОВА
Наконец, матрица Г попадания в поглощающие состояния
г = /												
	/1,11	0	0	0	0 >	/0,2		0,7 \		/0,22	0,78\	
	0,86	1,П	0	0	0		0,2	0		0,40	0,60	
	0,67	0,86	1,11	0	0	•	0,2	0	—	0,53	0,47	•
	0,52	0,67	0,86	1,11	0		0,2	0		0,63	0,37	
	\0,41	0,52	0,67	0,86	1,117	\0,2		0 /		к 0,72	0,28/	
Проанализируем полученные результаты. Компоненты вектора а
свидетельствуют о том, что студенты, достигшие 5-го курса, в средней
проводят в институте еще 1,11 года (сказывается возможность остаться
на 5-м курсе для повторного прохождения курса). Студенты, достигшие
4-го курса, в среднем проводят в институте еще 1,98 года (помимо упо-
мянутого выше фактора повторного обучения в данном случае дает себя
знать и перспектива досрочного отчисления). Воздействием этих двух
противоположных факторов (возможность остаться «на второй год» i
быть отчисленным досрочно) объясняются и средние времена пребывания
в институте студентов, начинающих третий год обучения (2,65 вместо
трех лет), второкурсников (3,17 вместо четырех лет) и поступивших на
1-й курс (3,58 года вместо пяти лет).
Второй столбец матрицы Г представляет нам следующую информаг
цию. При тех конкретных значениях переходных вероятностей, которые
мы использовали в своих расчетах, лишь 28% от поступивших в вуз его
успешно заканчивают. Аналогичный показатель для студентов, доучив-
шихся до 2-го, 3-го, 4-го и 5-го курса, имеет значения соответственно
37%, 47%, 60% и 78%.
Пример 5.5. Модель игровых возможностей двух шахма*
тистов. В этом примере главный вопрос, который нас будет интересо-
вать, это — кто из игроков (А или В) в длительном турнире (или в серин
турниров) выступит успешнее, т. е. наберет большее число очков? Для от-
вета на этот вопрос необходимо, по-видимому, подсчитать стационарное
распределение по «состояниям» (выигрыш-ничья-проигрыш) для каждого
из игроков. Поскольку матрица Р(А) переходных вероятностей, описыва-
ющая поведение игрока А, определяет последовательность независимых
испытаний (как частный случай цепи Маркова), то и стационарное рас-
пределение по состояниям для этого игрока останется тем же самым, т.е.
Р1°О)(л) = в; Р^°о)(Л) = н; р|оо)(А) = п,	(5.26)
где первое состояние соответствует выигрышу, второе — ничьей, а тре-
тье — поражению.
выводы
189
Система уравнений (5.21) для стационарных вероятностей игрока В
будет иметь вид:
Г ^’(В) • (в + е) +	 в + р<“>(В) - (в - е) = Р<“’(В)
j Р<ГЧВ)  н + Р^(В)  и + р<°°’(В)  в = р<?°Чв)
[р<оо)(В) + р‘о°>(В) + р<”>(В) = 1.
Решение этой системы дает:
Р(Г>(В) = B + s
В — п
1 -2е’
р^(В) = н; р^\в) = i - р1Г\в)
- Рз°Чв).
Сравнение соответствующих стационарных вероятностей для игро-
ков А и В, задаваемых соотношениями (5.26) и (5.27), позволяет сделать
следующий вывод: для игроков выше среднего уровня (т. е. при в > п) и
при «не слишком большой» эмоциональности игрока В (т. е. при е < п)
эффективность игры шахматиста В в длительном турнире окажется вы-
ше, чем А.
* ♦ ♦
Обратим внимание читателя на то, что во всех рассмотренных выше
примерах переходные вероятности pij считались априори заданными. На
практике они в большинстве случаев оцениваются статистически. В
некоторых случаях это делается достаточно просто с помощью соответ-
ствующих относительных частот. В общем случае проблема оценки пе-
реходных вероятностей может оказаться весьма сложной (см., например,
книгу Ли Ц., Джадж Д., Зелънер А. Оценивание параметров марковских
моделей по агрегированным данным. М.: Статистика, 1977).
ВЫВОДЫ
1.	Цепь Маркова с конечным числом состояний является про-
стейшим обобщением последовательности независимых испытаний. В
частности, она моделирует динамику (в дискретном времени) поведения
объекта, который может находиться в одном из N состояний, в ситуаци-
ях, когда вероятность оказаться объекту в заданном состоянии j в данный
момент времени t зависит только от того, в каком состоянии он находился
в предыдущий момент времени t — 1. Если в момент времени t — 1 объ-
ект находился в состоянии t, то вероятность оказаться в момент времени
t в состоянии j определяется так называемой переходной вероятностью
190
ГЛ. 5. ЦЕПИ МАРКОВА
Цепь называется однородной, если эти переходные вероятности
(для каждой фиксированной пары состояний i и j, i,j = 1,2,... ,Л) оста-
ются постоянными во времени, т. е. не зависят от t.
2.	Для вероятностного описания временнбй последовательности
состояний любой длины t достаточно задать (кроме матрицы Р = (pv)
переходных вероятностей) распределение объектов по состояниям в пер
вый (начальный) момент времени {pi,pa, • • • гДе Pi есть вероятность
того, что в начальный момент времени объект находился в состоянии t.
3.	Последовательность независимых испытаний, результатом ка-
ждого из которых может быть одно из N возможных событий, являет-
ся частным случаем однородной цепи Маркова с N возможными состоя*
ниями, в которой матрица переходных вероятностей Р определяется все-
го N различными числами, а именно, состоит из N одинаковых строк
(РиР2,* ,Рн)-
4.	Модель марковской цепи может оказаться полезной при решении
ряда важных прикладных задач, среди которых:
•	прогноз распределения объектов по возможным состояниям через за-
данное число тактов времени и в отдаленном будущем;
•	расчет среднего времени и вероятности пребывания объекта в задан-
ном состоянии или в заданном множестве состояний;
•	вычисление вероятности перехода объекта из определенного состоя-
ния i в заданное множество состояний за фиксированное число тактов
времени (в том числе, и за бесконечное время).
Б. Способ решения этих и других задач, связанных с анализом цепей
Маркова, зависит от типа анализируемой цепи, который, в свою оче-
редь, определяется типологией составляющих ее состояний. К основным
типам состояний марковской цепи относятся возвратные (вероятность
когда-нибудь вернуться в возвратное состояние равна единице), невоз-
вратные (вероятность когда-нибудь вернуться в невозвратное состояние
меньше единицы), поглощающие (попав в поглощающее состояние объект
с вероятностью единица остается в нем навсегда), периодические (объ-
ект не может вернуться в периодическое состояние за время, отличное от
времени, кратного заданному. периоду т), эргодические (все возвратные
непериодические состояния).
в. При анализе конкретной конечной цепи Маркова необходимо пред-
варительно ее классифицировать, определив, является ли она неприво-
димой (т.е. состоящей только из возвратных взаимодостижимых состо-
яний), и если «да», то являются ли эти состояния периодическими. В
условиях неприводимой непериодической марковской цепи справедливы
утверждения эргодической теоремы, в соответствии с которыми суще-
выводы
191
ствует единственное стационарное (финальное) распределение объектов
по состояниям и предлагается способ его расчета.
7. Если цепь не является неприводимой, то она может в общем случае
состоять из множества невозвратных состояний и какого-то числа по-
глощающих (замкнутых) множеств состояний (в частном случае погло-
щающее множество состояний может состоять из единственного состоя-
ния). При решении задач, связанных с анализом подобных цепей, следует
воспользоваться соотношениями (5.20), (5.22)-(5.25).

Раздел II
ГЛАВА 6. ОСНОВЫ СТАТИСТИЧЕСКОГО
ОПИСАНИЯ И СТАТИСТИКА
НОРМАЛЬНОГО ЗАКОНА
6.1. Генеральная совокупность, выборка из
нее и основные способы организации
выборки
Закономерности, которым подчиняется исследуемая случайная вели-
чина, физически полностью обусловливаются реальным комплексом усло-
вий ее наблюдения (или эксперимента), а математически задаются соот-
ветствующим вероятностным пространством {Q,C, Р}, или, что то же,
соответствующим законом распределения вероятностей. Однако при про-
ведении статистических исследований несколько более удобной оказывает-
ся другая терминология, связанная с понятием генеральной совокупности.
Генеральной совокупностью называют совокупность всех мы-
слимых наблюдений (или всех мысленно возможных объектов интересую-
щего нас типа, с которых «снимаются* наблюдения), которые могли бы
быть произведены при данном реальном комплексе условий. Поскольку
в определении речь идет о всех мысленно возможных наблюдениях (или
объектах), то понятие генеральной совокупности есть понятие условно-
математическое, абстрактное и его не следует смешивать с реальными
совокупностями, подлежащими статистическому исследованию. Так,
обследовав даже все предприятия подотрасли с точки зрения регистрации
значений характеризующих их технико-экономических показателей, мы
можем рассматривать обследованную совокупность лишь как представи-
теля гипотетически возможной более широкой совокупности предприятий,
которые могли бы функционировать в рамках того же самого реального
комплекса условий.
В практической работе элементы генеральной совокупности удобнее
связывать с объектами наблюдения, чем с характеристиками этих объ-
6.1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
195
ектов. Мы отбираем для изучения индивидуумов, семьи, предприятия,
регионы, страны, но не значения их характеристик. В математической
теории объекты и совокупность их характеристик не различаются и двой-
ственность введенного определения исчезает.
Как видим, математические понятия «генеральная совокупность»,
«вероятностное пространство», «случайная величина» и {закон распре-
деления вероятностей» физически полностью обусловливаются соответ-
ствующим реальным комплексом условий, а поэтому их можно считать в
определенном смысле синонимами. Генеральная совокупность называется
конечной или бесконечной в зависимости от того, конечна или бесконечна
совокупность всех мыслимых наблюдений.
Из определения следует, что непрерывные генеральные совокупности
(состоящие из наблюдений признаков непрерывной природы) всегда бес-
конечны. Дискретные же генеральные совокупности могут быть как бес
конечными, так и конечными. Скажем, если анализируется партия из N
изделий, когда каждое изделие может быть отнесено к одному из четырех
сортов, исследуемой случайной величиной £ является номер сорта слу-
чайно извлеченного из партии изделия, а множество возможных значений
случайной величины состоит соответственно из четырех точек (1,2,3 и 4).
В этом примере, очевидно, генеральная совокупность будет конечной (все-
го N мыслимых наблюдений). Как видим из примера, следует отличать
также совокупность всех мыслимых наблюдений от множества всех мы-
слимых (или теоретически возможных) значений исследуемой случайной
величины Наблюдений, вообще говоря, «больше», поскольку каждому
фиксированному возможному значению х может соответствовать несколь-
ко или даже бесчисленное множество мыслимых наблюдений.
Понятие бесконечной генеральной совокупности есть математическая
абстракция, как и представление о том, что измерение случайной величи-
ны можно повторить бесконечное число раз. Приближенно бесконечную
генеральную совокупность можно истолковать как предельный случай ко-
нечной, когда число объектов, порождаемых данным реальным комплек-
сом условий, неограниченно возрастает. Так, если в только что приведен-
ном примере вместо партии изделий рассматривать непрерывное массовое
производство тех же изделий, то мы придем к понятию бесконечной гене-
ральной совокупности. Практически же такое видоизменение равносильно
требованию N —* оо.
Выборка из данной генеральной совокупности — это результаты
ограниченного ряда наблюдений zi,£3,...,£n случайной величины £. Вы-
борку можно рассматривать как некий эмпирический аналог генеральной
совокупности, то, с чем мы чаще всего на практике имеем дело, поскольку
196
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
обследование всей генеральной совокупности бывает либо слишком тру-
доемко (в случае больших W), либо принципиально невозможно (в случае
бесконечных генеральных совокупностей).
В статистике интерпретация выборки и ее отдельных элементов
допускает в зависимости от контекста два различных варианта, при-
чем при изложении, как правило, специально не уточняется, о каком имен-
но варианте идет речь. В целях упрощения не делается различий и в
обозначениях. При первом (практическом) варианте интерпретации
выборки под а?2,... ,хп понимаются фактически наблюденные в дан-
ном конкретном эксперименте значения исследуемой случайной величи-
ны, т. е. конкретные числа.
В соответствии со вторым (гипотетическим) вариантом интер-
претации под выборкой xj,xj,...,хп понимается последовательность
случайных величин, t-й член которой (я^) лишь обозначает результат
наблюдения, который мы могли бы получить на i м шаге п-кратного
эксперимента1, связанного с наблюдением исследуемой случайной вели-
чины Если условия эксперимента не меняются от наблюдения к наблю-
дению и если n-кратный эксперимент организован таким образом, что
результаты наблюдения на каждом (t-м) шаге никак не зависят от пре-
дыдущих и не влияют на будущие результаты наблюдений, то, очевидно,
вероятностные закономерности поведения t-ro наблюдения гипотетической
выборки остаются одними и теми же для всех « = 1,2,..., п и полностью
определяются законом распределения вероятностей наблюдаемой случай-
ной величины, т. е.
•
Р{Х, <Х} = Р{£ < Х] = F((x).	(6.1)
При этом из взаимной независимости наблюдений выборки следует, что
последовательность случайных величин
• • • »
(6-2)
состоит из независимых компонент, т. е. их совместная функция распреде-
ления F(xi....,w)(^i,-..,a?n) = ^{*1 < *1,-
,хп < zn] может быть пред-
1 Говоря о «шаге п-кратного эксперименте», мы не имеем в виду жесткую связь
этих «шагов» с временными характеристиками проведения эксперимента. Переход
от i-го наблюдения выборки к i+1-му не обязательно выполняется в хронологической
последовательности: выбранные для наблюдения объекты могут образовывать так
называемую «пространственную выборку» и наблюдаться, например, одновременно.
6.1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
197
ставлена в виде
п	п
• • • > zn) = J"J -Р{г» < z*}	(6-3)
»=1	»=1
Если в рамках гипотетического варианта интерпретации выборки
ряд наблюдений (6.2) образует последовательность независимых и оди-
наково распределенных случайных величин (т.е, выполняются соотно-
шения (6.1) и (6.3)), то выборка называется случайной.
Число п наблюдений, образующих выборку, называют объемом вы-
борки.
Переход к группированным выборочным данным. Если объ-
ем выборки п велик (п > 50) и при этом мы имеем дело с одномерной
непрерывной величиной (или с одномерной дискретной величиной, число
возможных значений которой достаточно велико, скажем больше 10), то
часто удобнее, с точки зрения упрощения дальнейшей статистической об-
работки результатов наблюдений, перейти к так называемым «группи-
рованным» выборочным данным. Этот переход осуществляется обычно
следующим образом:
а)	отмечаются наименьшее zmin(n) и наибольшее zmax(n) значения в
g.	1
выборке ;
б)	весь обследованный диапазон [xminW, smax(n)] разбивается на
определенное число з равных интервалов группирования; при этом количе-
ство интервалов з должно быть в пределах 7-20. Выбор количества интер-
валов существенно зависит от объема выборки п ; для примерной ориента-
ции в выборе <з можно пользоваться приближенной формулой в ~ log2 п-|-1,
которую следует воспринимать, скорее, как оценку снизу для з (особенно
при больших п);
в)	отмечаются крайние точки каждого из интервалов Со, <?i, с2,..., св
0 0 о
в порядке возрастания, а также их середины Zi, z2,..., xa'y
г)	подсчитываются числа выборочных данных, попавших в каждый из
интервалов: Pj, i/2,..., ua (очевидно, i/i +р2 + ..	= п); выборочные дан-
ные, попавшие на границы интервалов, либо равномерно распределяются
но двум соседним интервалам, либо уславливаются относить их только к
какому-либо одному из них, например, левому.
1 Запись zmin(n) * zmax(n) подчеркивает тот факт, что наименьшее и наибольшее
значения в выборке, как и все другие характеристики, построенные по выборке объ-
ема п, конечно, зависят от п. Там, где этот факт не требует напоминания, мы будем
опускать п в записи выборочных характеристик.
198
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
В зависимости от конкретного содержания задачи в данную схему
группирования могут быть внесены некоторые видоизменения (например,
в некоторых случаях целесообразно отказаться от требования равной дли-
ны интервалов группирования; иногда крайние интервалы целесообразно
делать полу бесконечными слева или справа).
Репрезентативность выборки. Сущность статистических ме-
тодов состоит в том, чтобы по некоторой части генеральной сово-
купности (т. е. по выборке) выносить суждения о ее свойствах в qe-
лом. Поэтому один из важнейших вопросов, от успешного решения ко-
торого зависит достоверность получаемых в результате статистического
анализа выборочных данных выводов, является вопрос репрезентатив-
ности выборки, то есть вопрос полноты и адекватности представления
ею интересующих нас свойств всей анализируемой генеральной совокуп-
ности. В практической работе одна и та же группа объектов, взятых для
изучения, может рассматриваться как выборка из разных генеральных
совокупностей. Так, группу семей, наудачу отобранных из панельных до-
мов жилищно-эксплуатационной конторы (ЖЭК) одного из районов горо-
да для подробного социологического обследования, можно рассматривать
и как выборку из генеральной совокупности семей (в панельных домах)
данной ЖЭК, и как выборку из генеральной совокупности всех семей дан-
ного района, и как выборку из генеральной совокупности всех семей дан-
ного города, и, наконец, как выборку из генеральной совокупности всех
семей города, проживающих в панельных домах. Оценка степени репре-
зентативности имеющихся выборочных данных существенно зависит от
того, представителем какой генеральной совокупности мы рассматриваем
отобранную группу семей. Ответ на этот вопрос зависит от многих фак-
торов. В приведенном выше примере, в частности, — от наличия или от-
сутствия специального (быть может, скрытого) фактора, определяющего
принадлежность семьи к данной ЖЭК или району в целом (таким факто-
ром может быть, например, среднедушевой доход семьи, географическое
расположение района в городе, «возраст» района и т.п.).
Основные способы организации выборки. При оценке репрезен-
тативности выборки учитывается и то, насколько распределение в вы-
борке существенных для изучаемого вопроса показателей характерно для
анализируемой генеральной совокупности в целом. Первый путь повы-
шения степени репрезентативности — достижение полностью случайного
отбора объектов из генеральной совокупности — часто бывает труден в
организационном плане. Кроме того, сочетание регулярного и случайного
выбора иногда оказывается более эффективным. В любом случае способ
сбора исходных данных должен тщательно планироваться и его необхо-
6.1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
199
димо полностью описывать в отчетах о выполненной работе.
Использование для оценки репрезентативности сравнения распреде-
лений основных показателей в выборке и в генеральной совокупности так-
же имеет свои трудности, одни из которых носят чисто статистический
характер — недостаточный объем (число отобранных для обследования
объектов) выборки, неразработанность методов сравнения многомерных
распределений и т.п., а другие — содержательный, ведь часто заранее
неизвестно, распределение каких показателей следует сравнивать при до-
казательстве репрезентативности.
Опишем кратко основные способы организации выборки.
Простой случайный отбор — способ извлечения п объектов из ко-
нечной генеральной совокупности N объектов, при котором каждая из
возможных выборок (а всего существует, как известно, способов ото-
брать п элементов из множества N элементов) имеет равную вероятность
быть отобранной. На практике часто нумеруют объекты в генеральной
совокупности числами от 1 до N и затем, используя таблицы случайных
чисел или какой-либо другой метод, обеспечивающий равную вероятность
выбора объекта (например, урну с N шарами, занумерованными цифрами
от 1 до N), отбирают один за другим п объектов. Полученная таким спо-
собом выборка называется случайной, так как при этом обеспечивается
выполнение условий случайности (6.1) и (6.3).
Простой отбор с помощью регулярной, но несущественной для изу-
чаемого вопроса процедуры часто применяется вместо случайного отбо-
ра. На производстве изделия для контроля их качества часто отбира-
ют в определенный период времени, что удобно с организационной точки
зрения; в социологических обследованиях — по букве, с которой начи-
нается фамилия индивидуума, проживающего в домах данной жилищно-
эксплуатационной конторы, и т.п. Получаемые таким образом выборки
часто называют механическими.
Стратифицированный (расслоенный) отбор заключается в том, что
исходная генеральная совокупность объема N подразделяется на подсово-
купности объема ДГ1, iV2,...,	При этом подсовокупности не содержат
общих объектов и вместе исчерпывают всю генеральную совокупность,
так что JVi + Nt + ... + Nr = N. Подсовокупности называют стратами
или слоями. Когда слои определены, из каждого слоя извлекается про-
стая случайная выборка объема соответственно пг, п2,..., пц. Для того
чтобы можно было полностью воспользоваться выгодами от расслоения,
значения Ni/N должны быть известны. Стратифицированный отбор при-
меняется, когда слои однородны в том смысле, что входящие в них объ-
екты имеют близкие характеристики (средние значения которых могут
200
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
быть оценены по малым выборкам); либо когда целесообразно изучать
генеральную совокупность с равной тщательностью во всех слоях; либо
по организационным причинам, когда методы проведения отбора в слоях
должны быть разными. Выборки, полученные таким способом, называют
стратифицированными или расслоенными (иногда — районированными).
Частным случаем стратифицированного отбора является способ орга-
низации выборки, при котором страты (слои) генеральной совокупности
выделены по косвенному признаку, как-то связанному с изучаемым. Так,
изучая средний душевой доход семей, для получения стратифицирован-
ных выборок можно предварительно разбить исследуемую совокупность
семей на группы, однородные по какой либо из социально-экономических
характеристик главы семьи (например, по заработку). В подобных случа-
ях говорят о типическом способе отбора и соответственно о типических
выборках.
Методы серийного отбора (и соответственно серийные выборки) ис-
пользуются тогда, когда удобнее назначать к обследованию не отдельные
элементы генеральной совокупности, а целые «блоки* или серии таких
элементов. Так, при проведении выборочных обследований населения спо-
соб территориально-административного деления страны и характер ве-
дения соответствующей документации обусловливают большее удобство
сплошного способа обследования целых территориальных единиц (домов,
кварталов), а не отдельных семей. Подобный способ отбора часто назы-
вают также гнездовым.
Комбинированный (ступенчатый) отбор сочетает в себе сразу не-
сколько из описанных выше способов отбора, образующих различные сту-
пени (или фазы) выборочного обследования. Так, при выборочном обсле-
довании условий жизни и структуры семей какого-либо города на первой
ступени можно с помощью случайного отбора назначить городские рай-
оны, в которых будет производиться это обследование, затем способом
механического отбора определить подлежащие обследованию жилищно-
эксплуатационные конторы (ЖЭКи), а внутри ЖЭКов сделать серийную
(гнездовую) выборку домов.
6.2. Основные выборочные характеристики
и их свойства
В практике статистического анализа и моделирования, к сожалению,
точный вид закона распределения анализируемой генеральной совокупно-
сти, как правило, бывает неизвестен. Исследователь располагает лишь
выборкой из интересующей его генеральной совокупности и вынужден
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 201
строить все свои выводы на основании расчета ограниченного ряда вы-
борочных характеристик. Какие же выборочные характеристики несут
наибольшую информацию о генеральной совокупности, являются в этом
смысле основными? К основным выборочным характеристикам от-
носятся:
•	выборочная (эмпирическая) функция распределения F^n\x)\
•	выборочная (эмпирическая) функция плотности f^n\x);
•	выборочная (эмпирическая) относительная частота р\ появления
О	„	ч- ~
i-го возможного значения ж, дискретной случайной величины;
•	выборочные начальные и центральные моменты анализируемой слу-
чайной величины (rhk(n)um°k(n)) и, в первую очередь, выборочное
среднее значение х(п) — rh,i(n)u выборочная дисперсия я2(п) =
•	порядковые статистики х^у(п) (i = 1,2,...,п), т.е. члены ряда на-
блюдений выборки, расположенных в этом ряду в порядке их возра-
стания.
Нас будут интересовать в данном пункте определения и свойства этих
выборочных характеристик. Говоря о свойствах выборочных характери-
стик, мы постараемся ответить в числе прочих на следующие два вопроса:
•	стремится ли анализируемая выборочная характеристика к опреде-
ленному пределу при неограниченном увеличении объема выборки п (т.е.
при п -> оо)?
•	как «ведут себя» выборочные характеристики в роли случайных
величин (каковыми все они являются), т.е. что можно сказать о законе
распределения вероятностей каждой из них при достаточно больших (т. е.
при п —> оо) и ограниченных объемах выборок?
6.2.1.	Выборочные (эмпирические) функции распределения,
относительные частоты и функции плотности
Итак, объектом нашего анализа является генеральная совокупность,
отражающая поведение случайной величины £ с теоретической функцией
распределения (вообще говоря, нам не известной) F(x) = Р{£ < ж}. Мы
располагаем лишь случайной выборкой (6.2) из этой генеральной совокуп-
ности.
Эмпирическим (или выборочным, т.е. построенным по выборке объ-
ема п) аналогом теоретической функции распределения F(x) является
202
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
функция F^n\x), определяемая соотношением:
(6.4)
или, в случае группированных данных (см. п. 6.1),
Г<п)(г) = "1 + *2+*-+ Ц. ,	(6,5)
где i/(z) — число наблюденных значений исследуемой случайной величи-
ны в выборке Zj, х2,..., zn, меньших ж; — число наблюденных значений
в выборке, попавших в t-й интервал группирования, a ix — номер самого
правого из интервалов группирования, правый конец которых не превос
ходит х.
Из определения эмпирической функции распределения непосредствен-
но следует объяснение часто используемого ее другого названия — «но-
копленная относительная частота*.
Если анализируемая случайная величина £ дискретна и имеет воз-
можные значения z?(i = 1,2,...), принимаемые соответственно с вероят-
ностями pi = Р{£ = z?}, т.е. смысл ввести понятие выборочной (эмпи-
рическои) относительной частоты р\ , которая определяется как отно-
шение числа 1/д.о наблюдений в выборке, в точности равных z°, к общему
объему выборки, т.е.
4п)
И = —
Если £ — непрерывная случайная величина (генеральная совокуп-
ность) с функцией плотности вероятности /(z) и функцией распределе-
ния F(z), которая всюду непрерывна и дифференцируема, то, распола-
гая выборочными данными (выборкой) zj, x2t. -., zn, мы можем построить
выборочный аналог ^функции плотности — эмпирическую (выборочную)
функцию плотности f^n\x).
Для построения эмпирической (или выборочной) функции плотности
j (х) на всей области ее определения (т.е. для всех возможных зна-
чений исследуемой величины) используют предварительно сгруппирован-
ные данные (см. п. 6.1) и полагают
7П)(*) =	,	(6.6)
где к(х) — порядковый номер интервала группирования, который накры-
вает точку z; — число наблюдений, попавших в этот интервал,
Д*(х) — длина интервала.
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА
203
Геометрическое изображение эмпирической функции плотности носит
название гистограммы.
Пример 6.1. Анализируется выборка из ста малых предприятий
региона. Цель обследования — фиксация коэффициента соотношения за-
емных и собственных средств (zj на каждом t-м предприятии. Таким
образом, п = 100, а : = 1,2,...,п. Результаты обследования п = 100
малых предприятий представлены в табл.6.11.
Таблица 6.1. Коэффициенты соотношения заемных и собственных средств
предприятий
5,56	5,45	5,48	5,45	5,39	5,37	5,46	5,59	5,61	5,31
5,46	5,61	5,11	5,41	5,31	5,57	5,33	5,11	5,54	5,43
5,34	5,53	5,46	5,41	5,48	5,39	5,11	5,42	5,48	5,49
5,36	5,40	5,45	5,49	5,68	5,51	5,50	5,68	5,21	5,38
5,58	5,47	5,46	5,19	5,60	5,63	5,48	5,27	5,22	5,37
5,33	5,49	5,50	5,54	5,40	5,58	5,42	5,29	5,05	5,79
5,79	5,65	5,70	5,71	5,84	5,44	5,47	5,48	5,47	5,55
5,67	5,71	5,73	5,03	5,35	5,72	5,49	5,61	5,57	5,69
5,54	5,39	5,32	5,21	5,73	5,59	5,38	5,25	5,26	5,81
5,27	5,64	5,20	5,23	5,33	5,37	5,24	5,55	5,60	5,51
Требуется построить эмпирические функции распределения f^n\x) и
плотности f^n\x)t а также представить их геометрическое изображение
(графики).
Решение. Построим группированный ряд наблюдений:
а)	определим среди наблюдений (в выборке) минимальное zm;n = 5,03
и максимальное imax = 5,85 значения;
б)	разобьем весь диапазон [гт-1п, жтвх] на s равных интервалов груп-
пирования, где s ~ log2 п + 1 = 3,32Inn + 1 = 7,62 « 8, отсюда ширина
интервала Д =	—Жт|П = . 5,03 _ qjqj Примем Д = 0,11;
з	8
в)	определим крайние точки каждого интервала co,ci,c2,... ,сл в по-
оо о
рядке возрастания, а также их середины , х2,..., хв.
За нижнюю границу первого интервала предлагается принять вели-
чину Со = Zmin - f = 4,97.
1 Результаты обследования выстроены в таблице размером 10 х 10 в порядке регистра-
ции по строкам, так что 2-я строка начинается с 11-го наблюдения, 3-я — с 21-го и
т.д.
204
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Тогда Cj = со + А = 5,08; с2 = Cj + А = 5,19;
о
®2
Л	0 Ч) т С1
Определим середины интервалов: Ж] = —-—
С1 + с2 - . л О Сл_! + С,
—-— = 5,14,..., ха =----------------= 5,80.
J-г	л*
с8 = со 4- 8А = 5,85.
4,97 + 5,08
Таблица 6.2. «Группированный» ряд наблюдений
к	Интервалы 1 ^к	0 хк	”к		F(n)(z)	?"’(«)
1	4,97-5,08	5,03	2	2	0,02	0,18
2	5,08-5,19	5,14	3	5	0,05	0,27
3	5,19-5,30	5,25	12	17	0,17	1,09
4	5,30 5,41	5,36	19	36	0,36	1,73
5	5,41-5,52	5,47	29	65	0,65	2,64
6	5,52-5,63	5,58	18	83	0,83	1,б4
7	5,63-5,74	5,69	13	96	0,96	1,18
8	5,74-5,85	5,80	4	100	1,00	0,36
Границы последовательных интервалов и их середины представлены
в табл. 6.2.;
г)	подсчитаем числа выборочных данных, попавших в каждый из ин-
тервалов:	- - -, где pj + ... + иа = п.
Последовательно просматривая данные наблюдений, разносим значе-
ния признака по соответствующим интервалам. Так как значения могут
совпадать с границами интервалов, то условимся в каждый Jb-й интервал
включать наблюдения, большие или равные, чем нижняя граница интер-
вала, и меньшие верхней границы, т. е. наблюдения, удовлетворяющие
неравенствам сд._] х < с*. Общее число наблюдений, отнесенных к А-му
интервалу, равно частоте |/Л.
В табл. 6.2 приводятся также накопленные частоты , равные сумме
частот k-го и всех предшествующих интервалов.
Для построения гистограммы на оси абсцисс откладываются крайние
точки каждого из интервалов с0,с1,с2,...,са, а по оси ординат эмпири-
ческий аналог функций плотности f^n\x). Тогда Л-му интервалу будет
соответствовать прямоугольник, основанием которого является замкну-
тый слева интервал [cfc_!,cfc), а высота равна f^n\x) = Графики,
соответствующие эмпирической (/^(я)) и модельной (/(ж)) плотностям,
приведены на рис. 6.1. Для построения модельной кривой плотности ис-
пользовалась нормальная модель закона распределения, в которую подста-
6.2.	ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 205
влялись вместо неизвестных параметров — среднего а и дисперсии <т2 —
значения соответствующих выборочных характеристик х и з2 (подсчитан-
ные в примере 6.2, см. ниже).
Рис.в.1. Гистограмма
Если значения f^n\x) соотнести к серединам соответствующих ин-
0 0 о
тервалов	.,жя и соединить полученные точки, то получим лома-
ную линию (рис. 6.2), которую называют полигоном.
Геометрическое представление эмпирической функции распределения
fW(:r) называют кумулянтой или кумулятивной кривой (рис. 6.3). Для
этого на оси абсцисс откладывают границы интервалов Cq,C!,c2, ... ,св, а
по оси ординат значения F^n\x), взятые из табл. 6.2, причем значения
F^(x} относят к верхней с*, границе k-ro интервала (к = 1.2.я).
206
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ

Рис. в.2. Полигон
Рис. в.З. Кумулятивная кривая
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 207
6.2.2.	Выборочные аналоги начальных и центральных
моментов случайной величины
В основе объяснения перехода от теоретических характеристик, ко-
торые вычисляют на базе точного знания исследуемого закона распреде-
ления, к эмпирическим (или выборочным) лежит интерпретация выборки
(6.2) как модели генеральной совокупности, в которой возможными зна-
чениями являются наблюденные (т.е. практически реализованные) зна-
чения 24, жг,..., яп, а в качестве вероятностей их осуществления берутся
соответствующие относительные частоты их появления в выборке, т.е.
величины, равные 1/п. Таким образом, выборку можно представить в
табличном виде:
S1	х2	• • •	Хп
1 п	1 п	• • •	1 п
Условно рассматривая ее как табличную форму задания дискретной
случайной величины, возможные значения которой Xi,X2,. ..,хп появля-
ются с одними и теми же вероятностями pi — р2 — ... = рп = лег"
ко представить эмпирические аналоги рассмотренных выше начальных и
центральных моментов в виде:
1 к
™к = -5г,,
(6-7)
(6-8)
где средняя арифметическая х есть эмпирический аналог начального мо-
мента первого порядка:
Аналогичные формулы для группированных выборочных данных (см.
п.6.1) выглядят следующим образом:
j=l
. О 1 /О -
(6.7')
(6.8')
208
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
6.2.3.	Эмпирические аналоги центра группирования
генеральной совокупности
В статистической практике в качестве характеристик центра груп-
пирования значений исследуемого признака используют несколько видов
средних значений, моду и медиану (см. п. 2.6.2). Рассмотрим эмпири-
ческие аналоги этих числовых характеристик, которые вычисляются по
выборочным данным ,«а,..., хп.
Средняя арифметическая х (выборочная средняя) является, пожалуй,
основной и наиболее употребительной характеристикой центра группиро-
вания:
(6.9)
Геометрическое среднее определяется по формуле:
G = tyxi •х2•... •хп
(6.10)
Оно находит применение при расчетах темпов изменения величин и, в
частности, в тех случаях, когда имеют дело с величиной, изменения кото-
рой происходят приблизительно в прямо пропорциональной зависимости
с достигнутым к этому моменту уровнем самой величины (например, чи-
сленность населения), или же когда имеют дело со средней из отношений,
например, при расчетах «индексов цен».
Среднее гармоническое вычисляется по формуле:
(6.11)
Гармоническими средними иногда пользуются в экономике при анали-
зе средних норм времени, а также в некоторых видах индексных расчетов.
Следует от.мстить, что выборочное гармоническое среднее значение
Нп ряда чисел zj,a^,....zn всегда меньше выборочного геометрического
среднего значения Gn, которое в свою очередь меньше выборочного сред-
него арифметического х.
Выборочная мода хто^ представляет собой наиболее часто встреча-
ющееся в выборочных наблюдениях значение переменной, т. е. значение,
которое действительно является модным. Практическое отыскание эм-
пирического аналога моды по выборочным данным требует построения
группированного ряда наблюдений и будет подробно рассмотрено ниже, в
примере 6.2.
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА
209
Медиана, точнее, ее эмпирический аналог £med> определяется как
среднее (по местоположению) значение ранжированного, т.е. располо-
женного в порядке возрастания, ряда наблюдений X(i) Z(2)	я?(п)
(подробнее о таких рядах см. в п. 6.3). Если п нечетно, то £meti = Жрцр
а если п четно, то £med = |(z(^) 4- Z(*+l)).
6.2.4.	Эмпирические аналоги показателей вариации
рассеивания случайной величины
Каждая из описанных ниже характеристик степени рассеивания —
выборочные дисперсия, среднеквадратическое отклонение и коэффициент
вариации — дает представление о том, как могут отклоняться от своего
центра группирования элементы выборки.
2
Эмпирическую (выборочную) дисперсию з можно рассматривать как
приближенное значение теоретической дисперсии (см. (2.23) в п. 2.6.3):
(6Л2)
Выборочное (эмпирическое) среднеквадратическое отклонение име-
ет вид:
8 =
(6.13)
Оно используется наряду с выборочной дисперсией 82 для характери-
стики степени отклонения наблюдаемых величин х±, zj,..., хп от среднего
значения х и оказывается в ряде случаев более удобным и естественным,
так как з имеет ту же размерность, что и сама анализируемая случайная
величина, и соответственно характеристики центра группирования.
Несколько более точными приближениями к теоретическим значени-
ям дисперсии и среднеквадратического отклонения а и о при небольших
объемах выборки являются подправленные выражения з2 и з вида (подроб-
нее о точности в определении теоретических характеристик распределения
см. в п. 7.1.5):
Выборочный коэффициент вариации V используется в тех случаях, ко-
гда степень рассеивания естественно описывать некоторой относительной
210
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
характеристикой в соответствии со средним (см. п. 2.6.3). В частности,
V = - • 100%.	(6.15)
Как видим из (6.15), выборочный коэффициент вариации есть безраз-
мерная величина, измеряемая в процентах.
6.2.5.	Выборочные коэффициенты асимметрии и эксцесса
Выборочный коэффициент асимметрии является характеристикой
степени скошенности (см. п. 2.6.5) и подсчитывается с помощью вто-
рого и третьего центральных выборочных моментов по формуле:
(т®)^
1=1
1=1
(6.16)
Из формулы (6.16) следует, что для симметричных (относительно
среднего значения Е£) функций плотности распределений /Зг должен быть
близок к нулю, в то время как для распределения, гистограмма которого
имеет «длинную часть», расположенную справа от ее вершины, fa > 0, а
если слева — то fa <0. Выборочный эксцесс /32 является, как и соответ-
ствующая теоретическая характеристика /32 (см. п. 2.6.5), характеристи-
кой поведения плотности (полигона) распределения в районе ее модального
значения. Он подсчитывается по формуле:
А(0)
А = /Ж - 3 =	--------3.	(6.17)
(mJ')	8
Напомним, что своеобразным аналогом отсчета в измерении степени
островершинности служит нормальное распределение, для которого =
0. Для островершинного (по сравнению с нормальным) распределения —
> 0, а для плосковершинного — /?2 < 0.
Пример 6.2. По данным табл. 6.2 примера 6.1 рассчитать выбо-
рочные характеристики центра группирования, рассеивания, асимметрии
и эксцесса.
Решение. Для удобства вычислений целесообразно составить вспо-
могательную таблицу (табл. 6.3). В ней сохранены обозначения табл. 6.2
и введено одно новое: = ж° — ж (k = 1,2,..., 8).
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 211
Таблица 6.3. Вспомогательная таблица для вычисления выборочных характе-
ристик по группированным данным
к	0 Хк	”к	0	6к”к		6к”к	Як"к	н »к
1	5,03	2	10,06	-0,8712	0,37949	-0,1653	0,07201	2
2	5,14	3	15,42	-0,9768	0,31805	-0,10356	0,03372	5
3	5,25	12	63,00	-2,5872	0,55780	- 0,12026	0,025928	17
4	5,36	19	101,84	-2,0064	0,21188	- 0,02237	0,00236	36
5	5,47	29	158,63	0,1276	0,00056	0,00000	0,00000	65
6	5,58	18	100,44	2,0592	0,23557	0,02695	0,00308	83
7	5,69	13	73,97	2,9172	0,65462	0,14690	0,032996	96
8	5,80	4	23,20	1,3376	0,44729	0,14957	0,05002	100
Итого		100	546,56	0	2,80526	-0,08808	0,22008	
Пользуясь данными табл. 6.3, вычислим среднее арифметическое зна-
чсние
ч”4 ®
kXkVk 546,56
z = -*=------= —= 5,4656.
Е "к юо
к
Для проверки правильности вычисления х полезно убедиться в выполне-
нии условия 6kvk =	- fyk = 0.
На основании данных таб^т. 6.3 найдем выборочные:
•	дисперсию
Е _ 2>805
2>* “ юо
= 0,02805;
•	среднеквадратическое on клонение 8 = 0,167;
• коэффициент вариации
V = 4100% = г^100% ='3,06%;
х 5.466
212
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
• центральные моменты третьего и четвертого порядков:
. о
т3 =
-0,08808
100
= -0,00088;
0,22008
100
= 0,0022;
к
к
• коэффициент асимметрии:
01 =
Л о
т3
з
s
0,00088
0,00468
= -0,188;
• коэффициент эксцесса:
Л о
& = ^-з =
3
0,0022
(0,028)2
- 3 = -0,203.
Близость значении выборочных коэффициентов асимметрии и экс-
цесса 02 к нулю свидетельствует в пользу выбора нормального закона
распределения для анализируемой генеральной совокупности.
Как уже отмечалось, медиана zmed есть значение признака, приходя-
щееся на середину ранжированного ряда наблюдений. В нашем примере
п — 100 и imed =	Анализ таблицы исходных данных, пред-
ставленных в табл. 6.1, показывает, что наблюдения, расположенные в
упорядоченном ряду на 50-м, 51-м и 52-м местах принимают одно и то
же значение, равное 5,47. Другими словами, я?(но) = ®(51) = ®(52) = 5,47,
следовательно, imed = 5,47.
Мода, как отмечалось выше, равна значению признака zmod > которо-
му соответствует наибольшая частота. Как следует из табл. 6.3 наиболь-
шая частота р = 29 соответствует значению imod = 5,47.
Так как i,imed и zmod практически не отличаются друг от друга,
то есть основание предполагать, что теоретическое распределение симме-
трично относительно своего среднего значения, что является еще одним
доводом в пользу выбора модели нормального закона.
Построение модельной кривой плотности нормального закона рас-
пределения. При расчете модельных частот и? нормального закона рас-
пределения за оценку математического ожидания (Г и среднеквадратиче-
ского отклонения о принимают значения соответствующих выборочных
характеристик х и з, т.е. а = х = 5,466; о = з = 0,167.
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 213
Модельные частоты находят по формуле:
»к = пр*,
где п — объем выборки; р^ — вероятность попадания значения нор-
мальной случайной величины в к-и интервал.
Вероятности Рь в соответствии со свойством г) функции распределе-
ния (см. п. 2.5.1) определяются формулой
Р* = P{c*-i £ <
с*} = Ф(с*;л,з2) - Ф^-^з2),
(6.18)
где Ф(ж;о,<т2) — функция нормального распределения, имеющего среднее
значение а и дисперсию а2 (см. (З.в*) в п. 3.1.5). Чтобы вычислять зна-
чения функции Ф(с*;х,£2) для различных значений ск и при заданных
величинах х и з2 с помощью таблиц стандартной нормальной функции
распределения Ф(х) = Ф(эг; 0,1) (таблицы приведены в приложении 1), вос-
пользуемся результатом (4.9) из п.4.4,в соответствии с которым
Ф(ж; о, ст2) = Ф (-—0,1)
\ о /
(6.19)
Соответственно, возвращаясь к (6.18), в нашем случае имеем:
Р* = Ф(------------) - Ф(---------------),
X -S /	\	3	/
к = 1,2,..., 8,
2	_
где х и з — подсчитанные ранее значения выборочного среднего и вы-
t -£
борочной дисперсии, а Ф(^) = -^= е ^~dx — значение функции стан-
дартного нормального распределения, вычисленное в точке t.
Составим табл. 6.4 для вычисления вероятностей рд., модельных ча-
стот i/fc и модельной (нормальной) плотности распределения /м(г).
График плотности модельного (нормального) закона распределения
/м(ж) представлен на рис. 6.1. Этот график достаточно хорошо согласует-
ся с гистограммой — графиком эмпирического аналога плотности f^n\x).
214
ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Таблица 6.4 Расчет модельных частот и модельной плотности /к(х)
с*-] — Cfe	"к		1к		*(«*)	Рк	npk	Т Vk	ЛЮ
4,97-5,08	2	—оо	- 2,39	0	0,0082	0,0082	0,8	1	0,09
5,08-5,19	3	-2,39	- 1J1	0,0082	0,0446	0,0364	3,6	4	0,36
5,19-5,30	12	-1,71	- 1,03	0,0446	0,1587	0,1141	11,4	11	1,00
5,30-5,41	19	-1,03	- 0,35	0,1587	0,3632	0,2045	20,5	21	1,91
5,41-5,52	29	- 0,35	0,33	0,3632	0,6368	0,2736	27,4	27	3,45
5,52- 5,63	18	0,33	1,02	0,6368	0,8413	0,2045	20,5	21	1,91
5,63- 5,74	13	1,02	1,70	0,8413	0,9554	0,1141	11,4	11	1,00
5,74- 5,85	4	1,70	+оо	0,9554	1,0000	0,0446	4,4	4	0,36
	100	-	-	-	-	1,000	-	100	- 1
6.2.6.	Статистическая устойчивость выборочных
характеристик
Давно было замечено, что результаты отдельных наблюдений (будь
то экономические, демографические, физические, метеорологические или
иные наблюдения), хотя и произведенных в относительно однородных
условиях, колеблются, в то время как средние из большого числа наблю-
дений обнаруживают замечательную устойчивость. К такого рода вы-
борочным средним относятся и все введенные нами выше эмпирические
(т. е. построенные по выборке) характеристики: как выборочные момен-
ты (начальные и центральные) т^ и так и эмпирические функция
распределения F^n^(z), функция плотности f^n\x) и относительные часто-
ты р, (при интерпретации /Хп)^п) и р<п) в качестве выборочных средних
нужно лишь помнить о возможности их выражения в терминах сумм слу-
чайных величин £ 1,..., £п, где & равно 1 и 0 в зависимости от того, попало
или нет наблюдение z, в заранее определенную нами область возможных
значений (см. (4.4)-(4.6) в п. 4.2.2)).
Математическим основанием этого факта служат различные формы
закона больших чисел, который позволяет теоретически обосновывать
устойчивость основных эмпирических характеристик распределения —
среднего значения, дисперсии, асимметрии, эксцесса, функции распреде-
ления и плотности, построенных по выборке zj,Z2,... ,zn. При этом как
всегда, когда речь идет об исследовании выборочных характеристик, мы,
во-первых, подразумеваем, что имеем дело с выборкой, состоящей из не-
зависимых наблюдений, и, во-вторых, интерпретируем выборку во вто-
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 215
ром, гипотетическом, смысле как совокупность независимых наблюде-
ний, которые могли бы быть произведены над анализируемой случайной
величиной (см. п. 6.1, (6.1)-(6.3)). При такой интерпретации наблюдения
Т1,жз,...,жп суть независимые и одинаково распределенные случайные
величины и к ним применимы результаты п. 4.2. Покажем, как из закона
больших чисел и теоремы Я. Бернулли можно получить статистическую
устойчивость основных выборочных характеристик.
а.	Устойчивость выборочных начальных моментов т^п) и лю-
бых рациональных функций от них. Пусть существуют моменты т^ =
Е£*(Л = 1,2,...,2Ло) всех порядков (вплоть до заданного 2fc0) исследу-
емой случайной величины f. Тогда, применяя закон больших чисел к
случайным величинам ft = «1,53 = Xj,.. . ,fn = xn, где Xi — результат
i-го наблюдения исследуемого признака, мы немедленно получаем доказа-
тельство сходимости по вероятности всех выборочных начальных момен-
тов т^(п) = (£”=1 х^)/п к соответствующим теоретическим моментам
Непосредственно применить закон больших чисел к центрированным
наблюдениям хг — х(п),..., хп — х(п) нельзя, так как после центрирования
наблюдения становятся зависимыми.
Однако, воспользовавшись теоремой Е. Е. Слуцкого1 о том, что из схо-
димости (при п —► оо) по вероятности случайных величин &(п) к не-
которым постоянным числам a, (» = 1,2, ...,Ло) следует сходимость по
вероятности любой рациональной функции <р(€1(п),£2(п),.. ,,&0(п)) к 66
значению в точке (си, аз,...,а*0), т. е. к величине <p(ai, аз,..., а*0) (если
последняя существует), мы немедленно получаем доказательство сходи-
мости по вероятности всех интересующих нас выборочных центральных
моментов, асимметрии и эксцесса к соответствующим теоретическим зна-
чениям (если таковые существуют). При этом, конечно, мы учитываем,
что центральные моменты, асимметрия и эксцесс являются рациональны-
ми функциями от начальных моментов (см. соотношения (2.18) в п. 2.6.1).
б.	Устойчивость эмпирических функций распределения и плотно-
сти, а также относительных частот, т. е. их сходимость (при неогра-
ниченном увеличении объема выборки, по которой они построены) к со-
ответствующим теоретическим функциям и вероятностям, следует непо-
средственно из (4.3/)-(4.6). Продемонстрируем это на примере эмпириче-
ской функции распределения F^n\a;). Введем в рассмотрение случайные
Slutsky Е. Uber stochastische Aeymptoten und Grenzwerte — Metron, 5, X» 3
(19251 3.
216
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
величины
6== {J;
если
если
Xi X.
Очевидно, •••»€»* — независимые, одинаково распределенные
случайные величины, причем Е& = F(x) и Dft = F(z)(l — F(z)), где
F(x) — Р{£ < я} — функция распределения исследуемой случайной ве-
личины Легко видеть, что Ип\х) = [(£?=i&)/n] = f(n)» и» следо-
вательно, в соответствии с законом больших чисел F^n\x) —► F(x) (по
вероятности), когда п —> оо.
Таким образом, мы получили ответ на первый из вопросов, сформу-
лированных в начале пункта и относящихся к «поведению» основных вы-
бранных характеристик. Тот факт, что при неограниченном увеличении
объема выборки (ш. е. при п —> оо) все они стремятся по вероятности к
соответствующим теоретическим характеристикам, дает нам осно-
вание использовать выборочные характеристики для приблизительного
описания свойств всей генеральной совокупности в целом.
6.2.7.	Асимптотически-нормальный характер случайного
варьирования основных выборочных характеристик
Смысл результатов предыдущего пункта заключается, в конечном
счете, в том, что при осреднении большого числа (п) случайных слага-
емых все менее ощущается характерный для случайных величин некон-
тролируемый разброс в их значениях, так что в пределе по п —+ оо этот
разброс как бы исчезает вовсе или, как принято говорить, случайная ве-
личина вырождается в неслучайную. Однако при любом конечном (хотя
и большом) числе слагаемых п случайный разброс у среднего арифме-
тического этих слагаемых остается. Поэтому и был поставлен второй
вопрос в начале этого пункта относительно «поведения» основных выбо-
рочных характеристик: что можно сказать о характере их случай-
ного варьирования? Ведь этот характер должен существенно зависеть
от свойств той генеральной совокупности, по выборке из которой мы по-
строили наши выборочные характеристики. Хотя последнее утверждение
и верно (и, следовательно, характер случайного варьирования выбороч-
ных характеристик надо изучать отдельно для каждого типа генеральных
совокупностей), однако, оказывается, что по мере увеличения объема вы-
борки (т. е. при п —> оо) они начинают вести себя одинаковым образом
независимо от специфики генеральных совокупностей, по выборкам из
которых они были вычислены.
Поэтому ответ на вопрос о характере случайного варьирования основ-
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 217
ных выборочных характеристик следует формулировать в двух вариантах
в зависимости от размера объема выборки, по которой они строились:
(а)	асимптотически, т.е. для больших объемов выборок, что мате-
матически позволяет проводить соответствующее исследование в услови-
ях п —> оо;
(б)	доасимптотически, т.е. для ограниченных объемов выборок,
что требует проведения соответствующего исследования отдельно для ка-
ждого типа генеральной совокупности (для нормальной, экспоненциаль-
ной, равномерной, пуассоновской и т.д.).
Ответ в условиях асимптотики (т.е. при п —> оо) имеет общий ха-
рактер, практически не зависит от типа анализируемой генеральной со-
вокупности и основан на центральной предельной теореме (см. п. 4.3.1).
Опираясь на различные варианты формулировки этой теоремы, можно по-
казать, что при больших объемах выборок все основные выбороч-
ные характеристики ведут себя как нормально распределенные
случайные величины. Конкретизация закона распределения вероятно-
стей для каждой конкретной выборочной характеристики производится
с помощью подсчета ее среднего значения и дисперсии. Ниже приводятся
результаты для трех основных выборочных характеристик — среднего ж,
дисперсии з2 и функции распределения F^n\x):
(6.20)
F(">(z)€jV(F(Z);r(g)(1~F(g))
I	п
В соотношениях (6.20) N(m; Д2), как обычно, означает нормальный закон
со средним значением т и дисперсией Д2, а символика «£п 6 N(m; Д2)»
означает, что случайная величина £п асимптотически (по п —> оо) рас-
пределена нормально с указанными величинами среднего значения (тд) и
дисперсии (Д2). Параметрами а,<т2,/?2 и F(x) обозначены соответственно
среднее значение, дисперсия, коэффициент эксцесса и функция распреде-
ления анализируемой генеральной совокупности.
Вычислим приведенные в (6.20) средние значения и дисперсии выбо-
рочного среднего х(п) и эмпирической функции распределения /^”\ж), а
также среднее значение выборочной дисперсии з2(д) (вид ее дисперсии
218
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
приводится в (6.20) без доказательства):
= i  nF(x) = F(x);	(6.24)
п
OF*n\x) = D fl £ f.) = Л Е Of.-
= -4 • nF(x)(l - F(x)) =	-X1 ~ F^\	(6.25)
n	n
При выводе формул для EF^n\x) и DF^n\z) использовалось предста-
вление в виде ^п)(*) = (Е."=1f.)/п, где
(
I 0,
если xt < х;
если х^ z,
и учитывалось, что	 >£п — независимые, одинаково распределен-
ные случайные величины, причем Е£, = 1 • F(z) + 0 • (1 — F(z)) — F(x) и
Df, = (1 - F(xtf • F(x) + (0 - F(x))2(1 - F(xY) = F(x)(l - F(x)).
При выводе формулы для Ел было использовано тождество:
I	п
Е < 2(а - ж) - о)
I	»=1
= 2Е (а-х)
— па
= — 2пЕ(х - а)2.
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 219
Что касаетсся доасимптотического поведения основных выборочных
характеристик, то мы исследуем этот вопрос в следующем пункте это-
го п., но только для случая, когда выборка извлекается из нормальной
генеральной совокупности.
6.2.8.	Поведение выборочных характеристик в нормальной
генеральной совокупности (статистика нормального
закона)
Как и раньше, речь идет о свойствах выборочных характеристик,
проявляющихся при повторениях выборок того же объема из одной и той
же генеральной совокупности, в нашем случае — из (а, а2)-нормальной
генеральной совокупности. Соответственно наблюдения Xi,X2,...,xn,
образующие выборку, интерпретируются как независимые, одинаково
(в,а)-нормально распределенные случайные величины (см. п.6.1, со-
отношения (6.1)-(6.3)). Сформулируем основной результат, касающий-
ся распределения пары основных выборочных характеристик (it(n),s2(n))
(а, п2)-нормальной генеральной совокупности.
Теорема Фишера. Пусть х(п) и з2(п) — соответственно выбороч-
ная средняя и выборочная дисперсия, построенные по случайной выбор-
ке (Ж1,ат2,.. . ,zn) из (а,<т2)-нормальной генеральной совокупности. Тогда
при любом фиксированном объеме выборки п (а не только при п —> оо)
их совместный закон распределения описывается следующим образом:
распределение х(п) подчинено
(о, —)—нормальному закону,	(6-26)
пз2(п)	2
статистика ----1— распределена по закону х
о
с п— 1 ст. свободы*,	(6.27)
х(п) и 52(п) статистически независимы.	(6.28)
Мы не будем приводить здесь подробного доказательства этого важ-
ного результата. Отметим лишь, что нормальность х(п) вытекает из фак-
та нормальности любой линейной комбинации нормально распределенных
случайных величин, который в свою очередь получается, например, с помо-
щью индуктивного применения формулы композиции (см. (4.13) в п. 4.4)
сначала к сумме двух нормальных случайных слагаемых, затем трех и т.д.
Что касается вывода закона распределения статистики ns2/о2 и статисти-
220
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
ческой независимости выборочного среднего х(п) и выборочной дисперсии
з2(п), то в основе доказательства этих утверждений лежит последователь-
ный переход сначала от наблюдений х, к центрированным наблюдениям
= Xi — а, а затем к у» с помощью ортогонального преобразования (см.
приложение 2):
Vi =
при i = 1,2,
при i = п.
n- 1;
Несложно проверить, что полученные таким образом случайные величи-
ны 2/1/являются независимыми, одинаково (ОД)-нормалыю распределен-
ными и что интересующие нас характеристики х(п) и з2(п) выразятся в
терминах у\, уг, • • ♦ > Уп следующим образом:
*(п) = “7=Уп + «;
уп
па2(п) =	У?.
»=1
Отсюда и будет непосредственно следовать справедливость утверждений
(6.27) и (6.28).
Утверждения (6.26)-(6.28) теоремы Фишера позволяют сформулиро-
вать ряд следствий, которые окажутся весьма полезными в дальнейших
наших обсуждениях, в том числе при решении задач интервального ста-
тистического оценивания (см. п. 7.5.4) и статистической проверки гипотез
(гл. 8).
Следствие 1. Среднее значение и дисперсия эмпирической диспе-
рсии $2(п), построенной по случайной выборке объема п из
(а, а2)-нормальной генеральной совокупности, определяются формулами:
(6.29)
Выражение для Ез2(п) справедливо и в общем случае (не только для
нормальных выборок), см. выше вывод соотношения (6.23). Покажем, как
результаты следствия 1 получаются из (6.27). Известно (см. п. 3.2.1), что
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА
221
среднее значение и дисперсия %2(п — ^-распределенной случайной вели-
чины равны соответственно п — 1 и 2(п — 1). Поэтому
/ 2\	/ 2\
Е(^-|=п-1 и D f Ц- ) = 2(п — 1).
\	/	\ 67 J
Следовательно,
2
-^уЕл2(п) = п — 1 и ^Ds2(n) = 2(п — 1),
ст	(7
откуда непосредственно вытекают соотношения (6.29).
Следствие 2. Если х(п) и з2(п) соответственно среднее значение
и дисперсия у	построенные по случайной выборке из
(в, ст ^-нормальной генеральной совокупности, то статистика
(г - а)у/п - 1
3
с п — 1 ст.св.
распределена по закону Стъюдента
(6.30)
Для доказательства этого результата представим статистику t в виде
(6.31)
Легко устанавливается, что:
•	числитель дроби (в квадратных скобках) распределен по стандарт-
ному нормальному закону (с учетом (6.26));
•	подкоренное выражение в знаменателе дроби ведет себя как х(п —
^-распределенная случайная величина, поделенная на число степеней сво-
боды п — 1 (в соответствии с (6.27));
•	числитель и знаменатель дроби (6.31) статистически независимы (в
соответствии с (6.28)).
Но тогда правая часть (6.31) в точности удовлетворяет определению
«стьюдентовской» случайной величины с п — 1 степенью свободы (см.
п. 3.2.2), что и завершает доказательство следствия, 2.
Три следующих результата (следствия 3, 4 и 5) относятся к стати-
стике нормального закона, связанной с анализом двух независимых вы-
борок из нормальных генеральных совокупностей. А именно, пусть мы
располагаем случайной выборкой
из ген. сов. AT(oi,<t?)
(6.32)
222
ГЛ. в. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
и случайной выборкой
2
”21>®22)--->®2па из ген. сов. N(at,cr,),
(6.33)
статистически независимой от выборки (6.32).
Нас будет интересовать поведение различных комбинаций основных
выборочных характеристик xt (гц), Si(ni), ^(я?) и ^(яг)» построенных по
этим двум выборкам, где
1 пь
®fc(wfc) = ~~ xkit к = 1 j 2,
к *=1
«*(>»*) = 7" $2 (’*•' - *‘М’>
"* i=T
к = 1,2.
(6.34)
(6.35)
Следствие 3. В условиях (6.32)-(6.34) при известных значениях
дисперсий о2 и or2 имеет место следующий факт:
(	2	2\
(ei — <ъ); ~ ~ ) *	(6.36)
ni п2 J
В частности, при ai = a2i cr2 = <j2 = а2 и Л] = п2 = п
( 2о"^ \
(®1 («) - ®г(«)) € N ( 0;--).	(б.Зб')
\ я у
Утверждение (6.36) следует из (6.26) с учетом очевидных вычислений
теоретических среднего значения и дисперсии разности (sj(ni) — ^(nj)).
Следствие 4. В условиях (6.32)-(6.35) и при неизвестных, но оди-
наковых дисперсиях а2 = а2 = °*2 имеет место следующий факт:
[(®1(«1) - ЪМ) - (“» -
-------.	--- -	=-------С з.р.в. Стыодента с
V n?+na-2 (П1»1(П1) + ”а4(П2))
ni + я2 - 2 ст.св.	(6.37)
Для того чтобы убедиться в справедливости (6.37), следует проверить
правильность следующих утверждений:
а) Случайная величина
6.2. ОСНОВНЫЕ ВЫБОРОЧНЫЕ ХАРАКТЕРИСТИКИ И ИХ СВОЙСТВА 223
распределена по стандартному нормальному закону (следует непосред-
ственно из (6.36) с учетом trj = а2 = <т2 и независимости xi(nj) и £а(па)).
б) Случайная величина
2	_	_
подчиняется з.р.в. х с п1 + п2 ~ 2 степенями свободы. Этот факт осно-
ван на х2(п1 ~ 1)-распределенностй njsJ/cr2, х{п2 — 1)-распределенности
п252/(72 (и то, и другое — в силу (6.27)) и независимости з?(п1) и э2(па) (с
учетом того, что из определения ^-распределения следует, что если две
X2-распределенные случайные величины х\т1) и Х2(т2) статистически
независимы, то их сумма x2(mi) + №(m2) распределена снова по закону
X2, но уже с mi + степенями свободы).
в) Случайная величина 71 / ^Л1+*2_а72, с одной стороны, тождествен-
но равна левой части соотношения (6.37), а с другой стороны, распреде-
лена по закону распределения вероятностей Стьюдента с nj + па — 2 сте-
пенями свободы. Тождество проверяется непосредственно, а «стьюден-
товская» распределенность этого отношения следует из статистической
независимости 71 и 7а (в силу независимости выборок и (6.28)) и опреде-
ления случайной величины, подчиняющейся распределению Стьюдента с
т степенями свободы (см. п. 3.2.2).
Представляет самостоятельный интерес частный случай следствия 4,
когда Oi = а2:
-------------z---1--------€ з.р.в. Стьюдента с
s
П1 + п2 — 2 ст.св.,	(6.37*)
где величина
52 = „  1----9 (п1*1 (Я1) + П3«2(П2))
Т11 т~ Т12 — Z
V	V	2
является по существу оценкой неизвестной дисперсии а по объединенным
наблюдениям двух выборок (6.32) и (6.33).
Результат (6.37) используют, в частности, для построения статисти-
ческого критерия проверки гипотезы о равенстве средних в двух наблю-
даемых нормальных генеральных совокупностях (см. гл. 8).
224
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
Следствие 5. В условиях (6.32)-(6.35) и при неизвестных, но оди-
наковых дисперсиях <т? =	— °2 имеет место следующий факт:
п^)ЦП1-Х)	-1,п2-1).	(6.38)
П24(п2)/(п2 - 1)
В правой части (6.38) обозначен закон распределения вероятностей
Фишера с числом степеней свободы числителя, равным nj — 1, и числом
степеней свободы знаменателя, равным п2 — 1 (см. п. 3.2.3).
Справедливость (6.38) следует непосредственно из х(пк — ^-распре-
деленности случайных величин «^(«л)/^2, к = 1,2 (в соответствии с
(6.27)) и из статистической независимости s?(nj) и Зз(п2) (как следствие
независимости выборок (6.32) и (6.33)).
6.3.	Вариационный ряд и порядковые
статистики
Выше отмечалось, что выборка, т. е. совокупность имеющихся у нас
наблюденных значений Xi,X2t -. .,хп исследуемой случайной величины
является той исходной информацией, на основании которой исследователь
строит свои выводы о свойствах изучаемой генеральной совокупности в
целом и, в частности, составляет представление о функции распределе-
ния или плотности анализируемого закона распределения вероятностей.
Оказывается, что и каждый член выборки в отдельности может доста-
влять важную информацию о характере анализируемого закона расцре-
деления, если наблюдения предварительно расположить в порядке возра-
стания. Так, например: наименьшее и наибольшее выборочные значения
(соответственно гтш(п) и хтлх(п)) дают приближенное представление о
диапазоне изменения возможных значений исследуемого признака, а их
разность (zm„(n) — гт;п(п)) — о степени случайного разброса его наблю-
даемых значений; средний член упорядоченного ряда наблюдений — меди-
ана imed(n) — характеризует центр группирования наблюдений изучае-
мой случайной величины и так далее. Все это говорит о целесообразности
специального рассмотрения ряда наблюдений, расположенных в порядке
возрастания.
Итак, пусть Х\,Х2,-. .,хп — выборка, состоящая из п независимых
наблюдений исследуемой случайной величины £ с непрерывной функцией
распределения F^(x) и плотностью вероятности Построим новый
ряд из элементов имеющейся выборки, расположив x,(i = 1,2,...,п) в
порядке возрастания (неубывания) их значений. Обозначим член нового
6.3. ВАРИАЦИОННЫЙ РЯД И ПОРЯДКОВЫЕ СТАТИСТИКИ
225
ряда, стоящий на t-м месте, через х^у, чтобы отличать его от х,. Тогда
новый ряд будет представлен неубывающей последовательностью
®(1)j ®(2)> •   •> ®(п)-
(6.39)
Каждый член этой последовательности (я(,)) называется порядковой
статистикой, а сама последовательность (6.39) — вариационным рядом
случайной величины
Аппарат порядковых статистик широко используется как в теории и
практике статистического оценивания неизвестных параметров и стати-
стических критериев (особенно при построении устойчивых и «свободных
от распределения» оценок и критериев), так и непосредственно при мо-
делировании реальных систем и процессов. При исследовании качества
оценок, критериев и моделей, полученных с использованием порядковых
статистик, необходимо уметь описывать законы их распределения вероят-
ностей в схеме гипотетического варианта интерпретации выборки, ко-
гда члены вариационного ряда интерпретируются не как конкретные
числа, а как случайные величины, значения которых реализуются при
повторениях выборок того же объема из той же самой генеральной сово-
купности. И хотя члены вариационного ряда (6.39) в отличие от членов
исходной выборки уже не являются взаимно независимыми (по причине
своей предварительной упорядоченности) и соответственно их частные
распределения уже не являются одинаковыми, описываемыми, в частно-
сти, одной и той же плотностью f^(x) (см. (6.1)), однако, они могут
быть описаны в терминах этой плотности и соответствующей функции
распределения F^(x).
6.3.1.	Закон распределения вероятностей t-ro члена
вариационного ряда
Пусть FX(i)(x) = P{z(i) < х] и /х0)(ж), соответственно — непрерыв-
ные дифференцируемые функция распределения и функция плотности ве-
роятности t-й порядковой статистики, построенной на основании случай-
ной выборки Х],х2,...,хп из генеральной совокупности с функцией рас-
пределения Щх) и функцией плотности вероятности Д(х). Мы хотим
выразить FX(.)(x) и /Х(о(х) (для любого i = 1,2,...,я) в терминах функ-
ций F€(x) и Д(х).
Реализуем следующую схему вывода требуемых соотношений. Для
любого заданного значения х и некоторого достаточно малого положи-
I llpiiMJjiiiau ciai'iiiiiiKd и испоим иконометрики
226
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
тельного числа Д введем в рассмотрение событие
Л(х) =

А далее мы попытаемся выразить вероятность события А(я) одновременно
и в терминах вероятностных характеристик случайной величины хцу (что
тривиально, так как Р{А(ж)} = Pr(i)(z + у) -	“ у))» и в терминах
схемы п независимых наблюдений Xi,X2,---,xn анализируемой случайной
величины £. Для этого введем в рассмотрение наряду с событием A(i)
еще три события:
В терминах схемы п независимых наблюдений случайной величины
£ событие А(а?) эквивалентно следующему событию: i — 1 наблюдений (из
общего числа п) оказались меньше х— у {т.е. i — 1 раз состоялось собы-
тие Ai{x)), одно наблюдение попало в окрестность [ж — у, а: + у) точки
х {т.е. один раз произошло событие ^(я)) и остальные n — i наблюдений
оказались не меньшими, чем х + у {т. е. n — i раз произошло событие
Аз{х)). Чтобы подсчитать вероятность этого события (эквивалентного
событию А(я)) в терминах Frfx) и Д(аг), воспользуемся моделью полино-
миального распределения (см. п. 3.1.4). Действительно по существу речь
идет о производстве п независимых испытаний, в результате каждого из
которых может произойти одно из событий Aj(z), А2(ж) или А3(а:), причем
вероятности этих событий по построению равны:
Нас интересует вероятность того, что в результате этих п независимых
испытаний i — 1 раз произойдет событие Ai(x), (т.е. щ{п) = i — 1) одни
6.3. ВАРИАЦИОННЫЙ РЯД И ПОРЯДКОВЫЕ СТАТИСТИКИ
227
раз — событие Aafa) (т.е. ^(n) = 1) и n — t раз — событие А3(ж) (т.е.
р3(п) = п - *).
Воспользовавшись формулой (3.7) полиномиального з.р.в., имеем:
Р{4(г)} = /’{«'i(n) = I - 1,i>i(n) = 1,i*>(n) = п - «}
(6.40)
С другой стороны, Р{А(ж)} в терминах FX(i)(z) определяется в виде
Р{Л(г)} = FXM (х + у)
(6.41)
Приравнивая правые части (6.40) и (6.41), деля обе части полученного
таким образом выражения на Д и устремляя Д к нулю, получаем в пределе
/«.,(*) = (t-l)”(n-t)!^~1(a)(1 "	« = 1,2....,П.
(6-42)
Формула (6.42) позволяет описать з.р.в. в любой порядковой стати-
стике, зная з.р.в. анализируемой генеральной совокупности.
6.3.2.	Совместные (многомерные) распределения членов
вариационного ряда
Если в статистическом анализе или моделировании используются
функции от нескольких членов вариационного ряда (например, для оцен-
ки среднего значения симметрично распределенной случайной величины
может использоваться полусумма (жц) 4- Ж(п))/2, а для оценки диспер-
сии — статистика, пропорциональная разности Z(n) — a?(i)), то Для изу-
чения свойств таких функций необходимо уметь описывать совместные
(многомерные') з.р.в. для набора соответствующих порядковых статистик.
Вычисление плотностей вероятности для таких совместных з.р.в. в тер-
минах Д(х) и F{(x) не вызывает принципиальных трудностей, хотя и
реализуется в виде весьма громоздких выражений. Мы приведем здесь
228
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
без доказательства выражение функции плотности вероятности для лю>
бой пары порядковых статистик (я(«),®(у)), где i < j:
fawfa у) =	n)^-,(J:)[F€(») - *i(x)]
x[l-Fe(p)]“-7e(x)/e(y),	(6.43)
где нормирующий множитель K(i,j,n) определяется формулой
fi!
K^’j'= («- l)!(j — • - l)!(n — j)!'	(644)
Продемонстрируем способ получения этой формулы на одном важном
частном случае: выведем вид з.р.в. для пары крайних членов вариаци-
онного рядау т.е. для (x(i),®(п))- Для этого воспользуемся следующими
очевидными соотношениями между событиями:
{я(п) < У} = {^(1) < ж; ж(п) < у} + {«(1) ж; г(п) < у}
~ {®(1) < ®(п) < У1 “I"	v) * * * * х2у • • • > хп < У У-"
п
= {«(t) < х; г(„) < у} + J]{х О; < у}.
1=1
Соответственно имеем (учитывая независимость событий {г < х, < у}
для i = 1,2,..., п):
р{х(п) <У} = -Р{®(1) < г,г<п) < »} + [*№) - ^ё(г)Г>
v) = Р(ХМ < у] - [*е(гО - г«(г)]”•	(6.45)
Но событие {а?(п) < у} эквивалентно произведению независимых со-
бытий {я?! < у}, {г2 < У}, • • •, {*п < у}.
Поэтому из (6.45) получаем
у) = (») - [*№) - п (б-46)
или, после дифференцирования обеих частей по х и по у
Лх(п.х(.))(®. У) = п(п -	- Г{(®))П-2/е(г)Л(у).	(6.46')
Читатель может убедиться в том, что, подставляя в общую формулу
(6.43)-(6.44) значения t = 1 и j = п, мы получим то же соотношение
Г6.46 J.
выводы
229
6.3.3.	Порядковые статистики как эмпирические
(выборочные) аналоги квантилей и процентных точек
распределения
Из определения t-й порядковой статистики следует, что относи-
тельная частота (эмпирический аналог вероятности!) наблюдений выбор-
ки, меньше равна (i — 1)/п. А это означает, что порядковая стати-
стика является одновременно выборочным квантилем уровня (: — 1)/п
и выборочной 100( 1 — ~~)%-ной точкой анализируемого распределения.
ВЫВОДЫ
1.	Понятие генеральной совокупности является удобным (для ста-
тистических приложений) синонимом понятий «вероятностное простран-
ство», «случайная величина», «закон распределения вероятностей» и
определяется как совокупность всех мыслимых наблюдений, которые мог-
ли бы быть сделаны в данном реальном комплексе условий.
2.	Выборка — это статистически обследованная часть генеральной
совокупности, по которой мы хотим судить об интересующих нас свой-
ствах генеральной совокупности в целом. Вопрос представительности (ре-
презентативности) выборки с учетом обычной ограниченности времени и
средств на ее получение требует от исследователя знания и использования
различных специальных форм организации выборочных обследований.
3.	Следует иметь в виду, что, говоря о выборке (или о вариационном
ряде), в зависимости от контекста подразумевают один из двух различ-
ных вариантов интерпретации этого понятия. В первом (практическом)
варианте под х2,... ,гп понимают фактически наблюденные в данном
конкретном эксперименте значения исследуемой случайной величины, т.е.
конкретные числа или векторы. Во втором (гипотетическом) варианте
под Xi, х2, -.., хп понимают лишь обозначение тех п значений (чисел или
векторов), которые могли бы быть получены при реализации п-кратного
эксперимента (наблюдения) в реальном комплексе условий, индуцирую-
щем исследуемую генеральную совокупность. В последнем случае сами
Zj и любые функции от них выступают уже не в качестве конкретных
чисел или векторов, а в качестве случайных величин, поскольку их значе-
ния варьируют неконтролируемым образом при каждом новом извлечении
выборки того же объема п из той же самой генеральной совокупности.
4.	В практике статистического анализа и моделирования точный вид
з.р.в. анализируемой случайной величины, а соответственно и точные
значения ее основных теоретических числовых характеристик (среднего,
дисперсии и т.п.) бывают неизвестны. Исследователь располагает лишь
230
ГЛ. 6. ОСНОВЫ СТАТИСТИЧЕСКОГО ОПИСАНИЯ
выборкой из интересующей его генеральной совокупности, а потому вы-
нужден строить все свои выводы на основании ограниченного ряда вы-
борочных характеристик. К основным выборочным характеристикам од-
номерной случайной величины относятся: эмпирические функции распре-
деления и плотности	выборочная относительная часто-
-(п)	•	«г
та pl 1 появления i-го возможного значения, выборочное среднее значение
(я(п)), выборочная дисперсия (л2(п)), члены вариационного ряда («(;)).
5.	Осмысленное и обоснованное использование в статистическом ана-
лизе основных выборочных характеристик требует знания их свойств, в
том числе ответов на вопросы: 1) стремятся ли они к значениям своих
теоретических аналогов при неограниченном увеличении объема выборки
(т.е. при п —* оо)? 2) что можно сказать о з.р.в. каждой из выбороч-
ных характеристик? Оказывается, в асимптотическом смысле (т. е. при
п —* оо) ответы на эти вопросы практически не зависят от специфики
генеральной совокупности, из которой извлекалась выборка, и являются
следующими: основные выборочные характеристики с ростом объема
выборки стремятся к своим теоретическим аналогам и ведут себя при
этом как нормально распределенные случайные величины.
6.	Исследование поведения основных выборочных характеристик при
конечных (ограниченных) объемах выборок требует учета специфики ге-
неральной совокупности, из которой извлечена выборка. Пример резуль-
татов такого исследования дает теорема Фишера, описывающая поведе-
ние пары основных выборочных характеристик (i(n),s2(n)) для случая
нормальной генеральной совокупности. Ряд полезных следствий этой тео-
ремы {статистика нормального закона) используется в дальнейшем при
построении интервальных оценок и статистических критериев проверки
гипотез.
7.	Полезным приемом в исследовании свойств анализируемой слу-
чайной величины является расположение имеющихся наблюдений Zi,xj,
..., хп в порядке их возрастания: г(1),Х(2), • • • так что	—
это те же самые наблюдения	т°лько упорядоченные (т.е.
ж(»4-1) для всех 1 = 1,2,...,п — 1). Ряд {®(i)},=r^ называют вариаци-
онным рядом, а его члены — порядковыми статистиками. Они также
относятся к основным выборочным характеристикам и, в частности, ши-
роко используются при построении так называемых непараметрических
оценок и непараметрических критериев.
ГЛАВА 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
ПАРАМЕТРОВ
Одна из главных целей, которые ставит перед собой исследователь,
приступая к статистической обработке исходных данных, заключается в
том, чтобы добиться удобной лаконичности в описании интересующих
его свойств исследуемой совокупности (или исследуемого явления), т.е.
представления множества обрабатываемых данных в виде сравнительно
небольшого числа сводных характеристик, построенных на основании
этих исходных данных. При этом желательно, чтобы потеря информации,
существенной для принятия решения, была минимальной. Упомянутые
сводные характеристики являются функциями от исходных результатов
наблюдения Zi,^,... ,хп и называются статистиками (таким образом,
мы уже имеем, как минимум, три различных обиходных варианта тер-
мина «статистика»: научная дисциплина, исходная информация и любая
функция от результатов наблюдения). В предыдущей главе мы уже име-
ли дело с примерами таких сводных характеристик (статистик): к ним
относятся все выборочные (эмпирические) характеристики генеральной
совокупности — средние значения, дисперсии, коэффициенты эксцесса и
асимметрии, наконец, эмпирическая функция распределения и эмпириче-
ская плотность.
Добиться лаконичности в описании информации, содержащейся в мас-
сиве обрабатываемых данных, помогает целый набор прикладных мето-
дов математической статистики: выбор и обоснование математической
модели механизма изучаемого явления; изучение свойств анализируемой
системы или механизма функционирования с помощью небольшого числа
сводных выборочных характеристик (среднего, дисперсии и т.п.); нагляд-
ное представление (визуализация) исходных данных с целью формирова-
ния рабочих гипотез о механизме изучаемого явления; анализ относитель-
ных частот, выборочных функций распределения и плотности и другие
методы описательной (или дескриптивной) статистики; анализ приро-
ды обрабатываемых данных; описание интересующих исследователя ста-
232
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
тистических связей между анализируемыми признаками и т.Д. Все эти
методы в той или иной степени опираются на две основные составные
части математического аппарата статистики: 1) теорию статисти-
ческого оценивания неизвестных значений параметров, участвующих в
описании анализируемой модели; 2) теорию проверки статистических
гипотез о параметрах или природе анализируемой модели.
Изложению основных элементов первой из этих двух составных ча-
стей аппарата математической статистики и посвящена настоящая глава.
7.1.	Начальные сведения о задаче
статистического оценивания
параметров
7.1.1.	Постановка задачи
Пусть мы располагаем исходными статистическими данными — вы-
боркой
• • • »	(7-1)
из исследуемой генеральной совокупности и пусть интересующие нас свой-
ства этой генеральной совокупности могут быть описаны с помощью урав-
нения {математической модели)
М (z, 0) = О,	(7.2)
где х, — i-e наблюдение в выборке (7.1), х — текущее (т.е. подставляемое
по нашему усмотрению) значение исследуемого случайного признака, 6 =
(0^\. - . ,0^) — к-мерный параметр, участвующий в записи модели (7.2),
значения которого нам были не известны до получения выборки (7.1).
Задача статистического оценивания неизвестных параметров 6 по
выборке заключается, грубо говоря, в построении такой мерной век-
торной функции 0(жь...,жп) = (0*’'(«!,...,хп),...$к\хи...,хп))Т от
имеющихся у нас наблюдений (7.1), которая давала бы в определенном
смысле наиболее точные приближенные значения для истинных (не из-
вестных нам) значений параметров G = (0^\... ,0^)т. Здесь не уточ-
няется пока, в каком именно смысле приближенные значения 0'	0' 1
соответственно параметров 0^\..., 0^ являются наилучшими.
В качестве моделей (7.2) могут, например, рассматриваться модели
законов распределения вероятностей.
7.1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 233
Пример 7.1. Пусть нашей целью является исследование закона
распределения наблюдаемой непрерывной одномерной случайной величи-
ны с неизвестной плотностью вероятности Д(з?) и пусть предваритель-
ный анализ природы исходных данных (7.1) привел нас к выводу, что этот
закон может быть описан нормальной моделью. В этом случае
0 = (0(1),0(2))Т, где 0(1) = а = Е£ и 0(2) = а2 = Df;
1	(ж-**1))8
М (я; 0) = Д(х) = —Ц-
и можно показать, что вся информация о параметрах 0^ и 0^ (а следо-
вательно, и о всей модели) содержится всего в двух статистиках — х и
2
з , где
(7.3)
(7.4)
Выше показано, что есть основания использовать статистики (7.3) и (7.4)
в качестве приближенных значений (оценок) параметров а и о2, посколь-
ку по мере роста объема выборки, т.е. при п —> оо, эти оценки сходятся
по вероятности к соответствующим истинным значениям а и о2. Однако
вопрос о том, являются ли эти оценки наилучшими, пока остается откры-
тым. Чтобы иметь возможность обсуждать этот вопрос, нам придется
ввести и обсудить ряд понятий.
7.1.2.	Статистики, статистические оценки, их основные
свойства
Любая функция 7(^1,..., хп) от результатов наблюдения хг, аг2,•  • >
zn исследуемой случайной величины £ называется статистикой. Мы
уже познакомились с целым рядом статистик: выборочное среднее; выбо-
рочная ковариационная матрица; выборочные коэффициенты асимметрии
Й и эксцесса /32; эмпирические функции распределения F^n\x) и плотно-
сти f^n\x).
Статистика 0, используемая в качестве приближенного значения
неизвестного параметра 0, называется статистической оценкой. Так,
например, статистики x,s2,0i и можно рассматривать как статисти-
ческие оценки соответственно параметров а = Ef, D£, и поскольку,
234
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
как это следует из п. 7.2 все эти статистики при п —► оо сходятся по веро-
ятности к истинным значениям соответствующих параметров.
Обращаем внимание читателя на тот факт, что, говоря о статистиках
и статистических оценках, мы используем всегда гипотетический вари-
ант интерпретации выборки, т. е. вариант, при котором под zi,..., хп под-
разумеваются лишь обозначения тех п значений исследуемого признака
которые мы могли бы получить, проводя n-кратный случайный экспе-
римент (или производя п независимых наблюдений) в данном реальном
комплексе условий. Следовательно, все статистики и статистические
оценки являются случайными величинами: при переходе от одной выбор-
ки к другой (даже в рамках одной и той же генеральной совокупности)
конкретные значения статистической оценки, подсчитанные по одной и
той же формуле (7.3) (т.е. значения, полученные с помощью подстановки
в эту формулу соответственно различных конкретных значений аргумен-
та), будут подвержены некоторому неконтролируемому разбросу. Прав-
да, значения статистической оценки, подсчитанные по разным выборкам,
хотя и подвержены случайному разбросу, но должны (если наша оценка
«хороша»!) концентрироваться около истинного значения оцениваемого
параметра.
Возникает вопрос о требованиях, которые следует предъявить к ста-
тистическим оценкам, чтобы эти оценки были в каком-то определенном
смысле надежными. Эти требования формулируются обычно с помощью
следующих трех свойств оценок: состоятельности, несмещенности и эф-
фективности.
7.1.3.	Состоятельность
Оценка 0 = 0(a?i,..., жп) неизвестного параметра 0 называется со-
стоятельной, если по мере роста числа наблюдений п (т. е. при п -+ оо)
она стремится по вероятности к оцениваемому значению 0, т.е. если
для любого сколь угодно малого е > О Р{|0 — 0| > е} —> 0 при п оо (если
оцениваемый параметр 0 векторный, то для состоятельности соответ-
ствующей векторной оценки 0 требуется состоятельность отдельно всех
ее компонент). Заметим, что достаточными условиями состоятельности
оценки 0п параметра 0 являются следующие ее свойства:
1)	смещение Вп = Е0п — 0 оценки 0п равно нулю (Вп = 0) или стре-
мится к нулю при п —> оо, т. е. lim Вп = 0;
п—*оо
2)	дисперсия оценки D0n удовлетворяет условию lim D0n = 0.
п—»оо
Докажем, что эти условия являются достаточными. Согласно нера-
7.1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 235
венству Чебышева, можно записать
р(|0п - Е^| < £) > 1 -
Подставляя выражение Е0П = Вп — 0, получим
Переходя к пределу при п —* оо с учетом того, что по условию Вп = 0 или
lim Вп = 0, получим
П-+0О
lim р(\0п — 0| < е) = 1,
п—»оо \	/
что и требовалось доказать.
Все упомянутые выше опенки (х,л2, F^n\z),/^п\а?) и т.д.) являют-
ся, как это показано в п. 6.2, состоятельными оценками соответствующих
параметров.
С одной стороны, требование состоятельности представляется необ-
ходимым для того, чтобы оценка имела практический смысл (так как
в противном случае увеличение объема исходной информации не будет
«приближать нас к истине»), а потому это свойство должно проверяться
в первую очередь.
С другой стороны, свойство состоятельности —- это Асимптотиче-
ское (по числу наблюдений п) свойство, т. е. оно может проявляться лишь
при столь больших объемах выборок, до которых мы в нашей практике не
«добираемся». Кроме того, в большинстве ситуаций можно предложить
несколько состоятельных оценок одного и того же параметра. Например,
оценки 0i = х и 02 = (жт1п + гтах)/2 являются состоятельными оценками
неизвестного истинного среднего значения 0 = Е£ симметрично распреде-
ленной случайной величины, если это среднее 0 существует (здесь х —
выборочное среднее, определенное по формуле (7.3), a zmin и zmax — со-
ответственно минимальное и максимальное значения среди п наблюдений
исследуемого признака).
Более того, можно .привести примеры состоятельных оценок, уводя-
щих сколь угодно далеко от истины. Представим себе, что произведена
достаточно большая случайная выборка работников некоторой отрасли
экономики с регистрацией величины их заработной платы, т.е. мы рас-
полагаем выборкой вида (7.1). Заказчик поручает статистику построить
оценку теоретического значения средней заработной платы а = ана-
лизируемой совокупности с единственным требованием, чтобы эта оценка
236
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
была состоятельной. И представим себе, что статистик по тем или иным
причинам заинтересован в завышении реального результата (или в этом
заинтересован заказчик, о чем он проинформировал статистика). Тогда
статистик может предложить в качестве состоятельной следующую оцен-
ку:
ао при п < N —
х при n > TV — 1,
где а© — любое угодное статистику (или заказчику) значение, х — вы-
борочное среднее значение, построенное по выборке (7.1), a N — общее
число работников в анализируемой отрасли. Как легко видеть, состоя-
тельность оценки ап следует из состоятельности х (так как в процессе
п —> оо мы перейдем рубеж п = N — 1 и, следовательно, асимптотические
свойства ап будут определяться асимптотическими свойствами ж). В то
же время при всех реальных значениях объема выборки п оценка ап будет
давать заданное (угодное заказчику или статистику) значение а0, которое
никак не связано со свойствами анализируемой генеральной совокупно-
сти. И чтобы разоблачить недобросовестность статистика (заказчика),
потребуется в данном случае произвести сплошное обследование платы
работников анализируемой области.
Все это говорит о том, что свойства состоятельности недостаточно
для полной характеристики надежности оценки. Поэтому его надо допол-
нить рассмотрением двух других свойств.
7.1.4.	Несмещенность
Оценка 0 = #(zi,...,£n) неизвестного параметра 0 называется не-
смещенной, если при любом объеме выборки п результат ее осреднения
по всем возможным выборкам данного объема приводит к тонному ис-
тинному значению оцениваемого параметра, т. е. Е0 = 0 (если оцени-
ваемый параметр G векторный, то для несмещенности соответствующей
векторной оценки 0 требуется несмещенность отдельно всех ее компо-
нент).
Проверим, например, являются ли оценки (7.3) и (7.4) несмещенными
оценками параметров а = Е£ и а2 = Df:
7.1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 237
2
В ходе вычисления Ел мы воспользовались тем фактом, что в случае
независимых и одинаково распределенных, с дисперсией а2, наблюдений
ЖьЖз,... ,хп имеем
Мы видим, что х (6.21) является несмещенной оценкой параметра а, в то
время как оценка з (6.23) параметра а2 имеет отрицательное смещение,
равное сг2/п.
В отличие от состоятельности несмещенность характеризует «до-
асимптотические» свойства оценки, т.е. является характеристикой ее хо-
роших свойств при каждом конечном объеме выборки. Удовлетворение
требованию несмещенности устраняет систематическую погрешность оце-
нивания, которая, вообще говоря, зависит от объема выборки пив случае
состоятельности оценки стремится к нулю при п —♦ оо. Если смещение
оценки удалось определить, то оно легко устраняется. Так, в нашем при-
мере для устранения смещения достаточно перейти к оценке
«	2
n- Is
которая, как легко понять, уже будет несмещенной. Из сказанного сле-
дует также, что требование несмещенности (при соблюдении требования
238
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
состоятельности) особенно существенно при малом количестве наблюде-
ний.
7.1.5.	Эффективность
Представим себе, что мы имеем две состоятельные и несмещенные
векторные оценки 01 (34,..., хп) и ©2(24,..., гп) неизвестного векторного
параметра О. Для возможности геометрической интерпретации примера
будем полагать размерность k векторного параметра равной двум (к = 2).
Для анализа свойств двух конкурирующих оценок будем производить мно-
гократное (в данном примере двадцатикратное) оценивание неизвестного
параметра 0 = (0^\0^)Т каждым из двух рассматриваемых способов.
С этой целью подсчитываем значения 0ц и 02*(» — 1,2,..., 20), являющи-
еся результатом подстановки в функции 01 и 02 »-й по порядку выборки
объема п, т. е. извлекаем первую выборку объема п-хц ^12» — •,®1п, вста-
вляем эти наблюдения в качестве аргументов функций 0t и 02, получаем
первую пару оценок 0ц и 02i; затем извлекаем вторую выборку объема
п — 2?21,г22»---,®2п» вставляем эти наблюдения в качестве^аргументов
тех же функций 01 и 02 — получаем вторую пару оценок 0ц и 022, и
т.д. На рис. 7.1. по горизонтальной оси отложены первая компонента не-
известного (оцениваемого) параметра (0^) и первые компоненты ее двух
оценок (Йр на рис. 7.1. а и 0^ на рис. 7.1. б), а по вертикальной оси —
вторая компонента неизвестного (оцениваемого) параметра (0' ') и вторые
компоненты ее двух оценок (0^ на рис. 7.1. а и 0^ на рис. 7.1. б).
Рис. 7.1. Два способа состоятельного несмещенного оценивания многомер-
ного параметра 6 =	0^), характеризующегося разной эф-
фективностью: а) более эффективная оценка; б) менее эффектив-
ная оценка
7.1. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ 239
Таким образом, взаимное расположение точки	и крестика
(|	на рис. 7.1. а дает наглядное представление о близости оценки
полученной первым способом с использованием »-й выборки, к ис-
тинному значению оцениваемого параметра 0 (аналогичная картина для
второго способа оценивания представлена на рис. 7.1. б). Более тесная
концентрация оценок, полученных первым способом, около истинного зна-
чения, очевидно, склонит нас к мысли о большей эффективности оценки
§1 по сравнению с оценкой 02.
Именно этот критерий как мера разброса оцененных значений 02 око-
ло истинного значения 6 в соответствующем мер ном пространстве и
положен в основу определения эффективности оценки. Оценка 0 параме-
тра 0 называется эффективной, если она среди всех прочих оценок того
же самого параметра обладает наименьшей мерой/ случайного разброса
относительно истинного значения оцениваемого параметра. Эффектив-
ность является решающим свойством, определяющим качество оценки, и
оно, вообще говоря, не предполагает обязательного соблюдения свойства
несмещенности.
Остается уточнить^как именно измеряется степень случайного раз-
броса значений оценки 0 относительно истинной величины параметра 0.
В случае, когда 0 — скаляр (т.е. размерность оценки k = 1), в каче-
стве такой естественной меры берется средний квадрат отклонения, т. е.
величина Е(0 — 0)2, что для несмещенных оценок совпадает с их диспер-
сией, так как в этом случае D0 = Е(0 — Е0)2 = Е(0 — 0)2.
В случае, когда оценка 0 — вектор (т.е. размерность оценки к 2),
в качестве меры отклонения от истинного значения векторного параме-
тра 0 обычно рассматривается ковариационная матрица оценки 0, т. е.
симметричная и неотрицательно-определенная матрица размера к X fc, ко-
торую мы будем обозначать 53(0). Соответственно оценка 0j параметра
0 считается более эффективной, чем оценка 02, если существуют их
ковариационные матрицы S(0i) и Е(02) « матрица ДЕ = E(0i) — Е(02)
является неотрицательно- определенной.
Для векторных оценок возможны случаи, когда, несмотря на суще-
ствование матриц E(0i) и Е(02), нельзя ответить на вопрос, какая из
двух оценок эффективнее в указанном выше смысле. Эта неопределен-
ность устраняется, если в качестве меры отклонения векторной несмещен-
ной оценки 0 от истинного значения оцениваемого параметра 0 рассма-
тривать не саму ковариационную матрицу оценки Е(0), а ее определитель
det Е(0) (обобщенная дисперсия) или след tr Е(0).
Подчеркнем тот факт, что именно эффективность оценки, измеря-
емая средним квадратом ее отклонения от истинного значения пара-
240
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
метра, является решающим свойством, определяющим ее качество, ее
надежность. Бывают ситуации, когда требования несмещенности и эф-
фективности оценки оказываются несовместимыми. И тогда, как правило,
следует руководствоваться критерием эффективности.
Приведем такой пример. Речь идет о ситуации, в которой смещен-
ная оценка оказывается лучше несмещенной в смысле среднего квадрата
ошибки.
Пусть мы располагаем выборкой (7.1) из (а; а2)-нормальной генераль-
ной совокупности (см. пример 7.1) и нас интересует наилучшая (в смысле
среднего квадрата ошибки) оценка параметра о2 = Df. Мы уже знаем
(см. п. 7.1.4), что оценка
£>• - *о2
1=1
является несмещенной оценкой теоретической дисперсии а2. "'Воспользо-
вавшись соотношением (6.29), получаем:
2.2	т,_2 п, » 2х П2	2 П 2(п - 1) 4
E(s - а ) = Ds = -S ) = ------------• Ds = -----------------—а
п~ I (п - 1)	(п — 1) п
- 2g4
п — 1
Рассмотрим в качестве альтернативы к оценке з2 класс оценок {аз2}, где
а — любое положительное число, и попробуем подобрать а так, чтобы
Efas2 — а2)2 — min.
аг
Рассмотрим выражение среднего квадрата ошибки для оценок этого
класса:
Efas2 - <т2)2 = Е[а(з2 - а2) — а2(1 — а)]
2	, /1	\2 4
= а ------ + (1 - о) а .
п — 1
Легко устанавливается, что правая часть этого выражения, рассмат-
риваемая (с точностью до умножения на положительное число сг4) как
квадратный трехчлен относительно а:
------- + 1 )а2 -2а 4- 1
п — 1--}
имеет минимум в точке а = Подставляя это значение а, мы имеем
7.2. ФУНКЦИЯ ПРАВДОПОДОБИЯ
241
оценку
п — 1
п + 1
1
п 4-1
- ®)2
1=1
и ее средний квадрат ошибки
(n+lf
о 4
Легко видеть, что величина	будет всегда меньше величины
Е(52 - ст2)2 = ^-у-, а это и означает, что смещенная Оценка з* параметра
2	„	_2
а оказалась точнее несмещенной оценки з .
7.2. Функция правдоподобия. Количество
информации, содержащейся в
п независимых наблюдениях
относительно неизвестного значения
параметра
Пусть (7.1) — выборка, состоящая из п независимых одномерных на-
блюдений, извлеченная из исследуемой генеральной совокупности. Закон
распределения вероятностей наблюдаемой случайной величины £ описы-
вается функцией/(а:,©), зависящей от неизвестного параметра 0, причем
мы будем понимать под /(х,0) вероятность Р{£ = л}, если £ дискретная,
и значение плотности вероятности в точке х, если £ непрерывна. Если
рассматривать выборку (7.1) в гипотетическом смысле, то каждая кон-
кретная выборка (xi,x2,...,а?п) представляется определенной точкой в
n-мерном пространстве выборок переменных Xj, х2,..., хп и имеет смысл
говорить о совместном распределении вектора X = (х1?..., хп). Поскольку
при гипотетическом варианте понимания случайной выборки хх, х2,..., хп
суть независимые и одинаково распределенные случайные величины, то
для любого заданного набора значений xj, х2,... ,х„ их совместная плот-
ность (вероятность) будет
6) =	8).... •	8).	(7.5)
Таким образом, функция £(Х*,0), определенная равенством (7.5), задает
вероятность получения, при извлечении выборки объема п именно наблю-
дений xj,...,x„ (или величину, пропорциональную вероятности получе-
ния выборочных значений в непосредственной близости от точки X в
242
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
непрерывном случае). Поэтому, чем больше значение Л(Х*,0), тем прав-
доподобнее (или более вероятна) система наблюдений X* = (xj,...,!^)
при заданном значении параметра 0. Отсюда и название функции L —
функция правдоподобия.
Функция правдоподобия в зависимости от постановки задач и целей
исследования может рассматриваться либо как функция параметра 0 (при
заданных фиксированных наблюдениях xj,.. . ,х„), либо как функция те-
кущих значений наблюдений Xj,..., хп (при заданном фиксированном зна-
чении параметра 0), либо как функция обеих переменных X и 0.
Интересно попытаться проследить характер изменения вероятности
(7.5) в зависимости от изменения значения параметра 0. Очевидно, чем
резче проявляется эта зависимость, тем больше информации заключено в
конкретных значениях величин X и 0 друг о друге. При этом под инфор-
мацией о неизвестном параметре 0, содержащейся в случайной величине
X, понимают степень уменьшения неопределенности, касающейся1 неиз-
вестного значения 0, после наблюдения над данной случайной величиной.
Если по наблюденному значению X* случайной величины X можно с веро-
ятностью единица точно восстановить значение параметра 0, то это зна-
чит, что случайная величина (или ее наблюдение) содержит максимально
возможную информацию о параметре. И наоборот, если распределение
(7.5) случайной величины X одно и то же при всех значениях параметра 0,
то нет никаких оснований делать какие-либо заключения о 0 по результа-
там наблюдений этой случайной величины (ситуация нулевой информации
относительно значения неизвестного параметра, содержащейся в наблю-
дении). Чувствительность случайной величины к параметру может быть
измерена величиной изменения распределения этой случайной величины
при изменении значения параметра. Наиболее часто используемой харак-
теристикой, на основании которой измеряют изменение в распределении
(7.5) при небольшом изменении значения параметра 0, является так на-
зываемое количество информации Фишера (содержащееся в наблюдениях
X = (xi,X2,...,a?n))i которое определяется для скалярного параметра#
(т.е. при размерности параметра 0, равной единице) следующим обра-
зом:
1(9; X) = E
/dlnZV	Л T/v ЛЧ
dX. (7.6)
Интеграл в правой части (7.6) означает на самом деле п-кратное инте-
грирование подиитегрального выражения по всем возможным значениям
Xi,xj,..., хп; соответственно, под dX понимается n-мерный «элемент ин-
тегпипования». т. е. dX = dx^dx*.. ,dxn.
7.2. ФУНКЦИЯ ПРАВДОПОДОБИЯ
243
Учитывая независимость и одинаковую распределенность наблюде-
ний zi,£2,...,zn, получаем
1(0; %) = п у (dln^;e)) /(*! 9) dx = n 1(0; х).	(7.б')
Если параметр О = (^,...,0^) к-мерный, причем fc > 2, то вместо
количества информации (7.6) рассматривается информационная матрица
Фишера 1(0, X) размерности к х к с элементами
г /Л	dlnlA	.
у( ’) ( }
Эти понятия были введены Фишером в 20-х годах нашего столетия.
Воспользовавшись формулой (7.6), нетрудно подсчитать Количество
информации 1(0] г), содержащееся в одном наблюдении о параметре в
ряде конкретных примеров.
1. Одномерная величина X = х подчинена (а, а2)-нормальному закону
с плотностью <р(х] в, а2), в котором среднее значение а = 0 — неизвестный
параметр, а дисперсия известна. Тогда
— оо
2
9?(z;e,a2) dx
—оо
(7-8)
Результат, естественно, интерпретируется следующим образом: чем боль-
ше дисперсия а2, тем больше разброс в наблюденных значениях исследуе-
мой случайной величины, тем меньше информации о величине ее среднего
значения заключено в одном наблюдении.
2. Одномерная случайная величина X = х подчинена (а, а ^нормаль-
ному закону с плотностью tp(x] а,<т2), в котором среднее значение а извест-
но, а дисперсия а2 является неизвестным параметром. Тогда
оо	2 ч. 2
,, 2 •.	[ / о1п¥>(г;в,о-)\	.	2> .
7(а;ас)= J I--------y-j----'-\ <р(х;а,а ) dx
—ОО
(7-9)
<р(х] <х,<т2) dx =
1
2</
244
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
3. Одномерная случайная величина X — х подчинена гамма-распределению
с параметрами (а, 6), причем параметр а известен, а b является неизвест-
ным параметром. Тогда
г/i х f /'у(а,Ь)(3'У\ е f \ j ®
/(6; ж) — у	•—	j X f'rfa,b)(x) dx —
о
(7-Ю)
/
7.3,	Неравенство Рао-Крамера-Фреше и
измерение эффективности оценок
В п. 7.1.5 введено понятие эффективности оценки неизвестного пара-
метра О, которое определяется средним квадратом отклонения оценки от
истинного значения параметра, т.е. величиной Е(0 — О)2. В связи с
этим возникает вопрос: нельзя ли описать ту границу эффективности,
т.е. тот минимум (по всем возможным оценкам 0) среднего квадрата
Е(0 — 0)2, улучшить которую невозможно? Этот минимум и явился бы
тогда той точкой начала отсчета эффективности оценки, отправляясь от
которой можно было бы ввести абсолютную шкалу измерения эффективно-
ст и оценок. На этот вопрос дает ответ неравенство Рао-Крамера-Фреше,
известное также как неравенство информации.
Рассмотрим класс всевозможных оценок 0 скалярного параметра 9,
от которого зависит плотность вероятности f(x;0) исследуемой генераль-
ной совокупности. Пусть
Е?- У 0(xli...txn) L(xi,...,xn;0) dxl...dxn = 0 + 6^(0),	(7.11)
т. е. величина Ь$(0) дает смещение оценки 0 (очевидно, если оценка 9
несмещенная, то Ьд(0) = 0).
Если плотность f(x; 0) удовлетворяет некоторым условиям регуляр-
ности (в смысле характера ее зависимости от параметра 0), а именно:
а)	область розможных значений исследуемой случайной величины, в
которой f(x;0)	0, не зависит от 0;
б)	в формуле (7.11) и в тождестве J L(xi,..., хп; 0) dxi ---dxn = 1
допустимо дифференцирование по 0 под знаком интеграла;
в)	величина 1(0; х), определенная соотношением (7.6*), не равна нулю;
тогда для любой оценки 0 неизвестного параметра 0 имеет место еле-
7.3. НЕРАВЕНСТВО РАО КРАМЕРА- ФРЕШЕ
245
дующее неравенство:
Е(0-0)2 >
(1 + db^/de)1
nE [(In /(ж;0)/<10)2
(7-12)
или, что то же,
Е(0-0)2
(1 + dtgQQ/dO)2
п!{0\ х)
(7.12')
(доказательство этого факта см. в Приложении к гл. 7 на стр. 281).
Имеется обобщение неравенства (7.12) на случай к-мерного параме-
тра 0 = (0<г\ • • • А; > 2. В этом случае при тех же условиях регу-
лярности а)-в) для любой векторной несмещенной оценки 0 неизвестного
параметра 0 матрица
Е(0)-^Г'(0,г)	(7.13)
7*
является неотрицательно-определенной. Здесь Е(0) — ковариационная
матрица векторной оценки 0 = (0^\ ..., 0^), а I 1(0,х) — матрица,
обратная к информационной матрице, определенной соотношениями (7.7)
при X = х (т.е. при единственном наблюдении х).
Неравенства информации (7.12)—(7.13) дают возможность ввести ко-
личественную меру эффективности оценок в классе регулярных (в смы-
сле соблюдения условий а)-в)) генеральных совокупностей. Естественно,
в частности, измерять степень эффективности скалярной несмещенной
оценки 0 неизвестного значения параметра 0 отношением е(0) минималь-
но возможной величины дисперсии оценки, определяемой правой частью
неравенства (7.12), к дисперсии данной конкретной оценки 0, т.е.
e(g) =	.:Е(0-0)2.
4 '	п1(0;х)	'	'
(7.14)
тт	2
Подсчитаем эффективность некоторых оценок параметров а и а в
условиях примера 7.1.
1. Рассмотрим в качестве оценки среднего значения а нормальной слу-
чайной величины среднюю арифметическую (выборочное среднее), т.е.
положим
246
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Так как наблюдения ж, независимы и одинаково распределены, имеем:
Поскольку (см. (7.8)) /(а, ж) = 1/ст2, то в соответствии с (7.14) получаем,
что е(ж) = 1, т.е. оценка х в данном случае является неулучшаемой.
2	и w
2. Рассмотрим в качестве оценки дисперсии а нормальной случайной
величины «подправленную» на несмещенность выборочную дисперсию
-2
3 =
1
п — 1
1=1
—2	2
Выше получено, что Ез = or , т. е.
дисперсии а2. В п. 7.1.5 было показано,
s является несмещенной оценкой
что
П-2	2	4
Из =------- а
Поскольку (см. (7.9)) 7(а2,ж) = 1/2<т4, то в соответствии с (7.14)
получаем е(з2) = (п — 1)/п, т.е. оценка з2 не является эффективной, хотя
и близка к ней при больших объемах выборок. В то же время можно
2
показать, что если в качестве оценки а взять статистику
п 1=1
что в данных условиях допустимо, так как среднее значение а считается
известным, то она окажется точно эффективной.
Подчеркнем в заключение, что информационное неравенство спра-
ведливо лишь в классе регулярных (в смысле соблюдения условий а)-в)
§ 7.3) генеральных совокупностей. В частности, если область возможных
значений исследуемой случайной величины, для которых плотность /(ж; 6)
положительна, зависит от оцениваемого параметра, то неравенство ин-
формации «не работает». Именно такими нерегулярными плотностями
являются, например, равномерное распределение (в котором параметра-
ми служат концы диапазона изменения соответствующей случайной ве-
личины, см. п.3.1.7) и экспоненциальное распределение со сдвигом 0, т.е.
7.3. НЕРАВЕНСТВО РАО-КРАМЕР А-ФРЕШЕ
247
распределение, задаваемое плотностью
/(*;«)={
— (х — 9)	л
е '	' при ж > 0;
О при х <6.
Если, не обращая внимания на то, что эта плотность не удовлетворяет
условиям а)-в), вычислить по формуле (7.6) количество информации, со-
держащейся в п независимых наблюдениях, то получим 1(0,	. ,яп) =
п. Следовательно, в соответствии с информационным неравенством (7.12)
мы должны были бы прийти к выводу, что дисперсия любой оценки 0 па-
раметра 0 не может быть меньше 1/п. В то же время нетрудно вычислить
(см. ниже, (пример 7.6)), что для оценки
& — a'min(71) j
П
(7.15)
где, как обычно,жт-|П(п) — это минимальное значение в выборке «1,..., жп,
мы имеем:
Ев = в; Ов = -4.
п
Так что если для измерения эффективности оценки (7.15) восполь-
зоваться формулой (7.14), то получим, что эффективность оценки 0 ле
просто больше единицы, но и стремится к бесконечности по мере роста
объема выборки п (так как е(0) = J* = П)‘ В подобных ситуациях
оценки называют иногда «сверхэффективными».
Замечание о дискретных случайных величинах. Все изложенные вы-
ше результаты (понятие количества информации, неравенство информа-
ции, измерение эффективности оценки) распространяются на случай дис-
кретных признаков при соблюдении тех же ограничений а)-в) с помощью
внесения очевидных видоизменений: плотности f(z]0) заменяются веро-
ятностями Pi(0) = PR = ж? | 0}, а интегрирование — суммированием
по всем возможным значениям анализируемой дискретной случайной ве-
личины. Таким образом, в качестве дискретных аналогов количества ин-
формации (7.6) и информационного неравенства (7.12) будем иметь:
1(0] Т1,...,ЖП) = П 1(0] х) = п	) PiW't (7Лб)
\	U\7	]
I	z
(i+d6(ew .	(7.17)
»Е(^(^в)2А(в)
248
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
В качестве примера рассмотрим случайную величину £, подчиненную
распределению Пуассона, т.е.
Pi(A) = P{f = «|A} = ^-e \	. = 0,1,2,3,...
1'
т. е. дисперсия любой несмещенной оценки Л параметра А не может быть
меньше, чем 1/п/(А, я) = Х/п. Если рассмотреть в качестве оценки А
выборочное среднее я, то будем иметь:
ЕА = Е
DA = D
пЕя
=	= А;
п
1
= —у п D х = —.
п п
(7.18)
Таким образом, оценка А = х параметра А в распределении Пуассона
является эффективной.
7.4.	Понятие об интервальном оценивании
и доверительных областях (постановка
задач)
Вычисляя на основании имеющихся у нас выборочных данных оценку
0(Я1,..., хп) параметра 0, мы отдаем себе отчет в том, что на самом деле
величина в является лишь приближенным значением неизвестного пара-
метра 0 даже в том случае, когда эта оценка состоятельна (т. е. стремится
к 0 с ростом п), несмещенна (т. е. совпадает с 0 в среднем) и эффективна
(т. е. обладает наименьшей степенью случайных отклонений от 0). Возни-
кает вопрос: как сильно может отклоняться это приближенное значение
(оценка) от истинного} В частности, нельзя ли указать такую величи-
ну Д, которая с «практической достоверностью» (т.е. с заранее заданной
вероятностью, близкой к единице) гарантировала бы выполнение нера-
венства |0 — 0| < Д? Или, что то же, нельзя ли указать интервал вида
(^i>^2)j который с заранее заданной вероятностью (близкой к единице)
накрывал бы неизвестное нам истинное значение 0 искомого параметра?
При этом заранее выбираемая исследователем вероятность, близкая к еди-
нице, обычно называется доверительной вероятностью ь а сам интервал
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
249
(01,0г) — доверительным интервалом (или интервальной оценкой^ в от-
личие от точечных оценок 0). Доверительный интервал по своей природе
случаен (потому и идет речь о вероятности накрыть некоторую не из-
вестную нам, но не случайную точку 0) как по своему расположению, так
и по своей длине. Величины 01,0г и Д, как правило, тоже строятся как
функция выборочных данных а^,... ,гЛ^Ширина доверительного интер-
вала существенно зависит от объема выборки п (уменьшается с ростом п)
и от величины доверительной вероятности (увеличивается с приближени-
ем доверительной вероятности к единице).
Все данные здесь определения и понятия без труда переносятся на
случай векторного параметра 0 =<1(^1\...,0^^) с заменой доверитель-
ного интервала доверительной областью в соответствующем Л-мерном
пространстве.
7.5.	Методы статистического оценивания
неизвестных параметров
В предыдущем пункте рассмотрены различные варианты использо-
вания функций от исходных наблюдений a?i, х2,... ,жп в качестве оценок
неизвестных параметров, анализировались их свойства. Однако пока не
ясно, каким способом устанавливаются именно те комбинации результа-
тов наблюдений (статистики), с помощью которых производится (да еще
наилучшим в определенном смысле образом!) оценивание того или ино-
го параметра. Каким образом, например, было установлено, что именно
комбинации лучше всего использовать в качестве оценок неизвест-
ных параметров соответственно среднего значения а = Е£ и дисперсии
о = D£ нормальной генеральной совокупности? И как конкретно строить
описанные выше доверительные интервалы и области для неизвестных
значений параметров?
Описанию основных приемов, позволяющих получать ответы на дан-
ные вопросы, и посвящен настоящий пункт.
7.5.1.	Метод максимального (наибольшего) правдоподобия
В соответствии с этим методом оценка 0МП неизвестного параметра
0 по наблюдениям ®1э... ,хп случайной величины £ (подчиненной закону
распределения Д(г,0), где f — плотность или вероятность Р{£ = х})
определяется из условия
^(•^i»• • »®п,®мп) — max Z/(z],...,хП10),
(7-19)
250
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
где L — функция правдоподобия, определенная соотношением (7.5).
Таким образом, в формальной записи оценка максимального правдо-
подобия 0МП параметра 0 по независимым наблюдениям ,..., хп может
быть представлена в виде
©мп = arg max
е
П Л2” ®)-
(7.19')
Естественность подобного подхода к определению статистических
оценок вытекает из смысла функции правдоподобия. Действительно, по
определению (см. п. 7.2), функция Цх^,.. . ,жп; 0) при каждом фиксиро-
ванном значении параметра 0 является мербй правдоподобности получе-
ния системы наблюдений, равных х^, х2,. -., хп. Поэтому, изменяя значе-
ния параметра 0 при данных конкретных (имеющихся у нас) величинах
ха, • - . мы можем проследить, при каких значениях 0 эти наблю-
дения являются более правдоподобными, а при каких — менее и выбрать
в конечном счете такое значение параметра 0МП, при котором имеющаяся
у нас система наблюдений , хп выглядит наиболее правдоподобной
(очевидно, что это значение 0МП определяется конкретными величинами
наблюдений ж1,Я2» • • - ,яп, т.е. является некоторой функцией от них).
Так, например, пусть £ — заработная плата работников, подчинен-
ная логарифмически нормальному распределению (см. п. 3.1.6). И пусть
с целью приближенной оценки средней величины логарифма заработной
платы работников а = Е(1п£) мы зафиксировали значения заработной пла-
ты Xi = 190 ден.ед., х2 = 175 ден.ед. и ж3 = 205 ден.ед. у трех случай-
но отобранных из интересующей нас совокупности работников. Тогда,
расположив yi = 1пж,(« = 1,2,3) на оси возможных значений нормально
распределенной случайной величины Т) = 1п£^ мы будем стараться по-
добрать такое значение амп параметра а в (а, а)-нормальном распределе-
нии, при котором наши наблюдения у^, у2, Уз выглядели бы наиболее прав-
доподобными, а именно, при котором произведение трех ординат плотно-
сти у?(у;а;сг2), вычисленных в точках соответственно у^ = In 190 = 5,25,
у2 = In 175 — 5,16 и уз = In 205 = 5,32, достигало бы своего максимального
значения.
На рис. 7.2 изображены графики функции плотности </?(j/; а; ст2) при
значении параметра амп = у = 5,243, соответствующем наибольшей прав-
доподобности наблюдений у^ = 5,25, у2 = 5,16 и уз = 5,32 (сплошная
кривая), и при значении параметра а — 5,443, при котором наши наблюде-
ния выглядят явно неправдоподобными, — пунктирная кривая (значение
2	-
дисперсии сг определено в обоих случаях с помощью подправленной на
несмещенность оценки максимального правдоподобия и равно 0,0064).
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
251
Рис. 7.2. Графики нормальной функции плотности при двух значениях па-
раметра а
Отмеченная естественность подхода, исходящего из максимальной
правдоподобности имеющихся наблюдений, подкрепляется хорошими свой-
ствами оценок, получаемых с его помощью. Можно показать, в частности,
что при достаточно широких условиях регулярности, накладываемых на
изучаемый закон распределения f(x; 0), оценки максимального правдо-
подобия 0мп параметра 0 являются состоятельными, асимптотически
несмещенными (т. е. их смещения стремятся к нулю при неограниченном
увеличении объема выборки), асимптотически нормальными и асимпто-
тически эффективными (т.е. их ковариационная матрица S(0Mn) асим-
птотически имеет вид Е(0МП) = п 1 X I 1(0;ж), где 1(0; Аг) — инфор-
мационная матрица Фишера, определенная соотношениями (7.7) примени-
тельно к единственному наблюдению, т. е. при X = х).
Однако из этого не следует, что оценки максимального правдоподо-
бия будут наилучшими во всех ситуациях. Во-первых, их хорошие свой-
ства проявляются часто лишь при очень больших объемах выборок (т. е.
являются асимптотическими), так что при малых п с ними могут кон-
курировать (и даже превосходить их) другие оценки, например, оценки
метода моментов, метода наименьших квадратов и т.д. Во-вторых, и это,
пожалуй, главное «узкое место» данного подхода, для построения оценок
максимального правдоподобия и обеспечения их хороших свойств необхо-
димо точное знание типа анализируемого закона распределения /(я:;0),
что в большинстве случаев оказывается практически нереальным. В по-
добных ситуациях бывает выгоднее искать не оценку, являющуюся наи-
лучшей в рамках данного конкретного общего вида f(x- 0) (но, как часто
бывает, резко теряющую свои хорошие свойства при отклонениях реалъ-
252
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ного распределения от типа /(ж; О)), а оценку, хотя и не наилучшую в
рамках совокупности /(г; 0), ио обладающую достаточно устойчивыми
свойствами в более широком классе распределений, включающем в себя
/(я;0) в качестве частного случая (см. ниже, п. 7.5.4). Подобные оцен-
ки принято называть устойчивыми или робастными (английский термин
robust estimation означает грубое, или устойчивое, оценивание). И нако-
нец, оценки максимального правдоподобия могут не быть даже состо-
ятельными, если число к оцениваемых по выборке параметров 0i,...A
велико (имеет тот же порядок, что и обьем выборки п) и растет вместе с
увеличением числа наблюдений. Ниже приведен пример подобной ситуа-
ции (см. пример 7.6).
Попытаемся ответить на вопрос, как конкретно находятся оценки
максимального правдоподобия, т.е. как проводится решение оптимизаци-
онной задачи типа (7.19 ).
Если функция f(x; 0) удовлетворяет определенным условиям регу-
лярности (дифференцируемость по 0 и т.п., см. условия а)-в) п. 7.3) и
экстремум в (7.19) достигается во внутренней точке области допустимых
значений неизвестного параметра 0, то в точке 0МП должны обращаться
в нуль частные производные функции Ь(жь... ,агп: О), а следовательно, и
логарифмической функции правдоподобия
п
l(xi,..., хп; 0) = In L(xx,..., жп; 0) = In /(ж„ 0)	(7.20)
i=l
в силу монотонного характера этой зависимости: последняя удобнее для
вычислений. Значит, в данном случае оценка максимального правдоподо-
бия 0МП = (^ ,..., Slw) должна удовлетворять уравнениям:
х„;в) j =	(7.21)
и может определяться в качестве решения этой системы уравнений.
Однако могут быть ситуации (случай нерегулярных по О законов рас-
пределения), когда система (7.21) не определена или не имеет решений, в
то время как решение (7.19J существует. В подобных ситуациях оценку
0МП следует искать другими способами, в том числе с помощью непосред-
ственного подбора решения (7.19).
Пример 7.2. Исследуемая случайная величина £ имеет нормаль-
ную плотность вероятности
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
253
с неизвестным средним значением а = Е£ и неизвестной дисперсией а2 =
De.
В соответствии с (7.5) функция правдоподобия в этом случае будет
2\
zn;a;a ) =
... \
(2тг)7стп
Соответствующая логарифмическая функция правдоподобия
/(хь.
2ч ”] /о \ П 1	2	1
яп;а,<т ) = ——1п(2тг)— -Ina - —
z	*	2a
^(»i - о)2.
»=1
2
Дифференцируя I по а и а и последовательно приравнивая соответству-
ющие частные производные к нулю, получаем конкретный вид системы
(7-21):
2ч
•,2^0,^ )
да
. п	п
= -^53» = Х(^-а) = О;
°	i=l
д/(жь...,жя;а,а2)	п 1
да2	2 ’ а2
t=i
Решение этой системы относительно а и а2 дает оценки максимального
правдоподобия этих параметров:
МП —

Выше (см. п. 7.3) установлено, что оценка 0МП = х является эффективной
оценкой параметра а (так как ее эффективность е(вмп) = 1), а оценка
сгмп = <8 — асимптотически эффективной оценкой параметра а (так как
ее эффективность е(а„п) — (п - 1)/п).
Пример 7.3. Исследуемая случайная величина £ подчинена закону
распределения Пуассона, т. е.
/(z; А) = РЦ = z) = ^-е"Л
XI
(х = 0,1,2,...),
с неизвестным значением параметра Л.
254
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
В соответствии с (7.20) логарифмическая функция правдоподобия, по-
строенная по выборке Ж], ^2, -..,з?п> имеет вид
п
Z(a?i,..., хп, А) — 5 ( , In A ln(xt!) А)
»=1
п
= (1п А) • 52_ 52~ пХ‘
»=i
Отсюда после дифференцирования по А получаем уравнение метода мак-
симального правдоподобия
— п — 0
откуда
Легко видеть, что эта оценка несмещенная, так как
п =
Вычислим эффективность оценки Амп. Нижняя граница дисперсии по всем
возможным оценкам параметра А может быть вычислена в соответствии
с неравенством информации (7.12):
nE( In f(x, A))2 nE(J-l)2 пЕ(ж-А)2 п
Дисперсию оценки Амп вычислим, опираясь на следующий известный
факт: дисперсия суммы независимых случайных величин
равна сумме их дисперсий, т. е.:
Сравнивая (DA)m;n с DAMn, убеждаемся, что оценка максимального прав-
доподобия среднего значения пуассоновской случайной величины является
эффективной.
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
255
Пример 7.4. Исследуемая случайная величина £ распределена по
равномерному закону (см. л.3.1.7), т.е.
/(s;a,6)=|frTP еСЛИ ./*[«.4;
(О — в противном случае,
где параметры а и b неизвестны (подлежат оцениванию).
Легко проверить, что это — случай нерегулярный (в первую очередь
потому, что область возможных значений исследуемого признака, в кото-
рой плотность положительна, зависит от оцениваемых по выборке пара-
метров а и 6). Поэтому обычная техника, использующая уравнения (7.21)
метода максимального правдоподобия, здесь неприменима. Однако в этом
случае экстремальная задача (7.19) может быть решена непосредственно.
Действительно,
^'(^'1 , • • • ,	^) — 77	j
(6-а)
причем область допустимых значений параметров а и 6, где производится
поиск тех значений амп и 6МП, при которых 1/(6 — а)п = max, описывается
а,Ь
соотношениями:
а min {ж,} = ajmin(n);
Ь > max {х J = жт„(п),
где . •, хп — имеющиеся в нашем распоряжении наблюдения иссле-
дуемой случайной величины. Очевидно, решение экстремальной задачи
гаах /к 1	а «min(n)» b > ^max(n)
(6-а)
дается соотношениями:
®мп — ®min(^)> ^мп = а'гпах(^)-
Опираясь на результаты п. 2.6.4 (см. также п. 7.5.4), можно подсчи-
тать:
. b — а -
— E^'min(^) — ® Н ,
П
®ймп ~ ^*^min(^) — ~	о z	\	’
<П+1)(П + 2)	(7.22)
—	о — а
Е6МП = Ezmax(n) = b ;
О6МП = Dzmax(n) = -	2,	“ °) •
[п 4-1) (п 4- 2)
256
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Использовать неравенство информации для вычисления нижней гра-
ницы дисперсии этих оценок мы не можем, так как случай нерегулярный.
Из (7.22) видно, что величины DaMn и D6Mn характеризуют одновременно
средний квадрат отклонения «подправленных на несмещенность» оценок
'-г	__ / \	-^тах(^)	% min(^) *'
амп — ®min(w)	«	>
П — 1
\ . Я-тахС71) •rmtn(71)
Омп = ятах(п) 4--------—---------
п — 1
от истинных значений параметров а и Ь.
Пример 7.5. Снова рассмотрим задачу оценивания параметра
сдвига 0 в экпоненциальном распределении, задаваемом плотностью

/(*;*) =
при
при
х 0;
х < 0.
Ю
Как и в предыдущем примере, имеем дело с нерегулярным случаем.
Поэтому приходится непосредственно решать экстремальную задачу вида
max L(xly.. .хп\0} = шахе
о	v
0 min {я,-} = zrnin(n).	(7.23)
ISCiSin
Легко видеть, что 0МП = агп1]п(п) является решением этой задачи: при
любом другом 0, удовлетворяющем условию (7.23), очевидно
- 6) =	[l; - (»„„ - е)] =	- ?„„)
i=l	i=l	i=l
n
4"	^мп)
t=l
и, следовательно,
®n> ^мп ) > э • • • •> ^n> ^)*
Опираясь на результаты п. 2.6.4 (см. также п. 7.5.4), можно подсчи-
тать:
Е0МП = ЕжГП1П(п) = 4	5
П
О0мп = E(xmin(n) - Ezmin(n))2 = -4;	(7.24)
п
Е(0м„ - 0)2 = D9Mn + -4 = 4-
п п
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
257
Однако оценка 0МП = 0МП — получающаяся из оценки 0МП «подправле-
нием на несмещенность», будет иметь средний квадрат отклонения
в(й,„ - »)2 = 4-
п
(7-25)
Пример 7.6 (заимствован из [Ван дер Варден Б. Л., с. 187]). Рас-
смотрим ситуацию, когда метод максимального правдоподобия не приво-
дит к состоятельной оценке.
С целью оценки п концентраций некоторого элемента а^аз,... tan
в лаборатории производились двукратные измерения (xi,yi) каждой из
концентраций а,-. Предполагается, что все 2п результатов измерений
,1/1, «2, з/2 > • • •»Уп имеют одинаковую точность и являются независи-
мыми нормальными случайными величинами (см. п. 3.1.5), так что в ка-
честве функции правдоподобия получаем
^/(®1»3/1 , • • • > Уп) ®1 >	> • • • »	& )
=	1	.-A£-s, [(»<-()2+(и-«.)2]
(2тг)"<72п
Неизвестными параметрами являются п средних значений ai,O2>
...,ап и дисперсия <т2. Нетрудно получить оценки максимального прав-
доподобия параметров
®»мп — 9^’
Решая теперь уравнение максимального правдоподобия (7.21), в кото-
рое вместо а* подставлены значения а*мп» получаем
5м„ =	-9i)2-
4n
»=1
Нетрудно подсчитать, что Ебт„п = а2/2, т.е. метод максимально-
го	2
го правдоподобия дает в этом случае оценку параметра ст с постоян-
ным (асимптотически неустранимым) отрицательным смещением, рав-
ным -<72/2. В качестве наилучшей несмещенной оценки следовало бы
выбрать в данном случае статистику
i=l
258
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
7.5.2. Метод моментов
Пусть £ — исследуемая одномерная случайная величина, подчиняю-
щаяся закону распределения /(ж; О), где функция /(ж; 0) — плотность
вероятности, если £ непрерывна, и вероятность Р{£ = х | 0}, если £ дис-
кретна, зависит от некоторого, вообще говоря, многомерного параметра
0 = (0^,..., 0^). И пусть мы хотим оценить неизвестное значение этого
параметра, т. е. построить оценку 0 по имеющейся в нашем распоряжении
выборке, состоящей из независимых наблюдений Ж1,...,жп.
Метод моментов заключается в приравнивании определенного количе-
ства выборочных моментов к соответствующим теоретическим (т.е. вы-
численным с использованием функции /(я; 0)) моментам исследуемой слу-
чайной величины, причем последние, очевидно, являются функциями от
неизвестных параметров 0^\ ... ,0<*\ Рассматривая количество момен-
тов, равное числу к подлежащих оценке параметров, и решая полученные
уравнения относительно этих параметров, мы получаем искомые оценки.
Таким образом, оценки 0^„,..., Йм по методу моментов неизвестных па-
раметров 0^\...,0^ являются решениями системы уравнений:
/1 п
x‘-f(x-e)dx=	/=1,2,...,Л;	(7.26)
п 1=1
(очевидно, если анализируемая случайная величина £ дискретна, интегра-
лы в левых частях (7.26) следует заменить соответствующими суммами).
Число уравнений в системах (7.26) должно быть равным числу к оце-
ниваемых параметров. Вопрос о том, какие именно моменты включать в
систему (7.26) (начальные, центральные или их некоторые модификации
типа коэффициентов асимметрии или эксцесса), следует решать, руко-
водствуясь конкретными целями исследования и сравнительной просто-
той формы зависимости альтернативных теоретических характеристик
от оцениваемых параметров 0^\ ... В статистической практике де-
ло редко доходит даже до моментов четвертого порядка.
К достоинствам мегода моментов следует отнести его сравнительно
простую вычислительную реализацию, а также то, что оценки, получен-
ные в качестве решений системы (7.26), являются функциями от выбо-
рочных моментов. Это упрощает исследование статистических свойств
оценок метода моментов: можно показать (см. [Крамер Г., гл. 27 и 28]),
что при довольно общих условиях распределение оценки такого рода при
больших п асимптотически нормально, среднее значение такой оценки от-
личается от истинного значения параметра на величину порядка п"1, а
стандартное отклонение о(0мм) асимптотически имеет вид сп-1^2, где с —
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
259
некоторая постоянная величина.
В то же время, как показал Р. Фишер (Крамер Г.), асимптотическая
эффективность оценок, полученных методом моментов, оказывается, как
правило, меньше единицы, и в этом отношении они уступают оценкам,
полученным методом максимального правдоподобия. Тем не менее метод
моментов часто очень удобен на практике.
Иногда оценки, получаемые с помощью метода моментов, принима-
ются в качестве первого приближения, по которому можно определять
другими методами оценки более высокой эффективности.
Вернемся к нашим примерам.
В примере 7.2 в качестве системы (7.26) имеем:
2 1
<7 -4- а
что дает уже знакомые нам по методу максимального правдоподобия оцен-
ки для параметров:
Нормальное распределение, так же как и распределение Пуассона (в
чем легко убедиться, обратившись к примеру 7.3), относится к тем ред-
ким случаям, когда оценки по методу моментов совпадают с оценками по
методу максимального правдоподобия.
Построение системы (7.26) в примере 7.5 дает:
Откуда легко получаем оценки:
= х(п) — \/Зз(п);
= х(п) -Ь \ХЗз(п).
°мм — х
^мм = Х
(7.27)
260
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Можно сравнить асимптотическую эффективность оценок, получен-
ных методом максимального правдоподобия и методом моментов: учиты-
вая, что дисперсия оценок (7.27) как дисперсия функций выборочных мо-
ментов ж(п) и <82(п) имеет порядок п-1, и принимая во внимание соотно-
шение (7.22), в соответствии с которым дисперсии оценок максимального
—2
правдоподобия тех же параметров имеют порядок п , получаем, что эф-
фективность амм и 6ММ в сравнении с эффективностью амп и 6МП стремится
к нулю при п —> оо.
Реализация метода моментов в примере 7.5 дает
1 4- 0 = х(п).
Следовательно, 0ММ = х(п) — 1.
Для подсчета среднего значения и дисперсии оценки 0ии воспользу-
емся следующими фактами:
а)	случайную величину xty распределенную экспоненциально с пара-
метром сдвига 0У можно интерпретировать как частный случай гамма-
распределенной случайной величины с параметрами а = 1, b = 1 и с па-
раметром сдвига 0 (см. п. 3.2.5);
б)	сумма п независимых случайных величин ж2,..., хпу каждая из
которых распределена по закону гамма с параметрами а = 1 и b = 1 и с
параметром сдвига 0, подчиняется гамма-распределению с параметрами
а = п, Ь = 1 и с тем же самым параметром сдвига 0 (см. п. 3.2.5).
Поэтому
ES„M = Е(х(п) - 1) =	-1=9;
п
E(?MU - 9)1 = Пвии = D(Z(n) - 1) = 4 = 1.
п п
Учитывая выражение (7.25) для среднего квадрата ошибки «подпра-
вленной» оценки по методу максимального правдоподобия того же па-
раметра 0, получаем
- 0)2	Л	1
---= Л- =-------> 0 при п —► оо,
-0)2	I	"
т. е. и в этом случае асимптотическая эффективность оценки по методу
моментов стремится к нулю.
Е(УМП
Е $мм
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
261
7.5.3. Оценивание с помощью «взвешенных» статистик;
цензурирование, урезание выборок и порядковые
статистики как частный случай взвешивания
Выборочные моменты тпк всегда являются состоятельными оценка-
ми соответствующих теоретических моментов тк, если последние суще-
ствуют (см. п. 6.2). Однако не во всякой генеральной совокупности они
являются наиболее эффективными оценками. Так, например, мы видели
(см. п. 7.5.1 и 7.5.2), что эффективность оценки среднего значения иссле-
дуемой случайной величины с помощью выборочного среднего х = тг
существенно зависит от типа анализируемой генеральной совокупности:
для нормальной генеральной совокупности она равна единице (см. при-
мер 7.2 в п. 7.5.1), а для совокупности, подчиненной равномерному зако-
ну распределения, существенно меньше единицы и сильно проигрывает в
сравнении, например, с эффективностью оценки
а —
4" З'тах)*
(7.28)
Для построения оценки (7.28) нами использованы только два наблюдения
из п имеющихся — наименьшее и наибольшее, т. е. оценка (7.28) относит-
ся к классу «взвешенных» порядковых статистик 527=1 где —
i-e по величине (в порядке возрастания) наблюдение, aw, — его «вес»
(очевидно, в статистике (7.28) принято w-[ = wn = 0,5, а все остальные Wi
равны нулю).
Выборочная медиана £med демонстрирует удивительную устойчи-
вость своих хороших свойств в качестве оценки теоретического среднего
значения. Выборочная медиана £me<j также относится к классу «взвешен-
ных» порядковых статистик, т.е. статистик вида 527=1 для ее по-
лучения в качестве частного случая статистик этого класса достаточно
положить нулю все веса w,, кроме одного = 1, если п нечетно) или
кроме двух	если п четно).
Остановимся далее на описании основных подходов, связанных с ис-
пользованием взвешенных статистик, и на классификации их типов.
Взвешивание выборочных данных z1,...,zn. В общем случае
наблюдению ас, приписывается вес w,- = w(ac,) > 0, который определяется
как некоторая функция от его текущего значения. Обычно веса подчиняют
условию нормировки w(x*) = 1- В частности, можно рассматривать
w взвешенные моменты случайной величины £ с плотностью fe(x), как
262
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
выборочные rn*(n, IV), так и теоретические mjt(lV):
п
IV) = Xi • W(X&
i=l
7njfc(IV) = J vkw(x) dx.
Под IV понимается вектор весов (w^),..w(zn)) в выражении для вы-
борочных моментов и функция со значениями w(x) в выражении для тео-
ретических моментов.
Если имеют дело с результатами наблюдения одномерной случай-
ной величины аг1,...,а?п, то часто вес наблюдения х, определяют в за-
висимости от его порядкового номера в упорядоченном (по возраста-
нию) ряду наблюдений, т. е. располагают наблюдения в вариационный ряд
Z(i),ar(2),... ,Ж(п) и каждому члену вариационного ряда х^у ставят в соот-
ветствие некоторый вес wt.
Примеры такого рода взвешивания (которое приводит к так называ-
емым порядковым статистикам) приведены выше.
Цензурирование выборки. Этот прием заключается в приписы-
вании ряду «хвостовых» членов вариационного ряда нулевых весов, а
остальным — одинаковых положительных. Если приписывание нулевых
весов производится по признаку выхода текущих значений наблюдений за
пределы заданного диапазона [а, 6], т. е.
Wo > 0, если а
О, если Я7(ж) < « или > b,
то говорят о цензурировании 1-го типа. Очевидно, в этом случае число v
оставшихся в рассмотрении наблюдений есть величина случайная (и < п).
Если же нулевые веса приписываются фиксированной доле а крайних
малых значений и фиксированной доле /3 крайних больших значений, то
говорят, что производится цензурирование 2-го типа уровня	В
этом случае число и оставшихся в рассмотрении наблюдений является
величиной, заранее заданной и равной, в частности, п(1 — а — /3).
Исследователь может прибегнуть к цензурированию вынужденно иля
добровольно. Вынужденное цензурирование обусловлено соответствую-
щими условиями эксперимента: например, мы ставим на разрушающие
испытания п изделий, но можем производить эксперимент в течение огра-
ниченного времени Т. Очевидно, мы будем вынуждены произвести в
данном случае одностороннее цензурирование 1-го типа, при котором из
дальнейшего рассмотрения исключаются точные значения долговечностей
“(*(<)) =
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
263
(времени до разрушения) всех тех изделий, которые не разрушились за
время Т. С другой стороны, в классе оценок, построенных по цензури-
рованным выборкам, часто можно найти оценки, хотя и не являющиеся
наилучшими в жестких рамках генеральной совокупности определенного
типа, но обладающие выгодными свойствами устойчивости своих хоро-
ших качеств по отношению к тем или иным отклонениям от априорных
допущений.
Урезание распределения. Это понятие связано с ситуациями, ко-
гда исследуемый признак £ просто не может быть наблюдаем в какой-либо
части области его возможных значений. Так, например, если мы исследу-
ем распределение семей по доходу, но по условиям выборочного обследо-
вания лишены возможности наблюдать семьи со среднедушевым доходом,
меньшим некоторого заданного уровня а (тыс. руб.), то в подобных слу-
чаях говорят, что распределение урезано слева в точке а. В отличие от
цензурированных выборок в выборках из урезанных распределений мы не
имеем возможности оценить даже доли наблюдений, располагающихся за
пределами порога урезания.
Весьма подробные сведения об использовании в задачах статистиче-
ского оценивания параметров взвешенных и, в частности, порядковых ста-
тистик и статистик, построенных по цензурированным выборкам, с обсу-
ждением различных вопросов устойчивости получаемых при этом оценок
читатель найдет, например, в [Кендалл М. Дж., Стьюарт А., 1973, гл. 32]
и [Дейвид Г.].
7.5.4.	Построение интервальных оценок (доверительных об-
ластей)
В п. 7.4 введено понятие интервальной оценки неизвестного параме-
тра О = (^1\. ♦ .,</*)) Т, которую называют также доверительным интер-
валом, а при многомерном параметре, т.е. при к 2, — доверительной
областью. Как же конкретно построить по выборочным данным Ж1,..., хп
такую случайную область Д0р(а?1,. ..,жп), которая с наперед заданной
доверительной вероятностью Р накрывала бы неизвестное нам значение
параметра 0? Очевидно, эта область должна конструироваться вокруг
точечной оценки 0 параметра 0, а ее точный вид и объем определяют-
ся характером закона распределения случайной величины 0, в частности,
ее функцией распределения, которая, к сожалению, тоже зависит от неиз-
вестного истинного значения параметра 0.
Существуют два подхода к преодолению этой трудности. Первый
подход, если его удается реализовать, приводит к построению точ-
264
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ных (при каждом конечном объеме выборки п) доверительных областей
ДОр(а?1,...,а;п). А реализовать его удается в тех случаях, когда суще-
ствует принципиальная возможность подбора такой функции от резуль-
татов наблюдения хь^з,.. . ,жп (т.е. такой статистики), закон распреде-
ления вероятностей которой обладал бы одновременно следующими свой-
ствами:
(а)	не зависит от оцениваемого параметра О;
(б)	описывается одним из стандартных затабулированных распреде-
лений (стандартным нормальным, %2-, F-, Стьюдента);
(в)	из того факта, что значения данной статистики заключены в опре-
деленных пределах с заданной вероятностью, можно сделать вывод, что
оцениваемый параметр тоже должен лежать между некоторыми граница-
ми с той же самой вероятностью.
При этом в выражении самой этой статистики анализируемый пара-
метр 0 и его состоятельная точечная оценка 0 (полученная одним из из-
вестных методов — максимального правдоподобия, моментов и т.д.) обыч-
но участвуют в комбинациях разности (0 — 0) или отношения (0/0).
В качестве примера рассмотрим задачу интервального оценивания
параметров а и и нормальной генеральной совокупности (см. пример 7.2
в п. 7.5.1).	/
Как известно (см. п. 6.30), статистика
х — а ,--
----уп — 1
подчинена закону распределения Стьюдента с п — 1 степенями свободы.
Поэтому, определив из таблиц по заданной вероятности Р процентные
точки уровня g = (1 - Р)/2 и 1 — g = (1 — Р)/2 ^-распределения с п -1
степенями свободы, т.е. 100д%-ную точку tq(n — 1) и 100(1 — д)%-ную
точку ti_9(n — 1) (причем в силу симметрии ^-распределения ti_q(n-1) =
—tq(n — 1)), мы можем утверждать, что неравенство
выполняется с вероятностью Р = 1 — 2g. А это означает, что случайный
доверительный интервал
Д®р(®1э • • • j гп) — ® ^g(^l	1) ’ /	.= > "Ь ^) * /-----г
П — 1
(7.29)
накрывает неизвестное среднее значение а с заданной вероятностью Р.
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
265
Для построения интервальной оценки параметра ст2 воспользуем-
__2	2	/
ся тем фактом, что статистика подчинена % -распределению (хи-
квадрат) с п — 1 степенями свободы (см. п. 6.27). Поэтому, определив
из таблиц процентные точки %2-распределения с п — 1 степенями свободы
X?_g(n — 1) и — 1), где, как и прежде, q = (1 — Р)/2, а Р — заданная
доверительная вероятность, имеем неравенство
- 1) <
2
ns
Т
G
< Х?(» - 1)»
которое выполняется с вероятностью Р = 1 — 2g. Разрешая это неравен-
ство относительно ст2, получаем, что случайный доверительный интервал
Дстр(х1,
ns
ns
(7.30)
накрывает неизвестное значение дисперсии ст2 с заданной вероятностью Р.
Пример 7.7. Из многочисленного коллектива работников фирмы
случайным образом отобрано п = 25 работников. Средняя заработная пла-
та этих работников составила х = 700 ден. ед. при среднеквадратическом
отклонении з = 100 ден. ед. Требуется с доверительной вероятностью
Р = 0,95 определить интервальную оценку для:
а)	средней месячной заработной платы на фирме;
б)	суммы затрат фирмы на заработную плату отдела, состоящего из
520 сотрудников.
Решение.
а)	Среднемесячная заработная плата на фирме характеризуется гене-
ральной средней а. От нас требуется определить интервальную оценку а
с доверительной вероятностью Р = 0,95.
Согласно (7.29) имеем
а €
где i0025(24) — 2,5%-ная точка (-распределения.
По таблице процентных точек распределения Стьюдента приложе-
ния 1 находим для q =	= 0,025 и числа степеней свободы у = п— 1 =24
процентную точку (о,О2б(24) = 2,064. Тогда
а €
700 ± 2,064-^2=
д/24.
266
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Таким образом, с вероятностью Р = 0,95 можно гарантировать, что сред-
няя заработная плата на фирме находится в пределах: 657,88 ден. ед. <
а 742,12 ден. ед.
б)	Сумма затрат фирмы на заработную плату отдела составит
Na ден. ед. Поэтому с вероятностью Р = 0,95 можно гарантировать,
что затраты фирмы на заработную плату не выйдут из интервала:
520 • 657,88 Na < 742,12 • 520,
т.е.
342098 ден. ед. < Na 385902 ден. ед.
Пример 7.8. При анализе точности фасовочного автомата было
проведено п = 24 контрольных взвешиваний пятисотграммовых пачек ко-
фе. По результатам измерений рассчитано выборочное среднеквадрати-
ческое отклонение з = 0,8 г. Требуется с доверительной вероятностью
Р = 0,95 оценить точность фасовочного автомата, т.е. определить интер-
вальную оценку а.
Решение: Согласно (7.30) имеем интервальную оценку дисперсии
Г 2	2 1
_2 _ пз	пз
& €	2~»	2	’
. Xq Xl-g.
где q =	= 0,025. По таблице процентных точек х2~РаспРеДеления
(см. приложение 1) найдем:
Х?(п - 1) = X?,025(23) = 38,0757;
X(i-,)(n - 1) = Xo,97s(23) = 11,6885.
Тогда с вероятностью 0,95:
а2 €
24-0,64
38,0757’
24 ♦ 0,64'
11,6885.
Отсюда с доверительной вероятностью Р = 0,95 можно утверждать, что
среднеквадратическое отклонение а будет находиться в интервале
0,632 г. а 1,146 г.
Предположив, что ошибка фасовочного автомата есть нормальная случай-
ная величина с нулевой средней и среднеквадратическим отклонением а,
можно с вероятностью 0,954 утверждать, что вес пачек кофе будет в пре-
делах [500-2а; 500 +2а] = [500-2,292; 500 + 2,292] » [497,71г., 502,29 г.].
7.5. МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
267
Второй подход к построению доверительных областей более прост и
универсален, однако он основан на асимптотических свойствах оценок,
а поэтому дает приближенные результаты и пригоден лишь при доста-
точно больших объемах выборок п. Этот подход использует тот факт,
что как оценки максимального правдоподобия, так и оценки по методу
моментов имеют асимптотически нормальное совместное распределение,
т. е. распределение /г-мерного вектора £(п) = 5/п(0 — 0) стремится к мно-
гомерному нормальному закону с нулевым вектором средних значений и с
ковариационной матрицей Е(0), зависящей от неизвестного параметра 0.
При этом приближенном подходе допускаются две «натяжки»: во-первых,
асимптотический вид распределений случайной величины £(п) использу-
ется при конечных объемах выборки п и, во-вторых, вместо неизвестного
значения параметра 0 в матрицу Е(0) вставляется его оценочное значе-
ние 0.
Теперь, для того чтобы построить доверительную область для не-
известного параметра 0 = (^1\...,^*^)Т, мы должны воспользоваться
следующим известным фактом (см. [Андерсон, с. 77]): если А:-мерный век-
тор £(п) = ^/п(0 — 0) распределен нормально с параметрами 0 и Е(0), то
случайная величина
я(§ - ©)Т  s-1 (в)(ё - е)
имеет х -распределение с k степенями свободы.
Определив из таблиц по заданной величине доверительной вероятно-
сти Р процентные точки %2-распределения с к степенями свободы х?_9(/с)
и где q = (1 — Р)/2, и заменив в известной матрице Е(О) неизвест-
ное значение параметра 0 его приближенным значением 0, мы можем
утверждать, что неравенство
< »(0 - 0)т • з-'(0) • (0 - 0) < х?(*)	(7.31)
выполняется с вероятностью, приблизительно равной Р.
Замечание 1. В случае единственного оцениваемого параме-
тра О (т.е. при к = 1) можно воспользоваться непосредственно (Орто-
нормальностью разности 0 — 6 и записать вместо (7.31)
<е-е<и, о^е),	(7.31')
где «9 — 100^%-ная точка стандартного нормального распределения, а
— дисперсия оценки 0. Из (7.31х) следует запись соответствующего
268
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
доверительного интервала:
,..., жп) = [? - ид - ^),	•	(7.31И)
Замечание 2. Если в качестве 0 используются точечные оценки
максимального правдоподобия, то ковариационная матрица Е(0) вектора
у/п(& — 0) однозначно определяется информационной матрицей Фишера
(см. п. 7.2) 1(в) = Г*(в), где элементы матрицы 1(0) определяются соот-
ношениями (7.7).
Замечание 3. Положительная определенность и симметрич-
ность матрицы Е(0) обусловливают эллипсоидальный характер довери-
тельного множества, задаваемого соотношением (7.31).
Пример 7.9. Рассмотрим задачу интервальной оценки по наблю-
дениям zj,...,zn параметра р биномиального закона (см. п.3.1.1), т.е.
закона распределения дискретной случайной величины £, определяемого
вероятностями
/(я; р,N) = Р{£ = х) = CTNpz(l - p)N~z, х = 0,1.N,
где N — известное целое положительное число, а р — параметр, подле-
жащий оценке (0 < р < 1).
Сначала в соответствии с техникой, описанной в п. 7.5.1, подсчитаем
точечную оценку р максимального правдоподобия параметра р.
Логарифмическая функция правдоподобия в данном случае
п	п
1(®1, ®2,. .., Хп] p,Nj —	+ 1пр^х,
*=1	i=l
n
+ ln(l -p)	- Xi).
t=l
Соответствующее уравнение максимального правдоподобия
dl 1	1	S л
dp р£ l-p£f
Решая его относительно р, получаем оценку максимального правдоподо-
бия:
-	Е.=1г< _ ё(«)
Р nN N ’
Пользуясь независимостью и тем фактом, что Еж, = Np и Вж,- = JVp(l-p)
(см. и. 3.1.1), имеем:
р.	пА_Р(1-₽)
Ер = р; Dp =--------—.
7.6. БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 269
Задавшись доверительной вероятностью Р = 0,95, используя факт
асимптотической нормальности разности р — р и подставляя в выраже-
ние для дисперсии Dp вместо р его приближенное значение р, получим
в соответствии с (7.31w) интервальную оценку для р (с уровнем доверия
0,95):

, > - L- 1 Qg./Kl-P) а , по./рО-р)]
1,96^ nN ,p+l,96y nN j.
7.6.	Байесовский подход к статистическому
оцениванию
7.6.1.	«Философия» байесовского подхода
Байесовский подход является одним из возможных способов форма-
лизации и операционализации тезиса, в справедливости которого нет ви-
димых причин сомневаться: степень нашей разумной уверенности в не-
котором утверждении (касающемся, например, оценки неизвестного чи-
сленного значения интересующего нас параметра) возрастает и коррек-
тируется по мере пополнения имеющейся у нас информации относитель-
но исследуемого явления. Могут быть различные формы подтверждения
этого тезиса, в том числе не имеющие отношения к байесовскому подходу.
Одна из них выражена, например, в свойстве состоятельности оценки 0П
неизвестного параметра 0: чем больше объем выборки п, на основании
которой мы строим свою оценку 0П, тем большей информацией об этом
параметре мы располагаем и тем ближе (в смысле сходимости 0П к 0 по
вероятности, см. выше, п. 7.1.3) к истине наше заключение.
Специфика именно байесовского способа операционализации этого те-
зиса основана на двух положениях.
1)	Во-первых, «степень нашей разумной уверенности» в справедли-
вости некоторого утверждения численно выражается в виде вероят-
ности. Это означает, что вероятность в байесовском подходе выходит за
рамки ее интерпретации в терминах условий статистического ансамбля
(см. п. В.2.1 введения), но относится к одной из категорий субъектив-
ной школы теории вероятностей.
2)	Во-вторых, статистик при принятии решения использует в каче-
стве исходной информации одновременно информацию двух типов: апри-
орную и содержащуюся в исходных статистических данных (см. п. В.З
введения). Пои этом априорная информация предоставлена ему в виде
270
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
некоторого априорного распределения вероятностей анализируемого не-
известного параметра, которое описывает степень его уверенности в том,
что этот параметр примет то или иное значение, еще до начала сбора
исходных статистических данных. По мере же поступления исходных
статистических данных статистик уточняет (пересчитывает) это распре-
деление, переходя от априорного распределения к апостериорному, ис-
пользуя для этого известную формулу Байеса (см. п. 1.1.3; отсюда и на-
звание подхода).
7.6.2.	Общая логическая схема и базовые формулы
байесовского метода оценивания параметров
Общая логическая схема байесовского метода оценивания неизвест-
ных значений параметров представлена на рис. 7.3.
Рис. 7.3. Общая логическая схема байесовского подхода в статистическом
оценивании
Рассмотрим реализацию схемы байесовского оценивания неизвестного
параметра.
7.6. БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ
271
Априорные сведения о параметре 0 основаны на предыстории
функционирования анализируемого процесса (если таковая имеется) и на
профессиональных теоретических соображениях о его сущности, специфи-
ке, особенностях и т.п. В конечном итоге эти априорные сведения должны
быть представлены в виде функции р(0), задающей априорное распреде-
ление параметра и интерпретируемой как вероятность того, что пара-
метр примет значение, равное 0, если параметр дискретен, и как функция
плогности распределения в точке 0, если параметр непрерывен по своей
природе.
Примеры вероятностных законов, используемых в качестве априор-
ных распределений параметров, будут приведены ниже (см. п. 7.6.3). За-
метим лишь, что в ситуациях, когда априорные сведения об анализиру-
емом параметре слишком скудны, в качестве априорного распределения
р(0) используют, например, равномерное на отрезке [©min > ©max] распре-
деление, где [0mjn> ©max] — априорный диапазон варьирования возможных
значений оцениваемого параметра, т. е.:
р(0) = J ПР" ®т1"г^05>0пТ;	(7.32)
1 0	При 0 [©mini ©max -
Исходные статистические данные	• • •, хп — это не что
иное, как выборка объема п из анализируемой генеральной совокупности.
Получая исходные статистические данные, мы к имевшейся ранее априор-
ной информации о параметре присоединяем выборочную (эмпирическую)
информацию.
Вычисление функции правдоподобия	• • • >sn | ©) произ-
водится в соответствии с (7.5) по формуле
L(X1, z2,..., Х„ | 0) =	| 0) • /(x2 | 0) • ...  f(Xn | 0),	(7.33)
где f(x | 0) — функция плотности (или вероятность Р{£ = х | 0}), опи-
сывающая закон распределения вероятностей анализируемой генеральной
совокупности в предположении (или при условии), что значение оценива-
емого параметра равно 0.
Вычисление апостериорного распределения ^(0 | яь...,хп)
осуществляется с помощью формулы Байеса (см. п. 1.1.3, формула (1.19)),
в которой роль события Л, играет событие, заключающиеся в том, что
значение оцениваемого параметра равно 0, а роль условия В — собы-
тия, заключающееся в том, что значения п наблюдений, произведенных
в анализируемой генеральной совокупности, зафиксированы на уровнях
272
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
х1у х?у..., гп. Соответственно имеем:
(К© I,..., х„) =	р(е)^ь-^п|б)	(7.34)
J L(xiy...yxn | 0)-^(0)d0
Построение байесовских точечных и интервальных оценок
основано на использовании знания апостериорного распределения <р(0 |
х1у...ухп)у задаваемого соотношением (7.34). В частности, в качестве
байесовских точечных оценок 0^ используют среднее или модальное зна-
чение этого распределения, т. е.:
©<') = Е(0|хь...,1п)= /©¥>(© |®b...,xn) </©,	(7.35)
= arg max	| a?!,..., zn)-
Отметим, что для вычисления этих оценок нам достаточно знать
только числитель правой части (7.34), так как знаменатель этого вы-
ражения играет роль нормирующего множителя и от 0 не зависит (это
д(б)
существенно упрощает процесс практического построения оценок 0ср и
§(б) \
'“'мод/-
Отметим также одно важное оптимальное свойство оценки 0^.
Пусть 0(3?!,. ..,жп) — любая оценка параметра 0. Оказывается, если
качество любой оценки 0(Z],..., хп) измерять так называемым апосте-
риорным байесовским риском
К(б)(хг,..., хп) = Е{(0(®!,..., хп) - 0)2 | хг,..., агп}
= У (0(xi,...,xn)-0)2^(0 | xi,...,xn) d&
или его средним (усреднение — по всем возможным выборкам ж1}...,а!п)
значением то байесовская оценка (7.35) является наилучшей и в том
и в другом смысле.
Для построения байесовского доверительного интервала для параме-
тра 0 необходимо вычислить по формуле (7.34) функцию у(0 | х1э... ,жп)
апостериорного закона распределения параметра 0, а затем по заданной
доверительной вероятности Р определить 100^^- и 100^^%-ные точ-
ки этого закона, которые и дают соответственно левый и правый концы
искомой интервальной оценки.
Заметим, что байесовский способ оценивания может давать весьма
ощутимый выигрыш в точности при ограниченных объемах выборок. В
7.6. БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 273
процессе же неограниченного роста объема выборки п оба подхода будут
давать, в силу их состоятельности, все более похожие результаты.
7.6.3.	Примеры байесовского оценивания
Рассмотрим теперь на примерах, как практически реализуется опи-
санная в предыдущем пункте схема байесовского оценивания неизвестного
параметра.
Пример 7.10. Анализируется закон распределения вероятностей
(з.р.в.) семей определенной социально-экономической страты по величине
среднедушевого дохода f. Проведенные ранее исследования говорят о том,
что з.р.в. среднедушевого дохода внутри однородной страты описывается
логарифмически нормальной моделью (см. п. 3.1.6), а это значит, что слу-
чайная величина rj — Inf подчинена нормальному закону. Требуется по
результатам обследования среднедушевого дохода десяти семей, случайно
отобранных из всей совокупности семей анализируемой страты, а также
по некоторой априорной информации о величине теоретического среднего
6 = E(ln f ) построить байесовскую оценку для 0.
Математическая постановка задачи. Мы располагаем следую-
щей информацией об анализируемой генеральной совокупности.
1)	Логарифм (натуральный) от величины среднедушевого дохода
(i? — Inf) распределен нормально с неизвестным средним значением 0
и известной дисперсией а , т. е.
/г(«;0)=	<z = 0,28.
/
2)	Из предыстории и опыта обследований семей той же самой стра-
ты в других регионах известно, что величина 0 ведет себя как (tfoj^o)-
нормальная случайная величина, где значения 0q и ctq известны, т.е.
1 2
р(0) = -=-е а’о ; 0О = 0,60;	= 0,03.
V 2tt(Tq
3)	Имеются результаты обследования п (п = 10) случайно отобранных
от анализируемой страты семей по среднедушевому доходу, т. е. случайная
выборка значений , z2,..., тп, где х, = In од, а у, — среднедушевой доход
t-й обследованной семьи. Ниже приводятся конкретные значения х,-:
arj = 0,54; х2 = 1,20; х3 = 0,36; х4 = 0,80; х5 — 0,42; аг6 = 2,10;
= 0,70; х8 = 0,25; х9 = 0,90; ij0 = 0,48.
274
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Требуется на основании исходной информации 1) — 3) построить
байесовскую оценку для параметра в и сравнить эту оценку с оценкой,
полученной классическим методом максимального правдоподобия.
Решение. Поскольку мы уже располагаем априорным распределе-
нием р(0) и исходными статистическими данными хп, первые два
этапа схемы, представленной на рис. 7.3, можно считать реализованными.
На 3-м этапе вычисляем функцию правдоподобия. В нашем случае
имеем:

п
®п1«) = ПА(а'»<’) =
1=1
В этом выражении, как всегда, х =	хjn, s2 = (Е.П=1(^ - S)2)/» и
при его выводе использовано тождественное преобразование:
- 9)2 =	[(х; - х) - (в - х)]’ = f (х. - Х)2 + п(6 - Х)2.
«=1	i=l	»=1
Следующий (4-й) этап, на котором вычисляется апостериорное рас-
пределение <р(0 | 2?i,..., хп), является, как правило, самым трудным в тех-
ническом отношении. Мы будем вычислять функцию ip(0 | «1,...,яп) с
точностью до общего нормирующего множителя. Поэтому в тех местах
наших выкладок, в которых мы будем опускать отдельные сомножители-
компоненты этого общего нормирующего множителя, знаки равенства,
связывающие наши преобразования, будут заменяться знаком эквивалент-
ности
¥>(0 I
7.6. БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 275
где
(7.37)
Из (7.36) следует, что апостериорное распределение <р(0 | Ж1,...,жп),
аккумулирующее в себе как априорную, так и выборочную информацию
о параметре 0, снова является нормальным со средним значением а и дис-
персией определяемыми соотношениями (7.37).
Соответственно байесовская оценка параметра 0 в данном случае
определяется формулой
° ср — ° мод —
Как мы знаем (см. выше, п. 7.5.1), оценка параметра 0 по методу макси-
мального правдоподобия есть
^ип —
Мы видим, что байесовская оценка получается как взвешенное сред-
нее оценки 0МП и среднего значения 0$ априорного распределения параме-
тра 0, причем вес 0О тем больше, чем меньше дисперсия сг0 априорного
распределения и чем больше дисперсия анализируемой генеральной сово-
купности (т. е. чем менее точно производимые наблюдения xt характери-
зуют среднее значение своей генеральной совокупности).	,
Возвращаясь к конкретным числовым данным нашего примера, име-
ем: емп = х = 0,775; 6м = 0,687.
Пример 7.11. Рассмотрим задачу оценивания неизвестной веро-
ятности 0 в> схеме испытаний Бернулли (см. п. 3.1.1) на основе п неза-
висимых испытаний. Таким образом, можно сказать, что мы исследуем
биномиальную генеральную совокупность (см. формулу (3.3)) с неизвест-
ным значением вероятности «успеха» 0 в одном испытании, имея един-
ственное наблюдение — число «успехов» в серии из п независимых
испытаний. Распределение вероятностей f(x | 0) для числа успехов р#(п)
задается формулой
f(x I в) = Р{м«(п) = г} =	- J)”'
Анализ предыстории функционирования систем, аналогичных иссле-
дуемой, позволил определить в качестве априорного распределения р(0)
276
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
параметра О бета-распределение с параметрами а и b (см. п. 3.2.6, форму-
лу (3.22)):
Ptf) = {
- в/’1 при 0
О	при 0 [0; 1].
В нашем случае при единственном имеющемся наблюдении Xi функ-
ция правдоподобия L(xi | 0) = /(a?i | 0) =	— 0)п так что
апостериорная плотность <р(0 | a?i) определится в соответствии с (7.34)
соотношением:

- ey-'wa - в)"’11
j;	- «г11 $^“-*(1 -
Произведя очевидные сокращения в числителе и знаменателе правой
части этого выражения и учитывая тот факт, что в соответствии с опре-
делениями гамма- и бета-функций
[ ga-l+т, ц _ ^Ь-1+n-r,^ = В(а + Xi. ь + п _ г1)
о
Г(д + a?i)»Г(Ь + n - gj)
Г(с -|- Ь 4* w)
имеем:
?(*1 Х1> =	~х - в)ь+п"11''-
1 {а + a?i)l \р 4- п —
Но отсюда следует, что апостериорное распределение оцениваемого
параметра 0 снова является бета-распределением. Его среднее значение
известным образом выражается через его два параметра (см. и. 3.2.6),
так что
3(e) _ v(e I _ Ч_________a + si__________ Z1 4-0 _	;
ср	(а + а.1) + (г, + п_а.]) -п+о + ь - 1 + в±4-
Как мы знаем (см. п. 7.5.1), оценкой максимального правдоподобия
параметра 0 в данном примере будет отношение
Ь'мп —
П
Сравнение 0^ и 0ЫП показывает, что эти оценки могут достаточно
сильно различаться (в зависимости от значений а и 6) при небольших
7.6. БАЙЕСОВСКИЙ ПОДХОД К СТАТИСТИЧЕСКОМУ ОЦЕНИВАНИЮ 277
объемах выборок. Однако по мере роста п они, как и следует ожидать
при состоятельных способах оценивания, будут давать все более схожие
результаты.
Пример 7.12. При анализе распределения урезанной совокупно-
сти семей по величине среднедушевого дохода часто используют закон
Парето. А именно, если рассматриваются только семьи, душевой доход
которых превышает некоторый заданный уровень Со, то плотность рас-
пределения f(x j 0) описывается уравнением (см. п. 3.1.9):
f(x | в) = <	ПРИ х > со5
I 0	при х Cq.
Функция правдоподобия в данном примере имеет вид
Т(	1йЧ-	- *”**’
(*’.. - •, хл | 9) -	- s^e+1).
где Gn = (П?=1 xi)* — среднее геометрическое из имеющихся наблюдений
(см. п. 6.2.3, формулу (6.10)). Максимизация по 0 логарифмической функ-
ции правдоподобия Z(a?i,...,хп | 0) = In Цх^,...txn | 0) дает в качестве
оценки максимального правдоподобия статистику
Попробуем построить байесовскую оценку в условиях крайней скудно-
сти априорной информации. В частности, нам известно то, что значение
параметра 0 может с равной вероятностью оказаться в окрестности любой
точки достаточно широкого диапазона от 0 до С (С — некоторое известное
число). На языке априорного распределения это означает, что
’«-{Г
при
при
0 Ш С;
*Н0;С].
Тогда апостериорное распределение параметра 0 (с точностью до
нормирующих множителей, не зависящих от 0) будет

,яп) ~р(0) • Ь(«1,...,жп | 0)
0п
1
0пе“п(1п
(7.38)
278
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Но правая часть (7.38) задает (с точностью до нормирующего множи-
теля) гамма-распределение (см. п. 3.2.5, формулу (3.21)) с параметрами
a = n + 1 и b = nln(^j-).
Среднее значение гамма-распределенной (с параметрами а и Ь) слу-
чайной величины, равно, как известно (см. п. 3.2.5), отношению первого
параметра ко второму, так что в нашем случае имеем:
С = Е(« | Х1,

Сравнение оценок ' и вмп говорит о том, что, как и следовало ожи-
дать, при скудности априорных сведений об оцениваемом параметре бай-
есовский подход дает почти тот же результат, что и классический.
Пример 7.13. В данном примере речь идет об оценке параметра О
пуассоновского закона (см. п. 3.1.3, формулу (3.6)), т. е. анализируемая ге-
неральная совокупность описывается законом распределения вероятностей
вида
/(г I 9) = Р{{ = х I в} = ~уе~в (х = 0,1,2,.. .).
Априорное распределение вероятностей параметра 0 подчиняется
гамма-закону с параметрами а и b (см. п.3.2.5, формулу (3.21)), т.е.
р(в) = I
при
при
0> 0;
0<О.
о
Функция правдоподобия
L(xit...,xn\e)- n»=j(a..!)eE“,I‘e п<-
Как известно (см. п. 7.5.1), оценка максимального правдоподобия па-
раметра 0 имеет вид
л 1 V'
в~п - п2^я(-
Апостериорная плотность (с точностью до нормирующего множи-
теля) в соответствии с формулой (7.34) имеет вид
?(* | хи..., хп) ~
выводы
279
который соответствует гамма-распределению с параметрами а = а 4-
и = п + 6. Следовательно, байесовская оценка
= Е(0 | xi,
* * *
Применение байесовского подхода в эконометрике и, в частности, в
статистическом оценивании неизвестных значений параметров оказыва-
ется в определенных ситуациях крайне актуальным и достаточно эффек-
тивным [А. Зельнер]. Конечно, «узким» местом в его прикладной распро-
страненности является обоснованный выбор априорного распределения.
Бывают ситуации, когда информация о виде априорного распределения
имеется с точностью до небольшого числа неизвестных параметров, кото-
рые можно оценить по выборке одновременно с оцениванием параметра О.
В этом случае говорят, что применен эмпирический байесовский подход.
ВЫВОДЫ
1.	Одна из центральных задач статистического анализа реальной си-
стемы заключается в вычислении (на основании имеющихся статистиче-
ских данных) как можно более точных приближенных значений (стати-
стических оценок) для одного или нескольких числовых параметров, ха-
рактеризующих функционирование этой системы. Принципиальная воз-
можность получения работоспособных приближений такого рода на осно-
вании статистического обследования лишь части анализируемой гене-
ральной совокупности (т. е. на основании ограниченного ряда наблюдений,
или выборки) обеспечивается замечательным свойством статистической
устойчивости выборочных характеристик (см. п. 6.2).
2.	Статистическая оценка строится в виде функции от результатов
наблюдений, а потому сама по природе является случайной величиной.
При повторении выборки из той же самой генеральной совокупности и
при подстановке новых выборочных значений в ту же самую «функцию-
оценку» мы, вообще говоря, получаем другое число в качестве прибли-
женного значения интересующего нас параметра, т. е. имеется неконтро-
лируемый разброс в значениях оценки при повторениях эксперимента (в
данном случае — выборки)!
3.	В качестве основной меры точности статистической оценки О не-
известного параметра 0 используется средний квадрат ее отклонения от
280
ГЛ. 7. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
оцениваемого значения, т.е. величина Е(0 — 0)2, а в многомерном слу-
чае — ковариационная матрица компонент векторной оценки 0. Оче-
видно, чем меньше эта величина (или обобщенная дисперсия оценки 0
в многомерном случае), тем точнее {эффективнее) оценка. Для широкого
класса генеральных совокупностей существует неравенство (неравенство
Рао-Крамера-Фреше (7.12), (7.13)), задающее тот минимум A^in (по всем
возможным оценкам) среднего квадрата Е(0 — 0)2, улучшить который не-
возможно. Естественно использовать этот минимум Amin в качестве на-
чальной точки отсчета меры^эффективности оценки, определив эффек-
тивность е{в) любой оценки в параметра 0 в виде отношения
2
е(0) =	~	-
Е(е-9?
4.	Свойство состоятельности оценки 0 (см. п. 7.1.3) обеспечивает
ее статистическую устойчивость, т.е. ее сходимость (по вероятности) к
истинному значению оцениваемого параметра в по мере роста объема вы-
борки, на основании которой эта оценка строится. Свойство несмещенно-
сти оценки в (см. п. 7.1.4) заключается в том, что результат усреднения
всевозможных значений этой оценки, полученных по различным выборкам
заданного объема (из одной и той же генеральной совокупности), дает в
точности истинное значение оцениваемого параметра, т.е. Ев — в. Да-
леко не всегда следует настаивать на необходимом соблюдении свойства
несмещенности оценки: несущественное само по себе уже при умеренно
больших объемах выборки, оно может чрезмерно обеднить класс оценок,
в рамках которого решается задача построения наилучшей оценки.
5.	С учетом случайной природы каждого конкретного оценочного зна-
чения в неизвестного параметра в представляет интерес построение целых
интервалов оценочных значений Д0, а в многомерном случае — целых
областей, которые с наперед заданной (и близкой к единице) вероятно-
стью Р накрывали бы истинное значение оцениваемого параметра в, т. е.
Р{в € Др(0)} = Р. Эти интервалы (области) принято называть довери-
тельными (или интервальными оценками). Существуют два подхода к
построению интервальных оценок: точный (конструктивно реализуемый
лишь в сравнительно узком классе ситуаций) и асимптотически прибли-
женный (наиболее распространенный в практике статистических прило-
жений), см. п. 7.5.4.
в. Основными методами построения статистических оценок являют-
ся:
метод максимального правдоподобия (см. п. 7.5.1);
выводы
281
метод моментов (см. п. 7.5.2);
метод, использующий «взвешивание» наблюдений, — цензурирова-
ние, урезание, порядковые статистики (см. и. 7.5.4).
Различные варианты метода, использующего «взвешивание» наблю-
дений, находят все большее распространение в связи с устойчивостью по-
лучаемых при этом статистических выводов по отношению к возможным
отклонениям реального распределения исследуемой генеральной совокуп-
ности от постулируемого модельного.
7. Наличие априорной информации об оцениваемом параметре, позво-
ляющей сопоставить с каждым возможным значением неизвестного па-
раметра некую вероятностную меру его достоверности, т.е. сведений об
априорном вероятностном законе распределения оцениваемого параме-
тра, позволяет существенно уточнить оценки, полученные традиционны-
ми методами (методом максимального правдоподобия, методом моментов и
т.п.) в условиях отсутствия такой информации. Построение таких оценок
осуществляется с помощью так называемого байесовского подхода (см.
п. 7.6), а сами оценки называются байесовскими.
Приложение к гл. 7 (доказательство неравенства информации)
Рассмотрим тождества
О') dx\t.. .dxn = 0 + bg(O),
J L(si,...,zn; 0)dxi ...dxn = 1.
Их почленное дифференцирование по в (с учетом условий а) и б), см. с. 244, и обозна-
чения I = in L = in /(х<; ^)) дает
Применяя к левой части (♦) неравенство Коши-Бун яковского ([Е(£^)]а Е(аЕца)
и принимая во внимание тождества ~E(dl/d8) = 0, E(<W/d6)a = nE(dln/(x;0)/dfl)a, а
также — равенство левой и правой частей (*), получаем
^1 + —<Е(в-в) пЕ	J ,
откуда и следует непосредственно неравенство информации (7.12).
ГЛАВА 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА
ГИПОТЕЗ (СТАТИСТИЧЕСКИЕ
КРИТЕРИИ)
На разных стадиях статистического исследования и моделирования
возникает необходимость в формулировке и экспериментальной провер-
ке некоторых предположительных утверждений (гипотез) относительно
природы или величины неизвестных параметров анализируемой стохасти-
ческой системы. Например, исследователь высказывает предположение:
«исследуемые наблюдения извлечены из нормальной генеральной совокуп-
ности» или «среднее значение анализируемой генеральной совокупности
равно нулю». Будем обозначать в дальнейшем высказанное нами пред-
положение (гипотезу) с помощью буквы Н. Наша цель — проверить, не
противоречит ли высказанная нами гипотеза И имеющимся выборочным
данным.
Процедура обоснованного сопоставления высказанной гипотезы с име-
ющимися в нашем распоряжении выборочными данными х^, х2» • • •,хп> со-
провождаемая количественной оценкой степени достоверности получаемо-
го вывода, осуществляется с помощью того или иного статистического
критерия и называется статистической проверкой гипотез.
Результат подобного сопоставления может быть либо отрицатель-
ным (данные наблюдения противоречат высказанной гипотезе, а потому
от этой гипотезы следует отказаться), либо неотрицательным (данные
наблюдения не противоречат высказанной гипотезе, а потому ее мож-
но принять в качестве одного из естественных и допустимых решений).
При этом неотрицательный результат статистической проверки ги-
потезы не означает, что высказанное нами предположительное утвер-
ждение является наилучшим, единственно подходящим: просто ока не
противоречит имеющимся у нас выборочным данным, однако таким же
свойством могут наряду с Н обладать и другие гипотезы. Так что да-
же статистически проверенное предположение Н следует расценивать не
как раз и навсегда установленный, абсолютно верный факт, а лишь как
8.1. ОСНОВНЫЕ ТИПЫ ГИПОТЕЗ
283
достаточно правдоподобное, не противоречащее опыту утверждение.
По своему прикладному содержанию высказываемые в ходе стати-
стической обработки данных гипотезы можно подразделить на несколько
основных типов.
8.1.	Основные типы гипотез, проверяемых
в ходе статистического анализа и
моделирования
8.1.1.	Гипотезы о типе закона распределения исследуемой
случайной величины
При обработке ряда наблюдений
• • •, хп
(8-1)
исследуемой случайной величины £ очень важно понять механизм форми-
рования выборочных значений я,, т.е. подобрать и обосновать некоторую
модельную функцию распределения FMWJ(z) (например, из числа описан-
ных в гл. 3), с помощью которой можно адекватно описать исследуемую
функцию распределения F^(x). На определенной стадии исследования это
приводит к необходимости проверки гипотез типа
Я: F^x) = Гмад(х),
(8-2)
где гипотетичная модельная функция может быть как заданной однознач-
но (тогда F^(x) = F0(x), где Г0(я) — полностью известная функция), так
и заданной с точностью до принадлежности к некоторому параметри-
ческому семейству (тогда FMoa(3?) = F(s; 0), где 0 — некоторый, вообще
говоря, fc-мерный параметр, значения которого неизвестны, но могут быть
оценены по выборке (8.1) с помощью методов, изложенных в п. 7.5 и 7.6).
Проверка гипотез типа (8.2) осуществляется с помощью так назы-
ваемых критериев согласия и опирается на ту или иную меру различия
между анализируемой эмпирической функцией распределения F^n\a;) и
гипотетическим модельным законом FMOfl(s) (примеры реализации подоб-
ных критериев см. в п. 8.6.1).
284
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
8.1.2.	Гипотезы об однородности двух или нескольких
обрабатываемых выборок или некоторых
характеристик анализируемых совокупностей
Наиболее типичные задачи такого рода характеризуются следующей
общей ситуацией. Пусть мы имеем несколько «порций» выборочных дан-
ных типа (8.1):
1-я:
2 я:	J х22> • • •> x2n3i
(8-3)
1 я:	j ^i2i ’ - - >xini 
Эти порции могли образоваться, например, естественным образом —
в ходе проведения выборочного обследования (скажем, за счет разделен-
ности условий их регистрации во времени или пространстве). Обозначая
функцию распределения, описывающую вероятностный закон, которому
подчиняются наблюдения у-й выборки, с помощью Fy(x) и снабжая тем
же индексом все интересующие нас эмпирические и теоретические харак-
теристики этого закона (средние значения а; и aj; дисперсии и Uj и
т. д.), основные гипотезы однородности можно записать в виде:

F^x) = F2(x) =
= FM;
(8.4а)
Яа: ai = о, = • • • = aj;
(8.4.6)
ЯЛ	л	л
= • • • = <7/.
(8.4в)
В случае неотрицательного результата проверки этих гипотез го
ворят, что соответствующие выборочные характеристики (например,
ai, а2,...,в/) различаются статистически незначимо.
Отметим частный случай гипотез типа (8.4а), когда число выборок
I = 2, а одна из выборок содержит малое количество наблюдений (в част-
ном случае — одно). В таком виде проверка гипотез типа (8.4а) озна-
чает проверку аномальности одного или нескольких резко выделяющихся
наблюдений. Реализация конкретных критериев однородности описана в
п. 8.6.2.
8.1.3.	Гипотезы о числовых значениях параметров
исследуемой генеральной совокупности
Пусть, например, ряд наблюдений (8.1) дает нам значения некоторого
параметра изделий, измеренные на п изделиях, случайно отобранных из
массовой продукции определенного станка автоматической линии, и пусть
8.1. ОСНОВНЫЕ ТИПЫ ГИПОТЕЗ
285
До — заданное номинальное значение этого параметра. Каждое отдельное
значение х, может, естественно, как-то отклоняться от заданного номина-
ла. Очевидно, для того чтобы проверить правильность настройки этого
станка, надо убедиться в том, что среднее значение параметра у произво-
димых на нем изделий будет соответствовать номиналу, т.е. проверить
гипотезу типа
Я: = оо.	(8.5)
В общем случае гипотезы подобного типа имеют вид:
Hq' 0 € До»	(8*6)
где 0 — некоторый параметр (вообще говоря, многомерный), от которо-
го зависит исследуемое распределение, а До — область его конкретных
гипотетических значений, которая может состоять всего из одной точки.
Статистическая проверка гипотез о числовых значениях параметров
играет важную роль в эконометрическом моделировании, регрессионном
анализе, в широком спектре задач статистического исследования зависи-
мостей, существующих между анализируемыми показателями (этому кру-
гу вопросов посвящены гл. 10,11 и весь раздел IV данного учебника). В
частности, принятие решения о включении или исключении той или иной
переменной в анализируемую регрессионную (эконометрическую) модель,
о наличии-отсутствии статистической связи между наблюдаемыми при-
знаками существенно опирается обычно на проверку гипотез типа (8.6)
при До = 0. Такого же типа гипотезы приходится проверять ; ри устано-
влении факта независимости и стационарности имеющегося ряда наблю-
дений (см. п. 16.1).
Реализация некоторых конкретных критериев статистической про-
верки гипотез о числовых значениях параметров анализируемой стоха-
стической системы описывается в п. 8.6.3.
8.1.4.	Гипотезы об общем виде модели, описывающей
статистическую зависимость между признаками
В п. 8.1.1 речь шла, по существу о подборе подходящей модели для
описания закона распределения вероятностей исследуемой случайной ве-
личины. Не менее важное место в общем статистическом и эконометриче-
ском анализе занимает проблема подбора подходящей модели, с помощью
которой мы можем адекватно описать исследуемую статистическую зави-
симость между анализируемыми признаками. В качестве гипотетических
могут проверяться утверждения о линейном, квадратическом, экспонен-
циальном, степенном, логарифмическом, полиномиальном и т. п. типе нс-
286
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
комой зависимости. Подробнее эта проблематика обсуждается в гл. 10
данного учебника.
8.2.	Общая логическая схема
статистического критерия
По своему назначению и характеру решаемых задач статистические
критерии чрезвычайно разнообразны. Однако их объединяет общность
логической схемы, по которой они строятся. Коротко эту логическую
схему можно описать так.
1.	Выдвигается гипотеза HG.
2.	Задаются величиной так называемого уровни значимости критерия
а. Дело в том, что всякое статистическое решение, т. е. решение, прини-
маемое на основании ограниченного ряда наблюдений, неизбежно сопрово-
ждается некоторой, хотя, возможно, может и очень малой, вероятностью
ошибочного заключения как в ту, так и в другую сторону. Скажем, в
какой-то небольшой доле случаев а гипотеза Hq может оказаться отверг-
нутой, в то время как на самом деле она является справедливой, или,
наоборот, в какой-то небольшой доле случаев /3 мы можем принять нашу
гипотезу, в то время как на самом деле она ошибочна, а справедливым
оказывается некоторое конкурирующее с ней предположение — альтер-
нативная гипотеза Hi. При фиксированном объеме выборочных данных
величину вероятности одной из этих ошибок мы можем выбирать по сво-
ему усмотрению. Если же объем выборки можно как угодно увеличивать,
то имеется принципиальная возможность добиваться как угодно малых
вероятностей обеих ошибок а и /3 при любом фиксированном конкуриру-
ющем предположительном утверждении Hi. В частности, при фиксиро-
ванном объеме выборки обычно задаются величиной а вероятности оши-
бочного отвержения проверяемой гипотезы Яо, которую часто называют
«основной» или «нулевой». Эту вероятность ошибочного отклонения
«нулевой» гипотезы принято называть уровнем значимости или разме-
ром критерия. Выбор величины уровня значимости а зависит от сопо-
ставления потерь, которые мы понесем в случае ошибочных заключений
в ту или иную сторону: чем весомее для нас потери от ошибочного от-
вержения высказанной гипотезы Яо, меньшей выбирается величина
а. Однако поскольку такое сопоставление в большинстве практических
задач оказывается весьма затруднительным (часто трудно даже вообще
сказать, в какую сторону ошибка является для нас более опасной), то, как
правило, пользуются некоторыми стандартными значениями уровня зна-
чимости. К таким стандартным значениям можно причислить величины
8.2. ОБЩАЯ ЛОГИЧЕСКАЯ СХЕМА СТАТИСТИЧЕСКОГО КРИТЕРИЯ
287
а = 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Особенно распространенной является
величина уровня значимости а, равная 0,05. Она означает, что в среднем в
пяти случаях из 100 мы будем ошибочно отвергать высказанную гипотезу
при многократном использовании данного статистического критерия.
3.	Задаются некоторой функцией от результатов наблюдения (крити-
ческой статистикой) = 7(z1,z2,...,zn). Эта критическая стати-
стика как и всякая функция от результатов наблюдения, сама явля-
ется случайной величиной (см. 7.1.2) и в предположении справедливости
гипотезы Hq подчинена некоторому хорошо изученному (затабулирован-
ному) закону распределения с плотностью Д(»)(и).
Один из основных принципов построения критической статистики
(принцип отношения правдоподобия) описан в п. 8.3.1. Поясним здесь
лишь общий содержательный смысл этой статистики: как правило, ею
определяется мера расхождения имеющихся в нашем распоряжении выбо-
рочных данных (8.1) с высказанной (и проверяемой) гипотезой Но. Так,
в гипотезах типа рассмотренных в п. 8.1.1 критическая статистика 7^п^
определяет меру различия между анализируемой эмпирической функцией
распределения F^n\x) и гипотетической (модельной) функцией FM(W(z). В
гипотезах типа рассмотренных в п. 8.1.2 величина 'у^ измеряет степень
расхождения соответствующих выборочных характеристик в различных
выборках; в гипотезах типа рассмотренных в п. 8.1.3 — отклонения выбо-
рочных характеристик от соответствующих гипотетических значений и
т.д.
4.	Из таблиц распределения /у»)(и) находятся 100(1 — |^)%-ная точка
и 100f %-ная точка 717*^’ Разделяющие всю область мыслимых зна-
чений случайной величины 'у^ на три части: область неправдоподобно
малых (I), неправдоподобно больших (III) и естественных или правдопо-
добных (в условиях справедливости гипотезы Hq) значений (II) (рис. 8.1).
В тех случаях, когда основную опасность для нашего утверждения пред-
ставляют только односторонние отклонения, т. е. только «слишком ма-
ленькие» или только «слишком большие» значения критической стати-
стики 7^п\ находят лишь одну процентную точку: либо 100(1 — а)%-ную
точку 71т,"\ которая будет разделять весь диапазон значений 7^ на две
части: область неправдоподобно малых и область правдоподобных зна-
чений; либо 100а%-ную точку 7«тах\ она будет разделять весь диапазон
значений 7^ на область неправдоподобно больших и область правдопо-
добных значений.
5.	Наконец, в функцию подставляют имеющиеся конкретные вы-
288
ГЛ. в. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
, (п)
борочные данные z i,..., zn и подсчитывают численную величину 7' .
Бели окажется, что вычисленное значение принадлежит области правдо-
подобных значений 7^, то гипотеза Hq считается не противоречащей вы-
борочным данным. В противном случае, т. е. если слишком мала или
слишком велика, делается вывод, что 7 ' на самом деле не подчиняется
закону Д(.)(и) (этот вывод, как легко понять, сопровождается вероятно-
стью ошибки, равной а), и это несоответствие мы вынуждены объяснить
ошибочностью высказанного нами предположения Hq и, следовательно,
отказаться от него.
Таким образом, решение, принимаемое на основании любого стати-
стического критерия, может оказаться ошибочным как в случае отклоне-
ния проверяемой гипотезы Но (с вероятностью а), так и в случае ее приня-
тия (с вероятностью /?). Вероятности а и (3 ошибочных решений называ-
ют также ошибками соответственно первого и второго рода, а величину
1 — /3 — мощностью критерия. Очевидно, из двух критериев, характери-
зующихся одной и той же вероятностью о отвергнуть в действительности
правильную гипотезу Hq, следует предпочесть тот, который сопровожда-
ется меньшей ошибкой второго рода (или большей мощностью).
Рис. 8.1. График плотности распределения критической статистики уп и
выделение областей «правдоподобных» (II) к «неправдоподоб-
ных» (I и III), в условиях справедливости гипотезы Hq, значений
этой статистики
Если проверяемое предположительное утверждение сводится к гипо-
тезе о том, что значение некоторого параметра 0 в точности равно за-
данной величине 0О (см. выше гипотезы, рассмотренные в п. 8.1.3), то
эта гипотеза называется простой. В других случаях гипотеза будет на-
8.3. ПРИНЦИП ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
289
зываться сложной.
8.3.	Построение статистического критерия;
принцип отношения правдоподобия
Попытаемся выяснить, как конкретно получаются те функции ,от ре-
зультатов наблюдения (критические статистики 7^), по значениям ко-
торых принимается окончательное решение о том, соответствует ли про-
веряемая гипотеза имеющимся у нас данным (8.1) или противоречит им.
8.3.1.	Сущность принципа отношения правдоподобия
Для пояснения общего принципа, приводящего к построению наилу ч-
ших (наиболее мощных при заданной величине уровня значимости) кри-
териев, вернемся к условиям примера с заработной платой (см. п. 7.5.1)
и соответственно к рис. 7.2. В этом примере исследовалась логарифмиче-
ски нормально распределенная заработная плата £ работников определен-
ной совокупности, а в качестве исходных данных мы располагали тремя
наблюдениями (тремя обследованными работниками): zj = 190 ден. ед.;
Х2 = 175 ден. ед.; х$ = 205 ден. ед. Пусть мы хотим проверить основ-
ную гипотезу (простую) о среднем значении нормально распределенной
случайной величины Inf:
Но: E(ln f) = 5,240 = а0
против простои альтернативы
Нг: E(lnf) = 5,443 = ai.
Из рис. 7.2 видно, что гипотеза Яо не противоречит имеющимся на-
блюдениям (более того, в данном случае наши наблюдения выглядят наи-
более правдоподобными именно при гипотезе Яо), в то время как те же
наблюдения оказываются малоправдоподобными^в условиях справедливо-
сти гипотезы Hi.
В общем случае представление о сравнительной правдоподобности
имеющихся наблюдений xi,...,xn (в отношении проверяемой и альтерна-
тивной гипотез) дает нам сопоставление соответствующих функций прав-
доподобия (см. формулу (7.5)) и, в частности, их отношение
(п) _	_ 7/(zi,...,zn; 01)
Z^(zi,...,zn; 0) Z/(zi,...,zn; Go)
(8.7)
290	ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
где и Lffo — значения функций правдоподобия наблюдений Xi,..., хп,
вычисленные в предположении справедливости соответственно гипотез
Hi: 0 = 0i и Но: 0 = 0О. Очевидно, чем правдоподобнее наблюдения
в условиях гипотезы Яо, тем больше функция правдоподобия LHq и тем
меньше величина 7<п\ Если Д<«)(ц) — плотность распределения стати-
стики 7^ при условии справедливости гипотезы Яо, то построение кри-
терия проверки гипотезы Яо с заданным уровнем значимости а сводится
к определению 100а%-ной точки уа распределения /у»)(«) и к реализации
следующего правила:
если 7<п) > 7а, то гипотеза Яо отвергается
с вероятностью ошибиться, равной а, так как
в соответствии с законом /7(«>(и) и при справед-
ливости гипотезы Яо возможно осуществление
события {7^ > 7а} с вероятностью о, т.е.
оо
То
если 7^п^ < 7а, то гипотеза Яо не отвергается.
(8.8)
Критерии, основанные на статистиках вида (8.7) и процедурах
(8.8), носят название критериев отношения правдоподобия, а их практи-
ческая реализуемость и предпочтительность по отношению к другим воз-
можным критериям подкреплены следующими фактами (справедливыми
в достаточно широком классе ситуаций).
1.	Критерии отношения правдоподобия являются наиболее мощными
среди всех других возможных критериев (этот факт для случая сравнения
двух простых гипотез сформулирован и доказан в виде леммы Неймана-
Пирсона, см., например [Крамер Г.]).
2.	Плотность /7(»)(ц) распределения критической статистики у"п\ как
правило, без труда восстанавливается по функции правдоподобия L на-
блюдаемой случайной величины.
Так, в рассмотренном выше примере с проверкой гипотезы о сред-
чом luaunnuu wnnua nkTinu ГЛЧЧЯ.ЙНЛЙ величины f Гпои известном ЗНаЧбНИИ
8.3. ПРИНЦИП ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
291
2\
дисперсии а имеем:
Ljj.—	••
=	1 с-^ЕГв1(х.-аП3
(2я)^ап
®n5	)
и = 0,1),
так что
(n)	£я,	-5^
> т
LHo
VJ® с-у/п{аг - во) •
Поскольку в нашем примере п = 3; в2 = 0,16; в] = 5,443 и в0 = 5,240,
то с > 0, и если мы положим
сип ~ I С3
7а = е «о 5 ,
где Qa = 100 • 2а% и — (?%-ная точка стандартного нормального рас-
пределения, то неравенство
будет выполняться на множестве всех таких выборок (х1э..., zn), для ко-
торых у/п(х — во)	или, что то же,
Получившееся правило проверки гипотезы не зависит от альтерна-
тивного значения параметра ei, а потому является (принимая во вни-
мание лемму Неймана-Пирсона) наиболее мощным при всех возможных
альтернативных значениях параметра в] > во, или, как принято в таких
случаях говорить, равномерно наиболее мощным.
8.3.2.	Критерии логарифма отношения правдоподобия
для проверки простой гипотезы
Пусть известно, что ряд наблюдений Z],..., zn можно рассматривать
как независимую выборку из распределения, принадлежащего семейству
распределений F(z; G), где 0 — ^-мерный параметр. Требуется прове-
вить гипотезу о том. что 0 = 0п (гипотеза (8.6). п. 8.1.3).
292
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Рассмотрим критерий
7(n) = -21n{L(zi,...,zn;0o)/I(®i,...,JPn; О)}.	(8.9)
где 0 — оценка (введенная в п. 7.5.1) максимального правдоподобия (ОМП)
параметра 0 по выборке a?i,..., хп. Доказано, что при наложении на се-
мейство F(x; 0) и на значение 0О дополнительных требований, гаран-
тирующих оптимальные свойства оценок максимального правдоподобия
(см. п. 7.5.1), величина 7^ имеет асимптотически (при п оо) %2-
распределение с к степенями свободы (см. [Рао С. Р.]).
„	~(п)
В качестве примера применения критерия 7' рассмотрим еще раз
задачу проверки гипотезы о среднем значении нормальной совокупности,
приведенную в п. 8.3.1. В введенных там обозначениях с учетом того,
п
что оценка максимального правдоподобия параметра «о есть ® = п 53 xi>
i=i
имеем:
(Xj - op)2
2<т2
= п(х - Оо)2/сг2.
Поскольку в предположении справедливости гипотезы Но статистика х
-	2/	~(п)
нормально распределена со средним а$ и дисперсией ст /п, 7 имеет
X -распределение с одной степенью свободы (в данном случае это резуль-
тат точный, а не асимптотический !).
8.3.3.	Критерий отношения правдоподобия для проверки
сложной гипотезы
Рассмотрим модификацию критерия (8.9) для случая, когда в гипо-
тезе конкретизируются значения не всех параметров, как в предыдущем
пункте, а лишь части из них. Пусть 0 = (0j,..., 0*) — вектор неизвест-
ных параметров распределения и гипотеза состоит в том, что
Я01:^- = %, j = l,...,r<A.	(8.10)
Удобно разбить вектор 0 на две части: 0i =	и 02 =
(0г+1,...,0*). Обозначим 02 оценку максимального правдоподобия 02 по
выборке а?!,..., хп при известном значении 0i = 0qi и (Oi, ©2) — оценку
максимального правдоподобия (01,0г). Критерий для проверки гипотезы
Hqi имеет вид:
7(п) = —21n{Z(z1,...,a:n; ет,в2)/ЦХ1,...,хп-, 61,ё2)}.	(8.11)
ел. ХАРАКТЕРИСТИКИ КАЧЕСТВА КРИТЕРИЯ
293
Можно доказать, что при выполнении ряда дополнительных требований,
гарантирующих оптимальные свойства оценок максимального правдопо-
добия (см. п. 7.5.1), величина имеет асимптотически (при п —> оо)
X2-распределение с г степенями свободы.
8.4.	Характеристики качества
статистического критерия
Характеристиками точности статистического критерия проверки
простых или сложных гипотез типа (8.6) служат:
а(0) — вероятность отвергнуть основную гипотезу Яо, подсчитанная
в предположении, что истинное значение «проверяемого» параметра рав-
но 0; величину 1 — а(0) называют оперативной характеристикой крите-
рия, а значение а(0о) ® задаче проверки простой гипотезы «Но: 0 = 0О»
есть не что иное, как уровень значимости (размер) критерия (вероятность
ошибки первого рода);
/3(0) — вероятность отвергнуть конкурирующую (с основной) гипо-
тезу, подсчитанная в предположении, что истинное значение «проверяе-
мого» параметра равно 0; величину 1 — /3(0) называют мощностью (или
функцией мощности) критерия, а значение /3(01) в задаче проверки про-
стой гипотезы «Яо: ® = 0о» против альтернативы 0 = 01» есть
не что иное, как вероятность ошибки второго рода.
Обсудим эти характеристики и зависящие от них свойства критерия.
Пусть Гп — область возможных значений критической статистики
7^, а ] ° и Г^1 — описанные в п. 8.2 соответственно области «правдо-
подобных» и «неправдоподобных» (в условиях справедливости гипотезы
Hq) значений 7^п\ Тогда очевидно:
«„(6) = Рв{т(п) е г"1} = J Д<.,(и, 0) du; ’
г"1
/?«(©) = 1 - an(0) = Pe{7(n’ G Г"°)
= У Д(*>(«; О) du
г"°	'
(8.12)
где и Д(*)(и; 0) — соответственно вероятность события А и плот-
ность распределения критической статистики 7^п\ подсчитанные в пред-
положении, что истинное значение проверяемого параметра равно 0.
294
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
В условиях проверки параметрических гипотез вида (8.6) с заданным
уровнем значимости а0 критерий {7<"\г^°} называется несмещенным,
если
{ап(0) < «о	при всех 0 С До;
ап(0) > а0	при всех 0 £ До;
И, наконец, критерий {7^п\Г^0} называется состоятельным, если
lim on(6) = 1 при всех 0 £ До.
я—»оо
Последнее соотношение означает, в частности, что функция мощно-
сти состоятельного критерия 1 — /Зп(@) стремится (при п —> оо) к единице
при любом значении 0, не входящем в область До гипотетичных (в соот-
ветствии с гипотезой Но) значений параметра.
Из (8.12) очевидно, что при любом фиксированном объеме выборки п
перестройка критерия в направлении уменьшения уровня значимости а
(т.е. сужения области Г^1) связана с одновременным увеличением ошиб-
ки второго рода, а в общем случае — с уменьшением значений функции
мощности 1 — /3(0) (так как при этом расширяется область Г„/о отклоне-
ния альтернативы Н\). И наоборот, перестройка критерия (в любом фик-
сированном классе критериев, в том числе и в классе наиболее мощных
критериев) в направлении увеличения его мощности связана (при фикси-
рованном объеме выборки п) с неизбежным одновременным увеличением
его уровня значимости. В то же время неограниченным увеличением объ-
ема выборки (т.е. при п —> оо) можно добиваться сколь угодно малых
значений для вероятностей ошибок вида
ж | ап(0*), где 0* € До С До, или
“n = I S3? а^@У’
(/Зп(о**), гда 0** i до, или
™ ~ ] max /Зп(0).
Для больших объемов выборок (т. е. асимптотически по п —> оо) су-
ществуют соотношения, связывающие между собой характеристики
и п(см., например [Кендалл М. Дж., Стьюарт А., 1973. С. 310-311]). Оста-
новимся здесь на одном полезном соотношении такого типа, позволяющем,
в частности, определять объем выборки п(а,/3; р), необходимый в крите-
рии отношения правдоподобия (Неймана-Пирсона) для различения двух
простых гипотез
8.4. ХАРАКТЕРИСТИКИ КАЧЕСТВА КРИТЕРИЯ
295
Hq: выборка извлечена из генеральной совокупности
/(*; ©о);
Hi: выборка извлечена из генеральной совокупности
(8.13)
Л®; Qi)
с ошибками первого и второго рода, не превосходящими заданных зна-
чений соответственно а и /?; величина р = p(Ho,Hi), от которой также
зависит объем выборки п} характеризует «расстояние» между гипотеза-
ми Но и Ну и определяется по формуле р(Я0, Hi) = Jin [/(ж>©1)
-/(а:; ©о)] dar, где интегрирование ведется по всей области возможных зна-
чений наблюдаемой случайной величины ж, а /(«; 0) — ее плотность рас-
пределения. В [Айвазян С. А., 1959] показано, что в достаточно широком
классе случаев при различении близких простых гипотез (т.е. при малых
значениях р) справедлива приближенная (асимптотическая) формула
п(а;/3;р)«	Я,’)^ ’	(8'14)
в которой uqj как и прежде, квантиль уровня q (или ^-квантиль) стан-
дартного нормального закона распределения.
Замечание. Обратим внимание читателя на практическую не-
избежность проявления двух «невыгодных» для всей теории проверки
статистических гипотез эффектов: эффекта «слишком малого объема
выборки» и эффекта «слишком большого объема выборки».
Эффект «слишком малого объема выборки» состоит в том, что при
заданной величине уровня значимости критерия а и малом числе наблюде-
ний п, на основании которых принимается решение, мощность критерия,
т. е. вероятность отклонить проверяемую «нулевую» гипотезу Яо в ситу-
ации, когда она в действительности не имеет места, оказывается слишком
маленькой (приближенное представление о взаимосвязи величин а, (3 и п
дает формула (8.14)). Есть два выхода из этой ситуации: либо увели-
чить объем выборки п, либо несколько увеличить уровень значимости а,
что повлечет соответствующее уменьшение {3 (т. е. увеличение мощности
критерия 1 — /3).
Для пояснения эффекта «слишком большого объема выборки» под-
черкнем следующее: никто в действительности не считает, что какая-либо
гипотеза выполняется точно: мы просто строим абстрактную модель ре-
альных событий, которая в какой-то мере обязательно отклоняется от ис-
тины; однако, как мы видим, огромная выборка почти наверняка (т. е. с
296
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
вероятностью, стремящейся к единице при неограниченном возрастании
п)1 отвергает в этом случае нашу гипотезу при любом заданном уровне
значимости а.
Казалось бы, налицо «тупиковая» ситуация: при малых выборках
вывод статистически ненадежен, а при слишком больших — однозначно
предопределен. Так, например, авторы неоднократно наблюдали обеску-
раживающее действие эффекта больших п на прикладника-исследователя,
пытающегося с помощью критериев согласия подобрать подходящий мо-
дельный закон Fmoa(z) для описания распределения исследуемой генераль-
ной совокупности и неизменно приходящего при этом к отрицательному
результату (т.е. к отвержению проверяемой гипотезы).
Чтобы избежать эффекта большой выборки, априорное задание ха-
рактеристик точности критерия (уровня значимости а и ошибки второго
рода /?) необходимо увязывать с объемом имеющихся данных п: выигрыш
в «чувствительности» критерия, получающийся в результате увеличе-
ния п, целесообразно использовать для уменьшения как а, так и /?. В
частности, если определить уменьшение а при возрастании п, то очень
малые отклонения от Но уже не приведут к обязательному отвержению
этой гипотезы: вероятность этого факта будет зависеть от того, с какой
«скоростью» (с ростом п) убывает о.
8.5.	Последовательная схема принятия
решения (последовательные критерии)
8.5.1.	Последовательная схема наблюдений
Если число наблюдений, на основании которых статистик принимает
решение, не фиксируется заранее, но ставится в зависимость от резуль-
татов зарегистрированных на каждой данной стадии эксперимента на-
блюдений, то говорят об использовании последовательной схемы наблю-
дений. Поскольку результаты наблюдений на каждой фиксированной ста-
дии эксперимента представляют собой случайную выборку из генеральной
совокупности и, следовательно, случайны по своей природе, то и момент
прекращения наблюдений (определение которого зависит от этих резуль-
татов) также является величиной случайной.
Впервые идея об использовании последовательной схемы наблюдении
возникла в ходе конструирования экономных планов выборочного стати-
1 Это следует из свойства состоятельности критерия (см. выше).
8.5. ПОСЛЕДОВАТЕЛЬНЫЕ КРИТЕРИИ
297
стического контроля качества продукции1. Речь шла о выборочной про-
верке того факта, что неизвестная нам истинная доля р дефектных изде-
лий во всем производстве не превосходит некоторого порогового значения
(предельно допустимой доли брака) ро« Авторы упомянутой работы пред-
ложили для этой цели методику проверки с двукратной выборкой. На
первом этапе предложенной ими последовательной схемы извлекается од-
на выборка изделий объема nt и оценивается доля брака pi в этой выбор-
ке. Решение о необходимости контроля второй выборки принимается на
основании результатов наблюдений в первой выборке: грубо говоря, если
доля брака в первой выборке pi оказалась существенно меньше (или су-
щественно больше) заданного порогового значения р0, то необходимости
в повторной выборке нет и принимается гипотеза р р0 (или соответ-
ственно альтернатива р > Ро); если же доля брака pi в первой выборке
несущественно отличается от заданного порогового значения ро (или, как
говорят, находится в «зоне неопределенности», или в «зоне безразличия»),
то принимается решение о продолжении наблюдений и, в частности, об
извлечении второй выборки объема п2.
При такой методике достигается заметный выигрыш (в среднем) в
числе наблюдений, необходимом для различения интересующих нас гипо-
тез с заданными характеристиками точности (уровнем значимости а и
мощностью 1 — (3) по сравнению с критерием Неймана-Пирсона, являю-
щимся наилучшим (наиболее мощным, см. п. 8.3.1) среди всех критериев,
основанных на классической схеме наблюдений (т. е. построенных на ба-
зе выборок заранее заданного объема п). Поэтому к последовательной
схеме наблюдений целесообразно обращаться в ситуациях, когда каждое
наблюдение является дорогостоящим или труднодоступным и по услови-
ям эксперимента исследователь имеет практическую возможность реали-
зовать эту схему (далеко не всегда исследователь находится в подобных
условиях).
К величинам а(0) и /3(0), характеризующим «качество» всякого
критерия (см. п. 8.4), при рассмотрении последовательных критериев до-
бавляется еще средний объем выборки	необходимый для про-
верки гипотез вида (8.6) с заданными характеристиками точности (а, /?)
(нижний индекс 0 при знаке математического ожидания Е означает, что
усреднение проводится при истинном значении параметра, равном 0).
1 D о d g е H.F., R о m i g Н. G. A method of sampling inspection — The Bell System
Techn. Journ., 8 (1929), pp. 613-631.
298
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
8.5.2.	Последовательный критерий отношения
правдоподобия (критерии Вальда) и его свойства
Построение статистического критерия при фиксированном объеме
выборки п (см. п. 8.3.1) сводится в конечном счете к разбиению области
возможных значений критической статистики = 7(^1,... на две
части: область правдоподобных и область неправдоподобных (в условиях
справедливости проверяемой гипотезы Яо) значений 7<п\ При попадании
конкретного значения 7(a5i, • • •,хп) в область неправдоподобных значений
принимается решение об отклонении проверяемой гипотезы.
Последовательный критерий, т. е. критерий, основанный на после-
довательной схеме наблюдений, построен по той же логической схеме с
одним отличием: последовательно для каждого фиксированного объема
выборки р = 1,2, ...,п, п 4- 1,... область возможных значений кри-
тической статистики . .,xv) разбивается на три непересекающих-
ТГ '	ff
ся части: область Гр ° правдоподобных, область Гр неправдоподобных и
область Гр сомнительных (в условиях справедливости проверяемой гипо-
тезы Hq) значений, т.е.
Г„ = г"° U Г* U г;,	«/ = 1,2,...
На каждом р-m шаге последовательной схемы наблюдений, т.е. при
наличии наблюдений Zj,..., и = 1,2,..., решение принимается по сле-
дующему правилу:
если 7(a?i,..., х„) G Г^°, то проверяемая гипотеза Яо принимается;
если 7(3?!,.. .,Яр) € Гр1, то проверяемая гипотеза Яо отвергается
(или принимается некоторая альтернатива Я1);
если 7(ж1,...,Жр) € Гр, то окончательный вывод откладывается и
производится следующее (i/4-1 )-е наблюдение (поэтому область Г* иногда
называют областью неопределенности или областью продолжения наблю-
дений).
Таким образом, для того чтобы иметь какой-то конкретный стати-
стический критерий, надо конкретизировать: а) тип проверяемой гипоте-
зы; б) способ построения критической статистики 7(afi,-•-,«!/); в) способ
построения областей гУ°,Г^ и Г* по заданным (требуемым) значениям
характеристик точности критерия.
В качестве конкретного примера последовательного критерия рассмо-
трим известный критерий отношения правдоподобия Вальда, предназна-
ченный для различения двух простых гипотез вида (8.13).
Критическая статистика этого критерия для последовательности не-
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
299
зависимых наблюдений	.., х„ определяется соотношением
„ы = ]n /(gi;6i)--/(gy;Qi) = Vin
7	/(*,; 0i	0i)	/(*<;0о)’
(8.15)
«' = 1,2,...
Области правдоподобных (Г„), неправдоподобных (Г ) и сомни-
тельных (Г£), в условиях справедливости гипотезы Яд, значений крити-
ческой статистики 7^ приближенно задаются соотношениями:
(8.16)
Была доказана оптимальность этого критерия среди всех других воз-
можных последовательных критериев, а именно: среди всех критериев,
различающих гипотезы (8.13) с ошибками первого и второго рода, не пре-
восходящими заданных величин, соответственно а и /3, критерий (8.15)-
(8.16) требует наименьшего среднего числа наблюдений Е0 и(а,/3) как в
условиях справедливости гипотезы Я0(г = 0)» так и в условиях справед-
ливости гипотезы Я1(« =1) [Вальд].
Исследования показали, что этот критерий примерно в два-четыре
раза выгоднее (по затратам на наблюдения), чем наилучший из классиче-
ских критериев — критерий Неймана-Пирсона [Айвазян С. А., 1959].
8.6.	Методы проверки статистических
гипотез: примеры статистических
критериев	\
8.6.1.	Критерии согласия
Критерии согласия предназначены для статистической проверки ги-
потез о модельном виде закона распределения вероятностей (з.р.в.) иссле-
дуемой случайной величины. Пусть FMOfl(®;0i,...,#*) — гипотетичный
модельный вид функции распределения анализируемого з.р.в. Функция
Гмод(^;^1,  ..,£*) может однозначно задавать исследуемый з.р.в. (тогда
все значения параметров ,..., 0/t известны априори), а может обозначать
300
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
лишь гипотетичный тип искомого з.р.в., определяемый целым параметри-
ческим семейством {Гмод(ж; ,..., 0*)} (например, мы хотим проверить
гипотезу о том, что з.р.в. анализируемой случайной величины описыва-
ется нормальной моделью, см. п. 3.1.5).
Таким образом, описываемые в данном пункте критерии согласия
предназначены для проверки гипотезы
Яо: ад) 6 {ГМод(*;*ь...,»*)}>	(8-И)
1
на основании п независимых наблюдений (8.1) анализируемой случайной
величины £, функция распределения которой, как обычно, обозначена с
помощью	Критические статистики этих критериев основаны на
различных мерах расстояний между анализируемой эмпирической функ-
цией распределения F^n\x) (см. п. 6.2.1) и гипотетическим семейством
{^мод(®» ^1> — » ^fc)}-
Там, где речь идет о группированных выборочных данных, мы будем
придерживаться терминологии и обозначений п. 6.1.
Критерий согласия х2 Пирсона. Этот критерий позволяет про-
верять гипотезы вида (8.17) как для дискретных, так и для непрерывных
случайных величин в ситуациях, когда параметры 0i,...0* априори из-
вестны или являются неизвестными. Метод проверки (критерий) основан
на теореме Пирсона-Фишера, которые доказали, что если гипотеза (8.17)
истинна, то при некоторых достаточно общих условиях распределение
критической статистики
7(п) = у - «р/е))2	(818)
npj(Q)
сходится (при п —> оо) к/(5-^~ 1)-распределению.
Для объяснения обозначений в соотношении (8.18) разберем отдельно
случаи непрерывной и дискретной случайных величин.
В непрерывном случае статистика (8.18) строится по группированным
данным. Группировка данных (8.1) производится в соответствии с реко-
мендациями и обозначениями п. 6.1, т. е.: з — это общее число интервалов
группирования; i/j — число выборочных данных, попавших в j-й интервал
группирования; 0 = (01, - - -, 0fc) — векторный параметр, который участ-
вует в выражении модельной функции распределения FM<w(s; 01,.. .,0*),
а О — его состоятельная оценка (более корректным способом оценивания
считается тот, при котором в качестве 0 используется оценка максималь-
ного правдоподобия, построенная по группированным данным); при этом
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
301
к в теореме Пирсона-Фишера обозначает число неизвестных параметров,
оцениваемых по выборке, так что в случае априори известных значении
параметров к = 0; наконец, рл(0) — это результат модельного расчета
вероятности попасть в у-й интервал группирования, т. е.
Pj(®) = ^мод(с>»®) “ ^мод(су-15	(8.19)
где Cj_i,cj — соответственно левый и правый концы j-го интервала груп-
пирования (у = 1,2,..., s).
Случай анализа дискретной случайной величины отличается от пре-
дыдущего лишь тем, что мы работаем с исходной (а не группированной)
выборкой (8.1), Vj — это число выборочных данных, равных у-му воз-
о	«	« „
можному значению Xj, з — число всех возможных значении случайной
величины, а
Pj(§) =	= *°} = ^мол(®?+1) - ^моД(г“).	(8.19')
Итак, теорема Пирсона-Фишера дает нам основание следующим обра-
зом построить процедуру проверки гипотезы (8.17).
1)	По выборочным данным (8.1) (сгруппированным при анализе не-
прерывной случайной величины) строим состоятельные оценки в параме-
тров 0 = (#i,... А).
2)	В соответствии с формулами (8.18)-(8.19)-(8.19 ) подсчитываем
(п)
значение критической статистики 7' .
3)	По заданному уровню значимости критерия а из таблиц процент-
ных точек ^-распределения находим 100(1 — а/2)- и 100а/2%-ные точки
Х1-а/з(л — А: — 1) и Ха/г(л — fc — 1) «хи-квадрат» распределения с з — к — 1
степенями свободы.
4)	Если Х1-а/а(з - к - 1) <	- к - 1), то гипотеза (8.17)
не отклоняется; если же Xi-a/2(s ~к — 1) или	Ха/з(а ~ к — 1),
то гипотеза (8.17) отклоняется1.
1 Отвержение выдвинутой гипотезы в случае «слишком маленьких» значений ста-
тистики критерия 7^”) на первый взгляд противоречит здравому смыслу. Действи-
тельно, статистика характеризует степень отклонения эмпирического распре-
деления случайной величины ( от гипотетического F: чем меньше 7^п\ тем меньше
это отклонение. Казалось бы, идеальный случай достигается при 7^"^ = О. Однако
надо отметить, что хотя 7^п^ к является мерой отклонения гипотетического закона
F от истинного, но мерой случайной, т. е. величиной, подверженной обязательному
неконтролируемому разбросу. И в этом отношении одинаково неправдоподобными
(маловероятными) следует считать как слишком большие значения 7<п>, так и слиш-
302
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Так, например, при проверке гипотезы нормальности гипотетический
закон Гмод будет иметь вид:
1 f J
Р=— / е	аи,
—ОО
.2	2
а в качестве оценок а и а двух неизвестных параметров а и а будут
фигурировать величины
4.1у
-2	1	5
а “ п —Н
О
Xi
2
(через ж® обозначается, как и прежде, средняя точка интервала Aj)-
Значения F(cj\a,&2) = Ф(с^;а,а2), необходимые для подсчета веро-
ятностей pit можно найти, например, из таблицы значений функции стан-
дартного нормального распределения с учетом соотношения Ф(х;л,(72) =
Ф(£=а;0,1). Число степеней свободы закона распределения процент-
ные точки которого нам понадобятся, будет равно в данном случае з - 3,
где з — число интервалов группирования.
Критерий Колмогорова-Смирнова. Этот критерий позволяет
осуществлять проверку гипотезы (8.17) в условиях, когда модельная функ-
ция FMO„(z) = F0(z) известна полностью, т. е. не зависит от неизвестных
параметров.
Пусть F^n\x) —
эмпирическая функция распределения. Введем сле-
дующие меры уклонения (расстояния) между функциями F^n\x) и Fq(z):
ком малые. О чем же свидетельствуют слишком малые значения Одно* из
причин подобной «ненормальности» может служить неудачный выбор закона F —
искусственное завышение числа параметров, от которых этот закон зависит. Други-
ми причинами могут служить нарушения корректности или объективности техники
выборочного обследования, стремление «подогнать» экспериментальные данные под
желаемый результат и т. п.
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
303
c;=sup(F0(2)-F<")(a:)).
£
Статистики у/nDn и y/nDn являются статистиками критериев Колмого-
рова и Смирнова соответственно. При этом
Dn = max(£>i,Dn).
Для практического использования критерия Колмогорова-Смирнова ста-
тистики Dn, Dn, Dn представляются в виде:
i
п
Dn — max
D~ = max
* / ’
i — 1
n
Dn = max(p+,Z)“),
(^l<n
где tj = Fo(®(t))» т.е. это значение гипотетической функции распределе-
ния, взятой в i-й точке вариационного ряда.
Для статистик Рп, £)„ , Dn известны точные распределения [Большее Л.
Смирнов Н. В.]. Здесь приведем лишь распределение для
0, ds
[n—nd]
У=о
п-З
X
1-^-d
п
где [n — nd] — целая часть числа п — nd.
Для практических целей обычно достаточно предельных распределе-
ний статистик
lim P(y/nDn < А) = /С(А);
п—»оо
lim P(VnD* < А) = 5(A),
п—»оо
304
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
где
(1-2£(-1№*2Аа,
А) = < ы
I 0
А > 0;
А < 0;
5(A) =
А > 0;
А < 0.
Предельное распределение для статистики \/nDn в точности совпадает
с S(А).
8.6.2.	Критерия однородности
Переходим к описанию некоторых наиболее распространенных ста-
тистических критериев, предназначенных для проверки гипотез об од-
нородности двух или нескольких анализируемых генеральных совокупно-
стей, где однородность понимается в том или другом смысле (см. выше,
п. 8.1.2).
Критерий однородности Смирнова. Этот критерий предназна-
чен для проверки гипотезы совпадения з.р.в. в двух или нескольких ге-
неральных совокупностях по группированным выборкам, извлеченным из
этих совокупностей, т. е. речь идет о проверке гипотез типа (8.4а). Пусть
имеется I выборок (8.3) объемов соответственно п<, п2,..., п/ и пусть дан-
ные каждой из этих выборок сгруппированы так, как это описано в п. 6.1,
причем разбиение диапазонов исследуемых случайных величин на интер-
валы группирования во всех выборах произведено одинаковым способом
(при этом выбор общего диапазона варьирования анализируемого призна-
ка во всех выборках определяется наименьшим, по всем выборкам, из ми-
нимальных выборочных значений и наибольшим из максимальных выбо-
рочных значений). Итак, мы имеем з одних и тех же для всех выборок
интервалов группирования и пусть — количество элементов t-й выбор-
ки, попавших в j-й интервал (t = 1,2,...,/; j = 1,2,...,а). В качестве
критической статистики критерия используется величина
•	I
где i/f. = yij — ni — общее число элементов »-й выборки, i/j = vij —
J=1	«=1
общее (по всем выборкам) число выборочных данных, попавших в j-й ин-
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
305
I в
тервал группирования и п =	— суммарный (по всем выборкам)
i=i j=i
объем выборочных данных.
И. В. Смирновым было доказано, что при неограниченном росте объ-
емов всех выборок и в условиях справедливости проверяемой гипотезы
(8.4а) з.р.в. статистики (8.20) стремится к закону %2 с числом степеней
свободы, равным (/ — 1)(з — 1). Поэтому, в соответствии с общей логикой
статистического критерия (см. выше, п. 8.2) гипотеза (8.4а) отвергается,
если 7(n) Xi-f ((/ - l)(s - 1)) или 7(п) > х\(Ц ~ 1)(« - 1)), и принима-
ется при всех остальных значениях критической статистики 7^ (здесь,
как обычно, Xg(m — табличное значение 100д%-ной точки «хи-квадрат»
распределения с т степенями свободы).
В частном случае двух выборок (т.е. при I = 2) статистика (8.20)
может быть записана в виде
(п)
И) _ V2j \
n2 J
‘'Ч + ГЦ ’
(8.20')
и при условии справедливости гипотезы однородности она будет прибли-
зительно распределена (при больших объемах П] и п2) по закону у с а — 1
степенью свободы.
Пример 8.1. В табл. 8.1 приведены условные данные о заработной
плате работников двух отраслей. В данном примере число сравниваемых
генеральных совокупностей I = 2 и объемы выборок тц = п2 = 100. Про-
верим (при уровне значимости критерия a = 0,05) гипотезу о том, что
распределения работников по заработной плате не отличаются друг от
друга в двух анализируемых отраслях.
Вычисление критической статистики (8.20z) в данном случае дает:
= 14,58.
Из таблиц процентных точек х3-распределения (см. приложение 1)
определяем пятипроцентную точку «хи-квадрат»-распределения с семью
степенями свободы Xo,os(7) = 14,07. Следовательно, гипотезу о совпаде-
нии вероятностных распределений работников по заработной плате в двух
анализируемых отраслях мы должны отвергнуть (у > Хо,©5(7)). Веро-
ятность ошибиться при этом равна 0,05.
306
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Таблица 8.1
Номер интерв. группы О')	Интервал заработной платы (усл. цен. ед.)	Кол-во работников, попав- ших в данный интервал		"V + «Ь,	l/u - l/2y
		("у) из выборки 1-й отрасли	(**у) из выборки 2-й отрасли		
1	130-150	4	1	5	3
2	150-170	4	1	5	3
3	170-200	15	8	23	7
4	200-250	51	43	94	8
5	250-300	22	34	56	-12
6	300-350	3	7	10	-4
7	350-400	1	3	4	-2
8	400-500	-	3	3	-3
Описанный метод проверки однородности относится к непараметри-
ческим критериям, так как используемая в нем критическая статистика
никак не зависит от наших предположений относительно параметриче-
ского общего вида анализируемых распределений (или, как иногда гово-
рят, «свободна от распределения». В этом его преимущество перед па-
раметрическими критериями. Однако его реализация требует достаточно
больших объемов анализируемых выборок (по меньшей мере они долж-
ны содержать по несколько десятков наблюдений). Следующий критерий
также относится к непараметрическим, однако требования к объемам вы-
борок здесь существенно мягче.
Критерий Вилкоксона—Манна—Уитни. Этот критерий предна-
значен для проверки однородности двух генеральных совокупностей, по-
нимаемой в смысле отсутствия различий в значениях параметров место-
положений (средних значений, медиан) соответствующих распределений
(но не тождественного совпадения распределений, как это было в пре-
дыдущем критерии). Т.е. речь идет о проверке гипотез типа (8.46).
Итак, мы располагаем выборками (8.3), извлеченными из двух гене-
ральных совокупностей (/ = 2). Пронумеруем эти выборки так, чтобы
обеспечить выполнение неравенства п\ < п2. Объединим выборки и по
объединенной выборке объема гц + п2 построим общий вариационный ряд.
Обозначим — порядковый номер (ранг), который получает при этом
i-й член вариационного ряда, построенного только по первой выборке,
в общем вариационном ряду (т. е. Я^ — это ранг элемента в об-
щем вариационном ряду, где	.,®1(П1) — вариационный ряд,
построенный только по первой выборке).
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ	307
Критическая статистика описываемого критерия имеет вид
7(в) = £ Я?’	(8.21)
»=1
и носит название «суммы рангов*.
Удалось показать, что в условиях справедливости проверяемой ги-
потезы (8.46) статистика (8.21) ведет себя (асимптотически по ni —♦ оо
так, что Dmfnj/nj) = с > 0) как нормально распределенная случайная
величина с параметрами
а = Ey(n) =	+ п2 + 1),
!	(8.22)
а2 = D7(n) = —n1n2(n1 + n2).
Л-£
При этом сходимость к нормальному распределению очень быстрая:
оно уже эффективно работает при щ > 8.
Это позволяет построить следующее правило проверки гипотезы
(8.46).
1)	По заданному уровню значимости критерия а с помощью таблиц
квантилей (процентных точек) стандартного нормального распределения
определяем квантиль уровня 1-а/2 (или 100о/2%-ную точку) стан-
дартного нормального распределения.
2)	Вычисляем стандартизованное значение критической статистики
7<п)
7(n) = 7W-<»»(»,+*, + 1).	(8 23)
У Н”1П2(П1 +”2)
где значение вычислено по формуле (8.21).
3)	Если окажется, что
ITct’ |> “l-a/21
то проверяемую гипотезу следует отвергнуть (и соответственно принять
при всех других значениях стандартизованной критической статистики
7ст )'
Отметим в заключение, что существуют таблицы процентных точек
критической статистики (8.21) (подсчитанные при условии справедливо-
сти гипотезы однородности) и для доасимптотического случая, т. е. для
п < 8 (см. [Большей Л. Н., Смирнов Н. В.]).
308
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Строго говоря, описанные ниже критерии однородности (критерий
Стьюдента, или / критерий; критерий дисперсионного отношения, крите-
рий Бартлетта и др.) применимы только к выборкам (8.3), извлеченным
из нормальной генеральной совокупности: в этом случае, как легко понять,
неотрицательный результат одновременной проверки однородности сред-
них значений (т.е. гипотезы (8.46)) и дисперсий (т.е. гипотезы (8.4в))
достаточен для неотрицательного вывода по поводу гипотезы об однород-
ности самих законов распределения (т.е. гипотезы (8.4а)). Специальные
исследования показали, однако, что /-критерий является (особенно при
больших объемах выборок п) весьма устойчивым по отношению к откло-
нениям исследуемых генеральных совокупностей от нормальных. А это
значит, что он может применяться и к выборкам из негауссовских ге-
неральных совокупностей с той лишь оговоркой, что истинные значения
уровня значимости и мощности критерия в этом случае будут незначи-
тельно отличаться от заданных.
Критерий Стьюдента (/-критерий). Этот критерий предназна-
чен для проверки гипотезы однородности средних значений (8.46) в двух
нормальных генеральных совокупностях, имеющих одинаковую (хотя и не-
известную) дисперсию о2. В качестве критической статистики в данном
критерии используется величина
где Xj(nj) и sj(nj) — соответственно выборочные средние и выборочные
дисперсии, построенные по у й выборке (j = 1,2), а з2 вычисляется по
выборочным дисперсиям Si(ni) и а2(п2) по формуле
1
«1 + п2 - 2
-2
з
[П13?(П1) + П232(П2)].
(8.25)
При анализе статистики нормального закона (см. п. 6.2.8, формулу
(6.3/)) нами было показано, что в условиях справедливости гипотезы
(8.46) (и при дополнительном условии равенства дисперсий в двух ана-
лизируемых генеральных совокупностях) статистика (8.24) должна под-
чиняться распределению Стьюдента с ni + п2 — 2 степенями свободы. По-
этому, определив из таблиц (при заданном уровне значимости критерия а)
100а/2%-ную точку /a/2(ni +п2 —2) /-распределения с щ +п2 —2 степенями
свободы, мы принимаем решение об отклонении гипотезы однородности
(8.46), если окажется, что вычисленная по формулам (8.24)-(8.25),
по абсолютной величине превзойдет значение tQ/2 (щ + п2 — 2).
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
309
Замечание. Слишком большое значение статистики (8.24), т. е.
такое, при котором отвергается проверяемая гипотеза однородности, мо-
жет быть следствием как статистически значимого расхождения выбо-
рочных средних (т.е. невыполнения гипотезы (8.46)), так и статисти-
чески значимого расхождения дисперсий (т.е. невыполнения гипотезы
(8.4в)). Поэтому если мы хотим понять, за счет чего обнаружилась неод-
нородность анализируемых выборок, то необходимо произвести дополни-
тельно проверку однородности дисперсий, т.е. гипотезы (8.4в). Эта же
задача может являться и самостоятельной (автономной) целью исследо-
вания.
Критерий, дисперсионного анализа является обобщением
J-критерия на случай более чем двух сравниваемых совокупностей (т.е.
I > 2). В этом случае критерий принадлежности нескольких выборок
(8.3) из нормальных генеральных совокупностей с одинаковой (но неиз-
вестной) дисперсией к одной общей совокупности основан на критической
статистике
Тзт Е “ »)’
7(п) =----------3----------,	(8.26)
I
х = njXj(nj)/(ni -|-----F П[) — общее выборочное среднее значение, а
i=i
52 = Я1+.Е"^2(»>)-
J=1
(8.27)
Доказано, что если в рамках сформулированных выше условий спра-
ведлива гипотеза однородности (8.46) (а это будет означать, в силу нор-
мальности сравнимаемых совокупностей и одинаковости их дисперсий, и
справедливость более сильной гипотезы (8.4а)), то статистика (8.26) под-
чиняется F-распределению с числом степеней свободы числителя, равным
I -1, и числом степеней свободы знаменателя, равным ni +п3 -|-h П/ —
Поэтому, если окажется, что вычисленная по формуле (8.26) статистика
7(n) > Fa(l - 1;
52 п-> о>
J=1
(8.28)
то гипотезу (8.4а) об однородности выборок (8.3) следует отвергнуть
I
(в правой части (8.28) Fa(l — 1; S ” 0 — 100о%-ная точка F-
j=i
310
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
распределения с указанными выше числами степеней свободы числителя
и знаменателя).
F-критерий однородности дисперсий. Этот критерий предна-
значен для проверки гипотезы однородности дисперсий (8.4в) в двух нор-
мальных генеральных совокупностях. Он основан на использовании кри-
тической статистики
(п) = ^ГГ”14(»1)
^п2з2(п2)’
(8.29)
где все обозначения соответствуют ранее введенным.
При анализе статистики нормального закона (см. п. 6.2.8, Следствие 5,
формула (6.38)) нами было показано, что в условиях справедливости ги-
потезы (8.4в) статистика (8.29) должна подчиняться F-распределению с
числами степеней свободы числителя и знаменателя, равными соответ-
ственно Tij — l и п2 — 1. Поэтому при заданном уровне значимости критерия
а определяем 100(1—а/2)%-ную и 100а/2%-ную точки Fi_a/2(ni-l,n2-l)
и	— 1,п2 — 1) (см. таблицы в приложении 1). Если окажется, что
^1-а/2(«1 - 1,П2 - 1) < 7(П)
< ^а/2(П1 - 1,П2 - 1),
то гипотеза однородности дисперсий не отвергается (и отвергается при
всех других значениях статистики (8.29)).
Пример 8.2. Реклама утверждала, что из двух типов пластико-
вых карт «American Exspress» и «Visa» богатые люди предпочитают
первый. Другими словами, среднемесячные платежи одного среднестати-
стического обладателя «American Express» существенно (статистиче-
ски значимо) превышают среднемесячные платежи одного среднестати-
стического обладателя карты «Visa» . С целью статистической проверки
этого утверждения были обследованы среднемесячные платежи 32 обла-
дателей «American» (гц = 32) и 30 обладателей «Visa» (п2 = 30). В
результате первичной статистической обработки этих двух выборок были
получены следующие значения выборочных характеристик:
^(тц) = $563
з?(щ) = 31684
i2(n2) = $485
за(п2) = 38416.
Требуется проверить гипотезу (8.46) с уровнем значимости
а = 0,05.
Предварительный. анализ законов распределения месячных расходов
как среди обладателей «American» , так и среди обладателей «Visa» по-
казал, что и тот и другой з.р.в. достаточно хорошо описываются нор-
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
311
мольной моделью. Но перед тем, как использовать в решении поставлен-
ной задачи t-критерий (критерий Стьюдента), необходимо убедиться в
однородности дисперсий в анализируемых совокупностях, т. е. проверить
гипотезу (8.4в) при I = 2. С этой целью воспользуемся F-критерием.
Для экономии места таблицы процентных точек составлены только для
случая, когда числитель больше знаменателя, поэтому, если в статистике
(8.31) числитель оказывается меньше знаменателя, то следует изменить
нумерацию выборок. Поэтому в нашем случае выборкой 1 будем счи-
тать выборку из совокупности пользователей «Visa» (т.е. пг = 30).
Итак, в нашем примере отношение (8.29) оказывается равным
1,22. Из таблиц процентных точек находим пятипроцентную точку
^о,ов(29;31) » 1,84, а поскольку 1,22 < 1,84, то мы имеем основание при-
нять допущение о равенстве дисперсий в анализируемых совокупностях
в качестве статистически проверенной рабочей гипотезы.
Теперь мы имеем основания воспользоваться критерием Стьюдента
для проверки гипотезы о равенстве средних значений.
Вычисление критической статистики по формуле (8.24) дает:
7<"> = 7	485 ~ 563	= -1,61.
V 55+55^(30 • 1963 + 32 • 178=) (£ + £)
Из таблиц процентных точек находим <о,02б(30 4- 32- 2) = 2,00. И
поскольку |7^| = 1,61 < 2,00, то мы делаем вывод о непротиворечивости
гипотезы однородности средних значений имеющимся в нашем распоря-
жении статистическим данным. Следовательно, утверждения рекламы о
более высокой состоятельности обладателей «American Express» не имели
объективных оснований.
Критерий Бартлетта позволяет проверять гипотезу об однородно-
сти дисперсий в нескольких (в том числе более чем в двух) нормальных
генеральных совокупностях. Критическая статистика критерия предло-
жена Бартлеттом и имеет вид
л
•iM
В формуле (8.30) величина в определяется соотношением (8.27),
Sj(nj) = п,-з^(п,)/(п,- - 1), а
’ = 1 + з(ГЛ) “>»,+ • • • +’	(8 31)
7(п) = <?52(*Ъ-1)1п
j=i
(8.30)
312
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
При min(ni,..., п/) > 3 в условиях справедливости проверяемой гипо-
тезы статистика (8.30) распределена приблизительно по закону х* с I - 1
степенями свободы. Поэтому (при уровне значимости критерия а) если
оказалось, что вычисленная по формуле (8.30) величина 7n > XaG — 1)> то
гипотезу об однородности дисперсий в анализируемых нормальных гене-
ральных совокупностях следует отвергнуть {xa(J “ 1) — 100а%-ная точка
«хи-квадрат» -распределения с I — 1 степенями свободы).
8.6.3.	Проверка гипотез о числовых значениях параметров
Остановимся теперь на примерах статистических критериев, позво-
ляющих проверять гипотезы вида (8.6). При этом важные статистические
критерии такого типа, относящиеся к корреляционному анализу, моделям
регрессии, анализу временных рядов, системам одновременных уравне-
ний, будут обсуждаться в контексте изложения этих тем соответственно
в гл. 10, 11, 15, 16 и 17. В данном пункте мы опишем несколько приме-
ров статистических критериев, предназначенных для проверки простых
основных гипотез (чаще всего — при простых же альтернативах) отно-
сительно числовых значений параметров анализируемых законов распре-
деления вероятностей, т.е. речь идет о проверке основной («нулевой» )
гипотезы
Яо: О = О
против альтернативы	(8.32)
Hi: 0 = 0J (или 0 / 0О),
где 0О и 01 — заданные числовые значения параметра, который участ-
вует в модельном описании функции распределения вероятностей анали-
зируемой случайной величины £ (т.е. Р{£ < а:} = F^(z;0)).
Критерии проверки гипотез о числовом значении параметра
р биномиального распределения. Рассматриваемая задача относит-
ся к анализу результатов серии п независимых испытаний Бернулли (см.
п. 3.1.1). При этом в имеющейся у нас выборке объема п интересующее нас
событие произошло х раз. Можно интерпретировать эту серию (выборку)
как единственное наблюдение (п, р)-биномиальной случайной величины в
ситуации, когда параметр п известен, а параметр р нет. Далее речь пой-
дет о проверке гипотез типа (8.32), где роль параметра 0 играет параметр
р, т. е. о проверке (по имеющимся у нас результатам наблюдения) гипо-
тез о численном значении параметра р биномиального распределения при
различных альтернативах.
Принимая во внимание утверждение леммы Неймана-Пирсона о том,
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
313
что критерии отношения правдоподобия являются наиболее мощными
среди всех других возможных критериев (см. п. 8.3.1), попробуем вывести
критическую статистику критерия, руководствуясь именно этим принци-
пом. При этом нам удобнее будет, как это часто бывает при работе с функ-
циями правдоподобия, не само отношение правдоподобия, а его логарифм
(монотонность этого преобразования обеспечивает нужный результат).
Функция правдоподобия биномиального закона с параметрами п и
р при единственном наблюдении ж, как известно (см. п. 3.1.1), имеет вид:
Z(s|p;n) = C:/(l-p)n-r.
Так что критическая статистика критерия ^п\ определяемая лога-
рифмом отношения правдоподобия при произвольном значении параметра
р по отношению к основному гипотетическому ро, будет иметь вид:
j-» _ In Ц* I р; ”)
7 П£(х|ро;п)
= а: In
Р
1 -P
+ nln ——•
1 -Ро
(8.33)
Для того чтобы построить критерий при заданном значении уровня
значимости а, нужно уметь назначить такое пороговое значение са, при
котором
P{7(n) > са I Яо} = «•	(8.34)
А для того, чтобы вычислить ошибку второго рода /3 или мощность кри-
терия 1 — /?, нужно уметь вычислять вероятность
1 - р = P{7W > со I Я,}.
(8.35)
Из (8.33) следует, что обе эти задачи решаются, если мы будем знать
распределение случайной величины х как при условии справедливости
«нулевой» гипотезы Яо (т.е. при значении параметра, равном задан-
ной величине po)j так и при условии справедливости любой альтернативы
(т.е. при любом другом значении р анализируемого параметра). Но при-
знак х, по построению, есть (п,р)-биномиалъно распределенная случай-
ная величина со значением параметра р, определяемым в зависимости от
того, в условиях справедливости какой из гипотез мы ее рассматриваем.
Поэтому в дальнейшем мы в качестве критической статистики
будем рассматривать (п,р)-биномиально распределенную случайную ве-
личину или любую удобную для нас ее линейную комбинацию. Правда,
при переходе от непосредственно вычисленной критической статистики
7 , задаваемой соотношением (8.33), к ее линейным комбинациям смысл
314
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
неравенств в фигурных скобках (8.34) и (8.35) может меняться на проти-
воположный. Рассмотрим подробнее три возможных варианта анализи-
руемой задачи.
Вариант /. Проверяется простая гипотеза Hq: р = Pq при простой
альтернативе р = pi, причем pi > ро« Тогда смысл неравенств в
(8.34) и (8.35) сохраняется и при замене на х, а именно по заданному
уровню значимости а требуется найти такое са, что
Р{ж > са | ро} = а-
Но
п
> со | Ро} = 5Z - Ро)п~к = OL.
к=са
(8.34х)
(8.34")
Следовательно, требуется решить уравнение (8.34хх) относительно са.
Обычно для этого пользуются либо нормальным, либо пуассоновским при-
ближением, а именно:
• если гипотетичная величина ро «не слишком близка» к нулю или
единице (скажем, 0,10 ро < 0,90), а число наблюдений п составляет
хотя бы несколько десятков, то используют теорему Муавра-Лапласа (см.
п. 4.3.1) о приближенной (асимптотической) стандартной нормальности
случайной величины
= (п) = g~P
ys
Тогда при р = ро
(8.34'")
Следовательно, аргумент функции стандартного нормального распределе-
ния является ничем иным, как квантилем уровня 1—а этого распределения
(ui-a)- Так что определив из таблиц величину «1-а, имеем
(	Ро) / V	_	—	«•
\ п / / V	п
(8.36)
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
315
Из (8.36) определяем величину са, на которой основано правило проверки
гипотезы Яо: если окажется, что х cQi то гипотеза Но отвергается
(с вероятностью ошибки, приблизительно равной а).
Ошибка второго рода этого критерия подсчитывается также с исполь-
зованием нормальной аппроксимации биномиального закона, но при зна-
чении параметра р = pt, а именно:
/3 =	< са | Я1} = Р{х < са | pi}
= X сЫ(1 - р. Г ‘* (й - л)	; (8'37)
к=0	\	/
• если гипотетическая величина рд близка к 0 или единице (т.е.
Ро < 0,10 или ро > 0,9), а число наблюдений, как и в предыдущем случае,
составляет хотя бы несколько десятков, то для вычисления вероятностей
событий вида {ж = к], где х — (п,р)-биномиально распределенная случай-
ная величина, лучше пользоваться пуассоновской аппроксимацией, т.е.
Р{г = к] »	е-"”.	(8.38)
Использование таблиц пуассоновского распределения с параметром
А = пр позволит по схеме, аналогичной предыдущему случаю, определить
сначала са из условия
оо /	X к
Р{Х > СО I Ро} » £	= ! _ F(Ca | А = про) = а, (8.39)
Л=са
а затем вычислить вероятность ошибки второго рода
/3 = Р{х < са | рт} = F(ca - 1 | А = прг)	(8.40)
(в соотношениях (8.39) и (8.40) функция F(x | Л) обозначает функцию
распределения пуассоновского закона с параметром А).
Вариант 2. Проверяется простая гипотеза Яо: р = р0 при простой
альтернативе : р = pi, причем рг < р. Схема решения в точности по-
вторяет предыдущую с заменой смысла неравенства в соотношении (8.34z)
на противоположный. А именно критическая константа са по заданному
уровню значимости а определяется из условия
Р{х са | р0} = а.	(8.3б'а)
Соответственно меняется на противоположный и смысл неравенств в фи-
гурных скобках соотношений (8.34„), (8.34w/), (8.37), (8.39) и (8.40) с со-
ответствующими изменениями в последующих выкладках.
316
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Вариант 3. Проверяется простая гипотеза Яо: р = Ро против слож-
ной альтернативы	Ро- В этом случае одинаково «неестественны-
ми» (с точки зрения справедливости гипотезы Hq) будут большие откло-
нения х от про как в одну, так и в другую сторону. Это отразится на
схеме построения критерия следующим образом:
•	при использовании нормальной аппроксимации следует находить кон-
станту са/2, заменив в правой части (8.34w) величину а нае/2, тогда
решение об отклонении гипотезы Hq будет приниматься в случае
I® / /Ро(1 - Ро) .
\п~Ра / V п
(8-41)
где ич, как и прежде, квантиль уровня q стандартного нормального
распределен ия *,
•	при использовании пуассоновской аппроксимации потребуется вычи-
слить Эве критические константы: 100(1 — о/2)%-ную и 100«/2%-ную
точки (соответственно ci_q/2 и са/г) пуассоновского распределения с
параметром А = про; решение об отклонении гипотезы. Но будет
приниматься в случаях х < с\_а/2 и х > са/2-
Пример 8.2. Из массового стационарно функционирующего про-
изводства извлекается контрольная выборка изделий объемом 100 единиц
(я = 100) с целью проверки гипотезы Яо о том, что доля брака производ-
ства составляет ро = 0,05, против гипотезы Н\ о том, что эта доля равна
Р1 = 0,10. Построить наиболее мощный критерий проверки гипотезы Яо с
уровнем значимости а, не превышающим 0,05, и вычислить его мощность.
Решение. Условие задачи соответствует вышеописанному вариан-
ту /, а соотношение величин pq и п говорит за то, что следует воспользо-
ваться пуассоновской аппроксимацией при определении критической кон-
станты со,о5- В соответствии с (8.34п) и (8.39) с помощью таблиц пуассо-
новского распределения с параметром А = пр$ = 100-0,05 = 5 определяем:
Р{х < 8} и Г(9 | А = 5) = 0,932;
Р{х < 9} « F(10 | А = 5) = 0,968.
Так что выбрав са = 10, имеем величину уровня значимости кри-
терия, равную а = 1 — Г(10 | А = 5) = 0,032 < 0,05. Таким образом,
критерий задается критической статистикой — х-числом дефектных
изделий, обнаруженных в выборке объема п = 100, и критической кон-
стантой са = 9: если в выборке объема п = 100 окажется более 9 дефект-
ных изделии, то гипотезу о доле брака производства, равной 0,10, следует
предпочесть гипотезе о доле брака производства, равной 0,05.
8.6. ПРИМЕРЫ СТАТИСТИЧЕСКИХ КРИТЕРИЕВ
317
Подсчет мощности критерия (с учетом формулы (8.40)) дает:
® 1
1 - /? = 1 - Р{г < са | р = 0,10} » 1 - V - г е = 0,542.
к=а ’
Таким образом, ошибка второго рода, равная /3 = 0,458, оказывается
весьма большой.
Пример 8.3. Независимому статистику поручено проверить ин-
формацию маркетинговой службы некоторого туристического бюро о том,
что 70% клиентов выбирают в качестве формы обслуживания полупанси-
он. Статистик провел опрос 150 случайно выбранных туристов, из них
полупансион предпочли 84 человека. К какому выводу пришел статистик
при проверке гипотезы Но: р = 0,70 при альтернативе р / 0,70 при
уровне значимости критерия а = 0,05?
Решение. Условия задачи соответствуют вышеописанному вариан-
ту 3, а соотношение величин р0 = 0,70 и п = 150 говорит за то, что можно
воспользоваться нормальной аппроксимацией. Расчет величин, участву-
ющих в соотношении (8.41), приводит к следующим результатам:
(х „ } Z./Po(1_₽o) _ / 84 П 7^ / /°’7 ’ °>3 - Ч7Л
In - Ро) 'V —---------- (150 * °’7) 'V ПбО" - -3’74-
А поскольку ni-a/2 = «0,975 = lj96, то неравенство (8.41) имеет ме-
сто и, следовательно, есть основания подвергнуть сомнению данные мар-
кетинговой службы, т.е. отвергнуть гипотезу Яо.
Критерии проверки гипотез о среднем значении нормальной
генеральной совокупности. Все критические статистики, которые ис-
пользуются ниже для построения критериев проверки гипотез о среднем
значении нормально распределенной случайной величины, получаются с
помощью реализации принципа отношения правдоподобия (8.7), описан-
ного в п. 8.3.1. А потому и основанные на них критерии, в соответствии
с леммой Неймана-Пирсона, являются в определенном смысле наилучши-
ми (наиболее мощными). Мы не будем здёсь подробно расписывать ло-
гарифмы отношения правдоподобия для конкурирующих гипотетичных
нормальных законов: думаем, у читателя, овладевшего предыдущим ма-
териалом учебника, не возникнет принципиальных трудностей при само-
стоятельном выводе критических статистик в данном случае. Поэтому
ограничимся лишь сводкой результатов.
Итак, мы имеем случайную выборку (ij,^,.. .,жп) из (а,<т2)-нор-
лальной генеральной совокупности. Рассмотрим различные варианты по-
318
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
становок задач по статистической проверке гипотез о числовом значении
параметра а = Е£.
1)	HG: а = Oq при альтернативе Н^ а> а^а2 известна. Критиче-
ская статистика = (х — а^у/п/а.
Правило принятия решения: если	то гипотеза Hq от-
вергается с вероятностью ошибки, равной о (здесь и далее «^-квантиль
уровня q стандартного нормального распределения).
Обоснование: статистика 7^ в соответствии с теоремой Фишера (см.
п. 6.2) подчиняется стандартному нормальному закону в условиях справед-
ливости гипотезы Hq.
2)	Hq: а = а$ при альтернативе Hi: а < ад; о известна.
Критическая статистика:	= (х — а0)-\/п/а.
Правило принятия решения: если	то гипотеза Яо от-
вергается с вероятностью ошибки, равной а.
Обоснование: то же, что в предыдущем пункте.
3)	Яо: а = Oq при альтернативе Н\: а / «о» °"2 известна.
Критическая статистика:	= (я — ао)у/п/о.
Правило принятия решения: если 17^1 > «1-а/2» то гипотеза Яо
отвергается с вероятностью ошибки, равной а.
Обоснование: то же, что в предыдущих пунктах.
4)	Яо: а = а0 при альтернативах Hi', а > Oq; или Hi', а < Oq; или
Ну: а а0; о2 неизвестна. Схемы критериев для каждой из альтернатив
повторяют соответствующие схемы для известной дисперсии о со сле-
дующими изменениями, касающимися критической статистики и правила
принятия решения.
Критическая статистика: 7^ = (я — ao)\/n ~ 1/а.
Правило принятия решения: гипотеза Яо отвергается, если
7^ > ta(n — 1) при альтернативе Hi', а > ао;
7<n) < — tQ(n — 1) при альтернативе Hi', а < oq]
|7^n)| >	— 1) при альтернативе Hi', а uq
(здесь tg(n — 1) — 100<7%-ная точка распределения Стьюдента с п — 1 сте-
пенью свободы).
Обоснование: в соответствии со Следствием 2 теоремы Фишера (см.
П. 6.2, (6.30)) статистика распределена по закону Стьюдента с п — 1
степенью свободы.
выводы
319
Критерии проверки гипотезы о значении дисперсии нор-
мальной генеральной совокупности. По случайной выборке ($i,2:2,...
. ..,zn) из (а,а2)-нормальной генеральной совокупности получена выбо-
рочная дисперсия з\п). Требуется проверить гипотезу (при уровне зна-
чимости критерия a) Hq: а = <То, где oq — некоторое конкретное чи-
словое значение. При проверке этой гипотезы используют критическую
статистику
(п) _ пз (п)
7	—	2 ’
<*0
(8-42)
которая в соответствии с теоремой Фишера (см. (6.27) в п. 6.2.8) в услови-
ях справедливости гипотезы Но распределена по закону х2 с n—1 степенью
свободы.
Далее, как и в случаях проверки гипотез о параметре биномиального
закона р или о значении среднего нормальной генеральной совокупности
а, в зависимости от конкурирующей гипотезы Hi выбирают правосторон-
нюю, левостороннюю или двустороннюю критическую область:
1)	если Н\', <т = 6Т1 > а0, то гипотезу Но отвергают (с вероятностью
ошибки а) в случае пз2/о2 > Xa(n ~ 1);
2)	если Ht: а2 = а2 < <т2, то гипотезу Но отвергают (с вероятностью
ошибки а) в случае пз2/ctq < Х\-а(п ~ 1);
3)	если Hi: а2 £ сго, то гипотеза Hq отвергается (с вероятностью
ошибки а) при пз2/ао < Х1-а/г(п - 1)5 а также при пз2/а2 > Ха/г(та - 1).
Здесь, как обычно, %J(m) обозначает 100^%-ную точку ^-распределения
с т степенями свободы.
ВЫВОДЫ
1.	Процедура обоснованного сопоставления высказанного исследовате-
лем предположительного утверждения (гипотезы) относительно природы
или величины неизвестных параметров рассматриваемой стохастической
системы с имеющимися в его распоряжении результатами наблюдения,
сопровождаемая количественной оценкой степени достоверности получае-
мого вывода, осуществляется с помощью того или иного статистического
критерия и называется статистической проверкой гипотез.
2.	По своему прикладному содержанию гипотезы, высказываемые в
ходе статистического анализа и моделирования, подразделяют на следую-
щие типы:
об общем виде закона распределения исследуемой случайной величи-
ны;
320
ГЛ. 8. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
об однородности двух или нескольких обрабатываемых выборок;
о числовых значениях параметров исследуемой генеральной совокуп-
ности;
об общем виде зависимости, существующей между компонентами ис-
следуемого многомерного признака;
о независимости и стационарности ряда наблюдений.
3.	Все статистические критерии строятся по общей логической схе-
ме. Построить статистический критерий — это значит: а) определить
тип проверяемой гипотезы; б) предложить и обосновать конкретный вид
функции от результатов наблюдения (критической статистики 7^), на
основании значений которой принимается окончательное решение; в) ука-
зать такой способ выделения из области возможных значений критической
статистики уп области отклонения проверяемой гипотезы чтобы
было соблюдено требование к величине вероятности ошибочного отклоне-
ния гипотезы Яо (т.е. к уровню значимости критерия а).
4.	«Качество» статистического критерия характеризуется уровнем
значимости а, мощностью 1 — /?, свойствами несмещенности и состоя-
тельности. В состоятельных критериях можно добиваться сколько угодно
малых величин ошибок первого и второго рода (о и /?) лишь за счет уве-
личения объема выборки п, на основании которой принимается решение.
При фиксированном объеме выборки можно делать сколь угодно малой
лишь одну из ошибок (ft или /?), что сопряжено с неизбежным увеличени-
ем другой.
б. Наряду с классической схемой наблюдения, когда объем выборки п
заранее зафиксирован, в практике статистических исследований исполь-
зуется и последовательная схема наблюдения, при которой на каждом из
последовательно во времени проводимых этапов наблюдения принимает-
ся одно из трех решений: «принять гипотезу Яо», «отклонить гипотезу
Hq», «не принимать окончательного решения и продолжить наблюдения».
При этом выбор решения ставится в зависимость от результатов всех пре-
дыдущих наблюдений, а число наблюдений р, произведенных до момента
принятия окончательного решения, оказывается величиной случайной.
в. Оптимальные последовательные критерии отношения правдоподо-
бия (критерий Вальда, обобщенный последовательный критерий и др.)
оказываются более экономными по затратам на наблюдения, на основании
которых можно различить проверяемые гипотезы с заданной точностью
(ft,/?). Исследования показали, что, применяя последовательные крите-
рии, можно добиваться двух-, трех- и даже четырехкратного снижения
необходимого числа наблюдений по сравнению с классическими оптималь-
ными критериями.
Раздел III

ы X
Hr г*.
BbttJlWfc ’Wb
икла,
щ. .,
Статист!
41л Ле W*4* h	. .. .
’ >
И
□ИН
i О Г
ЖьМь 11
Г’ ' ~ .7? ’Л ', 
' 'Ж
1;W:
I: « '
Гдава 10. Статистическое исследование
’I	к, у1
зависимостей (основные ;
4	4 I >*4l
понятия ^постановки.задач)
1 11.  Корреляционный анализ
? i многомерной генеральной
k С^окупности
Распознавание обра юв и
тцпологизация объектов в
тащально-эконо^^ких
к исследованиях (методы
J
&	1
if
rj®
Й1
I.
Й)
Глава
1L '
'I; ЖжВнЙ,
4, ГТ.-iiU,
Иш>
aii.
1jl
О
Глава 13. Сниже
размерности
исследуемого многомерного
признака и отбор Наиболее
информативных показателей

ГЛАВА 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ
СТАТИСТИЧЕСКИЙ АНАЛИЗ
9.1.	Назначение и содержание прикладной
статистики
Во «Введении» к учебнику (см. и. В. 1.2) мы кратко обсудили вопро-
сы, вынесенные в заголовок этого пункта, дали определение прикладном
статистики как самостоятельной научной дисциплины, попытались по-
нять «взаимоотношения» прикладной статистики с теорией вероятностей
и математической статистикой, с одной стороны, и с эконометрикой — с
другой. В частности, было установлено, что теория вероятностей и мате-
матическая статистика являются по отношению к прикладной статисти
ке и эконометрике разработчиками и поставщиками существенной части
используемого в них математического аппарата. Однако доводка и разви-
тие этого аппарата, подчиненные требованиям и специфике различно-
го рода приложений, производятся уже в рамках дисциплин «приклад-
ная статистика* и «эконометрика*. Причем эконометрика (наряду
с другими сферами человеческой деятельности, в которых используют-
ся математико-статистические методы) является активным поставщиком
специального класса постановок задач для прикладной статистики. Да-
лее развиваются и комментируются некоторые из тезисно намеченных во
«Введении» к учебнику положений, относящихся к назначению и содер-
жанию прикладной статистики.
9.1.1.	Два подхода к интерпретации и анализу исходных
статистических данных
Первый подход (вероятностно-статистическим) развивается в
рамках классической математической статистики (т. е. в условиях хотя
бы приблизительного выполнения требований статистического ансамбля,
324
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
см. п.В.2.1) и предусматривает возможность вероятностной интерпрета-
ции анализируемых данных и получаемых в результате этого анализа ста-
тистических выводов. При подобной (вероятностной) интерпретации ис-
ходных статистических данных в поле зрения исследователя одновременно
попадают две совокупности объектов: реально наблюдаемая, статистиче-
ски представленная рядом наблюдений (т.е. выборка), и теоретически
домысливаемая (так называемая генеральная совокупность). Основные
свойства и характеристики выборки, называемые эмпирическими (или вы-
борочными), могут быть проанализированы и вычислены по имеющимся
статистическим данным. Основные свойства и характеристики генераль-
ной совокупности, называемые теоретическими, не известны исследовате-
лю, но назначение математике-статистических методов как раз в том и
состоит, чтобы с их помощью получить как можно более точное предста-
вление об этих теоретических свойствах и характеристиках по соответ-
ствующим свойствам и характеристикам выборок (см. гл. 6).
Важнейшим моментом в успехе статистического анализа и моделиро-
вания таких данных является удачное решение проблемы их генези-
са, т.е. правильный выбор вероятностной модели механизма генерации
этих данных (набор наиболее распространенных моделей подобного рода
описан в гл. 3). Именно отправляясь от решения проблемы генезиса ана-
лизируемых статистических данных, мы можем обоснованно ответить на
вопросы:
•	как наилучшим образом выбрать метод статистической обработки
этих данных, например, построить наиболее точную оценку неизвестного
среднего значения анализируемой генеральной совокупности?
•	каким должен быть общий вид модели, описывающий ту или иную
зависимость между анализируемыми признаками?
В обоих случаях критерий качества (оценки, степени адекватно-
сти модели) определится на основе принципа максимального правдоподо-
бия имеющихся у нас наблюдений, который в свою очередь базируется на
знании модели з.р.в. этих наблюдений (см. пп. 7.5.1, 8.3.1).
В принципиально иной ситуации оказывается исследователь, если он
не располагает никакими априорными сведениями о вероятностной при-
роде анализируемых данных, или если эти данные вообще не могут быть
интерпретированы как выборка из генеральной совокупности. Тогда
при выборе критерия качества (метода оценивания или степени адекват-
ности конструируемой модели) исследователь вынужден опираться на со-
ображения конкретно-содержательного плана: как именно получены ана-
лизируемые данные и какова конечная прикладная цель их анализа. По-
скольку эти соображения основаны на обычной логике и реализуются, как
9.1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ
325
правило, в виде критерия некоторого алгебраического вида, то и соответ-
ствующий подход принято называть логико-алгебраическим. Очевид-
но, в рамках логико-алгебраического подхода (в отличие от вероятностно-
статистического) исследователь не может претендовать на:
•	интерпретацию исходных статистических данных в качестве вы-
борки из некоторой (теоретически домысливаемой) генеральной совокуп-
ности;
v использование вероятностных моделей для построения и выбора
наилучших методов статистической обработки или наилучшего вида кон-
струируемой модели;
•	вероятностную интерпретацию выводов, основанную на статисти-
ческом анализе исходных данных.
В этом заключается главное различие двух возможных подходов к
статистическому анализу исходных данных. Однако и в том и в другом
подходе выбор наилучшего из всех возможных методов анализа и моде-
лирования данных производится в соответствии с некоторым критерием
качества метода или степени адекватности модели. Различие описы-
ваемых подходов проявляется здесь в способе обоснования выбора этого
критерия качества, а также в интерпретации самого критерия и получае-
мых статистических выводов. Но после того, как выбор конкретного вида
оптимизируемого критерия качества осуществлен, математические сред-
ства решения задачи статистического анализа и моделирования данных
оказываются общими для обоих подходов: и в том и в другом случае с
целью оптимизации выбранного критерия качества исследователь исполь-
зует методы решения экстремальных задач. Правда, на заключительном
этапе — на этапе осмысления и интерпретации полученных статистиче-
ских выводов — каждый из подходов снова имеет свою специфику.
Таким образом, общим для обоих описываемых подходов является на-
личие исходной статистической информации на «входе» задачи и необ-
ходимость наилучшего (в смысле оптимизации некоторого критерия каче-
ства) способа статистического анализа или моделирования этой информа-
ции с целью получения научных или практических выводов «на выходе».
Именно эта общая логическая схема и положена в основу методоло-
гического принципа разработки инструментария прикладной статистики.
Это позволило синтезировать два описанных выше подхода к статисти-
ческому анализу и моделированию. В результате прикладная статистика
объединила в себе как прикладные вероятностно-статистические ме-
тоды многомерного статистического анализа, включая модели регрессии
(существенно опираясь при этом на результаты математической стати-
стики, касающиеся методов статистического оценивания и статистиче-
326 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
ской проверки гипотез, см. гл. 7 и 8), так и логико-алгебраические ме-
тоды анализа данных, понимаемого в узком смысле, т. е. исключающего
использование в своих построениях вероятностных рассуждений и моде-
лей (достаточно полное представление об этих методах можно получить,
например, по книге [ДидеЭ. и др.]).
9.1.2.	Три центральные проблемы прикладной статистики
Перед тем как сформулировать три центральные проблемы приклад-
ной статистики, следует остановиться на двух основных формах записи
исходных статистических данных (и.с.д.). Первую, наиболее распростра-
ненную, форму представления и.с.д. обычно называют матрицей (или
таблицей) «объект-свойство». В своей наиболее общей записи эта ма-
трица имеет вид
(и.с.д.)!

где z^(tjt) — значение j-го анализируемого признака, характеризующего
состояние t-ro объекта в момент времени t^. Данные (9.1) образуют так
называемую пространственно-временную выборку, при формировании
которой статистическому обследованию подвергаются п объектов (как-то
размещенных в пространстве), причем на каждом из объектов регистри-
руются значения р характеризующих его признаков в N последовательные
моменты времени ti, <2,..., tN. Очевидно, что запись (9.1) в действитель-
ности определяет целую последовательность (а именно N штук.) матриц
«объект-свойство» . Можно также сказать, что данные вида (9.1) содер-
жат п реализаций р-мерного временного ряда (а^1^), a/2)(t),... ,a/p\f)).
Если мы располагаем так называемыми одномоментными наблюде-
ниями, то это соответствует случаю N = 1 в общей записи (9.1); при этом
для сокращения обозначений индекс времени t в записи (9.1) мы можем
опускать, а получающаяся выборка
(и.С.Д.)1 =
(9.1')
9.1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ
327
называется пространственной статической.
Другой частный случай и.с.д. мы получаем, если в (9.1) положить
п = 1 (т.е. обследуется во времени единственный объект). Тогда речь
идет об анализе единственной траектории р-мерного временного ряда, а
при дополнительном условии р = 1, — об анализе одного временного ряда.
Заметим, что для экономических приложений наиболее типична си-
туация, когда моменты времени t>, t2,..., tN, в которые производится ре-
гистрация значений анализируемых признаков, являются равноотстоя-
щими, т.е. t2 -	= tz — t2 = • • • = tN —	— At. В этом случае время
удобнее считать и обозначать в числе «тактов» At. Соответственно то-
гда вместо , t2,..., tN мы будем иметь t — 1,2,...,N.
В ряде ситуаций и в первую очередь в ситуациях, когда исходные
статистические данные получают с помощью специальных опросов, ан-
кет, экспертных оценок, возможны случаи, когда элементом первичного
наблюдения является не состояние i-ro объекта в момент t, а характери-
стика 7ij(t) попарного сравнения двух объектов (или признаков) соответ-
ственно с номерами i и у, отнесенная к моменту времени t.
Характеристика 7^ определяет результат сопоставления объектов О,-
и О; в смысле некоторого анализируемого отношения: 7<у может выра-
жать меру сходства или различия объектов О, и Oj, меру их связи или
взаимодействия в каком-либо процессе (например, поток продукции от-
расли «1» в отрасль «у»), геометрическое расстояние между объектами,
отношение предпочтения (тогда, например, полагают 7,, = 1, если объект
О, не хуже объекта Oj, и 7,j = 0 в противном случае), наконец, стати-
стическую меру взаимной коррелированности (если речь идет о призна-
ках, то в качестве 7у могут рассматриваться, например, коэффициенты
корреляции или ковариации признаков и ж^). Из данного выше по-
яснения смысла характеристик 7,у следует, что в большинстве случаев
(но не всегда*.) они оказываются симметричными, т. е. 7,у = 7^ (при-
мер с взаимными потоками продукции из одной отрасли в другую как раз
относится к исключениям из этого правила).
Таким образом, в описываемой ситуации исследователь располагает
в качестве массива исходных статистических данных временной последо-
вательностью матриц парных сравнений размера п х п (если рассма-
триваются характеристики парных сравнений объектов) или р х р (если
328
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
рассматриваются характеристики парных сравнений признаков):
(9.2)
В статическом варианте, т. е. при N = 1, исследователь рас-
полагает лишь одной матрицей парных сравнений (Ъ])> описывающей си-
туацию в один какой-то фиксированный момент времени.
Очевидно, что от формы записи (9.1) можно непосредственно перейти
к (9.2) (при наличии заданной метрики в пространстве объектов и в про-
странстве признаков). Однозначный обратный переход от (9.2) к (9.1) без
дополнительных предположений и специальных методов (скажем, много-
мерного шкалирования, см. п. 13.6), в общем, невозможен. Возможны и
другие формы представления и.с.д., однако они встречаются значительно
реже описанных двух, поэтому здесь не рассматриваются.
Теперь можно сформулировать три центральные проблемы приклад-
ной статистики. Не следует думать, что эти проблемы исчерпывают все
содержание прикладной статистики. Более того, то, что именно эти про-
блемы выделены в качестве центральных, имеет условный смысл и объ-
ясняется в первую очередь «эконометрическими интересами» данного
издания.
Проблема I. Статистическое исследование структуры и
характера взаимосвязей, существующих между анализируемы-
ми количественными переменными. При этом под «переменными»
понимаются как регистрируемые на объектах признаки	...,
так и время t. Методам и моделям, предназначенным для решения различ-
ных постановок задач в рамках этой проблемы, посвящен целиком раздел
IV данного учебника, который, в частности, охватывает регрессионный
анализ (гл. 15), анализ временных рядов (гл. 16) и системы одновремен-
ных уравнений (гл. 17).
Более подробное обсуждение обшей постановки и особенностей этой
проблемы мы откладываем до главы 10, специально этому посвященной.
Это объясняется тем, что по своему значению и в прикладной статисти-
ке, и в эконометрике проблема статистического исследования зависимо-
стей заметно превосходит две другие.
Проблема П. Разработка статистических методов клас-
сификации объектов и признаков. Говоря о классификации совокуп-
ности объектов подразумеваем, что каждый из них задан соответствую-
щей строкой матрицы (9.1 ) либо геометрическая структура их попарных
9.1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ
329
расстояний (близостей) задана матрицей (7^), М = 1,2,...,п. Анало-
гично интерпретируется исходная информация в задаче классификации
признаков с той лишь разницей, что каждый из признаков задается
соответствующим (j-м) столбцом матрицы (9.1 ) или, в случае задания
и.с.д. в форме (9.2), — у-ми строками и столбцами матрицы (9.2).
В дальнейшем, если это специально не оговорено, не будем разделять
изложение этой проблемы на «объекты» и «признаки», поскольку все
постановки задач и основная методологическая схема исследования здесь
общие.
В общей (нестрогой) постановке проблема классификации объектов
заключается в том, чтобы всю анализируемую совокупность объектов
О = {О,} (> = 1,...,п), статистически представленную в виде матриц
(9.1') или (lij), разбить на сравнительно небольшое число (заранее из-
вестное или нет) однородных, в определенном смысле, групп или классов.
Для формализации этой проблемы удобно интерпретировать ана-
лизируемые объекты в качестве точек в соответствующем признаковом
пространстве. Если исходные данные представлены в форме матрицы
(9.1*), то эти точки являются непосредственным геометрическим изобра-
жением многомерных наблюдений Xt, Xj» • • •»Хп в р-мерном пространстве
Ох^ ,...,Ох^ (т.е. X, = (z^\...,zJp))T). Если же исходные данные
представлены в форме матрицы парных сравнений 7,5, то исследовате-
лю не известны непосредственно координаты этих точек, но зато задана
структура парных расстояний (близостей) между объектами. Естествен-
но предположить, что геометрическая близость двух или нескольких точек
в этом пространстве означает близость «физических» состояний соот-
ветствующих объектов, их однородность. Тогда проблема классификации
состоит в разбиении анализируемой совокупности точек-наблюдений на
сравнительно небольшое число (заранее известное или нет) классов та-
ким образом, чтобы объекты, принадлежащие одному классу, находились
бы на сравнительно небольших расстояниях друг от друга. Полученные
в результате разбиения классы часто называют кластерами (таксонами,
образами)1, а методы их нахождения соответственно кластер-анализом,
численной таксономией, распознаванием образов.
Статистическим методам классификации.посвящена гл. 12 учебника.
1 Cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых
каким-либо общим свойством. Taxon (англ.) — систематизированная группа лю-
бой категории (термин биологического происхождения). Название «кластер-анализ»
для совокупности методов решения задач такого типа было впервые введено, по-
видимому, Трайоном в 1939 г. (см. : Tryon R.C, Cluster Analysis. II Ann. Arb.f
Edw. Brothers. — 1939).
330 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
В зависимости от наличия и характера априорных сведений о природе ис-
комых классов и от конечных прикладных целей исследования приходится
обращаться либо к методам дискриминантного анализа (они описаны в
п. 12.3), либо к методам расщепления смесей вероятностных распределе-
ний или процедурам кластер-анализа (и те и другие описаны в п. 12.4).
Проблема III. Снижение размерности исследуемого при-
знакового пространства с целью лаконичного объяснения приро-
ды анализируемых многомерных данных. Возможность лаконично-
го описания анализируемых многомерных данных основана на априорном
допущении, в соответствии с которым существует небольшое (в сравнении
с числом р исходных анализируемых признаков х^2\..., х^) число р
признаков-детерминант (главных компонент, общих факторов, наиболее
информативных объясняющих переменных), с помощью которых могут
быть достаточно точно описаны как сами наблюдаемые переменные ана-
лизируемых объектов, т.е. все элементы матриц (9.1) и (9.2), так и опре-
деляемые этими переменными свойства (характеристики) анализируе-
мой совокупности. При этом упомянутые признаки-детерминанты могут
находиться среди исходных признаков, а могут быть латентными, т.е.
непосредственно статистически не наблюдаемыми, но восстанавливаемы-
ми по исходным данным вида (9.1), (9.1') или (9.2). Гениальный пример
практической реализации этой идеи дает нам периодическая система эле-
ментов Менделеева: в этом случае роль идеально информативного един-
ственного признака-детерминанта играет, как известно, заряд атомного
ядра.
Необходимость снижения размерности исследуемого признакового
пространства с целью лаконичного объяснения природы анализируемых
многомерных данных может быть продиктована различными прикладны-
ми задачами статистического анализа и моделирования. Ниже кратко
формулируются несколько типовых задач такого рода.
Отбор наиболее информативных показателей (включая вы-
явление латентных факторов). Речь идет об отборе из исходного
(априорного) множества признаков X = (х^\.. .,ж^)Т или о построе-
нии в качестве некоторых комбинаций исходных признаков относительно
небольшого числа р переменных Z(X) = (z^(X),..., z^p \х))Т, которые
обладали бы свойством наибольшей информативности в смысле, опреде-
ленном, как правило, некоторым специально подобранным для каждого
конкретного типа задач критерием информативности Ip»(Z). Так, на-
пример, если критерий Ipt(Z) «настроен» на достижение максимальной
точности регрессионного прогноза некоторого результирующего количе-
ственного показателя у по известным значениям предикторных перемен-
9.1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ 331
ных	то речь идет о наилучшем подборе наиболее суще-
ственных предикторов в модели регрессии (см. п. 15.6). Если же крите-
рий Ip>(Z) устроен таким образом, что его оптимизация обеспечивает наи-
высшую точность решения задачи отнесения объекта к одному из классов
по значениям X его описательных признаков, то речь идет о построе-
нии системы типообразующих признаков в задачах классификации (см.
п. 12.3 и 12.4) или о выявлении и интерпретации некоторой сводной (ла-
тентной) характеристики изучаемого свойства (см. п. 13.5). Наконец,
критерий IP>(Z) может быть нацелен на максимальную автоинформатив-
ность новой системы показателей Z, т. е. на максимально точное воспро-
изведение всех исходных признаков х^2\..., а/р) по сравнительно не-
большому числу вспомогательных переменных	(/ < р). В
этом случае говорят о наилучшем автопрогнозе и обращаются к моделям
и методам факторного анализа и его разновидностей (см. п. 13.2 и 13.3).
Сжатие массивов обрабатываемой и хранимой информации.
Этот тип задач тесно связан с предыдущим и, в частности, требует в
качестве одного из основных приемов решения построения экономной си-
стемы вспомогательных признаков, обладающих наивысшей автоинфор-
мативностью, т.е. свойством наилучшего автопрогноза (см. выше). В
действительности при решении достаточно серьезных задач сжатия боль-
ших массивов информации (подобные задачи весьма актуальны и в плане
необходимости минимизации емкостей носителей, на которых хранится
архивная информация, и в плане экономии памяти ЭВМ при обработке
текущей информации) используется сочетание методов классификации и
снижения размерности. Методы классификации позволяют подчас пе-
рейти от массива, содержащего информацию по всем п статистически
обследованным объектам, к соответствующей информации только по к
эталонным образцам (к <С п), где в качестве эталонных образцов берут-
ся специальным образом отобранные наиболее типичные представители
классов, полученных в результате операции разбиения исходного множе-
ства объектов на однородные группы. Методы же снижения размерности
позволяют заменить исходную систему показателей X — (х^\...,х^)Т
набором вспомогательных (наиболее автоинформативных) переменных
Z(X) = (z^\x),...,z^p\x))T. Таким образом, размерность информа-
ционного массива понижается от р • п до р' • к, т. е. во многие десятки раз,
если учесть, что р* и к обычно на порядки меньше соответственно р и п.
Визуализация (наглядное представление) данных. При фор-
мировании рабочих гипотез, исходных допущений о геометрической и ве-
роятностной природе совокупности анализируемых данных Xr, Xj,..., Хп
важно было бы суметь «подсмотреть», как эти данные-точки распола-
332 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
гаются в анализируемом пространстве. В частности, уже на предвари-
тельной стадии исследования хотелось бы знать, например, распадается
ли исследуемая совокупность точек на четко выраженные сгустки в этом
пространстве, каково примерное число этих сгустков и т.д.? Но макси-
мальная размерность * фактически осязаемого» пространства, как из-
вестно, равна трем. Поэтому, естественно, возникает проблема: нельзя
ли спроецировать анализируемые многомерные данные из исходного про-
странства на прямую, на плоскость, в крайнем случае — в трехмерное
пространство, но так, чтобы интересующие нас специфические особенно-
сти исследуемой совокупности (например, ее расслоенность на кластеры),
если они присутствуют в исходном пространстве, сохранились бы и после
проецирования. Следовательно, и здесь речь идет о снижении размерно-
сти анализируемого признакового пространства, но снижении, во-первых,
подчиненном некоторым специальным критериям и, во-вторых, оговорен-
ном условием, что размерность редуцированного пространства не должна
превышать трех. Аппарат для решения подобных задач представлен в
учебнике методом главных компонент и факторным анализом1.
Построение условных координатных осей (многомерное шка-
лирование, латентно-структурный анализ). В данном типе задач
снижение размерности понимается иначе, чем прежде. До сих пор речь
шла о подчиненном некоторым специальным целям переходе от заданной
V /	(1) (2)	(р)\
координатной системы X (т. е. от исходных переменных ж' ж' , ж' ')
к повой координатной системе Z(X), размерность которой р существен-
но меньше размерности р и оси которой .., 0г^р конструируются
с помощью соответствующих преобразований исходных признаков. Од-
нако в данной постановке задачи исходной координатной системы не су-
ществует вовсе, а подлежащие статистическому анализу и моделирова-
нию данные представлены в статическом варианте (9.2), т.е. в виде
матрицы (7,j), i,j = 1,2,...,n — парных сравнений объектов. Ставится
задача: для заданной, сравнительно невысокой, размерности р' опреде-
лить вспомогательные условные координатные оси . ,0z^p и спо-
соб сопоставления каждому объекту О, его координат (жр\...,ж|р^) в
этой системе таким образом, чтобы попарные отношения 7ij(Z) (напри-
мер, попарные взаимные расстояния) между объектами, вычисленные на
базе этих условных координат, в определенном смысле минимально бы
1 Наиболее эффективные современные методы для решения задач подобного типа объ-
единяются в подходе, называемом «целенаправленным проецированием многомер
ных наблюдений», Однако описание этого подхода выходит за рамки целей данного
учебника.
9.1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ
333
отличались от заданных величин (t,y = 1,2, ...,п). В определенных
условиях (в первую очередь в задачах педагогики, психологии, построе-
ния различных рейтингов и т. п.) построенные таким образом условные
переменные поддаются содержательной интерпретации и могут тогда рас-
сматриваться в качестве латентных характеристик определенных свойств
анализируемых объектов (такого типа задачи называют часто задачами
латентно-структурного анализа). Снижение размерности происходит
здесь в том смысле, что от исходного массива информации размерности
п • п переходим к матрице типа «объект — свойство» размерности р • п,
где р' «С п. Аппарат для решения подобных задач состоит из методов так
называемого многомерного шкалирования и представлен в п. 13.6.
9.1.3.	Новые постановки задач и ослабление
ограничительных условий в канонических
математико-статистических и эконометрических
моделях
Формализация (математическая постановка) реальных задач стати-
стического анализа и моделирования экономических данных и на базе это-
го опыта выработка типовых математических постановок задач, выходя-
щих за стеснительные рамки жестких канонических моделей, составля-
ют, пожалуй, самый важный и самый трудный этап прикладного стати-
стического исследования. Одновременно это направление деятельности в
прикладной статистике является и самым неблагодарным, поскольку de
facto оказался как бы «незаконнорожденным дитем» теории и практики
статистического анализа данных. Искусство реалистического моделиро-
вания формально не предусмотрено ни в одном из разделов мате • гтико-
статистической науки, а его развитие никак и ничем не стимулируется в
рамках этой дисциплины.
Тем не менее за последние десятилетия прикладная статистика пред-
ложила и проанализировала ряд новых интересных типовых постановок
математико-статистических задач, непосредственно стимулированных за-
просами практики (в том числе в социально-экономической сфере). В этой
связи можно упомянуть об уже успевших стать каноническими постановки
задач обобщенного метода наименьших квадратов (см. гл. 15), о различ-
ных подходах к построению устойчивых статистических выводов, о раз-
3 В подобных ситуациях элементы nj матрицы (9.2) отражают обычно результаты
попарных сравнений объектов О,- и Oj по анализируемому качеству. Например,
численное значение может отражать степень уверенности эксперта (или каким-
то способом вычисленную вероятность) того, что объект О,- лучше объекта О].
334
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
витии методов целенаправленного проецирования и томографии в связи с
исследованием геометрической и вероятностной природы анализируемых
многомерных данных (9.1) (см., например, [Айвазян С. А., Енюков И. С.,
МешалкинЛ. Д., Бухштабер В. М., 1989), а в последние годы — о фор-
мулировке и исследовании таких моделей анализа временных рядов, как
модель коинтеграции, ARCH- и GARCH-модели (см.п. 16), модель много-
мерной развертки временного ряда [Бухштабер В. М.] и др.
9.2.	Основные этапы прикладного
статистического анализа
Для пояснения роли и места основных приемов статистического моде-
лирования и методов первичной статистической обработки исходных дан-
ных удобно разложить общую логическую схему статистического анализа
на основные этапы исследование. Подобное разложение носит, конечно,
условный характер. В частности, оно не означает, что этапы осуществля-
ются в строгой хронологической последовательности один за другим. Бо-
лее того, многие из этапов (например, этапы 4, 5 и 6) находятся в плане
хронологическом в соотношении итерационного взаимодействия: резуль-
таты реализации более поздних этапов могут содержать выводы о необ-
ходимости повторной «прогонки» (с учетом новой информации) преды-
дущих этапов.
Этап 1: исходный (предварительный) анализ исследуемой реальной
системы. В результате этого анализа определяются: а) основные це-
ли исследования на неформализованном, содержательном уровне; б) со-
вокупность единиц, представляющая предмет статистического исследова-
ния; в) перечень (х^\х^2\..,9х^) отобранных из представленного спе-
циалистами априорного набора показателей, характеризующих состояние
(поведение) каждого из обследуемых объектов, который предполагается
использовать в данном исследовании; г) степень формализации соответ-
ствующих записей при сборе данных; д) общее время и трудозатраты,
отведенные на планируемые работы, и коррелированные с ними времен-
ная протяженность и объем необходимого статистического обследования;
е) моменты, требующие предварительной проверки перед составлением
детального плана исследования (например, не всегда априори ясна воз-
можность идентификации единиц наблюдения); ж) формализованная по-
становка задачи, по возможности включающая вероятностную модель изу-
чаемого явления и природу статистических выводов, к которым должен
(или может) прийти исследователь в результате переработки массива ис-
ходных данных; з) формы, используемые для сбора первичной информа-
9.2. ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 335
цик и для введения ее в вычислительное устройство.
По затратам сил наиболее квалифицированного персонала, участву-
ющего в работе, трудоемкость первого этапа работы весьма значительна
и бывает даже сравнима с суммарной трудоемкостью всех остальных эта-
пов при условии, что обработка проводится с помощью подходящего па-
кета программ1. Поэтому максимального развития заслуживают методы
машинного ассистирования в проведении этой части работы. Оно может
заключаться в подсказке (с одновременной оценкой) форм документации
для сбора первичной информации, медицинских приложений), в автома-
тизированном режиме выбора подходящих моделей, в ведении тезауруса
исследования и т. п.
Этап 2: составление детального плана сбора исходной статисти-
ческой информации. При составлении этого плана необходимо по возмож-
ности учитывать полную схему дальнейшего статистического анализа, о
чем часто забывают. Априорное представление о том, как и для чего дан-
ные будут анализироваться, может оказать существенное влияние на их
сбор. При планировании особого внимания заслуживают случаи, когда:
а) используется аппарат теории выборочных обследований, т. е. определя-
ется, какой должна быть выборка — случайной, пропорциональной, рас-
слоенной и т. п.; б) хотя бы для части входных переменных эксперимент
носит активный характер, т.е. переменные допускают фиксацию в ка-
ждом конкретном наблюдении на определенном уровне, и выбор плана об-
следования осуществляется с привлечением методов планирования экспе-
риментов. В некоторых руководствах по статистике этот этап называют
этапом «организационно-методической подготовки*. Как уже было упо-
мянуто в п. 6.1, вопросы разработки методологии определения априорной
системы показателей, характеризующих исследуемый объект или процесс,
вынесены за рамки описываемых здесь этапов и должны быть отнесены к
области предметной (в нашем случае — экономической) статистики.
Этап S'. сбор исходных статистических данных и их ввод в вы-
числительное устройство. Одновременно в вычислительное устройство
вносятся полные и краткие (для автоматизированного воспроизводства в
таблицах) определения используемых терминов. В программном обеспече-
нии должны быть предусмотрены специальные меры, исключающие или
резко уменьшающие возможность появления расчетов не с тем подмноже-
1 В некоторых специальных статистических исследованиях социально-экономического
н других профилей, характеризующихся большими затратами времени и средств
на сбор исходных статистических данных, сформулированный тезис остается спра-
ведливым лишь при условии исключения этапа 3 из суммарной трудоемкости всех
остальных этапов.
336
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
ством данных или не для той подгруппы объектов.
Таким образом, независимо от того, производится ли исследователем
выбор метода и плана статистического обследования или он уже распола-
гал результатами так называемого пассивного эксперимента, к моменту
определения основного инструментария статистического исследования ис-
следователь в общем случае располагает в качестве массива исходных ста-
тистических данных матрицами наблюдении вида (9.1), (9.11) или (9.2).
Этап 4‘ первичная статистическая обработка данных. В ходе пер-
вичной статистической обработки данных обычно решаются следующие
задачи: а) отображение переменных, описанных текстом, в номинальную
(с предписанным числом градаций) или ординальную (порядковую) шка-
лу; б) статистическое описание исходных совокупностей с определением
пределов варьирования переменных; в) анализ резко выделяющихся на-
блюдений; г) восстановление пропущенных наблюдений; д) проверка ста-
тистической независимости последовательности наблюдений, составляю-
щих массив исходных данных; е) унификация типов переменных, когда с
помощью различных приемов добиваются унифицированной записи всех
переменных; ж) экспериментальный анализ закона распределения иссле-
дуемой генеральной совокупности и параметризация сведений о природе
изучаемых распределений (иногда этот этап называют процессом соста-
вления сводки и группировки). Кроме того, этап 4 включает в себя вычи-
слительную реализацию решения следующих вопросов: учет размерности
и алгоритмической сложности задачи и одновременно возможностей ис-
пользуемого вычислительного средства; формулировку задачи на входном
языке используемого программного обеспечения и т. п. (см. подробнее об
этом в описании этапа 6).
Остановимся на некоторых из затронутых вопросов подробнее.
Анализ резко выделяющихся наблюдений. Часто даже беглый пред-
варительный просмотр (визуальный или автоматизированный) исходных
данных (9.1) или (9.2) может вызвать у исследователя сомнения в истин-
ности (или правомерности) отдельных наблюдений, слишком резко вы-
деляющихся на общем фоне. В этих случаях возникает вопрос: вправе
ли мы объяснить обнаруженные резкие отклонения в исходных данных
(аномальные выбросы) лишь обычными случайными колебаниями выбор-
ки (которые обусловлены природой анализируемой генеральной совокуп
ности) или здесь дело в существенных искажениях стандартных условие
сбора статистических данных, а возможно, и в прямых ошибках регистра
ции (записи)? В последних двух случаях «подозрительные» наблюдения
очевидно, следует исключить из дальнейшего рассмотрения.
Единственным абсолютно надежным способом решения вопроса о(
9.2. ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 337
исключении резко выделяющихся результатов наблюдений является тща-
тельное рассмотрение условий, при которых эти наблюдения регистри-
ровались. Однако во многих случаях проведение такого содержательно-
го анализа объективно затруднительно или принципиально невозможно.
Тогда необходимо обратиться к соответствующим формальным (стати-
стическим) методам. Общая логическая схема этих методов следующая:
отправляясь от исходных допущений о природе анализируемой совокуп-
ности данных, исследователь задается функцией
p(X--,XitX2,...,Xn)	(9.3)
от всех имеющихся наблюдений, херактеризующей степень аномальности
(меру удаленности от основной массы наблюдений) «подозрительного»
наблюдения X*, а затем подставляет в (9.3) реальные значения наблю-
дений и сравнивает величину с некоторым пороговым значением ро1; если
р > р0, то подозрительное наблюдение X* или полностью исключается из
дальнейшего рассмотрения, или его вклад уменьшается с помощью весо-
вой функции, убывающей по мере роста степени аномальности наблюде-
ний (см. п. 7.5.3).
С одним из вариантов методов анализа резко выделяющихся наблю-
дений читатель познакомился в п. 8.6.
Восстановление пропущенных (стертых) наблюдений. В ма-
трицах исходных статистических данных (9.1) или (9.2) по разным причи-
нам (в том числе и в результате исключения резко выделяющихся наблю-
дений) могут быть пропуски отдельных элементов или каких-то частей
:трок или столбцов. Исключать по этой причине из дальнейшего рассмо-
грения весь объект (строку, в которой обнаружены пропуски) или при-
нтах (столбец, в котором обнаружены пропуски) слишком расточительно
: точки зрения потери полезной информации. Поэтому возникает задача
1аилучшего в некотором смысле восстановления пропущенных (стертых)
(анных. Конкретизация критерия качества восстановления стертых дан-
гых производится в зависимости от характера последующей обработки
[сходных данных, т. е. в зависимости от окончательных целей исследова-
[ия (см., например, [Айвазян С. А., Енюков И. С-, Мешалкин Л. Д., 1983]).
Проверка однородности нескольких порций исходных дан-
iwx. Объективные условия сбора исходных статистических данных, осо-
1 В вероятностной постановке задачи пороговое значение ро определяется из стандарт-
ных статистических таблиц с учетом знания закона распределения статистики р в
предположении необоснованности «подозрений» относительно наблюдения X*. В
других случаях ро определяется из содержательных соображений.
338
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
бенно в ситуациях пассивного эксперимента, могут быть такими, что об-
щая (р х п)-матрица наблюдений (см. (9.1)) получается составлением не-
скольких (р X ni)-, (р X па)—,...,(р х п*)-матриц (частных) наблюдении
(ni + Пэ + • —F Пк = п), г№ каждая из частных матриц задает порцию
исходных данных, относящихся к некоторой подсовокупности, состоящей
из ту объектов. При этом процессы (моменты) обследования этих сово-
купностей могут быть разделены в пространстве (во времени).
Очевидно, перед тем как подвергнуть исходные данные основной ста-
тистической обработке (т. е. применять к ним те или иные методы при-
кладного статистического анализа, выбор которых обусловлен конечными
целями исследования), исследователь должен ответить на вопрос: право-
мерно ли объединение имеющихся в его распоряжении порций (выборок) в
один общий массив или же каждая из порций имеет свою специфику, следо-
вательно, и обрабатывать их надо по отдельности? В рамках математико-
статистических моделей этот вопрос сводится к выяснению (с помощью
соответствующих статистических критериев), можно ли считать эти пор-
ции данных различными выборками из одной и той же генеральной со-
вокупности (см., например, пп.8.1.2, 8.6.3, 8.6.4).
Проверка статистической независимости последовательно-
сти наблюдений, составляющих массив исходных данных. При-
менение многих статистических методов является правомерным лишь в
ситуациях, когда справедливо допущение о статистической независимо-
сти обрабатываемого ряда наблюдений А\,Х2,.Хп- Этот же вопрос
возникает и применительно к рядам {ХД^),.. .,.¥,(7^}. Поэтому, перед
тем как подвергнуть имеющиеся результаты наблюдения основной стати-
стической обработке, необходимо выяснить (с помощью соответствующих
статистических критериев (см. п. 16.1)), являются ли они статистически
независимыми или их следует рассматривать как последовательности вза-
имозависимых величин.
Унификация типа переменных. Одна из сложностей автоматизи-
рованного анализа информации заключается в том, что среди компонент
а/2\...,хМ анализируемого многомерного признака могут быть по-
казатели трех разных типов: количественные, качественные (порядко-
вые, ординальные) и классификационные (номинальные). Их определение
и сущность приведены в п. 2.3.
В связи с этим возникает вопрос унификации записи единичного на-
блюдения, снятого с объекта i. В соответствии с одним из вариантов реше-
ния этого вопроса t-e многомерное наблюдение в унифицированной записи
представляется вектор-столбцом размерности mj +ma + * • -+mp, где m* —
число градаций (интервалов группирования, уровней качества или одно-
9.2. ОСНОВНЫЕ ЭТАПЫ ПРИКЛАДНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА 339
родных групп) признака х^к\ причем компонентами этого вектор-столбца
могут быть только нули или единицы. При таком подходе к достижению
единообразия записи наблюдений многомерного признака смешанной при-
роды мы вынуждены мириться, во-первых, с элементами субъективизма в
выборе способов разбиения диапазонов изменения анализируемых количе-
ственных признаков на интервалы группирования и, во-вторых, с опреде-
ленной потерей информативности исходных данных, связанной с перехо-
дом от индивидуальных к группированным значениям по количественным
переменным.
В качестве альтернативного подхода к способу унификации записи
исходных данных может быть использована идея, прямо противополож-
ная той, на основании которой построен только что описанный прием. В
частности, руководствуясь некоторыми дополнительными соображениями
(и допущениями), исследователь пытается преобразовать качественные
и классификационные переменные в количественные, используя процесс
так называемой «оцифровки», или шкалирования, неколичественных пе-
ременных, а также некоторые специальные модели (см. [Айвазян С. А.,
Енюков И. С., Мешалкин Л. Д., 1983, п. 10.2).
Экспериментальным анализ закона распределения исследуе-
мой генеральной совокупности и вопрос ее подходящей параме-
тризации. Эта часть предварительной статистической обработки ис-
ходного массива данных, представленных в виде (9.1), включает в себя
вычисление основных числовых характеристик распределения: среднего
значения, дисперсии, коэффициентов асимметрии и эксцесса, а в многомер-
ном случае — и элементов выборочной ковариационной матрицы. Кроме
того, исследователь проводит численный и графический анализ одномер-
ных законов распределения рассматриваемых показателей, заключающий-
ся в построении соответствующих полигонов частот, гистограмм, эмпи-
рических функции распределения. Результаты этого экспериментально-
го анализа, дополненные априорными сведениями о природе анализируе-
мой генеральной совокупности, зачастую оказываются достаточными для
формулировки одной или нескольких конкурирующих гипотез об общем
(параметрическом) виде закона распределения вероятностей, задающего
эту генеральную совокупность. Не следует пренебрегать такой возмож-
ностью, поскольку знание общего вида вероятностного распределения в
исследуемой генеральной совокупности позволяет сделать наилучший вы-
бор метода статистического оценивания параметров этого распределения,
а также метода последующей основной статистической обработки масси-
ва исходных данных (из набора конкурирующих методов). Как известно,
выяснение непротиворечивости высказанной исследователем гипотезы об
340
ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
общем виде распределения анализируемых наблюдений с природой и спе-
цификой имеющихся в распоряжении исследователя конкретных исходных
данных осуществляется с помощью тех или иных статистических крите-
риев согласия (см. пп. 8.1.1 и 8.6.1).
Этап 5: составление детального плана вычислительного анализа
материала. Этап начинается с составления справки по собранному мате-
риалу и результатам предварительного анализа. Определяются основные
группы, для которых будет проводиться дальнейший анализ. Пополняет-
ся и уточняется тезаурус содержательных понятий. Четко описывается
блок-схема анализа с указанием привлекаемых методов. Формулируется
оптимизационный критерий, на основании которого выбирается один из
альтернативных методов (или одно из альтернативных семейств методов)
основной статистической обработки исходных данных.
Этап 6: вычислительная реализация основной части статистиче-
ской обработки данных. Основная забота исследователя на этом этапе —
эффективное управление вычислительным процессом путем формулиров-
ки задачи обработки и описания данных на входном языке используемо-
го программного обеспечения. Учитываются размерность задачи, алго-
ритмическая сложность вычислительного процесса, возможности исполь-
зуемого вычислительного средства (длина слова, быстродействие, объем
оперативной памяти, организация базы данных и т.п.) и, наконец, осо-
бенности данных (степень обусловленности используемых при реализации
линейных процедур матриц, надежность априорных оценок параметров и
т.п.).
Этап 7: подведение итогов исследования. Этап начинается с по-
строения формального статистического отчета о проведенном исследова-
нии. При интерпретации результатов применения статистических проце-
дур (оценка параметров, проверка гипотез, отображения в пространство
меньшей размерности, классификация и т. п.) учитывается как место этих
процедур в блок-схеме анализа, так и соотношение объемов используемых
выборок, размерности пространства наблюдений, числа и значений пара-
метров. Теоретически эти вопросы, несмотря на их крайнюю актуаль-
ность, разработаны довольно мало.
Затем результаты исследования, его основные выводы формулируют-
ся в содержательных терминах. Если исследование проводилось в рамках
математико-статистических методов и моделей, то его выводы формули-
руются в терминах оценок неизвестных параметров анализируемой систе-
мы или в виде ответа на вопрос о справедливости проверяемой гипотезы и
сопровождаются гарантируемыми количественными оценками степени их
достоверности. Если же исследование осуществлялось средствами анали-
выводы
341
за данных (т.е. в рамках логико-алгебраического подхода), то его выводы
не претендуют на вероятностную интерпретацию.
В заключение проверяется, в какой мере достигнуты намеченные на
этапе 1 содержательные цели работы, и если достигнуты не все из них, то
объясняется, почему. Работа завершается содержательной формулиров-
кой новых задач, вытекающих из проведенного исследования.
В некоторых руководствах по статистике этапы 5, 6 и 7 объединены
в одном этапе, названном < Обработка и анализ* .
Резюмируя описание общей логической схемы статистического ана-
лиза исходных данных, отметим, что основные приемы статистического
моделирования и методы первичной статистической обработки являются
главными в ходе реализации важнейших этапов 1, 4 и 7, а также по мере
необходимости могут привлекаться при реализации этапов 3, 5 и 6.
ВЫВОДЫ
1.	Прикладная статистика заимствует часть методов статистиче-
ского анализа и моделирования у математической статистики и имеет пе-
ресечения в задачах и целях с эконометрикой. Однако основными харак-
терными чертами, отличающими прикладную статистику от этих двух
дисциплин, являются следующие:
•	основу методологии разработки инструментария прикладной стати-
стики составляет подход, позволяющий в рамках единой унифици-
рованной логической схемы синтезировать две автономно возник-
ших и какое-то время взаимонезависимо развивавшихся концеп-
ции анализа данных и моделирования — вероятностную и логико-
алгебраическую; в результате прикладная статистика объединила в
себе как прикладные вероятностно-статистические методы многомер-
ного статистического анализа, так и логико-алгебраические методы
анализа данных, не использующие в своих построениях вероятност-
ных рассуждений;
•	главный исследовательский интерес прикладной статистики сосредо-
точен на трех проблемах: (а) статистическом исследовании зависи-
мостей между анализируемыми показателями; (б) статистических
методах классификации объектов и признаков; (в) методах сниже-
ния размерности исследуемого признакового пространства с целью
лаконичного объяснения природы анализируемых многомерных дан-
ных;
•	прикладная статистика, в отличие от математической статистики
и в какой-то мере эконометрики относится к весьма динамичным
342 ГЛ. 9. ВВЕДЕНИЕ В ПРИКЛАДНОЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
по своему содержанию и постановкам задач научным дисциплинам:
она постоянно нацелена на выработку новых (стимулированных за-
просами практики) постановок задач и на достижение результа-
тов , позволяющих ослабить ограничительные условия в канониче-
ских математико-статистических и эконометрических моделях.
2.	Двумя наиболее распространенными формами представления ис-
ходных статистических данных, поступающих «на вход» прикладного
статистического анализа и моделирования, являются матрицы «объект-
свойство* вида (9.1) и JKamputfM парных сравнений (объектов или при-
знаков) вида (9.2). Первая из них содержит результаты измерении анали-
зе	v ( (1)	(2)	(р)\Т
зируемого набора признаков X = (аг , аг аг ') на статистически
обследуемом множестве объектов Oj, О2, ..., Опу а вторая (чаше всего по-
лучаемая с помощью специальных анкет и экспертных опросов) состоит из
характеристик попарных сравнений статистически обследуемых объектов
по некоторому анализируемому свойству.
3.	Проблема статистического исследования зависимостей состоит,
в самой общей формулировке, в выявлении и описании парных и множе-
ственных статистических связей (их смысла, степени тесноты, формы и
т.п.), существующих между компонентами анализируемого многомерного
признака X = (®^\«^2\...,ж^р^)т. Причем анализ этих связей произ-
водится на основании исходных статистических данных вида (9.1) или
(9.2). Описанию задач и инструментария, относящихся к этой проблеме,
посвящены гл. 10,11, 15,16 и 17.
4.	Проблема классификации объектов (в общей, нестрогой, постанов-
ке) заключается в том, чтобы всю анализируемую совокупность объектов
..,ОП, статистически представленную в виде матриц (9.1) или
(9.2), разбить на сравнительно небольшое число (заранее известное или
нет) однородных, в определенном смысле, групп или классов. Описанию
задач и инструментария, относящихся к этой проблеме, посвящена гл. 12.
5.	Проблема снижения размерности анализируемого признакового
пространства состоит в таком переходе от исходного набора р признаков
(ж^\ я/2\...»х^) к вспомогательному набору гораздо меньшего числа р
признаков-детерминант z^l\z^2\..., z^p \ при котором либо наблюденные
значения самих исходных признаков (т.е. данные матрицы (9.1)), либо
некоторые интересующие нас свойства или характеристики, определяе-
мые исходными признаками, могут быть наиболее точно (в определенном
смысле) оценены по совокупности значений вспомогательных признаков
z<	2),...tz^pK При этом упомянутые признаки-детерминанты могут
выбираться из числа исходных, а могут конструироваться в качестве не-
которых функций от исходных признаков. К методам снижения размер-
выводы
343
ности обращаются при решении ряда конкретных типовых прикладных
задач статистического анализа и моделирования, среди которых:
•	отбор наиболее информативных показателей в задачах классифика-
ции (п. 12.3 и 12.4), в моделях регрессии (п. 15.6) и при построении инте-
гральной латентной характеристики («агрегатного скалярного индикато-
ра») изучаемого свойства (п. 13.4);
•	сжатие больших массивов обрабатываемой и хранимой информации;
•	визуализация (наглядное представление) многомерных статистиче-
ских данных;
•	построение условных координатных осей для описания «состояний»
объектов, статистически заданных матрицей парных сравнений (9.2).
6. Общая логическая схема статистического анализа какого-либо про-
цесса или явления может быть условно разложена на следующие семь эта-
пов:
1)	предварительный анализ исследуемой реальной системы;
2)	составление детального плана сбора исходной статистической ин-
формации;
3)	сбор исходных статистических данных;
4)	преданализ или первичная статистическая обработка данных;
5)	составление плана моделирования и вычислительного анализа маг
териала;
6)	вычислительная реализация методов статистического анализа и
моделирования;
7)	интерпретация результатов и подведение итогов исследования.
В рамках этой схемы удобно комментировать роль и место основных
разделов и методов прикладной статистики.
ГЛАВА 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ
ЗАВИСИМОСТЕЙ (ОСНОВНЫЕ
ПОНЯТИЯ И ПОСТАНОВКИ ЗАДАЧ)
10.1. Общая формулировка проблемы,
пример
Любой закон природы или общественного развития может быть вы-
ражен в конечном счете в виде описания характера или структуры вза-
имосвязей (зависимостей), существующих между изучаемыми явлениями
или показателями (переменными величинами или просто переменными).
Если эти зависимости: а) стохастичны по своей природе, т.е. позволя-
ют устанавливать лишь вероятностные логические соотношения между
изучаемыми событиями Л и В, а именно соотношения типа сиз факта
осуществления события А следует, что событие В должно произойти, но
не обязательно, а лишь с некоторой (как правило, близкой к единице) ве-
роятностью Р»; б) выявляются на основании статистического наблюде-
ния за анализируемыми событиями или переменными, осуществляемого
по выборке из интересующей нас генеральной совокупности (см. гл. 6),
то мы оказываемся в рамках проблемы статистического исследования
зависимостей. Соответствующий математический аппарат, будучи та-
ким образом нацеленным в первую очередь на решение основной проблемы
естествознания: как по отдельным, частным наблюдениям выявить и опи-
сать интересующую нас общую закономерность, — занимает, бесспорно,
центральное место во всем прикладном математическом анализе.
Перед тем как перейти к формулировке общей и частных задач ста-
тистического исследования зависимостей, условимся описывать функци-
онирование изучаемого реального объекта (системы, процесса, явления)
набором переменных (рис. 10.1), среди которых:
а/1), а/2),...,х^ — так называемые «входные» переменные, они-
ЮЛ. ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР
345
сывающие условия функционирования (часть из них, как правило, под-
дается регулированию или частичному управлению); в соответствую-
щих математических моделях их называют независимыми, факторами-
аргументами, предикторными (или просто предикторами, т. е. предсказа-
телями), экзогенными, объясняющими (в книге мы будем использовать в
основном два последних термина);
у(Т)»	>У™ — выходные переменные, характеризующие пове-
дение или результат (эффективность) функционирования; в математи-
ческих моделях их называют зависимыми, откликами, эндогенными, ре-
зультирующими или объясняемыми (в книге используются в основном три
последних термина);
_(1) Анализируемая реальная система
С*
(2)	(объект)
с*
Случайные
факторы,
не подда-
ющиеся
учету
У(1)
„(2)
Механизм преобразования ___
входных переменных в --------
результирующие показатели----
резуль-
тирую-
щие пе-
ремен-
ные
Объясняю- '
щие пере-
менные <
(предик-
торные)
X
X

Рис. 10.1.
Общая схема взаимодействия переменных при статистическом ис-
следовании зависимостей
. .,£^т) — латентные (т.е. скрытые, не поддающиеся непо-
средственному измерению) случайные достаточные* компоненты, отра-
жающие влияние (соответственно на у^\у^2\... не учтенных «на
входе» факторов, а также случайные ошибки в измерении анализируемых
показателей (в математических моделях мы их, как правило, будем име-
новать просто «остатками»).
Тогда общая задача статистического исследования зависимостей (в
терминах изучаемых показателей) может быть сформулирована следую-
щим образом:
346
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
по результатам п измерений
{(»<’>,.............................................„ (ЮЛ)
исследуемых переменных на объектах (системах, процессах) анализиру-
емой совокупности построить такую (векторнозначную) функцию

,*<р)) =
(10.2)
которая позволила бы наилучшим (в определенном смысле) образом вос-
станавливать значения результирующих (прогнозируемых) переменных
Y = (у^\у^2\ • •	по заданным значениям объясняющих (экзоген-
\	v ( (Л (2)	(р)\Т
ныя) переменных X = (аг ,хх	.
Данная формулировка задачи нуждается в уточнениях. В частности,
прежде всего мы должны ответить на следующие вопросы:
а)	каково математическое выражение (или структура модели) ис-
комой зависимости между Y и X, записанное в терминах Y,X^f(X) и
e = (?’),£(2),...>eW)T?
б)	в соответствии с каким критерием качества апроксимации значе-
ний Y с помощью функции Г(Х) мы будем определять наилучший способ
восстановления значений результирующих показателей по заданным зна-
чениям объясняющих переменных?
в)	с какой именно прикладной целью мы проводим все наше исследо-
вание, т. е. для решения каких конкретных задач мы собираемся исполь-
зовать построенную в результате исследования функцию Г(Х)?
Прежде чем обсуждать эти вопросы, рассмотрим пример.
Пример 10.1. Анализируется «поведение» двумерной случайной
величины (£,*?), где £ (ден.ед.) — среднедушевой доход и т] (ден.ед) —
среднедушевые денежные сбережения в семье, случайно извлеченной из
рассматриваемой совокупности семей, однородной по своему потребитель-
скому поведению. В табл. 10.1 и на рис. 10.2 представлены исходные ста-
тистические данные вида (10.1), характеризующие среднедушевые вели-
чины дохода (zf) и денежных сбережений (у,) за определенный отрезок
времени, а именно за месяц, в каждой (t-й, i = 1,2,...,п) обследованной
семье рассматриваемой совокупности семей (в данном условном примере
объем п статистически обследованной совокупности семей равнялся 40). В
этом примере имелась возможность при отборе исходных данных (выбор-
ки) контролировать значения экзогенной переменной f, что позволило, в
10.1. ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР
347
частности, разбить статистически обследованные семьи на четыре равные
по объему группы по доходам.
Рис. 10.2. Графическое представление результатов обследования 40 семей
по их среднедушевому доходу (г,) и среднедушевым денежным
сбережениям (><)
Мы видим, что даже в пределах каждой из этих групп величины сред-
недушевых сбережений семей подвержены некоторому неконтролируемому
разбросу, обусловленному влиянием множества не поддающихся строгому
учету и контролю факторов (т.е. налицо упомянутый выше стохасти-
ческий характер зависимости между х и у). Однако это еще не значит,
что расположение точек	являющихся геометрическим изображе-
нием результатов обследования семей по доходу и сбережениям, должно
быть совершенно хаотичным и не должно обнаруживать некоторой вполне
определенной тенденции, характеризующей зависимость денежных сбе-
режений в семье (rf) от ее среднедушевого дохода (£). При исследовании
подобных зависимостей встают следующие основные вопросы (в скобках
после вопроса указываются главы и пункты настоящей книги, ему посвя-
348	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
тценные).
1.	Как исходя из конкретных прикладных целей исследования опре-
делить смысл, в котором понимается исследуемая зависимость? (п. 10.2 и
10.5).
2.	Имеется ли вообще какая-либо связь между исследуемыми перемен-
ными (а в случае многих переменных какова структура этих связей?) и
как измерить тесноту этой связи? (гл. 11).
3.	Каков общий математический вид искомой связи между rj и £,
т.е. как определяется общая структура соответствующей математиче-
ской модели? (п. 10.7).
4.	Как, отправляясь от принятой общей структуры модели, провести
необходимую вычислительную обработку исходных данных (10.1) с целью
получения конкретного вида зависимости т) от £, что позволит в данном
случае производить количественную оценку неизвестных денежных сбере-
жений семьи по заданной величине ее среднедушевого довода? (гл. 15, 16,
И)-
5.	Поскольку наши выводы основаны на обработке ограниченного ря-
да наблюдений, то их количественные характеристики, естественно, под-
вержены (при повторениях соответствующих выборочных обследований)
некоторому случайному разбросу. Как оценить степень точности наших
выводов? (гл. 15, 16, 17).	4
6.	Как решать сформулированные выше вопросы в ситуациях, когда
среди объясняющих (предикторных) переменных могут быть и неколиче-
ственные? (ответы на 2-й вопрос — в гл. 11).
Вернемся к нашему примеру и попробуем ответить на некоторые из
поставленных здесь вопросов, в том числе на принципиальные вопросы
а), б) и в), ответы на которые позволяют уточнить общую формулировку
задачи статистического исследования зависимостей, данную выше.
Начнем «с конца», т. е. с уточнения конечных прикладных исследова-
ний (см. вопросы 1, а также а) и в)). Известно, что из двух анализируе-
мых характеристик материальной состоятельности семьи характеристика
денежных сбережений (yj) относится к категории статистически трудно-
доступных: содержащиеся в ежегодных и единовременных выборочных
семейных бюджетных обследованиях Госкомстата РФ сведения о сбереже-
ниях, как правило, ненадежны и непредставительны. Поэтому главной
конечной целью нашего исследования (опирающегося, как мы будем все-
гда предполагать, на достоверную и репрезентативную выборку исходных
данных) является возможность восстановления (прогноза):
• удельной (т. е. в расчете на одного члена семьи за определенный от-
резок времени) величины денежных сбережений в конкретной семье (у(х))
10.1. ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР
349
ло заданному значению ее среднедушевого дохода х;
• удельной величины средних денежных сбережений (уср(х)) в семьях
данной группы х по доходам.
Этой цели мы сможем достигнуть, если сумеем математически опи-
сать закономерность изменения условных теоретических средних значе-
ний уср(х) = Е(»7 | £ = х) в зависимости от х, а также изучить характер
случайного разброса денежных сбережений у(х) отдельных семей данной
группы х по доходам относительно своего среднего значения уср(х) (при
любом интересующем нас значении среднедушевого дохода х). Это есте-
ственным образом приводит нас к необходимости рассмотрения матема-
тической модели вида
TJ = /(*) + в,	(10.3)
в которой остаточная компонента £ отражает случайное отклонение де-
нежных сбережений наугад выбранной отдельной семьи с доходом £ = х
от среднего значения уср(х) = E(i? | £ = х) этих сбережений, подсчитанно-
го по всем семьям данной группы по доходам, а функция /(х) описывает
характер изменения условного среднего уср(х) (при £ = х) в зависимости
от изменения х, если дополнительно прийти к соглашению, что харак-
тер случайного разброса величин у(х) = (г/ | £ = х) относительно своих
средних уср(х) таков, что Е(е | £ = х) = 0 при всех х.
Таким образом, из (10.3) мы непосредственно получаем
Уср = E(iy | С = х) = /(х).	(10.4)
Чтобы покончить с вопросами 1, а) и в), остается уточнить общую струк-
туру модели, т.е. определить, в каком классе F функций /(х) мы будем
производить аппроксимацию искомой зависимости &р(х).
В нашем случае, учитывая однородный (по характеру потребитель-
ского поведения) состав исследуемой совокупности семей, естественно ис-
ходить из гипотезы об одинаковой (в среднем) склонности семей к сбе-
режениям, выражающейся, в частности, в том, что все семьи начиная с
некоторого «порогового» уровня дохода склонны отделять в сбережения в
среднем одинаковую долю дохода. Математически, как легко понять, это
выразится в виде
уср(х) = 0о + 01®,	(10.5)
где 0Q и 01 — некоторые константы (неизвестные параметры модели).
Так что
F = {0o + 01x},	(10.6)
где под {/(х;0)} понимается семейство всех тех функций /(х;0), ко-
торые могут быть получены при подстановке вместо 0 ее оазличных
350
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
конкретных значений (0 — векторный параметр; в нашем случае О =
(во,в1)Т).
Таблица 10.1
Средне- душевой ДОХОД (ден.ед.)	Средне- душевые сбереже- ния (ден.ед.)	Средние сбережения для семей данной группы (ден.ед.)	Оценка среднеквадра- тического отклонения з и коэффициента вариа- ции V сбережений для семей данной доход- ной группы	
1	2	3	4	
	У1 = 15,2 1/2 = Ю,7			1 л
= Я!2 =	Уз = 18,5	II н	«(«?) =	111 |Е й 1—1
... = zI0 =	3/4 = Н,9	10 =	52 Vi = 17,9 i=i	-я*?))5	I4 = 6,4
= г? = 80	I/н = 24,1 3/6 = ю,з 1/7 = 14,2 3/8 = 31,о 1/э = 20,4 З/ю = 20,0		v(*?)	= 36%
	3/11 = 70,1 1/12 = 35,0			ол
*11 = г12 =	3/13 = 43,0	М»>) =	з(х$) =	1 Е (й)
. .. = 2?20 = = z” = 120	3/14 = 29,0 У15 = 17,0 3/16 = 48,2 3/17 = 18,9 1/18 = 53,0 1/19 = 39,4 1/20 = 46,2	20 = ТО Е Й = 40,0 1=11	-«(«?))’	1—11 = 16,0 = 40%
10.1. ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР
351
Продолжение таблицы 10.1
1	2	3		4	
Ж21 = Ж22 = • • • = ®зо = = г® = 160	У21 = 49,6 Угг — 69,4 1/гз = 77,8 1/24 = 43,0 1/25 = 31,8 Уго = 62,6 #27 = 100,2 Угв = 68,8 Угэ = 78,0 Узо = 29,6	_ 1 — 10	А со II II £ ЗМЗ	1 «и.	и "	wo 'ТГ*	wo wo	II •*	ы 		30 1 Е (й . »=21 i = 22,6 = 37%
	Уз1 = 125,5 Узг = 88,3				
*31 = *32 =	Узз = 62,0		»(*“) =	X«S) =	40 1 Е (и .*_41
...= Хм = = г$ = 200	S О to	-ч S W	lU II II И II II	II	II Ю СО Й СО -4 00	СЛ JO J» g СП JO рк ро Ч -QQ сл о о Ъо	_ 1 “ 10	40 Е й = 84,2 <=31	-s(*°))1 2 М)	t—«31 i = 28,9 = 34%
Такой выбор «класса допустимых решений» F = {/(г)} подтверждал
ется и характером расположения совокупности точек, являющихся гео-
метрическим изображением исходных данных в нашем примере (см. на
рис. 10.2 расположение «крестиков», ординаты которых определяются экс-
периментально подсчитанными, т. е. вычисленными на основании имею-
щихся выборочных данных, условными средними y(xi),i = 1,2,3,4)\
1 Обращаем внимание читателя на разницу в смысле и обозначениях эксперименталь-
ных (выборочных) и теоретических условных средних соответственно f (х) и Уср(*)>
Строго говоря, на практике теоретических средних мы никогда знать не можем, од-
нако мы опираемся в своем исследовании на тот факт, что в соответствии с законом
352	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
И наконец, следует уточнить, в соответствии с каким именно кри-
терием качества аппроксимации неизвестных величин среднедушевых
семейных денежных сбережений у(х) и уср(х) с помощью функции 0О 4~#iz
мы будем определять наилучший способ прогноза уср(я:) по х. Наиболее
обоснованное и точное решение этого вопроса опирается на знание веро-
ятностной природы (а именно типа закона распределения вероятностей)
остатков £ в модели (10.3). Так, например, известно (см. гл. 15), что
если предположить, что при любых значениях х распределение вероятно-
стей остатков £ описывается (0,<г2)-нормальным законом и что остатки
£(z,),i = 1,2,...,п, характеризующие различные наблюдения, статисти-
чески независимы, то наименьшая ошибка прогноза ycp(z) с помощью мо-
дели f(x) 6 F (т.е. функция f(x) подбирается из класса F) обеспечивается
требованием метода наименьших квадратов, в соответствии с которым
оценки 0О и #1 параметров 0О и определяются из условия минимизации
по 0О и 01 выражения
п
- е0 - о.ц)3.	(Ю.7)
»=1
В нашем примере явно нарушено условие постоянства дисперсии
остатков (см. табл. 10.1), т.е. условная дисперсия D(£ | f = я) =
D(tj — 0о - I € = ж) = существенно зависит от значения х. Мож-
но устранить это нарушение, поделив все анализируемые величины, от-
кладываемые по оси j;, а следовательно и остатки £(z), на значения s(s)
(являющиеся несмещенными статистическими оценками для <т(а:)), т.е.
перейдя к анализу остатков е(х) = е(х)/з(х). Тогда можно показать (с по-
мощью методов, описанных в п. 8.6.1), что гипотеза о (0; а2)-нормалъном
характере распределения остатков е(х) не противоречит имеющимся в на-
шем распоряжении данным (представленным в табл. 10.1) и, следователь-
но, требование (10.7) приводит к необходимости решения экстремальной
задачи вида
(10.7')
т. е. к системе из двух линейных уравнений с двумя неизвестными (0q и
больших чисел (см. п. 6.2) у(х) —» уСр(х) (по вероятности), когда число наблюдении,
по которым подсчитано §(х), стремится к бесконечности.
10.1. ОБЩАЯ ФОРМУЛИРОВКА ПРОБЛЕМЫ, ПРИМЕР
353
^1):
= -2 g «-’(«О • (и - е0 - 6iXi) = 0;
9A"ff’g,) = -2 £ r\Xi)  Xi  (у. -e0- e1If) = 0.
1^—1
(10.7")
Решение системы (10.7") дает нам в качестве оценок 60
известных параметров соответственно 0q и 0} выражения:
и 0i для не-
(10.7"')
где А, = 5 2 (г,).
Расчет по этим формулам с использованием данных табл. 10.1 дает
нам ответ на сформулированный выше вопрос 4:
01 = 0,685;
0О = -40,360,
так что статистическая оценка искомой зависимости средней величины
среднедушевых семейных сбережений уср(ж) от значения среднедушевого
дохода семей доходной группы х имеет в этом случае вид
ycp(z) = -40,36 + 0,685 • х.
При другой статистической природе остатков £ или при отсутствии
достаточной информации о типе их вероятностного распределения возмо-
жен иной, чем по (10.7), выбор критерия качества аппроксимации Дп. От-
метим, однако, что наиболее широкое распространение в статистической
практике получили именно различные варианты критерия наименьших
квадратов (10.7) (см. гл. 15).
Заканчивая обсуждение примера 10.1 и возвращаясь к общему опи-
санию задач статистического исследования зависимостей, отметим, что
354
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
функции f(A') = Е(г? | f = X), описывающие поведение условных средних
результирующего показателя г] (вычисленных при значениях объясняю-
щих переменных зафиксированных на уровне £ = X) в зависимости от
изменения X, принято называть функциями регрессии.
10.2	. Какова конечная прикладная цель
статистического исследования
зависимостей?
С этого вопроса должно начинаться любое статистическое исследо-
вание зависимостей. Ведь от ответа на этот вопрос существенно зависят
план исследования, выбор общей структуры математической модели, ин-
терпретация получаемых статистических характеристик и выводов и т. д.
Итак, для чего же строятся математические модели типа (10.3), опи-
сывающие статистические зависимости между исследуемыми переменны-
ми: результирующими показателями Y = (у , у,..., у '), с одной сто-
роны, и соответствующими объясняющими (экзогенными) переменными
X =	. .,ж^), с другой стороны?
Выделим три основных типа конечных прикладных целей подобных
исследований, расположив их как бы по нарастанию глубины проникнове-
ния в содержательную сущность анализируемой конкретной задачи.
Тип1: Установление самого факта наличия (или отсутствия)
статистически значимой связи между У и X. При такой постановке
задачи статистический вывод имеет двоичную (альтернативную) приро-
ду — «связь есть» или «связи нет» — и сопровождается обычно лишь
численной характеристикой (измерителем) степени тесноты исследуемой
зависимости. Выбор формы связи (т.е. класса допустимых решений F
и конкретного вида функции f(X) в модели (10.3)) и состава объясняю-
щих переменных X играет подчиненную роль и нацелен исключительно
на максимизацию величины этого измерителя степени тесноты связи: ис-
следователю часто не приходится даже «добираться» до конкретного вида
функции f(X) и тем более он не претендует на анализ причинных влияний
переменных X на результирующие показатели. Этой проблеме посвящена
гл.11.
Тип 2: прогноз (восстановление) неизвестных значений интересу-
ющих нас индивидуальных (У(Х) = (г) | £ = X)) или средних (Уср(Х) =
Е(т/1 £ = X)) значений исследуемых результирующих показателей по за-
данным значениям X соответствующих объясняющих переменных. При
такой постановке задачи статистический вывод включает в себя описа-
ние интервала (области) вероятных значений прогнозируемого показа-
10.2. КАКОВА КОНЕЧНАЯ ПРИКЛАДНАЯ ЦЕЛЬ?
355
теля Уср(Х) или У(Х) и сопровождается величиной доверительной ве-
роятности Р, с которой гарантируется справедливость нашего прогно-
за, формализуемого с помощью утверждения вида {У(Х) G Д[У(Х)]р}
или {Уср(Х) 6 Д[Уср(Х)]р) (см. определение доверительного интервала
в л. 7.4 и п. 7.5.4). Как и в предыдущем случае, выбор формы связи (т.е.
класса допустимых решений F и конкретного вида функции f(X) в мо-
дели (10-3)) и состава предикторов объясняющих переменных X играет
подчиненную роль и нацелен исключительно на минимизацию ошибки по-
лучаемого прогноза. Однако в данном случае (в отличие от предыдущего)
исследователь существенно использует значения функции f(X), которые
являются отправной точкой при построении прогнозных доверительных
интервалов. Последние обычно определяются в форме множества всех тех
значений У, которые удовлетворяют неравенствам
f(X) - еР(Х, п) У f(X) + еР(Х, п),	(10.8)
где еР(Х,п) — гарантируемая (с вероятностью, не меньшей заданного
значения Р) максимальная величина ошибки прогноза1 *. Таким образом,
исследователя интересуют в данном случае лишь значения функции f(X),
но не ее структура, определяющая, в частности, соотношение удельных
весов влияния объясняющих переменных	.,,х^ на каждый из
результирующих показателей у (k = l,2,...,m). Так, например, если
при статистическом оценивании неизвестной истинной зависимости
/(X) = Scp(®0),i(2)) = 1 + з/” + 5z(3)	(10.9)
исследователю удалось получить оценку функции /(X) в виде
/(X) = 1 + 6г(1> - х(3)	(10.9')
и при этом было установлено, что объясняющие переменные г1' и г*3*
связаны между собой «почти функциональной» линейной зависимостью3
г(1) га 2г<3),	(10.10)
1 Напоминаем читателю, что f,C и Y являются т-мерными векторами (см. (10.2)),
так что запись (10.8) означает справедливость т соответствующих покомпонентных
неравенств.
а Говоря о «почти функциональной» линейной зависимости между И1) и мы име-
ем в виду близость к единице (по абсолютной величине) коэффициента корреляции
между этими переменными (см. п. 2.6.6, соотношение (2.33)).
356	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
то функция /(X) будет обладать хорошими прогностическими свойства-
. .	(1)	(2)
ми, несмотря на существенное отличие ее коэффициентов при г ' и х'
от соответствующих коэффициентов истинной функции /(X). (Обращаем
внимание читателя на тот факт, что коэффициенты при я' ' в функци-
ях /(X) и /(X) отличаются даже по знаку!) При подстановке заданных
значений объясняющих переменных и х в правые части (10.9) и
(10.91), при условии, что эти значения связаны приближенным соотноше-
нием (10.10), мы будем получать совпадающие (или приближенно совпада-
ющие) результаты /(X) и /(X), характеризующие усредненную величину
3/ср(Х) исследуемого результирующего показателя.
Тип 3: выявление причинных связей между объясняющими перемен-
ными X и результирующими показателями У, частичное управление
значениями У путем регулирования величин объясняющих переменных
X. Такая постановка задачи претендует на проникновение в «физический
механизм» изучаемых статистических связей, т.е. в тот самый механизм
преобразования «входных» переменных X и е в результирующие пока-
затели У (см. рис. 10.1), который в большинстве случаев исследователь,
не будучи в состоянии его конструктивно описать, вынужден именовать
(следуя сложившейся кибернетической терминологии) «черным ящиком».
И при выявлении причинных связей, и при намерении исследователя
использовать модели типа (10.3) или (10.4) для управления значениями
результирующих показателей Уср(Х) или У(Х) путем регулирования ве-
личин объясняющих переменных X на первый план выходит задача пра-
вильного определения структуры модели (т. е. выбора общего вида функ-
ции f(X)), решение которой обеспечивает возможность количественного
измерения эффекта воздействия на У (X) каждой из объясняющих пере-
менных	в отдельности. Однако как раз это место (пра-
вильный выбор общего вида функции f(X)) и является самым слабым во
всей технике статистического исследования зависимостей: к сожалению,
не существует стандартных приемов и методов, которые образовывали бы
строгую теоретическую базу для решения этой важнейшей задачи (неко-
торые рекомендации по проведению этого этапа исследования содержатся
в п. 10.7).
Заметим, что исследователи, пожалуй, чаще других ставят перед со-
бой именно цели типа 3. И в таких прикладных задачах, как управле-
ние качеством продукции с помощью регулирования хода технологиче-
ских процессов, прогноз и анализ объемов произведенной продукции по
затратам на трудовые ресурсы и капитальные вложения, построение ин-
тегральных целевых функций описывающих эффективность функциони-
рования экономических единиц (предприятий, семей) по набору частных
10.3. МАТЕМАТИЧЕСКИЙ ИНСТРУМЕНТАРИЙ
357
характеристик и др., это вполне оправдано. Однако, к сожалению, далеко
не всегда целевые установки исследователей подкреплены объективными
возможностями их реализации.
10.3	. Математический инструментарий
Методы статистического исследования зависимостей составляют со-
держание специального раздела многомерного статистического анали-
за, который в свою очередь можно определить как важнейшую составную
часть прикладной статистики, содержащую инструментарий для постро-
ения оптимальных планов сбора, систематизации и анализа многомерных
статистических данных типа (10.1), нацеленный в первую очередь на вы-
явление характера и структуры взаимосвязей между компонентами иссле-
дуемого многомерного признака (X, Y) и предназначенный для получения
научных и практических выводов. При этом среди р + т компонент ис-
следуемого многомерного признака (Х,У) могут быть: количественные,
т.е. скалярно измеряющие в определенной шкале степень проявления изу-
чаемого свойства объекта (денежный доход и сбережения семьи, объем
валовой продукции, численность работников на предприятии и т.п.); по-
рядковые (или ординальные), т. е. позволяющие упорядочивать анализиру-
емые объекты по степени проявления в них изучаемого свойства (уровень
жилищных условий семьи, квалификационный разряд рабочего, уровень
образования работника и т. п.); классификационные (или номинальные),
т. е. позволяющие разбивать обследованную совокупность объектов на не
поддающиеся упорядочиванию однородные (по анализируемому свойству)
классы (профессия работника, мотив миграции семьи, отрасль промыш-
ленности и т. п.). Подразделы многомерного статистического анализа, со-
ставляющие математический аппарат статистического исследования за-
висимостей, формировались и развивались с учетом специфики анализи-
руемых моделей, обусловленной природой изучаемых переменных. Соот-
ветствующая специализация этих разделов отражена в табл. 10.2. В ней
же указаны главы данной книги, посвященные описанию указанных под-
разделов.
Из табл. 10.2 видно, что данная книга не охватывает методов иссле-
дования зависимостей неколичественного или смешанного (разнотипного)
результирующего показателя от количественных или смешанных объяс-
няющих переменных: объемность и специфичность указанной темы обу-
словливают целесообразность посвящения ей специального издания.
358
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Таблица 10.2
№ п/п	Природа резуль- тирующих пока- зателей (эндоген- ных переменных)	Природа объ- ясняющих (экзо- генных) пере- менных	Название обслу- живающих подраз- делов многомерно- го статистичес- кого анализа	Главы книги, посвя- щенные данным разделам
1	2	3	4	5
1	Количественная	Количественная	Регрессионный и корреляционный анализ	10, 11,14, 15, 17
2	Количественная	Единственная количественная переменная, ин- терпретируемая как «время»	Анализ времен- ных рядов	16
3	Количественная	Неколичественная (ординальные или номинальные пе- ременные)	Дисперсионный анализ	
4	Количественная	Смешанная (коли- чественные и неколичествен- ные переменные)	Ковариационный анализ, модели типологической регрессии	
5	Неколичественная (порядковые, или ординальные, переменные)	Неколичественная (ординальные и номинальные переменные)	Анализ ранговых корреляций и таблиц сопряжен- ности	11
6	Неколичественная (к л ассифи кацион- ные, или номи- нальные, пере- менные)	Количествен ная	Дискриминантный анализ, кластер- анализ, таксоно- мия, расщепление смесей распреде- лений	12
7	Смешанная (ко- личественные и иеколичественные переменные)	Смешанная (ко- личественные и неколичественные переменные)	Аппарат логи- ческих решаю- щих функций	
10.4. НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ
359
Кроме того, принцип систематизации различных схем, принятый в
табл. 10.2, не приспособлен для выделения одного важного (особенно в
области социально-экономических приложений) случая, когда связи меж-
ду количественными переменными X и Y описываются системой одно-
временных уравнений, в которых одни и те же переменные могут играть
одновременно (в различных уравнениях системы) и роль результирую-
щих, и роль объясняющих. Этому посвящена теория одновременных эко-
нометрических уравнений, основные результаты которой представлены в
гл. 14 и 17.
10.4	. Некоторые типовые задачи практики
эконометрического моделирования
Накопленный опыт практического использования аппарата статисти-
ческого исследования зависимостей позволяет выделить те типы основных
прикладных направлений исследований, в которых этот аппарат работает
особенно часто и плодотворно. Бели попытаться расщепить общую про-
блему оптимального управления сложной системой (т. е. центральную про-
блему кибернетики) на основные составляющие (рис. 10.3), то в качестве
этих составляющих как раз и фигурируют именно те направления при-
кладных исследований, в разработке которых существенную роль играет
математический аппарат статистического исследования зависимостей.
Остановимся кратко на роли методов статистического исследования
зависимостей в разработке каждого из упомянутых направлений.
I. Нормирование
Общая схема формирования нормативов с использованием методов
статистического исследования зависимостей может быть представлена
следующим образом. Нормативный показатель играет в моделях типа
(10.3)-(10.4) роль результирующей (объясняемой) переменной у, а факто-
ры, участвующие в расчете нормативного показателя, — роль объясняю-
щих переменных , я^2\..., я/р\ Предполагается, что привлечение для
расчета норматива у полной системы определяющих его факторов, т.е.
такой системы, с помощью которой возможно детерминированное (одно-
значное) определение величины у, либо принципиально невозможно, либо
нецелесообразно из-за чрезмерного усложнения расчетных формул. По-
этому анализируется связь между у и (ж^,®^,...,®^) вида
y = /(z(1),z(2)
,z(p); 0) + £,
(10.11)
360
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
где € — остаточная случайная компонента, обусловливающая возможную
погрешность в определении норматива у по известным значениям факто-
ров X =	а /(X; 0) — функция из некоторого извест-
ного параметрического семейства F — {/(X; 0)},0 € А, однако численное
Проблема оптимального управления сложной системой
III
IV
Оптнмальное
регулирова-
ние парамет-
ров функцио-
нирования
системы,
ситуационный
анализ
Нормирование
Прогноз,
планирова-
ние, диаг-
ностика
Оценка труд-
нодоступных
для непо-
средствен-
ного наблю-
дения и из-
мерения па-
раметров
системы
Оценка эф-
фективности
функциониро-
вания (или
качества)
системы
Исходные статистические данные
(информационная база)
Рис. 10.3. Основные направления практического использования аппарата
статистического исследования зависимостей и центральная про-
блема кибернетики
значение входящего в ее уравнение параметра 0 (вообще говоря, вектор-
ного) неизвестно. С целью подбора «подходящего» значения 0 проводится
контрольный эксперимент (наблюдение), в результате которого исследо-
ватель получает исходные статистические данные вида (10.1). Далее па
основании этих данных проводится необходимый статистический анализ
модели (10.11) с целью получения оценки 0 неизвестного параметра 0
и анализа точности полученной расчетной формулы К₽(Х) = /(Х;9),в
которой величина условной (экспериментальной) средней Кср(Х) интепре-
тируется как средний нормативный показатель при значениях определя-
ющих факторов, равных X.
10.4. НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ	361
Л
Данный подход использовался, в частности, при разработке методик
численности служащих (по различным их функциям) на промышленном
предприятии отрасли по набору технико-экономических показателей, ха-
рактеризующих предприятие, при построении автоматизированных си-
стем нормирования ремонтных работ и в других областях.
II.	Прогноз, планирование, диагностика
Отправляясь от общей формулировки задачи статистического ис-
следования зависимостей (см. п. 10.1) и от ее модельной записи (10.11),
определим в качестве результирующей переменной у интересующий нас
прогнозируемый (планируемый, диагностируемый) показатель, а в каче-
стве объясняющих переменных	— сопутствующие фак-
торы, значения которых содержат основную информацию о величине это-
го показателя1. Наличие остаточной случайной компоненты £, как и пре-
(1) (2)	(р)
жде, отражает тот факт, что переменные ж' ', аг ',... аг ' содержат не всю
информацию об у, и обусловливает неизбежность погрешности в опреде-
лении прогнозируемого (планируемого, диагностируемого) показателя по
известным значениям объясняющих факторов х^\х^2\... х^. Исходные
статистические данные вида (10.1) исследователь получает, регистрируя
одновременно значения у и (ж^,...,«^) на анализируемых объектах в
прошлом (в базовом периоде) или на других объектах, но однородных с
анализируемыми.
III.	Оценка труднодоступных для непосредственного
наблюдения и измерения параметров системы
Восстановление возраста археологической находки по ряду косвен-
ных признаков; прочности бетона с помощью косвенных (неразрушаю-
щих) методов контроля (например, по отношению диаметров отпечатков
на поверхности испытуемого образца бетона и на воздействующем на него
эталонном молотке); денежных сбережений семьи по ее доходу (в средне-
душевом исчислении) — во всех этих ситуациях исследователь вынужден
иметь дело с показателями, труднодоступными для непосредственного из-
мерения (они выделены в тексте курсивом). Очевидно, для того чтобы
иметь принципиальную возможность статистически выявить связь, су-
1 В моделях прогноза н планирования в качестве одного из объясняющих факторов
вводится в явном виде «длина прогноза», или «горизонт планирования», t (в
единицах времени).
362
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
шествующую между труднодоступным показателем у и косвенно связан-
ными с ним, но легко поддающимися наблюдению и измерению призна-
ками а/1), а/2\..., а^р\ исследователю необходимо располагать исходны-
ми статистическими данными вида (10.1), которые получают с помощью
специально организованного контрольного эксперимента или наблюдения.
После того как эта связь выявлена (и оценена степень ее точности), она
используется для косвенного определения значении труднодоступных по-
_	(1) (2)	(р)
к азател ей лишь по значениям объясняющих переменных г' , аг ',..., аг .
IV.	Оценка эффективности функционирования (или
качества) анализируемой системы
Пытаясь оценить (в целом) эффективность деятельности отдельного
специалиста, подразделения или предприятия, проранжировать страны по
некоторому интегральному качеству (например, по качеству жизни насе-
ления или по так называемому общему индексу человеческого развития),
наконец, проставить балльные оценки спортсмену — участнику команд-
ных соревнований в игровых видах спорта за качество его игры в опреде-
ленном цикле, мы каждый раз по существу решаем (на интуитивном уров-
не) одну и ту же задачу: отправляясь в своем анализе от набора частных
показателей а/^а/2),..., а/р\ каждый из которых может быть измерен и
характеризует какую-нибудь одну частную сторону понятия «эффектив-
ность», мы их как бы взвешиваем (т. е. внутренне оцениваем удельный вес
их влияния на общее, агрегированное, понятие эффективности) и выхо-
дим на некоторый скалярный агрегированный показатель эффективности
у. Этот показатель — латентный (скрытый), так как он принципиально
не поддается непосредственному измерению (не существует или нам неиз-
вестна объективная шкала, в которой он мог бы быть измерен). Но он с
некоторой точностью восстанавливается по значениям частных показате-
лей эффективности г^\ж^2\. ..,а;^р\ Это значит, что между латентным
агрегированным показателем у и набором частных критериев эффектив-
ности а/1), а/2\.. . ,а/р^ существует статистическая связь типа (10.11).
Главная особенность (и трудность) описываемой ситуации заключа-
ется в том, что при получении (сборе) исходной статистической информа-
ции вида (10.1) значения результирующего показателя у могут быть полу-
чены только с помощью специально организованного экспертного опроса
(значения частных критериев эффективности а?^\ х^2\..., а/р\ как прави-
ло, поддаются непосредственному измерению). Форма экпертной инфор-
мации о значениях у может быть различной (балльные оценки, упорядоче-
ния, парные сравнения). Но только располагая наряду со статистической
10.4. НЕКОТОРЫЕ ТИПОВЫЕ ЗАДАЧИ
363
информацией об X =	.. ,z^)T одной из форм соответствую-
щей экспертной информации об у, мы можем статистически построить
некоторую аппроксимацию уср(Х) = /(Х;0) для агрегированного крите-
рия эффективности функционирования системы и использовать ее затем
в качестве формализованного метода оценки интегрального понятия эф-
фективности (т.е. уже без привлечения экспертов, а лишь по частным
критериям	, х^). Такая модифицированная форма использо-
вания аппарата статистического исследования зависимостей предложена
в [Айвазян С. А., 1974] и носит название экспертно-статистического ме-
тода построения неизвестной целевой функции (см. п. 13.5).
В описанную схему вкладывается широкий класс задач теории и прак-
тики измерения комплексного понятия «качество» сложной системы: в
этих задачах у интерпретируется как агрегированный (комплексный) по-
(0 Р) (р)
казатель качества системы, аг , аг ,..., аг 7 — как отдельные частные
характеристики его качества (надежность, экономичность, удобство поль-
зования, эстетический вид и т. п.). В качестве параметрических семейств
F = {/(Х;0)}, привлекаемых при статистическом анализе задач данного
типа, чаще других используются функции линейные
f(X-, е) = «о + М(,) + • •  + 6гхМ	(10.12)
и степенные
f(x-t е) = в0(®<1))’1(®(2))‘1 •	(юле)
V.	Оптимальное регулирование параметров
функционирования анализируемой системы,
ситуационный анализ
Рассмотрим пример (заимствован из [Айвазян С. А., 1968]). При ана-
лизе производительности мартеновских печей на одном из заводов иссле-
довалась, в частности, зависимость между производительностью в тон-
но/часах (для исключения влияния задержек и простоев часовая произ-
водительность мартеновской печи определялась как частное от деления
массы плавки на продолжительность периода от начала завалки до вы-
пуска) и процентным содержанием углерода в металле по расплавлении
ванны (пробу брали через час после первого скачивания шлака). Результат
ты замеров по 130 плавкам (т.е. объем п обрабатываемой статистической
выборки вида (10.1) равен 130) приведены на рис. 10.4. Очевидно, величи-
ны производительности (у,) и процентного содержания углерода (ж,) под-
вержены некоторому неконтролируемому разбросу, обусловленному влия-
нием множества не поддающихся строгому учету и контролю факторов.
364
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Другими словами, последовательность пар чисел (z,»yj),t = 1,2,..., 130,
представляет в данном случае результаты 130 независимых наблюдений
двумерной случайной величины (£, 1/). Однако сквозь кажущуюся хао-
тичность расположения точек (а?,, у,-) на рис. 10.4 просматривается впол
не определенная закономерность зависимости условного среднего значе-
ния производительности уср(а?) =	| £ = г) от величины процентного
содержания углерода х. Поэтому, располагая статистической зависимо-
стью уСр(2)> мы можем дать рекомендации технологу по оптимальному
(с точки зрения максимизации производительности) управлению процес-
сом выплавки: поддерживать процентное содержание углерода в пределах
0,6-1,0%.
Рис. 10.4. Зависимость производительности (у, т/ч) от процентного содер-
жания углерода (z, %) в металле до расплавления
Мы не случайно начали с этого примера. Использование методов ста-
тистического исследования зависимостей в задачах оптимального регу-
лирования хода технологического процесса и построения соответствую-
щих автоматизированных систем управления технологическими процес-
сами можно отнести к примерам грамотных и относительно распростра-
ненных актуальных приложений этого аппарата. Общая схема таких при-
ложений предусматривает (в дополнение к приведенному выше частному
примеру): а) одновременное рассмотрение нескольких результирующих
показателей у^\	..., у^ (производительность, качество продукции,
расход сырья и энергии и т. п.) и многих регулируемых параметров тех-
10.5. ОСНОВНЫЕ ТИПЫ ЗАВИСИМОСТЕЙ
365
дологического процесса	... ,а/р\ б) возможность сбора исходной
статистической информации вида (10.1).
Менее освоенным (но не менее правомерным и актуальным) является
этот подход в задачах оптимального регулирования:
•	характеристик социально-экономического поведения людей и целых
коллективов в ситуациях, когда существует принципиальная возможность
выявления статистических связей между этими характеристиками и на-
бором объясняющих (и хотя бы частично регулируемых) факторов;
•	структуры и объемов нагрузок и видов заданий в процессе профес-
сиональной подготовки специалистов.
Особо выделим макро-уровень подобного моделирования с целью
оптимального регулирования параметров функционирования анализиру-
емой системы. В этом случае речь идет об оптимальном регулировании
тех макро-параметров национальной экономики, которые поддаются хо-
тя бы частичному управлению и планированию (институциональные и
структурные преобразования, налоговая и социальная политика, инвести-
ционная активность государства и т. п.). Построив и оценив статистиче-
ские связи, существующие между этими параметрами (так называемыми
экзогенными переменными), с одной стороны, и результирующими (эндо-
генными, т.е. формирующимися внутри и в ходе функционирования на-
циональной экономики) переменными — с другой, исследователь может,
придавая различные значения управляемым параметрам, отслеживать со-
ответствующие реакции на это эндогенных переменных. Т.е. происхо-
дит как бы многократная модельная «прогонка» различных сценариев
социально-экономического развития (такой способ исследования называ-
ют также ситуационным анализом). Реализуется этот подход, как
правило, с помощью систем регрессионных уравнений типа (10.3)-(10.4),
которые принято называть в эконометрике системами одновременных
уравнений (см. гл. 14 и 17).
10.5.	Основные типы зависимостей между
количественными переменными
При изучении взаимосвязей между анализируемыми количественны-
ми показателями следует установить, к какому именно типу зависимостей
относится исследуемая схема. Под типом зависимости мы подразумеваем
в данном случае не аналитический вид функции K-p(X) = f(X\ 0) в моде-
лях вида (10.11) (о выборе общего аналитического вида функции /(Х;0)
см. п. 10.7), а природу анализируемых переменных (Х,у) и соответствен-
но интерпретацию функции /(Х;0) в каждом конкретном случае.
366
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
Зависимость между неслучайными переменными (схема
А). В этом случае результирующий показатель у детерминирование (т.е.
вполне определенно, однозначно) восстанавливается по значениям неслу-
чайных объясняющих переменных X = (х^\х^2\. ..,ж^)т, т.е. значе-
ния у зависят только от соответствующих значении X и полностью ими
определяются. Это — обычная схема чисто функциональной зависимости
между неслучайными переменными, когда у является некоторой функцией
от р переменных X (т.е. у = /(X)), что является вырожденным случа-
ем зависимостей вида (10.11), когда остаточная случайная компонента е
равна нулю (с вероятностью единица).
Известно, например, что возраст дерева у (в годах) можно однознач-
но восстановить по числу колец х на срезе его ствола, а именно у = х.
Примеры адекватного описания реальных зависимостей с помощью чисто
функциональных (нестохастических) связей, к сожалению, крайне редки
в практике исследований. Кроме того, при проведении их анализа нет не-
обходимости использовать методы вероятностно-статистической теории.
Поэтому в дальнейшем изложении мы не будем больше возвращаться к
этому типу зависимостей.
Регрессионная зависимость случайного результирующего
показателя г] от неслучайных объясняющих переменных X (схе-
ма В). Природа такой связи может носить двойственный характер: а) ре-
гистрация результирующего показателя ту неизбежно связана с некоторы-
ми случайными ошибками измерения £, в то время как предикторные (объ-
ясняющие) переменные X = (ж^\г^2\...,я^р^)Т измеряются без ошибок
(или величины этих ошибок пренебрежимо малы по сравнению с соответ-
ствующими ошибками измерения результирующего показателя); б) значе-
ния результирующего показателя ту зависят не только от соответствую-
щих значений X, но и еще от ряда неконтролируемых факторов, поэтому
при каждом фиксированном значении X* соответствующие значения ре-
зультирующего показателя ту(Х*) = (ту | X = X*) неизбежно подвержены
некоторому случайному разбросу.
В этом случае объясняющие переменные X играют роль неслучайного
(векторного при р > 1) параметра, от которого зависит закон распреде-
ления вероятностей (в частности, среднее значение и дисперсия) исследу-
емого результирующего показателя ту. Удобной математической моделью
такого рода зависимостей является разложение вида
г)(Х) = /(X) + е(Х).	(10.14;
Модель (10.14) строится таким образом, что математическое ожидание
случайного остатка е(Х) равно нулю (Еб(Х) = 0) тождественно по X; по-
10.5. ОСНОВНЫЕ ТИПЫ ЗАВИСИМОСТЕЙ
367
этому функция /(X) описывает поведение условного среднего уср(Х) =
Е(т? | X) = f(X) в зависимости от X. Предполагается обычно, что
при всех X существует конечная дисперсия е(Х) (т.е. De(X) < оо), при-
чем величина этой дисперсии, вообще говоря, может зависеть от X (т. е.
De(X) = tf2(X)). Подчеркнем то обстоятельство, что в описанной модели
(10.14) ни природа случайной компоненты е(Х), ни соответственно харак-
теристики ее вероятностного распределения никак не связаны со структу-
рой функции f(X) и, в частности, не зависят от значений ее параметра 0 в
параметрической записи модели (т. е. когда вместо всех возможных функ-
ций f(X) рассматривают какое-либо параметрическое семейство /(Х;0),
см., например, (10.12), (10.13)).
Если вернуться к примеру 10.1, то можно убедиться, что он хоро-
шо укладывается в рамки модели (10.14). Для этого следует лишь заме-
тить, что имевшаяся в этом примере возможность контролировать зна-
чения объясняющей (предикторной) переменной £ по существу переводит
эту переменную из категории случайных величин в категорию неслучай-
ных (контролируемых) параметров модели. Дальнейший анализ примера
10.1 (см. табл. 10.1, формулу (10.5) и рис. 10.2) подсказал нам следующую
конкретизацию допущений о природе составных частей модели (10.14):
jfcp(ar) = Е(г) | X) = /(г) = 90 + 81Х;
\ f \	2 /	{ х\2	(10.15)
О (х) - D£(z) = <70 • (&р(*)) >
где Со — константа, не зависящая от х.
Подчеркнем тот факт, что именно зависимость по схеме В, т.е. ре-
грессионная зависимость результирующего показателя от неслучайных ве-
личин объясняющих переменных, лежит в основе большинства экономе-
трических моделей и, в частности, используется при построении и анализе
классической и обобщенной линейной модели регрессии (см. гл. 15).
Корреляционно-регрессионная зависимость между случай-
ными векторами т/ — результирующим показателем и £ — объяс-
няющей переменной (схема С). В данном типе моделей и компоненты
вектора результирующего показателя 1/, и компоненты вектора объясня-
ющих переменных ( зависят от множества неконтролируемых факторов,
так что являются случайными по своей физической сущности. Мы уже
сталкивались с такой ситуацией в примере, в котором исследовалась связь
между производительностью мартеновских печей и процентным содержа-
нием углерода в металле (см. рис. 10.4). Зависимости такого типа вообще
характерны для описания хода технологических процессов, реальные зна-
чения параметров которых £ =	Равно как и характе-
368	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
z (1)	(2) (т)Л
ризующие их результирующие показатели i; = (if	') , как
правило, флюктуируют случайным (но взаимосвязанным) образом около
установленных номиналов.
В подобных ситуациях оказывается полезным рассмотреть разложе-
ние исследуемого результирующего показателя т] на две случайные соста-
вляющие по формуле типа (10.3). Первая из них определяется некоторой
(векторнозначной) функцией f от объясняющей переменной а вторая
отражает остаточные влияния неучтенных случайных факторов на ана-
лизируемый результирующий показатель rj. Итак,
1?=Г(С + ®-	(10.16)
В частном случае единственного результирующего показателя (тп =
1) и линейного вида функции /(() имеем:
р
v = e0 + Y,^k} + e.	(10.17)
Подразумевая, как и прежде, под уср(Х) = Е(ту1 ( = X) условное ма-
тематическое ожидание результирующего показателя ту (при условии, что
объясняющая переменная ( приняла значение, равное X), мы от (10.17)
приходим к линейному уравнению регрессии
р
fc=l
Возможны случаи, когда вторая (остаточная) компонента в разложе-
нии (10.16) с полной мерой достоверности (т.е. с вероятностью единица)
равна нулю. При этом исследуемые случайные величины г] и ( оказыва-
ются связанными чисто функциональной зависимостью 7] = /(£), но ее
следует отличать от функциональной зависимости неслучайных перемен-
ных (см. выше, схема А).
Пример 10.2. Рис. 10.5 иллюстрирует связь между вакуумом в пе-
чи для обжига стекла £ и процентом брака Т] в стекольном производстве
[Айвазян С. А., 1968].
Случайные изменения свойств сырья, а также ряда неконтролируе-
мых факторов приводят к случайным колебаниям обеих исследуемых пе-
ременных. Однако расположение точек на рис. 10.5 свидетельствует о том,
что эти колебания взаимосвязаны, подчинены вполне определенной зако-
номерности: «облако» рассеяния вытянуто вдоль некоторой прямой, не
параллельной ни одной из координатных осей. Все это подтверждает це-
лесообразность разложения случайной величины ту по формуле (10.16) и
10.5. ОСНОВНЫЕ ТИПЫ ЗАВИСИМОСТЕЙ
369
исследования связи между rj и £, которая в этом случае носит название
корреляционной. К перечисленным вопросам регрессионного анализа (по-
строение конкретного вида зависимости меЖцу переменными, различные
оценки ее точности) в этом случае присоединяется круг вопросов, связан-
ных с исследованием степени тесноты связи между этими переменными.
Совокупность методов, позволяющих решать эти вопросы, принято назы-
вать корреляционным анализом (см. гл. 11).
Рис. 10.5. Графическое представление данных по связи вакуума в печи для
обжига стекла (£) и процента брака в стекольном производстве
(»?)
Зависимости структурного типа, или зависимости по схеме
конфлюэнтного анализа (схема D). В описываемой ниже схеме речь
идет о восстановлении искомых зависимостей по искаженным наблюдени-
ям анализируемых переменных, причем в отличие от регрессионной рсемы
В искаженными оказываются при наблюдении не только значения резуль-
тирующего показателя, но и значения объясняющих (предикторных) пе-
ременных	Этот тип связей упоминается в специальной
литературе как структурные зависимости [Кендалл М. Дж., Стьюарт А.,
1973, с. 500-557] или как зависимости по схеме конфлюэнтного анализа
[Айвазян С. А., 1979].
Таким образом, конфлюэнтный анализ предоставляет совокупность
методов математико-статистической обработки данных, относящихся к
анализу априори постулируемых функциональных связей между ко-
личественными (случайными или неслучайными) переменными Y =
(/г\...,^т^)Т и X = (а/1\а/2\..,,а^р))Т в условиях, когда наблюда-
370
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
ются не сами переменные, а случайные величины
й*> = гГ+^’, к=1)2)...,Р;
^•J) =	+4?» > = 1,2,...,m; i = 1,2,...,n,
(10.19)
где £ и с! — случайные ошибки измерений соответственно переменных
х^ и в t-м наблюдении, ап — общее число наблюдений. При этом
общий вид исследуемых функциональных (структурных) связей
(т))
(10.20)
между ненаблюдаемыми, а точнее, наблюдаемыми с ошибками переменны-
ми считается заданным (неизвестным является лишь значение векторного
параметра G = (0П.. . ,0/у), участвующего в уравнениях искомых зависи-
мостей (10.20)).
10.6.	Основные этапы статистического
исследования зависимостей
Весь процесс статистического исследования интересующих нас зави-
симостей удобно разложить на основные этапы. Эти этапы ниже описаны
в соответствии с хронологией их реализации, однако некоторые из них
находятся, в плане хронологическом, в соотношении итерационного вза-
имодействия: результаты реализации более поздних этапов могут содер-
жать выводы о необходимости повторной «прогонки» (с учетом добытой
на предыдущих этапах новой информации) уже пройденных этапов (см.,
например, схему взаимодействия этапов 3, 4, 5 и 6 на рис. 10.6).
Излагаемая ниже схема приспособлена в основном для исследования
зависимостей между количественными переменными, однако с минималь-
ными (и очевидными) модификациями она «работает» и при статистиче-
ском анализе связей между неколичественными и разнотипными перемен-
ными.
10.6. ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
371
Рис. 10.6. Схема хронолог и чески-итерацмонных взаимосвязей основных эта-
пов статистического исследования зависимостей
Этап 1 (постановочный). Прежде всего исследователь должен опре-
делить:
1)	элементарную единицу статистического обследования, или эле-
ментарный объект исследования О (это может быть страна, город, от-
расль, предприятие, семья, индивидуум, пациент, технологический про-
цесс, сложное техническое изделие и т. д.);
2)	набор показателей (ж' 1 ,х'	уу' '), регистрируе-
мых на каждом из статистически обследованных объектов, с подразделе-
нием их на «входные» (объясняющие) и «выходные» (результирующие)
и, если это необходимо, с четким определением способа их измерения; та-
ким образом, на этом этапе каждому элементарному объекту исследования
ставится в соответствие перечень анализируемых показателей, т.е.
0<=>(x<V2)........
3)	конечные прикладные цели исследования (см. п. 10.2), тип иссле-
дуемых зависимостей (см. п. 10.5) и желательную форму статистических
выводов (а иногда и степень их точности);
4)	совокупность элементарных объектов исследования, на которую мы
хотим распространить справедливость действия выявленных в результате
анализа статистических зависимостей (если, например, элементарная еди-
ница — семья, то анализируемой совокупностью могут быть семьи опре-
деленной социальной группы населения или семьи определенной страны и
т.д.);
5)	общее время и трудозатраты, отведенные на планируемое исследо-
вание и коррелированные с ними временная протяженность и объем необ-
ходимого статистического обследования (какую часть анализируемой со-
вокупности подвергнуть статистическому обследованию, производить ста-
тистическое обследование в статистическом или динамическом режиме и
172	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
г. д.). Заметим, что именно на этом этапе решаются задачи в) и 1, опи-
:анные в п. 10.1.
В решении всех перечисленных вопросов первого этапа исследования
'лавную роль, бесспорно, должен играть «заказчик», т. е. специалист той
федметной области, для которой планируется проведение этого исследо-
вания.
Этап 2 (информационный). Он состоит в проведении сбора необхо-
шмой статистической информации вида (10.1). При этом возможны две
финципиалыю различные ситуации: 1) исследователь имеет возможность
гаранее спланировать выборочное обследование части анализируемой со-
вокупности — выбрать способ отбора элементарных единиц статистиче-
:кого обследования (случайный, пропорциональный, расслоенный и т.д.,
:м. п. 6.1), хотя бы по части объясняющих переменных	...,
зазначить уровни их значений, при которых желательно произвести экспе-
эимент или наблюдения (условия активного эксперимента); 2) исследова-
тель получает исходные данные такими, какими они были собраны без его
участия (условия пассивного эксперимента). В любом случае «на выхо-
да» этого этапа исследователь располагает исходными статистическими
1анными вида (10.1), т. е. каждому (t-му) из статистически обследованных
элементарных объектов Ot поставлен в соответствие конкретный вектор
характеризующих его «входных» и «выходных» показателей:
О.	х<2>,....у!”, г/!2’...,i = 1,2,...п
"здесь п — общее число статистически обследованных элементарных объ-
ектов, т. е. объем выборки).
Говоря о проведении сбора статистических данных, мы не включа-
гм сюда разработку методологии и системы показателей отображаемого
эбъекта: эта работа предполагает профессионально-предметное (экономи-
ческое, техническое, медицинское и т.д.) изучение сущности решаемых
задач статистического исследования зависимостей, поэтому относится к
компетенции соответствующей предметной статистики (экономической и
г. д.) и входит в задачи 1-го этапа исследований.
Этап 3 (корреляционный анализ). Этот этап нацелен на решение
задачи 2 (см. п. 10.1), он позволяет ответить на вопросы, имеется ли во-
обще какая-либо связь между исследуемыми переменными, какова струк-
тура этих связей и как измерить их тесноту? Описанию методов, с помо-
щью которых проводится такой статистический анализ, посвящена гл. 11.
Поскольку перечисленные выше вопросы решаются с помощью вычисле-
ния и анализа соответствующих корреляционных характеристик, содер-
жание этапа можно определить как проведение корреляционного анализа.
10.6. ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
373
Этап достаточно полно оснащен необходимым математическим аппара-
том и программным обеспечением, поэтому может быть почти полностью
автоматизирован.
Этап 4 (определение класса допустимых решений). Главной целью
исследователя на этом этапе является определение общего вида, структу-
ры искомой связи между У и А”, или, другими словами, описание класса
функций F, в рамках которого он будет производить дальнейший поиск
конкретного вида интересующей его зависимости (см. задачи а) и 3 в
п. 10.1). Чаще всего это описание дается в форме некоторого параметри-
ческого семейства функций f(X; 0), поэтому и этап этот называют также
этапом параметризации модели. Так, определив в примере 10.1, что по-
иск зависимости среднедушевых семейных сбережений уср от величины их
среднедушевого дохода х мы будем производить в классе F = {0О +
линейных функций, мы тем самым завершили четвертый этап исследова-
ния (но конкретных числовых значений параметров и мы к этому
моменту еще не знаем).
Следует отметить, что, являясь узловым, в определенной мере решаю-
щим звеном во всем процессе статистического исследования зависимостей,
этот этап в то же время находится в наименее выгодном положении по
сравнению с другими этапами (с позиций наличия строгих и законченных
математических рекомендаций по его реализации). Поэтому его реализа-
ция требует работы специалиста соответствующей предметной области
(экономики, техники, медицины и т. д.) и математика-статистика, напра-
вленной на как можно более глубокое проникновение в «физический ме-
ханизм» исследуемой связи. Подходам и методам проведения этого этапа
исследований посвящен следующий пункте этой главы.
Существует подход к исследованию моделей регрессии, не требую-
щий предварительного выбора параметрического семейства функций F,
в рамках которого проводится дальнейший анализ. Речь идет о так на-
зываемых непараметрических (или частично-параметрических) методах
исследования регрессионных зависимостей. Однако возникающие при их
реализации проблемы (необходимость иметь очень большие объемы исход-
ных статистических данных, выбор сглаживающих функций — «окон» и
параметров масштаба, выбор порядка сплайна, числа и положения «уз-
лов» и т.п.) сопоставимы по своей сложности с проблемами, возникаю-
щими при реализации этапа 4.
Следующие два этапа — 5-й и 6-й — связаны с проведением опреде-
ленного объема вычислений и реализуются по существу параллельно.
Этап 5 (анализ мулътиколлинеарности предсказывающих перемен-
ных и отбор наиболее информативных из них). Под явлением мультикол-
374	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
линеарности в регрессионном анализе понимается наличие тесных стати-
_	(О (2)	(Р)
стических связей между объясняющими переменными х' ’,х' ',...,аг ,
что, в частности, проявляется в близости к нулю (слабой обусловленно-
сти) определителя их корреляционной матрицы, т.е. матрицы размера
рхр, составленной из парных коэффициентов корреляции Tij = r(o?^,«^)
(см. п. 2.6.6, соотношение (2.32)). Поскольку этот определитель входит
в знаменатель для важных характеристик анализируемых моделей (см.
гл. 15), то мультиколлинеарность создает трудности и неудобства при
статистическом исследовании по меньшей мере в двух направлениях:
а)	в реализации необходимых вычислительных процедур и, в част-
ности, в крайней неустойчивости получаемых при этом числовых харак-
теристик анализируемых моделей (так, коэффициенты при объясняющих
переменных в моделях типа (10.12), (10.13) и др. могут изменяться в не-
сколько раз и даже менять знак при добавлении (или исключении) к масси-
ву исходных статистических данных одного-двух объектов или одной-двух
объясняющих переменных);
б)	в содержательной интерпретации параметров анализируемой мо-
дели, что играет решающую роль в ситуациях, когда конечной целью ис-
следования является цель типа 3 («выявление причинных связей» и т.д.,
см. п. 10.2, соотношения (10.9) и (10.9#)).
Поэтому исследователь старается перейти к такой новой системе
объясняющих переменных (отобранных из числа исходных переменных
х(1),а;(2),...,зт(р) или представленных в виде некоторых их комбинаций),
в которой эффект мультиколлинеарности уже не имел бы места. Этап
проводится в основном силами математиков-статистиков с подключением
(в самом его конце) специалистов соответствующей предметной области
для выбора из нескольких предложенных вариантов наборов объясняющих
переменных одного, наиболее легко и естественно интерпретируемого.
Рекомендации по проведению этого этапа даны в гл. 15.
Этап 6 (вычисление оценок неизвестных параметров, входящих в
исследуемое уравнение статистической связи). Итак, в результате про-
ведения предыдущих этапов были решены, в частности, следующие зада-
чи:
а)	определены результирующие и объясняющие переменные и тип ис-
следуемой зависимости (В, С или D, см. п. 10.5);
б)	собрана и подготовлена к счету исходная статистическая информа-
ция вида (10.1);
в)	изучены характер и теснота статистических (корреляционных) свя-
зей между исследуемыми переменными;
г)	выбран класс допустимых решений F, т. е. класс (или параметри-
10.6. ЭТАПЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
375
ческое семейство) функций f(X), в рамках которого будет подбираться
наилучшая (в определенном смысле) аппроксимация f(X) искомой зависи-
мости типа (10.14), (10.16) или (10.20).
Теперь можно приступить к определению этой наилучшей аппрокси-
мации f(X), которая является решением оптимизационной задачи вида
f(X) = argextr An(f),	(10.21)
где функционал An(f) задает критерий качества аппроксимации резуль-
тирующего показателя т} (или У) с помощью функции f(X) из класса F.
Выбор конкретного вида этого функционала опирается на знание веро-
ятностной природы остатков е в моделях типа (10.14) и (10.16), при-
чем он строится, как правило, в виде некоторой функции от невязок
= 1,2,...,т), где 4^ =	(один из рас-
пространенных вариантов такого функционала, а именно функционал ме-
тода наименьших квадратов, упоминается в примере 10.1, см. соотноше-
ние (10.7')). Если в качестве класса F задаются некоторым параметриче-
ским семейством функций {f(X;0)}, то задача (10.1) сводится к подбору
(статистическому оцениванию) значений параметров 0, на которых до-
стигается экстремум по 0 функционала An(f(X;0)), а соответствующие
модели называют параметрическими. Эта часть исследования хорошо
оснащена необходимым математическим аппаратом и соответствующим
программным обеспечением (см. гл. 15 и 17).
Этап 7 (анализ точности полученных уравнений связи). Исследо-
ватель должен отдавать себе отчет в том, что найденная им в соответ-
ствии с (10.1) аппроксимация f(X) неизвестной теоретической функции
fr(X) из соотношений типа (10.14) или (10.16) (называемая эмпирической
функцией регрессии, см. гл. 15) является лишь некоторым приближени-
ем истинной зависимости Гт(Х)1. При этом погрешность 6 в описании
неизвестной истинной функции fT(X) с помощью f(X) в общем случае со-
стоит из двух составляющих: а) ошибки аппроксимации 6? и б) ошибки
выборки 6(п). Величина первой зависит от успеха в реализации этапа 4,
т.е. от правильности выбора-класса допустимых решений F. В частно-
сти, если класс F выбран таким образом, что включает в себя и неиз-
вестную истинную функцию f (т. е. Ст(-Х’) € F), то ошибка аппроксимации
= 0. Но даже в этом случае остается случайная составляющая (ошиб-
1 В дальнейшем, говоря о вектор-фу я кци и Гт(Х), вехтор-погрешности 6 я векторе
результирующих показателей Y(X), мы будем иметь в виду каждую из их компонент
в отдельности.
376
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
ка выборки) 6(n)t обусловленная ограниченностью выборочных данных
вида (10.1), на основании которых мы подбираем функцию f(X) (оцени-
ваем ее параметры). Очевидно, уменьшить ошибку выборки мы можем
за счет увеличения объема п обрабатываемых выборочных данных, так
как при fT(X) € F (т.е. при = 0) и правильно выбранных методах ста-
тистического оценивания (т. е. при правильном выборе оптимизируемого
функционала качества модели Дп(/)) ошибка выборки 6(п) —> 0 (по веро-
ятности) при п —> оо (свойство состоятельности используемой процедуры
статистического оценивания неизвестной функции Гт(Х)).
Соответственно на данном этапе приходится решать следующие
основные задачи анализа точности полученной регрессионной зависимо-
сти:
1)	в случае F = {/(Х;0)} и fr(X) 6 F, т.е. когда класс допустимых
решений задается параметрическим семейством функций и включает в се-
бя неизвестную теоретическую функцию регрессии f-j-(X), при заданных
доверительной вероятности Р и объеме выборки п указать такую пре-
дельную (гарантированную) величину погрешности £p,n(0fc) Для любой
компоненты неизвестного векторного параметра 0, что
|0* - 0*1 £p,n(0fc)
с вероятностью, не меньшей, чем Р (здесь — истинное значение к-н
компоненты неизвестного параметра 0, а 0* — его статистическая оцен-
ка);
2)	при заданных доверительной вероятности Р, объеме выборки п и
значениях объясняющих переменных X указать такую предельную (га-
рантированную) величину погрешности ^р,п(Кр(-^))» что
|Уср(Х) - f(X)| < «р,п(Уер(Х))
с вероятностью, не меньшей, чем Р (здесь KpPQ = Е(7? | -Д’) — неизвест-
ное условное среднее значение исследуемого результирующего показателя
при значениях объясняющих переменных, равных X, a f(X) — построен-
ная в соответствии с (10.21) эмпирическая функция регрессии);
3)	при заданных доверительной вероятности Р, объеме выборки п и
значениях объясняющих переменных X указать такую предельную (га-
рантированную) величину погрешности £рэП(У(Х)), что
|У(Х) - f(X)| « 6р,„(У(Х))
с вероятностью, не меньшей, чем Р (здесь У(Х) — прогнозируемое инди-
видуальное значение исследуемого результирующего показателя при зна-
чениях объясняющих переменных, равных X).
10.7. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
377
Описание методов анализа точности исследуемых регрессионных мо-
делей содержится в гл. 15.
Заметим в заключение, что часть исследования, объединяющая этапы
4, 5, 6 и 7, принято называть регрессионным анализом.
10.7. Выбор общего вида функции регрессии
Итак, как мы видим (см. предыдущий пункт), собственно регрес-
сионный анализ, т.е. конструирование по исходным данным вида (10.1)
неизвестной функции регрессии f(X) = E(i? | £ = X), начинается с этапа
4, т. е. с выбора семейства допустимых решений F — класса функций, в
рамках которого предполагается вести поиск наилучшей аппроксимации
/(X) для /(X)1.
Наиболее распространенными в статистической практике являются
параметрические регрессионные схемы, когда в качестве класса допусти-
мых решений выбирается некоторое параметрическое семейство функций
।
F = {/(Х;©)}вег.	(10.22)
В этом случае дальнейший поиск аппроксимации f(X) сводится к наи-
лучшему (в смысле заданного критерия адекватности, см. выше, этац 6,
соотношение (10.21)) подбору неизвестного значения параметра О, что в
свою очередь осуществляется с помощью полностью формализованного
алгоритма решения соответствующей оптимизационной задачи, составля-
ющей математическую основу процедуры, называемой статистическим
оцениванием параметра (см. гл. 7).
Но до перехода к процедуре статистического оценивания неизвест-
ного значения параметра мы должны сделать и обосновать выбор типа
параметрического семейства (10.22). Так, например, в качестве класса
допустимых решений можно использовать
р
линейные ф ункции : /(Х;О) = 0О 4-^0^ • х^;	(10.22*)
степенные функции : /(Х;0) = 0о(ж^1^)в1(а:^)ва .. .(хр)*г; (10.22**)
1 Начиная с этого момента мы будем рассматривать случай т = 1 общей постанов-
ки задачи статистического исследования зависимостей, т.е. случай единственного
результирующего показателя у.
378
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
алгебраические полиномы степени m > 2:
/(X; 0) = 60 + £в* 
*=1	*1=1 *2 = 1
*1=1 *m=i
(10.22'")
И т.д.
Следует подчеркнуть, что этап 4 (см. п. 10.6), т.е. этап исследова-
ния, посвященный выбору общего вида функции регрессии (параметриза-
ция модели), бесспорно, является ключевьмс: от того, насколько удачно
он будет реализован, решающим образом зависит точность восстановле-
ния неизвестной функции регрессии f(X). В то же время приходится
признать, что этот этап находится, пожалуй, в самом невыгодном поло-
жении: к сожалению, не существует системы стандартных рекомендаций
и методов, которые образовывали бы строгую теоретическую базу для его
наиболее эффективной реализации.
Остановимся на некоторых рекомендациях, связанных с реализацией
трех основных моментов, учет которых необходим при решении проблемы
выбора общего вида функции регрессии: 1) максимальное использование
априорной информации о содержательной (физической, экономической,
социологической и т. п.) сущности анализируемой зависимости; 2) пред-
варительный анализ геометрической структуры исходных данных вида
(10.1), на основании которых конструируется искомая зависимость; 3) раз-
личные статистические приемы обработки исходных данных, позволяю-
щие сделать наилучший выбор из нескольких сравниваемых вариантов.
10.7.1.	Использование априорной информации о
содержательной сущности анализируемой
зависимости
Анализируя содержательную сущность изучаемой зависимости, ис-
следователь еще до обращения к исходным статистическим данным может
(и должен!) попытаться ответить на ряд вопросов по поводу характера
искомой регрессионной связи:
а)	будет ли искомая функция f(X) монотонной или она должна иметь
один экстремум (может быть, несколько)?
б)	следует ли ожидать стремления (в процессе —+ оо) f(X) к асим-
птомам (по одной или нескольким предикторным переменным) и какова
их содержательная интерпретация? Так, например, если f(X) — сред-
10.7. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ	379
ний объем благ определенного вида, потребляемых семьями группы X по
доходам, то, очевидно, при X —* сю следует ожидать «насыщения», т.е.
/(X) будет стремиться (снизу) к горизонтальной асимптоте (см. п.4 в
табл. 10.3);
в)	какова принципиальная природа воздействия объясняющих пере-
(1) (2)	(р)	.
пенных х' , аг , ...,яг на формирование результирующего показателя
у — аддитивная или мультипликативная? Так, например, многие схемы
зависимостей в экономике характеризуются мультипликативной природой
воздействия предикторов на у (см. п. 1-3 в табл. 10.3);
г)	не диктует ли содержательный смысл анализируемой зависимости
обязательное прохождение графика искомой функции f(X) через одну или
несколько априори заданных точек в исследуемом факторном простран-
стве
Поясним необходимость и возможность максимального извлечения ин-
формации об общем виде анализируемой функции регрессии f(X) из со-
ображений профессионально-теоретического характера на примере.
Пример 10.3. На рис. 10.7 представлены 63 результата специаль-
ного эксперимента [Езекиэл М., Фокс К., с. 57]. Расположение точек на
рис. 10.7 не дает ответа на вопрос, описывать ли зависимость между ско-
ростью автомобиля (х миль/ч) и расстоянием (у футов), пройденным им
после поданного сигнала об остановке, линейной или параболической за-
висимостью.
у, футов
120
100
80
60
40
20
0 5 10 15 20 25 30 35 х, миль/ч
Рис. 10.7. График зависимости тормозного пути автомобиля (у) от скорости
его движения (z)
Этот вопрос остается без ответа и после построения соответствую-
щих кривых и применения известных статистических критериев, предна-
значенных решать, насколько хорошо согласуются кривые с эксперимен-
тальными данными. Однако несложные рассуждения профессионально-
380
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
теоретического характера все-таки позволяют сделать этот выбор. Дей-
ствительно, для каждого отдельного автомобиля и водителя расстояние,
пройденное до остановки, определяется в основном тремя факторами: ско-
ростью автомобиля (х) в момент подачи сигнала об остановке, временем
реакции на этот сигнал водителя (flj, ч) и тормозами автомобиля. Автомо-
биль успеет пройти путь в^х до момента включения водителем тормозов
и еще • х2 после этого момента, поскольку согласно элементарным фи-
зическим законам теоретическое расстояние, пройденное до остановки с
момента торможения, пропорционально квадрату скорости.
Итак, f(x) = в\Х + в^х2, что после оценивания и 02 с помощью
МНК (см. гл. 7) дает f(x) = 0,76а: 4- 0,056а:2.
10.7.2.	Предварительный анализ геометрической
структуры исходных данных
При выяснении вопроса о параметрическом виде исследуемой зави-
симости, как правило, идут от простого к сложному. Простейшей же
аппроксимацией неизвестной фушсции регрессии f(X) = Er; | £ = X)
является, естественно, линейная модель, т.е. функция вида
/Л(Х) = 00 + М(1) + - •  + 0„хМ.	(10.23)
Поэтому при предварительном анализе характера исследуемых зави-
симостей (т. е. проведения вычислительных процедур по оценке неизвест-
ных значений параметров, входящих в гипотетичные уравнения связей)
ограничиваются некоторыми приближенными эвристическими приемами,
связанными в основном с изучением «геометрии» парных корреляционных
полей и визуальной проверкой их линейности.
Содержание геометрического анализа парных корреляци-
онных полей. Под корреляционным полем переменных (и, и) понима-
ется графическое представление имеющихся измерений («i,Vi),(«2>
...,(un,vn) этих переменных в плоскости (u,v). Мы уже неоднократно
имели дело с корреляционными полями (см. рис. 10.2, 10.4, 10.5, 10.7).
Анализ парных корреляционных полей состоит обычно в следующем:
а) построение на основании имеющихся исходных данных вида (10.1)
t О)
корреляционных полей для всевозможных пар переменных вида \ х',х' ')
и (х 3\у)> отобранных из набора всех р 4- 1 исследуемых признаков
(а/1), а/2\..., х^; у\, всего таких пар будет, очевидно, р(р 4- 1 )/2, однако
процесс этот легко автоматизируется с помощью современных вычисли-
тельных средств;
10.7. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
381
б)	визуальное прослеживание характера вытянутости каждого кор-
реляционного поля: эллипсоидально-линейное (см. рис. 10.6), нелинейно-
монотонное (см. рис. 10.7), с наличием одного или нескольких экстремумов
(см. рис. 10.4) и т.п.;
в)	изучение поведения условных средних значений результирующего
показателя при изменения величины переменной, откладываемой по оси
абсцисс и играющей роль предикторной (см. рис. 10.2); для этого (если
значения предикторной переменной неконтролируемы в ходе наблюдения
или эксперимента) предварительно разбивают диапазон значений объяс-
няющей переменной на интервалы группирования (см. п. 6.1) и подсчиты-
вают средние значения ординат тех точек-наблюдений, которые попали в
общий интервал группирования.
В результате такого анализа обычно получают формулировку не-
скольких рабочих гипотез об общем виде искомой зависимости, оконча-
тельная проверка которых и выбор наиболее адекватной из них осуще-
ствляются (при отсутствии априорных сведений содержательного харак-
тера) с помощью соответствующих математико-статистических мето-
дов. Описание наиболее эффективных, с нашей точки зрения, приемов
такого типа приводятся в п. 10.7.3.
10.7.3.	Статистические критерии проверки гипотез об
общем виде функции регрессии
Подчеркнем сразу, что описанные ниже критерии проверки справед-
ливости сделанного выбора общего вида искомой функции регрессии не
могут ответить на вопрос: является ли проверяемый гипотетичный вид
зависимости наилучшим, единственно верным? Они лишь подтверждают
факт непротиворечивости проверяемого вида функции регрессии имею-
щимся у исследователя исходным данным (10.1) либо отвергают обсужда-
емую гипотетичную форму зависимости как не соответствующую этим
данным.
1.	Общий приближенный критерий, основанный на группированных
данных (или при наличии нескольких наблюдений при каждом фиксиро-
ванном значении аргумента). Пусть высказана гипотеза об общем виде
функции регрессии Но: E(q | f = X) = fa(X\0lie2i ...,0*) (Л(Х;0) —
известная функция, (01,02,-- .,0*) =0 — неизвестные числовые пара-
метры) и пусть вычислены (например, с помощью метода наименьших
квадратов, см. гл. 15) оценки 01,02, • • • ,0* неизвестных параметров, вхо-
дящих в описание уравнения регрессии. При группировке данных (или
при проведении эксперимента) мы должны соблюдать требование, в соот-
382	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
ветствии с которым число интервалов группирования (или число различ-
ных значений аргумента, в которых производились наблюдения) з должно
обязательно превосходить число неизвестных параметров fc, т. е. з — к 1.
Если высказанная гипотеза об общем виде зависимости является пра-
вильной, то статистика
ЛЕ^й-Л^,0;©)!2
= - ;=!—------------—	(10-24)
кЬ Ё Ё 1»ч - й1
1=1 J=1
должна приближенно подчиняться F(mi, т2)-расп ре делению с числом сте-
пеней свободы числителя mi = з — к и знаменателя = п — з. Все ве-
личины в формуле (10.24) соответствуют ранее введенным обозначениям.
В частности, X? — середина «-го гиперпараллелепипеда группирования
(или *-е значение аргумента, в котором было проведено щ наблюдений);
/а(Х,°; 6 — значение гипотетической функции регрессии, вычисленное в
точке X = Xi; у, — условное среднее из ординат, попавших в «-и гиперпа-
раллелепипед группирования (или из ординат, измеренных при »-м фикси-
рованном значении аргумента л,);	— J-e по счету значение ординаты
из числа попавших в *-й интервал группирования (или из числа измерен-
ных при i-м фиксированном значении аргумента X?). Легко понять, что
числитель в правой части (10.24) характеризует меру рассеивания экспе-
риментальных данных вокруг аппроксимирующей выборочной регресси-
онной поверхности, а знаменатель — меру рассеивания эксперименталь-
ных данных около своих условных выборочных средних у, (т. е. меру, не-
зависимую от выбранного вида линии регрессии). Причем и числитель, и
знаменатель являются практически независимыми (в некоторых частных
случаях — точно независимыми) статистическими оценками одной и той
же теоретической дисперсии ег31 = D(»71 f = X).
Соответственно получаем следующее правило проверки гипотезы об
общем виде функции регрессии. Задаемся, как обычно, достаточно ма-
лым уровнем значимости критерия а (например, а = 0,05). С помо-
щью таблицы находим 100(1 - f )%-ную точку и 100f %-ную точ-
ку t F(k — т,п — к)-распределения. Если окажется, что величина v2,
подсчитанная по формуле (10.24), удовлетворяет неравенствам
2	^2^2
Vl-f < V <
то высказанная нами гипотеза об общем виде функции регрессии призна-
ется не противоречащей экспериментальным данным (10.1). Если же эти
10.7. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
383
неравенства оказались нарушенными, то гипотеза об общем виде функ-
ции регрессии отвергается с уровнем значимости а. При этом если V2
«слишком мало» (т.е. v2 < v2_^), то, очевидно, при выборе общего вида
регрессии мы неправомерно реагировали на случайные отклонения точек
(XtiVi) от истинной функции регрессии и тем самым необоснованно за-
высили число параметров к, от которых зависит уравнение регрессии.
Напротив, если v «слишком велико» (т.е. v2 > t>^), то «гибкость» ап-
проксимирующей функции регрессии /а(Х;0) следует признать недоста-
точной, поэтому целесообразно увеличить число неизвестных параметров
регрессии (например, повысить порядок аппроксимирующего полинома).
Для случая, когда условная дисперсия зависимой переменной про-
порциональна некоторой известной функции аргумента, т.е. D,(X) =
(Т2/?(Х), формула (10.24) преобразуется:
тЬ Е - fa(Xi, ©)|
--------------й--------—•	(10.24*)
Й7 Ё “Ч 2 (»У - Й)
=1 j=l
где
W. = 1/Л2(Х,°).
Так, в примере 10.1: п = 40; s = 4; а = 0,05; к = 2; дисперсионное от-
ношение и , подсчитанное по формуле (10.24*), равно 1,04, в то время как
5%-ная точка ^(2,36)-распределения vo,os = 3,26. Это свидетельствует о
том, что гипотеза о линейном виде регрессионной зависимости в данном
случае не противоречит имеющимся в нашем распоряжении эксперимен-
тальным данным.
При проверке линейности регрессии (так же, впрочем, как и при про-
верке гипотезы о полиномиальном характере регрессии заданного поряд-
ка) в нормальных схемах зависимостей типа В и (см. п. 10.5) опи-
санный общий критерий является тонным. При этом в линейном случае
статистика v , определенная соотношением (10.24), может быть выраже-
на в более удобной форме, не требующей предварительного вычисления
выборочной аппроксимирующей функции регрессии, а именно:
(*-2)(1 -р*.<) '
(10.25)
Здесь и г — соответственно выборочные корреляционные отношения
(т/ по £) и коэффициент корреляции (см. гл. 11). Логическая схема исполь-
зования статистики (10.25) аналогична ранее изложенным критериям: за-
даются достаточно малым (0,05 ~ 0,15) уровнем значимости а; находят
384	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
по таблице 100а%-ную точку распределения F(a —2,п —л); сравнивают
величину v2, определенную с помощью (10.25), с процентной точкой
2^2
если оказывается, что v > vQi то гипотезу о линейном виде регрессии
считают статистически необоснованной.
Воспользуемся данным критерием для статистической проверки ли-
нейности регрессии в примере 10.2. Вычисления дают: г = 0,429,
р2^ = 0,459, так что v2 = 0,513. Принимая во внимание, что величи-
на 5% ной точки Г(4,37)-распределения равна Vo,os = 2,63, делаем вывод о
непротиворечивости гипотезы линейной регрессии и данных нашего экс-
перимента в данном примере (0,513 < 2,63).
2.	(Жций приближенный критерий, основанный на негру ппирован-
ных данных (при известной величине дисперсии остаточной случайной
компоненты).
Встречаются ситуации, когда в результате предварительных иссле-
дований или из других каких-либо соображений нам удается заранее опре-
делить величину дисперсии а2 остаточной случайной компоненты £ в раз-
ложениях вида (10.14) и (10.16) (например, когда е — ошибка измерения
и нам известны характеристики точности используемого измерительного
прибора). В этом случае можно отказаться от стеснительного требова-
ния группированности данных и для проверки гипотезы об общем виде
функции регрессии воспользоваться фактом х(п ~ ^)-распределенности
статистики
7 = Л~*Е(й-/«(^;0))2	(ю-26)
(который имеет место при условии справедливости нашей гипотезы).
Задавшись уровнем значимости критерия а и найдя с помощью табл,
величины 100(1 — у)%-ных и 100у%-ных точек %2-распределения с п - к
степенями свободы соответственно Xi-f (п ~ ^) и Х$(п ~ А), проверяем
выполнение неравенства
(п - к) < 7 < %^(п - к),
где 7 подсчитано по формуле (10.26). Если эти неравенства оказались на-
рушенными, то от гипотезы Яо об общем виде функции регрессии следует
отказаться. При этом если 7 «слишком мало» (т.е. 7 С Xi-$(n “ m))>
то, очевидно, при выборе общего вида мы неправильно реагировали на
случайные отклонения экспериментальных точек (Х,,у{) и тем самым не-
обоснованно завысили число параметров к, от которых зависит уравнение
регрессии.
10.7. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
385
Напротив, если 7 «слишком велико» (т.е. 7 > Х*(п — Л)), то «гиб-
кость» аппроксимирующей кривой регрессии	следует признать
недостаточной, поэтому целесообразно увеличить число неизвестных па-
раметров регрессии (например, повысить порядок аппроксимирующего по-
линома^ .
Для случая, когда дисперсия зависимой переменной (или, что то же,
дисперсия остаточной случайной компоненты) не остается постоянной при
изменении X, а пропорциональна некоторой известной функции аргумен-
та, т.е. Dr?(X) = ап(Х), формула подсчета статистики 7 несколько
изменится:
° п~к >=1
где w, = l//>3(Xj). В остальном схема проверки гипотезы об общем виде
функции регрессии остается той же самой, что и в случае Dtj(X) = сг2 =
const.
10.7.4.	Некоторые общие рекомендации
При выборе общего вида искомой функции регрессии /(X), помимо
соображений и приемов, описанных выше, полезно учитывать следующие
общие рекомендации.
1)	Не следует гнаться за чрезмерной сложностью функции, описы-
вающей поведение искомой функции регрессии, руководствуясь исключи-
тельно соображениями оптимизации критерия качества аппроксимизации
Дп(/) (см. (10.21)). Дело в том, что если и оценки 0 неизвестных параме-
тров модели 0, и значение критерия Дп(/) вычисляются на основании од-
ной и той же выборки, то за счет увеличения размерности к оцениваемо-
го векторного параметра 0 = (0j, 03,..., 0*)Т можно добиться, на первый
взгляд, идеального результата. Возможность эта основана на известном в
математическом анализе результате, в соответствии с которым для любой
заданной системы точек (®1,У1),(®2»1/2)>
»(®п»Уп) (с неповторяю
ся абсциссами) можно подобрать алгебраический полином степени п — 1,
проходящий в точности через все точки этой системы. А это значит, что
все «невязки» yt — на основании которых строится критерий Дп(/)
(а следовательно, и сам критерий, см. п. 10.6, этап 6), равны нулю, т.е.
«лучше» модели для описания поведения функции регрессии подобрать
невозможно. На самом деле при таком подходе мы как бы заставляем
функцию f(x) реагировать на случайные флюктуации, объясняемые наг
личием в представлениях типа (10.14) остаточной случайной компоненты
е(Х). Поэтому, если мы попробуем применить полученный таким образом
386	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
результат к другой выборке из той же самой генеральной совокупности,
то увидим явное рассогласование модельных (/(XJ) и наблюденных (у,)
значений результирующего показателя. Поэтому при подборе общего вида
функции регрессии, как правило, идут от простого к сложному, т. е. на-
чиная с анализа возможности использовать простейшую линейную модель
вида (10.23).
2)	Следует добиваться компромисса между сложностью регресси-
онной модели и точностью ее оценивания. Из общих результатов ма-
тематической статистики, относящихся к анализу точности оценивания
исследуемой модели при ограниченных объемах выборки, следует, что с
увеличением сложности модели (выраженной, например, размерностью k
векторного параметра 0, участвующего в ее уравнении) точность оцени-
вания падает. Например, ширина доверительного интервала Д[у(Х)]р
для неизвестного значения у(Х), при прочих равных характеристиках
анализируемой схемы, увеличивается с ростом размерности параметра
0, участвующего в вычислении функции регрессии /(Х;0) (см. гл. 15).
Именно поэтому в ситуациях, когда исследователь располагает ограничен-
ной исходной выборочной информацией вида (10.1), он вынужден искать
компромисс между степенью общности привлекаемого класса допустимых
решений F и точностью оценивания, которой возможно при этом добиться
(пример подобного рода действий по поиску компромисса будет приведен
в гл. 15 в связи с задачей определения оптимального числа объясняющих
переменных в линейной модели множественной регрессии).
3)	При обнаружении нелинейности в парных статистических связях
анализируемых переменных з и y(j = 1,2,...,р) следует попытать-
ся применить к этим переменным линеаризующие преобразования. Про-
стейший пример такого приема мы имеем, когда вместо анализа степенной
зависимости вида
у = 6o(i)e‘	(10.27)
исследователь рассматривает линейную зависимость между логарифмами
исходных переменных, а именно:
У =	(10.28)
где у = In у, х = Ina; и в0 = 1п0о- В зависимости от типа нелиней-
ной связи, существующей между исходными переменными, подбираются
и другие линеаризующие преобразования (см., например, [Айвазян С. А.,
Енюков И. С., Мешалкин Л.Д., 1985, п. 6.2.3]). Один из наиболее общих
подходов к линеаризации анализируемых зависимостей реализуется с по-
мощью так называемого преобразования Бокса-Кокса (см. гл. 15).
выводы
387
4)	Анализ регрессионных остатков. Ряд статистических критери-
ев проверки адекватности используемой аппроксимирующей модели ре-
грессии основан на анализе регрессионных остатков (невязок) е(Х,) =
у, ~ fa(Xi),i = 1,2, ...,п. В основе их конструирования — положение,
в соответствии с которым правильный выбор модели fa(X) предопределя-
ет асимптотическую (по п —► оо) независимость остатков e(JQ. Поэтому
статистическая проверка правильности выбора общего вида функции ре-
грессии сводится к проверке статистической независимости остатков, для
чего могут быть использованы, например, критерии, описанные в гл Л 6
(п. 16.2). В выражении для невязок £(Х,) под /а(Х4) понимается значе-
ние оцененной аппроксимирующей функции регрессии в точке X,, т.е.
/»№) = Л(Х,-; ©).
5)	Поиск модели, наиболее устойчивой к варьированию состава вы-
борочных данных, на основании которых она оценивается. Идея этого
подхода к выбору общего вида исследуемой регрессионной зависимости
основана на следующем простом соображении. Если общий параметриче-
ский вид зависимости /(я^\я^2\...ж^;0) «угадан» правильно, то ре-
зультаты оценивания 01,02,... параметра 0 по различным подвыборкам
выборки {arJ ,х} я;- ;у,будут мало отличаться друг от друга
(а следовательно, не сильно будут различаться между собой и соответ-
ствующие значения /(а/1),®^,..., а/р); 0i), /(я^\ж^2\.. .з/р\ 02),...).
И наоборот, при неудачном выборе общего вида искомой зависимости ре-
зультаты ее восстановления по различным выборкам, как правило, будут
сильно отличаться один от другого. Описание реализации этого подхода
читатель может найти в [Айвазян С. А., Енюков И. С., Мешалкин Л.Д.,
1985, п. 6.2.3].
ВЫВОДЫ
1.	Аппарат статистического исследования зависимостей — состав-
ная часть многомерного статистического анализа — нацелен на решение
основной проблемы естествознания: как на основании частных резуль-
татов статистического наблюдения за анализируемыми событиями или
показателями выявить и описать существующие между ними стохастиче-
ские взаимосвязи.
2.	Анализируемые переменные величины по своей роли в исследова-
нии подразделяются на результирующие (прогнозируемые) У и объясня-
ющие (экзогенные, предикторные) X. Среди компонент векторов У и X
могут быть и количественные, и порядковые (ординальные), и классифи-
388
ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
кационные (номинальные).
3.	Центральным математическим объектом в процессе статистиче-
ского исследования зависимостей является функция f(X), называемая
функцией регрессии Y по X и описывающая изменение условного сред-
него значения У^.р(Х) результирующего показателя Y (вычисленного при
фиксированных на уровне X значениях объясняющих переменных) в за-
висимости от изменения значений объясняющих переменных X.
4.	Конечные прикладные цели статистического исследования зависи-
мостей могут быть в основном трех типов: 1) установление самого факта
наличия (или отсутствия) статистически значимой связи между Y и X,
исследование структуры этих связей; 2) прогноз (восстановление) неиз-
вестных значений индивидуальных или средних значений результирую-
щего показателя по заданным значениям соответствующих объясняющих
(экзогенных) переменных; 3) выявление причинных связей между объясня-
ющими переменными X и результирующими показателями Y, частичное
управление значениями Y путем регулирования величин объясняющих пе-
ременных X.
5.	Разделы многомерного статистического анализа, составляющие
математический аппарат статистического исследования зависимостей,
формировались и развивались с учетом специфики анализируемых моде-
лей, обусловленной в первую очередь природой исследуемых переменных.
Так, изучение зависимостей между количественными переменными обслу-
живается регрессионным и корреляционным анализами и анализом вре-
менных рядов (гл. 11, 15, 16, 17); изучение зависимостей количественного
результирующего показателя от неколичественных или разнотипных объ-
ясняющих переменных — дисперсионным и ковариационным анализами,
моделями типологической регрессии; наконец, для исследования системы
зависимостей, в которых одни и те же переменные в разных уравнениях
этой системы могут одновременно выполнять и роль результирующих,
и роль объясняющих, служит теория одновременных эконометрических
уравнений (гл. 14 и 17). Аппарат исследования зависимостей неколиче-
ственных или разнотипных результирующих показателей от количествен-
ных или разнотипных объясняющих переменных в книге не рассматрива-
ется.
6.	К основным типовым задачам практики, в которых использование
аппарата статистического исследования зависимостей оказывается наибо-
лее уместным и эффективным, следует отнести задачи: 1) нормирования;
2) прогноза, планирования и диагностики; 3) оценки труднодоступных
(для непосредственного наблюдения и измерения) характеристик иссле-
дуемой системы; 4) оценки эффективности функционирования (или ка-
выводы
389
чества) анализируемой системы; 5) регулирования параметров функци-
онирования анализируемой системы. Все эти задачи являются основны-
ми составными частями центральной проблемы кибернетики — проблемы
«управления, связи и разработки информации» (см.: Математическая эн-
циклопедия. Т. 2 — М.: Советская энциклопедия, 1979, с. 850).
7.	По своей природе исследуемые зависимости могут быть разделены
на: 1) детерминированные (тип А), когда исследуется функциональная за-
висимость между неслучайными переменными; 2) регрессионные (тип В),
когда исследуется зависимость случайного результирующего показателя
от неслучайных объясняющих переменных — параметров системы; 3) кор-
реляционные (тип С), когда исследуется зависимость между случайными
переменными, причем объясняющие переменные могут быть измерены без
искажений; 4) конфлюэнтные (тип D), когда исследуется функциональная
зависимость между случайными или неслучайными переменными в ситуа-
ции, когда те и другие могут быть измерены только с некоторой случайной
ошибкой.
8.	Весь процесс статистического исследования зависимостей может
быть разбит на семь последовательно реализуемых основных этанов, хро-
нологический характер связей которых дополняется связями итерационно-
го взаимодействия (см. рис. 10.6): этап 1 (постановочный); этап 2 (инфор-
мационный); этап 3 (корреляционный анализ); этап 4 (определение класса
допустимых решений); этап 5 (анализ мультиколлинеарности предсказы-
вающих переменных и отбор наиболее информативных из них); этап 6 (вы-
числение оценок неизвестных параметров, входящих в исследуемое урав-
нение статистической связи); этап 7 (анализ точности полученных урав-
нений связи).
9.	Этап параметризации регрессионной модели, т. е. выбора параме-
трического семейства функций (класса допустимых решений), в рамках
которого производится дальнейший поиск неизвестной функции регрес-
сии, является одновременно наиболее важным и наименее теоретически
обоснованным этапом регрессионного анализа.
10.	Прежде всего исследователь должен сосредоточить свои усилия на
анализе содержательной сущности искомой статистической зависимости,
чтобы максимально использовать имеющиеся априорные сведения о «фи-
зическом» механизме изучаемой связи при выборе общего вида функции
регрессии.
11.	Важную роль в правильном выборе параметрического класса
допустимых решений играет предварительный анализ геометрической
структуры совокупности исходных данных и в первую очередь анализ
геометрии парных корреляционных полей, включающий в себя, в частно-
390	ГЛ. 10. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ
сти, учет и формализацию «гладких» свойств искомой функции регрес-
сии, использование вспомогательных линеаризующих преобразований.
12.	Сформулированные с помощью содержательного и геометрическо-
го анализа рабочие гипотезы об общем виде искомой функции регрессии
могут быть проверены с привлечением соответствующих математико-
статистических критериев. Среди фундаментальных идей, на которых
базируются эти статистические критерии, следует выделить: а) идею ком-
промисса между сложностью регрессионной модели («емкостью» класса
допустимых решений) и точностью ее оценивания; б) идею поиска моде-
ли, наиболее устойчивой к варьированию состава выборочных данных, на
основании которых она оценивается; в) идею проверки гипотез об общем
виде функции регрессии на базе сравнения выборочных критериев аде-
кватности и исследования статистических свойств получаемых при этом
оценок размерности модели.
ГЛАВА 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
МНОГОМЕРНОЙ ГЕНЕРАЛЬНОЙ
СОВОКУПНОСТИ
11.1. Назначение и место корреляционного
анализа в статистическом
исследовании
При исследовании реальных социально-экономических явлений и си-
стем статистику, экономисту приходится сталкиваться, как правило, с
необходимостью статистического анализа многомерной генеральной со-
вокупности, т.е. с ситуациями, когда на каждом из статистически об-
следуемых объектов этой совокупности регистрируются значения целого
набора признаков а/2\..., В дальнейшем мы будем обозначать,
как и прежде, этот набор признаков с помощью л = (аг аг аг ; ,
а результат регистрации значений этих признаков на t-м статистиче-
ски обследованном объекте — t-e многомерное наблюдение — с помощью
Xi =	Таким образом, «стартовая позиция» при
многомерной генеральной совокупности аналогична одномерному случаю:
исследователь по имеющейся у него случайной выборке
ХЬХ2,...,ХП	(11.1)
значений анализируемой многомерной случайной величины ( =
...,£^)Т должен сделать те или иные статистические выводы о ее
«поведении*.
Мы уже знаем (см. п. 2.6), что исчерпывающие сведения о поведе-
нии анализируемой случайной величины £ содержатся в ее законе рас-
пределения вероятностей (з.р.в.) /((X), где под Д(Х) понимается значе-
ние функции плотности вероятности в точке X, если случайная величина
{ непрерывна, и вероятность Р{£ = X} того, что случайная величина
392
ГЛ. II. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
примет значение, равное X, если £ дискретна. Однако з.р.в. анали-
зируемой случайной величины исследователю, как правило, неизвестен.
И если при описании поведения одномерных случайных величин исследо-
ватель еще имеет практически реализуемые возможности подбора и ис-
пользования подходящих модельных законов распределения (см. гл.З) с
последующей статистической оценкой участвующих в их записи параме-
тров (см. гл. 7), то при исследовании признаков размерности р > 2 ему
чаще всего приходится ограничиваться информацией, которую доставля-
ют оценки моментов первых двух порядков, а именно оценками вектора
средних значений М\ = (т^,	, mJp^)T и ковариационной матрицы
Е = (dij), —i,j = 1,2,... ,р (см. п. 6.2). Другими словами, можно сказать,
что за редчайшим исключением , все выводы многомерного статисти-
ческого анализа строятся на базе оценок М\ и Е.
Оценка Мг вектора средних значений дает представление о центре
группирования наблюдений анализируемого многомерного признака. От-
личие от одномерного случая, когда мы располагаем оценкой тх = х сред-
него значения анализируемой случайной величины, заключается лишь в
том, что Afj определяет точку в р-мерном пространстве, в то время как
выборочное среднее тг = х определяет точку на числовой прямой. По
существу вся специфика многомерного случая сосредоточена в ковари-
ационной матрице Е, а при статистическом анализе — в ее оценке Е.
Именно знание ковариационной матрицы позволяет исследователю стро-
ить и анализировать характеристики случайного рассеивания и статисти-
ческой взаимосвязи (коррелированности) компонент анализируемого мно-
гомерного признака. Данная глава как раз и посвящена так называемо-
му корреляционному анализу многомерной генеральной совокупности,
назначение которого — получить (на основе имеющейся выборки (11-1))
ответы на следующие основные вопросы:
•	как выбрать (с учетом специфики и природы анализируемых пере-
менных) подходящий измеритель статистической связи (коэффици-
ент корреляции, корреляционное отношение, какую-либо информацион-
ную характеристику связи, ранговый коэффициент корреляции и т. п.)?
•	как оценить (с помощью точечной и интервальной оценок) его
числовое значение по имеющимся выборочным данным?
•	как проверить гипотезу о том, что полученное числовое значе-
ние анализируемого измерителя связи действительно свидетельствует
1 Исключения относятся в основном к генеральным совокупностям, описываемым либо
многомерным нормальным, либо полиномиальным з.р.в. (см. соответственно (3.9')
и (3.7)).
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
393
о наличии статистической связи (или, кик говорят* проверить иссле-
дуемую корреляционную характеристику на статистически значимое
ее отличие от нуля?
• как определить структуру связей между компонентами исследу-
емого многомерного признака* сопоставив каждой паре компонент дво-
ичный ответ («связь есть» или «связи нет»)?
Какое место занимает корреляционный анализ в общем прикладном
статистическом исследовании? В гл. 9 обозначены три центральные про-
блемы прикладной статистики. Начнем с первой и наиболее значимой
из них — с проблемы статистического исследования зависимостей. В
соответствии с предложенным в предыдущей (10-й) главе разбиением
процесса решения этой проблемы на этапы (см. п. 10.6) корреляцион-
ный анализ составляет содержание, по существу, первого (после поста-
новки задачи и сбора необходимых статистических данных) этапа ста-
тистического исследования зависимостей. Действительно, при исследо-
вании зависимостей между анализируемыми переменными мы должны
дать в первую очередь ответ на вопрос: а существует ли такая за-
висимость или анализируемые признаки статистически независимы? И
только после утвердительного ответа на этот вопрос заняться выявле-
нием вида и математической формы этой зависимости. Корреляцион-
ный анализ как раз и предоставляет средства, позволяющие ответить на
первый вопрос. Выявление же вида и математической формы искомой
зависимости производится с помощью разнообразных методов и моделей
регрессионного анализа и анализа временных рядов, которым посвящены
гл. 14-17. В то же время рассматриваемые в рамках корреляционного
анализа характеристики статистической связи (ковариации, различные
коэффициенты корреляции и т.п.) используются в качестве «входной»
(базовой) информации при решении задач других двух центральных про-
блем прикладной статистики — классификации объектов и признаков и
снижения размерности анализируемого признакового пространства (ме-
тоды и модели, предназначенные для решения этих двух проблем, описы-
ваются в гл. 12 и 13). Поэтому именно с главы, посвященной корреля-
ционному анализу по существу начинается изложение методов и моделей
прикладной статистики и эконометрики.
11.2. Корреляционный анализ
количественных признаков
Здесь речь идет об измерителях степени тесноты статистической
связи между количественными компонентами вектора X = (х^*х^2\
394
ГЛ. И. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
... ,я^)Т. Напомним (см. п. 2.3), что значение количественной случайной
величины есть результат измерения степени проявления анализируемого
свойства статистически обследованного объекта в числовой шкале опре-
деленного физического смысла (в штуках, метрах, денежных единицах,
килограммах, единицах времени и т.д.).
В соответствии с изложенной в п. 10.1 общей логической схемой ста-
тистического исследования зависимостей анализируемые переменные по
своей роли делятся на результирующие и объясняющие. Поэтому, оста-
вив за компонентами вектора X роль объясняющих переменных, вве-
дем в рассмотрение результирующую переменную у. Тогда исходные
статистические данные (11.1) пополнятся еще одним вектором-столбцом
Y = (УьУз,* • ->Уп)Т» так что в дальнейшем предметом нашего анализа
будут исходные статистические данные вида
(D Y(2) y(p) v
(11-1')
где Х^ —	,а?2^,... , z^)T — вектор-столбец наблюденных значений
у-й объясняющей переменной (у = 1,2,...,р).
В п. 10.5 описаны основные типы статистических зависимостей (В, С
и Л), которые могут наблюдаться между исследуемыми переменными.
Умение правильно классифицировать каждую конкретную многомерную
систему наблюдений играет решающую роль при правильном выборе под-
ходящих математико-статистических методов анализа изучаемой зависи-
мости на стадии регрессионного анализа и при неформальной содержа-
тельной интерпретации выявленной связи.
Однако при решении задач корреляционного анализа удобнее исполь-
зовать единый (унифицированный) подход, при котором исследуемая объ-
ясняющая переменная (случайная при типах зависимостей С и D и
неслучайная при зависимостях типа В) интерпретируется как пара-
метр, от которого зависит закон распределения результирующе-
го показателя. Его мы и будем придерживаться в данной главе.
11.2.1.	Коэффициент детерминации как универсальная
характеристика степени тесноты статистической
связи
Основная идея, лежащая в основе определения коэффициента детер-
минации, состоит в следующем. Пусть нас интересует степень тесноты
статистической связи (с.т.с.с.), существующей между результирующим
показателем у и объясняющей переменной (вообще говоря, векторной) X.
Очевидно, степень тесноты этой связи может считаться максимальной,
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 395
если по заданному значению объясняющей переменной X можно однознач-
но (без всякой случайной ошибки) восстановить соответствующее значе-
ние результирующего показателя у(Х). И обратно: если значение величин
X не несет никакой информации о значении результирующего показате-
ля у, то связь отсутствует вовсе, и соответствующий измеритель степени
ее тесноты должен принимать минимальное (на выбранной шкале) воз-
можное значение.
Для того чтобы математически формализовать эту естественную посылку в виде
подходящего измерителя с.т.с.с., посмотрим, как она интерпретируется в терминах
регрессионной модели типа (10.14).
Итак, мы рассматриваем статистическую зависимость вида
S(X) = /(X) + е(Х),	(11.2)
где /(X) = Е(у | X) — условное среднее значение результирующего показателя (при
условии, указанном за прямой чертой, здесь и далее означает, что объясняющая пере
менная приняла заданное фиксированное значение X), т. е. ^ункдил регрессии у по
X, — а е(Х) остаточная случайная компонента, з.р.в. которой, вообще говоря, может
зависеть от X, но при этом предполагается:
Е(е|Х)=0*,
D(e |) = «г’(Х)
и е(Х) не коррелировала с /(X) в схемах зависимости типов С и D (в схемах типа В
величина /(X) не является случайной).
Отметим два важных соотношения, связывающих характеристики варьирования
(условные и безусловные) составных частей модели (11.2)-(11.2г):
= Е(/-Л)’+Ег’,	(11.3)
D(» | X) = D(« | X) = „’(X)	(11.4)
В соотношении (11.3), связывающем между собой безусловные характеристики
варьирования, уо = Еу, /о = Е/, а символ Е означает усреднение следующих за ним
величин по всем возможным значениям как у, так и X. Нуждается в пояснении слу-
чай зависимости по схеме В (см. п. 10.5), в которой объясняющая переменная X не
является случайной. В этом случае усреднение по X производится по всем наблюден-
ным значениям Xi, Ха,..., Хя, так что, например:
Л = Е, = 1 £ /(Х<) = i £ V, /(xf);
IS=1	J=1
4 = Е(/- /о)’ = i^/((X<) - /о)’ = 1Y,», (/(X?) - /о)’;
i=l	j=l
1 Знак тождества <=» означает, что среднее значение е равно нулю при всех возмож-
ных значениях объясняющей переменной X.
396
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
е*’ = £ Ё Ее’<х'>= Ё ">
(вариант формул для группированных данных дается в обозначениях п. 6.1). Что жа-
сается условных харахтеркстик, участвующих в (11-4), то они были определены выше
(здесь усреднение производится по всем возможным значениям у при заданном фикси-
рованном значении X).
Вернемся непосредственно к обсуждению возможного способа измере-
ния с.т.с.с. Из (11.2) видно, что однозначное восстановление у по X воз-
можно только в ситуации «вырождения» (отсутствия) случайной остаточ-
ной компоненты е(Х) при всех возможных значениях X, что равносильно
(при нулевом среднем значении е(Х)) отсутствию какого-либо разброса
значений £(Х) относительно нуля. А это означает на языке вероятност-
ных характеристик тождественное равенство нулю условных дисперсий
е(Х) и у(Х), т.е.
D(e | X) = D(y | X) = <z’(X) = 0.
(И.5)
Другой крайний (с точки зрения с.т.с.с.) случай — это ситуация, в
которой знание величины объясняющей переменной X не имеет никакой
информации о значении результирующего показателя у. Эта ситуация
возможна, в рамках модели (11.2), лишь тогда (и только тогда), когда
f(X) = с = const.	(11.6)
В этом случае поведение результирующего показателя у (определенного
соотношением (11-2) с учетом (11.6)) как бы повторяет, с точностью до
сдвига на постоянную величину с, поведение остаточной случайной ком-
поненты £ и, в частности, в силу (11.3) и с учетом тождества Е(/—/0)2 = О
имеет в точности ту же самую меру случайного рассеивания, т. е.
Е( V - й>)2 = Е?
или
Dy = D£.
(П-7)
Теперь мы подготовлены к тому, чтобы ввести и проинтерпретиро-
вать достаточно универсальный измеритель с.т.с.с. между у и X — ко-
эффициент детерминации у по X. Обозначим его с помощью Kd(y;X) и
определим соотношением
Kd(y,X) = 1 - —,
(И-8)
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 397
где De = Ее2 — безусловная дисперсия остаточной случайной компонен-
ты, которая может быть подсчитана как усредненная по всем возможным
значениям X условная дисперсия D(e | X), т.е.
De = Ex(D(e | X))	(11.9)
(нижний индекс х у символа математического ожидания Е означает, что
усреднение проводится по всем возможным значениям X), a Dy — без-
условная дисперсия результирующего показателя у, определенная соотно-
шением (11.3).
Легко видеть, что введенный соотношением (11.8) коэффициент
детерминации определяет в качестве шкалы измерения показателя
с.т.с.с. отрезок [0; 1], причем минимальное (нулевое) значение Kd(y;X)
соответствует полному отсутствию какой бы то ни было связи меж-
ду у и X (поскольку в этом случае, как мы видели, см. (11-7), De = Dy), а
максимальное значение Xj(y;X)—1 соответствует случаю чисто функ-
циональной зависимости между у и X, когда значение у может быть в
точности восстановлено по значению X с помощью формулы у = f(X)
(так как De, определенное формулой (11.9) с учетом тождества (11.5),
равно нулю). При этом из определения коэффициента детермина-
ции (11.8) с учетом соотношения (11 Л) следует, что численное
значение Kd(y;x) отражает долю обшей вариации результирую-
щего признака у, объясненную изменением функции регрессии
Кг).
До сих пор мы оперировали теоретическими характеристиками ана-
лизируемых переменных. Однако в статистическом анализе их заменяют
соответствующими выборочными характеристиками. Вычисление выбо-
рочного (эмпирического) значения коэффициента детерминации у по X
должно производиться по формуле
2
%) = 1 - 4.	(И.8')
3У
где
4 = 1
я, У =
п,
а выборочное значение дисперсии «невязок» е вычисляется по одной из
двух формул:
4 =4 £(»-/(*))’,
398
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
если предварительный анализ показал, что условная дисперсия D(e | X)
не зависит от X (т. е. D(e | X) =	= const);
=	(Ч-9")
J=11=1
если условная дисперсия D(e | X) зависит от значения объясняющей пе-
ременной X, или во всех случаях, когда вычисления ведутся по группиро-
ванной выборке.
В соотношении (11.9*) f(Xi) есть статистически оцененное значение
неизвестной функции регрессии /(X) в точке X = X,- (методы оценивания
функции регрессии описаны в гл. 15). В соотношении (11.9 ) использова-
ны группированные выборочные данные и обозначения п. 6.1. В частно-
сти, з — это общее число интервалов группирования, Uj — число выбо-
рочных данных, попавших в у-й интервал группирования, yji — значение
результирующего признака в i-м по счету наблюдении, принадлежащем
у-му интервалу группирования (нумерация наблюдений своя для каждо-
го интервала группирования), а yj. — среднее значение результирующего
признака, подсчитанное по наблюдениям, попавшим в j-k интервал груп-
пирования, т.е. у5, = (2?=i УзМуз-
Пример 11.1. Подсчитаем коэффициент детерминации /Q(y,X)
по данным примера 10.1 (см. табл. 10.1 и рис. 10.2). Вычисления по фор-
мулам (11.8Z), (11.9*) и (11.9**) дают:
1 40
У = 50,8; ej = -	- »)’ = 979,17;
»=1
j=l
= 4(40,96 + 256,00 + 510,76 + 835,21) = 369,96;
40
Kd(y,z) = 1 -	= 1 - °>377 = °>623-
Такое значение коэффициента детерминации свидетельствует о наличии
статистической связи между среднедушевыми денежными сбережениями
семей у (г/ — в обозначениях примера 10.1) и их среднедушевым доходом
х (£ — в обозначениях примера 10.1), причем степень тесноты этой связи
несколько выше среднего уровня. Более подробное обслуживание шкалы
значений так же как и вопросы проверки этих значений на стати-
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
399
стически значимое отличие от нуля, отложим до описания некоторых
частных версий этого важного индикатора.
11.2.2. Исследование линейной зависимости у от
единственной объясняющей переменной ж: парный
коэффициент корреляции
Рассмотрение этой схемы зависимости между у и х разобьем на два
случая: 1) переменные (ж, у) «ведут себя» как двумерная нормальная
случайная величина; 2) переменные х и у связаны линейной регрессионной
зависимостью типа (11.2)-(11.2*), т.е. у(х) = в04-^1ж + £(а:), где и —
некоторые неизвестные параметры, е(ж) и х взаимно некоррелированы, а
з.р.в. случайных величин у, е и переменной х не обязан быть нормальным.
1. Случай двумерной нормальности случайных величин
(ж, у). Эта схема зависимости относится к типу С по классификации, опи-
санной в п. 10.5. Займемся анализом двумерного нормального распреде-
ления (см. п. 3.1.5, формулу (3.9)) с целью конкретизации вида функ-
ции регрессии f(x) и других вероятностных характеристик модели (11.2).
Понимая под и из формулы (3.9) соответственно объясняющую
переменную х и результирующий показатель у и воспользовавшись ре-
зультатами п. 3.1.5, имеем:
а)
f(x) = Е(у I х) = е((<2) I «(,) = х) = е0 + е1Х, (11.10)
где
1/2
*1 = г“172» в° =	(11п)
*11
mJ’>=Ex, ,n=^ = E(x-n£>)2;
m1 = Еу, о22 = &у — Е(У “ т1 ) >
ЕК—-	(П.,3)
так называемый парный коэффициент корреляции между переменны-
ми ж и у;
б)
О(у | х) = £>(£<2) |	= х) = а2( 1 - г2).	(11.14)
Из (11.10) следует, что если анализируемые переменные подчинены
двумерному нормальному закону, то функция регрессии одной из них по
400
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
другой имеет линейный вид. Кроме того, из определения коэффициента
детерминации (11.8) с учетом соотношений (11.9), (11.4) и (11.14) следу-
ет, что парный коэффициент корреляции г и коэффициент детерминации
Kd(y,x) связаны простым соотношением
= г2(г,у).
(11.15)
При этом в отличие от коэффициента детерминации (который по
определению может быть только неотрицательным числом) коэффициент
корреляции может быть как положительным, так и отрицательным. А
поскольку он имеет одинаковый знак с угловым коэффициентом наклона
01 прямой f(x) = Оо + 01® (см. соотношение (11.11)), то положительное
значение г свидетельствует о положительном (монотонно возрастаю-
щем) характере парной связи у и х, а отрицательное значение г — об
отрицательном (монотонно убывающем) характере этой связи.
Сформулируем и докажем основные свойства парного коэффициен-
та корреляции (справедливые в рамках рассматриваемой двумерной нор-
мальной генеральной совокупности).
Свойство 1. Шкала возможных значений парного коэффициента
корреляции г ограничена отрезком от —1 до +1, т.е. — 1 < г < 1, или
И < 1-
Для доказательства этого свойства воспользуемся очевидными нера-
венствами
(11.16)
Вводя в квадрат сумму в круглых скобках, имеем
Поскольку
(г - m^Xy - т{2))
(	(2) \
+ Е(Ш_) >0.(11.17)
Е
2
= Е(г - mV*)2/^2 = 1
/	(2) \ 2
ЕН  TO1- ) =E(y-m(i2))2/<zJ = 1,
\ ау 7
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
401
а

(по определению),
то из (11.17) непосредственно следует, что г —1. Аналогично рассу-
ждая при анализе выражения, получающегося от возведения в квадрат
разности в круглых скобках левой части выражения (11.16), получаем,
что г 1. Объединение полученных двух неравенств дает нам доказа-
тельство свойства 1.
Свойство 2. Если случайные величины х и у статистически не-
зависимы, то г(я,у) = 0.
Доказательство этого свойства следует из определения (11.13) с уче-
том того, что для статистически независимых случайных величин их ко-
вариация равна нулю, т. е.
Е[(г - т’/’Х? - m(i2))] = [E(z - mJ1’)] [Е(» - mf0)]
= (т^ “	“ mi^) = 0-
Свойство 3. Из факта |г| = 1 следует наличие чисто функцио-
нальной линейной связи между х и у и наоборот: если х и у связаны чисто
функциональной линейной связью, то |г| — 1.
Для доказательства этого свойства следует обратить внимание на то,
что неравенства г 1 и г -1 обращаются в точные равенства тогда и
только тогда, когда обращаются в точные равенства неравенства (11.16)
(по построению). А неравенства (11.16) обращаются в точные равенства
тогда и только тогда, когда выражение в круглых скобках левой части
этого соотношения тождественно равно нулю. Но из равенства
(1)	(3)
х-тп\’ ± у-т\’
следует, что х и у связаны линейной зависимостью.
Свойство 4. Коэффициент корреляции является симметричной
характеристикой с.т.с.с. между х и у, т.е. r(z,y) = r(y,z).
Доказательство этого свойства следует непосредственно из определе-
ния (11.13).
Свойство 5. Из равенства нулю коэффициента корреляции (т. е.
из того, что г(х,у) = 0) следует статистическая независимость перемен-
ных X и у.
Чтобы доказать это свойство, надо показать, что из г(ж, у) = 0 сле-
дует представление двумерной совместной плотности /(rvj(u,v) в виде
402
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
произведения частных плотностей fx(u)fv(y). Для этого воспользуемся
общей формулой двумерного нормального распределения (3.9), подставив
в нее значение г = 0. Получаем (с учетом введенных выше преобразова-
ний):
е
2Tra;fo^
и еаа
(11.18)
Но правая часть (11.18) представляет собой как раз произведение частной
плотности распределения вероятностей случайной величины х на част-
ную плотность распределения вероятностей случайной величины у, что и
завершает доказательство.
Дав определение и познакомившись с основными свойствами парного
коэффициента корреляции г, мы должны привести формулу, по которой
вычисляется эмпирический (выборочный) аналог этой характеристики —
г(а,у):
Ё (xi ~ ®)(У< - У)
f(x,у) = ,	(П.13')
</£(«.•у)’
у i=l	i=l
Однако для проведения полноценного статистического анализа
свойств исследуемой генеральной совокупности, основанных на этой ха-
рактеристике, нам необходимо знать ее статистические свойства. Это
позволит судить о точности приближения (11.13 ) к неизвестному истин-
ному значению (11.13), строить статистические критерии для проверки
различных гипотез о численных значениях анализируемого коэффициента
корреляции.
В частности, какую величину выборочного коэффициента корреля-
ции следует считать достаточной для статистически обосгованного
вывода о наличии корреляционной связи между исследуемыми перемен-
ными! Ведь надежность статистических характеристик, в том числе и г,
ослабевает с уменьшением объема соответствующей выборки, а потому
принципиально возможны случаи, когда отклонение от нуля полученной
величины выборочного коэффициента корреляции г оказывается стати-
стически незначимым, т. е. целиком обусловленным неизбежным случай-
ным колебанием выборки, на основании которой он вычислен. Ответить
на этот вопрос помогает знание закона вероятностного распределения г.
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
403
Б случае совместной нормальной распределенности исследуемых перемен-
ных и при достаточно большом объеме выборки п (а именно при п > 200)
распределение г можно считать приближенно нормальным со средним,
равным своему теоретическому значению г, и дисперсией or = k
Однако следует учитывать, что при малых значениях пит, близких к
±1, это приближение оказывается очень грубым. Кроме того, при малых
п следует принимать во внимание, что величина г является смещенной
оценкой своего теоретического значения г, в частности Ег = г — [г(1 —
г2)]/2п.
Относительно хорошая степень приближения нормального распреде-
ления при малых значениях | г| позволяет получить простой критерий про-
верки гипотезы
Яо: г = 0,
т. е. гипотезы об отсутствии корреляционной связи между исследуемыми
переменными х и у. При этом используется тот факт, что статистика
при условии справедливости гипотезы Яо приблизительно распределена
по з.р.в. Стьюдента с п — 2 степенями свободы.
Поэтому если окажется, что
(11.20)
то гипотеза Яо °б отсутствии корреляционной связи между х и у отвер-
гается с вероятностью ошибиться, равной а (здесь, как и ранее, tq(m) —
100д%-ная точка /-распределения с т степенями свободы).
Доверительные интервалы для истинного значения коэффициента
корреляции г можно построить, используя следующее преобразование,
предложенное Р. Фишером:
Z = — In
2
(11.21)
Он показал, что величина z, определенная соотношением (11.21), уже
при небольших п с хорошим приближением следует нормальному закону
со средним Ez « | In 4- и дисперсией Dx = ^5. Это позволяет
404	ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
построить доверительный интервал [<гьг3] для Еж по формуле
1 , 1 4- г	г
г‘-’-21пГ^Т^Т5"2(П-1)
г
= arcth г 4=	— —----—,
7^3 2(п — 1)
откуда следует, что истинное значение коэффициента корреляции т с той
же доверительной вероятностью 1 — а заключено в пределах
th Zj < г < th z2.
(11.22)
Здесь th z — это тангенс гиперболический от аргумента z (определя-
ется с помощью соотношения th z = (ez—e-z)/(e*4-e-z)). Соответственно
функция, определяющая величину z с помощью соотношения (11.21), —
это функция, обратная к тангенсу гиперболическому; так что часто вме-
сто z = | In пишут z = arcth г (или z = tg-1f). Нахождение z по
данному значению г и, наоборот, определение г по заданной величине г
производятся с помощью специальной табл. (см. приложение 1), в кото-
рой в крайних столбцах (левом и правом) приведены значения |г|, а между
ними — соответствующие значения |z| = arcth |г| (знаки у аргумента и
функции совпадают, так что если, например, г отрицателен, то и соот-
ветствующее значение z = argth г также отрицательно).
Пример 11.2. По данным п = 39 предприятий получен коэффици-
ент корреляции г = —0,654, характеризующий тесноту связи между себе-
стоимостью продукции (у) и производительностью труда (ж). Построим
интервальную оценку для г, задавшись 95%-й доверительной вероятно-
стью.
По табл, из приложения 1 для г = —0,654 найдем z = —0,7823. Тогда
Z\ — —0,7823 —
z% — —0,7823 4-
= -1,1090;
1,96
v/36
-0,4556.
Теперь по табл, по найденным Zi и ж2 найдем соответствующие значения
И = —0,804 и ж2 = —0,426.
Таким образом, можно утверждать, что с доверительной вероятно-
стью Р = 0,95 истинное значение коэффициента корреляции г между се-
бестоимостью продукции у и производительностью труда х будет лежат!
в интервале от —0,804 до —0,426, т. е. —0,804 г —0,426.
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
405
Влияние ошибок измерения анализируемых переменных на величину
коэффициента корреляции г. Пусть мы хотим оценить степень тесно-
ты корреляционной связи между компонентами двумерной нормальной
случайной величины (ж, у), однако наблюдать мы их можем лишь с не-
которыми случайными «ошибками измерения* соответственно н €у
(см. схему зависимости D в п. 10.5). Поэтому экспериментальные данные
У»)» * = 2,..., п, — это практически выборочные значения искажен-
ной двумерной случайной величины (х',у), где х' = х + ех и у = у 4- еу.
Если предположить, что £х и еу взаимно независимы, не зависят от х и у,
нормальны, имеют нулевые математические ожидания и конечные диспе-
рсии, соответственно а? и то двумерная случайная величина (х', у) бу-
дет также подчиняться двумерному нормальному распределению. Однако,
как легко подсчитать, параметры этого распределения и, в частности, ко-
эффициент корреляции г между х м д будут соответственно отличаться
от параметров исходной двумерной схемы (ж, у). Действительно, в соот-
ветствии с основными правилами вычисления первых и вторых моментов
(см. п. 2.6) получаем
ах< = Ез/ = Еж = ах;
ар» = Еу? = Еу = ау;
2	2.2
<тх» — <7Х + ri;
(11.23)
Из (11.23), в частности, следует, что коэффициент корреляции при-
знаков, на которые наложены ошибки измерения, всегда меньше по аб-
солютной величине, чем коэффициент корреляции исходных признаков.
Другими словами, ошибки измерения всегда ослабляют исследуемую кор-
реляционную связь между исходными переменными, и это искажение тем
меньше, чем меньше отношения дисперсий ошибок к дисперсиям самих
исходных переменных. Формула (11.23) позволяет скорректировать иска-
женное значение коэффициента корреляции: для этого нужно либо знать
«разрешающие» характеристики погрешностей измерений (и, следова-
тельно, величины дисперсий ошибок о? и oj), либо провести дополни-
тельное исследование по их выявлению.
2. Общий случай парной линейной зависимости. Рассмотрим
регрессионную модель вида (11.2) в случае р = 1 и линейной функции
406
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
регрессии /(X), т.е.
у(я?) = 0о + М«(*)>	(11.24)
где Оо и — неизвестные параметры модели, единственная объясняющая
переменная х может быть случайной величиной или неслучайной, е(х) и
х взаимно некоррелированы, а Ee(z) = 0 и De(z) = <72(z). В отличие
от предыдущей схемы в данном случае не требуется двумерной нормаль-
ности анализируемой пары переменных (z, у). Очевидно, рассматривае-
мая модель может относиться к любому из типов зависимостей В, С и Л,
описанных в п. 10.5 (все зависит от конкретизации природы исследуемых
переменных).
Определенные соотношения (11.13) и (11.13*) — соответственно тео-
ретический и выборочный коэффициенты корреляции — могут быть фор-
мально вычислены для любой двумерной системы линейной статистиче-
ской связи между анализируемыми признаками.
Практически все свойства и рекомендации, касающиеся вычисления,
использования статистических свойств и интерпретации парного коэф-
фициента корреляции, определенного соотношениями (11.13) и (11.13*),
остаются приблизительно справедливыми и в рамках более общей схе-
мы (11.24) линейной зависимости между х и у. Так, например, из пяти
сформулированных выше свойств коэффициента корреляции первые че-
тыре остаются в силе и в рамках модели (11.24) («не работает» лишь
свойство 5: в общем случае из некоррелированности х и у не следует их
статистическая независимость).
Однако только в случае совместной нормальной распределенности ис-
следуемых случайных величин х и у коэффициент корреляции г имеет
четкий смысл как характеристика степени тесноты связи между ними. В
частности, в этом случае соотношение |r| = 1 подтверждает чисто функ-
циональную линейную зависимость между исследуемыми величинами, а
уравнение г = 0 свидетельствует об их полной взаимной независимости.
Кроме того, коэффициент корреляции вместе со средними и дисперсиями
случайных величин х и у составляет те пять параметров, которые дают
исчерпывающие сведения о стохастической зависимости исследуемых ве-
личин, так как однозначно определяют их двумерный закон распределения
(см. формулу (3.9)). Во всех же остальных случаях (распределения х и у
отклоняются от нормального, одна из исследуемых величин не является
случайной и т. п.) коэффициент корреляции можно использовать лишь в
качестве одной из возможных характеристик степени тесноты связи. При
этом, несмотря на то, что в общем случае пока не предложено характери-
стики линейной связи, которая обладала бы очевидными преимуществами
по сравнению с г, его интерпретация часто оказывается весьма ненадеж-
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 407
ной. Если же априори допускаете! возможность отклонения от линей-
ного вида зависимости, то можно построить примеры, когда, несмотря
на г = 0, исследуемые переменные оказываются связанными чисто функ-
циональным соотношением (следовательно, Kd(x,y) = 1). Поэтому о ве-
личинах, для которых т = 0, обычно говорят, что они некоррелированы, и
только после дополнительного статистического и профессионального ана-
лиза (исследование степени отклонения распределения рассматриваемых
величин от нормального и т. п.).
Замечания о необходимости известной осторожности при толковании
корреляционной связи никоим образом не обесценивают желательность
проверки значимости любого кажущегося соотношения. При этом сле-
дует использовать характеристики степени тесноты связи: коэффициента
корреляции г и корреляционного отношения р (см. ниже). Но не все-
гда знание этих характеристик оказывается достаточным для получения
информации о степени тесноты физической связи между исследуемыми
переменными и тем более об их причинной взаимообусловленности.
11.2.3.	Исследование парных нелинейных связей:
корреляционное отношение
При отклонениях исследуемой зависимости от линейного вида, как
уже отмечалось, коэффициент корреляции г теряет свой смысл как харак-
теристика степени тесноты связи. В этих случаях исследователь должен
воспользоваться имеющимися у него двумерными выборочными данными
(Х1>У1),(Х2>У2), • • • >(хп)Уп) с пелью построения оценок для определенной
выше в некотором смысле универсальной теоретической характеристи-
ки степени тесноты связи — коэффициента детерминации Kd(y;x) (см.
(11.8*)). Способ построения таких оценок выбирается в зависимости от
природы имеющихся у нас выборочных данных и от характера некоторых
дополнительных допущений.
Корреляционное отношение. Наиболее привлекательной в этом
смысле является ситуация, в которой характер выборочных данных (их
количество, «плотность» расположения на плоскости) допускает их груп-
пировку по оси объясняющей переменной и возможность подсчета так на-
зываемых «частных» средних ординат од. внутри каждого (j-ro) интерва-
ла группирования. Пусть такое группирование данных произведено. При
этом, как обычно, s — число интервалов группирования по оси абсцисс;
= 1,2,...,з) — число выборочных точек, попавших в i-й интервал
группирования; у;, = (53Л1 Уз')1уз — среднее значение ординат точек,
попавших в j-й интервал группирования. Тогда, как легко понять, выбо-
408	ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
рочным аналогом (оценкой) введенной ранее (см. п. 11.2.1) дисперсии
будет величина
4м = ~	- »)’•	(п-25)
j=l
где общее среднее у = £ -j узУ}.- Соответственно получаем оценку для
Kd(y; я) в виДе
& = 4ю/4>	(И.26)
где выборочная дисперсия sj индивидуальных результатов наблюдения
yji около общего среднего у вычисляется по формуле
‘И
j=l t=l
Величину рух принято называть корреляционным отношением зави-
симой переменной у по независимой переменной х. Его вычисление не
обременено никакими дополнительными допущениями относительно об-
щего вида регрессионной зависимости (11-2). Однако в отличие от ко-
эффициента корреляции корреляционное отношение несимметрично по
отношению к исследуемым переменным, т.е., вообще говоря, рух / pxv.
Кроме того, корреляционное отношение, по определению, является вели-
чиной неотрицательной1, так как под ним подразумевается результат из-
влечения арифметического значения корня квадратного из р .
В остальном свойства корреляционного отношения во многом похожи
на свойства коэффициента корреляции. Из (11.3) и (11.8), в частности, не-
медленно следует, что подобно коэффициенту корреляции корреляционное
отношение не может быть больше единицы.
Из |/>| = 1 следует наличие однозначной функциональной связи между
у и х, и, наоборот, однозначная функциональная связь между у и z сви-
детельствует о том, что |р| = 1. Далее, отсутствие корреляционной связи
между у и х означает, что условные средние уу. сохраняют постоянное
значение, равное общему среднему у, а потому ру/х = 0. Наоборот, если
Ру/г = 0, то у?. = у, и, следовательно, частные средние yj. не зависят от х,
т. е. соответствующая линия регрессии параллельна горизонтальной оси.
Отметим, что между pyjx и рх/у нет какой-либо простой зависимости.
Некоррелированность у с х (т. е. равенство нулю величины ру/х) не влечет
1 Иногда, в частности при монотонном характере функции регрессии f{x)t корреляци-
онному отношению приписывают знак, совпадающий со знаком первой производной
этой функции.
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
409
за собой непосредственно некоррелированности х с у. Возможны ситуа-
ции, в которых один из этих показателей принимает нулевое значение, в
то время как другой равен единице. Допустим, например, что у = х2 и
х принимает значения: —1,0 и +1 с вероятностями 1/3 каждое. В этом
случае pv/x = 1, px/v = 0 (в силу симметрии параболы относительно оси
у и симметричности распределения х).
Можно показать, что корреляционное отношение р не может быть
меньше абсолютной величины коэффициента корреляции г, характери-
зующего зависимость между теми же переменными. В случае линейной
зависимости эти две характеристики связи совпадают. Это позволяет
использовать величину разности	— г2 в качестве меры отклонения
регрессионной зависимости от линейного вида (см. соотношение (10.25) в
п.10.7).
И наконец, все замечания относительно смысловой интерпретации ко-
эффициента корреляции г (в частности, о логическом соотношении поня-
тий «корреляционная зависимость, связь между переменными, их при-
чинная взаимообусловленность») остаются в силе и для корреляционного
отношения.
Проверка гипотезы об отсутствии корреляционной свя-
зи. Какую величину корреляционного отношения можно признать ста-
тистически значимо отличающейся от нуля, т. е. достаточной для стати-
стически обоснованного вывода о наличии корреляционной связи между
исследуемыми переменными? Ведь так же, как и в случае прямолинейного
типа зависимости, принципиально возможны ситуации, когда отклонение
от нуля полученной величины корреляционного отношения р является ста-
тистически незначимым, т. е. обусловленным лишь неизбежными случай-
ными колебаниями выборки. Для построения соответствующего критерия
воспользуемся фактом приближенной F(s—1, n-з)-распределенности слу-
чайной величины
Ло) = -А- •	(11Л27)
справедливым в предположении, что х) = 0 (или, что то же, рух = 0)
и что условные распределения результирующей переменной у(х) при лю-
бом фиксированном х описываются нормальным законом с постоянной дис-
персией <г .
Поэтому если окажется, что
-2
Рух П — 3	2 .	.
-	•	> Vo(e 1» п 5)»
1 - рух а~1
410
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
то гипотеза Н: рух = 0 об отсутствии корреляционной связи между у их
отвергается с вероятностью ошибки а (здесь, как и ранее, v2 (з—1, п—з) —
100а%-ная точка F-распределения с числом степеней свободы числителя
з — 1 и знаменателя п — з находится из табл, приложения 1). При выпол-
нении обратного неравенства значение корреляционного отношения рух
признается статистически незначимым, т.е. делается вывод, что гипо-
теза об отсутствии корреляционной связи между у и х не противоречит
наблюдениям.
Доверительные интервалы для истинного значения корреля-
ционного отношения рух можно построить, опираясь на тот факт, что
статистика
(П) = (п ~	а- 1
(s-l)(l-pjr) а-! + «/>’*
приближенно описывается F-распределением с числом степеней свободы
числителя
= (а - 1 + »&)*	(п 28)
s 1 2прух
и числом степеней свободы знаменателя 1/2 = п — з (см. [Айвазян С. А.,
Енюков И. С., Мешалкин Л. Д., 1985, п.1.1.4]).
Таким образом, получаем следующее правило построения приближен-
ных доверительных интервалов для истинного значения корреляционного
отношения рух:
1)	пользуясь формулой (11.26), вычисляем точечную оценку рух для
истинного значения корреляционного отношения рух\
2)	по формуле (11.28) подсчитываем вспомогательное число степенен
свободы щ числителя для аппроксимирующего F-распределения;
3)	задавшись уровнем доверия Р = 1 — 2а, с помощью табл, приложе-
ния 1 находим 100(1 - а)%-ную точку v2_a(i/i*, п — л) и 100а%-ную точку
v2a(t/*,n —з) F-распределения с числом степеней свободы числителя.i/j и
знаменателя п — з;
4)	утверждаем, что приблизительно с вероятностью Р = 1—2а истин-
ное значение корреляционного отношения рух удовлетворяет неравенствам
(п-л)р^	а-1 „ 2 '	(п-«)р’г в-1
/1	-2 ч 2	„ Ру* .	„2 ч 2	„ *
«С1 “ PyxjVa П	»(1 “ PVx)Vl-a П
Проиллюстрируем работоспособность описанного метода на следую-
щем примере. Пусть в результате обработки 132 экспериментальных то-
чек (xi,yi)(i = 1,2,...,132) получено выборочное значение корреляцион-
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
411
кого отношения р = 0,60. При этом мы воспользовались разбиением диа-
пазона изменения независимой переменной на з = 12 равных интервалов
группирования. Соответственно получаем в качестве вспомогательного
числа степеней свободы числителя величину i/Г =	~ 27
(частное округляем до целого числа). Задавшись доверительной вероят-
ностью Р = 0,90, из табл, приложения 1 находим (полагая а = 0,05):
»o,os(27,120) = 1,58;
«о95(27,120) =
1
зд,о6(12О,27)
1
1,73
~ 0,58.
И наконец, в соответствии с формулой (11.29) находим левый (pmin) и
правый (Ртах) концы доверительного интервала для истинного значения
2
Рух'
л 120 0,36	11
Pm!n 132 0,64 1,58 132	’ ’
л _	120 0,36	11
Ртах - 132 о б41 58	132 “ » •
Таким образом, при точечной оценке рух = 0,6 истинное значение
заключено в пределах от д/0,24 до ^/0,87 с вероятностью, приблизительно
равной 0,9, т. е. 0,49 < рух < 0,93.
В этом примере хорошо видна существенная несимметричность кон-
цов интервальной оценки относительно точечной оценки (правый конец
интервальной оценки отстоит от точечной оценки на 0,33, в то время как
левый конец — всего лишь на 0,11).
а2
Для значении точечных оценок р , близких к нулю или к единице,
левый или правый конец интервальной оценки может терять содержа-
тельный смысл, выходя за пределы отрезка [0, 1]. В этом случае в ка-
честве левого или правого конца интервальной оценки следует брать со-
ответствующее граничное значение — нуль или единицу (причина подоб-
ных нежелательных ситуаций — в аппроксимационном подходе к реше-
нию данной задачи). Однако описанный прием все-таки следует признать
гораздо более точным, чем применяемый иногда метод построения интер-
вальных оценок для р^, необоснованно использующий приблизительную
(р, Ц£-)-нормальность статистики р^.
412
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11.2.4. Исследование линейной зависимости у от
нескольких объясняющих, переменных
а/1), х^,..., х^р\ множественный и частные
коэффициенты корреляции
Аналогично той схеме, по которой излагался п. 11.2.2, разобьем рас-
смотрение данной проблемы на два случая: 1) «поведение» вектора пе-
ременных	..., х^р\ у) описывается (р + 1)-мерным нормальным
законом (см. формулу (3.10) в п. 3.1.1); 2) результирующий показатель у
связан с объясняющими переменными	..., линейной регрес-
сионной зависимостью типа (11.2).
1) Случай многомерной нормальности векторного признака
(ж^\ж^2\... ,а/р\ у). Свойства многомерного нормального закона доста-
точно хорошо исследованы (см., например, [Андерсон Т.]). В частности,
имеют место результаты, аналогичные (11.10)-(11.14), которые были рас-
смотрены в рамках двумерной схемы в п. 11.2.2. А именно доказано, что
функция регрессии у по X имеет линейный вид:
f(X) = Е(у I X) = 00 + 01*(,) + • • • + «Г*М,	(11.30)
где коэффициенты 63 (j = 0,1,... ,р) явным образом выражаются в терми-
нах компонент вектора средних значений и элементов ковариационной
матрицы Е анализируемого многомерного нормального распределения, а
условная дисперсия у (при условии, что объясняющие переменные зафик-
сированы на уровне X) не зависит от X и тоже выражается в явном виде
через элементы ковариационной матрицы S.
Однако в анализе множественных корреляционных связей (так назы-
вают статистические связи между более чем двумя переменными в отли-
чие от парных связей, рассмотренных выше) есть своя специфика и возни-
кают принципиально новые проблемы. Эта специфика связана в первую
очередь с необходимостью уметь измерять степень тесноты связи между
результирующей переменной у и множеством объясняющих переменных
х^\х^2\..., х^р\ а также с возникающими трудностями в интерпретации
парных коэффициентов корреляции между у и х^\ обусловленными воз-
можным опосредованным влиянием на эту парную связь других (явно не
учтенных в вычислении г(у‘}х^)) объясняющих переменных / j).
Последнее обстоятельство, в частности, делает необходимым введение та-
ких измерителей статистической связи, которые были бы «очищены* от
опосредованного влияния других переменных, давали бы оценку степени
тесноты интересующей нас связи между переменными у и х^ (или z
и х^ ) при условии, что значения остальных переменных зафиксированы
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 413
на некотором постоянном уровне. В этом случае говорят о статистиче-
ском анализе частных (или «очищенных») связей и используют соответ-
ственно частные («очищенные» ) коэффициенты корреляции или другие
корреляционные характеристики.
Частные коэффициенты корреляции и их выборочные зна-
чения. Поставим в соответствие каждой из ранее введенных парных ха-
рактеристик статистической связи между переменными z^ и x^\i,j =
0,1,...,р; z = у) частную («очищенную» ) характеристику, опреде-
ляемую по той же формуле, но только для условного распределения (см.
п.2.5, (2.13)) y?(z^*\z^ | Х^''^ = х). Здесь у? — это функция плотности
вероятности переменных z^ и z^J\ — множество переменных, до-
полняющих пару (х^'\х^) до полного набора рассматриваемых (наблю-
даемых) переменных X = (z^°\ z^\..., z^), a z — (р — 1)-мерный вектор,
определяющий заданные уровни, на которых фиксируются значения «ме-
шающих» переменных Есть два взаимосвязанных обстоятельства,
которые препятствуют широкому практическому использованию частных
характеристик статистической связи в общем (т. е. негауссовском) случае:
• частные характеристики статистической связи, вообще говоря, зави-
сят от заданных уровней z мешающих переменных (как их выбирать
в каждом конкретном случае?);
• для подсчета выборочных значений частных характеристик стати-
стической связи необходимо иметь выборку специальной структу-
ры, обеспечивающей наличие хотя бы нескольких наблюдений при
каждом из заданного ряда фиксированных значений z мешающих пе-
ременных.
Однако можно показать, что если исследуемые случайные перемен-
ные (z^°\ z^\..., х^) подчиняются многомерному нормальному закону,
то указанные неудобства автоматически исчезают, так как в этом слу-
чае частные коэффициенты корреляции не зависят от уровней мешающих
переменных х, определяющих условие в соответствующем условном рас-
пределение В частности, имеет место следующая формула (при условии
невырожденности (р + 1)-мерного нормального закона):

—Rtj
(R„Rjj)^
(11.31)
где — частный коэффициент корреляции между переменными а
и х^ при фиксированных значениях всех остальных переменных
а К.*/ — алгебраическое дополнение (см. Приложение 2) для элемента
414
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
г/d в определителе корреляционной матрицы R анализируемых признаков
= у, х^\х^2\..., х^р\ т. е. в определителе
det R =
1 Пл Пи ... гОр
По 1 П2 Пр
где Tij = г(яР\х^).
1
Формула (11.31), примененная к трехмерному признаку (а/0^ = yf
х(1) х(2)) при t - 0 7 - 1 и	- х(2) дает-
к/ । X	H£JM 1 —• Vj J — А И -ZV	— Л ДСК1А.
ПЛ “ rO2r12
’’Ol.xW = r01(2) =	/ -	•
у (1 — Пв)(1 ~ Пг)
(11.32)
Последовательно присоединяя к мешающим переменным все новые
признаки из рассматриваемого набора, можно получить рекуррентные со-
отношения для подсчета частных коэффициентов корреляции roi(2...fc+i)
порядка к (т.е. При исключении опосредованного влияния к мешающих
переменных) по частным коэффициентам корреляции порядка к — l(fc =
1,2,...,р-1):
г01(2,3...к-Ц) =
П)1(2...к) ~ П)к+1(2.У) * rlfc+l(2dotjfc)
у(1 - »*0k+l(2...fc))(1 ” rlk+l(2...fc))
(11.32')
Выборочные (эмпирические) значения частных коэффициентов кор-
реляции вычисляются по тем же формулам (11.31) — (11.32') с заменой
теоретических значений парных коэффициентов корреляции их выбо-
рочными аналогами (см. формулу (11.13')).
Если исследователь имеет дело лишь с тремя-четырьмя переменными
(р = 2,3), го удобно пользоваться рекуррентными соотношениями (11.32').
При больших размерностях анализируемого многомерного признака удоб-
нее опираться на формулу (11.31), использующую расчет соответствую-
щих определителей.
Статистические свойства выборочных частных коэффициентное
корреляции (проверка на статистическую значимость их отличия от
нуля, доверительные интервалы). При исследовании статистических
свойств выборочного частного коэффициента корреляции порядка к (т. е.
при исключении опосредованного влияния к мешающих переменных) сле-
дует воспользоваться тем, что он распределен точно так же, ка^с и обыч-
ный (парный) выборочный коэффициент корреляции между теми же пере-
менными с единственной поправкой: объем выборки надо уменьшить на
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
415
k единиц, т. е. полагать его равным п — к, а не п. Поэтому при проверке
статистически значимого отличия от нуля выборочного частного коэффи-
циента корреляции и при построении для него доверительных интервалов
следует пользоваться рекомендациями п. 11.2.2 для парного коэффициента
корреляции с заменой п на п — к.
Рассмотрим некоторые конкретные числовые примеры, демонстриру-
ющие возможный характер искажающего опосредованного влияния «тре-
тьих факторов» на корреляцию между двумя анализируемыми перемен-
ными.
Пример 11.3. По итогам года 37 однородных предприятий лег-
кой промышленности были зарегистрированы следующие показатели их
работы: х' ’ = у — среднемесячная характеристика качества ткани (в
баллах); а/1) — среднемесячное количество профилактических наладок
(2)
автоматической линии; х' 7 — среднемесячное число обрывов нити.
По матрице исходных данных (®|°\	®^)»=Гз7 были подсчита-
ны (с помощью (11.131)) выборочные парные коэффициенты корреляции
= 0,1,2): г01 = 0,105; т02 = 0,024; г12 = 0,996.
Проверка «на статистическую значимость», проведенная в соответ-
ствии с рекомендациями п. 11.2.2, свидетельствует об отсутствии стати-
стически значимой парной корреляционной связи между качеством ткани,
с одной стороны, и числом профилактических наладок и обрывов нити —
с другой, что не согласуется с профессиональными представлениями тех-
нолога.
Однако расчет частных коэффициентов корреляции по формуле
(11.32) дает значения toi(2) = 9,907; ^02(1) = —0,906, которые вполне соот-
ветствуют нашим представлениям о естественном характере связей между
изучаемыми показателями.
Доверительные интервалы для истинных значений г01(2) и r02(i)
(в соответствии с рекомендациями п. 11.2.2) найдем с использованием
^-преобразования Фишера для доверительной вероятности Р = 1 — а. То-
гда
_ j- . 1 + г Цо/2________________г
*1,2 - 2 toj _ - ¥	_ 3	2[(П - 1) - 1]’
где ия — q- к ван тиль стандартного нормального распределения (см.
табл. Приложения 1).
В нашем примере п = 37, а = 0,05. Подставляя поочередно в эту
формулу значения roi(2) = 0,907 и коа(1) = —0,906 и пользуясь табл, (из
Приложения 1) значений z = |1п найдем:
1,16 < AfZoiCO < L>83
416
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
И
1,83 < MZ02(i) < 1Д6,
откуда, вновь воспользовавшись табл., окончательно получим:
0,820 < 6oi(2) < 0,950;
—0,950 < 7*02(1) < —0,820.
Пример 11.4. С целью исследования влияния погодных условий
на урожайность кормовых трав Хукер (Journ. Roy. Stat. Soc., 1907, v. 65,
p. 1) рассмотрел данные Министерства земледелия Англии за 20 лет, ха-
рактеризующие урожайность (в ц/акр), весеннее количество осадков
а/1' (в дюймах) и накопленную за весну сумму «активных» (т. е. выше
4-5,5°С) температур ж^2^ (в градусах по Фаренгейту) однородной в ме-
теорологическом отношении области Англии, включающей в себя группу
восточных графств. По выборке	®j2b«sl^j были подсчитаны
основные статистические характеристики изучаемой трехмерной случай-
ной величины:
= 28,02; т\1} = 4,91; т™ = 594,0;
419,54;	в?; л2 = 7225;
foi = 0,80;	г02 = -0,40; ня = -0,56.
Действительно ли высокая температура в период созревания трав от-
рицательно влияет на их урожайность (ведь г02 = —0,40) или здесь ска-
зывается опосредованное влияние «мешающего» фактора — количества
осадков
Вычисление частных коэффициентов корреляции по рекуррентной
формуле (11.32) дает:
Пи(2) = 0,759; Гог(1) = -0,097; г12(о) = —0,436.
Как видим, если исключить одновременное влияние количества осад-
ков на урожайность (с ростом а она повышается) и на сумму ак-
тивных температур (с ростом а/1) она понижается), то мы уже не обна-
ружим отрицательной корреляции между температурой и урожайностью
(г02(1) = 0,097, в то время как г02 = -0,40).
Построение доверительных интервалов для г01(2) и гог(1) (с Уровнем
доверия Р = 0,95) с использованием z-преобразования Фишера дает в дан-
ном случае:
0,448 < 7*01(2) < 0,890; -0,419 < П)2(1) < 0,525.
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
417
Последнее неравенство свидетельствует о том, что у нас нет осно-
ваний считать положительную очищенную корреляционную связь между
урожайностью и температурой (1*02(1) = 0>097) статистически значимой,
т. к. нуль находится внутри доверительного интервала.
Обратимся теперь к задаче измерения с.т.с.с. между результиру-
ющим показателем у и множеств ом объясняющих переменных X =
6 условиях многомерной нормальной совокупности.
В общем случае эта задача решается с помощью коэффициента детер-
минации Kj(ytX) (см. (11-8) и (11.8*)), который по построению обладает
следующими свойствами:
a)0^Kd(y;XH 1;
б) минимальное значение коэффициента детерминации (Kj(y-X) = 0)
соответствует случаю полного отсутствия корреляционной связи между у
и (s^\...,	так как это может быть только при <т2 = D/(£) = 0, т. е.
лри независимости значений функции регрессии f от величины ее аргу-
ментов X(f(X) = const); это соответствует ситуации, когда усредненная
дисперсия «регрессионных остатков» в точности равна общей вариации
результирующего показателя;
в) максимальное значение коэффициента детерминации (К^у;Х)
= 1) соответствует полному отсутствию варьирования «регрессионных
остатков» (Ее3 = 0), что означает наличие чисто функциональной связи
между у и (з/1),. ..,х<р)): у = f(x^\.. .х^). Следовательно, в этом слу-
чае мы имеем возможность точно (детерминированно) восстанавливать
условные значения у(Х) = {у | X} по значениям предикторных перемен-
ных X, и соответственно общая вариация результирующего показателя у
полностью объясняется контролируемой вариацией функции регрессии.
Из (11.8*) следует, что вычисление выборочного значения коэффици-
ента детерминации предусматривает проведение предварительных рас-
четов по статистическому оцениванию неизвестной функции регрессии
/(X), что противоречит хронологии исследований, описанной в п. 10.6.
Сейчас мы увидим, что свойства многомерных нормальных совокупностей
автоматически устраняют это неудобство, позволяя вычислять значение
Kd(y’tX) до проведения регрессионного анализа.
Множественный коэффициент корреляции Ry.x используется
в качестве измерителя с.т.с.с. между результирующим показателем у и
набором объясняющих переменных а/1 \ а^2\...	в моделях линейной
регрессии. Он определяется как обычный парный коэффициент корреля-
ции между у и линейной функцией регрессии у no X, т.е.
Ry.x = r(9; /(X)),	(11.33)
418
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
где
ДХ) = Е(у I X) = flo + М(,) + • • • + 0rzM
(можно показать, что следующее определение Ry.x является эквивалент-
ным определению (11.33): Ry.x — это парный коэффициент корреля-
ции между у и такой линейной комбинацией х^1\ х^2\..., для кото-
рой значение этого парного коэффициента корреляции достигает своего
максимума).
Можно показать, что при статистической обработке выборок, извле-
ченных из нормальных генеральных совокупностей, множественный ко-
эффициент корреляции Ry,x и его выборочное значение Ry,x обладают
рядом удобных свойств (приведенные ниже формулы и свойства теорети-
ческого множественного коэффициента корреляции Ry.x автоматически
переносятся на выборочный Ry.x заменой участвующих в них теоретиче-
ских характеристик соответствующими выборочными значениями).
1.	Вычисление Ry.x по матрице парных коэффициентов корреля-
ции. Обозначая, как и прежде, (р + 1)(р + 1)-корреляционную матрицу
(rij)ij=so,i,...>p через R, а алгебраическое дополнение элемента гм в ее опре-
делителе через |R|*z, имеем
—2	. det R
Ry X = ~ Ж"	( 34)
2.	Вычисление Яу.х по частным коэффициентам корреляции
Ry.x = 1 - (1 - Го1)(1 - Г02(1))(1 ” г03(12)) •• «(1 ~ гОр(12...р-1))- (11-35)
3.	Множественный коэффициент корреляции мажорирует любой
парный или частный коэффициент корреляции, характеризующий ста-
тистическую связь результирующего показателя, т. е.
Ry.x > 1го/(/>)1»
где j = 1,2,...,р, a Ij — любое подмножество множества индексов /о =
{1,2,... ,р), не содержащее индекса j (это соотношение следует из (11.35)).
Напоминаем, что = у.
4.	Присоединение каждой новой предсказывающей переменной не мо-
жет уменьшить величины R (независимо от порядка присоединения), т. е.
Яу.х(1)	Ry.(x^),xW) < Яу.(х<»,хЫ,х(з>) <	(11.37)
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 419
5.	Условная дисперсия результирующего показателя D(y | X) не за-
висит от условия (т. е. от значения X) и связана со значением множе-
ственного коэффициента корреляции Ry.x соотношением
D(»|X) = (l-«J.x)Dy.	(П.36)
Последний результат позволяет связать между собой две характери-
стики степени тесноты статистической связи — коэффициент детермина-
ции Kd(y;X) и множественный коэффициент корреляции Ry.x. Действи-
тельно, учитывая тот факт, что D(j/1 X) = D(e | X) (см. (11.5)), а значит,
и условная дисперсия остатков не зависит от X, получаем, что безуслов-
ная дисперсия De (как результат усреднения по X значений условных
дисперсий D(e | X), см. (11.9)) равна D(s | X). Но тогда мы можем
подставить в (11.36) De вместо D(y | X) и получим
De = (1 - ftJ.x)Dy,
(11.36')
откуда, учитывая формулу (11.8),
КЛ(У,Х) = ^.
(11.37)
Это означает, что в рамках статистического анализа многомер-
ной нормальной совокупности понятие введенного соотношением (11.8)
коэффициента детерминации Xd(y;X) совпадает с квадратом опреде-
ленного в (11.33) множественного коэффициента корреляции Ry,x м что
коэффициент детерминации Kd(y;X) может быть вычислен в данном
случае до проведения регрессионного анализа (т. е. до оценки функции
регрессии /(X)) с помощью формул (11.34), (11.35).
Для проверки гипотезы Яо: Ry,x = 0, т.е. для выяснения вопро-
са, можно ли считать выборочное значение множественного коэффициен-
та корреляции Ry,x статистически значимо отличающимся от нуля,
пользуются фактом F(p, п — р— 1)-распределенности случайной величины
F(fl) =
R — р — 1
Р
справедливым в рамках рассматриваемой многомерной нормальной со-
вокупности при условии, что истинное значение множественного коэф-
фициента корреляции Rv.x равно нулю. Если окажется, что F(R) >
va (р, п—р— 1), то гипотеза об отсутствии множественной корреляционной
связи между у и	отвергается при уровне значимости
420
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
критерия, равном а (здесь, как и ранее, v (р, n — р — 1) — 100а%-ная точ-
ка F-распределения с числом степеней свободы числителя р и знаменателя
п — р — 1 находится из табл. Приложения 1).
Знание следующих статистических свойств оценок Ry.x, определяе-
мых по формулам (11.34), (11.35) с заменой участвующих в них парных
и частных коэффициентов корреляции их выборочными аналогами, мо-
жет оказаться полезным при проведении корреляционного и регрессион-
ного анализов:
. ER2.X «	+ -Ц-(1 - R2„.x),	(11.38)
71 — 1
что означает наличие положительного смещения (асимптотически
устранимого) у оценки коэффициента детерминации
. DRl.x «	(И-39)
(п-1)(п -1)
(дисперсия DRy.x характеризует точность оценивания коэффициента де-
терминации Rv,x с помощью Rv.x и будет использована в регрессионном
анализе при определении числа объясняющих переменных, которые сле-
дует включить в линейную регрессионную модель);
***♦2
• подправленная на несмещенность оценка коэффициента де-
п2
терминации Ry.x имеет вид
Ry.x «1 - (1 - Ry.x) я"~тр	(11Л°)
Из последней формулы видно, что «подправленная» оценка R % все-
гда меньше смещенной оценки Ry.x.
Отметим, что при малых истинных значениях Ry.x и при «не слиш-
ком малых» величинах отношения р/п подправленные оценки, подсчи-
танные по формуле (11.40), могут принимать отрицательные значения.
Можно устранить абсурдность отрицательных значений оценки, исполь-
зуя в качестве «еще раз подправленной» оценки величину
Ry*x = тах(Й^х>0)
(правда, R уже не будет несмещенной оценкой).
Вернемся к ранее рассмотренным примерам и оценим в них степень
тесноты множественной связи между результирующим показателем, с од-
ной стороны, и набором объясняющих переменных — с другой. Будем
пользоваться рекомендациями (а именно формулами (11.34), (11.35)), пра-
вомерность которых, напомним, строго обоснована лишь в рамках много-
мерной нормальной генеральной совокупности.
11.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ
421
Пример 11.3 (продолжение). Оценка Ry.fx^x^) коэффициента
множественной корреляции между характеристикой качества ткани у и со-
вокупностью двух факторов: количеством профилактических наладок z^
и числом обрывов нити х<?\ подсчитанная с помощью формулы (11.35),
дает:
Bv.(«(Dc(3)) = 1 - (1 - Г01)(1 - ^02(1))
= 1 - [1 - (0,105)2] [1 - (0,906)2]
= 1 - 0,989 • 0,179 = 1 - 0,177 = 0,823.
Отсюда £v.(x(i)x(a)) = V®,825 = 0,9072.
Пример 11.4 (продолжение). Оценка Bv.(x(i)x(2)} коэффициента
множественной корреляции между урожайностью кормовых трав (у =
z^) и природными факторами — весенним количеством осадков (z^)
и накопленной суммой «активных» температур (z^), подсчитанная по
формуле (11.35), дает:
^у.(хП>г(2)) = 1 - (1 ~ Гщ ) (1 - ^02(1))
= 1 — [1 — (0,80)2][1 — (1,097)2]
= 1 — 0,36-0,99 = 0,6436.
Отсюда Rv,(x(i)x(2)) =	= 0,802.
2) Исследование линейных множественных связей (общий
случай). Речь идет о корреляционном анализе линейной модели вида
у = в0 +	+ • • • + в„хм + е(Х),	(11.41)
где 0 = (^о»^1>--ч^р)Т — неизвестные параметры модели, объясняющие
переменные, могут быть как случайными (схемы зависимостей типов С и
Р), так и неслучайными (схема зависимости типа В, см. п. 10.5), с(Х) и
X = (z^\z^2\..., z^), взаимно некоррелированы, а Ее(Х) = 0, De(X) =
а\Х). В отличие от предыдущего случая в модели (11.41) не требуется
совместной многомерной нормальности переменных (у, z^\z^2\...,z^).
В статистической практике свойства и рекомендации, справедливые в
условиях многомерной нормальной совокупности (относящиеся к частным
и множественным коэффициентам корреляции), обычно распространяют
и на общий случай (11.41). И, как правило, частные коэффициенты кор-
реляции, определенные соотношениями (11.31)-(11.32 ), являются удовле-
творительными измерителями очищенной линейной связи между z^ и
при фиксированных значениях остальных переменных Х^''^ и в случае,
422
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
когда распределение анализируемых показателей (х<°\	..., отли-
чается от нормального. При этом их можно интерпретировать как показа-
тели тесноты очищенной связи, усредненные по всевозможным значениям
фиксируемых на определенных уровнях «мешающих» переменных.
Точно так же множественный коэффициент корреляции Ry.x, опреде-
ленный формулами (11.34)-(11.35), может быть формально вычислен для
любой многомерной системы наблюдений. И в случае линейной зависи-
мости (11.41) результаты вычисления коэффициента детерминации, полу-
ченные по этим формулам, относительно слабо отличаются от результата
«прямого счета» по формуле (11.8*). Однако даже при незначительных
отклонениях типа функции регрессии f(X) от линейной доверять значе-
нию Я^.х как аппроксимации для величины коэффициента детерминации
Кд(у;X) не рекомендуется. В этом случае следует пользоваться непосред-
ственно формулой (11.8*), требующей предварительной оценки функции
регрессии /(X) в точках ХЬХ2,.. .,ХП. Возникающие при этом неудоб-
ства (особенно в условиях отсутствия априорной информации об общем
виде функции регрессии /(X)) преодолевают, в частности, следующим
образом:
а)	разбивают область возможных значений объясняющих переменных
на многомерные аналоги интервалов группирования — гиперпараллелепи-
педы группирования Д j, Д2,..., А
б)	подсчитывают условные средние j/j. результирующего показате-
ля по наблюдениям, попавшим в J-й гиперпараллелепипед группирования
(3 = 1»2,..., з);
в)	по наблюдениям, попавшим в Д^, оценивают условную дисперсию
2
результирующего показателя Sj по отклонениям этих наблюдении от сво-
его условного среднего yj, (j = 1,2,..., з);
г)	с помощью взвешенного усреднения условных дисперсий з* (j =
1,2,..., з) оценивают безусловную дисперсию остатков De, участвующую
в формуле (И.8*);
д)	оценив общую дисперсию зу = (Е(у{ - у)2)/п результирующей
показателя, подставляют оценку De и sj в формулу (П-в*) и вычисляют
Xd(y,X).
По существу эта процедура является многомерным аналогом проце
дуры вычисления парного корреляционного отношения.
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
423
11.3. Корреляционный анализ порядковых
(ординарных) переменных: ранговая
корреляция
Напомним (см. п. 2.3), что порядковая (ординальная) переменная по-
зволяет упорядочивать статистически обследованные объекты по степени
проявления в них анализируемого свойства. Исследователь обращается
к порядковым переменным в ситуациях, когда шкала непосредственно-
го количественного измерения степени проявления этого свойства в объ-
екте ему неизвестна (в том числе по причине объективного отсутствия
таковой) или имеет условный смысл и интересует его только как вспомо-
гательное средство для последующего ранжирования рассматриваемых
объектов. К подобным ситуациям относится рассмотрение таких пере-
менных, как «интегральный (сводный) показатель эффективности функ-
ционирования социально-экономической системы» (специалиста, пред-
приятия, научно-производственного объединения и т.п.), «качество (ме-
ра оптимальности) структуры потребительского бюджета семьи», «ка-
чество жилищных условий семьи», «степень прогрессивности предлагае-
мого проекта решения социально-экономической, технической или другой
проблемы» и т.п.
Таким образом, в отличие от статистического анализа Л-го (А =
0,1,2,... ,р) количественного признака х^к\ когда в результате его изме-
рения (наблюдения) на объектах мы могли каждому статистически обсле-
дованному объекту О, поставить в соответствие некоторую измеренную в
физически интерпретируемой шкале числовую характеристику ре-
зультатом измерения порядковой переменной является приписывание ка-
ждому из обследованных объектов некоторой условной числовой метки,
обозначающей место этого объекта в ряду из всех п анализируемых объ-
ектов, упорядоченном по убыванию степени проявления в них k-ro изуча-
емого свойства. В этом случае называют рангом t-ro объекта по к-ыу
признаку.
Процесс упорядочения объектов Oi,C>2,...,On производится либо с
использованием экспертной информации, т.е. с привлечением экспер-
тов, либо формализованно — путем перехода от исходного ряда наблюде-
ний некоторого вспомогательного (косвенного, частного) количественного
признака к соответствующему вариационному ряду (см. п. 6.3).
424
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11.3.1.	Исходные статистические данные (таблица или
матрица рангов типа «объект-свойство»)
Итак, в результате измерения р + 1 порядковых переменных =
у,х^\.. .tx^ на каждом из п анализируемых объектов Oi,O2l.. .,0п
мы получаем таблицу (матрицу) исходных данных следующего вида
(табл. 11.1).
В этой таблице элемент х\к^ задает порядковое место (ранг), кото-
рое занимает объект 0< в ряду всех статистически обследованных объек-
тов, упорядоченном по убыванию степени проявления А-го анализируемого
свойства (т.е. по переменной х^).
Очевидно, если рассмотреть столбец с номером к этой таблицы
(к = 0,1,...,р), то он будет представлять перестановку из п элементов,
а именно перестановку из п натуральных чисел 1,2,..., п, определяющую
порядковые места объектов O2i..., Оп в ряду, упорядоченном по свой-
(*)
ству х .
Замечание о случаях неразличимости рангов («объединенные ран-
ги»). При упорядочении объектов по какому-либо свойству х^к\к =
0,1,... ,р) могут встретиться ситуации, когда два объекта или целая груп-
па их оказываются неразличимыми с точки зрения степени проявления в
них этого свойства. Тогда каждому из объектов этой однородной груп-
пы приписывается ранг, равный среднему арифметическому значению тех
мест, которые они делят, а полученные таким образом ранги принято на-
зывать «объединенными» (или «связными»). Так, например, упорядо-
чивая семь альтернативных проектов Л,ByCyDyEyFyG перспективного
развития некоторой подотрасли с точки зрения их народнохозяйственной
эффективности, эксперт поставил на 1-е место проект С, на 2-е — проект
Л, далее располагал проекты B,D и Е, которые считал неразличимыми
(равноценными) по эффективности, а последнее место отвел проектам F
и G. Тогда соответствующий столбец таблицы «объект-свойство» будет
состоять из следующих компонент:
zf~xg'~ 2 “ 6>5'
Мы видим, что появление объединенных рангов может привести к
дробным значениям рангов, составляющих массив исходных статистиче-
ских данных (значения рангов, соответствующие 6-му и 7-му проектам).
При отсутствии объединенных рангов область возможных значений пере-
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
425
иенных очевидно, ограничивается множеством первых п чисел нату-
рального ряда, где п — число сравниваемых объектов.
Таблица 11.1
Порядко- вый номер объекта («объект»)	Порядковый номер исследуемой переменной («свойство»)						
	0	1	3	а а а	к	а а а	р
1 2 • • •	х<0) Х2	х™ Х1 М х2	4* 4”	а а а а а а а а а	4*> 4*>	а а а а а а • а а	4₽) г’”’ х2
1	40)		4”	а • а	4м	а а а	4₽)
а а а п	z(0)	z(1)	z<2)	а а а а а а	х<к} £п	а « а а а а	х(р)
Мы увидим далее, что наличие объединенных рангов несколько
усложняет вычислительные процедуры, связанные со статистическим
анализом соответствующих корреляционных характеристик.
11.3.2.	Понятие ранговой корреляции
Под ранговой корреляцией понимается статистическая связь между
порядковыми переменными. В статистической практике эта связь анали-
зируется на основании исходных статистических данных, представлен-
ных упорядочениями (ранжировками) п рассматриваемых объектов по
разным свойствам (см. столбцы табл. 11.1). Есть ли хоть какая-то со-
гласованность (или связь) между упорядочением анализируемых объектов
по свойству х^ и упорядочением тех же объектов по другому свойству
Можно ли измерить и проанализировать совокупную статистиче-
скую связь, существующую между ранжировками одних и тех же объек-
тов О1,Оз>--  tOn, полученными в соответствии со степенью проявления
в них сначала свойства х^к1^ (1-й способ упорядочения), затем — свой-
ства х^кз^ (2-й способ упорядочения)? Таким образом, речь идет о системе
понятий и методов, позволяющих измерять и анализировать статистиче-
скую связь, существующую между двумя или несколькими ранжировками
одного и того же конечного множества объектов 01,0а,..., Оп.
Система этих понятий и методов и составляет раздел математиче-
ской статистики, который принято называть анализом ранговых корре-
426
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
yurtfUtL Методы ранговой корреляции широко используются, в частности,
при организации и статистической обработке различного рода систем экс-
пертных обследований.
11.3.3.	Основные задачи статистического анализа связей
между ранжировками
Предположим, мы ввели измерители парной и множественной ранго-
вой статистической связи (см. ниже, пп. 11.3.4, 11.3.5 и 11.3.8), Тогда,
опираясь на эти характеристики, исследователь чаще всего пытается ре-
шить следующие три основные задачи статистического анализа структу-
ры и характера связей, существующих между изучаемыми порядковыми
переменными.
Задача А: анализ структуры имеющейся совокупности упоря-
дочений = (zifc\z2*\...,z^)T, к = 0,1,...,р. Интерпретируя
каждое упорядочение X как точку в n-мерном пространстве, можно
представить, например, три наиболее характерных типа такой структу-
ры: 1) анализируемые точки равномерно разбросаны по всей области сво-
их возможных значении (определяемой неравенствами 1	ж;- п, t =
1,2,...,л), что означает отсутствие какой-либо связи или согласованно-
сти в представляемых ими ранжировках; 2) расположение р + 1 точек
таково, что часть из них образует ядро из близко лежащих друг от дру-
га точек («сгусток»), а остальные произвольно разбросаны относительно
этого ядра. В этом случае существование ядра обеспечивает наличие под-
множества согласованных переменных; 3) анализируемые точки — ран-
жировки располагаются в пространстве несколькими относительно далеко
отстоящими друг от друга ядрами («сгустками»), что означает наличие
нескольких подмножеств переменных таких, что переменные внутри од-
ного подмножества обнаруживают высокую статистическую взаимосвязь,
тогда как согласованности между переменными, взятыми из разных таких
подсовокупностей, практически не существует.
Задача В: анализ интегральной {совокупной) согласованности
рассматриваемых переменных и их условная ранжировка по критерию
степени тесноты связи каждой из них с остальными переменными. По-
добные задачи возникают, например, при исследовании степени согласо-
ванности мнений группы экспертов и при попытках условного упорядоче-
ния последних по их компетентности. В основе этого анализа лежит рас-
чет коэффициента совокупной согласованности — коэффициента конкор-
дации для различных комбинаций исследуемых переменных (см. п. 11.3.8).
Задача С: построение единого группового упорядочения объек-
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 427
moe на основе совокупности согласованных упорядочений *ядраъ (или
нескольких групповых упорядочений — при наличии нескольких «ядер»).
Решение этой задачи сводится к построению такого упорядочения, которое
было бы, в определенном смысле, наиболее близким к каждому из упоря-
дочений заданной совокупности — «ядра». Именно с такой задачей стал-
кивается, например, исследователь, желающий установить неизвестное
истинное упорядочение заданной совокупности объектов по имеющему-
ся в его распоряжении набору экспертных ранжировок тех же объектов.
Для построения единого (группового) варианта упорядочения часто
используют в качестве ранга х^^ объекта Oi среднее арифметическое
или медиану имеющихся базовых рангов z^\^2\...,z|p^ этого объекта.
Обоснование способа построения единого варианта упорядочения может
быть получено, например, в рамках подхода, который опирается на меру
близости между ранжировками (определяется ранжировка Х<ад\ наиме-
нее удаленная, в смысле введенной меры близости, от всех ранжировок
Х^\х^2\..., Х^ базовой совокупности). Задача С может быть сформу-
лирована и как задача наилучшего (в определенном смысле) восстановле-
но)	-	(о)
ния ранжировки X 1, связанной с результирующей переменной у = х'
по ранжировкам Х^\Х^2\...,Х^Р\ индуцируемым соответственно объ-
ясняющими переменными а/2\..., В такой формулировке ее на-
зывают также задачей регрессии на порядковых (ординальных) перемен-
ных.
11.3.4.	Ранговый коэффициент корреляции Спирмэна
Для измерения степени тесноты связи между ранжировками Х^ =
...,а?п*))Т и Х^ = (z^\z^\...,z^)T К.Спирмэн еще в
1904 г. предложил показатель
(11.42)
названный впоследствии ранговым коэффициентом корреляции Спирмэ-
на. Прямым подсчетом нетрудно убедиться, что для совпадающих ран-
жировок (т.е. при = ж для всех i = 1,2,...,n)	= 1 а для про-
тивоположных (т.е. при = п — j Р + 1, i = 1,2,...,n) —	= — 1.
Можно показать, что во всех остальных случаях |f) | < 1.
Формула (11.42) пригодна лишь в случае отсутствия объединенных
рангов в обеих исследуемых ранжировках. Для ее распространения на об-
428
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
щий случай определим для каждой (fc-й) ранжировки Х^к* (к = 0,1,... ,р)
величину
т(к)
з44 = J £ Ы*’)3 - ««*’].	(и.4з)
1=1
(fc)	v (k)	(А)
где тп ' — число групп неразличимых рангов у переменной х' а п} ' —
число элементов (рангов), входящих в t-ю группу неразличимых рангов (в
частном случае отсутствия объединенных рангов имеем m ' = n, nJ —
г = ... = nJ*) = 1 и соответственно = 0; кроме того, группы
неразличимых рангов, состоящие из единственного элемента, по существу,
не участвуют в расчете величины Т^).
Тогда ранговый коэффициент корреляции Спирмэна между ранжи-
ровками и следует вычислять по формуле
z 1 (п3 п\ V”	Д*Ъ2
-(•) = el” ~ w) ~ 2^»=1(ж1 ~xi ) -1	-1
3 J i(n3 - n) - 2T(fc)] [i(n3 - n) - 2T0)]
(11.44)
Если и являются небольшими относительно |(п — п) вели-
чинами, то можно воспользоваться приближенным соотношением (а при
Т(А) = у(У) оно точное)
Правда, при этом же условии (относительная малость 4- по
сравнению с |(п3 — п)) и приближенная формула (11.42) дает хорошую
точность.
Пример 11.5. Два эксперта проранжировали 10 предложенных им
проектов реорганизации научно-производственного объединения (НПО) с
точки зрения их эффективности (при заданных ресурсных ограничени-
ях). Пронумеровав проекты в порядке ранжировки 1-го эксперта, по-
лучаем в качестве исходных данных:	= (1;2;3;4;5;6;7;8;9; 10)Т;
%(2, = (2;3;1;4;6;5:9;7;8;10)т.
Вычисления по формуле (11.42) дают:
= 1-95о'14 = °>915’
что свидетельствует о существенной положительной ранговой связи меж-
ду исследуемыми переменными.
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
429
Пример 11.6. Десять однородных предприятий подотрасли бы-
ли проранжированы вначале по степени прогрессивности их оргструк-
тур (признак я^), а затем — по эффективности их функционирова-
ния в отчетном году (признак я/2)). В результате были получены сле-
дующие две ранжировки: Х^ = (1; 2,5; 2,5; 4,5; 4,5; 6,5; 6,5; 8; 9,5; 9,5)Т;
Х(2) = (1;2;4,5;4,5;4,5;4,5;8;8;8;10)т.
В первой ранжировке имеем четыре группы неразличимых рангов,
число элементов в которых больше единицы, а во второй ранжировке —
две такие группы. В соответствии с формулой (11.43) получаем;
1м = А [(23 - !) + (23 - 1) + (23 - 0 + (23 - 0] = 75 = 2^3;
£ л»	1. jC
Т™ = Т^К4’ - + (З3 - 01 = 7’42-
JL Ла
Точная формула (11.44) дает = 0,917. Вычисление этого же коэф-
фициента корреляции по приближенным формулам (11.42) и (11.44') дает,
соответственно, значения 0,921 и 0,917. Все эти результаты оказываются
совпадающими при округлении до второго десятичного знака.
11.3.5.	Ранговый коэффициент корреляции Кендалла
Другой широко используемой характеристикой тесноты статистиче-
ской связи между двумя упорядочениями является ранговый коэффициент
корреляции Кендалла, определяемый соотношением
ЩХ™,Х<»)
Д*)
п(п — 1)
(11.45)
где у(Х^к\х^) — минимальное число обменов соседних элементов после-
довательности Х^\ необходимое для приведения ее к упорядочению Х^к\
Очевидно, величина 1/(Х^*\х^) симметрична относительно своих аргу-
ментов, так что с равным правом можно говорить о минимальном числе
«соседских обменов» элементов последовательности X \ необходимом
для приведения к виду Х^\
(к}
Из (11.45) сразу следует, что при совпадающих ранжировках X' 7 и
Х^ = 1 (так как и(Х^к\х^ = 0), а при противоположных (т.е.
при = п — х\^ Ч-1, i = 1,2,..., п, так что |/(Х^*\ Х^) = |n(n — 1)) —
= — 1. Нетрудно показать, что во всех остальных случаях |т^^| < 1.
430
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Вычисление связано с необходимостью подсчета величины
р(Х^к\Х^) и, следовательно, является более трудоемким, чем вычисле-
ние Однако, во-первых, коэффициент Кендалла обладает некото-
рыми преимуществами по сравнению с коэффициентом Спирмэна, глав-
ные из них: а) относительно большая продвинутость в исследовании его
статистических свойств и, в частности, его выборочного распределения
(см. ниже); б) возможность его использования и в частной («очищенной»)
корреляции рангов; в) большие удобства его пересчета при добавлении
к п статистически обследованным объектам новых, т.е. при удлинении
анализируемых ранжировок: для вычисления нового значения рангово-
го коэффициента корреляции приходится переранжировать значительную
часть объектов, что в случае 1 означает необходимость пересчета раз-
ностей z,* — при вычислении же т значения рангов не играют ни-
какой роли, важно лишь число необходимых «соседских обменов», которое
при добавлении новых объектов подсчитывается рекуррентным способом
(к старому значению и(Х^к\ Х^) может быть лишь дополнен некоторый
«добавок»).
Во-вторых, можно воспользоваться рекомендациями, упрощающими
подсчет числа и(Х^к\ Х^) как при ручном, так и при машинном счете.
Так, при ручном счете полезным оказывается известный факт то-
ждественного совпадения величин 1/(Х^к\х^) и ЦХ^к\х^), где число
инверсий 1(Х^к\х^3^) — это просто число разложенных в неодинаковом
порядке пар элементов последовательностей Х^ и Х^3\ являющееся есте-
ственной мерой нарушения порядка объектов в одной последовательности
относительно другой. Для удобства подсчета ЦХ^к\х^) перенумеру-
ем объекты в порядке, определяемом рангами последовательности X'
Тогда анализируемые ранжировки Х^к\х^ соответствующим образом
видоизменяются, т.е. преобразуются к виду соответственно
где Х^ = (1,2, ...,п)Т;	= (х^,х^,-чх!^)Т» а число инверсий
1(Х^к\Х^) = 7(Х^к\х^), а следовательно, и величина 1/(Х^к\х^)
определяется по формуле
9=i |=д+1
(11.46)
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
431
где
О -
если > х\^ (т. е. нарушен порядок
последовательности Х^)]
в противоположном случае.
Легко подсчитать, что число инверсий I(X^k\ Х^) может меняться от О
(что соответствует случаю совпадающих ранжировок) до |n(n — 1) (что
соответствует случаю противоположных ранжировок).
Формулы (11.45)-(11.46) пригодны для подсчета лишь в случае
отсутствия объединенных рангов в обеих исследуемых ранжировках. Со-
ответствующее «подправленное» значение т при наличии объединен-
ных рангов в анализируемых упорядочениях будет определяться соотно-
шением
4К)
kj	п(п —1)
/А	Wl 21/0)
У V	\	«б»-*)/
(11.45')
в котором коэффициент ’ вычисляется по формуле (11.45)-(11.46), а
«поправочные» величины определяются соотношением
m(i)
-1), l = k,j
(11.47)
(смысл величин rd и определен выше, см. (11.43)).
Для пояснения работоспособности формул (11.45)—(11.47) вернемся к
примерам 11.5 и 11.6.
Анализ степени согласованности ранжировок двумя экспертами де-
сяти проектов реорганизации НПО (пример 11.5), осуществленный с ис-
пользованием формул (11.45)-(11.46), дает:
432
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
"12 = 0;	"13	= 1»"14 = "15 = "16 = "17	= "18 = "19 = "1.10	= 0;
"23 = I?	"24	= "25 = "28 = "27 = "28 =	"29 = "2.10 = 0;
"34 = 1;	"35	= "36 = "37 = "38 — "39 =	"3.10 = 0;
"45 = "46 = "47 = "48 = "49 = "4.10 = 0;
"56 = I? "57 = "58 = "59 = "5.10 = 0;
"б? = "ев = "69 — "ело = 0;
"78 = "79 = "7.10 = 0;
"89 = "8.10 = о>
"9.10 = 0.
Таким образом, i/(X^\ Х^) = 14-14-1 + 0+1 + 0 + 2 + 0 + 0 = 6.
Соответственно
= 1 -	= 1 - 0,267 = 0,733
(напомним, что коэффициент Спирмэна в этом примере был равным
0,915).
При вычислении рангового коэффициента корреляции Кендалла в
примере 11.6 следует воспользоваться формулой (11.45*), так как исследу-
емые ранжировки содержат объединенные ранги. Используя результаты
расчета величин тг№ = 4,	= 2, пр = пр = пр = пр = 2,	=
4,п^ = 3, получаем (в соответствии с (2.8)):
l/(,) = |(2+2 + 2 + 2) = 4; UW = |(4-3 + 3 • 2) = 9.
At	АЛ
Обращаясь теперь к формуле (2.6*), имеем:
f«(K) =	1-8
” У(1 - &) О - й)
= 0,833
(напомним, что соответствующий коэффициент Спирмэна был равен
0,917).
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 433
11.3.6.	Обобщенная формула для парного коэффициента
корреляции и связь между коэффициентами
Спирмэна и Кендалла
Для удобства стандартной вычислительной реализации системы ал-
горитмов корреляционного анализа полезно ввести некоторый обобщенный
прием вычисления парных корреляционных характеристик, определенный
для любой двумерной системы п наблюдений
/ х(*)' \	/
\ XUY /	\
М х{к)
-U) x{j}
*1 j*2 >
х(к)
> *n
(11.48)
С этой целью определим некоторое правило, в соответствии с кото-
рым каждой паре (®^,®|^) компонент вектора (/ = k,j) ставится
в соответствие число («метка») причем это правило должно обла-
дать свойством отрицательной симметричности (т.е. а] = —а<2>1) и
центрированности (т.е.	= 0 при всех I = k,j и всех i = 1,2,...,п).
Тогда обобщенный коэффициент корреляции г^06^ переменных х^ и
определяется формулой
V? V? а№ а^.
= __________^»1=1 Z^«a=l ц«1»з *i»a_______	(ц
*' 7n.=i па=.(“&)2 • г?,,, е"=,(«;:1)2 ’
Легко видеть, что практически все введенные нами характеристики
парной корреляционной связи могут быть получены как частные случаи
формулы (11.49) при соответствующем выборе правила приписывания чи-
словых «меток» а,^а. Действительно:
а)	положив = а —	/ = fc,j, получаем формулу для
обычного парного коэффициента корреляции если х^ — значение
/-количественной переменной в i-м наблюдении (см. п. 11.2.2, формулу
(11.13*)), и формулу для рангового коэффициента корреляции Спирмэна
если — ранг i-ro объекта в ряду, упорядоченном по порядковой
переменной х (см. формулу (11.42));
б)	положив
(.I	(0 (О
4-1, если х-/<х-2;
О, если
-1, если <^2 >
434
ГЛ. И. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
получаем формулы (11.45) и (11.45') для рангового коэффициента кор-
реляции Кендалла если под понимать ранг i-ro объекта в 1-м
упорядочении.
Заметим, что значения ранговых корреляционных характеристик
' и довольно тесно связаны одно с другим. Это следовало ожи-
дать, так как обе характеристики являются линейными функциями от
числа инверсий, имеющихся в сравнении последовательностей Х^ и
различие этих функций состоит в том, что при подсчете коэффициен-
та Спирмэна инверсиям более отдаленных (по величине) друг от друга
элементов приписываются большие веса. Между масштабами шкал, в
которых измеряют корреляцию коэффициенты и т^К\ нет простого
соотношения. Однако уже при умеренно больших значениях п (п > 10) и
при условии, что абсолютные величины значений этих коэффициентов не
слишком близки к единице, их связывает следующее простое приближен-
ное соотношение « 1,5т^К\
11.3.7. Статистические свойства выборочных
характеристик парной ранговой связи
До сих пор речь шла о выборочные характеристиках ранговой связи.
Попробуем ответить на вопрос: как точно эти выборочные характери-
стики (определенные, в частности, формулами (11.42)-(11.47)) оценивают
соответствующие истинные (теоретические) значения?
Для этого в первую очередь следует пояснить, что в данном случае
понимается под теоретическими характеристиками.
Представим себе сначала конечную генеральную совокупность, состо-
ящую из N объектов	каждый из которых снабжен двумя
порядковыми номерами: Oi <-♦ (®1*\®<Л)> * - 1,2,.. .,7V, где означает
место объекта О, в общем ряду всех N объектов, упорядоченном по степе-
ни выраженности свойства x^(l = k,j). Будем полагать, что статисти-
чески обследованное множество объектов О,1ЭО4а,...,О,-я образуется как
случайная выборка объема п, взятая из совокупности Oj, О2,..., ON (п <
*)•
Определим теоретические (истинные) значения коэффициентов
и соответственно теми же соотношениями (11.42) (или (11.44),
(11.45) (или (11.45 ), что и выборочные с заменой объема выборки п объ-
емом генеральной совокупности N. При работе с выборкой производится
естественная перенумерация объектов и их рангов, не меняющая их упо-
рядоченности в генеральной совокупности ни по одной из переменных.
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
435
В дальнейшем нас будет интересовать, как сильно могут отличать-
ся выборочные значения тит от соответствующих теоретических,
в том числе в так называемых асимптотических ситуациях, т. е. при
N -+ оо и n(N) —► оо.
Проверка статистически значимого отличия от нуля ранговых кор-
реляционных характеристик осуществляется при «не слишком малых»
п, (п > 10) и заданном уровне значимости критерия а с помощью нера-
венства
Д /-(S)42
|f(s)|>t»("-2)V	(	} ;	(11.50)
2 У п — Z
(“•«)
в которых tg(v) и uq, как и прежде, соответственно 1009%-ная точка t(v)-
и 9-квантиль стандартного нормального распределения (см. табл, в При-
ложении 1). Выполнение неравенств (11.50) и (11.51) сигнализирует о
необходимости отвергнуть гипотезу о наличии статистически значимой
ранговой корреляционной связи. В случае небольших объемов выборок
(4 п 10) статистическая проверка гипотезы об отсутствии ранговой
корреляционной связи производится с помощью специальных таблиц (см.
Приложение 1).
Таблица значений вспомогательной величины Sc позволяет при ма-
лых п(п = 4,5,..., 10) построить то пороговое значение т^х» при пре-
вышении которого (по абсолютной величине) коэффициентом Спирмэна
следует признать наличие статистически значимой связи между ана-
лизируемыми переменными. Задавшись уровнем значимости критерия
а и числом сравниваемых объектов п, определяем из таблицы величину
Sc = Sc(ntQ), соответствующую нашему п и значению Q = а/2 (или
приблизительно равному а/2). Тогда
42, =	_ 1,	(П.52)
где Кп = |(т|3 — п) (значения этой вспомогательной константы приведены
в последней строке таблицы).
Так, в примере 11.5 для уровня значимости а = 0,06 имеем: п —
10; Q = 0,03; Sc = 5с(10; 0,3) = 268; К-щ = 330, так что в соответствии с
(11.52)
(S)	2- 268 _	2
тах 330	’
436
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Поскольку выборочное значение рангового коэффициента корреляции
Спирмэна т' ' в этом примере значительно превосходит пороговое зна-
чение [т = 0,915 > 0,624), то гипотеза об отсутствии корреляционной
связи отвергается.
И наконец, в таблице значений вспомогательной величины SK при-
ведены значения величин SK, позволяющих вычислить (при малых п =
4,5,...,10) то пороговое значение при превышении которого (по
абсолютной величине) коэффициентом Кендалла следует признать нали-
чие статистически значимой связи между анализируемыми переменными.
Для этого поступают следующим образом: задавшись объемом выборки п
и уровнем значимости критерия а, находят в столбце, соответствующем
данному п, величину, равную (или приблизительно равную) а/2; затем
находят значение SK = 5к(п,о) в левом столбце той же самой строки и
(К)	.
ВЫЧИСЛЯЮТ ПО формуле
(к) _ 25'д.(п, а)
^гпах — z 1 \ •
п(п — 1)
(11.53)
Если окажется, что	то гипотеза об отсутствии ранговой
корреляционной связи отвергается (связь статистически значима).
Так, в примере 11.5 при уровне значимости а = 0,06 имеем: п = 10;
0,23 < у < 0,36; следовательно, SK = 22 (оно лежит между 21 и 23), так
что
(К) = ^22 = 44 =
х 10-9	90
Поскольку т™ = 0,733 > 0,489, делается вывод о наличии статисти-
чески значимой корреляционной связи между исследуемыми переменными
в данном примере.
Построение доверительных интервалов для неизвестных истинных
значений ранговых коэффициентов корреляции возможно лишь прибли-
женно и только при измерении ранговой корреляции с помощью коэф-
фициента Кендалла. При этом используют (при п > 10 и значениях
не слишком близких по абсолютной величине к единице) прибли-
женный факт нормальности распределения величины № со средним зна-
чением Ет' « гк ' и с дисперсией Dr' , не превышающей величины
J[1 - (т^)2]. Можно утверждать, что с доверительной вероятностью, не
меньшей заданного уровня Р, истинное значение коэффициента Кендалла
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
437
заключено в пределах
(11.54)
где ич — g-квантиль стандартного нормального распределения.
11.3.8.	Коэффициент конкордации (согласованности)
как измеритель статистической связи между
несколькими порядковыми переменными
До сих пор мы рассматривали корреляцию между двумя порядковы-
ми переменными. Однако при решении основных задач А — С статисти-
ческого анализа ранговых связей (см. п. 11.3.3) возникает необходимость
уметь измерить статистическую связь между несколькими (более чем дву-
мя) переменными. С этой целью Кендаллом был предложен показатель
1У(т), названный коэффициентом конкордации (или согласованности),
вычисляемый по формуле1
(11.55)
где т — число анализируемых порядковых переменных (сравниваемых
упорядочений); п — число статистически обследованных объектов или
длина ранжировки (объем выборки);	— номера отобран-
ных для анализа порядковых переменных (из исходной совокупности
а;(0), ^t1), я?^2\...,х^р\ так что, очевидно, т р + 1).
Нетрудно устанавливаются следующие свойства коэффициента кон-
кордации:
а)	0 < W 1;
б)	W = 1 тогда и только тогда, когда все т анализируемых упорядо-
чений совпадают;
1 Мы приводим здесь формулу для подсчета выборочного значения W коэффициента
конкордации W. Интерпретация и вычисление теоретического значения IV непо-
средственно следуют из рассуждений, приведенных в л. 11.3.7 в связи с анализом
статистических свойств выборочных парных ранговых коэффициентов корреляции.
438
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
в)	если т > 3 и анализируемые ранжировки генерируются подобно
случайному независимому m-кратному извлечению из множества всех п
возможных упорядочений п объектов, то связи между ними нет и W = 0;
г)	пусть — среднее значение коэффициента Спирмэна, подсчи-
танное по значениям тп(т-1)/2 коэффициентов
j), характеризующих ранговую связь между всеми возможными парами
переменных (xki\x^) из анализируемого набора (^fcl\z^a\...,^**^);
тогда
_(s)	= тЩ-1
т — 1
в частности, из (11.56) следует для случая т = 2, что
^(2) =	+ 0.	(П-56')
т.е. коэффициент конкордации, исчисленный для двух переменных, про-
порционален введенному ранее парному ранговому коэффициенту корре-
ляции Спирмэна.
То, что шкала измерения IV(m) не включает в себя отрицательных
значений, объясняется следующим обстоятельством. В отличие от случая
парных связей при анализе m(m > 3) порядковых переменных противопо-
ложные понятия согласованности и несогласованности утрачивают преж-
нюю симметричность (относительно нуля); упорядочения, произведенные
в соответствии с переменными х^кл\х^к2\.. . могут полностью со-
впадать, но не могут полностью не совпадать в том смысле, который
мы вкладывали в это понятие при т = 2.
Формула (11.55) получена (и справедлива) в предположении отсут-
ствия объединенных рангов в каждом из анализируемых упорядочений.
Бели же таковые имеются, то формула должна быть модифицирована:
где поправочный коэффициент T^ki^ (соответствующий переменной
подсчитывается по формуле (11.43).
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 439
11.3.9.	Проверка статистической значимости выборочного
значения коэффициента конкордации
Как ведут себя выборочные значения W(m) коэффициента конкор-
дации при повторении выборок заданного объема п (из одной и той же
генеральной совокупности) при отсутствии какой-либо связи между ана-
лизируемыми т переменными? Другими словами, нас интересует ответ
на следующий вопрос. Предположим, что каждому объекту конечной ге-
неральной совокупности (состоящей из N элементов) приписан какой-то
определенный ранг по каждой из т рассматриваемых переменных. Так,
например, если т = 3 и объекту О{ приписана тройка (z^ = N; х^ =
1;	= 2), то это означает, что по переменной он стоит на последнем
(Af-м) месте в упорядоченном ряду всех объектов генеральной совокупно-
м (2)	- (3)
сти, по переменной z — на первом и по переменной х ' — на втором.
Тогда по исходным данным {(z^\zj2\.. •,	с помощью фор-
мулы (11.55) может быть вычислен теоретический (генеральный) коэф-
фициент конкордации W(m), характеризующий степень тесноты ранго-
вой связи между переменными z^\ z^2\...,Однако исследователю
/ (1) (2)	(т)
известны значения (z , z , ...,z'
) лишь для части объектов гене-
ральной совокупности, а именно для случайной выборки объектов объема
п(п < N). После естественной перенумерации рангов, сохраняющей праг
вило упорядочения объектов, но переводящей масштаб измерения рангов
в шкалу (1,2, ...,п) (для этого минимальный из оказавшихся в выборке
рангов по каждой переменной объявляется рангом, равным 1, следующий
по величине — рангом, равным 2, и т. д.), может быть вычислен (по той
же формуле (11.55)) выборочный коэффициент конкордации Ж(т). Извле-
кая другую выборку объема п из той же самой генеральной совокупности,
мы получим, вообще говоря, другое значение выборочного коэффициента
W(m) и т.д.
Спрашивается, как сильно могут^отклоняться от нуля выборочные
значения коэффициента конкордации Ж(тп) в ситуации, когда значение
теоретического коэффициента конкордации W(m) свидетельствует о пол-
ном отсутствии ранговой связи между анализируемыми переменными
z^\z^2\...,z^mh Для малых значений т и п(2 т 20, 3 п 7)
ответ на этот вопрос может быть получен с помощью таблицы значений
величины S. Обозначенная в ней величина S есть не что иное, как
(11.57)
440
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
«Входами» в эту таблицу является тройка чисел (m,n,S), «выхо-
дом» — вероятность того, что величина 5 может быть такой, какой она
является в нашей выборке, или большей в условиях отсутствия связи пере-
менных в генеральной совокупности. Если окажется, что эта вероятность
меньше принятой нами величины уровня значимости критерия а (напри-
мер, а = 0,05), то гипотезу об отсутствии связи следует отвергнуть, т.е.
признать статистическую значимость анализируемой связи. Таблица кри-
тических значений TF(m) построена несколько иначе. В ней при уровне
значимости а = 0,05 и в соответствии с «входами» (m,n) даны «кри-
тические» значения величины 5, т.е. такие значения, при превышении
которых следует отвергать гипотезу об отсутствии связей (признавать их
статистическую значимость).
При п > 7 для проверки статистической значимости анализируе-
мой связи следует воспользоваться фактом приближенной х(п — ^-рас-
пределенности величины т(п — 1) х IV(m), справедливым в условиях от-
сутствия связи в генеральной совокупности (значение W(m), как и прежде,
подсчитывается по формуле (2.16) или (2.16)). Поэтому, если окажется,
что
т(п - l)lV(Tn) > Ха(п~ 1),	(11.58)
-	-	(М
то гипотеза об отсутствии ранговой связи между переменными х ,
.. ,я(*т) должна быть отвергнута (с уровнем значимости крите-
рия, равным а); в (11.58) величина xi(n — 1) — это 100а%-ная точка
^-распределения с (п — 1)-й степенью свободы.
Можно использовать и другой способ проверки статистической зна-
чимости исследуемой ранговой связи между несколькими переменными,
основанный на том, что в условиях отсутствия таковой в генеральной
совокупности распределение случайной величины j In	прибли-
женно описывается Z-распределением Фишера с числом степеней свободы
числителя Pi=n — 1 — и знаменателя = (т — 1)^.
Строгих рекомендаций по построению доверительных интервалов для
истинного значения IV в условиях наличия ранговых связей в исследуемой
генеральной совокупности к настоящему времени не имеется.
Рассмотрим примеры, в которых реализуются приведенные выше ре-
комендации по статистическому анализу множественных ранговых связей.
Пример 11.7. Рассмотрим три порядковые переменные (з/1),^2),
а/3)) и соответствующие им упорядочения десяти объектов:
11.3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ 441
х(1)т	1	4,5	2	4,5	3	7,5	6	9	7,5	10
х(2)Т	2,5	1	2,5	4,5	4,5	8	9	6,5	10	6,5
Х(з)т	2	1	4,5	4,5	4,5	4,5	8	8	8	10
Сумма	5,5	6,5	9	13,5	12	20	23	23,5	23,5	26,5
В соответствии с формулами (11.57), (11.43) имеем:
(ч з
3	Q 11 \
£г(Л_3 И	=(_11)> + (_10)’ + (_7(5)’
i=i	J
+ (-3)’ + (-4,5)’ + (3,5)2 + (6,5)2 + 72 + 92 + 102 - 591;
Т0’ = ^(23 - 2)2 =
Т(2) =	- 2)2 = 1,5;
Т(3) = ^(43 - 4 + З3 - 3) = 7.
Следовательно, в соответствии с (11.55’)
^,,4______________591____________ 591	_
^32(102 - 10) - 3(1 + 1,5 + 7)	742,5 -28,5
Пример 11.8. Требуется проверить статистическую значимость
множественной ранговой связи 28 переменных (тп = 28), характеризуемой
величиной выборочного коэффициента конкордации IV(28) = 0,08, подсчи-
танного по 13 объектам (п = 13).
Воспользуемся фактом х2(12)-распределениости случайной величины
m(n - l)ir(m), который имеет место (приближенно) в случае, если в ис-
следуемой генеральной совокупности множественная ранговая связь отсут-
ствует. Тогда критерий сводится к проверке неравенства (11.57). Задав-
шись уровнем значимости критерия а = 0,05, находим из таблиц значение
5%-ной точки х2-распределения с 12 степенями свободы Хо,об(12) = 21,026.
В то же время т(п — l)J¥(m) = 28 • 12 • 0,08 = 27.
Поскольку т(п— l)W(m) > Xo,os(12), то оказалось, что даже такого
маленького числа, как 0,08, «хватило» для того, чтобы объявить связь
между 28 исследуемыми переменными статистически значимой.
442
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
11.4. Корреляционный
анализ категоризованных переменных:
таблицы сопряженности
Признак называют категоризованным, если его возможные «значе-
ния» описываются конечным числом состоянии или градации. Слово
«значения» взято в кавычки, так как речь идет, как правило, не о число-
вых значениях, а лишь об определенных условных метках возможных со-
стояний. Так, категоризованный признак «пол индивидуума» имеет две
градации, категоризованный признак «социальное положение респонден-
та» — столько градаций, сколько установлено социальных страт (сло-
ев) в данном обществе, категоризованный признак «уровень жилищных
условии семьи» — столько градаций, сколько их определено в данном
обследовании (например, при возможных ответах: «низкий», «удовлетво-
рительный», «хороший» и «очень хороший» мы будем иметь четыре
градации). Как мы видим, в класс категоризованных признаков попада-
ют те номинальные1 и порядковые (ординальные) переменные, возможные
значения которых описаны заданным (известным) набором градаций.
11.4.1. Исходные статистические данные (таблицы
сопряженности)
Мы ограничимся здесь задачей измерения парных статистических
связей между категоризованными переменными. Формально исходные
данные для пары категоризованных переменных будут иметь уже зна-
комый нам вид (9.1') таблицы «объект-свойство», в которой, правда, в
качестве элементов x\^(j = 1,2; i = 1,2, ...,п) будут обозначены услов-
ные метки (градации) состояния объекта t по переменной j. Однако мы
не можем работать с этими данными аналогично случаю количественных
переменных: скажем, среднее значение или дисперсия «пола» или «соци-
альной принадлежности» респондента лишены всякого смысла. Поэтому
при статистическом анализе двух категоризованных переменных исход-
ные данные преобразуют к виду таблицы перекрестных частот, называе-
мой двухвходовой таблицей сопряженности признаков и х^ (см.
табл. 11.2) или просто таблицей сопряженности.
1 Напомним, что случайная величина называется номинальной, если знание ее значе-
ний на статистически обследованных объектах позволяет разбить это множество на
не поддающиеся упорядочению однородные по анализируемому свойству классы (см.
п. 2.3)
11.4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТЕГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 443
Таблица 11.2
Градация признака	Градация признака z^2^						«».
	1	2	• • •	i	• • •	«32	
1	ПЦ	П12	• • •		•  •	^Im»	nb
2	«21	«22	• • •	n2j	 • •		«2.
«  •	• • 	• •	• • •	•	• » •	 	• 
t	"il	П<2	• • •		• • •		n«.
« •	• • •	• • •	• • •	• « «	• • •	• • •	•	1
	Я»П11	^mi2	• • •	nmjj	• • e	^mimj	
n.j	n.i	П.2	♦ • •	«J	• • •		«
В табл. 11.2 представлены результаты статистического обследования
побъектов по признакам а/1) и z^2\ В ней означает число объектов (из
общего числа п обследованных), у которых «значение» признака z^ ока-
залось зафиксированным на уровне t-й градации, а «значение» признака
а/2) — на уровне j-й градации; я,. = «tj — число объектов, зна-
чение признака z^ у которых оказалось зарегистрированным на уровне
t-й градации (при отсутствии каких бы то ни было условий на «значе-
ния» признака z^, a n.j = JSfci n»j — число объектов, значение призна-
ка а/2) у которых оказалось зарегистрированным на уровне j-й градации
(• = 1,2,...,Ш); j 1,2,...,tbj).
Переход к задаче измерения степени тесноты связи нескольких (более
двух) категоризованных переменных связан с необходимостью введения
многовходовых таблиц сопряженности и более громоздких обозначений
(количество нижних индексов у анализируемых часто приходится увели-
чивать до числа анализируемых переменных).
11.4.2. Основные измерители
степени тесноты статистической связи между двумя
категоризованными переменными
В статистической теории и практике в рамках данной проблемы суще-
ствует целый спектр характеристик с.т.с.с. Разные меры связи акцен-
тируют внимание на разных аспектах взаимоотношений между перемен-
ными, давая в целом многоаспектную информацию о природе изучаемой
444
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
зависимости. Поэтому вряд ли целесообразно давать универсальные ре-
комендации по поводу выбора наиболее предпочтительной характеристи-
ки «на все случаи жизни». Выбор описанных ниже измерителей с.т.сх
был основан на сочетании двух критериев: 1) наибольшей распростра-
ненности в практике статистических исследований; 2) умении описать
необходимые статистические свойства этих измерителей.
Построение подавляющего большинства используемых в данной про-
блеме характеристик с.т.с.с. основано на одной общей идее: характе-
ристика должна принимать тем большее числовое значение, чем боль-
ше анализируемая ситуация отклоняется от гипотезы взаимной ста-
тистической независимости исследуемых переменных	Как мы
знаем (см. п. 2.5.3), формализуется понятие статистической независимо-
сти условием представления двумерного закона распределения векторной
случайной величины X = (z^\x^2^)T в виде произведения частных зако-
нов распределения компонент этого вектора, т.е.
P{xW = х™ = ?2>°} = Р{«<” =	(11.59)
(1)°	(2)° к
где zj ' и х -' — обозначения принятых в данном исследовании меток
соответственно для i-й градации признака z^ и у-й градации признака
,(2)
Выборочный (эмпирический) эквивалент этого условия предусматри-
вает замену участвующих в нем вероятностей соответствующими отно-
сительными частотами (с заменой, конечно, точного знака равенства на
приближенный^, т.е.
п п п
или
(11.59')
Поэтому чем больше от нуля будет отличаться просуммированная по
i и j левая часть соотношения (11.59я), вычисленная по данным таблицы
сопряженности 11.2, тем более высокую с.т.с.с. между анализируемыми
переменными должны обозначать используемые измерители.
Характеристика X2 квадратичной сопряженности признаков
(О (2)
ж' ' и z ' определяется соотношением
mi mg
= П
(11.60)
11.4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТЕГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 445
Его значение может меняться от нуля (при строгой статистической неза-
висимости переменных я/1) и я^) до 4-оо. Являясь, как и всякая функция
от выборочных данных, величиной случайной, X2 ведет себя (в предпо-
ложении статистической независимости х^ и х^) приблизительно, —
2
асимптотически по п —* оо — как у -распределенная случайная величина
с числом степеней свободы, равным (mj — 1)(тп2 — 1). Это дает нам право
в случае
X2 > xl ((mi - 1)(™2 - 1))	(11.61)
заявить о том, что связь между анализируемыми переменными я^ и х '
является статистически значимой и она тем теснее, чем больше значение
X . Неудобство использования характеристики X связано с тем, что
ее верхняя граница стремится к бесконечности при возрастании объема
выборки п. Поэтому вместо X2 часто используют характеристику
nmm(m1 — 1, т2 — 1)
(11.62)
которая называется коэффициентом Крамера и которая обладает бо-
лее привычным для измерителей с.т.с.с. диапазоном изменения, а именно
) < С 1. При этом нулевое значение С свидетельствует о строгой стати-
стической независимости анализируемых признаков, а значение С, равное
единице, — о возможности однозначного восстановления значения одной
переменной по известному значению другой.
Информационная характеристика с.т.с.с. У2 признаков я^ и
(з)
I также основана на мере отклонения от выполнения соотношения неза-
висимости (11.59#), только вместо разности левых и правых частей этого
соотношения в ней используется их отношение. А именно измеритель У2
определяется соотношением
mi mj	z	\
°1-63’
Правую часть (11.63) можно преобразовать к виду, более удобному для
вычислений
(mj т?	mi	тд	\
52 УЗ “ УЗ П»-П«- “ УЗ п-3 In П.у + n In П 1 . (11.63')
1=1 j=l	1=1	/=1	/
Эта характеристика обладает теми же свойствами, что и X2'. ее зна-
чения варьируют от 0 (в случае статистической независимости я<^ и я^)
446
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
до 4-оо, и в условиях справедливости гипотезы о статистической независи-
мости анализируемых признаков она приблизительно (асимптотически по
п —> оо) подчиняется з.р.в. у3 с (mi — l)(m2 — 1) степенями свободы (дл!
достижения удовлетворительной точности последнего утверждения требу-
ется заполненность всех клеток таблицы сопряженности 11.2 ненулевым!
элементами, удовлетворяющими условию min,j ntJ- > 3).
Таким образом, если мы хотим проверить гипотезу о статистическк
значимом отличии от нуля характеристики с.т.с.с. Y2 (т. е. гипотезу о
(1)	(2)\	*	-
наличии связи между г и z' ), то необходимо убедиться в выполнении
неравенства
У2 > х’((п»1 - 1)("»2 - 1))>	(11-64)
где Ха(т)> как всегда, — 100а%-ная точка % -распределения с т степе-
нями свободы (см. соответствующую таблицу в Приложении 1), а а —
заданный уровень значимости критерия, т.е. вероятность принять ре-
шение о наличии статистической связи между анализируемыми перемен-
ными в то время, как в действительности они являются статистически
независимыми.
Если с помощью той или иной характеристики (X3 или У3) мы убе-
дились в том, что статистически значимая связь между и х дей-
ствительно существует, то возникает вопрос интервальной оценки харак-
теристики этой связи. Для приближенного построения такой оценки мы
должны уметь вычислить дисперсию соответствующей точечной оцем-
ки (см. п. 7.5.4), т. е. в нашем случае — дисперсии статистик X3 и У2
в условиях, когда оцениваемый с их помощью теоретический показатель
связи отличен от нуля.
Для характеристики X3 и основанном на ней коэффициенте Крамера
С существуют приближенные формулы1:
(11.65)
ст’ = DC rs
О
(11.66)
Заметим, что в формуле (11.65) первое слагаемое в квадратных скоб-
ках (т. е. X3) является главным членом, так что два других слагаемых
1 Точные формулы (они получены Холдуйном в 1939 г.) очень сложны, поэтому здесь
приводится только приближенный вариант, полученный К. Пирсоном в 1915 г.
J1.4. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ КАТЕГОРИЗОВАННЫХ ПЕРЕМЕННЫХ 447
I
играют роль остаточного члена. Поэтому другой, более грубый (менее
точный) вариант этой формулы имеет вид
= DX3 а 4Ха.	(11.65')
Соответственно в качестве приближенных доверительных интерва-
лов для истинных значений коэффициента квадратичной сопряженности
и коэффициента Крамера используются (при доверительной вероятности
Р=1-2а):
[-АГ — t£]_	Af3 + Н1_в(7^а]	(11.67)
Я
[С* —	С 4-	(11.68)
где как обычно, g-квантиль стандартного нормального распределения
(см. соответствующую таблицу в приложении 1), а вместо охг и ас под-
ставляются их приближенные значения, вычисленные соответственно по
формулам (11.65) (или (11.65*)) и (1.66).
Пример 11.9. В табл. 11.3 (из [Gilby W.Н., Biometrika, 8, 94])
дано распределение 1725 школьников (т.е. п = 1725) по значениям двух
анализируемых категоризованных признаков: по качеству одежды
я по их умственным способностям (z<3>). Были определены 4 градаций
(т.е. mt == 4) по первому признаку (1: «очень хорошо»; 2: «хорошо»;
3: «удовлетворительно»; 4: «плохо») и 6 градаций (т.е. т2 = 6) по вто-
рому признаку (1: «плохие»; 2: «ниже средних»; 3: «средние»; 4: «выше
средних»; 5: «высокие»; 6: «превосходные»).
Таблица 11.3
Градации признака J1) Л	Градации признака х^						Е
	1	2	3	4	5	6	
1	33	48	113	209	194	39	636
2	41	100	202	255	138	15	751
3	39	58	70	61	33	4	265
4	17	13	22	10	10	1	73
Е	130	219	407	535	375	59	1725
Нас интересует, существует ли связь между манерой одеваться и спо-
собностями, и если «да», то какова степень тесноты этой связи.
448
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Вычисление величины X2 по формуле (11.60) дает X2 = 174,92 и
соответственно значение коэффициента Крамера (см. формулу (11.62))
С = 0,184.
Поскольку даже при уровне значимости а = 0,001 соответствующее
пороговое значение Xo,ooi(15) = 37,697 оказывается намного меныпим ста-
тистики X2, то связь есть и, по-видимому, характеризуется достаточно
высокой степенью тесноты. Если сопоставить этот вывод с выборочным
значением коэффициента Крамера (С = 0,184), то мы получаем основание
относиться к этой шкале иначе, чем, например, к шкале абсолютных зна-
чений парного коэффициента корреляции |г|: если для |г| величина 0,184
означает отсутствие или крайне слабую связь между а/1) и z^2\ то для
С это значение, как мы видим, свидетельствует о наличии достаточно
тесной связи.
Величина <тс, вычисленная по приближенной формуле (11.66), ока-
зывается равной у/1/Зп = 0,014, так что в соответствии с (11.68) мо-
жем сделать вывод, что истинное (теоретическое) значение коэффици-
ента Крамера заключено в пределах от 0,184 — 1,96 • 0,014 = 0,157 до
0,184 + 1,96-0,014 = 0,211.
ВЫВОДЫ
1.	Трудности, стоящие на пути практического использования в стати-
стическом исследовании моделей многомерных з.р.в., обусловили тот факт,
что в подавляющем большинстве случаев все выводы многомерного ста-
тистического анализа строятся лишь на базе оценок вектора средних зна-
чений и ковариационной матрицы исследуемого векторного признака.
2.	Корреляционный анализ составляет содержание начальных этапов
исследования всех трех центральных проблем многомерного статистиче-
ского анализа. В проблеме статистического исследования зависимостей
корреляционный анализ позволяет выявлять сам факт существования ста-
тистических связей между компонентами анализируемого векторного при-
знака и оценивать степень тесноты этих связей. Для проблем классифи-
кации объектов и признаков и снижения размерности анализируемого
признакового пространства он предлагает и оценивает подходящие ха-
рактеристики парных отношений (ковариации, корреляции, разные виды
парных сравнений), которые используются в дальнейшем в качестве ба-
зовой исходной информации.
3.	Универсальной характеристикой степени тесноты статистической
связи (с.т.с.с.) между результирующим количественным показателем у я
выводы
449
объясняющими количественными переменными X = (г^\а:^2\. ..,г^)Т
является коэффициент детерминации у по X — К^у/Х). Другие распро-
страненные характеристики с.т.с.с. (парные, частные и множественные
коэффициенты корреляции, корреляционное отношение) представляют со-
бой те или иные частные версии коэффициента детерминации, реализо-
ванные в рамках различных конкретных схем зависимостей.
4.	Парные корреляционные характеристики позволяют измерять сте-
пень тесноты статистической связи между парой переменных без учета
опосредованного или совместного влияния других показателей, вычисля-
ются (оцениваются) они по результатам наблюдений только анализируе-
мой пары показателей.
5.	Факт установления тесной статистической связи между перемен-
ными не является, вообще говоря, достаточным основанием для доказа-
тельства существования причинно-следственной связи между этими пе-
ременными.
6.	Парные и частные коэффициенты корреляции являются измерите-
лями степени тесноты линейной связи между переменными. В этом слу-
чае корреляционные характеристики могут оказаться как положительны-
ми, так и отрицательными в зависимости от одинаковой или противопо-
ложной тенденции взаимосвязанного изменения анализируемых перемен-
ных. При положительных значениях коэффициента корреляции говорят о
наличии положительной линейной статистической связи, при отрица-
тельных — об отрицательной.
7.	При наложении случайных ошибок на значения исследуемой пары
переменных (например, ошибок измерения) оценка статистической связи
между исходными переменными, построенная по наблюдениям, оказыва-
ется искаженной. В частности, получаемые при этом оценки коэффициен-
тов корреляции будут заниженными. Существуют методы, позволяющие
учесть это искажение.
8.	Измерителем степени тесноты связи любой формы является кор-
реляционное отношение, для вычисления которого необходимо разбить
область значений предсказывающей переменной X на интервалы (гипер-
параллелепипеды) группирования. Возможна параметрическая модифи-
кация корреляционного отношения, при которой вычисление соответству-
ющих выборочных значений не требует предварительного разбиения на
интервалы группирования.
9.	Частный коэффициент корреляции позволяет оценить степень тес-
ноты линейной связи между двумя переменными, очищенной от опосредо-
ванного влияния других факторов. Для его расчета необходима исходная
информация как по анализируемой паре переменных, так и по всем тем
450
ГЛ. 11. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
переменным, опосредованное («мешающее») влияние которых мы хотим
элиминировать.
10.	Анализ статистических связей между порядковыми переменными
сводится к статистическому анализу различных упорядочений (ранжиро-
вок) одного и того же конечного множества объектов и осуществляется с
помощью методов ранговой корреляции. В зависимости от типа изучаемой
ситуации (шкала измерения анализируемого свойства не известна иссле-
дователю или отсутствует вовсе; существуют косвенные или частные ко-
личественные показатели, в соответствии со значениями которых можно
определить место каждого объекта в общем ряду всех объектов, упоря-
доченных по анализируемому основному свойству) процесс упорядочения
объектов производится либо с привлечением экспертов, либо формализо-
ванно — с помощью перехода от исходного ряда наблюдений косвенного
количественного признака к соответствующему вариационному ряду.
11.	Исходные статистические данные для проведения рангового кор-
реляционного анализа представлены таблицей (матрицей) рангов стати-
стически обследованных объектов размера п X (р + 1) (число объектов на
число анализируемых переменных). При формировании матрицы рангов
допускаются случаи неразличимости двух или нескольких объектов по
изучаемому свойству («объединенные» ранги).
12.	К основным задачам теории и практики ранговой корреляции от-
носятся: анализ структуры исследуемой совокупности упорядочений (за-
дача А); анализ интегральной (совокупной) согласованности рассматрива-
емых переменных и их условная ранжировка по критерию степени тесноты
связи каждой из них со всеми остальными переменными (задача В); по-
строение единого группового упорядочения объектов на основе имеющейся
совокупности согласованных упорядочений (задача С).
13.	В качестве основных характеристик парной статистической связи
между упорядочениями используются ранговые коэффициенты корреля-
ции Спирмэна и Кендалла Значения этих коэффициентов ме-
няются в диапазоне от —1 до +1, причем экстремальные значения ха-
рактеризуют связь соответственно пары прямо противоположных и пары
совпадающих упорядочений, а нулевое значение рангового коэффициен-
та корреляции получается при полном отсутствии статистической связи
между анализируемыми порядковыми переменными.
14.	В качестве основной характеристики статистической связи меж-
ду несколькими (т) порядковыми переменными используется так назы-
ваемый коэффициент конкордации (согласованности) Кендалла W(rn).
Между значением этого коэффициента и значениями парных ранговых
коэффициентов Спирмэна, построенных для каждой пары анализируемых
выводы
451
переменных, существуют простые соотношения.
15.	Если представить себе, что каждому объекту некоторой достаточ-
но большой гипотетической совокупности (будем называть ее генеральной
совокупностью) приписан какой-то ранг по каждой из рассматриваемых
переменных и что статистическому обследованию подлежит лишь часть
этих объектов (выборка объема п), то достоверность и практическая пер-
вость выводов, основанных на анализе ранговой корреляции, существенно
зависят от ответа на вопрос: как ведут себя выборочные значения инте-
ресующих нас ранговых корреляционных характеристик при повторениях
выборок заданного объема, извлеченных из этой генеральной совокупно-
сти. Это и составляет предмет исследования статистических свойств
выборочных ранговых характеристик связи. Результаты этого исследо-
вания относятся прежде всего к построению правил проверки статисти-
ческой значимости анализируемой связи и к построению доверительных
интервалов для неизвестных значений коэффициентов связи, характери-
зующих всю генеральную совокупность.
16.	Основными измерителями степени тесноты парной статистиче-
ской связи между категоризованными переменными являются коэффи-
циент квадратичной сопряженности X2 и информационная характери-
стика связи У2. Эти характеристики используют в ситуациях, когда
анализируемыми переменными являются ординальные или номинальные
признаки, шкала возможных «значений» которых определена заданным
набором их состояний (градаций).
ГЛАВА 12. РАСПОЗНАВАНИЕ ОБРАЗОВ
И ТИПОЛОГИЯ ОБЪЕКТОВ
В СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ИССЛЕДОВАНИЯХ
(МЕТОДЫ КЛАССИФИКАЦИИ)
12.1. Сущность, типологизация и
прикладная направленность задач
классификации объектов
Необходимость анализа и формализации задач, связанных со сравне-
нием и классификацией объектов, сознавали ученые далекого прошлого.
«Его (Аристотеля) величайшим и в то же время чреватым наиболее опас-
ными последствиями вкладом в науку была идея классификации, которая
проходит через все его работы ... Аристотель ввел или, по крайней мере,
кодифицировал способ классификации предметов, основанный па сходстве
и различии ...», — писал Дж. Берналл в «Науке истории общества» (М.:
Изд-во иностр, лит., 1956, с. 117). После Аристотеля с его «деревом вещей
жизни» имеется еще в докомпьютерной эре ряд интереснейших примеров
прекрасно построенных классификаций как в естественных, так и в об-
щественных науках. Упомянем здесь (в хронологическом порядке) две из
них: а) иерархическая классификация (основанная на понятии сходства)
растений и видов М. Адансона (1757 г.); б) знаменитая периодическая си-
стема элементов Д. И. Менделеева (1869 г.), представляющая собой по су-
ществу классификацию многомерных наблюдений (каждый химический
элемент может быть представлен в виде вектора характеризующих его
разнотипных признаков, включая характеристики конфигурации внешних
электронных оболочек атомов) с выявленным единым классифицирующим
фактором (зарядом атомного ядра) и с упорядочением элементов внутри
каждого класса.
Однако до разработки аппарата многомерного статистического ана-
лиза и, главное, до появления и развития достаточно мощной электронно-
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
453
вычислительной базы проблемы теории и практики классификации отно-
сились пе к разработке методов и алгоритмов, а к полноте и тщательности
отбора и теоретического анализа изучаемых объектов, характеризующих
их признаков, смысла и числа градаций по каждому из этих признаков.
Все методы классификации сводились по существу к методу так назы-
ваемой комбинационной группировки, когда все характеризующие объект
признаки носят дискретный характер или сводятся к таковым (пол или
мотив миграции индивидуума, уровень жилищных условий или число де-
тей в семье и т.п.), а два объекта относятся к одной группе только
при точном совпадении зарегистрированных на них градаций одновре-
менно по всем характеризующим их признакам (одинаковый пол, мотив
миграции и т. д.).
Однако по мере роста объемов перерабатываемой информации и, в
частности, числа классифицируемых объектов и характеризующих их
признаков возможность эффективной реализации подобной логики иссле-
дования становилась все менее реальной (так, например, число к групп
или классов, подсчитываемое при комбинационной группировке по фор-
муле к =	• m2 ... тпр, где т± — число градаций по признаку х^, а р —
общее число анализируемых признаков, уже при mj = 3 и р = 5 оказы-
вается равным 243). Именно электронно-вычислительная техника стала
тем главным инструментом, который позволил по-новому подойти к ре-
шению этой важной проблемы и, в частности, конструктивно воспользо-
ваться разработанным к этому времени мощным аппаратом многомерного
статистического анализа: методами распознавания образов «с учителем»
(дискриминантный анализ) и «без учителя» (автоматическая классифи-
кация, или кластер-анализ).
Развитие электронно-вычислительной техники как средства обработ-
ки больших массивов данных стимулировало проведение в последние годы
широких комплексных исследований сложных социально-экономических,
технических, медицинских и других процессов и систем, таких, как образ
и уровень жизни населения, совершенствование организационных систем,
региональная дифференциация социально-экономического развития, пла-
нирование и прогнозирование отраслевых систем, закономерности возник-
новения сбоев (в технике) или заболеваний (в медицине) и т. п. В связи
с многоплановостью и сложностью этих объектов и процессов данные о
них по необходимости носят многомерный и разнотипный характер, так
как до их анализа обычно бывает неясно, насколько существенно то или
иное свойство для конкретной цели. В этих условиях выходят на первый
план проблемы построения группировок и классификаций по многомер-
ным данным (т.е. проблемы классификации многомерных наблюдений),
454
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
причем появляется возможность оптимизации этого построения с точки
зрения наибольшего соответствия получаемого результата поставленной
конечной цели классификации.
Цели классификации существенно расширяются, и одновременно со-
держание самого процесса классификации становится неизмеримо богаче
и сложнее. Оно, в частности, дополняется проблемой построения самой
процедуры классификации, ранее носившей чисто технический характер.
Прежде чем переходить к примерам и типологизации (в прикладном
и математическом аспектах) задач классификации, определим сам термин
классификация.
В самой общей формулировке под классификацией жы будем пони-
мать разделение рассматриваемой совокупности объектов или явлений
на однородные, в определенном смысле, группы либо отнесение каждого
из заданного множества объектов к одному из заранее известных клас-
сов (при этом классифицируемое «заданное множество» может состоять
из единственного объекта). Заметим, что термин «классификация» ис-
пользуется, в зависимости от контекста, для обозначения как самого про-
цесса «разделения-отнесения», так и его результата.
Сделаем шаг в сторону формализации общей задачи классификации
и сформулируем ее теперь в терминах статичного варианта раз-
личных форм задания исходных статистических данных (см. (9.1) и (9.2)
при N = 1) по схеме «на входе-на выходе задачи».
На «входе» задачи исследователь имеет:
(а)	п классифицируемых объектов, представленных данными вида
(9.1) (тогда каждая t-я строка матрицы (9.1) отражает значения р харак-
теризующих t-й объект признаков	или данными вида
(9.2)	(тогда каждая t-я строка матрицы (9.2) задает попарные отноше-
ния , 7,2, • • • > 7»п 1-го объекта со всеми остальными классифицируемыми
объектами);
(б)	обучающие выборки
Xj2» • • • >	♦
j — 1,2,..., k,
(121)
каждая (j-я) из которых определяет значения анализируемых признаков
Xji = (^^),...,х^)Г на nj объектах (т.е. i = 1,2,...,п), о кото-
рых априори известно, что все они принадлежат j-му классу, причем
число к различных выборок (12.1) равно общему числу всех возможных
классов (так что каждый класс представлен своей порцией выборочных
данных); если классифицируемые данные представлены в форме (9.2), то
каждая (J-я) из обучающих выборок также представляется матрицей вида
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
455
(9.2) размерности пд* X nj, однако этот вариант задачи «классификации с
обучением» в книге не рассматривается не будет.
На «выходе» задачи мы должны иметь результат в одной из двух
форм:
(«) если число классов к и их смысл известны заранее, то каждое
из п классифицируемых многомерных наблюдений должно быть снабжено
«адресом» (номером) класса, к которому оно принадлежит;
(i>) если число классов и (или) их смысл выявляются в процессе клас-
сификации, то результатом классификации является разделение множе-
ства классифицируемых объектов на определенное число однородных (в
определенном смысле) групп, каждая из которых объявляется «классом».
Бели исследователь располагает на «входе» задачи не только класси-
фицируемыми данными (а), но и обучающими выборками (б) (см. (12.1)),
то говорят, что решается задача классификации при наличии обучающих
выборок («классификация с обучением*); в противном случае речь идет
о задаче «классификации без обучения*.
Для пояснения сущности основных прикладных типов задач класси-
фикации и конечных прикладных целей, которые ставит при этом перед
собой исследователь, рассмотрим примеры.
Пример 12.1. Выявление типологии потребительского по-
ведения населения, анализ сущности дифференциации этого по-
ведения, прогноз структуры потребления.
В качестве исходной информационной базы используются данные
бюджетных обследований семей. Поясним логическую схему исследова-
ния. Многомерная статистика рассматривает совокупность изучаемых
многомерных объектов как совокупность точек или векторов в простран-
стве описывающих их признаков. Применительно к схеме потребления
совокупностью объектов, подлежащих изучению, является множество эле-
ментарных потребительских ячеек — семей. Каждая семья характеризу-
ется, с одной стороны, некоторым набором X факторов-детерминантов
(социально-демографические и другие признаки, описывающие условия
жизнедеятельности семьи), а с другой — набором Y параметров поведе-
ния («переменных поведения»), в которых отражаются ее фактические
потребности.
В качестве социально-демографических факторов, имеющих суще-
ственное значение для изучения потребительских аспектов социальной
жизни, целесообразно использовать, например, общественную и нацио-
нальную принадлежность, уровень образования и квалификацию, харак-
тер труда, демографический тип и возраст семьи, тип населенного пункта
к характер жилища, размер и структуру имущества, уровень доходов.
456
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Различия в потребностях, складывающиеся под влиянием социально-
демографических и природно-климатических условий, являются объек-
тивно существующими; они формируют весь строй поведения потреби-
теля в конкретно-исторических условиях, а в конечном счете порождают
своеобразные типы потребителей, ориентированные на существенно раз-
ное потребление.
Весь комплекс социально-демографических и других факторов, суще-
ственно воздействующих на структуру потребления, будем называть ти-
пообразующим, Они имеют определяющее значение, в то время как все
другие дают лишь случайную вариацию в пределах одной группы (типа)
потребительского поведения.
В качестве признаков поведения Y можно рассматривать три группы
параметров: а) уровень и структуру потребления; б) характер (объем к
содержание) использования свободного времени; в) интенсивность измене-
ния социального, трудового, демографического статуса.
Итак, рассматриваются числовые характеристики и градации типо-
образующих и одновременно поведенческих признаков каждой семьи из
анализируемой совокупности.
Решение общей проблемы, связанной с выявлением и прогнозом
структуры и дифференциации потребностей населения, распадается на
следующие этапы.
1.	Сбор и первичная статистическая обработка исходных данных.
Исследуемые объекты (семьи) выступают в качестве многомерных наблю-
дений или точек в двух многомерных пространствах признаков. Фиксируя
в качестве координат этих точек значения (или градации) типообразую-
щих переменных X (т. е. факторов-детерминантов), рассматриваем их в
«пространстве состояния» П(Х) — пространстве, координатами кото-
рого служат основные показатели жизнедеятельности семей. Фиксируя
же в качестве координат тех же самых объектов значения показателей У
их потребительского поведения, рассматриваем их в «пространстве по-
ведения» П(У). Очевидно, при надлежащем выборе метрики в про-
странствах П(Х) и П(У) геометрическая близость двух точек в П(Х)
будет означать сходство условий жизнедеятельности соответствую-
щих двух семейъ так же как и геометрическая близость точек в П(У)
будет означать сходство их потребительского поведения. Среди мето-
дов первичной статистической обработки анализируемых данных, обычно
используемых на этой стадии исследования, широко распространенными
и весьма полезными являются методы изучения различных одно-, дву- и
трехмерных эмпирических распределений, которые сводятся к построению
и различным представлениям (графическим, табличным) упомянутых вы-
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
457
ше комбинационных группировок. Пример табличного представления од-
ной из таких двумерных комбинационных группировок приведен в табл.
12.1.
Эта комбинационная группировка построена на основе статистическо-
го обследования 400 семей по двум признакам из пространства П(Х): по
(руб.) — величине среднедушевого семейного дохода (с тремя града-
циями: «низкий», «средний» и «высокий»), и по — качеству жилищ-
ных условий (с четырьмя градациями: «низкое», «удовлетворительное»,
♦хорошее» и «очень хорошее»). Каждая клетка таблицы соответствует
классу, полученному в результате проведенной комбинационной группи-
ровки; внутри клетки обозначено число семей, имеющих данное сочетание
градаций анализируемых признаков (подобные таблицы называют также
«таблицами сопряженности», см. п. 11.4).
Таблица 12.1
Градация (1) признака х' ’ (доход)	Градация признака		(жилищных условий)		Сумма
	«Низкое»	«Удовлетвори- тельное»	«Хорошее»	«Очень хорошее»	
«Низкий»	24	12	4	0	40
«Средний»	20	100	140	20	280
«Высокий»	4	8	28	40	80
Сумма	48	120	172	60	400
Для более полного представления результатов подобной классификаг
ции можно было бы ввести в программу компьютера требование выпеча-
тывать номера семей, попавших в каждую из двадцати клеточек таблицы.
Заметим, что непрерывным аналогом комбинационной группировки
является обычный переход от исходных наблюдений непрерывной случай-
ной величины к «группированным» выборочным (см. п. 6.1). Результат
такого перехода представляется либо в виде таблицы, подобной табл. 12.1,
либо в виде графика (гистограммы).
2.	Выявление основных типов потребления с помощью разбиения ис-
следуемого множества точек-семей на классы в «пространстве поведе-
ния* П(У). Гипотеза существования «естественных», объективно обу-
словленных типов поведения, т. е. какого-то небольшого количества клас-
сов семей, таких, что семьи одного класса характеризуются сравнительно
сходным, однотипным потребительским поведением, геометрически озна-
чает распадение исследуемой в «пространстве поведения» совокупности
гочек-семей на соответствующее число «сгустков» или «скоплений» то-
458
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
чек. Выявив с помощью подходящих методов многомерного статистиче-
ского анализа (кластер-анализа, таксономии) эти классы-сгустки, тем са-
мым определим основные типы потребительского поведения.
3.	Отбор наиболее информативных типообразующих признаков
(факторов-детерминантов) и выбор метрики в пространстве типо-
образующих признаков. Очевидно, неправомерно рассчитывать на то, что
диапазоны возможных значений каждого из кандидатов в типообразую-
щие признаки окажутся непересекающимися для семей с разным типом
потребительского поведения. Другими словами, значения каждого из при-
знаков х^ в отдельности и их набора в совокупности подвержены неко-
торому неконтролируемому разбросу при анализе семей внутри каждого
из типов потребления. Естественно считать наиболее информативными
те факторы-детерминанты или те их наборы, разница в законах распре-
деления которых оказывается наибольшей при переходе от одного класса
потребительского поведения к другому. Эта идея и положена в основу
метода отбора наиболее информативных (типообразующих) признаков-
детерминантов.
4.	Анализ динамики структуры исследуемой совокупности семей
в пространстве наиболее информативных типообразующих признаков.
Конечной целью этого этапа является прогноз тех постепенных преобразо-
ваний классификационной структуры совокупности потребителей (семей,
рассматриваемых в пространстве типообразующих признаков), которые
должны произойти с течением времени.
5.	Прогноз структуры потребления. На этом этапе исследования
опираемся на результаты, полученные в итоге проведения предыдущего
этапа, т. е. исходим иэ заданной классификационной структуры потреби-
телей в интересующий нас период времени в будущем. Восстанавливая
классификационную структуру потребления (классификационную струк-
туру совокупности семей в пространстве признаков П(У), характеризу-
ющих потребительское поведение семьи) по классификационной структу-
ре потребителей (по классификационной структуре той же совокупности,
но в пространстве типообразующих признаков), будем относить каждую
конкретную семью к тому типу потребления, для которого значения ха-
рактеризующих ее типообразующих признаков являются, грубо говоря,
наиболее типичными.
Пример 12.2. Классификация как необходимый предва-
рительный этап статистической обработки многомерных дан-
ных. Пусть исследуется зависимость интенсивности миграции населе-
ния з р (профессиональной или территориальной) от ряда социально-
экономических и географических факторов х^2\..., таких, как
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
459
средний заработок, обеспеченность жилой площадью, детскими учрежде-
ниями, уровень образования, возможности профессионального роста, кли-
матические условия и т.п. Естественно предположить (и результаты ис-
следования это подтверждают), что для различных однородных групп ин-
дивидуумов одни и те же факторы влияют на х^ в разной степени, а ино-
гда и в противоположных направлениях. Поэтому до применения аппара-
та регрессионно-корреляционного анализа следует разбить все имеющиеся
в нашем распоряжении данные Xi =	, я^)Т (t = 1,2,..., п)
на однородные классы и решать далее поставленную задачу отдельно
для каждого такого класса. Только в этом случае можно ожидать, что
полученные коэффициенты регрессии х^ по з/ ,з/2\..., будут до-
пускать содержательную интерпретацию, а мера тесноты связи между
Р) (1)	(2)	(р-1)	ч.
х ’ иг зг ..,®	' окажется достаточно высокой.
Другой вариант такого рода примера получим, если в качестве объек-
тов исследования рассмотрим предприятия определенной отрасли, а в ка-
честве вектора наблюдений Xi — совокупность объективных (нерегулиру-
емых) условий работы t-ro обследованного предприятия (сырье, энергия,
оснащенность техникой и рабочей силой и т.п.). Классификация предпри-
ятий по X производится как необходимый предварительный этап для воз-
можности последующей объективной оценки работы коллективов и разра-
ботки обоснованных дифференцированных нормативов: очевидно, лишь к
предприятиям, попавшим в один класс по X, может быть применена оди-
наковая система нормативов и стимулирующих показателей. Далее можно
рассматривать задачу, аналогичную сформулированной выше, а именно:
У = (у >  • •,	— вектор показателей качества работы предприятия
(объем и качество выпускаемой продукции, ее себестоимость, рентабель-
ность и т.п.), a U = (t/1)
от которых зависят условия производства (число основных подразделе-
ний, уровень автоматизации и т.д.), то задачу описания интересующей
нас зависимости вида Y = f(U) естественно решать отдельно для каждо-
го однородного по X класса.
Пример 12.3. Классификация в задачах планирования вы-
борочных обследований. Здесь речь пойдет о планировании выбороч-
ных экономико-социологических обследований городов. Предположим, что
необходимо достаточно детально проанализировать подробные статисти-
ческие данные о городах с целью выявления наиболее характерных черт
в экономико-социологическом облике типичного среднерусского города.
Производить подробный, кропотливый анализ по каждому из городов Рос-
сийской Федерации, очевидно, слишком трудоемко, да и нецелесообразно.
По-видимому, разумнее попытаться предварительно выявить число и со-
1	А.
w ') — вектор регулируемых факторов,
460 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
став различных типов в совокупности обследованных городов по набору
достаточно агрегированных признаков	...,	характеризу-
ющих каждый город (например, понимать под число жителей горо-
да, приходящееся на каждую тысячу жителей, обладающих заданным j-u
признаком, скажем, высшим образованием, специальностью металлурга
и т.п.). А затем, отметив наиболее типичные города в каждом классе
(наблюдения-точки Х^ наиболее блйзко располагающиеся к «центрам тя-
жести» своих классов), отобрать их для дальнейшего (более детализи-
рованного) социально-экономического анализа. При этом, очевидно, мера
представительности отобранных «типичных городов» определится удель-
ным весом количественного состава точек данного класса среди всех рас-
сматриваемых точек (городов).
Анализ рассмотренных примеров с учетом, конечно, и другого на-
копившегося к настоящему времени опыта решения практических за-
дач классификации в экономике, социологии, психологии и других сфе-
рах практической и научной деятельности человека позволяет произвести
определенную систематизацию этих задач в соответствии с конечными
прикладными целями исследования (табл. 12.2).
Таблица 12.2
№ п/п	Тип задачи классификации	Варианты (примеры) конечных прикладных целей исследования для данного типа задачи класси- фикации
1	2	3
1	Комбинационные группиров- ки и их непрерывные обоб- щения	1.1. Составление частотных таблиц и графиков, характеризующих рас- пределение статистически обсле- дованных объектов по градациям или интервалам группирования характеризующих их признаков (см. п. 1 в примере 12.1)
2	Простая типологизация: выявление «стратификаци- онной структуры» множе- ства статистически обсле- дованных объектов, «на- щупывание» и описание четко выраженных скопле- ний («сгустков», «клас-	2.1. Классификация как необхо- димый предварительный этап ис- следования, когда до проведения основной статистической обработ- ки множества анализируемых дан- ных (построения регрессионных моделей, оценки параметров гене- ральной совокупности и т. д.) до-
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
461
Продолжение таблицы 12.2
£	2	3
	теров», «образов», классов) этих объектов в анализи- руемом многомерном про- странстве и построение правила отнесения каждого нового объекта к одному из выявленных классов	биваются расслоения этого мно- жества на однородные (в смысле проводимого затем статистиче- ского анализа) группы данных (см. примеры 12.1 и 12.2). 2.2. Выявление и описание рас- слоенной природы анализируемой совокупности статистически об- следованных объектов с целью формирования плана выборочных (например, экономико-социоло- гических) обследовании этой совокупности (см. пример 12.3). 2.3 Первый шаг в построении связных типологий (см. п. 3 таб- лицы и пример 12.1)
3	Связная неупорядоченная типологизация: исследова- ние зависимостей между не поддающимися упорядоче- нию классификациями од- ного и того же множества объектов в разных призна- ковых пространствах, одно из которых построено на результирующих (поведенческих) признаках (отражающих специфику функционирования объекта, его социально-экономичес- кое поведение, состояние здоровья и т. п.), а другое — на описательных (отражаю- щих условия функциони- рования и другие характе- ристики, от которых могут зависеть значения резуль- тирующих признаков)	3.1.	Прогноз экономико-социоло- гических ситуаций или отдельных социально-экономических показа- телей, включая задачу выявления так называемых типообразующих признаков, в том числе латентных, т. е. непосрественно не наблю- даемых (см. пример 12.1). 3.2.	Диагностика в промышленно- сти, технике, георазведке, меди- цине 3.3.	Кластер-анализ, автоматиче- ское (машинное) распознавание образов — зрительных, слуховых
462
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Продолжение таблицы 12.2
1	2	3
4	Связная упорядоченная ти- пологизация: модицикация связной неупорядоченной типологизации (см. п. 3 таблицы), обусловленная дополнительным допуще- нием, что классы, получае- мые в пространстве резуль- тирующих (поведенческих) признаков, поддаются экс- пертному упорядочению по некоторому сводному (как правило, латентному, не- посредственно не наблю- даемому) свойству: эффек- тивности функционирова- ния, качеству, степени прогрессивности (опти- мальности) поведения и т. п.	4.1. Построение и интерпретация единого (свободного) латентного признака-классификатора в виде функции от исходных описатель- ных признаков: классификация химических элементов по заряду их атомного ядра (периодическая система Д. И. Менделеева); по- строение фактора общей одарен- ности в педагогике и психологии; построение сводного показателя эффективности функционирова- ния предприятия (см. п. 13.5); по- строение интегральной характери- стики уровня мастерства спорт- сменов в игровых видах спорта (см. п. 13.5)
5	Структурная типологиза- ция: дополнение и развитие простой типологизация (см. п. 2 таблицы) в на- правлении изучения и опи- сания структуры взаимо- связей полученных клас- сов, включая построение соответствующих иерархи- ческих систем (на класси- фицируемых элементах и на классах элементов), анализ роли и места каж- дого элемента и класса в общей структурной клас- сификационной схеме. При этом структурная класси- фикационная схема опре- деляется составляющими ее	5.1.	Классификация задач много- целевого комплекса (крупной программы, научного направления производственного комплекса и т. п.) 5.2.	Классификация элементов и подсистем по их функционально- му назначению (производств — в территориально-производственном комплексе, территориальных еди- ниц — в народнохозяйственном разделении труда и потребления, элементов организационных структур и-т.п.). 5.3.	Классификация лиц, прини- мающих решение, по их роли и близости позиций в понимании ситуации и способе решения зада- чи.
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ 463
Продолжение таблицы 12.2
£	2	3
	классами (подсистемами) и характеристиками (правилами) их кзаимодей- ствия	5.4. Классификация исследуемых признаков и анализ структуры связей между ними
6	Классификация динамичес- ских траекторий развития систем: типологизация тра- екторий многомерных вре- менных рядов среди компонент которых могут быть как количественные, так и ка- чественные переменные	6.1. Задачи анализа типов динами- ки семейной структуры, потреби- тельского поведения семей и др.
В качестве комментария к табл. 12.2 поясним методологическую общ-
ность задач 3.1-3.3: прогноза экономико-социологических ситуаций, диа-
гностики и автоматического распознавания зрительных и слуховых обра-
зов. Для этого лежащую в основе их решения методологическую схему
связной неупорядоченной типологизации представим следующим образом.
Пусть в качестве исходных данных об объекте ОД» = 1,2, ...,п) име-
ем вектор описательных (объясняющих) признаков X, =	.. ,г^)Т
(это, в частности, характеристики условий жизнедеятельности i-й обсле-
дованной семьи в примере 12.1, значения параметров исследуемого тех-
нологического процесса или результаты обследований t-го пациента в за-
дачах диагностики, геометрические или частотные характеристики рас-
познаваемого образа в п. 3.3) и некоторую информацию У, о том резуль-
тирующем свойстве, по которому производится классификация объектов
(специфика социально-экономического поведения я-й семьи в примере 12.1).
Разница между задачами типа 3.1 и задачами 3.2 и 3.3 заключается
в том, что в задачах прогноза экономико-социологических ситуаций ин-
формация У, об исследуемом результирующем свойстве объекта не явля-
ется окончательной, т.е. не задает однозначно, как это делается в за-
дачах 3.2 и 3.3, образа (класса, типа), к которому относится этот объ-
ект. Эта информация в задачах типа 3.1 носит лишь промежуточный
характер и представляется, как правило, в виде вектора результирую-
щих показателей Y, = (ур\ • • •»У^)Т. Поэтому в отличие от задач 3.2 и
3.3 (в которых уже «на входе* задачи имеем распределение анализируе-
464 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
мых объектов-векторов Xi по классам, что и составляет так называемую
«обучающую выборку») в задачах типа 3.1 нужно предварительно осу-
ществить простую типологизацию множества объектов {OJ(i = !,...,»)
в пространстве результирующих показателей и лишь затем использовать
полученные в результате этой типологизация классы в качестве обучаю-
щих выборок для построения классифицирующего правила в пространстве
описательных признаков П(Х).
«На выходе» же всех задач типа 3.1-3.3 должны быть 1) на-
бор наиболее информативных объясняющих переменных (так называе-
мых типообразующих признаков) ^1\х),/2\х),...,/₽ \%), которые
либо отбираются по определенному правилу из числа исходных описа-
тельных признаков х , ...,:г либо строятся в качестве неко-
торых их комбинаций; 2) правило отнесения (дискриминантная функция,
классификатор) каждого нового объекта О*, заданного значениями сво-
их описательных признаков X*t к одному из заданных (или выявлен-
ных в процессе предварительной простой типологизации) в простран-
стве П(У) классов или образов. При этом типообразующие признаки
Z = (z^\x),.. .,г(р)(Х))Т и искомое правило классификации должны
быть подобраны таким образом, чтобы обеспечивать наивысшую (в опре-
деленном смысле) точность решения задачи отнесения объекта к одному
из анализируемых классов по заданным значениям его описательных при-
знаков X.
Типологизация математических постановок задач классифи-
кации. Целесообразность и эффективность применения тех или иных
методов классификации так же, как их предметная осмысленность, обу-
словлены конкретизацией базовой математической модели, т. е. математи-
ческой постановкой задачи. Определяющим моментом в выборе математи-
ческой постановки задачи является ответ на вопрос, на какой априорной
информации строится модель. При этом априорная информация склады-
вается из двух частей:
1) из априорных сведений об исследуемых классах; 2) из априорной
статистической (выборочной) информации, т.е. так называемых обуча-
ющих выборок (их определения даны выше).
Априорные сведения об исследуемых генеральных совокупностях от-
носятся обычно к виду или некоторым общим свойствам закона распреде-
ления исследуемого случайного вектора X в соответствующем простран-
стве и получаются либо из теоретических, предметно-профессиональных
соображений о природе исследуемого объекта, либо как результат предва-
рительных исследований. Получение априорной выборочной информация
в Экономике и социологии, как правило, связано с организацией систе-
12.1. СУЩНОСТЬ И ТИПОЛОГИЗАЦИЯ ЗАДАЧ КЛАССИФИКАЦИИ
465
яы экспертных опенок или с проведением специального предварительного
этапа, посвященного решению задачи простой типологизации анализиру-
емых объектов в пространстве результирующих показателей (см. пример
12.1).
Классификация задач разбиения объектов на однородные группы (в
зависимости от наличия априорной и предварительной выборочной ин-
формации) и соответствующее распределение описания аппарата решения
этих задач по пунктам данной главы представлены в табл. 12.3.
Таблица 12.3
Априорные сведения о классах (генераль- ных совокупностях)	Предварительная выборочная информация	
	Нет информации	Есть обучающие выборки
Некоторые самые общие предполо- жения о законе распределения ис- следуемого векто- ра: гладкость, со- средоточен ность внутри ограничен- ной области и т.п.	Классификация без обучения: кла- стер-анализ, так- сономия, распоз- навание образов «без учителя», иерархические классиффикации (см. п. 12.4)	Непараметрические методы дискриминант- ного анализа (см. п. 12.2.3)
Различаемые ге- неральные сово- купности заданы в виде параметри- ческого семейства законов распре- деления вероят- ностей (парамет- ры неизвестны)	Интерпретация ис- следуемой гене- ральной совокуп- ности как смеси нескольких гене- ральных совокуп- ностей .« Расщеп- ление» этой смеси с помощью мето- дов оценивания неизвестных пара- метров (см. п. 12.3)	Параметрические методы дискриминант- ного анализа (см. пп. 12.2.3, 12.2.4)
Различаемые ге- неральные сово- купности заданы однозначным опи- санием соответ- ствующих законов	Классификация при полностью описанных клас- сах: различение статистических ги- потез (см. гл. 8)	Обучающие выборки не нужны
466 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
12.2.	Классификация
при наличии обучающих выборок
(дискриминантный анализ)
12.2.1.	Класс как генеральная совокупность и базовая
идея вероятностно-статистических методов
классификации
Ставя задачу отнесения каждого из классифицируемых наблюдений
Xi = (х^,х^2\	i = 1,2,...,п, к одному из классов, необхо-
димо четко определить понятие класса. Во всех постановках задач это-
го и следующего (п. 12.3) параграфов juw будем понимать под «классов»
генеральную совокупность, описываемую одномодальной функцией плот-
ности f(X) (или одномодальным полигоном вероятностей в случае дис-
кретных признаков X).
Для пояснения общей идеи, заложенной в основу построения всех
вероятностно-статистических методов классификации, вернемся к приме-
ру п. 7.5.1 и рис. 7.2. По существу уже в этом примере мы имеем дело с
задачей отнесения трех наблюдений у\ = 5,16, У2 = 5,25 и у$ = 5,32 к од-
ной из двух гипотетичных нормальных генеральных совокупностей (т.е.
к одному из двух классов), различающихся между собой средними зна-
чениями. И решение мы приняли в пользу класса со средним значением
ai = 5,243 потому, что в рамках этого класса наши наблюдения выглядят
более естественными, более правдоподобными (что определяется произ-
ведением соответствующих им ординат плотности этого закона). Именно
этот принцип и положен в основу вероятностных методов классификации:
наблюдение будет относиться к тому классу (т. е. к той генеральной сово-
купности), в рамках которого (которой) оно выглядит более правдоподоб-
ным. Правда, во-первых, этот принцип может корректироваться с учетом
удельных весов классов и специфики так называемой «функции потерь*
c(j | i), которая определяет стоимость потерь от отнесения объекта i-ro
класса к классу с номером j. И во-вторых, для того чтобы этот принцип
практически реализовать, мы должны располагать полным описанием ги-
потетических классов, т.е. знанием функций fi(X),f2(X),..., Д(Х), за-
дающих з.р.в. соответственно для 1-го, 2-го, ..., Л-го классов. Последнее
затруднение обходят с помощью обучающих выборок в случае классифи-
кации с обучением, — и этому посвящен данный параграф, — и с помощью
модели смеси распределений в случае классификации без обучения (этому
посвящен jl. 12.3).
12.2. КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ
467
12.2.2.	Функции потерь и вероятности неправильной
классификации
Очевидно, желательно строить такие методы классификации, кото-
рые минимизируют потери (или вероятность) неправильной классифика-
ции объектов. Посмотрим, как эти две характеристики качества метода
классификации связаны между собой.
Мы уже ввели величину c(j | i) потерь, которые мы несем при отне-
сении одного объекта «-го класса к классу j (при i = J, очевидно, = 0).
Следовательно, если в процессе классификации мы поступили таким обра-
зом m(j | t) раз, то потери, связанные с отнесением объектов «’-го класса
к классу j составят m(j | *)c(j | «*). Для того чтобы подсчитать общие
потери Сп при такой процедуре классификации, надо просуммировать ве-
личину произведения m(j | i)c(j | «) по всем « = 1,2,..., к и j = 1,2,..., к,
т.е.
с„=Е Е «О’ । •>« I о-	(12.2)
i=l J=1
Для того чтобы потери не зависели от числа п классифицируемых
объектов (а величина Сп, очевидно, будет расти с ростом п), перейдем к
удельной характеристике потерь, разделив обе части (12.2) на п, а затем
перейдем к пределу по п —> оо:
fc к
С = lim
п—»оо
m(j | i) nj(n)
niM n
(12.3)
=EE «о ।	। *)•
<=1 >1
Предел в (12.3) понимается в смысле сходимости по вероятности
частот m(j | «)/п<(п) и пДп)/п соответственно к вероятностям P(j |
i), — отнести объект класса i к классу J, и тг,-, — извлечения объекта
класса t из общей совокупности анализируемых объектов; величину к,
называют также априорной вероятностью (или удельным весом) класса i
(о сходимости по вероятности относительных частот см. п. 6.2).
Величина
С(0 = ЕФ' I i)P(j I 0	(12.4)
определяет, как легко видеть, средние потери от неправильной классифи-
кации объектов «-го класса, так что средние удельные потери от недра*
468 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
вильной классификации всех анализируемых объектов будут:
(12.3*)
»=1
В достаточно широком классе ситуаций полагают, что потери c(j |:)
одинаковы для любой пары t и у, т. е.
c(j | i) = со = const при j / i; t, j = 1,2,..., k.
В этом случае стремление к минимизации средних удельных потерь С
будет эквивалентно стремлению максимизации вероятности правиль-
к
ной классификации объектов, равной $2 *fP(« | *)• Действительно,
»=1
с=। *)^(j I«) = со52^ [ 52 pw I о
t=l j=l	*=1	\ J=I
fc	/	к	\
=«>5X1 - р(» I *))=со 11 -52ж«р(* । *))
t=l	\	1=1	/
(при выводе этого соотношения мы воспользовались тем, что c(t | i) = 0 и
£*=1 ^0 I ») — 1 для любого »).
Поэтому часто при построении процедур классификации говорят не о
к
потерях, а о вероятностях неправильной классификации 1 — £ A\P(i |»).
t=i
12.2.3.	Принципиальное решение общей задачи
построения оптимальных (байесовских) процедур
классификации
Сформулируем постановку задачи построения оптимальной процеду-
ры классификации р-мерных наблюдений

(12.5)
при наличии обучающих выборок (12.1).
Классифицируемые наблюдения (12.5) интерпретируются в данной
задаче как выборка из генеральной совокупности, описываемой так на-
зываемой смесью к классов (одномодалъных генеральных совокупностей)
12.2. КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ
с плотностью вероятности
/(%)=
J=1
469
(12.6)
где — априорная вероятность появления в этой выборке элемента из
класса (генеральной совокупности) j с плотностью J (х) или, другими
словами, ttj — это удельный вес элементов j-ro класса в общей генеральной
совокупности (12.6).
Введем понятие процедуры классификации (решающего правила, дис-
криминантной функции) 6(Х). Функция 6(Х) может принимать только
целые положительные значения 1,2,... ,/с, причем те X, при которых она
принимает значение, равное j, мы будем относить к классу у, т.е.
S,,= {X: 1(Х) = Д У =1,2,...,*.
Очевидно, Sj — это р-мерные области в пространстве П(Х) возмож-
ных значений анализируемого многомерного признака X, причем функция
1(Х) строится таким образом, чтобы их сумма (теоретике - множествен-
ная, см. п. 1.2) S\ + 5*2 + ' •* + Sk заполняла все пространство П(Х) и
чтобы они попарно не пересекались. Таким образом, решающее правило
Я(Х) может быть задано разбиением
S’ = (S1,52,...,S'Jt)
(12.7)
всего пространства П(Х) на к непересекающихся областей.
Процедура классификации (дискриминантная функция) 6(Х) (или S)
называется оптимальной (байесовской), если она сопровождается ми-
нимальными потерями (12.3) среди всех других процедур классификации.
Оказывается (см., например, [Андерсон Т.]), процедура классифика-
ции 5,(опт'1 = (Si°nT'\...,5д°пт*^), при которой потери (12.3) будут опти-
мальными, определяется следующим образом:
5(опт> = |х:£^(Х)с(>|.) =
1=1
k
151/51.52’г*Л(х)с(,1’) '•
1 С л
(12.8)

Другими словами, наблюдение (о = 1,2,...,п) будет отнесено к
классу j тогда, когда средние удельные потери от его отнесения именно в
этот класс окажутся минимальными по сравнению с аналогичными поте-
рями, связанными с отнесением этого наблюдения в любой другой класс.
470
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Относительно простой вид приобретает правило классификации
(12.8) в случае равных потерь c(j | :) (т.е. при выполнении соотноше-
ния c(j | i) = со = const). В этом случае наблюдение^ будет отнесено к
классу j тогда, когда
^Л(^) = max
(12.8')
(т.е. максимизируется «взвешенная правдоподобность* этого наблюде-
ния в рамках класса, где в качестве весов выступают априорные вероят-
ности Kj).
Однако соотношения (12.8) и (12.8') задают нам лишь теоретиче-
ское оптимальное правило классификации: для того чтобы его реально
построить, необходимо знание априорных вероятностей яьтга,...,** и
з.р.в. /1(Х),/а(Х),..., fk(X). В статистическом варианте решения
этой задачи данные величины заменяются соответствующими оценка-
ми , построенными на базе обучающих выборок (12.1).
Априорные вероятности яу- (j = 1,2,..., к) оцениваются просто, если
ряд наблюдений, составленный из всех обучающих выборок (12.1), может
быть классифицирован как случайная выборка объема по<5 = nj +п2 4- • • •+
тц из генеральной совокупности (12.6). Тогда оценки
(12.9)
где nj — объем j-Й обучающей выборки.
Впрочем, величины тгу часто определяются априори самой содержа-
тельной сущностью задачи.
Что касается задачи оценки з.р.в. Л(Х),...»А(Х), то ее удобно раз-
бить на два случая:
i-й случай (параметрический дискриминантный анализ) характери-
зуется известным общим видом функций /у(Х), т.е. все классы описы-
ваются з.р.в. одного и того же параметрического семейства {/(Х;0)};
класс i отличается от класса j только значением параметра 0, т.е.
/у(Х) = /(Х;0у), у = 1,2,
(12.10)
Тогда в качестве опенок fj(X) неизвестных функций fj(X) исполь-
зуются функции fj(Xi; 0у), где 0у — статистическая оценка неизвестно-
го значения параметра 0у, полученная по наблюдениям у-й обучающей
выборки (12.1). Пример реализации этой схемы приведен в следующем
пункте.
13.2. КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ
471
2-й случай (непараметрический дискриминантный анализ) не преду-
сматривает знания общего вида функций fj(X) (j = 1,2,...,А). В этом
случае приходится строить так называемые непараметрические оценки
fj(X) для функции /j(X), например, гистограммного или ядерного типа,
либо пользоваться некоторыми специальными приемами (см., например,
[Айвазян С. А., Бежаева 3. И., Староверов О. В., с. 44-50]).
12.2.4.	Параметрический дискриминантный анализ в
случае нормальных классов
Предположим, что класс j идентифицируется р~мерной нормальной
генеральной совокупностью с вектором средних значений aj и ковариаци-
онной матрицей Б (общей для всех классов), j = 1,2, ...,&. Тогда при
реализации общих оптимальных правил классификации (12.8) и (12.8х) в
качестве функций fj(X) следует использовать р-мерные нормальные плот-
ности ^(A’jajjE) (см. (3.9х)), где оценки для векторов средних значений
ij = (a<l\aJ-2\... ,й^)Т и для ковариационной матрицы Б = (а/?), /,
q = 1,2,... ,р, получены с помощью метода максимального правдоподобия
(см. п. 7.5.1) по обучающим выборкам (12.1); они имеют вид
Z — 1,2,... ,р,
j = 1,2,...,А;
(12.И)
k ni
ъ = -—* i-а)’	<1212)
”««	* 4=1 i=l
— 1> 2,... tpt
Поб = «1 + П2 +  • ’ + пк-
Правило классификации (12.8х) наблюдений (12.5) имеет весьма про-
стой вид в случае к = 2. Действительно, правило (12.8х) эквивалентно
следующему: наблюдение относится к классу с номером jQ тогда и
только тогда, когда
> — для всех j = 1,2,...,А, (12.13)
или, что то же,
In > In — для всех j = 1,2,...,к,	(12.13х)
fi\Xv) 1Tja
472
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
В случае нормальных плотностей fj(X)t т.е. функций /ДХ), опреде-
ляемых по формуле 3.1 с заменой МиГ соответственно векторами а;
и матрицей S, определяемыми по формулам (12.11)-(12-12), соотношение
(12.13 ) эквивалентно соотношению
х,-
2
*jQ
для всех j = 1,2,...,Л.
(12.13")
Соотношение (12.13"), таким образом, задает вид дискриминантной
функции в задаче различения нормальных классов при постоянных значе-
ниях потерь от неправильной классификации. Особенно простым стано-
вится это правило классификации в случае двух классов (к = 2) и одинако-
вых априорных вероятностей (xj = х2 = 0,5). В этом случае наблюдение
Xv следует относить к 1-му классу тогда и только тогда, когда
X./ - -(«1 + «2)
Е 1(ai - а2) > 0,
(12.13"')
и ко 2-му классу во всех остальных случаях. Легко понять, что при клас-
сификации на два класса одномерных (р=1) нормальных наблюдений ре-
шение об отношении наблюдения xv к одному из двух классов будет опре-
деляться знаком произведения [z„ — (ai + a2)/2](dj — d2).
Пример 12.4. Специальное исследование показало, что склон-
ность фирм к утаиванию части своих доходов (и, соответственно, — к
уклонению от уплаты части налогов) в существенной мере определяется
двумя показателями:
а/1) — соотношением «быстрых активов» и текущих пассивов;
а ) — соотношением прибыли и процентных ставок (оба показателя
оцениваются по определенной методике в шкале от 300 до 900 баллов).
В табл. 12.4 представлены значения этих показателей (данные нало-
говой инспекции) по 10 фирмам, уличенным в тех или иных формах укло-
нения от уплаты налогов (ги = 10), и по 13 фирмам, не имеющим заме-
чаний по уплате налогов (п2 = 13). Кроме того, имеющаяся статистика
и специальные обследования свидетельствуют о том, что доля фирм, в
той или иной форме уклоняющихся от уплаты налогов, достигает 50%
(т. е. Xj = тг2 = 0,5). Наконец, статистическая проверка гипотез о нор-
мальном характере распределения двумерного признака X = (а^,®^)7
внутри каждой из анализируемых совокупностей фирм — уклоняющихся
от уплаты налогов (совокупности 1) и платящих налоги (совокупности 2)
12.2. КЛАССИФИКАЦИЯ С ОБУЧЕНИЕМ
473
дала неотрицательный результат, т.е. можно считать, что имеющиеся у
нас обучающие выборки (1) и (2) извлечены из нормальных генеральных
совокупностей.
Таблица 12.4
пп (0	Обучающая выборка (1) (фирмы, уклоняющиеся от налогов)		Обучающая выборка (2) (фирмы, не уклоняю- щиеся от налогов)	
	J1) г1»	хи	Jp x2i	J2) x2i
1	740	680	750	590
2	670	600	360	600
3	560	550	720	750
4	540	520	540	710
5	590	540	570	700
6	590	700	520	670
7	470	600	590	790
8	560	540	670	700
9	540	630	620	730
10	500	600	690	840
И	-	-	610	680
12	-	-	550	730
13	-	-	590	750
среднее	ар1 = 576,0	а,2) = 596,0	4° = 598,46	а’2) = 710,77
На фирме, не прошедшей проверку налоговой инспекции, зарегистри-
рованы значения переменных X = (x^1\x^)T:xq1^ = 740, х = 590.
Определить, к какой совокупности (1 или 2) будет отнесена эта фир-
на (т.е. наблюдение Xq = (:,х)Т), если воспользоваться методом
параметрического дискриминантного анализа (с учетом нормальности
анализируемых наблюдений).
Из условия задачи следует, что мы должны воспользоваться правилом
классификации, представленным соотношением (12.13").
Необходимые вычисления дают:
1)	оценки средних значений по каждой обучающей выборке (12.1),
подсчитанные по формуле (12.11):
ai = (576,0; 596,0)Т; а2 = (598,46; 710.77)Т;
474
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
соответственно:
ах - а2 = (-22,46; -114,77)т; (ах +а3)/2 = (587,23; 653,39)Т;
2)	оценка общей ковариационной матрицы Е производится по формуле
(12.12) или, что то же:
ё=- ЫЪ - «>)т
У=1 »=1
=	1	17 56240 17240\	/121569
10 + 13 - 2 [ V17240 33240) + \ 25615
_ /8467 2041 \
“ \2041 4273/*
25615\
56492/
в результате обращения этой матрицы получаем
Е’1 =
( 0,0001335
\ -0,0000637
—0,0000637 \
0,0002645; J
3) Е"1(а1-а2)
( 0,0043 \
V -0,0289 );
1 г . - ч _ (740 - 587,23 \ _ / 152,77 \
2 \а1 + а2) — 590 _ б53 39 J - —63,39; J
4)	поскольку численное значение выражения, определяемого соотно-
шением (12.13'"), в нашем случае равно
( 152,77 V ( 0,0043 \
V -63,39 )	\ -0,0289 J ~ и’
то наблюдение Xq должно быть отнесено к классу /, а это значит, что
есть основания к тому, чтобы диагностировать анализируемую фирму как
фирму, в той или иной форме уклоняющуюся от уплаты налогов.
12.3. Классификация без обучения
(параметрический случаи):
расщепление смесей вероятностных
распределений
В пп. 12.3 и 12.4 описаны методы классификации объектов (индивиду-
умов, семей, предприятий, городов, стран, технических систем, признаков
12.3. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
475
и т.д.) Oi,O2,...,On в ситуации, когда отсутствуют так называе-
мые обучающие выборки (12.1), а исходная информация о классифицируе-
мых объектах представлена либо в форме матрицы X «объект-свойство»
(см. (9.1)), либо в форме матрицы парных сравнений объектов (см. (9.2),
статический вариант), где величина = p,j характеризует взаимную
отдаленность (или близость) объектов О, и Oj.
Переход от формы исходных данных типа «объект-свойство» к фор-
ме матрицы попарных расстояний осуществляется посредством задания
способа вычисления расстояния (близости) между парой объектов, когда
известны координаты (значения признаков) каждого нз них.
В зависимости от наличия и характера априорных сведений о приро-
де искомых классов и от конечных прикладных целей исследования сле-
дует обратиться либо к данному пункту 12.3, где описаны методы рас-
щепления смесей вероятностных распределений, которые оказываются
полезными в том случае, когда каждый (j-й) класс интерпретируется
как параметрически заданная одномодальная генеральная совокупность
(j = 1,2,...,к) при неизвестном значении определяющего ее
векторного значения параметра и соответственно каждое из классифи-
цируемых наблюдений X, считается извлеченным из одной из этих (но не
известно, из какой именно) генеральных совокупностей; либо п. 12.4, где
описаны методы автоматической классификации (кластер-анализа) мно-
гомерных наблюдений, которыми исследователь вынужден пользоваться,
когда не имеет оснований для интерпретации классифицируемых наблю-
дений в качестве выборки из какой-либо вероятностной генеральной со-
вокупности или не располагает априорными сведениями, достаточными
для параметрического представления искомых классов. В том же пункте
кратко излагаются основные классификационные процедуры иерархиче-
ского типа, используемые в ситуациях, когда «на выходе» исследователь
хочет иметь не столько окончательный вариант разбиения анализируемой
совокупности объектов на классы, сколько общее наглядное представле-
ние о стратификационной структуре этой совокупности (например, в виде
специально устроенного графа — дендрограммы).
12.3.1.	Понятие смеси вероятностных распределений
Начнем пояснение понятия смеси распределений с рассмотрения ряда
конкретных примеров.
Пример 12.5. В отдел технического контроля (ОТК) поступают
партии изделий, составленные с помощью случайного извлечения из объе-
диненной продукции двух станков (станка А и станка В). Изделия кон-
476
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
тролируются по некоторому количественному параметру (линейному раз-
меру) € мм> так что результатом контроля :-го изделия партии является
число х^ мм. Изделия на станках не маркируются, так что в ОТК не
известно, на каком именно станке произведено каждое из них. Произ-
водительность станка Л в 1,5 раза выше производительность станка В.
Задано номинальное значение контролируемого параметра а = 65 мм и из-
вестно, что точность работы станков характеризуется одинаковой величи-
ной среднеквадратических отклонений од = и о*# = yDf#, равной
1,0 мм1. Позже выяснилось, что станок А был настроен правильно (про-
изводил изделие со средним значением Е£л = 65 мм, равным номиналу), в
то время как настройка станка В была сбита в направлении завышение
номинала (а именно Е£в = 67 мм).
Известно также, что распределение размеров изделий, произведенных
на каком-то определенном станке, описывается нормальным законом с па-
раметрами а7 = Е£у и = D£y (7 = А или 7 = В).
Очевидно, анализируемая в ОТК по наблюдениям хь xj,..., хп... ге-
неральная совокупность будет состоять из смеси двух нормальных гене-
ральных совокупностей, одна из которых представляет продукцию станка
А и описывается в соответствии с вышесказанным плотностью
2 1
/a W = ¥»(«; «а, ° а) = у---е 2"х ,
у 2згад
а другая — продукцию станка В и описывается плотностью
2 1
fB(x) = ¥>(х; ав, а в) = ~7= е *** .
у 2x0#
Обозначая 07 = (а7,(т7), а удельный вес изделий станка 7 через тг7
(7 = А, В), можем записать уравнение функции плотности /(х), описыва-
ющей закон распределения анализируемого признака ( во всей (объеди-
ненной) генеральной совокупности, в виде:
f(x) = 5Гд^(х; 0Л) + irBv>(x; 0В).	(12.14)
Учитывая, что в объединенной генеральной совокупности продукции
станка А в 1,5 раза больше, чем продукции станка В (поскольку произ-
водительность станка А в 1,5 раза выше), а также то, что = 65 ми,
1 Случайная величина £ ж ее числовые характеристики будут снабжаться нижним
индексом (А или В) в тех случаях, когда речь идет о продукции какого-то опреде-
ленного станка (соответственно станка А или станка В).
13.3. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
477
2
: , имеем:
Од = 67 ММ, (7^ = (7д = 1 ММ
е а
(12.14')
Правыми частями уравнении (12.14) и (12-14*) и представлен частный слу-
чай того, что принято называть смесью вероятностных распределений1.
На рис. 12.1 представлены графики функций плотности /д(х), fs(x)
«/(*)•
Рис. 12.1. Графики функций плотности отдельных компонентов и самой сме-
си из примера 12.5
В соотношениях (12.14) и (12.14*) величины тгл = 0,6 и хр = 0,4 пред-
ставляют удельные веса соответствующих компонентов смеси (их еще на-
зывают априорными вероятностями появления наблюдений из данного
компонента смеси), а 0д = (вд,(Ул) и 6в = (вв^в) — векторные пара-
метры, от значений которых зависят законы распределения компонентов
смеси.
Если сотрудники ОТК или потребители изделий-полуфабрикатов за-
хотят по наблюдениям zi,z2,... определить, на каком именно станке
произведено каждое из них, то как раз и возникает одна из типичных
задач классификации наблюдений в условиях отсутствия обучающих вы-
борок (конечно, в данном примере можно представить себе специально
1 Речь идет о частном случае, поскольку в общей модели смеси распределений, во-
первых, могут участвовать более чем два (и даже континуум) составляющих смесь
распределений, а во-вторых, анализируемые распределения могут быть многомерны-
ми и не обязаны быть однотипными (в данном примере оба компонента нормальные).
478
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
организованное производство этих изделий, в результате которого мож-
но получить отдельно изделия от станка А и отдельно — от станка В1
использовать их в дальнейшем в качестве обучающих выборок).
Пример 12.6. Речь идет о выявлении и анализе типов потреби-
тельского поведения по данным обследовании семейных бюджетов (см.
выше, пример 12.1). Здесь представлен один из фрагментов исследова-
ния, проведенного с целью изучения (на базе семейных бюджетов) диф-
ференциации потребностей, выявления основных типов потребительского
поведения и определения главных типообразующих признаков (социально-
демографической, региональной, экономической природы). Исследуемым
многомерным признаком является вектор Y показателей у , у' у''
потребительского поведения семьи, т. е. каждой (i-й) обследованной семье
ставится в соответствие многомерное наблюдение
где у|т) — удельное (т. е. рассчитанное в среднем на одного члена семьи)
количество m-го вида благ (товаров или услуг, включая сбережения), по-
требляемое t-й обследованной семьей за «единицу времени» (например,
за год) и выраженное в натуральных или денежных единицах.
В соответствии с одним из принятых в исследовании базовых исход-
ных допущений постулируется существование в анализируемом простран-
стве ПР(У) (У 6 ПР(У)) сравнительно небольшого (и неизвестного) числа
к типов потребительского поведения, таких, что различия в структуре
потребления У семей одного типа носят случайный характер (т.е. обу-
словлены влиянием множества случайных, не поддающихся управлению
и учету факторов) и незначительны по сравнению с различиями в потре-
бительском поведении семей, представляющих разные типы. При этом
предполагается, что случайный разброс структур потребительских пове-
дений У (j) внутри любого (j-ro) типа описывается многомерным (в на-
шем случае р-мерным) нормальным законом распределения с некоторым
вектором средних (и в то же время — наиболее характерных, наиболее
часто наблюдаемых) значений
12.3. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
479
SO) =
я с ковариационной матрицей
*п(» *1з(/) ••• *lp(j)
*31 СО *22(>) ••• *2р0)
*р10) *р20) ••• *РрО)
(см. сведения о многомерном нормальном законе в п. 3.1.5, формула (3.10)).
Однако в начале исследования нет сведений об упомянутых гипо-
тетических типах потребительского поведения: неизвестно ни их чи-
сло к, ни значения определяющих эти типы многомерных параметров
0, = (a(J),E(j)). Поэтому мы вынуждены рассматривать имеющиеся
в нашем распоряжении результаты бюджетных обследований семей
У1,У2,...,Уп	(12.15)
как выборку из генеральной совокупности, являющейся смесью много-
мерных нормальных законов распределения. Другими словами, функция
плотности /(У), описывающая распределение вектора У в этой объеди-
ненной генеральной совокупности, имеет вид
к
f(X) = Е	«О); SO)) >	(12.16)
J=1
где Kj (j = l,2,...,fc) — не известный нам удельный вес (априорная ве-
роятность) семей j-ro типа потребительского поведения в общей совокуп-
ности семей;
^.•OW)) =	1	
(2х)5|Е(»р
многомерная нормальная плотность, описывающая закон распределения
исследуемого признака Y(j) внутри совокупности семей j-ro типа потре-
бительского поведения (J = 1,2,..., к).
Далее необходимо по выборке (12.15) оценить неизвестные значения
параметров к, tti,%2,...,**-1, a(j) и E(j) (J = !,...,£) модели (12.16),
чтобы в конечном счете суметь расклассифицировать (в определенном
смысле наилучшим образом) семьи 12.15 по искомым типам потребитель-
ского поведения. Общая схема действий, увязывающая задачу статистиче-
ского оценивания параметров смеси типа (12.16) с задачей автоматической
классификации, изложена в п. 12.3.2.
480
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Общая математическая модель смеси распределений. Рас*
смотренные в примерах смеси (12.14) и (12.16) представляют собой част-
ные случаи общей модели смеси. Обобщение рассмотренных в примерах
смесей может быть произведено в направлении: 1) отказа от конечно-
сти и даже дискретности компонентов, составляющих смесь, распростра-
нения понятия смеси на непрерывную смешивающую функцию; 2) отка-
за однотипности участвующих в смеси компонентов (под однотипностью
компонентов-распределений понимается их принадлежность к общему па-
раметрическому семейству распределений, например к нормальному).
Итак, пусть имеется двухпараметрическое семейство р-мерных плот-
ностей (полигонов вероятностей) распределения
F = {/W(X; 0(w))},	(12.17)
где одномерный (целочисленный или непрерывный) параметр си в качестве
нижнего индекса функции f определяет специфику общего вида каждого
компонента-распределения в смеси, а в качестве аргумента при многомер-
ном, вообще говоря, параметре О определяет зависимость значений хотя
бы части компонентов этого параметра от того, в каком именно составля-
ющем распределении /ы он присутствует. И пусть
* = ty(w)}	(12.18)
— семейство смешивающих функций распределения.
Будем, как и ранее, понимать под f(X) функцию плотности, если
исследуется непрерывная случайная величина, и полигон вероятностей
Р{£ = X}, если анализируемая случайная величина дискретна. Анало-
гично значение функции	(си = 1,2,..., к) интерпретируется как
априорная вероятность появления элементов класса си, если смесь состо-
ит из конечного числа (fc) компонентов /ш(Х;0(си)), и — функция
плотности, если смесь состоит из континуального множества компонентов.
Функция /(X) называется смесью вероятностных распределений
(дискретной или непрерывной), если она представима в виде соответ-
ственно
к
=	(12.19)
j=l
или
ЛХ) = j /ДХ;0(си))^(си)Ли.	(12/19)
В данном пункте нас интересует использование моделей смесей в
теории и практике автоматической классификации, поэтому сузим дан-
ное выше определение смеси и будем рассматривать в дальнейшей
12.3. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
481
лишь случай конечного числа к возможных значении параметра
что соответствует ситуации, в которой величины будут играть
роль удельных весов (априорных вероятностей) xj компонентов смеси
(j = 1,2, ...,/г)1. Если же дополнительно постулировать однотип-
ность компонентов-распределений /j(X;0(y)), т.е. принадлежность всех
/ДХ;0(У)) к одному общему семейству {/(X; 0)}, то модель смеси может
быть представлена в виде
(12.19")
3=1
Интерпретация в задачах автоматической классификации j-ro ком-
понента смеси (j-й генеральной совокупности) в качестве у-го искомо-
го класса (сгустка, скопления) обусловливает естественность дополни-
тельного условия, накладываемого на плотности (полигоны вероятностей)
Jj(X;G(j)) и заключающегося в их одномодальности.
12.3.2. Задача расщеплении смеси распределении
Решить задачу расщепления смеси распределений — это значит по
выборке классифицируемых наблюдений
XltX2i...,Xn,	(12.20)
извлеченной из генеральной совокупности, являющейся смесью (12.19w)
генеральных совокупностей типа (12.17) (при заданном общем виде соста-
вляющих смесь функций fu(X; 0(о>))), построить статистические оценки
для числа компонентов смеси к, их удельных весов (априорных вероят-
ностей) 9Г1,7Г2,...,х* и, главное, для каждого из компонентов /w(X;0(u>))
анализируемой смеси (12.19„). В некоторых частных случаях имеющиеся
1 Модель смеси вида (12.19') с непрерывной смешивающей функцией ^&(w) также
является полезным инструментом социально-экономического анализа и моделиро-
вания. Так, например, при моделировании распределения населения по величине
среднедушевого дохода каждый компонент смеси интерпретируется как население
однородной (по источникам формирования доходов, территориальным и социально-
профессиональным признакам) страты, а все население — как континуальном
смесь таких страт. Подобный подход лежит в основе обоснования логарифмическн-
нор мольной модели распределения населения по доходу (см. Айвазян С. А. Модель
формирования распределения населения России по величине среднедушевого дохо-
да// Экономика и математические методы, том 33 (1997), Я» 4, с. 74-86).
Прикладная статистика и основы эконометрик (
482 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
априорные сведения дают исследователю точное знание числа компонен-
тов смеси к, а иногда и априорных вероятностей ЭГ1, ,..., Тогда зада-
ча расщепления смеси сводится лишь к оцениванию функций /W(X; 0(w)).
Отметим, что задача расщепления сохраняет смысл и применитель-
но к генеральным совокупностям, т. е. в теоретическом варианте. В этом
случае она заключается в восстановлении компонентов /W(X; 0(о>)) и сме-
шивающей функции по заданной левой части /(X) в соотношениях
(12.19) или (12.19') и называется задачей идентификации компонентов
смеси.
12.3.3. Общая схема решения задачи автоматической
классификации в рамках модели смеси
распределении (сведение к схеме
дискриминантного анализа)
Базовая идея, лежащая в основе принятия решения, к какой из к
анализируемых генеральных совокупностей отнести данное классифици-
руемое наблюдение Xi, состоит в том, что наблюдение следует отне-
сти к той генеральной совокупности, в рамках которой оно выглядит
наиболее правдоподобным. Другими словами, если дано точное описа-
ние (например, в виде функций /1(Х),.. .,Д(Х) плотности в непрерыв-
ном случае или полигонов вероятностей в дискретном) конкурирующих
генеральных совокупностей, то следует поочередно вычислить значения
функций правдоподобия для данного наблюдения X, в рамках каждой из
рассматриваемых генеральных совокупностей (т.е. вычислить значения
/1 PQ, ЛР^), • • •, и отнести X,- к тому классу, функция правдопо-
добия которого максимальна1. Если же известен лишь общий вид функции
/1 (X; ©j.), fi(X; 0г)> - • •, fk(%; 0*), описывающих анализируемые клас-
сы, но не известны значения, вообще говоря, многомерных параметров
01,02» • • • , ©*» и если при этом располагают так называемыми обучаю-
щими выборками, то данный случай лежит в рамках параметрической
схемы дискриминантного анализа (ДА) и порядок действий будет следу-
ющим (п. 12.2): сначала по j-й обучающей выборке оцениваем параметр
0j (у = 1,2,..., к), а затем производим классификацию наблюдений, руко-
водствуясь тем же самым принципом максимального правдоподобия, что
и в случае полностью известных функций fj(X).
В схеме автоматической классификации, опирающейся на модель
1 Для большей ясности здесь подразумевается простой случай равных априорных ве-
роятностей и равных потерь от неправильного отнесения наблюдения X,- к любому
из жлассов. Более общая схема и более подробно представлена в п. 12.2.
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
483
смеси распределений, как и в схеме параметрического ДА, задающие ис-
комые классы функции /^XjGj), ^(Х;©^,... также известны лишь с
точностью до значений параметров. Но в схеме автоматической класси-
фикации неизвестные значения параметров 0j,02,..., так же, впрочем,
каки параметров Л,ТГ1,1Г2,.оцениваются не по обучающим выбор-
кам (их нет в распоряжении исследователя), а по классифицируемым
наблюдениям Xi, Х2,..., Хп с помощью одного из известных методов ста-
тистического оценивания параметров (метода максимального правдоподо-
бия, метода моментов или какого-либо другого). Начиная с момента, ко-
гда по выборке (12.20) сумели получить оценки k, 7Г],?г2,...,я*, 0г,..., 0t
неизвестных параметров к, %1,я-2,...©пОг, - ,©*: модели (12.19"),
снова имеем схему дискриминантного анализа и собственно процесс клас-
сификации наблюдений (12.20) производим точно так же, как и в схеме
параметрического ДА (т.е. относим наблюдение Xi к классу с номером
jo, если *Л/л(Хг,ел) = max	§,)}).
Итак, главное отличие схемы параметрического ДА от схемы ав-
томатической классификации, производимой в рамках модели смеси рас-
пределений, — в способе оценивания неизвестных параметров, от ко-
торых зависят функции, описывающие классы. Но оценивание параме-
тров в модели смеси — процесс неизмеримо более сложный, чем оцени-
вание параметров по обучающим выборкам. Весьма подробное описание
процедур оценивания параметров смеси вероятностных распределений чи-
татель пайдет в книге [Айвазян С. А. и др., 1989].
12.4. Классификация без обучения
(непараметрический случай):
методы кластер-анализа
12.4.1. Общая постановка задачи автоматической
классификации
Итак, как и в п. 12.3, мы не располагаем обучающими выборками и
имеем лишь п подлежащих классификации наблюдений, заданных либо
матрицей X (9.1'), либо матрицей 7 (9.2) (в статичном варианте), со-
держащей все попарные расстояния (меры близости) между классифици-
руемыми наблюдениями. Однако в отличие от п. 12.3 в данном случае
отсутствует и априорная информация о характере распределения на-
блюдений X, внутри каждого из классов (в предыдущем пункте нам был
484
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
известен общий параметрический вид этих распределений). Теперь же
мы можем располагать лишь самыми общими сведениями об этих рас*
пределениях. Эти сведения могут относиться, например, к компактно-
сти или ограниченности диапазонов изменения компонент классифициру*
емых многомерных наблюдений, к свойствам непрерывности (гладкости)
соответствующих законов распределения вероятностей. Заметим, что па-
раллельно можно обсуждать задачу классификации признаков Х^ (а не
объектов X,), с той лишь разницей, что каждый из признаков задается со-
ответствующей строкой матрицы X. В дальнейшем, если это специально
не оговорено, не будем разделять изложение этой проблемы на «объекты»
и «признаки», поскольку все постановки задач и основная методологиче-
ская схема исследования здесь общие.
В общей (нестрогой) постановке проблема автоматической класси-
фикации объектов заключается в том, чтобы всю анализируемую сово-
купность объектов О = {О;} (i = 1,п), статистически представленную
в виде матриц X или у, разбить на сравнительно небольшое число (за-
ранее известное или нет) однородных, в определенном смысле, групп или
классов.
Для формализации этой проблемы удобно интерпретировать анали-
зируемые объекты в качестве точек в соответствующем признаковом про-
странстве. Если исходные данные представлены в форме матрицы (X),
то эти точки являются непосредственным геометрическим изображением
многомерных наблюдений Xi,X2,... ,Хп в р-мерном пространстве ПР(А')
с координатными осями Ох^,Ох^,... ,Ох^. Если же исходные дан-
ные представлены в форме матрицы попарных взаимных расстояний 7,
то исследователю не известны непосредственно координаты этих точек,
но зато задана структура попарных расстояний (близостей) между объек-
тами. Естественно предположить, что геометрическая близость двух иля
нескольких точек в этом пространстве означает близость «физических»
состояний соответствующих объектов, их однородность. Тогда проблема
классификации состоит в разбиении анализируемой совокупности точек —
наблюдений на сравнительно небольшое число (заранее известное или нет)
классов таким образом, чтобы объекты, принадлежащие одному классу,
находились бы на сравнительно небольших расстояниях друг от друга
Полученные в результате разбиения классы часто называют кластерами
(таксонами, образами)1, а методы их нахождения соответственно кластер
1 Cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых
каким-либо общим свойством. Taxon (англ.) — систематизированная группа лю-
бой категории (термин биологического происхождения). Название <кластер-аналкз»
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
485
анализом, численной таксономией распознаванием образов с самообучени-
ем.
Однако, берясь за решение задачи классификации, исследователь с са-
мого начала должен четко представлять, какую именно из двух задач он
решает. Рассматривает ли он обычную задачу разбиения статистически
обследованного (р-мерного) диапазона изменения значений анализируемых
признаков на интервалы (гиперобласти) группирования, в результате ре-
шения которой исследуемая совокупность объектов разбивается на неко-
торое число групп так, что объекты такой одной группы находятся друг
от друга на сравнительно небольшом расстоянии (многомерный аналог
задачи построения интервала группирования при обработке одномерных
наблюдений см. «Переход к группированным данным* в п. 6.1). Либо он
пытается определить естественное расслоение исходных наблюдений на
четко выраженные кластеры, сгустки, лежащие друг от друга на некото-
ром расстоянии, но не разбивающиеся на столь же удаленные части. В
вероятностной интерпретации (т.е. если интерпретировать классифици-
руемые наблюдения Xj, Х2,..., Хп как выборку из некоторой многомерной
генеральной совокупности, описываемой функцией плотности или поли-
гоном распределения /(X), как правило, не известными исследователю)
вторая задача может быть сформулирована как задача выявления обла-
стей повышенной плотности наблюдений, т. е. таких областей возможных
значений анализируемого многомерного признака X, которые соответ-
ствуют локальным максимумам функции f(X).
Если первая задача — построения областей группирования — всегда
имеет решение, то при второй постановке результат может быть и от-
рицательным: может оказаться, что множество исходных наблюдении не
обнаруживает естественного расслоения на кластеры (например, образует
один общий кластер).
Из методологических соображений (в частности, для упрощения пони-
мания читателем некоторых основных идей теории автоматической клас-
сификации и для создания удобной схемы исследования свойств различ-
ных классификационных процедур) будем иногда вводить в рассмотрение
теоретические вероятностные характеристики анализируемой совокупно-
сти: генеральную совокупность, плотность (полигон) распределения, те-
оретические средние значения, дисперсии, ковариации и т.п. Очевид-
но, если мысленно «продолжить» множество классифицируемых наблюде-
ний до всей генеральной совокупности, задача классификации заключа-
лся совокупности методов решения задач такого типа было впервые введено, по-
видимому, Трайоном в 1939 г. (Tryon R. С. Cluster Analysis//Ann. Arb., Edw.
Brothers. 1939).
486 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ется в разбиении анализируемого признакового пространства ПР(Х) на
некоторое число непересекающихся областей. Условимся в дальнейшем
называть такую схему теоретико-вероятностной модификацией задачи
кластер-анализа.
12,4.2. Расстояния между отдельными объектами и меры
близости объектов друг к другу
Наиболее труден и наименее формализован в задаче автоматической
классификации момент, связанный с определением понятия однородности
объектов.
В общем случае понятие однородности объектов определяется зада-
нием правила вычисления величины характеризующей либо рассто-
яние d(Oit Oj) между объектами О,- и из исследуемой совокупности
O(i,j = 1,2,...,п), либо степень близости (сходства) г(О,-,Оу) тех же
объектов. Если задана функция d(0„0j), то близкие в смысле этой ме-
трики объекты считаются однородными, принадлежащими к одному клас-
су. Естественно, при этом необходимо сопоставление d(O„Oj) с некото-
рым пороговым значением, определяемым в каждом конкретном случае
по-своему.
При задании расстояний и мер близости нужно помнить о необхо-
димости соблюдения следующих естественных требований: требования
симметрии (d(Oi,Oj) = d(Pj,O,) и	= г(О^,О,)); требования мак-
симального сходства объекта с самим собой (r(O<,Ot) =	г(О,,О^))
и требования при заданной метрике монотонного убывания rfO^Oj) по
d(O„Oj), т. е. из Ot) d(Oi,Oj) должно с необходимостью следовать
выполнение неравенства г(О*,О/) r(Oi,Oj).
Конечно, выбор метрики (или меры близости) является узловым мо-
ментом исследования, от которого решающим образом зависит оконча-
тельный вариант разбиения объектов на классы при заданном алгоритме
разбиения. В каждой конкретной задаче этот выбор должен производить-
ся по-своему. При этом решение данного вопроса зависит в основном от
главных целей исследования, физической и статистической природы век-
тора наблюдений X, полноты априорных сведений о характере вероят-
ностного распределения X. Так, например, если из конечных целей иссле-
дования и из природы вектора X следует, что понятие однородной группы
естественно интерпретировать как генеральную совокупность с одновер-
шинной плотностью (полигоном частот) распределения, и если к тому же
известен общий вид этой плотности, то следует воспользоваться общим
подходом, описанным в п. 12.3. Если, кроме того, известно, что наблюде-
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
487
ния X, извлекаются из нормальных генеральных совокупностей с одной и
той же матрицей ковариаций, то естественной мерой отдаленности двух
объектов друг от друга является расстояние махаланобисского типа (см.
ниже).
В качестве примеров расстояний и мер близости, сравнительно широ-
ю используемых в задачах кластер-анализа, приведем здесь следующие.
Общий вид метрики махаланобисского типа. В общем случае
зависимых компонент	,х^ вектора наблюдений X и их раз-
личной значимости в решении вопроса об отнесении объекта (наблюде-
ния) к тому или иному классу обычно пользуются обобщенным («взве-
шенным») расстоянием махаланобисского типа, задаваемым формулой1
ЫХьХД = у/(Х, - Х,)ТДТЕ-1Д(Х< - Xj).
Здесь Е — ковариационная матрица генеральной совокупности, из ко-
торой извлекаются наблюдения X,, а Д — некоторая симметричная
неотрицательно-определенная матрица «весовых» коэффициентов Amg,
которая чаще всего выбирается диагональной.
Следующие три вида расстояний, хотя и являются частными случа-
ями метрики d0 > все же заслуживают специального описания.
Обычное евклидово расстояние
р
\ *=1
К ситуациям, в которых использование этого расстояния можно признать
оправданным, прежде всего относят следующие:
• наблюдения X извлекаются из генеральных совокупностей, описы-
ваемых многомерным нормальным законом с ковариационной матрицей
вида <т2 • I, т. е. компоненты X взаимно независимы и имеют одну и ту же
дисперсию;
(1)	(2)	(р)	к	- V
• компоненты х' ,х'	.,х'г вектора наблюдении X однородны по
своему физическому смыслу, причем установлено, например с помощью
опроса экспертов, что все они одинаково важны с точки зрения решения
вопроса об отнесении объекта к тому или иному классу;
1 В случаях, когда каждый объект О, представлен вектором признаков Xi (т.е. в
случае исходных данных, представленных в форме X), часто удобнее в формулах и
различных соотношениях вместо О; писать сразу X,. Например, d(Xi,Xj) вместо
d(Oi,O;).
488
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
• признаковое пространство совпадает с геометрическим простран-
ством нашего бытия, что может быть лишь в случаях р = 1,2,3, и понятие
близости объектов соответственно совпадает с понятием геометрической
близости в этом пространстве, например классификация попаданий при
стрельбе по цели.
Взвешенное евклидово расстояние
Обычно применяется в ситуациях, в которых так или иначе удается при-
писать каждой из компонент х вектора наблюдении Л некоторый нео-
трицательный «вес» пропорциональный степени его важности с точки
зрения решения вопроса об отнесении заданного объекта к тому или иному
классу. Удобно полагать при этом 0 tv* 1, к = 1,р.
Определение весов связано, как правило, с дополнительным иссле-
дованием, например получением и использованием обучающих выборок,
организацией опроса экспертов и обработкой их мнений, использованием
некоторых специальных моделей. Попытки определения весов ык только
по информации, содержащейся в исходных данных, как правило, не дают
желаемого эффекта, а иногда могут лишь отдалить от истинного реше-
ния. Достаточно заметить, что в зависимости от весьма тонких и не-
значительных вариаций физической и статистической природы исходных
данных можно привести одинаково убедительные доводы в пользу двух
диаметрально противоположных решений этого вопроса: выбирать w*
пропорционально величине среднеквадратической ошибки признака а/*)
либо пропорционально обратной величине среднеквадратической ошибки
этого же признака.
Хеммингово расстояние. Используется как мера различия объек-
тов, задаваемых дихотомическими признаками. Оно задается с помощью
формулы
р
e=l
и, следовательно, равно числу несовпадений значений соответствую-
щих признаков в рассматриваемых i-м и J-м объектах.
Другие меры близости для дихотомических признаков. Меры
близости объектов, описываемых набором дихотомических признаков,
обычно основаны на характеристиках vjp и п,-7 =	где
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
489
— число нулевых (единичных) компонент, совпавших в объектах
X, и Xj. Так, например, если из каких-либо профессиональных сообра-
жении или априорных сведений следует, что все р признаков исследуемых
объектов можно считать равноправными, а эффект от совпадения или не-
совпадения нулей такой же, как и от совпадения или несовпадения еди-
ниц, то в качестве меры близости объектов X, и Xj используют величину
ГМ) =
Весьма полный обзор различных мер близости объектов чита-
тель найдет, например, в статье Г. В. Раушенбаха «Проблемы изме-
рения близости в задачах анализа данных» (сборник «Программно-
алгоритмическое обеспечение анализа данных в медико-биологических ис-
следованиях». — М.: Наука, 1987, с. 41-54).
О физически содержательных мерах близости объектов. В
некоторых задачах классификации объектов, не обязательно описываемых
количественно, естественнее использовать в качестве меры близости объ-
ектов (или расстояния между ними) некоторые физически содержательные
числовые параметры, так или иначе характеризующие взаимоотношения
между объектами. Примером может служить задача классификации с
целью агрегирования отраслей экономики, решаемая на основе матрицы
межотраслевого баланса. Классифицируемым объектом в данном примере
является отрасль экономики, а матрица межотраслевого баланса предста-
влена элементами Sij, где под 3ij подразумевается сумма годовых поставок
в денежном выражении t-й отрасли в j-ю. В качестве матрицы близости
(ty) в этом случае естественно взять, например, симметризоеанную нор-
мированную матрицу межотраслевого баланса. При этом под нормиров-
кой понимается преобразование, при котором денежное выражение поста-
вок из t-й отрасли в j-ю заменяется долей этих поставок по отношению
ко всем поставкам i-й отрасли. Симметризацию же нормированной ма-
трицы межотраслевого баланса можно проводить различными способами.
Так, например, близость между t-й и j-й отраслями можно выразить через
среднее значение их взаимных нормированных поставок.
О мерах близости числовых признаков (отдельных факто-
ров). Решение задач классификации многомерных данных, как правило,
предусматривает в качестве предварительного этапа исследования реали-
зацию методов, позволяющих существенно сократить размерность исход-
кого факторного пространства, выбрать из компонент х ',..., z наблю-
даемых векторов X сравнительно небольшое число наиболее существен-
ных, наиболее информативных. Для этих целей бывает полезно рассмо-
треть каждую из компонент	в качестве объекта, подлежа-
490
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
щего классификации. Дело в том, что разбиение признаков а^1),..
на небольшое число однородных в некотором смысле групп позволит ис-
следователю сделать вывод, что компоненты, входящие в одну группу, в
определенном смысле сильно связаны друг с другом и несут информацию о
каком-то одном свойстве исследуемого объекта. Следовательно, можно
надеяться, что не будет большого ущерба в информации, если для даль-
нейшего исследования оставим лишь по одному представителю от каждой
такой группы (процедура, реализующая эту идею, описана в п. 13.4.2).
Чаще всего в подобных ситуациях в качестве мер близости между от-
дельными признаками х и х^\ так же как и между наборами таких
признаков, используются различные характеристики степени их корре-
лированности и в первую очередь коэффициенты корреляции. Проблеме
сокращения размерности анализируемого признакового пространства спе-
циально посвящена гл. 13 данного учебника.
12.4.3.	Расстояния между классами объектов
При конструировании различных процедур классификации (кластер-
процедур) в ряде ситуаций оказывается целесообразным введение поня-
тия расстояния между целыми группами объектов. Приведем примеры
наиболее распространенных расстояний, характеризующих взаимное рас-
положение отдельных групп объектов. Пусть Si — t-я группа (класс,
кластер) объектов, п± — число объектов, образующих группу S',-, вектор
Х(:) — среднее арифметическое векторных наблюдений, входящих в Si
(другими словами, X(i) — «центр тяжести» t-й группы), a р(5|,5то) ~
расстояние между группами Si и Sm.
Ниже приводятся наиболее употребительные и наиболее общие рас-
стояния между классами объектов.
Расстояние, измеряемое по принципу «ближнего соседа»
(«nearest neighbour»)
Рт\п($Ь$т) —
Расстояние, измеряемое
по принципу «дальнего соседа»
neighbour»)

Расстояние, измеряемое по «центрам тяжести» групп
p(ShSm) = d(%(/),X(m)).
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
491
Расстояние, измеряемое по принципу «средней связи» опреде-
ляется как арифметическое среднее всевозможных попарных расстояний
между представителями рассматриваемых групп, т. е.
п‘Пт
Естественно задать вопрос: нельзя ли получить достаточно об-
щую формулу, определяющую расстояние между классами по заданно-
му расстоянию между отдельными элементами (наблюдениями), которая
включила бы в себя в качестве частных случаев все рассмотренные выше
виды расстояний?
Изящное обобщение такого рода, основанное на понятии так на-
зываемого «обобщенного среднего», а точнее, степенного среднего, бы-
ло предложено А. Н. Колмогоровым. Под обобщенным средним ве-
личин ci, с2,..., cN понимается выражение вида MF(ci, с2,..., cN) =
N
F	в котором F(tx) — некоторая функция и соответствен-
«=1
но F-1 — преобразование, обратное к F. Частным случаем обобщенного
среднего является степенное среднее, определяемое как
С2» • •
1/N
— геометрическое среднее;
, с2,..., Cjy
Нетрудно показать, что (при с,- > 0, i = 1,2,..., N)
-^—00(^1 > ®2»•• •»= ,
l<t<w
М+оо(с1» ^2> • • • >	~~,£? ах. ;
N
П С«
£=1
N
Afj(ci, с2,..., cN) = jj с« — арифметическое среднее.
(=1
Обобщенное (по Колмогорову) расстояние между классами,
или обобщенное расстояние, вычисляется по формуле
P(TK)(ShSm) =
(12.21)
XtGS,
В частности, при г —> оо при т —> —оо имеем
Роо ^m) = PmaxG>ih ^т)> Р—оо(*^'/, ^т) = PmlnC^h §тп)-
492
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Очевидно также
p\K}(Sl,Sm) = pcp(Sl,Sm).
Из (12.21) следует, что если 5(тп,д) = Sm U Sg — группа элемен-
тов, полученная путем объединения кластеров Sm и то обобщенное
X-расстояние между кластерами Si и S(m,g) определяется формулой
PTK\shS(m,q)) =
[/>№,Sm)T±n,[AK)(Si, «,)] I'
Понятие расстояния между группами элементов особенно важно в тах
называемых агломеративных иерархических кластер-процедурах (см. ни-
же п. 12.4.7), поскольку принцип работы таких алгоритмов состоит в по-
следовательном объединении элементов, а затем и целых групп, сначала
самых близких, а потом все более и более отдаленных друг от друга.
Учитывая специфику подобных процедур, для задания расстояния между
классами оказывается достаточным определить порядок пересчета рассто-
яния между классом Si и классом S(mt g) = SmU Sgi являющимся объеди-
нением двух других классов Sm и Sg, по расстояниям ptm = p(S/,5m),
pig = p(Si, Sg) и pmg = p(Sm,Sg) между этими классами. С этой целью
часто используется также следующая общая формула1 для вычисления
расстояния между некоторым классом Si и классом (тп, д):
Pi(m,g) —	= ^Plm 4" ^lq 4" 7Pmq 4"	—	(12.22)
где ot,/?,7 и — числовые коэффициенты, значения которых и определяют
специфику процедуры, ее нацеленность на решение той или иной экстре-
мальной задачи.
Так, например, полагая а = Р = — Я = | и 7 = О, приходим к расстоя-
нию, измеряемому по принципу «ближайшего соседа». Если же положить
а = р = 6 = I и 7 = 0, то расстояние между двумя классами определится
как расстояние между двумя самыми далекими элементами этих классов,
по принципу «дальнего соседа». И наконец, выбор коэффициентов соот-
ношения (12.22) по формулам
1 См.: Keller W. J. Statistical vio Personal Computers. «Compstat-86», Proceedings io
Computational Statistics. — Wien, Physica-Verlag, 1986, pp. 332-337.
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
493
приводит к расстоянию рср между классами, вычисленному как среднее
из расстоянии между всеми парами элементов, один из которых берется
из одного класса, а другой — из другого.
Расстояния между классами в теоретико-вероятностной схе-
ме кластер-анализа. В данной схеме анализируемая генеральная сово-
купность интерпретируется как смесь унимодальных генеральных сово-
купностей, каждая из которых и представляет один из искомых классов.
Если дополнительно ограничить себя рассмотрением только нормальных
классов, то каждый (Z-й) такой класс, как известно (см. п. 3.1.5, соот-
ношение (3.10)), определяется вектором средних значений а(1) и ковариа-
ционной матрицей £(/). Для измерения расстояния между нормальными
классами с номерами I ит используют так называемое «информационное
расстояние Каллбзка» (S. Kullback)
p\s„sm) = 1 (a(f) - a(m))T (£-’(/) +	(a(l) - a(m))
z	(12.23)
+ - tr { (E(/) - E(m)) (E-1 (Z) — E-1 (m)) } .
Если анализируемые классы (генеральные совокупности) различают-
ся только средними значениями а(/) и а(т) (т.е. ковариационные матри-
цы у них одинаковы), то расстояние между ними измеряется так назы-
ваемым «расстоянием Махаланобиса», которое вычисляется по формуле,
получаемой из (12.23) при £(/) = S(m) = Е:
p2(SbSm) = (a(Z) — a(m))T E-,(a(Z) — a(m)).	(12.24)
В статистической практике формулы (12.23) и (12.24) используются
для вычисления расстоянии между классами и при отклонении распреде-
ления наблюдений внутри классов от нормального с заменой теорети-
ческих характеристик а(у) и S(J) их оценками a(j) и Е(у), построенными
по наблюдениям, составляющим класс с номером j (j = см. выше
формулы (12.11) и (12.12).
12.4.4.	Функционалы качества разбиения на классы и
экстремальная постановка задачи кластер-анализа
Естественно попытаться определить сравнительное качество различ-
ных способов разбиения заданной совокупности элементов на классы, т. е.
определить тот количественный критерий, следуя которому можно бы-
ло бы предпочесть одно разбиение другому. С этой целью в постановку
494
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
задачи кластер-анализа часто вводится понятие так называемого функ-
ционала качества разбиения Q(S)t определенного на множестве всех воз-
можных разбиений. Функционалом он называется потому, что чаще всего
разбиение S задается, вообще говоря, набором дискриминантных функ-
ций tfi(X),	. Тогда под наилучшим разбиением S* понимается то
разбиение, на котором достигается экстремум выбранного функционала
качества. Выбор того или иного функционала качества, как правило, осу-
ществляется весьма произвольно и опирается скорее на эмпирические я
профессионально-интуитивные соображения, чем на какую-либо строгую
формализованную систему.
Приведем примеры наиболее распространенных функционалов каче-
ства разбиения.
Функционалы качества разбиения при заданном числе клас-
сов. Пусть исследователем уже выбрана метрика d в пространстве ПР(Х)
и пусть S = (51,5а,..., 5*) — некоторое фиксированное разбиение наблк>
дений Xi, %2»• • -»Хп на заданное число к классов 5i, 52,..., 5*.
За функционалы качества часто берутся следующие характеристики:
сумма («взвешенная») внутриклассовых дисперсий
=	(12.25)
/=1 XiES,
весьма широко используется в задачах кластер-анализа в качестве крите-
рийной оценки разбиения;
сумма попарных внутриклассовых расстояний между элементами
к
«г(Я) = Е Е АЗД)
/=1 XiJCjGSi
либо
в большинстве ситуаций приводит к тем же наилучшим разбиениям, что
и Qi(5), и тоже используется для сравнения кластер-процедур;
обобщенная внутриклассовая дисперсия <Эз(5) является, как известно
(см. п. 2.6.6, формула (2.30)), одной из характеристик степени рассеива-
ния многомерных наблюдений одного класса (генеральной совокупности)
около своего «центра тяжести». Следуя обычным правилам вычисления
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
495
выборочной ковариационной матрицы Е/, отдельно по наблюдениям, по-
павшим в какой-то один класс St, получаем
/ к	\
фз(£) = det	(12.26)
\/=1	/
где под det А понимается «определитель матрицы А», а элементы agf(/)
выборочной ковариационной матрицы Ej класса Si подсчитываются по
формуле
?,<(0 = Е	?,< =	(12.27)
x,es,
где — «-я компонента многомерного наблюдения X,, a x^v\l) — сред-
нее значение v-й компоненты, подсчитанное по наблюдениям 1-го класса.
Встречается и другой вариант использования понятия обобщенной
дисперсии как характеристики качества разбиения, в котором операция
суммирования Е/ по классам заменена операцией умножения
к
Qits) = n<det s<)ni •
1=1
Как видно из формул (12.26) и (12.27), функционал фз(^) является
средней арифметической (по всем классам) характеристикой обобщенной
внутриклассовой дисперсии, в то время как функционал (^(S) пропорци-
онален средней геометрической характеристике тех же величин.
Использование функционалов Q$(S) и Qi(S) особенно уместно в ситу-
ациях, в которых исследователь в первую очередь задается вопросом: не
сосредоточены ли наблюдения, разбитые на классы $2,$2,...,5*, в про-
странстве размерности, меньшей, чем р?
Функционалы качества разбиения при неизвестном числе
классов. В ситуациях, когда исследователю заранее не известно, на ка-
кое число классов подразделяются исходные многомерные наблюдения
Хь %2, • • • >	функционалы качества разбиения Q(S) выбирают чаще
всего в виде простой алгебраической комбинации (суммы, разности, про-
изведения, отношения) двух функционалов Д(5) и h(S), один из кото-
рых Д является убывающей (невозрастающей) функцией числа классов
к и характеризует, как правило, внутриклассовый разброс наблюдений,
а второй — возрастающей (неубывающей) функцией числа классов k.
При этом интерпретация функционала может быть различной. Под
496
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
12 понимается иногда и некоторая мера взаимной удаленности (близости)
классов, и мера тех потерь, которые приходится нести исследователю при
излишней детализации рассматриваемого массива исходных наблюдений,
и величина, обратная так называемой «мере концентрации» всей структу-
ры точек, полученной при разбиении исследуемого множества наблюдений
на к классов.
Весьма гибким и достаточно общим подходом, реализующим идею од-
новременного учета двух функционалов, является подход, основанный на
схеме, предложенной А. И. Колмогоровым. Эта схема опирается на поня-
тия меры концентрации ZT(S) точек, соответствующей разбиению S, и
средней меры внутриклассового рассеяния	характеризующей то
же разбиение S.
Под мерой концентрации ZT(S) предлагается понимать степенное
среднее вида
п
ZT(S) = МТ
v(X2)
п п
, (12.28)
V
где v(Xi) — число элементов в кластере, содержащем точку Х„ а выбор
числового параметра т находится в распоряжении исследователя и зави-
сит от конкретных целей разбиения. При выборе т полезно иметь в виду
следующие частные случаи ZT(5):
Z-i(S) = p
к
k
где к — число различных кластеров в разбиении 5; log Zq(S) = 52 log
i=l ” Я
— естественная информационная мера концентрации (здесь п,, как и ра-
нее, число элементов в кластере
Z«,(S) = max ;
Z-oo(S) = min ;
!<»</: \ П /
Заметим, что при любом т предложенная мера концентрации имеет ми-
нимальное значение, равное 1/п, при разбиении исследуемого множества
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
497
на п одноточечных кластеров, и максимальное значение, равное 1, при
объединении всех исходных наблюдений в один общий кластер.
При конструировании и сравнении различных кластер-процедур По-
лезно иметь в виду, что объединение двух кластеров Si и Sm в один дает
прирост меры концентрации Zi(S), равный
a v 1 Г/	2	2 1 2П/Пт
— 2 («i	Tim J —	2
П	П
Определение средней меры внутриклассового рассеяния ГТ '(S) так-
же опирается на понятие степенного среднего. В частности, полагают
ЛК)(5) =
(12.29)
где под
1
2
Q(*4Si) =
£ £ Л*).*)
x^eSi Xtes,
понимается обобщенная средняя мера рассеяния, характеризующая класс
5,. Числовой параметр т здесь, как и прежде, выбирается по усмотрению
исследователя. Полагая

1
v(X)
£ <Г(х,Х')
xtes(x)
где S(X) — кластер, в который входит наблюдение X, а «(X) — число
элементов в кластере 5(Х), формулу (12.29) можно переписать в виде
4Ю($) = л/т(«$к)(%1)......<?(Л’(хп))
п
(12.30)
X«€S(X.)
При конструировании и сравнении различных кластер-процедур по-
лезно иметь в виду, что объединение двух кластеров St и Sm в один дает
прирост величины п[Д*\5)]т, непосредственно характеризующей сред-
нюю меру внутриклассового рассеяния, равный
д[п(4к,Л
ntnm
ni + nm
{2[p<.K)(S(,Sm)]T - [<4К)(й)]т - [<3(TK)(Sm)]T} -
498
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Очевидно, если ориентироваться на сокращение числа кластеров при
наименьших потерях в отношении внутриклассового рассеивания, не обра-
щая внимания на меру концентрации, то естественно объединять два кла-
стера, для которых минимальна величина Д(п[/£К)]Т). Если же одно-
временно ориентироваться и на рост взвешенной концентрации Zi(S), то
объединение кластеров следует подчинить требованию минимизации ве-
личины
д[п(4к))т]	- |<?(,*)(яя,)Г} па
AZi(S)	n/ + nm
12.4.5.	Формулировка экстремальных задач разбиения
исходного множества объектов на классы при
неизвестном числе классов
Возможно множество вариантов таких формулировок. Рассмотрим
два из них, относящихся к наиболее естественным и часто используемым.
Вариант 1: комбинирование функционалов качества. Требуется
найти такое разбиение 5*, для которого некоторая алгебраическая комби-
нация функционала, характеризующего среднее внутриклассовое рассея-
ние (12.30), и функционала, характеризующего меру концентрации полу-
ченной структуры (12.28), достигала бы своего экстремума. В качестве
примеров можно привести комбинации, задаваемые формулами вида
аД(5) + /3/2(5) и [Zl(S)]“[Z2(S)]<’1	(12.31)
где Zi(S) = l[K\sy, Z2(S) = z 5a; а и /? — некоторые положительные
константы, например, а = /3 = 1.
Вариант 2; двойственная формулировка. Требуется найти раз-
биение S*, которое, обладая концентрацией Zr(S*), не меньшей заданно-
го порогового значения Zo, давало бы наименьшее внутриклассовое рас-
сеяние 7$К\5*), или, в двойственной подстановке: при заданном поро-
говом значении Iq найти разбиение 5* с внутриклассовым рассеянием
< Zo и наибольшей концентрацией ZT(S*).
12.4.6.	Основные типы задач кластер-анализа и основные
типы кластер-процедур
Прежде всего целесообразно подразделение всех задач кластер-анализа
на два основных типа: Б} и Б2 в зависимости от объема п совокупности
классифицируемых наблюдений Xi,Х2,...,Хп.
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
499
К типу Бх отнесем задачи классификации сравнительно небольших по
объему совокупностей наблюдений, состоящих, как правило, не более чем
из нескольких десятков наблюдений. Сюда, по-видимому, могут быть от-
несены задачи классификации некоторых макрообъектов, таких, как стра-
ны, города, фирмы, предприятия, типы технологических процессов и т. п.
К типу Б2 будем относить задачи классификации достаточно боль-
ших массивов многомерных наблюдений (п — порядка нескольких сотен
и тысяч; классификация индивидуумов, семей, изделий, некоторых про-
мышленных и технических микрообъектов). Подобное разделение задач
классификации на два типа хотя и условно, но весьма необходимо, и в
первую очередь с точки зрения принципиального различия идей и мето-
дов, на основании которых конструируются кластер-процедуры в том и в
другом случае. Например, для задач типа Б2 целесообразно построение
процедур последовательного типа, обладающих достаточно хорошими, хо-
тя бы асимптотическими по п, свойствами.
С точки зрения априорной информации об окончательном числе клас-
сов, на которое требуется разбить исследуемую совокупность объектов,
задачи кластер-анализа можно подразделить на три основных типа:
(а)	число классов априори задано;
(б)	число классов неизвестно и подлежит определению (оценке);
(в)	число классов неизвестно, но его определение и не входит в усло-
вие задачи; требуется построить так называемое иерархическое дерево
и следуемой совокупности, или дендрограмму,
В соответствии с подразделением задач кластер-анализа на типы
можно выделить следующие три основных типа обслуживающих их
кластер-процеду р:
•	процедуры иерархические (агломеративные и дивизимные). Пред-
назначены в основном для решения задач типа (в). Что касается объема
классифицируемой совокупности, то формально иерархические процедуры
применимы и для задач Б1, и для задач Б2. Однако поскольку эти проце-
дуры основаны на переборе элементов матрицы расстояний p(Xi,Xj) (или
матрицы соответствующих мер близости), то конструктивно реализуемы-
ми их можно признать лишь в пределах задач типа Bj. Следует отметить,
что иерархические процедуры применяются иногда и для решения задач
типов Б1,(а) и Б1,(б);
•	процедуры параллельные. Предназначены для решения задач типов
Бь(а) и Б1,(б). Они реализуются с помощью итерационных алгоритмов,
на каждом шаге которых одновременно (параллельно) используются все
имеющиеся у нас наблюдения;
•	процедуры последовательные. Предназначены в основном для реше-
500
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
ния задач типов Ба,(а) и Б3, (б). Они реализуются с помощью итерацион-
ных алгоритмов, на каждом шаге которых используется лишь небольшая
часть, например одно из исходных наблюдений, а также результат разби-
ения на предыдущем шаге.
12.4.7.	Иерархические процедуры
Как отмечалось выше, принцип работы иерархических агломератив-
ных (дивизимных) процедур состоит в последовательном объединении
(разделении) групп элементов сначала самых близких (далеких), а затем
все более отдаленных друг от друга (приближенных друг к другу). При
этом агломеративные процедуры начинают обычно с объединения отдель-
ных элементов, а дивизимные — с разъединения всей исходной совокуп-
ности наблюдений.
С некоторой точки зрения иерархические процедуры, по сравнению
с другими кластер-процедурами, дают более полный и тонкий анализ
структуры исследуемого множества наблюдений. Привлекательной сто-
роной подобных алгоритмов является и возможность наглядной интерпре-
тации проведенного анализа. Легко себе представить также использова-
ние иерархических процедур и для решения задач кластер-анализа типов
(а) и (б), т. е. для разбиения наблюдений на какое-то объективно обусло-
вленное число классов, заданное или известное. При решении задач типа
(а) для этого, очевидно, следует продолжать реализацию иерархического
алгоритма до тех пор, пока число различных классов не станет равным
априори заданному числу к. При решении задач типа (б) естественно бы-
ло бы подчинить правило остановки иерархической процедуры одному из
критериев качества разбиения.
К недостаткам иерархических процедур следует отнести громозд-
кость их вычислительной реализации. Соответствующие алгоритмы на
каждом шаге требуют вычисления всей матрицы расстояний, а следова-
тельно, емкой машинной памяти и большого времени. Поэтому реализа-
ция таких алгоритмов при числе наблюдений, большем нескольких сотен,
оказывается либо невозможной, либо нецелесообразной.
Кроме того, имеется широкий класс достаточно естественных приме-
ров, в которых иерархические процедуры, даже подчиненные на каждом
шаге некоторому критерию качества разбиения, приводят для любого на-
перед заданного числа кластеров к к разбиению, весьма далекому от опти-
мального в смысле того же самого критерия качества. Если прибавить к
этому широкое экспериментальное подтверждение того же эффекта, то
можно прийти к выводу, что «конечная неоптимальность» оптималь-
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
501
пого иерархического алгоритма является скорее правилом, чем исключе-
нием. Специфический характер метода образования групп, свойственный
иерархическим процедурам, оказывается, по-видимому, слишком жестким
ограничением с точки зрения экстремального подхода к решению задач
классификации наблюдений при определенном числе классов.
Приведем некоторые примеры иерархических алгоритмов:
•	агломеративный иерархический алгоритм «ближайшего соседа»
(или «одной связи»). Этот алгоритм исходит из матрицы расстояний
между наблюдениями, в которой расстояние между кластерами опреде-
лено по правилу «ближайшего соседа» (см. выше). На первом шаге
алгоритма каждое наблюдение Х,- (» = 1,2,...,п) рассматривается как
отдельный кластер. Далее на каждом шаге работы алгоритма происходит
объединение двух самых близких кластеров и соответственно пересчиты-
вается матрица расстояний, размерность которой, естественно, снижается
на единицу. Работа алгоритма заканчивается, когда все исходные наблю-
дения объединены в один класс. Поскольку расстояние между любыми
двумя кластерами в этом алгоритме равно расстоянию между двумя самы-
ми близкими элементами, представляющими свои классы, то получаемые
в итоге кластеры могут иметь достаточно сложную форму, в частности,
они не обязаны быть выпуклыми; ведь два элемента (наблюдения) попа-
дают в один кластер, если существует соединяющая их цепочка близких
между собой элементов (так называемый «цепочечный эффект»). Это об-
стоятельство можно отнести как к достоинствам алгоритма, так и к его
недостаткам.
Существуют различные способы устранения цепочечного эффекта
при образовании классов с помощью алгоритма ближайшего соседа. Наи-
более простым и естественным из них можно признать, например, введе-
ние ограничения сверху на максимальное расстояние между элементами
одного класса: если при формировании классов для некоторых элементов
получаемого кластера взаимное расстояние превысит некоторый задан-
ный порог, то эти элементы следует разнести по какому-то дополнитель-
ному правилу в разные классы.
•	агломеративные иерархические алгоритмы «средней связи» и
«полной связи» (или «дальнего соседа»). Эти. алгоритмы отличаются
от описанного выше алгоритма «ближайшего соседа» лишь способом вы-
числения расстояния между классами. В алгоритме средней связи под
расстоянием между кластерами понимается среднее из расстояний меж-
ду всевозможными парами представителей этих кластеров. В алгоритме
полной связи (или дальнего соседа) расстояние между двумя кластерами
определяется как расстояние между двумя самыми отдаленными друг от
502
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
друга представителями своих кластеров.
•	К-обобщенная иерархическая процедура, т.е. обобщенная по Кол-
могорову. Поскольку все вышеперечисленные виды расстояний между
кластерами могут быть получены в качестве частных случаев обобщенно-
го расстояния Колмогорова (12.21), то представляется естественным вве-
сти понятие К-обобщенной иерархической процедуры. Очевидно, в класс
lif-обобщенных иерархических процедур следует включить все обычные
иерархические алгоритмы, использующие в качестве расстояний между
кластерами обобщенное расстояние Колмогорова (12.21) при том или дру-
гом конкретном выборе числового параметра т;
•	процедуры иерархические, использующие понятие порога. Общая
схема подобных процедур отличается от обычной логической схемы ранее
описанных иерархических процедур лишь дополнительным заданием по-
следовательности, как правило, монотонной, порогов Ci,C2,...,ct, которые
используются следующим образом. Для определенности дадим пояснения
для агломеративных процедур. На первом шаге алгоритма попарно объ-
единяются элементы, расстояние между которыми не превосходит величи-
ны Cj, либо мера близости которых не менее Ci, На втором шаге алгоритма
объединяются элементы, или группы элементов, расстояние между кото-
рыми не превосходит с?, либо мера близости которых не менее с2, и т.д.
Очевидно, при с< = оо или, при сравнении мер близости, при с< = 0, на
последнем t-м шаге все элементы исходной совокупности окажутся объ-
единенными в один общий класс. Заметим, однако, что объединение в
кластеры, подчиненные подобным пороговым иерархическим алгоритмам,
приводит к образованию, вообще говоря, пересекающихся промежуточных
классов, которые могут не расцепиться вплоть до последнего шага. Поэто-
му эффективность подобных процедур, возможность выбора подходящих
пороговых значений cj,..., ct существенно зависят от внутренней геоме-
трической структуры исходного множества наблюдений. В частности, по-
роговые иерархические процедуры оказываются уместными и достаточно
эффективными в ситуациях, когда отсутствует (или слабо выражен) це-
почечный эффект в структуре исходной совокупности наблюдений и когда
последние, естественно, распадаются на какое-то количество достаточно
отдаленных друг от друга отдельных скоплений точек в исследуемом фак-
торном пространстве.
12.4.8.	Параллельные кластер-процедуры
В алгоритмах кластер-анализа реализуется обычно одна из двух
основных родственных идей, которой исследователь хочет подчинить свое
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
503
разбиение на классы. Это либо идея оптимизации разбиения в смысле
заранее выбранного функционала качества разбиения, либо идея образо-
вания кластеров по принципу определения мест наибольшей сгущенности
(плотности, концентрации) точек наблюдении в рассматриваемом фактор-
ном пространстве. Коль скоро характер параллельных процедур преду-
сматривает одновременный обсчет всех исходных наблюдений на каждом
шаге алгоритма, то естественно попытаться решать поставленную задачу
с помощью обычного перебора различных вариантов разбиения.
Однако нетрудно подсчитать, что уже при сравнительно небольшом
общем числе классифицируемых точек п (порядка нескольких десятков)
полный перебор всех вариантов разбиения на заданное, а тем более на
неизвестное число классов практически неосуществим. Следовательно,
основной смысл конструирования различных параллельных алгоритмов
классификации — в указании способа сокращения числа перебора вариан-
тов, в описании пути, приводящего, быть может, лишь к приближенному
решению доставленной задачи, но пути, конструктивно реализуемого и не
слишком дорогого.
а)	Алгоритмы, связанные с функционалами качества разбиения, К
таким алгоритмам следует в первую очередь отнести алгоритмы «после-
довательного переноса точек из класса в класс». Эти алгоритмы отпра-
вляются от некоторого начального разбиения S° =	..., S^}, полу-
ченного произвольно или с помощью какого-либо из методов предвари-
тельной обработки исходных наблюдений. Вычисляется значение приня-
того критерия качества разбиения Q(S), например, вида (12.25) при за-
данном числе классов к или вида (12.31) при неизвестном числе классов.
Затем каждое из наблюдений Xi поочередно перемещается во все кластеры
(при этом оно рассматривается как самостоятельный кластер, если число
кластеров неизвестно) и оставляется в том положении, которое соответ-
ствует наилучшему значению функционала качества Q. Работа алгорит-
ма заканчивается, когда перемещения наблюдений перестанут приводить
к улучшению (в смысле Q) качества разбиения. Часто описанный алго-
ритм применяют несколько раз к одной и той же исходной совокупности
наблюдений, начиная с разных начальных разбиений и выбирают в
итоге наилучший (в смысле Q) вариант разбиения.
б)	Алгоритмы, использующие понятие эталонных точек (мно-
жеств). Опишем общую формальную схему одного достаточного ши-
рокого класса алгоритмов, реализация которой может приводить как к
параллельным, так и к последовательным кластер-процедурам.
Под эталонными множествами Е^, Е2,..., Ek будем понимать каким-
то образом, в частности случайным, сформированные непересекающиеся
504
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
подмножества исходном совокупности наблюдений {Xi,Xj,. ..,ХП} зара-
нее определенных объемов соответственно	. ,тк. Как правило,
mj -f-m2 Н--l-mjt составляет лишь незначительную долю от общего числа
исходных наблюдений п. В частном случае тк = т2 = .. - = m* = 1 будем
иметь набор к эталонных точек. Пусть для любого набора эталонных мно-
жеств Е = {£i, £?,..., Е*}, для любого наблюдения X,, для любой группы
исходных наблюдений А и для произвольного I = 1,2,..., к заданы некото-
рые специальные функции у>(Х,, А) и ^(Х,, St, Е), характеризующие меру
типичности точки X, как представителя группы точек А (меру однородно-
сти наблюдений X, и группы наблюдений А) и меру типичности точки X,
как представителя класса Si, построенного с использованием эталонного
множества Ei из Е.
Будем для определенности считать, что чем меньше значения функ-
ций ср и тем типичнее соответствующая точка в указанном выше смы-
сле. Тогда общая схема эталонных алгоритмов может быть представле-
на следующим образом. При заранее заданном числе классов к каким-
то образом (случайным, с помощью обучающих выборок, из экспертно-
профессиональных соображений или с помощью методов предварительной
обработки исходных данных) выбираются числа mi,т2,..., тк и началь-
ная система эталонных множеств	Класс Sl
формируется из наблюдений, наиболее типичных с точки зрения предста-
ло)
вительства эталона EJ , т. е.
5/(0) = {Xi: VJ(Xi,E<0))<VJ(Xi,Ej0)), j = 1,2,... ,к, j*l}.
Если оказывается, что ^(Х,,Е,°^) = <p(Xi, Е^), то можно условиться
относить наблюдение X,- к тому из классов 5^ и который обла-
дает меньшим порядковым номером. Затем строится новая система
эталонных множеств Е = {Ep^Ej2^,. ..,Е[1^}, в которой эталон Е^
формируется из mi точек, дающих mi наименьших значении функции
V>(X,	Е(0)). После этого по тому же правилу строят новое разбие-
с(') гсО) с<‘)	v(l)
ние 5* ' = f,b2 , • • •, 5* }, но уже относительно эталонов Ек ' и т.д.
Итерации продолжают до тех пор, пока не получат устойчивых классов,
т.е. до такого номера v, при котором S^ =
Если число классов, на которое требуется разбить исходную сово-
купность наблюдений, заранее не известно, то в описанную схему необ-
ходимо ввести некоторые дополнения. В частности, на начальном этапе
устанавливаются: числа k(°\mi,m2,...,mk(o), система эталонных мно-
жеств Е<°) = {E|°\Ej°\...,E^o)}, а также величина — минимально
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
505
возможная типичность точки, представляющей свой класс, и — мини-
мально возможная нетипичность двух разных классов1. Как и прежде,
вначале подсчитываются Е/°) для всех наблюдений (t = 1,2,..., п)
и для всех эталонов (/ = 1,2,	Последовательно для каждого i
определяются эталоны Е^, для которых данное t-e наблюдение является
наиболее типичным, т. е.
Если ^(Х^Ец0^) то наблюдение включается в состав класса
5^; если же у>(Х1,Е^) > <^0, то наблюдение Xi принимается одновре-
менно за новый эталон Е*<о)+1 и за новый класс Sj$)+1. Затем та же про-
цедура сравнения производится с у>(Х2, Е и т. д. до 9?(ХП, E^j). Пусть
в результате у нас образовалось на этом этапе алгоритма fc^(0) классов
и столько же эталонов Е = {е}°\...,Е^^} (очевидно fc<o)(0) > к^).
После этого полученные классы	., ^(о (( проверяются на зна-
чимое попарное различие с помощью порога а- именно, если
^’= v>(40)--s(0))
£ ^,5(,Е(0>)4-^- Е ^№,S„E(0))
хТЙ.	x~ts,
< ito,
то классы Sg°^ я объединяются в один класс с номером z(g, /),
равным min(g,/), и с эталоном Е состоящим из raax[mqtmi) наблю-
дений, дающих соответствующее число наименьших значений функции
Последовательное вычисление величин	и
их сравнение с V’o производится до тех пор, пока не окажется, что
min № > V’o-
9,<	’’
Это означает окончание первой итерации алгоритма и образование новой
системы эталонов Е^ = {Е,11,..., ЕЙ}Л и соответствующих значимо
1 В наиболее общих процедурах «пороги» уо и V’O» так же как и общее число эле-
ментов (n<w> < п), составляющих классы ..., задаются переменными, т.е.
изменяющимися по определенному правилу при переходе от одного этапа алгоритма
к другому.
506
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
различимых классов = {S^S^,.. .,S^J(}. Затем процедура повто-
ряется применительно к эталонам и т. д. до получения устойчивого
разбиения S всех исходных элементов на некоторое число классов
При конструировании функций у>(Х,А) и V?(X, S/,E) можно исполь-
зовать заданную метрику (расстояние между точками) р(Х, Y) или меру
близости г(Х, У), а также подходящим образом выбранный вариант обоб-
щенного расстояния типа (12.21).
Используются, в частности, следующие способы задания ip и i/r.
¥>(Х,Л)= £ Р(Х,Х^,
XtEA
v(X,A) = р{Х,Х(А}),
где Х(А) — одна из разновидностей среднего значения всех наблюдений
Х<, принадлежащих группе А. Например, Х(А) может быть обычным
арифметическим средним, т.е. «центром тяжести» группы А;
V>(X,SbE) =
I2 ’
J=1
^(X,S/,E) = y?(X,S/).
В качестве примера параллельных кластер-процедур, укладывающих-
ся в описанную общую схему, рассмотрим теперь серию алгоритмов,
объединенных названием «Форель». Общую для этих алгоритмов
идею проиллюстрируем на примере алгоритма «Форель-1».
Пусть совокупность {Х],Хз,...,Хп} нужно разбить каким-то обра-
________________________________________________________ п
зом на некоторое число классов (заранее не известное). Пусть X = X,
«=1
и Ro — радиус минимальной гиперсферы с центром в X, содержащей все
точки исследуемой совокупности. Зададим произвольный радиус R < R$
и рассмотрим процедуру выделения классов для заданного R. Из любой
точки X, = Xi, принятой за Центр, радиусом R описывается гиперсфера
Ci- Находится центр тяжести Х2 точек совокупности, попавших в С\. Из
Ха радиусом R описывается гиперсфера С2 и определяется Хз — центр
тяжести точек исследуемой совокупности, попавших в С2- Процедура по-
строения гиперсфер и точек повторяется до тех пор, пока точки X* не
перестанут меняться. Точки совокупности, попавшие в «остановившую-
ся» гиперсферу, принимаются за первый класс S\. Для всех оставшихся
точек, т. е. не попавших в класс Si, вновь применяется описанная выше
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
507
процедура, выделяющая еще один класс S2i и т.д. до тех пор, пока все
точки совокупности не будут распределены по классам.
Применение описанного алгоритма для ряда последовательных зна-
чений R = Ro — vA, (Д =	= 1,2,...,7V — 1) позволяет ориен-
тировочно оценить наиболее предпочтительное число классов для данной
совокупности объектов. При этом основанием для выбора числа классов
может служить многократное повторение одного и того же числа классов
для нескольких последовательных значений R^ и его резкое возрастание
на следующем шаге.
Если ставится задача разбить совокупность на заданное число клас-
сов, то одна из моделей модификации алгоритма «Форель-1» — «Форель-
2» методом последовательных приближений позволяет находить мини-
мальный радиус йт|п, дающий разбиение на заданное число классов.
Покажем теперь, как процедура выделения одного класса точек из со-
вокупности, являющаяся основой алгоритмов типа «Форель», может быть
изложена в рамках описанной выше общей схемы «эталонных алгорит-
мов». Выделение класса точек из совокупности эквивалентно разделе-
нию совокупности на два класса. В качестве набора эталонных множеств
Е =	будем брать две точки Е = (е^ез). Функцию у?(Х,е<) опре-
делим следующим образом: <p(Xtex) = p2(X,ei); <p(Xi,e2) = R, где R —
выбранная величина радиуса. Функция ^(Х, S/, Е) может быть определена
многими способами, например так:
V-(X,S(,E)= £ р2е(Х,Х,).
xtest
12.4.9.	Последовательные кластер-процедуры
Если число п классифицируемых наблюдений Хх,Х2,... .,Хп доста-
точно велико (от нескольких сотен и более), то, как мы уже отмечали, ре-
ализация кластер-процедур иерархического и параллельного типов крайне
трудоемка, а иногда и практически невозможна. В этих случаях пользу-
ются итерационными алгоритмами, на каждом шаге которых последова-
тельно обсчитывается лишь небольшая часть исходных наблюдений, на-
пример одно из них. В том, что п велико, имеются не только неудобства,
но и свои преимущества. В частности, это позволяет исследовать асим-
птотические (по п) свойства соответствующих процедур, аналогичные,
например, свойствам состоятельности, асимптотической несмещенности
и т.п., анализируемым в теории статистического оценивания и статисти-
ческой проверки гипотез.
508 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
Как и в параллельных алгоритмах, основными средствами и идеями,
при конструировании последовательных кластер-процедур являются: ме-
ра близости или расстояние между группами; порог; эталонные множества
или точки; функционал качества разбиения.
Так же, как и прежде, более простой, а, главное, всегда имеющей ре-
шение, является обычная задача типизации, при которой исходное множе-
ство многомерных наблюдений разбивается на определенное число «обла-
стей группирования» по принципу наперед заданной взаимной близости
элементов, отнесенных к одной области группирования. Простейшим при-
мером такого рода является разбиение на интервалы группирования ис-
ходной выборки одномерных наблюдений, особенно необходимое как раз
при достаточно больших объемах выборки п.
Именно такую задачу решает, например, простой последовательный
алгоритм, использующий понятие порога с. В этом алгоритме случайным
образом выбирается точка X], которая объявляется центром ej первой
группы. Затем точка Х2 относится к первой группе, если р(Х2эе1) с.
В противном случае Х2 принимается за центр второй группы Х2 = е2 и
т. д. На l-м шаге, когда уже имеется г групп, точка Xt либо становится
центром (г — 1)-й группы, либо относится к той из групп, для которой
p(Xi9ej) с. Если таких групп несколько, то выбирается та, к центру
которой точка Xi ближе всего; если и таких групп несколько, то устана-
вливаются некоторые соглашения о том, куда относить Xj в этом случае.
Остановимся далее на описании двух наиболее общих и наиболее ис-
следованных последовательных кластер-процедурах.
а)	Метод fe-средних. Пусть наблюдения X\^X2i...tXn требуется
разбить на заданное число к (к п) однородных (в смысле некоторой
метрики р) классов.
Смысл описываемого алгоритма — в последовательном уточнении
E(v)	г («) (v)	(v)-i /
1 ' = {е, ',63	(v — номер итерации, v =
0,1,2,...) с соответствующим пересчетом приписываемых им «весов»
rk(v) Г (v)	(v)	(v)l тт	<-	n(0)
Я' = {(j) ',о>2	}- При этом нулевое приближение Е' 7 строится
с помощью случайно выбранных первых к точек исследуемой совокупно-
сти, т. е.
«4о) = 1, i = l,2,...,k.
Затем на 1-м шаге «извлекается» точка Хь+1 и выясняется, к какому из
(0)	-	тг	„
эталонов ' она оказалась ближе всего. Именно этот, самый близкий
к А*+1, эталон заменяется эталоном, определяемым как центр тяжести
старого эталона и присоединенной к нему точки (с увеличением на
12.4. КЛАССИФИКАЦИЯ БЕЗ ОБУЧЕНИЯ
509
единицу соответствующего ему веса), а все другие эталоны остаются неиз-
менными (с прежними весами) и т. д. Таким образом, пересчет эталонов и
весов на v-м шаге, т.е. при извлечении очередной точки Xk+vi происходит
по следующему правилу:
/ V" (v~0\	• /V (v—1) \
’ 1 •	 если p(X*+v) ej ’) = mmkp{Xk+v,e\
(v—1)
е- '	в противном случае,
(„)	+ если p(Xt+„,e^_'))= rnin p(Xt+„,e’v“l)),
I (v-1)
[	, в противном случае,
t = l,2,...,A.
При этом если обнаруживается несколько (по t) одинаковых мини-
мальных значений p(Xk+vi ejv-1^), то можно условиться относить точку
Xk+v * эталону с минимальным порядковым номером.
При достаточно большом числе итераций или при достаточно боль-
ших объемах классифицируемых совокупностей п и при весьма широких
ограничениях на природу исследуемых наблюдений дальнейший пересчет
эталонных точек практически не приводит к их измерению, т.е. имеет
место сходимость (в определенном смысле) к некоторому пределу при
и—► оо.
Если же в какой-то конкретной задаче исследователь не успел до-
браться до стадии практически устойчивых (по и) значений эталонных
точек, то пользуются одним из двух вспомогательных приемов. Либо «за-
цикливают* алгоритм, «прогоняя* его после рассмотрения последней точ-
ки Хп = Xjt+(n-fc) снова через точку затем Xj, и т.д., либо произво-
дят многократное повторение алгоритма, используя в качестве начального
эталона Е^° различные комбинации из к точек исследуемой совокупности
и выбирая для дальнейшего наиболее повторяющийся (в некотором смы-
сле) финальный эталон E<n-fc\
Окончательное разбиение S исследуемой совокупности многомерных
наблюдений на к классов производится в соответствии с правилом описан-
ного выше минимального дистанционного разбиения 5(E) относительно
центров тяжести (эталонов) Е = Е^п-*\ которое, кстати, является част-
ным случаем разбиений ранее описанной общей схемы эталонных алго-
ритмов, получающихся при
V?(X, Ej) = р(Х, Е/),
510
ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
т. е.
S((E)= {X: p(X,El)<p(X,Ej)-, 7 = 1,2,...,*; j / /}.
Если оказывается, что р(Х, Е() = р(Х, Ej)y то точку X относят к тому из
классов Si и Sj, который обладает меньшим порядковым номером.
Проведенные исследования свойств метода ^-средних (см., например,
[Айвазян С. А. и др., 1989] говорят о том, что в достаточно общих си-
туациях при больших объемах выборочных совокупностей этот алгоритм
строит разбиение, близкое к наилучшему в смысле функционала (12.25).
б)	Метод ^средних при неизвестном числе классов. Для обоб-
щения описанного метода на случай неизвестного числа классов следует
задаться двумя константами Фо и Фо, названными соответственно мерой
грубости и мерой точности. Работа алгоритма также состоит в после-
довательном построении эталонных точек = (EjV\..., и весов
w] ,..	но число классов k(v) может меняться при этом от итера-
ции к итерации.
Па нулевом шаге итерации берется любое начальное &(0) и полагайся
Затем производится процедура «огрубления» эталонных точек. А именно,
подсчитывается расстояние между двумя ближайшими эталонными точ-
ками и сравнивается это расстояние с заданной мерой грубости Фо. Если
это минимальное расстояние меньше Фо, то соответствующая пара эта-
лонных точек заменяется их взвешенным средним с весом, равным сумме
соответствующих двух весов. Процедура огрубления заканчивается то-
гда, когда расстояние между любыми двумя эталонными точками не мень-
ше чем Фо- Пусть в результате процедуры огрубления мы имеем число
эталонных точек fc(0)(fc(0)	fc(0)), эталонные точки E^°\j = 1,...,£(0))
и веса j = 1,..., fc(0)).
Па первом шаге итерации извлекается точка А\(о)ч-1 и вычисляет-
ся расстояние от Xjt(o)+i До ближайшей к ней эталонной точки EjQ\j =
1,...,Л(0)). При этом если это расстояние больше Фо, то Xjt(o)+i объ-
является новой эталонной точкой Efc(o)+i = -A a(o)4-i с весом Wfc(o)+i — Ь
а все остальные эталонные точки и соответствующие им веса остаются
неизменными.
Если это минимальное расстояние меньше чем Фо, то самый близ-
кий к Xfc(o)+i эталон заменяется эталоном, определяемым как центр тя-
жести старого эталона и присоединенной к нему точки Хцо)+1. Вес точки
выводы
511
^к(о)+1 считается равным 1. Вес этого нового эталона равен сумме весов
объединяемых точек (старого эталона и точки А\(о)+1)-
Все остальные эталоны и соответствующие веса остаются неизменны-
ми. Таким образом, пересчет эталонов и весов в этом случае происходит
точно так же, как и в обычном методе fc-средних.
После процедуры огрубления эталонных точек переходят ко 2-му ша-
гу итерации и так далее.
Выбирая различные константы Фо» мы будем с помощью этого
алгоритма получать различные разбиения. Выбор величин Фо и Фо мож-
но считать удачным, если разбиение, соответствующее этим величинам,
признается оптимальным или с точки зрения экспертов, или в смысле
принятых функционалов качества разбиения.
ВЫВОДЫ
1.	Разделение рассматриваемой совокупности объектов или явлений
на однородные (в определенном смысле) группы называется классифика-
цией. При этом термин «классификация» используют, в зависимости
от контекста, для обозначения как самого процесса разделения, так и его
результата. Это понятие тесно связано с такими терминами, как группи-
ровка, типологизация, систематизация, дискриминация, кластеризация, и
является одним из основополагающих в практической и научной деятель-
ности человека.
2.	Среди типов прикладных задач классификации следует выделить:
1) комбинационные группировки и их непрерывные обобщения — разби-
ение совокупности на интервалы (области) группирования; 2) простая
типологизация: выявление естественного расслоения анализируемых дан-
ных (объектов) на четко выраженные «сгустки» (кластеры), лежащие
друг от друга на некотором расстоянии, но не разбивающиеся на столь
же удаленные друг от друга части; 3) связная неупорядоченная типоло-
гизация. использование реализованной в пространстве результирующих
показателей простой типологизации в качестве обучающих выборок при
классификации той же совокупности объектов в пространстве описатель-
ных признаков; 4) связная упорядоченная типологизация, которая отлича-
ется от связной неупорядоченной возможностью экспертного упорядоче-
ния классов, полученных в пространстве результирующих показателей, и
использованием этого упорядочения для построения сводного латентного
результирующего показателя как функции от описательных переменных;
5) структурная типологизация дает на «выходе» задачи дополнитель-
но к описанию классов еще и описание существующих между ними и их
элементами структурных (в том числе иерархических) связей; 6) типоло-
512 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
гизация динамических траекторий системы. в качестве классифицируе-
мых объектов выступают характеристики динамики исследуемых систем,
например, дискретные или непрерывные временные ряды или траектории
систем, которые в каждый момент времени могут находиться в одном из
заданных состояний.
3.	Определяющим моментом в выборе подходящей математической
постановки для конкретной задачи классификации является ответ на во-
прос, на какой исходной информации будут основаны наши выводы. Ис-
ходную информацию целесообразно подразделять на: а) априорные све-
дения об искомых классах; б) предварительную выборочную информацию
(так называемые обучающие выборки); в) наблюдения, подлежащие клас-
сификации. Определение необходимого для решения анализируемой зада-
чи классификации математического инструментария (моделей, методов)
в зависимости от характера и состава исходной информации может быть
осуществлено с помощью табл. 12.3.
3.	Если исследователь (статистик, эконометрист) располагает, наря-
ду с классифицируемыми данными, так называемыми обучающими вы-
борками (12.1), то для решения задачи классификации он должен обра-
титься к методам дискриминантного анализа (см. п. 12.2). При этом
каждый класс интерпретируется как одномодальная генеральная совокуп-
ность, закон распределения вероятностей (з.р.в.) которой оценивается по
соответствующей обучающей выборке. Если априорные сведения позволя-
ют сделать вывод об общем параметрическом виде з.р.в. каждого клас-
са, то используют методы параметрического дискриминантного анализа
(ДА). Если общий вид закона распределения внутри классов неизвестен,
то обучающие выборки используются для получения непараметрических
оценок внутриклассовых з.р.в., а сами процедуры классификации называ-
ют непараметрическим ДА.
5.	Общая постановка задачи классификации объектов в условиях от-
сутствия обучающих выборок (т. е. задачи автоматической классифи-
кации) состоит в требовании разбиения этой совокупности на некоторое
число (заранее известное или нет) однородных в определенном смысле
классов. При этом априорные сведения об искомых классах могут давать
основания для того, чтобы интерпретировать каждый искомый класс как
параметрически заданную одномодальную генеральную совокупность, и
тогда для построения правила классификации может быть использована
модель смеси распределений. При более скудных априорных сведениях
о классах используются методы и модели кластер-анализа, включая ие-
рархические методы классификации. В обоих случаях исходная стати-
стическая информация (наблюдения, подлежащие классификации) пред-
выводы
513
ставлены матрицами вида (9.1*) «объект-свойство». В задачах кластер-
анализа исходная статистическая информация может быть представлена
также матрицей попарных расстояний (или близостей) вида (9.2). По-
нятие «однородности» основано на предположении, что геометрическая
близость двух или нескольких объектов означает близость их «физиче-
ских» состояний, их сходство.
6.	Решить задачу расщепления смеси распределений (в выборочном
варианте) — это значит по имеющейся выборке классифицируемых на-
блюдении, извлеченной из генеральной совокупности, являющейся смесью
генеральных одномодальных совокупностей известного параметрического
ввда, построить статистические оценки для числа компонентов смеси, их
удельных весов и параметров, их определяющих. После этого отнесение
классифицируемых наблюдений к тому или иному классу производится по
тем же правилам, что и в схеме дискриминантного анализа. В теоретиче-
ском варианте задача расщепления смеси заключается в восстановлении
компонентов смеси и смешивающей функции (удельных весов) по задан-
ному распределению всей (т.е. смешанной) генеральной совокупности и
Называется задачей идентификации компонентов смеси (эта задача не
всегда имеет решение).
7,	Базовая идея, лежащая в основе принятия решения, к какой из к
анализируемых генеральных совокупностей следует отнести классифици-
руемое наблюдение, является одной и той же как для модели дискрими-
нантного анализа (классификация при наличии обучения; см. п. 12.2), так
к для модели смеси: и в том и в другом случае наблюдение приписывают
к той генеральной совокупности (к тому компоненту смеси), в рамках
которой (которого) оно выглядит наиболее правдоподобным. Однако
главное отличие схемы параметрического ДА от схемы автоматической
классификации, построенной на модели смеси распределений, — в способе
оценивания неизвестных параметров, от которых зависят функции, описы-
вающие классы (в первом случае — по обучающим выборкам, а во втором
неизмеримо сложнее — в рамках одного из методов оценки параметров
смеси распределений).
8.	Основными «узкими местами* подхода, основанного на мето-
де максимального правдоподобия статистического оценивания параме-
тров смеси распределений, являются (помимо необходимости «угадать»
общий параметрический вид распределения, задающего каждый из клас-
сов) требование ограниченности анализируемой функции правдоподобия,
высокая сложность и трудоемкость процесса вычислительной реализации
соответствующих процедур и медленная сходимость порождаемых ими
терационных алгоритмов.
514 ГЛ. 12. РАСПОЗНАВАНИЕ ОБРАЗОВ И ТИПОЛОГИЗАЦИЯ ОБЪЕКТОВ
9.	Математическая постановка задачи автоматической классифи-
кации в рамках неиерархических схем кластер-анализа требует формат
лизании понятия «качество разбиения». С этой целью в рассмотрение
вводится понятие критерия (функционала) качества разбиения Q(S), ко-
торый задает способ сопоставления с каждым возможным разбиением S
заданного множества объектов на классы некоторого числа Q(S), оценива-
ющего (в определенной шкале) степень оптимальности данного разбиения.
Тогда задача поиска наилучшего разбиения S* сводится к решению опти-
мизационной задачи вида
Q(S} -*
О
где А — множество всех допустимых разбиений.
В статистической практике выбор функционала качества разбиения
Q(S) обычно осуществляется весьма произвольно и опирается скорее
на эмпирические и профессионально-интуитивные соображения, чем на
какую-либо точную формализованную схему.
10.	В статистических классификационных процедурах иерархическо-
го типа главной целью анализа является получение наглядного предста-
вления о стратификационной структуре всей классифицируемой совокуп-
ности в виде дендрограммы.
11.	Выбор метрики (или меры близости) между объектами, каждый
из которых представлен значениями характеризующего его многомерного
признака, является узловым моментом исследования, от которого решаю-
щим образом зависит окончательный вариант разбиения объектов на клас-
сы при любом используемом для этого алгоритме разбиения. В каждой
конкретной задаче этот выбор должен производиться по-своему, в зависи-
мости от главных целей исследования, физической и статистической при-
роды анализируемого многомерного признака, априорных сведений о его
вероятностной природе и т. д. В этом смысле схемы, основанные на ана-
лизе смесей распределений, а также классификация по исходным данным,
уже представленным в виде матрицы попарных расстояний (близостей),
находятся в выгодном положении, поскольку не требуют решения вопроса
о выборе метрики.
12.	Важное место в построении классификационных процедур, в пер
вую очередь иерархических, занимает проблема выбора способа вычисле-
ния расстояния между подмножествами объектов. Полезное обобщение
большинства используемых в статистической практике вариантов вычи-
сления расстояний между двумя группами объектов дает расстояние, под-
считываемое как обобщенное степенное среднее всевозможных попарных
расстояний между представителями рассматриваемых двух групп (см.
(12.21)).
ГЛАВА 13. СНИЖЕНИЕ РАЗМЕРНОСТИ
ИССЛЕДУЕМОГО МНОГОМЕРНОГО
ПРИЗНАКА И ОТБОР НАИБОЛЕЕ
ИНФОРМАТИВНЫХ ПОКАЗАТЕЛЕЙ
13.1. Сущность, типологизация и
прикладная направленность задач
снижения размерности
В исследовательской и практической статистической работе при-
ходится сталкиваться с ситуациями, когда общее число р признаков
(1)	(2)	(р)
г	, регистрируемых на каждом из множества обследуемых
объектов (стран, городов, предприятий, семей, пациентов, технических
или экологических систем), очень велико — порядка ста и более. Тем не
менее имеющиеся многомерные наблюдения
i — 1,2,..., п,
(13.1)
следует подвергнуть статистической обработке, осмыслить либо ввести в
базу данных для того, чтобы иметь возможность их использовать в нуж-
ный момент.
Желание статистика представить каждое из наблюдений (13.1) в ви-
де вектора Z некоторых вспомогательных показателей	. ..,z^₽ с
существенно меньшим (чем р) числом компонент р бывает обусловлено в
первую очередь следующими причинами:
•	необходимостью наглядного представления (визуализации) исход-
ных данных (13.1), что достигается их проецированием на специально
516 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
подобранное трехмерное пространство (р = 3), плоскость (р* = 2) илн
числовую прямую;
•	стремлением к лаконизму исследуемых моделей, обусловленному не*
обходимостыо упрощения счета и интерпретации полученных статисти-
ческих выводов;
•	необходимостью существенного сжатия объемов хранимой стати-
стической информации (без видимых потерь в ее информативности), если
речь идет о записи и хранении массивов типа (13.1) в специальной базе
данных.
При этом новые (вспомогательные) признаки z&\могут
выбираться из числа исходных или определяться по какому-либо правилу
по совокупности исходных признаков, например как их линейные комби-
нации. При формировании новой системы признаков к последним предъ-
являются разного рода требования, такие, как наибольшая информатив-
ность (в определенном смысле), взаимная некоррелированность, наимень-
шее искажение геометрической структуры множества исходных данных
и т. п. В зависимости от варианта формальной конкретизации этих тре-
бований приходим к тому или иному алгоритму снижения размерности.
Имеется, по крайней мере, три основных типа принципиальных предпо-
сылок, обусловливающих возможность перехода от большого числа р ис-
ходных показателей состояния (поведения, эффективности функциониро-
вания) анализируемой системы к существенно меньшему числу р' наибо-
лее информативных переменных. Это, во-первых, дублирование инфор-
мации, доставляемой сильно взаимосвязанными признаками; во-вторых,
неинформативность признаков, мало меняющихся при переходе от одно-
го объекта к другому (малая «вариабельность» признаков); в-третьих,
возможность агрегирования, т.е. простого или «взвешенного» суммиро-
вания, по некоторым признакам.
Формально задача перехода (с наименьшими потерями в информатив-
ности) к новому набору признаков z ,z' ,...	* может быть описана
следующим образом. Пусть Z = Z(X) = (^1\^2\...,^F^)T — некото-
рая р'-мерная вектор-функция от исходных переменных
(р* < р) и пусть Ipt(Z(X)) — определенным образом заданная мера инфор-
мативности р'-мерной системы признаков Z(X) = (л^(Х),..., z^v \%))Т.
Конкретный выбор функционала /р»(И) зависит от специфики решаемой
реальной задачи и опирается на один из возможных критериев: критерий
автоинформативности, нацеленный на максимальное сохранение инфор-
мации, содержащейся в исходном массиве {X,*}i=^ относительно самих
исходных признаков; и критерий внешней информативности, нацеленный
13.1. СУЩНОСТЬ ЗАДАЧ СНИЖЕНИЯ РАЗМЕРНОСТИ
517
МЯЮ)
на максимальное «выжимание» из {К-р:- информации, содержащейся
в этом массиве относительно некоторых других (внешних) показателей.
Задача заключается в определении такого набора признаков Z, най-
денного в классе F(X) допустимых преобразований исходных показателей
что
(13-2)
Тот или иной вариант конкретизации этой постановки (определяю-
щий конкретный выбор меры информативности IP>(Z) и класса допусти-
мых преобразований) приводит к конкретному методу снижения размер-
ности: к методу главных компонент, факторному анализу, экстремальной
группировке параметров и т. д.
Математическая модель, лежащая в основе построения того или
иного метода снижения размерности, включает в себя обычно три основ-
ных компонента.
1.	Форма задаяжя жсходном жнформацжж. Речь идет об отве-
те на следующие вопросы: а) в каком виде (т.е. в виде (9.1), (9.2) или
еще каком-либо) задана описательная информация об объектах? б) име-
ется ли среди исходных статистических данных обучающая информация,
т.е. какие-либо сведения об анализируемом результирующем свойстве?
в) если обучающая информация присутствует в исходных статистических
данных, то в какой именно форме она представлена? Это могут быть, в
частности, в привязке к объекту О, (i = 1,2,..., и): значения «зависимой»
количественной переменной («отклика») у, в моделях регрессии; номер
однородного по анализируемому свойству класса, к которому относится
объект в задаче классификации; порядковый номер (ранг) объекта
в ряду всех объектов, упорядоченных по степени проявления рассматри-
ваемого свойства, в задачах анализа предпочтений и построения упоря-
доченных типологизаций; наконец, значения У, = (ур\...,у{^)Т набора
результирующих признаков, характеризующих анализируемое в класси-
фикационной задаче свойство1 * 3 *.
1 Речь идет о нахождении (в виде функции от X) такого вектора Z(X) —
(л^1	*^9 >(Х))Т, который обращает в максимум или минимум (в зависимо-
сти от конкретного содержательного смысла оптимизируемого критерия информа-
тивности) значение Zpf(Z). Поэтому справа в данном соотношении записано extr
(«экстремум»).
3 Перечисленные варианты не исчерпывают всех возможных форм представления обу-
чающей информации. Так, например, при надлежащей интерпретации элементов
518
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
2.	Тип оптимизируемого критерия I^(Z) информативност!
искомого набора признаков Z =	...,к^р^)Т. Как уже отмеча-
лось, критерий информативности может быть ориентирован на достиже-
ние разных целей.
Следует выделить целый класс критериев автоинформативности,
т.е. критериев, оптимизация которых приводит к набору вспомогатель-
ных переменных Z = (z^\...,zp )Т, позволяющих максимально точно
воспроизводить (в том или ином смысле, в зависимости от конкретного
вида критерия) информацию, содержащуюся в описательном массиве дан-
ных типа (9.1) или (9.2). Если описательная информация представлена в
виде матрицы «объект - свойство» (9.1), то речь идет о максимально точ-
ном восстановлении рх п значений исходных переменных
по значениям существенно меньшего числа (р х п) вспомогательных пе-
ременных ...,	\ Если же описательная информация представле-
на в виде матрицы попарных сравнений объектов (9.2), то речь идет о
максимально точном воспроизведении п3 элементов этой матрицы (7,j)
(>, j = 1,...,п) по значениям существенно меньшего числа (рг х п) вспо-
могательных переменных .., zjp (t = 1,..., n).
Будем называть критериями внешней информативности (имеется в
виду информативность, внешняя по отношению к информации, содержа-
щейся в описательном массиве (9.1) или (9.2)) такие критерии 7p«(Z), кото-
рые нацелены на поиск экономных наборов вспомогательных переменных
Z(X) = (z^\x),	\х))Т, обеспечивающих максимально точное воспро-
изведение (по значениям И, а значит в конечном счете по значениям X)
информации, относящейся к результирующему признаку (варианты ее за-
дания перечислены выше, в п. 1).
3.	Класс F(X) допустимых преобразовании исходных призна-
ков X. Вспомогательные признаки Z = (z^\...,^p^)т в случае пред-
ставления исходной описательной информации в форме матрицы «объ-
ект - свойство» (т.е. в виде (9.1)) конструируются в виде функций от
X, т.е. Z = Z[X). Как обычно в таких ситуациях, чтобы обеспечить
содержательность и конструктивную реализуемость решения оптимиза-
ционной задачи (13.2), следует предварительно договориться об ограни-
ченном классе допустимых решений F(X), в рамках которого эта оптими-
зационная задача будет решаться. Очевидно, от выбора F(X) будет су-
Tij матрицы (9.2) она может быть также отнесена к разновидностям обучающе! кн-
формацим (если, скажем, 7<j понимать как результат сравнения ио анализируемому
результирующему свойству объектов О, и Oj).
13.1. СУЩНОСТЬ ЗАДАЧ СНИЖЕНИЯ РАЗМЕРНОСТИ
519
щественно зависеть и получаемое решение Z(X) = (z^\x),..., z^(X))T
упомянутой оптимизационной задачи.
Итак, следуя предложенной выше логике, мы должны были бы про-
извести типологизацию задач снижения размерности по трем «входам»
(или «срезам»): форме задания исходной информации, типу (смыслу)
оптимизируемого критерия информативности и классу допустимых пре-
образований исходных переменных. Однако в предлагаемой ниже форме
представления результатов типологизации задач снижения размерности
(табл. 13.1) эти принципы реализованы в упрощенном виде за счет следу-
ющих двух практических соображений: 1) подавляющее большинство ме-
тодов снижения размерности базируется на линейных моделях, т. е. класс
Таблица 13.1
(АИ — автоинформативность, ВИ — внешняя информативность)
№ п/п	Класс и смысловая нацеленность критерия информативности; форма задания исходной информации-	Название соот- ветствующих мо- делей и методов. Главы и пункты книги
1	2	3
1	АИ: максимизация содержащейся в z , доли суммарной вариабельности исходных 0)	(р) признаков х' ',..., аг. Описательная информация: в форме (9.1). Обучающая информация: нет	Метод главных компонент, п. 13.2
2	АИ: Максимизация точности воспроизведения корреляционных связей между исходными признаками по их аппроксимациям с помощью вспомогательных переменных	...,	\ Описательная информация: в форме (9.1). Обучающая информация: нет	Модели и методы факторного ана- лиза и главных компонент, п. 13.2 и 13.3
3	АИ: разбиение исходных признаков на группы высококоррелированных (внутри группы) ' переменных и отбор от каждой группы фактора, имеющего максимальную интегральную характеристику корреляционных связей со всеми признаками данной группы. Описательная информация: в форме (9.1). Обучающая информация: нет	Метод экстре- мальной груп- пировки пара- метров, п. 13.4
520
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Продолжение таблицы 13.1
1	2	3
4	АИ: приписывание каждому объекту 0, значении / (1)	(р')х условных координат (zj	z) ') таким образом, чтобы по ним максимально точно восстанавливалась заданная структура попарных описательных отношений между объектами. Описательная информация: в форме (9.2). Обучающая информация: нет	Многомерное шкалирование, п. 13.6
5	АИ: максимальное сохранение заданных описательным массивом (9.1) анализируемых структурно-геометрических и вероятностных свойств после его проецирования в пространство меньшей размерности (в пространство, натянутое на z ,..., z' , р < р). Описательная информация: в форме (9.1). Обучающая информация: нет	Методы целе- направленного проецирования и отбор типо- образующих при- знаков в клас- тер-анализе, метод главных компонент, п. 13.2 и гл. 12
6	ВИ: минимизация ошибки прогноза (восстановления) значения результирующей количественной переменной по значениям описательных переменных (предикторов). Описательная информация: в форме (9.1). Обучающая информация: в форме зарегистрированных на объектах Oj,..., Оп значений соответственно уг,..., уп результирующего количественного показателя у	Отбор сущест- венных предик- торов в ре- грессионном анализе, гл. 15
7	ВИ: минимизация вероятностей ошибочного отнесения объекта к одному из заданных классов по значениям его описательных переменных. Описательная информация: в форме (9.1). Обучающая информация: для каждого описанного с помощью (9.1) объекта указан номер класса, к которому он относится	Отбор типо- образующих признаков в дискриминантном анализе, гл. 12
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
521
Продолжение таблицы 13.1
1	2	3
8	ВИ: максимизация точности воспроизведения (по значениям вспомогательных признаков) заданных в «обучении» отношений объектов по анализируемому результирующему свойству. Описательная информация: в форме (9.1). Обучающая информация: в форме попарных сравнений или упорядочений объектов по анализируемому результирующему свойству (см. сноску к п. 1 о возможности использования формы (9.2) для представления обучающей информации)	Методы латентно-струк- турного анализа, в том числе построение не- которой свод- ной латентной характеристики изучаемого результирую- щего свойства, п. 13.5
9	ВИ: максимизация точности воспроизведения (по значениям условных вспомогательных переменных) заданных в «обучающей информации» попарных отношений объектов по анализируемому результирующему свойству. Описательная информация: нет. Обучающая информация: в форме (9.2) (см. сноску к п. 1)	Многомерное шкалирование как средство латентно-струк- турного анализа, п. 13.6
допустимых преобразований F(X) — это класс линейных (как правило,
подходящим образом нормированных) преобразований исходных призна-
ков я/1),...,	2) спецификация формы задания исходной информации
связана со спецификацией смысловой нацеленности критерия информатив-
ности, а поэтому их удобнее давать в общей графе.
Данная в табл. 13.1 типологизация, как и всякая иная классифика-
ция, не претендует на исчерпывающую полноту. Заметим, что пункт 9
этой таблицы повторяет по существу пункт 4, они отличаются только ин-
терпретацией исходных данных вида (9.2) и соответственно конечными
прикладными целями исследования.
13.2.	Метод главных компонент
13.2.1.	Основные понятия и определения
Во многих задачах обработки многомерных наблюдений и, в частно-
сти, в задачах классификации исследователя интересуют в первую оче-
522
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
редь лишь те признаки, которые обнаруживают наибольшую изменчи-
вость (наибольший разброс) при переходе от одного объекта к другому.
С другой стороны, не обязательно для описания состояния объек-
та использовать какие-то из исходных, непосредственно замеренных на
нем признаков. Так, например, для определения специфики фигуры че-
ловека при покупке одежды достаточно назвать значения двух признаков
(размер-рост), являющихся производными от измерений ряда параметров
фигуры. При этом, конечно, теряется какая-то доля информации (портной
измеряет до одиннадцати параметров на клиенте), как бы огрубляются
(при агрегировании) получающиеся при этом классы. Однако, как покат
зали исследования, к вполне удовлетворительной классификации людей с
точки зрения специфики их фигуры приводит система, использующая три
признака, каждый из которых является некоторой комбинацией от боль-
шого числа непосредственно замеряемых на объекте параметров.
Именно эти принципиальные установки заложены в сущность того
линейного преобразования исходной системы признаков, которое приводит
к главным компонентам. Формализуются же эти установки следующим
образом.
Следуя общей оптимизационной постановке задачи снижения размер-
ности (13.2) и полагая анализируемый признак X р-мерной случайной ве-
личиной с вектором средних значений а = (а^\..., и ковариацион-
ной матрицей S = (<т^) (t,j = 1,2,...,р), вообще говоря, неизвестными,
определим в качестве класса F(X) допустимых преобразований исследуе-
мых признаков	их всевозможные линейные ортогональ-
ные нормированные комбинации, т. е.
F= lz: = $Зс>(®(,/) “а(0)’ 3 = 1,2,...,р|,
'	i/=i	'
где
р	р
= 1 И	= 0	(13.3)
|/=1	1/=1
для j = 1,2,...,р и к = 1,2,...,р, но у / к, а в качестве крите-
рия (меры) информативности р'-мерной системы показателей Z(X) =
(z^\x), z^(X),..., х^г (X)) выражение
/F.(Z(X)) =
D z(1) + • • • + D
(13.4)
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
523
Тогда при любом фиксированном р = 1,2,... ,р вектор искомых вспо-
могательных переменных Z(X) =	.,z^F\x))T определяется
как такая линейная комбинация
Z = LX
(13.5)
(где
матрица, строки которой удовлетворяют условию ортогональности), что

5^(Х))= №/,№))•
Полученные таким образом переменные	и назы-
вают главными компонентами вектора X. Отсюда вытекает следующее
определение главных компонент.
Первой главной компонентой я^(Х) исследуемой системы
показателей X = (х^\. ,.,х^) называется такая нормированно-
центрированная линейная комбинация этих показателей, которая среди
всех прочих нормированно-центрированных линейных комбинаций пере-
менных х^\...,х^ обладает наибольшей дисперсией.
k-й главной компонентой 2^*\Х) (к = 2,3, ...,р) исследуе-
мой системы показателей X = (х^\... ,х^)Т называется такая
нормированно-центрированная линейная комбинация этих показателей,
которая не коррелирована с k— 1 предыдущими главными компонентами
и среди всех прочих нормированно-центрированных и некоррелированных
с предыдущими к — 1 главными компонентами линейных комбинаций пе-
ременных х^\..., хМ обладает наибольшей дисперсией.
Замечание 1 (переход к центрированным переменным). По-
скольку, как увидим ниже, решение задачи (а именно вид матрицы ли-
нейного преобразования L) зависит только от элементов ковариационной
матрицы Е, которые в свою очередь не изменяются при замене исходных
переменных х^ переменными х^ —с^ (с^ — произвольные постоянные
числа), то в дальнейшем будем считать, что исходная система показателей
уже центрирована, т.е. что Ех^ = 0, j = 1,2,. ..,р. В статистической
практике этого добиваются, переходя к наблюдениям х^ = х^ — х^\ где
sl (для упрощения обозначений волнистую черту над цен-
524
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
трированной переменной и над главной компонентой в дальнейшем ста-
вить не будем).
Замечание 2 (переход к выборочному варианту). Поскольку в
реальных статистических задачах располагаем лишь оценками а и S со-
ответственно вектора средних а и ковариационной матрицы Е, то во всех
дальнейших рассуждениях под а№ понимается а под а*,- — выбороч-
ная ковариация оц —	“ z^)(z|^ — z^)/n (j, k = 1,2,... ,р).
Замечание 3. Использование главных компонент оказывает»
наиболее естественным и плодотворным в ситуациях, в которых все ком-
поненты а/1),	..., хМ исследуемого вектора X имеют общую физиче-
скую природу и соответственно измерены в одних и тех же единицах. К
таким примерам можно отнести исследование структуры бюджета време-
ни индивидуумов (все z^ измеряются в единицах времени), исследование
структуры потребления семей (все z^ измеряются в денежных единицах),
исследование общего развития и умственных способностей индивидуумов
с помощью специальных тестов (все z^ измеряются в баллах), разного ро-
да антропологические исследования (все z<^ измеряются в единицах меры
длины) и т.д. Если же признаки z^\z^2\...,z^ измеряются в различ-
ных единицах, то результаты исследования с помощью главных компонент
будут существенно зависеть от выбора масштаба и природы единиц из-
мерения. Поэтому в подобных ситуациях исследователь предварительно
переходит к вспомогательным безразмерным признакам z , например,
с помощью нормирующего преобразования
*(«) _
и —
X
t — 1,2,...,р \
1/=1,2,...,п;’
где дц соответствует ранее введенным обозначениям, а затем строит глав-
ные компоненты относительно этих вспомогательных признаков X* и их
ковариационной матрицы Ех- > которая, как легко видеть, является одно-
временно выборочной корреляционной Матрицей R исходных наблюдений
13.2.2.	Вычисление главных компонент
Из определения главных компонент следует, что для вычисления пер-
вой главной компоненты необходимо решить оптимизационную задачу ви-
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
525
да (13.2), т.е. в данном случае:
D(ijX)-.
<1*7 = 1.
max;
h
(13.6)
где li — первая строка матрицы L (см. (13.5)). Учитывая центрирован-
ность переменной X (т.е. ЕХ = 0) и то, что Е(ХХТ) = Е, имеем
D(GX) = E(ltX)2 = E(liXXTli) = liEi}.
Следовательно, задача (13.6) может быть записана
ZiEZj -+ max;
(13.б')
м? = i,
Вводя функцию Лагранжа ^(Л, А) = G^i ~ A(Z]Zi — 1) и дифференцируя
ее по компонентам вектор-столбца Z^, имеем (см. Приложение 2):
= 2Е1, - 2А/Г,
dl]
что дает систему уравнений для определения />:
(Е - А1)ЛТ = 0
(13-7)
(здесь 0 = (0,0,...,0)Т — р-мерный вектор-столбец из нулей).
Для того чтобы существовало ненулевое решение системы (13.7) (а
оно должно быть ненулевым, так как l\l = 1), матрица Е — AI должна
быть вырожденной, т.е.
|Е-А1| = 0.	(13.8)
Этого добиваются подбором соответствующего значения А. Уравне-
ние (13.8) (относительно А) называется характеристическим для матри-
цы Е. Известно (см. Приложение 2), что при симметричности и неотри-
цательной определенности матрицы Е (каковой она и является как всякая
ковариационная матрица) это уравнение имеет р вещественных неотрица-
тельных корней Ai > Aj > • • • > Ар > 0, называемых характеристически-
ми (или собственными) значениями матрицы Е.
Учитывая, что = D(ZjX) = Z1EZ^r и ZjEZ^ = А (последнее
соотношение следует из соотношения (13.7) после его умножения слева
на Zlt с учетом ZJ^ = 1), получаем D z^(X) = А.
526
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Поэтому для обеспечения максимальной величины дисперсии пере-
менной нужно выбрать из р собственных значений матрицы Е наи-
большее, т. е.
D2(,)(X) = X1.
Подставляем Aj в систему уравнений (13.7) и, решая ее относительно
/ц,..., /1Р, определяем компоненты вектора /j.
Таким образом, первая главная компонента получается как линей-
ная комбинация z^fX) = liX, где Ц — собственный вектор матрицы
Е, соответствующий наибольшему собственному числу этой матрицы.
Далее аналогично можно показать, что z^*\x) = lkXt где lk — соб-
ственный вектор матрицы Е, соответствующий /с-му по величине соб-
ственному значению Хк этой матрицы.
Таким образом, соотношения для определения всех р главных ком-
понент вектора X могут быть представлены в виде (13.5), где Z =
(s' , ...,z4') , X = (ar x'rf) , а матрица L состоит из строк
/у = (lyi,.. . ,/ур), j = 1»р, являющихся собственными векторами матрицы
Е, соответствующими собственным числам Ау. При этом сама матрица L
в соответствии с условиями (13.3) является ортогональной, т.е.
LLT = bTL = I.	(13.9)
В дальнейшем в целях упрощения обозначений мы будем опускать
«тильду» над переменными главных компонент, т. е. обозначать главные
компоненты просто Z = (z^\z<2\..., z^p ^).
13.2.3.	Основные числовые характеристики главных
компонент
Определим основные числовые характеристики (средние значения,
дисперсии, ковариации) главных компонент в терминах основных число-
вых характеристик исходных переменных и собственных значений матри-
цы Е:
а)	ЕИ = E(LX) = L • EX = 0;
б)	ковариационная матрица вектора главных компонент:
Ег = E(ZZT) = Е ((ЬХ)(ЬХ)Т) = Е(1ХХТЬТ)
= L-E(XXT)-LT = L-S-LT.
Умножая слева соотношения
(3 - Д*1)£ = 0, к = Гр,
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
527
на lj (j = Т7Й» получаем, что
(13.10)
Из (13.10), в частности, следует подтверждение взаимной некоррели-
рованности главных компонент, а также D z^ = Л* (к = 1,р);
в)	сумма дисперсий исходных признаков равна сумме дисперсий всех
главных компонент. Действительно,
р
= trSz = tr(LEbT) = tr ((LS)LT)
*=1
p
= tr{bT(LS)) = tr((LTL)E) = trE = £OzW;
. г) обобщенная дисперсия исходных признаков X (det Ex) равна обоб-
щенной дисперсии главных компонент. Действительно, обобщенная дис-
персия вектора Z равна
det Ег = det(LSLT) = det((LS)LT) = det (LT(LS))
= det ((bbT)S) =det(E).
Следствие 1. Из б) и в), в частности, следует, что критерий
информативности метода главных компонент (13.4) может быть пред-
ставлен в виде
Jy.(Z(X)) =	(13.4')
где Xi,Х2,...,Хр — собственные числа ковариационной матрицы Е век-
тора X, расположенные в порядке убывания.
Кстати, представление Ipt(Z(X)) в виде (13.4х) дает исследователю
некоторую основу, опорную точку зрения, при вынесении решения о том,
сколько последних главных компонент можно без особого ущерба изъ-
ять из рассмотрения, сократив тем самым размерность исследуемого про-
странства.
Действительно, анализируя с помощью (13.4х) изменение относитель-
но доли дисперсь ’, вносимой первыми ] главными компонентами, в за-
висимости от числа этих компонент, можно разумно определить число
528
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
компонент, которое целесообразно оставить в рассмотрении. Так, при из-
менении /р», изображенном на рис. 13.1, очевидно, целесообразно было бы
сократить размерность пространства с р = 10 до р = 3, так как добавле-
ние всех остальных семи главных компонент может повысить суммарную
характеристику рассеяния не более чем на 10%.
Рис. 13.1. Изменение относительной доля суммарной
мых признаков, обусловленной первыми р'
тами, в зависимости от р* (случай р = 10)
дисперсии исследуе-
главмыми жомпонеи-
Следствие 2. Если X* — вектор нормированных признаков
т.е.	= 0 u = 1 для j = 1,р, то соглас-
но замечанию 3 ковариационная и корреляционные матрицы совпадают
(гм. е. = R) и из 6) и в) следует
tr'Sz = trEy = trR = р
или
*=1
Тогда критерий информативности (13.4') может быть представлен в
виде
/P,(Z(X)) = M-p + V.
(13.4")
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
529
Проиллюстрируем вычисление и анализ главных компонент на при-
мере.
Пример 13.1. При формировании типообразующих признаков
предприятий отрасли были обследованы 24 предприятия (п = 24) по
трем технико-экономическим показателям: объему выпускаемой продук-
ции основным фондам х^ и себестоимости х^ (все переменные изме-
рялись в денежных единицах). По полученным в результате обследования
исходным статистическим данным	t = 1,2,...,24, была
определена выборочная ковариационная матрица
(451,39 271,17 168,70\
271,17 171,73 103,29 ] .
168,70 103,29 66,65 /
Решая, в соответствии
Л) вида
451,39-А
271,17
168,70
с (13.8), кубическое уравнение (относительно
271,17	168,70
171,73-А 103,29
101,29	66,65-А
= 0,
находим Ai = 680,40, А2 = 6,50, А3 = 2,86.
Подставляя последовательно численные значения А1э А2 и А3 в систему
(13.7) и решая эти системы относительно неизвестных Ц = (in,
(i = 1,2,3), получаем
It = (0,8126 0,4955 0,3068),
i2 = ( -0,5454	0,8321	0,1006 ),
/3 =(-0,2054 -0,2491	0,9465).
В качестве главных компонент получаем
z(,) = 0,81х(1) + 0,50х(2) + 0,31х<3>,
= - 0,55х(1) + 0,83х(2) + 0,10х(3),
х(3) = - 0,21х(,) - 0,25х<2) + 0,95х(3).
Здесь под х^'\ з и х'3* подразумеваются отклонения объема выпускае-
мой продукции (х^), основных фондов (х*2’) и себестоимости (х^3*) пред-
приятия от соответствующих средних значений.
Вычисление относительной доли суммарной дисперсии, обусловлен-
ной одной, двумя и тремя главными компонентами, в соответствии с фор-
530
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
мулой (13.4х) дает
9(1) = . .	. = 0.9864;
<*1 + А2 + л3
9(2) = .	= 0,9958;
А] + А2 + A3
9(3) =1.
Отсюда можно сделать вывод, что почти вся информация о специфике
предприятия данного типа содержится в одной лишь первой главной ком-
поненте, которую и естественно использовать при соответствующей ти-
пологизации предприятий.
Матрица «нагрузок» А = (atJ-), itj = 1,2, ...,р, главных
компонент на исходные признаки также является важной характери-
стикой главных компонент. Если анализируемые переменные X =
/ (1) (з)	(р)\Т
(зг ',3!'	х'г’) предварительно процентрированы и пронормирова-
ны (см. выше замечания 1 и 3), т.е. если главные компоненты стро-
ятся для признаков X* = (z*^\z*^2\...,х*<₽>)т,	= 0,	= 1,
i = 1,2,...,р, то элементы матрицы нагрузок определяют одновре-
менно степень тесноты парной линейной связи (т.е. парный коэффициент
корреляции) между г '' и г ' и удельный вес влияния пронормированной
*(»)
j-и главной компоненты на признак х ' '.
Матрица нагрузок А определяется соотношением
А = ЬТА*,	(13.11)
Докажем, что элементы действительно обладают сформулирован-
ными выше свойствами. Введем в рассмотрение нормированные главные
компоненты ZB = (хг£х\,гг£2\..., получающиеся из обычных глав-
ных компонент домножением на А“^, т.е.
Z, =A-iZ.
(13.13)
Очевидно, что 2, =	/ v/Xj и соответственно
= 1.
(13.14)
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
531
Выразим из соотношения (13.5) X* через Z:
X‘ = L-,Z = bTZ
(13.15)
(при этом учтено, что мы, во-первых, упростили обозначения и вместо
Z теперь используем Z, а во-вторых, что матрица L — ортогональна по
условию (см. (13.3)) и, следовательно, L"1 = LT (см. Приложение 2)).
Принимая во внимание (13.11) и (13.13), из (13.15) получаем:
Х* = 1ТА^А_^Е = А2„,
(13.16)
= ап4,) +	+ • • • +	(13.16')
т.е. коэффициент действительно определяет удельный вес влияния J-й
нормированной главной компоненты z^ на t-и исходный признак.
Далее,
,/»(•) Aih Е[(®*(,) - Ег*< V» - Ez°>)]
r(x 'z	>/dz<W>
_ E(Z(,)z0)) _ / .(i) z(j)
= Е (г*(*,4,)) = Е [(<414'’ + • • • + ajpz^))z^)]
= ay Е ((4Л)’) = <М,	(13-17)
т.е. коэффициент а^ действительно определяет величину парного коэф-
фициента корреляции между х*( и (при выводе соотношения (13.17)
*(•)
использовались нормированность и центрированность переменных х и
а также тот факт, что z„J = z^/'
Отметим еще два свойства элементов матрицы нагрузок А.
Из определения матрицы А (13.11) следует:
АТА = (AJL)(LTAJ) = А^(ААТ)А^ = лМ = А,
а это означает, что сумма квадратов элементов любого j-го столбца
матрицы А равна дисперсии (j-й) главной компоненты Xj, т.е.
2	2	2
°lj +	4-----1" afi = Aj-
(13.18)
532
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Возводя в квадрат обе части соотношения (13.16*) и беря математи-
ческое ожидание от результата, непосредственно имеем:
D г*’ = Е (а^0 + - + а^>)’ = £ а?,- Е (4Я)’ = £ а?,-, (13.19)
i=i	i=i
т.е. с учетом	= 1 получаем, что сумма квадратов элементов
любой (i-й) строки матрицы нагрузок А. равна единице.
Приведенные здесь свойства используются, в частности, при содепжа-
тельной интерпретации главных компонент. Так, соотношение (13.16*) да-
ет основание придавать главной компоненте z содержательный смысл,
соответствующий исходному признаку для которого коэффициент
aioj достигает максимального значения (при условии, что |aioJ-1 > 0,6).
Пример 13.2. Компонентный анализ проведен по данным двадца-
ти сельскохозяйственных районов (п = 20) области, которые содержат
результаты измерений следующих показателей: ж^ — число колесных
тракторов на 100 га; ж1 1 — число зерноуборочных комбайнов на 100 га;
ж^ — число орудий поверхностной обработки почвы на 100 га; ж^ —
количество удобрении, расходуемых на гектар; ж' ' — количество средств
защиты растений, расходуемых на гектар.
Требовалось выделить р1 < 5 первых главных компонент для анализа
и дать им содержательную интерпретацию.
Расчеты проводились по нормированным данным и представлены в
табл. 13.2.
Таблица 13.2
Главные компоненты	/’>		г<3’		z<5>
Собственные значения А,-	3,04	1,41	0,43	0,10	0,02
Вклад t-й главной компоненты (%) в суммарную дисперсию	60,8	28,2	8,6	2,0	0,4
Суммарный вклад первых главных компонент (%)	60,8	89,0	97,6	99,6	100,0
При расчете относительного вклада главных компонент учитывалось,
что Si=i А, = р = 5. Для анализа были оставлены две первые главные
компоненты (р* = 2), на которые приходится 89% суммарной вариации.
Для интерпретации главных компонент построена матрица фактор-
ных нагрузок
' 0,95* 0,97* 0,94* 0,24 0,56 \Т
V-0,19 -0,17 -0,28 0,88* 0,67*) '
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
533
Звездочкой (*) отмечены элементы |в^| > 0,6, которые следует учитывать
(1)	(з)
при интерпретации главных компонент z' и z .
Из вида матрицы нагрузок А следует, что первая главная компонента
_	О)
наиболее тесно связана с показателями: х ' — число колесных тракторов
(ан = r(z^\z^^) = 0,95);	— число зерноуборочных комбайнов (aji =
r(x^2\z^) = 0,97); а ' — число орудий поверхностной обработки почвы
на 100 га (a31 = r(x^3\z^) = 0,94). Поэтому первая главная компонента
z^ интерпретирована как уровень механизации работ.
Вторая главная компонента z^ тесно связана с количествами удо-
брения (х^) и средств защиты растений (я ^), расходуемых на гектар.
Соответственно z^ интерпретируется как уровень химизации растение-
водства.
13.2.4.	Геометрическая интерпретация главных компонент
Всякий переход к меньшему числу (р) переменных z^\..., z^p \ осу-
ществляемый с помощью ортогонального линейного преобразования (ма-
трицы) С = (c,j), i = 1,2,...,р\ j = 1,2,... ,р, можно рассматривать как
проекцию исследуемых р-мерных наблюдений XiiX2i...1Xn в простран-
ство размерности р\ натянутое на оси Oz^\Oz^2\..., Oz^p \ где
•’ = 1.2,(13.20)
J=1
При этом проекциями р-мерных исходных наблюдений X, (» = 1,2, ...,п)
будут р'-мерные точки
Zi = CXit i=l,2,...,n.
(13.21)
Для пояснения сущности того линейного преобразования исходной си-
стемы признаков, которое приводит к главным компонентам, рассмотрим
его геометрическую интерпретацию на примере двумерной системы наг
блюдений (z^jS,2)), i = 1,2,...,п, извлеченной из нормальной генераль-
ной совокупности со средним значением а = (a^\a^) и ковариационной
матрицей
Е=(<т*	’№), НС1, > о, а2 >0.
О'] J
„22	(1)	(2)
Здесь ffi и о2 — дисперсии компонент соответственно г ' и г а г —
коэффициент корреляции между ними. Геометрически это означает, что
534 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
точки	будут располагаться примерно в очертаниях эллипсоидов
рассеивания вида (см. рис. 13.2а)
В этом случае для изучения	удобно перейти к новым координа-
там (z^\z^) с помощью преобразования:
z^ = (а^1) — а^) cos а + (ж^ — а^2^) sin а,
z = — (a/1) — </^) sin а + (a/2^ — </2^) cos а
где
tg2a =
2r<7j <72
~2	2 
<7! - <72
После этого преобразования точки (41\*РЬ также будут распреде-
лены нормально, но компонента z^ уже не будет зависеть от z^2\ Кроме
того, если выбрать направления так, что Dz^1^ > Dz^2\ то геометриче-
ски это будет означать следующее: сначала производится перенос начала
координат в точку (а^\ </’)), а затем оси поворачиваются на угол а так,
чтобы ось z^ шла вдоль главной оси эллипсоида рассеивания (рис. 13.2а).
Чем ближе |г| к единице, тем теснее группируются наблюдения около глав-
ной оси эллипсоида рассеивания (т.е. около новой оси z^) и тем менее
значащим для исследователя является разброс точек в направлении оси
z(2>, а следовательно, и сама эта координата. В предельном случае |r| = 1,
исследуемые наблюдения в координатах (z^\z^) вообще не отличаются
по координате z^ (см. рис. 13.26).
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
535
Рис. 1S.2. Эллипс рассеяния исследуемых наблюдений и направление коор-
динатных осей главных компонент и а) умеренный раз-
брос точек; б) отсутствие разброса точек в направлении второй
главной компоненты (вырожденный случай)
536
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
13.2.5.	Оптимальные свойства главных компонент
Описываемые ниже свойства первых р главных компонент во многом
объясняют их широкую распространенность в практике статистических,
в том числе эконометрических, исследовании. Оказывается, к главным
компонентам можно прийти, решая оптимизационные задачи, на первый
взгляд не имеющие ничего общего с оптимизационной задачей типа (13.2).
Свойство наименьшей ошибки «автопрогноза» или наилуч-
шей самовоспроизводимости. Можно показать, что с помощью пер-
вых р* главных компонент	... ,^₽ (р < р) исходных признаков
(1) Р) (р)
х ,х ,...,аг ' достигается наилучшии прогноз этих признаков среди
всех прогнозов, которые можно построить с помощью р линейных комби-
наций набора из р произвольных признаков.
Поясним и уточним сказанное. Пусть требуется заменить ис-
ходный исследуемый р-мерный вектор наблюдений X на вектор Z -
(z ,z , ...,zv ) меньшей размерности р, в котором каждая из ком-
понент являлась бы линейной комбинацией р исходных (или каких-либо
других, вспомогательных) признаков, теряя при этом не слишком мно-
го информации. Информативность нового вектора Z зависит от того, в
какой степени р* введенных вспомогательных переменных дают возмож-
ность «реконструировать» р исходных (измеряемых на объектах) призна-
ков с помощью подходящих линейных комбинаций z^, z^\...,	\ Есте-
ственно полагать, что ошибка прогноза X по Z (обозначим ее а) будет
определяться так называемой остаточной дисперсионной матрицей векто-
ра X при вычитании из него наилучшего прогноза по И, т. е. матрицей
д - (ди)» г№
Здесь bitz^ — наилучший, в смысле метода наименьших квадратов,
прогноз по компонентам z^\ z^2\..., z<p (см. гл. 15). Ошибка про-
гноза X по Z задается как некоторая определенная функция от элементов
матрицы Д, т.е. сг = /(Д), где /(Д) определяет некоторый критерий
качества предсказания.
Рассмотрим следующие естественные меры ошибки прогноза:
/(Д) — 1г(Д) — Дп -f- Д22 4- • • • 4- Дрр;
(13.22)
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
537
/(А) = IIДII =
(13.23)
Здесь tr(A) и ||А|| — соответственно след и евклидова норма матрицы
Д. Доказано, что функции (13.22) и (13.23) одновременно достигают ми-
(1)	(2)	(р’)	«-
нимума тогда и только тогда, когда в качестве г1 , z' z' ' выбраны
первые р главных компонент вектора X, причем величина ошибки про-
гноза о явным образом выражается через последние р-р' собственных
чисел исходной ковариационной матрицы Е или приближенно — через по-
следние р—р собственных чисел	, Ар выборочной ковариационной
матрицы S, построенной по наблюдениям Xi,X2,. ..,ХЯ. В частности,
при /(А) = tr(A): о » Ар»+1 4- Ар»+2 + • • • 4- Ар;
при /(А) = ||А||: о w JAj»+1 4- Ар,+2 4- * • • 4- Ар.
Поясним идею описания (прогноза) исходных признаков	...,
х{р} с помощью меньшего, чем р, числа их линейных комбинаций на при-
мере 13.1.
В этом примере р = 3. Зададимся целью снизить размерность ис-
ходного факторного пространства до единицы (f = 1), т. е. описать все
три признака с помощью линейных комбинаций только от одной вспомо-
гательной переменной.
В соответствии с описанным выше экстремальным свойством «ав-
топрогноза» главных компонент возьмем в качестве этой единственной
вспомогательной переменной первую главную компоненту, т. е. перемен-
ную
z(,) = 0,81а/1' + 0,50z(2) + 0,31®(3).
Метод наименьших квадратов приводит к следующему правилу вы-
числения неизвестных коэффициентов Ъц (см. гл. 15):
_ cov (a/’\z^)
i,=	D?)
0,81 cov	4- 0,50 cov (s/2\®^) 4- 0,31 cov (x^3\x^)
“	Б71)	*
Подставляя в эту формулу значения cov(z^’\®^), взятые из ковари-
538
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
анионной матрицы S примера 13.1, получаем
«<‘>=b/*’+ew = 0,805^” + е(1),
/”= 621/‘>+£(2>= 0,49г(,)+£(3),
a(3)=431^+e<=,)=0.310^ + ?3\
где — случайные (остаточные) ошибки прогноза исходных центриро-
-	ч	(1)
ванных компонент по первой главной компоненте z
Если в качестве относительной ошибки прогноза исходного призна-
ка х^ до первой главной компоненте рассмотреть величину =
(De^/D®^) • 100%, то несложные подсчеты дают = 2%,	= 1,2%
и = 0,8%.
Суммарная характеристика относительной ошибки прогноза призна-
ков	и по z^ (в соответствии с вышеописанным) может быть
подсчитана по формуле
«сУм.отЯ = 100%• —(1) tr(p}----(5,- = 100% •	= 1,36%.
D (ar J + s' ' + аг ')	А1 + Аз + Аз
Свойства наименьшего искажения геометрической структу-
ры множества исходных р-мерных наблюдений при их проекти-
ровании в пространство р первых главных компонент. Речь идет
о следующих трех оптимальных свойствах главных компонент (формули-
руются без доказательства).
Свойство 1. Сумма квадратов расстояний от исходных точек-
наблюдений Xi,X2,...,ХП до пространства, натянутого на первые
р* главных компонент, наименьшая относительно всех других подпро-
странств размерности р1, полученных с помощью произвольного линей-
ного преобразования исходных координат.
Наглядным пояснением этого свойства может служить рис. 13.2а, на
котором ось z^ соответствует подпространству, натянутому на первую
главную компоненту (т.е. р = 2 и р* = 1), а сумма квадратов расстоя-
ний до этого подпространства есть сумма перпендикуляров, опущенных
из точек, изображающих наблюдения Xi = (xj.1^,®^), на эту ось.
Свойство 2. Среди всех подпространств заданной размерности
р (р < р), полученных из исследуемого признакового пространства с
помощью произвольного линейного преобразования исходных координат
х^\ а/2\..., в подпространстве, натянутом на первые р* главных
компонент, наименее искажается сумма квадратов расстояний между
всевозможными парами рассматриваемых точек-наблюдений.
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
539
В данном свойстве за критерий наименьшего искажения геометриче-
ской структуры совокупности исходных наблюдений Xi,X2,.Хп при-
нимается величина
=Е - л>)т(* -
»=1 у=1
т. е. сумма квадратов евклидовых расстояний между всевозможными па-
рами имеющихся наблюдений.
После проектирования точек X, в р -мерное пространство, определя-
емое матрицей преобразования С, мы получим точки-проекции Z, = С X,
(i = 1,2,..., п) и соответствующую им сумму квадратов евклидовых рас-
стояний
Мр' (И(С)) = £ £(z, - z^z, - z,).
i=l J=1
Можно показать, что при р' <р МР(Х) Afp»(Z(C)).
Так вот, на преобразовании L, с помощью которого получают первые
р главных компонент, достигается минимум разности МР(Х)—Мр>(2(C)),
т.е.
Mt{X) - М„ (Z(D) = mm [м,(Х) - Mp,(Z(C))].
Свойство 3. Среди всех подпространств заданной размерности
Р (/ < Р)> полученных из исследуемого факторного пространства с
помощью произвольного линейного преобразования исходных координат
а/1),...,^ , в пространстве, натянутом на первые р' главных компо-
нент, наименее искажаются расстояния от рассматриваемых точек-
наблюдений до их общего «центра тяжести», а также углы между пря-
мыми, соединяющими всевозможные пары точек-наблюдений с их общим
«центром тяжести».
13.2.6. Статистические свойства выборочных главных
компонент; статистическая проверка некоторых
гипотез
Смысл математико-статистических методов, как известно, состоит
в том, чтобы по некоторой части исследуемой генеральной совокупно-
сти (по выборке или, что то же, по ограниченному ряду наблюдений
Х1эХ2,...,Хп) выносить обоснованные суждения о ее свойствах в целом.
Применительно к рассматриваемой задаче нас в первую очередь ин-
тересует, как сильно свойства и характеристики выборочных главных
540
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
компонент могут отличаться от соответствующих свойств и характери-
стик главных компонент всей генеральной совокупности и, в частности,
как эта мера отличия зависит от объема выборочной совокупности (п),
по которой эти выборочные главные компоненты были построены. Так,
например, для изучения природы внутренних связей между характери-
стиками различных статей семейного бюджета потребления и для вы-
явления небольшого числа наиболее существенных в этом смысле показа-
телей исследователь может обследовать какое-то количество (п) семей и
по полученным результатам наблюдения Xi,Xj,...,Xn построить глав*
41) 42)	4₽') гл
ные компоненты У* s'	. Однако, увеличивая объем выборки п,
т. е. добавляя к имеющимся наблюдениям результаты наблюдения по до-
полнительно обследованным семьям, естественно ожидать, что пересчет
главных компонент с учетом добавленных наблюдений^ вообще говоря,
изменит (хотя, быть может, и незначительно) ранее полученные значе-
ния интересующих нас характеристик: Л,-, /, (* = 1,2,...,р) и т.п. В то
же время существует, по-видимому, такое (столь большое) п, дальнейшее
увеличение которого уже не будет практически приводить к изменению
основных характеристик главных компонент (другими словами, мы впра-
ве ожидать, что в соответствии со свойством статистической устойчиво-
сти (см. п. 6.2) главные компоненты выборок достаточно большого объема
практически совпадают с главными компонентами всей генеральной сово-
купности).
Выяснению некоторых вопросов, связанных с оценкой близости раз-
личных выборочных (2^, Ц, А.) и теоретических (z^, AJ характеристик
главных компонент, и посвящен настоящий пункт. Приведенные ниже ре-
зультаты исследований неизменно опираются на допущение нормальности
исследуемой генеральной совокупности и взаимной независимости извле-
ченных из нее наблюдений. Как и прежде, под Xi,Xa,...,Xn будем по-
нимать центрированные наблюдения, которые, строго говоря, даже при
независимых исходных наблюдениях уже не будут независимыми. Однако
при достаточно больших п можно пренебречь этим эффектом нарушения
независимости. Таким образом, X, Е 7V(0,E), i = 1,2,...,п (как следу-
ет из предыдущего, вектор средних значений а = БХ определяет лишь
точку в р-мерном пространстве, в которую переносится начало координат
при переходе к главным компонентам, и с самого начала будем считать
этот перенос уже осуществленным).
Вспомогательные факты, относящиеся к свойствам выбороч-
ных характеристик главных компонент (см., например, [Андер-
сон]). Бели все характеристические корни А], Aj,..., Ар ковариационной
матрицы Б различны, что и имеет место в большинстве приложений ана-
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
541
лиза главных компонент, то справедливо следующее:
1)	характеристические корни Ai,A2,...,Ap и соответствующие им
собственные векторы	выборочной ковариационной матрицы
2 являются оценками максимального правдоподобия для соответству-
ющих теоретических характеристик (соответственно Ai, Аз,..., Ар
и /1,/з,...,/р) и обладают всеми хорошими свойствами этих оценок
(состоятельность, асимптотическая эффективность). Следовательно,
выборочные главные компоненты 2^ = 1,Х (о = 1,р) можно интерпре-
тировать как оценки главных компонент z^ всей генеральной совокуп-
ности. Если среди характеристических корней Ai,A2,...,Ap встречаются
равные между собой, то оценки максимального правдоподобия для А,* и I,
определяются иначе. Аналогичные результаты имеют место и при оценке
характеристических корней и соответствующих им собственных векторов
корреляционной матрицы^
2)	величины — 1(Aj — А^) (i = 1,р) асимптотически (по п —► оо)
нормальны со средним значением 0 и с дисперсией, равной 2А?, и незави-
симы от других выборочных характеристических корней',
3)	выборочный характеристический корень А,- распределен асимпто-
тически (по п —► оо) независимо от компонент соответствующего ему
собственного вектора I, (i = 1, р);
4)	ковариация между r-й компонентой выборочного собственного
вектора I, и q-й компонентой выборочного собственного вектора lj рав-
на величине
^i^j^ir^jq
(п-1)(А,-Х,)2’
В заключение приведем два факта, относящихся к ситуациям, в ко-
торых компоненты нормального вектора наблюдений X взаимно незави-
симы:
5)	пусть X Е А(а,Е), где ковариационная матрица имеет диаго-
нальный вид, т. е. cov,х^) = 0 при i £ j, i,j = 1,2,...,р. И пусть
|R| = det (r.j) — определитель выборочной корреляционной матрицы, по-
строенной по наблюдениям (Xj,..., Хп). Тогда при достаточно больших
п (п —♦ оо) статистика критерия отношения правдоподобия для про-
верки гипотезы о диагональном виде Е может быть определена в виде
у = —(n—	-)1п |R|, а для ее функции распределения справедливо при-
ближенное соотношение
а/р(р-1)
V 2
542
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
при относительной ошибке > не превосходящей сотых долей процента^
6)	пусть наблюдения Xj извлечены из так называемой сферической
р-мерной нормальной совокупности N(a\ a2I)r т. е. компоненты каждо-
го из векторов Xj взаимно независимы и имеют одинаковые дисперсии
равные о2. Тогда ковариационная матрица Б = о21 имеет един-
ственный корень (кратности р), оценкой максимального правдоподобия
которого является величина
причем величина Х/<т2 распределена по закону х\р(п ~ 1)).
Статистика критерия отношения правдоподобия для проверки гипо-
тезы о сферичности распределения исследуемого вектора наблюдений име-
ет вид
.., Ml
[ltr(nS)r
и при достаточно больших п (п —♦ оо)
„( ( 1 2р2 + р + 2\	1	( tfp(p+l) Д
I г- —ъ—J,nw<7 *д* (~2— 7
при относительной ошибке данного приближенного соотношения, не пре-
восходящей сотых долей процента.
13.2.7. Применение свойств выборочных характеристик
главных компонент
Опишем некоторые методы построения разного рода интервальных
оценок для интересующих нас неизвестных характеристик главных ком-
понент и критерии статистической проверки гипотез, относящихся к этим
характеристикам:
1)	интервальная оценка (доверительный интервал) для i-го харак-
теристического корня X, получается (при больших п) с учетом асимпто-
тической нормальности статистики у/п — 1 (Л^ — Л,):
1 5/iSr
(13.24)
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
543
где данное неравенство справедливо с вероятностью 1 — а (величиной а
заранее задаемся), a uq — g-квантиль стандартного нормального распре-
деления (находится из таблиц Приложения 1).
Возвращаясь к примеру 13.1, по формуле (13.24) находим 95%-ный
(а = 0,05) доверительный интервал для наименьшего характеристическо-
го корня А3 по его выборочному значению А3 = 2,86. В этом случае п = 24,
«о,975 = 1,96, так что 1,81 А3 6,78.
Возможно обобщение асимптотического (по п —> оо) доверительного
интервала на случай кратных, т.е. повторяющихся корней. Если г —
кратность корня А,, то 100(1 — а)%-ный доверительный интервал для не-
известного значения А,* задается неравенством
где
(13.25)
Вопрос о том, что неизвестный характеристический корень А< име-
ет кратность и, в частности, кратность, равную г, может быть решен с
помощью следующего критерия:
2)	проверка гипотезы о равенстве нескольких (о именно г) харак-
теристических корней: А,- = Ai+1 = ••• = A,-+r_i. Очевидно, аль-
тернативой этой гипотезе является утверждение, что не все корни среди
•• • равны между собой. Оказывается, в предположении
справедливости проверяемой гипотезы статистика
«+г—1
7г = (п-1)
j=i
4- (n — 1 )r In
распределена (асимптотически по п —* оо) по закону «хи-квадрат» с г(г +
1)/2 — 1 степенью свободы. Поэтому гипотеза А, = A,+i =  • = А,+г_1
отвергается (с вероятностью ошибиться, равной а), если
2
7г > Ха
/^(r+i) Л
\	2
где Ха(т) — 100а%-ная точка х -распределения с т степенями свободы.
Особый интерес может представить специальный случай t = р—r+1,
т. е. проверка гипотезы о равенстве последних г собственных значений А,
544
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
что будет означать независимость и сферичность т последних признаков
исследуемого вектора наблюдений.
Возвратимся к примеру 13.1. Тот факт, что оценка второго собствен-
ного значения (А2 = 6,50) попадает в доверительный интервал для Аз (си.
выше), приводит к мысли, что, возможно, А2 = А3. Проверим эту гипоте-
зу. В данном случае п = 24, р = 3, i = 2, г = 2, так что
7з = - 23(1п 6,50 + In 2,86) + 46In	_ 3 70
ЛА
А поскольку Xo,os(2) = 5,99 и, следовательно, 72 < Xo.os(2), то гипоте-
зу А2 = А3 следует принять. Но тогда следует пересчитать доверительный
интервал для А2 = А3 с учетом его кратности (в соответствии с (13.25)).
Несложные подсчеты (при а. — 0,05 и соответственно «1-^ = «0,975 — 1,96)
дают: 2,62 А2 6,21, последнее неравенство будет справедливо в сред-
нем в 95 случаях из 100;
3)	проверка гипотезы о независимости признаков х^\х^2\... ,а^р\
являющихся компонентами вектора наблюдений X. Такая проверка нуж-
на для установления целесообразности применения метода главных ком-
понент: если признаки являются взаимно независимыми, то переход к
главным компонентам сведется, по существу, лишь к упорядочению ис-
ходных признаков по принципу убывания их дисперсий. Воспользуемся
статистикой критерия отношения правдоподобия для проверки гипотезы
о диагональном виде ковариационной матрицы с целью проверки незави-
симости компонент вектора наблюдений в следующем примере.
Пример 13.3. Исследовалось время, затрачиваемое работниками
швейной фабрики на выполнение различных элементов операции глаженья
одежды. Эту операцию можно разделить на следующие шесть элементов:
1)	одежда размещается на гладильной доске (z^);
2)	разглаживаются короткие швы (г^);
3)	одежда перекладывается на гладильной доске (а/3));
4)	разглаживаются длинные швы на три четверти (z^);
5)	разглаживаются остатки длинных швов (г<&>);
6)	одежду вешают на вешалку (z<6>).
В этом случае Xv представляет собой вектор измерений элементов
1/-й выполненной операции. Компонента х^ — это время, затраченное на
выполнение i-го элемента операции, п — 76. Данные (время в секундах)
обработаны, получены выборочные вектор среднего значения а и корре-
13.2. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
545
ляцнонная матрица R:
25,56
13,25
31,44
27,29
/1,000	0,088	0,334	0,191	0,173	0,123 \
0,088	1,000	0,186	0,383	0,262	0,040
0,334	0,186	1,000	0,343	0,144	0,080
0,191	0,384	0,343	1,000	0,375	0,142
0,173	0,262	0,144	0,375	1,000	0,334
\ 0,123	0,040	0,080	0,142	0,334	1,000/
Для исследователей представляет интерес проверка гипотезы о взаим-
ной независимости шести случайных величин. Часто при изучении затрат
времени предлагается новая операция, в которой элементы комбинируются
иным способом. В новой операции некоторые элементы могут повторяться
по нескольку раз, а некоторые могут быть выброшены. Если оказываются
независимыми величины, обозначающие время, затрачиваемое на различ-
ные элементы операции, то естественно считать, что и в новой операции
они останутся независимыми. Тогда распределение затрат времени на
новую операцию можно будет оценить, пользуясь средними значениями
и дисперсиями, вычисленными для остальных элементов. Кроме того,
нас интересует возможность выделения небольшого количества вспомогаг
тельных признаков (двух-трех), с помощью которых можно производить
некоторую содержательную классификацию исследуемых работников (в
том или ином смысле).
В этой задаче статистика критерия отношения правдоподобия, опре-
деленная в соответствии с п. 5, имеет вид: у = —(n —	)ln |R| =
In 0,472 = 54,1, а р(р — 1)/2 = 15. Задавшись уровнем значимости
критерия а = 0,01 (вероятность ошибочно отвергнуть проверяемую гипо-
тезу), находим (из таблиц) величину 1%-ной точки £3-распределения с 15
степенями свободы: Xo,oi(15) = 30,6. Поскольку 7 > Xo,oi(15), то гипо-
тезу следует отвергнуть, т.е. приходим к выводу, что значения затрат
времени на различные элементы операции нельзя считать независимыми.
* ♦ *
Прикладная направленность компонентного анализа отчасти проде-
монстрирована приведенными в данном пункте примерами, но в основном
546
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
отражена в табл. 13.1. В частности, из оптимальных свойств главных
компонент следует, что они оказываются полезным статистическим ин*
струментарием в задачах «автопрогноза» большого числа анализируемых
показателей по сравнительно малому числу вспомогательных (латентных)
переменных, визуализации многомерных данных, построения типообразу-
ющих признаков; при типологизации многомерных объектов, при пред-
варительном анализе геометрической и вероятностной природы массива
исходных данных (это отражено в п. 1, 2, 5 упомянутой таблицы). Мы
увидим в гл. 15 и 17, что к методу главных компонент обращаются и при
построении различного рода регрессионных моделей.
13.3.	Факторный анализ
13.3.1.	Сущность модели факторного анализа
Развиваемые в рамках модели факторного анализа методы исходят
из общей базовой идеи, в соответствии с которой структура связей меж-
ду р анализируемыми признаками	может быть объяс-
нена тем, что все эти переменные зависят (линейно или как-то иначе)
от меньшего числа других, непосредственно не измеряемых («скрытых»,
«латентных») факторов	(р < р), которые принято на-
зывать общими и которые в большинстве моделей конструируются так,
чтобы они оказались взаимно некоррелированными. При этом в общем
случае, естественно, не постулируется возможность однозначного (детер-
минированного) восстановления значений каждого из наблюдаемых при-
знаков х^ по соответствующим значениям общих факторов
(в предположении, что мы их умеем вычислять): допускается, что каждый
из исходных признаков х^ зависит также и от некоторой своей («специ-
фической» только для него) остаточной случайной компоненты кото-
рая и обусловливает статистический характер связи между х^, с одной
стороны, и ...,	— с другой.
Конечная цель статистического исследования, проводимого с привле-
чением аппарата факторного анализа, как правило, состоит в выявлении
и интерпретации латентных общих факторов с одновременным противо-
речивым стремлением минимизировать как их число, так и степень зави-
симости х^ от своих специфических остаточных случайных компонент
и™. Как и в любой модельной схеме, эта цель может быть достигнута
лишь приближенно.
13.3. ФАКТОРНЫЙ АНАЛИЗ
547
В некотором смысле искомые общие факторы , f^p можно
считать причинами, а наблюдаемые признаки	— следствия-
ми. Принято считать статистический анализ такого рода успешным, если
большое число следствий удалось объяснить малым числом причин.
Таким образом, методы и модели факторного анализа нацелены, так
же как и метод главных компонент, на сжатие информации или, что то
же, на снижение размерности исходного признакового пространства. При
этом из трех упомянутых в п. 13.1 предпосылок возможности снижения
размерности (взаимная коррелированность исходных признаков, малая
«вариабельность» некоторых из них, агрегирование) методы факторно-
го анализа базируются в основном на первой.
Возникновение схемы и моделей факторного анализа обязано зада-
чам психологии, относится к началу двадцатого века и связано с именами
Ч. Спирмэна, Л.Тэрстоуна, Г. Томсона1. Однако в силу ряда историче-
ских причин и, в частности, из-за субъективных пристрастий и специ-
фических научных интересов первых исследователей, работавших в дан-
ной области, вероятностно-статистические аспекты этого раздела много-
мерного статистического анализа долгое время оставались практически
неразработанными, а интерпретации и анализу различных моделей фак-
торного анализа была присуща некоторая неопределенность. Лишь с се-
редины 50-х годов начинают появляться интересные результаты именно
вероятностно-статистических исследований этого аппарата, среди кото-
рых работа [Anderson Т. W, Rubin Н.] признается основополагающей.
Параграф посвящен описанию канонической линейной модели фактор-
ного анализа. Весьма обширный (и достаточно сложный) материал, ка-
сающийся подробностей вычислительной реализации разнообразных вер-
сий модели факторного анализа, обусловленных различными вариантами
априорных допущений о ее структуре (см. ниже п. 13.3.5), остается при
этом вне рамок нашего описания. Читателю, интересующемуся этими
аспектами проблемы, можно порекомендовать обратиться, например, к
[Харман Г.].
13.3.2.	Общий вид линейной модели, ее связь с главными
компонентами
Как и прежде, будем для удобства полагать исследуемые наблюде-
ния X],Х3,...,Хп центрированными. Переход от исходных наблюдений
1 В качестве первой опубликованной по этой теме работы называют обычно ста-
тью Spearman С. General intelligence objectively determined and measured /Amer. J.
Psychol, 1904, vol. 16, pp. 201-293.
548
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Хп к центрированным осуществляется с помощью простого пе-
реноса начала координат в «центр тяжести» исходного множества наблю-
дений. Тогда линейная версия модели факторного анализа представляется
в виде соотношений
X=QF + t7,
или в покомпонентной записи
*(t) = Е + «(,) (* = ГЙ
i=i
(13.26)
Здесь Q = (qij) — прямоугольная матрица размера р х р коэффи-
циентов линейного преобразования (нагрузок общих факторов на иссле-
дуемые признаки), связывающего исследуемые признаки с ненаблю-
даемыми (скрытыми) общими факторами . tf^p \ а вектор-столбец
U = («^\..., и(р ))Т определяет ту часть каждого из исследуемых призна-
ков, которая не может быть объяснена общими факторами, в том числе
включает в себя, как правило, ошибки измерения признака (сравнить
с (13.16)).
Применительно к каждому конкретному наблюдению Х„ (и =
1,2,..., п) соотношение (13.26) дает
или в покомпонентной записи
р»
4° = Е QijfP + 4° (»= КЙ " = Т7п
>=1
(13.26')
Будем предполагать, что вектор остаточных специфических факторов
U подчиняется р-мерному нормальному распределению JV(O, V), не зависит
от F и состоит из взаимно независимых компонент, т.е. его ковариаци-
онная матрица V = Е([717Т) имеет диагональный вид, где по диагонали
стоят элементы v,, =
Вектор общих факторов F = (/^,...,	^)Т, в зависимости от содер-
жания конкретной задачи, может интерпретироваться либо как р'-мерная
нормальная случайная величина со средним Е F = 0 (в силу центрирован-
ности исходных наблюдений) и с ковариационной матрицей специального
вида E(FFT) = 1^, либо как вектор неизвестных неслучайных параме-
тров, вспомогательных переменных, значения которых меняются от на-
блюдения к наблюдению. При последней интерпретации вектора общих
факторов более правильной является запись модели в виде (13.26J, причем
условия центрированности, независимости и нормированности дисперсий
13.3. ФАКТОРНЫЙ АНАЛИЗ
549
компонент вектора F в этом случае имеют вид:
Однако при обоих вариантах интерпретации вектора общих факторов
F исследуемый вектор наблюдений X оказывается нормально распреде-
ленной р-мерной случайной величиной: при первом варианте как линейная
комбинация двух нормальных случайных векторов (F и 17), а при втором
варианте за счет нормальности специфических факторов При этом
из (13.26) и из сделанных выше допущений немедленно следует, что
Е = 0	/ а** =	+ V”	1
I = QivQjv (bl = bp), I	27)
или в матричной записи
EX = 0, E = QQT + V	J
Примером достаточно прозрачной интерпретации модели факторного
анализа может служить ее формулировка в терминах так называемых ин-
теллектуальных тестов. При этом наблюдение по признаку выража-
ет отклонение оценки, например, в баллах, данной у-му индивидууму на
экзамене по t-му тесту, от некоторого среднего уровня. Естественно пред-
положить, что в качестве ненаблюдаемых общих факторов ..., f^p \
от которых будут зависеть оценки индивидуумов по всем р тестам, вы-
ступят такие факторы, как характеристика общей одаренности индиви-
дуума характеристики его математических технических
или гуманитарных способностей.
Отметим, что соотношения (13.26) формально воспроизводят за-
пись модели множественной регрессии (см. гл. 10), в которой под
(: = 1,2,...,;/) понимаются так называемые объясняющие переменные
(факторы-аргументы). Однако принципиальное отличие модели фактор-
ного анализа от регрессионных схем состоит в том, что переменные
выступающие в роли аргументов в моделях регрессии, не являются непо-
средственно наблюдаемыми в моделях факторного анализа, в то время
как в регрессионном анализе значения измеряются на статистически
обследованных объектах.
Замечание о связи метода главных компонент
и метода факторного анализа. Рассмотрим следующую об-
щую схему, включающую в себя в качестве частных случаев обе сравни-
550
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ваемые модели. Примем гипотезу, что существуют такие взаимно некор-
релированные факторы	что
или в матричной записи
Х = AF,
Д1) г(2) с
где по поводу случайных переменных / ,/ ',... без ограничения общ-
ности можно предположить, что D = 1.
Очевидно, представление (13.28), если оно существует, не единствен-
но, так как переходя от F с помощью произвольного ортогонального пре-
образования С к новым переменным Z = С F, будем иметь вместо (13.28)
следующее соотношение:
X = В Z, где В = АС-1.
Исследователю не известны коэффициенты atJ*, но он хочет научить-
ся наилучшим (в некотором смысле) образом аппроксимировать признаки
а/1),... с помощью линейных функций от небольшого (заранее опре-
деленного) числа т факторов	..., /^m\rn), которые поэтому есте-
ственно назвать главными или общими. Аппроксимация признаков X с
помощью	означает представление X в виде (13.28),
но с «урезанной» суммой, стоящей в правой части, т. е.
X(rn) = AmF(rn),
где Ат — матрица порядка р х т, составленная из первых т столбцов
матрицы A, a F(m) = (/^(пг),...,
Оказывается, что, по-разному формулируя критерий оптимальности
аппроксимации X с помощью F(m), придем либо к главным компонентам,
либо к общим факторам. Так, например, если определение элементов ма-
трицы Ат подчинить идее минимизации отличия ковариационной матри-
цы S исследуемого вектора X от ковариационной матрицы Sjf = Am • А^
аппроксимирующего вектора Х(т) (в смысле минимизации евклидовой
нормы ||S — EjJ|), то определяется пропорционально t-й главной
компоненте вектора X, в частности	где Aj — t-й по вели-
чине характеристический корень ковариационной матрицы S, a z^ — t-я
13.3. ФАКТОРНЫЙ АНАЛИЗ
551
главная компонента X; при этом i-й столбец матрицы Am (i = 1г..,т)
есть y/Xili , где — собственный вектор матрицы S, соответствующий
характеристическому корню А,.
Если же определение аппроксимирующего вектора Х(т) — AmF(m)
подчинить идее максимального объяснения корреляции между исходны-
ми признаками z^ и х^ с помощью вспомогательных (ненаблюдаемых)
факторов	...,	и, в частности, идее минимизации
величины
У' cov (»(,). Д0)) - cov (д<1>(">). *0>(т)) 1	(13.29)
«ил
при условии неотрицательности величин <Тц — то можно показать,
что t-я строка оптимальной в этом смысле матрицы преобразования Ато
состоит из т факторных нагрузок общих факторов
на i-й исходный признак z^ в модели факторного анализа вида (13.26).
Другими словами, сущность задачи минимизации (по Ат и F(m)) вели-
чины (13.29) состоит в следующем. Первый из т общих факторов /^(т)
находится из условия, чтобы попарные корреляции между исходными при-
знаками были как можно меньше, если влияние на них этого фактора
учтено. Следующий общий фактор f^2\m) находится из усло-
вия максимального ослабления попарных корреляционных связей между
исходными признаками, оставшихся после учета влияния первого общего
фактора	и т.д.
Из сказанного, в частности, следует, что методы главных компонент
и факторного анализа должны давать близкие результаты в тех случаях,
когда главные компоненты строятся по корреляционным матрицам исход-
ных признаков, а остаточные дисперсии оц сравнительно невелики.
13.3.3.	Основные задачи факторного анализа
При разработке моделей факторного анализа приходится последова-
тельно анализировать и решать следующие вопросы.
Существование модели. Далеко не для всякой заданной структуры
связей между исходными признаками X = (z^\...,z^)T можно (при за-
данном р < р) построить модель факторного анализа, т. е. указать такие
общие факторы	(или доказать их существование), которые
объясняли бы имеющуюся корреляцию между различными парами z^ и
в рамках модели (13.26). При каком характере связей между исход-
552 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ними признаками .,х<р\ т.е. при каких корреляционных (ковариа-
ционных) матрицах R = (г,у) (S = (cr.j)), а также при каком соотношении
между числом наблюдаемых признаков р и числом скрытых общих фак-
торов р (р < р) сделанное допущение о наличии определенных связей
между (i = 1,2,... ,р), с одной стороны, и (у - 1,2,...,р) — с
другой, является обоснованным и содержательным — в этом и заключа-
ется вопрос существования модели. В терминах модели (13.26) это озна-
чает, что не всякая ковариационная матрица S допускает представление
вида (13.27), а следовательно, не всякий вектор наблюдений X допускает
интерпретацию в рамках модели факторного анализа типа (13.26). Оче-
видно, условия представимости вектора наблюдений X в рамках модели
факторного анализа должны формулироваться в терминах свойств кова-
риационной матрицы Е, а также в виде некоторых соотношений между
размерностью исходного пространства р и числом общих факторов р.
Единственность (идентификация) модели. Оказывается, что если
р, £ и р таковы, что допускают построение модели факторного анализа,
то определение соответствующих факторов FT = (Z^,- ..tf^p ^) и коэф-
фициентов линейного преобразования Q = (ftj), связывающего X и F, не
единственно. Спрашивается, при каких дополнительных ограничениях на
матрицу преобразования Q и на ковариационную матрицу V = (v<j) оста-
точных специфических факторов и^,..., и^ определение параметров ис-
комой модели факторного анализа будет единственным?
Алгоритмическое определение структурных параметров модели.
При заданной ковариационной матрице S исходных признаков и извест-
ном числе общих факторов р (и в предположении, что решение задачи
определения структурных параметров Q и V существует) как конкретно
вычислить неизвестные параметры модели?
Статистическое оценивание (по наблюдениям Х\,Х2->. ..,Хп и при
заданном р') неизвестных структурных параметров модели.
Статистическая проверка ряда гипотез, связанных с природой мо-
дели и значениями ее структурных параметров, таких, как гипотеза об
истинном числе рг общих факторов, гипотеза адекватности принятой мо-
дели по отношению к имеющимся результатам наблюдения, гипотеза о
значимом отличии от нуля интересующих нас коэффициентов дц линей-
ного преобразования Q и т.п.
Построение статистических оценок для значений ненаблюдаемых
общих факторов	* (i = 1,2,...,п).
Далее мы кратко остановимся на решении некоторых из этих задач.
13.3. ФАКТОРНЫЙ АНАЛИЗ
553
13.3.4.	Вопросы идентификации модели факторного анализа
Будем в дальнейшем предполагать, что имеется по меньшей мере од-
но решение (Q,V) уравнений (13.27). При исследовании вопроса един-
ственности решения системы (13.27) относительно (Q, V) (при заданных
<Ту ) следует различать два аспекта проблемы. Во-первых, надо понять,
при каких дополнительных условиях на искомую матрицу нагрузок Q и
на соотношение между р и р не может существовать двух различных ре-
шений Q(l) и таких, чтобы одно из них нельзя было бы получить из
другого с помощью соответствующим образом подобранного ортогональ-
ного преобразования С (единственность с точностью до ортогонального
преобразования или с точностью до вращения факторов). Оказывается,
достаточным условием единственности такого рода является требование
к матрице Q, чтобы при вычеркивании из нее любой строки оставшуюся
матрицу можно было бы разделить на две подматрицы ранга рг, откуда
автоматически следует требование р' < (р— 1)/2.
Можно показать, что для р' = 1 и р = 2 это условие является одно-
временно и необходимым, откуда, в частности, следует, что случаи р = 2,
р = 1 и р = 4, р = 2 не допускают идентификации модели факторного
анализа в указанном выше смысле.
Будем предполагать далее, что имеется по меньшей мере одно реше-
ние (Q, V) системы (13.27) и что оно единственно с точностью до ортого-
нального преобразования.
Вставляя в уравнения (13.27) вместо найденного решения (Q, V) дру-
гую пару матриц (QC,V), где С — матрица (размера р х р;) любого
ортогонального преобразования, легко убедиться, что и она (эта пара
матриц) удовлетворяет данной системе уравнений. Следовательно, воз-
вращаясь к модели (13.26), получаем, что наряду с общими факторами
F = (/1)..../’У можно рассмотреть (при тех же нагрузках g,j) общие
факторы Z = С F. Поскольку, как известно (см. Приложение 2), ортого-
нальное преобразование координат F геометрически означает вращение
осей	) около начала координат на некоторый угол, то полу-
чается, что при отсутствии дополнительных условий на природу искомой
матрицы нагрузок Q общие факторы	..., * могут быть определены
лишь с точностью до вращения системы координат в соответствующем
р'-мерном пространстве. Существует несколько вариантов дополнитель-
ных условий на класс матриц Q, в котором следует искать решение систе-
мы (13.27), обеспечивающих уже окончательную однозначность решения
(Q>v). От конкретного содержания этих условий зависит и способ чи-
сленного выявления структуры искомой модели и соответственно способ
554
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
статистического оценивания неизвестных параметров дц, оц и факторов
Поэтому остановимся на них параллельно с описанием методов ста-
тистического исследования модели факторного анализа.
13.3.5.	Статистическое исследование модели факторного
анализа
Итак, в распоряжении исследователя — последовательность много-
мерных наблюдений X], ...., Хп, и с помощью модели (13.26) нужно пе-
рейти от исходных коррелированных признаков я/3\..., х^р\ являю-
щихся компонентами каждого из наблюдений, к меньшему числу некорре-
лированных вспомогательных признаков (общих факторов) ...,	\
Для этого надо суметь определить оценки неизвестных нагрузок й,- оста-
точных дисперсий и, наконец, самих общих факторов
Как упоминалось, в основной модели (13.26) при р > 1 оказывается
слишком много неизвестных параметров для однозначного определения.
Поэтому вначале исследователь должен выбрать какую-то систему допол-
нительных априорных соотношений, связывающих неизвестные параме-
тры модели, которые делают решение задачи однозначным и позволяют
получить относительно простое частное решение системы (13.27). За-
тем он может отказаться от этих дополнительных соотношений, подбирая
с помощью подходящего ортогонального преобразования (вращения осей)
тот вариант оценок нагрузок $ij и остаточных дисперсий иц, который ему
кажется предпочтительнее в основном в отношении возможности содер-
жательной интерпретации получаемых при этом общих факторов и их
нагрузок. Остановимся подробнее на основных этапах статистического
исследования модели факторного анализа.
Варианты дополнительных априорных соотношений между
 Vtb постулируемых исследователем с целью однозначной
идентификации анализируемой модели:
1)	решение (Q, V) системы (13.27) лежит лишь в классе таких матриц
Q и V, для которых матрица Q VQ имеет диагональный вид, причем
диагональные элементы ее различны и упорядочены в порядке убывания;
2)	из всех решений системы (13.27) выбирается лишь то, для которого
матрица QTQ диагональна, причем все диагональные элементы различны
и упорядочены (в порядке убывания);
3)	решение системы (13.27) ищут лишь среди таких матриц Q, кото-
рые для заранее заданной матрицы (размера р х р') В = (6<у), i = 1,... ,р,
13.3. ФАКТОРНЫЙ АНАЛИЗ
555
j = 1,. • • ,р, ранга р удовлетворяют требованию
BTQ = D =
0	...	О
^21	<^22	• • •	О
•р'1	^р'2	• • •	^р'р'
В частности, выбор
вт
01...О
0...0
0...0
\00...1 0...0/
приводит к ограничению на Q типа
/дп	0	0	...	0	\
921	922	0	...	О
9р'1	9р’2	9р’3	•••	9р'р'
' 9р1	9р2	9рЗ	• • •	9рр*	'
что означает: первый исходный признак z^ должен выражаться только
через один первый общий фактор второй признак х^ — через два
общих фактора и и т. д.
Содержательную интерпретацию условий 3) следует искать в ситу-
ациях, когда исследователь располагает некоторой априорной информа-
цией, из которой можно, во-первых, извлечь реальный гипотетический
смысл общих факторов и, во-вторых, постулировать наличие определен-
ного числа нулевых элементов в матрице нагрузок Q (с более или менее
точным указателем их «адреса»), что означает априорное отрицание за-
висимости исходных признаков z^ от некоторых их общих факторов
(j = l,2,...,j/). Эта же идея реализуется и в других, менее формализо-
ванных вариантах дополнительных условий («простые структуры», «ну-
левые элементы в специфических позициях»), на которых здесь не будем
останавливаться.
Описание общего итерационного подхода к выявлению струк-
туры модели факторного анализа. Конкретная реализация этого под-
хода зависит от выбора варианта идентифицирующих условий типа 1)-3).
556 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Как правило, исследователю известна лишь оценка Е ковариационной ма-
трицы S. Поэтому в дальнейшем мы будем писать S, подразумевая, что
это в действительности ее выборочное значение.
Логическая схема итераций следующая:
•	задаемся некоторым нулевым приближением матрицы V;
•	используя (13.27), получаем нулевое приближение 9^ = Е —
матрицы Ф = QQ = S — V;
•	по Ф с помощью некоторого специального приема (см. ниже) после-
(0) (0)	(0)	_
довательно определяем нулевые приближения q\ ,92	для столб-
цов ft, ft,..., qp> матрицы Q.
Затем определяем следующее (первое) приближение и т. д.
Специальный прием определения столбцов 9* (* = 1,2,... ,pf) матрицы
Q при известной матрице Ф = QQT опирается на то, что матрица Ф
может быть представлена в виде Ф = 919^ + 929^ + • • • + 9Р'9р'- Используя
специфику выбранных идентифицирующих условий, определяют вначале
столбец 91. Затем переходят к матрице Ф1 = Ф - 919^ = 9э9^ + • • * + 9Р’9Р*
и определяют столбец 92 и т. д.
Статистическое оценивание факторных нагрузок qij и оста-
точных дисперсий Vgj. Оценивание производится либо методом макси-
мального правдоподобия (см. гл. 7), либо так называемым центроидным
методом. Первый метод используется обычно при идентифицирующих
условиях типа 1) и 2). Он хотя и дает эффективные оценки для q^ и v,-,*,
но требует постулирования закона распределения исследуемых величин
(разработан лишь в нормальном случае), а также весьма обременитель-
ных вычислений. Центроидный метод используется при идентифицирую-
щих условиях типа 3). Давая оценки, близкие к оценкам максимального
правдоподобия, он, как и всякий непараметрический метод, является бо-
лее «устойчивым» по отношению к отклонениям от нормальности иссле-
дуемых признаков и требует меньшего объема вычислений. Однако из-за
определенного произвола в его процедуре, которая приведена ниже, стати-
стическая оценка метода, исследование его выборочных свойств (в общем
случае) практически невозможны.
Общая схема реализации метода максимального правдоподобия следу-
ющая. Составляется логарифмическая функция правдоподобия как функ-
ция неизвестных параметров q^ и v,i, отвечающая исследуемой модели,
т.е. с учетом нормальности Xit...,Xn модели (13.26) и соответственно
(13.27); в качестве дополнительных идентифицирующих условий берутся
условия 1) или 2). С помощью дифференцирования этой функции прав-
доподобия по каждому из неизвестных параметров и приравниванв я по-
13.3. ФАКТОРНЫЙ АНАЛИЗ
557
лученных частных производных к нулю получается система уравнений, в
которой известными величинами являются выборочные ковариации а
также числа р и р\ а неизвестными — искомые параметры g.j и И на-
конец, предлагается вычислительная (как правило, итерационная) проце-
дура решения этой системы. Реализация описанной выше (для случаев 1
и 2) общей итерационной вычислительной схемы с заменой неизвестной
ковариационной матрицы исходных признаков Е ее выборочным аналогом
Е приведет как раз к оценкам максимального правдоподобия параметров
9ij н va (* = 2,... ,р; j = 1,2,... ,pz). Отметим также, что при достаточ-
но общих ограничениях доказана асимптотическая нормальность оценок
максимального правдоподобия Q и V, что дает основу для построения со-
ответствующих интервальных оценок.
Как выше отмечено, центроидный метод является одним из спосо-
бов реализации вычислительной схемы, приспособленной для выявления
структуры модели факторного анализа и оценки неизвестных параметров
в случае идентифицирующих условий типа 3). Этот метод поддается весь-
ма простой геометрической интерпретации. Отождествим исследуемые
признаки ,..., х{р} с векторами, выходящими из начала координат не-
которого вспомогательного р-мерного пространства, построенными таким
образом, чтобы косинусы углов между z^ и равнялись бы их парным
корреляциям (ra-j), а длины векторов х^ — стандартным отклонениям
соответствующих переменных («т,1/2). Далее изменим, если необходимо,
направления, т. е. знаки отдельных векторов так, чтобы как можно боль-
ше корреляций стало положительными. Тогда векторы будут иметь тен-
денцию к группировке в одном направлении в пучок. После этого первый
общий фактор определяется как нормированная (т.е. как вектор еди-
ничной длины) сумма всех исходных векторов пучка, и, следовательно, он
будет проходить каким-то образом через середину (центр) этого пучка;
отсюда название «центроид» для общего фактора в этом случае.
Переходя затем к остаточным переменным z^’1^ =	под-
(1)	т
считывая ковариационную матрицу Е1 1 = 2 — для этих остаточных
переменных и проделывая относительно х^ и Е^ ту же самую проце-
дуру построения пучка и т.п., выделяем второй общий фактор («второй
центроид») и т. д.
Формализация этих соображений приводит к следующей итерацион-
ной схеме вычислений по определению факторных нагрузок и остаточ-
ных дисперсий Задаемся некоторым начальным приближением
55,8 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ многомерного признака
для дисперсий остатков V. Обычно полагают
»,(.0) =?« 1 - max |г,ч|
G#i)
Подсчитываем Ф = Е — V^°\ Выбираем в качестве нулевого приближе-
ния 6 первого столбца вспомогательной матрицы В столбец, состоя-
щий из одних единиц
Далее определяем нулевое приближение < первого столбца матрицы на-
грузок
(о) _	Ф(0)Ь<0)
’* (ь‘0)тФ<°>6<0))4 
Затем вычисляется матрица	Ф	и определяется нулевое
приближение второго столбца матрицы нагрузок
4 = (1330)
где вектор состоит только из 4-1 или —1, а знаки подбираются из
условия максимизации знаменателя правой части (13.30) и т.д. Получив,
таким образом, нулевое приближение Qдля матрицы
нагрузок Q, вычисляем = Е — Q и переходим к следующей
итерации. При этом матрица В не обязана совпадать с В^°\ Кста-
ти, как нетрудно усмотреть из вышесказанного, t-й столбец матрицы В
задает веса, с которыми суммируются векторы одного пучка для образо-
вания t-ro общего фактора («центроида»). Поскольку смысл центроидной
процедуры в простом суммировании векторов пучка, она иногда так и
называется — «процедура простого суммирования», то исследователю
остается определить лишь нужное направление каждого из векторов пуч-
ка, т. е. знаки единиц, образующих столбцы 6,. Непосредственная ори-
ентация (при подборе знаков у компонент вектора 6,) на максимизацию
выражений	хотя и несколько сложнее реализуема, чем неко-
торые эвристические приемы, опирающиеся на анализ знаков элементов
остаточных матриц , по быстрее и надежнее приводит к выделению
именно таких центроидов, которые при заданном р’ будут обусловливать
13.3. ФАКТОРНЫЙ АНАЛИЗ
559
возможно большую часть общей дисперсии исходных признаков, т. е. ми-
нимизировать дисперсию остаточных компонент и,.
Недостатком центроидного метода является зависимость центроид-
ных нагрузок от шкалы, в которой измерены исходные признаки. По-
этому исходные признаки обычно нормируют с помощью среднеква-
дратических отклонений oj/3, так что выборочная ковариационная ма-
трица Е заменяется во всех рассуждениях выборочной корреляционной
матрицей R.
Анализируя описанную выше процедуру центроидного метода, не-
трудно понять, что построенные таким способом общие факторы могут
интерпретироваться как первые р «условных» главных компонент ма-
трицы Е — V, найденные при дополнительном условии, что компоненты
соответствующих собственных векторов могут принимать лишь два зна-
чения: плюс или минус 1.
Оценка значений общих факторов. Это одна их основных за-
дач исследования. Действительно, мало установить лишь сам факт су-
ществования небольшого числа скрыто действующих общих факторов
...,	\ объясняющих природу взаимной коррелированности исход-
ных признаков и основную часть их дисперсии. Желательно непосред-
ственно определить эти общие факторы, описать их в терминах исходных
признаков и постараться дать им удобную содержательную интерпрета-
цию.
Приведем здесь идеи и результаты двух распространенных мето-
дов решения этой задачи, предложенных в разное время М. Бартлеттом
(1938 г.) и Г. Томсоном (1951 г.). В обоих случаях предполагаем задачу
статистического оценивания неизвестных нагрузок ( = (q\j) и остаточ-
ных дисперсий V = (»й) уже решенной.
Метод Бартлетта рассматривает отдельно для каждого фиксиро-
ванного номера наблюдения и (и = 1,2,...,п) модель (13.25) как регрес-
сию признака xv по аргументам 9-1,9.2» • ••>?₽'; при этом верхний индекс
: = 1,2,...,р у признака (и соответствующий первый нижний индекс у
нагрузок) играет в данном случае роль номера наблюдений в этой регрес-
сионной схеме, так что
р'
«1° = 52 №*3 +	(> = 1> • - ,₽)•
j=1
Таким образом, величины	интерпретируются как
неизвестные коэффициенты регрессии хи по 9'1»9*з>***»9*р'* В соответ-
560
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ствии с известной техникой метода наименьших квадратов (с учетом <не-
равноточности» измерений, т. е. того, что, вообще говоря, D а/’*) / D
при 1’1 / *з), определяющей неизвестные коэффициенты регрессии Fv =
(ff', ... ,	))Т из условия
получаем
Л, = (QTV-1Q)-,QTV-’Xv (iz=	(13.31)
Очевидно, если исследуемый вектор наблюдений X нормален, то эти
оценки являются одновременно и оценками максимального правдоподобия.
Нестрогость данного метода — в замене истинных (неизвестных нам) ве-
личин qij и их приближенными (оценочными) значениями Qij и
Модель Томсона рассматривает модель (13.26) как бы <вывернутой
наизнанку», а именно как регрессию зависимых переменных	...,
по аргументам	...,	Тогда коэффициенты с, у в соотношениях
(i= 1,...,р),
или в матричной записи
₽ = СХ,
где С — матрица коэффициентов размера р*Хр, находят в соответствии
с методом наименьших квадратов из условия
ЕЕ(& -=«й«ЕЕ - Е*М-
i/=l t=l х	J=1	7	* Р=11=1 х	j=l	7
Поскольку решение экстремальной задачи (13.32) выписывается в
терминах ковариаций и то отсутствие наблюдений по зависи-
мым переменным можно компенсировать знанием этих ковариаций,
13.3. ФАКТОРНЫЙ АНАЛИЗ
561
так как легко подсчитать, что
Отсюда, используя известные формулы метода наименьших квадра-
тов (см. гл. 15), получаем (с заменой матриц Q и V их выборочными
аналогами)
/^(I + rrVv-’X., (i/ = l,2,...,n),	(13.33)
где матрица Г (размера р X р) определяется соотношением
r = qTv-1q.
Сравнение выражений (13.31) и (13.33) позволяет получить явное со-
отношение между решениями по методу Бартлетта и методу Томсона
^т)
Г(Б) =(1 + Г-1)Г(т).
Если элементы матрицы Q,V-1Q достаточно велики, то эти два ме-
тода будут давать близкие решения.
Статистическая проверка гипотез. Проверка гипотез, связан-
ных с природой и параметрами используемой модели факторного ана-
лиза, составляет один из необходимых моментов исследования. Теория
статистических критериев применительно к моделям факторного анализа
разработана весьма слабо. Пока удалось построить лишь так называе-
мые критерии адекватности модели, т. е. критерии, предназначенные для
проверки гипотезы Но, заключающейся в том, что исследуемый вектор
наблюдений X допускает представление с помощью модели факторного
анализа (13.26) с данным (заранее выбранным) числом общих факторов
р. При этом критическая статистика 7(Xi,...,Xn), т.е. функция от
результатов наблюдения, по значению которой принимается решение об
отклонении или непротиворечивости высказанной гипотезы Но, зависит
от вида дополнительных (идентифицирующих) условий модели. Так если
рассматривается модель с дополнительными идентифицирующими усло-
виями вида 1), т. е. дополнительно постулируются диагональность матри-
цы Г = QTV~1Q, то гипотеза Яо отвергается (с вероятностью ошибиться,
562
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
приблизительно равной а) в случае
71 ton • • •, Хл) = n(In |V| + In |I + Г| - In |E|) > x’ to),
где число степеней свободы i/j = |[(р—р')2 — (р+р*)]; его положительность
обеспечивается условием р < (р — 1)/2, а Ха(^1) — как и ранее, величина
100а%-ной точки ^"Распределения с и\ степенями свободы (находится из
таблиц).
На языке ковариационных матриц гипотеза Яо означает в данном
случае, что элементы матрицы Е — (QQ + V) должны лишь статисти-
чески незначимо отличаться от нуля, или, что эквивалентно, матрица
Е — V должна иметь ранг, равный р\ А это в свою очередь означает,
что последние р-р* характеристических корней Ар«+1,...,Ар уравнения
|Е—V—AV| = 0 должны лишь незначимо отличаться от нуля. Статистика
71 (Xi,..., Хп) может быть записана в терминах этих характеристических
корней:
р
71(*1....Хп) = П У 1п(1 + \).
t=p‘+l
Если же в качестве идентифицирующих условий дополнительно к
(13.26), или, что то же, к (13.27), постулируется наличие какого-то за-
ранее заданного числа т нулевых нагрузок qij из общего числа р • р' на
определенных («специфических») позициях, то гипотеза Яо отвергается
(с вероятностью ошибиться, приблизительно равной а) в случае, когда
72(Х!,..., Хп) = n(ln |V|) + In |QTV-1 SV-1 Q| - In |Г| - In |S| > x’
где число степеней свободы i/2 = |р(р — 1) — (рр — т).
Иногда удобнее вычислять критическую статистику 72 (Хъ • • - ,ХЛ)
в терминах характеристических корней ,..., zp (нумерованных в по-
рядке убывания их величии) выборочной корреляционной матрицы R ис-
следуемого вектора наблюдений X:
, tv V \ _ (	2р+ 11	2р\
‘’У2СХ1, . ,ХП)—	g 3 /
Статистики 7i(Xi,. ..,ХП) и 7з(Хг,...,ХП) получены в результате
реализации известной схемы критерия отношения правдоподобия.
13.3. ФАКТОРНЫЙ АНАЛИЗ
563
До сих пор не удалось построить многомерной решающей процедуры
типа р (Е), т.е. оценки для неизвестного числа общих факторов р\ В
настоящее время приходится ограничиваться последовательной эксплуа-
тацией критериев адекватности Hq: р = ро (ро заранее задано) при аль-
тернативе Hi: р > ро- Если гипотеза отвергается, то переходят к
проверке гипотезы Но: р = ро + 1 при альтернативе Я{: р* > ро + 1 и
т. д. Однако по уровням значимости а каждой отдельной стадии такой
процедуры трудно сколько-нибудь точно судить о свойствах всей после-
довательной процедуры в целом.
Пользуясь асимптотической нормальностью оценок Q и V, можно бы-
ло бы попытаться строить критерии для проверки гипотез, касающихся
значений факторных нагрузок, например, гипотез о том, что некоторые
признаки не зависят от заранее определенных факторов, т. е. что на опре-
деленных местах матрицы Q стоят элементы, статистически незначимо
отличающиеся от нуля. Однако построение этих критериев затруднено
из-за сложности процедуры вычисления ковариационных матриц оценок
Q и V.
Продемонстрируем реализацию некоторых этапов факторного анали-
за на примере.
Пример 13.4. В табл. 13.3 приведены коэффициенты корреляции
между отметками по шести школьным предметам, подсчитанные по вы-
борке из 220 учащихся.
Таблица 13.3
Содержательный смысл признака	Номер признака						Нагрузка факторов на признаки	
	1	2	3	4	5	6	Ян	9*2
Отметка по гэльскому языку ж^	1	0,439	0,410	0,288	0,329	0,248	0,606	0,337
английскому (2) языку х '	0,439	1	0,351	0,354	0,320	0,329	0,611	0,197
(3) истории ж' '	0,410	0,351	1	0,164	0,190	0,181	0,458	0,384
арифметике ж^	0,288	0,354	0,161	1	0,595	0,570	0,683	-0,365
алгебре ж^6^	0,329	0,320	0,190	0,595	1	0,464	0,686	-0,335
(в) геометрии ж	0,248	0,329	0,181	0,470	0,464	1	0,575	-0,212
В последних двух столбцах таблицы даны факторные нагрузки дц, д,-3
на исследуемые признаки в бифакторной модели (р = 2), подсчитанные
564
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
по приведенной здесь корреляционной матрице с помощью центроидного
метода. Простой анализ величин и знаков этих нагрузок склоняет нас к
тому, чтобы интерпретировать первый фактор как фактор общей ода-
ренности, а второй фактор — как фактор гуманитарной одаренности.
Метод Г. Томсона (13.33) дает в качестве оценки общих факторов вы-
ражения:
= 0,245x(l) + 0,208х(3) + 0,158а:<3) + 0,278г<4) + 0,271z(S) + 0,157xW;
/3) = 0,352х(1) + 0,201х(2) + О,ЗО9т(3) - 0,351г(4) - 0,303z(t) - 0,126i(e).
В целях геометрической интерпретации центроидного метода рассмо-
трим рис. 13.3, на котором осями координат являются общие факторы '
и а координаты точек	определяются нагрузка-
13.4. НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 565
ми t-ro исходного признака на общие факторы (i = 1,2,...,6). Соот-
ветственно точку (9и»91з) удобно интерпретировать как изображение t-ro
исходного признака Расположение точек на рис. 13.3 свидетельству-
ет о естественном распадении совокупности исходных признаков на две
группы: группу гуманитарных признаков	и группу мате-
i СО (б) (б)\
матических признаков (х' ,х' \ху ).
Подобная геометрическая интерпретация помогает выбрать вращение
системы общих факторов, наиболее подходящее в отношении возможно-
сти их содержательной интерпретации. Дело в том, что, как уже отме-
чали, параметры модели факторного анализа, в том числе и сами общие
ж Hi) Я2) Ир’)
факторы Г ,...,f ч определяются не однозначно, а лишь с точно-
стью до некоторого ортогонального преобразования, т. е. с точностью до
вращения осей	. ff^p в пространстве. При этом выбор окон-
чательного решения, т. е. закрепление системы f^2\..., f в опре-
деленном положении, находится в распоряжении исследователя. Другими
словами, исследователь должен решить вопрос: как, располагая некото-
r(i) Я2) Ар*)
рым частным решением	Г , полученным, например, с по-
мощью центроидного метода, выбрать такое ортогональное преобразова-
ние, такой поворот осей	... ,f^p \ при котором получаемые при
этом новые общие факторы	... tf^p допускают наиболее есте-
ственную и убедительную интерпретацию. Рассматривая расположение
исходных признаков в плоскости	или в пространстве, натянутом
на первые три общих фактора, естественно повернуть координатную си-
стему таким образом, чтобы координатные осн прошли через наиболее
четко выраженные сгущения точек-признаков (см. поворот, намеченный
пунктирными осями и на рис. 13.3). При этом иногда бывает
полезно отказаться от ортогональности общих факторов, переходя к косо-
угольной системе координат.
13.4. Некоторые эвристические методы
снижения размерности
13.4.1. Природа эвристических методов
Описанные выше сокращения размерности исследуемого признаково-
го пространства (метод главных компонент и модели факторного анализа)
допускали интерпретацию в терминах той или иной строгой вероятност-
566 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
ной: модели и, следовательно, подразумевали возможность исследования
свойств рассматриваемых процедур в рамках теории математической ста-
тистики. В данном пункте речь пойдет о методах, подчиненных некото-
рым частным целевым установкам (наименьшее искажение геометриче-
ской структуры исходных «выборочных точек», наименьшее искажение
их эталонного разбиения на классы и т. д.), но не формулируемых в тер-
минах вероятностно-статистической теории1 Процедура выбора целевой
установки, подходящей именно для данной конкретной задачи, практиче-
ски не формализована, носит эвристический характер, т.е., как правило,
обусловливается лишь опытом и интуицией исследователя. Поэтому бу-
дем называть такие методы эвристическими.
При отсутствии априорной или выборочной предварительной инфор-
мации о природе исследуемого вектора наблюдений и о генеральных со-
вокупностях, из которых эти наблюдения извлекаются, точно в таком же
невыгодном положении находятся и методы факторного анализа и глав-
ных компонент. Однако для них все-таки существует принципиальная
возможность теоретического обоснования (при наличии соответствующей
дополнительной информации), в то время как лишь некоторые из эвристи-
ческих методов удается впоследствии теоретически обосновать в рамках
строгой математической модели.
Подчеркнем, что факт описания здесь методов снижения размерности,
не использующих предварительной информации, например, обучающих и
квазиобучающих выборок, целесообразно расценивать лишь как следствие
признания неизбежности ситуаций, в которых такой информации не име-
ется, но нс как стремление рекламировать эти методы в качестве наиболее
эффективных. В действительности же обоснование и эффективное реше-
ние задач снижения размерности без слепой надежды на удачу можно, по
нашему мнению, получить лишь на пути глубокого профессионального
анализа, дополненного статистическими методами, использующими пред-
варительную выборочную (обучающую) информацию.
13.4.2. Метод экстремальном группировки признаков
При изучении сложных объектов, заданных многими параметрами,
возникает задача разбиения параметров на группы, каждая из которых
1 Отсутствие строгой вероятностно-статистической модели, лежащей в основе тех или
иных методов, не исключает возможности использования отдельных вероятностно-
статистических понятий и соответствующей терминологии, как это имеет место,
например, в методе экстремальной группировки признаков, в методе корреляцион-
ных плеяд и некоторых других.
13.4. НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 567
характеризует объект с какой-либо одной стороны. Но получение легко
интерпретируемых результатов осложняется тем, что во многих прило-
жениях измеряемые параметры (признаки) лишь косвенно отражают су-
щественные свойства, которыми характеризуется данный объект.
Так, в психологии измеряемые параметры — это реакции людей на
различные тесты, а выражением существенных свойств, общими факто-
рами являются такие характеристики, как тип нервной системы, рабо-
тоспособность и т. п. Подобная природа формирования набора частных
характеристик объекта или системы присуща широкому классу явлений
и процессов в экономике, социологии, медицине, педагогике и т. д.
Оказывается, что во многих случаях изменение какого-либо общего
фактора сказывается неодинаково на измеряемых признаках, в частности,
исходная совокупность из р признаков обнаруживает такое естественное
«расщепление» на сравнительно (с р) небольшое количество групп, при
котором изменение признаков, относящихся к какой-либо одной группе,
обусловливается в основном каким-то одним общим фактором, своим для
каждой такой группы. После принятия этой гипотезы разбиение на груп-
пы естественно строить так, чтобы параметры, принадлежащие к одной
группе, были коррелированы сравнительно сильно, а параметры, принад-
лежащие к разным группам, — слабо. После такого разбиения для ка-
ждой группы признаков строится случайная величина, которая в некото-
ром смысле наиболее сильно коррелирована с параметрами данной груп-
пы; эта случайная величина интерпретируется как искомый фактор, от
которого существенно зависят все параметры данной группы.
Очевидно, подобная схема является одним из частных случаев об-
щей логической схемы факторного анализа. В отличие от ранее опи-
санных классических моделей факторного анализа при эвристнческн-
оптимизационном подходе группировка признаков и выделение общих фак-
торов делаются на основе экстремизации некоторых эвристически введен-
ных функционалов. Разбиения, оптимизирующие функционал Ji или J2
(см. ниже), называются экстремальной группировкой параметров. Во-
обще под задачей экстремальной группировки набора случайных величин
а/1),...,на заранее заданное число классов р' понимают отыс-
кание такого набора подмножеств ...,£?» натурального ряда чи-
сел 1,2,...,р, что иГ=1^ = {1,2,...,р}, a Si П Sq = 0 при I / д, и
таких р нормированных (т.е. с единичной дисперсией D = 1) фак-
торов	, ftp \ которые максимизируют какой-либо критерий
оптимальности.
Остановимся здесь на алгоритмах для двух различных критериев
оптимальности.
568
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
Первый алгоритм экстремальной группировки признаков в качестве
критерия оптимальности использует функционал
Л = £ [согг(х«/*>)]’ + ...+ £ Гсогг(х«,/^)]2.
•€Sj	i£S,t
в котором под согг (х, понимается обычный парный коэффициент корре-
ляции между признаком х и фактором /. Обозначим А{ = {а/*\ i G SJ, I =
1,2, ...,р. Максимизация функционала (как по разбиению признаков
на группы Ai,..., Ар», так и по выбору факторов , f^2\• отве-
чает требованию такого разбиения параметров, когда в одной группе ока-
зываются наиболее «близкие» между собой, в смысле степени коррелиро-
ванности, признаки: в самом деле, при максимизации функционала Jx, для
каждого фиксированного набора случайных величин f^2\..., f^p \ в
одну l-ю группу будут попадать такие признаки, которые наиболее сильно
коррелировали с величиной в то же время среди всех возможных набо-
ров случайных величин	f^2\...,	будет выбираться такой набор,
что каждая из величин в среднем наиболее «близка» ко всем призна-
кам своей группы.
Очевидно, что при заданных классах Si, Sa,... ,SP» оптимальный на-
бор факторов fl2\..., f^p) получается в результате независимой мак-
симизации каждого слагаемого
52 [согг =г> А
*€S|
откуда
р*
max Ji = V А?,
..../<‘> “
где А/ — максимальное собственное значение матрицы R/, составленной из
коэффициентов корреляции переменных, входящих в А/. При этом опти-
мальный набор факторов / = 1,2,... ,р\ задается формулами:
= /	* \п tn ’	1 = 1>2-(13-34)
где гу = согт(® а— собственный вектор
матрицы R/, отвечающий максимальному собственному значению А/, т.е.
13.4. НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 569
С другой стороны, считая известными факторы	, f^p \ не-
трудно построить разбиение S>,	, Sp>t максимизирующее при фик-
сированных f,	,..,	\ а именно:
Si = |i: coit2(z(’\/^) > corr2(a/*\/’)) для всех q = 1,2,...,p'J.
(13.35)
Соотношения (13.34) и (13.35) являются необходимыми условиями макси-
мума Л.
Для одновременного нахождения оптимального разбиения Si,S2,...,
Sp> и оптимального набора факторов , /^2\..., f^p предлагается ите-
рационный алгоритм, последовательно осуществляющий выбор оптималь-
ных (по отношению к разбиению, полученному на предыдущем шаге) фак-
торов, а затем выбор разбиения, оптимального к факторам, полученным
на предыдущем шаге.
Пусть на 1/-м шаге итерации построено разбиение параметров на груп-
пы Ai,..., Ар». Для каждой такой группы параметров строят факторы
по формуле (13.34) и новое (*/4-1) разбиение параметров Ai*'+1\..., ApV+1^
в соответствии с правилом: параметр х^' относится к группе А{*'+1\ если
согг2(ж(,),/ir)) > согг2(z(,\/to)	(q = 1,2,... ,р').	(13.36)
Если для некоторого параметра х^ найдутся два или более факторов
таких, что для и этих факторов в (13.36) имеет место равенство, то
параметр х' относится к одной из соответствующих групп произвольно.
Очевидно, что на каждом шаге итераций функционал Ji не убыва-
ет, поэтому данный алгоритм будет сходиться к максимуму. Максимум
может быть локальным.
Для описания второго алгоритма экстремальной группировки призна-
ков введем функционал
h =	|согг(а:(’),/1)) + |coit (z(,),/2))|
»€Si	i€Sa
+—i- 22 согг (z^>	|-
»esF»
В содержательном смысле функционал J3 похож на функционал Ji и
его максимизация также соответствует основному требованию к характе-
ру разбиения признаков на группы. Доказано, что необходимыми и доста-
точными условиями максимума функционала J2 являются следующие:
570 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
•	разбиение параметров на группы А1,...,Ар> таково, что функцио-
нал
j3=Е
1=1 )	'»€S|	'
(где gi — некоторые числовые коэффициенты, равные либо 4-1, либо -1)
достигает максимума как по разбиению на группы, так и по значениям
коэффициентов Здесь под Dz понимается, как обычно, дисперсия слу-
чайной величины z\
•	факторы определяются соотношениями
/(') =	^i€S| Si	(13.37)
yEijeSt Si9jrij
Логическая схема доказательства этого следующая. Сначала, варьи-
руя функционал J2 и используя метод множителей Лагранжа для учета
условия = 1, показывают, что в точке максимума функционала J2
фактор	имеет вид (13.37). Затем доказывается, что если имеет
вид (13.37), то при любом наборе коэффициентов = ±1 и любом раз-
биении параметров на группы имеет место соотношение J2 J31 а если
же J3 достигает максимума, то J2 = </3- Из этого утверждения следует, в
частности, что для нахождения групп Si и факторов достаточно мак-
симизировать функционал J3. При фиксированном разбиении на группы
функционал J3 достигает максимума тогда, когда для каждого I соответ-
ствующие коэффициенты <7, максимизируют величину
(13.38)
' t€S< '
Поэтому естественно воспользоваться рекуррентной процедурой мак-
симизации J3. В процедуре циклически перебираются переменные
а/ , з^2\..., х(р\ на каждом шаге принимается решение об отнесении оче-
редного параметра х^ к одной из групп Aj,..., Ар» и определяется знак
Пусть к //-му шагу алгоритма построены разбиения параметров на
группы AJ ,..., Ар,1, вычислены коэффициенты д{ ', ф ,..., <7р» , равные
4-1 или —1, и пусть на этом шаге рассматривается признак € А^.
Тогда строятся р вспомогательных коэффициентов (/ = 1,...,/)
13.4.	НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 571
по формуле
4‘1+1> = “Bn Е W *).
где
f 1
sign х = < О
1-1
при х > О,
при х = О,
при х < О
и для всех I = 1,2,..., р вычисляются разности
I
Е
i*»
("МяУ

Затем выбирается такой номер I = 1*, что
iShjp»
(i)	.	A
и признак x'1 исключается из группы Л/ и присоединяется к группе Л^;
остальные группы признаков на этом шаге не меняются. В результате
получаем новое разбиение признаков — Л^1^, Л^1^,..., Л^+1\ Новые
значения коэффициентов определяются по формулам:
(для 3 / •),
На следующем (р + 1)-м шаге алгоритма рассматривается параметр
(«4-1)	• _z (Л
or у если t / Ру и х 1 у если i = р.
Процедура заканчивается, если при рассмотрении всех признаков оче-
редного цикла сохранились как разбиения признаков на группы, так и зна-
чения всех коэффициентов; полученное разбиение и значения коэффициен-
тов рассматриваются как оптимальные (доказано, что на каждом шаге
алгоритма значение J3 не убывает).
Нетрудно проследить идейную близость метода экстремальной груп-
пировки факторов с методами, опирающимися на логическую схему фак-
торного анализа. Так, например, отправляясь от общей модели вида
(13.26)
д=1
572
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
первую компоненту р 1 и «нагрузки» 1ц в методе главных компонент
можно определять из условия минимума выражения В (х^ —
при нормирующем ограничении D = 1. Решение этой условно экстре-
мальной задачи очевидным образом сводится к нахождению максимума
выражения Jj-Ljcorrfa^,/^)]3 при условии В/^1^ = 1.
Для построения следующего фактора (второй главной компонен-
ты) рассматриваются случайные величины а/*3) =	согг(®^\/^1^)/1\
Для этих случайных величин аналогичным образом находится свой фак-
тор, который и является фактором , и т. д.
Очевидно, что при реализации первого алгоритма метода экстремаль-
ной группировки признаков для каждой группы признаков 4/ строится
фактор, имеющий смысл первой главной компоненты для признаков этой
группы.
В центроидном методе общий фактор ищут в виде
(13.39)
где 9i = ±1 и gt выбирается так, чтобы максимизировать величину
В
(13.40)
Сравнение выражений (13.39) и (13.40) с выражениями (13.37) и (13.38) по-
казывает, что максимизация функционала J3 приводит к построению для
каждой группы признаков фактора, отличающегося на некоторый мно-
житель от первого общего фактора, который был бы построен для этой
группы центроидным методом.
13Л.З. Метод корреляционных плеяд
Задача разбиения признаков на группы часто имеет и самостоятель-
ное значение. Например, в ботанике для систематизации вновь открытых
растений делают разбиение набора признаков на группы так, чтобы 1-я
группа характеризовала форму листа, 2-я группа — форму плода и т. д.
В связи с этим и возник эвристический метод корреляционных плеяд.
Метод корреляционных плеяд, так же как и метод экстремальной
группировки, предназначен для нахождения таких групп признаков —
«плеяд», когда корреляционная связь, т.е. сумма модулей коэффициен-
тов корреляции между параметрами одной группы (внутриплеядная связь'
13.4. НЕКОТОРЫЕ ЭВРИСТИЧЕСКИЕ МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ 573
достаточно велика, а связь между параметрами из разных групп (межлле-
ядная) — мала. По определенному правилу по корреляционной матрице
признаков образуют чертеж — граф, который затем с помощью различных
приемов разбивают на подграфы. Элементы, соответствующие каждому
из подграфов, и образуют плеяду.
Рассмотрим корреляционную матрицу R = (r,j), t,y = 1,2,...,р, ис-
ходных признаков. Нарисуем р кружков; внутри каждого кружка напи-
шем номер одного из признаков. Каждый кружок соединяется линиями со
всеми остальными кружками; над линией, соединяющей t-й и у-й элемен-
ты (ребром графа), ставится значение модуля коэффициента корреляции
|rtj|. Полученный таким образом чертеж рассматриваем как исходный
граф.
Задавшись (произвольным образом или на основании предваритель-
ного изучения корреляционной матрицы) некоторыми пороговыми значе-
ниями коэффициента корреляции го, исключаем из графа все ребра, кото-
рые соответствуют коэффициентам корреляции, по модулю меньшим г0.
Затем задаем некоторое ri > го и относительно него повторяем описан-
ную процедуру. При некотором достаточно большом г граф распадается
на несколько подграфов, т. е. таких групп кружков, что связи (ребра гра-
фа) между кружками различных групп отсутствуют. Очевидно, что для
полученных таким образом плеяд внутриплеядные коэффициенты корре-
ляции будут больше г, а межплеядные — меньше г.
В другом варианте корреляционных плеяд предлагается упорядочи-
вать признаки и рассматривать только те коэффициенты корреляции, ко-
торые соответствуют связям между элементами в упорядоченной системе.
Упорядочение производится на основании принципа максимального
корреляционного пути: все р признаков связываются при помощи (р — 1)
линий (ребер) так, чтобы сумма модулей коэффициентов корреляции была
максимальной. Это достигается следующим образом: в корреляционной
матрице находят наибольший по абсолютной величине коэффициент кор-
реляции, например, |г/,т| = (коэффициенты на главной диагонали
матрицы, равные единице, не рассматриваются).
Рисуем кружки, соответствующие параметрам и и над «свя-
зью» между ними пишем значение г^. Затем, исключив находим
наибольший коэффициент в m-м столбце матрицы (это соответствует на-
хождению признака, который наиболее сильно после х^ «связан» с а/т))
и наибольший коэффициент в /й строке матрицы (это соответствует наг
хождению признака, наиболее сильно после х^ «связанного» с х^). Из
найденных таким образом двух коэффициентов корреляции выбирается
наибольший — пусть это будет |r,j| = Рисуем кружок х^\ соединяем
574 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
его с кружком х^ и проставляем значение Затем находим признаки,
наиболее связанные с х^1\ х^ и х^\ и выбираем из найденных коэффи-
циентов корреляции наибольший. Пусть это будет |гд-9| =	. Требуем,
чтобы на каждом шаге получался новый признак, поэтому признаки, уже
изображенные на чертеже, исключаются, следовательно, q / /, q £ mt
„	»	(a)	(j)
Далее рисуем кружок, соответствующий х , и соединяем его с х
и т. д. На каждом шаге находятся параметры, наиболее сильно связанные
с двумя последними рассмотренными параметрами, а затем выбирается
один из них, соответствующий большему коэффициенту корреляции. Про-
цедура заканчивается после (р — 1)-го шага; граф оказывается состоящим
из р кружков, соединенных (р — 1) ребром. Затем задается пороговое зна-
чение г, а все ребра, соответствующие меньшим, чем г, коэффициентам
корреляции, исключаются из графа.
Назовем незамкнутым графом такой граф, для которого для любых
двух кружков существует единственная траектория, составленная из ли-
ний связи, соединяющая эти два кружка. Очевидно, что во втором ва-
рианте метода корреляционных плеяд допускается построение только не-
замкнутых графов, а в первом варианте такое ограничение отсутствует.
Поэтому разбиения на плеяды, полученные разными способами, могут не
совпадать.
В работе [Лумельский В. Я.] приводятся результаты эксперименталь-
ной проверки алгоритмов экстремальной группировки параметров, а так-
же сравнение полученных результатов с результатами, даваемыми мето-
дом корреляционных плеяд.
Эксперимент проводился на физиологическом материале: исследова-
лись влияния шумов и вибрации на работоспособность и самочувствие.
Регистрировались 33 признака (р = 33), из них 7 параметров, характе-
ризующих температуру тела; 4 — кровяное давление; 14 — аудиометрию
(порог слышимости на заданной частоте); 2 — дыхание; 4 — силу и выно-
сливость рук и 2 (обособленных параметра) — пульс и скорость реакции.
С точки зрения физиолога «идеальным* было бы разбиение, при ко-
тором все характеристики температур образовали бы отдельную груп-
пу; параметры, характеризующие давление, — свою отдельную группу и
т.д., обособленные параметры образовали бы группы, состоящие из од-
ного элемента. Наиболее близким к «идеальному» оказалось разбиение,
полученное вторым алгоритмом экстремальной группировки, хотя алго-
ритм и присоединяет обособленные параметры к другим группам. Наиме-
нее точные (среди трех сравниваемых алгоритмов) результаты дал метол
корреляционных плеяд.
13.5. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
575
Исторически раньше возникшие различные варианты метода корре-
ляционных плеяд являются в действительности несколько упрощенными
эвристическими версиями более совершенных в математическом плане ал-
горитмов исследования структуры связей между компонентами многомер-
ного признака, использующими графы-деревья и стохастические сети.
13.5.	Построение сводного (интегрального)
латентного показателя качества (или
эффективности функционирования)
сложной системы
13.5.1.	Общая постановка задачи
И в профессиональной деятельности, и в своей повседневной жизни че-
ловек постоянно сталкивается с ситуациями, когда ему приходится срав-
нивать между собой и упорядочивать по некоторому не поддающемуся
непосредственному измерению свойству ряд сложных систем. Речь мо-
жет идти, в частности, о сравнении стран по уровню или качеству жиз-
ни, предприятий отрасли по эффективности их деятельности, сложных
изделий (например, определенного программного или технического сред-
ства) — по обобщенной характеристике качества, специалистов — по эф-
фективности их участия в выполнении поставленной задачи, участников
игровых видов спорта — по уровню проявленного ими (в определенном
состязании) мастерства и т.д. При этом общее представление о степе-
ни проявления анализируемого латентного (т. е. не поддающегося непо-
средственному измерению) свойства складывается как результат опреде-
ленного суммирования целого ряда частных (и поддающихся измерению)
характеристику от которых зависит в конечном счете это свойство. Так,
различные интегральные характеристики уровня благосостояния обще-
ства («уровень жизни», «качество жизни», «индекс человеческого разви-
тия») определяются набором показателей структуры и объемов потребле-
ния, качества населения и социальной сферы, экологического состояния
окружающей среды. Точно так же эффективность работы предприятия
определяется в основном совокупностью таких параметров, как себестои-
мость и реализуемость продукции, фондоотдача, текучесть кадров, коли-
чество рекламаций и т. п. В том же плане можно рассмотреть задачу изме-
рения степени оптимальности социально-экономического поведения семьи
в зависимости от значений параметров, определяющих структуру и объем
семейного бюджета, времени и денег. Наконец, к типичным задачам тако-
576
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
го рода относится проблема измерения мастерства спортсмена в игровых
видах спорта по значениям частных числовых характеристик его игровой
деятельности (см. ниже пример с хоккеем).
Математико-статистической формализации подобных задач и вытека-
ющим из нее рекомендациям по построению некоторого условного число-
вого измерителя анализируемого латентного свойства сложной системы и
посвящен данный пункт.
13.5.2.	Сводный показатель («выходное качество») и его
целевая функция
Пусть обобщенная сводная характеристика f анализируемого свой-
ства объекта определяется набором частных критериев, задаваемых под-
дающимися учету и измерению переменными а/г\а/а\...,х^ (в даль-
нейшем будем называть их «входными»), однако сама эта характеристи-
ка является латентной, т.е. не поддается непосредственному количе-
ственному измерению (для нее не существует объективно обусловленной
шкалы). Естественно предположить, что интуитивное экспертное (про-
фессиональное) восприятие этой характеристики (обозначим его у) можно
представить как несколько искаженное значение . .,я:^), причем
это искажение 6 носит случайный характер и обусловленно как разреша-
ющей способностью такого «измерительного прибора», каковым в данной
схеме является эксперт, так и существованием ряда слабо влияющих на у,
но не входящих в состав X = (я^1\... ,х^) «входных переменных». То-
гда модель, связывающая между собой интуитивное представление о свод-
ном показателе качества (у), сам сводный показатель (/(X)) как функцию
от X и случайную погрешность £(Х), может быть определена в виде
у = /(Х)-Н(Х).	(13.41)
Практически, не ограничивая общности данной схемы, можно при-
нять естественные допущения относительно первых двух моментов оста-
точной случайной компоненты $(Х):
E«(X)sO, Df(X) = deg’(X)<oo.	(13.41')
Тогда, очевидно, обобщенная (сводная) характеристика f(X) может
интерпретироваться как регрессия у по X, и если бы в качестве исход-
ной статистической информации располагали бы наряду со значениями
Xi = (ж-1),... ,«-р^)Т и результатами регистрации соответствующих зна-
чений зависимой переменной yi (« — номер наблюдения), то данная схема
13.Б. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
577
непосредственно сводилась бы к обычной модели регрессии (см. гл. 10).
Специфика модели (13.41), (13.41#) состоит в том, что вместо прямых из-
мерений у можно получить (с помощью экспертов) лишь некоторые спе-
циального вида сведения о его значениях, чаще всего — сравнительного
плана (типа ранжировок или парных сравнении обследованных объектов
по свойству у). Это обусловливает и более скромные претензии в отно-
шении целей статистического анализа этой модели: вместо требуемого в
регрессионном анализе восстановления (оценивания) функции f(X) ста-
вится задача оценивания f(X) с точностью до произвольного монотон-
ного преобразования.
Определение. Целевой функцией исследуемого обобщенного
свойства («выходного качества») называется любое преобразование ви-
да <р(х^\... ,х^) = у>(Х), сохраняющее заданное соотношение порядка
между анализируемыми объектами	..,ОП по усредненным зна-
чениям выходного качества, т.е. обладающее тем свойством, что из
f(Xix) f(Xi2) >	> /(Х<ж) с необходимостью следует выполнение
неравенств y>(Xfl) > у>(ХВ1) > ••• > и> наоборот, из последней
серии неравенств вытекает выполнение соответствующих неравенств для
f(Xik), к = 1,2,...,п. Очевидно, данное здесь определение целевой функ-
ции неоднозначно. Действительно, если <р(Х) есть целевая функция и
(/(<£) — любая взаимно-однозначная монотонно возрастающая функция,
то всякая функция вида ф(Х) = (7[9?(Х)] также будет целевой функци-
ей. Это означает, что допущение о наличии определенной шкалы в из-
мерении единого сводного показателя играет во многих случаях чисто
вспомогательную роль и нацеливает на поиск, связанный с выявлением
этой шкалы лишь с точностью до произвольного допустимого преобразо-
вания шкал. Ведь в соответствии с данным определением само значение
целевой функции не отражает никакой реальной, физически содержатель-
ной количественной закономерности. Реальные закономерности отража-
ются только соотношениями «больше» или «меньше» между значения-
ми этой функции для различных наборов величин входных параметров
X = (х^\...,х^)Т. Тем самым эти соотношения отражают предпочте-
ние с точки зрения анализируемого выходного качества одних значений X
перед другими. Поэтому в задачах, в которых возможно регулирование
значений X (в некоторой допустимой области), наиболее рациональным
управлением естественно признать то, которое максимизирует, при за-
данных ограничениях на X, значения целевой функции.
Данное определение целевой функции предполагает ее содержатель-
ную (экономическую, социально-экономическую, квалиметрическую, пси-
хологическую и т. д.) интерпретацию в зависимости от контекста иссле-
578
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
дования.
Итак, функция /(X), с помощью которой можно было бы производить
сравнительную оценку анализируемого «выходного качества» на рассма-
триваемых объектах, определена лишь с точностью до произвольного мо-
нотонного преобразования. Тем не менее для построения алгоритма ее вос-
становления было бы удобно параметризовать модель (13.41), т. е. опреде-
лить параметрическое семейство F = {/(Х;0)}, в рамках которого будет
производиться поиск целевой функции f(X). Выбор этого параметриче-
ского семейства, как правило, не удается подкрепить исчерпывающим те-
оретическим обоснованием, а потому с этого момента исследователь имеет
дело не с целевой функцией /(X), а с некоторой ее аппроксимацией /(X).
Имея в виду достаточную однородность обследуемых объектов по
всем неучтенным переменным, т. е. по переменным, не вошедшим в со-
став ..., и ограниченность интервала времени, в течение которо-
го будем использовать искомую аппроксимацию целевой функции, а также
реализуя идею разложения любой функции в ряд Тейлора, ограничимся в
дальнейшем изложении аппроксимацией линейного вида, т. е.
р
7(X;e) = e0 + J2^(i).	(13.42)
«=1
Коэффициенты 0 = (^о>^1»--->^р)Т оцениваются статистически по
исходным данным, структура и происхождение которых описываются ни-
же.
13.5.3.	Исходные данные
Итак, пусть речь идет о построении непосредственно не поддающе-
гося измерению единого сводного показателя эффективности функциони-
рования (качества) объекта и пусть с этой целью были собраны исход-
ные данные по п таким объектам:	На основании этих
исходных данных как раз и оцениваются параметры 0 искомой целе-
вой функции /(Х;0). Эти исходные данные состоят их двух частей:
экспертной и статистической (отсюда название метода — экспертно-
статистический ).
Экспертная часть исходных данных. Эта часть исходных дан-
ных относится к сведениям о значениях случайной величины yt (i —
номер обследованного объекта) в модели (13.41) и получается с помо-
щью специально организованного опроса экспертов и соответствующей
статистической обработки экспертных оценок. При этом сведения об yt
(t = 1,2,..., п) получают от экспертов в одной из следующих форм.
13.6. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
579
Форма (а) — наиболее информативный (а потому наиболее трудный
для экспертов) вариант. Предусматривает получение экспертных балль-
ных оценок выходного качества
У12э» 3/22, > • • •> Уп2л
1/1 m,»1/2 т,? • • • > Уптя
где yija — оценка выходного качества объекта полученная от j-ro экс-
перта (здесь п — число оцениваемых объектов, т — число участвующих
в оценке экспертов).
Форма (б) — средний по информативности (и по степени трудности
для экспертов) вариант.
Предусматривает получение лишь экспертных упорядочений обсле-
дованных объектов по степени проявления в них анализируемого свойства,
т. е. ранжировок вида
Я11я,Я21,,. ..,ЯП1Э
^12.,Л2а>,...,7гп2э ,	(13.436)
^2т,> • • •, ^пт,
где Rijt — ранг (место), присвоенный объекту О, }~м экспертом в ряду
из п обследованных объектов, упорядоченном этим экспертом по степени
проявления анализируемого свойства.
Форма (в) — наименее информативный (и наименее трудный для экс-
пертов) вариант. Информация от каждого (J-го) эксперта поступает в
форме булевой матрицы парных сравнений
7л = (7*М>)» i,k = T^n, j = l,2,...,m.	(13.43в)
где life.». — результат парного сравнения j-u экспертом объектов О, и О*,
может выражаться либо единицей, либо нулем по одному из следующих
правил:
если эксперт производит сравнение объектов и 0 k типа их упоря-
дочения по анализируемому свойству, то
{1, если по мнению j-ro эксперта Oi не хуже	к
О в противном случае;	' *	'
если эксперт производит сравнение объектов О, и 0k лишь с точки
зрения принадлежности этих объектов к однородному (по анализируемому
580 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
свойству) классу, то

1, если объекты О; и Ok однородны,
0 в противном случае.
(13.43в")
Вычислительные трудности, связанные с реализацией алгоритма оце-
нивания параметров 6 искомой целевой функции /(Х;0), естественно,
возрастают по мере перехода от более информативных вариантов эксперт-
ной информации об к менее информативным.
Статистическая часть исходных данных. Как выше уже от-
мечено, входные переменные (частные критерии) а/2\..., на
основании которых формируется представление об исследуемом выход-
ном качестве, поддаются непосредственному измерению (регистрации) на
каждом из обследуемых объектов. Поэтому, статистически обследовав
анализируемые объекты Oi, О2,...,Оп по переменным а/2\...,
будем иметь статистическую часть исходных данных в виде матрицы
(таблицы) типа «объект-свойство»:
где z-’ — значение /-Й входной переменной, зарегистрированное на t-м
объекте.
Таким образом, приступая к оценке параметров О искомой целевой
функции /(Х;0) в модели (13.41), исследователь располагает исходной
информацией об объектах Oi,O2,...,On, состоящей из данных таблицы
(13.44) и одного из вариантов (13.43а)-(13.43в) сведений об jft.
13.5.4.	Алгоритмические и вычислительные вопросы
построения неизвестной целевой функции
Опишем вначале общую логическую схему оценивания параметров в
целевой функции (13.42). Располагая конкретными значениями Оо пара-
метров О, для каждого объекта Oi можем вычислить величину среднего
единого сводного показателя /(Х<; Од) и далее, ориентируясь на сравне-
ние значений 0о),/(^; во), • • • -/(^п, ©о), получить основанную на
целевой функции ранжировку объектов по искомому качеству
Я1(©о), Я2(0О), * • •, ЯП(0О)
(13.45)
13.6. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
581
либо их разбиение на однородные (по /) классы, которое так же, как и
уже имеющиеся экспертные разбиения (13.43в), может быть представлено
в виде булевой матрицы 7(60» А)-
Оценку О неизвестных параметров 0 предлагается подбирать таким
образом, чтобы: 1) минимизировать расхождения в экспертных	и по-
лученных с помощью целевой функции (/(Х»;0)) балльных оценках вы-
ходного качества (в варианте (а) экспертной информации); 2) максими-
зировать согласованность экспертных и полученной с помощью целевой
функции ранжировок объектов по анализируемому выходному качеству
(в варианте (б) экспертной информации); 3) минимизировать расхожде-
ния в экспертных и полученном с помощью целевой функции разбиениях
объектов на классы (в варианте (в) экспертной информации).
Из сказанного следует, что экспертно-статистический метод постро-
ения единого сводного показателя нацелен на формализацию (в виде со-
ответствующим образом подобранной целевой функции f(X\ 0)) тех кри-
терийных установок, которыми руководствовались привлеченные к кон-
трольному эксперименту эксперты при формировании своих оценок. По-
этому состоятельность и эффективность этого метода целиком за-
висит от компетентности и согласованности используемых в нем экс-
пертных оценок.
Оценивание неизвестных параметров целевой функции при
балльных экспертных оценках выходного качества. В этом случае
задача сводится к обычной схеме регрессионного анализа и соответствен-
но к использованию метода наименьших квадратов. Действительно, рас-
полагая данными вида (13.43а)-( 13.44), можем записать модель (13.41) в
виде
py, = /(x.;e)+M*);
1Е = О, D щх.) = <4	1
где величина (как правило, неизвестная) характеризует погрешность в
оценке j-м экспертом выходного качества «-го объекта. Критерий метода
наименьших квадратов дает нам оценку 0 векторного параметра 0 как
решение оптимизационной задачи вида (см. гл. 15)
Е Е 4 (»У. - f(Xi; ©))3 - min.	(13.47)
J=1 i=l
Если не располагают никакими сведениями относительно величин сг^,
то принимают упрощающее предположение cr,j- = const, и задача (13.47)
соответственно упрощается. В некоторых случаях удается априори за-
даться «весами» tUj, оценивающими сравнительную компетентность j-ro
582
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
эксперта (j = 1,2,, m). Тогда эти веса вставляются в (13.47) в качестве
сомножителей слагаемых вместо величин 1/(7?,.
Конкретные рекомендации по вычислительной реализации решения
задач типа (13.47) приведены в гл. 15.
Оценивание неизвестных параметров целевой функции при
экспертных ранжировках и парных сравнениях объектов. Ка-
ждая экспертная ранжировка Rj* =	(j-я строка в
(13.43в)) может быть представлена в виде булевой матрицы в соот-
ветствии с правилом (13.43в). Поэтому в дальнейшем (в данном пункте)
будем считать, что экспертная информация о выходном качестве объектов
представлена в виде матриц парных сравнений вида (13.43в).
В общем случае задача состоит в том, чтобы на основе известных
сравнений N пар объектов (не обязательно всех возможных пар из п объ-
ектов, т.е. N может быть меньше Сп) определить скалярную функцию
/(*;*>), такую, что парные сравнения, установленные по этой функции
относительно тех же пар объектов, минимально (в смысле заданного кри-
терия) отличались бы от экспертно установленных.
В случае парных сравнений в виде отношений предпочтения (см.
правило (13.43в') формирования элементов 7>fc.j,), поставив на первое ме-
сто в каждой из N экспертно оцененных пар лучший (не худший) объект,
будем иметь пары (*i> значения целевых функций элементов которых
должны были бы удовлетворять системе неравенств
(13.48)
V. 9 — 1,2,...,/».
Однако в общем случае эта система оказывается несовместной. По-
этому в каждое неравенство (iqtkq) вводится невязка
.	- / °>	если ®)_ Лх*,!е) °’
— (/(Хц5 0) —0)) в противном случае
и вектор оценок О определяется из условия минимума суммы невязок
SgLi	ПРИ некоторых ограничениях (типа нормировки) на ком-
поненты искомого параметра 01.
1 Алгоритм основан на результатах, изложенных в работе: Киселев Н. И. Экспертно-
статистический метод определения функции предпочтения по результатам парных
сравнений объектов //Алгоритмическое и программное обеспечение прикладного
статистического анализа: Ученые записки по статистике. — М.: Наука, 1980. Т. 36.
С. 111-122.
13.5. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
583
В случае парных сравнений, задающих разбиение объектов на
однородные классы (см. правило (13.43в') формирования элементов
7«к.ь)» матрицы 717m, задают т различных разбиений множества
{01,	..., 0п} на классы, элементы каждого из которых близки по ана-
лизируемому выходному качеству. Для любых двух разбиений 7, и уг
может быть введена мера близости этих разбиений
1 п
^(т8,7г) = 2	“ 7«i,r|’
W=1
Пусть f(X; 0) =	— некоторая линейная аппроксимация f.
Задавшись некоторым е > 0, можно с помощью /(X; 0) построить разби-
ение п объектов^ на классы. В один класс при этом попадут те объекты,
у которых 0 < /(Х;0) < е, в другой — те, у которых е < /(X; 0) < 2е и
т. д. Полученное разбиение у(€, 0) зависит, очевидно, от значений е и 0.
Подбираются такие значения £ и 0, чтобы величина ^(7»,»7(£*»®))
была минимальна.
Для наилучшего выбора вектора коэффициентов 0 можно использо-
вать также так называемый «метод голосования». При любом е > 0 с
помощью линейной функции /(Х;0) = $2?=i строится разбиение п
объектов следующим образом. Пусть в разбиениях классы пронумерова-
ны и 7^ — 1/-й класс в J-м экспертном разбиении. Для любого объекта
X, подсчитывается величина
r(Xi,%V’) = Е
где
1, если |	< £;
О, если |	М»!** ”	> £-
Объект Xi относится к тому классу, для которого величина Г(Х<, 7>*Ь
максимальна. Полученное разбиение обозначим через 7,(е;0). Параме-
тры £ и 0 подбираются из условия минимизации величины
EjLi ^(7j,>7j(£;®)) (при наличии априорных «весов компетентности»
Vi,..., vm минимизируется взвешенная сумма J^jLi vJ’^(7j», 7j(e> 0)))- Ис-
пользуется алгоритм эвристического типа.
Замечание. Выше отмечалось, что успех описываемого подхо-
да целиком зависит от качества экспертной части исходной информации.
Поэтому прежде чем непосредственно приступить к процедурам оценива-
ния параметров 0 целевой функции, необходимо тщательно исследовать
584
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
структуру и степень согласованности экспертных мнений. В варианте
балльных оценок это сводится в основном к анализу резко выделяющихся
наблюдений. В варианте ранжировок используется аппарат ранговой кор-
реляции (см. гл. 11) в первую очередь для того, чтобы проверить гипотезу
об отсутствии какой бы то ни было согласованности в упорядочениях раз-
личных экспертов. В варианте парных сравнений исследуется структура
попарных расстояний между экспертными разбиениями на классы.
13.5.5. Примеры построения интегрального показателя с
помощью экспертно-статистического метода
В п. 13.5.1 упоминались примеры реальных задач, в которых глав-
ной целью исследования было построение интегрального индикатора для
некоторого сводного латентного «выходного качества» системы. Вернем-
ся к некоторым из этих задач, чтобы дать краткое описание их решения
или ссылку на литературный источник, в котором это решение подробно
приводится.
1) Построение интегрального показателя уровня мастерства
хоккеиста, проявленного им в данном матче. В рамках создания
автоматизированной информационной системы для чемпионата мира по
хоккею 1973 г. (системы «АИС-хоккей-73») рабочей группой Централь-
ного экономико-математического института АН СССР была решена за-
дача построения интегрального показателя уровня мастерства хоккеиста
(отдельно для защитников и для нападающих) по одиннадцати частным
показателям его игровой деятельности:
— количество очков за результативность (по системе «гол-|-пас»);
(2)
яг ' — число бросков в створ ворот противника;
(з)
я: — число выигранных силовых единоборств;
(4)	-	--
я: 1 — число отборов шайбы у противника;
— разность шайб («забито—пропущено») в микро матче данного
игрока;
(6)	~
х' ' — общее число точных передач;
(7)
х — число точных длинных первых передач;
(в)	«
х * — число парированных бросков противника;
(»)
х — суммарное время участия хоккеиста в игре в период, когда его
команда играла в большинстве или меньшинстве;
х* ' — число удачно выполненных обводок;
(н)	.
х' ' — сумма штрафного времени.
Экспертная часть исходной информации была получена в результате
13.5. ПОСТРОЕНИЕ СВОДНОГО ЛАТЕНТНОГО ПОКАЗАТЕЛЯ
585
заполнения экспертами специальных анкет, в которых уровень мастерства
хоккеиста в данном матче оценивался по стобалльпой системе (т. е. имел-
ся вариант (13.43а) экспертной информации). «Съем» статистической
части информации (13.44) по каждому из участников хоккейного матча
производился специальными членами судейской комиссии.
В результате использования экспертно-статистического метода были
получены следующие два варианта аппроксимаций для линейных целевых
функций — отдельно для оценки мастерства защитников (/эащ(-^)) «
нападающих (/нап(Х)):
/МЩ(Х) = 10 + 4х(,) + xW + 4х(3) + х(5) + 0,2х(6) + Зх(8) + г<9) + х(,0);
/».„(%) = 8z(,) + хт + х<3’ + 0,5х<4» + 0,2х<в> + 4х<в> + 2х(9) + х<*°>.
Знание целевой функции позволяет в данном случае: 1) производить
формализованную оценку мастерства хоккеиста, проявленного им в дан-
ном матче или в серии матчей, основанную только на знании отдельных
числовых показателей, характеризующих его игру; 2) наиболее целесо-
образно строить индивидуальные планы тренировок, особое внимание уде-
ляя совершенствованию тех компонентов игры, которые вошли в целевую
функцию с относительно большими весами и за счет которых, следова-
тельно, можно добиться наиболее существенного прироста в оценках ма-
стерства.
Как и в любой работе такого профиля, в данной были последовательно
реализованы следующие семь основных этапов:
этап 1: постановка задачи;
этап 2: предварительный отбор входных параметров;
этап 3: организация экспертных обследований;
этап 4: организация службы наблюдений, т.е. съема значений вход-
ных признаков;
этап 5: вывод целевой функции (определение ее общего вида и вычи-
сление весовых коэффициентов);
этап 6: экспериментальная проверка адекватности целевой функции;
этап 7: рабочая эксплуатация целевой функции.
Ход и результаты данной работы подробно описаны в [Айвазян С. А.,
Бежаева 3. И., Староверов О. В., с. 218-223].
2) Построение сводного показателя эффективности деятель-
ности промышленного предприятия. Объектами исследования явля-
ются 17 промышленных предприятий, специализирующихся на выпуске
асинхронных двигателей переменного тока различного назначения. Цель
исследования — построение единого сводного показателя экономической
586
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
эффективности работы предприятия в форме линейной функции от ряда
частных показателей экономической эффективности. С помощью сочета-
ния экспертного анализа и статистических методов снижения размерности
(метода экстремальной группировки признаков п. 13.4.2, метода главных
компонент, — п. 13.2) из априорного набора, состоящего из 22 частных
показателей эффективности, было оставлено в качестве входных перемен-
ных экспертно-статистического метода восемь:
а/1 *) — удельный вес продукции высшей категории качества в общем объ-
еме товарной продукции (ТП) предприятия;
х1 ’ — динамика выпуска ТП на 1 рубль затрат;
х^ — выработка нормативно-чистой продукции (НЧП) на единицу про-
мышленно-производственного персонала (ППП);
х^ — выполнение плана выпуска НЧП на единицу ППП;
(5)	-
х' ' — динамика фондоотдачи;
х^6) — выполнение плана выпуска ТП;
х(7) — выполнение плана по оборачиваемости нормируемых оборотных
средств (отношение фактического числа оборотов к нормативно-
му);
х^ — выполнение плана по балансовой прибыли.
Из двенадцати привлеченных к задаче экспертов пять дали оценку
интегральной эффективности деятельности анализируемых предприятии
(по результатам их работы в 1982 и 1983 гг.) в десятибалльной системе,
остальные семь проран жировали предприятия, причем четверо из них до-
полнительно представили результаты своих парных сравнений. Поэтому
реализовывались все три версии оценивания неизвестных коэффициентов
линейной целевой функции. Приведем здесь для примера один из полу-
ченных с помощью ЭСМ вариантов решения, а именно вариант, ориен-
тированный на экспертные балльные оценки только одного из экспертов:
f(X; 0) = -2,944-0,10г(1)+0,07г(2) +0,55z(3)-0,13z(4) +O,O6ar(s)-0,03z(e)-
0,07z(7) - 0,02z(e).
Мера согласованности балльного оценивания предприятий, произве-
денного с помощью этого эксперта и данной целевой функции, характе-
ризуется величиной коэффициента корреляции, равной 0,77. Обращает
на себя внимание тот факт, что формализация критерийных установок
эксперта показала практическое игнорирование им при формировании ин-
тегральной оценки эффективности функционирования предприятия всех
1 Показатель Динамики исчисляется как отношение прироста анализируемого показа-
теля в данном периоде к его величине в предшествующем.
13.6. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
587
частных показателей выполнения плана (т.е. входных переменных
аг , зг В то же время если бы этому специалисту предложили не-
посредственно (экспертно) оценить значимость коэффициентов при этих
переменных, то результат, можно не сомневаться, был бы совсем иным!
13.6.	Многомерное шкалирование
13.6.1.	Постановка задачи метрического многомерного
шкалирования
Пусть исходная информация об объектах задана в форме матрицы
их попарных сравнений (9.2), где элемент 7^ этой матрицы интерпре-
тируется как евклидово расстояние между объектом О, и объектом О}
(i,j= 1,2,...,п), т.е.
где
711 712 ••• 7ш
721	722 • • • 72п
(13.49)
7п1	7п2	• • • 7пп
(13.50)
Однако ни координаты объектов X, = (xj’\... ,яг^)Т, ни даже раз-
мерность их признакового пространства р нам не известны. Требуется
на основании известных данных (13.49) восстановить неизвестную раз-
мерность р анализируемого признакового пространства и приписать ка-
ждому объекту Oi координаты X, = (zP\«^.,.,а?^)Т таким образом,
чтобы вычисленные по формуле (13.50) попарные евклидовы расстояния
по возможности совпали бы с заданными матрицей 7. При этом речь
идет о восстановлении координат Х2,...,с точностью до орто-
гонального преобразования, т.к. при ортогональном преобразовании си-
стемы координат попарные расстояния между объектами не меняются.
Таким образом, цель методов метрического многомерного шкалирования
состоит в том, чтобы отобразить информацию о конфигурации исход-
ных многомерных данных, заданную матрицей расстояний у, в виде гео-
метрической конфигурации п точек в соответствующем многомерном
пространстве.
588 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
13.6.2.	Решение задачи метрического многомерного
шкалирования
Введем в рассмотрение центрированную матрицу искомых наблюде-
ний
/ z(1) - х0* г(2) - z<2) z(p) -	\
Z(p)-Z<p)l	/юм.
Хц = х* х	х * ’' жз х I ,	(13.51)
и*> -' «$?’’-	/
а также матрицу В = (б,-,), i,j = 1,2, ...,п, скалярных произведений
Ьц = (Xi - X)T(Xj -Х) =	- ^)(х^ -	(13.52)
fc=l
Метод определения искомых координат Л\,Х2,...,Хп анализируе-
мых объектов (с точностью до ортогонального преобразования), а заод-
но и размерности р пространства, в которое они отображаются, основан
не на непосредственном использовании матрицы исходных данных 7 (см.
(13.49)), а на преобразовании ее в матрицу В. Можно показать, что эле-
менты матриц 7 и В связаны между собой соотношением
ь- = И - +	(13.53)
'	t=l	J=1	»=1 J=1
Далее используются следующие свойства матрицы В:
(i)	матрица В неотрицательно определена;
(ii)	ранг матрицы В равен размерности р искомого пространства ото-
бражения;
(iii)	ненулевые собственные числа А!,А2,...,Ар матрицы В, упорядо-
ченные в порядке убывания, совпадают с соответствующими соб-
ственными числами матрицы S2 =± Хц Хц, где матрица Хц определе-
на соотношением (13.51); отметим, что матрица = S2/n есть
выборочная матрица ковариаций искомого вектора признаков X;
(iv)	пусть lr = (Zri Jrp)T есть r-й собственный вектор матрицы
S2, соответствующий r-му по величине собственному значению Лг
(г = 1,2, ...,р); тогда вектор = (z{r\.,z£r^)T значений
r-й главной компоненты вектора X будет
№ = Хц/Г;	(13.54)
13.6. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
589
при этом, если lr = (lri, /г2,..., l“n) — r-й собственный вектор ма-
трицы В, соответствующий тому же собственному числу Аг (ш. е.
=	г = 1,2,...,р.	(13.55)
В конечном счете из приведенных свойств следует, что, решая про-
блему собственных чисел и собственных векторов для матрицы В и огра-
ничиваясь ненулевыми собственными числами Ai > А2 > • • • > Ар > О,
получим координатное представление (13.55) анализируемых объектов в
пространстве главных компонент искомого многомерного признака X. А
поскольку мы можем решить задачу только с точностью до ортогональ-
ного преобразования, то представление объектов в виде (13.55) и будет ре-
шением проблемы метрического многомерного шкалирования. Заметим,
что из построения следует возможность следующего выражения элементов
fty через 4г) и zjr) (г- 1,2,
(13.56)
Если же мы хотим представить имеющиеся данные в пространстве за-
данной (но меньшей, чем р) размерности р', то можно показать, что, беря
только первые р координат в выражении (13.55), мы обеспечим макси-
мальное (среди прочих представлений исходных статистических данных
в пространстве размерности р < р) приближение их геометрической
структуры, заданной элементами b*j матрицы В в смысле критерия
(13.57)
t=l J=1
В соотношении (13.57) величины tf£\x) означают значения геоме-
трических характеристик, вычисленных По формулам (13.53), в которых
стоящие в правых частях попарные расстояния вычислены в коорди-
натах предлагаемого ^/-мерного пространства (как следует из (13.56), в
случае р = р этот критерий принимает нулевое значение при использо-
вании представления (13.55)).
590
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
13.6.3.	Понятие о неметрическом многомерном
шкалировании (МШ)
В неметрическом МШ предполагается, что различия (близости) 7^
измерены в ординальной шкале, так что важен только ранговый порядок
различий, а не сами их численные значения. Процедуры неметрического
МШ стремятся построить такую геометрическую конфигурацию точек в
пространстве заданной размерности р, чтобы ранговый порядок попар-
ных расстояний между ними, по возможности, минимально отличался от
того порядка, который задан матрицей 7. Одна процедура неметриче-
ского МШ отличается от другой выбором вида критерия различия двух
разных упорядочений.
ВЫВОДЫ
1.	В исследовательской и практической статистической деятельно-
сти часто приходится иметь дело с исходными данными высокой размер-
ности, т.е. с ситуациями, когда число регистрируемых на каждом из
статистически обследованных объектов показателей составляет несколько
десятков, а иногда — сотни и даже тысячи. В подобных ситуациях лег-
ко объяснимо желание исследователя существенно снизить размерность
анализируемого признакового пространства, т.е. перейти от исходно-
го набора показателей к небольшому числу вспомогательных переменных
(которые либо отбираются из числа исходных, либо строятся по опре-
деленному правилу по совокупности исходных показателей), по которым
впоследствии он мог бы достаточно точно воспроизвести интересующие
его свойства анализируемого массива данных. Одним из наиболее рас-
пространенных методов снижения размерности исследуемого признаково-
го пространства является метод главных компонент»
2.	Имеется по меньшей мере три основных типа принципиальных
предпосылок, обусловливающих возможность практически «безболезнен-
ного» перехода от большого числа исходных показателей состояния (пове-
дения, качества, эффективности функционирования) анализируемого объ-
екта к существенно меньшему числу наиболее информативных перемен-
ных. Это, во-первых, дублирование информации, доставляемой сильно
взаимосвязанными показателями; во-вторых, неинформативность пока-
зателей, мало меняющихся при переходе от одного объекта к другому (ма-
лая вариабельность показателя); в-третьих, возможность агрегирова-
ния, т. е. простого или взвешенного суммирования некоторых физически
однотипных показателей.
3.	В оптимизационной постановке задачи снижения размерности
выводы
591
решение, получаемое с помощью метода главных компонент, максими-
зирует критерий информативности, определяемый суммарной дисперси-
ей заданного (небольшого) числа искомых вспомогательных переменных
(при соответствующих условиях их нормировки). Для вычисления к-н.
главной компоненты z^k\x) (к = 1,...,р) следует найти собственный
вектор Ik — (IkU' '•ylkp) ковариационной матрицы Е исходного набо-
ра показателей X = (z^\ ...,z^)T> т.е. решить систему уравнений
(Е - AfcI)/J = О, где А* — к-н по величине корень (при их расположе-
нии в порядке убывания) характеристического уравнения |Е — А1| = 0.
Компоненты (j = 1,р) собственного вектора являются искомыми
весовыми коэффициентами, с помощью которых осуществляется переход
V (1)	(р)	~	v\
от исходных показателей я ,..., аг к главной компоненте z' '(Л ), т. е.
4.	Основные числовые характеристики вектора Z = (г'1’,..., z^r
главных компонент могут быть выражены через основные числовые ха-
рактеристики исходных показателей и собственные числа их ковариаци-
онной матрицы Е (см. п. 13.2.3).
5.	Вектор р (р* < р) первых главных компонент Z^p \х) =
(z^\x),... ,z{p \Х))Т обладает рядом оптимальных свойству среди ко-
торых отметим следующие:
а)	свойство наименьшей ошибки автопрогноза или наилучшей само-
воспроизводимости: с помощью р' первых главных компонент z^,..., z^p
исходных показателей	..., я/р) (р* < р) достигается наилучший (в
определенном смысле) прогноз этих показателей среди всех прогнозов, ко-
торые можно построить с помощью р' линейных комбинаций набора из р
произвольных признаков;
б)	свойство наименьшего искажения некоторых геометрических ха-
рактеристик совокупности исходных многомерных наблюдений X],...,
Хп при их проецировании в пространство меньшей размерности, натяну-
t	(1)	(р')
тое на р первых главных компонент z' z' .
6.	Главные компоненты, построенные не по истинной ковариацион-
ной матрице Е вектора исходных показателей X = (ж^\.. . ,з/р))Т, а по
ее выборочному аналогу (оценке) Е, называются выборочными главными
компонентами и в определенных (достаточно широких) условиях обла-
дают (вместе с собственными числами и векторами матрицы Е) всеми
традиционными свойствами «хороших» оценок: состоятельностью, асим-
птотической эффективностью, асимптотической нормальностью.
7.	Геометрически определение первой главной компоненты равносиль-
592 ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
но построению новой координатной оси таким образом, чтобы она
шла в направлении наибольшего разброса исходных данных, т.е. в на-
правлении вытянутости анализируемого «облака» многомерных наблю-
дений. Затем среди направлений, перпендикулярных к Oz^, отыскива-
ется направление «наибольшей вытянутости» и т.д. Если харак-
тер вытянутости анализируемого «облака» данных в исходном признако-
вом пространстве существенно отличен от линейного, то линейная модель
главных компонент может оказаться неэффективной.
8.	Главные компоненты используются при решении следующих основ-
ных типов задач анализа данных:
1)	упрощение, сокращение размерностей анализируемых моделей ста-
тистического исследования зависимостей или классификации с целью об-
легчения счета и интерпретации получаемых статистических выводов;
2)	наглядное представление (визуализация) исходных многомерных
данных, получаемое с помощью их проецирования в пространство, натя-
нутое на первую, первые две или первые три главные компоненты;
3)	предварительная ортогонализация объясняющих переменных в за-
дачах построения регрессионных зависимостей как средство «борьбы» с
мультиколлинеарностью (см. гл. 15);
4)	сжатие объемов хранимой статистической информации.
9.	Различные версии моделей и методов факторного анализа (центро-
идный, максимального правдоподобия, экстремальной группировки пара-
метров, корреляционных плеяд и др.) основаны на общей базовой идее,
(1)	(р)
в соответствии с которой значения всех признаков х ,..., ж анализи-
руемого набора формируются под воздействием сравнительно небольшого
числа одних и тех же (общих) факторов	не поддающихся,
правда, непосредственному измерению (и потому называющихся латент-
ными). В определенном смысле эти общие факторы выступают в роли
причин, а наблюдаемые (анализируемые) признаки — в роли следствий.
10.	Поскольку число общих (латентных) факторов существенно мень-
ше числа анализируемых признаков, то методы факторного анализа в ко-
нечном счете нацелены (так же как и метод главных компонент) на сни-
жение размерности анализируемого признакового пространства.
11.	Статистическая реализация модели факторного анализа преду-
сматривает последовательное решение вопросов существования такой мо-
дели, ее идентификации (т.е. возможности ее однозначного восстано-
вления по исходным статистическим данным), алгоритмического опре-
деления ее структурных параметров (т. е. определения способа вычисле-
ния неизвестных параметров модели при точно известной ковариационной
матрице анализируемого многомерного признака) и их статистической
выводы
593
оценки по имеющимся наблюдениям, включая статистические оценки для
самих общих (латентных) факторов.
12.	Наиболее распространенной в практике статистических исследо-
ваний и наиболее теоретически разработанной является каноническая мо-
дель факторного анализа, в которой признаки линейно зависят от фак-
торов, факторы взаимно некоррелированы между собой и со случайными
остатками модели, а случайные остатки в свою очередь взаимно некорре-
лированы и нормально распределены.
13.	Между методом главных компонент и линейной моделью фактор-
ного анализа имеется идейная общность: и тот и другой метод можно
рассматривать как метод аппроксимации набора анализируемых переме-
щенных переменных с помощью линейных функций от сравнительно не-
большого числа одних и тех же вспомогательных переменных (главных
компонент — в одном методе и общих факторов — в другом). Их разли-
чие — лишь в конкретизации критерия точности аппроксимации.
14.	Наиболее «узкие места» в практической дееспособности модели
факторного анализа связаны с решением задачи оценки числа р общих
факторов модели и с содержательной интерпретацией найденных общих
факторов. Для успешного решения последней задачи широко пользуются
неоднозначностью (с точностью до ортогонального преобразования) опре-
деления общих факторов и соответственно возможностью их разнообраз-
ных «вращений» в факторном пространстве.
15.	Наряду с математико-статистическими методами снижения раз-
мерности, т.е. с методами, допускающими описание и интерпретацию в
терминах строгой вероятностной модели, существуют и широко использу-
ются в статистической практике так называемые эвристические методы.
Свое название они оправдывают тем, что порождаются обычно некоторы-
ми частными целевыми установками, выраженными в виде установлен-
ных на содержательно-субъективном уровне оптимизируемых критери-
ев качества решения задачи. К таким методам, в частности, относятся
методы экстремальной группировки, метод корреляционных плеяд.
16.	Задача построения не поддающегося непосредственному измере-
нию интегрального (агрегатного) сводного показателя у эффективности
функционирования (качества) объекта по заданным значениям частных
(1)	(2)	(р)
критериальных характеристик а; , аг ,..., ж' ' анализируемого свойства
может рассматриваться как задача снижения размерности исследуемо-
го признакового пространства до единицы. Эта же задача может быть
сформулирована в терминах построения целевой функции анализируемо-
го обобщенного свойства исследуемых объектов.
17.	Базовая идея экспертно-статистического метода построения
594
ГЛ. 13. СНИЖЕНИЕ РАЗМЕРНОСТИ МНОГОМЕРНОГО ПРИЗНАКА
единого сводного показателя эффективности функционирования (каче-
ства) объекта заключается в «настройке» искомых коэффициентов це-
левой функции ^(Х) на заданную (в различной форме) экспертную инфор-
мацию, относящуюся к сравнению статистически обследованных объектов
по анализируемому интегральному свойству. Название метода объясняет-
ся тем, что его реализация основана как на статистической информации
об объектах, так и на экспертной (это представленные в той или иной
форме экспертные оценки анализируемого интегрального свойства у).
18.	Вычислительная реализация экспертно-статистического метода
(т.е. алгоритм определения искомых «весов» 0j) сводится к известному
методу наименьших квадратов лишь в тех сравнительно редких случа-
ях, когда от экспертов удается получить балльные оценки у1э,..., уПл ана-
лизируемого интегрального свойства по каждому из исследуемых объек-
тов, Если же в распоряжении исследователя лишь сравнительные оценки
объектов по анализируемому свойству (упорядочения, парные сравнения,
классификации), то вычислительная процедура по определению коэффи-
циентов существенно усложняется (ее описание и обоснование требуют
специальной разработки).
19.	Экспертно-статистический метод имеет широкий диапазон воз-
можных применений, однако необходимым условием его достоверности и
эффективности является четкое определение анализируемого интеграль-
ного свойства и компетентность используемых экспертных мнений.
20.	Многомерное шкалирование — совокупность методов, позволяю-
щих по заданной информации о мерах различия (близости) между объек-
тами рассматриваемой совокупности приписывать каждому из этих объек-
тов вектор характеризующих его количественных показателей; при этом
размерность искомого координатного пространства задается заранее, а
«погружение» в него анализируемых объектов производится таким обра-
зом, чтобы структура взаимных различий (близостей) между ними, из-
меренных с помощью приписываемых им вспомогательных координат, в
среднем наименее отличалась бы от заданной в смысле того или иного
функционала качества. Процедуры многомерного шкалирования приме-
няются, когда данные заданы в виде матрицы попарных расстояний меж-
ду объектами или удаленностей или их порядковых отношений. В первом
случае используются методы так называемого метрического шкалирова-
ния, а во втором — неметрического шкалирования.
Раздел IV

ГЛАВА 14. ЭКОНОМЕТРИКА И
ЭКОНОМЕТРИЧЕСКОЕ
МОДЕЛИРОВАНИЕ: ОСНОВНЫЕ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
14.1.	Эконометрика и ее место в ряду
математико-статистических и
экономических дисциплин
Существуют различные варианты определения эконометрики — от
чрезмерно расширительных (при которых к эконометрике относят все,
что связано с измерениями в экономике) до узко инструментально ори-
ентированных (при которых под эконометрикой понимают определенный
набор математико-статистических средств, позволяющих верифици-
ровать модельные соотношения между анализируемыми экономическими
показателями и оценивать неизвестные значения параметров в этих соот-
ношениях на базе исходных экономических данных).
Название «эконометрика» было введено в 1926 г. норвежским эконо-
мистом и статистиком Рагнаром Фришем.
В буквальном переводе этот термин означает «измерения в экономи-
ке» и поэтому формально отвечает упомянутому выше расширительно-
му толкованию (сравните с биометрикой, наукометрикой, астрометрией и
т.п.). Однако ныне устоялся и широко распространен более ограничен-
ный взгляд на содержание и назначение эконометрики. Этот взгляд, в
частности, отражен в следующем определении.
Опр еделение 14.1. Эконометрика — это самостоятельная
научная дисциплина, объединяющая совокупность теоретических ре-
зультатов, приемов, методов и моделей, предназначенных для того,
чтобы на базе
(i)	экономической теории,
598 ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
I
(ii)	экономической статистики ,
(in) математико-статистического инструментария
придавать конкретное количественное выражение общим (качествен-
ным) закономерностям, обусловленным экономической теорией.
Именно это понимание и содержание эконометрики отражают сложив-
шиеся к настоящему времени в рамках этой научной дисциплины инсти-
туты и издания (международные научные общества; отделения, факуль-
теты и кафедры в университетах; конференции; монографии, учебники,
журналы и т.п.).
Таким образом, в соответствии с определением 14.1 суть эконометри-
ки — именно в синтезе экономики, экономической статистики и матема-
тики. Но при этом, говоря об экономической теории в рамках эко-
нометрики, мы будем интересоваться не просто выявлениен объективно
существующих (на качественном уровне) экономических законов и свя-
зей между экономическими показателями, но и подходами к их форма-
лизации, включающими в себя методы спецификации соответствую-
щих моделей с учетом проблемы их идентифицируемости (определение
этих понятии см. в п. 14.2). При рассмотрении экономической стати-
стики, как составной части эконометрики нас будет интересовать лишь
тот аспект этой самостоятельной дисциплины, который непосредственно
связан с информационным обеспечением анализируемой эконометрической
модели, хотя в этих рамках специалисту по эконометрике зачастую при-
ходится решать полный спектр соответствующих задач: выбор необхо-
димых экономических показателей и обоснование способа их измерения,
определение плана статистического обследования и т.п. И наконец, под
математико-статистическим инструментарием эконометрики под-
разумевается, естественно, не математическая статистика в традицион-
ном ее понимании, а лишь отдельные ее разделы (такие, как: классиче-
ская и обобщенная линейные модели регрессионного анализа, анализ вре-
менных рядов, построение и анализ систем одновременных уравнений),
снабженные определенными акцентами и дополненные некоторыми специ-
альными сведениями (специальные типы моделей регрессии и временных
рядов, подходы к решению проблем спецификации и идентифицируемости
моделей и т.п.).
Именно «приземление» экономической теории на базу конкретной эко-
номической статистики и извлечение из этого приземления с помощью под-
ходящего математического аппарата вполне определенных количествен-
ных взаимосвязей являются ключевыми моментами в понимании сущно-
сти эконометрики, обеспечивают разграничение эконометрики с такими
дисциплинами, как математическая экономика, описательная экономиче-
14.1. ЭКОНОМЕТРИКА
599
ская статистика и математическая статистика. Так, математическая эко-
номика, которая на самом деле является математически сформулирован-
ной экономической теорией, изучает взаимосвязи между экономическими
переменными на общем (неколичественном) уровне. Она становится эко-
нометрикой, когда символически представленные в этих взаимосвязях
коэффициенты заменяются конкретными численными оценками, полу-
ченными на базе соответствующих экономических данных.
Из определения эконометрики следует, что ее происхождение и глав-
ное назначение — это экономические и социально-экономические прило-
жения, а именно модельное описание конкретных количественных взаи-
мосвязей, существующих между анализируемыми показателями.
При всем разнообразии спектра решаемых с помощью эконометрики
задач их, тем не менее, было бы удобно расклассифицировать по трем
параметрам: по конечным прикладным целям, по уровню иерархии и по
профилю анализируемой экономической системы.
По конечным прикладным целям выделим две основные: (а)
прогноз экономических и социально-экономических показателей (перемен-
ных), характеризующих состояние и развитие анализируемой системы;
(б) имитация различных возможных сценариев социально-экономического
развития анализируемой системы, когда статистически выявленные взаи-
мосвязи между характеристиками производства, потребления, социальной
и финансовой политики и т.п. используются для прослеживания того, как
планируемые (возможные) изменения тех или иных поддающихся упра-
влению параметров производства или распределения скажутся на значе-
ниях интересующих нас «выходных» характеристик.
По уровню иерархии анализируемой экономической системы вы-
деляются макроуровень ( т.е. страны в целом), мезоуровень (регионы,
отрасли, корпорации) и макроуровень (семьи, предприятия, фирмы).
В некоторых случаях должен быть определен профиль эконометри-
ческого моделирования: исследование может быть сконцентрировано на
проблемах рынка, инвестиционной, финансовой или социальной политики,
ценообразования, распределительных отношений, спроса и потребления,
или на определенном комплексе проблем. Однако чем претенциознее по
широте охвата анализируемых проблем эконометрическое исследование,
тем меньше шансов провести его достаточно эффективно.
Представленная на рис. 14.1 схема, конечно, условна. Однако она
поможет читателю лучше понять нашу точку зрения на эконометрику и на
ее место в ряду математике-статистических и экономических дисциплин.
Заметим, что вынесенные в заглавие книги «Основы эконометрики»
подчеркивают то обстоятельство, что акценты в ней сделаны именно на
600
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
методах, в то время как приложения присутствуют в ней, как правило,
лишь в виде иллюстративных примеров.
Рис. 14.1. Эконометрика и ее место в ряду других экономических и стати-
стических дисциплин
14.2.	Эконометрическая модель и проблемы
эконометрического моделирования
14.2.1.	От простых количественных взаимосвязей между
экономическими переменными к эконометрической
модели
Первая же принципиальная идея, с которой встречается каждый изу-
чающий экономику, — это идея о взаимосвязях между экономически-
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
601
ми переменными. Формирующийся на рынке спрос на некоторый товар
рассматривается как функция его цены; затраты, связанные с изгото-
влением какого-либо продукта, предполагаются зависящими от объема
производства; потребительские расходы могут быть функцией дохода и
т.д. Все это примеры связей между двумя переменными, одна из кото-
рых (спрос на товар, производственные затраты, потребительские расхо-
ды) играет роль объясняемой переменной (или результирующего пока-
зателя) , а другие интерпретируются как объясняющие переменные (или
факторы-аргументы). Однако для большей реалистичности в каждое та-
кое соотношение приходится вводить несколько объясняющих перемен-
ных и остаточную случайную составляющую, отражающую влияние на
результирующий показатель всех неучтенных факторов. Спрос на товар
можно рассматривать как функцию его цены, потребительского дохода
и цен на конкурирующие и дополняющие товары; производственные за-
траты будут зависеть от объема производства, от его динамики и от цен
на основные производственные ресурсы; потребительские расходы мож-
но определить как функцию дохода, ликвидных активов и предыдущего
уровня потребления. При этом участвующая в каждом из этих соотноше-
ний случайная составляющая, отражающая влияние на анализируемый
результирующий показатель всех неучтенных факторов, обусловливает
стохастический характер зависимости, а именно: даже зафиксировав на
определенных уровнях значения объясняющих переменных, скажем, це-
ны на сам товар и на конкурирующие с ним или дополняющие товары,
а также потребительский доход, мы не можем ожидать, что тем самым
однозначно определяется спрос на этот товар. Другими словами, переходя
в своих наблюдениях спроса от одного временного или пространственного
тактик другому, мы обнаружим случайное варьирование величины спроса
около некоторого уровня даже при сохранении значений всех объясняю-
щих переменных неизменными.
В прикладном статистическом анализе анализируются различные ва-
рианты формализации понятия стохастическом зависимости между
результирующим показателем у и объясняющими переменными
..., хМ (см. выше, п. 11.5).
Наиболее распространенной в эконометрических приложениях формой
представления стохастической зависимости является аддитивная линей-
ная форма, которая и будет главным предметом исследования в нашем
изложении:
й = е» +	+ ...+еТг^+(u.i)
Здесь yt — значение результирующей (объясняемой) переменной, измерен-
ное в t-м временном (или пространственном) такте,	. .,zJF^ —
602 ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
значения участвующих в соотношении объясняющих переменных, полу-
ченные в том же t-м измерении,  • •»— некоторые параметры (как
правило, не известные до проведения соответствующего статистическо-
го анализа), а £< — случайная составляющая, характеризующая разницу
между модельным и наблюденным значениями анализируемой результи-
рующей переменной, зафиксированную в t-м измерении. Под модельным
значением результирующей переменной yt здесь и в дальнейшем мы бу-
дем понимать ее значение, восстановленное по заданным величинам объ-
ясняющих переменных при условии, что коэффициенты #о,01> нам
известны, т. е.
У1 = е0 + е1Х(^ + ...+врх\г\	(14.2)
При такой интерпретации модельного значения результирующей пе-
ременной случайную составляющую б можно интерпретировать как слу-
чайную ошибку прогноза у по заданным значениям
. ,.,z , причем, чтобы исключить систематическую ошибку в оценке
yt по yt, обычно полагают, что среднее значение случайной составляю-
щей 6t при всех значениях t равно нулю (т.е. E6f = 0). Очевидно,
чем больше информации заключено в значениях объясняющих переменных
а^1),..., х^р относительно величины у, тем надежнее будет прогноз и
тем меньше будет ошибка прогноза 6. А что значит малость случайной
величины? Это значит, что ее значения сосредоточены в окрестности нуля
с малой дисперсией.
Следующий шаг в развитии экономических теорий состоит в группи-
ровке отдельных соотношений в модель. Всякая математическая модель
является лишь упрощенным формализованным представлением реально-
го объекта (явления, процесса), и искусство ее построения состоит в том,
чтобы совместить как можно большую лаконичность параметризации мо-
дели с достаточной адекватностью описания именно тех сторон моделиру-
емой реальности, которые интересуют исследователя. Количество связей,
включаемых в экономическую модель, зависит от условий, при которых
эта модель конструируется, и от подробности объяснения, к которой мы
стремимся. Например, традиционная модель спроса и предложения долж-
на объяснять соотношения между ценой и объемом выпуска, характерные
для некоторого определенного рынка. Она содержит три уравнения, а
именно: уравнение спроса, уравнение предложения и уравнение реакции
рынка. В эти уравнения, помимо интересующих нас объема выпуска и
цены, будут входить и другие переменные; так, например, в уравнение
спроса войдет потребительский доход, а в уравнение предложения — цена.
Объяснение, достигнутое с помощью такой модели, обусловлено значени-
ями некоторых «внешних» по отношению к модели переменных и в этом
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
603
смысле модель является неполной, или условной. Более претенциозные
модели содержат гораздо больше уравнении и с их помощью пытаются
отразить поведение существенно большего числа переменных; однако и
они остаются условными, поскольку тоже содержат переменные, не опре-
деляемые или не объясняемые моделью.
Все экономические модели, независимо от того, относятся они ко все-
му хозяйству иля к его элементам (т. е. к макроэкономике, отрасли, фирме
или рынку), имеют некоторые общие особенности. Во-первых, они осно-
ваны на предположении, что поведение экономических переменных опре-
деляется с помощью совместных и одновременных операций с некоторым
числом экономических соотношений. Во-вторых, принимается гипотеза,
в силу которой модель, допуская упрощение сложной действительности,
тем не менее улавливает главные характеристики изучаемого объекта.
В-третьих, создатель модели полагает, что на основе достигнутого с ее
помощью понимания реальной системы удастся предсказать ее будущее
движение и, возможно, управлять им в целях улучшения экономического
благосостояния.
Чтобы проиллюстрировать сказанное и наметить пути для выяснения
специфической роли эконометрики, рассмотрим пример весьма общей и
приближенной макромодели.
Пример 14.1. Предположим, что экономист-теоретик сформули-
ровал следующие положения:
•	потребление есть возрастающая функция от имеющегося в наличии
дохода, но возрастающая, видимо, медленнее, чем рост дохода;
•	объем инвестиций есть возрастающая функция национального дохода
и убывающая функция характеристики государственного регулирова-
ния (например, нормы процента);
•	национальный доход есть сумма потребительских, инвестиционных и
государственных закупок товаров и услуг.
Наша первая задача — перевести эти положения на математический
язык. И тут мы немедленно сталкиваемся с многообразием открываю-
щихся перед нами возможных способов удовлетворения сформулирован-
ным априорным требованиям теоретика. Какие соотношения выбрать
между переменными — линейные или нелинейные? Если остановиться
на нелинейных, то какими они должны быть — логарифмическими, поли-
номиальными или какими-либо еще? Даже определив форму конкретного
соотношения, мы оставляем еще нерешенной проблему выбора для раз-
личных уравнений запаздываний по времени. Будут ли, например, ин-
вестиции текущего периода реагировать только на национальный доход,
произведенный в последнем периоде, или же на них скажется динамика не-
604 ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
скольких предыдущих периодов? Обычный выход из этих трудностей со-
стоит в выборе при первоначальном анализе наиболее простой из возмож-
ных форм этих соотношений. Тогда появляется возможность записать на
основе указанных выше положений следующую линейную относительно
анализируемых переменных и аддитивную относительно случайных со-
ставляющих модель:
^ = ao + a1(vP,-4,)) + ^).
.IM + lfW,
где априорные ограничения выражены неравенствами
0 < «1 < 1; Д > 0;	< 0.
Эти три соотношения вместе с ограничениями образуют модель. В ней
yj обозначает потребление, у^ — инвестиции, у{ — национальный до-
ход, z — подоходный налог, я — норму процента как инструмент
(з)
государственного регулирования, ж, — государственные закупки това-
ров и услуг, измеренные в ^момент времени* t
Присутствие в уравнениях (14.3) и (14.4) «остаточных» случайных
составляющих и обусловлено необходимостью учесть влияние со-
ответственно на ур) и yj ряда неучтенных факторов. Действительно,
нереалистично ожидать, что величина потребления у< будет однозначно
определяться уровнями национального дохода (у! ) и подоходного налога
(zj1^); аналогично величина инвестиций yj зависит, очевидно, не только
от достигнутого в предыдущий год уровня национального дохода (у) \) и
от величины нормы процента (а^), но и от ряда не учтенных в уравнении
(14.4) факторов.
Полученная модель содержит два уравнения, объясняющие поведение
потребителей и инвесторов, и одно тождество. Мы сформулировали ее
для дискретных периодов времени и выбрали запаздывание (лаг) в один
период для отражения воздействия национального дохода на инвестиции.
Мы привели здесь этот пример, чтобы пояснить общие черты од-
ного из важнейших этапов эконометрического моделирования, в процессе
которого исследователь математически формализует отдельные положе-
ния экономической теории и объединяет их в систему. В дальнейшем мы
используем этот пример для пояснения ряда основных понятий экономе-
трического моделирования.
(И.З)
(14-4)
(14-5)
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
605
14.2.2. Основные понятия эконометрического
моделирования
В любой эконометрической модели в зависимости от конечных при-
кладных целей ее использования все участвующие в ней переменные под-
разделяются на:
экзогенные, т. е. задаваемые как бы «извне», автономно, в опреде-
ленной степени управляемые (планируемые);
эндогенные, т.е. такие переменные, значения которых формиру-
ются в процессе и внутри функционирования анализируемой социально-
экономической системы в существенной мере под воздействием экзогенных
переменных и, конечно, во взаимодействии друг с другом; в эконометри-
ческой модели они являются предметом объяснения;
предопределенные, т. е. выступающие в системе в роли факторов-
аргументов, или объясняющих переменных.
Из данных выше определений следует, что множество предопределен-
ных переменных формируется из всех экзогенных переменных (которые
могут быть «привязаны» к прошлым, текущему или будущим моментам
времени) и так называемых лаговых эндогенных переменных, т.е. таких
эндогенных переменных, значения которых входят в уравнения анализиру-
емой эконометрической системы измеренными в прошлые (по отношению
к текущему) моменты времени, а следовательно, являются уже извест-
ными, заданными.
В нашем примере (14.3)-(14.5) из предыдущего пункта потребление
(уРЬ, инвестиции (j | и национальный доход (у| ) в текущий момент
времени t являются эндогенными переменными; подоходный налог (х^),
норма процента как инструмент государственного регулирования (х ) и
государственные закупки товаров и услуг (х ) — экзогенные перемен-
ные, которые вместе с национальным доходом в предшествующий момент
времени (з/{1\) образуют множество предопределенных переменных.
Таким образом, можно сказать, что эконометрическая модель слу-
жит для объяснения поведения эндогенных переменных в зависимости
от значений экзогенных и лаг о вых эндогенных переменных.
При построении и анализе эконометрической модели следует разли-
чать ее структурную и приведенную формы. Для пояснения этих поня-
тий условимся в дальнейшем обозначать латинской буквой X все предо-
пределенные переменные, Т.е. все экзогенные переменные и все участ-
вующие в модели лаговые эндогенные переменные. Пусть общее число
эндогенных переменных равно т, а общее число предопределенных пере-
606
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
менных — р. Примем (пока без объяснения)1, что общее число уравнений
и тождеств в эконометрической модели равно числу эндогенных перемен-
ных, т, е. равно т. И пусть из общего числа т соотношений модели мы
имеем mi уравнений, включающих случайные остаточные компоненты, и
т2 тождеств (mj + m2 = m)- Разобьем вектор эндогенных переменных
xz / (1) (2) (m)i\T	x/U) f (1) (2)
= (у}	) на два подвектора У/' =(yjу}yj 1J)
и Y* = (y<mi+1),.. , У<т1+та’ЬТ» ПРИ этом порядок, в котором перенуме-
рованы эндогенные переменные, не имеет значения.
Тогда общий вид линейной эконометрической модели может быть
представлен в форме
В1У(П) + в2у((2) + ад = д,
в3У,(1) + B4y((” + с2л, = о,
4 = 1.2,
(М.6)

где Bi =	— матрица размерности (mi X mj) из коэффициен-
тов при	в Ш] первых уравнениях; В2 = (Д^-)	ма-
трица размерности mi х т2 из коэффициентов при y{mi+1\...,	в
2 v f (О)	(1)	(2)	(р)\Т	_
mi первых уравнениях; Xt = (ж$ ,х\ ’ tx\ ',...,х\ ') — вектор-столбец
предопределенных переменных (в нем х^ = 1); Ст = (с^),вт^- — ма-
трица размерности mi х (р + 1) из коэффициентов при предопределен-
ных переменных в первых Ш] уравнениях (очевидно, коэффициенты с,0
играют роль свободных членов уравнений); В3 = (Aj).=,^+1'5*1-н*~3 — ма'
трица размерности т2 X mi из коэффициентов при yjl\.. .,y|mi^ в т2
тождествах системы; В4 =	— матрица размерности
+ma
т2 х т2 из коэффициентов при y|mi+1\.. .,у{т,+тз в т2 тождествах
системы; С2 ==	— матрица размерности т2 х (р + 1)
из коэффициентов при предопределенных переменных в т2 тождествах
системы; = (Лр\^2 3\...,^т,1)Т — вектор-столбец размерности mi
случайных остаточных составляющих пц первых уравнений системы и
0т2 — (0,0,..., 0)Т — вектор-столбец размерности т2, состоящий из ну-
лей.
1 Подробному анализу эконометрической модели, представленной в виде общей линей-
ной системы одновременных уравнений, посвящена гл. 17.
3 С помощью символов t = ni, п2 кратко обозначается тот факт, что индекс i может
принимать все целые значения от nj до nj, т.е. i = ni, ni + 1,...,п?.
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
607
Заметим, что исходными статистическими данными, необходимыми
для проведения статистического анализа системы (14.6) (а именно для
оценки неизвестных коэффициентов Ду и с,у, проверки статистических
гипотез, например, о линейном характере исследуемых зависимостей и
т.п.), являются матрицы
соответственно размерностей n X т и п X (р + 1), а все элементы матриц
Вз,В< и Cj являются известными (их числовые значения определяются
содержательным смыслом соответствующих тождеств системы).
Система (14.6) может быть записана также в виде
ВУ( + СХ( = Д(, t = l,2,...,n,	(14.б')
или в виде
Y • Вт + X • Ст = Д,	(14.6")
где
а матрицы Y и X определены в (14.7).
Определение 14.2. Система уравнений и тождеств вида
(14.6) (или эквивалентных ей записей (14.6*) или (14.6W)) называется
структурной формой линейной эконометрической модели. При этом
предполагается, что коэффициент при t-й эндогенной переменной в i-м
структурном стохастическом уравнении (t = 1,2, ...,m) равен единице
(правило нормировки системы), а матрицы В4 и В невырождены (допус-
каются и другие способы нормировки системы).
Замечание. Пользуясь тем, что эндогенные переменные у/2^ из
(14.6) могут быть явно выражены через у/1^ и Xt, их можно исключить
из общей системы и рассматривать систему, содержащую в качестве эн-
догенных переменных только переменные У/'\ а именно:
В*У,(,) + С*Х, = Д„ t = 1,2.....п,	(14.6е)
где В* = Bj — ВгВ^Вз и С* = CiBjB^Cj. Поэтому в дальнейшем,
говоря о статистическом анализе системы соотношений, описывающих
608
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
линейную эконометрическую модель, можно рассматривать системы, со-
держащие только тг эконометрических стохастических уравнений и не
содержащие тождеств. Правда, этот переход может приводить к опреде-
ленной «перепараметризации» модели, т. е. к утрате автономности перво-
начально введенных параметров (см. ниже реализацию данного перехода
в примере 14.1).
Поскольку при реализации конечных прикладных целей эконометри-
ческого моделирования (т. е. при прогнозе значений эндогенных перемен-
ных и при различных имитационных расчетах, см. п. 14.1) главный инте-
рес представляют соотношения, позволяющие явно выразить все эндоген-
ные переменные Yt через предопределенные Xit то одновременно со струк-
турной формой имеет смысл рассмотреть так называемую приведенную
(редуцированную) форму линейной эконометрической модели.1 Требуемый
результат мы получим, домножив слева обе части соотношений (14.б') на
матрицу В-1 и уединив затем У4:
Y, = -В"’С%( + В-,Д4> 1=1,2,...,п.	(14.8)
Аналогично можно поступить и со структурной формой, записанной
в виде (14.6е):
г/1’=-(В*)-*С’Х, + (В*)-1 Д«. 1 = 1,2,...,п.	(14.9)
В дальнейшем, говоря о приведенной (редуцированной) форме экономе-
трической модели, мы будем иметь в виду запись
yt = n.Xt + €b i=l,2,...,n	(14.8')
rt(1) = n’Xt + e*t, l=l,2,...,n,	(14.9')
где m X (p -I-1) матрица П, mj X (p+ 1) матрица П и векторы остаточных
случайных составляющих €t и £* определяются соотношениями
П = -В-1С,	(14.10)
‘	П* = -(В*)"’С*,	(14.11)
е, = В-1 Д„	(14.12)
е,* = (В*)-,Д<.	(14.13)
1 Более распространенный в русскоязычной литературе термин еприведеннал форма»
в действительности менее точно передает в переводе с английского смысл ereduced
form model>, так как основное отличие последней — в меньшем (редуцированном)
числе содержащихся в ней параметров по сравнению со структурной формой (более
подробно об этом см. ниже в п. 14.2.3).
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
609
Определение 14.3. Система соотношений (14.8х) (или (14.9х)),
6 которой все эндогенные переменные эконометрической модели явно ли-
нейно выражены через предопределенные переменные и случайные оста-
точные компоненты, называется приведенной формой линейной эко-
нометрической модели.
Проиллюстрируем введенные понятия на примере (14.3)-(14.5) (см.
п. 14.2.1).
В этом примере число эндогенных переменных, так же как и общее
число всех соотношений модели, равно трем (т = 3). Среди этих соотно-
шений мы имеем одно тождество (следовательно, т\ = 2,	= 1). Общее
число предопределеных переменных р = 4, в том числе три экзогенные
переменные	и одна лаговая эндогенная переменная (141\),
которую мы в соответствии с принятой договоренностью кодируем как
(т. е. = z(,4)).
Структурная форма модели в данном примере задается соотношени-
ями (14.3)-(14.5). В общих матричных обозначениях, использованных в
формуле (14.6), имеем:
1 "\0; 1J “ V О J ’ C1 “ V 0;	0;	0; -0J ’
В3 = (-1;-1); В4 = (1); С2 = (0;0;0;-1;0)
и
д< = (41,.^,)т.
Если же структурная форма записана в виде (14.6х), то в данном при-
мере участвующие в этой записи матрицы конкретизируются в виде
(1	0 -СЦ \	/ «о -<*1	0	0	0 \
0	1	0 1 ; С =	0	0 -ft 0 -ft I (14.14)
-1-11/	\ 0	0	0-10/
и
д, = («!”, «Р’,о)т.
Отметим, что, во-первых, выполнено условие нормировки (j входит
в t-e уравнение системы, : = 1,2, с коэффициентом единица); во-вторых,
значения элементов матриц Вз, В4 и С2 известны, они определяются содер-
жательным смыслом тождества; в третьих, требование невырожденности
матриц В4 и В соблюдено; и, наконец, в четвертых, матрицы В1э В2 и Cq
относительно «слабо заполнены» неизвестными (подлежащими стати-
стическому оцениванию) коэффициентами: их всего уетыре — ао, ^у,0х
610
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
и fa Последняя особенность рассматриваемой эконометрической моде-
ли является, к счастью, достаточно общей отличительной чертой систем
эконометрических уравнений. Если бы это было не так, т. е. если бы мы
были вынуждены иметь дело с системами, «сильно заполненными» неиз-
вестными коэффициентами, то задача статистического анализа таких си-
стем оказывалась бы принципиально неразрешимой: имеющихся в нашем
распоряжении исходных статистических данных просто нехватало бы для
корректного проведения такого анализа. Ведь при построении и анализе
систем эконометрических уравнений, описывающих макроэкономические
модели, исследователю зачастую приходится иметь дело с десятками и
сотнями эндогенных и экзогенных переменных!
Рассмотрим далее структурную форму в записи (14.6е), при которой
исключается часть эндогенных переменных У/ ' посредством их выраже-
ния через у/1^ из тождеств системы. В нашем примере эта структурная
форма имеет вид:
{/1 гу U1) „ гу 4- гу J1) гу -Л3) - Л*1)
~ aiPt —ao + aixt — aixt — Ct
„(2) fl fl - A(2)
Vt — Pixt ~ Pixt —	»
т.е. матрицы В' и С*, участвующие в общей записи (12.6е), в данном
примере конкретизируются в форме
т»* _ / 1 — <*1	— сц \	р* _ / —его	Qi 0	— tti	0 \
“ \ 0	1 J ’ V о	0	-02 о	-01)'
И, наконец, приведенная форма модели (14.9'), в которой все эндогенные
переменные выражаются через предопределенные, в данном примере име-
ет вид
[	= ——(«о - aiSt1* +	+ «143) + «1Д144))
I	1-0)
+	+ т^2))
< '	1 О1 '
U.(2) = ^2)+M4)+42’,
«
т. е. матрица П* и вектор случайных остаточных составляющих , участ-
вующие в общей записи приведенной формы (14.9х), в данном примере
конкретизируются в виде:
/ Qq	Qi П* = I 1 -	1-Q1 \ 0	0	Q1	а101 \ 1 — 0]	1 — 01	1 — 01 I 02	0	01 /
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
611
I
14.2.3. Основные проблемы эконометрического
моделирования
Для пояснения сущности именно эконометрической модели и описа-
ния основных возникающих при ее построении и анализе проблем нам
будет удобно разбить весь процесс моделирования на шесть основных
этапов.
1-й этап (постановочный) — определение конечных целей моделиро-
вания, набора участвующих в модели факторов и показателей, их роли;
5-й этап (априорный) — предмодельный анализ экономической сущ-
ности изучаемого явления, формирование и формализация априорной ин-
формации, в частности, относящейся к природе и генезису исходных ста-
тистических данных и случайных остаточных составляющих;
3-й этап (параметризация) — собственно моделирование, т. е. выбор
общего вида модели, в том числе состава и формы входящих в нее связей;
4-й этап (информационный) — сбор необходимой статистической ин-
формации, т.е. регистрация значений участвующих в модели факторов
и показателей на различных временных или пространственных тактах
функционирования изучаемого явления;
5-й этап (идентификация модели) — статистический анализ модели
и в первую очередь статистическое оценивание неизвестных параметров
модели;
6-й этап (верификация модели) — сопоставление реальных и модель-
ных данных, проверка адекватности модели, оценка точности модельных
данных.
Последние три этапа (4-й, 5-й и 6-й) сопровождаются крайне трудо-
емкой процедурой калибровки модели. Дело в том, что при постро-
ении эконометрической модели исследователь, как правило, находится в
ситуации, когда, с одной стороны, действует большое число «норматив-
ных» (т.е. определенных содержательным смыслом анализируемых свя-
зей) ограничений на коэффициенты матриц В и С, а с другой стороны, ему
приходится действовать в условиях определенной нечеткости (или непол-
ноты) исходной статистической информации (14.7). Процедура калибров-
ки модели заключается в переборе большого числа различных вариантов
«нормативные ограничения — значения отдельных переменных» (что свя-
зано с многократными «вычислительными прогонами» модели) с целью
получения совместной, непротиворечивой и идентифицируемой модели.
612
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Математическая модель, в том числе математическая модель эконо-
мического явления или процесса, может быть сформулирована на общем
(качественном) уровне, без настройки на конкретные статистические дан-
ные, т. е. она может иметь смысл и без 4-го и 5-го этапов. Тогда она не
является эконометрической. Суть именно эконометрической модели
заключается в том, что она, будучи представленной в виде набора мате-
матических соотношений, описывает функционирование конкретной эко-
номической системы, а не системы вообще (именно экономики России или
процесса «спрос — предложение» в данном конкретном месте и в данное
время). Поэтому она обязательно «настраивается» на конкретных стати-
стических данных, а значит предусматривает обязательную реализацию
4-го и 5-го этапов моделирования.
Обратимся теперь непосредственно к описанию основных проблем, ко-
торые приходится решать в процессе эконометрического моделирования.
Проблема спецификации модели. Эта проблема по-существу ре-
шается на первых трех этапах моделирования и включает в себя:1
(а) определение конечных целей моделирования (прогноз, имитация раз-
личных сценариев социально-экономического развития анализируе-
мой системы, управление);
(6)	определение списка экзогенных и эндогенных переменных;
(в)	определение состава анализируемой системы уравнений и тождеств,
их структуры и соответственно списка предопределенных перемен-
ных;
(г)	формулировка исходных предпосылок и априорных ограничений от-
носительно:
•	стохастической природы остатков Д^ (в классических вариантах
моделей постулируются их взаимная статистическая независи-
мость или некоррелированность, нулевые значения их средних
величин и, иногда, сохранение постоянными в процессе наблюде-
ния значений их дисперсий — гомоскедастичность);
•	числовых значений отдельных элементов матриц В и С в струк-
турной форме модели (14.6Г) или (14.6W).
Итак, спецификация модели — это первый и, быть может, важнейший
шаг эконометрического исследования. От того, насколько удачно реше-
1 Ниже описывается содержание проблемы спецификации эконометрической модели в
предположении ее линейности, т.е. при условии, что в результате проведения 3-
го этапа (этапа параметризации или выбора общего вида модели) эконометрист
пришел к выводу о непротиворечивости гипотезы линейности анализируемых свя-
зей имеющимся в его распоряжении исходным статистическим данным. Тому, как
поступать в противном случае, посвящен п. 15.12 учебника.
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
613
на проблема спецификации и, в частности, насколько реалистичны наши
решения и предположения относительно состава эндогенных, экзогенных
и предопределенных переменных, структуры самой системы уравнении
и тождеств, стохастической природы случайных остатков и конкретных
числовых значений части элементов матриц В и С, решающим образом
зависит успех всего эконометрического исследования.
Спецификация опирается на имеющиеся экономические теории, спе-
циальные знания или на интуитивные представления исследователя об
анализируемой экономической системе. Эти априорные сведения опреде-
ляют, в частности, природу матриц В и С. Например, информация (или
предположение) о том, что определенные переменные непосредственно не
участвуют в том или ином уравнении, означает равенство нулю соответ-
ствующих элементов в строках матриц В и С. Дополнительные сведения
о системе могут иметь вид ограничений на комбинации элементов матриц
В и С.
Проиллюстрируем сказанное на нашем примере из п. 14.2.1. Мы ви-
дим, что непосредственно из состава и смысла уравнений системы (14.3)-
(14.5) (т.е. из решения части вопросов проблемы спецификации модели)
непосредственно следует специальный вид матриц В и С (см. (14.14)) и,
в частности, их слабая заполненность априори не известными элемента-
ми (из 24 элементов этих матриц нам предстоит статистически оценить
лишь четыре:	и Д).
Априорные сведения о системе находят свое отражение при специфи-
кации модели не только в определении конфигурации матриц В и С, но и в
выборе предположений относительно стохастической природы участвую-
щих в уравнении переменных, в первую очередь относительно случайных
остатков Обычно принимаются допущения о том, что все случайные
остатки (j = 1,2,...,mi):
•	имеют нулевые средние значения, т. е. = О, t = 1,..., п;
•	не коррелируют друг с другом, т. е. Е(^	• 4* ) = 0, (j / /);
•	не имеют автокорреляций, т.е. Е(4 • 6^) = О, Ц £
•	не коррелируют ни с одной из предопределенных переменных.
Как правилд, подобные допущения в процессе спецификации модели
оказываются достаточно реалистичными. Однако обращаем внимание чи-
тателя на тот факт, что, к сожалению, ничего подобного нельзя сказать
о случайных остатках et и €* приведенной формы. Из (14.12), (14.13)
видно, что эти случайные остатки зависят (линейно) от элементов (в том
числе неизвестных) матрицы В , и это, как мы увидим позже, создает
свои трудности в статистическом анализе уравнении приведенной формы
(14.8*) и (14.9').
614
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Проблема идентифицируемости. При анализе эконометрической
модели, представленной системой уравнений вида (14.6) (или (14.6х)), ис-
следователи в конечном счете интересует прежде всего поведение эндо-
генных переменных Yt. Из соответствующей приведенной формы модели
(14.8) видно, что эндогенные переменные Yt являются по своей приро-
де случайными величинами, поведение которых определяется внутренней
структурой модели, а именно элементами матриц В и С и природой слу-
чайных остатков At. Возникает вопрос: а возможно ли, следуя в «обрат-
ном направлении», восстановить структурную форму (14.6х) (т.е. все эле-
менты матриц В и С), располагая знанием приведенной формы (14.8)
(т.е. знанием числовых значений всех элементов матрицы П и приро-
ды случайных остатков ef)? Именно этот вопрос и отражает сущность
проблемы идентифицируемости эконометрической модели (не смешивать
с проблемой идентификации модели, заключающейся в выборе и реализа-
ции методов статистического оценивания ее неизвестных параметров, см.
ниже).
Ответ на поставленный вопрос в общем случае, очевидно, отрица-
тельный: без дополнительных ограничений на внутреннюю структуру мо-
дели (т.е. без соблюдения некоторых условий идентифицируемости) по
mi X (р+1) элементам матрицы П невозможно восстановить гораздо боль-
шее число элементов матриц В и С (нетрудно подсчитать, что общее число
коэффициентов /3^ и clk в структурной форме равно х (т^ +m2 + р+1),
хотя, конечно, общее число коэффициентов, подлежащих статистиче-
скому оцениванию, оказывается меньшим).
В эконометрической теории приняты следующие определения, связан-
ные с проблемой идентифицируемости.
Определение 14.4. Уравнение структурной формы экономе-
трической модели называется точно идентифицируемым, если все
участвующие в нем неизвестные (т. е. априори не заданные) коэффици-
енты однозначно восстанавливаются по коэффициентам приведенной
формы без каких-либо ограничений на значения последних.
Определение 14.5. Эконометрическая модель называется
точно идентифицируемой, если все уравнения ее структурной формы
являются точно идентифицируемыми.
Определение 14.6. Уравнение структурной формы называет-
ся сверхидентифицируемым, если все участвующие в нем неизвест-
ные коэффициенты восстанавливаются по коэффициентам приведенной
формы, причем некоторые из его коэффициентов могут принимать од-
новременно несколько (более одного) числовых значений, соответству-
ющих одной и той же приведенной форме.
14.2. ПРОБЛЕМЫ ЭКОНОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
615
Определение 14.7. Уравнение структурной формы называет-
ся некдентифицируемым, если хотя бы один из участвующих в нем
неизвестных коэффициентов не может быть восстановлен по коэф-
фициентам приведенной формы. Соответственно модель называется
неидентифицируемой, если хотя бы одно из уравнений ее структурной
формы является неидентифицируемым.
Говоря о проблеме идентифицируемости модели, мы начали с того,
что исследователя в конечном счете интересует поведение эндогенных пе-
ременных, и с этой точки зрения может показаться несущественной, бо-
лее того, надуманной проблема «однозначного возврата» от приведенной
формы к структурной. Однако в действительности проблема идентифи-
цируемости крайне важна, в первую очередь с позиций выработки пред-
ложений по решению следующей проблемы — проблемы идентификации
эконометрической модели, т. е. проблемы выбора и реализации методов
статистического оценивания участвующих в ней неизвестных параметров.
Более подробное рассмотрение проблемы идентифицируемости эконо-
метрической модели, включающее в себя, в частности, формулировки не-
обходимых условий идентифицируемости отдельного параметра, целого
уравнения и всей системы уравнений структурной формы, приведено в
гл. 17, посвященной системам одновременных уравнений.
Проблема идентификации. Решение этой проблемы предусматри-
вает «настройку* записанной в общей структурной форме (14.6*) модели
на реальные статистические данные (14.7). Другими словами, речь идет
о выборе и реализации методов статистического оценивания неизвестных
параметров модели (14.6) (т.е. той части элементов матриц В и С, зна-
чения которых не являются априори известными) по исходным статисти-
ческим данным (14.7). Описание необходимых методов статистического
оценивания параметров в подобных моделях и в их отдельных фрагментах
приводится в гл.15-17.
Проблема верификации модели. Эта проблема, так же как и про-
блема идентификации, является специфичной, связанной с построением
именно эконометрической модели. Собственно построение эконометриче-
ской модели завершается ее идентификацией, т.е. статистическим оце-
ниванием участвующих в ней неизвестных коэффициентов (параметров)
Ьц и clk- После этого, однако, возникают вопросы: (а) насколько удачно
удалось решить проблемы спецификации, идентифицируемости и иденти-
фикации модели, т.е. можно ли рассчитывать на то, что использование
построенной модели в целях прогноза эндогенных переменных и имитаци-
онных расчетов, определяющих варианты социально-экономического раз-
вития анализируемой системы, даст результаты, достаточно адекватные
616
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
реальной действительности? (б) какова точность (абсолютная, относи-
тельная) прогнозных и имитационных расчетов, основанных на постро-
енной модели? Получение ответов на эти вопросы с помощью тех или
иных математико-статистических методов и составляет содержание
проблемы верификации эконометрической модели.
Методы верификации модели описаны в гл. 15-17. Здесь же отметим
лишь, что эти методы основаны на процедурах статистической провер-
ки гипотез (при ответе на вопрос (а)) и на статистическом анализе ха-
рактеристик точности различных приемов статистического оценивания
параметров (при ответе на вопрос (б)). Отметим также, что наиболее
распространенным и эффективным подходом к верификации эконометри-
ческой модели можно признать принцип так называемых ретроспектив-
ных расчетов. Конкретная схема построения таких расчетов зависит от
конечных прикладных целей моделирования, однако, их общая сущность
заключается в следующем.
Предположим, мы строим эконометрическую модель с целью прогно-
за эндогенных переменных или имитационных расчетов на т временных
тактов вперед. Тогда исходные статистические данные (14.7) делятся
на две части:
обучающую выборку
экзаменующую выборку
(14.7‘)
Далее все ранее принятые решения по проблемам спецификации, иден-
тифицируемости и идентификации модели применяются только к наблю-
дениям обучающей выборки (14.7е). Из полученной таким образом модели
подстановкой в ее приведенную форму значений экзогенных переменных
Xn_T+i,Xn_T+2,...,Xn получают модельные (ретроспективно прогноз-
ные) значения соответственно Ул-т+1Лп-т+2> • • .,УП« Сравнение этих
модельных значений с соответствующими реальными значениями экза-
менующей выборки Уп_т+1, Уп_т+2,..., Уп позволяет проанализировать и
адекватность модельных выводов реальной действительности и их точ-
ность. Более подробно реализация этого принципа будет описана в связи
с построением и анализом моделей регрессии (гл. 15), временных рядов
(гл. 16) и систем одновременных уравнений (гл. 17).
14.3. ИНСТРУМЕНТАРИЙ ЭКОНОМЕТРИКИ
617
14.3.	Математико-статистический
инструментарий эконометрики
В предисловии кратко упомянуто о том, что позиция авторов
данного учебника относительно понимания содержания математико-
статистического инструментария эконометрики несколько отличается от
общепринятой. В частности, современные продвижения в математико-
статистической науке (особенно в области многомерного статистического
анализа), с одной стороны, и заметное расширение круга экономических
задач, требующих эконометрического подхода в их решении, — с дру-
гой, создали все необходимые предпосылки для пересмотра сложившегося
взгляда на математико-статистический инструментарий эконометрики в
направлении его существенного пополнения.
14.3.1.	Традиционный состав математико-статистических
методов эконометрики
Подавляющее большинство учебников и учебных пособий по экономе-
трике предлагает читателю стандартный набор математике статистичес-
ких методов, представленных в следующих четырех разделах:
•	классическая линейная модель множественной регрессии (ЛММР)
и классический метод наименьших квадратов (МНК);
•	обобщенная ЛММР и обобщенный МНК;
•	модели и методы статистического анализа временных рядов;
•	анализ систем одновременных эконометрических уравнений.
При этом некоторые учебники не содержат описания моделей и ме-
тодов анализа временных рядов ([Джонстон Дж.], [Goldberger, A. S.]). И
действительно, упомянутые четыре раздела составляют математико-
статистическую базу эконометрического моделирования, предоставляя
исследователю разнообразные методы и модели статистического исследо-
вания зависимостей, существующих между экономическими показателя-
ми. Именно этим разделам посвящены гл. 15, 16 и 17 данного учебника.
14.3.2.	Некоторые задачи социально-экономической теории
и практики, решение которых требует методов
прикладной статистики, выходящих за рамки
традиционного эконометрического инструментария
Краткий перечень таких задач приведен в предисловии к данному
учебнику. Остановимся на некоторых из них подробнее.
1)	Типологизация и кластеризация социально-экономических объек-
618
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
тов. Моделирование и статистический анализ распределения по средне-
душевому доходу, выявление основных типов потребительского поведения
домашних хозяйств, задачи социально-экономической стратификации об-
щества, межстрановой макроэкономический анализ и многие другие реша-
ются сегодня с привлечением современного аппарата многомерного стати-
стического анализа — методов дискриминантного анализа, моделей рас-
щепления смесей распределений, методов кластер-анализа (см. гл. 12).
2)	Построение и анализ целевых функций и интегральных индика-
торов. Один из эффективных (и достаточно распространенных в теории
и практике экономических исследований) подходов к описанию и анали-
зу поведения хозяйствующего субъекта (индивидуума, домашнего хозяй-
ства, фирмы, предприятия и т.п.) связан с построением соответствующей
целевой функции, которая по-существу является некоторой сверткой ря-
да частных показателей его поведения. Аналогичные задачи возникают
при построении и анализе комплексных, агрегатных показателей какого-
либо сложного свойства — качества населения, качества жизни, научно-
технического уровня производственной системы и т.п. Как правило, при
решении подобных задач не удается обойтись привлечением только мето-
дов регрессионного анализа и анализа временных рядов. Чаще исследо-
вателю приходится обращаться к таким методам снижения размерности
анализируемого факторного пространства, как главные компоненты, фак-
торный анализ, многомерное шкалирование (см. гл. 13).
3)	Анализ динамики «состояний* объекта (типологии потребитель-
ского поведения семей, социально-экономической или демографической
структуры общества и т.п.). Эффективным средством решения задач по-
добного типа являются, как мы видели (см. гл. 5), модели марковских
цепей.
Упомянутый в п. 1)-3) инструментарий прикладной статистики, при-
способленный к специфике экономических и социально-экономических за-
дач, с полным правом может быть отнесен (наряду с указанными
в п. 14.3.1 четырьмя разделами) к математико-статистическому
инструментарию эконометрики. Однако, не столь важно, как назвать
эти методы. Важно, чтобы ими был оснащен современный специалист по
эконометрике!
ВЫВОДЫ
1.	Эконометрика — самостоятельная экономико-математическая на-
учная дисциплина, позволяющая на базе положений экономической тео-
рии и исходных данных экономической статистики, используя необходи-
выводы
619
мый математика-статистический инструментарий, придавать конкретное
количественное выражение общим (качественным) закономерностям, обу-
словленным экономической теорией.
2.	Эконометрическое моделирование реальных социально-экономичес-
ких процессов и систем обычно преследует два типа конечных приклад-
ных целей (или один из них): (а) прогноз экономических и социально-
экономических показателей, характеризующих состояние и развитие ана-
лизируемой системы; (б) имитацию различных возможных сценариев
социально-экономического развития анализируемой системы (многовари-
антные сценарные расчеты, ситуационное моделирование).
3.	При постановке задач эконометрического моделирования следует
определить их иерархический уровень и профиль. Анализируемые задачи
могут относиться к макро- (страна, межстрановой анализ), мезо- (регионы
внутри страны) и микро- (семьи, предприятия, фирмы) уровням и быть
направленными на решение вопросов различного профиля инвестицион-
ной, финансовой или социальной политики, ценообразования, распредели-
тельных отношений и т.п.
4.	Эконометрическая модель содержит набор уравнений регрессионно-
го типа, описывающих исследуемые стохастические связи между анали-
зируемыми экономическими показателями, а также какое-то количество
связывающих эти показатели тождеств, которые определяются экономи-
ческим смыслом проблемы. Наиболее распространенный математический
вид исследуемых связей — линейная (относительно анализируемых пере-
менных) и аддитивная формы. При этом возможны ситуации, когда одни
и те же показатели в одних уравнениях модели играют роль объясняемых,
а в других — объясняющих переменных (такие модели принято называть
системами одновременных уравнений).
Б. Эконометрическая модель служит для объяснения поведения эн-
догенных переменных в зависимости от значений экзогенных и лаговых
эндогенных переменных. Под экзогенными переменными системы понима-
ются показатели, значения которых задаются как бы «извне», автономно,
они являются в определенной степени управляемыми или планируемы-
ми. Значения эндогенных переменных формируются в процессе и вну-
три функционирования анализируемой Социально-экономической системы
в существенной мере под воздействием экзогенных переменных и во взаи-
модействии друг с другом. Лаговые эндогенные переменные — это такие
эндогенные переменные, значения которых входят в уравнения анализи-
руемой эконометрической модели измеренными в прошлые моменты вре-
мени, а следовательно, являются уже известными, заданными.
в. Эконометрическая модель, выраженная системой одновременных
620
ГЛ. 14. ЭКОНОМЕТРИКА: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
уравнений, может быть записана в структурной или приведенной форме.
Структурная форма отражает непосредственно результат формирования
уравнений связи между эндогенными и экзогенными переменными, опира-
ющегося на их экономическую сущность. При этом левая часть любого
уравнения структурной формы может содержать и эндогенные, и экзоген-
ные переменные без какого-либо разделения их ролей, а правая часть —
остаточную случайную компоненту. Приведенная форма системы есть
результат разрешения структурной формы относительно эндогенных пе-
ременных.
7.	К основным проблемам эконометрического моделирования следует
отнести:
•	спецификацию модели;
•	выяснение факта ее идентифицируемости;
•	идентификацию модели;
•	верификацию модели.
Сущность этих четырех проблем описана в п. 14.2.3.
8.	Содержание основного математико-статистического инстру-
ментария эконометрики в его традиционном понимании определяется сле-
дующими четырьмя разделами:
(1)	классическая модель регрессии и классический метод наименьших
квадратов;
(2)	обобщенная линейная модель регрессии и обобщенный метод наи-
меньших квадратов;
(3)	статистический анализ временных рядов;
(4)	анализ систем одновременных уравнений.
Однако в современном понимании эти разделы должны быть допол-
нены широким спектром методов многомерного статистического анали-
за и в первую очередь методами и моделями распознавания социально-
экономических образов, их типологизации и снижения размерности ис-
следуемого факторного пространства. Разделы (1)-(4) математического
инструментария эконометрики описываются в последующих трех главах
(см. гл. 15-17), а упомянутым здесь методам многомерного статистиче-
ского анализа и прикладной статистики посвящены гл.9-13.
ГЛАВА 15. МЕТОДЫ И МОДЕЛИ
РЕГРЕССИОННОГО АНАЛИЗА
15.1	. Введение в регрессионный анализ
(основные понятия и определения)
Регрессионный анализ занимает, бесспорно, центральное место во
всем математико статистическом инструментарии эконометрики. По су
ществу мы значительно раньше этой главы начали обсуждение проблем
регрессионного анализа. Ведь впервые условное математическое ожи-
дание одной случайной величины (f^) при условии, что вторая слу-
чайная величина £ зафиксирована на уровне х^3 (т.е. при условии
= я^}), обсуждается уже в п. 3.1.5 в связи с анализом условного
распределения одной из компонент двумерного нормального распределе-
ния. Общие постановки задач сзатистического исследования зависимо-
стей и основные типы регрессионных зависимостей между количествен-
ными признаками обсуждались в гл. 10 (см. п. 10.1, 10.2, 10.5). В пей же
впервые дано определение функции регрессии (см. конец п. 10.1). И, на
конец, в 1л. 11 дос1аточно подробно описан необходимый этап предрегрес-
сионпого анализа — так называемый корреляционный анализ, в процессе
которого оценивается степень тесноты статистической связи между
анализируемыми переменными (ведь именно от степени тесноты анализи-
руемой связи зависит прогностическая сила конструируемой регрессион-
ной модели).
Поэтому, приступая к изучению этой 1лавы, желательно освежить
в памяти сведения, почерпнутые читателем в результате чтения гл. 10
и 11. Самые необходимые из этих сведений мы приводим ниже в качестве
вспомогательной сводки понятий и результатов, предваряющей систе
магическое изложение содержания данной главы.
622	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
15.1.1	. Результирующая (зависимая, эндогенная)
переменная у
Переменная (или признак), характеризующая результат или эффек-
тивность функционирования анализируемой экономической системы. Ее
значения формируются в процессе и внутри функционирования этой си-
стемы под воздействием ряда других переменных и факторов, часть из
которых поддастся регистрации и, в определенной степени, управлению
и планированию (эту часть принято называть объясняющими перемен-
ными, см. ниже). В регрессионном анализе результирующая переменная
выступает в роли функции, значения которой определяются (правда, с
некоторой случайной погрешностью) значениями упомянутых выше объ-
ясняющих переменных, выступающих в роли аргументов. Поэтому по
природе своей результирующая переменная у всегда стохастична (слу-
чайна).
15.1.2	. Объясняющие (предикторные, экзогенные)
переменные X = (х^,х^2\... ,х^)Т
Переменные (или признаки), поддающиеся регистрации, описываю-
щие условия функционирования изучаемой реальной экономической систе-
мы и в существенной мере определяющие процесс формирования значений
результирующих переменных. Как правило, часть из них поддается хотя
бы частичному регулированию и управлению. Значения ряда объясняю-
щих переменных могут задаваться как бы «извне» анализируемой систе-
мы. В этом случае их принято называть экзогенными. В регрессионном
анализе они играют роль аргументов той функции, в качестве которой
рассматривается анализируемый результирующий показатель у. По сво-
ей природе объясняющие переменные могут быть как случайными, так
и неслучайными.
15.1.3	. Функция регрессии у по X = (а/’\	..., ж^р^)т
Функция /(%*) называется функцией регрессии у поХ (или просто —
регрессией у по X), если она описывает изменение условного среднего зна-
чения результирующей переменной у (при условии, что значения объяс-
няющих переменных X зафиксированы на уровнях X*) в зависимости от
изменения значений X’ объясняющих переменных. Соответственно мате-
матически это определение может быть записано в виде
/(%•) = Е(з/1 X = X’).
(15-1)
15.1. ВВЕДЕНИЕ В РЕГРЕССИОННЫЙ АНАЛИЗ
623
В дальнейшем в целях упрощения обозначений правую часть (15.1)
мы будем записывать просто Е($/ | X’) или даже Е(з/ | X) (в последнем
варианте не различаются обозначения самих, объясняющих переменных X
и их возможных значений X", однако, с учетом данного пояснения, это
не должно приводить к неправильному пониманию). Поэтому сокращенно
функция регрессии может быть определена также соотношением
/(%) = Е(У| X).	(15.1')
Замечание об этимологии слова «регресси я».
Строго говоря, по своей смысловой нагрузке слово «регрессия» не име-
ет отношения к существу стохастических связей, для описания которых
оно используется. Объяснение этому термину можно дать, лишь обратив-
шись к истории исследований в области статистического анализа связей
между признаками. Одним из первых примеров исследований такого рода
была работа шведских статис!иков, пытавшихся по наблюдениям значе-
ний пар признаков: х — отклонение от среднего уровня в росте отца;
у — отклонение от среднего уровня в росте взрослого сына этого отца, —
установить и описать стохастическую связь, существующую между х и
у. В процессе исследования была подтверждена естественная гипотеза о
наличии положительной сзатис! и ческой связи между ростом отца и сына
(«у высоких отцов в среднем высокие сыновья, и наоборот»), однако одно-
временно была подмечена тенденция регрессии (отступления, возврата)
в росте сыновей к среднему уровню, а именно: «у очень высокие отцов
сыновья в среднем высокие, но уже не такие высокие, как отцы, и наобо-
рот: у очень маленьких по росту отцов сыновья в среднем низкорослые,
но все-таки повыше, чем их отцы». Функцию, описывающую эту законо-
мерность, авторы назвали функцией регрессии, после чего этот термин и
стали использовать применительно к любой функции, построенной анало-
гичными методами.
Как было упомянуто выше, в соотношениях (15.1)-(15.1') объясняю-
щие переменные X могут быть как случайными величинами, так и неслу-
чайными параметрами, от значений которых зависит закон распределения
вероятностей случайной результирующей переменной у.
Пусть X — векторная случайная величина, а рУ|х(у, X) — функция
плотности (или полигон вероятностей), задающая совместный закон рас-
пределения вероятностей многомерной случайной величины [у, X) в точке
(у, X) (см. п. 2.5.3). Тогда, определив в соответствии с (2.13) условную
плотность ру(у | X = X*) результирующей переменной у при условии,
что объясняющие случайные переменные зафиксированы на уровнях X*,
мы получаем интерпретацию правой части (15.1) в виде математического
624
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
ожидания у, подсчитанного по условному распределению ру(у | X = X*),
т. е.
Е(У I X = X*) = J ypv(y | X = X*)dy	(15.2)
(интегрирование в правой части (15.2) ведется по всем возможным значе-
ниям у результирующей переменной у).
г?	V / (1)	(2)	(р)\Т	„
Если же X = (аг \х ,... , аг ’) — ряд неслучайных параметров, от
значений которых зависит одномерный закон распределения вероятное гей
ру(у; а/1),..., х^) результирующей переменной у, то правые части (15.1),
(15./) интерпретируются как математические ожидания у, подсчитанные
по безусловному распределению ру{у;х ,..., х ') при значениях параме-
тров, равных соответственно X и X, т.е.
Е(у|Х = Х*) = У УРу(у\х{1) ,х(2) ,...,х(р) )dy;
Е(у I *) = У
(15./)
15.1.4	. Уравнения регрессионной связи между у и X
Выше было отмечено, что в регрессионном анализе результирующая
переменная у выступает в роли функции, значения ко горой определяются
(правда, с некоторой случайной погрешностью) значениями объяспяю-
щих переменных X = (яг ,х' яг ') , выступающих в роли аргу-
ментов этой функции. Математически это может быть выражено в виде
уравнений регрессионной связи (см. также выше, соотношения (10.3)-
(10.4)):
Гз/(Х) = /(.¥)4-£(Х),
{ Ее(Х) ее 0.	(15 3)
Присутствие случайной «остаточной» составляющей («регрессионных
остатков») е(Х) в первом соотношении уравнений (15.3) обусловлено
причинами двоякой природы: во-первых, она отражает влияние на фор-
мирование значении у факторов, не учтенных в перечне объясняющих
переменных X; во вторых, она может включать в себя случайную по-
грешность в измерении значения результирующего показателя у (даже в
«идеальной» ситуации, когда по значениям объясняющих переменных X
в принципе можно было бы однозначно восстановить значение анализиру-
емой результирующей переменной).
I5J. ВВЕДЕНИЕ В РЕГРЕССИОННЫЙ АНАЛИЗ
625
Второе соотношение (тождество) в уравнениях (15.3) непосредствен-
но следует из смысла функции регрессии f(X) = Е(у | X), поскольку
усреднение (вычисление математического ожидания) левых и правых ча-
стей первого из соотношений (15.3) при любом фиксированном значении
X дает
Е<9(%) I X) = Е(/(Х)) + Е(е(Х)).
А так как Е(#(Х) | А") = /(X) по определению и Е(/(Х)) = /(X) (посколь-
ку величина /(X) при фиксированных значениях X не является случай-
ной), то Е(е(Х)) — 0 при любом фиксированном значении X.
Спецификация и способ статистического анализа моделей типа (15.3)
зависят от конкретизации требований к виду функции /(X), природе объ-
ясняющих переменных А'и стохастических регрессионных остатков е(Х).
Ниже в данной главе рассматриваются различные варианты конкретиза-
ции этих требований.
15.1.5	. Измеритель степени тесноты статистической связи
между у и X
Выше, в п. 11.2.1, с помощью соотношений (11.8)—(11.9) была введена
универсальная характеристика степени тесноты статистической свя-
зи (с.т.с.с.), существующей между результирующей переменной у и объяс-
няющими переменными X,— коэффициент детерминации Kd(y,X). Из
результатов, приведенных в п. 11.2, следовало, что в рамках исследования
линейных регрессионных связей типа (15.3) (т.е. при функциях регрессии
/(X) вида /(А') = 0О +	+ - • • + где 0Q,0t,...,0 — некоторые
числовые параметры) коэффициент детерминации совпадает с квадратом
2
множественного коэффициента корреляции Ry.x> определяемого соотно-
шениями (11.34) и (11.35). Принимая во внимание, что точность (прогно-
стическая сила) регрессионной модели определяется величиной условной
дисперсии результирующего показателя D(y | X) (она характеризует раз-
брос индивидуальных значений у(Х) около значения, лежащего на линии
регрессии f(X), при каждом фиксированном значении А'), а усредненная
(по всем значениям X) условная дисперсия Ех(Р(у | X)) определяется
формулой Ex(D(y | (X)) = (1 — Kd(y,X))Dy (см. соотношения (П.8)-
(11.9)), то можно сделать вывод, что величина коэффициента детермина-
ции Kd(y,X) (или квадрата множественного коэффициента корреляции
Ry.x пРи исследовании линейных моделей) является решающей характе-
ристикой прогностической силы анализируемой регрессионной модели.
626	ГЛ 15. МЕТОДЫ И MOHF ПИ РЕГРЕС t ИОННОГО АНАЛИЗА
15.1.6	. Исходные статистические данные
Все выводы в ре рессионном анализе, гак же как и в любом статисти-
ческом исследовании, строятся на основании имеющихся исходных стати-
стических данных.
В регрессионном анализе использую гся данные типа «объект-
свойства» (см. и.9.1.2, соотношения (9J) и (9 /)) Поскольку в регрес-
сионном анализе принято обознача ь результирующие переменные иначе,
чем объясняющие (первые обычно обозначаются латинской буквой у, а
вторые — я), то мы несколько видоизменим общие обозначения, приня-
тые в п. 9.1.2.
Итак, будем полагать в дальнейшем (в данной главе), что мы распо-
лагаем результатами регистрации значений анализируемых объясняющих
(ж^\я^2\. и результирующей (уУ переменных на и статистически
обследованных объектах. Так i о, если г номер обследованного объ-
екта, то имеющиеся исходные статистические данные состоят из п строк
вида
у.), i= 1,2,...,»,	(15.-1)
где х и у, значения соответ< 1 пенно j-и объясняющей переменной
(J — 1,2,...,р) и результирующего показателя, зарегистрированные на
г-м обследованном объек ie
Из чисто технических соображении (смысл которых станет попятным
несколько позже) данные (15.4) в pei рессионпом анализе обычно предста-
вляют в виде двух матриц вида:
матрица размера п х (р } 1), составленная из наблюденных значений объ-
ясняющих переменных, и
V--“	(15-4<5)
матрица размера п х 1 (т.е. вектор-столбец высочы л), составленная из
наблюденных значений результирующей переменной
Возможны ситуации, когда данные регистрируются на одном и том
же объекте, по в разные периоды («такты») времени. Тогда i будет
означать номер периода времени, к которому «привязаны» соответству-
ющие данные, а п — общее число тактов времени, в течение которых
15.1. ВВЕДЕНИЕ В РЕГРЕССИОННЫЙ АНАЛИЗ
627
собирались исходные данные (случай «ерел!енж5й» выборки в отличие от
предыдущей — «пространственной»).
Наконец, возможна ситуация, когда «отслеживается» каждый из п
объектов в течение N тактов времени («пространственно-временная»
выборка, или «панельные данные»). В любой из упомянутых ситуаций
исходные данные могут быть представлены в конечном счете в форме
(15.4а)-(15.46), которую мы и примем за базовую в дальнейшем изложе-
нии.
15.1.7	. Основные задачи прикладного регрессионного
анализа
В п. 10.2 описаны основные типы конечных прикладных целей, ко-
торые преследует регрессионный анализ. Резюмируя содержание этого
пункта, отметим лишь, что в конечном счете анализ регрессионных зави-
симостей вида (15.3), базирующийся на исходных статистических данных
(15.4л)-(15 4б), нацелен на решение следующих основных задач:
Задача 1. Для любых заданных значений объясняющих перемен-
V / П) (2) (рКТ
иых Л = (ж ',яг яг ') построить наилучшие в определенном смы-
сле точечные и интервальные (с доверительной вероятностью Р) одел
ки соответственно f(X) и A[/(A”)]p для неизвестной функции регрессии
/т.
3 а д а ч а 2. По заданным значениям объясняющих переменных
v / С1) (2)	(р)\Т
л =	,х' ,	построить наилучшии в определенном смысле
точечный и интервальный (с доверительной вероятностью Р) прогноз со-
ответственно у(Х) и Д[у(Х)]р для неизвестного значения результирую-
щей переменной у(Х).
Задача 3. Пусть известно, что искомая функция регрессии при
надлежит некоторому параметрическому семейству функций {f(X\О)},
где 0 = (0О,,0к)Т — векторный параметр, все или некоторые ком-
поненты которого допускают определенную экономическую интерпрета-
цию. Требуется построить наилучшие в определенном смысле точечные и
интервальные оценки для неизвестных значений этих параметров.
Задача 4. Оценить удельный вес влияния каждой из объясняю-
сь (2)	(р)	-	zv\
щих переменных х Jtx'	на результирующий показатель у(Х)
и, в частности, определить, какие из объясняющих переменных можно ис-
ключить из модели (15.3) как практически не влияющие на процесс фор-
мирования значений результирующего показателя.
628
ГЛ. J5. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Итак, собспзепно регрессионный анализ начинается с решения зада-
чи 1 и, в частности, с конструирования по исходным данным вида (15.4а)-
(15.46) оценки /(А) для неизвестной функции pei рессии f(X) = E(j/1 X).
Исходным (и по существу ключевым) этапом в решении этой задачи следу
ет признать гыбср параметрического семейства функций F = {/(X; 0)} —
класса допустщ ых решений, в рамках которого предполагается вести по-
иск наилучшеи (в определенном смысле) аппроксимации /(X) для f(X).
Этому этапу регрессионного анализа был посвящен специальный п. 10.7
данного учебника. В нем же приведены «некоторые общие рекомепда
ции» (см. н. 10.7.1), среди которых есть тезис о том, что «не следует
гнаться за чрезмерной сложностью функции, описывающей поведение
искомой функции регрессии». Следуя этой логике, при подборе общею
вида функции регрессии, как правило, идут от простого к сложному, т.е
начинают с аньлъ т возможности использовать простейшую линейную
модель вида (10.2?‘) Именно эта логика положена в основу изложения
материала данной главы
15.2	. Классическая линейная модель
множественной регрессии (КЛММР)
Классическая пинанная модель множественной регрессии (КЛММР)
представляет собой простейшую версию конкретизации требований к об-
щему виду функции pei рессии /(X), природе объясняющих переменных
X и статистических регрессионных остатков е(Х) в общих уравнениях
регрессионной связи (15.3)? В рамках КЛММР эти требования формули
руются следующим образом:
' у, = + 01*!1) + ... + 0pz<p) +et, i = 1,2,
Is t — 0, i — 1,2,...,n,
{2
67	ЛРИ ’ = ь
0	при г / j\
(x^1J,	, а/р)) — неслучайные переменные;
ранг :л<тгрицыХ = р ф1 < п
k (матрица X определена соотношением (5.4а)).
(15.5)
1 Процесс конкретизации подобных требований к структуре и характеру анализируе-
мых моделей ое’ оессионного типа обычно называют спецификацией модели (подроб-
нее о специфик г ,ик модели см. выше, и п. 14.2.3).
15.2. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 629
Из (15.5) следует, что в рамках КЛММР рассматриваются только
линейные функции регрессии, т.е.
/(X) = Е(у I X) = еа + et/’> +... + ерХм,	(15.6)
где объясняющие переменные аг*\аг ,...играют роль неслучайных
параметров, от которых зависит закон распределения вероятностей ре-
зультирующей переменной у. Это, в частности, означает, что в повто-
ряющихся выборочных наблюдениях (z, ,х\ 1;уг) единственным
источником случайных возмущений значений являются случайные воз-
мущения регрессионных остатков £t (подобную схему зависимости мы на-
блюдали в примере 10.1).
Кроме того, постулируется взаимная некоррелированность случай-
ных регрессионных остатков (Е(е,€7) = 0 для : / j). Это требование к
регрессионным остаткам Cj,...,еп относится к основным предположени-
ям классической модели и оказывается вполне естественным в широком
классе реальных ситуаций, особенно, если речь идет о пространствен-
ных выборках (15.4е) (15.4 ), т.е. о ситуациях, когда значения анализи-
руемых переменных регистрируются на различных объектах (индивиду-
умах, семьях, предприятиях, банках, регионах и т. п.). В этом случае дан-
ное предположение означает, что «возмущения» (регрессионные остатки),
получающиеся при наблюдении одного какого-либо обследуемого объекта,
не влияют на «возмущения», характеризующие наблюдения над другими
объектами, и наоборот.
Тот факт, что для всех остатков £t, £j,..., £п выполняется соотноше-
ние Ес? — сг2, где величина <г2 от номера наблюдения i на зависит, озна-
чает неизменность (постоянство, независимость от того, при каких зна-
чениях объясняющих переменных производятся наблюдения) дисперсий
регрессионных остатков. Последнее свойство принято называть гомоске-
дастичностъю регрессионных остатков.
Наконец, требуется, чтобы ранг матрицы X, составленной из наблю-
денных значений объясняющих переменных, был бы максимальным, т. е.
равнялся бы числу столбцов этой матрицы, которое в свою очередь долж-
но быть меньше числа ее строк (т.е. общего числа имеющихся наблю-
дений). Случаи р 4- I п не рассматриваются, поскольку при этом чи-
сло п имеющихся в нашем распоряжении исходных статистических дан-
ных оказывается меньшим или равным числу оцениваемых параметров
модели (р + 1), что исключает принципиальную возможность получения
сколько-нибудь надежных статистических выводов. Что касается требо-
вания к рангу матрицы X, то оно означает, что не должно существовать
строгой линейной зависимости между объясняющими переменными. Так,
630
ГЛ 15. МЕТОПЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
если, например, одна объясняющая пеоемениая может быть линейно вы
ражена через какое-то количество других, ч<* ранг матрицы X окажется
меньше р -|- 1, а следовательно, и ранг матрицы ХТХ будет тоже меньше
р +1 (см. Приложение 2). А это означает вырождение симметрической
матрицы ХТХ (т.е. det(XTX) — 0), что исключает существование матри-
цы (ХТХ) \ которая, как мед уридин, играет важную роль в процедуре
оценивания параметров анализируемой модели.
В дальнейшем нам удобнее будет оперировать с матричной записью
модели (15.5). При этом кроме обозначений (15.4а) (15.4 ) введем также
матрицы (векторы):
единичная матрица размерности и х п\
0--4W1................................*vT -
вектор-столбец неизвестных значений параметров;
е - (ei.£2, •>£г*)Т
вектор-столбец регрессионных остатков;
о„ = (0,0,••••()'
вектор-столбец высо1Ы п, состоящий из одних нулей;
(Е(И) E(£if*x) ... Е(Е]6П)^
Е £2tl)	Е(е2)	•••	Ц^п)
е’(£„£1) Е(£п«2) ... Е(е’) /
(15.7)
(15.8)
(15 9)
(15.10)
(15.11)
ковариационная матрица размерности п х н вектора остатков;

вектор столбец оценок неизвестных значений параметров;
2§ = Е[(6-0)(0-6)Т] = (^(0)),	= 0,1,2,...,?, -	(15.13)
15.2. КЛАССИЧЕСКАЯ ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ 631
ковариационная матрица размерности (р + 1) х (р + 1) вектора кесме
щепных оценок G неизвестных параметров О (в соотношении (15.13)
%(©) = е[(^ - et){s, - ^)]).
Тогда матричная форма записи КЛММР имеет вид:
У = ХО + е,
Ее — 0п,
< £. = ЛП,	(15.5')
, (1) <2)	<Р>\
(ас , х	згг') — неслучайные переменные;
ранг матрицы X — р -|- 1 < п.
Когда дополнительно к условиям (15.5) (или (15.б')) постулируют нор-
мальный характер распределения регрессионных остатков е — (£i,c2,...,
бп)Т (что записывается в виде! е € JVn(O; tr2In)), то говорят, что у и X
связаны нормальной КЛММР.
Пример 15.1. Исследуется зависимость урожайности зерновых
культур (у ц/га) от ряда переменных, характеризующих различные фак-
торы сельскохозяйственного производства, а именно:
— число тракторов (приведенной мощности) на 100 га;
(2)
т — число зерноуборочных комбайнов на 100 га;
(з)
х' ' — число орудий поверхностной обработки почвы на 100 га;
а/4) — количество удобрений, расходуемых на гектар (т/га)
(5)
х — количество химических средств защиты растении, расходуе-
мых па гектар (ц/га).
Исходные данные для 20 сельскохозяйственных районов области при-
ведены в табл. 15.1.
Таким образом, в данном примере мы располагаем пространственной
выборкой объема п = 20; число объясняющих переменных р = 5. Ма-
трица X будет составлена из шести столбцов размерности 20 каждый,
причем в качестве первого столбца используется вектор, состоящий из
одних единиц, а столбцы со 2-го по 6-й представлены соответственно 3-
7-м столбцами табл. 15.1. Вектор-столбец Y определяется 2-м столбцом
табл. 15.1. Специальный анализ технологии сбора исходных статистиче-
ских данных показал, что допущение о взаимной некоррелированности и
гомоскедастичности регрессионных остатков е может быть принято в ка-
честве рабочей гипотезы. Поэтому мы можем записать уравнения стати-
«	V f (!)	(2)	(3)	(4)	(5)чТ	/ir
стическои связи между & и л, = (□:'	',х\ ,х\ ’,х\ ') в виде (15.5 ).
632
гл. и. методы и модели регрессионного анализа
Таблица 15.1
* (номер района)	Ух	4*>				х<5>
1	9,70	1,59	0,26	2,05	0,32	0,14
2	8,40	0,34	0,28	0,46	0,59	0,66
3	9,00	2,53	0,31	2,46	0,30	0,31
4	9,90	4,63	0,40	6,44	0,43	0,59
5	9,60	2,16	0,26	2,16	0,39	0,16
6	8,60	2,16	0,30	2,69	0,32	0,17
7	12,50	0,68	0,29	0,73	0,42	0,23
8	7,60	0,35	0,26	0,42	0,21	0,08
9	6,90	0,52	0,24	0,49	0,20	0,08
10	13,50	3,42	0,31	3,02	1,37	0,73
11	9,70	1,78	0,30	3,19	0,73	0,17
12	Н) 70	2,40	0,32	3,30	0,25	0,14
13	12,10	9,36	0,40	11,51	0,39	0,38
14	н 70	1,72	0,28	2,26	0,82	0,17
15	7 00	0,59	0,29	0,60	0,13	0,35
16	7,20	0,28	0,26	0,30	0,09	0,15
17	8.20	1,64	0,29 .	1,44	0,20	0,08
18	8,40	0,09	0,22	0,05	0,43	0,20
19	13.10	0,08	0,25	0,03	0,73	0,20
20	8,70	1,36	0,26	0,17	0,99	0,42
15.3.	Оценивание неизвестных параметров
КЛММР: метод наименьших
квадратов и метод максимального
правдоподобия
Соотношения (15.5) и (15.5х) определяют специфицированные уравне
ния статистической связи, существующей между результирующей пере-
менной у и изменяющими переменными X. Однако значения участву-
ющих в этих уравнениях параметров 0 = (#0,0],... ,0р)Т и о2 нам не
известны- их гребхется определить (статистически оценить) по име-
ющимся в нашем распоряжении исходным статистическим данным вида
(15.4“)-( 15.46). Ниже описываются способы статистического оценивания
параметрон j о i рамках КЛММР (метод наименьших квадратов) и в
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛМЮ
633
рамках нормальной КЛММР (метод максимального правдоподобия).
15.3.1.	Метод наименьших квадратов (МНК)
В основе логики метода наименьших квадратов лежит стремление ис-
следователя подобрать такие оценки 0o,0i,-.-,0p Для неизвестных значе-
ний параметров функции регрессии соответственно вц, qi, .. 0р, при кото-
рых сглаженные (регрессионные) значения 0О +	. г 0»*^ резуль-
тирующего показателя как можно меньше отличались ок or соответству-
ющих наблюденных значений yt. Попробуем математически сформулиро-
вать этот принцип. Введем в качестве меры расхождения ci паженного и
наблюденного (в г м наблюдении) значений результируюлц, показателя
разность
- Уг -	~ •••-	(15.14)
(будем в дальнейшем называть г, «невязками»). Оч >и но з(усчения
0о,#1,... , 0р следует подбираю таким образом, чтобы «..мчлмизировать
некоторую интегральную (по всем имеющимся наблюдениям) характе-
ристику невязок. Примем за такую интегральную харэктгрнся ику под-
гонки (выравнивания) значений у, с помощью линей». >Й функции от
л; ,х; х\ (г - 1,2, ...,п) величину
п	п
<?(ё0, ё,,..., ё„) = £(у, - 6О - в, *<’> -... - ё^'”’ )2 = £ £. 05-15)
i=l	i=I
Очевидно, величина Q будет определяться при заданной системе на-
блюдений (15.4*)-(15.4 ) конкретным выбором значений оценок параме-
тров 0о, 01,. -., 0р. Оценки по методу наименьших квадратов (МНК-
оценки) 0о. мнк з 01 мню • • • ? 0р. мнк как Рпз и подбираются таким обра-
зому чтобы минимизировать величину Q, определенную соотношением
(15-15), т. е.
Wo МНК 1 01. МНК , • • - 1 0р. мнк) —	min ^(00,011--. Лр) (15.16)
или
ёмнк = argminQ(G).	(15.16х)
е
Опишем процедуру решения оптимизационной задачи (15.16 ). На
чнем с простейшего частного случая, когда рассматривается зависимость
у от единственной объясняющей переменной х (т.е. р — 1). Этот случай
634
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
в литературе обычно называют моделью парной линейной регрессии.
Первое из уравнений связи (15.5) в данном случае имеет вид:
Ух — 0о 4* 0i+ £», i — 1,2,...,л.
Критерий Q метода наименьших квадратов:
п
q<Mi) = £(».-0<. - W-
tx=l
(15.15')
Необходимые условия экстремума по в0 и 8t функции <2(0о.0):
^r = -2£>.-0o-<U) = °,
~ -2У^»>(й - 0о- М«) = 0,
991 fet	j
или, после раскрытия скобок и очевидных тождественных преобразований:
л	п
п0о 4-01
i=l	£=1
/ n \	п
(52ж») ^4-01 • 52*1
. \»=1 /	£=1
п
=
t=l
(15.17)
Система (15.17) из двух линейных уравнений относительно и
представляет так называемую стандартную форму нормальных уравне-
ний (для случая р — 1). Ее решения легко выписываются в явном виде:
п - ”££=i хм ~ (Stei *>) (Sfai у<) _	-^(у. -у)
1 мнк	v^n 2 Av'n \2	V'n	’
^O.MHK ~ У — 01.мнк^>
(15.18)
где х = 52”=1 Xi/n и у =r- Х;”=1 yjn.
Перейдем к случаю многих объясняющих переменных (р > 1). Как
обычно, в этом случае более удобной оказываемся матричная форма за-
писи всех необходимых в данной задаче условий в соотношений:
ё = у-хё = (у1-ёо-ё1г(11)-...-0Рх(1’,),...,у„-0о-01г(„’)-...-0Д’,))т-
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
635
вектор-столбец невязок;
п
=	 - ^|’,)1 = (^-хё)т(У-хё)- (15.19)
1=1
оптимизируемый (по 0 критерий метода наименьших квадратов.
Перед тем как выпи»аль необходимые условия экстремума функции
Q(0) по 0, преобразуем правую час гь (15.10):
с?(ё) = ут> -лё1 хту -г ётхтхё. (15.19')
В этом преобразования мы воспользовались правилом транспонирования
произведения матриц (см Приложение 2), а также тем, что 0ТХТК —
чнсло, а потому оно совпадай! со своим граиспонированным выражением
утхё.
Необходимые условия, которым удовлетворяют решения оптимиза
ционной задачи (15.16 ), получаются дифференцированием правой части
(15.19 ) по 6»ОЛЬ ... ,#р. При выписывании получающейся при этом систе-
мы уравнений относительно	.,0р мы воспользуемся матричным
обозначением производной
Эд(0) = аде) &Э(0)У
д& ~ \	’ дот. J ’
а также правилами записи матричного дифференцирования линейных и
квадратичных функций от 0 (см. Приложение 2):
^U-2Xri < 2ХгХб ер+1.	(15.20)
В (15.20) 0р+1 — это век тор-столбец размерности р + 1, состоящий из
одних нулей.
Разрешая систему уравнении (15.20) относительно 0, получаем:
и следовательно:
6MHk =(ХТХ)-'ХТУ	(15.22)
В основной формуле метода наименьших квадратов (15.22) лы вос-
пользовались невырожденностью матрицы ХТX, которая следует из тре-
бования максимального ранга для матрицы X, входящего в описание
КЛММР (см. (15.5) или (15.5?)).
636
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Применим общую формулу (15.21) к ранее рассмотренному частному
случаю парной регрессии (р = 1). Очевидно, в этом случае:
Подставляя эти выражения в (15.21), получаем:

т.е. ту же стандартную форму нормальных уравнений, с которой мы
встретились в (15.17), анализируя эгу же модель покомпонентно.
Пример 15.1 (продолжение). Применение формулы (15 22) к дан
ным табл. 15.1 позволяет получить следующие МИК оценки для парами
тров 0 =
00.мнк =3,515;	мнк = - 0,006; 02 мнк = 15,542; 03.мнк = 0, ПО;
04.«нм = 4,475; 05.мнк = -2,932.
Таким образом, оценка f(X) неизвестной функции регрессии ДХ) в дан-
ном случае имеет вид:
/(Х) = 3,515 - 0,006ж(1) + 15.542?2’ +0,110z(J) +<475/4) -2,932z(S).
(15.23)
Экономическое осмысление и интерпретацию полученных в данном
примере результатов отложим до того момента, когда мы будем в состо-
янии охватить весь комплекс вопросов прикладною регрессионного ана
лиза.
15.3.2.	Метод максимального правдоподобия (ММ 1)
Метод максимальною правдоподобия (ММП) может быть применен
в тех случаях, когда с точностью до неизвестных значений параметров
известен общий вид закона распределения вероятностей имеющихся вы-
борочных данных (см. п. 7.5.1). Поэтому, если мы проводим регресси-
онный анализ в рамках нормальной КЛММР, т.е. если дополнительно
15 3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
637
к условиям (15.5) постулируется нормальность регрессионных остатков
>^2> - • • >^п> то, учитывая их взаимную некоррелированюсть (которая в
нормальном случае влечет за собой их взаимную статистическую незави-
симость, см. Свойство 5 в п. 11.2.2), можно выписать функцию правдопо-
добия в терминах остатков (15.14) (см. п. 7.2):
.,еп | О;а2) = JJ
•=1

1	~	-00-01 х(£П-...-#7*?Ь3
\/2тго2
= ехр [~i(y "Х0)'(у -Х0) •
(Z7T6T	L 2(7
(15.24)
Оценки ©ммп и максимального правдоподобия определяются
как такие значения 0 и а , при которых функция правдоподобия L (или,
что то же, логарифмическая функция правдоподобия I — in L) достигает
своей максимальной величины. Соответствующие уравнения ММ II полу
чаются приравниванием к пулю производных функции I по 0 и ст2.
/(£Ь£2,- --,£n | 0;^2) = -|1л(2тг) -	1п(<72) -
-у(у - ХЙ)Т(У - хе);
2(т
[ де	2<т200^У	Х°)	Х0)]-Ор+15
) dl	п 1	1	т	(15.25)
Т^ = ~2‘^ + ^^(Г"Х0) (Г“Х0) = ’Ь
V до	* о 2(а	)
Первая строка (15.25) после сокращения левой и правой час гей на
-1/2сг2 повторяет систему уравнений (15.20) меч ода н; в*.”>чыних квадра
тов. Следовательно;
ёммп = Ом... = (ХгХГ’ХтУ.
(15.26)
Вторая строка системы (15.25) позволяет вычислите ММП оценку
2
для о :
*ммп = -(V - Х0)т(У - Х0) = 1	- во - М" - • • - «₽4₽))2,
71	71 —“*
t=I
(15.27)
где 0 = (^oj^i, • • • »^р) — оценки по мечоду наименьших квадратов (они
же — оценки по методу максимального правдоподобия) п '.^угстпых коэф-
фициентов регрессии 0. В дальнейшем оценки, полученные ио формулам
(15.26), мы будем обозначать просто 0 (без индексировав * метола).
638
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
15.3.3.	Анализ вариации результирующего показателя у и
выборочный коэффициент детерминации R2.x
Из структуры КЛММР (15.5) видно, что общая изменчивость (вари-
ация) результирующей переменной у обусловлена, во-первых, изменением
значений функции регрессии f(Xt) =	-Ь ... + 0рх\^ (которое
в свою очередь определяется варьированием значений объясняющих пе-
ременных X = (а/1\а/2\. ..,^)Т) и, во-вторых, поведением случайных
остатков
£» ~ 3/* f{ i)i * ~ 1 j 2,..., т1.
Определим выборочную (наблюдаемую) вариацию результирующей
переменной у величиной
ва₽ (У) = Е(». - У)’ = (У - У)Т(Г - Y),
i—1
п
где у = £ У»/п — выборочное среднее значение результирующей пере-
i=i
меяной у, Y - (уиу2,... Лп)Т, а У = (у,у,...,у)Т — n-мерный вектор-
столбец.
Обозначим значения оцененной функции регрессии
Л = /(х.) = во +	+ . • • + врХ\к\ i = 1,2,..., п.
Тогда
вар (у) = (У - У)Т(У - У) = £(у, - у)2 = £(у(	у)2
1=1 1=1
= £(й - /о2 + Е(/< - у)2+2Х(у. - /.)(/. - у)
1=1 1=1 »=1
= У 4 + вар (/) + 2 £ ё,(/. - у),	(15.27*)
1=1 1=1
где £\ = у, - 7 = yt - 0О -	- ... - 0Р^Р), а вар(/) = ^(7, - у)2 ~
i=i
вариация выборочной функции репрессии] она характеризует степень слу-
чайного разброса значений функции регрессии около среднего значения
результирующей переменной.
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
639
Чтобы получить требуемый результат, нужно показать, что послед-
няя сумма в выражении (15 27*) равна нулю ( этой целью докажем сна-
чала, что невязки £, ортогональны ко всем объясняющим переменным
(включая искусственную переменную = 1), т е. что
У2^> = 0 и	Ш1Я вссх J = 1>2,...,p.	(15.27^)
»=i	i=i
Действи тел ьно:
что и означает справедливость равенств (16.27 ) (при выводе этою соот-
ношения МНК-оценка 0 была заменена ее выражением по формуле (15.26);
0р+1, как и прежде, означает вектор столбец размерности р+1, состоящий
из одних нулей).
Теперь мы можем показать, что
£ Ш ~ ?) =-О-	(15.27*)
1=~1
Действительно, учитывая равенства (15 276) имеем:
22 “ у) “ 524 *	4 • • •+
t=l	t=l
= Л + ^£^!1)+...
»=1	i=l
4 «р У <Й₽) - У У ё, = 0.	(15.27')
Г = 1
Возвращаясь к (15.27е) и учитывая (15.27*), имеем:
вар (у) --= вар (/) + У" е •.	(15.27л)
640	ГЛ. 15 МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Поделив обе части (15.276) на вар (у), получаем:
=1 -	(15.27")
вар (у) мр (у)
или
%.Х = 1 - —-----------s-------------------•	(15.27’)
«=1
Сравнив левые и правые части соотношений (15.27е) и (15.27ж), а по-
следнее соотношение — с разложением (И.З) и ранее введенным коэффи-
циентом детерминации (11.8), с учетом результата (11 37) можно сделать
следующие выводы:
(i)	Характеристика, определенная соотношением (15.27ж), является
выборочным аналогом коэффициента детерминации (11.8) и одновременно
квадратом выборочного множественного коэффициента корреляции между
У и X;
(ii)	Выборочный коэффициент детерминации Ry.x> определенный со-
отношением (15.27ж), учитывая соотношение (15.27е), характеризует до-
лю общей вариации результирующего признака у, обьясненной иоведсни
ем (вариацией) выборочной функции регрессии /(А”) = 0$ +	+ ... +
(iii)	Принимая во внимание результат (11.37), для вычисления вы
борочного коэффициента детерминации Н^.х в рамках КЛММР можно
использовать (помимо формулы (15.27*)) формулы (11.34) и (11.35) с за-
меной участвующих в них коэффициентов парной и частной корреляции
их выборочными аналогами (оценками).
(iv)	Соответственно определенный формулой (15.27*) выборочный ко-
эффициент детерминации R^.x обладает всеми описанными в п. 11.2.4
(см., в частности соотношения (11.38)-(11.40)) статистическими свойства-
ми квадрата множественного коэффициента корреляции.
В заключение еще раз выпишем выведенное выше соотношение
(15.27д), но в матричной форме:
(У - У)Т(У - У) = (Х0 - У)т(хе - У) + ётё.
(15.27")
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
641
15.3.4.	Статистические свойства оценок параметров
КЛММР
При повторениях выборок того же самого объема п из той же самой
анализируемой генеральной совокупности и при тех же самых значени-
ях объясняющих переменных X наблюдаемые значения результирующего
показателя у будут случайным образом варьировать (за счет стохастиче-
ского характера остатков с), а следовательно, будут варьировать и зави-
сящие от yi, у2,..., уп значения оценок 0 и <т2, хотя каждый раз (т. е. для
каждой выборки (15.4а)-(15.46)) мы их будем вычислять по одним и гем
же формулам, соответственно (15.26) и (15.27). Другими словами, наши
оценки «ведут себяъ как случайные величины (см. также п. 7.1.2). По-
этому естественно попытаться проанализировать их поведение и в первую
очередь ответить на вопросы.
•	к чему стремятся (по вероятности) оценки О и а2 при неограни-
ченном росте объема выборки?
•	каковы средние значения этих оценок для выборок фиксированного
объема п?
•	каковы основные характеристики случайного разброса в значениях
этих оценок относительно истинных значений оцениваемых пара-
метров?
Состоятельность оценок 0 и д’мпп* В данном случае свойство
состоятельности наших оценок (см. п. 7.1.3) определяется структурой ма-
трицы X. Существуют различные формулировки условий (в терминах
элементов матрицы X), при которых оценки 0 и аммп являются состо-
ятельными. Пожалей, наиболее удобное для приложений условие состо-
ятельности оценок О и а^мп — следующее (см., например, [Себер Дж.,
в. 3.2]):
оценки 0 и оммп являются состоятельными тогда и только тогда,
когда наименьшее собственное значение матрицы ХТХ стремится
к бесконечности при п —> оо.
Напомним, что наименьшее собственное значение Amin матрицы X X
определяется как минимальный по величине корень уравнения |ХГХ —
А1р+1| = 0 (матрица ХТХ как симметричная и положительно определен-
ная имеет р Ц- 1 действительных положительных собственных значений
А], Лг,. • - Ар, см. Приложение 2). Можно показать, что сформулированное
условие состоятельности оценок 0 и «тммп Для случая, например, парной
линейной регрессионной зависимости (т.е. при р = 1) равносильно требо-
642
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
ванию:
п
— х)2 х п при п —* оо,	(15.28)
i=i
где символ х означает, что величины, стоящие слева и справа от него,
ведут себя асимптотически одинаково при п —♦ оо, т. е. :
—-----------► const при п —► ОС.
п
Так, например, условие (15.28) может быть нарушенным, если по мерс
роста объема выборки п наблюдаемые значения объясняющей переменной
будут концентрироваться в пределах неограниченно сужающейся окрест-
ности ее средней величины х(п). Грубо говоря, даже неограниченное до-
бавление наблюдений в бесконечно малой окрестности среднего значения
объясняющей переменной не несет полезной дополнительной информации
относительно расположения анализируемой прямой регрессии.
Несмещенность оценок. Напомним (см. п. 7.1.4), что оценка 0 па-
раметра 0 называется несмещенной, если Е0 — 0 (для векторного пара-
метра это равенство понимается одновременно выполняющимся для всех
компонент векторов 0 и 0).
Чтобы подсчитать среднее значение оценки (15.26), подставим в фор
мулу (15.26) вместо Y его выражение из основного (первого) соотношения
системы (15.5х):
0 = (ХтХ)-1Хт(Х0 + е) = 0 + (ХтХ)-,Хте. (15.29)
В последнем равенстве мы воспользовались тем, что (ХТХ) ,(ХТХ) =
1р+1- Таким образом, оценка 0 представлена как сумма истинного ( не
известного нам) значения 0 и линейной комбинации случайных остатков
• • • >£п- Беря математические ожидания от левой и правой частей
(15.29) с учетом того, что величины 0 и (ХТХ)-1ХТ неслучайны, а сред-
ние значения остатков равны нулю (т.е. Ее = 0п), получаем:
Е0 = Е0 + (ХтХ)'1ХтЕе = О.	(15.30)
Тем самым показано, что МНК-оцеики (они же ММП-оценки) 0 неизвест-
ных параметров КЛММР являются несмещенными.
Покажем, что в отличие от 0 оценка о’ммп параметра а2 оказывается
смещенной. Правда, проведенный ниже анализ позволяет «подправить»
оценку о^мп таким образом, чтобы смещение было устранено.
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
643
Итак, наша цель — вычислить математическое ожидание оценки
(15.27), т. е. определить значение
е 1(у - хё)т(У - хё) ,
- «
где 0 определено формулой (15.26). С этой целью выразим вектор невязок
Y — Х0 через остаточные случайные компоненты модели е:
У - хё = (X© + е) - Х[(ХтХ)-1Хт(Х0 + е)]
= е - Х(ХтХ)~'Хте = [ln - X(XTX)-,XT]e = Ze. (15.31)
В соотношении (15.31) использовано обозначение для (п х п)-матрицы
Z = In-X(XTX)"*XT.	(15.31“)
Отметим, что матрица Z является симметричной и идемпотентной (см.
Приложение 2), т.е. ZT = Z (симметричность) и Z2 = Z (идемпотент-
ность). Оба свойства устанавливаются непосредственной проверкой. Дей-
ствительно:
ZT = (In - Х(ХТХ)-’ХТ)Т = 1„ - Х(ХТХ)-1ХТ = Z
(при переходе к правой части использовались правило транспонирования
произведения матриц, а также симметричность матрицы (ХТХ) Х);
Z2 = ZZ = [1„ - Х(ХТХ)-1ХТ] [1„ - Х(ХТХ)-,ХТ]
= 1п -Х(ХТХ)-’ХТ - Х(ХТХ)-'Х + [Х(ХТХ)~1ХТ]
X [Х(ХТХ)-1ХТ] = 1„ - Х(ХТХ)-1ХТ = Z.
Теперь воспользовавшись (15.31), а также симметричностью и идем-
потентностью матрицы Z, мы можем вычислить величину
Е[(У - Х6)Т(У - Хё)] = E[(Ze)T(Ze)]
= E(eTZTZe) = E(eTZe) = a2 trZ
= a2 tr [I„ - Х(ХТХГ1ХТ]
l[( t Y^Yl-Y^l	(*5.32)
= а [trln — trX(X X) X J
= а2[п - tr(XTX)-’(XTX)]
= <z2(n - trlp+i) = a2 [n - (p + 1)].
644
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
В ходе преобразований мы воспользовались следующими двумя свойства-
ми (см. Приложение 2):
(а)	Е(еТАе) = о2 trA,
(б)	tr(ABC) = tr(BCA) = tr(CAB).
Из соотношения (15.32) следует, что опенка <7ммп> определенная фор-
мулой (15.27), является смещенной, так как
Е^ммп
-(у - хё)т(у - х§)
п
= ^е[(у - хе)т(У - хе)] = а2 (1 -
(15.33)
Воспользуемся вместо (Тммп оценкой
а2 =------—-<7ммп =---------гЦз/i -	- ... - Орх\р))2
п —р — 1	п — р-1
= -* -(У-§Х)Т(У-ёх).
п — р — 1
(15.34)
Очевидно, такой способ оценивания неизвестной дисперсии остатков £,
(так называемой остаточной дисперсии сг2) уже будет несмещенным.
П и м е р 15.1 (продолжение). Оценка остаточной дисперсии о2 по
данным табл. 15.1 по формуле (15.34) с использованием результатов оце
нивания функции регрессии (15.23) дает
а2 = 2,59.
(15.35)
Ковариационная матрица вектора О МНК-оценок. Ковариа-
ционная матрица Sg вектора 0 была введена соотношением (15.13) при
описании КЛММР в п. 15.1. С помощью ее элементов подсчитываются
основные показатели случайного разброса оценок 6$, ,.. .,вр около со-
ответствующих истинных значений анализируемых параметров и одно-
временно характеристики взаимозависимости полученных оценок. Дей-
ствительно, из определения Eg следует, что ее диагональные элементы
Е(0о - во)2, E(0i - 01)2,...,Е(0Р — вр)2 задают средние квадраты оши-
бок соответствующих оценок (а для несмещенных оценок, какими и явля-
ются МНК-оценки, это и есть дисперсии оценок!). В п. 2.6.6 был введен
многомерный аналог дисперсии случайной величины — так называемая
обобщенная дисперсия, количественно выражающая степень случайного
разброса значений векторной случайной величины около своего средне-
го в соответствующем многомерном пространстве (см. формулу (2.30)).
15 3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
645
Соответственно применительно к вектору оценок 0 эта степень случайно-
го разброса будет определяться величиной детерминанта ковариационной
матрицы Eg, т.е.
Do60 = det Eg.
Наконец, степень тесноты парных линейных связей между компонен-
тами и вектора оценок О (/,J = 0,	/ j) определяет
ся коэффициентом корреляции г(0^,0^) (см. (2.33) и п. 11.2.2), кото-
рый в свок^очередь выражается через элементы ковариационной матрицы
= 0, !,...,р:
*0

Все это говорит о том, что ковариационная матрица Eq вектора оце-
нок 0 содержит важнейшую информацию о качестве оценок 0. Опре-
делим ее в терминах параметров КЛММР и исходных статистических
данных (15.4*)-(15.4б). Для этого при выражении разности 0 — 0 вос-
пользуемся ранее полученным соотношением (15.29):
= Е[(0-е)(е-о)т]
= E{[(XTX)~,XTe][(XTX)~lXTe]T}
= E[(XTX)"’XTeeTX(XTX)-t]
= (ХТХ)-1ХТЕ(ееТ)Х(Х ГХ)“'
= (ХТХ)’,ХТ<721пХ(ХТХ)“1
= <72(ХтХ)чХ1 Х(ХтХ)“1 = <72(ХТХ)_'.	(15.36)
При выводе соотношения (15.36) мы воспользовались:
•	правилом транспонирования произведения матриц (см. Приложе
нис 2);
•	специальным видом ковариационной матрицы вектора остатков Ее =
Е(ееТ) = <т21п (см. (15.5х));
г 1
•	тем, что при умножении на единичную любая «подходящая» матри-
ца не меняется (в пашем случае X7 1п = ХТ).
Матрица А как сомножитель, стоящий слева от 1п, является «подходящей», если
длина ее строки (т.е. число ее столбцов) равна размерности п единичной матрицы
646
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Заметим в заключение, что в статистической практике пользуются
не самой матрицей а ее оценкой
= <z2(XTX)-1,
(15.36')
где а2 определяется по формуле (15.34). Кроме того, в большинстве слу-
чаев ограничиваются выводом на печать и использованием только сред-
пеквадратических ошибок
Si = а)/2(6) = а^/аЦ
(15.37)
оценок Of (I = 0,1,... ,р); в соотношении (15.37)	— /-й диагональный
элемент матрицы Eg (см. (15.36 )), д определено формулой (15.34), а ац —
I-й диагональный элемент матрицы А = (ХТХ) \ — I = 0,1,.. . ,р.
Пример 15.1 (продолжение). По формулам (15.34), (15-36*),
(15.37) подсчитаны среднеквадратические ошибки 5/ в оценивании коэф-
фициентов регрессии 0/ (I — 0,1,...,5). Стандартная форма компьютер-
ной выдачи результатов счета, объединяющая информацию о значениях
оценок регрессии 0{ и их среднеквадратических ошибках 3/, как правило,
имеет следующий вид:
/(X) = 3,515-0,006?° 4- 15,542?° 4-0,110?3) 4-4,475?° - 2,932?°.
(5.41)	(0,60)	(21,69)	(0,86)	(1,54)	(3,09)
(15.23')
В скобках под значениями оцененных коэффициентов регрессии 0( указа-
ны их среднеквадратические ошибки Анализируя полученный резуль-
тат, читатель даже на этой стадии подготовленности отметит для себя,
что средпеквадратические ошибки в оценке всех коэффициентов, кроме
04, превышают значения самих коэффициентов (что говорит о статисти-
ческой ненадежности последних). Позже мы вернемся к этому примеру,
чтобы более детально разобраться в возникшей ситуации.
Оптимальность МНК-оценок. При сравнении различных спосо-
бов оценивания решающей характеристикой качества оценки 0 неизвест-
ного числового параметра 0 оказывается средний квадратошибки Е(0—0)2
(см. п. 7.1.5). Поэтому говорят, что оценка 0j точнее (лучше, эффектив
нее), чем оценка 02, если Е(^ — 0) < Е(02 — 0). Соответственно оценка
0ОПТ является оптимальной в классе оценок М, если
Е(0ОПТ - #)2 = min Е(« - в)2,
ёгм
(15.38)
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
647
Анализируя КЛММР, мы имеем дело с вектором оценок 0 =
(00,01,... ,0р)Т. Как определить качество и оптимальность векторной
оценки? По-видимому, для подавляющего большинства практических за-
дач было бы достаточно, если бы удалось показать, что для любой линей-
ной функции СТ0 = 6с от неизвестных параметров 0о,0ь • •  оценка
СТ0Мнк является оптимальной для параметра 6с в смысле (15.38) в неко-
тором достаточно широком классе оценок М (здесь С = (co,ci,... ,ср)т -
(р+ 1)-мерный вектор-столбец произвольных констант Су). Действитель-
но, полагая СТ = (0,0,.. .0,1,0,.. .0), где единица стоит на j-m месте,
получаем оптимальность 0 с точки зрения точности оценивания параме-
тра 6j{j = 0,1,..., р). Полагая СТ = (l,^1^,.. .,ж^), получаем опти-
мальность 0 с точки зрения точности оценивания неизвестной функции
регрессии /(X) = 60 4- з/1 + ... + 6рх^ при любых заданных значениях
объясняющих переменных X. Как видим, подобная интерпретация опти-
мальности оценок 0МНК оказывается уместной по меньшей мере в двух из
четырех основных задач прикладного регрессионного анализа (см. зада-
чи 1 и 3 в начале гл. 15). Поэтому именно в таком смысле формулируется
основной результат, обосновывающий оптимальные свойства МНК-оценок
(теорема Гаусса-Маркова):
• Рассматривается задача статистического оценивания заданной
линейной функции 6С = СТ0 от неизвестных параметров регрес-
сионной модели (15.5х) (С = (cq, Cj, ... , ср)Т — вектор-столбец за-
данных констант). Пусть М = {В У} — класс линейных отно-
сительно У\,У2^‘  чУп « несмещенных оценок параметра 0С- (В =
(bi,bj,.. • ,bn)T — вектор-столбец коэффициентов, с помощью ко-
торых формируются оценки класса М). Тогда оценка СТ0МНМ явля-
ется оптимальной в классе М оценкой параметра 6с в смысле
(15.38), т. е.
Е(Ст0ии, - вс)1 < Е(В У - 6С)2	(15.39)
для любой оценки BTY из класса М.
Докажем это утверждение. Прежде всего отметим, что
оценка СТ0МНМ принадлежит классу М, так как, во-первых, она линейна
относительно У (см. формулу (15.26)), а во-вторых, она является несме-
щенной (так как Е(СТ0мнк) = СТЕ0мнк = СТ0 в силу того, что 0МНК
является несмещенной оценкой параметра 0, см. (15.30)). Наша цель —
доказать справедливость неравенства (15.39), поэтому проанализируем и
сравним левую и правую части этого соотношения. Заметим сначала,
что требование несмещенности оценок ВТУ из класа М обусловливает
648
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
существование определенных ограничений на компоненты векторов В, а
именно:
Е(ВТУ) = Е[Вт(Х0 + е)] = ВтХ0 = 9С = СТ0,
откуда следует, что
ВТХ = СТ.	(15.40)
Теперь вычислим и сравним средние квадраты ошибок для оценок В1Y
и С 0мнк:
Е(ВТУ - СТ0)2 = Е[ВТ(ХО + е) - СТ0]2
= Е(ВтХ0 + ВГе - СТ0)2 = Е(Ст0 + Вт е - Ст0)2
= Е(ВтееТВ) = ВтЕ(ееТ)В = <г2(ВтВ).	(15.41)
При выводе соотношения (15.41) мы воспользовались равенством (15.40),
специальным В|идом ковариационной матрицы вектора остатков е (Е(ее )
= сг21п) и возможностью представления квадрата числа В е в виде
Е(Ст0„„, - Ст0)2 = E[CT(0M„, - 0)]2
= Е[Ст(0и„. - 0)(0МИ1[ - 0)ТС]
= СтЕ[(0мн, - 0)(0И„, - 0)Т]С
= <72СТ(Х Х)-,С = а2ВтХ(ХтХ)_'ХтВ.	(15.42)
При выводе соотношения (15.42) мы воспользовались возможностью пред-
ставления квадрата числа СТ(0МНк~0) в виде СТ(0МНК —0)(0МНк~0)ТС,
знанием ковариационной матрицы вектора оценок 0МНК (см (15.36)) и вы-
ражением СТ через #ТХ (см. (15.40)).
Остается показать, что разность правых частей (15.41) и (15.42) все-
гда неотрицательна. Действительно:
Е(ВТУ - СТ0)2 - Е(СТ0мнж - Ст0)2 = а2(ВтВ)
- <72ВТХ(ХТХ)_,ХТВ = а2ВТ[1„ - Х(ХТХ)"*ХТ]В
= <72BtZB,	(15.43)
где матрица Z = 1п — Х(ХТХ)-1ХТ нам уже встречалась при анализе
смещения оценки ^ммп (см. (15.31*) и (15.32)). Было установлено, что
1Б.З. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
649
она — симметричная и идемпотентная. Кроме того, из хода преобразо-
вания в соотношении (15.32) следует, что матрица Z — неотрицательно
определенная, т.е. для любого вектора В = (^1,^2» • • • ,ЬП)П выражение
ВТ71В всегда неотрицательно (в ходе преобразований (15-32) показано,
что сумма квадратов невязок, являющаяся по определению существенно
неотрицательным числом, представима в виде eTZe, где вектор невязок
£ = (ei,C2,... ,£П)Т может быть составлен из произвольных действитель
ных компонент). А неотрицательность правой части (15-43) как раз и
доказывает справедливость неравенства (15.39).
Свойства оценок, справедливые только при дополнительном
условии нормальности регрессионных остатков (т. е. в рамках нор-
мальной КЛММР). Если мы несколько сузим класс рассматриваемых мо-
делей, добавив к условиям (15.5) КЛММР требование нормальности ре-
грессионных остатков, то соответствующая нормальная КЛММР может
быть кратк^ описана следующими условиями:
Y — Х0 4- с,
е е ап(0;	„
{,(1) ») М.	-	(15’5)
[ху	., х ') — неслучайные переменные;
l ранг матрицыХ = р + 1.
В (15.5,Z) JVjt(a; Е)> как и прежде, обозначает fe-мерный нормальный з.р.в. с
вектором средних значений, равным а, и ковариационной матрицей, рав-
ной X, а запись £ € 7Vjt(a;S) свидетельствует о том, что многомерная
случайная величина £ распределена по этому нормальному закону.
Сформулированные выше статистические свойства оценок 0МНШ и а2
справедливы и без предположения о нормальности остатков. Однако, да-
же располагая информацией о состоятельности, несмещенности и опти-
мальности оценок 0МНК и а2, мы не сможем решить задач с построением
точных доверительных интервалов для истинных значений этих пара-
метров, так же как и для неизвестных значений функции регрессии или
индивидуального значения анализируемого результирующего показателя
при заданных величинах объясняющих переменных (см. формулировки
задач 1-3 в начале этой главы). Необходимой базой для решения этих за-
дач является знание законов распределения вероятностей используемых
оценок. Именно это знание доставляют нам следующие (справедливые в
рамках нормальной КЛММР) результаты, являющиеся по существу мно-
гомерным обобщением известной теоремы Фишера о распределении выбо-
рочного среднего значения и выборочной дисперсии, построенных по вы-
борке из нормальной генеральной совокупности (см. п. 6.2.8, соотношения
650
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
(6.26)-(6.28)):
•	оценки 0МНК подчиняются (р + \)-мерному нормальному з.р.в. с век-
тором средних значений, равных истинным значениям анализируе-
мых параметров 0, и с ковариационной матрицей Xg, определяемой
соотношением (15.36), т. е.
6 ^+1(e;<72(XTX)-*);
(15.44)
•	случайная величина (п — р~ 1)а2/<72 подчиняется х -распределению
с п — р — 1 степенями свободы, т. е.
-2
СТ 2
(п-р - I)-у е X (п - Р - 1);
и
(15.45)
•	оценки 0МНК и д2 являются статистически независимыми. (15.45х)
Доказательство справедливости (15.44) основано на следующих фак-
тах: 1) среднее значение и ковариационная матрица вектора оценок 0МНК
были подсчитаны ранее (см. (15.30) и (15.36)); 2) оценки 0ММК строятся
как линейные комбинации нормально распределенных независимых слу-
чайных величин у, или с, (это видно соответственно из (15.22) и (15.29)), а
любая линейная комбинация независимых нормально распределенных слу-
чайных величин снова распределена по нормальному закону (что подтвер-
ждается, например, индуктивным применением формулы композиции^см.
п. 4.4). Утверждение (15.45) и статистическая независимость оценок 0МИК
и д2 следует, например, из теоремы 8.2.2 [Андерсон Т.].
Сформулируем одно важное следствие из приведенных выше ре-
зультатов, которое позволит нам в дальнейшем воспользоваться t-
распределением (см. п. 3.2.2) для проверки гипотез о численных значениях
каждого из регрессионных коэффициентов 0q,6i,. . .,вр и для построения
соответствующих доверительных интервалов.
Следствие. Пусть — истинное (гипотетичное) значение 1-го
коэффициента регрессии модели (15.5м). Тогда статистика
1 = 0,1,...,Р,
— * /-- ’
(15.46)
распределена по закону Стьюдента (t-распределения) сп-р-1 степе-
нями свободы. В (15.46) среднеквадратическая ошибка оценки 0,.мнк
определяется по формуле (15.37), д2 — по формуле (15.34) и ац — это
l-й диагональный элемент матрицы А = (ХТХ)-1.
15.3. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ КЛММР
651
Правило проверки гипотез вида Ho:0g = 6	(15.47)
Теперь мы можем сформулировать основанное на (15.46) правило про-
верки гипотез Яо- Пусть 0? — заданное гипотетическое значение Гго
коэффициента регрессии. По заданному уровню значимости критерия а
(см. п. 8.1.3 и п. 8.2) из таблиц процентных точек f-распределения (см.
Приложение 1) находим 100а/2%-ную точку распределения Стьюдента с
п-р — 1 степенью свободы fQp(n — р — 1). Если окажется, что абсолютная
величина статистики 7^, определенной соотношением (15.46), больше зна-
чения ta/2(n— р— 1), то проверяемую гипотезу (15.47) следует отвергнуть
(вероятность ошибиться при этом равна а). В противном случае (т.е.
при I7I	~ Р~ О) гипотеза Hq не отвергается. В распространен-
ном частном случае проверки гипотезы 0/ = 0 (что интерпретируется как
полное отсутствие влияния объясняющей переменной х^ на результи-
рующий показатель у в рамках анализируемой линейной модели и явля-
ется поводом к обсуждению вопроса об исключении х^ из этой модели)
решение о принятии или отклонении проверяемой гипотезы, следователь-
но, принимается на основании сравнения величины |0<мнк|/«/ со значением
^/а(« - р -1): при (|0/мнкI/-S/) > ta/2(n - р - 1) гипотеза «Яо: = 0» от-
вергается.
Построение доверительного интервала для неизвестного
значения коэффициента регрессии 0/
Приведенное выше следствие (15.46) дает нам возможность постро-
ить доверительный интервал для каждого «отдельно взятого» неизвест-
ного коэффициента регрессии 0t (о понятии доверительного интервала и
подхода к их построению см. п. 7.4 и п. 7.5.4). В частности, из (15.46)
следует, что с доверительной вероятностью Р = 1 — а истинное значение
1-го коэффициента регрессии должно удовлетворять неравенствам
0{.мнк	1)0/ О/.мнк + ^fa/2(n - Р- 1).	(15.48)
Проверка гипотезы об отсутствии какой бы то ни было
линейной связи между у и совокупностью объясняющих
(1) (2)	(Г)
переменных х ',х' аг
В п. 11.2.4 при описании корреляционных характеристик линейной за-
висимости у от нескольких объясняющих переменных
был приведен результат, в соответствии с которым в предположении спра-
ведливости гипотезы
Яо* 0\ — 02 — • - - — 0р = О
652
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
статистика
R2V х п — р—\
7	1 - R2v.x Р
должна подчиняться F-распределению с числами степеней свободы числи-
теля и знаменателя, соответственно равными р и п — р — 1 (см. п. 3.2.3).
Следовательно, гипотезу Яо можно проверить следующим образом. По
заданному уровню значимости критерия а определяем из таблиц Прило-
жения 1 100а%-ную точку F(p,n — р — 1)-распределеиия va(p, n — р — 1).
Если окажется, что
' ’ -—~“ > v2a(p,n-p - 1),	(15.50)
1 - Ry.x Р
то гипотеза об отсутствии линейной связи между у и X отвергается (с ве-
роятностью ошибиться, равной о), и принимается — в противном случае.
Пример 15.1 (продолжение). Отдельная проверка статистически
значимого отличия от нуля оценок коэффициентов ^1,^2, •••,^5 в модели
(15.23*), т.е. последовательное сравнение отношений 0(/sl с 2,5%-ной точ-
кой распределения Стьюдента с те — р — 1 = 20 — 5—1 = 14 степенями
свободы (<о.025(14) = 2,145), показывает, что гипотеза о нулевом значе-
нии коэффициента pci рессии оказывается принятой для всех объясняю-
щих переменных, кроме Другими словами, па этой стадии анализа
только переменная х' — количество удобрении, расходуемых на гектар
земли, — подтвердила свое право на включение в модель. В то же время
вычисление оценки R2 х для множественного коэффициента корреляции
между урожайностью зерновых культур у и совокупностью пяти факто-
ров сельскохозяйственного производства (Ry.x ~ 0,517) и проверка гипо-
тезы об отсутствии какой бы то ни были линейной связи между у и X
с помощью статистики (15.49) (7 — 0,517 • 14/0,483 • 5 — 7,238/2,415 =
3,00; t>o.os(5; 20) = 2,96) говорят за то, чтобы продолжить изучение ли-
нейной связи между у и (z^,^2 ,...,х^) в рамках КЛММР. Пытаясь
понять причины невыразительности проявления влияния на у факторами
ж(2)^ж(3) и и более внимательно анализируя с этой целью как их
содержательный смысл, так и подсчитанную матрицу парных корреляций
R (см. табл. 15.2), мы вынуждены придти к выводу, что в данном случае
наша КЛММР «отягощена» так называемым явлением мулътиколлине-
арносгпи. К исследованию природы и причин этого явления и описанию
способов преодоления возникающих при этом трудностей мы и переходим
в следующем пункте.
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
653
Таблица 15.2 Матрица R парных коэффициентов корреляции.
	У	х<”		•V	_(4) •С	z<5>
	1,100	0,43	0,37	0,40	0,58	0,33
z^	0,43	1,00	0,85	0,98	0,11	0,34
/2)	0,37	0,85	1,00	0,88	0,03	0,46
	0,40	0,98	0,88	1,00	0,03	0,28
	0,58	0,11	0,03	0,03	1,00	0,57
?5)	0,33	0,34	0,46	0,28	0,57	1,00
15.4.	Мультиколлинеарность и отбор
наиболее существенных объясняющих
переменных в КЛММР
Речь идет о мультиколлинеарности (т.е. совместной, или множе-
ственной, взаимозависимости} объясняющих переменных модели
...,а/₽\ Можно ли строго определить мультиколлинеарность, ка-
ковы внешние признаки ее присутствия, какие трудности она создает при
анализе линейной модели регрессии и как преодолевать эти трудности?
Попробуем ответить на эти вопросы.
15.4.1.	Признаки и причины мультиколлинеарности
Мультиколлинеарность в строгом смысле (или полная муль-
тиколлинеарность) определяется условием нарушения одного из требо-
ваний КЛММР, а именно, требования к рангу матрицы X (см. (15.5) или
(15.5*)): говорят, что объясняющие переменные модели (z^\ ..., z^)
характеризуются свойством полной мультиколлинеарности, если ранг ма-
трицы их наблюденных значений (15.4а) меньше р+1. Мы уже обсуждали
эту ситуацию в начале главы, комментируя смысл условия «ранг матрицы
X = р + 1». Напомним, что при нарушении этого условия между анали-
зируемыми объясняющими переменными существует линейная функцио-
нальная связь (т. е. значения по меньшей мере одной из них могут быть
выражены в виде линейной комбинации наблюденных значений остальных
переменных), а матрица ХТХ оказывается вырожденной, т.е. ее опреде-
литель равен нулю (а значит не существует обратная матрица (ХТХ)-1,
участвующая в основных соотношениях метода наименьших квадратов).
В практике статистических исследований полная мультиколлинеарность
654
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
встречается достаточно редко, так как ее несложно избежать уже на пред-
варительный стадии анализа и отбора множества объясняющих перемен-
ных.
Реальная (или частичная) мультиколлинеарность возникает в
случаях существования достаточно тесных линейных статистических
связей между объясняющими переменными. Точных количественных кри-
териев для определения наличия/отсутствия реальной мульти коллинеар-
ности не существует. Тем не менее, существуют некоторые эвристические
рекомендации по выявлению мультиколлинеарности.
1)	В первую очередь анализируют матрицу R парных коэффициентов
корреляции, точнее, ту ее часть, которая относится к объясняющим пе-
ременным. Считается, что наличие значений коэффициентов корреляции,
по абсолютной величине превосходящих 0,75-0,80, свидетельствует о при-
сутствии мультиколлинеарности. Отметим, чго анализ матрицы R в при-
мере 15.1 (см. табл. 15.2) выявляет три коэффициента: г(а/1\з/3)) = 0,98;
r(a/2\a/3)) = 0,88 и г(а/1\я^) = 0,85. Следует признать, что тесную
связь по меньшей мере в одной из этих пар можно было легко спрогнозиро-
вать и до статистического обследования регионов: орудия поверхностной
обработки почвы реализуются в подавляющем большинстве с помощью
тракторов, а потому з/3) обязано быть достаточно высоко коррелирован-
(1)
ним с ’.
2)	Существование тесных линейных статистических связей между
объясняющими переменными приводит к так называемой слабой обусло-
вленности матрицы ХТХ, т. е. к близости к нулю ее определителя. Поэто-
му, если значение det(XTX) оказывается близким к нулю (скажем, одного
порядка с накапливающимися ошибками вычислений), то это тоже свиде-
тельствует о наличии мультиколлинеарности.
3)	Важную роль в анализе мультиколлинеарности играет и минималь-
ное собственное число Amin матрицы ХТХ. Это объясняется двумя об-
стоятельствами. Во-первых, из близости к нулю Аш|п следует близость к
нулю величины det(XTX), и наоборот. Во-вторых, можно показать, что
среднеквадратическая ошибка оценки 07,мнк обратно пропорциональна ве-
личине Ат5п (см., например, [Джонстон Дж., п. 5.7]). Поэтому, наряду с
величиной det (ХТХ) (или вместо нее), вычисляют и сравнивают с накап-
ливающимися ошибками от округлений значение Amjn, т.е. минимальный
корень уравнения
|ХТХ - А/р+1| = 0.
4)	Анализ корреляционной матрицы R позволяет лишь в первом при-
ближении (и относительно поверхностно) судить о наличии/отсутствии
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
655
мультиколлинеарности в наших исходных данных (15.4*). Более внима-
тельное изучение этого вопроса достигается с помощью расчета значений
коэффициентов детерминации	каждой из объясняющих перемен-
ных х^ по всем остальным предикторам X(j) = (х^,...,
...,*(₽))Т. Это объясняется, в частности, тем, что среднеквадратиче-
ские ошибки Sj оценок 0,.мнк связаны с величиной Я^ь).х(у) соотношением
Ъ = ^’/”(1 - Я»о>.хо)).
5)	Наконец, о присутствии явления мультиколлинеарности сигнали-
зируют некоторые внешние признаки построенной модели, являющиеся
его следствиями. К ним в первую очередь следует отнести такие:
•	некоторые из оценок 0у,мнк имеют неправильные с точки зрения эко-
номической теории знаки или неоправданно большие по абсолютной
величине значения (см. пример в п. 10.2, соотношения (10.9)—(10-9*)—
(Ю.Ю));
•	небольшое изменение исходных статистических данных (15.4*)-
(15.46) (добавление или изъятие небольшой порции наблюдений) при-
водит к существенному изменению оценок коэффициентов модели,
вплоть до изменения их знаков.
•	большинство или даже все оценки коэффициентов регрессии оказы-
ваются статистически незначимо отличающимися от нуля (при
последовательной автономной проверке с помощью t-критерия
(15.46)), в то время как в действительности многие из них имеют
отличные от нуля значения, а модель в целом является значимой
при проверке с помощью статистики (15.49) (именно с такой ситу-
ацией мы столкнулись в примере 15.1).
Подобные не поддающиеся содержательной интерпретации особенно-
сти модели можно понять и предвидеть, если обратиться к основным соот-
ношениям (15.26) и (15.36), определяющим правила вычисления соответ-
ственно МНК-оценок 0МИК и их ковариационной матрицы. И в той и в дру-
гой формуле присутствует матрица (ХТХ)-1, элементы которой обратно
пропорциональны величине определителя det (ХТХ). Если эта величина
достаточно мала, то изъятие или дополнение одной-двух строк в матрице
X (что равносильно изъятию или дополнению одного-двух наблюдений в
массив исходных данных (15.4*)-(15.46)) может радикально (во много раз)
изменить значение det(XTX), а следовательно, и зависящие от него зна-
чения 0МНк и Sg- Одновременно малость величины det (ХТХ) влечет за
собой непомерно большие значения диагональных элементов матрицы Eg
(т.е. дисперсий з2 = D(0 — Oj)2), что может приводить к статистически
незначимым отклонениям от нуля критических значений |0Л мнк|/з7.
656
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
15.4.2.	Методы устранения мультиколлинеарности
I. Переход к смещенным методам оценивания. Как известно
(см. в предыдущем пункте формулировку теоремы Гаусса-Маркова, со-
отношение (15.39)), М НК-оценки являются оценками с минимальной сред-
неквадратической ошибкой в классе всех несмещенных и линейных отно-
сительно Y = (yi, Уз, • • •,Z/n)T опенок. Зададимся вопросом: может ли
существовать смещенная оценка 0СМ неизвестного параметра 0, более точ-
ная (в смысле среднего квадрата ошибки Е(0 — 0)2), чем наилучшая среди
несмещенных оценок? Оказывается, да, может! Поясним это на следую-
щей схеме (см. рис. 15.1). Пусть оценка 0МИК — наилучшая среди несме-
щенных оценок неизвестного значения в анализируемого параметра, т.е.
Е(0М11К — #)2	Е(0 — 0)2 в классе всех несмещенных оценок в. Повто-
ряя выборки одного и того же обьема п из анализируемой генеральной
совокупности и подсчитывая значения для каждой (/-й) выборки но
одной и той же формуле построения наилучшей несмещенной оценки (при
I = 1,2,...), мы будем иметь множество значений 0МНГ, во которым мож-
но оценить, например, плотность распределения оценки 0МНГ — функцию
fg (х). Поступая аналогичным образом с конкурирующей смещенной
оценкой 0СМ, мы получим плотное!ь ее распределения (х). Пусть да-
лее А опредсляез допустимый предел погрешности в оценивании истинно-
го значения 0 анализируемого параметра, т.е. если |0 — 0| А, то оценка
0 считается «хорошей», а при |0 — 0| > А — «плохой».
Простой визуальный анализ рис. 15.1 приводит нас к следующим оче-
видным выводам:
•	доля «плохих» оценок 0си (а она определяется, в соответствии с
вероятностным смыслом кривой плотности (z), величиной за-
штрихованной площади под кривой плотности Jq (z) вне интервала
[0 — Д,0 + А]) в несколько раз меньше доли «плохих» оценок 0МНК
(последняя аналогично определяется заштрихованной площадью под
кривой плотности ^(z) вне интервала [0 — А,0 | А]);
•	средний квадрат ошибок при оценивании метолом 0МНК (как результат
интегрирования величип (0МНК ~ 0)2 с весами, определяемыми функ-
2 Т 2
цией плотности fg (z), т.е. Е(0МНК - 0) = j (z — в) fg (x)dx)
— оо
будет превосходить средний квадрат ошибок, получаемых при оцени
вании с помощью смещенной оценки 0СМ (т.е. величину Е(0СМ — 0)2 =
7 (х - fe„.(x)dx)-
—оо
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
657
Рис. 15.1. Плотности распределения несмещенной (х)) и смещенной
(/^сы(г)) оценок истинного значения 6 неизвестного параметра
Таким образом, учитывая, что в условиях мульти коллинеарности
дисперсии даже наилучших несмещенных оценок могут быть слишком
большими, естественно попытаться отказаться от требования несмещен-
ности, чтобы в более широком классе оценок найти те, которые будут
обладать более высокой точностью.
Описание различных подходов к построению «хороших» смещенных
оценок коэффициентов регрессии в условиях мультиколлинеарности мож-
но найти в книге [Айвазян и др., 1985, пп.8.3-8.5]. Приведем здесь лишь
один из этих подходов, названный «ридж-регрессией» (или «гребневой
регрессией»). Он основан на рассмотрении однопараметрического семей-
ства несколько «подправленных» МНК-оценок, а именно оценок вида
бт = (ХТХ + т/р+1)-1ХтУ.	(15.51)
Добавление к диагональным элементам матрицы (ХТХ) «гребня» ,
«хребта» т (т — некоторое небольшое положительное число) с одной сто
роны, делает получаемые при этом оценки смещенными, а с другой, —
превращает матрицу ХТХ из «плохо обусловленной» в «хорошо обусло-
вленную». Соответственно в дальнейшем и, в частности, при вычислении
средних квадратов ошибок для оценок 0Т мы не столкнемся с чрезмерно
малыми значениями определителя матрицы ХТХ (теперь эго будет уже
определитель матрицы ХТХ + т/р+1) и связанными с этим неприятно-
658
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
стями. Целесообразность использования оценок вида (15.51) основана на
теореме (см. Hoerl А. Е., Kennan! R. W., Technometrics, 1970, vol. 12, N* 1,
pp. 55—67), утверждающей, что в условиях мульти коллинеарности най-
дется такое значение т0, при котором средние квадраты ошибок оценок
0То окажутся меньше соответствующих характеристик для МПК-оценок
0МПК. Универсальных рекомендаций по поводу выбора конкретного значе-
ния т нет (как правилб, эта величина определяется в диапазоне значений
от 0,1 до 0,4).
II. Переход к ортогонализированным объясняющим перемен-
ным с помощью метода главных компонент. Поскольку мультикол-
линеарность связана с высокой степенью корреляции между объясняющи-
ми переменными, можно попытаться обойти эту трудность, используя в
качестве новых объясняющих переменных некоторые линейные комбина-
ции исходных, выбранные так, чтобы корреляции между вновь введенны-
ми переменными были малы или вообще отсутствовали. Если объясня-
ющих переменных немного (как, скажем, в наших примерах 11.3 и 11.4)
или имеется некоторая априорная информация, то выбор таких комбина-
ций может быть осуществлен из содержательных соображений. В более
общей ситуации один из возможных подходов основывается на использо-
вании главных компонент вектора исходных объясняющих переменных
X =	(см. п. 13-2). Соответствующий прием известен
в литературе под названием «построение регрессии на главных компо-
нентах^. Ссылка на п. 13.2 требует пояснений. В п. 13.2 описывается
метод построения главных компонент многомерной случайной величины
X = (ж^\ж^2\..., аг<₽))Т, в то время как в нашей модели X — это неслу-
чайный векторный параметр, от которого зависит закон распределения
результирующего признака у. Поэтому, оставляя в силе все описанные в
п. 13.2 построения и результаты, мы должны сделать, тем не менее, ряд
пояснений:
(i) Вероятностная терминология применительно к переменным
(их математические ожидания, дисперсии, ковариации и т.п.) теряет
смысл, а вместо их вероятностных характеристик мы будем рассма-
тривать формально соответствующие им комбинации наблюденных зна-
чений. В частности, мы так же, как и в п. 13.2, перейдем к центри-
,	v { (1)	(1) (2)	-(2)	(р)	-(р)\Т
рованным наблюдениям Auj = (xj — х ,х\ ' — х ,. .-,а\ — х ) ,
где х^ = £Г=1	а вмест° теоретической ковариационной матри-
цы S = Е[(Х — ЕХ)(Х — ЕХ)Т], относительно которой решается задача
определения собственных чисел и собственных векторов, будем рассматри-
вать (рхр)-матрицу Хц Хц, где Хц — это (пхр)-матрица центрированных
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
659
наблюдений, т. е.
xW-xW	хМ-хМ
J») _±(1) /2>_г<2»	xM-xM
\x^-x^ x™-x™ ... x™-x™
(заметим, что матрица Х^Хц, поделенная на п, при случайных перемен-
ных X интерпретируется как выборочная ковариационная матрица век-
тора X).
(ii) Уравнение регрессии У по X в терминах центрированных пере-
менных Уц = У - У и Х'ц = X - X примет вид:
Е(У-У | Х-Х) = «1(х(1)-г(,))+в,(г(2’-±(2))+...+вр(а:(^-^₽))) (15.52)
так что свободный член 80 из исходного уравнения (15.5) может быть
выражен в виде
р
во = 3/-52^0),	(15.53)
з-i
где у = SiLi yJn^Y = (у, у,..., у)Т — п-мерный вектор-столбец.
С учетом сделанных замечаний реализация метода построения регрес-
сии У на главные компоненты вектора X предусматривает выполнение
следующих операций.
1)	Определяются и упорядочиваются собственные числа Aj и соответ-
ствующие им собственные векторы Zj = (Zji,Zj2,...,Zjp) матрицы ХцХц
(Ai > А3 > Ар > 0, см. п. 13.2.2).
2)	Составляется матрица коэффициентов преобразования
(15.54)
в которой j-й собственный вектор lj играет роль j-й строки. Отметим,
что из построения следует, что матрица L ортогональна, т. е. LT = L~1
и соответственно LTL = LLT = Ip.
3)	С помощью матрицы L переходят к вектору главных компонент
Z = (^,A...,^>)T = LXll.
(15.55)
660
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Соответственно t-e наблюдение вектора главных компонент определится
соотношением
!₽>)т = t%Hj>
(1) J2)
•	5
а матрица наблюдений главных компонент — соотношением
I
(15.56)
Отметим, что из построения следует:
(15.57)
и соответственно
(15.58)
Отметим также, что вектор центрированных исходных переменных Хц
может быть выражен из (15.55):
XU = X -X = L~'Z = LTZ.
(15.59)
4)	Возвращаясь к задаче регрессии, анализируем КЛММР Уц по Z:
Е(У„ | Z) = d?1’ + c2zW + ... + c„zM.
(15.60)
В соответствии с основными соотношениями метода наименьших квадра-
тов (15.26) и (15.36) получаем:
СмНК — (С1 МНК » 2 МНК , ' ' • •> Срмнк )
Ег... = a?«(ZTZ)-1,
где
А2 -	1	Г 7(,)- -Г
° г к ~	/ ДУт ЧмнкЧ ••• ермнмл| / 
С учетом (15.58) можно сделать вывод, что оценки qмнк,с2мнв,...,срм|Ш
взаимно некоррелированы и
Cjmhk =	(15.61)
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
661
-2
E(cJMnll - сД2 =	(15.62)
5)	Наконец, пользуясь формулами (15.61) и (15.62), последовательно
проверяем гипотезы (см. п. 15.2.3, (15.47))
Н0}: Cj = 0	(> = 1,2,...,р)
с помощью статистик
^гх/
I Ё
1=1_________
Обозначим JcyUi множество индексов тех главных компонент, для которых
гипотеза оказалась отвергнутой. Тогда оценка функции регрессии у
па главные компоненты может быть записана в виде
у-у = X Ь^з}'
?€Лу<п
(15.63)
В данном случае исключение из модели ряда объясняющих переменных
не приводит к необходимости пересчета оценок коэффициентов регрессии
для оставшихся главных компонент, так как вид матрицы (ZTZ)! (см.
(15.58)) обеспечивает независимость результатов вычисления оценок с;
от числа и состава включенных в модель главных компонент.
Если удается дать содержательную интерпретацию включенным в
модель главным компонентам, то представление оценки функции регрес-
сии в виде (15.63) может быть окончательным. В противном случае воз-
вращаются к исходным переменным. Оценки 0огх>^1гк> • * • >0Ргк для па-
раметров	исходной регрессионной модели (15.5) получаются
с учетом соотношений (15.52), (15.53), (15.55) и (15.63):
? — 1»Р>
до гх = y-^dqCKx{q).
9=1
Вообще говоря, полученные таким образом оценки для коэффициентов
регрессии 0g (q — 0,1,..., р) будут смещенными. Формулы для величин
смещений и средних квадратов ошибок этих оценок приведены в книге
[Айвазян С. А. и др., 1985, и. 8.5].
662
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
III. Отбор наиболее существенных объясняющих перемен-
ных в КЛММР. В п. 13.1 среди основных предпосылок, обусловливаю-
щих возможность перехода от исходного числа р анализируемых показа-
- П) (2)	(р)	1 с л
телеи х ,х , аг к существенно меньшему числу р наиболее инфор-
мативных (в определенном смысле) переменных, упоминалось дублирова-
ние информацииу доставляемой сильно взаимнозависимыми признаками.
Именно с этой ситуацией мы сталкиваемся при мультиколлинеарности
объясняющих переменных в модели регрессии, а потому стремление ис-
следователя попытаться уменьшить общее число предикторов, отобрать
из априорного набора объясняющих переменных лишь самые существен-
ные (с точки зрения влияния на у) представляется вполне естественной
реакцией на данную ситуацию.
Каким бы способом ни проводился отбор объясняющих переменных,
обусловленность матрицы ХТХ улучшается с уменьшением числа пре-
дикторов, включенных в модель. В действительности, процедура отбора
существенных переменных имеет самостоятельное (нс «привязанное» к
проблеме мультиколлинеарности) значение. Она может рассматриваться
как процедура выбора размерности линейной модели. Другими словами,
она полезна и должна применяться и в ситуациях, когда матрица ХТХ хо-
рошо обусловлена. Но особенно она необходима и эффективна в условиях
мультиколлинеарности. Так, если две какие-либо объясняющие перемен-
ные сильно коррелированы с результирующим показателем у и друг с
другом, то часто бывает достаточно включения в модель одной из них, а
дополнительным вкладом от включения другой можно пренебречь.
В предположении, что матрица данных X является неслучайной, воз-
можны две точки зрения на оценку уравнения регрессии, полученную по-
дле отбора существенных предсказывающих переменных.
Первая точка зрения исходит из того, что модель регрессии (15.5)
является истинной, и несмещенная оценка коэффициентов регрессии по-
лучается с помощью метода наименьших квадратов, т.е. путем решения
системы уравнений (15.21) (в условиях мультиколлинеарности эта оценка
может быть неудовлетворительной, но тем не менее несмещенной). То-
гда принудительное приравнивание части коэффициентов регрессионно-
го уравнения к 0, что и происходит при отборе переменных, естествен-
но, приводит, если матрица ХТХ недиагональна, к смещенным оценкам
коэффициентов при оставшихся переменных, т.е. мы приходим к классу
смещенных оценок, рассмотренных в п. 15.3.2. Вопросы анализа возника-
ющих при этом «ошибок спецификации» будут рассмотрены в следующем
пункте.
С другой стороны, процесс отбора существенных переменных можно
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
663
рассматривать как процесс выбора истинной модели из множества воз-
можных линейных моделей, которые могут быть построены с помощью
набора предсказывающих переменных, и тогда полученные после отбо-
ра оценки коэффициентов можно рассматривать как несмещенные. Этой
точки зрения мы будем придерживаться в данном пункте.
Для случая, когда переменные ., х р\у — случайные величины,
вопрос о правильности (истинности) модели не возникает. Все, что мы
ищем в этом случае, — это модель, сохраняющую ошибку предсказания
на разумном уровне, при ограниченном количестве переменных.
Существует несколько подходов к решению задачи отбора наиболее
существенных предикторов в модели регрессии. Мы остановимся здесь
на одном из них, с нашей точки зрения — наиболее распространенном
и эффективном. Речь идет о процедуре последовательного наращивания
числа предикторов, реализуемой в двух версиях: версии «всех возможных
регрессий» и версии «пошагового отбора переменных». Этот подход со-
ответствует общей логике, которой следует придерживаться при постро-
ении и анализе регрессионных моделей, а именно — реализации пути «от
простого к сложному».
Версия «всех возможных регрессий». Решается следующая за-
дача: для заданного значения к (к = 1,2, ...,р — 1) путем полного пе-
ребора всех возможных комбинаций из к объясняющих переменных, ото-
бранных из исходного (априорного) набора z^\a;^2\. ,.х^р\ состоящего из
р предикторов, определить такие переменные х' ' "tx ,..„,х	”,
для которых коэффициент детерминации с результирующим показателем
у был бы максимальным, т.е.
_ тах .	..(15.64)
41 *’«2 ₽«!*«
Таким образом, на первом шаге процедуры (к = 1) мы найдем одну
объясняющую переменную	которую можно назвать наиболее ин-
формативным предиктором при условии, что в регрессионную модель у
по X мы можем включить только одну из априорного набора объясня-
ющих переменных а/^а/2),... ,а/р\ На втором шаге реализация кри-
терия (15.64) определит уже наиболее информативную пару переменных
(аг ”,аг ' поскольку по построению среди всех возможных пар, ото-
бранных из исходных р переменных, эта пара будет иметь наиболее тес-
ную статистическую связь с результирующим показателем у. Отметим,
что, вообще говоря, в состав этой пары может и не войти переменная
х ' ’ ) объявленная наиболее информативной в классе моделей зависимо-
664
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
сти у от одной объясняющей переменной. На третьем шаге (А: = 3) будет
отобрана наиболее информативная тройка предикторов, на четвертом
(к — 4) — наиболее информативная четверка объясняющих переменных
и т.д. Строгих математических правил «останова» этой процедуры, т.е.
выбора оптимального числа к0 предикторов, которые следует включить
в модель, нет. Однако следующая приближенная рекомендация в боль-
шинстве случаев позволяет получить правильное решение этого вопроса.
Обратимся к рис. 15.2. Будем откладывать по оси абсцисс последова-
тельно увеличивающееся на единицу число к предикторов в модели, а по
оси ординат — соответствующие значения «подправленной на песмещеп-
ность» оценки	13л»к(*)>) (см. формулу (11.40)). Одновременно
нанесем на чертеж по оси ординат величину нижней доверительной гра-
ницы Йт.п(^) для R2(*)))> вычисленную по формуле
Ят» = «’’(*) - 2 J	7? 0 - «’(*))•
У (п- 1)(п - 1)
(15.65)
В соотношении (15.65) для большей краткости в обозначениях поло-
жено Й* (к) =	Й2(/с) = R2.(хОН*))а вычита-
емое в правой части приближенно равно удвоенной среднеквадратической
ошибке оценки R2(k) (см. формулу (11.40)). Предлагается выбирать
в качестве оптимального числа к0 предикторов регрессионной модели
значение к, при котором величина R^inW достигает своего максимума
(см. рис. 15.2).
Реализация описанного метода всех возможных регрессий, предна-
значенного для отбора наиболее существенных объясняющих переменных
регрессионной модели, требует больших объемов вычислений. Нетрудно
подсчитать, что при каждом фиксированном значении к число различных
наборов переменных будет равно числу сочетаний из р элементов по к
(Ср), а полное число анализируемых наборов переменных при изменении
к от 1 до р — 1 будет равно Ср + Ср 4- ... + Ср 1 = 2Р — 2 (так, при
р = 20 число всех возможных переборов составит величину, превосхо-
дящую 106). В практике используется два подхода к преодолению этих
вычислительных трудностей. Первый связан с использованием прибли-
женных (полуэвристических) методов оптимизации критерия (15.64) (по-
жалуй, наиболее распространенным способом реализации этого подхода
можно признать так называемый «метод ветвей и границ»; смысл этого
метода состоит во введении некоторого грубого правила, которое позво-
ляет отбросить большинство наборов объясняющих переменных, не вычи-
сляя для них значения критерия в силу их очевидной бесперспективности).
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
665
Другой подход основан на использовании так называемой пошаговой про-
цедуры отбора, к описанию которой мы и переходим.
1
Рис. 15.2. Зависимость нижней доверительной границы коэффициента де-
терминации от числа предикторов (пунктирная кривая)
Версия пошагового отбора переменных. Эта версия отличает-
ся от предыдущей только тем, что на каждом следующем шаге (т.е. при
переходе от отбора к переменных к отбору к + 1 переменной) учитывают-
ся результаты предыдущего шага. Так, при переходе от к = 1 к к = 2
перебираются не все возможные пары (а^ч\х^)9 а лишь те, в которых
непременно участвует переменная	отобранная на 1-м шаге. Соот-
ветственно при переходе от шага «А:» к шагу «к +1» первые к информа-
тивных переменных считаются уже определенными на предыдущем ша-
ге, так что при оптимизации критерия (15.64) остается перебрать р — к
оставшихся переменных, поочередно присоединяя каждую из них к уже
отобранной на предыдущем шаге группе переменных
ж(»1(1))} ^(2))
Все остальные характеристики процедуры (оптимизируемый крите-
рий, правило выбора оптимального числа предикторов и т. д.) остаются
теми же, что и в методе всех возможных регрессий. Нетрудно подсчитать,
что при пошаговой реализации процедуры отбора наиболее существенных
объясняющих переменных число необходимых переборов снижается с 2₽—2
до Р 4“ (Р - I) + (р — 2) -Ь ... + 2 = (р 4- 2)(р — 1 )/2 (т. е. при р = 20 вместо
666
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
1048574 переборов, необходимых в методе всех возможных регрессий, нам
понадобиться всего 209 переборов различных вариантов составов предик-
торов).
Следует, правда, признать, что пошаговые процедуры, вообще гово-
ря, не гарантируют получения оптимального (в смысле критерия (15.64))
набора объясняющих переменных при каждом фиксированном fc > 2. Од-
нако в подавляющем большинстве ситуаций получаемые с помощью по-
шаговой процедуры наборы переменных оказываются оптимальными или
близкими к оптимальным.
♦ ♦ ♦
В пакетах программ по статистическому анализу данных реали-
зованы различные варианты пошаговых процедур отбора существен-
ных предикторов: наряду с описанной выше процедурой последователь-
ного наращивания («присоединения») переменных имеются процедуры
«присоединения-удаления», «удаления» и др. Их описание содержится
в книге [Айвазян С. А. и др., 1985, п. 8.7].
Пример 15.1 (окончание). Напомним, что анализ матрицы пар-
ных корреляций (см. табл. 15.2) и проверка гипотез о статистически не-
. .	(1)	(2)	(5)
значимом отличии от нуля коэффициентов регрессии у по х' 'ж'
в сочетании со знанием оценки коэффициента детерминации Rv.x урожай-
ности у по всем пяти анализируемым факторам сельскохозяйственного
производства (Ry.x = 0,517) привели нас к выводу о наличии мульти-
коллинеарности в рассматриваемой модели. Чтобы избавиться от нее,
попробуем снизить размерность модели, т. е. исключить из модели «несу-
щественные» объясняющие переменные. Воспользуемся для этого поша-
говой процедурой последовательного наращивания (присоединения) пре-
дикторов.
1-й шаг (к = 1). В классе моделей регрессии у по единственной
объясняющей переменной выбирается наиболее информативный (в смысле
критерия (15.64)) предиктор. Поскольку при к = 1 величина Ry.x совпа-
дает с квадратом обычного (парного) коэффициента корреляции г(у,х), а
max г2(у, х^) = г\у,х^) = (0,58)2 = 0,336, то наиболее информатив-
ным предиктором в классе однофакторных (парных) регрессионных моде-
лей оказывается переменная х' ' — количество удобрении, расходуемых
на гектар площади (т/га). Подсчет подправленного (на несмещенность)
значения r (у,х( ') = R (1) и его нижней доверительной границы
15.4. МУЛЬТИКОЛЛИНЕАРНОСТЬ
667
соответственно по формулам (11.40) и (15.65) (при к = 1) дает:
Й’’(1) = 0,299 и Ят'ш(1) = 0,207.
2-й шаг (к = 2). Среди всевозможных пар объясняющих переменных
(а?^4\ж^), j = 1,2,3,5, выбирается наиболее информативная (в смысле
критерия (15.64)) пара предикторов. Поскольку
тпах Ry (xO)txO')j —	— 0,483,
O#«)
то наиболее информативной парой предикторов оказываются объясняю-
щие переменные
ж^4^ — количество удобрений, расходуемых на гектар площади,
и
аг ’ — число орудий поверхностной обработки почвы на 100 га
(коэффициенты детерминации на этом и последующем шаге подсчиты-
ваются как квадраты соответствующих множественных коэффициентов
корреляции по формуле (11.34)).
Подсчет подправленного (на несмещенность) значения коэффициента
""*2
детерминации Ry.(xwtT.wy = R (2) и его нижней доверительной границы
ftmin(2) соответственно по формулам (11.40) и (15.65) дает:
R (2) = 0,422 и Я<п(2) = 0,324.
Оценка уравнения регрессии урожайности зерновых культур у (ц/га)
по иа/4\ подсчитанная по формуле (15.26), имеет вид:
/(г(3),г<3)) = 7,29 + 3,48 z(3) + 3,48 г(4).
(0,66)	(0.13)	(1,07)
Заметим, что все три коэффициента регрессии статистически значи-
мо отличаются от нуля при уровне значимости а = 0,05 (см. выше о кри-
териях проверки гипотез вида <<//0: 0j — 0» с использованием статистик
(15.46); напомним, что в скобках под значениями оценок коэффициентов
регрессии приведены величины их среднеквадратических ошибок).
Целесообразность включения в модель в качестве второй объясняю-
(3)
щей переменной предиктора х' подтверждается сравнением нижних до-
верительных границ ^min(l) И Я^5п(2), T.K. /?min(l) < #min(2).
3-й шаг (к — 3). Среди всевозможных троек объясняющих перемен-
ных (a/4\a^3\a/^), j = 1,2,5, наиболее информативной оказалась тройка
668
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
f К) (3)	(5)ч
(г ',зг ), поскольку
m<LX	^у.(хО) >rO) tx(®) J	0,513
1 »2,5
(напомним, что x^ — это количество химических средств защиты расте-
ний, расходуемых на гектар, д/га).
Рис. 1Б.З. График изменения Я2(А) (сплошная линия) и	(пунктир)
в примере 15.1
По схеме, полностью повторяющей предыдущий шаг, находим:
Я* (3) = R*.(г<«),х(з)>х(5)) = 0,422 и 7Ййп(3) — 0,312.
Сравнение нижних доверительных границ Я^;п(2) и Ят1П(3) гово
-	(5)
рит, однако, о том, что третью объясняющую переменную х в модель
включать нецелесообразно, т. к. Я^.п (3) < fimin(2) (см. также рис. 15.3).
Этот вывод подтверждается также сравнением подправленных значений
коэффициентов детерминации Я* (3) и Я* (2): добавление х' ' в каче-
стве третьей объясняющей переменной в анализируемую регрессионную
модель практически не повышает значение к .
15.5. Ошибки спецификации модели
Выше (см. п. 14.2.3) было подробно описано содержание проблемы
спецификации эконометрической модели. Напомним, что к вопросам сне-
15.5. ОШИБКИ СПЕЦИФИКАЦИИ МОДЕЛИ
669
цификации модели относится, в частности, выбор общего вида зависимо-
сти между анализируемыми переменными (см. также и. 10.7), а в рамках
выбранного линейного вида зависимости — определение списка объяс-
няющих переменных и спецификация случайных регрессионных остатков
(«ошибок»), где под спецификацией ошибок понимается формулировка
исходных допущений и априорных ограничений относительно стохасти-
ческой природы регрессионных остатков. В данном пункте мы кратко
остановимся на ошибках спецификации (а не об упомянутой только что
спецификации ошибок), причем ошибки спецификации понимаются в весь-
ма узком смысле: речь идет только об ошибках той спецификации, которая
связана с выбором списка (состава) объясняющих переменных в рамках
КЛММР. Другими словами нас будут интересовать ошибки, возникаю-
щие при неправильной спецификации матрицы наблюдений X.
Итак, предположим, как и в (15.5х), что истинное уравнение связи
между у и X имеет вид
У = Х0 + £,
(15.66)
где, X, как и прежде, матрица наблюденных значений объясняющих пере-
менных размерности п х (р-Ь 1). Однако, в процессе анализа исследователь
вместо матрицы X ошибочно решил воспользоваться матрицей данных X
размерности п х к. При этом некоторые столбцы матриц X и X одина-
ковы, т.е. часть объясняющих переменных истинной модели (15.66) ис-
следователем включена верно. Однако, в матрице X могут отсутствовать
некоторые переменные, участвующие в истинной модели и одновременно
в нее могут быть включены столбцы наблюдений по так называемым не-
существенным (т.е. не участвующим в модели (15.66)) переменным. В
этом и заключаются те ошибки спецификации модели, которые мы рас-
сматриваем в данном пункте.
Соответственно, исследователь в качестве МНК-опенок неизвестных
параметров О получит оценки
е = (хтх)_,хту.
(15.67)
Подставим (15.66) в (15.67):
0 = (ХТХ)_1ХТХ0 + (ХТХ)~'ХТе,
так что
eg = во,
(15.68)
где
В = (ХТХ)"1ХТХ.
(15.69)
670
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Из сравнения вида к х (р 4- 1)-матрицы В = (/?;j), t = 0,1,..., к - 1;
j = 0,1,... ,р и формул для МНК-оценок коэффициентов регрессии следу-
ет, что матрица В состоит из столбцов	(j =
0,1,...,p), компоненты которых являются МНК-оценками коэффициен-
тов регрессии j-й исходной (существенной) объясняющей переменной по
всем к используемым исследователем предикторам X.
Используем теперь соотношения (15.68)-(15.69) в целях анализа точ-
ности оценок 0, получаемых при неправильной спецификации КЛММР.
1) Предположим сначала, что исследователь включил в свою модель
только к (из р 4- 1) существенных переменных (к < р4- 1), а остальные
р 4- 1 — к существенных переменных «выпали» из поля его зрения. Это
означает, что матрица X отличается от матрицы X отсутствием р 4-1 — к
последних столбцов, т. е.
X = (A'(0)X(,)...X(,,))
И
Х = (Х(0),Х(1),
Х{к)).
Здесь, как и прежде (см. (11.1')), Х^ — вектор-столбец размерности п,
состоящий из п наблюдений переменной у, т.е.:	= (1,1,..., 1)Т и
Х^ = (х^\ а:^,..., г* ЬТ Для 1 j р. Тогда к X (р4- 1)-матрица В
будет представлена в виде:
1	0	...	0	Pok	...	0ор
0	1	...	0	flik	...	/31р
(15.70)
0 0 ... 1 @к-1к ••• 0к-Лр
Действительно, если переменная х^ входит в состав отобранных ис-
следователем предикторов (а следовательно, наблюдения Х^ этой пере-
менной входят в состав матрицы X), то регрессия х^ на множество век-
торов X дает коэффициент регрессии, равный единице при и нулю
при остальных включенных в X объясняющих переменных. Последние
р 4- 1 — к столбцов матрицы В содержат коэффициенты регрессии по X
для тех	которые не вошли в матрицу X. Подставим
(15.70) в (15.68) и получим выражение для величины смещения в оценке
любого из оцениваемых с помощью 0 коэффициентов:
Eflj =	+ Pjk^k + Pjk+l^k+l + • ’  + Pjp6p’
(15.71)
15.5. ОШИБКИ СПЕЦИФИКАЦИИ МОДЕЛИ
671
Таким образом, оценки 0 коэффициентов регрессии 0 окажутся сме-
шенными по отношению к истинным значениям этих коэффициентов, а
степень смещения зависит от статистических связей между включенны-
ми в анализ и «проигнорированными» объясняющими переменными, а
также от значений коэффициентов регрессии при исключенных персмен-
H.TV	T(fc+1)
НЫЛ £ у £
2) Теперь предположим, что исследователь включил в рассмотрев
,	(о)
ние не только все «существенные» объясняющие переменные х' ’ =
1 (О (р)	*	/
1,х , ...,х но и какое-то количество т «несущественных» (т.е., в
действительности, не участвующих в истинной модели (15.66)). Тогда
матрица X отличается оз X дополнительными т столбцами, а матрица
В имеет порядок (р + 1 4- т) х (р 1) и принимает вид:
(15.72)
где1р+1 —единичная матрица порядка (р+l)x(p-f-l), aOm>p+l — матрица
порядка тх(р+1), состоящая из одних нулей. Подставляя (15.72) в (15.68),
убеждаемся, что оценки 0 в этом случае будут несмещенными.
* * *
Из проведенного выше анализа можно сделать следующие выводы.
(») Соотношения (15.70) и (15.71) свидетельствуют о том, что непра-
вомерное исключение из КЛММР объясняющих переменных может при-
вести к серьезным ошибкам. При этом не только оценки коэффициентов
регрессии окажутся смещенными, но и, в еще большей степени, будет
смещена оценка (15.34) остаточной дисперсии а2. А это значит, что не-
точность выводов, основанных на оценках 0, еще более усугубится.
(::) Если позволяет объем выборки (п), которой мы располагаем, то
лучше ошибиться, введя в модель «лишние» (несущественные) перемен-
ные, нежели исключив существенные. Как мы видели, полученные при
этом оценки остаются несмещенными (правда, несколько ослабевает точ-
ность статистических выводов, зависящая от отношения р/п). Кроме то-
го, увеличение числа предикторов может приводить к мультиколлинеар-
ности, с которой связаны свои «неприятности» (см. п. 15.3).
(ш) Рассмотренная схема служит предостережением против наивного
заключения о том, что МИК автоматически дает наилучшие линейные
несмещенные оценки. Следует помнить о том, что это справедливо лишь
в случае выполнения всех условий КЛММР (см. соотношения (15.5) или
672
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
15.6. Обобщенная линейная модель
множественной регрессии (ОЛММР)
и обобщенный метод наименьших
квадратов (ОМНК)
Естественно ожидать, что при моделировании многих реальных эко-
номических или социально-экономических процессов мы можем столк-
нуться с ситуациями, в которых условия классической линейной модели
множественной регрессии (15.5*) оказываются нарушенными. Так, если в
качестве исходных статистических данных (15.4“)-(15.46) мы используем
временные или пространственно-временные выборки, то чрезмерно огра
ничительным, нереалистичным становится, как правило, условие взаим-
ной некоррелированности и гомоскедастичности регрессионных остат-
ков, которое в терминах ковариационной матрицы Е< остатков выража-
ется в (15.57) соотношением Ee = а21п. Даже при соблюдении условия
взаимной некоррелированности остатков приходится часто анализировать
регрессионные модели, в которых разброс остатков около линии регрес-
сии не остается постоянным, а меняется, например, возрастая пропор-
ционально значениям функции регрессии.
С этой точки зрения весьма актуальным представляется расширение
КЛММР в направлении отказа от упомянутого условия
15.6.1. Обобщенная линейная модель множественной
регрессии (ОЛММР)
Формальная запись ОЛММР отличается о КЛММР только отказом
о г требования некоррелированности и гомоскедастичности регрессионных
остатков. Пусть Ео — некоторая симметричная, положительно определен-
ная матрица порядка п х п, где п, как и прежде, число исходных статисти-
ческих данных (15 4“)-(15.4б) (т.е. объем имеющейся в нашем распоряже
нии выборки). И пусть ковариационная матрица Ее регрессионных остат
ков е = (ej,£2»• -• ?£п) выражается через Ео соотношением Ес = ст2Г0
Будем предполагать, что в этом соотношении число а неизвестно, а ма
трица Ео известна. С точки зрения практической, прикладной последнее
предположение в большинстве случаев нереалистично; однако в дальней-
шем для некоторых частных случаев мы сможем отказаться от условия
априорного знания матрицы Eq.
Обобщенная линейная модель множественной регрессии описывает-
15.6. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ
673
си системой следующих соотношений и условий:
У — 0 Ч- е,
Ее = О
= <72Ео,
/ (О (2)	(р)\
(г , ж' ,...., аг ) — неслучайные переменные
ранг матрицы X = р + 1 < п,
(15.73)
где участвующие в (15.73) векторы и матрицы определены ранее соотно-
шениями (15.4а)-(15.46), (15.7)-(15.12).
Сравнение (15.73) с (15.5*) показывает, что ОЛММР отличается от
КЛММР только видом ковариационной матрицы ошибок Ее: в КЛММР
мы предполагали, что матрица с точностью до неизвестной положи-
тельной константы о2 равна единичной матрице 1п (что обеспечивало
некоррелированность и гомоскед астич ность остатков е), в то время как
в ОЛММР мы допускаем, что ковариации (а следовательно, дисперсии
и корреляции) остатков могут быть произвольными при сохранении,
правда, условия невырожденности матрицы
Именно в этом суть обобщения модели, именно поэтому модель (15.73)
называется обобщенной ЛММР. Рассмотрим два типа распространенных
в практике эконометрических исследований моделей, которые вкладыва-
ются в рамки ОЛММР, но не могут быть описаны в рамках КЛММР.
1) Линейная модель регрессии с гетероскедастичными ре-
грессионными остатками.
Впервые с линейной моделью регрессии, регрессионные остатки ко-
торой не отвечают требованиям гомоскедастичности (т.е. сохранения
постоянного уровня величины их дисперсии при переходе от одного наблю-
дения к другому, а точнее -— от одного значения объясняющей перемен-
ной к другому), мы познакомились в процессе анализа примера 10.1 (см.
п.10.1). Анализируя разброс значений удельных денежных сбережений в
семье у(х) при различных величинах семейных среднедушевых доходов
х, мы обнаружили явную зависимость несмещенной оценки з2(ж) услов-
ной дисперсии остатков D(e | х) от значения х (см. табл. 15.3; данные
составлены на основании информации, содержащейся в табл. 10.1).
Таблица 15.3
i	1	2	3	4
ж? (ден. ед.)	80	120	160	200
л(ж?) »	| ж?)	6,4	16,0	22,6	28,9
?(ж?) « D(e | xQi)	40,96	256,00	510,76	835,21
674
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Эти данные отражают, кстати, весьма естественную для практики
социально-экономических исследований ситуацию, когда более реалистич-
но постулировать постоянство относительного, а не абсолютного раз-
броса регрессионных остатков е(Х) около соответствующего регрессион-
ного значения результирующего показателя j/cp(X) = E(t/ | X) (относи-
тельный разброс измеряется соответствующим коэффициентом вариации
V(X) = yD(y I Х)/уер(Х), см. и. 2.6.3).
Отметим, что при соблюдении условия взаимной некоррелированно-
сти регрессионных остатков, ковариационная матрица вектора остатков
е в примере 10.1 может быть представлена в виде
где первые 10 диагональных элементов соответствуют первым десяти на-
блюдениям, сделанным при фиксированном значении среднедушевого се-
меиного дохода х-[, вторые 10 диагональных элементов соответствуют сле-
дующим десяти наблюдениям, сделанным при другом фиксированном зна-
0
чении среднедушевого дохода х2,ит.д.
Обобщая этот пример на случай зависимости результирующего пока-
зателя от многих объясняющих переменных, т. е. рассматривая линейную
модель множественной регрессии (ЛММР), условные дисперсии случай-
ных остатков которой D(e | X) оказываются величинами, зависящими от
значений объясняющих переменных, мы приходим к определению ЛММР
с гетероскедастичными некоррелированными остатками. Очевидно, ко-
вариационная матрица остатков е может быть представлена в данном
15.6. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ
675
частном случае ОЛММР в виде
(15.74)
К О
где в соответствии с описанием ОЛММР (см. (15.73)) величину ст2 мы
относим к неизвестным (оцениваемым по выборке) параметрам модели,
а значения Ai, А2,..., Хп пока считаются известными (в дальнейшем, при
определенных формах параметризации зависимости D(e | X) от X, будут
определены подходы и к статистическому оцениванию априори неизвест-
ных значений A,, i ~ 1,2,..., п).
2) ЛММР с автокоррелированными остатками.
Как уже упоминалось в начале п. 15.6, в ситуациях, когда исходные
наблюдения регистрируются во времени (тогда, очевидно, номер наблю-
дения «г» несет смысловую нагрузку времени регистрации наблюдения,
а потому индекс «г» часто во временных выборках заменяется индексом
«/»), регрессионные остатки (i = 1,2,.. .,п) оказываются статистиче-
ски взаимозависимыми, коррелированными, а значит и их ковариационная
матрица не может быть диагональной.
Естественным допущением относительно природы зависимости ос-
татков является гипотеза, в соответствии с которой эта зависимость осла-
бевает по мере их взаимного удаления друг от друга во времени. Одной
из простых и наиболее аналитически удобных (а потому и наиболее рас-
пространенных) математических форм реализации этого допущения (при
сохранении свойства гомоскедастичности остатков) является следую-
щая:
= /'1' я
(15.75)
где г(е,,€7) — коэффициент корреляции между б, и £j, а р — некоторое
число, по модулю меньшее единицы (очевидно, из (15.75) следует, что по
своему вероятностному смыслу р — это коэффициент корреляции меж-
ду соседними по времени остатками). Соотношение (15.75), в частности,
означает:
(t) корреляционная связь между регрессионными остатками зависит
только от меры их «разнесенности» во времени, но не зависит от того, к
каким именно «моментам» времени г и j они «привязаны» (т.е., скажем,
’(£1,^5) = г(бз,Е7));
(it) корреляционная связь между £, и исчезает вовсе при |t—J| —> оо,
т.е. при неограниченном удалении остатков б, иг,- друг от друга во
676
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
времени;
(in) ковариации остатков = Е(е^у) имеют вид
=
(15.76)
где а = D(e | X») — условная дисперсия остатков (не зависящая от ве-
личины Xt в силу гомоскедастичности); так что ковариационная матрица
остатков имеет в данном случае вид:

п-2
(15.76')
Заметим, что соотношение (15.76) следует из формулы, связывающей
г(Е»,£у) и crtJ = Е(е,€^): действительно, по определению (см. (2.33)),
г(£;,£у) = (Tij/y/bEi~	откуда и следует (15.76).
15.6.2.	Обобщенным метод наименьших квадратов (ОМНК)
Итак, нам предстоит провести статистический анализ зависимости,
описываемой ОЛММР (15.73). Это значит, что па основании исходных
статистических данных вида (15.4*) (15.4е) мы должны уметь решать
задачи 1-4, описанные в п. 15.1.7, и, в частности, в первую очередь, по-
строить паилучшие (в определенном смысле) точечные оценки неизвест-
ных значений параметров О и <т3. Выясним сначала, нельзя ли восполь-
зоваться уже известными нам МНК-оценками О и д2, определяемыми
соответственно соотношениями (15.26) и (15.36)?
Обычные МНК-оценки параметров ОЛММР. Можно пока-
зать, что определенные соотношениями (15.26) обычные МНК-оценки
0мнк остаются и в рамках ОЛММР состоятельными (при тех же тре-
бованиях к матрице наблюдений X) и несмещенными. В частности, дока-
зательство несмещенности оценок 0МНК в задаче оценивания параметров
ОЛММР в точности повторяет доказательство этого факта в условиях
КЛММР (см. (15.29), (15.30)).
Однако полученные ранее формулы (15.36) и (15.36*) для ковариаци-
онной матрицы Eg оценок Омнк и для оценки этой ковариационной
матрицы оказываются неработоспособными, неприменимыми в условиях
ОЛММР. Действительно, поскольку (15.29) справедливо и для ОЛММР,
15.6. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ
677
имеем:
- 6 = (XTX)-’XTe,
Чв. =	" 0)Т1
= Е[(ХтХ)-,ХтеетХ(ХтХ)-1]	(15.77)
= (XTX)-1XTE(eeT)X(XTX)-1
= <г3(ХтХ)_,ХтЕ0Х(ХтХ)-1.
Сравнение правой части (15.77) с формулой (15.36), справедливой
только в рамках КЛММР, позволяет установить факт существенного от-
личия истинных характеристик точности оценивания с помощью МПК
параметров ОЛММР от тех, которые мы получили бы, воспользовавшись
формулой (15.36) (ниже мы продемонстрируем существенность подобного
расхождения на некоторых примерах). Мы не обсуждаем здесь свойств
оценки о2, поскольку в общей схеме ОЛММР параметр а2 не имеет чет-
кой вероятностной интерпретации (в отличие от КЛММР (15.5*) и ЛММР
с автокоррелированными гомоскедастичными остатками, — см. (15.76*),
2
где параметр а имеет смысл дисперсии случайных регрессионных остат-
ков). Более детальный анализ (15.77) и ОЛММР показал, что оценки 0мнк
в условиях ОЛММР теряют свои оптимальные свойства и что можно
предложить другие оценки — так называемые оценки обобщенного мето-
да наименьших квадратов 0ОМНК > которые будут наиболее эффективными
в смысле теоремы Гаусса-Маркова.
Оценки по обобщенному методу наименьших квадратов опре-
деляются соотношениями
ё»мн. = (ХТЕо *Х)-1ХтЕо1У.	(15.78)
Можно доказать (Aitken А. С. On Least-Squares and Linear Combinations
of Observations. Proc. Royal Soc., Edinburgh, 1934, vol. 55, pp. 42-48), что в
классе линейных несмещенных оценок параметров О модели (15.73) оцен-
ки 0ОМНК, определенные соотношениями (15.78), являются оптимальны-
ми в смысле теоремы Гаусса-Марков а (см. 15.39).
Проведем доказательство этого утверждения.
Несмещенность оценок (15.78) устанавливается по той же схеме, что
и несмещенность 0мнк. В частности:
§оив, = (ХТЕо’Х)-’хТ£о '(X© + е)
= (ХтЕо‘1Х)“1Х So’X© + (Хг£о 'Х)~'ХТЕО *е (15.79)
= © + (ХТЕо 1Х)~1ХтЕо’е.
678
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Применение операции математического ожидания к левой и правой
частям (15.79) с учетом Ее — 0п дает:
Е60М„ = 0.	(15.80)
С целью доказательства оптимальных свойств оценок (15.78) восполь-
зуемся знанием матрицы £о Для того, чтобы преобразовать исходные дан-
ные (15.4“)-(15.4б) к виду, отвечающему требованиям классической (а не
обобщенной) модели. Это значит, что после произведенного преобразо-
вания случайные остатки модели е1|р должны удовлетворять свойствам
гомоскедастичности и взаимной некоррелированности, т.е.
S. = <?!„•
Выполнить необходимое преобразование позволяет известный резуль-
тат из матричной алгебры (см. Приложение 2), в соответствии с которым
всякая невырожденная симметричная (т X т)-матрица А допускает пред
ставлсние в виде
А = ССТ,	(15.81)
где С — некоторая невырожденная (гл X пг)-матрица (представление
(15.81) не единственно, однако для нас это не имеет значения). Восполь-
зуемся этим, чтобы представить в виде (15.81) матрицу Ео- Итак, суще-
ствует такая невырожденная ортогональная (n X п)-матрица С, что
So = ССТ.	(15.81')
Заметим, что тогда
C-,S0(C-,)T=In>	(15.82)
(C-1)TC-t = So1	(15.83)
(соотношение (15.82) получается из (15.81х) домножением левой и правой
частей последнего на матрицу С”1 слева и матрицу (СТ)-1 = (С ')Т
справа, а (15.83) получается из (15.81х) с учетом правила обращения про-
изведения квадратных невырожденных матриц (АВ)-1 = В-1А-1).
Теперь вернемся к ОЛММР (15.73) и, домножив все члены первого
соотношения этой модели слева на матрицу С-1, получим:
>пр = Хпр0 + епр,	(15.84)
где
ÄР= С-1У, Хпр = С-1Х и £пр = С-,£.	(15.85)
15.6. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ
679
Нетрудно проверить, что (15.84) удовлетворяет всем требованиям
классической модели (15.5Z). Для этого достаточно убедиться в том, что
Е<пр = Е(епр€гГр) = tf2In- Действительно,
S.„p = Е(спреУр) = Е^'е^Г1)1) = C-IE(eeT)(C-I)T
= С_1<г2£0(С’‘)т = <т2[С“1Е0(С",)т] = <z2In
(при переходе к правой части соотношения было использовано равенство
(15.82)).
Следовательно, в соответствии с ранее полученными для КЛММР
результатами наилучшей в классе всех линейных (относительно У) не-
смещенных оценок параметра 0 будет оценка
е = (Х,ТР Хпр)"’хУрУ„р,	(15.86)
ковариационная матрица которой определяется формулой
= ^(Х.УрХрр)-1.	(15.87)
Вернемся к исходным наблюдениям X и У. Оценки (15.86), выра-
женные в исходных наблюдениях, назовем оценками обобщенного метода
наименьших квадратов 0ОМНК:
... = ^(ХтЕо,Х)“1.	(15.87')
Как известно, МНК-оценки (15.86) являются по построению резуль-
татом минимизации по 0 критерия ^(0) - (Упр-Хпр0) Г(Упр-Хпр0) (см.
(15.19)). Выпишем вид этого критерия в исходных наблюдениях ОЛММР:
<?(©)= [С*‘(У-Х0)]Т[С-1(У-Хб)]
= (У - Х6)Т(С_1)ТС_,(У - Х0) = (У - Хб)т£о1 (У - Хб).
(15.88)
Поэтому ОМ НК-оценки 0ОМИК могут быть определены как «точка ми-
нимума» обобщенного критерия (15.88).
Анализ вариации результирующего показателя у и выбороч-
ный коэффициент детерминации в ОЛММР. В п. 15.3.3 бы-
ло получено разложение общей вариации результирующего показателя на
две составляющие, — вариацию, объясненную изменчивостью функции
680
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
регрессии (т. е. изменением значений объясняющих переменных), и вари-
ацию случайных остатков, — справедливое в рамках классической ЛММР
(см. (15.27д) и (15.27й)). Следовательно, в используемых в данном пункте
обозначениях мы, казалось быу можем записать это соотношение в виде
(пр Упр) (пр ^пр) ~ (^П) OMHI ^пр) (ХПр(Эомнк	УПр) + ^пр^пр"
(15.89)
Тогда возвращаясь с помощью (15.85) к исходным наблюдениям и па-
раметрам обобщенной ЛММР, из (15.89) мы бы получили:
(У-У)ТХ^*(У-У) = (X0OMH,-y)TSo’(X0<)MH1I-y)+eTSo12. (15.89')
Откуда, определяя, как и прежде, выборочный коэффициент детерми-
нации Ry x как Долю общей вариации признака у, объясненную изменени-
ем функции регрессии (или, что то же, изменением значений объясняющих
переменных X), имеем:
п2 ,_______________€ Ер £___________
-XVj/.A — *	__ т ,	___ •
(У - У)т3о *(У - У)
(15.90)
Однако, в действительности, мы не можем гарантировать справедли-
вости соотношений (15.89) и, соответственно, (15.89*), а следовательно,
и ограниченности значений коэффициента (определенного соотноше-
нием (15.90)) в пределах интервала [0; 1]. Причина в том, что базовое раз-
ложение (15.27й) выводилось в предположении наличия свободного члена
в анализируемой ЛММР. В то же время из построения видно, что мы
не можем гарантировать присутствия свободного члена в модели (15.84).
Поэтому определенный соотношением (15.90) коэффициент детерминации
Ry.x используется в ОЛММР лишь как приближенная эвристическая ха-
рактеристика.
Оценка параметра а2 в ОЛММР. Выше упоминалось о том, что
в отличие от КЛММР в рамках обобщенной модели мы уже не можем
интерпретировать (без дополнительных предположений о структуре ма-
трицы So) параметр о2 как величину дисперсии регрессионных остатков.
Однако он остается и в рамках ОЛММР неизвестным параметром модели,
который требуется статистически оценить.
С этой целью мы воспользуемся результатами решения этой задачи
для классической модели (см. п. 15.3.4) и, в частности, соотношением
(15.34) и свойствами (15.45)-(15.45^. В обозначениях и терминах ОЛММР
эти соотношения и свойства применимы по отношению к преобразованным
данным Х11р и Упр, что после обратного перехода к исходным данным X и
У обобщенной модели с помощью формул (15.85) дает:
15.7. ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
681
• оценка
? = n ~L i (у ~ Хвои„.)ТЕо’(У - хе^,,,)	(15.91)
является несмещенной оценкой неизвестного параметра о2 модели
(15.73);
• статистика (п—р— \)д/а2 подчиняется %2-распределению с п—р— 1
степенями свободы, а оценки <т2 и 0ОМ|1К, определенные соотноше-
ниями соответственно (15.91) и (15.78), являются статистически
независимыми.
* * ♦
Завершая описание общих сведений об обобщенном методе наимень-
ших квадратов, обратим внимание читателя на проблему практической
реализации этого метода. Ведь во всех основных формулах ОМ НК (см.
соотношения (15.78), (15.87*), (15.77)) мы исходим из того, что ковариаци-
онная матрица остатков известна (правда, с точностью до неизвестного
2
постоянного множителя а , несмещенную оценку для которого мы стро-
ить умеем (см. (15.91)). Однако ситуации, когда матрица £ нам извест-
на заранее, крайне редки в практике эконометрического моделирования.
Если же включать формально все элементы матрицы в множество па-
раметров модели (15.73), оцениваемых по выборке (15.4а)~(15.46), то мы
столкнемся с неразрешимой (без дополнительных априорных допущений
о структуре матрицы Eq) статистической задачей, поскольку число не-
известных параметров только в матрице Ео составляет п(п + 1)/2, что
превосходит объем располагаемых нами выборочных данных. Поэтому
для того, чтобы от общего описания ОМНК перейти к практически ре-
ализуемому обобщенному методу наименьших квадратов, нам придется
вводить дополнительные априорные ограничения на структуру матрицы
Ео, что и будет сделано в следующих трех пунктах.
15.7. ОЛММР с гетероскедастичными
остатками
В п. 15.6.1 описана линейная модель регрессии с гетероскедастичными
регрессионными остатками как один из частных случаев ОЛММР (15.77),
в котором ковариационная матрица остатков Еж имеет вид (15.74). Это
означает, что регрессионные остатки, как и в классической модели (15.5*),
взаимно некоррелированы (т.е. Е(€,-€у) = 0 для i / у), но в отличие от
условий (15.5*) не обладают свойством гомоскедастичности (т.е., вообще
682
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
говоря, ^4 Dej при i / j) или, как принято говорить, они гетерос-
кедастичны (неоднородны по характеристике случайного разброса). Как
было уже упомянуто в п. 15.6.1, гетероскедастичность остатков — вполне
естественная ситуация для анализа пространственных выборок: для них
чаще более оправданной является гипотеза постоянства относительного
разброса остатков, выраженная, например, в виде
D(e | Xi) = о-2[Е(у | А',)]2
(15.92)
или
<72(«+ frl-^)2,
D(f | Х() =
(15.92')
где — та объясняющая переменная, пропорционально квадрату кото-
рой возрастает условная дисперсия регрессионных остатков.
Кстати, данные табл. 15.3 и построенный на основании этих данных
рис. 15.4 свидетельствуют о том, что именно соотношение (15.92г) оказы-
вается подходящей формой допущения относительно поведения условной
дисперсии D(e | г») в примере 10.1.
Рис. 15.4. Зависимость условного среднеквадратического отклонения остат-
ков от значения объясняющей переменной в примере 10.1
15.7. ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
683
Попытаемся конкретизировать общие формулы ОМНК для данного
частного случая обобщенной линейной модели регрессии. С этой целью,
во-первых, выпишем конкретный вид (п х п)-матрицы С вспомогательно-
го преобразования (15.85). Отправляясь от вытекающего из (15 74) вида
матрицы Ео, определим
/ Va/^i
1/хА?
С =
(15.93)
\ о

Легко проверить, что в этом случае выполняются соотношения
(15.81 ), (15.82) и (15.83). Кроме того, определенный соотношением (15.88)
критерий ОМНК при матрице Ес вида (15.74) представим в форме
9(0) = (у - xe)TSo '(у - хе) = £>.(», - е0 -	------м'р))2-
(15.94)
Поэтому ОМНК в частном случае обобщенной ЛММР с гетероскеда-
стичными остатками часто называют методом взвешенных наименьших
квадратов или взвешенным методом наименьших квадратов (роль «ве
сов» в нем играют, как это видно из (15.94), диагональные элементы
матрицы Eq1)-
Соответственно несмещенная опенка о2 неизвестного значения пара-
метра а2 в выражении ковариационной матрицы остатков Ев (см. (15.73)),
определяемая формулой (15.91), в данном случае имеет вид
*2 = n_p_ 1 53 Ми - 4 - «1 х!*’------------------(15.91')
При определении ОМНК-оценок 0ОМНК для параметров регрессии G и
ковариационной матрицы Eg следует воспользоваться, соответствен-
но формулами (15.78) и (15.87*) с заменой в формуле (15.87*) неизвестной
величины а2 ее оценкой (15.91*) и с учетом того, что диагональный вид
матрицы Ео (а следовательно, и Eq 1) существенно упрощает сам процесс
вычисления.
684
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
15.7.1. Сравнение ОМНК- и МНК-оценок в моделях
регрессии с гетероскедастичными остатками
В общем виде ответ на вопрос, какие из оценок (ОМНК- и МПК-)
лучше и почему, мы уже имеем: хотя и те, и другие оценки являются со-
стоятельными и несмещенными, ОМ НК-оценки оказываются более эффек-
тивными, более точными. Проиллюстрируем этот тезис на примере 10.1.
Чтобы несколько упростить техническую сторону анализа, перенесем на-
чало координат по оси абсцисс в точку х = 40 (ден. ед.), т. е. будем изме-
рять значения объясняющей переменной в новой шкале Ох, где х связано
с х простым соотношением х = х — 40.
При таком преобразовании объясняющей переменной ее исходные зна-
чения автоматически уменьшаются на 40 ден. ед., а гипотетический ха-
рактер зависимости условной дисперсии остатков D(e | х) от х, как это
видно из рис. 15.4, может быть описан упрощенным вариантом соотноше-
ния (15.92/), а именно формулой
D(e | я) = aV	(15.95)
(в целях упрощения обозначений мы не будем с этого момента писать
волну над ж).
Для дальнейшего анализа этого примера выпишем основные формулы
ОМНК в схеме гетероскедастичных остатков для случая одной объясняю-
щей переменной.
Поскольку при р = 1
Х7Ео'Х =
то в соответствии с (15.78) получаем уравнения для определения ОМНК
оценок параметров и 0]:
0о £ А« + £ А»ж» = £ А»У»
i=l	i=l	i=l
00 £ Ai*i + 01 £ Ai*i = £
»=1	t=l	i=l
(15.96)
Откуда, в частности, и следуют использованные нами ранее формулы
(10.7я/) для ОМНК-оценок #о.омнх и 01 омнк-
15.7. ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
685
Приведенный выше конкретный вид матрицы ХТ£ё 1Х и формула
(15.87 ) позволяют выписать дисперсию оценки ОМ|1к:
D01.OMHK
— Е(^1.омнк ^1 )
(15.97)
Общая формула (15.22) для MIIK-оценок и ее частный случай для
р — 1 (см. (15.18)) дают нам способ вычисления обычных МНК-оценок
^о.мнк 11 ^1-мнк- Воспользовавшись формулой (15.77), мы можем выписать,
например, дисперсию оценки 0кмНк и затем сравнить ее с дисперсией оцен-
ки 01.ОМНК- Итак, из (15.77) для случая р= 1 следует:
= сг
О$1.МНК --	МНК
Нам известен общий результат теории ОМИ К, в соответствии с ко-
торым при известных значениях А, в условиях обобщенной линейной мо-
дели предпочти тельное оценивать 0 по формуле (15.78), чем по формуле
(15.22), поскольку ОМНК-оценки, найденные по формуле (15.78), являют-
ся наилучшими линейными несмещенными оценками. Попробуем конкрет-
но (численно) оценить потерю в эффективности оценивания при исполь-
зовании оценок 0Мцк вместо 0ОМН|С в нашем примере 10.1 (см. пп. 10.1 и
15.6.1) при гипотезе (15.95) относительно характера гетероскедастично-
сти регрессионных остатков. Эта гипотеза, в частности, означав!, что
числа А^ с помощью которых задастся матрица Ео (см. (15.74)-(15.73)),
определяются соотношением:
(15.99)
686
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
что в нашем конкретном примере 10.1 означает следующее:
А1 = Ад = • •	• —	Ajo =	(ХЪ)2 = 4Q a j
Ац =	А(2	=	• • •	=	А20	—	(г?)2	==	803 ’
А21 —	А22	=	•  •	=	Азо	—	(ХЬ)?	—	(120р ’
А31 =	А33	=	• • •	=	А40	-	pip-	=	(fe'opr-
(15.100)
Формулы (15.97) и (15.98) с учетом (15.95) принимают соответственно
вид:
DO
1.МНК —
(15.97')
Вычисление /J0i.Omhk й ^i.mhk с использованием формул (15.97')и
(15.98') по данным примера 10.1 и с учетом (15.100) дает:
ЯЯкомик = 0,1 Ост2,
Я01.МНЖ =0,17<Л
Отсюда следует, что D0|.omhk/^0i.mhk = 0,10<т2/0,17сг2 = 0,59, т.е.
эффективность обыкновенного метода наименьших квадратов составляет
в данном конкретном случае всего лишь 59% эффективности обобщенною
метода наименьших квадрагов.
15.7.2. Некоторые практические рекомендации по анализу
модели регрессии с гетероскедастичными остатками
Приступая к анализу ОЛММР, исследователь должен, во-первых, от-
ветить на все вопросы, связанные со спецификацией модели, и, во-вторых,
найти пути к определению ковариационной матрицы остатков Ее = сг2Е0
(либо на основе априорных теоретических сведений, что бывает достаточ
но редко, либо с помощью некоторых специальных способов статистиче-
ского оценивания на базе исходных данных X, У).
15.7. ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
687
Из вопросов, связанных со спецификацией модели, на стадии, когда
уже определены конкретные прикладные цели моделирования, анализи-
руемые переменные и общий вид зависимости (в нашем случае, т.е. в
рамках ОЛММР, он постулируется линейным по X), остаются только
вопросы, касающиеся вероятностной природы регрессионных остатков.
Это значит, что мы должны статистически проверить, находимся ли мы,
действительно, в условиях гетероскедастичности остатков с.
Проверка гипотез о гомо-/гетероскедастичности регрес-
сионных остатков. В специальной литературе ([Джонстон Дж.],
[Greene W. H.J, [Goldberger A.], [Pindyck R., Rubinfeld D. L.]) описываются
различные методы проверки гипотезы
Но: D(e | X) = const
(15.101)
при альтернативе, состоящей в том, что остатки £i,...,en гетероскеда-
стичны. Опишем некоторые из них.
1) Случай группированных данных и больших выборок. Это — наибо-
лее простой случай. Предполагается, что объем п имеющихся исходных
данных (15.4а)-(15.46) достаточно велик, и в частности, выборка может
быть разбита на определенное количество (k) подвыборок объемов, соот-
ветственно, Tij, п2> • • • 1 пк (П1 +п2 4-hnk = п) таким образом, что внутри
каждой из подвыборок значения объясняющих переменных либо совпада-
ют (как в нашем примере 10.1, в котором к = 4, а пг = п2 = тг3 = п4 = 10),
либо принадлежат одному интервалу (гиперпараллелепипеду) группиро-
вания (см. п. 6.1). Если среднюю точку j-ro интервала группирования
(или общее значение объясняющей переменной в j-й подвыборке) обозна-
чить Xj, то проверка гипотезы (15.101) сведется к построению статисти-
ческого критерия проверки гипотезы об однородности дисперсий
Яо= D(e | X?) = D(e | А'®) =
= D(e | A'J)
(15.10Г)
по величинам соответствующих выборочных дисперсий
1___
Пу — 1
- Si.)2>
где yji — значение результирующей переменной в i-м наблюдении j-й под-
выборки, а уу. = 52 Уц/п}.
i=l
В качестве такого критерия может быть использован, например, кри-
терий Бартлетта (см. п. 8.6.2, соотношение (8.32)). В случае отклонения
688	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
гипотезы (15.101*) значения л могут быть использованы для комплекта-
ции оценки матрицы Ес в качестве ее диагональных элементов.
2) Критерий Глейсера.1 В данном подходе рассматривается регрессия
абсолютных величин остатков |ej = |у,—^о.мнк~^1.ммкг?^--------^Р.мн»г^|
по некоторой функции от х^\ где х^ — это та объясняющая пере-
менная, от которой гипотетически зависит условная дисперсия остатков
D(c | х^). На практике рассматриваются простые функции от х^\ на-
пример:
Е(|е| | xU}) = а(1) 4- а(2)ж0),	(15.102е)
(2)
Е(|ё| | хМ) = а(,) +	(15.102е)
Ж*'
Е(|ё| | г0)) = а(1)(г0))°'”.	(15.102')
Решение о гомоскедастичности регрессионных остатков е принима-
ется на основе проверки МНК-оценок коэффициентов а^нк и ^мнк на их
статистически значимое отличие от нуля (см. п. 15.3.4, (15.47)). Преиму-
щество этого подхода состоит в том, что в случае отклонения гипотезы
«Яо: а' ' = 0» исследователь одновременно получает основание к вы-
бору формы параметризации матрицы Ео. Так, случай статистически
значимых коэффициентов и а^2^ в схеме (15.102*) соответствует пред-
положению
= ^(4»Н1С + ««Lhm®^),
где вспомогательные случайные величины имеют нулевые средние зна-
чения и дисперсии Ш, = а2. Тогда оценка значения i-ro диагонального
элемента матрицы Eq (т.е. величины А”1 в обозначениях (15.74)) опреде-
лится соотношением
= (« НК +
(15.103)
Заметим, что регрессия |е| может строиться не по одной объясняю-
щей переменной, а по нескольким или по определенной комбинации всех
fl)2 (212	z_\3
объясняющих переменных (например, по ж< = г; ' + ж^ +--Ь х\Р) ).
Состоятельное оценивание основных характеристик модели
регрессии с гетероскедастнчнымн остатками. Речь идет, конечно,
о ситуациях, когда матрица Eq, участвующая во всех основных формулах
1 Gejser Н. Л New Test for Heteroscedasticity. Journ. Am. Stat. Assoc., 1969, vol. 64,
pp. 316-323.
15.7. ОЛММР С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
689
ОМНК, неизвестна (когда Ео априори известна, ОМНК-оценки 0, ^вмжм и
Eg , определяемые соответственно формулами (15.78), (15.77) и (15.87 )
с заменой участвующего в них параметра а его оценкой (15.91), являются
состоятельными ).
1) Оценка ковариационной матрицы Sg обычных МНК-оценок
0МНК. В предположении, что мы находимся в условиях модели с некор-
релированными и гетероскедастичными остатками, можно показать1, что
(п	\
52ё?л;х,т)(хтх)-1,	(15.104)
»=1	/
где Ei — yi —	а- ЛГ» = (1,^^, -.• ,zJp))T является состоятельная
оценка матрицы ковариаций обычных МНК-оценок коэффициентов ре-
грессии 00,0|,..., 0р.
2) Оценка неизвестной ковариационой матрицы вектора остат-
ков е и коэффициентов регрессии О. Наиболее распространенный общий
подход к оцениванию неизвестной ковариационной матрицы Se в условиях
обобщенной линейной модели регрессии связан с экономной параметриза-
цией этой матрицы с последующей оценкой небольшого числа параметров,
в терминах которых она выражается (подробнее об этом подходе см. ни-
же, в п. 15.9). В условиях рассматриваемой модели с взаимпонекоррели-
риванными, но гетероскедастичными остатками этот подход может быть
реализован, папример, в рамках описанной выше общей схемы критерия
Глейеера, когда определенная форма параметризации матрицы Ес выте-
кает из избранною (гипотетичного) общего вида регрессии |е| по X (см.
соотношения (15.102*)—(15.102®)). Примером может служить регрессия
(15.102 ) и вытекающее из нее соотношение (15.103), при котором матри-
ца Ео определяется всего двумя параметрами а и
/(«<'>+ «<2>х</>)2	О \
(«<’> + а<2’^>)2
-о —
\	0	’ (а<” + а(2)х«>)2
(15.105)
Очевидно, возможны и другие формы регрессионной зависимости |е|
ог Х‘ конкретный выбор этой формы будет определяться спецификой ис-
1 White Н. A Heteroscedasticity-Consistcnt Matrix Estimator and a Direct Test for
Ueteroscedasticity. Econometrica, vol. 48 (1980), X« 4, pp. 817-838.
690
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
ходных данных (Х,У) и нашим умением адекватно подбирать общий вид
регрессионной зависимости (см. методы, описанные в п. 10.7).
15.8. ОЛММР с автокоррелированными
остатками
Мы уже познакомились в общих чертах в п. 15.6.1 с еще одним част-
ным случаем обобщенной линейной модели множественной pei рессии —
регрессионной моделью с автокоррелированными остатками. Там же об-
суждались реальные ситуации, естественно приводящие к необходимости
рассмотрения такого рода моделей (в первую очередь к ним относятся так
называемые «временные выборки» , т.е. ситуации, в которых исходные
статистические данные модели регистрируются во времени). Наконец,
была сформулирована базовая идея подобного рода зависимостей между
остатками: эта зависимость неограниченно ослабевает по мере удаления
остатков друг от друга по времени.
Рассмотрим теперь более систематически и подробно один из вариан-
тов математической формализации этой идеи — модель линейной регрес-
сии, в которой регрессионные остатки £i,£25 •••?£« связаны автокор-
реляционной зависимостью 1-го порядка1. Подобного рода зависимость
между остатками описывается соотношениями
€i = p£i-\ +	(15.106)
где р — некоторое число, по абсолютной величине меньшее единицы (т. е.
|р| < 1), а случайные величины 6, удовлетворяют требованиям, предъ-
являемым к регрессионным остаткам классической модели, т.е,
{2
<70	при 1-J-,	(15.107)
0	при 2 / J.
При этом полагается, что соотношения (15.106) справедливы для лю-
бого «момента времени» t, сколь угодно удаленного в прошлое или бу-
дущее, т. е. i может «пробегать» все целочисленные значения от —оо до
1 Регрессионные модели с более широким спектром типов взаимозависимостей, суще
ствующих между регрессионными остатками ej,€2,... ,сп, рассмотрены, например,
в книге: М. Песаран, Л. Слейтер. Динамическая регрессия: теория и алгоритмы
(пер. с англ.). М.: Финансы и статистика, 1984. — 312 с.
15.8. ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ
691
Отправляясь от (15.106) и (15.107), определим основные числовые ха
рактеристики (средние значения Ее,- и ковариационную матрицу =
Е(ееТ)) вектора регрессионных остатков е.
Из (15.106) следует:
£* — Р£:-1 +	— р(р£<-2 + ^i-1) +	— />2£ш-2 + Р^|-1 +
= Р {P£i-3 + ^i-2) + P^i-1 + t>i = p3£i-3 + p2&i-2 + P^i-l + $< = ...
= 6, 4- p£t-i 4- p2^i~2 4- .. =
(15.108)
Из (15.108) с учетом (15.107) непосредственно следует:
Ее, = 0,
о2 = D£i = Ее? = ЕЛ,2 4- р2ЕЛ,2_1 4- р4ЕЛ,2_2 4- • • •
2
2/1 ,	2 .	4 . ч &0
— (Tq(1 + р 4-р +••)— ------2'
1 -р
(15.109)
Для вычисления ковариаций E(£t£t_fc) (i = 1,2, ...,п; к —
1,2,..., i — 1) представим произведение £,£,_* с учетом соотношения
(15.108) в виде:
^i^i-k — [№ 4" p^t 1 4"  • • 4“ рк ^i-(fc-l)) 4- p\fit-k Ь	+’*•)]
X ($i-k 4-	4- • • •)•
Тогда, поскольку из взаимной некоррелированности следует взаим-
ная некоррелированность случайных величин (^,4-р^»-14-’ • •4-p*~1^i-(*-i))
и №-jt 4- p^i-h-i +••), получаем:
cov (£ь£^_л) = £(£,£,_*) = E[/'(<$,_k 4- p6trk_i 4- • • •/] = pfcE£?_fc = a2pkt
(15.110)
где дисперсия а определена соотношением (15.109).
Таким образом, мы пришли к тому, что автокорреляционная зави-
симость 1-го порядка (15.106), связывающая между собой регрессионные
остатки ОЛМНР, в терминах ковариаций этих остатков эквивалентна со-
отношениям (15.109)-(15.110). Это позволяет записать линейную модель
692
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
множественной регрессии с автокоррелированными остатками в виде:
y = хе + е,
Ее = 0п,
/ (1)	(2)	(Р)\
(аг ',аг ,... ,аг ') — неслучайные переменные;
k ранг матрицы X = р 4- 1 < п.
Таким образом, (n х п)-матрица S । определяется в данной модели
значением единственного параметра р по формуле
(15.112)
Понадобится нам и матрица Ео 1, участвующая во всех основных фор-
мулах ОМНК. Поэтому приведем здесь ее вид:
/1	-р	0	0	...	О	0	0	\
-р	1 + р2	-р	0	...	О	О	О
„-1	1	0 -р 1 + р2 -р ... О О О
Ьо = -------у
1 - Р .........................................j.....
О	0	0	0	...	-pl+p	— р
\ О	О	О	О	...	О -р	1 /
(15.113)
Становится понятным теперь и вероятностный смысл формально вве-
денного в (15.106) параметра/). Действительно, изопределения коэффици-
ента корреляции (2.33) и соотношений (15.109)—(15.110) следует, что ко-
эффициент корреляции r(£t,£i±jt) между регрессионными остатками, от-
стоящими Друг от друга по времени на к единиц, равен:
г(е,',— р , к — 0,1,2,...
(15.114)
Именно в такой математической форме реализуется в модели (15.111)
идея ослабления корреляционных связей между регрессионными остатка-
ми по мере их взаимного удаления во времени.
15.8. ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ
693
Как мы знаем (см. п. 15.6.2), общий прием, с помошью которого обоб-
щенная модель регрессии сводится к классической, заключается во вре*
менном переходе к преобразованным исходным данным (Хпр,Уор) с по-
мощью некоторым специальным образом подобранной (я X я) матрицы
преобразований С. Для модели с автокоррелпрованнымн регрессионными
остатками в качестве такой матрицы может быть использована матрица
1 о о • • • о о о		
	-р	1	0 ...	0	00	
С =	0	~р 1 ...	0	0	0	(15.115)
	0	0	0 ... -р 1	0	
	\	0	0	0 ...	0 -р 1/	
Соответствующие преобразованные исходные данные имеют при та-
кой матрице преобразования С следующий вид:
Упр = СУ = (71 - р2у1,у2 - рУ\,Уз - РЗ/2,---,Уп -
Хпр
= сх =
Л 2 (1)
V1 - р А
Г(,) -
Ж 2
71 - о2х{р} \
V1 Р xi
ХМ - ох^
Х2 рХу
х(1) - оя(,)
гп Рхп-1
Путем непосредственного перемножения соответствующих матриц
нетрудно убедиться в справедливости равенств (15.81 ), (15.82) и (15.83)
при матрице С вида (15.113), а соответственно и в справедливости соот-
ношения
Е(СееТСТ) = <721п.
15.8.1.	Искажение характеристик точности МНК-
оценок, обусловленное игнорированием
автокоррелированности регрессионных остатков
Под игнорированием автокоррелированности регрессионных остатков
мы понимаем ситуацию, в которой исследователь вместо ОМ НК-оценок
§омнк> определяемых формулой (15.78), и соотношений (15.77) и (15.87/),
позволяющих оценивать точность соответственно МНК- и ОМНК-оценок,
пользуется соответствующими формулами обычного метода наименьших
квадратов — (15.26) для 0мнк и (15.36) для ковариационной матрицы оце-
нок 0«ыи.
694
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
В этом пункте мы хотим проанализировать меру искажения харак-
теристик точности обычных МНК-опенок при использовании формулы
(15.36) (позволяющей оценивать ковариационную матрицу МН К оценок
6ЫИЖ только в условиях классической ЛММР) вместо действующей в усло-
виях обобщенной ЛММР формулы (15.77).
Заметим, что правомерность использования обычного МНК для по-
строения оценок 0МНЖ неизвестных параметров 0 подкрепляется сохране-
нием свойств несмещенности и (в широком классе ситуаций) состоятель-
ности оценок 0МНЖ и в условиях обобщенной ЛММР. Одпако неустра-
нимые искажения при этом возникают в оценивании их характеристик
точности, т.е. ковариационной матрицы Eg к-
С целью анализа этих искажений рассмотрим модель (15.111) зави-
симости у от единственной объясняющей переменной х без свободного
члена. Очевидно, в этом случае X = х, 0 — 0, т. е. yi — Oxi 4-а
матрица наблюденных значений объясняющей переменной х имеет вид
X = (я|, Zj,. •., з^п) •
Обычная оценка МИК, подсчитанная по общей формуле (15.26), в дан-
ном случае имеет вид
Е XiVi
«ин. =(ХТХ)-’ХТУ = ^----.
1=1
(15.116)
Подсчитаем дисперсию (средний квадрат ошибки) этой оценки парал-
лельно двумя способами: 1) по формуле (15.36), справедливой только в
рамках условий классической модели, т.е. игнорирующей автокоррелиро-
ванность регрессионных остатков, и 2) по формуле (15.77), учитывающей
эту автокоррелированность в рамках условий обобщенной модели (15.111).
Использование формулы (15.36) дает:
2
= -72(ХтХ)“1 = - - -.	(15.117)
Ех?
1=1
15.8. ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ
695
Проведем расчет величины по
правильной формуле (15.87):
Р0М11, = <72(ХтХ)',Хт£0Х(ХтХ)*1
2	1	(	ч
= °	(*1,*2---*п)
52*?
1=1
п—1	п—2	п—3	. I
V р р ... р 1 /
п—1	п—2
Е *.*•+!	Е
1 + 2р^л
Е	Е а
1=1	1=1
(15.118)
Возьмем для сравнения результатов (15.118) и (15.117) их отношение:
п—1
,nf Т - =1+2?i=1n	+ -+2рп~‘^Ч-	(15119)
(^^мяк )прибл	52	52 xi
i=i	•=!
Очевидно, правая часть (15.119) может существенно превышать еди-
ницу, например, при р > 0 и при положительной коррелированности зна-
чений объясняющей переменной х. При этом мы имеем в виду, что корре-
лированность значений х измеряется формально вычисленным коэффици-
ентом корреляции (в предположении нулевого среднего значения я), т.е.
r(fc) = r(x„xi+k) =
л—к
52 *<*•+*
t=i
к = 1,2,.. .,п — 1.
Тогда, придав определенное числовое значение р и положив, напри-
мер, т(к) = рк, можно численно оценить правую часть (15.119). Так, при
696
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
р = 0,8 имеем (при достаточно больших п):
1 +	+ - •  + 2р"-’	= 1 + 2р2 + 2/>4 + • • • + 2/п-,)
А	2	А	2
Е	Е
»=i	»=i
1	1 I 2
,2,4,	,	2(п—1)\	.	1	1	1 +Р ~ л
— 2(1+р +р +------р	2~1 — ~	2 ~ 4,56.
1-р 1-р
Мы видим, что игнорирование автокоррелированности остатков в
обобщенной линейной модели регрессии вида (15.117) при подсчете сред-
него квадрата ошибки МНК-оценки 0МНК приводит к неправомерному за-
нижению этой ошибки более, чем в 4,5 раза!
Обратим внимание читателя еще на одно обстоятельство. Выбран-
ный нами способ сравнения (£>0Мнк)прибл. и	позволил обойти еще
одно «тонкбе место» в оценивании характеристик обобщенной моде-
ли (15.111) методами, игнорирующими автокорреляцию регрессионных
остатков. Речь идет об оценивании параметра а2 (беря отношения срав-
ниваемых характеристик (15.117) и (15.118), мы сумели элиминировать
этот параметр из нашего рассмотрения). Проведенный аналогично толь-
ко что выполненному анализ результатов правильного (с помощью фор-
мулы (15.91)) и некорректного (с помощью формулы (15.34)) оценивания
параметра аг2 показывает, что расхождения здесь могут быть еще более
существенными, чем те, которые получаются при сравнении опенок для
(см., например, [Джонстон Дж., с. 246-248]).
15.8.2.	Проверка гипотезы о пали чин/отсутствии
автокоррелированности регрессионных остатков
Как это следует из предыдущего пункта, игнорирование автокорре-
ляции регрессионных остатков создает серьезные трудности для приме-
нения обыкновенного МНК. Поэтому важно владеть методами, позволя-
ющими устанавливать ее присутствие. Приведем здесь описание одного
из них, — известного в специальной литературе под названием критерия
Дёрбина-Уотсона (Durbin J., Watson G.S. Testing for Serial Correlation in
Least-Squares Regression. Biometrika, vol. 37 (1950), pp. 409-428; and vol.
38(1951), pp. 159-178).
15.8. ОЛММР С АВТОКОРРЕЛИРОВАННЫМИ ОСТАТКАМИ
697
Критическая статистика Дёрбина-Уотсона имеет вид
рё.-ё.-О3
----->	(15-120)
Е4
1=1
где Ei = yt — 0О.МНК —	—-----— невязки обыкновенного
метода наименьших квадратов. В упомянутой выше работе исследовано
распределение статистики d в предположении справедливости гипотезы
Яо:р = 0.	(15.121)
Поскольку, как оказалось, распределение статистики d (в предполо-
жении справедливости гипотезы Hq) зависит от наблюденных значений
объясняющих переменных X, Дёрбину и Уотсону удалось установить (для
двух заданных величин уровня значимости критерия а = 0,05 и а = 0,01)
лишь такие пороговые значения dh(a) и du(a) (dh(a) < <Zu(q)), которые
позволяют построить следующие два варианта процедуры проверки ги-
потезы (15.121) (в зависимости от альтернативы о наличии в остатках
положительной или отрицательной автокорреляции 1-го порядка):
а)	При d < 2 (альтернатива: существование в остатках положи-
тельной автокорреляции первого порядка):
•	по заданному а находим из таблиц (см. Приложение 1) пороговые
значения db(a) и du(a)\
•	по формуле (15.120) подсчитываем значение критической статисти-
ки J;
•	если d < d^(a)y то гипотеза Hq отвергается (с вероятностью оши-
биться, равной о) в пользу гипотезы о положительной автокорреляции;
•	если d > du(a), то гипотеза Hq не отвергается;
•	если dfi(ot) d < du(a), то сделать определенный вывод по имею-
щимся исходным данным нельзя.
б)	При d > 2 (альтернатива: существование в остатках отрица-
тельной автокорреляции первого порядка):
•	первые два действия — те же, что и п. а);
•	если 4 — d < dh(a), то гипотеза Яо отвергается (с вероятностью
ошибиться, равной а) в пользу гипотезы об отрицательной автокорреля-
ции;
•	если 4 — J > rfu(a), то гипотеза Яо не отвергается;
•	если dh(a) 4 — d du(a)} то сделать определенный вывод по
имеющимся исходным данным нельзя.
698
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Грубо говоря, в случае отсутствия автокорреляции в регрессионных
остатках значение критической статистики d должно «не слишком отли-
чаться» от 2.
Отметим, что данный критерий, строго говоря, выведен лишь для
неслучайных объясняющих переменных. Поэтому, если в составе объяс-
няющих переменных присутствуют, например, так называемые лаговые
значения результирующего показателя, то он должен быть соответствую-
щим образом модифицирован (см. [Джонстон Дж., п. 10.3]).
15.8.3.	Некоторые практические рекомендации по анализу
модели регрессии с автокоррелированными
остатками
В ситуациях, в которых значение коэффициента корреляции р меж-
ду соседними по времени регрессионными остатками известно, исследо-
ватель не должен испытывать затруднений в практической реализации
основных формул ОМПК (15.78), (15.77), (15.87) и (15.91).
Поэтому остановимся па ситуации (гораздо более реалистичной), ко-
гда значение параметра р априори не известно исследователю. Прак-
тически все процедуры, предложенные для реализации ОМ НК в моде-
ли регрессии с автокоррелированными остатками при неизвестном значе-
нии р, имеют итерационный характер (см [Pindyck R. S., Rubinfeld D. L,
и. 6.2.1). Приведем здесь описание одной из наиболее распространен-
ных процедур подобного типа, известной в литературе под названием
процедуры Кохрейна-Оркатта (Cochrane D.t Orcutt G. Н. Application of
Least-Squares Regressions to Relationships Containing Autocorrelated Error
Terms.«Journ. of the Amer. Stat. Assoc.», vol. 44 (1949), pp. 32-61):
1)	вычисляются обычные МНК-оценки Омнк по формуле (15.26);
2)	подсчитываются невязки 1-й итерации = у,—^о.мнк
____0 Лр).
•/p.MHK4zt 1
3)	первое приближение р№ оценки р неизвестного параметра р опре-
деляется в качестве МНК-оценки коэффициента регрессии р в модели
ер) =	где остатки удовлетворяют условиям классической
модели (15.5);
4)	вычисляются ОМНК-оценки ОомнДр^) по формуле (15.78) с ма-
трицей Ео(р^)» определенной соотношением (15.112), в котором вместо р
.(1)
подставлены значения р ,
5)	подсчитываются невязки 2-й итерации
— Vi “0.омнк\,Р ) ^1.омнк\Р )^i	“р.омнккР )	>
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
699
6)	второе приближение 𹑠оценки р неизвестного параметра р опре-
деляется в качестве М НК-оценки коэффициента регрессии р в модели
Е • =	4- с, , где остатки dj удовлетворяют условиям классической
модели (15.5);
7)	вычисляются ОМНК-оценки 0Омик(р^) по формуле (15.78) с ма-
трицей Ео(/Г определенной соотношением (15.112), в котором вместо р
-(2)
подставлены значения р — и т. д.
Процедуру заканчивают при стабилизации получаемых значений р^к\
т.е. на стадии, когда очередное приближение р мало отличается от пре-
дыдущего. «Тонкое место» метода определяется типовым недостатком
подобных процедур, заключающимся в возможности «скатиться» в ходе
итераций в локальный, а не глобальный минимум критерия наименьших
квадратов. В этом случае значение параметра р может быть определено
с большой ошибкой.
15.9. Практические рекомендации по
построению, анализу и интерпретации
регрессионной модели
15.9.1.	Построение и анализ обобщенной ЛММР
при неизвестной ковариационной матрице
регрессионных остатков (практически реализуемый
ОМНК)
В замечании, завершающем п. 15.6, мы уже обращали внимание чита-
теля на проблемы практической реализации ОМНК: в подавляющем боль-
шинстве ситуаций практики эконометрического моделирования ковариа-
ционная матрица регрессионных остатков не известна исследователю
заранее. В то же время ее значение необходимо для реализации основных
формул ОМНК: (15.78), (15.77), (15.87*), (15.90) и (15.91). Если элементы
матрицы нс связывать дополнительно никакими априорными ограни-
чениями и условиями, то мы приходим к практически неразрешимой зада-
че статистического оценивания п(п 4- 1)/2 неизвестных параметров (эле-
ментов матрицы S<) всего по п исходным наблюдениям. Именно поэтому
основной подход к статистическому анализу обобщенной линейной модели
множественной регрессии с помощью ОМНК в ситуации, когда ковариаци-
онная матрица регрессионных остатков неизвестна, базируется на предпо-
ложении, что задана структура матрицы Sc (и соответственно Ео), т.е.
700
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
форма ее функциональной зависимости от сравнительно небольшого коли-
чества параметров а , а , а ,..., а . Это значит, что матрица So рас
сматривается как функция известного вида от неизвестных параметров
а = (в ,	') и соответственно: S< = о S0(a ,... , а ') = аЕ0(а).
Так, в примере 10.1 удалось построить подобную схему с единственным
неизвестным параметром <т2 (т.е. при т = 0), так как в нем была ис-
пользована структура матрицы Sr, определяемая соотношением (15.74),
где А, = 1/г?-
В примере ОЛММР с автокоррелированными остатками (см. (15.7б'))
структура матрицы S< определяется двумя параметрами а и o' = р, так
что элементы матрицы So восстанавливаю 1ся по единственному параме-
тру р. Наконец, в описанном выше критерии Глейсера случай (15.103)
соответствует двухпараметрической структуре матрицы So (она опреде-
ляется параметрами а' ' и а следовательно, матрица будет опреде-
ляться значениями трех параметров:	и Главная идея обще-
го подхода заключается в следующем: по исходным наблюдениям (X, У)
сначала строятся состоятельные оценки а = (а а ') параметров
а = (а^\...,а^т^). Затем вычисляются оценки So = S0(a), д2 (по фор-
муле (15.91)) и Sc = о2Ео- При некоторых достаточно общих условиях1
удается показать, что использование полученных таким образом оценок
So и Sc в основных формулах ОМНК (15.77), (15.78) и (15.87z) вместо
неизвестных истинных значений So и Sc дает также состоятельные оцен-
ки соответственно для Sa , О и Sa . Подобный способ оценивания
принято называть в специальной литературе практически реализуемым
обобщенным методом наименьших квадратов.
Опишем общую схему процедуры практически реализуемого ОМНК,
которая используется в рамках нормальной ОЛММР, т.е. в рамках усло-
вий модели (15.73), дополненных условием (On;a2So(a)) — нормальности
вектора регрессионных остатков е.
В этом случае функция правдоподобия остатков е = Y — Х0 имеет
1 В качестве таких условий используются, например, условия сходимости по вероятно-
сти (при п —♦ оо): а) матрицы *	1X — к некоторой конечной невырожденном
матрице и б) вектора-столбца ^XTS^‘1e — к вектору-столбцу 0p + i, состоящему из
одних нулей.
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
701
х exp
---2(y-Xe)TSo-‘(a)(y-X0) .
. 2cr
Переходим к логарифмической функции правдоподобия I = In £ и,
приравнивая ее производные по О, <г2 и ак нулю, составляем систему урав-
нений для отыскания опенок максимального правдоподобия Оммп>^ммп и
А — I , . . . , ttm).
So(a)) = - £ 1п(2») - £ 1п(<т2 ) + | In (SJ*(«
- -^(У - X0)TSO-'(а)(У - хе);
2<г
2а2 де Г
п 1	1
о ~2 + о/ 2Ч2
* а 2{а )
(У - X0)Tw,(y - Х0)
Х0)'Ео*(а)(Г-Х0)] =0р+1,
(У - Х0)Т£о-’(а)(У - Х0) = 0,
(15.122)
д1
дв ~
д1
Я 2 ~
да
д1
даи} ~ (У-ХО)тЕо(о)(У-Х0)
ЭХо*(а) . . _
где и>, = -77Г-,	1=1,2,...,
П
т.
Анализ системы уравнений (15.122) позволяет сделать следующие вы-
воды:
1)	Решение первого уравнения системы доставляет минимум крите-
рию ОМНК (см. (15.88)), а следовательно, даже не производя диффе-
ренцирования по 0, можно заключить, что оценки параметров 0 в схе-
ме ОЛММР по обобщенному методу наименьших квадратов совпадают с
оценками по методу максимального правдоподобия (т.е. 0ОМНК = 0MMIJ,
где оценка 0ОМНК определена формулой (15.78)).
2)	Решение второго уравнения системы дает в качестве оценки <т„М11
гу же оценку а2 (с точностью до асимптотически устранимого смещения),
которая используется в ОМНК, т.е.
*ммп = ±(Y - Х0)тЯо’(У - Х0) = —f '
702	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
где опенка сг2 определена формулой (15.91).
3)	Сложность решения системы уравнений относительно оценок вспо-
могательных параметров а = (я^\ ..., ат) (эта система описана третьим
уравнением в системе (15.122), протиражированным для j = 1,2, ...,m)
зависит от принятой формы зависимости элементов матрицы So (или So!)
от этих параметров и от их общего числа т. При экономных и относитель-
но простых способах параметризации матрицы Ео решение этой системы
обычно не представляет трудностей. Что касается участвующих в этой
системе регрессионных остатков е — Y — ХО, то они заменяются соответ-
ствующими «невязками» е = Y — Х0 в режиме обычной (для ОМНК) ите-
рационной процедуры: сначала в качестве 0 в выражение е = Y -ХО под-
ставляется обычная МПК-оценка 0МНК; решают систему относительно а и
_	.(1) -(2)	.(т)
получают первое приближение оценок а ,а а и, соответствен-
но, первое приближение для So = S0(g^\-.. ,а^т^); затем используют
эту матрицу So для получения первого приближения для ОМПК оценок
0Омнк) по ним вычисляют «невязки» е = Y — Х0омнк и т. д. Получаемые,
в конечном счете, таким образом оценки при весьма слабых предполо-
жениях оказываются асимптотически эквивалентными оценками макси-
мального правдоподобия, а следовательно, в достаточно широком классе
случаев, — асимптотически эффективными. Заметим, что описанная вы-
ше итерационная процедура Кохрейна-Оркатта (см. п. 15.8.3) относится
к этому же типу методов оценивания.
15.9.2. Точечный и интервальный прогноз, основанный па
моделях линейной регрессии
Задачи, о которых идет речь в данном пункте, являются главным сти-
мулятором развития и применения разнообразных методов регрессионного
анализа. Потому с них мы и начали изложение материала данной главы
(см. задачи 1 и 2 в п. 15.1.7). Действительно, изучая зависимость между
результирующей (у) и объясняющими (X) переменными, исследователь,
в первую очередь, хочет уметь предсказывать значение у (или функции
регрессии у по X) по заданному значению объясняющей переменной X.
Построение прогноза для значения результирующего показателя з/(А")
или его условного среднего значения f(X) = Е(у | X) по заданным вели-
v ( (0 (2)	(р)\т
чинам объясняющих переменных X = (ж	х'г') основано па
решении задач анализа точности полученного уравнения регрессии /(X)
(см. «об основных задачах анализа точности полученной регрессионной
зависимости», описание этапа 7 в п. 10.6).
Начнем с задачи точечного (т.е. оцениваемого одним числом) про-
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
703
гноза значения результирующего показателя у по заданной величине объ-
ясняющих переменных.
Точечный прогноз значения результирующего показателя в
условиях ОЛММР. Пусть мы располагаем исходными статистиче-
скими данными (Х,У) (сл. (15.4а) (15.46)) и нам известно, что ста-
тистическая связь между у и X —	2\...	)7 может быть
описана регрессионной моделью вида (15.73), т. е. удовлетворяет усло-
виям обобщенной линейной модели множественной регрессии (ОЛММР).
Соответственно известна (или оценена методами, описанными в пре-
дыдущем пункте) ковариационная матрица регрессионных остатков Ег.
Помимо упомянутых исходных данных (Х,У) нам заданы также значе-
ния объясняющих переменных Xn+i = (1,	,...,	т.е. еще одна
(п + 1)-я строка матрицы X, однако соответствующее значение резуль-
тирующего показателя yn+j = y(Xn+i) нам не известно. Известен,
правда, характер ковариационных связей регрессионного остатка е„+1
из уравнения yn+i = Xn+10 4-£п+1 со всеми остальными регрессионными
остатками €^,^2, ..,£п, описываемый вектор-столбцом
— (E(£i£n+i),E(£2Cn+l)>---}E(£n€n+l)) ,
а также то, что Ееп+1 = 0 и Ее2 + | = А2- Требуется построить наи-
лучший (в смысле среднего квадрата ошибки) линейный относительно
У1»У2,--ч2/п и несмещенный прогноз для неизвестного значения уп+\.
Итак, по описанным выше исходным данным мы должны найти такой
вектор-столбец коэффициентов Со =	...,СдП^)Т, который обла-
дал бы следующим свойством:
Е(Уп+1 - С0ТУ)2 = min Е(»„+, - СТУ)2, (15.123)
С*
где минимум берется только но таким векторам-столбцам коэффициентов
г ( (О (2)	(")\т
С = (с , с ,..., с ') , которые дают несмещенные оценки для yn+i, т. е.
они должны удовлетворять условию:
Е(СТУ) = Еу„+1.	(15.124)
Обозначим
Sc(A'„+i) = CTY = СТ(Х© + е)	(15.125)
линейный прогноз для yn+l = y(Xn+i), удовлетворяющий условию несме-
щенности (15.124).
704
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Чтобы получить решение поставленной задачи, выпишем и проанали-
зируем средний квадрат ошибки прогноза (т.е. левую часть соотношения
(15.123))
Ус(Хп+г) — Уп+1 — СТ(Х0 4- е) — А'п+10 - еп+1
= (СтХ-%;+1)0 + (Сте-е„+1)
— С £	^-п+11
(15.126)
так как из условия несмещенности (15.124) следует:
Е(СТУ - уп+1) = (СТХ-Хпт+1
)0 + Е(СТе - en+i) = (СТX - xj+1 )0 = О,
т. е. вектор С должен удовлетворять условию
СТХ - %J+I = 0.
(15.121')
Поэтому, возвращаясь к (15.126), имеем:
E(yc(Xn+i) — Уп+i)
= Е(Сте-е„+1)2
= Е[(Сте - е„+1)(Ст£ - e„+i)T]
= E[(CTeeTC) +4+i - 2С1 ее„+1]
= СТЪ.С + Е(4+1) - 2СТо<п+1).
(15.127)
Далее минимизируем (15.127) при условии (15.124/) по С. С этой
целью выписываем соответствующую функцию Лагранжа 92(A), диффе-
ренцируем ее по С и по Л и приравниваем эти производные к нулю:
у(Л) = СТЕ«С + Д2 - 2Сто’"+’> - (СТХ - х7+1)Л,
(15.128)
гдаЛ = (А(0>,А(,),..„А(₽))т.
Система уравнений
МА) -
ЭЛ р+1’
Мл)
ас
= о
п
имеет вид
(15.129)
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
705
(0(р+1)х(р+1) — матрица размерности (р+ 1) х (р+1), состоящая из пулей).
Решение системы (15.129) относительно компонент вектора С и дает
нам по построению коэффициенты Со для оптимального прогноза:
Со = е;’[i„ -х(хте;1х)“‘хте;,]<7<"+” + ег1х(хте;’х)_,х-п+1.
(15.130)
Таким образом, наилучшим линейным несмещенным прогнозом зна-
чения уп+1 = y(Xn+i) будет
»С.(Хп+1) = СЬТУ = ЛЧ+1(ХТЕ<-’Х)-,ХТЕ.-,У
+ <т1п+,)ТЕ71у - <7*л+1,те71х(хтег|х)_|х' е^’у
= х;+10„мн« + <7<п+,)5^1(У - Х§оив1()
= xJ+iOohh, + а<п+1)Е.-'ё.	(15.131)
В преобразованиях, приведших к соотношению (15.131), мы восполь-
зовались правилом транспонирования правой части выражения (15.130),
формулой (15.78) для 0ОМИК и выражением вектора «невязок» е в виде
у-хёомнк.
Анализируя формулу (15.131), мы видим, что наилучший прогноз
значения у(Х'я+1) определяется оцененным с помощью ОМНК значени-
ем функции регрессии в точке Хп+1 (т.е. величиной А\+10омнк) только в
случае отсутствия корреляции между £п+1 и остальными регрессионными
остатками (из рассмотренных выше моделей этому условию удовлетво-
ряют классическая ЛММР и модель с взаимно некоррелированными, но
гетероскедастичными регрессионными остатками). В этом случае второе
слагаемое в правой части соотношения (15.131) тождественно равно нулю,
так как = (0,0,..., 0)Т.
Посмотрим, какой результат дает общая формула (15.131) в рамках
модели с автокоррелированными остатками.
Модель с автокоррелированными остатками предполагает, что мы
располагаем наблюдениями (Х,У) за п «тактов» времени, так что за-
данные значения объясняющих переменных А\+1 = (1,гя7п • *• >ЖЙ1)Т
интерпретируются как прогнозные (или планируемые) значения предик-
торов в будущем такте времени «п 4- 1».
По условиям модели (15.76z) регрессионные остатки е подчиняются
706
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
авторегрессионной схеме первого порядка, следовательно
так что вектор может быть получен умножением на р последне-
го столбца матрицы Ее, определенной формулой (15.76 ). Но поскольку
= In» го произведение	дает умноженную на р послед-
нюю строку матрицы 1п и, следовательно:
(<7<п+1))тЕ;1г = Рёп.	(is 132)
Возвращаясь к формуле (15.131) и принимая во внимание (15.132),
имеем:	~	_
#(^n+l) — ^^омнк + Р^п-	(15.133)
Строго говоря, использование прогноза (15.133) предполагает апри-
орное знание величины р (напомним, что и оценка 0ОМ||К вычисляется с
использованием этого значения). Однако она может применяться и при
неизвестном значении р, если заменить в ней величины р и 0ОМИК их зна-
чениями, полученными на последней итерации практически реализуемого
ОМНК (см. п. 15.8.3 и 15.9.1).
Интервальный прогноз значения результирующего показа-
теля в условиях нормальной ОЛММР. Условия предыдущей зада-
чи построения точечного прогноза должны быть усилены требованием
— нормальности регрессионных остатков е. Требуется при за-
данной величине доверительной вероятности Р построить основанный
на наилучшем линейном несмещенном точечном прогнозе y(Arn+j) ин-
тервальный прогноз для значения результирующего показателя y(An+j),
т.е. указать такой интервал значений (у^„(А'п+1), j/^x(Xn+i)], кото-
рый с вероятностью, не меньшей Р, накроет неизвестное значение
»(*-+! )•
По существу речь идет об оценке точности точечного прогноза,
а точность определяется средним квадратом (или дисперсией) ошиб-
ки. Средний квадрат ошибки оптимального прогноза сТпрогн(АГп+1) =
Е(ус0(-Хп+1) — 3/(Хп+1))2 получаем, подставив в правую часть соотноше-
ния (15.127) оптимальные значения коэффициентов Со, определенные фор-
мулой (15.130) (из-за громоздкости получающегося при этом выражения
не будем приводить здесь его явный вид).
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
707
Поскольку точечный прогноз ус0(Хп+}) по построению является ли-
нейной функцией от , y2i..., yni а последние в силу нормальности рас-
пределения ^остатков сами подчиняются нормальному закону, то и раз-
ность ус<>(Ап+1) — 1/(А'п+1) является нормально распределенной случай-
ной величиной со средним значением, равным нулю (в силу ^15.124), т.е.
из-за свойства несмещенности прогноза), и с дисперсией о,прогн.(Агп+1),
определяемой соотношениями (15.127) и (15.130). Следовательно, опре-
делив по таблицам квантилей стандартного нормального закона (см.
Приложение 1) квантиль ицр уровня (1 + Р)1Ъ мы можем вычислить
границы искомого интервального прогноза по формулам:
Ут1п(^п4-1) i/CoCA'n+l)	^прогн (Ап-ц)>
Утах (A^n-j-1 ) — УСо(Ап-ц) ^li^.^nporR.(Xn^_ j )i
(15.134)
где J/c0(An+i) вычисляется по формуле (15.131).
Другими словами, можно гарантировать (с заданной вероятностью
Р), что величина исследуемого результирующего показателя у при задан-
ных значениях объясняющих переменных Хп+1 будет заключена в преде
лах интервала [у^п(Хп4ч)> У™х(Ап+1)Ь где концы интервала определя-
ются по формулам (15.134), а участвующая в них величина ус (A’n+i)
по формуле (15.131).
Случай классической линейной модели регрессии. Полученный ре-
зультат весьма нагляден и прост в применении к классической ЛММР.
Действительно, в соответствии с (15.5*) в данном случае имеем:
£« = *21п
A2 = De,t] =А
а‘п+,> = 0л.
Соответственно, с учетом формул (15.130), (15.131) и (15.127), получаем:
Со = Х(ХтХ)-1Хп+11
Ус0 (1) = Ап+1ОМНК,
^poroX^n+i) = ff2[xJ+1(xTx)-‘xn+1 +1].
(15.135)
Применим полученный результат к построению интервального про-
гноза в классической модели парной регрессии (т.е. при р = 1). Ранее
(в и. 15.3.1) мы выписывали конкретный вид матриц X, ХТХ и ХТУ в
708
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
данной схеме. В частности:
Рис. 1Б.Б. Интервальный прогноз для значения зависимой переменной j/(zn+i)
при заданной величине объясняющей переменной хп+1
Подставляя полученное выражение в (15.135) и используя формулу
(15.134), с учетом свойств классической модели имеем: прогнозируемое
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
709
знание y(Xn+i) заключено (с вероятностью Р) между величинами
2
max
л
— #0. мнк
71	/	-\2
где ^о.мяк> ^х.мнк — оценки коэффициентов парной регрессии обычным
методом наименьших квадратов (см. (15.18)), zn+1 — заданное значение
объясняющей переменной, а о2 = De — дисперсия регрессионных остат-
ков в классической модели линейной регрессии.
Рис. 15.5 дает представление о зависимости (в рассмотренной моде-
ли) ширины интервального прогноза от удаленности заданного значения
объясняющей переменной zn+I от ее средней величины х.
* * ♦
Замечание. Условия ОМ НК, в рамках которых описаны про-
цедуры построения точечных и интервальных прогнозов, предполагают
априорное знание ковариационной матрицы остатков Ег. В наших по-
строениях считалась известной даже величина а2 (дисперсия остатков в
КЛММР и числовой параметр в соотношении Ег = (72Е0 — в ОЛММР).
Однако описанные процедуры могут применяться и при неизвестных Ео
2
и а , если заменить в них значения соответствующими оценками, полу-
ченными на последней итерации практически реализуемого ОМ И К (см.
пл. 15.8.3 и 15.9.1). При этом, правда, придется воспользоваться свойством
статистической независимости оценок а2 и 0ОМН|( (см. (15.91) и (15.9/))
и заменить квантили нормального распределения в формулах (15.134) на
соответствующие процентные точки t-распределения с п — р— 1 степенями
свободы.
Интервальные прогнозные оценки значений функции ре-
грессии в заданной точке. В некоторых ситуациях исследователя мо-
жет интересовать прогноз не «индивидуального» значения результиру-
ющего признака у при заданных величинах объясняющих переменных
Xn+i = G>®n+1>--->Z2+1)T» а условного среднего значения f(Xn+l) =
Е(у Xn+i). Так, в примере 10.1 (см. пп. 10.1, 15.6.1 и 15.7.1) вовсе не
надуманным выглядит вопрос об оценке (точечной и интервальной) сред-
них денежных сбережений семей с заданной величиной среднедушевого
дохода Яп+11 а это и есть задача опенки значения функции регрессии при
заданном значении аргумента. И следует отличать ее от предыдущей за
дачи оценки (или прогноза) индивидуального значения результирующей
710
ГЛ. 15 МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
переменной! В данном примере решение последней задачи потребовало
бы построения точечного или интервального прогноза для значения де-
нежных сбережений одной отдельно взятой семьи с уровнем душевого
дохода, равным zn+i.
Ответ на вопрос о наилучшей точечной оценке значения линейной
функции регрессии при заданном значении аргумента дается теоремой
Гаусса-Маркова для классической модели (см. п. 15.3.4) и ее расширением
на случай обобщенной модели (см. теорему Эйткена в п. 15.6.2): наилуч-
шая точечная оценка (наилучший точечный прогноз) определяется значе-
нием эмпирической функции регрессии 7(Xn+i) = Xn-цО при заданном
значении Хп-ы объясняющей переменной (в качестве оценок О использу-
ются МНК-оценки 0МНК в условиях классической ЛММР и ОМ НК-оценки
0ОМНМ в условиях обобщенной ЛММР).
Выведем формулу для интервального прогноза неизвестного значе-
ния линейной функции регрессии f(X) — Л'Т0 при заданном значении
X = А\+1 в условиях обобщенной ЛММР. Для этого вычислим сначала
средний квадрат ошибки наилучшего точечного прогноза:
<z}(A'n+i) = E(%J+1 ©<>„„« - А'„Т+,О)2
= Е[х^п(е«ив. - е)(0оМ.к - 0)тап+1]
= А'п+1Е[(9<,„„)1 — 0)(0омнк - 0) ]Ап4-|
При выводе соотношения (15.137) мы воспользовались возможностью
представить [АП_|_](0ОМ|||С	®)] виде [АП_|.](0ОМПК	€))][Апц.](0Омнк ~
0)]Т, а также видом ковариационной матрицы оценок 0ОМНК (см. формулу
(15.87')).
Итак, наилучшая линейная несмещенная точечная оценка Хп+]0ОЫЖ(
= Xj+i(XTEo *Х) Eq1 У неизвестного значения функции регрессии
Xn\i 0 — это нормально распределенная случайная величина (посколь-
ку она является линейно комбинацией нормально распределенных случай-
ных величин У) со средним значением, равным Л\У+10, и с дисперсией
сгу(Хп+1), определяемой по формуле (15.137). Поэтому, определив по за-
данной величине Р доверительной вероятности из таблиц (см. Приложе-
ние 1) значение (1 + Р)/2 — квантиля U(i+p)/2 стандартного нормального
распределения, мы имеем основания утверждать, что неизвестное значе-
ние функции регрессии /(А”п+]) = Х^+10 с вероятностью Р должно при-
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
711
надлежать интервалу
[-^п+1®омвк — «(1 + Р)/2^у(^п+1)э ^М-I^OMHIC + и(1 + Р)/2&/(^п+1)]> (15-138)
где величина среднеквадратической ошибки oy(Xn+i) оценки функции ре
грессии в точке Хп+] определяется по формуле (15.137).
Рекомендации для классической ЛММР получаются из (15.137)
(15.138) в качестве частного случая Ео = 1п. В частности, для класси-
ческой модели парной регрессии (т.е. при р = 1) нами было подсчитано
(см. (15.136)) выражение Х^|(ХТХ)	необходимое для вычисле-
ния aJ(Xn+i). Используя (15.136), с помощью формулы (15.137) получаем
выражение, для oy(Xn+j) в данном простом случае:
*/(*n+l) = <Г2
Подставляя это выражение в (15.138), получаем интервальный прогноз не-
известного значения функции регрессии в заданной точке zn+1 в условиях
классической линейной модели парной регрессии.
Замечание. Практическая реализация рекомендаций по постро-
ению интервального прогноза для неизвестного значения функции регрес-
сии в заданной точке Хп+i требует определенной модификации процеду-
ры. В частности, априори известные (в рамках условий ОЛММР) значе-
ния о и So заменяются их статистическими оценками сг и Soj получен-
ными на последней итерации практически реализуемого варианта ОМНК
(см. пп. 15.8.3 и 15.9.1). Из свойства статистической независимости полу-
ченных при этом оценок а2 и 0ОМ11К (см. (15.91) и (15.91х)) следует, что
величина
Ап-ц(€^омнк — ®)
йа/а:п+1(хтб(7,х)“,х„+1
подчиняется распределению Стьюдента с п — р — 1 степенями свободы
(или t (п — р — 1 ^распределению). Этот факт позволяет использовать в
качестве интервального прогноза для функции регрессии в точке Xn+i (с
доверительной вероятностью Р) интервал, определяемый соотношением
(15.138), с заменой в выражении (15.137) для <rJ(A^n+i) значений сг2 и Ео
их оценками а2 и Ео, а (1 + Р)/2 — квантиля стандартного нормального
712
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
распределения U(i + p)/2 100(1—Р)/2 — процентной точкой <(i_p)/2(«~P“l)
распределения Стьюдента с п — р — 1 степенями свободы.
15.9.3.	Исследование точности регрессионной модели в
реалистической ситуации
Неточный выбор общего вида функции регрессии, приводящий к на-
рушению базового допущения
е(у I х) = f(X) е № + 0, х(,) +... + e„zM],
на которое существенно опираются все выводы по оцениванию точности
регрессионной модели, и в частности, по их использованию в задачах про-
гноза, может заключаться как в неполном или избыточном представлении
набора объясняющих переменных х 2\..., х р\ так и в искажении са-
мой структуры модели, т. е. в отклонении ее общего вида от линейного.
Влияние неполного или избыточного представления набора объясняющих
переменных на свойства оценок и соответственно на точность статисти-
ческих выводов в регрессионном анализе (при правильном определении
структуры, т.е. линейного характера зависимости между Е(у(Х)) и X)
может быть учтено в рамках строгих математических конструкций (эти
вопросы были рассмотрены в п. 15.5). Наиболее неприятные последствия
влечет второй тип ошибок в спецификации регрессионной модели, а имен-
но, — неправильное, определение параметрического семейства функций,
к которому должна принадлежать искомая функция регрессии. В подоб-
ных ситуациях приходится говорить лишь об аппроксимационных вари-
антах регрессионных моделей. Применительно к построению и исследо-
ванию линейных регрессионных моделей (классической и обобщенной) это
означает, что функцию /а(^>®) = #о + 0\х^ + ... + 0рх^ мы долж-
ны рассматривать лишь как некоторую аппроксимацию неизвестной нам
функции f(X) = Е(у | X). Это мы и называем «реалистической ситу-
ацией» в регрессионном анализе. В подобных ситуациях необходимо ру-
ководствоваться следующими положениями при пос 1 роении прогнозов и
исследовании точности статистических выводов в регрессионном анализе:
1)	при анализе точности аппроксимационных вариантов регрессион-
ных моделей не следует претендовать на построение сколько-нибудь точ-
ных доверительных интервалов ни для неизвестных значений параметров
О (они, как правило, не имеют в данной ситуации самостоятельной со-
держательной интерпретации), ни для функции регрессии /(А') или ре-
зультирующего показателя ly(A') (поскольку, пользуясь аппроксимацией
fa(X), отличающейся по структуре от истинной функции регрессии /(А'),
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
713
мы не можем иметь достоверной априорной информации о вероятностной
природе остатков ё, = yi — fa(Xi)y
2)	имеющуюся выборку наблюдений Вп = {(X], j/[),..., (Хп,уЛ)} це-
лесообразно разбить (одним или несколькими различными способами) на
две непересекающиеся подвыборки объемов гц и п2 (тц + п2 = п): обуча-
ющую на основании наблюдений которой строятся оценки 0^П1^ не-
известных параметров аппроксимационной функции регрессии /а(Х;0),
и экзаменующую (или контрольную} В^, но наблюдениям которой оце-
ниваются основные характеристики точности анализируемой модели (в
первую очередь регрессионные остатки £, = у, — /а(Х^ 0^”*^)). Пусть
мы произвели такое разбиение исходной выборки Вп = (Х,У) на две под-
выборки — обучающую Bnij = (Xj(l),Yj(l)) и экзаменующую ВПъ =
(Xj(2),Yj(2)) к различными способами (т.е. j = 1,2,. ..,fc);
3)	основной (и по существу единственной) характеристикой точности
аппроксимационного варианта линейной регрессионной модели является
оценка д среднеквацратической ошибки аппроксимации ст, вычисляемая
по формуле
1	*
₽ = -к------------Е (у>(2) - X,(2)0fe))T(y#(2) - XJ(2)0<,"’'))
Е - Р - 1 >=|
5=1
(15.139)
при регрессионных остатках е, специфицированных в соответствии с усло-
виями классической модели (т.е. при Ес = ст 7П), или по формуле
1	k
а = -к——— Е (У>(2) - X>(2)0<X’)TSo ' (Xf(2) - Х(2)0<:«2)
Е n2j -р - 1 5=1
5=1
(15.139м)
при регрессионных остатках е, специфицированных в соответствии с усло-
виями обобщенной модели (т.е. при = ст2Х0). В соотношениях (15.139)
и (15.139й) оценки и &омн2 вычислены в соответствии с форму-
лами соответственно (15.28) и (15.78) обычного или обобщенного мето-
дов наименьших квадратов по наблюдениям только обучающей выборки
(соответствующей j-му способу разбиения выборки Вп на обучающую и
экзаменующую). Знание ст позволяет оценить максимально возможную
погрешность аппроксимации неизвестной функции регрессии f(X) (в пре-
делах обследованного диапазона значений X) приблизительно величиной
порядка	а результирующего показателя у(Х) — величиной по-
714
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
рядка ±2(7;
4)	следует проявлять известную сдержанность и осторожность при
использовании аппроксимационных вариантов регрессионных моделей для
решения задач интерполяции и (особенно) экстраполяции, т.е. при вос-
становлении неизвестного значения функции регрессии f(X) или резуль-
тирующего показателя ??(Х) по значению предиктора X, лежащему вне
статистически обследованной области значений объясняющих перемен-
ных.
Поясним подробнее реализацию положений 2) и 3) на примере исполь-
зования широко применяемого метода скользящего экзамена.1 Определим
п разбиений исходной выборки Вп = {(.¥], ),...,(Хп,уп)} на обучаю-
щую (В°6) и экзаменующую (#«*,) следующим образом:
(	= {(^I,3/1 )>•••>(^j-1>36-1)»36+1 )»•••>(^niУп)};
1С’ = {х„у,}, j = i,2,...,n.
Таким образом:	= п — 1 и П2} = 1 для всех j = 1,2, ...,п; j-н
вариант обучающей выборки содержит все наблюдения исходной выборки
Вп кроме одного — (JQ,^); соответственно j й вариант экзаменующей
выборки содержит единственное наблюдение — (Х7,у}). Применение к
такой последовательности обучающих и экзаменующих выборок формул
(15.139) и (15.139") и составляет метод скользящего экзамена оценки точ-
ности статистического вывода
Величина среднеквадратической погрешности <т, подсчитанная с по-
мощью метода скользящего экзамена, в аппроксимационных схемах ре-
грессии оказывается, как правило, существенно больше аналогичной ха-
рактеристики, вычисленной с помощью обычных формул (15.34) и (15.91).
Замечание (по поводу вычислительной реализации метода
скользящего экзамена). На первый взгляд реализация метода скользяще-
го экзамена связана с многократным повторением громоздких вычислений
на ЭВМ. Действительно, процедура предусматривает n-кратное вычи-
сление оценок 0^n,1\o^nia\...,0^ni“\ п2 * *-кратное вычисление выбороч-
ных функций регрессии /а(Х^ 0^n’J^)(i, j — 1,2,...,п) и т.д. Однако не-
посредственный анализ основных формул метода наименьших квадратов
в случае линейного вида аппроксимирующих функций /а(Х;0) = ХТ0
1 Этот метод (в зарубежной литературе он называется <методом складного ножа»
или <jackknife method») является одним из вариантов реализации общего подхода,
впервые предложенного, по-видимому, в связи с задачей устранения смещения в ста-
тистических оценках (см. [Кендалл М.Дж., Стьюарт А., 1973]).
15.9. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
715
позволяет установить полезные соотношения между интересующими нас
характеристиками, подсчитанными по всей выборке Вп, и геми же ха-
рактеристиками, подсчитанными по выборке, в которой пет наблюдения
{Xi, у,)-.
§(»<) = § + Ц-Г*1 е . (Хтх)-1 • х„
1 - <и
где q, = Xi • (ХТХ)’’ X,';
^т§(пн)=?тё+ й.^0.
1 - Qt
ё,(0(п,‘)) =	где ё.(0) = у,-0);
* Qi
£4(ё(я-’) = Е—4ё?(§).
«=1	1=1 U Qi)
Эти соотношения позволяют избежать многократной вычисли тельной
«прогонки» процедур метода наименьших квадратов на различных вари-
антах обучающей выборки за счет пересчета значений 0^П1,\ /(X,; 0^П1'^)
= А',Т0^П°^ и т. д. по соответствующим характеристикам, подсчитанным
по наблюдениям всей выборки Вп.
15.9.4.	Анализ эластичностей с использованием моделей
регрессии
Коэффициенты эластичности являются важным инструментом эко-
номического анализа. Они определяются на базе анализа функциональ-
ных зависимостей, существующих между некоторой интересующей нас
экономической характеристикой z (под z может пониматься, например,
спрос на определенный вид товаров или услуг или объем произведен-
ной продукции), с одной стороны, и набором объясняющих переменных
, и! (цены на рассматриваемый и другие товары, основные
факторы производства) — с другой. Пусть эта зависимость описывается
функцией
1 При самих естественных ограничениях на структуру матрицы X величина д,, несмо-
тря на зависимость от X,-, ведет себя при и —♦ оо (при фиксированной размерности
р + 1 оцениваемого параметра) как п-1; если же и р —► оо, то д, ~ (р + 1)/п.
716
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Коэффициент эластичности результирующего показателя z по
объясняющей переменной формально определяется как логарифмиче-
ская производная z по т.е.
a(inz)
cf(lnu^)	3(lnu^)
Из этого определения нетрудно вывести содержательный смысл коэф-
фициента эластичности. Действительно, анализируя процесс вычисления
_ #(1п z) __ (dz/z)
с?(1пи^)	(du^'/u^)
(Az/z) • 100%
= lim — ,/ ...-------------,
auG)_>0	. 100%
мы видим, что эластичность 9Z/Uo) показателя z по переменной
приблизительно определяет на сколько процентов изменится значение
z при изменении объясняющей переменной на 1%.
Теперь предположим, что зависимость f(u^\..., и^) получена на
v ( (!)	(р)\т
основе функции регрессии у по л = (ж , ...,z ) , построенной по ис-
ходным данным (X,-,у{), i = 1,2,...,п, где переменные у и X связаны
определенными функциональными соотношениями соотвегственно с пере-
менными z и U = (и(,),...,и<р>)Г. Можно ли по коэффициентеам постро-
енной функции регрессии что-либо сказать о значениях эластичностей z
по (у = 1,...,р)?
Рассмотрим две простейшие ситуации:
1)	Переменные X, у связаны с экономическими переменными U и z
логарифмическим преобразованием, т.е.
у — In z и ж^=1п«^\ j=l,2, ...,р.
Тогда оцененная по выборке линейная модель регрессии у по X в терминах
U и z выразится в виде
In Z = 0О + In l/1) + ... + 0р In .
Откуда в соответствии с определением эластичности имеем

C?(lfl z)
д(1пи )
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
717
2)	Переменные X и у, на основании наблюдений над которыми стро-
илась линейная функция регрессии, как раз и есть те экономические ха-
рактеристики, которые нас интересуют, т.е.
z = Е(у | X) и = х^.
Тоща оценка функции регрессии у по А дает нам зависимость
в виде
Z =	+ ... + Gpu^p\
Вычисление эластичности z ио на основе этой зависимости дает:
Э(1п2) (dz/z} dz
zfx" = а(й^) =	=	= 3'~'
Как видим, эта эластичность, в отличие от предыдущего случая, за-
висит от того, при каких конкретных значениях и z она вычисляется.
Однако часто в целях упрощения в этом случае пользуются приближен-
ным соотношением:
, й(>)	- z0)
^г/uO) ~	~	0j
‘	z J у
где значения х — ^х^/п и у = $2”^ yjn — выборочные средние
»=1
величины, соответственно, объясняющей переменной х^ и результирую-
щего показателя у нам известны (они подсчитаны в ходе статистического
анализа рассматриваемой регрессионной модели).
15.10. Линейные модели per рессии со
стохастическими объясняющими
переменными
До сих пор мы изучали линейную модель множественной регрес
сии (ЛММР) в предположении, что объясняющие переменные А' =
, (1) (2)	(р)\т
(хк ,х'	') , и соответственно матрица наблюденных значении
объясняющих переменных X, не являются случайными, стохастичны-
ми по своей природе. Дру1ими словами, значения	.. ,х^ (: =
1,2,...,и) играли роль неслучайных параметров, от которых зависит
закон распределения вероятностей случайной величины у, связанной с
718	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
х^\ ... соотношениями типа (15.2х). В этом соотношении функ-
ция регрессии Е(у | X), строго говоря, должна пониматься не как условное
математическое ожидание случайной величины у (при условии, что зна-
чения стохастических объясняющих переменных зафиксированы на уров-
нях X), а как безусловное математическое ожидание случайной
величины у при значениях параметров (от которых зависит ее
закон распределения вероятностей), равных X.
В ряде ситуаций «неслучайность» объясняющих переменных очевид-
на и обусловлена, например, способом получения исходных статистиче-
ских данных. Так, в примере 10.1 анализируемые семьи были предвари
тельно разбиты на 4 группы, однородные по величине объясняющей пере-
менной х: низкодоходные (х = х® =80 ден. ед.), с доходом ниже среднего
уровня (х = X2 = 120 ден. ед.), среднедоходные (z = z° = 160 ден.ед.) и
высокодоходные (z = z$ = 200 ден.ед.). Конечно, в данном примере объ-
ясняющая переменная играет роль неслучайного параметра х, от значения
которого зависит закон распределения интересующей нас случайной вели-
чины — суммы удельных сбережений в семье у(х). Однако, видоизменив
способ получения исходных статистических данных, а именно извлекая
случайным образом семью из анализируемой генеральной совокупности
семей и фиксируя в каждой такой (»-й) извлеченной семье одновременно
значения двух признаков (х,, у,), мы уже будем иметь дело с наблюдениями
двумерной случайной величины (х.у), так что и объясняющая переменная
х должна интерпретироваться при такой схеме наблюдений как слу-
чайная величина. Соответственно и функция регрессии f(x) = E(j/ | х)
должна пониматься уже в смысле (15.2), т.е. как условное магемати
ческое ожидание величины удельных денежных сбережений в семье при
условии, что значение среднедушевого семейного дохода зафиксировано на
уровне х.
Надо признать, что в практике статистических исследований и эко-
нометрического моделирования очень часто довольно трудно определить,
можно ли считать объясняющие переменные неслучайными. К тому же
существует весьма широкий спектр реальных задач регрессионного ана
лиза, в которых объясняющие переменные имеют явно стохастическую
природу. Помимо схем получения исходных статистических данных, ана-
логичных описанной выше видоизмененной схеме примера 10.1, к таким
задачам относятся все ситуации, в которых значения объясняющих пере-
менных могут измеряться только со случайной ошибкой, а также весьма
распространенные в эконометрических исследованиях задачи, в которых
в качестве объясняющих переменных используются значения случайных
по своей природе результирующих показателей в предыдущие моменты
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
719
времени. Поэтому хотелось бы уметь проводить статистический анализ
моделей регрессии, в которых объясняющие переменные стохастичны по
своей природе. Пам будем удобно разбить описание регрессионного анали-
за линейных моделей со стохастическими объясняющими переменными
на три случая:
•	объясняющие переменные X статистически независимы от регрес-
сионных остатков е и их распределение не зависит от оцениваемых
параметров модели 0 и а;
•	объясняющие переменные X коррелированы с регрессионными ос-
татками е;
•	объясняющие переменные могут быть измерены только со случай-
ными ошибками.
При этом, как и прежде, рассматривается ЛММР вида (обозначения
определены соотношениями (15.4а)~(15.46), (15.7)—(15.12))
Y = Х0 4- е,
(15.140)
где
ранг X = р (с вероятностью единица)1.	(15.141)
Что касается спецификации условий, определяющих природу регрес-
сионных остатков е = (ei,e2,... ,еп)Т, то пока мы их сформулируем в
достаточно общем виде:
Ее — Оп,
= Е(еет) = а2Е0,
(15.142)
(15.143)
где усреднение (операция вычисления математического ожидания Е) про-
изводится в безусловном смысле, т. е. по совместному з.р.в. случайных
величин е и X. При этом, вообще говоря, (п х п)-матрица Eq может зави-
сеть от неизвестных параметров, в том числе и от параметров 0.
15.10.1. Случайные остатки е не зависят от предикторов X
и оцениваемых коэффициентов регрессии 0
Из взаимной независимости е и X следует взаимная независимость е
и X. В этом случае безусловные соотношения (15.142) и (15.143) влекут за
1 Условие (15.141) сопровождается требованием его выполнения с вероятностью еди-
ница, поскольку матрица X в рамках данной постановки задачи формируется из
элементов случайной выборки (« = 1,2,..., п; j = 1, 2,..., р).
720
ГЛ. 15 МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
собой справедливость соответствующих соотношений для условных мате-
матических ожиданий
Е(е | X) = О„,	(15.142')
Е«(Х) = Е(еет | X) = <z2En,	(15.143*)
где матрица Ео не зависит ни от X, ни от 0.
Заметим, что условия (15.142*) и (15.143х) эквивалентны условиям
Е(У | X) = X©,	(15.142")
ЕУ(Х) = Е {(У - Х0)(У - Х0)т | х} = <г2Е0	(15.143")
и что из общих свойств многомерного нормального распределения следует,
в частности, выполнение этих условий в ситуациях, когда вектор анализи-
руемых стохастических переменных (ж^\	..., у) подчинен (р+1)-
мериому нормальному закону (см. [Андерсон Т.], теорема 2.5.1).
Покажем, что к модели, специфицированной соотношениями
(15.140)—(15.141)—(15.142г)-(15.143*), применимы все методы и
результаты, полученные нами в рамках КЛММР (при £0 = 1п) и
ОЛММР (при произвольной симметричной и положительно опре-
деленной матрице Ео). Правда, интерпретация этих результатов при
стохастических регрессорах базируется на понятии условного распре-
деления регрессионных остатков е — (ej, €2,...,£п)Т > в котором в качестве
условия используется заданность (фиксированность) матрицы X наблю-
денных значений объясняющих переменных.
Проведем доказательство возможности распространения формул
МНК и свойств МНК-оценок на случай некоррелированных с регресси-
онными остатками стохастических объясняющих переменных в рамках
условий классической ЛММР. Переход к обобщенной ЛММР аналогичен
тому, как это было сделано при неслучайных предикторах.
В рамках допущений классической ЛММР матрица So в (15.143х) по-
лагается единичной., т.е.
Е«(Х) = <721п.	(15.143*)
Мы будем предполагать также, что существуют следующие пределы
(по вероятности)’.
Е,	(15.144)
Ор+|,	(15.145)
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
721
где (р + 1) X (р+ 1)-матрица S положительно определена (а значит суще-
ствует матрица Е-1).
Заметим, что при интерпретации исходных статистических данных
(Х,У) как случайной выборки из некоторой (р+ 1)-.мерной генеральной
совокупности выполнение условий (15.144) и (15.145) обеспечивается дей-
ствием закона больших чисел (см. п. 4.2). Действительно, в этом случае в
соответствии с определением случайной выборки (см. п. 6.1) наблюдения
Х1,Х2,... ,Хп образуют последовательность независимых одинаково рас-
пределенных р-мерных случайных величин (X, =	.. .,х^)т).
То же самое можно сказать и о последовательности регрессионных остат-
ков £i,£2,••• »^п« Далее, (&,у)-й элемент матрицы (ХТХ)/п выражается
в виде суммы з^п) =	а l-я компонента вектора-столбца
»=1
ХТе/п — в виде суммы соу(ж^\е) = x^Ejn. А следовательно, при
»=1
существовании конечных моментов, скажем, 4-го порядка у случайных ве-
личин х^ (j = 1,2,...,р) и с учетом ранее сделанных предположений о
гомоскедастичности регрессионных остатков , е2,..., £п (см. (15.143*)) и
их некоррелированности с компонентами вектора X закон больших чисел
обеспечивает сходимость по вероятности (при п —» оо):
Wn) “♦	= Е(ж(МжЬ)), kJ = 1,2,... ,р;
cov(z^,e) -» Е(ж^е) = cov(x^,e) = 0, I = 1,2,... ,п.
Итак, рассмотрим МНК-оценку 0 = (ХТХ)“1ХТУ неизвестных пара-
метров 0 модели (15.140)-(15.141)-(15.142r)-(15.143*) и проанализируем
ее статистические свойства. Ее существование при любых выборочных
данных Х,У обеспечивается условием (15.141).
Состоятельность МНК-оценки 0 следует из ее представления в ви-
де
е = (ХтХ)-1Хт(Хе + е) = (ХтХ)_,(ХтХ)е + (ХтХ)-*Хте
(15.146)
В соответствии с условиями (15.144)-(15.145) второе слагаемое пра-
вой части выражения (15.146) стремится по вероятности к нулю при
п-> оо, а следовательно, 0 —> 0 (по вероятности) при п —> оо.
Анализ остальных статистических свойств оценок 0 и <7 2 в
рамках моментов соответствующих условных распределений (т. е. при
722
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
зафиксированных значениях элементов матрицы X), проведенный точно
так же, как это было сделано в п. 15.3.4, дает:
Е(ё | X) = 6	(см.( 15.29) - (15.30));
Sg(X) = Е{ [(§ - е)(ё - в)Т] I X} = <г2(ХТХ)-1	(см.(15.36));
ё(Х) = Y - Х§ = Ze (см.(15.31) - (15.31*));
Е(ё | X) = Оп;
Е*(Х) = Е(ёёТ | X) = E(ZeeTZT | X) = <z2Z;
Е(ётё | X) = <z2tr Z = <z2(n -р-1)	(см.(15.32));
Е(<т2 | X) = а	(см.( 15.34));
Е[ст2(ХТХ)-1 | X] = <72(ХтХ)-1.
Вывод этих соотношений опирается на тот факт, что сомножитель, зави-
сящий от «условия» (т. е. от матрицы X), можно выносить из-под знака
условного математического ожидания.
С помощью известного метода последовательного (повторного) вычи-
сления математического ожидания вида
Е(е,,)¥>((,>?) = Ел {Еч [*’({;’?) I ( = *]}’
1 Нижний индекс у знака математического ожидания Е определяет, по значениям ка-
кой именно случайной величины производится усреднение. Поясним смысл (выве-
дем) упомянутое правило повторного вычисления математического ожидания. Пусть
V’Ui1?) — некоторая функция случайных (вообще говоря, векторных) переменных
(€> п), совместное распределение которых задается функцией ,Ч)(Х, Y). Предпо-
ложим, что существует	ч)- Тогда, учитывая, что функция P(ft,)(XlF)
может быть представлена (см. (2.131)) в виде p((w)(X, Y) = рч(У | С = Х)р((Х),
имеем:
= J f ¥>(Х,У)р,(Г|е = Х)р{(Х)4Х4Г
X У
= J Е,(^(Х;ч) |х)р((Х)ИЛ = Ел-{Е,Р(Х;ч)|х]},
X
что и требовалось доказать.
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
723
легко доказывается и безусловная несмещенность оценок 0 и а3:
Е0 = Ех[Еу(§ | X)] = Ех(0) = О,
Ео2 = Ех[Еу(а2 | X)] = Ех(*2) =
Наконец, точно так же, как при неслучайных предикторах, доказы-
вается условная оптимальность МНК-оценок 0, а именно тот факт, что
среди всех линейных (относительно У) условно несмещенных оценок век-
тора 0 его МНК-оценка обладает «наименьшей ковариационной матри-
цей^ в смысле соотношений (15.38)-(15.39). При этом участвующие в
этих соотношениях моменты должны быть заменены на соответствующие
условные моменты (при условии, что матрица наблюденных значений объ-
ясняющих переменных равна X).
15.10.2. Общим случаи: стохастические предикторц X
коррелированы с регрессионными остатками е.
Метод инструментальных переменных
Из (15.146) видно, что если хотя бы одна из объясняющих переменных
X асимптотически (по п —♦ оо) коррелирует с регрессионными остатками
с, то ХТе/п не стремится (по вероятности) к нулевому вектору (т.е. не
выполняется условие (15.145)) и, следовательно, МНК-оценки 0 уже не
будут состоятельными. При этом всего один ненулевой элемент вектора
lim (ХТе/п) может приводить к несостоятельности всех компонент МНК-
п-»со
оценки 0. Действительно, возвращаясь к (15.146), имеем1:
lim 0 = 0 + lim
п—»оо	п—*оо
lim
п—*оо
Предположим, что в вектор-столбце lim (xJe/n) на l-м месте стоит по-
п—»оо
стоянная = cov(a?^,e) / 0, а на всех остальных местах — нули, и
пусть з = (з , з ,..., з ) — 1-н столбец матрицы Е , где матрица
Е определена соотношением (15.144). Тогда
lim 0
п—»оо
= 0 + Г131
1 Все участвующие в данном пункте пределы (по п —» оо) понимаются в смысле схо-
димости по вероятности, поскольку их обоснование опирается, в конечном счете,
на закон больших чисел (см. п. 4.2).
724
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
и, следовательно, все компоненты вектора О окажутся смещенными и не-
состоятельными оценками соответствующих компонент вектора 0 (за
исключением того редкого частного случая, когда все исходные объяс-
______	ji
няющие переменные ортогональны, так как в этом случае все з , кроме
одного — а11, равны нулю).
Мы видим, что корреляция между объясняющими переменными и ре-
грессионными остатками является серьезным препятствием к использова-
нию обыкновенного метода наименьших квадратов. Поэтому для анализа
моделей такого типа используется альтернативный метод, известный в
литературе как метод инструментальных переменных.
В качестве основного инструмента метода используются вспомога-
тельные (сопутствующие) переменные U =	...,«^)Т, которые
требуется подобрать таким образом, чтобы:
(:) имелась бы принципиальная возможность измерить их значения
на тех же объектах (или в те же «моменты времени» ), на которых (или
в которые) мы располагаем значениями исходных объясняющих перемен-
ных X = (l,^1),.. .,я/ '); следовательно, наряду с п х (р+ 1)-матрицей
значений X мы будем располагать и п х (р+ 1)-матрицей значений U;
(И) переменные U должны быть асимптотически (по п —> оо) некор-
релированы с регрессионными остатками е, т.е.
lim (1иТе) =0р+1;	(15.147)
л—*оо \ п	)
(Ш) перекрестные (смешанные) вторые моменты переменных U и X
в пределе (по п —> оо) не все равны нулю и образуют невырожденную
(положительно определенную) (р+ 1) х (р + 1)-матрицу Есгх, т. е.
lim ( —UTX ] = Есх;	(15.148)
л—»оо \ П	J
(tv) должна существовать положительно определенная матрица
такая, что
lim (-UTU ) = Есу.	(15.149)
n—oo \ П J
Отметим, что если некоторые из исходных объясняющих переменных
X можно считать некоррелированными с регрессионными остатками е, то
их можно использовать для формирования столбцов матрицы U и нахо-
дить дополнительно вспомогательные переменные только для оставшихся
столбцов.
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
725
Найденные в соответствии с условиями (i)-(tv) переменные U на-
зывают инструментальными, а оценки неизвестных параметров О в
модели (15.140) определяются по формуле
ёи = (UTX)"*UTK	(15.150)
В состоятельности оценки можно убедиться, подставив У, выра-
женное соотношением (15.140), в (15.150) и воспользовавшись свойствами
(i)-(w) инструментальных переменных U:
ёц = (итх)~’ит(хе+е) = (итх)"’(итх)е + (итх)_,ите
= e + (UTX)_,UTe.
Следовательно:
1)
(1	\1 X1
-и х lim I -ите
П	J п-+оо \Ц
= в + EtzxOp+i = 6»
2)
Е(©а|Х,и) = е и
Еву = ^x,v{^eu I Х,и)} = Ех,и6 = е,
т.е. оценка Ои является состоятельной, а также условно и безусловно
несмещенной.
Говоря о других статистических свойствах оценки 0^, следует отме-
тить, что она, вообще говоря, уже не является оптимальной. Оценка для
ее условной ковариационной матрицы Egy(X,U) = Е{(0(/—0)(0с7 —0)т |
X, U} может быть вычислена по формуле
Её„ =<7,(UTX)-1(UTU)(XTU)-,1	(15.151)
где
- X®l/)T(r - X®v)-	(15.152)
Анализ правой части (15.151) приводит к выводу, что чем выше кор-
реляция между U и X, тем точнее будут оценки метода инструмен-
тальных переменных 0(/. И наоборот: при слабой коррелированное™ ин-
струментальных переменных U с исходными объясняющими переменны-
ми X среднеквадратические ошибки оценок оказываются чрезмерно боль-
шими, устремляясь в бесконечность при приближении всех ковариаций
726	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
между и к нулевым значениям. Так, например, в случае един-
ственной объясняющей переменной (р = 1) «инструментальная» оценка
коэффициента наклона линии регрессии будет равна (в соответствии с
(15.150)):
Е(«< - «Хи “ У)
в\и =	,	(15-150')
£(и<-в)(х,--х)
1=1
а ее выборочная дисперсия (в соответствии с (15.151)—(15.152))
2
1=1
п
£(«.' - “)(* - ®)
(15.151')
Так что, если и и х слабо взаимно коррелированы, то знаменатель в вы-
ражении для будет близок к нулю и, следовательно, выборочная дис-
персия оценки 0iu окажется чрезмерно большой.
Отсюда следует, что при подборе инструментальных переменных на-
до стараться определить такие переменные U, которые практически не
коррелируют с регрессионными остатками е и одновременно достаточ-
но сильно коррелированы с исходными объясняющими переменными X. В
этом и состоит главная трудность реализации метода инструментальных
переменных (ведь истинное вероятностное распределение X, U и е нена-
блюдаемо и поэтому трудно быть уверенными в том, что подобранные
инструментальные переменные действительно практически некоррелиро-
ваны с £ и одновременно сильно коррелированы с X!).
Проиллюстрируем технику метода инструментальных переменных на
простом примере.
Пример 15.2. С целью оценки эластичностей потребления опреде-
ленного вида товаров (у) по доходу (х) на основании результатов выбороч-
ных обследований домашних хозяйств анализируется линейная регрессия
у по х
у = 0о + &гх + е.
(15.153)
В ходе выборочных обследований семей регистрировались значения
следующих показателей:
Vi — удельные (т. е. приходящиеся на одного члена семьи в «единицу
времени*) расходы на рассматриваемый вид товаров или услуг в
i-й обследованной семье;
1Б.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
727
х* — общие удельные расходы в той же семье (включая статью ^де-
нежные сбережения»)}
z, — объявленный среднедушевой доход в i-й семье (t = 1,2,... ,п).
Специальный статистический и профессиональный (экономический)
анализ позволил принять в качестве рабочих гипотез следующие допуще-
ния:
(а)	ненаблюдаемый истинный среднедушевой доход i-й семьи z, свя-
зан с общими удельными расходами z* соотношением
z,- = Xi
где случайная ошибка имеет нулевое среднее значение (Etf, = 0), не-
коррелирована с z,- (т.е. cov(z,£) = E[(z - Ez)tf] = 0) и с £, (т.е.
cov(tf,£) = E(te) = 0);
(б)	объявленный среднедушевой доход t-й семьи ж? дает заниженную
оценку для zj, некоррелирован ни с регрессионными остатками £,, ни со
случайными ошибками (т. е. cov(z ,£) = cov(z , 6) = 0), но весьма силь-
но коррелирован с истинным доходом ж,- и с общими расходами ж*;
(в)	общие удельные расходы z* практически некоррелированы с ре-
грессионными остатками £,-, т.е. cov(z*,£) = E((z* — Ez*)fi) = 0.
Проведем статистический анализ данной модели. Поскольку в соот-
ветствии с (а) общие расходы z* дают в среднем правильное представле-
ние о величине истинного дохода z, то вставим в (15.153) значения ж,-,
выраженные через наблюдаемые величины ж* и будем анализировать мо-
дель (15.153) на основании данных (ж*, у,), i = 1,2,.. .,n:
Ш = во + «I (4 - «;) + et = 00 + 91х* + е,-,	(15.153')
где £* = £, — Перепишем уравнение (15.153') в терминах центриро-
ванных переменных:
Vi ~ У = 01(®Г - х*) + £*.	(15.153")
Далее можно было бы попытаться воспользоваться МНК-оценками
параметров 0$ и по данным (ж*, &•), в частности (см. (15.18)):
Е(®*- »’)(₽.•-»)
91. мн. = *=4------------•	(15.154)
EW-i*)2
»=1
728
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Однако легко убедиться в том, что объясняющая переменная х* кор-
релирована с регрессионными остатками £* в модели (15.153*) и, следова-
тельно, в соответствии с (15.146) МНК-оценки будут несостоятельными
и обладать асимптотически неустранимым смещением.
Действительно:
cov(x*,£*) = Е((а:* — Ez*)e*) = E((z* - Ех*)(е - 0^))
= cov(z*,£) — Oi cov(z*, 6) = 0i cov(x 4- 6,6) = 0T cov(0, 0)
= O^s > 0,
где 67, = D£ — дисперсия ошибки 6. T. e. x* положительно коррелирова-
на се*.
Вычислим смещение оценки (15.154):

»=1
[сОу(ж*,е) — 0iCOv(z, 6) — 01 Л] .
В выполненных тождественных преобразованиях мы использовали
следующие обозначения:
з2. = £	(ж* — т*)2 — выборочная дисперсия переменной г*;
»=1
п	_
cov(f, rf) = £ 2 (& “ f Х7?»	— выборочная ковариация переменных
»=1
£кт)-,
з6 = cov(0,0) = £	“ О — выборочная дисперсия ошибки 0.
»=1
По закону больших чисел выборочные ковариации и дисперсии стре-
мятся (по вероятности) при п —> оо к соответствующим теоретическим
значениям, так что с учетом рабочих гипотез (а)-(б)-(в) имеем:
lim 01.МВк — 0i
п—*оо
2П=Й Л D* )
DZ/ 1 V Dz + DV
= в1гг™- О5-155)
1 +
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
729
А поскольку ни дисперсии Ш и Dx, ни их отношение нам не известны
(и, как правило, их не удается хорошо оценить по исходным статисти-
ческим данным), то придется обратиться к методу инструментальных
переменных для оценивания параметра Очевидно, в нашем примере
на роль инструментальной переменной вполне подходит переменная х° —-
величина объявленного среднедушевого дохода семьи: во-первых, она не-
коррелирована со случайными остатками £* = Е — ^6 (т.е. х° некоррели-
рована ни с е, ни с 6, см. рабочую гипотезу б)), а во-вторых, достаточно
сильно коррелировала с истинным среднедушевым доходом х и общими
расходами х*.
Поэтому в качестве состоятельной (и весьма эффективной) оценки па-
раметра #1 предлагается использовать оценку метода инструментальных
переменных
Е(*° - ®°)(я - у)
«i.« =	--------------•
-*’)(*? -®°)
»=1
15.10.3. Случайные ошибки в измерении значении
объясняющих переменных
Именно ситуации, в которых объясняющие переменные могут изме-
ряться только с некоторыми случайными ошибками, чаще других приво-
дят к необходимости рассматривать модели регрессии со стохастически-
ми объясняющими переменными и обращаться соответственно к методу
инструментальных переменных (заметим, что и в рассмотренном выше
примере 15.2 природа стохастичности объясняющей переменной и ее кор-
релированности с регрессионными остатками как раз и была обусловле-
на тем, что о значениях объясняющей переменной — истинного дохода х
мы могли судить лишь по соответствующим значениям общих семейных
расходов х*, представляющим собой измеренные с некоторой случайной
ошибкой величины х).
Прежде всего отметим, что случайные ошибки в измерении резуль-
тирующего показателя у (при условии их нулевых средних значений и
некоррелированности с объясняющими переменными X и регрессионны-
ми остатками е) приводят лишь к увеличению остаточной дисперсии (или
дисперсии остатка), но не влияют ни на несмещенность, ни на состоятель-
ность МНК-оценок. Действительно, пусть Ду — вектор-столбец (высоты
в) случайных ошибок измерения анализируемого результирующего пока-
зателя У, так что в качестве его наблюденных значений мы располагаем
730
ГЛ. 16. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
вектор-столбцом
У* = У + Ду.	(15.156)
Подставляя выраженные из (15.156) значения У в модель (15.140), полу-
чаем:
У* = ХО + (е + Ду).	(15.140*)
Анализ (по стандартной схеме, см. п. 15.3) полученных по наблюде-
ниям (Х,У*) МНК-оценок
Т„„, = (ХТХ)-’ХТГ* = (хтх)*’хт(хе + е + Ду), (15.157)
проведенный с учетом упомянутых выше свойств вектора случайных оши-
бок Ду (ЕДу = Оп, Е(Дуе ) = Оп>п, Е(ДуХТ) = ОПэР), подтвержда-
ет, что МНК-оценки (15.157) остаются несмещенными, состоятельными и
оптимальными (в смысле (15.38)-( 15.39)).
Теперь проанализируем, как влияют случайные ошибки в изме-
рении значений объясняющих переменных на МНК-оценки па-
раметров классической ЛММР (15.140). При этом мы будем предпо-
лагать:
Х* = Х + Дх;	(15.158)
ЕДл = Ор+1;	(15.159)
Е(Дхет) = Ор+1,я;	(15.160)
Е(ДхХт) = Ор+1,р+1;	(15.161)
Е(Х’ет) = Ор+),п;	(15.162)
ЕДх = Е(ДхД%).	(15.163)
В соотношениях (15.158)-(15.163) Дх = (Дх ,	•  - > А х ) —
вектор случайных ошибок в измерении объясняющих переменных X =
(1,г^\... ,а/р))Т; Д% — n X (р + 1)-матрица значений ошибок Д^ в изме-
рениях соответственно X* — п х (р+ 1)-матрица искаженных наблю-
денных значении объясняющих переменных, ал = (1, х ,..., х ') —
вектор наблюдаемых (искаженных) значений объясняющих переменных;
соотношения (15.160)—(15-161) свидетельствуют о некоррелированности
ошибок измерения с регрессионными остатками и объясняющими пере-
менными (откуда следует некоррелированность искаженных объясняю-
щих переменных с регрессионными остатками, см. (15.162)); и, наконец,
соотношением (15.163) определена ковариационная матрица вектора оши-
бок измерения Д%.
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ
731
Итак, мы рассматриваем классическую ЛММР со стохастическими
объясняющими переменными (15.140)-(15.142)-(15.143а)-(15.144)-(15.145)
в условиях случайных ошибок в измерении предикторов (15.158)-(15.163).
Подставим в модель (15.140) значения X, выраженные из (15.158) в терми-
нах наблюдаемых (но искаженных) значений объясняющих переменных:
Y = X 0 + (е — Д%0).
(15.140*)
МНК-оценка для 0 из (15.1406) есть
©м». = (Х’ТХ*)“1Х,ТУ = (Х*ТХ‘)_,Х*Т[Х‘0 + е - Дл0]
= 0 +
0
(15.164)
Проанализируем поведение правой части (15.164) при п —► оо.
Пт
п—юо
= Вт ( —(X 4- Дх)Т(Х + Дх))
п—юо	J
= Um (^ХТХ ) + lira (^д£х ) + Um (^ХТД
л—»оо уд у л—юо уп у п—+оо \ п	)
+ Um (-ДуДх ( =Х + Хд_	(15.165)
п—юо \ П	/
(полученный результат опирается на закон больших чисел (З.Б.Ч) и
соотношения (15.144), (15.161) и (15.163)).
2)
Um (-Х*Те) =O.+i	(15.166)
л—юо \ п	У
(полученный результат опирается на З.Б.Ч. и соотношение (15.162)).
3)
= Пт \— ХТДх ) + Пт ( —Д^Дх —	(15.167)
п—юо \ п	У п—юо \ П	У
(полученный результат опирается на З.Б.Ч. и соотношения (15.161)
и (15.163)).
732
ГЛ. 1Б. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Переходя к пределу (по вероятности) при п —> оо в (15.164) и учиты-
вая (15.165)-( 15.167), имеем:
lim б..,,, = е-(£+Хдх)-1ЕДх6 = [1р+1-(Х+£дх)-1Едх]0. (15.168)
л—*оо
Как видим из (15.168), оценка 0МИК в данном случае не являет-
ся ни состоятельной, ни несмещенной (ее асимптотически-неустранимое
смещение оказывается равным, в соответствии с (15.168), величине
-(Е 4- Едх)-1Едх0). Степень смещения оценки определяется истинным
значением параметра, структурой матрицы наблюденных значений объяс-
няющих переменных и ковариационной матрицей ошибок измерения. За-
метим, что в простейшем случае парной регрессии (т. е. при р = 1) форму-
ла (15.168), естественно, повторяет ранее выведенную нами (при анализе
примера 15.2) формулу (15.155).
Как же поступают при анализе подобных моделей? Это зависит от
априорной информации, которой располагает исследователь. Если из пре-
дистории или с помощью специальных экспертных опросов мы можем оце-
нить матрицы Е и Едх, то на основании (15.168) можно построить «под-
правленную МНК-оценкуэ»
= [Ip+1 - (3 + ЗдхГ’Едх]	(15.169)
В остальных случаях, как правило, обращаются к методу инструмен-
тальных переменных.
Следующий пример иллюстрирует возможность привлечения в каче-
стве инструментальных переменных не реальных показателей, а постро-
енных некоторым специальным способом искусственных признаков.
Вернемся к примеру 15.2 (см. модель (15.153)-(15.154)-(15.153,)-
(15.153w)). Предположим, что сведения о значениях объявленного дохода
о
х, утеряны и, следовательно, мы не можем использовать этот признак в
качестве инструментальной переменной. Пусть для определенности число
наблюдений п четно. Итак, для модели (15.153"), записанной в терминах
центрированных переменных:
и
= (й -У>У2-У^.^УП-У) •
Определим матрицу значений инструментальных переменных U следую-
щим образом:
15.10. СТОХАСТИЧЕСКИЕ ОБЪЯСНЯЮЩИЕ ПЕРЕМЕННЫЕ	733
где i-й элемент второй строки матрицы UT равен единице с плюсом или
с минусом в зависимости от того, будет ли соответствующее значение
z* - z* в матрице Хц выше или ниже медианы выборки (zj — x\zq -
— z*). В соответствии с (15.150) оценка по методу инструмен-
тальной переменной окажется равной в данном случае
= (л п/=* — 5г*	— а ’	(15.170)
у и 2 (Яц2 жц1)/	\ 2 (Ун2 Уц1) /
где zU2 и а?ц1 обозначают средние из отклонений значений zj" соответствен-
но вверх и вниз от медианы, а уЦ2 и j/ui — средние из соответствующих
этому разбиению значений у, - у. Из (15.170) получаем:
0<ш = О; eiv=	(15.171)
2?ц2	®ц1
Соотношения (15.170)-(15.171) определяют способ оценивания, впер-
вые предложенный Вальдом.1 Когда значение п нечетно, прежде чем при-
ступить к вычислениям, нужно исключить среднее значение. При весьма
общих предположениях оценка (15.171) состоятельна, однако ее выбороч-
ная дисперсия может оказаться большой. Бартлетт показал, что эффек-
тивность оценки можно повысить, разбив упорядоченные значения объ-
ясняющей переменной на три группы одинакового объема, из которых
первая содержит наименьшие значения z, а третья — наибольшие.2 3 Ис-
ключив центральные п/3 наблюдений, получим оценку для коэффициента
наклона линии регрессии
где Z,-, у, (i =1,3) обозначают средние для наблюдений, попавших в две
крайние группы.
Распространение метода Вальда и Бартлетта на случай двух и бо-
лее объясняющих переменных весьма трудоемко (см., например, статью
Hooper J. W.t Theil ff. The Extension of Wald’s Method of Fitting Straight
Lines to Multiple Regression. Rev. Intern. Statist. Inst., 1958, vol. 26,
pp.37-47).
1 Wald A. The Fitting of Straight Lines if Both Variables are Subject to Error. Ann. Math.
Stat., 1940, vol. 11, pp. 284-300.
3 Bartlett M.S. Fitting a Straight Line when Both Variables are Subject to Error.
Biometrics, 1949, vol. 5, pp. 207-212.
734
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Влияние ошибок измерения объясняющих переменных на
точность прогноза (в рамках КЛММР). Вернемся к задаче по-
строения точечного прогноза для неизвестного значения результирующе-
го показателя p(Xn+i) по заданному значению объясняющей переменной
= (1»®п+1»---»а;п+1)Т (см- П. 15.9.2). Пусть значение Xn+i задает-
ся со случайной ошибкой (что чаще всего и бывает в действительности,
так как в качестве Хп+1 берутся обычно прогнозные или планируемые
значения предикторов), т. е. мы располагаем значениями
Xn+i = Лп+1 + Ах,
где Дх — вектор-столбец ошибок измерений, не зависящий от
£п>€п+1» причем,
ЕДх = Op+i и ЕДх = Е(ДхДх) = ад Vh-
Тогда можно показать, что если мы проводим регрессионный ана-
лиз в рамках КЛММР со стохастическими переменными (т.е. в рамках
модели (15.140)-(15.142z)-(15.143B)-(15.144)-(15.145)), то наилучший ли-
нейный несмещенный прогноз y(Xn+i) неизвестного значения у(Хп+1) за"
дается формулой
у(Хп+1) =	(15.173)
а его средний квадрат ошибки определяется соотношением:
Е(р(Х„+1) - »(Xn+1))2 = а3 [1 + X;+1(XTX)-*X„+1 + d tr(XTX)-‘]
+ <т1Оте.	(15.174)
В соотношении (15.173) оценки 0МНк строятся по наблюдаемой матри-
це X* (т.е. 0МНК = (X* Х*)“ТХ* У). При статистической оценке величи-
ны среднего квадрата ошибки прогноза значения <т2,о-д и 0 заменяются
их статистическими оценками, а ненаблюдаемые вектор Хп+1 и матрица
X — соответственно наблюдаемыми Хп+1 и X*.
Сравнение правой части (15.174) с правой частью ранее выведенной
формулы (15.135) показывает, что ошибки в измерении значений объясня-
ющих переменных, как и следовало ожидать, увеличивают погрешность
прогноза (добавляются два новых положительных слагаемых, пропорци-
ональных дисперсии ошибки измерений <7д).
18.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
735
15.11. Линейные регрессионные модели с
переменной структурой (построение
линейной модели по неоднородным
регрессионным данным)
Линейные регрессионные модели с переменной структурой рассматри-
ваются в ситуациях, когда в ходе сбора исходных статистических дан-
ных Вп = {(Xi,yi),..., (Хп»Уп)} имеет место косвенное воздей-
ствие (во времени и/или пространстве) некоторых качественных факторов
(сопутствующих переменных}, в результате которого происходят скач-
кообразные сдвиги в структуре анализируемых линейных связей (т.е. в
значениях коэффициентов регрессии 0q,0i,...,0p). Попробуем формали-
зовать сказанное.
15.11.1. Проблема неоднородных (в регрессионном смысле)
данных
Пусть функция плотности вероятности анализируемого результиру-
ющего показателя у зависит не только от значений объясняющих пере-
менных (регрессоров) X =	но и от того, на каких
конкретных уровнях (градациях) зафиксированы так называемые сопут-
ствующие, как правило, качественные переменные Z = (л^\ z^, ...,
z ) , определяющие условия, в рамках которых проводится сбор исход-
ных статистических данных Вп = {(%!, уг),(Х2, Уг)> •  •, (Хп,Уп)}« Тогда
эта функция плотности ру(у | X; Z) интерпретируется как условная плот-
ность вероятности случайной величины у в точке у при значениях объяс-
няющих и сопутствующих переменных, зафиксированных соответственно
на уровнях X и Z, — если объясняющие и сопутствующие переменные
случайны по своей природе, — или как безусловная плотность вероятно-
сти случайной величины у в точке у при значениях неслучайных пара-
метров, равных соответственно X и Z, если векторные переменные X и
Z выполняют роль неслучайных параметров, от которых зависит закон
распределения вероятностей результирующей переменной у.
Бели исходить из допущения, что при любых условиях (т. е. при лю-
бых значениях сопутствующих переменных Z) функция регрессии у по
X остается линейной, то естественно предположить, что коэффициенты
этой линейной зависимости (т. е. параметры 0 = (0О,01,..., 0р)Т), вообще
говоря, зависят от Z, т. е.
/(% | z) = Е(» | х, z) = e0(z)+fi(z)x(1) +...+ep(z)xM. (15.175)
736
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Исходные статистические данные называются однородными (в
регрессионном смысле), если все они зарегистрированы при одних и тех
же условиях (т. е. при одних и тех же значениях сопутствующих пере-
менных Z*), т. е.
ё„ = {(x1,n,zt),(xi,^l2,z•),...,(xn,г|n,z•)}.
Если же эти данные объединяют в себе наблюдения, зарегистрированные
при различных условиях (значениях сопутствующих переменных Z), то
они, вообще говоря, могут быть неоднородными. Тогда соответственно:
Вп = {CXijJ/l, ^1)»(^2>У2» Z2),.. • ,(Хп,уп, Zn)J,
причем найдется по меньшей мере пара наблюдений (с номерами и i3)
таких, что / Z,a.
Проблема, которой посвящен данной параграф, состоит в следующем:
как наилучшим (в определенном смысле) образом использовать данные
Вп =	Для статистического анализа моде-
лей типа (15.175)? Казалось бы, ответ тривиален: разбить имеющиеся
в нашем распоряжении исходные статистические данные Вп на заведомо
однородные порции (т.е. на такие подвыборки, внутри каждой из кото-
рых значения сопутствующих переменных Z не меняются при переходе от
одного наблюдения к другому), а затем оценивать значения коэффициен-
тов Oq(Z),(Z),... ,0p(Z) одним из описанных выше методов (выбранным
с учетом природы регрессионных остатков модели) по каждой из таких
выборок отдельно. Тогда для каждого фиксированного сочетания града-
ций Z* сопутствующих переменных Z будет определена своя однородная
подвыборка Bn(z*) объема n(Z*) (n(Z*) < п) и каждой такой подвыборке
соответствует своя оценка искомой функции регрессии (15.175):
/(X I £•) = e0(Z‘) + «1(Z>(,) + ... + e„(Z')xM.	(15.176)
При этом оценки f(X | Z*) и f(X | Z**), полученные по двум различ-
ным однородным подвыборкам, могут, вообще говоря, статистически
значимо отличаться друг от друга, т. е. могут представлять собой эмпи-
рические версии двух различных теоретических функций регрессии.
Пример 15.3. Вернемся к условиям примера 15.2, в котором ста-
вилась задача исследования зависимости удельного потребления опреде-
ленного вида товаров или услуг (у) от величины располагаемого дохода
(ж) на основании результатов выборочных обследований бюджетов домаш-
них хозяйств. Роль сопутствующих переменных Z в данном примере мо-
гут играть как социо-демографо-экономические характеристики, опреде-
ляющие принадлежность семьи к той или иной социально-экономической
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
737
страте (или к тому или иному типу потребительского поведения), так
к индикатор сезонности, определяющий к какому именно времени года
«привязаны» собранные исходные статистические данные. Действитель-
но, предположим, что речь идет о потреблении продуктов питания. То-
гда количество потребляемого продукта у, определяемого «склонностью
к потреблению»(коэффициентом #i) и свободным членом (0о) в уравнении
(15.153), будет существенно различным для беднейших и состоятельных
социально-экономических страт общества: для первых величина может
достигать значений 0,6 ~ 0,7, в то время как для вторых она колеблет-
ся в пределах 0,2 ~ 0,4. Если же речь идет о потреблении, скажем пива
и прохладительных напитков, то даже в рамках одной и той же стра-
ты населения и одинаковых «склонностей к потреблению» количество
потребляемого продукта будет подвержено существенному сезонному ва-
рьированию: очевидно^ в модели регрессии, построенной по летним исход-
ным данным, оценка будет статистически значимо превышать оценку
0О, построенную, например, по зимним исходным данным. В дальнейшем
мы еще вернемся к рассмотрению примера 15.3.
К сожалению, предложенный выше рецепт преодоления проблемы ре-
грессионной неоднородности исходных статистических данных, заключа-
ющийся в необходимости предварительного разбиения имеющейся выбор-
ки Вп на однородные подвыборки	далеко не всегда дает наилуч-
шее решение, а в определенных ситуациях вообще не может привести к
сколько-нибудь удовлетворительному решению. Поясним этот тезис.
а)	Сопутствующие переменные Z ненаблюдаемы либо их зна-
чения не были своевременно зарегистрированы при сборе исход-
ных статистических данных. Обращаясь к примеру 15.3, мы можем
пояснить эту ситуацию следующим образом: при выборочном статисти-
ческом обследовании бюджетов домашних хозяйств не регистрировались
ни содио-демографо-экономические характеристики семей, ни времена го-
да, к которым относились данные Вп = {(хьУ1)»(ж2>0з)»---> (хп>Уп)}«
В этих случаях прямое (т.е. по значениям Z) разбиение выборки Вп на
регрессионно однородные подвыборки невозможно и с этой целью прихо-
дится привлекать подходящие методы кластер-анализа (в том числе ме-
тоды расщепления смесей вероятностных распределений) в объединенном
(р+ 1)-мерном пространстве (а^1\	...,	у). Описание этих методов
см. в п. 12.3 и 12.4 данного учебника.
б)	Сопутствующие переменные Z наблюдаемы (т. е. известны
значения Zi, i = 1,2,...,п)9 но прямое (т. е. по значениям Z) разби-
ение выборки Вп на регрессионно однородные подвыборки приво-
дит к слишком малым под выборкам #n(z-b т.е. к под выборкам
738
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
таких объемов, которых оказывается недостаточно для стати-
стически надежной оценки искомых функций регрессии (15.175).
В этих случаях для оценки искомых функций регрессии привлекают под-
ходы, связанные с введением так называемых фиктивных переменных1
или с использованием аппарата ковариационного анализа (описание ме-
тодов ковариационного анализа читатель найдет, например, в книге [Ай-
вазян С. А., Енюков И. С., Мешалкин Л. Д., 1985, п. 13.5]).
15.11.2. Введение «манекенов» (фиктивных переменных) в
линейную модель регрессии
Прием введения в анализируемую линейную модель регрессии так на-
зываемых фиктивных переменных (или «переменных манекенов»), отра-
жающих влияние на исследуемый результирующий показатель у сопут-
ствующих качественных переменных, используется обычно при работе
с неоднородными (в регрессионном смысле) исходными статистическими
данными в ситуациях, когда изменение значений сопутствующих перемен-
ных влияет на изменение значений только части коэффициентов регрес-
сии у по X. Использование этого приема в подобных ситуациях оказыва-
ется удобным и выгодным по меньшей мере в двух отношениях:
•	статистическая надежность (точность) получаемых при этом оценок
искомых коэффициентов регрессии будет выше той, которую мы бы
имели, оценивая эти коэффициенты отдельно по каждой однородной
выборке]
•	в ходе построения регрессионной модели с фиктивными переменными
мы получаем возможность одновременно проверять гипотезы о нали-
чии или отсутствии статистически значимого влияния сопутствую-
щих переменных на структуру анализируемой модели.
Учет влияния сопутствующих переменных на структуру модели осу-
ществляют, как правило, с помощью аддитивно-линейного введения в пра-
вую часть регрессионного уравнения определенного числа дихотомиче-
ских (бинарных, булевых) переменных, т.е. таких переменных, которые
могут принимать одно из двух возможных значений («нуль» или «едини-
1 В англоязычной литературе по эконометрике эти переменные называются «dummy
variables». В соответствующей русскоязычной литературе исторически «привился»
неудачный, на наш взгляд, перевод — «фиктивные переменные». Гораздо точнее
смысловую нагрузку этого термина передает перевод «переменные-манекены» илк
«манекенные переменные», так как из самой постановки задачи следует, что каждая
из переменных вполне реальна, а слово «dymmy» определяет лишь способ ее
кодирования в искомом уравнении.
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
739
ца»). При этом, если сопутствующая качественная переменная i имеет
kj градаций (т.е. может принимать kj возможных «значений»), то для
отражения ее влияния на структуру искомой регрессионной связи необхо-
димо ввести kj — 1 дихотомических переменных
Конкретная форма, в которой эти переменные будут представлены в ана-
лизируемом уравнении, будет зависеть от наших допущений о характере
влияния сопутствующей переменной на коэффициенты исходной модели
регрессии. Поясним это на примере 15.3.
Пример 15.3 (продолжение). Предположим, что К(РУб) — это
удельное (т.е. в расчете на одного члена семьи и один такт времени)
потребление пива и прохладительных напитков. Тогда векторная сопут-
ствующая качественная переменная Z состоит из двух компонент, т.е.
Z = (г'	) , где z' — номер социально-экономической страты (ти-
па потребительского поведения), к которой принадлежит статистически
обследованное домашнее хозяйство, a z — номер квартала (сезона). Бу-
дем предполагать, что обследуемая совокупность семей подразделяется по
уровню дохода на 3 страты: 1 - «низкодоходные», 2 -«среднедоходные» и
3 - «высокодоходные» (т. е. число градаций к\ качественной переменной
равно трем). Из определения z^ следует, что число ее градаций с2)
равно четырем (1 - зима, 2 - весна, 3 - лето, 4 - осень).
Чтобы учесть влияние сопутствующей переменной на структуру
модели (15.153), введем fcj — 1 = 2 фиктивные переменные:
{1, если t-e наблюдение относилось к домашнему хозяйству,
принадлежащему страте 2 (т. е. к среднедоходным);
О в противном случае;
{1, если t-e наблюдение относилось к домашнему хозяйству,
принадлежащему страте 3 (т. е. к высокодояоднылс);
О в противном случае.
Учет сезонности (т.е. влияния сопутствующей переменной z ) на
структуру модели (15.153) осуществляется введением — 1 = 3 фиктив-
ных переменных:
(2.1)	fl, если t-e наблюдение производилось весной;
*	I 0 в противном случае;
(2.2)	_ ( 1, если t-e наблюдение производилось летом;
•	[0 в противном случае;
(2.э)	_ f 1, если t-e наблюдение производилось осенью;
*	~ 1 0 в противном случае.
740
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Конкретная форма введения этих фиктивных переменных в уравнение
(15.153) зависит, как выше сказано, от допущений о характере влияния
z^1^ и z' на структуру модели. Рассмотрим два варианта таких допуще-
ний.
Вариант 1. Факторы z^ и z^ влияют на количество потребля-
емого продукта, но не влияют на склонность к потреблению (т.е. на
коэффициент 01).
Тогда анализируемое уравнение регрессии следует записать в виде:
У» = 0о+^1а;«4_^о1-г41’1^4"^о2-г<1 2^+0оз^2Л^+0о4-г;2’2^4"^О5-г^2	(15.177)
Далее, в зависимости от допущений о природе регрессионных остат-
ков Ei используем обычный или обобщенный метод наименьших квадратов
для получения оценок 0o,0i>0oi»0O2» 0оз>0о4 и 005- Располагая значениями
этих оценок и их среднеквадратических ошибок, мы можем выписать вид
искомой модели для любых сочетании значении сопутствующих перемен-
ных. А именно:
у, = 0о + 0i Xi 4 Ei — для семей 1-й страты в зимний период;
у, = (0о + 0оз) + &iXi Ei — для семей 1-й страты в весенний период;
yi = (0О + 0О4) 4- 6AXi + Ei — для семей 1-й страты в летний период;
Vi = (0о + 005) + 01 Xi 4 Ei — для семей 1-й страты осенний период;
Vi = (0о + 001) + 01 xi + £i — для семей 2-й страты в зимний период;
У» = (0о + 001 + 0оз) + 0i®t + £» — Для семей 2-й страты в весенний
период;
и т. д.........................................................
yi = (0О + 0О2 4 0О5) 4 0iZj 4- £» — для семей 3-й страты в осенний
период.
Мы видим, что в рамках допущений варианта 1 структурные изме-
нения модели при переходе из одной страты в другую и из одного сезона в
другой выражаются лишь в изменении значений свободного члена регрес-
сионного уравнения и не касаются значения параметра 01, определяющего
♦склонность к потреблению».
Сделаем ряд важных замечаний.
Замечание 1 (о статистической надежности метода оцени-
вания, использующего фиктивные переменные). Надежность статистиче-
ских выводов при построении модели, как мы знаем, существенно зависит
от соотношения объема исходных статистических данных (п) и числа оце-
ниваемых параметров модели (р+ 1). Это, в частности, видно из формул
(11.39) и (11.40) для вычисления оценки основной характеристики про-
гностической силы регрессионной модели (коэффициента детерминации
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ	741
R2) и ее среднеквадратической ошибки (\/DR2): чем больше отношение
п/(р+1), тем точнее соответствующие оценки. Попробуем сравнить вели-
чины отношений п/(р+1) в двух конкурирующих способах оценки модели
(15.153): в способе, использующем аппарат фиктивных переменных, и в
обычном методе, примененном отдельно к каждой из однородных подвы-
борок (предварительно полученных путем разбиения исходных неоднород-
ных данных Вп на однородные по значениям сопутствующих переменных
Z порции). Предположим для определенности, что в примере 15.3 ста-
тистическому обследованию подверглись 12 семей ( по 4 семьи от каждой
страты) в течение 12 тактов времени (затакт времени был выбран месяц).
Тогда вся совокупность исходных статистических данных будет состоять
из 144 наблюдений (п = 144), которые распадаются на 12 однородных (по
«стратам-сезонам») подвыборок, каждая из которых будет содержать 12
наблюдении (т.е. п> = па = ... = п1а = 12). Поэтому при изолированной
оценке параметров 0О и модели (15.153) отдельно по каждой однород-
ной выборке отношение n/(p + 1) составит величину 12/2 = 6, в то время
как при оценке семи параметров модели (15.177) по всем 144 наблюдени-
ям это отношение оказывается равным 144/7=20,57, т.е. почти в 3,5 раза
больше!
Замечание 2 (о выявлении наличия/отсутствия статистиче-
ски значимого влияния сопутствующих переменных на структуру моде-
ли). Предположим, метод наименьших квадратов дал следующий резуль-
тат статистического оценивания модели (15.177):
Vi = 6,8 + 0,025 х + 3,1 zj14) + 5,2 412) + 0,80z|21) 4,7z|2’2)
(2,1)	(0,006)	(1,2)	(2,1)	(1,20)	(1,1)
- 1,2 яр-3)+е<.
(11,8)
Отсюда непосредственно следует, что фиктивные переменные z^2,1^ и z^2*3^
статистически не значимо влияют на у, т. е. удельное потребление пива и
прохладительных напитков в зимние месяцы в среднем не отличается от
удельного потребления этих продуктов в весенние и осенние месяцы для
семей, принадлежащих одним и тем же социально-экономическим стра-
там. Этот пример демонстрирует возможности регрессионной модели с
фиктивными переменными в задаче выявления наличия или отсутствия
статистически значимого влияния сопутствующих переменных на струк-
туру регрессионной связи. В частности, если окажется, что ни одна
из фиктивных переменных 2^*Л\.. .,z^***-r~l\ введенных в модель с це-
лью учета влияния сопутствующей переменной z^\ не влияет на у, то,
следовательно, изменение значений этой сопутствующей переменной не
742
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
влечет за собой неоднородности соответствующих исходных стати-
стических данных.
Замечание 3 (о необходимости избегать «ловушек», связан-
ных с введением фиктивных переменных). Поясним смысл приведенной
выше рекомендации, в соответствии с которой для учета влияния сопут-
ствующей переменной z^J\ имеющей kj градаций, следует вводить kj — 1
фиктивных переменных. Предположим, что в примере 15.3 мы с целью
учета влияния фактора принадлежности семьи к той или иной социально-
экономической страте ввели не 2, а 3 фиктивные переменные, дополнив
определенные выше переменные z^1,1^ и z^1*2^ переменной
{1, если t-e наблюдение относилось к домашнему хозяйству,
принадлежащему низкодоходной страте;
О в противном случае.
Тогда, если сгруппировать имеющиеся п наблюдений таким образом, что
первыми пронумерованы все наблюдений, относящихся к семьям из
среднедоходной страты, затем п2 наблюдений, относящихся к высокодо-
ходной страте, и наконец, п$ наблюдений, относящихся к низкодоходной
страте, то столбцы матрицы наблюдений X, задающие наблюдения по пе-
(1.1) (1.2)	(1.3) -	t
ременным	' и z' , будут представлены в виде (см. табл. 15.4):
Таблица 15.4
1 (номер наблюдения)	4‘”	41Л>	4*л>
1 • • «1	1 • 1	0 0	0 • 0
ni 4-1 • • • 4~ я2	0 • 0	1 • 1	0 • 0
П1 + п2 + 1 • • • п =	4- П2 4- «3	0 • • 0	0 • « 0	1  • 1
4
Просуммировав эти три столбца матрицы X, мы получим столбец, со-
стоящий из одних единиц, т. е. столбец, повторяющий 1-й столбец общей
матрицы X, соответствующий свободному члену анализируемого уравне-
ния (15.177). А это значит, что столбцы матрицы X линейно зависимы,
следовательно, ее ранг меньше числа оцениваемых параметров. Таким
образом, мы оказываемся в условиях строгой мультиколлинеарности:
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
743
матрица ХТ X оказывается вырожденной и метод наименьших квадратов
«не работает» (см. п. 15.4.1). Легко видеть, что к такому же нежела-
тельному результату мы будем приходить всякий раз, когда число вве-
денных в модель фиктивных переменных, отражающих влияние любой из
сопутствующих переменных z^\ будет совпадать с числом градаций этой
переменной.
Вариант 2, Предположим теперь, что фактор принадлежности до-
машнего хозяйства к той или иной социально-экономической страте (г^)
влияет как раз на характеристику склонности к потреблению 01 (фактор
(2)	~
сезонности z , как и прежде, влияет лишь на количество потребляемого
блага). Тогда введенные выше фиктивные переменные следует предста-
вить в анализируемом уравнении регрессии в следующей форме:
Vi = 60+ егХ( +	+ вп(4’Л,х«) + в01г,-’Л)
+ в02422) + 0озгрЛ’ +	(15.177*)
При этом очевидным образом меняются способ и результат комплек-
тования общей (n X 7)-матрицы наблюдений X1 и соответственно резуль-
таты метода наименьших квадратов. Легко видеть, что в данном случае
в качестве оценок «склонности к потреблению» мы получим:
для страты 1:	#i;
для страты 2:	4- £п;
для страты 3:	0\ 4-
Сделанные выше замечания 1,2 и 3 в равной мере относятся и к ре-
зультатам анализа варианта 2.
Учет эффекта взаимодействия сопутствующих перемен-
ных. До сих пор введение фиктивных переменных отражало взаимоне-
зависимое влияние каждой из сопутствующих переменных на структуру
модели. Однако в ряде ситуаций может оказаться существенным влияние,
порожденное взаимодействием различных сопутствующих переменных.
Это взаимодействие также можно отразить в уравнении регрессии вве-
дением в него дополнительных (соответствующим образом построенных)
1 Очевидно, 3-й и 4-й столбцы матрицы X (соответствующие наблюдениям перемен-
ных = *<1Л>х и № = хС1*2)®) будут состоять теперь не из нулей и единиц, как
это было в варианте 1, а из нулей и значений г;, причем, = г,- для тех значений
«, которые соответствуют наблюдениям над среднедоходкьыш семьями (для осталь-
ных t: г j2) = 0), a Zj3) = si для тех значений >, которые соответствуют наблюдениям
над высокодоходными семьями (для остальных «: х^ = 0).
744
ГЛ. 1Б. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
фиктивных переменных. А именно: эффект взаимодействия сопутствую-
щей переменной z^ (представленной в уравнении фиктивными перемен-
ными	и сопутствующей переменной z (предста-
вленной в уравнении фиктивными переменными z	)
может быть учтен введением в анализируемое уравнение дополнительно
N = (А — 1)(Л/ — 1) фиктивных переменных i^, 5^,..., z^N\ образуе-
мых всевозможными попарными произведениями вида z = z^J’^z^l * g\ где
q = 1,2,— 1 и з = 1,2,...,kt — 1 (напомним, что kj и к( — это
числа градаций сопутствующих переменных соответственно z^ и z^).
Конечно, в ходе статистического анализа полученной таким образом ли-
нейной модели множественной регрессии оценки коэффициентов регрессии
при многих (или даже всех) переменных — «взаимодействиях» могут
оказаться статистически не значимо отличающимися от нуля, что будет
означать отсутствие влияния соответствующих взаимодействий на струк-
туру модели. Поясним это на примере.
Пример 15.4. Пусть у (руб.), заработная плата работника; X =
а/3 *\..., ®<р))Т — набор количественных признаков, от которых мо-
жет зависеть величина у (трудовой стаж; оценки, выставленные работ-
нику по ряду профессиональных тестов, и т. и.);1 z^ — сопутствующая
переменная, определяющая уровень образования работника (к\ = 3: «на-
чальное», «среднее» и «высшее») и z ' — сопутствующая переменная,
определяющая пол работника (к2 = 2: «мужской» и «женский»). В соот-
ветствии с приведенными выше рекомендациями вводим фиктивные пере-
менные:
4,л)={11
1о
г 1,
412) = 1
1о
J2-1) _ / h
*	"|0
если t-e наблюдение относится к работнику
со средним образованием;
в противном случае;
если t-e наблюдение относится к работнику
с высшим образованием;
в противном случае;
если t-e наблюдение относится к женщине]
в противном случае;
1 В действительности у и	—это логарифмы соответствующих характеристик, таг
как связь между заработной платой и определяющими ее признаками имеет муль-
типликативный (степенной) характер. Логарифмирование стеленной зависимого!
позволяет перейти к линейной аддитивной модели (см. ниже, п. 15.12).
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
745
4° =4>.«)4я.ц.
Таблица 15.5 отражает правила формирования элементов матрицы
наблюдений X в той ее части, которая относится к «значениям» фиктив-
ных переменных.
Таблица 15.5
Уровень образования	Пол	Фиктивные переменные				
		4’”	413>	431>	4°	42)
Начальное	Мужской	0	0	0	0	0
Начальное	Женский	0	0	1	0	0
Среднее	Мужской	1	0	0	0	0
Среднее	Женский	1	0	1	1	0
Высшее	Мужской	0	1	0	0	0
Высшее	Женский	0	1	1	0	1
Анализируемая линейная модель регрессии в данном случае имеет
вид:
Pi — 0о 4* 01	+ • • • + 0ргр) 4* 001	4- 0о2-гР'2)
+ W” + 0<м41) + 0os4” + е..
(15.178)
Подобный способ представления фиктивных переменных в уравнении ре-
грессии означает, что влияние рассматриваемых сопутствующих перемен-
ных (уровня образования и пола работника) может отразиться лишь на ве-
личине свободного члена уравнения. Это выглядит вполне реалистичным
с учетом того факта, что на самом деле мы рассматриваем линейную ад-
дитивную модель между логарифмами анализируемых переменных, так
что после возвращения к исходным переменным (т.е. после потенциро-
вания уравнения (15.178)) свободный член будет играть роль некоторого
поправочного множителя в степенной функции от	х^2\..., х^р\
Применение МНК с целью получения оценок коэффициентов регрес-
сии уравнения (15.178) позволяет выписать специфицированные (т.е. от-
носящиеся только к однородным по z^ и z^ ситуациям) модели зависи-
мости заработной платы от рассматриваемых объясняющих переменных,
см. табл. 15.6.
746
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Таблица 15.6
№ п/п	Сочетание значений сопутствующих пе- ременных («образо- вание — пол»	Соответствующая модель регрессии
1	«Начальное — мужской»	У, = 0о + 22	» _fc=i
2	«Начальное — женский»	Vi = (00 + 0оз) + 22 0fc®i*^ + £i *=1
3	«Среднее — мужской»	Vi = (00 + 001) + 22 0*®$*) + £i k=l
4	«Среднее — женский»	Vi = (00 + 001 + 003 + 0(m) + 22 0fc®i*^ + £i fc=l
5	«Высшее — мужской»	Vi = (00 + 002) + 22 0fc®j*^ + £i fc=l
6	«Высшее — женский»	Vi = (00 + 002 + 003 + 005) + 22 0*;®^ + £t
Знание оценок 0^ (к = 0,1,..., р), 0oj (j — 1,2,..., 5) и соответственно
их среднеквадратических ошибок (Dfljt)1^2 и (D0OJ)1/f2 позволит, в част-
ности, сделать ряд важных в прикладном плане выводов относительно
характера анализируемой зависимости. Так, например, если величина
0Оз окажется статистически значимо отличающейся от нуля отрицатель-
ной величиной, то придется признать, что существующая система оплаты
труда характеризуется определенным дискриминационным (по отноше-
нию к женскому труду) свойством. Статистически не значимое отличие
от нуля величин 0Q4 и #05 говорило бы о том, что взаимодействие двух
рассматриваемых сопутствующих факторов (уровень образования — пол)
никак не влияет на структуру анализируемой модели,^и т. д.
15.11.3.	Проверка регрессионной однородности двух групп
наблюдений (критерий Г. Чоу)
Предположим, сопутствующая переменная z принимала в процессе
сбора регрессионных наблюдений
В» = {(Х1,й),(Х2,И),.(15.179)
всего два значения: Zj и z2. Тогда общая выборка Вп может быть поделена
1S.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
747
на две подвыборки
....I * = *1}.	(15.1791)
I * = М	(15.179®)
таким образом, что все наблюдения внутри каждой из подвыборок были
произведены при одном и том же значении сопутствующей переменной
z: 1-я подвыборка — при z = и 2-я подвыборка — при z = z2.
Мы хотели бы получить ответ на вопрос: действительно ли подвы-
борки Вп? и В^? неоднородны в регрессионном смысле или переход от
градации z^ к градации в условиях сбора исходных статистических
данных никак не влияет на структуру линейной модели регрессии у по X,
и, следовательно, подвыборки Вп? и Вп? можно объединить и строить ис-
комую функцию регрессии по объединенной (общей) выборке Вп? Иными
словами, мы хотели бы статистически проверить гипотезу
Яо: е(,) = е(2), De(,) = De(2) = а’,
где 0^ = (вд	) и е соответственно коэффициенты регрес-
сии и случайные регрессионные остатки в КЛМНР (15.5), генерирующей
наблюдения выборки Вп? 0 = 1> 2).
Если ni > р 4- 1 и Па > р 4- 1, то можно предложить много способов
проверки гипотезы Hq (например, для принятия гипотезы Hq достаточ-
но проверить тот факт, что точечные оценки 6^ = (^о1^,^1^,... ,0р^)Т,
полученные по 1-й подвыборке, попадают внутрь интервальных оценок
коэффициентов регрессии, построенных по 2-й подвыборке).
Если же объем одной из подвыборок (например, второй) не позволяет
провести сколько-нибудь надежную оценку неизвестных коэффициентов
(это всегда так при Пз < р 4-1), то требуется более изощренная процеду-
ра проверки гипотезы Hq, Кстати, именно в такой ситуации достаточно
часто оказывается статистик-эконометрист, если к уже имеющейся у него
основной выборке Вп? он хочет присоединить полученную позже (или в
другом месте) небольшую дополнительную порцию данных вида , но
не знает, можно ли считать выборки Вп? и Вп? регрессионно однородны-
ми.
Г. Чоу (G.Chow, Econometrica, vol. 28, 1960, pp. 591-605) предло-
жил следующую процедуру для статистической проверки гипотезы Яо в
данном случае.
1)	По основной выборке Вп? строим МНК-оценки 0^ параметров
модели (15.5) и вычисляем вектор невязок = У^ — Х^0^\ а затем и
748
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
сумму квадратов этих невязок	(здесь У^ и Х^ соответственно
(пх х 1)-вектор и »i X (р+ 1)-матрица наблюденных значений анализиру-
емых переменных, соответствующие выборке В„^).
2)	По объединенной (общей) выборке Вп, содержащей в себе все наг
блюдения обеих выборок В^} и строим МНК-оценки О параметров
модели (15.5) и вычисляем вектор невязок е = У — Х0, а затем и сумму
квадратов этих невязок еТе (здесь У и X — соответствен© (n х 1)-вектор
ипх(р+ 1)-матрица наблюденных значений анализируемых переменных,
соответствующие объединенной выборке Вп, п — п\ + п2).
3)	Критическая статистика 7 вычисляется по формуле
_ (еТе-е<1)Те(1))/п2
В предположении справедливости гипотезы Hq статистика 7П|П1
должна «вести себя» как случайная величина, распределенная по за-
кону F(n2,ni — р - 1) (см. п.3.2.3 данного учебника). Поэтому, если
7п,П1 > Fe(n2,ni — р- 1), то гипотезу Hq о регрессионной однородности
выборок В$ и Вп} следует отвергнуть (и принять в противном случае).
Здесь Fa(n2,ni — р — 1) — 100о%-ная точка F-распределения с числами
степеней свободы числителя и знаменателя, равными соответственно п2
и пг — р — 1, a a — заданный уровень значимости критерия.
Замечание. Если объем «дополнительной порции» наблюдений
п2 достаточно велик для того, чтобы можно было иолучить статистически
надежные оценки 0^ неизвестных параметров регрессии и соответству-
ющие невязки	— Х^0^ только по наблюдениям 2-й подвы-
борки, то для проверки гипотезы Hq более предпочтительно использовать
критическую статистику
7ni’“a - (g(i)T2i +2(3)Tg(3))/(„i + „2 _ 2р_ 2)-
В предположении справедливости гипотезы Hq статистика 7щ,п3
должна «вести себя» как случайная величина, распределенная по закону
F(p+ 1,щ + п2 -2р —2). Так что, если 7П1,Па > Fa(p + 1,щ + п2-2р-2),
то гипотезу Но отвергают с уровнем значимости а (и принимают в про-
тивном случае).
15.11. МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ	749
15.11.4.	Построение КЛММР по неоднородным данным
в условиях, когда значения сопутствующих
переменных неизвестны
Бели воздействия сопутствующих качественных факторов на струк-
туру КЛММР скрыты, т.е. их «значения» не поддаются учету и кон-
тролю или не были своевременно (в процессе сбора исходных статисти-
ческих данных) зарегистрированы, то мы можем оказаться в ситуации,
когда собранные исходные статистические данные Вп в действительно-
сти представляют собой смесь нескольких регрессионно однородных под-
выборок, однако выявить эти подвыборки по значениям сопутствующих
переменных мы не можем. Игнорирование этого обстоятельства, выра-
жающееся в построении единой регрессионной зависимости на основании
всех имеющихся в распоряжении эконометриста исходных данных, являет-
ся причиной многих недоразумений и неудач в прикладных экономических
исследованиях. Для подтверждения этого тезиса рассмотрим следующий
пример.
Пример 15.5. В целях исследования зависимости интенсивности
региональных эмиграционных процессов (у%) от уровня (общей продол-
жительности) полученного образования (я: лет) были собраны исходные
статистические данные вида (15.179) за определенный промежуток време-
ни в анализируемом регионе. Так что элемент (ж,, у,) выборки (15.179)
интерпретируется в данном случае следующим образом: z, (лет) — об-
щая продолжительность процесса обучения взрослого (т.е. в возрасте
не менее 25 лет) жителя региона, у, — процент уехавших из региона
за рассматриваемый промежуток времени взрослых жителей среди всех
взрослых жителей с уровнем образования (лет). Несмотря на гипоте-
тическую уверенность специалистов в существовании достаточно тесной
статистической связи между гиу, регрессионный анализ данных (15.179)
свидетельствовал об отсутствии какой бы то ни было зависимости меж-
ду этими переменными. Обратившись к визуальному анализу исходных
статистических данных (их геометрическое изображение представлено на
рис. 15.6), естественно предположить, что наша выборка регрессионно не
однородна и состоит из двух пересекающихся «крестом» подвыборок, ка-
ждая из которых имеет вид линейно вытянутого эллиптического облака
точек-наблюдений. Более внимательный содержательный анализ каждой
из этих подвыборок позволил обнаружить и скрытый (не учтенный в ходе
сбора статистических данных) сопутствующий признак z. Им оказался
тип полученного образования с двумя градациями: 1 — гуманитарное,
2 — естественно-научно-техническое. Разделение всех имеющихся дан-
ных (15.179) на подвыборки (15.179*) и (15.1796) по этой сопутствующей
750
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
переменной и построение искомой регрессионной зависимости отдельно
для каждой из этих подвыборок дают две различные модели достаточно
высокой прогностической силы и противоположной направленности: если
для жителей с гуманитарным образованием (им соответствуют «крести-
ки» на рис. 15.6) интенсивность эмиграции падает (по линейному зако-
ну) с ростом уровня образования, то для жителей с естественно-научно-
техническим образованием (им соответствуют точки на рис. 15.6) мы
наблюдаем обратную картину.
(лет)
Рис. 15.6. Прямые 1, 2 к 3 — графики аппроксимирующих функций регрес-
сии, построенных соответственно по наблюдениям подвыборок: 1
(точки), 2 (крестики) и по объединенной выборке, состоящей из
тех и других наблюдений
Возвращаясь к общей проблеме построения линейной регрессионной
модели по неоднородным данным в условиях, когда значения сопутствую-
щих переменных неизвестны, отметим, что уже при трех объясняющих пе-
ременных (т. е. при р = 3) визуальный анализ геометрической структуры
исходной выборки (15.179) принципиально невозможен. Поэтому с целью
предварительного анализа геометрической стркутуры данных (15.179) и
выделения в них регрессионно однородных подвыборок необходимо исполь-
зовать методы кластер-анализа, в том числе методы расщепления смеси
многомерных распределений вероятностей (см. пп. 12.3, 12.4). Подчерк-
нем, что разбиение исходных данных (15.179) на регрессионно однород-
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ	751
вне подвыборки (кластеры) проводится в объединенном (р + 1)-мерном
пространстве (X, у) (а не в пространстве только объясняющих перемен-
ных X). Причем процесс этот либо предшествует процессу построения
регрессионных моделей, либо проводится в режиме итерационного взаи-
модействия с последним.
15.12. Нелинейные модели регрессии и
линеаризация
До сих пор мы рассматривали лишь линейные модели регрессионной
зависимости у от X = (z^\z^2\...,z^)T. Направления обобщений рас-
сматриваемых моделей касались только смягчения ограничений на при-
роду регрессионных остатков е (см. пп. 15.6-15.8). В то же время многие
важные связи в экономике являются нелинейными. Примеры такого ро-
да регрессионных моделей доставляет нам изучение так называемых про-
изводственных функций (зависимостей, существующих между объемом
произведенной продукции и основными факторами производства — тру-
дом, капиталом и т.п.), функций спроса (зависимостей, существующих
между спросом на какой-либо вид товаров или услуг, с одной стороны,
и доходом и ценами на этот и другие товары — с другой). Ниже мы
подробнее обсудим возможный общий вид этих и других моделей. Как
уже было отмечено выше (см. п. 10.7), этап параметризации регрессион-
ной модели, т.е. выбора параметрического семейства функций {/(X;0)},
в рамках которого производится дальнейший поиск неизвестной функции
регрессии /(X) = Е(у | X), является одновременно наиболее важным и
наименее формализованным и теоретически обоснованным этапом регрес-
сионного анализа. Если же в результате реализации этого этапа эконо-
метрист пришел к выводу, что функция /(Х;0) нелинейна, то далее он
обычно действует следующим образом:
• вначале он пытается подобрать такие преобразования к анализируе-
мым переменным у, z^\..., z^F\ которые позволили бы представить
искомую зависимость в виде линейного соотношения между преобра-
зованными переменными; другими словами, если ...,	— те
самые искомые функции, которые определяют переход к преобра-
зованным переменным, т.е. у = у>о(у), z^ = ^(z^),..., z^ =
<рр{х^), то связь между у и X = (z^\...,z^) может быть пред-
ставлена в виде линейной функции регрессии у по X, а именно:
й = 0о + М?) + • • • + 0p®iF) + е», « = 1,2,..., п;
752
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
эту часть исследования обычно называют процедурок линеариза-
ции модели;
• в случае невозможности линеаризации модели приходится исследо-
вать искомую регрессионную зависимость в терминах исходных пере-
менных, а именно:
Vi =	0) "Ь
если спецификация регрессионных остатков £< соответствует услови-
ям классической модели, то для вычисления МНК-оценок 0МНЖ век-
торного параметра 0 решается оптимизационная задача вида
п
= argmin V (и - /(%<; 0)) ;
О
»=1
о методах преодоления возникающих при этом вычислительных труд-
ностей читатель может узнать, например, из книги [Айвазян С. А.,
Енюков И. С., Мешалкин Л. Д., 4985, гл. 9].
15.12.1.	Некоторые виды нелинейных зависимостей,
поддающиеся непосредственной линеаризации
Итак, пусть у и X = (х^\х^,...,х^)Т — исходные анализируе-
мые переменные (соответственно результирующая и объясняющие), а е —
случайная остаточная компонента, участвующая в записи регрессионной
зависимости, связывающей между собой у и X. За редким исключением
вопросы линеаризации анализируемых связей решаются на основе рассмо-
трения пдрных зависимостей (и графически представляющих их парных
корреляционных полей) типа (xjJ\ У») и (х|^,х|^), t = 1,2,..., п. Поэтому
ниже будут представлены и проанализированы именно пбрные регресси-
онные зависимости, поддающиеся линеаризации.
Зависимости гиперболического типа
1)	Предположим, что анализируемые переменные и случайные регрес-
сионные остатки соответственно х, у и £ связаны между собой статисти-
ческой зависимостью вида
у = о 4- Oi —I- £
X
(О < х < оо).
Соответствующая кривая регрессии /(х; 0) = /(x;0o,0i) =	(см.
рис. 15.7) характеризуется двумя асимптотами (т.е. прямыми, к которым
график функции неограниченно приближается, не достигая их) — гори-
зонтальной (у = 0О) и вертикальной (х = 0). С помощью преобразова-
15.13. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ	753
им объясняющей переменной х = 1/а? (т.е. при переходе к новой объ-
ясняющей переменной х) эта зависимость приводится к линейному виду
у = 0О +	+ £. Соответственно при вычислении МНК-оценок пара-
метров Oq и второй столбец матрицы X должен быть сформирован из
чисел l/xi, 1/®2,
Рис. 15.7. График гиперболической зависимости вида У(х; 0) — So + ,
Рис. 15.8. График гиперболической
= 1/(®о + Й1*): *) случай So
зависимости вида /(х; 0)
< 0; Si > 0 (для х > -0о/01); б)
случай 0о > 0; 01 < 0 (для х > -0о/01)
2)	Пусть переменные х, у и случайные регрессионные остатки € свя-
754
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
заны между собой статистической зависимостью вида
У =
(см. рис. 15.8). Очевидно, мы придем к линейной модели j/ = #о +	+ е,
если в качестве результирующего признака рассмотрим переменную у =
1/у. Следует не забыть только, что при вычислении МНК-оценок 0q и
надо использовать в качестве вектора наблюденных значений зависимой
переменной вектор Y = (1/уь 1/уз?  • •»1/уя)Т«
3)	Если этап параметризации модели регрессии приводит нас к зави-
симости вида	*
х
OqX +	“F* Х£
(см. рис. 15.9), то линеаризацию исследуемой связи обеспечит переход к
новым переменным у = 1/у и х = 1/х. Легко видеть, что эти переменные
будут связаны между собой зависимостью вида
у = во + вгх + е.
Рис. 15.9. График гиперболической зависимости вида /(х;в) =	:
а) случай Йо > 0; 01 < 0 (для х > — Й1/Й0); б) случай Йо >0; Й1 >
0 (для х > -01/Йо)
Очевидно, что матрицы X и У, используемые^ в формулах метода
наименьших квадратов при вычислении оценок #о и , должны формиро-
ваться не из наблюденных значений, соответственно х^ и зд, а из обратных
к ним величин xt = 1/х, и у, = 1/у».
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
755
Заметим, что функции, изображенные на рис. 15.7 (вариант ^> < 0) и
15.9 (вариант б)) используются в определенных ситуациях при построении
так называемых кривых Энгеля^ которые описывают зависимость спроса
на определенный вид товаров или услуг (у) от уровня доходов (z) потреби-
телей. При этом спрос определяется либо абсолютными либо относитель-
ными (по отношению к общим потребительским расходам) расходами на
данный вид товаров или услуг. Функции, изображенные на рис. 15.7 (ва-
риант Oi > 0), 15.8. а) и 15.9. а) могут оказаться полезными при изучении
спроса на товар (у) в зависимости от его цены (z).
Зависимости показательного (экспоненциального) типа
4)	Достаточно широкий клаЛ экономических показателей характери-
зуется приблизительно постоянным темпом относительного прироста
во времени. Этому соответствует следующая форма зависимости этого
показателя (у) от времени (z):
у = еое 1	.
Действительно, если пренебречь влиянием случайной остаточной ком-
поненты е (т.е. положить е = 0, см. рис. 15.10.а)), то непосредственные
расчеты дают:
у = Мое*’*=в1у,
ах
Рис. 115.10. График показательной (экспоненциальной) зависимости вида
/(z;0) = Soe*1®: а) случай > 0; б) случай 6i < 0
так что относительный прирост у за единицу времени (т. е. за единицу
«количества» z) определяется выражением
dy
/у = &\ (в долях у).
756	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Легко видеть, что переход к новой переменной у = In у позволяет
свести исследуемую зависимость к линейному виду:
У = &о + OtX +€,
где 0о = 1п0о- Располагая наблюдениями (si,Vi),(s2>lft),-• • »(®п,Уп) и
формируя вектор-столбец У из In yi,lnya,..., 1пуп, мы с помощью МНК
можем построить оценки 4о и параметров в0 и #i, а затем получить
а
оценку Oq = е для параметра исходного уравнения.
5)	Если в результате параметризации модели мы пришли к необходи-
мости исследовать экпоненциальную статистическую зависимость вида
У = вое
(см. рис. 15.11), то линеаризация искомой зависимости достигается с помо-
щью следующих преобразований переменных: у = In у, х = 1/х. Очевид-
но, в терминах переменных (х,у) исследуемая зависимость будет иметь
вид
У —	4“ г 4"
Pmc.1S.11. График показательной (экспоненциальной) зависимости вида
/(г;©) =	а) случай 0i > 0; б) случай 01 < 0
где = In 00- Соответственно вектор-столбец У и матрица X, участ-
вующие в формулах МНК, определяются по исходным наблюдениям
{(«»»У»)}»=1,2,...,п следующим образом:
У = (lnyblny2,...,lnyn)T;
1
1/«2
Х =
1
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ	757
6)	Весьма гибкую форму параметризации искомой регрессионной за-
висимости представляет один из частных случаев так называемой логи-
стической кривой (см. рис. 15.12)
1
(О < х < оо).
Рис. 15.12. Графжж логжсткческой кривой вида /(к;в) = 1/(0о + lie"').
(Случай 0] > 0)
Кривая У(х; О) имеет две горизонтальные асимптомы у = 0 и у = 1/0о
и «точку перегиба» (z0 — ln(0> /0О), уо = 1/20о)- Линеаризация этой зави-
симости производится с помощью перехода к переменным у = 1/у и х =
е’г. Соответственно, вектор-столбец У и матрица X, участвующие в фор-
мулах МНК, определяются по исходным наблюдениям {(я», У»))»=1,2,...,п
следующим образом:
Y = (1/и> !/».•••> l/ffn)T; X =
1
е-х*
Логистические кривые используются для описания поведения показа-
телей, имеющих определенные «уровни насыщения», например, для опи-
сания зависимости спроса на товар (у) от дохода (х).
Зависимости степенного типа
7)	Широко распространены в практике социально-экономических ис-
следований так называемые степенные зависимости. Степенная модель
множественной регрессии имеет вид
« = е0(х™)'Чг11))'г   -(хм^е‘.
758
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Очевидно, при переходе к переменным у = In у, х^ = Inz^ (j =
1,2,... ,р) можно представить эту зависимость в виде КЛММР, а именно:
у = Go +	+ • • • + Gpx^ + е,
где ₽о = In Go. При оценке параметров до» >»* > участвующие в форму-
лах МНК вектор-столбец УЪ матрица X будут определяться по исходным
наблюдениям z$2\..., z|₽\ У»}|=1,2,...,п следующим образом:
У = (In yi, In уз,... ,1п уп)Т, а (у + 1)-й столбец матрицы X есть (lnzJJ\
In • • • i lnarn ))Т, 3 = 1»2,... ,p (первый столбец матрицы X, как обыч-
но, составлен из одних единиц). Графики зависимостей данного типа для
случая р = 1 представлены на рис. 15.13.
Рис. 16.13. График степенной зависимости вида /(х;О) = дох*1: а) случай
01 > 0; б) случай 01 < 0
Важную роль играют зависимости степенного типа в задачах постро-
ения и анализа производственных функций (у — объем произведенной
продукции,	... — основные факторы производства: труд, капи-
тал и т.д.). Достаточно часто используются степенные зависимости и
при построении и анализе функций спроса (у — спрос на определенный
вид товаров или услуг, — доход потребителя, z<2\a^3\... — цены на
данный и другие виды товаров).
Отметим, что при анализе степенных регрессионных зависимостей
прозрачную содержательную интерпретацию получают коэффициенты
01,02>--•>#₽, а именно: в соответствии с определением коэффициента
эластичности признака у по объясняющей переменной х^ (см. п. 15.9)
величина Gt = din f(X\6)/dlnx^ есть не что иное, как коэффициент
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
759
эластичности анализируемого результирующего показателя по ji-й объяс-
няющей переменной. Можно, кстати, показать, что если эластичность у
по каждой из объясняющих переменных х^ постоянна (т.е. не зависит
от того, при каких именно значениях объясняющих переменных она вычи-
сляется), то у и X могут быть связаны только зависимостью степенного
типа.
Зависимости логарифмического типа
8)	На рис. 15.14 представлены графики зависимостей логарифмиче-
ского типа:
у = 0О + вх In х + £	(0 < х < оо).
Рис. 16.14. Графхк логарифмической зависимости вида /(х; 6) = #о 4-01 In
а) случай 01 > 0; б) случай < 0
Кривые на рисунке 15.14 проходят через точку (1; 0О) и имеют в ка-
честве вертикальной асимптоты ось у (т. е. прямую х = 0). Переход к ли-
нейному виду зависимости осуществляется с помощью логарифмического
преобразования объясняющей переменной: х = In х. Соответственно, вто-
рой столбец матрицы X, участвующей в формулах МНК, будет иметь вид:
(1пж1,1пг2,...,1пгп)Т.
15.12.2.	Подбор линеаризующего преобразования (подход
Бокса-Кокса)
В предыдущем пункте описан набор зависимостей, поддающихся ли-
неаризации с помощью подходящих преобразований анализируемых пере-
менных. Но решение вопроса о том, к какому именно из перечисленных
линеаризуемых типов зависимостей следует отнести наш конкретный слу-
чай, является задачей не простой. Можно, конечно, действовать методом
«проб и ошибок»: последовательно построить по имеющимся у нас ис-
ходным статистическим данным (15.4) каждую из альтернативного набо-
760
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
ра линеаризуемых моделей, а затем выбрать из них наилучшую в смы-
сле какого-то «критерия качества» (например, по максимальному значе-
нию подправленной на несмещенность оценки коэффициента детермина-
ции R , см. формулу (11.40)).
Английские статистики Г. Бокс и Д. Кокс предложили более форма-
лизованную процедуру подбора линеаризующего преобразования1. Их ме-
тод основан на предположении, что искомое преобразование принадлежит
определенному однопараметрическому семейству преобразований вида
Й(А) =	-----> » = 1>2,...,п.	(15.180)
А	А
Точнее их гипотезу можно сформулировать следующим образом: су-
ществует такое вещественное (положительное или отрицательное)
число А*, что один из двух нижеследующих вариантов представления
искомой регрессионной зависимости между наблюдаемыми переменными
у «X = (аг(1),ж(2),...,г<р)):
»(>*) = е0 +	+ • • • + М5Р)(А’) + £-	(15.181)
или
= »о + 61Х^ +    +	+ £i, i=l,2,...,n,	(15.181')
будет удовлетворять всем требованиям нормальной классической ли-
нейной модели множественной регрессии (см. (15.5) и п. 15.3.2).
Замечание 1. Преобразования вида (15.180) применяются обыч-
но к переменным, принимающим только положительные значения. По-
этому, если это не так, то вначале подбирают «сдвиговые» констан-
ты с(0),Д...,сМ, которые обеспечивают положительность значении
у, 4- с(0) и 4- с^ (j = 1,2, ...,р), а затем к сдвинутым значениям
переменных применяют данное преобразование, т.е.:
(15.180')
Замечание 2. Семейство степенных преобразований вида
(15.180) (или (15.180')) весьма широко и гибко. При А = 1 модели (15.181)
1 См.: Box G.E.P. and Сох D.R. An Analysis of Transformations. <Journ. of Royal
Statist. Soc.» , Series B, vol. 26 (1964), pp. 211-243.
15.13. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ	761
и (15.181') являются линейными относительно у, и а?|1\	...,
При А = 0 мы имеем степенную зависимость между у и X вида 7)
(см. п. 15.12.1), поскольку у,(0) = lim (у* — 1)/А = In у, и х^(0) =
liin[(a! ') — 1]/А = 1пз^. При других значениях А уравнения (15.181) и
(15.18/) будут связывать между собой какие-то степени исходных пере-
менных.
Оценка неизвестного значения параметра А. Таким образом,
если исходить из справедливости сформулированной выше гипотезы, под-
бор линеаризующего преобразования анализируемых переменных сводит-
ся к оценке параметра А в формулах (15.180) или (15.180) по имеющимся в
нашем распоряжении исходным статистическим данным (15.4). Эта про-
блема решается с помощью метода максимального правдоподобия. Будем
исходить для определенности из справедливости нашего допущения при-
менительно к представлению искомой модели в форме (15.181'), т.е. в
матричной записи при неизвестном значении параметра А у (А) и X свя-
заны между собой уравнением
У(А) = Х0+е,
(15.181")
где У(А) = (yi(A), йг(А),..., у„(А))т, уДА) = (у* - 1 )/А (мы предполагаем,
что все yi положительны), X — матрица размерности п х (р 4- 1) ранга
р+ 1 из наблюдении значений объясняющих переменных (см. (15.4*)), а
е= (£1,Сз»--->£п)Т — вектор-столбец (0,ста)-нормально распределенных
н взаимнонезависимых регрессионных случайных остатков.
Для составления уравнений метода максимального правдоподобия от-
носительно неизвестных параметров А, 0 и ст3 при заданных значениях У и
X выпишем вначале функцию правдоподобия Ь(уь Уг, • • •»Уп I X; А,0,ст3)
для преобразованных значений у^(А), а затем, воспользовавшись прави-
лом вычисления закона распределения вероятностей случайных величин,
являющихся заданными функциями от известных случайных величин
(см. п.4.4, формулу (4.11)), определим нужную нам функцию правдопо-
добия L(j/i, уз,...,уп | X; А, 0, ст2) для непосредственно наблюденных зна-
чений у,-.
Опираясь на результаты п. 15.3.2 (см. соотношения (15.24)-(15.27)) и
с учетом взаимной независимости и (^о+^г^Ч- • +^0я?^р\<т3)-нормальной
762	ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
распределенности случайных величин у, (i = 1,2,...»п) имеем:
^(51,9а
(15.182)
Таблица 15.7
№ п/п	Смысл понятия или характеристи- ки, используемой в формуле (4.11)	Обозначения формулы (4.11)	Обозначения, при- нятые в данном пункте
1	Размерность анализируемых случайных величин	Р	п
2	Случайная ве- личина, распре- деление которой задано		Г(А) = (й(А),..., Уп(А))Т
3	Случайная ве- личина, распре- деление которой надо вычислить	»/ = (17(1),...,1?(р))	Y = (Уь--,Уп)Т
4	Преобразование, связывающее ис- следуемые случай- ные величины	ч = 9(f)	Y = 9(?(А)), где у, = (Ajf, + 1)1/А
5	Обратное пре- образование, свя- зывающее исследу- емые величины	f = 9~Чч) = (911(’l).--.9n,(’?))	У(А) = g-\Y) = (91 где 9."’(П = 91 = (9? - 1)/А
6	Определитель матрицы преобра- зования (якобиан)	/=Н(ЭД|, t,/ = 1,2,... ,р	J(A) = |det(jt/)|,rne г, = 1 У*	при t = /; 1 0	при i / /, t,/ = 1,2,...,п
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
763
Воспользуемся далее формулой (4.11), позволяющей перейти от из-
вестного распределения (15.182) многомерной случайной величины Y =
• • • ,Уп)Т к распределению случайной величины У, являющейся не-
которой (заданной) функцией от Y, Нижеследующая таблица, устанавли-
вающая соответствие между обозначениями формулы (4.11) и обозначе-
ниями, принятыми в данном пункте, облегчит читателю понимание этого
перехода.
Итак, в соответствии с формулой (4.11) имеем:
Ь(У1,№,I X; А,
_ J(A)
еХ₽
или (в терминах логарифмической функции правдоподобия I = In 1)
1(й, 1*2>  • -»»n I X; А, 0, <r2) = const + In J(A) - - In a1
1 ~ t ~	~	(15-183)
- —^У - Х0)т(У - X0),
2tT
где J(A) = (П yt) >0 (так как все у* > 0), a const — некоторая
t=i
постоянная величина, не зависящая от оцениваемых параметров А, 0 и
а2.
Предположим, что значение параметра А зафиксировано. Тогда диф-
ференцирование (15.183) по 0 и ст3 и приравнивание полученных частных
производных к нулю (см. (15.25)-(15.27)) дает:
0(A) = (ХТХ)-1ХТУ(А),
= |(?(А) - Х©(А))(У(А) — Х0(А)).
(15.184)
(15.185)
Для того, чтобы подобрать теперь оптимальное значение параметра
А, вернемся к соотношению (15.183), подставив в него оптимальные вы-
ражения (15.184) и (15.185) соответственно для 0(A) и <т3(А). Обозначим
полученное при этом значение I с помощью	Итак:
п
Uax(A) = ЦУь- -,1/n I X;A,?,ff3) = const + (А - 1)	- £ 1па3(А)
1=1
(15.186)
764	ГЛ. 15. МЕТОДЫ И ДОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
(при выводе (15.186) использован тот факт, что при оптимальных выра-
жениях для 0(A) и о2(А) последний член в правой части (15.183) равен
п/2, т. е. не зависит от А).
Далее анализируется функция /т*х(А) и отыскивается такое значе-
ние А*, при котором /щах(А*) = max/roax(A). С этой целью определяется
априорный диапазон (ATOin,Amax) возможных значений А (обычно доста-
точно рассмотреть в качестве области возможных значений А отрезок от
Дт;п = — 1 до Атах = 2), на этом диапазоне выбирается сетка («решето»)
значений А^ = Amin + t(Amax - Ат1п)/Л, t = 0,1,..., N и для каждого тако-
го значения А,- последовательно вычисляются 0(А,), о,3(Аа) и /тах(А»). То
значение А*, при котором
^швх(А ) = шах n*x( kt)>
А—Ао»А1 f«»«tA дг
и будет определять искомое линеаризующее преобразование (15.180).
Оценки А*, 0(А*) и ст2(А*) являются оценками метода максимального
правдоподобия, а процедуру их поиска часто называют «решетчатой*.
Замечание 3. Оценка параметра А в случае, если преобразова-
ния (15.180) применяются одновременно к результирующей и к объясняю-
щим переменным, производится тем же способом с единственным видо-
изменением процедуры: в формулах (15.181”), (15.192) ~ (15.186) матрицу
X следует заменить на матрицу Х(А) наблюденных значений преобразо-
ванных объясняющих переменных.
Пример 15.6 (заимствован из [А. Зельнер, с. 182-184]). Изложен-
ный выше подход к подбору линеаризующего преобразования с использо-
ванием метода максимального правдоподобия был применен в приложении
к анализу функции спроса на деньги. Результаты предварительного ана-
лиза показали, что функция спроса на деньги может быть записана в виде
= «о + «I---------+ 4г----т-----+в<, » =	(15.187)
А	А	А
где индекс t обозначает, что значение переменной относится к году i,
yi — денежная наличность, включая текущие и срочные депозиты (де-
флятированные индексом цен), — измеренный доход (дефлятирован-
ный индексом цен), — средняя норма процента по коммерческим
бумагам и с,- — остаточная случайная компонента, удовлетворяющая
всем требованиям нормальной КЛММР (исходные статистические дан-
ные (®|1\®<2\ув) представляют собой годичные наблюдения по экономике
США за 1869-1963 гг., причем i = 1 соответствует 1869 году, i = 95 соот-
ветствует 1963 году, а общее число наблюдений п = 95).
15.12. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ И ЛИНЕАРИЗАЦИЯ
765
При реализации «решетчатой» процедуры был определен диапазон
возможных значений А от Amln = -0,90 до Атак = 1,30 и «шаг»,равный
Д = (\nai - ^mjn)/y = 2,20/22 = 0,1. Затем для каждого значения Ау =
-0,90 + j • 0,1 (j = 0,1,.. .22) были подсчитаны:
?(А,) = (й(АД........Йп(А,)), где Й(А,) = Ц-^-
лз
Х(А>)=
^’’(Aj)
4”(Aj)
#’(А>)
где
а также значения О(Ау) и ^(Ау), соответственно, по формулам (15.184)
и (15.185) с заменой матрицы X матрицей Х(А); и, наконец, величина
п	2
^max(^j) = (Ay— 1) £ In у, — J In d (Ay) по формуле (15.186) (с исключением
»=i
константы).
График функции /max(A) изображен на рис. 15.15. Он позволяет вы-
числить А* « 0,20, т.е. такое значение А, при котором функция /т*х(А)
достигает своего максимума. Стандартный регрессионный анализ регрес-
сии у(0,2) по ж^\о^) и ж^2\о,2) дает:
Й(0,2) = - 1,055 + 1,112	- 0,097 £<2)(0,2) + е.; Я*’ = 0,72
(0.239)	(0,016)	(0,016)
(напомним, что в скобках под значениями оценок коэффициентов регрес-
сии 0О, 01 и указаны величины среднеквадратических ошибок этих оце-
нок).
Следовательно, отправляясь от (15.187) (при А = 0,20), можно по-
казать, что функция регрессии спроса на деньги (у) по доходу (г^1^) и
средней норме процента (ж^2^) в исходных переменных будет иметь вид:
Е(у|г(1),/2)) = (о,226 + 1,112^^-0,097^^) .	(15.188)
766
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Рис. 1Б.1Б. «Решето» значения логарифмической функции правдоподобия
(без учета величины константы)
Заметим, что близость к нулю оптимального значения А (А* = 0,2) го-
ворит о том, что и «логарифмический» вариант функции спроса на деньги
(т. е. переход к переменным у = In у, яг — In яг 'иг ' = In яг ') находит-
ся в приближенном согласии с имеющимися выборочными данными. Так
что наряду с функцией (15.188) можно было бы рассчитать и конкуриру-
ющую функцию регрессии вида
Е(у | х(1),г(2)) = e0(xm),\xW)e\
15.13. Дихотомические (бинарные)
результирующие показатели и
связанные с ними логит- и пробит-
модели
Представим себе, что результирующий показатель у, «поведение» ко-
торого существенно зависит от количественных объясняющих перемен-
15.13. ДИХОТОМИЧЕСКИЕ РЕЗУЛЬТИРУЮЩИЕ ПОКАЗАТЕЛИ
767
v	(1)	(2)	(р)\Т	Ч	У
них л = (1, ж' аг ,..., аг ’) , является качественной переменной, опре-
деляющей одно из двух возможных состояний характеризуемого ею объ-
екта. Так, например,объясняющие переменные X, могут описывать раз-
личные социально-демографо-экономические характеристики х-го индиви-
дума (его доход, возраст, стаж работы и т. п.), а результирующему пока-
зателю yi приписывается значение единица, если х-й индивидум оказался
безработным в обследуемом периоде времени, и нуль — в противном слу-
чае.
В подобных ситуациях вектор У = (У1,Уз,--.,уп)Т исходных стати-
стических данных зависимой переменной будет содержать только дихото-
мические (бинарные) признаки, т.е. его компоненты у, могут принимать
только два значения: «О» или «1». Можно ли построить линейную ре-
грессионную модель, описывающую зависимость у от X в данном случае?
Очевидно, непосредственное распространение описанной в предыду-
щих пунктах этой главы методики построения КЛММР или ОЛММР,
вряд ли, пригодно: неясно, как интерпретировать в этом случае регресси-
онные значения 0ТХ, измеренные в непрерывной количественной шкале.
Поэтому для исследования статистической связи между у и X строят
некоторую специальную регрессионную модель зависимости вероятности
Р{у = 1 | X} от линейной формы 0ТХ. Но описывать вероятность не-
посредственно линейной функцией 0ТХ, по-видимому, нецелесообразно,
так как в этом случае значения предсказанной (вычисленной по модели)
вероятности могут быть как отрицательными, так и превосходящими еди-
ницу. Вместо этого для моделирования значений Р{у = 1 | X) подбирают
функции, область значений которых определяется отрезком [0,1), а линей-
ная форма 0ТХ играет роль аргумента этой функции, т.е.
Р{у = 1 I X} = Г(втХ),	(15.189)
причем функции F(z) должны удовлетворять следующим требованием:
(а)
(б)
(в)
(г)
F(z) монотонно возрастает по z\
0 F(z) 1;
F(z) —* 1 при z —> оо;
F(z) —> 0 при z —> 0.
(15.190)
График одной из функций данного вида приведен на рис. 15.16.
Модели типа (15.189) при ограничениях (15.190) называют обычно
моделями бинарного выбора. Наиболее распространенными моделями би-
нарного выбора являются так называемые логит- и пробит-модели.
768
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
Логжт-модель. Модель типа (15-189)—(15.190) называется логит-
моделью, если в качестве F(y) рассматривается логистическая функция,
Рис. 1Б.16. График функции F(©TX), используемой в модели бинарного
выбора
Нетрудно проверить, что эта функция удовлетворяет условиям (15.190).
Непосредственной проверкой можно убедиться также, что эта функция
симметрична относительно точки вТХ = 0, т.е. A(—z) = 1 — A(z), где
А(*) =
1 + е”
(15.191)
Пробит-модель. Модель типа (15.189)-(15.190) называется пробит-
моделью, если в качестве F(z) рассматривается стандартная нормальна!
вероятностная функция распределения Ф(г), т.е.
Р{п = 11 xj = Ф(етй).
(15.189е;
где Ф(г) =
— ПО
15.13. ДИХОТОМИЧЕСКИЕ РЕЗУЛЬТИРУЮЩИЕ ПОКАЗАТЕЛИ
769
Так же, как и функция A(z), нормальная вероятностная функция рас-
пределения Ф(з) удовлетворяет всем условиям (15.19) и является симме-
тричной относительно z = 0 (т.е. Ф(—z) = 1 — Ф(г)).
Оценивание параметров в логит- и пробит-моделях. Опишем
здесь лишь случай «повторяющихся* (или группированных) исходных
статистических данных, т. е. данных вида
У11»У12,---»!/1п1; АГц = Х12 = ... = Х1п, = Xi\
У21 з У22 , • •  »У2п2 > 21	-^22 “ • • •	2п2	^21	(jg 192)
2/741» J/N2, • • •» VNtin »	= XN2 = ... = XNn„ = Xn.
Это соответствует ситуации, когда мы имеем по несколько наблюдений
зависимой переменной у при одном и том же значении объясняющей пере-
менной X (либо дихотомические наблюдения уд, J/J2,.. •,Vjn, произведены
при значениях объясняющих переменных, не выходящих за пределы j-ro
интервала группирования).
В этом случае от наблюдений (15.192) мы можем перейти к наблюде-
ниям вида
&»*>), J = 1,2,...,7V,	(15.192')
пз
где pj = 53 yjilnj — относительная частота появления «единиц» при
i=i
значениях объясняющих переменных, равных Xj.
Мы знаем (см. теорему Бернулли, формулу (4.6)), что относительная
частота pj связана с истинным значением вероятности Fj = F(0TX;)
соотношением
Pj = Fj^eh	(15.193)
где Efj = 0 и Dej = Fj(l — Fj)/n3.
Поэтому (15.193) можно рассматривать как нелинейную модель ре-
грессии с гетероскедастичными остатками. Роль функции регрессии
играет функция А(0ТХ) в логит-модели и функция Ф(0ТХ) в пробит-
ью дели. Следовательно, чтобы оценить параметр 0, например, в логит-
ьюдели, требуется реализовать итерационную вычислительную процедуру
поиска такого значения 0ОМНК» которое минимизирует взвешенную сумму
квадратов
N
£ [л(вт^)(1 - л(етху))]-' - A(eTXj)]2, (15.194)
J=1
770
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
где функция A(z) определена соотношением (15.191).
С этой целью на первой итерации определяют оценку 0^ по обычно-
му (а не взвешенному) методу наименьших квадратов, т. е. находят такое
0^\ при котором
Затем подставляют найденное значение ( в выражение «весов»
[A(OTXj) (1 — A(0TXj))]~1 в формуле (15.194) и находят следующие при-
ближение 0(3> для 6, минимизируя (15.194), и т.д.
Аналогичная процедура оценивания параметров О в пробит-ъмщш
производится точно так же с заменой функции A(z) на функцию Ф(х),
определенную в (15.1896).
Можно, однако, несколько упростить эту процедуру оценивания, при-
менив к обеим частям (15.193) преобразование F”1 и разложив получен-
ный результат в ряд Тейлора в окрестности точки £ = 0 (ограничившись
при этом членом линейного порядка):
Г"*(й) = F~l(F(6TX,) + е,) я F~l (F(0TX;))
(15.195)
+ dFj £i'
M	«
Ho f-’(F(eT x,)) = eTx„ 
dF~'(F)j) _	1	1	1	_ 1
dFj ~ dF(Fj)/dFj ~ f(Fj) - f^xs) ~ fi’
где fj = /(0TXj) — значение функции плотности з.р.в. F в точке 0ТXj.
Поэтому, возвращаясь к (15.195), имеем:
Уз “	Xj + £j,
(15.195')
где yj = F 1(pJ) — квантиль уровня pj функции распределения F, е,- =
ej/fj, причем Её> = 0 и Dej = F,(l - F,)/n>/’.
Таким образом, задача оценки параметра 0 в логит- и пробит-
моделях сводится к анализу линейной функции регрессии (15.195*) с гете-
поскедастичными остатками £j. При этом в качестве компонент вектора
15.13. ДИХОТОМИЧЕСКИЕ РЕЗУЛЬТИРУЮЩИЕ ПОКАЗАТЕЛИ
771
У = (У1 » , • • • 9 l/2v)T наблюденных значении зависимой переменной будут
использоваться:
•	в логит-модели: yj = 1п[р,-/(1 — pj)], так как непосредственно прове-
ряется, что именно у, является решением уравнения е*/(1 + е*) = Pj
относительно г, т. е. тот факт, что у; — квантиль уровня pj распре-
деления A(z);
•	в пробит-модели: у} — табличное значение квантиля уровня pj стан-
дартного нормального распределения.
Как известно (см. пп. 15.6.1 и 15.7), оценка параметров линейной ре-
грессионной модели с гетероскедастичными остатками производится с
помощью взвешенного МНК, в котором в качестве весов Wj используют-
ся величины, обратные Dcj. Соответственно для оценки параметров 0 в
мгит-модели мы должны решить оптимизационную задачу вида
min,
(15.196)
где = Hj-A(OTXj)(l - A(0TX)).
Данное выражение для весов получено с учетом справедливости
непосредственно проверяемого тождества:
1 _	\	_ "jAjU ~aj)
De,	Л(етХ,)(1 - Л(етХ,)) Л,(1-Л,-)
= п,Л,-(1 — Л,), где Л,- = Л(0тХ,).
Оценка параметров 0 в пробит-модели сводится к решению оптими-
зационной задачи вида
52	- ®т^)’ -* ™п>
j=i
(15.196')
где yj — табличные значения квантилей уровня pj стандартного нормаль-
ного распределения, «веса» = nJ-y>2(0TXJ)/$(0TXJ)(l - Ф(0ТХ?)),
a(/?(z) иФ(г) — значения функций соответственно плотности и распреде-
ления стандартного нормального закона в точке z.
Решение оптимизационных задач (15.196) и (15.196') осложнено тем
обстоятельством, что «веса» w^(0) и w^(0) зависят от оцениваемого
772
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
параметра 0. Однако эти вычислительные трудности обходятся с помо-
щью стандартной итерационной процедуры: на первом шаге подсчиты-
ваются значения 0^\ являющиеся решением задачи (15.196) (или задачи
(15.196*)) при Wj = 1. Полученные значения 0* используются для под-
счета весов wj^©^) (или wjn\0^)), после чего анализируемые опти-
мизационные задачи решаются уже с учетом этих весов. В результате
получают значения 0' ' и т. д.
Более подробное освещение регрессионных моделей бинарного выбора
читатель может найти, например, в книге [Greene W., Ch. 21].
ВЫВОДЫ
1.	Методы и модели регрессионного анализа занимают централь-
ное место во всем математико-статистическом инструментарии экономе-
трики. Постулируя возможность восстановления (с некоторой случай-
ной ошибкой £) значения анализируемого результирующего показате-
ля у по заданным значениям так называемых объясняющих переменных
X = (я^1),^2),.. .,а/р))Т, эконометрист по-существу рассматривает мо-
дель вида
у = /(X) + е.
Основная цель регрессионного анализа заключается в том, чтобы
на базе имеющихся наблюдений анализируемых переменных {(жр\ж^\
...,&)}«=!,2,...,п построить для заданных значений объясняющих пе-
v ' 7 (1) (2) (р)чТ
ременных Хо = (жд , Zq ,...уХц) , — наилучшие в определенном смы-
сле точечные и интервальные оценки для неизвестных значений /(Хо) и
УИо)-
2.	Следуя от простого к сложному, эконометрист рассматривает в
первую очередь линейные модели множественной регрессии (ЛММР),
т.е. модели, в которых функция регрессии /(X) представима в виде
/(Х) = в0 + М(,) + -.+«р®('’)-
В зависимости от принятой в модели спецификации случайных оши-
бок (регрессионных остатков) £ ЛММР называется классической (при
этом регрессионные остатки = у,- — /(X,), i = 1,2,...,п, полагают-
ся взаимнонекоррелированными и гомоскедастичными), или обобщенной
(при отказе хотя бы одного из вышеупомянутых свойств). Если в допол-
нение к упомянутым свойствам регрессионных остатков £, классической
выводы
773
ЛММР постулируется их нормальность, то ЛММР называется нормаль-
ной классической.
3.	В рамках классической ЛММР обычный метод наименьших ква-
дратов (МНК) позволяет получить состоятельные, несмещенные и в
определенном смысле наиболее эффективные оценки для неизвестных па-
раметров 0 = (0o,0i,.. • ,0Р)Т функции регрессии. Если исследуется обоб-
щенная ЛММР, то наилучшим способом оценивания неизвестных параме-
тров является обобщенный метод наименьших квадратов (ОМНК), в фор-
мулах которого участвует ковариационная матрица регрессионных остат-
ков Правда, и обычные МНК-оценки остаются состоятельными и не-
смещенными для регрессионных коэффициентов обобщенной ЛММР, од-
нако они утрачивают при этом свойство наибольшей эффективности.
4.	В большинстве ситуаций практики эконометрического моделирова-
ния ковариационная матрица регрессионных остатков Ее не известна ис-
следователю заранее, а следовательно, он не имеет прямой возможности
воспользоваться формулами ОМНК (в которых эта матрица присутству-
ет). Поэтому существует специальная итерационная процедура (называ-
емая практически реализуемым ОМНК), позволяющая получать, тем не
менее, именно ОМНК-оценки неизвестных параметров 0. Главная идея,
на которой основан практически реализуемый ОМНК, заключается в сле-
дующем: по исходным наблюдениям {(ж^,^2^,..сна-
чала строятся обычные МНК-оценки 0МВГ = (0омнк>0мвк> • • • »0р.мнк)Т
раметров 0; затем вычисляются «невязки» (первое приближение) .	=
Vt ~ 0о.мнк ~ 01.мнк— ... - 0Р.мнкя^ и по ним строится первое при-
ближение 5 оценки для неизвестной матрицы Ее; затем матрица Е,1)
используется для вычисления обобщенных МНК-оценок € к. После это-
го пересчитываются невязки 42) =	• -“^P.Imkk^
(т.е. вычисляется их второе приближение) и т.д. При этом, как прави-
ло, неизвестная ковариационная матрица остатков Ее каким-то образом
параметризуется, т.е. выписывается в форме, в которой все п(п 4- 1)/2
ее элементов являются функциями заданного общего вида от небольшого
числа (двух-трех) одних и тех же параметров.
5.	Основной характеристикой прогностической силы модели являет-
ся так называемый коэффициент детерминации R2, определяющий, ка-
кая доля общей вариации анализируемой результирующей переменной у
обусловлена изменением объясняющих переменных ж<1\ ж<2\..., Так,
например из R =1 следует, что вся вариация у обусловлена изменением
объясняющих переменных, а это значит: влияние регрессионных остатков
£ на формирование значений у сведено к нулю, т.е. мы имеем возмож-
774
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
ность практически без ошибок предсказывать значения у по заданным
значениям объясняющих переменных X = (z^\®^2\... ,z^)T.
6.	Говорят, что в анализируемой ЛММР присутствует свойство муль-
тиколлинеарностщ если включенные в модель объясняющие переменные
а/2\..., хМ характеризуются высокой степенью линейной взаимо-
зависимости (это может проявляться: в близости к единице, по абсолют-
ной величине, - значении парных и частных коэффициентов корреляции
между объясняющими переменными; в близости к нулю определителя ма-
трицы ХТХ, где X — матрица наблюденных значений объясняющих пе-
ременных, см. (15.4*); в близости к единице хотя бы одного из коэф-
фициентов детерминации RxU).x(j) каждой из объясняющих переменных
по всем остальным объясняющим переменным). Мультиколлинеарность
приводит к ряду осложнений в построении и интерпретации ЛММР,
среди которых: слишком большие значения среднеквадратических ошибок
в оценках коэффициентов регрессии; неустойчивость результатов оцени-
вания модели по отношению к небольшим изменениям исходных выбороч-
ных данных; знаки оценок коэффициентов регрессии, не согласующиеся с
содержательным смыслом влияния соответствующих объясняющих пере-
менных на у, и т. п.
7.	К основным методам устранения мультиколлинеарности в ЛМ-
МР относятся: модификация МНК-оценок в направлении перехода к сме-
щенным методам оценивания параметров регрессии (например, к методу
ридж-регрессии); предварительная ортогонализация объясняющих пере-
менных (например, с помощью метода главных компонент); исключение
из состава объясняющих переменных ряда признаков.
8.	Важным этапом спецификации ЛММР является отбор существен-
ных предикторов из априорного набора объясняющих переменных. Наи-
более распространенными и эффективными процедурами такого отбора
являются метод всех возможных регрессий и метод пошаговой регрес-
сии. Неправильный отбор объясняющих переменных в ЛММР приводит
к ошибкам спецификации модели. При этом неправомерное ущемление
(сужение) истинного набора объясняющих переменных приводит к сме-
щению в оценках коэффициентов регрессии при оставшихся предикторах,
в то время как избыточный (по отношению к истинному) набор объясня-
ющих переменных к смещению оценок не приводит (но может приводить
к мультиколлинеарности).
9.	Специального рассмотрения требует ЛММР, в которых объясняю-
щие переменные X = (®(1\аг2\...,ж^)Т стохастичны по своей приро-
де. К таким моделям относятся, например, ситуации, в которых значения
объясняющих переменных могут измеряться только со случайной ошиб-
выводы
775
кой, а также весьма распространенные в эконометрических исследованиях
построения, в которых в качестве объясняющих переменных используют-
ся значения случайных по своей природе результирующих показателей
в предыдущие моменты времени (так называемые лаговые результирую-
щие показатели). Если при этом случайные объясняющие переменные
X некоррелированы с регрессионными остатками £, то к рассматрива-
емой модели применимы все методы и результаты, полученные в рам-
ках классической или обобщенной (в зависимости от природы остатков е)
ЛММР. Правда, интерпретация этих результатов при стохастических
регрессорах X базируется на понятии условного распределения регресси-
онных остатков £, в котором в качестве условия используется заданность
(фиксированность) элементов матрицы наблюдений X. Если же стохасти-
ческие предикторы X коррелированы с регрессионными остатками £, то
МНК- и ОМНК-оценки неизвестных коэффициентов 0 перестают быть со-
стоятельными и несмещенными. В этом случае необходимо использовать
специальные методы, одним из наиболее распространенных среди которых
является метод введения инструментальных переменных.
10.	Иногда в ходе сбора исходных статистических данных имеет ме-
сто косвенное воздействие (во времени и/или в пространстве) некоторых
качественных факторов, в результате которого происходят скачкообраз-
ные сдвиги в структуре анализируемых линейных связей (т. е. в значени-
ях регрессионных коэффициентов 0о>	• • • ,0р)- В этих случаях говорят
об исследовании регрессионных моделей с переменной структурой или о
построении ЛММР по неоднородным данным, а само исследование в за-
висимости от условий проводится по одной из трех нижеследующих схем.
1) Воздействующие качественные факторы наблюдаемы в ходе сбора ис-
ходных статистических данных, а объем последних (п) позволяет разбить
всю имеющуюся выборку {(х^,®^, • • •,	У»)}«=1,з,...,п на регрессионно
однородные подвыборки таких объемов (nj, п2,...), которые обеспечивают
возможность статистически надежного регрессионного анализа отдельно
по каждой подвыборке; при этом воздействие качественных факторов мо-
жет приводить к скачкообразному изменению практически всех регрес-
сионных коэффициентов. В этом случае анализируется столько регресси-
онных зависимостей, сколько имеется регрессионно однородных подвыбо-
рок, причем построение и анализ модели регрессии производится
отдельно по каждой такой регрессионно однородной подвыбор-
ке. 2) Этот случай отличается от предыдущего тем, что воздействие
качественных факторов может приводить к скачкообразному измене-
нию лишь части регрессионных коэффициентов модели. Тогда анализ
регрессионной модели производится на базе объединенной (ре-
776
ГЛ. 15. МЕТОДЫ И МОДЕЛИ РЕГРЕССИОННОГО АНАЛИЗА
грессионно неоднородной) выборки с помошыо введения в модель
так называемых фиктивных переменных или в рамках модели
ковариационного анализа. Этот подход особенно актуален в условиях
дефицита исходных статистических данных. 3) Качественные перемен-
ные, под воздействием которых происходят скачкообразные изменения в
структуре модели, ненаблюдаемы или их значения не были своевременно
зарегистрированы при сборе исходных статистических данных. Это зна-
чит, что мы не имеем принципиальной возможности разбить имеющиеся
исходные статистические данные на регрессионно однородные «порции»,
ориентируясь при этом на значения этих качественных переменных. В
этих случаях сначала используют методы кластер-анализа или расщеп-
ления смесей распределений в пространстве	, х^р\ у) с целью
получения регрессионно однородных кластеров, а затем, так же как и
в случае 1), строят и анализируют искомую модель регрессии отдельно
по наблюдениям каждого такого кластера.
11.	Если в результате этапа параметризации модели исследователь
приходит к выводу, что искомая регрессионная зависимость /(X) нелиней-
на, то далее он действует следующим образом. Во-первых, он обращается
к процедуре линеаризации модели, т.е. пытается подобрать такие пре-
образования к анализируемым переменным	... ,х^ и у, которые
позволили бы представить искомую зависимость в виде линейного соотно-
шения между преобразованными переменными. Помимо определенного на-
бора стандартных преобразований (гиперболических, экспоненциальных,
степенных и т. п.) с этой целью используют также подход Бокса-Кокса,
при котором необходимое линеаризирующее преобразование подбирается
из некоторого однопараметрического семейства преобразований на базе
метода максимального правдоподобия.
Если же линеаризирующее преобразование подобрать не удается, то
приходится исследовать искомую нелинейную регрессионную зависимость
в терминах исходных переменных. Вычисление МНК- или ОМНК-оценок
неизвестных параметров потребует в этом случае привлечения соответ-
ствующих методов нелинейной оптимизации.
12.	Специальный класс логит- и пробит-моделей составляют за-
висимости дихотомического (бинарного) результирующего показателя
у от количественных объясняющих переменных х^\х^,... ,х^р\ К
этим моделям приходится обращаться, когда анализируемый социально-
экономический объект (индивид, домашнее хозяйство, фирма, предпри-
ятие и т.п.) в контексте проводимого исследования может находится в
одном из двух состояний в зависимости от значений ряда объясняющих
переменных (например, yi = 1, если i-й трудоспособный член общества
выводы
777
относится к категории «занятых», и у, = 0, если он относится к катего-
рии «безработных»; при этом переменные	характеризу-
ют его возраст, уровень образования, имеющийся стаж работы и т. д.).
В подобных случаях переходят к новому результирующему показателю
ft, определяющему вероятность события {у, = 1} как функцию специ-
ального вида F(z,), в которой в роли аргумента z, выступает линейная
функция от объясняющих переменных, т.е. z, = 0О +	+ •• • +
Если в качестве функции F(z) используют так называемую логистиче-
скую кривую, то модель вида у, = F(zj) называется ълогит-моделью*.
Если же в качестве функции F(z) используется функция стандартного
нормального распределения, то соответствующая модель носит название
«пробит-модели*. Очевидно, оценка параметров 0q, 0^,..., 6р в таких мо-
делях связана с необходимостью решения специального класса нелинейных
задач оптимизации.
ГЛАВА 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
(МОДЕЛИ И ПРОГНОЗИРОВАНИЕ)
Всякий эконометрический анализ основывается на исходных стати-
стических данных (и.с.д). Их общая форма была описана в п. 9.1.2 (см.
(9.1), (9.1#) и (9.2)). При этом если процесс регистрации и.с.д. происходит
во времени t и само время фиксируется наряду со значениями анализируе-
мых характеристик z^(ijt) (j = 1,2,... ,р; » = 1,2,..., n; k = 1,2,..., JV),
то говорят о статистическом анализе так называемых панельных данных1.
Если зафиксировать номер переменной j и номер статистически обследуе-
мого объекта i, то расположенную в хронологическом порядке последова-
тельность значений
(16.1)
называют одномерным временным рядом. Если же одновременно рас-
сматривать р одномерных временных рядов вида (16.1), т.е. иссле-
довать закономерности во взаимосвязанном поведении временных ря-
дов (16.1) для j = 1,2, ...,р, характеризующих динамику р перемен-
ных, измеренных на каком-то одном (i-м) объекте, то тогда гово-
рят о статистическом анализе многомерного временного ряда X(t) =
(z^\^),a:^2\zfc),..., x^(tk))T (k = 1,2,..., N). По существу, все задачи,
связанные с анализом экономической динамики, предусматривают исполь-
зование в качестве своей статистической базы временных рядов тех или
иных показателей.
Данная глава практически полностью посвящена методам построе-
ния, идентификации (т.е. — статистического оценивания параметров)
1 Напомним, что в принятых выше обозначениях j — номер анализируемой количе-
ственной характеристики (или переменной), i — номер статистически обследованно-
го объекта, а. к — порядковый номер времени регистрации значения анализируемой
переменной на t-м объекте.
779
и верификации (m. e. — статистической проверки адекватности) моде-
лей одномерных временных рядов. При этом с точки зрения прикладного
назначения этих моделей нас будет интересовать прежде всего проблема
прогнозирования экономических показателей. Это значит, что вне рамок
данной главы остаются такие важные (в первую очередь, в области си-
стем управления технологическими процессами) прикладные проблемы,
как анализ и построение так называемой передаточной функции систем
или проектирование регулирующих динамических схем с прямой и обрат-
ной связями (см., например, [Дж. Бокс, Г. Дженкинс]). Добавим к этому,
что в данной главе будут рассматриваться лишь дискретные (по времени
наблюдения) одномерные временные ряды для равноотстоящих момен-
тов наблюдения, т.е. = t3 — i2 = ... =	= А, где A —
заданный временной такт (минута, час, сутки, неделя, месяц, квартал,
год и т. п.). Поэтому в дальнейшем исследуемый временной ряд нам бу-
дет удобнее представлять в виде
®(1),®(2)....z(N),	(16.1')
где x(t) — значение анализируемого показателя, зарегистрированное в t-м
такте времени (t = 1,2,..., N).
Говоря о проблеме прогнозирования, мы имеем в виду кратко- и сред-
несрочный прогноз, поскольку построение долгосрочного прогноза подра-
зумевает обязательное использование методов организации и статистиче-
ского анализа специальных экспертных оценок. Тем не менее, использо-
вание доступных к моменту времени t = N наблюдений временного ряда
(16.1') для прогнозирования значения x(t) на один или несколько времен-
ных тактов вперед (т.е. — для прогнозной оценки значений x(N 4- I),
I = 1,2,3) может явиться основой для:
•	планирования в экономике, производстве, торговле;
•	управления и оптимизации протекающих в обществе социально-
экономических процессов;
•	частичного управления важными параметрами демографических про-
цессов и экологической ниши общества;
•	принятия оптимальных решений в бизнесе.
Отметим, что анализ и моделирование данных, представленных вре-
менными рядами (16.1*), потребует определенной ревизии принятого до
сих пор в данном учебнике понимания как механизмов генерации исход-
ных статистических данных, так и того, что мы называем выборкой
из генеральной совокупности.
780
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
16.1.	Временной ряд (определения, примеры,
формулировка основных задач)
Выше, говоря о расположенной в хронологическом порядке последо-
вательности наблюденных значений (16.1) или (16.1') какого-либо при-
знака, мы, по существу, уже дали определение временного ряда. Однако
в дальнейшем нас будет интересовать лишь некоторый подкласс подоб-
ных последовательностей, а именно тот, который связан с наблюдениями
стохастических по своей природе признаков. Другими словами, мы ис-
ключаем из рассмотрения детерминированные схемы динамических на-
блюдений, при которых элементы последовательности (16.1 ) могут быть
в точности вычислены как значения некоторой неслучайной функции
f(t), т.е. x(t) = f(t). Поэтому уточним понятие временного ряда, при-
нятое в данной главе.
Определение 16.1. Ряд наблюдений x(ti),x(t2), ••• ,®(<n) ана-
лизируемой случайной величины £(£), произведенных в последовательные
моменты времени , ij,..., tyy, называется временным рядом.
Как уже было отмечено, предметом нашего анализа в данной главе
будут временные ряды с равноотстоящими моментами наблюдений. А
это позволяет представлять их в форме (16.1).
Определение 16.1 опирается на понятие случайной величины f(t), за-
висящей от параметра Z, интерпретируемого как время. То есть, по суще-
ству, речь идет об однопараметрическом семействе случайных величин
{f(t)}. Это значит, что закон распределения вероятностей (з.р.в.) этих
случайных величин, и в частности, их первые и вторые моменты, также,
вообще говоря, могут зависеть от времени t.
В чем же состоят принципиальные отличия временного ряда
(16.1') от введенной в п.6.1 последовательности наблюдений хг,х2,...,
zn, образующих случайную выборку? Этих отличий два.
(а)	Во-первых, в отличие от элементов случайной выборки члены вре-
менного ряда не являются статистически независимыми.
(б)	Во-вторых, члены временного ряда не являются одинаково рас-
пределенными, т.е. P{x(ti) < я:} / P{x(t2) < при ti / t2.
Это значит, что мы не можем распространять свойства и правила ста-
тистического анализа случайной выборки на временные ряды. С другой
стороны, взаимозависимость членов временного ряда создает свою специ-
фическую базу для построения прогнозных значений анализируемого по-
казателя (т.е. для построения оценок x(N + к) для неизвестных значений
x(N -f- к)) по наблюденным значениям ж(1),я:(2),... ,x(N).
16.1. ВРЕМЕННОЙ РЯД
781
Генезис наблюдений, образующих временной ряд. Речь идет
о структуре и классификации основных факторов, под воздействием ко-
торых формируются значения элементов временного ряда. Целесообразно
выделить следующие 4 типа таких факторов.
(А)	Долговременные, формирующие общую (в длительной перспек-
тиве) тенденцию в изменении анализируемого признака x(t). Обычно эта
тенденция описывается с помощью той или иной неслучайной функции
/тр(0, как правило, монотонной. Эту функцию называют функцией трен-
да или просто — трендом.
(Б) Сезонные, формирующие периодически повторяющиеся в опреде-
ленное время года колебания анализируемого признака. Условимся обо-
значать результат действия сезонных факторов с помощью неслучайной
функции <p(t). Поскольку эта функция должна быть периодической (с
периодами, кратными «сезонам»), в ее аналитическом выражении участ-
вуют гармоники (тригонометрические функции), периодичность которых,
как правило, обусловлена содержательной сущностью задачи.
(В)	Циклические (конъюнктурные), формирующие изменения ана-
лизируемого признака, обусловленные действием долговременных циклов
экономической, демографической или астрофизической природы (волны
Кондратьева, демографические «ямы», циклы солнечной активности и
т.п.). Результат действия циклических факторов будем обозначать с по-
мощью неслучайной функции i/>(t).
(Г) Случайные (нерегулярные), не поддающиеся учету и регистра-
кии. Их воздействие на формирование значений временного ряда как
раз и обусловливает стохастическую природу элементов x(t), а следо-
вательно, и необходимость интерпретации z(l),a:(2),.. .,x(N) как на-
блюдений, произведенных над случайными величинами, соответственно,
((1),£(2),... ,f(Af). Будем обозначать результат воздействия случайных
факторов с помощью случайных величин («остатков», «ошибок») e(t)1.
Конечно, вовсе не обязательно, чтобы в процессе формирования значе-
ний всякого временного ряда участвовали одновременно факторы всех че-
1 Случайные факторы, в свою очередь, могут быть двоякой природы: внезапны-
ми (еразладочнымив), приводящими к скачкообразным структурным изменениям
в механизме формирования значений ®(i) (что выражается, например, в радикаль-
ных скачкообразных изменениях основных структурных характеристик функций
/тр(<)» v(0 и 1Ж) анализируемого временного ряда в случайный момент времени),
и эволюционными остаточными, обусловливающими относительно небольшие слу-
чайные отклонения значений x(t) от тех, которые должны были бы получиться толь-
ко под воздействием факторов (А), (Б) и (В). Однако в данном учебнике будут
рассмотрены схемы формирования временных рядов, включающие в себя действие
только эволюционных остаточных случайных факторов.
782
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
тырех типов. Из приведенных ниже примеров мы увидим, что в одних слу-
чаях значения временного ряда формируются под воздействием факторов
(А), (Б) и (Г) (см. пример 16.1), в других — под воздействием факторов
(А), (В) и (Г) (см. пример 16.2) и, наконец, — исключительно под воздей-
ствием одних только случайных факторов (Г) (см. пример 16.3). Однако
во всех случаях предполагается непременное участие случайных (эволю-
ционных) факторов (Г). Кроме того, мы примем (в качестве гипотезы)
для определенности аддитивную структурную схему влияния факторов
А, Б, В и Г на формирование значений x(t), которая означает правомер-
ность представления значений членов временного ряда в виде разложения:
х(0 = х(А)/тр(0-Ьх(Б)^) + х(В)^) + е(0, * = 1,2,..., АГ, (16.2)
где
{1, если факторы типа С участвуют в формировании
значений ж(/);
О в противном случае;
С = А, Б или В.
Выводы о том, участвуют или нет факторы данного типа в формиро-
вании значений х(1)> могут базироваться как на анализе содержательной
сущности задачи (т.е. быть априорно-экспертными по своей природе^
так и на специальном статистическом анализе исследуемого временно-
го ряда.
Примеры временных рядов. Рассмотрим несколько конкретных
временных рядов. Они иллюстрируют различные варианты вышеописан-
ной схемы генезиса исходных статистических данных, имеющих динами-
ческую природу. Одновременно эти данные понадобятся нам для иллю-
страции смысла и работоспособности описанных далее методов и моделей
анализа временных рядов.
Пример 16.1. В табл. 16.1 и на рис. 16.1 приведены данные о сум-
марных месячных расстояниях x(t) (в тысячах милей), пройденных бри-
танскими авиалайнерами за 96 месяцев с января 1963 г. по декабрь 1970 г.
(т.е. t = 1,2,... ,96; временной такт А равен одному месяцу).
16.1. ВРЕМЕННОЙ РЯД
783
Таблица 16.1. Расстояния, пройденные британскими авиалайнерами за месяц
(тыс. миль)
	1963	1964	1965	1966	1967	1968	1969	1970
Январь	6827	7269	8350	8186	8334	8639	9491	10840
Февраль	6178	6775	7829	7444	7899	8772	8919	10436
Март	7084	7819	8829	8484	9994	10894	11607	13589
Апрель	8162	8371	9948	9864	10078	10455	8852	13402
Май	8462	9069	10638	10252	10801	11179	12537	13103
Июнь	9644	10248	11253	12282	12950	10588	14759	14933
Июль	10466	11030	11424	11637	12222	10794	13667	14147
Август	10748	10882	11391	11577	12246	12770	13731	14057
Сентябрь	9963	10333	10665	12417	13281	13812	15110	16234
Октябрь	8194	9109	9396	9637	10366	10857	12185	12389
Ноябрь	6848	7685	7775	8094	8730	9290	10645	11595
Декабрь	7027	7602	7933	9280	9614	10925	12161	12772
Рис. 16.1. График данных мэ табл. 16.1 (расстояния, пройденные авиалай-
нерами Соединенного Королевства за месяц)
Пример 16.2. В табл. 16.2 и на рис. 16.2 представлены данные
Financial Times (FT) о квартальной динамике среднего индекса курса ак-
ций ведущих компаний на лондонской бирже за 1960-1971 гг. (соответ-
ственно: временной такт А равен одному кварталу, а общее число членов
временного ряда N — 48).
784
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Таблица 16.2. Индекс FT курса обыкновенных акций ведущих компаний: квар-
тальные средние за 1960-1971 гг.
Год и квартал	Индекс	Год и квартал	Индекс	Год и квартал	Индекс
1960 1	323,8	1964 1	335,1	1968 1	409,1
2	314,1	2	344,4	2	461,1
3	321,0	3	360,9	3	491,4
4	312,9	4	346,5	4	490,5
1961 1	323,7	1965 1	340,6	1969 1	491,0
2	349,3	2	340,3	2	433,0
3	310,4	3	323,3	3	378,0
4	295,8	4	345,6	4	382,6
1962 1	301,2	1966 1	349,3	1970 1	403,4
2	285,8	2	359,7	2	354,7
3	271,7	3	320,0	3	343,0
4	283,6	4	299,9	4	345,4
1963 1	295,7	1967 1	318,5	1971 1	330,4
2	309,3	2	343,1	2	372,8
3	295,7	3	360,8	3	409,2
4	342,0	4	397,8	4	427,6
Годы двадцатого столетия
График временного ряда, представленного данными табл. 16.2
(индекс FT, квартальные средние)
Рис. 16.2.
Пример 16.3. В табл. 16.3 и на рис. 16.3 представлены данные об
урожае ячменя в Англии и Уэльсе за 56 лет (с 1884 по 1939 гг.). Так что
временной такт Д в данном случае равен одному году, а длина временного
ряда N = 56.
16.1. ВРЕМЕННОЙ РЯД
785
Таблица 16.3. Урожайность ячменя в Англии и Уэльсе с 1884 по 1939 гг. (в
англ, центнерах на акр1, данные из «Agricultural Statistics»)
Год	Урожай- ность	Год	Урожай- ность	Год	Урожай- ность
1884	15,2	1903	15,1	1922	14,0
1885	16,9	1904	14,6	1923	14,5
1886	15,3	1905	16,0	1924	15,4
1887	14,9	1906	16,8	1925	15,3
1888	15,7	1907	16,8	1926	16,0
1889	15,1	1908	15,5	1927	16,4
1890	16,7	1909	17,3	1928	17,2
1891	16,3	1910	15,5	1929	17,8
1892	16,5	1911	15,5	1930	14,4
1893	13,3	1912	14,2	1931	15,0
1894	16,5	1913	15,8	1932	16,0
1895	15,0	1914	15,7	1933	16,8
1896	15,9	1915	14,1	1934	16,9
1897	15,5	1916	14,8	1935	16,6
1898	16,9	1917	14,4	1936	16,2
1899	16,4	1918	15,6	1937	14,0
1900	14,9	1919	13,9	1938	18,1
1901	14,5	1920	14,7	1939	17,5
1902	16,6	1921	14,3		
годы
Рис. 16.3. График временного ряда, представленного данными табл. 16.3
(урожайность ячменя, ц/акр)
1 Английский центнер равен 50,8 кг, один акр равен 0,405 га.
786
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Попробуем проанализировать приведенные примеры временных ря-
дов, опираясь на описанную выше общую схему их генезиса и вытекающее
из нее разложение вида (16.2).
Данные об авиалайнерах (пример 16.1) представляют собой ти-
пичный образец сезонных колебаний, наслаивающихся на монотонно ро-
ст ущий тренд. Сезонный эффект легко расшифровывается. Мы наблю-
даем в течение года три «всплеска» активности пассажирских авиапе-
ревозок, и все они объясняются перелетами в праздничный и отпускной
периоды: один из них приходится на пасху, второй — на лето и третий —
на рождественские праздники. Правда, перелеты на пасху приходятся,
как и сама пасха, то на одни, то на другие дни года, и картина колебаний
меняется из года в год частично из-за возрастающего парка авиалайнеров,
а частично из-за увеличения в настоящее время периода праздников.
Иногда требуется особая внимательность, чтобы не спутать се-
зонные циклические компоненты с такими колебаниями, как экономи-
ческие циклы или циклы проявления солнечной активности (послед-
ние правильнее отнести к колебаниям псевдоциклического типа). Так,
в примере 16.2 улавливается четырехлетний экономический цикл,
который, как считают некоторые специалисты, следует объяснять не дол-
говременной внутренней логикой экономического развития, а лишь при-
близительно таким же циклом проведения общих парламентских выборов
в Великобритании.
Наконец, анализ графика временного ряда, представленного в при-
мере 16.3 (см. рис. 16.3), приводит к гипотезе, что в генерировании этих
данных не участвовали ни долговременные (поскольку тренд, скорее всего,
отсутствует), ни сезонные, ни циклические факторы (поскольку осцилли-
рование значений x(t) около некоторого постоянного уровня носит, скорее,
случайный, а не строго периодический, характер).
Основные задачи анализа временных рядов. Отправляясь от
приведенного выше аддитивного разложения (16.2) временного ряда x(t),
можно дать общую формулировку базисной цели его статистического
анализа1:
• по имеющейся траектории (16.1*) анализируемого временного ряда
x(t) требуется:
1 Мы отличаем базисную цель анализа от конечных прикладных целей исследования.
Без достижения базисной цели невозможна реализация конечных прикладных целей
исследования. Другими словами, базисная цель формулируется внутри исследова-
ния и является необходимым этапом для достижения конечных прикладных целей,
результаты реализации которых формулируются «на выходе» исследования.
16.2. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
787
(i) определить, какие из неслучайных функций /Tp(t), fp(t) и |^(t) при-
сутствуют в разложении (16.2), т. е. определить значения индика-
торов х(С) (Р = А, Б, В) в разложении (16.2);
(Н) построить «хорошие» оценки для тех неслучайных функций,
которые присутствуют в разложении (16.2);
(iii) подобрать модель, адекватно описывающую поведение «случай-
ных остатков» e(t), и статистически оценить параметры этой
модели.
Успешное решение задач ( ) (tit), обусловленных базисной целью
статистического анализа временного ряда, является основой для достиже-
ния конечных прикладных целей исследования и, в первую очередь, для
решения задачи кратко- и среднесрочного прогноза значений временного
ряда.
16.2. Стационарные временные ряды и их
основные характеристики
Поиск модели, адекватно описывающей поведение случайных остат-
ков е(1) анализируемого временного ряда x(t) (см. выше формулировку
задачи (iii)), производят, как правило, в рамках некоторого специального
класса случайных временных последовательностей — класса стационар-
ных временных рядов. На интуитивном уровне стационарность временно-
го ряда мы связываем с требованием, чтобы он имел постоянное сред-
нее значение и колебался вокруг этого среднего с постоянной дисперсией.
В некоторых случаях временные последовательности этого класса могут
воспроизводить и поведение самого анализируемого временного ряда x(t)
(из приведенных выше примеров внешние признаки стационарного вре-
менного ряда демонстрирует график динамики урожайности ячменя, см.
пример 16.3).
Определение 16.2. Ряд x(t) называется строго стационар-
ным (или стационарным в узком смысле), если совместное распреде-
ление вероятностей т наблюдений s($i),a;(t2),... ,x(tm) такое же, как
и для т наблюдений x(t\ + т),х(12 4- т),...,х(1т + г), при любых т,
^132» • • • » Н Т.
Другими словами, свойства строго стационарного временного ряда не
меняются при изменении начала отсчета времени. В частности, при т = 1
из предположения о строгой стационарности временного ряда z(t) следует,
что закон распределения вероятностей (з.р.в.) случайной величины x(t)
не зависит от t, а значит, не зависят от t и все его основные числовые
788
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
характеристики, в том числе:
среднее значение Exft) = а
(16.3)
дисперсия Dx(f) = Е z(Z) — а)2 = о2.	(16.4)
Очевидно, значение а определяет постоянный уровень, относитель-
но которого флуктуирует анализируемый временной ряд x(t), а посто-
янная величина <г характеризует размах этой флуктуации. Поскольку
з.р.в. случайной величины x(t) одинаков при всех t, то он сам и его
основные числовые характеристики могут быть оценены по наблюдени-
ям х(1),ж(2),...,а:(А)1. В частности:
d = — У^ж(/) — оценка среднего значения, (16.3*)
1 п	2
д = —	(z(<) - д) — оценка дисперсии.	(16.4*)
t=i
Автоковариационная функция 7 (г). Из предположения о строгой
стационарности временного ряда x(t) при т = 2 следует, что совмест-
ные двумерные распределения для пар случайных величин
(ж(0), x(t2 - ii)), (х(т),г(/2 -	+ г)) совпадают при любых tj, t2 и т и
зависят только от разности t2 — G- Соответственно, ковариация между
значениями x(t) и x(t ± г) будет зависеть только от величины «сдвига
по времени» т (и не будет зависеть от t). Эта ковариация называется ав-
токовариацией (поскольку измеряет ковариацию для различных значений
одного и того же временного ряда z(t)) и определяется соотношением:
7(т) = cov (z(t),2;(< + г)) = E[(«(t) - a)(a:(t + г) - a)].	(16.5)
При анализе изменения величины 7(т) в зависимости от значения т
принято говорить об автоковариационной функции 7(т). Значения авто-
1 В общем случае (т.е. при отсутствии свойства стационарности) для оценки з.р.в.
случайной величины x(t) к ее основных числовых характеристик мы должны были
бы иметь по несколько наблюдений временного ряда для каждого фиксированно-
го «момента времени» I. Однако неизменность з.р.в. z(t) во времени t позволяет
(при некоторых дополнительных условиях эргодичности, см. теорему Биркгофа-
Хинчина в книге [М.Дж. Кендалл, А. Стьюарт, 1976]) оценивать среднее значение,
дисперсию и ковариации стационарного временного ряда по его единственной реа-
лизации (16.1').
16.2. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
789
ковариационной функции могут быть статистически оценены по имею-
щимся наблюдениям временного ряда (16. Iх) по формуле
7(г) = уз7 53 НО
(16.5')
где т = 1,2,..., N — 1, а а вычислено по формуле (16.3х).
Очевидно, значение автоковариационной функции при г = 0 есть не
что иное, как дисперсия временного ряда, т. е.
7(0) = о2 = Е(ж(«) - а)2
и, соответственно,
7(0) = *2 = Е МО - а)2-	(16.4")
Автокорреляционная функция г(т). Одно из главных отличий по-
следовательности наблюдений, образующих временной ряд, от случайной
выборки заключается, как мы видели (см. свойство (а) в начале п. 16.1), в
том, что члены временного ряда являются, вообще говоря, статистически
взаимозависимыми. Степень тесноты статистической связи между двумя
случайными величинами может быть измерена парным коэффициентом
корреляции (см. гл. 11). Так что степень тесноты статистической связи
между наблюдениями временного ряда, «разнесенными» (по времени) на
т единиц, определится величиной коэффициента корреляции
тМ = Е[И0-а)(з:(< + г)-0)]	. 7(т)	п fi
° [E(z(i)-a)2.E(z(« + r)-a)2]i	7(0)’
поскольку E(z(t) - а)2 = E(z(Z + т) - а)2 = 7(0).
Коэффициент г(т) измеряет корреляцию, существующую между чле-
нами одного и того же временного ряда, поэтому его принято называть
коэффициентом автокорреляции. При анализе изменения величины г(т)
в зависимости от значения т принято говорить об автокорреляционной
функции г(т). График автокорреляционной функции иногда называют
коррелограммой. Заметим, что автокорреляционная функция (в отличие
от автоковариационной) безразмерна, т. е. не зависит от масштаба изме-
рения анализируемого временного ряда. Ее значения, по определению,
могут колебаться от —1 до +1. Кроме того, из стационарности следует,
790
ГЛ. 1в. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
что г(т) = г(— т), так что при анализе поведения автокорреляционных
функций ограничиваются рассмотрением только положительных значе-
ний т.
Выборочный аналог автокорреляционной функции (ее статистическая
опенка г(т)) определяется формулой
wh Е (*(«) - a)(x(t + т) - а)
t=l
т = 1,2,...,7V— 1.
(16.6*)
Существуют ли какие-либо общие характерные особенности, отлича-
ющие поведение автокорреляционной функции стационарного временного
ряда? Другими словами, можно ли описать в общих чертах схематичный
вид коррелограммы стационарного временного ряда? Ответ — утверди-
тельный, и это обусловлено следующим общим соображением: очевидно,
чем больше разнесены во времени члены временного ряда x(t) и x(t + т)
(т. е. чем больше величина сдвига т), тем слабее взаимосвязь этих членов
и, соответственно, тем меньше должно быть по абсолютной величине зна-
чение г(т). При этом в ряде случаев существует такое пороговое значение
То, начиная с которого все значения г(т) будут тождественно равны нулю
(т.е. г(т) = 0 для всех т т0).
В левых частях рис. 16.4, 16.5 и 16.6 приведены графики автокорре-
ляционных функций для ряда моделей временных рядов, рассмотренных
ниже (см. пп. 16.4-16.7). Обращаем внимание читателя на тот факт, что
в отличие от теоретических автокорреляционных функций их выбороч-
ные (эмпирические) аналоги (16.6х) часто допускают нарушения свойства
монотонного убывания (по абсолютной величине) при возрастании аргу-
мента т.
*
Частная автокорреляционная функция гЧЛСТ(т). С помощью
этой функции реализуется идея измерения автокорреляции, существую-
щей между разделенными т тактами времени членами временного ряда
x(t) и x(t 4- т), при устраненном опосредованном влиянии на эту взаи-
мозависимость всех промежуточных (т.е. расположенных между x(t) и
x(t 4- т)) членов этого временного ряда. Идея «очищенной» от опо-
средованного влияния, т. е. частной, корреляции уже обсуждалась в этой
книге (см. п. 11.2.4). Поэтому нам остается лишь применить понятия,
результаты и формулы этого раздела корреляционного анализа к последо-
вательности членов временного ряда. Так, частная автокорреляция 1-го
16.2. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
791
порядка может быть подсчитана с использованием соотношения (11.32):
гч*сТ(2) = r(z(f),z(t + 2) | x(t 4-1) = в)
= r(z(t), *(* + 2)) - г(ж(<), x(t + 1 ))г(ж(14- 2), x(t + 1))
y/[l - ra(x(t),*(i+ 1))][1 - r’(z(i + 2),x(t + 1))]	(16.7)
r(2)-ra(l)
l-ra(l) ’
где a — среднее значение анализируемого стационарного процесса.
Частные автокорреляции более высоких порядков могут быть подсчи-
таны аналогичным образом с использованием либо рекуррентной формулы
(11.32 ), либо с помощью формулы (11.31) по элементам общей корреляци-
онной (N X N) — матрицы R, в которой = r(x(t),a;(i;)) = r(|t — j|), где
i, j = 1,2,..., N (и, очевидно, r(0) = 1). Так, например, частная автокор-
реляция 2-го порядка (т.е. корреляция между членами временного ряда,
разделенными тремя тактами времени, подсчитанная при условии, что
значения двух промежуточных членов временного ряда зафиксированы на
среднем уровне) может быть определена по формуле (см. (11.32х)):
г,„т(3) = r(i(t),i(t + 3) | x(t +1) = i(t+2) = а) = Г°зл ~ г°адГзал ,
у(1 ~ г02.1)(1 — ’’32.1)
(16.8)
где
Гозл = r(s(0,s₽(f 4- 3) I x(t 4-1) = а),
Пил = г(х(1),х(14- 2) | x(t 4-1) = а),
Г32.1 = r(x(t 4- 3), x(t 4- 2) I x(t 4-1) = а)
и в соответствии с формулой (11.32), имеем:
Гозл = r(x(t), x(t + 3) I x(t + 1) = а) = - ^(3) r0)r(2)	,
у(1 — ra(l))(l — ra(2))
«-02.1 = r(x(t),x(l + 2) I x(t + 1) = a) = ---- 5;-^,
1 - r (1)
Г32.1 = r(z(t + 3), x(t + 2) I x(t + 1) = a) = - r(1)~r(2)rW	.
V(1 - ra(2))(l - ra(l))
Эмпирические (выборочные) версии частных автокорреляционных
функций получаются с помощью тех же соотношений (16.7), (16.8) при
792
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
замене участвующих в них теоретических значений автокорреля-
ций г(т) их статистическими оценками г(т) (см. формулу
(16.6')).
Полученные таким образом частные автокорреляции гчаст(1)> ^чжстСЧ,
гчаст(3),... можно нанести на график, в котором роль абсциссы выполняет
величина сдвига т.
Знание автокорреляционных функций г(т) и гчаст(т) оказывает суще-
ственную помощь в решении задачи подбора и идентификации модели
анализируемого временного ряда. В правых частях рис. 16.4, 16.5 и 16.6
приведены схематические графики частных автокорреляционных функций
для рассмотренных ниже (см. пп. 16.4~16.7) конкретных моделей времен-
ных рядов. Заметим, что для тех временных рядов, которые «уклады-
ваются» в рамки той или иной конкретной модели (например, в рамки
модели авторегрессии, см. п. 16.4), можно избежать прямого вычисления
частных корреляционных функций по формулам (16.7)—(16.8), воспользо-
вавшись более простой процедурой.
Спектральная плотность p(w). Определим спектральную плот-
ность стационарного временного ряда x(t) через его автокорреляционную
функцию г(т) соотношением вида
?м= r(T)e‘rw>	(16-9)
т=—оо
где i = V—Т (мнимая единица). Благодаря тому, что г(т) = г(-т), спек-
тральная плотность p(w) может быть записана в виде
p(w) = 14- 2^ г(т) cos(rw).	(16.9*)
т=1
Мы видим, что функция (16.91) является гармонической и имеет пе-
риод 2ТГ1. Поскольку cos[(2tf - и)т] = соа(ь;т), то график спектральной
плотности р(о>), называемый спектром, симметричен относительное = я.
1 Аргумент ы намеряется в радианах на единицу времени и называется угловой ча-
стотой (т. к. значения соя (wt) повторяются с периодом 2x/w, то число циклов этой
функции в единице времени равно w/2x). Соответственно, период 2r/w имеет раз-
мерность времени i и называется длиной волны. Мы увидим ниже, что наличие или
отсутствие гармонических членов в разложении (16.2) анализируемого временного
ряда z(t) по-своему отражается на поведении спектральной плотности
16.2. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
793
Поэтому при анализе поведения функции р(о>) ограничиваются значения-
ми w, лежащими между 0 и тг. Ниже мы убедимся в том, что спектральная
плотность p(w) может принимать только неотрицательные значения.
Использование свойств этой функции в прикладном анализе времен-
ных рядов определяется как «спектральный анализ временных рядов*.
Весьма полное описание этого подхода читатель может найти, например,
в книге: Г. Дженкинс, Д. Вате. Спектральный анализ и его приложения.
М.: Мир, вып. 1 (1971); вып. 2 (1972). Применительно к статистическому
анализу экономических рядов динамики этот подход не получил широкого
распространения, т. к. эмпирический (выборочный) анализ спектральной
плотности требует в качестве своей информационной базы либо доста-
точно длинных стационарных временных рядов, либо по несколько тра-
екторий анализируемого временного ряда (и та и другая ситуация весьма
редки в практике статистического анализа экономических рядов динами-
ки). Поэтому мы ограничимся здесь обсуждением лишь следующих двух
важных свойств спектральной плотности.
1) Выражение автокорреляций через спектральную плотность р(и>).
Из обшей теории преобразований Фурье непосредственно следует
cos (Ли?)р(о>)
dw.
(16.10)
Этот результат получается, в частности, из соотношения (16.9#) после
его домножения на cos (Ли) и почленного интегрирования получившегося
выражения по w от 0 до л, с учетом того, что
Г
I cos (ги>) cos (Ли) da)
о
Г 0
I %/2
при т / Л,
при т = Л
2) Спектральная плотность р(о>) как индикатор наличия гармони-
ческих составляющих в представлении анализируемого временного ряда
x{t). Рассмотрим взаимосвязь наблюденного ряда (16.1*) (измеренного от-
носительно его среднего, т.е. мы полагаем, что Ez(0 = 0) с гармониче-
ским членом, имеющим период 2л/и. Пусть
a(w) =
J2*(0 cos (сЛ),
t=l
6(w) =
N
x(t) sin (art).
*=i
794
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Рассмотрим функцию = o2(w) + b2(w)t называемую интенсив-
ностью. Заметим, что поскольку a(w) и b(w) прямопропорциональны ве-
личинам коэффициентов корреляции наблюденного временного ряда x(t)
с гармониками, соответственно, cos(wf) и sin (art), то интенсивность 7(w)
можно рассматривать как характеристику степени тесноты связи меж-
ду x(t) и гармоническим членом, имеющим период 2зг/о/. В то же время
функция /(о?) может быть представлена в виде:
ЛГ-1 N—k
N—l
fc=l

г 2V
где <т2 = x\t)/N — оцененная дисперсия анализируемого ряда, а
t=i
r(k) = r(k)(N — k)/N — несколько «испорченная» оценка автокорреляции
r(fc). Однако, устремив N —* оо и переходя к пределу, мы получим:
ЭД =
1 + 2 r(k) cos (Ахи)
что, как это следует из (16.9*), эквивалентно
E(/(tv)) = __p(w)
(16.11)
(откуда, в частности, следует неотрицательность всех значении спек-
тральной плотности, поскольку усредняемая в левой части величина /(и)
неотрицательна по определению).
Таким образом, с учетом упомянутой выше интерпретации интен-
сивности 7(й>) мы получаем, что величина спектральной плотности при
16.2. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ
795
значении аргумента, равном и, характеризует силу взаимосвязи, суще-
ствующей между анализируемым временным рядом x(t) и гармоникой с
периодом 2тг/а>. Это позволяет использовать спектр как средство улавли-
вания периодичностей в анализируемом временном ряду: при движении
вдоль спектра в заданном диапазоне частот значения ординат должны
оставаться относительно малыми до тех пор, пока не достигнута часто-
та гармонического компонента анализируемого ряда; при этой частоте на
спектре обнаружится высокий пик. Соответственно, совокупность пиков
спектра и будет определять набор гармонических компонентов в разло-
жении (16.2). Отметим, что если в ряде содержится скрытая гармоника
частоты w (дающая в спектре пик в точке с*>), то, конечно, в нем присут-
ствуют также периодические члены с частотами cj/3, и/З и т. д. То есть,
скажем, месячная периодичность порождает эффект появления пиков, со-
ответствующих двухмесячным, трехмесячным и т. д. периодам. Это так
называемое «эхо», повторяемое спектром на низких частотах.
частота в циклах за единицу времени
Рис. 18.7. Спектральная функция очищенных от тренда данных о банков-
ском клиринге в США
796
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
На рис. 16.7 представлен пример графика спектральной плотности
(т. е. спектра), в котором присутствует упомянутый эффект «эха». При-
мер заимствован из статьи: Granger С. W. J.. The effect of varjing month-
length jn the analysis of economic time-series. L’Industria, 1 (1963), 3, Milano.
Анализировался ряд ежемесячных безналичных расчетов между банками
США за 1875-1958 гг. после исключения из него экспоненциальной не-
случайной составляющей. Как видно из графика, спектральная функция
этого ряда обнаруживает эффект появления пиков в точках, соответству-
ющих интервалам в 2 месяца, 3 месяца и т. д.
В заключение разговора о спектральном анализе стационарного вре-
менного ряда подчеркнем еще раз тот факт, что статистические оценки
(выборочные аналоги) введенных выше теоретических спектральных ха-
рактеристик, как правило, сильно флуктуируют и обладают весьма по-
средственной точностью.
И, наконец, можно несколько расширить класс моделей стационарных
временных рядов, используемых при анализе конкретных рядов экономи-
ческой динамики. С этой целью введем понятие стационарного в широком
смысле временного ряда.
Определение 16.3. Ряд x(t) называется слабо стационар-
ным (или стационарным в широком смысле), если его среднее зна-
чение, дисперсия и ковариации не зависят от t, т.е. если выполняются
соотношения (16.3)-(16.4)-(16.5).
Очевидно, все строго стационарные (или стационарные в узком смы-
сле, см. определение 16.2) временные ряды являются одновременно и ста-
ционарными в широком смысле, но не наоборот.
16.3.	Неслучайная составляющая
временного ряда и методы его
сглаживания
В п. 16.1 были описаны основные задачи (i) ~ (ш) статистического
анализа временного ряда (16.1х). Существенную роль в решении задач
выявления и оценивания трендовой (/тр(0), сезонной (tf>(t)) и циклической
(V’(O) составляющих в разложении (16.2) играет начальный этап анализа,
на котором:
• выявляется сам факт наличия/отсутствия неслучайной [и завися-
щей от времени t) составляющей в разложении (16.2); по существу,
речь идет о статистической проверке гипотезы
IIG: Еж(«) = а = const
(16.12)
797
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
(включая утверждение о взаимной статистической независимости
членов анализируемого временного ряда (16.1')) при различных вари-
антах конкретизации альтернативных гипотез типа
Hi'. Ez(t) / const;
(16.13)
• строится оценка (аппроксимация) для неизвестной интегральной
неслучайной составляющей f(t) = х(^)А₽(0 + х(^М0 + x(Q^(0»
т. е. решается задача сглаживания (элиминирования случайных
остатков e(t)) анализируемого временного ряда x(t).
Данный пункт посвящен именно этому начальному этапу статисти-
ческого анализа временного ряда.
16.3.1.	Проверка гипотезы о неизменности среднего
значения временного ряда
Критерий серий, основанный на медиане. Расположим члены
анализируемого временного ряда (16.17) в порядке возрастания, т.е. обра-
зуем по наблюдениям (16.1') вариационный ряд

Следуя рекомендациям п. 6.2.3, определим выборочную медиану
по формуле
{ж/«±1ъ если п нечетно,
(-F)
-(z(^) +	если п четно.
После этого мы образуем «серии» из плюсов и минусов, на статисти-
ческом анализе которых основана процедура проверки гипотезы (16.12).
В частности, возвращаясь к исходному временному ряду (16.1'), мы бу-
дем вместо каждого его члена ж($), t = 1,2,...,п, ставить плюс, если
z(t) > и минус, если x(t) < (члены временного ряда, равные
ггпе<1’ В полученной таким образом последовательности плюсов и минусов
не учитываются).
Образованная последовательность плюсов и минусов характеризует-
ся общим числом серий р(п) и протяженностью самой длинной серии
т(п). При этом под «серией» понимается последовательность подряд иду-
щих плюсов и подряд идущих минусов (в частном случае серия может
состоять только из одного плюса или только из одного минуса, и тогда ее
798
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
протяженность равна, единице). Очевидно, что если анализируемая после-
довательность (16.1*) состоит из статистически независимых наблюдений,
случайно варьирующих около некоторого постоянного уровня а (т. е. если
справедлива гипотеза (16.12)), то чередование плюсов и минусов в постро-
енной указанным выше способом последовательности должно быть более
или менее случайным, т. е. эта последовательность не должна содержать
слишком длинных серий подряд идущих плюсов или подряд идущих мину-
сов, и, соответственно, общее число серий v(ri) не должно быть слишком
малым. Так что в данном критерии целесообразно рассматривать одно-
временно пару критических статистик (i/(n); т(п)) (определение крити-
ческой статистики см. в п. 8.2).
Тогда, следуя общей логической схеме построения статистического
критерия (см. п. 8.2), мы должны были бы вывести и затабулировать
двумерный закон распределения случайной величины (i/(n); т(п)), спра-
ведливый при условии, что проверяемая гипотеза (16.12) верна. Мы огра-
ничимся здесь изложением приближенного критерия. Для его построения
воспользуемся:
•	(^2^»	— нормальным приближением одномерного (частного) рас-
пределения случайной величины i/(n);
•	приближенной оценкой для пятипроцентной точки то.О6(п) частного
распределения случайной величины т(п):
7b.os(n) « [l,431n(n+ 1)]
(здесь [ж] означает «целая часть числа ж»);
•	оценками сверху и снизу для вероятности
P{i/(n) < 1/0.95(п);т(п) > Т0.05(п)},
основанными на знании вероятностей P{i/(n) < Ц),95(п)} и Р{т(п) >
т0.05(п)} (здесь i/o,9s(n) — 95%-ная точка частного распределения
х/(п)).
Это позволяет сформулировать следующее приближенное правило
проверки гипотезы (16.12):
если хотя бы одно из неравенств
Ил) > |(п + 2 ~ 1>96л/п - 1) ,
л»
т(п) < [1,431п(п-|-1)]
(16.14)
окажется нарушенным, то гипотеза (16.12) отвергается с вероятностью
ошибки а, заключенной между 0,05 и 0,0975 (и, следовательно, подтвер-
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
799
ждается наличие зависящей от времени неслучайной составляющей в раз-
ложении (16.2) анализируемого временного ряда).
Пример 16.4. Имеются результаты испытаний на долговечность
58 образцов, отобранных в хронологическом порядке из текущей продук-
ции: 38, 33, 29, 16, 44, 21,16,17,19,1,22, 28, 22, 14, 7,13, 21,15, 34, 23,15,
19,32, 24, 14, 13, 22, 8, 30, 11, 15, 24, 2g, 14,11, 2g, 17,10,19, 5, 6, 16, 7,10,
1,5, 2, 8, 14,14, 15, 16, 13, 11, 9, И, 19, 21. (Подчеркнуты те выборочные
данные, на месте которых в соответствующей последовательности знаков
стояли бы плюсы.)
Ряд факторов, от которых существенно зависит качество образцов
(сырье, квалификация персонала, сменность и т.п.), подвержен неизбеж-
ным колебаниям с течением времени, характер которых может быть как
случайным, так и систематическим. Нас будет интересовать, было ли это
должным образом учтено при назначении способа отбора образцов, т. е.
производился ли отбор так, чтобы результаты наблюдений были бы стоха-
стически независимыми, образовывали бы случайную выборку? Так, ха-
рактер изменения выборочных данных во времени (порядок отбора образ-
цов из текущей продукции во времени определяется в нашем примере дви-
жением по строкам слева направо) наводит на мысль, что имела место
некоторая систематическая тенденция к монотонному снижению долго-
вечности. Ответить на вопрос, являются ли наши сомнения достаточно
обоснованными, нам поможет только что описанный критерий серий.
Необходимые подсчеты дают: £me<i(n) = 15,5; т(п) = 9; г(п) = 25.
Так что из двух неравенств (16.14) лишь одно (первое) оказалось вы-
полненным. Поэтому приходится признать, что результаты наблюдений,
представленные выше, не являются стохастически независимыми и обна-
руживают временную тенденцию к снижению долговечности.
Критерий «восходящих» и «нисходящих» серий. Этот крите-
рий «улавливает» постепенное смещение (по ходу выборочного обследова-
ния) среднего значения в исследуемом распределении не только монотон-
ного, но и более общего, например периодического, характера.
Так же, как и в предыдущем критерии, исследуется последователь-
ность знаков — плюсов и минусов, однако правило образования этой по-
следовательности в данном критерии иное. Исходным пунктом, как обыч-
но, является анализируемая последовательность результатов наблюдения,
т.е. ряд х(1),х(2),... ,ж(п); на i-м месте вспомогательной последователь-
ности ставится плюс, если ж(г-|-1 )-a;(i) > 0, и минус, если z(i-|-l)—а:(*) < 0
(если два или несколько следующих друг за другом наблюдений равны
между собой, то принимается во внимание только одно из них). Очевидно,
последовательность подряд идущих плюсов будет соответствовать тогда
800
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
возрастанию результатов наблюдения (восходящая серия), а последова-
тельность минусов — их убыванию (нисходящая серия). Критерий осно-
ван на том же соображении, что и предыдущий: если выборка случайна
(наблюдения независимы и одинаково распределены), то в образованной
нами последовательности знаков общее число серий не может быть слиш-
ком малым, а их протяженность (измеренная в количестве подряд идущих
плюсов или минусов) — слишком большой.
В частности, при уровне значимости 0,050 < а < 0,0975 количествен-
ное выражение этого правила имеет вид:
"(»)> |(2” -1) -1>96^16”90 29~
(16.15)
т(п) < т0(п),
где под i/(n) и т(п), как и прежде, понимается, соответственно, общее
число серий и количество подряд идущих плюсов или минусов в самой
длинной серии, а величина 7b(n) в зависимости от п определяется следу-
ющим образом:
п
то(п)
п < 26
т0 = 5
26 < п < 153 153 < п < 1170
то = 6	то = 7.
Если хотя бы одно из неравенств (16.15) окажется нарушенным, то ги-
потезу (16.12) следует отвергнуть (и, соответственно, признать, что в
разложении (16.2) анализируемого временного ряда присутствует неслу-
чайная, зависящая от времени t компонента).
Пример 16.5. Вернемся к данным примера 16.3 (см. выше
табл. 16.3 и рис. 16.3) и воспользуемся критерием восходящих и нисходя-
щих серий для проверки гипотезы о неизменности средней урожайности
ячменя в Англии и Уэльсе на отрезке времени с 1884 по 1939 гг.
Общее число наблюдений (длина временного ряда) п в данном приме-
ре равно 56, а образованная описанным выше способом последовательность
плюсов и минусов будет содержать 53 элемента (так как анализируемый
временной ряд содержит две пары совпадающих соседних наблюдений: за
1906-1907 гг. и за 1910-1911 гг.). Эта последовательность из плюсов и
минусов, в частности, имеет вид:
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА	801
№ п/п	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Член последо- ватель- ности	+	—	—	4~	—	+	—	4“	—	+	—	+	—	+	—	—	—	4“
п/п	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
Член последо- ватель- ности	—	—	4“	4-	—	-j-	—	—	4"	—	—•	4“	—	4-	—	4-	—	—
№ п/п	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53
Член последо- ватель- ности	4“	4-				-4-		—•	-4-	-f-	“Ь	-4-	—	—	—	4“	—
Анализ полученной последовательности плюсов и минусов дает:
i/(n) = 36 и т(п) = 4.
Воспользовавшись приведенной выше таблицей значений ть(п) и вы-
ражением для правой части первого из неравенств (16.15), определяем:
|(2-56- 1)- 1,96
16  56 - 29
90
= [30,92] = 30,
т0(56) = 6.
Поскольку оба неравенства (16.15) в нашем случае оказываются вы-
полненными, делаем вывод о непротиворечивости гипотезы о неизмен-
ности средней урожайности ячменя в Англии и Уэльсе в период времени
от 1884 до 1939 г.
Критерий квадратов последовательных разностей (критерий
Аббе). Если есть основания полагать, что случайный разброс наблюде-
ний ж(1),ж(2),..., х(п) относительно своих средних значений подчиняется
802
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
нормальному закону распределения вероятностей, то для выяснения во-
проса о возможном систематическом смещении среднего в ходе выбороч-
ного обследования целесообразнее воспользоваться критерием квадратов
последовательных разностей1.
Для проверки гипотезы (16.12) с помощью данного критерия подсчи-
тывают величину
(») _ «’(и)
» (»)
где g2(n) =	£ (*(• + О ~ «(О)’:
•=1
Если окажется, что
7(«) < 7«‘П(«)>	(1616)
то гипотеза (16.12) отвергается. При этом величина 7™ln(n) для п > 60
подсчитывается по формуле
min/ \	1 ,
7а (п) = 1 +
«а
У» + 0,5(1 + «а)
где иа — а-квантиль нормированного нормального распределения.
Величины 7а1п(п) при п < 60 для трех наиболее употребительных
значений уровня значимости а даны в табл. 4.9 книги [Большее Л. И.,
Смирнов Н. В.].
1 В этом случае данный критерий оказывается более мощным (см. гл. 8), чем преды-
дущий. Это означает, в частности, что если мы воспользуемся обоими этими кри-
териями при данном объеме выборки п и заданном уровне значимости а (т. е. при
заданной вероятности ошибочного отвержения гипотезы (16.12)), то вероятность
ошибиться в другую сторону (т.е. принять гипотезу (16.12), в то время как на са-
мом деле она является ошибочной) окажется меньшей в случае критерия квадратов
последовательных разностей.
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА	803
16.3.2.	Методы сглаживания временного ряда (выделение
неслучайной составляющей)
Методы выделения неслучайной составляющей в траектории, отра-
жающей поведение анализируемого временного ряда (16.1*), можно услов-
но разделить на два типа.
Методы первого типа (аналитические) основаны на допущении, что
кам известен общий вид неслучайной составляющей в разложении (16.2)
/(«) = x(A)Ap(t) +	+ x(C)lfr(t).	(16.17)
Например, рассматривая график временного ряда из примера 16.2
(см. рис. 16.2), исследователь может предположить, что неслучайная со-
ставляющая динамики курса анализируемых акций описывается линейной
функцией времени t, т. е.
f(t) = 0О 4- 6it>
где 0Q и ^1 — некоторые неизвестные (подлежащие статистическому оце-
ниванию) параметры модели. Тогда задача выделения неслучайной со-
ставляющей (или — задача элиминирования случайных остатков в раз-
ложении (16.2), или, что то же, — задача сглаживания временного ряда
(16.1’)) сведется к задаче построения «хороших» оценок 0О и 0j для пара-
метров 0О и 01.
Соответствующие методы мы назвали аналитическими, поскольку
«на выходе» задачи мы будем иметь явное аналитическое
задание (оценку, приближение) f(t) для искомой неслучайной соста-
вляющей f(t). Другими словами, f(t) будет представлена в виде форму-
лы f(t; О) функции известного вида, в которой неизвестные параметры
0 = (0о,0ь • • •) заменены их статистическими оценками О.
Методы второго типа (алгоритмические) не связаны ограничитель-
ным допущением о том, что общий аналитический вид искомой функции
(16.17) известен исследователю. В этом смысле они являются более гиб-
кими, более привлекательными. Однако «на выходе» задачи они доста-
вляют исследователю лишь алгоритм расчета оценки f(t) для искомой
функции f(t) в любой наперед заданной точке t и не претендуют на ана-
литическое (т. е. заданное в виде явной формулы) представление функции
(16.17).
Аналитические методы выделения (оценки) неслучайной со-
ставляющей временного ряда. Эти методы реализуются в рамках мо-
делей регрессии, в которых в роли зависимой (объясняемой) переменной
выступает переменная x(i), генерирующая анализируемый временной ряд
(16.1 ), а в роли единственной объясняющей переменной — время t.
804
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Таким образом, рассматривается модель регрессии вида
х(«) = /(«;0) + ф),	/ = 1,2,...,п,
в которой общий вид функции /(f; G) известен, но неизвестны значения
параметров 0 = (0о,0ь • • • »^т)Т* Оценки 0 параметров 0 строятся по
наблюдениям {t; a?(f)}t=i,2,...,n с помощью методов, описанных в гл. 15. Вы-
бор метода оценивания зависит от гипотетического вида функции /(<; 0)
и стохастической природы случайных регрессионных остатков e(t). Так,
например, если функция f(t; 0) имеет вид алгебраического полинома сте-
пени р, т. е.
/(«; 0) = 0О 4- 0^ + . • • + eptp,	(16.18)
и при этом длина временного ряда п существенно превышает степень это-
го полиномар1, а регрессионные остатки е(1),е(2),...,е(п) взаимно некор-
релированы, то оценки 0 параметров 0 могут быть получены с помощью
обычного метода наименьших квадратов (см. п. 15.3.1, формулу (15.22)):
0 = (ХТХ)-’ХТУ.	(16.19)
В этой формуле п х (р + 1) — матрица X наблюденных значений
объясняющих переменных имеет в данном случае вид:
/1 1 1’ ... 1₽\
х I 1 2 22 ... 2Р j
I ,	2 Р J
\ 1 П П	... П /
а вектор-столбец наблюденных значений зависимой переменной У =
(г(1),»(2),...,г(п))т.
Отказ от взаимной некоррелированности регрессионных остатков в
данной модели повлечет за собой необходимость использования практи-
чески реализуемого обобщенного МНК (см. п. 15.9.1); исследование моде-
лей (16.18), в которых неслучайная компонента /(t;0) нелинейна относи-
тельно оцениваемых параметров 0, потребует техники статистического
анализа нелинейных моделей регрессии (см. п. 15.12) и т.д.
Алгоритмические методы выделения неслучайной составля-
ющей временного ряда (методы скользящего среднего). В основе
1 Обычно удовлетворительная надежность статистических оценок О параметров 0
достигается уже при п > 4р, но, как минимум, требуется, чтобы n > р + 1.
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
805
этих методов элиминирования случайных флуктуаций в поведении анали-
зируемого временного ряда лежит простая идея: если «индивидуальный»
разброс значений члена временного ряда x(t) около своего среднего (сгла-
женного) значения а характеризуется дисперсией о2, то разброс среднего
из N членов временного ряда (ж(1) 4- ж(2) 4- • • • 4- x(N))/N около того же
значения а будет характеризоваться гораздо меньшей величиной диспер-
сии, а именно дисперсией, равной о2 /N. А уменьшение меры случайного
разброса (дисперсии) и означает как раз сглаживание соответствующей
траектории. Поэтому выбирают некоторую нечетную «длину усреднения»
N = 2m 4- 1, измеренную в числе подряд идущих членов анализируемого
временного ряда (конкретный выбор числа т зависит от специфики ис-
ходных данных, но, как правило, т выбирают таким образом, чтобы оно
удовлетворяло неравенству т < п/3’, обычно т не превышает трех; бо-
лее подробно о выборе m см. ниже). А затем сглаженное значение /(t)
временного ряда x(i) вычисляют по значениям x(t — m), x(t — т 4* 1),
..., x(i)t x(t 4- 1),..., x(t 4- m) по формуле
/(0 = 52	+ t = m+l,m + 2,...,n-m,	(16.20)
k~—m
где wjt (k = —m, —m 4- 1,... ,m) — некоторые положительные «весовые»
коэффициенты (или просто «веса»), в сумме равные единице, т. е. > 0
т
и 52 wk = 1- Поскольку, изменяя t от т 4- 1 до п — т, мы как бы
к=—т
«скользим» по оси времени (так что при переходе от t к t 4- 1 в составе
слагаемых правой части (16.20) происходит замена только одного слагае-
мого x(t—m) слагаемым x(t4-m4-l)), то и методы, основанные на формуле
(16.20), принято называть методами скользящей средней (МСС).
Очевидно, один МСС отличается от другого выбором параметров т
и	(А = —т, —т 4-1,..., т). Остановимся на этом подробнее.
Определение параметров основано на следующей процедуре. В
соответствии с известной теоремой Вейерштрасса любая гладкая функ-
ция f(x) при самых общих допущениях может быть локально (т.е. в
ограниченном интервале изменения ее аргумента t) представлена алге-
браическим полиномом подходящей степени р. Поэтому берем первые
2т 4- 1 членов временного ряда i(l),x(2),...,z(2m4 1), строим с помо-
щью МНК полином ^i(t) степени р, аппроксимирующий поведение этой
начальной части траектории временного ряда, и используем этот поли-
ном для определения оценки f(t) сглаженного значения /(х) временного
ряда в средней (т.е. (т 4- 1)-й) точке этого отрезка ряда, т.е. полагаем
806
ГЛ. 1в. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
/(m + 1) = -к 1). Затем «скользим» по оси времени на один такт и
таким же способом подбираем полином £j(0 той же степени р к отрезку
временного ряда ж(2), г(3),..., х(2т4-2) и определяем оценку сглаженного
значения временного ряда в средней точке сдвинутого на единицу отрезка
временного ряда, т.е. f(m 4- 2) = х2(т 4- 2), и т. д.
В результате мы найдем оценки для сглаженных значений /(f) ана-
лизируемого временного ряда при всех f, кроме f = l,2,...,m и t =
п,п — 2,...,n — m4-1.
Покажем, что подбор наилучшего (в смысле критерия МНК) ап-
проксимирующего полинома к траектории анализируемого временного ря-
да (на заданном временнбм интервале) действительно приводит к фор-
муле вида (16.20), причем результат (т.е. значения коэффициентов w*,
к = — тп, — т 4-1,..., »п) не зависит от того, для какого именно из «сколь-
зящих» временных интервалов был осуществлен этот подбор.
Начнем с простого примера. Будем полагать, что локальное поведе-
ние сглаженной функции /(f) описывается алгебраическим полиномом 1-й
степени ( р = 1), т.е. что на выбранном временном интервале (протяжен-
ностью 2т 4-1 временных тактов) неслучайная составляющая /(ж) может
быть аппроксимирована линейной функцией времени:
/(f) = ^04-^f, f = 1,2,..., 2т 4-1.
Без ограничения общности можно переобозначить моменты времени та-
ким образом, чтобы рассматривать нашу модель на временнбм отрезке
f' = -m, -т 4- 1, ...» -1,0, 1,...,тп- l,m (тогда средняя точка будет
соответствовать t* = 0). Очевидно, «новое» (условное) время f связано
со «старым» временем f соотношением t' = t — (m 4-1).
Итак, мы хотим подобрать коэффициенты 0$ и 0^ таким образом, что-
бы минимизировать критерий МНК, т. е.
Е (*(*') - 6о - »!<')’ -» min.
t'=—m
Дифференцирование левой части по 0о и и приравнивание получен-
ных частных производных к нулю дает систему уравнений для определе-
ния МНК-оценок 0q и
Im	m
(2m+1)0O+ 0i Е |,= Е «(<').
t=—m	t'=—m
m	m	m
E ''+«> E (*')’ = E
V-=—m	t’=—m	t»=—m
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
807
(16.21)
Поскольку	= 0, а оценка сглаженного значения временного ряда
t'=-m
определяется в средней точке рассматриваемого временного интервала
соответствующим значением функции во 4- при t' = 0, то:
/(m + l) = 4 + V]e>=e = «о = 2^П £ Х(?)
t'=—т
. 2m+l
= 2m+T g
Проделав тот же самый анализ для любого другого временного ин-
тервала $ = fc + 1, fc + 2, ..., fc 4- 2m 4-1 (k = 1,2,..., n - 3m — 1), мы
получим аналогичный результат. Таким образом, в общем случае имеем:
1 т
ло=£-п Е <t+k'><	(16-21)
Z<r7/€ **j“ А
fc=—т
т. е. при линейное характере локальной аппроксимации траектории вре-
менного ряда в качестве его сглаженного значения в точке t следует
брать среднее арифметическое из окаймляющих его 2т 4-1 соседних зна-
чений	x(t — тп4“1), •..., z(t4-m), или, в терминах весовых
коэффициентов: w_m = w_m+1 = • • • = wm = l/(2m 4-1).
Нетрудно показать, что если локальное поведение сглаженной функ-
ции f(t) описывается алгебраическим полиномом нулевой степени (р = 0),
т.е., другими словами, если функция f(x) локально ведет себя как по-
стоянная величина (f(t) = во = const), то оценка сглаженного значения
временного ряда в точке t определяется той же самой формулой (16.21).
Рассмотрим теперь случай р = 2, m = 2. Это означает, что в «сколь-
зящий» временной отрезок, по которому будет производиться усреднение
значений временного ряда, мы будем включать 5 точек (N = 2т 4* 1 =
2 • 2 4-1 = 5) и что локальное поведение сглаженного временного ряда вну-
три каждого такого отрезка мы будем аппроксимировать параболой 2-го
порядка, т. е.
/(«') = 00 + «1? + e2(«')2, t' = -2,-1,0,1,2
(здесь t' — уже «переобозначенное» время, т. е. сдвинутое по отношению
к реальному времени таким образом, чтобы точка I* = 0 была бы средней
па каждом временном отрезке усреднения).
Определяя оценкй и 02, соответственно, коэффициентов ^о,^1 и
по методу наименьших квадратов, имеем:
ГЛ. 1в. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
2
• критерий МНК: Q(0) = S (®(^) — 0о —	~ 02$ 2)2;
t'=-2
• система уравнений МНК:

E z(i') - 50o - *i E *'
*'=-2
= 0,
2
-0S E (*')’
t'=—2
2
t'=-2
-01 Е («')’ - 02 Е (I't
t»=-2	f=-2
2
= 0,
(16.22)
= -2 [ Е («')’*(«') - 0» Е («')’
а	Lt’=—2	t'=—2
-0i E («')3-02 E («V
t*=-2	t'=—2
= 0;
• решение системы уравнений МНК (с учетом того, что Е =
t'=-2
2	, я
Е («')’ = 0):
V--2
2	2	2	2
Е («')* • Е *(«') - Е (*')’ Е («')’*(«')
t=—2	t'=-2	t'=-2	t'=-2
Gq = -------------------------------------—5-----------
5 e a')4 - ( e (<')’)
t»=-2	\t'=-2	/
34 f z(t')-10 E (|')’г(4')
P=-2____________t'=-2__________
170 - 100
=	- M-2) + 12x(-l) + 17г(0) + 12г(1) - 3z(2)],
oo
E <'*(<')	.
01 =	--------= 7K [ ~ М-й) - *(-l) + x(l) + 2z(2)],
E («')’	10
t'=-2
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
809
3	3	2
5 Е (С’*(С - Е (t')2 Е »(<)
л t' = -2	t'=—2	t'=-2
₽2 — ------------------~-------Г“2-----
5 Е (С - ( Е (С2)
t*=—2	\t'=-2 /
= nl2x(-2) ~х(-1) _ 2х(0) _ х(1)+2х(2)Ь
Соответственно, оценка сглаженного значения /($) анализируемого
временного ряда в точке t определится значением оцененной параболы
+ dit' 4- 02(t')2 при I* = 0, т.е.
/ (0 = 0Q +	+ 0з(^)2]<»=:О =
= ~ [ - 3x(t - 2) + 12г(« - 1) + 17x(t) 4-12x(t 4-1) - 3x(t + 2)].
<50
Таким образом, мы снова получили формулу вида (16.20), в которой
w_2 = w2 = —3/35, w_j = Wi = 12/35 и w0 = 17/35.
Продемонстрированная на двух простых примерах процедура опре-
деления весов в формуле (16.20) имеет общий характер. Если по 2т + 1
точкам подбирают с помощью МНК алгебраический полином степени р,
то необходимо минимизировать критерий вида
т
Q(&) = Е (*(С-«0-Ы'-------W)”)3.	(16.23)
t'=-m
Минимизация Q(Q) по О приводит к уравнениям относительно О, анало-
гичным (16.22), которые разбиваются на две более простые подсистемы
т f к
из-за того, что £ (i) =0 при всех нечетных значениях k. Решения
i'=-m
этих систем зависят от численных значений сумм вида У2 (О (где
t'= —m
I	т I к i
четно) и линейных функций от x(t ) вида £ (t )	) (это следует из
t* =—ТП
самой формулы МНК-оценок (16.19) и вида вектора Y в данной задаче).
Оценкой /(I) неслучайной составляющей f(t) анализируемого временного
ряда x(t) в точке t = to (to = m 4- 1, m 4- 2,.. .,2n — m) будет величи-
на 0o, представляющая собой взвешенное среднее значений от ®(t0 — т)
до s(to 4- т). В таблице 16.4 приводятся подсчитанные указанным выше
способом значения весовых коэффициентов (fc = —т, —т +1,..., —1,0)
для ряда значений тир.
810
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Значения для положительных к не приводятся, так как в силу
имеющего место свойства симметрии этих коэффициентов Wk — w_k.
Таблица 16.4. Значения весовых коэффициентов в формуле метода скользяще-
го среднего (16.20) для различных длин отрезков усреднения т
и порядков аппроксимирующих полиномов р
т	Р	ш_т	W-m+l	« • •	W0
т0 5 7 9 7 9	0 или 1 2 или 3 2 или 3 2 или 3 4 или 5 4 или 5	1 2я1о+1 3 35 2 21 21 231 5 231 15 429	1 2m0+l 12 35 3 21 14 231 30 231 55 429	а • • 6 21 39 54 231 231 75 231 30 135 429 429	1 2mo+l И 35 7 21 59 231 131 231 179 429
Из самого хода процедуры вычисления оценок параметров G с помо-
щью минимизации критерия Q(O) (см. (16.23)) и вытекающего из него
вида (определяющего значения весовых коэффициентов ги* в формуле
(16.20)) можно вывести следующие важные свойства этих коэффициентов.
(1°) веса Wk симметричны относительно серединного значения w0, т.е.
Wk = W-k> & = 1,2,..., т (это следует из того факта, что они по-
лучены как функции сумм Е (*	), которые сами симметрии-
t*——т
ны);
m
(2°) сумма всех весов wk равна единице, т.е. £ wk = 1 (moi что это
к=—т
должно быть так, можно проверить на таком частном случае:
пусть все значения членов временного ряда на анализируемом вре-
менном отрезке равны одной и той же константе с; тогда сколь-
л	m	т
зящее среднее f(t) = Е + *) = с Е wk тоже должно
к=—т	к=—т
быть равно этой константе с, а это может быть только в случае
т
Е Wk = 1);
к=—т
(3°) при одной и той же длине N = 2т 4- 1 временнбго отрезка, по ко-
торому производится усреднение, веса Wk в формуле (16.20) для по-
линомов четной степени (т. е. для р = 21,1 = 0,1,2,...) будут теми
же самыми, что и для полиномов степени, на единицу бблыией (т. е.
для р =2/4-1); этот результат виден из того, что при составлении
систем уравнений, аналогичных (16.22), для р = 21 и для р = 214-1
мы получим две системы, каждая из которых распадается на две
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
811
подсистемы: одна из этих подсистем будет содержать параметр
6q в качестве неизвестного задачи, а вторая — нет; так вот, пер-
вые две подсистемы уравнений (гл. е. подсистемы, содержащие Oq)
в системах, соответствующих р = 21 и р = 21 4- 1, будут одними и
теми же, а следовательно, и решения для 0О будут одинаковыми (а,
ведь, именно значениями #о определяются веса w*);
Замечание 1 (определение сглаженных значений в крае-
вых точках).
В качестве сглаженных значений /(<) в т первых точках и в т по-
следних точках всего анализируемого временного интервала используются
соответствующие значения локально аппроксимирующих полиномов, по-
строенных, соответственно, по 2т 4- 1 первым и по 2т 4- 1 последним
точкам анализируемого временного ряда, а именно:
(	=	+	+	+	*=1,2,....m;
/(<) = < i„_2m(*) = e<0n-2m) +	+ ... + <?‘n-”n)*'>,
I	t = n — m +
(16.24)
В (16.24) ii(t) — сглаживающий полином, построенный по 1-му
интервалу сглаживания, т.е. — по точкам (l,i(l)),(2,z(2)),...,(2m 4-
1,з(2т 4-1)) (соответственно, j = 0,1,... ,р, — МНК-оценки параме-
тров этого полинома, вычисленные по точкам 1-го интервала сглажива-
ния), a in-2m(0 — сглаживающий полином, построенный по (п — 2т)-
му интервалу сглаживания, т.е. — по точкам (п — 2т,х(п — 2m)),
(я - 2m 4- l,z(n - 2m 4- l)),...,(n,a;(n)) (соответственно,	j =
0,1,...,p, — МНК-оценки параметров этого полинома, вычисленные по
точкам (п — 2т)-го интервала сглаживания).
Замечание 2 (усреднение по четному числу точек).
До сих пор мы использовали нечетное число (2m 4-1) точек в качестве
базы для расчета скользящего среднего. Однако специфика конкретной
задачи зачастую обусловливает необходимость использования интервала
скользящего усреднения, содержащего четное число точек. С подобны-
ми ситуациями мы столкнемся при вычислении среднесуточных часовых
данных (24 часа в сутках), среднемесячных недельных данных (4 недели
в месяце), среднегодовых квартальных или месячных данных (4 квартала
и 12 месяцев в году) и т. п.
В этих случаях, как и прежде, сглаженное значение f(t) временного
ряда x(t) вычисляется в средней точке скользящего интервала усреднения.
Очевидно, таковой (при длине интервала усреднения, равной 2m, и при
812
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
начальной точке к этого интервала) будет точка
+ fc + (fc + 2m)— 1	,	1	.	, «	»
t —-------—---------= к 4- т — к = 1,2, ...,п — 2т + 1.	(16.25)
Другими словами, мы будем получать при этом сглаженные значения ана-
лизируемого временного ряда не в точках его наблюдения t = 1,2,..., п, а
для моментов времени t* (см. (16.25)), лежащих посередине между точка-
ми наблюдения. Чтобы получить сглаженное значение временного ряда
x(t) именно в одной из точек его наблюдения (например, в точке t = к+т\
необходимо вычислить его сглаженные значения для двух окаймляющих
эту точку промежуточных моментов времени (т.е. для t* = к + т — | и
tJ = $J'4-l = fc4-m-f-|)H взять их среднее арифметическое, т.е.:
f(k + m) = |
к + т —
1\
9 ) +	( к + т + 9 )
“У	\.	“У
Предположим, например, что имеются помесячные наблюдения с ян-
варя по декабрь, «привязанные» к последнему дню каждого месяца. Про-
стое скользящее среднее (т.е. МСС с р = 0 или 1) по двенадцати точ-
кам (т. е. N = 2т = 2 • 6 = 12) дает оценку значения неслучайной со-
ставляющей для середины июля (т.е. для точки Г = (6 + 7)/2 = 6,5).
Поэтому, чтобы получить сглаженное значение на конец июляу мы возь-
мем арифметическое среднее сглаженных значений, вычисленных для се-
редины июля и середины августа. Нетрудно убедиться, что это экви-
валентно вычислению 13-месячного среднего с весами Wj =	= 1/24,
w2 = w3 = ... = w12 = 1/12. To есть при расчете сглаженного значения
берутся два январских наблюдения, но каждое входит с весом, в два раза
меньшим, чем наблюдения за другие месяцы.
Замечание 3 (влияние скользящего усреднения на оста-
точную случайную компоненту в разложении (16.2)).
При выделении неслучайной составляющей f(t) анализируемого вре-
менного ряда x(t) с помощью методов скользящего среднего мы должны
отдавать себе отчет в том, что получаемая при этом оценка f(t) лишь
приближенно описывает поведение функции (16.17) и сама продолжает
содержать в себе некоторую, хотя и менее ярко выраженную (в смысле
уменьшения дисперсии случайных колебаний) случайную составляющую
ё(0-
Рассмотрим теперь, как влияет выделение неслучайной составляю-
щей с помощью МСС на исходные случайные остатки е(1) анализируе-
мого временного ряда х(1) (см. (16.2)) в ситуации, когда эти исходные
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
813
случайные остатки взаимно некоррелированы и гомоскедастичны, т. е.
Еб(«)нО,
Е (e(t)e(t + т)) = ( ^ п₽и т = 0>	(16 26)
К k k ”	10	при т / 0.
Пусть wi, w2,..., w2m+l будут весами, используемыми при вычи-
слении среднего по 2m 4* 1 последовательным членам временного ряда
z(t-bl),... ,s(t4-2m), z(t + 2m +1). С теми же весами будут суммировать-
ся и остаточные компоненты e(t 4- 1), e(t 4- 2),..., e(t 4- 2m +1). Поэтому
случайный остаток e(t 4- m + 1), характеризующий оценку сглаженного
значения f(t 4- m 4- 1) в средней точке 14- тп 4-1, будет иметь вид
2т+1
е(«4-т4-1)= У^ 4- к).
Лс=1
Легко вычисляются:
Ee(t) = Ee(t 4- m 4-1) = 0,
2m+l	2 m 4-1
De(t) = De(i 4- m 4-1) = De(i) wk — ff2 У2 wj, (16.27)
k=l	Ы
cov (e(t 4- m 4- l),e(t 4- m 4-1 4- r))
= E[wic(t 4-1)4- w2e(t 4- 2) 4-... 4- w2m+if(t 4- 2m 4- 1)]
x [w1£(t -Ь 1 4- r) 4-... 4- w2m+1e(« 4- 2m 4-1 4- r)].	(16.28)
Учитывая взаимную некоррелированность исходных случайных ос-
татков £(1),£(2),...,е(п) (см. (16.26)), соотношение (16.28) может быть
преобразовано к виду
2тп+1—т
cov (ё(*4-тп4-1),е(*4-т4-14-г)) = ff2 wjwj+t, т = 1,2,...,2m.
i=i
(16.28х)
Из (16.28 ) и (16.27), в частности, следует, что автокорреляция меж-
ду преобразованными случайными остатками e(t), разнесенными друг от
друга на т единиц, равна
2 m 4-1— т
£ WjWy+T
rt — 2m+i » г = 1,2,..., 2m.	(16.29)
Е w?
J=1
814	ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Отсюда следует, что последовательность сглаженных значений /(<)
имеет ненулевые автокорреляции, определяемые формулой (16.29), вплоть
до порядка 2т (то, что автокорреляции более высокого порядка равны
нулю, следует непосредственно из (16.28)). Более того, для скользящих
средних, наиболее часто применяемых на практике, величина гг(1) = ry( 1)
будет положительной и может принимать достаточно высокие (близкие к
единице) значения. Таким образом, ряд сглаженных значений /(t) будет
более гладким, чем исходный временной ряд x(t) (так как дисперсия /(£),
равная дисперсии e(t), будет меньше исходной дисперсии ст2, что следует
из (16.27)), однако в нем могут появиться систематические колебания,
обусловленные автокоррелированностью его последовательных значений
(эффект Слуцкого-Юла).
Метод экспоненциально взвешенного скользящего среднего
(метод Брауна1). До сих пор все методы скользящего среднего постро-
ения оценок /(<) для неслучайных составляющих f(t) анализируемого
временного ряда x(t) основывались на критерии (16.23) классического
МНК, в соответствии с которым все исходные статистические данные
(t,□;(/)),t = 1,2, ...,п, имеют равный вес. Однако в задачах прогноза,
в которых сглаженная функция f(t) используется обычно для экстрапо-
ляции в будущее, кажется более естественным сравнительно «недавним»
исходным данным придавать, в определенном смысле, больший вес, чем
наблюдениям, относящимся к далекому прошлому (в таких случаях гово-
рят о дисконтировании наблюдений). Обратимся к одному из наиболее
распространенных методов выделения «более свежих» наблюдений — ме-
тоду экспоненциально взвешенного скользящего среднего (МЭВСС).
В соответствии с этим методом оценка сглаженного значения /(<) в
точке t определяется как решение оптимизационной задачи вида
<?(/) = £ А*(г(< -*)-/)’_ min,	(16.30)
fc=0	J
где А — некоторое положительное число, меньшее единицы (т. е. О < А <
1).
Мы видим, что веса А* при «невязках» в критерии Q(f) обобщенного
(«взвешенного») МНК уменьшаются экспоненциально по мере удаления
наблюдений x(t—к) в прошлое (т. е. по мере роста к), — отсюда и название
метода.
1 См. Brown R. G. Smoothing, Forecasting and Prediction. Prentice-Hall, Englewood
Cliffs, N.Y., 1963.
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
815
Решение оптимизационной задачи (16.30), т.е. дифференцирование
Q(f) по /, приравнивание полученной производной к нулю и решение обра-
зовавшегося таким образом уравнения относительно f дает:
1 А fc=0
(16.31)
Другими словами, речь вновь идет о скользящем усреднении исходных
значений я(0 анализируемого временного ряда. Однако в отличие от
обычного МСС в данном случае, во-первых, скользит только правый ко-
нец интервала усреднения (левый его конец закреплен в точке t = 1) и,
во-вторых, веса при x(t — к) экспоненциально уменьшаются по мере «уда-
ления в прошлое» (т.е. по мере роста к). Кроме того, формула (16.31)
дает оценку сглаженного значения временного ряда не в средней, а в пра-
вой конечной точке интервала усреднения.
Посмотрим, как преобразовались взаимно некоррелированные случай-
ные остатки е(0 из разложения (16.2) при переходе от исходных значений
временного ряда x(t) к сглаженным /(0 по формуле (16.31).
Поскольку преобразованные остатки eft) связаны с исходными остат-
ками eft) тем же самым соотношением, которым связаны значения fft) и
x(t) (см. (16.31)), то очевидно:
Ее(0 = О,
3(1 - А)(1 +Д«)
(1 + А)(1- А*)’
(16.32)
Из (16.32) видно, что при значениях А, не слишком близких к еди-
нице, и для достаточно удаленных от прошлого значениях t случайные
остатки е(0 (а следовательно, и сглаженные значения 7(0) подвержены
существенно меньшему случайному разбросу, чем х(0, т.е. ведут себя
более гладко.
Замечание 4 (случаи «бесконечно удаленного» прошло-
го).
Если анализируемый временной ряд достаточно длинный (т. е. п до-
статочно велико), то для представляющих главный интерес в прогнозе
«свежих» значений временного ряда а:(0 (т.е. при t близких к п) мож-
но приближенно допускать, что их прошлое как бы «уходит в бесконеч-
ность». Тогда соотношения (16.30), (16.31) и (16.32) могут быть замене-
816
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
ны, соответственно, соотношениями
<?(/) = 52 А*(з(1 -к)- f)2 — min,
Jt=O
оо
fc=O
(16.30')
(16.31')
(16.32')
Кроме того, в этом случае легко непосредственно проверить справед-
ливость следующего полезного рекуррентного соотношения
/(0 = Xf(t - 1) + (1 - А)ж(0.	(16.33)
16.3.3. Подбор порядка аппроксимирующего полинома с
помощью метода последовательных разностей
Реализация алгоритмических методов выделения неслучайной соста-
вляющей временного ряда, и в частности методов скользящего среднего,
связана с необходимостью подбора порядка р локально-аппроксимирующе-
го полинома. Эта же задача возникает и при реализации аналитических
методов выделения неслучайной составляющей (см. (16.18)). При реше-
нии этой задачи широко используется так называемый метод последо-
вательных разностей членов анализируемого временного ряда, который
основан на следующем математическом факте: если анализируемый вре-
менной ряд x(t) содержит в качестве своей неслучайной составляющей
алгебраический полином f(t) =	+ ... + 0ptp порядка (степени) р,
то переход к последовательным разностям1 я(1),а:(2),... ,я(п), повто-
ренный р 4-1 раз (гв. е. переход к последовательным разностям порядка
р+ 1), исключает неслучайную составляющую (включая константу 0О)>
1 Если имеется ряд чисел х(1), х(2),..., х(п), то последовательные разности этого ряда
обозначаются с помощью Ax(t) = x(i) — x(i — 1), t = 2,..., п. Последовательные
разности 2-го порядка — это разности от последовательных разностей, т. е. A3r(t) =
A(Ax(t)) — Ax(t) —Ax(t —1) = (x(t) —r(t —1)) —(r(t—1) —x(t —2)) = x(t) —2x(i —1)+
x(t — 2). Аналогично определяется последовательная разность любого (Л-го, к > 3)
порядка: A*z(t) = A(A*-1x(t)). Нетрудно показать (например, методом индукции),
что
Д*х(0 = x(t) - Cjx(t - 1) + Cjx(t - 2) - ... + (-1 )*x(t - fc),	(16.34)
где Сд — это число сочетаний нз к элементов по /.
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
817
оставляя элементы, выражающиеся только через остаточную случай-
ную компоненту e(t).
Продемонстрируем справедливость этого утверждения на простых
примерах.
1) Пусть р = 1, т. е.
x(t) = eQ +	+ e(i), t = 1,2,
Тогда
Az(f) = x(t) - x(t - 1) =	+ (e(0 - eft - 1)),
Д2x(t) = Дя(4) - Дх(£ — 1) = e(t) - 2c(t — 1) + e(t — 2).
Мы видим, что если неслучайная составляющая f(t) временного ряда
выражается линейной функцией времени (т.е. является алгебраическим
полиномом времени порядка р = 1), то последовательность вторых раз-
ностей Д2 x(i) анализируемого временного ряда уже не будет содержать
неслучайной составляющей, а может быть представлена только случайны-
ми остатками e(t), связанными с исходными остатками е($) соотношением
ЭД = е(0 - 2е(« - 1) + e(i - 2), t = 3,4,... ,n.
2) Пусть р = 2, т. е.
x(t) = ев + Bit + в212 + e(t), I = 1,2,..., п.
Тогда
д®(«) = е0 + + в3? -б0- «»(* -1) - e,(t -i)2 + (e(t) - £(t -1))
= Bl - Bl + 2Bit + (e(t) - e(t - 1)),
Д2г(<) = Az(t) - Дг(| - 1) = 2B3 + (e(i) - 2e(t - 1) + e(t - 2)),
Д3г(() = Д2®(0 - Д2а:(1 - 1) = e(t) - Зе(« - 1) + 3e(t - 2) - e(i - 3),
t = 4,5,...,n.
Мы вновь получили подтверждение сформулированного выше мате-
матического факта: при неслучайной составляющей временного ряда, вы-
раженной в виде алгебраического полинома времени t порядка р = 2, по-
следовательность третьих разностей Д3ж(/) уже не будет содержать не-
случайной составляющей, а будет представлена только в терминах слу-
чайных остатков е(2) разложения (16.2).
818
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Теперь рассмотрим общий случай. Пусть
z(t) = 0o+«i‘ + --- + V’ + e(t). t=l,2,...,n,	(16.35)
где случайные остатки e(t) удовлетворяют требованиям (16.26).
Последовательно переходя к разностям порядка р 4-1, с учетом (16.34)
получаем:
Д’>+1х(/) = £(1)-С^1£(1-1)
+ C’+ie(t - 2) - ... + (-l)”+l£(t - р - 1),	(16.36)
t = p + 2,p+3,...,n.
Вычислим среднее значение и дисперсию членов последовательности
Ар+1х(*):
E(Ap+1z(t)) = О,
D(A’+,a:(t)) = Dx(t) [1 + (<£+,)’ + (С’+1)2 +... + (C£+l)2 + 1] (16.37)
_____________ 2/^P+l
-° G2(p+1)-
При получении выражения для D(Ap+1z(t)) мы воспользовались вза-
имной некоррелированностью исходных остатков е(1), е(2),..., е(п), а так-
же тождеством
1 + (Ср+1)2 + • •  + (Ср+1 )3 + 1 = ^2(^+1) •
Для обоснования последнего тождества заметим, что из разложения
следует, что коэффициент при гЛ1-1 подсчитывается по формуле
*1 = i+(^p+i)2+---+(^J+i)2+i;
но тот же самый коэффициент, подсчитанный с использованием разложе-
ния
(1+г)з^*> = 1+c2’(p+1)z+...+свд-* +г’<₽+»,
оказывается равным
16.3. НЕСЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ ВРЕМЕННОГО РЯДА
819
Теперь можно обсудить способ подбора порядка р полинома, пред-
ставляющего собой неслучайную составляющую f(t) в разложении ана-
лизируемого временного ряда аг($). Заметим, прежде всего, что если
мы знаем, что среднее значение Е£ наблюдаемой случайной величины £
равно нулю, то выборочным аналогом ее дисперсии является величина
2 Л 2
р (n) = 2J & /п> где &»&»••• »€п — наблюденные значения этой случай-
is=l
ной величины. Если же Е£ / 0, то выборочным аналогом дисперсии будет
статистика ££?/» — (£ ft/»)2, так что величина д2(п) будет давать
t=i	t=i
в этом случае существенно завышенные оценки для Df. Возвращаясь к
последовательному переходу к разностям Afex(t), k = 1,2,... ,р 4- 1, — в
общем случае (16.35), отметим, что при всех к < р 4- 1 средние значе-
ния этих разностей будут отличны от нуля, так как будут выражаться не
только через остатки e(t), но и через коэффициенты ,..., и степени
t. И только начиная с к = р+1 (и для всех к > р4-1) оказывается справед-
ливой формула (16.37), а следовательно, при к > р4-1 можно утверждать,
что:
Е(Д*г(0) = 0 и «г2 = В(Д*г(0)/С5» п. (16.37')
С учетом этих замечаний можно сформулировать следующее правило
подбора порядка сглаживающего полинома р, называемое методом после-
довательных разностей.
Последовательно для к = 1,2,... вычисляем разности Д*я(4) (4 =
1,2,..., п — к), а также величины
*’(*)=
, Н	L	П
кЬ Е (Д*«(0)’
1=1_____________
^2*
(16.38)
Анализируем поведение величины д2(к) в зависимости от к. Учитывая
сделанные выше замечания, величина £?(&) как функция к будет демон-
стрировать явную тенденцию к убыванию до тех пор, пока к не достигнет
величины р 4- 1. Начиная с момента к = р 4- 1 величина (16.38) стабили-
зируется, оставаясь (при дальнейшем увеличении к) приблизительно на
одном уровне. Поэтому значение к = к0, начиная с которого величина
&\к) стабилизируется, и будет давать завышенный на единицу искомый
порядок сглаживающего полинома, т.е. р = ко — 1.
Для упрощения использования описанного метода в таблице 16.5 при-
ведены значения вспомогательных коэффициентов для к = 1,2,..., 10.
820
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Таблица 16.5. Значения вспомогательных коэффициентов
к	1	2	3	4	5	6	7	8	9	10
СяЛе	2	6	20	70	252	924	3432	12870	48260	184756
Этот метод привлекателен своей простотой, но его практическое при-
менение требует определенной осторожности. Последовательные значения
д?(к) не являются независимыми и часто обнаруживается тенденция их
медленного убывания (а иногда возрастания) без видимой сходимости к
постоянному значению. Кроме того, процесс перехода к разностям имеет
тенденцию уменьшать относительное значение любого систематического
движения, кроме сезонных эффектов с периодом, близким к временному
интервалу, так что сходимость отношения д2(к) не доказывает, что ряд
первоначально состоял из полинома плюс случайный остаток, а только
то, что он может быть приближенно представлен таким образом. Однако
для нас этот метод ценен лишь тем, что он дает верхний предел поряд-
ка полинома р, который целесообразно использовать для элиминирования
неслуч айной составляющей.
16.4. Модели стационарных временных
рядов и их идентификация
В п. 16.2 был введен в рассмотрение класс стационарных временных
рядов, в рамках которого подбирается модель, пригодная для описания по-
ведения случайных остатков анализируемого временного ряда (16.2).
В данном пункте мы займемся изучением определенного набора линей-
ных параметрических моделей из этого класса, в том числе методами
идентификации этих моделей, т.е. методами статистического оценива-
ния участвующих в описании модели параметров по имеющейся в нашем
распоряжении траектории (16.1*) анализируемого временного ряда.
Таким образом, речь пока идет о моделировании не самих анализи-
руемых временных рядов, а лишь их случайных остатков e(t), т. е. того,
что мы получаем после элиминирования из исходного временного ряда
x(t) его неслучайной составляющей (16.17) (см. п. 16.3.2). И наши усилия
направлены на построение такой модели случайного остатка, которая по-
зволила бы прогнозировать значения этого остатка по его же значениям
в предыдущие моменты времени.
Так что в отличие от прогноза, основанного, например, на классиче-
ской регрессионной модели (когда в качестве прогнозного значения мы ис-
пользуем значение функции регрессии при заданных значениях объясняю-
щих переменных, игнорируя значения случайных остатков, см. п. 15.9.2),
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
821
(16.39)
(16.40)
E(«(l)«(t ± т)) =
в прогнозе временных рядов существенно используется взаимозависи-
мость и прогноз самих случайных остатков.
Условимся об обозначениях, принятых в данном пункте. Посколь-
ку представленные ниже модели временных рядов предназначены для опи-
сания поведения случайных остатков, то анализируемый (моделируемый)
временной ряд мы будем обозначать с помощью e{t) и, соответственно, по-
лагать, что его среднее значение (математическое ожидание) тождествен-
но, т.е. при всех значениях /, равно нулю, т.е. Ee(t) = 0. Временные
последовательности, образующие так называемый «белый шул<», будем
обозначать с помощью £(t). Это значит, что
Е£(0 = 0,
2
<т0 при г = 0
0 при т 0,
причем величина дисперсии а0 не зависит от t.
Описание и анализ рассмотренных ниже моделей могут формулиро-
ваться в терминах общего линейного процесса, представимого в виде взве-
шенной суммы настоящего и прошлых значений белого шума, а именно:
оо
<•(0 =«(t) + дi(t -1).+ ргЦ1 - 2) +... = 52	- к), (16.41)
к~0
оо
где 0о = 1 и 52/3* < оо.
*=о
Таким образом, белый шум можно рассматривать как серию им-
пульсов, в широком классе реальных ситуаций генерирующих случайные
остатки анализируемого временного ряда.
Существует эквивалентная соотношению (16.41) запись общего ли-
нейного процесса, при которой анализируемый временной ряд £(f) полу-
чается в виде классической линейной модели множественной регрессии,
когда в роли объясняющих переменных выступают значения самого вре-
менного ряда во все прошлые моменты времени (включая и бесконечно
удаленные), т.е.
оо
e(t) = ir,e(t -1)4-5r2£(t - 2) 4-... 4-«(t) = 53^0 “ *) + SW- (16.41')
fc=l
При этом весовые коэффициенты тг^тга,... связаны определенными
условиями, обеспечивающими стационарность ряда e(t). Переход от фор-
822
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
мы (16.41х) к форме (16.41) осуществляется с помощью последователь-
ной (и повторенной бесконечное число раз!) подстановки в правую часть
(16.41х) вместо e(t — 1),e(t — 2),... их выражений, вычисленных в соответ-
ствии с (16.41х) для моментов времени t — 1, t — 2 и т.д.
Введем в рассмотрение, наряду с общим линейным процессом вида
(16.41) или (16.41х), процесс смешанного типа, в представлении которо-
го присутствуют как авторегрессионные члены самого процесса, так и
скользящее суммирование элементов белого шума:
£(() = 7^(1 - к) + й(0 + £>«(< - Д (16-41")
*=1 >=1
Мы будем подразумевать, что р и q могут принимать и бесконечные зна-
чения, а также то, что в частных случаях некоторые (или даже все) ко-
эффициенты т или /3 равны нулю. Нам понадобится в дальнейшем сле-
дующая специальная форма представления спектральной плотности р(ы)
(w = w/2tt, так что 0 < ш < 1/2), справедливая для процессов типа
(16-41**) (обоснование такого представления можно найти, например, в
книге [Бокс Дж., Дженкинс Г., выл. 1], с. 67, 98-99):
2
p(w) = 2(Т0
2’
(16.9Ж)
О С w С
где многочлены А(я) и B(z) определяются коэффициентами, соответствен-
но, тк(г = 1,2,...,р) и^ (j = 1,2,...,?):
р
Д(я) = 1 - $2 ****’
*=1
b{z) = 1 + £
3=1
сто = а * —	— мнимая единица.
Теперь перейдем к рассмотрению конкретных линейных моделей ста-
ционарного временного ряда.
16.4.1. Модели авторегрессии порядка р (АР(р)-модели)1
Начнем описание этого параметрического семейства моделей с анали-
за простейших частных случаев.
1 В англоязычной специальной литературе эти модели известны хак AutoTLegreseive
processes of order р и кратко обозначаются A R(p)-models.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
823
Модель авторегрессии 1-го порядка — АР(1) (марковский
процесс). Эта модель представляет собой простейший вариант линейно-
го авторегрессионного процесса типа (16.41*), когда все коэффициенты тгу
кроме первого равны нулю. Соответственно, она может быть определена
выражением
€(0 = oe(t -1)4- 6ft),	(16.42)
где а — некоторый числовой коэффициент, не превосходящий по абсолют-
ной величине единицу (|а| < 1), a 4(t) — последовательность случайных
величин, образующая белый шум (т. е. последовательность случайных ве-
личин, удовлетворяющая соотношениям (16.39)-(16.40)).
Внимательный читатель вспомнит, что мы уже имели дело с этой
моделью. Ведь именно соотношением (16.42) были связаны между собой
регрессионные остатки в обобщенной модели множественной регрессии
с автокоррелированными остатками (см. п. 15.8, соотношения (15.106)-
(15.107), в которых роль параметра а выполнял параметр р). В специаль-
ной литературе последовательности е($), удовлетворяющие соотношению
(16.42), называют также марковским процессом. Мы не будем повторять
здесь выкладки (15.108)-(15.110), из которых следовало:
Ее(О = 0,	(16.43а)
r(£(t),e(t± к)) =	в*,	(16.43е)
D«(0 =	(16.43е)
cov(£(i),£(l ± к)}	= akDe(t).	(16.43г)
Проанализируем некоторые свойства временной последовательности,
представимой в виде (16.42). Из представления e(t) в виде (15.108) следует,
что eft) зависит от 6 ft) и всех предшествующих 6, но не зависит от
будущих значений б, т. е. от 6 ft + 1), 6 ft 4- 2) и т. д.
Заметим, что формула (15.108) представляет eft) как скользящее
среднее с бесконечной длиной отрезка усреднения, но с весами, дающи-
ми в сумме не единицу, а 1/(1 - а). Может показаться, что случайная
величина е(£), представимая в (15.108) как взвешенная сумма большого
числа случайных слагаемых, должна быть распределена (в соответствии
с центральной предельной теоремой, см. п. 4.3.1) нормально. Однако одно
из условий Ц.П.Т. нарушено: веса в этом среднем — величины различного
порядка.
Одно важное следствие (16.43в) состоит в том, что если величина |а|
близка к единице, то дисперсия eft) будет намного больше дисперсии 6ft).
А это значит (с учетом того, что в соответствии с (16.436) а = г(е(<),е(1±
824
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
1)) = г(1)), что если соседние значения ряда e(t) сильно коррелированы,
то ряд довольно слабых возмущении будет порождать размашистые
колебания остатков e(t).
На графике марковский процесс представляется осцилляциями более
или менее регулярного типа (см. рис. 16.8). Может быть вычислено сред-
нее расстояние dcp между «пиками»1 такой осциллирующей ломаной (см.
[Кендэл М.], с. 78):
J / V __________2?Г_______
ср arccos [— ^(1 — а)]
В частности, для последовательности независимых и одинаково (0;
1)-нормально распределенных случайных величин (т.е. при а = 0) это
среднее расстояние оказывается равным 3,0 (т. к. arccos (—^) = |тг); для
примеров, представленных на рис. 16.8, эти средние значения между пи-
ками будут, соответственно, равны 2я/ arccos (—0,1) =	= 3,75 (для
а = 0,8) и 2тг/arccos (—0,9) = 360°/154° = 2,34 (для а = -0,8).
Исследуем теперь, опираясь на соотношения (16.43), основные харак-
теристики процесса авторегрессии 1-го порядка и попробуем о чить па-
раметры этой модели (а и <Tq) по имеющейся в нашем распоряжении реа-
лизации (16.1') анализируемого временного ряда x(t).
Условие стационарности ряда (16.42) определяется требованием к
коэффициенту а:
|а| < 1,	(16.42')
или, что то же, корень zQ уравнения 1—az = 0 должен быть по абсолютной
величине больше единицы2 3.
1 Диагностика модели по числу пиков в анализируемом временном ряду или по средне-
му расстоянию между пиками основан на том же подходе, который был использован
в п. 16.3.1 при построениях критериев для проверки гипотезы о том, что исследуе-
мый временной ряд представляет собой последовательность независимых и одинако-
во распределенных случайных величин (см. (16.12)). Обращаем внимание читателя
на то, что наличие «пика» определяется значением временного ряда, ббльшмм, чем
два соседних его значения, и что при таком понимании пика среднее расстояние
между пиками будет всегда несколько меньше периода (если таковой существу-
ет) или псевдопериода анализируемой временной последовательности.
3 Уравнение 1 — ах — 0 представляет собой частный случай характеристического
уравнения общего линейного процесса авторегрессии. Поскольку в общем случае у
характеристического уравнения допускается наличие комплексных корней, то вме-
сто требования к абсолютным величинам корней условие стационарности чаще фор-
мулируют так: «все корни соответствующего характеристического уравнения
должны лежать вне единичного круга» (см. ниже описание общей модели авторе-
грессии р-го порядка).
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
825

e(t) = -0,8e(t - 1) + ф)
Рис. 16.8. Реализация процессов авторегрессии первого порядка (а), соот-
ветствующие им автокорреляционные функции (6) и логарифмы
плотности (в)
Автокорреляционная функция марковского процесса определяется
соотношением (16.436):
г(т) = г(е(/),е(1 ± т)) = ат.	(16.44)
Отсюда же, в частности, следует простая вероятностная интерпретация
параметра а:
а = r(l) = r(e(0,£(t ± 1)),
826
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
т.е. значение а определяет величину коэффициента парной корреляции
между двумя соседними членами ряда е(0.
Из (16.44) видно, что степень тесноты корреляционной связи между
членами последовательности (16.42) экспоненциально убывает по мере их
взаимного удаления друг от друга во времени.
Частная автокорреляционная функция гЧЛСТ(г) = r(e(t),e(t 4- г)
e(t + 1) = e(t + 2) = ... = e(t + т — 1) = 0) может быть подсчитана
с помощью формул (16.7)-(16.8). Непосредственное вычисление по этим
формулам дает следующий простой результат: значения частной корреля-
ционной функции гчаст(т) равны нулю для всех т — 2,3,.... Это свойство
частной автокорреляции может быть использовано при подборе модели:
если вычисленные по оцененным «невязкам» e(t) = x(t) — f(t) выбороч-
ные частные корреляции гчвст(т) статистически незначимо отличаются от
нуля при т = 2,3,..., то использование модели авторегрессии 1-го порядка
для описания поведения случайных остатков анализируемого временного
ряда считается не противоречащим исходным статистическим данным.
Спектральная плотность p(fi) марковского процесса (16.42) может
быть подсчитана либо по формуле (16.9а), либо по формуле (16.9) с учетом
известного вида автокорреляционной функции г(т) = r(e(t),£($ ±т)) = ат:
1 + с? - 2ttcos(2xw)*
На рис. 16.8 видно, что в случае большого положительного значения
параметра а (при а = 0,8) соседние значения ряда е(/) близки друг к дру-
гу по величине, автокорреляционная функция убывает (оставаясь положи-
тельной) по экспоненциальному закону, а в спектре преобладают низкие
частоты (а значит, среднее расстояние между пиками осциллирующего
временного ряда e(t) достаточно велико). При большом по абсолютной
величине, но отрицательном значении параметра а (при а = —0,8) ряд
быстро осциллирует (в спектре преобладают высокие частоты), а график
автокорреляционной функции экспоненциально спадает до нуля с попере-
менным изменением знака.
Идентификация модели, т. е. статистическое оценивание ее параме-
тров а и Oq по имеющейся реализации (16.V) исходного анализируемого
временного ряда x(t) (а не его остатков, которые являются ненаблюдаемы-
ми), основана на соотношениях (16.43) (при Л = 0иЖ = 1)и может быть
осуществлена с помощью метода моментов (см. п. 7.5.2). Для этого следу-
ет предварительно решить задачу выделения неслучайной составляющей
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
827
f(t) (см. п. 16.3), что позволит оперировать в дальнейшем остатками («не-
вязками»)
ё(0 = z(t) - 7(t).	(16.44)
Затем подсчитывается выборочная дисперсия 5(0) остатков по формуле
(16.45)
N
где ё = (23	а «невязки» e(t) вычислены по формуле (16.44).
t=i
Оценку а параметра а получаем с помощью формулы (16.43е), подста-
вляя в нее вместо коэффициента корреляции r(e($),£(t±l)) его выборочное
значение r(e(t),e(t + 1)), т.е.
. ^Е£*(Ф)-ёМ‘ + 1)-0	......
=--------------W)--------------•	(1М6)
Наконец, оценка <7д параметра а? основана на соотношении (16.43*), в
котором величины De(t) и а заменяются их оценками, соответственно,
7(0) и а:
do = (1 - а2)1(0).
Заметим, что в большинстве методов сглаживания из самой техники
построения /(<) автоматически следует равенство нулю среднего значения
N
«невязок» (т.е. ё = (J3 е(0)/А = 0). В этих случаях в формулах (16.45)
t=i
и (16.46) значение ё следует положить равным нулю.
Обращаем внимание читателя на следующий факт: прямая оценка
значений автокорреляционной функции (т.е. оценка ее значений с помо-
щью формулы (16.6*)) при реалистичных соотношениях N и т дает, как
правило, неудовлетворительный результат (хотя и является состоятель-
ной). В частности, в то время, как теоретическая коррелограмма ана-
лизируемого ряда затухает, построенная с помощью (16.6х) выборочная
коррелограмма может сохранять колебательный (незатухающий эффект.
Поэтому, в частности, при анализе марковского процесса элементы его ав-
токорреляционной функции г(т) лучше оценивать по формуле: г(т) = аТ.
Модели авторегрессии 2-го порядка — АР(2) (процессы
Юла). Эта модель, как и АР(1), представляет собой частный случай ав-
торегрессионного процесса типа (16.41х), когда все коэффициенты я.- в
828
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
правой части (16.41*), кроме первых двух, равны нулю. Соответственно,
она может быть определена выражением
e(f) = ai£(f - 1) + a2e(t — 2) 4- 6(t),
(16.47)
где последовательность случайных величин 6(1),£(2),... образует белый
шум (см. выше).
Последовательно подставляя (бесконечное число раз) в правую часть
(16.47) вместо e(t- l),e(i — 2),... их выражения, вычисленные по формуле
(16.47), мы убедимся в том, что как и в АР(1)-модели, e(t) зависит от
£(Z),£(f — 1),6(t — 2),..., но не зависит от будущих значений т.е. от
ф+1),ф+2),....
Умножая обе части (16.47) по очереди на e(i — 1) и e(t — 2) и беря
математические ожидания от двух полученных таким образом соотноше-
ний, получаем систему уравнений, связывающих между собой параметры
модели и а2 с дисперсией 7(0) = Deft) и первыми двумя ковариациями
7(1) = E[e(i)e(f - 1)] и 7(2) = E[e(t)e(f - 2)] анализируемого процесса e(t):
7(1) “ «11(0) ~ «27(0 = О,
7(2) - 017(1) - 027(G) = О,
или, после деления обоих уравнений на 7(0):
r(l)-oi - а2г(1) = О,
г(2) — О1г(1) — а2 = 0.
(16.48)
Разрешая эту систему относительно Oj и о2, имеем:
г(1)(1 - г(2))
*	1 - г’(1) ’
_г(2)-г*(1)
Уравнения (16.48) могут быть решены относительно г(1) и г(2):
г(1)=Г^Р
r(2) =Q2+
Обобщая использованный прием, домножим обе части (16.47) нае(<-
к) (к — любое целое число, большее нуля) и возьмем математическое
(16.49)
(16.50)
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
829
ожидание от всех членов получившегося соотношения:
7(fc) = а^(к -1)4- а2у(к - 2),
или (после деления на 7(0)):
r(kj = ctir(k - 1) 4- a2r(k - 2).	(16.51)
Рекуррентная формула (16.51) используется для вычисления любо-
го значения автокорреляционной функции г(т) лишь по двум ее первым
значениям г(1) и г(2) (в модели авторегрессии 1-го порядка аналогичную
роль играет формула т(т) = гт(1)).
Наконец, для того, чтобы получить соотношение, связывающее между
собой параметры 7(0) = De(t) и <7q = D£(0, домножим обе части (16.47)
на e(t):
e(t) =	- l)e(t) 4- a2€(i - 2)e(t) 4- 6(t)[aie(f -1)4- a2e(t - 2) 4- £(0].
После операции усреднения (с учетом того, что 6(t) и е(1 — к) взаимно
некоррелированы при к > 1) получаем:
7(0) = «17(0 4- «27(2) 4- «о,
откуда
«о = 7(0) - «17(1) “ «27(2),	(16.52)
или в терминах 7(0) = D£(t),a1,a2,’’(l) и г(2):
4 = 7(0)(1 - a,r(l) - a2r(2)) = 7(0)ii^- [(1 - а2)2 - а?]. (16.52')
1 — ot2
Рис. 16.9. Временной ряд, генерируемый моделью авторегрессии второго по-
рядка
830
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
На рис. 16.9 изображен временной ряд, генерируемый моделью авторе-
грессии 2-го порядка при Oj = 0,75 и aj = —0,50. Чисто внешне его трудно
отличить от рядов, генерируемых, например, моделью авторегрессии 1-го
порядка: мы наблюдаем приблизительно такие же осцилляции так назы-
ваемого «псевдопериодического» характера. Можно было бы попытаться
отличать реализации АР(2)-модели по среднему расстоянию dcp(o1,o2)
между пиками ряда (наличие «пика», напомним, определяется значением
£(t), большим, чем два соседних значения), которое подсчитывается по
значениям Oj и &2 по формуле (см. [Кендэл М. , с. 81):
^cp(alia2) ~	г 5“7Z	J ГГ’
arccos [—1(1 — ai 4-aj)]
Однако диагностика модели, основанная на среднем расстоянии между пи-
ками, не очень чувствительна. Так, для белого шума это среднее расстоя-
ние, как мы видели, оказывается равным трем, для марковских процессов
оно варьирует в диапазоне от 3 до 4, а для процессов Юла — между 4 и
6. В частности, для ряда, изображенного на рис. 16.9, среднее расстояние
между пиками
d(a\\ «г) = </(0,75; -0,50) =
2тг
-------— 4,34.
arccos (0,125)
Более обстоятельные и обоснованные выводы о типе модели, генери-
рующей анализируемый временной ряд, делаются, конечно, на основании
комплексного анализа его основных характеристик — автокорреляцион-
ной функции, спектра и т.п. Условия стационарности ряда (16.47) мо-
гут быть получены из естественных требований к абсолютным величинам
автокорреляций т(1) и г(2), выраженным в терминах oi и (см. соотно-
шения (16.50)):
1—02
<	2	(16.53)
- 1 < а, + т—!- < k
1 — О2
Отсюда получаем следующие необходимые и достаточные условия
стационарности ряда (16.47):
1*1 К 2,
*2 < 1 ~ |*1|-
(16.53')
В рамках общей теории моделей авторегрессии те же самые условия
стационарности получаются из требования, чтобы все корни соответ-
ствующего характеристического уравнения лежали бы вне единичного
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
831
круга. Характеристическое уравнение для модели аворегрессии 2-го по-
рядка имеет вид:
1 —«1Z —	=0.
Кстати, из условий стационарности (16.52х) и выражений (16.50) для
т(1) и г(2) следует, что далеко не всякая лара значений г(1) и г(2), по
модулю меныпих единицы, годится для описания поведения первых двух
членов автокорреляционной функции процесса Юла. Используя упомяну-
тые соотношения, можно показать, что допустимые значения г(1) и г(2)
для стационарного процесса АР(2) должны лежать в области
[ - 1 <r(l)< 1,
J -1<г(2)<1,
( г(2) > 2г’(1) - 1.
Автокорреляционная функция процесса Юла подсчитывается следу-
ющим образом. Два первых значения г(1) и г(2) определены соотноше-
ниями (16.50), а значения г(т) для т = 3,4,... вычисляются с помощью
рекуррентного соотношения (16.51).
На рис. 16.10 представлен график автокорреляционной функции для
рассмотренного выше примера модели авторегрессии 2-го порядка (см.
Рис. 16.10. Автокорреляционная функция процесса авторегрессии второго по-
рядка e(t) = 0,75e(t - 1) - 0,50e(t - 2) + б(t)
Частная автокорреляционная функция гЧЛСТ(т) = r(c(t),£(t 4- т) |
e(t + 1) = e(t 4- 2) = ... = e(t -Ь т — 1) = 0) временного ряда, сгене-
рированного моделью авторегрессии 2-го порядка, обладает следующим
832
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
отличительным свойством:
гчаст(г) = 0 при Всех Т = 3, 4,... .
я
Этот результат доказывается прямым вычислением частных коэффи-
циентов корреляции по формулам (16.7)-(16.8) для т = 2,3 и с использо-
ванием рекуррентных формул (11.321) для т > 3. Действительно, подста-
вляя в формулу (16.7) значения г(1) и г(2), выраженные через и а2 с
помощью (16.50), получаем
Далее, числитель в формуле (16.8) для гчаст(3) приводится в нашем
случае к выражению, в свою очередь, числитель которого равен
(1 - г2(1))(г(3) - r(2)r(l)) - (r(l) - г(2)г(1))(г(2) - г’(1)).
Равенство нулю последнего выражения устанавливается на базе соотно-
шений (16.50) и (16.51).
Спектральная плотность p(w) процесса Юла может быть вычислена
с помощью общей формулы (16.9*):
,~ч _ __________2<уо__________
I,	—»2эго?	—t4irD|2
|1 — а^е — а2е
________________________2go_______________________ (16.54)
1 4- «1 4- «2 — 2fti(l — аз)cos (2тга>) — 2а2 cos(4та>) ’
л ~	1
0 w	-.
На рис. 16.11 представлен график спектральной плотности рассмо-
тренного ранее (см. рис. 16.9) примера модели авторегрессии 2-го порядка.
Из рисунка видно, что максимум спектра приходится приблизительно на
значение частоты w0 = 0,14 ~ 0,15. А это значит, что средний кажущийся
(«псевдо-») период То нашего временного ряда близок к 6 (т. к. То = 1 /ол0).
Кстати, обращаем внимание читателя на несовпадение (как и следовало
ожидать!) вычисленного ранее среднего расстояния между пиками этого
ряда (dcp(0,75; —0,50) = 4,34) и его псевдопериода Tq.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
833
I_______1______I_______L..... 1
0,125 0,25 0,375 0,5
w — частота ------>
Рис. 16.11. Спектральная плотность процесса авторегрессии второго порядка
Идентификация модели авторегрессии 2-го порядка основана, на со-
отношениях (16.49)~ (16.52*), связывающих между собой неизвестные па-
2
раметры модели сц, а2 и сг0 со значениями различных моментов «наблю-
даемого» временного ряда e(t) (с его дисперсией, автокорреляциями и
т.п.). Слово «наблюдаемого» взято в кавычки, поскольку в действитель-
ности наблюдается анализируемый временной ряд ®(t), а «наблюдаемые»
значения остатков с(<) получаются после выделения неслучайной соста-
вляющей f(t) и образования разностей £(t) = x(t) — f(t).
Итак, по значениям e(t) прежде всего вычисляются оценки 5(0), г(1)
и г(2), соответственно, дисперсии De(i) и автокорреляций г(1) и г(2). Это
делается с помощью соотношений (16.4W) и (16.6*):
7(0) = ^E(e(0-f)’,
t=l
.... 7т4Е^*(ад-ё)(Ф + к)-е-)
r(fc)=---------W)----------’
k = 1,2
834
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
(если из техники построения неслучайной составляющей /(t) автоматиче-
N
ски следует равенство £(0 = 0, то значение € в этих формулах следует
t=i
положить равным ну,лю).
После этого можно получить оценки и а2 для параметров ах иа2)
подставив в правые части формул (16.49) значения г(1) и г(2) вместо, соот-
ветственно, величин г(1) и г(2). Наконец, оценку параметра aj получаем
с помощью формулы (16.52'), заменив в ней теоретическую ковариацию
7(0) и параметры «1,03 ранее полученными оценками, соответственно,
7(0), «1 и а2.
Заметим, что при построении выборочной автокорреляционной функ-
ции г(т) ее значения для т 3 предпочтительнее вычислять с помощью
рекуррентного соотношения (16.51) на базе начальных значений г(1) и
г(2).
Модели авторегрессии р-го порядка — АР(р) (р > 3). Эти моде-
ли, образуя подмножество в классе общих линейных моделей (16.41 ), сами
составляют достаточно широкий класс моделей авторегрессии, включаю-
щий в себя в качестве частных случаев ранее рассмотренные АР(1)- и
АР(2)-модели. Если в общей линейной модели (16.41') полагать все па-
раметры 1Гу, кроме первых р коэффициентов, равными нулю, то мы при-
ходим к определению АР(р)-модели. Итак, авторегрессионной моделью
порядка р называется модель вида:
р
e(t) = Qje(t - 3) + «(«),	(16.55)
J=1
где последовательность случайных величин 6(1), 6(2),... образует белый
шум, т.е. удовлетворяет условиям (16.39)-( 16.40).
Условия стационарности процесса, генерируемрго моделью (16.55),
также формулируются в терминах корней его характеристического урав-
нения
1 — aiz — a2z2 — ... — apzp = 0.	(16.56)
Для стационарности процесса (16.55) необходимо и достаточно, чтобы
все корни уравнения (16.56) лежали бы вне единичного круга, т.е. превос-
ходили бы по модулю единицу.
Автокорреляционная функция процесса (16.55) так же, как и для
АЯ(2)-модели, может быть вычислена с помощью рекуррентного соотно-
шения по первым р ее значениям г(1),г(2),...,г(р). Это рекуррентное
соотношение выводится следующим образом. Умножим все члены соотно-
шения (16.55) на е($ - т) (т > р). Получим e(t - т)е(1) = ocie(t - т)г(1 -1)
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
835
+а2е(^ — г)£(* — 2) + • • • + ape(t ~ т)£(* ” Р) +е(* тЖ0- Переходя к
математическим ожиданиям величин, участвующих в этом соотношении,
получаем:
7(т) = ot17(r - 1) + а27(т - 2) + ... + арч(т - р).
(16.57)
Отметим, что E(e(t - k)S(t)) = 0 при к > 0, т.к. e(t - к), выраженное
через 6, может включать лишь импульсы 6(j) для j < t - к (т. е. e(t) не
зависит от будущих, по отношению к t, значений 6), Поделив все члены
(16.57) на 7(0), находим искомое рекуррентное соотношение, позволяющее
последовательно вычислять любой элемент автокорреляционной функции
процесса е(0 по первым р ее элементам г(1), т(2),..., г(р):
г(т) = О1г(т - 1) + а2г(т - 2) + ... + арт(т - р),
т=р+1,р+2,... .
(16.58)
Частная автокорреляционная функция гчаст(г) = r(e(t),e(i 4- т) |
e(I + 1) = e(t + 2) = ... = e(i + т — 1) = 0) процесса (16.55) будет иметь
ненулевые значения лишь при т р; все значения гчаст(г) ПРИ т > р будут
нулевыми (доказательство этого факта см., например, в книге [Бокс Дж.,
Дженкинс Г., вып. 1], с. 81). Это свойство частной автокорреляционной
функции АР(р)-процесса используется, в частности, при подборе поряд-
ка р в модели авторегрессии для конкретных анализируемых временных
рядов. Если, например, подсчитанные по исходным данным все частные
коэффициенты автокорреляции, начиная с порядка к, статистически не-
значимо отличаются от нуля, то порядок модели авторегрессии, подбирае-
мой для анализируемого временного ряда, естественно определить числом
р = к — 1.
Спектральная плотность р(ы) процесса авторегрессии р-го порядка
определяется с помощью формулы (16.9*):
- аре
—i2irpw
(16.59)
2 »
(здесь i = у—Т — мнимая единица).
Идентификация модели авторегрессии р-го порядка так же, как и
при анализе моделей 1-го и 2-го порядков, основана на соотношениях, свя-
зывающих между собой неизвестные параметры модели и автокорреля-
ции анализируемого ряда. Для вывода этих соотношений последовательно
836
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
подставим в (16.58) значения т = 1,2,...,р. Получим систему линейных
уравнений относительно ct], аа,..., ap:
r(l) = ai +a2r(l) + ...+ apr(p- 1),
т<2) = 0^(1) + aa 4-... + арт(р - 2),
(16.60)
r(p) = air(p - 1) + a2r(p - 2) 4-... + ap.
Они обычно называются уравнениями Юла-Уокера1. Мы уже рассма-
тривали частные случаи этих уравнений в АР(1)- и АР(2)-моделях (см.
(16.43е) и (16.48)). Оценки для параметров а* получим, заменив теоре-
тические значения автокорреляций г(Л) их оценками f(fc) (к = 1,2,...,р).
Для того, чтобы выписать решение в явном виде, перейдем к матричным
обозначениям:
(«1\ /ФА
«2 I I г(2)
. I, г=	.	,
ар/ \т(р)/
/ 1	г(!)	г(2)	•••	r(?-i)\
R= I	г(1)	1	r(l)	...	r(p-2)|
\r(p-l) r(p —2) r(p-3) ...	1	/
Тогда система (16.60) может быть представлена в форме
Ra = г,	(16.60')
а ее решение, соответственно, будет иметь вид:
a = R-1r.	(16.61)
Для вывода соотношения, необходимого при построении оценки й$
параметра = D^(t), помножим обе части (16.55) на e(t):
€2(t) = a^t - l)e(t) + a2e(t - 2)e(t) + ... 4- ape(t - p)e(t) 4- f(t)
x (a^t - 1)
4-	a2€(t - 2) 4-... 4- ape(t - p) 4- ОД)-
1 Cm. Yule G.U. On a method of investigating periodicities in disturbed series. «Phil.
Trans.», A226, p. 227, 1927. Walter G. On periodicity in series of related terms.
«Proc. Royal Soc.», A131, p. 518, 1931.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
837
Переходя к математическим ожиданиям участвующих в этом соотно-
шении величин и учитывая взаимную некоррелированность tf(t) и e(t — к)
при к = 1,2,... ,р, получаем:
7(0) = aiv(l) + а27(2) + ... + а₽7(р) +
Отсюда после деления всех членов на 7(0) имеем:
= 7(0)(1 - oir(l) - <*2г(2) - ... - Орф)). (16.62)
Оценка dg для параметра erg получается с помощью (16.62) заме-
ной всех участвующих в правой части величин их оценками (7(0),ai,S2,
. ..,ар).
16.4.2	. Модели скользящего среднего порядка q
(СС(д)-модели)
Рассмотрим частный случай общего линейного процесса (16.41), ко-
гда только первые q из весовых коэффициентов Pj ненулевые. В этом
случае процесс имеет вид
e(t) = £(*) - 6^(1 - 1) - е22Щ - 2) - ... - 0q6(t - q),	(16.63)
где символы — 01,— 02,...,— 0q используются для обозначения конечного
набора параметров Р9 участвующих в (16.41). Процесс (16.63) называет-
ся моделью скользящего среднего порядка q и сокращенно обозначается
СС(д)1. Особенно распространены в практике статистического моделиро-
вания СС-модели первого (g = 1) и второго (д = 2) порядка.
СС (1): е(0 =	- 06(t - 1),	(16.64)
СС (2): e(t) = 0(1) - М(* - 1) -	- 2).	(16.65)
Двойственность в представлении АР- и С С-моделей и поня-
тие обратимости СС-модели. В начале п. 16.4 были приведены две
эквивалентные формы записи общего линейного процесса. Из (16.41) и
(16.4Г) видно, что один и тот же общий линейный процесс может быть
1 Термин «скользящее среднее» здесь употреблен в несколько ином смысле, чем в
п. 16.3.2, где речь шла об алгоритмических методах сглаживания временного ряда.
В частности, в моделях СС(д) сумма весовых коэффициентов не равна единице. В
англоязычной специальной литературе СС(д)-моделк называются «Moving Average
models* и сокращенно обозначается МА (g)-models.
838
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
представлен либо в виде АР-модели бесконечного порядка, либо в виде СС-
модели бесконечного порядка. Именно это мы понимаем под «двойствен-
ностью» в представлении анализируемого временного ряда. Проанализи-
руем более подробно эту проблему в рамках конечных АР(р)- и СС(д)-
моделей, представляющих собой в совокупности некоторый подкласс в
классе общих линейных моделей.
Начнем с простейших представителей этого подкласса, а именно с
моделей АР(1) и СС(1). Мы уже видели (см. (15.108)), где АР(1)-модель
e(t) = ae(t — 1) + ^(0 может быть представлена также в виде
е(0 =	+ a6(t - 1) 4- a6(t - 2) 4- ...,
т. е. в виде модели скользящего среднего бесконечного порядка. При этом
оказалось, что для обеспечения стационарности e(t) необходимо и доста-
точно потребовать, чтобы параметр а по абсолютной величине был мень-
ше единицы (или, что то же, чтобы корень характеристического уравне-
ния 1 — az = 0 лежал бы вне единичного круга).
Рассмотрим теперь СС(1)-модель и попробуем выразить 6(0 через
текущее и все прошлые значения б(0. Уединяя 6(t) в соотношении (16.64),
имеем:
6(0 = e(t) 4-	-	1)	= е(0 4- 0[е(* -1)4- 06(1 -	2)]
= e(t) +	6e(t	-	1)	+ в2 [e(t - 2) + 06(t - 3)]
= e(t) +	0e(t	-	1)	+ - 2) + 03 [e(t - 3) +	9S(t - 4)]
= e(t) +	-	1)	+ fl2e(t - 2) + в3е(1 - 3) + ... .	(16.66)
Соотношение (16.66) можно переписать в виде
оо
Ф) = -£ ^(*-*)+«(«)•
(16.661)
fc=l
Это означает, что ряд е(0, сгенерированный СС(1)-моделью (16.64), мо-
жет быть представлен также в виде модели авторегрессии бесконечного
порядка. Заметим, что, в отличие от АР(р)-моделей, в СС(д)-моделях не
требуется накладывать никаких ограничений на параметры ^1,^2,
для обеспечения их стационарности: ряды вида (16.63) стационарны при
любых вещественных значениях параметров 0j (j = 1,2,..., q). Однако,
если, например, в модели СС(1) параметр 0 по абсолютной величине боль-
ше или равен единице (|0| > 1), то текущее значение анализируемого ряда
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ	839
e(t) в соответствии с (16.66*) будет зависеть от своих прошлых значений
e(t - 1), e(t — 2),..., берущихся с весами, бесконечно растущими по мере
удаления в прошлое. С целью избежать этой неестественной (с приклад-
ной точки зрения) ситуации потребуем, чтобы веса в обращенном разло-
жении (16.66*) образовывали бы сходящийся ряд, т.е. чтобы |0| < 1. Это
требование равносильно условию, сформулированному в терминах харак-
теристического уравнения модели (16.64) 1 — вг = 0 и заключающемуся
в том, чтобы корень этого характеристического уравнения был бы по мо-
дулю больше единицы («лежал бы вие единичного круга»). Итак, СС(1)~
модель называется обратимой, если в обращенном разложении (16.66*)
бесконечной ряд весов при e(t — k) (к = 1,2,...) сходится (или, что то же,
если |0| < 1). Еще раз заметим, что условия обратимости СС-моделей не
имеют никаких связей с условиями стационарности временного ряда.
Обобщим этот результат на случай СС(д)-модели при произвольном
конечном значении q. Уединяя 6(t) в соотношении (16.63), имеем:
6(0 = е(0 + ф - 1) +	- 2) + ... + 0q6(t - q).
(16.63')
Действуя аналогично тому, как мы это делали при выводе соотноше-
ния (16.66), т. е. заменяя бесконечное число раз 6(t — 1), 6(i — 2),..., 6(i — g)
в правой части (16.63*) их выражениями, вычисленными по формуле
(16.63*), получим разложение вида
6(0 = е(0 - xj- 1) - тг2£(* “ 2) - ...,	(16.67)
в котором коэффициенты эг, (j = 1,2,...) определенным образом выра-
жаются через параметры 0j,02,...,0р. Соотношение (16.67) может быть
записано в виде модели авторегрессии бесконечного порядка (т. е. в виде
обращенного разложения)
~ Я + *(*)•
j=i
(16.67')
Можно показать (см., например, [Бокс Дж., Дженкинс Г., вып. 1],
с. 84), что условие обратимости СС(д)-модели (т. е. условие сходимости
оо
ряда £ т,) формулируется в терминах характеристического уравнения
j=i
840
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
модели (16.63) следующим образом:
•все корни ZitZ2,...tZq характеристического
уравнения 1 — 0iz — 02z2 — ... — 0qz9 = 0
должны лежать вне единичного круга, т.е.
|zj| > 1 для всех j = 1,2,..., q.
(16.68)
Основные характеристики процесса СС(?). Получим вспомога-
тельные соотношения, связывающие между собой дисперсию и ковариации
процесса скользящего среднего порядка q с параметрами 0\, 02,..., 0q. Для
этого выразим e(t — к) в соответствии с (16.63)
e(t - к) = t(t -к)- 0^(1 - к - 1) - ... - 0qS(t -k-q),	(16.63*)
перемножим почленно выражения (16.63) и (16.63*) и вычислим матема-
тические ожидания всех членов получившегося соотношения (учитывая,
конечно, взаимную некоррелированность элементов белого шума ^(G) и
£(*з) при / t2). В результате получим следующее выражение для кова-
риации 7(т) = E(e(i)e(t — т)):
?(’) =
при т = 0;
при т - 1,2,...,?;
(16.69)
при т > q
(при этом, естественно, полагается, что 0j = 0 при j > q).
Автокорреляционная функция процесса CC(q) получается непосред-
ственно из (16.69):
{—0Г + 010Т-Ц + 020т+2 + • • • + 0q-?0q
1 + 01 + 02 + • • • + 0g
о
при т= 1,2,...,?;
при т > ?.
(16.70)
Мы видим, что автокорреляционная функция г(т) процесса СС(?) рав-
на нулю для всех значений т, ббльших порядка процесса ?. Это важное
свойство используется при подборе порядка СС(?)-модели по эксперимен-
тальным данным.
Спектральная плотность р(ы) процесса СС(?) может быть вычисле-
на с помощью соотношения (16.9*) с учетом того, что участвующий в нем
оператор B(z) для модели (16.63) имеет вид
B(z) = 1 — 0xz — 02z2 — ... — 0qzg.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
841
Соответственно имеем:
p(w) = 2(7?|1 -	- 02е'“™ -
л ~ 1
О < w < -.
~ - 2
- e,e-’”°|2
(16.71)
Идентификация модели CC(q) производится на базе соотношений
(16.70), а именно: 1) по значениям e(t) = x(t) — f(t) с помощью формулы
wb Е («(1)-€)(ё(<+Г)-в)
г(г) =--Ь1__--------------, г = 1,2.q, (16.6")
&ЕК0-О2
t=l
подсчитываются значения г(1),г(2),. . .,г(?); 2) в соотношения (16.70) по-
следовательно подставляются значения т = 1,2, ...,д с заменой в левой
их части величин г(т) полученными ранее оценками f(r); 3) полученная
таким образом система из g уравнений разрешается ^относительно неиз-
вестных значений 01,02, • • •, 09; решения этой системы 0г, 0},...,0Ч и дадут
нам оценки неизвестных параметров модели, соответственно, 0г, 02,..., 0д;
4) оценка параметра сто может быть получена с помощью первого из соот-
ношений (16.69) подстановкой в него вместо 7(0), 0i,02,. ..,0g их оценок,
соответственно, 7(0), 01,02, • • •, 09*
Заметим, однако, что в отличие от системы линейных уравнений
Юла-Уокера (16.60), выведенных в связи с задачей оценивания параме-
тров процесса авторегрессии, уравнения для определения оценок параме-
тров СС(д)-модели, полученные на базе соотношений (16.70), нелинейны.
Поэтому, за исключением простого случая q = 1, который будет рассмо-
трен ниже, эти уравнения приходится решать с помощью итерационных
процедур (одна из таких процедур описана, например, в книге [Бокс Дж.,
Дженкинс Г., вып. 1], с. 225).
Рассмотрим теперь специально два наиболее важных частных случая
СС(д)-модели.
Модель скользящего среднего 1-го порядка (СС(1)-модель).
Эта модель описывается соотношением (16.64) и, как уже было показано,
стационарна при любом значении параметра 0 и обратима при условии
1*1 < 1.
Автокорреляционная функция СС(1)-модели определяется соотноше-
842
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
ниями (16.70) при q = 1, т.е.
г(т) =
----S- при Т = 1,
1 + г
0 при т > 2.
(16.72)
Частная корреляционная функция гчаст(г) процесса скользящего
среднего 1-го порядка, определяющая степень тесноты корреляционной
связи между e(t) и e(t ± т) при фиксированных значениях всех проме-
жуточных элементов этого ряда, задается выражением
(16.73)
(вывод этого соотношения см., например, в книге [Бокс Дж., Дженкинс Г.,
вып. 1], с. 87). Мы видим, что (с учетом |0| < 1) кчаст(^)| < 0Т и ЧТО за-
тухающая экспонента определяет поведение частной автокорреляционной
функции. Если т(1) положительно (и, следовательно, 9 отрицательно),
гчаст(т) осциллирует с переменами знака. Если же г(1) отрицательно, все
значения гчаст(г) отрицательны.
Спектральную плотность СС(1)-модели получаем из (16.71) при
p(w) = 2ао|1 - бе *2ww|2
= 2а?(1 + 92 - 29cos(2ttw)),	0 < w <	(16.74)
Из (16.72) и (16.74) видно, что когда 9 отрицательно, то г(1) положи-
тельно и в спектре доминируют низкие частоты (т.е. соответствующие
временные ряды имеют относительно длинные псевдопериоды). Напро-
тив, при положительном 9 величина г(1) отрицательна, а в спектре доми-
нируют высокие частоты.
Идентификация СС(1)-модели сводится, в соответствии с описанным
выше общим процессом оценивания параметров СС(д)-модели, к решению
единственного уравнения
(16.75)
Из двух решений этого квадратного уравнения выбирается то, ко-
торое удовлетворяет условию обратимости СС(1)~модели (т.е. условию
|0| < 1). То, что такое решение существует и единственно, следует из
известного свойства корней приведенного квадратного уравнения: их про-
изведение равно свободному члену. В нашем случае это означает: если
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ	843
№ — корень уравнения (16.75), то величина 1/0^ является вторым кор-
нем этого уравнения. Поэтому, если один из корней по абсолютной вели-
чине меньше единицы, то другой будет больше единицы.
Модель скользящего среднего 2-го порядка (СС(2)-модель).
Эта модель описывается соотношением (16.65) и стационарна при любых
значениях параметров 0j и 02. Однако,как это следует из (16.68), СС(2)-
процесс обратим лишь при условии, что корни его характеристического
уравнения
1 — 9\z —	= О
лежат вне единичного круга, т. е.
/1*11 <2,
1*2<1-|*1|.
(16.68*)
Заметим, что эти условия аналогичны условиям (16.53') стационарности
процесса АР(2).
Автокорреляционная функция процесса СС(2) определяется соотно-
шениями (16.70) при 9 = 2, т.е.
г(1) =
г(2) =
-*1(1-*2)
1 + 0?+0? ’
~*2
1 + 0? + 02 ’
(16.76)
г(т) = 0 при всех т > 3.
Из (16.68*) и (16.76) следует, что первые две автокорреляции обрати-
мого процесса СС(2) должны лежать на плоскости г(1)0г(2) внутри пло-
щади, ограниченной отрезками линий
г(2) + г(1) = -0,5,
г(2) - г(1) = -0,5,
г2(1) = 4г(2)(1 — 2г(2)),
см. рис. 16.12. Рисунок позволяет оценить, согласуется ли вычисленная
по экспериментальным данным с помощью формулы (16.б") пара значений
f( 1), г(2) с гипотезой, что анализируемый временной ряд e(t) может быть
описан моделью СС(2).
844
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
г(1)
♦
Рис. 16.12. Допустимые области значений г(1) и г(2) для обратимого процес-
са СС(2)
Частная автокорреляционная функция имеет весьма сложную фор-
му аналитического представления. Однако можно показать, что главную
роль в этом представлении играет либо сумма двух экспоненциально убы-
вающих (с ростом г) членов (если корни характеристического уравнения
действительны), либо затухающая синусоида (если корни характеристи-
ческого уравнения комплексны). То есть эта функция ведет себя так же,
как автокорреляционная функция процесса АР(2).
Спектральную плотность p(w) процесса СС(2) получаем из (16.71)
при д = 2:
p(ur) = 2<т?| 1 - he-*™ - 02e-i4TC,\2
= 2а2(1 +	+ 02 — 20j(l — 02)cos(2xw) — 202 cos(4ttu>)),
1
0 < w < -.
2
Отметим, что этот спектр с точностью до постоянного множителя 2<т0
обратен спектру (16.54) процесса авторегрессии 2-го порядка.
Идентификация СС(2)-модели сводится, в соответствии с описанным
выше общим процессом оценивания параметров СС(д)-модели, к решению
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
845
системы из двух нелинейных (относительно неизвестных 01 и 02) уравне-
ний:
(16.78)
Взаимосвязь процессов АР(р) и СС(д). Результаты, изложенные
в пунктах 16.4.1 и 16.4.2, позволяют сделать ряд заключений о взаимо-
связях, существующих между процессами авторегрессии и скользящего
среднего.
1)	Для конечного процесса авторегрессии порядка р 6(t) может быть
представлено как конечная взвешенная сумма предшествующих е, или c(t)
может быть представлено как бесконечная сумма предшествующих 6. В то
же время, в конечном процессе скользящего среднего порядка q e(t) может
быть представлено как конечная взвешенная сумма предшествующих 6
или 6(t) — как бесконечная взвешенная сумма предшествующих е.
2)	Конечный процесс СС имеет автокорреляционную функцию, обра-
щающуюся в нуль после некоторой точки, но так как он эквивалентен
бесконечному процессу АР, его частная автокорреляционная функция бес-
конечно протяженная. Главную роль в ней играют затухающие экспо-
ненты и (или) затухающие синусоиды. И наоборот, процесс АР имеет
частную автокорреляционную функцию, обращающуюся в нуль после не-
которой точки, но его автокорреляционная функция имеет бесконечную
протяженность и состоит из совокупности затухающих экспонент и (или)
затухающих синсоид.
3)	Параметры процесса авторегрессии конечного порядка р не должны
удовлетворять каким-нибудь условиям, для того чтобы этот процесс был
обратимым. Однако, чтобы процесс был стационарен, корни его характе-
ристического уравнения должны лежать вне единичного круга. В то же
время параметры процесса СС не должны удовлетворять каким-нибудь
условиям для того, чтобы процесс был стационарным. Однако для того
чтобы процесс СС был обратимым, корни его характеристического урав-
нения должны лежать вне единичного круга.
4)	Спектр процесса скользящего среднего обратен спектру соответ-
ствующего процесса авторегрессии.
846
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
16.4.3	. Авторегрессионные модели со скользящими
средними в остатках (АРСС (р, д)-модели)
В п. 16.4.2 обсуждалась двойственность в представлении АР- и С Са-
моделен. В частности, мы видели, что конечный процесс скользящего
среднего, например,
e(t) = £(f) - Mft - 1),
может быть записан как бесконечный процесс авторегрессии
*(0 = -	е(< - *) + Ф).
fc=l
И обратно: простейший процесс авторегрессии может быть представлен
как бесконечный процесс скользящего среднего (см. (15.108)).
Но если мы анализируем процесс действительно типа СС(1), то его
представление в виде процесса авторегрессии неэкономично с точки зрения
формы его параметризации. Аналогично процесс АР(1) не может быть
экономично представлен с помощью модели скользящего среднего. Поэто-
му на практике для получения экономичной параметризации анализируе-
мого процесса иногда бывает необходимо включить в модель как члены,
описывающие авторегрессию, так и члены, моделирующие остаток в виде
скользящего среднего. Такой линейный процесс имеет вид
e(t) = «!£(*-!) + ... + ape(t - р) + 6(t) - tf(t -1) - ... - eg6(t - q) (16.79)
и называется процессом авторегрессии — скользящего среднего порядка
(p,q). Примем для него сокращенное обозначение АРСС (р, д)1.
Отметим, что, последовательно выражая бесконечное число раз в пра-
вой части (16.79) величины eft — 1), e(t — 2),...,с(< — р),... по формуле
(16.79), мы убеждаемся в том, что eft) не зависит от будущих значений
6, т. е. от + 1), 6ft + 2),....
1 Модель (16.79) может интерпретироваться как линейная модель множественной ре-
грессии, в которой в качестве объясняющих переменных выступают прошлые зна-
чения самой зависимой переменной, а в качестве регрессионного остатка — скользя-
щее среднее из элементов белого шума. Поэтому название этой модели, вынесенное
в заголовок данного пункта, лучше отражает ее сущность. Однако для краткости
чаще используется название «модель авторегрессии — скользящего среднего». В
англоязычной литературе эти модели называют AutoRegressive — Moving Average
Models, или сокращенно ARMA-models.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
847
Стационарность и обратимость АРСС (р, ц)-процессов. Записывая
процесс (16.79) в виде
«(о=- д+«,(').	<16-79')
У=1
где 6q(t) = £(t)-fli£(t —1) —•-0g6(t — q)t мы можем провести анализ ста-
ционарности (16.79*) точно по той же схеме, что и для АР (р)-процессов.
При этом различие «остатков» 6q(t) и 6(t) никак не повлияет на выводы,
определяющие условия стационарности процесса авторегрессии. Поэтому
процесс (16.79) является стационарным тогда и только тогда, когда все
корни характеристического уравнения АР (р)-процесса
1 — «iz — a2z2 — • * • — apzv = О
лежат вне единичного круга.
р
Аналогично, обозначив ep(t) = e(t) — 52	~ У) и рассматривая
j=i
процесс (16.79) в виде
e„(t) = «(t) - 0!6(t - 1)------0qs(t - q),	(16.79")
получаем те же выводы относительно условий обратимости этого процес-
са, что и для процесса СС (д), а именно: для обратимости АРСС (р,д)-
процесса необходимо и достаточно, чтобы все корни характеристического
уравнения СС (д)-процесса
1 -	— 02х2 —----0qzg = О
лежали бы вне единичного круга.
Автокорреляционная функция анализируется методами, аналогичны-
ми тем, что мы использовали при выводе автокорреляционных функций
для АР- и СС-процессов. Умножим все члены (16.79) нае(<—т) и перейдем
к математическим ожиданиям получившегося выражения:
7(т) = «!7(т - 1) 4-... ар7(т - р) 4- уе6(г) - ^7ев(т - 1) - ... - вд7е6(т - д),
(16.80)
где 7еб(Л) = Е(е(< —	— «перекрестная» ковариационная функция
случайных последовательностей e(t) и 6(t). Так как e(t - к) не зависит от
будущих (по отношению к моменту t - к) значений то yet(k) = 0 при
всех к > 0 и 7е«(£) / 0 при всех к < 0. Из (16.80) следует:
?(т) = Qi7(t - 1) 4- а2у(т -2) 4- *..4- ару(т - р) при т > g 4-1
848
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
и, соответственно (после деления всех членов на 7(0)),
г(т) = Л!г(т - 1) + а2г(т - 2) + ... + арг(т - р)
при т > g + 1. (16.81)
Анализ соотношений (16.80) и (16.81) позволяет сделать следующие
выводы.
1) Из соотношений (16.80) для г = 0,1,2, ...,д следует, что ко-
вариации 7(0)т7(1)»»**>7(9) и» соответственно, автокорреляции г(1),
r(2),...,r(g) связаны определенной системой зависимостей с q параме-
трами скользящего среднего	и р параметрами авторегрессии
• • ’tQp- При этом имеется в виду, что перекрестные ковариации
7<б(т), 7е«(т “ 0»• ,7с«(г “ при положительных значениях сдвига по
времени, как уже было подмечено, равны нулю, а при отрицательных —
тоже могут быть выражены в терминах параметров оц,..., ар, ,..., 09 с
помощью следующего приема: пусть к > 0; тогда yeg(—k) — E(e(t+k)S(1));
в произведении e(t + k)6(t) с помощью (к + 1)-кратной последователь-
ной подстановки первого сомножителя по формуле (16.79) он заменяется
линейной комбинацией e(t — 1), элементов белого шума 6 и параметров
модели, что после применения к получившемуся произведению операции
усреднения Е дает выражение, зависящее только от параметров модели
(поскольку E(e(t — 1 )£(<)) = 0).
2) Значения автокорреляционной функции г(т) для т > q + 1 вычи-
сляются по рекуррентному соотношению (16.81), которое в точности по-
вторяет аналогичное рекуррентное соотношение (16.58) для автокорре-
ляционной функции процесса АР(р). А это значит, что, начиная ст = д+1,
автокорреляционная функция процесса АРСС(р, д) ведет себя так же, как
и автокорреляционная функция процесса АР(р), т.е. она будет состоять
из совокупности затухающих экспонент и (или) затухающих синусоид, и
ее свойства определяются коэффициентами «1, а2,..., ар и начальными
значениями г(1), г(2),..., г(р).
Частная автокорреляционная функция гчаст(г) процесса АРСС(р,д)
при больших г ведет себя как частная автокорреляционная функция
СС(д)-процесса. Это значит, что в ней преобладают члены типа затуха-
ющих экспонент и (или) затухающих синусоид (соотношение между теми
и другими зависит от порядка скользящего среднего g и значений параме-
тров процесса).
Спектральная плотность р(й) процесса АРСС(р,д) может быть вы-
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
849
числена с помощью соотношения (16.9а):
р(й) = 2а0
|1 _ fa™ _ вае-й'“ _ ... _ в,е-а',й,|2
|1 - ate-a,,a - азе-^ - ... - аре-й'Й2 ’
(16.82)
_ 1
О < w < -.
~ - 2
Идентификация процесса АРСС(р,д) базируется (так же как и в АР-
и СС-моделях) на статистическом оценивании параметров модели с по-
мощью метода моментов. Соотношения, связывающие ковариации 7(т) с
неизвестными значениями параметров, могут быть получены различными
способами. Но большинство подходов к идентификации модели основано
на домножении соотношения (16.79) (или вытекающих из этого соотноше-
ния равенств) на е(А) (fc = t,t — l,f — 2,...), переходе к математическим
ожиданиям от получившихся выражений и использовании образовавших-
ся связей между автоковариациями процесса е(<) и параметрами АРСС-
модели для определения неизвестных значений этих параметров по не-
обходимому набору подсчитанных по исходным статистическим данным
выборочных автоковариаций у(т) (т = 0,1,2,...).
Наметим один из вариантов таких подходов. Разобъем процедуру
получения оценок параметров afc (Л = 1,2,... ,р), Ру (j — 1,2,...,^) и а?
на два этапа. На 1-м этапе мы получим оценки параметров сц, на 2-м —
оценки параметров Gj и <7q.
1-й этап. Перепишем соотношение (16.79) в виде
£(i) - £ ake(t - к) = «(О -	- j),
k=l	j=l
(16.79м)
домножим поочередно обе части этого соотношения на e(t — q — 1),
e(t - q — 2),..., e(t — q - p) и перейдем к математическим ожиданиям в
каждом из р получившихся таким образом соотношений. Учитывая вза-
имную некоррелированность каждого из упомянутых множителей со всеми
элементами белого шума, присутствующими в правой части (16.79м), име-
ем (после деления всех членов на 7(0)) следующую систему из р линейных
уравнений относительно неизвестных параметров ai,Q2,...,afp:
r(q + 1) - Qir(g) - a2r(q - 1) - ... - apr(q - p + 1) = 0,
r(g 4- 2) - a^q + 1) - a2r(q) - ... - apr(q - p 4- 2) = 0,
(16.83)
r(q + p) - <*\r(q + p - 1) - a2(q + p - 2) - ... - apr(q) = 0.
850
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Подставляя в (16.83)вместо г(к) их выборочные значения г(к) и решая
получившуюся систему относительно aj (J = 1,2,... ,р), получаем оценки
2-й этап. Подставим найденные оценки	в соотноше-
ние (16.79*) вместо, соответственно, аьа2, • ♦ •,ар и «протиражируем»
получившееся соотношение для моментов времени i, t 4- 1,..., t 4- q. В
результате получим следующий набор из q 4-1 соотношений:
e(t) - £ &ke(l - к) = 4(t) - £ 6^(1 - j),
к=1	J=1
Р	Я
e(t + 1)- £ °*£0+ 1 -*) = s(t + 1) - $2 W + 1 -д
fc=l	J=1
Р	я
e(t 4- q) -	**(< + ? “ *) = ^(* + “ 52	+ 9 “ •*)*
fc=i	j=i
Затем обе части 1-го из этих соотношений поочередно домножим на
самих себя, на 2-е, 3-е и т. д. до последнего. После перехода к математи-
ческим ожиданиям левые части каждого из (q 4- 1) получившихся таким
образом соотношений будут содержать различные комбинации автокова-
риаций 7(0),7(1),.. -, 7(? + ?) и оценок , S2,..., «р, а правые — будут
представлять собой некоторые нелинейные комбинации от неизвестных па-
раметров	Другими словами, мы получаем таким обра-
зом систему из q 4-1 нелинейных уравнений относительно Og » , ^2, • • •,
(т. к. все величины, участвующие в левых частях этих соотношений, нам
известны, поскольку вместо теоретических автоковариаций 7(A) мы под-
ставим их выборочные значения 7(^), * = 0,1,2,..., q+p). Вопросы суще-
ствования, единственности и практического получения решений этой си-
стемы в общем случае оставляем вне рамок учебника, однако ниже рассмо-
трим конкретный пример реализации описанного подхода в рамках модели
АРСС(1,1).
Процесс авторегрессии — скользящего среднего АРСС(1,1).
В соответствии с определением (16.79) процесс АРСС(1,1) описывается
формулой
£(t) = ae(t -1)4- Ф) - 06(t - 1),	(16.84)
или, что то же,
e(t) - ae(t - 1) = S(t) - 6S(t - 1).	(16.84')
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
851
Стационарность и обратимость. В соответствии с общей теорией
АРСС-процессов, процесс А РСС( 1,1) стационарен, если корень характери-
стического уравнения АР(1)-модели, т.е. уравнения 1 — az — 0, по модулю
больше единицы. Это значит, что стационарность гарантируется усло-
вием |а| < 1. Обратимость АРСС(1,1)-процесса обеспечивается требова-
нием, чтобы корень характеристического уравнения СС(1)-процесса, т.е.
уравнения 1 — Oz = 0, был бы по модулю больше единицы. Это означает,
что обратимость АРСС(1,1)-процесса гарантируется условием |0| < 1.
Автокорреляционная функция может быть построена с помощью со-
отношений (16.80), выписанных для т = 0, т = 1 и г > 2:
7(0) = а7(1) +	- 07е6(-1),
7(1) = «7(0) - М,
7(т) = а7(т — 1) при т > 2.
Чтобы выразить 7е$(—1) через параметры модели, умножим все чле-
ны (16.84 ) на S(t — 1) и перейдем к математическим ожиданиям от полу-
чившихся выражений:
7еб(“1) = («- 0)«о-
Теперь мы можем описать автоковариационную и автокорреляцион-
ную функции АРСС(1,1)-процесса в терминах его параметров:
7(°) =
7(1)=(1-4(°-*)
1 — а
2
и,следовательно,
(l-owa-0)
1 + в2 - 2ав
г(т) = аг(т - 1) = ат-1г(1)
для т > 2.
(16.85)
Мы видим, что автокорреляционная функция экспоненциально убы-
вает от начального значения т(1), причем это убывание монотонно, если
а положительно, и колебательно (знакопеременно), если а отрицательно.
Из (16.85) и условий стационарности и обратимости следует, что г(1)
852
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
и г(2) должны удовлетворять соотношениям:
к(2)| < |г(1)|,
г(2)>г(1)(2г(1)+1)
r(2) > r(l)(2r(l) - 1)
при г(1) < О,
при т(1) > 0.
Эти условия бывают полезными при проверке гипотезы о том, что
анализируемый процесс может быть описан АРСС(1,1)-моделью (по вы-
борочным значениям г(1) и г(2) коэффициентов автокорреляции).
Частная автокорреляционная функция гчаст(т) АРСС(1,1)-процесса
определяется единственным начальным значением гчаст(1), а затем экс-
поненциально убывает. При этом если 0 положительно, то она моно-
тонно убывает от значения гчаст(1), знак которого совпадает со знаком
(а — 0). При отрицательном 0 величина гчаст(г) убывает экспоненциально-
знакопеременно.
Спектральная плотность p(w) определится в соответствии с общим
соотношением (16.82), в котором следует положить р = q = 1:
/ - л л 2 1 + 02 — 20 сов(2тгй)
р(ы) = 2сг0------я--------------
1 + а — 2а cos(2?rw)
0 < w < -.
- “ 2
(16.86)
Идентификация АРСС(1,1)-модели может быть проведена в соответ-
ствии с общей двухэтапной процедурой, описанной выше (см. соотноше-
ния (16.79*), (16.83) и т. д.). Система (16.83) в нашем случае состоит из
единственного уравнения
г(2) - аг(1) = 0,
так что на 1-м этапе мы получаем оценку параметра а в виде
г(2)
Ф) ’
На 2-м этапе выписываем соотношения
е(0 - ac(t - 1) = 0(e) - 00(е - 1),
е(е + 1) -	= 0(е + 1) - 00(e).
(16.87)
(16.88)
(16.88')
Возводя в квадрат (16.88), перемножая почленно соотношения (16.88)
и (16.88*), переходя к математическим ожиданиям полученных выраже-
ний и заменяя y(k) их выборочными значениями 7(Л), имеем следующую
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
853
систему из двух уравнений относительно неизвестных 0 и
f 7(0)( 1 + а2) ~ 2ау(1) =	+ в2),
I 7(1)(1 + а2) - «(7(0) + 7(2)) =
Решение этой системы не представляет принципиальных трудностей.
Поделив 1-е уравнение на 2-е, получаем квадратное уравнение относитель-
но 0:
7(0)(1 + а3) - 2а7(1)	1+й3
7(1)(1 + а3) - 0(7(0) + 7(2))	9
Решив это уравнение относительно в и выбрав из двух корней тот,
который удовлетворяет условию обратимости |0| < 1, возвращаемся к лю-
_	2
бому из уравнении системы и определяем оценку параметра <т0.
Операторы F+ и F_ сдвига по времени и действия с ни-
ми. Удобным понятием при анализе АРСС-моделей является понятие опе-
раторов сдвига по времени анализируемого процесса на один такт време-
ни, соответственно, вперед (оператор F+) и назад (оператор F_). Опера-
торы F+ и F_ определяются с помощью следующих соотношений:
F+e(t) = e(t + 1);
F_e(t) = e(t -1).
Эта запись означает, что оператор F+ (или оператор F_), примененный к
значению с(0 временного ряда в точке Z, преобразует это значение в e(f+l)
(или, соответственно, в e(t — 1)), т.е. как бы «сдвигает» временной ряд
на один такт времени вперед (соответственно, назад).
Из данного определения операторов F+ и F_ непосредственно выте-
кают следующие простые правила действий с ними:
(!)Г+ = ГГ1.
Действительно, F+(F_e(t)) = F+F_e(t) = F+c(t-l) = е(<), т.е. F+F_ — 1.
(ii) F*£(t) = e(t + к) и	— к).
Действительно, например, F2 c(t) = F_(F_£(t)) = F_e(f — 1) = e(i — 2) и
т.д.
(iii) (c0 + cTF_ + ... + cmF?)e(t) = c0 + c^ft - 1) + ... + cme(t - m)
и аналогично
(со + CiF+ + ... + cmF™)e(t) = co + Cj£(t + 1) + . • • + cme(Z + m)
(в этих соотношениях Co, Q,..., cm — некоторые постоянные числа).
854
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
В частности, АРСС(р,д)-моделъ может быть записана в виде
4„(F_, а)е(1) = Л.(Г_в)«(0,	(16.796)
где
Xp(F_,a) = 1 - ajF- -	----- apFL (16.89)
И
= i -«iF_ -e„n. (16.89')
Приведем здесь еще одно полезное представление АРСС(р, ^-процес-
сов. Пусть	z2(a),..., zp(a) — корни характеристического уравнения
АР(р)-модели
Ap(z,a) = 0,	(16.90)
а ^1(0)j^2(0)j---j^(0) — корни характеристического уравнения СС(<?)-
модели
B,(z,») = 0,	(16.90')
где полиномы Ap(Z,a) и B9(z, 0) определяются соотношениями, соответ-
ственно, (16.89) и (16.89*). И пусть все эти корни удовлетворяют усло-
виям стационарности процесса АР(р) и обратимости процесса CC(q\
Тогда с помощью несложных рассуждений, используя представимость по-
лимов (16.89) и (16.89*) в виде
a) = (z - zj(a))(z - Zj(a)) •  • (z - z„(a)),
= (z - zj(e)) (z - z2(0)) • •  (z - z,(e)),
переходим от (16.796) к соотношению
1
Zj(a)
z/e)F-
«(0.
(16.79’)
представляющему собой еще одну форму записи АРСС(р, q)-процесса.
Наконец, отметим связь, существующую между оператором F_ и опе-
ратором введенной в п. 16.3.3 последовательной разности Д. Из опреде-
ления Д (напомним: Де(0 =	1)) и F_ непосредственно следует:
Д = 1- F_,
(16.91)
т.к. Де(<) = (1 — F_)e(J) = е(<) - e(t - 1).
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
855
Неоднозначность в определении параметров АРСС-моделей
и «прогноз назад». Как известно (см. п. 2.5.3), поведение всякой по-
следовательности случайных величин {£($)} полностью определяется со-
вместным законом распределения вероятностей для многомерных случай-
ных величин вида (£(<1),€(^)>-- -if(^v)) Для любого наперед заданного
N и любого набора значений	В данном пункте мы анали-
зируем определенный подкласс случайных последовательностей, а имен-
но стационарные в широком смысле временные ряды £(<), t = 1,2,...,
и, следовательно, каждый из них полностью определяется своей автоко-
вариационной функцией 7(т). О моделях (временных рядах, процессах),
имеющих одну и ту же ковариационную функцию, будем говорить как
о моделях с идентичной ковариационной структурой. В ходе анализа
АР(р)-, СС(д)- и АРСС(р,д)-моделей, идя от известной автоковариаци-
онной функции исследуемого процесса к определению неизвестных
значений параметров модели, мы видели, что одной и той же автоковари-
ационной функции могут соответствовать различные его представления в
виде линейных параметрических моделей (см., например, выше уравнение
(16.75) для определения параметра 6 в СС(1)-модели). Выбор единствен-
ного решения осуществлялся с помощью введения соответствующих огра-
ничений на значения параметров ak (к = 1,2,... ,р) и Qj (j = l,2,...,g),
обеспечивающих стационарность и обратимость АРСС-модели. Эти огра-
ничения в общем случае формируются в терминах корней Zi(a),..., гр(а)
и £1(0),..., £fl(0) характеристических уравнений, соответственно, (16.90) и
(16.901). Напомним, что стационарность процессов АР(р) обеспечивается
требованием, чтобы все корни ^(а) (к = 1,2,... ,р) лежали бы вне единич-
ного круга, обратимость процессов СС(д) — аналогичным требованием
к корням £j(0), j = 1,2, ...,g (СС — процессы стационарны при любых
значениях 0j), а для стационарности и обратимости АРСС(р,д)-процессов
необходимо и достаточно одновременного выполнения обоих этих требо-
ваний.
Теперь мы можем сформулировать три существенных факта, отно-
сящихся к проблеме неоднозначности в определении параметров АРСС-
модели (их обоснование можно найти, например, в книге [Бокс Дж., Джен-
кинс Г., вып. 1], с. 218-221).
1)	Все линейные параметрические модели вида
р /	1	\	4 /	1	\
П (1 - ~r^F-)	= П (1 - -^F-)
у к 2;(“) + /	\ zAe) +J
(16.92)
имеют идентичную ковариационную структуру. При этом допускается
любая комбинация знаков «+» и «-» в качестве нижних индексов опера-
856
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
тора F в левых и правых частях (16.92).
2)	Существует единственное представление (16.79в) (или равносиль-
ные ему представления (16.79), (16.79*), (16.796)), связывающее в рамках
модели АРСС(р,<?) значение e(t) только с прошлым этого ряда.
3)	Беря в левой и правой частях соотношения (16.92) оператор сдвига
F со знаком *+*, приходим к соотношению

(16.92')
или, что то же,
fi(l) = a1e(«+l) + ...+aJle(t+p)+i(t)-M(«+l)-.---M(t+?)- (16.92й)
Другими словами, существует стационарное обратимое представле-
ние, в котором e(t) выражено целиком через будущие значения е и настоя-
щее и будущие значения 6(f). На первый взгляд, с прикладной точки зре-
ния, представление (16.92п) (которое часто называют возвратным) кажет-
ся искусственным, странным, однако оно оказывается полезным в ситуа-
циях, когда требуется восстанавливать неизвестные (потерянные, «стер-
тые», незарегистрированные) прошлые значения анализируемого процес-
са, т.е. строить «прогноз назад*.
Проблема «перепараметризации» при подборе модели. Если
отправляться в представлении АРСС(р, д)-модели от (16.79б)-(16.79в), то
очевидно, что модель (16.796) идентична модели
(1 - АГ_)А„(Г_1О) = (1 - AF_)B4(F_,0)«(i),
в которой Л — некоторое число, а операторы авторегрессии и скользяще-
го среднего умножены на один и тот же множитель (1 — AF_). Поэтому
при подборе модели следует позаботиться о том, чтобы в ней не появля-
лись избыточные (с точки зрения экономной параметризации) или «почти
избыточные» множители подобного типа.
Например, общий множитель в модели АРСС(2,1)
(1 - 1,3F_ + 0,4F?)e(l) = (1 - 0,5F_)4(l)
можно увидеть только после разложения левой части на множители в со-
ответствии с (16.79в)
(1 - 0,5F_)(l - 0,8F_)e(0 = (1 - 0,5Г_ )$(*).
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
857
Так что на самом деле мы имеем не АРСС(2,1)-модель, а АР(1)-модель
вида
или, что то же,
<0 = O,8e(t-l)+ £(*)
На практике трудности вызывает не столько наличие одинаковых
множителей в представлении (16.79е), сколько ситуация, когда имеются
почти одинаковые множители. Например, пусть истинная модель имеет
вид
(1 - 0,4F_)(l - 0,8Г_)ф) = (1 - O,5F-M0.	(16.93)
Если делается попытка подогнать эту модель по экспериментальным дан-
ным, то можно ожидать крайнюю нестабильность в оценках параметров1
из-за близости множителей (1— 0,4Г_) и (1-0,5F_)b разных частях (16.93).
В подобных ситуациях следует идти на упрощение модели. Это достигает-
ся различными способами. Например, для близких значений корней *,•(<*)
и Zj(0) полагают z^a) & Zj(0) и сокращают соответствующие сомножи-
тели в левой и правой частях представления (16.79в). В нашем примере
(16.93) это привело бы к рассмотрению АР(1)-модели
(1-0,8Г_)£(0 = *(0
вместо АРСС(2,1)-модели (16.93), поскольку эти две модели на практике
оказались статистически неразличимы.
Можно подойти к этому вопросу с несколько иной точки зрения, «за-
гоняя» множители вида (1 —F_/zj(fl)) правой части (16.79в) в знаменатель
левой части этого соотношения и формально разлагая получившийся та-
ким образом оператор левой части
п ~
по степеням (F_/zj(0)) (при этом полагается, что |F_/zj(0)| < 1, исполь-
зуется формула суммы бесконечно убывающей геометрической прогрессии
1 Под нестабильностью в оценках подразумевается ях относительно большой раз-
брос, например, статистически незначимое расхождение в оценках параметра 0,4 в
левой части и параметра 0,5 в правой части представления анализируемого процесса.
Однако вопросы точности оценивания параметров моделей временных рядов оста-
лись за рамками нашего учебника (за исключением некоторых частных случаев).
858
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
и в получившемся бесконечном разложении ограничиваются двумя-тремя
первыми членами). Так, например, реализация этой процедуры примени-
тельно к (16.93) дает
(1 - 0,4F)(l - 0,8F) = (1 _ 0 4f )(1 _ 0 8F )
1 — и,О-Г_
х (1 + 0,5F_ + 0,25F“ + 0.125F3 + ...)
= 1 - 0,700F_ - 0,030Fl - 0,015/^
- 0,008fl - ... .
Ограничиваясь первыми двумя членами этого разложения, получаем
АР(1)-модель
(l-0,7F_)e(0 = ^),
также статистически неразличимую с истинной моделью (16.93).
Из сказанного следует, что окончательный выбор структурных па-
раметров модели (т.е. параметров р и q) надо производить лишь поем
идентификации первого (априорного) гипотетического вида АРСС(р,?)-
модели. Если в результате оценивания параметров ак и 0j и вычисления
корней характеристических уравнений (16.90) и (16.90*) (в которых вме-
сто значений параметров ак и подставлены их оценки, соответственно,
ак и 0j) окажутся близкие по величине пары я»(а) и £,(0), то в пред-
ставлении (16.79в) соответствующие сомножители в его левой и правой
частях должны быть сокращены. После этого значения р и q соответству-
ющим образом подправляются (в сторону их уменьшения, конечно) и весь
процесс анализа и идентификации модели повторяется заново.
Векторные модели авторегрессии — скользящего средне*
го. В эконометрической литературе и приложениях обсуждаются и ис-
пользуются также многомерные (или секторные) модели АРСС и, как
их частные случаи, векторные АР- и СС-модели. В сущности эта те-
ма больше относится к проблематике многомерной регрессии и систе-
ме одновременных уравнений (см. гл. 14 и 17), т.е. к ситуациям, когда
статистику-эконометристу приходится одновременно отслеживать пове-
дение многих показателей и исследовать существующие между этими по-
казателями статистические связи. Поэтому мы ограничимся здесь лишь
краткой справкой о векторных АРСС-моделях.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
859
Введем в рассмотрение многомерные временные ряды
а также последовательности матриц коэффициентов
/ а11	“12
а{к} “21	а(Аг) “22
	л(*)
'“ml	“m2
а1т
о(А)
а2т
а(А)
к — 1,2,... ,р,
/ дО)	М	д(»
д(5)	М	ди)
"21	"22	• - •	U2m
< й	Д	...
х ml m2	итт
j = 1,2,...,9.
Мы полагаем, как и прежде, что компоненты tr }(t) вектора 6(f)
образуют временные последовательности, именуемые белым шумом (см.
(16.39)-(16.40)). Однако это не значит, что 6^^(t) и №\з) взаимно не-
коррелированы ни при каких t и з, когда /1 / Z2*
Тогда векторная АРСС(р, <?)-модель может быть записана в виде
е(£) = ttle(t-l)+.. .+a„e(f-p)4-6(t)-0i6(f-l)-.. .-096(t~9), (16.94)
или в покомпонентной форме
mm	m
eW(0 = £	- 1) + £ «<?’?'>(! _ 2) + ... + £ a(?)£(')(t _ р)
/=1	1=1	/=1
m	m
+^°(0 - Е -1) -... - Е
(=1	/=1
»= 1,2,...,ш.	(16.94')
Однако по причине слишком большого числа участвующих в (16.94х)
параметров в эконометрических приложениях используется обычно упро-
щенный вариант этой модели, в котором отсутствует скользящее сум-
мирование элементов белого шума, т.е. векторная авторегрессионная
модель порядка р (сокращенно-векторная АР(р)-модель, или ВАР(р)-
модель):
e(i) = ai£(l - 1) + ... + a„e(t - р) + 6(f),
(16.95)
860
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
или в покомпонентной записи
тп	m
fi(’)(<) = 52 Qi?)e(00_1) + --- + 5L	» = 1,2,...,m.
/=1	1=1
(16.95')
Если остатки и №(t) взаимно не коррелировали при t / j,
то параметры т уравнений (16.96х) могут оцениваться отдельно для ка*
ждого уравнения с помощью обычного метода наименьших квадратов. В
общем случае (т. е. при взаимной коррелированности остатков) уравнения
(16.95х) можно рассматривать как один из типов систем одновременных
уравнений (см. гл. 14 и 17) и применять к ним соответствующие методы
статистического анализа.
Более подробные сведения о векторных моделях авторегрессии можно
найти, например, в книге [Greene W. Н.], гл. 19, 20.
16.4.4. Простая и обобщенная модели авторегрессионных
условно гетероскедастичных остатков
В ряде прикладных эконометрических работ, в частности, при анали-
зе и моделировании макроэкономических данных, характеризующих про-
цессы инфляции и внешней торговли, механизмы формирования нормы
процента и т. п.1, была выявлена некоторая общая закономерность в по-
ведении случайных остатков (ошибок прогноза) исследуемых моделей: их
малые и большие значения группировались целыми кластерами, или се-
риями. Причем это не приводило к нарушению их стационарности и, в
частности, их гомоскедастичности для относительно больших временных
интервалов, т.е. гипотеза De(t) = у(0) = const не противоречила име-
ющимся экспериментальным данным. Однако в рамках моделей АРСС
удовлетворительно объяснить этот феномен не удавалось. Требовалась
определенная модификация известных моделей.
Такая модификация была предложена впервые Р. Энглом в 1982 г.
(см. работу 1982 г. в сноске). Он рассматривал остатки e(t) как условно
гетероскедастичные, связанные друг с другом простейшей авторегресси-
1 См. Engle R. Autoregressive Conditional Heteroscedasticity with Estimates of the
Variance of United Kingdom Inflations. «Econometrics», 50 (1982), pp. 987-1008;
Engle R. Estimates of the Variance of U.S. Inflation Based on the ARCH Model.
«Journal of Money, Credit, and Banking, 15 (1983), pp. 286-301; Cragg J. More Efficient
Estimation in the Presence of Heteroscedasticity of Unknown Form. «Econometrics», 51
(1983), pp.751-763.
16.4. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
861
онной зависимостью, а именно:
[£(t)|e(t-l)]GJV(O;a?),
где <r? = D(e(t) | e(i - 1)) = в0 + 01£3(i - 1),
или, что то же,
£(О = в(О[«о+<’1Л‘-1)]>	(16-96')
где последовательность <5(t), t = 1,2,..., — образует стандартизован-
ный нормальный белым шум (т.е. 0(tj) и 6(t2) независимы при ti / t2 и
£(t) G N (0;l)), а параметры 0O и 0i должны удовлетворять ограничениям,
обеспечивающим безусловную гомоскедастичность e(t) (такими ограниче-
ниями являются требования > 0, |0i| < 1). При этом под [e(t) | е(« — 1)]
мы подразумеваем, что речь идет о случайной величине, рассматриваемой
в предположении, что ее значение в предшествующий момент времени за-
фиксировано (задано). Соответственно, ее поведение будет описываться
условным законом распределения вероятностей.
Следуя установившейся терминологии, будем называть модель (16.96)
авторегрессионной условно гетероскедастичной (сокращенно АРУГ).
В англоязычной литературе такие модели называют AutoRegressive
Conditional Heteroscedasticity (сокращенно ARCH-model).
Использование такой модели для описания поведения остатков моде-
лей регрессии и временных рядов в упомянутых выше типовых ситуаци-
ях оказывается более адекватным действительности и позволяет строить
более эффективные оценки параметров рассматриваемых моделей, чем
обычные или даже обобщенные МНК-оценки (см., например, описание ал-
горитма построения нелинейных оценок максимального правдоподобия для
параметров линейной модели множественной регрессии с авторегрессион-
ными и условно гетероскедастнчнымн остатками в книге [Greene W. Н ],
рр. 439-440; получающиеся оценки оказываются более эффективными, чем
даже наиболее эффективные, в классе линейных оценок, МНК-оценки).
Естественное обобщение моделей типа (16.96) было предложено Р. Эн-
глом и Д. Крафтом в 1983 г. (см. Engle R., Kraft D. in «Applied Time Series
Analysis of Economic Data», Washington D. C.: Bureau of the Census, 1983):
2	2	2	(16.96 )
где crt = 0O + 01 e (t - 1) + ... + 0g£ (t - q),
а параметры 0q,0i, • • •, 09 связаны некоторыми ограничениями, обеспечи-
вающими безусловную гомоскедастичность остатков e(t).
Модели (16.96м) называются моделями АРУГ порядка q (сокращенно
АРУГ(д)). Очевидно, модель (16.96) является АРУГ(1)-моделью и соот-
862
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
ветствует частному случаю (16.96*) при q = 1. Содержательно переход
к q > 1 в моделях (16.96* I означает, что процесс формирования значений
остатков e(t) имеет «более длинную память» о величинах предшеству-
ющих остатков e(i — 1), e(t — 2),... . Кстати, АРУГ(д)-модель (16.96а)
может рассматриваться как некая специальная форма СС^-модели, что
и используется при ее анализе.
Дальнейшее обобщение моделей этого типа было сделано в 1986 г.
Т. Боллерслевом (см. Bollerslev Т. Generalized Autoregressive Conditional
Heteroscedasticity. «Journal of Econometrics», 31 (1986), pp. 307-327). Он
предложил описывать поведение остатков e(t) с помощью обобщенной ав-
торегрессионной условно гетпероскедастпичной модели (ОАРУГ-модели,
или, в англоязычном варианте, — GARCH-model), которая записывается
в виде
[ КО I ^)] е Л(0;а?),
< где условная дисперсия	= D(e(f) | V’W имеет вид
Of = CViOf-i -f- ОС2(Ц-2 + + Qp°t-p + #0 +	— 1) + . • • +	— q).
(16.97)
В соотношениях (16.97) под подразумевается вся информация о
процессе e(t), которой мы располагаем к моменту времени t (т. е. — все
значения е(т) и oj для т < t), а параметры ак и 0j (к = 1,2,...,р; j -
0,1,...,д) связаны ограничениями, обеспечивающими безусловную го-
москедастичность остатков е(1). Модель ОАРУГ(р, д), задаваемая со-
отношениям (16.97), может интерпретироваться как специальная фор-
ма АРСС(р,д)-модели. На ряде примеров показано, что использование
ОАРУГ(р, д)-модели позволяет добиваться более экономной параметри-
зации в описании поведения остатков e(t), чем в рамках АРУГ(д)-моделей
(т. е. модели ОАРУГ(р, д) при малых значениях р и д оказываются более
точными, чем АРУ]Г(д)-модели при больших значениях д).
Достаточно полный критический обзор, посвященный описанию
АРУ Г- и ОА РУ Г-моделей и их приложениям в экономике и финансах,
читатель найдет, например, в журнале «Обозрение прикладной и про-
мышленной математики», серия «Финансовая и страховая математика»,
т. 3 (1996), вып. 6.
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
863
16.5. Модели нестационарных временных
рядов и их идентификация
В предыдущем пункте мы занимались анализом и моделированием
случайных остатков e(t), с которыми приходится иметь дело как в обоб-
щенных линейных моделях множественной регрессии (15.73), так и в мо-
делях временных рядов (16.2). Удовлетворительные (в прикладном смы-
сле) результаты в моделировании случайных остатков можно получить,
оставаясь в рамках класса моделей стационарных временных рядов. Од-
нако сами реальные временные ряды x(t), встречающиеся в экономике,
финансах, торговле, маркетинге, за редкими исключениями являются не-
стационарными. Правда, их нестационарность чаще всего проявляется
лишь в наличии зависящей от времени I неслучайной составляющей /(£).
В подобных случаях говорят о нестационарности на уровне первых мо-
ментов, или о нестационарных однородных временных рядах. Иначе го-
воря, временной ряд x(t) называется нестационарным однородным, если
его случайный остаток f(t), получающийся вычитанием из ряда x(t) его
неслучайной составляющей /(1), представляет собой стационарный (в ши-
роком смысле) временной ряд. Моделям именно таких временных рядов
z(t) и посвящен данный пункт учебника.
16.5.1. Модель авторегрессии-проинтегрированного
скользящего среднего (АРПСС(р,д,А;)-модель)
Эта модель предложена Дж. Боксом и Г. Дженкинсом (см. [Бокс Дж.,
Дженкинс Г., вып. 1], с. 102-132) и поэтому в специальной литературе из-
вестна также как «модель Бокса-Дженкинса* (в англоязычном вариан-
те — AutoRegressive Integrated Moving Average model, или сокращенно
ARIMA-model). Она предназначена для описания нестационарных вре-
менных рядов z(t), t = 1,2,...,N, обладающих следующими свойствами:
(i) анализируемый временной ряд включает в себя (аддитивно) соста-
вляющую /(t), имеющую вид алгебраического полинома (от параме-
тра времени t) некоторой степени к — 1 (к > 1); при этом коэффици-
енты этого полинома могут быть как стохастической, так и нестоха-
стической природы;
(ii) ряд t = 1,2,..., — к, получившийся из x(t) после применения
к нему fc-кратной процедуры метода последовательных разностей (см.
и. 16.3.3), может быть описан моделью АРСС(р,д).
Это означает, что АРПСС(р,д, к)-модель анализируемого процесса
864
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
x(t), t = 1,2,..., N, может быть записана в виде
xk(t) = агхк(1 - 1) + a2xk(t - 2) + ... + apxk(t - p) + 6(t)
- O^t - 1) - ... -	- g),	(16.98)
где
z*(t) = A*Xt) = x(t) - dz(t - 1) + cfa(t - 2) -... +	- *),
1 — к 1,A; 4" 2,...,TV.
С учетом представления APCC(p, д)-модели в виде (16.796) и связи
между операторами Д и F_ (см. (16.91)) модель АРПСС(р, д) может быть
записана в форме
Ar(F.,а)(1 - F_)‘z(() = B,(F_, W0,	(16.98*)
или, что то же,
AP(F_, а)Д*г(0 = B,(F_,W0,	(16.98")
где полиномы Ap(F_,a) и Bg(F_,tf) определены соотношениями, соответ-
ственно, (16.89) и (16.89х), а под &kx(t) понимается к-я последовательная
разность анализируемого процесса x(t). Обозначив произведение операто-
ров Ap(F_,a) и (1 - F_)k с помощью ^(F_,a), т.е. полагая
^F_,a) = Ap(F_,a)(l-F_)*,	(16.99)
представление АРПСС(р,д,А;)-модели можно записать в виде	ф
V(F_,a)z(0 = Bg(F_,0)£(<)-	(16.98*)
Оператор y>(F_,a) принято называть обобщенным оператором авторе-
грессии, в то время как Ap(F_,ct) — просто оператор авторегрессии,
Bq(F_,(T) — оператор скользящего среднего.
Из определения (16.99) следует, что y»(F_,a) есть полином от F_ сте-
пени р 4- к со свободным членом, равным единице, т. е.
<p(F.,a) = (1 - a,F_ - atFL - ... - arFl)(l - F_)k
= l-^F_-ViFL-...~ <рг+кР^к, (16.99*)
где коэффициенты ^i, ^2, • ♦ • ? <Pp+k очевидным образом выражаются через
«1, а2,... ,ар. Например, для модели АРПСС( 1,1,1) имеем в соответствии
с (16.89) и (16.99)
y?(F_,a) — (1 — aF_)(l — F_) = 1 — (1 4- a)F_ 4- aJPL,
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
865
так что форма (16.98*) для модели АР ПСС( 1,1,1) будет иметь вид
[1 - (1 + а)К_ + af?]a(l) = (1 - вГ_)«(1),	(16.100)
или, что то же,
a(t) = (1 + a)x(t - 1) - ax(t - 2) + 4(t) - W(t - 1).	(16.100')
Для многих целей, и в частности для вычисления прогнозов (см.
и. 16.6), уравнения типа (16.100z) являются наиболее удобной формой опи-
сания АРПСС-моделей.
Поясним теперь слово «проинтегрированного» в названии АРПСС-
моделей. С этой целью введем в рассмотрение бесконечный оператор сум-
мирования S, определенный как
t
Sx(t) = x(i) + x(t - 1)+ x(t - 2) + ... =	х(т).
т=—оо
Непосредственно из определения операторов , Д и S следует:
5 = Д"’=(1-F_)-1 = 1 + F_ + F’+... .	(16.101)
Соответственно определяются степени оператора S:
t I
s2i(t) = s(si(t)) = si(t)+sa(t-i)+...= 52 52 г(г)>
1= —оо т=—оо
S3x(t)= S(S2x(t)) = 52 5Z	итд-
V— — OO /= —OO T=—co
Из (16.101) следует (и непосредственной проверкой можно в этом убе-
диться), что процесс x(t) можно получить из процесса х^(1) = Afci(Z)
суммированием (интегрированием) последнего к раз, т. е.
a(t) = 5*(A*i(t)).
Применяя эту операцию к обеим частям АРПСС-процесса, записан-
ного в форме (16.98”), имеем
4„(F_,a)a(i) = S*(B,(F_, 0)ф)),	(16.986)
т.е. имеем именно процесс авторегрессии (левая часть) — проинтегриро-
ванного скользящего среднего (правая часть). Правда, правильнее было
бы сказать «просуммированного» вместо «проинтегрированного».
866
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Заметим, что при описании несезонных временных рядов (сезонные
модели будут рассмотрены в п. 16.5.2) редко встречаются с ситуацией, в
которой порядки р, q или к были бы больше 2. Наиболее распространенные
в прикладных эконометрических исследованиях АРПСС-модели имеют по-
рядки
1)р=0, g = l, fc=l;
2)	р = 0, q = 2, к = 2;
3)р=1, д=1, к=1
4)р= 1, g = О, к= 1;
5)	р = 2, q = 0, к = 1.
(см. (16.100'));
Идентификация АРПСС-моделеи. В первую очередь, следует по-
добрать порядок к модели. При этом руководствуются соображениями
двух типов. Первый тип эвристического критерия описан в п. 16.3.3. Он
основан на отслеживании поведения величины д2(к) (см. (16.38)) в за-
висимости от к: в качестве верхней оценки для порядка к определяется
то значение к0, начиная с которого тенденция к убыванию ст3 (Л) гасится
и само значение д2(к) относительно стабилизируется. Второй тип со-
ображений, на которых основан подбор порядка к модели АРПСС(р,д,Л),
относится к анализу поведения автокорреляционных функций процессов
Az(£), A2z(t),... . Последовательные преобразования анализируемого
процесса x(t) с помощью операторов Д, Д3 и т.д. нацелены на устра-
нение его нестационарности. Пока мы не «доберемся» до нужного поряд-
ка к (т.е. при всех I < к) процессы Afz(t) будут оставаться нестацио-
нарными, что, в частности, будет выражаться в отсутствии быстрого
спада в поведении их выборочной автокорреляционной функции. Поэто-
му предполагается, что необходимая для получения стационарности сте-
пень к разности Д достигнута, если автокорреляционная функция ряда
хь(1) = &кх(1) быстро затухает. На практике к обычно равно 0, 1 или
2. Поэтому достаточно бывает вычислить по несколько первых значений
автокорреляций исходного ряда x(t), его первых и вторых разностей (т.е.
рядов a?i(0 = Дг(<) и ®j(t) = Д2х(£)).
После подбора порядка к мы практически анализируем уже не сам
ряд x(t), а его к-е разности, т.е. ряд Xk(t) = Д*г(1). А идентификация
этого ряда сводится к идентификации АРСС(р, q)-моделей. Процедуры же
идентификации моделей АРСС(р, д) описаны в п. 16.4.3.
Коинтеграция временных рядов в регрессионном анали-
зе. Временной ряд x(t) называется интегрируемым порядка к, если он
становится впервые стационарным после ^-кратного применения к нему
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
867
разностного оператора Д. В регрессионном анализе обычно одновременно
рассматривается несколько временных рядов. Очевидно, если sc(t) — ин-
тегрируемый временной ряд порядка fcj и y(t) — интегрируемый времен-
ной ряд порядка fc2, причем > А, то при любом значении параметра О (в
том числе при в — 0МИК, гдс — МНК-оценка коэффициента регрессии
в модели парной регрессии у по х) случайный остаток e(t) = y(t) — 0x(t)
будет интегрируемым временным рядом порядка fc2. Если же ki = fc3 = k,
то константа в может быть подобрана так, что e(t) будет стационарным
(или интегрируемым порядка 0) с нулевым средним. При этом вектор
(1;-0) (или любой другой, отличающийся от этого сомножителем) назы-
вается коинтегрирующим. При регрессионном анализе временных рядов
x(t) и y(t) их коинтеграция (согласование порядков их интегрируемости)
производится обычно по следующей схеме: 1) рассматривается модель
y(t) = 6x[t) 4- e(t) и строится МНК-оценка 0МНК для параметра 0; 2) ряд
e(t) = y(t) — 6мнкх(1) анализируется на стационарность в рамках одной из
моделей АРСС(р,^); например, в рамках АР(1)-модели проверяется гипо-
теза |а| < 1 в представлении е(0 = ae(t — 1) + 0(0; 3) если результат от-
рицательный, то возвращаются к спецификации исходной модели, пробуя
в качестве зависимой и объясняющей переменных различные варианты
Подробнее с проблемой коинтеграции временных рядов можно позна-
комиться в книге [Greene W. H.J, § 19.6.
16.5.2.	Модели рядов, содержащих сезонную компоненту
В разделе п. 16.1, посвященном генезису наблюдений, образующих
временной ряд ж(0, мы подразделяли факторы, под воздействием которых
формируются значения з;(0, на долговременные, сезонные, циклические и
случайные. В примере 16.1 и на рис. 16.1 был описан типичный представи-
тель временных рядов, в формировании значений которых существенную
роль играют сезонные факторы. В дальнейшем под временными рядами,
содержащими сезонную компоненту, мы будем понимать процессы, при
формировании значений которых обязательно присутствовали сезонные
и/или циклические факторы.
Напомним, что построение модели временного ряда — на самоцель,
а лишь средство его анализа и прогнозирования. Один из распростра-
ненных подходов к прогнозированию состоит в следующем: решают за-
дачу разложения ряда на долговременную, сезонную (объединяющую в
себе собственно сезонную и циклическую компоненты) и случайную соста-
вляющие; затем долговременную составляющую стараются «подогнать»
868
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
полиномом, сезонную — рядом Фурье, после чего прогноз производится
экстраполяцией этих «подогнанных» значений в будущее. Однако такой
подход может оказаться неэффективным, более того, приводить к серьез-
ным ошибкам, по двум причинам. Во-первых, короткие участки в дей-
ствительности стационарного ряда (а в экономических приложениях мы
редко имеем достаточно длинные временные ряды) могут выглядеть при-
близительно как фрагменты полиномиальных или гармонических функ-
ций, что повлечет за собой их неправомерную аппроксимацию и предста-
вление в качестве долговременных или сезонных неслучайных составля-
ющих (см. ниже пример 16.13 в п. 16.6.2). Во-вторых, даже в случаях,
когда анализируемый ряд действительно включает в себя неслучайные
полиномиальные или гармонические компоненты, их формальная аппрок-
симация может потребовать привлечения слишком большого числа пара-
метров, т. е. получающаяся параметризация модели оказывается неэко-
номичной. Так, например, потребуется много гармонических компонент,
чтобы описать в динамике данные о сбыте товаров, на который влияют
всевозможные праздники и сезонные распродажи.
Принципиально другой подход основан на модификации описанных
выше конструкций АРПСС-моделей с помощью так называемых «упроща-
ющих операторов». Мы уже, по существу, пользовались этим приемом,
когда для элиминирования нестационарности из анализируемого времен-
ного ряда x(t) применяли к нему оператор Д* = (1 — F_)k. Оценивая затем
параметры в упрощенной таким образом модели стационарного временно-
го ряда Zfc($) = (1 — F_)kx(t) и возвращаясь с помощью обратного опера-
тора Sk = (1 — F_)~k к исходному ряду xft), мы получали в итоге модель
именно для ряда x(t). В данном случае в роли упрощающего оператора
выступал оператор 1 — F_. В других задачах может оказаться полезным
применение других типов упрощающих операторов. В частности, для
временного исключения (в целях упрощения) из анализируемого ряда x(t)
сезонной составляющей, имеющей период Т, в левую часть АРПСС(р,д)-
модели, представленной уравнением (16.98*), мультипликативно вводит-
ся упрощающий оператор Vy = 1 — Fl в «подходящей» степени А, а в
правую часть — множители (упрощающие операторы) вида 1 - (таг
кие модели называются мультипликативными) либо в оператор-полином
Bq(F_,0) добавляются члены вида -OtFI и/или
Ниже описываются четыре относительно простые конкретные модели
такого типа (1-я и 2-я — мультипликативные, 3-я и 4-я — не мультипли-
кативные), которые успешно удовлетворяют потребности эконометриче-
ского моделирования в достаточно широком спектре приложений.
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
869
Модель сезонных рядов 1. Уравнение модели имеет вид
AfcV*z(t) = (1 - 0F_)(1 -	(16.102)
или, что то же
A*v*z(t) = i(t) - 9i(t -1) - 6"i(t -т) + ee’t(t - т -1),
т>з.
При идентификации модели подбор параметров к, К, Т производится
в процессе сочетания статистического и качественного анализа с исполь-
зованием приведенных выше рекомендаций. Оценка параметров основана
на следующих соотношениях, связывающих автоковариации процесса
х\.	= AkV^z(t) с неизвестными параметрами сто = D£(f) и 0*:
1(0) = <го(1 + f2)(i + е”);
7(1) = -<7^(1 + е*2);
7(Т-1) = 7(Т+1) = <7>*;
7(Т) = -<^*(1 + в2)-
Все остальные ковариации равны нулю.
Модель сезонных рядов № 2. Уравнение модели имеет вид:
(1 - «Fj)A*V*z(0 = (1 - «F_)(l - 0*FZ>(i),	(16.103)
или, что то же,
A*V*z(0 - aA*V«z(l - Т)
= S(t) - 6S(t - 1) -	- Z) + 00*6(1 - T - 1),
T>3, |a| < 1.
Идентификация модели включает в себя подбор параметров к, К
и Т (см. выше), а также оценивание остальных параметров методом
моментов с использованием оценок у(т) автоковариаций 7(т) процесса
sJJkW =	и связей, существующих между этими ковариациями
870
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
2	*
и неизвестными параметрами <т0 = D£(t),a, 0 и 0 :
7(0) = оЛ(1 + в2) (1 + Ц—;
7(1) =-а?в (1 + (*
\ 1 ~ а /
7(Т - 1) = 7(7 + 1) = (г - а - °(*
у	1 — а
7(7) = -а?(1 + в2) (в*-а- °(*	;
\ 1 —а /
7(т) = в7(т - Т) при т > Т 4- 2;
Модель сезонных рядов X* 3. Уравнение модели имеет вид:
A*V^i(t) = (1 - в£_ - 6* Fl)6(t),
(16.104)
или, что то же,
a*v*®(z) = ед - юр -1) - e*6(i - т),
7>3.
Идентификация модели включает в себя подбор параметров к, К и
Т (см. выше), а также оценивание остальных параметров методом мо-
(Т)
ментов с использованием оценок 7(7) ковариаций 7(7) процесса =
A*V£s(t) и связей, существующих между этими ковариациями и неиз-
вестными параметрами его = D6(t), 0 и 0*:
7(0) = ао2(1 + 02 + 0*2);
7(1) = -аов;
7(7 - 1) = <&6*;
7(Т) = -<&*;
все остальные ковариации равны нулю.
Модель сезонных рядов К1 4. Уравнение модели имеет вид:
(1 - af?)A*V*z(i) = (1 - 6F_ - 9*FI)4(t),	(16.105)
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
871
или, что то же
z(t) -	- 7) = S(t) - M(t - 1) - e'S(t - 7),
7>3, |a| < 1.
Оценивание параметров a, Oi = D4(i), 6 и 6 производится мето-
дом моментов с использованием оценок ковариаций у(т) процесса
^,к(0 = Д vf«(t) и связей, существующих между этими ковариациями
и неизвестными параметрами:
7(0) = <г? 1 +
-°)2
2
7(1) = -<& (1 - а~л—;
7V*	1) —	2 j
1 — в
1-а’
Схематично процедура построения сезонных моделей, основанных на
АРПСС-конструкциях, модифицированных с помощью упрощающих опе-
раторов VT = 1 — Fl, может быть описана следующим образом:
1)	применяем к наблюденному ряду x(t) операторы Д и VT для до-
стижения стационарности;
2)	по виду автокорреляционной функции преобразованного ряда
х^я(0 подбираем пробную модель в классе АРСС- или модифицирован-
ных (в правой части) АРСС-моделей;
3)	по значениям соответствующих автоковариаций ряда а .(/) полу-
чаем (методом моментов) оценки параметров пробной модели;
4)	диагностическая проверка полученной модели (анализ остатков в
описании реального ряда x(t) с помощью построенной модели) может либо
подтвердить правильность модели, либо указать пути ее улучшения, что
приводит к новой подгонке и повторению всей процедуры.
Более детальное описание этих процедур можно найти в книге
[Бокс Дж., Дженкинс Г., вып. 1].
872
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
16.5.3.	Регрессионные модели с распределенными лагами
Вернемся теперь к проблематике гл. 15, т. е. к построению и анализу
линейных регрессионных моделей. Уместность рассмотрения некоторых
специальных вопросов этой проблематики в главе, посвященной времен-
ным рядам, объясняется тем, что в качестве исходных статистических
данных мы располагаем наблюдениями двух временных рядов

(16.106)
Нашей целью является построение линейной регрессионной моде-
ли, позволяющей с наименьшими (в определенном смысле) ошибками
восстанавливать и прогнозировать значения y(t) по значениям ®(i),
x(t — 1),... ,x(t - Т) для t > Т 4- 1 (при этом предполагается, конечно,
что Т < N). Иначе говоря, мы будем рассматривать модели вида
т
y(t) = со +	~к) +
к-0
t = Т+1,Т+2,...,	(16.107)
где 6(t), t = 1,2,..., TV, как и прежде, последовательность гомоске-
дастичных и взаимно не коррелированных (и не коррелированных с
x(t),x(t - l),...,®(t — Т)) регрессионных остатков, а со, ^о,^,...,^ и
ад = Dtf(i) — неизвестные параметры модели. При этом, для «очень
длинных» (теоретически-бесконечных) временных рядов (16.106) в анали-
зируемой модели (16.107) допускается случай Т = оо, т.е. суммирование
в правой части (16.107) ведется по А: от 0 до оо.
Подобные модели оказываются естественными (и, соответственно,
правильно специфицированными) в ситуациях, когда две переменные х
и у связаны так, что воздействие единовременного изменения одной из
них (ж) на другую (у) сказывается в течение достаточно продолжитель-
ного периода времени (71)» т.е. наблюдается распределенный во времени
эффект воздействия. В частности, такие связи возникают, в первую оче-
редь, между регистрируемыми во времени входными и выходными харак-
теристиками процессов накопления и распределения ресурсов (например,
процессов преобразования доходов населения в его расходы) или процессов
трансформации затрат в результаты (например, процессов воспроизвод-
ства основных доходов). Рассмотрим эти примеры.
Пример 16.7. Зависимость общих расходов населения (y(t)) от
его наблюдаемых доходов (x(t)). При такой интерпретации участвую-
щих в модели (16.107) переменных x(t) и у(<) коэффициенты регрессии 0*
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
873
имеют прозрачный содержательный смысл, а именно: это, грубо го-
воря, доля дохода, которая тратится через к лет после его приобретения.
Можно было бы обойтись без «грубо говоря», если бы в качестве я($) мы
располагали бы величиной истинного (а не наблюдаемого) дохода, полу-
ченного в году t. В действительности же наблюдаемый доход в среднем
несколько меньше истинного, поэтому вместо естественного соотношения
Т
Е = 1 (ПРИ 0 <	< 1) мы будем иметь обычно	Обраща-
ло
ем внимание читателя на тот факт, что вытекающие из содержательного
смысла коэффициентов 0^ ограничения на их значения задают некоторую
их априорную структуру.
Пример 16.8. Зависимость объемов введенных основных фондов
(у(0) от капитальных вложений (z(£)). В данном случае значения коэф-
фициентов регрессии 0q,#т показывают, какими долями реализу-
ются капитальные вложения зс(т), соответственно, в году т, т+1,..., т+Т.
В силу существования определенной доли «нефондообразующих» капи-
тальных вложений (которая идет на постройки временного типа, содер-
жание управленческого аппарата, обучение персонала в период строитель-
ства и т. п.) в данном случае мы будем иметь
т
Р = £ 0* < 1,	0 < ek < I,
fc=O
где /3 мы можем интерпретировать как долю фондообразующих капиталь-
ных вложений.
Прежде чем перейти к систематическому анализу подобных моделей,
зададимся двумя вопросами:
1) Почему модель типа (16.107) требует специального рассмотрение
а не может быть проанализирована и идентифицирована в рамках класси-
ческой линейной модели множественной регрессии (КЛММР, см. п. 15.2)
или модели со стохастическими предикторами, не коррелированными с ре-
грессионными остатками (см. п. 15.10.1), в которой роль Т + 1 объясняю-
щих переменных играют члены временного ряда x(t), x(t— 1), • • -, x(t — Т)?
2) В чем заключается общая специфика того подкласса КЛММР, ко-
торый принято называть моделями с распределенными лагами и которому
посвящен данный пункт учебника?
Формально при сделанных предположениях о природе регрессион-
ных остатков А(£) в (16.107) и о некоррелированности 6(t) и z(<),
x(t — l),...,z(i — Т) модель (16.107), действительно, может быть отне-
сена к КЛММР (при неслучайном характере временного ряда x(t)) или
к линейным регрессионным моделям со стохастическим предикторами, не
874
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
коррелированными с регрессионными остатками. И в том и в другом слу-
чае статистический анализ этой модели может быть произведен с помо-
щью обычного метода наименьших квадратов (МНК). Однако при прак-
тической реализации этого метода в данном случае возникают принци-
пиальные трудности. Так, величина Т, определяющая число включенных
в модель объясняющих переменных, как правило, относится к неизвест-
ным параметрам модели. Чтобы определить значение Т, приходится, вы-
брав вначале его достаточно большим, исследовать статистическую зна-
чимость получающихся при этом оценок коэффициентов регрессии 0* для
различных значений к. Но здесь нас подстерегают две серьезные (взаимо-
связанные) «неприятности»: высокая корреляция между объясняющими
переменными (и, следовательно, высокая степень мультиколлинеарности)
и слабая статистическая достоверность наших выводов, недостаточная
их точность (из-за низких значений отношения числа имеющихся в на-
шем распоряжении наблюдений к числу оцениваемых параметров модели).
Именно эти обстоятельства стимулируют поиск некоторых специальных
подходов к анализу моделей типа (16.107).
Что касается второго вопроса, то ответ на него как раз и подсказывает
направление этого поиска. Общая специфика моделей (16.107) заключает-
ся в том, что из их содержательной сущности, как правило, вытекают
определенные априорные сведения о значениях и взаимосвязях, существу-
ющих между весовыми коэффициентами 0o,0i,...,0т, или, иначе говоря,
об их структуре. Так, например, в некоторых ситуациях коэффициенты
0* экспоненциально убывают по мере роста kt т. е. 9* = с0^, где 0 < 0О < 1,
а это значит, что вместо Г 4-1 неизвестных параметров нам придется оце-
нивать всего два: с и 0q!
Таким образом, главная идея, на которой базируется общий
подход к анализу и построению моделей вида (16.107), может быть
сформулирована следующим образом:
• отправляясь от содержательной сущности моделируемых зависи-
мостей и смысла весовых коэффициентов (к = 0,1,2,...), опреде-
лить их структурные связи с помощью введения небольшого числа
параметров оц,... ,am (m <С Т), по значениям которых можно вос-
становить значения всех неизвестных коэффициентов регрессии 9^
(т. е. речь идет об экономичной параметризации последовательно-
сти 0i, 02,...); после этого задача сводится к оценке параметров
£11	• • • 1
Модели (16.107), рассматриваемые в рамках этого общего подхода,
называются, как мы уже упоминали, регрессионными моделями с рас-
пределенными лагами или просто моделями с распределенными лага-
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
875
ми. Поясним это название.
Бели переменная (эндогенная или экзогенная) участвует в записи ана-
лизируемой модели, будучи измеренной в один из прошлых (по отношению
к текущему моменту времени t) временных тактов t — к (к > 0), то эту пе-
ременную называют лагов ой или запаздывающей, а число единиц времени
запаздывания (к) — лагом (запаздыванием). А поскольку эти лаги к в мо-
дели (16.107) распределены по объясняющим переменным с весами Вк, то
естественно называть такие модели моделями с распределенными лагами
(ниже мы увидим, что при некоторых способах параметризации весов 0к
их пронормированные значения могут интепретироваться как элементы
закона распределения вероятностей, что снова подтверждает правомер-
ность использования слова «распределенные» в названии соответствую-
щих моделей). Последовательность весовых коэффициентов	на-
зывают структурой лага (конечной или бесконечной в зависимости от ко-
нечности или бесконечности их числа Т). Если все в3 > 0 (j = 0,1,2,...),
Т
то последовательность коэффициентов w0,Wi,W2,..., где Wj = Qj/ ^6j,
i=o
называют нормированной структурой лага модели (16.107) (очевидно,
Е «,• = 1)-
j=0
Нормированная структура лага как распределение вероят-
ностей. Можно воспользоваться формальным сходством нормированной
структуры лага и закона распределения вероятностей дискретной случай-
ной величины (см. п. 2.5). Для этого введем случайную величину т («вре-
мя задержки») с законом распределения вероятностей
P{r = k} = wk,	к = 0,1,2,..., Т,	(16.108)
где Т может принимать и бесконечные значения.
Подобная интерпретация нормированной структуры лага открывает
широкие возможности в построении экономичной параметризации после-
довательности весов wk с помощью различных широко известных мо-
делей законов распределения для дискретных случайных величин (см.
пп. 3.1.1~3.1.3). Кстати, интерпретация весов w* как вероятностей в ряде
ситуаций оказывается вполне оправданной. Так, в примере 16.7 случай-
ная величина т в (16.108) интерпретируется как число тактов времени,
прошедших с момента получения дохода до момента расходования одной
случайно выбранной из него единицы. Тогда вероятность Р{т = к} = wk
определится, очевидно, отношением У^т/х^ где — истинный доход, по-
лученный в t-м такте времени, a ytfT — та его часть, которая израсходова-
на в (t + т)-м такте времени. Точно так же вероятностная интепретация
876
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
механизма зависимости (16.107) в примере 16.8 может быть сформулиро-
вана следующем образом: некоторая случайным образом выбранная еди-
ница фондообразующих капитальных вложений будет освоена на объекте
в том же году с вероятностью w0, в следующем году — с вероятностью
т
через 2 года — с вероятностью w2 и т. д. (здесь wk = Зк/ J 0к). При та-
fc=i
кой интерпретации вполне определенный смысл приобретают и основные
характеристики вероятностных распределений. Так, среднее значение Ет
в примере 16.8 будет задавать средний срок реализуемости фондообразу-
ющих капитальных вложений, дисперсия Dr будет характеризовать точ-
ность в определении среднего срока с помощью Ет и т. д.
Итак, из описанного выше следует, что одна типовая модель распре-
деленных лагов отличается от другой способом параметризации весовых
коэффициентов	т.е. способом параметризации своей лагов ой
структуры. Опишем несколько наиболее распространенных в практи-
ке эконометрического моделирования способов параметризации лаговых
структур.
Полиномиальная лаговая структура Ширли Алмон (си.
Almon S. The Distributed Lag between Capital Appropriations and Expen-
ditures. «Econometrica», 30 (1965), pp. 178-196). Мы рассмотрим здесь
простейший вариант этой модели.
Подход основан на полиномиальной форме параметризации конечной
лаговой структуры 0О>01,- • ч^т- А именно, опираясь на теорему Вейер
штрасса (которая утверждает, что непрерывная на замкнутом интервале
функция может быть приближена на всем отрезке многочленом подходя-
щей степени от ее аргумента, отличающимся от этой функции в любой
точке меньше, чем на любое заданное число) и рассматривая весовые ко-
эффициенты вк как функции к, автор предложила выразить их в виде
полиномов невысокой степени т (т < 3) от А, т.е.
вк = а0 4- arf 4- а2к2 4-... 4- аткт,
* = 0,1,2,...,Т,
(16.109)
где ao,ai,...,am — некоторые неизвестные параметры, которые опре-
деляются из условия наиболее точной (в определенном смысле) подгонки
модели (16.107).
16.Б. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
877
Подставляя последовательно в (16.109) к = 0,1,2,.. . ,Т, получаем:
= «о>
i = <*о + <*1 + •
< #2 = «о +	+
• 4"
.. + 2тато,
(16.109')
О'Р — «о 4- Tot\ + • - - + Ттат.
Возвращаемся к анализируемой модели (16.107J, заменяя в ней коэф-
фициенты их выражениями по формулам (16.109):
т
у(0 = с0 4- 52^®(« - к) 4- Л(0 = со
fc=o
4- «о®(0
+ aox(t - 1) 4- aix(t - 1) 4-... 4- <*mx(t - 1)
4- aQx(t - 2) 4- 2а!ж(/ - 2) 4-... 4- 2mamx(t - 2)
+ a0*G - T) 4- TaAx(tT) 4-... 4- Tmamx(t - T) 4- *(*).
(16.110)
Суммируя co и остальные слагаемые правой части (16.110) по столбцам,
получаем:
1/(0 = с0 4- «о [z(0 4-	- 1) 4-... 4- x(t - Г)]
+ ai [s(t -1)4- 2x(t - 2) 4-... 4- Tx(t - 7)]
+ am [®(t -1)4- 2mx(t - 2) 4-... 4- Tmx(t - T)]
+ Ф).	(16.110')
Обозначая первую квадратную скобку в правой части (16.110') как
($'), вторую — как i^2\f'),..., m-ю — как i^m\t'), где «новое» время
/ «привязано» к моменту времени t — Т (т.е. t' = t - Т), получаем:
y(t'+T) = Co+aoi(1)(<')+aii(2)(*')+-”+“mi(m,(«') + «(i'+T), (16.110")
i = X,2,...,N-Т.
В результате мы свели задачу оценивания Т 4- 2 неизвестных весовых
коэффициентов со,^о»^1,• •  к статистическому анализу стандартной
878
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
линейной модели множественной регрессии всего с т + 1 (т < 3) неиз-
вестными параметрами (при этом предполагается, конечно, что длина
исходных временных рядов N много больше, чем Т + т). Так что оценки
со и otj параметров с0 и aj (j = 1,2,..., т) получаются с помощью обыч-
ного МНК (см. п. 15.3.1), после чего по формулам (16.109') вычисляются
оценки (к = 0,1,... ,Т).
Заметим, что мы полагали в данной схеме максимальную величину
лага Т известной. В действительности она, как правило, определяется
статистически. Обычно проводят описанные выше расчеты для несколь-
ких предположительных значений Т и окончательный выбор между ними
производят на основании диагностики полученных моделей, т. е. — путем
сравнения различных характеристик их точности.
Геометрическая лаговая структура Койка (см. Коуск L.M.
Distributed Lags and Investment Analysis. North-Holland Publishing
Company, Amsterdam, 1954). В данном подходе рассматривается беско-
нечная лаговая структура (т.е. в (16.107) полагается Т = оо), поэтому
он применим лишь к достаточно длинным временным рядам (16.106).
Общим (и естественным!) допущением при анализе бесконечных лаго-
оо
вых структур является требование сходимости ряда /3 = £ 6^ т е.
*=о
т
lim J2 = Р < и, следовательно, lim 0^ = 0. Это означает, что
Т-кю fc_0	fc—юо
влияние x(t) на y(t 4- к) уменьшается до нуля по мере неограниченно-
го увеличения временного интервала к, что естественно, т. к. текущее
значение у практически не должно зависеть от поведения х в бесконеч-
но далеком прошлом. Койк в своем подходе конкретизировал и усилил
это допущение. В частности, он постулировал, что все нормированные
оо
веса = в к/ У2 являясь положительными, убывают с ростом к по
>=о
геометрической прогрессии, т.е.
w* = (1 - А)А*, где 0 < А < 1	(16.Ш)
(множитель (1 — А) в соотношении (16.111) нужен для того, чтобы обеспе-
оо
чить условие нормировки £ w* = 1).
*=1
Как мы сейчас увидим, это допущение приводит к огромным упроще-
ниям модели (16.107), т.к. вместо оценивания бесконечного ряда весовых
коэффициентов 0о>01>02>*- - нам придется оценить лишь два (!) параме-
тра: А и р = S
fc=0
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
879
Действительно, возвращаясь к (16.107), имеем:
У(0 = со + £	- к) + S(t) = со + /3 £(1 - X)Xkx(t - к) + 6(t)
fc=0	fc=0
= с0 + 0(1 - А) A*FM z(t) + d(l),	(16.112)
\*=o	/
где F_, как и прежде (см. п. 16.4.3), оператор сдвига назад на единицу,
т.е. F_x(t) = x(t — 1). Произведя формальные операции с операторами
сдвига, получаем
y(t) = Со + 0(1 - А)[1 + XF_ + X2fI + .. .>(t) + tf(t)
= с» + 0(1 - Х)-^ + 4(t),
1 — АГ _
или, что то же
(1 - AF_)y(l) = (1 - AF_) со + 0(1 - A)x(t) + (1 - AF_)f(t). (16.112')
Применяя, в соответствии с этим соотношением, оператор сдвига F_ к с^,
y(t) и £(1), получаем
У(<) = (1 - А)с0 + 0(1 - A)z(t) + Ay(t - 1) + (f(t) - Af(t - 1)). (16.112')
В результате мы получили уравнение регрессии y(t) по объясняющим
переменным х(1) и y(t — 1) всего с двумя неизвестными коэффициентами
Р и А (не считая свободного члена Со и дисперсии остатков Оо = Dtf(f)).
Однако поскольку в правой части уравнения остаточная случайная ком-
понента e(t) = 6(t) —	— 1) зависит от оцениваемого параметра А и,
вообще говоря, коррелирована, по крайней мере, с объясняющей перемен-
ной y(t — 1), метод оценивания параметров /3 и А нестандартен и зависит
от дополнительных предположений относительно природы остатков 6(f)
и/или e(i).
Процедуры состоятельного оценивания параметров модели (16.112*)
при нескольких вариантах специфицирующих условий, касающихся при-
роды случайных остатков и e(t), описаны, например, в [Джонстон
Дж.], с. 303-320.
Замечание 1. Финальный вид (16.112*) модели Койка может
быть получен и без помощи операций с оператором сдвига F_. Для этого
выпишем исходный вид модели для двух текущих моментов времени t и
880
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
t-1:
оо
»(0 = с» + 0(1 - А) £	- *) + «(«)>
*=0
оо
У(1 - 1) = q, + 0(1 - А) £ A*i(t - 1 - k) + f(t - 1).
Jt=O
Умножив второе уравнение на Л и вычтя полученный результат из первого
уравнения, приходим к (16.П2* 1 2).
Рассмотрим две хорошо известные динамические модели экономиче-
ских процессов, сводящиеся к модели Койка, хотя их базовые априорные
допущения прямо не формулируются в виде (16.111).
Модель частичного приспособления (или — «частичном кор-
ректировки»)1. Предположим, что желаемое (или оптимальное, целе-
вое) значение y*(t) некоторого экономического показателя определяется
уравнением
У*(0 = 0О + 01X(t) + £(*),	(16.113)
где регрессионные остатки 6(1) удовлетворяют условиям (16.39)-(16.40), а
x(t) — переменная, выполняющая роль объясняющей, не коррелировала с
6(f). Однако желаемое значение исследуемой результирующей переменной
не всегда является наблюдаемым. Экономический объект, характеризуе-
мый этой переменной, может не иметь возможности сразу (т. е. в точно-
сти к моменту времени t) «выходить» на желаемое значение y*(t). Так
что фактическое (наблюдаемое) значение y(t) этого показателя будет
со временем как бы «подтягиваться» к желаемому у*(1)ъ соответствии
с правилом, формализуемым с помощью соотношения
»(0 = 9(i - 1) + 7(/(t) - 9(t - 1)) + 4(1),	(16.114)
0<7«l,
где 6(t) удовлетворяет условиям (16.39)-(16.40). Из (16.114) следует, что
на каждом следующем временном такте наблюдаемое значение y(t) будет
«подправляться» в направлении целевого значения y*(t) на величину,
1 Впервые подобная схема модели была описана в работах:
1) Nerlove М. Estimates of the elasticities of supply of selected agricultural commodities.
«Journ farm econ.» , 38 (1956), pp. 496-509;
2) Nerlove M. The dynamics of supply: estimation of farmers response to price. The
Johns Hopkins Press. Baltimore, 1958.
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
881
пропорциональную разнице между оптимальным и текущим уровнями ре-
зультирующего показателя. Соотношение (16.114) может быть переписа-
но в виде
9(0 = 79*(0 + (1 - 7)»(t - 1) + «(«)>	(16.114')
откуда следует, что наблюдаемое значение исследуемой результирующей
переменной есть (с точностью до регрессионного остатка 6(0) взвешенное
среднее желаемого уровня (на данный момент времени) и фактического
значения в предыдущем такте времени. Подставляя модельное оптималь-
ное значение (16.113) в (16.114*), имеем
9(0 = 7«о + тМ) + (1 - 7)»0 " О + (<(0 + 7^(0)-	(16.114")
Сравнивая это соотношение с (16.112*), мы видим, что исследуемая
зависимость относится по своему типу к геометрической структуре Кой-
ка. В этом можно еще раз убедиться, «разматывая» (16.114*) в обратную
сторону по сравнению с тем, как мы это делали при выводе финального
соотношения структуры Койка. Действительно, выразим y(t — 1), руко-
водствуясь соотношением (16.114"):
j/(« - 1) = 7#о + 7^1	- 1) 4- (1 - 7)j/(t - 2) + (6(t - 1) + 7^(t - 1)).
Подставив это выражение y(t — 1) в (16.114"), получим
2/(0 = 7(2 - 7)0о + 701®(О + 7(1 — 7)0is(* - 1) + (1 - 7)22/0 “ 2) + е(0,
где
ЗД = [6(0 + (1 - 7W - 1)] + 7 [6(0 + (1 - 7» - 1)].
Неограниченно продолжая подобную подстановку, т. е. последователь-
но выражая у(1 - 2), y(t - 3) и т. д. по формуле (16.114") и подставляя их
в соответствующее выражение для y(t), получим в конечном счете
9(0 = «о + «о[х(0 + О ~ 7>(« - О + (1 - 7)’«(« - 2) +...] + е(0, (16.115)
где свободный член получен в результате бесконечного суммирования ве-
личин 7#o+(l — 7)70q+(1 ~7)270о+* • -j коэффициент 0О = 7^, а случайные
остатки г(0 получаются как бесконечные скользящие средние исходных
остатков и 6(0, а именно:
«(0 = £ {(1 - 7)*[«(« - *) + 7«(< - k)]} •
fc=0
882
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Сравнив (16.115) со средним выражением в соотношении (16.112),
убеждаемся в том, что модель частичного приспособления действитель-
но относится к классу геометрических структур Койка (с точностью до
условии, специфицирующих случайные остатки).
Схема «частичного приспособления» имеет довольно широкий
спектр экономических приложений. Упомянем о некоторых из них.
Пусть x(t) в соотношении (16.113) определяет уровень продаж неко-
торого товара, а y*(t) — соответствующая оптимальная (с позиций рав-
новесия) реакция со стороны производства (т.е. — оптимальный объем
предложения этого товара). Если принимать в расчет затраты двух ти-
пов — потери, связанные с нарушением равновесия, и затраты, связанные
с изменениями состояния производителя, — и если полагать, что оба типа
потерь, составляющие суммарные потери £, пропорциональны квадратам
соответствующих отклонений, т. е.
Ь(?(0) = с1(у(0 " У*(0)2 + сз(у(0 “ ~ О)2» ci>c2 > о,
то задача состоит в выборе (при заданных величинах y(t — 1) и !/*(<)) зна-
чения y(t), минимизирующего потери I(y(t)). Приравняем к нулю произ-
водную
"	= 2С* М “ У*^ +	~ у^ ~ = °'
Отсюда определяем
»(<) = »(г-1) +„	(»*(0-»(<- о).
С1 + с2
что в точности соответствует основному принципу (16.114) частичного
приспособления.
По совершенно аналогичной схеме может быть рассмотрена модель,
связывающая между собой доход x(t) с оптимальной (y*(t)) и реальной,
т.е. наблюдаемой (y(t)), величинами потребительских расходов. Ведь по-
требитель не располагает всей необходимой информацией о своем «про-
странстве потребностей», так что не может мгновенно оптимально среа-
гировать в своих расходах на изменение (в большую или меньшую сторо-
ну) своего дохода. Этой мгновенной реакции препятствуют также опреде-
ленная инерционность потребительского процесса, наличие определенных
(пусть неформальных) обязательств, связанных с прежним уровнем его
дохода.
Наконец, модель частичного приспособления используется при кор-
ректировке (в динамике) доли прибыли, выплачиваемой компанией в виде
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
883
доходов своим акционерам. При росте прибыли x(t) выплачиваемые диви-
денды y(t) также увеличиваются, но, как правило, не в той же пропорции
О, которая определена компанией в качестве целевой долгосрочной доли
выплат. Это объясняется рядом причин, в том числе осторожностью ру-
ководства компании: возрастание прибыли может оказаться временным,
поэтому если при этом сохранить долю 0, то в случае последующего пони-
жения прибыли дивиденды придется сокращать, а это — серьезный удар
по репутации фирмы. Как следствие, динамика выплаты дивидендов y(t)
в зависимости от текущей прибыли x(t) и желаемого (в долгосрочной пер-
спективе) объема выплат дивидендов у (t) = Ox(t) регулируется во многих
случаях соотношением (16.114).
«Узкое место» модели частичного приспособления состоит в том,
что иногда предположение о зависимости оптимального значения y*(t)
только от текущего значения x(t) оказывается не адекватным действи-
тельности. Другими словами, часто решающим мотивом для принятия
ответственных решений не может служить единственное значение объяс-
няющей переменной. Один из способов преодоления этой ограниченности
отражен в описываемой ниже модели адаптивных ожиданий.
Модель адаптивных ожиданий. Моделирование закономерностей
с учетом ожидаемых ситуаций — одна из важнейших проблем приклад-
ной экономики. Это, в первую очередь, верно для макроуровня, на ко-
тором инвестиции, сбережения и спрос на активы оказываются особенно
чувствительными к ожиданиям относительно будущего. Бели в модели
частичного приспособления в роли корректируемой величины выступа-
ла зависимая переменная (результирующий показатель) y(t), то в модели
адаптивных ожиданий корректируется объясняющая переменная z*(t-H),
которая определяет ожидаемое на момент $ +1 (но экспертно формируемое
в момент t) значение аргумента в исследуемой зависимости вида
y(t) = 0о +	+ 1) + ф),	(16.116)
где возмущающее воздействие удовлетворяет условиям (16.39)-(16.40)
и не коррелировало с наблюдаемым значением аргумента z(t). В соответ-
ствии с основным допущением модели механизм формирования ожидаемо-
го значения x*(t + 1) описывается соотношением
+ 1) = г*(0 + т(»(0 - “*(*))>
(16.117)
или, что то же,
x’(t + 1) = 7z(t)+ (1 -	(16.117')
884
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Это означает, что значение объясняющей переменной, ожидаемое в мо-
мент времени t + 1, формируется в момент времени t как взвешенное сред-
нее ее реального и ожидаемого значений в текущий момент времени. От
значения 7 зависит скорость адаптации ожидаемых значений к реально-
сти. Мы видим, что, в отличие от процесса частичного приспособления,
который базируется на инерции и проймой динамике показателей, про-
цесс адаптивных ожиданий направлен в будущее. Другими словами, мы
формируем значение результирующего показателя на текущий момент
еремени с учетом будущего значения объясняющей переменной.
Покажем, что и процесс адаптивных ожиданий вкладывается в об-
щую схему моделей с распределенными лагами, имеющих геометрическую
структуру Койка. Для этого перепишем (16.117*) в виде
ж*(Г + 1) - (1 - 7>*(0 =
или, что то же,
[1 - (1 - 7)F_]x*(t + 1) = 7«(t),
где с помощью F_, как и прежде, обозначен оператор сдвига функции
времени на один временной такт назад. Выражая отсюда x*(t + 1) и под-
ставляя это выражение в (16.116), получаем
»(0 = + °' 1	+ *(')•	(16118)
1 - Ц - У)Г-
После домножения всех членов этого выражения на 1 — (1 — 7)F_ и при-
менения этого оператора к #(/), и 6(t) получаем
»(<) = уё0 + (1 - 7)v(t - 1) + 7М(0 4- («(I) - (1 -	-1)). (16.118')
Сравнение модели (16.118*) с финальной формой (16.112*) модели Койка
свидетельствует об их эквивалентности.
Модель гиперинфляции Кагана и модель потребления Фридмана
(основанная на «гипотезе о перманентном доходе») представляют собой
наиболее известные примеры эконометрических приложений модели ада-
птивных ожиданий1. В модели гиперинфляции исследуется соотношение
между спросом на денежные остатки и ожидаемым изменением уровня
инфляции. В несколько упрощенном (по сравнению с первоисточником)
1 См. Cagan Р. The Monatary Dynamics of Hyperinflation. In: «Studies in the Quantity
Theory of Money» . Chicago, University of Chicago Press, 1956.
Friedman M. A Theory of the Consumption Function. Princeton, N.J.: Princeton
University Press, 1957.
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
885
|M(t)
варианте модель может быть описана следующим образом. Изменение
спроса на денежные остатки в момент времени t определяется показате-
лем
y(i) = In
где Af(t) — индекс изменения объема денег в обращении, a P(t) — ин-
декс цен. Зависимость изменения спроса на денежные остатки в момент
t от ожидаемого в момент t 4- 1 уровня инфляции х*(£ 4-1) определяется
уравнением
У(О = -^о -	4-1)4- АО» > 0, 0, > 0.
Адаптивные ожидания уровня инфляции определялись формулой (16.117).
Модель рассчитывалась по месячным данным, характеризующим семь ин-
фляционных периодов в США в промежутке 1921-1956 гг. (как отдельно
для каждого периода, так и агрегированно по совокупности всех семи пе-
риодов).
Модель потребления Фридмана основана на двух постулатах. Один
из них выделяет эту модель среди других многочисленных моделей, ис-
следующих зависимость объема потребления (у) от дохода (ж) (в данном
учебнике эта задача тоже рассматривалась в п. 15.10.2 в связи с методом
инструментальных переменных, используемым в проблеме построения ре-
грессионной модели со стохастическими предикторами). В соответствии с
этим постулатом фактический объем потребления y(t) и фактический уро-
вень дохода x(t) складываются из перманентной (постоянной) и временной
(случайной) составляющих, т. е.
АО = У*(0 + УвР(0»
АО = г*(0 + жв₽(0-
Предполагается, что временная составляющая потребления уВр(0 и
временная составляющая дохода гвр(0 являются случайными переменны-
ми со средними значениями, равными нулю, и постоянными значениями
дисперсий и что распределены они независимо от постоянного дохода, по-
стоянного потребления и друг от друга.
Второй постулат не отличается от базовых допущений большинства
других аналогичных моделей и состоит в допущении, что x*(l) и у*(0
связаны между собой классической линейной регрессионной моделью, т. е.
/(0 = 0О + М*(0 + АО’	(16.119)
Однако величина постоянного дохода z*(t) (впрочем, так же, как и вели-
чина в модели (16.119) ненаблюдаема. Эта проблема обходится с
886
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
помощью предположения, что изменение постоянного дохода x*(t) подчи-
няется закону адаптивных ожиданий (16.117). Другими словами, домаш-
ние хозяйства (индивиды) корректируют свое представление об ожидае-
мом постоянном доходе по мере роста (убывания) фактического дохода,
но не на полное значение прироста (убывания), сознавая, что изменения
фактического дохода частично объясняются вариацией врёменной его со-
ставляющей.
Возвращаясь к (16.119) и подставляя вместо y*(t) разность y(t) -
yBp(t), а вместо a?*(t) его выражение, полученное из соотношения (16.117),
имеем
»(0 = во + 81 1 - (1 - 7)Г- + (Ф) + ?ч>(г))’	(16Л20)
Сравнивая это выражение с (16.118) и учитывая эквивалентность
(16.118), (16.118*) и (16.112*), мы видим, что модель потребления Фрид-
мана также может быть отнесена к моделям распределенных лагов с гео-
метрической структурой.
Замечание 2. И в моделях частичной корректировки, и в мо-
делях адаптивных ожиданий мы сталкиваемся с проблемой оценки вели-
чины 7. Один из распространенных подходов к решению данной зада-
чи — это использование эвристического по своей природе общего мето-
да перекрестного анализа дееспособности модели (в англоязычной ли-
тературе он известен как «cross validation method*). Применительно к
данной проблеме это означает следующую последовательность действий.
Все имеющиеся в нашем распоряжении исходные статистические данные
M(1,7V) = {z(t),p(t); t = 1,2, ...,7V} разбиваются на две части: «обу-
чающую» Мов(1,ЛГ1) = {x(f),y(t); t = l,2,...,7Vi (Ni < TV)} и «экза-
менующую» M3KS(7Vi + 1,-АГ) = {z(t),y(t); t = Ni + 1, Ni + 2, ...,JV}.
Задаются сеткой значений параметра 7 на интервале [0; 1]. Для каждого
значения 7 из этой сетки по «обучающим» данным Моб(1,^) строится
модель (16.120). Затем по «экзаменующим» данным M3K3(jV1 4- 1,7V) вы-
числяется значение критерия качества полученной модели (роль такого
критерия в данной задаче обычно играет соответствующий коэффициент
детерминации №, см. п. 15.3.3). Выбирают то значение 7, при котором
значение критерия качества модели максимально.
Лаговые структуры, основанные на вероятностной параме-
тризации. Мы уже упоминали, что одним из способов экономичной па-
раметризации лаговых структур является их интерпретация в терминах
вероятностных распределений (см. (16.108)). Приведем в заключение два
примера такой параметризации: один — для бесконечной лаговой струк-
туры (структура Паскаля), другой — для конечной лаговой структуры.
16.5. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
887
Лаговая структура Паскаля была предложена в 1960 г. Р. Солоу1.
Она основана на так называемом отрицательном биномиальном распре-
делении (см. п.3.1.1), т.е. элементы wk нормированной бесконечной ла-
говой структуры Паскаля (А = 0,1,2,...) определяются в соответствии с
(16.108) с помощью соотношений
W* = (1-P)MC'U*-1P*,	* = 0,1,2,...,	(16.121)
где р (0 < р < 1) и М (М — любое целое положительное число) —
оо
два параметра, определяющие (наряду с /3 = 0fc) конкретную лаго-
л=о
вую структуру в данном параметрическом семействе. Отметим, что из
свойств отрицательного биномиального распределения следует:
(«) элементы wk нормированной лаговой структуры при М > 1 сначала
возрастают (при к < (рМ — 1)/(1 — р)), а затем убывают (при к >
(рЛ/- 1)/(1-р));
(й) среднее значение лага (Ет) и его дисперсия (Dr) являются возраста-
ющими функциями как М, так и р, а именно:
Ет =
Dr =
рМ
1-р;
рМ
(1-р)2'
Лаговая структура, основанная на биномиальном законе распределе-
ния вероятностей, является естественным аналогом структуры Паскаля
в классе конечных моделей с распределенными лагами. Ее нормированные
элементы wk задаются с помощью соотношений
«<к = Стр*(1-р)Т"*,	* = 0,1,...,Т.	(16.122)
Мы видим, что данный класс конечных лаговых структур описывается
однопараметрическим семейством (параметр р — некоторое число между
0 и 1). Из свойств биномиального распределения (см. п. 3.1.1) следует, что
последовательность (16.122) образует так же, как и в структуре Паскаля,
унимодальный ряд, причем Ет = рТ и Dr = р( 1 - р)Т.
Описанные вероятностные лаговые структуры применимы в ситуаци-
ях, когда из содержательного смысла анализируемых зависимостей вида
(16.107) следует, что весовые коэффициенты 0* (а значит, и w*) начинают
1 См. Solow R. М. On & family of lag distributions. «Econometrics», 28 (1960), pp.
393-406.
888
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
монотонно убывать не сразу, а только после некоторого к0. С подобны-
ми ситуациями исследователь имеет дело, например, при анализе зависи-
мостей, связывающих между собой входные и выходные характеристики
процессов накопления и распределения ресурсов (см. выше примеры 16.7
и 16.8).
16.6.	Прогнозирование экономических
показателей, основанное на
использовании моделей временных
рядов
Познакомившись в п. 16.3 с различными способами сглаживания вре-
менного ряда, а в пп. 1^.4 и 16.5 — с разнообразными моделями, соответ-
ственно, стационарных и нестационарных временных рядов, рассмотрим
теперь, как все эти методы и модели используются при прогнозировании
экономических показателей. Причем наше внимание будет сконцентри-
ровано на методах автопрогноза, в которых имеющийся в наличии ряд
экстраполируется вперед, а другие ряды, которые, возможно, тоже не-
сут определенную информацию о поведении нашего ряда (как это и име-
ет место, например, в регрессионных моделях с распределенными лагами,
см. п. 16.5.3), остаются без внимания. Это объясняется просто: единствен-
ный тип не авторегрессионных моделей, рассмотренный в данной главе
(см. п. 16.5.3), как мы видели, сводится к относительно простым классиче-
ским или обобщенным моделям регрессии, а задача прогноза, основанная
на этих моделях, была обсуждена в п. 15.9.
Отметим прежде всего, что не существует универсально предпочти-
тельных методов прогнозирования на все случаи жизни. Выбор метода
прогнозирования и его эффективность зависят от многих условий, и в
частности от:
(а)	требуемого горизонта I прогнозирования, т. е. от того, на сколько вре-
менных тактов (/) вперед мы собираемся строить наш прогноз; при
I 3 прогноз обычно называется краткосрочным, при 3 < I 6 —
среднесрочным, а при I > 6 — долгосрочным (приведенная здесь клас-
сификация, конечно, условна; она может зависеть от конкретного смы-
сла одного такта времени — подразумевается ли под ним день, неделя,
месяц, квартал, год и т. д.);
(6)	длины N анализируемого временного ряда (условно говоря, при N
50 ряд считается коротким, а при N > 50 — длинным);
(в)	наличия или отсутствия в анализируемом ряду сезонной составля-
ющей или каких-либо «нестандартностей» (скачкообразных измене-
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
889
ний в поведении тренда, слишком большой величины дисперсии а
случайных остатков и т. п.).
Поэтому выбор метода прогнозирования следует производить с уче-
том всех специфических особенностей как целей прогноза, так и анализи-
руемого временного ряда.
Кстати, с точки зрения целевых установок мы ограничим наше рас-
смотрение задачами кратко- и среднесрочного прогноза, которые могут
решаться (и весьма эффективно) с привлечением только статистически-
экстраполяционных методов. Серьезное решение задач долгосрочного
прогноза требует использования комплексных подходов и, в первую оче-
редь, привлечения различных технологий сбора и анализа экспертных
оценок.
16.6.1. Прогнозирование на базе АРПСС-моделей
Из результатов пп. 16.4-16.5 следует, что АРПСС-модели охватывают
достаточно широкий спектр как стандартных, так и нестандартных вре-
менных рядов, а небольшие модификации этих моделей позволяют весьма
точно описывать и временные ряды с сезонностью (см. п. 16.5.2). По-
этому начнем обсуждение проблемы прогнозирования временных рядов
с методов, основанных на использовании АРПСС-моделей. Мы говорим
об АРПСС-моделях, имея в виду, что сюда входят как частные случаи
АР-, СС- и АРСС-модели. Кроме того, мы будем исходить из того, что
уже осуществлен подбор подходящей АРПСС-модели для анализируемого
временного ряда, включая идентификацию этой модели. Поэтому в даль-
нейших наших рассуждениях предполагается, что все параметры модели
уже оценены, т.е. известны. Для упрощения обозначений мы будем ис-
пользовать при записи моделей в качестве ее параметров символы р, q, к;
Q1,... ,ар; 0J,..., подразумевая при этом их оценки, соответственно,
р, q,k; di,..., ар; 0j,..., 0q (значениями которых мы располагаем).
Итак, займемся прогнозированием неизвестного значения x(t + /),
/ > 1, полагая, что x(t) — это последнее по времени наблюдение анализи-
руемого временного ряда, которое имеется в нашем распоряжении (будем
говорить, что t — это текущий момент времени). Другими словами, мы
делаем прогноз в момент времени t на I тактов времени вперед (или с
упреждением I). Обозначим такой прогноз i(t;/).
Заметим, что хотя z(t;Z) и x(t — 1; / -Ь 1) обозначают прогноз одного
и того же неизвестного значения z(Z + 0» но вычисляются они по-разному,
т. к. являются решениями разных задач. Поэтому мы не используем, каза-
лось бы, естественное обозначение x(t 4-I) для прогноза величины ж(< -Ь О-
890
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Известно (см. (гб-Эв^Хб-Эв1)), что анализируемый в рамках
АРПСС(р, д, £)-модели ряд ас(т) представим (при любом т > Л + 1) урав-
нением вида
(1 - a, F_ - ... -	- &х(т - 1)+ ... + (-1)*г(г - к))
= «(т) - М(г - 1) - ... - 6,6{т - д),	(16.98е)
где F_, как и прежде, оператор сдвига функции времени на один вре-
менной такт назад (соответственно, оператор FL сдвигает функцию, к
которой он применяется, на j тактов времени назад).
Перепишем соотношение (16.986 последовательно для т = t — g, i —
g 4-1,..., t + 1, t + 2,... ,t + /, уединив при этом ®(т) в левой его части:
®(4-9)= | ^2aiF- | *(*-«)+ ( 1~52°>^
V=i /	\
X (C'kx(t - q - 1) - ... + (-l)*l(t - q - k))
+ ф - q) - M(t - g - 1) - ... - egS(t - 2g),	(16.123)
®(t - g + 1) = [ 52 aiF1- 1 ®(4 - g + 1) + | 1 ~ 52 aiF-
V=i /	\ j=i
x (Clx(t - g) - ... + (-1)4* - 9 + 1 - *)) + 4(‘ - « + 1)
- ^S(t — g) — ... — 0q6(t - 2g + 1),	(16.123')
x(cUt)-.-.+(~i)*«(‘ + i-*))
(16.123")
+ ф + 1) - M(0 - • - • - 646(t + 1-9),
x (С*х(« + 1-1)-... + (-1)*г(< + 1-A:))+ «(« + /)
- 9,«(t + / - 1) - ... - 9,6(t + l-g).	(16.123'")
Обращаем внимание на тот факт, что правые части этих соотноше-
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
891
ний представляют собой линейные комбинации р + к предшествующих
(по отношению к левой части) значений анализируемого процесса ас(т),
дополненные линейными комбинациями текущего и q предшествующих
значений случайных остатков 6(т). Причем коэффициенты, с помощью
которых эти линейные комбинации подсчитываются, известны, т. к. выра-
жаются в терминах уже оцененных нами параметров модели , аа,..., ар
и #1,02,.. .,0д.
Этот факт и дает нам возможность использовать соотношения
(16.123)-(16.123w) для построения прогнозных значений анализируемого
временного ряда на I тактов времени вперед. Теоретическую базу такого
подхода к прогнозированию обеспечивает известный результат, в соот-
ветствии с которым наилучшим (в смысле среднеквадратической ошиб-
ки) линейным прогнозом в момент времени t с упреждением I является
условное математическое ожидание случайной величины x(t + /), вы-
численное при условии, что все значения х(г) до момента времени t
(включительно) известны (этот факт является частным случаем более
общих результатов теории прогнозирования, развитой Волдом, Колмого-
ровым, Винером1).
Условное математическое ожидание E(z(t + I) | ж(1),®(2),.. .,®(t))
получается применением операции условного усреднения к обеим частям
(16.123w) с учетом следующих соотношений:
E(®(t - j) | х(1),..., x(t)) = x(t - j)
при всех j = 0,1,2,... ,t - 1; (16.124*)
E(z(t + j) | z(l),...,s(t)) = x(t; j) при всех j = 1,2,...;(16.124е)
E(tf(t + j) I	= 0 при всех j = 1,2,...;	(16.124*)
E(^(f - j) | z(l),..., x(t)) = x(t - j) - x(t - j - 1; 1)
при всех j = 0,1,2,...;	(16.124r)
Таким образом, определяется следующая процедура построения про-
гноза i(t; I) для значения x(t 4-1) анализируемого временного ряда по из-
вестной до момента t (включительно) его траектории х(1), ®(2),..., x(t):
1) на 1-м этапе используются формулы (16.123), (16.123*), ... для вы-
числения ретроспективных прогнозов x(t — q — 1; 1), x(t — q; 1) и т.д. до
1 См.: 1) Wold Н. О. A Study in the Analysis of Stationary Time Series. Almquist and
Wieksell, Uppsala, 1932; 2) Kolmogoroff A. Sur ^interpolation et 1’extrapolation des
suites stationaires. Com pt. Rend., 208 (1939), p. 2043; 3) Wiener N. Extrapolation,
Interpolation and Smoothing of Stationary Time Series. John Wiley, New York, 1949.
892
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
x(t — 1; 1) по предыдущим значениям временного ряда; при этом при вы-
числении начальных прогнозных значений i(t — q + т — 1) для x(t — q + т)
(m = 0,1,...) по формулам (16.123)-(16.123 )-... вместо условных сред-
них E(tf(< — q 4- т — j) | ж(1),..., x(t — q + m)) (которые в общем случае
следовало бы вычислять по формулам (16.124г), однако на начальном эта-
пе значения i(t — j — 1; 1) нам не известны) подставляются их безусловные
значения, равные, как известно, нулю; ретроспективный прогноз нужен
для того, чтобы при построении обычного прогноза (начиная с x(t\ 1) для
x(t 4 1) по формуле (16.123//)) мы могли бы подсчитать в правой части
(16.123) значения E(0(t - j) | z(l),..., x(t)) (j = 0,1,..., q - 1) по форму-
лам (16.124г);
2) на 2-ом этапе используются формулы (16.123 ),..., (16.123 ) и
правила (16.124*)-(16.124г) подсчета условных математических ожиданий
участвующих в правых частях (16.123”),..., (16.123 ') выражений для вы-
числения прогнозных значений i(<; 1), £(<; 2),..., ®(t; I).
Замечание. Возможен и упрощенный варианту при котором сра-
зу приступают к реализации 2-го этапа, начиная с формул (16.123”); при
этом те значения Е(£(< - j) | ж(1),.. .,«(<)), которые должны были бы, но
еще не могут, быть вычислены по формуле (16.124г), аппроксимируются
нулями.
Описанная процедура выглядит достаточно сложной. Мы сейчас по-
кажем на примерах, что при реалистичных значениях параметров p,q и к
(как правило, не превышающих двух) эта процедура в действительности
оказывается весьма простой. Тем не менее, в качестве альтернативно-
го способа построения прогноза, казалось бы, могла бы рассматриваться
следующая схема.
Из (16.986) непосредственно следует, что описываемый АРПСС(р,
q, к)-моделью временной ряд х(г) может быть представлен в форме мо-
дели авторегрессии вида
г(т)=52	~
j=l
(16.125)
где коэффициенты тг7 очевидным образом выражаются в виде линейных
комбинаций параметров а и 0, а случайные остатки е(т) — в виде ли-
нейных комбинаций элементов белого шума 6. Почему бы, не проводя
предварительную процедуру статистического оценивания параметров а и
0, не оценить параметры тгу с помощью обычного или обобщенного метода
наименьших квадратов по наблюдениям (ж(т), х(т 4-1),..., х(т4р4к -1);
х(т 4 р 4 к))у г = 1,2,	— р — А? А получив оценки параметров Xj и
подставив их в (16.25) при т = <4-1, можно было бы вычислить прогнозное
16.в. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
893
значение £(/; 1) для а:(/4-1), по нему — прогнозное значение f(t +1; 1) для
z(t + 2) и таким рекуррентным способом добраться до x(t 4- /).
К сожалению, эта схема в общем случае не позволяет получить
состоятельные оценки параметров ttj по той причине, что регресси-
онные остатки е(т) в модели (16.125) оказываются существенно корре-
лированными с объясняющими переменными х(т — j) (см. п. 15.10.2).
Рассмотрим ряд примеров.
Пример 16.9. Прогнозирование ряда, описываемого моделью
АРПСС(1,0,1). Анализ и идентификация имеющегося временного ряда
х(т) привели нас к АРПСС(1,0,1)-модели вида
(l-0,8F_)(l-F_)x(r) = 6(r),
или, что то же,
(1 - 1,8Г_ + 0,8Г1)г(т) = #(т).
Воспользуемся упрощенным вариантом описанной выше процедуры
прогнозирования. Уравнения (16.123w), (16.123w) в данном случае имеют
вид
x(t 4-1) = 1,8 x(t) - 0,8 x(t - 1) +	+ 1),
................................................. (16.126)
x(t + I) = 1,8 x(t +1 - 1) - 0,8 ®(t +1 - 2) 4- £(i 4- /)-
Мы знаем, что прогнозные значения x(t',m) для x(t 4- тп) (тп =
1,2,...,/) получаются вычислением условных математических ожиданий
Е(ж(/ 4- тп) | x(l),z(2),...,ar(f)). Для этого в правых частях соотноше-
ний (16.126) фиксируются значения х(т), известные к моменту времени t
(т. е. ж(1),..., x(t)), а будущие значения x(t 4- тп) заменяются их прогноза-
ми x(t; тп)\ вместо будущих значений 6 и тех прошлых значений, которые
нельзя подсчитать по формулам (16.124г) из-за нехватки прогнозных зна-
чений x(t — j — 1; 1), вставляются нули, а остальные прошлые значения 6
подсчитываются по формулам (16.124г). В результате от (16.126) прихо-
дим к следующим выражениям для прогнозов:
х(Р, 1) = 1,8х(/)-0,8®(/- 1);
i(t; 2) = 1,8 х(Р, 1)-О,8ж(0;
£(«; I) = 1,8 z(t; I - 1) - 0,8 i(t; 1-2), I > 3.
Пример 16.10. Прогнозирование ряда, описываемого моделью
АРПСС(0,1,1). Анализ ежедневных данных о биржевых ценах акций
1 Пример заимствован из [Бокс Дж., Дженкинс Г.], с. 188-190.
894
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
IBM в период с 17 мая по 2 ноября 1962 г. (общая длина ряда N = 369)
показал, что исследуемый временной ряд х(т) хорошо может быть опи-
сан АРПСС(0,1,1)-моделью с параметром В = 0,1. Э’то значит, что он
может быть представлен в форме Дх(т) = £(т) — В6(т — 1), где Дя(т) =
х(т) — х(т — 1). Поэтому уравнения (16.123”), (16.123”*) в данном случае
имеют вид
x(t + 1) = x(t) +	+ 1) - 0,1 ОД,
x(t + /) = х(« +1 -1) + ф + /) - 0,1 ад.
Отсюда в соответствии с описанной выше процедурой получаем
x(t- 1) = s(f) - 0,1
i(i; /) = x(t; I - 1) при I > 2.
Мы видим, что для всех упреждений (в момент t) прогнозы будут сле-
довать прямой линии, параллельной оси времени. Учитывая то, что
Л($) = x(t) — x(t - 1; 1), прогноз x(t; I) можно записать также в виде
ад о = (1 - *)ад + аф - г, i),
что в нашем конкретном случае дает
£(<; I) = 0,9 x(t) + 0,1 x(t - 1; I).
To есть прогноз в момент t с упреждением I есть взвешенное среднее те-
кущего значения х t) и аналогичного прогноза в предыдущий момент вре-
мени. Причем если В близко к нулю (в нашем случае В = 0,1), то прошлый
прогноз i(t — 1;/), представляющий собой взвешенное среднее данных «о
прошлом» (т. е. — до момента t — 1), практически игнорируется и прогноз
«на все будущие времена» определяется текущим значением x(t). Мы
еще вернемся к этому примеру в п. 16.6.2 в связи с сопоставлением описы-
ваемогр метода прогнозирования с методом экспоненциально взвешенного
скользящего среднего Брауна.
Пример 16.11. Прогнозирование ряда., описываемого моделью
АРПСС(0,2,2). Анализируемый временной ряд х(т) представим в форме
Д2х(т) = ад)-01£(т-1)-0^(т-2),где Д2х(т) = х(т)-2х(т-1)+ж(т-2).
Поэтому уравнение (16.123й) в данном конкретном случае имеет вид
x(t + /) = 2x(t + 1-1)- x(t + l-2) + 6(1 + 1)-0i$(t + /-l)-02$(t-H-2).
Беря условные математические ожидания (при известном до момента I
прошлом) от обеих частей этого соотношения, получаем для / = 1, / = 2
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
895
и в общем случае
i(i; 1) = 2®(0 - x(t - 1) - М(0 - 026(t - 1),
x(t\ 2) = 2i(t; 1) — ж(0 - 02^(0»
i(<; I) = 2x(t; I - 1) - z(t; I - 2) при I > 3.
Напомним, что в этих выражениях £(0 = x(t) — x(t — 1; 1), 6(t — 1) =
x(t — 1) - x(t — 2; 1), и процесс прогнозирования можно начинать подста-
новкой вместо неизвестных значении 6 их безусловных математических
ожиданий, равных нулю.
Пример 16.12. Прогнозирование ряда, описываемого моделью
АРПСС(1,1>1). Подчиняющийся закономерностям этой модели временной
ряд представим, как известно, в форме
(1 - aF_) Az(r) = 6(т) - 06(t - 1),
где Дя(т) = г(т) — х(т — 1). Применяя к Д®(т) оператор (1 - qF_) и
уединяя ж(т) в левой части, можно выписать уравнение (16.123w):
+ 0 = (1 + a)x(t +1 - 1) - ax(t + I - 2) +	+ 0 - 06(t + 1-1).
Беря условные математические ожидания от обеих частей этого соотноше-
ния (при условии, что все прошлое этого процесса до момента t известно),
получаем для I = 1 и в общем случае
r(i; 1) = (1 + а) «(О - ax(t - 1) - 0«(4),
х(1; 0 = (1 + a) x(t; l — l) — ax(t; 1-2) при I > 2.	' ’
Значение 6(i) можно вычислить по формуле <5(0 = ®(0—x(t — 1; 1), постро-
ив предварительно ретроспективный прогноз i(t — 1; 1) так, как это было
описано выше. В упрощенном варианте значение 6(t) полагается равным
нулю.
Можно показать, что объединенной формой соотношений (16.127)
является эквивалентное им представление прогноза £((; 0 в виде
6 — а
1 — а
0 — а
1 — а
I) =
(1 -«')]
»(0 +
(1 - а')гв(« - 1),
(16.127')
1 -
где xe(t — 1) — экспоненциально взвешенное скользящее среднее (с па-
раметром 0) — см. выше п. 16.3.2 — анализируемого <длинного» ряда,
просуммированного от бесконечно удаленного прошлого до момента вре-
мени t — 1, т.е.
ie(t-i) = (i-6)£
j=i
(16.128)
896	ГЛ, 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Из (16.127*) следует, что прогноз получается в результате линейной
интерполяции величин x(t) и xg(l — 1) с весами 1 — А(/) и A(Z), где А(/) =
(0-а)(1 -</)/(! -а), т.е. x(t]l) = (1 - A(Z))a:(£)A(Z)±e(t- 1) (напомним,
что |а| < 1 и 0 < 1, т. к. это обеспечивает условия, соответственно,
стационарности и обратимости анализируемого ряда, см. п. 16.4.3).
Мы не касались здесь важных вопросов оценки точности получаю-
щихся прогнозов. Теоретические аспекты этой проблемы рассмотрены,
например, в [Бокс Дж., Дженкинс Г.]. Некоторые общие эвристические и
имитационные подходы к оценке точности «подгонки» модели по экспери-
ментальным данным и точности получающихся с ее помощью прогнозов
будут рассмотрены в конце гл. 17 (см. п. 17.5).
16.6.2. Адаптивные методы прогнозирования
Считается, что характерной чертой адаптивных методов прогнози-
рования является их способность непрерывно учитывать эволюцию дина-
мических характеристик изучаемых процессов, «подстраиваться» под эту
эволюцию, придавая, в частности, тем больший вес и тем более высокую
информационную ценность имеющимся наблюдениям, чем ближе они к
текущему моменту прогнозирования. Однако деление методов и моделей
на «адаптивные» и «неадаптивные» достаточно условно. В известном
смысле каждый из рассмотренных в данном учебнике методов прогнози-
рования адаптивный, т. к. практически все они учитывают вновь посту-
пающие наблюдения, в том числе сделанные с момента последнего прогно-
за. Общее значение термина заключается, по-видимому, в том, что «ада-
птивное» прогнозирование позволяет обновлять прогнозы с минималь-
ной задержкой и с помощью относительно несложных математических
процедур. Но, как мы увидим, это вовсе не значит, что в любой ситуации
адаптивные методы оказываются эффективнее тех, которые традиционно
не относятся к таковым.
Методы экспоненциального сглаживания (Брауна1). Про-
стейший вариант этого метода был описан в п. 16.3.2 в связи с задачей
выделения неслучайной составляющей из анализируемого временного ря-
да. Постановка задачи прогнозирования с использованием простейшего
варианта метода экспоненциального сглаживания формулируется следу-
ющим образом.
Пусть анализируемый временной ряд ж(т) (г = 1,2,...»«) представлен
1 См.: Brown R.G. Smoothing, Forecasting and Prediction of Discrete Time-Series.
Prentice-НаЛ, New Jersey, 1962.
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
897
в виде
х(т) =	+ е(т),	(16.129)
где а0 — неизвестный параметр, не зависящий от времени, а е(т) — слу-
чайный остаток со средним значением, равным нулю, и конечной дис-
персией. Как мы знаем (см. п. 16.3.2), экспоненциально взвешенная сколь-
зящая средняя (ЭВСС) ряда х(т) в точке t x\(t) с параметром сглажива-
ния (или — параметром адаптации) А (0 < А < 1) определяется формулой
1 — А
®л(0 =  ---П £	(1613°)
1 Л j=0
которая дает решение задачи на минимум экспоненциально взвешенного
критерия метода наименьших квадратов, а именно:
t—1
®>(0 = arg mjn [«(* “ j) “ а] •
j=0
Коэффициент сглаживания А можно интерпретировать также как ко-
эффициент дисконтирования, характеризующий меру обесценивания наг
блюдения за единицу времени.
Для рядов с «бесконечным прошлым» формула (16.130) сводится к
виду
оо
xx(t) = (1 - Л) £ *'«(* - Л-	(16.130')
j=0
В соответствии с простейшим вариантом метода экспоненциального
сглаживания прогноз i(t; 1) для неизвестного значения x(t -I-1) по извест-
ной до момента времени t траектории ряда х(г) строится по формуле
i(Z; 1) = xA(t),	(16.131)
где значение x\(t) определено формулой (16.130) (для короткого времен-
ного ряда) или формулой (16.130') (для длинного временного ряда).
Формула (16.131) удобна, в частности, тем, что при появлении следу-
ющего (t + 1)-го наблюдения x(t 4-1) пересчет прогнозирующей функции
x(t 4-1; 1) = x\(t 4-1) производится с помощью простого соотношения
xx(t 4-1) = Xxx(t) 4- (1 - A)x(t 4-1).
(16.132)
898
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Для вывода этого соотношения выпишем (16.130*) для моментов вре-
мени t 4- 1 и t:
®а($ + 1) = (1 ~ А)[®($ + О + Ах($) 4- A2®(t — 1) 4-...],
«а(0 = С1 - А)[«(0 +A®(t- 1)4-A2®(t- 2) + ...].
Вычтя из первого соотношения второе, умноженное на Л, получим
xk(t 4- 1) — Ажд(0 = (1 — X)x(t 4- 1), что и доказывает справедливость
(16.132). Для конечных временных рядов соотношение (16.132) имеет при-
ближенный смысл, поскольку в аналогичных выкладках мы должны бу-
дем пренебречь разницей в знаменателях правых частей (16.130) (легко
видеть, что приближение это высокой точности, т. к. разность
1 1
1 - А<+1 i — а*
достаточно быстро стремится к нулю при t —> оо).
Метод экспоненциального сглаживания можно обобщить на случаи
полиномиальной неслучайной составляющей анализируемого временного
ряда., т.е. на ситуации, когда вместо (16.129) постулируется
®(t + г) = во + ахт + ... 4- актк 4- е(т),	(16.129')
где k > 1. В соотношении (16.129') начальная точка отсчета времени сдви-
нута в текущий момент времени t, что облегчает дальнейшие выкладки и
вычисления. Соответственно, в схеме простейшего варианта метода про-
гноз x(t; 1) значения х(1 4-1) будет определяться соотношениями (16.129*)
при т = 1 и (16.131):
i(t; 1) = i(t + 1) = a^(t; А) + А) + ... + alkk\t-, А),	(16.132')
где оценки ao(t; Л), ai(t; А),.. .tak(t\ А) получаются как решение экспонен-
циально взвешенной оптимизационной задачи метода наименьших квадра-
тов, т.е.
Vs AJ[z(i - j) - ao-a^j -	— ajJ*]2 -> min .	(16.133)
"	..a*
j=0
Решение задачи (16.133) не представляет принципиальных трудно-
стей (см. описание взвешенного метода наименьших квадратов в п. 15.7).
Мы выпишем здесь решения задачи (16.133) для случаев & = 1иА = 2я
для рядов с «бесконечным прошлым».
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
899
1) Случай линейного тренда, т. е. Ex(t + т) = oq 4- ajr.
a£’(t; А) = i>(t) = (I - A) £ AJx(£ - j),
>=° oo	(16134)
aV’ft; A) = (1 - A)SX(<) + (1 - A)2 £ (j + l)A<r(t - j).
J=o
Так что прогноз x(t; 1) будущего значения z(t4-l) при линейном трен-
де ряда будет вычисляться в соответствии с (16.132)
X(t- l) = a<1)(t;A) + a(11)(t; Л),
где коэффициенты $\t; А) и (^(t; А) определяются по формулам (16.134).
Пересчет коэффициентов о и dj при появлении следующего
(t + 1)-го члена ряда производится по формулам
4”(t + 1; А) = (1 - A2) x(t + 1) +	+ A’aV’Ct),
a^\t + 1; A) = (1 - A)2 x(t + 1) - (1 - A)2a<’>(«) - (1 - A)’a<1>(t) + ^\t).
2) Случай квадратичного тренда, m. e. Ex(i 4- r) = Oq 4- air 4- a2r2.
Мы выпишем для этого случая лишь так называемые «формулы
обновления», позволяющие пересчитывать оценки 6^(5; A), dj2\a;A) и
d22\s; А), полученные как решения оптимизационной задачи (16.133) при
t = з, когда появляется очередное (э 4- 1)-е наблюдение временного ряда
я(з 4-1):
4”(в + 1; А) = a'2)(e; А) + а|2)(а; А) + а'2)(«; А) + (1 - А3)ф + 1),
а(,2)(« + 1; А) = а<2>(з; А) + 2а<2)(а; А) + |(1 - А)(1 - А2)ё(з + 1),
а<2»(Я + 1; А) = а<2)(з; А) + 1(1 - А)3ф + 1),
где £(з 4-1) = х(з 4-1) — d02\e; -М “ А) — d22\s;	— ошибка прогноза
на последнем шаге. Решив для сравнительно небольшого t = з оптимиза-
ционную задачу (16.133), затем последовательно пересчитывают по этим
формулам значения прогнозирующих коэффициентов dj2\s 4- m; A) (j =
0,1,2,; т = 1,2,...), пока не «доберутся» до текущего момента времени
t.
900
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Пример 16.13. Мы возвращаемся к примеру 16.10 (см. п. 16.6.1),
чтобы сравнить эффективность применения квадратичного варианта ме-
тода Брауна и метода, основанного АРПСС(0,1,1)-модели, к решению од-
ной и той же задачи — прогнозу биржевых цен на акции IBM на три
дня вперед. Описание исходных данных задачи и результатов построения
АРПСС-модели было дано выше. На рис. 16.14 наглядно представлено
сравнение двух методов, а в табл. 16.6 приведены результаты расчетов
среднеквадратических ошибок прогнозов на базе ряда цен акций за пери-
од с 11 июля по 10 февраля 1961 г. (150 наблюдений). Для этого участ-
ка ряда опенка параметра в в модели АРПСС (0,1,1) оказалась равной
0 = 0,1, а это значит, что прогнозы по АРПСС-модели на 3 дня впе-
ред, грубо говоря, эквивалентны использованию сегодняшней цены (т.к.
x(t; 1) = 0,9гс(1) + 0,1 x(t — 1; /)), что тем не менее оказывается значительно
точнее, чем прогнозы, полученные с помощью существенно более сложной
методики Брауна.
Таблица 16.6. Сравнение среднеквадратичных ошибок прогнозов, получен-
ных при различных упреждениях, по наилучшему из процессов
АРПСС(0,1,1) и по методике Брауна
Упреждение 1	1	2	3	4	5	6	7	8	9	10
СКО (Браун)	102	158	218	256	363	452	554	669	799	944
СКО АРПСС (9 = 0,1)	42	91	136	180	282	266	317	371	427	483
Попробуем понять причины неудач применения квадратичного мето-
да экспоненциального сглаживания в данном случае.
1)	Выбор вида прогнозирующей функции, основанный на подборе опе-
раторов авторегрессии (1 — 'EotjFL) и конечных разностей Д* = 1 -
нам представляется более гибким и обоснованным, чем формальная ап-
проксимация полиномом траектории анализируемого ряда. Посмотрим,
например, на траекторию биржевых цен акций IBM на рис. 16.14. Видно,
что квадратичная функция может быть использована для аппроксимации
лишь коротких участков ряда, причем эта аппроксимация носит чисто
формальный характер и не имеет отношения к описанию генезиса анали-
зируемых наблюдений.
2)	Узким местом всех адаптивных методов, и методов экспоненциаль-
ного сглаживания в частности, является подбор подходящего к данной
конкретной задаче параметра сглаживания (адаптации) А. По этому
поводу мы могли бы только в точности повторить наше «Замечание 2» из
п. 16.5.3, в котором формулируются рекомендации по подбору параметра 7
16.6. ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
901
в моделях с распределенными лагами, обладающих геометрической струк-
турой Койка. Но даже при оптимальном подборе параметра А модель
Брауна существенно уступает в точности прогноза АРПСС(0,1,1)-модели.
3)	Наконец, в моделях экспоненциального сглаживания вся специфика
анализируемого ряда должна быть отражена в единственном параметре
А. Это, конечно, сильно ограничивает класс допустимых в рамках этого
метода моделей.
Кратко описанные ниже методы также используют «идеологию» экс-
поненциального сглаживания, но развивают методы Брауна в различных
направлениях.
Метод Хольта. По-видимому, Хольт первым попытался ослабить
ограничения метода Брауна, связанные с его однопараметричностью, за
счет введения двух параметров сглаживания Ai и А2 (0 < А> < 1,0 < А2 <
I)1. В его модели прогноз х(1‘Г) на / тактов времени в текущий момент t
также определяется линейным трендом вида
f(<; /) = ao(t' Ai, А2) 4- Zai(t; Ai, A2),
где обновление прогнозирующих коэффициентов производится по форму-
лам:
e0(t 4- 1; Ai, А2) = Ai®(t) + (1 — Ai)(a0(t; Ai, А2) 4- di(t; Аь A2)),
di(Z 4- 1; Ai, A2) = A2(do($4-1; Ai, A2) — di(Z; Ai,A2))
4- (1 — A2)di(Z; Ai, A2).
Таким образом, прогноз по данному методу является функцией про-
шлых и текущих данных, параметров Ai и А2, а также начальных значе-
ний do(0;Ai,A2) и ei(0;Ai,A2).
Метод Хольта—Уинтерса. Метод Хольта был развит Уинтерсом
(см.: Winters P.R. Forecasting Sales by Exponentially Weighted Moving
Averages. Mgmt. Sci., 6, p. 324) так, чтобы он охватывал, помимо ли-
нейного тренда, еще и сезонные эффекты. Прогноз, сделанный в момент
t на I тактов времени вперед, равен
I) = [d0(t) 4- lai(t)]u(t + l-T)t
где w(r) — так называемый коэффициент сезонности, а Т — число вре-
менных тактов, содержащихся в полном сезонном цикле, т. е. в одном году
1 См.: Holt С.С. Forecasting Seasonal» and Trends by Exponentially Weighted Moving
Averages. Carnegie Inst. Tech. Res. Mem. X» 52. 1957.
902
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
(например, при месячных данных Т = 12). Мы видим, что сезонность в
этой формуле представлена мультипликативно. Метод использует три
параметра сглаживания (адаптации) А1,А2,Аз (0 < Aj < 1, j = 1,2,3),
а его формулы обновления (пересчета прогнозирующих коэффициентов)
имеют вид:
®о(4 4-1) -	+	+ МО]»
+ 1) = ^2\ "/ТгА + 0 “ A2)w(I + 1 - Т),
Оо(ь + 1)
ai(£ + 1) = Аз[а0(« + 1) — Оо(0] 4- (1 — Аз)а>(0.
Как и в предыдущем методе, прогноз здесь строится на основании
прошлых и текущих значений временного ряда, параметров адаптации
Ai, А2 и Аз, а также начальных значений по(0), oi(0) и w(0).
Аддитивная модель сезонности Тейла—Вейджа. Надо при-
знать, что в экономической практике чаще встречаются экспоненциаль-
ные тенденции с мультипликативно наложенной сезонностью. Поэтому
перед использованием аддитивной модели члены анализируемого времен-
ного ряда обычно заменяют их логарифмами и тем самым преобразуют
экспоненциальную тенденцию в линейную и одновременно — мультипли-
кативную сезонность в аддитивную. Преимущество же аддитивной мо-
дели — в относительной простоте ее вычислительной реализации. Будем
считать, что логарифмическое преобразование исходных данных уже вы-
полнено, и рассмотрим аддитивную модель вида
x(r) = Oq(t) 4- w(r) 4- d(r),
а0(т) = а0(т - 1) 4- ai(r),
где по (г) — уровень процесса после элиминирования сезонных колебаний,
ах(т) — аддитивный коэффициент роста, и(т) — аддитивный коэффици-
ент сезонности и 6(т) — белый шум.
Прогноз, сделанный в момент t на I временных тактов вперед, под-
считывается по формуле
0 = ®о(0 4- ^«1(0 4- w(i — Т 4- /),
где коэффициенты do, d] и ы вычисляются рекуррентным способом с до-
выводы
903
мощью следующих формул обновления:
«оО”) = Оо(т - 1) + &1(т - 1) + Aj [ж(т) - х(т - 1; 1)];
Л1(т) = ai(Ti) + A!A2[x(t) - х(т - 1; 1)];
w(r) = w(r - Т)+ (1 - Ai)A3 (а;(т) - х(т - 1; 1)].
В этих соотношениях, как и прежде, Т — это число временных тактов,
содержащихся в полном сезонном цикле (как правило, в году), а А], А2 и
Аз — параметры адаптации.
Мы уже упоминали при рассмотрении примера 16.13, что подбор
подходящих значений для параметров адаптации является узким местом
всех методов, основанных на экспоненциальном сглаживании. Обычно вся
сложность решения этой проблемы перекладывается на компьютер: запа-
саются наборами значений — «кандидатов» в параметры сглаживания,
для каждого набора значений подсчитывают серию прогнозов по данному
методу и на основе сравнения получающихся при этом среднеквадратиче-
ских ошибок прогнозов выбирают оптимальные значения для Ау.
ВЫВОДЫ
1. Большинство математике-статистических методов, описанных в
главах 6-13 данного учебника, имеет дело с моделями, в которых наблю-
дения предполагаются независимыми и одинаково распределенными. При
этом зависимость между наблюдениями чаще всего рассматривалась как
Помеха в эффективном применении этих методов. Однако разнообразные
данные в экономике, социологии, финансах, коммерции и других сферах
человеческой деятельности поступают в форме временных рядов, в кото-
рых наблюдения зависимы, и характер этой зависимости как раз и пред
ставляет главный интерес для исследователя. Совокупность существую-
щих методов и моделей исследования таких рядов зависимых наблюдений
называется анализом временных рядов.
2. Главная цель эконометрического анализа временных рядов состо-
ит в описании по возможности простых и экономично параметризованных
моделей, адекватно описывающих имеющиеся ряды наблюдений и соста-
вляющих базу для решения, в первую очередь, следующих задач:
•	вскрытие механизма генезиса наблюдений, составляющих анализиру-
емый временной ряд;
•	построение оптимального (т. е. наиболее точного) прогноза для бу-
дущих значений временного ряда;
904
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
•	выработка стратегии управления и оптимизации анализируемых
процессов.
3.	Говоря о генезисе образующих временной ряд наблюдений, следует
иметь в виду (и по возможности моделъно описать) четыре типа факторов,
под воздействием которых могут формироваться эти наблюдения: дол-
говременные, сезонные, циклические (или конъюнктурные) и случайные.
При этом не обязательно в процессе формирования значений конкретного
временного ряда должны одновременно участвовать факторы всех четы-
рех типов. Успешное решение задач выявления и моделирования действия
этих факторов является основой, базисным отправным пунктом для до-
стижения конечных прикладных целей исследования, главные из которых
упомянуты в предыдущем пункте.
4.	Приступая к анализу дискретного ряда наблюдений, расположен-
ных в хронологическом порядке, следует, в первую очередь, убедить-
ся, действительно ли в формировании значений этого ряда участво-
вали какие-либо факторы, помимо чисто случайных При этом под
«чисто случайными» понимаются лишь те случайные факто-
ры, под воздействием которых генерируются последовательности взаим-
но не коррелированных и одинаково распределенных случайных величин,
обладающих постоянными (не зависящими от времени) средними значе-
ниями и дисперсиями. Ответ на поставленный вопрос получают, проводя
статистическую проверку соответствующей гипотезы с помощью одного
из «критериев серий» или критерия Аббе (см. п. 16.3.1).
5.	Если в результате проверки такой статистической гипотезы выяс-
нилось, что имеющиеся наблюдения взаимно зависимы и неодинаково рас-
пределены (т.е. образуют действительно временной ряд), то приступают
к подбору подходящей модели для этого ряда. Множество моделей, в рам-
ках которого ведется этот подбор, ограничивается обычно двумя классами
линейных моделей: классом стационарных временных рядов (которые ис-
пользуются, в основном, для описания поведения «случайных остатков»)
и классом нестационарных (но однородных) временных рядов.
6.	Стационарные (в широком смысле) временные ряды ж(<) характе-
ризуются тем, что их средние значения Еж(1), дисперсии Dz(t) и ковари-
ации 7(т) = Е[(а?(£) - Ez(t))(z(f + т) - Ех(7 + т))] не зависят от t, т.е.
остаются постоянными при изменении момента времени t, для которого
они подсчитываются (см. п. 16.2). Взаимозависимости, существующие
между членами стационарного временного ряда, как правило, могут быть
адекватно описаны в рамках моделей авторегрессии порядка р (АР(р)-
моделей), моделей скользящего среднего порядка q (СС(д)-моделей) или
моделей авторегрессии со скользящими средними в остатках порядка р
выводы
905
и q (АРСС(р, д)-моделей), см. п. 16.4.
7.	Ряд z(t) называется нестационарным однородным, если существует
такой порядок Л, что последовательные разности д\г(£) этого ряда поряд-
ка к образуют стационарный временной ряд. Другими словами, нестаци-
онарный однородный ряд характеризуется тем, что после вычитания из
него локального среднего уровня он становится стационарным. Поведение
нестационарных однородных временных рядов, в том числе рядов, содер-
жащих сезонную компоненту, в эконометрических прикладных задачах до-
статочно успешно описывают с помощью моделей авторегрессии — про-
интегрированного скользящего среднего порядка p,q и к (АРПСС(р,д, к)-
моделей) или некоторых их модификаций (см. пп. 16.5.1-16.5.2).
8.	Подобрать модель для конкретного временного ряда {а;(0}, t =
1,2,..., А, — это значит определить подходящее параметрическое семей-
ство моделей в качестве допустимого множества решений, а затем стати-
стически оценить параметры модели на основании имеющихся наблюде-
ний ж(1),х(2), ...,ж(А). Весь этот процесс принято называть процессом
идентификации модели, или просто идентификацией,
9.	В ситуациях, когда нестационарные однородные временные ряды
{ж(<)} и {у(0}»	— 1,2,. ..,А, являются исходными данными для по-
строения регрессии у по х, причем, воздействие единовременного измене-
ния одной из них (ж) на другую (у) растянуто (распределено) во време-
ни, большой прикладной интерес представляют так называемые модели
с распределенными лагами. В рамках этого специального класса моде-
лей проводится, в частности, интересный эконометрический анализ таких
важных экономических явлений, как «процесс частичного приспособле-
ния» , «модели адаптивных ожиданий» и др. (см. п. 16.5).
10.	Важную роль в системах поддержки принятия экономических ре-
шений играет прогнозирование экономических показателей. В гл. 15 мы
рассматривали методы прогнозирования, основанные на моделях регрес-
сии. В данной главе внимание было сконцентрировано в основном на ме-
тодах автопрогноза, в которых имеющийся в наличии ряд экстраполиру-
ется вперед только на основании информации, содержащейся в нем самом.
Такого рода прогноз может оказаться эффективным лишь в кратко-
и, максимум, в среднесрочной перспективе. Серьезное решение задач
долгосрочного прогнозирования требует использования комплексных под-
ходов, и в первую очередь привлечения различных (в том числе, стати-
стических) технологий сбора и анализа экспертных оценок.
11.	Наиболее эффективный подход к решению задач кратко- и средне-
срочного автопрогноза — это прогнозирование, основанное на использова-
нии «подогнанных» (идентифицированных) моделей типа АРПСС(р,д,&),
906
ГЛ. 16. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
включая, в качестве частных случаев, и модели АР-, СС- и АРСС.
12.	Весьма широко распространены в решении прикладных задач
кратко- и среднесрочного автопрогноза и так называемые адаптивные ме-
тоды, позволяющие по мере поступления новых данных обновлять ранее
сделанные прогнозы с минимальной задержкой и с помощью относительно
несложных математических процедур.
ГЛАВА 17. СИСТЕМЫ ЛИНКИНЫХ
ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
Изучение взаимосвязей между экономическими переменными — стер-
жневая, базисная цель всяких эконометрических методов, моделей, прило-
жений вне зависимости от того, чтб является конечной прикладной целью
исследования — прогноз, управление или сценарные расчеты. До сих пор
мы осваивали методы и модели, предназначенные для автономного анали-
за и оценивания одного уравнения, отражающего интересующие нас взаи-
мосвязи, будь то корреляционно-регрессионные связи (гл. 10, 11), зависи-
мости, позволяющие решать задачи типологизации объектов (гл. 12) или
отбора наиболее существенных показателей (гл. 13), уравнение регрессии
(гл. 15) или модель временных рядов (гл. 16).
Тетдерь мы расширим рамки нашего анализа. Во-первых, интересую-
щие нас зависимости будут описываться целой системой взаимосвязан-
ных соотношений, что ставит новые вопросы, связанные с правильной
(т. е. непротиворечивой, идентифицируемой) комплектацией такой систе-
мы. Во-вторых, мы должны выяснить, можно ли применять техниче-
ские приемы и методы, используемые в анализе и оценивании отдельного
уравнения, последовательно к каждому из соотношений системы. Или
же специфика взаимосвязей соотношений, из которых составлена систе-
ма, требует разработки специальных методов для оценки одновременно
всех неизвестных параметров этой системы?
Напомним, что системой одновременных уравнений (СО У) называ-
ется набор взаимосвязанных регрессионных моделей, в которых одни и
те же переменные могут одновременно играть роль (в различных урав-
нениях системы) результирующих показателей (объясняемых перемен-
ных) и предикторов (объясняющих переменных), и что введению в круг
сформулированных выше проблем была посвящена гл. 14. Поэтому чита-
телю, принимающемуся сразу за изучение данной главы, мы рекомендуем
обратиться предварительно к гл. 14 и, в частности, внимательно озна-
комиться в ней со «сквозным» примером 14.1 (с. 603 и далее), определе-
908 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
ниями эндогенных, экзогенных и предопределенных переменных модели
(с. 605), определением и общими формами записи (структурной и при-
веденной) системы одновременных уравнений (с. 605-610), формулиров-
ками проблем спецификации, идентифицируемости и верификации эко-
нометрической модели, представленной в форме системы одновременных
уравнений — СОУ (с. 612-615), а также с понятиями неидентифицируе-
мой, идентифицируемой и сверхидентифицируемой СОУ (с. 614-615).
Мы же сосредоточим внимание в данной главе на проблеме иденти-
фикации СОУ, понимаемой в широком смысле, т. е. при включении в нее и
проблемы идентифицируемости (отдельных уравнений и всей системы), и
проблемы статистического оценивания неизвестных параметров систе-
мы. В заключительном пункте главы мы собираемся рассмотреть задачи
точечного и интервального прогноза значений эндогенных переменных в
рамках моделей СОУ.
Начнем рассмотрение указанных выше проблем с анализа относитель-
но простого примера — «модели спроса-предложения».
17.1. Модель спроса-предложения как
пример системы одновременных
уравнений
Мы располагаем наблюдениями (xt,ур\ у|2^), t = 1,2,..., п, характе-
ризующими динамику среднедушевого дохода (xt), предложения некото-
рого товара (уР\ которое совпадает со спросом на этот товар в условиях
равновесия) и цены на него (уР^). Нам будет удобнее в дальнейшем опе-
рировать не с самими наблюдаемыми переменными (я, у' и у' '), а с их
отклонениями от своих средних уровней, т.е., соответственно, с наблюде-
= (1)	~(1) ~(1)	(2)	~(2) ~(2) (
ниями xt = xt - х, yj ' = у} - уи Уе = у\ 1 - у (черта сверху озна-
чает усреднение соответствующей переменной по всем ее наблюденным
значениям). Для центрированных таким образом переменных известные
линейные уравнения спроса и предложения запишутся в виде
J yj1) = 6jyJ2) 4- Яр) — уравнение предложения,	(17.1)
1 ур) = 62у|2) + ca?t + 4^ — уравнение спроса,	(17.2)
t = 1,2,. ,.,п,
где 61, Ь2 ис — некоторые неизвестные коэффициенты, а каждая из после-
довательностей {Яр)} и } (t = 1,2,..., п) представляет собой ряд вза-
имно не коррелированных случайных величин, имеющих нулевые средние
17.1. МОДЕЛЬ СПРОСА-ПРЕДЛОЖЕНИЯ
909
2	2
значения и дисперсии, соответственно, и ст2, не зависящие от t. Кроме
того, предполагается, что регрессионные остатки и не коррели-
рованы между собой, а также не коррелированы с переменной xt.
Заметим, что в модели (17.1)~(17.2) значения цены и спроса-
предложения у формируются как бы «внутри* нее, в процессе взаи-
модействия связей, описываемых этой моделью. В то же время значения
среднедушевого дохода х поступают в систему как характеристики внеш-
ней среды, в которой взаимодействуют эти анализируемые связи. Поэтому
в данной модели спрос-предложение и цена отнесены к эндогенным пере-
менным, а доход — к экзогенным.
Отправляясь от описанной выше спецификации модели, проведем ее
анализ по схеме: а) основные структурные характеристики системы (чи-
сло уравнений, эндогенных и экзогенных переменных, структурная и при-
веденные формы); б) идентифицируемость уравнений системы; в) стати-
стическое оценивание параметров системы (включая анализ свойств обыч-
ных МПК-оценок, понятие о косвенном и двухшаговом методах наимень-
ших квадратов и связь с методом инструментальных переменных).
Основные структурные характеристики модели. Анализи-
руемая модель описана системой (17.1)—(17-2), состоящей из двух урав-
нений (в обозначениях гл. 14 т = 2) с двумя эндогенными и одной (р = 1)
предопределенной (она же — экзогенная) переменными. Балансовых то-
ждеств система не содержит (т.е. т2 = 0 и, следовательно, = т).
Структурная форма модели (см. определение 14.2) задана уравнениями
(17.1)—(17.2). Решая эти уравнения относительно эндогенных переменных
ур) и получаем приведенную форму СОУ (см. определение 14.3):
(17-3)
(17.3')
(17.3")
yt(2) = TT2Xt +	t = 1,2,..., n,
где
bYc	с
= 6, -6j’	= bt-bt’
L ;(2)	। с(1)	г(1)
(1) _ Mt -b26t	(2) _ bt -btl
‘ ' bi-b2 ’	‘ - bi-b2
В рамках сделанных выше предположений о постоянстве дисперсий
D#, и Di5 и о некоррелированности i и <5 между собой и с экзо-
генной переменной zt из (17.3й) следует, что случайные остатки е,1’ и
е[ приведенной формы также имеют не зависящие от I дисперсии, не
910
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
коррелированы между собой и с экзогенной переменной xt в уравнениях
(17.3).
Идентифицируемость уравнении системы. Следуя определени-
ям 14.4~ 14.7, попробуем ответить на вопрос об идентифицируемости пара-
метров 61,62 и с структурной формы, т. е. о возможности их однозначного
выражения через параметры и %2 приведенной формы. Поделив первое
из уравнений (17.3х) на второе, получаем
Ь, = £1.	(17.4)
ТГ2
Однако соотношений (17.3*) оказывается недостаточно для того, чтобы
определить из них значения коэффициентов 62 и с второго уравнения
структурной формы. Это значит, что первое уравнение структурной фор-
мы анализируемой СОУ идентифицируемо, а второе и вся система — не-
идентифицируемы.
Статистическое оценивание параметров СОУ. Попробуем сна-
чала формально воспользоваться обычным методом наименьших квадра-
тов, примененным в отдельности к каждому из уравнений (17.1) и (17.2),
и проанализируем состоятельность полученных оценок.
1)	Несостоятельность обычных МНК-оценок параметров уравнений
структурной формы. Начнем с уравнения (17.1) и воспользуемся форму-
лой (15.18) для вычисления МНК-оценки в простейшем варианте модели
регрессии с единственной объясняющей переменной (в уравнении (17.1) ее
роль выполняет цена товара у^):
Ё 14’М2)
Ё (^>)2 ’
4=1
(17.5)
Как обычно это делается при исследовании свойств несмещенности
и состоятельности оценки, подставим в правую часть (17.5) вместо пере-
менной у*1) ее модельное выражение из (17.1):
Ё(б1^,+41))^	1 Ё
L	— t=1	— A. J	£=1
°1мнк —	п	1	
£ (?!2))2 t=l	1Ё (»!2))2 4=1
(17.6)
Исследуем поведение (при п —> оо) 2-го слагаемого в правой части
(17.6), поскольку от него зависят свойства несмещенности и состоятся ь-
17.1. МОДЕЛЬ СПРОСА-ПРЕДЛОЖЕНИЯ
911
ности оценки мяж. Если принять естественное допущение о существова-
нии пределов (при п —► оо) числителя и знаменателя этого отношения, то
в силу закона больших чисел будем иметь:
М 11Е ) = Е гё*М2>)=-v (4”. »!”).	(17.7)
lim
п—»оо
= Е (у,(2))2 = DS$2)
(17-8)
(в этих соотношениях учтено, что по построению ЕЯ, = Ej = 0 при
всех tt а сходимость пределов понимается «по вероятности»). Остается
выразить значения cov(6p\y|3^) и Dj в терминах параметров модели.
Для этого воспользуемся выражением yj 1 из второго соотношения приве-
денной формы (17.3) анализируемой СОУ (с учетом (17.3х) и (17.3W)):
cov(«Jl),y|2)) = Е
6<’>
- <<»)
61 — 62
= №(1’> г<)
T2Z, +
Cov(<p),42>)-Pfp) =	<г?
6| — Ь2	bi — 62'
(17.9)
DyP) = Е /сЖ|+(42)-41))\ =	1	(£;JdI( + WU) + цдЮ)
\	01 - &2	/	(6j - Ь2)
(17.10)
Теперь мы можем вычислить предельное выражение (при п -+ оо)
для 61мик, вернувшись к (17.6) и учтя (17.7)-(17.10):
Um - 61 +	- bi- (bi - 6j) 2	1	2- (17.11)
—8	с uxt + oi + о2
Мы видим, что обычная МНК-оценка 6iMHK параметра имеет в
общем случае (т.е. при ЬА / 62 и а / 0) асимптотически неустранимое
смещение, а следовательно, она не является ни несмещенной, ни (что
более важно) состоятельной. Поскольку результат — отрицательный,
оценивание 2-го уравнения системы с помощью обычного МНК, очевидно,
не имеет смысла.
2)	Использование косвенного метода наименьших квадратов. При
переходе к приведенной форме (И.З^И.З'^И.З”) было подмечено, что
912 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
регрессионные остатки в уравнениях (17-3) удовлетворяют условиям клас-
сической модели регрессии. Следовательно, оценки параметров я-! и ^2 мо-
гут быть получены с помощью обычного метода наименьших квадратов, и
при этом они будут несмещенными и состоятельными. Но в случае иден-
тифицируемости параметров структурной формы они по определению мо-
гут быть выражены через параметры приведенной формы. Поэтому если
в эти выражения мы вместо параметров т3 подставим их МНК-оценки тг;-,
то получим (в соответствии с теоремой Слуцкого) состоятельные оценки
для соответствующих идентифицируемых параметров структурной фор-
мы. Такой способ оценивания идентифицируемых параметров структур-
ной формы называют косвенным методом наименьших квадратов. В на-
шем примере идентифицируемым является только 1-е уравнение. В со-
ответствии с (17.4) получаем состоятельную оценку косвенного метода
наименьших квадратов для параметра ЬА:
=	(17.12)
*2mhk
где тг,Мнк — обычные МНК-оценки параметров itj в уравнениях (17.3)
приведенной формы анализируемой СОУ.
3)	Использование метода инструментальных переменных. Причи-
на непригодности обычного метода наименьших квадратов в оценива-
нии параметров 1-го уравнения структурной формы, как мы знаем (см.
п. 15.10.2), — в коррелированности объясняющей переменной (в нашем
случае — у, ) с регрессионными остатками (в нашем случае — с ^ ).
В соответствии с рекомендациями п. 15.10.2 в уравнении (17.1) в качестве
инструментальной переменной естественно использовать доход х, посколь-
ку:
•	xt не коррелирован по условию с
•	xt по построению достаточно сильно коррелирован с у (что, в
частности, подтверждается осмысленностью рассмотрения 2-го урав-
нения приведенной формы (17.3)).
Тогда в соответствии с (15.150*) оценка параметра по методу
инструментальных переменных будет
Л (О
Е yt xt
-- 	(плз)
t=l
Если принять во внимание, что МПК-оцепки к3 параметров к3 урав-
17.1. МОДЕЛЬ СПРОСА-ПРЕДЛОЖЕНИЯ
913
нений приведенной формы (17.3) имеют вид
£ Е уУ*<
~	4=1	о <=1
то сравнение оценки (17.12), полученной с помощью косвенного метода
наименьших квадратов, с оценкой (17.13), полученной с помощью метода
инструментальных переменных, приводит к выводу, что в данном случае
эти оценки совпадают.
4) Двухшаговый метод наименьших квадратов. В ходе применения
косвенного метода наименьших квадратов мы выяснили, что 2-е уравне-
ние анализируемой системы (т.е. уравнение (17.2)) неидентифицируемо,
и, соответственно, параметры 62 и с остались не оцененными. Прямому
применению к этому уравнению обычного метода наименьших квадратов
препятствует коррелированность значений объясняющей переменной i
с регрессионными остатками Чтобы обойти эту трудность, пред-
лагается следующая двухэтапная процедура оценивания. На 1-м этапе,
чтобы избавиться от у\ в правой части уравнения (17.2), мы заменяем
эту переменную ее аппроксимацией с помощью линейной функции от х.
Аппроксимацию строим с помощью обычного метода наименьших квадра-
тов, который, с учетом центрированности обеих переменных, дает:
»<” =	+ е«,	(17.14)
где МНК-оценка параметров парной регрессии i по ж, как из-
вестно, имеет вид
t
= ‘-А	(17.15)
£ 4
4=1
а остатки в соответствии со свойствами МНК не коррелированы с пре-
диктором
Теперь, на 2-м этапе оценивания, мы можем возвратиться к оценива-
емому уравнению (17.2) и заменить в нем объясняющую переменную у^2^
ее аппроксимацией (17.14). В результате вместо (17.2) получаем уравне-
ние
У*^ =	/Xxt + et) + cxt -f- tf|2) = (b20y&)fx + c)xt 4- (42) + b2et). (17.2')
914
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
В этом уравнении остаток + 62£t по условию и по построению не кор-
релирован с предиктором a?f, а поэтому мы можем использовать обычный
МНК для оценки параметра 0va)/x = 62^(2)4- с:
— п
(17.16)
t=i
Таким образом мы получаем линейное соотношение, связывающее
между собой оцениваемые параметры 62 и с:
62^v(2)/x + С =
(17.17)
в котором величины 0у<з)/х и ^(о/х определены соотношениями (17,15) и
(17.16). Для того, чтобы отсюда извлечь опенки 62 и с, надо вернуться к
соотношениям (17.3*), связывающим между собой параметры приведенной
и структурной форм:
Ь{с
(17.18)
^2^1Д2)/х + С = #y(D/r-
Решая эти три уравнения относительно параметров структурной фор-
мы 61,62 ней воспользовавшись значениями уже подсчитанных оценок тг1}
Tri, 0уо)/х, 0у(2)/Х1 а также известной теоремой Слуцкого, получаем
7^	*, _^1/(1)/х+^1 А _ 0у(1)/х^2 —
— тг- \ о2 —	’ ё — л ZT”
^2	0у(2) ]х 4- fT2	0y(3) [х 4- *2
Описанный (для данного частного случая) способ получения оценок
параметров отдельного уравнения системы носит название двухшагового
метода наименьших квадратов. Ниже (см. п. 17.3.3) мы опишем этот
метод для общего случая СОУ.
Замечание. Заменяя в ходе 1-го шага процедуры объясняющую
переменную у ее аппроксимацией Ovw/Cxt мы тем самым сознательно
идем на чистую мультиколлинеарность (см. п. 15.4.1) в получающейся
модели
= b2(Syw/xxt) 4- cxt 4- e(t).
17.2. УСЛОВИЯ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ СИСТЕМЫ
915
Так что мы, конечно, не можем претендовать на получение состоятельных
МНК-оценок отдельно для коэффициентов Ь2 и с: в силу вырожденности
матрицы наблюдений объясняющих переменных	= Ov^)/Xxt и = xt
получающаяся в результате применения МНК система нормальных урав-
нении будет содержать два одинаковых уравнения для определения оценок
параметров 62 и с. Однако с учетом уже имеющихся у нас соотношений
(17.3 ), связывающих между собой параметры структурной и приведенной
форм системы, мы получаем как раз ту связь между этими параметрами,
которой не хватало для определения оценок параметров неидентифициру-
емого уравнения.
Итак, мы обсудили и предварительно «прочувствовали» на примере
модели спроса-предложения основные проблемы, возникающие при анали-
зе СОУ: спецификацию, идентифицируемость, статистическое оценивание
параметров модели. Теперь мы приступаем к общему описанию этих про-
блем и методов их решения.
17.2. Условия идентифицируемости
уравнений системы
Сама проблема идентифицируемости СОУ, ее отдельных уравнений
и даже отдельных параметров была сформулирована в гл. 14 (см. с. 614-
615). Эта проблема логически предшествует статистическому оценива-
нию параметров системы, поскольку от ее решения зависит и выбор ме-
тодов оценивания. Отсутствие идентифицируемости СОУ означает, что
существует бесконечно много моделей, не противоречащих имеющимся
в нашем распоряжении наблюдениям. В результате анализа проблемы
идентифицируемости конкретного структурного параметра системы мы
приходим к одной из трех принципиально возможных ситуаций: 1) этот
параметр может быть однозначно выражен через коэффициенты приве-
денной системы; 2) структурный параметр допускает несколько разных
вариантов определения с помощью косвенного МНК; 3) структурный па-
раметр не может быть выражен через параметры приведенной формы.
Очевидно, идентифицируемость или неидентифицируемость системы, ее
уравнений и параметров зависят только от внутренней структуры мо-
дели (числа уравнений, соотношения количеств эндогенных и предопреде-
ленных переменных в системе и в каждом уравнении, мультиколлинеарно-
сти анализируемых переменных, некоторых свойств матриц структурных
коэффициентов), но никак не связаны со статистическими свойствами ис-
ходных наблюдений, например с их количеством.
Следуя, в основном, обозначениям, введенным в гл. 14 (см. (14.6),
916 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
(14.7), (14.6Z), (14.6й), (14.6е) и т. д.), мы будем полагать, что балансовые
тождества уже исключены из анализируемой системы (см. замечание на
с. 607), так что ее структурная форма имеет вид:
Byt + CXt = Af, t = l,2,...,n,	(17.19)
где В = (Ду) — матрица размерности т х ту (т.е. i = l,2,...,m;
j = 1,2,...,7Пу) коэффициентов при ту эндогенных переменных Yt =
(уР\уГ\*• -»У«туЬТ» С = (cv) — матрица размерности т х р (т.е.
i = l,2,...,m; j = 1,2,...,р) коэффициентов при р предопределенных
v ( (1)	(2)	(р)\Т	_
переменных А< = (ж) \х\ , ...,ж} ') , в состав которых, если необхо-
димо, включен и свободный член; а вектор-столбец случайных остатков
удовлетворяет в общем случае следующим усло-
виям: EAt = 0т; ковариационная матрица остатков Ед = E(AtA^) по-
ложительно определена и не зависит от 1; векторы и Ata взаимно
не коррелированы при / t2> а не коррелированы со всеми предо-
пределенными переменными системы, т.е.	— Еа )] = 0 при
i = 1,2,..., m, j = 1,2,... ,р. Коэффициенты Ду пронормированы с помо-
щью условия Д, = 1.
Таким образом рассматривается система из гп уравнений, содержа-
щая ту эндогенных и р предопределенных (т.е. экзогенных и лаговых
эндогенных) переменных.
Прежде всего, для того, чтобы мы могли уединить эндогенные пере-
менные У4, выразив их через предопределенные переменные Xt (т.е. —
осуществить переход к приведенной форме и установить соотношения,
связывающие коэффициенты структурной и приведенной форм), необхо-
димо потребовать, чтобы матрица В была квадратной и обратимой (т.е.
невырожденной). Так мы приходим к формулировке 1-го (необходимого)
условия идентифицируемости:
1-е условие (необходимое) идентифицируемости: число урав-
нений системы (т) должно быть равно числу анализируемых эндогенных
переменных (пгг), т. е. т = ту = т, а матрица В должна быть невы-
рожденной.
Тогда приведенная форма анализируемой системы будет иметь вид:
yt = nXt + €t, t = l,2,...,n,	(17.19е)
где
П=-В"*С	-	(17.20)
матрица размерности т х р коэффициентов приведенной формы, а е4 =
t (1) (2)	(m)J D-1 А	_
(е}	') = В — вектор-столбец остатков.
17.2. УСЛОВИЯ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ СИСТЕМЫ
917
Очевидно, необходимым условием возможности оценить все коэффи-
циенты матрицы П параметров приведенной формы (17.19а) является
требование, чтобы предопределенные переменные Xt не были мультикол-
линеарны. Итак,
2-е условие (необходимое) идентифицируемости: матрица на-
блюдений предопределенных переменных X = (ж^), t = 1,2,. ..,n; j =
1,2,...,р, — размерности п X р должна иметь полный ранг р (очевид-
но, при этом число наблюдений п должно существенно превышать общее
число анализируемых переменных т + р).
На интуитивном уровне достаточно очевидна «перегруженность»
модели (17.19) неизвестными значениями параметров и cik (t =
1,2, к = 1,2,...,р). Более того, можно доказать (см., например,
[Джонстон Дж.], с. 357), что если не дополнить модель (17.19) никаки-
ми априорными ограничениями относительно числовых значений этих па-
раметров, то ни одно из уравнений не может быть идентифицируемо.
При этом априорные ограничения носят чаще всего исключающий харак-
тер, т.е. они определяют в каждом (t-м) уравнении «адреса» (i,J) и (x*,fc)
тех коэффициентов, которые априори считаются нулевыми (априорные
ограничения могут быть сформулированы и в виде определенных линей-
ных связей, априори существующих между оцениваемыми коэффициента-
ми). Поставим в соответствие каждому (х-му) уравнению системы (17.19)
(т 4- р)-мерный булевский (т.е. состоящий только из нулей и единиц)
вектор 7» = (7i »..•,?< 7 7i , ...,7i h задающий исключающие
априорные ограничения для параметров этого уравнения по следующему
(fc)
правилу: нулевые значения компонент у,- ' определяют «адреса» отсут-
ствующих в уравнении переменных, или, что то же, априори равных нулю
параметров t-го уравнения структурной формы.
3-е условие (необходимое) идентифицируемости: среди ис-
ключающих априорных ограничений у» = (ур\...,71-m+p^), i = 1,2,...,т,
не должно быть одинаковых.
Пример 17.1. Чтобы пояснить, к чему может приводить наруше-
ние этого условия, вернемся к рассмотренному в предыдущем пункте при-
меру (17.1)-(17.2). Очевидно, анализируемая модель спроса-предложсния
может быть записана в следующем виде, эквивалентном (17.1)—(17.2):
+	(пл')
»«3) =	б2»‘2) + сг<	+ «!2)>	(И.2')
уГ) =	»$3)-	(17.2й)
По сравнению с прежними обозначениями	изменено только обозначение
918
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
спроса: в данной записи для спроса введена специальная переменная
и, соответственно, появилось одно тождество (17.2,z).
Желая несколько упростить модель, положим, что спрос так же,
как и предложение зависит только от цены товара у\ (т.е. не за-
висит от дохода). Тем самым мы воспользовались двумя одинаковыми
исключающими априорными ограничениями — ив первом, и во втором
уравнениях системы «обнулили» коэффициент при доходе х. В результа-
те получаем систему
(= М2М”.
us,=u2)+e.
Ы”=»Г.
Рис. 17.1. Линии предложения (А), спроса (Б) и наблюдения (крестики),
произведенные в условиях равновесия
На плоскости, где по оси ординат откладываются значения предложе-
ния и спроса, а на оси абсцисс — значения цены, равновесие представля-
ется как пересечение линий предложения (А) и спроса (Б), см. рис. 17.1.
Поскольку мы собираем исходные статистические данные
t = 1,2,..., п, в условиях равновесия, то различие в наблюдаемых значе-
ниях обусловлено только случайными остатками и что, кстати,
17.2. УСЛОВИЯ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ СИСТЕМЫ
919
подтверждается и приведенной формой этой модели
И2’=^(42М*>),
так как правые части уравнений выражаются только в терминах случай-
ных остатков модели. Очевидно, располагая только разбросанными около
точки равновесия значениями случайных остатков и е (см. (17.3х)
и (17.3м)), мы ничего не можем сказать о самих функциях предложения
(А) и спроса (Б). А это и значит, что мы не можем оценить параметры
6] и bj в уравнениях (17.1х) и (17.2х), т.е. оба анализируемых уравнения
неидентифицируемы.
Заметим, что к точно такому же результату мы пришли бы, если бы
пошли по линии некоторого усложнения (а не упрощения) модели (17.1)-
(17.2), введя в 1-е уравнение системы доход ж. Это снова означало бы
использование идентичных векторов априорных ограничений и привело
бы к неидентифицируемости системы.
Выведем еще два важных условия идентифицируемости отдельного
уравнения системы (17.19). Для этого выпишем i-e уравнение этой си-
стемы, полагая (без ограничения общности), что анализируемые перемен-
ные системы перенумерованы таким образом, что участвующие в этом
уравнении рх предопределенных и переменных (р, р) и т, эндогенных
переменных (тх С т) идут первыми в общих перечнях, соответственно,
предопределенных и эндогенных переменных. Тогда это уравнение может
быть записано в виде
+ (en ... c,w0.. .OX®!*’.	. .x(rt)T = 4°> (17.21)
или, что то же,

(17.21х)
где
/^(*) = (Д»1> • • • iflimi) 1 с(') = (c*l 1 • • • 1 cipi) 1	(17.21 )
yt(i) = (ур\..., У<т‘>)т, Xt(i) = (?;>,....	(17.21xxx)
Нас будут интересовать соотношения, связывающие между собой ко-
эффициенты структурной и приведенной форм именно i-ro уравнения си-
стемы (17.19) с точки зрения возможности однозначно выразить ко-
эффициенты структурной формы /3(i) и c(i) по известным значениям
920
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
коэффициентов приведенной формы (т.е. по элементам матрицы П из
(17.19*)). Для этого мы, конечно, используем в качестве отправного пунк-
та базовое соотношение (17.20), а точнее, — эквивалентное ему соотноше-
ние
ВП = -С.	(17.20')
Для того, чтобы извлечь отсюда интересующие нас соотношения, свя-
зывающие i-e строки матриц, стоящих в левой и правой частях (17.20*),
нам придется разбить матрицу П на четыре блока двумя воображаемы-
ми линиями: одна (горизонтальная) отделяет первые mt строк от т — mt
последующих, а вторая (вертикальная) — первые р, столбцов от р — pt
последующих (см. п. П2.8 в Приложении 2):
п(<)
т4хр<
"I, х (р-р,)
mxp
Xfm-mjxp, : (m - m,) x (p - Pi)J
(под матрицами указаны их размерности).
Тогда мы можем записать приведенную форму (17.19*) анализируе-
мой СОУ в виде
где УД1) и Х*(») определены в (17.21'"), a Vt(i) = (ytTO,+1\...,y^)T и
хдо = (4₽i+,)....х(1₽,)т-
Теперь выпишем вытекающее из (17.20 ) равенство »-х строк матриц
ВП и -С:
(17.23)
(векторы /3(») и c(t) определены в (17.21")).
17.2. УСЛОВИЯ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ СИСТЕМЫ
921
Произведя перемножение матриц в левой части (17.23), получаем
Г /3Т(.) П(«) = -с(.),	(17.24)
1/Зт(|)Пл(0 = Ор_п.	(17.25)
Мы получили систему уравнений, связывающих элементы t-й стро-
ки структурной формы СОУ с параметрами приведенной формы. Эта
система, как мы видим, распалась на две подсистемы: (17.25) и (17.24).
По-видимому, сначала надо попытаться решить подсистему (17.25) отно-
сительно коэффициентов /?(х), а затем, подставив найденные решения в
(17.24), решить эту подсистему относительно параметров c(t).
Поэтому определим, в первую очередь, условия, при которых подси-
стема (17.25) имеет хотя бы одно решение. Соотношения (17.25) предста-
вляют собой систему из р - р, уравнений относительно Д1, Дг,. - . ,^т, с
пг, — 1 неизвестными (поскольку в соответствии с условием нормировки
один из коэффициентов 0^ равен единице). Для того, чтобы параметры
/3(i) в подсистеме (17.25) можно было бы выразить через элементы ма-
трицы Пх(«), необходимо, чтобы число уравнений в (17.25) было бы не
меньше числа неизвестных, т. е.
р-р, > т, - 1.
Таким образом, мы пришли к еще одному необходимому условию
идентифицируемости уравнения системы.
4-е условие (необходимое) идентифицируемости (правило по-
рядка): число исключенных (при спецификации модели) из i-го уравне-
ния системы предопределенных переменных (т. е. число (p — pi)) должно
быть не меньше числа включенных в него эндогенных переменных, умень-
шенного на единицу. Сформулированное условие называется правилом
порядка. Заметим, что выполнение условия р — р, = mt — 1 является не-
обходимым условием точной идентификации t'-ro уравнения, в то время
как при р — Pi > mi — 1 уравнение будет сверхидентифицируемым. Из
анализа подсистемы уравнений (17.25) можно извлечь также необходимое
и достаточное условие идентифицируемости i-ro уравнения СОУ. Извест-
но, в частности, что для разрешимости системы (17.25) относительно 0(i)
необходимо и достаточно, чтобы матрица Пх(х) имела бы ранг, равный
числу неизвестных (т.е. т,- — 1). Таким образом получаем
5-е условие идентифицируемости отдельного уравнения систе-
мы (условие называется ранговым и является необходимым и достаточ-
ным): ранг матрицы Пх(‘) =	— 1.
922 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
Следует отметить, что в отличие от правила порядка (см. 4-е усло-
вие), которое может проверяться на стадии спецификации системы, со-
блюдение рангового условиями можем проверить в общем случае только
после вычисления матрицы Пх(*)>т*е* после применения обычного МНК к
приведенной форме (17.22) анализируемой системы. Правда, в отдельных
простых случаях это можно сделать и до применения МНК, просто ана-
лизируя элементы матрицы Пх(»), выраженные через параметры струк-
турной формы 0ij и сн (что мы и продемонстрируем сейчас на примере).
Пример 17.2. Снова несколько видоизменим пример, рассмотрен-
ный в п. 17.1. Полагая, что и ставка процента может влиять на спрос,
мы решили дополнить наши наблюдения за среднедушевым доходом (ft),
предложением некоторого товара (у*1 ) и ценой на него (j регистраци-
ей во времени этой величины. Тогда, как и прежде, переходя от значений
самих анализируемых величин к их отклонениям от средних (соответ-
ственно	и а^) и вводя в модель еще одну экзогенную пере-
менную г ) в виде аргумента функции спроса (т.е. в уравнение (17.2)),
мы получаем СОУ:
yj1) = bjyJ2) -Ь £	— уравнение предложения;	(17.1а)
„(») - Ьо«(2) 4- с^(1) 4- сож(2) 4- Л(2)
Vt —	+ clxt » c2xt • °4
— уравнение спроса, (17.2е)
I — 1,2,..., п,
в которой для удобства доход (в отклонениях от среднего) и коэффициент
при нем мы, теперь обозначаем, соответственно, и с1в Структур-
ные параметры этой системы: число уравнений равно общему числу
эндогенных переменных и равно т = 2; общее число предопределенных
переменных р = 2; число эндогенных и предопределенных переменных,
включенных в 1-е уравнение, соответственно, тг =2, pi =0; число эн-
догенных и предопределенных переменных, включенных во 2-е уравнение,
соответственно, т2 = 2,pj = 2; матрица В коэффициентов при эндоген-
ных переменных (при канонической записи системы)
Таким образом, 1-е условие идентифицируемости будет выполнен-
ным, если потребовать det В / 0, т.е. b2 / bi (и Ь2 / 0).
Для проверки 2-го условия надо убедиться в том, что наблюдения
и (t = 1,2,...,п) не связаны пропорциональной зависимостью,
т.е. что
17.2. УСЛОВИЯ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ СИСТЕМЫ
923
Очевидно выполнение S-го общего условия идентифицируемости си-
стемы, т. к. векторы исключающих ограничений первого (71) и второ-
го (72) уравнений системы различны, а именно: 7! = (1,1,0,0); 72 =
(1,1,1,1).
Теперь сосредоточимся на проверке идентифицируемости отдельного
(например, 1-го) уравнения системы. Правило порядка (4-е условие) вы-
полняется со строгим знаком неравенства, т. к. число исключенных в 1-м
уравнении предопределенных переменных равно двум (р — рг = 2 — 0), а
число включенных в него эндогенных переменных, уменьшенное на еди-
ницу, равно единице (mi — 1 =2—1). Это означает, что 1-е уравнение
системы является сверхидентифицируемым, т.е. его структурные пара-
метры (в данном случае это один параметр 61) допускают неоднозначное
выражение через параметры приведенной формы. Этот факт в анализиру-
емом примере легко проверить непосредственно. Действительно, решение
системы (17.1*)-(17.2а) относительно и у[2^ дает нам приведенную
форму
Ji)	,(2)	(1)
Vt — ^nxt + *i2®t + £t ,
„(2) _ - JO . ~ J2) 1 _(2)
2/t — *21^1 + *22®t +	,
где
61 cx _ bi c2
= 7----*12 — 7--------7“,
bi — 02	bi — O2
Cl _	c2
*21 = 7---7“,	*22 = 7---7“,
©1 — £>2	t>i — t>2
a ej1) и такие же, как в (17.3я). Мы видим, что структурный ко-
эффициент bi может быть определен по параметрам приведенной формы
двумя различными способами, которые дают, вообще говоря, два разных
результата.
тгц
1-й вариант:	щ	;
*21
Л Ч	L	*12
2-й вариант:	6Х	= —.
*22
Для полноты картины проверим выполнение 5-го (необходимого и до-
статочного) условия идентифицируемости 1-го уравнения так называе-
мого рангового условия, хотя мы уже знаем, что 1-е уравнение сверхиден-
тифицируемо.
В нашем случае матрица П%(1), имеющая размерность mx х(р—pi) =
924
ГТ 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
2x2, совпадает со всей матрицей П,
61 — 62
~ I C1 С2 I '
\ 6] — 62 61 — 62 /
«Невооруженным глазом» видно, что строки этой матрицы связаны
пропорциональной зависимостью (2-я строка получается из 1-й делением
на 61), так что ранг матрицы Пх(1) равен единице, что и требуется в
ранговом условии (т. к. в нашем случае = 2 и, следовательно, ранг
nx(l) = mj-l = l).
17.3. Идентификация систем одновременных
уравнений (статистическое оценивание
неизвестных значений параметров
системы)
В данном пункте речь идет только о той части проблемы идентифика-
ции СОУ, которая связана с методами статистического оценивания неиз-
вестных значений параметров /3tj и с,* (» = 1,2,..., тп; j = 1,2,..., тп; к =
1,2,... ,р) в уравнениях (17.19) по имеющимся в нашем распоряжении на-
блюдениям
Y= 14”
(2)
„(2)
(т)
У2
-0) z(2)
Я] ж,
-(П ж(2)
*2 х2
ж(₽)
>)
х2
. (17.26)
,0) J2)
и™ «<т>/	\х(1) ж(2)	х(р)/
Мы будем предполагать, что число наблюдений п «много больше»,
чем т + р (п > т + р), матрица В в (17.19) невырождена и что предопре-
деленные переменные	немультиколлинеарны, т.е. матрица
X имеет полный ранг р. Среди столбцов матрицы X может присутство-
вать столбец, состоящий из одних единиц (если в правую часть модели
(17.19) включен свободный член). Другие структурные предположения
о модели (17.19), и в частности, допущения о природе случайных остат-
ков Д«, будут формулироваться в ходе изложения того или иного метода
статистического оценивания.
Мы уже убедились в том, что независимо от того, хотим ли мы оце-
нить только одно из уравнений системы (17.19) или же намерены оценить
все уравнения этой системы, в общем случае мы оказываемся в ситуа-
ции, когда известные нам по гл. 15 методы регрессионного анализа (МНК,
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
925
различные версии ОМНК) не обеспечивают удовлетворительную процеду-
ру оценивания. Причина подобной ситуации заключается в том, что при
отсутствии специальных предположений о структуре СОУ (например, о
ее рекурсивном характере, см. ниже) в анализируемом уравнении среди
объясняющих переменных присутствует одна или несколько эндогенных
переменных, которые коррелируют с регрессионными остатками. Прав-
да, существует достаточно простой — так называемый косвенный метод
наименьших квадратов, когда с помощью обычного МНК, примененного
к каждому отдельному уравнению приведенной формы (17.19*), сначала
оцениваются элементы тг,у матрицы П, а затем, используя соотношение
(17.20) (в которое вместо матрицы П подставляется ее оценка П), опре-
деляются значения оценок Д; и параметров структурной формы. Но
этот метод применим лишь к точно идентифицируемым уравнениям.
Переходя к описанию специальных методов оценивания структурных
параметров модели (17.19), разделим их на два класса: методы, позволяю-
щие оценивать каждое отдельное уравнение системы (17.19) поочередно, и
методы, предназначенные для оценивания всех уравнений сразу. Правда,
существует специальный тип СОУ — так называемые рекурсивные си-
стемы, — для которых прц, определенном выборе порядка и взаимосвязей
оцениваемых отдельных уравнений системы процедура МНК приводит к
оцениванию всех ее уравнений. С точки зрения задач статистического
оценивания этот тип СОУ является простейшим, поэтому мы с него и
начнем.
17.3.1. Идентификация рекурсивных систем
Во многом потому, что рекурсивные СОУ относительно просты для
решения задачи статистического оценивания структурных параметров, в
большом числе прикладных работ (может быть, в бблыпей их части!) при
спецификации модели стараются построить ее так, чтобы она удовлетво-
ряла свойству рекурсивности. Для этого действуют следующим образом1.
В качестве 1-го уравнения системы специфицируют соотношение, в кото-
1 Следует, правда, признать, что в ряде публикаций ведущих эконометристов (в том
числе, например, в работах X. Волда) делаются серьезные попытки дать содер-
жательное (исходящее из сущности реальных экономических систем) обоснование
правомерности использования именно рекурсивных СОУ. Главные доводы их аргу-
ментации основаны на тезисе, что большинство реальных механизмов формирования
рассматриваемых в модели экономических показателей функционирует в рекурсив-
ном (а не одновременном) режиме. Так, например, трудно представить себе ры-
ночные механизмы, одновременно формирующие цены и количества предлагаемых
товаров (см. ниже пример 17.3).
926 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
ром присутствует только одна эндогенная переменная \ (соответствен-
но, и индексируют ее первым номером). Так что 1-е уравнение системы
содержит ni] = 1 эндогенных переменных и какое-то количество pi пре-
допределенных переменных. Второе уравнение системы может содержать
не более двух эндогенных переменных; это, если необходимо, эндогенная
переменная («участница» 1-го уравнения) и, кроме нее, еще толь-
ко одну эндогенную переменную (обозначим ее у^2^). При комплектации
состава и числа р? предопределенных переменных руководствуются содер-
жательными соображениями и «правилом порядка» (см. правило иден-
тифицируемости N* 4 в предыдущем пункте). В третье уравнение, кроме
уже участвовавших во 2-м уравнении эндогенных переменных у^ и у^2\
можно включить еще опять только одну эндогенную переменную у^ и
т. д. В результате мы получим модель вида (17.19), в которой матрица В
является нижней треугольной матрицей, т. е. = 0 при j > i для всех
i = 1,2,...,т (при сохранении условия нормировки 0ц = 1). Оказыва-
ется, если для систем такого вида дополнительно потребовать взаимную
некоррелированность случайных остатков и \ при всех t и для
всех i‘i / <2 (*1,«2 = 1,2,...,т), то оценки структурных параметров в
каждом отдельном уравнении системы с помощью прямого метода наи-
меньших квадратов будут состоятельными, а при нормальности <5 —
и асимптотически эффективными. Под прямым МНК понимается следу-
ющая процедура, последовательно примененная к i-му уравнению системы
(t = l,2,...,m): с помощью обычного МНК строятся оценки коэффици-
ентов регрессии у] по всем включенным в это уравнение эндогенным и
предопределенным переменным.
Достаточно естественно выглядит приведенная выше схема специфи-
кации модели в виде СОУ при описании процесса формирования равно-
весных цен и количеств предлагаемых на рынке товаров. Рассмотрим
пример.
Пример 17.3. Пусть у — цена некоторого товара в момент вре-
мени t, а у} ' — объем продаж этого товара в тот же момент времени.
Естественно предположить, что объем продаж yj зависит от цены yjlj и
от объема продаж в предыдущим момент времени у*2 . В свою очередь,
цена товара yj1' зависит от объема его продаж в предыдущий момент вре-
мени (т.е. от у$1\). В данной схеме цена j и объем продаж у^ играют
роль эндогенных переменных, а лаговой переменной у естественно от-
вести роль единственной предопределенной переменной xt (т.е. xt = yj!2\).
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
927
В результате анализируемая модель будет описана системой
(s‘(1)+с>‘*‘=(1727)
Первое уравнение системы без дополнительных ограничений является
идентифицируемым, т.к. приведенная форма модели (17.27) имеет вид
Гу!1’ = -сп®< + г((’) = ’гц®<+«<”,	.
lyS2) = №icn-C21)I( + (^-j32I^) = T214I> + 42>>	1	’
где Сц = —7Гц, a ~ С21 = ^21 •
Однако если дополнительно потребовать некоррелированность остат-
ков и т.е. диагональности ковариационной матрицы остатков
V _ (cov(^(1),^(1)) cov($t(1),^2))\
Л \cov(42\^1)) cov(4’\42))/
то коэффициенты /?21 и с2г 2-го уравнения (17.27) могут быть состоятельно
оценены с помощью обычного МНК, примененного к уравнению регрессии
у по и xt. Действительно, перепишем 2-е уравнение (17.27) в виде
l/t(2) = -02iyti} - C21®t +	t = 1,2,.. .,n.
Поскольку объясняющая переменная = -СцХ^ + в правой ча-
сти этого уравнения не коррелирована с tfj2^ (т. к. ни xt, ни не корре-
лированы по условию с Я^), то в соответствии с общей теорией КЛММР
(см. пп. 15.2-15.3) МНК-оценки параметров 021 и c2i будут состоятель-
ными.
Замечание. Очень важным моментом в правильной специфика-
ции модели, рассмотренной в примере 17.3, является выбор продолжи-
тельности такта времени. Действительно, продавец устанавливает це-
ны, а покупатель на них реагирует. При этом торговые запасы будут
либо накапливаться, либо рассасываться. Продавец среагирует на эту
динамику и т.д. Если выбрать в качестве такта времени один день, то
сделанные нами в модели примера 17.3 допущения выглядят естественны-
ми, поскольку последовательность причинных связей у{2\ —> д	—► у
является линейной цепью (т. е. не содержит никаких петель обратной свя-
зи). Это позволяет нам, в частности, предположить возмущения, влия-
ющие на спрос (^) и предложение (tfj I, независимыми. Однако если
928
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
бы публиковались, скажем, только недельные данные о средней недель-
ной цене (j/f1)) и среднем объеме дневных продаж (у*2 ), то вынужденное
агрегирование соответствующих возмущений и 4 в системе (17.27)
делает эти возмущения взаимно коррелированными, а саму модель — не-
идентифицированной. Введение же в модель дополнительных переменных
с целью достижения идентифицируемости модели (если бы такие пере-
менные существовали), как правило, превращает рекурсивную модель в
обычную СОУ со всеми вытекающими отсюда проблемами ее оценивания.
Перейдем к описанию процедуры статистического оценивания струк-
турных параметров общей рекурсивной модели СОУ. Пусть анализи-
руется система из т стохастических уравнений с т эндогенными пере-
менными Yt —	и р экзогенными переменными Xt =
ВУ( + cxt = д„
(17.28)
t — 1,2,..., п,
где В — (т х т)-матрица коэффициентов при эндогенных переменных
(t,j = 1,2,.. .,т; рц = 1 — условие нормировки), С — (т х р)-матрица
коэффициентов Cjj при предопределенных переменных (» = 1,2,..., т; j =
1,2,... ,р), а вектор = (£р\^2\...,^т^)Т — вектор-столбец возмуще-
ний (или случайных остатков), не коррелированных с предопределенными
переменными.
Определение 17.1. Система одновременных уравнений (17.28)
называется чисто рекурсивной, если:
(i) матрица В является нижней треугольной, т. е.
Pi3 = 0 при j>i для всех i = 1,2,	1;
(и) ковариационная матрица Ед случайных остатков диагональна и
не зависит от t, т. е.
= Е(Д,дГ) =
0	0 ... О	О
О ^22 0 ... О	О
О 0 0 ... О
Иногда при спецификации модели удобнее ориентироваться на экви-
валентное (и) условие:
(ii ) случайные возмущения	,..., обладают тем свойством,
что 6^ не коррелирует со всеми «предшествующими» эндогенными
переменными, т. е. с	..., у(к~^ (к = 2,3,..., т).
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
929
Если выполняется только условие (t), то система называется фор-
мально рекурсивной, или просто рекурсивной.
Выпишем теперь явный вид МНК-оценок структурных коэффициен-
тов t-ro уравнения системы (17.28). Пусть Л < Уз < ••♦ < Jmj-i и
fci < к2 < ... kPi — номера, соответственно, эндогенных (кроме перемен-
- (»)\
нои у ) н предопределенных переменных, участвующих в t-м уравнении
системы (в силу ее рекурсивности, очевидно, < t). Тогда t-e уравнение
можно записать в виде
У?’ = -0ihVt,l} ~	°
••• <-|fcPi-bf T Ut ,
t = 1,2,
(17.29)
Обозначим и соответственно, /-й столбец матрицы Y и q-н
столбец матрицы X (см. (17.26)). Пусть A(t) = (^$*\^*\.. .,^)Т, 0(t) =
, -.., J —»• • • > ~cikVi )T — вектор-столбец, составленный из
коэффициентов правой части (17.29), а
Z(i) = (У(л)

(^»J)
матрица размерности п X (m, — 1 фр,), составленная из столбцов, отобран-
ных из матриц Y и X. Тогда уравнение (17.29) может быть представлено
в виде
У(0 = Z(i)©(>) + Д(0>	(17.29')
а МНК-оценки коэффициентов 0(i) в соответствии с общим результатом
(15.22) (см. с. 635) можно вычислить по формуле
©(.) = (ZT(i)Z(i))-IZ(i)y(,>.
(17.30)
При этом, конечно, необходимо, чтобы матрица Z(t) имела бы полный ранг
(т.е. ранг Z(t) =	— 1 ф р,), или, что то же, матрица ZT(t)Z(i) должна
быть невырожденной.
17.3.2. Косвенный метод наименьших квадратов
Сущность и реализация косвенного метода наименьших квадрат
тов (КМНК) были продемонстрированы на примере модели спроса^
предложения, рассмотренной в п. 17.1. Мы лишь кратко повторим здесь
процедуру КМНК применительно к общему случаю СОУ.
930
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
Косвенный МНК предназначен для оценивания структурных параме-
тров отдельного уравнения системы и может дать результат (без сочета-
ния с другими методами, например, с двухшаговым методом наименьших
квадратов) только в применении к точно идентифицируемому уравнению.
Итак, рассмотрим систему (17.19) и ее приведенную форму
У^ПХе + Et, t = l,2,...,n,	(17.31)
в которой
П = -В"‘с-	(17.32)
матрица коэффициентов предопределенных переменных (i = 1,2,
..., т\ j = 1,2,..., р), переменные Xt-немультиколлинеарны, а
€t — В	t — 1,2, ...,n,
(17.33)
вектор-столбец случайных остатков, не коррелированных с предопреде-
ленными переменными Xt = (х} zj ,..., xt ') по условию (т. к. все ком-
поненты вектора At не коррелированы с Xt).
Наша цель — оценить структурные параметры i-ro уравнения си-
стемы (17.19). Для анализа i-ro уравнения воспользуемся общей схемой
(17.21)-(17.25), которая была рассмотрена в п. 17.2 при выводе 4-го и 5-го
условий идентифицируемости отдельного уравнения системы.
Процедуру статистического оценивания структурных параметров
i-ro уравнения системы (17.19) разобьем на 2 этапа.
На 1-м этапе оцениваем с помощью обычного МНК все пара-
метры Ki] (i = 1,2,j = 1,2,...,p) приведенной формы (17.31),
последовательно (и автономно) решая эту задачу для каждого отдельного
уравнения системы (17.31). Хорошие свойства получаемых МНК-оценок
(их состоятельность, а в случае нормальности (5^ — и их эффектив-
ность) обеспечиваются тем, что в модели (17.31)-(17.33) выполняются все
условия классической линейной модели множественной регрессии.
На 2-м этапе используются соотношения (17.24)-( 17.25), свя-
зывающие структурные параметры i-ro уравнения системы (17.28) с па-
раметрами приведенной формы. В случае точной (или сверх-) иден-
тифицируемости i-ro уравнения структурной формы (т.е. при выполне-
нии условии 4 и 5 или только условия 4 со знаком строгого неравенства)
его параметры Д(>) и c(i) однозначно (или неоднозначно) определяются
из системы (17.24)-( 17.25) по значениям Подставив в эти соотноше-
ния вместо я-,,- их оценки и решив систему уравнений (17.24)-(17.25)
относительно 0(i) и c(i), мы получим состоятельные оценки и c(i)
структурных параметров i-ro уравнения системы (17.19).
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
931
В случае неидентифицируемости анализируемого уравнения струк-
турной формы (т.е. при невыполнении 4-го условия идентифицируемо-
сти) число взаимно независимых связей между /3(1), c(i) и тгч-, содержа-
щихся в системе (17.24)-(17.25), будет меньше общего числа т,+р1 — 1
неизвестных. Поэтому без дополнительной информации мы не сможем
из (17.24)-(17.25) определить значения структурных коэффициентов /3(1)
и c(i). Один из самых распространенных способов получения необходи-
мой дополнительной информации в данном случае, который в результате
позволяет получать оценки структурных параметров неидентифицируе-
мого уравнения, — это двухшаговый метод наименьших квадратов. К
его рассмотрению мы и переходим.
17.3.3. Двухшаговыи метод наименьших квадратов
оценивания структурных параметров отдельного
уравнения.
Снова вернемся к рассмотренному выше примеру (17.1)-(17.2), в ко-
тором анализировалась модель спроса и предложения (см. п. 17.1). Напо-
мним реализацию «шагов» в двухшаговом методе наименьших квадратов
(2 МНК), использованном в этом примере. Чтобы обойти главное препят-
ствие в применении обычного МНК к отдельному неидентифицируемому
уравнению (в данном примере это было уравнение (17.2), описывающее за-
висимость спроса ур^ от цены j и дохода xt: yj = b2y{2) фса^ фЛр^) —
коррелированность играющей роль предиктора эндогенной переменной
j со случайными остатками 6$2\ — на 1-м шаге строится регрес-
сия эндогенной переменнои-предиктора yj ' по предопределенной пере-
менной xt. В результате получаем оцененное регрессионное уравнение
у<2> = dyW/xXt + et. На 2-м шаге в правую часть анализируемого
уравнения (17.2) вместо эндогенной переменной ур вставлялось ее ре-
грессионное выражение через xti в результате чего получали уравнение
уР* = (ОД<*>/* + c)xt + (^t2) + 62£f).	(см. (17.2'))
После этого к данному уравнению применялся обычный МНК с целью со-
стоятельного оценивания коэффициента	+ с (очевидно,
вести речь об отдельном оценивании коэффициентов Ь2 и с в уравнении
уР> =	+ cxt + (^ + b2Et)i в котором х{2^ = 0yC2)/xa:t, не имеет смы-
сла, т. к. переменные xt и xt связаны чистой мулътиколлинеарностью по
построению). Получив оценку 9у^/х параметра 0уа)/х =	+ с, мы
к имеющимся уже двум соотношениям, связывающим параметры струк-
932
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
турной и приведенной форм (вытекающим из общей формулы (17.32)),
добавили еще одно: 0v(i)jx = 62^(2)/г 4- с. После этого, решая систему
(17.18), мы смогли получить оценки параметров 62 и с неидентифицируе-
мого уравнения.
Точно такая же процедура 2 МНК предлагается и в общем случае.
Правда, в отличие от упрощенной модели спроса-предложения (17.1)—
(17.2), содержащей единственную предопределенную переменную (что и
явилось причиной мультиколлинеарности переменных и xt), в реали-
стичных эконометрических моделях мы будем крайне редко сталкиваться
с проблемой чистой мультиколлинеарности объясняющих переменных на
2-м шаге процедуры, т. к. состав предопределенных переменных в каждом
отдельном уравнении почти никогда не исчерпывает всего их априорного
набора.
Итак, пусть, как и прежде, i-e уравнение системы представлено в
форме (17.29), и пусть
Y(t) = (у<**>у<л>...у<*"<-')) _	(17.34)
матрица размерности п х составленная из соответствующих
столбцов матрицы Y (см. (17.26)),
X(t) =	...%<*«>) _	(17.35)
матрица размерности n х pt, составленная из соответствующих столбцов
матрицы X (см. (17-26)), a XoCT(i) — матрица размерности п х (р — р»),
составленная нз тех столбцов матрицы X, которые остались после отбора
из нее столбцов для матрицы X(i). Тогда анализируемое (£-е) уравнение
системы (17.29) можно представить в виде
У0) = Y(i) 6_(i) + X(i) c_(i) + A(i),	(17.36)
где 6-(i) — (—Aji»—> • • • > —	) » c-(0 =	• • • > ~ciAPi)
и, как и прежде, A(i) = (6$*\...,£n>)T-
1-й шаг 2 МНК. С помощью обычного МНК строится регрессия
выступающих в роли предикторов в уравнении (17.36) эндогенных пере-
менных Y(i) по всем предопределенным переменным X. В результате по-
лучаем регрессионную аппроксимацию Y(i) эндогенных переменных Y(i)
в виде линейной комбинации всех предопределенных переменных в форме
Y(i) = ХвГ1/х,	(17.37)
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
933
где = С^ТХ) 1XTY(i), аХ = (X(t) :XOCT(i)) — матрица размер-
ности п х р наблюденных значений всех предопределенных переменных,
составленная из матриц X(t) и XOCT(i).
2-й шаг 2 МНК. С помощью обычного МНК строится регрессия эн-
догенной переменной по Y(t) и X(i). Другими словами, в уравнении
(17.36) объясняющие переменные Y(t) заменяются на их аппроксимации
Y(i), выраженные формулой (17.37). Реализация МНК в данном случае,
проведенная в соответствии с общей теорией классической линейной мо-
дели множественной регрессии (см. п. 15.3, и в частности соотношения
(15.21) на с. 635), приводит к следующей системе нормальных уравнений
относительно оценок 6_(i) и с_(») неизвестных параметров, соответствен-
но, 5_(t) и c_(i):
YT(i)Y(.) = YT(i)-X(.)
X(«)-Y(i)  XT(i)-X(i)

(17.38)
Заметим, что квадратная матрица А, являющаяся первым сомно-
жителем в левой части соотношения (17.38) (она составлена из матриц
YT(t)Y(i), YT(i)X(i), XT(i)Y(i) и XT(i)X(i)), имеет размерность (т,- —
1 +pt) х (mi — 1 4- р^ и может оказаться вырожденной в силу мультикол-
линеарности, возникающей (по построению) между объясняющими пере-
менными Y(i) и Х(») в силу X = X (как это было в нашем примере). В
этих случаях явные выражения оценок b_(i) и c_(i) из (17.38) получить
невозможно. Однако так же, как и в рассмотренном выше примере модели
спроса-предложения, объединение соотношений (17.38) и системы (17.24)-
(17.25) даст нам систему линейных уравнений относительно b_(i) и c_(t)
(т.е. относительно неизвестных параметров г-го уравнения структурной
формы), которая позволит вычислить значения всех этих параметров. В
остальных же случаях матрица А обратима и, следовательно, мы имеем
возможность получить явные выражения оценок, а именно:
М«)\ =А-'
£-(*)/ \XT(i)YW7’
где (mt - 1 + р^ x (mi — 1 + pt) — матрица А имеет вид
YT(i)Y(.) : YT(i)X(i)>
XT(i)Y(i) 
(17.39)
(17.40)
934
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
или, что то же,
(YT(i)X(XTX)XTY(.) : YT(i)X(i)\
А = I ................................ .	(17.40')
\ XT(t)Y(i) ; XT(i)X(i)/
Заметим, что первые ш, — 1 компонент вектора-столбца, являющегося вто-
рым сомножителем в правой части (17.39), могут быть также представле-
ны в терминах исходных наблюдений, а именно:
YT(«)Y(0 = YT(«)X(XTX)_1XTY(<).	(17.41)
В задачах анализа точности 2 МНК-оценок отдельного уравнения
СОУ важную роль играет ковариационная матрица Е этих оценок. Можно
показать (см., например, [Джонстон Дж.], с. 383), что при большом числе
наблюдений (т. е. асимптотически по п —► оо) матрица S может быть оце-
нена (в случае невырожденности матрицы А) с помощью матрицы
Е = ?А"1,	(17.42)
где матрица А определяется соотношениями (17.40) или (17.40'), а
в2 =-------Ц------ (Y(i>-Y(i)j_(i)-X(i)c_(i))T
п -	-1 - Pi 4	"	(17.43)
x(Yw-Y(.)L(i)-X(i) £-(•))
Использование метода главных компонент в 2 МНК. В двух-
шаговом методе наименьших квадратов, как мы видим, на 1-м шаге вычи-
сляется регрессия Y(i) по всем (!) р предопределенным переменным, т. е. в
каждом U3mi~l регрессионных уравнений (17.37) приходится оценивать
р параметров. В моделях небольшой размерности, т.е. при относительно
малых значениях р, это не создает трудностей, но в средних и больших мо-
делях общее число предопределенных переменных (р) может быть одного
порядка с общим числом наблюдений (п), и тогда статистическая надеж-
ность выводов становится неудовлетворительной (бывают случаи, когда
р > п; однако при этом состоятельное оценивание параметров модели
становится в принципе невозможным). В подобных ситуациях возникает
необходимость снизить общее число предопределенных переменных, че-
рез которые выражается Y(t) (т.е. число р участвующих в правой части
выражения (17.37) предопределенных переменных X). Клоек и Меннес
предложили с этой целью использовать в качестве аргументов аппрок-
симирующей функции Y(t) не все предопределенные переменные Х(») и
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
935
Хост(*) (что предусмотрено в (17.37)), а лишь те, которые участвуют в i-
м уравнении (т. е. X(i)), плюс небольшое количество главных компонент,
построенных по прочим предопределенным переменным Хост1- Что каса-
ется переменных X(t), то, с одной стороны, их не следует трогать, т. к.
они включались в :-е уравнение и по содержательному смыслу, и с учетом
выполнения условия 4 идентифицируемости (см. выше), а с другой сторо-
ны, ими нельзя ограничиваться при построении аппроксимации Y(i) для
Y(t), т. к. в этом случае мы столкнулись бы со строгой мультиколлинеар-
ностью.
Поэтому предлагается следующая процедура.
1)	Матрица XOCT(i) размерности n X (р — р,), состоящая из наблюде-
ний предопределенных переменных, не вошедших в анализируемое (t-e)
уравнение, стандартизируется, т. е. из каждого наблюдения переменной
вычитается ее выборочное среднее значение и результат делится на ее вы-
борочное среднеквадратическое отклонение. В результате получаем ма-
трицу ХоСТ(»).
2)	По наблюдениям стандартизированной матрицы XoCT(i) строятся
главные компоненты	.. .,t4?)T, I = 1,2,..., р — р, (см.
п. 13.2).
3)	Из р — Pi построенных главных компонент V отбирается срав-
нительно небольшое число к (к < 4) наиболее информативных с точки
зрения точности аппроксимации значений У^*^ в виде функции от X(t) и
, U^tk\ В качестве критерия информативности можно ис-
пользовать, например, величину коэффициента детерминации Я2 3, опреде-
ляющего степень тесноты связи между У^*\ с одной стороны, и набором
X(i),	...,	— с Другой.
Иначе говоря, главные компот
щего числа р — pi в соответствии с
0	д/( *) rnax^	,...1и<,*>)-
нты •.., отбираются из об-
условием^
1 См.: KLoek Т., Mennea L.B.M. Simultaneous Equation Estimation Based on Principal
Components Variables. «Econometrica>, vol. 28 (1960), pp. 45-61.
3 В эконометрической литературе и практике предлагались и использовались и другие
критерии отбора главных компонент: критерий минимизации мультиколлинеарно-
сти между Х(») и ..........критерий максимальной дисперсия, когда отбира-
ются главные компоненты, соответствующие максимальным характеристическим
числам (см., например, [Джонстон Дж.], с. 393-395). Однако предложенный нами
критерий представляется более предпочтительным.
936
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
4)	В качестве 1-го шага 2 МНК строится регрессия ¥(») по Х(»),
(а не по X(t), XOCT(t), как это рекомендовано в обычном
2 МНК).
Замечание. Иногда строят главные компоненты по всей матри-
це X и тогда аппроксимация Y(i) осуществляется только по к главным
компонентам этой матрицы, причем к должно подбираться с учетом усло-
вия 4 идентифицируемости уравнения. Тем самым обходится неудобство
этого метода, возникающее при необходимости оценивания сразу несколь-
ких (а тем более — всех) уравнений системы. В вышеизложенном вариан-
те тогда придется строить главные компоненты для каждого уравнения
в отдельности. Однако существуют работы, демонстрирующие преиму-
щества (в точности) именно изложенного выше метода по сравнению с
подходом, в котором главные компоненты строятся по всей матрице X
для всех уравнений системы.
В заключение отметим, что эконометрическая теория и практика сви-
детельствуют о том, что 2 МНК являются, пожалуй, наиболее важным и
широко применяемым методом оценивания структурных параметров от-
дельного уравнения СОУ.
17.3.4. Трехшаговый метод наименьших квадратов
одновременной оценки всех параметров системы
Трехшаговый метод наименьших квадратов был предложен впервые
Зельнером и Тей лом1 в качестве метода статистического оценивания од-
новременно всех уравнений модели (17.28) с учетом возможной взаим-
ной коррелированности регрессионных остатков различных уравнений
этой системы. Этот метод оказывается более эффективным, чем 2 МНК,
если случайные остатки oj	',...,оJ ' различных уравнении систе-
мы (17.28) взаимно коррелированы, т.е. если их ковариационная матрица
Ед =	..„) отлична от диагональной. Хотя отметим, что
и в этой ситуации 2 МНК-оценки структурных параметров системы оста-
ются состоятельными.
В трехшаговом методе наименьших квадратов (ЗМНК) сохранены
первые два шага 2 МНК. Однако полученные в результате этих двух
шагов, автономно для каждого отдельного (»-го) уравнения, оценки струк-
турных параметров (32м„,(«) = —6_(») и с2м„(1) = -£-(’)• » =
(6_(i) и с_(«) определены соотношениями (17.39)), не являются оконча-
1 См.: Zellner A., Theil Н. Three-fltage Least-squares: Simultaneous Estimation of
Simultaneous Equations. <Econometrica>, vol. 30 (1962), pp. 54-78.
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
937
тельными, а пересчитываются на 3-м шаге следующим образом: оценки
flz мнк и мнк используются для подсчета выборочной ковариационной ма-
трицы случайных остатков Ед, а последняя, в свою очередь, используется
для одновременного вычисления оценок всех структурных параметров В
и С системы (17.28) с помощью обобщенного метода наименьших квадра-
тов в рамках соответствующим образом построенной обобщенной линей-
ной модели множественной регрессии (см. и. 15.6).
Рассмотрим подробнее, как реализуется описанная выше общая схема
3 МНК. Можно было бы начать сразу с 3-го шага, т. к. первые два, как
было отмечено, совпадают с соответствующими шагами 2 МНК. Однако
мы вернемся вначале к 2 МНК, чтобы описать прием, эквивалентный двум
шагам этого метода, поскольку он приводит к тем же самым оценкам
(17.39), что и 2 МНК.
Замечание о 2 МНК-оценках. Итак, снова рассмотрим отдельное
(i-e) уравнение (17.36) анализируемой СОУ (17.28). Так же, как и при
анализе рекурсивных систем, введем матрицу
z(’)=(y(») : X(i))>	(17-44)
составленную из матриц Y(i) и X(t), и вектор-столбец неизвестных пара-
метров
®(*) = (— Piji > • • • j —	~c*fci»• • • > —C»*F. ) >	(17.45)
составленный из векторов 6_(») и c_(t). Тогда мы можем записать урав-
нение (17.36) в виде
Y(i) = Z(>) 0(i) + A(t).	(17.36')
В 2 МНК мы обходили неприятности, связанные с взаимной коррелиро-
ванностью объясняющих переменных Y(i) и остатков A(t), подстановкой
в уравнение (17.36) вместо Y(i) их регрессионного выражения через X
(см. формулу (17.37)). Оказывается, можно добиться того же и прийти к
2 МНК оценкам (17.39), действуя формально несколько иным способом. А
именно, домножим все члены уравнения (17,36*) слева на матрицу ХТ:
ХТУ(,) = (XTZ(i)) 0(|) + ХТД(1),	(17.36")
или, что то же,
У<0 = Z(i) 0(1) + Д(|),	(17.36'")
где
y(i) = XTy(i),	(17.46)
938
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
Z(i) = XTZ(.),	(17.47)
4(i) = ХТД(£).	(17.48)
Можно показать, что в уравнении (17.36***) объясняющие переменные
Z(i) не коррелировали с остатками Д(») и что ковариационная матрица
ES(t) остатков Д(») имеет вид
Ед(0 = Е(Д(.)ДТ(<)) = <г«(ХтХ),	(17.49)
где <ru = Dcr}*\
Соотношение (17.36 ) (и эквивалентное ему (17.36**)) можно рас-
сматривать как обобщенную линейную модель множественной регрессии
(15.73), в которой у(’) играет роль вектора наблюдений зависимой пере-
менной, Z(i) — матрица наблюдений объясняющих переменных, 0(») —
вектор-столбец оцениваемых параметров, а Д(») — вектор-столбец ре-
грессионных остатков с заданной (с точностью до постоянного множителя
о-,,) ковариационной матрицей1. Тогда в соответствии с формулой (15.78)
ОМНК-оценок получаем:
0»м».(О = [ZT(i)(XTX)-,Z(t)] ,ZT(t)(XTX)-1y(0
= [ZT(t)X(XTX)-1XTZ(i)]“1ZT(£)X(XTX)-1XTy(i)(17.50)
Сравнение правых частей формул (17.50) и (17.39) с учетом соотноше-
ний (17.40*), (17.44) и (17.45) приводит к заключению об эквивалентности
2 МНК-оценок и оценок (17.50).
3-й шаг ЗМНК. От отдельных уравнений (17.36**) вернемся ко
всей СОУ (17.28). С этой целью, составив уравнения (17.36**) для t =
l,2,...,m, объединим их в одной обобщенной линейной модели множе-
ственной регрессии вида
XTZ(1) о	о ...	о
О	XTZ(2) 0 ...	0
О О О ... XTZ(m)/
0(1) \
0(2)
м

0(тп)/
1 Если в состав предопределенных переменных X входят помимо неслучайных экзоген-
ных переменных лаговые эндогенные переменные (которые по своей природе явля-
ются стохастическими), то, как известно (см. п. 15.10.1), обобщенный метод наи-
меньших квадратов будет продолжать давать тем не менее состоятельные оценки
параметров, если эти стохастические предикторы не коррелированы с регрессион-
ными остатками (что и имеет место в нашем случае).
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ 939
ХТД(1) \
ХТД(2)

\ХтД(т)/
(17.51)
Матрица ковариаций Ед вектора случайных остатков А = (А (1), А (2),
..., Дт(т))т = (ДТ(1)Х:ДТ(2)Х:
:ДТ(т)Х)Т будет иметь вид
— Ед ® X X,
(17.52)
где через обозначена ковариация случайных остатков «-го и у-го урав-
нений структурной формы (она по условию не зависит от i, т.е. =
cov(A^, A</>) = E(^°^j))), Ед =	..а символ ® означает
кронекерово перемножение матриц (см. Приложение 2).
Чтобы воспользоваться обобщенным методом наименьших квадратов
в одновременном оценивании параметров 0(1), 0(2),..., 0(т) обобщенной
линейной модели множественной регрессии (17.51), необходимо знать ко-
вариационную мазрицу остатков Ед. Из (17.52) видно, что для этого
нам необходимо знать матрицу Ед ковариаций случайных возмущений
анализируемой структурной формы (17.28). Сущность 3-го шага трех-
шагового метода наименьших квадратов как раз и заключается в том,
что для построения оценки Ед неизвестной матрицы Ед используются
2 МНК-оценки 02мнк(») параметров 0(«), а именно: («,у)-й элемент
этой матрицы оценивается по формуле
= i (У(0 - Z(i)§2„„(i))T(y(j) - Z(j)02mh,(j)),	(17.53)
n
где Z(/) и 02 мнк(0 определены соотношениями, соответственно, (17.44) и
(17.39) (или (17.50)), а У(<) = (у}0, у^..., у!,'))Т, 1 = 1,2,... ,т.
После этого мы можем воспользоваться формулой (15.78) обобщенного
метода наименьших квадратов, примененного к модели (17.51):
взм»« = (ZT^,Z)-1ZTS~’y,
(17.54)
940
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
где
(0(1)
0(2)
\0(тв);
ацХ^Х
а21хтх
ат1ХТХ
<rm2XTX
ffi2X^X
^22^ X
&ij определены формулой (17.53), а
XTZ(1)	о	о	...	о
0	XTZ(2)	0	...	0
0	0	0	...	XTZ(m)
(напомним, что Z(i) и O(t), * = 1,2, ...,т, определены соотношениями,
соответственно, (17.44) и (17.45)).
Как уже было упомянуто в начале этого пункта, процедура ЗМНК
обеспечивает лучшую по сравнению с двухшаговым методом эффектив-
ность оценок линте в случае, когда матрица Ед не является диагональной,
т.е. когда случайные остатки , входящие в различные структурные
уравнения, коррелируют друг с другом. Если матрица ковариаций Ед для
структурных остатков может быть приведена (соответствующим упоря-
дочением уравнений системы) к блочно-диагональному виду, то всю про-
цедуру трехшагового оценивания лучше применять отдельно к каждой
группе уравнений, соответствующих одному блоку. Тем самым суще-
ственно снижается трудоемкость вычислительной реализации ЗМНК.
17.3.5. Другие методы оценивания СОУ и некоторые общие
рекомендации.
Помимо методов статистического оценивания СОУ, описанных выше,
в эконометрической литературе и практике существуют и другие процеду-
ры. Так, если дополнительно постулировать нормальность структурных
возмущений то для оценки отдельного уравнения наряду с 2 МНК
может быть использован метод максимального правдоподобия с ограни-
ченной информацией, или, что то же, метод наименьшего дисперсионно-
17.3. ИДЕНТИФИКАЦИЯ СИСТЕМ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
941
го отношения . Для одновременной оценки всех параметров системы в
рамках тех же условий нормальности разработан также метод мак-
симального правдоподобия с полной информацией1 2. В расширении класса
методов оценивания СОУ можно идти также по линии введения целых
параметрических семейств методов, когда при конкретном выборе зна-
чения свободного параметра этого семейства мы приходим к тому или
иному уже известному методу как к частному случаю. Именно такого
рода семейство процедур представляют собой так называемые «оценки
класса k$>, которые содержат в себе в качестве частных случаев проце-
дуры оценивания отдельного уравнения структурной формы по прямому
методу наименьших квадратов (при к = 0) и по двухшаговому методу
наименьших квадратов (при к = I)3.
Мы оставили эти методы за рамками учебника, поскольку трудоем-
кость их вычислительной реализации, по меньшей мере, не уступает опи-
санным выше косвенному, двухшаговому и трехшаговому методам наи-
меньших квадратов. В то же время они требуют дополнительных мо-
дельных ограничивающих предположений. Поэтому, наверное, они реже
других методов применяются в эконометрической практике.
В заключение приведем несколько общих рекомендаций по построе-
нию и статистическому анализу СОУ.
1)	Прежде всего следует провести процедуру исключения из СОУ всех
уравнений, являющихся тождествами.
2)	В ходе этапа «спецификация модели» надо стремиться к обеспече-
нию выполнения условий 1~5 идентифицируемости отдельных уравнений
и системы в целом. Если среди конечных прикладных целей моделиро-
вания ставится задача интервального прогноза значений эндогенных пе-
ременных (см. ниже, п. 17.4), то следует стремиться к обеспечению нор-
мальности и взаимной независимости (по t) случайных возмущений
3)	Приступая к статистическому оцениванию СОУ, следует приме-
нить, в первую очередь, 2 МНК последовательно ко всем уравнениям си-
стемы и использовать полученные оценки структурных параметров для
оценки ковариационной матрицы Ед структурных остатков (см. формулу
(17.53)).
1 Метод впервые предложен в работе: Anderson Т. W.f Rubin Н. Estimation of the
Parameters of a Sing] Equation in a Complete System of Stochastic Equations. «Ann.
Math. Statistics», 20 (1949), pp. 46-63.
2 Cm. Hood W. C., Koopmans T. C. (eds). Studies in Econometric Method. Wiley, New
York, 1953.
3 См. Тейл Г. Экономические прогнозы и принятие решений. (Пер. с англ.). М.:
Статистика, с 281-282.
942
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
4)	По полученной оценке Ед ковариационной матрицы Ед проверить
гипотезу о ее диагональной (или блочно-диагональной) структуре. Если
гипотеза о диагональности Ед не отвергается, то использовать получен-
ные ранее 2 МНК-оценки структурных параметров В и С для вычисления
оценок П параметров приведенной формы по формуле П = — В”1 С и да-
лее — для прогноза и имитационных расчетов.
5)	Если гипотеза о диагональности матрицы Ед отвергается, то сле-
дует использовать полученную ранее оценку Ед для реализации процеду-
ры ЗМНК.
6)	Если в процессе статистического анализа оценки Ед выяснится,
что блочно-диагональная структура матрицы Ед не противоречит имею-
щимся наблюдениям, то процедуру ЗМНК следует применить отдельно к
каждой группе уравнений СОУ, соответствующих тому или иному блоку
матрицы Ед.
17.4. Точечный и интервальный прогноз
значений эндогенных переменных
Можно выделить два основных типа конечных прикладных целей,
преследуемых при построении эконометрических моделей в виде СОУ.
Один из них связан с получением сведений о структурных параметрах
модели и (или) коэффициентах приведенной формы. Это бывает обычно
в ситуациях, когда интересующие исследователя параметры модели име-
ют четкую экономическую интерпретацию (они могут играть роль раз-
личных эластичностей, мультипликаторов, характеристик «склонности к
сбережениям» и т. п.). Другой тип конечных прикладных целей заключа-
ется в стремлении осуществить с помощью анализируемой СОУ условный
прогноз эндогенных переменных (при определенных условиях, накладыва-
емых на значения предопределенных переменных), произвести многова-
риантные (в соответствии с различными вариантами условий) сценарные
расчеты, показывающие, как себя «будут вести» эндогенные переменные
при различных условиях, касающихся значений предопределенных пере-
менных.
Если интерес сосредоточен на структурных параметрах В и С, то сле-
дует воспользоваться состоятельными методами их оценивания (2 МНК,
3 МНК) и по той же исходной информации оценить точность применен-
ных процедур (либо с помощью аналитических методов, т.е. выводя и
статистически оценивания ковариационную матрицу используемых оце-
нок параметров, см., например, (17.42)-( 17.43), либо с помощью разно-
го рода компьютерно-имитационных методов, о последних см. ниже,
17.4. ТОЧЕЧНЫЙ И ИНТЕРВАЛЬНЫЙ ПРОГНОЗ
943
п. 17.5).
Если же нас могут удовлетворить коэффициенты П приведенной фор-
мы (сами по себе или как средство получения точечного прогноза эндо-
генных переменных по формуле Уп+т = ПХп+т, где Хп+г — заданные
для момента времени п 4- т значения предопределенных переменных, а
г — «глубина» прогноза), то анализ точности полученных оценок и (или)
прогноза можно проводить одним из двух способов. В первом из них (бо-
лее сложном) отправным пунктом служат состоятельные оценки В и С
(структурных параметров В и С) и их ковариационные матрицы Sg и
Eg, а точнее, — состоятельные оценки Eg и Eg этих матриц. По ним
строят оценки П = —В“1С (см. (17.20)) и стараются вывести общий вид
состоятельной оценки Ед ковариационной матрицы Ед. Решение послед-
ней задачи составляет аналитическую базу для решения задачи построе-
ния интервального прогноза для эндогенных переменных Y и интерваль-
ных оценок для параметров приведенной формы П. Этот путь анализа
точности точечного прогноза Yn+r и точечных оценок П считается бо-
лее предпочтительным в ситуациях, когда есть основания полагать, что
спецификация модели в ее структурной форме осуществлена правильно1.
Однако сопутствующие этому пункту громоздкость вывода вида ковари-
ационной матрицы Ед и связанные с этим аналитико-вычислительные
сложности побудили нас не включать подробное описание данного под-
хода в учебник (интересующийся читатель может обратиться непосред-
ственно к работам: 1) Goldberyer A.S., Nagar A. L., Odeh H.S. The
Covariance Matrices of Reduced-Form Coefficients and of Forecasts for
a Structural Econometric Model. «Econometrica», 29 (1961), pp.556-
573; 2) Humans S. H. Simultaneous Confidence Intervals in Econometric
Forecasting. «Econometrica», 36 (1968), pp. 18-30).
Мы же остановимся здесь подробнее на относительно более простом
пути построения интервальных оценок для эндогенных переменных и для
отдельных параметров приведенной формы. Этот путь основан на непо-
средственном вычислении оценок П коэффициентов приведенной формы
П с помощью обыкновенного метода наименьших квадратов, применен-
ного к каждому уравнению системы (17.19*). Состоятельность и несме-
щенность этих оценок обеспечивается стандартными модельными допу-
щениями, относящимися к системе (17.19), а их ковариационная матрица
выводится на базе фундаментальных соотношений классического МНК.
Итак, по исходным статистическим данным (17.26) анализируется
1 См. Klein L. R. The Efficiency of Estimation in Econometric Models. Cowles Foundation
Paper, N* 157, Yale University, 1960.
944
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
приведенная форма СОУ вида
Yt — IIXt 4- £*,
t — 1,2,... ,n,
(17.55)
v / (1) (2) (m)xT v ( (1) (2) (p)xT
где Yt = (y) y\ . , y} ') и Xt = (zj x\ ., х^1) — векторы на-
блюденных в момент времени t значении, соответственно, эндогенных и
предопределенных переменных, П = (т,,)*-1.з.т( — матрица коэффици
ентов приведенной формы, а случайные остатки Et = (ej1^,^2^,... ,4m^)T
имеют нулевые средние значения, постоянные (не зависящие от времени)
дисперсии и не коррелированы с предопределенными переменными Xt.
Заметим, что модель (15.55) состоит из т обобщенных линейных мо-
делей множественной регрессии вида
У(,) = ХП(.)+ £(«•),
(17.55')
t — 1,2,..., го,
где У(,) =	—	П(0 = (’г»1,*12»---,я‘йп)Т — * й столбец
матрицы ПТ, e(t) =	а X — матрица наблюдений пре-
допределенных переменных (см. (17.26)).
Даже при взаимной коррелированности остатков	..., (а
они могут быть тчковыми в нашем случае, если не потребовать некор-
релированности структурных возмущений и 6^ разных уравнений
для разных моментов времени) обычные оценки наименьших квадратов
Ямнж(0 параметров тг(») в уравнении (17.55х) являются состоятельными
(см. пп. 15.6, 15.9, 15.10.1). Применяя известную формулу (15.22) для
вычисления МНК-оценок, получаем
Пи».(«) = (XTX)-‘XTy(i),
i = 1,2,
(17.56)
Матрицу, составленную из столбцов ПМНК(1),ПМНК(2),..., Пмнк(пг), оче-
видно, можно записать в виде
(пмв.(1) : Пмик(2) :	: Пнв,(го) :) = (ХТХ) ’хт¥, (17.57)
V	ez v(l) v(2) xz(Tn)
где матрица Y составлена из столбцов У ,У , ...,У' \ т.е. является
матрицей наблюденных значений эндогенных переменных, представлен-
ной в (17.26). Но матрица, стоящая в левой части (17.57), есть не что
иное, как МНК-оценка для ПТ, следовательно, вместо (17.57) мы можем
записать
fiL, = (XTX)-IXTY,
(17.57')
17.4. ТОЧЕЧНЫЙ И ИНТЕРВАЛЬНЫЙ ПРОГНОЗ
945
или, транспонируя обе части этого соотношения (воспользовавшись пра-
вилом транспонирования произведения матриц, см. Приложение 2), полу-
чаем:
пми. = YTX(XTX)-‘.	(17.58)
Точечный прогноз эндогенных переменных Yn+r на т тактов
времени вперед, т. е. точечная оценка значений Уп+т по заданным значе-
ниям предопределенных переменных Хп+т, опирающийся на наблюденные
значения этих переменных до момента времени t = п (т. е. на исходные
данные (17.26)), строится с помощью формулы
Пмнк-^n+rj
(17.59)
где матрица МНК-оценок Пмнк коэффициентов приведенной формы мо-
дели (17.19) определена соотношением (17.58). Заметим, что истинные
значения эндогенных переменных в прогнозируемый период будут равны
в соответствии с (17.55)
— ПХп+т +
Следовательно, ошибка е(т) прогноза (17.59) может быть выражена в виде
^(^") — Уп+т ^п+т — (ПМНк И)-^п+т £п+т-
(17.60)
А поскольку БПМ(|К = П (в силу свойства несмещенности МНК-оценок в
обобщенной линейной модели множественной регрессии, см. п. 15.6.2) и
Ебп+т = 0т, то, применяя к (17.60) операцию усреднения Е, убеждаемся
в несмещенности прогноза (17.59), т.е. в том, что Ее(т) = 0т.
Интервальный прогноз эндогенных переменных Yt или постро-
ение совместных доверительных интервалов для различных сочетаний
компонент этого вектора на т тактов времени вперед возможны, если мы
будем знать (сможем оценить) ковариационную матрицу ошибок прогноза
ё(т) = Уп+т - Уп+т, т.е. матрицу
S£(T) = Е(ё(г)ёт(т)) = Е[(Уп+т - Ув+т)(У„+т - Ув+т)т].
(17.61)
В условиях соблюдения стандартных модельных допущений, сформу-
лированных, в частности, при описании модели (17.19), удается получить
несмещенную оценку Ег(т) для ковариационной матрицы Её(т) в виде
Si(T) = [1 + Х„т+т(ХтХ)-1Х„+т]§£,
(17.62)
946
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
где матрица Se является несмещенной оценкой ковариационной матрицы
остатков приведенной формы	= (^tj)i,j=i,2,...,Tn и задается
формулой
S„ = — (Y - XnL.)T(Y - X nJ.,.)	(17.63)
п—р
(вывод соотношения (17.62) дается в конце данного пункта).
Теперь, если дополнительно предположить нормальный характер
распределения случайных возмущений структурной (6^), а значит, и
приведенной (е ) форм анализируемой модели, мы располагаем всем не-
обходимым для построения интервальных (как совместных — одновре-
менно по набору эндогенных переменных, — так и покоординатных —
для каждой эндогенной переменной в отдельности) прогнозов.
Отклонения значений Yn+r = (у„+т»Уп+т1 • • •»£п+т)Т эндогенных пе-
ременных, спрогнозированных на г тактов времени вперед, от их ис-
тинных будущих значений Уп+т с заданной доверительной вероятностью
Р = 1 — а должны концентрироваться внутри эллипсоида рассеяния, опре-
деляемого уравнением
х п m”!' i F«(m;n “ Р - m + 1),	(17.64)
п — р — тп + 1
где Лп+т = («n+ri^n+r»- • чхп+г) — заданные (на прогнозный пери-
од) значения предопределенных переменных, a Fa(m-n — р — т+1) —
100а%-ная точка /"-распределения с числами степеней свободы числителя
и знаменателя, равными тип — р — m + I1.
С практической точки зрения бывает удобнее знать гарантирован-
ные (одновременно для всех эндогенных переменных) пределы варьирова-
ния каждой из компонент j [_т (« = 1,2,...,п), обозначенные на своей
координатной оси Геометрически эти покоординатные интервалы
определяются проекциями эллипсоида (17.64) на каждую из координат-
ных осей 0j/*\ Хьюмане показал2, что эти проекции могут быть заданы
1 Этот вывод опирается на результат Хупера и Зельнера, которые показали, что ста-
тистика	1	“ У»+г )ТЕГ(г)(У»+г - У) подчиняется F(m; в - р - т +1)-
распределению. См. Hooper J. W.f Zellner A. The Error of Forecast for Multivariate
Regression Models. «Econometrica», 29 (1961), pp. 544-555.
a Cm. Human» S.H. Simultaneous Confidence Intervals in Econometric Forecasting.
«Econometrica», 36 (1968), pp. 18-30.
17.4. ТОЧЕЧНЫЙ И ИНТЕРВАЛЬНЫЙ ПРОГНОЗ
947
соотношениями вида (одновременно выполняющимися для всех с ве-
роятностью Р = 1 — а):
i = l,2,...,m,
(17.64')
где
са = [1 + Aj+T(XTX)-,Xn+r] ~ Р)*". п - р - т + 1),
1	П — р — 771+1
a Sjg — t-й диагональный элемент матрицы Se, определенной соотношени-
ем (17.63).
Соотношения (17.64) и (17.64) задают совместные доверительные
области (интервалы) для всех анализируемых эндогенных переменных од-
новременно. Если же нас интересует интервальный прогноз одной от-
дельно взятой эндогенной переменной выполняющийся с заданной
вероятностью Р = 1 — а, то он определяется неравенствами
Уп+т - л/^а(т; П-Р-7П + 1)зй- <
< Уп+т + >/Fe(m; п - р - m + 1)в«.	(17.65)
Из общих соображений следует ожидать (и это можно доказать строго ма-
тематически), что ширина интервального прогноза (17.65) для одной от-
дельно взятой эндогенной переменной всегда существенно меньше, чем
ширина интервального прогноза для той же самой переменной, получаю-
щаяся в рамках задачи построения совместных доверительных интерва-
лов (17.64').
Вывод формулы (17.62) для несмещенной оценки ковариаци-
онной матрицы ошибок прогноза. Вернемся к задаче вычисления ко-
вариационной матрицы ошибок прогноза E^(r) (см. (17.61)) и построения
ее несмещенной оценки Бг(т)-
1) Подставим в правую часть (17.61) вместо ошибки прогноза Уп+т —
Г„+т ее выражение из (17.60):
2е(т) — Е|[(ПМНК — П)Хп+т £п+т][(Нмнк П)Хп+т £п+т] }
= Е[(Пмик — П)Хп+тХп+т(Пмнк - П)Т] + Е(£п+т£п+т)
мнк
(17.61')
948
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
Два последних члена в правой части этого выражения равны нулю. Дей-
ствительно, рассмотрим, например, произведение £п+т4^п+т(Пмнк—П)Т].
Его первый сомножитель (£п+т) не коррелирован со вторым, т. к. еп+т не
коррелироваиы и с предопределенными переменными (по условию),
и с (П — П)Т, т. к. последнее выражение зависит только от прошлых (по
отношению к моменту времени п 4- т) наблюденных значений и у
(j= 1,2, ...,р; I = 1,2, I = 1,2,...,п), см. формулу (17.58). А по
условию случайные возмущения приведенной формы не коррелироваиы ни
с предопределенными, ни с лигированными (т. е. измеренными в прошлом)
значениями эндогенных переменных. В точности те же доводы относятся
и к последнему члену правой части соотношения (17.611). Таким образом,
получаем:
£г(т) = Е[(ПИ1Ж - П)Хп+тХ^+т(Пнвк - П)т] + Se,
(17.66)
где Ес = E(£te^) = Е(£п+т£^+т) — ковариационная матрица остатков
приведенной формы (она по условию не зависит от t);	= cov (4‘М^) =
Е(£^£^) — (i,j)-H элемент этой матрицы.
2) Займемся теперь приведением первого слагаемого правой части
(17.66) к «работоспособному» виду, т.е. постараемся выразить его в тер-
минах имеющихся у нас наблюдений (17.26). С этой целью вернемся к
оценке Пмнк и подставим в правую часть соотношения (17.58) матри-
цу Y, выраженную в терминах приведенной формы анализируемой мо-
дели, т.е. Y = ХПТ + е, где матрица е составлена из столбцов е(») =
(•' = 1,2,.
Пив. = YTX(XTX)-1 = (ХПТ + е)тХ(ХтХ)'*
= ПХТХ(ХТХ)-1 + етХ(ХтХ)-1 = П + етХ(ХтХ)~’,
откуда
Пмн. - П = еТХ(ХтХ)-1.	(17.67)
Подставим это выражение в первое слагаемое правой части (17.66) и по-
пробуем упростить получившееся выражение с учетом представления ма-
трицы е в виде е = (е(1):е(2):.. .:е(т)):
Е[(ПМИ. - П)Хп+тХ;+т(Пивв - П)т]
= Е [вТХ(ХТХ)-' Xn+TX^.T(XTX)-1 ХТе]
17.4. ТОЧЕЧНЫЙ И ИНТЕРВАЛЬНЫЙ ПРОГНОЗ
949
/ ет(1)МтМе(1)
Е ет(2)МтМе(1)
ет(1)МтМе(2) ...
ет(2)МтМе(2) ...
UT(m)MTMe(l) eT(m)MTMe(2) ...
eT(l)MTMe(m) \
eT(2)MTMe(m) I
I 9
£T(m)M^Me(m) /
(17.68)
где M = Xj+T(XTX) *XT — строка длины n (т.е. матрица размерно-
сти 1 х п). Заметим, что все элементы матрицы, стоящей в правой ча-
сти (17.68), являются числами, или, формально, матрицами размерности
1x1. А такие матрицы равны своему следу. Мы воспользуемся этим
при вычислении элементов правой части (17.68), а также известным свой-
ством коммутативности при вычислении следа произведения квадратных
матриц (т.е. tr(AB) = tr(BA)):
E(eT(i)MTMg(j)) = E[tr(sT(i)MTMe(j))]
= E[tr (Me(j)eT(i)MT)| = tr {M[E(e(j)eT(i))]MT}
= tr (Mcov	= cov(e^\e^’)tr(MMT)
= s,jX^.T(XTX)-1X„+T.
(17.69)
При выводе (17.69) мы воспользовались также следующими фактами:
(i) значения М неслучайны, т. к. выражаются только через наблюденные
в прошлом и заданные на прогнозируемый момент значения предик-
торных переменных;
(ii) ММТ = [Л-;+т(ХтХ)-*Хт][Х(ХтХ)-1Х„+т] = Х^+т(ХТХ)-1Хп+1;
(MAi) МА')	ММ \
tj tj tj to •••	\
MM MM	MM I
£2 £j	£2	... £2 £n I
MM *”(’/)’(0.......7(01(0	/
fcn	fcn	• • • fcn fcn /
/COV(£^,£^)	0	...	0	\
_	0	COV(£^,£^) ... О I т
I —
\	0	0	... СОУ(£^,£^)/
где In — единичная матрица n x n (в данных выкладках исполь-
зовались модельные допущения о равенстве нулю ковариаций ви-
да cov(€^,£^) при it / Z2, а также независимость ковариаций
cov(£^,£^) от времени t).
950
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
3) Теперь вернемся к матрице (17.66), подставим в нее правую часть
(17.68) (с учетом (17.69)) и получим окончательный вид для матрицы
Sf(r). Действительно, после подстановки в правую часть (17.68) элемен-
тов этой матрицы, выраженных соотношениями (17.69), имеем:
Е[(пмвм - П)Х„+тХ„т+т(Пм„. - П)т] = х;+т(ХтХ)-1Х„+т£с, (17.70)
где матрица Е. составлена из элементов = сот(е ,е^). Подставляя
(17.70) в правую часть (17.66), получаем:
= [1 + х;+т(ХтХ)-1Х„+т]Х..
(17.71)
4) Несмещенная оценка 2г(т) матрицы £г(т) получается подстановкой
в правую часть (17.71) вместо теоретической ковариационной матрицы
ее несмещенной оценки (17.63). Вывод формулы (17.62) закончен.
17.5. Некоторые общие подходы к анализу
точности оценивания и к сравнению
методов и моделей
Подавляющее большинство методов и моделей эконометрики базиру-
ется, как мы видели, на математическом аппарате многомерного стати-
стического анализа. Соответственно, «болевые точки», «узкие места»,
словом, главные трудности этого аппарата как бы ретранслируются на
эконометрический инструментарий. Среди этих главных трудностей, в
первую очередь, следует упомянуть о проблемах, вынесенных в загла-
вие данного пункта учебника. Действительно, мы неоднократно видели,
как непросто достаются результаты, связанные с аналитическим выводом
характеристик точности статистически построенных методов и моделей,
их прогностической силы (вывод формулы (17.62) в конце предыдуще-
го пункта — последнее тому доказательство). Более того, даже тогда,
когда нам удается аналитический способ исследования качества методов
статистического оценивания неизвестных значений параметров модели и
построенных на их основе прогнозов, следует помнить, что, как правило,
полученные результаты имеют асимптотический (по п —> оо) характер
(свойство состоятельности оценок, например, или асимптотический вид
ковариационных матриц и т. п.). В эконометрической же практике рабо-
тают с конечными выборками (т. е. при существенно ограниченных п), и
поэтому важно уметь проанализировать свойства различных способов
оценивания и различных методов прогнозирования в условиях относи-
тельно малых выборок. К сожалению, как правило, это не удается еде-
17.5. НЕКОТОРЫЕ ОБЩИЕ ПОДХОДЫ К АНАЛИЗУ ТОЧНОСТИ ОЦЕНИВАНИЯ 951
лать с помощью аналитических методов и приходится прибегать к разного
рода имитационно-компьютерным экспериментам. Мы уже упоминали
о подобных подходах: в п. 16.5.3 — о так называемом методе ^перекрест-
ного анализа дееспособности* (модели или метода) в связи с подбором
конкретного значения для свободного параметра дисконтирования А в гео-
метрической лаговой структуре Койка и в п. 16.1.1 — в связи с оценкой
качества и сравнением различных прогнозных методов, основанных на тех
или иных моделях временных рядов.
Ниже мы кратко остановимся на описании трех наиболее распростра-
ненных в эконометрической практике подходах такого типа.
Метод Монте-Карло (статистических испытаний). Сущность
метода статистических испытаний заключается в следующем. В компью-
тер закладываются все параметры анализируемой стохастической моде-
ли, после чего компьютер с помощью специальных датчиков случайных
чисел генерирует требуемое число еыборок заданного объема, которые,
соответственно, интерпретируются как наблюдения, произведенные над
данной моделью. Затем эти выборки используются в той статистической
процедуре (в статистическом оценивании параметров анализируемой мо-
дели, в построении различного рода прогнозов и т.п.), качество которой
мы хотим исследовать. Наличие большого числа сгенерированных ком-
пьютером выборок заданного объема п позволяет исследовать поведение
интересующих нас выходных характеристик анализируемой процедуры
(оценок 0(п) или прогнозов уп) и, в первую очередь, оценить их смещение
и среднеквадратическую ошибку. Конечно, результаты такого исследова-
ния как бы «условно-локальны», т. е. зависят от тех численных значений
параметров модели, которые мы заложили в компьютер и которые, соот-
ветственно, определяют специфику сгенерированных «наблюдений». Од-
нако подобные эксперименты, проведенные в большом объеме и в широком
диапазоне значений закладываемых в компьютер параметров, способны
доставить исследователю ценную информацию.
Конкретизируем описанную процедуру применительно к анализу ме-
тодов оценивания параметров СОУ и точности построенных на основании
этой модели прогнозов. Итак, зададимся:
1)	структурными параметрами СОУ, т.е. числом уравнений и эндоген-
ных переменных т, а также числом предопределенных переменных
р;
2)	конкретными значениями структурных параметров В и С;
3)	вероятностными распределениями структурных возмущений
4)	требуемым объемом генерируемых выборок п;
952
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
5)	конкретными «наблюденными» значениями предопределенных пере-
менных	t = 1,2,. ,.,n;
6)	значениями предопределенных переменных в прогнозный период вре-
мени (при анализе качества прогноза);
После этого:
7)	с помощью компьютерного датчика случайных чисел моделируются
случайные остатки	t = l,2,...,n;
8)	в соответствии с соотношениями приведенной формы Yt = —B-1CXt+
вычисляются значения Yty t = 1,2, ...,n.
В результате пп. 1)-8) сгенерирована 1-я выборка объема п: {Х(1),
Затем пп. 7)-8) повторяются еще N — 1 раз, в результате чего получа-
ем еще N — 1 выборок того же самого объема из той же самой генеральной
совокупности (т.е. для той же самой модели).
Таким образом, в нашем распоряжении оказываются N выборок объ-
ема п, сгенерированных в рамках одной и той же модели:
{X(l), Y(l)}, {Х(2), Y(2)},.... {Х(ДГ), Y(7V)}.	(17.72)
По «наблюдениям» каждой (j-й) выборки строим интересующие нас
выходные характеристики анализируемой процедуры (оценки структур-
ных параметров B(J),C(j), прогнозы Yn+r(j) и т.п.). Сравниваем полу-
ченные оценки B(j), С(у) и прогнозы Yn+T(j) с имеющимися у нас ис-
тинными значениями, соответственно, В, С и Уп+т: оцениваем среднюю
(по всем выборкам) величину смещения, среднеквадратическую ошибку и
другие интересующие нас характеристики качества анализируемой про-
цедуры.
Проиллюстрируем применение метода Монте-Карло на примере.
Пример 17.4. (заимствован из: Simister L. Т. Monte Carlo Stadies
of Simultaneous Equations System. Ph. D Thesis, University of Manchester,
1969). Автор этой работы исследовал с помощью метода Монте-Карло
влияние различных способов спецификации структурных остатков си-
стемы из двух уравнений (i = 1,2) на точность прогноза, осуществляемого
разными методами. Из методов, описанных выше в данной главе, сравни-
вались три процедуры:
• «МНК», непосредственно примененный для оценивания параметров /3
и с каждого из двух структурных уравнений; затем на основании соот-
ношения (17.20) определялись оценки параметров приведенной формы
и строился прогноз для j/1) и у по формуле (17.59);
17.5. НЕКОТОРЫЕ ОБЩИЕ ПОДХОДЫ К АНАЛИЗУ ТОЧНОСТИ ОЦЕНИВАНИЯ 953
•	*МНК без ограничений (МНК Б О) применялся непосредственно для
оценивания параметров к приведенной формы, после чего строился
прогноз для j/1) и у по формуле (15.59);
•	<с2МНК», с помощью которого оценивались параметры структурной
формы, по ним (с помощью (17.20)) — параметры приведенной фор-
мы, а затем строился прогноз по формуле (15.59).
В качестве возможных спецификаций структурных возмущений rf1)
и рассматривались 4 варианта:
(i)	4 и £ (t = 1,2,.. .п) образуют белый шум;
(ii)	бр) связаны автокорреляцией 1-го порядка с параметром pi = г(1) =
0,9, а £ связаны автокорреляцией 1-го порядка с параметром р2 =
г(1) = 0,225;
(iii)	на стандартные возмущения i накладываются ошибки в измерении
переменных модели (вариации ошибок составляли 10% и более от ва-
риаций соответствующих переменных);
(iv)	на случайные возмущения марковского типа (Н) накладываются
ошибки (iii) в измерении анализируемых переменных.
В таблице 17.1 приведены результаты оценки с помощью метода
Монте-Карло среднеквадратических ошибок прогнозов значений перемен-
СО (2)
ных у' * и у' для различных сочетании «метод оценивания — вариант
спецификации структурных возмущений модели». Величина среднеква-
дратической ошибки прогноза, получаемой при оценивании параметров
модели с помощью 2 МНК при спецификации остатков типа (t), принята
за эталонную единицу в сравнении различных методов.
Таблица 17.1 Среднеквадратические ошибки прогнозов i и у$Г при раз-
личных методах оценивания параметров модели
Метод оценивания	При прогнозе у^				При прогнозе j/2)			
	Вариант спецификации возмущений Я*1)				Вариант спецификации возмущений			
	0)	(«)	(«О	(iv)	6)	(»)	(iii)	(iv)
2 МНК	/\	1,47 А	1,83 А	2,25 А	Д'	1,86 Д'	3,1 д'	2,98 Д'
МНК	3,59 А	1,36 А	2,39 А	2,74 Д	12,32 Д'	1,64 Д'	8,4 Д'	8,12 Д'
МНК БО	1,13Д	2,98 А	3,86 А	2,36 А	1,17 Д'	2,44 Д'	5,53 Д'	3,06 д'
Из анализа табл. 17.1 следует, что 2 МНК оказался самым точным
во всех ситуациях, кроме случая автокоррелированных возмущений
954 ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
и В последнем случае несколько неожиданно лучше других проявил
себя обыкновенный метод наименьших квадратов, примененный в отдель-
ности к каждому из двух уравнений структурной формы.
Бутстреп метод «тиражирования» наблюдений. Этот метод
получил весьма широкое распространение в последние два десятилетия
в задачах статистического анализа, основанного на относительно малых
выборках. Заложенная в его основание идея внешне выглядит несколь-
ко странной: метод предлагает тиражировать уже имеющиеся в нашем
распоряжении наблюдения, генерируя их, как и в методе Монте-Карло, с
помощью специальных компьютерных датчиков случайных чисел. Однако
в методе Монте-Карло эти датчики «настраиваются» на экзогенно задан-
ные параметры модели (там мы «на старте» не имели никаких наблю-
дений), в то время как в бутстреп-процедурах «настройка» датчиков
определяется структурой и спецификой уже имеющейся в нашем рас-
поряжении выборки. Грубо говоря, схема действия бутстреп-процедуры
заключается в следующем: по имеющейся выборке строится некоторая
опенка (параметрическая или непараметрическая) закона распределения
анализируемой генеральной совокупности, а затем генерируются (в необ-
ходимом количестве) наблюдения, подчиняющиеся этому закону распре-
деления вероятностей. Как обрабатываются полученные таким образом
«наблюдения» и какие с их помощью решаются задачи оценки качества
модели или прогноза — это предмет для специального обсуждения, и мы
оставляем его за рамками данного учебника1.
Перекрестный анализ дееспособности модели (или ПАД-проце-
дура)2 3. Идеи этого подхода были сформулированы достаточно давно, од-
1 Интересующемуся этой проблематикой читателю мы можем порекомендовать, на-
пример, книгу: Б. Эфрон. Нетрадиционные методы многомерного статистического
анализа. (Перев. с англ.) М.: Финансы и статистика, 1988.
3 Здесь предложен вариант перевода английского названия этого подхода, впервые
достаточно полно описанного как «Cross-validation method», по-видимому, в англо-
язычной специальной литературе (см., например, Stone С. Cross-validatory choice
and assesment of statistical predictions. «Journ. Roy. Stat. Soc.», Ser. B, 36 (1974),
pp. 111-147). К сожалению, нет единой точки зрения на состав методов, объединя-
емых этим названием. Некоторые специалисты включают в рамки этого подхода к
бутстреп-метод, и различные варианты метода «скользящего экзамена», о котором
мы упоминали в п. 15.9.3 (см. Htnkhey D. V. Jackknife, bootstrap and other cross-
validation methods. London-New York: Chapman and Hall, 1983). Нам представляет-
ся, что из методических соображений удобнее несколько сузить столь широкое тол-
кование «Cross-validation», акцентируя внимание на многократных вычислитель-
ных «прогонах» ужё оцененных моделей при различных вариантах значений их
свободных (т. е. не поддающихся статистическому оцениванию) параметров.
17.Б. НЕКОТОРЫЕ ОБЩИЕ ПОДХОДЫ К АНАЛИЗУ ТОЧНОСТИ ОЦЕНИВАНИЯ 955
цако высокую прикладную значимость и популярность различные версии
ПАД-процедур обрели лишь с появлением современных вычислительных
мощностей. Их сущность заключается в следующем.
Пусть мы решаем проблему подбора модели по имеющимся в на-
шем распоряжении исходным статистическим данным, но не уверены в
ее общем виде, в ее структуре. Так, если речь идет о подборе регрес-
сионной модели, то мы не знаем, является ли она линейной, степенной
или еще какой-нибудь, нужно ли проводить линеаризующие преобразо-
вания переменных, каким выбрать значение «гребневого» параметра в
методе ридж-регрессии (см. (15.51), с. 657) и т.д. Бели речь идет о мо-
дели временных рядов, то мы обычно испытываем затруднения в выборе
структурных параметров p,q и к АРПСС-моделей, параметров адапта-
ции (сглаживания) Ai,A2,A3 в различных процедурах экспоненциального
сглаживания или параметров дисконтирования А или 7 в моделях рас-
пределенных лагов с геометрической структурой. Аналогичные вопросы,
связанные с подбором значений некоторых свободных (или структурных)
параметров модели, возникают при построении и исследовании моделей
дискриминантного или факторного анализа, систем одновременных урав-
нений и т.д. При этом под свободными (структурными) параметрами
модели А = (Ai,А2,...,Ат) мы в общем случае будем понимать параме-
тры, от которых зависит общий вид (структура) модели, но для которых
не существует математически корректных процедур статистического
оценивания. И пусть существует некоторый экзогенно заданный крите-
рий качества модели
А(А; 0; Хэкз),	(17.73)
значение которого зависит от значений использованных в модели свобод-
ныхпараметров А, статистических оценок неизвестных параметров моде-
ли 0 и состава «экзаменующей выборки» Хэкз, т.е. от состава тех экс-
периментальных (наблюдаемых) данных, на которых была проведена ве-
рификация построенной модели. В моделях регрессии и временных рядов
в качестве критерия К чаще других используется среднеквадратическая
ошибка прогноза, в моделях дискриминантного и кластерного анализов —
доля неправильно расклассифицированных наблюдений из состава Хэкэ и
т.п.
Тогда общую схему процедуры перекрестного анализа дееспособно-
сти модели можно описать в виде реализации следующих двух этапов.
1-й этап. Все имеющиеся в нашем распоряжении наблюдения X
(исходные статистические данные, результаты эксперимента) случайным
образом разбиваются на две части Хоб и Хэкз. Первая из них (X^g) ис-
пользуется для подбора («настройки») модели. Этот подбор обязательно
956
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
включает в себя определение значений свободных параметров А и, если не-
обходимо, статистическое оценивание параметров 0. Поэтому эту часть
исходных статистических данных называют обычно «обучающей выбор-
кой» (хотя, строго говоря, это может не совпадать с классическим по-
нятием обучающей выборки, принятым в математической статистике).
Данная стадия процедуры, в частности, включает в себя выдвижение и
предварительную проверку рабочих гипотез о структуре модели, пере-
бор различных вариантов моделей с целью «нащупывания» относительно
устойчивых результатов и т. п. При этом перебор различных вариантов
модели обычно включает в себя задание некоторой сетки возможных зна-
чений структурных параметров Aj, Aj,..., Am и проведение полного цикла
всех необходимых вычислений по идентификации модели для каждого фик-
сированного сочетания этих значений (т.е. оценку параметров 0 и т.п.).
2-й этап. На этой стадии каждый из вычисленных на предыдущем
этапе вариантов модели верифицируется (с помощью критерия (17.73) на
данных «экзаменующей выборки» Хэкз). Поскольку модели «настраива-
лись» на данных Хоб, очевидно, значения критерия качества на данных
Хэгз будут существенно менее оптимистичными, чем на данных Хо6. Из
всех возможных значений структурного параметра А выбирается такое
(Ао), при котором значение критерия X”(A0; 0;ХЗКЗ) оптимально. Заме-
тим, что в современных процедурах метода ПАД при делении массива ис-
ходных данных X на Хоб и Хэкз действуют так же, как и в методах скользя-
щего экзамена (и в частности, в методе «складного ножа» — «jackknife»,
см. п. 15.9.3): в составе Хэкз оставляют единственный элемент, по осталь-
ным данным подбирают модель и вычисляют значение критерия К в этой
единственной точке; затем в качестве Хэжз берут другой элемент из X
и т.д. до тех пор, пока роль единственной «экзаменующей» точки не
исполнят поочередно все элементы из массива исходных статистических
данных X. «Настройка» модели на обучающих данных Xog и после-
дующая перекрестная «перепроверка» (верификация) модели на других
(экзаменующих) данных Хэжз с непременным многовариантным перебором
значений структурных параметров на 1-й стадии процедуры — в этом и
состоит сущность метода перекрестного анализа дееспособности модели
(кстати, в некоторых переведенных с английского на русский язык рабо-
тах, относящихся к данной тематике, метод «Cross-validation» переведен
как «перепроверка», см. книгу [Эфрон Б.]).
выводы
957
ВЫВОДЫ
1.	Эконометрическая модель, выраженная системой одновременных
уравнений (СОУ), служит для объяснения поведения эндогенных (т.е.
формирующихся в процессе и внутри функционирования описываемой
социально-экономической системы) переменных в зависимости от значе-
ний экзогенных (задаваемых извне) и лаговых эндогенных переменных.
СОУ широко используются в проведении многовариантных сценарных
расчетов, касающихся социально-экономического развития анализируе-
мой системы, а также в задачах прогноза экономических и социально-
экономических показателей.
2.	Общая проблема идентификации СОУ является, наряду со спе-
цификацией модели, центральной в построении и анализе модели. Она
включает в себя проверку соблюдения условий идентифицируемости ка-
ждого отдельного уравнения и всей системы в целом (см. п. 17.2), а также
реализацию процедур статистического оценивания неизвестных значе-
ний параметров системы (см. п. 17.3).
3.	Проверка и соблюдение условий идентифицируемости производит-
ся как на стадии составления уравнений системы (1-е, 3-е и 4-е условия)
и формирования массива исходных статистических данных (2-е условие),
так и на стадии анализа результатов статистического оценивания неиз-
вестных параметров системы (1-е условие в части, касающейся обратимо-
сти матрицы В, а также 5-е условие).
4.	Методы статистического оценивания параметров СОУ подразделя-
ются на два класса: 1) методы, предназначенные для оценки параметров
одного отдельно взятого уравнения системы (МНК, косвенный МНК,
2МНК, метод максимального правдоподобия с ограниченной информаци-
ей, «оценки класса А:»); 2) методы, предназначенные для одновременного
оценивания параметров всех уравнений системы с учетом их взаимосвязей
(ЗМНК, метод максимального правдоподобия с полной информацией).
б. Если уравнения структурной формы модели могут быть располо-
жены в таком порядке, что *-е уравнение (1 = 1,2,...,т) может содер-
жать в качестве объясняющих эндогенных перемепных только переменные
у , у' ',..., jr (или часть из них), а случайное возмущение ’ этого
уравнения не коррелирует со всеми этими эндогенными переменными, то
такая система называется рекурсивной^ и последовательное применение к
каждому уравнению такой системы обычного МНК дает состоятельные
оценки ее структурных параметров (см. п. 17.3.1). Класс рекурсивных
систем является простейшим с точки зрения решения задачи оценивания
структурных параметров СОУ.
в. Если исследователя интересуют только параметры приведенной
958
ГЛ. 17. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
формы и задача прогноза эндогенных переменных, то он может ограни-
читься применением обычного метода наименьших квадратов к каждо-
му отдельному уравнению приведенной формы (с последующей оценкой,
если это необходимо, идентифицируемых параметров структурной фор-
мы). Такой образ действий называют косвенным методом наименьших
квадратов, или методом наименьших квадратов без ограничений, а оцен-
ки, полученные с его помощью, будут состоятельными (см. п. 17.3.2).
7.	В ситуациях, когда среди уравнений системы имеются неидентифи-
цируемые, так же как и в случаях, когда оценивание и анализ параметров
структурной формы представляют для исследователя самостоятельный
интерес, рекомендуется применять двухшаговый метод наименьших ква-
дратов (2МНК). Этот метод предназначен для оценивания параметров
отдельного уравнения структурной формы, а его последовательное при-
менение к каждому из уравнений структурной формы СОУ позволяет по-
лучить состоятельные оценки всех структурных параметров (хотя 2МНК
и не учитывает возможные взаимосвязи между уравнениями системы).
8.	Сущность двух шагов 2МНК заключается в следующем. На 1-м
шаге для каждой эндогенной переменной, играющей роль объясняющей
в анализируемом уравнении структурной формы, с помощью обычного
МНК строится регрессия на все предопределенные переменные X. На 2-м
шаге эта эндогенная переменная заменяется в рассматриваемом уравне-
нии ее регрессионным выражением через X, после чего в правой части
этого уравнения остаются только предопределенные переменные и к нему
применяется обычный МНК. В моделях с большим числом предопреде-
ленных переменных в целях снижения размерности рекомендуется на 1-м
шаге строить регрессию предикторной эндогенной переменной не на все
предопределенные переменные, а лишь на небольшое число их главных
компонент (см. п. 17.3.3).
9.	Если структурные случайные возмущения различных уравне-
ний системы взаимно коррелированы, то для оценивания структурных
параметров рекомендуется применять трехшаговый метод наименьших
квадратов (ЗМНК). Этот метод предназначен для одновременного оце-
нивания структурных параметров всех уравнений системы и дает их со-
стоятельные оценки, по эффективности превосходящие в данном случае
оценки (тоже состоятельные) 2МНК.
10.	ЗМНК использует полученные на первых двух шагах 2МНК оцен-
ки структурных параметров для вычисления оценки ковариационной ма-
трицы возмущений различных уравнений структурной формы. Затем на
3-м шаге оценки структурных параметров системы пересчитываются с
помощью обобщенного МНК в рамках соответствующей схемы обобщен-
выводы
959
ной линейной модели множественной регрессии, в которой в качестве ко-
вариационной матрицы остатков используется полученная ранее оценка
ковариационной матрицы возмущений (см. п. 17.3.4).
11.	В ряде ситуаций могут оказаться полезными и другие методы ста-
тистического оценивания параметров СОУ. Для оценивания параметров
одного отдельно взятого уравнения — это метод максимального правдо-
подобия с ограниченной информацией (требующий, правда, дополнитель-
ного априорного предположения о нормальном характере распределения
структурных возмущений модели), «оценки класса Л»; для одновремен-
ной оценки всех структурных параметров системы — это метод макси-
мального правдоподобия с полной информацией. Однако эти методы из-за
их относительно сложной вычислительной реализации и дополнительных
априорных допущений существенно реже используются в эконометриче-
ских приложениях.
12.	Одна из главных конечных прикладных целей построения и ана-
лиза эконометрических моделей в виде СОУ — это точечный и интер-
вальный прогноз эндогенных переменных по заданным значениям предо-
пределенных переменных и связанная с этим задача проведения многова-
риантных сценарных расчетов, показывающих, как будут «себя вести»
эндогенные переменные при различных сочетаниях значений предопреде-
ленных переменных. « Точечное решение» этих задач основано на подсче-
те значений эндогенных переменных с помощью статистически оцененной
приведенной формы СОУ. Для получения «интервальных» вариантов
решения необходимо уметь оценивать ковариационную матрицу ошибок
точечного прогноза, что является задачей аналитически достаточно слож-
ной (см. п. 17.4).
13.	Важные средства анализа качества построенных моделей, точ-
ности получаемых с их помощью прогнозов, наконец, решения задачи
выбора наилучшей модели предоставляют исследователю разного рода
имитационно-компьютерные системы экспериментирования. Среди них
следует выделить метод Монте-Карло, бутстреп-метод, а также схему
перекрестного анализа дееспособности модели (или метода).
ЛИТЕРАТУРА
Айвазян С. А. (1968). Статистическое исследование зависимостей. М.: Метал-
лургия.
A de озим С. Л. (1974). Об опыте применения экспертно-статистического метода
построения неизвестной целевой функции. — В кн.: Многомерный статистический
анализ в социально-экономических исследованиях. М.: Наука, С. 56-86.
AdeasHwC. А. (1979). Конфлюэнтный анализ. — В кн.: Математическая энци-
клопедия. М. Т. 2. С. 1083.
Айвазян С. А. (1980). Вероятностно-статистическое моделирование распредели-
тельных отношений в обществе. — В кн.: Статистическое моделирование экономиче-
ских процессов. Ученые записки по статистике. М., Статистика, Т.37.
Айвазян С. А., Енюков И. С., МешалкинЛ.Д. Прикладная статистика. Исследо-
вание зависимостей. — М.: Финансы и статистика, 1985.
Айвазян С. А., Бухштабер В. М., Енюков И. С., МешалкинД.Д. Прикладная
статистика. Классификация и снижение размерности. — М.: Финансы и статисти-
ка, 1989.
Андерсон Т. Введение в многомерный статистический анализ. М., Фиэматгиз,
1963.
Бокс Дж,, Дженкинс Г. Анализ временных рядов. Прогноз и управление. /Пер.
с англ./ — М.: Мир, 1974, вып. 1 и 2.
Большее Л. Н., Смирнов Н. В. Таблицы математической статистики. М., Наука,
1965.
Боровков А. А. Курс теории вероятностей. М.: Наука, 1972.
Бухштабер В. М. Метод многомерной развертки в анализе временных рядов. Обо-
зрение прикладной к промышленной математики. Т. 4 (1997): № 6.
Вальд А. Последовательный анализ. /Пер. с англ./ — М.: Фиэматгиз, 1960.
ДжонстонДж. Эконометрические методы. /Пер. с англ./ — М.: Статистика,
1980.
Дидэ Э., и др. Методы анализа данных: подход, основанный на методе динами-
ческих сгущений. /Пер. с франц./ — М.: Финансы и статистика, 1985.
Езекизл М,, Фокс К. Методы анализа корреляций и регрессий. /Пер. с англ./ —
М.: Статистика, 1966.
КемениДж., СнеллДж. Конечные цепи Маркова. /Пер. с англ./ — М.: Паука,
1970.
Кендалл М. Дж., Стьюарт А. Теория распределений. /Пер. с англ./ — М.: На-
ука, 1966.
Кендалл М. Дж., Стьюарт А. Статистические выводы и связи. /Пер. с
англ./ — М.: Наука, 1973.
Кендалл М. Дж., Стьюарт А. Многомерный статистический анализ и времен-
ные ряды. /Пер. с англ./ — М.: Паука, 1976.
Колмогоров А. Н. Основные понятия теории вероятностей. М. — Л., ОНТИ, 1936.
Крамер Г. Математические методы статистики. — 2-е изд. /Пер. с англ./ — М.:
Мкр, 1975.
ЛИТЕРАТУРА
961
Лумелъский В. Я. Агрегирование объектов на основе квадратичной матрицы. Ав-
томатика и телемеханика, 1970. N« 1. С.133-143.
Майстров Л. Е. Развитие понятия вероятности. М.: Наука, 1980.
МаленвоЭ. Статистические методы в эконометрии. /Пер. с франц./ — М.:
Статистика, 1975, вып.1; 1976, вып.2.
Митоян А. А. Потребительское поведение семей: дифференциация, динамика,
классификация. М.: Экономика, 1990.
Феллер В. Введение в теорию вероятностей и ее приложения. /Пер. с англ./ —
2-е издание. М.: Мир, 1964.
Харман Г. Современный факторный анализ. /Пер. с англ./ — М.: Статистика,
1972. Мир, 1983.
Эфрон Б. Нетрадиционные методы многомерного статистического анализа.
/Пер. с англ./ — М.: Финансы и статистика, 1988.
Anderson Т. W., Rubin Н. Statistical inferences in factor analysis. Proc. 3 Berkeley
Symp. Math. Statist, and Probab. — Univ. Calif. Press, 1956. Pp. 11-50.
Berndt E. R. The practice of econometrics. Classic and contemporary. Addison-
Wesley Publishing Company. Reading-Massachusetts-Menlo Parc-California, 1990.
Dougherty C. Introduction to econometrics. Oxford University Press. New York-
Oxford, 1992.
Goldberger A. A course in Econometrics. Cambridge-Mass.: Harvard University
Press, 1990.
Green W. H. Econometric analysis. Macmillan Publishing Company, New York, 1993.
Magnus J. R., NeudeckerH. Matrix Differential Calculus with Applications in
Statistics and Econometrics. New York, John Wiley, 1988.
Ptndyck R., Rubmfeld D. L. Econometric models and economic forecasts. MeGraw-
НШ Kogakusha Ltd, Tokio, 1976.

ПРИЛОЖЕНИЕ 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Таблица П1.1. Значения функции плотности ф(х) = 0(х;О;1) стандартного
нормального закона распределения.	Ф(х) —
X	0(х)	X	0(х)	X	0(х)	X	0(х)	X	ф(х)	X	0(Х)
0,00	0,3989	0,50	0,3521	1,00	0,2420	1,50	0,1295	2,00	0,0540	2,50	0,0175
0,05	0,3984	0,55	0,3429	1,05	0,2299	1,55	0,1200	2,05	0,0488	2,55	0,0154
0,10	0,3970	0,60	0,3332	1,10	0,2179	1,60	0,1109	2,10	0,0440	2,60	0,0136
0,15	0,3945	0,65	0,3230	1,15	0,2059	1,65	0,1023	2,15	0,0396	2,65	0,0119
0,20	0,3910	0,70	0,3123	1,20	0,1942	1,70	0,0940	2,20	0,0355	2,70	0,0104
0,25	0,3867	0,75	0,3011	1,25	0,1826	1,75	0,0863	2,25	0,0317	2,75	0,0091
0,30	0,3814	0,80	0,2897	1,30	0,1714	1,80	0,0790	2,30	0,0283	2,80	0,0079
0,35	0,3752	0,85	0,2780	1,35	0,1604	1,85	0,0721	2,35	0,0252	2,85	0,0069
0,40	0,3683	0,90	0,2661	1,40	0,1497	1,90	0,0656	2,40	0,0224	2,90	0,0060
0,45	0,3605	0,95	0,2541	1,45	0,1394	1,95	0,0596	2,45	0,0198	2,95 3,00	0,0051 0,0044
Замечание 1. Значения функции плотности ф(хо\ а;<т2) нормального
закона со средним а и дисперсией ст2 подсчитывается по формуле
Ф(хо;а;<^ ) = -Ф I—-—;0;11 = -ФI—-—I
<Г\СГ	/ (У X <г /
(П1.1)
(если величина аргумента (хо — а)/(Т попадает между табличными значениями
х, то для определения	пользуются линейной интерполяцией функции
Замечание 2. При определении значений функции ф(х) для отрица-
тельных величин аргумента х следует использовать тождество (выражающее
свойство четности функции ф(х))
ф(-х) = ф(х).
(П1.2)
Пример П1.1. Требуется определить значение ф(хо\а',а2) при хо =
3,36, а = 1 и а2 = 4.
Решение: х = ypJ~a = 3,3д~* = 1,18. Два окаймляющих х соседних та-
бличных значения аргумента — это xj = 1,15 и Х2 = 1,20, поэтому, используя
линейную интерполяцию, получаем:

[<£(1,15) — 0(1,20)] =0,199.
Значение 0(3,36; 1; 4) получаем по формуле (П1.1):
ф(г0 = 3,36; 1; 4) = | #1,18) = |0,199 = 0,0995.
964
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.2. Значения функции Ф(я) = Ф(ж; 0; 1) стандартного нормального
X 2 /
распределения.	ф(х) = —4= J* e-t '2dt.
^2,г —оо
X	ф(*)	X	ф(г)	X	ф(«)
0,00	0,500000	1,00	0,841345	'>,00	0,977250
0,05	0,519939	1,05	0,853141	2,05	0,979818
0,10	0,539828	1,10	0,864334	2,10	0,982136
0,15	0,559618	1,15	0,874928	2,15	0,984222
0,20	0,579260	1,20	0,884930	2,20	0,986097
0,25	0,589706	1,25	0,894350	2,25	0,987776
0,30	0,617911	1,30	0,903200	2,30	0,989276
0,35	0,636831	1,35	0,911492	2,35	0,990613
0,40	0,655422	1,40	0,919243	2,40	0,991802
0,45	0,673645	1,45	0,926471	2,45	0,992857
0,50	0,691463	1,50	0,933193	2,50	0,993790
0,55	0,708840	1,55	0,939429	2,55	0,994614
0,60	0,725747	1,60	0,945201	2,60	0,995339
0,65	0,742154	1,65	0,950528	2,65	0,995975
0,70	0,758036	1,70	0,955434	2,70	0,996533
0,75	0,773373	1,75	0,959941	2,75	0,997020
0,80	0,788145	1,80	0,964070	2,80	0,997445
0,85	0,802338	1,85	0,967843	2,85	0,997814
0,90	0,815940	1,90	0,971283	2,90	0,998134
0,95	0,828944	1,95	0,974412	2,95	0,998411
				3,00	0,998650
Замечание 1. Значение функции распределения Ф(®о*> о; о-2) нормаль-
2	-
кого закона при среднем значении а и дисперсии а в заданной точке хо подсчи-
тывается по значениям функции Ф(х) = Ф(ж; 0; 1) с помощью формулы
2\	~ о л Л - (— а\
Ф(®о;а;<г ) = Ф (-------; 0; 11 = Ф (------)
\ а /	\ и J
(П1.3)
(если величина аргумента (жо—а)/^ попадает между табличными значениями х,
то для определения Ф((«о "_°)/0’) пользуются линейной интерполяцией функции
♦(«))•
Замечание 2. При определении значений функции Ф(ж) для отрица-
тельных величин аргумента х следует использовать тождество
Ф(х) = 1 - Ф(—х).
(П1.4)
Пример П1.2. В условиях примера П1.1 имеем:
Ф(х0 = 3,36; а = 1;а2 = 4) = Ф(1,18)
= Ф(1,15) +
1,18-1,15
1,20-1,15
[ф(1,20) — Ф(1,15)] =0,881.
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
965
Таблица П1.3. Значения g-квантилей uq стандартного нормального распреде-
ления.
Q	«9	9	«9	Я	«9	Я	«<7
0,50 51 52 53 54 0,55 56 57 58 59 0,60 61 62 63 64 0.65 66 67 68 69	0.000000 025069 050154 075270 100434 0,125661 150969 176374 201893 227545 0,253347 279319 305481 331853 358459 0,385320 412463 439913 467699 495850	0,70 71 72 73 74 0,75 76 77 78 79 0,80 81 82 83 84 0.85 8б 87 88 89	0,524401 553385 582842 612813 643345 0,674490 706303 738847 772193 806421 0,841621 877896 915365 954165 994458 1.036433 080319 126391 174987 226528	0,00 91 92 93 !495 96 97 971 972 973 974 0,975 976 Ж 979 0,980 981 982	Г281552 340755 405072 475791 554774 1,644854 750686 880794 895698 911036 926837 943134 1,959964 977368 033520 2,053749 074855 096927	0.983 984 0,985 986 989 0,990 991 992 993 994 0,995 996 999	120072 144411 2,170090 197286 ш 290368 2,326348 365618 408916 457263 512144 2,575829 652070 И 3,090232
Пример П1.3. Найти 0,9-квантиль но,9. Величину 1*0,9 находим из та-
блицы в графе, расположенной справа от соответствующего значения q = 0,9,
т.е. 1*0,9 = 1,281552.
Замечание 1. Если заданная величина q попадает между двумя со-
седними табличными значениями и qi (qi < да 5 это может случиться при
графической проверке нормальности распределения), то следует воспользовать-
ся линейной интерполяцией, а именно формулой
“9 = «91 +	_ qi («91 “ «91)-
Замечание 2. При нахождении g-квантилей для значений q < 0,5 сле-
дует воспользоваться соотношением ug = — ui-g. Например, uo,4 = —ui-0,4 =
~uo,6 = —0,25335.
Замечание 3. При отыскании 100<2%-ных точек Wq следует восполь-
зоваться соотношением Wq — Например, wo,O5 = «0,95 = 1,64485.
Д X2-распределения c v степе-
Таблица П1.4. Значения 100Q%-hux точек
нями свободы.
V		 Q									
	0,995	0,990	0,975	0,950	0.900	0,100	0,050	0,026	0,010	0,005
1	392704-10-ю	157088-10'®	982069-10'»	393214-10'»	0,0157908	2,70554	3,84146	5,02389	6,63490	7,87944
2	0,0100251	0,0201007	0,0506356	0,102587	0,210720	4,60517	5.99147	7,37776	9,21034	10,5966
3	0,0717212	0,114832	0.215795	0,351846	0,584375	6,25139	7,81473	9,34840	11,3449	12,8381
4	0,206990	0,297110	0,484419	0,710721	1.063623	7,77944	9.48773	11,1433	13,2767	14.8602 *
5	0,411740	0.554300	0,831211	1,145476	1,61031	9,23635	11,0705	12,8325	15,0863	16,7496
6	0,675727	0,872085	1.237347	1,63539	2,20413	10,6446	12,5916	14.4494	16,8119	18.5476
7	0,989265	1,239043	1.68987	2,16735	2.83311	12,0170	14.0671	16,0128	18,4753	20.2777
8	1,344419	1.646482	2,17973	2,73264	3,48954	13,3616	15,5073	17.5346	20.0902	21.9550
9	1,734926	2,087912	2.70039	3,32511	4.16816	14,6837	16,9190	19,0228	21,6660	23,5893
10	2,15585	2.55821	3,24697	3,94030	4,86518	15,9871	18,3070	20.4831	23,2093	25.1882
11	2,60321	3,05347	3,81575	4,57481	5,57779	17,2750	19,6751	21,9200	24.7250	26,7569
12	3,07382	3,57056	4,40379	5,22603	6,30380	18,5494	21,0261	23.3367	26,2170	28,2995
13	3,56503	4,10691	5,00874	5.89186	7,04150	19,8119	22,3621	24.7356	27,6883	29,8194
14	4,07468	4,66043	5,62872	6,57063	7,78953	21,0642	23,6848	26,1190	29,1413	31,3193
15	4,60094	5,22935	6,26214	7.26094	8,54675	22,3072	24,9958	27,4884	30,5779	32,8013
16	5,14224	5,81221	6,90766	7,96164	9,31223	23,5418	26.2962	28,8454	31,9999	34,2672
17	5,69724	6,40776	7,56418	8.67176	10,0852	24,7690	27,5871	30,1910	33,4087	35,7185
18	6,26481	7,01491	8.23075	9,39046	10,8649	25,9894	28,8693	31,5264	34,8053	37,1564
19	6.84398	7,63273	8,90655	10,1170	11.6509	27,2036	30,1435	32,8523	36,1908	38.5822
906	П 1., ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
20	7,43386	8,26040	9,59083	10,8508	12.4426	28,4120	31,4104	34,1696	37,5662	39,9968
21	8,03366	8,89720	10,28293	11,5913	13,2396	29,6151	32,6705	35,4789	38,9321	41,4010
22	8,64272	9,54249	10,9823	12,3380	14,0415	30,8133	33,9244	36,7807	40,2894	42,7956
23	9.26042	10,19567	11,6885	13.0905	14,8479	32,0069	35,1725	38.0757	41,6384	44,1813
24	9,88623	10,8564	12,4011	13,8484	15,6587	33,1963	36,4151	39,3641	42,9798	45,5585
25	10,5197	11,5240	13,1197	14.6114	16.4734	34,3816	37.6525	40,6465	44,3141	46,9278
26	11,1603	12,1981	13,8439	15,3791	17,2919	35,5631	38,8852	41.9232	45.6417	48,2899
27	11,8076	12,8786	14,5733	16,1513	18,1138	36,7412	40,1133	43,1944	46,9630	49 ,*6449
28	12,4613	13,5648	15,3079	16,9279	18,9392	37,9159	41,3372	44,4607	48,2782	50,9933
29	13,1211	14,2565	16,0471	17.7083	19,7677	39,0875	42,5569	45,7222	49,5879	52,3356
30	13,7867	14,9535	16,7908	18,4926	20,5992	40,2560	43,7729	46,9792	50,8922	53,6720
40	20,7065	22,1643	24,4331	26,5093	29,0505	51,8050	55,7585	59,3417	63,6907	66,7659
50	27,9907	29,7067	32,3574	34,7642	37,6886	63,1671	67,5048	71,4202	76,1539	79,4900
60	35,5346	37,4848	40,4817	43,1879	46,4589	74,3970	79,0819	83,2976	88,3794	91,9517
70	43,2752	45,4418	48,7576	51,7393	55,3290	85,5271	90,5312	95,0231	100,425	104,215
80	51,1720	53,5400	57,1532	60,3915	64,2778	96,5782	101,879	106,629	112,329	116,321
90	59,1963	61,7541	65,6466	69.1260	73,2912	107.565	113,145	118,136	124,116	128,299
100	67,3276	70,0648	74,2219	77.9295	82.3581	118,498	124,342	129,561	135,807	140,169
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ	967
968
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П 1.5. Значения 100Q%-hux точек v^(vi,P2) F-распределения с чи-
слом степеней свободы числителя iq и знаменателя i/j.
	1	СООТСО<0 О C4N (О 5ON О ЮО СОСЧОТС0СО CO5j<-,S —« Г" xf СЧ — OOOTOOOQ Г- Г-. СО СО <О ююююю *	*	* м	ММммм	м м М 4» м	ММммм	ммммм
	120	чроо'Фоо сч хг от сч co go о ср до ср от из сч от n- 'Фсчооь Ov-N _ ь. со — О О ОТ СО <30 Ь» С’- Ь« СО СО ОоОюЮ
	о «о	ON ЮО>	xt« О •—	хГ	_	«— СО СО О СО	СЧ сою NO	ср <0 xf< СЧ _ N- хГ —«N-	_ N- UP	СО	СЧ	-0 010)00	СО ь- n- с- Ь-	<О СО СО Ю со СЧ ОТ UP СО	СО СЧ СЧ	СЧ	СЧ	C4N---	— —. _ _ _	_ _ _ _ _ со
	о тг	СО N СО О СО ОО хг СО СО СО UP ОТ СО ОТ up _ 00 Ю со — ON Юч?	“ UW— ОО —< N- Up СО СЧ —0 0)0)00 ОО СО С*» Г- N N- СО СО <О СО
	о со	СО со Г* СЧ	Г* О	со ОО U3	со др —<О _	N-	х£ _	со со СЧ	О СП N сч хг —«со	—« оо	Ш СО СЧ	— о со от от	ОО	оо 00	Г» Г*-. Г- Г—	N. tO U счОТ СО СО	СОСЧ	СЧ СЧСЧ	СЧ СЧ СЧ _ _	—	— —<	_ _ — _	_ —1 _ из	_	_ _ _
	м	8S2S 2S338 22S3X 8S33K К£йй£ СО
	о сч	хГ xj« 00 х|« —•'Г ONO О СЧ to _ <0 СЧ ОТ tO xf _ ОТ 00 <ОхГ <О NV — со СЧ СО US xt* СО N —ООО) ОТ ОО 00 ОО 00	Г- N. N. Г-х e CJD		
	to	NNQN	хг	N- Ср	СО	ХГ	«TN	ОЮ—	Г»	-Ч* —« ОТ	СО	xf*	ео _ О	СО СЧ хГ СЧ аО	СЧ СОСО	со	СЧ —	— О О	ОТ	ОТ ОТ ОО	ОО	оо	00 оо оо	с- _ ОТ UP СО	СО СЧ СЧ	СЧ	СЧ	СЧ СЧ	СЧ СЧ СЧ	—	—. —« _	—	—	_ _ _	_ со		
	сч	— - NO	NQNOOQ	др	_ up о	из	СЧ ОТ <О СО	—	Г- р х£	ср N- хг сч от	сч от со из со	сч	сч — —	о	о от от от	от	оо	оо со со	со МММ*	• М • М М	МММММ	М М М м	М	МММММ О ОТ Ш СО	со сч сч сч СЧ	СЧ	СЧ СЧ СЧ	СЧ	сч —• _ —«	—	_	_ _ _	_ со			
	о •м	О О	СО СЧ	О	хг О хг СЧ	СЧ up ОТ	хГ ср	со CO	Q	др <р	xf сч 0 О со —«	_ СО	СЧ О	со	PNn’t	СО СЧ —•	— —•	О О	О	ОТ ОТ	О) О) О СО СО О	g 0	tn СО	СО	сч сч сч сч	сч сч сч	сч сч	сч сч	сч	— —«	_____
	а>	СО	00 XJ"	сч	СО СЧ	СО	хг	Ю N -« СО 04	ОТ (О	Ср О др	СО 1П СО СЧ — о»	ОО	СО СЧ ОТ	СО	О) N	tn	хг	со СЧ СЧ — —«	о о	о о от	от от от от от ОТ	ОТ UP со	со	сч сч	сч	сч	сч сч сч сч сч	сч сч	СЧ сч —•	_____ из	
	во	хг с—	up up	хг др и? от in	соохгою	сч от «о хг сч	о	оо с* цр хг хГ СО	СЧ От	СО ОТ Г— tn Xf	<0 СО СЧ СЧ —«	— О О О О	<	ОТ ОТ От От О) ОТ	ю со	со сч" сч сч" сч"	сч" сч" сч" сч" сч"	сч" сч" сч" оГ сч"	сч	—’ —“ _“ _" tn
	n-	— m N	до	N- — 00 СЧ _	— xj> 00 со ОТ	СО	со О	оо сП	ХГ СЧ _ ОТ ОО ОТ со СЧ	От	NONtOm	ХГ со сч сч —	—	—< _	О О	ООООТОТ м	•	М	м	Ш М М М М	« М М М М	МММММ	М М М М М eg от ю	со	со со сч сч сч	счсчсчсчсч	сч	сч сч	сч сч	сч сч сч — _
	«о	О СО ОО •—<	О ио ср N tn	СО ОТ СО 00 хг	_ оо ио СО _	от др СО UO Tf СЧ со СЧ О	X? о со СО Ю	ХГ со со СЧ СЧ	СЧ — — —< _	ООООО оо" от in хг’	со" со сч" сч" сч"	сч” сч" сч" сч сч	сч" сч" сч" сч" сч"	сч" сч" сч сч’ сч" ио
	«о	хг ОТ — up ио — ар СО —« СЧ и? ОТ up —« IN xt* СЧ О CO to xt* СО _ со СЧ СЧ СО О хг _ 00 г- UP U0 хг со со со сч сч СЧ сч _ _____ Гх." От ио" хг" со" со” сч сч сч сч" сч сч" сч" сч" сч" сч" сч" сч" сч" сч" сч" сч" сч" сч" из
	•ч*	со хг хг _ сч ОО ио — ОТ _ xf ар СО от <О ср — ОТ N- up со сч _ ОТ ао сч со — ио —• от со <о союхгхгео со со со сч сч сч сч сч сч — ММММ	МММММ	МММММ	МММм*	МММММ tg ОТ ио Xt* СП со сч сч сч счсчсчсчсч счсчсчсчсч счсчсчсчсч
	СО	ОТ to ОТ ОТ сч ОТ IN СЧ	_	СО tp _ to СЧ	ОТ <О Х#« СЧ О	со Ю ио X*	оо го—«со— СО СЧ О ОТ	ОО	NtOCOlOtQ	XT xf Xj* ХГ	СО СО СО СП	СП eg ОТ tn ^*" со" со" со" сч	сч	сч" сч" сч сч’ сч’	сч" сч" сч" сч сч"	сч" сч" сч" сч	сч"
	сч	О Q to СЧ со «о со — — сч to —х СО СО о IN XJ СЧ _ От IN <0 tn Xt* изо xt* со г- xt* сч —'О от<х>оог- t- to coco со иоизизшио от" от" ю’ <*" со" со" со’ со со" сч" сч" сч" сч сч" сч" сч’сч’сч" сч сч" сч сч" сч" сч"
	•м	<0 СО хг хг	со со ОТ Ю со	ОТ	со QO хг О	r_tneO_OT<Ncpu3xf«eo 00 tn up up	OtNUpxrcO	сч	сч — _ _	о О О О ОТ ОТ От от от от от СО to xt*	Х1« со со со со	со	со со со со	со СО СО СО СЧ СЧСЧСЧСЧСЧ СО
•*		_ СЧ СО Xi* to <О tN СО ОТ О _ СЧ со хГ из СО |N СО ОТ О — СЧ СО xf _____ _____ СЧСЧСЧСЧСЧ
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
969
<NOO)OON U3 U3 ЧУ чф чф	to оо ст сь о ЧУ СО СМ — О •—•	"И •—I »	
СО чф ср СМ — ЮиЭЩЦЭ ш в—Ч	<5 см io to гч из Чф ср CM -— От	от	от	от	от	
ст со гч ю из из из из из из	чф Гч О СМ чу иЗ чф Чф СР СМ	
••и •—< •—« •—« ОТ—	ОТ— ОТ—	X—4	•—	
СО -Г о ст оо со со со из из ОТ — ОТ ОТ ОТ ХМ ОТ— сот-4 от—4 —1	Гч — чф Г- о ио ио чф со со От	от	ОТ	ОТ	от	
СО U3 чф со см со со со <о со от от от л — ОТ—4 — ОТ— ^м4 ОТ—	—• чф ОО —' чф СО ио чф чф со ОТ	ОТ	ОТ	от	от ОТ— — ОТ— ОТ—	
О ОО Гч ср ю to to to to to	чф [Ч — ио оо СО ио V0 чу со	
ОТ^ *—< от—4 гМ от—4	—— ОТ— Ф— ОТ—	
СМ — О СП оо Г» t^> Ь» to to ОТ	ОТ	—	ОТ	ОТ —от—4 от— от— ••—	Г- — Чг со сч со <£> lq хг а.	От	ОТ	ОТ	от ОТ— — ОТ— ОТ— ОТ—	
Г- (XJ ю	со С4» <** Is*	с** от от от от от *>М	CM to CD ио О (ч СО СО U3 чф от от от от от ОТ— •— от— ОТ—	
см — о сп оо до СО ООГч Гч ОТ	ОТ	ОТ	ОТ	ОТ OT-W *—4 от— от— от—	г- ~ч to сэ из Гч гч to со ио ОТ	ОТ	ОТ	ОТ	от От—4 От—4 •—4	
(ч СО U3 чф ср СО СО во СО СО «ц	—	ОТ	ОТ	ОТ	СМ СО — U3 Q СО Гч <4 СОСО ОТ	ОТ	от	от	от отЧ ОТ—4 ОТ—4 —— ОТ—	ио о о
СТ 00 г* <ч to со со со со оо —4 •—м — —— •—*	и? СП чф со со оо t— Гч <О СО ОТ	от	от	от	от	II О»
СО СМ —• О СП а ст ст о> со * От от М — ОТ— ОТ— — •—* от—	СО CQ Гч СМ Гч оо оо гч гч со От	от	От	от	от 4—4 от— ОТ—	—	
Ь* СО VO ЧГ оо о> о> о> о о от от от от от от^ от— от—	со гч см г— см О ОО ОО ь- Гч от	от.	от	от	ОТ	
8Б888 см см см см —	ср СО Сч см £ч СТ О> ОО ООСч от	От	от	от	—	
8SS88	88888	
СМ СМ СМ СМ СМ	СМ см — — —•	
О0Г>Г*<£1Ю — — от—	от—	ЧГ СТ чг СТ чф — О О СТ СТ	
СМ СМ см см см	СМ СМ СМ — —	
СМ —« О СТ оо со ср ср см см	оо со оо со др см см —< — о	
см см см см см	см см см см см	
со см —«о о U3 U3 U3 МО U3 см’ см" см’ см’ см’	СТ чу СТ ио о Чф ’Ф СО СО со см см см см см	
см •—• О СТ ст &) СТ СТ 00 оо см см см см см	со чф Ст ио —• 00 оо Гч (ч Сч см см см см см	
U3 СОГчСОСТ СМ СМ СМ СМ СМ	О О О О О СО ч* <о см о	
со о со ср “U0 ио to ио СТ оо иэ СМ -ч			Ср Гч ср СО — со СО СМ СТ Гч ЧГ со со см см						Чф о о —1 СО иЗчфСОСМ — см см см см ем			
СО СТ ио <£ - Чф ио СС со • - ио ст оо сх- ем —«		) )	Q О Гч Гч LO * ГЧ см СТ Гч чу со со см см						СО из Чф из 00 из чф СО см — см см см см" СМ			
СМ 00 ГЧ СТ •ЧУ ио сэ СМ - - - ио СТ оо ио см »			ГО Чф о — ст чу ГчСООГч Чф СО СО со см						см ст «3 чу см см	со о см со со см см см ем		
— гч ст СМ -чу из гч V-«	"	•	•» VJ стоо U0			со Чф чф		Гч чф чу С* >- Ср се СО со сое*.			) [_ г	tD СО СО Чф Гч to из чф со см см см см’ см см"			
с и	- со см ио “ЧГ о ГЧ- । ст со ио’		О оо др сэ ио со со о со Чф СО СО со см						О ГЧ гч ср — Гч из чф со СО см см см см см			
—• ио чу <ч -чу to Гч ст - - - ЧУ ст оо ио ем —			с* и-	> — — см о чу — — см и: ) ОО ЧУ —• СТ Гч со из Чф СС • со со со см см" см см см ем								
о ио to о -чу to 00 оо - - ЧУ Ст ОО ио см —			СО ГЧ «ф LO чф из СО ЧГ — ст чф со СО СО см						ГЧ из чф (_р СТ г- со из ’3F се см см см см см			1 1
Ст СО о to СМ чу — СМ —“ -чу сч СО to СТ ио СМ О ио - - - - -- -- ЧУ СТ СО ио чу СР Ср ГО ГО см —									из см см со О СО Гч to из чф см см см см см			
СТ —1 Чф — -чу Гч ст Ср - - - чу СТ во ио см —			ОО О Гч оо Гч Ю О ио см о Чф чф со со со						— ст ст о со СТ гч. to со иэ см" см см ем" см			
СТ О СТ to Ф to ЧУ ио чф - чф |ч СТ Гч О Ю СР — Чф Ст СО ио чу чф ср СР Ср см —									ОО из из Гч о СТ СО Гч to to см см см см см			
ио др •— о “СР СО О о - - - Чф ст СО to см —			г- о со ст со см о о — и: гч — to СО — ОСТСОГЧ-tC чу" чф со СО со СО CM CM CM CS									!
СТ Гч ио Чф CM ио СР Чф СО Гч ио ио Гч о -СР СО о СО Гч чф см О СТ СО Гч Гч СО ст" СО со чф’ чф ср ср’ СО СР см’ см см см’ см —												
оо ио СТ СТ “СР со о to - - - СТ со to		С§ см Чф чф				ст ост гч из см со со со		—ч О СТ СО Гч СО со см см см				
О СО Чф со -СО ст —< ст со со			Л 00 Гч се гч см ст о см из ст см со из со см о о ст со Чф ЧУ со СО СО Ср со со см см									
см О — со О“СР О см Ср ст" СТ СО см —•		ио СТ Гч СТ 00 СО О —' СО <р О СР ст to чф СР СМ — О ст ио чф Ср СР ср СР СР ср СР см										
cou^^i ст см ст ст<со СМ ““		СТ СО СМ чу Ср cotoepco — — U0 — оо to Чф со СМ —< —1 ио-ф^срср ср СО СО СР со										
(ч СО оо ст -— см ио ио “ - • —• Ст Ст со см —		— со ио Гч СО —« Ст СТ —' чу чф Гч со О СО Гчиочучфср Ю^чф'фСр со СО со со со										
10 Q ио Чф “О ио ст 8> СТ СТ СО «от^ от—4			Ст чф чф to to Гч — Гч чф см из из Чф чф" чф					о др ст —* -ф — СТ 00 СО Гч Чф" со со со со				
ф —в СР — “U0 —* ГЧ — - " • СО со О Гч —ч —* ——«		— СП ст см см со ст ио со —• to ио ио ио ио						4,96 4,84		из Гч с Гч СО t чф чф 1		
	СМ ср Чф	ио со				Гч	со ст	О -И СМ СО чф				
970
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение таблицы П1.5
	S	SS8SS 33888	S3S83 	 	 ст* сч —
	120	-зз&з 8SS3BS sssse ssssss 		2о»‘осо" -	 СП <N -
	| 60	2 = 8S8 S?g!8S$ SSSSe K3S35S 25ЙЗ 		‘	Sooco” 					СТ* СЧ
	о	5^ *2 2 42 £2 2 !£ S _ 01 s uo v cn — ст» cn ст* о ст*	ь- —- ю » e	ст* co CO CO CO GO co Г-— о to Ю CO	CO "Ф M о»о»счсч"сч —о ст*" о” co’
	1 30	822=S 3sS?8?3> SJ83S8 SStSBS счсчсч’счсч” счсч"—" — —." —" —" —" —* — —- —Sen о co .	СТ* СЧ —
	>г |	ст*фст»ш — ooj5S2-2 otoco — о o*o*o—сч	to co о co СМСЧ — — —. CO О О CO CT* O* O* O* CT* CT) co r-1*. co to	co ф CO CT* 		О* CN —
	| 20	888.22 ^°o38 33S.S3 8S8Ste	3S33 СЧСЧСЧСЧ*СЧ Сч’сЧСЧСЧСЧ сч"—" —Г — —Г —Г	ОСПсо’чг 									 							 О* СЧ —
	91 |	SJ!£lz:£;£3	осою со —	2*£г4?^£Э	«счфюг-	r-cot<"o"_ •Ф СО СО СЧ СЧ	СЧ_ — — — —	О О О О О	О СТ* ОО Г*- со	Ю ф СО СЧ СЧ СЧ СЧ СЧ СЧ	СЧ СЧ СЧ СЧ СЧ	СЧ сч сч сч" СЧ	сч"	—	со О* со Ф 	-	О* СЧ —
	1 12	22 £! 22 — — 22 Ю 52 S 00 4о ю со сч о ст* о сч со ш	> сч ю г^ ф ф со со со сч сч сч сч —• ~~ —- —- —• •— о О ст* со Г"'-	оф о со сч сч сч сч сч сч сч сч сч сч сч сч сч" сч" сч" сч" сч" —* — —•	О О* Г*." ф” 		 СТ) сч —
	о	СТ) Ш — СО	to СЧ О Г", ю	Ф сч О Ст) ОО	СО ор СТ* — СО	,	СО	О СО ю	" СО	CO_COCO<NC4	СЧСЧСЧ-——	— о ст* ст* со	£	to	сч to СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	СЧ СЧ — —" —>	со	СТ* < тг 			 .	СП сч
	а>	Ч? "Т ’СТ СЧ	O1 N Ч* CN О	СО Г- IZ) V (N	—. сч 'Ф со со	II *	СЧ СТ) ю со IO IO •чг	СО СО^ СО СО СО	СЧСЧСЧСЧСЧ	СЧ—ОСЬоО	СЧ со со to СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	сч" СЧ СЧ — —	§О*Г-Гч*«" -	сп сч —
	«о	ГЭС SJ 42 75 °5	«стечог-со	«ф сч — о* °Q	ь-	со о сч ч*	сч г-~ ст* о to to IO to-Ф	"Ф -ф «ф СО СО	СОСОСОСЧСЧ	СЧ	—— ОО*	ОО СО -Ф СО СЧСЧСЧСЧСЧ	счсчсчсч'сч	сч" сч" сч" сч" сч"	сч	сч" СЧ СЧ —	ЮстГьГ'ф" ст* сч —
	ь.	Г* S? тх 92	•-•СТ*<р'Фсч о о* г*, со ш со to t*. ст* —•	“оо <о г^. со " 1 r^totototo to	ф -ф <Ф СО со со со сосч«-«оо	CNCOtOCT* СЧСЧСЧСЧСЧ СЧСЧСЧСЧСЧ сч" СЧ СЧ* СЧ сч" СЧСЧСЧСЧСЧ	S СТ* Г—" ф" —		СТ* сч —
	9 1	ип СО —	СТ)Г*<ОЮСО	СЧ ЧГ LQ Г-	о	СТ1СО — — t^r^r^co <о	totototoio	'Ф_'Ф-ф-ч	«ф о сч—>	—	tn со а* сч СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	СЧСЧСЧСЧСЧ	сч" сч" сч" СЧ сч”	tOO*r»TiO О* "Ч —
	« 1	t^StSSto SS?xot8tf3 Й-фсосчсч СЧСЧСЧСЧСЧ сч’счсчсчсч счсчсчсч’сч" счсч сч"счсч	locnooto -	СТ) сч —
		5₽Z?5C52S	сч оюо	tO’e’co—о	о* —союс^	to io — об	’ Ос^о^ст^ст*,	OOCOoOQOt^-	S'- Г«- Г''- с*, г».	40 <о ю м* со	СЧ СЧ г», ст* СО СО СЧ СЧ СЧ СЧСЧСЧСЧСЧ СЧСЧСЧСЧСЧ сч” сч* сч сч СЧ*	g 30 to
	1 3	° С: JQ S3 ss encototoco счффсоо	"соь.<ост* ^.^Ч0.0. СП СП О* СТ) СТ) СТ* СО t4* 40 40	О— ЧГ 40 со со со со со со со со со со счсчсчсчсч сч”сч*счсч сч
	! 1	5R £3 S22 J2 S3 32 52 2! S* ° ст* ь» *о ф* со сч со «о г- о	ю о сч о 4040X01010 ФФФФФ СО СО со со со со сч — о о	«оооо со со со со со Чо со со со со со со со” со со со со со со со	§ споаГ --	V О* со —
		Й8Й88 33882 C-33S53 'ggsg' ’ чф чф чф чф «Ф чф Чф чф -Ф «Ф чф чф "Ф чф чф" чф -ф СО СО	ф Ср ф — -	СТ) СО сч
1	►	ьо <£> >. оо СТ* О — СЧСОчф хОСОЬоСОСТ» ОООО о	— СЧСОчф СЧСЧСЧСЧСЧ СЧСЧСЧСЧСЧ СО Чф со СЧ о
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
971
сч ср © © — О оо со со со	— о © г», о СТ» со СО — о	ь» to v? ь- ст» СО Г. © © хф	ечсо — со — ч со со сч сч	1=2283	— О О 00 о О 00 СО СО о
СТ» СО © Хф Хф	со со СО СО со	сч сч сч сч сч	сч сч сч сч сч	сч сч сч’ сч сч’	сч — —> — —.
—• Гх. "'Г © о — СП С*- О чг	О СТ» СО © СТ» о © хф сч о	СО Ч* СО СО ОО О* оо Г- со to	сч со о Ю — ю ч ч со со	сх. со О [х- чф сч сч сч — —	— СЧ со СО сч —- ст» сх. ио со
© © © хф хф	хф СО со СО со	сч сч сч сч сч	СЧ СЧ сч сч сч	сч сч сч сч сч	сч — — — —
О СО СЧ СО оо сч о со О хф СП г*, © СО хф	др оо хф хф оо Ot^-tOcO — ч* со со со со	© СО ср © Гх. о ст> с с— со со сч счсч сч	— to О to о со ю ю ч ч сч сч сч" сч сч"	to СО СТ» Ю со со со сч сч сч сч сч сч сч сч	—4 СЧ Хф ср (X- СЧ О 00 со хф СЧ сч — — —
ст* хф — сч г— сч —< ст» — © СТ» Г- со сО хф	г~ со сч СО г- —< ю о ч* с ч* со со со со	СО СЧ СЧ хф со — о о» оо п СО СО сч сч сч	О» ч оо ч СТ» СО СО to to ч сч сч сч СЧ сч	U0 сч со to СО Яф Хф со СО СО сч сч сч сч сч	о —. Хф СО СТ) со — О* fx~ Щ сч сч — — —
© со ст» о 42 СО СЧ СТ» СЧ © СТ* Г*. СО СО хф	© ХГ О — со СЧ СТ) Г*- to СО ч* со со со со	со со со" сч сч	Sff&SS сч сч сч" сч сч	ЧФОП^’Ф — to Ю хф чф сч сч сч сч* сч"	СТ» © ер сО О СО сч о 00 Гх. сч сч сч — —
г-. —< с- оо со Хф СО О СЧ Г СТ) г«- СО Ю хф	со сч оо ст* со со о г* © хф ч> ч* со со со	СТ» об	? сч СЧ —< О о СТ» СО со со со сч	СО О to О <Р 00 ОО По Го СО сч сч сч сч сч	СЧ op to сч СТ) СО to to to чф сч сч сч сч сч	Г- СТ) сч ш ст> Ф ч — ст» г сч сч сч — —
Ю О со СО —- Ю  ' - со оо	— О © © — хф — ОО © to	Гх © © ср О со сч — о о	.94 ,88 .83 .78 .74	ОЧЭСрОГ- Г. to СО со ю	О Гх. с СО р in со сч о «5
СТ» с* © © хф	хф хф СО СО со	СО СО со СО СО	сч сч сч сч сч	сч сч сч сч сч	сч сч сч сч —
СЧ СО —' сч © © со © ст»	© © — сч © to СЧ О 00 со	сч — — СО © © Хф со сч •—	СТ* со ОО СО ст» о о ст» ст» оо	42 — 00 to СО ОО ОО Гч г.	О CM tn СТ* хф Гх 1П СО — О
ст* г- со © ч*	ч* ч* ч* со со	СО СО со СО СО	со со сч сч сч	сч сч сч сч сч	сч сч сч сч сч
ст» сч г— гх. — ОО С- хф со —*	— О СО СО О сх. хф — О* ©	N л	О СО © ч* со со	СО Г- СЧ со СЧ — —1 о о	ст» ip со о г- О» О* О* СТ» Q0	хф со О хф СО 00 ю щ со —
ст* г. © © ©	Ч* ч* Ч" со со	со со СО СО СО	СО СО СО со со	сч сч сч сч сч	сч сч сч сч сч
СО г— СЧ — со О СО СО 00 СЧ	© хф О О хф об СО СО — СТ»	о О* СТ» — СО 00 © © © ч*	с^. — со —. ь- со СО СЧ СЧ —	2S888	ОО О СО гх, сч СТ» 00 со хф СО
О Г- СО со ю	Ч* Ч* Ч* ч* со •	СО СО СО СО СО	со со СО СО СО	СО СО СО СО СО	сч см сч сч сч
со оо СЧ —- со — C1N (7) С*3	хф СО СТ) СТ» СО СП со со — о	СТ) ОО ОО о сч ОО Гх. © со ©	<О О 42 О со ХГ ф со со сч	сч со ю сч g	СХ.ОСЧСО — О оО Гх- Щ хф
© г*х © © ©	хф хф ч* ч* ч*	СО СО СО СО СО	СО СО СО СО СО	со со со' СО со	со сч сч сч сч
.29 .10 .84 .03 .47	.06 .74 .50 ,30 .14	О СТ» СТ» —< ср О 00 Г» Г- ©	со _ U0 >-« СО to Ю 'Ф хг СО	СЧ СТ» со СО о со сч сч сч сч	(х-осчср — — О* О0 to in
о оо со со to	ю ч* ч* ч* ч*	хф СО со со со	СО СО СО СО СО	со со со со со	со сч сч сч сч
©©ст*© — со* — © О оо со со ю	О СТ* хф ч* со Сч оо © хф сч to ч* ч* Ч* Ч*	Хф СО СО хф *"• — © О* СО Г- хф ч* со со со	О V о*ч<о г- со ю to to СО СО СО СО СО	(О СЧ СТ* со ср «Ф хф со со со СО СО СО СО со	О СЧ tn СТ» Хф со —« о* г- © со со сч сч сч
h-b-OlN О СО хф •—। СО ОО	о* п- сч сч СО со О 00 <О ч*	сч о о —« ч* со сч — о ст»	— to — г- 00 ОО Гх- г» <о	ср о* Ср СО О СО to to to tn	ГХ CD CM too хф СЧ -х СТ) оо
о оо Г- со © т—	© © ч* ч* ч*	Ф ч* ч* ч* со	СО СО СО СО СО	co co CO CO CO	СО со со сч сч
г- 1О СО СО СО сл с~» ч* со О О 00 Г- со со	ч> сч © СО СТ) СО со о оо со © © © хф хф	<О Ч* Ч" to г» ЮЧСОСЧ — Ч* ч* Ч" ч ч*	О 5 О)^ О  о СТ» СТ» СТ» ЧГ ЧТ со со со	42 сч oo tn co ОО ОО Г. r. r* co co co co co	О —« Хф гх. см Г- tn СО — о со со со со со
сп © © —* сч CO—CQ О хф	СТ» гх. —« — ч* Ст) СО хф сч о	СТ) - с^- Ор О 00 Ь» <О io to	со г- —-со сч чг СО со сч сч	CO Хф — C> «ф x— — —«о о	сч со ио оо сч О со <о Хф со
—’ ст» г-1" со	© © to to ©	ч ч* ч» ч* ч	<ф чг «г Чф чг	хф хф хф ХГ Хф	Хф со со со со
ср оо СО СТ» СТ* О г— ч* ю, ст»	© СЧ © хф © © сч ст» Г- ©	сч ст» оо ст» ~ Ч1 сч —о о	г— сч со сч СТ» ОО 00 г*- г»	Ср -ф О Гч Хф со со to tr и:	— — со tn «о to со — ст> г-
СЧ О* QOC-. со	со со to ю to	Ю to ю ю ю	чф чГ чГ чф Чф	Хф хф хф хф хф	Хф Хф хф СО СО
СЧ СО СО сч Q)1 СТ» Ю СО О	СР — СО О —• © СЧ। Ст) to	<о со — — со со сч —> о ст»	ю °О сч со —• 00 Г- СО со	Гч со о» ю сч in to Хф хф Хф	СТ»ООООСТ> — СО — СТ» Сх. to
СО О СТ» 00 оо	г- г- со со со	со со со <о to	*л ю ю т tn	tn to m tn in	tn tn хф хф хф
СО сО СО СО СО СЧ Г- СЧ СЧ со	хф © Ср С*. © О СО СО Q QO	оо со О О* QO СО to ч сч —	о сч ю др сч — О О* оо со	«х» сч CO Хф о Гх Г- to со СО	© — до ш со Ю СО о оо ©
СО со сч — о	О СТ» Ст) СТ» оо	00 со ОО 00 оо	со оо г- г- г»	Г» С*“ Г» Г- г«	ГХ. (X- Гх. © ©
to со г-~ оо СТ)	о — сч со ч*	to СО Г- 00 ст»	о — сч со чг сч сч сч сч сч	со СО Г- 00 ст* сч сч сч сч сч	О О О О о СО Хф © см о
V
ж
а
я
ST
V
31
X
о.
С
972
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.6. Значения 100ф%-ных точек tq(v) распределения Стьюдента с
I/ степенями свободы.
V	0*0.4 2Q—0.8	0.25 0.5	о. 1 0. 2	0.05 0. 1	0.025 0.05	0.0! 0. 02	0.005 0.01	0.0025 0.005
1	0,325	1 .000	3,078	6,314	12,706	31.821	63.657	127.32
2	289	0,816	1,886	2,920	4,303	6,965	9.925	14,089
3	277	765	1 ,638	2,353	3,182	4,541	5,841	7,453
4	271	741	1.533	2.132	2,776	3,747	4,604	5.598
5	0,267	0,727	1,476	2.015	2.571	3,365	4,032	4,773
6	265	718	1 .440	1,943	2.447	3,143	3.707	4,317
7	263	711	1,415	1 .895	2,365	2,998	3,499	4.029
8	262	706	1 .397	1,860	2,306	2,896	3,355	3.833
9	261	703	1.383	1,833	2.262	2.821	3,250	3,690
10	0.260	0,700	1,372	1,812	2.228	2,764	3,169	3.581
11	260	697	1,363	1,796	2,201	2,718	3,106	3,497
12	259	695	1,356	1 .782	2,179	2,681	3,055	3,428
13	259	694	1,350	1,771	2,160	2,650	3,012	3.372
14	258	692	1,345	1,761	2.145	2,624	2.977	3,326
15	0,258	0,691	1,341	1.753	2,131	2,602	2,947	3.286
16	258	690	1.337	1,746	2,120	2,583	2,921	3,252
17	257	689	1,333	1,740	2,110	2,567	2,898	3.222
18	257	688	1,330	1,734	2,101	2.552	2,878	3,197
19	257	688	1,328	1,729	2,093	2,539	2,861	3,174
20	0.257	0,687	1.325	1,725	2,086	2,528	2,845	3, 153
21	257	686	1,323	1,721	2.080	2,518	2.831	3. 135
22	256	686	1,321	1,717	2,074	2,508	2,819	3.119
23	256	685	1,319	1,714	2,069	2,500	2,807	3,104
24	256	685	1.318	1,711	2,064	2,492	2,797	3,091
25	0,256	0,684	1,316	1,708	2,060	2,485	2,787	3,078
26	256	684	1 ,315	1,706	2,056	2,479	2,779	3,067
27	256	684	1,314	1,703	2,052	2,473	2,771	3.057
28	256	683	1,313	1,701	2,048	2,467	2,763	3,047
29	256	683	1,311	1,699	2,045	2,462	2,756	3,038
30	0,256	0,683	1,310	1,697	2,042	2,457	2,750	3.030
40	255	681	1,303	1,684	2,021	2,423	2.704	2,971
60	254	679	1.296	1,671	2,000	2,390	2,660	2,915
120	254	677	1,289	1,658	1,980	2,358	2,617	2,860
оо	253	674	1,282	1,645	1,960	2,326	2,576	2,807
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
973
Таблица П1.7. Преобразование Фишера (z-преобразование) выборочного коэф-
фициента корреляции г (г = arcthr).
г	, 000	, 002	,004	.006	.008 1	г	, 000	,002	,004	,006	,008
0,00	0000	0020	0040	0060	0080	0,50	5493	5520	5547	5573	5600
1	0100	0120	0140	0160	0180	1	5627	5654	5682	5709	5736
2	0200	0220	0240	0260	0280	2	5763	5791	5818	5846	5874
3	0300	0320	0340	0360	0380	3	5901	5929	5957	5985	6013
4	0400	0420	0440	0460	0480	4	6042	6070	6098	6127	6155
0,05	0500	0520	0541	0561	0581	0,55	6184	6213	6241	6270	6299
€	0601	0621	0641	0661	0681	6	6328	6358	6387	6416	6446
7	0701	0721	0741	0761	0782	7	6475	6505	6535	6565	6595
8	0802	0822	0842	0862	0882	8	6625	6655	6685	6716	6746
9	0902	0923	0943	0963	0983	9	6777	6807	6838	6869	6900
0,10	1003	1024	1044	1064	1084	0,60	6931	6963	6994	7026	7057
1	1104	1125	1145	1165	1186	1	7089	7121	7153	7185	7218
2	1206	1226	1246	1267	1287	2	7250	7283	7315	7348	7381
3	1307	1328	1348	1368	1389	3	7414	7447	7481	7514	7548
4	1409	1430	1450	1471	1491	4	7582	7616	7650	7684	7718
0,15	1511	1532	1552	1573	1593	0,65	7753	7788	7823	7858	7893
6	1614	1634	1655	1676	1696,	6	7928	7964	7999	8035	8071
7	1717	1737	1758	1779	1799 (	7	8107	8144	8180	8217	8254
8	1820	1841	1861	1882	1903	8	8291	8328	8366	8404	8441
9	1923	1944	1965	1986	2007	9	8480	8518	8556	8595	8634
0,20	2027	2048	2069	2090	2111	0,70	8673	8712	8752	8792	8832
1	2132	2153	2174	2195	2216	1	8872	8912	8953	8994	9035
2	2237	2258	2279	2300	2321	2	9076	9118	9160	9202	9245
3	2342	2363	2384	2405	2427	3	9287	9330	9373	9417	9461
4	2448	2469	2490	2512	2533	4	9505	9549	9594	9639	9684
0.25	2554	2575	2597	2618	2640	0,75	0,973	0,978	0,982	0,987	0,991
6	2661	2683	2704	2726	2747	6	0,996	1,001	1,006	1,011	1,015
7	2769	2790	2812	2833	2855	7	1,020	1,025	1,030	1,035	1,040
8	2877	2899	2920	2942	2964	8	1,045	1,050	1,056	1,061	1,066
9	2986	3008	3029	3051	3073	9	1.071	1,077	1,082	1,088	1,093
0,30	3095	3117	3139	3161	3183	0,80	1,099	1,104	1,110	1,116	1,121
1	3205	3228	3250	3272	3294	1	1,127	1,133	1,139	1,145	1,151
2	3316	3339	3361	3383	3406	2	1,157	1,163	1,169	1,175	1,182
3	3428	3451	3473	3496	3518	3	1,188	1,195	1,201	1,208	1.214
4	3541	3564	3586	3609	3632	4	1 ,221	1,228	1,235	1,242	1,249
0,35	3654	3677	3700	3723	3746	0,85	1,256	1,263	1,271	1,278	1,286
6	3769	3792	3815	3838	3861	6	1,293	1,301	1.309	1,317	1,325
7	3884	3907	3931	3954	3977	7	1,333	1,341	1,350	1,358	1,367
8	4001	4024	4047	4071	4094	i 8	1,376	1,385	1,394	1,403	1,412
9	4118	4142	4165	4189	4213	I 9	1,422	1,432	1,442	1,452	1,462
974
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение табл. П .7
г	.000	, 002	. 004	.006	,008	г	.000	, 002	. 004	, 006	.008
0,40	4236	4260	4284	4308	4332	0,90	1.472	1,483	1,494	1.505	1,516
1	4356	4380	4404	4428	4453	1	1,528	1,539	1,551	1,564	1.576
2	4477	4501	4526	4550	4574	2	1,589	1,602	1,616	1,630	1,644
3	4599	4624	4648	4673	4698	3	1.658	1,673	1,689	1 .705	1,721
4	4722	4747	4772	4797	4822	4	1,738	1,756	1,774	1,792	1,812
0,45	4847	4872	4897	4922	4948	0,95	1.832	1,853	1,874	1 ,897	1 ,921
6	4973	4999	5024	5049	5075	6	1.946	1 .972	2,000	2,029	2,060
7	5101	5126	5152	5178	5204	7	2,092	2,127	2,165	2,205	2.249
8	5230	5256	5282	5308	5334	8	2,298	2,351	2,410	2,477	2,555
9	5361	5387	5413	5440	5466	9	2,647	2.759	2,903	3,106	3,453
г	,000	,002	,004	,006	,008	|	,000	,002	.004	,006	,008
Примеры.
1.	Дано г = 0,206. Определить z = arc th 0,206.
Находим (в левом столбце таблицы) строку, соответствующую г =
= 0,20. Чтобы получить заданное значение г, к 0,20 надо прибавить
0,006, а потому искомое число находится (в этой строке) в столбце, рас-
положенном под 0,006. Итак, z = arc th 0,206 = 0,2090.
2.	Дано г — —0,515. Определить z = arcth (—0,515).
Находим (в левом столбце таблицы) строку, соответствующую
г = 0,51. Чтобы получить значение г = 0,515, к 0,51 надо прибавить
0,005, а потому arc th 0,515 находится как среднее арифметическое двух
чисел данной строки, расположенных в столбцах, соответствующих
верхним индексам 0,006 и 0,004, т. е.
arc th 0,515 =
0,57094-0,5682
2
0,56955.
Соответственно z = arc th (—0,515) = —arcth 0,515 = —0,56955.
3.	Дано z = 0,8752. Определить r = th z.
Находим в таблице число, равное 0,8752, и определяем, какому
значению г оно соответствует. В нашем случае г = 0,704.
Примечание. В тех случаях, когда в таблице не найдется
в точности заданного числа, берут два приближенных (ближайших к не*
му) значения — с недостатком н с избытком. Искомое значение г бу-
дет лежать между двумя значениями гх и га, соответствующими этим
приближенным величинам z.
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
975
Таблица П1.8. Верхняя граница доверительного интервала для истинного зна-
чения коэффициента корреляции при условии отсутствия ли-
нейной корреляционной связи (при доверительной вероятности
Р = 1 - 2Q).
п — 2	Q					
	0.00	0,020	0,01	0,005	0.0025	0,0005
1	0,9877	0.92692	0,92507	0,93877	0.9*692	0,9»877
2	9000	9500	9800	9*000	9*500	9*000
3	805	878	9343	9587	9740	9*114
4	729	811	882	9172	9417	9741
5	669	754	833	875	9056	9509
6	0,621	0,707	0,789	0,834	0,870	0,9249
7	582	666	750	798	836	898
8	549	632	715	765	805	872
9	521	602	685	735	776	847
10	497	576	658	708	750	823
И	0,476	0,553	0,634	0,684	0,726	0,801
12	457	532	612	661	703	780
13	441	514	592	641	683	760
14	426	497	574	623	664	742
15	412	482	558	606	647	725
16	0.400	0,468	0,543	0,590	0,63!	0,708
17	389	456	529	575	616	693
18	378	444	516	561	602	679
19	369	433	503	549	589	665
20	360	423	492	537	576	652
25	0,323	0,381	0,445	0,487	0.524	0,597
30	296	349	409	449	484	554
35	275	325	381	418	452	519
40	257	304	358	393	425	490
45	243	288	338	372	403	465
50	0.231	0,273	0,322	0,354	0,384	0,443
60	211	250	295	325	352	408
70	195	232	274	302	327	380
80	183	217	257	283	307	357
90	173	205	242	267	290	338
100	164	195	230	254	276	321
Примечание. Верхний индекс (2,3 н т. д.) над цифрой 9 оз"
начнет, что эта цифра занимает первые 2,3 и т. д. разряда десятичной
дроби. Например, 0,9*692 = 0,9999692.
Пример. Если мы оцениваем корреляционную связь по п = 20
наблюдениям, то при доверительной вероятности Р = 0,95 (т. е. при
2Q = 0,05) значение коэффициента корреляции, не превосходящее по
абсолютной величине 0,444, еще не говорит о статистической значимости
этой корреляционной связи (т. е. о том, что истинное значение
коэффициента корреляции г отлично от нуля).
976
И 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.9.
Проверка статистической значимости корреляционной связи
с помощью рангового коэффициента корреляции Спирмэна т(5)
п*	а 4	л кз 5	л	=>6	л «= 7 л	л = 8	л=9	л»= 1 0
sc	Q	SC Q	sc	Q	SC Q	Q	Q	SC	Q
12	0,458	22 0,475	50	0,210	74 0,249	108 0,250	156 0,218	208 0,235
14	375	24	392	52	178	78	198	114	195	164	168	218	184
16	208	26 342	54	149	82	151	120	150	172	125	228	139
18	167	28 258	56	121	86	118	126	108	180 089	238	102
20	042	30 225	58	088	90	083	132	076	188 060	248	072
		32 0,175	60	0,068	94 0,055	138 0,048	196 0,038	258 0.048
		34	117	62	051	98 033	144	029	204	022	268	030
		36	067	64	029	102	017	150	014	212	011	278	017
		38 042	66	017	106 0062	156 0054	220 0041	288	0087
		40 0083	68	0083	110 0014	162 ООН	228 0010	298	0036
			70	0,0014				308 0.001
20		40	. 70		112	168	240	330
Таблица П1.10.
Проверка статистической значимости корреляционной связи
с помощью рангового коэффициента корреляции Кендалла т(К>
	п				SK	л		
	4	5	8	9		6	7	10
0	0,625	0.592	0,548	0,540	1	0,500	0,500	0,500
2	375	408	452	460	3	360	386	43!
4	167	242	360	381	5	235	281	364
6	042	117	274	306	7	136	191	300
8		042	199	238	9	068	119	242
10		0,0083	0,138	0,179	11	0,028	0,068	0,190
12			089	130	13	0083	035	146
14			054	090	15	0014	015	108
16			031	060	17		0054	078
18			016	038	19		0014	054
20			0,0071	0,022	21		0,0002	0,036
22			0028	012	23			023
24			0009	0063	25			014
26			0002	0029	27			0083
28				0012	29			0046
30				0,0004	31			0,0023
					33			ООП
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
977
Таблица П1.11*. Вероятности того, что критическая статистика проверки
статистической значимости выборочной величины коэффи-
циента конкордации IV(m) достигнет или превзойдет та-
бличное значение S (при п = 3 сравниваемых объектах).
	т = 2	т — 3	т=4	5	т=6	т=7	т= 8	nt = 9	/Я== 1 0
0	1,000	1,000	1,000	.000	1,000	1,000	1,000	1,000	1,000
2	0,833	0,944	0,931	0,954	0.956	0.964	0,967	0,971	0.974
6	0,500	0.528	0,653	0,691	0.740	0,768	0.794	0,814	0,830
8	0,167	0,361	0,431	0,522	0.570	0,620	0.654	0,685	0,710
14		0,194	0,273	0,367	0,430	0.486	0,531	0,569	0,601
18		0.028	0.125	0,182	0,252	0,305	0,355	0,398	0,436
24			0,069	0,124	0,184	0,237	0,285	0,328	0,368
26			0^042	0,093	0,142	0,192	0,236	0,278	0,316
32			0^0046	0.039	0,072	0,112	0.149	0,187	0,222
38				0,024	0,052	0,085	0,120	0,154	0,187
42				0,0085	0.029	0,051	0,079	0,107	0,135
50				0,0’77	0,012	0,027	0,047	0,069	0.092
54					0,0081	0,021	0,038	0,057	0.078
56					0,0055	0,016	0,030	0,048	0,066
62					0,0017	0,0084	0,018	0,031	0,046
72					0,043	0,0036	0,0099	0 019	0.030
74						0,0027	0,0080	0,016	0,026
78						0,0012	0,0048	0,010	0,018
86						0,0*32	0.0024	0.0060	0,012
96						0,0*32	0,0011	0,0035	0,0075
98						0,0*21	0,0’86	0.0029	0,0063
104							0,0*26	0,0013	0,0034
114							0,0*61	0.0*66	0,0020
122							0,0*61	0,0*35	0,0013
							0,0*61	0.0*20	0.0*83
126							0,0*36	0,0*97	0,0*51
128									
134								0,0*54	0,0*37
146								0,0*11	0,0*18
150								0,0*11	0,0*11
152								0,0*11	0,0*85
158								0,0*11	0,0*44
162								0,0*60	0,0*20
168									0,0*11
182									0,0*21
200									0.0’99
978	П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение
Вероятность того, что данное значение <$ будет достигнуто
как превзойдено* для п—4, т=3 н т®=5
3	тявЗ		3	гпс 5
1	1,000	1,000	61	0,055
3	0,958	0,975	65	0,044
5	0,910	0,944	67	0,034
9	0,727	0,857	69	0,031
11	0,608	0,771	73	0,023
13	0,524	0,709	75	0,020
17	0,446	0,652	77	0,017
19	0,342	0,561	81	0,012
21	0,300	0,521	83	0,0087
25	0.207	0,445	85	0,0067
27	0,175	0,408	89	0,0055
29	0,148	0,372	91	0.0031
33	0,075	0,298	93	0,0023
35	0,054	0,260	97	0,0018
37	0,033	0,226	99	0,0016
41	0,017	0,210	101	0,0014
43	0,0017	0,162	105	0,0364
45	0,0017	0,141	107	0,(НЗЗ
49		0,123	109	0,0321
51		0,107	113	0,0314
53		0.093	117	0,0*48
57		0,075	125	0,0530
59		0,067		
Продолжение
Вероятность того, что данное значение S будет достигнуто
май превзойдено, для п==4 в т=2, ю=»4 н /п«=6
S	т»2		т-6	S	
0	1,000	1,000	1,000	82	0,035
2	0,958	0,992	0,996	84	0,032
4	0,833	0,928	0,957	86	0,029
6	0,792	0,900	0,940	88	0,023
8	0,625	0,800	0,874	90	0,022
10	0,542	0,754	0,844	94	0,017
12	0,458	0,677	0,789	96	0,014
14	0,375	0,649	0,772	98	0,013
16	0,208	0,524	0,679	100	0,010
18	0,167	0,508	0,668	102	0,0096
20	0,042	0,432	0,609	104	0,0085
22		0,389	0,574	106	0.0073
24		0,355	0,541	108	0,0061
to — — — — — OOoCTi^tOOOiTi^WO	(л
ооооооооо — *- 2? ri 9° °°	to'cd q о ООЮ(7)УД“А^«)5о ЮООО—СЛ д- tooooo	2 В- ы
Ji.A.COCJCOWCOtObQtOtO ЮОООС» д (О осой д ю	Сл
ооооооооооо ММ WW Д 4*. А. 4» сл СЛ О> СлсОеО4к.фСЭ*^1СОСЛС04к. со—0*ЦСПКЭСЛСлЭСОСЛсО	9 И
Ологспслслспслслд'Д'^ь. ДЮООЭО>ДМООо(ЛЛ>	И
ооооооооооо 	4	*	*	«	v яр	•	*	* OOQOO — •— — — N3K3 SC 219S 45	- со CnO>COOoS*J“*IWN3WO	в и ы
<Г>аооОэх1-^^^^0т ОО'МОООО^ДМООо^	<л
ооооооооооо 2§88882288S s8g§aau"j»“®	т — 3
о
Qj
о
ь
X
<ъ
%
Е
ГЬ
OOOO^bjOOOOAbJOOCD^WOOsClAbJOOOO^^WOW
OOQoOpPООоpppppppppppооооо
З *§ о 3 3 В "2 '2 2 *8 "8 8 8 8 "8 2 S X сл <5 о 1о
-qy3<DlC>^tOtOO»<5»tO.fr‘t£>Q0Q)b0.UQ0-4.UCn—OOOOK34*
МДДДСПЧ^ЮЮ
*- ьо
05-'4000,>СЛС(ЛСЛСЛЛ4>к4*.£ООЭСОМСОКЭЮКЭЬО’“"“’—’‘“
со д юо» amowo^o&G) дюоаомооо сп а о
Ч ‘г7? <г<г<г«г<г2<?2<г,?§§§§228
— to 00 — •— Ю 4*> О С0 ♦— КЭЮКЗС*Э.КСП*4ООц!>^ьэЬэЙ)СоХсл
С»э4кОюаэ»КОЬЭСЛЬЭЬ0«Д>000>О&1С0-ЧОслОС*Э00С*>О'Ч
Сл
э
и
to
9
и
3
в
§
Й
*
<9
X
X
а
я
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ	979
980
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.116. Критические значения статистики S при уровне значимости
а = 0,05 для проверки статистической значимости выбороч-
ного значения коэффициента конкордации W'(m).
m	n					Дополнительные значения для п = 3	
	3	4	5	6	7	m	S
3			64,4	103,9	157,3	9	54,0
4		49,5	88,4	143,3	217,0	12	71,9
5		62,6	112,3	182,4	276,2	14	83,8
6		75,7	136,1	221,4	335,2	16	95,8
8	48,1	101,7	183,7	299,0	453,1	18	107,7
10	60,0	127,8	231,2	376,7	571,0		
15	89,8	192,9	349,8	570,5	864,9		
20	119,7	258,0	468,5	764,4	1158,7		
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
981
Таблица П1.12а. Значения статистик d;, и dy критерия Дербина-Уотсона при
уровне значимости а = 0,05 (n-число наблюдений, р-число
объясняющих переменных).
п													P = 4			P = 5	
	dL	dU	,d4	dU	dL	dU	dL	dU	dL	dU
15	1,08	1,36	0,95	1,54	0,82	1,75	0,69	1,97	0,56	2,21
16	1,10	1,37	0,98	1,54	0,86	1,73	0,74	1,93	0,62	2,15
17	1,13	1,38	1,02	1,54	0,90	1,71	1,78	1,90	0,67	2,10
18	1,16	1,39	1,05	1,53	0,93	1,69	0,82	1,87	0,71	2,06
19	1,18	1,40	1,08	1,53	0,97	1,68	0,85	1,85	0,75	2,02
20	1,20	1,41	1,10	1,54	1,00	1,68	0,90	1,83	0,79	1,99
21	1,22	1,42	1,13	1,54	1,03	1,67	0,93	1,81	0,83	1,96
22	1,24	1,43	1,15	1,54	1,05	1,66	0,96	1,80	0,86	1,94
23	1,26	1,44	1,17	1,54	1,08	1,66	0,99	1,79	0,90	1,92
24	1,27	1,45	1,19	1,55	1,10	1,66	1,01	1,78	0,93	1,99
25	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89
26	1,30	1,46	1,22	1,55	1,14	1,65	1,06	1,76	0,98	1,88
27	1,32	1,47	1,24	1,56	1,16	1,65	1,08	1,76	1,01	1,86
28	1,33	1,48	1,26	1,56	1,18	1,65	1,10	1,75	1,03	1,85
29	1,34	1,48	1,27	1,56	1,20	1,65	1,12	1,74	1,05	1,84
30	1,35	1,49	1,28	1,57	1,21	1,65	1,14	1,74	1,07	1,83
31	1,36	1,50	1,30	1,57	1,23	1,65	1,16	1,74	1,09	1,83
32	1,37	1,50	1,31	1,57	1,34	1,65	1,18	1,73	1,11	1,82
33	1,38	1,51	1,32	1,58	1,26	1,65	1,19	1,73	1,13	1,81
34	1,39	1,51	1,33	1,58	1,27	1,65	1,21	1,73	1,15	1,81
35	1,40	1,52	1,34	1,58	1,28	1,65	1,22	1,73	1,16	1,80
36	1,41	1,52	1,35	1,59	1,29	1,65	1,24	1,73	1,18	1,80
37	1,42	1,53	1,36	1,59	1,31	1,66	1,25	1,72	1,19	1,80
38	1,43	1,54	1,37	1,59	1,32	1,66	1,26	1,72	1,21	1,79
39	1,43	1,54	1,38	1,60	1,33	1,66	1,27	1,72	1,22	1,79
40	1,44	1,54	1,39	1,60	1,34	1,66	1,29	1,72	1,23	1,79
45	1,48	1,57	1,43	1,62	1,38	1,67	1,34	1,72	1,29	1,78
50	1,50	1,59	1,46	1,63	1,42	1,67	1,38	1,72	1,34	1,77
55	1,53	1,60	1,49	1,64	1,45	1,68	1,41	1,72	1,38	1,77
60	1,55	1,62	1,51	1,65	1,58	1,69	1,44	1,73	1,41	1,77
65	1,57	1,63	1,54	1,66	1,50	1,70	1,47	1,73	1,44	1,77
70	1,58	1,64	1,55	1,67	1,52	1,70	1,49	1,74	1,46	1,77
75	1,60	1,65	1,57	1,68	1,54	1,71	1,51	1,74	1,49	1,77
80	1,61	1,66	1,59	1,69	1,56	1,72	1,53	1,74	1,51	1,77
85	1,62	1,67	1,60	1,70	1,57	1,72	1,55	1,75	1,52	1,77
90	1,63	1,68	1,61	1,70	1,59	1,73	1,57	1,75	1,54	1,78
95	1,64	1,69	1,62	1,71	1,60	1,73	1,58	1,75	1,56	1,78
100	1,65	1,69	1,63	1,72	1,61	1,74	1,59	1,76	1,57	1,78
982
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.126. Значения статистик и d(j критерия Дербина-Уотсона при
уровне значимости а = 0,05 (n-число наблюдений, р-число
объясняющих переменных).
	к1 -	= 1	fc'	= 2		= 3	fc' =	= 4	k'	= 5
п	dL	du	dL	dU	dL	du	dL	dU	dL	dU
15	0,81	1,07	0,70	1,25	0,59	1,46	0,49	1,70	0,39	1,96
16	0,84	1,09	0,74	1,25	0,63	1,44	0,534	1,66	0,44	1,90
17	0,87	1,10	0,77	1,25	0,67	1,43	0,57	1,63	0,48	1,85
18	0,90	1,12	0,80	1,26	0,71	1,42	0,61	1,60	0,52	1,80
19	0,93	1,13	0,83	1,26	0,74	1,41	0,65	1,58	0,56	1,77
20	0,95	1,15	0,86	1,27	0,77	1,41	0,68	1,57	0,60	1,74
21	0,97	1,16	0,89	1,27	0,80	1,41	0,72	1,55	0,63	1.71
22	1,00	1,17	0,91	1,28	0,83	1,40	0,75	1,54	0,66	1,69
23	1,02	1,19	0,94	1,29	0,86	1,40	0,77	1,53	0,70	1,67
24	1,04	1,20	0,96	1,30	0,88	1,41	0,80	1,53	0,72	1,66
25	1,05	1,21	0,98	1,30	0,90	1,41	0,83	1,52	0,75	1,65
26	1,07	1,22	1,00	1,31	0,93	1,41	0,85	1,52	0,78	1,64
27	1,09	1,23	1,02	1,32	0,95	1,41	0,88	1,51	0,81	1,63
28	1,10	1,24	1,04	1,32	0,97	1,41	0,90	1,51	0,83	1,62
29	1,12	1,25	1,05	1,33	0,99	1,42	0,92	1,51	0,85	1,61
30	1,13	1,26	1,07	1,34	1,01	1,42	0,94	1,51	0,88	1,61
31	1,15	1,27	1,08	1,34	1,02	1,42	0,96	1,51	0,90	1,60
32	1,16	1,28	1,10	1,35	1,04	1,43	0,98	1,51	0,92	1,60
33	1,17	1,29	1,И	1,36	1,05	1,43	1,00	1,51	0,94	1,59
34	1,18	1,30	1,13	1,36	1,07	1,43	1,01	1,51	0,95	1,59
35	1,19	1,31	1,14	1,37	1,08	1,44	1,03	1,51	0,97	1,59
36	1,21	1,32	1,15	1,38	1,10	1,44	1,04	1,51	0,99	1,59
37	1,22	1,32	1,16	1,38	1,11	1,45	1,06	1,51	1,00	1,59
38	1,23	1,33	1,18	1,39	1,12	1,45	1,07	1,52	1,02	1,58
39	1,24	1,34	1,19	1,39	1,14	1,45	1,09	1,52	1,03	1,58
40	1,25	1,34	1,20	1,40	1,15	1,46	1,10	1,52	1,05	1,58
45	1,29	1,38	1,24	1.42	1,20	1,48	1,16	1,53	1Д1	1,58
50	1,32	1,40	1,28	1,45	1,24	1,49	1,20	1,54	1,16	1,59
55	1,36	1,43	1,32	1,47	1,28	1,51	1,25	1,55	1,21	1,59
60	1,38	1,45	1,35	1,48	1,32	1,52	1,28	1,56	1,25	1,60
65	1,41	1,47	1,38	1,50	1,35	1,53	1,31	1,57	1,28	1,61
70	1,43	1,49	1,40	1,52	1,37	1,55	1,34	1,58	1,31	1,61
75	1,45	1,50	1,42	1,53	1,39	1,56	1,37	1,59	1,34	1,62
80	1,47	1,52	1,44	1,54	1,42	1,57	1,39	1,60	1,36	1,62
85	1,48	1,53	1,46	1,55	1,43	1,58	1.41	1,60	1,39	1,63
90	1,50	1,54	1,47	1,56	1,45	1,59	1,43	1,61	1,41	1,64
95	1,51	1,55	1,49	1,57	1.47	1,60	1,45	1,62	1,42	1,64
100	1,52	1,56	1,50	1,58	1,48	1,60	1,46	1,63	1,44	1,65
ПРИЛОЖЕНИЕ 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ
МАТРИЧНОЙ АЛГЕБРЫ
Все модели и методы эконометрики, эксплуатирующие понятия и при-
емы многомерного статистического анализа, — а это и классификация
многомерных данных (гл. 12), и всевозможные конструкции факторного
анализа, включая метод главных компонент (гл. 13), и множественная ре-
грессия (гл. 15), и, конечно, системы одновременных уравнений (гл. 14 и
17), и все, что связано с решением систем алгебраических уравнений (а
сюда относятся и корреляционный анализ, и анализ временных рядов), —
требуют, для своего компактного и эффективного описания и анали-
за, использования аппарата матричной алгебры. И если при описании
этих моделей мы еще, как правило, можем обойтись без такого аппара-
та (правда, за счет утомительных и чрезвычайно громоздких выкладок и
выражений, приводящих к покомпонентной записи требуемых соотноше-
ний), то при анализе их свойств и выводе связанных с этим мате-
матических результатов без использования методов линейной алгебры
мы вынуждены были бы в ряде ситуаций просто отступить, не добившись
желаемого.
Поэтому специалисту (или студенту, готовящемуся стать таковым),
предполагающему всерьез работать с эконометрическими методами и мо-
делями, необходимо внутренне настроиться на неизбежность расходования
некоторого времени и интеллектуальных усилий на овладение определен-
ным минимумом сведений из матричной алгебры.
При описании этих сведений мы будем следовать обозначениям, при-
нятым в данном учебнике, а именно: буквы, набранные жирным шрифтом,
будут обозначать матрицы, а буквы прописные будут использоваться для
обозначения векторов (представляющих собой, правда, важный частный
случай тех же матриц). Доказательства приводимых здесь фактов из ли-
нейной алгебры будут, как правило, опускаться.
П 2.1. Виды матриц и действия с ними
Матрицей называется прямоугольная таблица чисел (элементов)
вида
(ап fl12	fllm \
°22 • • • °2”* .	(П2.1)
ап1 ап2 • •  апт'
984
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
В общем обозначении элемента aig матрицы А первый нижний индекс (t)
указывает номер той строки, а второй нижний индекс (j) — номер того
столбца, на пересечении которых находится этот элемент. Если матрица
А содержит пт элементов, расположенных на п строках и т столбцах, то
говорят, что .мы имеем п х т-матрицу А или матрицу А размерности
пхт.
Квадратной матрицей называется матрица, у которой число
строк равно числу столбцов^ т.е. пх п — матрица (при любом целом
п > 1). Элементы ац,Ц22,  ..,аПп квадратной матрицы образуют ее глав-
ную диагональ.
Среди квадратных матриц выделим:
•	диагональную матрицу D, у которой все элементы, кроме элементов,
стоящих на главной диагонали, равны нулю, т. е.
(dn 0 0 ... О 0 \
О ^22 0...0	0 | Д' t А А АХ
= diag(dn,d22,..-,dnn);
О 0 0 ... О dnn /
заметим, что ковариационная матрица Е = (atJ) любой последо-
М /-(2) r(n)	X
вательности f	взаимно не коррелированных случай-
ных величин является диагональной, т. к. <7^ = Е	-
= 0 при любых t / j.
•	единичную матрицу 1п, которая является частным случаем п х п диа-
гональной матрицы, поскольку все ее диагональные элементы равны
единице:
/1	0	0	...	0	0\
т | 0	1	о	...	о	о |
\0 О О ... 0 1/
нижний индекс п определяет размерность матрицы, и в тех случаях,
когда эта размерность очевидна из контекста, он может опускаться.
•	симметрическую (симметричную) матрицу, а именно такую матри-
цу, у которой элементы, симметрично расположенные относительно
главной диагонали, равны между собой, т.е.	для всех i,
j = 1,2, ...,п; заметим, что всякая ковариационная матрица S =
(ff.j) является симметрической по определению, т. к. = Е[(^	-
Ef(i))(£u) - Ef°’)] = Е[«(Л - Ef°’)(f(i) - Ef(i))] =
Равенство матриц. Две матрицы А = (а^) и В = (Ьу) называются
равными, если они имеют одну и ту же размерность и если atJ == 6,j для
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
985
всех i it j. Это означает, что равные матрицы совпадают поэлементно.
Вектор-строка — это матрица размерности 1 х т (тп > 1),
т.е. матрица, состоящая из единственной строки длины т. Напри-
мер, результаты наблюдения значений р анализируемых переменных
И) (2)	(р)	с
ж1 ,х' ,...,х' на одном объекте, зарегистрированные в определенный
момент времени t, образуют вектор-столбец
,*(Л.
(П2.2)
Вектор-столбец — это матрица размерности п х 1 (n > 1), т.е.
матрица, состоящая из единственного столбца длины п. Например, ре-
зультаты наблюдения одной какой-либо переменной х^ на п статистиче-
ски обследованных объектах (или на одном объекте, но зарегистрирован-
ные в п последовательных моментов времени) можно представить в виде
вектора-столбца
(J) =
(П2.3)
Чтобы выделить эти специальные частные случаи матриц, мы бу-
дем обозначать векторы-строк и и векторы-столбцы прописными буквами
алфавита, а их компоненты — теми же самыми, но строчными буквами.
Условимся обозначать в дальнейшем вектор-строку длины тп, состо-
ящую из одних нулей, с помощью 01>т (или просто 0ш, если из контекста
ясно, что речь идет о строках). Аналогично вектор-столбец из нулей дли-
ны п будем обозначать 0яЛ (или просто 0п).
Перейдем к описанию действий над матрицами.
Транспонирование матрицы А определяется как действие, в ре-
зультате которого из А получается новая матрица АТ, строками которой
служат столбцы матрицы А, а столбцами — строки матрицы А при со-
хранении их порядка. Таким образом, первая строка матрицы А стано-
вится первым столбцом матрицы АТ, вторая строка матрицы А — вто-
рым столбцом матрицы АТ и т. д., так что (t, j)-it элемент матрицы А
становится (j,«)-m элементом матрицы АТ. Так, при построении регрес-
сионных моделей мы оперировали как с п X (р + 1)-матрицей наблюдений
986
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
объясняющих переменных
(П2.4)
так и с транспонированной (р 4- 1) X п-матрицей
1	1
(D JO
1	Х2
(р) *''(р)
1 х2
(П2.5)
Заметим, что из определении операции транспонирования и свойства
симметричности матрицы следует непосредственно, что транспонирова-
ние не меняет симметрическую матрицу, т. е. если А — симметрична, то
АТ = А и обратно: если АТ = А, то матрица А квадратна и симметрична.
Очевидно также, что последовательное двукратное применение к ма-
трице А операции транспонирования приводит к исходной матрице А, т. е.
(Ат)т = А.
Сложение двух матриц. Если А и В-матрицы одной размерности,
то можно определить новую матрицу С = А 4- В, которая будет иметь ту
же размерность, что и А и В, а ее элементы c,j определяются для всех i
и j соотношениями ctj =	4- Ьу. Заметим, что из определений операций
транспонирования и сложения непосредственно следует, что
(А + В)т = АТ + ВТ.
(П2.6)
Умножение матрицы на число. Произведение матрицы А на чи-
сло Л определяется как
А А - (Аа,,)
т. е. каждый элемент матрицы А умножается на это число.
Произведение матриц. Если число столбцов п X m-матрицы А рав-
но числу строк тп X к-матрицы В, то может быть определена операция
умножения АВ матрицы А на матрицу В (при этом говорят, что «маг
трица В умножается на матрицу А слева»). Элементы c,j такого про-
изведения С = АВ определяются для всех t = 1,2,...,п и j = 1,2,...,к
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
286
соотношениями
Qnb[j.	(П2.7)
1=1
Таким образом, элемент произведения С вычисляется как скаляр-
ное произведение t-й строки матрицы А и j-ro столбца матрицы В, т.е.
как сумма попарных произведений элементов t-й строки первой матрицы
на соответствующие (т. е. стоящие на тех же по порядку местах) элемен-
ты j го столбца второй матрицы. При этом автоматически определяется
размерность матрицы-произведения С: она будет иметь столько же строк
(п), сколько имел первый сомножитель, и столько же столбцов (А), сколько
их имел второй сомножитель.
Заметим, что при перестановке сомножителей произведение В А мо-
жет просто не существовать, но даже если оно существует (как это и
бывает в случае, если матрицы А и В — квадратные и одной размерно-
сти или если сомножители имеют размерности п х т и т х п), то, вообще
говоря, коммутативный закон для умножения матриц не имеет места,
т. е.
АВ / ВА.	(П2.8)
Отметим еще несколько полезных для эконометрических приложений
свойств произведения матриц.
Ассоциативный закон:
АВС = (АВ)С = А(ВС).	(П2.9)
Дистрибутивный закон:
А(В 4- С) = АВ + АС, (В + С)А = BA + СА. (П2.10)
Умножение на единичную матрицу: для любой п х n-матрицы А име-
ют место тождества
А1П = ^А = А.	(П2.11)
Транспонирование произведения матриц:
(А, А2... А*)т = A* A J_i... A J А^	(П2.12)
(доказывается индукцией: непосредственным сравнением элементов ма-
триц (А1Аг)Т и А^ А^ доказывается справедливость (П2.12) для случая
k = 2 и т. д.).
Произведения вида ААТ и АТ А играют заметную роль в эконометри-
ческих построениях. Так, произведение ХТХ, в котором матрица X опре-
делена соотношением (П2.4), является непременным «участником» всех
988
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
основных формул классического метода наименьших квадратов. Заме-
тим, что если А — матрица размерности n X тп, то произведение ААТ
будет иметь размерность п х п, в то время как произведение АТА — это
матрица размерности т х т. Но в любом случае произведения вида ААТ
и АТА всегда являются квадратными симметрическими матрицами.
Обратим внимание на специальный случай, когда X = (xi,x2,...,
ХП)Т — это вектор-столбец, состоящий из п элементов (или вектор-
столбец длины п). Тогда
»=1
(П2.13)
это 1 х 1-матрица, т. е. число, а
хпх1
хпх2
хгхп
х2хп
(П2.14)
3?2 1
2
Я2
это матрица размерности п х п.
Матрицы типа (П2.13) и (П2.14) играют заметную роль в регресси-
онном анализе и в системах одновременных уравнений (см. гл. 14, 15, 17).
Действительно, если в качестве компонент xt вектора X рассмотреть ре-
грессионные «невязки» у, —	— ... — 0рх\р) (i = 1,2,.. .,п), то
произведение (П2.13) даст нам сумму квадратов «невязок», которая игра-
ет важную роль в анализе точности регрессионной модели. Если же в
качестве компонент х, вектора X рассмотреть отклонения i-й объясня-
ющей переменной от своего среднего значения а№ (i = 1,2,...,р),
то произведение (П2.14) после применения к нему операции усреднения
(математического ожидания) Е даст р х р-ковариационную матрицу объ-
ясняющих переменных
Прямое (или кронекерово) произведение п X т-матрицы А и
k х / матрицы В обозначается А ® В, имеет размерность пк х ml и под-
считывается по формуле
А® В =
«нВ в12В ... а1тВ
в21В а22В ... а2тВ
ащВ впгВ • • ♦ ®пт В
(П2.15)
где правая часть представляет собой матрицу, составленную из блоков
вида a,jB. Каждый такой блок сам является матрицей и, как легко видеть,
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
989
имеет размерность к х I. Повторенные п раз по строкам, они дают общее
количество строк, равное а повторенные тп раз по столбцам, они дают
общее количество столбцов, равное ml (подробнее о матрицах блочного
типа, или о составленных матрицах, так же, как и свойствах прямого
произведения, см. ниже в п. П2.8).
Отметим, что некоторые эконометрические построения (в первую оче-
редь, связанные с вычислительными проблемами систем регрессионных
уравнений, см. гл. 17) значительно упрощаются, если использовать поня-
тие прямого (кронекерова) произведения.
Матричное дифференцирование. Достаточно полное изложение
аппарата векторного и матричного дифференциального исчисления чита-
тель найдет в книге [Magnus J.R., Neudecker Н.]1. Мы же остановимся
лишь на тех определениях и результатах, которые непосредственно ис-
пользованы в нашем учебнике.
Пусть 0 =	— пз х 1-матрица (т.е. вектор-столбец
длины т), компоненты которой играют роль неизвестных параметров
эконометрической модели, а 4(0) = (а1(0)>аз(0),... ,ап(0))Т — п х 1-
матрица (т.е. вектор-столбец длины п), компоненты который интерпре-
тируются как некоторые характеристики этой модели, зависящие от 0.
Производной п х 1-векторной функции 4(0) по т х 1-векторному
аргументу 0 называется т X п-матрица
04(0)
де
8а де) ве2	8аа(е) 9«Т(е) ёе2	• • 	8а, (О) вех 8а, (в)
0ai(6)	8аДв)	• • •	
(П2.16)
Матрицы вида (П2.16) используются, в частности, в качестве матриц
преобразований («якобианов») в теории преобразований случайных вели-
чин (см., например, п.4.4).
Рассмотрим важные для эконометрических приложений частные слу-
чаи функции 4(0):
1°. 4(0) = Х0, где X — симметрическая матрица размерности п х т.
о Тогда ^1 = ^ = Х.
2.4(0) = 0 В0, где В — симметрическая квадратная матрица размер-
ности т X т.
Тогда 9^1 =	= 20тв
1 Готовится русский перевод этой книги.
990	П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
3°. А(0) = ХТ0, где X — вектор-столбец длины т.
Тогда ^ = ^=ХТ.
П2.2. Основные числовые
характеристики квадратной
матрицы: определитель, след
Любой квадратной матрице А можно сопоставить некоторый набор ее
числовых характеристик. В данном пункте остановимся на двух из них.
Одна из таких характеристик называется определителем (детерминан-
том) матрицы А и обозначается det А или |А|, а другая определяется как
след матрицы А и обозначается tr(A).
Определитель (детерминант) п х n-матрицы А вычисляется по
формуле
det А =££... £	...anj„ (П2.17)
л=1 Ja=l
где суммирование ведется по всем возможным комбинациям различных
столбцов (т.е. по всем возможным перестановкам вторых индексов), а
i/(y’i, у2,.. .,jn) — это минимальное число инверсий (т.е. парных обменов
местами), которое надо совершить с элементами исходной перестановки
(1,2, ...,п), чтобы получить перестановку (Ь»Л»**ч Очевидно, об-
щее число слагаемых в правой части (П2.17) составит при таком опреде-
лении n-факториал (п!).
Для малых размерностей матриц это определение приводит, в част-
ности, к следующим результатам:
а)	п = 2 :	det А = det 1		<*12 1	| — <*11 <*22 — <*12<*21 i
			<<*21	<*22 )	
			(<*ii	<*12	<*13 \
б)	п — 3 :	det А = det	<*21	<*22	<*23 1
			\<*31	<*32	<*33 /
= П11<Х22аЗЗ + <*13<*21<*32 + <*12<*23<*31 — <*13<*22<*31 ~ <*11<*23<*32 — <*12<*21<*33«
Приведем здесь важнейшие свойства определителя:
1)	det(A В) = det (В А) = det А  det В;
2)	det(AA) = An det А (А — число , п — размерность матрицы А);
3)	det[diag(an,a22,..., <*nn)] — <*11<*22 * • • • * <*nnj
4)	detln = 1;
5)	det Ат = det А;
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
991
6)	det А = 0, если о матрице А есть две одинаковые строки (два оди-
наковых столбца)-,
7)	инверсия (обмен местами) двух строк (столбцов) матрицы А при-
водит к изменению знака ее определителя-,
8)	значение определителя матрицы А не изменится, если к любой
его строке (столбцу) добавить линейную комбинацию других строк
(столбцов).
Последнее свойство нуждается в пояснении. Обозначим А,. =
(ай»в«2>♦ • •»aim) — i-ую строку п х тп матрицы А. Линейной комбинацией
строк с номерами , i2,..., ik называется строка, определяемая в соответ-
ствии с правилами действий с матрицами по формуле
где At, А2, • • • >	— некоторые числа. Точно так же определяется линейная
комбинация столбцов Aj = (ai>,a2j,... ,anj)T, у = л, j2,..., ji;
9)	разложение определителя no элементам строки (или столбца).
det А = «ij( -l)*+j det А,,,
j=i
где Ajy — (п — 1) х (п — 1)-матрица, получающаяся из матрицы А
вычеркиванием из нее t-й строки и j-ro столбца. Величина detA(J-
называется минором матрицы А, а величина (—l),+j det A,j — алге-
браическим дополнением элемента а,у в матрице А. Кстати, понятие
алгебраического дополнения используется в учебнике, например, при
вычислении коэффициента детерминации R2 и частных коэффициен-
тов корреляции по корреляционной матрице R исследуемого много-
мерного признака (см. п. 11.2).
Отметим, что если квадратная матрица имеет отличный от нуля
определитель, то она называется невырожденной.
След квадратной п X n-матрицы А (обозначается tr А, от англий-
ского слова «trace» ) определяется как сумма ее диагональных элементов,
т. е.
tr А = Пц -f- а22 +••• + апп.	(П2.18)
Основные свойства следа матрицы:
(i)	tr(AB) = tr(BA);
(ii)	trln = n;
(iii)	tr(AA) = AtrA, где A — число;
(iv)	trAT = trA;
992
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
(v)	tr(A + В) = trA 4- trB;
(vi)	в качестве частного случая свойства (i) особо отметим ситуации, в
которых роль А играет вектор-столбец X = (xi,z3,. ..,гп)Т, а роль
В — л ; и хотя ни для X, ни для X след не определен, их произве-
дения ХХУ и Х^X являются квадратны миу соответственно, п х п-
и 1 х 1-матрицами и для них действует правило (1), т.е.
tr(XXT) = tr(XTJf),
где, обращаем внимание читателя, матрица X X — Х\ Ч-Яз+• •	—
это число.
Заметим, что и определитель, и след матрицы имеют четкую ве-
роятностную интерпретацию, например, когда в качестве А рассматри-
вается ковариационная матрица многомерной случайной величины
С =	В этом случае и trS^ и detS^ характеризуют
степень многомерного рассеяния значений этой случайной величины, а
det называется обобщенной дисперсией £ (см. п. 2.6.6).
П2.3. Обратная матрица и ее свойства
В операциях с числами для любого отличного от нуля числа а су-
ществует число а-1 = 1/а, которое мы называем обратным и которое
обладает тем характеристическим свойством, что аа-1 = а”1 а =1. В
матричной алгебре роль единицы, как мы видели, выполняет единичная
матрица 1п, поскольку при умножении на 1п любой квадратной матрицы
размерности п х п справа и слева эта матрица не меняется (см П2.11).
Поэтому по аналогии с алгеброй чисел определим:
• пусть А — квадратная невырожденная (т. е. det А / 0) матрица]
тогда матрица А-1 называется обратной, если АА-1 = А-1 А = I.
Можно показать, что такое определение обратной матрицы А-1 =
(a°J₽) приводит к следующей формуле для вычисления ее элементов а^р:
обр___ ( 1)’ det Aj,
a,i ~ det А
(П2.19)
где Ал — как и прежде, матрица, получающаяся из матрицы А вычер-
киванием из нее у-й строки и i-го столбца (т. е. числитель правой части
(П2.19) является алгебраическим дополнением элемента ау, в исходной ма-
трице А, или, что то же, — алгебраическим дополнением («,у)-го элемента
в транспонированной матрице АТ).
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
993
Пример П2.1. Двухпродуктовая версия статической модели
^затраты-выпуска Леонтьева. Пусть — затраты продукта i на вы-
пуск единицы продукта j (itj = 1,2). И пусть xt — общий выпуск про-
дукта i и — конечный спрос на этот продукт. Тогда уравнения, свя-
зывающие между собой введенные выше величины, будут иметь вид (в
предположении, что нет ни потерь, ни излишков продуктов):
f <*п®1 4- ai2x2 + С1 = Xi,
I <12121 4" <122 х2 + с2 — x2i
или, после приведения подобных членов,
{(1 — <*llkl — <*12^2 = с1»
— 021^1 + (1 — <*22)^2 = с2-
Запишем эту систему, используя матричные обозначения:
АХ = С,
(П2.20)
где X = (жЬ22)Т, С = (сьс2)т, а
~<*12
1 - а22
Мы хотим разрешить систему (П2.20) относительно хг и х2, т. е. опре-
делить, какое общее количество первого и второго продукта должно быть
произведено, чтобы обеспечить производственное потребление и конечный
спрос. Чтобы уединить X в уравнении (П2.20), дом нож им обе части этого
уравнения на матрицу А”1 слева:
где в соответствии с (П2.19)
А-1
1
det А
1 — «22
а21
<112
1 — <1ц
С учетом того, что det А = (1 — <хц )(1 — агг) — <*12а21> имеем:
X1 = 71 z. Vi	—V—— К1 “a22)ci 4-012С2],
(1 — «И — «22) “ в12<*21
«2 = 77 V1	—Т —	[<*21<-1 + (1 - <*11 кг] •
(1 - <*11Д1 “ <*22/ “ <*12<*21
994
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Основные свойства обратной матрицы:
1)	матрица А” для любой невырожденной матрицы А — единствен-
на;
2)	det А-1 = (det А)-1;
3)	(АТГ* = (А-1)Т;
4)	(А-1)-1 = А;
5)	(АВ)-1 = В-1А-1,
(АВС)-1 = С-1В-1А-1 и т.д.
(напомним, что все матрицы, участвовавшие в формулировке свойств
обратной матрицы, — квадратные и невырожденные).
Теперь мы можем дополнить перечень основных типов матриц, при-
веденный в п. П2.1. Введем в рассмотрение класс ортогональных матриц,
определив:
• квадратная невырожденная матрица А называется ортогональ-
нои, если А = А
Из определения ортогональной матрицы непосредственно следует, в
частности, что А А = ААТ = I. Нетрудно также вывести, что определи-
тель ортогональной матрицы всегда равен по абсолютной величине еди-
нице, т.е. ]det А = 1. Действительно, поскольку det А = det АТ (свой-
ство 5) из п. П2.2), a det (АВ) = det A-det В (свойство 1) из п. П2.2), то для
ортогональной матрицы det(AAT) = det A det АТ = (det А)2 = det 1=1.
Отсюда получаем, что | det А| = 1, если А ортогональна.
Мы еще будем обращаться к ортогональным матрицам в пп. П2.5 и
П2.6.
П2.4. Ранг матрицы и линейная
зависимость ее строк (столбцов)
Наряду с рассмотренными в п. П2.2 двумя основными числовыми ха-
рактеристиками квадратной матрицы — ее определителем и ее следом,
в общем случае, включающем и прямоугольные матрицы, существует еще
одна очень важная числовая характеристика матрицы — ее ранг.
Перед тем, как сформулировать строгое определение этого понятия,
рассмотрим понятие линейной зависимости строк (столбцов) анализиру-
емой п х m-матрицы А.
Строки Aj. = («й»а»2,-•	» = 1,2,...,п, матрицы А называ-
ются линейно зависимыми, если существуют числа А|, Aj,. ..,АП, не
все равные нулю, и такие, что
Ai Ai. 4- AjAj. + ... + AnAn. = 0i.m
(П2.21)
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
995
(здесь 01, т, в соответствии с принятыми выше обозначениями, — это
строка длины т, состоящая из нулей).
Аналогично: столбцы А.; =	. ,anj)T, j = 1,2, . ..,m, ма-
трицы А называются линейно зависимыми, если существуют числа
ке все равные нулю, и такие, что
^-1 + М2^-2 4--h	= 0п.i.	(П2.21;)
В противном случае строки (столбцы) называются линейно незави-
симыми.
Можно доказать, что максимальное число линейно независимых
строк п х т-матрицы А совпадает с максимальным числом ее линейно
независимых столбцов и, одновременно, — с максимальным порядком
ее не равного нулю минора (напомним, что минором порядка к матрицы
А называется определитель к X ^-матрицы, получающейся из матрицы А
вычеркиванием из нее п — к строк и тп — к столбцов).
• Ранг п х m-матрицы А (будем обозначать его ранг А) определяется
как максимальное число ее линейно независимых столбцов.
Очевидно, что в силу приведенного выше свойства, ранг матрицы А
может быть определен и как максимальное число ее линейно независимых
строк, и как максимальный порядок ее отличного от нуля минора. Кста-
ти, последнее определение часто бывает наиболее удобным с точки зрения
возможности практического вычисления ранга конкретной матрицы. При
этом, определяя ранг матрицы как максимальный порядок ее отличного от
нуля минора, подразумевается, что достаточно того, чтобы нашелся хотя
бы один ненулевой минор порядка к, в то время как все миноры порядка
к + 1 уже будут равны нулю. Так, например, в 4 X 3-матрице
(4 8 2 \
2 4 4 |
2 4-21
3 6 -3/
все четыре минора 3-го порядка равны нулю. Следовательно ранг А < 3.
И хотя большинство миноров 2-го порядка тоже равно нулю, все-таки
существуют миноры этого порядка, отличные от нуля. А это значит, что
ранг А = 2.
Заметим, что применительно к матрице X наблюденных значений
объясняющих переменных (см. (П2.4)) в регрессионном анализе линей-
ная зависимость столбцов означает линейную зависимость объясняю-
щих переменных.
996
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Из определения ранга матрицы более или менее непосредственно вы-
текают следующие его основные свойства:
1)	ранг А min(n, тп); если ранг А = min(n, m), то говорят, что матрица
А — это матрица полного ранга;
2)	ранг 1п = п;
3)	ранг (diag(an,022, -  ,ann)) = где к — число ненулевых элементов
В ряду О11»а22,-	Опп 5
4)	ранг (АВ) пнп{ранг А, ранг В};
5)	ранг В = п, если В — квадратная невырожденная матрица размер-
ности п X п;
6)	ранг (А В) = ранг А, если А — произвольная матрица размерности
n X т, а В — невырожденная т х ш-матрица;
7)	ранг (В А) = ранг А, если А — произвольная матрица размерности
п х т, а В — невырожденная п х п-матрица;
8)	ранг (Bi А В2) = ранг А, где А — произвольная матрица порядка пх
тп, a Bi и В2 — невырожденные квадратные матрицы размерностей,
соответственно, (п х п) и (тп х ш);
9)	ранг А = ранг АТ.
Отметим также один важный для эконометрических приложений
(особенно для проблемы идентифицируемости модели) факт, связанный
с понятием ранга матрицы. Пусть X = (х^1^,^2^,.. .,х^)Т — набор
переменных (среди которых, в целях большей общности, мы допускаем
присутствие и переменной, тождественно равной единице), а А — матри-
ца размерности п х р. Система уравнений относительно X может быть
записана в виде
АХ = ОпЛ.	(П2.22)
При решении системы (П2.22) важным моментом является соотношение
между числом неизвестных и числом линейно независимых уравнений, со-
держащихся в системе. Так вот, оказывается, что число линейно незави-
симых уравнений в системе (П2.22) равно рангу матрицы А.
П2.5. Характеристические
(собственные) числа квадратной
матрицы и соответствующие им
собственные векторы
Широкий крут задач многомерного статистического анализа и эконо-
метрики сводится (в вычислительном плане) к необходимости анализа и
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
997
решения параметрического семейства систем уравнений типа
(А - А1Я)Х = 0пЛ>	(П2.23)
где А — некоторая п X п-матрица, X = (хх, х2,. • • > жп)Т — вектор-столбец
неизвестных, а А — некоторый числовой параметр. Для того, чтобы су-
ществовало нетривиальное (отличное от нулевого) решение, необходимо,
чтобы матрица А — А 1п была вырожденной, т. е. необходимо потребовать,
чтобы
det(A - A In) = 0.	(П2.24)
Из правил вычисления определителя матрицы (см. (П2.17)) следует,
что левая часть (П.24) представляет собой алгебраический полином от А
степени п, так что соотношение (П.24) — это алгебраическое уравнение
степени п относительно А. Само это уравнение, а следовательно, и его
корни Ai, А2,..., Ап по построению полностью определяются элементами
матрицы А. Приходим к определению:
•	Характеристическими (собственными) числами пхп-матрицы
А называются корни характеристического уравнения (П.24)-
Беря любое из собственных чисел А, и подставляя его в исходное со-
отношение (П.23), мы получаем уже конкретную систему уравнений (от-
носительно X) вида
(А-АДП)Х = ОП,1.	(П2.24*)
Существование нетривиального решения X(i) этого уравнения обеспечи-
вается равенством нулю определителя det(A — АДП). Соответственно, при-
ходим к еще одному определению:
•	Вектор-столбец X(i) —	• ->хпЬТ> являющийся решением
уравнения (П.24'), называется характеристическим (собствен-
ным) вектором матрицы А, соответствующим характеристи-
ческому (собственному) числу А,.
А поскольку алгебраическое уравнение степени п имеет п корней (сре-
ди которых, вообще говоря, могут быть совпадающие и комплексные), то
всякая квадратная п х n-матрица А имеет п собственных чисел (не обя-
зательно различных) и п соответствующих им собственных векторов.
В дальнейшем, отправляясь от интересов прикладной статистики и
эконометрики, мы сосредоточим свое внимание на свойствах характери-
стических чисел и характеристических векторов только действительных
симметрических положительно (или неотрицательно) определенных ма-
триц А (будем для краткости их называть далее, соответственно, спо- и
998	П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
сно-матрицами)1.
1)	Всякая спо- (сно-) п х n-матрица имеет п положительных (нео-
трицательных) действительных характеристических чисел; и наоборот,
матрица, все характеристические числа которой положительны (неотри-
цательны) является спо- (сно-) матрицей.
2)	Собственные векторы X(i) и X(j), соответствующие разным соб-
ственным числам, всегда взаимно ортогональны, т. е.
ХТ(.)Х(» = О при А,#АУ.
Поскольку собственный вектор определяется с точностью до коэффициен-
та пропорциональности, то можно пронормировать собственные векторы
Х(1),Х(2),...,Х(п) так, что все они будут образовывать ортонормиро-
ванную систему, т.е.
при»#;’ мявсех «,; = 1,2,...,п.
Заметим, что п х п-матрипа А, составленная из столбцов Х(«) (i =
1,2,..., п), т. е. матрица
х=(х(1) : Х(2) : ... : Х(п))
будет ортогональной, т.е. X X = 1п.
3)	Всякая спо- и сно- матрица А может быть приведена с помощью
ортогонального преобразования X к диагональному виду, в котором на
диагонали будут стоять характеристические числа, т. е.
XTAX = diag(A1,AJ,...,An).
П2.6. Некоторые свойства
симметричных положительно
(неотрицательно) определенных
матриц
На протяжении всего данного пункта мы будем полагать (если спе-
циально не оговорено другое), что А — симметрическая положительно
1 Симметрическая п х п-матрица А называется положительно (неотрицательно)
определенной, если для любого ненулевого вектора X = (ri, za,... ,zn)T выполня-
ется неравенство ХТАХ > О (ХТАХ > 0). Более подробно о сжмметржческжх
положительно и неотрицательно определенных матрицах см. в п. П 2.6.
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ	999
определенная матрица размерности п, т. е. для любого ненулевого векто-
ра X = (a?i, х2,..., sn)T выполняется неравенство
ХТА X > 0.	(П2.25)
1)	При любой т X «-матрице В матрица В В будет всегда симме-
трична и неотрицательно определена. Действительно, для любой (n х 1)-
матрицы X (т. е. для вектора-столбца длины п)
п
ХТ(ВТВ) X = (В Х)ТВ X = УТУ = У2 »’ > °.
»=1
т. к. произведение вектора-строки УТ = (ВХ)Т на вектор-столбец У =
В X приводит, очевидно, к неотрицательному числу.
2)	Если л > и и пх т-матрица В — матрица полного ранга (т. е. ранг
В = т), то матрица ВТ А В — положительно определенная; в частном слу-
чае п = т В является невырожденной квадратной матрицей размерности
п X п.
3)	Матрица А-1, обратная к А, также является симметрической и
положительно определенной.
4)	Единичная матрица 1п является симметрической положительно
определенной (т.к. для любого векторагстолбца X длины п ХТ1пХ =
Xх х = £ г? > 0).
»= 1
5)	det А > 0, т.е. определитель любой спо- матрицы положителен;
отсюда, в частности, следует, что и все главные миноры матрицы А поло-
жительны (минор матрицы называется главным, если он является опреде-
лителем подматрицы, образованной из исходной матрицы вычеркиванием
из нее строк и столбцов, имеющих одинаковые номера).
6)	След матрицы А может быть вычислен как сумма ее собственных
значений, т.е.
trA = Aj 4- А2 + • •  4- Ап.
где, напомним, А — спо- матрица размерности п х n, a Aj, А2,..., Ап — ее
собственные числа.
Пример П2.2. Продемонстрируем использование свойств симме-
трических положительно определенных матриц при анализе многомерных
распределений и их статистик. Пусть X = (х\,х2,... ,жп)Т — последова-
тельность одинаково (0,сг2)-нормально распределенных случайных вели-
1000
П 2. необходимые: сведения из матричной алгебры
чин, т.е.
Ez, — 0, t = 1,2,.. . ,п;
Dz,-= Ez2 = tr2, i = 1,2, . ..,п;
COV (zB, Xj) = E(zBzj) = 0 при i / j,
или, в компактной записи, X € АГп(ОпЛ; ^2In)- И пусть в процессе анализа
модели нам пришлось заниматься исследованием квадратичной формы от
анализируемых случайных величин вида ХТАХ, где А, как и ранее, спо-
матрица.
В соответствии со свойством 3) спо- и сно- матриц (см. п. П2.5) су-
ществует такая ортогональная матрица С, с помощью которой матрица
А может быть приведена к диагональному виду, а именно:
СТ АС = diag (Ai, А2,..., Ап),
где Ai, А2,..., А„ — собственные числа матрицы А, а элементы матрицы
С полностью определяются собственными векторами той же матрицы А.
Введем вспомогательные переменные
У = с'х
(соответственно, X = CY)
(П2.26)
и посмотрим, как будет выражаться анализируемая квадратичная форма
ХТАХ в терминах этих новых переменных:
ХТАХ = (СУ)ТАСУ = УТ(СТАС)У
п
= yTdiag(Al,Aj.....АП)У = ^Vi-
1=1
(П2.27)
Следовательно, для того чтобы понять, как «ведет себя» квадратич-
ная форма ХТАХ, необходимо выяснить, какому закону распределения
вероятностей подчиняются переменные yi, у2, -.., уп.
Из (П2.26) следует, что У, будучи линейной функцией от X, также
подчиняется нормальному закону со средним значением
ЕУ = Е(СТХ) = СТЕХ = 0„,1
и с ковариационной матрицей
Еу = Е(УУТ) = Е(СТХХТС) = СТЕ(ХХТ)С
= СТЕХС = Ст(а21„)С = а2СтС = <?1п
П2.7. ИДЕМПОТЕНТНЫЕ МАТРИЦЫ
1001
(в этой выкладке мы воспользовались тем, что ковариационная матри-
ца вектора X равна по условию а 1П, а также — ортогональностью
матрицы С, из чего следует СТС = !„).
Таким образом, мы убедились в том, что вспомогательные пе-
ременные	так же» как и исходные случайные величины
а?1,а:2,..., хп, (0, ст3)-нормальны и взаимно независимы. А это позволяет
описать распределение интересующей нас квадратичной формы (П2.27)
законом суммы масштабированных %2(1) — распределенных случайных
величин.
П2.7. Идемпотентные матрицы
Особенно важны в прикладной статистике и эконометрике соотноше-
ния типа (П2.27), в которых матрица А относится к классу так называе-
мых идемпотентных матриц.
• Идемпотентной называется симметрическая1 матрица А, облада-
ющая тем свойством, что она совпадает со своим квадратом, т. е.
А = А2.	(П2.28)
Перечислим основные свойства идемпотентных матриц.
1)	Любая целая положительная степень к идемпотентной матрицы А
дает снова исходную матрицу А, т. е. А* = А (следует непосредственно из
определения).
2)	Собственные числа идемпотентной матрицы могут принимать
только одно из двух значений: 0 или 1; а следовательно, в соответствии
со свойством 1) из п. 112.5 все идемпотентные матрицы неотрицательно
определены.
Докажем справедливость этого утверждения. В соответствии с ха-
рактеристическим уравнением (П2.23)
АХ = XX.
После домножения обеих частей этого характеристического уравнения сле-
ва на матрицу А имеем:
А2Х = А (АХ) = А (АХ) = АаХ.	(П2.29)
1 Иногда требование симметричности не включают в определение идемпотентной
матрицы.
1002
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Но одновременно с этим, используя идемпотентность матрицы А, мы мо-
жем записать:
А2Х = АХ = АХ.	(П2.29*)
Сравнивая правые части (П2.29) и (n2.29z), получаем
(А2-А)Х = 0п.,,
а т.н. X / 0n.i> то
А2 - А = 0,
т.е. либо А = 0, либо А = 1, что и доказывает свойство 2).
3)	Ранг идемпотентной матрицы равен числу ее ненулевых собствен-
ных чисел, что совпадает со следом исходной матрицы.
4)	Если ранг п х n-идемпотентной матрицы А равен п — к, то ис-
пользование ее собственных векторов для преобразований типа (П2.26)
будет приводить квадратичную форму ХТАХ относительно п независи-
мых (0, о )-нормально распределенных случайных величин к виду
XTAX = s? + ^ + ... + y2_*,	(П2.30)
где элементы УьУз»   • >Уп-* также взаимно независимы и (0,<т2) — нор-
мально распределены. А это значит, что квадратичная форма ХТАХ
подчиняется (п — ^-распределению.
П2.8. Матрицы блочной структуры
Содержание анализируемой задачи зачастую обусловливает целесо-
образность разбиения матриц, которыми мы оперируем, на отдельные бло-
ки. Так, например, при анализе модели многомерной регрессии или систем
одновременных уравнений в рамки нашего анализа попадают т зависи-
мых (эндогенных) переменных Y =	., у^)Т и р объясняющих
(экзогенных, предопределенных) переменных X = (я^1\я^2\... ,х^р^)Т.
Важным объектом анализа является при этом ковариационная матрица
всего вектора переменных Z = (х )» которая будет состоять, соответ-
ственно, из четырех блоков Еуу, ^ух> ^xy и ^хх> а именно:
£

(П2.31)

хх
П а. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
1003
Очевидно, матрица будет иметь размерность (m+p) X (тп-Ьр), в то вре-
мя как блок Еуу (матрица ковариаций между компонентами вектора У)
имеет размерность т х т, блок ЕуХ (матрица «перекрестных» ковари-
аций эндогенных переменных с предопределенными) имеет размерность
т х р, блок Гху (матрица «перекрестных» ковариаций предопределен-
ных переменных с эндогенными) имеет размерность р х т, и, наконец,
блок (матрица ковариаций между компонентами вектора X) имеет
размерность р х р.
Заметим, что для того, чтобы пользоваться некоторыми общими пра-
вилами оперирования с блочными матрицами, следует соблюдать необхо-
димые требования при их разбиении, а именно:
• блоки, стоящие друг над (или под) другом по вертикали, должны
иметь одинаковое количество столбцов] а блоки, стоящие рядом
(слева или справа друг от друга) по горизонтали, должны иметь
одинаковое количество строк.
Сложение блочных матриц. Если две матрицы А и В одина-
ковой размерности разбиты на блоки, соответственно, А|?- и Bu- (t =
l,2,...,&i; j = 1,2, ...,fc2) одинаковым образом (т.е. размерности бло-
ков AtJ- и B,j совпадают), то их сложение производится по правилу
Ац + Вц
А21 + В21
Au + В12
А22 + В22
Afcii + Bjfe12
Ацка + Bi*a '
A2/t3 + B2*a
A*jfc3 + BjtjJta /
Afc^ + Ajt^
Умножение блочных матриц формально также производится по
правилам умножения обычных матриц, однако разбиение А и В на бло-
ки А-ij и B,j должно быть произведено таким образом, чтобы количество
столбцов в первом сомножителе совпадало бы с количеством строк во вто-
ром сомножителе. Например:
I Ап А12 | { Вц	В12 1
АВ =	.......... ...............
\A2i : А22 / \В21	В22 /
(АцВп 4- А12В21	АцВ]2 + А12В22
А21Вц + А22В21 A2iBj2 + А22В22
1004
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
Определитель блочной матрицы. Пусть матрица А разбита на 4
блока
(П2.32)
таким образом, что блоки Ац и А22 являются квадратными матрицами
(как это было в нашем примере (П2.31)). Тогда можно воспользоваться
следующей общей формулой подсчета определителя матрицы А, во многих
случаях существенно упрощающей вычисления:
det
— det Ац • det А22 — Ац Ац Aj2
— det А22 • det Ац — Aj2A22 A2j).
В частном случае блочно-диагональной матрицы А (т. е. когда матри-
цы А12 и A2j состоят из одних нулей) данная формула принимает вид
Обращение блочной матрицы (П2.32) производится по формуле
где
А22 = (А22 — А21А1/А12) 1 и А11 = (Ац — Ai2A221A21) \
Прямое (кронекерово) произведение п х m-матрицы А и
k X /-матрицы В было введено в п.П2.1 (см. соотношение (П2.15)). По-
кольку результат такого перемножения матриц А и В представляется
патрицей блочной структуры, рассмотрим несколько полезных свойств
трямого произведения:
1)	если матрицы А и В квадратны и обратимы, то
(А® В)-1 = А-1 ®В-1;
1005
П 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ МАТРИЧНОЙ АЛГЕБРЫ
2)	если А — п х n-матрица, а В — к х к-матрица, то
det (А 0 В) = (det A)n(det В)*;
3)	(А 0 В)т = (Ат 0 Вт);
4)	tr (А ® В) = tr А - trB.